\\n\",\n \"\\n\",\n \"This version of the network uses `tf.layers` for almost everything, and expects you to implement batch normalization using [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization) \"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We'll use the following function to create fully connected layers in our network. We'll create them with the specified number of neurons and a ReLU activation function.\\n\",\n \"\\n\",\n \"This version of the function does not include batch normalization.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 2,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"\\\"\\\"\\\"\\n\",\n \"DO NOT MODIFY THIS CELL\\n\",\n \"\\\"\\\"\\\"\\n\",\n \"def fully_connected(prev_layer, num_units):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Create a fully connectd layer with the given layer as input and the given number of neurons.\\n\",\n \" \\n\",\n \" :param prev_layer: Tensor\\n\",\n \" The Tensor that acts as input into this layer\\n\",\n \" :param num_units: int\\n\",\n \" The size of the layer. That is, the number of units, nodes, or neurons.\\n\",\n \" :returns Tensor\\n\",\n \" A new fully connected layer\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)\\n\",\n \" return layer\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We'll use the following function to create convolutional layers in our network. They are very basic: we're always using a 3x3 kernel, ReLU activation functions, strides of 1x1 on layers with odd depths, and strides of 2x2 on layers with even depths. We aren't bothering with pooling layers at all in this network.\\n\",\n \"\\n\",\n \"This version of the function does not include batch normalization.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 3,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"\\\"\\\"\\\"\\n\",\n \"DO NOT MODIFY THIS CELL\\n\",\n \"\\\"\\\"\\\"\\n\",\n \"def conv_layer(prev_layer, layer_depth):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Create a convolutional layer with the given layer as input.\\n\",\n \" \\n\",\n \" :param prev_layer: Tensor\\n\",\n \" The Tensor that acts as input into this layer\\n\",\n \" :param layer_depth: int\\n\",\n \" We'll set the strides and number of feature maps based on the layer's depth in the network.\\n\",\n \" This is *not* a good way to make a CNN, but it helps us create this example with very little code.\\n\",\n \" :returns Tensor\\n\",\n \" A new convolutional layer\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" strides = 2 if layer_depth % 3 == 0 else 1\\n\",\n \" conv_layer = tf.layers.conv2d(prev_layer, layer_depth*4, 3, strides, 'same', activation=tf.nn.relu)\\n\",\n \" return conv_layer\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Run the following cell**, along with the earlier cells (to load the dataset and define the necessary functions). \\n\",\n \"\\n\",\n \"This cell builds the network **without** batch normalization, then trains it on the MNIST dataset. It displays loss and accuracy data periodically while training.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 4,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Batch: 0: Validation loss: 0.69066, Validation accuracy: 0.10020\\n\",\n \"Batch: 25: Training loss: 0.40348, Training accuracy: 0.07812\\n\",\n \"Batch: 50: Training loss: 0.32874, Training accuracy: 0.10938\\n\",\n \"Batch: 75: Training loss: 0.32664, Training accuracy: 0.07812\\n\",\n \"Batch: 100: Validation loss: 0.32607, Validation accuracy: 0.09900\\n\",\n \"Batch: 125: Training loss: 0.32351, Training accuracy: 0.14062\\n\",\n \"Batch: 150: Training loss: 0.32545, Training accuracy: 0.15625\\n\",\n \"Batch: 175: Training loss: 0.32736, Training accuracy: 0.10938\\n\",\n \"Batch: 200: Validation loss: 0.32522, Validation accuracy: 0.11260\\n\",\n \"Batch: 225: Training loss: 0.32507, Training accuracy: 0.14062\\n\",\n \"Batch: 250: Training loss: 0.32610, Training accuracy: 0.09375\\n\",\n \"Batch: 275: Training loss: 0.32387, Training accuracy: 0.18750\\n\",\n \"Batch: 300: Validation loss: 0.32564, Validation accuracy: 0.11260\\n\",\n \"Batch: 325: Training loss: 0.32367, Training accuracy: 0.14062\\n\",\n \"Batch: 350: Training loss: 0.32777, Training accuracy: 0.06250\\n\",\n \"Batch: 375: Training loss: 0.32563, Training accuracy: 0.12500\\n\",\n \"Batch: 400: Validation loss: 0.32574, Validation accuracy: 0.11000\\n\",\n \"Batch: 425: Training loss: 0.32619, Training accuracy: 0.04688\\n\",\n \"Batch: 450: Training loss: 0.32667, Training accuracy: 0.10938\\n\",\n \"Batch: 475: Training loss: 0.32398, Training accuracy: 0.20312\\n\",\n \"Batch: 500: Validation loss: 0.32535, Validation accuracy: 0.09240\\n\",\n \"Batch: 525: Training loss: 0.32837, Training accuracy: 0.04688\\n\",\n \"Batch: 550: Training loss: 0.32466, Training accuracy: 0.20312\\n\",\n \"Batch: 575: Training loss: 0.32340, Training accuracy: 0.12500\\n\",\n \"Batch: 600: Validation loss: 0.32493, Validation accuracy: 0.11260\\n\",\n \"Batch: 625: Training loss: 0.32785, Training accuracy: 0.15625\\n\",\n \"Batch: 650: Training loss: 0.32530, Training accuracy: 0.14062\\n\",\n \"Batch: 675: Training loss: 0.32741, Training accuracy: 0.12500\\n\",\n \"Batch: 700: Validation loss: 0.32513, Validation accuracy: 0.09860\\n\",\n \"Batch: 725: Training loss: 0.32644, Training accuracy: 0.10938\\n\",\n \"Batch: 750: Training loss: 0.32451, Training accuracy: 0.14062\\n\",\n \"Batch: 775: Training loss: 0.32561, Training accuracy: 0.04688\\n\",\n \"Final validation accuracy: 0.09900\\n\",\n \"Final test accuracy: 0.10090\\n\",\n \"Accuracy on 100 samples: 0.11\\n\"\n ]\n }\n ],\n \"source\": [\n \"\\\"\\\"\\\"\\n\",\n \"DO NOT MODIFY THIS CELL\\n\",\n \"\\\"\\\"\\\"\\n\",\n \"def train(num_batches, batch_size, learning_rate):\\n\",\n \" # Build placeholders for the input samples and labels \\n\",\n \" inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])\\n\",\n \" labels = tf.placeholder(tf.float32, [None, 10])\\n\",\n \" \\n\",\n \" # Feed the inputs into a series of 20 convolutional layers \\n\",\n \" layer = inputs\\n\",\n \" for layer_i in range(1, 20):\\n\",\n \" layer = conv_layer(layer, layer_i)\\n\",\n \"\\n\",\n \" # Flatten the output from the convolutional layers \\n\",\n \" orig_shape = layer.get_shape().as_list()\\n\",\n \" layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])\\n\",\n \"\\n\",\n \" # Add one fully connected layer\\n\",\n \" layer = fully_connected(layer, 100)\\n\",\n \"\\n\",\n \" # Create the output layer with 1 node for each \\n\",\n \" logits = tf.layers.dense(layer, 10)\\n\",\n \" \\n\",\n \" # Define loss and training operations\\n\",\n \" model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\\n\",\n \" train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)\\n\",\n \" \\n\",\n \" # Create operations to test accuracy\\n\",\n \" correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))\\n\",\n \" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\\n\",\n \" \\n\",\n \" # Train and test the network\\n\",\n \" with tf.Session() as sess:\\n\",\n \" sess.run(tf.global_variables_initializer())\\n\",\n \" for batch_i in range(num_batches):\\n\",\n \" batch_xs, batch_ys = mnist.train.next_batch(batch_size)\\n\",\n \"\\n\",\n \" # train this batch\\n\",\n \" sess.run(train_opt, {inputs: batch_xs, labels: batch_ys})\\n\",\n \" \\n\",\n \" # Periodically check the validation or training loss and accuracy\\n\",\n \" if batch_i % 100 == 0:\\n\",\n \" loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,\\n\",\n \" labels: mnist.validation.labels})\\n\",\n \" print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))\\n\",\n \" elif batch_i % 25 == 0:\\n\",\n \" loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys})\\n\",\n \" print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))\\n\",\n \"\\n\",\n \" # At the end, score the final accuracy for both the validation and test sets\\n\",\n \" acc = sess.run(accuracy, {inputs: mnist.validation.images,\\n\",\n \" labels: mnist.validation.labels})\\n\",\n \" print('Final validation accuracy: {:>3.5f}'.format(acc))\\n\",\n \" acc = sess.run(accuracy, {inputs: mnist.test.images,\\n\",\n \" labels: mnist.test.labels})\\n\",\n \" print('Final test accuracy: {:>3.5f}'.format(acc))\\n\",\n \" \\n\",\n \" # Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.\\n\",\n \" correct = 0\\n\",\n \" for i in range(100):\\n\",\n \" correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],\\n\",\n \" labels: [mnist.test.labels[i]]})\\n\",\n \"\\n\",\n \" print(\\\"Accuracy on 100 samples:\\\", correct/100)\\n\",\n \"\\n\",\n \"\\n\",\n \"num_batches = 800\\n\",\n \"batch_size = 64\\n\",\n \"learning_rate = 0.002\\n\",\n \"\\n\",\n \"tf.reset_default_graph()\\n\",\n \"with tf.Graph().as_default():\\n\",\n \" train(num_batches, batch_size, learning_rate)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"With this many layers, it's going to take a lot of iterations for this network to learn. By the time you're done training these 800 batches, your final test and validation accuracies probably won't be much better than 10%. (It will be different each time, but will most likely be less than 15%.)\\n\",\n \"\\n\",\n \"Using batch normalization, you'll be able to train this same network to over 90% in that same number of batches.\\n\",\n \"\\n\",\n \"\\n\",\n \"# Add batch normalization\\n\",\n \"\\n\",\n \"We've copied the previous three cells to get you started. **Edit these cells** to add batch normalization to the network. For this exercise, you should use [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization) to handle most of the math, but you'll need to make a few other changes to your network to integrate batch normalization. You may want to refer back to the lesson notebook to remind yourself of important things, like how your graph operations need to know whether or not you are performing training or inference. \\n\",\n \"\\n\",\n \"If you get stuck, you can check out the `Batch_Normalization_Solutions` notebook to see how we did things.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**TODO:** Modify `fully_connected` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 15,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"def fully_connected(prev_layer, num_units, is_training):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Create a fully connectd layer with the given layer as input and the given number of neurons.\\n\",\n \" \\n\",\n \" :param prev_layer: Tensor\\n\",\n \" The Tensor that acts as input into this layer\\n\",\n \" :param num_units: int\\n\",\n \" The size of the layer. That is, the number of units, nodes, or neurons.\\n\",\n \" :returns Tensor\\n\",\n \" A new fully connected layer\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)\\n\",\n \"\\n\",\n \" layer = tf.layers.batch_normalization(layer, training=is_training)\\n\",\n \" layer = tf.nn.relu(layer)\\n\",\n \" return layer\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**TODO:** Modify `conv_layer` to add batch normalization to the convolutional layers it creates. Feel free to change the function's parameters if it helps.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 16,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"def conv_layer(prev_layer, layer_depth, is_training):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Create a convolutional layer with the given layer as input.\\n\",\n \" \\n\",\n \" :param prev_layer: Tensor\\n\",\n \" The Tensor that acts as input into this layer\\n\",\n \" :param layer_depth: int\\n\",\n \" We'll set the strides and number of feature maps based on the layer's depth in the network.\\n\",\n \" This is *not* a good way to make a CNN, but it helps us create this example with very little code.\\n\",\n \" :returns Tensor\\n\",\n \" A new convolutional layer\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" strides = 2 if layer_depth % 3 == 0 else 1\\n\",\n \" conv_layer = tf.layers.conv2d(prev_layer, layer_depth*4, 3, strides, 'same', activation=tf.nn.relu)\\n\",\n \" conv_layer = tf.layers.batch_normalization(conv_layer, training=is_training)\\n\",\n \" conv_layer = tf.nn.relu(conv_layer)\\n\",\n \" return conv_layer\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**TODO:** Edit the `train` function to support batch normalization. You'll need to make sure the network knows whether or not it is training, and you'll need to make sure it updates and uses its population statistics correctly.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 22,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Batch: 0: Validation loss: 0.69055, Validation accuracy: 0.09860\\n\",\n \"Batch: 25: Training loss: 0.62911, Training accuracy: 0.10938\\n\",\n \"Batch: 50: Training loss: 0.54283, Training accuracy: 0.15625\\n\",\n \"Batch: 75: Training loss: 0.48776, Training accuracy: 0.07812\\n\",\n \"Batch: 100: Validation loss: 0.46307, Validation accuracy: 0.11260\\n\",\n \"Batch: 125: Training loss: 0.44106, Training accuracy: 0.10938\\n\",\n \"Batch: 150: Training loss: 0.41721, Training accuracy: 0.07812\\n\",\n \"Batch: 175: Training loss: 0.39374, Training accuracy: 0.07812\\n\",\n \"Batch: 200: Validation loss: 0.38370, Validation accuracy: 0.08680\\n\",\n \"Batch: 225: Training loss: 0.37264, Training accuracy: 0.09375\\n\",\n \"Batch: 250: Training loss: 0.36432, Training accuracy: 0.09375\\n\",\n \"Batch: 275: Training loss: 0.35929, Training accuracy: 0.06250\\n\",\n \"Batch: 300: Validation loss: 0.35560, Validation accuracy: 0.09240\\n\",\n \"Batch: 325: Training loss: 0.35081, Training accuracy: 0.03125\\n\",\n \"Batch: 350: Training loss: 0.35347, Training accuracy: 0.12500\\n\",\n \"Batch: 375: Training loss: 0.35275, Training accuracy: 0.06250\\n\",\n \"Batch: 400: Validation loss: 0.34188, Validation accuracy: 0.11760\\n\",\n \"Batch: 425: Training loss: 0.30678, Training accuracy: 0.23438\\n\",\n \"Batch: 450: Training loss: 0.25516, Training accuracy: 0.37500\\n\",\n \"Batch: 475: Training loss: 0.22896, Training accuracy: 0.48438\\n\",\n \"Batch: 500: Validation loss: 0.20522, Validation accuracy: 0.50360\\n\",\n \"Batch: 525: Training loss: 0.20960, Training accuracy: 0.54688\\n\",\n \"Batch: 550: Training loss: 0.21292, Training accuracy: 0.46875\\n\",\n \"Batch: 575: Training loss: 0.15521, Training accuracy: 0.50000\\n\",\n \"Batch: 600: Validation loss: 0.15440, Validation accuracy: 0.67700\\n\",\n \"Batch: 625: Training loss: 0.15890, Training accuracy: 0.62500\\n\",\n \"Batch: 650: Training loss: 0.15213, Training accuracy: 0.64062\\n\",\n \"Batch: 675: Training loss: 0.15449, Training accuracy: 0.65625\\n\",\n \"Batch: 700: Validation loss: 0.15554, Validation accuracy: 0.69280\\n\",\n \"Batch: 725: Training loss: 0.14911, Training accuracy: 0.75000\\n\",\n \"Batch: 750: Training loss: 0.16774, Training accuracy: 0.68750\\n\",\n \"Batch: 775: Training loss: 0.11901, Training accuracy: 0.71875\\n\",\n \"Final validation accuracy: 0.78440\\n\",\n \"Final test accuracy: 0.77810\\n\",\n \"Accuracy on 100 samples: 0.78\\n\"\n ]\n }\n ],\n \"source\": [\n \"def train(num_batches, batch_size, learning_rate):\\n\",\n \" # Build placeholders for the input samples and labels \\n\",\n \" inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])\\n\",\n \" labels = tf.placeholder(tf.float32, [None, 10])\\n\",\n \" \\n\",\n \" #boolean to hold if network is training\\n\",\n \" is_training = tf.placeholder(tf.bool)\\n\",\n \" # Feed the inputs into a series of 20 convolutional layers \\n\",\n \" layer = inputs\\n\",\n \" for layer_i in range(1, 20):\\n\",\n \" layer = conv_layer(layer, layer_i, is_training)\\n\",\n \"\\n\",\n \" # Flatten the output from the convolutional layers \\n\",\n \" orig_shape = layer.get_shape().as_list()\\n\",\n \" layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])\\n\",\n \"\\n\",\n \" # Add one fully connected layer\\n\",\n \" layer = fully_connected(layer, 100, is_training)\\n\",\n \"\\n\",\n \" # Create the output layer with 1 node for each \\n\",\n \" logits = tf.layers.dense(layer, 10)\\n\",\n \" \\n\",\n \" # Define loss and training operations\\n\",\n \" model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\\n\",\n \" with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):\\n\",\n \" train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)\\n\",\n \" \\n\",\n \" # Create operations to test accuracy\\n\",\n \" correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))\\n\",\n \" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\\n\",\n \" \\n\",\n \" # Train and test the network\\n\",\n \" with tf.Session() as sess:\\n\",\n \" sess.run(tf.global_variables_initializer())\\n\",\n \" for batch_i in range(num_batches):\\n\",\n \" batch_xs, batch_ys = mnist.train.next_batch(batch_size)\\n\",\n \"\\n\",\n \" # train this batch\\n\",\n \" sess.run(train_opt, {inputs: batch_xs, labels: batch_ys, is_training:True})\\n\",\n \" \\n\",\n \" # Periodically check the validation or training loss and accuracy\\n\",\n \" if batch_i % 100 == 0:\\n\",\n \" loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,\\n\",\n \" labels: mnist.validation.labels,\\n\",\n \" is_training:False})\\n\",\n \" print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))\\n\",\n \" elif batch_i % 25 == 0:\\n\",\n \" loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys, is_training:False})\\n\",\n \" print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))\\n\",\n \"\\n\",\n \" # At the end, score the final accuracy for both the validation and test sets\\n\",\n \" acc = sess.run(accuracy, {inputs: mnist.validation.images,\\n\",\n \" labels: mnist.validation.labels,\\n\",\n \" is_training:False})\\n\",\n \" print('Final validation accuracy: {:>3.5f}'.format(acc))\\n\",\n \" acc = sess.run(accuracy, {inputs: mnist.test.images,\\n\",\n \" labels: mnist.test.labels,\\n\",\n \" is_training:False})\\n\",\n \" print('Final test accuracy: {:>3.5f}'.format(acc))\\n\",\n \" \\n\",\n \" # Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.\\n\",\n \" correct = 0\\n\",\n \" for i in range(100):\\n\",\n \" correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],\\n\",\n \" labels: [mnist.test.labels[i]],\\n\",\n \" is_training:False})\\n\",\n \"\\n\",\n \" print(\\\"Accuracy on 100 samples:\\\", correct/100)\\n\",\n \"\\n\",\n \"\\n\",\n \"num_batches = 800\\n\",\n \"batch_size = 64\\n\",\n \"learning_rate = 0.002\\n\",\n \"\\n\",\n \"tf.reset_default_graph()\\n\",\n \"with tf.Graph().as_default():\\n\",\n \" train(num_batches, batch_size, learning_rate)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"With batch normalization, you should now get an accuracy over 90%. Notice also the last line of the output: `Accuracy on 100 samples`. If this value is low while everything else looks good, that means you did not implement batch normalization correctly. Specifically, it means you either did not calculate the population mean and variance while training, or you are not using those values during inference.\\n\",\n \"\\n\",\n \"# Batch Normalization using `tf.nn.batch_normalization`\\n\",\n \"\\n\",\n \"Most of the time you will be able to use higher level functions exclusively, but sometimes you may want to work at a lower level. For example, if you ever want to implement a new feature – something new enough that TensorFlow does not already include a high-level implementation of it, like batch normalization in an LSTM – then you may need to know these sorts of things.\\n\",\n \"\\n\",\n \"This version of the network uses `tf.nn` for almost everything, and expects you to implement batch normalization using [`tf.nn.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/nn/batch_normalization).\\n\",\n \"\\n\",\n \"**Optional TODO:** You can run the next three cells before you edit them just to see how the network performs without batch normalization. However, the results should be pretty much the same as you saw with the previous example before you added batch normalization. \\n\",\n \"\\n\",\n \"**TODO:** Modify `fully_connected` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.\\n\",\n \"\\n\",\n \"**Note:** For convenience, we continue to use `tf.layers.dense` for the `fully_connected` layer. By this point in the class, you should have no problem replacing that with matrix operations between the `prev_layer` and explicit weights and biases variables.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 27,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"def fully_connected(prev_layer, num_units, is_training):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Create a fully connectd layer with the given layer as input and the given number of neurons.\\n\",\n \" \\n\",\n \" :param prev_layer: Tensor\\n\",\n \" The Tensor that acts as input into this layer\\n\",\n \" :param num_units: int\\n\",\n \" The size of the layer. That is, the number of units, nodes, or neurons.\\n\",\n \" :returns Tensor\\n\",\n \" A new fully connected layer\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)\\n\",\n \" gamma = tf.Variable(tf.ones([num_units]))\\n\",\n \" beta = tf.Variable(tf.zeros([num_units]))\\n\",\n \"\\n\",\n \" pop_mean = tf.Variable(tf.zeros([num_units]), trainable=False)\\n\",\n \" pop_variance = tf.Variable(tf.ones([num_units]), trainable=False)\\n\",\n \"\\n\",\n \" epsilon = 1e-3\\n\",\n \" \\n\",\n \" def batch_norm_training():\\n\",\n \" batch_mean, batch_variance = tf.nn.moments(layer, [0])\\n\",\n \"\\n\",\n \" decay = 0.99\\n\",\n \" train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))\\n\",\n \" train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))\\n\",\n \"\\n\",\n \" with tf.control_dependencies([train_mean, train_variance]):\\n\",\n \" return tf.nn.batch_normalization(layer, batch_mean, batch_variance, beta, gamma, epsilon)\\n\",\n \" \\n\",\n \" def batch_norm_inference():\\n\",\n \" return tf.nn.batch_normalization(layer, pop_mean, pop_variance, beta, gamma, epsilon)\\n\",\n \"\\n\",\n \" batch_normalized_output = tf.cond(is_training, batch_norm_training, batch_norm_inference)\\n\",\n \" return tf.nn.relu(batch_normalized_output)\\n\",\n \" \"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**TODO:** Modify `conv_layer` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.\\n\",\n \"\\n\",\n \"**Note:** Unlike in the previous example that used `tf.layers`, adding batch normalization to these convolutional layers _does_ require some slight differences to what you did in `fully_connected`. \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 33,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"def conv_layer(prev_layer, layer_depth, is_training):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Create a convolutional layer with the given layer as input.\\n\",\n \" \\n\",\n \" :param prev_layer: Tensor\\n\",\n \" The Tensor that acts as input into this layer\\n\",\n \" :param layer_depth: int\\n\",\n \" We'll set the strides and number of feature maps based on the layer's depth in the network.\\n\",\n \" This is *not* a good way to make a CNN, but it helps us create this example with very little code.\\n\",\n \" :returns Tensor\\n\",\n \" A new convolutional layer\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" strides = 2 if layer_depth % 3 == 0 else 1\\n\",\n \"\\n\",\n \" in_channels = prev_layer.get_shape().as_list()[3]\\n\",\n \" out_channels = layer_depth*4\\n\",\n \" \\n\",\n \" weights = tf.Variable(\\n\",\n \" tf.truncated_normal([3, 3, in_channels, out_channels], stddev=0.05))\\n\",\n \" \\n\",\n \" bias = tf.Variable(tf.zeros(out_channels))\\n\",\n \"\\n\",\n \" conv_layer = tf.nn.conv2d(prev_layer, weights, strides=[1,strides, strides, 1], padding='SAME')\\n\",\n \" conv_layer = tf.nn.bias_add(conv_layer, bias)\\n\",\n \" gamma = tf.Variable(tf.ones([out_channels]))\\n\",\n \" beta = tf.Variable(tf.zeros([out_channels]))\\n\",\n \"\\n\",\n \" pop_mean = tf.Variable(tf.zeros([out_channels]), trainable=False)\\n\",\n \" pop_variance = tf.Variable(tf.ones([out_channels]), trainable=False)\\n\",\n \"\\n\",\n \" epsilon = 1e-3\\n\",\n \" \\n\",\n \" def batch_norm_training():\\n\",\n \" # Important to use the correct dimensions here to ensure the mean and variance are calculated \\n\",\n \" # per feature map instead of for the entire layer\\n\",\n \" batch_mean, batch_variance = tf.nn.moments(conv_layer, [0,1,2], keep_dims=False)\\n\",\n \"\\n\",\n \" decay = 0.99\\n\",\n \" train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))\\n\",\n \" train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))\\n\",\n \"\\n\",\n \" with tf.control_dependencies([train_mean, train_variance]):\\n\",\n \" return tf.nn.batch_normalization(conv_layer, batch_mean, batch_variance, beta, gamma, epsilon)\\n\",\n \" \\n\",\n \" def batch_norm_inference():\\n\",\n \" return tf.nn.batch_normalization(conv_layer, pop_mean, pop_variance, beta, gamma, epsilon)\\n\",\n \"\\n\",\n \" batch_normalized_output = tf.cond(is_training, batch_norm_training, batch_norm_inference)\\n\",\n \" return tf.nn.relu(batch_normalized_output)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**TODO:** Edit the `train` function to support batch normalization. You'll need to make sure the network knows whether or not it is training.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 34,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Batch: 0: Validation loss: 0.69116, Validation accuracy: 0.08680\\n\",\n \"Batch: 25: Training loss: 0.61918, Training accuracy: 0.09375\\n\",\n \"Batch: 50: Training loss: 0.57291, Training accuracy: 0.14062\\n\",\n \"Batch: 75: Training loss: 0.54827, Training accuracy: 0.12500\\n\",\n \"Batch: 100: Validation loss: 0.51580, Validation accuracy: 0.08680\\n\",\n \"Batch: 125: Training loss: 0.47078, Training accuracy: 0.12500\\n\",\n \"Batch: 150: Training loss: 0.41947, Training accuracy: 0.09375\\n\",\n \"Batch: 175: Training loss: 0.37808, Training accuracy: 0.06250\\n\",\n \"Batch: 200: Validation loss: 0.37041, Validation accuracy: 0.11000\\n\",\n \"Batch: 225: Training loss: 0.37841, Training accuracy: 0.04688\\n\",\n \"Batch: 250: Training loss: 0.39858, Training accuracy: 0.09375\\n\",\n \"Batch: 275: Training loss: 0.38057, Training accuracy: 0.15625\\n\",\n \"Batch: 300: Validation loss: 0.40183, Validation accuracy: 0.11000\\n\",\n \"Batch: 325: Training loss: 0.44106, Training accuracy: 0.01562\\n\",\n \"Batch: 350: Training loss: 0.42878, Training accuracy: 0.07812\\n\",\n \"Batch: 375: Training loss: 0.45432, Training accuracy: 0.15625\\n\",\n \"Batch: 400: Validation loss: 0.44503, Validation accuracy: 0.32180\\n\",\n \"Batch: 425: Training loss: 0.30620, Training accuracy: 0.48438\\n\",\n \"Batch: 450: Training loss: 0.07195, Training accuracy: 0.87500\\n\",\n \"Batch: 475: Training loss: 0.34081, Training accuracy: 0.53125\\n\",\n \"Batch: 500: Validation loss: 0.11314, Validation accuracy: 0.81720\\n\",\n \"Batch: 525: Training loss: 0.48202, Training accuracy: 0.40625\\n\",\n \"Batch: 550: Training loss: 0.17013, Training accuracy: 0.73438\\n\",\n \"Batch: 575: Training loss: 0.02425, Training accuracy: 0.96875\\n\",\n \"Batch: 600: Validation loss: 0.03587, Validation accuracy: 0.94600\\n\",\n \"Batch: 625: Training loss: 0.01194, Training accuracy: 0.96875\\n\",\n \"Batch: 650: Training loss: 0.01723, Training accuracy: 0.96875\\n\",\n \"Batch: 675: Training loss: 0.00529, Training accuracy: 0.98438\\n\",\n \"Batch: 700: Validation loss: 0.02844, Validation accuracy: 0.96120\\n\",\n \"Batch: 725: Training loss: 0.01406, Training accuracy: 0.95312\\n\",\n \"Batch: 750: Training loss: 0.01881, Training accuracy: 0.96875\\n\",\n \"Batch: 775: Training loss: 0.01447, Training accuracy: 0.96875\\n\",\n \"Final validation accuracy: 0.96460\\n\",\n \"Final test accuracy: 0.96360\\n\",\n \"Accuracy on 100 samples: 0.99\\n\"\n ]\n }\n ],\n \"source\": [\n \"def train(num_batches, batch_size, learning_rate):\\n\",\n \" # Build placeholders for the input samples and labels \\n\",\n \" inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])\\n\",\n \" labels = tf.placeholder(tf.float32, [None, 10])\\n\",\n \" \\n\",\n \" # boolean variable if network is training\\n\",\n \" is_training = tf.placeholder(tf.bool)\\n\",\n \" # Feed the inputs into a series of 20 convolutional layers \\n\",\n \" layer = inputs\\n\",\n \" for layer_i in range(1, 20):\\n\",\n \" layer = conv_layer(layer, layer_i, is_training)\\n\",\n \"\\n\",\n \" # Flatten the output from the convolutional layers \\n\",\n \" orig_shape = layer.get_shape().as_list()\\n\",\n \" layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])\\n\",\n \"\\n\",\n \" # Add one fully connected layer\\n\",\n \" layer = fully_connected(layer, 100, is_training)\\n\",\n \"\\n\",\n \" # Create the output layer with 1 node for each \\n\",\n \" logits = tf.layers.dense(layer, 10)\\n\",\n \" \\n\",\n \" # Define loss and training operations\\n\",\n \" model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\\n\",\n \" train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)\\n\",\n \" \\n\",\n \" # Create operations to test accuracy\\n\",\n \" correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))\\n\",\n \" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\\n\",\n \" \\n\",\n \" # Train and test the network\\n\",\n \" with tf.Session() as sess:\\n\",\n \" sess.run(tf.global_variables_initializer())\\n\",\n \" for batch_i in range(num_batches):\\n\",\n \" batch_xs, batch_ys = mnist.train.next_batch(batch_size)\\n\",\n \"\\n\",\n \" # train this batch\\n\",\n \" sess.run(train_opt, {inputs: batch_xs, labels: batch_ys, is_training:True})\\n\",\n \" \\n\",\n \" # Periodically check the validation or training loss and accuracy\\n\",\n \" if batch_i % 100 == 0:\\n\",\n \" loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,\\n\",\n \" labels: mnist.validation.labels,\\n\",\n \" is_training:False})\\n\",\n \" print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))\\n\",\n \" elif batch_i % 25 == 0:\\n\",\n \" loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys,\\n\",\n \" is_training:False})\\n\",\n \" print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))\\n\",\n \"\\n\",\n \" # At the end, score the final accuracy for both the validation and test sets\\n\",\n \" acc = sess.run(accuracy, {inputs: mnist.validation.images,\\n\",\n \" labels: mnist.validation.labels, is_training:False})\\n\",\n \" print('Final validation accuracy: {:>3.5f}'.format(acc))\\n\",\n \" acc = sess.run(accuracy, {inputs: mnist.test.images,\\n\",\n \" labels: mnist.test.labels, is_training:False})\\n\",\n \" print('Final test accuracy: {:>3.5f}'.format(acc))\\n\",\n \" \\n\",\n \" # Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.\\n\",\n \" correct = 0\\n\",\n \" for i in range(100):\\n\",\n \" correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],\\n\",\n \" labels: [mnist.test.labels[i]], is_training:False})\\n\",\n \"\\n\",\n \" print(\\\"Accuracy on 100 samples:\\\", correct/100)\\n\",\n \"\\n\",\n \"\\n\",\n \"num_batches = 800\\n\",\n \"batch_size = 64\\n\",\n \"learning_rate = 0.002\\n\",\n \"\\n\",\n \"tf.reset_default_graph()\\n\",\n \"with tf.Graph().as_default():\\n\",\n \" train(num_batches, batch_size, learning_rate)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Once again, the model with batch normalization should reach an accuracy over 90%. There are plenty of details that can go wrong when implementing at this low level, so if you got it working - great job! If not, do not worry, just look at the `Batch_Normalization_Solutions` notebook to see what went wrong.\"\n ]\n }\n ],\n \"metadata\": {\n \"anaconda-cloud\": {},\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.5.3\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 2\n}\n"},"license":{"kind":"string","value":"mit"}}}],"truncated":false,"partial":true},"paginationData":{"pageIndex":18,"numItemsPerPage":100,"numTotalItems":47214,"offset":1800,"length":100}},"jwt":"eyJhbGciOiJFZERTQSJ9.eyJyZWFkIjp0cnVlLCJwZXJtaXNzaW9ucyI6eyJyZXBvLmNvbnRlbnQucmVhZCI6dHJ1ZX0sImlhdCI6MTc1MTcxNzk3NSwic3ViIjoiL2RhdGFzZXRzL2NvZGVwYXJyb3QvZ2l0aHViLWp1cHl0ZXIiLCJleHAiOjE3NTE3MjE1NzUsImlzcyI6Imh0dHBzOi8vaHVnZ2luZ2ZhY2UuY28ifQ.6Z24dBVWazMX0WdrB7r-f_f0At4VAzxZYKhBdUFDqPLJzdlRQ3L98WOshfR3UXj3E2IDWi1qeB8Oy54BQnHUDA","displayUrls":true},"discussionsStats":{"closed":2,"open":0,"total":2},"fullWidth":true,"hasGatedAccess":true,"hasFullAccess":true,"isEmbedded":false,"savedQueries":{"community":[],"user":[]}}">
repo_name
stringlengths 6
92
| path
stringlengths 7
220
| copies
stringclasses 78
values | size
stringlengths 2
9
| content
stringlengths 15
1.05M
⌀ | license
stringclasses 15
values |
|---|---|---|---|---|---|
t-vi/pytorch-tvmisc | wasserstein-distance/Pytorch_Wasserstein.ipynb | 1 | 180292 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# An efficient implementation of the Sinkhorn algorithm for the GPU\n",
"*Thomas Viehmann <[email protected]>*\n",
"\n",
"Recently the Wasserstein distance has seen new applications in machine learning and deep learning. It commonly replaces the Kullback-Leibler divergence (also often dubbed cross-entropy loss in the Deep Learning context). In contrast to the latter, Wasserstein distances not only consider the values probability distribution or density at any given point, but also incorporating spatial information in terms of the underlying metric regarding these differences. Intuitively, it yields a smaller distance if probability mass moved to a nearby point or region and a larger distance if probability mass moved far away.\n",
"\n",
"There are two predominant variants of Wasserstein distance approximations used in machine learning:\n",
"- Stochastically optimised online estimates of the Wasserstein distance. This is the concept underpinning many of the GAN applications using a (heuristic approximation of) the Wasserstein distance as a *discriminator*. Starting from the [Wasserstein GAN](https://arxiv.org/abs/1701.07875) as an improvement over the KL-based DCGAN, with improvements to how to estimate the Wasserstein distance in [WGAN-GP](https://arxiv.org/abs/1704.00028), and [SN-GAN](https://openreview.net/forum?id=B1QRgziT-).\n",
"- Direct computation of the Wasserstein distance as a replacement for the cross-entropy loss in mini-batch training. This is commonly done using the entropy regularised Wasserstein distance and the Sinkhorn iterations [Cuturi](https://papers.nips.cc/paper/4927-sinkhorn-distances-lightspeed-computation-of-optimal-transport). In the context of deep learning this has been proposed by [Frogner et al.](http://cbcl.mit.edu/wasserstein/), but there is also earlier work in image retrieval using the (non-regularised) Wasserstein distance, see e.g. [Y. Rubner et al](http://ai.stanford.edu/~rubner/emd/default.htm). A comprehensive treatment is given in [Peyré and Cuturi's book](https://arxiv.org/abs/1803.00567), R. Flamary's [Python Optimal Transport](https://github.com/rflamary/POT/) library provides implementations for many algorithms in this area.\n",
"\n",
"This code is concerned with this latter use of the Wasserstein distance. One of the challenges is the numerical stability of the Sinkhorn iteration and carrying that over to mini-batch computations efficiently. While the ingredients appear to be readily available, it seems that they have not been put together in recent implementations we observed.\n",
"\n",
"\n",
"The following is the code for [Thomas Viehmann: \n",
"Implementation of batched Sinkhorn iterations for entropy-regularized Wasserstein loss, arXiv 1907.01729](https://arxiv.org/abs/1907.01729). If you use the code in academic work, please cite this paper.\n",
"The paper has a self-contained writeup of the key calculations to derive the algorithm.\n",
"\n",
"First we need the some imports."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import math\n",
"import time\n",
"import torch\n",
"import torch.utils.cpp_extension\n",
"%matplotlib inline\n",
"\n",
"from matplotlib import pyplot\n",
"import matplotlib.transforms\n",
"\n",
"import ot # for comparison\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## The kernel\n",
"\n",
"The following GPU kernel computes\n",
"$$\n",
" \\log v_{bj} := \\log \\nu_{bj} - \\operatorname{logsumexp}_{i} (-\\frac{1}{\\lambda} c_{ij} + \\log u_{bi}).\n",
"$$\n",
"\n",
"This has two key properties that shape our implementation:\n",
"- The overall reduction structure is akin to a matrix multiplication, i.e. memory accesses to $c_{ij}$ and $\\log u_{bi}$\n",
" to compute the result $\\log v_{bj}$, with the additional input $\\log \\nu$ following the same access pattern as the result. We parallelize in the independent dimensions ($b$ and $j$) and split the reduction over $i$ amongst multiple threads then combine their intermediate results. We have not employed tiling, which is commonly used to speed up the memory accesses for matrix multiplication.\n",
"\n",
"- In our implementation, the stabilisation of the `logsumexp` calculation is carried out in an online fashion, i.e. computing the stabilisation and the reduction result in a single pass, similar to the Welford algorithm for the variance.\n",
"\n",
"I explain a bit about the reduction (in particular the bits about `WARP_SHFL_XOR`) in [this blog post](http://lernapparat.de/sinkhorn-kernel/)."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"cuda_source = \"\"\"\n",
"\n",
"#include <torch/extension.h>\n",
"#include <ATen/core/TensorAccessor.h>\n",
"#include <ATen/cuda/CUDAContext.h>\n",
"\n",
"using at::RestrictPtrTraits;\n",
"using at::PackedTensorAccessor;\n",
"\n",
"#if defined(__HIP_PLATFORM_HCC__)\n",
"constexpr int WARP_SIZE = 64;\n",
"#else\n",
"constexpr int WARP_SIZE = 32;\n",
"#endif\n",
"\n",
"// The maximum number of threads in a block\n",
"#if defined(__HIP_PLATFORM_HCC__)\n",
"constexpr int MAX_BLOCK_SIZE = 256;\n",
"#else\n",
"constexpr int MAX_BLOCK_SIZE = 512;\n",
"#endif\n",
"\n",
"// Returns the index of the most significant 1 bit in `val`.\n",
"__device__ __forceinline__ int getMSB(int val) {\n",
" return 31 - __clz(val);\n",
"}\n",
"\n",
"// Number of threads in a block given an input size up to MAX_BLOCK_SIZE\n",
"static int getNumThreads(int nElem) {\n",
"#if defined(__HIP_PLATFORM_HCC__)\n",
" int threadSizes[5] = { 16, 32, 64, 128, MAX_BLOCK_SIZE };\n",
"#else\n",
" int threadSizes[5] = { 32, 64, 128, 256, MAX_BLOCK_SIZE };\n",
"#endif\n",
" for (int i = 0; i != 5; ++i) {\n",
" if (nElem <= threadSizes[i]) {\n",
" return threadSizes[i];\n",
" }\n",
" }\n",
" return MAX_BLOCK_SIZE;\n",
"}\n",
"\n",
"\n",
"template <typename T>\n",
"__device__ __forceinline__ T WARP_SHFL_XOR(T value, int laneMask, int width = warpSize, unsigned int mask = 0xffffffff)\n",
"{\n",
"#if CUDA_VERSION >= 9000\n",
" return __shfl_xor_sync(mask, value, laneMask, width);\n",
"#else\n",
" return __shfl_xor(value, laneMask, width);\n",
"#endif\n",
"}\n",
"\n",
"// While this might be the most efficient sinkhorn step / logsumexp-matmul implementation I have seen,\n",
"// this is awfully inefficient compared to matrix multiplication and e.g. NVidia cutlass may provide\n",
"// many great ideas for improvement\n",
"template <typename scalar_t, typename index_t>\n",
"__global__ void sinkstep_kernel(\n",
" // compute log v_bj = log nu_bj - logsumexp_i 1/lambda dist_ij - log u_bi\n",
" // for this compute maxdiff_bj = max_i(1/lambda dist_ij - log u_bi)\n",
" // i = reduction dim, using threadIdx.x\n",
" PackedTensorAccessor<scalar_t, 2, RestrictPtrTraits, index_t> log_v,\n",
" const PackedTensorAccessor<scalar_t, 2, RestrictPtrTraits, index_t> dist,\n",
" const PackedTensorAccessor<scalar_t, 2, RestrictPtrTraits, index_t> log_nu,\n",
" const PackedTensorAccessor<scalar_t, 2, RestrictPtrTraits, index_t> log_u,\n",
" const scalar_t lambda) {\n",
"\n",
" using accscalar_t = scalar_t;\n",
"\n",
" __shared__ accscalar_t shared_mem[2 * WARP_SIZE];\n",
"\n",
" index_t b = blockIdx.y;\n",
" index_t j = blockIdx.x;\n",
" int tid = threadIdx.x;\n",
"\n",
" if (b >= log_u.size(0) || j >= log_v.size(1)) {\n",
" return;\n",
" }\n",
" // reduce within thread\n",
" accscalar_t max = -std::numeric_limits<accscalar_t>::infinity();\n",
" accscalar_t sumexp = 0;\n",
" \n",
" if (log_nu[b][j] == -std::numeric_limits<accscalar_t>::infinity()) {\n",
" if (tid == 0) {\n",
" log_v[b][j] = -std::numeric_limits<accscalar_t>::infinity();\n",
" }\n",
" return;\n",
" }\n",
"\n",
" for (index_t i = threadIdx.x; i < log_u.size(1); i += blockDim.x) {\n",
" accscalar_t oldmax = max;\n",
" accscalar_t value = -dist[i][j]/lambda + log_u[b][i];\n",
" max = max > value ? max : value;\n",
" if (oldmax == -std::numeric_limits<accscalar_t>::infinity()) {\n",
" // sumexp used to be 0, so the new max is value and we can set 1 here,\n",
" // because we will come back here again\n",
" sumexp = 1;\n",
" } else {\n",
" sumexp *= exp(oldmax - max);\n",
" sumexp += exp(value - max); // if oldmax was not -infinity, max is not either...\n",
" }\n",
" }\n",
"\n",
" // now we have one value per thread. we'll make it into one value per warp\n",
" // first warpSum to get one value per thread to\n",
" // one value per warp\n",
" for (int i = 0; i < getMSB(WARP_SIZE); ++i) {\n",
" accscalar_t o_max = WARP_SHFL_XOR(max, 1 << i, WARP_SIZE);\n",
" accscalar_t o_sumexp = WARP_SHFL_XOR(sumexp, 1 << i, WARP_SIZE);\n",
" if (o_max > max) { // we're less concerned about divergence here\n",
" sumexp *= exp(max - o_max);\n",
" sumexp += o_sumexp;\n",
" max = o_max;\n",
" } else if (max != -std::numeric_limits<accscalar_t>::infinity()) {\n",
" sumexp += o_sumexp * exp(o_max - max);\n",
" }\n",
" }\n",
" \n",
" __syncthreads();\n",
" // this writes each warps accumulation into shared memory\n",
" // there are at most WARP_SIZE items left because\n",
" // there are at most WARP_SIZE**2 threads at the beginning\n",
" if (tid % WARP_SIZE == 0) {\n",
" shared_mem[tid / WARP_SIZE * 2] = max;\n",
" shared_mem[tid / WARP_SIZE * 2 + 1] = sumexp;\n",
" }\n",
" __syncthreads();\n",
" if (tid < WARP_SIZE) {\n",
" max = (tid < blockDim.x / WARP_SIZE ? shared_mem[2 * tid] : -std::numeric_limits<accscalar_t>::infinity());\n",
" sumexp = (tid < blockDim.x / WARP_SIZE ? shared_mem[2 * tid + 1] : 0);\n",
" }\n",
" for (int i = 0; i < getMSB(WARP_SIZE); ++i) {\n",
" accscalar_t o_max = WARP_SHFL_XOR(max, 1 << i, WARP_SIZE);\n",
" accscalar_t o_sumexp = WARP_SHFL_XOR(sumexp, 1 << i, WARP_SIZE);\n",
" if (o_max > max) { // we're less concerned about divergence here\n",
" sumexp *= exp(max - o_max);\n",
" sumexp += o_sumexp;\n",
" max = o_max;\n",
" } else if (max != -std::numeric_limits<accscalar_t>::infinity()) {\n",
" sumexp += o_sumexp * exp(o_max - max);\n",
" }\n",
" }\n",
"\n",
" if (tid == 0) {\n",
" log_v[b][j] = (max > -std::numeric_limits<accscalar_t>::infinity() ?\n",
" log_nu[b][j] - log(sumexp) - max : \n",
" -std::numeric_limits<accscalar_t>::infinity());\n",
" }\n",
"}\n",
"\n",
"template <typename scalar_t>\n",
"torch::Tensor sinkstep_cuda_template(const torch::Tensor& dist, const torch::Tensor& log_nu, const torch::Tensor& log_u,\n",
" const double lambda) {\n",
" TORCH_CHECK(dist.is_cuda(), \"need cuda tensors\");\n",
" TORCH_CHECK(dist.device() == log_nu.device() && dist.device() == log_u.device(), \"need tensors on same GPU\");\n",
" TORCH_CHECK(dist.dim()==2 && log_nu.dim()==2 && log_u.dim()==2, \"invalid sizes\");\n",
" TORCH_CHECK(dist.size(0) == log_u.size(1) &&\n",
" dist.size(1) == log_nu.size(1) &&\n",
" log_u.size(0) == log_nu.size(0), \"invalid sizes\");\n",
" auto log_v = torch::empty_like(log_nu);\n",
" using index_t = int32_t;\n",
" \n",
" auto log_v_a = log_v.packed_accessor<scalar_t, 2, RestrictPtrTraits, index_t>();\n",
" auto dist_a = dist.packed_accessor<scalar_t, 2, RestrictPtrTraits, index_t>();\n",
" auto log_nu_a = log_nu.packed_accessor<scalar_t, 2, RestrictPtrTraits, index_t>();\n",
" auto log_u_a = log_u.packed_accessor<scalar_t, 2, RestrictPtrTraits, index_t>();\n",
" \n",
" auto stream = at::cuda::getCurrentCUDAStream();\n",
"\n",
" int tf = getNumThreads(log_u.size(1));\n",
" dim3 blocks(log_v.size(1), log_u.size(0));\n",
" dim3 threads(tf);\n",
" \n",
" sinkstep_kernel<<<blocks, threads, 2*WARP_SIZE*sizeof(scalar_t), stream>>>(\n",
" log_v_a, dist_a, log_nu_a, log_u_a, static_cast<scalar_t>(lambda)\n",
" );\n",
"\n",
" return log_v;\n",
"}\n",
"\n",
"torch::Tensor sinkstep_cuda(const torch::Tensor& dist, const torch::Tensor& log_nu, const torch::Tensor& log_u,\n",
" const double lambda) {\n",
" return AT_DISPATCH_FLOATING_TYPES(log_u.scalar_type(), \"sinkstep\", [&] {\n",
" return sinkstep_cuda_template<scalar_t>(dist, log_nu, log_u, lambda);\n",
" });\n",
"}\n",
"\n",
"PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {\n",
" m.def(\"sinkstep\", &sinkstep_cuda, \"sinkhorn step\");\n",
"}\n",
"\n",
"\"\"\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Incorporating it in PyTorch\n",
"\n",
"We make this into a PyTorch extension module and add a convenience function (and \"manual\" implementation for the CPU)."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"wasserstein_ext = torch.utils.cpp_extension.load_inline(\"wasserstein\", cpp_sources=\"\", cuda_sources=cuda_source,\n",
" extra_cuda_cflags=[\"--expt-relaxed-constexpr\"] )\n",
"\n",
"def sinkstep(dist, log_nu, log_u, lam: float):\n",
" # dispatch to optimized GPU implementation for GPU tensors, slow fallback for CPU\n",
" if dist.is_cuda:\n",
" return wasserstein_ext.sinkstep(dist, log_nu, log_u, lam)\n",
" assert dist.dim() == 2 and log_nu.dim() == 2 and log_u.dim() == 2\n",
" assert dist.size(0) == log_u.size(1) and dist.size(1) == log_nu.size(1) and log_u.size(0) == log_nu.size(0)\n",
" log_v = log_nu.clone()\n",
" for b in range(log_u.size(0)):\n",
" log_v[b] -= torch.logsumexp(-dist/lam+log_u[b, :, None], 0)\n",
" return log_v"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We use this update step in a building block for the Sinkhorn iteration:"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"class SinkhornOT(torch.autograd.Function):\n",
" @staticmethod\n",
" def forward(ctx, mu, nu, dist, lam=1e-3, N=100):\n",
" assert mu.dim() == 2 and nu.dim() == 2 and dist.dim() == 2\n",
" bs = mu.size(0)\n",
" d1, d2 = dist.size()\n",
" assert nu.size(0) == bs and mu.size(1) == d1 and nu.size(1) == d2\n",
" log_mu = mu.log()\n",
" log_nu = nu.log()\n",
" log_u = torch.full_like(mu, -math.log(d1))\n",
" log_v = torch.full_like(nu, -math.log(d2))\n",
" for i in range(N):\n",
" log_v = sinkstep(dist, log_nu, log_u, lam)\n",
" log_u = sinkstep(dist.t(), log_mu, log_v, lam)\n",
"\n",
" # this is slight abuse of the function. it computes (diag(exp(log_u))*Mt*exp(-Mt/lam)*diag(exp(log_v))).sum()\n",
" # in an efficient (i.e. no bxnxm tensors) way in log space\n",
" distances = (-sinkstep(-dist.log()+dist/lam, -log_v, log_u, 1.0)).logsumexp(1).exp()\n",
" ctx.log_v = log_v\n",
" ctx.log_u = log_u\n",
" ctx.dist = dist\n",
" ctx.lam = lam\n",
" return distances\n",
"\n",
" @staticmethod\n",
" def backward(ctx, grad_out):\n",
" return grad_out[:, None] * ctx.log_u * ctx.lam, grad_out[:, None] * ctx.log_v * ctx.lam, None, None, None\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We also define a function to get the coupling itself:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def get_coupling(mu, nu, dist, lam=1e-3, N=1000):\n",
" assert mu.dim() == 2 and nu.dim() == 2 and dist.dim() == 2\n",
" bs = mu.size(0)\n",
" d1, d2 = dist.size()\n",
" assert nu.size(0) == bs and mu.size(1) == d1 and nu.size(1) == d2\n",
" log_mu = mu.log()\n",
" log_nu = nu.log()\n",
" log_u = torch.full_like(mu, -math.log(d1))\n",
" log_v = torch.full_like(nu, -math.log(d2))\n",
" for i in range(N):\n",
" log_v = sinkstep(dist, log_nu, log_u, lam)\n",
" log_u = sinkstep(dist.t(), log_mu, log_v, lam)\n",
" return (log_v[:, None, :]-dist/lam+log_u[:, :, None]).exp()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We define some test distributions. These are similar to examples from [Python Optimal Transport](https://github.com/rflamary/POT/)."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAD4CAYAAADiry33AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABEjUlEQVR4nO3dd3xUVf7/8deZSe+kkZAACSGE3jsoTbqAuth1F2miIFhX3eKuq36ta0FRpIqiIiooIkrvNZTQCSShJJRU0kjPnN8fN+GHbEIGMsmdcp6PxzzIzNyZ+7lM8p57zz33HCGlRFEURbFfBr0LUBRFUeqWCnpFURQ7p4JeURTFzqmgVxRFsXMq6BVFUeyck94FVCUwMFBGREToXYaiKIrN2LdvX4aUMqiq56wy6CMiIti7d6/eZSiKotgMIcTZ6p5TTTeKoih2TgW9oiiKnVNBryiKYuesso1eURSlLpWWlpKSkkJRUZHepdw0Nzc3wsPDcXZ2Nvs1KugVRXE4KSkpeHt7ExERgRBC73LMJqUkMzOTlJQUIiMjzX6darpRFMXhFBUVERAQYFMhDyCEICAg4KaPRFTQK4rikGwt5CvdSt2q6cZGlZWbSEy/wuHzOVwpLmNMx0b4ebjoXZaiKFZIBb2NKTdJ3lsTz8LtpykqNV19/K3fTnB/t8ZM6BtJY38PHStUFMXaqKC3IVeKy5ixJI51x1MZ1aERA1sG0S7Ml5IyybxtSSzedZZv9pxj4bhu9GkeqHe5iqJYCbPa6IUQw4QQ8UKIBCHES1U8L4QQMyuePySE6Hzd80YhxAEhxEpLFe5oLuYUcu/snWw4kcq/R7Xm4wc7cXencJoHe9O6kQ/v39eRLX8dQGSAJ5O/3MvhlBy9S1YUpQb9+/cnPj4egMzMTNq2bVsn66lxj14IYQRmAYOBFCBWCLFCSnnsmsWGA9EVtx7AZxX/VpoBHAd8LFS3QyktNzHpy72cyypg/rhuDIgJrnK5Rn7uLBrfnT99toNxC/fwwxO9iQz0rOdqFcW2vPrLUY5dyLXoe7Zu5MO/RrWpcbmEhASio6MBOHToEO3atbNoHZXM2aPvDiRIKZOklCXAEmDMdcuMAb6Uml2AnxAiFEAIEQ6MBOZZsG6H8smGBI6cz+W9e9tXG/KVQnzd+GpCdyTw6PzdZBeU1E+RiqLclLNnzxIWFobBoMXwoUOHaN++PUlJSUyYMIGxY8dabF3mtNGHAcnX3E/hj3vr1S0TBlwEPgT+CnjfcpUO7HBKDp9sTOCujo0Y1jbUrNc0C/Ji/l+68qfPdvD+2pP8Z0zdHA4qij0wZ8+7LsTFxdG+ffur9/ft28f9999Ps2bNmD9/vkWD3pw9+qo6bUpzlhFC3AmkSSn31bgSISYLIfYKIfamp6ebUZb9Kyot59mlcQR5ufLq6JsL605NGvBoz6Ys3nWW4xcte1iqKErtHTx48OqFT6dOneLnn3/WtekmBWh8zf1w4IKZy/QBRgshzqA1+QwUQiyuaiVSyjlSyq5Syq5BQVWOne9wPlp/ilNp+bw9tj2+HuaPa1HpmcEt8HV35t8rjiLl9d/NiqLoKS4uDpPJRIcOHfjPf/5Dq1atWLRoUZ2sy5ymm1ggWggRCZwHHgAeum6ZFcA0IcQStGadHCnlReDlihtCiP7A81LKRyxTun3LyC9m4fbT3N0pjH4tbu2Lz8/DheeHxvD35Uf49fBF7mzfyMJVKopyqw4dOsSBAwfw9v5jq3ZmZiZ///vfOXDgAG+++SYvv/xyrddVY9BLKcuEENOA1YARWCClPCqEmFLx/GxgFTACSAAKgMdqXZmDm7s1iZIyE08NbF6r93mgWxO+3nWON349zsCWwXi4qEsnFEVveXl5GAyG/wl5gICAAGbPnm3R9Zn1Vy+lXIUW5tc+NvuanyUwtYb32ARsuukKHVDWlRK+2nmWO9s3olmQV63ey2gQ/GtUa+6fs4ulscmM62P+iHeKotQNb29vTp48WW/rU4OaWaEF205TUFLOtFruzVfq0SyAzk38WLD9DOUm1VavKI5GBb2VySksZdGOMwxvG0KLhpbrkTqhbzPOZRWw7niqxd5TURTboILeynyx/Qx5xWUW25uvNLRNQ8L83Jm/7bRF31dRFOungt6KlJab+GrXWQbEBNGmka9F39vJaOCxPhHsOZ3FkfNqHBxFcSQq6K3IhhNpZOQX80jPpnXy/vd1a4yni1Ht1SuKg1FBb0W+i02moY/rLfebr4mPmzP3dWvMLwcvcCnH9iZFVhTl1qigtxIXcwrZFJ/GvV0a42Ssu49lXO8IykySH/en1Nk6FEWxLirorcQPe1MwSbiva+OaF66FpgGedI/wZ9n+FDUsgqI4CBX0VsBkkizdl0zvqACaBNT9NIB3dw67Ot+soij6sZqJR5S6tzMpk+SsQp4fElMv6xvRLpR/rTjKsv3naR/uVy/rVBSr9dtLcOmwZd8zpB0Mf6vGxaxp4hGlji2JTcbX3ZmhbULqZX2+7s7c0SqYXw5eoLTcVPMLFEWxuOomHvnpp5+YNGkSY8aMYc2aNRZZl9qj19mV4jLWHL3E/d0a4+ZsrLf13t0pnFWHL7HlZDqDWjWst/UqitUxY8+7LlQ38cjIkSO56667uHz5Ms8//zxDhgyp9brUHr3ONpxIo7jMxMh25s0eZSn9WgTRwMOZZQfO1+t6FUXR1DTxyOuvv87UqTccK9JsKuh1turwRYK8Xeka4V+v63VxMjCqQyPWHkslt6i0XtetKEr1E49IKXnxxRcZPnw4nTt3tsi6VNONjq4Ul7ExPo37ujbGaKhqNsa6dXenML7ceZbfj1yq826diqL8UXUTj8ycOZN169aRk5NDQkICU6ZMqfW6VNDraMOJNIpKTYyo52abSh0b+xHm585qFfSKUq9uNPHI9OnTmT59ukXXp5pudLTq8EUCvVzpVs/NNpWEEAxp05CtCRnkF5fpUoOiOCI18YiDKCjRmm2Gtw3Rpdmm0tA2IZSUmdgcn65bDYqi1C0V9DrRu9mmUtemDfD3dGHNsUu61qEoSt1RQa+Tymab7pH6NNtUcjIaGNQymA0n0igpUxdPKYo9UkGvg6LScjaeSGdom4a6NttUGtomhLyiMnYmZepdiqIodUAFvQ52JmVSWFrOHa2t44rUvtGBeLgYWX1UNd8oij1SQa+DjSfScHc20qtZgN6lAODmbKR/TBBrj6ViMqmhixXF3qigr2dSStYfT6NP88B6HdumJkPbhJCeV8yB5Mt6l6IoioWpoK9nJ1PzOZ9dyKBWwXqX8gcDWgbjZBCsPZamdymKoliYCvp6tv5EKgADYqwr6H3cnOka0YBN8SroFaW+qIlH7NSG42m0DfMhxNdN71L+x4CYYN787QQXcwoJ9XXXuxxFqRdv73mbE1knLPqeLf1b8mL3F2tcTk08YoeyrpSw/9xlBra0jt421+tfcZShrpJVlLpX3cQjx48fZ8qUKYwdO5bPPvvMIutSe/T1aPPJNEwSBrW0rmabSi0aehHq68am+HQe6N5E73IUpV6Ys+ddF6qbeKRVq1bMnj0bk8nEpEmTLLIutUdfjzacSCfQy5V2Yb56l1IlIQT9Y4LZlpChrpJVlDp2o4lHVqxYQd++fRk0aJBF1qWCvp6UlZvYHJ/GgJggDFZwNWx1+scEkV9cxr6zqpulotSl6iYeARg9ejQ7duzg66+/tsi6VNNNPTmYkk1uURkDrLTZplKf5oE4GwWbTqbRK8o6LuhSFHtU3cQjmzZtYtmyZRQXFzNixAiLrEsFfT3ZcjIDg4DeVh6eXq5OdG3qz+b4dF4e3krvchTFLt1o4pH+/fvTv39/i65PNd3Uk62n0mkf7oefh4vepdRoQMsgTlzK40J2od6lKIpdUhOP2KGcwlLikrO5PTpQ71LMcrWb5UnVzVJR7IEK+nqwIyEDk4TbWgTpXYpZooO9aOTrxhYV9IpiF1TQ14MtpzLwdnWiY2M/vUsxixCCPs0D2ZGYSbkazVKxU1La5u/2rdStgr6OSSnZcjKdXlEBOBtt57+7b3QgOYWlHDmfo3cpimJxbm5uZGZm2lzYSynJzMzEze3mhlBRvW7q2JnMAs5nFzKlf5TepdyUPs218wnbEjLoYCNHIopirvDwcFJSUkhPt73mSTc3N8LDw2/qNSro61hlO7etnIitFOjlSqtQH7adymDqgOZ6l6MoFuXs7ExkZKTeZdQbs9oShBDDhBDxQogEIcRLVTwvhBAzK54/JIToXPG4mxBijxDioBDiqBDiVUtvgLXbeiqdJv4eNA3w1LuUm3ZbdCD7zl6msKRc71IURamFGoNeCGEEZgHDgdbAg0KI1tctNhyIrrhNBiqHXCsGBkopOwAdgWFCiJ6WKd36lZab2JmYye0tbGtvvlLf5oGUlJvYfVpNGq4otsycPfruQIKUMklKWQIsAcZct8wY4Eup2QX4CSFCK+7nVyzjXHGzrbMftRCXnM2VknL6NrfNoO8W4Y+L0cD2hAy9S1EUpRbMCfowIPma+ykVj5m1jBDCKISIA9KAtVLK3VWtRAgxWQixVwix1xZPkFRle0IGQkBPK5kE/Ga5uxjpGtGAradU0CuKLTMn6KsaavH6vfJql5FSlkspOwLhQHchRJVzZUkp50gpu0opuwYF2caFRTXZkZBJ20a+NjHsQXX6Rgdy4lIe6XnFepeiKMotMifoU4DG19wPBy7c7DJSymxgEzDsZou0RQUlZRxIvkzv5ra5N1/ptubal+6ORLVXryi2ypygjwWihRCRQggX4AFgxXXLrAD+XNH7pieQI6W8KIQIEkL4AQgh3IE7AMtOzmilYs9cprRc0ifKNtvnK7Vu5IOfh7NqvlEUG1ZjP3opZZkQYhqwGjACC6SUR4UQUyqenw2sAkYACUAB8FjFy0OBRRU9dwzAUinlSstvhvXZkZCBi9FAtwh/vUupFaNB0KtZADsTtasIhbDeSVMURamaWRdMSSlXoYX5tY/NvuZnCUyt4nWHgE61rNEmbU/MoFMTP9xdjHqXUmu9owL47cglkrMKaRLgoXc5iqLcJNsZfMWGZBeUcPRC7tVhBGxdr4rmJ9VOryi2SQV9HdCaOax/NilzRQV5Euztyo5EdeGUotgiFfR1YEdiJp4uRrsZDEwIQe+oAHYk2t5of4qiqKCvE9sTM+ge6W9TwxLXpHdUIBn5xSSk5de8sKIoVsV+kshKXMopIin9it20z1fqVdEMpZpvFMX2qKC3sJ1J2gnLXnbSPl+psb8Hjf3d1bg3imKDVNBb2I6ETPw8nGkV4qN3KRbXu1kgu5LU9IKKYmtU0FvYzqRMekT6YzDY34VFvZsHkFtUxrELuXqXoijKTVBBb0HJWQWkXC6kt40Pe1CdXs0q2+lV842i2BIV9Ba0s+JEpb21z1cK9nGjebCXOiGrKDZGBb0F7UzKJNDLhehgL71LqTO9mgUQeyaL0nKT3qUoimImFfQWIqVkZ2ImPZoF2PXAX72iAigoKedQSo7epSiKYiYV9BZyOuMKl3KLrrZj26vK2bJ2JanmG0WxFSroLWRnRfDZy/g21fH3dKFliPfV8xGKolg/FfQWsjMxk4Y+rkQGeupdSp3r2SyAvWezKC4r17sURVHMoILeAqSU7ErKpJedt89X6hUVQFGpiYPJqp1eUWyBCnoLOJWWT0Z+id12q7xez8gAhEA13yiKjVBBbwGVgWevF0pdz9fDmdahPlfH9VEUxbqpoLeAHYkZhPm509jfcabZ69UsgP3nsikqVe30imLtVNDXkskk2X06y2GabSr1igqgpMzE/nOX9S5FUZQaqKCvpeOXcskuKLX7/vPX6xbpj0HALtVOryhWTwV9Ldn7+DbV8XFzpl24nxr3RlFsgAr6WtqVlElEgAeN/Nz1LqXe9WoWwMGUbApKyvQuRVGUG1BBXwvlDto+X6lXVACl5ZK9Z1Q7vaJYMxX0tXD0Qg55RWVXx39xNN0iGuBkEKr5RlGsnAr6WqgMOEc7EVvJw8WJjo39ro7zoyiKdVJBXws7EzOJCvIk2MdN71J00zsqgMMp2eQWlepdiqIo1VBBf4tKy03EnslymKthq9MzKgCThNjTWXqXoihKNVTQ36JDKTkUlJQ77InYSp2bNMDFyaDa6RXFiqmgv0U7KybIdtQTsZXcnI10adJADXCmKFZMBf0t2pGYSatQH/w9XfQuRXe9ogI4fimXy1dK9C5FUZQqqKC/BUWl5ew9e9nuZ5MyV++oAKSE3afVXr2iWCMV9Ldg/7nLlJSZ6NNcBT1A+3A/3J2NqvlGUayUCvpbsCMhE6NB0C3CX+9SrIKLk4Fukf5sV0GvKFZJBf0t2JGYQftwX7zdnPUuxWr0jgogIS2ftNwivUtRFOU6KuhvUn5xGQdTclT7/HX6VFxPoLpZKor1UUF/k2JPZ1Fukg5/odT1Wjfywdfdme0JanpBRbE2Kuhv0o7EDFycDHRp2kDvUqyK0SDoHRXA9oQMpJR6l6MoyjWc9C7A1mxPyKRLkwa4ORv1LsXq9G4eyG9HLnEms4DIQM9bfp/0gnROXT7FqexTJOUkkVaQRmZhJllFWZSaSpFSYsKEh5MHfq5++Lr60sirEZE+kUT6RtLSvyUNPRtacMsUxbaZFfRCiGHAR4ARmCelfOu650XF8yOAAmCclHK/EKIx8CUQApiAOVLKjyxYf726fKWEYxdzeW5wC71LsUp9Ks5bbE/IuKmgzynOYdv5bey5tIfYS7Ek5yVffc7fzZ+GHg0JdA+kRYMWuBpdEUIgEBSUFZBdnE12UTabkjexrGjZ1deFeYXRObgzPUJ70C+8H35ufpbaTEWxOTUGvRDCCMwCBgMpQKwQYoWU8tg1iw0HoituPYDPKv4tA56rCH1vYJ8QYu11r7UZuyqG4+2t+s9XKTLQk1BfN3YkZvBIz6Y3XDa/JJ+1Z9ey+uxqdl/YTZksw9vFm64Nu/JAzAO0CmhFlF8U/m7md2HNKc7hdM5pjmQcYX/afnZc2MEvSb9gEAa6NOzCkKZDGB45HF9X39puqqLYFHP26LsDCVLKJAAhxBJgDHBtWI8BvpRa4+wuIYSfECJUSnkRuAggpcwTQhwHwq57rc3YmpCBl6sT7cP99C7FKgkh6B0VyIYTqZhMEoNB/M8yxzKPsTR+KatOr6KwrJAwrzAebf0odzS9gzYBbTAabr1JzNfVl47BHekY3JFHWj+ClJJjWcdYf3Y9G85t4I3db/De3vcY3HQw97a4l07BndAORhXFvpkT9GFA8jX3U9D21mtaJoyKkAcQQkQAnYDdVa1ECDEZmAzQpEkTM8qqf9tOZdCzWQDORnUOuzp9mgfw4/4Ujl3MpW2YtucspWTnhZ3MPTyXval7cTO6MTxyOGNbjKVdYLs6C1shBG0C2tAmoA3TO0/nWOYxlp1axq9Jv7IyaSXtg9ozvu14BjQegEGoz1SxX+YEfVV/hdd3q7jhMkIIL+BH4GkpZW5VK5FSzgHmAHTt2tXqum2cyyzgXFYB4/tE6F2KVevTvLI/fQZtGvmw9fxWPo37lKOZRwn2COaFri9wV/Rd+Lj41HttrQNa0zqgNc92eZYViSv44ugXPL3xaZr5NuOpTk8xqMkgtYev2CVzgj4FaHzN/XDggrnLCCGc0UL+aynlMmzUtor+4X2jg3SuxLo19HEjKsiTNQn72F34f+y5tIdwr3D+3evfjIoahYtR/9E+PZw9eKDlA4xtMZa1Z9fy2cHPeGbTM7QLbMczXZ6hW0g3vUtUFIsyJ+hjgWghRCRwHngAeOi6ZVYA0yra73sAOVLKixW9ceYDx6WU71uw7nq3LSGdUF8txJTqZRZm4ha6lPjSrfhdbsDL3V/m3hb34my0vuEinAxODI8czuCmg/kl8Rdmxc1i/OrxDI0YyvNdnyfEM0TvEhXFImpsmJRSlgHTgNXAcWCplPKoEGKKEGJKxWKrgCQgAZgLPFnxeB/gUWCgECKu4jbC0htR18pNkh2JmfRpHqgO7athkiaWxi9l1E+jOF+2k+KMfvy705c81Oohqwz5azkZnLg7+m5W3r2SqR2nsil5E6N/Gs2CIwsoM5XpXZ6i1JpZ/eillKvQwvzax2Zf87MEplbxum1U3X5vU45eyCG7oJTbotWwB1U5m3uWf2z7B3HpcXQP6c4znV7krg8T2Hu6iEExeldnPjcnN6Z0mMKdze7k7di3+WDfB/x++nde6/MaMf42tCGKch3V1cAMW09p7fNqfJs/MkkTi48tZuyKsSTmJPJG3zeYN2QebYNb0LlpA7aeSte7xFsS7h3OxwM/5v3+75NakMoDvz7AZwc/o9RUqndpinJLVNCbYdupDFqGeBPk7ap3KVYj9Uoqk9ZM4u3Yt+ke2p2fxvzE6KjRV5u2bo8O5Mj5XDLzi3Wu9NYNbjqYn8b8xJCmQ/g07lPG/T7uD1ftKoqtUEFfg8KScvadvayaba6xKXkTY38Zy+GMw7za+1U+GfgJwR7Bf1jmtoreSdtsfDTLBm4NePv2t3m337uczj7Nvb/cyy+Jv+hdlqLcFBX0NdhzJouScpPqVgmUlpfy9p63eWrDU4R6hvLdnd9xT/Q9VZ6gbhvmi5+H89VmL1s3LGIYP4z+gZgGMfxt2994ZfsrFJWpSVYU26CCvgZbT6bj4mSgu4NPG5hWkMb41eNZfHwxD7d6mMUjFhPpG1nt8kaDoE/zQLaeSrebYYsbeTViwdAFTG4/meUJy3n0t0dJzlVNOYr1U0Ffg00n0+kR6Y+7i+MOSxx7KZb7frmP+MvxvNvvXV7q/pJZFz7dHh1Iam4xp9Ly66HK+mE0GHmq01PMGjSLC/kXuH/l/WxJ2aJ3WYpyQyrobyDlcgEJafn0a+G4zTbfnfiOyWsm4+3izbcjv2VYxDCzX1vZ3LXlpG32vrmR28NvZ+mopYR7hzNt/TTmH55vN0cuiv1RQX8DW05q7cv9Yxwv6EtNpby+63Ve3/06vRr14puR3xDlF3VT7xHm505UkKfNn5CtTphXGIuGL2JoxFA+3P8hL219SbXbK1ZJzTB1A5vi0yrCykvvUupVTnEOz216jt2XdvNYm8eY0XnGLQ8ffFt0EEtiz1FUWm6Xs3K5O7nzzu3vEOMfw8z9M0nJS+GjgR8R6K56aSnWQ+3RV6OkzMSOxEz6xQQ51LAHKXkpPPrbo+xL28frfV7n2a7P1mqM+P4xQRSVmth9OsuCVVoXIQQT203kgwEfcPLySR5Z9QiJ2Yl6l6UoV6mgr8b+c5fJLy5zqPb5w+mHeXjVw2QWZjJn8BzGNB9T6/fs2SwAN2cDG0+kWaBC6zaoySC+GPYFxeXFPLLqEXZd3KV3SYoCqKCv1qb4dJwMgt5RjjFt4ObkzYxfPR53J3e+GvGVxYbqdXM20jsqkE3x9h/0AG0C2/DNiG8I8QzhiXVPsCppVc0vUpQ6poK+GptPptOlaQO83ax75EVLWH5qOTM2zqCZXzO+HvE1zXybWfT9B8QEcSazgKR0++lmeSOhXqEsGr6IDkEdeHHriyw6ukjvkhQHp4K+Cqm5RRy/mEv/mOCaF7ZhUkrmHprLKzteoUdoDxYOXUiAu+WPYCr/HzfG2183y+r4uPjw+eDPGdJ0CO/tfY/3Yt9T3S8V3aigr8Lmin7f9tw+b5Im3ol9h5kHZnJnszv5ZOAneDh71Mm6Gvt7EB3s5TDNN5Vcja682+9dHmz5IIuOLeKf2/+pxrdXdKG6V1Zh44k0Gvq40irUW+9S6kSZqYx/7fgXKxJX8EirR3ih2wt1Pjn2gJbBfLH9DFeKy/B0dZxfO4Mw8HL3l2ng1oBP4z4ltySXd/u9i6tRjYSq1B/H+YszU3FZOVtOpjOmU5hddqssLi/mhc0vsDF5I1M7TuXx9o/Xy3b2jwlizpYktidkMKSNY03RJ4TgiQ5P4Ofqx5u73+TJdU8yc+BMPJ09wWSComwoyNL+Lc6DkitQWgjlJdqt8ihACBAGcHIDJ1dwcgdXb+3m5gMeAeDqoy2nKNdQQX+dXUlZXCkp545W9tc+X1BawPSN09l9cTcvd3+Zh1pdP/Vv3ena1B8vVyc2xqc7VtAX50NWImSd5sHLqfh4teHvl/YweXEfPs0qwDc/HaTJcuszuoBHIPiEgk8j8AkDv6bQIAL8I8G/mfYloTgUFfTXWXcsFfeKLoH2JLckl6nrpnIo4xBv9H2D0VGj63X9Lk4GbovWullKKe3vaKm8FNJPwKUjkHoEUo9CxknIPf+HxUa6+eHuH8LzroWMb+jP5+3uJdA7TNsbd/Ot2EP3AmcPLbSNLnDtBWumcigvhrJiKC3QvkiK8yqOCjLhSjpcyYDcC5B+EhI3Qsk1vZ2EQQv9wBho2BpC2kHDdtoXgEGdsrNXKuivIaVk/fFU+kYH2tXl+peLLvP42sc5lX2K9/q9x+Cmg3WpY0DLYH47comjF3JpG+arSw0WISXkJMO53ZCyBy4cgEuHoXKcG6MrBLeEiNsgsDkERGtB2qApuPkyEJh1YSczNs7gsSuHmNvnKUI86+goR0qtWejyacg6rX35ZMRDejycWgOyXFvO1QcadYRGnSG8GzTpCZ72tbPjyFTQX+PYxVwu5BTx9B0t9C7FYjIKM5i0ZhLJecnMHDCT28Jv062WQS2DMQhYeyzVtoJeSshKgjNb4fRWOLsd8i5qzzl7agHZbSI06gQh7bVQN974T6tXo158Pvhznlj3BON+H8f8ofMJ8wqzfO1CgGeAdgvv+sfnSou0o5DUI9qX1fl9sHMWVM6NG9AcmvaGiNsh8jbwdqAmNzsjrLFvb9euXeXevXvrfb0z15/ig3Un2fO3O+xiftjUK6lMXDOR1IJUPh74MT1Ce+hdEvfN3klecRm/zdDvC8cshdmQtBESN2jNHzkVE4x4NYSmfbQAbNwdgtvUGOo3ciTjCI+vfRwPZw/mDZlHU5+mlqn/VpUWwcU4OLcLzu2EszuhOEd7LjAGmg+CqEEQ0Qec3XUtVfkjIcQ+KWXXKp9TQf//jf5kG0aDYPmTfep93ZZ2If8CE1ZP4HLxZT4d9CmdG3bWuyQA5m1N4vVfj7P1rwNo7F83/fZvWcYpiF8FJ1drQSfLwdUXmt0OzfpDZD9tL9fC5xfis+KZtGYSTgYn5g2dZ/Erk2vFVA4XD2pHM4kb4ewO7RyBkzs06wcthkKLYdqJX0VXKujNkJpbRI//W88LQ2OYOqB5va7b0pLzkpm4eiJ5JXnMHjyb9kHt9S7pqrOZV+j37ib+eWdrJvStfirCeiGl1mRx/Bc4sVJrvwbt5GSLIRA9BMK61mqP3VwJlxOYuGYiEsm8IfOIbhBd5+u8JSUFWtifWgMnf4Psc9rjYV2g5Z3QarR2XkKpdyrozfDN7nP8bflhVj99OzEhtnuh1Lncc4xfPZ7CskLmDplL64DWepf0P4Z9uAVfd2e+e7xX/a9cSm0P9egyOPoTZJ8FYYSIvlpQtRwBvuH1XxeQlJPExNUTKTOVMXfIXGL8Y3Spw2xSam388au0L8sLB7THQ9pBm7uhzT1al06lXqigN8O4hXtITM9nywsDbLbr3+mc00xcPZESUwnzhsyz2qB4f008n2xMYO8/BuPvWfPcsxaRlQSHvofD30PmKTA4ac0xre+CliPBwzomfz+be5YJqydQVF7EnMFzrPKLulrZyVrgH10GKbHaY2Fdof19WvB72d+1KdZEBX0NcgpK6frGWsb3ieTlEa3qbb2WlJSdxIQ1EzBJE3OHzKVFA+vtOXQ4JYdRn2zj3bHtubdr47pbUWE2HF0OB5dA8i5AaCdS242F1mOsJtyvl5yXzITVE8gvzWfu4Lm0CWyjd0k3L/scHFkGh3+A1MPaUVPzO6DjQxAzXF20VQdU0Nfgh30pPP/9QX6a2oeOjf3qbb2WUtm+CzB/6Pybntu1vkkp6f3WBtqG+TL3z1X+Xt46kwnOboP9X8HxFVrf9sAY6PggtLtXt2aZm3U+/zwTVk8gtziXzwd/TrugdnqXdOvSjmtftoe+07qluvlpe/md/6w18ygWoYK+BhO+iOXEpTy2vWh7zTYnL59k0ppJGIXR+nps3MC/fj7CkthkDrwyGA8XC5zszEuFuK9h/yK4fEbrLdNuLHR6WLsIyMY+V4CL+RcZv3o82cXZzB48mw5BHfQuqXZM5ZC0Sfucjv+ijeMT2hG6jNM+K1fbPTdmDW4U9A5/zXNuUSlbT2UwvG2IzYV8fFY8E1ZPwEk4sWDoApsJeYChbUMoLjOx8UQtxqiXEpI2w9I/wwetYf2r4BMOd8+B507Ane9rvUFs7HOtFOoVysJhC/F38+fxtY8Tlxand0m1YzBq/fDHLoDn4mH4O9rQESufhv+2hF+e1q4wVizO4YN+w/E0SspNDG8XqncpN+V45nEmrJmAq9GVhcMWEuEboXdJN6VHZACBXq6sPHTh5l9clAu7ZsOs7vDlaDi9BXpMgWl74bFfocP94GJlffRvUYhnCAuGLiDIPYjH1z7O/tT9epdkGR7+0ONxeGI7TFinnTM5uARm94X5Q7UT52UleldpNxw+6FcdvkiIjxudbKht/mjmUSaumYiHkwcLhy2kiU8TvUu6aUaDYGS7EDacSCO/2MzJONJPwq/Pw/ut4PcXtUP9u2bDs8dh6BsQaKV9z2upoWdDFgxdQEPPhkxZN4XYS7F6l2Q5QkDjbnDXp/DccRj6f3AlDZZNhA/awMY3Ie+S3lXaPIcO+vziMjadTGdY2xAMBts4vD+cfphJqyfh5ezFwmELaexdh71W6tioDo0oLjOx7lhq9QuZTHBqHXx1D8zqprXBtxoFkzbCpA3aSVYHuBQ/yCOIBUMX0MizEU+ue5LdF3frXZLluTeAXlNh2j545Edt7KDNb2uB/+MkOG8nRzM6cOig33AijZIyEyNspNkmLi2OyWsn4+vqy8JhC+tmEKx61LlJA0J93apuvikthL0L4dMe8PWftIG3BvwdnjkGd8+GMOsY0qE+BboHMn/ofMK9w5m6fio7zu/Qu6S6YTBoXTEfXgpP7YNukyD+N5g7ABYMg2MrtBO7itkcOuh/PXSBIG9XujRtoHcpNdqfup/H1z6Ov5s/C4ctpJGX7Y8tYjAIRrYLZfPJdHIKKkZMzE+DDW9oe3Ern9b21u+eA08fgX5/BS/7ncfXHAHuASwYuoAInwie2vAUW1O26l1S3QqIguFvwbPHYOib2jj7Sx+FjzvD7s+18fiVGjls0OcUlLLxRDqj2jfCaOXNNrGXYpmybgrBHsEsGLqg7sYu18GoDo0oLZfs2LMTfpkBH7SFLe9C4x4w7leYvFk7uepUT1fQ2oAGbg2YN2QeUX5RzNg4g43nNupdUt1z84FeT8L0A3Dfl+AZDL/9VdshWP+atoOgVMthg37l4QuUlJu4p7N1N3/suLCDJ9c9SSPPRiwctpCGng31Lsmi2st4vvT8iKGbRkPct9qVk9Ni4cFvtfFnbLRrZF3zc/PTxsNpEMOzm55l7dm1epdUPwxGrYfOxLUwYa02Tv7W/2o7CCumQ0aC3hVaJYcN+uX7zxMd7EWbRj56l1KtrSlbeWr9UzTxacKCYQsIdLeTGX+khJNrYMFwxIIhdOM4n5bfRdbk/TDqQ7vtPWNpvq6+zBkyhzaBbXhh8wusSlqld0n1q3F3uH+x1o7f8SGte+YnXeG7RyBln97VWRWHDPpzmQXsPXuZuzuHWe1FUuvPrmf6xulE+UUxf8h8/N2sc1yWm1JepvWP/qwPfHOvNh7K0Dc5N24P75Xey88JpXpXaHO8Xbz5fPDndAzuyEtbX+KnhJ/0Lqn+BURpOwjPHIHbntWuq5g3EBaN0sbQt8Kr/+ubWUEvhBgmhIgXQiQIIV6q4nkhhJhZ8fwhIUTna55bIIRIE0IcsWThtbH8wHmEgLs6Wmezza9Jv/Lc5udoE9CGeUPn4efmp3dJtVNaBLHztRNoyyZqE3rcNRtmxEGvJ4lpHErbMB++35uid6U2ydPZk8/u+IyeoT355/Z/8t2J7/QuSR9ewTDoFXjmKAx5Xbvu4qu7YE7/ip46Jr0r1E2NQS+EMAKzgOFAa+BBIcT1Y6cOB6IrbpOBz6557gtgmCWKtQQpJcsPpNAzMoBGftbX/3r5qeW8vPVlOjfszJzBc/Bxsd6mpRoV58H2j+Cj9vDrs+AZBA98A0/s1Pq/G52vLnpvl8Ycu5jL0Qs5OhZsu9yd3Pl40Mf0D+/P67tf54sjX+hdkn5cvaH3U/D0IRj1ERTnaj11Pu0Bcd9owy44GHP26LsDCVLKJCllCbAEGHPdMmOAL6VmF+AnhAgFkFJuAbIsWXRtxCVncyazgLs7Wd/e/OJji3llxyv0btSbWYNm4eFso5fxF2TBxv/TTpCtfQWCW8FffoGJ67Sx3w3/+2s3pmMjXIwGtVdfC65GV97v/z5Dmg7hv/v+y6y4WVjjoIX1xslVGzBt2l5tfB2jK/z0BMzsDHvmatdqOAhzgj4MSL7mfkrFYze7zA0JISYLIfYKIfamp9dioKsaLD9wHlcnA8PbWU8XRSklnx/8nLdj3+aOJncwc+BM3J2s72ijRnmXYM0/tIDf/LbWa2bSBvjzzxB5+w170Ph5uDC4dUN+jjtPSZnjHmLXlrPRmXduf4e7mt/F7IOzeXfvu44d9qD11Gn7J5iyFR76HnxCYdXz8GF77YizOE/vCuucOePDVvXXef1vjjnL3JCUcg4wB7Rhim/mteYqLCln+YHzDG0Tgrebc80vqAdSSj7Y9wELjy5kdNRoXu39Kk6Gup+j1KKyz2l/MPu/AlOp9kfV91loeHOzI43tGs6vhy+y/niqzQ0yZ02MBiOv9n4VDycPvjr2FVdKr/BKz1cwGox6l6YvISrmAh4MZ7fDlve0I86t70PPJ6D7ZKudjKa2zEmUFODaAVXCgeuvWTdnGd2tPHSBvKIyHu5hHYOAlZnKeG3Xayw7tYwHYh7g5R4vYxA21BEqIwG2va9NKIHQ2t37PK31grgFt0cH0dDHle/3paigryWDMPBS95e0XjmHPievJI+3bnsLF6O68AwhtKPNiL5aN8yt78GmN2HHx9Btojbejp1Ne2hO0McC0UKISOA88ADw0HXLrACmCSGWAD2AHCnlRYtWagFf7z5H82Avukfq/61dXF7Mi1teZP259UzpMIUnOzxptV09/8elI9pFKkeXa+2g3SZqJ79qOXuT0SC4p3M4n29OJC23iGAfNwsV7JiEEEzrNA1fV1/eiX2H/JJ8Phzwoe2e+6kL4V20i/Mqf6e3fwS7Z0Pnv0Cf6TYzI1lNatx9lFKWAdOA1cBxYKmU8qgQYooQYkrFYquAJCABmAs8Wfl6IcS3wE4gRgiRIoSYYOFtMMuR8znEJWfzcI8mugdqfkk+T657kvXn1vNS95eY2nGq7jWZJWUffPsgzO4Dp9ZCnxnw9GEY/rbF/iDu7RKOScJ3sck1L6yY5dHWj/J6n9fZc2kPE1ZPIKvIavpGWI+QtnDvQu3EbduxsHc+fNQRVjylTSxv4xxmKsG/LT/Msv0p7H75Dnw99GufTy9I54l1T5CYnch/+vyHUVGjdKvFLFLCmW3a4W3SJm2+z55PaJNGuNfNYHCPzt/NydQ8tr04EGejDTVlWbmN5zbywpYXCPEMYfYdswn3to+91TpR1Xmn257TepBZKYefSjC/uIyfD5xnVPtGuob8mZwzPPrbo5zLO8fHgz627pC/OkzBUFh0J6Qeg8GvaVcf9n+pzkIeYFzvCFJzi1l9VE04YUkDmgxg7pC5XC66zKO/PcqJrBN6l2S9/JrAyP9qffF7TYUTq+DTnrDkYZscF98hgv6nA+e5UlLOQzqehD2YfpA///ZnCssKWTB0AX3D+upWyw2ZyuHoT/D57dowBbkXYMR72i98n+n1MoFz/5hgmvh7sGjHmTpfl6PpFNyJRcMWYRRGxv0+jh0X7HRMe0vxDtGusn3mCPR7Ec5s1cbF/+pu7UjXCltEqmL3QS+lZPGus7QK9aGjTtMFrju7jgmrJ+Dl4sWXw7+kbWBbXeq4obISOPA1zOoB3/8FSgtgzCxtWNjuk+p1FiejQfDnXk2JPXNZXSlbB5o3aM7iEYsJ8wpj6rqpjjk+zs3y8IcBf9PmRbjjVW0S8y9Gake8J1dbfeDbfdBvOZXBiUt5TOgbWe8nPKWUfHXsK57d9Cwx/jEsHrGYpj5N67WGGpVcgV2fwcxO8POTWqDfuwim7oFOj/xhmIL6dG/Xxrg7G9VefR0J8Qxh0bBFdA3pyj+3/5NP4z5VF1aZw80H+j6tdUIY8R7kXoRv7tMmNT/8gzZwnxWy+6D/fHMiIT5ujO5QvzMylZpKeWP3G7wT+w4Dmwxk3pB51jUCZUEWbH4HPmwHv78EDZrCwz/C41ugzV3a1YQ68nV35u7OYfwcd4HLV0p0rcVeebl48emgTxkTNYbPDn7GS1tfori8WO+ybIOzu3akO32/NkBfeSn8OAE+6QJ7F2gD+VkRuw76wyk57EjMZHzfCFyc6m9Tc0tymbpuKt/Ff8djbR7jv/3+az1DGuSch9V/14Yp2PgGhHWF8avhsVUQfYdVTfQxrncExWUmvtp1Vu9S7Jaz0ZnX+rzGjM4zWHV6FRNXTySzMFPvsmyH0Vm7UPDJXXD/1+ARACuf0Xagtr4Phdl6VwjYeffKad/sZ3N8OjteHlhvQx6cyz3HUxue4lzuOf7Z65/cE31Pvay3RmnHYftMOLxUa09sN1brB9+wjd6V3dDERbHsPXuZ7S8OxNPVxoaGsDFrzqzhb9v+RoBbADMHziTGP0bvkmyPlNoJ220fQuJ6cPGGruOg55PgU7etCg7ZvfJcZgGrDl/koZ5N6i3kd5zfwQO/PkBmUSZzhszRP+SlhNNb4ev7tK5hx37SrmKdEQf3zLH6kAeYOqA52QWlLFZ79XVuSMQQFg1bRJks49HfHmXd2XV6l2R7hNAG8Ht0mdYM2mIo7JylDaD205PaDpcO7Dbo529LwmgQjO8TWefrklKy6Oginlj/BCGeISwZuYRuId3qfL3VKi+DIz9q3cAW3Qnn90H/v2kTMgx/W+sjbCM6NWnAbdGBzN2aRFFpud7l2L02gW1YMnIJ0X7RPLPpGWbFzcIk1WiityS0A4ydr/Vc6/qYNmTIpz1h8VhI2lyvPXXsMugv5RSxJDaZuzuF0bCOx0spKC3gxS0v8t7e9xjUZBCLhy/W74rDolxt72FmJ/hhvHb/zg8qLnJ60WZH5ps2oDkZ+SUs2XNO71IcQpBHEAuGLWBM1BhmH5zNtPXTyClW3VxvWYMIGPGutqM14B9wMQ6+HA2f36bNc1tW950N7LKN/uVlh/lhXzIbnutPY/+6G8DpdM5pntn4DKdzT/NUp6cY33a8PqNPXj4Luz+HA19ps+k07QO9pkGLYVVO8mGL7pu9k3NZBWz+a39cnRx8uN16IqVkafxS3op9ixCPED4c8KFqt7eE0iLtXNnOWZB+ArxDtSbVruNrtTPmUG30pzOusHRvMg/3aFqnIb/6zGoe/PVBsoqymH3HbCa2m1i/IS8lnNmuzXg/syPs+VxrD5y0UetB03KE3YQ8wLSBzbmUW8RSNdhZvRFCcH/L+1k4dCEl5SU8vOphfjz5o+pvX1vObtD5z1pPnYd/0MbP2fAavN8afplRJ10z7a4bw/trT+LqZGDqgOZ18v7F5cW8G/su38V/R/vA9rzX7z1Cvepx7PTSQq39ffds7eo89wZa75luk8DX+qZHtJTbogPpHuHPh+tOcVenMKuZOMYRdAzuyNJRS3lp60v8e+e/iU2N5ZWer6jhjmtLCG0SlOjB2knaXZ9Cxilt6G9Lr8oav51vtenm6IUcRs7cxrQBzXl+qOUPMZNykvjr5r8SfzmecW3GMb3zdJwN9RQ42ecgdj7s/xIKsyCoFfScAu3uAxfH+IM7lJLN6E+282T/KP46rKXe5TicclM5cw/P5bODn9HEuwlv3f4WbQKsv+eWTTGZbvlI/EZNN3a1R//u6nh83Z2ZdHszi76vlJLvT37Pu7Hv4ubkxqxBs7g9/HaLrqNKJhMkboDYeXDyd20PoOVI6P64NjuOFV3cVB/ah/txV8dGzNt2mod6NCG8gWN8wVkLo8HIlA5T6NKwCy9tfYlHVj3CjE4z+HObP9vWzGjWrI6aW+3m08ktKiU5q4An+kfh6265veysoiymb5zOa7teo3PDzvw4+se6D/n8dNj2AXzcCb7+E5zfq42F/fRhuH8xRN7mcCFf6YVhLRFoX+qKPrqFdOPHUT/SP7w//933XyavnczFfKubUE65hl013ZSVmzBJLDbcwdqza3l91+vkleTxTJdneLjVw3W352IywZktsG8RHP9Fm+ygaV+t/22r0eCk5vqs9O7qE8zamMhPU/voNiKpoh3p/njqR96JfQejMPJi9xcZEzXGNmZLs0M3arqxq6C3lMtFl3lz95v8duY3Wge05o0+b9C8Qd2c3CXnPBz8VusaefmMdnK1w4PQZRwEqa5sVckvLmPAe5sI8nLl52l91CxUOkvOS+Yf2/7B/rT99Avvxz96/oMQzxC9y3I4KujNJKXk19O/8s6ed8grzWNK+ymMbzfe8idcy4oh/jc4sFgbD0OaIOI2bULiVqO07lfKDf1+5BJTFu/jhaExddbDSjGfSZpYfGwxHx/4GCeDE890eYaxLcaqtvt6pILeDCl5Kby+63W2X9hO+8D2/Kv3v2jRoIXlViClNhRB3Dda98iibPAJg44PaTd/y55AdgRTv97P2mOp/Dq9L9EN637mK6VmybnJvLrzVXZf2k3n4M78s+c/6+5oWPkDFfQ3UFxezIIjC5h/eD5GYWRG5xncH3M/RkuNx551Gg4thUPfQVYiOLlpe+0dHoRm/XUf992WpecVM+SDzTQN8OTHJ3pjNKi2YWsgpWR5wnL+u/e/FJQW8EjrR3iiwxOq330dU0FfBSklm1M28/aet0nJT2FYxDCe6/qcZdoW81K1AYwOf6/1mAGtaab9fdB6DLj51n4dCgA/x51nxpI4Xh7eksf7ReldjnKNrKIsPtz3IcsTlhPsEcyzXZ5lROQIdbK2jqigv058Vjzv7n2X3Rd3E+kbyd96/I2eoT1r96ZXMuDYz1rAn92utbs3bAft/gRtx4JfY8sUr/yBlJInFu9n7fFUvp3Uk+6Rtjlwmz2LS4vj/3b/H8ezjtM+qD0vdnuR9kHt9S7L7qigr3Ax/yKfHvyUnxN+xsfVhyc7PMm9Mffe+snWvEtaV8jjK7RxZ2Q5BERDm7uh7Z8gWF29WR9yi0oZ88l2rhSXsXJ6X4K91clsa2OSJlYkruCj/R+RUZjBkKZDeKrTU0T4Ruhdmt1w+KDPLMxk3uF5fBf/HQLBgy0fZFL7Sfi63kITSmYinFgJx1dCSiwgIbCF1te9zd3aZB7q0LTenbiUy12zttM+3I9vJvbASXW5tEpXSq/wxdEvWHR0ESXlJdwTfQ+T209W3TEtwGGDPqMwgy+OfMHSk0spKS/hruZ3MaXDlJv7pTKVQ/IeOPkbxP8OGRVXZIZ2gJiRWpu72nO3CssPpPDMdwcZ1zuCf41qrdqCrVhGYQZzD81l6cmlCAT3RN/DxHYTVeDXgsMF/fn883x17Ct+OPkDpaZSRkaOZFL7SUT6mjnbVH66NsbMqTVaP/fCy2Bw0sZ5jxmujTdjQ7M0OZLXVh5j/rbTPD+kBdMGRutdjlKDC/kXmHd4HssTlgMwOmo049qMM/9vVbnKYYL+eOZxFh5dyJozaxAIRjYbyeT2k2niU0MolxVre+2JG7Rgv3hQe9wzCJpXDCPafJDqLWMDTCbJ898fZNmB87w2pg2P9orQuyTFDBfzLzL/yHx+SviJkvISBjYZyF/a/IWOQR3VkZmZHCLo80vyGfj9QAzCwL0t7uXhVg9XfxhoKtfC/MxWOL0Fzu6A0gIQRmjcHaIGQfOBENrJribvcBSl5SaeWLyf9SdSef++DtzdSaepHZWbllmYyTcnvmHJiSXkluTSOqA1D7d6mKERQ3E1Wn6cdnviEEEPsOPCDtoFtsPb5bqrJMvL4NJBLdDPbNf+rZwDM7CFduFSswEQ0UfttduJotJyHlsYy86kTP4xshUTb1NXHtuSgtICViat5Jvj35CYk4ivqy+jo0YzNnoszfzUZ1kVhwn6qwqzteEGknfDuZ2Qsg9Kr2jP+UdpgR5xuzamu089zg6l1Kui0nKe+S6O345cYnyfSP4xshUGdfWsTZFSsvvSbn44+QPrz62nzFRGh6AOjI4azdCIobfWc85OOUbQlxXDr89Cyl5IjwckCAM0bAtNemq3pn3AW53VdyTlJslrK4/xxY4zDG3TkHfGdrDofAVK/ckszGRF4gp+TviZxJxEnA3O3BZ2G8Mih9EvvJ/DD7HgGEEPMLsveDeC8G7QuBuEdQFXNdiVo5NSMn/bad767QQNfdz48IGOdItQV9DaKiklx7OO80viL6w+s5r0wnRcja70DevLgMYD6BfeDz83P73LrHeOE/SKcgNxydlM//YAKZcLeLJ/c6YNbI6bsxpUzpaVm8o5kHaA38/8zsbkjaQVpGEQBjoGdaRvWF/6hvUlxj/GIYZLVkGvKBXyikr514qjLNt/njA/d/4+shXD24aoLnx2QErJscxjbEjewNaUrRzPOg6Av5s/3UO60y2kG91DutPUp6ldft4q6BXlOjsSM/jPL8c4cSmP7hH+TB3YnNujA+0yABxVRmEG289vZ9fFXey5uIe0wjRAC/5OwZ3oFNyJtoFtaeXfyi7a91XQK0oVyspNfBubzCcbTpGaW0yrUB8m3RbJ8LahuLuoJh17IqXkbO5ZYlNjiUuLY3/qflLyUwAwCANRflG08m9FK/9WxPjH0KJBC5vr0aOCXlFuoKTMxE9x5/l8cyKJ6VfwcnViWNsQ7u4URvdIfzUnrZ3KKMzgaMZRDmcc5kjmEU5kniCzKPPq80HuQUT5RdHMtxkRvhFE+ETQxKcJIR4hlpuYyIJU0CuKGUwmya7TmSzff57fjlwiv7gML1cnekcF0C8miC5NGxAd7K1msrJj6QXpnMg6QWJ2IqeyT5GYncjpnNMUlBVcXcbJ4ESYVxhhXmGEeoYS5hVGiGcIDT0aEuwRTLBHsC5NQbUOeiHEMOAjwAjMk1K+dd3zouL5EUABME5Kud+c11ZFBb2it8KScjafTGfzyXS2nEznfHYhAJ4uRtqF+9IyxIfohl40D/KiaYAnwd6u6mIsOyWlJL0wndM5p0nOS756u5h/kQtXLpBVlPU/r/Fw8iDII4gAtwD83fzxd/PHz80PP1ft5uvqi4+Lj3Zz9cHL2QtXo2utzhHVKuiFEEbgJDAYSAFigQellMeuWWYE8BRa0PcAPpJS9jDntVVRQa9YEyklZzILOHDuMnHJ2RxMzuZUWj4FJeVXl3E2CkJ93Wno40qQtyuBXq74ebjg5+6Mr7szXm5OeLk64enqhLuzETdnA27ORlydDDgbDbg4GXAyCHUy2AYVlhWSVpBG6pVUUgtSSStII6Mwg/TCdLKKssgqzCKrKIuckhxM0lTt+1QeKay8e+Ut1XGjoHcy4/XdgQQpZVLFmy0BxgDXhvUY4EupfWvsEkL4CSFCgQgzXqsoVk0IQWSgJ5GBntzTWRsgzWSSXMwt4lRqHimXC0m5XMj57ELS84qIv5THtrwMcovKbnpdTgaB0SCu/lt5E0JgEGAQAlFRkxDaHDeCip8rHgft5/+/AVX+WOsvFfWVVBWfilvzPzzqCgRhQopCTOIKJkMBUhRgElcqHitEGorIL66bq7bNCfowIPma+yloe+01LRNm5msBEEJMBiYDNGmixnpXrJvBIAjzcyfMz73aZcpNktzCUnIKS8kvLuNKcRlXSsooLDFRVFpOUVk5JWUmSspMlJabKCmXlJWbKDdJykyS8sqblEipHVmUmyQSrt7Xfv7/jwFce4x+7RH7H47da3lqTtb2DRyWz42fddMv6Kv64r7+U65uGXNeqz0o5RxgDmhNN2bUpShWzWgQNPB0oYGni96lKA7OnKBPARpfcz8cuGDmMi5mvFZRFEWpQ+Z0EI4FooUQkUIIF+ABYMV1y6wA/iw0PYEcKeVFM1+rKIqi1KEa9+illGVCiGnAarQukguklEeFEFMqnp8NrELrcZOA1r3ysRu9tk62RFEURamSumBKURTFDtyoe6W6tltRFMXOqaBXFEWxcyroFUVR7JwKekVRFDtnlSdjhRDpwNlbfHkgkGHBcmyBI24zOOZ2O+I2g2Nu981uc1MpZVBVT1hl0NeGEGJvdWee7ZUjbjM45nY74jaDY263JbdZNd0oiqLYORX0iqIods4eg36O3gXowBG3GRxzux1xm8Ext9ti22x3bfSKoijKH9njHr2iKIpyDRX0iqIods5ugl4IMUwIES+ESBBCvKR3PXVFCNFYCLFRCHFcCHFUCDGj4nF/IcRaIcSpin8b6F2rpQkhjEKIA0KIlRX3HWGb/YQQPwghTlR85r3sfbuFEM9U/G4fEUJ8K4Rws8dtFkIsEEKkCSGOXPNYtdsphHi5It/ihRBDb2ZddhH0FZOQzwKGA62BB4UQrfWtqs6UAc9JKVsBPYGpFdv6ErBeShkNrK+4b29mAMevue8I2/wR8LuUsiXQAW377Xa7hRBhwHSgq5SyLdrw5g9gn9v8BTDsuseq3M6Kv/EHgDYVr/m0IvfMYhdBzzUTmEspS4DKScjtjpTyopRyf8XPeWh/+GFo27uoYrFFwF26FFhHhBDhwEhg3jUP2/s2+wC3A/MBpJQlUsps7Hy70ebJcBdCOAEeaLPS2d02Sym3AFnXPVzddo4Blkgpi6WUp9Hm/uhu7rrsJeirm5zcrgkhIoBOwG6gYcWsXlT8G6xjaXXhQ+CvgOmax+x9m5sB6cDCiiareUIIT+x4u6WU54H3gHPARbTZ6tZgx9t8neq2s1YZZy9Bb/Yk5PZCCOEF/Ag8LaXM1bueuiSEuBNIk1Lu07uWeuYEdAY+k1J2Aq5gH00W1apokx4DRAKNAE8hxCP6VmUVapVx9hL05kxgbjeEEM5oIf+1lHJZxcOpQojQiudDgTS96qsDfYDRQogzaM1yA4UQi7HvbQbt9zpFSrm74v4PaMFvz9t9B3BaSpkupSwFlgG9se9tvlZ121mrjLOXoHeYSciFEAKtzfa4lPL9a55aAfyl4ue/AD/Xd211RUr5spQyXEoZgfbZbpBSPoIdbzOAlPISkCyEiKl4aBBwDPve7nNATyGER8Xv+iC081D2vM3Xqm47VwAPCCFchRCRQDSwx+x3lVLaxQ1tcvKTQCLwd73rqcPt7It2yHYIiKu4jQAC0M7Sn6r411/vWuto+/sDKyt+tvttBjoCeys+75+ABva+3cCrwAngCPAV4GqP2wx8i3YeohRtj33CjbYT+HtFvsUDw29mXWoIBEVRFDtnL003iqIoSjVU0CuKotg5FfSKoih2TgW9oiiKnVNBryiKYudU0CuKotg5FfSKoih27v8ByhJZML+dtKsAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# some test distribution densities\n",
"n = 100\n",
"lam = 1e-3\n",
"x = torch.linspace(0, 100, n)\n",
"mu1 = torch.distributions.Normal(20., 10.).log_prob(x).exp()\n",
"mu2 = torch.distributions.Normal(60., 30.).log_prob(x).exp()\n",
"mu3 = torch.distributions.Normal(40., 20.).log_prob(x).exp()\n",
"mu1 /= mu1.sum()\n",
"mu2 /= mu2.sum()\n",
"mu3 /= mu3.sum()\n",
"mu123 = torch.stack([mu1, mu2, mu3], dim=0)\n",
"mu231 = torch.stack([mu2, mu3, mu1], dim=0)\n",
"cost = (x[None, :]-x[:, None])**2\n",
"cost /= cost.max()\n",
"pyplot.plot(mu1, label=\"$\\mu_1$\")\n",
"pyplot.plot(mu2, label=\"$\\mu_2$\")\n",
"pyplot.plot(mu3, label=\"$\\mu_3$\")\n",
"pyplot.legend();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We run a sanity check for the distance:\n",
"(This will take longer than you might expect, as it computes a rather large gradient numerically, but it finishes in $<1$ minute on a GTX 1080)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"OK? True took 32 sec\n"
]
}
],
"source": [
"t = time.time()\n",
"device = \"cuda\"\n",
"res = torch.autograd.gradcheck(lambda x: SinkhornOT.apply(x.softmax(1), \n",
" mu231.to(device=device, dtype=torch.double),\n",
" cost.to(device=device, dtype=torch.double),\n",
" lam, 500),\n",
" (mu123.log().to(device=device, dtype=torch.double).requires_grad_(),))\n",
"print(\"OK? {} took {:.0f} sec\".format(res, time.time()-t))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We might also check that sinkstep is the same on GPU and CPU (Kai Zhao pointed out that this was not the case for an earlier versions of this notebook, thank you, and indeed, there was a bug in the CPU implementation.)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"res_cpu = sinkstep(cost.cpu(), mu123.log().cpu(), mu231.log().cpu(), lam)\n",
"res_gpu = sinkstep(cost.to(device), mu123.log().to(device), mu231.log().to(device), lam).cpu()\n",
"assert (res_cpu - res_gpu).abs().max() < 1e-5"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can visiualize the coupling along with the marginals:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmAAAAI/CAYAAADQs2XyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAACHz0lEQVR4nOzdd5hdV3n3/e+99t7nnOkzkka9N/cubIwLmBZTDQkhEBIImDgESEKe8CQQkrzJ8yR5eVMJgUAINiUQDEkoTiB0jLFxk3tVsYrVR33qKXvv9f6xzozGQrLGtjRnyu9zXXNp5px9Zu7jIv201r3vZd57RERERGT8uEYXICIiIjLdKICJiIiIjDMFMBEREZFxpgAmIiIiMs4UwERERETGmQKYiIiIyDiLG13AMzFr1iy/dOnSRpchIuPonnvu2ee97250HSIiJ9OkCmBLly5l7dq1jS5DRMaRmW1tdA0iIiebtiBFRERExpkCmIiIiMg4UwATERERGWcKYCIiIiLjTAFMREREZJwpgImIiIiMMwUwERERkXGmACYiIiIyzibVIFaRk2GgkrLj0BC7DpcZqmbEzmguRiye0cy8jiYiZ40uUUREpjgFMJny0izntif28/1H93D3lgM8vrvvuNcWYsdFi7u4bOVMfu6suaya0zaOlYqIyHShACZT1r7+Ctffupn/uGc7e/sqtBQiLlzSxSvOnsfSWc3M72yiKYnIvae/nLL1wCAbe/q5/Yn9/M131/M3313PBYs7+eWLF/O6CxaQRNqxFxGRk0MBTKacw4M1/vGHG/jCnVuppDkvOX0Ob7hoAVedPptiHB33dS8Y9XlPX5lv3LeTG+9+kv/9Hw/ysR9t5H0vXcU15y3AaYtSRESeI/PeN7qGMVuzZo3XYdxyPN57vnrvDv7yW49xcLDK6y5YwHuuWsmK7tbn9D2//1gPf/e99Ty2q5eLlnTx//78OazW1uS4MbN7vPdrGl2HiMjJpAAmU8K+/grv//cHuHndXi5c3Mn/fd3ZnDW/46R9/zz3fPW+Hfz5Nx9loJLyvpeu5jdfuEKrYeNAAUxEpiJtQcqk99ON+/idL9/P4aEa/+eas/iVS5ac9GDknPGGixZy1Wnd/MlNj/DX31nHnZsP8PdvPI+ZrcWT+rNERGTqU1exTGr/esdWfvWGu+hoSvjGey7jrZcuPaWrUjNbi3zszRfwF68/mzs27efV/3grj+/uPWU/T0REpiYFMJmUstzzZ//1CH/89Yd50epuvv6eyzhjXvu4/Gwz4y2XLOGrv/kCcu/5xU/czq0b9o3LzxYRkalBAUwmnTTLef+/P8BnbtvC2y9byqfeuobW4vjvpp+9oIOvvfsy5nc28WufuYv/fnDnuNcgIiKTkwKYTCrVNOe3b7yPr923g/e/fDX/z2vOaujk+vmdTfz7b17KBYs7+Z0b7+cb9+9oWC0iIjJ5KIDJpJHlnt/98v1866Hd/NGrzuC9L17V6JIAaC8lfPbtF3PRki5+98sKYSIicmIKYDIpeO/50Nce4psP7eKPXnUG77xieaNLeoqWYsxn3/48nrd0Br/3lQe4eV1Po0sSEZEJTAFMJoX/79vruPHubbz3qpUTLnwNay7EfPpta1g9p43f/MK93PfkwUaXJCIiE5QCmEx4X7rrST754yf45UsW83svX93ocp5WWynhs+94Ht1tRd7x2bvZdmCw0SWJiMgEpAAmE9pPN+7jj7/+MFeu7ub/vPYszCb+5PnZbSU+946LyT1c+7m76SvXGl2SiIhMMGMKYGZ2tZmtM7ONZvaBYzxvZvbR+vMPmtmFo567wcx6zOzh43zv95uZN7NZz/5tyFS0df8Av/nFe1k2q4WP/fIFxNHk+fvCslktfPyXL+SJvQP8zo33k+WT58gvERE59U74J5qZRcDHgVcAZwJvNrMzj7rsFcCq+sd1wCdGPfdZ4OrjfO9FwMuAJ59p4TK1DVUz3vWFewG4/m3Po72UNLiiZ+7yVbP409ecyQ8f7+EffrCh0eWIiMgEMpYlhYuBjd77Td77KnAjcM1R11wDfN4HdwCdZjYPwHt/C3DgON/774HfB7Q8ICO89/zR1x/m8d29fOSXzmfxzOZGl/Ss/crzl/ALFy7kH3+4gR+v39vockREZIIYSwBbAGwb9fX2+mPP9JqnMLPXAju89w+MoQaZRr589zb+897t/NaLV3HV6bMbXc5zYmb8+evO5rQ5bbzvxvvYeWio0SWJiMgEMJYAdqyu56NXrMZyzZGLzZqBDwF/csIfbnadma01s7V792oFYarb2NPHn/7XI1y+cha/85KJMWj1uWoqRPzTWy6kmua8T/1gIiLC2ALYdmDRqK8XAkcfejeWa0ZbASwDHjCzLfXr7zWzuUdf6L3/lPd+jfd+TXd39xjKlcmqkmb81pfup7kQ83dvPK+hRwydbMu7W/nz15/NXVsO8MkfP9HockREpMHGEsDuBlaZ2TIzKwBvAm466pqbgLfW74Z8PnDYe7/reN/Qe/+Q9362936p934pIcBd6L3f/ezehkwFf/XtdTy2q5e/+oVzmd1eanQ5J93rzl/Aa8+bz99/bz33bzvU6HJERKSBThjAvPcp8F7gO8BjwFe894+Y2bvM7F31y74FbAI2Av8CvHv49Wb2JeB24DQz225m157k9yBTwB2b9nP9rZv5lecv5qVnzml0OaeEmfF/X3c2c9pLvO/G+xiqZo0uSUREGsS8nzz9KGvWrPFr165tdBlykg1UUq7+h1twZvzP71xBcyFudEmn1O1P7OfN/3IH77hsGX/ymqMnusjRzOwe7/2aRtchInIyTZ7JljJlffh/Hmf7wSH++g3nTfnwBXDpipm89dIlfOanm7lr8/EmtIiIyFSmACYNdcem/fzrHVt5x2XLuHjZjEaXM27+4OrTWdDZxO//xwPaihQRmYYUwKRhyrWMP/zqQyye0cz7X35ao8sZVy3FmL96w7ls2T/IR36wvtHliIjIOFMAk4b5+I82smnfAH/x+rNpKkSNLmfcvWDFLN64ZiGf/slmHtvV2+hyRERkHCmASUOs293HJ25+gp+/cAFXrJq+890++Ioz6GhK+OBXHyLXgFYRkWlDAUzGXTjr8SHaSjF/9KrpfRdgV0uBP371Gdy/7RBfvHNro8sREZFxogAm4+5r9+3g7i0H+YOrT2dGS6HR5TTc685fwGUrZ/LX31nH/v5Ko8sREZFxoAAm4+rwUI2//NZjnLeokzeuWXTiF0wDZsafvfYsBqsZf/XtdY0uR0RExoECmIyrv//eevYPVPnza87GTaGzHp+rlbPbeMfly/jy2m3c9+TBRpcjIiKnmAKYjJsNe/r41zu28ssXL+achR2NLmfC+e2XrGJOe5E/+cYjasgXEZniFMBkXHjv+b/ffIyWQsTvTbOZX2PVWoz54CvO4KEdh/nqfTsaXY6IiJxCCmAyLn60rodb1u/ld166Wo33T+O1583nvEWd/NW3H2egkja6HBEROUUUwOSUq6Y5f/7fj7G8u4W3Xrqk0eVMaM4Zf/LqM+npq/DJHz/R6HJEROQUUQCTU+7f7tzKpn0D/NGrziCJ9J/ciVy0pIvXnDefT92yiR2HhhpdjoiInAL601BOqd5yjX/4wQZesGImV502u9HlTBp/cPVpeOBvv6uxFCIiU5ECmJxSn7z5CQ4O1vjgK87ATGMnxmphVzNvf8FSvnbfDh7dqXMiRUSmGgUwOWV2Hhri+ls387rz52vsxLPw7hetpL2U8OFvP97oUkRE5CRTAJNT5iPfX4/38P6f09iJZ6OjOeG9V63klvV7+cmGvY0uR0RETiIFMDklNvb08R/3bOdXL13Cwq7mRpczaf3qpUtY0NnEX317Hd5rOKuIyFShACanxN98Zz3NhZh3v2hFo0uZ1EpJxPteuoqHdhzm2w/vbnQ5IiJykiiAyUn3wLZDfPuR3bzzimXMbC02upxJ7+cvXMjK2a38zXfXkWZ5o8sREZGTQAFMTrq//s46ZrQUeOcVyxtdypQQOeP9L1/NE3sH+JqOKBIRmRIUwOSkumPTfm7duI93v2gFrcW40eVMGT931lzOXdjBR76/gWqqVTARkclOAUxOGu89f/fd9cxpL/Irz9eRQyeTmfF7Lz+NHYeG+MrabY0uR0REniMFMDlpbt24j7u2HOA9V62klESNLmfKuXLVLC5a0sXHfriRci1rdDkiIvIcKIDJSeG952+/u575HSV+6XmLGl3OlGRm/N7LVrO7t8yNdz3Z6HJEROQ5GFMAM7OrzWydmW00sw8c43kzs4/Wn3/QzC4c9dwNZtZjZg8f9Zq/NrPH69d/zcw6n/O7kYa5ef1e7t92iN96ySqKsVa/TpVLV8zkkmUz+PjNTzBU1SqYiMhkdcIAZmYR8HHgFcCZwJvN7MyjLnsFsKr+cR3wiVHPfRa4+hjf+nvA2d77c4H1wAefafEyMXjv+cj3N7Cgs4lfuHBho8uZ0syM//Wy1eztq/BvWgUTEZm0xrICdjGw0Xu/yXtfBW4ErjnqmmuAz/vgDqDTzOYBeO9vAQ4c/U2999/13qf1L+8A9Cf3JPXj9Xt5YNsh3vvilRRi7Wqfapcsn8nzl8/gkz9+Qr1gIiKT1Fj+tFwAjL7tanv9sWd6zdN5B/A/z+B6mSC0+tUYv/OSsAqmXjARkclpLAHMjvHY0YfSjeWaY39zsw8BKfDF4zx/nZmtNbO1e/fqQOKJ5pYN+7h/2yHec5VWv8bTpStmcvGyGXxCq2AiIpPSWP7E3A6Mvq1tIbDzWVzzM8zsbcCrgbf445w07L3/lPd+jfd+TXd39xjKlfHivecff7CB+R0l3nCRVr/G2/tesoo9vRXNBRMRmYTGEsDuBlaZ2TIzKwBvAm466pqbgLfW74Z8PnDYe7/r6b6pmV0N/AHwWu/94LOoXRrszs0HWLv1IO960QqtfjXApStmsmZJF5+8+QlNxxcRmWRO+KdmvVH+vcB3gMeAr3jvHzGzd5nZu+qXfQvYBGwE/gV49/DrzexLwO3AaWa23cyurT/1MaAN+J6Z3W9mnzxZb0rGx8d+uJHutiJvXKO5X41gZrznxSvZebjM13VGpIjIpDKmw/q8998ihKzRj31y1OceeM9xXvvm4zy+cuxlykRz75MHuXXjPj70yjM09b6BXrS6m7MXtPNPN2/k5y9cQBxpJVJEZDLQ79byrHz8hxvpak745UsWN7qUac3MeO9VK9myf5BvPvS0u/4iIjKBKIDJM/bYrl5+8HgPb79sGS3FMS2iyin08jPnsmp2Kx//0UbyfEw3H4uISIMpgMkz9ombn6ClEPG2S5c2uhQBnDPefdUK1u/p54eP9zS6HBERGQMFMHlGtuwb4L8f3MmvXLqEjuak0eVI3WvOnc/Crib+6eaNHGeii4iITCAKYPKM/PMtm4gjx7WXL2t0KTJKHDl+48rl3PvkIe7a/DMnf4mIyASjACZj1tNb5j/v2c4vXrSQ2W2lRpcjR/nFNYuY1Vrgn25+otGliIjICSiAyZhdf9tm0jznN65c0ehS5BhKScTbL1vGj9fv5ZGdhxtdjoiIPA0FMBmT3nKNf7vjSV55zjwWz2xudDlyHL966RJaizH//ONNjS5FRESehgKYjMkX73iSvkrKu16o1a+JrL2U8JZLFvPfD+5k2wGd8CUiMlEpgMkJlWsZ19+6mStWzeLsBR2NLkdO4O2XLSNyxqd/olUwEZGJSgFMTuhr9+1gX39Fq1+TxNyOEq+/YAFfXruN/f2VRpcjIiLHoAAmTyvPPf9yyybOXtDOC1bMbHQ5MkbXXbmcci3nc7dvbXQpIiJyDApg8rS+99geNu0b4LorV2BmjS5Hxmjl7DZeesYc/vX2LQxVs0aXIyIiR1EAk6f1qVs2sbCriVeePbfRpcgzdN2Vyzk4WOM/7tnW6FJEROQoCmByXPdsPcA9Ww9y7eXLiCP9pzLZPG9pF+cv6uTTt24m0yHdIiITiv5UleP65x9voqMp4Y1rFjW6FHkWzIzfuHI5W/cP8p1Hdje6HBERGUUBTI5p874BvvfYHn71+UtoKcaNLkeepZefNZclM5v551s26ZBuEZEJRAFMjun6WzeROMdbX7Ck0aXIcxA5452XL+OBbYdYu/Vgo8sREZE6BTD5GQcGqvzHPdt53QXzdej2FPCGixbR2ZzwqVs0mFVEZKJQAJOf8YU7tlKu5bzziuWNLkVOgqZCxK8+fwnff2wPm/cNNLocERFBAUyOUq5lfP72LVx1Wjer57Q1uhw5SX710iUkznH9rVoFExGZCBTA5Cm+cf8O9vVXtfo1xcxuK/G6C+bz72u3c2Cg2uhyRESmPQUwGeG959M/2cwZ83Ts0FT0ziuWU0lzvniHjicSEWk0BTAZ8eP1e9nQ08+vX7FMxw5NQavntPHC1d187vatVFIdTyQi0kgKYDLi+ls3M7utyKvPnd/oUuQUeecVy9jXX+Gm+3c2uhQRkWltTAHMzK42s3VmttHMPnCM583MPlp//kEzu3DUczeYWY+ZPXzUa2aY2ffMbEP9167n/nbk2Xp8dy8/2bCPt71gKYVYuXyqunzlLE6b08b1t27WYFYRkQY64Z+0ZhYBHwdeAZwJvNnMzjzqslcAq+of1wGfGPXcZ4Grj/GtPwD8wHu/CvhB/WtpkOt/spmmJOItlyxudClyCpkZ116xjMd393Hrxn2NLkdEZNoay1LHxcBG7/0m730VuBG45qhrrgE+74M7gE4zmwfgvb8FOHCM73sN8Ln6558DXvcs6peToKevzDfu38kbLlpIZ3Oh0eXIKXbN+fOZ1Vrk+ls3N7oUEZFpaywBbAGwbdTX2+uPPdNrjjbHe78LoP7r7DHUIqfAF+54kmqW8/bLlja6FBkHxTgMZr153V429vQ1uhwRkWlpLAHsWLfDHd08MpZrnhUzu87M1prZ2r17956MbymjlGsZX7xjKy89YzbLu1sbXY6Mk7c8fzGF2HHDbVsaXYqIyLQ0lgC2HVg06uuFwNG3UI3lmqPtGd6mrP/ac6yLvPef8t6v8d6v6e7uHkO58kx8/b4d7B+o8o7LlzW6FBlHs1qL/PwFC/jqvds5qMGsIiLjbiwB7G5glZktM7MC8CbgpqOuuQl4a/1uyOcDh4e3F5/GTcDb6p+/DfjGM6hbTgLvPTfcFgavXrpcg1enm3dcvoxyLeff7nqy0aWIiEw7Jwxg3vsUeC/wHeAx4Cve+0fM7F1m9q76Zd8CNgEbgX8B3j38ejP7EnA7cJqZbTeza+tPfRh4mZltAF5W/1rG0U827GP9nn6uvVyDV6ej1XPauGLVLD730y1U07zR5YiITCvxWC7y3n+LELJGP/bJUZ974D3Hee2bj/P4fuAlY65UTrrrb93MrNYirzlvXqNLkQa59vJl/Npn7uabD+3k9RcsbHQ5IiLThiZuTlMbe/r48fq9vPXSJRTjqNHlSIO8cHU3K2e3ajCriMg4UwCbpq6/dQuF2Gnw6jRnZrzjsmU8vKOXuzYfa1yfiIicCgpg09DBgSpfvXc7rz9/ATNbi40uRxrs9RcsoLM50WBWEZFxpAA2Df3bXU9SSXONnhAAmgrhCKrvPbaHrfsHGl2OiMi0oAA2zVTTnM/fvoUrVs3itLltjS5HJoi3XrqUyIzP/nRLo0sREZkWFMCmmW89tIs9vRXecZlWv+SIOe0lXn3uPP597Xb6yrVGlyMiMuUpgE0jw4NXl3e38MLVOlVAnuray5fTX0n58t3bTnyxiIg8Jwpg08g9Ww/y4PbDvP2yZTinwavyVOcs7OB5S7v47E+3kOUaSSEiciopgE0j19+6mY6mhF+4cEGjS5EJ6h2XLWP7wSG+9+juRpciIjKlKYBNE9sODPKdR3bz5osX01wY0wEIMg29/Ky5LOxq4oZbtzS6FBGRKU0BbJr43E+3YGa89dIljS5FJrDIGb/2gqXcteUAD20/3OhyRESmLAWwaWC4sfqV58xjfmdTo8uRCe6Nz1tESyHihts0mFVE5FRRAJsG/mPtNvoqKddq8KqMQXsp4RfXLOK/H9zJnt5yo8sREZmSFMCmuCz3fOanW7hwcSfnL+psdDkySbz9sqWkuecLd2xtdCkiIlOSAtgU98PHe9i6f5BrL1/e6FJkElkys4WXnjGHL9yxlXIta3Q5IiJTjgLYFHf9rZtY0NnEz501p9GlyCRz7eXLODhY4+v37Wh0KSIiU44C2BT2yM7D3LHpAG97wRLiSP+q5Zm5ZNkMzprfzg23bcZ7DWYVETmZ9KfyFHbDrVtoLkT80vMWN7oUmYTMjHdctoz1e/r5yYZ9jS5HRGRKUQCbonr6yvzXAzt5w0UL6WhKGl2OTFKvPm8e3W1FjaQQETnJFMCmqC/cvpVanvP2yzR6Qp69Yhzxq89fws3r9rKxp6/R5YiITBkKYFNQuZbxhTuf5CWnz2bZrJZGlyOT3FsuWUwxdtxw25ZGlyIiMmUogE1B37h/BwcGqrxDg1flJJjZWuT1FyzgP+/ZzoGBaqPLERGZEhTAphjvPdffupkz5rVz6fKZjS5Hpoh3XL6MSprzb3dqMKuIyMmgADbF3LpxH+v39HPt5csws0aXI1PE6jltXLFqFp+/fSvVNG90OSIik54C2BTz6Z9sZlZrkdecN6/RpcgUc+3ly+jpq/BfD+xsdCkiIpOeAtgUsmFPHz9ev5e3XbqEYhw1uhyZYl64upuVs1u5/lYNZhURea7GFMDM7GozW2dmG83sA8d43szso/XnHzSzC0/0WjM738zuMLP7zWytmV18ct7S9HXDbZspxo63PH9Jo0uRKcjMuPbyZTy6q5fbN+1vdDkiIpPaCQOYmUXAx4FXAGcCbzazM4+67BXAqvrHdcAnxvDavwL+zHt/PvAn9a/lWdrfX+E/793BL1y0kBkthUaXI1PU6y9YwIyWAjfcqsGsIiLPxVhWwC4GNnrvN3nvq8CNwDVHXXMN8Hkf3AF0mtm8E7zWA+31zzsANZY8B1+880mqac47NHhVTqFSEvErz1/C9x/rYdPe/kaXIyIyaY0lgC0Ato36env9sbFc83SvfR/w12a2Dfgb4INjrlqeolzL+PztW3jRaaFHR+RU+tXnL6EQOa7XKpiIyLM2lgB2rFkGR3fgHu+ap3vtbwK/671fBPwucP0xf7jZdfUesbV79+4dQ7nTz03372Rff5Vfv2J5o0uRaaC7rcjrLpjPf967nYMazCoi8qyMJYBtBxaN+nohP7tdeLxrnu61bwO+Wv/83wnblT/De/8p7/0a7/2a7u7uMZQ7vXjv+fStmzhjXjsvWKHBqzI+3nnFcsq1nC9qMKuIyLMylgB2N7DKzJaZWQF4E3DTUdfcBLy1fjfk84HD3vtdJ3jtTuCF9c9fDGx4ju9lWrplQxi8+k4NXpVxtHpOG1eu7uZzt2+lkmaNLkdEZNI5YQDz3qfAe4HvAI8BX/HeP2Jm7zKzd9Uv+xawCdgI/Avw7qd7bf01vw78rZk9APwl4e5JeYY+/ZNNzG4r8prz5je6FJlmfv2KZeztq/CN+3X/jIjIMxWP5SLv/bcIIWv0Y58c9bkH3jPW19YfvxW46JkUK0/12K5efrJhH//7506jEGumroyvy1fO4vS5bVz/k8384kULtQIrIvIM6E/tSezTP9lMcyHiLZcsbnQpMg0ND2Zdt6ePWzbsa3Q5IiKTigLYJLX7cJmbHtjBG9csorNZg1elMV57/nxmtxX59E82NboUEZFJRQFskvrsT7eQ5Z5rL9fgVWmcYhzxa5ct5Scb9vHozt5GlyMiMmkogE1C/ZWUL965lVecPY9FM5obXY5Mc2+5eAnNhUirYCIiz4AC2CT05bu30VdOeecVWv2SxutoTvil5y3ipgd2suvwUKPLERGZFBTAJplalnPDrZu5eOkMLljc1ehyRAB4x2XL8MBnbtvS6FJERCYFBbBJ5lsP7WLHoSGuu1LHDsnEsWhGM688Zx7/dueT9JZrjS5HRGTCUwCbRLz3/POPN7Giu4UXnz670eWIPMVvXLmc/krKl+58stGliIhMeApgk8htG/fz6K5errtyOc5p6KVMLGcv6OCylTO54bbNVNO80eWIiExoCmCTyD/f8gTdbUVed8GCRpcickzXXbmCPb0VvnH/jkaXIiIyoSmATRIP7zjMTzbs4+2XLaUYR40uR+SYrlw1izPmtfOpWzaR577R5YiITFgKYJPEP9+yidZizFsuWdLoUkSOy8z4jSuXs6Gnnx8+3tPockREJiwFsEngyf2DfPPBnbzlksV0NCWNLkfkab363Hks6Gzikz9+otGliIhMWApgk8C//GQTkTPeoWOHZBKII8evX7GMtVsPsnbLgUaXIyIyISmATXD7+it8Ze02Xn/BAua0lxpdjsiYvPF5i+hqTrQKJiJyHApgE9xnb9tCNcv5jReuaHQpImPWXIh52wuW8v3Heli3u6/R5YiITDgKYBNYX7nG527fwtVnzWVFd2ujyxF5Rt526VKaC5FWwUREjkEBbAL74p1P0ldO+c0XafVLJp+ulgJvvngxNz2wk20HBhtdjojIhKIANkGVaxnX37qZy1fO4tyFnY0uR+RZeecVy3AGn7plU6NLERGZUBTAJqj/vHc7e/sqWv2SSW1eRxM/f8FCvrJ2G3v7Ko0uR0RkwlAAm4DSLOeTP36C8xd18oIVMxtdjshz8hsvXE41y7nhts2NLkVEZMJQAJuAQs/MEO+5aiVmOnRbJrfl3a288px5/OvtWzk8WGt0OSIiE4IC2AST555/uvkJTp/bxktOn93ockROive8aCX9lZTP/nRLo0sREZkQFMAmmO8+upuNPf28+6qVOKfVL5kazpzfzkvPmM1nfrqZgUra6HJERBpOAWwC8d7zsR9tZOnMZl51zrxGlyNyUr3nqpUcGqzxxTu3NroUEZGGG1MAM7OrzWydmW00sw8c43kzs4/Wn3/QzC4cy2vN7Lfqzz1iZn/13N/O5PajdT08vKOXd1+1kkirXzLFXLC4i8tWzuTf7nySPPeNLkdEpKHiE11gZhHwceBlwHbgbjO7yXv/6KjLXgGsqn9cAnwCuOTpXmtmVwHXAOd67ytmNq0bnrz3fPQHG1nY1cTrL1jQ6HJETom/eN05dDQl2l4XkWlvLCtgFwMbvfebvPdV4EZCcBrtGuDzPrgD6DSzeSd47W8CH/beVwC89z0n4f1MWrdu3Mf92w7xmy9aQRJpZ1impqWzWuhqKTS6DBGRhhvLn/QLgG2jvt5ef2ws1zzda1cDV5jZnWb2YzN73jMpfKr5xx9sZF5HiTdctLDRpYiIiMgpNpYAdqy9gqMbOI53zdO9Nga6gOcD/xv4ih1j6JWZXWdma81s7d69e8dQ7uRz+xP7uWvLAX7jyuUU46jR5YiIiMgpNpYAth1YNOrrhcDOMV7zdK/dDny1vm15F5ADs47+4d77T3nv13jv13R3d4+h3MnnI99fz+y2Im+6eHGjSxEREZFxMJYAdjewysyWmVkBeBNw01HX3AS8tX435POBw977XSd47deBFwOY2WqgAOx7rm9osrn9if3cufkA737RCkqJVr9ERESmgxPeBem9T83svcB3gAi4wXv/iJm9q/78J4FvAa8ENgKDwNuf7rX1b30DcIOZPQxUgbd576fdven/8AOtfomIiEw3JwxgAN77bxFC1ujHPjnqcw+8Z6yvrT9eBX7lmRQ71dyxaT93bDrAn77mTK1+iYiITCOad9Ag3nv+7rvrmdOu1S8REZHpRgGsQW7duI+7thzgvVet1OqXiIjINKMA1gDee/72u+uZ31Hijc9bdOIXiIiIyJSiANYAP1rXw/3bDvFbL1mluV8iIiLTkALYOMvzsPq1aEaTpt6LiIhMUwpg4+zbj+zmkZ29/O5LV+vMRxERkWlKCWAcpVnO3353Hatmt3LN+UcfpykiIiLThQLYOPrafTt4Yu8Av/fy04jcsY7JFBERkelAAWycVNKMj3x/A+cu7ODnzprT6HJERESkgRTAxskX73iSHYeG+N8/dxpmWv0SERGZzhTAxkFfucbHfrSRy1fO4opV3Y0uR0RERBpMAWwc/MstmzgwUOUPrj690aWIiIjIBKAAdort7avw6Vs386pz53HOwo5GlyMiIiITgALYKfaR76+nmua8/+WnNboUERERmSAUwE6hjT193Hj3Nn7l+UtYNqul0eWIiIjIBKEAdgp9+H8epzmJ+O2XrGp0KSIiIjKBKICdIrc/sZ/vP9bDb161ghkthUaXIyIiIhOIAtgpkOeev/jWo8zvKPGOy5Y1uhwRERGZYBTAToH/vHc7D+/o5Q9ecTqlJGp0OSIiIjLBKICdZAOVlL/6zjouWNzJa8+b3+hyREREZAJSADvJPvnjJ9jbV+GPX32mjhwSERGRY1IAO4m2HRjkU7ds4rXnzefCxV2NLkdEREQmKAWwk+gvv/UYzowPvlJHDomIiMjxKYCdJLdt3Mf/PLyb9754JfM6mhpdjoiIiExgCmAnQS3L+dObHmHxjGauvVxjJ0REROTpjSmAmdnVZrbOzDaa2QeO8byZ2Ufrzz9oZhc+g9e+38y8mc16bm+lcT730y1s6Onnj199psZOiIiIyAmdMICZWQR8HHgFcCbwZjM786jLXgGsqn9cB3xiLK81s0XAy4Ann/M7aZA9vWU+8v0NXHVaNy89Y3ajyxEREZFJYCwrYBcDG733m7z3VeBG4JqjrrkG+LwP7gA6zWzeGF7798DvA/65vpFG+fNvPkY1y/nT156lsRMiIiIyJmMJYAuAbaO+3l5/bCzXHPe1ZvZaYIf3/oFnWPOEcdvGffzXAzt594tWsGRmS6PLERERkUkiHsM1x1rWOXrF6njXHPNxM2sGPgS8/IQ/3Ow6wrYmixcvPtHl46Zcy/ijrz/MkpnNvOuFKxpdjoiIiEwiY1kB2w4sGvX1QmDnGK853uMrgGXAA2a2pf74vWY29+gf7r3/lPd+jfd+TXd39xjKHR//dPMTbN43wJ+/7mw13ouIiMgzMpYAdjewysyWmVkBeBNw01HX3AS8tX435POBw977Xcd7rff+Ie/9bO/9Uu/9UkJQu9B7v/tkvbFTaWNPH5+4eSOvO38+V6yaOKFQREREJocTbkF671Mzey/wHSACbvDeP2Jm76o//0ngW8ArgY3AIPD2p3vtKXkn4yTPPX/41YdpLsT80auPvhlURERE5MTG0gOG9/5bhJA1+rFPjvrcA+8Z62uPcc3SsdQxEfzbXU9y15YD/H+/cA6zWouNLkdEREQmIU3CfwZ2Hhriw//zOJetnMkb1yw68QtEREREjkEBbIy89/zR1x8myz3/7+vP1cwvERERedYUwMboa/ft4IeP9/D+nzuNxTObG12OiIiITGIKYGOw+3CZP73pES5a0sWvvWBpo8sRERGRSU4B7AS893zgqw9SzXL+5hfPI3LaehQREZHnRgHsBL6ydhs3r9vLB64+nWWzdNyQiIiIPHcKYE9j6/4B/s9/Pcqly2fy1kuXNrocERERmSIUwI4jzXJ+98v345zxt288D6etRxERETlJxjSIdTr6xM1PcO+Th/iHN53P/M6mRpcjIiIiU4hWwI7hnq0H+cgPNvDa8+ZzzfkLGl2OiIiITDEKYEc5PFTjt790H/M7S/z5689udDkiIiIyBWkLchTvPX/41YfY01vm3991Ke2lpNEliYiIyBSkFbBRvnjnk3zzoV38r5ev5oLFXY0uR0RERKYoBbC6h7Yf5v/816Ncubqbd125otHliIiIyBSmAAYcHqzx7n+7h5mtBT7yS+dr5ISIiIicUtO+ByzPPb/37/ez61CZL//GpcxoKTS6JBEREZnipv0K2D/+cCPff6yHP3rVGVy0RH1fIiIicupN6wD2g8f28JEfrOfnL1jA216wtNHliIiIyDQxbQPYxp5+3vfl+zlzXjt/+fPnYKa+LxERERkf0zKAHRqs8s7P3U0xdvzzr15EKYkaXZKIiIhMI9OuCb+W5bz7i/ey81CZL113CQu7mhtdkoiIiEwz0yqAee/50Nce4qdP7OdvfvE8Lloyo9EliYiIyDQ0rbYgP/bDjXxl7XZ+68UrecNFCxtdjoiIiExT0yaAfe2+7fzt98Idj//rZasbXY6IiIhMY9MigP1oXQ//+98f5NLlM/nwL5yrOx5FRESkoaZ8ALtn60F+8wv3cNrcNj711osoxFP+LYuIiMgEN6Y0YmZXm9k6M9toZh84xvNmZh+tP/+gmV14otea2V+b2eP1679mZp0n5R2N8tiuXt7x2buZ217is2+/mLZScrJ/hIiIiMgzdsIAZmYR8HHgFcCZwJvN7MyjLnsFsKr+cR3wiTG89nvA2d77c4H1wAef87sZZWNPP7/y6TtpLkT867WX0N1WPJnfXkRERORZG8sK2MXARu/9Ju99FbgRuOaoa64BPu+DO4BOM5v3dK/13n/Xe5/WX38HcNJuS9y6f4C3fPoOzIwvvvMSFs3QrC8RERGZOMYSwBYA20Z9vb3+2FiuGctrAd4B/M8YahmTg4M1mpKIL77zEpZ3t56sbysiIiJyUoxlEOuxbhn0Y7zmhK81sw8BKfDFY/5ws+sI25osXrz4RLUCcP6iTr7/v15IHKnhXkRERCaesSSU7cCiUV8vBHaO8Zqnfa2ZvQ14NfAW7/3RoQ4A7/2nvPdrvPdruru7x1BuoPAlIiIiE9VYUsrdwCozW2ZmBeBNwE1HXXMT8Nb63ZDPBw5773c93WvN7GrgD4DXeu8HT9L7EREREZnwTrgF6b1Pzey9wHeACLjBe/+Imb2r/vwngW8BrwQ2AoPA25/utfVv/TGgCHyvPhj1Du/9u07mmxMRERGZiOw4O38T0po1a/zatWsbXYaIjCMzu8d7v6bRdYiInExqlBIREREZZwpgIiIiIuNMAUxERERknCmAiYiIiIwzBTARERGRcTap7oI0s73A1jFePgvYdwrLOZVU+/ibrHXD5K19rHUv8d6PfQqziMgkMKkC2DNhZmsn663rqn38Tda6YfLWPlnrFhE5GbQFKSIiIjLOFMBERERExtlUDmCfanQBz4FqH3+TtW6YvLVP1rpFRJ6zKdsDJiIiIjJRTeUVMBEREZEJaUoGMDO72szWmdlGM/tAo+s5HjNbZGY/MrPHzOwRM/ud+uMzzOx7Zrah/mtXo2s9HjOLzOw+M/vv+teTonYz6zSz/zCzx+v//C+dDLWb2e/W/1t52My+ZGaliVq3md1gZj1m9vCox45bq5l9sP7/7Doz+7nGVC0iMj6mXAAzswj4OPAK4EzgzWZ2ZmOrOq4U+D3v/RnA84H31Gv9APAD7/0q4Af1ryeq3wEeG/X1ZKn9H4Bve+9PB84jvIcJXbuZLQB+G1jjvT8biIA3MXHr/ixw9VGPHbPW+n/3bwLOqr/mn+r/L4uITElTLoABFwMbvfebvPdV4EbgmgbXdEze+13e+3vrn/cRQsACQr2fq1/2OeB1DSnwBMxsIfAq4NOjHp7wtZtZO3AlcD2A977qvT/EJKgdiIEmM4uBZmAnE7Ru7/0twIGjHj5erdcAN3rvK977zcBGwv/LIiJT0lQMYAuAbaO+3l5/bEIzs6XABcCdwBzv/S4IIQ2Y3cDSns5HgN8H8lGPTYbalwN7gc/Ut08/bWYtTPDavfc7gL8BngR2AYe9999lgtd9lOPVOin/vxURebamYgCzYzw2oW/1NLNW4D+B93nvextdz1iY2auBHu/9PY2u5VmIgQuBT3jvLwAGmDjbdsdV75e6BlgGzAdazOxXGlvVSTPp/r8VEXkupmIA2w4sGvX1QsI2zYRkZgkhfH3Re//V+sN7zGxe/fl5QE+j6nsalwGvNbMthG3eF5vZF5gctW8Htnvv76x//R+EQDbRa38psNl7v9d7XwO+CryAiV/3aMerdVL9fysi8lxNxQB2N7DKzJaZWYHQ2HtTg2s6JjMzQh/SY977vxv11E3A2+qfvw34xnjXdiLe+w967xd675cS/hn/0Hv/K0yO2ncD28zstPpDLwEeZeLX/iTwfDNrrv+38xJC3+BEr3u049V6E/AmMyua2TJgFXBXA+oTERkXU3IQq5m9ktCfFAE3eO//orEVHZuZXQ78BHiII31Uf0joA/sKsJjwh+4veu+PbmaeMMzsRcD7vfevNrOZTILazex8ws0DBWAT8HbCX0gmdO1m9mfALxHuoL0PeCfQygSs28y+BLwImAXsAf4f4Oscp1Yz+xDwDsJ7e5/3/n/Gv2oRkfExJQOYiIiIyEQ2FbcgRURERCY0BTARERGRcaYAJiIiIjLOFMBERERExpkCmIiIiMg4UwATERERGWcKYCIiIiLjTAFMREREZJwpgImIiIiMMwUwERERkXGmACYiIiIyzhTARERERMaZApiIiIjIOFMAExERERlnCmAiIiIi40wBTERERGScKYCJiIiIjDMFMBEREZFxpgAmIiIiMs4UwERERETGmQKYiIiIyDhTABMREREZZwpgIiIiIuNMAUxERERknCmAiYiIiIwzBTARERGRcaYAJiIiIjLOFMBERERExpkCmIiIiMg4UwATERERGWcKYCIiIiLjbMIEMDO72szWmdlGM/tAo+sREREROVXMe9/oGjCzCFgPvAzYDtwNvNl7/2hDCxMRERE5BSbKCtjFwEbv/SbvfRW4EbimwTWJiIiInBJxowuoWwBsG/X1duCSp3tBUmjxpeau8EV9Ec+GF/O8D495sOEVPu9HPV5/cuTzI78eWRH0I99XRMZPmQGqvmKNruNkmzVrll+6dGmjyxCRcXTPPffs8953H+u5iRLAjvWb7c/EHzO7DrgOoFjs4OIL3v3UC/L6dfmRsOXSHLzH0hzyHMs81NL6YxmkGeQ5Pk0h95CmkGUhiNVqoZAsBx++uc/9yOfhAaU0kZPpTv+DRpdwSixdupS1a9c2ugwRGUdmtvV4z02UALYdWDTq64XAzqMv8t5/CvgUQEfzfB/1ViEyvDNw9V8BLHxuHvJCFB5LPOZ9CGBpHFbGakcCmNVDGdUaPs0wn4fv4z3m6iHNe4wMiI4EMTOFMBEREXlGJkoAuxtYZWbLgB3Am4BfftpXeI+r1PDOYbHDm2GRhdBkQFRvbxu1tubNIALDHdlqjAzLPN65EMScCytjeY6PorCaVl8VY9SqGFlO+EH1VbHwyUhtIiIiIsczIQKY9z41s/cC3wEi4Abv/SNP+6Isww72YnEcwpZz+DiCyOGjCOqhjNjh66tk3hkeg2R0KvOYB8tyyD2W5WG7MvNhVWx4dSzNsCzD12rhNbUUPxzKsixsX3oLYcxQGBMREZHjmhABDMB7/y3gW8/gBSEM5XkIYWaY9/jcYbnHE2OR4b1hWX31C8IKWTQqgJnhPZgLW4mWOZwL/WIQmvg9YGYQuXq2qj/nDJ/lYZHNcnwG5oZ7xdyRLcp6vSIiIiIwgQLYM5Z7/FAZi6Kw4uUManEISnGMxVFYFUvCCpklET4OK2V54kb6xHxkYNQfAzzk9QZ+aw7N/C4tjqyKueqRXrGwWpZBrRb6w6o18HkIZVl9G1MN/CIiInKUSRvAvM/xlQreHDgLwStJwmpVHIcQFjksSUI4KyRYEuOdw/k4hK9CBBjejDyp9485jvSNDY+3yELzvss8rppAHn61NMdq2UgYI47DdmSaho/h/jE18ItMSWZ2NfAPhNaJT3vvP9zgkkRkkpi0AQwfVpTM5ZA7vCOsOsHItp/Prb49GH4NdzSG5nyL6ndJ5r5+92QE5snj+t2UxkgQG+khi8K1lnt8vXnfpXlYXcs8lsRYvVeMau1I036Whab9+qoY3td7xnI18ItMUvUTPD7OqBM8zOwmneAhImMxeQMYQJ7hvQEZmMPX0tCXVUtHVsXC9qQ70qwfRbhCIYytKCS4JMbHDl9M8JGRFyPy2JHHNrItGULZU3+05aE/zFJwqcdyT1TJsNRjtQxXSUMjf6UaQlma4avV0Ohfq4atyTwPK2QQwhlHbVMqjIlMZCMneACY2fAJHpM6gHnvw46CiJxSkzuAwaiQUu+zygDzmDe8haZ5sixsTXoXrrew3Whm9cdDSMO7sG1pPlwS+3DXZH01zBsjs8ZseNJ+BD4Cy8L4C5d63PA1w6tbLh1p4CfPw8+MsjAQtv4ePIRw5vLQwD/qPSmIiUxIz/gEj8ngz/7rUZ48MMgrz5nHy86cQ0dT0uiSRKakyR/Ahg2HFLN6IzwhJY1eTTILQau+QkatVl8Zi7BCgo8crljA1xv282KMj40sCY37PjLyQj2IRVb/gKwQtjMtDwHPZeBqCZZ7XM1jqcdVM6JK2IJ05fpYi1oaGveHx1vUtyl9fVXMj4y30FalyAR0whM8Rp/esXjx4vGo6TnrbivyvUf38MPHe0gi44pV3bzqnHm8VGFM5KSaOgFs2Ohg4oe3KAnBxtxTtyjrd1Ba5KBSD2KVGhZH+CTGmgph0GtTTF6IyAsubHVGkMZGHoUVsTzmSL+YWdierH9EtdDAH9UionI4EikqZ6F3rJLhylXIcqxShTSEr+G7KalZ/VgkqzfwHzXeQiFMpJFOeILH6NM71qxZMyn+h33PVSt594tWcP+2Q3zroV1866HdI2HsylXdvPysOVx12mxmt5caXarIpDb1AtjRjl4Zy11o3M/CX1Utz/F5VN+qrG8P5jE2POurPlHf0hxXi7AsIo8tjKuI6ytgOfVBr0B999CHHc2w1ZmHa/PYY7kjL7gQyio5rhRjWY4rh7sqqdawSr2Bv1KFfHgAbHrU0Fetiok02DM/wWOSMDMuWNzFBYu7+MNXnsH92w7xzQd38T8P7+YHj/cAcNb8dl58+mxedNpszl/USeTUNybyTEz9ADZsOJyMXhXL60NWXYqv1sKqWGXUqlh9ezIqFKC+KhaVEnCOrDkZWRVLmxzeGWnJ6kEL8gQwSOvHI4WfHRr3Xc1hObgaRNUw3iIeyrE0hLKonIbANxhWxaxaCytk3uMr1RC+amkIZsOhDDXwi4ynZ3WCxyQ0Oox96FVn8PjuPn60rocfPd7Dx3+0kX/84Ua6mhNeuLqbq06fzWUrZzGrtdjoskUmvOkTwEY7unE/d0AWGvepr4plYaI+0c+uihFHuMhGAlVe7wVz9a3I4YPA/XDzfv08cG+En+EAD9HIWIt6037GyAgMq4VxFZZGIzcMkB45+qg+M3ZkUr8a+EXG3zM+wWOSMzPOmNfOGfPaefeLVnJosMotG/Zx8+M93Lx+L1+/P+zAnjanjUtXzOQFK2ZyyfKZ6h0TOYbpGcCGHesOytyHBn1z+CyrB580rGIlcViJMiMaKuLiCJKYqCk08GfNSVgBK45eFSOsiMWQJyF8Da+O5cUQ4vBQTaN6074jqsZY5onLRVzmicqeeCgNzfyDNSzLsHINVw2N+75aHRkAO7xVqQZ+ETnVOpsLvPa8+bz2vPlkueehHYf56RP7uP2J/dx495N89qdbcAZnze/gBStmcumKmTxv6QxaitP7jx4RmO4BbNgxG/frs8UAS9Mwcb9i4a5J57BqFVyExRHRUDHcQVku4pOIvJTgKhF54rDckSVGVgyDXLHQvJ/H9T6xaPjnAhguI8wWy4xoKNxRGZUhGXK41BP3R7jUEw3WcOVamMY/FIXVsVoNovrg15qNBDE18IvIqRY54/xFnZy/qJN3v2gllTTjgW0hkP30if185rYt/PMtm4idceb8di5a0sWaJTO4aEkXczvU0C/TjwLYsQyPrPBHtiiHJ+6HqfbZyCwv7+MwJiwKSSpMw88hL4Rp+XlMlDiymuHSEL4sBT/cKzY81qJ+BJI38EkIZsN3VGYJZEWHZZAUXb1nLCIqF3BpTjRQCEGsUm/gzzKsEoa9WpqGsRZHDX3VqpiInErFOOLiZTO4eNkM3vdSGKpm3LP1ILdv2sfaLQf50l1P8pnbtgCwoLOJNUu7WLOki4uWzOC0uW1q6pcpTwHseI6zKuaz4bsi0yPnUEb1Pq1CASKHSxJcIYEoImkaXhWLSZsTfGzUWiOyJDTtp00hjKVN9VWxGPLEh/4xV+8by8OgV8vBVa2+KhbGWrgUCv3FsDo2mIetylpONFCtr45Vjswaq29VqoFfRMZbUyHi8lWzuHzVLABqWc6jO3tZu/Ug92w9wO1P7Ocb9R6y1mLM+Ys6OW9RB+ct7OS8RZ3M0dgLmWIUwMbqRI37ZvhqNcwW8x7zHqIoBLQ0wnlPZBYGvEaGZfU+s8jIc49Lwt/2slFHHvmo3iLmwlR+6uMu8mx4+9JwNcCDS62+khbjqnn9sRwzC9P903rjfp5j5sK8sfpUfgAjUwO/iIybJHKctyiEq2svX4b3nu0Hh7hn60HWbj3AvVsP8ckfbyKrr9bPaS9y7sKwxXnuwg7OXdBJR7Oa+2XyUgB7po7TuB+2JHO8S7FqFZ8koYG/UgnnTyYJri/BxxFxb5i2n5Vi0pYYHw2vikFaMrKmsD2ZNoUQlhd8aNx3kDWF1bE0J9yFmUNUNcghqkRE5QiXQjJQwKWeZNATDeVE1Zx4IPSMuaHayBmVlCvhXMrh8ymzTA38IjLuzIxFM5pZNKOZ112wAIByLeORnb08sO0QD24/xIPbD/O9R/eMvGbpzGbOW9TJOQs6OHtBB2fOb6e9pFAmk4MC2LN11BZleKgeysyNbFGGZv36TLEkBhfhBsNcMVcsEA0UIXZE5QJ5wVFrcdSqLgQurH7HpI1sS2ZFD5HHOz8y9DXNwt2UrmK4muGqUBs0LDWSfk885IiqnmKvw1JP0h/jynGYxO9cGK9RdqGJP3PHbuDP6u9VDfwiMk5KScRFS7q4aEnXyGOHh2o8vOMw99dD2V2bD4xsXQIsntHMWfPb6x8dnDW/XVP7ZUJSADsVRk3c9xmjhsD60LgPWOrCUFbvIY5IvCdPIlwtJqpG5InhUhdWxZqNqFJfFauFrcc8qa+KWT2IWb13LApjLvIkzBXLikZUDb1jtWYLq2ODEfFQIayK9RfrQ19rYeBrLcXKlSNDX+srYqN7xrQqJiKN0tGUcNnKWVy2ctbIY3v7Kjyy8zCP7Ozl0Z29PLLzMP/z8O6R52e1FjlzJJSFYLZ4RrMa/aWhFMBOpqMb93NGpuCPnEMJEJXD9mSS1MdaGFGhQBTHxKUChfqB4KXWAnniSFsiai1hnEW1PayKpc1G2hKGwGYteRhxUfCQhL6u3EIt1ZqDzLDU4QYdLoO4PyIqQ1SBQl+Cq3kK/TnxUE5UyYh6q2HW2GBl5MBwX61iuQ+/qoFfRCaQ7rYiLzotHIs0rK9c47FdfSPB7JGdvfzLLZtI63+BbEoiVs9t44y5bZw2t43T57Zz+tw2uloKjXobMs0ogJ1qo3rGfAaYCw3v5jBq+DwPW5QQjh3yPqyU1SJw4JJo5Fu5gpHHLoyuiCyMuUg8eSFsQXrnwwQN57HIYwa5hYZ8n3oy8+RpuL3SxyHImTcsJTwWGXkS+sksy4nMoFzDoghzbiRwjR7FAWrgF5GJp62UjIzBGFZJM9bv7uexXb08vruPx3f38p1HdnPj3dtGrpnbXuL0eSGUnTG3ndPntbF8ViuF2B3rx4g8awpg4+Vngli9x8qlYPX+K+dC0/5Q6BWLBosQOaJigULT8KpYQp44ai0RtWYjKxi1NldfFYtImz15DFlLBpGHQo5LclycQVOYA5ZlRpo5fGoMlSPIjHjAiMqOqBqR9Ca41FPoayIue6JyTtJXw6U5rr+KVWu4Whoa+PMcKpXjN/APr4w95Z+BiMj4K8YR5yzs4JyFHSOPee/Z21cZCWSP7+rjsd193LZxH7Us/J6VRMbyWa2sntvG6tmtrJoTApq2MeW5UAAbb6MOBQ9fHjVfLErDxP3hOyidQVLAFeuN+wMlfOyIW4oUmmOyoqNSDj1j1fbQhJ8VAOdCT1jsMeeJopxSsUbkcsw8ziDNHJVaTJ4b1cECtYrDyhFJa/g+abMRD4Um/rxouKoniR1RJcEqNZxZaOA3O9LAXwUshMyRsylHhzARkQnEzJjdXmJ2e4krV3ePPF7LcjbvGxhZLVu/u4/7tx3kvx440vBfjB0rZ7eyek4bq+a0ctqcNlbPaWNBZxNOwUxOQAGs0Y6eup/VD+w2N3IGpVG/wzKKMO/DlmDmcbWEKImwLAx4jaoR8aCRFSGq1FfFWh1pU0yW5NSaEyzOiZOMOM4wgyjKw28UzVWyQkTWlFEthVWxtDkiqkBUNip9cVgV642Iy564nJP0Nx0Z+lpN65P46437oxr4UQO/iEwySeRYXQ9U14x6fKCSsrGnn3V7+tiwp491e/q5Y9N+vnbfjpFrmgsRq+orZeHXVlbNVjCTp1IAmwiOO3U/rJJZJQxtxY06i7KQECVJaNxvKoJzlFqL5KWErBhR7YjJE6PSbqGBv+SodkTkCVTbMmrNKXGS0dJcIYkzSi0pxTgl90bujSx39FcKVNOYaiVmsL8AqZEcjoiGHPFgROFwTFSFYm+JaCgnHsqI+yphAv9A+akN/MeYwB/CmLYoRWTyaCnGIwNkRzs8VGNjTx/r9/SzbncfG3r6uHndXv7jnu0j1zQlEStmt7BqdhsrZ7eOhDRtZU5PCmAT0TGm7pvLIePI1H0IvVZpikE4AskZloUGfu8gLzi8i45Myo+s3sDvyImpFY1KkpF5I3I5iTeceRKX4eu/GdSSlEEX7grKUkfNQ5640KxPfRI/jrhg4WYAA6vlxGZQOaqB36pHnaXJU1fF1MAvIpNUR1PCRUtmcNGSGU95/NBglY09/Wzo6WfDnn427u3nzqNWzAqxY/mslpEVs5X1j6UzW9T8P4UpgE1ko/rFwqoYR6buZzneVUMYq1SxyMFgGRdHuEJCdLgIcUSpuUDWHIdVsfaIPA6rYmlzTNoUU+soUI09fW0ZrjklSjLaWsokUU5TUqM5qdJRLEN76FcbqBWoZhFD1YShwSJ5zdHXGxOVHfFgTOFwjKtB4XBT2KYczEl6UyzNifrCuZSuWjv2BP5aWn+79bsttU0pIpNcZ3OBNUtnsGbpU4NZX7nGE3sH2LCnbySgHd1jFjljycxmVnYfCWWrZrexYnYLzQX98T3Z6d/gZPEzzfvHmLofVfBRFA4Hrx8GHjWVcIWEuJAQ9xfxiSMZSKg1O9Imo1IOd1JWUyOtOmpNGUNxThpntBSqtCYVCi6jszCEw5NjZN7oq5U4UGmmksXsbW+lUk4oDyTUWsK2ZFoy4qGIpN9RSkIDf8EZrhLjhuJwRmU6vBKWhen7+XDgGnXeps81fV9Eppy2UsL5i8LZlqMNVlM27R1gY0//yMeGnj5++HjPyAwzgAWdTayY3crK7tBjtrL+ueaYTR4KYJPVqOb94YPBRx73PmxLujQEnHovluU5PnZhi3AgJmtyRJVwB2U8FJru06aISn/MUCGnv63ErqZ2SoUaXc1DJC4bCWQ5RnuhTO6N2OVUWmL6Wwv0t5ZIU0eto4ArG/GAo9wbVsWKh2KiiicZyEn6W3C1nKi/cqSBf6gcDguv1sKKWJpqrIWITCvNhZiz62dbjlbLcrbuD8FseCtzY08/d23eT7l25PfFWa0FVnS3jvSYraz3m81pL4a762XCUACbzJ5uVcxVw3ND9an7UYQVCpgzklKJJInxSUxTSxhrUWsvkjU5as2OSqcjK8RUOmPSlhKHWjyHulqIk4wZHQN0loZoL5SZW+olsYzW9gqJZZTzhKEsoZIn7BxqZ6BWZN9gM4f7mskqEdGBhKhsJH0xxYMRrgqlQ8UwZ6w/Je6rQJrjBoaglkKthlUqYdu1Wg3vN/dHtijVMyYi00QSuXqYauPqs488nueeHYeGnrJitnFvP//1wE56y+nIdW3FOKyYzR4dzlpZ2KUbABpFAWwqeZqp+yPP1afuW5ZgWdjeszgidobLYiyL8ZGRJWHavuWGZVCLE2pJxOE4J8sdtTyiFNUougxnnuaoSmQ5rXGFYp5SKcY0xzWsfiRSpZQwkBt5OcJH4fDKkBEdcdnwcbhJwNVycGC1DCuHg8x9nmPOoN4rhrN6EGPk/T71/YuITA/OGYtmNLNoRjNXnX7kKCbvPXv7K08NZj39/Hj9U+/MLMaO5d0hkK2eE1bMVs1pZcmMZuJINwCcSgpgU9HPNO9nYYxFlo1M3ffOhVWxwQRcRNwXmvaTQkKxtYhPImrtBbJifVWsw5EXIiqdCYebWznQ7NncNYsoyenqGKCtWKGjMMTcpj4KLmVOsZeSq4WJ/V0RNR+xZ14b5SyhZ7CN/QPNVKoxfQdLuLIj6Q1jLVwVSgdKRFVPoS9M4LdaRtRXxtIQyny5AnmGr9Ygz/FpeuxtSgUyEZmmzIzZbSVmt5V4wYpZT3nu8GCtvoV55AaAe7Ye5KZRNwAUIsfy7paRxv/Vc0Kv2ZKZLSQKZieFAthUd4wwNjJ131mY0WWGL5fDjLE4PnIEUl8TeSmm0JRQ6E/ICo540JE2G9U2o1otkhU9B7wx1JyQtTg6CmUcno7iIB3RECWr0uKqZBh9TU3UfMSutk62D3XRlxbZ3DKTwUrC4KEm0uaYqGL42BGVPVnByOOwKlYAXDUbGUw70rA/fCB4mkJ9XIea90VEjq+jOeGiJV1ctKTrKY8PVFKe2NvP+j2h8X/jnn4e3H6Ybz60a+S30iQyls0Ks8xWzWnl9LlhWO2SmS3aynyGFMCmk2PNFxt9MHiW1QelHpm67yoxrlzAVTN8EhFVkjDUtcVR6Q+zvyp9JYaaimxtbWFXZzuFQsrc9tl0FIboKgwxpxh6xdqicugZi8osa95HOU9oiysMZAX2tLexf2YzlUpC78wSVnEkvRaGvVagdDDcXZn0ZST9Ka6WEfVVoJbiKlWoVEMIq9aOTN/Phk8XGDXWQoFMROSYWoox5y7s5NyFnU95fKia8cTeEMo27AkB7eGdh/nWw0eCWTF2rJoTjmUaDmWnzW1jbntJzf/HoQA2HY1eFcsBM3xK6BlzVRiqT92PohDE4piokGDOEbc0QRKTlwpk7QXy2FHpiklLRrUtptKVUCvCE7Pa8E0ZTe1lFnQdpiWuclr7HmbEA8yK+5hbOkSEx7XmRJZzKGthf9bK4ayJ9QNz6UuLbO3tYv+hVmrlmIG9BVwFiocSCodi4oqndKBIVMmJB2ohjKUZNjAUxnLUalDfoiS1+halaYtSROQZaipEx7wzc6iasbGnn8d397J+Tx+P1w8x/+q9R4bMtpdiTpsbwthpc9o4fV47p89to62UjPfbmHAUwOSpIy0ywHw4jxLC6Io8D+dROgtT7dMMl3tw4JKovk3owDu8C2dR+tiRVo0hX2J3lNNUqFGKa/QVSpQLCZHlJJbRGQ2Ah8RSOqMBCpYyWCrSnxVJ87BVOlAp0JcZVolCU35kpOXwN6qoGlFIHEnkQq9YOGW83sAfesWoupFeMbNRQUzN+yIiz1pTIeKchR2cs/CpwezQYJV1u/tGQtn6PX184/6d9I26K3PJzGbOnNcePuaHj+m2WqYAJsFTQkg9iA1P3Xdp2N4DrFwJK2NJTNRbCMNe9xfDqlhzgbS1QF5wVDoi0pKj2lag2lGgrwh3zZyBL+UU2it0d/TTklRZ0b6PGckAs5I+5saHaXNl1rRsIsIz0Fqkr7tEX9bElkUz6U2beLK/i919bQyWE3r3N2EVo3gwIelNiMue0oHm0MDfmxL318KMsYHQwE+5ElbGslEN/Fmu5n0RkZOos7nAJctncsnymSOPee/ZdbjM47t7eXRnL4/uCr/+z8O7R67pak5CGBsOZfM6WN49dZv+FcDkZ/3MfDE7cgdlVh9rUTEsroSDwcv1IDZQxNXvpoz7S+TFiGp7TKUvIiuCq0RkpYjqYMTuNKJQrBG5nP5Sgchy5saHSSxlQXSYZhcCX4Sn7CN2FNsZ9EU2tMxhc3s3PeVWNpS6KVcShppKpE0R8aDhzRFVwgiNPDKiSkzsPdQywumV4F2E1eeJWf1tqnlfROTUMTPmdzYxv7OJF58+Z+Tx/krK47uOBLJHd/Xyudu3Uk3DX4iLsePsBR2ct7CT8xZ1cP6iThbPaJ4SK2UKYHJix5i6P7JFaaN+zbKw0uQccZrhk5hoqEBSv4MyGYxIi0a13VE90ERaLPHYzCasKeP+9gXc2b6U1qTC6tYeOuIhZsV9dMe9YbuSjGarsLywl+64j0PNzcxvOsxAWmTLzBns7W+hPFTg0P4SrmIUDkYkfVFYFTtYJKrmJL0ZcX8VV82wgTLuKati+ciwV19LNXlfRGQctBbjnzkrM81yNu0b4JGdh3l4Ry8PbDvEF+/cyg23hd+PO5sTzl3YyfkLOzhvUbhpoLut2Ki38KwpgMnYHL0qlhNWwwCqtTAodchh0UBYFTscY1FEVEiIS0WIIppaS/hCTNpaoNYWkxWNoRkxaVNCtaPEhhkd5KWcx2fPoa2pzJL2g5zWuoeueIAzizvojAZZmhyirT7ctdwKNYxtaTs7al3sS9u5v28hvdUmNh2cQd+hZvxgRKknxlUcpQMRhZGtyiJWy4l6K2FbtZbCYDn0jEVhm3LkA9QzJiIyTuLIsXpOuJPy9ReEx2pZzvo9fTyw7TAPbj/E/dsO8bEf7WX4eMwFnU1cuKSLS5bN4PnLZ7Ciu3XCr5IpgMmz9zOT9+tfZ0dmdBmEFbI4xpxhtWzkPzpXdeSxEVUADMyRlYyBuIlyU4Esd+Te6CoMEuGZEfczNz7E3Kgfhyeq/7w2V2ZufJiCZRxubuJwoYlqHrHb5fSXilTyJly5/v0LRjzkwQrhgPDIEQ3FWDXFudCsT7kSQmX9PEryPLwnNe+LiDREEjnOmt/BWfM7+OVLFgPh4PLhFbL7tx/izk37+a/6MNlZrQUuWTaTS5bP4JJlM1k1uxU3weaUjWsAM7NFwOeBuYQ/xT7lvf8HM5sBfBlYCmwB3ui9PzietclzMDqIpcPhpD6DK02xSoQ3wwbi0CtWKBAVC/g4otTahE8i0taEWuvwqlhCVizQ39HEvZ0zyUueH81aRalUY357L8vb9tMZD3J6007aozLdUS8L4vBxZnEXALs72jiQtbI3beexwXn01kpsPDSLg33NVAcKxHuT+tT9mKS3RDLkKR5sq29VVnGDVajWcIPlsNJXnzNmWTZyQLjmi4mINE5zIebiZTO4eFnYvvTes2X/IHdu2s+dmw9wx6b9fPOh8GdCV3PCxctmcPnKWbzkjDnM72xqZOnA+K+ApcDvee/vNbM24B4z+x7wa8APvPcfNrMPAB8A/mCca5PnalQI8Wka+sbqTfvmrD4GwvDlCpaEMObKVYgcrr9E3FIkL0TEgwWykqPc70gGHGkJyrVm+ppyttZianlEV3GQjniIsh+g0w3SbIOUDGZERRyOJXEvFX+I/ZmxpLCXQ1kzc4qL2dw6k57BNnYlHaRDMT4KoS8dMPAQVcPdNnFkuHIE3oe+Nu/DNmvNwopYFP4m5YdvTtCqmIhIQ5mFKf3LZrXwposX471n24Eh7ti8nzs3hUD2nUf28MffeISzF7Tz8jPn8rIz53D63LaGbFeab+AfGGb2DeBj9Y8Xee93mdk84Gbv/WlP99p2m+EvsZeMR5nyXIz6j9qiKHwSReFzM6xQgMhhxSIUEnwSk7eVRs6irLWGxv3yDEdWhGqnp9qZ40s5LbMGaS5WWdx+kGUt++mIh1hd2kWLq9DpBmlzVXJvVHHk3rEj7WJ/1kpPrZ31A7PprTax9VAXfQMlsv6EZH84Cql4AJJ+TzzkKR3McLWwKmZDNaxaw4ZXxapVqKX4ka1KnUd5Mtzpf0CvPzCx9gpOgjVr1vi1a9c2ugyRaW1jTz/ffXQ333t0D/dvO4T3sLCriZedOYefO2sulyybcVLDmJnd471fc8znGhXAzGwpcAtwNvCk975z1HMHvfddx3kpoAA2qQ3/x11fGcMcFrkjwayQhM9LRXypiE9iso5SmC/WmVBtdaRNUJ5lZCVPdWaO66rQ3Fzh9Fk9dBUGObtlJ6uKu+l0gyxPyhTNkRARmTGY19ibewbzmEeq89lamcX2ShcP7p/PQKXAob2tuN6YpN8o7TWiiqd0MCfpz4mHMpJDZawWpu5TS8NMsUoF73046FyzxZ4TBTARGQ89fWV+8FgP33t0D7du3Ec1zVnR3cKvXbaMn79gAS3F575J+HQBrCFN+GbWCvwn8D7vfe9Y06aZXQdcB1Ci+dQVKKfWMcZajDzufThsO8qPHLydZUSxw1XrvWQ+Iqo38OfFMPurlhfpG4zZ6GbRWqyS5hF9WYlZSR9VdtJiVWa4Ki3OyLwnAZpdSnfUC0WILKe/o0BvtYk0dwwWi1RKCRDhKoZ3jrTkSAbDtH9Xy4mTCKvUwtT9yIVG/chBLQ3vpZYCUX2bEvWKiYhMILPbSrz54sW8+eLFDFRSvvPIbj770y388dcf5q++/Thvet4i3nrpUhbNODV5Y9xXwMwsAf4b+I73/u/qj61DW5DT16gVMTiyVTncJ2aRg2IxLAs3lfClQmjcby/hE0e1Iw6rYiULq2IFqM7IyTtqJE01Fs06RFtS4bT2PSwr7qUzGmR5oYeSZbRYSmJQ9kZfnlD2MRuqc9lT62BbeQbremfTXy2wZ28Hvj8m7o0o7TdcFZr25ySDnnggo3C4itUyXF8Zq9bC4eDV6s9M3X9K4z4okB2DVsBEpFG899z75CE++9Mt/M9Du8i959rLl/H7V5/+rCbyT5gVMAtLXdcDjw2Hr7qbgLcBH67/+o3xrEsa7Gcm79fvoMyy0LxvDqvWwupXpQqFBBfHJEPVcCTSQJGkNTTuR5WYrABx2VEdKJC2JDyZO4qlGjlG2uqYWzxMd9wLrky3S5kRHRngl/mUudEmDhULbCnOYmahn4O1Zh6MFrCvv4XB5hJlK+CqYN6RFTyF2LDM49KYJPOhp80M8/5npu6HN6ap+5OBmf018BqgCjwBvN17f6j+3AeBawnLt7/tvf9Oo+oUkZPHzLhoSRcXLeli9yvP4KM/3MC//GQzd285yMd++QIWdp281bBxXQEzs8uBnwAPMXLbGH8I3Al8BVgMPAn8ovf+wNN9L62ATXHHWhVzFn6NojBXrBiOQPJNRSgWyAsxaUdx5CzKWouj1mxUZkBW9FRnZri2GqXmKktmHByZur+wcIDOaJD5yUFKVqNAjjPPYJ6wP2+hnBfYWJlDT7WNHeVONh2ayVA1oX9fC24gIu4zSgcMVyH0ig3lxP1ZaNyv5bj+oTDo9TirYuoXe6qJsgJmZi8Hfui9T83s/wPw3v+BmZ0JfAm4GJgPfB9Y7X39bxDHoRUwkcnpmw/u4g/+80Gcwb9eewnnLeoc82snzAqY9/5W4Hi/sSpNyRHHWxWDI837g1HYlkwSLHK4OKa4twSRo9TSRN6UkJcSqp3hKKShGRG11pi0pYl13W3kpZyHu+cxu72f2c19nN++nRlxP6cXdzE/7qMzTjnb1QC4omkXZe/ZnRXZMGsuh7Jm7p23hF1D7ezqbefQ3lasElHuiYgHHIXeiKYDMVHFUziYEJVT3FAtNO6nGZTLkKahiT9NMfMa9DrBeO+/O+rLO4A31D+/BrjRe18BNpvZRkIYu32cSxSRcfCqc+dx9oJ2rvn4bXzmts185E0XnJTvq0n4MjkMh5FRzftGfcYYNXxe3+qr31FpzuG8x9KcxBlRweGjGJc6XM3wkQtDX62Z7dWYg81N5N7oSMr0tZZYlIRVsUXxofrUfYgIh4PPjPpJLGVx0wGaohrOPGnuqFRiKnkTaZMjL4TG/agKeVwkHkqI+2Pi2GFpjsVRaNKv1rBRd1DifVghy/2Rxv3R718a5R2EYdEACwiBbNj2+mMiMkUtmdnCS8+Yw3cf2U0ty59VP9jRFMBkchm1Mua9ARk+c5hL671i1XD00eDQyFZl4UARIkexpYm8FIdVsY6EvGCUOyNqLc3UWpt5YEYnedFz86xVtLSWmdE8xGmde2iPy6xq2sPsuJc2N8TcqJf58WFWJHup+Yj9XS1smz2Tw1kzj/TP40ClhZ297Rzc3wqViMLeiHgwnENZOlAiqnqKB1uJyinRQHXkYHA/VMaGV8Wq1RDKRp9FqTB20pnZ9wkncxztQ977b9Sv+RBhiPQXh192jOuP+S9l9J3bixcvfs71ikjjlGsZ/ZWUgUpKZ3PhOX8/BTCZvI4TxgAsy8Pdk85BrRrCWKVKVCzgCgmuHIa9RuVi6BVrcURVIysa5bRIX1vMUFsRM09HoUzRpQC4OGdu1E9iOTNcSsGM7jyEsr68RGtUpqfWTnsym41RzmClwIBvIRtw+MhhuRFVDJdF5ImBGVEWgpZloSnf19+b5Xn4PPeMjOqQk8p7/9Kne97M3ga8GniJP9Iwux1YNOqyhcDO43z/TwGfgtAD9pwLFpGG+Oq92/nvB3fxuy9dfVLCFyiAyVQx6jxKqLeO+Tw08ed5CGJZBtUqliRE1Vo4i3KoRqEYkzUnFA/HZAWjeMCRNifUWhKenFnCFz2PzphLa0uZmS2DLG/bR2tUYWlpPzPifkpWo80NAbAgOUh33MusuJ9FzQfpS0ts6OjmcLnEwcMtDB0q4MqO0r6YqExYFTtUDL1ih1pxlRQ3WMMNDIUm/cEy5PWm/VptZFUs9IqhVbFTyMyuJhyJ9kLv/eCop24C/s3M/o7QhL8KuKsBJYrIKdZbrvGxH27kM7dt5uKlM3jvi1eetO+tACZTy+hVsZywohQWr7BqNQQyZ1gcg3NYISGKY+JCgUJTEZKYlvYSWVNM2hxRnhGRFYzyrBYGWpo51N7F5u6ZFIs1ls08wJxSHwubDnJGaSfNrsL8+CAtlnJ6YQ+1ZkfZx2xp7+ZQ1syGoTls7Oumt1Jix95O8oGY+GBM5UCEq0DzXkdcLpD0phQOJ2GuWBSF4FiuQMWFPrdqdVSvmMZZnEIfA4rA9+rDou/w3r/Le/+ImX0FeJSwNfmeE90BKSKTS5Z7/n3tNv7mu+vYP1DlDRcu5IOvPIPInbwbtBXAZGobnrpPvY+KDPNhm88sbAGS+/C1M0gzoshwaY7lCT6CrBCa9qOK4WpGhRKDxQKbvLGvuYW9La30txZpjSsjg14TSylZjcw7InJaXIVZST8DTUWa4yoD1YTBYpGyK1G2mKgS5opFZU+xkJAnjqiak8QOq6ZYEofQmGVhO3X4/MksC/Vr2v5J570/7l91vfd/AfzFOJYjIuOgp6/MN+7byVfWbmNDTz9rlnTxmV+7mHMWdpz0n6UAJlPfz4y0GBW60nTkLErfH86itN4w6DVKEgrNJYgjWtpL5MWItCWi3BmRJxHlme30NrWzv62bh2YuxBUzZs7op6s0xJzmXpY176fZVZmTHKbZVVhd2sXq0i7KecKezg76sxJPDs3gyf4u+ipF9u1rw5cj4oMxxUMJURma9iVhe7I3I+mt4aoprjfMFbNKFV+uhLtCq7UQwobDGGh7UkRkDMq1jO8/tof/vGc7t2zYR5Z7zlvUyUfffAGvOXfeST2cezQFMJl+vH9qGLP6pPoox7sUS1P88LDXWg3imLiW4gsJ0WCCqxXJE8OymLQZoopR8QlZIWa/wWBzgWoe0RTVaI0qdESDlKxGs6vQ7spUXUSLq1L2Cc2uSlNU40C1mSw3BstFypQwYqKy4WqOeMhjHizzRLHDahnEUbgVL8/DKliWhwWw+gofjLxFERE5Sl+5xk+f2M/N63r45oO76C2nzG0vcd2Vy/mFCxewcnbbKa9BAUymN39k8KnPCDcb5vXxD8MfzqBWw8UxbiAhGgh3UCb9RbJiRK01orwvzP4q720ibSrxZFsbW7tm4QoZ3V19tBcqzCwNsKDpEEWX0hEPkliGs5yFxYPMSAZoiaoMZAV2tnewf1YzlUpCZWYRV3YUDkUUD0dEFU/pQCGsivXViPqrWCULTftpFlbEalV8lmNHN+1rRUxEpqk89zy6q5cfr9/LLev3cs/Wg6S5p6UQ8bIz5/ALFy3kBStmndQerxNRABMZy9T9ofKRqftxjEWOwv4mSGJKTUWaWwrkhYhqV4G0ZFTaHZUZRbIC9HSX2N2UkXRU2N7VSXNSZWXbPjqTQWbEA8wp7AdgZWkPmXfsauukp9rGoVoTT8yYRX+5SO/BZiqHEqIho9YahV6xQ47i4ZionJMcjELTfhLDUBSm7ZuFAGkGWR4m7Q9/rRAmIlOY954dh4a4e8sBfrJ+H7ds2Mu+/ioAZ81v59evXM4LV3dz4eIuCvFzH6r6bCiAiRxt9NR9QvO+mcfjw9R9QsO8r1axPMe8JwJcNcLHDld1mAdw5AXAHFmTUas6dqQRSSGlnCa0F8vMLA4wr9hK4jKKlhJZTs1HJJbRFNXoKJYpRBlp5hgE8lKEZRFRxfCRkcdGXPF4B1EtJypGuCQOZ0/G9SBWq4ap+1kW7gLV2ZMiMsWkWc6ju3pZu+Ug9zx5kHu2HGR3bxmAGS0Frlg1iytXdXPF6lnMbis1uNpAAUzkeJ7SKza8TelCj5g5rFzBOxfuTuyNMRdRPFgaOSC8pb4qVutISEuOapuj0tFEXoQdM1p5ssnj21JaOocoJjUWtPfSGldoS8p0JkPMdAN0dg6Re+NAWwuHZ5foq5bYObedSiVm6FCJ+HBEVHaU9oVZYqVDRQq9zUSVjPhQBVdNscFyqDXNwrFHWRbOoayHsCNN+wpiIjI5HB6qcd+TB7ln60HWbjnI/dsOMVQLv5fN7yjxvGUzWLOki4uWdHHmvHbcOG4tjpUCmMhYjBr0GjJZBj4KT2VZuJsyiiDPwEVYLSWqpURJjGWeuBgRVcNZlGnR8GZkg0Y1ixmwEuViQiHOqBTC/5KtUQUcNLsqkeU48zRFNZrjKtU8olyK2Zc7UgrkBUdUCWdbWgZ4RxwbrppD7HD1VTpzKT7Pwpaq93gyyB315TpAIyxEZOLpLdd4eMdhHtp+mId2HObhHYfZsj/MRnYGZ85v55eet4iL6oFrfmdTgyseGwUwkWdiVEAZWTnKffgY2eazsMJUrWLOEVfCUUjx4SKFQyEwlQ7FZEWj2mZUO0Kv2N6uEntKng2tNZrbKhTilO6WAYpxSimqUYpq5N4xszRAmkckLqe/tcBQpcBgWxGqjsqhiKQvIi5DaX9EVPUUDpdI+lNcJSU6PARZhhuq4CsVyPLwa57js1zbkyLSUE8XtgAWdDZx9oJ23nDRQi5Y3MX5izppKU7OKDM5qxaZCJ5yFuXwFmUIZVaphIGpZtjAIDjDFYtEpSJEEYW2JnwSkbYVqLaHI5CGZjqyoqPaETHUWWCglNPfVaJQTJnRMsispn4KUcbM4gCReWYWB6h5R3+tyJ62Nsq1mMMdLQz2JbhBR9rkcFWj1GwU+hzxUEIxdrhajosibLhHDEJwTNOwmmd+1FFOatgXkZPPe8/2g0M8tquXx3f38fjuXh7d2XvcsHX2gg7OWdDBzNZiA6s+uRTARE6Go8+izN1I4z5pCmaYudDAX7+L0uIo/A/oISs6vDOyIrjMcKkjKxnVvEStkFMpJ/S1FCkmKZ2lIQpRhsPjLKeaxyQuhyRlqFijkkPuYqo1w1XBvJHHjrgJoIirhQn70UCMVdJwd2f9nEyqtfA5AFE9UGo1TESevYFKyro9fSFs7Qph6/FdffRV0pFrlsxs5oy5UzdsHYsCmMjJdJxVMXOGr9bCxH3nsIEEoogoSYhKxXAweEtpZFWs1hq2KMtdjqwQUW1PGOhoorfg2dOZ4goZTc1V2prKROZpSaqUYk+pM6XWFlFOY3o7S6RpRN/hAtGAIxoySgdiXAVKB2MK/UWioYzCoRJWy7CBMq5cxddq2FAZ732YJTa8NalmfRF5GmmWs2X/IOv39LF+T99I2Np6YHDkt43WYszpc9t43QULOH1eG6fPbef0uW2TdhvxuZh+71hkvBzduG/13ipzYYK9c0em2Ef1g7bjiDjzWOrJCw5vYXsS7wAjKhqVOCIvOMoGzuUU44xinBKTk7iMxGVELifLjVoW0Z86MovxzlGrGFECtaqFURoOokqCix1RLRxlZIBP03DeZB6F96FmfRGpy3LPtgODrNvTx4Y9fazf08/6PX1s2jtANQt/8TSDpTNbOHN+Oz9/4UJOn9vGGfPaWdjVdMqO9plsFMBETrUTBbFaGlbF6ndSRpUqrj+BJCYeKJHHjlJ7Qq3F1VfFIvIC1NpiBltK9Bdz9rWluCQnKaQUCynOwuyyyDyl5ippISVtjhkqxVjNUWs14gFHPOQotodm/eLhInF/jaiSHTlvcqiMr9VCf1i1Fpr107R+sDk6/FtkCsvzMMx0Q08f63b3h7DV08eGPf1U0nzkugWdTZw2t40XntbNaXPaWD2njRXdrTQVogZWP/EpgImMl9Hbkzlghk8Zmbbvq1XMDD8Ypu0TOeK+JogcSUsTeVNCXowpHUzIio5Ku6PaZmRNEZUuR554Km0xaWuKizJamqrEUU4cVTHz1NKIoVJClkZUigVqQ2FbMisYUTX8WmhyxEM5BQOr5bjIYeUq1GrhoG8fVsgY2ZZEjfoik1ya5Tx5YJANPf1s7AlBa+Pe8Hm5diRozW0vsWpOK7/6/CWsntPG6rltrJzdSus03D48GfRPTaRRvK+Hlzw07ZOFAa9HT9t3DjPDeY+lOYkzooIDH2OZIxsCvJEnRi010oojK3h6axEWeeI4I4pyvDfyvL70n+Tk9Wn9aauR1cAyw0euvuVZJKrmxI5wvFG1diR4DY/ZyI/8xqz+MJGJr5rmbNk/wIY9/Wzo6QuBa08/m/cd2TqEMMh05Zw23nLJTFbNbmXl7FZWzWmjoylpYPVTjwKYSCM9pWnfgOzY0/YHYkhiLI4pHKyPsmgukTeHVbFqR0JeCGdQ1loishJUO8JWZbUlx5dyiHOiYoYzT9yU4psgb3aUm2IsM9K2sCIWDxrV9gRXhdKhmKQ/IxpKiYsFSDNsYAgq1RDC6jPEMFc/ZxJtS4o02EAl5Yn6CtbGnn429PTzRE8/Ww8MktXbB8xgUVczq2a38qLTu1k1u41Vs1tZoRWtcaN/yiITxYl6xbIMi9KwOuYcDrA8x1UzcJAloWnfckdagzw28ip4c2QGPjPyyEMU+sOceYg9WSHHZ0ZWrK+OeSOqGC7ypGWH1f9i7CoxVjOsGmPeh8PK6yM28B7zdqQ3TNuSIqfcgYHqSMgKQauPJ3r62Xm4PHJN7Iyls1pYPaeNV54zj1VzworWiu5WSol6tBpJAUxkojleEMtyvKvfnegcVqthQ6FfLBkqkcQRSX+RrBSTlSIqhyPyGKrtRtockRWg1h7hI8iacnziw/d29Z9WyvFJ2Mr0sWGpkZWMeMiIByNKTREu9RQOFXBDNaxcww0UQoN+uYyv1WtLw2wfbUuKPHfee3b3luu9Wf0jvVkbe/o5MFAdua4piVgxu4WLl81gZX3bcOXsNpbMbCaJXAPfgRyPApjIRHWM7UlgZFCqr1axKAoT94eGwnFHAyWiQoIvJSR9JfLEUR2IqTU50iajUjHyBGptjqzkyRPwpbCCRpLjC5DFjjwJAcxH4XVxCbwLd0tCMZxtORCFvrRaGlbAzIXw5etHM42s4Gk1TOREstyz/eDgSMga/vWJnn76Rw0s7WhKWDm7lZefOSesZM1uZdXsVuZ3NE3IA6fl+BTARCaD4YZ9GNnmC5P2s9AcX61BFMKOeQ95TmSGSyIwcNWIqOrAO/IkNNxnJSMveNJahHfgE4+PPJYbeAODPAlbi5mHWs3IC+BSRx4nJM6IvcdqWVhEi0OzPhC2TNMwYT/Uq2n6IgC1LGfrSCN8/8idh5v2PnW0w+y2Iitnt/ILFy4YWc1aObuVWa0FzdGaIhTARCaLUSti4ct683stxaLwN+SRMyjjGNdfgCjCHSpSKBbICzFN7QWyxFHtiEmbjLRkVNsdPoa0GbKix0eQFzwYYZWs6MmKYUyFS42sGBGVPcmAo9gU4ao5hUKMG6pBpYqLXJieXy7XB81m+Nrw3+DVoC/TQzUNQWv98B2H9V837xuglh35f2DRjCZWdrdy+cqZrJrdxor69qHuOJz6FMBEJit/ZGXJZ4RZYrUUy3P88IgIZ/WzHnNcmkDssNjhY4flocE+jyFPjDwCb4aPfVgRq7eN+Pog/jwJq3BZITzo0nCGJQZ5MQbvcXkOcYxZBpHD53n4+W5Ug77IFFLLcjbvG2D9niMha0N9tEM66o7DxTPCHYcvOWMOq2a3snpOG8u7W2gu6I/h6Ur/5kUms6dp2CfLjhx3FEVYkoQp+3FENFgiL8bkTTGF3oQ8MaptjrQEWdFIWwzvICuCj+s/w0Eee9LmcGh4noRDvl0t9IxF5YS4PyFOIizNwzDZ4QO+K5UQDIen6GtUhUwyee7ZfnCIdfVzDtftDh+b9vWPrGg5gyUzW0KP1llzWFXfNlw5W3ccys9SABOZCo43T8xZOAzcDB9FWKUKkcNVargkxpcKuKEiPomIKglpkwvbkrVwN6TlkBUsbEsmHqKwTWl56BHDDFcDyyPiJMe7BMs9rprh0voh5BDujsyy0KxPhs8d2o6Uich7z97+Cut397NuTx/rdveybk+YDj9YzUauW9jVxGlz2njxGbNHjt9Z3t2ioCVjpgAmMtUcd8L+8CHb9TCW55j3RGb42JGMNOtHmHfkcWjWj4qQJyGIUe/PH5bX/6zJioQjlTy4aowrRCRpDlGY4u9zj+UZDIX5YUamY4yk4Sppxsaefh7b1cdju3p5bFcvj+/ue8p4h1mtBVbPaeOXnrcoBK25IWxpWKk8V/ovSGQqOtGE/TTFm2FJDINFnHMkA00khYS8mFBoL5DHjmp7HLYkS0atJayEZaUjwStPwMcARpqGYbB5lBDVPN6FbcmoEOPMIK2vHlRr4WxJOHKHpEKYnGL7+isjIWs4cG3s6R/p0yrGjtPntvGyM+Zw+ry2kbA1q7XY4MplqlIAE5nqjl4Rc/mRbUkI87sih1ViyH0YKTHosMQRJw7zBoTxFXkEPqqPw3D1Bv16kz5RCGN5AhC2MF3m8EmEj6MwLsNFWJTh8wiyvF4LWgmTk8Z7z7YDQzy88zAP7TjMIztD6NrbVxm5Zm57iTPmtfHi02dzxrx2zpjXzrJZLUSaoyXjSAFMZDo4ulk/96Fj+CnN+vUtw6GEqFzCxRFuqEReislLEclAHJr1WxxZob4tWRzuBaM+N8yoNYNLQ19YVnIksSMxOzIvrJqEMyThyFBZrYTJs5Dnnq0HBnl4x2Ee3hEC18M7DtNbDmNPYmesmtPGlau6OWNeG2fOa+f0ee3MaCk0uHIRBTCR6eV4d01CGJ4aRWGLMM2wyBGlGa6ckJcKWOrJE4flEWnR1c+ODFuNeUK4SzICCoaPPGnNhcGuGbg0xqoOqxRCVqvfmekhBD+ynylVZLThla37th3koe2HeXjnYR7Z0UtffUp8IXKcNreNV507n7MXtHPOgg5Wz2lTU7xMWApgItPR6CCW1wd+ZUdWoKxWxecRVgnN+i4PZ0a6yIEVcFVPmoZhYT7yYSxFNGr7xhPunPT1sRa1iMgZvpgcmdafplgWHVkFy0I9aBFMgMNDNR7cfoj7njzE/dvCx3BzfCF2nDGvnWsumM/Z8zs4ux62CrHOPJTJQwFMZDrzvj7F1fBpmKxP/UBtM4NaGlbFCglRuRgm65dL+EJM1pQQt8b42Ki21nvERnrA6p+PhLKIvOqwtIirRESAZTmhcz8Lv0KoQaadNMt5fHcf928bDlwHeWLvwMjzK2e38uLTZ3PB4k7OX9TJ6jltOmBaJj0FMBE57ugK6odrmzOoOojy0KwPOGdEiSPPjag6HLRsZIL+yLc2wztPHhs+NnxWn8QfubBM5iz8bGchAMqUV65lPLDtEHdvOcCdmw9w79aDDNRnbM1sKXD+ok5ed/4Czl/cybkLO3Usj0xJCmAiEvzMtmS9L6t+nuPwaphlGRbHWKmAq2b42BFVC2QFR1ZypCVXP7rIRmaG5Ulo1k+bIlziwINlHmoplqYQ1aBc/1laBJtyess17tl6kLs3H+DuLQd4YNthqln4F716Tiuvv3ABz1s6gwsWdbFoRpMOm5ZpQQFMRJ5q9LZkRshhuQ9N+q6+QhXVsDz0jFkSE5vhClHo6bL61qMd2YL09Qb9fHiYa8GRF+JwV2Qch5EUURRW3dAfvpNduZZxz9aD/GTDPm7buI9Hdh4m9xA54+wFHbztBUu4eNlM1izpokt3JMo0pQAmIsc26rBvfD2MDTfPexcGutYHrDrnII2J66toeeJGpukPzwkzH7Yj85hwhmQxIgeiJMa8x+dZuFOy1qg3LM9Wnnse393HrRv38pMN+7h7ywHKtZzYGRcu7uK9L17FxUtncMHiTlo0QV4EaFAAM7MIWAvs8N6/2sxmAF8GlgJbgDd67w82ojYRGaUeqHyWhQRVXw3zzrBaCrUqxDGWZkRJjKsUcdUCeRKR1mLygiMvGFlyZCUMM7Kiw7IY5wxXLmBm4bzIKAr9YDLhHR6qcfO6Hn74eA+3bdzHvv5wh+LK2a286XmLuWLVLC5ZPlNH9ogcR6P+z/gd4DGgvf71B4AfeO8/bGYfqH/9Bw2qTUSOdtRqGHn9bknnMNKRuxiJI6wW4QCXRuD8U7Yin/ItneGdgatP4jfDIs1smsi2Hxzk+4/u4XuP7eHOTQdIc8/MlgKXr5rF5StncfmqWczraGp0mSKTwrgHMDNbCLwK+Avgf9UfvgZ4Uf3zzwE3owAmMrHU75QcWQ3z+ZG7J+FIg36a4eOIOPP4xJE3xVgWh6OLonCeJEa4I9I78lIcwlcthWo13A05gZjZ+4G/Brq99/vqj30QuJawJvjb3vvvNLDEU8Z7z2O7+vj2w7v43mM9PLarFwirXO+8YjkvO3MO5y/q1BE+Is9CI1bAPgL8PtA26rE53vtdAN77XWY2uwF1iciJHG9cRbUGUVghM8DiGBdH+DwGZ7iofmdk8UiTvXdGHllY/Yo9Po7ARUykJnwzWwS8DHhy1GNnAm8CzgLmA983s9Xe+ykzzn/bgUG+cf8OvnH/Tjb09OMM1iyZwR++8nReduZcls1qaXSJIpPeuAYwM3s10OO9v8fMXvQsXn8dcB1AieaTW5yIjM1R4ypGDvfO87BCVp90b+Vw4LYj3P3m66sk/qhp5T5y+NhjUYTF0UTKXwB/T/gL4zdGPXYNcKP3vgJsNrONwMXA7Q2o76Q5MFDlmw/u5Ov37+SeraEF93lLu/jz153NK86ey8zWYoMrFJlaxnsF7DLgtWb2SqAEtJvZF4A9Zjavvvo1D+g51ou9958CPgXQbjN0YIlII9X7wkYf7u29HznnEe+xOIY8J/I+NNgDPqmfHxnXA1lk5ERYEmOFZMI04ZvZawk3Cj1w1FyqBcAdo77eXn9s0vHec/eWg/zrHVv59sO7qGWe0+a08ftXn8Zrz5vPwi79RVfkVBnXAOa9/yDwQYD6Ctj7vfe/YmZ/DbwN+HD9128c73uIyAQyqgfM5x4zD94fCWJmWJpB/Yghy+LQPxaDecOG/xplQP0OyfFcAjOz7wNzj/HUh4A/BF5+rJcd47Fj/oVw9Kr94sWLn2WVJ19/JeVr9+3gC7dvZd2ePtpLMW+9dCm/uGYhp89tP/E3EJHnbKLcH/xh4Ctmdi2h1+IXG1yPiIzVqDskR7qg6gdsjxxl5P3IHY4+icgL8VMji9Xvhkzicd2C9N6/9FiPm9k5wDJgePVrIXCvmV1MWPFaNOryhcDO43z/kVX7NWvWNHzVfk9vmX/+8Sa+fPeTDFQzzl7Qzl/9wrm85rz5NBV0B6rIeGpYAPPe30y42xHv/X7gJY2qRUSeo1HN+XgL9wZmGT4PE+6pOog9VgvBzDmHj+zI6pmFIa3mJsYkfO/9Q8DIzUBmtgVY473fZ2Y3Af9mZn9HaMJfBdzVkELHaOehIT754ye48e5tZLnntefN520vWMp5Czt07I9Ig0yUFTARmeyGx1Tk9YWeLAt/uNfSI435lTj0i5nhotCwPzJ2InTrT4T89bS894+Y2VeAR4EUeM9EvQOyp7fM339/A/9xzzYA3nDRQn7zhStZPFO9XSKNpgAmIifP6IGtWcboFi9fP+/R6tuTzizMBUuiI3dIOjdhmvBH894vPerrvyDMMpyQqmnOZ27bzEd/sIFa5nnT8xbzrhetYEGnhqSKTBQKYCJyco1aCbP6nZFkWVjYqjfmk+eQ5xgOH/kJGbomqx+v38uf3fQIm/YN8JLTZ/PHrz6TpZrbJTLhKICJyMk3akSFUe+39x4qVcjysDVpBsNHEOU+LJy5p/2u8jQGqyn/978f5Ut3bWPZrBY+82vP46rTNdNaZKJSABORU2p4PIUnG9l+JI2wNMYDlufhTEmvlbBn66Hth/mdG+9j8/4B3vXCFfzuy1ZRjHVXo8hEpgAmIqfG8MR8I9wdmbswMR/waYbV0hC6kvipZ0rKM/KVtdv40NceYmZLkS++8xJesGJWo0sSkTFQABORU6t+biRkkFqYC1Y/msjyGJIY81HoG4sUwsbKe8/ff38DH/3BBq5YNYt/fPMFdDYXGl2WiIyRApiInHo+B6s3eOV5GEWR+5FmfLLQDzbhZ1BMEHnu+eBXH+LLa7fxixct5C9//hySSA10IpOJApiInFqjh7RmGd4cpGn9DskYqyWQezyxhoKOgfee//Pfj/Lltdt471Ur+b2Xr9Y/N5FJSH9lEpFTr94P5nNf7werr4JlefgYXgkbda0c28d/tJHP/nQL77hsmcKXyCSmFTARGR/egw2HsFGzwdIUAHMOPxzC5JhuXtfD33x3Pa87fz5/9KozFL5EJjEFMBEZP/7IlHzMwnywNA1BLHKQRU89pFtG9PSVef+/P8Dpc9v48C+ci3MKXyKTmbYgRaQhvK+vhHkfPh9eGVMCO6Y/+trD9FdS/vHNF1BKNONLZLJTABOR8TMcuPKwBemzDGpp2IbMcyzTFuSx3LZxH999dA+/9eJVrJrT1uhyROQkUAATkcbJ/chZkWRZPaA1uqiJxXvPn3/zMRZ2NXHt5csaXY6InCQKYCIy/nweVsFg5I5In+WQZiiBPdWP1+/lsV29vO+lq7X1KDKFqAlfRBrD5+AtbEUCNjyeQvnrKa6/dTOz24q89rz5jS5FRE4irYCJyPgbPRds+Gvvj8wCEwB2HhriJxv28ZZLllCI9du1yFSiFTARaSif5eF8yCwLc8A0iHXENx/cBcA152v1S2Sq0V+pRKQxvD8yFwyOnA8pI7776G7Omt/O0lktjS5FRE4yBTARaSyfH7kbMlcT/rCBSsp9Tx7iytXdjS5FRE4BBTARaaiR8yGzrD6MtdEVTQxrtx4kzT0vWDGz0aWIyCmgACYijXN0v5dXE/6wh7YfAuC8RZ0NrUNETg0FMBFprOGZYHkeGvK1BAbAwzt6WTarhfZS0uhSROQUUACT/7+9+42VrK7vOP7+sLssrIhAFQSWrUuzaND6B690ta2lQCKxTdc21ewDIhrtRmOs2gcthKTGBySWmEZNWpMN2mBrpVtEITb4B1prmhToqqgLK7KKhZWVxWqVWtl/99sHc9Drdi572Zn9zZy571cyuTPnzJn7/e7M/uYzv3PmXGkq1BOzYeYvAO7f+xgbTj9p0mVIOkYMYJImrzsQ3/OADRyaLx76wU9Z/yy//SjNKgOYpMlaeBzYoUOTq2OKPPLjx9l/aJ51p62ZdCmSjhEDmKTp8MQB+J6Ile/9+HEAznrGiROuRNKxYgCTNHlP/GmiKg8BA/Z2Aez0k1dPuBJJx4oBTNJUKM+C/zP/9ZP9ADzzJAOYNKsMYJKmhyEMgB92AeyUNZ6CQppVBjBJ06M8DxjAY48f5IRVx7F65YpJlyLpGDGASZoOngX/Zx7bd5CTVjv7Jc0yA5ikqVH+LUgA/nffQdYc7+yXNMsMYJI0ZX564JABTJpxBjBJmjI/PTDP6lUGMGmWrZx0AZIEdOcC8zgwgP0HD7F6pZ+PpVnm/3BJmjL7D85z/AqHZ2mW+T9ckhaR5O1J7ktyT5JrFyy/Ksmubt2rxv17DxwqVq3IuB9W0hRxF6QkDZHkt4FNwAural+S07vl5wObgecDZwG3JTmvqsb2l8QPzhcrjvPzsTTLmv8PT3JKkhuTfCPJziQvT3Jaks8nub/7eWrruiTpMG8F3ltV+wCqam+3fBNwQ1Xtq6oHgF3AheP8xYfm550Bk2bcJD5ifQD4TFU9D3gRsBO4Eri9qjYAt3e3JS03NVUnATsP+M0kdyb51yQv65afDTy04H67u2Vjc3C+OO44A5g0y5rugkxyMvBK4A0AVbUf2J9kE3BRd7frgS8Af9ayNknLT5LbgGcPWXU1g/HxVGAj8DJgW5JzgWHJaGhyTLIF2AKwbt26Jdc1P1+siAFMmmWtjwE7F3gU+JskLwK+BLwDOKOq9gBU1Z4njrWQpGOpqi5dbF2StwI3VVUBdyWZB57JYMbrnAV3XQs8vMjjbwW2AszNzS15em++YIUzYNJMa70LciVwAfChqnoJ8BOewu7GJFuSbE+y/QD7jlWNkgTwKeBigCTnAccD3wduATYnWZ1kPbABuGucv3i+aug0m6TZ0TqA7QZ2V9Wd3e0bGQSyR5KcCdD93Dts46raWlVzVTW3itVNCpa0bH0EODfJDuAG4IoauAfYBtwLfAZ42zi/AQmDQ+HiLkhppjXdBVlV30vyUJLnVtV9wCUMBrF7gSuA93Y/b25ZlyQdrjtG9fJF1l0DXHMMfzfmL2m2TeI8YG8HPpbkeODbwBsZzMRtS/Im4EHgtROoS5KmwnyBh4BJs615AKuqu4G5IasuaVyKJE2loohHgUkzzVMtS9IUchekNNsMYJI0ZabrfLSSjgUDmCRNmcIZMGnWGcAkaSqZwKRZZgCTJElqzAAmSZLUmAFMkqaMB+FLs88AJklTyIPwpdlmAJMkSWrMACZJktSYAUySJKkxA5gkSVJjBjBJkqTGDGCSJEmNGcAkSZIaM4BJkiQ1ZgCTJElqzAAmSZLUmAFMkiSpMQOYJElSYwYwSZKkxgxgkiRJjRnAJEmSGjOASZIkNWYAkyRJaswAJkmS1JgBTJIkqTEDmCRJUmMGMEmSpMYMYJIkSY0ZwCRJkhozgEmSJDVmAJMkSWrMACZJktSYAUyShkjy4iR3JLk7yfYkFy5Yd1WSXUnuS/KqSdYpqZ9WTroASZpS1wLvqapbk7y6u31RkvOBzcDzgbOA25KcV1WHJlirpJ5xBkyShivg5O76M4CHu+ubgBuqal9VPQDsAi4csr0kLcoZMEka7p3AZ5O8j8GH1Vd0y88G7lhwv93dMklaMgOYpGUryW3As4esuhq4BHhXVX0iyeuADwOXAhly/1rk8bcAWwDWrVs3lpolzQYDmKRlq6ouXWxdko8C7+hu/iNwXXd9N3DOgruu5ee7Jw9//K3AVoC5ubmhIU3S8uQxYJI03MPAb3XXLwbu767fAmxOsjrJemADcNcE6pPUY81nwJK8C3gzgyn7rwNvBNYA/wA8B/gO8Lqq+mHr2iRpgT8CPpBkJfA43a7EqronyTbgXuAg8Da/ASnpqWo6A5bkbOCPgbmqegGwgsHXua8Ebq+qDcDt3W1Jmpiq+reqemlVvaiqfq2qvrRg3TVV9StV9dyqunWSdUrqp0nsglwJnNh9qlzDYJp/E3B9t/564DUTqEuSJKmJpgGsqr4LvA94ENgD/KiqPgecUVV7uvvsAU5vWZckSVJLrXdBnspgtms9gzNIPy3J5U9h+y3dnwTZfoB9x6pMSZKkY6r1LshLgQeq6tGqOgDcxODkho8kOROg+7l32MZVtbWq5qpqbhWrmxUtSZI0Tq0D2IPAxiRrkoTBiQ53Mvha9xXdfa4Abm5clyRJUjNNT0NRVXcmuRH4MoOvb3+FwUkKTwK2JXkTg5D22pZ1SZIktdT8PGBV9W7g3Yct3sdgNkySJGnmeSZ8SZKkxgxgkiRJjRnAJEmSGjOASZIkNWYAkyRJaswAJkmS1JgBTJIkqTEDmCRJUmMGMEmSpMYMYJIkSY0ZwCRJkhozgEmSJDVmAJMkSWrMACZJktSYAUySJKkxA5gkSVJjBjBJkqTGDGCSJEmNGcAkSZIaM4BJkiQ1ZgCTJElqzAAmSZLUmAFMkiSpMQOYJElSYwYwSZKkxgxgkiRJjRnAJEmSGjOASZIkNWYAkyRJaswAJkmS1JgBTNKyluS1Se5JMp9k7rB1VyXZleS+JK9asPylSb7erftgkrSvXFKfGcAkLXc7gD8AvrhwYZLzgc3A84HLgL9OsqJb/SFgC7Chu1zWrFpJM2HlpAuQpEmqqp0AQyaxNgE3VNU+4IEku4ALk3wHOLmq/r3b7qPAa4Bbx1XTtX/4q5z+9BPG9XCSppABTJKGOxu4Y8Ht3d2yA931w5ePzcXPO2OcDydpChnAJM28JLcBzx6y6uqqunmxzYYsqydZPuz3bmGwq5J169YtoVJJy4UBTNLMq6pLj2Kz3cA5C26vBR7ulq8dsnzY790KbAWYm5sbGtIkLU8ehC9Jw90CbE6yOsl6Bgfb31VVe4DHkmzsvv34emCxWTRJGsoAJmlZS/L7SXYDLwf+KclnAarqHmAbcC/wGeBtVXWo2+ytwHXALuBbjPEAfEnLg7sgJS1rVfVJ4JOLrLsGuGbI8u3AC45xaZJmmDNgkiRJjRnAJEmSGjOASZIkNWYAkyRJaixV/Tw1TZJHgZ8A3590LWPwTPrfxyz0ALPRR997+OWqetakixi3bsz6z6ewSd+fxyOxv36zv6VZdDzrbQADSLK9quYmXceoZqGPWegBZqOPWehBs/882l+/2d/o3AUpSZLUmAFMkiSpsb4HsK2TLmBMZqGPWegBZqOPWehBs/882l+/2d+Ien0MmCRJUh/1fQZMkiSpd3obwJJcluS+JLuSXDnpepYiyTlJ/iXJziT3JHlHt/y0JJ9Pcn/389RJ13okSVYk+UqST3e3+9jDKUluTPKN7jl5ed/6SPKu7rW0I8nHk5zQtx6WmyONXRn4YLf+a0kuWOq202DE/j6SZG+SHW2rXrqj7W+x8X8ajdDjCUnuSvLVrsf3tK/+yEZ5jXbrf+H976hVVe8uwArgW8C5wPHAV4HzJ13XEuo+E7igu/504JvA+cC1wJXd8iuBv5h0rUvo5U+Avwc+3d3uYw/XA2/urh8PnNKnPoCzgQeAE7vb24A39KmH5XZZytgFvBq4FQiwEbhzqdtO+jJKf926VwIXADsm3csxeP6Gjv+T7mnMPQY4qbu+CrgT2Djpnsb5Gu3W/8L739Fe+joDdiGwq6q+XVX7gRuATROu6Yiqak9Vfbm7/hiwk8Gb6CYGYYDu52smUuASJVkL/A5w3YLFfevhZAaD/YcBqmp/Vf03PesDWAmcmGQlsAZ4mP71sJwsZezaBHy0Bu4ATkly5hK3nbRR+qOqvgj8oGnFT81R9/ck4/+0GaXHqqr/6e6zqrtM24HmI71GF3n/Oyp9DWBnAw8tuL2b6XwhLyrJc4CXMPiEcEZV7YFBSANOn2BpS/F+4E+B+QXL+tbDucCjwN90U8nXJXkaPeqjqr4LvA94ENgD/KiqPkePeliGljJ2LXafPox7o/TXB2Pp77Dxf9qM1GO3e+5uYC/w+aqath5HfQ7fz/9//zsqfQ1gGbJs2lL2opKcBHwCeGdV/XjS9TwVSX4X2FtVX5p0LSNayWBXx4eq6iUM/qzVVB5Ts5ju2K5NwHrgLOBpSS6fbFU6gqWMXYvdpw/j3ij99cHI/fVg/B+px6o6VFUvBtYCFyZ5wXjLG9lR9zfu97++BrDdwDkLbq9lsOtl6iVZxeA/38eq6qZu8SMLpjfPZPDJYVr9OvB7Sb7DYOr24iR/R796gMFraPeCT2c3MghkferjUuCBqnq0qg4ANwGvoF89LDdLGbsWu08fxr1R+uuDkfpbZPyfNmN5DrtDOr4AXDb2CkczSn+Lvf8dlb4GsP8ANiRZn+R4YDNwy4RrOqIkYXDM0c6q+ssFq24BruiuXwHc3Lq2paqqq6pqbVU9h8G/+z9X1eX0qAeAqvoe8FCS53aLLgHupV99PAhsTLKme21dwuC4kj71sNwsZey6BXh9902sjQx2Le9Z4raTNkp/fXDU/T3J+D9tRunxWUlOAUhyIoMPid9oWPtSHHV/T/L+d3RGOYJ/khcG31L4JoNvM1w96XqWWPNvMJjq/Bpwd3d5NfBLwO3A/d3P0yZd6xL7uYiffwuydz0ALwa2d8/Hp4BT+9YH8B4GA9wO4G+B1X3rYbldho1dwFuAt3TXA/xVt/7rwNyTbTttlxH7+ziD4xkPMJiFeNOk+xlXf4uN/5PuZ8w9vhD4StfjDuDPJ93LuF+jCx7jIkb8FqRnwpckSWqsr7sgJUmSessAJkmS1JgBTJIkqTEDmCRJUmMGMEmSpMYMYJIkSY0ZwCRJkhozgEmSJDX2f5T/naBw2XrOAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 720x720 with 3 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"coupling = get_coupling(mu123.cuda(), mu231.cuda(), cost.cuda())\n",
"pyplot.figure(figsize=(10,10))\n",
"pyplot.subplot(2, 2, 1)\n",
"pyplot.plot(mu2.cpu())\n",
"pyplot.subplot(2, 2, 4)\n",
"pyplot.plot(mu1.cpu(), transform=matplotlib.transforms.Affine2D().rotate_deg(270) + pyplot.gca().transData)\n",
"pyplot.subplot(2, 2, 3)\n",
"pyplot.imshow(coupling[0].cpu());\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This looks a lot like the coupling form Python Optimal Transport and in fact all three match results computed with POT:"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"1.2526288628578186e-07"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD7CAYAAACscuKmAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAvBUlEQVR4nO29W6xk2Xnf9/vWZe9dVefW3dNz4XAYitaElGRYkUNENyMQTDtwFMHSiww5UMAEAviSRLJhQKGSpzwEEBAjsIAEBgg5BhMLtgVZsATBsC2MozwEMCXqAl1IUSJFYTjDnu6e7j7XqtqXtb48rF3nHB5293RP387p+n5AYZ/adar2qtP9399a3/ouoqoYhvH84571AAzDeDqY2A1jTTCxG8aaYGI3jDXBxG4Ya4KJ3TDWhEcSu4j8DRH5koh8WUQ+/bgGZRjG40fe7z67iHjgT4C/DrwF/Bbwt1X1C49veIZhPC7CI7z3PwG+rKp/BiAi/wz4YeCeYo/VTJvpJVjdXxQEQLWcU0V09fzkHJx9Xo66+hCLCzIMAJYc0Wkrd3vtUcT+KvC1U8/fAr777C+JyKeATwHUkx2+66/8JJJBsiKDjseMGzKSFOkGSIp0PeSMtOWoXQ85QUpoPxSxpwRZQTM6HoGTG4JhrBmf0zfu+dqjiP1ud49vUpmqfgb4DMDWxqta3enKO+Ub367eoU4RHyErUnvIIE1CcoZ+QNJ4HAY0Z2QYjsUv9xN/GcgjfFXDuPg8itjfAl479fyDwNfv9wbJil/0aHAggnpBRU7EP57DKTgpwnWg2eNE0JzBCeIdMqRyZ3G+3HWyri6CJhCX0Tz6HzWXzzfBG2vMo4j9t4DXReRbgLeBHwP+y/u+I2Xc7iEaPDgHwaPOQXCjyN3xDUCdgHflxgDkJiBapvwkRVJC+gQpI/0wTvk7VMclgOb3nu6D3QCMteF9i11VBxH574B/A3jg/1TVP7rvm3JCD4+QGMF7iAG8G48egpaP8pD9yvq7b1gwSNZR7AE3ZBgyrhvF7n2Z8jtXpvniIKVi1VNCVRAS4MsNAMziG2vDo1h2VPVfAf/qgd+QFW07SGU6Th8Q5yAEJHg0eCQG1LmyZneOHEfRh2Lt1ZUbgKiS1ZfjUNb5rk+QtIh/SMXip4R0PTokJCfoh2L9+x5VNQefsTY8ktgfFtWMLhao94gI+DKNlxCK4L2DGIvwU1Wm+k0ozjvxIEIOggaHOk4s/rg755IiSXFdRlLGtQMyZKQbilc/JVjdbLxDsqJDmRWQMqgU0WOiN54/nqrYUdCsCAkVV/bVR8ebaEazL+eGYrlxDqdabghZ0eCQ4NCoZD+KXihxgAJZBEK5IUhyuMqP23oR6SukT0hblyn/sisiH7f0pB/QlJCUji3+8VTfLL7xHPB0xQ5l3a4CFCGpOMQNZR/dCeI9KoKM63hZVOVcU4H3uCaiVSBXnlSDBiF5h3qK1XecbOupIrlYfNeXfX3fZmTI+OVo9Rddmeovu7KlN4xbeymfTPVH0R+Lf/xsw7hIPH2xw4lQRMb1sgMSooJCsfYray5SLLEI+FFsSXE5F097HL31vgi8rOm1ePNFyk1AynkJivpi9TW4IvrxSAxlnd/1xdoPqSwtUjqZ6ku5lqZUlhBm8Y0LxLMR+4rj0NfRcuroNRdXrCtAW9b3GuO4pq9wwUMVcVWEGPCTiHpHmkbUC8PEkyPkKORQPPt6KuVHlBKtlyG0Ou7/Z1yv+OWA61JZ5y86ZEjIsi1LjbYt0/tR/JqyOfeMC8OzFftZVM9Ye47X90KPZj8a1OKFL9twuQTcBFcceV5wQZAsIK4sCWRl6UFd8eeJk/EHkFz29t2gaBB865Do8c6hQz4O4jne0htFzzCu80XNuWece86X2OHu1p6Epm9e20sY9+ePIs45XFOjwRMmFRo9aRLHtb0jNY4chaEep/axCH+Yrtb3Uiz+4HFDxPeKbxvcoISjhEuKP+qRPuOWHfRDOQ4D2vdlS2815YcyQzGLb5wjzp/Yz3IskhIGi2hZ22ct62jnyrraj9Y+hOKYi+WrSVJEfbHgKmTvyAjE8eO9HE/xVcCVoDxyDymO1t4Lri/+A5cyOJAhlGt3/ehUbJHkj8dcfA+6umdhFt941px/sa84K/pjay/jVFrQrkO8h2WJ0POHFT4UT36si5WvppFcOYapIwehnzhy4Niznz1oBamR4yn+cgDJ4FuPJIiLerT4Gd9l/DLh5n3Z2lu2Zcq/bMuavm2LR/+UZ19Xcfxm9Y2nyMUR+4rTwtBxGy+PltRnlL5kw4lA1RePetcjVSyPPqO1R1Ikx7JPn2NJwMmiEAQNFNF7jvP4JIMbBEmQmvJzqAXfOeLcESqHaxPeCwxl92CVrCN5PKZ0bPGP/RKn4/QN4wly8cR+Fj1ximm6y2tdB32ANiAh4NsODR53WKPREw4jGh39LJBqYZiUdX2uII3r+1QBUqw/jFZfwfWCS+Baj28DvoM4L+v8eLCB6zN+3hWLPx8tftuVNf4wnCTq9MM4fgviMZ4cF1/scBen3kr85bl0/sSpN1+MwTl1OR41ZftuVpHrQL8RSBNHPxH6GeSqbN+ph1SXlNvsKVF7uWy3u24Ufg9h7nGdUm04fA/xIOC7TDiIZUtv3pa9/LYD3x0H7JBXAj9l8S1Jx3iMPB9iP8up9T2Ue8A3OPX86EhzchyW64eEiwHXRnIdCFNPXHhSJfiFkCP4WbH0Q1PEr0GPPfs56jjFF2QQ+g3BDRCPBBmgOgz4TglHE/wylf38+RmvftedVOJJyfbxjcfK8yn2FacsvmZKRN0AiCt75eKQxRJEkMMK8Y7QFEsfm4o8Ha39ZnHqtduOFIVuS8h12bZLTslVeeBAfamJJ4NALjcKlyAc+jLNP/SEOcRFJh40+DYTDlqkT7jDZbH082UpwdWNyTvjw/bxjUfh+Rb7Wc4E7YgbC1y4stcu3hcH2hCQnHEpI20sCTzBgUZyJUh25KpM3VMtpEZIjZI95Ho1twdEyU2ZTKiDYaDMFDagW3jizBFapZp5XK+EgxrXp7K0GC2+9sXhqF2P5DxG71larvHwrJfY4a7WHih17JzAwpWwXF9y68V74p0GgidOG9R7Jls1ufJ024GhcfSzMm0fJtBvOHKEtJHLNH82IE4ZpHjhu95DEqR1uIXDd0I8iLgO6t2I75R6dzqu83v8okcWHW7ZwpDQZbH+x+K3qb7xgKyf2M9yZv9ePOhQkmxQBT8KKIRSKs978ILrSqCO6zySHZIdrgco63vEkaOSKVN7iRm8IiGDBxUleSV3JW7f9SVZx/UlRdd3jqpy+GUgzCP+KJZ4/TFhh+WyRP90XRmnTfWN98DEvmIUhq726FcJOU7QZVuceaFYetmPiPfUk4YqBnRakyeRNCne/KGRsr6vHN1OmfJ3WxmtFZ0kfJ1wdUeMJyHBKTmO2oAODjn0uE6I+4GwDMSDing4JS4y1X7Ct4mwN67zjxYnFn+1nWfOPeMumNjvxn1CdNWVstWl6IYiwSMpl730PiJZR6svpEpLNl5dcu1TkmLNnSKiiCScywSXSdkRQiIlR+cjqXeoD6RlsfSpgjR3qCtWX0VwXcKLIP1QUoCHoWznrQQ/DBayaxxjYr8fp9f3q4IbYxFLFYd0Xcm7P5pDFfEh4JuaGAPNrEGjp9+qSLWj3fYMjdBtBYZpYJgp880GrTNuo8eHxKTpaaqenY0FAN3gSdmxbCOLNqALjz/w+NZT7QZcB83taVnn7yX8MhEOO9y8K9t5bVdmKovl3UN2zeKvFSb2B+Uuwv+G2PyuKzn3bQch4Lq+OPn6KRo9rqtIjcf3jn4pdH2JwkuNJ4WMVgJNjxOYVR3RJZyUa877iuUQOGor5tOabhnIsYhdveCXJZknLEuKbwgOFz3iBOl9mYHcJWRXExa8s0aY2N8PZ6f5eWxqkTL4vhTK7LsSobdYQgg0+w0aA/VmTZoEhpmn2yyRet1ORapgfqnmsFLe3e7xdWI6bZlWPU0Y2K6XbNdL8pbQJ8/ByxXdEDg8aNDe4XcDrnVUezXxqCYeKvV+xi8z1W6H6zNuf1Eq7i6W6JCg72yNv0aY2B+F+wXtdF05rmrpzedICMTDhlBFqmlNtVGRpoH2oDj1lkspzr0hkpvAnOK8q3xiFlumoWcnLsgISYUuB25e2mAxRK5f2qRdRo52K8KBJ+4L/YYnzB2pdvhlpvZSnHrelQKbi7HmX9eX4iBjXX0L130+MbE/Tr6p0s6qZl4ac+9LAgwh4NqOOK8ITSQc1uTaUx1EUiUs7wipcXQ7U5aTCV/b2uDtzR3qpufSxpzKJ640RzhRdqoFW3HJZmzpsufOpUmZ7s9rFvsVbuGodss6v7k1rvN3Z/hlJu6f7OPLsoWuPwnZHRtrropxmMW/+JjYHzdnk3Jy6UizymyTpf+GSjsSA7GqoIpUswkaPdNLk+LUuxTop0J7KdBtBdrNmmuXa+Kkh8swix0vzm4zCy3bfkHjepY50qvnZrfJjXaDW8sZ13a3WCwjixs1vhWam4GwUJrbYZzyD4SDFrcckMN52cf3Y+hu54pPwiz+hcfE/jQ4k4a7qqJbmlOMfeiGVNpXx0BUJVQBN9RUjSMsPfFA6Dcc7VFFair+/KjC14kbOxtMY8/Ls31mvmMWWia+p3Y9Lzf7zELHLHYcdDU3Jht0beRwq8YtheVtR1g4qj1PdVgRjzLV3hTXJ/z+soTszpfFurdjMY6+t/X9BcXE/rQ4u74fveLfkJTjXSl1VdeIdzRjUs5kNiFPI2kWaXciw0RYXKlIDdy52vDuJPP1F7aZTVte3d7j1ekuV6tDXq+uEyUxcy2devbSjHmu+JOjlzgYar5y5wqH84aDOw1x1xP3A/VtT1jA9N0a12aq3RbpBtxBce7pclnaaaVUliSrZhqr0tom+nOLif1Zcdqjf3p9vyq44cbqukMoOTUplf70CmFRUnSHutTGT7VnmSfsTiraPnBnY8LVyRG70ymz0PJS3CdK+fza9bzS7LGTIlmFvemEd6pNjiYNw2ZkmDjCQkhNwLcwmXhcl6mmVZnmzxuk7UrH3Ha1vu/u3kzDhH+uMLE/a1S/uejG8fp+DNM9KGG6rorUdV2s/bRBq0C/05ys7yeB9vIWtze3eGc78/uXO5pZx4cu32GnXvBtG++w6Zf8pembNNLjt8v1bg5b3B42eLvd4atHV3h3scHXb22TFoF4PRIWgebdSJhDs5uIByV4xx8Wp547WpStvLb9ZosPZvHPCSb288T9im74VV57Lkk5qsjSEwFfFUsflg7RElcvg6PLFYul5y2n7DYTKjewExdESWz7I3b8nEZ6dvycqWuJkgguc6kqEXwHy5pd3WBYetSVPPwcPFXjqCaOWHl8m3Del/177yCVuvpF9DKm48rJ+t5E/8wQfYp//C25rN8tn3hq13tuEDluPSXeHyfllPV96YEnkxK0kzcm5EkpuNFverqZo70sDA0sX8zkSWZ69YhZ0/GtO+/ySrPHa81tPhDvMHMtm25JVseRVhzlmi8vX2YvTfijvVe4s5xw/dY26SASdz31bSEcweTdTGgz9a0e1w74vVPBO31pp6VjQw0L1X2yfE7fYF9vy91eM8t+EVhN9UVK+u0Yn39ylOP9e98PuKOIWzSEeUWcBXzv6SelokZqHHNmLKY10SeWKeBEmbqOShIz6fCivCSH9Dh23JyDPGHqOm52m3wxDNyczTioZmQfidPyuWFRwn99G6igtMt2grThOHuQ5Eu5b0vOeSaYZb+oyEl1HaBYdxGkGi19XUFdoVUkb0zQ2tPt1KRaWFz2pAaWV4RhQ+kvDcTtlp3NBR/ZucXlas53zN5m5lpei7eIkvCjKG+mLXbTlK+2V3lzcZlr8y3evH2JdhGR6zV+KUxuSNnHv5MJR5lqv8cftsiyR44WJRV3uTzZyrPknMeGWfbnkXvl3w/D8XaehFAq5x6OWXkHU3IViAcNqXHEw0A/g3Y/0l4K3NyuWfaBy9MFlRt4MR7wcthj0y152bdMRXg9LkiqfL1+i7enO3xt6wq/N/sQ15eb/El9lW4RyaEmzIUcHHHi0CDE6AhH487CWEL7OClnFLo4q6z7JDHL/jyx6ku/mjaP1p4YS7ReXUEI6GyCxkDaqklNoNsJdBuOblNoL8EwU/oXBtxk4NWru2zVS75t6x1erPZ5Ld7matinkZ5GBpYaOMgTdtOUL7cvcaef8oe7H2Cvbbjx7hZ6FKhue6o9Ie4rzR0lLDP1ra7k49v6/rHySJZdRF4D/i/gZcoC6zOq+nMichn458CHgT8H/paq3nlcgzbeB/cK3On6Iv75ONXfr8baehNi8NSzCXlaMWxWtDuRfiosrkaGSeStl2t0krj2yiZXZ0d856W3+QvNDf5CdZ3Xwpyp9Gw7JXPIwfQt5qr8wfYL3Bo2+PdXv5Wvz7f58q0XOLw9we8Guncd4cgxbVxx6q08+nu+BOssStAOwwB9Dynb+v4x8SDT+AH4e6r6OyKyCfy2iPw68F8Db6jqz4rIp4FPA//Dkxuq8dCcraY7tr8+HbSDd0jK+GWHW9T4RbH2cREZaiEeFqfe/u4V7swu8WdXrrCzueCDm7u8vnmTl+I+31q/w8y1XHEZJ8pVf8COm1NtJXZnU/544xXeurrD24fb3Ly9RToMLG4G/CIwuelL8M6tCWGRiPul+Ia0HbJoS0LOuJWntn//SDz0NF5EfgX438fHD6jqNRF5BfgNVf3o/d5r0/hzwt2m+6sW2FVEYkRnE6giw/aEXHuWL0SGRlhcdXSb0F3O8ELL1uaC77j6Di/V+3zf5pe54g/5aNxn0wVqiTiEO3nBXla+0l/iC+2rfG15md++9SHuzCfsX9vEzx2T645wCJPbpc5ePBgI+8u7OvW060z09+CxOehE5MPAdwGfA15S1WsAo+BfvMd7PgV8CqBh+jCXM54Ud7P440sCqCoC0A8EQKvy3yQ1HskQD4WwdLTzhr3Nit9cVMwmHdde2OZyNecvbXyNK/6QV8Mdtt0SELzAjp/zev0Om24JwO2tGX8YXuFoWXE4meKPPN22o9p3VPuBZjcS5om415zE5w8JXSzK9H6VjmuJOQ/EA1t2EdkA/l/gf1HVXxaRXVXdOfX6HVW9dL/PMMt+jrmHc0+qqgTxNM2Jc6+JDJs1/VaknzkWVxzDVFi8qKRppn5lzuZ0yXdceYcPTW7zbc3Xeb26zmXXcdWXG0evmSPN/Nmwwe20wW8efoTr7RZ/cOsV7uzNSLdr6nc94RCmN5SwVCY3O1yXCXfmxQ9xtDCn3hke2bKLSAT+BfALqvrL4+nrIvLKqWn8jcczXOOZcCYx55vW91Ja2shYzTaoIknxbQACw9yBCEPjWbopy0nN72fh2myLO1tTbk03eDXe4SPxXSKZTZfJwI5bUpH4DyfvcCke0ebAtbrl63GbZZjgD3ypq7cQsq8IrdIEKe2xq4iMhTVp22/unIMl5ZzmPS27iAjwWeC2qv6dU+f/V+DWKQfdZVX96ft9lln2C8ZZa78qs7Wy+Kv1/bRBq0jabkoG3pXSKWf5QumE217J5J2e2faSj1y5xUvNAf/x5p+z4+d8rHqHqRtoRHHAXvYc5Iqv9C/y1fYqX52/wBfuvMT+vGFxbQO3cEyuC2EO03cz8SgR93rCYVcq7qz5+v5RLfv3A/8V8Aci8nvjuf8R+FngF0XkJ4A3gR99DGM1zhNnK+rKOD1ehekOA4TSi05iRHLGR4/kybi+98SpIMnRtxVHrecrCrdmU6JLXK0OmLqWHT/nVX/IVGDbJTbdAifFw7/hy/r++mSTLydHt4i0qWaYC6LC0ATUCRocIfrjoB2BMj4oY3Vj4FEee22f/n5rggXVGA/H3az9qjdeVZWtvNkUvCdvTtAq0G1XDBuedtPTXhqt/QuZNMlMXypJOR+7fJ2X6gNen1zn5bDLjp+z45b06o4Dd77SvcidYcbv7L7GXjfhzRuXGQ4j8Vag2hOqPaW5rcR5pr7d4doBtzcfi2uOHXO6/rjazjdYe3guxG/hssbj457184exA42UVtPe49oOYqCZl6CdaiNSHZWgnbB0DBPHYthgPi2fdWO6CUDfeLxkrrgFM9cxlY6lzrnqDzjIDVPXcXuYEV3i5tGM23GTVEdSVTrlDBNBcsS1niopritdfOhKbIEC4k6Efhyi+5xjYjfeP/eon7+aLcowFKu/WOJjxDUV8VaN1pHpO6VpxuJtT2ocRy+8wP70Cl+68ip+s+fS9hGvbd3hanPIR6fX2fBLXg67VJL49uZtEsKH6lvspQlffulF3p7vcO1gkzu3N9CjQHMj4pcwuVERlkpza5OwHHvkzdtSaWe+svZntvCeU6eeid14dO4SpgucaoO9PKmmW9e4KtLsNlBF6jsTUu1p7kT6ibC4Ghg2AreuVNy5MmV7c87RlZoX6kOaWceOn/OhcIdaEq+FXbIKH62vcXNziz/Zfpkvbb3E9fkG70x2YOHJIeCXUtJx557aO0Ll8UehzELarow9Jei6sXY+J91wnyPBm9iNx8/ZNtiM4llV02192ScPntD1hOAJ8xKp1+xF+qmj3Xa0O1MONyb8f1d2kOnAv3/hw8yqjo9u32AzLPlgdYdNv8CRaVzPt9Q32b604NbGjK9Mr7LXNby1c4lF61lerQhzT3PLEw8r6v1MtbuBXw6E3UWppHs4R3MuSTlnw3Ofg3W9id14cpxOwwV0OFVxZ7EswTqHR4gI/nZDCIE4Bu2kzYZuK9JvOBZXPMM0cOvFmhvTzNsvbzObtHz08k1eafb4cHOL16pbXPGHfHvzNsscub2xwW6a8oVLH+B2N+MLV17icF6zd2NC3HfUdzz1bUd1GGiaUEQfPJzuiDsW1CyDlxNrf+q7XSRM7MbT4y718+n70gm3bYuDD5CuR4aM62riPOC7UvXWt47UeJbzDXabGb+5P2MybXl564BXpntcrua8Wt/Bo9Sup1fPpTindgPLS4GDWcNbcZvFTk2/WdFtOeJh6bkXFpFmM+LbTLwzhuceLsr4xm64crpm/gVc15vYjafLmfX9sWiWbVnfHx4dr+9dFfExUk0atI5srpJyrlQMtbC4OqGfTfjq5W2+vP0y1XbLBy7vcame87HN60x9x4eqW0QZ+NjkGr163rx8hd1hyp8dXOHa/haHBw3zm6XYxuR6RVgo03cDfpGpbzfIolTPlWVbHHldX6x9P1w40ZvYjWfL3ZJysp68NiblSEp4EVz01CKE2oEEwpHgBqFbBvqF583Oc32yyUHfMAsdH97YoHYDm36JG9N9Jq7jcj0nbTq8y+xmoZsGUF9q6YnHLz0ahDCPhCbgjipk2SGLVYec7htFfwHi8S2oxjh/3C8F13tkOoHg0Y1SZmvYrscW2J7ljjDMhOVVJTWKXG2p6p5XL+2xXS14uTlgKyxwonjJHA41N7sN9rsJb+7tsGgr2htT3EJobjriETS3M9V+Jh4OxN0l0vbIwfzeYbnPUPQWVGNcLO6WlLPy5q8KbIaAAG7sjee6iAwRyYF+CSpCaoSlq1jUga+Lstc0dDlwpa6O++IlHBuhI6vj0nRBFRI3twOpCnS9kKOAOrIXNAA0+GXAZ717WC6cW2eeid04v4wltE9H6kFfylY5KT3vvUf2amLwxKZmMm3ITaDfLp1ylpc9qQ4sX9jmoIFbl6+QZ4m4WarpzqqOq5NDgmQ+tHGHPntenB3SDoF3rm6ybCO7dxr8gafaC9R3AmGuTN9t8G2mur0szrz9OYy98LTrz6Uzz8RunH9Ot8EWKdF6Y8SeugFJqVj8vkf6Ab+IyJDRKiC5JlcO1JcwWnX0S6FPwq4K7SRQuUQdBmo/EF1iKy4ZgqPLnkUVuZUcg4904pHsyFHwvSMsBddVuNYjfUKcQ/K42wAIfRmrnOr08wwFb2I3LhZne+ONGXgqDulKs0nxDjma40Jgsls64dbvFk9+txPoJ45229NvzeimM/700jZaZ+LOkhgTW9MltU94l9msW8LlTLsVONypWbxQoQvP8qrHLxzNuw7flq63vs1Ud1rcvMPNlyU4ZxiTcFRLD79naOlN7MbF5S7TfBmGUfg96v1x/fy47NAY8PMJ9SQQ55Hu0NFtCK4tlXY6beirjAh0sWdnsiS6RKwT1FCHgYM4sGginTS4pQN1hCW4VDz5kiqCFzyUfny9L/35Uioiz+5UqvDTrY1vYjcuPmcTcs7k3av3SN9DCIS2iD7sNTSzimEW6LY8QyMsbwZSDe3lyLJSbm8lXDMQ64G6GooH32XqekAuLRn6Ms13naOfOXzraXcc8ShS79XE/Sl+0eP2S218dziHnNBlW8Y1DE91y87Ebjw/3DX9tkyZpSuJLzpflICdgwpXV4SmptpsyHWg3qtKBd2DUj67vSwMk0C7NTBsDMRqYNq0NHFgUvUMyTGvKobBs6wq3NKRoyMeCUMtNLUjHJW4AGl7XM4wpOJrGMauOKu+d0/B0pvYjeeTM+2vVw0zBE72wocB6frSDLOOSJ/IlScsK1ItxCPHMBG6rVhmABNlOWuQmAn1cHwpAWgyOSidQpoIqRaGiScelRuHX9bUVUD6hNsLJ1Vy+5Ji+zQ89yZ24/nmbDLO2P1Wuu6kys5haY8VdmsIgXh7ikbPZKdhaDztTqDbEPpNR7flSBOl3/YQFD8bcC4TpyVVdqgDaXD0G4GwJcRDYZh6wsKTo8MvE5VzpaCGdyUSz5WCH5rSE02vNbEb68cqNNetUnD7ktrqBIZUovZiIIjg2oAo+M7jO4frS7CO6z25gqF3JK9QZcQpmkvraoKSaxgySBJyBDc4fOfK5y1L+K9UsXTiDW1xKnbdScurovzHJnoTu7FenC20IYIOjNb+JFgH55C9puTaTxqapiLPSrZcmjiWlzxDLbSXPTlCt6XkStFJhqBolUkVpKkwzBy+ldGJB/1kLIk9C4SjAX9Q4Q6XxcrPS3VcjsNv4XFZeRO7sd6cTsQZ024VSk67d2j2JVhGS6nrCLhUKtr6RlDvyJWgIqMld+RKwYN6RbKgDrKHXJdLDlNQL/jWo05KOa8M4mQMEHInhT5WNfIeg+BN7IZx1ot/ttf9YjlWz434qsLXFXHaoFVgstOQK8fyUiBVQrftGCYwTCBNtQi9UjQo/aYiUyFXguthmHj80tFsOOJhRTxo8E2NtB0uhOJnWCxL//rT23TvU/QmdsM4zZkknBKXS+kyA6MVzmMvvEDwQq4ClRdS41DvkARlwS1F6GPDXARUIMcym0hNOTm0pba+6z2uLZKUrj+u1KsAKR/7GN7vFp2J3TDuxiosVwQd8kl0nvdI62GxhBjw8yU+eMJ+8eA32zVD4+k3Pf20WPl+w5FjsfbqFFwRfD8ThgZydHQbSj+L1FOPXySq2iNtwoVQkmrmi2Lp+7Gn3fuY1pvYDeN+3K1cdkplTT0WpMS7Yse9J6jiJhFJEUkBN0ix5lVZu6sXUq3FyodSejvVAMIwgOvLNCAvIk4EXcayO9D3ZTaR8/tex5vYDeNBOCN6zVpEmHNpfDkMEAKu63Ex4A4nVHuRNA1U+5FUC+3WaOFnQg6QA+UG4DgWvHoYGo/6Cr+MVE5wXcKJlKo480Xx1A9DSax5CMGb2A3jYbiH6DWlsl++En0/oMsKWdRIn8m1R3IkVYIopEoYJpDj+LGesm+PoKJ0gyMExbcRDQ5p6+M1vKRUxrHqXTdmAb4XJnbDeD/cqzY+jHXptHTE6ctD64D0Dbny+C6Qo9BtCKkqU/wcxrR3AQ1lLa9ecH3Adb5U260CDiB4WLbj9tzoOHwAL72J3TAehVU4bioVNTSVCDwdhtIBZxlgWeNiJLZDSbNty3ad68v0vp+WaXwOpfRV9sBE0KBIcvhO8V1VOuQO+XjtLqtOusf96u5v4U3shvE4OFs3T/Q4Hn+VfCMiSPDgS5VcFSHVDkmOoXfkqOPavdTQg3IDEKVs6wm4Npa21DmfxNKnVOr06Riqew9M7IbxODkuqHEqn77rS9LLqrtt10PwuEWpjhu3KvppIE0c/VTIQUhVUW2OZTovyeNrh2QIweFVkazHwT/HMQD3wcRuGE+CsfvN6YQbxhz2YydbDLic0egofrqAihuddmXLrphuTkJuo5Cjx1UBiaHUvBsDcUhpFQN0V0zshvGkOFM26xuq54iUcFzvCcsObSr8tCJtVKTa0294sodUl7h79ZClpMuqLxF0QfV4xiDeF7/BcNeS8YCJ3TCePGOyTdmmy8fr92NLPzaTdK6E25KLBZcoqBfUabHyULz1TtDgypZc8EjwqObymffhgcUuIh74PPC2qv6QiFwG/jnwYeDPgb+lqnfez9/CMJ57Tlv5XCLndKFFoCmVphdth29rfF3h+rpM1zfDGHUnReRjNF5x7FUA+LYplr3tkPbegnf3fOWb+Sngi6eefxp4Q1VfB94YnxuGcT9UT8pPpVRaR/VDSXjpeqTtoe1wywHXDvg243pFEsjogNNj615SbDX4ErL7Hpb9gcQuIh8E/gvg50+d/mHgs+PPnwV+5CG/tmGsJ2PDSh3LS2vXk9u2dJM5PEIO57i9I/zunLjXEvc64sFAPMz4VnGpxNbn6MiVR5uI1hXUdam2cw8edBr/D4CfBjZPnXtJVa+Vses1EXnxbm8UkU8BnwJomD7g5QxjTThVNIN+LI9FKZ4hOeMWoXS3Ca7kwDgHqQhanYCXkokXcnHW8QhiF5EfAm6o6m+LyA889HdR/QzwGShdXB/2/Ybx3HI2d37lsFsxjI68GMZ21Q7JkVy5Y4edOkHjWFEnxpMOuHfhQSz79wN/U0R+EGiALRH5J8B1EXlltOqvADfez/c1jLXn9J78qf70qxJVMiRc8GjyxVtPCbTJYbTwwZWml8Hfz7C/95pdVX9GVT+oqh8Gfgz4d6r648CvAp8cf+2TwK+8z69qGMbKcTeWntJhKI927F+3aJFFcdz55YDriuNuLJhXtva8e2TLfi9+FvhFEfkJ4E3gRx/hswzDWFn4M1l0khLqBBli2YtPAZrISr4r7zwx8Ehr9m8ci/4G8Bvjz7eATzz0FzIM496cCcBhlfAyxr9LH0u5a+8Rn8dSd6PARe47jbcIOsM4b5yy8EDpAguIH0o9+5RO1t+h9JeD0VP/hKbxhmE8Kc5aeFVUdexY48px1b/OlzTY9/LAmdgN47xyyktPP8AYU685HUfLSQysak/ez6qDid0wzj+ax4LzDlUtW3IplU6wziHJCk4axsVnVfYqK5BKDfnswXes0t0JperNe03jHyYRxjCMZ4UWJ52msQdcSiW0dnzIGGZ7P8yyG8ZFYZzOa2LMgXfFO+9LZJ1IvO/bTeyGcRE4NZ1feedJCR298gLFW3+fctImdsO4SKzKRqfSh06GAYZxQz7dfypvYjeMi4bmk55zYztnkbEV1X0c8+agM4yLxHEv+YyuAm1G0ZfXbBpvGM8PqmXtToK+B+/G+vHJLLthPHfoqfX5mBZrvd4M4zlFsxanXErIIMVRdx/Bm2U3jIvKyrqrFuv+HoE1ZtkN4yKyyopLqVSUFbPshvH8shJ2PvHQ3w+z7IZxkVllxKU0BtWYZTeM5xrVlUf+3r9jYjeMC47mlYPu/kE1JnbDuMisLDoUZ51ZdsN4znmAoBoTu2E8B+gD7LOb2A3jecL22Q3jOWZV2CLl+y3ZTeyG8VzwHgE1YGI3jOcHtaAawzAwsRvGc0Np93zv103shvE88B577GBiN4znh/dw0pnYDWNNMLEbxppgYjeMNcHEbhhrwgOJXUR2ROSXROSPReSLIvK9InJZRH5dRP50PF560oM1DOM+PKast58D/rWqfgz4TuCLwKeBN1T1deCN8blhGOeU9xS7iGwB/ynwjwBUtVPVXeCHgc+Ov/ZZ4EeezBANw3gcPIhl/whwE/jHIvK7IvLzIjIDXlLVawDj8cW7vVlEPiUinxeRz/e0j23ghmE8HA8i9gD8ZeAfqup3AUc8xJRdVT+jqh9X1Y9H6vc5TMMwHpUHEftbwFuq+rnx+S9RxH9dRF4BGI83nswQDcN4HLyn2FX1HeBrIvLR8dQngC8Avwp8cjz3SeBXnsgIDcN4LDxok4j/HvgFEamAPwP+G8qN4hdF5CeAN4EffTJDNAzjcfBAYlfV3wM+fpeXPvFYR2MYxhPDIugMY00wsRvGmmBiN4w1wcRuGGuCid0w1gQTu2GsCSZ2w1gTTOyGsSaY2A1jTTCxG8aaYGI3jDXBxG4Ya4KJ3TDWBBO7YawJJnbDWBNM7IaxJpjYDWNNMLEbxppgYjeMNcHEbhhrgondMNYEE7thrAkmdsNYE0zshrEmmNgNY00wsRvGmmBiN4w1wcRuGGuCid0w1gQTu2GsCSZ2w1gTTOyGsSaY2A1jTTCxG8aa8EBiF5G/KyJ/JCJ/KCL/VEQaEbksIr8uIn86Hi896cEahvH+eU+xi8irwE8CH1fVvwh44MeATwNvqOrrwBvjc8MwzikPOo0PwEREAjAFvg78MPDZ8fXPAj/y2EdnGMZj4z3FrqpvA38feBO4Buyp6r8FXlLVa+PvXANevNv7ReRTIvJ5Efl8T/v4Rm4YxkPxINP4SxQr/i3AB4CZiPz4g15AVT+jqh9X1Y9H6vc/UsMwHokHmcb/NeCrqnpTVXvgl4HvA66LyCsA4/HGkxumYRiPyoOI/U3ge0RkKiICfAL4IvCrwCfH3/kk8CtPZoiGYTwOwnv9gqp+TkR+CfgdYAB+F/gMsAH8ooj8BOWG8KNPcqCGYTwaoqpP7WJbclm/Wz7x1K5nGOvG5/QN9vW23O01i6AzjDXBxG4Ya4KJ3TDWBBO7YawJJnbDWBNM7IaxJpjYDWNNMLEbxppgYjeMNcHEbhhrgondMNYEE7thrAkmdsNYE0zshrEmmNgNY00wsRvGmmBiN4w1wcRuGGuCid0w1gQTu2GsCSZ2w1gTTOyGsSaY2A1jTTCxG8aaYGI3jDXBxG4Ya4KJ3TDWBBO7YawJJnbDWBNM7IaxJpjYDWNNMLEbxppgYjeMNcHEbhhrgondMNYEE7thrAkmdsNYE0RVn97FRG4CR8C7T+2ij84LXJzxXqSxwsUa70UZ63+gqlfv9sJTFTuAiHxeVT/+VC/6CFyk8V6kscLFGu9FGuu9sGm8YawJJnbDWBOehdg/8wyu+ShcpPFepLHCxRrvRRrrXXnqa3bDMJ4NNo03jDXBxG4Ya8JTE7uI/A0R+ZKIfFlEPv20rvugiMhrIvL/iMgXReSPROSnxvOXReTXReRPx+OlZz3WFSLiReR3ReTXxufneaw7IvJLIvLH49/4e8/reEXk747/B/5QRP6piDTndawPw1MRu4h44P8A/nPg24G/LSLf/jSu/RAMwN9T1W8Dvgf4b8cxfhp4Q1VfB94Yn58Xfgr44qnn53msPwf8a1X9GPCdlHGfu/GKyKvATwIfV9W/CHjgxziHY31oVPWJP4DvBf7Nqec/A/zM07j2I4z5V4C/DnwJeGU89wrwpWc9tnEsH6T8p/urwK+N587rWLeArzI6hE+dP3fjBV4FvgZcBgLwa8B/dh7H+rCPpzWNX/0BV7w1njuXiMiHge8CPge8pKrXAMbji89waKf5B8BPA/nUufM61o8AN4F/PC47fl5EZpzD8arq28DfB94ErgF7qvpvOYdjfVieltjlLufO5Z6fiGwA/wL4O6q6/6zHczdE5IeAG6r62896LA9IAP4y8A9V9bso+RHncho8rsV/GPgW4APATER+/NmO6vHwtMT+FvDaqecfBL7+lK79wIhIpAj9F1T1l8fT10XklfH1V4Abz2p8p/h+4G+KyJ8D/wz4qyLyTzifY4Xy7/+Wqn5ufP5LFPGfx/H+NeCrqnpTVXvgl4Hv43yO9aF4WmL/LeB1EfkWEakoDo9ffUrXfiBERIB/BHxRVf+3Uy/9KvDJ8edPUtbyzxRV/RlV/aCqfpjyt/x3qvrjnMOxAqjqO8DXROSj46lPAF/gfI73TeB7RGQ6/p/4BMWZeB7H+nA8RcfHDwJ/AnwF+J+etbPiLuP7K5Slxe8Dvzc+fhC4QnGE/el4vPysx3pm3D/AiYPu3I4V+I+Az49/338JXDqv4wX+Z+CPgT8E/m+gPq9jfZiHhcsaxppgEXSGsSaY2A1jTTCxG8aaYGI3jDXBxG4Ya4KJ3TDWBBO7YawJ/z9bPgtvR75eGwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"o_coupling12 = torch.tensor(ot.bregman.sinkhorn_stabilized(mu1.cpu(), mu2.cpu(), cost.cpu(), reg=1e-3))\n",
"o_coupling23 = torch.tensor(ot.bregman.sinkhorn_stabilized(mu2.cpu(), mu3.cpu(), cost.cpu(), reg=1e-3))\n",
"o_coupling31 = torch.tensor(ot.bregman.sinkhorn_stabilized(mu3.cpu(), mu1.cpu(), cost.cpu(), reg=1e-3))\n",
"pyplot.imshow(o_coupling12)\n",
"o_coupling = torch.stack([o_coupling12, o_coupling23, o_coupling31], dim=0)\n",
"(o_coupling.float() - coupling.cpu()).abs().max().item()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Performance comparison to existing implementations\n",
"\n",
"We copy the code of Dazac's recent [blog post](https://github.com/dfdazac/wassdistance/) in order to compare performance.\n",
"\n",
"Dazac uses early stopping, but this comes at the cost of introducing a synchronization point after each iteration. I modified the code to take the distance matrix as an argument."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"46 ms ± 37.1 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)\n"
]
},
{
"data": {
"text/plain": [
"68"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD7CAYAAACscuKmAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAwYklEQVR4nO29a4yk2Xnf93vOOe+lqvo2PZe9UyTttWRZhiyFiSgrCATTDhxZMP1FhhwoYAIBzIckVhwHNpl8ygcDBGIY1ofAAGHFYGLBtkATJiEYtoVNZCBAQIgSGUviiiItksvdHc61e/pS9d7OefLhvNXdOzszO7Nz6556fkDj7arq6jrbO//3Oee5iqpiGMazj3vaCzAM48lgYjeMFcHEbhgrgondMFYEE7thrAgmdsNYER5K7CLyF0XkGyLyLRH51KNalGEYjx55v3F2EfHAHwJ/AXgT+C3gr6nq1x/d8gzDeFSEh3jvfwR8S1X/CEBE/inwceCuYi+LmdbVFpLGG0xS0BNfLL+H45tQfmwYxnvTcEinrdzptYcR+0vA9048fhP4idt/SEQ+CXwSoC43+eif+q+RboCoSNcjQ4R+gL5HY4K+G699FnyMaFLQlH+hZfwZxl35sr5219ceRux3unu8S4mq+lngswCb0xdV+ngsWO/yG5wgTpCYUCdIjCCSf67v83UpeiEL30RvGA/Ew4j9TeCVE49fBt5+z3cN6fh7EfCjj9B7EEFUQQRVRWJEk0dU0aSIS1nwy/ea4A3jvnkYsf8W8KqIfAh4C/h54D+/5ztSQtoOnAN3YmPgHSqSXxcBDYj3ECP4Pp/tl49jHM/66Xh7b6I3jPfkfYtdVQcR+W+Bfw144H9X1d+/95tA+gENHtRlqy6j6L2Akyx61XxGCD7v2mPKj8efVSIkB0QQB9h53jDei4ex7KjqvwT+5f2/IUHbIVrkrXrw2covt/MiEDyoHot+ubXvejQlZBjyDSNGJLp3OvFM9IZxVx5K7A9MUrTr8nbduSx677PoId8A/GjpC5+1GzwkRbzPjrshoK5HUkS7HkkJBUQUVEz0hnEXnqzYVXOYDVDnEeeykFWzV947kFH4XsCD4vMhAfK23g35fcMAzkOK0DlICR2G/Haz9IbxLp6o2FWV1LbZQjuXheo8UhZZ8OMZHedQGZ12xXhOr7KllxiRIcEQka6HmCB0EPNjvVO4zkRvGE/YskP2pMcx1t4LFKCD5LM5oG4MxSVBnMv6FBnP9aOll/zzCvlIMF5VXN7eA5JSfk9Mtr03DJ7CNl6HHjTvyzXG7HALAR235TLE8Zxe5m19GVAPWnj0ZLhOwQ0pi70frX3XIzEhTYum5eOYf/cYstMYjxNzxjUZxirw5C07HCXGiGgOo41WnYJ8FgcIo/UP4zk+5WSbHJ4DUUiFQ9J4A3DuOEynigzZwjPIcdguxuUC0LQs+LM4vbEaPHmx6/F2WiMQyRbXDcgwZAee9/l7748891oXqPf57O4d6gQNo2DrMAq8hKS4rkKGlHPw+xyqkzbn3Eu/vFruvbFaPBXLfiyoY9EL/sjKo5q38KpIP8bigx+ts0OdAmMCjjBaekGcIklJBMQnHOQbxbhzkCGimhBJOWY/RgFENN94lmsywRvPIE9H7EtOiP6klcfl1FmcG1Nm81legkfrEikDWngkBdQJqXSoQCpzYo5U+fe6vkAGRYaE64Z8tm9ypZ202YOvfT9e87leY3pnKu471mkYZ5enK/YlqqN5l3xRGS3ueB2r4ySFnDs/Ik5y8g3ks7zPlj6N2/sUBEnguoQGhwwJ7xw6pFxlN8QxAuCPIgFCn9fgxnO9Jiu6MZ4JTofYl4zneV06zBmv0SFJ0TGLTro+x+b7Mos4lqgTYh3QIKRAPtN7IRWQCo8kh0SIk4AkxTdltviLPsfs2y5v89su+wuWXvwxWQcwa2+caU6X2OFIRDp6znNpq+Qw3bLyrQg5ZDd+79JxaE6TI/ls7VOQHLYTQPINQ8Ybh68cEpVQ+iz6eciOvOChH3IqrpOjIhxVRYhm7Y0zy+kT+5Kxrn0ZJstC0+PXxpZWMsRs9cNY9x4cEgtS4YiVy5a+EJJXVEALyZ2uvM/OvCKLP0wC0ifcosJ1Q47Rj510tG1zY42uy59xMmYPVmZrnAlOr9jhWEAaURUgZgvvJIu1Czk81xZICDldNnikr9HC42YFsXCgHq2EFPK2XsWhY9TORUUS+M7jhry9923EtRE/77NTb17AEKEJYy5+duplR+LSk2/be+N0c7rFfpKlpWfc2ovms7SO2/xlOWwMOcFmCNkzX3pEQdSRCmEgh+5SGMN2To6En0LeAaRCcKVDC4f0CV94GBKuCDkHv+1y0U3XH5famhffOOWcHbHDsdceUE0gDh2TZnCChDaf65sK8Q4/r3FFwE9K0qQgVR43C1n0E0fyEKt8rh8mY2ZeEkTB9R7fBdwAYV7hBqXYr5GY8PttTtZpuyz4vj8SPsNgabnGqeRsif0ky0w8GR1mKcfkdWnpk8818OOOwEnecnvvkJg99TI68JKCFoyW/rhrpjrBDQDZmQcFrk+oCK4bcMFnZ2Eb8rFiGI7KbRlk/MVWhGOcDs6u2OHI0h+f592R5x7IDjbvoChxZYErC/xBhRaeuFaRCke/li19PxViKaSSbPnLsV5HR2ufwLc5fBcWBb5XwmHCtwm/GPDzDukG3KKFIaJNA0unniXrGKeAsy32Jbdl4h2l3fR9vgGQt/2yLIcdAi44JPox8caRiqxsHZtm4DhxlgdJjG2ucygvDnnbr2E88zvBtT7P0xpi3lEsvfXj9l5jfHdq7jvWbxiPj2dD7EvuFaMXQYsCaVoIAb9oIXj8fvbcF2slqfQMM88wcQyVMEyylY91tvJ9lT9G1nP4znceGcC3ntCAb5XicIrrE8V+j+sT7qCBIeIWbU7N7fqjkltddu2xEJ7xBHi2xL7k9pz7Zb790toOQxbW8kwfPAFIpQfKfGhXQb0DlFRm650t+NjYViAVIBHSuP33Lah3uD7vLVyvFKosB2PIsqmmk9y4g7GmX5ffY8k6xmPj2RT7kjuJPo7tp5dTZ8amGa7tccHjD2uKOhAnBcMskEpHt+6IhdCv5VTcOIHkQUMWfKxzfb0Mgutl9OA7XA/lQYHrlXJ/husS4bBHFj3SduP5fkCXRTnjVn+5/T+2+CZ+4+F5tsW+5A7JOUdOsmU/vL6DkFNm/TzgJhW+rYiVR1JBLB2Iy0k5IZ/Xk4NUaE7J9ZobaaR8vg9TQYYc0vOdEivBt0pZOnzl8QuPcy6n6IqgY1EOR+22FPEce/JN8MZDshpiP8lyvNTSwg/DOGiC3DgjpiPRu67PHvy2IpUe3xSkUvCNJxXQrwmxEmIFscrneg15u9+vKaJ5FyBR6DYF10Fx6PBNQbGoKA6m+DYS9rucqXfY4IaILpp8ExrP98v0XDSZtTfeN6sndrhrGi4ch+t07pGyzM68wxrvPf5ggpaBcFiSKkfbePpJ3t5LzI68oVA0KKlKOSwwlu+5MWzn54JvhGLuKQ4cvgnUuyFv9XcLpI+4/SInCi0a6Ps8FGPpzQeL2xvvi9UU+0lu65qDynGJ7TJGDkjwuQa+8ZSqpNIjsSRMHKEV+kYYasF1ghbCMBXUK6nUHMYr9Mjqxzpb/H4q+BaGqcf1UM0cvlPKvRLpEv6wzc022u4oRVfbLg/GOJmpBxa7N94TE/uSZdhuGPI2fyCXxTqBts1594dz8B6/V+FDIKxN0KpgWCsZZoFh5mk3HEMN3Vautus2Uz7nTyIUCbyCU/oodIOD3uHmDtcJ5a1R9Due0CrVrYowj4TDHneQU3PdvMlOvaa5cy89s/jGXTCx34k7ldcuz/eq0I0TZxcOhkiAsVZegYBvc5FNLAUVRyqVQX0O4RWaRQ9ISNnRB2gpdLicnuuEvhNiIYTGUe57iknANRFf5i2+FAUyDGjTWrts474wsd+Ne53rG58Lb+YLxDtkt6SoSoqyoFqr0TLQb1bEytGc88RSaM85Yu3oN5RhmtA64aYDoewpNgdUBVUhJeFwUaCD4PZDPt/vBYrDQDhU6ls1vlHK3Q7XRfytRRb/onln0s7JDjvm1DMwsd8fdzjXE/OZHu+P03FjxAFaFYQxfVZ99thrcAyD5EEX6hh0bKhRCM4nnFO8T3g/pvyn/DNaOtTl8txYCjiHbwBKXJ8onSBtxPkcxqNp8/irfshjtEanHpjoVx0T+4NwWzouSd9ZYut9PtcXgbBXQ/AUNydo4Zls1MTK0W0F+mlO1Ok2SuJE6bYKtFT8Rof3idmkI/gEG7nNddMHui4wbwMHBwWucZS7AddBfaPAt1DvzgiLRNjvc1HOonvv871t81cKE/v74cQWf9kR96gNdkr5bB9jjtcnRYInqOKr4qhWXmLOvx0GIQVHqpRYBrSMpEoQUeowUPhIHQZiLczbksMiMrSB1pX4VhDNHn3wFJU7arTpg8t98/uxwccyqnBixLVGsH56q4OJ/WE52QZ7SO8osxWRHCrzDrdoIATcbkVZlUzWSoZZwTD1NFueWAnN+ZJUwsG5ir064TZ6ympgWrfMyp6t6YILa4cMybG4WNANnv2DCXFw7O8W+MZR7haEw4JyX6n21giLRLnb47qIuzXPs/Tmi3yeP5m0Y9b+mcfE/qi43aEXswdfYsqlsf2Qu+i0Ha4skKbCzStCXYxpubnkNlaAOuJE6By0SQghMit7Kj+wXc1xkj9rUMeN2Yx2CFybrNG1gcWkJBw4hqkQS0cxzxNxfJcoVXPNvWpO1GHsvd+LTcZZAUzsj4O7TLpRN7a/bj20be5kWwT84YRUBoqDilg6qluBWAnt9UA/DTQbFd/bWEOmA7ONhjIMXJjOKXxks1xACRtVw5Acu9sTDtuS+WHFfL/Azx3lTsjn+hsFvlXqm+v4NlHstbhFnwty2g7temhb9KhnviXtPEu8p9hF5BXg/wCeJ7ujP6uqvywi28A/Az4IfAf4q6q68/iWega5vWceZIeeE2h9Dt2FAAeH+BBw+1MoAuWtCanyNLdKhonQnHN0m4F+w3PQetx0oPCJWdlxsT5g5jtmoaV2PQdDRZsKrrZrXFussTufcGtnhjaeft3jm2z1w0KpJ45wWBIOCtxhizTd2KAjwliJlxdt03GeBe7Hsg/A31TV3xGRdeC3ReQ3gP8SeE1VPyMinwI+Bfztx7fUM85Ja3+yD34at8vLTrkh4GPCF7mPfawDYRHo9hz9GrR7BcMkcGWvgCpxdXuNSdlzaXbAWtEy8x0T37NZNMxCx35dcWO64LArubkxo2097XaBb4XqZkE4DFR7JeXelDCPFHtt3urvL3J7rcXiqL2WzcI727yn2FX1MnB5/H5fRF4HXgI+Dvz0+GOfA34TE/t7s+yblzhOyx2nz7BoclrufgneU9yscqLObEKalsRZQbtVMEwciwuBYQKLSwWHk8TuhQlr05aXN2/xwuQWF8t9XihvAeAk0aaCy90me0PNt/Yust9WXL++jh4GypuecjdQ7nvqm4GwUKqb1ejUK4+Lcro+35T6Pt8ArL3WmeKBzuwi8kHgx4AvA8+NNwJU9bKIXLrLez4JfBKgZvpQi33muFda7tEQitw3zw0RGRIkCBMPBIYqz6uOlaftp+xMK+ZNydW1NbYnc65N15mFlnNhDsDUdxQSGdY8h5OSwkf2m4qD6ZR+I9DtO7p1T1jAZM3hW6VaK3FtJOxlsbtFezQPz6z92UL0Pv+niMga8G+Bv6OqXxCRXVXdOvH6jqqeu9fv2JBt/Qn52MOs99lnOaV2WYQjDiny5Bspi1x2Wxbo2pRUBvpzOVmnOe/pp0JzXug3lH4rUm43rE0bXt2+zmax4AenV5i6li0/p5DIfqppUsEb7XmutBu8ebjFm7ubLA4r3NUSvxAmV/P5fnIjEeaR8laHm3fIvEUW7Xs79Uz0T5Qv62vs6U2502v3ZdlFpAD+OfCrqvqF8ekrIvLCaNVfAK4+muWuOLdbe5eyU29MhgGytRfBdYHCC770qK/GApzcA08GT58m7KwF/r3ARt3gRZn5lg9UN5m6Fi+JqWu5VO5RuEhwufvt7mTCNVmnWwSQnJ+fQg7jxdpR7BeEeYnfL/MRZF7AMObnq+ZMvZg46plv1v5UcD/eeAF+BXhdVf/eiZe+BHwC+Mx4/eJjWeEqcjJmf/vZflmEc3CIeI/brfDBE65OoAisrdfEaUG3GWg3PP1axeH5mltT5Y8uXcJPIi9f3GGrWvDq+lVeKG9xIezxavV9mAHbsB8nfO8D2+z0M35v70X22po3r28RDwuK64FiL1DtltQ7U8IiUd3o8ny8W3NcP6DzxbjN73PmXj/YNv8UcD+W/aeA/wL4XRH52vjc/0QW+a+JyC8CbwA/91hWaNw7bq8K3o1dcgM+Ka4dkKHC9QWh9aDkZhquIE49l8MG+9OSOvQkFZwkZq5j5lrW3YJaemrXsxdqAHaHKUmFW9OaPZkRq4AGh3ohHApQ4ptEBdmTLzIW4rS5t59Ino1nPfOfKvd9Zn8U2Jn9EXGnc71347k+t9KSukLrEq1K4kZFrAPN+Zyss7iYG2w0FxNpFpmcX3Bp44DnZ3v8ybXvsxnmfLi8SimRWnoArsZ15qniDxfPc6Xd4DsH21ze3WCxXxGuloSFUF+F0CiTG5GwSBS7LW4+Nty4n6QdE/5D89BnduOUccdae4e43KtOvM8Wtcljr6StCWWBbyfEyuP6IrfQGhz9mqMZHG91gXlfMPE9F8qK58MtSj/noj+kkMRz/oCE8Hy4xY3pGq/XL/KH9SXeXtvkctikOSyAfL5HPcUiN/EMhQcvuaWXc2Mp8FjHK0vrnqxn/hPALPuzwu3W3ufBlksvPiEgkxotAmkjp+d250qGicsZehtCvwHt+YhOI+cu7rNRt/zIuctsFXP+RH2ZLT9nwzXU0tNowaGWXBs2+HZ7kWvdOl/feZ79tuTmlQ1k4amueYoDqHaUai9RHCbK3RbXDLi9eQ7bHc4taecRYpZ9FbjdqbcsxHGSW1d5lxNjvMcfzHMPvVtTUlVQb1V0G9mh1+x4+jXP7nyLnWmkjZ5z9QK/nXip3GGrepuLfsFUFqy7wFxvcKP+DjdTzddmP8D1fp0vr32Qm4spV2ZbtPuBYeYYdjzlnkM9+EVBMU7ClTRmD5L7/wl9LiJ0J1J0jUeCif1ZZRxpnbfHY895VURyRR7jiGlfFrimJuyVVNOSeqdgmDrmO55Ye65fu8SVifKtSxeZTVs+dO4GL093eaW+yYfLa6y7Bef9IYVE/kz9XZqq4IVyl1txwte3X+TKYp3v7W6xuztB9grq6wVhDpNrJb5VJtfXjpJ2pOnH2H2Xy2/vZu3N0r8vbBu/Stxlq3+0za9rdFKhVcmwVRNrz+JiPt/PnxeGqdI9N1Butry4fYs/fe5tXqlv8h9Ovs2WW/ChIlHgAUgkvjsou6nia80P8I3583xr/yLfvn6eZr+ivFzg58L0iuaknetD7qS71+SEnaY7zstvW+upd5/YNt7I3Ck9N42Ciemoo410PYUqvgxIglg53JBz8Zt5Qb8R+M5OzeXtDbbWFnx9+0W2i0N+dPYGG77hxbBDnWdZse46Xi2/z5af83y5x3OTfa4s1vn2+nmaRUG/WeEbodkuCXNlslNSHETCQY/fa3P77MNFtvAn22uZtX9gzLKvOnez9mFM0Z1OIHjS+gytPP1WTb+Wu+u054R+HZrnIjobeOmFHbYncz567tu8WO7ww9VbPO9bNp1nKiWt9uyngSux4Pe7F7nSb/L/3Pxj3GxmvPH9bfQgUF8NlLeyU6/ejYSDSLnT5Kaa+4e5Em8+ir/r3t1Tb8VFb5bduDv3tPZjMU4IOOfQLoyOtQKJ4AZHWAgkzzBzvJW2uTLZoB0C5+tDrmxs8kKxwweKmzznDygl4YBKIi+FHWauZX+z5sZ0BsDOfMJesUa/7unXHP0sUBx6JhOPbxPlTpGTdvYKGCIsxky9fshOPmu2cU/Mshvv5qS19/kMflSMU5XZ6k/y+T5NCvrNmjhxzC8EYg3z54Q4VfrnOibrLR/Y3uFPbFzlw5Nr/On6e2y5Ba+EniLfWuhV+e4wYTdN+Z35B3mzPcfru8/x1o1N+r2K8kogLM/3TT7f+0Uk3Fogiy479Zqxk27XH53vVzF8Z5bdeDBuT89dEmNutlGEfL4fIq4v81SrJqAixFpQ5xgmglKyWHi+k4RmKNhdn5DUcSHsAW8zlYEtp3gRtn3D1PUc1pdZz43xCS5xpV5jX9cY5h5Rh18IEAiNp/KCnxe50UcRcr29X07AdflqY7GOMMtu3B/3OtuXRb5OJ2gRiJsTUhVozxf0y6SdTeg2leFCTzHr+dClG5yr5/wHm9/lYtjPTjzXUkukENhPnt1U8dZwjtcXL/F2u8m/u/EiB03FweU1/KFnck0o9pV6Ryn3IsXhQNhtkG5A9ufv6JmvXbcS6blm2Y2H53Zrn0bHWIz53Ow9EhPiHT7GbG2HKcUk4LtAWOTzfTMUDGuBb8s216YzJr7nUrXP1LXEcIuX/AFTEWqf2HZztlzLzLV8v9wC4EY74+vR0cxLmlTlaTtOSB5SkQfn+WbAxXTcM38M2b2rp96KWXuz7Mb7R+TdxTjO5bi998gkl92m2QSdFAxrufS2nzoW5x1xAotLiTRRqktz1qcNf3zrOq9Md/hAdYMPlteYSceWWxCR3GxDC/6gfYFbw5T/79ZLXF+scfnGJsOtkuKWp7ouFIfK5HoiNEp1oz3umd/1aNMez8MbQ3jPklPPLLvxeLi9n17MxS9H47C6Pg++nC9wZYmbVIS9mjgpKPdL+qnDL7Lo5+2Ma9MJTR+4sT7jcKPCk3i+uMVz/oBaEq+EnqjKi+EW+6nkQrHP1X6Dr9av8ObaJruzGSmUDAcOcIQFSMrlt0VUXBvy3DsRcIKOLb/yf8tt/olnELPsxqPjxLkeyJ58J0gYHWhFiVS5rVYap9122zWxdCzO+5y0c14Y1nNbrWp7wcYsW/vtcs4PTr/Pul9wMexREOnxRHW83Z/j+rDOdxfn+aP98+zMJ+xcW0cWnvqKxzcwuZYz9eqdgXA44A9a5LBB2v7dmXrLhJ0zmKlnlt14MpycgcdtvfJbAd8cV+LtlbgQmNzMTr36+pRYB9rtgm7maLYD3bl1bmzOuPncjOm05ebFKReqA3587bts+wNeCrusu55Xi+skhLemG3xv4zxvdtt8dfMVbjZT3lzbRheeYZLDd0NdUO17ytpTFB5pBpyTHLeH0ZPfoSrjiPvRk3+GBH83TOzG4+NOTr3RsUdKLOdTi3P4lHvlu3ZCVXvKg4Jux9GtOdqbU5rphP/3+gw/iXztwstsVA1/fP0aF4oDLoR9tsMBSR0z1/JCuQtbsDNMWStb9tqa729s0swD7flAse8pb3mq3YJirtQ3J7g2z7qnH3CHC3SIudHGMzQLz8RuPH7eUX47DsHss4dcFk3e6u/tI94TbtRIUVBOKnRaEWcl3VaZK/EuFMRJyeXnat6cJr753EU2Zg1/7Nx1Pjy9zgvlLT5cXWHbH/CnqjfpNXB1fZ39OOF3L77MzW7K6zee59b+hMXNmvKGo9h3TK7VuRjnWoFvI2GnyP3+Dj30fXbsLdt7n+G4vYndePLosVg0gqjkG4AqMratEtUcyhsSkpQwD6AFsRJIjlh7mnbG9bWaWwc139nY5tLsgA/OLrERGl4odykkb82TCudCbp893yy5Uc24UqyzqGr6g0CsclgwVrnstp54fBMJe9VR2S1Ne9QrX06W3Z6hc72J3Xg63NZsYyka6br8/JiwI97jq4oQPOVanoW3vjUhlZ7m/Dgd5/wae+trXN+8yO9eeIly2vPBCzdZLxt+aP0K677h5fImtev5ocllevVcvrTF280WlxcbfHfnHPN5xeGVirAQJleqsey2OuqV7/fz8Et3MM9WfjkL7/bOuadY9CZ243QwFuRojDlmT8x98lVHR1lA5g6CJ4iQykDlhDD2uvOd4AahTSX9LPBt3WZS9wzJs1a0fGBykzXfUriBQiIOZauY0ybP4VrJXhi42Tm6qUeGsZcejuJQUC8UhccvCpxzObToF7n4Rtq89n449X3yLfRmnE7u1kHXOaSq8jn/tqSdfr2k2wwMEzlK2mkuKHGSCBca6knHixt7XKgP2S4POVfMjz5uHkuutOsc9BXf2d1m0ZY01yf4Q0d1w1HuQbmnTG4O+EWi2GlyW629wzEtt31Hos7T2uJb6M04e9zeQXdsrbWM4R/dDFqPSwntSso+4vqKYZb/WQ91TqWNlad1NfuTgreBZihoJoGkjonvmPqOyg1sFQsqFzmcVRyUPVd6TywCXSxQl3+XJE9ROVwsSV0gpAT9cf9+BcSNacRwqpx5Jnbj9LPM1Dtqmx1zI81hQETQpsmZekVJWVcUVUE9G5N2zlVHSTuxdjTb57g82+KNzQQbPeWk58LGIZOi52J9QHCRF2d5+u3FySGLoeDqxTUOFyWLvYrD3UCYO+rrE3yjTK9X+EYpbza4dhx13XY5QWf04r9rIs5TEr2J3Tg73G7tk2ZLGlO2uv2Q++UvAq7toQhU3YCWAddXxInD9Z5+JvjW03VCOwvcEKjLnsoP1L7nXLmgcBFXHZIqwbvErapmJyQWriZWAYkO3wiu94RKcX2JLzxEzT3yRUYrnyfx5iSd+FQLcEzsxtlktPZ5tNS4vR8nzYjIWNvucWP77MneBK0C9bWaYeLpNwLteu6G022tM58oX9/eRMtEtdlQlgMbdUsVBoIk1ssWv64s6o5FVzDfrNHW0W4HfONY3KjwC2WyUxEOI8X+2EOv7XDzJp/nF83xNJynkKRjYjfONrdb+2W//GHITr22zWG8JqfqFvsTQllQrtdUayXDzNPs+ezUm+f22W0vtFUibjmmVc9G3TALHaVfsFUvWAwFu2VP0wcOwpS+c6j3ubGGcxR19uCXIrjG41SR3ufjxzgNR+HY0j+h3vgmduPZ4fb0XDnRSy8lcNn6Swj4tsMdVoS6pDgoGWpPuZdn4TU7gVhBd67gZq1cXxvw04GiiEyqDhHNrflcolpviYOndQXSOYapI8wd5Zaj2vMU84pqp8I1kXBrktNxD+bokLvl3nHK7WOy8iZ249njXum5TZvDdmXupefKAn+zoigLqrUJqQ5MzpXE2rHYdgwTR7dV0q8VNOuRbiMQisjatKEIkbrsURUOJyXD4GmmFX3j6dcd/Z6j2IehEopFovKC6yJecvkvMMbqR2fjyTP9YxC8id149tGT4S+ByNimKmXLmjT3p1fFNQGJiVR6XF8y1Dlxp18T+r1Av+cZauXmeomERKgGnNMxUgBSJJSxiM45UiGod/QLIfkK3ypVcLmhRlkgbZdTcdv23V1yH7GVN7Ebq8EoGj3Rokr7IXvLFzl0x8Eh4h1hp4YQKK4te+rVDLNAv+ZpNxz91NGeK0mV0m0VaKnIdMCHRCgHXK0ME8/QO/pFoNvw+Ba69VxbP506fJuo6oBf9Lj9BlmU0HXI6MSjI2fkPcLEHBO7sZosZ+Ell4dIRvJQyeRBOhi9+lIEcCB9gQwlkjy+dYgKscpJNrFUhl4YCoUyISFBkvwRoqQqAY5hChqg7XLozw0FqfS5F3/wyMJnx91tPfMeVWKOid1YXW5vqzWQPfjjeVrmi6NGGyEEQl1RTSpSXRI3SmLlac4FYim05zyxhm5dSRXESYIygYBOI7FKNLVDeqGfOXwL/VrAN1DvBor9iuKgxu9VSNNByN1xWTTIyT74D3GeN7EbBrxzMk7MyTAaYxYaQMz96kQVF1O29l2g9EKqBPWe2JJ75/cgyTEkAa9oGMXpQD2kMgfehomgAn0niHokgQwJJ4Kc6H2vyzl8D+nAu2+xi4gHvgK8pao/KyLbwD8DPgh8B/irqrrzwCswjNPC3WbcD0O+LhZQ5B75fq/MM+6XbbU2KlLlcyFO7ejWswWPNfQzRUMWuQrESvP3QXC9MEwd7cJRbniqPY9fJKqbJdL2uFsFMkT08PDYgfc+Z9s9iGX/JeB1YGN8/CngNVX9jIh8anz8tx/g9xnG6eYOM+4ZB0miua2WABLyiCxXjdfOjyYc3CCoCKnIgQBxkEIWffKgokgliGYduz4X+sQ64ASkKRHpc7POcU15Oz867kTuW/D3JXYReRn4S8DfAf6H8emPAz89fv854DcxsRvPGnfIxz/y5HuHju2yXZMz9dz+hLIIVOsVw7QgThzthieWQrchaIB+mq/qFXWgBfQeUhBiKfSNEEuHbwuq0uPbiCtC9iUcjv3vu+6Bz/H3a9n/PvC3gPUTzz2nqpfz30Mvi8ilO71RRD4JfBKgZnqfH2cYp5CT1XeiY/rrWIQzTsORGKEo8EPENSVxWiCxJNYC+NHCZ0sfK4GgqFPUgyQhTgARXA/JuzxDLziKtoQxGUePdhfjOT5yXxb+PcUuIj8LXFXV3xaRn37wv49+Fvgs5OYVD/p+wzh13KGHnnbd2GlnFH3fI/MCOSzxhxWpCoSDklQ62kNPKoRuTUiFkEpIoxLVQSyhnwmxBEkB3yswxTcD3rvcEy+EHJMfhtz6OulRC++7cT+W/aeAvywiPwPUwIaI/GPgioi8MFr1F4Cr7/dvZxhnjrsV4Jwot5UiQFPimg43tsnWMuC6klQ53JC39/1UiPV4zA+Ah1jnbb3EseVWF/LjPuIYy3qHITfI6IecK6AC9zCn7yl2Vf008GmA0bL/j6r6CyLyvwKfAD4zXr/4EH86wzi73B62Uznqn8fYokr6gFNFi0CpSio8MhSk0uFbx1BnCx+rnHarbvQJhuyKG6YODeD7EpzLgldFXe52e9zi+u48TJz9M8CvicgvAm8AP/cQv8swzjZ3s/Qub/HF+5wH7x2+7fDe4+d5tHWYlzm9duropxyf5xkn03roI8TCIUNBCI5ijPeLSO6BNww58+4e1bIPJHZV/U2y1x1VvQFY90jDuJ2Tlj45RBQlj5US71Hfjm2yHX5IuQovKpI8qDsaPY3krT3ksJ16IZVCTA5fBaQu8md1Xd7Oew/DHXtNApZBZxiPh3dY+hOddJZJOt4jbRZ9mNf4uiRMS4ppSZx4wponBaGfCOqAMS4/VELyDkkFAN45XD/krrtdh3QmdsN4eryr6Can4eJdnoIzJuc4l1tlo5qdcUUWtrps1XWpY8k3gFQ4XOHR4JGYB2rcCxO7YTwJTsbol40yVfOZux/G1lktfl7lhhpNTSo9fr1AgzBMHMlL3to7iJUDHX9HV+ebRFPBoVl2wzgdnGykMW7rGYZxqoxDnMspuE323vvSk6LgihxWe4eFd+R+9sEhweeafEzshnF6WDbSiPGdwy9izF1xyyKfw4uA9BEtPG6ocjpt7dFAFr4TUuFI9Xh+r/OknLthYjeMp8UdzvLAkWddVJEmIFFxZUDUocGRON7OLyfVsDzvm2U3jFPKycq6pOPXWNgSQpZu8ARAC48MSipdtuhekJRLZVNwuKo4Hot1B0zshvG0ub0FtqZxTlyOwTOOrmYIuOCOgu8qLjv7RMDlBhr3MOwmdsM4VYyJOIzdaejGSjrnkFjgvEOGkHPgl/eIpcC9mGU3jDPBbRb+qJrO+/w1RMQ5GCLLiLr67I0H0OCOPfV3wMRuGKeNk467MdVW+gG8Qtfn8dDB43zuSZ+O3nNvTOyGcRo54bg7svDO5TP8EBARHNlphxs76NxjCw8mdsM4vZyw8KjmFNuYx1kxROjH3vbD/Q2GNLEbxmlmKfh+yBa8G5134nI9uyoyOuaWZ/e7YWI3jDOCptG6i0DKDSskJoi5Wy331rqJ3TBOPSd73i3z6LusbAHwLsfh3fGU6jvxHvcCwzBOBSe97cssuxjRlLJ1T+meXWrALLthnB1Uj4tnxo40Ii5n2I3huHuF4EzshnEWSScm04wZdsR7m3YTu2GcJZbnd5XcCKMfwPe5Br4I97TsdmY3jLPGct7bOBXmaNJrSvfsG29iN4yziCY05TN8Fnoct/F2ZjeMZ5OlhY/L9lZ3/1Gz7IZxVtE8bYaUsnXXk3Wv78bEbhhnkWUfu6RZ6DGOCTd3f4uJ3TDOKrd73s2yG8YzzLiV13G4o1l2w3iGOZremsyyG8azjabceNIsu2E8wxwNkEz3zJ4DE7thPBPoyX7zd8HEbhjPCKp6r128id0wzjx60kF3dyxd1jCeBTRXwt0Ls+yG8UzxkGd2EdkSkc+LyB+IyOsi8pMisi0ivyEi3xyv5x7Zeg3DeGA06SMJvf0y8K9U9YeAHwVeBz4FvKaqrwKvjY8Nw3ga3MdEmPcUu4hsAP8J8Cv5d2qnqrvAx4HPjT/2OeCvvM9lGobxKNB7t6W6H8v+YeAa8I9E5Ksi8g9FZAY8p6qXAcbrpTu9WUQ+KSJfEZGv9LQPtnjDMB4Z9yP2APw48A9U9ceAQx5gy66qn1XVj6jqRwqq97lMwzAelvsR+5vAm6r65fHx58nivyIiLwCM16uPZ4mGYTwK3lPsqvp94Hsi8oPjUx8Dvg58CfjE+NwngC8+lhUahnF/vIeT7n6Tav474FdFpAT+CPivyDeKXxORXwTeAH7uIZZpGMZj5r7ErqpfAz5yh5c+9khXYxjGY8My6AxjRTCxG8aKYGI3jBXBxG4YK4KJ3TBWBBO7YawIJnbDWBFM7IaxIpjYDWNFMLEbxopgYjeMFcHEbhgrgondMFYEE7thrAgmdsNYEUzshrEimNgNY0UwsRvGimBiN4wVwcRuGCuCid0wVgQTu2GsCCZ2w1gRTOyGsSKY2A1jRTCxG8aKYGI3jBXBxG4YK4KJ3TBWBBO7YawIJnbDWBFM7IaxIpjYDWNFMLEbxopwX2IXkb8hIr8vIr8nIv9ERGoR2RaR3xCRb47Xc497sYZhvH/eU+wi8hLw14GPqOqPAB74eeBTwGuq+irw2vjYMIxTyv1u4wMwEZEATIG3gY8Dnxtf/xzwVx756gzDeGS8p9hV9S3g7wJvAJeBW6r6b4DnVPXy+DOXgUt3er+IfFJEviIiX+lpH93KDcN4IO5nG3+ObMU/BLwIzETkF+73A1T1s6r6EVX9SEH1/ldqGMZDcT/b+D8PfFtVr6lqD3wB+LPAFRF5AWC8Xn18yzQM42G5H7G/AXxURKYiIsDHgNeBLwGfGH/mE8AXH88SDcN4FIT3+gFV/bKIfB74HWAAvgp8FlgDfk1EfpF8Q/i5x7lQwzAeDlHVJ/ZhG7KtPyEfe2KfZxirxpf1Nfb0ptzpNcugM4wVwcRuGCuCid0wVgQTu2GsCCZ2w1gRTOyGsSKY2A1jRTCxG8aKYGI3jBXBxG4YK4KJ3TBWBBO7YawIJnbDWBFM7IaxIpjYDWNFMLEbxopgYjeMFcHEbhgrgondMFYEE7thrAgmdsNYEUzshrEimNgNY0UwsRvGimBiN4wVwcRuGCuCid0wVgQTu2GsCCZ2w1gRTOyGsSKY2A1jRTCxG8aKYGI3jBXBxG4YK4KJ3TBWBBO7YawIJnbDWBFEVZ/ch4lcAw6B60/sQx+eC5yd9Z6ltcLZWu9ZWesPqOrFO73wRMUOICJfUdWPPNEPfQjO0nrP0lrhbK33LK31btg23jBWBBO7YawIT0Psn30Kn/kwnKX1nqW1wtla71la6x154md2wzCeDraNN4wVwcRuGCvCExO7iPxFEfmGiHxLRD71pD73fhGRV0Tk/xaR10Xk90Xkl8bnt0XkN0Tkm+P13NNe6xIR8SLyVRH59fHxaV7rloh8XkT+YPwb/+RpXa+I/I3x38Dvicg/EZH6tK71QXgiYhcRD/xvwH8G/DDw10Tkh5/EZz8AA/A3VfVPAh8F/ptxjZ8CXlPVV4HXxsenhV8CXj/x+DSv9ZeBf6WqPwT8KHndp269IvIS8NeBj6jqjwAe+HlO4VofGFV97F/ATwL/+sTjTwOffhKf/RBr/iLwF4BvAC+Mz70AfONpr21cy8vkf3R/Dvj18bnTutYN4NuMDuETz5+69QIvAd8DtoEA/Drwn57GtT7o15Paxi//gEveHJ87lYjIB4EfA74MPKeqlwHG66WnuLST/H3gbwHpxHOnda0fBq4B/2g8dvxDEZlxCterqm8Bfxd4A7gM3FLVf8MpXOuD8qTELnd47lTG/ERkDfjnwH+vqntPez13QkR+Friqqr/9tNdynwTgx4F/oKo/Rq6POJXb4PEs/nHgQ8CLwExEfuHprurR8KTE/ibwyonHLwNvP6HPvm9EpCAL/VdV9Qvj01dE5IXx9ReAq09rfSf4KeAvi8h3gH8K/DkR+ceczrVC/v//pqp+eXz8ebL4T+N6/zzwbVW9pqo98AXgz3I61/pAPCmx/xbwqoh8SERKssPjS0/os+8LERHgV4DXVfXvnXjpS8Anxu8/QT7LP1VU9dOq+rKqfpD8t/y/VPUXOIVrBVDV7wPfE5EfHJ/6GPB1Tud63wA+KiLT8d/Ex8jOxNO41gfjCTo+fgb4Q+DfA//z03ZW3GF9/zH5aPHvgK+NXz8DnCc7wr45Xref9lpvW/dPc+ygO7VrBf4M8JXx7/svgHOndb3A/wL8AfB7wP8JVKd1rQ/yZemyhrEiWAadYawIJnbDWBFM7IaxIpjYDWNFMLEbxopgYjeMFcHEbhgrwv8P4h0ik6MxsFcAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Copyright 2018 Daniel Dazac\n",
"# MIT Licensed\n",
"# License and source: https://github.com/dfdazac/wassdistance/\n",
"class SinkhornDistance(torch.nn.Module):\n",
" r\"\"\"\n",
" Given two empirical measures each with :math:`P_1` locations\n",
" :math:`x\\in\\mathbb{R}^{D_1}` and :math:`P_2` locations :math:`y\\in\\mathbb{R}^{D_2}`,\n",
" outputs an approximation of the regularized OT cost for point clouds.\n",
" Args:\n",
" eps (float): regularization coefficient\n",
" max_iter (int): maximum number of Sinkhorn iterations\n",
" reduction (string, optional): Specifies the reduction to apply to the output:\n",
" 'none' | 'mean' | 'sum'. 'none': no reduction will be applied,\n",
" 'mean': the sum of the output will be divided by the number of\n",
" elements in the output, 'sum': the output will be summed. Default: 'none'\n",
" Shape:\n",
" - Input: :math:`(N, P_1, D_1)`, :math:`(N, P_2, D_2)`\n",
" - Output: :math:`(N)` or :math:`()`, depending on `reduction`\n",
" \"\"\"\n",
" def __init__(self, eps, max_iter, reduction='none'):\n",
" super(SinkhornDistance, self).__init__()\n",
" self.eps = eps\n",
" self.max_iter = max_iter\n",
" self.reduction = reduction\n",
"\n",
" def forward(self, mu, nu, C):\n",
" u = torch.zeros_like(mu)\n",
" v = torch.zeros_like(nu)\n",
" # To check if algorithm terminates because of threshold\n",
" # or max iterations reached\n",
" actual_nits = 0\n",
" # Stopping criterion\n",
" thresh = 1e-1\n",
"\n",
" # Sinkhorn iterations\n",
" for i in range(self.max_iter):\n",
" u1 = u # useful to check the update\n",
" u = self.eps * (torch.log(mu+1e-8) - torch.logsumexp(self.M(C, u, v), dim=-1)) + u\n",
" v = self.eps * (torch.log(nu+1e-8) - torch.logsumexp(self.M(C, u, v).transpose(-2, -1), dim=-1)) + v\n",
" err = (u - u1).abs().sum(-1).mean()\n",
"\n",
" actual_nits += 1\n",
" if err.item() < thresh:\n",
" break\n",
"\n",
" U, V = u, v\n",
" # Transport plan pi = diag(a)*K*diag(b)\n",
" pi = torch.exp(self.M(C, U, V))\n",
" # Sinkhorn distance\n",
" cost = torch.sum(pi * C, dim=(-2, -1))\n",
" self.actual_nits = actual_nits\n",
" if self.reduction == 'mean':\n",
" cost = cost.mean()\n",
" elif self.reduction == 'sum':\n",
" cost = cost.sum()\n",
"\n",
" return cost, pi, C\n",
"\n",
" def M(self, C, u, v):\n",
" \"Modified cost for logarithmic updates\"\n",
" \"$M_{ij} = (-c_{ij} + u_i + v_j) / \\epsilon$\"\n",
" return (-C + u.unsqueeze(-1) + v.unsqueeze(-2)) / self.eps\n",
"\n",
" @staticmethod\n",
" def ave(u, u1, tau):\n",
" \"Barycenter subroutine, used by kinetic acceleration through extrapolation.\"\n",
" return tau * u + (1 - tau) * u1\n",
"\n",
"n = 100\n",
"x = torch.linspace(0, 100, n)\n",
"mu1 = torch.distributions.Normal(20., 10.).log_prob(x).exp()\n",
"mu2 = torch.distributions.Normal(60., 30.).log_prob(x).exp()\n",
"mu1 /= mu1.sum()\n",
"mu2 /= mu2.sum()\n",
"mu1, mu2, cost = mu1.cuda(), mu2.cuda(), cost.cuda()\n",
"sinkhorn = SinkhornDistance(eps=1e-3, max_iter=200)\n",
"def x():\n",
" mu1_ = mu1.detach().requires_grad_()\n",
" dist, P, C = sinkhorn(mu1_, mu2, cost)\n",
" gr, = torch.autograd.grad(dist, mu1_)\n",
" torch.cuda.synchronize()\n",
"\n",
"dist, P, C = sinkhorn(mu1.cuda(), mu2.cuda(), cost.cuda())\n",
"torch.cuda.synchronize()\n",
"x()\n",
"%timeit x()\n",
"pyplot.imshow(P.cpu())\n",
"sinkhorn.actual_nits\n"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3.08 ms ± 2.68 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)\n"
]
}
],
"source": [
"def y():\n",
" mu1_ = mu1.detach().requires_grad_()\n",
" l = SinkhornOT.apply(mu1_.unsqueeze(0), mu2.unsqueeze(0), cost, 1e-3, 200)\n",
" gr, = torch.autograd.grad(l.sum(), mu1_)\n",
" torch.cuda.synchronize()\n",
"y()\n",
"%timeit y()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With this problem size and forward + backward, we achieve a speedup factor of approximately 6.5 when doing about 3 times as many iterations."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Barycenters\n",
"\n",
"We can also do barycenters. Let's go 2d to do so. I use relative small $N$ because at the time of writing, my GPU is partially occupied by a long-running training."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"tensor([0.0143], device='cuda:0')"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD6CAYAAABnLjEDAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAALX0lEQVR4nO3dX4ild33H8fen20gsUsw2k7BkQ8eLpRikJjCkKelFSVzYpuLmRkjAsheBvbEQQZBNCwXvciXe9GapwQVFCSjsEgRZVkMpSMxook26xk1LqotLZmIR2xtp9NuLebTDzuyes3P+zDnzfb/g8JznOTP7fGbYz/zO7zfPOZOqQtLB93v7HUDSfFh2qQnLLjVh2aUmLLvUhGWXmpio7ElOJHkjyZtJzkwrlKTpy15/z57kEPBj4DhwFXgZeLKq/u1Gn3PnnXfW6urqns4nabS33nqLd955J7s99vsT/LsPAm9W1X8AJPkqcBK4YdlXV1dZX1+f4JSSbmZtbe2Gj03yNP4e4Kfb9q8OxyQtoEnKvttThR1zgiSnk6wnWd/c3JzgdJImMUnZrwL3bts/Cvzs+g+qqrNVtVZVaysrKxOcTtIkJin7y8CxJB9I8h7gCeDCdGJJmrY9L9BV1btJ/hb4JnAIeK6qXp9aMklTNclqPFX1DeAbU8oiaYa8gk5qwrJLTVh2qQnLLjVh2aUmLLvUhGWXmrDsUhOWXWrCsktNWHapCcsuNWHZpSYsu9TERC9x1WjJrm/0eVP+ZV3NgiO71IRll5qw7FITztlvwV7m3/M6j/N8jeLILjVh2aUmLLvUhGWXmnCBbjCvxbdZ2S2/i3bazpFdasKyS01YdqmJtnP2ZZ+jj+P6r9E5fG+O7FITll1qwrJLTbSZs3eYo4/iHL43R3apCcsuNWHZpSZGlj3Jc0k2kry27djhJBeTXBm2d8w2pqRJjTOyfxE4cd2xM8ClqjoGXBr2tWSS7Ljp4BpZ9qr6Z+C/rjt8Ejg33D8HPD7dWJKmba9z9rur6hrAsL3rRh+Y5HSS9STrm5ubezydpEnNfIGuqs5W1VpVra2srMz6dJJuYK9lfzvJEYBhuzG9SJNzLirttNeyXwBODfdPAeenE0fSrIzzq7evAN8B/iTJ1SRPAc8Cx5NcAY4P+5IW2Mhr46vqyRs89OiUs0iaoTYvhNF4fLHMweXlslITll1qwrJLTVh2qQnLLjVh2aUmLLvUhGWXmjgQF9X4QhdpNEd2qQnLLjVh2aUmLLvUhGWXmrDsUhOWXWrCsktNWHapCcsuNWHZpSYsu9TEgXghzPXvgOoLY6SdHNmlJiy71IRll5o4EHN2TY9/AebgcmSXmrDsUhOWXWrCsktNWHapCcsuNWHZpSZGlj3JvUm+neRykteTPD0cP5zkYpIrw/aO2ceVtFfjjOzvAp+uqg8CDwGfTHIfcAa4VFXHgEvD/kKoqh037eT3qZeRZa+qa1X1/eH+fwOXgXuAk8C54cPOAY/PKKOkKbilOXuSVeAB4CXg7qq6Bls/EIC7pp5O0tSMXfYk7wO+Bnyqqn55C593Osl6kvXNzc29ZJQ0BWOVPcltbBX9y1X19eHw20mODI8fATZ2+9yqOltVa1W1trKyMo3MkvZgnNX4AF8ALlfV57Y9dAE4Ndw/BZyffrzpcSFK3Y3zEteHgb8B/jXJq8OxvwOeBZ5P8hTwE+DjM0koaSpGlr2q/gW40Zu6PTrdOJJmxSvopCbavlNNx3ekda2iN0d2qQnLLjVh2aUm2s7Zr7fbfHaZ5vHOxzWKI7vUhGWXmrDsUhOWXWrCBbqbGLXoNa8FPBffNA2O7FITll1qwrJLTThnn4Bz6dlyTWS6HNmlJiy71IRll5pwzq59sUgvMhqV5aDM6R3ZpSYsu9SEZZeasOxSEy7QaeoWafFtGnb7epZx0c6RXWrCsktNWHapCefsmthBm6OP4/qveRnm8I7sUhOWXWrCsktNOGeXpmAZ5vCO7FITll1qwrJLTYwse5Lbk3w3yQ+SvJ7ks8Pxw0kuJrkybO+YfVxJezXOyP4r4JGq+jBwP3AiyUPAGeBSVR0DLg37OuCS7Lhpp0X8Po0se235n2H3tuFWwEng3HD8HPD4LAJKmo6x5uxJDiV5FdgALlbVS8DdVXUNYNjedYPPPZ1kPcn65ubmlGJLulVjlb2qfl1V9wNHgQeTfGjcE1TV2apaq6q1lZWVPcaUNKlbWo2vql8ALwIngLeTHAEYthvTDidpesZZjV9J8v7h/nuBjwA/Ai4Ap4YPOwWcn1FGSVMwzuWyR4BzSQ6x9cPh+ap6Icl3gOeTPAX8BPj4DHNKmtDIslfVD4EHdjn+c+DRWYSSNH1eQSc14avedFOLcDGIpsORXWrCsktNWHapCefs0pzs97vZOLJLTVh2qQnLLjVh2aUmLLvUhGWXmrDsUhOWXWrCsktNWHapCcsuNWHZpSZ8IYw0J/v9Z5wd2aUmLLvUhGWXmrDsUhOWXWrCsktNWHapCcsuNeFFNbqp6y8E8S/ELC9HdqkJyy41YdmlJpyzSzOw3y962Y0ju9SEZZeaGLvsSQ4leSXJC8P+4SQXk1wZtnfMLqakSd3KyP40cHnb/hngUlUdAy4N+zrgqmrHTcthrLInOQr8NfBP2w6fBM4N988Bj081maSpGndk/zzwGeA3247dXVXXAIbtXbt9YpLTSdaTrG9ubk6SVdIERpY9yUeBjar63l5OUFVnq2qtqtZWVlb28k9ImoJxfs/+MPCxJI8BtwN/mORLwNtJjlTVtSRHgI1ZBpU0mZEje1U9U1VHq2oVeAL4VlV9ArgAnBo+7BRwfmYptdBcsFuO78Ekv2d/Fjie5ApwfNiXtKBu6XLZqnoReHG4/3Pg0elHkjQLXkEnNeELYTR1Hd7wYlHn5TfjyC41YdmlJiy71IRzds3cbvPbRZ7HL+N8fByO7FITll1qwrJLTVh2qQkX6LQv9rIItpdFvYO62LYXjuxSE5ZdasKyS004Z9fScP49GUd2qQnLLjVh2aUmLLvUhGWXmrDsUhOWXWrCsktNWHapCcsuNWHZpSYsu9SEZZeasOxSE5ZdasKyS01YdqkJyy41YdmlJiy71IRll5rIPN+xM8km8J/AncA7czvx5JYp7zJlheXKuwxZ/7iqVnZ7YK5l/91Jk/WqWpv7ifdomfIuU1ZYrrzLlHU3Po2XmrDsUhP7Vfaz+3TevVqmvMuUFZYr7zJl3WFf5uyS5s+n8VITcy97khNJ3kjyZpIz8z7/zSR5LslGkte2HTuc5GKSK8P2jv3M+FtJ7k3y7SSXk7ye5Onh+KLmvT3Jd5P8YMj72eH4QuYFSHIoyStJXhj2FzbrOOZa9iSHgH8E/gq4D3gyyX3zzDDCF4ET1x07A1yqqmPApWF/EbwLfLqqPgg8BHxy+F4uat5fAY9U1YeB+4ETSR5icfMCPA1c3ra/yFlHq6q53YA/B765bf8Z4Jl5Zhgj4yrw2rb9N4Ajw/0jwBv7nfEGuc8Dx5chL/AHwPeBP1vUvMBRtgr9CPDCMv1fuNFt3k/j7wF+um3/6nBskd1dVdcAhu1d+5xnhySrwAPASyxw3uFp8avABnCxqhY57+eBzwC/2XZsUbOOZd5lzy7H/HXABJK8D/ga8Kmq+uV+57mZqvp1Vd3P1qj5YJIP7XOkXSX5KLBRVd/b7yzTNO+yXwXu3bZ/FPjZnDPcqreTHAEYthv7nOd3ktzGVtG/XFVfHw4vbN7fqqpfAC+ytT6yiHkfBj6W5C3gq8AjSb7EYmYd27zL/jJwLMkHkrwHeAK4MOcMt+oCcGq4f4qtufG+SxLgC8DlqvrctocWNe9KkvcP998LfAT4EQuYt6qeqaqjVbXK1v/Rb1XVJ1jArLdkHxY+HgN+DPw78Pf7vWhxXbavANeA/2XrWchTwB+xtVBzZdge3u+cQ9a/YGsK9EPg1eH22ALn/VPglSHva8A/DMcXMu+23H/J/y/QLXTWUTevoJOa8Ao6qQnLLjVh2aUmLLvUhGWXmrDsUhOWXWrCsktN/B+xRi0uAJLuNgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"N = 50\n",
"a, b, c = torch.zeros(3, N, N, device=\"cuda\")\n",
"x = torch.linspace(-5, 5, N, device=\"cuda\")\n",
"a[N//5:-N//5, N//5:-N//5] = 1\n",
"b[(x[None]**2+x[:,None]**2 > 4) & (x[None]**2+x[:,None]**2 < 9)] = 1\n",
"c[((x[None]-2)**2+(x[:,None]-2)**2 < 4) | ((x[None]+2)**2+(x[:,None]+2)**2 < 4)] = 1\n",
"pyplot.imshow(c.cpu(), cmap=pyplot.cm.gray_r)\n",
"coords = torch.stack([x[None, :].expand(N, N), x[:, None].expand(N, N)], 2).view(-1, 2)\n",
"dist = ((coords[None]-coords[:, None])**2).sum(-1)\n",
"dist /= dist.max()\n",
"a = (a / a.sum()).view(1, -1)\n",
"b = (c / b.sum()).view(1, -1)\n",
"c = (c / c.sum()).view(1, -1)\n",
"SinkhornOT.apply(a, b, dist, 1e-3, 200)\n"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"def get_barycenter(mu, dist, weights, lam=1e-3, N=1000):\n",
" assert mu.dim() == 2 and dist.dim() == 2 and weights.dim() == 1\n",
" bs = mu.size(0)\n",
" d1, d2 = dist.size()\n",
" assert mu.size(1) == d1 and d1 == d2 and weights.size(0) == bs\n",
" log_mu = mu.log()\n",
" log_u = torch.full_like(mu, -math.log(d1))\n",
" zeros = torch.zeros_like(log_u)\n",
" for i in range(N):\n",
" log_v = sinkstep(dist.t(), log_mu, log_u, lam)\n",
" log_u = sinkstep(dist, zeros, log_v, lam)\n",
" a = torch.sum(-weights[:, None] * log_u, dim=0, keepdim=True)\n",
" log_u += a\n",
" return (log_v[:, None, :]-dist/lam+log_u[:, :, None]).exp()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It's fast enough to just use baricenters for interpolation:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"res = []\n",
"for i in torch.linspace(0, 1, 10):\n",
" res.append(get_barycenter(torch.cat([a, b, c], 0), dist, torch.tensor([i*0.9, (1-i)*0.9, 0], device=\"cuda\"), N=100))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7fc899008be0>"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2cAAAB2CAYAAABMKevGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAB1iElEQVR4nO29W6is3ZoW9oyahzrXPK3///une+/svuiLmEAUNkbom0YT0oli50bRoHRA6BsFJQbd7U3IRaAhIOYiudhESQcl2qCgiCDSSRMCQe02BtN2TBrbuHfvf//rMA8163z6crHWM+bzvXOMr76asw7fXGs8UFTNmlXf4a1xeJ/3ecc7XJZlSEhISEhISEhISEhISDgsaoe+gISEhISEhISEhISEhIREzhISEhISEhISEhISEiqBRM4SEhISEhISEhISEhIqgETOEhISEhISEhISEhISKoBEzhISEhISEhISEhISEiqARM4SEhISEhISEhISEhIqgGeRM+fcTzvn/oVz7jedc9/Z1kUlJCQkJCQkJCQkJCR8anBP3efMOXcE4P8B8O8D+D6Afwzgj2ZZ9s+3d3kJCQkJCQkJCQkJCQmfBp6jnP1uAL+ZZdm/zLJsBuCvA/iZ7VxWQkJCQkJCQkJCQkLCp4XjZ3z3RwF8T/7+PoB/t+gLr169yr71rW8945QJCQkJCQkJCQkJCQkvF7/2a7/2Nsuyz0L/ew45c4H3HuVIOud+DsDPAcA3v/lN/Oqv/uozThlHLD3TudBlJiQkJCQkJCQkJCQk7B/Ouf8v9r/npDV+H8A35O8fA/AD+6Esy76bZdm3syz79mefBQnik5Fl2UaPhM2R7JeQkJCQkJCQkJCwHzxHOfvHAH7COffjAH4bwB8B8J9s5aoKoERBicNqtfLvAe8Vs9iD/094gJIvtW8I1obJlutRhtwmOyYkJCQkJCQkfNp4MjnLsmzhnPtTAP4+gCMAfyXLsl/f2pU9Pp9/VkLGZ7625KxWq6FWq/nXStD4uU8ZlpSF7EwoGQvZ7VO3ZQgh0huCcy5o64RySLZLSEhISEhI+BjwHOUMWZb9PQB/b0vXEjvHIyK2XC6xWq2wWCywXC4xn8/969Vq5YnY0dERjo6OcHp6ilqthpOTE0/Wjo6OcoTtU4IlYFQdSXKV7PIZQI7k6iOpk+9hFccY2Q0RiVqt5v+OKZOfmj0VMZK7jvDqc+h/CQ8om7qcbJeQkJCQkLA7PIuc7RLWmV0ul/6xWCywWCwwm838sxI0ADg6OsLJyQmOj49Rr9dxfHyM09NTHB8f4/j4/W3TIf5UCJoSBas6Kukl8eV7/A4J7fHxcY78WrJLuwIfvyO3johZkhsiZ7QbgBzZDRE2/v2xoyjNNmZzAI/sVIbgfgr2VIRImH0v9BnaKWRr+5mE90iENyEhISFhU1SSnKljS8JAIjadTjGbzTCbzTAajTCfzzEajfz7i8UCzjkcHR2hXq/j9PQU7XYbp6enaLVa/r1Go+EJG4CcM/wxwpIFS3ZVgVTiu1gs/PePj4/hnPNk9+TkBCcnJ54Ik6zxc0ouPkbYAEIR4VXiS6USeCBjSnKtMmnTcoGP26Z8VvKl6u66gj9WxVXiG/p/lmXRVN2PBaF1pEWkN4ZYoECJ26ccSCh6r8wxiuz1KdiyDBLhTUhI+NhRKXKmjhjVG6pio9EIs9kMw+EQ4/EYk8kE9/f3mE6nGAwGmEwmnlAAwMnJCer1Our1Onq9Hur1OrrdLtrtNprNJnq9Hk5PTz3poJr2sTlpljyQiNGu8/kck8kkR3z1vdls5o9DAtZoNHBycpIjuc1m0793enrqSZqSi48F1qaaZrtarTCfzz3xnc/nj96jGgnA2ydGcvmeKpWx9ZMvGSGiq+m1y+Uy90y7W1XSrjWNkdwY8f2YyG8spbbsw2IdyQ2lNX/MNtXnov+tIxMh+2z63ktHWYK7KemN2WfT9z8GbGq7TfEx2y4hYd+oFDkDkHO85vO5JwwkYP1+H4PBAOPxGHd3d56kTSYT/1nnHE5OTtBsNlGv1zEajdBsNjGbzTCdTtHpdHB0dITlchkkZR/bIEOnliRhsVh4e02n06ACOR6PMZ/PMZvN/KDONFESsUajgVarhdPTUyyXS9Trda9wkFAQHwtBs6mhqjxqmq0qkPo/Tb0F4JWyer3u10cyWECSu1qtcHx8/GjtH/HS7RpKYbaptapA6v+VsCk5UyXSqpL6HlXeLMtyRM0qQC8NVnVUwmsJbSz1NqZGhght6DXt+LGkOcfIrr637rXCktiy74Xa5ku1axG5LfqM/X8ZsqWvQ0olbRv6/EvDOiK2LaIWsmmZz37s2MS+n5JdEsqjMuRMnQcShOFwiLu7O4zHY3z99dcYjUa4vr7G3d0dhsMhbm9vMZ1OPTkj8QCA4+NjNBoNr5w1m01cXV3h/Pwc5+fnGI1G6HQ6WC6XaDabaDabaDQa0XU+LxGaWkdFbDAYYDqdot/vexXy7u4uR4CVsFH5AeCJA211enrqVcnz83O02220222cnZ2hXq+j3W779Eeb6vgSoc4slTASXNpvsVh4lXc2m3kFks980KGgOsZUUVUlm81mLi23Xq/n0nF1rd9Lba9KyEh0SWin06nv09Pp1Kc3W1WS9qRNSbpIwqwqSfvS7laxtDZ9SXYNqY8MCNC+IeKrpFjJLvC48q2m3tp1qLS9JcNK2PSYLwHWpjEl15LbIrILhJXHUIElq/jGPveSgoubqLchghtTd0OEls/r3lun+FbdrmWDAuv+XocygYEYKX5p6m+ZwMCuUcY+636DqmEfdtsl9mHbSpAzncxIJCaTCYbDIe7v7zEYDHB9fY3BYIC3b9/i7u4Oo9HIk7PhcOgdZBKJWq3mCcRsNkOz2cw5Ko1GA6vVCq1Wy0faqVh8DGul1KZ0eGkrErL7+3tPgCeTiSdu0+kU4/E4l9YIwNun0Wh44jufz70tSVhUlVQ146WvmbIO73w+x3g8zqXZkqTR3iFyRodO252SM6aGzmYznJ6eYrVaoV6ve8Xt5OTEO8TAe/UNeHk2tc6uqrq0LdXb6XSaUyD5WUvO2MZIzlSB5BpJkrOTkxOvSq5WK/838JBuSrwk22q/V7sy2KLEVgmbrotUdRdAkIhZBVLJsKbqrlYr/zng5ThmhFV0NT3Z2swqkSGCFiIBRQSMdo+tR7VEjceuKkIBhJiqGyNqZdXIGOnie6FCTPqb6Pf0+FVDyF6692uI3Op3y2Id6dLXZclw6BiHRlEwIGavbRCObRCxKhO1sgGDqqHIfruybWXImabcDQYDDIdDvH37Fl9//TVub2/xve99D/1+H2/evPGpjYPBIOfEcaIEkCNbnU4HjUYD19fXuLy8xMXFBRaLBc7Pz+Gc846fcw6np6d+IixKl6gy1JmgszsYDDAajfD69Wvc39/jzZs3nqDd3Nx4MqwFV+gME3S6SMyonDUaDVxeXuLs7Ay9Xg+z2QztdhtZlqHZbKLVagGAV89eUtScsDYlIVOSSzv2+31PcKfTqVd+SM7YRtnOVMGhbev1um+3Z2dnaLfb6HQ6mM1maDQayLLMkwwAL4742oAMgwK032w282tKJ5NJjqjRjiHlTNUbS85UlWQ6brvd9ook/0/CpmoQUH27qj1VeWQ75MO2x5Caplto0FENETFdF0mVnIGGUJVcq6rx+FUE75/EQUmupjCrKpllmX8OETaFkjGrROpzyN60I/+2iqaeo0qw/V7X6dq05XVkzapnRaQ39p61d+g3sIRZz1UF2CBXLFiwTonUZ0UR2bLPMSIc+z2qutY3pICHyC7/Dn2/LGL3XEReY2Q4FnwoOs8+oDaL2fElIGRrfX+bODg5U6eXa8z6/b4nED/84Q9xfX2NH/zgB/49qj+j0SiX8mTJGR+LxQInJyfeEZlOpzg9PcVkMkGj0fBRYkbQqUgAL3OtlFXMxuMx7u/vvf36/T5++MMfemJxe3uL+XyO4XCYc0DUnsBD9HwymXgFYjqdotFoeBI4mUxQq9UwHo9xdHTk16w557BarfxE95KIr22jTLklIbu9vUW/38f19XWOnGlaozofSs5oU932gQ7ucDj0ayVHo5EnKK1WC1mWeZIGvDzia206mUwwGo1yJPf29ta3KSq5DKQoqdDtHkLKGRUcBhS0cut0OkW9Xker1fLpo1TRSC4AVNIpU1ilXEkZ0745ZnKcjZEzW1EUQJCcqTpGJZLpt1zzq4WZqAxT6VUyXVW7WrLLPs2+OJlMfBu2apqmh9qiNUB+30irjml6rSq/dj1qrGJuFQsGaZ/XFGbOHaryWnJRtkorn2NrIC0hjq1Dte08lFFTBdsq0dXsFTs+xlJs16lqZdWvIiKmfTykAut79rz7hg3I2KCVDbQUkbR1xGNTBWwTu1t7H3L+smNgLGign68CQvaP2Tj0+eeiMuSMAwvXO9HZfffuHd6+fesVn+vra69a0PHVaBGhBiQ542eY5rhYLNDpdLyT0W634ZxDo9HINeiXBB181fEdDAbepnd3d3j79i1ub2/9+yRxmvJko706mDIaPp/PfSEQpk2dnp76dEcA3kF2znlHukoT3DrEHN/RaIS7uzvc3Nzg7u4O7969w3g89vbkQ9uoTRdT54BOFx8kvlyHuVgsfHtmyii/Czz8PlUnvjqx0ZFgyu1gMPBpyzc3N7m0UY4PGnXXiCbwMICqQsP1eVTGlJSxkA2PVa/Xc4UsYlHiKsIqEhwj7+/vMRqNPPll+7VOnC2wQvCe1Wnls10zSSLGMeD09NS3f/4ODCRoMRY9TxVgx1ESCQ0iaPq37rNpt80oImch5UzJglUlOe4qGV4ul358tcev2lhg2yjVXQYNdLxcZ0cdR6yzGlqbZ9Uxuz5SVWC1O7/H81QlUGPVHc7d+lB1ch3BXUfOrBoTUmliJNi2b1WDQ989JDQgoIHqmB35Hf2+PZ7FOhXM/h1TbEJBCB1D9DOxc+wSto2GyO5LUNBCYzbHjl2NCQclZ1bhGY1GGAwGeP36Na6vr/H9738f3/ve9/Du3Tv84Ac/8GvQOKBbEmEHFT4WiwWOjo68czccDlGr1dDv9wHAl+E/Pj72JfZJ0KoyYJSFDtR0JG5vb/H27Vu8e/cOv/3bv427uzt89dVXPh1vMBj4FEa75iTmTEynU6+MnZyc+LVWPFa328VqtfIRZv0d6Ei8BLvGFJ7r62v0+3189dVXuL6+xs3NjVfO6ADzEYsShQZUdcRGoxFOTk4wmUzQarW8AtJut7FcLtHpdLxDrYrESyASbGN0ePv9Pm5vb3F7e4sf/vCHGA6HuUAM+3xIlbABBHUM1BlQx5bFVgaDAZrNJtrttq/qulgs0Gw2/TmYzltFZ5fQ1DuShru7O79Ol31zOBzm1vDpGkhbCIT3qg9VdNShVdty3aTuL8n00cVigXq9nvvtTk5OAFSvvWobZZot56C7uzs/l7CfK6kIEQlLQouUBbuGT8kZK+VqRWIWYDo5OQna9NC2tc6ZZnRMp1NflIrqpF0Lqcfg6zLkDEAwVZQ21/WRoUADA2VcQ83jVWHZg871LPilQYOQn1S0ns+q5USIjMUeti2HAg06XtgMBXu+fUL7rGZZMTA4mUxy5GIdsd1EOQv105g6BoSJMMlCqPAVv7Nv21r/SVPqbbu03zs07G+hbdkGyrIs27qCVgnlzDpq4/HYKzqDwcBPihpBVzVCmTmhEQU6sNPp1L93f38P5xzu7u783mfD4dATDaY42mhnlaEDhE6CGu1leuNwOPSpcrqOx3YUvffVauUdB3Y4596nK2qFO6bd9Xo970h0u12fYsqBxB6/qrDKmbZTpjfyoSl4IcdXoQ4DUz75WTokqpI553zaXavVQq1W8+ulWITlJZDekBJp2ymDBnQ0bJ8PreEhrANG2zBlmb8F2yL/ZvEKBmboCNdqNd/2q4hQv6czQZuqXTUdz6br8DhKJIqcXKpfLASka4ioRLLtrlbvC9s457wDoYS3SmNBSDnTYkmj0chnJNgCNUXpTyHCqw6tttmQQ8vxgEqk9gESspBtqwLbRmlPkgnORzbN1pKJIiKhkewYAbYKjq6JpBKp52M713Haku1DwLZRElz1lWhPm2ar3+frEHQMKEvOrAqsATISW16DKukcZw9lU/VHtY1qZpGSM7WjHiP0WhFTsmJKGVGkTrItMy2fnwcexm4bHN4HrE0ZSGAQJjafH4qgWbto+2YQh+MA8NB+tz3WHoycWQeNEx1T7l6/fo3Xr1/jzZs3XqXgoBNKd+Ax9fjAA+PVwYkKzmQyyRGNXq/nUx01esnjVGmSi8GqPNxy4Pr62qtnTG/kAK6KWciWdqCgEkbb6OL46XQKABiNRjg+PsZi8X5rA62OCTw06CoTCY0oMnhAQsZ0xnfv3uH6+tqrPtbxDQ3ewIMtdTIiUeBgS4d3uVx6B2a5XGI4HHolmO0UAOr1OoBqFwfRfq8BGaoRVCAHgwFubm68amFV8pBzpvdtJzFbTIHKL1NHdT1frVbDfD73jgUHZXX6qmZXmyo2Go18IIb27Pf7ucIqVn0MTYY2YqvkTB2vyWTyKKI4Ho+9gjabzbxtOf7yt7FVRw8N20Y144IKL1NuSc44hqpCtM65sGlHfIScWqugUflttVo+TZ/znE23qQpBU3WXYynV3Ovr6xw5s2nLNgARgu3/+l7IoeVYQBuT1HKtZKvV8tvG0OnVtb08xyFggwdso9wDtt/v+y1dNBU81N/LKjyhsSBkWwA5AqxjL7eCYWErzncM8PL32DfxtcTfjqO0baiv8/v6bI9NhBx/+zpG0EL2VhtzfNCiYiQNJMQatAxdzzYRsqdWs7aF/GJz0CFhgw5U0ulrca4Dtp9GfvC0RqoE6vje39/7oiCq7ugPadMdQscmdDAnWRiPx3DOod/v+wH47u4OJycnGI/HXpHgGpSXAB2suYCdAwyj5rSnTRMrIhIxqFLD3xCAX2t2f3/vU8isKkniUXWEoueMnPOhUUqNoMdsagmE2lA/S0JCwuucw3A4RJZlGAwGOD4+RqvV8gVu6PRWXe21jq9GezWNUYkZVTN+P2RP67TpxMR+r44eJzV+j9FGBhbYR3S9atXsap0tKra6lQMfWq2RbauImAFhx4A2sKqXDYAB8BFGOrXT6dSvVa3ypAw8VnnUprru2aaHrhtHtb2GiC8dVpJgDdJowEsDObVaDbPZzH9O0/AObduQ6qWqhLZTq5yVJRLWobXOZ0idtASYqiQAb3M+OLZaJe/QqpmmimpWh9oyRs70ODGUVXJCJE1TdPkAHqo+k4zR1jHiuM/AuPWhbJ9XJTI0dm3S19apZ4S1sSVnfPA3VsJGH20+n3sb77PIlbZRDSLYQIxNqa8KaBvaVP0QcoNQius2bFoZ5UzTmhhNY/l3m8rIzlPmh+RnNE2MDq9zDoPBwEfI7u7uUK/XMR6P/doTToD7juRsClV5Qul3JGiWSNBJ0t/Dooic8rvz+dxfx3g8BgAMBgMfOR+NRqjX67m9u3QgrqpdAUQnQEskVJEoM9ioNE5HzRYM0c8A74kDn09PTz3RZnGLsv3i0FCbUm1UJ01tattoSIXkMx/st/o/Ja8AvHLGv7mNxmQy8fvMKdmucntVcqSOr7WnrjUrSyKAsALBc2o6rqpgSuSoPE6nU185V8mZXkcVbKvjoU0Z00eogEUZ2LapxBeAd7aUnJE8aIodI+a6/1+orVahzYbaqLUp5yZtG2VtCpRfH2XXn/GatLAK1TQSCNteeU9VIGjaRpWgxcgZv7sO69QcfR1SJ0l8bbvV6tmh1NVQeuM+7Gztaef7UBbHU8jZpgpajJxpNggAPyZwvFgsFp6c8XpVVd4VtI3FxlFdUvOUtrlL2N9A15nShiS8GoTfJg5CzkLEjIuDmTbCxexW5dmEmOn5gAeClmWZV3nu7++91H5zc4PT01P0+300Gg10Oh20Wq0XofAAjyO9JGVMbwqRXTsg8jhAPsKrBFURUhMmkwmA9+SsXq/7c7MCIVUeRtCqCjuwhNZF0Z66Cfo6YqbvW/KlBI02JfEF3tvWOefJLvsHBzm7VuLQDplC7ak2VdVM9+SKrS0tcx5GtHS9GG3Lv/kMwBMHPlvFrkya2qFgI+h23YkSCTqZ69qoOvS0lQ1SxRRfXg8dYNrSkrIyyt2+YcfDkHKmRFcruRXdi3W+dDJX4mvJFB0w67jQ0Q0Rw6rY0sKqEiFypsGYEHFXhBzaEMEPKQ86BnCM0DV7GhHXc4RUHB1H7Ll3iZDjS5tqcRWSs6c6kXZ+Kkse+LDzXZFN+burMqTH0/PuAtambI/a3znX8n70u+sQuvZ1bUfv25JfptoCyC3D4W/N+ZTrp5nqqHt47rq92jaq7dL69lUhZ0C+rdutNEIBxm1f88GVs1jEJxQ53wZD1WikVuSxE27I8FVydC2sU6GTn6o6tkpOjJjxtSVo9px0JNZNFC/F0bUI3RfvjfdkU5pi0bRY+6Ejy89ap0HJjF6DOmVVdHSLEGor1q72nkJRdJtaB+SJhbUtoc6ZJSxqT3vNVYYlvvbe9H9FE6ElCXwvFKRRO9vPqB1D9jyEQ7spQv3P2jPUTmOwNuU5QkEqfpZtPvYb8H/Waa4iQgGaUHuNzUn2WErKQgqhEmENslplhjaNEYcQMYvNlfzurhAal9Smakd9bx3ZDV23DSQAj9PhYjayvoEeUwmGEjP+P7R+eNc+mP09dY5Su9q1kE+ZF8qSNPqqtp3rdYYC5PStleiS7DKAq/e5C7vG2qkGaELBwqrMs3Y8ZZqoVXsV27TlwcgZb073NqPCQ6WFrN/+cE/98bRBssGH1BBN/bMRyapPfLSpva9QZUbr7Jaxqx1krXNGUsg1EBrFe6oScgjYgcTm82sAwcryIWLG17b9hJxgvm8dXTuYhWxZVXsS9l5spJd9LkQ6Q4EZtVHMUbMOiTq9lqSE7BeLmFcBvF51HjTaq2t1Y20l1qeLCJo9P1/Trvo9IL9HIp0E65xVycbq7GpARp9D7ZTf3QQhu/I4OraGHFytNKgbUmvBFe0X9rz7grY52tQGmmwVvNj8ZK87RGxDZElTnfkdS37VgeWDqoNuSs3jKZRU7HrMsP5QKIBgiUUZJTI0FvA1ob+Jjr1Kumx71hRHtalmz3A5RJZlvg1rwQUeZx9KT4jsWtV/kz5fdM0hQhx6Vrvq70Jb6b6T9Ktpd147VR8twrJL2Lk11lY180C/d0iE+q/2q21wkiLsnZzZH8nmoeqeRkW5vc+Bdfh0ErYqnTaWqjgOIcRsqukNMeUq5PQ+5fyx96rU4TaFHUxU3bHrILdxf2XamY08qsNR5TZKhKJntu89d+B7Sn9VAqET3b4crqci5kxYBy1EcGORv6fYTx0ybZ+0pzq7MQJRFcScX/vgZ/V7644bi4JbZylEMGhXtanu4ce/1xEze/x92N/255Cqam0eunZLGGyApsjGFnYcte1USYSWzLZrNvV3ocOs59g1rN1if/OzsWPo9ZaxY5Hqq6mJlpTxWddG0UEHkFujpsfjfeyS9PI5Ngc9ZW6KkWH9Xyy4GPpeaE2fppFzfLJjsKo+sevaFWyfjj32fV0h2MBEUTvYFQ6a1qiESBcEhxau20F8W+fXyCjPZVMoD91Q1kEbtEbPVbnS9NBtkgl7HbEJWFFFZywES3iVlIWqMoac33XHD9nBTor2t7KDsxI0tW3VbBxydmN9TxXrbZ47ZhNLynQTYCURVYVtq6FUzU1IhH6u6L6tY0EokVCHl06uXfNQVdva4EwZNTd2HL3HIruGnGKNnlub6mbJGlBQdUiPTcQi9tuGPb8luNo+yxIJ/s8StNj/Q/YO2VRJRMiuVDKzLL9pu66v2mewLBREKCIPMbvatsn37OsQadCggg1iWWWX9qRNWViB648JG2Tg73MIX6yIRPD/ZRGzs/1bbW2/p/O/2lbJGX1nncdIzva9tKSoDRbZdZvz/yYIpY3bMWkftjv4JtQ2xemlrk06NHRwtuW0rRJpbapFE3isp0wqdmB27qGaUCgtpMpOGZBXeGxRAJLedSRik3SG2Gc0KstBVvfbsOlMVbZryKa6ds+20W31/xh50BQmbp/BrTUajUbOiagaQQs5ZpoiZoNbu45K2gpibJ/1eh3NZjP3YLu1xLfMte3L4V2nQoa+s01oG7UpYWyf7XYbzWYTrVbLb/2iRIKpd6Hsk5DqHlJBtoGQc2MJ2jbsF5u7Qgok2yrHU22rrVbLV3FuNpu5rSC0b/G6OfbS/sDjfex2hZiTu4lDGbJb0Xv6P1XLda4KjautVsurZsvl0hfUor9CcOzVgiCqXPJ8u8A6wms/t+mxgcckLXYv6/wpjqPcO261WuWUM/18KCuMj33Pa0V2OxQps+ePkbR94eD7nIVe7wNWLo+pDy8JdkCJ5UevQ+jeN62URKdCN6CschpTDGrTonzjXQ8odnDWyHmI9FYZ1m5WKYu1UwYR7HtlESJoIcXM2rXqhBcIO7wxpwJ4vL5E3y/6O/R5HUtDNlUFwrbXkOMamxesg70PhJw0e20hpeE5KFIhbYqYBmjUrrwuVXn0+vV4lhwfgkjwf/uCnfc16GXbq1bAs2sPef2qBgMP1d303rZt1xjhDZEI+73Y8Z56jSF/imNnSDUH4APyJLwkZ/QdnHOPAvX79hOfSr6A4jHK2roMQdP9y9S+bHO0VSgIb32Xp9xbQhi7suNByVlowrGTDDspEK6o9Jxza0QytKCakZqqO2YWoYkvBN5XlmVBx5ewDnAsMsmH5uwzEsmorioRVbartSEHt1AhAILtuUwb1cnMPtvX2k5tZDcUMa+awkOEgge2KICdVNQebKcWMWe2KIKujgM3Sm+32+h0On4LDavwlBkLDhWFtOvNirIPykSfN70HHa/Z/xktp03VrpoqRoTIpF57aO3fLhxePlubFiln64jZU0mvbadq01arhU6ng3a7jVar5dsqx3J11HT9NoDcvMe5T8eNXbThENHdttNddN2qDlriwP7PLXQajYa3KVWJxWLhl10wi4LXzeOsViuv+PB69qmchf7eBdQniwUPqH7RthxPnXu/FYwuZSHZ5XHYfuv1ulfhNeC0jzF2E4IbsvVzya7aVcfW4+Njv/0TtyVirQb2edvP7J5yNhB6iHlLz08cWjVTxNZTErsmtwcjZ3aQ1CggX9vo6rZIGQ2uE5SeP+boVtHhVYQ6s0ZXrINpHbR1KkQocq3ftal3TGcgeaBdlZzZ41YVoWvV17Xaw35PSibKHCukStrfUsluiPBqiph+v4ooipyvc3DLBBti76vD65zzToS201hKoyWJ9lpCr/fRvu15rcNbZNOYPcsSiZADoWoZHVxrU9tWreoXctqt0qFrqvahSBS1UzuWliVp9rpD5DOk6tj0W44BJAS63pCp15qCzeNyTOF7x8fHOYdkV+12034fgx1/Q/+3wS6rlLH/q011rsqyDPP53BMI3XeV5Mw5h9PTUyyXS7+R/WKx8OdZFwjZFp7rH5W5vlggzM796lM1Go3cZt6r1cpXjiY5Y0CJv8/p6WluXbcqPrzXfY2rRe9tC7EgbWhs1fV4umbb7rkIPGxmH5oTqqKcJSUvjL2TMztQ6qQTm3B0se22zm3z+Ok80IGw534psBO6LWygzuk6h9MeV5/te+r42t9Tf9OXsjaKWOfshxyq2PdCiKmSGpTQAEZoTURs/U7VsW6i2GQtZIjYxj7Dfm9tSruyvdoCC3rMMs6lvY59OLtlCyuwr8dsG3IWQvcVcs44fqpNbVtV0mtT76hQ8z54Dn7Hlta217ctxGy6CYpsqq91HNCxVOcou3ZHbarkTNdyklQwqs5y8rVaDfV63duc3yWZ2JY9YyS3TBvdNkLkzAa7rLJLx3c0GmE+n2M4HOaKbGVZ5p1kKj0kZyR3uyQS64hubFwqY+t1Y61VzbSt2kAC+z3Xa49Go9yaeN2T6+joCLPZzAc8Q9WzdwVrP6vk7OMaioIJSs4A5LZN0aweHiNWzCih+jiYckayxUmn1Wqh2+1iOByi1+thMpmg2WzmpFoAwUG9LHTC43mbzSa63S56vR7Oz8/R6/XQ6XT8pPcSHN7QAGmdTiWdnIw5sajEXXSfITKm5EFTxDqdDs7Pz3F2dpazK68jtt6kKohFrjT1NbaWjo6WDuwh21qVi//XoAADB0xhOjs7e2TTsm31ORPythGyb4jslr2m2Gftcfnb0XHodDrodruPbKopTZpaXYYI8TqUXIcI/L6g52R/t8GYMsTMtlfenzoNTGFqtVro9Xp+bLU25XVoqnCoMIwqPXSYleAx9XwXY0nI4S0i4vx/UWDAjqH2MyFlh/273W6j2+2i3W6j1+v5cYHEjJFzOrx0gknSrANMkrdcLv18QKdv0yBTWZSN3uv5Q4EFhSXotq/Fglycq+h76FjqnPMq2XQ6xWAwyJEztlUAuSp4/O58Ps+lje6CpFm7rCO6RaQs1Bbta33PKthaoELbK229Wq0wGo1yJJekQtdIsd3TfrZI1KHSGtehTDuN/S/Ubq3PQdvyb7Y3rteze9fyOAzGhPpdldSzquMQdlpLzpxz3wDwPwL4EQArAN/Nsuy/cc5dAvgbAL4F4F8B+MNZlt2UPbE69pZMaCrc6ekpJpOJl2ef2imt48eGbxWemBJRVRJhYSPYdhNNHVA5oITuzTqaodf82/6WNk2ETllof6OXALYXVSBDtuRnaVclvnZi02PHHnouS7ZVjbSponquUBS1yLmM/b1NxJyokEPFzxUpu0VkwtrTRnc1nVGDGFbdUdup0qPPOtlpGjH/tr/7LrGODBT1/dD39f0im2qa2Lp0RpIvOrrq9E4mE29rVdhOTk6CTsyusI6U0SZKcmNjZ+y9UEBC1V1tq6pE6BozADnbcW1UjJyR1HKMWSwWfo6lM7erNhoiFUUouo5Y5oF9T0mvtaldTsHfcDab+bU89pkKBYAc4bVre3blANtxvegcmxKH0OdC44HalfdvN+7mGMgqglrp2G5Jo8e16zt3rfgUHbvsee04UPS52Hs6rtnCHzp22rXaaitVx4uU64Rqo4xytgDwZ7Ms+yfOuS6AX3PO/QMA/ymAX86y7Becc98B8B0Af77MSUMEidHA+XyOV69eYbVaod/vP2pwnDTYeYHizmMncQ4gjPCenZ3h8vISr169wqtXr3B1dYVer4d2u52L8vJYVYV2aFUFW62Wj2SzeAQnHgA+KkWbxo6tr3UgoX3oNNCmZ2dn+Oyzz3B1dYXLy0sfPVebliG9ZSN9u0AogKBOkqZq0PY2UqVrDuy1hxxnHYSpmnU6HfR6PVxcXODy8hLn5+e4uLjw0V7m9CsZAOKV0UJKqSVF1lncpj21rdqiBLx/pmZYmxY5GpYAW+dBSS77BNUy2pUFFkLOBcchOhOa46+To7YZjm/sl0omtmXbEFmxD/uZdQuv1xEI+/uRhFGFbLfb3p52PAWQS8UZj8eYz+e59TyTycSP8WwTVIm63S6WyyUajUZuDNqmTa0dioIIZYKG6wII+mzHGio6zO6ggkZHmKrjcDjEZDLBaDTythwMBp6wsX3yN9NtFur1OgB4cqKO3bZsWibdjs8MbgHxIgExxUz/p+MplVdNX+52u/6Z4ygJxHA49LZkGh7TRKlSOPdejef9TKdTr/zwt9mXMxwKvj3lt1sXsFHSwAACbad+RqPRAABfLn86nWI4HPr2qETWju2qBoWqTu9aiSwKIGxKvGL/D40toTRGVcxUGeda0lChIp3jQxke9l6r7NtWDfsitmvJWZZlXwH46sPre+fcbwD4UQA/A+CnPnzsFwH8CkqSMyDv+FrC1Ov1MJ1O0ev1/MQ9mUzgnMulOAKPB27b0HgONnxbRZAV2pguwoGFkfNdOKm7gHZ0du5Q3ne9Xvf58JreyMmwTJoJkE9rsJXEtOod05l035IyqXdFA2UoQrWL38c6olotyVb1tFGtdce157COtW4uq2mNJA8hhZfQwVcntaI0PF2PqK/VSdoW7CRkHzEywd/d/tYxIqHPdrKjUtZut32/t2uirLPAFDwWV2BKiUZ/aS9VrrMs84rPttf2rGtLIUJh+846xyP0e4QIqCrlOpZqYRVVy+gEM2VsPB5jMpnkyBnHKNqLY5f2E7Vr7B6eY9sYMYuda51za4mZ2pVjiV0PpWvMWKmtVqvlFMfhcOgJGckElTM6cWyLbOOnp6eeEHNO2JVKEXJMY/bSdqrBhNhYFDqeDVDY9e1aAIT9lO2QtmNVwfF47G1tCQUAn2oWqjyrY+2hHGEdO8sGPGOkN6SW2YJutEeWZV7JZX/X4hW6hYpzLrpGqmprpYrs+NTjxcgZ+3qounFo3zJCbVbGr0qoFjZac+ac+xaA3wXgHwL44gNxQ5ZlXznnPo985+cA/BwAfPOb37T/84MmI4TL5RKXl5deOeOi28lkglqt5sutkqCRsOkxCeuk6QBCR/f8/NwrEWdnZz6SZhWelwC1py4gpwPKUsGLxcJPRqqmxCLAIedX1R06EkXrotaVew/J7/o+X4cmjNh1PgchsqtpW0X7C1H1iU2IIcfODspapIbrdvRBgqZFK9TZ1hK6nOz0wc/YIIkWkbH3sC27hgiTqkr64P2UVShiSoRVlNkfaM9ut+udXyW8odQ7OrOj0cgXW+BkyWvVUtLaJlSZ2HZ7Vbsq8dVzWcLL99bZU6/ZuQe1SteZagBBgwiWTDByTnWn3+97kkYHbjqdetuzjaxWK38s3hvX+Gj64zYRImTWZlaJLEohKyLTdk0UbUeiq1sRcPwmiZhOp7i/v8dkMsH9/X2OYDDCzmvTdbMcP2azmVfTNL1xF3NfyB5lCFrsOCESbUmZDVbSjropMtPsqEAOBgPfRknOSCo0wEF/hIqZfm6XSs9TESIWZYmZ2jaWysx5XsdJptkyvVbtqPOQJWQhxeylItT39XXIB7DFPyy51Y3QQz5GLHumanas2vVUAaXJmXOuA+BvAvgzWZb1yw4yWZZ9F8B3AeDb3/62/wX4fXWaOp0OnHP4/PPP/WBZq9XQaDSwWq1wf38P51wu/YUpTx/OpdfrHyxAoZHdq6srnJ+f40d+5EfwxRdf4NWrVzg/P/fpDU9VeQrsl3veBdTRphI5m81wdnbmF+D2+3045zCbzXLXYgfB0LWrAskJjwSBZOz8/Nzb8vLyEmdnZ9HUO7VfaEC2ETNObnYgC6kE27SnkjOdhKbTKRqNRm5C5sSXfUiBW+d8qApRq9VyxI+E4fLyEhcXF77N8n275kRtxr7BwVzX8zDgwevTlB9N12Q63rYU5HWTkO6Dp9fGewqliIaObx0IHpNObrfb9Xbksy2sAiA3CdLZZYoTU3SoANlF7SQsjUYDy+USzWYTwMNkqdf43PYa6g9KYJR8q6IaShtTJ9gSE16rbirLdkgbakCG6aEkVmrH4XCIwWCAyWSCfr/v7WnLlJNMkDCQRGh/4TVtK5AQum/tp2pTFoXg94qOqTa2x+Y9cu4hGWM6I/8mOWV/Ho1Gnkzc3d155UxJLp04guMrifXR0VGOnLGABbB9pSfUnux7sXPHVPOQk6vBQ5IvtlVbSIk+BdWdu7u7XLCAtqRyTvvxt+M4wXHLBsS0r+0DsbFaSVnsN40RiBDZ5VzB9qoFxyaTiR8ftfiH2tGSViVnMWJ2aGJhx0dg80Jb1iew7VWzLjT9mH0+lEpvr0H7SpHdEimqLkqRM+fcCd4Ts7+WZdnf+vD21865Lz+oZl8CeP2UC1Bnn1V9uKbg/PzcR6fv7u48qdDBmxOkJRXqtGuuOaOPZ2dn6PV6Xi2LRc5DsCqPfU/vjc92Ytk2SdNz6YRvy4S3Wi0sFgsMBoOcksJrjykU6qCo2sEBmkoEnTS7ka9VY9RWOgjrxKbv8/OhydeStG3aN0QmOAlpxTj+jwEFkokisqs2ZR+wxT/smkE6/FqwgtCUEBIxpgVrSonmqfP8nGR1jQRJyrZIhEJtalND9XmxWAQdjZCTYR0+Pbau4QmliWmKKI+vihkDQsPhMJc+puXK2U45udLGdAC1H2zLyShyTNXG1gnWPhhTJUIP/a1sOrMtVqP2pENBB5ikYjweeyeYThwdOYKEgUE2tmWbGqVBum20VUsi7PjFz6xTIRQhYmYDQHYrEnWCaU86uuPx2D80BU9Jro6heg20dcjZs2l720aRs6rzZWg+jR1Dfys7ttjy7rHiH1pMhcRM10aR5NJGQD4opnPqvlPxYoTM/h27pph/YhUzDQDp2Mr5SDfp1sIfqiYWkQobrK0CKXtOP1jX1jluWT+D74dSGW0RKttPQv+rgh0TyqNMtUYH4C8D+I0sy/6i/OvvAPhZAL/w4flvb3pybZinp6c+SrpcLtFqtXy649nZGY6OjnB7e4t6vY67uzsMh0Pc398/WhQJPDRyOrCc4DSF6csvv8T5+Tm++c1v4tWrV/jss89wfn6eSxVTh7RI5bGDiN6fnYh1oLMddRtg52Y0CwAuLy99usp4PM6tO9N0Iw6eer96fRrV4STHtXqvXr3yCs+XX37piyyQWNCx4LEsIeP5SSA04qu2pQ3p6DabTT9B2D3UnhuttJEtVcw6nQ4WiwV6vV5uUqbzaAm5vrbkTNUdkjHatNvt4osvvsDZ2Rmurq5wdnb2qHQ+VTASCXXQ7u/v/d9K1Cw5Y8EGrr9sNptYrVY+LY+pFc8laXaSV6dJNyxdLpf+nCRooWCIJSdKIOiUUcFhEZWLiwu8evUKnU4HFxcXnqyR6LM9kkQwmj4ej3F/f+8VH5Iz3aeH96eFHAD4ojG8XpsK+xSbahuzZFRTYnQ937riKnps4OH3VlKmqWFUdS4vL3PbZ1AByrIs1x5px36/79PG7u/vvXNs1+9pMKhWq/mNfvlbtVotT3y3EUSwNrUkVwMHqu4CeYfdQn/nUECGwQGmglLVZdEaOsB00Pr9vie2akeumVLSFbomKmfT6TT3zEIWmvb+HFh72vu38+Imc6K2UT6H0u05XnJc4zYEmno3GAxy6Yy0Y2wNGc/HOUkdaLbhXe4tZW0VC75YW9l+H/scn63yrqqOBl9ZUEYVSK53VIKrqYy8Hp6PQc116pl+bx9Y1yZj42gZUqZkjGMr50X6trqRvAZgi+wR8ltDzwnVRRnl7CcB/HEA/8w5908/vPcX8J6U/ZJz7k8A+NcA/tBTL0InKgBoNpvIsswXBgGAwWDgF5lqBTTt/NrRNarDtVZMu+v1evjiiy+8o8bqYho9tx1RCRgH3VAkIxShtJEmjWZvU+nhIMFJg44vHf75fI5er4csyzAYDPy1apEVq/boZEqCpSWyWZGNxEwrM2oxAE4YGhmj/TgAMRKsE6PN8acd6cQvFguvUmRZ9igFb1t2VTKhJK3ZbOby6dk+tD0Cj8mZjewq2WXqHVNCqUbaVEbnXI4YUlFQNeLu7i5Xwc2SM7bN2WzmU/DYJuhch9Ian2tXtYFGtukYMpjA9mKLrISi5sAD6dFUSRamUFWXQQPt8zwPo720I1PGlJxROaPdlUyo+rxardButz1pZzU3OvYxJ+kp9gw5vBqs4P813Xbd8dQxo51sQRVVITXzgO2SKWJ8Ho1GnlSwbdpy7/y9NZgzm81wdHTk7aj7om3bCbZkwqqR+n87VpY5ns5RWlAhtBk6+zvbGtMZx+OxryhIxUcL1tgIO88fCooVlYDfhYIWG6NDZCHmeOpnbZu3almo+IdmFmiFS7t3lLUjQbVWVbOiFLxDKJE6HsU+H/oeEFbMlJxxbtdCMrQf58RQxcVQ2wrZKqSa7ZJUFLXDTb5b5rM6DoSyR0LFP2JpniGEbJYI2stCmWqN/xuAWMv7fc+9AB0IOAm1223vENZqNR/F7/V6OD4+RqfTQb/f9w4yHXmd0DXl7uzszK8zY7GKL774Ap1OB59//nkuBz20LkpVMl3MqtXauOZEnUir4Kn8zxQdfk5t8Vx78niMZvEaa7WaJ7lUdzhwcw2a5oPzeCSUdBS0wMjV1RU6nY5Xd7jWjIRQVUgAOTLBwZtpYhpFZ/SSn+H10EmkGnd+fu6LnFDpseT3qXbVtmmJGYvXdLvd3P5Czjnv/FLxAfITM69NFT8GB7gGqtfreXWHqoS2UXUK2A4Z+R0Oh7i7u8NoNMLt7a134rjeZzqd+u9yYqAzqA4eSa+Ss20pPVY5sylHuvZF07Ji51VFg+SdvxUJL5UzqjskFZwU2S6plg0GA69QvH371q+P4v9Ho5FPfVTnh+mt/B+3r+Bvx+tjf1Ml6ykIESmt9KUTv45PRdFeS3bV2aXd2E65fQb7PFUs9l9mOYzHY1xfX2M8HnuySzsWFQnIssyTMudcbs8pW8hCnZLn9vsQ2Q2pPaqcrfuNrBKpYwqVa7ZZvrbreCaTCW5vb33xj1BFQdtv2M60rSgxs3tOWWVjG4gFEPQ9SyZC/cK2UavuqBLJAAILq3CssRUuue6RdrRKRcgemrVAh7lMFb1tIhYwi7X9IrKrr/W3sGq8pt1zfmfQgPZksFLHx1AARdulJbX60O/twpbr7FLm/aLP2jGF7ZXBZl0iAeBRv4yRf+BxllOozyQi9vKwUbXGXUEHBAA54gLA75fBtMPb21vc39/j+vrar1XQRc/WQWPqEvcw63a7nkDwmFoERB1qdgjtLLqoXTemZJSDICnhIKYTRLvdzkWfOAiqPZ5qSw4AdG65zsymNXLy4uBKO+pWBTrh6eJ/EtpXr16h3W7js88+8yrP+fm5d7R5bxxgNf98OBxiNpt5IkFnmE6HrdrGAY1kptFoYDgc+j2V5vM5ms2mJ+dMySuKaJeBEgkWp+l2uwDg1RPeG6OytKM67fxtaBPd5kCLfyg50zZKIkECyPaoqXej0Qj9ft+TspubG69OkHhpQRA636PRyBeQIVlXkmQdKxvxfkr7VHLWarV86iWDMVTNVYUKTaC8JjplbKskC0wPY1vlOlN+1jnnlZvZbOYJ2P39vbfp9fV1roIb0x7tOhT+vnxvuVxiMBjAOZdbf6ntNDahlrWnEl6d7FWJ1IIFtCm/HzqmdRw0IEJCpql3tCfTcZgqxr5Mksv2yP9pWmhonY6OxUwNZaXHer3u0/HUGeY4+hwoiVHVQB8a+FnnyGmfYXCFZJ3BHgYSmXrH/zOrgG3SFv+wdmQwy6rNmoapUXmbihdSibZpzxBJs//bxKbaVnV9OddCa7VgkntN++b4qOv0bHsMpYbyfZuOZ7+7axVS7Ruypdozdn59T9s2g9UMInDu5fjCfkn1m74Rg6ohW1hbriNoSoz3TTJsMDJky9g16Wdtu+c8Qdtq8IzzL+3H/lykyhL297VqZFLNXg4qQc6A/IBLh0kn2/l87gcDpn9wjxZubKjkjIMJU++azaZ3fOmwkSxplTiNgnKC09Q7rYZFh4MPXgMbPiMhWhJ5uXy/eaqmF9nJZlu2ZCSZ9sqyzJMKRv3VMWW0W9fPaNRM00NZROXq6grNZtNvjso1E1qwgmSCBIYRSq0yNhgMcH9/7yPC3EZBlTNez+npKSaTiVcfqAoy6kQyrxHV5zi/fFYHoNlsYrFYoNVq5ar3ZVnm2wrvm+1BB2U6ZUy3oVPGNFHd1iGUzkiCy4mRTvBwOMTt7a0nZ7QnnREl31QkmMrK9siF8qPRyCvZ7B9KJtQ+m9pUiaqqyuyL8/nctz1OUBwT7HHUYVYHwu4NRwKsexnSsWIf0H2i+v1+jqiprenQalSd10TbsA1MJhPvZDOqHCpk8VTEiISqZ5qJkGUPhX+Ax+s+aFM6ZzqW0uHVtZG2XL6mhbLwB0mtquRaLCC0pof3pETXqj32d+D3tzWOriMT69JE7TH097BFarSwigYO2G6475bdFFntqOtR9LfltdhMEI3Il02Z2qZNY0RCU4NDsIqbDSRo4IvtluOcFv/QbAJNw7PrekLkTAMHMed5H4RinS1pL9qzSCGybVvX8NmAD/0FLf6ha6RCpCJkRwC5awsRs33B2s3+z/5dhpjpezaVUYt/0F+g7exymU3blI4BlqQlVB+VIWcAHg3OHBzoSGlZeC4q50CrC585CdLRY3l8OrucBLWUsC7O58CsOelMHxkMBri5ufHRdDoeutknQQVQ1xGxSMbnn3/uF9TT+SVpe44ywfsHHsgJQVWHka9ut4t+v49ut+udezo8qgLQTrTjxcWFd3ovLi7QaDTQ6/UeVRXjZEiVIWTH4XCIN2/e+FQ8rpEaDAa5yoJKzpQoDgYDdLtd7/SdnZ35qLQO9iRuT7Ep28XJyYmfRHq9Ho6O3peg5uSVZRlGo5FPwbJKqiUQJA3tdtsruVdXV7mN0akq2Vx0XbzO9mjtqEUCtNy7RtR53Ol0inq97ifWyWTi/1YlexuFQSzR5bosTXN1znlVmg6qKqi8dpJJttFOp+PTXTudDnq9nlfOGZDR1FAluFTJ3r596/9mAEaLVoTW82hb0RTr5XKJ+/t7ZFnmA0pHR0fodrtwzuX6/HNIhdrUOqdUylkNF3io0miJEK9FC24whYlqDgMxVM95LqbeUc159+5djuTqGMMxO+TE2XsCHlKztV0wOEeF16Y+PYegWQfVFllh0IAqnV1DyGPwWdNDOZ9R0dEiPOfn5/73I2lgoIVFVGJ2ZNAllpJYRHY1rTFElJ8DVRmsbWMpjjGnXOfGEHHQ4h+0LYkZCRjnIFvURwuLFSlmhLY1Jbf2oQ71NoIGateyj1C7tHYNEQfOVTpuMtCrQRYt/qHjY8iOMXJoyUTo732pZ5bgFv1uZQIzNp2ZQWZb/IOBqqLKlkXql9oydF32O4moVReVImeEEjRGD5vNpp8IOcExwh4qCKILVzWVUNe2aNRCFTNNv+MgfnNz49UdOh1v3771pbVD5IwTOVPGuC1Ap9Pxjr1Gs3k9OqA+l6ApoQHgq8cxtY3OtjrjunZPyRknOlXJmM7EgZtpEJrKSHJGVYLpi+/evcNwOPTPVNA0xVK3TuBvT8dIiytwAgGATqcDALkKbs9Revg9HVxZdr7VankHaTQa+egX1zXQgVcHjamkJOZUctUBVnWHJCTLslxqLdfysHrp7e0thsOhd4Y13URJtzoKmlICvCc8k8kEx8fHGA6HOD4+9qmGnEQ0ZXZTm2q7VnvaxftKJmhDtSXbAvs5+zQdXhb54dodOhccE3jvdPQZZKFNqZbRGdZKgkUFKEh6+DkSQI3O78IJVnvGiqxo+nRMNeP/bfEf3XeLRCJUYIEOGxUzLZlPZdLaUZUea0sl47SXLdQQcmK24QTHSIQtDqLE0kbKVb1XVUeLf2gBEAZCNMtAszPYFjWFUQluGQc2pJ7tQzWzNgXypMA+QoqyEjgtVGPVXbZNZgFYxUzboo6NaocYyeV9cOy0Ss8+7BiDDeqWIRdWLeP4rj4U+zmzlzSbyCrgtj8WETOL0HgasuM+7Wrb4bqxxQYhtC2Hin9wTNOUWA38hcjYuv5tCe+67yRUD5UlZ/pgQ+bg2+l0clEaLQFPaAdgiohWF9IJluCAotF0krLXr1/j7u4ONzc3XqFghJ3OB5UegtFnVtrrdru4u7tDt9vFYrHA+fm574QkbOqMbCPdSY/BiUTz8kejEVqtll9Dp7ZUcsZILxU0ddqoUnLg4fXTidJUsTdv3qDf7+P6+hpv3rzBYDDwdqRzrIuJQ6Sba+dIkFhQgApLq9XyhM1GWZ/iuClx4fdbrZZP4eJvTbLGgitUgmh72tKu3WEJclUg6WTQCeGArRul9vt93Nzc4O3btzk7klzYTWhtH9E2ok4y2yFJLlN/j4+PfeVBttOnOMHaLunYt1ot3/YGgwGA92WZVbFTRZcRc7ZjBl+YHkolkum3/D/tyd+G7e7u7g7v3r3zdqRapuljSqhCtiTYThgAYcow09IajcajtVJPnTjVEeC90YniBukku7r/kCXpSpRpU6rrJGa07cXFha+CyT5Gh5epycPhEDc3N17xYVptSDGLRYKVlPFZlZ4Y0X0OQuqOJQFsdyTf7DN0REPqjjq57E+0J5UzBhjYz0ludfuBUEXBUOrTOqgTrQ5hUbT+uYTXOqsaGNV1Tla10N9FSbHt//QNOI5yXqK9mJrMFFtVwjU1lu2tSKHgNSkBOQRJK6uc0XZAfgN6/YwSB7ZX2pZ9ncE7qmWh9Y7WjpvYUov6xB6HglXS2Cf0mkLjhx2bdR1flmU+iBtK8Y6pZjGE+qm1WxVsmbAelSRnhKpKOpBz0LWRdXXidWLkd/UYOhHweyQDTHe4v7/H119/jX6/j+9///u4vb31zjCJm67nsQ4wzzkcDtFoNPz6FZazZ6oUI/i1Ws2vo2IHtqmJT7UhX5NE8RwkWZoio+mh1mFjsQWul2CEXfOmVTHjYuvb21sMBgN8/fXXuL29xbt37zypUDuGJstQdJ8kmsoE8N7RXywWfm2fFnjRdTc81qZ25G8KwBcb4Ro+KkksVKC59/wenQnaT9dAKYHg5MhrV/WRDtv19TXu7u5wfX2N169f54pW6OJ2rYBnHXLel40QU6G+v79HrVbD/f29V52ZxmmL9mxqS+2jVD15rb1eD7Vaza/VOj4+9mSdypRzzq9z0mps3GOL6ba6BlKLtZAoUK29vr72acpMrWXqqKbXavGPWESdvzk/yxLwurmtVsazE+9zCK86VyRllpzZcU/7Ofs00xlJIFikhunhmpLKVFQSCSq5TGXkOildH6brHmOpY0rElTxoIQslKCFS8RxY0sq2yLa0XD7sxcfrVWeM479mepCMce2uEoqjo6NcMEsVXB0fQyrFOqVHoYrPunVn+js815Z8LlIi6ZwX/RaWQLCtMtDFtg8gRyL4rJt020p4of4YChpo39HPWX9kX05wTHXUvq5zmP2sVcuoOpKUMWjArVrsesfQOj2ijA0s0SlDzLbRLmOIEVz7GXsNlgxrIIG2pa+ky2eKAi1FxKzIBqHP73sNX8LTUWlyBoQjZhzA6RCHJiUbtQilT+hndZLSvaJYXOHNmze4vb3F9fW1T8NjJE7z1UPVGrWiIyMlHOw4AALv0/Gcc97x3UY6Hr+r0UpVgjQKzH26lJzpoE1ixxQHOh5qW+BBgaQzRrLLKoLX19e4ubnxa850PY9dTByKSvH3ZwXKLHuvBvb7fU8mmDZIx5zXROLxVKiSA8BXb2QqG9NoSM5oSxIaJWeabsdJkE6aknK2Sy2ycH9/71MaqThq9VC1Y5Gzxbahail/s9Fo5IuvqBK4jXUU6mxlWZZTe1itsdPp5NKfeN7Q2j3akASCtuXDrtnTIgtMaVQ7UgnSqGaRs2BtwPRPVS1ja3u2pfhof7Wpolw7yKCCtgVVd/h53ZScypnuvcXfgGSBTi/VQRKyWCrjJs6rdX6t2rMtG8bsadUzjoe0m814AB7Sl9jnda8tDSYwBY/jspYhpz1pQ7Uj22OITMUcMPYla09+t6xD+BybWtvaFNGQQ1xG3dH9DKnys89xTNRxzKoUfFj7hGDn5FBb3qUdY/ZcR9B4HaHPWWVHU8XZ3tl/bSqjkgrblmL3rvOGnUMOregUzWcxoqbfi40dmrXFebZIsbYEVxH6n7Whvc5D2zVhM1SenAGP5WR1kGMN2HYU+55+R9MZWSnw3bt3ePPmDb73ve/h3bt3+K3f+i1P1BhZZ7EQmyes16CTOtevNJtNzOdzn64ym81wdXWFWq2GXq/nryvLMp/a9twIkab0qeOwXC69MxwiRKEIp1Ugea/8LidFLev++vVr3NzceAXy+vraVxJktc3YZGnvg7amY08SROeGlRS1Ip9WcHyqPTVQwOMCj9dAnp2d5aKJ+h06aiRiIQWSbVaDBSRk19fXXtFlKh73jmJaqm4/QNIVc17Zn7Qf0NkcDoc4OjryRWPo5GsxhOcQNLYp4P36QCoP/O0A5CLdtKUWVqDaqOui7FYVPAcdC+6zxdRkriNlYRUWW7DV24ocrpCjxEANj6VOti7+fi6x0HNqQRAGfaju8hx0rghGdZXMsqCCVrVlAEHL5ZOEMf375uYGt7e3uQqXRWW1ixw4DU4wgKCEt0g54zGfOm5ashsqsrJarXwxkhAxYx/XAALVHa4vpT35mzC74vb2NlcplHOTjiv2ftdFxVUxCxHdkIK0bYfOEixVJDXYpr+BtSl/C5IyBmRIdhk0YJotlUcW/6AdNQi4KTEtUnn0t7Ht8TnjZew61FYxwqup6EB+GwISBrZV3bCbwUcGsnQds6Yo67pgvVciRtD0HvS9UACnbDBnWyhSz2JKmooCSsbYLpndQ4Wc83sROVtnxyKUacuJtFUTL4KcKWwHKdOwQqRMwQFVlR7dd4vre1gtK7SeJxZNt4P28fExVquVV3kYna7Vari8vMTR0VFuktHS5c8d0K0DoYMOI+jWnjrYhAb8UHSGNqFDqsoE1Qk6dbb0Lgcnm/fPa+HaMp6X32N0VAuwaPqKdYKfak8bJGCAgGRKqwAqWbcRX10LqcUaNFWQgzXbGtsl1R1Vy2yqnE2PiIGfseSak4au7bGpeM8lFLRbKB0PgE+f4/tqSyVnjJhr0Q+7BlL7N22pSg/biqbp8FHGOYi9Z9PG7Lq1baiQtKd10NSRpVrPLQpIWJ1zubU7usm6qhF03KgYazBLUxdVLdMtA2LETO2m5EKzBnidOjZYB7go6vwUW/K3sO1TCcViscilNRKa/mgDCCwAxLQx3qeOl+tUHksmLCkrQ3RDhGGbNozZNaQq2DRHJRMh5VI3QdZn7mPGMVOzMXR8tI5waDyz9277ZujvIod6F7a0do2pj6FAtdpVx1i2WS30Q3Jm13mWIROhv0NQe+7adkUo8hXXkTT9P9ur2pf9zir/oTTYpxCz2PyRyNfLxIsjZ8DjDvEcaGdhZSyu5Xnz5g2+/vprvH37Fm/evMltpqrromKTJPCg9NBh50AHwEeearUaxuMx2u22r1LH9Dg+P3V9j4WSMToGJBgx4hJSBfR9a0c6wCy0wHV6WryC6XgkVkooykTcaDf9DInvzc0Njo6OcHZ25gts0CndRuRSiSkHYq4/Wa1WviCJdTY1t98qkJrGqLbUFFvaku2TUWFNZ9SB3w7wIeJNMGoNwK8HYgVPdbpDjuJz7QjAVxOlU0ZypY4VHUslZ1oQgE4bHWMenw4Z+zfTQVm8gv2alULt4nZ14NapE7wH7Sdse5rWGCtk8VyCpgEDW72UtqOTxc/T4VUiRnJGJZK/B/CgvGnQhfbr9/s+LVQjwyHnH4irPao4829NbQ2t1dh2eqPakynoVjmjkkz1jGO2Lf6h6g7Xb1KB1D3MVC3T9qjrHi2xIMo4cjYIo7+LBhK27RSHggdWOeND74tt1hb/4D57LP7BYBfJGIt+3N/fPyqiEitTvm68tMEC24atc73NtmhtyeOGCG8R0bXkgZkcmm7PrIOjoyNvO84B7Pu6flQzNCzptwjNQWVIxSEIRkw14//s3zqX6bjKNp5lWS7YYtfV27Hxqff/XP8moRp4keRsW9BJSotXUC1jig4dDy38EVq8yWMCD52XSg//x7UCw+EQwHvng/uGvHv3DkdHR+j1er4KYqvV8oOpHve5sNHhMg58LKqkk5EWW9B1Znd3d76KG523UN6/vYbYoESbayRwOp3i6Ogopy7ZYi2cpJ4LPa8O4EwLtI6TEjoSMRvp1HvTdVF0gFlsQdeZMdXEVskKTZKxaDCJOtuqpo9pCXgbNd2WA6dOMIBH+5Bp1UvaXKuv6gTI7+lvoOmMXOPY7/c9udW+relO1nkrq1DY9DEdZ5SYhUjFc4gZbcP7p9rIPf/4Ph0rtj1GyemcMUWU79GJ43VSdaQttXgFSbyqZtbxiJFc6/wC+cpy+l2rSIZSyJ4DGwVnO6NCwy1JdE0hbc/gmqbaacEfEl32L6uEq5Jrlf9Ye1zXF7Wvx2wZst+2glk6L4bW4eheT8CDwqd93W6LQ1s2Gg0/t1olV1OJbWptWWJmg2z6/zJqz66Ihc7HlpTpekiO6xznnXsoOMZ2StsyqMDAg6YwKjHbpIBKkQ20bW07IPBUhNTGosC0jhMkZbrelMsEQuM/8HjtJ98jPgVipmNEwnt88uSMA4ymxjEirM6bXdgecoLtsRWcvPldVVHu7+/92h6Wt9dJmY7mtjudHWBi5yhzXiVnsWILofSxIjLBv4vAiYcOp13bY9e86GT8XHuGBvAsy6eH6nnsIK/r9QiNoun+WDadUZUsGyywg3zMntZZIzFTB57OTIhQxAIST7GhEmbaEECuUhivUSPvjKprGolOouzb7N+6B1fR/luWWIUUilAgg9dI55KvLaGwdtzWxKT20W0K9P+8R45BWvWOaU1UJbU4kaa70gEu2sfMqo+x+yx6T8ku3w8RC/t7bcuW6vjaIivso7oGk2t3WJnR7rFJuzr3UDQotJdZaK3euvZYZM9Q2wx9Z5cOsrWnJWi0L/AQ9NJql9o2dV842p/jvbVhaO1oUSCQz6EAgg3uWRJXJoCzTYTmlNAyBP6uum5cAw5ajOr4+DinMtr94GyK8jqCVsYGVSQVIWKmSqR+zrZpnZcYONb5MzRXJyQoPllyppOcTcN7+/atfzDtyRKmTVI/Qg6zLsjnotu3b9/i+PgYFxcXODs78xFXDqYx5WpbeMpxeV+69osRdZbLZ0qjbjLNlCclZuuUMzuA839MKWKZd6YBkhDyt2N0NrS27qmwxMuSs9hn7XvaHqn08Npvbm58lVBNZ1RnOJa7rnaKpd3yf5xkVEGj86hVIG0ZbxKp59rQpuGoWqNpTqFIsVUgaUdWuByPx14FZ7VQBmB0k2lNVY45ckUBGf2NlUDEilhsk6BZoqvbHZyenmI6naLVavnroc20oqAqkHQs2L/ZDqg6skAS+zvtHFqLW5SGt+6+leCGlDJL0LYBVRroaOnWLavVytuN16DptlqdkWl4/D/bGccn3X6ARVTUjqE1dmrDTR1iGwwq851twDqxGnhhCm6WZV7xpZNLpZIVbrkWku1b9zHjsgNWAGYqnl3rGevLRWMlwf+VGfdsVsS2oeNhiOza9hIq/qGK+Wq18nM4nxmMCQWvivrzU9tT0dy5LxQRM52jGAxUu2u9AF3mwfnIZmXo/FIm0GLfL2Obos9UjRRXHfuy1ydLzgjrEDNlhxF2q/I8N0JLJ5iTLtMpmS9vF4Nbp7uKHckSNLWj7i8Tup91k2ToXIQSm5AqEUsh03Ns054h0rXucxZ6D+ui6qECCxYhZ8OqEkA+XccqE6GiDmrHbUBtwmtRx9f+7naiVCdIr58E0/ZtW3AhVuK9LDGztgUe+nooHU2fN40yl7ElnTXgYT2fOhVUAGyKk13Azutnf7JkPRQgiKWMhexUdO9Fav5zHcAyUKKtyhkLrCgBz7LMO75My9VCKlwDCSDnsIXsuK7ggtqgLDGLBbYOgZByxu1OOPYByCmVJGe0rRZT0SI/mgoa2guuyE4xYhZql3xfX9vP7Hqutu0zpuAwXVyVSK7RpcrLMYLpjLb4R1FabawdhhCbv8vMl/uwpz5C79HGvGZV1fXBOcxmSYTsSBtYlO2jVfULE56HT5acKaHgQMQUPEYydR2FLoDl4tennBN4SMXjug9utnt/f49Wq+UX1bdaLb/g3KZTVAXWjoy20Y5cb0ZbFqXqPCXyRrto+p1WNrTpf7sgFoqnDpJKJtSOLF6ha80Gg8GjiVMXZBeRC3tOgnYMkTK2/VARi20GDVR9tGu27OdCz3r/akem3qkdGWEPldXeVlSY96JO3yaT81OgNtFtIxjF1d9OSZw+8zsAcimh7E9Uztge+b51iJ9CdDVwwGvUZ9px3f1vC7Qj8LDxPN+fz+d+C4gsy3LbdpBAKOHVlFCqO9ysm+se1Y5cnxxziK3NYmSjDCkLOabbhHVulehmWeaVRfZ7ALlqo1qsgqqELf7BdbjarzUgWJQCu4lzXETK7BrkfWS7aD/W9FASXv2MpjAr6a3VarlS+XwdK6JSNK+EUCZgELs3vrbv7RqW8OprQtNENfMgy7JH+8GVXe9oX1tsassQid+nHT8GHMJWnyw5A8KpZJqzzsE/VADhOc6UdVhsGWVdVK9rifjdKnUqex9cPGzLlNuJct2gtEkETh1yOkG65sVG/qqGovZgN/bVhe0xtccSmrI25URur+cpxOQ5UIdcnXL7Gft5Xhvbgq4jVRuq46ETpn6/aKIsskPsevm/fThvluAyksviALx2nlML1KjNLcm1WzloBTdd0xOKqMfUiCJioba0yqpVT3dhS22HmopH0AHmfdLOmtZEBVL7tWZmqJJrq+DF+rO14br3YyTX3quS8l2RNas2aNEavsfr06qXJLwkc9q31ZahteGhlNoYnjo/xPq2td+2bRkiZ7qRtHMP288wRZTFP5iCyz5O29k1j+uCmpu0zdDnrE2svWLtcNeEV9uqtk2trEy1nG1Vi3+o/cpmFOwbVfIlE/L4pMkZ8Fix0EXaGu0goXiuc68TpCU1PLc+dpVGtk2oDZXk2j1mVJ2IRdEtYvbW1AJL9ELpeE+J9u0TllTY/bjsuigluDEbhYhVmesIXde+bRYjX0XRQbWH2tEGPUJ7HsXWkIaCAPZ9+3mNqtvfZl/OWyjiTAdOrz12LbRHyI760Gqam0aEN7Vl0T3a1NZtwao9iuVy6ckZ8BBF1wI1HKfopNkAoBZI0qqrodTvUD/fJJgVso0WJbIqwbahv5cWTciyzBej4Fps5/JrIVlIhdsW6DxtN3cvWs9Zdjx7zv9jfWqbwQM7Jmo6o6pnJGf8n6bcqj01zXZdem1sHi0bLHjKvYZe7wKx4ITaV9VIBmDYVp17KLikxEwrMz4lcPoxYxcByo8Bnyw5s+qAqiwclHRzZH5Hn7d5HSRpen51Hrd93m1AbcjJUCdMTdOhvM97LYq2FTkjhKbhaafm36GJscqd3xJ1jQizvDadEFuZcVvnt1Anis6prYi4L7uuO4fty3Q2WPKdD1Ze1cImIdXMpjSGJtRQ+9S0rND/1HlS2+6KWPC8et0hoqskSNuiVmaMVV4tWtvzHMVH1R77vhIh2jJUGGYbsOOI3VqA1x0qUEOb2ErA3MuMfdymXq8juNtyhNWW6oDusk2qCqnVK3WuVcdXFUiSB9qPNlWiu2/VzN5bTEXbBaxqxqI1TBNlMFSL1VBV4zipa8OV5Ma2cNgHYiok73mXc05IMWM7tH2cKaGnp6e5uZtjZ6iK8nMDnkrM+XfRZ/m8z/m6LOy1cE10FbBuGdGu7fjJkjMiFlU7hGIQ+rGr1JFiUIcupliVteW6KPE6e4SUAutsVMmmIadL188pUacd16k8IXLxVKhqEHI+qwa1oQY71NnYVRn7GOxkr+1yH20yRG7WIRQwUkW/aP3hJniK7TWazWcAO2uTShJ1wraOhF6Xfk8DBnysS3naF6wysMtx0tqR4wqJ2XK5zPUJkm5+Rvu1Fq2IEbJ9qhIhdSykmm37nFbdIelluijbolbH1LQ8bZOx4lmxeWWT64z9BuuIRcyeuwbPpetxtTqnBodoYx0v1X5PGR+LbMb/P/f+EraDXdnykydnh4YdWDVSqJEafraqUHJmS4XrmrmnHtu+du5hw2cFB0xORNzHRasoVc2OIdsVOcPW6XiuQxwLCmh7pB1Z4EAJb1VgVXBdxxmqLGij6uvsWMbOVHQJS8h0TYi2yX3Ysoz6yHtQJVyrhaqCGyJoZRELLKy7fht0sVHtXRKLEEmLRbCVSGhKqN1o2qrhVo3bBbEIOfWhxy6VMwA5YsZ0MaaMAciNMSSzNqPAVl19TuGnTaL2RWTMKpH7IGhMuW00Gv6cNuWW6bbOOV8qn2twQ9VCNw1gKaGIqTuh99QuIbVsn2Oj/R1pt8Vi4dfnMZ2ZvsZyuXyk2mo6Y4yYFdlLr2mTNhwjtKFx8ZBzd9G5leweAjp/H9Jmnzw5086v5Wc58dMR4Ge3eV5VJUgm9KE7zFfNEY4hNMDsI+Jlo1yslMaH7tu0zwjcJrBpdfoIRS11EKbTWEZdXIdQsEAJRcgRPrQ9rdqtlSbLKhTW+Q7Ze5PIp3V+bUpjiJhVxY5KckMq7nOVx1CbDR3HOhrq+OpYvU9n2F6/hW2HVr1V5Sy0tsw6sJs4bWXbqCVlatt9OCQ8P23I61Zyxv9rW7TrokIbTAPrHdqYndjvi+xo25cquCH1cdfjo/YHLVjD1FsdzzUrwwb+ygRadFwM9V37GogHMBQxIlHkKO8CdszmfGfTtjVt2c41RUsOYnO1HUvK2Gzdfdh7OtR8bc8VI48KVX0PgaJr3Jf9PllyFhoE1IEqSofbxEkLnVehAwDVCW5iSme4Ss6bRWwACl2vbdxFTtkm0N+QxIz590py1ZZVIBQhlCVmu4IGK2JqT6jkelVg7RdLsVXUajVfxfC57TE0oagtLUGrWntU9cwWVontHVWEGLko8z37Wu0UK/+/j3Fy3TxgAyxKbjd1hvWcRQGDdTYNzWF2XU1RauM27anHYoGamCOv/Zd2s3a0SniZdLCQY1yGBCsh498xUrHrQKAel9fDIiDOOV9dUK9rPB57RTxW6r2M0mPfKyJlITvq+yHHV22363RbC+sP6h587Ndst7YvF80zIWK2zmaKsmNmrE0e2oekXWPXWDWE2qWdl3Z53Z8sOQPyTtPJyQmazSYajQba7Tba7TZarZaXsrlg25ajfs55dUf5ZrOJbreLTqeDXq+HTqeDdrvtVZ8qOsJAfkCwRJMbXJIgMX0FeIiKhqLPZQchHbCtLfU35F4u6oBUFXaCt6muulZJbWjXmIUinHoOOwmEzklyy37BgIGmx1ShTRY5yPa+rX1Dk1aIGOh5aD/rLNuJR8cWq4yzX1cp1VZVhxC5tRFha0sgn4qiTkhIkQg5K/pdPYc6S1piXe14iDYZG7us4hMiuLH2qXMMkC8yo3bc9Br1+FbJ1cc+Mgx4bNpA7xF4SAtVcqtVGtUpDh2XdlJ1zipz+h09t61oGrp2IJyyvM6O27Ynj8e2r/vqWQWXKqMSs1iAIOY4W1Kr9lxHykJ2t/egQSz7eh8EQ/uIbt2gRYCyLItWBtVjaDvUNhVSd2Nz2KbXzudQNhjtuU9SFCI3NvMhVJCrCtBrP4QdP2lyBjwYng5wo9HIPXTip8Py3PNpx1Eyw00h1emoYnTdItTh7No5bdjrnAsd1Pi3HeCtTZTs6j4vSiZ0IXRV7ahOfSjNVgeHxWIRbBNKHtTJs5+xCClm+ju+tDTbogmB/VmdNwtLKNTZUBuvO2fIeYul4lUZNn2LrzU6r8TC3pPt+zFiRhT9dvaxazKxCUJOV1GGgSUTsfExRnSLbMjzAA/Bg1AaXlGmyC5hCfk6JTJEaPmstgwFT4Bicmvnmdhvxme1n7Wl2ngf9tT71uvXQAsQLnqmx+BxQtC2pn2e/wMQJb9FsESiSM3dJUJjN8drguvCLWHVY6j9bEAqZJ91JK3ofZ7T3oNti0Xq4y6Jbui6LNmxbZOvDwnrJ2pgvGid+DZtWZqcOeeOAPwqgN/OsuwPOOcuAfwNAN8C8K8A/OEsy262dmU7hnXq6/U6Op0OZrMZLi4uMBqNMBgMcHNzgyzLMB6PATxEhlXmLns+4CHCpdH0druNbreL8/NznJ2d4ezsDO122+9JUlVnWDs6I9q8n/l8jm63m9u8FgBms1lusNKIE2GjxDwXYVMeaMtGo4Fms4lOp4Nut4tut+vtqMpZ1ewIPI7YkajPZjO0Wi2/GJ77AHGC4PYEAHJELERCi5wN2kaDBc1mE61Wy6uQDBxooZoqOMTWqdJJiW1yNpuhXq9juVz6zaeBvNLDKDydnHXOsr0GPb/akqnKzWbTP7S4ShWDLzZQoET99PQUq9XKV4QD8koR/+ZzSLGwJC10fuBh+wEN+NCeVHNDQYOq2JFQZ4kFBnQDa9qaa6fY7lRhs45xkcMXOr/Od6rkqh0PoUKGCJptP/bz6uBpxTy1HxWjECGx5GSToKsNYhWp4vuwoyWoem+r1So351rlW/uXjuu27cXstu657DXz99S2yYB1SIncFdQm+h6LgMznc4xGo9z4xD4FwO8pZ0mxLTpVRj3b1Lfka52D1I6hQPW++rf2V6qR9Xodzr3PerKZBFUjZ7x2ZoPtY87ZRDn70wB+A0Dvw9/fAfDLWZb9gnPuOx/+/vNbvbodw05WTGns9Xro9/ueKGVZhuFwCCC/sa9NJSs6j3YYdcLpAJNQdDodtFot7wRXlZgR1hlVUtHpdHJ7JK1WK0wmk1yEDyi2XUiZ4PskZrQlHTYlE+xMNtpRFXtap54TFNNC5/O5J2dcBO+c82lS9jh0jmljplOEFrmHIlmWTDAtlA5cVZUzG/VkwIV2XCwWaDabyLIst/cPHTmSXUZGdZLg5Mzz2AnE/oaccDS9Vx+h9aRVsGUscqxtYrVaodFoeDuw7UynU29L/R8dZPteETEDHpMJToyhzIaqFfuxDqf2LQYL2A41sk3HTtNJ2UaVaAB5BaQoDU+vxQZ/lJxZh0PteAh7htoir30+n/tAi7axo6MjH6xiH9Z1QlaBA8KpVOsUMz7Yf9WWoZTlfak+2q/0fRtooR1pH+DB+bTrSdVppr+jQcBNyVmISGiAkHZj/7YZRPsKZNHv0EAxbUCyyL3NtP9q+re2OWtDItbunkrM+MzfmvZbN+9s25baHm0gg0E99tlQynxVECK7++rjpciZc+7HAPx+AP8VgP/sw9s/A+CnPrz+RQC/ghdEzmxk9vj4GM1mE/P5HL1eD+fn5xgOh+h2u1gul7i7u8NqtcJ8PvcOHCdFThJAvFSsSsu6nqfRaOSUHiVn3OCQA8WhnY4YNOpFcrZYLNDpdHy53sFggCzLMJlMAOQVM50k1p2Hzzphc3K0a824ZpB7u+wzWrQpbKCA97NcLtHpdHKLuJ1znqRxAlBCoUSCNg45cJbMWEJBlUftWDVHWBEjFbRju90GgJzjyzVBltyyT9u1GDrB6r3baDr7uCq6JLk2XTqWRnQohCZTjlVZ9n69BZ0V9n0Afm0Q7abP2sdDDrGeG3hwjjQVVBUzXc9axSBWaIxaLpeo1+s+qMI5hDako8f5hQ4Lx0pNAYoVHSi6jpDDpoGXKiqQet3ap2kTVczYXrXKqC2qFHOWQ46zXkMoAKNKQCz4Ytem7BLWUWffCxHc09NTAA+qqwYC1FkuIhpW6SjjXFuSCzzYV/t6SM3dF8nlM+cR/tbL5TJHzADkfEFdI1lkM+BpClro3kPkTPu7FkdToruv8dK2PV4L5wSqZjZgUgWE/E0GsWIF+/R7z0VZ5ewvAfhzALry3hdZln0FAFmWfeWc+3wrV7Rn6IRF5+3Vq1e+sYzHY68E9ft91Go1DIdDv3eNRoOBBzVNCVUoms6iH69evcJnn33mH1dXVzg7O/MErWpOhwWvS6Nx3W4XtVoNn3/+uW+8WZah1Wp5FXI4HGI8HmM+n2M6neYmBjuI2YavaVZ0Lnq9nrfdq1evcHV1hfPzc7Tbbe8Mc6KsGthGAPjBK8synJ2d4fj4GNPpNDcYjEYjHB0dYTKZ4PT09NH+NNYhCS32VgeDgw6VXKbV0obn5+fodrtotVqVLlCjEyptSOLKaB2JZqPRwGQy8ZF43SuJNlTnriiFmXa0ygTTFy8vL9HpdHBxceH7vQYN9uW8rYMl68D7fZOILMvQaDS8Usa9urgXGosN6B4/1kFm6miof2u7tCT75OQEnU4HzWYT5+fn6PV6fpzU/n1oUmGVClbPa7Va/vqOj499mi3bHlNtZ7OZJ7m0HQMvmjZqHb+iawCQWytBR63Vavl+3e12fXtVUnEo8NrpwNXrda9OaBo77cdMAvZdBlG1/YVIWkgNUlilxrZNjabX63X0er1c6rKdd/ZhU1UtNEWPYyAJB/fu0u0yypCz2Po1fS90TXy2r7XPc47jXMM+v8+sDW17eq0MlgPwpJyBAp13bTsD8MhmfE3EiEmob4f+tjZVex4dHXkb2kyiXY6Vdj5hH+Y8oEEWm/ZZJahNtY5Cs9nMpdxu25ZryZlz7g8AeJ1l2a85535q0xM4534OwM8BwDe/+c1Nv75TcBDTiBLXTHU6HZ/WuFwuvYLGCYDRJp0AeEw+64M/oE6MnU4nV51RB6KqOBvroPfLiAyjxK1WC7PZDNPpFIPBAABy6aE2qk672ii7EkCNYHDQUcWMdqTTpmTiJSmQbIur1QqdTscPaLPZDLVaDdPpNHcfSrY06m4X0dt2SdvQVlxjpmvNVMm1k2NVbKkOidqRKiAAtNttH1Fmegr7tDpcMYKmjoh1MtTxVsUulGZrnbYq9W+1o9pwuVyi2Wx6B5kOnrah+Xzu7WedPbU58HiNj9pBVW46Egyesa8rKbNrIA8NdUqoWGsamdqBNuM6NAapdO8uTdGzjp86NTGSq78l56Dj42NvT67JDW0wfwh7WnKhdjw9PfXXpM6nzs3qLFtyVmS/IpIbIhK0p1Yk1vn7kGnLtCHtlGUPFQcBeCW2Vqt5m2nJ+DKENqYKhRRInXtjdmXbo3Km2Qf7DlLbuRVAri/zfc4nob75XNWsKBgYex2zqY6Vh1hTavuw2s76KFWEVctpx1328TLK2U8C+IPOuf8IQANAzzn3VwF87Zz78oNq9iWA16EvZ1n2XQDfBYBvf/vblbM+De6cQ6PRQK1Ww+XlpR/4F4sFer2eT4viBDYej72joqWRuW5AJxYOLiw6Uq/X8fnnn+P8/BxffPEFvvGNb+Dq6gqff/45zs7O0O12vbOspKKq0M5HJ4oDPaNLtVoN9/f3ODo6Qr/fR6vVwt3dnV+TpqWRNUKsx9f0OxZLocpzcXGBL774AmdnZ/6Zyhmdkao4byGoY0oHhPYDkEvTHA6HqNfrGI/HuL+/x3A49OqFOimMIFtoBJLOLwlYp9PB+fk5Op0OvvzyS3S7XVxeXqLX66HVavlBqUqEglDniYoF+zajXJPJxBP46XSKdruN6XSK8Xjst8ugihFSL3QCYURao2eaFsrf6/LyEu12G5eXl769WrWnKlDHk+vLNOV1Npuh0WhgNpthMpl49Zt9mKm3VIE0Rc86MfacHEPU8dWqqxw7tdiPbjdSlbRl3g/wUGgHQK4i72KxQLvdzpU212I1tJ2uAaItAeSCL6FzW2VcHV9Vyakid7tdTzKqsBbSRt01wMn1ozYIYPtrzGm2pAMIE4oYKbNtVdso5yUdKw9J0GywmESWRX1U8SkiZTofr1POYtei16HXpuRH5yWSCl2Ltk9b6vVpgJh9KJbCGFPJypCwIuUsdM8homYDXZwPNfCrY8Qubal243MoS6rKxAyIr93UcWDbtlxLzrIs+3kAP//hAn8KwH+eZdkfc8791wB+FsAvfHj+21u7qj1CG/Tx8bFP3Wm321gul56o3d/f+0EkyzKMRiOvYDClTOVZ/ngaWeMk2Gq18Nlnn+H8/Nyn4F1cXORSx6pOJizUIWFkqdVq+UFrOp16507XNmhqmU0rI1TZVEm5Xq97InFxcYGrqyv0ej2/dk/X9lRNobCw0WJOAM45tNvtXKSJhG00GuWqEdJR1r2UlFRoeq11fBlBp5LbbrdxdnZWWKCmirbUCZUTAtMHqViwXzKdlrYLkTONxFsFkufgMe06M67pOT8/94qPpujYlKkqQe+PYPTdfVC02H7m87lfHK9EQ9fnhlL0iJjDq21UAwiqnO0rRecpsMECdfC5xocpt+yv3FdT5xNLbEPkgudTB4L21Igv5yNd92zX7h06pVHvB3hQfmzfpvKtio9d96POs3WgY+Qi5ORq+7LE166L1GBNlRRIgtfE/lxEXovUn9jr2LXY55DSw2f2F7s2d9+21HPZjBHa77kKWZm/Q9cTei/Wdi2R2JdvGbOftd1LQGh8tWPDNvGcfc5+AcAvOef+BIB/DeAPbeeSDgOdyFqtln9vMpmgXq9jMpnk1k8NBgM453ypeFYrY6oeHRim3pHwnZ+fo9Vq4csvv8T5+Tk+//xzr5gxX70q0ctNYMlZrfawbw+j8M1m00fj6dyNx2Ocnp76SLxG3QmbekcHrdFo4OLiwitnV1dXXunRdJ2XQnTVhs453w4A5KrSMTDA9ZCtVsuvAVL1gkqkkjOd8EgiVJUgOWu1Wt6OtDXbc5XtqJE6tScLfKhDynU/JGcMtNg1LHSW6biwTyop42/DSC+JGZUePmvVy6q2Sb0mtSNJxfHxsV+vwnZGNcgGBuzaM0vOLJFQ8qdRatpUAzOaile1sdISC/7evKfVauVJhWYM2HU/NiXPKmihyLr+ZpacWeLLh9p7n85bEaxDT6JB+4UIWIiMFRGNWFpjiDyESIR1fDlXVYGcqe30+tUxLrJNGbJRREDsNYSux14bH2y3VQhiaV/m39YG6whYyC5l3yu6pqL3Y21X72MfCNkPiK9PrDKK2uy2sRE5y7LsV/C+KiOyLHsH4Pdt/YoOADupUZlgVKndbiPLstz6sMFggLdv3/q0PKoWdN50fRkXW5OcdTodfPHFF+h2u7i6usLV1ZXf6yzkcLwUsPNrKg8nfOccOp0OTk5OMBgMcH5+jouLC4zHY/T7fcxmM4xGI0wmE+8ME3TONGWE6YokuywQQKWCqWVVSncqA9pQHToAj9K7Wq2WTysbjUY55YzFLegscxBkmyI50Ig508M0fbLb7eZSdKrgbJSBTgZ8TVuyYl69XvepZZbQMkBA+6lyxoCDOg4a3aVKp9Wx2G5DVRqraktrQ07qulZPiRftFFrvE1I0VPEJEQhLZqj4qPJDZ9gqA1WBncjZr+kYM1PDEo2i9VEh5ceez/5mllDYVEebolOlNmlJro28A4+Lo5QhGUUEI+bg2r9jZM2mjB3aljbYsu7+yyo+68hH0bXECBufrW1D39snQjYEnkbAnvKZstcW+1+oDe8TocBACFUja2VJ8C7wHOXso4NOXpqa55zD+fm5/xwjxc45jMdjDAYDX62MRS1IJpScdbtdXFxcoNVq4erqKre+h5+t2uL2TaGDqtpR03g0tUwrDrbbbW9HJWeM7jLlk0S3Xq/j7Owstx0BHe9D5/s/ByFyoYMb1TQSeaZFsfoRi7DwNQe8GDnTtqp7w1kyUXXVTBFzSLRvaZtUxUcJmabm0Qnkb6HKmSUQuviaFQ6rUnChLLTtqeOq/VvTRZWIWaKh5AzIb5xsSUOIQKgaoeTW9pGqwV6T9mM+h5SM0BqW2LoWey7r1Nq/rRpqyUQVYdui2pHEbRPSsU7xCREGPhcRtX1E1J+KkO2U7BKbEo5NHOqQPcoQtdh394l1117WDrsmIGVtfAisO/ehf+Oy2Md1JnImoME1kuuc86lKvV4PFxcXuLy8xHg8xs3NDUajkd9kmRF4OhBcI8F0RW5w3Wg0cH5+7lMdGVmvaorOpuBkaVM8mI40nU5xcXHhFR8+TyYTTCaTR+RM15zonmZUekgkSDRYgOQlqo8EnSe+VhLAFFElFdykmqRC1R9OBnTCaE9NlaTio6SCv99LbZPqhPBvOma2MplVd2KKjx47RiDseyFV4qXYMuQkqSNsVYuYumPXSKkttW2F8vhD6s9LtKN1hNm/Y2RhU1JRhkjo6yo6wEWw11hEEtaRik0d5CLnNmS7qtqx6BoPQS6K7FRVGwLrCdBTsakC+VLx0q9/H0jkzEAHWjrEwIOCRkeLig/TGrXiIB0xEgeuNWHBBb6nJXhVmXgpDkcReP10pOjoM0pMoqFrV1TxseSM5I4klkSMxNlusPix2FCjm5rGAzxUCTw5OfHpeiRkTDdTUkFyFlJ8LJFWcvESiZkiFGEHHuyxWj1s8EsCEXpYR9gqD6GHBnleGqGwsO1Rya8qk5ZMxNLL9Lhl1IdQitNLtaP9uyhNat17RccPEbai55cEq1qE7jtEXvU7TznXpu+9FKy79lDa577O/akg2SGBSOQsADpeWZbl1CxN+5rP5zg7O/MFQTStkY4Z1R2WlmcFNyUVfNCJ4/k/BqgdNRWJ631YIETXR+naFcKu59FUOyVkmq7zUh03i5j6o2lQWu44lFpmj6WL/lUltkSs6iljm8A6biEViDZeV6lMj6G2Ah5vWmvP97HY0RK1dWlR60hFGdLwsdiQWEcmLJ6iWMRs9bHYkHjqfZax6cdmq6ci2SEhYX9I5CyCULSWZIBlo1lMgEUY6Bhr+hgruGnKGIsIvJR8/+dAHVVdZ0HFJ8syv9myrVBGhFLGQgqFpgF+bLbU9sjnGIEIrU2xx7Ak1truY3OEiXXkQokv/7ZkY1M14mOzIWHJRSyyvm6NSkhJKjrXx4yi+1QbP+c4CQ9IdkpISKgiEjkrQMjJIhmgesM0skajkSulryliVt15qetPngMlBnRwNc0xtn+PkocQma1KNad9IeYQ2/UoofUpVskJ2e1TsSNQTALKrE8JKR9Fx/7YUaReFKWXlTlGwnsk+yQkJCR8/EjkbA2UVGiKHlMebWqZOsJl1px8SpOtTSezzyFCod8LpYnx708NofZTdsF7IhKPUdYmdm1LQjkkmyUkJCQkJJRDImclEXLeGBFmUQEgr1LEHqHjfWoI2TNULMB+/lMnZUXYxB7Jdk9DsltCQkJCQkLCLpHI2YYIqT/2tf28PifkESNbZdOgEsJINktISEhISEhIeHlI5OwZWOcAJwf56Ui2S0hISEhISEhI+NSQyNmWkMhEQkJCQkJCQkJCQsJz4La52/vakzn3BsAQwNu9nTQhoTxeIbXNhOoitc+EqiK1zYSqIrXNhKri38iy7LPQP/ZKzgDAOferWZZ9e68nTUgogdQ2E6qM1D4TqorUNhOqitQ2E14iaoe+gISEhISEhISEhISEhIREzhISEhISEhISEhISEiqBQ5Cz7x7gnAkJZZDaZkKVkdpnQlWR2mZCVZHaZsKLw97XnCUkJCQkJCQkJCQkJCQ8RkprTEhISEhISEhISEhIqAD2Rs6ccz/tnPsXzrnfdM59Z1/nTUggnHN/xTn32jn3f8l7l865f+Cc+38/PF/I/37+Q3v9F865/+AwV53wKcA59w3n3P/inPsN59yvO+f+9If3U/tMOCiccw3n3D9yzv2fH9rmf/nh/dQ2EyoB59yRc+7/cM793Q9/p7aZ8KKxF3LmnDsC8N8C+A8B/A4Af9Q59zv2ce6EBMH/AOCnzXvfAfDLWZb9BIBf/vA3PrTPPwLg3/rwnf/uQztOSNgFFgD+bJZl/yaA3wPgT35og6l9JhwaUwC/N8uyfwfA7wTw086534PUNhOqgz8N4Dfk79Q2E1409qWc/W4Av5ll2b/MsmwG4K8D+Jk9nTshAQCQZdn/CuDavP0zAH7xw+tfBPAfy/t/PcuyaZZlvwXgN/G+HSckbB1Zln2VZdk/+fD6Hu8djR9Fap8JB0b2HoMPf558eGRIbTOhAnDO/RiA3w/gv5e3U9tMeNHYFzn7UQDfk7+//+G9hIRD44ssy74C3jvIAD7/8H5qswkHgXPuWwB+F4B/iNQ+EyqAD2lj/xTAawD/IMuy1DYTqoK/BODPAVjJe6ltJrxo7IucucB7qUxkQpWR2mzC3uGc6wD4mwD+TJZl/aKPBt5L7TNhJ8iybJll2e8E8GMAfrdz7t8u+Hhqmwl7gXPuDwB4nWXZr5X9SuC91DYTKod9kbPvA/iG/P1jAH6wp3MnJBTha+fclwDw4fn1h/dTm03YK5xzJ3hPzP5almV/68PbqX0mVAZZlt0C+BW8X6+T2mbCofGTAP6gc+5f4f1ymd/rnPurSG0z4YVjX+TsHwP4CefcjzvnTvF+Qebf2dO5ExKK8HcA/OyH1z8L4G/L+3/EOVd3zv04gJ8A8I8OcH0JnwCccw7AXwbwG1mW/UX5V2qfCQeFc+4z59z5h9dNAP8egP8bqW0mHBhZlv18lmU/lmXZt/Der/yfsyz7Y0htM+GF43gfJ8mybOGc+1MA/j6AIwB/JcuyX9/HuRMSCOfc/wTgpwC8cs59H8B/AeAXAPySc+5PAPjXAP4QAGRZ9uvOuV8C8M/xvpLen8yybHmQC0/4FPCTAP44gH/2YW0PAPwFpPaZcHh8CeAXP1S1qwH4pSzL/q5z7n9HapsJ1UQaNxNeNFyWpXTbhISEhISEhISEhISEQ2Nvm1AnJCQkJCQkJCQkJCQkxJHIWUJCQkJCQkJCQkJCQgWQyFlCQkJCQkJCQkJCQkIFkMhZQkJCQkJCQkJCQkJCBZDIWUJCQkJCQkJCQkJCQgWQyFlCQkJCQkJCQkJCQkIFkMhZQkJCQkJCQkJCQkJCBZDIWUJCQkJCQkJCQkJCQgXw/wNxlBC0dD8RVgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 1080x360 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"pyplot.figure(figsize=(15,5))\n",
"pyplot.imshow(torch.cat([r[0].sum(1).view(N, N).cpu() for r in res], 1), cmap=pyplot.cm.gray_r)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.1+"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
lang-uk/lang.org.ua | __notebooks/POS tagging and compression.ipynb | 1 | 17736 | {
"cells": [
{
"cell_type": "code",
"execution_count": 3,
"id": "d6215d5e",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-25T22:51:42.289906Z",
"start_time": "2022-01-25T22:51:41.049137Z"
}
},
"outputs": [],
"source": [
"import os, sys\n",
"sys.path = [\"/Users/dchaplinsky/Projects/lang-uk/lang.org.ua/languk/\"] + sys.path\n",
"os.environ[\"DJANGO_SETTINGS_MODULE\"] = \"languk.settings.dev\"\n",
"import django\n",
"\n",
"django.setup()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"id": "97d31865",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-25T22:51:43.049330Z",
"start_time": "2022-01-25T22:51:43.043502Z"
}
},
"outputs": [],
"source": [
"import pymongo\n",
"from django.conf import settings\n",
"from corpus.mongodb import db\n",
"from corpus.udpipe_model import Model as UDPipeModel"
]
},
{
"cell_type": "code",
"execution_count": 5,
"id": "50e5bbff",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-25T22:53:39.707242Z",
"start_time": "2022-01-25T22:51:43.921259Z"
}
},
"outputs": [],
"source": [
"model = UDPipeModel(settings.UDPIPE_MODEL_FILE)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"id": "20331227",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-26T00:03:36.071921Z",
"start_time": "2022-01-26T00:03:36.046511Z"
}
},
"outputs": [],
"source": [
"test_doc = db.fiction.find_one({\"_id\": \"e0555ead86335ee058bf2eef5758839f0f124ee7\"})"
]
},
{
"cell_type": "code",
"execution_count": 8,
"id": "e99a89ac",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-26T00:03:37.151159Z",
"start_time": "2022-01-26T00:03:37.130710Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"'e0555ead86335ee058bf2eef5758839f0f124ee7'"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"test_doc[\"_id\"]"
]
},
{
"cell_type": "code",
"execution_count": 9,
"id": "353d55c5",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-26T00:03:37.945211Z",
"start_time": "2022-01-26T00:03:37.839143Z"
}
},
"outputs": [],
"source": [
"import logging\n",
"logger = logging.getLogger(\"decompress\")\n",
"logger.setLevel(logging.INFO)\n",
"\n",
"from collections import OrderedDict\n",
"\n",
"from corpus.ud_converter import (\n",
" DECOMPRESS_UPOS_MAPPING,\n",
" DECOMPRESS_FEATURES_MAPPING,\n",
" DECOMPRESS_FEATURE_VALUES_MAPPING,\n",
" grouper\n",
")\n",
"\n",
"\n",
"def unpack_values(param_name, s):\n",
" def _unpack_value(v):\n",
" if param_name == \"ud_postags\":\n",
" try:\n",
" return DECOMPRESS_UPOS_MAPPING[v]\n",
" except KeyError:\n",
" logger.warning(\n",
" f\"Cannot find the upos '{v}' in the mapping, skipping it for now\"\n",
" )\n",
" return \"UNK\"\n",
"\n",
" elif param_name == \"ud_features\":\n",
" res = []\n",
"\n",
" for c_cat, c_val in grouper(v, 2):\n",
" try:\n",
" cat = DECOMPRESS_FEATURES_MAPPING[c_cat]\n",
" except KeyError:\n",
" logger.warning(\n",
" f\"Cannot find the feature '{c_cat}' in the mapping, skipping it for now\"\n",
" )\n",
" cat = \"UNK\"\n",
"\n",
" try:\n",
" val = DECOMPRESS_FEATURE_VALUES_MAPPING[cat][c_val]\n",
" except KeyError:\n",
" logger.warning(\n",
" f\"Cannot find the value '{c_val}' for the feature '{cat}' in the mapping, skipping it for now\"\n",
" )\n",
" \n",
" val = \"UNK\"\n",
"\n",
" res.append((cat, val))\n",
" return OrderedDict(res)\n",
"\n",
" else:\n",
" return v\n",
"\n",
" if param_name == \"ud_postags\":\n",
" return [[_unpack_value(w) for w in l] for l in s.split(\"\\n\")]\n",
" else:\n",
" return [[_unpack_value(w) for w in l.split(\" \")] for l in s.split(\"\\n\")]\n",
"\n",
"\n",
"def decompress(tokens=None, ud_lemmas=None, ud_features=None, ud_postags=None):\n",
" params = locals()\n",
"\n",
" assert any(\n",
" map(lambda x: x is not None, params.values())\n",
" ), \"at least one param should be not None\"\n",
"\n",
" zipped = {}\n",
"\n",
" for param_name, param_value in params.items():\n",
" if param_value is not None:\n",
"# if param_name == \"tokens\":\n",
"# # TODO: validate if this workaround can be properly fixed\n",
"# param_value = param_value.strip()\n",
" zipped[param_name] = unpack_values(param_name, param_value)\n",
" \n",
"\n",
" sentences_length = set(map(len, zipped.values()))\n",
" assert len(sentences_length) == 1, f\"Text contains different number of sentences: {sentences_length}\"\n",
"\n",
" res = []\n",
" param_names = list(zipped.keys())\n",
" param_values = list(zipped.values())\n",
"\n",
" for sent in zip(*param_values): \n",
" word_length = set(map(len, sent))\n",
"\n",
" assert len(sentences_length) == 1, f\"Text contains different number of words in sentence: {sent}\"\n",
"\n",
" res.append(\n",
" [OrderedDict(zip(param_names, word_info)) for word_info in zip(*sent)]\n",
" )\n",
"\n",
"\n",
" return res\n",
"\n",
"\n",
"_ = decompress(\n",
" tokens=test_doc[\"nlp\"][\"text\"][\"tokens\"],\n",
" ud_lemmas=test_doc[\"nlp\"][\"text\"][\"ud_lemmas\"],\n",
" ud_features=test_doc[\"nlp\"][\"text\"][\"ud_features\"],\n",
" ud_postags=test_doc[\"nlp\"][\"text\"][\"ud_postags\"],\n",
")\n"
]
},
{
"cell_type": "code",
"execution_count": 10,
"id": "bca41b30",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-26T00:03:41.623317Z",
"start_time": "2022-01-26T00:03:40.348185Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from ufal.udpipe import Sentence\n",
"\n",
"from deepdiff import DeepDiff\n",
"\n",
"def compare_article(article):\n",
" for f in [\"title\", \"text\"]:\n",
" if \"nlp\" not in article:\n",
" logger.warning(f\"Cannot find field 'nlp' in the document {article['_id']}\")\n",
" continue\n",
"\n",
" if f not in article[\"nlp\"]:\n",
" logger.warning(f\"Cannot find field {f} in the document {article['_id']}\")\n",
" continue\n",
"\n",
" if \"tokens\" not in article[\"nlp\"][f]:\n",
" logger.warning(\n",
" f\"Cannot find tokenized version of field {f} in the document {article['_id']}\"\n",
" )\n",
" continue\n",
"\n",
" if \"ud_lemmas\" not in article[\"nlp\"][f]:\n",
" logger.warning(\n",
" f\"Cannot find lemmatized version of field {f} in the document {article['_id']}\"\n",
" )\n",
" continue\n",
"\n",
" if \"ud_features\" not in article[\"nlp\"][f]:\n",
" logger.warning(\n",
" f\"Cannot find udpipe features of field {f} in the document {article['_id']}\"\n",
" )\n",
" continue\n",
"\n",
" if \"ud_postags\" not in article[\"nlp\"][f]:\n",
" logger.warning(\n",
" f\"Cannot find udpipe postags of field {f} in the document {article['_id']}\"\n",
" )\n",
" continue\n",
" \n",
"\n",
" decompressed_result = decompress(\n",
" tokens=article[\"nlp\"][f][\"tokens\"],\n",
" ud_lemmas=article[\"nlp\"][f][\"ud_lemmas\"],\n",
" ud_features=article[\"nlp\"][f][\"ud_features\"],\n",
" ud_postags=article[\"nlp\"][f][\"ud_postags\"],\n",
" )\n",
" udpipe_res = []\n",
"\n",
" for s in article[\"nlp\"][f][\"tokens\"].split(\"\\n\"):\n",
" tok_sent = Sentence()\n",
" for w in s.split(\" \"):\n",
" tok_sent.addWord(w)\n",
"\n",
" model.tag(tok_sent)\n",
"\n",
" udpipe_res.append(\n",
" [\n",
" {\n",
" \"tokens\": w.form,\n",
" \"ud_lemmas\": w.lemma,\n",
" \"ud_postags\": w.upostag,\n",
" \"ud_features\": OrderedDict(\n",
" (f.split(\"=\") for f in w.feats.split(\"|\"))\n",
" ) if w.feats else OrderedDict(),\n",
" }\n",
" for w in tok_sent.words[1:]\n",
" ]\n",
" )\n",
"\n",
" comparison = udpipe_res == decompressed_result\n",
" if not comparison:\n",
" print(f\"Comparing {f} for the {article['_id']}: {comparison}\")\n",
" \n",
" if not comparison:\n",
" with open(\"udpipe_res.json\", \"w\") as fp_out:\n",
" json.dump(udpipe_res, fp_out, indent=4, ensure_ascii=False, sort_keys=True)\n",
" with open(\"decompressed_result.json\", \"w\") as fp_out:\n",
" json.dump(decompressed_result, fp_out, indent=4, ensure_ascii=False, sort_keys=True)\n",
"\n",
" return False\n",
"\n",
" return True\n",
"\n",
"\n",
"compare_article(test_doc)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"id": "b0a68265",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-26T01:52:07.565621Z",
"start_time": "2022-01-26T00:03:41.626527Z"
}
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "21012dd8489d4d46924168acf473d752",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"0it [00:00, ?it/s]"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"Cannot find field title in the document 3eafcb11ef77e173a6c2cebdb49ca58baad12c71\n",
"Cannot find field text in the document 3eafcb11ef77e173a6c2cebdb49ca58baad12c71\n",
"Cannot find lemmatized version of field title in the document d6c6f1f0fc7c6bce04bd2a3b84d92a2d5f9bddb0\n",
"Cannot find lemmatized version of field text in the document d6c6f1f0fc7c6bce04bd2a3b84d92a2d5f9bddb0\n",
"Cannot find field 'nlp' in the document 80fc9ef85762e377b10eba8a36f31416962ceb16\n",
"Cannot find field 'nlp' in the document 80fc9ef85762e377b10eba8a36f31416962ceb16\n",
"Cannot find field 'nlp' in the document 011039174c48261a23a403c00d96c3754af9e4d9\n",
"Cannot find field 'nlp' in the document 011039174c48261a23a403c00d96c3754af9e4d9\n",
"Cannot find field 'nlp' in the document 44ca9029164a35c86a70469082770d9e8aa065b0\n",
"Cannot find field 'nlp' in the document 44ca9029164a35c86a70469082770d9e8aa065b0\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Comparing text for the 0d9b2526dffb75c06ecd52ad7d44f9c752c60cba: False\n",
"Comparison failed on 0d9b2526dffb75c06ecd52ad7d44f9c752c60cba\n"
]
}
],
"source": [
"from tqdm.notebook import tqdm\n",
"for test_doc in tqdm(db.fiction.find()):\n",
" if not compare_article(test_doc):\n",
" print(f\"Comparison failed on {test_doc['_id']}\")\n",
" break\n",
"\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 13,
"id": "e394af51",
"metadata": {
"ExecuteTime": {
"end_time": "2022-01-26T08:47:34.951623Z",
"start_time": "2022-01-26T08:47:34.946235Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"'https://javalibre.com.ua/java-book/book/1202'"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"test_doc[\"url\"]\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 6,
"id": "b817566c",
"metadata": {
"ExecuteTime": {
"end_time": "2021-12-15T13:16:15.211403Z",
"start_time": "2021-12-15T13:16:15.207009Z"
}
},
"outputs": [],
"source": [
"s = \"\"\"Звернімося просто до його творчої біографії яка починається ще на порозі юності збіркою 1910 року На білих островах і поки що доходить до книжок віршів виданих у 1957 1959 роках\n",
"За підрахунком одного з критиків М. Рильського у цілому це складає більше 25 збірок оригінальних поезій і понад 250 тисяч рядків поетичних перекладів а до того слід додати ще численні статті і дослідження з історії літератури народної творчості театру багато публіцистичних виступів\n",
"Початкове формування таланту М. Рильського припадає на роки 1907 1917\"\"\"\n",
"\n",
"s = \"так-сяк понад 250 тисяч\""
]
},
{
"cell_type": "code",
"execution_count": 15,
"id": "f5c8b23b",
"metadata": {
"ExecuteTime": {
"end_time": "2021-12-15T13:17:57.505845Z",
"start_time": "2021-12-15T13:17:57.498932Z"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"так так ADV\n",
"- - PUNCT\n",
"сяк сяк ADV\n",
"понад 250 понад 250 NUM\n",
"тисяч тисяча NOUN\n"
]
}
],
"source": [
"for ss in s.split(\"\\n\"):\n",
" tokenized = model.tokenize(ss)\n",
" for tok_sent in tokenized:\n",
" sent_lemmas = []\n",
" sent_postags = []\n",
" sent_features = []\n",
"\n",
" model.tag(tok_sent)\n",
"\n",
" for w in tok_sent.words[1:]:\n",
" print(w.form, w.lemma, w.upostag)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"id": "966b5d48",
"metadata": {
"ExecuteTime": {
"end_time": "2021-12-15T13:17:56.003289Z",
"start_time": "2021-12-15T13:17:56.000276Z"
}
},
"outputs": [],
"source": [
"model.tokenizer = model.model.newTokenizer(model.model.TOKENIZER_PRESEGMENTED)"
]
},
{
"cell_type": "code",
"execution_count": 26,
"id": "a6c19e82",
"metadata": {
"ExecuteTime": {
"end_time": "2021-12-15T13:23:09.513741Z",
"start_time": "2021-12-15T13:23:09.509577Z"
}
},
"outputs": [],
"source": [
"tokenizer = model.model.newTokenizer(model.model.TOKENIZER_NORMALIZED_SPACES)"
]
},
{
"cell_type": "code",
"execution_count": 30,
"id": "03cd238d",
"metadata": {
"ExecuteTime": {
"end_time": "2021-12-15T13:25:21.790161Z",
"start_time": "2021-12-15T13:25:21.784103Z"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"понад 250\n",
"понад 250\n",
"понад 250\n"
]
}
],
"source": [
"import ufal.udpipe\n",
"\n",
"\n",
"for tok in [model.model.TOKENIZER_PRESEGMENTED, model.model.TOKENIZER_NORMALIZED_SPACES, model.model.TOKENIZER_RANGES]:\n",
" tokenizer = model.model.newTokenizer(tok)\n",
" tokenizer.setText(s)\n",
"\n",
" error = ufal.udpipe.ProcessingError()\n",
" sentences = []\n",
"\n",
" sentence = ufal.udpipe.Sentence()\n",
" while tokenizer.nextSentence(sentence, error):\n",
" sentences.append(sentence)\n",
" sentence = ufal.udpipe.Sentence()\n",
"\n",
" print(sentences[0].words[4].form)\n",
" "
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "6eb65b2d",
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.12"
}
},
"nbformat": 4,
"nbformat_minor": 5
}
| mit |
california-civic-data-coalition/python-calaccess-notebooks | calaccess-exploration/decoding-filing-periods.ipynb | 1 | 27307 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# Decoding Filing Periods"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The raw data tables mix together filings from different reporting periods (e.g. quarterlys vs. semi-annual vs. pre-elections). But we need these filings to be sorted (or at least sortable) so that or users, for example, can compare the performance of two candidates in the same reporting period."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are two vectors at play here:\n",
"1. The \"Statement Type\", as described in CAL-ACCESS parlance, which indicates the length of time covered by the filing and how close it was filed to the election.\n",
"2. The actual time interval the filing covers, denoted by a start date and an end date."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This notebook is pulling data from the downloads-website's dev database, which was last updated on..."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from calaccess_processed.models.tracking import ProcessedDataVersion"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"<ProcessedDataVersion: 2016-09-26 11:20:39+00:00>"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ProcessedDataVersion.objects.latest()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Will also need to execute some raw SQL, so I'll import a helper function in order to make the results more readable:"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from project import sql_to_agate"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's start by examining the distinct values of the statement type on `CVR_CAMPAIGN_DISCLOSURE_CD`. And let's narrow the scope to only the Form 460 filings."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|--------+---------|\n",
"| upper | count |\n",
"|--------+---------|\n",
"| SA | 62,439 |\n",
"| PE | 48,984 |\n",
"| QT | 4,208 |\n",
"| TS | 4,152 |\n",
"| SY | 1,829 |\n",
"| SE | 696 |\n",
"| ** | 96 |\n",
"| | 56 |\n",
"| PR | 5 |\n",
"| S2 | 4 |\n",
"| S1 | 3 |\n",
"| QS | 2 |\n",
"| YE | 1 |\n",
"| S | 1 |\n",
"|--------+---------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT UPPER(\"STMT_TYPE\"), COUNT(*)\n",
" FROM \"CVR_CAMPAIGN_DISCLOSURE_CD\"\n",
" WHERE \"FORM_TYPE\" = 'F460'\n",
" GROUP BY 1\n",
" ORDER BY COUNT(*) DESC;\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Not all of these values are defined, as previously noted in our [docs](http://calaccess.californiacivicdata.org/documentation/calaccess-files/cvr-campaign-disclosure-cd/#fields):\n",
"* `PR` might be pre-election\n",
"* `QS` is pro probably quarterly statement\n",
"* `YE` might be...I don't know \"Year-end\"?\n",
"* `S` is probably semi-annual\n",
"\n",
"Maybe come back later and look at the actual filings. There aren't that many."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There's another similar-named column on `FILER_FILINGS_CD`, but this seems to be a completely different thing:"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|-------------+----------------------+------------|\n",
"| STMNT_TYPE | CODE_DESC | count |\n",
"|-------------+----------------------+------------|\n",
"| 10,004 | REDESIGNATE THE A... | 335 |\n",
"| 10,006 | LOG/AMENDMENT | 97,221 |\n",
"| 10,007 | AS FILED BY COMMI... | 1,281 |\n",
"| 10,002 | AMENDMENT | 108,166 |\n",
"| 10,003 | TERMINATION | 57,391 |\n",
"| 10,005 | LOG | 459,319 |\n",
"| 10,001 | ORIGINAL/INITIAL | 1,191,192 |\n",
"|-------------+----------------------+------------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT FF.\"STMNT_TYPE\", LU.\"CODE_DESC\", COUNT(*)\n",
" FROM \"FILER_FILINGS_CD\" FF\n",
" JOIN \"LOOKUP_CODES_CD\" LU\n",
" ON FF.\"STMNT_TYPE\" = LU.\"CODE_ID\"\n",
" AND LU.\"CODE_TYPE\" = 10000\n",
" GROUP BY 1, 2;\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"One of the tables that caught my eye is `FILING_PERIOD_CD`, which appears to have a row for each quarterly filing period:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|----------+-----------+------------+------------+-------------+--------------+------|\n",
"| id | PERIOD_ID | START_DATE | END_DATE | PERIOD_TYPE | PER_GRP_TYPE | ... |\n",
"|----------+-----------+------------+------------+-------------+--------------+------|\n",
"| 124,529 | 889 | 2182-01-01 | 2182-03-31 | 1,500 | 1,500 | ... |\n",
"| 124,530 | 890 | 2182-04-01 | 2182-06-30 | 1,500 | 1,500 | ... |\n",
"| 124,531 | 891 | 2182-07-01 | 2182-09-30 | 1,500 | 1,500 | ... |\n",
"| 124,532 | 826 | 2166-04-01 | 2166-06-30 | 1,500 | 1,500 | ... |\n",
"| 124,533 | 827 | 2166-07-01 | 2166-09-30 | 1,500 | 1,500 | ... |\n",
"| 124,534 | 828 | 2166-10-01 | 2166-12-31 | 1,500 | 1,500 | ... |\n",
"| 124,535 | 829 | 2167-01-01 | 2167-03-31 | 1,500 | 1,500 | ... |\n",
"| 124,536 | 830 | 2167-04-01 | 2167-06-30 | 1,500 | 1,500 | ... |\n",
"| 124,537 | 831 | 2167-07-01 | 2167-09-30 | 1,500 | 1,500 | ... |\n",
"| 124,538 | 832 | 2167-10-01 | 2167-12-31 | 1,500 | 1,500 | ... |\n",
"| 124,539 | 833 | 2168-01-01 | 2168-03-31 | 1,500 | 1,500 | ... |\n",
"| 124,540 | 834 | 2168-04-01 | 2168-06-30 | 1,500 | 1,500 | ... |\n",
"| 124,541 | 835 | 2168-07-01 | 2168-09-30 | 1,500 | 1,500 | ... |\n",
"| 124,542 | 836 | 2168-10-01 | 2168-12-31 | 1,500 | 1,500 | ... |\n",
"| 124,543 | 837 | 2169-01-01 | 2169-03-31 | 1,500 | 1,500 | ... |\n",
"| 124,544 | 838 | 2169-04-01 | 2169-06-30 | 1,500 | 1,500 | ... |\n",
"| 124,545 | 839 | 2169-07-01 | 2169-09-30 | 1,500 | 1,500 | ... |\n",
"| 124,546 | 840 | 2169-10-01 | 2169-12-31 | 1,500 | 1,500 | ... |\n",
"| 124,547 | 841 | 2170-01-01 | 2170-03-31 | 1,500 | 1,500 | ... |\n",
"| 124,548 | 842 | 2170-04-01 | 2170-06-30 | 1,500 | 1,500 | ... |\n",
"| ... | ... | ... | ... | ... | ... | ... |\n",
"|----------+-----------+------------+------------+-------------+--------------+------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT *\n",
" FROM \"FILING_PERIOD_CD\"\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Every period is described as a quarter, and the records are equally divided among them:"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|--------------+--------|\n",
"| PERIOD_DESC | count |\n",
"|--------------+--------|\n",
"| QUARTER 3 | 362 |\n",
"| QUARTER 4 | 362 |\n",
"| QUARTER 1 | 362 |\n",
"| QUARTER 2 | 362 |\n",
"|--------------+--------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT \"PERIOD_DESC\", COUNT(*)\n",
" FROM \"FILING_PERIOD_CD\"\n",
" GROUP BY 1;\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The difference between every `START_DATE` and `END_DATE` is actually a three-month interval:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|-----------+--------|\n",
"| duration | count |\n",
"|-----------+--------|\n",
"| 89 | 275 |\n",
"| 91 | 724 |\n",
"| 90 | 449 |\n",
"|-----------+--------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT \"END_DATE\" - \"START_DATE\" AS duration, COUNT(*)\n",
" FROM \"FILING_PERIOD_CD\"\n",
" GROUP BY 1;\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And they have covered every year between 1973 and 2334 (how optimistic!):"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|--------+--------|\n",
"| year | count |\n",
"|--------+--------|\n",
"| 2,334 | 4 |\n",
"| 2,333 | 4 |\n",
"| 2,332 | 4 |\n",
"| 2,331 | 4 |\n",
"| 2,330 | 4 |\n",
"| 2,329 | 4 |\n",
"| 2,328 | 4 |\n",
"| 2,327 | 4 |\n",
"| 2,326 | 4 |\n",
"| 2,325 | 4 |\n",
"| 2,324 | 4 |\n",
"| 2,323 | 4 |\n",
"| 2,322 | 4 |\n",
"| 2,321 | 4 |\n",
"| 2,320 | 4 |\n",
"| 2,319 | 4 |\n",
"| 2,318 | 4 |\n",
"| 2,317 | 4 |\n",
"| 2,316 | 4 |\n",
"| 2,315 | 4 |\n",
"| ... | ... |\n",
"|--------+--------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT DATE_PART('year', \"START_DATE\")::int as year, COUNT(*)\n",
" FROM \"FILING_PERIOD_CD\"\n",
" GROUP BY 1\n",
" ORDER BY 1 DESC;\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Filings are linked to filing periods via `FILER_FILINGS_CD.PERIOD_ID`. While that column is not always populated, it is if you limit your results to just the Form 460 filings:"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|------------+------------+------------+-------------+--------|\n",
"| PERIOD_ID | START_DATE | END_DATE | PERIOD_DESC | count |\n",
"|------------+------------+------------+-------------+--------|\n",
"| 450 | 2072-04-01 | 2072-06-30 | QUARTER 2 | 1 |\n",
"| 227 | 2016-07-01 | 2016-09-30 | QUARTER 3 | 53 |\n",
"| 226 | 2016-04-01 | 2016-06-30 | QUARTER 2 | 2,612 |\n",
"| 225 | 2016-01-01 | 2016-03-31 | QUARTER 1 | 2,786 |\n",
"| 224 | 2015-10-01 | 2015-12-31 | QUARTER 4 | 282 |\n",
"| 223 | 2015-07-01 | 2015-09-30 | QUARTER 3 | 2,330 |\n",
"| 222 | 2015-04-01 | 2015-06-30 | QUARTER 2 | 409 |\n",
"| 221 | 2015-01-01 | 2015-03-31 | QUARTER 1 | 2,780 |\n",
"| 220 | 2014-10-01 | 2014-12-31 | QUARTER 4 | 2,934 |\n",
"| 219 | 2014-07-01 | 2014-09-30 | QUARTER 3 | 2,676 |\n",
"| 218 | 2014-04-01 | 2014-06-30 | QUARTER 2 | 1,563 |\n",
"| 217 | 2014-01-01 | 2014-03-31 | QUARTER 1 | 4,522 |\n",
"| 216 | 2013-10-01 | 2013-12-31 | QUARTER 4 | 452 |\n",
"| 215 | 2013-07-01 | 2013-09-30 | QUARTER 3 | 2,595 |\n",
"| 214 | 2013-04-01 | 2013-06-30 | QUARTER 2 | 488 |\n",
"| 213 | 2013-01-01 | 2013-03-31 | QUARTER 1 | 2,881 |\n",
"| 212 | 2012-10-01 | 2012-12-31 | QUARTER 4 | 3,181 |\n",
"| 211 | 2012-07-01 | 2012-09-30 | QUARTER 3 | 2,710 |\n",
"| 210 | 2012-04-01 | 2012-06-30 | QUARTER 2 | 1,537 |\n",
"| 209 | 2012-01-01 | 2012-03-31 | QUARTER 1 | 4,379 |\n",
"| ... | ... | ... | ... | ... |\n",
"|------------+------------+------------+-------------+--------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT ff.\"PERIOD_ID\", fp.\"START_DATE\", fp.\"END_DATE\", fp.\"PERIOD_DESC\", COUNT(*)\n",
" FROM \"FILER_FILINGS_CD\" ff\n",
" JOIN \"CVR_CAMPAIGN_DISCLOSURE_CD\" cvr\n",
" ON ff.\"FILING_ID\" = cvr.\"FILING_ID\"\n",
" AND ff.\"FILING_SEQUENCE\" = cvr.\"AMEND_ID\"\n",
" AND cvr.\"FORM_TYPE\" = 'F460'\n",
" JOIN \"FILING_PERIOD_CD\" fp\n",
" ON ff.\"PERIOD_ID\" = fp.\"PERIOD_ID\"\n",
" GROUP BY 1, 2, 3, 4\n",
" ORDER BY fp.\"START_DATE\" DESC;\n",
" \"\"\"\n",
").print_table()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Also, is Schwarzenegger running this cycle? Who else could be filing from so far into the future?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"AAANNNNYYYway...Also need to check to make sure the join between `FILER_FILINGS_CD` and `CVR_CAMPAIGN_DISCLOSURE_CD` isn't filtering out too many filings:"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|------------+-----------+---------------------------------------------------------------|\n",
"| FILING_ID | FORM_TYPE | FILER_NAML |\n",
"|------------+-----------+---------------------------------------------------------------|\n",
"| 591,533 | F460 | Damian Jones for Assembly |\n",
"| 602,619 | F460 | United Teachers Los Angeles-Political Action Council of E... |\n",
"| 670,063 | F460 | Carl Washington For CA St Assembly 52nd District |\n",
"| 786,716 | F460 | Ernst & Young LLP - Los Angeles Political Action Committee |\n",
"| 983,030 | F460 | John Doe for Senate |\n",
"| 1,643,669 | F460 | TEST EFS 2012 CAMPAIGN 460 |\n",
"| 1,643,696 | F460 | TEST EFS 2012 460 CTL CMTT |\n",
"|------------+-----------+---------------------------------------------------------------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT cvr.\"FILING_ID\", cvr.\"FORM_TYPE\", cvr.\"FILER_NAML\"\n",
" FROM \"CVR_CAMPAIGN_DISCLOSURE_CD\" cvr\n",
" LEFT JOIN \"FILER_FILINGS_CD\" ff\n",
" ON cvr.\"FILING_ID\" = ff.\"FILING_ID\"\n",
" AND cvr.\"AMEND_ID\" = ff.\"FILING_SEQUENCE\" \n",
" WHERE cvr.\"FORM_TYPE\" = 'F460'\n",
" AND (ff.\"FILING_ID\" IS NULL OR ff.\"FILING_SEQUENCE\" IS NULL)\n",
" ORDER BY cvr.\"FILING_ID\";\n",
" \"\"\"\n",
").print_table(max_column_width=60)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So only a handful, mostly local campaigns or just nonsense test data."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So another important thing to check is how well these the dates from the filing period look-up records line up with the dates on the Form 460 filing records. It would be bad if the `CVR_CAMPAIGN_DISCLOSURE_CD.FROM_DATE` were before `FILING_PERIOD_CD.START_DATE` or if `CVR_CAMPAIGN_DISCLOSURE_CD.THRU_DATE` were after `FILING_PERIOD_CD.END_DATE`."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|--------------------------------------------+---------|\n",
"| test | count |\n",
"|--------------------------------------------+---------|\n",
"| filing from_date before period start_date | 12 |\n",
"| filing thru_date after period end_date | 54,769 |\n",
"| okay | 67,688 |\n",
"|--------------------------------------------+---------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT \n",
" CASE \n",
" WHEN cvr.\"FROM_DATE\" < fp.\"START_DATE\" THEN 'filing from_date before period start_date'\n",
" WHEN cvr.\"THRU_DATE\" > fp.\"END_DATE\" THEN 'filing thru_date after period end_date'\n",
" ELSE 'okay'\n",
" END as test,\n",
" COUNT(*) \n",
" FROM \"CVR_CAMPAIGN_DISCLOSURE_CD\" cvr\n",
" JOIN \"FILER_FILINGS_CD\" ff\n",
" ON cvr.\"FILING_ID\" = ff.\"FILING_ID\"\n",
" AND cvr.\"AMEND_ID\" = ff.\"FILING_SEQUENCE\"\n",
" JOIN \"FILING_PERIOD_CD\" fp\n",
" ON ff.\"PERIOD_ID\" = fp.\"PERIOD_ID\"\n",
" WHERE cvr.\"FORM_TYPE\" = 'F460'\n",
" GROUP BY 1;\n",
" \"\"\"\n",
").print_table(max_column_width=60)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So half of the time, the `THRU_DATE` on the filing is later than the `FROM_DATE` on the filing period. How big of a difference can exist between these two dates?"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|------------+---------|\n",
"| date_diff | count |\n",
"|------------+---------|\n",
"| 91 | 23,057 |\n",
"| 92 | 16,499 |\n",
"| 47 | 3,029 |\n",
"| 52 | 1,722 |\n",
"| 49 | 1,657 |\n",
"| 275 | 1,605 |\n",
"| 50 | 1,586 |\n",
"| 23 | 1,509 |\n",
"| 22 | 394 |\n",
"| 183 | 343 |\n",
"| 18 | 301 |\n",
"| 16 | 260 |\n",
"| 20 | 205 |\n",
"| 51 | 186 |\n",
"| 21 | 173 |\n",
"| 19 | 166 |\n",
"| 4 | 137 |\n",
"| 17 | 113 |\n",
"| 32 | 96 |\n",
"| 6 | 92 |\n",
"| ... | ... |\n",
"|------------+---------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT \n",
" cvr.\"THRU_DATE\" - fp.\"END_DATE\" as date_diff,\n",
" COUNT(*) \n",
" FROM \"CVR_CAMPAIGN_DISCLOSURE_CD\" cvr\n",
" JOIN \"FILER_FILINGS_CD\" ff\n",
" ON cvr.\"FILING_ID\" = ff.\"FILING_ID\"\n",
" AND cvr.\"AMEND_ID\" = ff.\"FILING_SEQUENCE\"\n",
" JOIN \"FILING_PERIOD_CD\" fp\n",
" ON ff.\"PERIOD_ID\" = fp.\"PERIOD_ID\"\n",
" WHERE cvr.\"FORM_TYPE\" = 'F460'\n",
" AND cvr.\"THRU_DATE\" > fp.\"END_DATE\"\n",
" GROUP BY 1\n",
" ORDER BY COUNT(*) DESC;\n",
" \"\"\"\n",
").print_table(max_column_width=60)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ugh. Looks like, in most of the problem cases, the from date can be a whole quarter later than the end date of the filing period. Let's take a closer look at these..."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|------------+----------+------------+------------+------------+-------------|\n",
"| FILING_ID | AMEND_ID | FROM_DATE | THRU_DATE | START_DATE | END_DATE |\n",
"|------------+----------+------------+------------+------------+-------------|\n",
"| 2,025,877 | 1 | 2016-07-01 | 2016-12-31 | 2016-07-01 | 2016-09-30 |\n",
"| 2,025,893 | 0 | 2016-07-01 | 2016-12-31 | 2016-07-01 | 2016-09-30 |\n",
"| 2,025,877 | 0 | 2016-07-01 | 2016-12-31 | 2016-07-01 | 2016-09-30 |\n",
"| 2,002,159 | 0 | 2016-07-01 | 2016-12-31 | 2016-07-01 | 2016-09-30 |\n",
"| 2,002,159 | 1 | 2016-07-01 | 2016-12-31 | 2016-07-01 | 2016-09-30 |\n",
"| 2,076,271 | 0 | 2016-01-01 | 2016-07-01 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,670 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,664 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,657 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,650 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,624 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,622 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,584 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,575 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,574 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,571 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,566 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,537 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,444 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| 2,063,428 | 0 | 2016-01-01 | 2016-06-30 | 2016-01-01 | 2016-03-31 |\n",
"| ... | ... | ... | ... | ... | ... |\n",
"|------------+----------+------------+------------+------------+-------------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT \n",
" cvr.\"FILING_ID\",\n",
" cvr.\"AMEND_ID\",\n",
" cvr.\"FROM_DATE\",\n",
" cvr.\"THRU_DATE\",\n",
" fp.\"START_DATE\",\n",
" fp.\"END_DATE\"\n",
" FROM \"CVR_CAMPAIGN_DISCLOSURE_CD\" cvr\n",
" JOIN \"FILER_FILINGS_CD\" ff\n",
" ON cvr.\"FILING_ID\" = ff.\"FILING_ID\"\n",
" AND cvr.\"AMEND_ID\" = ff.\"FILING_SEQUENCE\"\n",
" JOIN \"FILING_PERIOD_CD\" fp\n",
" ON ff.\"PERIOD_ID\" = fp.\"PERIOD_ID\"\n",
" WHERE cvr.\"FORM_TYPE\" = 'F460'\n",
" AND 90 < cvr.\"THRU_DATE\" - fp.\"END_DATE\" \n",
" AND cvr.\"THRU_DATE\" - fp.\"END_DATE\" < 93\n",
" ORDER BY cvr.\"THRU_DATE\" DESC;\n",
" \"\"\"\n",
").print_table(max_column_width=60)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So, actually, this sort of makes sense: Quarterly filings are for three month intervals, while the semi-annual filings are for six month intervals. And `FILING_PERIOD_CD` only has records for three month intervals. Let's test this theory by getting the distinct `CVR_CAMPAIGN_DISCLOSURE_CD.STMT_TYPE` values from these records:"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"|--------+---------|\n",
"| upper | count |\n",
"|--------+---------|\n",
"| SA | 37,523 |\n",
"| TS | 1,393 |\n",
"| PE | 502 |\n",
"| QT | 85 |\n",
"| ** | 19 |\n",
"| SY | 16 |\n",
"| | 6 |\n",
"| SE | 4 |\n",
"| S2 | 4 |\n",
"| S1 | 3 |\n",
"| S | 1 |\n",
"|--------+---------|\n"
]
}
],
"source": [
"sql_to_agate(\n",
" \"\"\"\n",
" SELECT UPPER(cvr.\"STMT_TYPE\"), COUNT(*)\n",
" FROM \"CVR_CAMPAIGN_DISCLOSURE_CD\" cvr\n",
" JOIN \"FILER_FILINGS_CD\" ff\n",
" ON cvr.\"FILING_ID\" = ff.\"FILING_ID\"\n",
" AND cvr.\"AMEND_ID\" = ff.\"FILING_SEQUENCE\"\n",
" JOIN \"FILING_PERIOD_CD\" fp\n",
" ON ff.\"PERIOD_ID\" = fp.\"PERIOD_ID\"\n",
" WHERE cvr.\"FORM_TYPE\" = 'F460'\n",
" AND 90 < cvr.\"THRU_DATE\" - fp.\"END_DATE\" \n",
" AND cvr.\"THRU_DATE\" - fp.\"END_DATE\" < 93\n",
" GROUP BY 1\n",
" ORDER BY COUNT(*) DESC;\n",
" \"\"\"\n",
").print_table(max_column_width=60)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"At least this is mostly true."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Django Shell-Plus",
"language": "python",
"name": "django_extensions"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
CompareML/CompareML-Manuscript | ReproducingMLpipelines/Paper1/.ipynb_checkpoints/paper1selection-checkpoint.ipynb | 1 | 35071 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Classification on paper1 feature selection\n",
"\n",
"Summary of paper1 feature selection:\n",
"- Data:\n",
" - Train: 38*7129 (27ALL/11AML)\n",
" - Test: 34*7129 (20ALL/ 14 AML)\n",
"- Preprocessing:\n",
" - Thresholding\n",
" - Filtering\n",
" - Transformation\n",
" - Normalization\n",
"- Feature Selection:\n",
" - Neighborhood analysis\n",
" - Informative genes selection\n",
" \n",
" <img src=\"../../Part3 Related Articles/paper1.png\">"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"suppressMessages(library(e1071))\n",
"suppressMessages(library(fastAdaboost))\n",
"suppressMessages(library(caret))\n",
"suppressMessages(library(sparsediscrim))\n",
"suppressMessages(library(tree))\n",
"suppressMessages(library(fastAdaboost))\n",
"suppressMessages(library(bnlearn))\n",
"library(ropls)\n",
"library(MASS)\n",
"\n",
"set.seed(201703)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Data"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"# golub_test_50, golub_test_response, golub_train_50, golub_train_response\n",
"load(\"../transformed data/golub50gene.rda\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Paper1 classifiier"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"get_p = function(train_d, train_r){\n",
" tr_m_aml = colMeans(train_d[train_r == \"AML\",])\n",
" tr_sd_aml = apply(train_d[train_r == \"AML\",], 2, sd)\n",
" tr_m_all = colMeans(train_d[train_r == \"ALL\",])\n",
" tr_sd_all = apply(train_d[train_r == \"ALL\",], 2, sd)\n",
" p = (tr_m_aml-tr_m_all)/(tr_sd_aml+tr_sd_all)\n",
" return(p)\n",
"}\n",
"classifier1 = function(train_p, train_r, test_p, test_r){\n",
" train_m_aml = colMeans(train_p[train_r == \"AML\",])\n",
" train_m_all = colMeans(train_p[train_r ==\"ALL\",])\n",
" b = (train_m_aml+train_m_all)/2\n",
" p = get_p(train_p, train_r)\n",
" #train\n",
" train_vote = t(p*t(sweep(train_p, 2, b)))\n",
" train_V1 = apply(train_vote, 1, function(x) sum(x[x>0]))\n",
" train_V2 = abs(apply(train_vote, 1, function(x) sum(x[x<=0])))\n",
" train_pred = (train_V1-train_V2)/(train_V1+train_V2)\n",
" train_pred_r = ifelse(abs(train_pred)>0.3, ifelse(train_pred>0, \"AML\", \"ALL\"), \"Uncertain\")\n",
" train_table = table(Train_Predict = train_pred_r, Train_Actual = train_r)\n",
" ##train_table\n",
" #test\n",
" test_vote = t(p*t(sweep(test_p, 2, b)))\n",
" test_V1 = apply(test_vote, 1, function(x) sum(x[x>0]))\n",
" test_V2 = abs(apply(test_vote, 1, function(x) sum(x[x<=0])))\n",
" test_pred = (test_V1-test_V2)/(test_V1+test_V2)\n",
" test_pred_r = ifelse(abs(test_pred)>0.3, ifelse(test_pred>0, \"AML\", \"ALL\"), \"Uncertain\")\n",
" test_table = table(Test_Predict = test_pred_r, Test_Actual = test_r)\n",
" ##test_table\n",
" return(list(train = train_table, test = test_table))\n",
"}"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 26 0\n",
" AML 0 11\n",
" Uncertain 1 0"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 19 0\n",
" AML 0 12\n",
" Uncertain 1 2"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"paper1 = classifier1(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper1$train\n",
"paper1$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Paper 3 classifier\n",
"\n",
"- NN"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 19 0\n",
" AML 1 14"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# helper function\n",
"cl_nn_helper = function(new_s, train, train_label){\n",
" # use Pearson correlation\n",
" corr = apply(train, 1, cor, new_s)\n",
" train_label[corr==max(corr)]\n",
"}\n",
"\n",
"classifier3nn = function(train_p, train_r, test_p, test_r){\n",
" nn_train_pr_p1 = apply(train_p,1, cl_nn_helper, train_p, train_r)\n",
" nn_test_pr_p1 = apply(test_p,1, cl_nn_helper, train_p, train_r)\n",
" train_table = table(Train_Predict = nn_train_pr_p1, Train_Actual =train_r)\n",
" test_table = table(Test_Predict = nn_test_pr_p1, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper3nn = classifier3nn(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper3nn$train\n",
"paper3nn$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- SVM"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predicted ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predicted ALL AML\n",
" ALL 20 1\n",
" AML 0 13"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# linear SVM\n",
"classifier3lsvm = function(train_p, train_r, test_p, test_r){\n",
" r_train = data.frame(train_p, Y = factor(train_r))\n",
" r_test =data.frame( test_p, Y = factor(test_r))\n",
" svm_linear = svm(Y~., data = r_train)\n",
" svm_l_trpr = predict(svm_linear, r_train)\n",
" svm_l_tepr = predict(svm_linear, newdata = r_test)\n",
" train_table = table(Train_Predicted = svm_l_trpr, Train_Actual = train_r)\n",
" test_table = table(Test_Predicted = svm_l_tepr, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper3lsvm = classifier3lsvm(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper3lsvm$train\n",
"paper3lsvm$test"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predicted ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predicted ALL AML\n",
" ALL 20 1\n",
" AML 0 13"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"classifier3qsvm = function(train_p, train_r, test_p, test_r){\n",
" r_train = data.frame(train_p, Y = factor(train_r))\n",
" r_test =data.frame( test_p, Y = factor(test_r))\n",
" svm_quad = svm(Y~., data = r_train, kernel = \"polynomial\", degree = 2, gamma =0.01, coef0 = 100)\n",
" svm_q_trpr = predict(svm_quad, r_train )\n",
" svm_q_tepr = predict(svm_quad, newdata = r_test)\n",
" train_table = table(Train_Predicted = svm_q_trpr, Train_Actual = train_r)\n",
" test_table = table(Test_Predicted = svm_q_tepr, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper3qsvm = classifier3qsvm(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper3qsvm$train\n",
"paper3qsvm$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Adaboost"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 18 1\n",
" AML 2 13"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"classifier3Ada = function(train_p, train_r, test_p, test_r){\n",
" r_train_p1 = data.frame(train_p, Y = factor(train_r))\n",
" r_test_p1 =data.frame( test_p, Y = factor(test_r))\n",
" ada_cl_p1 = adaboost(Y~., data = r_train_p1, 100)\n",
" ada_train_pr_p1 = predict(ada_cl_p1, r_train_p1)\n",
" ada_test_pr_p1 = predict(ada_cl_p1, newdata = r_test_p1)\n",
" train_table = table(Train_Predict = ada_train_pr_p1$class, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = ada_test_pr_p1$class, Test_Actual =test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper3Ada = classifier3Ada(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper3Ada$train\n",
"paper3Ada$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Paper 6 classifier"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"pca_helper = function(train_p, train_r, test_p, test_r, K=3){\n",
" pca_slt = getLoadingMN(opls(train_p, printL = F, predI = K))\n",
" pca_train_s = t(t(pca_slt)%*%t(train_p))\n",
" pca_test_s = t(t(pca_slt)%*%t(test_p))\n",
" return(list(pca_train = pca_train_s, pca_test = pca_test_s))\n",
"}\n",
"pls_helper = function(train_p, train_r, test_p, test_r, K=3){\n",
" pls_slt = getLoadingMN(opls(train_p, train_r, printL = F, predI = K))\n",
" pls_train_s = t(t(pls_slt)%*%t(train_p))\n",
" pls_test_s = t(t(pls_slt)%*%t(test_p))\n",
" return(list(pls_train = pls_train_s, pls_test = pls_test_s))\n",
"}\n",
"\n",
"classifier6logit = function(train_p, train_r, test_p, test_r, dr = \"pca\"){\n",
" if(dr == \"pca\"){\n",
" pca_result = pca_helper(train_p, train_r, test_p, test_r)\n",
" train_data = data.frame(response = train_r, pca_result$pca_train)\n",
" test_data = pca_result$pca_test\n",
" }else{\n",
" pls_result = pls_helper(train_p, train_r, test_p, test_r)\n",
" train_data = data.frame(response = train_r, pls_result$pls_train)\n",
" test_data = pls_result$pls_test\n",
" } \n",
" ld_s = train(response~., data = train_data, method = \"glm\", family = \"binomial\", trControl = trainControl(method = \"LOOCV\"))\n",
" ld_tr = predict(ld_s)\n",
" ld_te = predict(ld_s, data.frame(test_data))\n",
" ld_ac = mean(ld_te == test_r)\n",
" ld_re = c(LOOCV = ld_s$results$Accuracy, Test = ld_ac)\n",
" train_table = table(Train_Predict = ld_tr, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = ld_te, Test_Actual =test_r)\n",
" return(list(train = train_table, test = test_table, re = ld_re))\n",
"}\n",
"classifier6qda = function(train_p, train_r, test_p, test_r, dr= \"pca\"){\n",
" if(dr == \"pca\"){\n",
" pca_result = pca_helper(train_p, train_r, test_p, test_r)\n",
" train_data = data.frame(response = train_r, pca_result$pca_train)\n",
" test_data = pca_result$pca_test\n",
" }else{\n",
" pls_result = pls_helper(train_p, train_r, test_p, test_r)\n",
" train_data = data.frame(response = train_r, pls_result$pls_train)\n",
" test_data = pls_result$pls_test\n",
" } \n",
" qda_s = train(response~., data = train_data, method = \"qda\", trControl = trainControl(method = \"LOOCV\"))\n",
" qda_tr = predict(qda_s)\n",
" qda_te = predict(qda_s, data.frame(test_data))\n",
" qda_ac = mean(qda_te == test_r)\n",
" qda_re = c(LOOCV = qda_s$results$Accuracy, Test = qda_ac)\n",
" train_table = table(Train_Predict = qda_tr, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = qda_te, Test_Actual =test_r)\n",
" return(list(train = train_table, test = test_table, re = qda_re))\n",
"}\n",
"classifierlogit = function(train_p, train_r, test_p, test_r){\n",
" train_data = data.frame(response = train_r, train_p)\n",
" test_data = test_p\n",
" ld_s = train(response~., data = train_data, method = \"glm\", family = \"binomial\", trControl = trainControl(method = \"LOOCV\"))\n",
" ld_tr = predict(ld_s)\n",
" ld_te = predict(ld_s, data.frame(test_data))\n",
" ld_ac = mean(ld_te == test_r)\n",
" ld_re = c(LOOCV = ld_s$results$Accuracy, Test = ld_ac)\n",
" train_table = table(Train_Predict = ld_tr, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = ld_te, Test_Actual =test_r)\n",
" return(list(train = train_table, test = test_table, re = ld_re))\n",
"}\n",
"classifierqda = function(train_p, train_r, test_p, test_r){\n",
" train_data = data.frame(response = train_r, train_p)\n",
" test_data = test_p\n",
" qda_s = train(response~., data = train_data, method = \"qda\", trControl = trainControl(method = \"LOOCV\"))\n",
" qda_tr = predict(qda_s)\n",
" qda_te = predict(qda_s, data.frame(test_data))\n",
" qda_ac = mean(qda_te == test_r)\n",
" qda_re = c(LOOCV = qda_s$results$Accuracy, Test = qda_ac)\n",
" train_table = table(Train_Predict = qda_tr, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = qda_te, Test_Actual =test_r)\n",
" return(list(train = train_table, test = test_table, re = qda_re))\n",
"}"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1] \"pca, logit\"\n"
]
},
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 20 1\n",
" AML 0 13"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1] \"pca, qda\"\n"
]
},
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 20 2\n",
" AML 0 12"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1] \"pls, logit\"\n"
]
},
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 20 1\n",
" AML 0 13"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1] \"pls, qda\"\n"
]
},
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 20 1\n",
" AML 0 13"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1] \"logit\"\n"
]
},
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 12 2\n",
" AML 8 12"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1] \"qda\"\n",
"Something is wrong; all the Accuracy metric values are missing:\n",
" Accuracy Kappa \n",
" Mode:logical Mode:logical \n",
" NA's:1 NA's:1 \n"
]
},
{
"ename": "ERROR",
"evalue": "Error: Stopping\n",
"output_type": "error",
"traceback": [
"Error: Stopping\nTraceback:\n",
"1. classifierqda(golub_train_50, golub_train_response, golub_test_50, \n . golub_test_response)",
"2. train(response ~ ., data = train_data, method = \"qda\", trControl = trainControl(method = \"LOOCV\")) # at line 67 of file <text>",
"3. train.formula(response ~ ., data = train_data, method = \"qda\", \n . trControl = trainControl(method = \"LOOCV\"))",
"4. train(x, y, weights = w, ...)",
"5. train.default(x, y, weights = w, ...)",
"6. stop(\"Stopping\", call. = FALSE)"
]
}
],
"source": [
"options(warn=-1)\n",
"pca_logit = classifier6logit(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"print(\"pca, logit\")\n",
"pca_logit$train\n",
"pca_logit$test\n",
"pca_qda = classifier6qda(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"print(\"pca, qda\")\n",
"pca_qda$train\n",
"pca_qda$test\n",
"pls_logit = classifier6logit(golub_train_50, golub_train_response, golub_test_50, golub_test_response, \"pls\")\n",
"print(\"pls, logit\")\n",
"pls_logit$train\n",
"pls_logit$test\n",
"pls_qda = classifier6qda(golub_train_50, golub_train_response, golub_test_50, golub_test_response, \"pls\")\n",
"print(\"pls, qda\")\n",
"pls_qda$train\n",
"pls_qda$test\n",
"print(\"logit\")\n",
"logit = classifierlogit(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"logit$train\n",
"logit$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Paper 9 classifier"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- NN"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 26 0\n",
" AML 1 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 19 0\n",
" AML 1 14"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Distance measure used in the paper\n",
"Distance = function(predictor, test){\n",
" 1- apply(predictor, 1, cor, test)\n",
"}\n",
"# NN classification process\n",
"paper9_nn = function(test, pk, learning, response){\n",
" distance = Distance(learning, test)\n",
" index = order(distance)[1:pk]\n",
" cl = ifelse(sum(response[index] == \"AML\")>sum(response[index]==\"ALL\"), \"AML\", \"ALL\")\n",
" cl\n",
"}\n",
"# leave-one-cross-validation to tune k\n",
"mycv= function(pk,learning,response){\n",
" error = 0\n",
" for(i in 1:nrow(learning)){\n",
" cl = paper9_nn(learning[i,], pk, learning[-i, ], response[-i])\n",
" error = error+(cl == response[i])\n",
" }\n",
" error\n",
"}\n",
"classifier9nn = function(train_p, train_r, test_p, test_r){\n",
" k = seq(1, 21, 2)\n",
" choose_k = sapply(k,mycv, learning = train_p, response= train_r)\n",
" nn_train = apply(train_p, 1, paper9_nn, k[which.min(choose_k)], train_p, train_r)\n",
" nn_test = apply(test_p ,1, paper9_nn, k[which.min(choose_k)], train_p ,train_r)\n",
" train_table = table(Train_Predict = nn_train, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = nn_test, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9nn = classifier9nn(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9nn$train\n",
"paper9nn$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Decision Tree"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_Predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_Predict ALL AML\n",
" ALL 18 1\n",
" AML 2 13"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# test_paper3 test_response train_paper3 train_response loaded\n",
"classifier9dt = function(train_p, train_r, test_p, test_r){\n",
" cbine_data = data.frame(response = factor(train_r), train_p)\n",
" tree_mdl = tree(response~.,data = cbine_data)\n",
" tree_tr = predict(tree_mdl, data.frame(train_p), type = \"class\")\n",
" tree_te = predict(tree_mdl, data.frame(test_p), type = \"class\")\n",
" train_table = table(Train_Predict = tree_tr, Train_Actual = train_r)\n",
" test_table = table(Test_Predict = tree_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9dt = classifier9dt(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9dt$train\n",
"paper9dt$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Bagging"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_predict ALL AML\n",
" ALL 19 0\n",
" AML 1 14"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"my_baghelper = function(train, test){\n",
" bg = sample(nrow(train), replace = T)\n",
" temp_md = tree(response~., data = train[bg, ])\n",
" predict(temp_md, test, type = \"class\")\n",
"}\n",
"classifier9bg = function(train_p, train_r, test_p, test_r, B = 50){\n",
" cbine_data = data.frame(response = factor(train_r), train_p)\n",
" t_tr = replicate(B, my_baghelper(cbine_data, data.frame(train_p)))\n",
" pred_tr = apply(t_tr, 1, function(x) ifelse(sum(x == \"AML\")>sum(x ==\"ALL\"), \"AML\", \"ALL\"))\n",
" t_te = replicate(B, my_baghelper(cbine_data, data.frame(test_p)))\n",
" pred_te = apply(t_te, 1, function(x) ifelse(sum(x == \"AML\")>sum(x ==\"ALL\"), \"AML\", \"ALL\"))\n",
" train_table = table(Train_predict = pred_tr, Train_Actual = train_r)\n",
" test_table = table(Test_predict = pred_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9bg = classifier9bg(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9bg$train\n",
"paper9bg$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Bagging with CPD"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_predict ALL AML\n",
" ALL 19 1\n",
" AML 1 13"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"CPD = function(x1, x2, d = 0.75){\n",
" a = runif(nrow(x1), 0, d)\n",
" a*x1+(1-a)*x2\n",
"}\n",
"# helper function for each bagging with CPD\n",
"my_cpdhelper = function(train, test){\n",
" id1 = sample(nrow(train), replace = T)\n",
" id2 = sample(nrow(train), replace = T)\n",
" temp = CPD(train[id1, -1], train[id2,-1])\n",
" temp_md = tree(response~., data = data.frame(temp, response = train$response[id1]))\n",
" predict(temp_md, test, type = \"class\")\n",
"}\n",
"classifier9bgcpd = function(train_p, train_r, test_p, test_r, B = 50){\n",
" cbine_data = data.frame(response = factor(train_r), train_p)\n",
" t_tr = replicate(B, my_cpdhelper(cbine_data, data.frame(train_p)))\n",
" pred_tr = apply(t_tr, 1, function(x) ifelse(sum(x == \"AML\")>sum(x ==\"ALL\"), \"AML\", \"ALL\"))\n",
" t_te = replicate(B, my_cpdhelper(cbine_data, data.frame(test_p)))\n",
" pred_te = apply(t_te, 1, function(x) ifelse(sum(x == \"AML\")>sum(x ==\"ALL\"), \"AML\", \"ALL\"))\n",
" train_table = table(Train_predict = pred_tr, Train_Actual = train_r)\n",
" test_table = table(Test_predict = pred_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9bgcpd = classifier9bg(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9bgcpd$train\n",
"paper9bgcpd$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- FLDA"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_predict ALL AML\n",
" ALL 19 2\n",
" AML 1 12"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"classifier9flda = function(train_p, train_r, test_p, test_r, B = 50){\n",
" cbine_data = data.frame(response = factor(train_r), train_p)\n",
" flda_md = MASS::lda(response~., data = cbine_data)\n",
" flda_tr = predict(flda_md, data.frame(train_p))$class\n",
" flda_te = predict(flda_md, data.frame(test_p))$class\n",
" train_table = table(Train_predict = flda_tr, Train_Actual = train_r)\n",
" test_table = table(Test_predict = flda_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9flda = classifier9bg(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9flda$train\n",
"paper9flda$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- DLDA"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_predict ALL AML\n",
" ALL 19 1\n",
" AML 1 13"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"classifier9dlda = function(train_p, train_r, test_p, test_r, B = 50){\n",
" cbine_data = data.frame(response = factor(train_r), train_p)\n",
" dlda_md = dlda(response~., data = cbine_data)\n",
" dlda_tr = predict(dlda_md, data.frame(train_p))$class\n",
" dlda_te = predict(dlda_md, data.frame(test_p))$class\n",
" train_table = table(Train_predict = dlda_tr, Train_Actual = train_r)\n",
" test_table = table(Test_predict = dlda_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9dlda = classifier9bg(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9dlda$train\n",
"paper9dlda$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- DQDA"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_predict ALL AML\n",
" ALL 19 2\n",
" AML 1 12"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"classifier9dqda = function(train_p, train_r, test_p, test_r, B = 50){\n",
" cbine_data = data.frame(response = factor(train_r), train_p)\n",
" dqda_md = dlda(response~., data = cbine_data)\n",
" dqda_tr = predict(dqda_md, data.frame(train_p))$class\n",
" dqda_te = predict(dqda_md, data.frame(test_p))$class\n",
" train_table = table(Train_predict = dqda_tr, Train_Actual = train_r)\n",
" test_table = table(Test_predict = dqda_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper9dqda = classifier9bg(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper9dqda$train\n",
"paper9dqda$test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Paper 29 classifier"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
" Train_Actual\n",
"Train_predict ALL AML\n",
" ALL 27 0\n",
" AML 0 11"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
" Test_Actual\n",
"Test_predict ALL AML\n",
" ALL 19 8\n",
" AML 1 6"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"classifier29 = function(train_p, train_r, test_p, test_r, B = 50){\n",
" train_data = data.frame(train_p, class = train_r)\n",
" test_data = data.frame(test_p)\n",
" eg = empty.graph(c(\"class\", colnames(data.frame(train_p))))\n",
" arcs(eg) = matrix(c(rep(\"class\", 50), \n",
" colnames(data.frame(train_p))), \n",
" ncol = 2, byrow = F, \n",
" dimnames = list(c(), c(\"from\", \"to\")))\n",
" fitted = bn.fit(eg, train_data)\n",
" predict_tr = predict(fitted, node = \"class\", method=\"bayes-lw\", train_data)\n",
" predict_te = predict(fitted, node = \"class\", method=\"bayes-lw\", test_data)\n",
" train_table = table(Train_predict = predict_tr, Train_Actual = train_r)\n",
" test_table = table(Test_predict = predict_te, Test_Actual = test_r)\n",
" return(list(train = train_table, test = test_table))\n",
"}\n",
"paper29 = classifier29(golub_train_50, golub_train_response, golub_test_50, golub_test_response)\n",
"paper29$train\n",
"paper29$test"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "R",
"language": "R",
"name": "ir"
},
"language_info": {
"codemirror_mode": "r",
"file_extension": ".r",
"mimetype": "text/x-r-source",
"name": "R",
"pygments_lexer": "r",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
adamsteer/nci-notebooks | data_days2016/PDAL on the VDI.ipynb | 2 | 34704 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<img src=\"http://nci.org.au/wp-content/themes/nci/img/img-logo-large.png\", width=400>\n",
"\n",
"\n",
"# Point data manipulation with PDAL\n",
"\n",
"#### This notebook is an incomplete training document for NCI systems. All pipelines and commands used here have been tested against PDAL 1.3 on a centOS system, although you will need to modify path and file names to suit your systems. \n",
"\n",
"### PDAL is not yet installed as a production system at NCI. We expect it will be available via NCI's virtual desktop infrastructure for NCI users in early 2017. Keep an eye on http://vdi.nci.org.au/news for details. \n",
"\n",
"### In this notebook:\n",
"- manipulating point data on the NCI filesystem using PDAL (http://pdal.io, v1.3)\n",
"\n",
"#### The following material uses Geoscience Australia's Elevation Data Collection which is available under the Create Commons License 4.0 through NCI's THREDDS Data Server. For more information on the collection and licensing, please [click here](https://geonetwork.nci.org.au/geonetwork/srv/eng/catalog.search#/metadata/f9082_1236_9859_8989)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What is PDAL?\n",
"\n",
"http://pdal.io\n",
"\n",
"PDAL (the **Point Data Abstraction Library**) is an open source library for handling massive point data sets. It's name is derived from GDAL - since it aims to sit in the same space for point data.\n",
"\n",
"PDAL is actually a C library - if you're writing applications you can insert it into your code. It also has python bindings. Today we'll explore some of PDAL's capabilities using it's command line applications - which are mostly wrappers to PDAL's **pipeline** functions.\n",
"\n",
"We'll also us a sneaky bit of LibLAS: http://www.liblas.org\n",
"\n",
"...but you'll hopefully see why we'd prefer PDAL in the end.\n",
"\n",
"## Why would I use PDAL? Why is it here on data day?\n",
"\n",
"If you deal with:\n",
"- LiDAR elevation observations\n",
"- 3D photogrammetry\n",
"- Any other data which consists of dense, ungridded points\n",
"\n",
"...PDAL can make your life a lot simpler with some basic processing tasks. \n",
"\n",
"PDAL is demonstrated at this workshop because point data exist on NCI's filesystem, and the VDI is the perfect place to work on them without having to ship unneccessary data. Using the VDI as a front end for development is an excellent way to protoype point data analyses on data that exist in the NCI filesystem; or define specific subsets to take away for analysis."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Agenda for this workbook\n",
"\n",
"A lightning speed overview of point data handling and manipulation:\n",
"1. <a href=\"#info\">Getting information about a point dataset</a>\n",
"2. <a href=\"#subset\">Collecting a subset from a LiDAR survey</a>\n",
"3. <a href=\"#classes\">Requesting only a specific point class from a dataset</a>\n",
"4. <a href=\"#ground\">Classifying ground (in case you don't like the vendor's version of 'ground')</a>\n",
"5. <a href=\"#DEM\">Generating a bare earth DEM and a DSM</a>\n",
"6. <a href=\"#HAG\">Requesting 'height above ground' instead of 'absolute height'</a>\n",
"\n",
"We will do all this on the command line, viewing results in CloudCompare or QGIS. These tasks are based on the PDAL workshop here: http://www.pdal.io/workshop/index.html, and are very much 'learn by doing'. PDAL is very well documented, please keep reading for more information.\n",
"\n",
"...so feel free to zoom ahead, create and share!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Set up\n",
"```\n",
"module purge\n",
"module load QGIS GDAL PDAL cloudcompare```\n",
"\n",
"(to verify)\n",
"\n",
"A canned QGIS project with all the layers shown in this workbook is here:\n",
"\n",
"```\n",
"/path/to/materials/pdal_demo.qgis\n",
"```\n",
"\n",
"Feel free to explore it, or build your own example and apply the tools you see here."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Locate data\n",
"\n",
"We will use a LiDAR survey over Merimbula in 2013, from the Geoscience Australia elevation reference collection. Here is it's catalogue entry:\n",
"\n",
"*THREDDS*\n",
"\n",
"http://dapds00.nci.org.au/thredds/catalog/rr1/Elevation/Merimbula0313/catalog.html\n",
"\n",
"*Geonetwork*\n",
"\n",
"https://geonetwork.nci.org.au/geonetwork/srv/eng/catalog.search#/metadata/f9082_1236_9859_8989\n",
"\n",
"Licensed under Creative Commons (CCBY4): http://dapds00.nci.org.au/thredds/fileServer/licenses/rr1_licence.pdf\n",
"\n",
"The path to the data on your VDI desktop is:\n",
"\n",
"```\n",
"/g/data1/Elevation/Merimbula0313/\n",
"```\n",
"\n",
"...and LAS tiles are in:\n",
"\n",
"```\n",
"/g/data1/Elevation/Merimbula0313/Tiles_2k_2k```\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## <a name=\"info\"></a>1. Basic information\n",
"Try:\n",
"\n",
"```\n",
"pdal info /path/to/Elevation/Merimbula0313/z55/2013/Mass_Points/LAS/AHD/LAS/Tiles_2k_2k/Merimbula2013-C3-AHD_7605910_55_0002_0002.las ```\n",
"\n",
"...and compare with:\n",
"\n",
"```\n",
"lasinfo /path/to/Elevation/Merimbula0313/z55/2013/Mass_Points/LAS/AHD/LAS/Tiles_2k_2k/Merimbula2013-C3-AHD_7605910_55_0002_0002.las ```\n",
"\n",
"\n",
"<br />\n",
"<div class=\"alert alert-info\">\n",
"Lasinfo gives more compact results - but can only read LAS. PDAL's info function can tell you about dimensions in any dataset it has a schema for reading: http://www.pdal.io/stages/readers.html, which hints also that PDAL can <i>process</i> point data in a diverse range of data formats.</div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## <a name=\"subset\"></a>2. Clipping point data with PDAL\n",
"\n",
"Straight into the fire! We're going straight to PDAL's **pipeline** architecture, which gives it an enormous amount of felxibility and power. A pipeline is a set of operations chained together and defined in a JSON file. You'll see it in action here \n",
"\n",
"### a. Why do we want to clip LAS data?\n",
"\n",
"LAS tiles are pretty hard to handle - you get a lot of extra data that you may not want, and they are pretty much always boringly square. If we only need a certain region, we can get just those points using PDAL.\n",
"\n",
"### b. An example - selecting Merimbula town\n",
"\n",
"The image here shows a lot of data - an index of LiDAR tiles labelled by filename, an OpenStreetMaps layer giving us an idea of where Merimbula town is, and a polygon roughly around the urban area. These are all in the QGIS project given above.\n",
"\n",
"The image here shows that Merimbula town covers several LIDAR tiles. This is an excellent challenge - it means some tiles have a **lot** of data we don't want, and it means we have to sift through multiple tiles to find our data of interest. We can see a rough polygon surrounding our region of interest, which is defined in QGIS and save as GeoJSON.\n",
"\n",
"\n",
"\n",
"Here's the GeoJSON polygon:\n",
"\n",
"```\n",
"{\n",
"\"type\": \"FeatureCollection\",\n",
"\"crs\": { \"type\": \"name\", \"properties\": { \"name\": \"urn:ogc:def:crs:EPSG::28355\" } },\n",
"\"features\": [\n",
"{ \"type\": \"Feature\", \"properties\": { \"id\": 0 }, \"geometry\": { \"type\": \"Polygon\", \"coordinates\": [ [ [ 759094.480855233967304, 5913008.271593709476292 ], [ 758464.699909413931891, 5912716.199270982295275 ], [ 757743.646362751838751, 5912898.744472593069077 ], [ 757716.26458250079304, 5913304.907546310685575 ], [ 757373.992329337401316, 5913418.998297326266766 ], [ 757018.029186049010605, 5913724.761510098353028 ], [ 757556.537531022448093, 5913784.088700683787465 ], [ 757828.153738587978296, 5913997.946465536952019 ], [ 757828.153738587396219, 5914326.52782854065299 ], [ 758357.534823469701223, 5914381.291389083489776 ], [ 758877.788648267393, 5914554.709330711513758 ], [ 758850.406868015765212, 5914810.272613044828176 ], [ 759042.079329782165587, 5914837.654393311589956 ], [ 759151.606450793216936, 5914673.363711818121374 ], [ 759370.660692813224159, 5914709.872752171941102 ], [ 759361.533432727912441, 5915102.34493575617671 ], [ 760593.713544093072414, 5915138.853976195678115 ], [ 761177.858189482591115, 5915047.581375411711633 ], [ 761123.094628979102708, 5914235.255227984860539 ], [ 761260.003530243760906, 5914007.07372591085732 ], [ 761570.33037310524378, 5913952.31016543880105 ], [ 761369.530651255394332, 5913559.837981833145022 ], [ 761141.349149147979915, 5913459.438120897859335 ], [ 760484.186423085397109, 5913377.292780089192092 ], [ 759817.896436938317493, 5913632.856062367558479 ], [ 759516.696854161447845, 5913550.710721591487527 ], [ 759416.29699323582463, 5913286.020179163664579 ], [ 759094.480855233967304, 5913008.271593709476292 ] ] ] } }\n",
"]\n",
"}\n",
"\n",
"```\n",
"\n",
"...but PDAL needs WKT (for now) - using this website: http://rodic.fr/blog/online-conversion-between-geometric-formats/, we can get a WKT polygon:\n",
"\n",
"```\n",
"POLYGON((759094.480855234 5913008.2715937095,758464.6999094139 5912716.199270982,757743.6463627518 5912898.744472593,757716.2645825008 5913304.907546311,757373.9923293374 5913418.998297326,757018.029186049 5913724.761510098,757556.5375310224 5913784.088700684,757828.153738588 5913997.946465537,757828.1537385874 5914326.527828541,758357.5348234697 5914381.2913890835,758877.7886482674 5914554.7093307115,758850.4068680158 5914810.272613045,759042.0793297822 5914837.654393312,759151.6064507932 5914673.363711818,759370.6606928132 5914709.872752172,759361.5334327279 5915102.344935756,760593.7135440931 5915138.853976196,761177.8581894826 5915047.581375412,761123.0946289791 5914235.255227985,761260.0035302438 5914007.073725911,761570.3303731052 5913952.310165439,761369.5306512554 5913559.837981833,761141.349149148 5913459.438120898,760484.1864230854 5913377.292780089,759817.8964369383 5913632.856062368,759516.6968541614 5913550.7107215915,759416.2969932358 5913286.020179164,759094.480855234 5913008.2715937095))\n",
"```\n",
"\n",
"### c. Making a list of LIDAR tiles.\n",
"\n",
"We need to know which tiles contain our data - by labelling the tile index layer in QGIS we can pick out the following set:\n",
"\n",
"```\n",
"Merimbula2013-C3-AHD_7565916_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7565914_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7565912_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7585916_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7585914_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7585912_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7605916_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7605914_55_0002_0002.las\n",
"Merimbula2013-C3-AHD_7605912_55_0002_0002.las\n",
"```\n",
"<br />\n",
"<div class=\"alert alert-info\">\n",
"PDAL supports filename globbing for pipelines - so you could just send \"../merimbula2013/Tiles_2k_2k/*.las\" to the pipeline below. However, you'll find pretty quickly that PDAL's *tindex* application, and using the resulting index to tell us where tiles and polygons intersect (without needing to know tile names) is vastly more efficient. However, for this demonstration we want to avoid creating extra datasets - so we list our tiles of interest.</div>\n",
"\n",
"### d. Constructing a PDAL pipeline\n",
"\n",
"We create a JSON file which tells PDAL what to do:\n",
"\n",
"```\n",
"nano merimbula_clip.json\n",
"```\n",
"..and paste in the following:\n",
"\n",
"```\n",
"{\n",
" \"pipeline\": [\n",
"\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7565916_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7565914_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7565912_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7585916_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7585914_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7585912_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7605916_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7605914_55_0002_0002.las\",\n",
" \"../merimbula2013/Tiles_2k_2k/Merimbula2013-C3-AHD_7605912_55_0002_0002.las\",\n",
" {\n",
" \"type\": \"filters.crop\",\n",
" \"polygon\": \"POLYGON((759094.480855234 5913008.2715937095,758464.6999094139 5912716.199270982,757743.6463627518 5912898.744472593,757716.2645825008 5913304.907546311,757373.9923293374 5913418.998297326,757018.029186049 5913724.761510098,757556.5375310224 5913784.088700684,757828.153738588 5913997.946465537,757828.1537385874 5914326.527828541,758357.5348234697 5914381.2913890835,758877.7886482674 5914554.7093307115,758850.4068680158 5914810.272613045,759042.0793297822 5914837.654393312,759151.6064507932 5914673.363711818,759370.6606928132 5914709.872752172,759361.5334327279 5915102.344935756,760593.7135440931 5915138.853976196,761177.8581894826 5915047.581375412,761123.0946289791 5914235.255227985,761260.0035302438 5914007.073725911,761570.3303731052 5913952.310165439,761369.5306512554 5913559.837981833,761141.349149148 5913459.438120898,760484.1864230854 5913377.292780089,759817.8964369383 5913632.856062368,759516.6968541614 5913550.7107215915,759416.2969932358 5913286.020179164,759094.480855234 5913008.2715937095))\"\n",
" \"outside\": false\n",
" },\n",
"\t\"./merimbulatown_clip.las\"\n",
" ]\n",
"}\n",
"\n",
"```\n",
"\n",
"### e. Apply our clipping operation\n",
"\n",
"Then we execute the task using:\n",
"\n",
"```\n",
"pdal pipeline merimbula_clip.json\n",
"```\n",
"\n",
"*Time to execute on an 8 core, 16GB RAM VM: 1 minute 12 seconds*\n",
"\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-warning\">\n",
"<h3>Can we do better that that?</h3>\n",
"<p>\n",
"**Yes!** If we first generate a tile index and give PDAL a better idea of which data to use, we can do this job in **49 seconds** including compression to LAZ using PDAL's <a href=\"http://www.pdal.io/stages/readers.tindex.html\">tindex reader</a>. This still generates a 46 mb LAz file (388 mb uncompressed LAZ), so a roundtrip time of a couple of minutes would be expected from a web-based request to a data subset on your machine.</p>\n",
"\n",
"<h3>Note</h3>\n",
"<p>\n",
"PDAL also supports file name globbing in pipelines. However, giving our clip \n",
"\n",
"</div>\n",
"\n",
"This will result in a set of points inside your polygon being written into a .LAS file at the location specified in the pipeline file. Now you have a template for doing this job with pretty much any LAS tiles!\n",
"\n",
"How much data do we have? ```pdal info ./merimbulatown_clip.las``` tells us we have 11948596 points - so our time to process is really not bad (read 9 las tiles, do some clipping, merge and write an 11.9 million point dataset).\n",
"\n",
"So let's explore our new dataset. In a new terminal, type:\n",
"\n",
"```\n",
"cloudcompare &\n",
"```\n",
"\n",
"...and use it's file/open menu to navigate to your newly made LAS file. Take a look at it there (hint - use the projections menu to convert the Z dimension to a scalar field to colour your points by height).\n",
"\n",
"Here's an example. **Note** Cloudcompare's default point colouring scheme is 'point source' - which is useful but not pretty. Use the 'scalar fields' dropdown in the lower left panel to change your colour scheme - the screenshot here uses intensity.\n",
"\n",
"\n",
"\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-warning\">\n",
"<h3>Caution</h3>\n",
"<p>\n",
"If your polygon is quite large, or your points very dense, or both, you can still get a massive dataset! Use pdal info to get an estimate of how dense the data are, and figure out how much area you are clipping to estimate the final file size before going ahead.</p></div>\n",
"\n",
"<div class=\"alert alert-success\">\n",
"<h3>Extension</h3>\n",
"<p>\n",
"Colour your points by height.</p>\n",
"</div>\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## <a name=\"classes\"></a>3. I want only buildings\n",
"\n",
"If you only want a specific classification from your cloud, here's how to filter it out using PDAL. We take advantage of the LAS specification, and know that the numerical tag for points of class 'building' is 6.\n",
"\n",
"See Table 4.9 in this document: http://www.asprs.org/wp-content/uploads/2010/12/LAS_1-4_R6.pdf for a list of standard classification codes.\n",
"\n",
"Save the following in merimbula_buildings.json:\n",
"\n",
"```\n",
"{\n",
" \"pipeline\": [\n",
" \"./merimbulatown_clip.las\",\n",
" {\n",
" \"limits\": \"Classification[6:6]\",\n",
" \"type\": \"filters.range\"\n",
" },\n",
" \"./merimbulabuildings.las\"\n",
" ]\n",
"}\n",
"```\n",
"...and execute:\n",
"\n",
"```\n",
"pdal pipeline merimbula_buildings.json\n",
"```\n",
"\n",
"*Time to execute: 6.071 seconds*\n",
"\n",
"...and add a new layer in cloudcompare - here the point cloud of buildings we just made is coloured by point source, since it contrasts nicely.\n",
"\n",
"\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-success\">\n",
"<h3>Extension</h3>\n",
"<p>\n",
"Can you do this job using las2las? Why would you use PDAL instead?</p>\n",
"<p>\n",
"When writing your own data, using ASPRS classification codes to flag bui;dings, ground, trees etc. is a good start - it helps to integrate with a lot of existing analysis tools.\n",
"</p>\n",
"</div>\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## 4. I don't like the vendor's ground classification, and want to try my own\n",
"\n",
"Vendor-supplied ground can be poorly documented, or may not meet your requirements for other reasons. You can use PDAL to construct your own, with more control over how ground is parameterised. Also, PDAL implements some relatively recent ground classification algorithms.\n",
"\n",
"Here use a Simple Morphological Filter (Pingel, T.J., Clarke, K.C., McBride, W.A., 2013. An improved simple morphological filter for the terrain classification of airborne LIDAR data. ISPRS J. Photogramm. Remote Sens. 77, 21–30.).\n",
"\n",
"```\n",
"{\n",
" \"pipeline\":[\n",
" \"./merimbulatown_clip.las\",\n",
" {\n",
" \"type\":\"filters.smrf\",\n",
" \"extract\": false,\n",
" \"cell\": 2.0,\n",
" \"window\": 42.0 \n",
" },\n",
" \"./merimbulatown_smrf.laz\"\n",
" ]\n",
"}\n",
"```\n",
"\n",
"```\n",
"pdal pipeline merimbula_smrf.json\n",
"```\n",
"\n",
"This takes some time - and the results need inspecting. Did these parameters do a better job than the vendor?\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-info\">\n",
"These ground filters don't need to have LiDAR data to work, but they do rely on sufficiently dense input data. 3D photogrammetry works equally well, swath sonar is also a candidate - or essentially anything with points separated by a few metres or less. So the next few steps which rely on this - finding height above ground and making DEMs would work equally well on any dense data structure. Be sure to read the docs and tune your ground detection parameters to suit your data.\n",
"</div>\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 5. All I want is a better DEM than SRTM\n",
"\n",
"PDAL and GDAL are hand-in-glove, wih PDAL employing GDAL's ```gdal2dem``` to create raster elevation models. Here we look at two types, the DSM and the DTM/DEM.\n",
"\n",
"\n",
"### a. The easy one - a DSM\n",
"First a DSM - Digital Surface Model - meaning the top of everything in the point cloud.\n",
"\n",
"This is relatively simple given what we've accomplished already. Here's the pipeline to do it:\n",
"\n",
"```\n",
"{\n",
" \"pipeline\": [\n",
" \"./merimbulatown_clip.las\",\n",
" {\n",
" \"filename\":\"./merimbula_dsm\",\n",
" \"output_format\":\"tif\",\n",
" \"output_type\":\"all\",\n",
" \"grid_dist_x\":\"2.0\",\n",
" \"grid_dist_y\":\"2.0\",\n",
" \"type\": \"writers.p2g\"\n",
" }\n",
" ]\n",
"}\n",
"```\n",
"...and we get the pattern by now:\n",
"```\n",
"pdal pipeline merimbula_dsm.json\n",
"```\n",
"*Time to execute: 27.356 seconds*\n",
"\n",
"\n",
"\n",
"### b. The slightly less easy one - the DTM/DEM\n",
"\n",
"For this one we need to ignore everything that is not 'ground' - let's do this **without** creating a new .las file containing only ground points. In this example we *pipe* the result of a filter into another process - starting to show how PDAL operations can be chained. In the first block we limit our selection to points of class 2 (ASPRS LAS for 'ground'), and then pass the result to our raster generator in the second block.\n",
"\n",
"```\n",
"{\n",
" \"pipeline\": [\n",
" \"./merimbulatown_clip.las\",\n",
" {\n",
" \"limits\": \"Classification[2:2]\",\n",
" \"type\": \"filters.range\"\n",
" },\n",
" {\n",
" \"filename\":\"./merimbula_dtm\",\n",
" \"output_format\":\"tif\",\n",
" \"output_type\":\"all\",\n",
" \"grid_dist_x\":\"2.0\",\n",
" \"grid_dist_y\":\"2.0\",\n",
" \"type\": \"writers.p2g\"\n",
" }\n",
" ]\n",
"}\n",
"```\n",
"...and once more:\n",
"```\n",
"pdal pipeline merimbula_dtm.json\n",
"```\n",
"*Time to execute: 12.34 seconds*\n",
"\n",
"\n",
"\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-success\">\n",
"<h3>Extension</h3>\n",
"<ol>\n",
"<li>You can see that the raster elevation models in this example are hillshaded - replicate this! How many steps did your method take?</li>\n",
"<li>We made a DTM on a 2 m grid. Make a 1 m DTM and compare the two (do we have enough point density to make a 1 m DTM? Or even a 2 m DTM?)</li>\n",
"</ol>\n",
"</div>\n",
"\n",
"### Quick aside - point density map\n",
"\n",
"Not even a pipeline! PDAL can create a set of hexagonal bins to show the actual point coverage and density. While the metadata for this survey gives an average density for the entire dataset, what does it look like in real life?\n",
"\n",
"First, let's set ourselves a sane sample area, say 20 m per cell. PDAL lets us set an edge size - so how long are edges in a 20 m^2 hexagon?"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from math import sqrt\n",
"def hexside(area):\n",
" return sqrt(area / (3 / 2 * sqrt(3)))"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"2.7745276335252114"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"hexside(20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"OK, apply! This gives us a 20 m binned sqlite dataset that can be loaded straight into QGIS:\n",
"\n",
"```\n",
"pdal density -i ./merimbulatown_clip.las -o merimbuladensity_20m.sqlite --filters.hexbin.edge_size=2.7745276335252114\n",
"```\n",
"\n",
"\n",
"Looking at our density map, classified by point count per hexagon, we see that most of the coverage has fewer than 3 points per square metre (cyan), and a reasonable proportion has fewer than 1 point per square metre (blue). The overall density metric has been tweaked a bit by swath overlaps, with up to 10 points per square metre!\n",
"\n",
"Based on this information, a 2 m DTM is reasonable for a lot of the data (at least two samples per cell), but a 5 m DTM might be more realistic (at least 5 samples per cell).\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-success\">\n",
"<h3>Extension</h3>\n",
"<p>\n",
"How could we use PDAL to give us a consistent point density across our dataset?<br />\n",
"*Hint: check out http://www.pdal.io/stages/filters.dartsample.html*\n",
"</div>\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 6. Where is the tallest building in Merimbula?\n",
"\n",
"Sometimes we want relative height above ground (HAG). You might be interested in the tallest tree, or the mean height of shrubs, or in this case, finding the tallest building in a region. We now know how to pipe PDAL operations together, we're going to do some of that right now!\n",
"\n",
"```\n",
"{\n",
" \"pipeline\":[\n",
" \"merimbulatown_clip.las\",\n",
" {\n",
" \"type\":\"filters.height\"\n",
" },\n",
" {\n",
" \"type\":\"filters.ferry\",\n",
" \"dimensions\":\"HeightAboveGround = Z\",\n",
" },\n",
" \"merimbulatown_hag.las\"\n",
" ]\n",
"}\n",
"```\n",
"```\n",
"pdal pipeline merimbula_hag.json\n",
"```\n",
"*Execution time 35 seconds*\n",
"\n",
"...gets us height above ground! Here's a profile view of the data. The new height-above-ground points are coloured, original data in grey (translated 100 m upward).\n",
"\n",
"\n",
"\n",
"But where is the tallest building? One approach is to make a dataset of building heights and consult ```pdal info``` for some guidance.\n",
"\n",
"```\n",
"nano find_tallest.json\n",
"```\n",
"\n",
"```\n",
"{\n",
" \"pipeline\":[\n",
" \"merimbulatown_hag.las\",\n",
" {\n",
" \"limits\": \"Classification[6:6]\",\n",
" \"type\": \"filters.range\"\n",
" },\n",
" \"merimbulabuildings_hag.las\"\n",
" ]\n",
"}\n",
"```\n",
"This is our pipeline for selecting a single class. Use ```pdal info ``` to find out how tall the tallest buidling is, and use it to guide the next pipeline - which adds a height filter and returns a comma delimited text file.\n",
"\n",
"```\n",
"{\n",
" \"pipeline\": [\n",
" \"./merimbula_hag.las\",\n",
" {\n",
" \"limits\": \"Classification[6:6]\",\n",
" \"type\": \"filters.range\"\n",
" },\n",
"\t{\n",
" \"limits\": \"Z[23.5:25]\",\n",
" \"type\": \"filters.range\"\n",
" },\n",
"\t\"./merimbulabuildings_hag_tallest.txt\"\n",
" ]\n",
"}\n",
"```\n",
"\n",
"```\n",
"pdal pipeline find_tallest.json\n",
"```\n",
"\n",
"...which we can inspect in our QGIS project. Load the CSV file up and see where Merimbula's tallest 'building' is - styled as a red dot in the map below. Do you think they're really buildings?\n",
"\n",
"\n",
"\n",
"<br/>\n",
"<div class=\"alert alert-success\">\n",
"<h3>Extension</h3>\n",
"<ol>\n",
"<li>What's the address of the building?</li>\n",
"<li>How can I quickly assess whether the points identified are really a building?</li>\n",
"</ol>\n",
"</div>\n",
"<div class=\"alert alert-info\">\n",
"<p>\n",
"This is a pretty clunky way of finding the highest point in a dataset. An alternative might be writing a custom filter - or using PDAL's python binding to ingest data into a numpy array. For the second approach, just be mindful of memory consumption.</p>\n",
"<p>\n",
"***Note:*** using the PDAL-python approach, you could achieve most of the outcomes here using array operations - the main limitation being that you need to ingest all the data into memory at once (PDAL streams data - keeping only chunks at a time in memory).\n",
"</div>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 7. Awesome! But my points are not .LAS tiles\n",
"\n",
"PDAL has a wide range of readers built in - including a configurable text reader. Because is it is built with GDAL in mind it will generally ingest GDAL formats.\n",
"\n",
"Let's try reading a gridded NetCDF file as a point cloud:\n",
"```\n",
"{\n",
" \"pipeline\":[\n",
" {\n",
" \"type\":\"readers.gdal\",\n",
" \"filename\":\"./IR_gravity_anomaly_Australia_V1.nc\"\n",
" },\n",
" {\n",
" \"type\":\"filters.ferry\"\n",
" \"dimensions\":\"Latitude=Y, Longitude=X, grav_ir_anomaly=Z\",\n",
" },\n",
" {\n",
" \"type\":\"writers.laz\",\n",
" \"filename\":\"./gravityanomaly.laz\"\n",
" }\n",
" ]\n",
"}\n",
"```\n",
"Did this work? <b>No!</b> Why not? Because we have not built (yet) a schema to read out the gridded gravity anomaly!\n",
"\n",
"**Why include a broken example? To inspire you! What *could* we do if this function worked?**\n",
"\n",
"*Also waiting to see if I can get a hold of some experimental geophysics point data... depending on how they're packed this might work a lot more easily! Then the open-ended question is 'why use PDAL and not a natove netCDF IO?'* \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Summary\n",
"\n",
"**Points are no longer your enemy!** Using a completely open source stack and the VDI, you can whip point data into shape quickly and easily. You don't need to copy the raw tiles anywhere, only your derived datasets.\n",
"\n",
"Still, keep an eye on those - they can get quite large.\n",
"\n",
"Just to reiterate, PDAL and cloudcompare will happily handle data from 3D photogrammetry, terrestrial scanners, mobile (non airborne scanners), Zebedees, sonars, radars.. whatever produces data which are arranged as points in space. \n",
"\n",
"## Future things\n",
"\n",
"This workbook only goes through simple pipelines - a more complex example might clip, classify, and compute height above ground in one step.\n",
"\n",
"PDAL also underpins processing for visualisations like web-based massive point cloud rendering - we've used PDAL to apply colour from aerial imagery to LiDAR points prior to indexing for interactive web display.\n",
"\n",
"PDAL Python bindings are also on the way - meaning that point data can be piped straight into Numpy arrays. The *disadvantage* of this approach is that all the points need to be held in memory at once, so the subsetting feature demonstrated here will be a critical first step.\n",
"\n",
"### Caveats\n",
"\n",
"- PDAL does not yet handle full waveform LiDAR data. We're looking at PyLIDAR as a package for handling full waveform data, alongside other methods for handling points + pulses.\n",
"- PDAL is not parallel by nature (yet). Processing multiple tiles can be done using a parallelisation wrapper (eg Gnu Parallels), but tasks need to fit. We're not ready for vastly parallel jobs with PDAL just yet!\n",
"\n",
"### Where to get help?\n",
"\n",
"...ask us! But we don't know everything - so we might point you to:\n",
"\n",
"- http://www.pdal.io/community.html\n",
"- The PDAL list: [email protected]\n",
"- The PDAL gitter channel: https://gitter.im/PDAL/PDAL\n",
"\n",
"### ...but PDAL doesn't do my specialised thing X, why not?\n",
"\n",
"Because you didn't build it yet! Fork PDAL and have your merry way with it: https://github.com/PDAL/PDAL\n",
"\n",
"### Is PDAL ready to use for analysis, given that this workbook identifies some unresolved issues?\n",
"\n",
"Yes! PDAL is actively maintained and developed - with a lot of interest in the community to keep it's momentum up. The glitches we see all have workarounds - and their presence on the list of issues means that they are being attended to."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
deebuls/RecommenderSystemInRobotics | experiments/DataAnalyzer.ipynb | 1 | 188885 | {
"metadata": {
"name": "",
"signature": "sha256:a0e15f6e7e6c5d5669c2d6c10a3cbdea099b4f0fc87422745f851ebddf434f4c"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#TO DO\n",
"\n",
"* ~~Why does the code fail ?~~\n",
"* ~~Histogram how to handle the precision effect ?~~ np.around(data, decimal=2)\n",
"* ~~Why in move base the base footprint dsnt ave zero entropy ?~~ changed the range in histogram \n",
"* Remove cases where both initial and final are same \n",
" * ~~approach both conditional entorpy are same~~\n",
" * Compare in direct data and find a thershold of change in data \n",
"* ~~Create Database for skill to template or feature~~\n",
"* Re do the relative distance movebase experiment -> Experiments not correct .\n",
"* Evaluation : Total number of demonstration required for sucessfully determining the importatn features\n",
"* Experiments :\n",
" * ~~Move to Base Absolute~~\n",
" * Move to Base Relative \n",
" * ~~Move to Arm Absolute~~\n",
" * Move to Arm Relative\n",
" * Pick up Pre grasp \n",
" * Place\n",
" * Press\n",
" * \n",
"* Determine if a feature has changed ? Filter out first all the features who have not changed\n",
"* Template creation -> need to find alternatives \n",
" * using just the robot feature and calculating all the environment feature \n",
" * adding environment feature in the template\n",
" \n"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#%matplotlib inline\n",
"import glob\n",
"import json\n",
"import pandas.io as io\n",
"import pandas as pd\n",
"import numpy as np\n",
"import quaternion\n",
"import sklearn.preprocessing as pre\n",
"import pprint\n",
"import matplotlib.pyplot as plt\n",
"from collections import defaultdict\n",
"\n",
"##Library based on statsmodel for information theory\n",
"import infotheo\n",
"\n",
"class DataAnalyzer:\n",
" def __init__(self, folderPath, skill):\n",
" self.skill_being_learned = skill\n",
" self.initial = io.json.read_json( folderPath + \"/INITIAL.json\", typ='frame')\n",
" self.final = io.json.read_json( folderPath + \"/FINAL.json\", typ='frame')\n",
"\n",
" #Deleting state column as not reqired for calculations\n",
" del self.initial['state']\n",
" del self.final['state']\n",
" \n",
" print \"Are the inital and final features equal : \", (self.initial.columns.values==self.final.columns.values).all()\n",
" \n",
" self.readExpertKnowledgeBase()\n",
" number_of_demonstrations = self.initial['arm_joint_1'].count()\n",
" print(\"Data has been succesfully read. Nu of Demonstrations : \", number_of_demonstrations)\n",
" \n",
" #Duplication rows if the Number of Demonstrations are less than 3\n",
" if (number_of_demonstrations < 3):\n",
" self.initial_copy = self.initial\n",
" self.final_copy = self.final\n",
" \n",
" for i in range(number_of_demonstrations-3):\n",
" self.initial = self.initial.append(self.initial)\n",
" self.final = self.final.append(self.final)\n",
" \n",
" number_of_demonstrations = self.initial['arm_joint_1'].count()\n",
" print(\"Data Duplication, No of Demonstrations : \", number_of_demonstrations)\n",
" \n",
" print self.initial['arm_joint_1'][0], self.final['arm_joint_1'][0]\n",
" print self.initial['base_link_y'][0], self.final['base_link_y'][0]\n",
" \n",
" def mad_based_outlier(self, points, thresh=3.5):\n",
" \"\"\"\n",
" http://stackoverflow.com/questions/22354094/pythonic-way-of-detecting-outliers-in-one-dimensional-observation-data\n",
" Removes outliers based on MAD.\n",
" Returns boolean map with false value in outliers\n",
" \"\"\"\n",
" if len(points.shape) == 1:\n",
" points = points[:,None]\n",
" median = np.median(points, axis=0)\n",
" diff = np.sum((points - median)**2, axis=-1)\n",
" diff = np.sqrt(diff)\n",
" med_abs_deviation = np.median(diff)\n",
"\n",
" modified_z_score = 0.6745 * diff / med_abs_deviation\n",
"\n",
" return modified_z_score > thresh\n",
" \n",
" def readExpertKnowledgeBase(self):\n",
" '''\n",
" The function reads the knowledge base to extract the mappings between the \n",
" skill to features.\n",
" \n",
" ---------------------------------------------------------------\n",
" |skill \\ Features || Feature1 | Feature2 | Feature3 | Feature4 |\n",
" ---------------------------------------------------------------\n",
" |skill1 || * | | | |\n",
" |skill2 || | * | * | |\n",
" |skill3 || | | | * |\n",
" |skill4 || * | | * | * |\n",
" ---------------------------------------------------------------\n",
" \n",
" TODO :\n",
" how to represent the knoweldge base\n",
" how to intutively add the knowledge base\n",
" \n",
" '''\n",
" #Database Path\n",
" self.skills_db = './knowledge_base/skills.csv'\n",
" self.robot_features_db = './knowledge_base/robot_features.csv'\n",
" self.environment_features_db = './knowledge_base/environment_features.csv'\n",
" self.templates_db = './knowledge_base/templates.csv'\n",
" \n",
" #Reading knowledge Base\n",
" self.skills = []\n",
" self.robot_features = []\n",
" self.environment_features = []\n",
" templates = []\n",
" self.templates = defaultdict(list)\n",
" with open(self.skills_db, 'rb') as f:\n",
" for line in f:\n",
" self.skills.append(line.rstrip('\\n'))\n",
" with open(self.robot_features_db, 'rb') as f:\n",
" for line in f:\n",
" self.robot_features.append(line.rstrip('\\n'))\n",
" with open(self.environment_features_db, 'rb') as f:\n",
" for line in f:\n",
" self.environment_features.append(line.rstrip('\\n'))\n",
" with open(self.templates_db, 'rb') as f:\n",
" for i, line in enumerate(f):\n",
" templates.append(line.rstrip('\\n').split())\n",
" for temp in line.rstrip('\\n').split():\n",
" self.templates[i].append(temp)\n",
" \n",
" self.features_without_positions = {'arm_joint_1','arm_joint_2','arm_joint_3','arm_joint_4','arm_joint_5'} \n",
" self.manipulate_templates()\n",
" \n",
" \n",
" print \"Database reading Complete:\"\n",
" print \"Skills : \",len(self.skills),\" Robot Features : \",len(self.robot_features)\n",
" print \"Environment Features : \",len(self.environment_features),\" Templates : \", len(self.templates)\n",
" \n",
" \n",
" def manipulate_templates(self):\n",
" '''\n",
" The expert only specifies the feature name in the template\n",
" Internal replresentation conatins splitting data in x y z and orientation\n",
" This funciton splits the template feature name into internal representation\n",
" \n",
" This function also adds the distance feature of all the features with the environment features.\n",
" \n",
" '''\n",
" for i, temp in self.templates.iteritems():\n",
" for feature in temp[1:]:\n",
" if feature not in self.features_without_positions:\n",
" self.templates[i].remove(feature)\n",
" self.templates[i].extend([feature + \"_x\", feature + \"_y\", feature + \"_z\",\n",
" feature + \"_ox\",feature + \"_oy\",feature + \"_oz\", feature + \"_ow\"])\n",
" for env_feature in self.environment_features:\n",
" self.templates[i].append(\"d_linear_\"+feature+\"_\"+env_feature)\n",
" \n",
" \n",
" def recommend_using_knowledge_base(self):\n",
" \"\"\"\n",
" After Calculation of the entropy.\n",
" The Templates for each action are used to determine the feature \n",
" with lowest entropy\n",
" \"\"\"\n",
"\n",
" print \"skill being learnt : \", self.skill_being_learned\n",
" for key, temp in self.templates.iteritems():\n",
" entropy_sum_template = 0\n",
" if self.skill_being_learned == temp[0]:\n",
" for feature in temp[1:]:\n",
" try:\n",
" entropy_sum_template += self.condEntropyFinalGivenInitial[feature]\n",
" except :\n",
" print \"feature not available : \", feature\n",
" continue\n",
" \n",
" print \"FOR template : \", key, \" Summed Entropy : \",entropy_sum_template\n",
" \n",
" def dataManipulation(self):\n",
" '''\n",
" TODO : Remove this once the camera based object detector is ready\n",
" '''\n",
" #Assigning griper palm co - ordinates as the object point\n",
" self.final = self.final.assign(object_1_x = self.final.gripper_palm_link_x, \n",
" object_1_y = self.final.gripper_palm_link_y,\n",
" object_1_z = self.final.gripper_palm_link_z,\n",
" object_1_ox = self.final.gripper_palm_link_ox,\n",
" object_1_oy = self.final.gripper_palm_link_oy,\n",
" object_1_oz = self.final.gripper_palm_link_oz,\n",
" object_1_ow = self.final.gripper_palm_link_ow)\n",
"\n",
" self.initial = self.initial.assign(object_1_x = self.final.gripper_palm_link_x, \n",
" object_1_y = self.final.gripper_palm_link_y,\n",
" object_1_z = self.final.gripper_palm_link_z,\n",
" object_1_ox = self.final.gripper_palm_link_oy, #mixing the pose to get different pose between initial and final\n",
" object_1_oy = self.final.gripper_palm_link_ox,\n",
" object_1_oz = self.final.gripper_palm_link_ow,\n",
" object_1_ow = self.final.gripper_palm_link_oz)\n",
"\n",
" \n",
" \n",
" \n",
" def dataCalculatingRelativeDistances(self, from_frame, to_frame):\n",
" '''\n",
" This function calculates all the relative distance between all the frames .\n",
" Both linear distance and angular distance.\n",
" '''\n",
" linear_distance = \"d_linear_\"+from_frame+\"_\"+to_frame\n",
" angular_distance = \"d_angular_\"+from_frame+\"_\"+to_frame\n",
" from_x = from_frame+\"_x\"\n",
" from_y = from_frame+\"_y\"\n",
" from_z = from_frame+\"_z\"\n",
" to_x = to_frame+\"_x\"\n",
" to_y = to_frame+\"_y\"\n",
" to_z = to_frame+\"_z\"\n",
" from_ox = from_frame+\"_ox\"\n",
" from_oy = from_frame+\"_oy\"\n",
" from_oz = from_frame+\"_oz\"\n",
" from_ow = from_frame+\"_ow\"\n",
" to_ox = to_frame+\"_ox\"\n",
" to_oy = to_frame+\"_oy\"\n",
" to_oz = to_frame+\"_oz\"\n",
" to_ow = to_frame+\"_ow\"\n",
" \n",
" '''\n",
" self.final = self.final.assign(d_linear_m0_gripper = lambda x: np.sqrt((x.gripper_palm_link_x - x.object_1_x)**2 +\n",
" (x.gripper_palm_link_y - x.object_1_y)**2 +\n",
" (x.gripper_palm_link_z - x.object_1_z)**2 ))\n",
" \n",
" self.initial = self.initial.assign(d_linear_m0_gripper = lambda x: np.sqrt((x.gripper_palm_link_x - x.object_1_x)**2 +\n",
" (x.gripper_palm_link_y - x.object_1_y)**2 +\n",
" (x.gripper_palm_link_z - x.object_1_z)**2 ))\n",
" '''\n",
" try :\n",
" # Calculating Distance between gripper and object and assigning \n",
" final_distance_col = np.sqrt((self.final[from_x] - self.final[to_x])**2 +\n",
" (self.final[from_y] - self.final[to_y])**2 +\n",
" (self.final[from_z] - self.final[to_z])**2 )\n",
" init_distance_col = np.sqrt((self.initial[from_x] - self.initial[to_x])**2 +\n",
" (self.initial[from_y] - self.initial[to_y])**2 +\n",
" (self.initial[from_z] - self.initial[to_z])**2 )\n",
"\n",
" self.final[linear_distance] = final_distance_col\n",
" self.initial[linear_distance] = init_distance_col\n",
" #self.final = self.final.assign(linear_distance = final_distance_col)\n",
" #self.initial = self.initial.assign(linear_distance = init_distance_col)\n",
"\n",
" # Calculating angular distances between the frames \n",
" diffAngle = []\n",
"\n",
" for index, row in self.final.iterrows():\n",
" q0 = np.quaternion(row[to_ox], row[to_oy], row[to_oz], row[to_ow])\n",
" q1 = np.quaternion(row[from_ox], row[from_oy], row[from_oz], row[from_ow])\n",
" _ = q0.inverse()*q1\n",
" diffAngle.append(_.angle())\n",
"\n",
" self.final[angular_distance] = diffAngle\n",
"\n",
" diffAngle = []\n",
" for index, row in self.initial.iterrows():\n",
" q0 = np.quaternion(row[to_ox], row[to_oy], row[to_oz], row[to_ow])\n",
" q1 = np.quaternion(row[from_ox], row[from_oy], row[from_oz], row[from_ow])\n",
" _ = q0.inverse()*q1\n",
" diffAngle.append(_.angle())\n",
"\n",
" self.initial[angular_distance] = diffAngle\n",
"\n",
" except :\n",
" print \"Feature not present in Readings : \", from_frame,\" \",to_frame\n",
" \n",
" def createRelativeDistanceData(self):\n",
" '''\n",
" Calculates the relative distance between the features which are relevant\n",
" This is a general function to keep adding the features between which the \n",
" data has to be calculated.\n",
" The the distance between Robot features and environment features.\n",
" Features :\n",
" Robot Features :\n",
" \"arm_link_0\", \"arm_link_1\", \"arm_link_2\", \"arm_link_3\", \"arm_link_4\",\n",
" \"arm_link_5\", \"gripper_palm_link\", \"gripper_finger_link_l\",\"gripper_finger_link_r\",\n",
" \"base_footprint\", \"base_link\", \"wheel_link_bl\", \"wheel_link_br\", \"wheel_link_fl\", \"wheel_link_fr\" \n",
" \n",
" Environment Features :\n",
" \"table_1\",\"table_2\",\"table_3\",\"table_4\",\"table_5\",\"table_6\",\"table_7\",\"object_1\"\n",
" '''\n",
" \n",
" #TODO the base frame for TF transformation was taken as arm_link_1 so its missing in the \n",
" #data collection. So need to update .\n",
" robot_features = [\"arm_link_0\", \"arm_link_2\", \"arm_link_3\", \"arm_link_4\",\n",
" \"arm_link_5\", \"gripper_palm_link\", \"gripper_finger_link_l\",\"gripper_finger_link_r\",\n",
" \"base_footprint\", \"base_link\", \"wheel_link_bl\", \"wheel_link_br\", \"wheel_link_fl\", \"wheel_link_fr\" ]\n",
" \n",
" env_features = [\"table_1\",\"table_2\",\"table_3\",\"table_4\",\"table_5\",\"table_6\",\"table_7\"]\n",
" print \"env : \",self.environment_features\n",
"\n",
" for robot_feature in self.robot_features:\n",
" if robot_feature not in self.features_without_positions:\n",
" for env_feature in self.environment_features:\n",
" self.dataCalculatingRelativeDistances(robot_feature, env_feature)\n",
" \n",
" print(\"Relative Distances are calculated . Data is ready for analysis\")\n",
" print \"Total number of features : \",len(self.initial.columns.values)\n",
"\n",
" \n",
" \n",
" def discribeData(self):\n",
" #print \"INTIAL DATA :\", self.initial.describe()\n",
" #print \"FINAL DATA :\", self.final.describe()\n",
" self.initial.boxplot()\n",
" self.final.boxplot()\n",
" \n",
" def discribeParameter(self, name):\n",
" print \"Parameter :\", name \n",
" print \"INITIAL :\", self.initial[name]\n",
" print \"FINAL :\", self.final[name]\n",
" #plt.savefig(\"/data/dataDeebul/rnd/RecommenderSystemInRobotics/experiments/\" + name + \"Box\")\n",
"\n",
" pdf, H, xedges, yedges = self.jointProbabilityDensityFunction(name)\n",
" px = pdf.sum(0)\n",
" py = pdf.sum(1)\n",
" print \"pdf Initial Values, pdf Final Values :\", px, py\n",
" print \"check sumpx, sum py, sumpxpy : \", sum(px), sum(py), sum(px)+sum(py)\n",
" print \"H_FinalGivenInitial : \", np.float16(infotheo.condentropy(py, px, pdf)), \"H_InitialGivenFinal :\", np.float16(infotheo.condentropy(px, py, pdf))\n",
" \n",
" initialValue = np.asarray( self.initial[name] )\n",
" finalValue = np.asarray( self.final[name])\n",
" \n",
" \n",
" labels = list('IF')\n",
" plt.boxplot(np.vstack((initialValue,finalValue)).T, labels=labels)\n",
" plt.show()\n",
" #min_max_scaler = preprocessing.MinMaxScaler()\n",
" #initialValue = min_max_scaler.fit_transform(initialValue)\n",
" #finalValue = min_max_scaler.fit_transform(finalValue)\n",
" \n",
" initialValue = np.around(initialValue, decimals=4)\n",
" finalValue = np.around(finalValue, decimals=4)\n",
" \n",
" #Return a boolean map of data, with false at place of all outliers\n",
" #So replacing all the outliers with the std mean \n",
" initialValue[self.mad_based_outlier(initialValue)] = np.median(initialValue, axis=0)\n",
" finalValue[self.mad_based_outlier(finalValue)] = np.median(finalValue, axis=0)\n",
" \n",
" \n",
" myextent =[xedges[0],xedges[-1],yedges[0],yedges[-1]]\n",
" plt.imshow(H.T,origin='low',extent=myextent,interpolation='nearest',aspect='auto')\n",
" plt.plot(finalValue, initialValue,'ro')\n",
" plt.colorbar()\n",
" plt.ylabel(\"Initial Values\")\n",
" plt.xlabel(\"Final Values\")\n",
" plt.title(\"Parameter : \"+name )\n",
" #plt.savefig(\"/data/dataDeebul/rnd/RecommenderSystemInRobotics/experiments/\" + name + \"JoinPDF\")\n",
" plt.show()\n",
"\n",
" xx = np.floor(100 * initialValue )\n",
" yy = np.floor(100 * finalValue )\n",
" \n",
" \n",
" \n",
" def jointProbabilityDensityFunction(self, feature, bins=5):\n",
" \"\"\"\n",
" Creates the Joint probability distribution based on the initial\n",
" and final values of the feature.\n",
"\n",
" \"\"\"\n",
" initialValue = np.asarray( self.initial[feature] )\n",
" finalValue = np.asarray( self.final[feature])\n",
" \n",
" if (np.allclose(initialValue, finalValue)):\n",
" print \"feature same final intial : \", feature\n",
" \n",
" #min_max_scaler = preprocessing.MinMaxScaler()\n",
" #initialValue = min_max_scaler.fit_transform(initialValue)\n",
" #finalValue = min_max_scaler.fit_transform(finalValue)\n",
" \n",
" initialValue = np.around(initialValue, decimals=3)\n",
" finalValue = np.around(finalValue, decimals=3)\n",
" \n",
" #Return a boolean map of data, with false at place of all outliers\n",
" #So replacing all the outliers with the std mean \n",
" initialValue[self.mad_based_outlier(initialValue)] = np.median(initialValue, axis=0)\n",
" finalValue[self.mad_based_outlier(finalValue)] = np.median(finalValue, axis=0)\n",
" pre.normalize((initialValue,finalValue),copy=False)\n",
"\n",
" #scalling both the axes on the same scale \n",
" #since intital and final values are measured of a single feature\n",
" #The histogram should be on same scale \n",
" #from larget value of both to smallest value of both\n",
" value_max = max(initialValue.max(), finalValue.max())\n",
" value_min = min(initialValue.min(), finalValue.min())\n",
" range_value = [[value_min, value_max],[value_min, value_max]]\n",
" H, xedges, yedges = np.histogram2d(finalValue, initialValue, bins=bins, range=range_value)\n",
" return H/float(len(initialValue)), H, xedges, yedges \n",
"\n",
" def condEntropyFinalGivenInitial(self):\n",
" \"\"\"\n",
" Calculates the conditional entropy of the features. It calculates the \n",
" final entropy given initial \n",
" \"\"\"\n",
" \n",
" self.condEntropyFinalGivenInitial = {}\n",
" for featureName in self.initial.columns.values:\n",
" pdf, _, __, ___ = self.jointProbabilityDensityFunction(featureName, 5)\n",
" #pdf of initial values\n",
" pInitial = pdf.sum(0)\n",
" #pdf of final values\n",
" pFinal = pdf.sum(1)\n",
" \n",
" #Entropy of Final given Initial\n",
" self.condEntropyFinalGivenInitial[featureName] = np.float16(infotheo.condentropy( pFinal, pInitial, pdf))\n",
" #self.condEntropyInitialGivenFinal[featureName] = np.float16(infotheo.condentropy( pInitial, pFinal, pdf))\n",
" #print \"Entropy : \",featureName,\" : \",self.condEntropyFinalGivenInitial[featureName],\" : \", np.float16(infotheo.condentropy( pInitial, pFinal, pdf))\n",
" \n",
" print sum( x == 0.0 for x in self.condEntropyFinalGivenInitial.values() )\n",
" return(self.condEntropyFinalGivenInitial)\n",
"\n",
" def condEntropyInitialGivenFinal(self):\n",
" \"\"\"\n",
" Calculates the conditional entropy of the features. It calculates the \n",
" final entropy given initial \n",
" \"\"\"\n",
" \n",
" if (self.initial.columns.values==self.final.columns.values).all() == False :\n",
" print (\"Columns are not same. Error in data collection\")\n",
" \n",
" self.condEntropyInitialGivenFinal = {}\n",
" for featureName in self.initial.columns.values:\n",
" pdf, _, __, ___ = self.jointProbabilityDensityFunction(featureName, 5)\n",
" #pdf of initial values\n",
" pInitial = pdf.sum(0)\n",
" #pdf of final values\n",
" pFinal = pdf.sum(1)\n",
" \n",
" #Entropy of Final given Initial\n",
" self.condEntropyInitialGivenFinal[featureName] = np.float16(infotheo.condentropy( pInitial, pFinal, pdf))\n",
" \n",
"\n",
" return(self.condEntropyInitialGivenFinal)\n"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 133
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"move_arm = DataAnalyzer(\"./movetoArmSingleDemo\", \"move_to\")\n",
"move_arm.createRelativeDistanceData()\n",
"h_F_I = move_arm.condEntropyFinalGivenInitial()\n",
"\n",
"move_arm.recommend_using_knowledge_base()\n",
"'''\n",
"h_I_F = move_arm.condEntropyInitialGivenFinal()\n",
"zeroEntropy = []\n",
"for key1, key2 in zip(h_F_I.keys(), h_I_F.keys()):\n",
" \n",
" if h_F_I[key1] == 0.0 and h_I_F[key2] != 0.0:\n",
" zeroEntropy.append(key1)\n",
" \n",
"pprint.pprint(sorted(zeroEntropy))\n",
"'''\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Are the inital and final features equal : True\n",
"Database reading Complete:\n",
"Skills : 13 Robot Features : 20\n",
"Environment Features : 11 Templates : 4\n",
"('Data has been succesfully read. Nu of Demonstrations : ', 1)\n",
"('Data Duplication, No of Demonstrations : ', 1)\n",
"2.54486122593 2.424795999\n",
"0.251524564165 0.157192282386\n",
"env : ['table_1', 'table_2', 'table_3', 'table_4', 'table_5', 'table_6', 'table_7', 'object_1', 'object_2', 'object_3', 'object_4']\n",
"Feature not present in Readings : arm_link_0 object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_1 object_4\n",
"Feature not present in Readings : arm_link_2 object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_3 object_4\n",
"Feature not present in Readings : arm_link_4 object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_5 object_4\n",
"Feature not present in Readings : gripper_palm_link object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" gripper_finger_link_l object_4\n",
"Feature not present in Readings : gripper_finger_link_r object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" base_footprint object_4\n",
"Feature not present in Readings : base_link object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" wheel_link_bl object_4\n",
"Feature not present in Readings : wheel_link_br object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" wheel_link_fl object_4\n",
"Feature not present in Readings : wheel_link_fr object_4\n",
"Relative Distances are calculated . Data is ready for analysis\n",
"Total number of features : 480\n",
"feature same final intial : arm_link_0_ow\n",
"feature same final intial : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_0_ox\n",
"feature same final intial : arm_link_0_oy\n",
"feature same final intial : arm_link_0_z\n",
"feature same final intial : arm_link_1_ox\n",
"feature same final intial : arm_link_1_oy\n",
"feature same final intial : arm_link_1_z\n",
"feature same final intial : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_angular_wheel_link_br_table_1\n",
"feature same final intial : d_angular_wheel_link_br_table_2\n",
"feature same final intial : d_angular_wheel_link_br_table_3\n",
"feature same final intial : d_angular_wheel_link_br_table_4\n",
"feature same final intial : d_angular_wheel_link_br_table_5\n",
"feature same final intial : d_angular_wheel_link_br_table_6\n",
"feature same final intial : d_angular_wheel_link_br_table_7\n",
"feature same final intial : d_angular_wheel_link_fl_table_6\n",
"feature same final intial : d_angular_wheel_link_fl_table_7\n",
"feature same final intial : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_angular_wheel_link_fr_table_1\n",
"feature same final intial : d_angular_wheel_link_fr_table_2\n",
"feature same final intial : d_angular_wheel_link_fr_table_3\n",
"feature same final intial : d_angular_wheel_link_fr_table_4\n",
"feature same final intial : d_angular_wheel_link_fr_table_5\n",
"feature same final intial : d_angular_wheel_link_fr_table_6\n",
"feature same final intial : d_angular_wheel_link_fr_table_7\n",
"480\n",
"skill being learnt : move_to\n",
"feature not available : d_linear_gripper_palm_link_object_4\n",
"feature not available : d_linear_base_link_object_4\n",
"feature not available : d_linear_base_footprint_object_4\n",
"FOR template : 0 Summed Entropy : 0.0\n",
"FOR template : 1 Summed Entropy : 0.0\n",
"feature not available : d_linear_base_link_object_4\n",
"feature not available : d_linear_base_footprint_object_4\n",
"FOR template : 2 Summed Entropy : 0.0\n",
"feature not available : d_linear_gripper_palm_link_object_4\n",
"FOR template : 3 Summed Entropy : 0.0\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 134,
"text": [
"'\\nh_I_F = move_arm.condEntropyInitialGivenFinal()\\nzeroEntropy = []\\nfor key1, key2 in zip(h_F_I.keys(), h_I_F.keys()):\\n \\n if h_F_I[key1] == 0.0 and h_I_F[key2] != 0.0:\\n zeroEntropy.append(key1)\\n \\npprint.pprint(sorted(zeroEntropy))\\n'"
]
}
],
"prompt_number": 134
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"move_base_relative = DataAnalyzer(\"./movetoBaseRelativePosition\", \"move_to\")\n",
"\n",
"move_base_relative.createRelativeDistanceData()\n",
"h_F_I = move_base_relative.condEntropyFinalGivenInitial()\n",
"\n",
"move_base_relative.recommend_using_knowledge_base()\n",
"\n",
"'''\n",
"move_base_relative.discribeParameter('d_linear_base_footprint_object_1')\n",
"\n",
"h_F_I = move_base_relative.condEntropyFinalGivenInitial()\n",
"h_I_F = move_base_relative.condEntropyInitialGivenFinal()\n",
"zeroEntropy = []\n",
"for key1, key2 in zip(h_F_I.keys(), h_I_F.keys()):\n",
" \n",
" if h_F_I[key1] == 0.0 and h_I_F[key2] != 0.0:\n",
" zeroEntropy.append(key1)\n",
" \n",
"pprint.pprint(sorted(zeroEntropy))\n",
"'''"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Are the inital and final features equal : True\n",
"Database reading Complete:\n",
"Skills : 13 Robot Features : 20\n",
"Environment Features : 11 Templates : 4\n",
"('Data has been succesfully read. Nu of Demonstrations : ', 12)\n",
"0.00884526338301 2.29815502717e-06\n",
"0.203341135413 0.26976739659\n",
"env : ['table_1', 'table_2', 'table_3', 'table_4', 'table_5', 'table_6', 'table_7', 'object_1', 'object_2', 'object_3', 'object_4']\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_0 object_2\n",
"Feature not present in Readings : arm_link_0 object_3\n",
"Feature not present in Readings : arm_link_0 object_4\n",
"Feature not present in Readings : arm_link_1 table_1\n",
"Feature not present in Readings : arm_link_1 table_2\n",
"Feature not present in Readings : arm_link_1 table_3\n",
"Feature not present in Readings : arm_link_1 table_4\n",
"Feature not present in Readings : arm_link_1 table_5\n",
"Feature not present in Readings : arm_link_1 table_6\n",
"Feature not present in Readings : arm_link_1 table_7\n",
"Feature not present in Readings : arm_link_1 object_1\n",
"Feature not present in Readings : arm_link_1 object_2\n",
"Feature not present in Readings : arm_link_1 object_3\n",
"Feature not present in Readings : arm_link_1 object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_2 object_2\n",
"Feature not present in Readings : arm_link_2 object_3\n",
"Feature not present in Readings : arm_link_2 object_4\n",
"Feature not present in Readings : arm_link_3 object_2\n",
"Feature not present in Readings : arm_link_3 object_3\n",
"Feature not present in Readings : arm_link_3 object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_4 object_2\n",
"Feature not present in Readings : arm_link_4 object_3\n",
"Feature not present in Readings : arm_link_4 object_4\n",
"Feature not present in Readings : arm_link_5 object_2\n",
"Feature not present in Readings : arm_link_5 object_3\n",
"Feature not present in Readings : arm_link_5 object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" gripper_palm_link object_2\n",
"Feature not present in Readings : gripper_palm_link object_3\n",
"Feature not present in Readings : gripper_palm_link object_4\n",
"Feature not present in Readings : gripper_finger_link_l object_2\n",
"Feature not present in Readings : gripper_finger_link_l object_3\n",
"Feature not present in Readings : gripper_finger_link_l object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" gripper_finger_link_r object_2\n",
"Feature not present in Readings : gripper_finger_link_r object_3\n",
"Feature not present in Readings : gripper_finger_link_r object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" base_footprint object_2\n",
"Feature not present in Readings : base_footprint object_3\n",
"Feature not present in Readings : base_footprint object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" base_link object_2\n",
"Feature not present in Readings : base_link object_3\n",
"Feature not present in Readings : base_link object_4\n",
"Feature not present in Readings : wheel_link_bl object_2\n",
"Feature not present in Readings : wheel_link_bl object_3\n",
"Feature not present in Readings : wheel_link_bl object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" wheel_link_br object_2\n",
"Feature not present in Readings : wheel_link_br object_3\n",
"Feature not present in Readings : wheel_link_br object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" wheel_link_fl object_2\n",
"Feature not present in Readings : wheel_link_fl object_3\n",
"Feature not present in Readings : wheel_link_fl object_4\n",
"Feature not present in Readings : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" wheel_link_fr object_2\n",
"Feature not present in Readings : wheel_link_fr object_3\n",
"Feature not present in Readings : wheel_link_fr object_4\n",
"Relative Distances are calculated . Data is ready for analysis\n",
"Total number of features : 383\n",
"feature same final intial : arm_link_0_ow\n",
"feature same final intial : arm_link_0_ox\n",
"feature same final intial : arm_link_0_oy\n",
"feature same final intial : arm_link_0_oz\n",
"feature same final intial : arm_link_0_x\n",
"feature same final intial : arm_link_0_y\n",
"feature same final intial : arm_link_0_z\n",
"feature same final intial : arm_link_2_z\n",
"110"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"skill being learnt : move_to\n",
"feature not available : d_linear_gripper_palm_link_object_2\n",
"feature not available : d_linear_gripper_palm_link_object_3\n",
"feature not available : d_linear_gripper_palm_link_object_4\n",
"feature not available : d_linear_base_link_object_2\n",
"feature not available : d_linear_base_link_object_3\n",
"feature not available : d_linear_base_link_object_4\n",
"feature not available : d_linear_base_footprint_object_2\n",
"feature not available : d_linear_base_footprint_object_3\n",
"feature not available : d_linear_base_footprint_object_4\n",
"FOR template : 0 Summed Entropy : 25.498046875\n",
"FOR template : 1 Summed Entropy : 0.0\n",
"feature not available : d_linear_base_link_object_2\n",
"feature not available : d_linear_base_link_object_3\n",
"feature not available : d_linear_base_link_object_4\n",
"feature not available : d_linear_base_footprint_object_2\n",
"feature not available : d_linear_base_footprint_object_3\n",
"feature not available : d_linear_base_footprint_object_4\n",
"FOR template : 2 Summed Entropy : 17.4599609375\n",
"feature not available : d_linear_gripper_palm_link_object_2\n",
"feature not available : d_linear_gripper_palm_link_object_3\n",
"feature not available : d_linear_gripper_palm_link_object_4\n",
"FOR template : 3 Summed Entropy : 8.0380859375\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 135,
"text": [
"\"\\nmove_base_relative.discribeParameter('d_linear_base_footprint_object_1')\\n\\nh_F_I = move_base_relative.condEntropyFinalGivenInitial()\\nh_I_F = move_base_relative.condEntropyInitialGivenFinal()\\nzeroEntropy = []\\nfor key1, key2 in zip(h_F_I.keys(), h_I_F.keys()):\\n \\n if h_F_I[key1] == 0.0 and h_I_F[key2] != 0.0:\\n zeroEntropy.append(key1)\\n \\npprint.pprint(sorted(zeroEntropy))\\n\""
]
}
],
"prompt_number": 135
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"movebase = DataAnalyzer(\"./movetoBaseAbsolutePositionWithEnv\")\n",
"\n",
"#movebase.dataManipulation()\n",
"movebase.createRelativeDistanceData()\n",
"\n",
"#movebase.condEntropyFinalGivenInitial()\n",
"#movebase.discretizeData()\n",
"#movebase.discribeParameter('base_footprint_y')\n",
"\n",
"h_F_I = movebase.condEntropyFinalGivenInitial()\n",
"h_I_F = movebase.condEntropyInitialGivenFinal()\n",
"zeroEntropy = []\n",
"for key1, key2 in zip(h_F_I.keys(), h_I_F.keys()):\n",
" \n",
" if h_F_I[key1] == 0.0 and h_I_F[key2] != 0.0:\n",
" zeroEntropy.append(key1)\n",
" \n",
"pprint.pprint(sorted(zeroEntropy))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
" Are the inital and final features equal : True\n",
"Data has been succesfully read.\n",
"Relative Distances are calculated . Data is ready for analysis"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Total number of features : 348\n",
"Entropy : arm_joint_1 : 0.0 : 0.0\n",
"Entropy : arm_joint_2 : 0.0 : 0.0\n",
"Entropy : arm_joint_3 : 0.0 : 0.0\n",
"Entropy : arm_joint_4 : 0.0 : -inf\n",
"Entropy : arm_joint_5 : 0.0 : -inf\n",
"Entropy : arm_link_0_ow : 0.0 : 0.0\n",
"Entropy : arm_link_0_ox : 0.0 : 0.0\n",
"Entropy : arm_link_0_oy : 0.0 : 0.0\n",
"Entropy : arm_link_0_oz : 0.0 : 0.0\n",
"Entropy : arm_link_0_x : 0.0 : 0.0\n",
"Entropy : arm_link_0_y : 0.0 : 0.0\n",
"Entropy : arm_link_0_z : 0.0 : 0.0\n",
"Entropy : arm_link_2_ow : 0.0 : 0.0\n",
"Entropy : arm_link_2_ox : 0.0 : 0.0\n",
"Entropy : arm_link_2_oy : 0.0 : 0.0\n",
"Entropy : arm_link_2_oz : 0.0 : 0.0\n",
"Entropy : arm_link_2_x : 0.0 : 0.0\n",
"Entropy : arm_link_2_y : 0.0 : 0.0\n",
"Entropy : arm_link_2_z : 0.0 : 0.0\n",
"Entropy : arm_link_3_ow : 0.0 : 0.0\n",
"Entropy : arm_link_3_ox : 0.0 : 0.0\n",
"Entropy : arm_link_3_oy : 0.0 : 0.0\n",
"Entropy : arm_link_3_oz : 0.0 : 0.0\n",
"Entropy : arm_link_3_x : 0.0 : 0.0\n",
"Entropy : arm_link_3_y : 0.0 : 0.0\n",
"Entropy : arm_link_3_z : 0.0 : 0.0\n",
"Entropy : arm_link_4_ow : 0.0 : 0.0\n",
"Entropy : arm_link_4_ox : 0.0 : 0.0\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_4_oy : 0.0 : 0.0\n",
"Entropy : arm_link_4_oz : 0.0 : -inf\n",
"Entropy : arm_link_4_x : 0.0 : 0.0\n",
"Entropy : arm_link_4_y : 0.0 : 0.0\n",
"Entropy : arm_link_4_z : 0.0 : -inf\n",
"Entropy : arm_link_5_ow : 0.0 : -inf\n",
"Entropy : arm_link_5_ox : 0.0 : 0.0\n",
"Entropy : arm_link_5_oy : 0.0 : -inf\n",
"Entropy : arm_link_5_oz : 0.0 : -inf\n",
"Entropy : arm_link_5_x : 0.0 : -inf\n",
"Entropy : arm_link_5_y : 0.0 : -inf\n",
"Entropy : arm_link_5_z : 0.0 : -inf\n",
"Entropy : base_footprint_ow : 0.0 : -inf\n",
"Entropy : base_footprint_ox : 0.0 : -inf\n",
"Entropy : base_footprint_oy : 0.0 : -inf\n",
"Entropy : base_footprint_oz : 0.0 : -inf\n",
"Entropy : base_footprint_x : 0.0 : -inf\n",
"Entropy : base_footprint_y : 0.0 : -inf\n",
"Entropy : base_footprint_z : 0.0 : -inf\n",
"Entropy : base_link_ow : 0.0 : -inf\n",
"Entropy : base_link_ox : 0.0 : -inf\n",
"Entropy : base_link_oy : 0.0 : -inf\n",
"Entropy : base_link_oz : 0.0 : -inf\n",
"Entropy : base_link_x : 0.0 : -inf\n",
"Entropy : base_link_y : 0.0 : -inf\n",
"Entropy : base_link_z : 0.0 : -inf\n",
"Entropy : gripper_finger_link_l_ow : 0.0 : -inf\n",
"Entropy : gripper_finger_link_l_ox : 0.0 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" gripper_finger_link_l_oy : 0.0 : -inf\n",
"Entropy : gripper_finger_link_l_oz : 0.0 : -inf\n",
"Entropy : gripper_finger_link_l_x : 0.0 : 0.0\n",
"Entropy : gripper_finger_link_l_y : 0.0 : -inf\n",
"Entropy : gripper_finger_link_l_z : 0.0 : -inf\n",
"Entropy : gripper_finger_link_r_ow : 0.0 : 0.0\n",
"Entropy : gripper_finger_link_r_ox : 0.0 : -inf\n",
"Entropy : gripper_finger_link_r_oy : 0.0 : -inf\n",
"Entropy : gripper_finger_link_r_oz : 0.0 : -inf\n",
"Entropy : gripper_finger_link_r_x : 0.0 : -inf\n",
"Entropy : gripper_finger_link_r_y : 0.0 : -inf\n",
"Entropy : gripper_finger_link_r_z : 0.0 : -inf\n",
"Entropy : gripper_palm_link_ow : 0.0 : -inf\n",
"Entropy : gripper_palm_link_ox : 0.0 : -inf\n",
"Entropy : gripper_palm_link_oy : 0.0 : -inf\n",
"Entropy : gripper_palm_link_oz : 0.0 : -inf\n",
"Entropy : gripper_palm_link_x : 0.0 : -inf\n",
"Entropy : gripper_palm_link_y : 0.0 : -inf\n",
"Entropy : gripper_palm_link_z : 0.0 : -inf\n",
"Entropy : table_1_ow : 0.0 : -inf\n",
"Entropy : table_1_ox : 0.72705 : -inf\n",
"Entropy : table_1_oy : 1.0459 : -inf\n",
"Entropy : table_1_oz : 0.0 : -inf\n",
"Entropy : table_1_x : 0.50977 : -inf\n",
"Entropy : table_1_y : 0.0 : -inf\n",
"Entropy : table_1_z : 0.86475 : -inf\n",
"Entropy : table_2_ow : 0.0 : -inf\n",
"Entropy : table_2_ox : 0.0 : -inf\n",
"Entropy : table_2_oy : 1.1777 : -inf\n",
"Entropy : table_2_oz : 0.0 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" table_2_x : 0.0 : -inf\n",
"Entropy : table_2_y : 0.0 : -inf\n",
"Entropy : table_2_z : 0.0 : -inf\n",
"Entropy : table_3_ow : 0.0 : -inf\n",
"Entropy : table_3_ox : 0.97754 : -inf\n",
"Entropy : table_3_oy : 0.69434 : -inf\n",
"Entropy : table_3_oz : 0.0 : -inf\n",
"Entropy : table_3_x : 0.65869 : -inf\n",
"Entropy : table_3_y : 0.0 : -inf\n",
"Entropy : table_3_z : 0.0 : -inf\n",
"Entropy : table_4_ow : 0.76025 : -inf\n",
"Entropy : table_4_ox : 0.69189 : -inf\n",
"Entropy : table_4_oy : 0.65869 : -inf\n",
"Entropy : table_4_oz : 0.0 : -inf\n",
"Entropy : table_4_x : 0.0 : -inf\n",
"Entropy : table_4_y : 0.0 : -inf\n",
"Entropy : table_4_z : 0.0 : -inf\n",
"Entropy : table_5_ow : 0.29492 : -inf\n",
"Entropy : table_5_ox : 0.80518 : -inf\n",
"Entropy : table_5_oy : 0.50098 : -inf\n",
"Entropy : table_5_oz : 0.0 : -inf\n",
"Entropy : table_5_x : 0.0 : -inf\n",
"Entropy : table_5_y : 0.69189 : -inf\n",
"Entropy : table_5_z : 1.3418 : -inf\n",
"Entropy : table_6_ow : 0.0 : -inf\n",
"Entropy : table_6_ox : 0.0 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" table_6_oy : 0.97754 : -inf\n",
"Entropy : table_6_oz : 0.0 : -inf\n",
"Entropy : table_6_x : 0.0 : -inf\n",
"Entropy : table_6_y : 0.0 : -inf\n",
"Entropy : table_6_z : 1.1592 : -inf\n",
"Entropy : table_7_ow : 0.29492 : -inf\n",
"Entropy : table_7_ox : 0.0 : -inf\n",
"Entropy : table_7_oy : 0.43237 : -inf\n",
"Entropy : table_7_oz : 0.0 : -inf\n",
"Entropy : table_7_x : 0.54541 : -inf\n",
"Entropy : table_7_y : 0.0 : -inf\n",
"Entropy : table_7_z : 1.1592 : -inf\n",
"Entropy : wheel_link_bl_ow : 0.43237 : -inf\n",
"Entropy : wheel_link_bl_ox : 0.0 : -inf\n",
"Entropy : wheel_link_bl_oy : 0.44141 : -inf\n",
"Entropy : wheel_link_bl_oz : 0.0 : -inf\n",
"Entropy : wheel_link_bl_x : 0.0 : -inf\n",
"Entropy : wheel_link_bl_y : 0.36353 : -inf\n",
"Entropy : wheel_link_bl_z : 0.0 : -inf\n",
"Entropy : wheel_link_br_ow : 0.25049 : -inf\n",
"Entropy : wheel_link_br_ox : 0.0 : -inf\n",
"Entropy : wheel_link_br_oy : 0.0 : -inf\n",
"Entropy : wheel_link_br_oz : 0.0 : -inf\n",
"Entropy : wheel_link_br_x : 0.0 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" wheel_link_br_y : 0.36353 : -inf\n",
"Entropy : wheel_link_br_z : 0.0 : -inf\n",
"Entropy : wheel_link_fl_ow : 0.0 : -inf\n",
"Entropy : wheel_link_fl_ox : 0.0 : -inf\n",
"Entropy : wheel_link_fl_oy : 0.0 : -inf\n",
"Entropy : wheel_link_fl_oz : 0.0 : -inf\n",
"Entropy : wheel_link_fl_x : 0.47681 : -inf\n",
"Entropy : wheel_link_fl_y : 0.25049 : -inf\n",
"Entropy : wheel_link_fl_z : 0.0 : -inf\n",
"Entropy : wheel_link_fr_ow : 0.0 : -inf\n",
"Entropy : wheel_link_fr_ox : 0.72705 : -inf\n",
"Entropy : wheel_link_fr_oy : 0.86475 : -inf\n",
"Entropy : wheel_link_fr_oz : 0.0 : -inf\n",
"Entropy : wheel_link_fr_x : 0.7959 : -inf\n",
"Entropy : wheel_link_fr_y : 0.50098 : -inf\n",
"Entropy : wheel_link_fr_z : 0.86475 : -inf\n",
"Entropy : d_linear_arm_link_0_table_1 : 0.7959 : -inf\n",
"Entropy : d_angular_arm_link_0_table_1 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_0_table_2 : 0.47681 : -inf\n",
"Entropy : d_angular_arm_link_0_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_0_table_3 : 0.54541 : -inf\n",
"Entropy : d_angular_arm_link_0_table_3 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_0_table_4 : 0.54541 : -inf\n",
"Entropy : d_angular_arm_link_0_table_4 : 0.32812 : -inf\n",
"Entropy : d_linear_arm_link_0_table_5 : 0.0 : -inf\n",
"Entropy : d_angular_arm_link_0_table_5 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_0_table_6 : 1.1729 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_angular_arm_link_0_table_6 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_0_table_7 : 0.44141 : -inf\n",
"Entropy : d_angular_arm_link_0_table_7 : 0.25049 : -inf\n",
"Entropy : d_linear_arm_link_2_table_1 : 0.93311 : -inf\n",
"Entropy : d_angular_arm_link_2_table_1 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_2_table_2 : 0.43237 : -inf\n",
"Entropy : d_angular_arm_link_2_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_2_table_3 : 0.54541 : -inf\n",
"Entropy : d_angular_arm_link_2_table_3 : 0.54541 : -inf\n",
"Entropy : d_linear_arm_link_2_table_4 : 0.54541 : -inf\n",
"Entropy : d_angular_arm_link_2_table_4 : 0.25049 : -inf\n",
"Entropy : d_linear_arm_link_2_table_5 : 0.32812 : -inf\n",
"Entropy : d_angular_arm_link_2_table_5 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_2_table_6 : 1.1592 : -inf\n",
"Entropy : d_angular_arm_link_2_table_6 : 0.50098 : -inf\n",
"Entropy : d_linear_arm_link_2_table_7 : 0.44141 : -inf\n",
"Entropy : d_angular_arm_link_2_table_7 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_3_table_1 : 0.93311 : -inf\n",
"Entropy : d_angular_arm_link_3_table_1 : 0.54541 : -inf\n",
"Entropy : d_linear_arm_link_3_table_2 : 0.43237 : -inf\n",
"Entropy : d_angular_arm_link_3_table_2 : 0.72705 : -inf\n",
"Entropy : d_linear_arm_link_3_table_3 : 0.50977 : -inf\n",
"Entropy : d_angular_arm_link_3_table_3 : 0.18176 : -inf\n",
"Entropy : d_linear_arm_link_3_table_4 : 0.54541 : -inf\n",
"Entropy : d_angular_arm_link_3_table_4 : 0.29492 : -inf\n",
"Entropy : d_linear_arm_link_3_table_5 : 0.57861 : -inf\n",
"Entropy : d_angular_arm_link_3_table_5 : 0.47681 : -inf\n",
"Entropy : d_linear_arm_link_3_table_6 : 1.0459 : -inf\n",
"Entropy : d_angular_arm_link_3_table_6 : 0.43237 : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-inf\n",
"Entropy : d_linear_arm_link_3_table_7 : 0.44141 : -inf\n",
"Entropy : d_angular_arm_link_3_table_7 : 0.7959 : -inf\n",
"Entropy : d_linear_arm_link_4_table_1 : 0.93311 : -inf\n",
"Entropy : d_angular_arm_link_4_table_1 : 0.7959 : -inf\n",
"Entropy : d_linear_arm_link_4_table_2 : 0.43237 : -inf\n",
"Entropy : d_angular_arm_link_4_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_4_table_3 : 0.0 : -inf\n",
"Entropy : d_angular_arm_link_4_table_3 : 0.98682 : -inf\n",
"Entropy : d_linear_arm_link_4_table_4 : 0.62305 : -inf\n",
"Entropy : d_angular_arm_link_4_table_4 : 0.32812 : -inf\n",
"Entropy : d_linear_arm_link_4_table_5 : 0.57861 : -inf\n",
"Entropy : d_angular_arm_link_4_table_5 : 0.54932 : -inf\n",
"Entropy : d_linear_arm_link_4_table_6 : 1.0459 : -inf\n",
"Entropy : d_angular_arm_link_4_table_6 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_4_table_7 : 0.36353 : -inf\n",
"Entropy : d_angular_arm_link_4_table_7 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_5_table_1 : 0.61426 : -inf\n",
"Entropy : d_angular_arm_link_5_table_1 : 1.0557 : -inf\n",
"Entropy : d_linear_arm_link_5_table_2 : 0.54541 : -inf\n",
"Entropy : d_angular_arm_link_5_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_5_table_3 : 0.50977 : -inf\n",
"Entropy : d_angular_arm_link_5_table_3 : 0.97754 : -inf\n",
"Entropy : d_linear_arm_link_5_table_4 : 0.25049 : -inf\n",
"Entropy : d_angular_arm_link_5_table_4 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_5_table_5 : 0.69189 : -inf\n",
"Entropy : d_angular_arm_link_5_table_5 : 0.93311 : -inf\n",
"Entropy : d_linear_arm_link_5_table_6 : 0.62305 : -inf\n",
"Entropy : d_angular_arm_link_5_table_6 : 0.0 : -inf\n",
"Entropy : d_linear_arm_link_5_table_7 : 0.62305 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_angular_arm_link_5_table_7 : 0.43237 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_1 : 0.50977 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_1 : 0.47681 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_2 : 0.54541 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_2 : 0.54541 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_3 : 0.84033 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_3 : 0.65869 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_4 : 0.43237 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_4 : 0.0 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_5 : 0.73096 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_5 : 0.62305 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_6 : 0.87354 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_6 : 0.25049 : -inf\n",
"Entropy : d_linear_gripper_palm_link_table_7 : 1.1592 : -inf\n",
"Entropy : d_angular_gripper_palm_link_table_7 : 0.0 : -inf\n",
"Entropy : d_linear_gripper_finger_link_l_table_1 : 0.68262 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_1 : 0.43237 : -inf\n",
"Entropy : d_linear_gripper_finger_link_l_table_2 : 0.43237 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_2 : 0.78662 : -inf\n",
"Entropy : d_linear_gripper_finger_link_l_table_3 : 0.25049 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_3 : 0.25049 : -inf\n",
"Entropy : d_linear_gripper_finger_link_l_table_4 : 0.44141 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_4 : 0.36353 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_linear_gripper_finger_link_l_table_5 : 0.0 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_5 : 0.61426 : -inf\n",
"Entropy : d_linear_gripper_finger_link_l_table_6 : 1.1592 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_6 : 0.43237 : -inf\n",
"Entropy : d_linear_gripper_finger_link_l_table_7 : 0.69189 : -inf\n",
"Entropy : d_angular_gripper_finger_link_l_table_7 : 0.61426 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_1 : 0.61426 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_1 : 0.0 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_2 : 0.0 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_2 : 0.50098 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_3 : 0.54541 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_3 : 0.43237 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_4 : 0.53613 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_4 : 0.65869 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_5 : 0.0 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_5 : 0.69189 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_6 : 0.73633 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_6 : 0.47681 : -inf\n",
"Entropy : d_linear_gripper_finger_link_r_table_7 : 0.69189 : -inf\n",
"Entropy : d_angular_gripper_finger_link_r_table_7 : 0.32812 : -inf\n",
"Entropy : d_linear_base_footprint_table_1 : 0.86475 : -inf\n",
"Entropy : d_angular_base_footprint_table_1 : 0.65869 : -inf\n",
"Entropy : d_linear_base_footprint_table_2 : 0.43237 : -inf\n",
"Entropy : d_angular_base_footprint_table_2 : 0.93311 : -inf\n",
"Entropy : d_linear_base_footprint_table_3 : 0.72705 : -inf\n",
"Entropy : d_angular_base_footprint_table_3 : 0.0 : -inf\n",
"Entropy : d_linear_base_footprint_table_4 : 0.62305 : -inf\n",
"Entropy : d_angular_base_footprint_table_4 : 0.25049 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_linear_base_footprint_table_5 : 0.0 : -inf\n",
"Entropy : d_angular_base_footprint_table_5 : 0.86475 : -inf\n",
"Entropy : d_linear_base_footprint_table_6 : 1.0557 : -inf\n",
"Entropy : d_angular_base_footprint_table_6 : 1.1592 : -inf\n",
"Entropy : d_linear_base_footprint_table_7 : 0.65869 : -inf\n",
"Entropy : d_angular_base_footprint_table_7 : 0.65869 : -inf\n",
"Entropy : d_linear_base_link_table_1 : 0.68262 : -inf\n",
"Entropy : d_angular_base_link_table_1 : 0.7959 : -inf\n",
"Entropy : d_linear_base_link_table_2 : 0.36353 : -inf\n",
"Entropy : d_angular_base_link_table_2 : 0.93311 : -inf\n",
"Entropy : d_linear_base_link_table_3 : 0.36353 : -inf\n",
"Entropy : d_angular_base_link_table_3 : 0.57861 : -inf\n",
"Entropy : d_linear_base_link_table_4 : 0.54932 : -inf\n",
"Entropy : d_angular_base_link_table_4 : 0.25049 : -inf\n",
"Entropy : d_linear_base_link_table_5 : 0.0 : -inf\n",
"Entropy : d_angular_base_link_table_5 : 0.32812 : -inf\n",
"Entropy : d_linear_base_link_table_6 : 0.97754 : -inf\n",
"Entropy : d_angular_base_link_table_6 : 0.84033 : -inf\n",
"Entropy : d_linear_base_link_table_7 : 0.69189 : -inf\n",
"Entropy : d_angular_base_link_table_7 : 0.47681 : -inf\n",
"Entropy : d_linear_wheel_link_bl_table_1 : 0.50098 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_1 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_bl_table_2 : 0.62305 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_bl_table_3 : 0.54541 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_3 : 0.43237 : -inf\n",
"Entropy : d_linear_wheel_link_bl_table_4 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_4 : 0.25049 : -inf\n",
"Entropy : d_linear_wheel_link_bl_table_5 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_5 : 0.98682 : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"-inf\n",
"Entropy : d_linear_wheel_link_bl_table_6 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_6 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_bl_table_7 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_bl_table_7 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_1 : 0.50977 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_1 : 0.54541 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_2 : 0.18176 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_2 : 0.68262 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_3 : 0.43237 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_3 : 0.43237 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_4 : 0.73633 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_4 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_5 : 0.58984 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_5 : 0.54541 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_6 : 0.43237 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_6 : 0.43237 : -inf\n",
"Entropy : d_linear_wheel_link_br_table_7 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_br_table_7 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_1 : 0.54932 : -inf\n",
"Entropy : d_angular_wheel_link_fl_table_1 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_2 : 0.36353 : -inf\n",
"Entropy : d_angular_wheel_link_fl_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_3 : 0.54541 : -inf\n",
"Entropy : d_angular_wheel_link_fl_table_3 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_4 : 0.73096 : -inf\n",
"Entropy : d_angular_wheel_link_fl_table_4 : 0.25049 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_5 : 0.35449 : -inf\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" d_angular_wheel_link_fl_table_5 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_6 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_fl_table_6 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fl_table_7 : 0.25049 : -inf\n",
"Entropy : d_angular_wheel_link_fl_table_7 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_1 : 0.72705 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_1 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_2 : 0.18176 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_2 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_3 : 0.43237 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_3 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_4 : 0.47681 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_4 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_5 : 0.73096 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_5 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_6 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_6 : 0.0 : -inf\n",
"Entropy : d_linear_wheel_link_fr_table_7 : 0.0 : -inf\n",
"Entropy : d_angular_wheel_link_fr_table_7 : 0.0 : -inf\n",
"Columns are not same. Error in data collection\n",
"["
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"u'arm_joint_4',\n",
" u'arm_joint_5',\n",
" u'arm_link_4_oz',\n",
" u'arm_link_4_z',\n",
" u'arm_link_5_ow',\n",
" u'arm_link_5_oy',\n",
" u'arm_link_5_oz',\n",
" u'arm_link_5_x',\n",
" u'arm_link_5_y',\n",
" u'arm_link_5_z',\n",
" u'base_footprint_ow',\n",
" u'base_footprint_ox',\n",
" u'base_footprint_oy',\n",
" u'base_footprint_oz',\n",
" u'base_footprint_x',\n",
" u'base_footprint_y',\n",
" u'base_footprint_z',\n",
" u'base_link_ow',\n",
" u'base_link_ox',\n",
" u'base_link_oy',\n",
" u'base_link_oz',\n",
" u'base_link_x',\n",
" u'base_link_y',\n",
" u'base_link_z',\n",
" 'd_angular_arm_link_0_table_1',\n",
" 'd_angular_arm_link_0_table_2',\n",
" 'd_angular_arm_link_0_table_3',\n",
" 'd_angular_arm_link_0_table_5',\n",
" 'd_angular_arm_link_0_table_6',\n",
" 'd_angular_arm_link_2_table_1',\n",
" 'd_angular_arm_link_2_table_2',\n",
" 'd_angular_arm_link_2_table_5',\n",
" 'd_angular_arm_link_2_table_7',\n",
" 'd_angular_arm_link_4_table_2',\n",
" 'd_angular_arm_link_4_table_6',\n",
" 'd_angular_arm_link_4_table_7',\n",
" 'd_angular_arm_link_5_table_2',\n",
" 'd_angular_arm_link_5_table_4',\n",
" 'd_angular_arm_link_5_table_6',\n",
" 'd_angular_base_footprint_table_3',\n",
" 'd_angular_gripper_finger_link_r_table_1',\n",
" 'd_angular_gripper_palm_link_table_4',\n",
" 'd_angular_gripper_palm_link_table_7',\n",
" 'd_angular_wheel_link_bl_table_1',\n",
" 'd_angular_wheel_link_bl_table_2',\n",
" 'd_angular_wheel_link_bl_table_6',\n",
" 'd_angular_wheel_link_bl_table_7',\n",
" 'd_angular_wheel_link_br_table_4',\n",
" 'd_angular_wheel_link_br_table_7',\n",
" 'd_angular_wheel_link_fl_table_1',\n",
" 'd_angular_wheel_link_fl_table_2',\n",
" 'd_angular_wheel_link_fl_table_3',\n",
" 'd_angular_wheel_link_fl_table_5',\n",
" 'd_angular_wheel_link_fl_table_6',\n",
" 'd_angular_wheel_link_fl_table_7',\n",
" 'd_angular_wheel_link_fr_table_1',\n",
" 'd_angular_wheel_link_fr_table_2',\n",
" 'd_angular_wheel_link_fr_table_3',\n",
" 'd_angular_wheel_link_fr_table_4',\n",
" 'd_angular_wheel_link_fr_table_5',\n",
" 'd_angular_wheel_link_fr_table_6',\n",
" 'd_angular_wheel_link_fr_table_7',\n",
" 'd_linear_arm_link_0_table_5',\n",
" 'd_linear_arm_link_4_table_3',\n",
" 'd_linear_base_footprint_table_5',\n",
" 'd_linear_base_link_table_5',\n",
" 'd_linear_gripper_finger_link_l_table_5',\n",
" 'd_linear_gripper_finger_link_r_table_2',\n",
" 'd_linear_gripper_finger_link_r_table_5',\n",
" 'd_linear_wheel_link_bl_table_4',\n",
" 'd_linear_wheel_link_bl_table_5',\n",
" 'd_linear_wheel_link_bl_table_6',\n",
" 'd_linear_wheel_link_bl_table_7',\n",
" 'd_linear_wheel_link_br_table_7',\n",
" 'd_linear_wheel_link_fl_table_6',\n",
" 'd_linear_wheel_link_fr_table_6',\n",
" 'd_linear_wheel_link_fr_table_7',\n",
" u'gripper_finger_link_l_ow',\n",
" u'gripper_finger_link_l_ox',\n",
" u'gripper_finger_link_l_oy',\n",
" u'gripper_finger_link_l_oz',\n",
" u'gripper_finger_link_l_y',\n",
" u'gripper_finger_link_l_z',\n",
" u'gripper_finger_link_r_ox',\n",
" u'gripper_finger_link_r_oy',\n",
" u'gripper_finger_link_r_oz',\n",
" u'gripper_finger_link_r_x',\n",
" u'gripper_finger_link_r_y',\n",
" u'gripper_finger_link_r_z',\n",
" u'gripper_palm_link_ow',\n",
" u'gripper_palm_link_ox',\n",
" u'gripper_palm_link_oy',\n",
" u'gripper_palm_link_oz',\n",
" u'gripper_palm_link_x',\n",
" u'gripper_palm_link_y',\n",
" u'gripper_palm_link_z',\n",
" u'table_1_ow',\n",
" u'table_1_oz',\n",
" u'table_1_y',\n",
" u'table_2_ow',\n",
" u'table_2_ox',\n",
" u'table_2_oz',\n",
" u'table_2_x',\n",
" u'table_2_y',\n",
" u'table_2_z',\n",
" u'table_3_ow',\n",
" u'table_3_oz',\n",
" u'table_3_y',\n",
" u'table_3_z',\n",
" u'table_4_oz',\n",
" u'table_4_x',\n",
" u'table_4_y',\n",
" u'table_4_z',\n",
" u'table_5_oz',\n",
" u'table_5_x',\n",
" u'table_6_ow',\n",
" u'table_6_ox',\n",
" u'table_6_oz',\n",
" u'table_6_x',\n",
" u'table_6_y',\n",
" u'table_7_ox',\n",
" u'table_7_oz',\n",
" u'table_7_y',\n",
" u'wheel_link_bl_ox',\n",
" u'wheel_link_bl_oz',\n",
" u'wheel_link_bl_x',\n",
" u'wheel_link_bl_z',\n",
" u'wheel_link_br_ox',\n",
" u'wheel_link_br_oy',\n",
" u'wheel_link_br_oz',\n",
" u'wheel_link_br_x',\n",
" u'wheel_link_br_z',\n",
" u'wheel_link_fl_ow',\n",
" u'wheel_link_fl_ox',\n",
" u'wheel_link_fl_oy',\n",
" u'wheel_link_fl_oz',\n",
" u'wheel_link_fl_z',\n",
" u'wheel_link_fr_ow',\n",
" u'wheel_link_fr_oz']\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n"
]
}
],
"prompt_number": 68
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"reachData = DataAnalyzer(\"./reach\")\n",
"reachData.dataManipulation()\n",
"reachData.dataCalculatingRelativeDistances()\n",
"\n",
"reachData.condEntropyFinalGivenInitial()\n",
"#reachData.discretizeData()\n",
"reachData.discribeParameter('arm_joint_2')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Data has been succesfully read.\n",
"Relative Distances are calculated . Data is ready for analysis\n",
"Columns are not same. Error in data collection\n",
"Entropy : arm_joint_1 : 0.0\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_joint_2 : 0.0\n",
"Entropy : arm_joint_3 : 1.7754\n",
"Entropy : arm_joint_4 : 0.0\n",
"Entropy : arm_joint_5 : 0.0\n",
"Entropy : arm_link_0_ow : 0.0\n",
"Entropy : arm_link_0_ox : 0.0\n",
"Entropy : arm_link_0_oy : 0.0\n",
"Entropy : arm_link_0_oz : 0.0\n",
"Entropy : arm_link_0_x : 0.0\n",
"Entropy : arm_link_0_y : 0.0\n",
"Entropy : arm_link_0_z : 0.0\n",
"Entropy : arm_link_2_ow : 0.53027\n",
"Entropy : arm_link_2_ox : 1.5801\n",
"Entropy : arm_link_2_oy : 1.1455\n",
"Entropy : arm_link_2_oz : 0.27759\n",
"Entropy : arm_link_2_x : 0.0\n",
"Entropy : arm_link_2_y : 0.21191\n",
"Entropy : arm_link_2_z : 0.0\n",
"Entropy : arm_link_3_ow : 1.2891\n",
"Entropy : arm_link_3_ox : 1.5215\n",
"Entropy : arm_link_3_oy : 0.91553\n",
"Entropy : arm_link_3_oz : 1.4053\n",
"Entropy : arm_link_3_x : 1.3848\n",
"Entropy : arm_link_3_y : 1.4219\n",
"Entropy : arm_link_3_z : 0.99561\n",
"Entropy : arm_link_4_ow : 0.61865\n",
"Entropy : arm_link_4_ox : 0.67334\n",
"Entropy : arm_link_4_oy : 0.21191\n",
"Entropy : arm_link_4_oz : 0.82715\n",
"Entropy : arm_link_4_x : 0.24963\n",
"Entropy : arm_link_4_y : 0.83496\n",
"Entropy : arm_link_4_z : 0.52734\n",
"Entropy : arm_link_5_ow : 1.8262\n",
"Entropy : arm_link_5_ox : 0.68115\n",
"Entropy : arm_link_5_oy : 1.251\n",
"Entropy : arm_link_5_oz : 0.94336\n",
"Entropy : arm_link_5_x : 0.57764\n",
"Entropy : arm_link_5_y : 0.51953\n",
"Entropy : arm_link_5_z : 0.0\n",
"Entropy : gripper_finger_link_l_ow : 1.1934\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" gripper_finger_link_l_ox : 1.1631\n",
"Entropy : gripper_finger_link_l_oy : 1.5088\n",
"Entropy : gripper_finger_link_l_oz : 1.4053\n",
"Entropy : gripper_finger_link_l_x : 1.0469\n",
"Entropy : gripper_finger_link_l_y : 0.68115\n",
"Entropy : gripper_finger_link_l_z : 0.58545\n",
"Entropy : gripper_finger_link_r_ow : 0.89307\n",
"Entropy : gripper_finger_link_r_ox : 0.15381\n",
"Entropy : gripper_finger_link_r_oy : 0.79736\n",
"Entropy : gripper_finger_link_r_oz : 0.58545\n",
"Entropy : gripper_finger_link_r_x : 1.0771\n",
"Entropy : gripper_finger_link_r_y : 0.82715\n",
"Entropy : gripper_finger_link_r_z : 1.3574\n",
"Entropy : gripper_palm_link_ow : 0.73926\n",
"Entropy : gripper_palm_link_ox : 1.3262\n",
"Entropy : gripper_palm_link_oy : 0.73145\n",
"Entropy : gripper_palm_link_oz : 0.37354\n",
"Entropy : gripper_palm_link_x : 0.64355\n",
"Entropy : gripper_palm_link_y : 0.36572\n",
"Entropy : gripper_palm_link_z : 0.21191\n",
"Entropy : marker_0_ow : 0.24963\n",
"Entropy : marker_0_ox : 1.2012\n",
"Entropy : marker_0_oy : 0.65332\n",
"Entropy : marker_0_oz : 0.74902\n",
"Entropy : marker_0_x : 0.0\n",
"Entropy : marker_0_y : 0.0\n",
"Entropy : marker_0_z : 0.0\n",
"Entropy : d_linear_m0_gripper : 0.0\n",
"Entropy : d_angular_m0_gripper : 0.0\n",
"Parameter : arm_joint_2\n",
"INITIAL : 0 1.107059\n",
"1 0.926407\n",
"2 0.943948\n",
"3 0.957602\n",
"4 0.656764\n",
"5 1.058616\n",
"6 1.058626\n",
"7 0.976129\n",
"8 0.976129\n",
"9 0.355977\n",
"10 0.656915\n",
"11 1.004393\n",
"12 1.224939\n",
"Name: arm_joint_2, dtype: float64\n",
"FINAL : 0 0.057868\n",
"1 0.029140\n",
"2 0.055199\n",
"3 0.060838\n",
"4 0.077029\n",
"5 0.077029\n",
"6 0.064715\n",
"7 0.064715\n",
"8 0.084813\n",
"9 0.084803\n",
"10 0.104760\n",
"11 0.104760\n",
"12 0.059529\n",
"Name: arm_joint_2, dtype: float64\n",
"pdf Initial Values, pdf Final Values : [ 0. 0. 0.15384615 0.46153846 0.38461538] [ 1. 0. 0. 0. 0.]\n",
"check sumpx, sum py, sumpxpy : 1.0 1.0 2.0\n",
"H_FinalGivenInitial : 0.0 H_InitialGivenFinal : -inf\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n"
]
}
],
"prompt_number": 139
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"reachData.discribeParameter('arm_joint_1')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Parameter : arm_joint_1\n",
"pdf Initial Values, pdf Final Values :"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" [ 0.23076923 0.30769231 0.15384615 0.23076923 0.07692308] [ 0.23076923 0.30769231 0.15384615 0.15384615 0.15384615]\n",
"check sumpx, sum py, sumpxpy : 1.0 1.0 2.0\n",
"H_FinalGivenInitial : 0.21191 H_InitialGivenFinal : 0.15381\n",
"SINGLE pdf Initial Values, pdf Final Values : [ 0.23076923 0.30769231 0.15384615 0.23076923 0.07692308]\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWYAAAEBCAYAAABL1w/0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAADchJREFUeJzt3X2IZXd9x/HPZ3ca0rXVS1prtIZeRQVLpDdplUiQva19\nWGriQ+0/oU83BcE/GhOoRREko0grReimLf2jjWYilP4TUYio8WlPWa1Nq91ZtLu2oiwkVWtAoYmp\nRrNf/9gzs+Nk5t57Zu49v4f7fsEm85t7d+/3hNlPznzuOb9xRAgAkI8jqQcAAPw4ghkAMkMwA0Bm\nCGYAyAzBDACZIZgBIDMzg9n2wPZ9ts/bPmf7hj4GA4BVtTbHc+6S9JGI+F3ba5KetuSZAGCledoN\nJrafIelMRDy/v5EAYLXNqjKeJ+kR2/fY/g/b/2D7WB+DAcCqmhXMa5Kul/R3EXG9pO9KeuvSpwKA\nFTarY35Y0sMR8e/t+j7tCmbbbLYBAAcQEd7r81ODOSK+afsh2y+KiP+W9OuS/nOP5y1mSmDB1tfX\ntb6+nnoM4CnsPTNZ0nxXZdwm6R9tXyHpq5JuXdBcwNJduHAh9QhAZzODOSLOSnppD7MAAMSdf6jc\nZDJJPQLQ2dTrmOf6A+ygYwaAbmzv++YfZ8yoWtM0qUcAOiOYASAzVBkAkABVBgAUhGBG1eiYUSKC\nGQAyQ8cMAAnQMQNAQQhmVI2OGSUimAEgM3TMAJDAtI55nm0/gSxM2792kTjRQGoEM4pxkMC0G0WM\nFz8MsER0zACQGc6YUYyDVhldfxtVBlLjjBnFiIjOv44f7/57gNQIZlRtfb1JPQLQGcEMAJnhOmYA\nSIC9MgCgIAQzqsZeGSgRwYyq3XFH6gmA7uiYUTVb4ssTOaJjBoCCEMyoXJN6AKAzghkAMjNXx2z7\ngqT/k/SkpB9ExMt2PEbHjGzRMSNXi9iPOSSNI+LbixsLWL7jx1NPAHTXpcroZ5dyYIHYKwMlmjeY\nQ9InbX/e9huWORAArLp5O+ZnR8Q3bD9T0ick3RYRp9vH6JgBoKNDd8wR8Y3234/Y/qCkl0k6vfX4\nZDLRcDiUJA0GA41GI43HY0mXb4llzZo161VeN02jjY0NSdrOy/3MPGO2fUzS0Yh41PbTJH1c0jsi\n4uPt45wxI1tN02z/JQFyctg7/54l6bTtTUkPSvrwVigDuWOvDJSIvTJQNa5jRq7YKwMACkIwo3JN\n6gGAzghmAMgMHTOqRseMXNExY2WxVwZKRDCjauyVgRIRzACQGTpmAEiAjhkACkIwo2pbm8gAJSGY\nUTX2ykCJ6JhRNa5jRq7omAGgIAQzKtekHgDojGAGgMzQMaNqdMzIFR0zVhZ7ZaBEBDOqxl4ZKBHB\nDACZoWMGgATomAGgIAQzqsZeGSgRwYyqsVcGSkTHjKpxHTNyRccMAAUhmFG5JvUAQGcEMwBkho4Z\nVaNjRq7omLGy2CsDJZormG0ftX3G9v3LHghYJPbKQInmPWO+XdI5SXxTCABLNjOYbT9X0m9LulvS\nnn0IkKvxeJx6BKCzec6Y/0rSn0m6uORZAACS1qY9aPsmSd+KiDO2x/s9bzKZaDgcSpIGg4FGo9H2\nmcrWXgWsWadYnzx5kq9H1lmsm6bRxsaGJG3n5X6mXi5n+88l/YGkH0q6UtLTJX0gIv5wx3O4XA7Z\nGo0abW6OU48BPMW0y+Xmvo7Z9nFJb46Im3d9nmBGtriOGbla5HXMfIkDwJJx5x+qZjeKGKceA3gK\n7vwDgIJwxoyq0TEjV5wxY2WxVwZKRDCjauyVgRIRzACQGTpmAEiAjhkACkIwo2pbexUAJSGYUbU7\n7kg9AdAdHTOqxnXMyBUdMwAUhGBG5ZrUAwCdEcwAkBk6ZlSNjhm5mtYxT/3RUsAyHTnST2h6yT9C\n2JYu8hMxsUBUGUgmYvm/Tp1qenkdYJEIZgDIDB0zkqml/63lONAvrmMGgIIQzKgae2WgRAQzAGSG\njhnJ1NLN1nIc6BcdMwAUhGBG1eiYUSKCGQAyQ8eMZGrpZms5DvSLjhkACkIwo2p0zCjRzGC2faXt\nB21v2j5n+y/6GAwAVtVcHbPtYxHxuO01SZ+R9OaI+Ez7GB0zDqSWbraW40C/Dt0xR8Tj7YdXSDoq\n6dsLmg0AsMtcwWz7iO1NSf8r6VREnFvuWMBi0DGjRHP9BJOIuChpZPsZkh6wPY6IZuvxyWSi4XAo\nSRoMBhqNRhqPx5Iu/8VgzTrFenNzs5fXk/I4Xtb5rpum0cbGhiRt5+V+Ol/HbPvtkv4/It7TrumY\ncSC1dLO1HAf6daiO2fbP2h60H/+kpN+QdGaxIwIAtszTMT9b0qfbjvlBSfdHxKeWOxawGJerBqAc\nMzvmiPiipOt7mAUAIPbKQEK1dLO1HAf6xV4ZAFAQghlVo2NGiQhmAMgMHTOSqaWbreU40C86ZgAo\nCMGMqtExo0QEMwBkho4ZydTSzdZyHOgXHTMAFIRgRtXomFEighkAMkPHjGRq6WZrOQ70i44ZAApC\nMKNqdMwoEcEMAJmhY0YytXSztRwH+kXHDAAFIZhRNTpmlIhgBoDM0DEjmVq62VqOA/2iYwaAghDM\nqBodM0pEMANAZuiYkUwt3Wwtx4F+0TEDQEEIZlSNjhklWks9AFZXyNKe38iVJXb8E1iEmR2z7Wsk\nvV/Sz+nSV9/fR8Rf73icjhkHUks3W8txoF/TOuZ5gvlqSVdHxKbtn5L0BUmvjYjz7eMEMw6klkCr\n5TjQr0O9+RcR34yIzfbjxySdl/ScxY4ILAcdM0rU6c0/20NJ10l6cBnDAAA6vPnX1hj3Sbq9PXPe\nNplMNBwOJUmDwUCj0Ujj8VjS5TMW1qxTrLc+t+zXk/I4Xtb5rpum0cbGhiRt5+V+5rrBxPZPSPqw\npI9GxMldj9Ex40Bq6WZrOQ7061Ads21Leq+kc7tDGcjd5TNaoBzzdMw3Svp9Sb9q+0z768SS5wKA\nlcVeGUimlgqgluNAv9grAwAKQjCjanTMKBHBDACZoWNGMrV0s7UcB/pFxwwABSGYUTU6ZpSIYAaA\nzNAxI5lautlajgP9omMGgIIQzKgaHTNKRDADQGbomJFMLd1sLceBftExA0BBCGZUjY4ZJSKYASAz\ndMxIppZutpbjQL/omAGgIAQzqkbHjBIRzACQGTpmJFNLN1vLcaBfdMwAUJC11ANgtXnP84VFaiSN\nl/oKyz8GrBqCGcn08e0/NQNKRMeMqhHMyBUdMwAUhGBG5ZrUAwCdEcwAkBmCGVU7fnycegSgs5lv\n/tl+n6RXSfpWRLxkj8d58w8AOjrsm3/3SDqx2JGAfrBXBko0M5gj4rSk7/QwCwBAc17HbHso6X6q\nDABYDK5jBoCCLOSW7MlkouFwKEkaDAYajUYaj8eSLnd8rFmnWL/gBSd19918PbJOv26aRhsbG5K0\nnZf7ocpA1exGEePUYwBPcagqw/Y/SfoXSS+y/ZDtWxc9ILA849QDAJ2xiRGqxiZGyBVv/mGFNakH\nADojmAEgMwQzqsZeGSgRHTMAJEDHjJW1dR0pUBKCGQAyQ5UBAAlQZQBAQQhmVG00alKPAHRGMKNq\nZ8+mngDojo4ZVeOWbOSKjhkACkIwo3JN6gGAzghmAMgMwYyqsVcGSsSbfwCQAG/+YWWxVwZKRDAD\nQGaoMgAgAaoMACgIwYyqsVcGSkQwo2rslYES0TGjauyVgVzRMQNAQQhmVK5JPQDQGcEMAJkhmFE1\n9spAiXjzDwASONSbf7ZP2P6y7a/YfsvixwOWh70yUKKpwWz7qKS/lXRC0i9KusX2i/sYDFiEzc3N\n1CMAnU2tMmy/XNKdEXGiXb9VkiLi3TueQ5WBXth7fte3cHw9ow+HqTJ+XtJDO9YPt58DehcRnX/d\neeednX8PkNqsYOarFEW7cOFC6hGAztZmPP4/kq7Zsb5Gl86af0xf32ICB3HvvfemHgHoZFbHvCbp\nvyS9UtLXJf2bpFsi4nw/4wHA6pl6xhwRP7T9J5IekHRU0nsJZQBYrkPfYAIAWCxuyQaAzBDMqIrt\nX7Z914zn3DzrLlbbv2D7lhnPucr2KduP2v6bg8wL7IUqA9mxfSQiLiaeYSzpTyPi5inPOSbpOknX\nSro2Im7raTxUjjNm9M72B21/3vaXbL+h/dxjtt9je1PSy9v1X7bP+YTtG2z/s+2v2p4WlmPb97cf\nX2X7Q7bP2v6c7Ze0n59sneHa3rB9l+3Ptn/269s/6t2SXmH7jO3b93qtiHg8Ij4r6fuL+68DEMxI\n448j4lckvVTSm2xfJemYpH+NiFEbdsckfSoirpX0qKR3Svo1Sa9rP57HOyR9ISJ+SdLbJL1/n+dd\nHRE3SrpJlwJZkt4i6XREXBcRU6sRcSMWFmzWDSbAMtxu+7Xtx8+V9EJJT0r6wI7nPBERD7Qff1HS\n9yLiSdtfkjSc83VulPQ7khQRp2z/jO2f3vWckPSh9jnnbT+r/Tx3TSEZghm9arvbV0q6ISK+Z/uU\npCt1KXh3nnn+YMfHFyU9IUkRcbG98Wnul9y13uvs9okpzwd6R5WBvj1d0nfaUH6xpBuW+FqnJf2e\ntP0/hEci4rE5f++jknafXe+HMMdCccaMvn1M0httn9Ol2/0/135+95nstPW0Tjd2PL4u6X22z0r6\nrqQ/2uM5+/3ZZyU92b4Zec9+PbPtC7oU4FfYfo2k34yIL0+ZD5iJy+VQlfaqipsi4tbUswAHxRkz\nqmH71ZLeJYlQRtEIZhTJ9m/p8qVtW74WEQv/0WdTXuv1ez0fOCyqDADIDFdlAEBmCGYAyAzBDACZ\nIZgBIDMEMwBk5kfgVRMHYSWQIwAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fd392bcef10>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWEAAAEZCAYAAABGjpR7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmcHVWd9/HPN2lCEkgIGGSXAhVHRA0giKChgw6DKNFx\nHMV1WgS3iejM87gxozSjoM7gQ9QY0cgSlwFnQAZRRB2h2WSRpdkCKmCxyL4KJCyd/J4/qjq5uel7\nb1X1rXuqun/v1+u+uuveulXf3CSnT//q1DkyM5xzzoUxJXQA55ybzLwRds65gLwRds65gLwRds65\ngLwRds65gLwRds65gLwRdq4FSa+TdEvGfb8t6V/LzuQmHvk44XAkxcDzgdXAU8AvgEVm9lTIXO1I\nioDbgT4zWxM2TT1JOhW4y8w+n2HfRcAAsBtwmpl9oNx0rte8JxyWAW82s1nAHsCrgFy9KaXKCNfp\n1IXeJPV1O0jT8UN9HmX5M/BF4OTQQVw5vBGuCDO7BzgP2E3SHEk/k/SApEcknSNpu9F9JQ1J+pKk\nS0l60DtL+oCkFZL+Iuk2SR9q2L9f0t2SPpUe8x5Jb5V0sKQ/SHpY0mcb9pekz0q6VdJDkn4safP0\n5YvSr49JekLSq9P3HJae/xFJ50l6QcPx1kj6mKQ/Ar/P+9nk/DyeTD+PNZI+KumP6Wfyb5JeKOky\nSY9JOl3SRh3O2y/probtl6bnelTSjZIOaXjtVElfbPq8/1nS/ennPZC+9iHg3cCn08/v7HYZzOws\nMzsbeDjv5+bqwRvh8AQgaQfgjcA1JH8vJwEvSB+rgCVN73svcDiwKXAHcD/wJjObDXwAOEHS7g37\nbwVsDGwDfAH4HvAeYHfgdcAXJO2Y7nsksBCYn+7/KPCt9LXXpV83M7NZZnaFpLcAnwP+FpgLXAyc\n1pT3LcBewK5jfgjSdZIObfEZ5fk8ZgF3ps8dmP759gE+AywD3pUe4+Xp95mkDfY5JD8otwQ+DvxI\n0i7pLpY+Rm0FzAa2BT4IfEvSZmb2XeBHwFfTz+8tWSNkzepqxsz8EegBxMATJI1cTNKwbDzGfvOA\nRxq2LwAGOxz7LODI9Pt+YCXrrgHMAtYAezXsfxWwMP3+ZuCAhte2AZ4laQyj9L1TGl7/BXBYw/YU\nkh76Dun2GqC/i59bx88jPedrmv58n2rYPh44ocN5+klqt5D88Lm36fX/BI5Ovz8F+GLT5934Gd0P\n7N28b44/8xeBU0L/m/VH9x+l1udcRwa8xczOb3xS0kzgBOBvgNEywKaSZOn/SOCupve8ETgaeDFJ\nIzgTuL5hl4cb3rsq/Xp/w+urSHrVADsCZ0lqvPA2QtK7G8uOwNclfa3p+e0act5FQUU+j1Tzn695\ne+scMbYd4xx3pM+P5WFb/8LlStZ9vkV4T3iC8nJENf0fYBeSntNmwP4k/wkb/yOu/dVX0sbAmcC/\nA883s82Bcyn+H/dO4CAz27zhMdPM7mX9X7kb9/9Q0/6bmNnlY+UtINfnUZJ7gB2aLvrtSHLhLG+G\nIll9GNME5Y1wNW1K0lN7XNIWJD3cZo2NwbT08RCwJu0VHziO858IHDd6cU3SlpIWpq89SPKr/gub\n9j9K0q7p/ptJ+vtxnL9Z3s+jFbX4PosrSHqzn5a0kaR+4M3A6Q3Hy3rM+4Gds+woaaqk6UAfMFXS\nxpKm5kruKs0b4WpaDMwgaVR/S1Jzbe4Jrd02sydILqb9F/AIyQWn5qvuLd8/hq8DPwV+JekvwGXA\n3um5VgLHApemowT2NrP/Ab4KnC7pceAGktJBlnMBkI42aHWhLNfn0eac1vR95t6lmT0LHEJy8fRB\nkvr9+8zsDy2O1+7YJwG7pp/fTzqc+vMkjf9nSC4+rgL+JWtuV32l3qwhaQ7JVfiXkfyjPKzpV1Tn\nKkvSAcAyM3thx53dpJH+JnIVcLeZHTLG698g+WG9Ehgws2vbHa/sC3NfB841s7crGaS/Scnnc66b\ndiO5O9C5Rp8AVpCMMlqPpIOBF5nZi9Mx9N8mGSLZUmnlCEmbAa8zs5MBzGzEzB4v63zOFSHpqPSm\niebHuST/2Y4p+fwvaHH+v0javsxzu/zSv5ODSX7DH+sawEJgOYCZXQHMkdRqVBFQbk94J+BBSacA\nrwSuBj6R1hSdqwQzOw44LuD572SMHpWrrBOAT5HciDOWxmGZAHcD27P+8Mj1lHlhro9kPoSlZrYH\nyeD9z7Z/i3POVZOkNwMPpDXediNhml9re+GtzJ7w3SSF69+l22fQ1AhL8rGPzrnMzGxcN63kbXOa\nzrcvsDCt+04HZkv6vpm9v2GfPwM7NGxvz/pjyTdQWk/YzO4D7mq4t/4NwE1j7Ferx9FHHx08w0TP\nXLe8nrk3j275UsbHGG3VUWa2g5ntBBwKnG/rN8CQDO18P4CkfYDHzKxlKQLKHx0xOsnJNOA2koll\nai2O49ARcqtb5rrlBc9cJ22nzsvHACR9GMDMvmNm5yqZnfBWkhJsxzav1EbYzK4jmTnLOecqoRuN\nnpldCFyYfv+dptcW9TrPpDIwMBA6Qm51y1y3vOCZ62RG6ABNgi5vtP4kWM4515okrAsX5pZl3PcI\nxn8hMAufOyKnoaGh0BFyq1vmuuUFz1wnfRkfvczjnHOTRhcvzHWFlyOcc7XQrXLE6Z13A5IxaL0o\nR3hP2Dk3qVStJ+w14ZzqWEerW+a65QXPXCcbZXz0iveEnXOTig9Razy514Sdcxl1qyZ8QcZ9F+A1\nYeec6zqvCddcHetodctct7wwuTMvHRzknXPnMjBnDu+cO5elg4NdOW5ZfJywc27CWDo4yPXHHsuP\nR0bWPveRY49lKfCxijbGVesJV6YmfPvtj/Dww6uCZXEuuG23C50gt6/sNpczH3t4g+cPfd7zOP2h\nh7p6rm7VhK/LuO8rmWQ14X/7twtZvjzrx+PcBFTRnmM7b1k1Mubz00fGfr4KqtYT9ppwbnHoAAXE\noQPkFIcOUEAcOkB+fxoa9yGemDJ2P+7pvsr07zYwI+OjmaTpkq6QNCxphaQvj3V8Sf2SrpV0o6Sh\nTnm8EXbOFXbD3ov4oNZvcD/c18f8Rbmm1O2pojdrmNnTwAIzmwe8Algg6bWN+0iaA3wLOMTMdgPe\n3ilPdX9cVVYUOkABUegAOUWhAxQQhQ6Q30794z7EgwsGOQd4/ZVL2LZvhOemJQ1wVS/KwfgaPVu3\nWvw0YCrwSNMu7wbONLO70/07Fsa9EXbOjcuDCwY5f8Egtx0JO28eOk1nG2Vt9cYoa0uaAlwDvBD4\ntpmtaNrlxcBGki4AZgFfN7MftDuNN8K5xdSv1xNTr8wx9coLtcz8p6Gu9IbrplW5+uLVcMma9u81\nszXAPEmbAb+U1G9mQw27bATsAbwemAlcJulyM/tjyzx5wjvnXN1tNHXs5w+YCgc0bH/lqdbHMLPH\nJf0ceBUw1PDSXcBDZrYKWCXpIpLRbi0bYb8wl1sUOkABUegAOUWhAxQQhQ6Q3yTsBUPSE87yaCZp\nbnrhDUkzgL8Grm3a7WzgtZKmSpoJvBpoLlmsn6cbfyjnnKuLjTYu/NZtgOVpXXgK8AMz+03Tkve3\nSDoPuB5YAywbo268Hm+Ec4upX68npl6ZY+qVF2qZeZLWhIu2emZ2A0m9t/n55iXvjweOLzmOc87V\nVMVavYrFqYModIACotABcopCByggCh0gv8nYC4bKtXoVi+OccyVrMToiFB8dkVscOkABcegAOcWh\nAxQQhw6QXxfmjqilik0o7D1h59zkUnx0RClKb4QlxcBfgNXAc2a2d9nnLFcUOkABUegAOUWhAxQQ\nhQ6Qn9eEK6EXcQzoN7PmiS6cc673KtYI96omXPrs9L0Thw5QQBw6QE5x6AAFxKED5DdZa8JTMz56\npBeNsAH/K+kqSUf04HzOOdfaJLwwt5+Z3StpS+DXkm4xs4t7cN6SRKEDFBCFDpBTFDpAAVHoAPl5\nTbgSSo9jZvemXx+UdBawN7C2ER4YGCCKIoaHbwYeB7Zm3T/oOP3q2749CbZHywOjjWPNti+/ZIg7\nZ0F/f7I9NJS8XnR78eLFDA8PE0URXVWxRrjU1ZbTWYSmmtkTkjYBfgUcY2a/Sl9fu9rywMBZNVno\nM6Z+vZ6YemWOqVde6ErmXq9G0eW5I8qe1L1bqy3bwoz7/nRirLa8FXCWpNFz/Wi0AXbOuSAq1hMu\nNY6Z/QmYV+Y5ei8KHaCAKHSAnKLQAQqIQgfIb7LWhAuOfJA0HbiQ5HaPacDZZva5pn3eA3yaZETY\nE8BHzez6dset2M8E55wrWfGpLJ+WtMDMVkrqAy6R9Fozu6Rht9uB+enKGwcB3wX2aXdcnzsitzh0\ngALi0AFyikMHKCAOHSC/yTpOeBxD1Dqttmxml5nZ4+nmFcD2neJ4I+ycm1zGcbOGpCmShoH7gQs6\nrJrxQeDcTnG8HJFbFDpAAVHoADlFoQMUEIUOkN9krQm3aPWG7oGhe9u/NcNqywBIWgAcBuxXMI5z\nzk1Q08d+un/n5DHqmOYlPBu0WW0ZSa8AlgEHmdmjneJ4OSK3OHSAAuLQAXKKQwcoIA4dIL/JWhMu\nWI7IstqypBcAPwHea2a3ZonjPWHn3ORSvNXruNoy8AVgc+Db6f0RHafv9UY4tyh0gAKi0AFyikIH\nKCAKHSA/rwnnkmW1ZTM7HDi8B3Gcc66mfI25uotDByggDh0gpzh0gALi0AHym6w14Uk4laVzzlVH\nxVq9isWpgyh0gAKi0AFyikIHKCAKHSC/yVoTnmwLfTrnXKVUrNXzmnBucegABcShA+QUhw5QQBw6\nQH5eE/aasHPO9VzFRkd4I5xbFDpAAVHoADlFoQMUEBV+55ZcwMv5HbO+vJgnpvRxw96LeHDBYNeS\ntTRZa8IVa/UqFse5yWVLLuAQLuYkDJ5ZBcAHLzqWc6A3DfFkVLFWr2Jx6iCmfj21mHpljimS91/t\n2W4HySweuoOof8fc7xueeyUnPbz+Oo8n2Qivv3IJ55fdCHd5jbna8HKEc27UzJE1Yz4/a81Ij5NM\nIi1mUQvFG+HcotABCohCB8gpCh0gtyK9YICVfWMPUHpiSg/+a07GXjBUrtXzIWrOBTRt0Z4c0bf+\nquqHKbk450oyjpU1yuCNcG5x6AAFxKED5BSHDpBbPHRHofftOjifR/5lXw553gzeuvFmvH7G8/jZ\n/H/pzUU5Hyeca5ywpB0kXSDpJkk3SjpyjH3mSjpP0nC6z0CWOM65gHYdnA+D8/nSMceFjjI5FG/1\nngP+ycyGJW0KXC3p12Z2c8M+i4BrzexzkuYCv5f0QzNrWeT3nnBuUegABUShA+QUhQ6QW9GacFCT\ntSZcsBxhZveZ2XD6/ZPAzcC2TbvdC8xOv58NPNyuAQbvCTvnJpsujI6QFAG7kyxr32gZcL6ke4BZ\nwDs6Hct7wrnFoQMUEIcOkFMcOkBuRWvCQU3WmvA4L8ylpYgzgE+kPeJGRwHDZrYtMA/4lqRZ7eJ4\nT9g5N7m0WvL+ahi6pv1bJW0EnAn80Mz+Z4xd9gWOBTCz2yT9CXgJcFXOOK61KHSAAqLQAXKKQgfI\nzWvCNdKi1et/dfIYdcxJ67+uZOXOk4AVZra4xdFvAd4AXCppK5IG+PYCcZxzboIq3urtB7wXuF7S\n6FL3RwEvgLULfh4HnCLpOpJy76fN7JFy4mQkaSpJV/xuMzuk7POVL6Z+PbWYemWOqVfe4nNHBOVz\nR+RiZpfQ4TqamT0E5GrnetET/gSwguRKoXPOhVWx3/9LHR0haXvgYOB7gDrsXhNR6AAFRKED5BSF\nDpBb7XrBMDl7wZCsMZfl0SNl/0w4AfgU6wYvO+dcWBXrCZcWR9KbgQfM7FpJ/a32GxgYIIoihodv\nBh4HtmZdTyhOv1Zp+z5gnwrlybI9+lxV8nTaHn0u3/tHx+qO9kp7ud04Trjo8daO2x3toZa9fdli\n2Hpe1453+SVD3DkL+vuT7aGh5PWi24sXL2Z4eJgoiuiqijXCMrPOexU5sHQc8D5ghOQeldnAmWb2\n/oZ9bPT8AwNnsXz5daVk6a6Y+v26HFOvzDGTZVL3Rj2fO6LLF+ZuOxJ23rxrh9uAJMxsXGVNSWYP\nZNz3+Yz7fFmUVhM2s6PMbAcz2wk4FDi/sQGuryh0gAKi0AFyikIHyM1rwvVhU7M9eqWXHfNyutzO\nOZfD6oqVI3oyd4SZXWhmC3txrvLFoQMUEIcOkFMcOkBuPndEfazuy/bolYr9THDOuXI9s/G0jHv2\n5hpDx0Y4nTFolZmtlvQSknuhf2Fmz5WerpKi0AEKiEIHyCkKHSA3rwnXx+qp1VpuOUs54iJgY0nb\nAb8kGfFwapmhnHOuLKuZmunRK1kaYZnZSuBtwFIz+3tgt3JjVVkcOkABcegAOcWhA+TmNeH6GGFq\npkevZKoJS3oN8B7gg+lTPhm8c66WVlfsUliWxvSTwOeAs8zsJkkvBC4oN1aVRaEDFBCFDpBTFDpA\nbl4Tro+i5Ygsqy037LuXpBFJb+uUp+OPBDO7ELhQ0ibp9m1Ay5M751yVjaPem2W15dHpe78KnEeG\nics69oQl7StpBcmM8UiaJ2lpkT/BxBCHDlBAHDpATnHoALl5Tbg+nmFapkezjKstA3ycZA26B7Pk\nyVIcWQwcBJydnnxY0v5ZDu5cFa0YvIhnl1zNzJE1rOybwrRFe7Lr4PzQsVyPdKMm3Gq15XQU2VuA\nA4C9yHCncKY0ZnZnsrzSWiPZok5EUegABUShA+QUlXbkFYMXscWxv2XZyLr/G0cc+1tWwLgaYq8J\n18d4h591WG15MfBZM7N0TbqO5YgsjfCdkvZLTz6NpB58c/u3OFdNzy65er0GGGDZiHHIkmvAe8OT\nQqtG+Kqhp7hqaGXb92ZYbXlP4PS00zoXeKOk58zsp62OmaUR/ijwdWA74M/Ar4B/zPC+CSqmfj3L\nmHpljulm3sbyw7THx74VdebI6nGdw9eYq49WY4Dn9c9mXv+69Se+e8xD672eZbVlM9u5Yf9TgHPa\nNcCQbXTEg8C7O+3nXBU1lx/+tcV+K/uqdSurK884asJZVlvOLcvcEac0PWXpCQ8rcsL6i0IHKCAK\nHSCnqGtHai4/HAj8C3Bswz6H94lpi/YY13lq1wuGSdkLhuI14SyrLTft/4Es+2X5kfBz1l3hmwH8\nLXBP1iDOhTRzZM1626NV3zcDm2w2jZV9U5m2aA8fHTGJPDvG8LOQspQjzmjclvSfwKWlJaq8mPr1\nLGPqlTmmW3lX9m3YcZkP/MfzZrDLQ5/syjnAa8J10st5IbIoMgfELsCW3Q7iXBmmLdqTI/rWHyXU\njfKDq6/V9GV69EqWmvCTrCtHGHA/8JkyQ1VbFDpAAVHoADlFXTvSroPzWQEcsuQaZo6sLq38ULte\nMEzKXjCMf5xwt2UpR2zaiyDOlWXXwfk+BtitVZtGWNKetLnlzsyuKSVR5cXUr2cZkyVzyCXjGxWt\nr35JIS+4xIz/38XguFPkE9PVf8vvOxI236J7xytJ1WrC7XrCX6P9fc8LupzFOedK9ywbh46wnpaN\nsJn19zBHjUShAxQQhQ6QSy3rqzX7jBNR6ABB1KYc0UjSy4GXAtNHnzOz75cVyjnnylK1ckSW+YQH\ngW8AS0hKEP8OLCw3VpXFoQMUEIcOkEst5+at2WeciEMHCKJqQ9SyjBN+O/AG4N70NrxXAnNKTeWc\ncyWp2mrLWZr7VWa2Ol0vaTPgAWCHknNVWBQ6QAFR6AC5eE24V6LQAYKoY034KkmbA8uAq4CngN+W\nmso550pStUa4ZTlC0lJJrzWzj5rZo2Z2IskkVP+QdXagiSkOHaCAOHSAXLwm3Ctx6ABBPMPGmR69\n0q4m/AfgPyTdIenfJe1uZn8ys+uyHlzSdElXSBqWtELSl8cf2Tnniit7yXtJ35D0R0nXSdq9U56W\njbCZLTaz1wD7A48AJ0v6vaSjJe2S5Q9rZk8DC8xsHvAKYIGk12Z5b3VFoQMUEIUOkIvXhHslCh0g\niHFcmBtd8v5lwD7AP0p6aeMOkg4GXmRmLwY+BHy7U56OoyPMLDazr5jZ7sChJPMJZ15jzsxGF22a\nBkwladCdcy6IEaZmejTLuOT9QmB5us8VwBxJW7XLk2WccJ+khek8wucBtwBvy/BnHX3/FEnDJLOv\nXWBmK7K+t5ri0AEKiEMHyMVrwr0Shw4QRDfGCbda8p5kLc67GrbvBrZvd6x2E/gcSNLzfRNwJXAa\n8KExlnhuy8zWAPPS4W2/lNRvZkOjrw8MDBBFEcPDNwOPA1uz7tekOP1ape37KpYnyzYdXk+2Rxu/\n0XJAqO21aXO+vzqfd1227+vq8S6//BLuvHM2/f39AAwNDQEU3l68eDHDw8NE0ej5uqPV6Ih46A7u\nyNAB6LDkPWy4zH27OXiQ2divSzqfpOE908y6UkKQ9HmSccfHp9s2ev6BgbNYvjzzNT9XgqrMolZU\n2FnU3G23HcnOO5c3i5okzKy5gct7DDvKPp9p3+P0xQ3Oly55/zPgF2OtuCzpRGDIzE5Pt28B9jez\n+1udp90EPgdkStqGpLnAiJk9JmkG8NfAMeM9rnPOFfVMwTXmsix5D/wUWAScLmkf4LF2DTBknMBn\nHLYBlkuaQlJ//oGZ/abkc5Yspn5XlWPqlLmW67XV7DNOxNQv8/iVueS9mZ0r6WBJt5Lc2NbxnopS\nG2EzuwHwxbycc5VR9pL3ZrYoz3F7N1XQhBGFDlBAFDpALvXrBUPdPuNEFDpAEFW7bbnd6IjGBT6b\nmZnNLieSc86VpzbzCZvZpmY2q8VjEjfAcegABcShA+Ti44R7JQ4dIIiqzSec+UySns/6K2vcWUoi\n55wrUW3KEaMkLSRZ9HNbkrmEdyS5Xe9l5Uarqih0gAKi0AFy8Zpwr0ShAwTxbMEhamXJsrLGl4DX\nAH8ws52A17PhrXrOOVcLReeOKEuWRvg5M3sImCJpqpldALyq5FwVFocOUEAcOkAuXhPulTh0gCDq\nWBN+VNIs4GLgR5IeAHLNH+EmvhWDF/HskquZObKGlX1TmLZoT3YdnB86lnMbqF1NGHgrsAr4J+A9\nwGwm9a3HUegABUSlHn3F4EVscexvWTaybkTjEcf+lhVQqCH2mnCvRKEDBFG1RjjL3R9PmtlqM3vO\nzE41s2+Y2cO9COfq4dklV6/XAAMsGzGeXXJNoETOtVabmrCkS9OvT0p6ounxl54lrJw4dIAC4lKP\nPnNkTYvnVxc6nteEeyUOHSCI2tSEzWy/9OumPUvjamll39g/y1f2VevXPueghkPUJP0gy3OTRxQ6\nQAFRqUeftmhPjuhbf5rXw/vEtEXF5m7ymnCvRKEDBFG1ckSWPvdujRuS+oA9y4nj6mjXwfmsAA5Z\ncg0zR1azsm8q0xbt4aMjXCUVLTVIOplkpaEHzOzlLfbpB04ANgIeMrP+TsdtN4HPUcDngBmSnmh4\n6Tngu5mTTzgx9etBxJSdedfB+dClRtfnE+6VmPplHr9xjI44Bfgm8P2xXpQ0B/gW8Ddmdne6qEVH\n7SbwOc7MZgHHN03es4WZfbbAH8A554IruuS9mV0MPNrm0O8mWQ7u7nT/h7LkadcT/iszuwX4b0kb\nFPfMbJKOP4pCByggCh0gl/r1gqFun3EiCh0giBLHCb8Y2EjSBcAs4Otm1vH6WbviyP8BjiCZvGes\neYUXFEnpnHMhPcPGZR16I5KVhF4PzAQuk3S5mf2x3ZvaDVE7Iv3a38WQE0BM/XoQMXkyh74F2WvC\nvRJTv8zj16onvHLod6wcumo8h76L5GLcKmCVpIuAVwLFGuFGkvYl+dtau7+ZjVmcdvXW7VuQnaua\nVo3wxv37sHH/Pmu3HznmxLyHPhtYImkqsDHwauD/dXpTlvmEfwjsDAwDjbdATdJGOAodoIAo856t\nbkE+ZMk1XRv90En9esEw0f9dTCRFxwBLOg3YH5gr6S7gaJISxOhKy7dIOg+4HlgDLDOzFZ2Om6Un\nvCewq5m1Wm/OTSDdvgXZuaopOk7YzN6VYZ/jgePzHDfLfMI3AtvkOejEFocOUECcec8q3ILsc0f0\nShw6QBBFh6iVJcuPhC2BFZKuBJ5JnzMzW1herPo5usKze8Zk+8XzGB3NluzNB7mYkxoGxByGuOLh\nvfiZenXP/UZQsfv73cRRtaksszTCg2WHqJcodIDcoqbtm4CngU2Ap0hWbx1dMPBBFnAO8Hp+xyzW\n8ARTuIG9eLCnIxKjHp6rW6LQAQqIQgcI4plnq/UDvmMjbGZDPcjheuQmYA6wrOG5I9LnRz3IAs73\nYeBuglo90rtpKrNoN5/wWPMI+3zCNayjxQ3fP836DTDp9tM9S5NFHDpAAXHoAAXEoQMEsXpkaqZH\nr7S7WcPnEZ6ANsn5vHMTTS8b2CxK7ZdL2oFkPPHzSW59/q6ZfaPMc5YvCh0gl9H679Mk9d8nWuz3\nVM8SZRGFDlBAFDpAAVHoAEGMPDeJGmGSaS//ycyGJW0KXC3p12Z2c8nndYxd/z0MeBvwk4bnDie5\nOOfcZLBmdU1qwt1gZveZ2XD6/ZPAzcC2ZZ6zfHHoAJmN1n+HGp47GVgJHAIcmn59nHWjI6ohDh2g\ngDh0gALi0AHCGJma7dEjPfuRICkCdgeu6NU5J7tWdd45wF/1MohzVfJ0tXrCPUmTliLOAD6R9ojX\nGhgYIIoihodvJumTbc26WlWcfq3aNmO+XpV0o9t3kPSC+9PtofTrUy32D5+4zttRxfJk2R59rjvH\nu/zyS7jzztn09/cDMDQ0BFB4e/HixQwPDxNFjXm7YKS7hxsvlT0lhKSNgJ8BvzCzxU2vrZ2SYmDg\nLJYvv67ULGWq4h1zY9WED6d1+eEYju5FLDdB3Xbbkey88xalHV8SZqbOe7Y9hnFdxjbvleM/XxZl\nj44QcBKworkBrq+YulxVfhlJQ/waYEc2vDuuumLq8hmvE+OZa6JiPeFSL8wB+wHvBRZIujZ9HFTy\nOV2DlwEvIakB70kdGmDnSvZcxkcTSSdLul/SDWMdVtJ7JF0n6XpJl0p6RZY4pfaEzewSym/oeywK\nHSC3KHRBKqH/AAAPmElEQVSA3KLQAQqIQgcoIAodIIzis7K2XW0ZuB2Yb2aPp53N7wL7tNh3rWpd\nJnTOubIVLEeY2cXpKK9Wr1/WsHkFsH2W406wXmovxKED5BaHDpBbHDpAAXHoAAXEoQOE8XTGx/h8\nEDg3y47eE3bOTS4lX5iTtIDk5tT9suzvjXBuUegAuUWhA+QWhQ5QQBQ6QAFR6ABhtGqEbxiCG4fG\ndej0Ytwy4CAzezTLe7wRds5NLq0a4Zf2J49Rp+cb+y/pBSTTsrzXzG7N+j5vhHOLqVsPIsYTly/G\nM9fEGMPPsui02jLwBWBz4NvJLRI8Z2Z7dzquN8LOucml4BC1Tqstm9nhJDel5uKNcG5R6AC5RaED\n5BaFDlBAFDpAAVHoAGFU7I45b4QDaLfQpnOuZNVay8vHCecXj+vdo5PqnAOcnn6dw/oLbXZbXOKx\nyxGHDlBAHDpAAXHoAGGMZHz0iDfCPVaPhTadm8Aq1gh7OSK3aFzvDrHQZlTiscsRhQ5QQBQ6QAFR\n6ABheE14cmu1oGa1Ftp0bgIrOEStLF6OyC0e17unA0c0PVf2QptxiccuRxw6QAFx6AAFxKEDhLE6\n46NHvCfcY6MTrR+Cj45wLoiKXYDxRji3aNxH6HWDG/X4fOMXhQ5QQBQ6QAFR6ABheE3YOecC8ppw\n3cWhA+QWhw6QWxw6QAFx6AAFxKEDhOE14cnF745zrmK8HFF3UeY9x1py/oj0+V42xFEPz9UdUegA\nBUShAxQQhQ4QRsUaYS9HlMjvjnOuggqutlwWb4RzizPvGeLuuLHEPT7f+MWhAxQQhw5QQBw6QBjP\nZHyMQdJBkm6R9EdJnxnj9bmSzpM0LOlGSQOd4ngjXCK/O865Cio4d4SkqcAS4CBgV+Bdkl7atNsi\n4Fozmwf0A1+T1Lbs641wblHmPUPcHTeWqMfnG78odIACotABCohCBwijeDlib+BWM4vN7DmSiRDf\n0rTPvcDs9PvZwMNm1rYK7RfmSuR3xzlXQcWHn20H3NWwfTfw6qZ9lgHnS7oHmAW8o9NBvRHOLSZP\nD6IKDW5M3fo8MXVL7JlrpFW/9KEheHio3Tstw9GPAobNrF/SC4FfS3qlmT3R6g3eCDvnJpdWjfCc\n/uQx6g8brLb8Z2CHhu0dSHrDjfYFjgUws9sk/Ql4CXBVqziVaYRPfd/ZnLrX8tAxCtOio0NHmECi\n0AEKiEIHKCAKHSCM4sPPrgJeLCkC7gHeCTQv/nkL8AbgUklbkTTAt7c7aKmNsKSTgTcBD5jZy8s8\nl3POZdJi+FknZjYiaRHwS2AqcJKZ3Szpw+nr3wGOA06RdB3JwIdPm9kj7Y5bdk/4FOCbwPdLPk/P\nDP0B+ncJnSKvmHr1emLqlRc8c42M4445M/sF8Ium577T8P1DJNfiMyu1ETazi9Ouu3POVUPFZlGr\nTE24LurXC4b69Xai0AEKiEIHKCAKHSCMHs6QloU3ws65yaViE/gEb4QHBgaIoghuH2bOUzBv+3W9\nzaE/JF9DbX/y+3DddbCjYNUU2GY3iLaHTx4w9v7r7sWPKrY9+lxV8nTaHn2uKnmybI9+X5U8WbYv\nB7bu2vEuv/wS7rxzNv39/QAMDQ0BFN5evHgxw8PDSfvQTRVrhGWWZfzxOE6Q1ITPGWt0hCRbe/7f\nDMAt1RmitvTncP0v4cQ16577yBSY/ipY/P4N96/2ELWYev3qGVOvvOCZ4bbbjmTnnbfo2vGaScLM\nNM5jGC/K2ObdOv7zZVHq3BGSTgN+C+wi6S5JHyjzfN104YXrN8CQbN93U5g84xOFDpBTFDpAAVHo\nAAVEoQOEMY5Z1MpQ9uiI5oHMtTFjzdjPT69YUd85l1PFyhE+i1oLq1p8Mnf2NkaXxKED5BSHDlBA\nHDpAAXHoAGH4pO71sP/+SQ240YenwCteESaPc65LfKHPevjYm2ApcOhFSQni6akwf37yfP1EoQPk\nFIUOUEAUOkABUegAYVSsHOGNcBsfe1NdG13nXEsVa4S9HJHT6NjgeolDB8gpDh2ggDh0gALi0AHC\nqFhN2HvCzrnJxXvC9eZzR/RCFDpAAVHoAAVEoQPUTqfVlhv220vSiKS3dTqmN8LOOZdBxtWWR/f7\nKnAe0PGOuwlVjlj68+ROtxlrknG+++/f/QtrPp9wL8TUKy945klh7WrLAJJGV1u+uWm/jwNnAHtl\nOeiEaYRH53r4ceNcD79Mhpn5CAfn3DqFr7p1XG1Z0nYkDfMBJI1wx4kqJkwjfOGF6zfAkMz1cOhF\n3W2E69cLhvr1dqLQAQqIQgcoIAodIJBWV+YuSh8tZZn5ZzHwWTMzSWIylSN8rgfnXDatesKvSR+j\njmveIctqy3sCpyftL3OBN0p6zsx+2irNhLkw12quh6endvc8Pk64F+LQAQqIQwcoIA4dIJBVGR8b\nWLvasqRpJKstr9e4mtnOZraTme1EUhf+aLsGGCZQI9xqrof588Pkcc5VVbG7NcxsBBhdbXkF8OPR\n1ZZHV1wuYsKUI3o114PXhHshCh2ggCh0gAKi0AECKX63RqfVlpuezzR/+oRphMHnenDOZVGt5ZYn\nTDmiV7wm3Atx6AAFxKEDFBCHDhDISMZHb0yonrBzznVWrZ6wN8I5eU24F6LQAQqIQgcoIAodIJAx\nRz4E442wc26SqdY0al4Tzslrwr0Qhw5QQBw6QAFx6ACBVGtCYe8JO+cmmWr1hL0Rzslrwr0QhQ5Q\nQBQ6QAFR6ACB+IU555wLqFo9Ya8J5+Q14V6IQwcoIA4doIA4dIBAvCbsnHMB+RC1WvOacC9EoQMU\nEIUOUEAUOkAgXhPewNLBQS484TRmPFveskTOOZeYRDXhLCuTLh0c5Ppjj+XHf3mWU5+GH69Mlila\n+vMykxXnNeFeiEMHKCAOHaCAOHSAQIrXhLO0aZK+kb5+naTdO6UprRHOujLphUuWcOLI+j+ZTlwD\nF7VdZSSc4eZ59GvhvtABcqpbXvDMdVJsAp8sbZqkg4EXmdmLgQ8B3+6UpsxyRKaVSWeMjP2rwfQp\nm8A7Li4xXjGPxSfCOz6ywfPX7Lt1gDTZnHjiE3zkI4XnnO65uuUFzwyw3Xazu3aschWuCWdp0xYC\nywHM7ApJcyRtZWb3tzpomY1wx5VJAVb1jR3h6WnTYcuOPfne22SbMXPtvmWALBlts80sdt99m9Ax\nMqtbXvDM9VK4JpylTRtrn+2Blo1wmTXhLCuTsv+iRXykqSH+cF8f8xctKiXUeMVxHDpCbnXLXLe8\n4JnrpfAac5naNDZcYbnt+2SW9bj5SNoHGDSzg9LtzwFrzOyrDfuUc3Ln3IRkZh2XkG8nb5vTeL6M\nbdqJwJCZnZ5u3wLsH6ocsXZlUuAekpVJ39W4w3g/UOecy2OcbU7HNo1k9eVFJMve7wM81q4BhhIb\nYTMbkTS6MulU4CQzu7nD25xzrpJatWmjKy2b2XfM7FxJB0u6FXgK6LjYZ2nlCOecc50Fm8Any6Dn\nKpF0sqT7Jd0QOksWknaQdIGkmyTdKOnI0Jk6kTRd0hWShiWtkPTl0JmykDRV0rWSzgmdJQtJsaTr\n08xXhs6TRTrU6wxJN6f/NvYJnalbgvSE00HPvwfeAPwZ+B3wriqXKyS9DngS+L6ZvTx0nk4kbQ1s\nbWbDkjYFrgbeWuXPGEDSTDNbKakPuAT4v2Z2Sehc7Uj6Z2BPYJaZLQydpxNJfwL2NLNHQmfJStJy\n4EIzOzn9t7GJmT0eOlc3hOoJrx30bGbPAaODnivLzC4GHg2dIyszu8/MhtPvnyQZUL5t2FSdmdnK\n9NtpJHW3SjcUkrYHDga+x4ZDk6qsNlklbQa8zsxOhqQ2O1EaYAjXCI81oHm7QFkmvPRq7u7AFWGT\ndCZpiqRhksHtF5jZitCZOjgB+BSwJnSQHAz4X0lXSToidJgMdgIelHSKpGskLZM0M3SobgnVCPvV\nwB5JSxFnAJ9Ie8SVZmZrzGweyV1G8yX1B47UkqQ3Aw+Y2bXUqGcJ7GdmuwNvBP4xLbVVWR+wB7DU\nzPYgGXXw2bCRuidUI/xnYIeG7R1IesOuiyRtBJwJ/NDM/id0njzSXzd/DrwqdJY29gUWpjXW04AD\nJH0/cKaOzOze9OuDwFkk5cEquxu428x+l26fQdIoTwihGuG1g54lTSMZ9PzTQFkmJEkCTgJWmNni\n0HmykDRX0pz0+xnAXwPXhk3VmpkdZWY7mNlOwKHA+Wb2/tC52pE0U9Ks9PtNgAOBSo/4MbP7gLsk\njS6p8AbgpoCRuirIpO51vJFD0mnA/sDzJN0FfMHMTgkcq539gPcC10sabcg+Z2bnBczUyTbAcklT\nSDoIPzCz3wTOlEcdymxbAWclP6PpA35kZr8KGymTjwM/Sjttt5HhJoi68Js1nHMuIF9t2TnnAvJG\n2DnnAvJG2DnnAvJG2DnnAvJG2DnnAvJG2DnnAvJG2HUkaXU67eG16b37O0q6dBzHO1XS3zU99w+S\n/rPpubmSHkjv/BvrOAOSvlk0h3NVEORmDVc7K9O5BhrtN47jGRve2PAT4HhJM8xsdJXFtwM/TWfa\na3Uc52rNe8KuEElPpl/7JQ1J+u90wu0fNuzzeUlXSrpB0neaD9G4YWZPABcChzQ8/U7gNElvlnR5\n2gv/taTnj5Fnvd71aL70+0+lOa6TNJg+t4mkn6cTyN8g6R3FPw3nivNG2GUxo6EccWb6XGMvdB7w\nCWBXYGdJo73kJWa2dzoJ/ox01rF2TiOZgwFJ2wK7AOcDl5jZPukMWj8GPp3u39iQN/eKLT3OgcCL\nzGxvkuk890xnDfsb4M9mNi/NV+Xbud0E5uUIl8WqMcoRja40s3sA0rmAI+BSklnFPgXMBLYAbgR+\n1uY45wJL0wlm3gGcYWaWLtX0X8DWJJO9354j+4HAgQ3zZ2wCvIhk1Y6vSfoK8LOqr97hJi7vCbtu\neKbh+9XAVEnTgW8Bf2dmrwCWAdPbHSStBZ8HvI20FJG+9E3gG+lxPgzMGOPtI6T/ntMJgKY1vPZl\nM9s9fexiZqeY2R9JesY3AF+S9Plcf2LnusQbYVeW0Qb34XRi+b/P+L7TgH8Gnm9ml6fPzQbuSb8f\naPG+mGSdN4CFwOiIil8Ch6XTNiJpO0lbStoGeNrMfgQczwSan9bVi5cjXBZjjUKwdq+b2WOSlpGU\nIO5jw6WVWo1s+F+SKS2/1/DcIPDfkh4lqRHv2HCM0eMsA85OyyHnkSzKipn9WtJLgcvS6RufAN5H\nUpL4D0lrgGeBj7bI41ypfCpL55wLyMsRzjkXkDfCzjkXkDfCzjkXkDfCzjkXkDfCzjkXkDfCzjkX\nkDfCzjkXkDfCzjkX0P8HDhO7a4SoD3cAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fd391f29ed0>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"INITIAL : \n",
"[ 5.52168137 4.39171494 3.48558698 2.30818451 2.13802498 1.30728517\n",
" 0.57634128 0.07523712 0.91886551 1.5767573 2.02673003 2.61355336\n",
" 3.56882912]\n",
"FINAL : \n",
"\\begin{tabular}{lrrrrr}\n",
"\\toprule\n",
"{} & Discrete actual & Discrete mul & actual & mul by 100 & normalized \\\\\n",
"\\midrule\n",
"0 & 5 & 5 & 5.444571 & 544 & 5.445312 \\\\\n",
"1 & 5 & 5 & 4.391725 & 439 & 4.390625 \\\\\n",
"2 & 4 & 4 & 3.485587 & 348 & 3.486328 \\\\\n",
"3 & 4 & 4 & 2.308185 & 230 & 2.308594 \\\\\n",
"4 & 3 & 3 & 2.138035 & 213 & 2.138672 \\\\\n",
"5 & 2 & 2 & 1.307285 & 130 & 1.307617 \\\\\n",
"6 & 1 & 1 & 0.489937 & 49 & 0.489990 \\\\\n",
"7 & 1 & 1 & 0.075257 & 7 & 0.075256 \\\\\n",
"8 & 2 & 2 & 0.918866 & 91 & 0.918945 \\\\\n",
"9 & 2 & 2 & 1.418902 & 141 & 1.418945 \\\\\n",
"10 & 3 & 3 & 2.026730 & 202 & 2.027344 \\\\\n",
"11 & 4 & 4 & 2.613563 & 261 & 2.613281 \\\\\n",
"12 & 5 & 5 & 3.568839 & 356 & 3.568359 \\\\\n",
"\\bottomrule\n",
"\\end{tabular}\n",
"\n"
]
}
],
"prompt_number": 179
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"reachData.discribeParameter('d_linear_m0_gripper')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Parameter : d_linear_m0_gripper\n",
"pdf Initial Values, pdf Final Values :"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" [ 0.23076923 0.15384615 0.53846154 0. 0.07692308] [ 0. 0. 1. 0. 0.]\n",
"check sumpx, sum py, sumpxpy : 1.0 1.0 2.0\n",
"H_FinalGivenInitial : 0.0 H_InitialGivenFinal : -inf\n",
"SINGLE pdf Initial Values, pdf Final Values : [ 0.23076923 0.15384615 0.53846154 0. 0.07692308]\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAW8AAAEBCAYAAAC3wiQ+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFUJJREFUeJzt3X2QXXd93/H3J+ua1ilm7ZKaGWHYCSjE7mAvMAiHlHRT\n3GZDHkRiWuO0hE0YomlG8E86VZ1miuhDGvdhQloHooKGdfJH5AyPSsEIhvqSlDi2hR8oRWKkELWS\n3YRgMINJHKT62z/27Pr6anfvPt3de+59v2ZWur9zfnvO9+7sfve33/P7nZOqQpLULt+x0wFIktbP\n5C1JLWTylqQWMnlLUguZvCWphUzektRCfZN3ktkkJ5OcSnJgmf1XJPlwkoeT3Jvkbw0mVEnSolWT\nd5IJ4HZgFrgWuCXJNT3dfhF4oKquB34a+LVBBCpJelq/kfce4HRVnamq88ARYG9Pn2uAuwGq6kvA\nVJLv2vJIJUlL+iXvXcDZrva5Zlu3h4GfBEiyB3gh8PytClCSdLF+yXsta+d/BZhM8iCwH3gQ+H+b\nDUyStLJL+ux/BLi6q301C6PvJVX1TeBnF9tJ/hj4cu+BkngTFUnagKpK77Z+yfs4sDvJFPAocDNw\nS3eHJM8B/qKqvp3krcBnquqJFQLYQNjSYB08eJCDBw/udBjSspKL8jbQJ3lX1YUk+4FjwARwuKpO\nJNnX7D/EwiyU+WZk/QXgLVsZuDRoZ86c2ekQpHXrN/Kmqu4C7urZdqjr9T3AS7Y+NGl7/Mmf7HQE\n0vq5wlJj73nPm9vpEKR1M3lr7E1Nzex0CNK69S2bSKOo01n4AHjnOzvADAAzMwsf0rDLds0ASVLO\nNtEwmpvrMD8/s9NhSMtKsuxUQcsmGnuWTdRGJm+NPcskaiOTt0RnpwOQ1s3kLUkt5AVLSRpiXrCU\npBFi8tbY6yxO+JZaxOQtSS1kzVuShpg1b0kaISZvjT1r3mojk7cktVDf5J1kNsnJJKeSHFhm/3OT\nfCLJQ0m+kGRuIJFKAzLj+ni10KoXLJNMAF8CbmThYcT3A7dU1YmuPgeBZ1XVrUme2/S/qqou9BzL\nC5aStE4bvWC5BzhdVWeq6jxwBNjb0+f/Apc3ry8HHutN3NIws+atNur3MIZdwNmu9jngVT193gv8\n9ySPAs8G/uHWhSdJWk6/5L2WOscvAg9V1UySFwGfSnJ9VX2zt+Pc3BxTU1MATE5OMj09vVRvXBz9\n2La93e2ZmZmhisf2eLc7nQ7z8/MAS/lyOf1q3jcAB6tqtmnfCjxVVbd19fk48G+r6rNN+9PAgao6\n3nMsa96StE4brXkfB3YnmUpyKXAzcLSnz0kWLmiS5CrgJcCXNx+ytD0WRz1Sm6xaNqmqC0n2A8eA\nCeBwVZ1Isq/Zfwj4ZeD9SR5m4ZfBP6uqrw04bkkaa97bRJKGmPc2kaQRYvLW2LPmrTYyeUtSC1nz\nlqQhZs1bkkaIyVtjz5q32sjkLUktZM1bkoaYNW9JGiEmb409a95qI5O3JLWQNW9JGmLWvCVphJi8\nNfaseauNTN6S1ELWvCVpiG245p1kNsnJJKeSHFhm/z9N8mDz8T+TXEgyuVWBS5IutmryTjIB3A7M\nAtcCtyS5prtPVf3HqnpZVb0MuBXoVNXjgwpY2mrWvNVG/Ubee4DTVXWmqs4DR4C9q/T/KeC3tyo4\nSdLy+iXvXcDZrva5ZttFklwG/BDwwa0JTdoeMzMzOx2CtG6rPj0eWM8Vxh8D/sdqJZO5uTmmpqYA\nmJycZHp6eukHZ/FPV9u2bdse53an02F+fh5gKV8uZ9XZJkluAA5W1WzTvhV4qqpuW6bvh4E7q+rI\nCsdytomGUqfTWfohkobNRmebHAd2J5lKcilwM3B0mYM/B/gB4KNbEawkaXWrlk2q6kKS/cAxYAI4\nXFUnkuxr9h9qur4eOFZVfzHQaKUBcNStNnKRjiQNMW9MJa1g8WKR1CYmb0lqIcsmkjTELJtI0ggx\neWvsWfNWG5m8JamFrHlL0hCz5i1JI8TkrbFnzVttZPKWpBay5i1JQ8yatySNEJO3xp41b7WRyVuS\nWsiatyQNMWvekjRC+ibvJLNJTiY5leTACn1mkjyY5AtJOlsepTRA1rzVRqs+Bi3JBHA7cCPwCHB/\nkqNVdaKrzyTw68APVdW5JM8dZMCSpP4j7z3A6ao6U1XngSPA3p4+PwV8sKrOAVTVV7c+TGlwfIal\n2qhf8t4FnO1qn2u2ddsNXJnk7iTHk7xpKwOUJF1s1bIJsJbpIX8FeDnwWuAy4J4kf1hVp3o7zs3N\nMTU1BcDk5CTT09NLo57FuqNt25ttJxddmB+Iu+++eyjer+3Ranc6Hebn5wGW8uVyVp0qmOQG4GBV\nzTbtW4Gnquq2rj4HgL9WVQeb9vuAT1TVB3qO5VRBDaVOp7P0QyQNm41OFTwO7E4yleRS4GbgaE+f\njwJ/O8lEksuAVwFf3Iqgpe1g4lYbrVo2qaoLSfYDx4AJ4HBVnUiyr9l/qKpOJvkE8HngKeC9VWXy\nlqQBcoWlxp5lEw0zV1hKK2iuDUmt4shbYy8BvzU1rBx5S9IIMXlLdHY6AGndTN6S1ELWvDX2rHlr\nmK1U8+63PF7aUVdeCV//+uDPM+gV9VdcAV/72mDPofFi2URD7etfXxgVD/Lj7rs7Az/HdvwC0ngx\neUtSC1nz1lAblXr0qLwPbT/neUvSCDF5a+wt3ktZahOTtyS1kDVvDbVRqRWPyvvQ9rPmLUkjpG/y\nTjKb5GSSU80jz3r3zyT5RpIHm49fGkyo0mBY81YbrbrCMskEcDtwI/AIcH+So1V1oqfrZ6rqxwcU\no8ZYEdie5wkPVHX9K22Ffsvj9wCnq+oMQJIjwF6gN3mPwI+XhlGogdeKZwZ7eKCpeW/DeTQ++pVN\ndgFnu9rnmm3dCnh1koeTfDzJtVsZoCTpYv2S91oGCw8AV1fV9cB/AT6y6aikbWTNW23Ur2zyCHB1\nV/tqFkbfS6rqm12v70ry7iRXVtVF91Cbm5tjamoKgMnJSaanp5ce/Lr4A2Tbdnd7sagxLPFstA0d\nOp3hicf28LY7nQ7zzYNVF/Plclad553kEuBLwGuBR4H7gFu6L1gmuQr4SlVVkj3A71TVRWd0nrc2\nYlTmR4/K+9D229D9vKvqQpL9wDFgAjhcVSeS7Gv2HwLeAPyTJBeAPwfeuOXRS5KewRWWGmrbMWLt\ndDpd5Y3BcOStjXKFpSSNEEfeGmqjMmIdlfeh7efIW5JGiMlbY+/paYlSe5i8JamFrHlrqI1KrXhU\n3oe2nzVvSRohJm+NPWveaiOTtyS1kDVvDbVRqRWPyvvQ9rPmLUkjxOStsWfNW21k8pakFrLmraE2\nKrXiUXkf2n7WvCVphJi8NfaseauN+ibvJLNJTiY5leTAKv1emeRCkp/c2hAlSb36PcNygoVnWN7I\nwsOI76fnGZZd/T7FwmPQ3l9VH1zmWNa8tW6jUiselfeh7bfRmvce4HRVnamq88ARYO8y/d4GfAD4\ns01HKknqq1/y3gWc7Wqfa7YtSbKLhYT+nmaT4wu1ijVvtVG/5L2WRPwu4J83NZE0H5KkAbqkz/5H\ngKu72lezMPru9grgSBKA5wI/nOR8VR3tPdjc3BxTU1MATE5OMj09vfTU7sXRj23b3W0Y/PlmZmYG\n/n6gQ6ez819P28Pf7nQ6zM/PAyzly+X0u2B5CQsXLF8LPArcxzIXLLv6vx/43ar60DL7vGCpdRuV\nC32j8j60/TZ0wbKqLgD7gWPAF4E7q+pEkn1J9g0mVGl7PT3Kl9qjX9mEqroLuKtn26EV+v7MFsUl\nSVqF9zbRUBuVcsOovA9tv5XKJn1H3tJOywjMX7riip2OQKPG5K2hth2j1aRD1czgTyRtIW9MJUkt\nZM1bY896tIaZ9/OWpBFi8pbo7HQA0rqZvDX23vzmnY5AWj9r3pI0xKx5S9IIMXlr7HlvE7WRyVuS\nWsiatyQNMWve0goOHtzpCKT1c+Stsee9TTTMHHlL0gjpm7yTzCY5meRUkgPL7N+b5OEkDyb5XJK/\nO5hQpUGZ2ekApHXr9wzLCRaeYXkjCw8jvp+eZ1gm+c6q+lbz+qXAh6vqxcscy7KJhpI3ptIw22jZ\nZA9wuqrOVNV54Aiwt7vDYuJu/HXgq5sNVtpenZ0OQFq3fsl7F3C2q32u2fYMSV6f5AQLz7p8+9aF\nJw2e9zZRG/V7ks6a/pisqo8AH0nyGuC3gJcs129ubo6pqSkAJicnmZ6eZmZmBnh6lZtt29vdnp+f\nGap4bI93u9PpMD8/D7CUL5fTr+Z9A3Cwqmab9q3AU1V12yqf80fAnqp6rGe7NW9JWqeN1ryPA7uT\nTCW5FLgZONpz4BclC4+ITfJygN7ELQ2zxVGP1Carlk2q6kKS/cAxYAI4XFUnkuxr9h8CbgJ+Osl5\n4AngjQOOWZLGnissJWmIucJSWoH3NlEbOfLW2PPeJhpmjrwlaYQ48tbYc3m8hpkjb0kaISZvyXub\nqIVM3hp73ttEbWTNW5KGmDVvSRohJm+NPe9tojYyeUtSC1nzlqQhZs1bWoH3NlEbOfLW2PPeJhpm\njrwlaYQ48tbY894mGmabGnknmU1yMsmpJAeW2f+Pkjyc5PNJPpvkuq0IWpK0vL7JO8kEcDswC1wL\n3JLkmp5uXwZ+oKquA/418F+3OlBpcDo7HYC0bmsZee8BTlfVmao6DxwB9nZ3qKp7quobTfNe4Plb\nG6Y0ON7bRG20luS9Czjb1T7XbFvJW4CPbyYoaTvNz8/sdAjSuq369PjGmi/lJPlB4GeB719u/9zc\nHFNTUwBMTk4yPT3NzMwM8PQSZdu2bdse53an02F+fh5gKV8up+9skyQ3AAerarZp3wo8VVW39fS7\nDvgQMFtVp5c5jrNNNJQ6nc7SD5E0bFaabbKWkfdxYHeSKeBR4Gbglp6Dv4CFxP2Pl0vc0nZKLvo+\nHwgHI9pJfZN3VV1Ish84BkwAh6vqRJJ9zf5DwL8ErgDe0/zgnK+qPYMLW1qZSVXjwEU6kjTEXB4v\nrWDxYpHUJiZvSWohyyaSNMQsm0jSCDF5a+xZ81YbmbwlqYWseUvSELPmLUkjxOStsWfNW21k8pak\nFrLmLUlDzJq3JI0Qk7fGnjVvtZHJW5JayJq3JA0xa96SNELWlLyTzCY5meRUkgPL7P/eJPckeTLJ\nL2x9mNLgWPNWG/V9DFqSCeB24EbgEeD+JEer6kRXt8eAtwGvH0iUkqRnWMvIew9wuqrOVNV54Aiw\nt7tDVf1ZVR0Hzg8gRmmgfHK82mgtyXsXcLarfa7ZJknaIX3LJsCWTRGZm5tjamoKgMnJSaanp5dG\nPYt1R9u2t7vdXfMehnhsj3e70+kwPz8PsJQvl9N3qmCSG4CDVTXbtG8Fnqqq25bp+w7giar6T8vs\nc6qghlKn01n6IZKGzWamCh4HdieZSnIpcDNwdKXzbCJGaUeYuNVGa1qkk+SHgXcBE8Dhqvp3SfYB\nVNWhJM8D7gcuB54CvglcW1VPdB3DkbckrdNKI29XWGrsWTbRMHOFpSSNEEfekjTEHHlL0ggxeWvs\ndc/zltrC5C1JLWTNW5KGmDVvSRohJm+NPWveaiOTtyS1kDVvSRpi1rwlaYSYvDX2rHmrjUzektRC\n1rwlaYhZ85akEdI3eSeZTXIyyakkB1bo85+b/Q8nednWhykNjjVvtdGqyTvJBHA7MAtcC9yS5Jqe\nPq8DXlxVu4GfA94zoFilgXjooYd2OgRp3fqNvPcAp6vqTFWdB44Ae3v6/DhwB0BV3QtMJrlqyyOV\nBuTxxx/f6RCkdeuXvHcBZ7va55pt/fo8f/OhSZJW0i95r3V6SO+VUKeVqDXOnDmz0yFI63ZJn/2P\nAFd3ta9mYWS9Wp/nN9suklw020UaCnfcccdOhyCtS7/kfRzYnWQKeBS4Gbilp89RYD9wJMkNwONV\n9ae9B1punqIkaWNWTd5VdSHJfuAYMAEcrqoTSfY1+w9V1ceTvC7JaeBbwM8MPGpJGnPbtsJSkrR1\nXGEpSS1k8taWSXIwyS+ssG8+yU3N6/f2LvYaJkmeleTOZtXwHyZ54RYd951JXrsVx5L6XbCU1mO1\nGlwt7q+qtw4yiCSXVNWFTRziLcBjVbU7yc3AbcAbNxnTd1TVOzZzjDWcY7PvWy3iyFubkuRfJPlS\nkt8HXrLGz+kkeXnz+okk/ybJQ0nuSfI3m+3fleQDSe5rPl7dbN+T5A+SPJDks0m+p9k+l+Rokk8D\nn1rhvDNJPpPkI0n+KMmvJHlTc/zPJ/nupuvSqmHgg8CKo+UseHeSE0k+meRjXX9hnGnO8TngH/T8\n9XEmyW3Nee9N8qJm+3yS30hyf/N1/ZFm+0SS/9DE+nCSn+t6T7+f5KPA/1rL11+jweStDUvyCham\nj14PvA54JWtboNXd5zLgnqqaBn4PWByV/xrwq1W1B3gD8L5m+wngNVX1cuAdwC93HetlwE1V9YOr\nnPs6YB9wDfAm4EXNOd4HvK3ps7RquBnJfiPJlSsc7ybghVW1eLzv63p/BXy1ql5RVXfS9ddH8//j\nVXUdC/cPelfXMV9QVa8EfgT4jSTPYuGvgcebWPcAb22m8C6+77dX1Zp+eWo0WDbRZrwG+FBVPQk8\nmeQoF6+27efbVfWx5vXngL/XvL4RuKZrYdezk1wGTAK/meTFLCTA7u/hT1ZVvxuV3L+4DqGZ3nqs\n2f4FYLWkv5LvB34HoKr+NMndPfvvXOVzf7v5/wjwq83r6jre6SRfBr4X+PvAS5O8oel3OfBi4AJw\nX1X97w3ErhYzeWszimcm640sxDrf9fopnv6eDPCqqvp2d+ck7wY+XVU/0VxI7HTt/vM1nO8ve873\nl12vF8/9CPAC4NEklwDPqaqvrXLM1b4G31pDTND/egHA/qp6Rkkoycw6zqERYtlEm/F7wOuT/NUk\nzwZ+lK27r80ngbcvNpJc37y8nIXVvjC4BWFHgTc3r98AfHqVvp8Fbmpq31cBf2cd57m56/8/aF6H\nhfp4mjr4dwMnWfgL4eebXyYk+Z7mLxGNKUfe2rCqejDJncDDwFeA+zZymJ7Xi+23A7+e5GEWvk8/\nA/w88O+BO5L8EvAxnllD7veLY7U+3fsOA7+V5BTwGKvPNFm8oPlFFurkDwDf6BPHoiua9/ckT992\nooD/w8LX8nJgX1V9O8n7gCnggSzUkr4C/ESf96QR5gpLaZOSfGdVfSvJ3wDuBV5dVV/p8zl/DLyi\ntxyT5P3A71bVhwYXsUaBI29p8/5bkkngUuBf9UvcDUdN2hRH3tpSSW5nYQZGt3dV1bbdczXJS4Hf\n7Nn8ZFV93zAdU9oMk7cktZCzTSSphUzektRCJm9JaiGTtyS1kMlbklro/wP+Dc0Hl8Hh+gAAAABJ\nRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fd3932f2b90>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWoAAAEZCAYAAAC+bm+MAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmcHVWd///XmyQQwtZicAO0RKMjigaYRNywFZWwOy4w\nqGADIgpBfuMufh2bUVQcGOOYBBlE3A0jiIAQEIVGZQATpdmSKKilhEUImywBs3x+f1R1cnNz7+2q\n21X3VHU+z8fjPvpW3XOr3rnp/nT1qVOnZGY455yrrs1CB3DOOdeZF2rnnKs4L9TOOVdxXqidc67i\nvFA751zFeaF2zrmK80LtekrSWkm7jNLmW5I+lz5/naRlvUlXb5LeLemK0Dlc8bxQd0FSLOkJSY9K\nulfSuZK2Cp2rE0lRWiTr8H9u6QMz+5WZ/VPgPGMm6TRJK9LHl8rYh5l938z2LWPbLqw6/NBWkQEH\nmtk2wB7APwP/L88GlCoj3Gi77upN0sSig4y2yx7vb8OdSxMK3NZxwCHAy9PHQem6whSZt0773lR4\noR4jM7sbuBx4maQ+ST+VdJ+kByVdImnHkbaShiR9XtK1wOPALpKOkrRE0t8l/VHS+xva90taLulj\n6TbvlvRWSftL+oOkByR9sqG9JH1S0h3pkdt5kp6WvvzL9OvD6V8Cr0zfc3S6/wclXS7puQ3bWyvp\neEm3A7/v5vNJs9+d/juO7uL9/ZLubFiOJX1E0k2SHpa0QNIWDa8fKGlY0kOSrpW0W8NrI5/N3yXd\nJumtDa8NpO3/S9IK4LMdMjW2fSjd5qvT/8u/SvqbpCMb3vJe4HQzuzv9fjkdGMjwb3+LpN+n/855\nkq6RdEybvIPpul81vH+tpBPT76v7JX155OCg4f1fS7e/VNIbG967naRzGv7vPqf0r7E8n5UriJn5\nI+cD+DOwT/p8Z+BW4BRge+BfgMnA1sD/Ahc2vG8IiIGXkPySnAjsDzw/fX1vkgK+e7rcD6wiOVqf\nALwPWAF8H9gK2BV4Anhe2v4k4P+A5wCTgK8DP0hfex6wFtisIc8hwO3Ai9M8nwaubXh9LXAF0Ads\n0eazuAn41zavzQLuTXNOAX6QbnOXUT7fc4HPNXwGdzZ99tcDzwKeBiwBjktf2x34GzCD5Ij8yLT9\npPT1dwDPSp8fCjwGPDNdHkg/6xPSz2Jyh3wjbd+b7udzwHLga+nn/mbg78CUtP3DwIyG9+8J/H2U\nz2Aq8Ajw1jTPh4B/AEe3y5uu+1XT/98v0v+/nUl+2R7T9P6T0u+tQ9OcfenrFwJnAlsCOwA3AO/P\n+1n5o6CaEzpAHR8kxfZR4KH0+dxWhQyYDjzYsHw1MDjKti8EPpQ+7ycpxEqXt0l/+Bp/6BcDB6fP\nlwJvbHjt2ekP92ZAxMaFeuHID366vBnJL4qd0+W1QP8YPqdvAl9oWJ5GMYX6XQ3LpwFnps/PBP6j\naVvLgL3b7OfGhs9uAPhLxn/XAPCHhuXd0n/XDg3rVgAvT5+vBl7U/DmMso8jafilma77KxsW6r+0\nyNVcqN/SsPxB4OcNbe9qev8NwHuAZwJP0lCAgcOBq/J+Vv4o5tHrfsfxwoBDzOyqxpWSpgBfAfYl\nOdoD2FqSLP0OB+5ses9+JH86TiMplFOAmxuaPNDw3pXp1781vL6S5OgdkqPmCyWtbXh9NckPXivP\nA74q6Yym9Ts25LyT7j0bWNSw/NcxbKvRvQ3PV5L8BQHJv+dISSc2vD4pzUHaHfFvJL+0IPncnt7Q\nNs+/tfn/ADO7v2ndyP/LY8C2Da9tl67r5DkkR+mNmpez5G1s81fWf1YAdzW1/Uv6+nNJPrd7tP40\nymZs+P83lu8Ll5P3URfrI8CLgJlmth3wepI/jRtPjK2brjDtW70A+DLwDDN7GnAZ3Z9I+yswy8ye\n1vCYYmb3NO63qf37m9pvZWbXt8rbhXtIfuhHPLddwxby7Hek7V+BU5v+PVub2XmSngf8D8mf69un\nn/WttPm/KdhtJH9djXhFuu9O7gZ2GllI+5Z3amqTJW/z599YnHdsavu89PU7gaeApzd8jtuZ2W4N\nbX3azR7yQl2srUmOpB6RtD2tT7I0FobN08cKYG16dP2WMez/68AXRk4IStpB0sHpa/eT/Cn8gqb2\nJ0vaNW2/naR3jmH/zf4XGJD0kvSvjawnnZp/uWVpD3A28AFJM9MTq1tJOkDS1iR9+kbyWW8m6Sjg\nZTn2MRbfAT4s6TlKTi5/GPjWKO+5FNhN0iFKRtycQNIvn9dHlZzk3pmkn/u8hteeIelDkial/+//\nBFxmZvcCPwP+S9I2kjaT9AJJe3exf1cAL9TFmkNy8mUFyUm9hWx85LFu2cweJfnh+V/gQZJ+wIva\ntW+z3OirwMXAzyT9HbgOmJnu6wngVODadKTCTDP7CUkf7wJJjwC3kHTbZNkXAJJulXR4q9fM7HKS\nz+Qq4A8kJ7ayHImtG0edIUfjmOvfAseSnDN4kORE6ZHpa0uAM0g+k3tJivSvO+wzT76OGc3sLOAS\nks/3ZuASM/ufjjswewB4J8lfWytITkAvJjnS7ZShed1FwG9J+uN/CpzT8NoNJF1u95OcEH27mT2U\nvnYkyUHEEpLP8kes/0WR57NyBRg5SVXOxqVZJD+oE4BvmNlpTa8/jeSE0y4kJy+ONrPbSgvkXE2l\nQ+PuJDmRek3G96wFXmhmf2rx2gDJCJDXFRrUlaK0I2olg+DnkgzR2hU4XNJLmpqdDPzOzF5B8hv8\nq2Xlca5u0nHUfem5jJPT1dd3eo8bn8rs+pgJ3GFmsZmtAhaQjNtt9BKSIWuY2e+BSNIOJWZyFZFe\ncPJoi0fLbpRek/T1NvnmF7iP17XZx9/TJq8C7iDpmjgAeKuZPdV2gxvL1GXkqq+0rg9J7wD2NbNj\n0+X3AK80sxMb2pwKbGlmH5Y0E7iWZMTEjaWEcs65GirziDrLb4AvAX2SbgRmk5zwWFNiJuecq50y\nL3i5i+Sy1RE70zRgPx31sG7+B0l/Blqd+PA/0ZxzmZnZmCb1yltzxrq/0ZR5RL0YmKZkes3NgcNI\nho6tk47b3Tx9fixwjZm1vGIr9CWceR+f/exng2cYz3k9s+dt9yjK5zM+eqG0I2ozWy1pNsmkPhOA\nc8xsqdLpHS0ZW7or8K30t9etwDFl5em1OI5DR8ilbnnBM/dC3fIWaVLoAA1KnevDzBaSXPTRuO6s\nhufXkczc5pxzlVKliZD8ysSSDAwMhI6QS53yzh8c5LCpU7n3/PM5bOpU5g8Oho6UWZ0+Z6hf3iJt\nmfHRC6VemViUDSefc5uy+YOD3HzqqXx99ep16z4wcSIv//SnOb5GBduVRxJWwMnEszO2PZbyTyZu\n0oX6a1+7gUsu6erGJaN68MGlbL9984WY1VVq3q2PHL1NRhN+OpWFqx4Akrsw9Kfr95v0dNYcuKKw\n/fDYd4rbVgP/vljvoINezIknvrLw7RZVqM/N2PYoyi/UVeqG6blly1Zw5ZUbjQYsyD3AFqO2qo4S\n8/YVt6lDVq1uuX6LVau56Ori9sPD/n2RKC/vtGlPH71RQJvMycRNWxQ6QE5R6ACZPNrwLdvfZn21\nRaED5BSFDhBMlb6j/GSiq5VbNp/NMU0/QkczkVs2nx0okRuvJmV89EKVfmmMMzH1OhqJqUPe+6cM\ncgmwzz/m8hRPsgWTuWXz2dw/ZTB0tIxi6vA5rxdTr7zF8a4P58bg/imDXDVlEFYNwaT+wGnceNWr\noXdZeKEuTRQ6QE5R6AD51bJIR6ED5BSFDhBMlYpjlbI451xlVKnrw08mliYOHSCnOHSA/FYNhU7Q\nhTh0gJzi0AGCmZjx0Up6Z57zJS2VtETSXm3azZC0WtLbRsvinHOuyRiPqL9Kckf3d6R3kd+quUF6\nu8LTgMuBjhfMeKEuTRQ6QE5R6AD5eR91D0ShAwTTbXGUtB3wOjN7LyQziQKPtGh6InA+MGO0bXrX\nh3POtTCGcdTPB+6XdK6k30k6W9KUxgaSdiS5h+yZ6aqOc2R4oS5NHDpATnHoAPl5H3UPxKEDBDOG\n2fMmAnsA881sD+Bx4JNNbeYAn0wnMRLe9eGcc/m166P+P+C6zm9dDiw3s0Xp8vlsXKj3BBZIApgK\n7CdplZldTAteqEsThQ6QUxQ6QH7eR90DUegAwbQrjnunjxFfaXrdzO6VdKekF5nZH4A3Abc1tdll\n5Lmkc4FL2hXpTlmcc26TNilrdWw9oeOJwPfTe8L+ETi66TaEuXihLk1MvY5GYuqVl5peQh5Tr885\npl55izNxDIXazG5i49EcLQu0mR012i5KPZkoaZakZZJul/SJFq9PlXS5pGFJt0oaKDOPc85lNWlC\ntkcvlFao08Hcc4FZJHcbP1xS860iZgM3mtl0kumFz0gHh48DUegAOUWhA+RXu6NpqN/nHIUOEMzE\nidkePclS4rZnAneYWQwgaQHJuMGlDW3uAV6ePt8WeCAdHO6cc0FNqtCNeMrs+tgRuLNheXm6rtHZ\nwEsl3Q3cBJxUYp4ei0MHyCkOHSA/H0fdA3HoAOGMZbKPEqKUJcvdaE8Ghs2sX9ILgCslvcLMHm1u\nODAwQBRFAPT19TF9+nT6+/sBGBoaAsi9vF6cfo0KXL634O2VvVxi3pGCOtJVUdTyiFK2H1Ot/5/x\nuJyca+v253dkec6cOQwPD6+rD4WpUCdsaXchT2eLGjSzWenyp4C1ZnZaQ5vLgFPN7Np0+RfAJ8xs\ncdO2SrkL+QknXMr8+YtGb+jGpm8wdIL8Hh4MnWDcO/74Gcybd0Dh2y3qLuTrRzqP0vZP5d+FvMyu\nj8XANElROpbwMKB5QPcyksHgSHom8GKgrNs/O+dcdhMyPnqgtEKdnhScDVwBLAHOM7Olko4bGfgN\nfAH4Z0k3AT8HPm5mD5aVqbfi0AFyikMHyM/7qHsgDh0gnE2kjxozWwgsbFp3VsPzFcBBZWZwzrmu\nVGjUR4W6y8ebKHSAnKLQAfLzcdQ9EIUOEE6FqmOFojjnXIVUqDr6fNSliUMHyCkOHSA/76PugTh0\ngHAqdDKxQr8znHOuQipUHSsUZbyJQgfIKQodID/vo+6BKHSAcCpUHSsUxTnnKqRC1dH7qEsThw6Q\nUxw6QH7eR90DcegA4WyR8dEDFfqd4ZxzFVKh6lihKONNFDpATlHoAPl5H3UPRKEDhDOGER2SYuDv\nwBpglZnNbNGmn+SWi5OAFWbW3257Xqidc66VsVVHA/rbTYkhqQ+YB+xrZsslTe20Me+jLk0cOkBO\ncegA+XkfdQ/EoQOEM/a5PjrNqPcu4AIzWw7rptNoywu1c861MrYLXgz4uaTFko5t8fo0YHtJV6dt\njugUxbs+ShOFDpBTFDpAft5H3QNR6ADhtKmOQ3fD0D2jvvs1ZnaPpB1IboiyzMx+1fD6JGAPYB9g\nCnCdpOvN7PYcUZwrkE/C7+pocuvV/bskjxGn3LhxGzO7J/16v6QLSe4h21io7yQ5gbgSWCnpl8Ar\ngJaF2rs+ShOHDpBTHDpAF+LQAboQhw6QUxw6QDhddn1ImiJpm/T5VsBbgFuaml0EvFbSBElTgFeS\nzNvfkh9RO+dcK91Xx2cCF0oa2cr3zexnIzdMMbOzzGyZpMuBm4G1wNlm5oW696LQAXKKQgfoQhQ6\nQBei0AFyikIHCKfL6mhmfwamt1h/VtPy6cDpJUZxzrlxrkdTmGbhfdSliUMHyCkOHaALcegAXYhD\nB8gpDh0gnArdM7HUQi1plqRlkm6X9IkWr39U0o3p4xZJq9MrdpxzLqwKFerSdiNpAjAXeBNwF7BI\n0sVmtnSkTWMfjaQDgf/PzB4uK1NvRaED5BSFDtCFKHSALkShA+QUhQ4QToVublvmEfVM4A4zi81s\nFbAAOKRD+3cBPywxj3POZVehI+oyC/WOJIO6RyxP120kHUe4L3BBiXl6LA4dIKc4dIAuxKEDdCEO\nHSCnOHSAcCpUqMvcjeVoexDw607dHgMDA0RRBEBfXx/Tp0+nv78fgKGhIYDcy+vF6deowOV7C95e\n2ct1y9uoKnl8Od/yDKD7n9+R5Tlz5jA8PLyuPhSmQqM+ZJannubYsLQXMGhms9LlTwFrzey0Fm0v\nBM4zswVttmVl5DzhhEuZP39R4dt1zo3u+ONnMG/eAYVvVxJm1mnmuizbMPt6xrYfYMz7G02ZXR+L\ngWmSIkmbA4cBFzc3krQdsDfJJZXOOVcNFer6KK1Qm9lqYDZwBck17OeZ2VJJx41cSpl6K3BFOjnJ\nOBKHDpBTHDpAF+LQAboQhw6QUxw6QDhjm+a0UKX+PjCzhcDCpnXNl1F+G/h2mTmccy63NrPnheCX\nkJcmCh0gpyh0gC5EoQN0IQodIKcodIBwKlQdKxTFOecqpEKjPnyuj9LEoQPkFIcO0IU4dIAuxKED\n5BSHDhBOhU4m+hG1c861UqHqWKEo400UOkBOUegAXYhCB+hCFDpATlHoAOF414dzzlXc5IyPNtLb\nbN0o6ZIWr02VdLmkYUm3ShroFMULdWni0AFyikMH6EIcOkAX4tABcopDBwhn7OOoTyK5hqTVZdWz\ngRvNbDrQD5whqW0Phxdq55xrZQwnEyXtBOwPfANodXn5PcC26fNtgQfSiwTbRnGliEIHyCkKHaAL\nUegAXYhCB8gpCh0gnLFVx68AH2N9MW52NnCVpLuBbYBDO23Mj6idc66VLo+o05ug3GdmN9L6aBrg\nZGDYzJ5DciPceZK26RTFlSKmXkcjMfXKC565F2LqlbdAbfqfhxYljw5eDRwsaX+S043bSvqOmR3Z\n1OZUADP7o6Q/Ay8mmcxuI16onXOulTbVsf9VyWPEKWdu+LqZnUxyxIyk1wMfbSrSAMtIblN4raRn\nkhTpP+WM4sYuCh0gpyh0gC5EoQN0IQodIKcodIBwirtnogGMzBqaTkz3BeBcSTeRdEF/3MwebLcB\nL9TOOddKAdXRzK4Brkmfn9WwfgXJna0y8ZOJpYlDB8gpDh2gC3HoAF2IQwfIKQ4dIByf68M55yqu\nQtWxQlHGmyh0gJyi0AG6EIUO0IUodICcotABgrEKzfXhhdo551pYU6Hq6H3UpYlDB8gpDh2gC3Ho\nAF2IQwfIKQ4dIJg1E7M9eqHU3UiaBcwhGTr+DTM7rUWbfpLLLScBK8ysv8xMzjmXxVNbbJ6x5T9K\nzQEZCrWkrYGVZrZG0otJBmYvNLNVo7xvAjCXZFD3XcAiSReb2dKGNn3APGBfM1suaeoY/i0VE4UO\nkFMUOkBmO3A1u7GIbVjLo2zGLczgft4QOlZGUegAOUWhAwSzZkJ1OqmzdH38EthC0o7AFcARwLcy\nvG8mcIeZxWlRXwAc0tTmXcAFZrYc1o0tdK6tHbiag/gVv2AlP+EpfsFKDuJX7MDVoaO5cWYNEzI9\neiFLoZaZPQG8DZhvZu8EXpbhfTsCdzYsL0/XNZoGbC/pakmLJR2RJXQ9xKED5BSHDpDJbizinHR6\n36F03TkYu9F58oXqiEMHyCkOHSCY1UzI9OiFTH3Ukl4FvBs4Jl2VpcC3miy72SRgD2AfYApwnaTr\nzez25oYDAwNEUQRAX18f06dPp7+/H4ChoSGA3MvrxenXqMDlewveXtnL5eV9L6cUtrVlrC/QI4YA\nYyWfTfcztrTJ8rd5b0GJfbn98gyg+5/fkeU5c+YwPDy8rj4UZU2FBsXJrHM9TScV+QhwrZmdJukF\nwElm9qFR3rcXMGhms9LlTwFrG08oSvoEsKWZDabL3wAuN7Pzm7Zlo+XsxgknXMr8+XU5EquvkQJa\nhN8CG93XiORa3D0L2wucwmcL3Jpr5fjjZzBv3gGFb1cSZtZuetGs27C/2DMytX2e7hvz/kYz6pGx\nmV1jZgeTnBjEzP44WpFOLQamSYokbQ4cBlzc1OYi4LXpvcWmAK8kuXWNcy1NBo5tWvc+Ot66zrmu\nVKmPOsuoj1eT3E5mG2BnSdOB95vZ8Z3eZ2arJc0mOQE5ATjHzJY2ziBlZsskXQ7cDKwFzjazcVKo\nY+p1xjymDnlfCtxGcgT9OLAVSZF+achQucTU4XNeL6ZeeYvzFFmH55UvSyfMHGAWydEvZjacdoeM\nyswWAgub1p3VtHw6cHqmtM6xvijHbKolxPVClfqoMyUxs79KG3TBtL0JoxsRhQ6QUxQ6QG5R6ABd\niUIHyCkKHSCYXnVrZJGlUP9V0msA0r7mDwFLO7/FufLcBjxJ0u3xOHXr+nB1UaVCnWWY3QeBE0jG\nQN8F7J4uu47i0AFyikMHyOQ2oI9k5McH0q996fp6iEMHyCkOHSCYWo2jNrP7Sa4gdC64J4Gzm9ad\nTY5bZTiX0Vj7qNNpNBYDy81so29RSf8N7Ac8AQykdy1vKcuoj3ObVhmAmR2dJ/SmJwodIKcodIBM\ntmp43t9mfbVFoQPkFIUOEEwBXR8nkQw33qb5hfQO5S80s2mSXgmcCezVbkNZfmVcyvqrDLcE/gW4\nO29i54rwcM71znXrH2MYnidpJ2B/4FTgwy2aHAx8G8DMbpDUJ+mZZva3VtvLcsHL+WZ2Qfr4HvBO\n4J+7/hdsMuLQAXKKQwfI5EnWf9cPpV//DXgqSJpuxKED5BSHDhDMGPuovwJ8jOT6kFZazYW0U7uN\nddMJ8yJghy7e59yYTQYeAT5D8l3+C+DvwBYhQ7lxqV0f9c1DD3HzUPu/4SQdCNxnZjem8+23bdq0\n3HaejCx91I81bMCAvwGfGO19LgodIKcodIBMBJzTYv1+vQ7StSh0gJyi0AGCaddH/dL+qby0f/3U\n+d8/5S/NTV4NHJz2Q08GtpX0HTM7sqHNXcDODcs7petayjLqY+vR2jjXK1vmXO9ct7o9mWhmJwMn\nw7pJ7T7aVKQhmfdoNrAgncDu4Xb909ChUEvakw6H4mb2uxzZN0Ex9ToaialD3sbbCg2xfuRHx9sN\nVUpMHT7n9WLqlbc4BY6RNoCmeY4uk7S/pDtIrts6qtMGOh1Rn0HnOaXrcu8jN45MBo4Gvtmw7mh8\n9jxXvH8UcObDzK4BrkmfN89zNDvrdtoWar/J7FhFoQPkFIUOkNnDJCcTJ5CcTHw4fV4PUegAOUWh\nAwRTpUvIs97hZTfgJTQcuJjZd8oK5Vw7T9L+xgHOFalXl4dnMeo4akmDwH+T3DjgDcCXSQZru47i\n0AFyikMHyKTxCsShNuurLQ4dIKc4dIBg1jAx06MXskzK9A7gTcA9ZnYU8AqSeXCc67nHc653rlu1\nusMLsNLM1khaLWk74D42HP/nWopCB8gpCh0gk8nA24BdSb55f04ymUJ9TiZGoQPkFIUOEEzd+qgX\nS3oaySRli0kOXv6v1FTOddAHfL5h+Wjg0UBZ3PhVi0ItaT7wAzP7YLrq65KuALY1s5t6kq7WYup1\nNBJTh7xPAj9Knw+RjKP+JnU6mRhTh895vZh65S3OUxWamKBTH/UfgP+U9BdJX5a0u5n9OU+RljRL\n0jJJt0va6LJzSf2SHpF0Y/r4f938I9ymo91Jw/qcTHR1UYs+ajObA8yRFAH/CnxT0hTgB8APzewP\nnTacTpo9l+RE5F3AIkkXm1nzbbyuMbNxOIokCh0gpyh0gEwaTxr2t1lfbVHoADlFoQMEU6WujyzT\nnMZm9iUz252kYP8L2e6ZOBO4I33/KmABcEiLds0zSDnX1mTg2KZ176NOJxNdXVTpVlxZxlFPlHSw\npB8AlwPLSE68j6bVfKs7NrUx4NWSbpJ0maRdM+augTh0gJzi0AEyeSnJlYgHAW9Mvz5CnW5uG4cO\nkFMcOkAwVRpH3elk4ltIjqAPAH4D/BB4v5k9lnHbneYJGfE7YGcze0LSfsBPSOa73sjAwABRFAHQ\n19fH9OnT6e/vB2BoaAgg9/J6cfo1KnD53oK3V/ZyeXmLTrtV+nh6ui5mw1Nexeyv+C36cvPyDKD7\nn9+R5Tlz5jA8PLyuPhSlSl0fMmtdTyVdRVKcLzCzB3NvOJm6b9DMZqXLnwLWmtlpHd7zZ2DP5v1J\nsnY5x+KEEy5l/vxFhW/XbeiznBI6Qm6n8NnQEca944+fwbx5BxS+XUmY2Zi6VCXZyfaZTG2/oM+N\neX+j6XQy8Y1j3PZiYFp6MvJu4DDg8MYGkp5JcicEkzST5BdH7l8KbtNyG8kwva1ITiJOpk5dH64u\nnhrDPROLluUS8q6Y2WqSibGvILl47DwzWyrpuJF5WUkuT79F0jAwh6SrZZyIQwfIKQ4dIJPbSC54\nuQT4QPq1L11fD3HoADnFoQMEU4s+6iKY2UJgYdO6sxqezwPmlZnBjS9Pklwi2+hs6nTBi6uLKvVR\nl3ZE7aLQAXKKQgfIpPHClv4266stCh0gpyh0gGC6veBF0mRJN0galrRE0hdbtHl3OtrtZknXSnp5\npyydRn003tS2mZnZtqP8O50rnM+e53ql2zHSZvakpDeko9kmAr+W9Foz+3VDsz8Be5vZI5JmAf8D\n7NVum22PqM1sazPbps3Di/So4tABcopDB8ik8YKXofRrvS54iUMHyCkOHSCYsfRRm9kT6dPNSW5A\n9GDT69eZ2SPp4g0kdyFvK3MftaRnsOEdXv6a9b3OFeWlJCcODyI5ij4DH/XhyjGWPmpJm5FcJ/IC\n4EwzW9Kh+THAZZ22N2qhlnQwyc/Dc0jmon4eySXk/rPRURQ6QE5R6ACZ1fsbLwodIKcodIBg/jGG\n4XlmthaYns7hf4WkfjMbam4n6Q0kM/W+ptP2shxRfx54FXClme2ebviI3MndJuuU7xV/sVLp3jMY\nOoELrF0f9X1DS7lvaFmmbaR90JcC/8yGd48jPYF4NjDLzB7qtJ0shXqVma2QtJmkCWZ2taSvZkq5\nSYup19FITL3yAkuGYNf+0ClyiqnX5xxTr7zFadf//PT+3Xh6/27rlpecctEGr0uaCqw2s4clbQm8\nGTa8PFfSc4EfA+8xsztGy5KlUD8kaRvgV8D3Jd0HZJ3vwznnamkMfdTPBr6d9lNvBnzXzH4xcqFf\nei3JvwNPA86UBMkB8cx2G8xSqN8KrAT+DXg3sC3UcPKGnotCB8gpCh0gv9odTUP9PucodIBgui3U\nZnYLsEdoan0WAAAW/UlEQVSL9Y0X+72PZMBSJqMW6obZ8tYA38q6Yeecq7NezTWdRdtx1JKuTb8+\nJunRpsffexexruLQAXKKQwfIb8lQ6ARdiEMHyCkOHSCYWsz1YWavSb9u3ZMkzjlXIWMZnle0LHd4\n+W6Wda5ZFDpATlHoAPl5H3UPRKEDBFOlW3FlOW5/WeNCeu36nuXEcc65auhVt0YWnfqoT5b0KLBb\nY/80ydWJF/csYW3FoQPkFIcOkJ/3UfdAHDpAMN3OnleGTn3UXwC+IOlLZvbJnqRxzrmKqNJ81J2m\nOf0nM1sG/EhSqzGBvys1We1FoQPkFIUOkJ/3UfdAFDpAMLUo1MBHSGaUPIPW81K/oZREzjlXAU+x\nRegI63Tq+jg2/drfszTjSky9jkZi6pUXn+ujJ2Lqlbc4dTmiXkfSq0n+t9a1N7PvZHjfLJKb1k4A\nvmFmp7VpNwO4DjjUzH6cJZNzzpWpVoVa0veAXYBhksvIR3Qs1JImAHOBNwF3AYskXWxmS1u0Ow24\nHFCu9JUWhQ6QUxQ6QH61O5qG+n3OUegAwVTpEvIsR9R7AruaWd5JhWcCd5hZDCBpAXAIyU0HGp0I\nnA/MyLl955wrTS3GUTe4lWTavrx2BO5sWF6erltH0o4kxfvMdFUNZ5hvJw4dIKc4dID8fBx1D8Sh\nAwRTi3HUDXYAlkj6DfBUus7M7OBR3pel6M4BPmlmpmRS1rZdHwMDA0RRBEBfXx/Tp0+nv78fgKGh\nIYDcy+vF6deowOV7C95e2csl5h0pqCNdFWNc3u7rA+yy+EKmrF3DFptP5rfTD+SRvQcK236yHGf/\n9/lyl8vJH9Hd/vyOLM+ZM4fh4eF19aEoVeqj1mg9GpL6W61vdf+vpvftBQya2ax0+VPA2sYTipL+\nxPriPBV4AjjWzC5u2lYXPS+jO+GES5k/f1Hh23VNvjdY2KZ2uGCQgy46lXPWrl637pjNJnLJIZ/m\n/rcXtx+/FVf5jj9+BvPmHVD4diVhZmM63yXJtnvqnkxtH9ni2WPe32iyzEc91OW2FwPTJEXA3cBh\nwOFN295l5Lmkc4FLmou0c412u3LuBkUa4Jy1q9nnyrlcVWShdpu8Natr0EfdZh7qzPNRm9lqYDZw\nBbAEOM/Mlko6buSWNONbHDpATnHoAJlss2Z9kR5qs77a4tABcopDBwhmzeoJmR7NJO0s6WpJt0m6\nVdKH2u1D0gxJqyW9rVOWThe8jHkeajNbCCxsWndWm7ZHjXV/bvx7dPU/cq13rlutinBGq4B/M7Nh\nSVsDv5V05ViGJmcZ9eG6EoUOkFMUOkAmTwKfTp/3p19PZv1Z7uqLQgfIKQodIJjVqyZkejQzs3vN\nbDh9/hjJkOTntNjFyNDk+0fLUp1OGOcy2GHi5uy7aiWfIbncdQ0wC1gysTp343Djw9o1Yy+P6Tm6\n3YEbmtaPDE1+I8nwl46jJbxQlyamXkcjMXXI++iEiewN7E3SR92frj9lQl2+lWPq8DmvF1OvvAVq\n1/Vx3TVw/TWjvj3t9jgfOKnhJuEjMg9NBi/UrmZuefNsjmkannf0ZhO55c2zA6Zy49KTbcrj7vsk\njxFzPrdRE0mTgAuA75nZT1psZU9gQVKjmQrsJ2lVu1FvXqhLE4UOkFMUOkAm9799kEuAfa6cyzZr\nVvO5CUmRLnQMdami0AFyikIHCKfLgUTpEfI5wBIzm9OqTd6hyV6oXe3c//ZBHzPtytf9iM/XAO8B\nbpZ0Y7ruZOC50H7kWydeqEsTU6+jkZh65cXno+6JmHrlLVCXhdrMfk2OEXVZhiZ7oXbOuVZWhQ6w\nnhfq0kShA+QUhQ6QX+2OpqF+n3MUOkA4a0Zv0iteqJ1zrpUKzUrgVyaWJg4dIKc4dID8fD7qHohD\nBwjnyYyPHvAjaueca6VCR9ReqEsThQ6QUxQ6QH7eR90DUegA4Xihdq57O1wwyG7pBS+P1u6CF1cb\nXqg3BTH1OhqJqUPeHS4Y5DUX/gcvxVgOvAzY9sL/4FqoSbGOqcPnvF5MvfIWyIfnuU3J6999eWHb\nWnvsF9kV4/Osn5Tp0xgPXP5Fdv3xXoXt55r3FLYpV1cVGp7noz5KE4UOkFMUOkAm26z8B6emz/vT\nr6cC266sy40DotABcopCBwhndcZHD/gRtauVLdqs99moXeF6NPQuCz+iLk0cOkBOcegAmTy65fqS\nPNSw/rEt61Kq49ABcopDBwinQkfUpRZqSbMkLZN0u6RPtHj9EEk3SbpR0m8lvbHMPK7+Hv74OzhK\nG86xfpTEQx9/R6BEbtyqUKEuresjvXHjXOBNwF3AIkkXN93g8edmdlHafjfgQuCFZWXqrSh0gJyi\n0AEy2WrwCG4F9pv7U7ZavZrTJk5kxewD2WrwiNDRMopCB8gpCh0gnE1keN5M4A4ziwEkLSC5R9i6\nQm1mjze03xpYUWIeN05sNXgEKwePYOXIctA0btyq0PC8Mrs+dgTubFhenq7bgKS3SloKLAQ+VGKe\nHotDB8gpDh0gt4eHbg4doQtx6AA5xaEDhLMm46MHyjyi7nhX3XWNkvuJ/UTS64DvAi9u1W5gYIAo\nigDo6+tj+vTp9Pf3AzA0NASQe3m9OP0aFbh8b8HbK3u5vLwjBbWv/+WFLo8oZ/txYf9+X263PAPo\n/ud3ZHnOnDkMDw+vqw+F6XLUh6RvAgcA95nZbm3a9ANfASYBK8ysv+M2zTLV09wk7QUMmtmsdPlT\nwFozO63De/4IzDSzB5rWWxk5TzjhUubPX1T4dt2GXm/FXYjSK9fo+tARxr3jj5/BvHkHFL5dSZhZ\nx7t6Z9iG8amMNeeLG+4vPeh8DPhOq0ItqQ+4FtjXzJZLmmpmHbt9y+z6WAxMkxRJ2hw4DNjg5o2S\nXpDeCBJJewA0F2nnnAtiVcZHEzP7FfBQhy2/C7jAzJan7Uc9N1daoTaz1cBs4ApgCXCemS2VdJyk\n49JmbwduSW8A+VXgX8vK03tx6AA5xaED5OZ91L0Qhw4QTnl91NOA7SVdLWmxpFGHLJV6ZaKZLSQ5\nSdi47qyG518GvlxmBuec60p5w/MmAXsA+wBTgOskXW9mt7d7g19CXpoodICcotABchs5+VcvUegA\nOUWhA4TTrlDfNQR3D41ly3eSnEBcCayU9EvgFYAXauecy6XdOOpn9CePEYtPybvli4C56UWBWwCv\nBP6r0xt8ro/SxKED5BSHDpCb91H3Qhw6QDhPZXw0kfRD4P+AF0u6U9LRjefmzGwZcDlwM3ADcLaZ\nLekUxY+onXOulS77qM3s8AxtTgdOz7pNL9SliUIHyCkKHSA376PuhSh0gHAqdAm5F2rnnGvF7/Cy\nKYhDB8gpDh0gN++j7oU4dIBwNoVpTp1zrtY2kWlON3FR6AA5RaED5OZ91L0QhQ4QjvdRO+dcxbUY\neheK91GXJg4dIKc4dIDcvI+6F+LQAcLxPmrnnKs47/rYFEShA+QUhQ6Qm/dR90IUOkA4FRqe54Xa\nOedaqdCoD++jLk0cOkBOcegAuXkfdS/EoQOE433UzjlXcd5HvSmIQgfIKQodIDfvo+6FKHSAcCo0\nPM8LtXPOtbIp9VFLmiVpmaTbJX2ixevvlnSTpJslXSupjodJLcShA+QUhw6Qm/dR90IcOkA4Xd7c\ntgylHlGndzCYC7wJuAtYJOliM1va0OxPwN5m9oikWcD/AHuVmcs550a1CQ3PmwncYWYxgKQFwCHA\nukJtZtc1tL8B2KnkTD0ShQ6QUxQ6QG7eR90LUegA4WxCXR87ktzIccTydF07xwCXlZrIOeeyGMPw\nvAxdvlMlXS5pWNKtkgY6RSm7UFvWhpLeABwNbPSPqqc4dICc4tABMnt88LtMnnootvVbmTz1UB4f\n/G7oSDnEoQPkFIcOEE6XfdQNXb6zgF2BwyW9pKnZbOBGM5sO9ANnSGrbw1F218ddwM4NyzuTHFVv\nID2BeDYwy8wearWhgYEBoigCoK+vj+nTp9Pf3w/A0NAQQO7l9eL0a1Tg8r0Fb6/s5fLyjpz0G+mq\nGMvy44Pf5RmfW8DH1q4FoP/xpzjgcwu4I/4bz/7WRwvcX1za5+HLI8szgO5/fkeW58yZw/Dw8Lr6\nUJjuuz5G7fIF7gFG+u62BR4ws7Z7lFnmg97c0t8Qvwf2Ae4GfgMc3ngyUdJzgauA95jZ9W22Y2Xk\nPOGES5k/f1Hh23Uber0Vd2548tRDufyBRzdav9/Tt2XlivMK2881avmt6Ap0/PEzmDfvgMK3Kwkz\n0xi3Ydk7BDbcn6R3APua2bHp8nuAV5rZiQ1tNiOpey8CtgEONbOF7fZQ6hG1ma2WNBu4ApgAnGNm\nSxtum34W8O/A04AzJQGsMrOZZeYa8Z//+WZOPfWNvdjVJm1Cgd9ms1e3/vl7xmqYyz6F7WfNQ68v\nbFuutc03nxA6QpeG0kdbWSr8ycCwmfVLegFwpaRXmNnGRyH04IKX9LfEwqZ1ZzU8fx/wvrJztDJl\nyuZMmVLOtoeGhtb9aVYHdcn75MRJ654PkXTuATw1cRLbMKnFO7rUV+C2GtTlcx5Rt7y90c/67zyA\nU5obZOnyfTVwKoCZ/VHSn4EXA4tb7dEnZXK18vrZs/nAxA2PL46bOJG9Z88OlMiNX11f8bIYmCYp\nkrQ5cBhwcVObZSTXlyDpmSRF+k/tkpTaR12UsvqoXT3NHxzkl3PnMnn1ap5Mi/Txg4OhY7mKKK6P\n+omMradstD9J+wFzWN/l+8XGLl9JU4FzgeeSHDB/0cx+0DZPHQqgF2rnXFbFFepHMrbebsz7G413\nfZRk4yGA1Va3vOCZe6FueYu1MuOjfD57nnPOtVSdCam968M5N64U1/Xx54ytn19614cfUTvnXEvV\nOaL2PuqS1K1vr255wTP3Qt3yFqs6N030I2rnnGupOkfU3kftnBtXiuujzjrfy17eR+2cc2FU584B\n3kddkrr17dUtL3jmXqhb3mJV56aJfkTtnHMtVeeI2vuonXPjSnF91FnvCri/91E751wY1Tmi9j7q\nktStb69uecEz90Ld8hbL+6idc67iejPhUhbeR+2cG1eK66M+N2Pro7yP2jnnwtiE+qglzZK0TNLt\nkj7R4vV/knSdpCclfaTsPL1St769uuUFz9wLdctbrO77qEere2mb/05fv0nS7p2SlFqoJU0A5gKz\ngF2BwyW9pKnZA8CJwOllZum14eHh0BFyqVte8My9ULe8xepuUqYsdU/S/sALzWwa8H7gzE5Jyj6i\nngncYWaxma0CFgCHNDYws/vNbDFVmgGlAA8//HDoCLnULS945l6oW95idX1EPWrdAw4Gvg1gZjcA\nfelNblsqu1DvCNzZsLw8XeeccxXX9TSnWepeqzY7tUtS9snETXaoRhzHoSPkUre84Jl7oW55i9X1\n8Lysda95pEjb95U6PE/SXsCgmc1Klz8FrDWz01q0/SzwmJmd0eK1TbbgO+fyK2Z4Xnf7y1L3JH0d\nGDKzBenyMuD1Zva3Vtsv+4h6MTBNUgTcDRwGHN6mbdsPtuwxis4512iMNSdL3bsYmA0sSAv7w+2K\nNJRcqM1staTZwBXABOAcM1sq6bj09bMkPQtYBGwLrJV0ErCrmT1WZjbnnCtDlrpnZpdJ2l/SHcDj\nwFGdtlmLKxOdc25TVslJmSRtL+lKSX+Q9DNJfW3a9Uk6X9JSSUvSPyF6LmvetO0ESTdKuqSXGVvk\nGDWzpJ0lXS3pNkm3SvpQoKyFXjxQtgwXeb07zXmzpGslvTxEzqZMo37GabsZklZLelsv87XIkeV7\noj/9WbtV0lCPIxbLzCr3AL4MfDx9/gngS23afRs4On0+EdiuynnT1z8MfB+4uOqfMfAsYHr6fGvg\n98BLepxzAnAHEAGTgOHmDMD+wGXp81cC1wf8XLPkfdXI9yrJRRHB8mbN3NDuKuCnwNurnBfoA24D\ndkqXp4b8jMf6qOQRNQ2DwdOvb21uIGk74HVm9k1I+oXM7JHeRdzAqHkBJO1EUlS+QYeTpz0yamYz\nu9fMhtPnjwFLgef0LGGi8IsHSpblIq/rGr5Xb6DD+NkeyfIZQ3IF8fnA/b0M10KWvO8CLjCz5QBm\ntqLHGQtV1UL9TFt/BvRvQKsfuucD90s6V9LvJJ0taUrvIm4gS16ArwAfA9b2JFVnWTMDkJ7B3p2k\nsPRS4RcPlCzvRV7HkP1WImUZNbOkHUmK4cilziFPbmX5jKcB26ddd4slHdGzdCUINnuepCtJ/rRu\n9unGBTOzNmMaJwJ7ALPNbJGkOcAngX8vPCxjzyvpQOA+M7tRUn8ZGVvsc6yf8ch2tiY5kjrJej8a\np/CLB0qWeb+S3gAcDbymvDiZZMk8B/hk+r0iwv5FmCXvJJL6sA8wBbhO0vVmdnupyUoSrFCb2Zvb\nvSbpb5KeZWb3Sno2cF+LZsuB5Wa2KF0+n6RQl6KAvK8GDk4nY5kMbCvpO2Z2ZEmRi8iMpEnABcD3\nzOwnJUXt5C5g54blnUn+7zu12SldF0KWvKQnEM8GZpnZQz3K1k6WzHuSjPkFmArsJ2mVmV3cm4gb\nyJL3TmCFma0EVkr6JfAKoJaFuqpdHxcD702fvxfYqECY2b3AnZJelK56E8nJgxCy5D3ZzHY2s+cD\n/wpcVWaRzmDUzOmR0znAEjOb08NsjdZdPCBpc5KLB5qLw8XAkbDuqrCOFw+UbNS8kp4L/Bh4j5nd\nESBjs1Ezm9kuZvb89Pv3fOCDgYo0ZPueuAh4bTrKagrJSeYlPc5ZnNBnM1s9gO2BnwN/AH4G9KXr\nnwNc2tDuFSQXy9xE8o0fatRHprwN7V9P+FEfo2YGXkvSnz4M3Jg+ZgXIuh/JiJM7gE+l644Djmto\nMzd9/SZgj8Cfbce8JCeTH2j4TH8TMm/Wz7ih7bnA26qeF/goycHbLcCHQn/GY3n4BS/OOVdxVe36\ncM45l/JC7ZxzFeeF2jnnKs4LtXPOVZwXauecqzgv1M45V3FeqF0hJK1Jp5S8MZ175XmSrh3D9r4l\n6e1N694r6QdN66ZKui+9grLVdgYkfa3bHM5VQbBLyN2484SZNc8DPZY5LIyN53T4MXC6pC0tuTQY\n4B0kFw+t6rAd52rNj6hdaSQ9ln7tlzQk6UdKbvLwvYY2n5H0G0m3SDqreRONC2b2KHANcFDD6sOA\nH0o6UNL16dH8lZKe0SLPBkfpI/nS5x9Lc9wkaTBdt5WkSyUNp/kO7f7TcK57XqhdUbZs6Pq4IF3X\neDQ7HTgJ2BXYRdLI0fZcM5tpZrul2zhwlP38kGSuFCQ9B3gRyWT2vzazvcxsD+A84ONp+8Zi33x0\nbel23gK80Mxmkkzluqek1wH7AneZ2fQ03+UZPgfnCuddH64oK1t0fTT6jZndDSBpmOTuHNcCb5T0\nMZKpKLcHbiW5g0g7lwHzJW0DHAqcb2am5LZh/0syrevmwJ9yZH8L8BZJN6bLWwEvBH4NnCHpS8BP\nzezXObbpXGH8iNr1ylMNz9cAEyRNBuaR3NZpZNrPyZ02kvZNXw68jbTbI33pa8B/p9s5DtiyxdtX\nk37PS9qMpKCP+KKZ7Z4+XmRm51oyd/HuJJP6fF7SZ3L9i50riBdqF9JIUX4gvTnBOzO+74ck9558\nhpldn67bFrg7fT7Q5n0xybzKkNy+a2SkyBXA0ZK2guRuJpJ2SOfpftLMvg+cTjIRvXM9510friit\nRldYp9fN7GFJZ5N0d9zLxrf5ajdi4+fAs0mmCx0xCPxI0kMkfdbPa9jGyHbOBi5Ku14uBx5Lc1wp\n6SUkdwEBeBQ4gqT74z8lrQX+AXywTR7nSuXTnDrnXMV514dzzlWcF2rnnKs4L9TOOVdxXqidc67i\nvFA751zFeaF2zrmK80LtnHMV54XaOecq7v8HFqjthUtIMWcAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fd392fb2fd0>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"INITIAL : \n",
"[ 0.87399842 0.55698544 0.53254873 0.37791788 0.32340168 0.48135461\n",
" 0.55050018 0.56948357 0.51526644 0.192667 0.31971078 0.38866229\n",
" 0.60102601]\n",
"FINAL : \n",
"[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n"
]
}
],
"prompt_number": 168
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"reachData.discribeParameter('marker_0_x')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Parameter : marker_0_x\n",
"check pdf :"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" [[ 0.38461538 0. 0. 0. 0. ]\n",
" [ 0. 0.07692308 0. 0. 0. ]\n",
" [ 0. 0. 0.23076923 0. 0. ]\n",
" [ 0. 0. 0. 0.07692308 0. ]\n",
" [ 0. 0. 0. 0. 0.23076923]] [[ 5. 0. 0. 0. 0.]\n",
" [ 0. 1. 0. 0. 0.]\n",
" [ 0. 0. 3. 0. 0.]\n",
" [ 0. 0. 0. 1. 0.]\n",
" [ 0. 0. 0. 0. 3.]]\n",
"pdf Initial Values, pdf Final Values : [ 0.38461538 0.07692308 0.23076923 0.07692308 0.23076923] [ 0.38461538 0.07692308 0.23076923 0.07692308 0.23076923]\n",
"check sumpx, sum py, sumpxpy : 1.0 1.0 2.0\n",
"H_FinalGivenInitial : 0.0 H_InitialGivenFinal : 0.0\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAEBCAYAAACDu+UiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEehJREFUeJzt3X+MZWV9x/H3x10wNY2dUlpU0E6jaK0VBltx/dEyRlo3\n1EK1PyhV2/FHu0m71rZ/FLGJ3cSoIf1DYtpQSpGhjRGM2nZtKAhkbzSgCNFZBHbpbugmCyhtVUir\naQvut3/MZfdmmJm7s2fm3jnnvl/Jhnnufe485yHMh7Ofc++ZVBWSpG55xrgPQJK0/gx3Seogw12S\nOshwl6QOMtwlqYMMd0nqoMbhnuTjSR5N8vUVnn9rkr1J7klye5Kzmq4pSVrdepy5XwtsX+X5B4Gf\nr6qzgA8Cf7MOa0qSVtE43Kvqi8B3Vnn+S1X1eH94J3BG0zUlSasbdef+LuDGEa8pSRNn66gWSvJ6\n4J3Aa0e1piRNqpGEe/8i6tXA9qp6WoWTxBvcSNIJqKos9/iGh3uSFwCfBd5WVQdXmucNzLRZ7dq1\ni127do37MKSnSZbNdWAdwj3JJ4HzgFOTHAb+HDgJoKquAj4A/DBwZf9Anqiqc5uuK43KoUOHxn0I\n0po1DvequmTI8+8G3t10HUnS8fMTqtIQc3Nz4z4Eac2yGbruJLUZjkOS2iTJihdUPXOXhuj1euM+\nBGnNDHdJ6iBrGUlqKWsZSZowhrs0hJ272shwl6QOsnOXpJayc5ekCWO4S0PYuauNDHdJ6iA7d0lq\nKTt3SZowhrs0hJ272shwl6QOsnOXpJayc5ekCbPhvyBb2kxW+4XC68m/iWrcPHPXRKmqNf/Zs2fP\nml8jjZuduyS1lJ27JE0Yw10aYmamN+5DkNasUbgn+XiSR5N8fZU5H0tyIMneJOc0WU8ah717x30E\n0to1PXO/Fti+0pNJLgBeVFVnAr8HXNlwPWkMZsd9ANKaNQr3qvoi8J1VplwIXNefeycwleS0JmtK\nkobb6M79dODwwPgh4IwNXlNaZ71xH4C0ZqO4oLr0bTq+51GSNthGf0L1YeD5A+Mz+o89zdzcHNPT\n0wBMTU0xMzPD7OwscOyufI4dj2N89tmLj22W43E8ueNer8f8/DzA0bxcSeMPMSWZBj5XVS9f5rkL\ngJ1VdUGSbcAVVbVtmXl+iEmS1mjDPsSU5JPAHcBLkhxO8s4kO5LsAKiqG4EHkxwErgJ+v8l60jg8\ndeYktUmjWqaqLjmOOTubrCFJWjvvLSNJLeW9ZSRpwhju0hDeW0ZtZLhLQ3hvGbWRnbs0RAL+56nN\nyM5dkiaM4S4N1Rv3AUhrZrhLUgcZ7tIQ5503O+5DkNbMC6qS1FJeUJUa8N4yaiPDXZI6yFpGklrK\nWkaSJozhLg3hvWXURoa7NIT3llEb2blLQ3hvGW1Wdu6SNGEMd2mo3rgPQFozw12SOshwl4bw3jJq\nIy+oSlJLeUFVasB7y6iNGod7ku1J9ic5kOTSZZ4/NclNSRaS3JtkrumakqTVNaplkmwBHgDOBx4G\n7gIuqap9A3N2Ac+sqsuSnNqff1pVPTkwx1pGktZoI2uZc4GDVXWoqp4ArgcuWjLnG8Cz+18/G/jW\nYLBLktZf03A/HTg8MH6o/9igq4GXJXkE2Au8t+Ga0kh5bxm10daGrz+eLuX9wEJVzSZ5IXBLkrOr\n6r8GJ83NzTE9PQ3A1NQUMzMzzM7OAscuaDl2PI7x3r0L9Hqb53gcT+641+sxPz8PcDQvV9K0c98G\n7Kqq7f3xZcCRqrp8YM6NwIeq6vb++Dbg0qq6e2COnbs2Le8to81qIzv3u4Ezk0wnORm4GNi9ZM5+\nFi+4kuQ04CXAgw3XlSStolG49y+M7gRuBu4HbqiqfUl2JNnRn/Zh4GeT7AVuBf60qr7dZF1ptHrj\nPgBpzfyEqjRE0qNqdtyHIT3NarWM4a5We8YzutGHJ3DkyLiPQm2zWrg3fbeMNFZV3Ql3aT15bxlp\niKfeiia1ieEuSR1k565W68p70LuyD42Wt/yVpAljuEtD2LmrjQx3SeogO3e1Wle66q7sQ6Nl5y5J\nE8Zwl4awc1cbGe6S1EF27mq1rnTVXdmHRsvOXZImjOEuDWHnrjYy3CWpg+zc1Wpd6aq7sg+Nlp27\nJE0Yw10aws5dbWS4S1IH2bmr1brSVXdlHxotO3dJmjCGuzSEnbvaqHG4J9meZH+SA0kuXWHObJKv\nJbk3Sa/pmpKk1TXq3JNsAR4AzgceBu4CLqmqfQNzpoDbgTdW1UNJTq2q/1zyfezcdUK60lV3ZR8a\nrY3s3M8FDlbVoap6ArgeuGjJnN8CPlNVDwEsDXZJ0vprGu6nA4cHxg/1Hxt0JnBKkj1J7k7y9oZr\nSiNl56422trw9cfzF8mTgFcAbwCeBXwpyZer6sDgpLm5OaanpwGYmppiZmaG2dlZ4NgPl2PH4xgv\nLCyMZD3YHPt1vHnHvV6P+fl5gKN5uZKmnfs2YFdVbe+PLwOOVNXlA3MuBX6gqnb1x38L3FRVnx6Y\nY+euE9KVrror+9BobWTnfjdwZpLpJCcDFwO7l8z5J+B1SbYkeRbwKuD+hutKklbRKNyr6klgJ3Az\ni4F9Q1XtS7IjyY7+nP3ATcA9wJ3A1VVluKs1jtUmUnt4+wG12ijqjF6vd7T/3CjWMjoRq9Uyhrta\nrSuh2JV9aLS8t4wkTRjDXRrCzl1tZLhLUgfZuavVutJVd2UfGi07d0maMIa7NISdu9rIcJekDrJz\nV6t1pavuyj40WnbukjRhDHdpCDt3tZHhLkkdZOeuVutKV92VfWi07NwlacIY7tIQdu5qI8NdkjrI\nzl2t1pWuuiv70GjZuUvShDHcpSHs3NVGhrskdZCdu1qtK111V/ah0bJzl6QJY7hLQ9i5q40ah3uS\n7Un2JzmQ5NJV5r0yyZNJ3tJ0TUnS6hp17km2AA8A5wMPA3cBl1TVvmXm3QJ8D7i2qj6z5Hk7d52Q\nrnTVXdmHRmsjO/dzgYNVdaiqngCuBy5aZt57gE8D/9FwPUnScWga7qcDhwfGD/UfOyrJ6SwG/pX9\nhzw/UavYuauNtjZ8/fEE9RXA+6qqkgRY9q8Qc3NzTE9PAzA1NcXMzAyzs7PAsR8ux47HMV5YWBjJ\nerA59ut48457vR7z8/MAR/NyJU07923Arqra3h9fBhypqssH5jzIsUA/lcXe/XeravfAHDt3nZCu\ndNVd2YdGa7XOvWm4b2XxguobgEeAr7DMBdWB+dcCn6uqzy553HDXCelKKHZlHxqtDbugWlVPAjuB\nm4H7gRuqal+SHUl2NPne0mZxrDaR2sPbD6jdsuxJy7rq8VQbvsH8GdAabVgts14Md52ortQZXdmH\nRst7y0jShDHcpSHs3NVGhrskdZCdu1qtK111V/ah0bJzl6QJY7hLQ9i5q40Md0nqIDt3tVpXuuqu\n7EOjZecuSRPGcJeGsHNXGxnuktRBdu5qta501V3Zh0bLzl2SJozhLg1h5642MtwlqYPs3NVqXemq\nu7IPjZaduyRNGMNdGsLOXW1kuEtSB9m5q9W60lV3ZR8aLTt3SZowhrs0hJ272qhxuCfZnmR/kgNJ\nLl3m+bcm2ZvkniS3Jzmr6ZqSpNU16tyTbAEeAM4HHgbuAi6pqn0Dc14N3F9VjyfZDuyqqm1Lvo+d\nu05IV7rqruxDo7WRnfu5wMGqOlRVTwDXAxcNTqiqL1XV4/3hncAZDdeUJA3RNNxPBw4PjB/qP7aS\ndwE3NlxTGik7d7XR1oavP+6/SCZ5PfBO4LXLPT83N8f09DQAU1NTzMzMMDs7Cxz74XLseBzjhYWF\nkawHm2O/jjfvuNfrMT8/D3A0L1fStHPfxmKHvr0/vgw4UlWXL5l3FvBZYHtVHVzm+9i564R0pavu\nyj40WhvZud8NnJlkOsnJwMXA7iWLv4DFYH/bcsEuSVp/jcK9qp4EdgI3A/cDN1TVviQ7kuzoT/sA\n8MPAlUm+luQrjY5YGrFjtYnUHt5+QK02ijqj1+sd7T83irWMTsRqtYzhrlbrSih2ZR8aLe8tI0kT\nxnCXhrBzVxsZ7pLUQXbuarWudNVd2YdGy85dkiaM4S4NYeeuNjLcJamD7NzVal3pqruyD42Wnbsk\nTRjDXRrCzl1tZLhLUgfZuavVutJVd2UfGi07d0maMIa7NISdu9rIcJekDrJzV6t1pavuyj40Wnbu\nkjRhDHdpCDt3tZHhLkkdZOeuVutKV92VfWi07NwlacIY7tIQdu5qo8bhnmR7kv1JDiS5dIU5H+s/\nvzfJOU3XlCStbmuTFyfZAvwlcD7wMHBXkt1VtW9gzgXAi6rqzCSvAq4EtjVZVxqUZRvH9TS70QuM\nYA+aNI3CHTgXOFhVhwCSXA9cBOwbmHMhcB1AVd2ZZCrJaVX1aMO1pZFchPRip9qoaS1zOnB4YPxQ\n/7Fhc85ouK40Qr1xH4C0Zk3P3I/3fGbpXzqf9rq5uTmmp6cBmJqaYmZmhtnZWeDYBS3HjscxhgV6\nvc1zPI4nd9zr9Zifnwc4mpcrafQ+9yTbgF1Vtb0/vgw4UlWXD8z5a6BXVdf3x/uB8wZrGd/nrs3M\nWkab1Ua+z/1u4Mwk00lOBi4Gdi+Zsxv47f6BbAMes2+XpI3VqJapqieT7ARuBrYA11TVviQ7+s9f\nVVU3JrkgyUHgu8A7Gh+1NEJnn91jFO+YkdaTtx+Qhuj1egP9u7R5rFbLGO6S1FLeW0aSJozhLg3x\n1FvRpDYx3CWpg+zcpSFmZ8GTd21GXlCVGvBDTNqsvKAqNdIb9wFIa2a4S1IHWctIQ1jLaLOylpGk\nCWO4S0Ms3ltGahfDXRriiivGfQTS2tm5S1JL2blL0oQx3KUhvLeM2shwl6QOsnOXhvDeMtqsvLeM\n1IAfYtJmtVq4N/odqlLbJMv+HBzH69Y235MVjZuduyZKVa35z549e9b8GmncrGUkqaV8n7skTZgT\nDvckpyS5Jcm/Jvl8kqll5jw/yZ4k9yW5N8kfNjtcafR8n7vaqMmZ+/uAW6rqxcBt/fFSTwB/XFUv\nA7YBf5DkpQ3WlEZuYWFh3IcgrVmTcL8QuK7/9XXAryydUFXfrKqF/tf/DewDntdgTWnkHnvssXEf\ngrRmTcL9tKp6tP/1o8Bpq01OMg2cA9zZYE1J0nFY9X3uSW4BnrPMU382OKiqSrLi212S/CDwaeC9\n/TN4qTUOHTo07kOQ1uyE3wqZZD8wW1XfTPJcYE9V/eQy804C/hn4l6pa9s7Yq/2PQZK0so34hOpu\n4HeAy/v//MelE7L4ccBrgPtXCvbVDk6SdGKanLmfAnwKeAFwCPiNqnosyfOAq6vql5K8DvgCcA/w\n1EKXVdVNjY9ckrSiTfEJVUnS+vITqpLUQYa7JlqS2SSfW+fv+cwkNyQ5kOTLSX58Pb+/dDwMd02s\nJI1ueZ1kywpPvQv4VlWdCXyUxTcdSCNluKt1kkwn2Z/k2iQPJPlEkl9Mcnv/Xkev7P+5I8lX+4+/\nuP/auSS7k9wG3MqxC/30X/PVJD+R5GeS9JLcneSmJM/pz+kl+WiSu4CV7pU0+OntzwBvWGUvb05y\na//r5/b382ON/yVp4vnLOtRWLwR+FbgfuAu4uKpem+RC4P3A24Gfq6rvJzkf+DDwa/3XngO8vP/u\nrlmAJK8BPsZiMD8KfAL45ar6VpKLgQ+xeEZewElV9cpVju104DBAVT2Z5PEkp1TVt5dOrKp/SPKW\nJDuBNwIfqKp/b/DvRQIMd7XXv1XVfQBJ7mPxLBzgXmAamAL+PsmLWAzkwf/WP19VgzeMeSlwFfAL\n/Q/l/TTwMuDW/m9u2gI8MjD/hnXey3uA+4A7qmq9v7cmlOGutvrfga+PAP838PVW4IPAbVX15v4F\nzd7A/O8NfF3AN4BnAq8AbgQC3FdVr1lh7e8OObaHWfz8xyP9Xv+HljtrH/B84PvAafE312id2Lmr\niwI8m2Nn2+8YMvcx4E3AR5KcBzwA/GiSbbB4C40kP7WG9Z/69DYsVkG3rbj4YvhfA/wmsB/4kzWs\nI63IcFdbLT27HRwfAf6CxbD+Kou1Sg3MqyWvq37P/Sbgr4CzWQzly5MsAF8DXr2GY7sG+JEkB4A/\nYvnfdfCUy4AvVNUdLAb7u5O8ZA1rScvyE6qS1EGeuUtSB3lBVTpBSd4P/PqShz9VVR9ZZu7Lgb9b\n8vD/VNVa6h7puFnLSFIHWctIUgcZ7pLUQYa7JHWQ4S5JHWS4S1IH/T/9AUtxBxSMzQAAAABJRU5E\nrkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x7fd3925be210>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAWMAAAEKCAYAAADHOTRzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XucHXV9//HXO9lAwIALBlAhMlKjQKoEFcQbrmLbQBVa\nSiteqgEvqKTa/upPRHyU5fETW/rr79eUhlspUqz9iTfUaAl4Y70VkSgLQZJKqmO5yCUBIobrJp/f\nHzO7nJzM95w5Z84539ndz/PxmEfOzHzPzDu7Z787+53vfL8yM5xzzsU1J3YA55xzXhk751wteGXs\nnHM14JWxc87VgFfGzjlXA14ZO+dcDXhl7JxzNeCVsXM5SdslHRQ7h5udvDKOTFIq6RFJD0u6R9Ll\nkp4WO1crkpK84vLPT4fyr911krZKWi/pmNiZXD34D1N8BrzBzPYAXgy8FPhYJwdQrh/h2p26qzdJ\nQ70OUkUv85Q41meAHwN7A2cBX5C0sFfnd9OXV8Y1YmZ3A9cAvy1pWNLXJN0n6QFJX5W0/2RZSWOS\nPi7pB8BW4CBJp0i6TdKvJf2XpPc0lB+RdKek/5kf825JfyDpOEk/k7RZ0kcaykvSRyRtlLRJ0mcl\n7ZXv/m7+70P5Ff3L8vecmp//AUnXSHpOw/G2S3q/pNuB/+z0a9NF/iMlXS/pwbzsP0qaVzaPpFdJ\n+m9JR/fq/ybp+cDhwNlm9riZXQXcAvxRm//7RZK+0LB+nqRvlvm6uWnEzHyJuAC/AI7JXy8CbgXO\nIbty+kNgPrAA+BzwpYb3jQEpcAjZL9Uh4Djgufn+o8kq6cPz9RHgSbKr7rnAu4BNwL8BTwMOBR4B\nDszLfxD4D+DZwDzgYuD/5fsOBLYDcxrynADcDrwgz3MW8IOG/duBa4FhYNfA1+Jm4OTAvk7zvxg4\nMs9yIHAb8MFWefJtBwHLgP8GXtqr/1te7g+B25q2nQ+c3+YzshtZJf8O4NXA/cCzY392fentEj3A\nbF/yCvVh4MH89aqiH2hgKfBAw/p1wGibY38J+ED+eiSvrJSv75FXIkc0lF8LHJ+/Xg+8rmHfs4An\n8sooKaiM1wCnNqzPIftlsChf3w6MVPg6lc1/QuD9fw5c1bC+U55825n59+HQXv/fgD8Frm/a9nHg\n8hLvPRJ4IM/2ptifW196v9Sq7W6WMrIK5NuNGyXtDvw98HvAZPPAAkmy/KcTuKPpPccCZwOLySqM\n3cn+DJ60ueG9j+b/3tuw/1Gyq3DIria/JGl7w/4JYL/A/+NA4B8k/Z+m7fs35LyDasrkfxpMNQn8\nX+AlZF+HIbLKulFRng8AnzKz2xq29er/9htgz6Ztw8Cv273RzH4k6efAQuDzJc7lphlvM66vvwSe\nDxxpZk8HXkN2w6zxptnU+KeSdgW+CPwtsK+Z7QVcTZc32cj+TF9mZns1LLub2a8az9tU/j1N5Z9m\nZj8syjsAF5E1TTwv//qdxc6f96I8fwz8oaQPNGzr1f/tp2Rt+wsath2Wb29J0unALsDdwIdLnMtN\nM14Z19cCsiu9LZL2JrvibdZY0e6SL5uA7flV8u9WOP/FwCcmb1RJ2kfS8fm++8n+NP+tpvIflXRo\nXv7pkv64wvmrWkDW/POIpIOB95V8393AMcAHJb0339aT/5uZ/QwYB86WNF/SicBvk/0SDcqv8v8X\n8Fbg7cCHJR3W6fldvVWujCV9UtK9ktYF9r9V0s2SbpH0A0kvqnrOWWIl2Y2bTWQ30taw89XX1LqZ\nPUz2J/bnyNoW3wx8JVQ+sN7oH4DVwNcl/Rq4nqzdEjN7BDgX+EHeW+FIM/sycB5wpaQtwDqyJpYy\n5wJA0q2S3tyiSCf5PwS8hawJ4J+AK5vKF73XAMzsDrIK+SOSTu3F/63ByWTdFx8g+xr+kZltDhXO\nu8r9K/A3ZrbOzDYCHwX+tbF3iBssZc8H3CLpJkk/CpQ5X9Ltef13eNtjPtUE13WoV5O1hX3KzF5Y\nsP/lZHeQt0haRnbT6ahKJ3XOuYgk/QJ4iZk9ENh/HLDCzI7Lu37+Q7t6r/KVsZl9j6wnQGj/9Wa2\nJV+9ATig6jmdc64GWt2POR64AsDMbgCGJYVufgODbzN+J9lNJedmJEmvzh+EaV5a9piQdHHgfRcO\nKrvriAHflLRW0rsL9jf2tAG4kzYXogPr2ibptcCpwCsHdU7nBi3/S3GPLt73XuC9bQu6unilmf1K\n0j7ANyRtyL/3jZqvnFu2CQ+kMs5v2l1K1lVqpyYNST5FtXOuNDOrNBZLp3VO8/nyLp6Y2f2SvkR2\nc7uxMr6L7InaSQfk24L63kyRd426Cnhbfie4UOynX0LL2WefHT2D55rZ2TxXZ0uvfLzkUlCn7S5p\nj/z108i6kDb3JltN1g0RSUcBD5nZvbRQ+cpY0mfIHkhYKOkOsv6w8wDM7BLgr8ieILtI2cBiT5rZ\nkVXPOyhpmsaOUMhzda6u2TxXHBX6Be5H9nQqZHXov5nZ1yWdBlm9Z2ZX54NYbSR7dP6UdgetXBmb\nWat+oZjZu8gGdXHOudrotvIzs1+QjRXTvP2SpvUVg8gzayxfvjx2hEKeq3N1zea54tgtdoAmlR/6\n6EmIHca+cc65MElYD27gXVqy7LupfsOwDB+boo2xsbHYEQp5rs7VNZvnimOo5DLIPM45N+vUbWAP\nb6Zwzk0rvWqmuLJk2ZMZTDOFXxk752alul0Ze5txG3VtN/NcnatrNs8Vx7ySy6D4lbFzblbyrm1F\nIbzN2DlXUq/ajK8rWfa1eJuxc871jbcZTzN1bTfzXJ2razbPFYf3M3bOuRqo25Wxtxk756aVXrUZ\n31yy7GF4m7FzzvVN3a6Mvc24jbq2m3muztU1m+eKY7eSS4ikuZJukvTVgn0jkrbk+2+S9LF2ebwy\nds517cLRUd60cCHLh4d508KFXDg6GjtSaT146OODwG2E57b7jpkdni9Fk4bswNuMnXNduXB0lFvO\nPZeLJyamtr13aIgXnXUW7+9jpdyrNuN7SpZ9Jju3GUs6APgX4Fzgf5jZG5v2jwB/2by9ZaY6VIJl\nK+NNm7byta/9bACJnIvjjcvT2BFKe+/Ct/P5zb/ZafvJz3gGV27a1Lfz9qoy3lzyjtkzJgor488D\nnwD2BD5UUBm/hmzuzzvJJiL9kJnd1uo80+oGXpo+xCmnfGXQZwWSAZ+zjBTP1amUemZLmcz14+Wf\nixlkB2vHtvLSkacF9+86sbVw+/yGK+U6GwrUft/bBt/fHn6fpDcA95nZTfkVcJGfAIvM7BFJxwJf\nBp7fMk/7yM45t7NHh0RRc+ljoVquZubNLd7+urnwuob1v9n5d84rgOMlHQfMB/aU9Ckze/tkATN7\nuOH1GkkXStrbzB4I5fEbeG0lsQMEJLEDBCSxA7SQxA4QkMQOUKjVVTHAISv24rSmeve0oSGOXtHR\nPJzRDA2VW5qZ2UfNbJGZPZdsuONvN1bEAJL2Uz59tKQjyZqEgxUx+JWxc65LJ47uy1XASaseZLcJ\n8eTQMEevWNHXm3e9NG/Xnh3KACSdBlOzRJ8EvE/SBPAIWaXd0rS6gbd27V0ccUTZaQR7JaWeVy4p\nnqtTKfXMljLVZmzTp8240Xyex6Gs7nOiTK9u4NmzS5a9expMSCrpk5LulbSuRZnzJd0u6WZJh1c5\nn3PO9UzNRgqq2mZ8ObAstDNv4H6emS0G3gNcVPF8ESSxAwQksQMEJLEDtJDEDhCQxA5QqOxV8bQ1\nkypjM/se8GCLIscDV+RlbwCGJe1X5ZzOOdcTc0suA9Lv3hT7A3c0rN8JHNDnc/ZYGjtAQBo7QEAa\nO0ALaewAAWnsAIXWjhX3I54xanZlPIhTNTd8F96pW758OUmSADA8PMzSpUsZGRkBnhqwZMGCxXnp\nNP83mcXr99Qsz3RYp83+WOv37LA+WQlONhPEWp9UpvwubOLQkaz85M9r889vt+srV65kfHx8qn7o\nmd71puiJyr0pJCXAV83shQX7LgbGzOzKfH0D8Bozu7epXI17Uzg3OHXqTdGJadmb4qUly66dBr0p\nSlgNvB1A0lHAQ80VsXPORVGzZoqqXds+A/wH8AJJd0g6VdJpDZ2frwZ+LmkjcAnw/sqJBy6NHSAg\njR0gII0doIU0doCANHaAQjO+zbhmN/Aq1ftm9uYSZabHs5HOzRJXjd7H+lUPstuE8eiQOGTFXpw4\num/sWINXs+ePaxanjpLYAQKS2AECktgBWkhiBwhIBnamq0bv4/5zN/PFqYHVjNPO3cxVsFOFPCv6\nGdeIDxTk3CyyftWDXNI0wuUlE7BhVavHBWaomdRmPDuksQMEpLEDBKSxA7SQxg4QkA7sTLtNFPda\nml+wfca3Ge9achmQml2oO+f6KTwGcd97btVPzWo/vzJuK4kdICCJHSAgiR2ghSR2gIBkYGcqGoP4\nPUNw8Iq9dio749uMK/amaDU7dL6/o0HSava7wTnXT41jEM+fMB4bEgd7b4puTc4OvUfzjsZB0iS9\njGyQtKP6G2fGS6nnFVWK5+pUSj2zpQwy14mj+0KJyreT8YynpQq1Xz479HHks0MXFNlhkDRJw5L2\na/XQmzdTOOdmp2rNFH8P/E8gNHVpx4Ok+ZVxW0nsAAFJ7AABSewALSSxAwQksQMUmtFXxRCs/cbu\nhrFfhd9WcnZoKDlIWps4zrnpwp+o69L84s0jB2XLpHNu2qlI29mhgbuARQ3rB+TbgryZoq00doCA\nNHaAgDR2gBbS2AEC0q7fOfVE3ebtfHqL8cXN27n/3M1cNXpf5VQzvp9xl80UZWaHpotB0rwydm4a\n8yfqKujdE3hTs0NXGSTNmynaSmIHCEhiBwhIYgdoIYkdICDp+p2dPFHXqdnaZtwJM/sO8J389SVN\n+zoaJM0rY+emMX+iroIBDo9ZhjdTtJXGDhCQxg4QkMYO0EIaO0BA2vU7O3mirlMzvs24ZgMF+ZWx\nc9OYP1FXQc1qv5rFqaMkdoCAJHaAgCR2gBaS2AECkkrvLvtEXadmfJtxzSYk9crYOTc71az28zbj\nttLYAQLS2AEC0tgBWkhjBwhIYwco5G3GeJuxc871Xc16U3hl3FYSO0BAEjtAQBI7QAtJ7AABSewA\nhWZ8m3HNar+axXHOuQGpWe3nbcZtpbEDBKSxAwSksQO0kMYOEJDGDlBoxrcZV5zpo9cqV8aSlkna\nkE8vckbB/oWSrpE0LulWScurntM55yqbX3IZkEoX6pLmAquA15MND3ejpNVmtr6h2ArgJjM7U9JC\n4D8lfdrMJgoOWUNJ7AABSewAAUnsAJk3jMZO0JWXTNOnmJcs2Ydbb42dokMzrJniSGCjmaVm9iRw\nJXBCU5lfAXvmr/cENk+fitg5N2PNsGaKoqlF9m8qcymwRNLdwM1kk/hNI2nsAAFp7AABaewAYZvG\nYicoVtdcdf5e9kKX/YwlzZd0Q970epukvy4oMyJpSz579E2SPlYmThVlxun7KDBuZiOSfgv4hqTD\nzOzhxkLLly8nSRIAhoeHWbp0KSMjIwCMjY0BsGDB4rx0mv+bzOL1e2qWp2brm8Zg4Ui22lzZTa43\n74+1vmV8x/U6fP120L781q1PjZ88+fPa/PPb7frKlSsZHx+fqh96psvaz8wek/RaM3tE0hDwfUmv\nMrPvNxX9jpkdX/a4Mut+3NN8BPtRM1uWr58JbDez8xrKXA2ca2Y/yNe/BZxhZmsbyliZHGvX3sUR\nR1zadV43i0zTNmO+Nho7QVeyNuPTB3IuSZhZpdZ1SWbXliz7ewTPJ2l3svGM32FmtzVsHwH+0sze\nWDZT1WaKtcBiSYmkXYA3kU030mgD2Q0+JO0HvAD4ecXzOjdt7LNhlNddu5AT1gzzumsXss+G0diR\nHFTqTSFpjqRx4F7gusaKOGfAKyTdLOlqSYe2i1OpMs5vxK0ArgVuAz5rZusbpx8BPgG8VNLNwDeB\nD5vZA1XOO1hp7AABaewAAWnsAGER2mb32TDKGzeey7ee3MyXt23hW09u5o0bz92xQvY24zgq3MAz\ns+1mtpRsotGjC2aJ/gmwyMwOA/4R+HK7OJU7d5jZGmBN07ZLGl5vAkpfqjs3k7zwl6u4jB07D13G\nBMf8chXfPng0TiiXCdR+Yz+GsZ+UO4SZbZH078BLgbGG7Q83vF4j6UJJe7e6EK1ZT7s6SmIHCEhi\nBwhIYgcIm7pBNjh7bC/uxbnD9gi5ykliB+ivQO038rJsmXTOZTvuz5+XmDCzhyTtBvwOcE5Tmf2A\n+8zMJB1Jdn+uZYuAV8bO9dHDc4ZgW2C7i6v7b8GzgCskzSFr6v1XM/tWw8zQlwAnAe+TNAE8Apzc\n7qA+NkVbaewAAWnsAAFp7ABhEdpm1x24gnc2/dSfyhDrDmyYONjbjOPoss3YzNaZ2YvNbKmZvcjM\n/ne+/ZLJJlozu8DMfjsv8woz+2G7OP7r2bk+uv/gUb4KHPPLVeyxfYKH52QV8f3eXhxfzWq/msWp\noyR2gIAkdoCAJHaAsEhts/cfPNr6Zp23Gcfhc+A551wN1Kz28zbjttLYAQLS2AEC0tgBwuraNlvX\nXHX+XvaCz4HnnHM1ULPar2Zx6iiJHSAgiR0gIIkdIKyubbN1zVXn72UPmE9I6pxz8W2rWe3nbcZt\npbEDBKSxAwSksQOE1bVttq656vy97IFtQ+WWQanZ7wbnnBuMx3fdpWTJJ/qaY5JXxm0lsQMEJLED\nBCSxA4TVtW22rrnq/L3sgW1z69Vo7JWxc25W2jbICe5K8DbjttLYAQLS2AEC0tgBwuraNlvXXHX+\nXvbABHNLLYPiV8bOuVlpW82qP78ybiuJHSAgiR0gIIkdIKyubbN1zVXn72UPbGNuqaVZmdmh83Ln\nS7o9n3rp8HZ56vWrwTnnBqTbNuMys0NLOg54npktlvQy4CLgqFbH9SvjttLYAQLS2AEC0tgBwura\nNlvXXHX+XvbA4+xSailiZo/kL3chG/W4eRaP44Er8rI3AMP57B9BXhk752albQyVWoqUmB16f+CO\nhvU7ySYvDfLKuK0kdoCAJHaAgCR2gLC6ts3WNVedv5c90G2bMZSaHRpAzW9rlcfbjJ1zs1Kool07\ntpW1Y48U7msWmh0auAtY1LB+QL4tyK+M20pjBwhIYwcISGMHCKtr22xdc9X5e9kDoX7FS0f25F2j\nz5xamklaKGk4fz05O/RNTcVWA2/PyxwFPGRm97bKU/nKWNIyYCVZI/Y/m9l5BWVGgL8H5gGbzGyk\n6nmdc66KCv2M284ObWZXSzpO0kZgK3BKu4NWqowlzQVWAa8nuwS/UdJqM1vfUGYYuAD4PTO7U9LC\nKuccvCR2gIAkdoCAJHaAsLq2zdY1V52/lz1QoWvbOuDFBdsvaVpf0VymlapXxkcCG80sBZB0JXAC\nsL6hzFuAL5rZnXnATRXP6ZxzlT0R6LYWS9U246LuG/s3lVkM7C3pOklrJf1pxXMOWBo7QEAaO0BA\nGjtAWF3bZuuaq87fyx6YaWNTtOyqkZtHdkl/DLA7cL2kH5rZ7Y2Fli9fTpIkAAwPD7N06VJGRkYA\nGBsbA2DBgsV56TT/N5nF6/fULE/N1jeNPfXnf3NlN7nevD/W+pbxHdfr8PXbQfvyW7c+OFV68ue1\n+ee32/WVK1cyPj4+VT/0St3GppBZmfo08ObsLuGomS3L188EtjfexJN0BrCbmY3m6/8MXGNmX2go\nY2VyrF17F0cccWnXed0s8obR2Am687XR2Am6smTJPtx66+kDOZckzKy5D2+nx7Cv2TGlyr5B36p8\nvjKqNlOsBRZLSiTtAryJrEtHo68Ar5I0V9LuwMuA5qdVnHNuoKo89NEPlSpjM5sAVgDXklWwnzWz\n9ZJOa+jmsQG4BrgFuAG4tODRwRpLYwcISGMHCEhjBwira9tsXXPV+XvZAzOtzRgzWwOsadrW3MXj\n74C/q3ouN3g/ts91VH7t2FZeOvK0PqUp7yWFf1Sm7PiQVF2k1DPXzPYEu8aOsIN6tWDXUhI7QEAS\nO0ChOlTEYUnsAAFJ7AABSewAfVW3aZe8MnbOzUqDbIIow8emaCuNHSAgjR2g0NqxrbEjtJDGDhCQ\nxg4QkMYO0FdVhtDsB78ydtPKVaP3sX7Vg+w2YTw6JA5ZsRcnju4bO5abhryZYtpJYgcISGIHKNTP\nNuOrRu/j/nM388WJyS3Gaedu5iooWSEnfctWTRI7QEASO0Bf1a0y9mYKN22sX/Ugl0zsuO2SCdiw\n6sHiNzjXwozqZzw7pLEDBKSxAxTqZ5vxbhPFT2nOD2zfWdqzLL2Vxg4QkMYO0FePs2upZVC8MnbT\nxqNDxU+kPhbY7lwr3V4ZS1qUD3z2U0m3SvpAQZkRSVsk3ZQvH2uXxyvjtpLYAQKS2AEK9bPN+JAV\ne3Fa012O9wzBwSv2KnmEpNeReiSJHSAgiR2gryo0UzwJ/IWZLQGOAk6XdEhBue+Y2eH58vF2efwG\nnps2Thzdl6uAk1Y9yPwJ47EhcbD3pnBd6rafsZndQzZsImb2G0nrgWez4zjusPOEpC15ZdxWSj2v\nEFLqmKvfj0OfOLovdF35ptTxa+a54uhFH2JJCXA42bg7jQx4haSbyWZB+lC7MXm8MnbOzUqhnhLp\n2C/55dgv275f0gLgC8AHzew3Tbt/Aiwys0ckHQt8GXh+q+N5ZdxWEjtAQBI7QKFurooH9yBH0odj\n9kISO0BAEjtAX4Uq40UjB7Fo5KCp9e+e8/2dykiaB3wR+LSZfbl5v5k93PB6jaQLJe1tZg+E8nhl\n7KKq/iCHc915vMs58CQJuAy4zcxWBsrsB9xnZibpSLKJPIIVMXhvihLS2AEC0tgBCnXaz3iwD3Kk\nfThmL6SxAwSksQP0VYWxKV4JvA14bUPXtWMbx3EHTgLWSRoHVgInt8vjV8YuquoPcjjXnW6frjOz\n79PmQtbMLgAu6OS4Xhm3lcQOEJDEDlCo0zbj7EGOnSve/jzIkfThmL2QxA4QkMQO0Fc+NoVzDao/\nyOFcd+o27ZJXxm2lsQMEpLEDFOq0zfjE0X3Z56xncNIz5vC2p4uTnjGHfc96Rp9u3qV9OGYvpLED\nBKSxA/SVj2fsXJNqD3I41526NVN4ZdxWEjtAQBI7QCGfA68bSewAAUnsAH31RJdd2/rFK2Pn3Kzk\nc+BNO2nsAAFp7ACFfA68bqSxAwSksQP0Vd3ajCtXxpKWSdog6XZJZ7Qod4SkCUknVj2nc85VVbeZ\nPipV+5LmAquA15ONTHSjpNVmtr6g3HnANXQ4rFx8SewAAUnsAIW8zbgbSewAAUnsAH1Vtxt4Va+M\njwQ2mllqZk8CVwInFJT7M7LRje6veD7nnOuJmdbPeH/gjob1O/NtUyTtT1ZBX5RvmmbPuaaxAwSk\nsQMU8jbjbqSxAwSksQP0Vd3ajKueqUzFuhL4SD56kQg0UyxfvpwkSQAYHh5m6dKljIyMADA2NgbA\nggWL89Jp/m8yi9fvGdj5JivYySaI6bGeFvx/aFov9//v//o9NcszuU6b/U+tb9361MBOkz+vzT+/\n3a6vXLmS8fHxqfqhV+rWtU1m3V+oSjoKGDWzZfn6mcB2MzuvoczPeaoCXgg8ArzbzFY3lLEyOdau\nvYsjjri067yucz+2zxVuH9wYxN15if4kdoRZZcmSfbj11tMHci5JmFmle0+S7FX29VJlv6/frXy+\nMqpeGa8FFudTj9wNvAl4c2MBM5sapVnS5cBXGytiN/34GMRuJui2CULSIuBTwL5krQP/ZGbnF5Q7\nHziW7AJ0uZnd1Oq4ldqMzWwCWAFcC9wGfNbM1jeN6znNpbEDBKTRztxqDGJvM+5GGjtAQBo7QF/1\nc3ZoSccBzzOzxcB7eOqeWVDl1mkzWwOsadp2SaDsKVXP5+LzMYjdTFBhPOMys0MfD1yRl7lB0rCk\n/czs3tBx/XHotpLYAQKSaGduNQax9zPuRhI7QEASO0Bf9aKfcYvZoYt6mh0ABCtjfxzadczHIHYz\nwePsWmoJaTM7NOzcc6zln45+ZdxWSj2vEFJi5TpxdF+uAk5a9SDzJ4zHhsTBeW+KtWNba3x1nOLf\ny06k1DNXb4SujB8Zu5FHxta2fG+72aHJnkhe1LB+QL4tyCtj1xUfg9hNd6HKeNeRo9h15Kip9QfO\nuXiH/WVmhwZWk3VuuDLvAvxQq/Zi8Mq4hCR2gIAkdoBC9b0qhrp+zTxXHBUedZ6cHfoWSZPd1T4K\nPAeyDgxmdrWk4yRtBLYCbTsveGU8KG8YjZ2gKy+ZZsM6OVdWt/2My8wOnZdb0clx/QZeW2nsAMU2\njcVOEJDGDtBCGjtAQBo7QEAaO0BfzaghNJ1zbrqq2xCaXhm3lcQOUGzhSOwEAUnsAC0ksQMEJLED\nBCSxA/TV40/Ua6Agr4ydc7PStol6VX/eZtxWGjtAMW8z7kIaO0BAGjtAQBo7QF9tm5hbahmUev1q\ncM65ARlkRVuGV8ZtJbEDFPM24y4ksQMEJLEDBCSxA/TVxJNeGTvnXHTbt9Wr+vM247bS2AGKeZtx\nF9LYAQLS2AEC0tgB+mtibrllQOr1q8E55wblsXpVf/VKU0tJ7ADFvM24C0nsAAFJ7AABSewA/TXR\nvsggeWXsnJudalYZe5txW2nsAMW8zbgLaewAAWnsAAFp7AD9NVFyGRCvjJ1zs9OTJZcmkj4p6V5J\n64oOK2lE0hZJN+XLx8rE8WaKtpLYAYp5m3EXktgBApLYAQKS2AH6a1vX77wc+EfgUy3KfMfMju/k\noF4ZO+dmpy6bIMzse/lEpK10PBK4N1O0lcYOUMzbjLuQxg4QkMYOEJDGDtBfj5VcOmfAKyTdLOlq\nSYeWeVPlyljSMkkbJN0u6YyC/W/NQ90i6QeSXlT1nM45V1n/buD9BFhkZoeRNWcUTVi6k0rNFJLm\nAquA15PNfHqjpNVmtr6h2M+Bo81si6RlwD8BR+18tLpKYgco5m3GXUhiBwhIYgcISGIH6K9QRbtu\nDG4d6/qwZvZww+s1ki6UtLeZPdDqfVXbjI8ENppZCiDpSuAEYKoyNrPrG8rfQDZltXPOxRWqjA8Z\nyZZJV57TgnXQAAAPVklEQVTT0WEl7QfcZ2Ym6UhA7SpiqN5MsT9wR8P6nfm2kHcCV1c854ClsQMU\n8zbjLqSxAwSksQMEpLED9Ff3Xds+A/wH8AJJd0g6VdJpkk7Li5wErJM0DqwETi4Tp+qVsZUtKOm1\nwKlk01zvZPny5SRJAsDw8DBLly5lZGQEgLGxMQAWLFicl07zf5Pps75p7KmmhcmKtMr6lvHeHq/V\neh2+fj1Zp83+WOv31CzP5Dpt9j+1vnXrg1OlJ39em39+u11fuXIl4+PjU/VDz3TZtc3M3txm/wXA\nBZ0eV2al69Od3ywdBYya2bJ8/Uxgu5md11TuRcBVwDIz21hwHCuTY+3auzjiiEu7zhvVG0ZjJ+jO\n10ZjJ3DTwJIl+3DrracP5FySMLOOu441HcO4omTd947q5yuj6pXxWmBx3ufubuBNwA6/NSQ9h6wi\nfltRReycc1F0122tbyq1GZvZBLACuBa4Dfisma1vaj/5K2Av4KL80cAfVUo8cGnsAMW8zbgLaewA\nAWnsAAFp7AD9VbOxKSo/gWdma4A1TdsuaXj9LuBdVc/jnHM9VbNR2/xx6LaS2AGKeT/jLiSxAwQk\nsQMEJLED9JdXxs45VwMF3dZi8rEp2kpjByjmbcZdSGMHCEhjBwhIYwfor20llwHxK2Pn3OxUs94U\nXhm3lcQOUMzbjLuQxA4QkMQOEJDEDtBf3mbsnHM14G3G000aO0AxbzPuQho7QEAaO0BAGjtAf3mb\nsXPO1YA3U0w3SeUj7MN1vPDaVeyxfYKH5wyx7sAV3H/waLWDeptxF5LYAQKS2AECktgB+ssr49ll\nH67jjXyPy57MByXZBu/ceC5fheoVsnOue95mPN2kld79Qm7ksqaRRi9jghf+clWl43qbcTfS2AEC\n0tgBAtLYAfrr8ZJLE0mflHSvpHWhQ0s6P5+K7mZJh5eJ41fGfbAP1/FCbmQPtjOn6LsJ7LG9Zn8j\nOTfbdP8jeDnZ3HafKtop6TjgeWa2WNLLgIsoMdXctKqMn8WvOJvOpkAZtJ8Cw8DkqMsfC5R7eNsT\nPRgreKzi+/shiR2ghSR2gIAkdoCAJHaA/uqymcLMvpcPGxxyPHBFXvYGScOS9jOze1sd15speuwx\nnqqIAX4XOKupzKmIdRwxuFDOuZ31r2tb0XR0bef+nFZXxjGkdHZ98LSm9aPzf38fmMeuPMwc1nEE\n9/PaAScblJR65oL6ZkvxXBGEmik2jcHmsapHb54ZpO20Il4Z99jWgm1HA+ewG1fz4UHHcc6FhCrj\n4ZFsmfSzjptG7wIWNawfkG9ryZsp2kg6LD8feHfTtndBH5olkh4fr1eS2AFaSGIHCEhiBwhIYgfo\nry5nhy5hNfB2mJon9KF27cXgV8Y9t4TsJt4byZostpJV0NWbJZxzPVXc0aktSZ8BXgMslHQHcDYw\nD7JZjszsaknHSdpIVgWcUua4Xhm3kdL59cGSgm1fqJykWUo9r1xS6pkL6pstxXNF0GXXNjN7c4ky\nKzo9rlfGzrnZqWZP4Hll3EYSO0BQEjtAQBI7QAtJ7AABSewAAUnsAP01wBHZyvDKuISfkvUfbmwD\nLmqKcM5NIzV7CNZ7U7RxHdkTdV8Frsz/HSaroONKYwcISGMHaCGNHSAgjR0gII0doL8mSi4DUrky\nlrRM0oZ8UIwzAmU6HjSjLp5gxyfqyNdrNn2Wc65T/eva1pVKzRSS5gKrgNeTdWq+UdJqM1vfUKar\nQTPq4sDA9uYn7QYviR0gIIkdoIUkdoCAJHaAgCR2gP7qsmtbv1S9Mj4S2GhmqZk9SfaX/AlNZXYY\nNAMYlrRfxfMOTNETda22O+emiRnWTFE0IMb+Jcq0HTSjLn5N8RN18yNk2VEaO0BAGjtAC2nsAAFp\n7AABaewA/TWTmikoMfhFru2gGcuXLydJEgCGh4dZunQpIyMjAIyNjQGweMEC4KmPSJL/28/15wI/\nA15O1mSxlayCfm5D9nLHS3uc8J4eH282rNNmf6z1e2qWZ3KdNvufWt+69cGp0pM/r80/v92ur1y5\nkvHx8an6oWdq1rVNZmXr04I3Z89dj5rZsnz9TGC7mZ3XUOZiYMzMrszXNwCvaXxWW5KVyXHX2rVc\nesT0HHryHM6OHcG5vlmyZB9uvfX0gZxLEmbWfIHX6TGMPUrWfQ9XP18ZVZsp1gKLJSWSdgHeRDZI\nRqOuBs1wzrm+qlmbcaVmCjObkLQCuBaYC1xmZuslnZbv73rQjH4r+yBHSl3vKafUM1lKPXNBfbOl\neK4IZtrj0Ga2BljTtO2SpvWOB83op+apkSC7SfdT/Mk652YNfwIvvuapkSD8IEfS9zTdSmIHCEhi\nB2ghiR0gIIkdICCJHaC22j3sJmlE0hZJN+VLaDrMKbNybIrQAxvxH+RwztVdmYfdct8xs+PLHndW\nXBn/FPgxsCH/955AuaIHOdI+ZaoujR0gII0doIU0doCANHaAgDR2gLoq87Ab7Nylt6UZXxlPtg83\nDvRzEHBiU7l6PMjhnBucrp/6KPOwmwGvyMfjuVrSoe3SzPhmiqL24U8Cy9h5aqSim3dJP8NVksQO\nEJDEDtBCEjtAQBI7QEASO0Cfhe7gfTdfgsp0UP4JsMjMHpF0LPBl4Pmt3jDjK+NQO/AwcPAggzjn\naibUt+3l+TLpE80Fmmd/XkR2dTzFzB5ueL1G0oWS9jazB0JpZnwzRdWBftIe5ei9NHaAgDR2gBbS\n2AEC0tgBAtLYAfrs0ZLLTto+7CZpP0nKXx9J9rRzsCKGWXBlPJ+sD3FjU4W3Dzvnun3qo8zDbsBJ\nwPskTQCPACe3O+6Mr4yXkN3EK9M+XCTpT6weSGIHCEhiB2ghiR0gIIkdICCJHaDPun/qo93DbmZ2\nAXBBJ8ec8ZUx+FN1zrki9Xoeesa3GVeVxg4QlMYOEJDGDtBCGjtAQBo7QEAaO0Cf1WukoFlxZeyc\nczur15WxV8ZtJLEDBCWxAwQksQO0kMQOEJDEDhCQxA7QZ4U9JaLxytg5N0vVa9g2bzNuI40dICiN\nHSAgjR2ghTR2gIA0doCANHaAPqvXJHjT5sr4wtFRrlu5krl03j3NOed2Vq8r42lRGV84Osot557L\n5yee+uINajD4pM/H714SO0BAEjtAC0nsAAFJ7AABSewAfVavG3jTopniO6tWcfHEjr/FQoPBO+dc\nOd61rWO7TRR/Qfbec0/+6sEHC/f1ytjY2NSU4VX8VfUoO+hVrl6ray6obzbPFUu9roynRWX86FBx\nzMfnzWPOnP5e3M+ZM6fv5+iG5+pcXbN5rljq1bVNZmWG5uxzCMla5ZhsM25sqjhtaIjDzjqL94+O\nDiChc64uJGFmHc2iUXAMg8tLlj6l8vnKmBZXxu8fHeVC4ORVq5g/McFjQ0McvWKFV8TOuQrq1Zui\n679BJO0t6RuSfibp65KGC8osknSdpJ9KulXSB7o93/tHR7ly0yb+5aGHuHLTpoFVxGNjYwM5T6c8\nV+fqms1zxdJ9P+N2s0PnZc7P998s6fB2aao0CH0E+IaZPR/4Vr7e7EngL8xsCXAUcLqkQyqcc+DG\nx8djRyjkuTpX12yeK5buelM0zA69DDgUeHNzvSbpOOB5ZrYYeA9wUbs0VSrj44Er8tdXAH/QXMDM\n7jGz8fz1b4D1wLMrnHPgHnroodgRCnmuztU1m+eKpesr4zKzQ0/Vj2Z2AzAsab9WaapUxvuZ2b35\n63uBlieSlACHAzdUOKdzzvVI1/2My8wOXVTmgFZpWt7Ak/QN4JkFu85qXDEzy+5OBo+zAPgC8MH8\nCnnaSNM0doRCnqtzdc3muWLpumtb2S5ozT0wWr/PzLpagA3AM/PXzwI2BMrNI5sr6s9bHMt88cUX\nX8ou3dZb3dY5Te89CrimYf1M4IymMhcDJzfVl/u1ylSla9tq4B3Aefm/X24ukM+Oehlwm5mtDB1o\nEH34nHNuUsU6Z2p2aOBustmh39xUZjWwArhS0lHAQw3NuoW6fuhD0t7A54DnkI219ydm9pCkZwOX\nmtnvS3oV8F3gFrLfMABnmtk1XZ3UOedqQNKxwEqemh36r5tmh0bSZI+LrcApZvaTlseswxN4zjk3\n20V58HzQD4yUyNPzDtyDyibprXmmWyT9QNKL6pCrodwRkiYknViXXJJGJN2Uf67G6pBL0kJJ10ga\nz3MtH1CuT0q6V9K6FmUG/tlvlyvW576vqjaEd9l4/rfAh/PXZwB/U1DmmcDS/PUC4D+BQ/qQZS6w\nkWzw1nnAePN5gOOAq/PXLwN+OKCvU5lsLweenr9eNohsZXI1lPs28DXgj+qQCxgmGwr7gHx9YU1y\njQJ/PZkJ2AwMDSDbq8m6nK4L7I/12W+Xa+Cf+34vsYZkqtMDI33pwD2obGZ2vZltyVdvoE1fxkHl\nyv0ZWZfG+weQqWyutwBfNLM7AcxsU01y/QrYM3+9J7DZzPo+eIKZfQ9oNQ5tlM9+u1yRPvd9Fasy\nrtMDI33pwN0jZbI1eidwdV8TZdrmkrQ/WYUz+RjoIG5OlPl6LQb2zpvA1kr605rkuhRYIulu4Gbg\ngwPIVUasz34nBvW576u+jdo2jR4YKVtJdNaBuzdKn0PSa4FTgVf2L86UMrlWAh/Jv79i569fP5TJ\nNQ94MXAMsDtwvaQfmtntkXN9FBg3sxFJvwV8Q9JhZvZwH3OVFeOzX8qAP/d91bfK2Mx+J7Qvb5h/\nppndI+lZwH2BcvOALwKfNrOd+jH3yF3Aoob1RWS//VuVOSDf1m9lspHfvLgUWGZm/Z36pHyul5D1\nsYSsDfRYSU+a2erIue4ANpnZo8Cjkr4LHAb0szIuk+sVwLkAZvZfkn4BvICsT2tMsT77bUX43PdV\nrGaKyQdGoOIDIz0w1YFb0i5kHbibK4zVwNvzXKU6cA8qm6TnAFcBbzOzjQPIVCqXmR1kZs81s+eS\n/WXzvj5XxKVyAV8BXiVprqTdyW5K3VaDXBuA1wPkbbIvAH7e51xlxPrstxTpc99fMe4aAnsD3wR+\nBnwdGM63Pxv49/z1q4DtZHeeb8qXZX3KcyxZb42NZA+lAJwGnNZQZlW+/2bgxQP8WrXMBvwz2Z33\nya/Rj+qQq6ns5cCJdckFfIisR8U64AN1yEX218NX88/XOuAtA8r1GbKnyJ4g+6vh1Dp89tvlivW5\n7+fiD30451wNzOTZBp1zbtrwytg552rAK2PnnKsBr4ydc64GvDJ2zrka8MrYOedqwCtj55yrAa+M\nnXOuBv4/faFSxIEGhoIAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x7fd392594190>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"INITIAL : \n",
" Discrete actual Discrete mul actual mul by 100 normalized\n",
"0 5 5 0.895326 89 0.895508\n",
"1 3 3 0.378905 37 0.378906\n",
"2 2 2 -0.039802 -4 -0.039795\n",
"3 2 2 0.018108 1 0.018112\n",
"4 2 2 0.080845 8 0.080872\n",
"5 4 4 0.533948 53 0.534180\n",
"6 5 5 0.958832 95 0.958984\n",
"7 5 5 1.058258 105 1.058594\n",
"8 4 4 0.770940 77 0.770996\n",
"9 4 4 0.475365 47 0.475342\n",
"10 3 3 0.100056 10 0.100037\n",
"11 1 1 -0.143746 -15 -0.143799\n",
"12 1 1 -0.064413 -7 -0.064392\n",
"FINAL : \n",
" Discrete actual Discrete mul actual mul by 100 normalized\n",
"0 5 5 0.895326 89 0.895508\n",
"1 3 3 0.378905 37 0.378906\n",
"2 2 2 -0.039802 -4 -0.039795\n",
"3 2 2 0.018108 1 0.018112\n",
"4 2 2 0.080845 8 0.080872\n",
"5 4 4 0.533948 53 0.534180\n",
"6 5 5 0.958832 95 0.958984\n",
"7 5 5 1.058258 105 1.058594\n",
"8 4 4 0.770940 77 0.770996\n",
"9 4 4 0.475365 47 0.475342\n",
"10 3 3 0.100056 10 0.100037\n",
"11 1 1 -0.143746 -15 -0.143799\n",
"12 1 1 -0.064413 -7 -0.064392\n"
]
}
],
"prompt_number": 129
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#ceDict = reachData.condEntropyFinalGivenInitial()\n",
"zeroEntropy = []\n",
"for key in ceDict.keys():\n",
" if ceDict[key] == 0.0:\n",
" zeroEntropy.append(key)\n",
"\n",
"pprint.pprint(sorted(zeroEntropy))\n",
"pd.DataFrame.to_latex(sorted(zeroEntropy))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[u'arm_joint_5',\n",
" u'arm_link_0_ow',\n",
" u'arm_link_0_ox',\n",
" u'arm_link_0_oy',\n",
" u'arm_link_0_oz',\n",
" u'arm_link_0_x',\n",
" u'arm_link_0_y',\n",
" u'arm_link_0_z',\n",
" u'arm_link_2_ow',\n",
" u'arm_link_2_x',\n",
" u'arm_link_2_z',\n",
" 'd_angular_m0_gripper',\n",
" 'd_linear_m0_gripper',\n",
" 'marker_0_ow',\n",
" 'marker_0_ox',\n",
" 'marker_0_oy',\n",
" 'marker_0_oz',\n",
" 'marker_0_x',\n",
" 'marker_0_y',\n",
" 'marker_0_z']\n"
]
},
{
"ename": "TypeError",
"evalue": "unbound method to_latex() must be called with DataFrame instance as first argument (got list instance instead)",
"output_type": "pyerr",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[1;31mTypeError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-176-e79e3543717c>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[0;32m 6\u001b[0m \u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 7\u001b[0m \u001b[0mpprint\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mpprint\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0msorted\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mzeroEntropy\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m----> 8\u001b[1;33m \u001b[0mpd\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mDataFrame\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mto_latex\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0msorted\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mzeroEntropy\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[1;31mTypeError\u001b[0m: unbound method to_latex() must be called with DataFrame instance as first argument (got list instance instead)"
]
}
],
"prompt_number": 176
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"toolTipAllign = DataAnalyzer(\"./reach\")\n",
"toolTipAllign.dataManipulation()\n",
"toolTipAllign.dataCalculatingRelativeDistances()\n",
"\n",
"toolTipAllign.condEntropyFinalGivenInitial()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Data has been succesfully read.\n",
"Relative Distances are calculated . Data is ready for analysis\n",
"Columns are not same. Error in data collection\n",
"{"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"u'arm_joint_1': 0.15381,\n",
" u'arm_joint_2': 1.0771,\n",
" u'arm_joint_3': -inf,\n",
" u'arm_joint_4': -0.79834,\n",
" u'arm_joint_5': -inf,\n",
" u'arm_link_0_ow': 0.0,\n",
" u'arm_link_0_ox': 0.0,\n",
" u'arm_link_0_oy': 0.0,\n",
" u'arm_link_0_oz': 0.0,\n",
" u'arm_link_0_x': 0.0,\n",
" u'arm_link_0_y': 0.0,\n",
" u'arm_link_0_z': 0.0,\n",
" u'arm_link_2_ow': 0.0,\n",
" u'arm_link_2_ox': 0.14075,\n",
" u'arm_link_2_oy': -0.21362,\n",
" u'arm_link_2_oz': 0.1781,\n",
" u'arm_link_2_x': -inf,\n",
" u'arm_link_2_y': 0.15381,\n",
" u'arm_link_2_z': 0.0,\n",
" u'arm_link_3_ow': -0.0057831,\n",
" u'arm_link_3_ox': -inf,\n",
" u'arm_link_3_oy': -inf,\n",
" u'arm_link_3_oz': 0.82471,\n",
" u'arm_link_3_x': 0.53271,\n",
" u'arm_link_3_y': -inf,\n",
" u'arm_link_3_z': 0.91162,\n",
" u'arm_link_4_ow': 0.39185,\n",
" u'arm_link_4_ox': 0.09906,\n",
" u'arm_link_4_oy': 0.47461,\n",
" u'arm_link_4_oz': 1.1895,\n",
" u'arm_link_4_x': -inf,\n",
" u'arm_link_4_y': 0.41528,\n",
" u'arm_link_4_z': 0.82715,\n",
" u'arm_link_5_ow': -0.16101,\n",
" u'arm_link_5_ox': 0.26147,\n",
" u'arm_link_5_oy': -inf,\n",
" u'arm_link_5_oz': 0.68701,\n",
" u'arm_link_5_x': 0.48779,\n",
" u'arm_link_5_y': 0.15381,\n",
" u'arm_link_5_z': 0.87207,\n",
" 'd_angular_m0_gripper': -inf,\n",
" 'd_linear_m0_gripper': -inf,\n",
" u'gripper_finger_link_l_ow': 0.75635,\n",
" u'gripper_finger_link_l_ox': -inf,\n",
" u'gripper_finger_link_l_oy': 1.251,\n",
" u'gripper_finger_link_l_oz': 0.70557,\n",
" u'gripper_finger_link_l_x': -inf,\n",
" u'gripper_finger_link_l_y': 0.44849,\n",
" u'gripper_finger_link_l_z': 0.73926,\n",
" u'gripper_finger_link_r_ow': 0.32666,\n",
" u'gripper_finger_link_r_ox': -0.013069,\n",
" u'gripper_finger_link_r_oy': 0.67529,\n",
" u'gripper_finger_link_r_oz': 0.089966,\n",
" u'gripper_finger_link_r_x': -inf,\n",
" u'gripper_finger_link_r_y': -inf,\n",
" u'gripper_finger_link_r_z': 0.15649,\n",
" u'gripper_palm_link_ow': -inf,\n",
" u'gripper_palm_link_ox': 0.63428,\n",
" u'gripper_palm_link_oy': 1.0391,\n",
" u'gripper_palm_link_oz': 0.7334,\n",
" u'gripper_palm_link_x': 0.36768,\n",
" u'gripper_palm_link_y': 0.302,\n",
" u'gripper_palm_link_z': 0.50635,\n",
" 'marker_0_ow': 0.0,\n",
" 'marker_0_ox': 0.0,\n",
" 'marker_0_oy': 0.0,\n",
" 'marker_0_oz': 0.0,\n",
" 'marker_0_x': 0.0,\n",
" 'marker_0_y': 0.0,\n",
" 'marker_0_z': 0.0}\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"infotheo.py:237: FutureWarning: comparison to `None` will result in an elementwise object comparison in the future.\n",
" if pxpy != None and not _isproperdist(pxpy):\n",
"infotheo.py:239: FutureWarning: comparison to `None` will result in an elementwise object comparison in the future.\n",
" if pxpy == None:\n"
]
}
],
"prompt_number": 22
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"toolTipAllign = DataAnalyzer(\"./toolTipAllign\")\n",
"toolTipAllign.dataManipulation()\n",
"toolTipAllign.dataCalculatingRelativeDistances()\n",
"\n",
"ceDict = toolTipAllign.condEntropyFinalGivenInitial()\n",
"zeroEntropy = []\n",
"for key in ceDict.keys():\n",
" if ceDict[key] == 0.0:\n",
" zeroEntropy.append(key)\n",
" \n",
"pprint.pprint(sorted(zeroEntropy))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Data has been succesfully read.\n",
"Relative Distances are calculated . Data is ready for analysis\n",
"Columns are not same. Error in data collection\n",
"Entropy : arm_joint_1 : 0.0\n",
"Entropy : arm_joint_2 : 0.0\n",
"Entropy : arm_joint_3 : 0.0\n",
"Entropy : arm_joint_4 : 0.0\n",
"Entropy : arm_joint_5 : 0.72461\n",
"Entropy : arm_link_0_ow : 0.0\n",
"Entropy : arm_link_0_ox : 0.0\n",
"Entropy : arm_link_0_oy : 0.0\n",
"Entropy : arm_link_0_oz : 0.0\n",
"Entropy : arm_link_0_x : 0.0\n",
"Entropy : arm_link_0_y : 0.0\n",
"Entropy : arm_link_0_z : 0.0\n",
"Entropy : arm_link_2_ow : 0.0\n",
"Entropy : arm_link_2_ox : 0.0\n",
"Entropy : arm_link_2_oy : 0.0\n",
"Entropy : arm_link_2_oz : 0.0\n",
"Entropy : arm_link_2_x : 0.0\n",
"Entropy : arm_link_2_y : 0.0\n",
"Entropy : arm_link_2_z : 0.0\n",
"Entropy : arm_link_3_ow : 0.0\n",
"Entropy : arm_link_3_ox : 0.0\n",
"Entropy : arm_link_3_oy : 0.0\n",
"Entropy : arm_link_3_oz : 0.0\n",
"Entropy : arm_link_3_x : 0.0\n",
"Entropy : arm_link_3_y : 0.0\n",
"Entropy : arm_link_3_z : 0.0\n",
"Entropy : arm_link_4_ow : 0.0\n",
"Entropy : arm_link_4_ox : 0.0\n",
"Entropy : arm_link_4_oy : 0.0\n",
"Entropy : arm_link_4_oz : 0.0\n",
"Entropy : "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" arm_link_4_x : 0.0\n",
"Entropy : arm_link_4_y : 0.0\n",
"Entropy : arm_link_4_z : 0.0\n",
"Entropy : arm_link_5_ow : 1.0\n",
"Entropy : arm_link_5_ox : 0.87549\n",
"Entropy : arm_link_5_oy : 0.87549\n",
"Entropy : arm_link_5_oz : 1.0264\n",
"Entropy : arm_link_5_x : 0.19995\n",
"Entropy : arm_link_5_y : 1.2002\n",
"Entropy : arm_link_5_z : 0.0\n",
"Entropy : gripper_finger_link_l_ow : 0.75098\n",
"Entropy : gripper_finger_link_l_ox : 0.75098\n",
"Entropy : gripper_finger_link_l_oy : 0.92432\n",
"Entropy : gripper_finger_link_l_oz : 0.75098\n",
"Entropy : gripper_finger_link_l_x : 1.2754\n",
"Entropy : gripper_finger_link_l_y : 1.0752\n",
"Entropy : gripper_finger_link_l_z : 0.47559\n",
"Entropy : gripper_finger_link_r_ow : 0.0\n",
"Entropy : gripper_finger_link_r_ox : 0.0\n",
"Entropy : gripper_finger_link_r_oy : 0.0\n",
"Entropy : gripper_finger_link_r_oz : 0.0\n",
"Entropy : gripper_finger_link_r_x : 0.27539\n",
"Entropy : gripper_finger_link_r_y : 0.6001\n",
"Entropy : gripper_finger_link_r_z : 0.36108\n",
"Entropy : gripper_palm_link_ow : 0.36108\n",
"Entropy : gripper_palm_link_ox : 0.0\n",
"Entropy : gripper_palm_link_oy : 0.0\n",
"Entropy : gripper_palm_link_oz : 0.0\n",
"Entropy : gripper_palm_link_x : 0.75098\n",
"Entropy : gripper_palm_link_y : 0.3999\n",
"Entropy : gripper_palm_link_z : 0.76074\n",
"Entropy : marker_0_ow : 0.87549\n",
"Entropy : marker_0_ox : 1.2852\n",
"Entropy : marker_0_oy : 0.6001\n",
"Entropy : marker_0_oz : 0.87549\n",
"Entropy : marker_0_x : 0.0\n",
"Entropy : marker_0_y : 0.0\n",
"Entropy : marker_0_z : 0.0\n",
"Entropy : d_linear_m0_gripper : 0.0\n",
"Entropy : d_angular_m0_gripper : 0.0\n",
"["
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"u'arm_joint_1',\n",
" u'arm_joint_2',\n",
" u'arm_joint_3',\n",
" u'arm_joint_4',\n",
" u'arm_link_0_ow',\n",
" u'arm_link_0_ox',\n",
" u'arm_link_0_oy',\n",
" u'arm_link_0_oz',\n",
" u'arm_link_0_x',\n",
" u'arm_link_0_y',\n",
" u'arm_link_0_z',\n",
" u'arm_link_2_ow',\n",
" u'arm_link_2_ox',\n",
" u'arm_link_2_oy',\n",
" u'arm_link_2_oz',\n",
" u'arm_link_2_x',\n",
" u'arm_link_2_y',\n",
" u'arm_link_2_z',\n",
" u'arm_link_3_ow',\n",
" u'arm_link_3_ox',\n",
" u'arm_link_3_oy',\n",
" u'arm_link_3_oz',\n",
" u'arm_link_3_x',\n",
" u'arm_link_3_y',\n",
" u'arm_link_3_z',\n",
" u'arm_link_4_ow',\n",
" u'arm_link_4_ox',\n",
" u'arm_link_4_oy',\n",
" u'arm_link_4_oz',\n",
" u'arm_link_4_x',\n",
" u'arm_link_4_y',\n",
" u'arm_link_4_z',\n",
" u'arm_link_5_z',\n",
" 'd_angular_m0_gripper',\n",
" 'd_linear_m0_gripper',\n",
" u'gripper_finger_link_r_ow',\n",
" u'gripper_finger_link_r_ox',\n",
" u'gripper_finger_link_r_oy',\n",
" u'gripper_finger_link_r_oz',\n",
" u'gripper_palm_link_ox',\n",
" u'gripper_palm_link_oy',\n",
" u'gripper_palm_link_oz',\n",
" 'marker_0_x',\n",
" 'marker_0_y',\n",
" 'marker_0_z']\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n",
"/home/deebuls/anaconda/lib/python2.7/site-packages/sklearn/utils/extmath.py:68: DeprecationWarning: Implicitly casting between incompatible kinds. In a future numpy release, this will raise an error. Use casting=\"unsafe\" if this is intentional.\n",
" np.sqrt(norms, norms)\n"
]
}
],
"prompt_number": 140
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"a = [ 0.07354736, 0.07354736, 0.07348633, 0.07354736, 0.07348633, 0.0736084,\n",
" 0.07348633, 0.0736084, 0.07354736, 0.07348633, 0.07366943, 0.07354736] \n",
"b = [ 0.07354736, 0.07354736, 0.0736084, 0.07513428, 0.07354736, 0.07348633,\n",
" 0.07446289, 0.07366943, 0.07501221, 0.07537842, 0.07354736, 0.07348633]\n",
"\n",
"np.histogram2d(b,a,bins=5)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 32,
"text": [
"(array([[ 2., 3., 0., 2., 1.],\n",
" [ 0., 0., 0., 0., 0.],\n",
" [ 1., 0., 0., 0., 0.],\n",
" [ 0., 0., 0., 0., 0.],\n",
" [ 1., 2., 0., 0., 0.]]),\n",
" array([ 0.07348633, 0.07386475, 0.07424317, 0.07462158, 0.075 ,\n",
" 0.07537842]),\n",
" array([ 0.07348633, 0.07352295, 0.07355957, 0.07359619, 0.07363281,\n",
" 0.07366943]))"
]
}
],
"prompt_number": 32
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sklearn import preprocessing\n",
"\n",
"data_start = np.arange(10,20.0)\n",
"data_start = np.array([5,5,5,5,5,5,5,5,5.0])\n",
"\n",
"data_end = np.arange(0.1,1.1,0.1)\n",
"'''\n",
"data = np.append(data_start,data_end)\n",
"print data\n",
"min_max_scaler = preprocessing.MinMaxScaler()\n",
"data = min_max_scaler.fit_transform(data)\n",
"print data\n",
"data_start, data_end = np.split(data,2)\n",
"data_start = min_max_scaler.fit_transform(data_start)\n",
"data_end = min_max_scaler.fit_transform(data_end)\n",
"print data_start\n",
"print data_end\n",
"'''\n",
"\n",
"data_max = max(data_start.max(), data_end.max())\n",
"data_min = min(data_end.min(), data_end.min())\n",
"print x_max, x_min\n",
"\n",
"\n",
"H, xedges, yedges = np.histogram2d(data_start, data_start, bins=5)\n",
"pdf = H/float(len(data_start))\n",
"px = pdf.sum(0)\n",
"py = pdf.sum(1)\n",
"print \"pdf Initial Values, pdf Final Values :\", px, py\n",
"print \"check sumpx, sum py, sumpxpy : \", sum(px), sum(py), sum(px)+sum(py)\n",
"print \"H_FinalGivenInitial : \", np.float16(infotheo.condentropy(py, px, pdf)), \"H_InitialGivenFinal :\", np.float16(infotheo.condentropy(px, py, pdf))\n",
"\n",
"myextent =[xedges[0],xedges[-1],yedges[0],yedges[-1]]\n",
"plt.imshow(H.T,origin='low',extent=myextent,interpolation='nearest',aspect='auto')\n",
"plt.plot(data_start, data_start,'ro')\n",
"plt.colorbar()\n",
"plt.ylabel(\"Initial Values\")\n",
"plt.xlabel(\"Final Values\")\n",
"plt.show()\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"19.0 0.1\n",
"pdf Initial Values, pdf Final Values : [ 0. 0. 1. 0. 0.] [ 0. 0. 1. 0. 0.]\n",
"check sumpx, sum py, sumpxpy : 1.0 1.0 2.0\n",
"H_FinalGivenInitial : 0.0 H_InitialGivenFinal : 0.0\n"
]
}
],
"prompt_number": 174
}
],
"metadata": {}
}
]
} | mit |
keras-team/keras-io | examples/keras_recipes/ipynb/tensorflow_numpy_models.ipynb | 1 | 15853 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"# Writing Keras Models With TensorFlow NumPy\n",
"\n",
"**Author:** [lukewood](https://lukewood.xyz)<br>\n",
"**Date created:** 2021/08/28<br>\n",
"**Last modified:** 2021/08/28<br>\n",
"**Description:** Overview of how to use the TensorFlow NumPy API to write Keras models."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Introduction\n",
"\n",
"[NumPy](https://numpy.org/) is a hugely successful Python linear algebra library.\n",
"\n",
"TensorFlow recently launched [tf_numpy](https://www.tensorflow.org/guide/tf_numpy), a\n",
"TensorFlow implementation of a large subset of the NumPy API.\n",
"Thanks to `tf_numpy`, you can write Keras layers or models in the NumPy style!\n",
"\n",
"The TensorFlow NumPy API has full integration with the TensorFlow ecosystem.\n",
"Features such as automatic differentiation, TensorBoard, Keras model callbacks,\n",
"TPU distribution and model exporting are all supported.\n",
"\n",
"Let's run through a few examples."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Setup\n",
"TensorFlow NumPy requires TensorFlow 2.5 or later."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"import tensorflow as tf\n",
"import tensorflow.experimental.numpy as tnp\n",
"import keras\n",
"import keras.layers as layers\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"Optionally, you can call `tnp.experimental_enable_numpy_behavior()` to enable type promotion in TensorFlow.\n",
"This allows TNP to more closely follow the NumPy standard."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"tnp.experimental_enable_numpy_behavior()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"To test our models we will use the Boston housing prices regression dataset."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"(x_train, y_train), (x_test, y_test) = tf.keras.datasets.boston_housing.load_data(\n",
" path=\"boston_housing.npz\", test_split=0.2, seed=113\n",
")\n",
"\n",
"\n",
"def evaluate_model(model: keras.Model):\n",
" [loss, percent_error] = model.evaluate(x_test, y_test, verbose=0)\n",
" print(\"Mean absolute percent error before training: \", percent_error)\n",
" model.fit(x_train, y_train, epochs=200, verbose=0)\n",
" [loss, percent_error] = model.evaluate(x_test, y_test, verbose=0)\n",
" print(\"Mean absolute percent error after training:\", percent_error)\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Subclassing keras.Model with TNP\n",
"\n",
"The most flexible way to make use of the Keras API is to subclass the\n",
"[`keras.Model`](https://keras.io/api/models/model/) class. Subclassing the Model class\n",
"gives you the ability to fully customize what occurs in the training loop. This makes\n",
"subclassing Model a popular option for researchers.\n",
"\n",
"In this example, we will implement a `Model` subclass that performs regression over the\n",
"boston housing dataset using the TNP API. Note that differentiation and gradient\n",
"descent is handled automatically when using the TNP API alongside keras.\n",
"\n",
"First let's define a simple `TNPForwardFeedRegressionNetwork` class."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"\n",
"class TNPForwardFeedRegressionNetwork(keras.Model):\n",
" def __init__(self, blocks=None, **kwargs):\n",
" super(TNPForwardFeedRegressionNetwork, self).__init__(**kwargs)\n",
" if not isinstance(blocks, list):\n",
" raise ValueError(f\"blocks must be a list, got blocks={blocks}\")\n",
" self.blocks = blocks\n",
" self.block_weights = None\n",
" self.biases = None\n",
"\n",
" def build(self, input_shape):\n",
" current_shape = input_shape[1]\n",
" self.block_weights = []\n",
" self.biases = []\n",
" for i, block in enumerate(self.blocks):\n",
" self.block_weights.append(\n",
" self.add_weight(\n",
" shape=(current_shape, block), trainable=True, name=f\"block-{i}\"\n",
" )\n",
" )\n",
" self.biases.append(\n",
" self.add_weight(shape=(block,), trainable=True, name=f\"bias-{i}\")\n",
" )\n",
" current_shape = block\n",
"\n",
" self.linear_layer = self.add_weight(\n",
" shape=(current_shape, 1), name=\"linear_projector\", trainable=True\n",
" )\n",
"\n",
" def call(self, inputs):\n",
" activations = inputs\n",
" for w, b in zip(self.block_weights, self.biases):\n",
" activations = tnp.matmul(activations, w) + b\n",
" # ReLu activation function\n",
" activations = tnp.maximum(activations, 0.0)\n",
"\n",
" return tnp.matmul(activations, self.linear_layer)\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"Just like with any other Keras model we can utilize any supported optimizer, loss,\n",
"metrics or callbacks that we want.\n",
"\n",
"Let's see how the model performs!"
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"model = TNPForwardFeedRegressionNetwork(blocks=[3, 3])\n",
"model.compile(\n",
" optimizer=\"adam\",\n",
" loss=\"mean_squared_error\",\n",
" metrics=[keras.metrics.MeanAbsolutePercentageError()],\n",
")\n",
"evaluate_model(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"Great! Our model seems to be effectively learning to solve the problem at hand.\n",
"\n",
"We can also write our own custom loss function using TNP."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"\n",
"def tnp_mse(y_true, y_pred):\n",
" return tnp.mean(tnp.square(y_true - y_pred), axis=0)\n",
"\n",
"\n",
"keras.backend.clear_session()\n",
"model = TNPForwardFeedRegressionNetwork(blocks=[3, 3])\n",
"model.compile(\n",
" optimizer=\"adam\",\n",
" loss=tnp_mse,\n",
" metrics=[keras.metrics.MeanAbsolutePercentageError()],\n",
")\n",
"evaluate_model(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Implementing a Keras Layer Based Model with TNP\n",
"\n",
"If desired, TNP can also be used in layer oriented Keras code structure. Let's\n",
"implement the same model, but using a layered approach!"
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"\n",
"def tnp_relu(x):\n",
" return tnp.maximum(x, 0)\n",
"\n",
"\n",
"class TNPDense(keras.layers.Layer):\n",
" def __init__(self, units, activation=None):\n",
" super().__init__()\n",
" self.units = units\n",
" self.activation = activation\n",
"\n",
" def build(self, input_shape):\n",
" self.w = self.add_weight(\n",
" name=\"weights\",\n",
" shape=(input_shape[1], self.units),\n",
" initializer=\"random_normal\",\n",
" trainable=True,\n",
" )\n",
" self.bias = self.add_weight(\n",
" name=\"bias\",\n",
" shape=(self.units,),\n",
" initializer=\"random_normal\",\n",
" trainable=True,\n",
" )\n",
"\n",
" def call(self, inputs):\n",
" outputs = tnp.matmul(inputs, self.w) + self.bias\n",
" if self.activation:\n",
" return self.activation(outputs)\n",
" return outputs\n",
"\n",
"\n",
"def create_layered_tnp_model():\n",
" return keras.Sequential(\n",
" [\n",
" TNPDense(3, activation=tnp_relu),\n",
" TNPDense(3, activation=tnp_relu),\n",
" TNPDense(1),\n",
" ]\n",
" )\n",
"\n",
"\n",
"model = create_layered_tnp_model()\n",
"model.compile(\n",
" optimizer=\"adam\",\n",
" loss=\"mean_squared_error\",\n",
" metrics=[keras.metrics.MeanAbsolutePercentageError()],\n",
")\n",
"model.build((None, 13,))\n",
"model.summary()\n",
"\n",
"evaluate_model(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"You can also seamlessly switch between TNP layers and native Keras layers!"
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"\n",
"def create_mixed_model():\n",
" return keras.Sequential(\n",
" [\n",
" TNPDense(3, activation=tnp_relu),\n",
" # The model will have no issue using a normal Dense layer\n",
" layers.Dense(3, activation=\"relu\"),\n",
" # ... or switching back to tnp layers!\n",
" TNPDense(1),\n",
" ]\n",
" )\n",
"\n",
"\n",
"model = create_mixed_model()\n",
"model.compile(\n",
" optimizer=\"adam\",\n",
" loss=\"mean_squared_error\",\n",
" metrics=[keras.metrics.MeanAbsolutePercentageError()],\n",
")\n",
"model.build((None, 13,))\n",
"model.summary()\n",
"\n",
"evaluate_model(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"The Keras API offers a wide variety of layers. The ability to use them alongside NumPy\n",
"code can be a huge time saver in projects."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Distribution Strategy\n",
"\n",
"TensorFlow NumPy and Keras integrate with\n",
"[TensorFlow Distribution Strategies](https://www.tensorflow.org/guide/distributed_training).\n",
"This makes it simple to perform distributed training across multiple GPUs,\n",
"or even an entire TPU Pod."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"gpus = tf.config.list_logical_devices(\"GPU\")\n",
"if gpus:\n",
" strategy = tf.distribute.MirroredStrategy(gpus)\n",
"else:\n",
" # We can fallback to a no-op CPU strategy.\n",
" strategy = tf.distribute.get_strategy()\n",
"print(\"Running with strategy:\", str(strategy.__class__.__name__))\n",
"\n",
"with strategy.scope():\n",
" model = create_layered_tnp_model()\n",
" model.compile(\n",
" optimizer=\"adam\",\n",
" loss=\"mean_squared_error\",\n",
" metrics=[keras.metrics.MeanAbsolutePercentageError()],\n",
" )\n",
" model.build((None, 13,))\n",
" model.summary()\n",
" evaluate_model(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## TensorBoard Integration\n",
"\n",
"One of the many benefits of using the Keras API is the ability to monitor training\n",
"through TensorBoard. Using the TensorFlow NumPy API alongside Keras allows you to easily\n",
"leverage TensorBoard."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"keras.backend.clear_session()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"To load the TensorBoard from a Jupyter notebook, you can run the following magic:\n",
"```\n",
"%load_ext tensorboard\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"models = [\n",
" (TNPForwardFeedRegressionNetwork(blocks=[3, 3]), \"TNPForwardFeedRegressionNetwork\"),\n",
" (create_layered_tnp_model(), \"layered_tnp_model\"),\n",
" (create_mixed_model(), \"mixed_model\"),\n",
"]\n",
"for model, model_name in models:\n",
" model.compile(\n",
" optimizer=\"adam\",\n",
" loss=\"mean_squared_error\",\n",
" metrics=[keras.metrics.MeanAbsolutePercentageError()],\n",
" )\n",
" model.fit(\n",
" x_train,\n",
" y_train,\n",
" epochs=200,\n",
" verbose=0,\n",
" callbacks=[keras.callbacks.TensorBoard(log_dir=f\"logs/{model_name}\")],\n",
" )"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"To load the TensorBoard from a Jupyter notebook you can use the `%tensorboard` magic:\n",
"\n",
"```\n",
"%tensorboard --logdir logs\n",
"```\n",
"\n",
"The TensorBoard monitor metrics and examine the training curve.\n",
"\n",
"\n",
"\n",
"The TensorBoard also allows you to explore the computation graph used in your models.\n",
"\n",
"\n",
"\n",
"The ability to introspect into your models can be valuable during debugging."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Conclusion\n",
"\n",
"Porting existing NumPy code to Keras models using the `tensorflow_numpy` API is easy!\n",
"By integrating with Keras you gain the ability to use existing Keras callbacks, metrics\n",
"and optimizers, easily distribute your training and use Tensorboard.\n",
"\n",
"Migrating a more complex model, such as a ResNet, to the TensorFlow NumPy API would be a\n",
"great follow up learning exercise.\n",
"\n",
"Several open source NumPy ResNet implementations are available online."
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "tensorflow_numpy_models",
"private_outputs": false,
"provenance": [],
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
bcbi/julia_tutorials | plotting/seaborn.ipynb | 1 | 386414 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Seaborn\n",
"\n",
"[Searborn](http://seaborn.pydata.org/index.html) is a Python library for Statistical Data Visualization. It provides a high-level interface and many \"out-of-the-box\" plotting functionality for easy exploration. [Seaborn.jl](https://github.com/JuliaPy/Seaborn.jl) is a Julia wraper of the python library."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Imports"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"using Seaborn\n",
"using Pandas\n",
"using PyPlot\n",
"using PyCall\n",
"\n",
"@pyimport numpy"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Visualizing linear relationships:\n",
"\n",
"Seaborn is not a regression library itself. For quantitative measures related to the fit of regression models, you should use GLM.jl. However, Seaborn provides regression plots in seaborn that helps emphasizing patterns in a dataset during exploratory data analyses. \n",
"\n",
"#### Functions for linear-regreassion models\n",
"\n",
"* `regplot`: In the simplest invocation, draw a scatterplot of two variables, x and y, and then fit the regression model y ~ x and plot the resulting regression line and a 95% confidence interval for that regression. Inputs x,y can be in a variaerty of formats.\n",
"\n",
"\n",
"* `lmplot`: Uses regplot.\n",
"Inputs must be Pandas.DataFrame format.\n",
"\n",
"\n",
"* `jointplot`: Use regplot together with dictribution plots to provide and alternative visualization of the relationship\n",
"\n",
"[More info](http://seaborn.pydata.org/tutorial/regression.html#regression-tutorial)\n"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/plain": [
" day sex size smoker time tip total_bill\n",
"0 Sun Female 2 No Dinner 1.01 16.99\n",
"1 Sun Male 3 No Dinner 1.66 10.34\n",
"2 Sun Male 3 No Dinner 3.50 21.01\n",
"3 Sun Male 2 No Dinner 3.31 23.68\n",
"4 Sun Female 4 No Dinner 3.61 24.59\n"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#for some strange reason loading doesn't work the first time\n",
"tips = nothing\n",
"try\n",
" tips = load_dataset(\"tips\");\n",
"catch\n",
" tips = load_dataset(\"tips\");\n",
"end\n",
"\n",
"\n",
"head(tips)"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAH7CAYAAAAJoc3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xt0G+WZP/DvzOhqW7IlS7ETx3YSX3IhJHZIA00LhDYsW8rCrzTdXqHddk9pdnuBLeyhpz0sW9pDL2y7SyltOactu/TGLgF2C7SUlIXCAoUQJxBIsB07tnEcR/Lduo/m/f0h27FsS5ZtXUbS93MOp7UynnlHryQ/et/nfV5JCCFARERERKRTcq4bQERERESUDANWIiIiItI1BqxEREREpGsMWImIiIhI1xiwEhEREZGuMWAlIiIiIl1jwEpEREREusaAlYiIiIh0jQErEVEC3FeFiEgfGLASUd679dZbsXHjxqT/XXfddSmf7/Tp0/jbv/1bDA4OLqkdH/3oR/GpT30q4b+/8MIL89q1detW7N27F3fddReCweC8Yw8dOgQAuPnmm3H55ZcDAFRVxcaNG3HvvfcuqX3p9v3vf3/R5326zbPbT0S0VIZcN4CIaKX+7u/+Dh/5yEdmfr733nvx5ptv4p577pl5rKysLOXz/d///R+ee+65tLZxtq9//evYuHEjACAQCOD48eO4++67MTQ0hDvvvBMAsG3bNjz44INobGzMWDtW6qMf/Sguu+yymZ8ffPBB/Pd//zd+9atfzTxmNpsBAF/84hfh8/my3kYiKgwMWIko79XV1aGurm7mZ6fTCZPJhJaWlhy2KrGGhoa4tr3zne/E2NgY7rvvPtx2222wWq0oKyvTbfunVVdXo7q6eubn//3f/wWABds9u3+IiJaKKQFEVHR++9vf4tprr0Vrayve/e534/bbb8f4+DgA4L/+67/wta99DQBw6aWX4qtf/SoAwO/347vf/S4uv/xybN26FTt27MBnPvMZnDhxIi1tstvtkCRp5ue5KQFL8eijj2Ljxo04efJk3OO///3vsXHjRrz11lsAgPvvvx9XXHEFzj//fFxyySX453/+54yNgs5NCbjkkktw99134xvf+AZ27tyJCy+8ELfeeutMPxARzcaAlYiKyg9+8APccsst2LFjB37wgx9g//79+N3vfodPfvKTCIfDeO9734sbbrgBAPCjH/0In/vc5wAAt9xyCx599FHs378fP/vZz3DrrbfixIkTuOWWW5bcBk3ToKoqVFWF3+/HoUOH8Itf/AIf/OAHYbVaV3yPl19+OaxWK5544om4xx9//HFs2rQJGzduxKOPPorvfe97uP766/HTn/4U+/fvxyOPPIJvfvObK75+qh544AG89tpr+Pa3v42bbroJf/zjH3HDDTdwsRsRzcOUACIqGsPDw/jJT36Cj33sYzOjqO9+97vR0NCAT37yk3jkkUfw4Q9/GLW1tQCALVu2oLq6GqFQCMFgELfddhuuuOIKAMCuXbswNjaGu+66C8PDw3A6nSm3Y6EFYHV1dfjCF76QhrsESktLsXfvXjz++OMz55ycnMSzzz6LG2+8EQDwyiuvoK6uDh/72McgSRJ27doFq9Wa1TxTRVHws5/9bCa/uKKiAl/60pfw4osvYvfu3VlrBxHpHwNWIioaR44cQSQSwfvf//64xy+66CJUVVXh5Zdfxoc//OF5v2c2m/HTn/4UAHDmzBmcOnUK3d3d+NOf/gQAiEQiS2rHN77xDWzatAkAEA6H0dvbi5/85Cf40Ic+hAcffDAuL3S5rrnmGvz2t7/Fm2++iS1btuCpp56Cqqq46qqrAAAXXnghHnroIVx77bXYu3cvLr30UlxzzTVxaQmZdvnll8cthtu7dy9kWcbLL7/MgJWI4jBgJaKiMTY2BgBwu93z/s3lciXNn3z22Wdx5513oru7G2VlZdi4cePM9P1Sp7DXr1+P888/f+bnCy64ADt37sTll1+On//85/jKV76ypPMtZPfu3XC73XjsscewZcsWPPbYY3jnO9+JVatWAQCuvvpqAMCvf/1r/PCHP8Tdd9+NtWvX4h//8R9nRpEzraqqKu5ng8GA8vLymX4iIprGHFYiKhrl5eUAAI/HM+/fPB4PHA7Hgr/X3d2Nz3/+89i6dSsOHjyIV199Fb/61a9w6aWXpq1ttbW1qKioQE9PT1rOpygKrrrqKvz+97/H8PAwXnrppZkgddrVV1+NX//613jppZfw/e9/H3a7HV/+8pfh9XrT0obFjIyMxP0ciUQwNjaGysrKrFyfiPIHA1YiKhotLS0wGo14/PHH4x5/6aWXcPbsWVxwwQUAAFmO/2g8duwYwuEwbrjhhpn8VgAzKQGapq24bb29vRgbG0N9ff2KzzXtmmuuQX9/P+69916YTKa4Vfpf+MIX8MUvfhFArELBlVdeic997nOIRCILBvSZ8Mwzz0BV1Zmfn3rqKWiahosuuigr1yei/MGUACIqGk6nE5/5zGfwk5/8BLIsY8+ePejt7cXdd9+N5uZmXHPNNQBiARwAPPnkk7j44ouxZcsWKIqC7373u/jUpz6FYDCIAwcO4PnnnwcQK/6/FCdPnoTBEPv4FULg7bffxr333guLxYJPfOITabvfzZs3o7m5Gb/61a9w1VVXoaSkZObfLrroInz961/Hd77zHVxyySUYGxvD3XffjfXr16O5uRlALIgeGRnB9u3b09am2fr7+7F//3584hOfQH9/P77//e/jsssuw86dOzNyPSLKXwxYiaio3HTTTVi1ahV++ctf4je/+Q0cDgfe//7340tf+hIsFguAWCH/iy66CN/97nfx0ksv4Uc/+hHuuusu3HPPPfjc5z6HiooKtLS04N///d9x/fXX49ChQ2hoaEi5DbfddtvM/5dlGRUVFdixYwe+973vxY3gpsPVV1+Nu+66a146wMc//nFEIhH853/+J375y1/CYrHgXe96F2655RYoigIAuPvuu/HEE0/gzTffTGubpv3VX/0VSkpKcOONN6K0tBT79u2bqWJARDSbJFjwjoiIsuySSy7BxRdfnNW6r0SUv5jDSkRERES6xoCViIiIiHSNKQFEREREpGscYSUiIiIiXWPASkRERES6xoCViIiIiHSNASsRERER6VpBbxzg8Uzkugm0RLIsweksxfCwD5rG9YCFgv1amNivhYn9Wpj03K9ut23RYzjCSroiyxIkSYIsS7luCqUR+7UwsV8LE/u1MOV7vzJgJSIiIiJdY8BKRERERLrGgJWIiIiIdI0BKxERERHpGgNWIiIiItI1BqxEREREpGsMWImIiIhI1xiwEhEREZGuMWAlIiIiIl1jwEpEREREusaAlYiIiIh0jQErEREREemaLgLWcDiMq666Cn/+859nHuvr68OnPvUptLS04Morr8Tzzz+fwxYSERERFS4hBHrOTOBY9xB6zkxACJHrJsUx5LoBoVAIX/7yl9HR0THzmBACf//3f4/m5mYcOHAABw8exOc//3k88cQTWLNmTQ5bS0RERFRYjveM4OChPgxPhGYec9rM2LuzFpvrHTls2Tk5HWHt7OzEX//1X6O3tzfu8Zdeegl9fX34+te/joaGBtxwww1oaWnBgQMHctRSIiIiosJzvGcEDz3TGResAsDwRAgPPdOJ4z0jOWpZvJwGrC+//DIuvPBCPPjgg3GPHz16FFu2bEFJScnMYxdccAGOHDmS7SYSERERFSQhBA4e6oOWYPZfE8DBQ326SA/IaUrAxz72sQUf93g8WLVqVdxjlZWVOHPmzJLOL8sSZFladvso+xRFjvtfKgzs18LEfi1M7NfCtFC/nhoYx8hkCFKSUGlkMoT+IR/WVdsz3cSkcp7DupBAIACTyRT3mMlkQjgcXtJ5nM5SSMl6gXTLbrfmugmUAezXwsR+LUzs18I0u1+7z/pgSOGLiZAVOBylmWzWonQZsJrNZoyOjsY9Fg6HYbFYlnSe4WEfR1jzjKLIsNutGB8PIBrVct0cShP2a2FivxYm9mthWqhfpWgUagp9LGlRjIz4Mta2VIJhXQasVVVV6OzsjHvM6/XOSxNYjKYJaIkSM0jXolENqsoPykLDfi1M7NfCxH4tTLP7tcZVCkeZed6Cq9mcNjNqKktz/lrQZYLK9u3b8cYbbyAYDM489uqrr2L79u05bBURERFR4ZAkCXt31iLRZLQsAXt31uoivVKXAeuuXbuwevVqfOUrX0FHRwfuu+8+vPbaa9i3b1+um0ZERERUMDbXO7BvTyOcNnPc406bGfv2NOqmDqsuUwIURcG9996Lr371q7j22mtRX1+PH/7wh9w0gIiIiCjNNtc7sKmuAr2Dk5gIhGGzmlBXVaaLkdVpuglY33rrrbif6+vr8Ytf/CJHrSEiIiIqHpIkob7alutmJKTLlAAiIiIiomkMWImIiIhI1xiwEhEREZGuMWAlIiIiIl1jwEpEREREusaAlYiIiIh0jQErEREREekaA1YiIiIi0jUGrERERESkawxYiYiIiEjXGLASERERka4xYCUiIiIiXWPASkRERES6xoCViIiIiHSNASsRERER6RoDViIiIiLSNQasRERERKRrDFiJiIiISNcYsBIRERGRrjFgJSIiIiJdY8BKRERERLrGgJWIiIiIdI0BKxERERHpGgNWIiIiItI1BqxEREREpGsMWImIiIhI1xiwEhEREZGuMWAlIiIiIl1jwEpEREREusaAlYiIiIh0zZDrBhARERHROUII9A5OYiIQhs1qQl1VGSRJynWzcooBKxEREZFOHO8ZwcFDfRieCM085rSZsXdnLTbXO3LYstxiSgARERGRDhzvGcFDz3TGBasAMDwRwkPPdOJ4z0iOWpZ7DFiJiIiIckwIgYOH+qCJhf9dE8DBQ30QIsEBBY4BKxEREVGO9Q5OzhtZnWt4IoTewckstUhfGLASERER5dhEIJzW4woNA1YiIiKiHLNZTWk9rtAwYCUiIiLKsbqqMjht5qTHOG1m1FWVZalF+sKAlYiIiCjHJEnC3p21kBOUW5UlYO/O2qKtx8qAlYiIiEgHNtc7sG9P47yRVqfNjH17Gou6Dis3DiAiIiLSic31Dmyqq+BOV3MwYCUiIiLSEUmSUF9ty3UzdIUpAURERESkawxYiYiIiEjXGLASERERka4xYCUiIiIiXWPASkRERES6xoCViIiIiHSNASsRERER6RoDViIiIiLSNQasRERERKRrDFiJiIiISNcYsBIRERGRrjFgJSIiIiJdY8BKRERERLrGgJWIiIiIdI0BKxERERHpGgNWIiIiItI1BqxEREREpGsMWImIiIhI1xiwEhEREZGuMWAlIiIiIl1jwEpEREREusaAlYiIiIh0jQErEREREekaA1YiIiIi0jUGrERERESkawxYiYiIiEjXGLASERERka4xYCUiIiIiXdN1wDowMIAbbrgBO3bswHve8x7cf//9uW4SEREREWWZIdcNSObGG2/EmjVr8PDDD6OzsxM333wzampqcPnll+e6aURERESUJbodYR0bG8ORI0ewf/9+rFu3Dnv37sXFF1+MF198MddNIyIiIqIs0m3AarFYYLVa8fDDDyMSiaCrqwuHDx/G5s2bc900IiIiIsoi3QasZrMZt912Gx588EFs374d73vf+3DJJZfgQx/6UK6bRkRERERZpOsc1pMnT+Kyyy7D3/zN36CjowN33HEH3vnOd+Lqq69O6fdlWYIsSxluJaWToshx/0uFgf1amNivhYn9WpjyvV8lIYTIdSMW8uKLL+LGG2/Es88+C4vFAgD40Y9+hP/5n//B7373u5TOIYSAJDFgJSIiIspnuh1hPXbsGOrr62eCVQDYsmULfvzjH6d8juFhH0dY84yiyLDbrRgfDyAa1XLdHEoT9mthYr8WJvZrYdJzvzocpYseo9uAddWqVejp6UE4HIbJZAIAdHV1Ye3atSmfQ9MENE2XA8i0iGhUg6rq6w1FK8d+LUzs18LEfi1M+dqvuk1keM973gOj0Yivfe1r6O7uxtNPP40f//jHuO6663LdNCIiIiLKIt2OsNpsNtx///345je/iX379sHpdGL//v348Ic/nOumEREREVEW6TZgBYDGxkb8/Oc/z3UziIiIiCiHdJsSQEREREQEMGAlIiIiIp1jwEpEREREusaAlYiIiIh0jQErEREREekaA1YiIiIi0jVdl7UiIiKi9BJCoHdwEhOBMGxWE+qqyiBJ3Mac9I0BKxERUZE43jOCg4f6MDwRmnnMaTNj785abK535LBlRMkxJYCIiKgIHO8ZwUPPdMYFqwAwPBHCQ8904njPSI5aRrQ4BqxEREQFTgiBg4f6oImF/10TwMFDfRAiwQFEOcaAlYiIqMD1Dk7OG1mda3gihN7BySy1iGhpGLASEREVuIlAOK3HEWUbA1YiIqICZ7Oa0nocUbYxYCUiIipwdVVlcNrMSY9x2syoqyrLUouIloYBKxERUYGTJAl7d9ZCTlBuVZaAvTtrWY+VdIsBKxERURHYXO/Avj2N80ZanTYz9u1pZB1W0jVuHEBERFQkNtc7sKmugjtdUd5hwEpERFREJElCfbUt180gWhKmBBARERGRrjFgJSIiIiJdY8BKRERERLrGHFYiIiIiyjohBCKqltKxDFiJiIiIKGs0IRAIqfAFVSgpVqhgwEpEREREGadGNfhDKgIhFULEHlMUBqxERERElGMRNQpfUEUwHF32ORiwEhEREVHaBaZGU8Mp5qkmw4CViIiIiNJiOj/VH1QR1UTazsuAlYiIiIhWJKpp8AXj81PTiQErERERES1LOvJTU8GAlYiIiIiWZHraPxJdeX5qKhiwEhEREdGiMpWfmgoGrERERESUUKbzU1PBgJWIiIiI5pnOTw2Fo8hRnDqDASsRERERzQiGY9P+6aifmi4MWImIiIiKXC7zU1PBgJWIiIioSOkhPzUVDFiJiIiIioye8lNTwYCViIiIqEgEwyrGJ8O6yk9NBQNWIiIiogKmCQFfIIKQ5sPIRAjRaD6MqcZjwEpERERUgGbnp8qyhHJj/oZ9+dtyIiIiIpon3/JTU8GAlYiIiEgnhBDoHZzERCAMm9WEuqoySJKU0u/qsX5qujBgJSKioraSAIEonY73jODgoT4MT4RmHnPazNi7sxab6x0L/o7e66emCwNWIiIqWssJEIgy4XjPCB56phNzY87hiRAeeqYT+/Y0xr0m86V+arrIuW4AERFRLkwHCLODVeBcgHC8ZyRHLaNiI4TAwUN984LVaZoADh7qgxACETWK0ckQvKNB+IPFEawCDFiJiKgILSVAIMq03sHJeV+c5vKOBfF61xCGxkMIFtBiqlQxYCUioqKTSoAwPBFC7+BkllpExWwiEF7wcSEEoppARNUQ1QTGfAsfVwyYw0pEREUnUYCw3OOIVsJmNcX9LISAJgS0OYv9S83GLLZKXzjCSkRERWdugLDS44hWoq6qDE6bGUIIqFENanR+sFpeasJqV0luGqgDDFiJiKjoTAcIyThtZtRVlWWpRVTMQpEodm2ugqaJBRdRyRKwe2t1UZdbY8BKREVHCIGeMxM41j2EnjMTBb2wppjudSkkScLenbWQE/z9lyVg787aog4QKLM0IeALRuAZDWB0Moz6ahuu2FWH8tL4Uf3yUhOu2FWHhpryHLVUH5jDSkRFpZjqbhbTvS7H5noH9u1p5HNEWZWsfmpDTTk2rLFjwOuHLxRBqdmI1a4SfnECA1YiKiJLLcydz4rpXldic70Dm+oquNMVZVxEjcIXVBFapCSVJElY4y7NWrvyBQNWIioKqdbd3FRXkffBSjHdazpIkoT6aluum0EFKhiObZsaVrXFDy4SmhDoHhhHW7sXpwbG8e+3/+Wiv8OAlYiKwlLqbuZ78FJM90qkR5oQCIRigWo00TfHInR2JIC2Dg+OdHiXXFOWASsRFYViqrtZTPdKpCdqVIM/tHB+arGaDETw2skhtHV40O/xLfs8DFiJqCgUU93NYrpXIj0IR6byUyPRXDdFFyKqhhO9I2hr96K9bxRakuh9blWERBiwElFRmK67mWyqvFDqbhbTvRLlihACwXAU/qCKSJT5qUII9AxOoK3di9e7hhAMJw7eTQYZ5613orXZjY1rK1I6PwNWIioK03U3F1o5DxRW3c1iuleibNM0AX9IhT+kQmN+KobGgmjr8KCtw4uRJF+SJcTKdrU2u3DeOidMRgUAICcqhjwHA1YiKhrFVHezmO6VKBsiqgZ/MILgImWpioE/qOL1rlheau/gZNJjqxxWtDa7sb3RlfL0/0IYsBJRUSmmupvFdK9EmcKyVDFqVEN73yja2r040TuStPpBmdWI7Y2VaG1yY3VlejY+YMBKREWnmOpuFtO9EqULp/1jhBB42+NDW4cHr3UOwR9SEx5rUCRsWedEa5MLjWsroKQ41Z8qBqxEREREiI0i+oIqgiG1qKf9RyZCONrpxeF2D7xjwaTHrl9tR2uTC1s3OGExZS6sZMBKRERERS0UjsIXjBT1tH8wrOJY1zDaOrzoHhhPeqyr3ILWJjdamlxw2MxZaR8DViIiIio63I0KiGoCnW+Poq3DizdPDUONJn4eSswGbGusxI4mN2rcpVnPhWfASkREREVDjWrwB1UEwsW5G5UQAqe9sbzUo51DmAxEEh6ryBI21Tuwo8mFptoKGBQ5iy2Nx4CViIiICl4oHIU/VLy7UY1NhvDnEx68cLQfZ4YDSY+tr7KhpcmFbQ2VsJr1ESrqoxVEREREaaYJgeDUtL9ahNP+oUgUb3bH8lJP9o8lXUjmtJnR0uRCa5MbleWWrLUxVQxYiYiIqKCoUQ3+kIpAqPim/TVNoOv0ONo6PHijezjpQjKLScG2hli9VL3XaGbASkRERAUhFInCHyzOaf/BYT/aOjw40jmEcV844XGyLGFjbQVam1zYWOeA0ZC7vNSlYMBKREREeUsIgUAoCn8oknSVeyGa8Ifx2skhtLV7cHrIn/TYtatK8a5tNWhea4c1g/VSM0XXLQ6Hw7jzzjvx2GOPwWg0Yt++fbjpppt0PWRNRETpJ4TgFrMUJ6pNrfYPqSim9NSIquF4zzDa2r3oeHs06b2Xl5rQ2uRCS3Nsi9Ty8hKMjfkRzcPAXtcB6ze+8Q38+c9/xk9/+lP4fD7cdNNNWLNmDT7ykY/kumlERJQlx3tGcPBQH4YnQjOPOW1m7N1Zi831jhy2jHIhHJla7R+OFs1uVJoQ6DkzgbZ2D17vGk6a8mA2Kti63onWZhfWrbZDLpAvdroNWEdHR3HgwAH8/Oc/x7Zt2wAAn/70p3H06FEGrEREReJ4zwgeeqZz3ijS8EQIDz3TiX17Ghm0FgEhBIJTu1EV07S/dzSAtg4v2jo8GJ1MnJcqSUDT2nK0NrmxeZ0DJoOSxVZmh24D1ldffRVlZWXYtWvXzGOf/exnc9giIqLCpccpdyEEDh7qSzjlqQng4KE+bKqryHlbKTOimhbLTw1Gimba3x+M4OjJIRzp8KLv7GTSY1dXlqC1yY1tjZWwl5iy1MLc0G3A2tfXh5qaGjz66KP48Y9/jEgkgmuvvRb79++HLKe2ok2WJcgyP8TyiTK1i4aSw900KP3Yr/r25qlh/OHlPgxPBGcec9os+Itdtdiyzpnw9zLdr6cGxjEyGUKyWHRkMoT+IR/WVdsz0oZipIf3a1iNwh9QEYxEIYSAJEsovDHDc9SohhM9Izjc7sGJntGkW8XaSoxobXJhx0Y3VleWpnyN+H5NXOoq25QUqxToNmD1+/3o6enBb37zG9x5553weDy47bbbYLVa8elPfzqlczid2d/rltLDbrfmugmUAexX/Xmt04MDz3ZBCBG37eK4P4wDz3bBZrNgW6M76Tky1a/dZ30pbQUpZAUOR+p/uCk12X6/xlb7q5gMRKBChslqgqmAPzKEEOg+PY6Xjg3g0PFB+INqwmONBhmtG1fhoq3V2FTvXNFgXFmZvjYFSLWslm4DVoPBgMnJSfzLv/wLampqAACnT5/Gr3/965QD1uFhH0dY84yiyLDbrRgfDyAa1c83QFqZQu1XMbUQYsIfga3EiPpqW159SRZC4MAfOxBREy/gePjpDqx1Whe8r0z3qxSNQk3hvJIWxciIL+3XL1bZfr9qmoA/pMIfjCQdWSwUQ+NBtLV7cLjdi6GxYMLjJAAbauy4oNmNrRsqYTbFxpgnJpJvq5qIosgoK7NgcjKoq89ho0HBKkfJosfpNmB1u90wm80zwSoArF+/HgMDAymfQ9MEtCJ48ReiaFSDmmR3DspPhdSvhbByvefMBIbGE//BBADvWBBd/eOor7YlPCZT/VrjKoWjzBz3HM/ltJlRU1laMK8rPcn0+zWiavAHIwgWwWr/QEjFsa4hHO7woufMRNJj3RVW7Gh2YXujCxVl5pnHV16KSps6j6arslZyiukJug1Yt2/fjlAohO7ubqxfvx4A0NXVFRfAEhHlQqGsXJ8IJF51vJzj0k2SJOzdWbvgcw0AsgTs3VmbV6PaBATDKvxBNemWoYUgqmno6BvD4Q4PTvSMJK1uUGoxYFujCzuaXFjjYjrjQnQbsG7YsAF79uzBV77yFdx+++3weDy47777sH///lw3jYiKWCGtXLdZU1tVnOpxmbC53oF9exrzfjS72M1M+4fUgp75FELgtNeHtg4vjnZ64UuSl2pQJGyud6C1yY2m2nIoKS4oL1a6DVgB4K677sIdd9yBj370o7Barfj4xz+O6667LtfNIqIi1js4mXSKGoiNtPYOTiadRteDuqoyOG2LT7nXVZVlsVXzba53YFNdhe7KbtHi1KgGX1BFMKQW9LT/6GQIRzu9ONzuhWc0eY5pfbUNO5rd2LreCatZ12GYruj6mbLZbPjOd76T62YQEc3Q+zT6UuTTlLskSbr/AkDnFMO0fygcxRunhnG43YPu0+NJA/JKuwWtzS60NLrgtOtrlX6+0HXASkSkN/kwjb4UnHKndNGmylL5g2rBrvbXNIHO/jEc6fDijVPDiCQJyK1mBdsaXGhtcqF2FWcEVooBKxHREuTLNPqXVPc0AAAgAElEQVRScMqdVkKNavAHVQTCKkRhxqkYGPLhSIcXRzq9mPBHEh6nyBI21lWgtcmNjXUVKdURptQwYCWiorWc7UjzaRp9KTjlTksVCkfhD6kIRRLX8c1n4/4wjnZ6caTDi4Ehf9Jja1eVobXJhW0NlSixGLPUwuLCgJWIitJK6qhyGp2KlSYEglPT/moBTvuH1SjePDWCtnYPOvvHko4YO2xmtDTGpvxdFQW8JZdOMGAloqKTjjqqnEafbzkj1pQf1KgGf0hFIFR40/6aEOgeGEdbuxfHuocQjiTOSzUbFZzfUInWJhfqq22Q+fpesVSfQgasRFRU0llHldPo5xTCzl80XygShT9YmNP+Z0cCaOvw4EiHF2O+xFU9ZAloWluB1mY3Ntc7YDQwL3WlFFmC2ajAbFRgMqb2fDJgJaKiUkh1VPXizVPDBbHzF8UIIeALROAdDSAYLqxAdTIQwWsnh9DW4UG/x5f02DWu0pm8VFtJflT90CsJgGkqODUblWUtRmPASkRFpZDqqOqBEAJ/eLkwdv4qdtO7UYUiUdiiQCRaGDVUI6qGE70jaGv3or1vFFqSnAZ7qQktjZVoaXKj2lmSxVYWnrmjqCt9/zNgJaKiUmh1VHPtZP8YhieCSY/hiLW+zd2NSlHy/4uFEAI9gxNoa/fi9a6hpCPFJoOM89Y70drkxoY1dshy/t9/LkgAjAYZZpOy7FHUZBiwElFRKcQ6qrk0niT3bzaOWOtPIeanDo0H0dYey0tN9h6XADTUlKO1yYUt650wG5XsNbKAzB5FNRrljC5CY8BKREWlUOuo5oq9lCPW+UQIgWA4Cl8wAjVaGMv9/UEVr3fF8lJ7ByeTHlvlsKK12Y3tjS6Up/japXMyPYqaDANWIio6rKOaPg015XDaLBgaT5wWwBHr3JvOT/WHVGgFUD9VjWpo7xtFW7sXJ3pHkm4FW2Y1YntjJVqb3FhdWcIvo0skz4yiyjAZlZyV8mLASkRFiXVU00OSJPzFrlo8+McOjljrUCFtmyqEwNueSbS1e/HaySH4Q2rCYw2KhC3rnGhtcqFxbQUU5qWmLJejqMkwYCWiosU6qumxZZ2TI9Y6U0j5qSMTQbR1xLZI9Y4lX+C3frUdrU0ubN3ghMXEECdVehlFTYa9SUREK8YR69wTQiAQisIfjOT9tqnBsIpjXcNo6/Cge2Ai6bGucgtam9xoaXLBYTNnqYX5bXoU1TS9YCoPNkNYdsB66tQptLe3Q5ZlnHfeeVi9enU620VERHmGI9a5EdWmpv1DasJ6uPkgqgl0vj2Ktg4v3jw1nHRRWInZgG1Tealr3aX8YpQCRZZQYjFA1syQJUmXo6jJLDlgnZycxD/8wz/gueeeg5hKiJEkCVdeeSXuvPNOmExcdUdERJRp4UgUvjyf9hdCYGDIj7YOD452DmEyEEl4rCJL2FTvQGuTC821FbrJrdQzo3IuF9VqMcBhs2BEjUJV829TiCUHrN/85jfR3d2N++67D62trdA0DYcPH8Ydd9yB733ve7j11lsz0U4iIqKiVyhlqcZ8YRzt9KKt3YPBkUDSY+uqytDa5Ma2hkpYzcxkTEaSAJNBgWUqSC2kTRCW3PMHDx7Evffei3e84x0zj+3Zswcmkwk333wzA1YiIqI0K4Rp/3AkijdODaOt3YuT/WNIdhtOmxktTS60NrlRWW7JWhvzkSJLM6OoJsPKt0DVqyUHrIqiwGabn6PkdruhqolLTBAREdHSRNSpaf9wNGmAp1eaJtB1ehxtHR680T2McJKpaItJwfkbKrGj2c0Fe0notexUpi05YL3++utxxx134N/+7d/gcrkAxPJa//Vf/xXXX3992htIRERUTKan/f1BFZFo/uUaAsDgsD9WiqrTm3T7XlmSsLGuAi1NLmyqc+TFavVckCXERlCNCswmfZadyrQlB6zPP/88Xn/9dbz3ve/FunXrYDAYcOrUKfh8Phw/fhyPPPLIzLF//OMf09pYIiKibBFCZLVMV77vRjXhD+O1k0No6/DitNeX9Ni17lK0NrlxfkMlyqzGLLUwvxgVGSajDItJgdGg5Lo5ObfkgHX37t3YvXt3JtpCRFQUsh0I0dId7xnBU6/04sxIAJomIMsSqh1WXP6OurRvhBBRNfiDEQTzcNo/omo43hPLS+14ezRpfm1FmQktjS60NLuxqsKavUbmCWlqFHX6v0JaMJUOSw5YP//5z2eiHZRj/ANKlB3He0byekeo2Z8VFWVmVFSU5LpJaXe8ZwQPPHkCY74IorOm5McmwzgzfALXXbEpLX0VCMUWUSXL69QjTQj0nJlAW7sHr3cNJy2rZTYq2LreidZmF9atthflVHYy06Oo08X7+Xc3sZQC1nvuuQef+cxnYLVacc899yQ9lgFt/sn3P6BE+eJ4zwgeeqZz3ijU8EQIDz3TiX17GnX9npv7WSFJQNVLvbisdQ2a11bkuHXpIYTAI386GbvHOf0UjWoYngjhkT+dxKZPXLCs4CKfp/29owG0dXjR1uHB6GTivFRJAprWlqO1yY3N6xwwcTp7RlwuKkdRlySlgPXhhx/Gxz/+cVitVjz88MMJjxNCMGDNM/n+B5QoXwghcPBQX8IpU00ABw/1YVNdhS5HWRJ9VgyNBfCfT3fig5c2FMRnRc+ZCfR7/fOC1RkC6Pf60XNmAutW21M+rxrV4AuqCIbUvJr29wcjOHpyCEc6vOg7O5n02NWVJbF6qY2VsJdwEyEgP7dA1auUAtann3467ucDBw7A4Yj/YBocHMTVV1+dvpZRxuX7H1CifNI7OBk3i7GQ4YkQegcndbe96UKfFeFIFJoQMBoUGGSpYD4rTp4ei0sDWEg0qqFrYCylgDUYVuEP5te0vxrV0PbWWTx/5G2c6BlFNMlIsM1qREuTCy1NLqyuLM1iK/XLIEvnAlSjzDSINEkpYH3iiSfw3HPPAQAGBgZwxx13wGw2xx3T398PWeY3h3ySz39AifLNRCDxFOpyjsum2Z8VwbCK8encTgmQIEGRJQTCakF8VkhIMbgQiY/ThEAgFAtUkwV7eiKEQN/ZSRxu9+D1riEEQonzUo2KjPPWO9HS5EJDTTmUIp/Wnt5dKjbVLxdNXdRsSylgbW1txW9+8xsIISCEwOnTp2E0nitDIUkSSkpK8K1vfStjDaX0y+c/oET5xmZNbYo01eOyafozIBhWMbJAbqeqaRiZCOGNU8N5H7BuWGOHoshJR1kVRcaGmvmjq2p0ajeqsAqRH3EqhseDsXqpHV4MjQcTHicBWL/GjtYmF7aur4TZVNx5qbMXS5mMxf1cZEtKAevq1avxH//xHwCA6667Dj/84Q9ht6eeu0P6lM9/QKlwpKtChd4qXcxtT+2qUjht5qSzGk6bGXVVZSmfM1v3OP0ZMO6LJM3tfP3kEN53Yd2ibUrHfWTquaivtqHGVYresxML36sEuMotmPCH0XNmAnVVZQhHNPhDatLV8noSCKk41jWEwx1e9JyZSHqsu8KKHc0ubG90oaLMnPA4IQQGvH74QhGUmo1Y7SpJ22szk+dOlSxhZpo/k4ul9PY5pidLLmv1wAMPZKIdlAN1VWUr/gNKtBLpqlCht0oXidrTXFuBl48PLpg3LkvA3p21Cf845fIe66rKYDEqi446ppIWkI77yORzIUkSPnDJBjzw5FsY84Xj7jnWNwLhSBQHnu2CEICtxIh3nleNhpryFV0306Kaho6+MRzu8OBEzwjUaOIh4FKLAbvOq8bW9Q5UOxYPDk/2j+GFY2cwNmtHq/JSE3ZvXfnzkslzL8agSDMBajZGUfX2OaY3yu233357rhuRKX4/p7KTkSQJ9lITjvcMLziQIEvAVbvXw53FAs+yLMFqNSEYjORdyRdKbKF+nV517p+TKxcIR3G8ZxirHCUpvfbSdZ50Sdae014fdm2umpo2PvfvTpsZV+1en/CPUq7vUZIkjPvDeKtvdM4/nMv5rCg1wWhQ0FBjxyrHwrVZ03Ef2Xgu3BVWrHGVYtwXhibE1E5DMqKaBnuJCSaTgqgGCAEEw1F0nR6D026B025Z0XXTTQiBfq8Pzx49jQPPnMShtzw4OxJY8AuTQZFw3non/nJXHa69dAPesXUNzIq0aGrDyf4xPPlyL4Lh+P4IRVb+vGTy3AuRJMBiUlBqMcJeakSZ1QSzUYGShZzUbLyu9fz3tbQ08ej9tCWPsFJh2VzvwL49jfxWR1mVrgoVeqt0kUp72vtG8fcf2Iq+s76Upv30co/nrXPiuaOnMe6PL6ZvUCSUlZhgMcX+nCRKIUrHfWTzudhc78Cmugr0Dk5i3B/GYy+cgj8YgYAEbc5AsyaAF46dwYY1dl1M345OhnC004vD7V54RgNJj11XbYvlpW6ohNUc60NFSe0ehBB44diZpP2x3Oclk+eeLdujqAvRy3tc7xiwUtwHM/NmKBvSVaFCb5UuUm1P31lfyu3Ryz3WVZVhjasU5vEgwqoGTRNQFAklZgOimoAQyVOI0nEf2X4uJEnCKocVY5Mh+IIqkKSCwJgvjAGvH2vcuSntFApH8capYRxu96D79HjSWq+Vdgtam11oaXStaIRywOuPm6pfyHKfl0yde/b2pyajDEUH1Y308h7XOwasBCD2wVzMbwTKrnRVqNBbpYtMtEcv9yhJEvburMVDz3TCPDUSJUnn8joXy8FNx31k67mYW5ZqLMX0Ml8osqLrLpWmCXT2j+FIhxdvdA8jkiTH2GpWsK3BhdYmF2pXpWdAItX7Xc7zks5zzx5F1eP2p3p5j+sdA1Yiyrp0VajQW6WLTLRHT/eYKIWo0m7Be3asTZpClI77yPRzoWkCvmAEgZAaNz1bajYm/qVZUj1upQaGfDjS4cWRTi8m/IkDNkWWsLGuAq1Nbmysq0h7fdBMPi8rOffsuqhmkz5GUZPR03tczxiwElHWpatChd4qXWSiPXq7x9kpRP6QippqOxwlBkSTrDoH0nMfmXouFts2dbWrBOWlpqRT1OWlJqx2LbzYLB0m/GEc7RxCW4cHA0P+pMfWripDa5ML2xoqUWLJXBCdyedlqefW+yhqMnp7j+uVvr92EFFBmp5eTlTKcLHp5XSfJ10y0R693eN0m+qrbTi/oRINa1NbCJKO+0j3cxFRoxiZCME7FkQgQbA6fd3dW6uTXnf31uq090FYjeJIpxf3/+44vvXLw3jipZ6EwarDZsZlrTX4h7/ejv3/bysuOq86o8EqkNnnJZVz72mtQUWZGasqrHCVW2ErMcFkVPIqWAX0+R7XI5a1Il3Rc9kNWr6F+tVdYcUqRwkGhnxLKvE0V7rOky6ZaI/e7nHaUt+v6biPdJwjtr1sGJOB1LdOnS6h5BkNxG0QUF5qwmWtNWmrCaoJga6BcTz9aj8OPHsSr50cwtD4wiNvZqOC1mY33v/Oerzvono01pSnJUiVZQkWixGhUGTRslaZfF7mnluSAFkGXHYL/t/FG7C90ZV3o6mJZOM9rue/r6mUtZKEyJcN5JbO40m+gwfpj8Egw+EoxciID6qaeAEB5Zdk/VosO12loz16u8flvl9zsdOVEAKBUBT+YATqCv5YZ2rXpbMjAbR1eHCkw5t0GlyWgKbaCrQ2ubC53gmjIf0TpYoioby8BGNj/kVTPaZl4nmZXtFvMsgYHA7AF4ro4nWfSZl8j+v576vbvfiibwaspCt6fkPR8rFfC1M+9KumCfhDKvwhVXejSpOBCF47GctL7ff4kh67xlU6k5dqK8ns4htFkWC3W3H8pAcT/uxuh2qQJZhMykygWqiBaS7o+f2aSsDKRVdERBmgt9HQYhNRNfhDiRdS5UpE1XCidwRt7V60941CSzJmVF5qwvbGWCmqKmfmFnTNdbJ/DC891YGhscBMSkCmtkM9t6JfhsmopL2SARUOBqxERGnGPcFzJxSOwheMIJyDEaRE0+JCCPQMTqCt3YvXu4bmbTU6m8kg47z1TrQ2ubFhjR1yopU4GXKyfwxPvtILec6XqzFfGE++3IsrdtWtOGjlKCotBwNWIqI0mt4TfO7s8/BECA8904l9exoZtKbZ3EL/uXCyfwwvHDsTl39qNSmwl5rQc2YiackiCUBDTTlam1w4b70zp1uEvnDsTGxUdYEYcrnboUoATEaOotLKMGAlIkoT7gmeXTP1U8PqoqvZM+lk/xiefLkXmojlzAamcmYji4zyVjmsaG12Y3ujC+WluS8KP70darKXZqrboRpkaSpIjW2Bytc7rRQDViKiNOGe4NkRDMdGU3Mx7T+XEAL/9/oAfEEVgZCadLofAEqtRrQ0VqK1yY3VldlZyJSqlWyHylFUyjQGrEREacI9wTNHD9P+swkh8LZnEs+/NjC1eCr58U1ry7F7azUa11ZAyXJeaqqWuh2qIp/bXYqjqJRpDFiJiNKEe4KnnxrV4A+qCOR42n/ayEQQbR1eHOnwwjsWTHqsySijxGyAxWTAu7etRtPaiiy1cnmmt0MdT7LpjsNmQnNdOSwmA0dRKasYsBIRpQn3BE+fUCQKf1CN2z0pV4JhFce6htHW4UH3QPL63gZFgtVsgNUcH9ClOnqZS9PboT75Sm/c47IU+zdFBq68aB3K+IWLcoABKxFRmkzvCb5QlQCAe4InI4RAz5kJDE0EYZBlrHJYc/o8RTWBzrdH0dbhxZunhqEm2fFJkSVYTAqsZsOCW4WWl5qw2pW9Oqor0VBTjr8yrcfLx8/CM+qHNFUugGXZKNcYsBIRpdHmegf27WlkHdYleKN7GH94pRdD4+eer0wVqk9GCIGBIT/aOjw42jmEyUDiRUiKLGFTvQM7mlxQFDlhdQhZAnZvrdb1l5TpLVCn/1u7qgzve9cGHDl+BqOTIW58QbrAgJWIKM021zuwqa6CO10tQo1qONLpxf883z0v2EtnofrFjPvCONLpRVu7B4MjgaTH1lWVobXJjW0NlbCaz/0JVWRpXh3WXATdqTIo5xZMLTQqLEkS1q22624LTypeDFiJiDJAkiSWrkogokYxGYjVT/3fw/1J69Yup1B9KsKRKN44NYy2di9Onh5LuqDLaTOjpcmF1iY3KsstCx7TUFOODWvsC+50pQeyhLi6qIrMBVOUXxiwEhFRVgTDKnwBFZFobNRuulB9MqkWqk+Fpgl0nR5HW4cHb3QPJ63jajEpOH9DJVqbXaivsqUUeEqSlJZ2potRkWE2xWqjGg252T2LKF0YsBIRUcYIIRAIReELRubVT11JofqlGBz2x0pRdXoxniRAliUJG+sq0NLkwqY6B4yG/BqFlKdyUadHUmWd1nslWg4GrERElHaaEPAHVfiDkYRT/kstVL8UE/4wXjs5hLYOL057fUmPXesuRWuTG+c3VKLMqv/yU9MkAEaDPBOg5luATbQUDFiJiDJMCFE0C7CimjazTelihf6nC9UnSwtYSkmoiKrheE8sL7Xj7eS7T5WXmtDa5EJLsxurKqwpnV8P5JndpWKBqlygryOiuRiwEhFl0PGekaIocRVRNfiDEQTDUaS6IdVMofqXe5ddEkqbqt/a1u7B613DSTcaMBsVbF3vRGuzC+tW2/Mm2DuXi8pRVCpeDFiJ8kwxjdYtJB/uf7qNb5waxgvHBmBQ4ssGDU+E8NAzndi3pzHvg9ZgSMXweBD+oLqs32+oKccVu+qWXBLKOxpAW4cXbR0ejE4mHqGVJKBpbTlamtzYss4BUx4sPppbF5W5qEQMWInySrGM1iWSD/c/u41nRwKIRjUoigx7iRGWWXU7NQEcPNSHTXUVugu4FzO9kCqkRlGqihVvn5pqSSh/MDKTl9p3djLpOVdXlsTqpTZWwl6i/61EDbIE09QoqmmBuqhExY4BK1GeON4zsuCWn4U0WpdMPtz/7DaGI1FEp8o3RaMaRiZDcABxQevwRAi9g5N5U681qmnwT+WnagJQlPQFVYlKQqlRDW/1jqKtw4O3ekfnVRqYzVZiREujCy1NLqyu1E95qYVImK6LGstFNSic6idKhgErUR4QQiTc+hHI79G6VOTD/c9toza3sQIY90dgNilxbZwIJK9DqgfLyU9dCSEE+s5Ooq3Di9dOehEIJR7BNSoyzpvKS21YU67r6XNFPre7lMnIUVSipWDASpQHegcn46bBF6K30brZuaYVZWZUVKS20nsh+XD/c9u4UOAUjWqIqBpMxnN5lDarfqerg2EV/qAaV2BfCDEzdW8rMcJuT98K++HxYKxeaocXQ+PBhMdJANavsWNHsxvnrXPCbNJnXup02SmLSeEoKtEKMWAlygOpjsLpZbRubq6pJAFVL/XistY1aF5bseTz5cP9z722yahAUeSZtIBps6e0nTYz6qrKstK+VMXyU1X4guq86feT/WNxi6MkCag8MoCLtqzCumr7sq4XCKl4vSuWl9pzZiLpse4KK3Y0u7C90YWKMvOyrpdp08X7zVNBar5UIiDSOwasRHkg1VE4PYzWJco1HRoL4D+f7sQHL21Ycq5pPtz/Qte2lxoxMhHC7Hl0ZWrkVZaAvTtrdTMtPDc/da6T/WMLlp8anQjiiZd6cMU76hKu6F/oWu19Y2jr8OBEzwjUaOJEg1KLAdsaXdjR5MIaV6lunq/ZDEpsqt9iUrgFKlGGMGAlygN1VWVw2sxJp8X1MFq3eK6pWFauaT7c/0JttJgMcNiAcV9kplqA0SDrqrJBKvmpQgi8cOxMwn4VAnjh2BlsWGNP2K9CCPR7fWhrj+Wl+pKUwTIoEjbVO9Da5EZzbTkUWV9T6ecWTCkwm2TdtY+oEDFgJcoDkiRh787aBUcuAf2M1mUq1zQf7j9RGy0mAywmAyKqht1bq3HeOqcuaseGIlH4ApG4/NREBrz+pLtRAcCYL4wBr3/eSv/RyRCOdHjR1uGFZzSQ9Bzrqm1obXJh64ZKWM36+vM0vcOUhQumiHJCX58IRJTQ5noH9u1pTGsd0nQX4V9KrulC1waQsD2ZuP9003sbhRAIhqPwBSNJp+Hn8oUiSzouFI7ijVPDONzuQffp8aSVBSrtFrQ0udDa5ILTbkm5TdnAHaaI9IMBK1Ee2VzvwKa6irQEmZkowp9qDql3NIh7Hn497tpGRQYgEInGL0qa3Z503n+m6LGNmibgD6nwh9T55bZSUGo2LnqMEAJDo0G0tXfije5hRKKJR26tZgXbGmJBau0q/fSfJAEmQywXlTtMEemLJITIRlm9nPB4kq84Jf0xGGQ4HKUYGfFBTWGqkpYn0cIoIDa9vtwi/EKIeYEoEAsEDIoMNarF/leNQuBcMBAMq7HFSQAcZea44voraU+xU6NTC6nCKlbySS+EwC/+0D4vLUCSYqW6JgMqgmE16aitIktorq3AjmY3NtZV6KbEkyJLM6Oo3GEqhp/DhUnP/ep2L54iljcjrJ/97GfhdDrxrW99K9dNoTTIh/3gVyKb9zd9rXF/GL5ABKVWA+wl5oTXXGxhVFQT+J/nu6FGNdhLFp+qn22xXFMJEiAEBCQIIRBWNWiawNhkGEITkCRpXnH9dG8KkMvXXrquLYRAz5kJnDw9BgkSNqyxo77aNnOuiBqFL6giGF7ZlqnTJEnC7q3VM1UCopqGQCiKQFBNOpIKALWrytDa5MK2hkqUWBYfqc206dqo00GqXgLnpSj0z0+iheRFwPr444/j2WefxQc+8IFcN4XSINlU9PkNlTlsWXpkc7/76WudHvLFrUS3lxixxlW64DWTLYwKhlSM+2Pn+c0fO2AyKjAqEgApLjBJdj+J8jhdFVZsqq3A/7b1x11HiNhIICQgttPn/OL66doUIJt9k6lrH+8ZwSN/Ool+r3+mxquiyFhTWYL3716HWnfZokHkctRWlaGxphyvnDibdIU/ADhs5lheaqMLror0bSywXNO1UU1T9VHzuTZqLl/DRLmk+5SA0dFRXHPNNXC73WhsbFzSCCtTAvRnsanoD7+3Ce9qrdXllEUqMjXVnuxa/pA6r9YnpNjUeonFMO+ax7qHcODZrnnnC4ZUjEyeO4/DFivMPjIZmvnZYkp9qj5upyubGS2bqvHcq334j9+fiLuOJgSis6aSFVmCs9wyb5X4By/dgK3rl/+FJpt9k6lrH+8ZwQNPnogFK1PnmvkIl4DyUjOueff6lOuhLkYTAt0D42hr9+JY9xDCkcTvSbNRwfkNlWhtcqG+2pbzoHC6Nup0oFoIsvUa1vPUMS2fnvu1IFICvv3tb+Oaa67B2bNnc90UWqFU9oN/6pU+7G5Zm92GpUk297uffa1xXwTzlmHP2rd+7jUXWhglhMC4P/48kgSMzTr3uC8SF7Audj+SJM2MiBqmcgPLrIb514GE2Q9EhcBCa11sVtOyp0Kz2TeZurYQAk+90jvTJ/PGGgQw4Y8sWg81FWdHAmjr8OBIhzdpOStZAs7bUInzNzixsdaR05X00wumCrU2ai5fw0R6oOuA9cUXX8ShQ4fw29/+FrfffvuSf1+WJa7y1JFTA+MYmQwh2Wfp8HgIXf1jcNv1ue1iMqnc38hkCP1DvmVvYzn3WhE1iqgWm06fK6ppiES1edfcUGNHpd2C4Ylze7WHVS3uPAY5FmDOfiyqaYio0bjRqlTvR5nKE5QVOXa6We2VEAs2xJyfZz+PlXYLghEVP3zkWFy7nTYL/mJXLbascya9fjb7JlPXPjUwjjMjfqjRqbzUBc6nCQ1D4wEMjvpR41raJgqTgQiOdnpx+C0P3vb4kh5b4ypFa7MbF2xyY/UqOyYng/O2oM0GgyKf2wa1wBdMZfM1PP1+VfIwv5cSy/d+1W3AGgqF8E//9E+47bbbYLEsrzaf06nPbfyKVfdZX0oLHMZ8YTQsY7/5XEv1/oSswOEoXfS4VK4VjmhTI5QLkxD7oz73mh98bxPuf+zNmVG6cCQad54KuxkQYoFzS/PucSn3o0kyKuxmDI2eCzohxT5A1Vn5mJJ07pgAf+kAACAASURBVDqSJKFl4yo8/KduCCHirj/uD+PAs12w2SzY1uhOeN1s9k0mrh1RNUz0jE6VpFrsM02CkBSUl5cses2IGsVrnV78+dgZHOsaSlryqsJmxoXnVePC86qxxh0fDJeVZad+qgTEFkuZDLCY8nPB1HLl4jVst+c+/5jSL1/7VbcB6z333IOtW7fi4osvXvY5hod9HGHVESkanQlKEh4DCeWlJoyPB3IyYrMSqdwfAEhaFCMjyUewUr+WgEhSll0gtqBp7jVrK0vwwUs34KlX+jA0HoSYOpNBlmEvNcFkkBGKRBc4t5h3j6ncj6LIsNutUCBgMshw2MwY94WharFzTU/nYtYdqVENlXYLLt+5Fn945W1E1MQr3h9+ugNrndaEX1Cz2TfpvHZoqsh/KBJFKBCa6o3Flh0ISCKKsTH/wv8qBE6dmcDhdg9e6xxKWknAZJCxdUMlLtjoxoY19pnP0+lzK4qMsjJLRkdYDfK5Ff0mowxJ0xAJhhEJLv67hSSbr+Hp92s+fg5TYnru11S+ZOk2YH388cfh9XrR2toKAAiHY3lUTz75JNra2lI6h6aJZRXJpsyocZXCUZZ8P/jKcjM21JRjdNSvu6TwxaRyf06bGTWVpSu+t9nXUmR5wQ8fRZFhVGQ4yha+ZvPaCjTVlE+VxArhiRd7EYzEghchYoX8Z59bUWQYDUpcPc+l3k+te6rdIgS3yYpwJApNE5BlaSbVwGpS8L6L6mZKc/UOTmJoPHl04h0Loqt/PGEVgWz2zUqvLYRAIBSFPxiBOuvzq8pRgkqbBeOTEWjawm2UZRmVdiuqKkriFrIBwNBYcCYvNVlbJAlorClHS5ML561zzvSLEJh3TiDWjmhUW+DflidZ2anYNYrzMz0Xr+FoVMu7z2FaXL72q24D1gceeACqeq50yl133QUAuPnmm3PVJFqhVPaDv/wdud0PfiWyud/97GvZS40LVgmwlxihyFLSa55bGGWDQVHi2i5JEuwlxpkqAfbS+Bqay7mfuc/R3NXbsgT81bvWx610Xsp2r6led6509s1yr60JAX8ggkBIXbiGrSThXeevhncsEFsINfcYCbCVGLF7a/XMffiDKl7vGkJbhwe9g5NJ21nlsGJHsxvbG12wl6a2Y1m6FFLZqUzJ5WuYSA+U25ezmikL7HY7KioqZv7705/+BJPJhH379qV8Dr8/tT90lD3uCitWOUowMORDYNZUpNNmxlW712PrhkpYrSYEg5G8HB1f7P7SWTZp+lqe0QDUqIaIKiCEgKLIqCg1YY2rdEnXXKjtBoMMp82M8jJzXBCx1PuRZWmmXyvtliU9R4FQFEc6vYte48LNVagoS7xYL5t9s5Rr/+WF9VjrLsW4L4KwqiUdP3ROPXdnR/zwh6IzOciyLKO6sgRXXlSP+mobTvSO4A8v9+HR57pwvGck4Ur/MqsRuzZX4ep3r8fenWtRX22H2ZR6CShZlmCxGBEKRZa8k5ZBlmA1G2AvMcJeGiuZZizwhVMrla3X8Oz3az5+DtPC9NyvpaWLL7TW7QgrFS497rWeTtm8v9nXSnWnq2Q21VXAYpTx6lseBCJRNK6x48ItVZAkKa33s5TnqK6qDE7b4lOh0ztypeu6y5Gs7FZ8X4VgNhrgtJuhRkVc8LGYhppybFizFac9PvSenYAECWtXlUITwJEOL359sAP+UOLC/gZFwpZ1TrQ2udC4tgJKFvP8TXm+w5QeFPrnJ1Eiut84YCW4cUD+0XNh40IX20GpC/1eX1zeao2rBB+4pGFFozcr7ddcFv1PVSo7EGmagD+kwh9S0zLCMTIRwpEOL9o6PPCOJc/zXb/ajtYmF7ZucMbV010JRZFQXl6CsTH/gjms04vpLFNBKhfB5gd+DhcmPfdrQWwcQETxMrGPeGwHpbdiNU5nxR3RqIbes5N44MkTuO6KTTkLChNt96qXLSkTBdTDEyE89EwnPnDxBtRW2RAMqSteMhQMqzjWNYy2Dg+6B5J/KXeVW9Da5EZLk2tm57JMk+XYDlOW6VX9HPkjojRgwEqURzKxj7gQAk8d6lt4IQ8AiNiOV0+90pvTXXT0OhWabAciTRNQhcDv/tyLT/xF87LbGtUEOt8exeF2L473DENNsiK/xGzAtoZKtDa7sdadnVrURkWGxSjBYlJgNOT/NqiZ+FJIRCvDgJUoTyw2irfcafHewUkMDvuT1uWLRjUMjgTQOziZsHRUNsze7lUvegcn475ACCEgRCxYne6qMV8YA14/1rhTL+guhMDAkB9t7R4cOTkEXyCS8FhFlrCp3oEdTS401VZkPD9UQqzCQ4nVgGpnCcYNku6mGJcrE18KiWjlGLAS5YFM7iM+EQinlE8Z1UTKJaaKyfRzIsT/Z+/dguO6zrPNd6197DO6cSIBEjyAoEhJlAlZVmL5bEeR/zhJlZ38MzWZSVUmU5ObeHLhm1TlSlWpTE2VysmNJxeZ1GRSsWPPxJby2/NnIp8SSZbkSLZASZQoETyBJAiAaKDR531ec7F7b/Rh9xHdQKO5nipbJLh77bX2bvR++1vf936u73OzS1nUmwvOarJFA29fS2Pp6iY2MuWWx85NR7G4MInH5scRUgb7ce5t9SsShSy51lOiSA9tm8cgBvWlkMPh7B0uWDmcQ0B9FC+I7bzeUwQ0FpI7KoYRKEEstL/+nMNAs+1h7+d37xdQ1kyIbbbCI4rU9N8M08Z7t7axdDWN66vZlnmuyZiCxYUJLC5MYjwx2JaookCgyiIUiY7EVn8rBvmlkMPh7B0uWDmcQ0A/zPObMTcdxXQqjJ2C0TQtQBAoppOhjqyjRolm28MLxxK4spLBVk4HYwzZognARDQsQpEaP1YTERlHJ8I1P3Mchhv3clha3sR7N7dhtNhSV2UBF06P4/GzkwPNp/S2+hVJgCK7nc4eFAb5pZDD4ewdLlg5nENAp5HNXiKghBA8/cRxrG+VGlwC3AOARETC0x+be6AiS0Hbw4wx3N0s4PLNLcTDMhRZBCEE0ZCIXMlArmggHkGNaKUENd2nNrZLWFpO49K1NHJNDP3d1xGcPT6GxbMTODeXhCQORjzyqn6X+i97QW2Dg47jcDj7AxesHM4hoJ/m+UGcP5HE7z/zEF545QZWN/vvw3rYqN8eZozBdtxiqlzRBBhQKFuQJQGEECiyiDjcnxVKFpSE+9GaiMh46tEjmEqG8Oq7a1haTuNeutjy3McmI7hYyUuNhpqnEewFUaiI1BGp6u8H3pc9zbCQK5o1uw2CQBGPSFBl8YFMi+FwhgEuWDmcQ0A3fcTrcy6PT0Vw534RuZKOYtlCJCQhHm606jk3N4bf+8ICrq9msZ3XkYrLmJ8Zw4kjsY6ibv2wAmKMYWU9jxv3cmBgmJ9J+OfvZvy9zuX2RgFbOc2t9q9U/QOAadlwHFfIOI4Dy3Z8wafIImRJgGk7eOLsJGYmIsgUdPzsnTUs391pmhsJuMJ2cWECFxcmMZUMdTzPbuBdplozNx2FJFCs5fWGXQbbdpDJ65iblh+4tJgHCW5nNtxwwcrhdMhBf5h1Yp5fn3Op6RY0wwalgGY4sG3HjxbNjEeavs4bd2aiM7HaDyugVp22PvrQFK7e2elo/PdvbeMHr95CpqC727kixXhc7XgujsNwf6cU6HXquSkw5lpWlQ0bDK4PqXedGAOu3M7gxTfvQDebt1xVJAGPnkph8ewETh6Ng/b5vVSdj6rKvMtUZ7RxyxjdxpAPPNzObPjhrVk5Q8Wwto4bpg+zZsK5PudS0y1kCjocm8FmDAIlu6KIuNXmYUXEk+en8caVjZ7bnnbSNvXC/HjL+9qs0xbgRjgBYDyhNrQUrZ/fi2/cxg9evQWrfjs3LCGsii3XYloOSpoJzbCxulnE86/cCDjGxnZWg6dlRUpACABCIFICw3JgtwilEgIsHEtgcWES508mIfd5O54SVAqmBN96apAM6+9rL6ys5/F//esH0HQLuVJASkBYgqqI+IMvnhv5oqtRuq+dcBhaP/eDYb6vvDUrh9MHhs2bMcg8PyjnMlcywRxXrIK5PqpUqAiYSi6mIgn41/+4jbEmbTvbWfl0agX06OlU0/W067TlCcBswYCaqv3Iqp7fByuZBrEKVLZzC+4XjaC16IaNombWVOkfnQgjEZHdOVWfz2GoDrw6jIE5AANDK5fVo+Nh1y/1zDji4f7mQIqU+Fv91cVBnO7wiqlURYQiCzAsB47jftGTxN0IOi+6Gi24ndnhgQtWDqcFh+XDrN6Sx7Dc7X8G7IpA5u5oetO0bQclzUJZtxBWxaZip5WVT6dWQCsbeaRSwbl/rTptOWx3/pbtwDDthnl6438/QKz6MCBXMqHkNNzeKGBuOoqybqOkmbACbi4hBE89egQvvnG75ktAvmSCEvg/a5WXGgtLuHhmAhcXJnB0vPMOV/6UGcNauoSibiKiSDg6EQYhBASAJFKolSgqz0ftD9XFVIS4RWntjuMcfrid2eGBC1bOSNKvfNPD8GHGGMO11R2UdcvP2fQ7V9UJKgYGV/K4eAKvXaerZlGljv1hi83jj607bbGaPzY77sZqDjuF1vfJrgje+zslhBShpdgEgPnZBJ55cg6vvruGdFZDoWy29Er1eOj4GJ66cATzM4me80avr2bx2uX1mghvKqbgCx89hgvz4wPf6n8QGbQTB2c4GaTHNae/cMHKGTn6mW867B9m3lrXt0vYqaxXEChCciU6VKdrSN0PvOhcO2HVLKrUsT9spLk9U+tOWwS+aCUt5klYyzV4qfqG5UAgtK1YBYDtnIZb63ls7pSxlWsthiWRIqKKUGURT104goVjY+1P0ITrq1m8+MZtMLjrpcSN+OXLJr7/6k3IkjAS+XTDRjdOHJzRYZAe15z+wgUrZ6Tod77pMH+YVa9VlgQIAoVtu6kA+bINSggIw67mI7vpAIArbMOqCNNyWuY+tooqdRqVOjHdPPp8fCqCeFjGdk6D7bjCwIMSwK78XRRo4DxTMQWnjybwirTuXwOP+prSRLix41Q1Zd3C5RtbeGs5jZX11kWbokAQUkSEFRFC1bZ8qxasrSDEdRt488oGKCWBwmhYUlBGlU6cODijBY+sHx64YOWMDIPINx3WD7OgtcYjEjIVD0kC4mpUQiAQwIZbPOJD3OMFSvDFX5lr6RLQKqq016iUFyHeKeiwHdec3wZqHA28eSeijV8KvPFPHIkhFVOgGRa2cwHdugAIlOJzj882zMV2HCzfyeKt5U18sJIJtLPaHYNAlQWEVLHGysojqAVrKyglUCWvYIri9kYB2ZLZ8v150Ckoo875E0mcmxvjfpwPCDyyfnjggpUzMgwi33RYP8yC1qrKIpIx7HbpYUA0LMG2WVsf1rnpWM9RpV6jUtURYlURMR5XsVPQd62hKCCJAuY69GH93OIsvvvv1xCPyCiULN/gH3DF6uc/Ooszla16xhhW00UsLafxzrU0iprVdH0CJTh/MonHFyYhUIIfNflSVN+CtRmSsGvgX99uddhTUB4Ugpw4OKMLj6wfDrhg5YwMg3rYD+OHWbM1qLKbR+n1QX/6ieP47OJMYKcrrwPW5ZtbiIVk/PGXH8Wd+8WeokrdRqWCIsSqImK6YidkGDbCqoj/8T+dw8mjcRBC8OsfOx44vmZYKGkWJsZCePpjc3jt8joUyah0pWJIRGR8bnEW88fGsFPQ8fa1NN66msbmTrnlmmSRIqSKiCgifuX8NOZnEwDcqGh9QZTXgtU7pppuDPyHOQWFwxlleGR9+OGClTMyDPJhP2wfZu3W4OV6zs8mQCmtRIt2I0ZXVjL431+43CDAv/DRY4iFZOTLhm//1Okau4lKNYuGe3ZCnqUQpbvb7tXjOw5DUbNQ0q0a54D52QROz8Rr7KCSMRmvXd7Af/2P21jfKrWcl0AJwqqIkCLW2EW9dnkdp2dc4Rx0Ds9yyoMSt1WrIlEoknDoU1A4nAcBHlkfbrhg5YwMg37Y7/XDrJ+tXeemo0hGZaxnynAc5ttZVY/XbK3NCtPupYv46xcuIxaR/I5S/Y4iM8awsp7Huze3oJt2w5zrqY8km5aDkm5B062mTTQJIZgeD+P6ahb/33+s4MZarmVHTUUSIAgEYUWsMYivJls0sJYuYWYy4p/D+7OHSAlkWYC6BwP/YU1B4XA4nIOGC1bOyDDMD/t+t3b94PYOCuXaAqPq9pHN1tqsMM1r4+p1wPIEaz+7eb1zbRPf+8kytnIaDNNtcVo95yBiIRmMMWiGjbJutfVBXdty81LfXk4jX27Vewo4MR3FJx+bgUCBH/9yte38i3rjeF4+qir3z8B/GFNQOBwO56DhgpUzUgzjw75Xq61mEdnq8ZIxxS+y8lqQzoUlfPnT84FjBm3Fe21cPeFr13WU6tVKqXr+2zkdr15eh2nZAGptuDIFHUmgQbQmozJScQWbWa1lY4NcycDb19K4tJzGWpstf0mkCCvuln9YlfDwySTW0q1f4xFRpJp8VEWmEOhgukwNWwrKftLPnQgOhzM6cMHKGTmG6WHfq9VWs4jsFz56DD/55V1/vPoiK0oJYmEZ5+aCjeuDirW8Nq4186qbcLfuCtXzZ4zhfsYtcApV+rTLIq2x4cqVTCiym+vpMLeH7BPnpppW7xuWjfdvZXBpeRPLd7Mtt/wFWvFLVWvzUr1t/qMTYSQick0RVT2pmIKHTyb9Oe4H1SkoD4qI6/dOBIfDGR24YOWMJMOSPN+L1VariOw//vgqbIf5W/Ye1TmTrcRlULFWUPQyqJK9U3eF+vnnyyZ0042s6qYNgRJIooB4WPIjxJZlQzdsiAJFvFJxf3qmtuLeYQw313JYuprGeze3/TGDkEQKSXCr/FvlyRZ11/P0qUeP4MU3bvtzJgAIBSghECjBf/rVE03TFgbNlZUMfvSLO9jYLvlfSqZTYTw9YiKu3zsRHA5ntOCClcMZIN1abbWLyFo2Q75kNgjWTs8bVJhWL06FJh2lOnFXqJ+/plvI10UubYeBVlIBxiIyxuMKdNPGY2fG8dCxZEPF/f1MGUvLm7i0nG4ZBaUEWDg+hsWFCYxFFHz/tVtt5+t1pZqfTeBLHz+J1y6vIVs0/PMfdHTvykoG//Dih8gWjZoo+E7BwPpWCb//zEMHLloZY7i1lsNOQe9ZMPZ7J4JHZDmc0YMLVg5ngHRrtdUuIkspacgxDaJQMn1/1WoBUV+Yxhhz25cSwKm0RY1HGluLduquUD1/PzfW7w2Lys/dqC4hQLZoIhWnkEQBDx1L+pX3hbKJd65vYWl5E6ubxZbnnJmIYHFhAo/NjyMWlv1zt9vmT0RknDwagyqLUGSKI6kwnjw/NTTROsYYXnj5BrbzjZ27bNvBdl7DC6/cwLm5xw9sju/f2sa/LV3GxnbRT8voRTD2eyeiX4WCHA5neOCClcPZI622JLu12moXkZVFCkGgTYuQNMOCptv41zduN40SeoVpL7x8HavpMmzbgeMw2IxBEBtFcDfuCtXz93JjKQFsoCbPlIGBgMBxHFi2g4lECBNjKt69sYWlq2lcvbPj5rI2IR6RcfHMBBYXJjCdamyFGrTNv/tvrgXVlz5+Aqm42vC6YUglAYCV9TxW08XANrMAAAasbhaxspHHySPxfZ0b4ArG7710vSFC34tg7PdORK+FghwOZ3jhgpXD2QPttiSDIpqG5fi5iKpEa8Rgu4gsIQTxsAQhwEJJMyxk8jqSUaXmId1MQNgOw1hU9ufiOG5ENJPXkYy5BV3dRsuq5+84legtXNFrV4kLAnd+jDHopg2HMfxv33oLmtE8L1UWKR45lcLi2UmcPhpv2TEKcLf5n3lyDq+/t45cyd3mJwDG4+qh2DK+cS/XUAxXj207uLGa23fBuisYGSga70O3grHfOxFA94WCHA5nuOGClcPpkeotyWohumba+Kd/W8Z//twCzp9IBkY0AXd7fyIRws21HEKyG9nMlXSAMbeDE3OFnkAJGNwIJaUER8fdgpsf//JuzUNb020kowpURWwQxrJI8eNf3MFDxxO4vVHA8y9dR9moNe43TBuxkAiHuf6iD8+NIRlXEJIFOI7Tsm2rF2XOlQwoIsVOUYduOP4aKCUgBLBtVlkLg+24wcNc0USuuBN4jQmAoxNhPHIyhacePQKlTe6uhyy6ebi/8vA0Pv7INN64ch/pnIaJuIonz0+BDsiOqp+wpqHVOkjr4zotSuqmeMkTjK20aDeCsd87ER7dtmE+DHRynwZRiMaL2zgHDResHE4PVG9JarqFXMmsiYYJAsULL1/Huf/ho/6HenVE07QdlHUb9zMl/PMrN/CDV11RSuAWVtmVvU4v+5MQQCAEVCCIqhJACL76lQv+A6RQMv00gGbzyRcNPPftS8iVDGxlNf/nqkyhGe72vcPcczMGrKWLbiSXuAI2Gg7ugOVFmbdyGsqGhWzegGG5qQAOc9MBBOpGhwl19ZXdRosJlegpAcNWVsdbVzdxd7OIpx49gvnZRMPxnj+qKrseqV70NSgC/uYH9w9FhHV+JuF71TZDEChOH228Hh6dFiV1W7zUb8HYbdOPQbZhHmY6uU+DKETjxW2cYUB49tlnnz3oSQyKUmn0vl2POpQShEIyNM1saRZ/0NzeKOD19zf8DlGsbq6MMWRLbiTixJEYvvOTZZR0G4JAYdkOciUDzGFu7qjDYFX+bFXEYhAMQDwsQRIFXFnZxlQyjDPHEphKhrFT1HFlZafpfGzbQdmwYdtuxNXbercdVzgzx43nWVVK0o+E2q7A1gwbskQhChRlw8aVlW1oho0fvnkbBc1ESbeQLRgAcwV29RQYQyUS3TwlkxBAlQVEQiJMywYlBIQQN23AsmHZDlY28kjFVaTiKihxmw3EQhLiERmhutaqXgS8pNemGXhzn0qGMTkWanerD4xEVMbb19LINvscI8DxyQh+86mTgZGuTtffy3Uq6zYuXUuDVKLnzfKNf+X8NMaiSkfrnRwLYSoZxtpWEeWq1JBUTMFvPnWqRhglIjLevbFVc1w9qZiCpz82Om1sO7lP6azWl/d89efweze3D/XvEWeXYX6+RiLtPyd4hJXD6YF82WjoENUAA169vIaTR2KNlfOVNAKb7W78Vg9DAv4uUgLNcBALMzggNTmCXgvToPl45wEDyoYFVdn9YLAd9+c2GFhAIM9xDQTcYxyGXNGAKrspB5YD/MvrK4iGJRBCUChZ/roA+BHWdoQUASFFRKFkgjFXDJH6vEgGFMoWFFnAG1c28LFzk5Cl5h9f/SzKOaitUEIIvvzpefzDix8gW2yMmCcibkezZtv7naz/oeOJnq6Tt4WfKXS2hd8pnTb9GOY2zIOgk/v5ozdvA4T0tRCNF7dxhgkuWDmcHoiF5MAOUfWUNAs31rL+36tfw/z/a6RerHo/s20HpuVAloSaHMG56ShCshg4H/88ZLdJgCBQWJaDQLUc8HpPtJqmg7JuQRQoTMuGZlhQFTf/1rZtOKwzkSqLrql/SBZBKYFp2WDMjTIzMNCAh5/jOGCVrlhrW+WWuZH9Kso56K3Q8yeS+P1nzuFHb97GeqYMx2EQKMF0MoSnPzbXdA6drv+NK/d7uk6eYPzeS9cDX7MXwdipU8MwtmEeFJ3cz/VM2U+NaUa3hWgr63le3MYZGrhg5XB6YG46iogiYrvFMb4BP9t9aNdsw3S4I1MtGEHg57cCuzmChBBcmB/HzfVc47iV13l5oY7DEI9Ifh5rJ1PZ1bUMtu1ArFhrMcZQ0izopg2rtXaHQAlkiSIWlmtapHpz8sbfXTD8tXl4a6/PjayPguZKrR+yHq1yLIfF57OXVsOd5o6mc1r7g5qMd/5EEv/N58/g3y/dw/rWrlfufgv6YWnDPEg6uZ+OwwL8Gnobyz+2ZHZ23AgWt3GGDy5YOZweIITgExeO4js/XQ5We1UG/Kdn43jv1ja283qtFVOHz1RS9wehaozqopJHTqbwyjv3kAvYPobj+FFLSglkSUAiIrvRE9aYgtB8Lm61v2ZYKJZNWA5gaVbL16iygFglbQBgDWLVm5M3PiiaCg5v7dXrDoqCqpIATbfatlNtVpQzbFuh3frDdlpsNFHnQ9vteA+fTOGpi8dw6cr6njpd7YVh8s4dFJ3cT0obEml6Hss/NtzYRGSvY3I4vTL83i4czpDymYszmJuKNXiiCgJFMqb4PqYnpmP4tSeOg5Jd43+goj8rTxiCWv3a8OAh7s8EgUIS3dfX5wjOTUcxMx7BVDKE8YSKZEzBeELFdCoEqdIQoLrtajQsQ5UFd0yJQhbbfxwwMGznDGzndOhm85AqgesMIIvutZAlAUfGwxhPhGBaNnTDcgurKIEoEIRVCaIoQJKEQEHrzV0Sac26vSho/balZtrIl0xoenMx3SrHspuUgmHEyzFtRSqm4MnzUx0d1yoXlRCCk0fjePTUOE4ciY1cdHMY6OR+HkmGAptoVNNtXvGJI7E9vz84nH7BBSuH0yNuUcxpHEnVCsSpZAiqLNbk8Xn5duNxFfGw5ApQQiCJFKJAaqKmQQiEgFC3aQAhJDBH0MsrpKRi8aSIkCXBbzZQHfX1iEdkEMKQCMuIRaS287AdNK0IFwUCSgGRen8mfmSVEODsXBJlzcJOQUeuaCBbcO21dNOtPk5EZCQiEhJRuVGxE9chQaDEX3e7KGgsIiFfMv0isGra5Vgedp/P6vdCEN76KaUdHcdF6MHSyf18+mNzeLrP97LT9xF/f3D2A25rxRkqhtl2IwjPiud+pgzTZn70NMiKZ3IshCfPT2Hh2BhScRWm5biiUqSwHAZSEXqkImYF6gpaKhCIooCxiAxVEQPHrp9PvTXQVDKET144CsN07a0Yc+2zklEFj5+dhGE5sGwGSSQwLaejwilvnedOJBFRRSiyaytl2e78Y2EJiiwiFZNxcWECl5bTcBiDJFCYNqvMgUEzokpRaAAAIABJREFUbKTiKv7bzy/gI2cmsLlThmU7MC333wWBYiwiY2YiUrNuz1qsGaJAIQiug4JVtaBW18/Ds21qRze2TftNpzZR3dhJ1XPYfl8PM53cp73cy2qq7+t4XO3LmJyDZ5h/XzuxtSIsKPwwImxu5g96CpwuEUWKZDKCTKboVrEfMIPoEhT0mqjqRj7zZQPFsoWIKqKoWYiERMTCsmvrpJk9jV39Gk23cG01i0xBR0SRcHQiDEIIbNvBLz7YxOVbW1hZL8Bq4X6gSBSPzU/g8bOT/riMMaylSyjqJiKqCFkUYFg2UjEVc9NR/PU/v4dcyYBlOdBNu9KkwP0A9are/5ffecwfy+uaVSybiIRExMNKw7ov39zC91660fI6AMBXPn0a8bDc9b35xvPvtu289NWvXBj66NIg38PD9vv6ILAfna6C7ivvdHX4Gebf18nJ9nnovOiKw2lCdTGP1+o0ooj4xIWj+MzFmYbt+G4LPwZZLFI9tmnZuLKSwXZeQ1h2RepExeh7Y7uEpeVNXLq2hVyx+Y4EJQRnj49h8ewEzs0l/TxaD4ESzM/GocoiZInWXBvXGkeDYTnYyek1YlgQKOIRCZmC4VvjdHpdOi30iIflnu7NqPh8dno9H4TipVGgk/s0iHvJ3x+cg4YLVg4ngGpLo+pWp9sAvvPTZbx2eR1f/vTpod0OcxwGzbDw7o1tvPT2PWxlXQ9PSgkSUQXjcRV37hdwL11sOc6xyQguLkzisflxREO1+a+UAIokBIrUavJlA5puI5PXweq8CGzbQSavIxnrPh+02/7z3fIg+XxyOBzOsMMFK4dTR3Uxj9fqtEZnMWA1XdxXL85O8PJBNcOGYdq4tprFf/nZTeRLJmzb9tujbu5ouIZs03ESETfndPHsJKbqWi4S4lpGtROp1URVqWX0FgzIFc0GQdyO/YiCPig+nxwOhzPscMHK4dThWRq1ar1q2w40wz7wtoReqoIrVC14GemMMfzwjdvIFDQ4DtAuU12WKC6cGsfi2QmcPBqv6TRFCaDIIlRJ6FikNsyzbwfVsh9RUL4VyuFwOAcPF6wcTh3e1nS71quOww6kLSFjDIbpQDNdP9P66GJ6p4yXL93Dnc3W2/0AMDcVxccfPYLzJ5OQxd2WjpQSqJIARRagtGj12AkFzUQ8ImEn3yTKWrGsKmidddWph0dBORwOZ/ThgpUzlDDGsLKePxAB4hXzBNl+uD9ye4d63Zn2w4vTF6mG2wa1fmolzcQ717ewtJzGnfudm9nrpo1oSIIsChAogSILCMmC32igH8RCMkKKCIFS7OQDiq7CElRF3FO3HB4F5XA4nNGGC1bO0PHOtU187yfL2Krqc76fhS5eMc+aues56DDm9rH3hCJh2CkYiEekgbYl1E03JzUokmrZDj68vYOl5U18eHvHnV+XlA0bP/rFHcQjMi6cHu/TrGtxr6eKXMmAJBLopgPHYb7PLCGEd8vhcDgcTku4YOUMFe/f2sb3XroB07Jrfr6d1/etyMkr5vmnf1uGIFCYll0nVl0bJ9t2kC+aKPa4ld0MoyJStQCRyhjDnfsFLC2n8c71NMq6HTyIvxY3B7VZZkNYcTth/fvSKh49lRpIFJsQgl9/8ji+99INEEIaUgyG1SJqFH0nR3FNHA7nwYALVs7Q4BYK3QlspQm42/H7VeR0/kQS//lzC3j+peu4sZZrEKuUEIAAsbCEn/zyLs6fSO5pTlaliKusW4GR0u2chqXlNC4tp2siz/UQAKdn41g8M4Gfv7eOjZ0ymAPUVzQRAJJEIVfE46BzcR8+mUIspuL5ny4jnT2YyHk3VHvwegzrXDtlFNfE4XAeHLhg5QwNbnW+BlGgTY/pt7BqFXE6fyKJ//7ps/jGC++iWDbhOG7EEqjNvex1Tp5Xalm3YQaEQMu6hcs3tvDWchor6627tk0lQ1hcmMDFMxNIVFqFjsVU/Jef3UC2oAN1w3vyVTdtqLL7MTDoXNzHzkziWCqEG6u5oY7wVXvwVrOfUf5+M4pr4nA4DxZcsHKGhk4FU7Pjut3urI446YYFw3QQVkV8fnEWn1mcBSEEBc31B5VECsN0VZ9SiUxWj50vGx21FLUdB7rnlRrQGs92HCzfyeKt5U18sJKBZTfPS5VFitnJCJ54aAofOTMOSikIAFkSEFIEfPyRaSRjCr7946u4W+cYIFICMPim/aq8W/Q0yG3jYS+OqvbgDWI/o/z9YhTXxOF0Ak+BGS24YOUMDZ0WLwUd1+12pxdxKukWMnkdpuX4Au6bP7qKn7y1it97+izSOxo2d7QaeyvNoIiHAVXZ/fVJ72j4xvPv4t5WEbmi2xXLi8IeHQ/jUx+ZwYnpWKBIZYxhNV1081KvpVHUrKZrF6ibA2pYDhzHwZ2NAu5uFvCzd+7hdz87j4+cmfTdCwDg3NwYxuPK7hrcTIbdD+2Kaf/MeARz09EHftvY8+BtxUFYme2FUVwTh9OOB/2zbBQRnn322WcPehKDolQavN0Qp38kIjIu39iu2DYFh4NSMQVPf6y2QGdXfNYWIJUNG1dWtjGVDGOyqmMTYwzf+ckytvM6trIaLKvxXIWyifdvZbCynodu2jV5tYwxaKYNSaAQRQpJpLi5lkWmoLvtRx0Gxhgch6FsWNANt+tUIqogFVf9cXYKOn7+3gb++ZWbeOnSPdy9X3CFcwAnj8TwyKkU8mUTZcMCYwy240bHHAcoli1cupaGLAk4M5vwX3d7o4CfX7kPUSDQLRsEpCHCwMDwhcePQTPsrq5jN1BKEArJ0DSzwS7Mi4Lc3SygrNtIROQDi4Lc3Szgykqm7XHzs3FMJcP7MKO9M8g1tbqvnMPLYb+v3T4THhSG+b5GIkrbY3iElTM0VFeTBxFUTd7LdqcXccoWjKZWUA4DsgUdiiwiHpYC27PmSiZCigAwBgaCbMEAayjrBwplC7Ik4LXL65idiOC9W9tYWk7j5r1cy+ZO43EVi2fdvNRkTME//PAqimULjuOK1XpJZ1gOvv+zmzg+FcXDJ1MAdtMnVEVEEu6c7QAf1PGEeiDbxsMWBdlLlH9YGcU1cTjN4CkwowsXrJyhottq8l62O/NlA4Zpuwb2LRSjwwDLckApQTKm+Fv91ZybS+LyrW3oht20K5Zt2yhpJnYKOv7Xb/6yZV5qSBHw2PwEFhcmcHxqN99qY7uETE6D4zhwWKNYBQAwwLQd/ODVW75rQbUIURURiuylE9T6oBbL5r5vGw9jIZDnwdvqWhw2z9hRXBOH0wyeAjO6cMHKGTq6qSbvpVArFpLd7ZA2OyIE7na54zCoighVFl0Df4cBhEAUKGzG4DjBXbEYY+6WPQOyxeZerQIleGhuDIsLk3hobsx3SaDELYYKKSLS2fLurJqkS7gnBTKF3Q/jerES5IOaiimIhDr7KOiXk8CwRkE8D94gIQ0Mr2dsK0ZxTRxOM/ZavMsZXrhg5QwlnVaT97LdOTcdxVhUaeln6s8DBIS4gtRhDJRS0CrXrWTFQsordKoWqe04PhXFxYUJfGR+HGFV8n8uixQhRYQq7zoRxEIyKCVgHahsgRL/w7idWDEtB/OzCRTLzQu9qunXtvEwR0HOn0jidz97ZqhSFfbKKK6JwwmCp8CMLlywcg41rbY7GWMwLAcRRQRjbiEUIW7R0W9/4iS+8fy7sB27MdJKAAr3x1QgoJQG5romIjIemx/H29e2sLFjwXJYy+An4Arciwvulv9EVdI/Je6WfVgRA31o56ajmE6FsZ3TYdtNulsRQBTcIrDqD+MgsaIZFjTdhioLePOD+2CMIVswoCqC78va7jruhWGPgpw/kcS5ubGRssQZxTVxOPXwFJjRhQtWzqGmWQRR0y23wMhxwGIK/v7FD2uiSedPpvDbnzyFf37lBgzTqdGsAqlUUyoiZFFoOCcAEDCcPBLD8y/fxI21XNPqfvdYIKSK+OzFWTx14YjbJauCJFCE1dpoarN1Pv3EcaxvlXA/U/KFcfW8RUKQiMgYj6sNH8bVYuW9W9t47fIaEtHdanxCCFRZqPFl7eQ69sphiIIMu2dsL4zimjicangKzOjCba04Q0UvthuTYyFMJcNY2yqibNjQdAuZgg5KCMaisi++6i1N5mfiODYZxZ37eWimDQoCgRIIgoAj42H81lOncG4uic2dMnTTjWqalgPLclzbq5UM1rZKTedJCRAJiTh1NI4vffwELi5MVCK8QFgREY/IiIYlv/Cpk3XOTERway2PfNlsCAyLIkVYEfHlT88HWraQiqB98Y3bMCyn4ZyiSCEJFJphQ1XEjq9jJ9Tf10RExrs3tlA2mkSLEWxhxhkuhtkmh9M7h/2+1j8TPFIxBb/51KkHNgVmmO8rt7XiPDB4EcSV9Ty+9eOroJRAlhqjo7bD8OIbt3EkFYJhOTgyHsEff+Ux3Nss4vb9PAgIjk9HMTMR8YXSdDKEV95Zw5WVTI1zQRCTYypOHY3jSCqEVFxFVJVxdCIMQkhgbmqneF6ltuPg84/P4r++voJ8yYTjuP5WlBAIlKKJf4BPu9xRz0ng1584hp8urTa9jnstiqqPgnhpB47DQCmBKlEeBeFwOD3DU2BGDy5YOSODl59q2axGZLl5l4BT+W86q+HmvTxmJiP+62anopiZjGAtXUJRN3Fno4BsUcfS8hau3tlp2sgAAOIRGRfPuHmp06la4/V2uamt8ETqe7e28e71LWiVBgabO65oTsUVUEp8keetuZWQ7CQnlBCCkm41XMd69loU5eXWvvDydaymy74tmCBQRCciPY3J4XA4HjwFZrTggpUzUniCzKvW98SqB2MMpu3gw7tu5x8v+nl9NYtX313DZlZDWbdQ1q2WBVSySPHIqRQWz07i9NF4TTtU79/ro6nd9LX2DPXvpYt+0wJBoAgpgi/sMgUdyZhS0yIWaC0kO80JJW0itR79KIqyHYaxqFwjvE3bOTAvVg6Hw+EMH1ywckYCb0uZgjQtgNINC4WyBcdxcGk5jfduZpCIyJhKqnjraholzWra+QoACAHmZxJYXJjAI6dSDdFHQoCQLCKsNkZTu+no5Bnq2w5DrmT6lVW27SBXdPOxKCFut62i2VDVDzQXkp1W0J6eieOVd9eaHuOxl6Koai/WQaQd1J+Lbw1yOBzO4YULVs6hhTEGw3SgGRZ004bDgGRcQSIiI1usFWy6YSFXMgAGUEohUIpi2cTmTrltn3VFovjc4iw+sjCJRKRRoEmCG00NKcG5qd10dKoWcYblBHbPsh0GKrjnsW0Hhmk3CL5mQrLTCtoTR2IDt4bZLy/WYWv/yuFwOJzu6S6pjsM5YBzGUNYt7BR03N8pI1PQUTZsX3wRQvDUo0dQvUPPGEOhbIFVzP8ZY1jfLiFbNJpGYykhiKgiJsdUpOIqzsyO1YhVAiAkCxiPKxhPqAirYqBY7bSjE6vkH1SLuKAqTu8M1ekK9ce1E5Je7mgqVluVmYopvnj2hC1tEoTshzXMfnixel8W6oWx92Wh3ZcVDofD4QwHPMLKGXpsx4FuONBNG4Zpt+v1hPnZBJ55cg6vXV7HTkFHSbdgWrui1naae6aGFAEhRYQi1UZLi7rbWlWkBCFVREgWG/JWg2gVRTRMG47DsG7aWNnI4+SReI04CxqfEAKBuC1jvTzT6uM6FZKdVNAOujvSoL1Yh7X9K4fD4XC6hwtWzlBiWg6KZRO6YcMM2BZvRyquYnYygrWtIrKF1hE6AlfoxaMyQooUeEwqqiIVU1pWzQcRFB3UDAu5olmz3f+tH17FVz4zXyPOZJFCEGhDWgClBNGwhLLu5rN6c+pWSHZSQTtIa5hBd6QZ5vavHA6Hw+kOLlg5Q4FXNFXSLegOsJ0tw7a7MzbWDAuXb2xjaXkTN9fyLY8VBVLJOxWRLRhwHKehUIpU/E3H4woePpXsSaTVRwc1w0Imrze0gy3plpvP+pl5X8QRQhAPS75LgIcgUMTCMuJhhk9/ZBYTY+pAC4kGZQ0z6I40w97+9SDhRWgcDuewwQUr58BwHAbdtKEZNgzLBmOAIBCITaKcQdgOw7W7O1haTuP9W9uwWohcSuCL1OruUtGwiGLJ8gUrqbRmpYSAEuDpj831/DCvjyLmimaDWBUECkmkcBjwo1/cwYXT4/jhL+6AEAJFFjAWkZH1IrIUGAuLI1M0NMi0g36nHIyKyONFaBwO5zAy1IJ1Y2MDf/EXf4Gf//znUBQFv/Ebv4Gvfe1rUJT2Lbw4vbOXB3O711q24wpU04YRVPDEgJX1HO5vFqBIFJs7ZewUDYxFZEyOhVA2bIRlESDApeU03r6+hULZbDofgRKcO5HE0VQYV1a2war8RU3LzSEVBIovfHQWt+8XcC9dhO0wiAJFRBUxFlXw6rv3sHo/j/nZBADgxloOBASnZ+I4PhXBmx9sIp3TMBFX8bFzk7i7WfLXf2wyjJmJCG6u5wAGmKYFSqsiuQSIhyUQQqDpFj7MlLGRKQOAH/l1GOA4DggIREJAQZCMyVhN57GT1xANy4iHexNQgxJh9eOeno37P19Zz9ecb1BpB3PTUSSjMtYz5V2P17o2uO1SDuqbN5QNy399MqbgsdPjA49wt5pXt9erG8eKTudx7e4O7q3nEFZEHJ+K4M794qEX9RwOZ/gYWsHKGMOf/MmfIB6P41vf+hay2Sz+7M/+DJRS/Omf/ulBT29k2Uv0Jei1yaiMzyzO4tSROHTTbulzen01i9ffW0ehbCJb0N3Wo8yNeHpV8YpEYTusZSQVACSRYjyu4tc+egwPn0oBAE5MR/FvS6tIZzW3vzRjoAJFPCzhreU0sgXdtZJyvI5YwMpGAQDw2uUNAG6U1ou+MrhRYgL3Zw5j+D//5QpiYQnxiIJc0V2DhzcuZW76gVA5t6qI0HTL3/p3HOY2A6h05XIcVgnKMlgOw3qmjPVM2ZXexF1rMqZgZjzSVZRsUJG2oHHH4yoWz01h6YP72MrttretPl+/0w4+uL2DQtnCdk7zo9rV17xdyoHfvGGr6KdxeK8HAT68Xcb7t7aRjLrNG/YrStnrfet3EdqVlQx+8su7yJUMWLaDsm5B022osuA3s+CRWw6H0y+EZ5999tmDnkQQN27cwNe//nX84z/+I44fP46ZmRkkk0n83d/9Hf7wD/+wozFKpQcvN20veNGXUqWYx6Ns2Liyso2pZBiTY6G2r/W6TDkOQ1Gz8MFKBrGwjLFY88j49dUsXnzjNjTTRrFkYqdoBroB2A5r+sAF3Cr/VFxFLCyDEIKVjTxScRWZvI7X3tvAVraMvGaCOQyUUoxFZVi2g3RWc0UwQ8sOVwzwO2h5AtRhbtW+wwDmAFolzaGoWWCO+xpKCARCXVstAGFVRCwsVdbkIFdy5wQAkZAEQaBIZ8swO8jjdRwGzXC/DCzf3Wl5nzz2cq97GXcnr+ON9zdgWnZNrvBez9duHrbDIIkUpsUqXc8YNNNGKqbgdz7TPJpYvY7tnO7fG8YYSpVOaN4b1LQZwqoIbUBraTavajq5jrc3Cnj9/Y2W45cNG6eOxjEWbb2L5c2jbFiglKCkubnZluVAM21IAoUo0oHdX85goZQgFJKhaWagvR7ncDLM9zUSab9zPrQ+rJOTk/jbv/1bTExM1Py8UCgc0IxGm279QquxHQf/+h8rKGgW8iUDJd2CbTu+8HMY8Nrl9cDXeud+7fK6e24G7LSp6q+HUkCggEjdlINq2yovL/Rf/2MF2YKOkm6DgkCoiKZMXnddBCpCtdPf4frjHGdX6DIGaIa9m6vKXKFNiBstBoB8yUR6p4xMXkc6q0EzLDjMTU+QJaF5ykQTbIe5KQQt7pPHXu51K1qNmyu61zhfNBvG7fV8nc5DlUVMJUMYT6hIxhSMV77QnJsba/t6w7QbXBpsx/uy4p7Ath3fz7ffa2m1rnranbtfRWhB8/Dur3sA3C9glXkM8ppwOJwHh6FNCYjH4/jUpz7l/91xHHzzm9/Er/7qr3Y8BqWkI69MDnBrLYdMQUerncBMQcfqVhEnj8RhO24uqm7YePnSPVy9k4XDdh/slFBEw6LfNjRXMrCxU8LsRGO+4Opm0d9WzBaNtj6rHn6grlLN71EsWVATbp4rGHA/U0YiJoMSd9ueVL0nmOM+UPv2LqmcE5X/VF9PL9JqVx7cjNQebzsMcVkAIa5Q6vb5bjkOTMuuuU9BdHuvO6XZuIZpw6rk4FqOA9N2oNTZg/Vyvm7noci752x1vurXO6z2zVF9T1jVFxCHMf/P/VxLs3k1o9W5x6JKy9f6x8UUiGLzWEb1PAgINMO9v9XXya67z4O6JpzB4H2hF4ShjWlxeuCw39ehFaz1PPfcc3j//ffx3e9+t+PXpFIRnvDfITfvFxtsnepxGEPRcGAyAtMhIKKIldUcfvbumvtgr3piOYwhVzQhUAq1IhQYEZBIhGvGzBUNLF3bxv1MuWnXqSDcXFLqRm3qlKHNWCUPVIBhuZFeofLvpE6a7nfUhzG2q1EZAQGpPPjd6KpuulvmhNJqLdsRpKKARYGCUQHJZCTwuE7uNYCWY3QzrmE6/nUnlT8FHdft+bqdR6fnq369JAo17xlWdUcII/7niywKNefs11qazasVzc49NhbG9M9vYytbbvraibEQLp470vJzs34euskafq8ANNznQVwTzmCJx3kaxyhyWO/roRCszz33HP7+7/8ef/VXf4WzZ892/Lrt7SKPsHYIsW1YdVufbs4f/JxUACiXdaS3K2kZDHjx9VvuH5pIq1zBgJhQQAgBYTay2RJMy8b7tzJ46+omrt7e6Xgbvma+BP45GWENj0ubOWAQYNkOWJXMYHXz9J7L+yFbWSV/FQQgDIiFJSiViGq2YMB2GEzbQUkzIQsE3SpWRtz7YNkOiGMjkykGHhd0rwOPazFGd+MyvzOXdy+Cjuv2fN3Po7PzVb9epAQCdSPD9TDirkWkFJTWrqlfa2k2r5bHtTj35xZn8P/89FrlC2YtlBB89uIMdnZKHc+DwN3Fqv+9AtBwnwdxTTiDQRAo4vEQcrlyQ0oM5/AyzPe1ky+zQy9Y//zP/xzf/va38dxzz+GZZ57p6rWOw4YusXhYmZ2IIBlVsJXT/KKi+mdaIiJjeizsG/rf2yxip2BAFARQQuEEPNRt5ub3jcdVlMoW/umn1/DujW3opt1wbDd4elWgBAzEL4rxIkMCpW5FPiEQKIXkbYXQ2s5RpOq/fXmnVA1Cqv9Oav+dUIJYWPItruJh+C4Btu26BMgihW52/qEiUgpJFJCMKpgdj8BqErH27nW7DlOtxuhmXEkUIFLX3UGs3Iv691Yv5+t2Hp2er/71sYjkuwRUfzEilU0Ft3iO+Gvq51pazSuIduc+e2wMv/OZ+aYuA2ePjbWdd808CIMqu/e3WpwKQu19HtQ14QwW23b4PRtBDut9HepEhm984xv4zne+g7/8y7/El770pYOezkjiMIaybiFXNPDEuSlf5NcLCkqApx6t3Sos6ruWTdGwGJgIyhhDoWzi7mYRf/v/XsEvPtwMFKsErj2TJARtLtYi0oowJUA8ImMsIoPQ3e1Zr3AJAFRZwOxE2I3wVjpHVZ+AEFIRvbstWjuh/jhKd6O1hLjnrVbDAiW726YESFSJVQBQFRHJqAJBoP6uwFhMgdQil7AagRIkonJH3aG8DlPN1tprh6lW48YjsivuIlLDuHvtaNXNPDo5X/3rVVlEMqbs5n9Voq5i5cuBZ+E0iLW0mlc9nZ77/IkkvvqVC/iDL57D73zmNP7gi+fw1a9c6Kqlb/08vPvrHrDrLdzNvDgcDqcVQ2trdf36dXzta1/DH/3RH+GZZ55BqVTy/xeJdJYHxW2tgrFsB2XDQqFkIl8yoZk2LJshGVOQiqvY3CnXiMpERMbnFmd943wPXbdx5XYGgJurJgoEpsWqzO7dgibLZk0r3o+Oh/GpjxzFEw9NYjVdgGVViqJY4yYjIUA8IiESlmHbDGNRBSFVgiQKkAQK03Y3nMeiMkSBIhVT8JtPncL5E6lK0wBAFKl/rO24nqu0IkC8GVLSPNpKiduNS6CusCRw82MFSv0OWYmIjPFECIQApu1UOmYR3yUgEZYRD7ANEkWKY5MR/N6vncWZYwl84tGjePzsJO5nSq5FFna/SJDK9SAEkCSKVFzFzHikst72wmNyLISpZBhrW0XXk7bC7jXrzTez2bhHUmH8+q+eQKlsoqRbfTtft/Po9Hz1rxcFikhIwtRYCJ++OIvHz066UYqqHZxBraWf6/IghGAsqmAqGa4UY3UnJr15bGyXoJs2KHVzpwkIYiGpxod10NeE03+G2f6I0zvDfF87sbUibEi9Rv7mb/4GX//61wP/7cMPP+xojM3N1v3kHyQM04Zm2jAMu+YhGwRjDGvpEoq6iYgi4WglQhl03Dd/eNWt7GeuF2hZt1xLpxbEwhIunpnAxYUJHB2P1IwDMNgOYNmusb9lM9gMiIck/HdfOAMHQDysoKiZ+Mkv79Zsa6oSxbGpGI6mwjg9G8eJ6Zg/73qz9bJmIlc0oaoCQrLoRzJLmgXLcfDUw9M4Oh7BzbUcNNPGyekYzhxLgLGqTlezcRyfbN/pqvrfY2EJz798IzBvlxIEdhryukNdv5cFmOvhWtIsgABhRey505U37o17OTAwzM8kcOJIrC+RsKBOV6lUFNvbBdxYze1bJ6S9dvJq9fqDbNU6LG1iBYFgu2TxTlcjhihSJJMRZDLFQ7l1zAlmmO/r5GT7xjFDK1j7wYMsWBlj0E0buulAN6yeCps6Ocfr763j395aRUm3WtowSSLFIydTWDw7gfmZhL/tzRjD29fS+PEv7/qtM0WB+qb8pGJZRSnBH3zxXE03pFZtM4M67HjH50o6/uV1t0lBM1IxBV/9yoWBPGyHoZf7fs9hmD8oOb3D7+towu/raDLM97UTwTr0RVecznEcV6Rqhu092Ov5AAAfxklEQVT6eA7oPNs5DUvLaVxaTte02QxifjaOxYVJPHIyVeODCbjdrV67vI77mRLyRTd9g1KKRFSGIlKYjmtJRSmBTIUGQ3NCCEq6hV9+eL/SwnVXXAb1RieE4MSRGFbW0VKseq+/vVHoe7tQwM0hPDc3dmARsn73k+dwOBwOZ9BwwXrIsWzHjaQa3XVG6paybuHyjS28tZzGynrryHUypuDJc1O4uDCBRJMWj14rVqciSD0c5mA7p7mFUFWCShAo0ju14rjX3ui9dvzp5zasJ573m373k+dwOBwOZz/ggvUQYlpOJZJqweqg13yv2I6D5TtZvLW8iQ9WMi3PFVFFfOTMBBYXJjAz0bphQ00rVgCyJEAQaKWdK/GLocRK9b4rXB28dOkuplNhP/p3e6PQ0uIHCI6UxkJyR+uvPm4YtvH7Qa/XjMPhcDicg4QL1kMAY26VvW64hVODrO5jjGE1XcTSchrvXEujqFlNjxUFgnMnknh8YRILxxMQaGcWTGvpErJFw6+qp8S1ZMrkddiVKDFjgFklkG2H4c5mCd/60VX8+f/0JAghHUdKcyUdK+vwI6PHpyJIxdr7Wc5Nu21k92MLfb+KaPrVT57D4XA4nP2EC9YhxctH9f436NK4nYKOt6+l8dbVNDZ3mrduBIATR2J4fGECj54eR0jp7i1EidtMQBRIjSBTZRGxkINMXm+6VsdhuJcu4v/4/vv4n3/74Y4ipZpuNRRYpWIKzh4fwxtXNppW63u+kfuxhb6f0dteosscDofD4Rw0XLAOEfuVj+qhGzYu39zC0nIaN+/lWhZpjcdVLJ6dwMUzE0jF1a7PJVKCsCohpAgo63aguHO9XGnbtb/xwQY008LTTxxvGSnVdAv5kllj7A64kdE3rmzgyfPTuHpnp6VQrN5C9yLdTsW7VRYpCCF72kLf7wKoueloV9FlDofD4XCGAS5YDxDGGAzT8aOo9j4Y+doOw/XVLJaWN/H+zQzMFv2EQ4qAC6fH8fjZSRyf6n6LmsDNTw2rIhRp1yGgmWiyHdbWIxZw0wXubhbx3Zeu48nz04GRUsYY8iUTsYgUOIbDgKt3dvDHX360pW+ktzWu6RZyJbOmrasgUMTDrkl6L1voQdFbo5LyQSmBLAl9L4DyuhQFiWSAdyXicDgcznDCBes+40VRDdMZqPVUPWtbbl7q28tp5Mtm0+MESvDQ3BgWFybx0NwYRKH77r2UACFFRFgVA/Na60WTZljIFV0xyDoU7Zbt+KLzdz4z39BEICSLiEUkqHLzt/h2Xsed+8WWkdFYSIamW8gU9Ib2V7btIFPQkURvW+jV0dvqa+AhCBSaYfW9AOr8iSR+97NnRqKIjMPhcDgPBlywDpiDiKJ65EoG3r6WxtLVNNa3Sy2PPT4VxeLCBB6bH0dYDY5KtkMSKMKqCFUWOupn/rufPYMXXrmBta1dMSgIpCPnA09Ib+d1RFQJX/3KhZqipVzJwPMv32g7TrvI6PGpiNu5q9mUGKAZNo5PddYuOOjcmmEhk28iiPM63ru13feK/YP2guVwOBwOpxu4YB0AtuNW9Ov7HEUFAMOy8f6tDJaubuLaarZlsVYypuBixYpqYizU9bkYY1jbKsEwbVi2g0RURjzcef7jubkxRFURqbgKx2EQKnmhd+4X4bSYOCHwW6kCrjCvF14r63no1dvrlXzT+i33aEjCynq+qWi7c78IVRFQNqxg0UoAVRHaRmqD8KKyuaLZMDZjDBU3L7x5ZQNffPI4aIcuDJ2yFy/YYWkNOorwa8vhcDiNcMHaJ/bLGzUIhzHcXMth6Woal29uwTCb56UqkoAL8+NYXJjAiSMx0B4fhDfXcvj5e+vYyJSQL1mwbcfP6ZyZiHS0tXx7o4BMwajJbyUESMUVbOW0lmJ7M1OGIFCEFAH/8vpKjQuAJLhryhYMf4udkIomrBpTEim+9cOrNXmz9dvi+bIBVRaRjCFwyz5eSTvoJYd1bjoKVRJqxgRcNwSbMXeuBFjbKuG5b1/Cb3/y1FBs14+KJ+0wwq8th8PhBMMFa49Ue6Pu91a/x/1MGUvLm7i0nEa22FwwUQIsHB/D4sIEzp9I1UQnm8EYw1q6hIJmoKRZCKsSoqqEuSNRrG4W8aM3b6Ns2NgpGL4I9HI6AbStcGfMLf7SdMuPdnqMxRQ4DsNOQQ8sDGIMsBmD5bjXHmBIRF3nAk23sFaZQ0SVUNTcqn7bdgWgQAkoJXCYaxt2Z7OAZEzxc13rq/O9KKgqi1BlsSFC69FLDishBBfmx3FzPedfQ8dhu+8l4s4XcG3HhqFtKm/rOjj4teVwOJzmcMHaBZ43qmbYMKzBe6MGUSibeOf6Fi4tb+LuZrHlsTMTET8vNRbuXFBdX83itcvruJ8poVC24DiOH02cmYiiUDLAQAK3ssGAXMmEIjevcPeiSGvbJTd3E7vRSs/XNR6VEQtLyOR1lHQLDmNgTQLH2aIJRRKhyAJypd05aYaNZFRBOqvtimrmdtACq4RcmRs5rS7OqvZWrXc0qBapHnuxgXrkZAqvvH0PuZIJy7LdyCrgi1UvAu6K7INtm8rbug4Ofm05HA6nNVywtsHb6tcNu6UF1KDn8MHtDJaupnH1zk7L/M54RMbFMxO4uDCBI6lw1+e6vprFi2/cRlm3kCsZNZG/nYIB284jXzYRDUkNW9ketu3AtJxAf9LqKJIsUr8lq1dgREAQDVciwITg6HgEmbyGdE5HjTom7l8J3P/uFAyMxeSaOdm22+JVoF6TAgYC1w+2UDJrjjNMu0aMVs99kDZQc9NRzExEoOQ0FDUL2YJ7DaqHEwTqz+0g26bytq6Dg19bDofDaQ0XrAEYptsCVTcOZqsf2C28eOvqJt69seVWqjdBFikeOZXC4tlJnD4aB6W9iSfGGF67vA6HMbclK0OtEGNuhBcMKJZNMMaaCjXvulXndtZHkQghiIelXcsoBuSKBqJh16WAEuDC/Dh+9u4aRErgVIlOhso2v38+JzB316oIWPeSkJq5VRPU7tab+yBtoKotvqojqrsHAPE6L9n9bpvqvRffvbkF3bT9ArZm8Lau3cNb5nI4HE5ruGCFW7RkmG5Vv25YTbfl9oOtnIalq25eaquICyHA/EwCi2cn8MjJVOBWddfnzmooaCYc5gq4IFHiVDRhVU1QIF7uZXVuZ1AUSVVEJAHflN+qOCxMJUP4/OPHEFZEvPz2PQC1opOxSoi1AmkykyAf2aCfBYn86rkP0gbKE8Tf/9lN7FRdn+qirmbzGjTVRUCGaWM7q9U0TAiCt3XtHt4yl8PhcFrzwArW6jaopuXsq/VUPWXdwjvXt7C0vInbG4WWx04nQ1g8O4mPnJlAIrL3hxfxTP4VEelsGZSQwGhj9fGEuIKV+KX3tQgChSTShtzO+uiQV7jG4EYRPQn6pU+exsfPT8K2GRhjSEaVGiEHuOLV9l5QmZMiUWgG9dMCBIEiooooalbNz8KKgJJWe1y94A/KS92LDVQ7zp9I4qHjCTz37UvYKegNRV2t5jUo6ouAZEnwUzi8hgn1opW3de0N3jKXw+FwWvPACNaDNPAPwrIdXL2zg6XlND5YybScTzQk+XmpR8fDfYnqiZS4Jv+K6G9De9GbdikF0ZDk57F6KQI+BIiHJQiUNOR2VkeHmrY6jUg4dyK5m3NKCH7rEyfx1y9c9rf3/eMp8XNUPdEZD8N3KohHJIAQxCOSX9wVD0uglO6mIqBxy/2g2pNSSvHbnzw1FG1TmxUB+deyqrjOmw9v69o7vGUuh8PhtGakBatVKaY5CAP/IBhjuLtZxNLVTbxzfQsl3Wp6rCgQPHwyhcfPTmJ+NuFvse8VRRIQVtyK+nq8KM9WTvMjafUIAkU0LCMZVxFVRaxtl3x/0nY+rN7499LFpq1O8yUThbKJVJWIfPhkCr/1iZP4wau3akSrJAqIyQJ0w0YsLIEQAlURMRd2happuceqsoi5aRlgDGYl7zXoOODgPS+HpW1qsyKgek9a03IgS8KBX7dRYFjuPYfD4QwjIy1Y01ntoKcAAMjkdVxaTmNpebPtnE4djePxsxN45FSqIXexVwgBQrKIsCoG5m/uHrcb5akphvIPcCNslABf/tRpP6czV9SxspEHAzCZCOHJ81OBXZkIIfjCR4/hr1+43LRrVCwk4f/+0Yd45snjiCiSvwV6bi4J23Hwiw82UdIttyuWJ5Q+egxhVarJLQXQkG/a6c8OOoo1DG1TWxX3VHvSfvzRI7hwanwortsoMAz3nsPhcIaRkRasB4lmWLh8YxtLy5u4uZZveexEQsXjlbzUZEzp2xyCtv3bUR3lAXaLoXwf1vHa6GlJt/Dvl+7VRITe/OB+04hQRJUQi0iBXaNUmSJXMrFT2MFWtgxJFCAJFMBuZNTLab0wP45HTqZaPsyD8k07/dlBM8h82U7opLhHlgRcODU+lNfvMHPQ957D4XCGES5Y+4jtMFy76+alvn9ru2WL1rAi4rEz43h8YRKzk5G+RlAUSUBYFWtannZDdZQnV9JRLFuIhCTEw7XRnl4683itTuu7RjkO83NKCdzcVNuwsFYRwsmoAlURQQiBZtr45Yf3ceponEeeBgQvAuJwOBzOMMEF6x5hjGFtq4Sl5U28fW3LLUJqgkAJzs0lsXh2AmePj7Xcnu8WWqn2Dymtt/07ZTfKExzp6bUzT3XkzquCZ4xhc0er8ckSKEEmv9u4oL7Ah3f+GSy8CIhzGPA8gnn6BIcz+nDB2iPZooG3K3mpG5lyy2PnpqNYXJjEhdPjCKv9veSiQBBWJIQUYV8/qHvtzBMUuTMspyY9QBRcu6z6rlVegU+r8Tn9gxcBcYaZao9gD/7e5HBGFy5Yu0A3bbx/cxtLy2lcX822dB1IxhQsLkxgcWES4wm173NRJAERVexLw4Be6LUzT1Dkrt73NRFTAh0Kgqy/eOefwcKLgDjDSC/pSBwO53DDBWsbHIfhxr0clpY38d7NbRhWo5DyUGUBF06PY/HsBE5Mx/r+UCeomPy3qfbfD/bSmac+cuf5vgoCRSIiI6yIKGmNqRVB1l6D6PzDtxlr4UVAnGGi13QkDodzuOGCtQnr2yVcWnZbpOZKzfNSKSE4e3wMi2cncG4uCUnsv5CklCBc6UbVztR/v9hrUU59Yde/vH4bmmnDe77IolDjBet1z+p0/F7h24wcznDTazoSh8M53HDBWkW+ZODta1u4tLyJe1ullscem4zg4sIkHpsfRzQktTy2V0SBIKJKUOX9zU/thH4U5VQXdomCgO/++7XdNAuChg5V1WMNouiHbzNyOMNPr+lIHA7ncPPAC1bTcnBlZRtLV9NYvrvTdJsJABIRGRcrealTydDA5rRXW6r9op9FOd5YP33rLrJF90ET1KGq1/HbwbcZOZzDwV7SkTgczuHlgRSsDmNYWc9j6eom3r2xDd20mx4rSxQXTo3j4tkJnDoaDzTgZ4xhLV1CUTcRUSQcnQh3LWoI3HahkR7yU/uRc9nrGP0syjl/IolHT6ewXbJwbz2HsCLuWzeqlfU81rZLvi+sLNKGcxyWbUaeg8sZZbhHMIfzYPJACdb0ThlLFSuqnULz7SJCgIVjCSwuTOL8ySRksXmk8/pqFq9dXvejgoAbiX3q0SOYn020nRMlQFiVes5P7UfO5V7H6GdRDiEEZ46NYTwiwaoqcBukSLyyksHzL1/HdlXbXEGgiIclqErtr8iwbzPyHFzOqMM9gjmcBxPCGGvlzvT/t3f3QVHW/R7HPwvLLrAkD7Im2RydG8K0CDcK64x2FOmQ6eQEMXY8o+OUmlNKM5oPiZZOmqM0SmpqZvZgD1Y+MDo0WTpm0m2YmCaaJlDeonce1zQn5cGRPX8Ym5tiKCt7Xcv7NbN/7M+La3+/viN+uq7ffi9T23vwuM7VnteeypPafcitI//3+1WPT2gfKddtTt2V1F7tIv/+dlLl0d+0cce/mvylmZX+H02G1ouPTW1Z/9Sm9lw2fn5z9lz64xz+ZLWGKDbWoVOnzvoE1hulcf219Rd08pLAKkmy/PmErUbDH7rdsFdYjVbLS7V2XdE6AllX/ufsxuHva3Aycl2dzr//dzWor7C+9/lBHfzX6Sv272x0U2SYeiTFq8dt8Upo72j2uT0ej/5Z/stV9zz+s/wX/eMW38eH2sNCFWm3ym5r2f5Uf+y5bOv7Ni9dvy3MtyvBxQN8n7Bl5NuMbb2WaHvoEQy0LUEdWPf/fOqK42HWEN3RJU6u5Hgl3hJ9Xbfi/+0+57MN4Ep+O1uvf7vPqVMHhyJs/u2f6o/WLm29Pcxf1+/tSnBJ6Gt8wla4LdTQtxnbei3RNtEjGGg7gjqwXsoi6R+d2sl1m1N3dIlr8RXOs3VN92b1fqZF8sgjZ0zEFb+s1RL+aO3S1tvD/HVd4TarYm+Szpw973OlNdJuVfZ/JRr6NmNbryUAILgFfWDtEBsh123x6pEUr+gou9/O67A33XvVYrnY7D/EYlF8tP/DquSf1i5tvT3MldYVbrMq3GZV/fkL3o4B//vfyerSsV0AZth8bb2WAIDgFtSBNe+xu3RzbMQNuY2bEB+paIfNZ1tASMjFJ181ft6N3PPoj9Yubb09zNXWb/ujB27cTXZ1vtn4txzbei0BAMEtsA+kv8E6xl17P9Tmslgs+s87Oyrkj6up1lCLQkP+7N15o1urNLZ2aWr7bXOfNNXSc5hZMK0/mNYCAMBfBXVgvZFs1hDdnezU/2Qmyxkd7hME4m6yt0oLocanQ8Xd5LvV4Vo+3x/nMLNgWn8wrQUAgEsFfR9Wf2p8GlWk3aow659ZP9BPFgrkk678LVB94oyyfn8w4lqM3P8P14+6BifqGpyMXNc234fVX0JDLIoMtyrCduWnUQW6tYo/Pj/Qawi0YFp/MK0FAACJwHpVYaEhF4Oqnf9MAAAAgUISuwJ7WKgc4VbvN8UBAAAQOATWPzTuT3X48WlUAAAAaLk2H1hDLFJkeJgi7VfenwoAAIDAarOB1RpiUWR4mCLsoQH/BjUAAACa1uYCq80aIkd4mOw29qcCAACYQZsIrBZJdtvFL1KFWQmqAAAAZhLUgdVikSL++CJVaAhfpAIAADCjoA6szpgIhbA/FQAAwNSC+rIjYRUAAMD8gjqwAgAAwPwIrAAAADA0AisAAAAMjcAKAAAAQyOwAgAAwNAIrAAAADA0AisAAAAMjcAKAAAAQyOwAgAAwNAIrAAAADA0AisAAAAMjcAKAAAAQyOwAgAAwNAIrAAAADA0AisAAAAMjcAKAAAAQyOwAgAAwNAIrAAAADA0i8fj8QR6EgAAAEBTuMIKAAAAQyOwAgAAwNAIrAAAADA0AisAAAAMjcAKAAAAQyOwAgAAwNAIrAAAADA0AisAAAAMjcAKAAAAQyOwIuDq6+s1cOBAlZaWeseOHDmi4cOHq0ePHnr44YdVUlISwBniWhw/flx5eXlKT09X7969NXv2bNXV1UmirmZ2+PBhPfnkk3K5XOrTp4+WL1/u/TPqan6jRo3S5MmTve/379+v3NxcpaamKicnR+Xl5QGcHa7VF198oa5du/q88vLyJJm3tgRWBFRdXZ3GjRunQ4cOecc8Ho+eeeYZxcfHa82aNRo0aJDGjBmjY8eOBXCmaA6Px6O8vDzV1NTo/fff1/z587VlyxYVFhZSVxNraGjQqFGjFBsbq3Xr1mnGjBlasmSJNmzYQF2DQHFxsbZu3ep9f+7cOY0aNUr33HOP1q5dK5fLpaeeekrnzp0L4CxxLSoqKtS3b1+VlJR4XzNnzjR1ba2BngDaroqKCo0fP14ej8dn/JtvvtGRI0e0atUqRUZGKjExUdu3b9eaNWs0duzYAM0WzVFVVaXdu3fr66+/Vnx8vCQpLy9Pc+bM0QMPPEBdTcrtdqtbt26aPn26oqKi1KVLF91///0qKytTfHw8dTWx06dPa+7cuUpJSfGOffrpp7Lb7Zo4caIsFovy8/P11Vdf6bPPPlN2dnYAZ4vmqqysVHJyspxOp8/46tWrTVtbrrAiYHbs2KGePXvqo48+8hnfs2ePunfvrsjISO9YWlqadu/e3dpTxDVyOp1avny5N6w2+v3336mriXXo0EGFhYWKioqSx+NRWVmZvv32W6Wnp1NXk5szZ44GDRqkpKQk79iePXuUlpYmi8UiSbJYLLr77rupqYlUVlaqS5cul42bubYEVgTMkCFDNGXKFEVERPiMnzhxQh06dPAZa9++vX755ZfWnB6uQ7t27dS7d2/v+4aGBr333nu67777qGuQyMjI0JAhQ+RyuZSVlUVdTWz79u3auXOnnn76aZ9xampuHo9HP/30k0pKSpSVlaXMzEy98sorqq+vN3Vt2RIAw6mpqZHNZvMZs9lsqq+vD9CMcL0KCgq0f/9+rV69Wm+//TZ1DQILFiyQ2+3W9OnTNXv2bP6+mlRdXZ1efPFFvfDCCwoPD/f5M2pqbseOHfPWsLCwUNXV1Zo5c6Zqa2tNXVsCKwzHbrfr9OnTPmP19fWX/VKFsRUUFOidd97R/PnzlZycTF2DRONex7q6Oj333HPKyclRTU2NzzHU1fgWLVqkO++80+eOSCO73X5ZgKGm5tGpUyeVlpYqOjpaFotF3bp1U0NDgyZMmKD09HTT1pbACsO5+eabVVFR4TPmdrsvu40B43rppZf04YcfqqCgQFlZWZKoq5m53W7t3r1bmZmZ3rGkpCSdP39eTqdTVVVVlx1PXY2tuLhYbrdbLpdLkrwhZuPGjRo4cKDcbrfP8dTUXGJiYnzeJyYmqq6uTk6n07S1ZQ8rDCc1NVX79u1TbW2td6ysrEypqakBnBWaa9GiRVq1apXmzZunAQMGeMepq3lVV1drzJgxOn78uHesvLxccXFxSktLo64mtHLlSm3YsEFFRUUqKipSRkaGMjIyVFRUpNTUVH333XfeDi4ej0e7du2ipiaxbds29ezZ0+fOxw8//KCYmBilpaWZtrYEVhhOenq6EhIS9Pzzz+vQoUNatmyZvv/+ez322GOBnhr+RmVlpRYvXqyRI0cqLS1NJ06c8L6oq3mlpKTojjvu0JQpU1RRUaGtW7eqoKBAo0ePpq4m1alTJ3Xu3Nn7cjgccjgc6ty5sx566CGdOXNGs2bNUkVFhWbNmqWamhr1798/0NNGM7hcLtntdk2dOlVVVVXaunWr5s6dqxEjRpi6tgRWGE5oaKgWL16sEydOKDs7W+vXr9drr72mW265JdBTw9/YvHmzLly4oCVLlqhXr14+L+pqXo21i4iI0ODBg5Wfn6+hQ4dq2LBh1DUIRUVF6fXXX1dZWZmys7O1Z88eLVu2zKd1GYwrKipKb775pn799Vfl5OQoPz9fgwcP1ogRI0xdW4vnr13bAQAAAAPhCisAAAAMjcAKAAAAQyOwAgAAwNAIrAAAADA0AisAAAAMjcAKAAAAQyOwAgAAwNAIrADQQseOHVNxcXGzj9+yZYsqKiqaffzQoUM1efJkvx1fWlqqrl27qrq6WpKUkZGhhQsXSpLWrl2rrl27NvuzAKA1EFgBoIUmTZqkbdu2NevYo0ePavTo0Tp58uQNnlXTXC6XSkpKlJCQELA5AMC1sAZ6AgDQlhjh4YI2m01OpzPQ0wCAZuMKKwC0wNChQ7Vjxw6tW7dOGRkZqq2tVWFhofr166eUlBQNGjRIGzdulCRVV1erX79+kqRhw4Z5b8Nv2rRJubm56tGjh1JSUpSdnd3sK7ZNOXv2rMaPH6/U1FT16tVLCxYsUENDg6TLtwQAgNERWAGgBRYuXCiXy6X+/ftr9erVGjdunIqKijRt2jStX79emZmZevbZZ7Vp0yYlJCTok08+8f7cE088ofLyco0dO1YDBgzQhg0b9PHHHysuLk4TJ05UfX39dc/r888/V2xsrNauXauJEyfqrbfe0rvvvuuvZQNAq2JLAAC0QExMjMLCwhQeHq5Tp05p8+bNWrp0qfr06SNJGjt2rA4cOKClS5cqMzNTcXFxkqTo6Gg5HA6FhoZq2rRpGjJkiPecw4YN08iRI3Xy5Mnr3mfavXt3TZ06VZKUmJioyspKrVixQsOHD2/RegEgEAisAOAnBw8elCSlpaX5jN97772aN2/eFX+mW7duio6O1rJly1RVVaXDhw/rwIEDkqQLFy5c91z+Ooe77rpLS5cu1ZkzZ677nAAQKGwJAIAbzOPxyGq98vWBHTt2KCsrS3v37tXtt9+uMWPGqKCgoMWfGRLi++u9oaFBFotFYWFhLT43ALQ2rrACgJ809i8tKytT3759veM7d+5UUlKSJMlisfj8zIoVK9SzZ0/vF7AkaeXKlZJa1lFg3759Pu/Lysp06623KiIi4rrPCQCBQmAFgBZyOBw6evSoHA6H+vbtqxkzZshisahz584qLi7W5s2bVVhYKEmKjIyUJP3444/q3r27EhIStGnTJu3cuVMdO3ZUaWmpXn31VUlq0Zeudu3apYKCAmVnZ2vXrl364IMPNH369BavFQACgcAKAC30+OOPa9KkSXrkkUf05Zdfat68ecrPz9eZM2eUnJyshQsX6sEHH5QkxcbGKicnR3PnztXhw4eVl5cnt9ut0aNHS5KSkpL08ssva8KECdq7d68SExOva065ubn6+eef9eijjyouLk7jx49Xdna239YMAK3J4jFCF2sAAACgCXzpCgAAAIbGlgAAMIk33nhDixcvvuoxU6ZMUW5ubivNCABaB1sCAMAkfvvtN50+ffqqx7Rv315RUVGtNCMAaB0EVgAAABgae1gBAABgaARWAAAAGBqBFQAAAIZGYAUAAIChEVgBAABgaARWAAAAGBqBFQAAAIZGYAUAAICh/T8jif1fsrHWCgAAAABJRU5ErkJggg==",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x3230a2908>)"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"PyObject <matplotlib.text.Text object at 0x32307d3c8>"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g = regplot(x=\"total_bill\", y=\"tip\", data=tips)\n",
"title(\"Total Bill vs. Tip\") #current active figure PyPlot\n",
"# alternatively\n",
"# g[:figure][:axes][1][:set_title](\"Total Bill vs. Tip\")\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### One discrete variable:\n",
"\n",
"* Simple scatter plot is not optimal\n",
"* Add random noise \"jitter\" to the points (only on plot) to see their distribution more clearely\n",
"* Collapse the observations to the mean along with a confidence interval\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAHmCAYAAAC26dynAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XuUHGWdP/73U9WX6dtM90ySyWQyM4FMbqCAEEEIasB4CQuKbBABQfCy6ln/2Nv5nePZPZ51WXf37MWz53t0ZVkVFETUgEGRqASIYEQwKCAhJJlc5hImk8v0/VLdVfX8/uj0ZDozPemZ6eqq7nm/PIrU1HQ9XdNP96efy+cjpJQSREREREQOpdjdACIiIiKimTBgJSIiIiJHY8BKRERERI7GgJWIiIiIHI0BKxERERE5GgNWIiIiInI0BqxERERE5GgMWImIiIjI0Vx2N8BKJ04k7W7COSmKQHt7AOPjaZjmwqzhwHtQVO19WLw4VMdWVYd9rTHwHhQ1al9rhH5WstBfawv5+c/luVfT1zjCajNFERBCQFGE3U2xDe9BEe+DtXh/eQ9KeB+st9Dv8UJ+/lY9dwasRERERORoDFiJiIiIyNEYsBIRERGRozFgJSIiIiJHY8BKRERERI7GgJWIiIiIHI0BKxERERE5GgNWIiIiInI0BqxERERE5GgMWImIiIjI0RiwEhEREZGjMWAlIiIiIkdjwEpEREREjsaAlYiIiIgcjQErERERETkaA1YiIiIicjRHBKz5fB7XX389XnzxxYljw8PDuOuuu3DJJZfguuuuw29+8xsbW9i8pJQYPJbE64dPYfBYElJKu5tE1LSklBhKjmDvqf0YSo6wvxERVclldwM0TcPf/u3f4sCBAxPHpJT4y7/8S6xevRqPPvooduzYgS9+8Yt48sknsWzZMhtb21z2DkaxY/cwxpPaxLH2kBeb1vdgXV/ExpYRNZ/90QE8O7wLMS02cSzsDeOang1YHem3sWVERM5n6wjrwMAAPvaxj2FoaKjs+O9+9zsMDw/jn/7pn7By5Up87nOfwyWXXIJHH33UppY2n72DUWzdOVAWrALAeFLD1p0D2DsYtallRM1nf3QA2wa2lwWrABDTYtg2sB37owM2tYyIqDHYGrC+9NJLuOKKK/DDH/6w7Pirr76KCy64AH6/f+LYZZddhldeeaXeTWxKUkrs2D0Ms8JspCmBHbuHOV1JVANSSjw7vAsS5vQ/h4mdw7vY34iIZmDrkoDbbrtt2uMnTpzAkiVLyo51dHTg2LFjs3p8RRFQFDHn9tWDqipl/6yHI6MJRFMaxAy3JprScPRUGiuWtlreHjvugRM18n1gX6tsKDGCWD6OmTpcNB/HaPYYelu7LW1LI7/GaqlR70Mj9LOSRr3HtbKQn79Vz932NazTyWaz8Hg8Zcc8Hg/y+fysHqe9PQAxU1TmIK2tvrpd6/DxNFxVvJCkoiISCdShRUX1vAdO1oj3gX2tsiHNqKq/wavXrb814mvMCo12Hxqpn5U02j2utYX8/Gv93B0ZsHq9XsRi5Wu98vk8WlpaZvU44+Npx38bVVUFra0+JBJZGMb0U4a1JgwDehXXEqaBaDRteXvsuAdOVO19qOeXiGqxr81AU6vqb9Bclvc39rWiRu1rjdDPShb6a20hP/+5PPdq+pojA9bOzk4MDJRvQjh58uSUZQLnYpoSZqWFmg5jGCZ0vT4v6u5FAUSC3ikbriZrD3nR3RGoW5uA+t4DJ2vE+8C+VlmXrwthT9uUDVeTRbxhdPmW1q1djfgas0Kj3YdG6mcljXaPa20hP/9aP3dHLq64+OKLsWfPHuRyuYljL7/8Mi6++GIbW9U8hBDYtL4Hlb6oKwLYtL6n4aaeiJxICIFrejZAVHi7FVCwsWcD+xsR0QwcGbBefvnl6Orqwpe+9CUcOHAA9913H1577TVs2bLF7qY1jXV9EWzZ2I/2kLfseHvIiy0b+5mHlaiGVkf6cWP/ZkS84bLjEW8YN/ZvZh5WIqJzcOSSAFVV8T//8z/4+7//e9x0003o6+vDN77xDRYNqLF1fRGs7Q1jaCyFZDaPkM+D3s4gR3qILLA60o9V4ZUYTh1FOp9B0BPA8uAy9jcioio4JmDdt29f2b/39fXhoYcesqk1C4cQAn1LQ3Y3g2hBEEKgN7Tc7mYQETUcRy4JICIiIiIqYcBKRERERI7GgJWIiIiIHI0BKxERERE5GgNWIiIiInI0BqxERERE5GgMWImIiIjI0RiwEhEREZGjMWAlIiIiIkdjwEpEREREjsaAlYiIiIgcjQErERERETkaA1YiIiIicjQGrERERETkaAxYiYiIiMjRGLASERERkaMxYCUiIiIiR2PASkRERESOxoCViIiIiByNASsRERERORoDViIiIiJyNAasRERERORoDFiJiIiIyNEYsBIRERGRozFgJSIiIiJHY8BKRERERI7GgJWIiIiIHI0BKxERERE5GgNWIiIiInI0BqxERERE5GguuxtAC5uUEkdGEzh8PA1hGOheFIAQwu5mETUVKSWGU0eRM7LokosQRrvdTSIimhUGrGSbvYNR7Ng9jGhKg0tVoBsmIkEvNq3vwbq+iN3NI2oK+6MDeHZ4F2JaDBACrsMKQq4QNi7fgNWRfrubR0RUFS4JIFvsHYxi684BjCe1suPjSQ1bdw5g72DUppYRNY/90QFsG9heDFYniWpxbBvYjv3RAZtaRkQ0OwxYqe6klNixeximnP7npgR27B6GlBVOIKJzklLi2eFdkDCn/zlM7BzexX5GRA2BASvV3dBYasrI6tnGkxqGxlJ1ahFR8xlOHZ0ysnq2qBbDSOqtOrWIiGjuGLBS3SWz+ZqeR0RTpfOZqs5L5dMWt4SIaP4YsFLdhXyemp5HRFMFPP6qzgt6Aha3hIho/hiwUt31dgbRHvLOeE57yIvezmCdWkTUfHqC3Qh7wzOeE/GGsTy4rE4tIiKaOwasVHdCCGxa3wOlQrpVRQCb1vcwHyvRPAghcE3PBogKb/MCCjb2bGA/I6KGwICVbLGuL4ItG/unjLS2h7zYsrGfeViJamB1pB839m9G5KyR1vaWMG7s38w8rETUMFg4gGyzri+Ctb1hHD2ZhlRVCNNAdwcrXRHV0upIP1aFV05Uulq2aDHaZASGwXRWRNQ4GLCSrYQQWNHVikgkgGg0DV2fPmckEc2dEAK9oeVwuZSJvgYwYCWixsElAURERETkaAxYiYiIiMjRGLASERERkaMxYCUiIiIiR2PASkRERESOxoCViIiIiByNASsRERERORoDViIiIiJyNAasRERERORoDFiJiIiIyNEYsBIRERGRozFgJSIiIiJHY8BKRERERI7GgJWIiIiIHI0BKxERERE5GgNWIiIiInI0BqxERERE5GgMWImIiIjI0RiwEhEREZGjMWAlIiIiIkdjwEpEREREjsaAlYiIiIgcjQErERERETkaA1YiIiIicjQGrERERETkaAxYiYiIiMjRGLASERERkaMxYCUiIiIiR2PASkRERESOxoCViIiIiBzN0QHr6OgoPve5z+HSSy/FtddeiwceeMDuJhERERFRnbnsbsBM/uqv/grLli3DY489hoGBAfzd3/0duru78f73v9/uphERERFRnTh2hDUej+OVV17BF77wBaxYsQKbNm3Cu9/9brzwwgt2N42IiIiI6sixAWtLSwt8Ph8ee+wxFAoFHDp0CH/4wx+wbt06u5tGRERERHXk2CUBXq8XX/7yl3HPPffge9/7HgzDwE033YSbb7656sdQFAFFERa2cv5UVSn750LEe1DUyPeBfa0x8B4UNep9aIR+VtKo97hWFvLzt+q5CymlrOkj1tB//Md/YHR0FHfffTcOHDiAe+65B1/5ylfw4Q9/uKrfl1JCiMbo3ESNjH2NyHrsZ7SQOXaE9YUXXsDWrVvx61//Gi0tLXj729+OsbExfPOb36w6YB0fTzv+26iqKmht9SGRyMIwTLubYwveg6Jq70MkEqhjq6rDvtYYeA+KGrWvNUI/K1nor7WF/Pzn8tyr6WuODVhff/119PX1oaWlZeLYBRdcgHvvvbfqxzBNCdN07AByGcMwoesL60V9Nt6Doka8D+xrjYX3oKjR7kMj9bOSRrvHtbaQn3+tn7tjF1csWbIEg4ODyOfzE8cOHTqE5cuX29gqIiIiIqo3xwas1157LdxuN/7hH/4Bhw8fxjPPPIN7770Xd9xxh91NIyIiIqI6cuySgFAohAceeABf/epXsWXLFrS3t+MLX/gCbrnlFrubRkRERER15NiAFQD6+/tx//33290MIiIiIrKRY5cEEBEREREBDFiJiIiIyOEYsBIRERGRozFgJSIiIiJHY8BKRERERI7GgJWIiIiIHM3Raa2o+UkpcWQ0gcPH0xCGge5FAQjRGLWyiRqJlBJDiREMaQagqejydbGvEVHDYMBKttk7GMWO3cOIpjS4VAW6YSIS9GLT+h6s64vY3TyiprE/OoBnh3chlo9P9LWwpw3X9GzA6ki/3c0jIjonLgkgW+wdjGLrzgGMJ7Wy4+NJDVt3DmDvYNSmlhE1l/3RAWwb2I6YFis7HtNi2DawHfujAza1jIioegxYqe6klNixeximnP7npgR27B6GlBVOIKKqSCnx7PAuSJjT/xwmdg7vYl8jIsdjwEp1NzSWmjKyerbxpIahsVSdWkTUnIZTR6eMrJ4tqsUwknqrTi0iIpobBqxUd8lsvqbnEdH00vlMVeel8mmLW0JEND8MWKnuQj5PTc8joukFPP6qzgt6Aha3hIhofhiwUt31dgbRHvLOeE57yIvezmCdWkTUnHqC3Qh7wzOeE/GGsTy4rE4tIiKaGwasVHdCCGxa3wOlQgpIRQCb1vcwRyTRPAkhcE3PBogKb/UCCjb2bGBfIyLHY8BKtljXF8GWjf1TRlrbQ15s2djPPKxENbI60o8b+zcjctZIa8Qbxo39m5mHlYgaAgsHkG3W9UWwtjeMoyfTkKoKYRro7mClK6JaWx3px6rwSoxmRwGvAWgudPmWsq8RUcNgwEq2EkJgRVcrIpEAotE0dH36fJFEND9CCPS2LmdfI6KGxCUBRERERORoDFiJiIiIyNEYsBIRERGRozFgJSIiIiJHY8BKRERERI7GgJWIiIiIHI0BKxERERE5GgNWIiIiInI0BqxERERE5GgMWImIiIjI0RiwEhEREZGjMWAlIiIiIkdjwEpEREREjsaAlYiIiIgcjQErERERETkaA1YiIiIicjQGrERERETkaAxYiYiIiMjRGLASERERkaMxYCUiIiIiR2PASkRERESOxoCViIiIiByNASsREREROZrL7gbQwialxJHRBA4fT0MYBroXBSCEsLtZRE1FSonh1FHkjCy65CKE0W53k4iIZoUBK9lm72AUO3YPI5rS4FIV6IaJSNCLTet7sK4vYnfziJrC/ugAnh3ehZgWA4SA67CCkCuEjcs3YHWk3+7mERFVhUsCyBZ7B6PYunMA40mt7Ph4UsPWnQPYOxi1qWX2KI00/2HfcRwZTUBKaXeTqAnsjw5g28D2YrA6SVSLY9vAduyPDtjUsvqTUmIoOYK9p/ZjKDHCPkbUYDjCSnUnpcSO3cMwK3xemBLYsXsYa3vDC2J5AEeayQpSSjw7vAsS5vQ/h4mdw7uwKryy6ftZ2SgzAAiBJcMdeE/XlVjZer69jSOiqnCElepuaCw1ZWT1bONJDUNjqTq1yD4caSarDKeOThlZPVtUi2Ek9VadWmSPSqPM45koHtv/8wU1ykzUyBiwUt0ls/manteoqh1p5tQlzUU6n6nqvFQ+bXFL7HOuUWYTEjuHd7GPETUABqxUdyGfp6bnNSqONJOVAh5/VecFPQGLW2IfjjITNQ8GrFR3vZ1BtIe8M57THvKitzNYpxbZgyPNZKWeYDfC3vCM50S8YSwPLqtTi+qPo8xEzYMBK9WdEAKb1vdAqbDPQxHApvU9Tb8RhCPNZCUhBK7p2QBR4W1eQMHGng1N3c84ykzUPBiwki3W9UWwZWP/lJHW9pAXWzb2L4jd8RxpJqutjvTjxv7NiJw10treEsaN/ZubPg8rR5mJmgfTWi1wUkoMjaWQzOYR8nnQ2xms24jLur4I1vS0Yfe+E0gXTAQ8CtavXgxFWRjfo0ojzVt3Dky78WqhjDQvJKWKU+l8BgGPHz3Bbsv/vqsj/VgVXomh5AiGUyPw+73odHdimb/5g7TSKPO2ge3TbrxSIJp+lJmoWTBgXcBK+T8nb/xpD9Uv/+d0+Udf3DO2oPKPlkaaS/ehpJ5/B6qPKblAAYS9YVzTY33FqQOxg8Vr5+MTfS3saavLte1WGmXeObwL0Un3vsMfwbuZh5WoYQjZxPk8TpxI2t2Ec3K5FEQiAUSjaej69KlXrFDK/1lpZM/qafnJ1xcCEx+iUtbn+k4jpcTRk2lIVYUwDXR3BCqO+ixeHKpz686NfW1mpVyg043yCSiWTs+XXVuIib4GKS2/tpNMHt1u84VwUe8qxGKZGV8LTutrjdDPSuzsb06wkJ//XJ57NX1tYcy9Uhm783/afX0nEkJgRVcrLl2zBCuWtnKKsolUW3HKite7ndd2GiEEekPLsa5jNXpbrV+KQUS1xYB1AbI7/6fd1yeqJztzgTIPKRE1CwasC5Dd+T/tvj5RPdmZC5R5SImoWTBgXYDszv9p9/WJ6snOXKDMQ0pETifN6ta5MmBdgOzO/2n39Ynqyc5coMxDSkROJnUdRiJe1bkMWBcguytN2X19onqys+IUq10RkVNJ04Qei0IaHGGlGdhdacru6xPVU6WKUxGv9RWn7Lw2EdF0pJTQYzFI3aj6d1g4YAFb1xfB2t6wrZWu1vaGq84/SlgQ6YeaVaniVCkXaNATwPLgsrq83kvXHs2OAl4D0Fzo8i1lXyMiWxiJBGR+dhurGbAucEII9C21Lzl2Kf/oQk2wPFvxdB5L7G4EzVkpF6ht125dzr5WpWQ+hcVwVuEAokYgdR2mrlf8uZFOw8xmZ/24DFiJGkQik0cuX/30CRHNTbqQQVbP2d0MooYT/81zOP7QgxCKwNI77kTwyqvLfm7mcjCSc6vYxjWsRA0gkysgk6v8jZWIaiOr55AqMC8t0WyZhQJO/PAHkHoBZj6PYw8/DLNQKPu5Hq8uI8B0GLASOVwuryORKZz7RCKal7xRQDI/t9EfooXOiMfKpvrNbAZGvFhpTxoG9FgUmMc+DAasRA5W0A3EU6z4RWQ13dQR1xLgtkai2iplBECV6asqYcBK5FC6YSKa1PgBSmQxU5qIaQmY4EY0oloz4jHIwvxnCRmwEjmQaUpEkxpMRqtElpJSIq4lYEhuaCSqNSOdhpnTavJYDFiJHEbKYrBqMFolslwin0Te5BpxIisYmUzNHosBK5HDRJMaCvNc60NE55bKp5EzajP6Q0TWYsBK5CCxpAatwKlJIqtl8lmkC7Ub/SEiazk6YM3n8/jKV76Cd77znbjqqqvwta99jaUpm4yUEkdGE/jDvuM4MppY0H/fVLaAdI5Tk2QtKSWGEiPYe2o/hpIjC7LP5Y084hrTVxE1EkdXuvrnf/5nvPjii/j2t7+NdDqNv/7rv8ayZcvw8Y9/3O6mUQ3sHYxix+5hRFMaXKoC3TARCXqxaX0P1vVF7G5eXWU1HalcAW1tju6S1OD2jQ/guT0v4Hjy1EQ+xLA3jGt6NmB1pN/m1tVHwdSR1BMIeVvsbgpRU7H6u69jR1hjsRgeffRR3HPPPbjoootw5ZVX4lOf+hReffVVu5tGNbB3MIqtOwcwnixfPzae1LB15wD2DkZtaln9aQUDiTRzrZK19kcH8Nj+n2M8U963YloM2wa2Y390wKaW1Y9hGohr8QU5qkxkNSNl7ayFY4dzXn75ZQSDQVx++eUTx/7iL/7CxhY1JyklhsZSSGbzCPk86O0MQghh+TV37B6umLLJlMCO3cNY2xu2vC120w0TsRRzrTY7KSWGU0eRzmcQ8PjRE+yu62tbSolnh3fBhISCqdeVMLFzeBdWhVc2bZ8r5Vo1pAmXc8dqiBpSMX1VztJrODZgHR4eRnd3N7Zt24Z7770XhUIBN910E77whS9AUap7s1EUAUVx9puvqipl/6ynN46M41cvDWM8eeZF1h5qwQcu78EFK9otu+6R0QSiKQ2lz0Vx+gNUQACiGLpFUxqOnkpjxdJWy9phN8M0kUwWJl6j5a+FxsoSwL5W2b7xATw9+Dyi2pka2hFvG97X926saa/PNPxQYgSxfHwiVBUA5FmBaTQfx2j2GHpbu+vSpnqL5pKAUgxWFbX43BVVVAxenRi4N0I/K7Hzs80JFtLzNzUNRjYFVZ362lRVAdU182tWOcfPSxwbsGYyGQwODuKRRx7Bv/7rv+LEiRP48pe/DJ/Ph0996lNVPUZ7e8CRbzrTaW311fV6rw2cwKO/PgQpJVyTOlQik8ejvz6EUKgFF/UvtuTah4+ny65ZUnyxn/l7SUVFJBKwpA12M02Jk/EsAqGp6+iCwcZbW8e+Nr3Xx/bh8UPbp/SzpJ7E44e24/bgR/G2zjWWt2NIM8quX/FD1Ks3ZZ+L5xJocaloQfnffqa+Nt1ItN0aqZ+V1PuzzWma/fmbhQK0XAJo9UMrZKf8PBTywdvqn/ExFI+7qms5NmB1uVxIpVL4r//6L3R3F7/xv/XWW/jBD35QdcA6Pp529LdRKSWGT6RhQECFRM/i+rwZSSnx6NMHUNArp0967JkDWN7us6Q9wjCgT8ozKiCgqgKGISEnTY4L00A0mq759Z1gPJGbkr5KVRUEgy1IpXIwZsjD2r04aHXzZq0R+trR9ChMdwFKwY3uQFddlr48vuepGfvZT9/YgWXuOiwP0FTohgmB4uvMMMzpl6Forqbrc+lCBql8+XNSVDHR10xj+gU5QggsDdWjhdVzej+bTFUVtLb6kEhkZ3w/a1YL4flLw0Dh1ClIs/geV0hODViTySxy7pnTxyluN5ZUMT7m2IB18eLF8Hq9E8EqAJx33nkYHR2t+jFMU8J0aLUgO3fIDx5L4lRi5rUmJ+M5HDqaQJ8F79jdiwKIBL1nNlwJCUBAQk7sMmwPedHdEYCuN19HT6TzyGj6ND8pPlfDMGFU+BB1Kif3tf3RATw7vAuxfHyir4U9bZbvjB9KjiCai814zng2iiOxEfSErJ2G7/J1IexpQyxfXJYggSlbeiPeMLp8S5uqz+V0DfH81I0gpWUApiHLvjxPJhw4wurkflaJYZhN9ZqarWZ9/lJK6OPjkIUzn2XTfW4ZhoSiz/yaNUV1r2nHLq64+OKLoWkaDh8+PHHs0KFDZQFso7J7h3wyW92O9GrPmy0hBDat70GlgQJFAJvW9zTc1Fc10rlChWCVrLA/OoBtA9sR08oDx3rsjE/nq0tKf/bonxWEELimZ0PFaW4BBRt7NjRVnysYBSTyCbubQdSUjHgcslDfvOGODVjPP/98bNy4EV/60pfw5ptv4vnnn8d9992HW2+91e6mzUu1O+StTLsS8nlqet5crOuLYMvGfrSHvGXH20NebNnY35R5WHN5HckMCwPUS2lnvKywga20M96qvhbwzLxuqyToqc+a0dWRfty0+s/Q4S/vWxFvGDf2b26qPKy6qSOmJZh9g8gCRjJpeUaA6Th2SQAA/Od//ifuuece3HrrrfD5fLj99ttxxx132N2seRkaS00ZWT3beFLD0FjKkul4AOjtDKI95J2xHe0hL3o7rV0rua4vgrW9YRw9mYZUVQjTQHdH420qqEZBNxBPMddqPQ2njk4ZWT1bVIthJPWWJVPyPcFuhL3hGdsQ8YaxPLis5teuZE17P644/yK8NrQf8WwKQU8Ay4PLmqrPldJXmQ2WaYOoERjZLIy0PevcHR2whkIh/Pu//7vdzagpu6fjgTNT8lt3Dkw70lvPKXkhBFZ0tSISCSAaTTflWp+CbiKaZK7VerN7Sr40Db9tYPu0o7x2TcMLIdDbuhy6v/n6mpQSMS0OQ1be6EZEc2Pm8zAS8XOfaBHHLgloVk6YjgcW5pS8HXTDRDSlVVwCQtZxwpT86kg/buzfjIg3XHa8GafhnSCeT6Bgco04Ua1JXYcei8HOkRdHj7A2I6dMxwNnpuTrXelqoTBNiVhSa7hdvc3CKVPyqyP9WBVeOVHpqhmn4Z0gkU9CM7jshqjWpGlCj0UB095ZGY6w1pnTdsgLIdC3NIS3ndeBvqUhfojWiJQSsZQGncGqbUpT8qJSJaM6TskLIdAbWo51HavRE6pvWdaFIF3IIKvXfxMIUbOTUkKPxSBnyCddLwxYbVCajo8EPdAKBjK5ArSCgUjQw+n4JhFL5ZFvwvW4jWbylLyUEpqeR1bPwat68ZGVH+KUfBPI6jmkCs1V7IDIKYxEAjJv3cyFlBK5ocGqzmXAaidRSk19+p8cdWkKiUx+ShUrss/qSD/eu3wDfC4vDGlCFQpyhoadI7+1NA8rWS9v5JGcpjAAEc2fkU7DzE6tXlUrZi6Hse/8H0a/8f+qOp8Bqw1KhQOiSQ0etwp/iwset4ponQoHOImUEkdGE/jDvuM4MpqwNP9sPaRzBWRy3PThJPujA3j84HbkjDz87hZ4VA8E6lM8wEmklBhKjODVY29gKDHS8H2twFyrRJYxNQ1G0rovg0Y6hWPf+T/kDh+q+ne46arOqi0csLY33PTr3OwsT2uFrGZtYQApJQbHknj7mk7LrtFsyosHTO1PpeIBq8Irm7q/2VWe1iqGaSCuxSEtCleHEiN4Zvh5/Gff31vy+EROZhYKxYwAFtETcYzd/y0UTpyY1e9xhLXOZlM4oJnZXZ621vIFA4m0det8TFNi2/OHcd9P37DsGs1oNsUDmpWd5WmtUCwMEIchrVkjvnd8Px7c+yMMJUcseXwiJ5OGUcwIYNEMTOHUKRy7797yYFWpLhRlwFpnTigcYDcnlKetJd0wEUtZVxigoJt4eMd+/P7N4xZdoXnZXTzAbnaXp601KSXiWgK6RYUB/nD8NWzd/1MWHqAFSZom9Og4YFjzZTA/NoZj37q3GBCfJlwudN55d1W/P+emU+RCAAAgAElEQVQlAUeOHMH+/fuhKAouvPBCdHV1zfWhFhSnFA6wkxPK09aKYRarWFmVvSqr6XjwV/twZNTajSXN2p+dUDzATnaXp621RD6JvFn7ZTdSSux660U8M/x8zR/7bM3a16ixFdNXRS1LX6WNDGPsu/fDzJ4ZRBAeD5Z84pPwr1lb1WPMOmBNpVL4m7/5Gzz//PMT38qFELjuuuvwr//6r/B4mjfQqgUnFQ6wS7OMMptSIprUYFgUrSYyeTzw5Js4Nl7dKOFcNHt/dkrxALs00whzMp9Czpj5i+5cSCnxq8Fn8eKxl8uO1/o10ex9jRqbEY9D5q3Zg5E9dBDHH/puWXosxedH5yfvhnd5T9WPM+slAV/96ldx+PBh3Hfffdi9ezdeeuklfPOb38Qrr7yCr33ta7N9uAXHaYUD7NAMo8xSSsRTeeiGNcHqyXgW//v4nrJgVQC44aoVNb1Os/dnJxUPsEOzjDBnChlk9Nqn1zFMA48f3D4lWO0Pn4c7191S02s1e1+jxqUnEjBz1hTeyB06iOPfu78sWFVDISz9zOdmFawCcwhYd+zYgX/5l3/Bu9/9bgSDQbS2tmLjxo2455578NOf/nS2D7cglQoHtIe8ZcfbQ94FUTigNMo8E6ePMifS1uVaHTmewv8+vgfRSaPwqiJwy/v6ceXbltb0WguhP5eKB7S3hMuOR7xh3Ni/uSF3yVerNMI8E6ePMOf0HJIWFAbIG3n84M2f4LWTe8qOv33ROtyy+qNwq+6aXm8h9DVqPEY6DTNj3Szeqcd/AqmfSfXoCkew9LOfh6dz9tluZr0kQFVVhEJT1xUuXrwYus78k9Va1xfB2t4wjp5MQ6oqhGmguyPQtCM9k5VGmbfuHJh27afTR5mTmTyyeWuC1b1HxvG/P92DfOHMonePW8En3r8G/cvban69hdKfV0f6sW7RKsQwjtFTJ+FT/VgeXObY11itlEaYtw1sn3bjldNHmPNGAQkLCgNk9RweeOknOBQdKjt++dJL8cG+ay25Hwulr1HjMHNZS3OtFi9y5n3HvXgJOu/+NFytc/ssm/UI65133ol77rkHJ0+enDiWSqXw3//937jzzjvn1IiFSgiBFV2tuHTNEqxY2urYDw0rNOoocyZXQNqiwgCvDpzE13/0SlmwGmhx4bPXX2BJsAosrP4shMD57b24YNEa9IS6F0x/m1yedjKnjzDrpo64BYUBkvkUvvOnh6cEq9f0XG1ZsAosrL5GzmdqGvR4vG7X8yzrxtLPfG7OwSoACDnLfCa33XYb/vSnP0FRFKxYsQIulwtHjhxBOp3GsmXlIxZPP/30nBtWCydOOL9kn8ulIBIJIBpNQ1+AteellA0zypzVdMQtyrX629eP4ee/PVL24RwJeXH3dWuxqM1Xdm4tCwfUqj+zrzmflBKj2VHAawCaC12+pY7ta4ZpIKrFa55eajwXxUN7f4yYVv5B/WfnvR+XdV5SdkxA4MK+82p27Vr0tUboZyULvb85+fmbhQL08fGa51rNj5/CW1/7jynHvX0r0HnHXVBaWqb9PeF2Y9naFed8/FkvCbjqqqtw1VVXzfbXiKZVGmV2ascusaowQDEn7Qie/ePRsuNdHX58cvNatPqt3XjG/rxwCCHQ27rc8X2tWBggUfNg9Vh6DN9/cyvShTPr9VSh4qP9f4YLOtbU9FrTYV8jJ7CqMIA0TcSfnfpFy3ve+cVgtQZZMGYdsH7xi1+c90WJGklBNxG1oDCAYUo8/pvD2H1WQYDzukL4xAfWwOe1vnIy+zM5yZnCALVddnMkMYwf7nsMmnHmS6dX9eDjaz+KvlBvTa9VCfsa2c2qwgDSMHBy26NI//EPU37W8ZGP1iRYBaoMWL/+9a/j05/+NHw+H77+9a/PeC47JTUTwzwdrNY4Wi3oJn74zAG8caS8BO0lqxdjy3vPh2LhVC37MzlVIp+qeWGAfeMHsPXAz8pGbP0uHz5/+ScQFu3QLarqA7CvkXNYVRhA6jpO/OgHyLyxZ9qfC1Wt2bWqClgfe+wx3H777fD5fHjssccqnielZKejpmGaEtGEBrPGhQEqVa+6fN0S3HXD25BMZmFYlN8VYH8mZ0oV0sgZtc0F+crxP+Fnh34JOWl+pNUTwicvvAW94W4k4rXP7ToZ+xo5hZGofWEAM5/H8e8/iNzBAzV93EqqClifeeaZsn9/9NFHEYmU7+IeGxvDhz/84dq1jMhGUkrEUhr0GgeriXQeD2yfWr3qmku78cHLe6BUqihRQ+zP5DRZPVu2trQWfvvWS9gx9OuyY4t8HfjE2pvR7rcm68bZ2NfICYxUCma2tl8GjWwWxx98ANrQYE0fdyZVBaxPPvkknn++WGN5dHQU99xzD7ze8nRER48ehaLMOksWkSPFUnnka7wp5WQsi/u3v1lWEEAAuH7DClx5Yf12bLM/k5NoRh6JfKpmjyelxI6hX+OF0d+XHe8OduHWNX8Ov9tX4Tdrj32N7GZqGoxU7foXUAyAx777beRHR8uOt228FvGd5V/SCidOwB1pr8l1qwpY3/GOd+CRRx6BlBJSSrz11ltwu89UARFCwO/349/+7d9q0ihaOKSUODKawOHjaQjDQPci+9NaWVHFauRECt/d/mZZDldVEbj5mn5ctLKjptc6F/bnhUlKiaHECIY0A9BUdPm6bO9rBaOAuFa7XJCmNPHEoV/ilROvlx0/v20FPrb6I/Co9S33zL5GdpK6Dj0Wq+lj6rEYjj3wLeiT8glDCLTf8BFk9r4x5fzjjzwM/6pVWHTzLVBc86seV1XA2tXVhe9973sAgDvuuAPf+MY30NraOq8LE+0djOJXLw3i6KkMTFNCUQS6O/z4wOV9thUOSOcKyGi13aE8MBLHQ0/tm1q96gNr0N9dn6nJydifF5594wfw5JGnEc8n4FZUGKYJv8uPd3Vdhg3LrrAlcDVMA7EaFgYomAU8duAJ7IsOlB2/sGMtblx5HVSldps/qsW+RnYpZgSobfqqwsmTOHb/t2DEJwXBqorFN9+C9J9eQ+7A/qm/lNeQ2fM6TgJYcusn5nX9WefNefDBB+d1QTrDiaOL9bJ3MIpvPbEH8XQBk2tXjCc0DB1P4TPXX1i3oFVKiaGxFE4mshBSoGuRv2Z/h9cOnsSPnz0IY9Ja2ECLC3dtXovuxcGaXGM+Flp/Lo0yxrMpBDx+9ASbv+LV00PPYfuRp2GYOkxpwpDFL06qUHE09RZePPYybjj/g3WpeCWlxHDqKJJaCgYMLPEtrsn9z+kaHtn3GIaSI2XH39n5Dnxoxfsc8TdeaH2N7FPMCBCDNGo3U5g/NopjD3wb5qTlBcLtxuJbPwFXayuyBw/O+PvZgweRHxuDp3PuhW+sT/RI09o7GMWO3cOIpjS4VAW6YSIS9GLT+h7HliWtFSklvv/UPsRSeUCiuJCz9DNTIpbK4/tP7cM9n7Z+5Kf0dzgZz00ElW0BD65621KsnOfoZ6XqVZ+6bh062qav+EHW2Tc+gOf2vIDjyVMTow5hbxjX9GxwbHnS+do3PjBtsArgdJonFaPpMWwbeBI39l9n6X3YHx3As8O7EM1FYUgDEhKtnlZcsfRSrGjrm/PjpvJpPPzmVhzLlOczfu/yDXhP95WOCFaJ6slIJiHztSt0kxsewvHvfgdm7szGLeH1ovOOu9Cy4jyc2PYYZG7mjBsyl0X8d7uw+CM3zbkdXOltg72DUWzdOYDxSZtvAGA8qWHrzgHsHYxW+M3mcGQ0gWPjWVScC5TAsfEsjowmLG1H6e9wKpErGwGNp/P45UtDOHh0bmvrpJT41e+H8cRZwWpXhx+f+8iFDFZtsD86gMf2/xzjmfK+FdNi2DawHfvPmkZuBlJKbD+yA4apQ0pZFqyWGNKAbhrQjDx2Du/CLCt1V21/dADbBrYjpsVgSHMizVQin8COoedwJD63ncbRXAz373l4SrC6ecUmvHf5VQxWacExMhmYmdpl3MgeHMDY/d8qC1YVfwBLP/VZtKwoli6WWpUZCHLauc+ZAQPWOiuW4hxGpWxJpgR27B627IPDCXbvOw456QZICUCWL7WRpsTL+49P/eUaKf0dDFNCnybnqSmLI6Sz/TsYpsRPnj+MnWeVWj2vK4TP3nCB5aVWaSopJZ4d3gWzwjckCdPSYM0uw6mjiGnFL31nPzM5+T+ng9moFsNI6q2at6N0/yVMGKYBifLAWcLES8f+MOv7P5Y+jvv3PIyodmY9nSIU/Hn/DXjn0nfUpO1EjcTM52EkazfQk3nzDYw9+EDZaK0aasXSz3wO3u7lE8eEt8pBmBbvuc+ZAQPWOhsaS00ZWT3beFLD0Fht01A4iXZ689HpOHXi/599LJe3rgLN0FgKpxK5aYPVkng6j9GT1X9TLegmHn5q/5RSqxesiOCuzevQ4uEKHDsUA7eZd8paFazZKZ3PQBWlt3h5+n9lWRJ9oDjKapjFjYapfLrm7Sjdf0OaMDF9n47nExjLVP8FdSgxggfeeASpwpn2uhU3bl1zEy5ctHbebSZqNBMZAWr0vTv16is4/vBDgH5mE7Ir0o6ln/08PEuWlJ3b9q6rIFpmThcnWnxoe9eGebWJAWudJbPVrSup9rxGtHJZa9m61WkJzHsN6UwSGa1sGUAlaa26yiBZTcf9T+6dspzjnWuX4LZNq+F2savZJZ2v7kuHFcGanQIeP9yq+/TueDElUJ0sVUgjp2sIegI1b0c6n4EpTZhy5g0g6UJ1Vaf2Rw/iob0/hmac+eLvc7XgjnUfw8rwefNqK1EjkqYJPR4DzNoM8iRe/B1Obv1h2eO5l3Ri6Wc/D3f71JyqnqVL4Vu5csbH9K3sn9eGK4Cbruou5Js0JSyLG4wMU0JVBNoCHuD0mquy8yxU2iGfzOYR8nnQ2xm0fN3X5euW4DtPvgljhilARQhcvnaxJdeXUgJSTCxBkFIip+nQTQmXItDidU3cg4D33HnjKlWvuvbSbrzvsuVV3U/TNPHawXFkCyZ8bgVvO6+dycRrJOD2I28UoBl5mMKAIlV4VQ/cqrvse5MVwdrZSrvk0/mM5VkKeoLdiHjD0HQNp/TxiuepopjuKWdo6A501bwdbtVdHF2VgKbnoEsDLqHC62rB5MJugSoS+r92Yg8eP7h9SqnV29duwWL/onP+vpQSo+ljGM0cQ0vUg0WuRVjiW8K1rtTQjEQcsnBmJLSUHUCos0/lFn9uJ6K/+kXZMU/3cnR+8m6o/srvkYtuvgXH8/mpqa08XvhXrcaimz8267acjQFrnfV2BtEe8uLASBypbPnoXSyVR9DnxqrlbejttD7lUWmH/OQlCu0h6zMVjJzIoDXgRjRZeRS5NeDGyIkM+paGan79eDqPReEWtAU8OHoyhWSmULZ+VqTzCPnd6F4URNci/4yPVal61Q0bVuBdFy6tqj2/ee0tPPfqKLSCfvq3JZ747SDec3EXrr5o2eyfIE3YHx3ATw/+AmOZE2VBjoCAW3Uj7GlFi8uLiDeM5UFr73Vpl/zk5QlWZikQQuCang145M2fQFEUGNOMvkwO01pUL46mR9ET6q5ZGwqmjlZ3ELqp42R2vPxvkE8i6PYj6AmgzdOKTv+SGR4JeGH093hqcGfZsY6Wdnxi3c1o8547t+mR+CCeGdqFE7kTME0TEAKKEFjsW4Rre66eV6YCIrsYqRTMSZuZki//Hqd+9jgEgPYbbkTosvVVPY6UErGnfon4czvLjntXnIfOT3wSSsvM61QVlxsdH74RR//r38uOL7n1dvhXra6qDefCIZw6E0LAlHJKsFqSyhZgSlmXdE52ZSqwc1lEIpNHLm9ACIGQ341EujxYBYqbvxLpAkJ+94x/h5ETKdz70z1lwaqqCHx806pZBatP7R6Gli8vVqDldTy1exi/ea251lXW0/7oAB7Z9xMMJ9+aMh0uIZE38hjXYtCMPDb2bLC0z03eJT9ZXbIUzPC0JIprWP0uH1pc3pouizBMA3Etjt+O/h7j2di0f4NkIY10PoPLl15a8f5LKfH00HNTgtVlgaW4+8Jbqw5Wf37oKYxlxorB6mmmaWIsfRw/P/zUnDMVENnFzOXKyq5KXcf4k08Aul78/9ufgNTPXQhHmibGn3h8SrDqW7MWnZ/81DmD1Zm4F5175qNaDFjrzDAM7DlceXoOAPYcHodRw4S/Z7M7U0HA60I8Xaj4OSoAxNMFBFpqOwGQzhWQOV0a1TRNvHEkCrVCD1AV4I0j0bIPt8kOjMTwrSfemHg8oFi96q7Na/H286srtWqaJp57dXTG9F7PvTpasQ1UWXFn+m+Q0JIwpAFR4dVmmiYCrgBWhWdefzX/tuyasjt+4ucWZSkoXdejeqCIym/1KhRoZh4StVsWYUoTMS0B3dDx29HfQxECKqafniyYOvpCPRUf54nDv8Kut14sO35eay/uuOAW+N0zz4AAxfvwu9GXkdIrB+OpQhovziFTAZFdzEIBerw89aKeTEBqZwZQZC4H/RxZA6Rh4OSjP0byxd+VHQ+8/WIsue0OKO75lVOtJQasdbb9d0MwDDljsGYYEttfHLKsDXZnKjg2npn4YBAoLtud+O/pc6SUOHaquk0Y1chqOpKZM6Parx08BS2vQxECblVAVQRUBXApxX9XhICW1/HawVNTHuvVgZP43i/KS60GfG589oYLZ7VRrNSGmVRqA81sOHUUxzMnUZBn7u90QauAQEbPWJohwK4sBaXrFozTszYV/gMhYJgGWtSWmiyLkFIiriWgSx1/OrUXeb34XqMIAZdwQRUqVChQhQqXcEE3dbx+6s0pj6ObOrYe+Cn+ePy1suPr2lfj1rV/Dq9a3Tr/Y5kxjOfGZ/ziZ5omTmXHZ5WpgMgu0jRhxGLzLrtqFgo4/sj3kX71j2XHg+svx6Kbb5nTGlgrcQ1rnY3FzgRhYuJ/Tpv02huL1i5YO5vdmQpOJTWoiiju0p+uv4ni1PqpZJXJiM8hXzCQSJc/l2iqPGBXpvwxpj+vltWrzn7s+Z5HZ6TzmWKi/LPe0M8OWoUADGlamiHAriwFpesa0oRAcXOVMe1O/WK5uQs71tRkWUQin0TeLH45TGjJsp8JYCJIniyulY8CabqGH+7fhiOJ8i/uly25GJvP2zTjiPHZMoXcjBs8Swwpq85UQGQXKSX0aHTeZVdNTcPx7z+I3KHy5UitG96NyIeuc+RGRAasddYZPvdOWADojFR33lxUm4HAqkwFi1pboAgBKJiaWup0sKoIgUWt868IpRsmYiltSlwcCVaXwLh0npQST+0emVIQoKvDj09uXjunggCzbQNVL+DxF3OQCnGOvIQCqlAszRAQ8Jx72hqofZaC0nVLuVgVIQChwpRGWRyvKiraPK1Y275q3tdM5lPITUo31eqtbtPk5HWo6UIaD7/5KEbTY2XnvLv7SmxcPvu1xn53C9QqfkcVoixTgeLAD2wiIx6HLFSXbrHiY2QzOP69B6ANl38hDG/6ANree01dg1XhdkFtPfc6dIBLAupu87t6oaozvxhUVWDzFb2WtaGUqWAm7SGvZZkKLl+3BD6v6/R0vALXpP+6VQWKEPB5Xbh83cy7hs/FME2MJ7Vp1+petLID3nMk8vd6XLhoZYdl1atm04YSl8IP0Wr0BLuxxL8IbjHz/XUpKpb4F1uaIaAn2I2wNzzjOVZkKShd90wuVkCBgEtxQVVUqEKBR3VjcUsHugKd875+ppBBRi8foXx7xzp4XDO/13hcXryto5jsP5aL4/49P5gSrH6w71pc03P1nD5Il/o70d4yc5o4RVHQ4WufyFTgUdyInONvRlRvejJRViJ1LoxUEse+fd+UYLX9z25AeOO1dQ1WlYAfrvaOqtfJMmCtM1VVcfVFXZV37grg6ou6oFq4dkQIgU3re1Ap9lEEsGl9j2UvXEVR8KEreifugRDF0YyJywngQ1f0zisPqWlKRBMazAo7yxRFwXsunvnv8J6Lu2CYmLZ61YUr2uddvaraNpTug9/rmvWyg4WqmNLparR6QxN5Rs+mCgVt3lZcY3GGgFJ6KVHh7VZAsSRLQem6ChSE3JO/fAooEFCEgjZPK1TFNe/r5/QckoWpSxqEouCqrndiphf5VV3vhFAUHM+cwP17HsZ47kyGEkUo+Gj/n+GKrsvm3DYhBN7VdRmCrsoj2EF3AFeczlQQcPkRaQlPBPlETmBk0jDT1VdenI4ejWL0//4XhWPHzhwUAotuuhmtV86vCtWsqApckQhcodZZve+o//iP//iP1rXKXpmMM6tFXdy/CPG0hpETqfKpOVXgPRcvw50ftL604OKwD0sifoyeSiObP7MWpj3kxfVXnWdpHlYA6O9ug9ulYPBYErphTqwt9HlduOGqFfjg5XMfYTalRDSpQT9HJavezhDcqoKjJzMwjDMbMrweF669tBuXrVmC7/7iTQwcLd+Jefm6JdiycSVclVIMzEJZG0wTpQ/2UhuuvmgZFEUgHPAi4Cum2QoEnLdEwIl9rcPXjq5AJ45nTiBdOL2m9TS34kJv63LctOp6S3KgTteWxf4OjKVPIGecGSGJeMP40HnXWtaG0nVPZcehmzoKUoeEnFgG0BXonPf1NSOPRL7yTuSeUDdcioq3MmMwzDPvNR6XF+/ufheuXPZODCeP4qG9P0ZGP/OB7FJc+NjqG7GuY/45HMMtYSzxd+BkZhwZI1vc9CkEFEVBp38JPtC3ESvD5yHsbYPPfeZLodP6mhP7WSWKIuDzeZDLFSoOHDSzWj5/U9NgnJURYNrzclkkX9hVdqz1qg1QfT4UTpzAse/cByM6KWWlqmLxLbchePEl82pfNdcvUXwtcIUjU0ZVq+lrQjZxHo8TJ5LnPslGhmHgFy8NI5YpIBJw44Pv7LF0ZHU6dlS6msw0TezedwLpgomgR8FlqxfPa2RVng5W83r1qaCKVaZOIZrSEAl6cdHKDqSy+ryrV82GaZp4/XCx0pXfo+DCFcUpTK9bRVvAA2XScPjixbUvpjBfTu5rUkoMJ49iMDmErMjAJwPoC/WgJ2RdlakZ23K60lXQE8Dy4LK6tKF03ayRgXQbEHkVftf8r583CohpsarKl0vTxJ9O7UVCS6LN24q3dayFUBQciB7Cjw88Dt08k9GhRW3BrWtvqmkRA6C80pWvxYMO12Is8S1Gi8uLVk9oymYup/U1J/ezs7lcCiKRAKLRNPRZvB83i1o9f7NQgD4+XlVGgEJ0fEri/u6//f9g5nIYe+DbMNNnZkGE240lt98JX//8166f6/ruSDugKHC1tlbM6VpNX+OmKxupqoqPvPt8Wzu1EMKSalKzuf6yRQFIVYUwjHl9eMrTpW5nE6wCxan5S1adKQNbqXrV9RtW4MoqCwLMlqIoeMfqxWhr8yMez8A0JEJ+D/w1zkW7EAkh0Nu6HOe399r+ASqEQG9ouS3XBoo79Je1LkUY7TCM+Y1VFEwdMS1eVbAKFJcHXLT4wrJjfzr5Bh4/uB3mpNHvkDuI29dtwRJ/7UszCyGwLNiF3rZutLb5kIhn4VP88FdRFpao3qRhQI9F55W+Sjt6FKe2PQo5ae2raGlB5x13oaVvRQ1aeW7C64WrtXXeabL4aUi22TsYxVO7h3E8mkGpJOmSiB/vn2Np2Hg6D60wv1QfI8dTeOAXb5YVBFAVgY9d2191QYD5crtUBIOumiw5ICqVhI1qMRTMAiCAVncQH+rbhDXtc1sKUKpidXb1qtl4cfRl/HLwmbJj7S0RfGLtzQi3VJ/PeK5cigvtvgiEyX5GziNNE3p0HDDm9+X61NYfQepnsgoogQA6P/kpeJfVdvaiEjUYgjtSmyWGDFjJFnsHo3jwl/sQT+dhmMU1rBIS0WQex05lcMcH18wqaI2niyVX5+PASAzf/9X+shFar1vF7R9Yjf5ZFASYq2K5WA98KuY9+kUEnCkJm9WzSBZSxTWkQmA8E8X/vf4gNq94H97X+55ZPWaxilW8bE3wbEgpsXNkF54/+kLZ8a5AJ25b++cIuK1LMVbic7Vgsb8dsXwGOivJkcNIKaHHYpD6/CteTg5W1dY2LL37M3Avrv3sRSWqr3YbhRmwLnB2rGGVUuInzx3CeDJXylk+wTBMjCdz+Mnzh7C2t3J98ckSmTyy2rnrJc/k1YGT2LrzYFle2IDPjbs2r0X3Ius/QF2qQEdrC1oDHkTzBZwjeSg1qMlrWAMeP3qC1q2jLZVmzepZxLSpGzYMU8f2I09jebALa6rMwVoKVvVpCxBU9/vbD+/Ay8dfLTve19qDj6/+KLznSIE1XwoUhDxBBL0+RyZGJwIAIxGHzNd2g52rowNL7/oMXDUa7bQDA9YFbO9gFDt2D5eVaW0PebFpjlPy1Ro8lsTRk+nKMZkEjp5IY3AsiRVLZ04onMoWyqbv5+K3r4/iid8Olh2ba/Wq2RIoBsaBFhfcLk5NNrPS1PzkMq1hbxjX9GywJEvAcOoooloMyULlEsuloHV1pP+cAZyUEol8EgVzbv1NN3VsG3gSb4zvKzu+tn0Vbuq/Hi7F2o8jj+JGqyfEdFXkaEYqBTNbmyqPJe7Opei869Nwhazdr2J1KVd+Qi5Qewej2LpzoCxYBYDxpIatOwewdzBa4Tfn79BbibI0UtMxDBOHjlZOlQMA6VwBqezcK35IKfGrl4amBKtdHX58/iMXWh6sulSB9tYWBE+nq6LmVZqanxysAkBMi2HbwHbsjw5U+M25S+czKBiFslRS04lpcYyk3jrn4yXyKWjG3EZ9NCOPH7z56JRg9R1LLsKWVR+2PFgNuJlblZzPyGZhpCp/wZyJlBLJF1+Yctzd1YWln/4Ly4NVxe+HK9Ju7TUsfXRyJCklduwenrYCFACYEtixexhWZTyreqOGqHxeVtORzMw9WDXM4rKEna+Uf1Cf19WKz95wAUJzrF5VDQEg6HOjo7WFo6oLQIuArREAACAASURBVGlqXmL6L2kSJnYO76p5fwt4/FWtM1WFglR+atL/yVL5dFn+2NlIFzJ48I0f4nCivLLO1cvehevP+8CUVFK1pAoFEW8YwTqsiyWaD1PTYCTOnWt1OlJKRH+5HYnfPD/lZ4u2fAyqv7ry0HOinC4C0NoKq8dduCRgARoaS00ZWT3beFLD0FjKkpRXK5e1QVWVGUdZVVXB+V3Tb3TS8gYS6bmv7ynoJh55+sCUUeQLV7TjY9f2WxpEulSBtoCXgeoCMpw6OmVk9WxRLYaR1Fs1zTtaLM3aivg061dLVEWFW3Ej6Kkc0GX1LNL63CrsxLUEHtr7Y5zKjZcd/0DfNXhX1/o5PWa1WlQvQp6gpQExUSVS12Hq1S2fMQsF6LHYnLYuSNPEqZ89jtTvX5z254rHunXhwuuFq60NYh6502eDPXkBSmarC/aqPW+2+paG0L3IP2NJ0u5F/mmD5YJuIJbW5rwlKavpuP/JvVOC1cvXLcGtm1ZZGkj6W1wcVV2A0vnqgr1zjXLOlhACm1dsgjrDdHvIHUR7SwTLg8um/XlO15DIz22K8kT2FO7f83BZsCogcOPK6ywNVhUoaPOE0OZtZbBKtoj/5jm8+fnP4cVb70Ds+edmPFea5pxzrUrDwMmtP6wYrFpGAGqomK6qXsEqwIB1QQr5qpvurva82RJC4KPvWYn2kBfqWblGVVVBe8iLj75n5ZR1nYZpIprKzzmHciKdx//97A0cOVZeLebaS7vxkavPK6smVUuKIhAJedHq93Ct6gIU8FQ3HTfTKOdcrWnvx+YV75sStKqKWixD6vJhY8+GaV+X+XOUXJ3JSPItPLDnYSTyZ/qaS3HhljUfnVI8oJY8ihvtLWG0uKxdf05UiVko4MQPfwCpF2Dm8zj28MMwC9MvXyumr4rOKdeqWSjg+A8eQvq1V899cg0JVYWrvR1qoP7LbLgkYAHq7QyiPeSdcVlAe8iL3s6gZW1Y1xfBHR9ci1+9NIijpzIwTQlFEeju8OMDl/dNyVJgni65OteazCdjWXznyb2Ipc6MGgsAN2xYgXdZVL0KAFo8KloDHigMVBes4tR8eMZlARFvuOIo53y9r/c9WB7swpOHd+CkFoUqBFzChU7fYlzTe/W0GQoKRgExLTGnmYyDscP40f7Hi0UKTmtRvfj42pssq/IlAATdQVasItsZ8RjMbHbi381sBkY8BmXR1NynRiIBmZ/9XgxT03D8oe8id/hQ2fHgO6+wdLRV8bVADbXWdVS17Pq2XJVsJYTApvU9qDSgqAhg0/qeuowGCkWBx6WgxeOCx6VU7AjxVB76HJPpjxxP4d6f7ikLVlVF4OObVlkWrAoBtAU8CAe9DFYXOCEErunZAFHh7VZAqTjKWcs2+N0+tKgeuNXTWSkqXE439dPB6uz7256Tb+IH+x4rC1aD7gA+eeGtlgWrbsWF9pYIg1VqKEYmXRbYVv97GRy7/1tTgtXw+z+Etve8t1bNKycEXOE2uNrCtgWrAAPWBWtdXwRbNvajPVS+ILs95MWWjf2W5mEFzqTViiY1eNwq/C0ueNwqotOk1UrMo+TqgZEYvvXEG2W5Wr1uFXdtXmtZqVW3qqCjtQU+LycwqGh1pB839m9GxBsuOx7xhnFj/2ZL8rCWnEmpFYdH9cDvboFH9SCmxaek1DJMAzEtDrNCRoOZ/P7YH/HowM9gTspMEPGGcfeFt6HTX/vKOgKn01V5w5anxSKqJVPTYCST5z7xLHoygWPf/l/kR4bLjrff8BGE37uxRq0rJ9xuuDs6oLTY/4WQvXwBW9cXwdresC2VrqpJq7W2N4yMpiMzxypWrw6cxI+fPQhT1q96VdDnRtDntuSxqbGtjvRjVXjlRKWroCeA5cFllva3alNqrQqvhIRETEvMuuSqlBLPHf0tfj3y27LjS/1LcNvaLZaszXUJF1q9IbgZqFKDkboOPR6fdUaAQnQcY/d/G/r4qTMHFQWLbroZwUveUdtGlh4+4IcaDDlm7wV7+wInhLAkddVMqk2rNTASRygwt41f01Wvag95cbdF1atURSAc9MDtYmJyqkwIYdnU+HRmk1Ir5AlCl7P7ciilxC+OPI3fj/2x7HhfqAe3rPkoWiwotRpw+RFw+x3zIUpULSkl9HgMMGf3pTB/4jjG7v8WjMSkTZCqisW33IbABRZsYlQUuNraoHitLZU8WwxYqe6qSZclpcSxaGbWAauUEk/9fnhKQYCuDj/u2rzWkoIAPo+KEDdWkQNVm1LrePokPOrs+oZhGth28EnsOfVm2fE1kX78+aobaj5N7xIqWj0huFXOYFBjMuIxyMLsvhRqbx3F2APfgZk5k/ZOeDxYcvud8K2s/VIi4fEUc6taXGZ1LhiwUt2dK12WlBK6IRHwzu6DyTAlHn/+EHbvO1F2/LyuVtzxwdVo8dT25S4E0Or3cK0qOVY1KbVMacI1yw+nvJHHj/Y/jkPxI2XHL1n8dlx/fu2rV/ldPgTdAY6qUsPSkwmYuZlnFs+WO3IEYw/+/+y9Z3AcV372+5yOkwMAIhAEmMBMiQpUWJIKlCjJ1Cqsclhpl9pXu2uX3yrXveXPtj/avq665Vu+t9b7yq/WyoFU1kpcURKpFRVWVBYTBFIkQBKBACaHnu4+535ozGAaEzAAZgZB51cl09tzprsxMz39zDn///M8DqaNP09wOND8i0fg6Fxa3RMkgOj2QPTUzh1opvA7LafuTLTVyugmMjoFwCCJAkzK4HcraGuqPE6u3ulViiTA71EgzmLHJIczGVlLrZAWhm7qoKCQmQRx7KufMgqP7EaLq7nifSb1FJ49vgdn4/227VvaLsf1nVdXVVSKRIRP8Ux59pfDmUuYqRQEY2qNw6nvuzH0zJNgeR6ugtuD1l2/gtJWXQs8IooQA34I8ty+zrhgnUUopfjo20EkdAq3LGDzmkUQfgQCKGur9eTe44gkMjApBQEBZRSiIMDjlLHl8taKb3wpzcCTe48XBAJcvq4Zt22tbiAAgdW4xRur5g+UUhwa+gqRTAQdja1Y710326dUNwgh6Aosx1un3oVJjexGiESAR3JDFmVc3npJxddaRIvi6WO7MZwasW3f0XkNtiy+vKrn7pQc8MhunlbFmfeY8TiEYEPF4xOHv8X5F54DzHGRK/r9aH3kUchF/Fxnwmx7q04FLlhnib1/6cVbn5xGMmOAMAJGGJ55R8LOK5fipss7Z/v06kRhm6TV0F95+2Q0kcEf3jqGgVF7rd51l7Tj+kuXVHW2RxII/Lyxal7xbu8H2Nd7AGkjDcYY2EkrDemK1s24a9UtC36JuTvUg88Hv4ZXdiOmx2FS6wZomAaiLI6rm3+CZf7KlhaHUyN46uiLtvQqAoJbV9yEi5ovqNo5i0SAV/FC5bOqnB8hsS8OYeTlPbaoVqmpCa27HoUUCJR55hQRBEg+HwRH9ZqQRX8AgtOZ85cVnC6I/uqdMxess8Dev/Riz4ETMHO+Tta/sZSOPQdOAMCCFq1ZWytVkbBIFqGbFIwymIxBEgQQQvDRdwNYsdhXVlCUTK/atgxXrq9uIIBTleBzyQte4Cwk3u39AG+c/BMABsqoZdfEgBQ1sf/MhzgW6sa9q2+vqQfqbJJvaeWQVKiiAp0ZYKAwKYNERPTFzuBKtnnSz/XZeD+eObYHKWPc6FwkIu5edSvWNKyq2jk7RBVexcNnVTk/SqIfH8Tom6/btsmtbWjd9SuInuq5+RBFtkIAqtxYJcgyFt33IIaeegJEIGh98EEIcvVWI7lgrTOUUrzx0SmY2dSm/PsEA0yT4Y2PTuGGzUsWbHlAvq0VIQSyKACi1TSV/VEZSWTQP5zE4kXFPRzPDMXxh7eP2QIBRIHg3uu6qhoIIBDA51aq3rDFqS2UUuzrPQCbWJ3AYPI8Xu75I+7ounlBitaJllaEEMhEBhEYdMMEwBDJRDGYHEKru6Xkfk5GTuGF468gk5depYoK7l9zJ5b6OqpyrgIEeBU3HFL1Lec4nLkOYwyR/e8h/O47tu1qRyeaf7ELorPyfo7JEN1uCJ7a+a37t12Fhm1bEQi6EYlpMIyph5CUYmEqojnMp0cGJzXCT2oGPj0yWKczqj/5tlaUsryZZjsJrXjGcr3Sq1RZRKPfwcXqPOTQ0Fe5MoBSRviMMST0JPb3HQRj04v9ncsUs7SijNqCNAAgoZeOhzwychzPHNtjE6tu2YVfrr+/amJVFRU0OoNcrHIWBGyKzVWMMYTe/mOBWHWs7ELLrv9RPbEqCpCCQYje2gcBEEmCIFX/vsnvxHWm51w0V6JZrFyTjG07cS6Kn2xsq+/J1YmsrRVlllgtde0Us7UqlV71yM61WFyl9CoCwOOS4XbUr7GKMYZT/VH8MJQAMU20N3ELn5kQSlsziwwAK1ITTcaWNgxq5IzzO7zt9TzFmjPR0sqkJigYxAnzFG65eOTiocGv8Mcf7DfRgOrHQ+vuQYNj5tHNBARexQNnHYUqYwx98bNImym0sSYEUHkjDIczGYxSGNHIlMaPvPoy4p9/ZtvuWrceTfc+ULXldKIokAKBedFYVQ4uWOuMU7ZqRkrN5zBYgskhL9zGns4WDwJuBecj6ZJjitlalUyv+uk6NPqqc9OTRAK/W626DVY5jp4OYd+hPoTiGiRRgGFSBD0qdmzuwLqlMxcGP0aCDqvQn5aaXQUDAcmZ28cziaLj5jNZS6uwFrZmVkFhr0EC/IqvwNKKMYY/n/0E+898aNve4lqEB9feDa8yc59GVVTglT0Qhfp9z3WHevB+30GrTIIQSD8I8EpeXLtk64IsCeHUF0YpjNAomFnZDCszDJzf8wKS335j2+6+6GI03XF31epLRZcbcsPC+GE2v+X2POTSNYtKzihmIQTYvLa61hVzCZMyXLauBaXcpgQCbNk4bmvFGMPev/QWiNW2Rhd+e/uGqolVl0NCo89Rd7G6e39PQVTtaEzD7v09Bb6ynMrY3HwRJEEaE2mlcUnW7GIt8u5nG0IItndsBWOAyQpvogRCgaUVYwx7T79XIFY7vO345fr7ZyxWCQh8igcB1V93sfpKz1sFMbUhLYJXet5Cd6inbufCWXgwxmCES6dY6eftYTZU1zH07FMFYtV7xU/QdOc9VW2GEt3Vq3+dbbhgrTNLW71QJpk9VWQRnS3V6wicS1DKEIppWLHYh5su74R/QvSq363gpss7sbLdD8ASty9/cBIHJkStLm/z4de3rq9K1KogEAS9Knwupa7L8Fm3hBIlvKAM2Heob0HWV9YaQgj8qi+39F8MSRABMATVAJZ4qmvEPVdY7luK7R3b4Fd8tu1+1YcdnVfbLK2sqNU38ZeBL2xjVwVW4qG198y4xlQRZDQ6gnBKxUsQakW+W0LRx0EXbB0zpz6Y0QhYJgNq6Bh57ZWCx4eeewZDzz4Fauig6TQG//t/I3XcHmnsv2Y7Gm65bd4v29cSXhJQZ/qGEvB7FOjhdNFmI3HM67NvKIGlrQtLtFJmidXs372y3Y8Vi30YDCXBBBGEmWgJuHKisWR61fIG3Lu9OulVDkWEz6VUNVygUvLdEkoxGtPQOxhfcJ+FWtMXPwtZkOBXfYhqUdAJRTgiEUFAYFAT13ZsXZD1wgY1ENaiWObvxFJfBwaSg9DMNJqDDfAyv+37J2NmsPv719AT/sG2jwubNuDWFTfNaDaUAPDIbrjk2ZnpmeiWUIyFWsfMqT1mLAaassrbhl98HunvuwsHZTQkD3+H84YBMx5H5uwZ28PBm3bCf9U1Mz+Zhfc1ZoML1joTS2XgUCQ0BRyIJjLQMmaublVVxJyFUn4n/UKAMYZIPAPdtM9yEELQvsgDv9+FSCSZs/tKaQae2Hscp2uUXiUIBH6XAlWZvVrhSt/jhfZZqAfZDnmf4oFX9iCsRZA0kqCMgRACQghEQcQVbZcuyPpFk5oIa5FcSQQhBG3uVkiiAJ/fiWgkhWwlfcpI4dljL+FM3L6KcWXbZtzQee2MxLwsSPAp3lyt8GxQzC2hGAuxjplTW8xkAmbC+txkBvqROnGi7PhU93FbIAAIQcOtt8N3+ZUzPhciiZACC7vngQvWOpPtkE+kDKS08boyBiClmRAFAw5Fyo1bKEQTGWh6ZcXo0UQGj//xKAZDdrud6y9dgusuaZ/xbJhLleBxyRBmeVat0vd4oX0W6kF+h3xMjyOhJ3KzrIxZ3qxgqGuHer2gjCKsRUvaeeUTzcTw9NHdOJ8atm2/ruNqbF18+bSvNQLALbvhnqVZ1XwmuiWUYiHWMXNqB02nYUbHJ1Qin3wMli5tEQfALlYFAU133QvPpotmfC6C0wnR54MxMjz54HkMF6x1prPFg3hKRzxV3GM0ntLhUER0tsy8E3euEEtmkMpUJlbPh1N4vEbpVZJA4HMrk9YQ14vOFg8avGrZsoAGr7qgPgv1Itsh3xs7g7BW3GbGYAbeOrkPza6mBTPLyhhDRIvCYOW9ngFgJDWKp46+iEgmmttGQPDTFTfikuYLp30OEpHgU72QZ3FWNZ98t4RSLOQ6Zk71oXoGRsT+eWJaadebAiQJzfc/CNfa9TM7EUIg+X0QHKXrwjP9A5CbFkYT99z4RqmA3/zmN2hoaMA///M/z/apzAhKKUKx8h/s0VgalFKIVY5NK4ZhGHj23R4MhlJoCTrxwPVdkKpo+JtM60ikS988KaX45sQoUjpFMpXBwW8HCtKr7ruuCxtnEAhAYHm1uh3SnKpVJIRgx+YO7N7fU7TxSiDAjs0dc+qc5wuEEFzTvgX/7zf/VXZcRI/hvdN/xqrAypq9zowx9MXO4ofoaTDKkDRSEIiABmcQm5svqlqiHWNWclW+yf9EKKU4dOYbdA/9gK+GDiNDx38YikTEXatuwdqG1dM+B5fkhEeeWx7CWbeEV3reKtp4RSAs2DpmTvVhhgEjFC70UFcrXK0RBLT84hE4V6yc0XlMjFeluo7Bp54oGHfuP/8/uDdsQOujv61qTOpsMC8E65tvvokDBw7gjjvumO1TmTFvfdKLyVbqGAXe+rQXt2xZXtNz+ffdX+ObnpHcdXfkVAj7vzyHC7sa8Xd3b5rx/tMZA9Fk6Zvnh9+cwwdf90PTDVCKgiY0VRbx0I2rc44B02E2fFWnwrqlQdx9bVfOhzVLg5f7sM6UqB6bdAwDw+lYb80abrpDPXj95F70JwaRMTO2ZXqJSHi5503s6LwG13dePeNjRTNxaGbpeuePz32Gj/o/Q9pIF9hcKaKC+1bfgeX+zmkdW4AAn+qFKs7N8pXVwS78rGsn9vcdRChvprXBEcA17VsWzAw7p7ZYXqshgBbexP1XbkHyu28nLQtouuu+GYtV0e2G6LU34g489p9Ifvdt4TmnU4h/fggDABb/zf+c0XFnmzkvWMPhMP71X/8VF1xwwWyfSlUYDKdKhgZkYUBB/Wa1+ffdX+PrnpGix/66ZwT/vvvrGYlW3TARiZe+eX74zTm8c6gPYNnEK/vjiizg17eun1F6lUuV4HXJc37mZN3SINZ2BnB2OAEmiiDURHvj3Jqlmo+E0uGSwQH5JIwUjo1+X3XB2h3qwXPHX0YoHYbJzIKaUoMZSOopvHHyTwAwI9EazySQNkuv3Hx87jPs7zsIykyYRWYZL150wbTFqiLI8CneuvqqTofVwS6sCqzMJV0tbloEPwvmGj05nHJkxWqpYACltRXOlSuRPPxdyX04Vq6CZ9MMJoNEAZLPD0FVbZu1M31IHj1a9qnJo0ehnT0LtX3+OmHMzWmnPP7lX/4Ft99+O7q6FsYv4KC7st8IQXftpu4Nw8A3RcRqPt/0jMAwJq+DK7p/kyIU00oKc0opPvi6H2DWrOpEsQoAkiCgtWF6fo2EWH6uPnd9fVVnAiEEy9p8uGRNM5a1+ubNec9lvFJltb+MAYdHjlfVh9Py/vwQ0UwMDCjZAGUwAwwM+3oPgBaZtamEpJ5CwijdCc8oxUf9n5UUqxJEfDdyDGyKxycAvLIbQUdgzovVLIQQdHqXYH3TGiwP8nIbTuUYkQiYXnrFEACa7rkPcmvxSHVH12o0P/yLaR+fqCrkxqYCsQoAoffeBU2Wd7mgyQRC771TdsxcZ07PsH788cc4dOgQXn/9dfzTP/3TlJ8vCGRW/DXLcaI/XtG4HwZikGq0jP3Un05UNMv7/Psn8Mud66a0b0oZYjEdRCAodQv75sQo0hkdlKJo7aYkArpp4vCpUVy0amrF4rIoIOBVIYlz/rdYAeLYOYvz8Nzn4rV2JHS84rGaqaE/NYBOX3VmH3qjZzCUGoZJzUlneRkY0kYaX418i8vbLp7ScdKGhhRNlv28fzVyBCk9VTT1S4IIQggyhoaj4W5cuKiyJhCRCPCrPsji/KyJm6/X2ly8zkoxX1/jYhiRCAQzA0jlX/vEl19BHxwo2L7ovvvhu3hq1/Y4BJLXC9FdZrWx0oYvLV0zXZFPrd77OStYNU3DP/7jP+If/uEf4HBMz3qmoWHuLauGyiyT5zMSyyAYrI3NymiNzoFShuFICm5v+fcrkTFhUrvDB2DNjIoCyb1nyQyF31+ZJU22sWo+zaqWwuerbxJQNZiL11pYL28Wn4UQYn2Jq0bVrrlezbQ+lIQUNGeUOAkkEZ/S8TNGBulUAr4yHcKUUXx55NsCsUpArPCEvPcshSR8/sk/ew5RRcDhq1qz2Gwy3661uXidTcZsvcZ0bIVQmGETsR6NwZABTGLRNvjuezi/5+WijzVvXAvVN3WLNyJJUBqCkzZLjQS8iJYdYeH0e2umK4pR7fd+zgrW//iP/8DGjRtx1VVXTXsfo6OJOfdrNOhRMDAyuZF1o1dBKFQbI+sGT2WNEVM5BzaWYjWZ12pGN/H50cESYtX6N3uHdykCIpHJXytZFOD3qKC6gXB4emUMcwFRFODzORGNpmAWq5MYo55fOJUyF6+1gBIA0FfBSAbDoIAmVe+a00TrY1xpmQFjcMFT8fENaozV6Jbev0lNvNrzNn4I9dq2ExCIEKxQnLznO+EaCxQojUdxg8gyIlpta+xrzXy91ubidVaKSl/jWhD64AAGnngCIEDbL36JwFXTqw83U6kC+6qJMMYQ2rcPoXf3lRwTi6WQlisLsMgiOpwQHU6k4hkA5SeZ3FddC+HDj0ATpb8/BLcb7qu310xX5DOd976Sa23OCtY333wTw8PDuHhsGj2Tsd6wvXv34ssvv6xoH5Qy0FJB7bPEz7YuxdHTk8/83LZlqXUTrQH3X7cS739xtuzEDwFw3/aVFZ9DJK5N6rWa0gw88fZxnBu2X7gCsZa6CEFuNkpVJGxY1lC2IcJmVwXU7PWqN6ZJ593fMhevtV+uuR9fDhV2zU5EgABVVNHmbK3a697mbEOzswkRLQpGUdCVnw8BgUNy4KLGCyo6vklNhLRI2X3qpo49Pa+jO2RP3snNrE4Yr0gq1gVWwyhxcxGJCJ/ihULkeffZLMd8u9bm4nU2GfV+jamuY/DZZ8AMq9504Jmn4dp8xZQtnaimwQiHyq6QMEox+tabiH18sOy+TJNBMCp838a8VeFwWv0dFdSWS63tcK1dh/jnh0qOca1dD6llcV3fi2q/93NWsD755JO2pp9/+7d/AwD8/d///WydUlXQTGsmsdyPDlGwxtUKSZJwYVdjUZeALBd2NVbsxxpP6ZOK1VLpVZZYxdgy19gFTYCrN7WVXXKc63ZVnNlHlmW0uBZhMHm+5BgCqwRlQ+Oaqi61Wt6f2zCYPI9QOgyRCEUbryQigYBgR+c1FS2xj6dYlb7e0kYazx5/CX2xs7btAgQIY3+vfeaXYEvbZSAlju8QHfAqbgiEX2ucuY8ZCYOmxu8zNJWCGQlDmIJ5PtUzMMKFXqv5MEox8spLiH9hF4mOVauR/r57yucNAESWLG/VaZQxtD76W5zTtAJrK+Jwwr1hI1of/c20zmkuMWe/gdrb27F06dLcf263G263G0uXLp3tU5sRXqeCJc1elKpFFgVgSbO35nGcf3f3JmzqaiyYaSEANk3BhzWZNkqmdmU5H07hd69+ZxOrBMCGZUG4HHbbKVWRcMPmDmy7sHTqjEuV0OhzcLHKmZRdGx6ATIrPrFgzmyoCqh9rG1ZV/dirg124f80d6PC2QxEViBMEn0QkuGQnbllxY0WWVpWkWMUycfzhyLMFYnV7xzZc13EVHLK9vlyRVFzbsRU/WXxZwb4ECPArPvhVLxernB8N48EApdUqMwycf/7ZArHqvvgSNNxy27SOKzgdkBoapyVWAUCQZbQ8VOhCsPiv/xaL/+Zv531oADCHZ1gXKtk4TsBqLBuJ6TApgygQNHplqKpatzjOv7t7ky3pqrXBifuvqzzpSsuYiCXL19b0DcXx328dQ1Kzp1fde10XLljRCNMw8OYnvQgndQRdMm6+shNiieMLBPC5FTgU/rHlVEaHpx1rG1bhXLQfMTMOk5oQBREe0QVFViALMhocwZrFcq4OduH/uGTleNIVA1J6EoQIaHQ24NLmTRU3L02WYjWaDuGpoy8WRNHevPwGbG65CIwxrAh04MuRbxFNxdHmbsW2tisgFEnUU0UFXtkzb+yqOJxqwCi1ygDKLMPTTAbnn30KqQmzqN6fbEHDzlsmrXktgACi1wfRNfWmrEpQWltqst/ZYN7c+ed7JGuWbBznk3uPIZKkIIRAFgUwMESSFH5iYMfmrrp1gkqShIdvWjvl5+mGiXCitNcqAHT3hfHMO93I5NWw5KdX5SddWXOuDN/+EMLVm9oKZlitxiplXtpVcWaP78MnkDASiJmWnZwoShCJAEmSoYhKXWI5CSHo9C1Bp2/JtPcRmyTFaiAxiKeP7UZCH68PF4iAO7tuwfrGNTgVOY33+j7E+dSw1ajFGE5F+9ATOoXrOrdimd9auSIAPLIHLnl+dc9zONXACIfBjNLlNjSdxuCTf4B2+pRtu//aSkinaAAAIABJREFU6xC4/oYpf48QUYQY8EOQ52ZC3Fxj3gjWhUepD3Z9O0AZY+gdjCOWysDrVNDZ4pn0otMNitGYVrYB+queYex+/4Sti9njlLFr51osbnLbkq7y/2QtY1jbgZxodTkkeJ1zP7GKM7foDvXk8uMDqh8xPQ6TUZjURFiLoENuxy0rb6xrLCdjDH3xs0hkknArLnR42if9XMf1BJJG6a7809E+PHf8JZuglQUZ9635GVb4l+FU5DTe/OEdRLWxqNqx41FKMZgcxJsn38FPV9yAVcGV8CleSAK/LXB+fBixKFim9I9CMxHH4H8/jsw5e7lN8K9uhn/b1F0IBIcK0ecvWTvOKYR/M9UZxhj2HeqDqohoVpzQDRPZ2UVZspbf9h3qw9rOQM0F2tHTIew71IfRWOUZ9laKVbqsWD34bT/e/Pi0bVuDT8UjN69Do89hS7pijFmalQGMMBBm1RZ+8HU/tl3QhqDXAVXhy5KcqWElTR0EG/MfdUgqHJIDJgzopgEBAtyKG6sCM8v0ngrdoR6833cQ4bws+4AawPaOrSVFc1JP2WZNJ3J89Hvs/v51WxOWU3LiwbV3od3TBsYYPh34HHF93MqGMTaW6mX9WozpcRwa+AqXtVyyILxVOZypYiYToInS15kRjWDw8cegn89r4CQEjbfdAe9ll0/tYAQQvV6IrrllmTYf4N9OdaZ3MG4TiIoswuWQoMjjomw0pqF3sLJErOly9HQIu/f32M4le+zd+3tw9HSo4DkmtSJXS7mqMMaw9y+9BWJ1caMLv71tAxp9VsPHNydGoGUMUMpgUMA0AYOysX8t6xYtY+DkuSgXq5xp0Rc/axOGAAACqJICh+SAIsoIa2GciZ+ry/lkZ3snnlNYC+OVnrfQHeopeE7aSCOml/4e+GroW7zQ/apNrPoULx7Z8ADaPVY85EByECOpUC72lTIKgxkwYcW0mjCRoTr6k4M4m+ivxp/K4cwrzFQKZjRW8nF9ZAQDv/+dXawKAhbde/+UxSqRREgNjVysThMuWOtMLFVZylSl46ZDdpa3lPCkzJrlzc9Wp2PBAGaJJ5mU4aUPTuLAV3YBsGKxD4/euh5e13iNTiiugVKGUharplVih9G4VnwAhzMJiUxlJt3xTO1NtCfO9hY8Dor9fQdt11vGzCCaKX0T/ejcX/DaybfB8qrIm5yNeGTDg2hyNua2JfU0zLH9UkZhFjkHAoJYJo5jo99P+W/jcOYzVNNgRiMlH88MDmDgsd9ZjVhjEElC889/AfcFlTnpZBGcTkiNTQuiW3+24IK1zlRqV1VLW6uJs7zFyJ/lZYwhHNNglFCYGcPE03/qxufH7X6XG5c3YNfOtQVd/QG3UlKsAlaBhMkYGsfcFDicqeJWKuu49Si1n+koOts7gVDebK9u6ghr0aINjYwxvHN6P/b1HrBtb/e0Ydf6B+BXfbbtLtkBkRAwxoqK1RyE4PDIcZto5nAWMswwynqtamf6MPDY72HGxn84ElVFyy9/BdeaqTUqSz4fJL+f92HMEC5Y60y+rVUpam1rlT97yxiDpptIaQY03bTdsLLjIomMrdM/n5Rm4PE3j+FYr72E4Ir1Lbj/+lVFu/oXBZwoly7IAAiEoK2xNjYfnIVPh6cdATVQdkxQDdTMziqf/NlexhgyZgYpI42MmbFdb/FMAgY1xsRq4V2UMorXT76Nj/s/s21f4V+Gh9fdW7Szv9XVgkZnsGxjBwODAAFpM123EgkOZzZhpgkjFCrptZo6eQID//t/gabyXDecLrT+6tdwLF8x5eMJKp98qQZcsNaZrK1VKcEmEGDH5o6a/hLLzt6mNQPnw2mMRtIIxzSMRtI4H04jPeaZ6nUqiCYzSJdIsYokMvj9a4dxetC+dHn9pUtw29ZlJTOvUxlzUi9Vpyohni5tkM7hlMNKmtoKUuIrrh52Vlmys71pQ8NwehSj6TAiWhSj6TCG06NIG9Zqh0t2IqxFQYvMhOpUxwvdr+Kr89/Ztm9oXIsH1twJRSy+IkMIwRWtl8Ihlr9hUkahGVpdSiQ4nNkk67XKzOL3teTxYxh64nGbY4Do9aL10d9CbZ++NR1n5nDBOgusWxrE3dd2IehRoOkmkmkdmm4i6FFw97VdJTv0q0VniweySBCKazAnZMSaJkUorkEWCRp8KpIlRONQOIX/LJJedfu25bj+0iVlhYBLkWBSVlK0iwKBSRk8Tl7rw5k+q4Nd+FnXTgTHZloZY9CMDCQiYsviy+rmENDhaYdEZIS1CExqv0lmLbYkSHBLrqKRq2lDwzNH9xQ0Zl3WcjHu7LplUnP/5f5luLFzO4QiX/cEBBKRIBDLLcAt81UNzsKFMWaJVb34fS3+zdcYevoJsLxYeCkQROuv/xpKS2UG/KRIEAenOnBbq9mEkDELUgIClvNHrNPByz5KGRBP6UWFZ6n0qvuuX4WNyxsqOzqxnpOtr2Njfz7JvSYom+PM4VTC6mAXVgVW4sNzn+AvA19AYyYMauLguU9xeOR4WUupqkLKxDwyBhMmDGYWXG/xTALPHNuNgeSQbfs1S7bg6vYtk84Qy4IEn+LFyuAyqKICnRm5MgQCYr/eOJwFjhmJgGWKp8XFPvsUI6+9YisTkBc1o+WR/wHJ569o/4LDAYlbw9UM/srOAllLqVA0jVhSRyimWf9G0yUtpapJ72AcukkR9KoAKHSDImNY/wIUfo+CdMZE/3Bhp3V3Xxj/9cYRm1hVZRG7bl5bkVgVBQJBBPxuBUSwbpaEEAhC3s2TAD6XjHi6dAwlh1Mp34dP4KNznyGiRRFORTGcGkFcTyKULm0pVU36YlZQgCzIMKgJnerIUB0mpSAg8KleZGgGgxNEaSgdxuOHnykQqzuX7cA1S8qXMxAAbtmFoBqAJEhI6il4ZHfuesv9l/ccr+wp6/nK4cxnjFgUNJ0u+ljkzwcw8urLNrGqLG5H66O/rUysEkD0+SAFApCCQQjO8XpywemC6C9fT8+pDD7DWmeyllIDo0mkNPvyXyypw6mKNQ8OyDZTjUY15K+MMAAZAwhFNTQHXUhodsE4WXpVOQisxCqPU0YybcChSnDrJiJJ3dZ4QgiB3yXDoUo1dUrg/DhgjOH5468UiL6kkUIIYfhVH/b3HcSqwMqaXG/doR48d+wVDKbOFzxmwgTo+D0yoY+X1wwmhvD0sd02w3+BCLhj5U+xoal8h7JIBPgUHxRxvKRmOD2CuJGwZnMZzRsrQhYleGUPHJJaF9cEDqfemMkUhCKRq4wxhPf9CZED79u2q0uXoeXhXRAcjkn3TWQJkj8AIllySpBlLLrvQQw99QSIQND64IPcyqpKcMFaZ3oH4zjWGyoQq1lSmoljvSH0DsaxtNVbk3PwOhWcG06MzagWYpgMQ6Ek3Or4RVY0vcqr4pGfrssFApRCFgX4PUrOMSBbQ5vQDIgEYAIBYSSXdJXQDDT6HTV1SuD8OHjs26cKxGoWBoawZnkwnomfQ4e3varH7g714InDzyOUKe3zaMJESAsjiADcY13+vdEzePb4S9DMces5WZBx7+rbsTKwvOwxFUGGX/VBIOOLZ92hHnx8znIWEIgAQoS8pCvAI7nhkNS6uSZwOPXGTMQhKPYVQEYpRv/4BmKffGTb7ly9Bovu/zkEZfIJE8HtgujxFvzY9W+7Cg3btiIQdCMS02CUuNdypgYXrHUmHE+VFKtZUpqJcDyFpaiNYG1rUEuK1SyGybAooIAxhj991lcQCLC40YVf7lxrCwQohscpw+2QisxejVXvEpKrXbVV+XG/Os4MOTbyPb4Z/m7ScREtiqgWQzUvN8YYXuvZi3AmOvlYMGimhhbnInSHTmB392sw2PjSh1Ny4IE1d2GJt7yYdMsueGT7DOl4aAGDV/YgrEXySgGs/xs3EnBKzrq5JnA4sw0zTQy/sgeJL7+wbXdtvACL7r4vN1taEkGA5PeXtasikgRBkgDwAJxqwQVrnfnwm8riDz/8ZgCbupprcg6PvXmsonEvvH8CDkXG59325cwVi3146MbVZa2pCAECbrVotGp+DW00YdXyZRFFAT63DN2gNZ1l5ixsGGN45eQfQSvo3GNg6IudnXSpfSr0xs7gXLK/qJ9qKf587hMcOPOR7Tk+xYufr70bi1xNJZ9nlQB4i1pb5YcWOCQVQRJATI/DMO1d0lvbL69P8xmHMwvo589DDlozrMwwcP6FZ5E8ctg2xnPpZjTefmdZz2IAIIpihQBwN4C6wwVrnekfraypoX+0dn6IZ85Xtu/vz0QLAgM2Lm/Avdd1FQ0EyCIJBAGvWnJMtobWoUhwKBJ0w4Q128MgS2LBOA5nqvTFz1qzphUSSU8+EzoVTkX6CiysyqFTA/vPHLRta3Q04KF19xSkV+VTrAQgn4kRtaqkwq06kcykYVIKkQiQRRmNjsrcPTicuQzVdQw+9UTB9qHnnoFr1So03H4Hhp9/DukT9hhi35atCO68pfwKAwFEjxeim9d5zxZcsNYZh1zZS17puOngdSkYGE1NOm6iWL1ifQtu3VI6EACwHAP8HgVCmQt/YjOVIouQRAGGSW3BI7zpijNdEpkkpEn8SfNxyFVOoiEMk1nH5ZOh9h9ni92teHDtXXCV8UX1yO5JfVNLRdQqogIIec2TvNmKswAYeOw/kfzu28IHMhqSh79D+oeToEn7j7jAdTvg3359edcNUYQY8EOQ+T1pNuG2VnXm2ovaKhq3/eLKxk2Hu69eNuXnTJZeRYhlVRX0qmXFKjA34mk5Cxu34oKAygXrpqaNVT3+ct/SKQlm+3M78fD6+0qKVZEICKqBikz+51JELYdTS7QzfUgcOVJ2zESxGrz5FgSu21FWrAoOFVJjIxercwAuWOvM4qbKRFhbY+3EmjCF2htCJk+vkgSCRp8DTrWyWeG5EE/LWdgscS+GRrWSS+X5SESCUGWz7w5vOxZ7WiFO8St2XcNqPLD2LqglolZVUUGDI2izrCrHXIqo5XBqyei7+8BSFfoIE4LGO+6Cf8u2MmOsSFYpEJy0rpVTH/i7UGd+GIhBLLOkDljm+qcGK6+/mwqUMvSPpiBLk9+gBELwwPWrcMX60pF0DkVEg99Rtqa1GNl42okzrQ1etS7xtJyFzZnEOThEtWgc6UQ8sqvqhvmEENy64iZ4lMp/eF7avAl3rboVklD4w48A8CkeBFR/RSI8n4kRtVmCagA/69rJm604CwIzVmEdOiFYdN8D8F56WekhogipoYHXq84xeA1rnbHiECcZQwCw6s94UMYwGksjnswADBAFwCzjbnX1pjZsXNFY/BwBeF0yXI7pGyKvWxrE2s4Azg4nwEQRhJpob3Tz2R7OjElkknBIKryKZeVUqltfgICkkcJIerTq57DcvwwXNK3Dh+c+nXTsmmAXbl5+Q9HPvkRE+FQf5CJCtlKyEbX9qX5ANQFNQpuzlV9rnAWBGYuBSJXdi9RVq+DeeGHJx4mqWi4AfFZ1zsHfkTqzvM1raywqBmPAisXVtXNijCEc02CYDC6HtQQqEFJyWV6WBCxrK34OkkDQ4HPMSKxmIYRgWZsPl6xpxrJWH7+BcqpCttlIFiSQMs1PAhEgCiIODx+zJa7NFIMaCKcjWOrtgCooEIkIocR5iETE5uaLin72HaIDQUdgRmI1CyEEnb4l2NS6Hp2+dn6tcRYEZiIBM5GA/8otIA5n+cGKgsabflr8MQKIHg/kIC8BmKvwd6XOkDIiMYv1eHVvJuF4Jtf173Eo8DglGJSBFrlHCwTwuWR4HIV1dC5VQqPfAVniHx3O3KXD0w5JkDCaDoOi9DICY2OG+pkIzsTPlRw3FQxqIJSOgILCpTjhlt1gjBX1hCUg8Cu+gm5+qwTAC7/qnXIJAIfzY8FMpWDGrPI5pbUVzpUry453rVoDpaWwxC1XAuDhjb5zGf5NWGdiqQzMYioxD5OyqnqQRhIZaPq4J2RroxO6QUvO9BICuB0S2prGb6KCQBD0qvC5FT4zw5kXpPS0LTGqGBTj10U8M3Pv43yxCgCtrhaIRCwpmgUQuCUXWlzjISESERF0BOGUJs8x53B+rNB0GmbEHnvsunBT8ZREWYZrwwVouufegocEp5O7AMwTeA1rnYnGtaKzmvlQBkTj1RGs0WQGKW38pm1Shpc/+AHRpF4wViDWf0QgtoveqYjwust7q3I4c4ne2BmEtcik4xiAUDqMVnfzjL1IJ4pVAOgJn8RweqRgrAABAoj14y/vslJFBT6Fz6pyOOWgmgYjErZti3/1JYZfehHFZmKaH3wYrlWr7RsFAZLPB8HBfxjOF/i3Yp05cipU0bijpysbV454SkcyPS5WM4aJp//UjS8mRK0CY0KVkLFoVAWGydA/koTPpcDvmdxblcOZS5yK9EGfZHY1i84MqKI6Iy/SYmL12+EjeO74ywUNX1mhKgoivIoXBtMxmByCW3ZNywWAw/kxQdNpGOEQ8i+r6F8+wfCeFwBafCVDbrJHGxNFgdzYyMXqPIPPsNaZ85HJE6YAYChc2bhSJNM64qnxWdSUZuCJt4/j9AS7LEEgIIwBuYmesf9LAFEkcDlq+xFhjOFUfxQ/DCVATBPtTdwlgFMFCAMrcfMqRrunbdqfu2Ji9dP+z7H39Hv2U4Lle5prAiN5jzACj1xbCx3GGHqjZ9CrmYAmos05/b+Zw5kNaDptzazmidXwgf0Iv/N2xfsQPR5eqzpP4YJ1zjL9juWUZtiW/CNxDY+/dQxDIbsIFgRAALNKAMaglCKayEASBQTcVY6rnMDR0yG881kvBsMpEFh/cUvAiRsu6+Q+rJwZsdy3FIIgwKxQtMrC9BwvDGogrI2LVcYY9p85iD+f/bhgrAjRJhAppYhlYhCJHw3O8mlUM6U71IP3ej/E+fSwFRvLCBY5mnBd5zbuw8qZF+TKAMZujYwxhN/Zi8gH+23jlCUdyJzpK9yBKEDy+SGotb2vcWoHF6x1xueurLDbX+G4iaQ0A5HEeP3rUDiFP/zxKMJ5NbGEAIokgtLsTRZgYDmPWAKCtGaio7l2Mz5HT4fw5N5jiCR0mJSCgICBIRzLYGD0GB6+aS0XrZxp0+FtR4OjAYPJoYrGh9JTL8HJilWTWdcRZRRv/bAPnw99bRsnEAECs+rCKZh1wx27zggAjWbQ7q5dFHN3qAfPHXsZUT0Gk5rWFwBjiGhRDB07j/vX3sFFK2dOQzXNVgbAKMXom68h9ukntnHONWsRvGknzv0//7dtO1FUyI1N3K5qnsPfvTqjypXFoiry1H9LTBSrfUNx/P7VwzaxKokEf3VZJzxOCZQx6CaDQRlMChiUjVldMTgUEX1DM++aLgZjDC9/cAKjMQ3mhOQC06QYjWl4+YMTVfXF5Py4IIRg06INFY8fSA5N6fNmUtMmVg1q4KXv3ygQq8t8nfDLPjAABjNgMhMmTOtfZoIBcIgqzib6Kz72VGCM4fUTf0JIC1tidcLfENLCeOPEn/i1xpmzFIhV08TwnhcKxKr7gk1ofvBhELlwtUT2+7hYXQDwd7DO1GqGNZm2i9XuvjAee+MIknkOAaosYtfOtWhtchXYvBJM2ERQVWutfE4PxHB2OFm66oEBZ4eTOD1Qm3hazo+DVf4VFUWzAoDJaMU+rFmhlxWrmpnBs8dfwpHR47ZxlzRfiJ+0XT5WBmD/sI+HGVjbq2GpVYze2Bn0JwfKjjmXHEBf7GxNjs/hzISJDVZU1zH03NNIfP2VbZzn0svQdM99IGJlE0Kc+QkvCagzDd7KuhKDvsrrbJJp3Vaz+tX3w9i9/wRo3qyJxylj1861WNzkxtmhOOJJA0J2iRK5VUoQBgiEIJrQ4XHOPMmqGCfORXIzq5QxUJPlji8IBAIhME2Kk/0RLGvz1eQc8mGMoXcwjlgqA69TQWeLhzejLADcsqtsaEAWWZAhi3JFonGiWE3qSTxzbA/OJeyicOviK3Bdx1UYSAwiYVj7FUDywgMYBIggIIjpcbhle3BAtTgV6YNJrZlcyigoozmxTMhYUQI1cSrSi07fkpqcw0QYY+iLn0Uik4RbcaHDw1O3OIXQdApGJDIuVjUNQ08/ifTJHts437arEbxpJ/8M/QjggrXOpDOVWe2kNXPyQQBiyQwSedZVB7/tx5sfn7aNafCp+NXN69DgyxPLBNBN+6wPG/tPNyhEUZhJ31dZsjdM3bBn/zAA1GQgYFaSFqv9F9DR0yHsO9SH0ZiW29bgVbFjcwevoZ3nDFRYvwpYP5Ym82GdWLMa0aJ46uiLGEmP2sbduHQ7rmzbDMCqDTdMA+YE4cwAmDBBGQGhNfycEzZWfjB+/JzN1tg/AhOqHaxXku5QD97vO4iwNu6hGVAD2N6xldfRcnLQdApGeNxH2UwlMfTEH6D19drGBXbcCP81221iVXTV1m2DM3vwkoC6U707QyQxLlYZY3j7094Csbq40YXf3rbBJlZ1Skv61QFjwpVSxNOF4QLVYMViHwyzWFDl+PENk2JFe21nV4+eDmH3/h6bWAWA0ZiG3ft7quKFy5k99p56t6JxOtWR0JNlfVgnitXzqRE8fvgZm1glILh95c6cWAWAL4a+LRCr+TBYNePHQz0lx8yE88lRm1gtBgXFULIw3KDadId68ErPWzaxCgBhLYxXet5Cd41eA878wnIDyBOr8RgG/uv3BWK14ae3InDtdeNilRBIwSBEd21WKzizDxesdSYarawuM1ZmHGMM4biWS7AyKcNLB07ig6/tNXgrFvvw6K3r4XWN18N6nDKa/Q5oRvnp07RO4VJqUw/U3uSsKO2rvdFZk+MD1mu471BfyfOgDNh3qI83o8xTDMPAYGq44vEj6VDONaNgX2M+q1nhdyZ2Dn84/AyimfFrVCIS7ltzBzYt2pjbRhjBsZHuvHrVEjCGwyPHq/5Zo5Ti0OCXk44jIPh88KuSf381YIzh/b6DYCXEOwPF/r6D/Hr7kTOxwcoIhdD/v34HfSCv5IYQNN15D3w/2Tq+SRKtIABuWbWg4YK1zrz/TWU30fdKjKOMIRTTkM5YJQNWetVxfD4hvWrjigbs2rkWDsWq+iAECHgUeJwyDp8aLdhvMQ7XaIbxufdOVDTu+fcrGzcdegfjBTOrExmNaegdjNfsHDi1Y3fPa1N+zju9+wu26RNCAU6Ef8CTR19AykjnxjhEFQ+tuwergytz21RRwQ/R0xWlbRGBIG2mK276qpRDQ19BM7VJBTMh1vEnOhxUk7742YKZ1YmEtHDVXwPO/IHqGRjhcZ9Vffg8+h/7HYyRvNl/UcSi+38OzyWX5jYRVYXU0Agi8QrHhQ5/h+vMZDOL5caZlCIU02CM1Z4m0wae3FuYXnXl+hbcsmUZhLFAAEEgCHpUqy4UwFA4jUqYGDRQLQYr3O/AaG2OD1TugFArpwRObTmfmvoS98Tn6KaOsBbNidXDw8fw8ok3QfOW2D2yGz9fezda3M22bW7ZhbAWsRoJCYFZZuZQFhQQVN8pIJS2BGKhR8EExjoeR6fhRVspiUyyonG1ckvgzG2orsMIhS1TcABa/zkM/uG/QBPjnwciy2h+8GE4V63ObRPdboheb93PlzM7cMFaZyQRMCrop5ImrMYbpiVWzTElWyq9asfmJdh+8XjXrSIJCHjUnHgFrDSpyW5iBEBLsDZL8i1BB46cqmRc7UoCvM7KbMMqHceZWyxyNuJY6PspPyeLbuoIaZFcg9JnA1/irVP7bOODagAPrbsHQYeVUkVA4FO8cEjWsmRuOxGAMnWkTsn6jE3W9DVVgo6A1cg4SfckAwWDiAZH7ZoM3UpldYXVfg04cx9LrIZyfRXp3tMYfOJxsPT4xApxONDy8C44li4b2wCIPj9EZ+3uEZy5By8JqDP/128unXzQhHEZ3cRoNJ0Tq0PhFH736mGbWCUEuH3bclx3yZKcWHWqEoJeu1gFgJ1XdkIUSc57Nfto/v8WRYKdV3RO74+chC0bWisat3VjS02ODwCdLR40eMvXOzV4VXS28Mzp+cjdXbdNub3xhs5rAQAZM5MTq4wxHDhzsECstrgW4ZEND+ZEqUgEBB2BnFgFgM3NF8EhOcYSrUjB0jwBgUAEOEUngmqgbNPXdNjcfBGUCiJnGQBFlHFp86aqHj+fDk87Amr5+NlavAacuc1EsZrq+R6Djz9mE6uC243WX/06T6wSSIFgSbEq+gMQ8h4TnE6I/tpGH3PqAxesdcbnq6zzPTsumTYQimm5EoG+oRh+/+phW0iAJBI8sGM1rlg/LvC8Lhl+t1LUm04URWy7sM1mWDAxNGDbhW0Qa2TCnNIpHJM0dDkUEclM7ZpACCHYsbkDQglVIxBgx+YO7u03T5EkCRsa1lY8/qrFV0IURWTMDMJ5YvXtU+/iwJmPbGM7vUvwy/UP5GYDZUFCUA1AFuwLVoIgYEfnNSAgEIn1eZ8oXn2yB6Ig4dqOrVX/rAmCgIuaL5i8hhUEFy26AEINk4AIIdjesRWkxC2HQKjJa8CZu9BMBsboaE6sJo58h8En/wCmj7vTiD4/Wh/9LdTF7WMbBEgNDWWbqwRZxqL7HgSRJJCx/18okn7FmX/wkoA60zsYR0uDE4Nl6jNbGpzoHYwj6FORzPNY7e4L4+l3uqEb40JOlUU8fNMarFhsCVxCgIBbhTqJIPzFTdbN/MNv+mHm+bGKIsG2C9tyj9cCr1NBS4MLg6PJXPNYPg5FREuDq+bL8euWBnH3tV3ch3WB8tOVN6I7fBIZWr4O+eJFF+D+tXfmiVUrIOCVE3/E4ZFjtrFrgl24c9UtkMdmLlVRgV/xlRRa13deDQDY13sAST0Fk1mfd0IIfLIHS30duLaGHqTb2q/A4eGjiOpxW+1tFoEI8MkeXNV+ZU2On8/qYBd+1rUT+/sOIpTXgBVUAzV9DThzj4luAPEvv8Dwy7ttdotSYyNadz0KKWh9DxNFhhQIVhT5ejHPAAAgAElEQVSx6t92FXxX/sR6Hm/GWjDwd7LORJMZRBM6FEmASSnMvHuIKACiICASz+DccMImOoulV3mdMnbdvBZtjdZMj0CAoFeFPLEAtgS/uGktfr5jFd76pBeD4RRagk7svKKzZjOrWfKX46lpIhTPwKQMokAQ9CgQRLFuy/HrlgaxtjPAk64WIPFMAqIgQIYMk5pFU6+cogNbFl+OtKEhmomCwSoJeKH7VZyMnLKNvWjRRtyy4iYIxLphuiVXRTWX13deje1LtuHQ0FdWYxOzlsh9Di+WeBbX9LPW4WlHp68Do+kQUkYKummAEQYBBJIgwSk50egI1m0pfnWwC6sCK3NJVx7FXfPXgDO3MFMpmNHxBKvoJx9j9I1XbWPklha07HoU0lhDleB0QPT5p/Q54UJ14cHf0TqTSOm5WFJREEAIA2PWzKhACBhjME2GSGJ8xu/Db/rxx0/sgQCNPgceuXltLhBAEggCXhWSOLVlPUEQcMHKJiwbE2u1XBbMkl2O372/BxBFNAWckETBChNg9V+OJ4RgaSvvNF1oxPUETGpaNdmCCAFCzueTgIAQApOZGE2H0eiMAgCSegrPHt+Ds/F+275+0naZtbxPrAV2r+KBU6q84UMQBFzWcrEtkrQeQi27FP9Kz1tW/KtCctcaGJuVpXhCCDq99YmB5cwtzHgcZtyyCmSMIfLBfoTf2WsboyzpQMsvHoHoshr1uBMAJwsXrHXG7ZQgigIyuplrohqHQSCALIlwOSQwxrD3L7344Gv7zXNxkxu7dq6Fx2ktSxZzAqiE2YwlzV+OD8X5cjyn+ngkN0RBhG7qMFhh6QlhBBKRIIzVeEa1GJ469iKGJ9hb7ei8BlsWX249BwQB1QdFnFq5ymxGktqW4jPjCUJ8KZ5TLxhjMCMR0LFmKsYYQn96G9E/H7CNcyxfgeaHfpmrURV9Xh61ysnBBWud8blUiAKKiFULyqzSAJciY8+Bk/hiQiDAisU+PHTj6lwggMshweuUpzxDko0lnXga2VjSu6/tqotoXdsZwNnhBJgoglAT7Y1uvjzIqQoe1Q0BQlGxClixqAYzEM5EMJwawVNHX7SlVxEQ3LriJlzUfAEAywkgoPohCVP72sxGkk5MecpGkv6sa2ddROuqwEr0p/oB1QQ0CW3OVn6tcWoGMwxQwwCjFMboaK6ZilGKkddfRfyzT23jnWvXjTdIEUDyByA4HMV2zSlB1iGBpqwemYXmkMAFa51Zsshla6QqRlIz8e4XfTjeF7Ft37iiAfdu74IkWnNCPrcCpzr1t7DSWNK1nYG6LFkua/MhGHQjFErAMGrnDMD5cZHMpJAyyodPMDB8O3QE7/d9iGTeWJGIuHvVbVjTYAlJiUgIqD6IwtTquyuNJF0VWFmXa63Tt4Rfa5yaE/nwAww99SSIADT97E64LrwYAMBME8N7XkTim69s490XXoSmu+4BEUVAECAFAxBk7oE9VbIOCUNP/TdAyIJzSOCCtc58emSworSriWI1P71KIEDAo0KRp9ccNTGWNKOboJRBEEhun9lYUl7byZmPMMbw9ul3J7HMt+hNnLX9b1VUcP+aO7HU1wEAUAQZftWXa7aaCvmRpAxWIIHJKEQiQBZlEIxHknZ426e8fw5nrkF1HeeffxbM0MEADL/2KjrWXwDGGM4//wxSx47axnsuuwKNt94OIgggoggpGOQNUzNgITskLKy/Zh7w9YnhKT/n+kuX4LpLrPSq6TZX5ZONG01nDEQT401gACCKAnxuGQ5F4rGknHlLX/wshlMjuaSqSnHLLvx87d1odVuexg5RhU/xTnv2MxtJmjY0xPQ4TDpeniAKIryyBw5J5ZGknAWDGQnnlqQBgKbTyIycR+iN15H+4aRtrO+qaxC88a+sZkZJhBRssGZZOTNioQnVLAvzr5rDMDYFW46x9KrL11k3z+k2V03E61SQzliBBBPv5+ZYBGzQy2NJOfMXSyhO7ToJqH48tO6eXESpS3LCq8zMWs2tuJA2NIS1SMFjJjUR1iIIwM8jSTkLBjORLNg2/OIL0AfszcOBG25C4JrtAAAiS5ZYrYNLDWf+wj8ddeaCFY2TD4JlcfXAjtU5sarKYtGY1enQ0exGWjMLxGoOBqQ1Ex3N/CbKmZ+4FRcUUZk05SlLQPXjkQ0P5sSqV3bPWKwCwBL3YqRNreyYtKmh3d0242NxOLONEY3CTBauFkwUqw233j4uVhWFi1VORfBPSB1JaQa62iuLZt21czU2Lm8AADhVCQFP8ZjV6dA3lLCiUUvtjlhpU31DfJmSMz/p8LTDLTkrKgmQiIhFjgZ4ZOsHmk/xwiW7qnIeZxLn4BBLx0gCVtnB2UR/2TEczlyGMQYjHIIRjWDktVdKDyQCmu6+D74rrBpLweGwala5WOVUAP+U1AHGGKKJDCKJDM4NJ0vm12chAJyq1dnnccrwu6snVgGrhtWhSgh6VIgTamFFUUDQo8Kh8hpWzvyFMQaDmjmP1XI4RAfiRgKDySEEVD+cUvWsdBKZJBySioDqL3AYEAURAdXPa1g58xpmmjBGR0HTGoZffB7p77tLjlWWLIHnIssxQHC5IAVq70TDWTjwGtYaY1KKcCwDfayxqXcwNqlLAAPQOxDDuqUNcDmq/xZla1MdqgRFFpDUTBgmhSQKcKliLu2qHjWsjDGc6o/ih6EEiGmivYn7sHJmhklNHBk9jgzNQCQiKCtvIxc3EiACgQAB6hQDASbDrVgztaqogMADjeogABRBgSKO+yfXs4aVMYbe6BlEUnG4FRc6PO38muNMC5rJwIiEAZMiM9CP1IkTZcfr588jMzgIx4rlkLyVrTZyOFm4YK0hmm4iEtdsAjUUK+8LmSWVMWoiVgGgs8WDBq+Kc8MJRJN2l4BkWoDPJWNxkxudLTOv4StHNmkrFNdycZFBD0+64kwfnRqIaBHEMgkYVIc+iVjNEs8k4FOqb+HW4WmHRGT0pwZsDgFpQYMXlkNAUA1giWdx1Y9djOOjPfjg8McYio0AYzG19Urc4iwszGQSZiya64WIfPIxWHoS3+N0CrHP/wLPpk11OEPOQoOXBNSIRFpHKGYXqyZlOHI6XPpJeSTTeo3OzDIQX90RQCiu2cQqMOYSENewuqO2SzXZpK2RaBqabiKZ1qHpJkaiaeze34Ojp0M1OzZnYZI2NITSYZiMwiU7EEnHJn/SGAwMg8nzkw+cIt+HTyBhJGxiFRh3CNCMDK7t2FrzGU7GGD48+wmePrIH/dFBMDb+xZRN3OoO9dT0HDgLBzMWgxmN2hp3jeEKrx+jePIchzMZfIa1yjDGEE3qSGn2mZ2MYeK5fd9jNFZZXWg8ma7F6QGwzrG7L4ygVy3pw9rdF8aNl3XU5EaaTdpKpg1rhpdSEBAwMIiCNcNbr6QtzsIgnkkgYYzb6UhMgo7KZlezjKRGq3pO2ZQrVVQQUP1FfVg9ihurAiuretyJdId68H7fh/g+fNI6PiEQiZDzgAXqm7jFmb8wxmBGI6Ap+/0p8d230E6fqmgfxMnjVjnTgwvWKkIpQziuITMh8jCZNvDE3mPoHYxXvK+ec7VrwsgmXTkUCQ5FqnvSVe9gHOeGEwjFx3xg8+6P2Rne7DietMUph0lNRDMxZOj4ikR/YhB/OPLslPcVzVQ+I1sJ+SlXDkmFKqkFSVc61WuactUd6sErPW9BMzWbWM73gM2KVp64xSkHoxRGOASWsa/+xb44hJGX9+RKTMohuNwIXndDrU6Rs8DhgrVKGGOG++aEjqpIXMPjbx3DUKiy2tXc/irJb50mE7v/S0W81solIJrUEE3qZX1go0kd0aQGgAtWTnHShoZYJg6K8R+IP0R68Xz3y9Dp1EtqfGp1m0CyKVdZCABFLMz1rpVDQHaGl4HCZLTomJgetxrCxmZVuVsBpxj5zVX5RD8+iNE3X694P65166G28x9EnOnBBWsVSGkGoslMwQ/MoVAKj//xKCKJqQs/j1q7t6bS7v9auQQkUkZB7exETJMikZraki7nxwFjDHE9gaRh/xF4bLQbe75/AyabXo1ck7OhGqeXI+sQMBm1cgjIn+EVSfF2BZOa0KkOZcwdgSducSZiJhIwY/bVB8YYIvvfQ/jdd2zblSUdIIoC7aTdLYA4nHBv2IjWR39T8/PlLFx409UMiSYtf9WJYrVvKIb/fO2wTaxKIsGOSypLtPn1rWuqeZo2si4B5WjwqjVzCXA7ZZv/K2MAZcz2GoqiALezcDaK8+PGoAZG06ECsfrF0Dd4sfu1aYtVj+TGpc3V7Vzu8LQjoAbKjqmlQ0D+DK8syhAFERQMlFHQvEiF7OxrPd0KOHMfqwQgXFSsht5+s0CsOlZ2ofWRR9F0x10F+1r813+LxX/ztxBk/p3OmT5csE4TyhhCMQ3JdOEs4PHeEB5746it8UqVRezauQ7bL+2cNDhAFIDVnU3VPuUchBDs2NyRO4+MbiKtGcjo1s1eIMCOzbVpuAIAn0uBzy2DMkA3KYy8/3STgjLA55bhc9XeB5Yzf0gbGkbTYRh5opQxhoNnP8UbJ/faUq0WOZtwQeP6ivYrQMCNy7bn/IerBSEE2zu2goAgY+pIGRoypp47SwKhpg4B+TO8mqHBpBQmNXP/GdQAZQwiEWp+Lpz5BTMMGKFR0LS9uYpRipFXXkL04Ie27a5169H80C8hqCpQ5DOktLbU9Hw5Pw54ScA00A0T4XimoF4VAL7sPo89B06C5k0Xep0ydt28Fm2N1nLbb27bgN+9erjk/v/P+y6u+Y1j3dIgLl/Xgrc/7f3/27vzKKnKM3/g3/cudWtfeqH3bpZmEwERBCKgqBjAaFTcokZjnEjWw5zfjDNm5kySyXFGTkJc5gwTl5gxJkTAYDATF0hAENEIQSNGIUCD0M3Wa1V1V3Vtd/n9UV3dXV1LV0Pdququ5+PhJNy+3fetpp6qp977vs8Tl1ibJAErFtTrWge1vsIKm8mATm+qSggabGaD7nVgyeiQagmApmn4Y/NuvH/uQNzxWms17p62CibBBHfQjdNp2p6KTMRNk5bjuvqrdBk7APBMgDfc0b/pied4VFsqcePEz+ta+zQ2w3ve3wpPyNt/bVVT+u9mKJoCs2DGTZOWUx1WAgBQgwHI3u6ETVSaLKP9lZfR+9eP445bLpuDsltvB+N5gONgrK8HZzJBDUTjlTOZwTvS32kgJBM0wzoCmqbBF4igqztxcxUA7P34HH6z+3hcslpqN+LrN8/oT1YNAoeu7iBEPvmvXuQ5NLdmd7dyModPubH/cCscVgNKHEY4bRJKHUY4rAbsP9yagzqo0aoEIs9BGPRH5DlwHMtoxykZ+2K72Ycmq4qq4HfH30xIVhudE3Df9DthEkw46T2FoBxK+bNNnBHfmPWAbslqbIe+rEVQZixBidEJh2SHw2BDRNF/fTZjDEtrF6EnMrCRigODwAngOR484+CU7LCK+pfWIoVP0zTIXi9kjzfh9VcNh9H20q8SklXbgs+hbNUd/cmq4HKBN1tQftc9YIIIzmBA5T330FIAkhU0w5ohWVHh9Q20WB1M0zRs29eMdz6On8mpKbPgKyunwdq3FlMSedjNArbvbwFjgMABqhZ9bWAseiueMWDbvmZcP68267coB493x4GWhBaxsb+qGnStg9rc6kNE0eCySinrsEYUjcpaFbmwEoY31BNXBQAAIkoEW479Hsc88Rs7ZpZNxxcnrgTP8dA0DfvO/QU+2Q+RE6FBg6oOrNxkYFCgYPfpdzG1pDHrz/PBO/SBaPIociKgRstahdUQdjXv1b3uqUk0wiZahtSAZRA5vr8OqyfspXJWRU6TZcheD7RI4gcpNRhE64YXETr5Wdxxx9XXwLns89Hnb1+yGktMHYuXoGTxIjhdFnh7QpDl9JtsCckEJawZCIUVeP2hhAQPABRVxdY9J/Dh0Y6445Nq7Pjy9VMhGaIlowwCB6fVgH2HWhEIyYgoatyH2OjGI4BpKhCSsf9wGxbOqNTl8cTqsAZDckJrVp6PJoxd0K8OaqxcllESIBl4RBQVDNGEWeS5/jdwvcpqkcLnj/TCF0kssRSUg9h45Ldo6TkTd3x+5eVY3nBt/3OnI9AJT8gNWVWgaErc+lYg2tkqrKr4m/so3j27D4trFmZ1/IN36EfHHUpoHOAN9+hy7cH84d5oDVjegIgagQINBl4AB35w+WMqZ1XEhrZYjf+aH60vvoDwmdNxx13LV8Kx5OroXxiLS1ZjmCCAEwQAqe9yEDISlLCmoWkaegKRpBurgGj3qo07juFIc3y71ZkTS3DHNY0Q+m77izwHp00CYwwd3cGEZDX+mtGNSB3d+nW66gmEEQzJcPtC0NS+t/K+Av6arMDtU+GCfgnj4HJZjDFIIg+B5yAP+b3oVVaLFC5VU9Ed7kFISXzu9YR9eOlvWxJaqC6tXYwlNQv7k1WBCWBgCCrhpMnqYBFVxpsnd2KcuSyrazgH79CPtYyNjiIaaAzRZQ07m9/J+rUHi228YoxFS1cx1h9rg4ONylkVn1Rdq2Lk7m60/uJ5RNraBg4yhpKbboZ9ft+HLIakySoheqCENQVZUeHxhSAryd/sUnWvWjijAjdeOR5c7M2TZ3DZpP6/uyzisMszNQ1wWfVL1qxGEd29EaiKBkXT4j9ZM4DvK9xvNerzIhQrq9XVk/qTt55ltUhhklUZ3lB3XBWAmK6gGxsO/6Z/81DMDROux7yKy/r/LjAeLqMD/ogfQSWYNlmNCchB7MpyW9JYoqhpGjwhb9LHxIMDx5iuLVFjG68Gz/YOReWsik+6JQAAEOnqROsLP4fsHtSumONQdtudsM4eFG8OBzgDTSyQ3KBNV0kEQjI6u4Mpk1WvL4Tnfv9pQrK6bF4tbhqcrHIMJTZjdBNRn87uzG6PdHr1vY0SLXGjJd4G0gBF1aCoalzL1GwaWlZrKL3LapHCE1LCCSWrYs77W/HCpy/FJasc43D75C/GJavRTUQOcIyDBq1vHnN4siqjrbcdp31nL/6B9Iklir6IHxE1eVKgaNEOVLGWqHoYKK2V/KWeylkVH6W3F5HOzpTJaritFed/9mx8sioIGHfPl+OSVd5qBWc06T1cQvpRwjpEqkYAMW3uAJ753adxrVYZA25dMgHXXl47cFuSY3DZpbhkNfr98e0aU2lz67emrCcQjr6Vp3qPYtEv9fTqt4Z0eoMLty9tTGhgUGKTcPvSRl3LapHC4o/0whPyJp0NPdXdghcPbYI/MqgIPifi7qm34ZLSgeYaDAwOyQGei64Z740EYBMzm6FXNRWyqmR1HWd0h/6V8EdSt2TmGQ9fxBetPqLjGtIprkbc0rgSriFNDFySE7c0rqRyVkUi2gjADaU7sWRVTOjMaZx//tnomtY+zGBAxf1fhXnaQF1j3mIBb6U7YCS3aElAH0WNVgEIp9nN2Nzagxe3HYmrWyrwDHdeOxmXThho68j3Jat8kl3+6X7+YJEUs7vZ4A/I0LToOBNmWVn0uKZB99ao0xtcmFbvxJkOPzSeB1MV1JRaaLanSKRbrwoAR7qa8Mqx30PWBp6HZsGEu6fdhhrrQMc4BsApOSByAy9nFoMZPMeBA4M6zLIALVpDIOvrOE2iCVbRDPeQZQxANFnlGOtvjar3GtIprkZMdk7CucA5QFKAkIAqUyXFWpFQI2HIHg+QpiV28LMTaN3wIrTQwN09zmRCxf1fhVRXP3DMYgZvo+otJPcoYQUQiijw+pJXAYg50uzGSzuOITIo4ZREHvctn4qJ1fb+YxwXXbOaLFkFgNpyKw4c6Uj6tcFqyvR7A+tvjaqo4Phochq7hRp7/8pVa1TGGMZX2eFyWeB2+6n8SZGI1VdNtgQAAD5q+wS/P7EtbtbVbrDhy9PvQJmpNO5cu8EOAx//XK2z1sAkmIH++hOpMTDYDfasr+P0h3thMVgQUILRZQF9GxvZkMUKZsGckzWkjDHU22sp1oqMEghA6famDYPeo0fQ/tKvoMkDHw45qxWVD3wNhsqBajWcyQTBZk/2IwjRXVEnrLFGAP4UVQBi/nKsHa/sTt+9CoiuvXRZpf7qAMmMc5nBhqmLz1j0PL3EWqO6e0LAoAnWvvdTgFFrVKKfoBxCd7gn5Yao987ux47mt+OOlZlK8eVpd8Auxc/s2A02GIX4ZSVA3wchez0+6z417Hg4xmFh1dyszzZaDGYwADbRCk/IC5VFiy5rfUEWu9oCHa5NCAAoPT1Q/OmXm/j/+jHaf7MJUAeVN3Q6UfnVr0EsHWgRzhmNEBwO3cZKyHCKdg1rRFbR2R0cNlnd+/E5/GZX+u5VQF+yajNCFNL/Sq+YVg4+1W6jPjzHcMW08gwexYWpr7CiutQCi1GMbrBSVChK3/+qGixGEdWlFtqlT7JK0zT0hH3whruTJquapuGPp3YnJKs11io8cMndSZNVk2BMea2OQCdElv4uAQcODfY6LKpeMMJHM7zYxisAQN/tf0VToagKZFUGA0OdrUaXa5Pi1r9edZhktefAn9H+8sa4ZFUoK0fVQ9+MS1aZQQRPySrJs4KeYW1tbcV//ud/4v3334ckSbjhhhvwD//wD5CkxBmVTGmaBn9Qhj8QSXujUNM0bN/fjD0H03evAqIzopkkqwBwur0XNpMIty/1hiabScTp9l7dujwxxjClzolPT3aBQeuf8WUMYNDgD0YwpU6fLldDybKMDX84ji5fGCVWA7507SQIQm6flpoW7arVEwjDZjKgvsJKM15ZpqgKvOHulDvmVU3Faye246P2T+KOT3SMx51Tbo7WEB3EJlpTJqtAtHC/N+yFRTTBE46kPM9hsOGmiZ/X5d+bMYZG5wT8resYAA0846FoCmL3MhRVwayyGTl5rqmqigOtH+FkzylogooqqRLjbQ2os9Xk9LmuaRpafGf6lkuYUWfN7fWLgRoKQe72pl2vCgDed9+B+83X444ZqqpR8cCD4C0DkxVM4CE4XfTvRPKuYBNWTdOwZs0a2O12/PrXv4bX68W//uu/guM4PPLIIxf0M4errRqTafcqIJrkldikjJJVILpDPzLM2rGIrOra5UnTNBxt8YBjQFgdfDzabcsoAEdbPPj8FfqWlvqvLQfxcVNn3AeHXR+ewazGUvz97bN1u+5gh0+5seNAS1xN2BKbhGXz6qhSQZYE5RB6wr6EFqsxETWC3x57DUfcTXHHZ5ROwy2Tbujf+R9jEcwwi+nL6fjDvQjKIXjC3WnPc4e92HzkVXxv4cMZPJKR0TQNTZ7P4JTsfSW7BifrGmQoePPkDtTZajC1RL+d+jub92DbyZ3oleMrFoicgDpbDW6auDwnlQKOupuwq+XduJqwTsmJa+oWUaWCLNA0DUpPD9Te9JVoNE2D560d8O7aGXdcqm/AuPseAG8aFFs8F01WdWoTTshIFOyz8MSJE/joo4+wdu1aTJ48GfPmzcOaNWvw2muvXdDPG662akxYVrDhD0cTktWZE0vxlRXT4pNVAE6rBFHgkSmzgYdvmGUIvqAMsyHznzlSza0+HDvtQTCcPIEIhlUcO+1JqDObTf+15SAODklWgejc08GmTvzXloO6XTvm8Ck3tuxuSmhg0NUTwpbdTTh8yq37GMYyTdPQHe6BN9ydMlkNyiG8dPiVhGT1ioo5WNV4Y0KyahZMGe2oN4smtAWG39wIAOd72/Do+z/J6NyRiLVnDSvhIcnqgKASwguHXsLRIY8/W3Y278H/ndiWkKwC0S5fp7pPY9ORrbpdP+aouwmvNr2Z0MDAE/Lg1aY3db/+WKfJMuSuzuGTVVWF+83XEpJVY+NkVDzwd/HJKmPRZDXHd7wISaVgE9by8nI8//zzKCsrizvu840sidI0DV5/Ym1VTdNwtt2PY6c9ONvuh6Zp6A3K+N/XDye0Wl04owJ3XdcYt5kqlqxK4sgSyz0fZPbC/M6H+r2Ae3xB+IYpWeULyPD49GkPK8syPm7qTHvOx02dkGX9ymppmoYdB1pSVoZQNWDHgRZow7UlI0lFVBldQTcCchCapuGc/zyOe07inP98/+/UF/bjl4c24VRPS9z3Xl17JVaMvy5hdt8kGGEzZLauOhQaWeON871tCIeze1fDH+6FqmnwhnuGOc+PXS17s/5cU1UVO5rfhpxiGQYAKJqC7lAPdrW8q9tzXdO06M9P8aFFg4rdOl5/rFODQUS6ulI2AojRVBWdr76C7vfejTtuvmQGKr78lfiOVdRylRSggv3oZLfbsWTJkv6/q6qKDRs2YOHChRn/DA0avL0RRGQFPD/w5nf8jBd7Pz4Hr3/gDcosCejwBqM75wf5/Pw6XHt5/DorxhicVgOMhpH/+vYcSn+LMubtT7vxd7fq83nirye6hj8JwCefdWHutIqsX3/DH44P2zBTA7B513F8ZeX0rF8fAE6e64bbF0K6FQ9uXwhnOv0YX5mbMi583wciPk2ViULFcay/SYY/0gtfxA9wQIu3BX86cyAuaXMYbLi0fBreat6LruDAh0MG4AsTr8f8qssTfr5RkOCQMv93+OXRl0f8GJ799EX8vyu+PuLvS8VhsiIgB4ZtD6tCw1n/eZwLnEe9vSZr19937qOkM6tDhdUI2gLtWb9+THP3aXjCXqQLNnfYq9v1kxmtsTY4zjRNg9LdDS3QC54DUrYORHQGtvU3m+D/61/jjtvmzkX5qtvA+PiJF9HpAmdMvUY8E6P1d5wtxfz49XrsBZuwDrVu3TocOnQIW7Zsyfh7ZHAwW+I3aB051YXt+6MzZ7Hd+hFZxYmz3dEi+n0YA+5ZPg1LLkt8AXXZJJiN+n/ydLl0qsWa4XokjXG6jKErzYazwTp7wrr9Dj5r86ctPxajcbx+/w4p2O2jr91hSYkFiqbCE/SCE1TYTSYc6/gMO1r2RGNt0O+6K+zBb4+9AVUbVEaHcbh39ipcXn1pws82CUa4TC1XUpIAACAASURBVCPboRzMIFEbqi3YntV/a6dzCoyfGoBhblQwMKhQAEnO6vUD50bQPYsh69ePaQ4pGcWaXtdPZ7TFWklJtLGKKssId3VBEwGI6UsgquEwTjz3C/gPHY47Xr70atTeviphfarodECwZO/fYbT9jrOtmB9/th/7qEhY161bhxdffBFPPvkkpkyZkvH3ud29YINjUQO2/+kk5EG7J8MRBR3eYNxyAYFnuHvZZFw6wQWvN35NkNMqIRQII6TjpqgYt07tWV2WzJLtEquoyxhKrJnVdy21GXT7HTBFiXsepDxPVXQbw1A8z8FuN6G7OwAlzdhy/aaeiTNtHfDLvf23dTVNw85j70KW4xsDhJUwuoKeuFlHkRNx97Rb0WiZgG5vfKJp4EUYJR7u4Mj+DcyCGQFlZMsCLLw56//Ws0pn4ExP67DnceCBkJDV65swgueJhqxfv1+IzyjWdLt+EqM11rq6/NBCwejMqjb871QJBnD+F79A8OTJuOOua6+D7frr0T1k2RdvtUIIA8hCq+BMf8djVTE//gt57JnEWsEnrI8++ig2btyIdevWYfny5SP6XlXTgEHvl2fb/fAMmt3zBcLo9seXvGEMuOnK8ZjeUAJlyAYtm1mEyHMX1SFmdr2Ig82py+zEXNYg6taJZsX8Ovxu72dpN6AJPMPyK+p0GcOXrp2EXR+eSXujlAG465pJuv0OasoscFmlhA1Xg5XYJNSUWnLeEUhR1FHXhcgTjF+nec5/Ht4hO/QDcgieIW1KJd6Ae6fdgVpbdUJSIzABFoO1Lw5Htr7x1vFfwPNHNozoe+6YdHPWf+83jP88dre8h4CSfJo12l2OodpSiSpTZVavP6d0FrYIv0f3MGtoDZyIcabyrF8/pspUBafBkbDhajCX5NTt+umMtliL9Pig9KT/94yRu7vR9qtfIHzubNxx14ob4Fh8FVQFGBxXnMkEGLP/ejfafsfZVsyPP9uPvaAXV6xfvx6bNm3CE088gS984QsX/fP8oWiiGIrIaHP3Jk1WyxwmOG2JdV7NRgGWLCwD+OLSWRmdd9PVmZ13IXiex+JZVX11Vwew2B8GLJ5VBZ7Xp1KBIAiY1Via9pxZjaW61mNljGHZvLqUy744Biybp29Zr7GsNxKfoHWHfAnJKgDMKZ+JWltiW1Ke8XAZHeDYhb1EldpLhjRATU/iREwsGX9B10qH4zisnLAMAouPJTaoQavDYMM1dYuz/lzjOA7L6q+GwKWOI57xsEs2XFO3SLfnOmMs+vNTvN0wcFiq4/XHEk1J3sp4KM/ePTj948fik1XGUHrzKjgWX5VwPmeUqIsVKXgFm7AeP34cP/3pT/HQQw9h7ty5aG9v7/9zoSySiFBEhrsneS1WnosWMLdI8YmpycBnrU3p+Co7qsvSrzmqLjNjfJW+G33uXz4NV19WDZ5n/YkqAPA8w9WXVeP+5dN0vf7f3z4bsxtLE1IKBmB2juqwTm9w4faljSgZ8gGlxCbh9qWNVIf1IpjFgQ0b3mAP/HJiuR0BPI57TuKkN759KgcOTsl+wckqEO0yNbPskozO5cDhG7O/qlvCdF39VfjipJUwC6a4RJUxhkrLONx/yV261SG9rv4qfHHiCliExNcckRMw3l6HL029Vfc6qFNcjbilcSVcsc5ffVySE7c0rqQ6rFkUbmuFZ9sb8Qc5DuV3fgm2K+YnnM9EEbzDmXCckEJTsEsCdu7cCUVR8PTTT+Ppp5+O+9qRI0cu6GeOKzGi2x8Z3IUOQDRJ4rnorEcorKKydGChsEHgYLdkJ1kFom9SS2ZVY8vu43GbvGJ4Lvr1XMw23L98Gu5dNhlvvt+MVk8AFS4TVi6o121mdai/v302ZFnGpreina5KbQbcdU1uO11Nb3BhWr2TOl1lWaW5AjbRhjP+c+hV4telMgA8ePA8D57jsf/8h2iw14OxaDLnlOxpZwUzEZvV84a64fa50a0lL4cnQkCJWf8PJtfVX4Vrahfjz61/wcnuZki8hDnlM1Fvr9X9uRa7dqzTFQSgUqrAeFt9TjtdTXE1YrJzUn+nK6vBglprbl7rikW49TzO/+/PEo6X3nwrLDMTJwEYz0NwURcrMjoUbMK6evVqrF69Oms/T1FVvPTHYwldpvqT1b7745LI4XxnANXlFgg8g9MmZTWYY12m7BZDQgktALBbDDnpMhXD8zxuXDRB9+ukIggCHrhhOlwuC9xuf17W+jDGdGuDW6y0vv/8kfiZVQYGHhwYY7AIFjAGeMPdaO1tQ5WlAg7JDpHPTgWO2KzeW6feweGuo5AHLWhnYDDwIhwGOyTegN0t72Kyc5KuMcdxHBZUzcWCqrm6XSPdtedXXY4r6+blPdbqbbU5v24xCJ1uQeuLL0ANJN7NME6clPgNPBdNVqmLFRkliuKZGo4o2LD9KP42pCEAYwPJKsdxsJsNkAwC/KEIeI7BZZPAZfkNrLnVh7Odfnj9yTf7eP0hnO3069plihA9yaqMLcf+D8c8J+KOx5JVnudhM9ggCQOJqT8SiB7js3c3I+Zcb1tcsgpEE2pFVeAJeRGUQ3CHPDjtO5viJxBS2AInjuP8//4sabKaFMdBdJVQFysyqoz5Z2tvMIJfbj+SkACajQJMEg9Ni96GF3iuf3bFahThskngdfjk2d0bRqc3mLAsIUZVgU5vEN29+pfNIiTbQnIIm4++ipPdzXHHjbwBRt4EgeMgcGJCDfkyUwlMwsUVKh/qqLsJm45sRUcweVc1WVMgAOiJ+CAJEnxZKOVDSK71/u0w2jb9Gsi0MyADBIeDklUy6ozpZ6zHF8ILb/wN7Z74NXQ2swirSUx6+89hMWDGBFdmha4vQI8/+YavwWRFQ0+KGdhsU1UV+w+3oaM7iDK7EfOnjwNHt4jIBfBH/Hjpb6/gnD++7mip0QWRE1Lebi+RXJjsnJjVsUTbge5FZyB9VzdZU8AUhogSgdWgX81NTdPQ4jsDX9gPX8QPq2CBVbKgzpq7NaRk7PF9fBAdWzZj8AwI73BA8SZW5Oj/us0GTkqshENIoRvTCeuzv/s0rv0qY8CiSytx8nxP0h7yHIu2YjWI+v1aTrdndqv/dLv+sz3b9zdj275mBEIDn8w3v9WEFQvqsXx+ve7XJ2OHJ+TFhsO/QVfQHXd8ecO1qDCXYUfznqS95HkIWNZwddaTthbfGbT0nIWsDV8GSANgFkyotSaW18qGo+4m7Gp5F+f9reiJ+KCoCniOh020otJSgWvqFtEueTJiPX/ej87/24rBXW/E8nEovfU2nH/u6aTfw1nM4M2F1QyBkEyN6YR1cLIq8Axfum4yLhlfguNnvHjvk/NxX3dYDLj+ijrMnlSm65g6vJnNnHZ4h+nneJG272/G1ndOJNRjD4Tk6HGAklaSsRc+eQk9kYEPYxzjcPOklf2lpZbVX4X95z+MayZQIrmwrOFqXZK16ExmZh8ONahYUDVXl5nOo+4mvNr0JgJyIK4ObWz9LAC82vQmlXYiI+LduwfuIaWrDNU1qPjKg1DDyd9jOJMJgk3fcomE6GlMJ6wxRgOP+5ZPxYS+2qaTahyYWG3HuY5e+EMRWCQRk+scsGWp1mo6opjZm6JB1O+2vKqq2LavOXXzIA3Ytq8Z18+rpeUBJCODk1WBE3DH5Jsx2TVwm3+8owEN9nqc721FbySIUqMLU1z67cr3RfzRTncZkDgJi6oXZH0M0WUJ70KFGvf7Gawn4stZlQIy+mmaBveOP8C7+62441LDeFTc9wA4ozFpwspJ1BiAjH5jPhuxmUU8dNMl/clqDGMM1eUWTK51orE2N8kqAIwfl1n5pIZxVt3GsP9wW9wygGQCIRn7D7fpNgYyNhl5CfdNvzMuWY1hjKHKUomZZdMxtaRR1+TMKlgSukulEtFkHHUfz/oYWnxn4Al5EFEiUNTkSxMUVUFEjVCVApKRzq2vJCSrpslTUPGVB8EZU29a5GlmlYwBYzphnVrvxNe/OANVpanX7BgNfFYbAwzHbMxsUttsyk4tymQ6ujNbbpDpeYQAgE204oEZd6POVpPyHCNvhM2g34exGKtkgc2QeW3dN0/uhJbhjGym/OFoiSFFS1/vNPZ1qlJAhtO9d0/c382XzsS4e+8HZ0j/HkYT92QsGNMJ61dWTEOJPfWnToPAwZHDZBUAznRm9qZ0tkO/N6+yNL+TCzmPkBprFb464x6MM5enPEfiDXBIuWnQUGetgdPoAJfQ/DdRbD1ptmc4LYZoO1R+mBazsa/rWaWAjD3WufNQfufdVJ6KFI0xnbCmI/Jc1rtYZSIUGn7XMgAEwxnW1LsA86ePg0lK/yJnkgTMnz5OtzGQseXBGffCaUy9Rk7iDXAYcndbkjGGS0unARkkrCpUcGBZn+Gss9bAKTkh8iJ4LvnyBJ7jIXIiXJJTtyoFZOyxX7kYpbfcRl2qSFEpyme7oFMXq0xketNR0/RtEbliQX3q93IGrFhQTxuuSMbSffAzcNEWqLn+cDjV1Zi0lFYysiZnfYaTMYZr6haBAwebmHwZhE20gmM8ltYtog1XZFjGSY0ovWUVXCu/kPr5Qs8jMkYV3b0EjmNw2iRwXGEHNWPZXU83VKxk1dA6rCZJoDqsJGtEToBDyn2yCgDbTu7M+ANiWInoMsM5xdWIWxpXYnfLuwCQUIe1ylKBpVSHlWSo+ttroPamab/KAMFOG6zI2FRUCSvHAJdV0q2LVUZjyHDGhxtmo0Y2LJ9fj+vn1VKnK6ILgfFwSg5ww6zh1IOiKPhrx6GMzw9EgtA0TZfEeoqrEZOdk/o7XfkjflgEC2ySFbXWappZJVkjOBxQfIkl1MLnzkMsS72+nJDRoGgSVsYAl02CKOQ3GTtwtCOj8/58tAP3rtB5MIguD1g4o1L/C5GiwjMub8kqAPyheRfUjOdXAQUKPmg7iCsq5+gyHsYY6m21uvxsQgCAt1oBXkDrhl8mfO3ssz+FZcYMVH7t6+BE/SrQEKKnophKYwCcVgmikFldRj31BjPbdNWb4eYsQgoNA+Aw2FNuNMqFjkDXiL9naFtZQkYLzmQEb7Xi/PPPoveTvyZ8XQsG4PvgAM4//2weRkdIdhTFDKvdYoAk5j9ZBQCOAzJZFcDnaI2tpmlobvWhJxCGzWRAfYWVblGSi2I32CDy+Z3FKTOVjOh8DRpKjC6dRhONsxbfGfjDvbAYzKiz1lCckaxgBgN4uwOh0y3oPXw47bm9hw8jdOYMpJrUtZIJKVRjPmG1mw3DlnDKpcZqOw41dw973qRq/etVHj7lxo4DLejqGWjlV2KTsGxeHaY36PfmTcYum2iFUch//d7P11+D1z/7I7QMlwUIEDB33GxdxnLU3YRdLe/CE/L0H3NKTlxDm63IRWICD8HpBGMM7rd2Qu1NX5pN7fXD/dYfUXnfA7kZICFZNKaXBFhNYsadpXKloiSz0jkVLn2LiB8+5caW3U1xySoAdPWEsGV3Ew6fotujZGQsghlm0ZTvYQAAeJ7HJa4pGZ8/o2yqLpsNj7qb8GrTm3HJKgB4Qh682vQmjrqbsn5NUiR4DoKrpL8WqxoMZPRtWoA6GJLRacwnrIWmsdaZ2Xl1+t6e3HGgBWqKySdVA3YcaMl6q0oydpkEY8F1arqxcTkM3PCvATzjsGL8dVm/vqZp2NXybspasBpU7G55l+KMjBzHQXSVgPEDS904Y2YfFpkp/3dACLkQYzphLUQLLqmA0ZB+Pa3RwGOBjl2mmlt9CTOrQ3X1hNDcmlgehZBk7IbctFwdiTprDWqsVcOe12CvQ50t+2v6WnxnEmZWh3KHPFlvCUvGOMYguFwJLVld1y4DZ07/oZEzW+C69no9R0eIbihhzTHGGErsUtpzSuz6toztCYSzeh4hhYqBA5/mZU7kBNw4Ybku8eYPpynwPki2W8KSsYv1JavJSlNJtbUwT5+e9vvN0y+hDVdk1KKENceaW30QBR4in/wNUuQZRIHXdXbTZjJk9TxCClGL7wx8EV/KVpU84+GSnLqtu7UYzBmdV2hLKUjh4iwWcIbUr8uVX/s6zJfOTDjOjCZY516Byq+t1nN4hOiKEtYc6wmE0ekJIKIkX7cWUTR0egK6zm7WV1hRYhtmltcmob4ief9zQkaDI11N6Ax2QdGS1zRWNAVhJazbDGedtQZOKf2adZfk1KUlLBmb2DAbAzlRRMWX7084Xv2Nb6P6m9+mpgFkVKOENcfMBh6+oJz2HF9QhnmYda4XgzGGZfPqkKrUK8eAZfPqqE4kGbU0TcMnHYehDNPi2BvugVnQZ4aVMYZr6haBpXiZZeCwtG4RxRnRnaGyIt9DIOSiUcKaY5+ezKwDz6c6l5Wa3uDC7UsbE2ZaS2wSbl/aSHVYyajW4jsD9zAbnoBow4C2QLtu45jiasQtjSvhGjLT6pKcuKVxJdVhJYSQDBVWkdIi0ObJrAZemzuzmnoXY3qDC9PqndTpiow5/nAvgnL6ShgAwIFDV3D4xPZiTHE1YrJzUn+nK6vBglprNcUZIYSMACWsOTbOkVkNvHHO3NTKY4yhobLwShIRcjHMoglhNTLseQxM15as/ddhDPW2Wt2vQwghYxUtCcixGRMz63F+6YSR9UInhAxgYBDY8OvAJcGgW0tWQggh2UMJa471hhSYpPRvpCaJhz+UfGczIWR4/kgvJCF9JQwAmDNuli4tWQkhhGQXvVLnmNUoAmDgUqxfix5nBdlWlpDRwiKaEVJCEJiAVCtFRU7A4uoFOR0XIYSQC1O0a1hVVcX+w23o6A6izG7E/OnjcjrTIvAMGhhkRYWmRWubCzw38OZK7cXJGKGqKg60fQR30AOX0Yl54y7TPda0vgDiGANjIjRNg6qp/ccZY+DAQdMo0AghZDQoyoR1+/5mbNvXjEBooB7q5reasGJBPZbPr9f12r5gBHaziHZPEOqgN0tNAyKyCo4xuGwifMHhN4wQUuh2Nu/Bjua3EZQHqmNsbXody+qvxnX1V+l23d5IADbRCk/ICwZA7fsvRtM0hLQwfvbJr3D/JXdSeSlCCClwRbckYPv+Zmx950RcsgoAgZCMre+cwPb9zbpe32YywB+U45LVwVRNgz8oU1tUMurtbN6D1078IS5ZBYCgHMRrJ/6Anc17dLu2xWCGUZDglBzQNC1lAwF3yINfHtqMo+4m3cZCCCHk4hVVwqqqKrbta059u10Dtu1rhqqm745zMWrKTPAH0s+e+gMR1JTp032HkFxQVRU7mt9GumDb0fy2brEWa4tq4A2QU7RmBQCGaLert5r30vIAQggpYEWVsO4/3JYwszpUICRj/+E23cawbV/LsMtTNQDb9rfoNgZC9Hag7aOEmdWhgnIQH7Qd1OX6sbaoQTnYv241xZnQNA1n/edw2ndWl7EQQgi5eEWVsHZ0Z9ZlKtPzLkSrJ5By13IMA9Cag05XhOjFnWH3qK6gfi2Ip7gaMcU1CSxFxA0+LqsKfGG/bmMhJFd4hxOcaeAOHWcygXc403wHIaNDUSWsZfbMukdlet6FqHBGX0hY3x8M+d/Y/69w0ZIAMnq5jJm9QerdZWqyaxL4IQ0EonEWn8QKHA+rwaLrWAjJBU4UUX7XPWCCANb3/zmRyiSS0a+oEtb508fBJKUvjGCSBMyfPk63MaxcWA+eH3iz7Cu7isFlWXmeYeUCfasVEKKneeMug1FI/8HPKBh17zI1b9xlMAsmsEH/YUiyyhhDtaUKtdZqXcdCSK44Fi9B4/pn0PjfT8OxeEm+h0NIVhRVwspxHFYsqB/6fjWAASsW1OtaI5LneSyeVZV2DItnVYHnh28rSUih4jgOy+qvRron+rL6q3Wvx8pxHJY1XJ0wyzqYw2DDtfWLwVI08yBkNGKCACYUZeVKMkYV3bM5Vmd1aB1WkyTkpA4rANy/fBoAYO/H56CoAxtCeJ5h8ayq/q8TMprF6qwOrcNqFIy612FNNo7tp95CQA4gVgyAMYZKcznumHIz1WElhJACx7QxXMulvb0n5dfy3ekKABRFwbb9LfD0RuCyiFh+RV1RzqwKAgeXywK32w9Z1q+kWKHL9PdQXm7L4agyM1ysxTpdlRhdmDtuds5jDQA4Dvi0+xA+OXcUBmbAZeUzUW+vLaqZVYq1qNEaa+nirNAU+3OtmB//hTz2TGKt6GZYYziOw8IZlXkdA8/zuHnJxKJ9UpPiwHEc5ldenu9hgOM4XDVhAWY6L6VYI4SQUaao1rASQgghhJDRhxJWQgghhBBS0ChhJYQQQgghBY0SVkIIIYQQUtAoYSWEEEIIIQWNElZCCCGEEFLQKGElhBBCCCEFjRJWQgghhBBS0ChhJYQQQgghBY0SVkIIIYQQUtAoYSWEEEIIIQWNElZCCCGEEFLQKGElhBBCCCEFjRJWQgghhBBS0ChhJYQQQgghBY0SVkIIIYQQUtCYpmlavgdBCCGEEEJIKjTDSgghhBBCCholrIQQQgghpKBRwkoIIYQQQgoaJayEEEIIIaSgUcJKCCGEEEIKGiWshBBCCCGkoFHCSgghhBBCCholrIQQQgghpKBRwkoIIYQQQgoaJax50traijVr1mD+/PlYsmQJ1q5di1AolO9h5dXq1avx3e9+N9/DyItwOIwf/vCHuOKKK3DllVfiiSeeADWhyx6Kt3jFGmsUZ/qjWBtQjHGmZ4xRwpoHmqZhzZo1CAQC+PWvf40nn3wSu3btwlNPPZXvoeXN66+/jrfffjvfw8ib//iP/8B7772Hn//853j88cfx8ssvY/Pmzfke1phA8RavmGON4kxfFGsDijXO9IwxSljz4MSJE/joo4+wdu1aTJ48GfPmzcOaNWvw2muv5XtoeeHxePDjH/8YM2fOzPdQ8sLj8eCVV17Bo48+ilmzZuFzn/scHnzwQRw8eDDfQxsTKN4GFHOsUZzpj2ItqljjTO8YE7LyU8iIlJeX4/nnn0dZWVnccZ/Pl6cR5dePfvQj3HzzzWhra8v3UPLigw8+gNVqxfz58/uPrV69Oo8jGlso3gYUc6xRnOmPYi2qWONM7xijGdY8sNvtWLJkSf/fVVXFhg0bsHDhwjyOKj/+9Kc/4cCBA/jWt76V76HkTUtLC2pqavDqq69ixYoVuO666/A///M/UFU130MbEyjeooo91ijO9EexVtxxpneM0QxrAVi3bh0OHTqELVu25HsoORUKhfCDH/wA3//+92E0GvM9nLzp7e3FqVOnsGnTJqxduxbt7e34/ve/D5PJhAcffDDfwxtzijHeKNYozvKh2GKt2ONM7xijhDXP1q1bhxdffBFPPvkkpkyZku/h5NT69etx6aWXxn0iL0aCIMDn8+Hxxx9HTU0NAODs2bPYuHEjvZFmWbHGG8UaxVmuFWOsFXuc6R1jlLDm0aOPPoqNGzdi3bp1WL58eb6Hk3Ovv/46Ojo6MGfOHADRchgAsH37dvzlL3/J59Byqry8HJIk9Qc4AEyYMAHnzp3L46jGnmKON4o1irNcKtZYK/Y40zvGKGHNk/Xr12PTpk144oknsGLFinwPJy9+9atfQZbl/r//5Cc/AQA8/PDD+RpSXsyePRuhUAifffYZJkyYACC623Zw0JOLU+zxRrFGcZYrxRxrxR5nescYJax5cPz4cfz0pz/F6tWrMXfuXLS3t/d/rby8PI8jy62hT2KLxQIAaGhoyMdw8mbixIlYunQp/uVf/gX//u//jvb2djz33HP45je/me+hjQkUbxRrAMVZLhR7rBV7nOkdY5Sw5sHOnTuhKAqefvppPP3003FfO3LkSJ5GRfLpJz/5CR599FHcfffdMJlMuPfee3Hffffle1hjAsUbiaE40xfFGtEzxphGfekIIYQQQkgBozqshBBCCCGkoFHCSgghhBBCCholrIQQQgghpKBRwkoIIYQQQgoaJayEEEIIIaSgUcJKCCGEEEIKGiWshBBCCCGkoFHCSgghhBBCCholrGRE9u3bh6lTp+L06dP5HgohYxrFGiH6ozgbPajTFRmRcDgMr9eLkpIS8Dyf7+EQMmZRrBGiP4qz0YMSVkIIIYQQUtBoSQBJ6u2338aqVaswe/ZsfO5zn8N3v/tdeL3euNsnv/3tbzF16tSkf86cOQMAOH78OB566CHMmTMHixcvxj/+4z+ivb09z4+OkMJBsUaI/ijORj9KWEmCrq4ufOc738Ftt92GN954A+vXr8ef//xn/PjHP44774YbbsDevXv7//zud79DaWkpVq1ahZqaGrS2tuKee+5BQ0MDtmzZgmeeeQY+nw933XUXent78/ToCCkcFGuE6I/ibGwQ8j0AUnhaW1sRDodRXV2Nmpoa1NTU4JlnnoGiKPB6vf3nGY1GGI1GAEAoFMJ3vvMdTJw4ET/84Q8BABs3bkRlZSX+7d/+rf97nnrqKSxcuBDbtm3DqlWrcvvACCkwFGuE6I/ibGyghJUkmD59Om688UZ84xvfQHl5ORYtWoSlS5fi+uuvxwcffJBwvqZpeOSRR9DV1YWXX34ZBoMBAHDo0CEcO3YMc+bMiTs/FArh+PHjOXkshBQyijVC9EdxNjZQwkqSevzxx/Htb38be/bswXvvvYd/+qd/wty5c/Gtb30r4dynnnoKe/fuxebNm+FyufqPq6qKhQsX4gc/+EHC99hsNl3HT8hoQbFGiP4ozkY/WsNKEhw8eBCPPfYYJk6ciAceeADPPfccHnvsMbz//vvo7OyMO3fr1q14/vnn8dRTT2HSpElxX5s8eTKOHz+OqqoqNDQ0oKGhAQ6HA4899hiOHj2ay4dESEGiWCNEfxRnYwPNsJIEVqsVL730EkRRxJ133olQKIQ33ngD48ePj/u0uX//fnzve9/Dww8/jEsuuSRup6TNZsM999yDzZs34+GHH+7/FPujH/0IR44cwZQpU3L+uAgpNBRrhOiP4mxsoDqsJKldu3Zh/fr1OHHiBDiOi5e7SQAAAMdJREFUw8KFC/HII4/g3LlzuP/++7Fz506sX78eW7duTfr9a9euxapVq3Do0CE8/vjj+PDDD8HzPC6//HL88z//MxobG3P8iAgpTBRrhOiP4mz0o4SVEEIIIYQUNFrDSgghhBBCCholrIQQQgghpKBRwkoIIYQQQgoaJayEEEIIIaSgUcJKCCGEEEIKGiWshBBCCCGkoFHCSgghhBBCCholrIQQQgghpKBRwkoIIYQQQgoaJayEEEIIIaSgUcJKCCGEEEIK2v8HfDgIrWeMbm4AAAAASUVORK5CYII=",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x321a18a90>)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"f, (ax1, ax2,ax3) = subplots(1, 3, sharey=true)\n",
"regplot(x=\"size\", y=\"tip\", data=tips, ax=ax1);\n",
"regplot(x=\"size\", y=\"tip\", data=tips, x_jitter=.05, ax=ax2);\n",
"regplot(x=\"size\", y=\"tip\", data=tips, x_estimator=numpy.mean, ax=ax3);"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Higher order models"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAHkCAYAAADvrlz5AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xl8FHWeP/5XdyedTjpX5yTkJuTqQABxQBQUEORMUAYvxhMhDh6sM+P+dpxx0R3cdcdjd3a+M6NyeIsnKAnhMKigIIjckvsiBwTI1bmTTnfV7w9GtNIEOiHdVd15PR8PHzz4VKXz5mMnr66qd31KJYqiCCIiIpKVWu4CiIiIiIFMRESkCAxkIiIiBWAgExERKQADmYiISAEYyERERArAQCYiIlIABjIREZECMJCJiIgUwEPuAhypvr7NIa+rVqsQFKRHU1MHBIELnV0O58o+nCf7ca7sw3myn6PnKjTUz746hvw7DwNqtQoqlQpqtUruUhSPc2UfzpP9OFf24TzZTylzxUAmIiJSAAYyERGRAjCQiYiIFICBTEREpAAMZCIiIgVgIBMRESkAA5mIiEgBGMhEREQKwEAmIiJSAAYyERGRAjCQiYiIFICBTEREpAAMZCIiIgVgIBMRESkAA5mIiEgBGMhEREQO0NjSjY++KrN7fwYyERHREDtYeA6rXz+IHd9V2/01Hg6sh4iIaFjp6rHgvbwSfHvy7IC/loFMREQ0BMpOt2BdTj7qTd2D+noGMhER0VWwCgJyv61C9r5TEERRsm3MqCC7X4eBTERENEj1pi6syylA2ekWybiHRo3bZyRg1sQou1+LgUxERDQI+/PP4t3Pi9HVY5WMR4XqkZWRhqgw3wG9HgOZiIhoADq7LXj382IcKDhns232tdFYMn0UPD00A35dBjIREZGdSmpMWJdTgMZWaeNWgF6LhxakYsyo4EG/NgOZiIjoCixWAdn7TiF3/yn06dvC+NEheGB+Cvx9tFf1PRjIREREl3GuuRNrswtQWdcqGdd6qHHXzYm4afxIqFSqq/4+DGQiIqJLEEURe3+ow8a8UvT0Shu3YsJ8kZWZhpEh+iH7fgxkIiKiPjq6e/HWjmIcKjpvs23u5BjcNm0UPD2GdvVpRaxlbTabsXDhQnz33XcXx2pqavDAAw9g/PjxmD9/Pvbu3StjhURENFwUVTVj9YaDNmEc6KvFk3eNxx0zRg95GAMKOELu6enB7373O5SWll4cE0URjz76KJKSkrBp0ybs2rULjz32GLZt24aRI0fKWC0REbkri1XAx7vLsONANfr0beGapFA8MC8Fvt6eDvv+sgZyWVkZfve730Hs07J24MAB1NTU4IMPPoCPjw8SEhKwf/9+bNq0CY8//rhM1RIRkbuqPd+GP7/9PU7VtUnGtZ5qLJ2VhGnpEUPSuHU5sgbywYMHMXnyZPzmN7/B+PHjL44fP34cRqMRPj4+F8cmTpyIY8eOyVEmERG5KVEU8dWR09i4qwQ9ZmnjVuwIPzycmYYRQT79fPXQkjWQly5desnx+vp6hIWFScaCg4Nx9uzAH2dFRER0KW2dZry5vQhHSxsk4yoA86fEYtHUeHhonNdqJfs15Evp6uqCViu9wVqr1cJsNg/oddRqFdTqoT/FoPnn/yCNE/9HuSrOlX04T/bjXNmH83R5JysasTY7H6Z2aa4E+Xvh14vGICXW4PSaFBnIXl5eMJlMkjGz2QydTjeg1wkK0jv0nL+/v7fDXtvdcK7sw3myH+fKPpwnqV6LFW9vK8Rne8pttk0dNxKPLhkH36tccWuwFBnI4eHhKCsrk4w1NDTYnMa+kqamDocdIfv7e6O1tQtWqzDkr+9OOFf24TzZj3NlH86TrdP17Xjls5OoPtcuGddpNVj5y3RMTAxBb08vmnt6h/T7Ggz2LR6iyEAeN24c1q5di+7u7otHxYcPH8bEiRMH9DqCIEIQ+javDx2rVYDFwje6PThX9uE82Y9zZR/O0z8bt46exodflqG3z1wkjPTHr28dg5SEUDQ3d8g6V4oM5EmTJiEiIgJPPfUUHnnkEXz11Vc4ceIEnn/+eblLIyIiF9LaYcbr2wpxorxRMq5SAQunxCFzahy8tMqIQmVU0YdGo8E//vEP/PGPf8TixYsRGxuLv//971wUhIiI7PZDRSM25BaitUPauBUSoMOKDCMSowJlquzSFBPIxcXFkr/Hxsbi3XfflakaIiJyVb0WKz7+qhy7DtfabLsuLRz3zE6Gj04x8XeR8ioiIiIapNrz7XgtJx+n6zsk495eGtxzSzKmpI2QqbIrYyATEZHLE0QRXxyqxce7y2Hp01U+OioAWQuNCAlU9i1gDGQiInJpLe092LCtECcrmiTjapUKmVPjsGBKLDRq5S+QwkAmIiKXday0Aa9vK0R7l/Te4dBAHbIy05AwMkCmygaOgUxERC6np9eKj74sw1dHT9tsu2HsCCydlQRvL9eKONeqloiIhr3qc214LTsfdY2dknEfLw/cNzcZk1LDZars6jCQiYjIJQiiiM8P1mDTnnJY+6zCmBwdiOULjQgOGNgzD5SEgUxERIrX3NaD9VsLUFjVLBnXqFW4dVo85k2OdcizC5yJgUxERIp2uLgeb24vREe3RTIebvBGVmYa4iP8ZapsaDGQiYhIkbrNFnzwRSm+Pl5ns+3GcRG4++YkeGk1MlTmGAxkIiJSnMq6VqzNzse55i7JuF7ngQfmpWJicqhMlTkOA5mIiBRDEERs/64Kn31TadO4ZYwz4KEFRhj8vGSqzrEYyEREpAhNrd1Yl1OA4hqTZFyjVuGXNyXglknRUKtcu3HrchjIREQku4OF5/D2jmJ09kgbtyKCffBwZhpiwv1kqsx5GMhERCSbrh4LNu4qwb4fztpsmzEhEnfMHA0vT/dp3LocBjIREcmi/EwL1mbno97ULRn39fbEsvmpGJ8YIlNl8mAgExGRUwmCiNz9p7Bl7ykIorRxa0x8EB5akIoAX/ds3LocBjIRETlNg6kL67YWoLS2RTLuoVHj9hkJuHlilFs3bl0OA5mIiJxif/5ZvPt5Mbp6rJLxyFA9Hs5IQ1SYr0yVKQMDmYiIHKqz24J384pxIP+czbZZE6OwZHoCtMOkcetyGMhEROQwpbUmrMspQEOLtHHLX6/FsvmpSE8Ilqky5WEgExHRkLMKAnL2nULOt6fQp28L4xKC8eD8VPjrtfIUp1AMZCIiGlLnmzuxLqcA5WdaJeOeHmrcNXM0pk+IhGqYNm5dDgOZiIiGhCiK+PbkWbybV4Ies7RxKzrMF1mZaYgM0ctUnfIxkImI6Kp1dPfi7R3F+L7ovM22OZOisfjGBHh6qGWozHUwkImI6KoUVzdj3dYCNLX2SMYDfLVYvtCItLggmSpzLQxkIiIaFItVwJa9ldi2vwp9+rYwITEED8xLgZ8PG7fsxUAmIhokQRRRUm1CUXUzus1W6LQapMQYkBQT6ParTZ1t6sTa7HycOtsmGdd6qnH3zYm4cdxINm4NEAOZiGgQKutasWVvJVo6zJLx4+WNCNBrsWhqPOIj/GWqznFEUcQ3J+qwcVcJzL2CZFvsCD9kZRgREczGrcFgIBMRDVBlXSs25pXAIvQ9UXtBS4cZG/NKsHR2kluFcntXL97aXoTDJfWScRWAedfF4tZp8fDQsHFrsBjIREQDIIgituyt7DeMf2QRLuy3akm6W5y+LjjVhPVbC2Bql54RMPh5YflCI1JjDTJV5j4YyEREA1BSbbI5Td2flg4zSmtMSI5x3bDqtQj49OsK7DhYbbPt2pQw3D83GXqdpwyVuR8GMhHRABRVNw9o/8KqZpcN5DMNHVibnY/q8+2ScS+tBr+alYQbxo5g49YQYiATkUv4saO5pNYEUaWGShSQFBXo9I7m7j4rUA31/kogiiJ2HzuDD78ohdkibdwaNdIfKzKMCDf4yFSd+2IgE5Hi/byjWaW68DB7i1XA0dIGp3c067QDe0zgQPe/Wlf7waW104w3txXhWFmDZFylAhZOiUPGDXFs3HIQBjIRKZrSOppTYgw4Xt5o9/7ObHa62g8uJysasT63EK19rpEH+3thRUYakqIDHf1PGNb4MYeIFGugHc1C3+f8OUBSTCAC7HxsYIBei0QnhdiPH1z6azj78YNLZV2rzbZeixUbd5Xgfz46bhPG1xnD8R/LJjOMnYCBTESKNZiOZkdTq1RYNDUeHurLn/71UF/YzxnXt6/mg0vt+Xb86a1D2HWoVrKvt5cGKzKMyMpMg4+OJ1OdgYFMRIo1mI5mZ4iP8MfS2Un9HikH6LVOXRRkMB9cRFFE3qEa/OmtQzhd3yHZZ3RkAJ59cBKmpI1wRLnUD37sISLFUnJHc3yEP1YtSUdpjQmFVT+tZZ0aa0BitHM7vwf6weVoaT1yD1ThZEWTZFytUiFzahwWTImFRs3jNWdjIBORYim9o1mtUiE5xiD7fcYD+SDS2W3BV0fPoLfP7UwhATpkZaZhdGTAUJdHdlL0R6DGxkasWrUK1157LWbPno3NmzfLXRIROVHKAINuuC7faM8HEUEU0djajXpTl00Y3zBmBP5j2SSGscwUe4QsiiIeffRRCIKAt99+G+fOncO//du/wdfXF7fccovc5RGRE/zY0WzP9VFndjQrzZVuxTL3WtFg6kavVRrE3l4euG9OMiYbwx1dItlBsUfIJ0+exNGjR/Hyyy/DaDRixowZWL58OTZs2CB3aUTkJErsaFai/m7FEkURLe1m1DV22oRxUnQg/rRsEsNYQRQbyDU1NQgKCkJ0dPTFseTkZJw8eRK9vb0yVkZEzqS0jmYlutQHF4tVwJmGTjS39djs+8ubRuH/u3sCggN0zi6VLkOxp6xDQkLQ1taGrq4ueHt7AwDOnj0Li8WCtrY2BAUFyVwhETnLzzuai2t+WhIyOTrQ6R3NSvXjB5cteytR19iBxpZu9L0tOcjfC4/eNnZYf3hRMsUG8rhx4xAWFoY1a9bg6aefRn19Pd544w0AsPsIWa1WQX2FU12DofnnOq4arud6RZwr+3Ce7JM2KhjpiaHw9/dGa2sXrH1Oww53MeF+CPL3wolLXE++cfxI3HNLEnRaxf7al41Sfv5UouiEteYG6cSJE3jiiSdQV1eH4OBgLF++HM8//zyOHDkCvV5/xa8XRZGPBiOiYaGsxoSX3rNd5MPPxxOP3T4e16ePlKkyspeiPyqlp6fjyy+/RH19PQwGA/bt2weDwWBXGANAU1OHw46Q+QndPpwr+3Ce7Me5khIEEdsPVOGT3eWw9jlHnT46BCsyjAjQa9Hc3NHPK5Cj31MGg32ZpdhANplMWLlyJf7xj38gNDQUALB7925MmjTJ7tcQBBHCFdZ2vRpWqwCLhb8Q7MG5sg/nyX6cK6CptRvrtxagqFq6hrdGrcIdM0fjrjmpaGnpHPbzZC+531OKDeTAwEB0dnbixRdfxMqVK3HgwAFs2rQJ7777rtylERHJ7vui83h7RxE6ui2S8YhgH2RlpCEhKsAhZwjJcRQbyADwv//7v3jmmWeQkZGBqKgo/N///R/S09PlLouISDZdPRa8v6sUe3+os9k2Y0Ik7pg5Gl6ezl1ClIaGogN51KhReOedd+Qug4hIEcrPtGBddgHOm7ok477ennhwfgomJIbKVBkNBUUHMhE5nyCKKKk2oaj6pycYpcQYkBTD+33lIggicg9UYcs30mcZA0BafBAeWpCKQF8vmaqjocJAJqKLKutasWVvpc3a0cfLGxGg12LR1HguKuFkDS1dWJdTgNLaFsm4h0aF26ePxs3XRvGDkptgIBMRgAthvDGvBJZ+7kxo6TBjY17JsF+m0pkOFJzFOzuL0dUjfbxiZIgeWZlpiA7zlamygeFZF/swkIkIgihiy97KfsP4Rxbhwn6rlqTzF6kDdXZb8F5eMfbnn7PZNmtiFJZMT4DWRRq3eNbFfgxkIkJJtcmuRxwCF46US2tMSB7gs4rJPqW1JqzLKUBDS7dk3N/HE8sWpCI9IUSmygaOZ10GhgvnEhGKqpsHtH9h1cD2pyuzCgI++6YC//3eEZswHpcQjD89NNmlwnigZ136NqsNRzxCJiJ0m61X3ukq9qfLO2/qwrrsfJSfaZWMe3qocefM0ZgxIdLl1uXnWZeBYyATEXTagV2PHOj+dGmiKOLbk2fxbl4Jevp8yIkO80VWZhoiQ+xbB1lpBnPWhYFMRMNeSowBxy/xyL7+pMYO71+cQ6Gzuxdv7yzGwcLzNttu+UU0fnlTAjw9XPeqIs+6DBwDmYiQFBOIAL3WrlOMAXotEqMDnVCV+yqubsa6rQVoau2RjAf4arF8gRFp8UEyVTZ0eNZl4Fz34xcRDRm1SoVFU+PhcYWHEXioL+zHW54Gx2IVsGlPOV7YeNQmjCckhuBPyya5RRgDF866DATPuvAImYj+KT7CH0tnJ13ynlEAvGf0Kp1r6sRr2fk4dbZNMq71VOPumxNx47iRLte4dTk86zJwDGQiuig+wh+rlqSjtMaEwqqfVlVKjTUgMZqrKg2GKIr45kQdNu4qgblX+qzd2HA/ZGUaERHsmo1bl/PjWZfL3YcM8KzLzzGQiUhCrVIhOcYw7Dteh0J7Vy/e2l6EwyX1knEVgLnXxeC2aaPgoXHfK4c86zIwDGQiIgcoPNWE9bmFaG6TXis2+Hlh+ULjsLlmyrMu9mMgExENIYtVwOavK7Dzu2r0PVF7bXIo7pubAl9vT1lqkwvPutiHgUxENETqGjvwWnY+qs+1S8a9PDVYOisRU9Mj3Kpxi4YWA5mI6CqJoojdx87gwy9KYbZIG7fiI/yRlWlEuMFHpurIVTCQiYiuQmunGW9uK8KxsgbJuEoFLJgSh8wb4ty6cYuGDgOZiGiQTlY0YkNuoU0HcbC/F1ZkpCGJ99bSADCQiYgGqNdixSe7K5B3qMZm22RjOO69JQk+uuHVuEVXj4FMRDQAtfXtWJudj9r6Dsm4TqvBvbck47q0cDZu0aAwkImI7CCKIr44XIuPviqHxSpt3EqI9MeKjDSEBXrLVB25AwYyEdEVtHSY8XpuIX6okD6iUqUCMm+Ix8LrY6FRs3GLrg4DmYjoMo6XNeD1bYVo6+yVjIcE6JCVkYbRUQEyVUbuhoFMRHQJ5l4rPv6qHF8cqbXZdv2YEfjV7CR4e/FXKA0dvpuIiPqoPteGtTkFONMgbdzy9vLAfXOSMdkYLlNl5M4YyERE/ySIInZ9X4NP9pTDYpWuRJ0UHYgVC40IDtDJVB25OwYyEREAU3sPNuQWIr+ySTKuUatw67R4zJscC7WatzOR4zCQiWjYO1pSjze2F6G9S9q4FWbwxsOZaXxeLzkFA5mIhq0esxUfflmK3cfO2Gybmh6BpbMSodPy1yQ5B99pRDQsVZ1tw2vZ+Tjb1CkZ1+s8cP/cFFybEiZTZTRcMZCJaFgRRBE7v6vG5q8rYBWkjVspMYFYvtCIIH82bpHzMZCJZCSIIkqqTSipNUFUqaESBSRFBSIpJhBqroc85Jpau7F+awGKqk2ScY1ahcU3jcKcSTGcd5INA5lIJpV1rdiytxItHWaoVICHRg2LVcDR0gYE6LVYNDWezURD6FDReby1owgd3RbJ+IggHzycmYbYEX4yVUZ0AQOZSAaVda3YmFcCS59Tpj9q6TBjY14Jls5OYihfpW6zBRt3lWLviTqbbdPHj8SdMxPhpdXIUBmRFAOZyMkEUcSWvZX9hvGPLMKF/VYtSedp1EGqONOKtTn5ON/cJRn39fbEg/NSMCEpVKbKSAmUdsmIgUzkZCXVJrR0mO3at6XDjNIaE5JjDA6uyr0IgojcA1XI3ltp07iVFmfAsgVGGPy8ZKqOlECJl4wYyEROVlTdPKD9C6uaGcgD0NDShfU5BSipbZGMe2hUWHJTAmb9IppnHIY5pV4yYiATOVm32erQ/YezAwVn8c7OEnT1SBu3RobokZVhREw4G7eGOyVfMmIgEzmZboANRAPdfzjq7Lbgvbxi7M8/Z7Pt5muicPuMBGg9OY+k7EtGaqd8l0Gqq6vDww8/jGuuuQYzZ87Em2++KXdJRFctZYA/3KmxPF19OWW1LXj2jYM2Yezv44knbk/Hr25JYhjTRYO5ZOQsij5CfuKJJzBy5Ehs3rwZZWVlePLJJxEZGYnZs2fLXRrRoCXFBCJAr7XrU3qAXovE6EAnVOV6rIKAz76pQM63pyD2OfuYnhCMB+enIkCvlac4UiwlXzJS7BFyS0sLjh07hpUrVyIuLg6zZs3CtGnTsH//frlLI7oqapUKi6bGw+MKj/LzUF/Yjw1Its42duA/3z6M7H3SMPb0UONXs5PwL0vSGcZ0SUq+ZKTYQNbpdPD29sbmzZvR29uLiooKHDlyBKmpqXKXRnTV4iP8sXR2Ur+hEaDXclGQSxBFEftO1GHVy7tR1qeLOirUF6vvvxY3T4yCih9iqB9KvmSk2FPWXl5eWL16NdasWYO3334bVqsVixcvxu233y53aURDIj7CH6uWpKO0xoTimp8WJkiODkRiNNey7quzuxdv7yzGwcLzNttmXxuNJdNHwdOD14rp8pR8yUixgQwA5eXlmDFjBh588EGUlpZizZo1mDJlCjIzM+36erVaBfUVTgsOhkajlvxJ/eNcXVnaqGCkJ4bC398bra1dsFoFuUtSnOLqZrz6WT4aW7sl4wG+WmRlpGFsQrBMlSkXf/b6t/imUXhnZwmswoWfNRVUP/2punANRKNWY/FNzu3OV4li33YIZdi/fz+eeOIJ7NmzBzrdhUehvfLKK8jOzsb27dvteg1RFHnqisiFWawC3v+8GJ98UYK+t41OThuBx+8YjwBfrrhFA1dS3Yz3Py+Gqa3bZlugnw5L5yQjMdq5dzgo9gj55MmTiI2NvRjGAGA0GvHqq6/a/RpNTR0OO0Lm0Yx9OFf24TzZOtfUiVc+O4mKM62Sca2HGituHYspxjAIvRY0N1v6eYXhje+pywv10+KxxWNQUm1CYVUzBKighojUWMPFtaybmzuG5HsZDHq79lNsIIeFhaGqqgpmsxla7YXGl4qKCkRFRdn9GoIgQrjCaixXw2oVYLHwjW4PzpV9OE8XzmztPVGHjbtK0dMrveUkJtwXj9w2FmmJYWhu7hj2c2UPvqcub3RkAFJiDTAY9BffU4JVhADnnzxW7MWFmTNnwtPTE08//TQqKyvx5Zdf4tVXX8W9994rd2lE5CDtXb34x2cn8cb2IkkYqwDMmxyDp++7FiND7DvaIHI1ij1C9vPzw5tvvon//M//xJIlSxAUFISVK1fizjvvlLs0InKAwqpmrN9agOa2Hsm4wc8LyxekIjUuSKbKiJxDsYEMAKNHj8Ybb7whdxlE5EAWq4BPv67Aju+qbU4STkwOxf1zU+Dr7SlLbUTOpOhAJiL3VtfYgbXZBag61yYZ9/LUYOmsRExNj+CdEjRsMJCJyOlEUcSeY2fwwRelMPdpOIqP8ENWRhrCg3xkqo5IHgxkInKqtk4z3txehKOlDZJxFYD5U2IvrPPNxSxoGGIgE5HT5Fc2Yf3WAptlC4P8vbBiodFpz50lUiIGMhE5XK/Fik17KvD59zU22yalhuG+Ocnw0bFxi4Y3BjIROdTp+na8ll2A2vp2ybhOq8E9tyRhStoINm4RgYFMRA4iiiK+PHIaH31Vht4+jVsJkf5YkZGGsEBvmaojUh4GMhENuZYOM97YVogT5Y2ScZUKyLg+Dhk3xEGjZuMW0c8xkIloSJ0ob8DruYVo7eyVjIcE6JCVkYbRUQEyVUakbAxkIhoS5l4rPt5dji8O19psm5I2AvfckgRvL/7KIeoPfzqI6KrVnG/H2ux8nG6QPq7O28sD985JwnXGETJVRuQ6GMhENGiCKGLXoVp8srsMFqt0JerEqACsyDAiJICNW0T2YCAT0aCY2nvwem4hTlY2ScbVKhUWTYvHgutioVbzdiYiezGQiWjAjpbW441tRWjvkjZuhQV6IyszDaNG+stUGZHrYiATkd16eq348Msy7D562mbb1PQI3H1zIhu3iAaJPzlEZJeqs214LTsfZ5s6JeN6nQfun5uCa1PCZKqMyD0wkInosgRRxM6D1di8pwJWQdq4lRITiOULjQjy18lUHZH7YCATUb+aWruxIbcQhVXNknGNWoXFN47CnMkxUHMdaqIhwUAmoks6VHQeb+0oQke3RTI+IsgHWZlGxI1g4xbRUGIgE5FEt9mC93eV4psTdTbbpo8fiTtnJsJLq5GhMiL3xkAmoosq61qxNjsf55q7JOO+3p54YF4KrkkKlakyIvfHQCYiCIKI7d9V4bNvKm0at9LiDFi2wAiDn5dM1RENDwxkomGusaUb67YWoKTGJBn30Kiw5KYEzPpFNBu3iJyAgUw0jB0sPIe3dhSjq0fauDUyRI+sDCNiwv1kqoxo+GEgEw1DXT0WvJdXgm9PnrXZdvM1Ubh9RgK0nmzcInImBjLRMFN2ugVrs/PR0NItGffz8cSy+akYNzpEpsqIhjcGMtEwYRUE5H5bhex9pyCI0satMaOC8ND8VAT4snGLSC4MZBo2BFFESbUJRdXN6DZbodNqkBJjQFJMoNs3LdWburAupwBlp1sk4x4aNe6cORozr4mEys3ngEjpGMg0LFTWtWLL3kq0dJgl48fLGxGg12LR1HjER7jnylP7T57FO58Xo9tslYxHheqRlZmGqFBfmSojop9jIJPbq6xrxca8Elj63F/7o5YOMzbmlWDp7CS3CuXO7l68+3kJDhScs9k269oo3D49AZ4ebNwiUgoGMrk1QRSxZW9lv2H8I4twYb9VS9Ld4vR1SY0J63IK0NgqbdwK0Gvx0IJUjBkVLFNlRNQfBjK5tZJqk81p6v60dJhRWmNCcozBwVU5jsUqIHvfKeTuP4U+fVsYPzoED8xPgb+PVpbaiOjyGMjk1oqqm6+8088UVjW7bCCfa+7EupwCVJxplYxrPS40bk2fwMYtIiVjIJNb69vINNT7K4Eoitj7Qx025pWip1daf0yYL7Iy0zAyRC9TdURkLwYyuTXdAB8TOND95dbe1Yu3dxbjUNF5m21zJ8fgtmnnxpcnAAAgAElEQVSj4OmhlqEyIhooBjK5tZQYA46XN9q9f2qs65yuLqpqxrqtBWhu65GMB/pqsXyhEca4IJkqI6LBYCCTW0uKCUSAXmtXY1eAXovE6EAnVHV1LFYBn35TgR0HqtG3d3xiUijun5cCX29PWWojosFjIJNbU6tUWDQ1/rL3IQOAh/rCfkq/5amusQNrswtQda5NMu7lqcHSWYmYmh7Bxi0iF8VAJrcXH+GPpbOTLrlSFwCXWKlLFEV8ffwM3v+iFOZeQbItboQfsjLTMCLIR6bqiGgoMJBpWIiP8MeqJekorTGhsOqntaxTYw1IjFb2WtZtnWa8ub0IR0sbJOMqAPOnxGLR1Hh4aNi4ReTqGMg0bKhVKiTHGFzqPuP8yiaszy1AS7v0yD7I3wsrFhpd6t9CRJen2EDevHkznnrqKZtxlUqFoqIiGSoicp5ei4DNX5dj58Eam22/SAnDfXOTodexcYvInSg2kOfPn49p06Zd/LvFYsH999+P6dOny1cUkROcbujA2ux81Jxvl4x7aTW4Z3YSrh8zgo1bRG5IsYGs0+mg0+ku/v21116DKIp48sknZayKyHFEUcSuQzV4f1cpei3Sxq2Ekf5YkWFEmIGNW0TuSrGB/HMmkwnr1q3Dc889B62WC+OT+2ntMOP/bf4B3/d5VKJKBWRcH4eMG+KgUbNxi8iduUQgv//++wgLC8PcuXPlLoVoyJ0ob8Tr2wrR2ueWrJAAHVZkGJEYpfzFSojo6ik+kEVRxMcff4zly5cP+GvVahXU6qG/1qb55y0mGt5qckWcq/6ZLVZ8+EUZ8r63bdy6fswI3Dc3BT46xf+IOh3fU/bhPNlPKXOlEsW+T01VlhMnTuDuu+/Gt99+i4CAgAF9rSiKbH4hRTpV14qX3j2EqrPSFbd8dB5YuTgd0ydGy1QZEclF8R+/v/nmG1x77bUDDmMAaGrqcNgRsr+/N1pbu2C1Clf+gmGMcyUliCLyvq/BR1+UobfPfKTGBeHhRWkI8vNCc3OHTBUqH99T9uE82c/Rc2Uw2Pf4U8UH8okTJ3DNNdcM6msFQYRwmfWLr5bVKsBi4RvdHpwrwNTeg9dzC3GyskkyrlapcNuN8bh3QRpaW7uG/TzZi+8p+3Ce7Cf3XCk+kEtLS5GZmSl3GURX5VhpA17fVoj2rl7JeFigN1ZkGJEca5D9+hURyUvxgdzQ0AB/f+Uu+k90OT29Vnz4ZRl2Hz1ts23q2AjcPSsR3l6K/zEkIidQ/G+CEydOyF0C0aBUnW3D2px81DV2SsZ9vDxw/7wU/CIlTKbKiEiJFB/IRK5GEEV8frAGm/aUw9qnhyE5OhArMowI8tf189VENFwxkImGUHNbD9ZvLUBhVbNkXKNW4bYbR2HupBiHdP4TketjIBMNkcPF5/Hm9iJ0dFsk4+FBPng404i4EeyFIKL+MZCJrlK32YIPvijF18frbLbdOC4Cd9+cBC+tRobKiMiVMJCJrkJlXSvWZufjXHOXZFyv88AD81IxMTlUpsqIyNUwkIkGQRBEbP+uCp99U2nTuGWMM+ChBUYY/Lxkqo6IXNGAA3nPnj248cYbuUY0DVuNLd1Yt7UAJTUmybiHRoXFNybglknRUPPng4gGaMCBvGrVKgQEBGDRokVYvHgx4uPjHVEXkSIdLDyHt3YUo6tH2rgVEeyDhzPTEBPuJ1NlROTqBhzI+/btQ25uLj777DOsW7cO48aNw+LFi7FgwQL4+vo6okYi2XX1WPBeXgm+PXnWZtuMayJxx4zR8PJk4xYRDd5VPX6xqqoKOTk52LlzJ2pqajBr1iwsWbIE11133VDWOGj19W1X3mkQPDzUMBj0aG7u4KLtV+AOc1V+ugVrc/JRb+qWjPv5eOLBeakYnxhy1d/DHebJWThX9uE82c/RcxUaat+Zs6tq6ho5ciSSk5NRVVWFmpoaHD58GF9++SUiIyPx4osvIiUl5WpenkhWVkFA7rdVyN53CkKfz61jRgXhofmpCPBl4xYRDY1BBfKRI0ewZcsW7NixAz09PZg1axZeeeUVTJkyBR0dHfjjH/+IJ554Ajt27Bjqeomcot7UhXU5BSg73SIZ99CocceMBNw8MYqNjUQ0pAYcyLNnz0ZtbS2MRiP+5V/+BRkZGfDz++lwXK/XY968edi3b9+QFkrkLPvzz+Ldz4vR1WOVjEeF6pGVkYaoMPZKENHQG3Agz5w5E4sXL0ZycnK/+0yZMgU7d+68qsKInK2z24J3Py/GgYJzNttmXRuF26cnwNODjVtE5BgDDuSnnnrqivvw+cXkakpqTFiXU4DGVmnjlr9ei4cWpGLsqGCZKiOi4YIrddGwZrEKyNl3Clv3n0Lf+w3GJQTjwQWp8PfRylIbEQ0vDGQats43d2JtTgEqzrRKxj091Lhr5mhMnxDJxi0ichoGMg07oihi3w9n8d6uEvSYpY1bMWG+yMpMw8gQvUzVEdFwxUCmYaWjuxdv7yjG90XnbbbNmRSNxTcmwNNDLUNlRDTcMZBp2Ciqasa6rQVobuuRjAf6avHQQiPS4oJkqoyIiIFMw4DFKuDTbyqw40A1+q4Te01SKB6YlwJfb09ZaiMi+hEDmdza2aZOvJadj6qz0nXNtZ5q3H1zIm4cN5KNW0SkCAxkckuiKOLr42fw/helMPdKF4uPHeGHhzPTMCLIR6bqiIhsMZDJ7bR39eLN7UU4UlIvGVcBmD8lFoumxsNDw8YtIlIWBjK5lfxTTdiwtQCmdrNk3ODnhRULjUiJNchUGRHR5TGQyS30WgRs/rocOw/W2Gy7NiUM989Nhl7Hxi0iUi4GMrm80w0dWJudj5rz7ZJxL60G98xOwvVjRrBxi4gUj4FMLksURXx19DQ+/LIMvRZp49aokf7IyjAizMDGLSJyDQxkckmtHWa8sa0Qx8sbJeMqFbBwShwybohj4xYRuRQGMrmcHyoasSG3EK0d0satYH8dVmQYkRQdKFNlRESDx0Aml9FrseLj3eXYdajWZtt1xnDcc0syfHR8SxORa+JvL3IJtefb8VpOPk7Xd0jGvb00uOeWZExJGyFTZUREQ4OBTIomiiJ2Ha7Fx1+Vw2KVNm6NjgpA1kIjQgK9ZaqOiGjoMJBJsVrae7BhWyFOVjRJxtUqFTJviMOC62OhUbNxi4jcAwOZHEIQRZRUm1BSa4KoUkMlCkiKCkRSTCDUdtwTfKysAa/nFqK9q1cyHhqoQ1ZGGhIiAxxVOhGRLBjINOQq61qxZW8lWjrMUKkAD40aFquAo6UNCNBrsWhqPOIj/C/5tT29Vnz0VRm+OnLaZtsNY0Zg6ewkeHvxbUtE7oe/2WhIVda1YmNeCSxC3ycPX9DSYcbGvBIsnZ1kE8rV59rwWnY+6ho7JeM+Xh64b24yJqWGO6xuIiK5MZBpyAiiiC17K/sN4x9ZhAv7rVqSDrVKBUEUkfd9DTbtKYfFKv3a5OhALF9oRHCAzpGlExHJjoFMQ6ak2oSWPot19Kelw4zSGhPCDD7YkFuAglPNku0atQq3TovHvMmxUKu5DjURuT8GMg2ZourmK+/0M18eqUXBqWZ0dFsk4+EGb2RlpvV7nZmIyB0xkGnIdJutdu0nCCKa23pQdbbNZtuN4yJw981J8NJqhro8IiJFU3Qgm81mPP/889i6dSs8PT2xZMkS/OY3v+Gj9BRKZ0eI9vRa0WDqsrlWrNd54IF5KZiYHOao8oiIFE3Rgfzcc8/hu+++w4YNG9DR0YHf/OY3GDlyJO666y65S6NLSIkx2Dx96UeiKKKl3QxTu+015tRYA5YvNMLg5+XoEomIFEuxgWwymbBp0ya88cYbSE9PBwAsW7YMx48fZyArVFJMIAL0WpvGrl6LgLNNXejpc0pbo1bhlzcl4JZJ0XYtFkJE5M4UG8iHDx+Gr68vJk2adHEsKytLxoroStQqFRZNjZfch9zR1YvGlm70vRMqOECHxxePRUy4nwyVEhEpj2IXAq6pqUFkZCQ+++wzzJ07FzfffDP+/ve/QxCEK38xySY+wh9LZyfB19sTDS1dqDfZhvHEpFA8t3wyw5iI6GcUe4Tc2dmJqqoqfPDBB3j++edRX1+P1atXw9vbG8uWLbPrNdRqlUPuYdVo1JI/SUqtVqHe1IWOLuntTN5eHsjKNLJx6xL4nrIf58o+nCf7KWWuFBvIHh4eaG9vx8svv4zIyEgAwJkzZ/D+++/bHchBQXqHdmT7+/Oxfz9nFUR88kUJNn5eDKHPYfE1yWF44q4JMPhzxa3L4XvKfpwr+3Ce7Cf3XCk2kENDQ+Hl5XUxjAEgPj4edXV1dr9GU1OHw46Q/f290draBauVp9ABoN7Uhde25KOkxiQZ99So8cBCI24cFwHRakVzc4dMFSob31P241zZh/NkP0fPlcGgt2s/xQbyuHHj0NPTg8rKSsTHxwMAKioqJAF9JYIg2hypDSWrVYDFwjf6gfyzeOfzYnT1SLuoI0P1eOS2sUhPDkdzcwfnyg58T9mPc2UfzpP95J4rxQbyqFGjMH36dDz11FN49tlnUV9fj7Vr12LlypVyl0b/1NltwXt5xdiff85m26yJUVgyPQE+3p4yVEZE5HoUG8gA8NJLL2HNmjW4++674e3tjV/96le499575S6LAJTVtmBtTj4aWrol4/4+nli2wIj0hGCZKiMick2KDmQ/Pz+88MILcpdBP2MVBOTsO4Wcb09B7HM1YFxCMB6cnwp/vVae4oiIXJiiA5mU5bypC+uy81F+plUy7umhxl0zR2P6hEiuM05ENEgMZLoiURTx7cmzeDevxGb5y+gwX2RlpiEyxL4uQiIiujQGMl1WR3cv3tlZjIOF5222zZkUjcU3JsDTgwsPEBFdLQYy9au4uhnrthagqbVHMh7gq8XyBUakxQfJVBkRkfthIJMNi1XAlr2V2La/Cn3v4p6QGIIH5qXAz4eNW0REQ4mBTBJnmzqxNjsfp862Sca1nmrcfXMibhw3ko1bREQOwEAmABcat745UYeNu0pg7pWuVBM7wg9ZGUZEBLNxi4jIURjIhPauXry1vQiHS+ol4yoAc6+LwW3TRsGDT4whInIoBvIwV3CqCeu3FsDUbpaMG/y8sGKhESmxBpkqIyIaXhjIw1SvRcCnX1dgx8Fqm23XpoTh/rnJ0Ou4DjURkbMwkIehMw0dWJudj+rz7ZJxL60Gv5qVhBvGjmDjFhGRkzGQhxFRFLH72Bl8+EUpzH0eMRYf4Y+sTCPCDT4yVUdENLwxkIeJ1k4z3txWhGNlDZJxlQpYOCUOGTfEsXGLiEhGDORh4GRFI9bnFqK1Q9q4Feyvw4oMI5KiA2WqjIiIfsRAdmO9Fis+2V2BvEM1NtuuM4bjnluS4aPjW4CISAn429hN1da3Y212PmrrOyTj3l4a3HNLMqakjZCpMiIiuhQGspsRRRFfHK7FR1+Vw2KVNm6NjgzAigwjQgO9ZaqOiIj6w0B2Iy3tPXh9WxF+qGiUjKtVKmROjcOCKbHQqNm4RUSkRAxkN3GsrAFvbCtEW2evZDwkQIeszDSMjgyQqTIiIrIHA9nF9fRa8dFXZfjqyGmbbTeMGYGls5Pg7cX/zURESsff1C6s+lwb1uYU4ExD38YtD9w/NxmTUsNlqoyIiAaKgeyCBFFE3vc12LSnHBarKNmWFB2IFQuNCA7QyVQdERENBgPZxTS39eD13ALkn2qWjGvUKtw6LR7zJsdCreY61EREroaB7EKOlNTjze1FaO+SNm6FG7yRlZmG+Ah/mSojIqKrxUB2AT1mKz74shR7jp2x2TYtPQJ3z0qETsv/lUREroy/xRXu1NlWvJZdgHNNnZJxvc4DD8xLwcTkMJkqIyKiocRAVihBELHzYDU2f10BqyBt3EqNNWD5QiMMfl4yVUdEREONgaxATa3dWL+1AEXVJsm4Rq3CL29KwC2ToqFWsXGLiMidMJAV5lDReby1owgd3RbJeESwD7Iy0hA7wk+myoiIyJEYyArRbbZgY14p9v5QZ7NtxoRI3DFzNLw8NTJURkREzsBAVoDyMy1Yl12A86YuybivtycenJ+CCYmhMlVGRETOwkCWkSCIyN1/Clv2noIgShu30uKD8NCCVAT6snGLiGg4YCDLpKGlC+tyClBa2yIZ99CocPv00bj52ig2bhERDSMMZBkcKDiLd3YWo6vHKhmPDNEjKzMN0WG+MlVGRERyYSA7UVePBe9+Xoz9+edsts2aGIUl0xOgZeMWEdGwxEB2krLaFqzNyUdDS7dk3N/HE8sWGJGeECxTZUREpAQMZAezCgJy9p1Czren0KdvC+kJwVg2PxX+eq08xRERkWIwkB3ovKkL63LyUX66VTLu6aHGHTNGY+Y1kVCxcYuIiMBAdghRFPHtybN4L68E3WZp41ZUqC8ezjQiMpSNW0RE9BMG8hDr7O7F2zuLcbDwvM22W34RjV/elABPD7UMlRERkZIxkIdQcXUz1m8tQGNrj2Q8QK/FQwtTMSaejVtERHRpig7kvLw8PPbYY5KxOXPm4K9//atMFV2axSpgy95KbNtfhT59W5iQGIIH5qXAz4eNW0RE1D9FB3JZWRlmzJiBNWvWXBzz8lLWUpLnmjqxNicflXVtknGthxp3zUrETeNGsnGLiIiuSNGBXF5ejqSkJISGKu/hCqIoYs/R03j38xL09Eobt2LD/ZCVaUREsF6m6oiIyNUoPpCvv/56ucuw0d7Vi1ezv8e3J6SPSlQBmHtdDG6bNgoeGjZuERGR/RQbyKIoorKyEnv37sVrr70Gq9WKuXPnYtWqVdBq5bseW3iqCetzC9HcJm3cMvh5YflCI1JjDTJVRkRErkyxgXzmzBl0dXVBq9XiL3/5C2pra/Hcc8+hu7sbTz/9tF2voVaroFYPzfVbi1XAJ7vLsf0SjVu/SAnDgwtS4evtOSTfy51o/nmmQMMzBpfFebIf58o+nCf7KWWuVKLYd0FH5TCZTAgICLjYFLVz507867/+K44ePQqN5soPYRBFcUgaqmrOteGl9w6j4rT0UYk6rQYP3zYWN/8iho1bRER0VRR7hAwAgYGBkr8nJCSgp6cHLS0tCAoKuuLXNzV1XNURsiiK+OrIaWzMK4HZIki2JUYH4te3jkFogA4mU+egv4e702jU8Pf3RmtrF6xW4cpfMExxnuzHubIP58l+jp4rg8G+Bl/FBvI333yDJ598Ert374a3tzcAoLCwEIGBgXaFMQAIgghBGNwJgLZOM97cXoSjpQ2ScRWAjBvi8OCisWhr7YLFwje6PaxWgXNlB86T/ThX9uE82U/uuVJsIE+YMAFeXl54+umn8eijj6KmpgYvvPACli9f7vDvfbKyERu2FqKlwywZD/a/0LiVNiqYXdRERDSkFBvIvr6+2LBhA/7rv/4Lv/zlL6HX63HXXXc5NJB7LVZ8srsCeYdqbLZNSg3DfXOS4aNj4xYREQ09xQYyACQmJuKNN95wyveqrW/H2ux81NZ3SMZ1Wg3uvSUZ16WFs3GLiIgcRtGB7AyiKOKLw7X46KtyWPpczB8dGYAVGUaEBnrLVB0REQ0XwzqQWzrMeD23ED9UNErG1SoVMm+Iw4LrY6FR81oxERE53rAN5ONlDXh9WyHaOnsl4yEBOmRlpmF0ZIBMlQ2MIIooqTahqLoZ3WYrdFoNUmIMSIoJhJqn2ImIXMawC2RzrxUffVWGL4+cttl2/ZgR+NXsJHh7uca0VNa1YsveSptu8OPljQjQa7FoajziI/xlqo6IiAbCNZJniFSfa8PanAKcaZA2bnl7eeC+OcmYbAyXqbKBq6xrxca8Elj6uc+6pcOMjXklWDo7iaFMROQChkUgC6KIXd/X4JM95bBYpQGWFBWA5RlGhAS4TuOWIIrYsrey3zD+kUW4sN+qJek8fU1EpHBuH8im9h5syC1EfmWTZFyjVmHR1HjMvy52yB5A4Swl1Sab09T9aekwo7TGhOQYPoWKiEjJ3DqQj5bU443tRWjvkjZuhRm8kZWRhlEjXfNUblF184D2L6xqZiATESmcWwfy/9v8g83Y1PQILJ2VCJ3Wdf/p3WarQ/cnIiLnc91UGiC9zgP3z03BtSlhcpdy1XTaKz968mr2JyIi5xsWgZwSE4jlC40I8tfJXcqQSIkx4Hh545V3/KfUWJ6uJiJSOrcOZA+NCrdNG4U5k2Pcqss4KSYQAXqtXY1dAXotEqMDr7gfERHJy63XhfzL41Mx77pYtwpj4MLSnoumxsPjCt3hHv/sJHe3fz8RkTty60B250clxkf4Y+nsJATotZfcHqDXclEQIiIX4tanrN1dfIQ/Vi1JR2mNCYVVP61lnRprQGI017ImInIlDGQXp1apkBxj4H3GREQuzq1PWRMREbkKBjIREZECMJCJiIgUgIFMRESkAAxkIiIiBWAgExERKQADmYiISAEYyERERArAQCYiIlIABjIREZECMJCJiIgUgIFMRESkAAxkIiIiBWAgExERKQADmYiISAEYyERERArAQCYiIlIABjIREZECMJCJiIgUgIFMRESkAAxkIiIiBWAgExERKQADmYiISAEYyERERArAQCYiIlIAlwnkrKws/P73v5e7DCIiIodwiUDOzc3Fnj175C6DiIjIYRQfyCaTCS+88ALGjh0rdylEREQO4yF3AVfy5z//GYsWLcL58+flLoWIiMhhFH2EvH//fhw6dAiPPPKI3KUQERE5lGKPkHt6evDMM89g9erV0Ol0g3oNtVoFtVo1xJUBGo1a8if1j3NlH86T/ThX9uE82U8pc6XYQP7b3/6GMWPGYNq0aYN+jaAgPVSqoQ/kH/n7ezvstd0N58o+nCf7ca7sw3myn9xzpRJFUZS1gn7MnDkTDQ0N0Gg0AACz2QwA0Gq1OHr0qF2v0djY7rAjZH9/b7S2dsFqFYb89d0J58o+nCf7ca7sw3myn6PnymDQ27WfYo+Q33nnHVgslot/f+mllwAATz75pN2vIQgiBMFxnzesVgEWC9/o9uBc2YfzZD/OlX04T/aTe64UG8iRkZGSv+v1Fz5hxMbGylEOERGRQ/FqPxERkQIo9gi5r//+7/+WuwQiIiKH4REyERGRAjCQiYiIFICBTEREpAAMZCIiIgVgIBMRESkAA5mIiEgBGMhEREQKwEAmIiJSAAYyERGRAjCQiYiIFICBTEREpAAMZCIiIgVgIBMRESkAA5mIiEgBGMhEREQKwEAmIiJSAAYyERGRAjCQiYiIFICBTEREpAAMZCIiIgVgIBMRESkAA5mIiEgBGMhEREQKwEAmIiJSAAYyERGRAjCQiYiIFICBTEREpAAMZCIiIgVgIBMRESkAA5mIiEgBGMhEREQKwEAmIiJSAAYyERGRAjCQiYiIFICBTEREpAAMZCIiIgXwkLsAVyKIIkqqTSipNUFUqaESBSRFBSIpJhBqlUru8oiIyIUxkO1UWdeKLXsr0dJhhkoFeGjUsFgFHC1tQIBei0VT4xEf4S93mURE5KJ4ytoOlXWt2JhXgpYO8yW3t3SYsTGvBJV1rU6ujIiI3AUD+QoEUcSWvZWwCOJl97MIF/YTxMvvR0REdCkM5CsoqTb1e2TcV0uHGaU1JgdXRERE7kjRgVxVVYWHHnoIEyZMwPTp07F+/Xqn11BU3Tyg/QurBrY/ERERoOCmLkEQkJWVhbFjx+LTTz9FVVUVfvvb3yI8PBwZGRlOq6PbbHXo/kRERICCj5AbGhqQmpqKZ599FnFxcbjpppswZcoUHD582Kl16LQah+5PREQEKDiQw8LC8Je//AW+vr4QRRGHDx/G999/j0mTJjm1jpQYw4D2T40d2P5ERESAgk9Z/9zMmTNx5swZzJgxA3PmzHHq906KCUSAXmtXY1eAXovE6EAnVEVERO7GJQL5r3/9KxoaGvDss8/i+eefx9NPP23X16nVKqjVV7+C1uKbRuGdnSWwCgIAQAXVT3+qLtzmpFGrsfimBGg9ecr65zQateRPujTOk/04V/bhPNlPKXOlEkXXuXF2x44dePLJJ3HkyBFotdor7i+KIlRDtKRlSXUz3v+8GKa2bpttgX46LJ2TjMRonq4mIqLBUewRckNDA44dO4ZZs2ZdHBs9ejR6e3vR3t6OoKCgK75GU1PHkBwhA0ConxaPLR6DkmoTCquaIUAFNUSkxhourmXd3NwxJN/LnWg0avj7e6O1tQtWqyB3OYrFebIf58o+nCf7OXquDAa9XfspNpBra2vx2GOPYc+ePQgPDwcAnDx5EkFBQXaFMQAIggjhCitsDdToyACkxBpgMOjR3NwBi0WAYBUhwGVONMjCahVgsfCXwpVwnuzHubIP58l+cs+VYi8ujB07FmlpafjDH/6AsrIy7NmzBy+++CJ+/etfy10aERHRkFNsIGs0GvzjH/+At7c37rzzTvzxj3/Evffei/vuu0/u0oiIiIacYk9ZA0B4eDj+9re/yV0GERGRwyn2CJmIiGg4YSATEREpAAOZiIhIARjIRERECsBAJiIiUgAGMhERkQIwkImIiBSAgUxERKQALvW0JyIiInfFI2QiIiIFYCATEREpAAOZiIhIARjIRERECsBAJiIiUgAGMhERkQIwkImIiBSAgUxERKQADORBysrKwu9//3u5y1Ass9mM//iP/8AvfvELXH/99fif//kfcA2aS6urq8PDDz+Ma665BjNnzsSbb74pd0mKYjabsXDhQnz33XcXx2pqavDAAw9g/PjxmD9/Pvbu3Stjhcpxqbk6duwY7rrrLkyYMAFz5szBxx9/LGOFynGpufpRW1sbpk2bhs2bNzu1JgbyIOTm5mLPnj1yl6Fozz33HL799lts2LABL7/8Mj766CN8+OGHcpelSE888QR8fHywefNm/OEPf8Bf/vIX5OXlyV2WIvT09OC3v/0tSktLL46JoohHH30UISEh2LRpE3GuinMAAAbSSURBVBYtWoTHHnsMZ86ckbFS+V1qrurr67FixQpMmjQJn376KVatWoU1a9Zg9+7d8hWqAJeaq5978cUXcf78eSdXxUAeMJPJhBdeeAFjx46VuxTFMplM2LRpE9asWYP09HRMmTIFy5Ytw/Hjx+UuTXFaWlpw7NgxrFy5EnFxcZg1axamTZuG/fv3y12a7MrKynDHHXegurpaMn7gwAHU1NTgT3/6ExISEvDwww9j/Pjx2LRpk0yVyq+/udq1axdCQkLw29/+FnFxcViwYAFuvfVW5OTkyFSp/Pqbqx8dOnQIBw4cQGhoqJMrYyAP2J///GcsWrQIo0ePlrsUxTp8+DB8fX0xadKki2NZWVl4/vnnZaxKmXQ6Hby9vbF582b09vaioqICR44cQWpqqtylye7gwYOYPHmyzZmV48ePw2g0wsfH5+LYxIkTcezYMWeXqBj9zdW0adMu+XPX3t7urNIUp7+5Ai6cxv73f/93rF69Glqt1um1eTj9O7qw/fv349ChQ8jJycGzzz4rdzmKVVNTg8jISHz22Wd49dVX0dvbi8WLF2PlypVQq/kZ8Oe8vLywevVqrFmzBm+//TasVisWL16M22+/Xe7SZLd06dJLjtfX1yMsLEwyFhwcjLNnzzqjLEXqb66ioqIQFRV18e+NjY3Izc3F448/7qzSFKe/uQKAV199FUajEVOnTnViRT9hINupp6cHzzzzDFavXg2dTid3OYrW2dmJqqoqfPDBB3j++edRX1+P1atXw9vbG8uWLZO7PMUpLy/HjBkz8OCDD6K0tBRr1qzBlClTkJmZKXdpitTV1WVz9KLVamE2m2WqyDV0d3fj8ccfR0hICO688065y1GcsrIyfPDBB8jOzpatBgaynf72t79hzJgxmDZtmtylKJ6Hhwfa29vx8ssvIzIyEgBw5swZvP/++wzkPvbv349PPvkEe/bsgU6nw9ixY3Hu3Dm88sorDOR+eHl5wWQyScbMZjM/KF9GR0cHHnnkEZw6dQobN26Et7e33CUpiiiKePrpp7Fq1SqEhITIVgcD2U65ubloaGjAhAkTAODip/GdO3fi6NGjcpamOKGhofDy8roYxgAQHx+Puro6GatSppMnTyI2NlYSJkajEa+++qqMVSlbeHg4ysrKJGMNDQ02p7Hpgvb2dixfvhzV1dV46623EBcXJ3dJinPmzBkcPXoUxcXF+POf/wzgwpmYZ555Btu2bcP69eudUgcD2U7vvPMOLBbLxb+/9NJLAIAnn3xSrpIUa9y4cejp6UFlZSXi4+MBABUVFZKApgvCwsJQVVUFs9l88TRsRUWF5LofSY0bNw5r165Fd3f3xQ8yhw8fxsSJE2WuTHkEQcBjjz2G2tpavPPOO0hISJC7JEUKDw/H559/Lhm79957ce+99zr1TBU7bOwUGRmJ2NjYi//p9Xro9XrE/v/t3SFIM3EcxvHndWcwOEGDaDlZWdB8WS0mEeQMYwyjDMaKIIwJhp1JwSCKzCKISYNhIFcsFq0ic2BYkZWlgUnQ903vC0Pft73+f5zfT7yyp2zfuz9j833X08zJZDKanZ1VpVJRq9XSzc2N6vW6crmc62nmzM/Pa3BwUJubm2q327q+vtbR0ZEKhYLraWYFQaCJiQlVKhU9PT2pXq/r/v5eYRi6nmbOxcWF7u7uFEWR0um0ut2uut3uhyP/787zvL7Pd9/35XmexsbGND4+/nU7vuyV8K3s7u6qVqspl8tpaGhI+XyeyHxieHhYJycn2t7eVhiGGh0dVbFY5Es3/5BKpXR4eKhqtarl5WX5vq+DgwNNTk66nmZOHMd6f3/X2tpa3/UgCHR6eupoFf7mx09+zxAAAOc4sgYAwACCDACAAQQZAAADCDIAAAYQZAAADCDIAAAYQJABADCAIAMAYABBBgDAAIIMAIABBBkAAAMIMoA+cRwrm80qjuM/19bX1zU3N6der+dwGZBsBBlAn4WFBS0tLalWq6nX66nRaOjq6ko7OzsaGRlxPQ9ILP7tCcAHLy8vWlxc1MzMjG5vb7W6uqpSqeR6FpBoBBnAp36HeHp6Wufn50qlUq4nAYnGkTWATz08PMjzPLXbbXU6HddzgMTjCRnAB61WSysrK9ra2tLl5aXe3t50dnamgQHu4YH/hXcXgD6vr6/a2NhQEAQKw1BRFKnZbOr4+Nj1NCDRCDKAPnt7e3p+flYURZKkqakplctl7e/v6/Hx0fE6ILk4sgYAwACekAEAMIAgAwBgAEEGAMAAggwAgAEEGQAAAwgyAAAGEGQAAAwgyAAAGECQAQAwgCADAGAAQQYAwACCDACAAb8A8TOBZy67PjEAAAAASUVORK5CYII=",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x321a377b8>)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"anscombe = load_dataset(\"anscombe\");\n",
"head(anscombe)\n",
"\n",
"lmplot(x=\"x\", y=\"y\", data=query(anscombe, \"dataset == 'II'\"),\n",
" ci=nothing, scatter_kws=Dict(\"s\"=> 80));"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAHjCAYAAADyq2xBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xl8VPW9P/7XmZlMZjLJJJMVshIgQFjCKptEETdEEUWt1tYu1mKpltrW3lavdSl+L6201v5ur9rbeuutVusCynWpCCKbsoddQgLE7GTfk1nP+f0RmeRkgRlI5nNm5vV8PHrlczIzed8PIa/5nPkskqIoCoiIiEgonegCiIiIiIFMRESkCQxkIiIiDWAgExERaQADmYiISAMYyERERBrAQCYiItIABjIREZEGGEQXcCnq6tqG7bV1Ognx8RY0NnZAlrl3yoWwv/zD/vId+8o/7C//BKK/kpJifKtlWL57CNDpJEiSBJ1OEl1KUGB/+Yf95Tv2lX/YX/7RUn8xkImIiDSAgUxERKQBDGQiIiINYCATERFpAAOZiIhIAxjIREREGsBAJiIi0gAGMhERkQYwkImIiDSAgUxERKQBDGQiIiINCOrDJYiIAk1WFBSVNaOwrAl2pwcmox4TMm0YlxkHnSR+P2QKXgxkIiIflVS3YsPOErR0OFXXD59uQKzFiGULspE90iqoOgp2vGVNROSDkupWvLapqF8Yn9PS4cRrm4pQUt0a4MooVDCQiYguQFYUbNhZAvcFzst1y92PkxWeQ0z+4y1rIgp7iqLA7vSgpcOJlnYHWjqcaOt0we50o8vhQXVDB05XtkABAAXd/4UCQIIkARIASBJ0EtDU5sCrH5/EqBFWWEwGxFoiERdjRFx0JAx6joFocAxkIgob7V0uVNa1o7K+A7VNXahr7kJdsx11LV1wOD1D9n22HqwCUNXvekxUBBKsJqTERyHFZkaKLQop8VFIS7Qg0qgfsu9PwYmBTESadG42c1FFMxRJB0mRMS49zufZzI2tdpRUt+JMdSvKzrahoq5j0M9/A6Wt04W2The+PNumui4BSI6PQkZyNDKSozF6pBWjU60wR/JXdDjh3zYRaU7v2cySBBj0Org9Mg4W1w84m1lRFFTWd+DkV8uRTle2oLl9+MJX8v4fYCg+LlYA1DR2oqaxE/sLa73fIzXJgjGpschJj8XEUfGwxUQO+hqX+gaGxJMUJXhnH9TVtV34QRfJYNDBZrOgqakDbrc8bN8nVLC//MP+Gty52cznJlD1DuRzv60MOgk3L8hGc5sDR0sacbKsCW2dLr+/l14nIcFqQlKcCfFWE2KjIxFrMSLWYoTVYoQ50gCzUY/y2nZs+Kzkq3r6h5uiKFDQHc6yrOCamelIijOjw+5Cc5sDTe0ONLU50NzmQF2LHU1tjovqm5EJUZiYFY+Jo2zIHWWDyWjw9tlAb2AUBVyOdQGB+LeYlBTjWy3D8t2JiC7C+WYzK4oCh0tGl92NLocbf3jzsM+va9DrkJZoQVpS9//Sk6KREh+FBGsk9LoLT7SKjzVh2+GqQW95S5LkHTXHx0Tiimmp5x2VOpwe1DR1orapC1X1HSirbUd5bRvqmu3nraO6oRPVDZ34pKACBr0OuVk2ZCRbcLyksfudywDOLce6+9pxDGWNYyATkWYUlTWrQk9RFDhdMpodDrR3ueD2+HZDb0R8FMakdn8Om51qRXpS9CXNcNZJEpYtyFaN3Adi0HU/7kK3iCONemSmxCAzRT1y6nK4UVbThlOVLThd2YpTlS1o7xp45O/2yDh6pgFHzzQAAIwROlhMEbCYDf3+fz23HGvV7Xm8fa1hDGQi0ozCsiYAgMsto8PuQoePIZwSH4XczDhMyLJhfEYcYqMH/6z1YmWPtOLua8cNuFMXMDS3hs2RBozPtGF8pg1A9xuSmqYunChtwokvG3GitAkddveAz3W6ZDhd3bfGTUY9okwGWEwR0Om6A7ilw4ni8mbva5P2MJCJSBMcTg9OV7bgbEMnHK7zL0GS0D3KHDUiBt9dkoukOHNAasweacWq2/NQXN6ME6U9e1nnZtmQkzH0k6ckScKI+CiMiI/CVdPTIMsKSmvacPR0Aw6eqkfp2YHn0didHtidHjS1OrqD2RwBk1GPE6VNDGQNYyATkVCV9R3YWlCJz49Xo8sxeBBLUvcI0mIywBRpgE6SMC4jLmBhfI5OklSj2IB+b52E7JFWZI+04uYF2Xj5XydwrKQRnXY37AOso1YAdNjd6LC7oddLiIzQ4+qZTsREGQNeO10YA5mIAk6WFRQU1eGTAxU4Wd486OMkAGaTAVaLEcYIHSSoR6C5WeE92ouLjkRMlBExUUZ4PDI6Hd3hO9AmJx6PguKKFvzsvz7HnInJuHpmOkaN4CQvLREayA0NDXjqqafw+eefw2azYeXKlVi+fLnIkohoGNmdbuw8Uo1N+8vPO6M4MkIPi7n7M1C9Xuq37Ano/sw2JyMuAFVr14RMGw6f7p7UpdfrEBPVvVxLUYCWdgfaOl3w9JmE5vbI+OzoWXx29Cxy0mNxw5ws5I1N4GQvDRAWyIqi4IEHHoAsy/j73/+Ompoa/OIXv0B0dDSuu+46UWUR0TBo7XRi075yfFpQiU7HwJOSLCYDLp8yEmPTYrFxb9mQzGYOdeMy4xBrMfabZBZh0CEuJhJWixF2pwftXS502d3o26PFFS0orjiCkQlRWDwnE/MmjeB+2wIJC+Rjx47h4MGD2Lx5MzIyMjBx4kTcd999eOmllxjIRCGipd2Bj/aW4dODlXC6Bt50IXukFYtmpOGyCckwRnTv55wQaxrW2cyh4kLLsSRJgjnSgBhzBJZePgpfVrfh00OVaOmzi1l1Qyf+9mEh3t1RgiVzs3DF1FREGBjMgSYskMvLyxEfH4+MjAzvtfHjx+OPf/wjXC4XIiIiRJVGRJeoud2BD3eVYtvhKrgG2P1IAjBjXBKun52Jsemx/b7eezbzyfKerSDHZ8QNy2zmYObPcqy8MYlYMi8LBUV1+GhPWb89tZvaHPjHpiJ8uLsUN83LwoI8BnMgCQvkxMREtLW1oaurC2Zz9yzJs2fPwu12o62tDfHx8Rd8DZ1O8q6xG2r6r27b6Hn7xifsL/+Ean912F348PNSbNxXNuCI2GjQ4Yppqbh+diZS4qMu+HqTRicgLycJVqsZra1d8Hi4zehAcjLi8NO7pqGorHs5lgwJOijIzbL128vaYNBh/pSRmDd5BE6UNuHDXaU48tXn0Oc0tTnwysdF+GB3KW69YjTy81KH7XetaFr6tyhsL2uHw4EbbrgBc+fOxWOPPYa6ujrcf//9KCkpwfbt25GSknLB11AUZcB9ZYkosOxONz7YWYK3txQPuLOUyajHjZdn45YrxyLuPAckkBglVS14c3MRdh7uf2QkAGSkxOA7N07EZRNT+Dt3GAk9XOLIkSN46KGHUF1djYSEBNx3331Ys2YNCgoKYLFYLvj8hob2YR0h812579hf/gmV/pIVBbuPncWbW06hcYADE0xGPa67LAPXz8m86LWvodJXgXIp/VVR2453dpzBvhO1A359fEYc7romB2PS+n/MEKwC8fNls104zwDBy57y8vKwZcsW1NXVwWaz4bPPPoPNZvMpjIHutYzyeWZiDgWPR+ZpPH5gf/knmPvrdGULXv+kGGeqWvt9zaDX4eqZaVgyN8sbxJf6/2cw95UIF9NfI+KjsHLZZCyd1x3MB4vrVV8/Wd6Mp/62D5dPHoHbFo5B3DBsUSqKFn6+hAVyc3MzVq5cieeffx5JSUkAgK1bt2L27NmiSiIiHzS3O/Dmp6ew+3hNv69JEpCfNxI3X56NeKtJQHU0FNKTo/Gj2/JQXNGMtz49jVOVLaqvf3bsLPYX1WHp/FG4dlYGJ34NEWGBHBcXh87OTqxduxYrV67E7t27sW7dOrz66quiSiKi8/DIMrYUVOLdHWcG3OIyb0wCvnbVWKQm+naHi7QvJz0Oj3xzBg4V1+PtbadR3dDp/ZrD6cHbW09j++Eq3HPdeEzKvvBEXDo/obes//CHP+CJJ57A0qVLkZ6ejj/+8Y/Iy8sTWRIRDeB0ZQte2XgSZbXt/b6WmmjBXYvGYvLoBAGV0XCTJAnTxyVhypgEfFpQiXd3lqCr1+YutU1d+P0bhzBnYgruWjR2WE7aChdCJ3Vdqrq6gU86GQoGgw42mwVNTR3CP1cIBuwv/2itv2RFQVFZMwrLek4wmpBpQ0ZKNNZvP4NPCyr7PScq0oBbrxiNhdNTodcN3y1LrfWV1g13f7V2OvHu9jPYdqiq385f5kgDbl84BldOSw2ateKB+PlKSoq58IPAwyWIwl5JdeuAm0rs/qIGTW2OATf2uHzKCNyxcCysFp4aFG6sUUZ8a/EEXDktDa98fFI1qa/L4cYrG09izxc1+O6SCUixRQ36Zq/v+mjiCHlQfFfuH/aXf7TSXyXVrf22XfTICppa7eiw999zOi3JgnuuG49xATzUQSt9FSwC2V+yomDboSq8vfW06jY20L0JzJXTUnG2sROtnf3XpmtlC1SOkIlIOFlRsGFniSqMO+1uNLTa+y0nlCTg1itGY/HsTB4+QF46ScJV09MwIycR/9xyCnu+6Jl573TL2LS/ApEROiTEmvvNxG7pcOK1TUW4+9pxwkNZK/gviyhMFZU1e29Ty7KChhY76pq7+oVxZIQeIxMsyEmLZRjTgGKjI3H/zZPw49vzYOuzE5vDJaO6vgNtnU70vSHrlrvfFMrBe6N2SPFfF1GYKixrAtC97WV1Q0e/LS8lCYi3RiIlvnt0c6K0SUSZFESmjk3E6u/NwZQ+M+4VAI2tDtQ29d8Nq6XDieLy5gBWqV0MZKIw1elwo7nNgZrGLrg9/UfFqQkWxEQZvXsX25391x4T9RVlMiB7ZAySbWbo+2xtbHd6UFXfiU67+s0f3+x1YyAThaGGFjsKiuoGPK7PFtM9Kjb0+czPZNQHqjwKcnanB+ZIA1ITLbCY1FOVZEVBXbMdja127y1svtnrxkldRGFmf2EtXv5XITr7zIqNMOiQGGuCMWLg4M3NsgWiPAoB59686XQSEuPMMHe50NhqR+/pCW2dLtidHiTFmflm7ysMZKIw4fbIeOOTU/ikoKLf12KiImCLiRz0aL1YixE5AVzqRMFtQqYNh3udsWwxRyDSqEdDi101Gna5ZVQ3dECWE0WUqTkMZKIw0NBixwsbjvU7mSnKZIA1KgKRxsF/FRh0EpYtyOYmDuSzcZlxiLUYVR+JGPQ6JNvMaO1worm957qiAO/vKkVrpwvfuDYHEYbwHS3zM2SiEHfsTAOeenlfvzCeOMqGp++bg+8vnYTYQXbcirUYuU6U/KaTut/EGfpM6pIkCbHR3XMU+k742n64CmteLUB9S1cgS9UU7tQ1CO4O5B/2l38C0V+youD9z77Ehp0lqj2HJQDL8rNx0/xR3lGvrCgoLm/GidKe7Q1zs2zIyRC/vSF/tvyjpf4abFtWALCYDHC5ZRRXqI92jDZH4P6bJwXs9Cju1EVEw6rL4cZf3/+i3wHzg/2y00kSxmfaMD6TE7do6GSPtGLV7XmDvtmTAHy0pwxvbzuNc0PD9i4Xnn3jEJZfORpL5mYNOq8hFDGQiUJMTVMn/nPdUVTVd6iuj0m1YuUtkxFvNQmqjMLRhd7s3TA3C6NGxODF/zuOtq/2vFYArNt2BuW17fjuklxEDjLzP9TwM2SiEHLsTANWv7y/XxhfNSMNv/jGDIYxaVLuqHg88Z3LMDpVPVdh74la/ObVAjS22gVVFlgMZKIQoCgKNu0vxx/eOqxaX2zQS/jODRNwz3XjuQ81aVq81YRf3D0DV0xNVV0vrWnDr/93P4orQn97Tf4LJQpyHlnGq5uK8PrmYvSeohkbbcS/DfALjkirIgw6fHvxeHzj2nGqyYStHU6sff0gdh0/K7C64cfPkImCWKfdjRc3HMOxkkbV9eyRVjy4fEq/k3eItE6SJFw9Mx2pCVF4/t1j3nO53R4Ff3nvC9Q1dWHp5aNCcrIXR8hEQaq+pQv/8eqBfmE8OzcZv7h7OsOYglruqHj86juXIS3Rorr+7s4S/PX9E3CF4BI4BjJRECqracP/+/uBfpO3ls4fhRU3Txp0P2qiYJIcZ8Yj35zZb5neruNn8fs3DvU7MjTYMZCJgszxkkas+UdBn20JJXz/pom49YrRwjfyIBpKUSYDfnx7Xr+5EEXlzfjNP0JrBjYDmSiIfH6sGs+9dRiOXhv0W0wGPHzXdMybPEJgZUTDx6Dvnux1x1VjVNer6jvw/145gIq6dkGVDS0GMlEQUBQFH+4uxV/fPwFPrzPsEqwmPHrPTIzjSUwU4iRJwg1zsvDDWyarlvA1tTnwm1cLcLKsSWB1Q4OBTKRxiqLgrU9P4+2tp1XXM1Oi8e/fmomRCZZBnkkUemZNSMbP7pwKc2TPIqFOhxu/f+MwDpysE1jZpWMgE2mYR5bxt38V4qO9Zarrk7Lj8Yu7ZyAumjOpKfyMz7ThkW/MUK0kcHtkPP/uUXx2tFpgZZeGgUykUS63By+8exw7j6h/wcydmIIf356nGiEQhZv05Gg8+s2ZGJkQ5b2mKMBLH5zA5v3lAiu7eAxkIg2yO9147q0jKChS34JbNCMN9y2dyG0wiQAkxJrwyDdnYkyfPbBf21yM9z4rQbCdLsx/1UQa02l349k3D+NEqXqSys2Xj+q3pSBRuIs2R+Bnd01Dbpb6NKl3dpTgzU9PBVUoM5CJNKS9y4Xfv3EQp/oc2v71a3JwS/7okNwukOhSmYwGPHRHHqbnJKqub9xbjn9sKoIcJKHMQCbSiNZOJ373+kGUVLd5r0kScO+SXFw7K0NgZUTaF2HQY+UtkzFvUorq+paCSryy8WRQhDIDmUgDWtodeOa1gyir7dngQCdJWLF0EhbkjRRYGVHwMOh1+N5NE3HV9DTV9W2HqvDyh4WQZW2HMqdpEgnW0uHEM68fRHVDp/eaXifhB8smY+b4JIGVEQUfnSThm9eNg14nYfOBCu/1nUer4ZFl3HtjLvQ6bY5FGchEASQrCorKmlFU0QxF0sHhcGHfiVo09NqP16DX4cHlk5E3JvE8r0REg5EkCV+/Jgd6vYSNe3uWQO06XgMA+N6NE6HTaW8+BgOZKEBKqluxYWcJWjqcODc3q7KuQ3WMXIRBh1W35fU73YaI/CNJEr521VgY9Dp8sKvUe33X8RrodBK+uyRXcysWGMhEAVBS3YrXNhXB/dVnWB6PjJrGLlUYSwDuWDiGYUw0RCRJwvIrRkOvk/B/n33pvf7Z0bPQSRLmTkxBcWULFEkHSZExLj0O4zLjhAU1A5lomMmKgg07S3rCWFb6hTEAJNnMOFbSiEUz0zX3zp0oWEmShGULsuGRFdVIeceRahwsrkdCbCQiDHq4PTIOFtcj1mLEsgXZyB5pPc+rDg9tfrJNFEKKypq9ZxfLsoLaps5+YZxsM8McaUBLhxPF5c0iyiQKWedGyjfMyVRdb+9yobHVodo8pKXDidc2FaGkujXQZTKQiYZb4VfHwnWHcRecroHD+Jy+O3QR0aWTJAnLrxyNxFiT6npbZ3co9+aWu+9qBXrtMgOZaJjZnR4oioK65i44XB7V15Jspn6HRNid6scQ0dAoLm9BlMmAmKgI1fWmNgda2tWhLOJuFQOZaJgZDTrUNdv7BW1KvBkWU0S/x5uM+kCVRhRWCsuaIEkSbDGRiDb3DWUn2jqdqmuBvlvFQCYaRrKioKS6FV0Ot+p6QmwkYqKMAz6n7yb5RDQ0zr0pliQJ8dZIRJnUd6caWx1o73L1e3ygCA3k6upq3H///ZgxYwYWLVqEl19+WWQ5RENKURS8ueUUjn+pfpdtixk8jGMtRuRkxAWiPKKw0/vukyRJSIw1wRypviPV0GJHp93d7/GBIDSQH3roIURFRWH9+vV49NFH8dxzz2HTpk0iSyIaMh/uLsXH+9QHpcdGG2G1DBzGBl338gwueSIaHhMy1XefJElCks3cL5Trm7tgd7oDfrdKWCC3tLTg0KFDWLlyJUaNGoVrrrkG+fn52LVrl6iSiIbM1kOVWLftjOra7NxkZCZHD/j4WIsRd187TsjaR6JwMS4zDrF93hDrJAkjEywwRvTEoQKgvtkOsymwW3UI2xjEZDLBbDZj/fr1+NnPfoby8nIUFBTgoYce8vk1dDpp2PYj1et1qv/S+bG/euwvrMUrG0+qrs2fPAIrlk0C0L0u+URpE2RI0EFBbpZN6O5AWsefLf+wv85v+ZWj8crGInjk7uWHErpzZER8FKrqO+H2dF/3yAr++NYR/Orbs5AYZw5IbZKiiDskcv369Vi9ejUcDgc8Hg+WL1+ONWvW+Px8RVF4YDtpyvEzDfjVnz9XbfwxKzcF//7d2TDwFySRJhSVNeH1j0+iuc2uuu5yy6iqV+8vn5ZkwW8fzEdsdOSw1yU0kNeuXYvq6mp897vfRXFxMVavXo2nnnoKN998s0/Pb2hoH9YRstVqRmtrFzwe+cJPCHPsL6CyvgNPv7wPHfaeGdU56bH4t2/MQGSE+jMq9pfv2Ff+YX/55tzJa33vVlnMBvzH3w+o/h2PSYvFL7/Z/9+xr2w2i0+PE3bLeteuXXj77bexbds2mEwmTJkyBTU1NXjhhRd8DmRZVob9wGmPR4bbzR9qX4VrfzW1OfC71wpU/4hHJkThR7flQS9Jg/ZJuPbXxWBf+Yf9dWFj02IxIcsGm82CpqYOb3/9+Pap+N0/D8L5Vft0ZQueX38UD9w6ZViPbRR2D+3YsWPIysqCydSzjdnEiRNRVVUlqiSii9LlcOO5tw6jodf2e7HRRvzka1P7bT5ARNo3Nj0WP1g2Gb0/ET1YXI/XNxdjOG8qCwvk5ORklJaWwuns2RnlzJkzSE9PF1USkd/cHhnPv3MU5bXt3msmox4/uWMqEmMDMxGEiIbetJxEfPO68aprnxRUYOPe8kGecemEBfKiRYsQERGBxx57DCUlJdiyZQtefPFF3HPPPaJKIvKLoih49eMi1cYfep2EB5dPQWZKjMDKiGgoXDU9DUvmZqmuvfnpKew9UTMs309YIMfExODll19GXV0dbr/9dqxZswYrV67EnXfeKaokIr98tLcM2w+rP2K5d0kuJo6KF1QREQ215VeOxtyJKaprf33/BE5Vtgz59xI2qQsAxo4di7/97W8iSyC6KPsLa/HWp6dV127Jz8a8ySMEVUREw0EnSfjuklw0tztQWNZ9+pPbI+M/1x3BY9+ahaQhXKPMhZFEfjpd1YK/vP+F6tr8ySOwdP4oMQUR0bCKMOjw4PIpGJkQ5b3W1unCH98+4t33eigwkIn8UN/Shf98+4hq44DxGXH4zg0TuEkNUQiLMkXgx7fnqVZOVNV34IUNx7y7fl0qBjKRj+xON/5z3VG0dvYcz5YSH4UHlk/hLlxEYSDZFoUf3TYFBn3Pm+/jJY14bdPQLIfibxEiH8iKgr+894VqeVO0OQI/uSOPa42JwkhOehy+uyRXde3Tg5X49GDlJb82A5nIB+9sP4ODxfXetl4n4YFbJyPZFnWeZxFRKJo3aQRuvnyU6tprm4px4svGS3pdBjLRBew+fhYf7CpVXfvmdeMwPjOwZ6USkXYsW5CNyyYke9uyouD5d4+htqnzol+TgUx0HiXVrfifDwtV166ZlY4rp6UJqoiItECSJNx7Yy4yU3rOOO+wu/H/rTuKLsfFzbxmIBMNoqXdgT+tP+o9HxUAJmfH485FYwVWRURaERmhx6rb8mCNUs+8/u//O35RBx8xkIkG4PbI+K93j6GprefAiBHxUfjBsknQ6/jPhoi6xVtNeHB5nmrm9eHTDXh3Z4nfr8XfLEQDeH1zMU5V9GyNZ47U40e3TUGUiTOqiUhtbHos7rlefRDF+59/iYKiOr9eh4FM1Me2Q+olDBKA7y+dhJEJvh0yTkThJz8vFdfOylBd++v7X6CqvsPn12AgE/VyqrIFr35cpLp2S342po1NFFQREQWLO64agwmZcd623enBn9Yf9fn5DGSir7R0OPH8O0fh6TUZY+a4JNzIPaqJyAcGvQ4/WDYZ8dZI77Wzjb4vg2IgEwHwyDL+vOEYmtud3mtpiRbce2MudNyjmoh8ZLUY8cCtF7edLgOZCMC6bWe8R6sB3ZO4Hlw+BeZIoSeUElEQyh5pxbf6TPLyBQOZwt7+wlp8tKdMde2+GyciJZ7bYhLRxVmQNxKL52T69Ry+/aewVt3Qgf/58ITq2o3zsjB9XJKgiogoVHztqrGYOd733yUcIVPYcjg9+K93jsHu9Hiv5WbZcGv+aIFVEVEoGZMa6/NjGcgUlhRFwSsfn1StEbTFROL+ZZOg03ESFxEFHgOZwtLOI9X4/NhZb1uvk/DDWyfDGmUUWBURhTMGMoWd8tp2vLpJvfnH1xaN9evWEhHRUGMgU1jpcrjx/LvH4HL3nOA0c3wSrpmZLrAqIiIGMoURRVHwvx8VoqbXzjlJcSZ894ZcSNz8g4gEYyBT2Nh+uAp7T9R62wa9hB/eMgVRJq7+IyLxGMgUFirr2vHa5mLVta9fMw5ZI2IEVUREpMahAYUkWVFQVNaMwrImdHS5sLewVvW58WUTkrFwWqrAComI1BjIFHJKqluxYWcJWjq6D4poaLGjvcvl/XpctBHfXjyBnxsTkabwljWFlJLqVry2qcgbxh12lyqMAcBiikBNk+9HohERBQIDmUKGrCjYsLME7q/OM3a5ZTS02FWPiYuJhMGgw4adJZAVZaCXISISgoFMIaOorNk7MlYUBQ0tXeiduSajHtaoCABAS4cTxeXNA70MEZEQDGQKGYVlTd4/t7Q74XD1TOLS6yQkxppUnxufKG0CEZFWMJApZJw7tcnudHtHyuckxJqg1+sGfDwRkRYwkClkmIx6yLKC+j6fG8dERcAc2X9BgcmoD1RpREQXxECmkDEh04bGVjs8np4PjiMMOthiIgd8fG6WLVClERFdEAOZQkZjmx0ddre3LQFIjDMNuN441mJETkZcAKsjIjo/BjKFhIYWO/7R50hFmzUSRkP/29IGnYRlC7Kh48YJ6zulAAAgAElEQVQgRKQh3KmLgp6sKHjpgy/Q5eiZpBUTFYFoc0S/x8ZajFi2IBvZI62BLJGI6IIYyBT0Nu0rR2FZz5rimKgIPHXvbNQ0duJEaRPsTg9MRj1ys2zIyYjjyJiINImBTEGtsq4d67adUV37zg0TEBcdibjoSIzP5MQtIgoO/AyZgpbbI+Mv730Bt6dnA5D8vJGYnpMksCoioosjbIS8fv16PPLII/2uS5KEwsJCARVRsNmwswRlte3edmKsCXddnSOwIiKiiycskJcsWYL8/Hxv2+1249vf/jYWLlwoqiQKIqcqW/Dh7lJvWwJw300TB9wAhIgoGAj77WUymWAymbztP//5z1AUBQ8//LCokihIOFwevPT+F6qDI26Ym4VxXFdMREFME8OJ5uZm/OUvf8HTTz8No9Ho8/N0Ogk63fDMmD2373Hf/Y9pYIHsr39uKUZNU5e3nZEcjdsWjoHBEDx/V/z58h37yj/sL/9oqb80Ecivv/46kpOTsXjxYr+eFx9vGXAXpqFktZqH9fVDzXD319HT9fh4b7m3rddJePibs5CcFDOs33e48OfLd+wr/7C//KOF/hIeyIqi4K233sJ9993n93MbGzuGdYRstZrR2toFT69ZvDSwQPSX3enGH14rUF1blp8NW5QBTU0dw/I9hwt/vnzHvvIP+8s/gegvm83i0+OEB/LRo0dRU1ODG2+80e/nyrICWVYu/MBL4PHIcLv5Q+2r4eyv1zYVo66551Z11ogYLJ6dGdR/P/z58h37yj/sL/9oob+E3zTfsWMHZs2ahdjYWNGlkIYd/7IRWw9WetsGvYT7bsyFQQOf+xARDQXhv82OHDmCGTNmiC6DNKzL4cbLH6rXpt+SPxppSdGCKiIiGnrCA7m4uBhjx44VXQZp2Lptp9HQave2R6dasXh2psCKiIiGnvBArq+vh9XKk3doYCfLmrClQH2r+t4lucM2mY+ISBThk7qOHDkiugTSKIfLg7/9S32retmCbKQm+jZjkYgomAgfIRMN5p3tZ1Db1GdW9Rzeqiai0MRAJk06XdmCTfvUG4DcuyQXeh1/ZIkoNPG3G2mOyy3jfz48gd4rzG+cl4WMZM6qJqLQxUAmzflg15eobuj0ttOSLLhp/ihh9RARBQIDmTSlsq4dH+zqdayiBNy7hBuAEFHo42850gxZVvDyvwrh6bUd6rWzMpA9ksviiCj0MZBJMz49WInTVa3edmKsCbfmjxZYERFR4DCQSRMaWux4e9tp1bVvLR6PSKNeUEVERIHFQCbhFEXBKx+fhMPp8V6bP3kEJmcnCKyKiCiwGMgk3L7CWhw53eBtx0RF4K6rcwRWREQUeAxkEqrT7sLrm4tV175+TQ6izRGCKiIiEoOBTEKt23YGLR1Ob3vy6HjMyU0RWBERkRgMZBLmVGULth7sOcnJaNDhnuvGQ5J4khMRhR8GMgnh9sj4+0eFqu0xb16QjaQ4s7CaiIhEYiCTEJv2l6OirsPbTkuy4LrLMgRWREQkFgOZAq6+uQsbdpSorn37+gncHpOIwhp/A1JAKYqCVzcVwemWvdcWTkvF2PRYgVUREYnHQKaAOlRcr1pzbLUYcdvCMQIrIiLSBgYyBYzD6cFrm4tU1+5aNBYWE9ccExExkClg3vv8SzS0OrztCZlxmDORa46JiAAGMgVIZX0HNu4t87b1Ognf5JpjIiIvBjINO0VR8I+PT6rOOV48JxOpiRaBVRERaQsDmYbd7i9qUFjW7G0nWE24af4ocQUREWkQA5mGVZfDjTe3nFJdu/vaHERG8JxjIqLeGMg0rDbsLFEdHjF1TAKm5yQJrIiISJsYyDRsKuvasXl/hbdt0Otw97XjBFZERKRdDGQaFoqi4B+biiArPRO5lszN5OERRESDYCDTsNhXWKuayJUYa8KSuVkCKyIi0jYGMg05u9ONN/pM5Lrr6hwYOZGLiGhQDGQacu9/Xoqmtp4duSaPjsf0nESBFRERaR8DmYZUdUP/HbnuvmYcd+QiIroABjINqdc2Fat25Lp+diZGxEcJrIiIKDgYRBdAwU1WFBSVNaOoohlnm7pw+FS992tx0UbcNJ8TuYiIfMFApotWUt3aa+MPBVX1naqvL5yeBpORP2JERL7gLWu6KCXVrXhtU5F3F67WDhdcbtn79cgIHY6cqkdJdauoEomIggoDmfwmKwo27CyB+6vPij0eGc3tDtVjbFYTPEr31pm9NwchIqKBMZDJb0Vlzar9qZvbneiduRZzhPfwiJYOJ4rLm/u+BBER9cFAJr8VljV5/+xwedDe5fK2JQmwRRtVjz9R2gQiIjo/BjL5ze70AOjer7qpVX2rOi46Enq9bsDHExHR4BjI5DeTsft2dKfDDYerJ2wjDDpYLRGDPp6IiAYnNJCdTieeeuopXHbZZZg/fz6effZZKJwApHkTMm3do+M29eg4MdY04I5cuVm2QJVGRBS0hC4Sffrpp7Fnzx689NJL6OjowE9+8hOkpqbirrvuElkWXcC4zDg4XTI8np43TyajHlEmg2qXLgCItRiRkxEX6BKJiIKOsBFyc3Mz1q1bh9WrVyMvLw/z5s3Dvffei8OHD4sqiXzU1ulCY5tddS3eGtlvdGzQSVi2IBs67mNNRHRBwkbIBw4cQHR0NGbPnu29tmLFClHlkB/e2X4GTlfPJiDR5oh+RyvGWoxYtiAb2SOtgS6PiCgoCQvk8vJypKWl4d1338WLL74Il8uF5cuXY+XKldDpfBu463QSdLrhGX2dmyncd8ZwuCs924Ydh6u8bXOkHt+7MRdlte2QIUEHBblZNozLjOPI+Dz48+U79pV/2F/+0VJ/CQvkzs5OlJaW4p///CfWrFmDuro6PP744zCbzbj33nt9eo34eMuwH+tntZqH9fWDiaIo+N0/D6H3p8R3XTse18zLFlZTsOPPl+/YV/5hf/lHC/0lLJANBgPa29vx+9//HmlpaQCAqqoqvP766z4HcmNjx7COkK1WM1pbu+DxyBd+Qhg4VFyPI71Oc0qOM2PB5BFoaupgf/mJ/eU79pV/2F/+CUR/2WwWnx4nLJCTkpIQGRnpDWMAyM7ORnV1tc+vIcsKZHl4l0l5PDLcbv5Qe2QZr28uUl27feEYSICqf9hf/mF/+Y595R/2l3+00F/CbppPnToVDocDJSUl3mtnzpxRBTRpx/bD1ahu6DlecWx6LGaOTxJYERFRaBEWyKNHj8bChQvxyCOPoLCwEDt27MB///d/4+tf/7qokmgQXQ43Nuw4o7p256Kxw/75PRFROBG6Mcjvfvc7rF69Gl//+tdhNpvxjW98A/fcc4/IkmgA/9pTitbOngMkZucmY0xqrMCKiIhCj9BAjomJwTPPPCOyBLqAxlY7Nu4t97YNegm3XTlGYEVERKFJ/MIr0rT128/A1WuiwzUzM5AUJ355ABFRqGEg06DKatqw69hZb9tiMuDG+VkCKyIiCl0MZBrUW1tPqzYBWXp5Niym/scrEhHRpWMg04COf9mI4yWN3nZSnAmLZnBJGhHRcGEgUz+youCtT0+pri2/YgwMGtjrlYgoVPE3LPWz54salNW0e9ujRsTgstxkgRUREYU+BjKpuNwy3tmu3gTkjqvG8uQmIqJhxkAmlU8LKlDfYve2p4xOQG6WTWBFREThgYFMXp12F977/EtvW0L3ARJERDT8GMjk9a89Zeiwu73t+ZNHICM5WmBFREThg4FMAIDmdgc27eu9RaYOt+SPFlgREVF48TuQt23bBkUZ3jOIKfDe++xLOFVbZKYjIdYksCIiovDi9+ESq1atQmxsLJYtW4bly5cjOzt7OOqiAKpp6sT2w1XetjlSjyXzuEUmEVEg+T1C/uyzz/DAAw9g//79uOGGG3DnnXfijTfeQHt7+4WfTJr0zvYz8Mg9dz0Wz8lCtJlbZBIRBZLfgRwdHY0777wTr7/+OjZu3Ij8/Hy8+uqrWLBgAR5++GHs3r17OOqkYVJ6tg17T9R621aLEdfNyhBYERFReLqkSV2pqakYP348JkyYAAA4cOAAfvjDH2Lp0qUoLCwckgJpeK3bflrVvvnyUYg06gVVQ0QUvi4qkAsKCvDEE09gwYIF+PnPfw5FUfDCCy/g008/xY4dOzBmzBg89NBDQ10rDbHC0iYcO6M+QOKKqakCKyIiCl9+T+q69tprUVFRgYkTJ+LHP/4xli5dipiYGO/XLRYLbrjhBnz22WdDWigNLUVRsG6benR8a/5oHiBBRCSI34G8aNEiLF++HOPHjx/0MfPmzcPGjRsvqTAaXodPNeB0Vau3nZ4UjdkTUwRWREQU3vwO5EceeeSCj7FarRdVDAWGrChY3+cAiduuHM0DJIiIBOL9yTC0v7AWFXU9y9TGpFmRNyZBYEVERMRADjMeWcY7O0pU1267Ygwkjo6JiIRiIIeZz4+eRU1jp7c9cZQNE3i8IhGRcAzkMOJyy/i/z9Sj4+VX8HhFIiItYCCHkW2HKtHQ6vC2p+ckYnQqJ+AREWkBAzlMOJwevL+r1NuW0L3umIiItIGBHCa2HKxAa4fT254zMQXpydECKyIiot4YyGGgy+HGv3aXeds6ScKyBTw2k4hISxjIYWDzgQq0d7m87flTRiAlPkpgRURE1BcDOcR12l3YuKdndKzXSVg6f5S4goiIaEAM5BD38b5ydDrc3nZ+3kgkxZkFVkRERANhIIew9i4XNu0v97YNegk3cXRMRKRJDOQQtnFvGbocHm/7yqlpiLeaBFZERESDYSCHqNZOJzbvr/C2Iww63Dg/S2BFRER0PgzkEPXRnjI4XD2j46umpyEuOlJgRUREdD4M5BDU2uHEloKe0bExQocb5nJ0TESkZQzkEPTR3jI4XbK3vWhGOmItRoEVERHRhTCQQ8xAo+PFszMFVkRERL5gIIeYgUbHVo6OiYg0j4EcQjg6JiIKXkIDedOmTRg/frzqf6tWrRJZUlD7aA9Hx0REwcog8pufOnUKV111FVavXu29FhnJpTkXg6NjIqLgJjSQT58+jXHjxiEpKUlkGSHhoz1lcLo5OiYiClZCb1mfPn0ao0aNEllCSGjtdGLLQY6OiYiCmbARsqIoKCkpwc6dO/HnP/8ZHo8HixcvxqpVq2A0+jay0+kk6HTSsNSn1+tU/9WyzfsrVJ8dXz0zA/Gxgd2zOpj6SwvYX75jX/mH/eUfLfWXsECuqqpCV1cXjEYjnnvuOVRUVODpp5+G3W7HY4895tNrxMdbIEnDE8jnWK3aPqqwrdOJTw70nOhkjNDj64snwBYj5hAJrfeX1rC/fMe+8g/7yz9a6C9JURRF1Ddvbm5GbGysN1Q3btyIn//85zh48CD0ev0Fn9/Q0D6sI2Sr1YzW1i54PPKFnyDIuq2nsWFnibd9/ewMfOO68QGvI1j6SyvYX75jX/mH/eWfQPSXzWbx6XFCJ3XFxcWp2mPGjIHD4UBLSwvi4+Mv+HxZViDLw/t+wuOR4XZr84e60+7Cx/t6n3esw3WXZQqtV8v9pUXsL9+xr/zD/vKPFvpL2E3zHTt2YM6cOejq6vJeO3HiBOLi4nwKYwI2H6hAl8PtbV8xdSRsMVw2RkQUjIQF8vTp0xEZGYnHHnsMZ86cwbZt2/DMM8/gvvvuE1VSUOlyuLGp1+hYr5OwhCc6EREFLWG3rKOjo/HSSy/hP/7jP3DbbbfBYrHgrrvuYiD7aEtBBTrsPaPj/LyRiLeKmchFRESXTuhnyDk5Ofjb3/4msoSg5HB6sHEvR8dERKFEaCCT72RFQVFZMwrLmnCyrBntXS7v1+ZNHoHEOPFT9omI6OIxkINASXUrNuwsQUuHE4qioLKuQ/X1qWMSBFVGRERDRfzWJHReJdWteG1TEVo6nACA9i4XPL2WekWZDPhoTxlKqltFlUhEREOAgaxhsqJgw84SuL8KYEVR0PpVMJ8TazHCLXc/Tha3xwsREV0iBrKGFZU1e0fGANBhd8Pt6Qldc6QBxojuHc1aOpwoLm8OeI1ERDQ0GMgaVljW5P2zoihoae8zOo5WH8JxorQJREQUnBjIGmZ3erx/7nS44e61z6rJqEdkhH7QxxMRUXBhIGuYydgduIqioPUCo+PejyciouDDQNawCZk2AN0jX2evTc8jI/QwGfuvWMvNsgWsNiIiGloMZA0blxmHWIvxgp8dA92zrXMy4vpdJyKi4MBA1jCdJGF6TiIcrp7Pho0GXb9b0wadhGULsqGThudsaCIiGn7cqUvjDhbXq9rWaCOkXsEbazFi2YJsZI+0Bro0IiIaQgxkDSuracOR0w3ednxMJOZNTIHDJcNk1CM3y4acjDiOjImIQgADWcM+3F2qai9bkI38qamCqiEiouHEz5A1qqapE/sKa71tW0wk5k0eIbAiIiIaTgxkjdq4pwy9t6a+/rIMGPT86yIiClX8Da9Bze0O7Dxa7W1bTAZcMY23qomIQhkDWYM+3leuOkTimlkZA24EQkREoYOBrDGddhe2Hqz0tiMj9Lh6ZrrAioiIKBAYyBrz6cFK1SERV05LRbQ5QmBFREQUCAxkDXG5Pdi8v8Lb1uskXHdZhsCKiIgoUBjIGvL5sbNo6ejZt3ruxBTEW00CKyIiokBhIGuELCv4aE+Z6triOZmCqiEiokBjIGtEQVEdapq6vO2pYxKQlhQtsCIiIgokBrIGKIqCf+1Rb5N5w9wsQdUQEZEIDGQNOFnWjJLqNm97TJoVOemxAisiIqJAYyBrwId9RsdL5mSpjlgkIqLQx0AWrKK2HcfONHrbIxOiMDUnUWBFREQkAgNZsI17+8ysnp3J842JiMIQA1mgpjYHdn9R423HWoyYO4lHLBIRhSMGskCb95fDI/c+RCIdEQb+lRARhSP+9heky+HG1kPqQyQWTk8TWBEREYnEQBZk++EqdDl6DpG4YmoqLCYeIkFEFK4YyAK4PTI27S/3tnWShGsv4xGLREThjIEswL7CWjS2Orzty3KTkRhrFlgRERGJxkAOMEUZ4BCJ2TxEgogo3DGQA+yL0iaU17Z727lZNmSNiBFYERERaQEDOcD6bgRyPUfHREQEBnJAVdapt8lMTbRgyuh4gRUREZFWMJAD6ON95ar2dZdl8BAJIiICwEAOmJYOJ3Yd79km0xoVgXmTUgRWREREWqKZQF6xYgV++ctfii5j2HxaUAG3R/a2F81IR4RBL7AiIiLSEk0E8gcffIBt27aJLmPYOF0ebCno2SYzwqDDwhncJpOIiHoID+Tm5mY888wzmDJliuhShs3nx8+ivcvlbc+fPALWKKPAioiISGsMogv47W9/i2XLlqG2ttbv5+p0EnS64ZkUpdfrVP+9WLKiYFOfyVw3zM2CIcROdRqq/goX7C/fsa/8w/7yj5b6S2gg79q1C/v378d7772HJ5980u/nx8dbhn2WstV6aVta7vviLKobOr3tWbkpmJSTfKlladal9le4YX/5jn3lH/aXf7TQX8IC2eFw4IknnsDjjz8Ok8l0Ua/R2NgxrCNkq9WM1tYueHpNxvLX258Uq9rXzEhDU1PHpZanOUPVX+GC/eU79pV/2F/+CUR/2WwWnx4nLJD/9Kc/YfLkycjPz7/o15BlBbKsDGFV/Xk8Mtzui/tLKq9txxdf9mwEkpEcjZz02It+vWBwKf0VjthfvmNf+Yf95R8t9JewQP7ggw9QX1+P6dOnAwCcTicAYOPGjTh48KCosoZU7yMWAW4EQkREgxMWyK+88grcbre3/bvf/Q4A8PDDD4sqaUi1djixu/dGIBYjZudyIxAiIhqYsEBOS1Ovw7VYuu+xZ2VliShnyG09WKneCGR6GiJCbGY1ERENHSbEMHC5ZWw52LMRiEGvw8Lp3AiEiIgGJ3wd8jm/+c1vRJcwZPaeqEFrh9PbnjspBVYLNwIhIqLBcYQ8xJQBNgK5blaGoGqIiChYMJCH2MmyZpTVtnvbuVk2pCdHC6yIiIiCAQN5iPVd6nTtZRwdExHRhTGQh1BtcxcOFdd72yk2M/LGJAisiIiIggUDeQhtOVCB3vuGXTMrAzpuBEJERD5gIA+RLocbO45UedvmSD3mTx4hsCIiIgomDOQh8vmxs+hyeLzt/LxUmCM1s6qMiIg0joE8BGRFweYDFd62BGDRzHRxBRERUdBhIA+B4yWNqGnsOfN46thEJMeJP1uTiIiCBwN5CPRd6nTNLI6OiYjIPwzkS1Td0IFjZ3rOPE5LtCA3yyawIiIiCkYM5Ev0Sa/PjgHg6lnpPPOYiIj8xkC+BJ12Nz47etbbtpgMmDeJS52IiMh/DORLsPNoNRyunqVOV0xNRWSEXmBFREQUrBjIF0lWFGwp6LXUSQKumsEzj4mI6OIwkC/SsTONqG3q8ran5yQhMZZLnYiI6OIwkC9Sv8lc3AiEiIguAQP5ItQ0deLomQZvOy3RggmZcQIrIiKiYMdAvghbDlSq2otmcqkTERFdGgayn+xON3Ye7X2qkwHzJqUIrIiIiEIBA9lPu47X9DnVaSRMRp7qREREl4aB7AdFUbClz6lOXOpERERDgYHsh8LSJlTWd3jbU8YkIMUWJbAiIiIKFQxkP3xSoJ7MxaVOREQ0VBjIPmpsteNgcZ23nWwzY1J2vMCKiIgolDCQfbT1UCUUpae9aHoadFzqREREQ4SB7AOXW8b2Qz1LnYwGHS7PGymwIiIiCjUMZB8cOFmL1k6Xtz13UgospgiBFRERUahhIPtgS5/JXItmcDIXERENLQbyBZSebcOpyhZve2xaLDJTYgRWREREoYiBfAF9T3VaxI1AiIhoGDCQz6O9y4XPj1V72zFREZg5PllgRUREFKoYyOfxyb4yOF2yt33F1FREGNhlREQ09HgqQh+yoqCorBkny5uwudcxi5IELJzG29VERDQ8GMi9lFS3YsPOErR0OGF3utHR1bPUKSYqAq2dTiTEmgRWSEREoYr3X79SUt2K1zYVoaXDCQBo67XuGABMRgNe21SEkupWEeUREVGIYyCj+zb1hp0lcMvde2O6PTI67W7v1w16CSajHm65+3Fy7z00iYiIhgADGUBRWbN3ZAx0z67uLSbKCOmrfatbOpwoLm8OaH1ERBT6GMgACsuavH9WFAXtfW5XW8zqbTJPlDaBiIhoKDGQAdidHu+fuxxueOSeW9IWswF6nTTo44mIiIaC0EAuLS3F9773PUyfPh0LFy7EX//6VyF1mIx675/7TuaKiTKe9/FERERDQdiyJ1mWsWLFCkyZMgXvvPMOSktL8dOf/hQpKSlYunRpQGuZkGnD4dMNcLll1eg3MkKHyIj+71lys2yBLI+IiMKAsBFyfX09cnNz8eSTT2LUqFG48sorMW/ePBw4cCDgtYzLjEOsxYi2TqfqutUS6Z3MdU6sxYicjLhAlkdERGFA2Ag5OTkZzz33HIDuiVQFBQXYt28fnnjiCZ9fQ6eToOvz+e7FWnr5KKx5pcDblqTuzUAUBYDU/ZmyXqfD8ivHwBjBW9Z96fU61X/p/NhfvmNf+Yf95R8t9ZcmdupatGgRqqqqcNVVV+H666/3+Xnx8ZZ+I9iL1Xm6QbW+2Bpl7BX2EuJiTLj7+vHIyeDt6vOxWs2iSwgq7C/fsa/8w/7yjxb6S1IU8btcHD16FPX19XjyySdx7bXX4rHHHvPpeQ0N7UM2Qv71y/twqqLn3OOrZ6Yj2hIJHRTkZtkwLjMOuiEK/1Ck1+tgtZrR2toFj0e+8BPCHPvLd+wr/7C//BOI/rLZLD49ThMj5ClTpgAAHA4HHn74Yfzbv/0bjMb+s5v7kmUFsnzp7ycqattVYZyTHotv3zABNpsFTU0dcLtlyB4FMoS/d9E8j0eG281fAr5if/mOfeUf9pd/tNBfQid1bd68WXVt7NixcLlcaG9vD2gtWw9VqtoLp/NUJyIiCixhgVxRUYEHH3wQNTU13mvHjh1DfHw84uPjA1aHw+nBruNnve1ocwRmjU8K2PcnIiICBAbylClTMGnSJDz66KM4deoUtm3bhrVr1+IHP/hBQOvYc6IGXY6etcfzJ49AhIGzqImIKLCEBbJer8fzzz8Ps9mMO++8E//+7/+Oe+65B9/61rcCWsfWg+rb1VdOSw3o9yciIgIET+pKSUnBn/70J2Hf/8uzrfjybJu3PSEzDiMTfJsNR0RENJTEr4QWaOvBKlWbk7mIiEiUsA3kLocbe77omVBmjYrAjHGczEVERGKEbSDvPn4WDlfPZK4FeakwaGDrNCIiCk9hmUCKomDbIfXt6is4mYuIiAQKy0D+8mwbymp7Nh+ZlB2P5Djx+5gSEVH4CstA7js6vnIqR8dERCRW2AVyv8lcFiOm5SQKrIiIiCgMA3nPiRr1ZK4pIzmZi4iIhAu7JNredzLX1JGCKiEiIuoRVoFcerZNtTNXbpYNybYogRURERF1C6tA3na4z2QuLnUiIiKNCJtAtjvd2N3rmMUY7sxFREQaEjaBvPdELezOnslcl3MyFxERaUjYJNL2w30nc/F2NRERaUdYBHJFbTvOVLV62xMy4zAinpO5iIhIO8IikDk6JiIirQv5QHa5PdjVazKXxWTAzPGczEVERNoS8oF8oKgOHXa3tz1v0ghEGPQCKyIiIuov5AO5785c+bxdTUREGhTSgVzT1InCsmZvO3ukFRnJ0QIrIiIiGlhIB/LOI9WqNvetJiIirQrZQPbIsiqQIyP0mJ2bIrAiIiKiwYVsIB851YCWDqe3PTs3GeZIg8CKiIiIBheygcy1x0REFExCMpCb2hw4cqbB205LtGB0qlVgRUREROcXkoH82dFqKEpPO39qKiRJElcQERHRBYRcIMuKoprMpddJmDeJk7mIiEjbQi6Qi8ubUdvc5W1PH5eEmCijwIqIiIguLOQCefvhPmuP87j2mIiItC+kArnT7saBk7Xedrw1EhNHxQusiIiIyImcoxMAAAtRSURBVDchFch7T9TA6Za97csnj4ROx8lcRESkfSEVyDuOqNceL+DtaiIiChIhE8gVte0oqW7ztnOzbEiKMwusiIiIyHchE8jb+4yO8zk6JiKiIBISgexyy9h9vMbbjoo0YMa4JIEVERER+SckAvnQqXq0d7m87bmTUmCM0AusiIiIyD8hEch9zz3Oz+NBEkREFFyCPpCb2hw4VtJzkERGcjSyRsQIrIiIiMh/QR/Inx9THySxYAoncxERUfAJ6kBWBjhIYi4PkiAioiAkNJBramqwatUqzJ49G/n5+VizZg0cDofPzz9V2YKapp6DJKblJPIgCSIiCkoGUd9YURSsWrUKVqsV//jHP9DS0oJHH30UOp0Ov/jFL3x6jb6TuXi7moiIgpWwEfKZM2dw6NAhrFmzBjk5OZg1axZWrVqF999/3+fX2FvYc5BEbLQRk0fzIAkiIgpOwgI5KSkJf/3rX5GYmKi63t7e7vNrOJwe75/nTx4BvS6oPxInIqIwJuyWtdVqRX5+vrctyzJeffVVzJ0796Jeb+H0NBgMQxfIer1O9V86P/aXf9hfvmNf+Yf95R8t9ZewQO5r7dq1+OKLL/D222/7/dwJWTZMHJs8DFUBVisPqPAH+8s/7C/fsa/8w/7yjxb6SxOBvHbtWvzv//4v/vCHP2DcuHF+P3/epBFoauoY0pr0eh2sVjNaW7vg8cgXfkKYY3/5h/3lO/aVf9hf/glEf9lsFp8eJzyQV69ejddffx1r167F9ddf7/fzjQYdZo1Pgts9PB3p8cjD9tqhiP3lH/aX79hX/mF/+UcL/SU0kP/0pz/hn//8J5599lksXrz4ol7jutkZMEcKf19BRER0SYQl2enTp/H8889jxYoVmDlzJurq6rxfS0ry7ejEn901DbmZtuEqkYiIKGCEBfInn3wCj8eDF154AS+88ILqaydPnvTpNSaN4rpjIiIKDcICecWKFVixYoWob09ERKQp4hdeEREREQOZiIhICxjIREREGsBAJiIi0gAGMhERkQYwkImIiDSAgUxERKQBDGQiIiINYCATERFpAAOZiIhIAxjIREREGsBAJiIi0gAGMhERkQYwkImIiDSAgUxERKQBkqIoiugiiIiIwh1HyERERBrAQCYiItIABjIREZEGMJCJiIg0gIFMRESkAQxkIiIiDWAgExERaQADmYiISAMYyERERBrAQD6PFStW4Je//KXoMjTN6XTiqaeewmWXXYb58+fj2WefBTd/G1x1dTXuv/9+zJgxA4sWLcLLL78suiRNcjqduOmmm7Bnzx7vtfLycnznO9/BtGnTsGTJEuzcuVNghdoyUH8dOnQId911F6ZPn47rr78eb731lsAKtWWg/jqnra0N+fn5WL9+fcDrYiAP4oMPPsC2bdtEl6F5Tz/9ND7//HO89NJL+P3vf48333wTb7zxhuiyNOuhhx5CVFQU1q9fj0cffRTPPfccNm3aJLosTXE4HPjpT3+K4uJi7zVFUfDAAw8gMTER69atw7Jly/Dggw+iqqpKYKXaMFB/1dXV4fvf/z5mz56Nd955B6tWrcLq1auxdetWcYVqxED91dvatWtRW1sb4Kq6MZAH0NzcjGeeeQZTpkwRXYqmNTc3Y926dVi9ejXy8vIwb9483HvvvTh8+LDo0jSppaUFhw4dwsqVKzFq1Chcc801yM/Px65du0SXphmnTp3C1772NZSVlamu7969G+Xl5fj1r3+NMWPG4P7778e0adOwbt06QZVqw2D9tXnzZiQmJuKnP/0pRo0ahRtvvBG33HIL3nvvPUGVasNg/XXO/v37sXv3biQlJQW4sm4M5AH89re/xbJlyzB27FjRpWjagQMHEB0djdmzZ3uvrVixAmvWrBFYlXaZTCaYzWasX78eLpcLZ86cQUFBAXJzc0WXphl79+7FnDlz+t1lOXz4MCZOnIioqCjvtZkzZ+LQoUOBLlFTBuuv/Pz8Af8dtre3B6o0TRqsv4Du29i/+tWv8Pjjj8NoNAqoDjAI+a4atmvXLuzfvx/vvfcennzySdHlaFp5eTnS0tLw7rvv4sUXX4TL5cLy5cuxcuVK6HR8r9dXZGQkHn/8caxevRp///vf4fF4sHz5ctxxxx2iS9OMu+++e8DrdXV1SE5OVl1LSEjA2bNnA1GWZg3WX+np6UhPT/e2Gxoa8MEHH+BHP/pRoErTpMH6CwBefPFFTJw4EQsWLAhgRWoM5F4cDgeeeOIJPP7/t3c/IU33ARzHP0+udEgFZQ718NM8BKZIBIMOQXbpZEIsQmJEEUSiXhJBEj1sEZLRoX8yOxhDE/IQ0R/WIRAP1SGEGKb4ZxqyiHlQWGWjtEOwHPXgc/L79dn7BR78Xfxc9P37fTdcR4fy8vJMz7Hely9fNDc3p8HBQV29elWJREIdHR1yu906d+6c6XlWmp6eVk1Njc6ePavJyUkFAgEdOnRIx48fNz3Nal+/fv3jqWXbtm1KpVKGFm0ey8vLampqUkFBgU6dOmV6jpWmpqY0ODiox48fG91BkNe4deuWKisrdfjwYdNTNgWXy6VkMqnr16+rpKREkhSPx/XgwQOC/BevXr3S0NCQhoeHlZeXp6qqKn369El3794lyOvIzc3V4uJixrVUKsWN8zo+f/6shoYGzc7OamBgQG632/Qk66yurqq9vV3Nzc0qKCgwuoUgr/H06VMtLCzowIEDkpS++45EIhodHTU5zUp79uxRbm5uOsaSVFZWpo8fPxpcZa9oNCrHcTIiUlFRoZ6eHoOrNgePx6OpqamMawsLC38cY+O3ZDKp8+fP68OHD7p//75KS0tNT7JSPB7X6OioJiYm1NXVJenXiUxnZ6eePXume/fubdgWgrxGOBzW9+/f0993d3dLklpaWkxNslp1dbW+ffumWCymsrIySdLMzExGoPFbYWGh5ubmlEql0sevMzMzGa/14e+qq6sVCoW0vLycvqF5+/atDh48aHiZnVZWVtTY2Kj5+XmFw2GVl5ebnmQtj8ejFy9eZFzz+/3y+/0bfnLFO2/WKCkpkeM46a/8/Hzl5+fLcRzT06y0d+9eHTlyRG1tbRofH9fIyIhCoZDq6+tNT7PS0aNHtXXrVrW3tysWi+nly5fq6emR3+83Pc16Xq9XRUVFamtr0+TkpEKhkN69eyefz2d6mpWGhob05s0bBYNB7dixQ4lEQolE4o9jf/x66W3t333HceRyubR79255PJ6N3bKhPw3/O93d3QoEAqqvr5fb7dbp06cJzL/Yvn27+vr6dOXKFfl8Pu3atUsXL17kjTb/QU5Oju7cuaPLly/rxIkTchxHt2/fVnFxselpVopEIlpZWdGFCxcyrnu9XoXDYUOrsJ5/Vvk/hwAAGMeRNQAAFiDIAABYgCADAGABggwAgAUIMgAAFiDIAABYgCADAGABggwAgAUIMgAAFiDIAABYgCADAGABggxkuUgkon379ikSiaSvXbp0STU1NVpaWjK4DMguBBnIcseOHVNdXZ0CgYCWlpb05MkTPX/+XNeuXdPOnTtNzwOyBp/2BEDJZFK1tbWqrKzU69evdebMGTU2NpqeBWQVggxAktIh3r9/vx4+fKicnBzTk4CswpE1AElSNBqVy+VSLBZTPB43PQfIOjwhA9D4+LhOnjypzs5OPXr0SD9+/FB/f7+2bOGeHdgo/LYBWS6VSqm1tVVer1c+n0/BYFBjY2Pq7e01PQ3IKgQZyHI3btzQ/Py8gsGgJKm0tFTNzc26efOm3r9/b3gdkD04sgYAwAI8IQMAYAGCDACABQgyAAAWIMgAAFiAIAMAYAGCDACABQgyAAAWIMgAAFiAIAMAYAGCDACABQgyAAAW+Alab3gDjchp1wAAAABJRU5ErkJggg==",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x32232c080>)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"lmplot(x=\"x\", y=\"y\", data=query(anscombe, \"dataset == 'II'\"),\n",
" ci=nothing, scatter_kws=Dict(\"s\"=> 80), order =2);"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Joint Plot with marginal distributions"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAkQAAAJICAYAAACAIvshAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xd4W+WhP/Dv0R6WbXlvO4Mkzl4EMoCQxQyFNFB2KfeW0XLb0sKPyywXSrlwgRYokFIoo4PRBGgJoxBICCQhZCcOGXa8V7y19zm/P+SIOLIdx5Z9NL6f5/ET55xj6X0lWfr6nYIkSRKIiIiIEphC7gIQERERyY2BiIiIiBIeAxERERElPAYiIiIiSngMRERERJTwGIiIiIgo4TEQERERUcJjICIiIqKEx0BERERECU8ldwGGU2urTe4iRJxCISAtzYiODgdEMb4XGWdd41Mi1RVIrPqyroOTmWmKUKloKNhCFGMUCgGCIEChEOQuyrBjXeNTItUVSKz6sq4UyxiIiIiIKOExEBEREVHCi+sxRETH27C7IeK3uXB6fsRvk4iIRh5biIiIiCjhMRARERFRwmOXGVEvJEmC0+OHJAEKQYBCASgVCqhV/BuCiCgeMRBR1Fq/sx4GgxZOpweBYV7TpMvmQV2LHZ02DywOL6wOb6/3qdcqkZasQ1qyDunJWrg8fui1/DUiIop1fCenhGWxe1DVZEPNURssdu+AfsblCaCh1YGGVgcAYPO+Zkw/LQNzJ+Vg0qg0qJRsQSIiikUMRJRwOqxu7KloR12LvcdxQQBSk7RIMWqQkqRBslEDpUKAKEoQJcDvF9Fp96DD6kanzQN/QILXL+KbAy345kALkvRqLJldgKWzC9lqREQUY/iuTQmjy+bBnoo21Bz9LggJApCTZkBxjglF2UnQaQb2KyFKEtotbnh9Ir45cBQ2pw92lw/vfVmFT7fV4fwzirBoZgGDERFRjOC7NcW9gChiT0U79ld24NioIJVSwPgiMyaWmAcVWhSCgMxUPRZOz8cPFo3F/qoOfLq9Dt9Wd8Lh9mPNF5X49zd1WLlwDBZMzYVC4PL+RETRjIGI4lq71Y1Ne5vQ1T1GSKkQML4oFZNGpUWs9UalVGDa2AxMG5uBQ7WdeO/LKhyq64Ld5cOrHx3E5rJm/PD88chNN0bk/oiIKPIYiCguSZKEfZUd2FPRBqm7WSgnzYB5U3KQpFcP2/2OLzLjrmvM+La6A39fV47GNgcO13Xh13/+BheeWYyL55Vw4DURURTiOzPFHZ9fxIZdjdhdHgxDKqWAOaVZWHp6wbCGoeNNLEnDgz86HZedNQoqpQB/QMK/NlXjt3/ZgaMdzhEpAxERDRwDEcUVu8uHj7fWhmaQZaTocPG8EkwoNkMY4XE8KqUCy+ePwkP/cQbGF6YCAKqbbXjwlW3YtK8JkjS8aysREdHAscuM4kZrlwvrdzbA7Q0AAEblmjBvcg6Uw9hFNdANY+dMzIJRr8Ku8jZ4fAG8/MEBfLazHnMn5UCtUkCpEGAwaHHGhMxhKysREfWNgYjiQmObA+t3NoRWl55+WgamjE4b8VahvgiCgMmj05GTZsCXe5tgc/pQ3WRDp9WDc2bkIT1ZJ3cRiYgSGrvMKOY1tDrweXcYUioEnDM9D1PHpEdNGDpeRqoeF88rwahcEwDA4vDiwy01qG6yylwyIqLExkBEMa2+1Y71uxogihJUSgGLZxWgOMckd7H6pVYpsGBqLuaUZkEhAP6AhPW7GrFpbyMCoih38YiIEhIDEcWs+hY7NuxsDIWhRbMKkJNukLtYAyIIAiYUm3HenKLQeki7D7fiiTd2w+7yyVw6IqLEw0BEMam53YkNuxohSt0tQ7MLkJMWG2HoeJlmPS6eV4ycND0AYH9VBx56dVvYPmtERDS8GIgo5nTa3MFusu4wtGR2IbLNsReGjtFrVThvThGmjM0AALRZ3HjkL9ux7WCLzCUjIkocDEQUU+wuH9Ztb4DPL0IQgHOm5yPLrJe7WEOmUAg4e3o+/vPiiVApBXh9Il54rwxrvjgCUeR6RUREw42BiGKG2xvAZ9vr4fL4AQDzJucgPzO+9gc7e3oe7rpmJlKTNACAD7bU4OnVe+Fwc1wREdFwYiCimBAQRazf2QCLI7hJ68xxGRiTnyJzqYbHmLwUPHDD6RjbXb99le14+NXtaGjluCIiouHCQERRT5IkfL3/KFq7XACACcXB3erjWWqSFv/v6hlYOD0PANDS5cJvXt+Bbw4clblkRETxiYGIot7+qk4caQguXFiQacTsCVlRuehipKmUClx//gRcf/54KBUCPL4AVv1zP95YVw5/gOsVERFFEgMRRbWaZiu2d8+2Sk3SYMG0XCgSIAwdb+H0fPz3NTNhNmkBAJ9ur8Pjb+xCp80jc8mIiOIH9zKjqGWxe/DJ1hpIADRqBc6dmQ+NSil3sYbV+p31of3YTrT09AJ8uacJTe1OVNRbcO+fvsaCqbnIy+h7YPnC6fnDVVQiorjCFiKKSk63H+t2NMDrC06vXzg9HyaDRu5iyUqnUWHx7AJMGR0cP+X2BrBuez12HGrl1HwioiFiIKKoI0kSXv7gW1i7Z5SdMTE7ZrbkGG4KQcCMcZlYPCsfWnWwtWx/VQc+3loLm9Mrc+mIiGIXAxFFnQ+/rsGu8jYAwIRiMyYUpcpcouiTn5mE5fNLQtuVtFncWLupBhX1FkgSW4uIiE4VAxFFlf3VHXhnYyUAIC1Zi3NmFiTEjLLBMOhUWHJ6AaaflgFBAHwBEZvLmrF+V2No8UoiIhoYBiKKGu0WN/74z/2QJMCoU2HRzHyolHyJ9kchCJg6Jh3nn1GEZIMaAFDfYse/vqpGdbONrUVERAPETxuKCj6/iOffK4Pd5YMA4MfLJyX8IOpTkZmqx8XzS0Ldix5fABt3N+LZNfvQYXXLXDoioujHQERR4c3Py1HVFFx88ZIFozB1TLrMJYo9KqUCcyZmY+npBTDqgitq7K5ow30vbcVnO+ohsrWIiKhPDEQku6/3N2P9zgYAwJTR6Vg+v0TeAsW43HQjLlkwCqXFZghCcHr+3z49jEde347KRqvcxSMiikoMRCSrhlY7Xv34IAAgPVmLHy+fmHArUQ8HtUqB00uzcN/1s1GYlQQAqGqy4Tevb8efPzgQ2iSXiIiCGIhINi6PH8+9WwavT4RKKeAnl01Bkl4td7HiyqjcZNz/w9m4ctFY6LXBdYu+2teEe17cgo+21sDnD8hcQiKi6MBARLKQJAmvfHQQzR1OAMBVi0/DqNxkmUsVn1RKBZbNKcJvb5qL+VNyAAAuTwD/WH8E97z4NTaXNXF8ERElPAYiksW/v6kLbdp65qRsLJzBPbeGW4pRg/+4aCLuvX4WxuQHw2e71YOX1h7AQ69sw56KNk7TJ6KExc1dacQdqOnEPzZUAAAKMpPww/MmcPHFYbJhd0Ovx+dNzkFhVhJ2HmqF1elDbYsdT6/ei4wUHaaNzUBehqHX54SbxRJRvGIgohHVYXVj1T/LIEmAQavCbSsmQ6uJ7x3so5EgCCjKNqEgMwnl9V3Ye6QdLk8AbRY3PttRj8xUHaaMSUd+hpFhlYgSAgMRjRifX8Rz75bB5vQBAH68fCKyzNy0VU4KhYDxRWaMyU9BeZ0F+yrb4fYG0Nrlxuc7GmA2aTF5VBqKc0xQKBiMiCh+cQwRjQhJkvDXTw6FFl/83oJRmDY2Q+ZS0TEqpQKlJWasOGc0Zo/PDM1I67R58OXeJrz3ZRUOVHdyjzQiiltsIaIRsW57Pb7c2wQAmDqGiy9GK5VSgYmj0jC+KBVHGq3YX9UBm9MHu8uHbQdbUFbVjrOm5mHxrAJkpurlLi4RUcQwENGw21fZjjc/LwcA5KYbcNPySVx8McoplQqMK0zF2IIU1DTb8G11J9otbrg8AXyyrQ6fbq/D1NHpWDgjH1NGp7M7jYhiHgMRDaumdkdoELVRp8LPVk6FQceXXaxQCAJG5SajJMeE1i432ixu7DjUAkkC9hxpx54j7UhP1uGc6XmYPyUXZpNW7iITEQ0KP5lo2NhdPjy9ei9cngCUiuBK1NkcRB2TBEFAllmPK84di3aLG1/sacDGPU2wOrxot7rxzsZKvPtlJSaPSsdZU3MxbWwG1CoOUSSi2MFARMPC6wvg2TV70dLpAgBcvXQcSovNMpeKIiE9RYcVZ4/BJfNHYVd5G9bvrMfB2i5IUrB7dF9lO4w6FU6fkIUzJ+VgbEEKu0iJKOoxEFHEBUQRq/65H+X1FgDA4pkFOJcrUceF3hZ6nDMxG6UlZhxpsKKiwQKn2w+H248NuxuxYXcjjDpVsNst1wSzSQuVUgGDQQun04OzpubJUAsionAMRBRRkiThL/8+hN0VbQCA2eMzcdWS02QuFQ03k0GD6adlYOrYdDS3O1HZaEXtURv8AQkOtx9lVR0oq+qAyaDGqNxkTBiVDoOarUZEFD0YiChiNuxuwK7yNuw70g4AyEkzYHxxKjbubRzU7Sk5cynmKAQBeRlG5GUY4fNno77FjsomK5raHBAlwOb0Ye+Rduw90o4kvRqNbU7MHJeJsfkpnKlGRLJiIKKI2V/VEQpDZpMWC2fmQangwNpEpVYpMCovGaPykuHxBVB31I6aZhsa2x2QpOCg+0+21eGTbXUwGdSYOjod08ZmYNKoNOi1fGsiopHFdx2KiPc3V2PHoVYAQJJejSWzC6BRcY8yCtKqlRhbkIKxBSnwB0S0dLlxuLYTze1OeP0ibE4fNpU1Y1NZM1RKAeMLUzFlTAamjE5DTlrvG80SEUUSAxENiSRJ+OdXVfjXpmoAwTC0bE4h/8KnPmnVSowvTkNhphFzSrOxv6oDuyvasLeiDVanD/6AhP3Vndhf3Yk3PwMyUnSYMjodk0elYUKxma8tIhoWfGehQZMkCe9srMQHW2oAAMkGNZbOKYRRp5a5ZBQrtGolZo7LxMxxmRAlCVWNVuyuaMO+ynbUHrUDANosbqzf1YD1uxqgVAgYk5eMSaPSMLEkDSW5JnbLElFEMBDRoPgDIl7/9yF81b0/WW66AfOn5HIVaho0hSBgTH4KxuSn4PvnjEGX3dO9rlEHDlR3wOH2IyBKOFxvweF6C979sgp6rRLjC80oLQ5+5WUaueYREQ0KP73olFmdXjz/zj4c7l5nqCDTiDuunIGd5a0yl4ziSWqSFmdNzcNZU/MgihKqmoKbzZZVdaCy0QpRkuDyBLC7oi20zEOSXo0JRakYX2TG+MJUBiQiGjAGIjol9a12PLN6L9osbgDBnetvvmQSx3XQoPS20GN/kpM0mDclB7NLM9HS4UJTuxNN7Q502b0AgjPXth9qxfbuAf5GnQqnFaTitO4B3SU5Jqg52J+IesFPMRoQSZKwuawZf/v0MNzeAABg2emFuOLcsVw/hkacRqVEQVYSCrKSAAAujx9HO5xo7nDC6vChucMJAHC4/T1akFRKASU5yRid1/2Vm4z0FB1nsRERAxGdnNXpxesfH8LOw8G/upUKAdedNx5nT+O2CxQd9FoVSnKTUZKbjIXT82FxeFFe14VDdV0or+tCXasdkgT4AxIqGiyoaLCEftZkUKM4x4Ti7OBXUXYSMlL17GojSjAMRNSvXYdb8drHB2F1+gAAWWY9fnzxRIzJT5G5ZES9O74bLj/TiPxMI7z+ANq63GjpdKG1y4V2ixtevwgguHp2WWUHyio7Qj+nUgpITdIi1aTF7HGZyEk3IjfdgPQUHYMSUZxiIKJe1bfY8fb6CpRVffchce6MfFxx7lhoNRyDQbFFo1KGthQBgl3ANqcPrV0udFg9aLe60WF1wx+QAARbktosbrRZ3Kio/641Sa1SINusR2aqHtlmA7K6v89I0SEtWQe1iksAEMUqBiLqodPmwXtfVuKrfU2Qgp8NSE3S4MYLSzF5dLq8hSOKEEEQkGzUINmowZj84DFJkmB1+NBp96DL5kGnzYMuuwe27tZRAPD5RdS3OlDf6uj1dvVaFYw6FYx6dfBfnRomgxppqQYoIUGjVuDcGQUjUUUiOkUMRAQAqGm2Yd2OOmz9tgX+QLArQaNS4Lw5RTj/jCLOIqO4JwgCUpI0SEnSADmm0HF/ILi1iMXhhaU7INmcXticvtAEg2NcHj9cHn9oFmb4fQAfbKmBOUkb6pJLTdIgxagN3rcx+GUyaDhZgWiE8VMugbk8fuypaMP6XQ0oP65bQAAwf2ouLjtrNMwmrXwFJIoCKqUCZpO2+3fB1OOc1x+Aw+WD3eWH3emD3eWDw+2Dw+2HwxUemCQJ6LB60GH19HufAoAkgxrJRg1MejWS9GqYDJpQy5NBp4JBq4ZBp4Jeq4ROo4JOo4ROo4RGpRxymDrV5RCOUSoEGAxaOJ0eBEQpdHzh9PwhlYdoJDAQJRi7y4d9R9qx/VAL9lV2hFqDgGCL0LzJOVg8uxD53WMtiKhvGpUSGpMSZlPv5wMBER5fAAFJQHuXE3aXD2nJOnTZPOiye9Fp88Di8ITGLh0jAd0tUb7eb/gkVEoFtGoFNGol1EoF1CoFVCoF1EoFVEoh9L1apYDqhH81KgXqW+1QKhRQqYTgzxx3vUalhEYd/J7LFVA8YSCKY5IkocPqQVWTFYfqunCotgsNrXZIJ1yXnqzDoln5OGtqHpL03IeMKFKUSgVMaiUMBi1SjWoERCmstUSSJDjcfljsHnQ5vLA5vLA6vLA6fbA6vLC7gi1PNpcPdqcXTo8/NL6vL/6ACH9AhMPtH8baARq1Alq1MvilUcKgVcFk1EApCNB2t1jptSrYnF4Y9WrO0KOoxkAUB9xeP9q63Gi1uNDW5UZzpxMNLXbUtTrg8vT+hpiRokOWWY/iHBMyuhem236oZYRLTpR4BtIdpdEokaFRIiNVF3ZOkiT4AiK8PhFeXwC+gAifP/jl94vwByT4RRGBgAR/QERAlIJfARHise9FqY/vu3+u+9jJBMsgwob+W7Le31QNpSI4kP3YOKmUJE33/7XBAe7HuggNGhh0KoYnGnEMRDIRRan7r7jgm5ff/92bmi8gwu0NwOMNwO3zw+0NwOX2w+H2w+X1wxuQ0NbpRJfdC6vDA5cncNL7M+pUGFeYinGFqZhQZEZRdhK+2NM4AjUlokgSBCHYbaVSAsPYoitKEgIBKRi0jgtdXn8gGIT8AXh8IjzeADy+7ver7u/dHn9YS3RAlNDZPXvvZBSCgCT9sdl6x8ZNqWHQqqDXBVud9BpVsBWqu3XqWPfgse48tVIBpfLYvwKUCoFdfNQvBqIBeH9TFTaXNUOSAKn71/xYk/V3TdcSRCn415vUfVwUJUhS8LgoBf/iOvZ18r+9Bs9s0qIgMwkFmUYUZCWhMCsJeRnc5JKIBk4hCFCohFNaW+nYoGq7ww2n2w+31w+XJ4DibBMs3V2Bx2brHft/b916oiQFuwwHOYaqLwpBgEIRDEcKRfD/giBAIQSDpnD8vwCA4PcAvvsXAkwGNX50USnMZo61jCeCJJ2sN5qIiIgovnFZVSIiIkp4DERERESU8BiIiIiIKOExEBEREVHCYyAiIiKihMdARERERAmPgYiIiIgSHgMRERERJTwGIiIiIkp4DERERESU8BiIiIiIKOExEBEREVHCYyAiIiKihMdARERERAlPJXcBhlNrq03uIkScQiEgLc2Ijg4HRFGSuzjDinWNT4lUVyCx6su6Dk5mpmnQPxuPn3ORNtDHly1EMUahECAIAhQKQe6iDDvWNT4lUl2BxKov60qxjIGIiIiIEh4DERERESU8BiIiIiJKeAxERERElPAYiIiIiCjhMRARERFRwmMgIiIiooTHQEREREQJj4GIiIiIEh4DERERESU8BiIiIiJKeAxEREQxZtu2rbjuuiuwePF8/Oxnt6Chob7PayVJwssv/xHLly/DBRcswmOPPQKPxxM6v2fPLtx447VYsmQBbrjhamzbtnUkqjAgu3btwA03XI3Fi+fjpptuQHn54V6v+/DD97Fgweywr7POOn3Q911fX4df/vI2LF16FlasuAh///vrvV5nt9tw6aUX4MMP3x/0fVF0YCAiIoohzc3NuOeeO3DhhZfgT396HampZtxzzx2QpN53XP/rX1/Du+/+Aw8++AiefPIZ7Ny5Da+88icAQGdnB+6663YsWbIMr732JhYtWoK77/4VWlqOjmSVetXY2IA77vgZzj57IV599Q2MGXMa7r77V/D5fGHXLl68FP/858ehrzVr1qKgoBCXX37loO5bFEXceefPkZpqxp///DfceefdeO21l/HJJx+HXfvcc8+gra11UPdD0YWBiIgohqxd+x7Gjy/FVVddi9Gjx+Cee36NpqYm7Nq1I+zaQCCAt976G376019g1qzTMXHiZPzHf9yMQ4cOAAD27t0DpVKJq6++Hvn5Bbj++huh0Wixf/++ka5WmDVr3sLEiZNx4403obCwCD//+a+gUChQXV0Vdq1Wq0N6ekbo65NPPoIkSbjllv8a1H13dHTgtNPG4447/huFhUWYO3cBZs2ag717d/e4bvv27di27Rukp6cP6n4oujAQEVHUaWpqxIIFs/HJJx/j0ksvwPnnL8Tvf/8E/H5/6JovvliPa6+9HIsXz8ePf3x9j0DgcNjx29/+Dy6+eCkWLjwTV1/9fWzcuCF0fsGC2XjppVW46KLFuOuu2+H3+/HYY7/BRRctxtKlZ+Guu25Ha2tL6PpNm77EjTdeg0WL5uPaay/HF198Hjp322034bXXXsYvf3kbFi2ajyuvXIGtW7eEzp955kw8/fTTOO+8RbjrrtvD6vrIIw/22t2zcuXyXh+b/fv3Yfr0maH/63Q6jBs3vtcQU1VVCYulC2edtTB0bNmyC/C73z0HAEhJSYHFYsEXX3wOSZKwceMGOJ0OjBkzFsB3XVF9WbBgNtaufQ9XXPE9LF16Nh544F44HI5erz3Veu7atQPnnHNuj3q+/fY/cdpp4/osDwBYrRb87W+v4ZZbboNGowkd7+/1cqKMjAw89NCjMBiMkCQJe/fuxp49OzFjxqzQNV6vF/fffz/uvPO/oVZr+rwtih0quQtARNSXV155Ef/zP48iEPDj4YcfgF6vx803/xTl5YfxyCMP4o477sbEiZOwZcsm3HHHz/Daa2+ioKAQTz/9JOrqavC73/0BOp0ef//763jssYcxd+58qNVqAMCmTRvxwgsvIxAQsWbNW9i1ayeeeuo56HQ6PPHEo3jmmafw8MP/ix07tuHee+/ET37yM5x55nxs3vwlHnjgbvzxj69iwoRSAMDrr/8Zv/rVf+NXv/pvrFr1Bzz22G+wevX7UCiCf3OuX78eL774Z3i9/rA6/vznd+CWW24LO65QKHt9TNrb25CRkdHjWFpaOlpaWsKubWxsQHJyMvbt24MXX3wOFosF55yzCLfe+l/QaDSYNm0GVqy4HPfddxcUCgUCgQDuuefXKCoqARDsijrjjLn9Pkd/+tMLuOuu+5GWloZHH30IDzzwAO6776Eh17OxsQE6nQ733XcX9uzZhVGjRuP22/8fRo0a3W953n13NTIyMnHuuUtCx072eunPypXLcfRoM+bNOwsLFy4KHX/ttZcxceLEkz4+FDvYQkREUesnP/kZpk2bjpkzZ+M///MWvP/+e5AkCW+++RcsX34pli07PzRW5Mwz5+Hdd1cDAKZPn4k777wHp502HoWFRbjqqmthsVjQ0dEeuu3vfW8FiopKMGrUaDQ1NUGr1SI3NxfFxSW4994Hce21NwAA1qx5GwsXLsYVV1yNoqJiXHnltVi4cBHeeOMvoduaO3cBLrxwOfLzC/DDH/4HWlqO9rivH/zgByguLun1wzwpKalHd8+xL7PZ3Otj4na7w1ok1Go1fD5v2LUulxNutxurVv0Bt912O+6++35s2rQRzz33+9D5xsYG3HjjTXjxxddw/fU34ve/fwI1NdUAvuuK6s8119yAefMWYMKEifjlL+/ERx99BLvdNuR6ulwuvPDCs5g+fQaeeOIZZGVl4xe/+AmcTmefZZEkCWvX/hPf//4Pehw/2eulP4888jgee+x3qKg4jGeffQpAsOXtnXfW4O677z7pzw83ry8gdxHiBluIiChqTZkyPfT9hAkT0dXVia6uLlRXV6Oych3+9a93Qud9Ph/mzAn+tX7++Rfhyy834F//ehc1NdU4dOgggOBg2WNycvJC319yyWVYt+7fuOSS8zBjxiycffa5uPDCiwEANTVV+N73vt+jXJMnT8MHH/wr9P/CwqLQ90ajEQB6dO/l5+f3Wcf/+7/f4pNPPgo7np2di7/+9e2w4xqNNiz8+Hw+mEymsGuVSiU8Hg9+8Ys7Qt09t912Ox588F78/Od34G9/ex2SBPzoRz8GAIwfPwHffluGf/zjDdxxx8A+7KdOnRb6fsKEiQgEAqitrcW4caVDqqdSqcT8+Wdj5crgwOi77roPK1ZchK++2ohly87vtSwHD36LlpajWLx4WY/j/b1empubcd11l4eOL1t2Ae68854edQIAr9eDhx66Hz/5yc/x+OO/wU033YKMjAx0dvbeRThS3l5fgWuXjZe1DPGCgYiIopZK9d1blCgG/xJWKAQEAgFcc80Pcf75F/W4XqvVAgB+85tfY9++vTj//Atx6aUrkZ6egVtu+VGPa48fXzJ69BisXv0+Nm/+Cps3f4k//vEP+PTTj/Hcc3/qcd3xZTlWnhPLeczxs76Olas3//mft+Cqq67rt+7Hy8zMRHt7e49jHR3tvY6tOda6U1xcEjpWVFQMr9eDrq5OHDp0AGPHntbjZ8aNG4/KyiN9lvdESuXxz1EwcCoUQth1p1rP9PQMFBUVh/6vVquRk5OLlpbmPsuydesWTJ8+E8nJyT2O9/d6MZvT8Morfw8dMxqN6OhoR1nZPpx99sLQ8ZKS0fD5fOjoaMe+fXtRUVGOZ5/9PSRJgtvtxhNPPIrPPvsUTz75TJ/lGw5HO/puMaNTw0BERFGrvPxQqGXj4MEDyMjIREpKKoqKitHU1NBj/Mfzzz+NwsJiLFq0BJ9++jFefPFVlJZOAgBs2fIVAPQ5Nf2jj9ZCo9Fg8eJlWLRoCcrK9uGWW35e37mzAAAgAElEQVSEzs4OFBUVdw9Yvip0fVnZvh4f1kNhNqfBbE4b8PWTJk3B3r17Qv93u904fPgQbrzxprBrx40bD7VajYqKcsyZE5wJVVNTBYPBiOTkFGRkZKK6urLHz9TUVCM3t+8WrRNVVBwOhbEDB76FWq0OjUE63qnWc+LEyaioKA/93+fzoampAbm5eX3+zLfflmHKlGlhx/t7vSxffmnYOKKysn2499478c47HyAzMwsAcOjQAaSmmpGRkYk333wXSqWAlBQDLBYnfvKTm7By5Q+wbNkFA65fpPT+iqbB4BgiIopaTz/9JA4e/Bbbtm3FSy+twooVwa6NK664GuvWfYJ//ONNNDTU4+23/4633vo7CguLoNFoodPpsWHD52hqasTWrVvw1FP/BwC9rmEDBGelPf30k9i+/Rs0Njbg008/QlZWNlJSUnHFFddgw4bP8Pbbb6CurhZvvfU3bNy4HpdddnmvtzXcLrroEuzbtwd/+curqKw8gt/+9n+Qm5sXCo5OpxOdnZ0AAKMxCcuXX4rf/e5xlJXtQ1nZXrzwwrNYvvx7UKlUuPjiS/H115vx1lt/Cz2OW7duwWWXrQQAeDxutLe39Vuel15ahV27dmD//jI89dTjuOyyy2AwGIZczyuuuBpffPE53n13NerqavHUU49Bo9Fi3ryzAAB2ux1Wq6XHz1RWHkFJyaheb6uv10tvSksnYvz4Ujz66EOoqqrEli1f4fnnn8H1198IlUqFgoJCFBYWobi4GIWFRVAqlTCb00LhiWITW4iIKGotXrwUd975C0iSiEsvXRka6Dx58hTcf/9D+POfX8Tzzz+N/PwC/PrXj4Smoz/wwEP4wx9+j9Wr30Rubj5++MMb8ac/vYDDhw/26D46ZsWKK9DS0oKHH34ANpsV48eX4n//90kolUpMmjQ5dF8vvPAMioqK8dBDj2LWrMGvgjwUubl5eOSRx/HMM0/i1Vf/hMmTp+HRR5+AIAS7qd544y/46KO1WL06uHLyf/3XL/H888/gzjt/DkmScN55F+Dmm4OzvSZPnoJHHnkcL730R7z00ioUFhbj//7vaYwePQYA8Nlnn+K3v/0ffPXV9j7Lc8EFF+ORRx6E3W7D0qXn4/7774fD0XvwPBWTJk3GQw89ihdeeBbPPvsUxo8vxRNPPAO9Xg8AePrpJ9DU1Ig//OHF0M90dHTAZEoOu62TvV5OpFQq8b//+ySeeupx3HLLj6DT6bFy5Q8GvdDjcOqj0ZMGQZD6akOOA62t4TMdYp1KpYDZbERnpwN+v3jyH4hhrGt8Gkhdm5oacfnll+Af//hXv10ksSDWn9vbb/9paN2iEy1YMBvPPLMKM2cG1yqK9bqeikjWNTMzfED8QP2/ZzbizqtmDOn+491AH192mRERUa/27NmFrKxsuYtBNCLYZUZERL2aNGkKpk6dfvILSTZx3Mkz4hiIiCjq5Obm9TtuhUZGX1Pij+FzRPGEXWZEREQxig1EkcNAREREFKPYZRY5DEREREQxinEochiIiIiIYhQbiCKHgYiIiChGscsschiIiIiIYpTIPBQxDEREREQxii1EkcNAREREFKNEBqKIYSAiIiKKUcxDkcNAREREFKNEDiKKGAYiIiKiGMUus8hhICIiIopRAbYQRQwDERERUYxil1nkMBARERHFKLYQRQ4DERERUYwKBES5ixA3GIiIiIhiFFuIIoeBiIiIKEb5GYgihoGIiIgoRgUCDESRwkBEREQUoziGKHIYiIiIiGKUBCAgMhRFAgMRERFRDGO3WWQwEBEREcUwPwNRRDAQERERxTA/xxFFBAMRERFRDONaRJHBQERERBTD2EIUGQxEREREMYyBKDIYiIiIiGIYZ5lFBgMRERFRDOMYoshgICIiIoph7DKLDAYiIiKiGMYWoshgICIiIophbCGKDAYiIiKiGCZKbCGKhKgIRF6vFxdffDG2bt0aOlZXV4cbbrgB06dPx4UXXoivvvpKxhISEdGpkiQJNc02lFW1o6bZBokf3MNCZJdZRKjkLoDH48GvfvUrlJeXh45JkoSf/vSnGDduHNasWYN169bhtttuw4cffoi8vDwZS0tERANxoKYT67bXocPmCR1LM2mxZHYhSovNMpYs/nAMUWTI2kJUUVGBK664ArW1tT2Of/3116irq8NDDz2EMWPG4Oabb8b06dOxZs0amUpKREQD9W11B1ZvqOgRhgCgw+bB6g0VOFDTKVPJ4hPXIYoMWQPRN998gzPOOANvvfVWj+N79uzBxIkTYTAYQsdmzZqF3bt3j3QRiYjoFEiShE++qUNfjRaiBKzbXsfuM4o6snaZXX311b0eb21tRVZWVo9j6enpaG5uPqXbVygEKBTCoMsXjZRKRY9/4xnrGp8Sqa5AYtVXqVTgSIMFnTYPhH7eejvtHjS0O1CSkzxyhYuwaHpeBYUAlUr+csQ62ccQ9cblckGj0fQ4ptFo4PV6T+l20tKMEPr7rYxhycl6uYswYljX+JRIdQUSp74VTTYolQKA/t97JYUSZrNxZAo1jKLheTUYNHHxWMotKgORVqtFV1dXj2Nerxc6ne6UbqejwxGXLUTJyXpYrS4E4nztCdY1PiVSXYHEqq9SqUCyUYNAQIKE/rvEBDGAzk7HCJUs8iL5vA41zNhs7ph+LIfbQB/fqAxE2dnZqKio6HGsra0trBvtZERRitvpiIGACL8/vt9cj2Fd41Mi1RVInPqOyU+B2aRFu9Xd5zVpJi3y041x8XhEw/MaCEiylyEeRGWn47Rp07B//3643d/9Qu3YsQPTpk2TsVRERHQygiBg2ZxC9NU4rxCAJbML43Y4A8WuqAxEc+bMQW5uLu6++26Ul5fjxRdfxN69e7Fy5Uq5i0ZERCcxsSQNKxeORZpJ2+N4mkmLlQvHch2iCDtZ9yQNTFR2mSmVSjz//PO49957sWLFChQXF+O5557jooxERDGitNiMCUWpqD1qh83lhUmvQVF2EluGhgFXMIiMqAlEhw4d6vH/4uJi/PWvf5WpNERENFSCIKA4xyR3MeIeM2ZkRGWXGREREdFIYiAiIiKihMdARERERAmPgYiIiCiGCSdZFZwGhoGIiIiIEh4DERERUSxjA1FEMBARERFRwmMgIiIiooTHQEREREQJj4GIiIiIEh4DERERESU8BiIiIiJKeAxERERElPAYiIiIiCjhMRARERHFMknuAsQHBiIiIqIYJjERRQQDERERESU8BiIiIqIYJrGBKCIYiIiIiCjhMRARERFRwmMgIiIiooSnkrsAREQUvSRJQu1RO2wuL0x6DYqykyAIgtzFIoo4BiIiIurVgZpOrNtehw6bJ3QszaTFktmFKC02y1gyOh7zaWSwy4yIiMIcqOnE6g0VPcIQAHTYPFi9oQIHajplKhmdSAATUSQwEBERUQ+SJGHd9jqIfUznFiVg3fY6SJzvHR2YhyKCgYiIiHqoPWoPaxk6UYfNg9qj9hEqEfWHeSgyGIiIiKgHm8sb0etoeHGQe2QwEBERUQ8mvSai19HwUigYiCKBgYiIiHooyk5Cmknb7zVpJi2KspNGqETUH8ahyGAgIiKiHgRBwJLZheir4UEhAEtmF7KrJkrweYgMBiIiIgpTWmzGyoVjw1qK0kxarFw4lusQRRElu8wiggszEhFRr0qLzZhQlMqVqqMcxxBFBgMRERH1SRAEFOeY5C4G9YMtRJHBLjMiIqIYxjwUGQxEREREMUyp5Ed5JPBRJCIiimEcQxQZDEREREQxjGOIIoOBiIiIKIYpOOsvIhiIiIiIYhhbiCKDgYiIiCiGcQxRZDAQERERyUSUpCHfBluIIoOBiIiISAZOtx9dNs+Qb0dgIIoIrlRNREQ0gkRRgsXhhccXgDoCawgpOag6IhiIiIiIRojHG4DF4YE49J6yEI4higwGIiIiomEmShJsTh9cHn/Eb5t5KDIYiIiIiIaRzx9Al92LQCSbhY4jsMssIhiIiIiIhoEkSXC4/bC7fMN7R8xDEcFAREREFGH+gAiL3QtfQBz2+2IeigwGIiIioghyuv2wOb0Yng6ycOwyiwwGIiIiogg4fjr9SJIisLgjMRARERENmdvrh9Xhjeh0+oFiHIoMBiIiIqJBEqVgq9BwTKcfMCaiiGAgIiIiGgSPL4D2LveId5GdiF1mkRHVe5k1NTXh5ptvxsyZM7Fo0SK8+uqrcheJiIgSnCRJsDm9aOtywS8O/yyyk5Gjmy4eRXUL0S9+8Qvk5eXhnXfeQUVFBe644w7k5+dj6dKlcheNiIgS0LHp9CIkpGjUchcHAFuIIiVqW4gsFgt2796NW2+9FSUlJViyZAnOOussbNmyRe6iERFRAnK6fWi3uEdkbaFTMVwrYCeaqA1EOp0Oer0e77zzDnw+HyorK7Fz506UlpbKXTQiIkogAVFEp80Dq9MXleOXRQaiiIjaQKTVavHAAw/grbfewrRp03DBBRfg7LPPxuWXXy530YiIKEG4vX60W+QfON0fPwNRRET1GKIjR47g3HPPxY9+9COUl5fj4Ycfxty5c3HJJZcM6OcVCgGKONsGWKlU9Pg3nrGu8SmR6gokVn3jqa6iJMHaPZ1eUAhQnnC+Z10H34WmVA39sRIEQBWB20l0URuItmzZgtWrV+OLL76ATqfDlClTcPToUbzwwgsDDkRpaca4XdI8OVkvdxFGDOsanxKprkBi1TfW6+rxBdBpdUOj00Cj0/R7bVKSbkj3pY5AkDEYtTCbjUO+nUQXtYGorKwMxcXF0Om+e7FNnDgRq1atGvBtdHQ44rKFKDlZD6vVhUCUDeyLNNY1PiVSXYHEqm+s11WSJNhdvgHtTq9UKpCUpIPd7h5SXdUqJbLMhkH/PAB0djnRmdR/cEtkAw2LURuIsrKyUFNTA6/XC40m+ERXVlaioKBgwLchilLcDjYLBET4/bH3hjMYrGt8SqS6AolV31isqz8gosvugT8w0M+MYP0CARGBAf9MOMUQutuO8XoDMfd4R6Oo7XRctGgR1Go17rvvPlRVVeHzzz/HqlWrcN1118ldNCIiiiOO7un0Aw9D0SXalgGIVVHbQmQymfDqq6/ikUcewcqVK5GWloZbb70VP/jBD+QuGhERxYGAGFxk0RvjrSt+f2wGuWgTtYEIAMaOHYtXXnlF7mIQEVGccXn8sDnl2Z0+0vxsIYqIqA5EREREkSRKEmwOL1ze6F1X6FSxyywyGIiIiCgheH0BdDm8cTfZhgOqI4OBiIgoQiRJQu1RO2wuL0x6DYqyk+QuEqF7d3qXD063X+6iDAu2EEUGAxERUQQcqOnEuu116LB5QsfSTFqcd0YR5nPRPNn4/CIsjlOZTh97fGwhiggGIiKiITpQ04nVGyrCBuh22Dx4+/MKmEw6FKYPbfE9OnUOtw/2KN2QNZIYiCIjatchIiKKBZIkYd32uj5nK4mShPe/rIQkxfvHcvQIiCI6rG7YEiAMAQxEkcJAREQ0BLVH7T26yXrT1uVCzVHbCJUosbk8wd3pY31toVPBQBQZDERERENgc3kHdp3j5Ptj0eCJkgSL3QOLIzbWFvL5RXy+sx5PvLlryLfl9cfPEgJy4hgiIqIhMOkHtqmmyage5pIkLp8/gC67F4EYSEKSJKGsqgMffV2DLvvAwvTJJFJr2HBiICIiGoKi7CSkmbT9dptlpOpRnG0a0iag1Du7yweHKzbGCjW1O7B2cw2qmqwRvV2vjy1EkcBAREQ0BIIgYMnswl5nmQGAQhCw/KzREAQBiImP7djgDwT3IYuFNXicbh8+3V6Pbw4cxYlj6xXC0G/f64v+xyAWMBAREQ1RabEZKxeO7XMdoqljM9HZ6ZCxhPHF6fbD5vKGhYtoExAlbP32KD7bUQeXJ7wVZ0x+Mi6dP2rI9+NhC1FEMBAREUVAabEZE4pSw1aqVquVchctboiiBIvDGxMBoKLBgrWbq9HS6Qo7ZzZpcdHcYpQWm6FRDf314Y6jfdnkxEBERBQhgiCgOMckdzHiktvrhzUGZpB1WN348OsafFvdGXZOo1Jg4Yx8zJ+SC7UqcpO8YyEgxgIGIiIiilqxsju9xxfAhl0N+GpvU6+z3WacloHz5hQh2TiwWYmndN/e+NyjbaQxEBERUVTy+ALBdYWiuFlIkiTsKm/Fv7fWwuoMX2uqINOIi+eVoCh7+FoOexufRKeOgYiIiKJKrOxOX91kxd8/PoDao/awc0l6Nc6bU4gZ4zKhECIwlawfLq8fkiR1z2SkwWIgIiKiqOHzi7DYPfBHcauQzenFp9vrsP1ga9g5pULA/Ck5WDgjHzrNyHzESlJwYLVey4/0oeCjR0REUSHaF1n0B0RsLmvG+p0NvQ5knlBkxoVzi5CRoh/xsrk8fgaiIeKjR0REsvIHRFgd3qjdgkKSJByq7cIHX9eg3eIOO5+ZqsNFc0swrjBVhtIFOT1+pMl27/GBgYiIiGTj8vhhdUbvIostXS58uKUah+ssYef0WhUWzyrAGROzoFTIu1e6w8XNg4eKgYiIiEZctC+y6PL48fnOemwpOwrxhLQmADi9NAuXLx0P0eePij3q7K7oHoAeCxiIiIhoRHm8AVic0TmdXhQl7DjUgk+21cHRyyy34hwTls8rQWF2EkwGDSyW6AgiDjdbiIaKgYiIiEaEJEmwOX1weqIjRJyoutmKtZuq0djuDDuXYtTggjOLMGV0elRNb1cpBfgDEuzsMhsyBiIiIhp2Pn8AFrs3KqfTd9k9+HhrLfYeaQ87p1IKOHtaHs6elgdNFO5Ll6RXo8vuhc3plbsoMY+BiIiIhlW0Tqf3+UVs3NOIjbsb4QuEz3CbPDoNF5xRDLNJK0PpBsZk0HQHIrYQDRUDERERDQt/QITF7u01bMhJkiSUVXXgo69r0GUPb1nJTTfgorklGJ2XLEPpTo2/+7GtabZhw+4GAMDC6flyFilmMRAREVHEOd1+2FzRN52+qd2BtZurUdVkCztn0Kqw9PRCnD4hCwpF9IwT6o9OE+zGc0f55rexgIGIiIgiJiBK6LR5om5dHIfbh0+31WHbwZawkKYQgDMm5WDJrIKYW+352PYgbu54P2Sx9cwTEVHU8ngDaOlwRtWHc0AUsfXbFqzbXtdrK8rY/BRcNLcY2WkGGUo3dMe3EHGD16FhICIioj5JkoTao3bYXF6Y9BoUZSeFfeiK3dPpvf4AUlKiJ1hU1Fuwdks1WjpdYefSTFpcOLcYpcXmmA4RxwJRQJTgD0hQq2K3LnJjICKiuDOQD3E6uQM1nVi3vQ4dNk/oWJpJiyWzC1FabAYQnE7fZfciIEpQKqPjMe6wuvHBlhocqOkMO6dRKXDuzHzMn5ILlVLe7TYiQXdcF5/b64dapZGxNLGNgYiI4spAPsTp5A7UdGL1hgqcuGxQh82D1Rsq8P1zxqAo2xRVCwJ6fAFs2NWAr/Y2IdDLekczTsvAeXOKkGyMn9CgO25tJLc3AFP0NNDFHAYiIoobJ/sQX7lwLEPRAEiShHXb68Iex2MCooSPvq7B1UvHRUXLmyhJ2FPRhn9vrYW1l/V4CjKNWD6/BIVZJhlKN7y0mp6BiAaPgYiI4sLJPsRFCVi3vQ4TilKj4kM8mtUetfdoYTueKErBmWR2L5ranMjLNI5w6Xqqa7Fj7eZq1LXYw86Z9Gosm1OIGeMyoYjT51zXIxBFz2D2WMRARERxob8P8WM6bB7UHrWjOCf+WgoiyeYKX6xQkoJB6Pgp6w6PfN1lVqcXn3xTi52H28LOKRUC5k/Jxbkz8nu0oMQjtUoBhRAM/B62EA0JAxERxYXePsSHcl0iM+l7jrE51ip0IqNWPVJFCvEHRGze14zPd9XD6wtfAbu02IwLzyxGeopuxMsmB0EQoNUo4fIE4PExEA0FAxERxYUTP8SHel0iK8pOQppJi3arG6Io9doNmWLUIDdj5EbwSpKEg7Vd+HBLDdqt7rDzmal6XDS3GOMKU0esTNFCq+4ORN7o2iIl1jAQEcURuaabR8M092Mf4v11m6WZtCjKThrBUsUmQRBwzvT8XgeoA8GVnedNzhmx57il04UPtlSjvN4Sdk6nUWLxrAKcOSkbSkXsT6MfjGPdgm62EA0JAxFRnJBrunm0THMXBAFLZhf2+yG+ZHYhB1SfhCRJsLt8yDLrcd6cImwua4bF8V03Y4pRg3mTczAmP2XYy+Ly+PH5jnps2X8U4gn7bQgATi/NwpLZhUjSj3zXXTTRdk+99zIQDQkDEVEckGu6ebRNcy8tNmPlwrFREdBikT8gosvugT8QfELH5KdgdF4ymtqccHh8MGrVyM0wDHuoFEUJ2w+14JNtdXC6w2dOleSYcPG8EuRlyDvDLVpougMRxxANDQMRUYyTa7p5tE5zLy02Y0JRquxdeLHG6fbB5vThxKdTEIQRnVpf1WTFB5ur0djuDDuXYtTggjOLMGV0Op/P47CFKDIYiIhinFzTzaN5mrsgCJxaP0ABUYTF7oXXL++A3C67Bx9vrcXeI+1h51RKAWdPy8PZ0/OgUcX3NPrB0KiDY6c8XhGS1MdfKHRSDEREMU6u6eac5h77XB4/bE5vn618I8HnF7FxTyM27m6ELxAeyqaMTsP5ZxTDbNLKULrYMGVUOnYdboMoSZg3OVfu4sQsBiKiGCfXdHNOc49doiTB5vDCJeNCfpIkoayqAx99XYMue3hozk034KK5JRidlyxD6WKLQffdR7nT7Q91odGpYSAiinFyTTfnNPfY5PUFYHF4e11ocaQ0tTuwdnM1qppsYecMWhWWnl6I0ydkQaGI73FCKqUAo37oH8NG3Xez7JxuH1vTBomBiCjGyTXdnNPcY8ux6fSOXmZtjRSH24dPt9Vh28EWnDjURSEAZ07KweJZBdBr4/ujSatWwqBTRawl5/gWIjmf31gX3686ogQh13RzTnOPDSdOpx9pAVHE1m+PYt32+l53ZD+tIAUXzi1GtnnkVr4eaYIA6DUqGHQqqJSRXUDSeNw6TA63fPvLxToGIqI4Idd0c05zj24Otw/2XqbTj5Ty+i58sKUGLZ2usHNpyVpcdGYxJhSb4/b1olAIMGhVMGhVw9YFmHTCGCIaHAYiojgi13RzTnOPPnJPp2+3uvHhlhocqOkMO6dRK3DujHzMn5Ib8daSaKFWKmDQqaDTKIc97Om0KggCIEmAw8UWosFiICIiijNyTqd3e/z46OsafLmnqdeB2zPHZWDZnCIkG+Jz9qFWrYRRpwqtHj0SFIIAo04Nu8sHGwPRoDEQERHFCVGSYHV4ex2nMxL3vftQG/79TS0svUyjL8g0Yvn8EhRmxV9L4nCODxook6E7EDkZiAaLgYiIKA54uqfTizI0C9W12LF2czXqWuxh50x6Nc47owjTT8uAIs7GCSkVApINGqhVCtnrlmzQoKndCZuTC6EOFgMREVEMkyQJNpdPlsG0VqcXn3xTi52H28LOKRUC5k/Jxbkz8qHVxNdCgWqlAslJGmSnGdDV5YRf5m1PgGALERB8TmhwojoQeb1ePProo1i7di3UajVWrlyJ22+/PW5nIxBR3yRJ4ky2E/j8IiyOkZ9O7w+I2LSvCet3NcDrCw8DE0vMuOCMYqSn6Ea0XMNNpwmOD1KrlFCpFFH1+ksxBhdj7LIxEA1WVAei3/zmN9i6dStefvllOBwO3H777cjLy8OVV14pd9GIaAQdqOnkWkcnkGM6vSRJOFjbhQ+31KDd6g47n2XW48pl45GfpkdApjWPIk0QAH33tPlonhGXltwdiOweiKIU96t8D4eoDURdXV1Ys2YNXnnlFUydOhUAcOONN2LPnj0MREQJ5EBNZ6+rYXfYPFi9oQIrF45NqFAk13T6lk4XPthSjfJ6S9g5nUaJxbMKMH9KDtLSkmCxOEe0bMNBqRBg0Kmg16pkHx80EObuQBQQJVgcXm7fMQhRG4h27NiBpKQkzJkzJ3TspptukrFERHQqItHFJUkS1m2v63P6uCgB67bXYUJRalR1XwwXl8cPq9Mbtu3FcN/nZzvq8fX+5rDnQQBwemkWlswuRJJeDaUy9p8DjerY+kFR+/HYqzTTd92THTY3A9EgRO0zXldXh/z8fLz33ntYtWoVfD4fVqxYgVtvvRUKxcCaLRUKIe6aDZXdTbbKKG66jRTWNXZ9W92BT76pQ4ftu26VNJMOy+YUYsqYDAADq2t1kxWddg/6yzqddg8a2h0oyYnOXdEj8dyKYnA6vcvrH7H3NFGUsO1gC/69tbbX/bFG5ZpwyYJRyMswho71rKv8A40HShAE6NRKGPQqaFQDGwAeLb+zCkGASqVATvp32560W9wYX5Q4raaRErWByOl0oqamBm+++SYeffRRtLa24oEHHoBer8eNN944oNtISzPG7V+Nycl6uYswYljXyJIkCUcaLLA6vEg2ajAmPyWivyd7K1qx5otKSJLUY8yF1enFmi8qYTLpMDVZP6C6VrU4BjRuQ1IoYTYbT3qdnAb73Lq9fnTZPNDoNdDoR2Yxw/LaTry97nCv0+jNyVp8/9zTMGtCVp+vm6Sk2BhMrRCC3WLB1q3BBRu5358MRg22HmyFJElQqxTw+UV0On1R//sQjaI2EKlUKtjtdjz55JPIz88HADQ2NuKNN94YcCDq6HDEZQtRcrIeVqsLgUDs/AU2GKxr5PXXcjOxJG3Ity9JEtZ8Vg6fv++FAd9dX4EpYzJgs7lPWlchEIB/AI+HIAbQ2ek45fKOhME+t5Ikweb0jehmnZ02Dz7cUoO9R9rDzqlVCpwzPQ/nTM+DRq2E1Rq+N5lSqUBSkg52+8mfWzmpurfV0GhVEH1+WH2nvmRBJH9nhxJenA5vqAU12aBGu9WDqgZL1P4+yGGgj2/UBqLMzExotdpQGAKAUaNGoampacC3IYqSLIuUjYRAQIyKtS9GAusaGX0NTm63uvep9twAACAASURBVPHWZ+URGZxc02zrdfbR8dosLlQ2WJBmVJ+0rvkZRpiTtD1ml50ozaRFfrox6l8jp/Lc+vwiLHYP/CP0/uX1B/DlniZs3N0IXy8f7lNGp+OCM4uQmtQ9cLfPGWRi93kxKmeZnTg+SAxIEIc4T0/u9ydRknCsCiajBu1WDxpbHVH/+xCNojYQTZs2DR6PB1VVVRg1ahQAoLKyskdAIqKBGanByTbXwNZAsTi8SDOqT3qdIAhYMruw1yAHAAoBWDK7MK66xu0uHxyukZlOL0kS9lV24OOtNejqZbuN3HQDLp5XglG50Tk+ayAEBGfBGXRqqFXxMUavL+YkLaphQ1O7Az5/AOoBjoeioKgNRKNHj8bChQtx991348EHH0RraytefPFF3HrrrXIXjSjm1B6199vKAgSnsdcetQ9p13rTAMe4pBgHPhamtNiMlQvHxv06RP6ACKtj5KbTN7Y5sHZLNaqbbGHnDDoVlp1eiNnjs2J22MGx9YOMOhWUA5yIE+uOLYQZECXUtTgwOi92g6wcojYQAcATTzyBhx9+GFdddRX0ej2uueYaXHfddXIXiyjmDLTlZqDX9aUoOwlppv67uNKTdRidn4KuroGvVVNabMaEotS4Xal6JKfT210+rNteh20HW8LuTyEImDspG4tmFUCvjeqPhz4pFAKMMbR+UCSlJX83mL262cpAdIqi+hVvMpnw+OOPy10Mopg30JabgV7Xl4F0cS09fXBdXIIgDKn1KhqJogSrc2R2pw+IIr7efxSf7ajv9f7G5qfg4nklyDLH5qxOlVKAUaeGTqOMm6B8qnQaJZL0wV3vqxqtwEy5SxRbojoQEdGp621BxIG03KSZtCjKThry/Z+siysSs9niwUjuTl9e34W1m2vQ2hU+MywtWYuLzizGhGJzTAYJjUoBo14NrZrjZQAgM1UHu8uHQ3Vdchcl5jAQEcWR/vb8GsnByQPp4pIkCTXNtrjsAuvPSO5O325x44MtNThY2xl2TqNW4NwZ+Zg/JTeq9+jqTSINlD5VOekGVDXZ0GZxo7XLhczU2GzxkwMDEVGcGMieXyM5OLm/Lq69Fa1Y81l5jyn68TZIujf+gIgu+/DvTu/xBrB+Vz027WtGoJcEPHNcBpbNKUKyYWQWeoyURBwofapy0r5bsfpgTScD0SlgICKKAwOdVn/biimyD07+troDa76oDFu8Md43a3W4feiyeoZ1Or0oSdhd3oZ/b62FzRW+oGNBphHL55egMCu2xmIl8kDpU5WkVyM9WYd2qxvf1nTirGl5chcpZjAQEcWBU51WL9fgZEmS8Mk3dZD6mE4Vj5u1iqKEdosLVod3WMNQXYsN72+qRn1r+ArFJr0a551RhOn/n703D47ruu98v+euvTca+0Is3EWKlEiJoijKsmRZsmRZcWI7TjLPsZ/fS16qJnFlqjyuiit/JE7pueLEKcepJ7tqEs9k4mXiZLQ4smRLlmSLokWJpDaKC7QQJAASO9CN3vuu5/1x+zZ6ud3oBrqBBnA+VRLJvqfvOef2cn/9W76/3e0byqBgidK1QwjBgR2tOPH2JC5cWYBhmsybViXMIGIwNgFrVVa/WizDLVMxZ6UeekjNgqIZSGY0+PyNC1vEUiqeOz2Otz6YLznGcwQfuqkH9xzqgyxtnKRjlii9Om7e1Y4Tb08imdFx+XqUNXqtEmYQMRibgLUqq18tG8VwWy2UUktxOqOD5xvj2dANE6+cn8Kv3pqAqpWKOe4bDOGhOwbRFtgYjVZZonT92D8YgiRwUHUT50YWmEFUJSs2iEZHR/H++++D4zjceOON6Onpqee6GAxGDaxlWf1q2CiG22rQdBPRZOMSpymleHcsgmdeG0M4Vvp6d4bc+MQdg9i9raUh89cblihdfySRx77BEM6NLOCt9+fw2Xt2spBjFdRsECUSCXz5y1/GyZMnc3kAhBA89NBD+Ou//mtI0sb9ImMwNiobpeeXZbi5EEuV9wA1g+G2Uhrdh2wmksIzp8ZweSJacswl8bjvyDbcvr9rQxgWLFG6sdyytwPnRhYwE0ljYi6JbZ0b8zO1ltRsEH3961/H1atX8Y//+I84fPgwTNPEm2++iUceeQTf+ta38NWvfrUR62QwGMuwEXp+EULwsaP9ePzEFcfjzWK41Uqj+5ClFR0vvHEdpy9Olxi8hAC33dCJ+2/rh9e1fMPc9YYlSjeel96egKIaIASgFHjsxAgO7W6v+vn3HNqaTdRrNoheeOEFfPe738Vtt92We+yee+6BJEn4yle+wgwiBmMd2Qg9v/YPtcLvd+GJX36A+ejG1yFqZB8y06Q4++4snj97DSmlVMhxe48fDx8fQk+bt/6T1xlJ4OB1iRsquXsjI0s8uls9mFpIYWw6XpNBtFWp2SDieR5+f2n1R0dHB3S98cqrDAajMhuh59dNuzqwrdWNKxOxpjXclsOkFLFk4/qQXZmM4ZlXRzG1UNoEt8Un4ePHBnFge2tTXzOWKL2+DHb7MbWQQjSpYjGuoMUvr/eSmpqaDaIvfOELeOSRR/AP//APaG+3LM5EIoFvf/vb+MIXvlD3BTIYjM3JRjDcyqFm+5A5qUCvlkhcwc9Pj+HClXDJMZHn8OFDvbjr5h5IQvN6WjhCILt4lii9zgx0+XD64gwogLGZODOIlqFmg+jXv/41zp8/j49+9KMYGhqCIAgYHR1FMpnE8PAwnnzyydzYF198sa6LZTAYjPUkv5y+3qi6gZffnsTL5yYdK9QO7mjDx48NoMXXvDc1niMIeCW4eMBscHsSxvK4JAFdrR5Mh62w2c27WNisEjUbRMePH8fx48cbsRYGg8GoO5TSuuRU6YaJaEKFZtQ3cZpSindGFvDs6XFEk6XVdz1tHjx8fAjbewJ1nbee2InSPo8Iv0dCRNFgNlSXm1Etg91+TIdTWEyoiCYUBJvYoF5vajaIvvSlLzViHQwGg1F3hscieP7sOKYjaZgmBccRdIfcuP+2gZqSt1MZHfF0/ROnJ+eTePrUKEan4yXHPC4BH7utH0f2doLjmjNPqDhRupnzmbYqA10+nL40A8BSij/IDKKyVGUQPfroo/iDP/gDuN1uPProoxXHMoOJAdTvVzljbWn060YpxehUDFdnkyCGgb52b8PeF8NjEfzguXcRTWow8rw60YSK6fC7+PwDNyxrFBmmiVhSg6LVN3E6kdbw/NlreP3d2RI/CkcI7rixC/feug1uufmaCRBYFUxelii9IXDLAjpa3JhbTOPabAIHd7at95Kalqo+bU888QQ+97nPwe1244knnig7jlLKDCIGhsciTa2Fw3Cm0a+bff5IQoHAc9ANEyFfY94XlFI8+fKItZcii8MwTITjCp58eQQ3/P6tZQ2ytKIjnlIdhS5XimGaeO3iDF5847pjddrubUF84o4hdIYa1/tspTBF6Y1Lf6cXc4tpzEczSCt6UxrazUBVV+WXv/xlwb8ff/xxhEKFX2AzMzP45Cc/Wb+VMTYkw2MRR7XkcFzBYy9dxm/fs4sZRU1Io1+3/PPn2x+Nel+MTccxMZ8qMYZyUGBi3ko0HSrKzTFNinhKRbrO5fTvjS/ip69cxdxipuRYW8CFT9wxiL0DLU3nSWWK0huf/k4f3nzfav57fTaB3f0bo63LWlOVQfSzn/0MJ0+eBABMTU3hkUcegSwXxiEnJibAsV8NWxpKKV54/VrZX9QmBV54/RpuaMIv/a1Mo1+34vOrmpFtRkohCnxD3hcjk9GCMJkThmHiylS0wCBSVAPRlAqzjm6h+cU0fvT8B3jncmk3eknkcO/hbTh+sBsC31zfnyLPweMSmKL0JiDgleD3iIinNEwupJhBVIaqDKLDhw/jxz/+MSiloJRicnISorgkEU8IgcfjwTe+8Y2GLZTR/IzPJCo2FwUsj8D4TGLD6s9sRhr9utnnz6g6YkkNhmmCgICCguc4BLwiwnHU9X1BUOUNnFrjTEoRT2lIO6hBrxRFNfCrt67jlfPTjnpFt+zpwMeO9iPgaa7+j7Jo6QdJYvPqHDFqgxCCnjYP4qkophdSoJQyI9eBqgyinp4efP/73wcAfP7zn8d3vvMdBALNWwLKWB/i6fINO1cybqtSTWJzvZKfKaUYmYgio+jgOFLxJhhLqRibjtc8ZzytIqPqiNj5PHlPMQwTkbiCkB/ZKq7K+6p23zt6A+B5ztFLRClAQSHwHHb0+qFoBmJ1FFk0KcVb78/hF2euIZ7WSo73d/rwG8eH0NfhxdR8CjPhFLyyiJ52T9nrSSnF1HwKSUVbduxKILDygzwuocBTxYojNg/dbV68fy0KRTOwmFAQ8rvWe0lNR82ZVT/4wQ8asQ7GJsDvru6XbrXjtiKXRsN47vR4xcTmeiU/2+eZCqcsYwUAz1seG5dU+NWQUXX87NUxZPKqraqd0+cSEUtqFfN5YkkNc4tpPPrE+bL7qmXfg91+9LV7MT4bz81rUmoZPVmjjCMmHj9xBcdu7MbOvuAyV6s6rs3G8dNXRnF9LllyzO8R8eDRAdy8ux1XJ2P44S/eL9AdCnolHD9QupaRiShOXZiuamytcByBRxbgkYWS0n5WHLG56G5dStSfWkgxg8gB/mtf+9rX1nsRjSKV2nyeCI4jcLslZDJaXfMc6kHQK+H8lYWKyaitfhn331ZdN/Nm3mu94TiCDyai+OGz75Y08UyrBobHwugMeTAfzeCxly4jpRhlx3S0LF+hZCc5pxQDPEeQVo1cSDyjGhAFLucpyKg64kkNksgVvG7VzrmYUHDqwjSoLeJDnEJaFFMLSah64etsz5FRDTz/+rWq900IQXuLGx9ci0LVTRimWWQMAS1eGZpBcWUyitaAC62Bld8gYkkVT71yFT89NYZYqtArxHMEDxwbxO/duwt9HT5cmYzhuTPjJVVmimaUrGVkIlr12FoQeAK/R0LQK0EWS3OE8t8f+Sz3mm+1z2y99ur1rlwb6NKV0tw0JwSew9h0PPv55jFUITw91L25IkDVXt/myuJjbGgIIbjvSD/KachxBLjvSHXG0FaDUoqnXr4Cs4zyn514/PzZ8WWTn+ky6oHFSc6EEAQ84lIoK+uxsYknNfg9ouPrVs2ciYxWeP5iiGWnlMuBNkyKZ0/Xvu99gyF8/oG9uGGgBTzHgecIeI5AFjm0+GRIWS+YSVFosNWAbpg48fYEvvVvb+OtD0pvTPsGQ/ivv3cIv3X3LsgSD0opTl2YrrgXey21jK0WWeQR8stoD7rhlgXH17TaJPuVXC/G+tIetIzYhWhppSNjBSEzBqMS+wZD+O17djFXe42MTcexEE1XHDMdtrqeV8rzqSb52SmJ2iULCAGIpSwRQ8MwoWoGgtnqFFcF3ZLl5vS7pcLzm0uWD89zcMs8EikNfBlLWtVNpBUdngqJvuXWsG8wBLfEYyqcgmGYINk5iw2BaFLF1HwKvR3esvvMh1KK4bEIfvbaGMKx0oT0zpAbn7hjELu3tYDnl+aamk85tudwWov992rGVlo3gfX6eovyg8rBiiM2L+1BFy5PRJFIa8ioeklofKvDrgaj7uwbDOGGgRaWjFkD8VRp8m0xpkmr6g61XNJ6ueMuWYAs8VB1E6ZJ8dFb+9DR4sYTL19d1ZwDXT60+mWEYSkca1nDhMIq7VZUAzzPlVU9tsMRy4Ulyq0hkdEg8tyyGjpJZfnXAABmIik8c2oMlyeiJcdcEo/7jvTj9v1djgZetXNUO67SWI4AHpfomB9UCVYcsfG551Cf4+PbuwN4LdvGo7fNi5t2smav+TCDiNEQCCHs12MN+D3ismOqvaktl7Re6TghBHLWC7Ozt3qtkuXOed+RfkuYEdb5baVqSrOJ3GVCcsDSvpfbv9MaTJOCmqiqgswrV34N0oqOF964jtMXS8NYhABH93XhviPb4HWVP89yc9Q6zmmswBF4XCLc8sr0g1hxxOalr8MLniMwTIprswlmEBXBDCIGowkY7PajLejGTLi0Osmmu9UDSikiifK/zFv9Mga6fBXnynlsKoRF8s9Ty9hy5IdSI4miUOqt2/DCG9fLziEJHNxyZV0cpzVYukcq2ltcCHqliuGnoFdCT7vH8ZhpUpx9dxbPn71WkvAOANt7/Hj4+BB62pYPt/W0e2paSy1jixutrpRa3x+MjYPAc+hu82BiLokJh0rIrQ4ziBiMJoAQgk9+eAf++39cgOGQrGonpANwbLGRP2Y5r0CBx6aK89QythJ2KHViPgnK8yCmgb62bHNXQsrOwXMED94+gDPDM1WtoVhkkRCC4we68dwZ58RsjgDHD3Q77uHKZAxPnxrN5W/l0+KT8PFjgziwvbVqT0yta1lu7J0Hu62y+To2Wq31/cHYWGzr8GFiLukoDbHVYWX3GwxW1ro54TiCob4WBNwCJueSBdIFrX4ZDx/fjn2DIXS0uNEZ8mBqofyYasg/TzSpQtNNmJSio8Vdcp56zQlYN9vWoAs7toXgEjjYtt9ycxy7sbuqNWi6gUhcgaoXlqzZ5elzi+mCzvVBr4SPHO4r0fOJxBU8efIKnj09jkSRuKLIc7j31j787r270WMbdBXgCMHMYhrjUzFkFAMDXT60VbmWcutu8Up48NggjuztgFsWyyakr5SVvuZb7TPbrGX3lcrmZ8IpDI9FkMxoeOjYYE35ZRuVaq8v8xAxGE3E/qFW7O4LVkxIr2fSOqVWojbN+7cTa5Eov9wcyx1PpLUS4yWfnX1B7OgNVFR8VjUDJ85N4uS5SehG6bW4aWcbHrx9AC2+6r5gRyaiePXiNBJpDYZJQemSqOLvf2xPVerT+etOqxraAm7s7g82vOM8K47YnPS1W6FOw6SYCafQ18FCnzbMIGIwmoxqEtJXm7Se331ezsvNiSTUst3n1yJRfrk5nI7rholoQoW2TDNX+/l2iXp+OwyPJGA+lsGzp8cdc3Z62zx4+M6hmgTrbFFFChR4cKJJFc+dGccDRweqVpqWBB77hkJwV5A/aASsOGLzsS1PouH6XJIZRHkwg4jB2GI0urv9WpJWdMRSKmrVCMxvh6HqBmIJtSTMBgBel4CPHR3ArXs6agot5IsqOl1CW1RxR2+g4jWWRR4+twBRYI1WGfWhLeiCLPFQVAPX5xK4HV3rvaSmgRlEDMYWYzMI75mUIpZUS1paVIPtudEMinhSdawc4wjBHQe6cO8t21bklalFgLFYVJEQwC2VNlplMOoBIQTb2r0YmYzh2mxivZfTVDCDiMHYYmx04T1NN7CYWFl3ekopXjk/hVhKQ7yMZ8nrEvCHD+9HV6tzGX41rESAMddo1SUsKyLJYKyGwW4/RiZjGJ2KgVLa9J7gtYL9/GAwthgbVXiPUopEWkM4pqzIGAKA1y7O4PJEFLFkqTHEcwStARkBrwTDIaG6FmoRYBR4gqBXQkfQBZ9bZMYQo+Hs7LVy12IpDfOsr1kO5iFiMLYYG0V4j1Kaq3DySAICPsmx8qsa5qNp/OzVMbw7vlhyjBDA7xbhdS+pZdfSOsOJagQYQz4J+4dCFfvEMRiNYEffUnHAyGQUHS3udVxN88A+iQzGFmMjCO8Nj0VyDYINk8I0aa5cvdrKLMBSq/7VmxM4dWHa0avklgUEvGJJCXstrTOcyBdgLJ6VEEDgCR66Y4gZQ4x1obPFDZ9bRCKt4YNrURzb373eS2oKWMiMwdiC2K00Wv2Fejqtftmx5H4tsSUBFmIZ6IaZE72zy9VHHJqqFmNSijfem8W3/u0cTr4zVWIMiQKH9qALIb9cYgxVauNRCzv7gnjg6ABafFbokcsaQp0tbvzOR3av6zVmbG0IIbn33zsjC2X1x7Ya7OcJg7FFaUbhPVsSQDeoo0enmnL18Zk4nj416tiaIOARcXh3By5PLIKi9PmV2nishF3bgji8px0Zk2BmNg6PLKz7NWYwAODmXW04++4sFmIZTMwnsY3pETGDiMHYyjSb8N7oVByzi+mKukLlytVjSRXPnh7H25dLWxnwHMFdN/Xg7sN9kEUeuyaCOR0im5WE5MqRXzEmiTwGQ150+iXoDlpHDMZ6cHBHGwgslfpzl+eZQQRmEDEYDBQmMK+Xpyit6Lg+n6hKZDE/6VnTTbxyfgovvTXhKK64fyiEh44NojXgyj1WTRuPlSBwBB6XCLfMMy8QY9146e2Jqsa1t7gwt5jBr96agNe9fN7cPYf6Vru0poYZRAzGFic/gdmm1S/jviP9a5LnYpoUsZQlslhLuTqlFJdGI/jZa2OIOFTMdYbcePiOIeza5uzxyW/jsVpEnoPXLcAlsa9UxsZhe28Ac4sZhGMKFqIZtAVdyz9pE8M+vQxGlay3F6UR818aDeN/vfA+dIOC4wgkgQMhBOG4UranWT1RNAPRpJpLnK6mXD3olcBxwP/42TBGJmIlx90yj4/e2o/b93fVvQt8MbLIw5sNizEYG40dPQG88e4cDJPi/WuLuCO4tavNmEHEYFTBentRGjH/8GgY//TTS0jnta7geQ4BjwiXLDS0pxnNtt6IFRk++eXqjtqL1EqFfvSJ8yXHCQGO7uvCfUe2wetaXdl8JQgAl8TD4xIhCqxQl7FxkUQeQz1+jEzEcHUqhiM3dG7p9/TW3TmDUSV2GXixkKHtRRkei2y4+YfHIvjRCx8UGEMAYBgmIgkFmezjdk+zeqLpJmYjaSQzzuKHdrl60LuklE0phWGaWIgpuDQWKTGGtvcE8KVPH8Rvfmh7w4whAsAjC2gLuhD0yVv6xsHYPOzpbwEA6AbFe9dKhUu3EsxDxGBUoNGd4e0wWErR0dutodUjlByv9/z2OQ2jTMUTtST9ZclKDK5XTzNKKd4bX0Q4nkFHuw8trvJfP/lJz5cnF3F2eA4LsdIWAy0+CR8/NogD21sbFr7kCOBxifDIQk0d7xmMjUB70IWOFjfmFtO4eCWMvf0tW9bYZwYRg1GBRnaGzw+DWerFHAIeCR+9dVsuDNaI+e1zVrq5G4YJTTchiXxdeppduBrGc6fHEEmoIMQqg/e5RdxxY/ky98WEgpfensCFq+GSYyLP4e7Dvbjrpt6GfXnzHIHXJcAtC6xijLFpIYTg0O42PH/2OhTNwHvjERzY0bbey1oXmEHEYFSgUZ3h7TBYsecnHM8UJDM3Yn57rCTy4HmurKfIMGldepq9/cE8nnh5pGSvtvL0A0cHCowiVTNw4twkTp6bdOxddtPONjx4+wBafHLJsXog8ARelwiXxErnGVuD7lYPOkNuzEbSuHg1gr0DoS3pJWIGEYNRgUZ0hq8lDNaI+fPHBryiVbLusBaBJ6vqaWaaFIsJBc8vs1dbeRqw2gg8e3rcscqst92Lh48PYqg7UHKsHkgCB69LhCyxijHG1oIQgpt3LXmJ3hmZx617O9d7WWsOM4gYjAqspDP8cuXx1YbBxmbiALXE/pKKniuJX27+WvbkkgSE/EAsqRV4ityygP/jvj0rrmBTVAPRlIrrM4mKJfSA5Sk6d3kBp4dnMDYdLznudQl44OgAbtnT0ZAcHlnk4XMLEAVmCDG2Lj1tXmzr8OL6XBKXRiPY1RdEsEFe2GaFGUQMRgVq7QxfTXl8xfAWtUJGGcXA/3hmGBxHoGgGInEFPLdUEl9u/pXsySVZgoKqZsA0KXiew+fu2419Q61VnzO3fEoRT2lIZavU8hWlnTBMinhSxb//6nLJMS5bgn/vrX11FzwkAFyyAK9LgMBvvdAAg+HEbfs6MbkwCtOkODM8i/uObNtSYeMN803wR3/0R/jqV7+63stgbEGq7QxfbXl8ufBWStExG0ljbjGNxaSC6XAKc4sZgAKh7Nz5JfGr6UzvtCdJ5NHb7sXn7t+zImNI0w0sRDM5YwhAWeVp23CajaQKxtvs6W/Bf/nsTXjojsG6GkMcAXxuER0tbgS9EjOGGIw8/B4JB7Zbn/2phZSjx3YzsyE8RM888wxOnDiBT33qU+u9FEaDyQ83tfhktLR41mSu5ZSf8zvDx1IKEikNqYyOyfkE3BKPgS5fSV4QpRSqbsIwTJgUePzEZfz+/Xsdw3AZxfICmaa5lEhMKXTdQCRhIuST0RlyQ9UMeFwCPnffHgx2+0vWu9I9xdMqfFn9nkRGw9h03PG5pmnizPAs5mMZtAdcOLqvExzHIZHWkExrJalITsrTGUVHNKk6Jky3BVz4xPFB3DBQX7FLkefgcQmrTpReb7VyBqPRHNjRiiuTMSTSGs4Mz6K7zbNlWtI0/S4XFxfxt3/7tzh48OB6L4XRYIrDTYQAXa+N4yOHe7FnW0tD5wKWV34mhCCl6PjpK2OYmE/mcm54nkN7QIaqm7lwVkbREUtp0DQDBqUABcKxDL7z5HkMdPmxp78FZ4ZncgZULNu+Qs+zqAwTAKHg83SBJJGHblAQQkpuxCvd02C3H8NjEfz01GjF5z53ZhzPnh4vEHP88Ysf4MOHenH8QE/Z89vK06puIppQoWhGyThZ5HHvLX2440B33bw2S4rS9ckPWm+1cgZjLRB4Dsdu7MILr19HRjXw2sUZ3H2od0sY/vzXvva1r633IirxV3/1V7jlllsgy5Zr/7777qv6ualUfQTlmgmOI3C7JWQyWq7/02bADjellKWbJSFWcu6FK2F0tLjR0eJu2FwAkFYNDI+F0RnyOM41PBbBD557D9ORFGjetaeUIp7WkM4mPutZtWdDN2EUvUZq9rHZSBpH93UhlbG8JfGUWjA2/6uHUmsOlyzAMCk03UTIL2Oox1+Qu7SSPVX73Dffn8OTJ69Az+smTymFbpgYmYxC5DkMdDnrIHlcAkan47g6FS+5HgBw694O/P7H9mB3f0tdkqY5ziqbb/HJcMsCeG71BtZqru9m/cw6wfa6MrzelScvX7oyv6q5nfB7JKQVHQsxBdGkiqBPsr5zGlTh2Wiqvb5NHUB/9dVX8frrr+OP//iP13spjAayfBm6xUM7ywAAIABJREFUdZzS1X/BVlvyXjwXpRTPv37NCv04PJeAwDApoknrC4Sa1PIMOYyLJTWYFHj/2iL+5FMH8JHDveA5AoHnIHAETiaBYVLMR9NYiGYQiSt48c3rePSJ8xgei6x4T7Vcj5+/NpbbN6W08FwUePncFEzTLHouxRvvzeJb/3YO56+UiisOdPnwx586gM/cvRN+z+rFHyWBQ4tPQkfQBZ9brFtF2mquL4OxUbl1byd8biuMfvrSDFKZ0ly/zUbThswURcFf/uVf4i/+4i/gcrlWdA6OI5tOap/PhhP4TZQMOjoVQyRhqTXnY5sGBASRhIKJheSqf6GUmysfp7lGp2KYjaRgmCacLBaS/U83KEDo0hhSNIYAhmlC0w1EEgomwykEvDIorKoqSgBi0gKby77PmpRahhPHQRI5RBIKHj8xgg/f3LuiPVV7Pa7PJpBSdWt9lDruX9F0XBwN49DuDgDA2HQcT/36Kq7PJUvGBrwSPnPvbuwfCK76lzVHCNyyAE8Dq8VW+p6x2Yyf2XKwva49HCEV35srhZd4fOimbjx7+hpUzcSvz0/h4eNDm+6emk/TGkSPPvooDhw4gLvuumvF52ht9W7auGcgUJ/wUTNwdTZZ8WbG85a5QTkeoZC3oXPZFM91dTYJyzQr834i1hejaVJwuTGFN3uez9cRsjxClOPR0+mHyHNWbhAIeN4Ku5VMQa35W/xyQU7Ma5dmVrQne1/LPdegAExk/cnlP08p1YTJcfjJSyM4fXG65LjAc7jv6AAerEPlmMhz8LpFeFyNb6ux0vdMMZvpM7scbK9rh8crlf9eWiU7PTJuWczgzffmML2QwgtvTeB379vbkLmagaY1iJ555hnMz8/j8OHDAABVtfKBnnvuObz11ltVnSMcTm46a5bnOQQCbsRi6fLNOTcYxDCcDQAQ8DyBYVBQUBDTQCRS6nGox1wl44rmIoYBwFpH2edkS7oV1YBOl+YgADiOAyHIe76Vf0NMA6CA3yshElOsfRKA5ziYpon8KIzAcwj6JUhiocGUzGggsMrma9mTva/lrgcHCkoq7dwKK12dWMTPT41C1UvPd2B7Kx46Poi2gAu6qgOSgEQiU9N7mBACl8jD4xYgEgI1o0LNND5PcKXvGZvN+JktB9vryljND71UUm2Ih8jm4PZWRBMKRiZi+F/PvoftnT7s7q9vkUujqfb6Nq1B9IMf/AC6vhSz/Lu/+zsAwFe+8pWqz2GadNMm9hmGWZDgupHpa/ci5HNQgyYUAAEFRcgno6/Nu+o9l50rj1Z/6Vx97V50hjyIxNWyX348z2F7jx8UwEw4hXBMyUsipgAluXGiwOf2BAC9bV5wHMFiTIFumOAIwPEcKKz3scBz6Ai5wHEcilNVRJ6DKHCOZeyV9rTc9aCUwqQUHSEP0qoB1aE6jFLLUDIp8M5IaZ5QV8iNTxwfwq5srzIj526y3sNGhTXbEGIpZ3tdSwnSa/neX+l7ppjN9JldDrbXtcPMVrE2kj/6jRvxtX8+g7Ri4DtPnsfX/q+jufyizUTTBnr7+vowODiY+8/r9cLr9WJwcHC9l8aoM7ZycjlnHkdW11OrtrmclZ8JIbj/SD+CXsk5akSAoFfE/bcN4GO3DUDRTGiGVVFmmBS6QXMVZgGvWDAPIQQfO9oPr0tEZ8iNtqALIb+MtqAL7UEXeJ6gxSeBK1MtRQjBnQd6at6Tramzsy8ITTcKkoIptdYNChw/0I27D/WW7NsaY8kDFBtpbpnHbxwfwpc+c1POGKqVnIhi0I2AR6pLtdhKWOl7hsHYLHS0uPF/PngDACAcU/BPP71kGWKbjKYvu7d54YUXALCy+81a1trR4kZnyIOphSTSquWJIATobPXgE3fUV6jPaS7A+pX/8PHtZTVl2oMuCDyH6XAaGdXIGQE8z6G/w4vf/ajV++vN9+dw7vK8c1USBYJeGb/70d0F83S1erCjvwVjUzEomglB4MDzHDpa3HBLfFljyF7373xkV017Gh6L4McvfoBXL81gcj4JTTeRTFseWcJZFXNBr4SPHO7Dzr4gBrqsPKeJ+RR03YBJs7lFRRACHNvfhd//2B7s6A2CczASOI7A5RKhKFqJIQVYvdt8bglBnwRZbI6O8yt9zwCb9zPrBNvrymi2svtihroD6OvwIZZSMToVx2wkDY4j2FtnAdVGUe31bdqQWTHf+MY31nsJjAZTrJzc4pdx6IZuLC6m6u6SLp5rOdXhfFE+IeuxEXgOewdCuPNAd0412jRNPHt6HIQQiDyBSQFKzaWkRwLEUyr29pd6TW7a1YFtrW5cmYgVrOnd8cWqeqlVuydbUyf/fC5JgCzyUFQDNw6FsLuvBT3tnoLn3nGgBzxH8NzZa9C10tdjR28ADx8fQnfrytTFJcFWk67f11I9laVrfc8wGJuN37t3N0an4rg6FcN/nLyKnb1B3Li99jY/zcqGMYgYWwNbORkAhDLd3RsxVyWKDQhCCOTsTfvKZBS37OnIrfPM8GyBkjNHAJBC705GNXBmeBbHbuyuak1237FqVJKX21M5TR0zG9rjeQ7jMwl8+OZCZdork1E8fWoM0+FUyTlbfBIeOjaIG7e31vx6LalJixCF+obEGqEsXe17hsHYjIgCh//8Wzfir/75LJIZHf/tqYv4yy/ehrbgyqRxmg1mEDEYFahWlO+GgRYQQjAfy1R13mrH2dTLOzE2Hcd0OGXJA3AEosDBMGlB6CqaVDE1n0JvhxeReAY/f20cF66WJkyLAoe7D/Xirpt6azZmOELg90iQeK4hlaBOXjBgqdHuSpviMhhbnfagG3/0yRvx7X8/h0Raw3d/ch5f/dwtdWmPs94wg4jBqMD4TKJidRFg3WTHZxIY7PajPVDdL6Vqx+WzUu+EHTa6OBrGaxensRDN5B7neA4+twBZLPwqWEwquDgWxslzk47VazfvasODRwcQ9NWW+8BxBAGPhK5WD6LR+odCgdqNWAaDURsHd7ThNz+0HT/59VVcnYrjR89/gC9+/Ib1XtaqYQYRg1GBeLq6xHx73NF9nfi3X14uCJsV45YFHN3XWZf1LYcdNppcSCISV6wGsgYFz1leGtMwEUuqCHgBWRRAKUVaNfCTk1eRSGsl5+tr9+Lh40M1G2YcR+BzCXDLAkSRb6g+WLERq2pGziNmazXlG7EMBqN2Hr5zCFenYjg3soCXz01iR28AH765d72XtSqatuyewWgG/O7qemzZ4ziOw4O3D5QXdCbAg7cPVKwaqxd22CgcVxBLapZWSTY2ZphYKpulQCKlQ9UNLEQzWIwrJcaQ1y3i0x/egf/8qQM1GRF81iPUEXTB4xLXxCNjG6cZVcdsZKn/20I0g9lIGhlVLxjHYDBqhyME/89v7EdntqnxD3/xHkanY+u8qtXBPEQMRgUGunxo9ZcXLlR1Ex6Jx8RcHB9MLIIDwd7+FvzmnUP4+WvjyKgGQCz7yOMS8eDtA3jg6EBJ9dOOvkDJucem47gyGQMFxY6eAAghSGS0gvyhclVU+WEjVTOg67aUAQFPKAxqGUUcb+/DwPxiqfAiRwiOH+zGvbf01VT9JXAEXrcIt7z2XzF+t4SMqiMSV0oE6wzDRCSuIOSv3tjdqNSzwo7BcMLjEvGlTx/E//v916HqJr775AX8xRdv27CijcwgYmwJVnpzsEX5ihN0M4qOWEqDphsgAP77z94FYHlEOI5A5Dn43CJcsgDdMBH0yvjsPTuwf3ubY/VTW8CFz3x0N/rbPBgei+DJl69gYj4JwzBhUgqTAgJPEPLLcEkCWv0ydm8L4tzlBUQSihUOEji0BVy470g/PLKQO3++srbdnJVkxW11o3xLjr39LXjojkF0tFTfq0ngibXvOpbO10p/pxcZxSiv3kuBjGKgv3N1ffGamUZU2DEYTmzr9OELD+7F954exnw0g+89fQl/+ts3OWqQNTvMIGJselZ7cygue88oOiIJ61wmpchrW2YlIBsUmm5C0Uy0BWV43Vbi8eMvX8G1uSTODM84VD9l8D+fvoQjezvwqzcnEI5nAGqd31aM1kyKhWgGbUEXRqdVnLs8D46QXD4Oz3NQVAOPvXQZt+7tzLXesKcyTVoipuhkM7QHXfjEHYM1ia5JAgevS4QsrX+lybXZJFwSj7SqO2+QWKX+12aTmzKHiFXYMdaa4wd6cPl6FC+9PYl3RhbwzKtj+I3jQ+u9rJphBhFjU1Ovm4Nd9j42HccPn38PumEillILjKGCKShgmCZiSS3nLTEp8OzpcQR9kqN3yjRN/OzVMaj6knfDNoZsDJMiEstYnh0KGKAg1PJkGYaZM9TeGZnPNiQlVjkscVaWzkcWedx7ax/uuLE7192dUoqp+RSSigavLJaINbokHl6X0FQlt/G0CpcsIAQgltIKPGQ8zyHgsTx3mzGHiFXYMdaL/3TfblydjmNsOo6fnLyCvf0t2LPBmsAyg4ixYVkuDFbvmwMhBKPTcUwtpKHpRsVmqtYCrCakqmZAEnmomoG0osPjEhw70yuaiZRieTUIsdZX4uGggKrTpZztrL2U/+9oUrXaY4g8FN20GrAu03fI6xLwp5+5CX7vUl7NyEQUpy5MI5pcMhyCXgl3HuzBge2t8LiEnOHUTNi5QS5ZgCzxUHUTpknBZ3WX7Nd6M+YQ1SoTwWDUC1Hg8Se/dQB/+c9nkVZ0/NNPL+Kv/u+j8Lg2Tj4RM4gYG5JqwmD1vjkMj0Xw3Nlxy+OwvC0EAoCC5voc2X8aZSw00zRzhgulJNdJPt9Uo3l/5htBIMg91zAodMPEnp1tuHBlAbGUCr00XxqAZXgFvCK8LgnxlJYziEYmonjuzHiJMRlPa3jh9XGE/HLThl3yE+EJIZAdjM9Wv4yBLt86rK6x1CoTwWBUw0tvT1Q99sgNHTh5bgoLMQV/9+O3cdfNPQ31Rt5zqK9u52q+n3cMxjLkl5PnY4fBhsciAOp7c7C9TblEwWU+3yT351KOTy7Xp4wGD8dxVhjMpDAMM2c4OTmKSNE/ij1Ahknhc4lIZnQk0qWaSIQAfo+I7lYPvC7LCEoqWm6vpy5ML7Uqya5Z4Al4joCC4IXXry3rdVovtnJ3+lplIhiMerO9J4Cd2arZ0Wyl7EaBGUSMDUW1YTBKaV1vDra3SRJ58Dy3nD1kQax+bHZ4TBJ5S5iwTJsLwyxUbS6eo8ArRJYeK24ZTylFKqPj8ZevYDFRauz53CK6Wj3wewpzmbyy5dqemk8hmlRBSNYQEqz2Gvljbc9as2Inwrf6C5W0W/3ypk4qtr1jldis3jFG83B0Xxf8Huv7pLi/YzPDQmaMDUUtYbBKGkI21d4c8r1IAa+ISNyEQAG9jGVGAfCEwC3zyCi6ldMj8Xjw9gHHKjNQIJbUEPCKiKe0kmRqG54j4HkOhmlaitPE8oiYFLkQG6WArpbGyAgAngdkiSspiQ16JfS0W13qVcOAwJNlPSjNHnbZit3py8lE2Gxm7xijeRAFDh862IOfnx6Hpps4++7shlCxZh4ixoailjBYLaETWwjxwtUFjE3HS8JBtheJUgpCCDwuATzPgS86N8n706TUUkiOZbCYUMFzBANdfkfPhVsWEPRKCPpktAVckAQuJ+iYT9AnIegTIfAcAl4RHE+gGVZpvmUUle5T4AkCHhGCQEBAkEgV/lrjCHD8QDfcsoD2oAs9rd6qbpgbIexi9387sL0Ng93+LWEIbFXvGKO56Ai5sac/CAAYnYpjcj65zitaHuYhYmwoag2DFWsI2eQnYFeToD3Q5YPIE0zMpwvKuAWBh1/iYGZ7gNkKrfGUCiu5x/rD7xGgGTRX6v+lTx/E+EwCsZSKZFrDQiyD1y7NIKPqoABa/DIIAFWz5hIFAsJxOLK3A9u7A0hmNLzwxnWkMlo2ebsUAiDgleBxCSDEqrBKpHWYpglNNyAKPIJeCR853IdDu9tzFWP19KytBqa0vHK2oneM0Xwc3tOB8ZkEMqqB05dm8Mk7h8A3YWWqDTOIGBuKldysK90cltMp+szdO+F1ibg4GkYkrhYYQ0A2X0e11Kpb/S7IEo+5xQw4kv3QZ+8/8ZQOtywWlPqnFB0vvTWBcFxBPKkgEletUFu28aog8DnNHJoVaBzqCqCn3YtkWkMsWb56jCOAwHM5YwgAZMkq99cME4f3dODmHe3Y0x8s+YJqhrALU1pePbZ3jMFYL2SRx5EbOvHrd6YQT2l4/3q0qT+/zCBibChWerN2ujksl6Cdyuj4p59eQtAnYW4xA8Mws+elBaEpLhtyszVvio0mwGqfYesRheMKTrw9iZPvTMKkQCyhYDGp5rw8hgmYoKDUQCRhImhSiKLlzelsdeO1i9N47sw1KFqpNSQKHKhp5sKAumEWiCYSQuCWBBzb14WhnkDJ821KPGuUIpnRIQocbt3Tgb1ZV3gjYErLDMbmYXuPH8OjESzEMrh4JWz9CFuD5tYroTlXxWBUoF45EpUStO32HGlFRyqj54wcO3HZ7xER8stoC7oQ8EqgFNCyAoDlyD/2yvkpmBRIKxoWs8KHxXpDuklh6CZiKQ0EFEPdfnz3yQt46pXREmOI56w+Z+1BF3h+yQDK1zyyS+fbg66qPAf7BkP40qcPYk9/EHOLGSwmFMwvpvGLs9fwX79zCs+dGV/2HE5QSnH5+iLOj5Tma1VbRWiaZsWcLwaD0RwQQnBwZysAIKXoGLnevGX4zEPE2JCsJkfCzk05f3UBimZAylMvto/HUlouMUcv9vhQIKUY6GwRoeomdN2ESa1xdvjJuqFbCUR2UretQ6RqBlRY3pxoQluqp3dIBjIowFHr/D8/XWqAEAA+jwifW8ztwecREEuqAM1WpXEEJFuNVmu46xdnr+HE25MARUFlWlrR8eTJKwCAB44OVHUuwPL+vPjG9axYpAlKC0Nh1VQRTs4n8c1/fRuZPKOQhdMYjOalv9OHkF9GJK7gwtUwdm0L5r4PmwlmEDE2LCvJkcjPTVE1A+FopqC/FYCSsJdTewpNNzAdTi+pQ2f7lrklDrpJQXMuDgqDWM1PbT0ij0uAppvWPGZpeC23v9xcFFMLqZLjAa8Et8SX5ADJooCg10rIdkl87ounVqPBNE08e3q8Ytf4Z0+P4/4j28BV4QK3Q2EUhdc0PxRW6XoAKGisa79exedgRhGD0VwQQnBwRytePjeFRFrD1EISfR3Np4XFDCLGliE/N8UOfYFYxk04biAEGYQQJNM6DNPq/8VxgKLqME2rBYedK23ZOya4rAYQzxEomgFFM0BIaaNXVTcRiWfglgUc2duJd0bmkVH0pW70DkZHOTukr8OLh+8Ygm6YBe01NN0ApQDPE/g9En777p3wuMQVVxlVI6iWVnScvjSD3nZfwTwACrx3/Z3eXCjMaQl2KKxSh+x8z53Tr8u1aFxaXPnW3+nFtdlkVdfYlnZgVV+MrchAlx+SOANVM3F1Ks4MIgZjvcjPTckoeq4Lupmt3gIFZiOZkueZBhDPb32R392eAppplmj/OKWz0KzwYjqj49SFacSSatmeZpVo9Ut44Lb+nGfsgaMDeP71a5iNpHNJ3zzPwe8WgVVWGc3HSq9HMaZJ8fSrYwXNakWeA0Ch5TW/dYk8FpMKXFL5r5xwXAEIylYR2p47nuccm+Pa52hU49LiyreMoiOjGnDJfG5f5bxw71yew+MvfoCFvGvKwnyMrQTHEQx2+fHB9SiuzSRyn+VmorlWw2A0CDs3xQ652CExjhCrSmwF5yynJl0JzbDEGms1hggAgbOaqz71ylWMTERBAMgSDwKKFr+MUMCFtqALHS2unOaR3ddtJbQHXBWPm6ZlTGr6kpWYUXWMz8YxPptAJs+7FEkoiMQVZNTKHqdEWisrpmmaFMg2o61EIxS0i/vn5Sfd5++ruJ8eAFwaDeN/Pn0J4Xihgek0lsHYzGzPVrZqhonrc80n1MgMIsaWIJ5WS5KlbcxVVCgVd6NvFDTvL/G0jtOXptEWkPHqhWmAcJCzfdIkkc+FYVZbkXV0XyfcsrNHh1IKg1JwHIHXtTQmltRy3WhjKS03F8eRXHuSSkak3y2VrSIM+WSE/HJFL5N9jnpSXPlW8j6y95Ulv58epRS/OFO+EW7+WAZjs9PZ6oZLsry7zahczUJmjC2B3y05agTRMu0umhHb+DINE/PRDJ49PY6J+SQ4jpRUytmspiKL4zg8ePuAVU1WHBbM/hnwSrmkIFUzCq6vYZjQdBOSyEMSOKsHm2FC1Q0IDg1u8wU1naoI+zu9+M6TF9ZcQbu48s3pfZSvMwUUNr8NxzOOifk2jQzzMRjNBEcIOkNujM8kMLeYXu/llMAMIsaWYKDLB68sIFz0OF1RsKyUcu0z6goFCEdgmhThuIJfvjWBVMYK1RRXygH1qciyS+qfPT1ekGAtCTxkibcMoixOGkx2aJAQq59aJOEcLnSSA3CqIlwPBe3iEFw5ranix2sJ3TV7o1wGoxL3HOqremxGMTA+cxnRhIrb93WV9UKvB82zEgajgRBCcOfBHvz4lx8UWC5kbUyZVUOwZAwZptVgNt/rYBgmIgkFISDX6qNeFVkPHB3A/Ue24czwLOZjGbQHXOgKufH9X7xfMM5pHj7vMZcsIASrxYmW52GpJbm4mt509aY4BFdOP6X48VpCdxuhUS6DUQ929ll5RBTAlakYbhxqXd8F5cEMIsaW4e5DvTh1YRoT88lcyIMQ66ZtUitBuhrTiOTZUNTh8XqbV8T+H6UwsnEzQbByd5J5Ktp23k5+C5F6VWRxHIdjN3bn/k0pLakGk0Q+FxYDLK+VWBQa62334r989iZE0gYmp2PwyELN5edr3bi0uH9efvjPpvg654fuWv0uxFLlPUBr0SiXwWgWBrv8uZ+hE7OJpjKIWFI1Y8tACMGnPrwD3a1utAVdudYb7UGX5ckgcKxuKobnCFr8Mrpa3WgNyOB5y1sj8hx4vrabMkHph5AvWgQFwFtS07njdu5OwCsWZHXbeTuNrsiye8oVX6/ceggQ8IgFRood0uI4Dru2teDgzjYMdvtXZMjY4bQD21d+jlrmyt+rHf7LXfei65wfuiOE4GNHy4fx1qJRLoPRTEgij7agVcE6HWmuPCJmEDE2PbYg3oWrC/DIAj5z9050t3rgylZluWQBQz0B9LR5IEsChDJWEQEgiRyGuv34w4f34/MP3IDBLj9aAzI4jsAwLaHGgFeES+QqVp8JHIHAW53tzey5RcHyqNheq/x7JCHIJU+3BV25SiuXJCDklwv0PAyTrklFllM1mEsSMNDlx0CnryBvqdY+c81G8V5dsoCQT4ZbFgqus9M+9w+14osP70dbkYzBRr8mDMZK6W71AABmwqUK/OsJC5kxNjXDYxE8f3Yc05E0TNMqE+8OuXH/kf4SFWcAGJuOY2QyClDA7eKRylg6M6BAa1DGzt6WQo8EpXjqlVGoqgHdIOA4q5JCN53TtQe7/Lj75l7sGbAapg6PhvH6+3MgANKqAU23qsEIrNCMxyWAgODYjZ3oa/fhF69fLzmnSxLgkgSomgHTpPjND23H0X2da1KRVS58BWDNQlprRbnKt2qUqm/a1YFtrW5cmYhtqmvCYKyErlYPLlwNY5oZRAzG2jA8FsEPnnsX0aRWkO8RTaiYDqfw+QduwIHtbQXPGeoJYCgrHlbN+b//3HuIJlXougEKoLgPrE13qwefuGMQO/uCEHkOPo+I3nYfeJ7g3JUFROIKCKwQi50zRCmQzOgI+WXcMNiKG4da8fp7c2WNHEnk0eqXcfv+rlyYZy0qssr1lNuMZeROe612nyvpvcdgbEZsD1EkrkDRDMhl8hzXGhYyY2xKKKV48uURhOOKo2ZMOK7gyZdHViyIZ5gmHvvVZYTjGei6AcN0NobcsoBP3jmEP/n0Qeztb0GLT0Jb0JX7AvC5xAJRv9KNWKJ/djf7cirOQKmRU07gkIVqGAzGetIZcuf+3kx6RMxDxGhqKKUYnYphMaHUFGYYm45jYj5VUPJl5rqoEnAAJuZTGJuOV+0RskkrOt4di2Sr1aijB8bmnkM9uPNgD3xucXV6G9k5ai07X+uKLAaDwViOfINoNpLGtiZp9MoMIkbTcmk0jF+9dQEz4WROTbpavZmRyWjOM5TfwNWCwiDW41emolUbRIpqIJ5WoWgmXnprAqpeJj6Wx6uXZnDj9jZ0tLgdjycyWk6w0JFstVYis+RFqtXIYaEaBoPRTLQFXOCIJXcyE2mePCJmEDGakuGxCB4/MVIidletynI2E8fBGMpCrWqs6YXl3bWKZiCR0qAZJkYmonj61ChmqiwXJSB48Y3r2DcYcjRY/G7JqlgiyM6xtNB89eniarBajBxK6Zp4iNZqHgaDsbEReA6dITemwylMNFGTV2YQMZqOpWaaFE7F68upLFNK4ZZ5gACGUVkp8dpsApRSx/NouolEWoOiGQjHMvj5a+O4OFrc/KM8BIAschUFEG3Rv0gC8LlFpBQdhkHBcyRbgk9WVQ02PBZZE1XntZqHwWBsDvo7fZgOp3BtNrHeS8nBkqoZTUdxM00nFmIZnL40U9LBfXgsgv/vifN46pWrMAwTWQHqgv9sBJ7DbCSFx166jNGpWO4chmkimlSxEMsgllLxizPj+Pb/PleTMYTsXKpmIKPoGJmIOiZwLyVKWxVmxV3rV1MNNjwWwWMvXS65lraXbXgsUvM513MehjP5Olv5nwUGo5np77R+5E3OJ6GXK89dY5iHiNF0LKeenFF0xFIa/uPXV3Pif61+GXv6W3Di7UmE4xloulm2i739sKabWEyoeP7sdbz09hR629z4+LEh9LV7YVKKc5cX8OyZccSSzuvhufJl9jaRhAqR5/Dim9dxcTRcNvH5d+7dhZfensT0QhKUUqi6Ca8s4M6DPbhhoKXyJE57zHnZnI/X0susGeZhOMM8c4yNim0QGSa+PVoeAAAgAElEQVTFxFyyKfIcmYeI0XRUUk+2O7gbhlmQX7QQy+AnJ69idjEFTTNrayhGAF03MD6bwI9ffB+vXpzGf3vqIv79V5fLGkPA8sYQAawO9cQKf1XymOwfasWff/Eo7jnUZ4XKAOgmxYlzk3j0ifM1e1mq8bLZobzVsFbzMEphnjnGRmZ7XjHLB9cX13ElSzCDiNF02Hk1xeR3cC9upqnqJhTNgLnU57QqrEp8azQ1KcIxFU+9MrqiGzhPACHbyyzfF+KW+Zx3xPaYOIU1zo/M4+Vzk9ANWrC3ldzgqu1RttJeZms9D6OQaj1zLHzGaFYCXgk9bZZA43vXmEHEYDiSn1eTj93B3alpqaoaK5rL/gAYJoVuWlVpxUhFHdtJ3n/58DxnqU3nDeQ5UqI/5OQxoZTiqZevOM4P1H6Dq7ZH2Wp6ma3lPIxCmGeOsRnYO2CFdd8bX2wK453lEDGakuK8GgAwTWqVonvFik1La/1YlZMTag+6cHhPO85cmoWqqxWbtQKA1y0AINkwGwUBgSjyEIXS3x3FHpOx6TgWopVL+StVqxVje9ka3ctsreZhFMI8c4xm4qW3J1b0PCPr0k+kNfzk11cRcogMrJR7DvXV/BxmEDGalv1DrTh+aBveHp7GYkJBIqXhubPXCsbYCcj5vy4IqjeKnGwhAuD4gW48cPsAonEVrw/PFhhD5c6tGSY0jcLMxTEoONNERtXBcVyuuawkcCUek3iqQvuO/HFV3uDWqpfZWvZMYyzBPHOMzYAdMgOsarN6GkQrgYXMGE0NIQRDPQEc2N6G2/d3FeQWZRQdc4sZhKMZJDN67vFKxtByt2WOEOzsC+CTHxpCZ4sb+7eH0BnyWM1WK5ybwGrpQSnNxdN4jsA0KOYWM5hfTGMxriAczSCaUJHKFBpAfo/oeN5iarnBrVUvM9Yzbe0pl2eXD/PMMZodlySgLeACAEzMr79AI/MQMTYM+d6IVMaqNsu3UASeg2GWL7cnFVxHBADPAy0+CQ/ePoj2oDvn1fjknUP49mPvQKvQqkMWOQT9MigFdN1EPK2CmlZuEmD9yfEEIIBL5vHYiRH8NiE5Y2Gw24+2oBszYetLwfZ85XuV2gKumm9wa9XLjPVMW1uYZ46xWejt8GIhlsFsOA1NNx1TDNYK5iFibCj2DYbwmbt3IqMaBcYNz3NoDUhoD7pylV4cKfQI2SKNxfAEEAUO2zp8+MKD+3DLno7cjYRSiulw5V47PEdAgZyoot8rIeSTC8NxFOA4gpBfhksSSpKkCSH45Id3gCOkwPNle5XmFzPY078yLR+7zceB7W0Y7PY37Ca5VvMwLJhnjrEZ6Gu3wmbN0NeMeYgYGw6vS0SLX4bHJcA0KQgBBIGHYZjQDBNuWUBa0SAKHHSdFvQHsxF4gkO72tHZ4oYoctg70AKXKCCR0TA2HcdAlw/vji/iyZdHMDoTh6E7u5YkgYPXJSKZ0aDpZq5cnuM5CByBmXVLERAEvFJBMnhxkvRNuzpw+/4u/MfJq7nGtIBl7Pm9Is4Mz2Cgy+94o2N9xLYmzDPH2Oi0B90QeALdoJgJr2/ne2YQMTYcdmKxKHAwKYVpAumMhkRah24YOcHEcnLwB3a04uO3DyDkd8EjC7g+l8DzZ68XVEqJPId4SkEspecyr+1bDIXlFeIIAc8TuGQeyYyWC48ByCVWW9qR1jN5rvQmlZ8kTSnFe+OL6Ai5oWrGUrgsa2SVU31masVbm1oa/TIYzQbHEXS0uDG1kMLMMt74hq9lXWdnMFaAzyXCME3ohmUMKaqOWEqFkWcMOSHwHAa6fPhPH92NjqAbrX4ZE/NJPH5ipKRsfGI+iXBMhaYZJZnYBJZ7l9jNY2F5cfINHq7I+CkWkrTJT5IemYgiHM8AACSRhyvb0yyfYm0ZplbMYDA2Ol2tVthsIZapmKvZaJhBxNgwmJQikdbgkvmcIUEpRSKtg2aFFcsR8IroaHFBNygicQVtQRdEgXNU+02mNWi6AZNSy+tjV47lQ3MC1zBNir4OL2Rx6eMkCRx4PvtvByFJoLQKqFKbkHxsrxJTK2YwGJuBzpAbgPWdGsn+KFwPmEHEaHpM0zKE5hfTSKQ1AATHD3SDI4CiGdB0o6wxxBFA4KyEZ44QCDzJendIidpvRtUxG0ljMaHAMCxjiML6kPIOORkUS96hT921A5/9yO5cgishBAGPCIHnconUxesqrgIKeGvTlmFqxQwGYzMQyJMdyZdQWWtYDhGjadENE4txBbOLaehFFs9Qjx/bOnw4Mzzj6CEhsLrRL1WLATxPQAjJGRT5+TsZVUckbpXxE5CcsQMABgW4bIgs39lCYLXl+Nx9u3O5OsUJrqmMhhfeuF5Vfs/OviBa/S4sxMr/Qsr3KtWiVrxWSdcsuZvBYNSKSxZy368pZhA5MzMzg69//et47bXXIMsyHnroIXz5y1+GLK+vmiWjOpa7OZY7rukmEmkVYzNxmITg/dGwVU0Ggt4OLxbjKl69OI3ZRedWF3a5PYXlXTKpFY5KZXSE/BKePzsGWRJAKUUyrYJSIJpQl0QVHTCBgpp9AisM9sWP34B9Q61LjxOCgS5fwb7+5FMHcG026Xgd7GuQUnT0dqm4aWcrfn56HBwhJflDxV6l/LBhsWZR/nWei6Txt6feQiShWLlNlMLrFnHngR7cfai3JoOl0mtabXI3pRSXry9iYjqKWEKF1y0g4JGZ8cRgbFE4QuCWBKQUnRlETlBK8ad/+qcIBAL40Y9+hGg0ij//8z8Hx3H4sz/7s/VeHmMZlrs5Oh1v8Uo4fqAHqm7g1IVpTM4nEE9pZXNkisne65HXOSOHqptQdRMpRcfEfIVKhirnorDCUf/64mV87n4ud8OvtO8D29sKzpE/VlENxFMqTAq4RA4ZzfKI2X3bnAyLgS4fRJ5gYj5dUqYf8IhwyQI03cDjJ65AN8ylnCgA/GIG12YTOHVhCp/68M6qqtEq7Q2Ao0igndxt6+IMj0Xw4hvXMR1JYTGmQDfM3Hp7272sMo7B2KJIIoeUAqj6yhp11wNCmzTjcmRkBA899BBeeeUVtLe3AwCefvpp/M3f/A1OnjxZ1Tnm5uKNXOK6IAgcQiEvIpFkSRipWbArn8op6B7d11UQ6rJK5ykoBVRNB0Cg6gZiyer6e3EEVRtN9YYAaPHL+MOH9wNwNgoAa435Ynn518gO1+WH6lq8EjieA6UUD9w24OjJGR6L4AfPvWdVphXPSQCvzCOlWH3elhLEl4bwnNV8tivkwmc/sruiIbLca8pzxFHvyabVL+O+W7fhsRMjSCsGInHF2qv9FAKEfJa21GYTFdwIn9l6wfa6Mjo6Vi6b8L+ff3dVczcLP37hA6i6iYM7WnF4T8eqz5ff3LXa69u0SdUdHR343ve+lzOGbBIJliDazFRT+fTz18aQVnQkMxpSGQ26brXboJQintIRT6lVNzu1z7leUADRpIpfnBnD81VWfBVfoxLDjwLxtA5J4OCSBJy/slA6b/YcssQj5JeXKtqy8BxBRjVhZrtJFxtDAGBQCl03oGhmxWq05V7TjGpgYj5VsZptIZbBU6+M5sKXpZMAsZSl5cQq4xiMrYWqG1CzRqXXXV1fx0bQtCGzQCCAu+66K/dv0zTxwx/+EMeOHav6HBxHSvRgNjr2ja/4BtgsjE7FEEkoKJcKEksoiKU0pBQ9N4YjHHweARxHYFIz5y3aKFBKMTaTgMdVqhuUTyShYGIhCVDkrpGqGTDMol+XBDBMS3VbFvnc84a6A7kh+dfZLQtwSwJU3YBhUksPicLKsSKF5y1ZO7E8dE5zOM3lhOV9WlqvE6puQkkq4DkC3TRB7MXkndM+R6W1bESa/TNbT9he1x6OkLKfzY1COi9vKOARHUVsa0VYQU+0pjWIivnmN7+JS5cu4bHHHqv6Oa2t3k2bpBkIuNd7CY5cnU1CcPiCsBKYdcQKPD/Wa2NSilhSg0fmQSkqiis2K1ZuDnHcez6UswwGe5yq5RkHQNHfl8ZRjkco5M0dc7rO+V8AqYxuvfcpyiaKAwChBJLAQ+C5kjkqzZWPKPAg2ZWXG6dqBiSBh5FNji/ea2492XOUW8tGplk/s42A7XXt8Hglx8/SevLgHUM1jX/ypcu5v3/2/hvQ3bY+n/0NYRB985vfxL/8y7/g7//+77Fnz56qnxcOJzelhygQcCMWK0ykbRaIYRS0zKDZ/CDDtAQRC6EF4xJpWtD+YiNh/aKhZduF2BDTakq7NI7m8oaKy/0plsYR00Akklw6T9F1LoWCwPKSGhXcbTxHwHHWPMVzVDuXwJFcg9ty44JeCWnF8obRbG836pDBbp+j3Fo2Is3+ma0nbK8rYzXGfyqpNp2HqJbPrkkpnv71FQDA7m1ByFxtz6+Gaq9v0xtEjzzyCP71X/8V3/z/27vz8CjLc3/g3/edfSb7QgiBJCwCASKJgSCLFhFEBZcj2tNqtV62pZ669He0inrailft8VKOlKNW3A6t9bTaunGqVFGoVSh7kCVokDUkJEACWUhmn/f5/fHODJPMJJkkk8xk5vu5Li7NO5N3noeEzJ3nee77XrECCxcu7NXnKorw95SKNx6PEpOHFvOyLEhPMqCx1d5h60tNC1fUN2lfF3rvuSEB36rQ0PtaSfD2kspJgiTLIYK+CzKSDcjz/uaTnmTAufMO6LQaaGS547aZUH/Y6jQyhLjweYFfb9/fc1eFGXVaDUwGLQx6Gc1tTv99Ow9eraAtIT0p+DXCfS0AGJFtgdvtCbnVKUvAopmF2Oitx6SV5QuBb+Ahb++cuxvLUBar/2YHAuc6eBQRfD4w2nrz91F57CzONKklVOaW5kX17zKmN3pfeOEFvPXWW1i5ciUWLVoU7eFQGOxOD8qLciA6nQPyB6YSkGTWAZIaDHmU2Nwi8wVu4Twx1aLHVeUFWDBtFCQIOFwe2BxuOFwe/+HgwBpCkiRh/rRR/vsHtfWQ1H10SZJCVrQGEHSPzmQJuHpGPixGHdKTDdBrNUHnidIsepiMui5fozev1blSt09GsgE3zx2HSYUZ/nuErMgtXTg70N1YiCh+CCHwyc4aAECSSYdpE4ZFdTwxu0J05MgRvPjii1i6dCnKysrQ0NDgfyw7u/8peRQ5Qghv1pgbHkWgYHgyFpbnY0vlKbR4M4rUA+7q4WmdRgOnS4G9i3oTBp26guDxhNpUCc1Xgwjo/S9Lvob0QgCSBOi0sj/tva3dCavDHTrdXJYwPMOM2xaM99fY0Wo0aGmy+5fQNRoZeVnmoFo/RQXpuHnuOG9dHyAjWcJ5qxNCSEj21hDqqWN9x3uErveUn5OMDbtqYNRr0WZ1+lufpCbpYDLoenyN3rwWEFypO7DYou8ef99dC1kjsQ4RUYLbtK8elUfPAQC+VTICuj4chI6kmA2INm7cCI/Hg9WrV2P16tUdHjt48GCURkWBFEWg3e6CLUTAMDYvFWNGpKC+0Yp2hwtmvRYbdtfi1DkrmlqtIQMMg04Dg06CwyUAoUCW1XR1CWo/Mlmjgd3pUVtyAICkZhHqNTKsDjdkX6sOoQYrRr265eR0K9BpZEzIT8PYEUk42WiDXqdBWpIe+TnJanVUmxunmmyoOX0edpfH/yaeOyoN8y7Jw3mrCw3NNjS32QGoVVXLJmajcHgKJEnqUKdnWLoJTpfHXzm6q3NRRQXp/gDC6nBjxPAUtLZY0dIeftuLwHt0FYQEPp5k0gECaLO7et1ao6fXUr8kEgqGd13zo6ggHVPGZOCc1c1K1UQJrP5sO/604RsAarf7xb08iD0QYjYgWrp0KZYuXRrtYVAIbo+Cdrsbdoe729UYSVJbbQDA8VOtaGy2oaUtuAaNRpaQatFj9IgU7DvSCF+9PkVR/ysAOD0APB5oNRKSzXrotLJaWFAr+6tQS5KE1CQ9NHJw2wshBMomDEOSWYeiwuwu33z70osrVJ2ewNf31SCamJ8WcuurYHjyhSJvFl2v99B7CkJ6ejySrxXuPcaNTENmH+ZKREOfy63g5b8egNOlQCNLuPv6yTDouy5ZMlhiNiCi2ONweWC1q2djwtXc5sDH209g35Hg4oKAum+cl2XBnOLh+Pvuk4Dw1bUJfT+3R8Du9HQ4h+LxtqWA9xC9sdM/LLtDTff/v83HYDSo3/JdbRX53vB9gdGB4+d6DIx603U+UoEJEdFQpAiBN9YfxInTapHlJd8aGzM/FxkQUbeEUAOQdrsL7m5aM3TmcivYtK8On++pgyvEKsC4vFSUjs9CTpoZuVlm1Dda4XArkGUZrh4CLpvDjdZ2J1IsejXYaXfB4x1bc5sD7Xa3v5eX3eFGU5vDv43m07nHVqBwm5T69KbrPBFRolKEwB8+rsLm/fUAgCmjM3BV+agoj+oCBkQUkqII9WyNw92r0gVCCFQeO4ePtlVfSPcOkJtpxqKZhRgzomMV4naHWrDRYtTA6fL0eDC6+bwDeq2EpjbnheKDQq3l4/FWO06D2grEFwwJqMGUryO8AiloKyvwLFDgOaDuAihf1/mehPs8IqJ4owZDB/HFXjUYGjsiBf924xTIMXRukAERdRDu+aBQ6s+248Mt1ThW3xr0mNmgxYLpozB94rCQxTIzkozQaiS16rEsQfQQhAkAZ1sc/ntpZAmKIi4UKBNAS5sLiqKo8ZIAzrXY/Z/vy2w6B/i3snxngaz+VadOHeQtupBngfJzkpCR3H2dnoxk9dAwEVGi8W2TfbG3DgAwZkQK/v3bJTAZYisEia3RUNT05XyQT7vdhU931mBn1ZmgwnyyBMyYPBzzy0aG/OaXJSDVYkBOugmZXxpx6pwV4TYycysCOkk99yPL6mFru9PjD2Q8/p5Zwb3RfKtI6biwlXXidBvqzrarxRVDPd8b8HQ+C+Sr09NdN3jW1iGiROR0ebDmb19jx9dnAKjB0APfLoHZGHvhR+yNiAZNX88H+XgUBdu/OoMNu2pgdwYHUuPyUrFoZgFyMswdXrOuoR01Z9qg1UqYVJCB7DSTP6h4Y/3BXjV29SgCWq2EJKMOep2sZp15gzq1PpKn6z4/3g7rSUa1MGKr1al2ng94fV8lbd+2XEubE63W4K3AcOv09CWLLVqG0liJKPY0nXfghff24Vj9eQDA6NzYDYYABkQJSQkopNjX1iaHa1vw4dbj/pLrgTKSDbh2ZgEm5qehvtGKrZX1avNPCdh9qAFnmu1QPGqa/Efba/yFCyeMSoVOI0GrkeAKM0BThHqA23dw2t/LVLpQrFGWpe73qb0Ptds6bpMpilD7gAUMxaN4cKimGcVjMoNu01Odnu4OaxePDb5fNPX2YDkRUaBj9a14/t19/rOkZROy8cNFk2Iivb4rDIgSiNujwOpww+Zw92oVJtDZVjv+trUaX1c3BT2m18q44pI8zC7ORfWp83jlrwdwuskORVE6pNJrJPVMDqBuRZ0404bXPvwKSUYtTocIsHrSeS6+M0MeoZ4t8igCkBEcFHl7eanVmwGLSQuNRlbT+JWuG83uPHgGRYUZIQODrur0BB7WDuQ7rK3RSJgdI93dexprqIPlREQ+O74+jTXrvobTm2F83axC3HDZ6Jg6QB0KA6IE4HR5YHW4Q25rhcvh8uAfX57E5n31IQOF0ouysLA8HykWPY6cbMH/bT6qtu3wPjWwrpBHAJI3ewtQV2Ka2xxos6nPlyQJOg3CXiUKRUANvBQh1E7s/qUjle+QtFGv9Wd/pZgN6kHr8/bQHeIlb3d4KTg7rduxhCjcGEgRwKc7azCrZGTvJxph4Yy1N3MnosThUQR2H2zw/8Ks08r4waIilBflRHlk4WFAFMdsDjesdjdc/eieqgiBvYca8fGOEzhvdQU9PjLbgsWzCpGfo66KCCHwz/31/nR39VrwfT3ejDBJ8q7gCLUytSRd6CAvScGHocOlkdStMkURkCBBltWmohrZ2+7DW0k6MPsrPycJI7IsF7bgAnmDIZ1WA71O06tCi9WnzqP+nNWfwq/XykHBxNlWO46ebEFG50avg4xFJomoL9psLnyxpw6N3mzetCQ97ltyMUbnpvTwmbGDAVGcUYSAPaDRan/UnGnDh1uOo+ZMW9BjySYdFs7IR8lFWR2WQesbrWhsVbfJ/EIsJPhaclz4H2+HeVmC+qnCV1qo1y4EVBI0EiCgBkUaWfJXqgaCs798B7v/sL4KOo3sXSUR/vNPvi02n3AKLX5d3YT3vjgSMuXf2CnrrqXdGfWAiEUmiQgA5pbkhf3cvYcb8e4/jqDd7gYATCpMx9LrJnfoKDAUMCCKE901Wu2t81Yn1u+owe5vGoIe08gSZhcPxxWlI0Mejmt3uDoc1PY1W5UQonO9AIQkAj4UUAT8Vaf7NQ1vECbLEpLMOtgcng71j7o6IFxUkI6F0/Px9j+OePf5vHWOArbYfHoqtOg7i9N5qzIw5T8wKEqNgR8eLDJJROFyexS8v+koPtp2AoD60/KGOaOxeFZhyHpzsY4B0RDXn0KKoe61Zf8p/P3LWjhdwdtsE/PTsWhmATJTjV3ew2LUQavpuCXkW10JGqAEf50gQI0/dN6tqc7ZXf77BF/ufEvvfVUajYxksx75w/S4fvbosLq8f6tkBPYdPYvTgdtcnZrF9lRoMfAsjl6n8R/WvvAENeXfoNdAkiRkphgxJi8Vzc3WbmY38FhkkojC0dhiw8t/PYAjJ9VCvClmHZZePxmTCjOiPLK+Y0A0RDlcHrS2OftUSLEzIQSqTjTjb1urcbbVHvR4dpoJi2YWYPyotG7vo9VImDI6A5v3mXHe2qnSsywF1ToSQvgPDQkBaGXJu9UFtVGrBATuvMmSpDZx7YHGu13m2+KSJWDB9HwUhrmXLUkSFvSz0GLnszgpFl1QwUePR4HLrcCo12DB9Ngo3Mgik0TUk4qDZ/C7v1XB6lC3yCaMSsOPb5iMtCRDlEfWPwyIhhDhrR/kOmfFuVa7f2upP8402bBu63Ecqm0Jesyo1+DKspG4dHIONLLc7X3MRi2STTo1mJiej1PnqtSAwDtEWZKg1ajbYb5RKwoASYFOI8OtKB2yzkJNLfBMlG8lSCNJ3hT+gG02cWGLa0SmpU+1c8IttNiVzmdsjHot0pMR1BLEbNDipm+Njanfqvo7dyKKTy63B2/9/TA+230SgPr77PWzR+O6IbpF1hkDoiFAEQJWu9poVZKA1NT+F7ayOdz4e0Utth44HbTqIgGYXjQM86eNQpKp+0O+GllCqkXfYUupqCAdty+ciPe/OIKTjVZ/AKCRZWhkAbNJB9/RIb1OPbx8rtUOSIDiCaj/IwXvtMneekIaWUJ5UQ6KCtJhMemQbNYBQg1E2m1uWEw6pJj7V125p0KL3Ql1xsao18Ko13ZoGnvbVeNRODz2sjD6M/eBxgraRIOv/mw7Vq89gNoGNckmLUmPH18/GRPy4+cXJAZEMcyjqOeDAgspajT9+8GvKAIVB8/gk501/oyAQIW5yVg8sxAjsnouEmgyaJFs1oUstlVUkI6J3ytD9anzOFKnrj7trDoDu9MT9ObldHkgS2p9H0kD/wEgjyIunAcS6txlWUJGsgF6nQZtNhdmTMoZ0DfDrgot9qS7sziBKf8FObGbut7XuQ8kVtAmGnzbvzqN339cBYc3QeTisZn4waIiJJvjK7mCAVEMcrkVWO0u2J2efh+UDnSsvhUfbjmO+rPBB3dTLXpcc2kBisdk9BhgyN5VIYOu+5UqSZJQmJuCwtwUVJ86j837T4W8t+/Qscut9h1TzwoBHdaGJG+laXEhpT6W6+HwLE7ksYI20eByuRW8tfEQPvtS3SLTyBJunjsWV8XImcdIY0AUQ+xOtZCir9x5pDS3OfDRthPYf/Rs0GM6jYzLS0bgsqm50Gt73ooz6TVItuh7XYK9p7o1KRYdzrZ4/DWDOueSaQL2pwPPEnV332hvrfAsTuSwgjbR4DrTbMPqtZWoPqU2Zs1IMeDfbpiCsXmpUR7ZwGFAFGW+juxWuwvu/hYQ6sTp9mDT3np8sacuZLXq4jGZuObS/LAyA2QJSDbrYTL07Vump7o1Rr0WKRY92m1uNfvMGxSpxRplBJ7XCwyOurpvrGytxPJZnKGEFbSJBk/NmTa8/dkR2LxZZMVjMvGj6yb1eKZ0qGNAFCWR6DjfFSEEKo+dw0fbqv2dhgPlZpqxeFZh2CXV9VoZqUn6HjPNuhNOfZv8YWptm9NNNngUgdZ2J9RyRBeKD2k0MnRadRxd1cOJta2VWDyLM9SwgjbRwBNCoPLoOXx5qBGAmkV20+VjcM2lBTHfmDUSGBANMkURsDrcsNpd/a4oHUr92XZ8uOU4jtWfD3rMbNBiwfRRmDYhG6fP2XCothkWgw65WeaQKxYSgCSzDhZjx98KwtmKCvWcns7ULJieDwD+58iSpNbuCRhQillN7e/qDI4QAp/uPAGb0xOyd1gkt1aivSWXSFhBm2hg+QrzHvdukSWbdfi3G6ZgYgJt7TMgGiRujwKrL2NsAO7fbnfh05012Fl1JqghqiwBl04ejivLRqKusR1/2nBI7UTvlWrRY9aU4R32hnUadVVIq+m4KhTOVlR3zwnnTI3vOU1tDmRqjGhudUAA/v5f3W19fb6nDgdrWjoWhezUOywSWyuxsiWXKFhBm2jgtNtc+OzLkzjXqv77Sk824NHvXYKsVFOURza4GBANsIHKGPPxKAq2f3UaG3bVBvXMAoBxealYNKsAOelmHDnZgvU7TgSt0LS0O7F+xwksLM/HuLxUWEw6WIzaoNWOcLaiAPT4nHtvKu52ZcV37uZkYzuERgPJ44HbrfTYduPr6ias33miY4sMhO4d1p+tlVjbkksEzNojGhiNLTb8veKk//2jICcJs4pzEy4YAhgQDRiHy4N2myviGWOBDtU2Y93WapxpsgU9lpFiwKJLCzCxIB2SJEEIgS2Vp7rN0tl24GrZn1YAABnaSURBVBSmT8yGXhf8bRFOls+nO08A/pT50M/xbVf1tDrjS9lPT7egqakd7h7+Hn3j63Kfu1PvsL5urTDbKXqYtUcUWfVn2/HZ7pP+tkol4zJRPDYzYX92MSCKICEE7E4P2u2uoL5dkdTQZMWb66vw1fGmoMf0OhlXlOZhdnFuh+2u+kZrh22yzmRZwnmbC/VnbSGDlXCyfE412SABQY1QAw1UJpBvfCEbqXr5eocNzzD3eWuF2U7Rxaw9osioPnUem/bWQxECsiRhztRcFCb4zywGRBHgPyjtiHzGWCCH04PP957E5n31IQOu0ouysHBGPlJCVA9td7hC3lPydpf3vaF0tZUUzhaTogiE87Y0EJlAgfcM1UjVRxGiX1srzHaKPmbtEV0wtySv15/zxd46fLG3DkIABr0G991UHFP9FKOFAVE/DPT5IB9FCOw51Ij1O07gvDU4sBmZbcF1swsxaljXbxIWQ3D9CFmWOtT0AbrO0glni0mWpbACooHIBAq8Z1eNVDUaGQun5/dra4XZTkQ0lH2yswZvbTwEAEgy6fDv354adgmWeMeAqA8c3m2xgTwf5FNzpg0fbjmOmjNtQY8lm3RYOCMfJRdl9VgjIjfLjFSLHi3tzqBVIZ/usnTCyfIZnm4COqfKdzJQmUCdxxeqkerwDDO+VTIioq8TCrOdiCgWbdpX5w+G0pMN+Nl3SpCb2XPfykTR90p7CcjmcKOxxYamNseAB0OtVife+cdhrF5bGRQMaTUS5paOwAP/WoJLxmeHVTBLkiTMLh4OrUaCViMHBUM9Zen4snzkLl7KV0doQQ/PGahMoK7Gp9dpYDRoYdRrIvLa4fw9MNuJiGLN7m8a8PuPqgB40+pvu4TBUCdcIeqBr7VGu93VoYfWQHF7FPxzfz0++/IknK7goGtSYTq+s3AiDDLg6cXBbZ1GRnlRDtKTjX3O0gk3yydamUCDlYXEbCciGkq+rm7CS/9XCSEAi1GLB/61BFlpiZdW3xMGRF0YrIPSPkIIVFU3Yd22an9xrEDZaSYsnqWm0aemmtHSEtyxPhQJ6FBXqL9ZOuF8fjQzgQbrtZntRERDwcmGNjz37j64PQIGnQb/79tTkZfFlaFQGBB14q8o7XQHVXweKGeabFi39TgO1bYEPaZu9YzEjEk5ve4lppUlpCYZ/L2/fPqbpRPO50czE2iwXpvZTkQUy+xON15cWwmH0wONLOHem4oxdkT8dqvvLwZEXg6XB1a7Gw5XcLXngWJzuLGxohbbDgQXTJQkYPrEYZg/bVSfOgybjVokm3RcsSAiSkBCCPzh44OoP6vuJty2YDwmj2ZqfXcSOiAarEKKnSmKwK6DZ/DJzhpY7e6gxwtzk7F4ZiFG9GFZUyNLSLXouy2OSERE8e3zvXXY9tVpAMCMSTn9zrBNBAkZEClCwGofvPNBgY7Vt+LDLcf9UXugtCQ9rrm0AFNGZ/RpZcdk0CLZrAsr64yIiOJTXWM7/vSpml4/PMOMOxZO4G5BGBIqIPIoCtp9HecHNw5Cc5sDH22rxv6j54Ie02lkXF4yApdNzYVe2/uVHVkCUix6GPUJ9eUkIqJOhBD446ffwO1RoNXI+MmNU2Ay8L0hHAnxt+T2KGi3DXxF6VCcbg827a3HF3vq4ArRX6t4TCauuTQfaUmGPt3foNMg1aKH3FVhHCIiShi7Djbg62q1z+WimQUYOYxFYsMV1wGRy+1Bm21wD0r7CCGw/+g5fLy9Gs1twX2tcjPNWDyrsM8l0yVJQopZB7Mxrr+EREQUJofT469EnZVqxDUz8qM8oqElrt9Nz4ao5zMY6hrb8eHW4zhefz7oMbNRi6umj8K0CcP6vKqj08rISjWGbF5KRESJ6eMdJ/ytk7575UVMrumluA6IBlubzYUNu2qws+pM0BklWQIunTwcV5aN7PN+rgQg2azHsHQzmpra4R6EXmpERBT7HC4PNlbUAlA7GpRclBXlEQ09DIgiwKMo2HbgNDZW1MLuDN6eu2hkKq6dWYCcdHOfX0OrkZBqMcDELTIiIupka+UptNlcAIBrLy1gVlkf8N21nw7VNuPDLdVoaLYFPZaRYsCimYWYmJ/Wr29Oi1GLJBZZJCKiEBQhsH5nDQBg1LAk9lPsIwZEfXS2xY6/bav2n+YPpNfJuKI0D7OLc6HV9K7dRiAWWSQiop58dewcTp9Ta9tdNX0Uf3nuIwZEveRwevDZlyfxz/318IQo6njJ+GxcVT4KKWZ9v17HpNcg2aJnkUUiIurWroNnAKi7CTMm5UR5NEMXA6IwKUJgz6FGrN9+Aue9+7SBRg1LwuJZhRjVz5oPLLJIREThUhSB3d80AgBKxmX1a1ci0fFdNww1Z87jg38eR21De9BjyWYdri7Px9SLsvq9mmPQaZBi0fW6qz0RESWmQ7XN/sPUl0zIjvJohjYGRN1obXdi/Y4T+PJQY9BjGlnCnItzMbc0D4Z+nvFR0+l1MBt739WeiIgSl+/9yaDTYHIhu9n3BwOiEFxuBVsq6/HZ7pNwhqj1U1SQjmtnFiAzxdjv19JqJKQlGbjMSUREvXbkZAsAYPyoNCbg9BMDogBCCHxd3YS/ba3GufPBVa6HpZuweGYhxo1MjcjrMZ2eiIj6o/q02hFhbF7f2kDRBQyIvE43WbFuSzUOe6PtQEa9BvOnjcKMSTnQRKCJKtPpiYgoEtweNdt5zAgGRP2V8AGRzeHGxopabDtwCp2z6CUJKC/KwfxpI2GJ0PkeptMTEVGkjeljo3C6IGEDIkUR2Fl1Bp/urIHV4Q56fHRuMhbPKkRupiUirydLah+yvvYxIyIiCiU92cCknAiI6Xdnh8OBJ554Ap988gmMRiPuuusu3HXXXf2+79G6Vqzbehz1Z61Bj6Ul6XHNpQWYMjojYmd79FoZqUl6ptMTEVHE5aSboj2EuBDTAdEzzzyDyspKvP7666irq8OyZcswYsQIXH311X26X9N5Bz7aXo3Ko+eCHtNpZFxeMgKXTx0BnTYygYsEIMmsi9h2GxERUWfDGBBFRMwGRFarFW+//TZeffVVTJ48GZMnT8ahQ4fwxz/+sdcBkdPtwRd76vDF3jr/AbRAF4/NxNUz8pGWZIjU8P3d6SMVXBEREYWSncaAKBJiNiCqqqqC2+1GaWmp/1pZWRleeuklKIoCOYztJyEE9h89i4+2nUBLuzPo8RGZZiyaVYjRET6MZjZqkcx0eiIiGgSR/GU+kcVsQNTQ0ID09HTo9ReapGZlZcHhcKC5uRkZGT1X5Hz1g69w/NT5oOtmoxYLp49C2YRhkCOQRu8je9Pp+1u5moiIKFwplv41EydVzAZENputQzAEwP+x0xm82hNK52BIliXMmjIc86eNjHi2l8mgRcogpNNrvBWtNQlQ2ZpzjU+JNFcgsebLuUZHerIBWh7P6LeYDYgMBkNQ4OP72GjsfcuMSaMzcMuV45GbFZk0eh9ZkpCWbBj0dPqUlMTZM+Zc41MizRVIrPlyroMrLzcV6enmaA9jyIvZgCgnJwdNTU1wu93QatVhNjQ0wGg0IiUl/DM/malGXDerEBML0iBJElpaglPt+8qg0yAtyQC71QG7NbjVx0DQaGSkpJjQ2mqDxxPcZy2ecK7xKZHmCiTWfDnXvklP798v6k67E01NwQlDpAr37zdmA6KioiJotVrs2bMH06ZNAwBUVFSguLg4rAPVALDkW2MwdVwWtBoZigIAkfmGkSQg2aSH2aiFoggonUtcDwKPR4E7ROPZeMS5xqdEmiuQWPPlXAeXVpaiPoZ4ELObjiaTCTfeeCOWL1+Offv2YcOGDVizZg3uuOOOsO9RNmFYxLvI6zQyMlOMMBtjNpYkIqIEodPKLPobITH9rv7oo49i+fLl+P73v4+kpCTcd999uOqqq6IyFgmAxaSDxahlOj0REcUEZjVHTkwHRCaTCU8//TSefvrpqI5DK0tITdJDp+U3HhERxQ4W/42cmA6IYoHJoEWKmUUWiYgo9mg1fG+KFAZEXZAlINVigEHPVSEiIopNkT4nm8gYEIVg0GmQatFHtIo1ERFRpDEgihwGRAEC0+mJiIhi3UB3R0gkfOf30mlkpCbpGW0TEdGQwZ2MyEn4gMiXTp9k0kV7KERERL3CEkSRk9ABEdPpiYhoKMvLSor2EOJGwgZEZoMWyUynJyKiIey2BeOjPYS4kXABkSxLSDXrmU5PRERDHgszRk5CBURMpyciIqJQEiIgkiQgxayHyZAQ0yUiIqJeivsIQa+VkWJhOj0RERF1La4DoiSm0xMREVEY4nrZhMEQERERhSOuAyIiIiKicDAgIiIiooTHgIiIiIgSHgMiIiIiSngMiIiIiCjhMSAiIiKihMeAiIiIiBIeAyIiIiJKeAyIiIiIKOExICIiIqKEx4CIiIiIEh4DIiIiIkp4DIiIiIgo4TEgIiIiooTHgIiIiIgSHgMiIiIiSngMiIiIiCjhMSAiIiKihMeAiIiIiBKeJIQQ0R4EERERUTRxhYiIiIgSHgMiIiIiSngMiIiIiCjhMSAiIiKihMeAiIiIiBIeAyIiIiJKeAyIiIiIKOExICIiIqKEx4BoiHA4HHjssccwbdo0zJkzB2vWrIn2kAaE0+nE4sWLsX37dv+1mpoa3HnnnSgpKcG1116LzZs3R3GE/Xf69Gncf//9KC8vx2WXXYannnoKDocDQPzNtbq6Gj/4wQ9QWlqKuXPn4rXXXvM/Fm9zDbR06VI88sgj/o+/+uor3HLLLZg6dSqWLFmCysrKKI4uMj799FNMmDChw5/7778fQPzN1+l04oknnsD06dMxa9YsrFy5Er6axvE210TGgGiIeOaZZ1BZWYnXX38djz/+OF544QV8/PHH0R5WRDkcDjzwwAM4dOiQ/5oQAvfccw+ysrLw7rvv4oYbbsC9996Lurq6KI6074QQuP/++2Gz2fDHP/4Rv/nNb/DZZ59h1apVcTdXRVGwdOlSpKen4/3338cTTzyB1atX44MPPoi7uQZat24dPv/8c//HVqsVS5cuxbRp0/Dee++htLQUP/7xj2G1WqM4yv47fPgwrrjiCmzevNn/58knn4zL+T755JPYsmUL/ud//gfPPvss/vKXv+DPf/5zXM41oQmKee3t7aK4uFhs27bNf+23v/2t+N73vhfFUUXWoUOHxPXXXy+uu+46MX78eP9ct2zZIkpKSkR7e7v/ud///vfFc889F62h9svhw4fF+PHjRUNDg//aBx98IObMmRN3cz19+rT46U9/Ks6fP++/ds8994jHH3887ubq09TUJC6//HKxZMkSsWzZMiGEEG+//baYN2+eUBRFCCGEoihiwYIF4t13343mUPvtwQcfFM8++2zQ9Xibb1NTk5g0aZLYvn27/9rLL78sHnnkkbiba6LjCtEQUFVVBbfbjdLSUv+1srIy7N27F4qiRHFkkbNjxw7MmDEDf/7znztc37t3LyZNmgSz2ey/VlZWhj179gz2ECMiOzsbr732GrKysjpcb2tri7u5Dhs2DKtWrUJSUhKEEKioqMDOnTtRXl4ed3P1efrpp3HDDTdg3Lhx/mt79+5FWVkZJEkCAEiShEsuuWTIz/XIkSMoLCwMuh5v862oqEBSUhLKy8v915YuXYqnnnoq7uaa6BgQDQENDQ1IT0+HXq/3X8vKyoLD4UBzc3MURxY5t956Kx577DGYTKYO1xsaGjBs2LAO1zIzM3Hq1KnBHF7EpKSk4LLLLvN/rCgK/vd//xeXXnpp3M010Lx583DrrbeitLQUCxcujMu5bt26Fbt27cJPfvKTDtfjca5CCBw7dgybN2/GwoULMX/+fPzXf/0XnE5n3M23pqYGeXl5WLt2La6++mpceeWV+O1vfwtFUeJurolOG+0BUM9sNluHYAiA/2On0xmNIQ2aruYeL/NesWIFvvrqK7zzzjv4/e9/H7dzfe6559DY2Ijly5fjqaeeiruvq8PhwOOPP45f/vKXMBqNHR6Lt7kCQF1dnX9eq1atQm1tLZ588knY7fa4m6/VakV1dTXeeustPPXUU2hoaMAvf/lLmEymuJtromNANAQYDIagf2C+jzv/8I03BoMhaBXM6XTGxbxXrFiB119/Hb/5zW8wfvz4uJ5rcXExADVw+NnPfoYlS5bAZrN1eM5QnusLL7yAKVOmdFj98+nq3+9QnSsA5OXlYfv27UhNTYUkSSgqKoKiKHjooYdQXl4eV/PVarVoa2vDs88+i7y8PABqQPjmm2+ioKAgruaa6BgQDQE5OTloamqC2+2GVqt+yRoaGmA0GpGSkhLl0Q2snJwcHD58uMO1xsbGoGXqoeZXv/oV3nzzTaxYsQILFy4EEH9zbWxsxJ49ezB//nz/tXHjxsHlciE7OxtHjx4Nev5Qneu6devQ2NjoP+fne5Ncv349Fi9ejMbGxg7PH8pz9UlLS+vw8dixY+FwOJCdnR1X883OzobBYPAHQwAwevRo1NfXo7y8PK7mmuh4hmgIKCoqglar7XBQr6KiAsXFxZDl+P4STp06FQcOHIDdbvdfq6iowNSpU6M4qv554YUX8NZbb2HlypVYtGiR/3q8zbW2thb33nsvTp8+7b9WWVmJjIwMlJWVxdVc33jjDXzwwQdYu3Yt1q5di3nz5mHevHlYu3Ytpk6dii+//NJft0YIgd27dw/ZuQLApk2bMGPGjA6rfF9//TXS0tJQVlYWV/OdOnUqHA4Hjh075r929OhR5OXlxeXXNpHF97tpnDCZTLjxxhuxfPly7Nu3Dxs2bMCaNWtwxx13RHtoA668vBy5ubl49NFHcejQIbzyyivYt28fbr755mgPrU+OHDmCF198ET/60Y9QVlaGhoYG/594m2txcTEmT56Mxx57DIcPH8bnn3+OFStW4O677467uebl5aGgoMD/x2KxwGKxoKCgAFdffTVaW1vx61//GocPH8avf/1r2Gw2XHPNNdEedp+VlpbCYDDg5z//OY4ePYrPP/8czzzzDH74wx/G3XzHjBmDuXPn4tFHH0VVVRU2bdqEV155Bd/97nfjbq4JL3oZ/9QbVqtVPPzww6KkpETMmTNH/O53v4v2kAZMYB0iIYQ4fvy4uO2228SUKVPEokWLxD//+c8ojq5/Xn75ZTF+/PiQf4SIr7kKIcSpU6fEPffcIy655BIxe/ZssXr1an/Nlniba6Bly5b56xAJIcTevXvFjTfeKIqLi8XNN98sDhw4EMXRRcY333wj7rzzTlFSUiJmz54tnn/+ef/XNt7m29raKh566CFRUlIiZs6cGddzTWSSEN61PiIiIqIExS0zIiIiSngMiIiIiCjhMSAiIiKihMeAiIiIiBIeAyIiIiJKeAyIiIiIKOExICIiIqKEx4CIiIiIEh4DIqIhrq6uDuvWrQv7+Z999llQE9nu3H777XjkkUci9vzt27djwoQJqK2tBQDMmzcPzz//PADgvffew4QJE8J+LSKiSGFARDTELVu2DJs2bQrruSdPnsTdd9+Ns2fPDvCoulZaWorNmzcjNzc3amMgIupMG+0BENHgiYVOPXq9HtnZ2dEeBhFRB1whIhrCbr/9duzYsQPvv/8+5s2bB7vdjlWrVuHKK69EcXExbrjhBqxfvx4AUFtbiyuvvBIAcMcdd/i3qTZs2IBbbrkFJSUlKC4uxk033RT2ilNX2tvb8eCDD2Lq1KmYM2cOnnvuOSiKAiB4y4yIKBYwICIawp5//nmUlpbimmuuwTvvvIMHHngAa9euxS9+8Qv89a9/xfz58/HTn/4UGzZsQG5uLt5++23/5911112orKzEfffdh0WLFuGDDz7AX/7yF2RkZODhhx+G0+ns87g++eQTpKen47333sPDDz+M3/3ud/jDH/4QqWkTEUUct8yIhrC0tDTodDoYjUY0NTVh48aNeOmllzB37lwAwH333Yeqqiq89NJLmD9/PjIyMgAAqampsFgs0Gg0+MUvfoFbb73Vf8877rgDP/rRj3D27Nk+n/OZNGkSfv7znwMAxo4diyNHjmDNmjW48847+zVfIqKBwoCIKE4cPHgQAFBWVtbh+vTp07Fy5cqQn1NUVITU1FS88sorOHr0KKqrq1FVVQUA8Hg8fR5L5zFcfPHFeOmll9Da2trnexIRDSRumRHFOSEEtNrQv/vs2LEDCxcuxP79+zFx4kTce++9WLFiRb9fU5Y7/mhRFAWSJEGn0/X73kREA4ErRERxwle/p6KiAldccYX/+q5duzBu3DgAgCRJHT5nzZo1mDFjhv+ANQC88cYbAPqXkXbgwIEOH1dUVGDkyJEwmUx9vicR0UBiQEQ0xFksFpw8eRIWiwVXXHEFnnjiCUiShIKCAqxbtw4bN27EqlWrAABmsxkA8M0332DSpEnIzc3Fhg0bsGvXLgwfPhzbt2/Hf//3fwNAvw5V7969GytWrMBNN92E3bt3409/+hOWL1/e77kSEQ0UBkREQ9x3vvMdLFu2DNdffz3+8Y9/YOXKlfiP//gPtLa2Yvz48Xj++eexYMECAEB6ejqWLFmCZ555BtXV1bj//vvR2NiIu+++GwAwbtw4/Od//iceeugh7N+/H2PHju3TmG655RYcP34c//Iv/4KMjAw8+OCDuOmmmyI2ZyKiSJNELFRqIyIiIooiHqomIiKihMctMyIKy6uvvooXX3yx2+c89thjuOWWWwZpREREkcMtMyIKS0tLC5qbm7t9TmZmJpKSkgZpREREkcOAiIiIiBIezxARERFRwmNARERERAmPARERERElPAZERERElPAYEBEREVHCY0BERERECY8BERERESU8BkRERESU8P4/H7G5pjrdQBYAAAAASUVORK5CYII=",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x321b90748>)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"jointplot(x=\"total_bill\", y=\"tip\", data=tips, kind=\"reg\")\n",
"savefig(\"./test.svg\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Conditioning on another variable\n",
"\n",
"* Must use `lmplot` instead of `regplot`"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAHjCAYAAADrFv8WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xl0U+edPvDnape1WF7A2MYLtoEAWSAhJAQIJCFpaNYS2mmbXzpd5rQn3bJMTpvOtJ1MaEpnpm1m0jaT0zM96cyk0840OEmbNmlLEpYQShayUQhgG2MDxoAtWbvu1b3v7w9jY1myLNtaruzn808b6Vr6+mKsh3f5vpIQQoCIiIioSBgKXQARERHRRDC8EBERUVFheCEiIqKiwvBCRERERYXhhYiIiIoKwwsREREVFYYXIiIiKioML0RERFRUTIUuIJfOnAkUuoSiYDBIKC93oL8/BE1jz8KJ4v2bGt6/qeM9nJp83r9Zs1w5ff2ZgiMvBINBgiRJMBikQpdSlHj/pob3b+p4D6eG96/4MLwQERFRUWF4ISIioqLC8EJERERFheGFiIiIigrDCxERERUVhhciIiIqKgwvREREVFQYXoiIiKioMLwQERFRUWF4ISIioqLC8EJERERFheGFiIiIigrDCxERERUVhhciIiIqKgwvREREVFRMhS6AiIhIj4QQ6A6eQEgOw2EpQZ2zFpIkFbosgk7CiyzL2LhxI771rW/hiiuuAAB0d3fjW9/6Ft555x3U1NTg7/7u77B69eoCV0pERDPBYW8bXuneDV/MN/yYx+rBNXWrsKCspYCVEaCDaaNYLIb7778fR44cGX5MCIEvfelLqKysxNatW3Hbbbfhy1/+Mk6ePFnASomIaCY47G3Ds20vJAQXAPDFfHi27QUc9rYVqDIaUtDw0tbWho997GPo6upKePzPf/4zuru78fDDD6O5uRlf+MIXsHTpUmzdurVAlRIR0UwghMAr3bshoKV+Hhq2d++GECLPldFIBZ02ev3113HFFVfgvvvuw9KlS4cff/fdd7F48WKUlJQMP3bZZZfhnXfemdDrGwwSDAbOT47HaDQk/C9NDO/f1PD+TR3v4dSMvH9d/uPwyQNAmrUtXnkAPZFTqHfX5qtEGqWg4eWTn/xkysfPnDmD2bNnJzxWUVGBU6dOTej1y8sdXFw1AW63vdAlFDXev6nh/Zs63sOpcbvtQFiFKZMQaI2jrMyR+6IoJV0s2B0tEonAYrEkPGaxWCDL8oRep78/xJGXDBiNBrjddvj9Eahq6qFSGhvv39Tw/k0d7+HUjLx/iBkRz+QexkzwekMTfi8GnuzQZXixWq3w+RIXSsmyDJvNNqHX0TQBTeO8ZKZUVUM8zl98k8X7NzW8f1PHezg1qqqh2l4Nj6U0abHuSGVWD6rtc3ivC0iXE6RVVVU4e/ZswmNnz55NmkoiIiLKJkmScE3dKkhjfDxKMGBd3SouSSgwXYaXSy65BH/5y18QjUaHH3vrrbdwySWXFLAqIiKaCRaUteD2lg0os3oSHi+zenB7ywb2edEBXU4brVixAtXV1fjGN76BL37xi3jllVfw3nvvYcuWLYUujYiIZoAFZS2Y72ke7rDrtDgw11nDERed0GV4MRqNePzxx/H3f//32LhxIxoaGvCTn/wENTU1hS6NiIhmCEmSUO+aW+gyKAXdhJdDhw4l/HdDQwOeeuqpAlVDREREeqXLNS9EREREY2F4ISIioqLC8EJERERFheGFiIiIigrDCxERERUVhhciIiIqKgwvREREVFQYXoiIiKioMLwQERFRUWF4ISIioqLC8EJERERFheGFiIiIigrDCxERERUVhhciIiIqKgwvREREVFQYXoiIiKioMLwQERFRUWF4ISIioqLC8EJERERFheGFiIiIigrDCxERERUVhhciIiIqKgwvREREVFQYXoiIiKioMLwQERFRUWF4ISIioqJiKnQBRERE2SCEQFdvEIGIDJfdgvoqJyRJKnRZlAMML0REVPQOHvNi25vd6A/Ehh8rd1mxfnkdFjWUFbAyygVOGxERUVE7eMyLp7e3JQQXAOgPxPD09jYcPOYtUGWUKwwvRERUtIQQ2PZmNzSR+nlNANve7IYQY1xARYnhhYiIilZXbzBpxGW0/kAMXb3BPFVE+cDwQkRERSsQkbN6HRUHhhciIipaLrslq9dRcWB4ISKiolVf5US5y5r2mnKXFfVVzjxVRPnA8EJEREVLkiSsX14HwxjtXAwSsH55Hfu9TDMML0REVNQWNZRh07qWpBGYcpcVm9a1sM/LNMQmdUREVPQWNZThgnoPO+zOEAwvREQ0LUiShIY5rkKXQXnAaSMiIiIqKgwvREREVFQYXoiIiKioMLwQERFRUWF4ISIioqLC8EJERERFheGFiIiIigrDCxERERUVhhciIiIqKgwvREREVFQYXoiIiKioMLwQERFRUWF4ISIiyoO4qhW6hGmD4YWIiCjHonIc/f5oocuYNkyFLoCIiGi6EkIgEFEQjsYLXcq0wvBCRESUA6qmYSAoQ45zuijbGF6IiIiyLKaoGAjGoIlCVzI9MbwQERFlUTCiIBhRCl3GtMbwQkRElAWaJjAQkhFT1EKXMu0xvBAREU2RElfhC8pQOU+UFwwvREREUxCOKgiEFTC25A/DCxER0SRoQiAQkhGROU2UbwwvREREExRXNfgCMcQ5TVQQDC9EREQTEInF4Q/LEMwtBcPwQkRElAEhBAJhBeEYu+UWGsMLERHROFRNgy8gQ+Hhirqg64MZe3p68IUvfAGXXnoprr32Wvz85z8vdElERDTDxGQVfQNRBhcd0fXIy7333ouamhq0traira0NDzzwAGpra3H99dcXujQiIpoBAmEZIR6qqDu6HXkZGBjAO++8g7vvvhuNjY1Yv3491qxZgz179hS6NCIimuY0TaDfH2Vw0SndhhebzQa73Y7W1lYoioKOjg7s27cPixYtKnRpREQ0jcmKirP+KE+D1jHdThtZrVZ8+9vfxubNm/Ff//VfUFUVGzduxEc/+tGMX8NgkGAwSDmscnowGg0J/0sTw/s3Nbx/U8d7ODUj79/QoYqSBBiN/PzQK92GFwBob2/HNddcg8985jM4cuQINm/ejJUrV+LWW2/N6OvLyx2QJP7wZcrtthe6hKLG+zc1vH9Tx3s4eaomoAjAYDbBbdb1RyNBx+Flz549ePrpp7Fjxw7YbDZcdNFF6O3txb//+79nHF76+0McecmA0WiA222H3x+BytX0E8b7NzW8f1PHezg1qhCICwkDebh/tbOcOX39mUK34WX//v1oaGiAzWYbfmzx4sV44oknMn4NTRPQ2Lo5Y6qqIc453knj/Zsa3r+p4z2cuGBEQVRR4XbboaoaVJWfGcVAtxOks2fPxrFjxyDL8vBjHR0dmDt3bgGrIiKi6UDTBLyBGIIRBYJ9/ouObsPLtddeC7PZjG9+85s4evQoXn75ZTzxxBO46667Cl0aEREVsaHdRDGFp0EXK91OG7lcLvz85z/HI488gk2bNqG8vBx33303/uqv/qrQpRERUZEa2k1ExU234QUAWlpa8OSTTxa6DCIiKnKaJuALxti7ZZrQdXghIiKaqpiiYiAkcwPHNMLwQkRE0xaniaYnhhciIpp2VE3DQFDmNNE0xfBCRETTSkxRMRCMgbNE0xfDCxFRkRBCoKs3iEBEhstuQX2Vk0egjCCEQDCi6PIk6F5vGHv2n8JFC6sKXcq0wPBCRFQEDh7zYtub3egPxIYfK3dZsX55HS5qrihgZfqg12kiVdOw452TeGXfCagcCsoahhciIp07eMyLp7e3JU2D9AdieHp7G4xGCavKHIUpTgdisoqBkP6miU6eDWHrjnb09IULXcq0w/BCRKRjQghse7N7zA9mTQB/eqMbVy2deUenCCEQiCgI62yaKK5qeHnfCex854TuAtV0wfBCRKRjXb3BhKmiVPr8UXScGEC5w5ynqgovrg5OEyk6O0W7qzeArTs6cMYXSXhcAnDlkjmFKWoaYnghItKxQEQe/yIAAyF5xoSXqBzHQEiGns5TlOMqtr1xHLvf78HosipLbdi4tgmNc9wFqW06YnghItIxl92S0XWljsyuK2ZCCATCCsIxfU0TdZz0o3VnO/r9iSNkkgSsubga111WB7NJt+cgFyWGFyIiHauvcqLcZU07dVThtqGpthQ+3/RdGKrHaaKYrOLF17uw90Bv0nNVZXbcsbYZc2c7C1DZ9MfwQkSkY5IkYf3yupS7jQDAIAHXX143rfu9RGJx+MP6miY63O3Ds7s64AsmTusZJAnrltVg3bJamIwcbckVhhciIp1b1FCGTetaxuzzsrixvIDV5Y4ep4kisTh+v+cY3jp8Jum52koHNq5tQnXFzN22ni8ML0RERWBRQxkuqPfMmA67cVWDLxhDXNXPcMuBzn48t+soAqMOejQZJVx32VysvrgGRsP0/PPQG4YXIqIiIUkSGua4Cl1GzultmigYUfDb3Z14v6Mv6bn6KifuWNuMWR57ASqbuRheiIhIF4QQ8IcVRHQyTSSEwHvtffjta51JjfDMJgM+tKIOVy6eAwNHW/KO4YWIiApOb9NE/pCM5149ioPHvEnPNdW4sfHqJpS7bQWojACGFyIiKrBILA5/SE5q7lYIQgjsO3wGv9tzDFFZTXjOajZiw5X1uPyC2dN2rVGxYHghIqKC0IRAICQjMiokFIo3EMPW7e04cnwg6bmFdR7ctmYePE5rASqj0RheiIgo75S4hoFgDHEdnFyoCYEd+45j6ytHICuJTfDsViNuXtmIpfMrOdqiIwwvRESUV+FoHIGwPqaJ+gaieGZXBzpO+pOeW9JYjltXN8JVMv2PXig2DC9ERJQXmhDwh+SktSQFqUUTeG3/Kfzpje6kIwccdjNuXdWIi5oqClQdjYfhhYiIck5P00S93jBad3Sg+3Qw6bmlLZW46aoGOGwz44TuYsXwQkREORWOKgiElYJPE6mahp3v9ODlfcehjgpRpU4rPrJmHhbUeQpUHU0EwwsREeWEnqaJTp4NYeuOdvT0JZ+8ffmi2fjEhy6AElOg6qTPDKXH8EJERFmnxAebzo0e4ci3uKrh5X0nsPOdE0mncpe5rPjImiYsbPCgxGbGQExJ/SKkOwwvRESUVXrZTdR9OoCtOzpw2htJeFwCcOWSObhhRR2sZmNhiqMpYXghIqKs0EvTOTmuYtsbx7F7f0/S4Y6VpTZsXNuExjnuwhRHWcHwQkREUxZXNfgChd9N1HHSj9ad7ej3xxIelyRg9UXVWL+8DmaToUDVUbYwvBAR0ZREYnH4w3LSKEc+xWQVL77ehb0HepOem11mx6a1zZg721mAyigXGF6IiGhShBAIhBWEY/GC1nG424dnd3XAF5QTHjdIEtYtq8G6ZbUwGTnaMp0wvBAR0YTFVQ0DQTmpO20+RWJx/G7PMew7fCbpuZpKB+5Y24TqCkcBKqNcY3ghIqIJicpx+ENy0tbjfDrQ2Y/ndh1FIJK4vdlklHDdZXOx+uIaGA08SHG6YnghIqKMCCEQiCgIRws3TRSMKHj+tU68196X9Fx9lRMb1zZjtsdegMrGxyyVPQwvREQ0LlXT4AsUbppICIH3O/rw292dCI0KT2aTATdcXoeVS+bAoMOEIAGw20xw2nleUrYwvBARUVqFnibyh2U8t+soDh7zJj3XVOPGxqubUO62FaCy8VnNRrhKzFwwnGUML0RElFKhp4mEENh3+Ax+t+dY0vlIVrMRH76yHssvmA1JkiCEQM/ZMEIxBQ6rGdWVJZCkwo3CmIwSXCUWdvDNEYYXIiIMflB29QYRiMhw2S2or3IW9MOv0Aq9m8gbiOHZXR04cnwg6bmFdR7ctmYePE4rAKD9xABe238KA6HzW6VLHRZcdeEcNNeW5q1mADAYJLjsZtit/HjNJd5dIprxDh7zYtub3egPnO/KWu6yYv3yOixqKCtgZYURleMYCBWm6ZwmBF4/2IsX93ZBVhKDk91qxM0rG7F0fuVwsGw/MYA/vN6VNKU1EJLxh9e78KEV9XkJMBIAh92MEpsJhhkcevOF4YWIZrSDx7x4entb0odffyCGp7e3YdO6lhkTYArddK5vIIrWne042hNIem5JYzluXd0IV4ll+DEhBF7bf2rMtTiaAF7bfwpNNe6cjqLZLUY4S8wwGriuJV8YXohoxhJCYNub3Wk//La92Y0L6j3TfgqpkNNEmjYYQv70RnfS+zvsZty6qhEXNVUkfV3P2XDCVFEqAyEZPWfDqJmV/WZ1FpMBrhIzzKbx17UoWhwhJYRZcGW9jpmI4YWIZqyu3mDCVFEq/YEYunqDaJgzfT90CjlN1OsNo3VHB7pPB5OeW9pSiZuuaoDDlnqLcSimpHx8stdlymiQ4Coxw2YZ/yNU1VQElRCiavqfM5oYhhcimrECkfT/ap/odcWmkNNEqqZh5zs9eHnfcaijhr7cJWbctqZp3Ok6hzWzvimZXjceg3RuXYvVNO5InKqpCMXDiMajKOw529MTwwsRzVguu2X8iyZwXTGJqxp8wRjiav4/Wk+eDWHrjnb09IWTnlt+wWxsuKI+o9061ZUlKHVY0k4dlTosqK4smVK9w03mbOZxm+BpQkNICSMSjzC05BDDCxHNWPVVTpS7rGmnjspdVtRXOfNYVe5FYnH4w/mfJoqrGl7edwI73zkJbdSbl7ms+MiaJrTMzXxnkCRJuOrCOSl3GwGDIyVXXThnSuuVbBYjnPbxm8xpQkM4HkFYiUAwtuQcwwtRERBCoDt4AiE5DIelBHXOWl0tINV7fWORJAnrl9el3G0EDH74rV9eVxTfSyYKOU3UfTqArTs6cNobSXhcAnDlkjm4YUXdpBq6NdeW4kMr6rPe5yXTxbhCCETiEYSUCDQU7oTtmYbhhUjnDnvb8Er3bvhivuHHPFYPrqlbhQVlLQWsbJDe6xvPooYybFrXMu37vBRqmkiOq9j2xnHs3t+TNNJTWWrDxrVNaJzjntJ7NNeWoqnGnZUOuybDuc64lvGD1GBoCUMVDC35JglRiPXl+XHmTHKvAEpmMhlQVuaA1xtCPM6/hBOVy/t32NuGZ9tegEjxLzoJBtzesqGgASEb9enl56+YO+yOdw8LNU3UcdKP1p3t6PcnTstJErD6omqsX14Hs6nwvVGMRgnlZQ6ochyWDOqJxqMIKWHEhTrutaNd2NA0mRJpFI68EOmUEAKvdO9OGQwAQEDD9u7dmO9pLsiHrN7rmyhJkqbdduhCTRPFZBUvvt6FvQd6k56rKrPjjrXNmDtbH+uIJABOuxmzy0owMBBOG6BjqoygHEJcFKaJH53H8EKkU93BEwlTMal4Yz4cD55Enas2T1Wdp/f6ZjpV0+AL5L/p3JHjPjyzswO+YOIOIIMkYd2yGqxbVqubE5aHOuNaLaa0u4hkVUFICUHWstsvhiaP4YVIp0Jy8jbSVIJyKMeVpKb3+maymKxiIBQbs3NwLkRicfz+z8fw1qEzSc/VVDpwx9omVFdkv8vtZGS6GHeoK25MnZ59fooZwwuRTjksmfWmcFoK84Gg9/pmqmBEQTCS3xGCg539ePbVowiEE9/XZJRw3WVzsfriGhjH6Y+SD5l2xmVXXP1jeCHSqTpnLTxWT9qpmTKrB3OdNXms6jy91zfTqJpAvz+KcDR/6zGCEQXPv9aJ99r7kp6rr3Ji49pmzPbY81bPWCRpcF3LeJ1xVU2FXw6yK24R0MfEIxElkSQJ19StgjTGX1MJBqyrW1WwxbB6r28mkeMqznjDiCkT3/0yGUIIvNd+Fv/663eTgovZZMBNKxvw+VuWFDy4SABKrCbMKrXDYTOP+bOoCQ3+aABnI/2IMLgUBY68EOnYgrIW3N6yAdu7d8M7YoSjzOrBOh30UdF7fTNBOKogLKtwu/MTFPxhGc/tOoqDx7xJzzXVuLHx6iaUu215qSUdq9kIV0n6zrhDXXFlOQaXufA1U+YYXoh0bkFZC+Z7moc72DotDsx11uhmREPv9U1XmhDwh2REZRVGY+7vtRAC+w6fwe/2HENUThzhsZqN2HBlPZZfMBuGAv+5m4znmsyl6dY7uiuuXnY/UeYYXoiKgCRJqHfNLXQZY9J7fdNNXNXgC8QQz9N2Im8ghmd3deDI8YGk5xbUeXD7mnnwOK15qWUsBglw2i0osaX/WGNX3OmB4YWIqIjks1uuJgReP9iLF/d2QVYSP+ztViNuXtmIpfMrCzrKJgEosZngsJvTjvpMpSsu6Q/DCxFRERBCwB9WEMlTt9y+gSi27mxHZ0/yMStLGstx6+pGuEoseallLJmc+MyuuNMTwwsRkc7FVQ0Dwfx0y9U0gd37e7DtjeNJ7+ewmXDr6nm4qKki53WkYzYONpmzpFnXwq640xvDCxGRjuWzW26vN4zWHR3oPh1Mem5pSyVuuqoBDps594WMwWCQ4LKbYbeO/dHFrrgzA8MLEZFOBcIyQnloOqdqGna+04OX9x2HOioluUvMuG1NExY1lOW8jrFIABx2M0pspjHXtbAr7szC8EJEpDOaJuALxiCnOeE4W06eDaF1RztO9iWfVbV84SxsuLIh7UhHrg0dnmg0pF7XomoqQvEwu+LOMAwvREQ6IisqfCEZWo7nieKqhpf3ncDOd05CG7V1yeO04CNXN2H+XE9Oa0jHbDTA7Rj78ERNaAgpYUTiEYaWGUjX4UWWZWzZsgXPP/88zGYzNm3ahPvuu4/Nr4goJSEEunqDCERkuOwW1Fc5i+r3RSiqIBhWcv5h3H06gK07OnDaG0l6buWSObhhRV3aJm+5ZDRIcKZZ1zLUFTesRCAYW2YsXYeX73znO9i7dy9+9rOfIRQK4b777kNNTQ0+/vGPF7o0ItKZg8e82PZmN/oD59c8lLusWL+8rqDrNTIxsltuLslxFdvePI7d7/ck9YmpKLVh49VNmFftzmkNY5EkwGEzw2FLfXji6K64NLPpNrz4fD5s3boVTz75JC6++GIAwGc/+1m8++67DC9ElODgMS+e3t6WtCOnPxDD09vbsGldi24DjBLXMBDMfbfcjpN+tO5sR78/cUGrJAFrLq7GdZfVwWwqTJt8u9UEp9005rqWSDyKkBJiV1waptvw8tZbb8HpdGLFihXDj33+858vYEVENBm5nsoRQmDbm91jbiXWBLDtzW5cUO/R3RRSJBaHPyTndPIjJqt48fUu7D3Qm/Tc7DI77ljbjLrZzhxWMDaLyQBXiWXM0BSNxxBSQuyKS0l0G166u7tRW1uLZ599Fk888QQURcHGjRtx9913wzBGOh/NYJBgMOjrl5UeGc91pzTycLJJ4f0b24HOfvzx9W70B6LDj5W7bLhhRR0WN5YDmPr96+zxwxuMIV0u8QZjONEXQuOcwkyJjCbOTROFY3EYsnCoYuI9PD86cbjbh63b2+ELJvY8MRgkXLOsFtdeVluQQwlNRgPcJRZYLanX1cjnuuIqWhwwACbktsahPwODUcr5e1F26Da8hMNhHDt2DL/61a+wZcsWnDlzBt/+9rdht9vx2c9+NqPXKC936O5fWnrmdtsLXUJR09P9E0Kg/cQA/CEZbocFzbWlef+78F7bGWzd0QEhRMIHpD8sY+uODrhcNlzcMmv48cnev6OnQxl9AAuDEWVljkm9RzbFVQ39/ijMNgtKbdltr+902gAMLvzd+tIRvPZ+T9I19VUufOrDizC3ypXV986EQZLgcljGXNciqwoCsSBUVYbdaoYd+W2IN3T/SP90G15MJhOCwSB+8IMfoLa2FgBw8uRJ/PKXv8w4vPT3hzjykgGj0QC32w6/PwI1D+3Hpxu93b9MRjtyTQiBrS8dgRIfe7i/9eUjmFtuh8lknNL9k1QV8Qy+TtJUeL2hCb9+NsVkFb5gLGlr8lQZjQY4nTYEg1G813YWz+zsQCCc2BbfZJSwfnkdrl5aA6NBwsBAcl+XXJEkCQ6bCTa7GUpUhi+aOBIU1+IIyoXrimswSsP3T1Nzu/aoJv+ZcVrSbXiZNWsWrFbrcHABgHnz5qGnJ/lfEmPRNJHzXgnTiapqiOehKdZ0pYf7N9bC1T5/FP/70pG8LVw9diqAPn807TVnB6LoOOFH89xSAJO/f7WVDpQ5rQm7jEYrd1lRW+Eo6J9PbrvlagiEZTz14gd4t60v6dn6Kic2rm3GbI8dEICa4w/okUYuxtVUAW3ECp/BrrhhRNX0Pyu5NjRVpKkioyBMhafb8HLJJZcgFovh6NGjmDdvHgCgo6MjIcwQ0Xl6WrgaiGT2L+hMr0tHkgZHFFKFNgAwSMD65XUFm0LOdbdcIQTebevDb17tRDCSONpiNhpww4o6rFwyJ++j0FazEa6S1Cc+q5qKcDzCBnM0aboNL01NTVi3bh2+8Y1v4KGHHsKZM2fw05/+FHfffXehSyPSpa7eYNrRB2Bw63BXbxANc3I7du2yZ7aWI9PrxrOooQyb1rXors9Lrrvl+sMyntt1FAePeZOea6pxY+PVTSh353cdh8kowVViSdnkThMawkoE4XiYoYWmRLfhBQC+//3vY/PmzfjEJz4Bu92OO++8E3fddVehyyLSpXyOdoynvsqJctf4Uzn1VdnboruooQwX1Ht002E3l91yhRDYd/gMfrfnWFJjO6vZiA1X1uPyC2bn9XtPd+KzEGK4Ky4bzFE26Dq8uFwu/PM//3OhyyAqCvke7UinUFM5kiTlfFRpPLnulusLxvDMzg4cOT6Q9NzCeg9uWz0PHqc1J++dSrrOuINdcaMIx8NsMEdZpevwQkSZK8RoRzp6ncrJpbiqwRfITbdcTQi8cfA0Xth7DLKSGATsViP+6vqFuGCuG1oeM0K6zrjReAxBJQSVDeYoBxheiIqEEALdwRMIyWE4LCWoc9Ym/EtXjwtX9TaVk0u57JbbNxBF6852HO0JJD23uLEMG9c2YW6159z259yvJknXGVdRFQSVEGRNSfGVRNnB8EJUBA572/BK9274Yr7hxzxWD66pW4UFZS3Dj+lxtEMPUzm5JISAP6wgEsv+NmhNE3ht/yn86Y1uKKO28DpsJtyyah4uaioHmzI8AAAgAElEQVSHKU9nEpkM5xbjpuiMO7jtOYSomn7ROFE2MLwQ6dxhbxuebXsBYtRCR1/Mh2fbXsDtLRuSAkyxjnbk+hykbIurGgaCclKwyIZebxitOzrQfTqY9NzSlkrcdFUDHLb8dKA1SIDz3GLc0X8e3EFEhcDwQqRjQgi80r07KbgMPw8N27t3Y76nOWkKqdhGOw509uMPe7t0M2I0npisYiAUG7OvzmSpmoZd7/bgpbeOQx314u4SM25b05S3+yEBsNtMcNrNMKQIkZF4BEE5zB1ElHcML0Q61h08kTBVlIo35sPx4EnUuYq3geN7bWfwfy+3JX1Y9wdieHp7W946A2cqV91yT54NYeuOdvT0JbfuX75wFjZc2ZByK3IupGsyJ6syAnIIcZGrjsFE6TG8EOlYSM7s/JmgXNgze6ZCCIHf7OwY87yffHYGHk+uuuXGVQ2v7DuBHe+cTLoPHqcFH7m6CfPnerL6nmMxGw1wlZhhSdFkLq7FEVQKdwYR0RCGFyIdc1hKMrrOaSn8acmTdexUAH0DkbTX5KszcDpKXIU3mP1uud2nA9i6owOnvcn3YOWSObhhRV3KbrXZlq7JnCY0hJQw2/mTbjC8EOlYnbMWHqsn7dRRmdWDuc6aPFaVXaNPPx7zujx0Bh5LLrrlynEVL715HK++34PRg04VpTZsvLoJ86rdWXzH1MZvMhdBUAlDMLaQjjC8EOmYJEm4pm5Vyt1GACDBgHV1qwo+nTIVrpLMdszkozPwaLnqlnu0x4/WHR1JJ29LErD6omqsX16XsodKtqVvMhdFUAmzyRzpEsMLkc4tKGvB7S0bsL17N7wjRmDKrB6sG9XnpRg1zHGhotSO3v6x1+3kszPwECWuYSCY3W65MVnFi693Ye+B3qTnZpfZccfaZtTNzv33ma7JnKzKCCohKBoX45J+MbwQFYEFZS2Y72ke7rDrtDgw11lT1CMuQyRJwq1XN+Fnz+2HmmLRbiE6A4ejcQTC2e2We+S4D8/s7IAvmDj9ZZAkrFtWg3XLalPu7MmmdE3mFC2OoBxkZ1wqCgwvREVCkiTUu+YWuoycuLhlFj52bUvB+7yIc9NEkSxOE0Vicfx+zzG8dfhM0nM1lQ7csbYJ1RW5XXCdrsncYGfcMKJqdIyvJtIfhhci0oXFjeWYX1tasA67uThU8UBnP5579WjSomSTUcJ1l83F6otrYDTk7vtL12ROCIFwPIIQF+NSEWJ4ISLdKFRn4EgsDn9YTtr1M1nBiILnX+vEe+19Sc/VVzmx8epmzC6zZ+fNxmCzGOG0JzeZE0IgqkYRUiJcjEtFi+GFiGasbB+qKITA+x19+M3uToRHdeA1Gw24YUUdVi6ZA0MOR1vGajLH0ELTCcMLEc1IcVWDLxhDXM3OcIs/LOM3rx7FgU5v0nNNNW585OomVLhtWXmvVIwGCR6nFeYUIy2ReBTheBiq4BlEND0wvBDRjJPNaSIhBN4+chbPv9aZ1A/Gajbixivqcfmi2SkPNswGSQJcJRZUlZfA5wsjfu7oAk1og6FFifDgRJp2GF6IaMYQQiAQVhDOYJpICIGes2GEYgocVjOqK0uSFg/7gjE8s7MDR44PJH39gjoPbl8zDx6nNWv1j2a3muCym2GxGIdrY2ihmYDhhYhmhLiqYSAoQ1HH/0BvPzGA1/afwkDofE+WUocFV104B821pdCEwBsHT+OFvccgK4mvZ7cacdPKRiybX5mznVKpmswJIRBWIhiIBBladEQIge7ACRzoP4R2Xyf+veGRQpc0LTC8FAkhxHCDMoelBHXO2mnRoIwKZyb9TMVkFQOhGDLZBd1+YgB/eL0LqiagqBo0TcBgkOALxvCH17uwcskcvHnoDI72+JO+dnFjGW5bPQ+uktwcZTBWk7loPIozoQgCMoOLHggh0BU4gYP9h3Cw7zACSrDQJU07DC9F4LC3Da907044nM9j9eCaadAangpDDz9TQgh09QYRjsVRM0dBeUn2fx0JIRCIKEk7f9Jd/9r+U4jE4ghG4tC080FAkiSYjBKe3tGetFbGYTPh1tXzcOG88pwEwMEmcxaU2BLv0VArfyFpcNtyu/Wa0tOENjjC0ncIB/sPI6iMfdwFTd2kf1t0dnbi8OHDMBgMWLJkCaqrq7NZF51z2NuW8lA+X8yHZ9tewO0tGxhgaEL08DN18JgX297sRn8gBkkCTEYD3CUWXHfZ3Kx101W1wWkiOZ75SETP2TBOe8Pwh2WM7NsmhEBcFZBTZKBLWipw81WNcNgyO2ByIiQAJTYTHKOazMW1OIJKCDF1cFor18cKUGqa0NAVOIEDfR/gg/4j4wYWuyl3u81mmgmHl2AwiPvvvx+7du2COPfPD0mS8OEPfxhbtmyBxZL/k1+nKyEEXunenfI0YQAQ0LC9ezfme5qn7XA/ZZcefqYOHvPi6e1tw1M4sqJCVjSEowqe3t6GTetaphxgJjJNNFIwKiMYiQ8HFyEENIGUr+MuMeO2NU05O7ogVZM5VVMRiocRibOVf6FoQkOX/zgO9A+OsISUcNrr7SYbLiibj8UVC9Hors9TlVP34IMPoqysDF//+tcLXUpKEw4vjzzyCI4ePYqf/vSnWLZsGTRNw759+7B582b88Ic/xIMPPpiLOmek7uCJhGH9VLwxH44HT6LOVZunqqiYFfpnSgiBbW92QxNAVI7DH1KgahokSBAQMBoMeGZXBy6ov3TS4SkQlhHKcJpotHD0/FSREAJjDdrMq3bh/92wEHZr9qe6BhfjmmE2nV/XogkNYSWCcDzMRv4FMPHAYscF5fOxuHwBGt31MBqSD8KkqZnw37xt27bh8ccfx+WXXz782Lp162CxWPDAAw8wvGRRSE7/F2RIUObcKmWm0D9TXb1B9AdiiMpxeAOxwRGOERlFVTV09Qaw452TWLdsYuFpMtNEo5XYzJAkCXFVG3PUxmw0YO3S2qwHF6NBGj48cchgg7kIQtz2nHea0HDMf3xw0W2GgWVR+XwsKl+IRnddXgLLv/zLv+DZZ5+FpmlYvHgxHnroIfzkJz9BeXk59u3bhw8++AAXXnghvva1r+G73/0uDh06hKVLl+JHP/oRnE4nzp49iy1btuDVV1+FzWbDTTfdhHvvvTdpBmXPnj2455578Oijj2LVqlU4dOgQvvOd7+DgwYOorq7GAw88gLVr1wIArr32WqxatQp//OMfceONN+If//Efc/K9T/hvn9FohMuVfPbIrFmzEI9np8U2DXJYSjK6zmnJ7Ym0NHFDi1EzPWBwotdPtqaAEkQkHoNRMsBsNGOsdxj5M5XN2gKRwTUa/pCCMYcQBLD7/R6sXVqT8D7p6hg9TSSEwKlID8LxMEpMJZhjr86o5mBYgaqJlMHFIA02hLNbjQhHFQghsvJnJEmAw2aGw2bKWa+WTHrWjPf1p8K9CCtRlJhtmFNSpbup6ql+jwCgCg1HB47hQN8hfOA9knFgGZoSMkj5W3u0Z88evPDCC3j++efhcrnwD//wD/jRj34Eg8GA1tZWPPXUU6iursYdd9yBL37xi/jP//xPVFZW4mMf+xiee+453Hnnnfjyl7+M2tpavPTSSwiFQvjSl76Exx57DA888MDw+7z99tu477778MMf/hCrVq1CMBjE5z73Odx999148skn8dZbb+ErX/kK/vd//xfz5s0DAJw8eRI7duzIaSaYcHj51Kc+hc2bN+Pf/u3fUFlZCWBwHcy//uu/4lOf+lTWC5zJ6py18Fg9aYf5y6wezHXW5LEqGs/IxahDyl1WrF9el3J9xESvn4yh3UXeqBdBJQhVU2E0GOEyO2EzJTZRG/kzle3aXHYLZEWFOk6vlXAsjq7e4PAhjenqmDvLkTBN1Bk4ir1n/oyAcn4rs8vsxhWzrkSja17K95PjKl568zhefb8nZdfdkUcRxRQNu97rwfsd/cN9XyarxHruxGdD7hrMtZ8YwJ79p+Ab0bPG47BgZYa1dw4cw95T++CXz99Pt8WNK+ZcisbShqzUOFVT+R41oaHD143D3W14t+fAuIGlZGhKqACBZSSz2Yy+vj78+te/xvr167F582YYDAY8+OCDuOaaa9DSMrjo/qKLLoLFYkFzczMA4JJLLsGJEyfQ1dWFt99+G48//jicTiecTifuuecePPjgg8Ph5fDhw3j66afx9a9/HatXrwYA7NixA+Xl5bjzzjsBAFdccQWuu+46PPPMM7j//vsBAB/60Idgs+V2cfKEw8urr76K999/H9dddx0aGxthMpnQ2dmJUCiEgwcP4plnnhm+9qWXXspqsTONJEm4pm5Vyp0hACDBgHV1q3T3L6CZbPRi1CH9gVjKxagTvX4yRu4ukiQJLrMTvtgAVE2FLzYAD0qHA8zIn6lc1FZf5USJzYS+5Ia0w4xGA8wmw/AozVh19Pmj+NVLh3HD5fXDH1CdgaN4qedPw5sJhgQUP17q+ROuw/VJAeZojx+tOzrQ509eBGu3GmEySIjI6uAolQQ47YMjJAMhGX94vQsfWlE/4QBjNRvhKjm/GFcTGsLxCMJKBCKLq1qGetaMvne+DGvvHDiGbV07k37/+GU/tnXtxPr6qwseYCbzPWpCQ6e/Gwf7DuFg/xGE4+MFlpLBKaGKwSmhQgWWkZYvX44tW7bgf/7nf/DYY4+htrYW3/jGNwAApaXnv1+j0Qi32z383waDAUII9PX1oaSkBOXl5cPP1dTU4OzZs1AUBQCwd+9eLFu2DM8//zw2bdoEYHBUpb29HcuXLx/+OlVVcf311w//99DARi5NOLxcddVVuOqqq3JRC6WwoKwFt7dswPbu3fCOGIEps3qwjn1edGXkYtRUNAFse7MbF9R7IEnShK+fbE2jdxfZTFZ4UIrAuRGYgBKE1WRF+YifqVzVJkkSVl1YjV+dPpJ62kga3MUjSRJcdsuYdWhCQD13oOJr+0+hqWbwl/PeM39OCi4j78XrZ/eiwdkISZIQk1W8+HoX9h7oTbrW47TC47RAjmvoG4hCwuAvfafdBKvl/K9NTZx//0zuw+gmc+cX4mY3tACD3++e/afS/hnuSVO7EAJ7T+1LuzPt9VP70OCuL9g/oCbyPQqISQWWxRUL0aCTwDJST08Pmpqa8NRTTyEUCuEXv/gF7r33Xlx//fUZ/XnU1NQgHA6jv79/OMAcP34cHo8HZvPgtv+Pf/zj+OpXv4oNGzbg6aefxqZNmzBr1iwsXboUv/jFL4Zf69SpU7Baz4/g5uPnYcLh5ctf/nIu6qA0FpS1YL6nebgbqtPiwFxnDUdcdObYqUDCtEYq/YHY8HTI0OLVTK+fjLF2F9lMVliNFiiaAlVouK7uaiyvWjr8M5XL2tYurcFr+3tw4mw4YfrIZBjcZWOzmlDusqK+ypmyDlUT0EZ8Wg2EZPScDUNyDCRMFaXilwdwKnIKwX47ntnZAV9QTnjeIElYt6wG65bVwmiQ8G7bWWx76ziMBgkmoyHl37mh96+ZNfbas9FN5jShIaQMbnnOdmgZ0nM2nDCNkoovTe2nwr0JU0WpDMh+9IZPY46jakq1TtZ436OAhjPKSfz6YBu6wkcRjkfSvp7DXDK8rVmPgWWkd999F1u2bMFTTz2Furo6uN1uuN1uGI2ZLRSuqqrCypUr8cgjj+Dhhx9GMBjEY489hltuuWX4GrPZDLfbjQcffBCbN2/G2rVrsW7dOvzTP/0Tnn/+eWzYsAGdnZ349Kc/ja9+9av46Ec/mqtvN0lG4eXHP/4xPve5z8Fut+PHP/5x2msZbnJDkiTUu+YWugxKIxBWMrvu3HTI0P9mev1kpNtdJEkSLMbBXQVOsyPhgzmXtUmShI9c3Yxfv3IEUUWDEAIWkxEGAwBIMEjA+uV1kCQp4fWFEFA1kXJNSiimwGAdfyeVGjfgD7tP4fDR5GBWU+nAHWubUF1x/oPcYTfDZhn/12QolvrPfnSTOVVTEY5HEIlHcr7leayaMr0urGTWSyakpA8EuZSqdgENcWs/ZNspyLZeCKOCD9JkMIe5BIsrFmJFw8WYZZwNrUg2dd144404dOgQPvGJTyAUCmHevHl47LHH8Ktf/Srj1/j+97+PRx55BNdddx0A4NZbb8Xf/u3fJl13yy23oLW1FQ8//DB+9KMf4T/+4z/w3e9+Fw899BBKSkrwiU98Iq/BBcgwvLS2tuLOO++E3W5Ha2vrmNcJIRheaMZylWTWYdVltyT8b6bXT8Zkd6zlurZFDWX46DXzse3NbniDMZiMBsRVDWXOxMXAQ68/1OF2LA6rGZIp/fcaOuvG2SNzocqJwcVklHDdZXOx+uIaGA2JIysOa2Z/pqmus1kG17UYDYZz03P5CS3paprIdSXmzBZcOsyFO5ZgqPZUgSXt15lLsKh8ARaXL0S9ey4sJhPcpXb4B4prS/o999yDe+65J+GxpUuXJvz39773vTH/u7KyEo8++mjK1x79dU8++eTw/1+yZEnCtNFIL7/88viFZ0FG4WV0MVu3bkVZWeJCvd7eXtx6663Zq4yoyDTMcaHcZU073TI0HQIMLl6dyPWTMdkda/mobVFDGS6o9+DE2RCE0QhJU1FbkTgCVF/lhLvEjD7/2HWUOiyoriwBUAKX2Z00daQqRpxtq0XodPLi4voqJzZe3YzZZak/gKsrS1DqsCScLj32+w8a2WRO1VT45QCi8Wjem8tVV5bA47CknVbxjKp9pDklVXBb3GmnjkotblSVzJ5yrZOhairCptNQKg8gaOyZcGDR85QQjS+j8PL73/8eu3btAjC4SGjz5s0Ji3MA4MSJEzAY+MNAM5ckSVi/vC7lzhgACdMhk7l+sjVNZsdaPmobep/GajfKyhzwekOIj2gwpwmBgaCMFYuqUu4mGarjqgvnDNdxxawrh3cbCQGEzpTibFstNCVxdMFsNOCGFXVYuWTO8Dblseq76sI5Gb3/yCZzhQwtQyRJwspxal854t6l+vor5lyacrcRMPizs2LO5DshT4aqqej0d53rw9KGSDwCpBn8k1Qr5pc248r6i1HvqmVgmUaMDz300EPjXeR0OtHa2gq/348TJ07A4XAgFArB7/fD7/cjEAigpKQE9913HxobG3NfdYbC4cmvFZhJDAYJdrsF0aiSsBCSMjPy/lW4bZhdVoKevhAisjp8TbnLipuvmpe0tXiWxz6h6yejwl6OWSUV6A2dQVQ9v46hzOrBjfOuHXPHWj5qA1L//ClxFd5ADIqqodxtQ7nbhjO+CGLK+TpKHRZcs6w2YRusx1qGcks5evxeHP9LFXxdcyC0xAWM86rd+PSHL8DC+rKMPnjHe//5c0vhLDGj1GGBwQAElRACcgCKlr+mnQaDBKvNjFgsDm3EoqCh2s/6IoiOqN3jsGDdqHuXisfmQbnNg75IP2Lq+dGvUosba2qvzMs2aVVT0TFwDLtP7MVvj/4B+06/h1Ph04iPcX8l1QprpBaz5SW4uWU91rZcDI+1NO2f9Vj3Lxdme3JzFtZMI4mx9hWO4a677sJPfvKThH3jenXmTKDQJRQFk8mQ8l++lJlU90+vHXYns2Mt17WNvn/hqIJAWEkascikg6oQAvsOn8Hv9hxDdETgAgZ7q9x4RT0uXzQ74YTmTI1+/5rKEpTYzXDazQDEud1D+VvTMpLRIMEPH874vLAakzvgZrPDrsNsR1XJ7JyOuKiaiqNDIyz9RxJCdypOswOLyhegytgAh1QBl806oe/RZDQMr3mJj9NAcaoubGjK6evPFBMOL8WE4SUzDC9TUyz3Lx8BaTKG7l9ffxD9A9Gk0JEpXzCGZ3Z24Mjx5A54C+o8uH3NPHic1hRfOXFDJz4bDMhJc7mJ6Bw4htdP7UNQDZ3bei501wE3E0MjLAf7D+GD/raMAsviioVYVL4Q9a7aKf0sM7wUn+wfiUpEupOPIwimQomr6PNFE6ZlMqUJgTcOnsYLe49BVhI/eOxWI25a2Yhl8yuzEtSGFuOajIbBAxNjhd2dcr4DroDReH49h5464KYzFFgO9B/CoQwCi8vsxKKKwUW3dVMMLFTcGF6Iprl8HEEwFaGogkhcID6JBht9/ihad3TgaE/yjpjFjWW4bfU8uEomv9V8yNBiXJvFiKgaxUA0jLimTvkgwKlI7ICbokOuDjrgpjIcWPo+wCFvG6Jq+maIDCyUCsML0TSWjyMIJksTAv6QDEXVUFo6sV9Fmibw2v5T+NMb3VBGDfM7bCbcunoeLpxXnoXdUOdPfI6qMfRH/YgLdcqHHWZDMXTAHaJqKtoHOnGw79DEAkvFQtQ5GVgoGcML0TSWjyMIJkOJa/AFY1A1AaNxYh9Mp70RbN3Rju7TwaTnLmmpwM1XNcJhy6xBWzp2qwlOmwmyiKEvGoAqBqe0pnrYYbbovQNuXIufG2EZDCyx8QKLxYnF5QuxqGIBAwuNi+GFaBrLxxEEEzXWbqLxqJqGXe/24KW3jkMdlRzcJWbctqYpK9NfVrMRTrsJccjwysHh0AJM/bDDbNJjB9zzgeUDHPK2ZxxYFlcs5HltRWDhwoW4+eab8YMf/CDh8dbWVvz4xz/OW3ddgOGFaFrLxxEEmRpqOjeZRbknz4bQuqMdJ/uSzy9avnAWNlzZALt1ar/Ohk581gwKBpSBhNAyZKqHHWaTXjrgxrV4wpRQTE1/f9wW12CnWwaWKRNCoP3EAPwhGW6HBc216fvZZMPzzz+PTZs2YeXKlTl9n/EwvBBNY/lo858JJa7CF5STRkzGE1c1vPL2Cex4+2RS8zCP04KPXN2E+XM9U6pt8MRnMwwmFUFlAPH42OFqqocdZlNiB9zk+5rLDriTCSyLKxZicflC1DqrGViy4L22M/jNzg70DZyfFqwotePWq5twccusnL1vbW0tHn74YTz33HOwWHL/j56xMLwQTWP5avOfzmSnibpPB7B1RwdOe5PXbFy5uAoXN1dAUTWcPBOa1E4fCYDdZoLZIhBWgojL43fEnephh9nWWNqA9fVX4/XetxGMn18DVGpxY0WW+7zEtTjafUcHtzV72yGPE1hKLe7hXUIMLNn1XtsZ/Pz5Axjdpq1vIIKfP38An755cc4CzL333ouHHnoIP/vZz3D33XenvObUqVPYsmUL9uzZA0mScMstt+BrX/taVsMOwwvRNLeooQyb1rXkvc/LZKeJ5LiKl948jlff78HoFpoVpTZcubgKHSf9eH7PseHHSx0WXDWBnT42ixEWCxDTwojImY+STPWww1xoLG1Ac1njcIddmzF7HXDjWhxtvqM40HcIh30MLHoghMBvdnYkBZeRz/92Vwcuas5Ob6PRqqqq8NWvfhWPPvoobr75ZtTV1SU8L8sy/vqv/xoNDQ347//+b/T39+Nb3/oWAOCb3/xm1upgeCGaAYZOcM5Xh93JThMd7fGjdUcH+vyJO2kkCVh9UTWaatx46a3jSaNIAxnu9DEbDbDZAFlEEIhPfGpnqocd5ookSagrrUGpVDblDrGKpqDd1zkYWLxtkLX096nU4h6cEqpYiBpH/r/3mab9xEDCVFEqZ30RdJwYQPMUp1THctddd6G1tRWPPPIInnjiiYTndu3ahd7eXvzf//0fSksH/y5++9vfxt1334377rsPDkd21oIxvBDNEJIk5WU79GSmiaKxOJ7d2YE9f+lNem52mR13rG3G3FkOPPXHw2l3+rw2xk4fg0GCzQqoUhRBdWrrUZprS/GhFfUF7/OSTYOB5SgO9B1mYNE5/zgLxocMZHjdZBiNRjz00EP45Cc/iW3btiU8197ejsbGxuHgAgCXXnop4vE4urq6sGjRoqzUwPBCRFkx2Wmiw90+PLPzKPpHjbYYJAnrltVg3bJamIwGnDwTGvcX8sConT6SBFgsAIwxRDQF2Tp+qLm2FE017oJ22J0qRVOGp4SOeNvHDSwea+nwLiEGlsJxOzJbN1Ka4XWTdemll+KOO+7AI488gr/5m78ZftxqTT4/TFXVhP/NBoYXIpqyyUwTRWJx/P7Px/DWoTNJz9VUOnDH2iZUV5wfYp7oTh+zGZBMMmShIBfHD0mSlPPt0Nk2MrAc9rZDySCwDPVhqXZUMbDoQHNtKSpK7Wmnjio9djTlYQTwgQcewI033oif/exnw4/NmzcPnZ2d8Pl88HgGp63eeecdmEwm1NfXZ+29GV6IZphsny4diioITnCa6GBnP5579Sj84cQPT6NBwvrlc7H64hoYDYk1ZbqDx1VigskqIy5lb6SlmCmqgjZfBw70H84osJRZS7Ho3LZmBhb9kSQJt17dlHK30dDzt6xpysufW1lZGR544AF885vfRG1tLQBg1apVqKurw9e+9jX87d/+LbxeLzZv3oybb74Zbrc7a+/N8EI0g2TzdOnJTBOFogp+u7sT77X3JT1XX+XExqubMbssdUfY6soSlDosaaaONHg8EuZUA6qU+z4reqaoCo74OganhHwdGQeWJRUXYE6WdipR7lzcMgufvnkxfrurA2d950dgKj123LImt31eRtu0aRO2bt2K06dPAxhcD/P4449j8+bN+NjHPgaHw4FbbrkF999/f1bfVxJj7beaBs6cCRS6hKJgMhlQVuaA1xtCPJ6D8fU8EUKgO3gCITkMh6Ukb+ejTOb+ZXv0I5P323nkA/xpXxugWmFSPJBGnERskDCh06UnOk0khMD7Hf347e6jCEUT+6mYTQbcvrYZl7ZUJG2NHi3VuUICGiSTAoNJwY1XNBTlgtmpMhkNsDmNeKvzL3j/zAcZBhbP8KLbmR5YTEYD3KV2+AciU96tNZ4LG5qy9lojO+yWOixoykOHXb3gyAtNC4e9bXilezd8Md/wYx6rB9fUrcKCspYCVpYsm6MfmRi8N6/i8KlTiJcOfuobVDtKAvNhiQ22jp/I6dITnSbyh2X85tWjONDpTXpuXrUbH72mGU315RgYCENV07/q0E6f11ObQpIAACAASURBVPafgi8UhWSSIRnjKHNasfLCmRdcZFVGm+8oDvYPjrDI4+ykKrd5sKicgWW6kCQJLTnaDq13DC9U9A572/Bs2wsQo1Zl+mI+PNv2Am5v2aCbAHPwmDdlt9v+QAxPb2+b0OhHJobuTVSJIz4iGGjGCIKe9+D0XTwcYMY7XXqi00RCCLx95Cyef60TUTnxa6xmI268oh6XL5oNs8kwoe9pXo0L9TUWnPb7EVHiRbnTZypkVR6eEmrzHR13hIWBhaYjhhcqakIIvNK9Oym4DD8PDdu7d2O+p7ngv7SFENj2ZnfaPiWZjn5k+n5D90Yb403DriMwx2YNTyGNdbr0RKeJfMEYnt3VgcPdA0nPLajz4PY18+BxJm+pTEcTGhREYTKrsJgMmGvP7XlMejIysBzxdSCupT/KoNxWdm6X0IKsddsl0hOGFypq3cETCVNFqXhjPhwPnkSdqzar7z20xiaqRlAtKuFBedrru3qDaQ9IBMYf/ZiIkffGYEj94aUZI4ibfTArg6M9qU6Xnsg0kSYE3jh4Gi/sPQZZSQyUdqsRN61sxLL5g23LhRDoORtGRI5j9qw4PLbUv46E0BATMRhNcdgsBgATG6kpVrIq44i3Awf6MwsssxwVWFS2ABeULUBVySwGFprWGF6oqIXkcEbXBeVQVt83YY2NJMF01ACXyYV1c8deYzPWqMZkrxvPyHtjMRtgMkoJU0dDNGMMUJJPl57oNFGfP4rWHR042uNPem5xYxluWz0PrpLBcNR+YgCv7T+FgZAMSRrcIu20m7FyyfkOtUJoiKlRSObB0CJJ0z+0yKqMw952HOgfnBIaL7BU2MqwqGIhLp61CPOr6xHwR3O+4JRIDxheqKg5LJkdgOe0ZK+Z2FhrbLyxgbRrbFKNaqSS6XXjGXlvJAAuhwXeQCyp94lBtSadLj2RaSJNE3ht/yn86Y1uKKM+OB02E25ZNQ8XNZUPv3aqHUPA+fOJbri8DrVzrBAGGfYSAwwG48S/+SKSEFi8RxEX4wWW8sFdQuULMPvcCIvJaOBIC80oDC9U1OqctfBYPWmnjsqsHsx11mTl/aayxqa+yolylzXt1NHo0Y+pGH1v7BYj4LIiEJKHR2AMqh2zbVW4fnn98ELhiUwTnfZGsHVHO7pPB5Oeu6SlAjdf1QiH7XxzOSEGg06qTCQgoEoKXv2gHf+vYT7M5un76ymmyjjibR9edJtxYKlYiNn23JwWTFRMpu9vB5oRJEnCNXWrUo6EAIAEA9bVrUr5y34yvVYmssZmrrMm6fXXL69LudsIQNLox1Slujd2ixE2ix2yokFowDXV12FN04WQJGlC00SqpmHXuz146a3jSaMz7hIzblvTlHLXVM/ZcFKTOQEBTYpDM0VhkICQLOGML1p0rffHE1NlHPa24UDfIbT7OscNLJW28nON4xZiFgMLUQKGFyp6C8pacHvLBmzv3g3viGBRZvVg3Rh9Xibba2W8NTYCg91Nt7e/g1OdhxHyOYZ38gy9/qZ1LXnr85Lq3kgA5jjLE+7NRKaJevpC2LqjAyfPJq8jWr5wFjZc2QC7NfWvlpHnEwkICIMCGBUYzRKM2lB1mZ9jpHcjA0ub7yhUkT4YVtorsPjc4YcMLERjY3ihaWFBWQvme5qHO+w6LQ7Mddak/OU/lV4r6dbYxOIx+OUAFDWOMwP7IFlNMFSebwY38vW/vPGivHXYHe/ehKMKAhlME8VVDa+8fQI73j4JbVQrXI/Tgo9c3YT54zTMcljNENAgDAqEQYHBIGAwSDBIBghJGu6wm+k5RnoUi8dw2NeecWCZZa8Y7sMyu6QyT1USTcz999+Pt956Cy+++CLs9sQjPD7zmc8gEongl7/8Zd4CN8MLTRuSJKHeNTftNVPttTLWGpuIEoU36oMAoKkSJG1wkenoZnAjXz8b26EzlereTGSaqPt0AFt3dOC0N/kk2yuXVOFDK+phNadfWKsJFa5SDQ63jGBEgdEgQZIMGH2bPQ4LqiszW4itFwwsVAhCCBz1diMgB+GyODGvLHvTzqN9/etfx4YNG/DEE0/gvvvuG378j3/8I9544w20trbmdaSwaMLL5z//eZSXl+N73/teoUspeqPPAJrnqSt0SVk9l2jotYJyCEElBKfJAafVgTpn7Zi9VoQQkOODzdx6FBWdPX4YXYGkelKusRHAQGzwHC1NExCqGZDiACRAGCFBSmgGN9FeLrk4s0lW4jjQ6UMgIqftUCvHVbz05nG8+n5P0rlDFW4rNq5txrzq9CfFCiEQUSOIqhEYDRJWX1yDl95KHSANErDywjlFMV0SjccGp4T6D6M9o8BSicUVC7CoPDGwDPW7CcWUGdctmCZvf+8h/P7IK+gPnz92o7ykDB+efw0urFqY9ferqqrCV77yFTz66KPYtGkT6urqEI1G8b3vfQ+f+cxnsGDBgqy/ZzpFEV5+97vfYceOHfjI/2fvzYMju+773s85d+sdjR0YrLMvHFIiRXJEUqRIkTZFKY4kl5/fe+VS1cvLq3Je5blcSZyqxK7EdHkpb8kfjlIVv4qrlPi5osQSbUmRZdK0uIk7RVLkcPYNwAwGO9D7cpfz/rjdjW50YxkMBoOZuZ8qEgPg9u3TB8C93/4t39/Xvnazl3LL02oGUHsoyVfu+hkGzLWjFtu5ps3OJaqeayo3TcbO4noumtSIGzH6or2M6nc3PaZYckjnbdxqm29snm988BbxpOd36KxYz8o6krJXxvH8G5cQAqWVaykYoSTCtUCjwQxuo14uN2Jm0wdnZ3nxvcsNhbNtUZOHj/Y1zAa6eDXNc69eYD5VXHEGhdkzRXJvDhFLAquLl5JbJO/kQShiYQPL1EjGLXRN8ObxKZbq1pCMWXz2SO+Onk+0LFj8otuNCpYjHQfpbhFhOX8l1bwPUZOHVvwsAgLqOT59mr/46K9YOVd5Ib/IX3z0V/zSPV+7IQLm61//Os899xx/9Ed/xJ/8yZ/wn//zf0ZKyT/9p/8UgFKpxB/8wR/wgx/8ACEEjz32GL/xG79BW5v/u/zNb36T//Jf/gtzc3McPHiQX//1X+e+++7b1Fp2/FTppaUlvvKVr9Dd3c2+ffuuKfISTJVuZDV/EoTA0DW+sucZ9ia2buLpda0Jv1PoWuYSVc9VcAoslZpt6ZNWG1KZFMeWBxIWSw6L2Trvk9g8cuAUuiYQUtAet2oCZuV6qhGR04tn+fGVt0iXsniKliZh0gkTX7oXq9gHwP/xxUPrRl62cm/ATxP95NQs33/j4qpRj6cfHGawO8bz74zz1onp5mNCeayh82gRv1i3LWrx5ZEvMhrf3XBc2S2Td/N4yiFsGYQtrSmaUO+w29sdoy2kb3j8wHZSFSyfzJ/mQmp9wdIT7uJwpa25O9y56nGr+d3A8s9iowJmO6ci347cSlOllVL80et/2hBxWUlnpJ1fe+SXb0gE79133+XrX/863/jGN/iX//Jf8id/8ic8+uijAPzO7/wOn3zyCf/6X/9rTNPk3/27f4fnefzZn/0ZH330Eb/0S7/EN77xDfbu3cs3v/lNXnjhBV555ZVNrXPHR17+4A/+gK985SvMzMzc7KXc0qzrT6IUPxr/MXvu2r1tIeutnEtUPZeHR8Zu9hwByNhZOkMdOO0XMKa6QUE6b9eZtilkzyWE8CMoKMjkyoTMMKLFeqp1JJoUvDD2MkDlsTSlWJRWQri++VxH3EIpxfGL86sW6271zCbbcVnMlHj5wytr1vu88O4EmXyZpezKyJCH0TuJ2XMFIZdPkC3YvDP7NiOxUYQQOJ5N3sljezYhUycSspCytTOuEIJd3dGGG0eTg95NougUOb14jhPzZzYmWCJdlVlCB+laQ7BUUUrx5ip+N+D/LN48PsWeXYkghRTQwMXFiTWFC8B8fpFLS5fZ3b71JQEPPPAAP/dzP8ev/uqv8vTTT9eESzab5Vvf+hbf/e532bt3LwB/+Id/yEMPPcT58+e5cuUKUkoGBgYYHBzkn/2zf8aTTz6J53lo2rUbUe5o8fLmm2/y3nvv8f3vf59nn332mh8vpVh1psudxnj6MkvlFE3VkVSbU2GxuMTVwhTDia2dAbSZNVVZLKc2tKbquWzPxvVa32hcz8VRDpG4h7eYwsnFcT1veQPCaTALaFLWvuZ4CtvxMCvFqK3WU39zFvhW966rmm7DQkDZdskWbP7rC6drX++Ih/jZB4c4Mro8G2kr9yZXsMkUbCbnc6Tz5Zan9DxFKlcmX2z2HpHhnB9tCTe3ibuex3xxkaniJAkzQdkrYxoabZEw+iqipen8mqh91G/i3KKCU+TUwlk+mTtdqWFZ+x14b6Sbu7oOclfnIboj6wuWei7PZkmt8rOoksqXmV4qMNi1vmnhTtnDW5Vbaf8y5dZvzlaSLt24zMM/+Sf/hO9973u1dBHAxMQEtm3zC7/wCw3HKqW4ePEijz32GHv37uXLX/4yd911F1/4whf4xV/8xU0JF9jB4qVUKvGbv/mb/Nt/+28JhUKbOkdHRzR411JhvOSia2v/UWqaBMuhvX17zME2siZgQ2uqnqvsseYNH6GIRUyOfa6fN35ss5BaLt7VTAepSWTT40XjOlesZ7zk0GbFWSj43UZSCIRQfvi5omA0z8IMedgFgYKG86XzZb7zygXi8RD37OtueD3rssbeuJ5iKVNEGDoJQ0fN5dFaiPl8yWExXWpK2UgpiCSKMPwJQiiWVd4yCoWnPDJiif54J72RCJa5uYtRLLa5v/PrIW8XOD59mg+vfsLpufPrCpZd8V4+3X8Xn+o7Qm/sOrqE5vO+SF4P4UelNsrN2MPbiVth/+Lmxhy4E9aN62a0LKvhI4Dj+G98/vt//+8NXwfo6uoiGo3y7W9/m7fffpuXXnqJ73znO3zrW9/iueeeo6en55rXsGPFyze+8Q2OHj1aC0lthoWFXBB5qVLSVs3lCnzh4roelHQWF7d2iOFm1tR43AbWVD2XojlnU48SOK7Hns5ORp6M8aff+wTXU37bbjhOWogWiQvVuM4V65G2QdgIkfTaSJczuJ6LAAxNIpCEtSgh3SJUCIMuV33Nz/3oLIMdYV9wX+felB2XVKaM4y2fQ3hug0BxPUUqW6JQao5UDffGeOxT/fzdJ5+QE17TnvhxJQVCodCJSgtDKEqFMqXmbuo1kZogFguRzRbxWgyO3GoKTpFT82c5Pn+KC0uX1hUsfdEe7uo8xF1dB+kKV6JjLpU01ybxPD/qtx7K29DzbPce3m7cyP0TQqALDU1q6FKH69QUu9uH6Ii0r1vzMprc3gaMkZERNE1jaWmJBx98EIDZ2Vn+zb/5N/zGb/wGp06d4r333uOXf/mXeeihh/gX/+Jf8NnPfpYPPviAp59++pqfb8eKlx/84AfMzc1x7733AlAu+zn4559/ng8++GBD5/A8hbcDCwBvBv3hfpJmW0tre1WJNLSHkvSH+3Cc7Sn4W2tNVdqtja2peq7F0hKa1FqmjjSpYQiddrON/nAfhKG3PVJrnVZ2EumE8bTlm4WuCQxd1gRRq/UMRPvpiLTjuB5dmont2rjKQxMSQzMQgEWMpaVIi9jFMnOpIheupBnpi1/X3qw2m6i3PUIiYrKULVEsu6SypaaaCyHgmWPDPHy0HyHgvdM9FJwwnu7vSb1oAdCEpCfWxkC8b9OFjtUwveeqG1YsWXCKnF44y4mF01xIjeGtJ1giPX7RbcdBOsPLhoVbtb7e9jBtEbOhy2glyahJbzK8oefcjj28ndmK/dOEhi61uo86utSQWzwNXQjBl/Y/0bLbqPr9Z/Y/se1Zh0Qiwc///M/zm7/5m/zWb/0W7e3t/N7v/R6zs7MMDAyQSqX4D//hP9DV1cWxY8d46623KJVKm26x3rHi5c///M9rYSiAP/7jPwbg137t127Wkm5p1p0BJARfGP7ctv7CX89corXOFTdiLbuN4kYMKbSGc9bPGhIIIpn9ZJMfVRdAPGrWBMdq66leTP7r+9/BQ2Fqje6wAsnh6L28xfpmcNUW6s3sTbVuZTXTOSEEn97XyV+9dpFiufkYy5D8w0d2c++B7trXHjnaz//8aB/Z9o9BeDXR4q9BEI+YHOv7zI5MzxacAqcWfGv+i+mNCZbq8MOO0NaOaViJEIKHjvat2W10q/jd3EkIRIMwqRcs2/mzOtp7kF+652v88OxLzNdFYDoj7Txzg3xeNsKv//qv8/u///v8yq/8CrZt8+CDD/Knf/qnSCk5evQov/3bv81/+k//iWeffZaBgQH++I//mN27d69/4hbs+FbpKv/qX/0rgKBV+jo5s3iuaQZQR7idf3jkKQbMwW2Luqy3prXmEm3kXFdb+Lz0R3tbnvPk2CIvvDvGZO4qriyhjDxaco5I3Km1Sa+1Hl2XtLdHeev8T/n7S6+1fB1WqZdv/u2pdde/soV6o3tjOy6L2XJTpLHajpwtlpmYzvH68atNwkUIPyrzpc8Os2+Fvb9SHicuz/DK+Q9JmRfw9AICgSYFPfF2vjD6IKNtI+u+rrXYyjbVvF3g9OLZimAZX1ew9Ed7K063B264YGnFVvm8BK3S10f9/rmuh1ZJ89SLk+rXrpfu7q2rRal32E1YcUaTg3eM4N2xkZeAG0OrOTejyUE6OmLbV+uygTWtNpfoWs6VLefI2TmiepS4FVv1nJcLY0zGXqUQyVItS9WIclf80xwdGNzweg527GNPfHfL16GUoiNutXT3rdIRtxjubSzG28jerDab6PyVFG8cn2I+XVx1DMBAd5Sn7hvkwIpxCEp5FN0iBbdAX7fO/95zP+ncPUwXZxCaw1BnO33R3h1xoczbBU5VBMulW0Cw1LN3oI09uxKBw+5NwBckEl3qWIZBZziBWQ6jvFtn74UQ7OkYvtnLuCncMpGXzRBEXjZGNXKwuJi7KZGXrUAptalBh3936kN+cPGHLd1FBPDl3c/wM4c+veY5Nrp/qw2EBD9NsNZAyFYopUjnyhRapIDOX0nxt2+PkS04pPPlphpms5oi2t+1QrSommhRykMIiIQMQuaNC4tvJmqQt/Ocqkxrvpgao7kxvZH+aC9HOg5yeAcIlhtBEHlpTXOaR6JJHX1Fmmc7r4FbGXm5kwkiLwG3PCfHFnnxvYmGqEZH3OKp+4fWFAOe5/HipVdXve0p4MVLr/HkgXtWNVq7Fg6PtPMLj+/b1FpX4rgeS9kSTovOCKUUL39whdmlIuUWF+KQqTHUE2sQLkopSl6JgpOvRS5Cpk40pCN2SMde3s5zqlJ0ezE1vjHBUim6bQ+tPe16JUoppvLT5O0iESNEX2RnRJkCWtNcLLt1aZ6AnUkgXgJuaVaLZixkSnz75XNrRjPeHTtHUa2dKiuqLO+NnePB3VszdOzwSDuHhpObihJVKZRaR1PAL9r927fHuTCZbrq1SwFtMYuQqZErOlydy9PfFaboFim6xZpoMXRJNGSg6zffrCtXJ1gubUCw7Ir2cbgyS+haBUuVS6kx3p56n3Q5XftawkxwrO++667vCdgcEokmJZrwu3eqwkSvfB4IyzuPQLwE3LIopXjxvdbTicG3WH/xvQkOrajnqLKQT7d4VDPzGzxuowghNjxRuh5PKTKrpIkAZhYLfOeV80zMNDtwhi2NRNSqmdQpPOYLKULlYq3dUpOCaNiouQnfLDYjWI50HuRwx4FNC5Yql1JjvDj+alOHV7qc5sXxV3lq+LFAwNwANLFSmEhkpSZluzt5Am4NAvEScMsyPp1dswAW/AjM+HS2pVjoiKw+Dbmezg0edyOxHZelbLnl4ELHdfmbN8d559RMS18jXZNEQjqaFChcf+q1cND1DpRSyEpdi3UD61rWI1vK8e7URxyfPcml9MSGBcuRjoMkQ1szfVkpxdtT7685T+qdqfcZSQwHN9NrRFBN7eiVLh5ZS+0EkZOAzRCIl4BblqonymaPe2BkH8+djq6ZOgqJGPePXFu79lazmukcwDsnp/nbt8db+rYIAZoAgSKdLxBLgOnPhiQeNujpCBOyKnUtN+HmkbNznFo4y8mFMxuqYdkV7edIJSW0VYKlnqn8dEOqqBWpcprp/Ax90d4tf/7bhWrdiV4tkm1RIBsQcL0E4iXgliUeNq/rOCklT40+tma30VOjj25Jse5m8CrdRK2EieN6PPfKBT48N9fysbIy3VpID/QySI98SWCaFhJ44HAP7XHLn2e1jeTsHCcX/LbmsQ1EWAZi/bUuoaS19YKlnrxdrP1bAY7r4CqFJgS6ptfMCnP2dYwFuI2obzXWKwJFuwGOsgEBrQjES8Aty3BvbFPeKfVU26BfvPQaRbVcKxISMZ4afbSpTbpVS/aNwHE9ljIlnBZpoImZLN955Twzi803USkqwkV6YJSRmkd1hI7nKSxD8sR9gxwa3r524Ww5x6mFM5xYOLPjBEs9EcMfyldybHJODq9u9pCUkqgexdINosbGByXeymhC1mpQ6otkgzqUgJ1AIF4Ctg2lVM1sLWpGGIoNXNcFUAjRYO+/Eingyc8MMj6dJZ0vkSs4REI6+aJDNGyQiPji46mDn+JAfyfvXz5LyXbZnRjmgdH9TRGX1Vqynz42zCMtJjsrpZjIXOHCzBzKMdjdNsRwb4yJmdyqnUae5/HG+TNMphZJWnGO9o/W1mE7Hi++N8GPP77a1GkkpUCgENJB6XatbiNmGQgp8TyFrgm+cN8AB7dBuGTLWT/CsnCa8fTldQXLSHKQQ8n9HGo/QJt1c2qM+iK9aEInU15o+p7neWTKGaJGL72Ra5+Au1OpChE/eqI1CJUbIU62+hoQcOcSiJeAbeHM4jlemni9YdBg0kryxCZGANSzlnfKgaEkf/+Ty0zO5UjnbWzbxcMXNYaukYgatPVm0HvHcLV87bGp7CTtKa1hXWu1ZP+PH50jHg8x1BlpeL3fO/0SV9Pzy14sdghmdxNxewmZem2dVY+XF05+wN9deo0SyxGgFyaiPNz7EP2hYZ579QLzqSIriYZ1QiGXpUIet14kKMgWHeJhk0ilriUetpoev1XUC5ax9MS6xw/GdnGk8yB3dx9iqKd3ZxisqXVupLewpWc1xWNIA6OS6tnOFM+NugYE3JkEDrsBN9xd8sziuTUHDH513zPXffFamc7JF22+/cp58kWHxWwJz1XLnTrCbwuWiQWMoTNICe1xqzbHaOW6lFJ847mPV01PCQF9nVH+76/chesqziye47+d+D4LmWLtZucphet5oATe5CHaxa6agJECRveXeS/1alOEQrmS8tVh7Pm+pufVNUEiITEsh7LttJxQrAmB1CARMeltj/BLP3tgS9/p+oLlDCfmzzCW2bhgOdyxHGHZKe6wV3NT/M8Lz6+bNvq5PV/ccQW7K/dQIGoCxagIlptp2LYd14DrIXDYvfUIIi8BNxSlFC9NvL5m++nLE6+zP7n3ulNI1XboqthwPUU6b6M8hasaIxKu56F3X8LzPKSQZHJlQma4VpRZv66NtGTPLRUYm84w0BnlpYkfk86VGt6le56qfK6Q3ZdIj3XVxIvtebw9/RbSUlC3BU6mjdLEHpTdGC2RQvDwPd1cTc+TLdoopciXHKSgITIkACn915srODz0uY1NKV7PXXYrBMtOpFqwa+kGppbE8ezlgl1pUN2CnVSw67cg64R0g4QZQ1gGwpM7yll2u64BAXcWgXgJuGauZY7QRPZKQ5i4FYulJS5nJxmKD2zJ+samMlxdyFMqu9jVd1Er4osinAajgFL+63FcKNselrEcRq+uK1MIbeh5MzmbCesK09nFBtt+pRQNAU6jgGsuUbb9bp+8mK9Ma5YIQLkapckRnIXm2oreDouffbiHng6L8WnJjz+apOQqPE8hhQAUnqoKF/9noklJNKITttb/c1/NXfbuzsNknTwn5k8znrm87nmG4gN+0W3HARLWrfFOs1qwC340zdAMjBbH3YyC3fralAYL/IpI0XVJzIpi6+y4+WQ34xoQcPsTiJeAa+Ja5wjlyvmmr7UiW96aidYnxxZ57tXzLKSKeJ6fKqrKhnp5JXS7NkG6+rGVwVu2nCMe3li0IB41yJTzeJ7nC5a68zehlbAdDyEEnu7vpVIKN91O6fIelLOivVt4jO5WfPXhwZpL7nBvjM/ds4vXP56kmiDVpMCUkpCpoWkCKQWG7t/gciV7zfWvdJd1PZeiW2K+sMjpxXPrvv5bUbDU0xfpJWEm1vR6aTMTN6xgVyCWhUnF+l6Teq3r51Zlu68BAXcGgXgJ2DCbmSMUNSNshJjZ3K2z2fXVfFFWBINU3ZeUY9T+Xf0oWwwgjJlRBjvWb8nuSoYZ6Y3zo5MuqWy5sXZDiIbn9p/fRFT++qSyUI5OaXoP7lJX07llJI01fI6jIw/XhEuV0f44HfFR/urHF/3oS51YWUnUahVHqKyn4i7reDZFt0TBKWF7a4sdqBMsnQdImLeeYKlHCMGxvvtajgcAvzbjwb77rju1sXJ44Mooyu3Gdl4DAu4cAvESsCE2O0doKDZA0kquGTZut5IMxnZt2fpMQ0PTJMpxVw19qEIC7DDCLCKEQNcEptH47ra6rvVbsgU/9+geTo4t8sqbGegMI0RuOVVU+ViLxJTDyFISI6ShlMLLJyjN3QvuCnEhXMz+MfTuq1hE2N/TGFJP58o4nkfUMuhqC5NqUbBbJRk16e9qfRNJlzO8ffU9LqTGNiRYhuODtRqWuHljfG5uFqNtIzw1/BjvTL1Pqi4C02YmePAaBjNWa1FWRlHuRKfZ7boGBNxZBOIlYENsdo6QEIInhh5Zs9Pg8aFHrvuCvnJ9iajBYsZDU+CqFT08wq8D8WZHMYbOgIB41GxMK61Y11ot2U8fG+buvV08+/++iVKCSGY/TttHuJ7bQjgJ1OwI8YiB63mkslUH3UbhImMprKFzSKsICO7t+DRSCAQwtZDn/TOzpPLLSZvQQgAAIABJREFUQkPXBGXbbTlUUQp46GhjsW66nOHk/BlOLJxmInNl3f01pUFIt3hy6HHu7j687vG3MqNtI4wkhmtFy1EjTG+kZ9Xf0XqXWUMaNafZAJ/tugYE3FkE4iVgQ1zPHKED7fv46r5neHnidRbr3n21W0ke3yKPh5XPGzJ12uOQztlgu76AUX4hZjW1EnH7CGfCWLsm0IwiJdvD8xRJq41n9n6+aV2HR9o5NJxsKlY2DI3zV1J+azRglnpIpO4hGz2DI/MopSoRlxBifg8xrwfXUyykC01mc0gXc9dF9I5pX2Q5YQ7Gj/Lpwf2Yhsb0Qp5XfjrZFAHyC4QVuiYbUlbJqMlDR/vYO9BGupTh5MIZPpk/xeXs5Lp7WhUsIc2q3Yy7Ix0b+nnc6ggh6I82tqfXp3j8j35k5VauR9kutuMaEHBnEYiXgA1xvXOEDrTvY39yb81dM2ZGaymZVlxLR1P98yoUjrGEp5XQDItuM4lte7iuh6fgZx8YJJWzOTm2QKHkIvNdZE4kKcgFzJCDJSMs2UleGM/j3b/YVMNT35JdT3pFysYs9ZAsdlHWFymrItgGmp3k858a4N1TM4xPZ5vOMborwpOf7eLEVcnZqTacsobptTExL/jh3BiP3N3P2yemV03dmYZO1NL4wn0j5MsOUcsgGnc5uXiGV46f3rRgqXIji1V3CgLRIEw0Ie/YdM9Wc63XgICAtQjES8CG2Io5QkIIhuOD6z7XtXY0VddntS8yrZ3A05Z9OKQbJpLZT7jUQ0fcYldXjDc/OV+rjSmWHJayZVAxSmnQ4xaGKdYsQm5FPGJgG4u4soR0LWSpDc8DzW0njC/G8rbD916/tNy+XcEyJY/f38Vde+NMzOS4dEmh0YmGbzInpCBdsPn+m5dwXQ/LXP3PNpW3yblZFrTLvDZ9msvn1xcsI/EhjnQeJGaEeX3y3RtarLpTkEgMTb9jimZ3Chu9BgQErEcgXgI2xEbmCD11/9B139w209EEcHbpPKWuT/DqXG0BPK1ANvkR8dQ9PPWZh3jxJ5dr51bKN7GrHa/8NFPVPG61IuQq1ejQmaXznC5+QL5rGsdVKBTSCWOl9mEUe7Bdl1S2RNlu3rh9Q1GePNZNLKKjgA/OzvojDAAhRcPzuq5HruBgGs1RAFcWsMPTlMJX+dZYas09FgiGE4OVtub9xOqKbsN6+LqLVbeL9cz0qkgkutT8epSK42wgUgICbm0C8RKwYdYqWl0rKrJRrqWjCaiFnyNGmJcmfkzIlLTHLTK5coNJnK4J2ndfJWzpDesuO346qR7X9RoKX1sVIcNydGiqPEE2+VHFPFfhKd8sztML5No/RkzcQy4VbpqZEw5pPPlgFwdGltNhswsFsgUbbYVoqSKlwPU8HNfD0DVcrUA5NEU5PIVrri9YRhJDHOk4wKGOA6u2pV5rserNYjUzvYf67+dA+76aNf52z+8JCAjYHgLxEnBNrFa0uhU3t412NL124Tgnc+/XWi/LbplUOUPciBE2LUJmmHKl+FZKvwXaIcfFVKMzbCtTulZfX1kMXI0OuUqR7TiD43q1tmgFKKFQpRDlK/vw8s3tyYdGYzzxYDeRUN0sJQEenj8depW9NHQNzSxTil0lH5vZuGDpPMih9v0b9tGoFqsqz+PjyXHOTH5CMhzj7l3DCHnzhYBvpvca4CGRtf3K23lemnidNisRFIAGBNzmBOIl4JpZrWj1etlIR1PZmuGlq2cIWcs3UVd5uJ7LUilFkjZCutVg819F6I3nb2VK1+rr9UXI9dGhPPPYIleXpvI7fuzZQZyZYVCNa4iGNZ76bA/7hhpFhGloREM6pbLXUrjUR1jYlWKtXRIIRquCpWM/UWNzxl9vXDjJG5ffpcRy/dALF8I8PPgAD+/Z+lZppRST2SkypXxDCqjeL8WoWON/MHMcXUr85NqK86yYk6OUqkXoomaEodjAjosiBQQEXDuBeAnYMazX0aRQ5ONnsVbcs7S6tEDGzmLpVs2brj4Cs7u7k4/ji7XojqELtFgGVxTBMaGQQNO0Bq+UlUXI1eiQUoqsk6MqWBDgFSLYV/ajis3C7ui+BJ+/v5NQ3eRqTQqiYaP2fP1dEZJRk6VcGVfLUw5NbyglhIKw28Xd3Yd5dM89RI2NOZquxhsXTvLy5VebLGpKFHj58qsAWypgLqbGePfshyzkl/ytFIKk1cYTg49wuPNgw7HjmcukymvvR3VOTsEp8NLE6w3maEkryRNBa25AwC1PIF4Cbhor26GHeqJrdjQ5xhLSLGKuGIxnSANNariei+u52K6N68qG2hfphvnuiwscHGrnnZPTFM0Z8vGzSJlHeZ6vQewwkdx+cP3ztypCzhTKKBQFp4jrumjCQ3kCZ2YYd3aQldEAzSrxxLF2PjW63GIsBIQtg7DVWHibKqVpG55mfPYUzgZSQv3hAQasUQ4k97Ont3NLIgrK83jj8rut5zHhb9Mbl9/jodGD15VCEoAudcbTl/n7sdfQNN/orWp8kyln+P6FF9Ck1iA0Njon59TCWT6Y+bipc2qptMRfn/shX933TCBgAgJuYQLxEnBTWK0d+sBQkndO+l4mSinKznLkRISKTU644L9Tjxsxlkr+Db9g2+SqQZEKkcx+Fktl3jk5zZ79Nu9nj+O5nj/HWUrfSC5Uohz+hPKSRp851FSE7HgOQitTFhlsHChHcDMdOFOjqFJzekbvukr/3iXuGf252tdChkYkrCMrN/7F4hInFk5zcv4Mk7kp/6BVAlACwe62YY50+CmhyHVGWFrx8eR4Q6qoFSXyfDw5zj2Do+uerzoNWdZ9rHb+APzl1PdAVOt8GiXTyhQQbGxOjlKKT+ZPtWz5Xu28AQEBtxaBeAnYdurboesFylXbZTFT5NiRPn5yeoYrcwUcx0Xh16G0h0xst4xdcnGViyY1TGmAp6OUTlSLU/TyFIouKD8VI90w4fQ+VK6TgueAVHyQeYN4HFxPQyqJpwRS+ikm1/XQey/xpQMPo2kaH1+Yw7Kgq0MjWyqBbmNEs2RFFieXQI0dYeUESGEWMAbPosczHE48wmxhhpl0GlMLMZLopyxznFzwrfmv5qbX2S1Bt9HPgwN3cbjzwA0RLPUsFZrN89Y7zp+GLJnOz1J0SsStGCPxIXSpIRCr1pyMZy77KZ01BEQ1BTQU9+c6bWROTkgPUXRLTSJ3rfPeTFary9lsvU5Q5xNwJxCIl4Btpb7gtVhySOfthnZlTZO89tFVTF0QtjRynofnAdF5Um2nEfbSivHMgKch3TBSGeiqA33mAEbIRboWTjZGKu/gukWIzSN7ziJkinJR+B0+rkA5Jp6j1zqGMizw+3/9I3Q3RiIuMQxJLGwwOGxzoXSCOTyKc3tR5ZVCQqF1XUHrGUO4Ju5iN29576Nmi3h4KGmjZlyQzpp7JBCE7C5Ergez2IvrmZycM0ketdl7g++1yfA6gxaVv8LeaCdJqw1daJxPXWxZW7IvuZtzSxdXrTnZaAooW87V/r2ROTl3dR7i/ZmfXtN5bxZnFs9tau9W4/TCOV689FpQ5xNw26M9++yzz97sRdwo8vmNzeO505FSEA6bFIv2qu3DW8X4dJY3T0xTLDksZkuoFc+nlCKVK+O6ikLZ8Qs44/PIoeMQzoHw5wQ1TIsWCiUdUBrG7GEyczFCKoEqWyxly/5zxOaRA6dAL4Pm+JpH+UXAStgoT/jdQaJafBvFLZsUyw6aFBS1OS7aH7F0qY/ylX3NE6A1GxFdQhoOZLqhFEXrvoyr5fD0EuglkC6I1qkMgWBv2ygHIveQv7QXIzeEbrchKhGkou1yYTJFRyJERyK0lT+SBnpiCd4ZP4mLUxMq/n+yskpJWMT5P+//BxiazrmlC/z1uR9SdBtTTUulFB/NncDxHL+WpULRLXJ64TzdkU4iRpjjcydBCKQUeE2Dnnw+0/tp2qxE7fPOcAfdkU6mc7MU3WLt6+1Wki/u/gJ90R7/vOuw8rzbzZnFc5veu85w44wpKQXn0xf51vHvUnAaz7fW4wJ8tvMaGI1aN/T8dwpB5CVgW8kUys3OtnWoSvNOtmijSz86InsuglGq3fgVvsZoQCikZ2KUukGVSOfLtXOBQvZc8j+pmMUpBYLqtGmFMMqo8nIBqnINv49IQb5oI2OLFM/ci7JXCgcPrfsysm0a9/JhhA1achbROQGau2bqAiXYmxzhSOchDrbvI6yH+IsXzoDXWnR7Ct48PsWeXYmGNIBSiqtzeXIlm6hl0N8VueY0gcAvfDZ0gy8Mf56/HXuBlemw6nFPjT6KrNQJvTTxelMEROF3fYHyu780s3G9lZqT/+vo1/0U0BrdQ+1WksHYrqavrzUnRym1bmpptfNuF6vunVKNe1fpnKt9f5V6HaUUf3P2JbxVSq2DOp+A241AvARsK/Gw2dLZtoqqCgpVESnhNFg5kM03yIZLsBIoaSMjGbRsqDI/yHe7JZwGo/Ju1JO+gBErLvPC85/Dk6iyhSr6BbhKQdkWqEsHmtYqw1nM4bOIUAZP2GgHfoIIrV3s6isiDeEZxBaP8sS+B9nV7T/X5GyOpdza0cKlXJmrc/naY85fSfHm8amGx9VPkl4NTUhfrEij5kZbvak9c+R+dKnz4qXXKKrl2paQiPHU6KP8zKFPA77DcSuBYLs2rucC+N1fno2pNVYhL5aWuJK7yhNDj/Dd8z9suUaB5PGhR1a92a42J2cjqaW1zrsdrLp33oq9c21MrTHK16peZyJzhYX84prPuZPqfAICrpdAvARsK8O9MaKWzsIq3xcIhFA1+xT0coswS2sUCk8rkYjGmU8Vl0M0RgHwKhkQhfBMlFaiKfQj/MiMOz8ACJSrgW2iVpqhCQ9j8Bx69xWQNkivcoTdel2VuhzhGUhlICqyS0lFrmTXZvScW5rD0VNoTqJ2TCtyJf95zl9J8fw7403jFJZyZZ5/Z5ynHxxm70AbAlETKIbUa63la/Ezhz7Nkwfu4d2xcyzk03RGEtw/sq/WJQWrty27ylvz8yrZco7DnQf4+QNf5rWrbzKdma99r91K8vh11GkcaN/HV/c9w8sTr7NYJxKu97xbxVbs3Vqfr8ZOqPMJCNgKAvESsK0IIXjk7n6+9aOzLdNGQoIuJI5TERuO2TQXaNVzI5CuhW5KEnFBrlTya2GqokUIhJQIJXEdQCs31KCosok7M4KbTYJtgdf45yGsHFrvGHr3JEJbu+gWBcrTwNHA1QGB1GTDu33pmqS8Gf7HmZdIl9OUbUUuWUK6IUK5EYxyZ8tTRy0DpRRvHp9qEi5CCUADT/LORyke2DOCseKd+0aRUnJsd3PEqbaOVdqWtRWzhFZ+XqU6ruBgxz6O7bmHj8bPkCpkG1JA18NaqaWbzVbt3Wqfr8ZGjwsI2OkE4iVg2/n8p3fxxvEprszlmjqNElEDFMylin7soZCAUtSvedH8Y1veepREuGGE0nH1HP29Jp7SmE8X8bwOikRAW/aUEa4GXhglPZTyUI5F+cJR8AxfuFSeRYRyaO1TaJ1TyEhmzdelPAG5dlS6C5mY9aNGFXEhhFghXEJEIvBh6q1a5Y1hCDQpcCmST5wmkj7YJGCSUZP+rghX5/Kksg5CGQglEWj+HtTtTirjMTlbZKRvc+JlPVZrWza0ZdNArc7TpZ6VNSdC+JOunUjrSMNmWS21dLNZde/kir1rITxb1esMxQfoiLQzUxe92sjjAgJuVW7+lLWAOw4hBF97bA99HWE620K0xy0620L0tIcJmTqRkM6jn+rH0DVA4M3sBtuq3KSrJ6k7oRII1yScGwF8Z9yHjvbxyN39WIaGZepE8qMNa5BSIKRAooGn41wdBTsMdggRyqHvOo919HVC97yGMXR2deGiQLka3swg7qnP4o0fRS314c4NoZSoNeyIFfOSQvlh9K7JmnCpvqRoePlmVYyO1b4vlEBTOl/41B46Qu3obgzNjaJ5IaQyEUprmWrayLyozVKtLRErLiMCiBsxwDcPXBnp2Ak1JzebVfeuYrhY27uVj1tl74QQfGn/E8hV0o3BngfcbgSt0gE3vE2wOgbg8myWQsmlLWrSnQzT0x5hZrGA7So0zb+Id8Qt/sHDu3nqM0Ps7o8zu1RA2Ra6G8MzsyjdXq6BEQAamp0gmjmEUe4kGTV5/N4B9g601dqK55YK2EULzYng6jmk7hKPGpi6hipbuJcP4RRC6N1XMEZOYgyeQ0ssIIxVfn8UoHSEa0I+jpjeT5u3G03olQnTIJwQlMNo4QKGoWo3DemG6HIOcuzgIFedC02n1jWBpklc18PFxSx1o9ttdMUS/MOH9nP37h40qVEsuXx4bm7dvT92uJdk7Ma1Zq7Wttwd7uKz/fdje3bLdub6mpPtbFPdSWzF3lWRUjDS1U9cJriandnw4wJ8glbpWw+h1CrmCrcBs7Nrh/kDfHRd0t4eZXEx59eabCGrjQGoWu+vnG803BtDoSi7NmWvTMkpcXk2S65kEzF1RDjDlcxVUnaGNjPOQKwfVYiTLzurtgkrpZiczTE+k0F5ChnJYYQ80rkS718aJ2NMICNrO8tqQmNP2yhHOg6QtBJML+VYSnkcP+WnhnIFB8fzUJUxSVJCxDKIhDQ+fyxB0S2iXIPBWB+7uqNcSI3xo4lXKmcXlULl2r9ACMq2xwNtj3Kk8yDDvbGm1thvPPfxqnOgqvv8//z83dvybrve1XVl2/J6NSc38vfvVuB69q5K/R7atrsj63x2Mtv5O9jd3Ty4NeDaCWpeAm4Ya40B+MuXzvK/PLGfQ8NJdnWHsD0d23NYKC7iKLfhPNW2YJ8Yu+L9jU+0zrXgwmSaN45PMbOYx5ZZvNgMbmwGZWahbfXcqRSS0dgId3cf4mDHfkL68jumkTY4e3mJj9VF0rlyLWXjCxBAQb5ko+uCMO3cM5KsPVYACSuGFFotzN/q5mIZkqPD/QzFm1+gEIKn7h+q7W/z2puHSt5I1mpb3ok1JzuJrd67YM8D7gQC8RJwQ2g9BqDiMCs8NAP+8vWP+OWuI6tU4G4N56+keO6tj8ibV6FvFhFa25JeIhmOjbA/sY+7eg6QCK0+Syhi6uTya3QdKcjlHWIhE0szMaWBXvFV6Q538fqVd67LSO3wSDu/8Pi+NSNbAQEBAbcjgXgJuCGMTWWYz+Yo2CVSpaLfKaQvh2NdYHKhxDsnp3nwSO+WP/9Mfo4T86d4/dLHuAPZtfWRJ+nSB/hUz0F2x3eTjMYIW9rmoxZKgue3KyMMkkY7yRY29FthpHZ4pJ1Dw8mm1FuQJggICLidCcRLwJbgKQ/bc7ArtSqXM3M4Mk+2vGzr34SC98/O8sDhni252fqC5TQnF04zW6i0jK7SJaw8iZfqwkt18+V77mbfri4M3R/AWC0eXo982SEa1knnbN8TxpPgatQSUQISUYtssbV53VYZqQkhGOkL8ugBAQF3DoF4CQD8NM+lq2mWsqU13717ysNVnv/Rc3GVb/9ue43pk6hlYLseruetePzyv6WAQslpsLu/1jXPFnzBcmLhDHOF1T0uYFmwuAt9uItdoHkIzeWNj+doi8auKc1iSJ3OSIKIlkBaHrm8g+2t8KyJGIQsnXjYXPU8O9lILSAgIGCnEoiXAE5cWuClD44zvZBDVSYtt8d1Pn9vP3sH47jKrQgVr8GXZC36uyJETJ0Ufi2Gp2hqQVRC4HmqZne/ETYlWJa6cBf7cBd7/AiJZoNRpqoPSrbHS+9fxtTlqvOANKFhagamNDE1Aykk7QOKztg0i/iCL19ycF2FJgWG7rvpdsQthntja64xKLAMCAgIuDYC8XKHc+LSAt957QxCerjSQeGhhMdcAf7qzaXafJxrRQjBfQe6+cFbOTyvWbj4x0A6X2YxvXq7L/iCZaYiWE7On2auuNpkpMp5lYaz1IU734u71FNn8++BUURoy91MAr+rp9XEZlMafqGtZqLL5j+VasfPd145jxACy9BQdYdtR8dPq1bzmxm1qW/vjZoRhmIDQRQpICBgywnEyx2CUgpXuTiVVI/jOTieww8/OIEty2hS+sKlTmO0uqFv5HmuzuXJlWwGuqL0d0a5PNM8DE5KgRT+7JbT44tNdS/1guXE/Gnm1xEsmtDoMQaZH+skdaWjeS6RZqP05WgL+MJF10XFydcfaDi7UGZvXyeWZq47vBD8gtlf/MI+Xv5wkqn55de5HR0/63nobDdnFs/x0sTrDR1USSvJEztgEGJAQMDtRSBebkOqxbNO7T8XVzlNCZ/J2RxLucYb+kqWcuVaTUp1+nHeLhIxQvRFehsEx/krKd44PsXsUh7b8Z9N13zzNSkEKpRBao4/P6gYAwHRsM5cushbn0wRNnXKeoope5yJwsV1BYsuNIajI4xG9zJ5IcGHn+SaXmMsoiGMEkXHxmm0j6kda9sQ0iyE0pmdAeHkiYedDUcxjox28PCnB/nw5NS6NUNbRb2HTj0LmRLffvkcv/D4vm0VMGcWz7XsnFoqLfHX537IV/c9EwiY25wg6hawnQTi5RZHKYVTiaTYno3t2k0mb6ux0VqTXMnmUmqMt6feJ11O176eMBMc67uP0bYRzl9J8d0fXySVK+E4jXdUEV1C676C0OsHI4bQ08Pk0glsI8PzF08hEnMIq7DmWnShsze5m93RvQxFhpmedfmblybJZFdGdxSxXTM8/cAwWqmbVz68wsxSse7b/qwgSgapkoYTgmK5xN+/fxnT8CMu1xLFEEIw2p/YFofYeg+dVngKXnxvgkPDyW1z131p4vWWLd8ACo+XJ15nf3JvcDO7TQmibgHbTSBebiHc+pSPcrFdp2VEZaNErY1NG055M3w4/nbTzSldTvPi+Ks8OfQYf/delsVMqam2RUSX0PsuglAIWZ2srFB6AbvnOHQLDHPtGVS61Nmf3MPhjgMMhkdwbUHJ9nj13Xk+PJ1qOl6Espijx3FjaV6YOMNjvZ+nI26xlHFwbQGe7g8yrNxIPaVIZUtYpoahL7dJX08U40bWooxPZ9ccCwD+2sens9vSQj2RvbKm2R7AYmmJy9lJhuIDN3w9AdtLEHULuBkE4mUHUm1DdpSf8vGjKs6GO302Sn9XhGTUJLXGAMu2qMH5wvE131W/Mv4u0wtDLYpyFVrXlcogRYXCQ+guSjogvHWN44xiN+0M8o8eewQNg2zBxrE9xibzvPDWDOnsCndb4aH3XUTvv4CQ/locUeKV8fcIzx8jaSZZLFdu+nVP7noKFIQtvUlgbCaKcaNrUTY6KfpGTpSuJ1de27W4SrbcXPsUcGsTRN0CbhaBeLnJNNenOBtO+1wvQggeOtrHC+9OtPy+FHDogMGH2bUHXC4WUzhGEuzGlmARyiDMPEJ3QXMQcm35pTyJynSg0t2Q6SAei2BrkstTRZIxj0LZ5ZX35jl+Lt30WBFJY45+goysWKvw8PQ8WW+JbquX9phVGVXgX2yrBcqaFOirmNNdSxRjO2pR1vKN2cxx10vUXH2EQj0x89q9fAJ2NkHULeBmEYiXbaS+gNZRDrbr4K3yjmW72DvQxjOa4J2TM8wuLdebJKMmDx3tg+girD1wGfC7eXwUIpxDts2iJWcQ66SElAKVb0Mt7IJMB6jlDh/XVUihWMyVmFu0efGtGbKFFcJOeJgD55E9l2rRlso3lv8lFI4oYjseIUvHMrXakEjH8cjkywgh0OTq7ww3EsXYrlqU4d4YHXFr3YnS6/nLbBVDsQGSVvK65jQF3JoEUbeAm0UgXraYeudZV3m1Th/H23xtyo1m30CSew/3cfL8HJl8mahl0N8VQQjB1dzaBbQAhiaRugN9F9Ha5hBWcd3H4OoIT0fZEjW11+8+qlDfru168JOP01yabF5HV4eGGPmIvDFdl7JqFgUCiaZCfnoIap4sADnPRuF3Q9XXu6xkI1GMsanMttSi7MSJ0lsxpyng1iOIugXcLALxco2s9Eupus/6tvnujhUo6yGEYLA7huM23nz6Ir0kzERDl5ECymUPWznYXgkXGzk0x1oTgZQCTRkkwmEszWIxXcZVCuUaLYWLEALbFuTSklmvUbjomuDRe7s4dlcPP7h8hvGcTtlrPd1ZKIl0YkRkJ3pdZKVYdkjn/PSRX/PiMbtUJBE1CJk6SqladKY9ZjHUs/7FN5PfWPfWVtSi7LSJ0ls1pyng1iKIugXcLALxsgpKqVr9ieM5DYLlTkIIwbG++3hx/FU85ZIrlcnZBTxhVwpxV0e5Ei8fR5glNHTaYiFClehGNGyQyZUJ5UfJCVB1mkkpwLFI55rl0HBfhK8+upu+9jimLvni7sf5y3N/zUxuoSFiU1u/axHNHKCvM8aTnxnk739ymcn5HIuZEih/BlE0pJMrObiux2KmRDTkUix7fl2M8J2A/+NfHV9XFMQjG+ve2qpalJ02UTqY03TnEUTdAm4WgXiBhjoUx3MqnT53lkhZDaUUpmbRbrVxavE8rnJYK8QiPA0v04G71A3ZdnSp095bIDowgyuX8+O9sSSfaT/E+bxgOlwgW7BxXQWejls2UKrxYmcaki8+OMyDR3rRpCAeNomEdDrYz/+mfY0//+n3WSjPoqoTrJVEFOOElu4ipHp46uGh2s3+j/7bh34kqG4GkWlopPM2tu2ylC1jaNIfrliJxGyk4HakL77ttSg7baJ0MKfpziOIugXcDO4o8bIcTfFbj6/XJ+V2RSnFZG7KnyW0cIalUrOXSgOehlnsoV0N8o8+/xCzCzZj02myapG2NsFw5zB9kUeZKsyQt4tEjTC9kR5KZY+DHWWmFwrMpUu8dzzF7EJz6mX/YBtfe2wPyZiFqUvaYiZSCMamMqTzJc5OCOwzx7C0BUrGgj/JOpeEQhsFTeOpR3prgmNiJkfRdglbjb/6IUvHNCQzi0XwPBJRk2i4MZKyXsFtfS2K6y2nnaQUmLpEk2Jba1ECAraLIOpb1zLSAAAgAElEQVQWsN3c1uKl7No1sVLt9AmESmuUUlzOTPLx7KlrEixmsQ+j2IVAwwbmFh1sa54Js+LGm4aP0stuvHuToziOy1K2hOuqyiykMq/+ZJ6y3fjTCZka/+DhUe7d34Wsi7ZUfVQm53KkcmVKth8l02QUQ48Tt3R0XSLb/IjKmYklfvYBXzSsVW9iV9Yj1+g8Wq/g9vBIOw8e7uVv3x6nUFquwwlbOl88NnxTZg4FBGwHQdQtYDu5rcXL4jr+A3c6SimuZK9yavEMJxfPsFi4dsECvv2co6fwtDIfzme4Uj7XVA+TLqf5u/FXeKT3EXpMv3hvKWPzwpszTEw1dxIdHmnns0d6QcDcUpHDo0l0Tav5qOSLDovZiqNv5alcT4HjkfFs2uNWzea/XnCsVW9Sb7InN9k2fXJskXdOTpOMW0RC+nLkxdB45+Q0w73xDQuYnTYxOiAgIGCncFuLl4BmqoLlxMJpTs6fIVVuNnyrx9RMDrbvpU8f5b33nZpgqWKb8xSjY3ia3x7901QBKQVRPYqlL6ddPA88z+MnMx/ys7v6+fBUih9/MI/jNoqcaEjnwcO9XJ3P8fy7E2hSIKWg40OLpz4zyIs/uYzrKdJ52xct9Q9XvoCRQpDO2YTM5V/vquBYyyOlKlg0TdaETytWE0ArfV5WnuNafF522sTogICAgJ1EIF7uAK5VsFiayYH2fRzpOMje5Ci69FuHz58+w1JuOepgm/PkE6drn0vN9YcAeIpMOQPEMTUDz/PXALCYsvmLn15idr65IPqevZ0c3d3Bqz+dRFGdSO3f5BcyJf7ixbO4roeQouaQ22TrovxuJdf1KNtuTUBUBcdaHimmLtE1STy6etfQWgW3W+XzstMmRgcEBATsNALxcpuilOJydrJWdJsur23xH9ItDrbv41DHAfa2+YKlnuoogeffGcfP1CiK0bGGYyxLo1TRJArI2jkSKoEQAqUgfbmP1Fg/rOjkikcMvvK53Rweaef/e+EMCNHgyVLFdT3SeZtYeHltovq/uhu9QiEQtTTQSsGxmkdKZyLEQ3f18c7J6U2Zv22Fz8tOmxgdEBAQsBMJxMttxLUKFkvzBcvd3Ye4d/gw+azdZFJXz96BNp5+cJg3j08xV5qtpYo0KYiGDTTNo+Qu6wjP8437vFychbOjlLPNbpyfOdjNlz47QtjSmZ7PkyvaDcWyCoVjLOFpJTyh42ZCeKpOvAiBJsCtM3kRlXCMlGJVwbGWR8pwb3xTKZut8HnZaROjAwICAnYigXi5xdmsYDnSeZA9bSPoUkfXJLqmA+tHDvYOtLFnV4J3xz3envNblg3DlwtKSYSQKK8y9NATpMcGyF4ZgBW+LcmYydce28P+wSQAEUtHajSIjLI1Qz5+Fk9bLujVEiZeeh9asb2WOqrWqlQFjBB+3UpfR2RNwbGaR8pmzd+2wudlp02M3gxBoXFAQMCNJhAvtyCbESyH2vdxuE6wXA9CCIa62vlp2nerU/gziJSnCGsRciqLm0lQvHgEr9B8o/7skV6efnAYy9SQUtAWMbFMjUTEqh1TtmbIJj9qeqy0StjdJ4iIu8jMJlDe8qRqKSERMTENjacfGObzn968z8RmzN+2YubQZidGK6VqHhtRM8JQbOCmCIag0DggIGA7CMTLLUL15nRi/jTHZ0+Td9ee0mppFsORUfrNUfa2jTLYHW95M1NKMZmd4nLR4ezlaTxbpz0coysZouCWiBgh+iK9lboVxdW5PLmSTcSMkTDjLBUztdoSx1XgGLiXj5Cf7GdlNa1hOTx0cIBkb5kPp07giCKWDNMdbaMn1Ee26GDqggV3hmLiY8BGoNfSQACGLgiHJEXtNKHyITLzYQhnELoNjkG20Mahzg46Ehbj09k13/Vfzw2/PrqQjFm0tYW5dDWN63k8es8uPr4wv6kbeLUbaj5TrKXLpGuh28naPtRHb5RSvD75Nm9d/QkFJ48hDRACiyhHovdxqGP/lkQ+NrJXmy00VkpxYWGcq/NzhGQYhSJvF26qCAsICNjZ7GjxMj09ze/+7u/y1ltvYVkWX/rSl/jn//yfY1nW+g++DVBKMZG54ncJLZwhU86ueXxIszjYsZ92NcjYeZ35CYd54DhjJKMmDx3tY+9AW+34S6kx3p56n8nMLFk7h6oOGFIgJiRRM0LMCmFJkw65i5krIfLpMAJfyOixbsodS7iuolBycbIJShN7UOXwyleC1nsJuesc72gezOogFUIoQIBtQSmGVujCicyhrCzC9FNFQkmEZ6EpE0/aSNMm73l4psIdfA9ryEM5Gnj+r7Iqh/hkaoRPvr1AW8xktC/RUjScWTzHSxOvNwyUS1pJntiAnfnK6EKp7FKyf4ppyFp7dnvM5POf2kVXMnRNqRMhBIfu8vjhuTdw69Jl0g0TyewnVO6pRW/OLJ7j+xee53Jmsu4MEmWbKCfPpbnnefWnV+kzh64r8rGRvdpsofGZxXO8fPl1Mk6GXKlQiyLGjRgh3drwzyQgIODOQnv22WefvdmLaIVSin/8j/8xmqbx7//9v+fxxx/nz/7sz5iZmeFzn/vchs4xk1q8wavceqqC5c2r7/I/LzzPO9PvcyV7lbLbusZBeAZWoZ9H+x/hf73ry5jFXt78IEWx3Fh4W7RdLkym6EiE6EiEuJQa48XxV5nPpyptzRXTFFH5D0XZLVNwSqTLGSYLk2TFDI61AI4OTphCxiI9a1EiT3l6EHtyD7iNRasilMHc/z569xWEVH4wRvPqTOwUaA5K2qj4DEgXIQCt4k4rFEo6gEIaZar3Pcf1UNIF4SE0BzzpzzPSHLTEAl4xQjFjUbQdLkym6WmP0J30RdWZxXP89bkfUnQbzfGKbpHTC+fpjnTSGe5oud81k7xKW1Wx7LCYKeE4ikLZwdAkui4pll0mZjIc3d3JvsG2DUcPziye4+Wpv0eaLo7j1cSAkg5edJbH7zrAsX27K6/hb5jOz9ba0D2lsF3PH5qpJAINx0jjLfVzamyxYQ82ykb3anz6/2/v3oPjrM7Dj3/Pe9m7VjfLtozvV2xijDGxSbmEW2NIaCAm/NKhA820CWVacH8TGkggackkaQbcAA0UKKG0NElJE3A88CNpElxwsAN2MBhjg7Flg235LksrabX39z2/P1a70mpX8sqyLa30fGY8WO/unj17ZPQ+OpfnifL6e0cGbCuecpjRGKYm5C1oO+4kSDpJWuMRtM5mOU44SSzDIqMzJ/yeiOy+L7/fQyKRLki2KMpzJscvGBwbv3yfbiN25mXPnj1s2bKFDRs2MG7cOABWrlzJ/fffz9133z3MvTu1XO2yv/MA77fu5P3jO+lMDzzDolwbO96d6TZZj8JgX9rDJTMVv992iJSZzXZrOB7MTDi/3OBqeH3bYWY2VrHx8Fu42iWa6rX81DsrbvffHZ0hG3EotJkiQwwn3IR11KYrUkPGaYC2cRQlXFEu5sQ9WJN2Z4OWog+Ry4ybfZ2yU9mvrVR2JqaARptJHNfA7U7fj3JB91SIVHYKnTSz7SmNNWEvqc462rvSVAU8+d/6AV7Zv6FkBdzsO7m8un8Dc2pmFQUcpWYXOroKNzl3xNJ4PSZKqUEfa9Za5/vm95j4PH5S6V71kWyDD1Pv4Lrn8sr+DSSdFI7rdPe7O8Nwri0zic5YuGacjB1BpWsHfcS6d39ONFaD3Whc0LZWtCeL9211pqN4TQ+o/r8nQoixacQGLw0NDTz11FP5wCUnGh34xt6bodSAad6Hk6td9nUcYFvLDt47/gHR9MB7WJRr96Tm7w5Ysg9k/9MeS/HKB9tp9ryF60/kX2c4Pvyxadip+vzzth/eR0eqk0Q63evGNMBvG7mHlAtolFIkgvtwjlSTC2wK+urrxJ61FSMw8EbifH4WRXcwkw1KNNnlIlTPTVMrjdIarRWOdrOHl3p3WblguOBmk9IpbwIV6ETHw8ST2VICB453YQQ6iKTaYYCbYFuqnUPxw0wNn1Vw/aNDHbRFk/mXptJOtghkL47rknZcvN3J8XLvO31ieOCxAPZ1NBf0TQFeT2GW3rZUO1uObyWSasftFVTo7uR8PePlguGAttBmEpUZXF9K9aeU3FjVhKoGelpeTZUXyzIK2k47aTJucdJCx3VI6wwew9Pv90RkmaZR8F8xODJ+lWfEBi/hcJhLLrkk/7Xruvz4xz/mwgsvLLuN6hr/iPpNzdUue1r3seXwdrYefp+O5MCBWMD2c+6Es6llCm9uTvUELCX+/0rbLWyN7kab6YJQQpsJYlU7qYrOw05nA8GEm8I0jYKbX1Gm2pIUCkW6vYZk84yi48+gMcfvw5z4IYY3UbKFst5FaXTag/Ik6YludL6bGgpmXXpeWBiAKSuVn5GwTANtmOB1sMr5AeXNUFsbLLj04dGugtem0m7BZuLc3xUUPE8bZlFbpexLlte3GNl+2NrqCSy0LvEtzF6z8efbLbcvg+kP3gznTZ3IhDf2cby9uE5VzrgaP+edPRGlVEHbqdyMUan/V5Xu6UOJ74koFA4PbllQFJLxqxwjNnjpa9WqVbz33ns899xzZb+mPRIf9pkXV7vs7Whme8sO3ju+84QzLAHLz/z6OZxTfzYzqqdiGibNx6JscndDv9P3mqj/I4Kqv/mT7ONVyVoUCp/hwXFcjN5RUC5GKKl72Shtk9g3F6dtfOmn+aJYDQcG/Hzl0FqBa6JT3ctJqtdv5dpAuRbaKJFLpW8wlckeJzYNRcZxUa4DSXPARHx5SYu2tsLvlXKcPq/V6HxQpfJ/11DwPOU6RW2Vfs/y+hYgSMZxMbEwlVGwdFRIYWT8qGSYTPe/nbL7Moj+kLSIRGJcvngSP/vfJlxd3BNDKS47bxKRSKyobaV7ArAiWvX0ocT3RGSZpkE47KejI95TOkOU7UyOnwTgp0ZFBC+rVq3imWee4aGHHmLu3Lllv87VGtcZYDnkNMkFLO93nxLqSscGfL7f8nN23RwW1M1lejgbsED2Z3nGcZlQ66c64CmoK9RbxupA2Ul8Hi+xRKZg70O+T2aCjNnBOG8D50ycyvbOKrTuQCWN7qWjvuswPbQGt208qX3z8wFBX5YBmUQInfKhPBp0smgmpLjh3v/N3cCM/NIPrgVJC4wMyk5juj6UtgCd3ZTaa1kp+7pesx1JHzpWhTIUfq9FbcjLWfVBIEiNp7rg5Exftd4aGv0TyWQKf4idNS5IbagnCZ1tmZiGUbB0ZBoGtmnk78N1Vdn37dtWKY3+xrL6dl79ufzh0DtEkhGq7BCRZDtKZScucu+rusfR3zkHtEIPsi+D6U9urOZOruGGT87qN8/L3Mk1+ffu3bZt2FiGScbJFLRtGia2skDrfr8nopDjuDJGQyDjVzlGfPDy7W9/m2effZZVq1axfPny4e5Ov04mYJlfN4f5dfOYHp6SD1hK6VtXqIiZIui3UQqCfpuOfoIczBSf+NhElGGwbOL5/L+mVzAcDxkjQX7qRfVZfkj7SO9dUHK2RUH+pqmUwjQgc3ga9pSdvZZ9+qEL98rotAdlZSDjKQ6jXBtv20yccG5WR2G6Plwrnj9po9Oenva0InNkGihFddDGNFRBcrjLp1zEmqZfldyIqjC4bMpFJZcbSyWhCwdt2nrdqMMBO//acpLS9W2/nL4ZhpF/ns/yUkM1nekoWut8lW4zHSbU/jE8yfEn1ZfB9Kd3m+VmJy5oW2mqvVUcjxWeDqyys68b6HsihBiblNal5mpHhkcffZTHH3+c73//+1x99dWDfv22vXtOQ696ZAOW/bx3/AN2tO0qO2BZUD+P6eGpGGpwm8N2H2jn9W2HC2ZgaoIe5s212BJdn7+WSLl0xdMFMzCmobjqrCu5YMasfFsvbnmbeGAvaTMKRhKdy7vSHci4bRNJ7T276PgzhoM/lMKNBQl11/PpjKVIZbLvZ1Qdx5qwFyPUnj09lJuByS0PZPrP8+L4W8BOZJdgNKhMNr9JyG0sKBdgmQqfHzqTcZy0gZvpnq1K+rKBS9c4qoP2gHleXt2/gbZeswq13houO+k8L05BnpehZJUtt2+9n6eBtJMGx0a3TsY9PqUgqd1Q87yc7FiV0/a6A7+nI91RMs/LqXqf0c6yDGprg7S1dcnMwUk4k+PX0CA1yU6FERu87N69mz/5kz/h1ltv5c/+7M8KHmtoaCirjdMRvAw2YAnkloROMmDpq3eW26DXpnFcttjhz3auoSPV0fM8IJ3W+aPF44LV/J+51+cz5f741zuJdGjcjIX2tqPNJCmdwE3bqIyPVJeXeLz4N11fTQcL5/tZOmEx8VSG17cfoSUSpy2aALKnu0I+G9tWOJ52tJVg+oxsIBI0q5kdOJuUpw1lpYlnYuB4qA9WM947ga5khqDP4mj8MDsOHeX93V14ndqCMdNoXE+EixbXs2DyRCYFJvLmvt20dLUTadNUqXoMw2DqhCqqg94Bk8O5rssf9jbRGuugPhDmgmmzMYzyvj8FGXarvCyaN4F3dhwhEk2ekno+vTPahjxBJodKlzoo9TzglNcWKrc/J8M0FRFaizLsnur3Gc0keBkaCV4qz4gNXp588km+//3vl3zsgw8+KKuNUxW8uNrlo479vH/8A95v3UUsU27AcjbTw1OGHLCUI5d0rr/p/aumXsr06mmYGBw8kuanL39IxtG4rsY0FT7bJJHKEEs4xBKZot0vhuVQM3Mf4QntGIaiyg5z4fgLOXf8XH7w/LtEosnuXCTFy191VV5uX7Fw0Deh01kn51S2LTeOoZHxGzoZw6GR4KXyjNjg5VQYSvCSDVj2ZWdYWpvKCFgC+SWhaWcoYOnro/a9bDr8Fu29ZmCqPWGWTjyfObWzUI6HdNrglbeaefXtg7jdG01dDW6vAod9BerbGTenGcvbs6FSKYVlGnyi7nJeee3Ex6K/ePXZgy50CKenQnF/NXgguzekvxo8/ZEbx9DI+A2djOHQSPBSeUb8ht0zqTBg2UUs03/OCoCgHeDs2uENWHqbXj2NaeGpHI4dIZZOELT9TK2ajIWPZDK7mXP3gQhv72rJBy6Oq/utR6MUTJh7CP+EowUpOAxDYRrZvTGbjr2BZlFBvpNSOuOpkwpETqa680BOtgaPEEKIkWPMBy+udvmwfR/vt5YfsMyvm8v8unlMC08e9oClL6UUjcGJ+EwvXsNHPKHpSnfnAdGa3287jGUaGIaB4zj93sQBAtVdxAP7CShvrnFMQ5FLnaOB9lQHCY5jp2vxWEa/N/yWSIJHV787pGWaoVSBztl3JFrQh1JaO5PsOxI9pUGTEEKIU2dMBi+9A5b3W3cRLzNgWVA3j6kjMGDpzWd68Vt+kklNe1fh3pVDLTHau7IzIKYByXSpFjR4Yhi+OAm7C08mQzpj47FNTEPlZ2DiKYfOrhQZR5NJx3Da/dlETwEbn7fwn5VtKl7berAoUGrtTPLcq01lLdMMpQp0b4OtwSOEEGLkGTPBi+M62SWh1p3sGGUBC4DX9BC0g2TSEOksXRm1K5kmnXGJRJOkS63r2gnsKR9g+LuzmBoO2k6Sck0CZiD/tHjKyeY26X6LoB2gQ2UTPLVFk9RCPoDJpkfLFlTUaDJ2BNdMYjherHQNrlYnXKbJVR/uuxk5koywpulXXD/7mrIDmCp/6SR7J/s8IYQQZ96oDl4c1+HDjn28332sOZ4ZeGNpyA5ml4Tq5zG16qwRH7BAT9CCq+joTJPuJ7V1xnHZtqeVY5HSQZvyd+CZsb0wK253ptuo04kvY+KzvGigsyuVD1wMx0+Aeswqh46uNI7j5isr14d9LJxZz7p3DhbkaMkxnGwOl9bO8f0u0/SuPqyhqMoyA1SBLmXqhBB1Vd4Bl47qqrJHrIUQQoxMozp4efCtx8oOWBbUz2NKhQQsAB7DJmQHMZRJNJYmniquypvTfDTK8+t2c6Stv9kmjT25qWQ6/2zm2xSd6She00Mq05PFFSDQOSdbL8lj4fNYpNIOrqu5eulUli2YwPaPWkl5jxKt2VrUtmvGidZsJRQ5l874zJI92x89QCQZKVimyrFMRVXQA0Rojh5kStWJKw6XypLb28lkohVCCHFmjergpb/ApVIDFgBLWVR5gtiGTVciQ1cigdalk9dlnOzJmvXvHipZ885Q2dM1KtCB8vQT5LkWAdNDyo3TmUiCNtFolGvhTTSCa5GyW9FmCsPxYlNDOu3S0pFg35EoQa9FrGrXgJ8pVrWLkO+Sko91pWJFy1QaDcoh5Wpao2lqgwGiqfIL9s2fVsvnL5tddp6X03Fce6QaS59VCFG5RnXw0lvIDrKgfh7z67JLQpX2A9lUJiE7gM/ykUhlaOlM5NP/7z7Qzu+3Haa9u2xAOuOgoDu4KSx2pxSEfBbJtIvuLlyprJI7d/OiUY1SfuyuqaR1Csd3GMPKkAh9SCy8I9uu4wXXwk16cY5M5/VtsPmDY/iro2h/vL+ajwAYngRGsAMIFz0WtAMFy1SuSqPNJLpXUcbWRIKW+PETjGChcmvwnM5EeSPNWPqsQojKNqqDl7Cnqrtac3aGpdICFgADg6AdwG/5cFxNa0eCVK/NtrsPtOcLNibTGTq70mQct+SSyPhaP5csbOR3Ww9iWy5aQzLtEs/YxU/uxXE1Ck0mo3FqDoLj4pBBmT2zNdqKo1NesFzMyTvQHV5ITSCSjOJ6s50pOf4KqoKefsssuF1h3JQPzDiuSuNaxUtfWsOr+zYyIdgwqJNHJ8oh018yu8GckqoUY+mzCiEq36gOXv7v+bcNdxdOmkLlgxa0ojOWJpbM5JeHookUcdXKGzv3kbJNMl0h2jtT9LNfl/Nm13Pe7HGsfauZSK/frA3TIKDrSKd8/S8dAW7KS9x7EJtskjrHSuYLUQPZv1spcE0MwyAebsLTMh7D8WYrA6tscchSe1b8HpOQJ1jyfaOJNIHOOXTWvIM2S2+yNVwvjju4jbsnMphkdpVOEvcJISrNqA5eKpFCEbD8BGw/hjKIJdJE42lc3bM81OI0k6xuwjHjOD6N4TFJRmfiuONKtlkT8tDameS3b+4n2eeItOu4pLUiGJ1DrG4bJdd3tMKNNKDGN+O4CsN0UYYueKpGoxQoU2OgcM04GTuCla7BcPy4ZpzqUDbZXe/TQopsheJcQcG+qvwePMnx+KMz6ap5t3CstIHhelGujWEo2pLlb9w9kcEks5s1uXrI7zecJHGfEKLSSPAyQijAb/kJ2gEMZZBMO3TG4vmZitzyUNJ7lHjdtuzJIFfjdNSQODgTMt6iNg3V/cdQHGmNEw7a2N3ZdXPlAXK/ScdaqtGxeTD+o4IZGJ304RyZlj+JlK1SrfOdNo1sJpfu5rJJ7HL7U8wkKq0IdM4hWrMV19X4vYWFGxUGl025qN/f6HNHm5PpIGYmhFaZbF+0QunsP1/LzB2bZlAbdwcylpLZjaXPKoQYHSR4GWa5oCVg+TENk4zj0h5Lkkz3HH3OpfV3tCZZnT3SrDMWiQPTcCINJds0jZ7ARLsa13VxXI1tKcJBO7u5t3dKFw06Wo/TUYsZ7ERZaZyUjY5VAQoVaO/uDGjdE2gola1q5HY31rvGkeFkAypPcjyhyLnUjDtMkmj+8VpvDZedIENu7mjzsxsOZ7/WVuHkUPeemdy79rf8NBha6+zx82QmO0M0QNmD0ZDMThL3CSEqjQQvw6Rv0KK1JhpP0xVPFy3c5NL6O55IdqkoUkfywAx03422ysEavw+i9ahEdinDMIx8Sn/LUFimwjItMq6mK57GdcHo7o9hKMDASGT3ceheG2h0LIzO7YtxTZQ2wHDzbSsFuAbo7MyK4fix0j37QSZ6pvA3S66huesgXakYIU+QyaFJZe2hmD+tlj/VF/DMjh0kdM/MSu89MzDw8lO5ep+46Yxlk+71V/ZgtCSzk8R9QohKUzkJTkYJhSJoBRjnr6fKE8I0zOzR5/YE0RKBC2TT+gM4pEnsnUti79yiwEUF2vHMegdr3CEMO5V7M0J+C9M0ME0Dr8ckmXI4FknQFUujXQ1oUFAd8vCpj0/pDmCyTEP1bMhVCn10Orm5FcP1YhrZPSvZmR4D5XrzMy+55HXQk/jNMAymVk1mfv3cQZ/+WjC9jr9Y+mnGVfuprfJSX+2jodafD1xOtPxUjtyJm9xNPBy0oVfZg0Sy59j5aEpml5vdMvr5KKPpswohRgeZeTlD+m7EBUhnXDpjqYKjz6UEPBaxRJr24wG07rMsYjh4Gveiqg/nAw2d8WAYBiG/hddjYZuK6qCHzliatmhPsrfckg9ALOmwYHot7++NcKClC8dxMZQCI3sUWSlQXeNQhwz8U5vxhzIow0dnOrsMVGOH0B6LeKeN1TYTT3I8cGrzhMyrm80X5l/Lq/s30NarQGM5y08nUurEjc9jUVtFybIHoy33yWAT9wkhxHCS4OU0UygCdnZ5KBe0uK6mM57dU3EikWiS327eTySaAgp/8zWrIngn78HwpDANC5/HJB61UdRj+BSGoRhX7WX50mlorXnsF9uKDhNprdGA12PwwoaPuO6iaTy7tolEd7kBr8fEYxmkMi6u1iz/+DIuXXR9fvknaAfQaGLpOCFPkLOCjew/2nXaMrTOrZ3NnJpZ7I8eGPTy00D6O3HTX9mD0TgLUW7iPiGEGG4SvJwmBgZ+21cQtGitu7Pepkum6+9Na80fdhzlV2/sK9i8C4CZwTtpL1btsfyek5DfAhR1ybPpsky0zi77GEb2vYM+m6qgnZ9FgGwQ5QIGiq5Yhl3Rdv716HvYpkEi7eI4LvGUQzhoM6k+WPAb+NSqyf32/XQfp1VKDfj+J+NEJ2k8dnZ5KhSwR/XN/ESJ+4QQYiSQ4OUUMzAI2H78lq+gZlIilcluAO0vE1gvrR0JVv9uD3sOdhQ9FvLbeGpiZMJduCq71yTktwgYVXTsnYSO1+LzqPzelbbuDKlL5o0vmEVIJBaXERAAABj9SURBVDNE4xms7k0rrtY4riaRckgZLjUhT/eRao1pKK5cMnlULx3IiRshhKgcErycIn3ztORkHJeOrhPva4HsTMjr2w/zmz/sJ93n+QGfxWcvms7HZtRx+HicaGIxCaONQJVL0Azw2/UdWIk0pqmKZgZcDdv2HEdrjVIK2zKIRHtOCqHJz8YoFGjojGVoqPHl21q7uZn502pH7ayDnLgZfbTW+eXFoCfAlFBllggRQhST4OUU8JoequzsyaEc180efY4nMwPVJMw7Gomzet1u9h2JFj127qx6rv2j6YT82RNGkxqCQBDIzoQcbOmiK96KZfZ/eCyecvB7LBJph1TGzQcrkN0Gk8v0n/vZ7jgu6YybXy4Z7RlWcyduStX3ATlxU2l2tjXxyv4NRHpt7K7x1nD5EDd2CyFGBglehsBj2ATtAB6zcCmhd0r/E3FczfqtB1m7ubmg7g9AVcDm+otnMH96Xb+vtwyFaVBwxLk/C2fVs/mDo7h9Oqa7N+Dk9sf07ltvoz3Dqpy4GR12tjWxpulXZHd09YgkI6xp+hXXz75GAhghKpwELyfBa3oIWgFsszDXSjalf6ooCOnPoeNdrF63hwMtxSntl8xr4NMXTsPv7f9b5PeYhIMeuhInPrUEcM70OmY0hnlh/YcFxRkt00ApXZDaH7rzvPQy2P0elThtLyduKpvWmlf2bygKXPKPc2oLeAohhocEL2VSgM/Knh6yjMJhyzgunbF08amgfmQcl1ffPsCrbx/E7XPsqCbk4XOXzmTO5P6rFSsF4YAnH9gMZr+GUop5U6pZ9ewWItEkhqHw2ibHInHSvZaSTNPAtoyi15erkqft5cRN5dofPVDwb66UU1nAUwgxPCTD7gkYGATtbEbcsKeqIHBxtaYzluJ4e6LswKX5aJR/Wf0u//vWgaLAZdmCCfzt5xcNGLjYpkF92FcwIzPYDKmGYfDZi2cQ8FnZPS0Kqqt6FXZUEO51JHiw+z1y0/Z9byK5afudbU1ltSPEYHWlYmU971QV8BRCDA+ZeemHqUwCVvbIc6mbdiyRIRpPlbWvBbLZdF9+cz/r3z1UlOOlLuxlxaWzmDkpPGAbQZ9FyF86z8hg92v0fn5bNEnAa1FX5SOezODzmPk6PoPd7zHSpu211rIENIYEPYGynncqCngKIYaPBC99WMokYAfwmV6UUtmbX2dzft/GeM9EovE0mXKjFuCjwx08v24Px9sTBdeVgnPm+rl4cT1TqvpfpjAMRThgc6Q1zt4jnf3ehAe7XyP3/AMtXWjTRLkOk+oCQ8qQuz96gLZEG2k3jaNdTGVgG4UB15matu9dZDFHNt+OblNCZ1HjrRlw6ehUFPAUQgwvCV66WcoiaPvxWb78td77NrTOnr4JWVUsa7iQ6VUzTthmMu3w60372Lj9SNFxaW8wRf3cvcTCMX5zCKpawiXb9XlMDhzr4r/X7irrJjzY/RpKKaY3hqmtDdLW1kUm4w5pv8cHrU20JFpx3J5lNNMwqbJD+KyepanTPW2fK7LYN8Zs7U7a9/nLZksAMwoppbh8ykUlTxvBqSngKYQYfmN+z4ulLKo9Yer9tUWBy5qmX9GWiOA4mozjorWmM93B2kO/5aPODwdst6m5nR88t5U3+gQuSkHttCNMOn8HvnDP+nzfdpWC6qCHQ8djrP7d7qLNuLmb8Pt724Y+CKfIzrYmNh7eXBC4ADiuQyTZTiLT8xlO57R9qSKLvbkaXn5zf/6IuBhd5tbO5vrZ11DrLdw7VuutkWPSQowSY3bmxTYsAlagYDYgR2vN/+5fT8Z1inKi5B7f1LKRaaHpRb/BJVIZfvnGPt7ccbTodY31AUKzduH4W0r2KdfunJqZ1FR5MZQq6yZ89tSaYf9NMrfXxTIsTMMsCmAAOtNRvKaHOl/taZ2276/IYm+jPeneWHe6CngKIUaGMRe82IZF0A7iNfvPWdLUuo+WWISBqid2pNo5HD9MY6Axf23H3jbWvLaHjli64Lmmobji/MnMmQv/c+D1AfsXzXQQM1qpN85i7+HOirkJ546oKqDKDhFJthc9x3EdMq5z2qfty02mN9qT7o11p6OApxBiZBgzwUt/2XB7S6UdOmNpjna2Dxi45MQy2X0bXYk0L/1+L1uaimdUpowPseKTM5lQG2B3xwBHhJXCMhRK9ewHqaSbcO8jqj7LSw3VdKajRXtfljUuOe3T9lJkUQghRrdRH7zYhkXIDg4YtPRNMhewyjtu6TcDvLvnOC+s/7Aoy61tGvzxx6fwRx+bmE/d31+7hlIYpiI3F5HbD1JJN+G+R1R9lhev5SXt9Dp1ZNqcXTfntPdFiiwKIcToNqqDl1pv9YBBi+tqook08URh8cSJ/kaq7DCd6Y5+X+vXdbyyoZPtH+0remxGYxUrLp1FfbWv4Hqpdk3DoHdJod7HOCvpJlzqiKoCPL1KKJypI6pSZFEIIUa3UX3aqL/ARWtNVyJNS3ucWKK46rNSimUNF5a8uWkN0SO1NL0xle0fFZ708dgG1108g7+8dkFR4NK3XaUUllkYuPQ9xjnYzLnDKXdEVfXzT+pMH1HNJeGrqyrckF1X5ZVj0kIIUeGUHsXnRY8d6yy6Fk9miMbTRRWTS/mo80M2tWykI5XdfJpJ2LQ1TafzePHyz5zJ1Xzu0pnUhIpPL/V1KLmPTcc2FsxS1HpruKyfuj+nO9maZRkFeV6GYmdbE6/u30BbmZ/tdDsTGXZP5fiNRTJ+QydjODRncvwaGuSE46kwZoKXdCa7GTc1yH+YWmsOxQ7y9gdtbHqni3S6cLh8HpPPfGIa589tOOFN0VBQHfTi9ZgFFZfLOcZ5Om/Cp/p/3MF+tkonN46hkfEbOhnDoZHgpfKM6j0vkN2MG42nSaTKK5zYV1tnkl/+rp09B6NFj82fVst1l8wgHDjxhlmPZVAd8mB2rxMN9hhnJVU6liOqQgghTqdRHbx0xFJFm3HL5bqa17cf5jd/2E+6TyQe8Fl89qLpLJxZf8IZBQUE/TYhvz3g84QQQghRnlEdvMT6HF8u19FInNXrdrPvSPFsy7mz6rn2j6aXFYwYhqI25MG2zJPqhxBCCCGKjergZbAcV7N+60HWbm4m4xTO11QFbK67eAYLpteV1ZbXNqkOevI5XoQQQghxakjw0u3Q8S5Wr9vDgZbiasdL5jbw6U9Mw+898XDJMpEQQghxeo354CXjuLz69gFeffsgbp+DVzUhD9dfMpO5U2r6eXUhw1DUBD14bFkmEkIIIU6XMR28NB+N8vy63Rxpixc9tmzBBK5eOhWvp7xAxGMZ1IS8skwkhBBCnGZjMnhJZ1zWbt7Pa1sPFdVfrA/7+NylM5k5KVx2e0GfRVUZx6WFEEIIMXRjLnj56HAHq9ftoaU9UXBdKbhoYSNXXTAZT5mng3onnRNCCCHEmTFmgpdk2uE3m/bzxvbDRXlfxtf6ueGTM5kyvvwkcLaZTTpnmaO6PJQQQggx4oyJ4KWpuZ1fvLaHtj7VmQ2l+OR5k7j8/LMGFYQEvBZVAXtUp7wXQgghRqpRHbwkUhl++cY+3txxtOixSfUBVnxyFpPGBctuTykIBzxlHZkWQgghxOkxqu/CD/98Kx1dqYJrpqG4cslkLlnUmK8zVA7LUNRUeWWZSAghhBhmozp46Ru4TG4IcsMnZzGhLjCodnwek3DQgyHLREIIIcSwG9XBS45lKj718an80ccmDioPiyJbFiDgk2y5QgghxEgx6oOXGY1VrLh0FvXVvkG9zjQUNSEvtiXLREIIIcRIMqqDl1uWz2Pu1JpBL/fIMpEQQggxco3q4OXsabWDen52mchDwDeqh0UIIYSoaHKX7ianiYQQQojKIMEL4O9eJpKkc0IIIcTIN6aDF0k6J4QQQlSeMXvXtszsaSJZJhJCCCEqy5gMXqQ2kRBCCFG5xlTwYiioDnrxeszh7ooQQgghTtKYCV48lkF1yDOoekZCCCGEGHlGffCigKDfJuSXFP9CCCHEaDCqg5dsin8PtiXLREIIIcRoMaqDl/pqn6T4F0IIIUaZEb0BJJlMcs8993DBBRdw8cUX8/TTTw/q9RK4CCGEEKPPiJ55eeCBB9i2bRvPPPMMBw8e5O6772bSpElcffXVw901IYQQQgyTERu8xGIxfv7zn/PDH/6Qc845h3POOYddu3bxk5/8RIIXIYQQYgwbscHLjh07yGQyLF68OH9tyZIlPPHEE7iui1HGkWfDUBiGLB2diNmdZdiUbMMnRcZvaGT8hk7GcGhk/CrPiA1ejh07Rm1tLR6PJ39t3LhxJJNJIpEIdXV1J2yjri4oWXQHIRz2D3cXKpqM39DI+A2djOHQyPhVjhEbvMTj8YLABch/nUqlymqjtbVLZl7KYJoG4bCfjo44juMOd3cqjozf0Mj4DZ2M4dCcyfGrrQ2e1vbHihEbvHi93qIgJfe1z+crqw3X1biuPuV9G60cxyWTkR98J0vGb2hk/IZOxnBoZPwqx4hd4JswYQJtbW1kMpn8tWPHjuHz+QiHw8PYMyGEEEIMpxEbvMyfPx/LstiyZUv+2ubNm1m4cGFZm3WFEEIIMTqN2CjA7/dz/fXXc99997F161Zefvllnn76aW655Zbh7poQQgghhtGI3fMC8PWvf5377ruPP//zPycUCnHHHXfwqU99ari7JYQQQohhpLTWo3ZH67FjncPdhYpgWQa1tUHa2rpks9pJkPEbGhm/oZMxHJozOX4NDVWntf2xYsQuGwkhhBBClCLBixBCCCEqigQvQgghhKgoErwIIYQQoqJI8CKEEEKIiiLBixBCCCEqigQvQgghhKgoozrPixBCCCFGH5l5EUIIIURFkeBFCCGEEBVFghchhBBCVBQJXoQQQghRUSR4EUIIIURFkeBFCCGEEBVFghchhBBCVBQJXoQQQghRUSR4EUIIIURFkeBljEqlUlx77bVs3Lgxf23//v188Ytf5LzzzuPTn/4069evH8YejkxHjhxh5cqVLF26lEsuuYTvfe97JJNJQMavHHv37uUv//IvWbx4MZdddhlPPfVU/jEZv8G59dZb+drXvpb/+r333uPGG29k0aJF3HDDDWzbtm0Yezdy/fa3v2XevHkFf1auXAnIGFYSCV7GoGQyyVe+8hV27dqVv6a15m/+5m8YN24czz//PNdddx233347Bw8eHMaejixaa1auXEk8HucnP/kJDz30EK+88goPP/ywjF8ZXNfl1ltvpba2ll/84hd861vf4vHHH+fFF1+U8Rukl156iXXr1uW/jsVi3HrrrVxwwQWsXr2axYsX81d/9VfEYrFh7OXI1NTUxOWXX8769evzf77zne/IGFYYa7g7IM6spqYm7rzzTvqWtHrjjTfYv38/P/3pTwkEAsyaNYvXX3+d559/njvuuGOYejuy7Nmzhy1btrBhwwbGjRsHwMqVK7n//vu59NJLZfxOoKWlhfnz53PfffcRCoWYPn06n/jEJ9i8eTPjxo2T8StTJBLhgQceYOHChflrv/zlL/F6vdx1110opbj33nv53e9+x//8z/+wYsWKYeztyLN7927mzp1LQ0NDwfXnnntOxrCCyMzLGLNp0yaWLVvGf//3fxdcf+edd1iwYAGBQCB/bcmSJWzZsuVMd3HEamho4KmnnsoHLjnRaFTGrwzjx4/n4YcfJhQKobVm8+bN/OEPf2Dp0qUyfoNw//33c9111zF79uz8tXfeeYclS5aglAJAKcX5558v41fC7t27mT59etF1GcPKIsHLGHPTTTdxzz334Pf7C64fO3aM8ePHF1yrr6/n8OHDZ7J7I1o4HOaSSy7Jf+26Lj/+8Y+58MILZfwG6YorruCmm25i8eLFLF++XMavTK+//jpvvvkmf/3Xf11wXcavPFprPvzwQ9avX8/y5cu56qqr+Kd/+idSqZSMYYWRZSMBQDwex+PxFFzzeDykUqlh6tHIt2rVKt577z2ee+45/uM//kPGbxB+8IMf0NLSwn333cf3vvc9+fdXhmQyyT/8wz/w93//9/h8voLHZPzKc/DgwfxYPfzwwzQ3N/Od73yHRCIhY1hhJHgRAHi9XiKRSMG1VCpV9ENSZK1atYpnnnmGhx56iLlz58r4DVJuv0YymeTv/u7vuOGGG4jH4wXPkfEr9Oijj/Kxj32sYPYvx+v1Ft1kZfyKnXXWWWzcuJHq6mqUUsyfPx/XdfnqV7/K0qVLZQwriAQvAoAJEybQ1NRUcK2lpaVoGlXAt7/9bZ599llWrVrF8uXLARm/crS0tLBlyxauuuqq/LXZs2eTTqdpaGhgz549Rc+X8evx0ksv0dLSwuLFiwHyN9pf//rXXHvttbS0tBQ8X8avtJqamoKvZ82aRTKZpKGhQcawgsieFwHAokWL2L59O4lEIn9t8+bNLFq0aBh7NfI8+uij/PSnP+XBBx/kM5/5TP66jN+JNTc3c/vtt3PkyJH8tW3btlFXV8eSJUtk/E7gRz/6ES+++CJr1qxhzZo1XHHFFVxxxRWsWbOGRYsW8fbbb+dPEWqteeutt2T8+njttddYtmxZwSzf+++/T01NDUuWLJExrCASvAgAli5dSmNjI1//+tfZtWsXTz75JFu3buXzn//8cHdtxNi9ezePPfYYX/7yl1myZAnHjh3L/5HxO7GFCxdyzjnncM8999DU1MS6detYtWoVt912m4xfGc466yymTZuW/xMMBgkGg0ybNo2rr76ajo4Ovvvd79LU1MR3v/td4vE411xzzXB3e0RZvHgxXq+Xb3zjG+zZs4d169bxwAMP8KUvfUnGsMJI8CIAME2Txx57jGPHjrFixQpeeOEF/uVf/oVJkyYNd9dGjLVr1+I4Do8//jgXX3xxwR8ZvxPLjZHf7+cLX/gC9957LzfffDO33HKLjN8QhUIh/vVf/5XNmzezYsUK3nnnHZ588smCo+ciO07/9m//RmtrKzfccAP33nsvX/jCF/jSl74kY1hhlO6brUwIIYQQYgSTmRchhBBCVBQJXoQQQghRUSR4EUIIIURFkeBFCCGEEBVFghchhBBCVBQJXoQQQghRUSR4EUIIIURFkeBFCCGEEBVFghchKtTBgwd56aWXyn7+K6+8UlQ8ciA333wzX/va107Z8zdu3Mi8efNobm4G4IorruCRRx4BYPXq1cybN6/s9xJCjG0SvAhRoe6++25ee+21sp574MABbrvtNo4fP36ae9W/xYsXs379ehobG4etD0KI0cEa7g4IIU6/kVAFxOPx0NDQMNzdEEKMAjLzIkQFuvnmm9m0aRO/+MUvuOKKK0gkEjz88MNceeWVLFy4kOuuu45f//rXADQ3N3PllVcCcMstt+SXal5++WVuvPFGzjvvPBYuXMiKFSvKnsnpT1dXF3feeSeLFi3i4osv5gc/+AGu6wLFy0ZCCHGyJHgRogI98sgjLF68mGuuuYbnnnuOr3zlK6xZs4ZvfvObvPDCC1x11VX87d/+LS+//DKNjY38/Oc/z7/uL/7iL9i2bRt33HEHn/nMZ3jxxRf52c9+Rl1dHXfddRepVOqk+/Wb3/yG2tpaVq9ezV133cW///u/85//+Z+n6mMLIQQgy0ZCVKSamhps28bn89HW1sbatWt54oknuOyyywC444472LFjB0888QRXXXUVdXV1AFRXVxMMBjFNk29+85vcdNNN+TZvueUWvvzlL3P8+PGT3peyYMECvvGNbwAwa9Ysdu/ezdNPP80Xv/jFIX1eIYToTYIXISrcBx98AMCSJUsKrn/84x/nwQcfLPma+fPnU11dzZNPPsmePXvYu3cvO3bsAMBxnJPuS98+nHvuuTzxxBN0dHScdJtCCNGXLBsJMUpprbGs0r+fbNq0ieXLl/Puu+9y9tlnc/vtt7Nq1aohv6dhFP5IcV0XpRS2bQ+5bSGEyJGZFyEqXC4/yubNm7n88svz1998801mz54NgFKq4DVPP/00y5Yty2/eBfjRj34EDO1k0vbt2wu+3rx5M5MnT8bv9590m0II0ZcEL0JUqGAwyIEDBwgGg1x++eV861vfQinFtGnTeOmll1i7di0PP/wwAIFAAICdO3eyYMECGhsbefnll3nzzTeZOHEiGzdu5J//+Z8BhrRh96233mLVqlWsWLGCt956i//6r//ivvvuG/JnFUKI3iR4EaJC/emf/il33303n/3sZ3n11Vd58MEHuffee+no6GDu3Lk88sgj/PEf/zEAtbW13HDDDTzwwAPs3buXlStX0tLSwm233QbA7Nmz+cd//Ee++tWv8u677zJr1qyT6tONN97IRx99xOc+9znq6uq48847WbFixSn7zEIIAaD0SMheJYQQQghRJtmwK4QQQoiKIstGQogB/fCHP+Sxxx4b8Dn33HMPN9544xnqkRBirJNlIyHEgNrb24lEIgM+p76+nlAodIZ6JIQY6yR4EUIIIURFkT0vQgghhKgoErwIIYQQoqJI8CKEEEKIiiLBixBCCCEqigQvQgghhKgoErwIIYQQoqJI8CKEEEKIivL/ASlychlQV9WUAAAAAElFTkSuQmCC",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x322a2ad68>)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"lmplot(x=\"total_bill\", y=\"tip\", hue=\"smoker\", data=tips);"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA9gAAAHjCAYAAADYCLc2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xt4VNW9B/zvnsnM5Da5cQkhkHAJEBQFFLGoKCAK4l2pVStKOW19bc/T1p6ec7S1V9tD9fT0bZ+etup5WxVpay2i1gugiCAoYhFvWAKESxJugZBk7re993r/CAnZ5EIys28z8/08z3l6WJnMXtnOmr1/e/3Wb0lCCAEiIiIiIiIiSonD6g4QERERERERZQIG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2NTDpEmTsHr1aqu70cPmzZuxZMkSXHDBBZg6dSquv/56PPHEE0gkElZ3jchSmT5mP/jgA2zfvt2gXhIZx25j8ze/+Q0mTZrU7/8dOnQIDzzwAJYsWWJ1d4lswW7jGAAeeOCBPsfwN77xjT5/7ze/+Q3mzZtnYk+zU47VHSAaiHfeeQf33Xcf7r//fvzoRz9CTk4OduzYgeXLl+PAgQNYvny51V0kom70HLN33nknli9fjhkzZhjYY6LMt2zZMtx+++1d/168eDEWLVqEZcuWdbWVlZVZ0TUiGqTp06fjN7/5TY92j8fT5+8sW7YMX/ziF43sFoEBNqWJv/71r5g9ezb+5V/+pauturoa0WgUP/nJT/Dggw+iqKjIwh4SUXccs0T2U1BQgIKCgq5/O51O5OfnY9iwYRb2ioiS4XK5Bj12z/wOIGMwRTzLHTt2DPfddx+mT5+Oyy+/HC+//LLm56qq4vHHH8eCBQswZcoUXHDBBfjyl7+MxsZGAMB//dd/Yf78+ZrfCQQCOP/887Fx48Yex9u2bVu/qWl9kSQJdXV1aG5u1rTfdNNNeOWVV5Cfnw8AWLJkCR544AHNa7q3bdu2Deeccw42bdqE6667DlOmTMHChQuxfv36gZ0wIotl2pj1+Xx46KGHMHv2bJx77rmYNWsWHnroIUQiEQDoOsaDDz7YY2wT2Um6jM2BSiQSeOSRR/C5z30O06ZNw9e+9jW0tLQAAA4dOoRJkyZh27ZtXa8/s+2BBx7AN77xDSxbtgwXXHAB/u///i/lPhEZLZPGcW9jkCni5uAMdhaTZRlf/vKXUVhYiJUrVyIej+PHP/6x5jUrVqzAH/7wBzzyyCOYOHEiGhsb8f3vfx8///nP8bvf/Q633HILnn76aWzfvr0rffO1115DUVERZs+e3eOY06dPx5YtWwbd13vuuQdLly7FvHnzMGPGDFx00UWYOXMmLrjgAowfP35Q76UoCv77v/8b3/ve91BRUYFf/vKX+M///E+8/fbbfKpHtpaJY/aBBx5Ac3Mz/vd//xdDhgzBjh078N3vfhc1NTVYunQptmzZgssuuwzf/e53ccsttwy6H0RmSKexOVAffvghxo8fjz//+c84ceIE7r//fjz66KN49NFHB/we69atw7//+7/j+9//PnJzcw3rK5EeMnEcnzkGV61aZdix6DQG2Fls69at2Lt3L9544w1UVVUBAJYvX46bbrqp6zVVVVV45JFHMHfuXABAZWUlFi5ciLVr1wIAamtrce655+Lvf/971xfJCy+8gBtuuAFOp7PHMd1ud1KpaBdccAFWr16NJ598Eps2bcJ7770HABg+fDh++MMf9nhaeDbf+ta3MGvWLADA1772Naxbtw579uzB9OnTB903IrNk4pi99NJLcdFFF3U9qR81ahRWrlyJPXv2AEDXsb1eL7xe76D7QWSGdBqbAzVs2DA8/PDDcDgcGDduHBYtWoR33313UO9RXFyML3/5ywb1kEhf6TaOt2/f3uO+deTIkXj11Ve7/s0xaA0G2Flsz549KC4u7voSAYDJkydrnjLPmzcPH3/8MX7961/jwIEDOHDgAOrr61FeXt71mltvvRW/+tWv8NBDD+Ho0aP48MMP8bOf/azXY27fvh1f+cpX+uzThx9+2OfPampqut5337592Lx5M1auXIlvfvObWL169aBSacaNG9f1/xcWFgIAq5GT7WXimL3zzjuxYcMGvPDCCzh48CDq6+tx6NAhzRglsrt0G5sDUVVVBYfj9ErC4uJiRKPRQb1HdXV1Sn0gMlO6jeMpU6bgF7/4haYtJ0cb2nEMWoMBdhaTJAmqqvZo7z44n3jiCfz2t7/FzTffjFmzZmHp0qV48803NU/Hrr/+ejzyyCN46623sGfPHpx//vl9pm1PmTIFL7744qD6GQ6H8ctf/hK33norJk+eDAAYP348xo8fjxtuuAFz587Fli1b+gywZVnu0eZ2u3u0CSEG1S8is2XamJ0wYQLuvfde7N27F9dddx0WLVqEc889F9///vcHdTwiq6XL2ByM3mbb+qMoSo82poVTOkm3cZybm3vWAJpj0BoMsLPY5MmTEQgEsHfvXkyYMAEAcPDgQQSDwa7XPPbYY/j617+Or371q11tf/jDHzTBaFFREa666iq88cYbqKur67f8/0C+DHr7nZdffhmJRKLHWpiCggI4nU4MGTIEQEdFxe79V1UVTU1NfIJHGSHTxuyuXbvw9ttv47nnnsPUqVMBdGSSNDY2YvTo0YM6JpGV0mVs6sXlcgGA5u87ePCgJX0h0ku2jWMyDgPsLHbxxRdj6tSp+I//+A/88Ic/hNPp7Fpv1amiogLvvPMO5s2bB4fDgZdeegmvv/46hg4dqnmvW2+9Fffddx+EELj22mt17afD4cB3vvMdPPTQQ13HKisrQ2NjI/74xz+ioqICCxcuBABMmzYNTz75JN5++21UV1fjqaeegt/v17U/RFbJtDHr8/mQk5ODNWvWoKysDO3t7Xjsscdw4sQJxOPxrvfLz8/Hvn370NbWhtLSUl37SqSHdBmbehk+fDgqKyvx9NNPY8yYMWhvb8evf/1rSJJkddeIkpZt45iMw226spjD4cDjjz+OcePGYdmyZbj33ntx7bXXoqysrOs1jz76KKLRKG699Vbcdddd2LNnD3784x/j5MmTOHLkSNfrZs2ahdLSUsyfP9+QvW0///nP4/HHH0djYyO+8pWvYOHChfjud7+L6upqPPPMM10pMMuWLcOVV16Jb37zm7jtttuQn5/PLzbKGJk2ZsvLy/Hzn/8cGzZswKJFi/DNb34T5eXlWLp0KXbu3Nn1XsuWLcPKlSvx4IMP6t5PIj2k09jUgyRJePTRRxEMBnHjjTfiBz/4Ab797W9rAhGidJNt45iMIwkuPCUdhEIhXHbZZfjtb3+LSy65xOruENFZcMwS2RPHJlH64zjObkwRp5T4fD689957WLNmDSorK7u2viIie+KYJbInjk2i9MdxTAADbEqRoij43ve+h7KyMvzqV7/i+isim+OYJbInjk2i9MdxTABTxImIiIiIiIh0wWoURERERERERDpggE1ERERERESkAwbYRERERERERDrI6CJnJ08GUVZWgNbWEFSVS80Hw+GQeO6SkA3nbdgwr+7vybGavGz4zBkhG84bx6q9ZMNnzgjZcN44Vu0lGz5zRsiG8zbQsZrRM9gOhwRJkuBwsILfYPHcJYfnLTk8b8njuUsOz1tyeN6Sx3OXHJ635PC8JY/nLjk8b6dldIBNREREREREZBYG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpAMG2EREREREREQ6YIBNREREREREpIMcqztAREREvRNCoLE5iEAkDm+eG1XlhZAkyepuERERUR9sMYMdj8dx3XXXYdu2bV1tTU1NWLp0KaZNm4ZFixZhy5YtFvaQiIjIXLsa2vC/qz/FU2vr8Pym/XhqbR3+d/Wn2NXQZnXXiIiIqA+WB9ixWAzf/va3sXfv3q42IQS+/vWvY+jQoXj++edx44034l//9V9x5MgRC3tKRERkjl0NbVi1sR6tgZimvTUQw6qN9QyyiYiIbMrSALu+vh633XYbGhsbNe3vvfcempqa8JOf/ATjx4/Hvffei2nTpuH555+3qKdERETmEEJg/fYmqKL3n6sCWL+9CUL08QIiIiKyjKVrsN9//31cfPHFuP/++zFt2rSu9o8//hjnnHMO8vPzu9ouvPBCfPTRR4N6f4ejY52a02n5RH3a6TxnPHeDw/OWHI7V5PEzlxw7n7eDR/1oC8bQ31LrtmAMh0+GMGZEkXkdA8dqKuz8mbMznrfkcKwmj5+55PC8nWZpgH3nnXf22n7ixAkMHz5c0zZkyBAcO3ZsUO9fVJSn+V8aPJ675PC8DQ7Haup47pJjx/N24HgIOQO4QREOJ0pLC0zo0Wkcq6njuUsOz9vgcKymjucuOTxvNq0iHolE4Ha7NW1utxvxeHxQ7+P3R1BcnA+/PwJFUfXsYsZzOh0oKsrjuRukbDhvRtzQc6wmLxs+c0aw83mTFAXyAPokqQra2kJ9/pxj1V7s/Jmzs2w4bxyr9pINnzkjZMN5G+hYtWWA7fF40N7ermmLx+PIzc0d1PuopxawKYoKWc7M/9BG47lLDs/b4HCspo7nLjl2PG+VQwtQWujpUeCsuzKvB5VDCkzvO8dq6njuksPzNjgcq6njuUsOz5sNqoj3pry8HC0tLZq2lpaWHmnjREREmUaSJMyfMRqOPtZgOyRg/ozR3A+biIjIhmwZYE+dOhWfffYZotFoV9sHH3yAqVOnWtgrIiIic0yuLsXiOTUo83o07WVeDxbPqcHk6lKLekZERET9sWWK+MyZM1FRUYEHH3wQX/va1/DWW2/hk08+wfLly63uGhERkSkmV5eitqoEjc1BBCJxePPcqCov5Mw1ERGRjdkywHY6nfjd736H733ve7jllltQXV2N3/72txg5cqTVXSMiIjKNJEmoHuG1uhtEREQ0QLYJsHfv3q35d3V1NVauXGlRb4iIiIiIiIgGx5ZrsImIiIiIiIjSDQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSAQNsIiIiIiIiIh0wwCYiIiIiIiLSQY7VHSAiIso2Qgg0NgcRiMThzXOjqrwQkiRZ3S0iIiJKEQNsIiIiE+1qaMP67U1oDcS62sq8HsyfMRqTq0st7BkRERGliiniREREJtnV0IZVG+s1wTUAtAZiWLWxHrsa2izqGREREemBATYREZEJhBBYv70Jquj956oA1m9vghB9vICIiIhsjwE2ERGRCRqbgz1mrs/UGoihsTloUo+IiIhIbwywiYiITBCIxHV9HREREdkPA2wiIiITePPcur6OiIiI7IcBNhERkQmqygtR5vX0+5oyrwdV5YUm9YiIiIj0xgCbiIjIBJIkYf6M0XD0sd21QwLmzxjN/bCJiIjSGANsIiIik0yuLsXiOTU9ZrLLvB4snlPDfbCJiIjSXI7VHSAiIsomk6tLUVtVgsbmIAKROLx5blSVF3LmmoiIKAMwwCYiIjKZJEmoHuG1uhtERESkM6aIExEREREREemAATYRERERERGRDhhgExERERFZQFFVq7tARDpjgE1EREREZAFfMG51F4hIZwywiYiIiIhMFo4mEJc5g02UaRhgExERZRhZ4U07kZ3JiopAOGF1N4jIAAywiYiIMgzTTonsSwgBXzAOYXVHiMgQDLCJiIgySDCSQIIz2ES2FYrKHKNEGYwBNhERUYZIyCpCEaadEtlVQlY4RokyHANsIiKiDCCEgC8UY9opkU0xNZwoOzDAJiIiygCBSAKywlt3IrsKhBOQVY5RokzHAJuIiCjNxRMKwlHZ6m4QUR9icQXhGMcoUTZggE1ERJTGVCHgC7FqOJFdqaqAL8wxSpQtGGATERGlsUA4AYVpp0S25Q/HoXKMEmUNBthERERpKhZXEGHaKZFtRWIyonHF6m4QkYkYYBMREaUhpp0S2ZuiqvBzjBJlHQbYREREaYhpp0T25gvGIThEibIOA2wiIqI0w7RTInsLRROIy6rV3SAiCzDAJiIiSiOKqiLAtFMi25IVFcFwwupuEJFFGGATERGlEV8wDmaGE9mTEALtwRg4RImyFwNsIiKiNBFm2imRrQUjCcgKw2uibMYAm4iIKA3IiopAhGmnRHYVTygIRbltHlG2Y4BNRESUBvwhViQmsitVCPhCrI1ARAywiYiIbC8YYWo4kZ0FwgkoLI5ARLB5gH306FHce++9uOCCCzBv3jw89dRTVneJiIjIVAlZRYip4US2FYsriMSYGk5EHXKs7kB/vvWtb2HkyJFYvXo16uvr8Z3vfAeVlZW46qqrrO4aERGR4YQQ8IVYkZjIrlS1Y4wSUWaLJZQBv9a2M9g+nw8fffQR7rvvPowZMwbz58/H7NmzsXXrVqu7RkREZApWJCayN1+I2+YRZTpZUeELDvxBmm1nsHNzc5GXl4fVq1fj3/7t39DU1IQdO3bgW9/61oDfw+GQAABOp22fI9hW5znjuRscnrfkcKwmj5+55KTDeYvLCqIJBU6nZHVXunCsJi8dPnN2ZOfzFonJkFXVVmO0E8dq8uz8mbOzTD1vqhAIBhOQHAMf55IQ9q1Junr1ajz88MOIxWJQFAW33HILli9fPuDfF0JAkuz3pUdEWhyrRFpCCBxvi0BWki9sVjmsUMcedeBYJeogKyqOt4V1qezPsUpkX63+aFeNhYGOVdvOYAPAvn37MHfuXHzpS1/C3r178fDDD2PWrFm44YYbBvT7fn8ExcX58PsjUFK4SclGTqcDRUV5PHeDlA3nrbS0QPf35FhNXjZ85oxg9/PmD8URiqZW2MyIm3aO1eTZ/TNnV3Y9byd9UcTlga/J7A/Hqr3Y9TNnd5l43oKRBALh09vvpX2AvXXrVqxatQqbNm1Cbm4uzjvvPDQ3N+P3v//9gANs9dSiGEVRIXN7k6Tw3CWH521wOFZTx3OXHDuet4SswG/T/XQ5VlPHc5ccO523UDRh+6rhHKup47lLTqact1hcQfsg1l13Z9sk+Z07d6K6uhq5ubldbeeccw6OHDliYa+IiIiMI4SAL2jP4JqIOrbNC4a5bR5RJpMVFe0p7A5g2wB7+PDhaGhoQDx++kZj//79GDVqlIW9IiIiMk4wkoDMksREtsRt84gynyoE2gOxlOor2DbAnjdvHlwuFx566CEcOHAAGzZswGOPPYYlS5ZY3TUiIiLdJWQFoai9006Jshm3zSPKfL5gPOUH3bZdg+31evHUU0/hZz/7GRYvXoyysjLcd999+MIXvmB114iIiHTVMTPG1HAiu4on+ACMKNMFIwnEEqkXL7RtgA0ANTU1ePLJJ63uBhERkaFCUZkzY0Q2pfIBGFHGiyUUBCP61FewbYo4ERFRNkjIKkI6XdSJSH+BcAIKayMQZSxFVeFLsmJ4bxhgExERWUQIAX8ozqJJRDYVjcu235KLiJInhEB7IA49n6HZOkWciIhIL0IINDYHEYjEUVLoQUlJvtVdQigqI6Gk/36hRJlIVYVt96QnIn0EIgndr8MMsImIKOPtamjD+u1NaA10pIBJElD+XiPmTh+JiaNKLOmTrDA1nMjOfCF9Z7WIyF6icRlhA4oXMkWciIgy2q6GNqzaWN8VXHc66YvguQ312NXQZkm/fEGmhhPZVTgq61JNmIjsSVZUw4oXMsAmIqKMJYTA+u1Nfc5Cqad+LoS5oW4oqn9KGhHpQ1ZUBCJMDSfKVEIItAdjMOrSzwCbiIgyVmNzsMfM9ZlaAzE0NgdN6lHHzXswzNRwIrvyh+KG3XgTkfX84YShW2MywCYioow10FkoM2ermBpOZF/BSAJxmdklRJkqEjN+ZwAG2ERElLG8eW5dX5eqoAHVSolIH9yTniizyYoKf9j4B+oMsImIKGNVlReizOvp9zVlXg+qygsN7wtv3onsSwgBXyhmenaJyjLlRKbo2O/auHXX3THAJiKijCVJEubPGA2H1PvPHad+Lkl9vEAnVt28E9HAhKKyoWsye7PvsA+P/nmHqcckylb+UByySQ+0GGATEVFGm1xdisVzanrMZA8tycNt82owubrU8D4EIsYWVCGi5CVkxfTskiMtITzz+m74WfCQyHDhqIxI3Lxt93JMOxIREZFFJleXoraqBI3NQQQicZR4PZhWOwLt7WHIBhc0iicUhKPGFlQhouQIIUwvPNgejGHF2jrEE6zHQGS0hKwiYMK66+4YYBMRUVaQJAnVI7wAgJwch+Fp4UDHPtu+EPfTJbKrQCRhWtooAETjMlas5cw1kRlUIeALmr88iyniREREBgmEE1BYxIjIlszOLlFUFX9+Yy+OtYa72nLdTtOOT5RtfEHz1l13xwCbiIjIALG4Yvhem0SUHGFydokQAi9tPoD6w76uNqdDwl1XTzKtD0TZJBhJIJYwb911dwywiYiIdKaqHVXDiciezM4u2fTREWzffULTdssV4zBuZJFpfSDKFrG4gqCF22IywCYiItKZLxQHM8OJ7CmWUBA2Mbvk4/oWvP6PJk3b/BmjMH3CMNP6QJQtZEVFu8UPuBlgExER6SgSky1LSyOi/qlCwG9iaviBo36s2rhP03bhpGGYO73StD4QZQtVFWgLxCAsfsDNAJuIiEgniqrCb/J2IEQ0cGamhp9oj2Dl67s1x6upLMZNs8easosBUTYRQqA9GLNFYVEG2ERERDrxBeOWPzknot6ZWXgwGEng6TV1iMROZ7OUl+bhzqsmwOng7TeR3vzhBOKyPfaW5wgnIiLSQThqn4s7EWmpQsBnUnZJXFbwzLrdaA2cXgfqzXfhnmtqkevOMaUPRNkkHE3YatcOBthEREQpkhUVgbB1FUvP1NgcsLoLRLYSCMWhmpA6qqoCf9uwD03Hg11t7hwH7llYi5JCj+HHJ8o2sYQCv42uvwADbCIiopQIITpSw63uyClvfnAIj730mdXdILKNaFxGJG5O4cG12xrx2cHWrn9LEnDH/AkYObTAlOMTZRNZUdEetN+WmAywiYiIUhCKykgo9kgNf3fnMbz5wSGru0FkG6pqXtXwrTuPYcunRzVtN1w6FpOqSk05PlE2UVWBdhtUDO8NA2wiIqIkJWQFoYg9UtM+rm/BK+8etLobRLbiD5uzJ/2ug614ZetBTdvs8ytw8Tnlxh+cKMt0VgyXbVAxvDcMsImIiJJgp9TwPU3t+Ntb+87+QqIsEonJiJqQGn7oRBDPbqjXzKRNGVuGBRdXGX5somwUsFHF8N4wwCYiIkpCIJKwxdPzpuMB/OmNPVC73d2PrfBa2CMi6ymqioAJVcPbAjGsWLsbiW43+1Xlhfj83Bo4uNc1ke7CURlhG1UM7w0DbCIiokGKJRSEo9Zf4JvbwnhqjfbmvmJIPpYsmGRhr4is5w8lDE8Nj8RkPL22DsFuy0TKijy46+pJcOXwFptIb7GEYsqDs1Rx9BMREQ2CKgR8JhVN6k97MIanXqvT7P1ZVuTBUu61S1kuHJURSxibGi4rKv70xh4cb4t0teV5crB0YS0K81yGHpsoG8mKCl8wZotlWWfDAJuIiGgQzNpPtz+haAJ/fHWXJtD35rmwbNFkePPdFvaMyFqyoiIQMfYBmBACL7y9H/uP+LvanA4JSxZMxNCSPEOPTZSNVNFRMdwGq7IGhAE2ERHRAJm5n25fYgkFT6+pQ4sv2tWW63Zi6aJalBXlWtgzImt1FR40+CZ8w47D+HBvi6Zt8ZzxGDOiyNgDE2UpXzBui5onA8UcMiIiogHQcz9dIQSOtoQRiiVQ4HGhYmg+pAEURJIVFX96fQ8OnQh1teU4JSxZMAkVQwp06RtRugpGEobvSb9jz4kee80vmDkaU2uGGnpcomzlD8cNX/KhNwbYREREA+AL6bOf7r7DPry785gmvbu4wI1LpozA+MriPn9PVQX+9tY+1B/2dbU5JOCO+RMxtoIzZ2QdIQQam4MIROLw5rlRVV44oAdGeoolFIQMLjy477APqzft17RdVDscl08daehxibJVOCrboqDoYDHAJiIiOotwNKHLE/R9h31Y935jj0DdF4pj3fuNWDCzqtcgWwiBl989iE/3n9S033LFeEyuLk25X0TJ2tXQhvXbm9AaiHW1lXk9mD9jtGmfTVU1vvBgc1u4x3Z4E0cX44bLxpr+MIEoG8TTpGJ4b7gGm4iIqB+yoiIQTpz9hWchhMC7O4/1OQuuCuDdnccgellA+uYHh7Dtn82atms+V4ULJg5LuV9EydrV0IZVG+s1wTUAtAZiWLWxHrsa2kzph8/gwoOBcBxPr6lDtFv9hYoh+bjjyolwOhhcE+lNVlS0p0nF8N4wwCYiIuqDEEK3i/zRlvBZZ9l8oTiOtoQ1bVs/O4YNOw5r2i6fOhKzz2daKllHCIH125v6fWC0fntTrw+M9KRXdklf4gkFK9buRnvw9NgtKnDj7oW18Lidhh2XKFupp667aVTTrAcG2ERERH0IRBKQFX2u8qHYwGbBu7/uk30teOWdg5qfXzhpGBbMHK1Ln4iS1dgc7DFzfabWQAyNzUHD+qBXdklfVFXg2TfrcbjldFFBt8uBexZOQnEBt8MjMoIvGNftumsVBthENGCRWPoVmiBKViyh6FpcpcDjGtTr9h5qx9/e2qeZPZ9cXYqbZo/jmk+y3ED3mjZqT2o9s0v6ev9Xth5EXePpNHeHBNw5fyIr9hNDaZegAAAgAElEQVQZJJCGFcN7wwCbiAYkHE0YXkSGyC6MKJpUMTT/rLNexQVuVAzNR9PxAP70+h4o3XLkxlR4cfuVE7jmk2zBmzewGdyBvm6wgjpml/TmnU+P4b3PtHUPbrxsLCaOLjHsmETZLBKTDd8JwCwMsCllQgg0HAtg54GTaDgWMHy9FZkvGEnAb2AaHqWnTB77RhRNkiQJl0wZgb7iY4cEXDJlBE60R/H0mt2Iy6f3860Yko+7F0yCK4eXbbKHqvJClHk9/b6mzOtBVXmh7sdOyMZuybXzQCvWvNegabti2khcNLncsGMSZbOErMCfQZM43KaLUmKH7TnIWP5QHGGmhtMZMnnsh6OyYSlq4yuLsWBmVZ/7YA8pzsXjL32mGXNlRR4svaYWuW5essk+JEnC/BmjsWpjfa/FiBwSMH/GaN2XMwgh4AsadyPedDyA5zbs1aSenz9+CK66iHUPiIygqCraAulbMbw3vFpT0jq35zjzwtq5PcfiOTVpf6OdzYToSJHtvi0JEZDZY19WVMPWjHYaX1mMcSOLcLQljFAsgQKPCxVD8xGJyXj8759pAm9vngvLFk2GN58Flch+JleXYvGcGlMftgXCCcgGlRdu9UexYu1uTep59Qgvbr1iPByse0CkO1UItAXSu2J4bxhgU1IGuj1HbVUJi/GkoY7iMZlRaIL0lcljv3NmzIxMd0mSMHLY6UJJsYSCp9bU4UR7tKst1+3E0kW1KCvKNb5DREmaXF2K2qoSNDYHEYjE4c1zo6q80JDxH0sohmVUhaMynlpTp0k9H1qciyVXT+TSDCKDZELF8N4wwKakDGZ7juoRXpN6RXpQhUB7IKZZ/0nUKZPHfjCSQEIx/3MvKyr+/MYeHDpxeiugHKeEJQsmsVoxpQVJkgwf70YUHuwkKypWvrEbLb7TD7jyc3NwzzW1yM8dWPV/IhqcTKkY3hsG2JQUq7fnIGOoakeqjhVBBqWHTB378YSxRZP6ogqBVRv3Ye8hX1ebQwLuuHICxlYUmd4fIrsyovAg0JG5snrTfhw8Guhqy3FKuHvBJAxh9giRITKpYnhvGGBTUqzenoP011lkIhNTdUg/mTj2VSHQbkH1UiEEXn23AZ/sO6lpv/nycZg8psz0/hDZVSiSQDRuzM34+u2H8FF9S9e/JQC3za1BVbk5GTguJ9PPKbtkWsXw3nBUU1Ks3J6D9CcrKlr9DK7p7DJx7PsNmhk7m7c+PIytnx3TtF1zcRUunDTc9L4Q2ZWsqPAF+1+Wkqztdcfx1oeHNW0LP1eFKeOGGHK8M7lzHCgt6v/7lCiTKKqKtmA8oyqG94YBNiWlc3uO/vZzNWJ7DtKfrKhoDcSgZFoJRzJEpo39SEy2pFL+e/88hvXbD2naZp9fgdlTR5reFyK7Eqdqghhxddp7qB0vbt6vabv4nHJcdl6FAUfryeNyotTrYXVyyhod49maB9pmY4BNSevcnuPM2awyryett+nJJglZQas/mhVfdqSfTBn7iqJakqb26f6TeHnLQU3bhROHYeHFVab3hcjOAgYVHjzWGsaf39ir2Q2htqoE110yxpSHgx6XEyWF7rR5EEmkB38onjU1frgGm1Ji5vYcpK9YXEF70JiZAcp8mTD224MxqGbsydVN/SEfnttQrxl3k6tLcdPl49Lq3BEZLZZQEI7KcDr1HRf+UBxPr6nTVC8eObQAX7hyApx9peboKNftRHEBg2vKLqFoAhELssWswgCbUmbG9hykr3BUhj+c2QUmyHjpPPYjMRnC6TT1mIeOB7Hy9d2a5RhjRnhxu0k39kTpwqgtuWJxBU+vrdO8d3GBG3cvnASPy/jvgzxPDooL0qcAJJEeYgkFgXDC6m6YiiniRFkmGEkwuKaspqjmp4Yfb4/gqbV1mv3lK4bkY8mCSXDl8FJM1J0/rP86TUUVePbNvTh6MtzV5nE5cc81tSjKNz7ozc9lcE3Zx8gihWZqOh7EH17954BfzxlsoiwhhIA/FM+qFB2i3vhDCVNTw33BGJ58dRfC3fb8LPV6cM81tcjz8DJM1J0RhQeFEHj5nQPY3dTe1eaQJHzx6okYUZav67F6U5jnQmGey/DjENmJKsSppVhW9yQ1n+xrwaqN+wa10w6v7ERZQD1VibX77BlRNorEZMQSiu7rOvsSjibw5BptSmphngvLrp1syqwZUTqRFdWQDKvNnxzF+7uOa9puvnwsaiqLdT/WmRhcU7byBeNpvf2rEAKbPjqC1//RNOjfZYBNlOEUVUVbgHtcE6mqQMDE5RHxhIKn1+7G8bZIV5vH5cTSa2oxpCjXtH4QpQMhBHzBOPROLvl0/0ms3daoaZt3QaUp+80X5buQn8vgmrJPMJLQFBJMN7Ki4sXNB7Bjz4mkfp8BNlEG69zjmttwEQG+UNy0VDVZUfHn9XvQdDzY1ZbjlLBkwSSMHFpgTieI0kjQgC25Go4F8Le36jVt02qG4soLR+l6nN4UF7i5BISyUiyuIBhJ36Jm4aiMP72xBweO+jXt40YWDfg9OPKJMlQ8oWTE2hciPXSmhptBFQLPb9qHPU2+rjZJAm6/csKgLtBE2SKWUBDqVqNADyd9UTyzbrcme2tsRRFuucLYLfEkAEUMrilLJWQV7Wlc1OykP4qn19ShxRfVtM+YNAw3XDZ2wO9j69Efj8exfPlyvPLKK3C5XFi8eDHuv/9+7h1I/RJCpPXevHqIxuWOVDurO0JkA2amhgsh8OrWBnxcf1LTfvPscThnTJkpfSBKJ0ZsyRWKJvDUmjqEY6eD9mElebjr6onIcRpXtV8CUFLogcdt7haARHagCoFWf9TUIqJ6OnjMj5Xr9mi+NwBg4cwqzJ5aMahYwtYB9k9/+lNs27YNf/jDHxAKhXD//fdj5MiRuP32263uGtnUroY2rN/ehNbA6adnZV4P5s8YjcnVpRb2zDzc45pIy8zU8I0fHsHWncc0bQtmjsaMWuPXexKlI19I3y25ErKKlev24KT/9AxUQZ4LS6+ZZOissiSdCq5N2E+byI7aAzHk5nus7kZSPqpvwfMb90Hp9l2U45Tw+bk1OG/ckEG/n20332xvb8fzzz+Phx9+GOeffz5mzZqFZcuW4eOPP7a6a2RTuxrasGpjvSa4BoDWQAyrNtZjV0ObRT0zD/e4JtIyMzX8/V3NeGO7ttroZedX4PKpI005PlG60Xt8qkJg1cZ6NDQHutpcTgfuWTAJpV7jCgtKElDK4JqyWCAcT8uiZkIIvPnBITy3oV4TXBfmufCV689NKrgGbDyD/cEHH6CwsBAzZ87savvqV79qYY/IzoQQWL+9qc9ZKlUA67c3obaqJGPTxf3huGafXSIz2XFphpmp4Tv3n8RLWw5o2qZPGIqFF1dZfh6I7MiILblef78Jn+5v7fq3BOALV9Zg1PBCXY/TnUMCSr25cOXYds6KyFCRmIxQVDZt+0u9yIqKF97ejw/3tmjah5fm4Z6FqT2Us22A3dTUhMrKSrz44ot47LHHkEgkcMstt+C+++6DwzGwLzGHo+M/tNPA9TaZqvOcpcu5O3jUj7ZgDP3dx7YFYzh8MoQxI4wrMmTFeROiY/2amXv76o1jNXl2GKv/PNiK199vQmvgdEpmmTcXV88cbem647ZADJJDQm9zStrzllrl4vpDPvx1Q71me6HJ1aX4/NzxGfeZ5lhNnh3Gqp34w/Guz1N/BjpW3/usGW9/fETTdv2lY3De+ORmoAbC6ZBQVpRr6LruZHGsJo9jdeASsopwrCO41vO6arRQNIFn1u7GgaMBTfuEUcX44tUTU15OYtsAOxwOo6GhAc8++yyWL1+OEydO4Ac/+AHy8vKwbNmyAb1HUVGe5n9p8NLl3B04HhrQBU44nCgtNX6LHLPOmzhVUMKd64Y7123KMY3AsZo6q87dJ/Un8Pym/RBCaMagPxzH85v2w+vNxfk1w0zvVziagEcW8OT1Py4KC1NLG2045seKdbs1qWXjRxXjvsVT4c7AdFGO1dSlcu6EENh32Ad/KI6iAjfGVxanZYZEMBxHbr7AYEZff2N1574WvLRZm0Eyb8ZoLJo9Pskenp3TIWFoSZ4tg2uAY1UPPHf9U1SBE21heM84T6leV43W3BrG71/8DCfaIpr22dNG4varJunyYMW2AXZOTg6CwSD+53/+B5WVlQCAI0eO4C9/+cuAA2y/P4Li4nz4/REoOu+tmOmcTgeKivLS5txJigJ5AP2UVAVtbSHD+mHmeVOFQHsgZvqal8ph+qfacawmz8qxKoTA82/uRULu+zO4esNejCrLMzUIUFQVLe39VzJ1Oh0oLMxFMBhN+rydaI/g9y/sRCx++u8fUZaPu66eiEg4hkg/v2sGjlV7SXWs2jVTZLBkRUWLLwoxwErDZxurh0+E8MSLOzXj/dyxpbjqwkr4fGHd+t2dy+lAaZEHAb8+o9yIB/8cq8lLt3tgq7T6o5p7UD2uq0bbf8SPZ9bu1lQKlwAsmlWN2VMrEAxG+/5lDPy6atsAe9iwYfB4PF3BNQCMHTsWR48eHfB7dFalVBQVsmzP/9B2ly7nrnJoAUoLPT0KnHVX5vWgckiBKX+P0edNFQJt/hgSNv0CGyyO1dRZce4ajgU0lXp70+KLYv9hP6pHeE3qVUdqeOKs56Lj54qiQlEGX8HYF4rj/3v5n5q9e0u9Hiy9phaeHGdS75kOOFZTl8y56yzieWadkZP+KP765l4snlOTFjtlCCFw0h/V7E19dn2P1fZgDE+9tgvxbudz1LACfH5uDYSAIePQneNAUYEbQgVk1b5jgGM1dTx3feu97k9q11Wj7dhzAi+8vV+TceZyOnDbvBqcO7YMHcNZn37bM68FwNSpUxGLxXDgwOmUn/3792sCbqJOkiRh/ozR6Gs5l0MC5s8YnZapdGdS1Y608EwJril9BSIDK1A00NfpIRxNGJ7VEY7KePK1XWgPnv67CvJc+NKiWhQVpO9SDbKngRbxHOiMsJVCUXmQwXXfonEZK9buhj+c6Gor9XqwZMEkuHOMWZ7hcTlR6vXAkQH3EkTJisTktCqqK4TAG9ubsOqMbbi8eS585YZzcO5Y/TOAbBtgjxs3DnPmzMGDDz6Iuro6bN68GU888QTuuOMOq7tGNjW5uhSL59SgzKvdg6/M60mbp/tno6gqWgf99J/IGN6zrG8e7OtSJSsqApHE2V+YgrisYMW6OhzvtnbL43LiS9fUYmgx1+uR/hqbg/1mZwEd21E2NgdN6lFyErKCkE7jU1FV/GX9XhxrPZ0Cnut24p6FtfDmG/N9k+d2oqTQnREP6omSlZBV+EPpsx1sQlbx1w31eGvHYU37iLJ83HfzFIwyYCkVYOMUcQD4xS9+gYcffhh33HEH8vLy8MUvfhFLliyxultkY5OrS1FbVWK77YL0ICsq2gIxzdM3IitVlReizHv2pRlV5cZtkdOdPxSHkZN4iqriL2/s1QQyToeEuxZMxMihxhdPpOxkx0yRwRJCwBeM65J8KYTAS1sOYu8hX1eb0yHhrqsnYnipMQ+58j05zE6hrKeqAm3BmE5J1MYLRhJY+fruHg8fJ44uxu1XTkCu27gw2NYBttfrxaOPPmp1NyjNSJJk6npPM8iKitZArGtNFZEddC7N6G1tKGDu0oxgJKFZh6k3VQg8v3E/dje1d7VJEnD7lRMwfmSxYcclslumSDIC4QRkna5fmz46gu11xzVtt14xHuMMGof5uTkoMmhWnChdCCHQHkyf+9DjbRE8vbYObWdMAFx8Tjmuu2QMnAPYIjAVtk0Rp/QihEDDsQB2HjiJhmOBtFgLli4SckdaeLp8qVF2scPSjISs6pZ62hshBF7b2oCP6ls07TfNHmfI2i2i7jozRfpjZqbIYMXiiqZibyo+rm/B6/9o0rTNnzEK0yYM1eX9z1SY52JwTYSOh2RGPsTW077DPjz20k5NcC0BuHZWNW641PjgGrD5DDalh10NbVi/vUmTJlrm9WD+jNEZse7ZSglZQWsgZmjaK1GqrFyaIYToSA038BibPjqCd3ce07RdfdFoXFQ73MCjEnWwU6bIYKmqgC+sT+r6/iN+rNq4T9N24aRhmDvdmOK33nwXCnJdhrw3UTqJxGTdHpIZbXvdcby4+YBm2z53jgNfuHKCqTEJA2xKSV9bh7QGYli1sd6wGSwhREaus+4ullDQHmRwTenBqqUZoahsaEX9f+xq7jFjdumUEbhi2kjDjkl0ps5MkXR7mO0LxXXJvjp2MoQVa+s0NUhqKotx0+yxhlz7i/JdyGdwTZQ2Rc1UIfDGP5qw6aMjmvaifBfuXlhrep0UBtiUtIFuHVJbVaLrBTAbZsxj8VPBtdUdIbIxWTE2NXzngVa8uOWApm1azVBcM6s64x7okf2lWxHPcFTWZcu8YDiB37/0GSKx0+9VXpqHO6+aAKdD/5WOxQVu5Hl4e0ykCgFfGtyLJmQVf3urHjsPtGraK4bk4+4Fk1Bc2P8SGyPwG4SSNpitQ/Sa2bJqxtxMkZhseMorUSbQqypxb/Yd8eGvb+7VZJBMqirBrXPGcQ9csky6FPHs2DIv9VmvuKzgqTV1aGk/vS2eN9+Fe66p1b0CsASgiME1URd/KK5bcUKjBMJxPLNuNw6dCGnaa6tK8IUrJ8DjclrSL36LUNLM3jrEqhlzM4WjMvw6rVcjymTBSMKw1PDDLSGsXLdHk45aVV6IO+YbM2NGlEm6tuRK8b5cVQWe21CPpuOnt9hx5zhw98JalOg8IyUBKC50G7ptD1E6CUUTiMZTz0AxUnNrGE+vrUN7UHvfPGvKCFz7uWo4TChm1hd+k1DSzN46xIoZczMFIwkEDUx31UP3WQQiqxiZGt7ii+Cp13ZpUlvLS/Nwz8JauHOseRJOlE70evi1ZlsD/nmwrevfkgTcPn8CKnVeSykBKPF6LJvpIrKbhKwgGLb3/ejeQ+348xt7NddqSQKumzUGs6aMsLBnHRhgU9I6tw7pL+jVc+sQs2fMzeQPxxGO2rdCYziawGvvNWLHnhOYe/EYq7tDWaxzL04jktb8oTiefK0OoW5jsaTQjaWLJjNtlGgA4glFM36StXXnMbzzqbZy/42XjUVtlb5LwCQJKC30wM3gmghAR+ZIm4HLr/Tw/q5m/H3LAU1Gq9vlwB1XTsAknb8jksU7Bkqa2VuHmD1jbobOLYYiNk3DEULg4/qTeGXrQVs/AKDsEYgkICv6X/ojMRlPvrZLs29mQW4Oli2ajOKC9PlOIbKKKgTadag2vKuhDa9sPahpmz+zCrOmjICi49iXpI5JABczU4i6tAdjulT+N4IqBNZta8TmT45q2osL3Lh74SRUDDG3Unh/GGBTSszcOsTsGXOjdczExXWpsmqEVn8UL205gL2HfFZ3hQhAR3V9Ix70xGUFK9buRnPb6SUQHpcTS6+pxdCSPN2PR5SJ/DpsyXX4RBDPnlFc8LxxZbhlbg0Cfv2WKDkkoNSbC1cOayoQdQpGEojLxm17mYq4rOC5DfWaZSMAMHJoAe5eMAlFNnsQzgCbUmbW1iFmz5gbSRUC7YGYLb/IFFXFO58ew5vbD/VYR+fmzQhZRFUFfAYUAFQUFX9ZvxcNzYGuNqdDwl1XT0TlsPR4WEdktUhMTrkgUlsghhVrdyPR7bpYVV6IL1xZo2vlfodDQpnXgxwnr2dEnWJxxbZ1gPynKoUfPqNS+OTqUnxhXo0tl3gwwCZdmLV1iJkz5kZRVYHWQNSQNNdUHToexAub9+PoyXCPn9VWleCGy8Za0CsiwKfD7NiZVCGwauM+7G5s72qTJOAL82owvrJY12MRZSpZUVPe/SISk/H02joEut3glxV5cNfVk3RN4WZwTdSToqrwhfovImyVoydDWLF2N3xnLD+57PwKLJxZZWml8P4wwKa0Y9aMuRFkRUV7IGa7fQVjCQXr/9GEdz871mNrFW+eC9ddOgZTxpalxTmmzBOOJnRfSiGEwOoN9dixp0XTfuNlYzFl3BBdj0WUqfTYkktWVPzpjT043m2JRr4nB0uvqUVhnkuHXnZwOiSUFXm41R5RN0IItAfifW6Ba6U9Te34y3ptpXCHBFx/6VhcfE65hT07OwbYlJbMmjHXk6yoaA3Yr3hEXUMb/v7OgR77CALAzMnDsWBmFSsok2VkRUXAgO1CNn10BOv/0ahpu2rGaMycbO+LNpGdhKJySltyCSHw4ub92H/E39WW45Rw14KJGFqsX/2DHIeEUgbXRD0Ewvpsq6e39/55DC+/c1Dz8M7jcuKO+RMwcXSJdR0bIN41E5kgIStoC8Rs9YQwEI7j5XcPYuf+1h4/G1aSh5svH4sxI4os6BlRh67ZMZ3fd3vdcax5TxtcXzJlBOZMH6nzkYgyVzyR+prNDTsO98giWTxnvK7XnhynhDJvrm1TSYmsEonJCMfstUOMqgqs2dbQY5u+kkI37l5YixFl+Rb1bHAYYBMZLBZX0B6KpZRCpydVCHxQdxxrtjX2KErjdEiYM70SV0wbyTVqZLlUZ8d688+DrXhh835N29SaIVg0q5pLIIgGSBWix5rIwdqx5wTe/OCQpm3BzNE4f/zQlN63O3eOAyVej65F0ogygR61E/QWS3RUCt/VoK0UPmpYAZYsmARvvr0qhfeHATZlLSGE4eu4IzEZ/pD+M3DJOt4ewYtv78fBY4EePxtT4cXNs8dhGLclIhtIyApCOlc03X/E12MLoImjS3DrFeN5A040CIFQHEoKKVn7DvuwepP2QddFtcNx+VT9skg8LidKCt18cEZ0BnFqJxu7TPwAHYVMn1lbhyNnFNk9d2wZPj93PNxptl89A2zKSrsa2gyvRB6JySk/4deLrKjY9NERbPzwcI+boly3E9d8rhoXThrGIINswYjU8CMtITyzbo+mev+4ymIsWTAx49ZlSgAKdCwORdRdJCYj0seWXEIIHG0JIxRLoMDjQsXQ/B4BbnNbGH96Yw/Ubnf3E0YV44bLxuoWDOe5nSgqYHBN1Bt/KG6rYrtHWkJYsW43/GfcM18+dSSunjk6Le9NGWDryIwZ0Wym1/nd1dDW617arYEYVm2sx+I5NSkH2aFowjbB9YGjfry4eT9OtEd7/Oy8cUNw3SXVaZV2Q+aw8vssEEnoevE/6YviyTV1mkqkw0vz8PXFUyHHE1BsuGVesnKcEooLPHBxz3oyQH9ppfsO+/DuzmOaa19xgRuXTBnRte1dIBzH02vqNMuTKobk4875E+HUaY10fm4OinhNI+pVONr3AzIr1DW24dn1exGXTy8Hc0gSbpw9FhfVDrewZ6lhgK0TM2ZEs5le51cIgfXbm/osNqYKYP32JtRWlSQdTATD8R5P4awQiclYu60R/6g73uNnJYVu3HjZWEyq4meTerLy+yyWUBCO6ld0xR+O44+v7dKkm5cUuvEv101GQZ4Lvrj+Fcqt0DlrXZCbwwe7ZBh/qPctufYd9mHd+409rq2+UBzr3m/EgplVGD28ECvW7dbsWFFU4MbdCybB49Yn/dOb70JBLrM3iHqTkFUEbLTu+t2dR/Hq1gbNd0qu24k7r5qImlMP5dIVA2wdmDEjms30PL+NzUFN0NCb1kAMjc3BpLYBC0YScMjWzoYJIfDp/la88u7BHhVeJQm4dEoFrpwxCh5Xeq1nIXNY+X2mCqHrw6lITMZTr9WhrduYz8/NwbJFk1FS6NHtOFZzOR0oLnSzMCEZKhhJaGaZOgkh8O7OY/0+uH7n06OABBw+Eepqd7scuGfhJBTrNBaLC9zcUpKoD6oq0B6M2aImkKIKvLr1IN77rFnTXur14J6FtRhear9aQDlOaVCZMfwmSpEZM6LZrLfzG08oUFUBh0OC2+Uc1PkNRAZ28z7Q12l+JxxHNKGguNi6YdUWiOHv7xzA7sb2Hj8bOSQfN18+DpXDCi3oGaUDq7/PAuFESoWTuovLClas3Y1jracLprhdDiy9phZDM6SQX+esdSHXW5PB+is6eLQl3O+SKCEEmo4HEeqWmeKQgDvnT0TFkIKU+yYBKC50I9fNW1qivvhSLEyol1hcwbNv7sXuJu19alV5Ie66epLtrmcOCSjMcyM/d3DfL/w2SpHRM6LZrvv5jcZl+EMJKN227XE6HYjG5QGfX2/ewJ4+DfR1nfzhOMJRGU6nNQ9RVFVg62fH8MY/mnrMMLicDsyfMQqXnFeh2xo3ykxWfp/FEgoiOu3HqagCz66vR0Pz6Wr5ToeEu66ehFEZ8oCJs9ZkFlUItPdTdDAU63+ZRSgqa4JrALjxsrGYOLok5b5JElBa6IGbGVlEfQqE45oaJFZpD8bwzLrdOHpGpfDzxpVh8Zwa29UOyffkoDDPBUcS984MsFNk5Iyo1YQQOHjUj/ZgrEeRI7MKIHWet2hc7kjzPOMKrygq2gIxfHawdUA3/FXlhSjzenoEEd1nxUeU5aOqfOA34f5QHGGdAoNkHGkJ4YXN+zWpd50mji7GDZeORVlRrgU9o3TjD8d7ZIj0Jtnvs76+N/TYU7eTKgReeHsf6hpP76MpAbhtXk3ar+kCOv6WQq4zpX7ofX3u3JKrrwrhBZ6+P4udW1V2d8W0kbhocnnS/ensRzieQEVZAYZ3y0hhsVkirXA00eMBlxUOnwhixbrdCIS1D+TmTK/E/BmjbFUp3J3jgDffnVLAzwA7RUbNiFrtnwdb8daHO9HcGuoqPtBZ5AiAaQWQOs+bP5ToEVx3EcCn+07imourznohlSQJ82eM7lpj2mNWXAIKcnNQ19g+oL/FF4rrNus2WHFZwZvbD+GdT4/2SOl1SMCIIQW47LwKBtc0ILsa2vDa1gac9J2uNu90OlBU4OqRepnM91l/hdNGDi2AqlPq2rptjdixp0XTdsNlY3HeuCG6vL+V3DkOFBVw1pr6pneBws4tufqrED5uZBGKC9w9HpLFEwraz6iG4I4AACAASURBVHiYff74IbjqotGD7ken7v3IcUqQJMmSexOidBCNy/CHrS/kuetgK57dUI9EtwxLp0PCzZePwwUTh1nYMy2HQ4I3z6VLLQdepVPUOSPanzKvZ1Azolbb1dCG5zbU46QvomlvDXSkdjyzrq7HDHBnAaRdDW3QU1V5IXJdTk1a+JmcTgcip9LEB2JydWlXKkpbINb13k6nA6WFHiQUcda/RQiBtkDMsuB6T1M7fv23T7D5k57Bdb4nB8NL8wEAr/+jCfsO+yzoIaWTzsJmkbgMZ7fgrTNDJBo//TlP5vus8/17+9547q292Ln/ZGp/wClvf3wEmz85qmmbP2MULj4n+dkyO5DQUR25rCiXwTX1qb9xlsz1WVE7Kg53Vgg/M4DurBC+/4gfl0wZge5ZlLKiotUf1TwXrx7hxa1XjE96pqp7PzqD686/75l1dXhm3W7T7k2I7E5WVMu3ixVCYMsnR7Hy9T2a4DrP48SXFtXaJriW0DG5Nqw4V7dCibxSp6hzRrSv9HyHBMyfMTptUpROFznqfTbJF4rDF0pA9PLzzgJIvf0sWZIk4bzxQzo+/b2+ACjKd0GSpEGlrdZWlaAwNwdlRbko8XowpDgXw0pykXtqYPX3t6iqQKs/Zsl6lmAkgec21OOpNdrKyADgdEoYcurv6Vwvogrg3Z3HdP1vQpmle2EzSZJQlO/SjjdxKoMEyX2f9Vc4TQiBhCx0+Yx+sPs41m5r1LTNOncE5k6vTOl9rebOcWBIcS5TwqlfAy1QOJhx5gt2pIafrUL4uzuPYdzIIiyYWYXiAvepa2RU8ztDi3Ox5OqJSadcdt6oCwFNcN35M18o0WcwYcS9CZGdCXGqYriFH3lFFXhpywG89l6D5kFbWZEH/8+NUzBupD2WbHlcTgwpzoU3361rrJZ0gH3w4EG8/vrrWL9+PY4ePXr2X8hgnTOiZ85kl3k9abdFV39FjuIJBYqiQlFUzZOo7joLIOnp3DFlKC30aGbWgNMzzp1B8WDSVhubg2gLxuFxOZHnyYHb5ewxsHr7W2RFxUl/FIl+ZtSNIITAB7uP4/997mN8VN/S4+eFeS4ML8nrdS9RXyiOoy3hHu1EQM8xn+vJ6THeFEVFntuZ1PdZf98pnWnhqX5Gdx1sxeq392vazh8/BNdeUp02DzfPJJ16eMhZaxqIwRQoHIjOLbnOViEcOD1+x1cW4/Yra+CQJMjK6Vvq/Nwc3HNNLfJTeEjU2ByALxSH84zgGgDistp1bxLv48G3EfcmRHblD8U1Y9Bs0biMFWvr8P6u45r26nIv7rtpCobZYCePHIeEUq8HpV6PIdfYQc+DB4NBfPvb38bmzZu7ngZKkoRFixZh+fLlcLvTa62xXiZXl6K2qiTti2v0NwvcfY1kf6X+9S7oVlVeiJFDC+DxRxGXVaiqgNMhwZXj6Dq/g01bTaY4XTyhoD0Y6/NJvlFafBG8uPkA9h/x9/hZ55fU2WYFzlbllbJXb2Mh15MDj9upGW/XfK4qqYeFfY01VRWasZTsZ/TAUT/+8uZezZP6CaOKsXhO8qmoVuNaaxosPQuudt+Sa6DjMhTryGxb/fZ+HDl5uuBmjlPC3QsmYUiKtUCiMQU5Tgm9pbN1vzfpr5ZDOhabJRqscLSjboJVTvoi+P0LO3GsVbvMdGrNENx6xXjLr2sSOh76Fea5DI3RBh1g/+xnP8OBAwfwxBNPYPr06VBVFTt27MDDDz+MX/7yl3jggQeM6GdakCQp7bfi6m8WuHuZ+v62e9K7oFv3wmSeXqoaJ5O2OtjidJ2VUM2MrWVFxZZPjmLDjkM9nkR6XE4smDkao4cV4oUtB876Xv1VeaXs1tdYkCRJM96K8vuvNTGY9xdC9HhIl8xn9OjJEFas3a0ZH6OHF+KLV020/CKeDEnqOF+D3W+TSK+Cq0II+LptyTXQcVngcWH99kP4uP50PQUJwG1za1BVntp9kSvHiVGnJix6S3ntfm/S33Y66VZslmiwEnJH3QSrNDUHsGLdnh47B8y7oBJXXjjK8klHMx9eD/oqvn79evzud7/DRRdd1NU2Z84cuN1ufOc738nqADsTdBZtawv2TDVzu5xdaaN9zZgaVdCtMw1frwqhfW3X1V3n3xKKJnpsK2C0xuYAXnh7P5rbIj1+ds6YUlx/6VgUF7ghhOi1emt3xQVuVAzNN7K7lMYGMxb0ev8zg+tkPqMn/VE8+VqdphbC8NI83LOwNi33xHXndOxr7XSk34MBsp5e49gfTkDuNj4rhuYP6Bpz+GQQb314WNO+8HNVmJJi9X53jgNlRR6UlRagzJuLk/5or6/pvDfpa+ynW7FZosFShYAvGDN1Iqi7nftP4m8b9/WoFH7LFeMwfYK1xcyseHg96CM5nU54vT2fRg4bNgyybP0+a5Saztni5zft6/XnxQVuAKLXp1BGF3TTMw3/zO26ztT5twTCCVP3uI7GZax7vwnv/7O5x5dkUYEbN1w6BueMKetqkyQJl0wZgXXvN/b5d1wyZYTlTw3JvgY6FpL9DJ35/qoqNLNQyXxGA+E4nnx1F4KR0w++igvc+NI1tWk3+8tZa9KDHuM4Gpd77IwxkGtMdXkhXtp8UNP+uXPKcdl5Fcn8KV3cOQ6Uej1wSB3rrq+eORp/fXNvj35IkoTiAhf6qoaabsVmiZLhD8U1D8fMIoTA5o+PYu372iKjeZ4c3HX1RIytKDK9T915XE4UFbhMf3jt/NGPfvSjwfxCPB7HypUrccUVVyA/v2PGIRgM4qc//Snmz5+PmTNnGtHPpESjCeTluRGNJnTbYzUbDCvJw4gh+TjeHtXcwJZ5Pbj58nGYWjMUR0+GNGs8yrweXHfJWMMLukmShJJCD4aX5qOk0JPSBXNYSR6Gl+b3+rdcO2sMKoYUIDrIdSwOh4TcXBdiscSgqzd+dqAVK9bW9VhrLaGjGvIXr5qAiiEFPX6vrCgXZUW5ONEe0czmFRe4MXd6JcZX6lupsXyo/rMAHKvJcziklM9df2NBj3Hd+f5HWoIIRk7fwCfzGY3EZPzxtV040X56Jivfk4MvX3/OoNZ5pjJW9eJx/f/svVeQW1d27/3fJyKjc2QHNjOHGomSSElUliiR0mgUJnnGGo2crqtc1374qvxsT5VfxlWuuvVVjb/rKte9HoXxJI3CzEiMyhIlkQqUxEw2m91kR3ZCBk7a38Ppg8YBDtAAGuhGd++fy5Z5cBLQZ52919pr/RePer/sWPpSCbze8tL6C8FstXwqYauFWIwd64aB2Yjz6lehMebGDY048uk1aBnCn1u76/Dd+zYWTNdeCMs2CCHp383vEtAUdDt+v6fu2bCsc5PFwmy1tqi2rVaaeFJDLLn0i5y6YeC1D67gvS9HbNubgi78zWPb0FmF+WKxcMRcmPJ7pIrqsRRrq4SW2Lfgz//8z/H111+D4zj09vZCEARcuXIFsVgMHR0dNofnzTffLO2uK8zMTAz19V7MzMSg5VG9ZjgjCBzq6jw4eXYMs9FUzmoxpXTFC7pZZH+XdS1ehKIKlDKeGZ4nCAY9CIXi0ItUcAzFFPzxwwGcuZLbp7OtwYOn7lmPrpaFa9gopRidjCOWUuGVRbQ3earyN7lhS+V7CjNbLR9B4Cr221XbrqfDSVwZjZT9jKqagf964yyujEXS2ySBw988th3rWkobyMux1UrBEcDvkSrWbzMfzc2V1wRhtlo+lbTVQpRjxzORhVtPZo8xXreA/3jttC19vKPJi//x7e2LChrJIo8633zLnOzfrdD3W6lzE2artcVS2WolULXcnvNLQSKl4VdHL+LScMi2vavVj3u+2YZ6n6tq89CFcEu86VgvIsiXj2JtteTRfc+ePdizZ0/JN8RYeRBC0NsecHy5lCroVsuDXuZ3MQyK6UhySdobGJTikzPjOHz8as7ERuAJHrh5He6+sb3otBZCCDqac1e4GYxiqaZQYyKlQdGMsp9R3aD49ZsXbc41zxH8+OEtJTvXy8lypasx1g6l2nEsqS7oXFvntew3per4zz/YneugV8JP9m9ZlHPtknjU+QqvEBX6fqtBbJbBKBbD6ne9xNedDifx3MHzuD5r1wkKeiWAGnjn5AgoNf+9Z0dbxTMp88FxBEGP5Niydqkp2cH++7//+2rcB2MVc3ZwpmLiZNVE0w3MRFIFW5BVirHpOF59/7JjX84NnQE8eVcfGoOLa2vCYNQKurE4ZVNKKV597zLODtqzPO6+sR0eWQClzroQtcRSrVozGKWgagaiJYp46gbFr49exMjUfO96WeTx7CNbEfCUr9TtloU5nRcGg1EM4ZiyJHPWTIbGI3jh0PmclPSAx8xqIYTAqrsKxRQcOj6Efbu7q+5ke2QBPo9YM+05ixrpf/7zn+Ov//qv4Xa78fOf/7zgvswBZ2RydnDGUXRlOpLCS+9cwvfu21gTTraqGZiJpqpea6NqBt7+YhjvnRyBkVWd4ZEFPHpHD3Zuaqp5Z4HBKIVwTF1U//hDx4fw2YXrtm1Br4QLV0O4cDW05FHyUpFFHkFvddLVGIxyoZQiFCtt9YtSij9+OIDzV2fT2zhC8PTDm9HWUH63Co8sIMCcawajaOJJtWSdoMXyVf8UXnrnki3LU+AJWupN23eauhoUOHZqDH0dgarMbQWOIOCVaq57SFEO9ssvv4ynn34abrcbL7/8ct79KKXMwWakoZTi6KdX806sDQoc/fQqtnbXLatDqag6ZqKpqgsd9Q+H8Or7A45tRm7a2IRH7+iBz836VTNWF/GkVlT6aT7e/3IE7305atvm94jwZtjKUkbJS4GtWjNqmUhCLbkc6v2vRnH87IRt23fu7cPGRdidxyUsauWbwVhrqJq+pO1jKaV49+QIDp+4atvucQl4ZHc3PjozXvD4UEzB6GS8omWMZO76PrdYk4tSRY36b731lu3fv//971Ffb191HB8fx+OPP165O2OseIbGowV7cgLmSvbQeHTZaqZSil71+pV4UsUbHw/h86wVOACo98t48u712LSurop3wGAsD5puIJIoPzX88wvXceATe+sPa0DNptpR8lJxSTwCVRJZYTAWi6LqiJeoOvz15SkczLLHB27uxM2by+9x63OLLLDMYJSAWXetLFndtaYbePX9gZw5bHOdCz/ZvxXTDotGTsRSlQsIiDyHgFeCKNSulklRDvYbb7yB999/HwAwOjqKf/mXf4Es20UohoeHwTHRFkYGxU6sFzMBXwyJlIZwrHovKUopvuyfwuvHruTUqnAEuOubHXjglk5IQm2ltTAYlSIcU8rODDk7OIOX3+23bXNJZqp1Pge6GlHyUrFag7gktmrNqE0MSm3iZMUwOBbB796+ZNu2c1MTHrxlXdn3wZxrBqN0QtGlq7uOJzX88sgFDIza28f2dQTw9EOb4ZYFpFLFZah55cXbOgHg84jwumr/vVHUDGDnzp349a9/DUopKKUYGRmBKM5/OUIIPB4Pfvazn1XtRhkrD7+7uJSvYverJNGEauvxXWmmwkm88u5lXLwWyvlsXbMXT97dh44mpvjNWL1E4uW1ugOAgdEwfnX0gq28pKPJW5SYWSWj5KXCVq0ZK4FIXC1pgj4VSuKFQ+dt6eTr2wN46p6+srNF/Ctkksxg1BLxIhX/K8FUKInnDp7DZMi+Qn3LlmY8cdd6CLy5qNre5EHQKxUM2gW9EtqbytdoAMyWnAGvlL5urVOUg93e3o7nn38eAPDMM8/g3//93xEIBKp6Y4yVT3erDw1+uWCaeINfRndrZVrsFNsKLBxTEE+VlhpXLLpu4NDHg/jTB5ehZjkXksjh4V1duH17G5uAM1Y1iqrnZG0Uy+hULGcyv67Zi0dv78GfPhpc8PhKRMlLheMIAh6RrVozap6UoiNRwvgXS6r4xYFztjGzuc6NHz+8ueyJbsAjweNitsJglMJS1l1fGQvjxUMXcubK+3Z34Z4bO2xza0II9uxow6HjQ44ZoRwB9uxoKzsYR4i5ELfS3hkl3+0LL7xQjftgrEIIIdh7a5ejijhgGt3eW7sqUi9ZTCswwzD7BZa7qrYQ165H8cp7lzGa0brEYmt3PR6/q3fB/p61DAFqTqWRUXsYlGK2xPRTi+lwEr9445xNGbW5zoVnH9kKz1wLn2pHyUvFLfHws1VrxgrAoBShEtrlqZqBFw6dtwlzet0i/uKRLWUL9wW9TPSPwSiVpay7PnlpEr9/p9+W5SLwBN+/fyNu6Gt0PGZDZxD7dnfj4zNjtiDAYjt8yCKPgFcEvwJLkNlbjlFVtvXU43v3baxqH+xiWoFt6AhgNqZUpQ1XStVx9MRVHDs9llNv6neL+PadvfjG+oaaEF4qB4En8MgCXJLAnAjGgoTLtLNIXMH/feMsIgn74PyXj25Lp5JaUfJ8AbvFRMlLheMIgh4JssSCToyVQaQE2zQoxUvvXMLQeDS9TeQ5PLtvC+r9rpKvTWBqEzDnmsEonaWou6aU4q3Ph/HmZ9ds271uEc88vBndrYXFiDd0BrG5qw6zSQ0T16NwSwLamzxljcmrISts5d45Y8WwraceW7vrikrfLpViWoEd/GQQP3pwk3ODvkVybmgGf/hgALPR3FWB3dtasG9394qcUHAEcEkC3LJQ0yqNjNoikdLK6suZVDT84sA5TIfng3AeWcBfPrrNlvVhRcmPnRqzrWQvdR9st8TD75XArdCgGWPtkVQ0JEqwzcPHr+Lry9PpfxMAf/bgRqxrKb2kiwAI+pjwH4NRDrElqLvWdAMvv3sZJy9N2ra31Lvx7P4SgmoE6GkLoM4tQC+xBaCFWxbg94grfnxlbzvGkkAIqUorrkKtwCilMAyKqXAKIxVWFo7EFfzp2BXbBMSirdGDJ+9ej+6W5Wk9thhkkYdLMv93pa64M5YHTTcQLiH91MJKQ80srZAEDs8+shUt9e6c/Td0BtHXEcDoZByxlAqvLJYdJS8VphDOWIkYBkW4hLKNT86M470vR2zbvrWnB9t7G0q+NgFQ55NZpgeDUQYpVUe0ynXX8aSKFw9fwJWxiG37xs4g/vyhTUs23vEcQcArQV4lpYhslsBY0eRr8UUphW7QdMp2pZSFDUrx2bkJHPhkKGeljucIHrilE4/fuwnxWLLs6N1SI3AELlmAW+ZXZJ0LY/mhlCIULb0ll25Q/OatixgYnR/YeY7g6Yc3o6vAShkhZMlbcTGFcMZKJRxX8mZ5ZXN+aAZ//HDAtu3OHW3Ys6O95OsSMudcr5IJM4OxlGi6gVA0VdW668nZBJ47aNdZAIBdW1vw+F29SzYn9LoE+NziqlrYYQ42Y8koVuW7FJxafGU710BllIUnZhN49b3LOVE+AOht9+Opu/vQ1uhZESnVxEoBl3gmXMZYNNGEClUvTTyQUorXPhjAmSsz6W0EwPfv34BN6+oqfIflwxHA72G1o4yVSSllGyOTMfzqzYs2Z3x7bz0eub2n5OsSAtT7ZDa+MBhlQKkpylvNsuuB0TBePHzB1lWAANh/ezfuuqF9SZxdgScIeuUVMW8uFTZjYCwJxah8l0N2KzBKKXSd2iJ+i1UW1nQD754cwTtfDOeITLgkHo/c1o1btrasiHoRSeDglgXIEr8i7pdRHuUGs8o5rtyWXIdPXMWn5yZs2x67sxff3NBU8rmqxUpWMGUwdMNApMiyjdloCs8fPAdFnQ+UrWv24gcPbCw5a4MjQL1fhigw55qxPFRjQWcpCcdVW6vKSvPFhet4+b3LtjmtyHP4wQMb8Y31pZeClAohgM8twiMLK+rvUgrMwWZUnWJUvst1sjNbgekGzXkhLVZZeGA0jFffv4zrs8mcz27oa8Rje3rg9+SuotcSHGepgPNl9y1lrBzKDWaVc5xBacG2Wfn44KtRvHvSXuP5wM2duOMbbSWfqxqs1L6bDEYm4Zha1ApYUtHw/MHzCGfUetb7ZTyzbwukEp1k07l2rcoVKcbKoFoLOktFIqWV1Ku+FCilePOza3jr82Hbdr9bxDP7t2Bdc+kihqXiknj4Pas/cL26vx1j2SlG5fvop1dBSy3ezGBbTz2euKsPPpc9DTzolbBvd3dZysKJlIZX3ruM//zjmRznus4n4dn9W/CjvZtq2rmWBA51PgktdW743CJzrtcAVjArW/jPCmadHZyp6HGRuFpy65DPL1zHGx8P2rbdtr0VD96yrqTzVAtJ4NAYcDHnmrGiSaS0opSHdcPAr45exNj0vMigS+Lx7P6tJY9vHEfQEGDONWP5KHcsqxU03ShJkLAUVM3Ab966lONctzV48HdP7ai6cy1wBPV+GXU+edU71wBbwWZUmUIq3xbTkRSGxqNlq4ynFB2t9W48/fDmRSsLU0rx9eVpvH7siq0fL2Cuau3Z0Ya9t3bVrGgLIWaLA48sMId6jVFsMGtrd53NLso9LqXoJUfZzw3O4OV3+23bbuhrwLf39C57mhgB4POI6Z7bDMZKRTeKU/SnlOK19wdw8VoovY3nCH788BZHBf9C8HOTZzbuMJaLcseyWsGqu65GYng0oeKXhy9gcNyuIbS5K4gfPlhdpfC1kA7uBHOwGVUln8p3uftlk0hpCMcUUCxeWXg2msJrHwzg/NBszmcdjR48dU8fOpcgfaYceI7A6xLgkgVWW71GGRyLlBXMKicIZhgUoRJbcg2ORfDfRy/YJj8bO4P4/v2l13hWGpHnEPRJzDlgVAWrHjSe0tDRpqLBU92pV7GK/u+eHMGn56/btn3nnj70dQRKup7AEdQH1saqFKN2WYoFnWpSrbrridkEnj9wLue3uW17Kx7b0wu+iuOvW+LhX6PdN5iDzagqTirfi9kvk1hSRaQC/QENg+Kj02M4cuIqFM2uhCzyHPbuWoc9O9qr+hIqF0ng4HWJrMcoo2hbyA5mlRMEC8cVGCWkho9Nx/HcwXO2ycO6Zi+efmjzsjq1BKZCuKtGM1IYK5/MelBCAIHnEPBIePCWdVWpB40n1ZxxzImTlyZx+MRV2za/R8SpgWkEvFLRpVUCT9Dgd63JCTSjtqj2gk41qVbddf9wCL88csHWSYAAePSOnkXpEy2EKPCo8/JrWuiQOdiMqpKt8u1Eg19Gd2tpK8PhmIJ4BV5GI5MxvPL+ZQxfj+V8trkriMfvXI+GgGvR16kkBIBrLg2c1boxLPye4lKbs4NZpQbBSmn7AwDT4ST+642ztmOagi78ZP/WZQ0MiTyH5no3opEktCIcEgajVPILfCYXLfDphKYbRQXaBkbDeOkde6mGWzb70IZiCg4dHypKv0QSONT5ZZY1xagJqrmgU000vbiSjlL57PwEXnlvAEZGOoskcPizBzdVTeyNIwR1Phkegaz5cZU52Iyqkqny7bTgxRFg761dRUfRDMOsUSkmQl8IRdPx5qfX8OHXozn35XUJ+NaeXty4obGm6kUEjqQda7ZawMimp81fVjCrlCBYqROBSFzBf71xzjbpD3gl/NW3tsHnXr5aZ69LQB1rI8SoIktdD1ps/eb12QRePHzeloEiiaYgpnUfBgWOnRpDX0cg773JIm87hsFYbqq1oFNNDEoxG0kVVdJRyjmPnLia06kj4BHxk/1b0dFUfillIdyygHq/DK9bhJKsvSyBpYYtfzGqzraeenzvvo1o8Mu27Q1+uaQIvqrpmAwnF+1cX7g6i//3d1/h/a9ynetbNjfj//nBTbhpY1NNTBxEnoPPLaIxIKNpTg2cOddrB0opBsciODUwhcGxyIJq+zf0NSKpmOrB2fvmC2ZZQbB8j1XmceFYcbWdgNn657kD5zAVnlfhd8s8/vLRrajzyQWOrB4CR9AYkOH3MMeAUV1KqQetBJEi6jejCRXPHTiHRGo+m8RK8c62h1BMwehkPPsUAJhzzahNShnLaoVQVIFWYieOQqiagd+8eTHHuW5v9ODvntxRFefa7LwhI+hdm7XW+WAr2IwlYVtPPbZ212FoPIpIQoHfLaG71Vf0iy5TzKxcogkVb3w0iJOXJnM+awy68OTd67Gho/SWXpWGKYEzgNJ6eX55cQIvvnEW05EUNN1APKmBEIKAR4RLFhbsAWoFwQpdL5oorrYTMAf5Fw5dwMjU/ARdFDg8u38rWus9pfwMFcMjC/B7xJqaXDFWL0tZD5pUtAVLpkybPG+zb6utVr5JcSyVm27ulngElylAxmAsRDFjWa0QjitFtdIrlkhcwYuHL+DqhD1ot6W7Dj98cFPFu9/wHIHfI1ZVgXwlw34VxpJBCClLuTGaUBFNlC9mRimd6707lCMiwRGCe2/qwH07O5e9npkjgMclwuNiSuBrnfy1m6mc2s0DHw/iDx8OQNUMWBEonufglnmAAPfe2IF7b+pY0LEsFARTVL1oGzQMit+8dREDo+H0No4QPP3QZnS3Lr1yK8cRBL1SzbbWY6xOlqoe1DDogn1zDYPit29dsk28CYCGQOG2Wl7ZXsbhcQkIlNgbm8FYaha7oLMUxJMa4snKiZqNz8Tx/MHzmMnKmtmzow2P3t5T0ZVlQgCvS4TXtbbabpXKinGw//Zv/xYNDQ342c9+tty3siisdh1LZfRLcb1ir1HqvVBqThwSJQgqZTMVSuKV9y/j8kg457PuVh+evLsPbQ3Fr6hRShfdazsbniPwuAS4WYutVUk5z32xtZvnBmfw2vsD0LN21nUD0YSBep+Mry9P4d6bOoq6V6cgmEEpZheYwGfe+2sfDODMlRnb9u/dvwGbu+qKOkclcUs8/F6J2RWjYhSyZ+uzcDyFaFwFzxHEUxokgbPtk1J16DpFvU9GV8viUjbDccXxXZE5Vn1xYRKnr0ynPyME6Gzy2cSPsgl6JbQ3zY+NPre4rLoJDEYplLugsxSkFB2RDC2Txc4rL16bxX8fuWhbDScEeOyOXtyxo62i9+6WePg8ImvJVwQrwsF+/fXX8e677+Kpp55a7ltZFKWk2B90vQAAIABJREFUfK6U6xV7jVLvxRJ+KLfeWtMNfPDVKN76/FpOXZos8ti3uwu7t7eWNPHuHw7h2KkxhDKcjaBXwp4dbUW3NLEgxLwPtySwFlurmHJssNjazcGxCP7w4RVohgECh+eYmn015XByUX0/w7HiW3IdOXEVJ85N2LY9tqcHN21sKuva5cJxBEGPxGyLUVEK2TNgBr5GJmMIx1XougFCAN0wyyMCHhEgQDSuQtXNcY0Q4N9fOVX2mJxP0T9zrIolVNuYBQDf3tOL5jo3Dh0fyis+mtnCx+8R4XUx55rBWCyqZmA2Ni9GuNh55Ymz43jtgwGbHUsihx89uAlbuivnV4g8B79HhMQywYqG/+lPf/rT5b6JQszOzuIf/uEfsH79ejQ0NGDv3r1FH5tMqnC7JSSTakk9W6uBlfIZT9kHw4Si4+zgNFrqPWiuc9fM9TiO5Px2VnT+2vUoEikdo5MxvPRu/4LXKPVeDINiOpKEuoBgSz6GxiN4/uB5fNU/lTN5+EZvA559ZCs2dAZLihD2D4dw6PhQzmQmpeq4PBJCQ8CVrmVzuUSkUmqOGBQB4JJ4+D0SAh4J7hVaY+31Vr7+rpZstVKUa4PXrkdxdnAmZ3s2fo+IM1dmkFR0Zwcbps3KEo/N3XVoKaP2OZ7UECsyje3Dr0dx5NNrtm337+zEfTs7S77uYnBJPOp98oIlH07vuNUGs9XKUcieP79wHV/1TyISVzETTYFm/C4UFAQEsaQ6V6JEIHAcgj4JLkkoew6gG4ajanjmWJVMaZiN2p3rG/oa8MjtPekx6/pswrbyFfRKuH9npzlGzv3bs8zONbPV8lirtloJqvHM6YaB6QzF8GLnlU4YlOLgJ0M4dOKq7R0Q9Er4629tQ297oCL3zBHA75EQ9Engi5ivMludp+ZXsP/1X/8VTzzxBCYmJhbeuUZZjnYdlb5eduSeUopQVIFL5h0FDqxrbOkKlnQvmm5gJpLKSXkthqSi4fDxq/jkzHjOpCPglfD4nb3Y3ttQ8nkppTh2aqzgd7BamsDB0eE4Ag9rr7WmWIwNFluTSUCKep50g5ZV56npRtECTF9cvI7XPxq0bdu9rQV7b11X8nXLxZoIuOWaH9YYK4yF7DkUU0ApBSFA9uDDEQJCaDqlsrneDYEjtt3KGZND0dzU8MyxStH0nHpMl8RD1Yy5eyXY0BlEX0fAMT2VAOkgAIPBWByGQTETTtkWrIqdV2a/ExRNx+/e6reVfQBAZ5MXz+zfUhGdBALA7RLMzjWsxKosavrN+dFHH+HTTz/FH//4R5Sz0G5NPouJulSTK6NhzERTKPSMzkRTGJ6Kobdt8VGnSlzP+s14nsOZK9P4/bv9MKwJBABFM5BQNCQUDQ1+ApecmzYyE03hs/PXi76X9kavmSZDAJ4vzaBPD0zj1fcHcsReCIA7bmjDvt1dZU8Uhq/HEI4rBb9DOK5gfDaO7lbz9+R5DpIwX1vNKEyt2GqlWIwN9nUG0BhwYTqSzHMk0BhwYVNXEB98PQqB4+YDUg7XawzI6OvM38/WCbOnrlqUA39ucAa/f/eybdsNfQ146p6+JQsouSQBAW9pdWGZ7zhG8aw2Wy2GQvasqDp0wzDHRxDHfTSDgsBMCTf/m+uJlzIHiMQV6JTmjJPWWKUbBqbD9tVtUeDQEJARSagYn42js8nqBUzQ1WbvC8wRgjq/XDPCgMxWy2Mt2mqlqOQzR+d0TGjG3LaUeeW8rZq2/4sD53BtImbbd3tvPX60d1NFUrhlkUfAK5WVYclsdZ6anfmnUin88z//M/7pn/4JLpdzisRCBAJu23+Xi4GJWFEPKuV41NcvvkddJa/n97vw9hcj4DgCLmP2rqjzaamRuAKfx/k8UdUo6l7iKoVOOPhL/FvNRJL4zZELOHnhes5nHc1e/Hj/NvSVWB+dzbWpBPgiHAVKeAQDbnhcIlrqPcuuSr6SqBVbrRSLtcHvPrgJv/jTGce+14QQfOeBTbhhQxPe+OQqFN3A1GzSMU1cEDg8/cg2NDT4cj4rxGwkBU8Rh/Rfm8WLhy/YUsG29NTjb79z45I8/zxHEPTJiwpirZZnbqlYbbZaDIXsWVFNDQRCARA42mHmZ7pBIUsETtGwYsZkRdUR1yiCUm7a9rWpBAiA6VDKZpMCT9BS706PY5TwCAadS0YIARqD7ppxrjNZS89cJViLtlppKvHbzYSTyJ4ilzSvnLPV4Yko/r9XTmM6bA++793Vje/cv3HRAe1KjKcW7JmrYQf75z//OXbs2IG777677HOEwwkEgx6EwwnoenliWZWA6Dq0Iq5PDB0zM7EF91uK6/E8h0DAja8uTGB8OncfCrO2DABUnSKeVB0jZz6RK3gvlFIYBkU8nkQoVPzjaFCKT06P48DHQzl9BAWeYO+tXbjnxnbwPIdQKJ7nLMVBDH3BlHVCgICbh0fkEPBKCIcTiC7jM1dNKhEEyqZWbLVSLNYGuxo9+O69fThy4iqmMgbTxoALD+3qQlejB7Ozcdy/swO/fesSGutcmJ3rgW0h8Bwev7MX3U3ekt4rSUXLSS11Ymwqjv949ZTZHmyOzmYvnt67CfFY/tX3SkCIWXbh8ohIxlNIxhe+32ysd9xqeeacYLZaGQrbMzX/h5gr2DSnQAm2z3iOQNep434LzQEMSjE1m4RmON+Loam4PptIi6gB5thk1XFa4xihuuO4yBGzL3Y8msTiRs3Kwmy1PNairVaKSj1zsaTq2EavmHklMG+r54dm8MvDdqVwjgBP3L0et3+jDZFIoux75AiB1y3C7RLKHk8tmK3OU7MO9uuvv47JyUns3LkTAKAo5gN66NAhfPHFF0Wdw4rg6roBrUw16krQ2eRFvU8uqAzc4JfR2eityH1W8nqhDEGGTESeA89xaQPSdQqa9TQ1+GXcsqUZH58Zd7wXSil0gyLgkdBa54FepKjZ2HQcr75/GUPj0ZzPNnQG8ORdfWgMutL3tVha6z0IeKQcJVYA4Djz5dQYcKGvLZDxeyzvM7fSqBVbrRSVsMHN6+qwqTPo2BLIOmbzujr84IGNeOfkCCSeQ0rVYRgU9X4Z397Ti229DSX9nrphYCqUdLT5TGYiSfyfP52xtdBrDLrw7P6tEHiuInaXD0ng4PdIEAUOhk5hODgqpbBanrmlYrXZajEUsmdR4MFzHLi5EiqnZ1/guHRdsyzx0HQjx8aKGZND0VROQNmCUopjX48jpdqPbwi4IPBc+npBr/N4y3EEQZ8EAtTs33UtPXOVYC3aaqVZzG+nqDpmI7lChEDheaWFZasffj2KP354xfbOkEUeP9q7CZu76hY13ma23TLPUyFBN/bM1a6D/cILL0DT5tVr/+3f/g0A8I//+I/LdUtlQ4i5ovrSO5fytsTYe2tXxfpTV/J6fo+zeighBAGPiJloCqDISU2xrsFxnOO9UEqh6TSnHUghVM3A218M472TIzn9Oz2ygEfv6MHOTU0V7/NNCMGeHW22liY8Z9baEUIq/vdjrHwqZYOEEHS1eHH8bAxXxiIYnYph97YWcBm1xtt7G7DnpnU4eXYMs9HUovrdh6LKgs51NKHi/75xDuG4mt4W8Ij4q0e3VbVPLhMxYywXC9lz0CsBoKAU6TFx/mCkHdd8NlnM+yCpaLaAVjZvfT6MLy5O2rbVZ9VR5xtvBc6suV6JXS0YjFpE051V/i2c5pWZcAS4/RuteOPjQXz49ZjtszqfhJ/s34q2htI7g1gIPEHAI7G2W1WkZmcqnZ321i5er7kk39PTsxy3s2i29dTje/dtXLI+2JW6Xk+bHw1+58i9SxZQDyCp6DYjzbwGpRQeWcAtW1rwdf8UEooGSs1UtVJ6/fWPhPDq+wOYCuWmnu7c1IRHbu+p6uR+Q2cQj+3pzelXWM0+5oyVTSVs8NDxIRz8ZGiuvY/Jb966hP23dWPf7u70NkIIetsDi4oYRxPqgn3nk4qGXxw4Z7NDt8zjLx/dhnp/5dvMpK8x196OqfAzlouF7BkwlcABpPtg8zyHgFdER6MXe2/tAs8TvHNyBGNTsZzjC70PDIM6pplafH7hOt78zN4ir7nObdNByDfeCjxBg9/FbIvBqBAGpZiNpvIqhFts6Axi3+5uxz7Yu7a24OPT4zktO9c1e/HMvi3wl6kUzhHA55bgcdWs+7dqYL/wErKtpx5bu+scUz4rjeXY3rezA7GEBq9bRMBT+vUWitx7XAKe2bcFXpeY852yW3sBgMRz2LAuiE2ddel2IIWIJ1W88fEQPncQMav3y3jy7vXYtK6u6O9TKhwxFYrdsoC2Bg92bW1Zkr8fY3WwGJs/dHwIr7x/OSdjK5HSzO2AzcleDKqmI5ZQF9jHwIuHL2Bkct45EHkOz+7fitZFRNILwRGzxR5rFcSoBRayZ+uzcDzlOO4KAldWtkkoltuSy6J/OISXs1T8d21twRN39WJsKpHTfisTkedQ75eZc81gVAiD0jk9lOJSrZ1a5XncQs5YCwDfWN+A79+/AZJQ3qqzWxbgd4vM3peIFTNr+dnPfrbct1ARCCHoafNX9RpOjq0VJS/HGSxnJe7s4IzNKbfqrVXNbKm1rrnwpIJSii8vTeFPH11BPKnZPuMIcNc32/HALevKftFQSh17fwJI18m5JB6yyNvucyn+fozVRTnPjGEYOPjJUP5yKAoc/GQID926DsDi0jrNaLtSsPLKMCh++/YlXB4Jp7dxhODPH9qE7tbq2IPZKqS01lsMRrUpZM/zn+W3iVKzTeJJLW/d9fhMHL88csFWMrVpXRCP37UeHEfQ0ZxfjEcSONT5ZdbjlsGoEIZBMR1JFu1cWxAyb6sjkzH8x2unczJW7rmxHQ/v7i7LXsW5TBqxzPkyozxWjIPNKI5sx9ZiOpLCS+9cwvfu21hWOnMpK3GUUhz99GqOc23NAQwKHDs1hr4O59680+EkXvtgABevhXI+W9fsxVP39KG9sXzFzf7hkGNKzp03tOObGxrhkQUW4WMsK8fPTtjSwp1IpDQcPzuBu27sWNS1IjGloJoppRR/+HAApwembdu/e18ftnRXvjSC58zaMFlikwHG2kbTDUQSzqnhkbiC5w6cQzKjLrutwYMf7d20YPsfWeRR55NY9hWDUSEopZgpYeXaiXNDM/j10Yu2Ui2OAE/ctR67trWWfD6OI/C5RJYOvkywX30Vke3YZmNQs0Zsa3ddWQNrsStxQ+PR9Ep3StGgagY4jtiiZ6GYgtHJuC3CrhsUH349ijc/vWZrMwKY0faHd3fh9u1ti3J++4dDOaIShJj1p0c/HUK9X2b11IxlZzJcXJurYvfLRyJVWDgJAI5+eg3Hz07Ytn3rjh7s3NS8qGtnQwB43SK8LoFN/BkMAOGYs+igoup4/uB5zEbnne+AV8Kz+7csWE7hlngEvMy5ZjAqSSim5MxbS+HYqTG8/pFdKdwlmUrhpZZBWmOpxyWwDJVlhDnYq4hMxzYf05EUhsajVU1zjiQUJBUNoahi64PHcRx8HgGyaD52sdR8zee161G88t5ljE7ldt/c2l2Hx+9ajzrf4kSUKKU4dmoMBjWdao7MK4EDZjbuYgIQDEalaJrrW1up/ZzQdAOhWAoj151LJQDg2KlRvP3FsO24+27qwJ03tJd9XScEjiDok22iTAzGWiaWdBYdNAyKX795CcMZ9ZmyyOPZ/VsQXGCM9MgCAt7yxJEYDIYz0YRqyyQpBcOgeP2jQXx02q4UXu+X8ZP9W9BaX5q+iSzy8HtE1hGgBmAO9ioiXypZufuVy8R0AtPhZE79qGEYCMcUBLyALArwyiJSqo6jJ67i2OmxnEi93y3isTt7sWN9Q0Uc3rGpOCJxBTxP8kb1liIAwWAsxO5tLfjNW5cKpom7ZQG7t7WUdX5KKT47fx3vfTmSUyphKQ2fvDSJPx0btB23a2sLHtrVVdY18+GWBQQ8IgtqMRhzaLqBaDxXdJBSij99dAXnhuaVhTkC/GjvpgXLprwuoWzlYQaD4UxK0RFdQCC00LG/fusizg/N2rZ3tfjwzL4tJXXGYYKgtQf7S6wi/O7iBs9i9yuHRErFZxcmwBEOBnVIl6FANK6hpcODUDyFF4/Y09wsdm9rwb7d3RXpeStwBB6XiOtCHHxGVE9RdRgGBccRW5uxagcgGIyF4DgO+2/rdlQRBwAQYP9t3bZ+2KXw+cVJvP7RlZxyklBMwaHjQ9je24Cjn9rb/nyjtwFP3LW+Yo4wmxAwGM6EY86ig8dOjeHj0+O2bU/ctR6buwqnkPo9Iryu6rWxZDDWIlYWWDmEoik8f+h8TtbmDX0N+N59G0vK5mLq4LUJm9msIrpbfY49qymlSKk6FNWA1yXAMAwYhoGrEzGbYBmAtIhZnU9GXZ0HlFJcGQ3j8kgYBgx4ZRE+j5TT8sugFJG4iv5rIYRiKnxuAeG44ugc6IaOcEzBC4cu5HzWXOfGU/esR29bYNG/hyzy8LgEyHPOc8Bjps8lFQ3hmGpLX7f6lbokoaoBiFKhlLK2YGsUqwVXdh9styzk9MEuhaSi4a3PruXVakgqOo58etWWUdLXEcAPHthYsQFcEjgEfRJTCGeseCr9jo7nSQ0/PTCNNz6yZ5Tce1PHguJHAQ/rectgVBpdN3D68jTCCSVvG7x8DE/G8PzBc4hkZancd1MH9u7qKrpuWuAJgl6JqYPXKOytu4pw6lmdTGmYiaagzg3YkbiCf/3VFxB5Dj6PmF49EnkOAIU6p4BICOB68yIiMQXT4RRUTU8rDYuC2Tuzo9GLvbd2YX27H+G4CsOg6bpqWRLgpxSRhAZDN0zVBQoQjkDXYasfA0zl4Pt2duLemzoWVTtC5vpWe11Cznm6W30QeQ6jkVSO46/rBmYiKXS3zgcblptC7daYENvaYN/ubjx06zocPzuByXASTQEXdm9rKWnlOtMB8MoiZiJJW1p4JqpmYCqctDnXHU1e/PjhzRWpj7bEV0pJfWMwapVKv6M13ciZdAPA1YkofvvWJduw9c0NjQXLNQjMDJFKZIExGLVArSw4nLkyjQMfD2Im6lxetdCxv3nrUnpODpjz3yfvXo9bthRf8iWLPII+iYmY1TDszbvKyOxZPTIZw1Q4CV2nADGNGBRQVQOqZiClGmicexeMzk0Q6n0yXLKARErD8PUYNN0AR4jZZ3NudFdVA1OhJCil+PWbF/Dwru70S8UrmxPnlKIhltQBaiqKUWq26aIOLQx62/x48p4+tNS5y/7eHAE8LrGIFlsLtFBwkmxdBqrVbo2x8uA4Drd/o62sY7MdANOeTfuUs1KzNT3XuW4MuPAXj2ytSBq3JHAIeCUmvsJYFVT6HU0pxWw0lTNCTYeTeP7gOZtCcU+bH9+9d0PeyTUBUOeTWas7xqqhVhYcTAf5IrIFw63yqn27ux2dbEopPvx6DAc+HrTZuEvi8eOHN6Ovo7BjnomPBalXBGymswrZ1lOP//nUDgS9EniOQOA5iDwHAkC3Zs8U0A0D4ZhqNrSn5jZzJdqYT6GmZvus7FFf0ylmowp0w6wLo3PnbW/yQOCAcFyBYRhzjjWFwyngkng8dU8f/ubb28t2rjmOwO8R0VTnhm+BGpSh8ShUnaLeJ9tqsQEzRbzeJ0PVzQjpclJsuzVaI8EARm1iOQDWhMTqRZ9UdITjClLKfNq5blBMhZMwMh46j0vAX31r66IHco6YaaoNARdzrhmrgmq8o6MJNaeHbjyp4RcHziGWnLfVpqALzxTIKCEA6vzMuWasHrLHMgsrmHV2cCbPkZWFUoqDnwzlONcWBrXPhy10g+K1DwbwRpZz3RCQ8XdP7ijauSbEXARjzvXKgK1gr1KuTsQQTqjWAjKAOQc307opoGo6CEh6H103EE/p0HTD8rltZP5b1w2omu7Q03q+Ljvfi+ibGxrxrTt6ylY15TkCr0uEW+aLThGyxMtcsgBZ4qFoBgyDgucIRIFLn2e5Rc5qpd0aozC1kq7mRLYDYFCadp5FgQdHOEQTGiSRB6XmKpmeMbnnOIK//tY21Ptd6fONTuZv55UPWeQR9EpMfIWxqhgci2BsOu4okmlRyjs6peo2JxowM0pePHIek6H5Xvcel4BnH9kKTx7BMmsC7nQ/DMZKpNhg1lK0Vz07OLPg3Cx7PpxUNPzq6EVcvBay7dfT6seP920uWnyQZYCtPJiDvUqJJBTbahQAx+xoSgEQCoL5F5OmGzkROMd3G0X6Glbt9ehkHIpmppWrDm9EjpjR9Xu+2VGWc81xBL4SHWuLTPEyQkha/KzQfstBrbRbY+SnVtLV8pEZpKGU2pxnAPB5BIRjClRNRziu2urBCIBHb+tOt/3pHw7h2KmxvO28nCAAfEy5mLEKOTs4g5ff7cdUhuObKZKZSTHvaIPSHE0ESil+/24/roxG0tsEnuAn+7agMeByPA9zrhmrkVpZcIjEFUyFkwvviPn58EwkhecPnsP4TML2+Y0bG/GdezYUpWtCiNmyNl9QjVG7sFDIKsXvdlg1cvBHCYHNuQYAgeeKc14J0tfwyiIopTh1ZQoTMwmk1Nyla69LQEuDBy5JSL+AioUQs+6kKeiCxyWUFam0VNYL0eCXl13krBbarTHyUyvpaplYav+nBqYwOBYxFfzn0B0CXbIowO8REUtqULJsde+t67DnhnYApnN96PhQjgNg1Zv1D9uj8oD5Tqj3y8y5Zqw6LNuPZfWnt0Qyk4p9ezHv6HAsNxh+9NNr+PLSVPrfBMD379+I7lZnB4I514zVSi0sOIRiCmJJLa0xtBBeWcS1iSj+96uncpzrB27uxA/uL64NlyRwaAy4mHO9QmEr2KuU7lYf2urdCEWVdDsqYv0faywnmJP3n1/h4nkOHplHPMlBc2gVkgnPcxAFMwXU7eLx/KHzOD80m7OfyHMI+iVIGa0Ein1RccRsS+R1Lb7Hn5PKeva19t7atexpvvnarWVSC4GAtUgtpatZnLkyjbe/OIXx6VhaoMwl8kgqGiSBd9Tto5QiqRhIpHTb9u/d14ebN7ek9zl2aqzgdz12agx9HYH0dxV5DnV+1n6LsfrItH1J4MDznK3VIygQjqnpVexi3tHxpIakYrfBT89N4O0vhm3b9t/WjRv6Gh3PwZxrxmpmuRccwjEl3SazvcmDoFfK24UDMLO7piJJvPR2v02YkOcIvnNPH3Zubi7qul6XUHYJJaM2YLOgVQohBA/t6kbQK6ZXrgkh4K1JPwF4zkxrC3glcx8CBDwiCCHwuQXwvLmvk1/Lc4DfI4KAIuCV8L9++6Wjc+1x8Wiqc9mc66BXQnuTp+D98xxBYE68zO+pXA2npbKevZLd4JdrRpnbCgTk+8q1EghYi5SSrrZYKKUYHIukV6WdBJPODs7gt29dwlTIHiVPKBrCUQXxPJkikbiKeFbN56O396Sda8As9yg0kQDm680AMxDWEJCZc81YlWTaPiHm+JSdFabrBhRVL+odrWoGInG7fV28NotX3x+wbbtteyvu+ma74zmYc81Y7Sxn5mEkriCWnB9DCSHYs6Mt79yMgMLnFvGroxdtzrVbFvBX39pWlHNNYM6RmXO98mEr2KuYbT31eGbfVrzyXj+GJ+PQdQMcR8DxJKcPdnerBGoYSGkUmk4hiTy62/yIxVXMRhVoup4WLBMFgoBXQsAjIRJX8cmZ8ZxrEwLwxJxEKJoOWTSvwxFgz462vBMPgSPwukW4pNJrrEv5XbZ219WsQBVgb7dWq3W+a5GlSlcrpsZ7fkWNgnOo//C6BETjGuSg/TUfS6iIJuyO9703deRM4ost44ilVAQ8EjwuNpwwVi/ZNu2SBdTD7LyhZ61U3bKlBR5ZAKXUcVwxKEUoqyXX2HQc/33kotkSc46t3XV4bE+v4zkIMd8JosCca8bqZbkyD2NJFUTLveCGziD27e7GsVNjmI2moOqmWG7ALUKSBJw4N2HbvzHowrP7t6ApuHCnHFnk4feITMhslcBmRCuchZSMt/XUY+uPb8HgWAT9IyEQEPR1BtDd4sPViVj6uJZ6FyJxFdcmYoilVPi9Irb1NSMcSmBoLIKrE1FQULgkHrIk4PTANL68NJnzwuMIEPDJ4EARS+owDCM9yS8kjCTwlir40jyShJCaV+BeCYGAtcZSpKsV21/XWlFzehwMg0KSBHgBuEQOybk663hKy1mVvnVLMx7e1ZVzjmLLODoavcy5Zqx6LJumlKY7UHAcQVPQbO+YTGlIzHXgOHFuAifOTeQNiIajCrQMAw/HFDx34BxS6ny6eEeTF3/24CbwDstlHAHq/a6i6jgZjJXOUi84RBMqEoqGYNB5XNvQGQQoxVufD0NRdRAAI9PxHD2T3nY/fvzQ5gVrqMlcK8ulmv8ylgb211zBFKtkTAhBb3sAve0B2/E9bX4kUhpiSRWhmLlaZbUW4HliOnIE6GzxobPFTL+xUthmHNJkPbKAQEZLHlkS0tG9u25ow40bm3KcQ0ng4HWLeRW91zorIRCwlqh2fXwpNd7WippZT62bLfcIgcCR9PGyJOCemzrgc0m4cG0GRz+9Zjvf9t56PHF3n2PQZqF6M46YPXn7OgKOnzMYq4nuVh9EnmB4MmFfseY5uEQO8ZQGnuMgZyiJZwfFgPnJu0VK1fH8wXM5Kv0/2b/FcVzk50QE2SoXYy2xVAsO4biCeFJLl0g60T8cwqET5jjN8xymw8mcHvY7NzXhqXv6FrRTgSeo8zF7Xo0wB3uFUuwqVz6SioZoQs15KeQjmlDxxkeDOHlpMucznjNfELJknwwQQtK11163aHsRWinqlXSsa7kvMWN1UMl0NafntZQab59LNCcDCRUGndMvpBQcz8HnEtITfZ9Lgk4NvP3FiO2e17f78WcPOK+QWd91z442HDo+lPNdeY5A4E2dB2ZjjLXAuaFZRBMadMO+SqXrBmYVbc7xzV2pygyKKZqORHTevnXSxeP5AAAgAElEQVSD4tdHL2JkKp7eJos8nn1kKwIONZgCbzrXTOeAsRap5oIDpdQUNMsSHXTazxL/VFQd0+FkzvjYHHThu/f2gVvATj2y2c2DjaGrE+Zgr0AWo2RcqmNNKcVn5yfwxsdDaSVFC54j2LmpCcOTsQVfEFa6KccR+N2VTwWv9b7EjNVDJdLV8j2v+fpKZ3P6yjS+uHgdM2G7M276ygbCcQUBAC31HvA88H/+eN7W67q90YNn9m1ZMMU0s94sFDO1GECBQMCFb+/pZbbFWBNYY64s8aj3ywjH5uuurXGY50jegPF0JIUroxEE/RJ8fnf6nH/8cADnr86Lg3KE4OmHN6OtIVcEVOQ51Pvligl+MhiMeWajiq1EIx+W+GcipTlmctb5ZYgij7GpRDojNBtCzCwVl8RcsNUM++uuQEpZ5bKifVYqeLGONQCMT8fx/Otn0D8czvmsu9WHp+7uQ0u9Gy8evrBg24KuVh98DuJllVh1zreaPxVO4pdHzmPPjnZ8o7eBrWgzKsZi0tUKZZ+MnxqDrhtwFQhAJRUNH349gqlwytZ1DzAn+9SgEDiCWELDDbc04BcHztuCY40BF/7ika1FD+6W0//uyRGE4wZ4niCe0nD0s2sAIczJZqx6MsdclyTAJQlQVB2GQaFqBqIJFZSaop75FL3HZmLweedXuD/4ahTHz9oFkZ66Zz02OgTZJIFDnV8Gx8YvBqPihOPFOdcAEE0qiMQVROJ2EVCOAA0BV9r+84mEijyHoE9iKeFrAOZgr0CKVSgOxVKIJlxIpDTo+Za7HdB0A++eHMWbnw1D0+3pcLLIY99tXdi9rTU92OdLIwXMdl77dnejuS5XQbESq875VvOTKS2t7vr6R4MFBWcYjHIoJ11toewTUeAQS6iQ5wJR2YJKksAhmdLBcYCqOveppxQAAdwuHkdOXLMFv/xuEX/56NaSWoAMjUfw5mdXQUFsmScLlaOwkg3GasFpzLUm0hynp1X5842zukEhC/O281X/FA58MmTb54GbO3HLlpbsQ+GSeAS9ErMdBqMKJFJaTsvKfGi6gU9OT+Q41wJP0BBw2ZxmJ5FQj0uA381SwtcKzMFegfhcIlJz0XNr0p29KmwYZrut7HY8CzE0HsEr713G+Ewi57PtvfX49p3rEfTaJ+fZaaSAWQ/aFHTh4d3djpPvxdaQz99v7mp+MqVhJppKL+1ZvUlLPTeDUWmKyT4ReGKuiMF8lvWMrBOOI3CJHGLJherEgGhCs6WFuyQef/HoVjQEXEXdKwHgcwv45Mw4qEMbMCB/OQor2WCsJgp1BZBEHjzPQdcNRz0Dg1L43SLam8y078vDIfzmzYu2fW7a2IQHb1mXc6wlHMpgMCpPIqUhXCD7MnvfXx65gMsj9oxOSeTQ4HfZSjeCXilt7wBLCV+rsL/2CuPs4AyOfHoVoaiSrgEjhMAt85Alfm6AJ6aBN+bWceUjqWg4fPzq3GTaTsAr4fE7e7G9tyHv8Rs6g+jrCGB8Og7NMNAUcKOnze8YqVtMDXk22SsLlFKE4yqyv4Qxd7FSzs1gVJpC2SdJRUvXdkoih9hcVJ3nCDhC5tSKeUQTKvS5Xrn58lLMUpD5TwWe4Jl9W9De6FwTlo2VxjZ8PVZyOUqlgmcMRq2wUPeAgFdEJKbmaBpQSkENij072kAIwWQogf/9ymlbqdb69gC+c2+ukr/PLcLnLq5VHoPBKI1oQi16AWoqnMRzB85hMpS0bffIAoI+e3YJR5C2d8As7wj6JCZMuAZhDvYKInPiGvCKmArNtwZIqTp4AggCD79HwJ4dueq+lFKMTsYRTaqIJZS56J2KeErF2cHZ9ITeggC4Y0cb9t66bsHIm8AReFwS2ho8Czqu5dSQ5yN7ZUHRDFsLFYvM6GKx5y4XSimujIYxG02x1Ng1TnaatFc2azd13YBu0Awn1Mw2ISAwKEVS1ecGZHMHv0eEzyNBUXVEEoo5cS/yHjgC/GjvZqxvX7idFoGp+G9N7BcqR7FS2L8emAIAdLV4KxY8WwyZv7tvrgdpNKkye2SUxULdAzyygPtu6sSFq7OYjqTSdiELHDZ0BqEbBvqvhfDahwO2SX29X8YdO1oxMZ1Ae5MnXRYSiiqYDCXY88pgFEkp73yrFVcxXBkN47kD5xHPEvm9dUszognVXNCZI+iVsGdHW1q3xOsSSirHWuh7sffByoI52CuE7FVfSilo1kCvU4DHXAFmFv3DIRw7NYaJ2TjCMdWWOupEW4MHzz62HQ1e0Zaimk05quDF1pAXs1/2yoLhMPvheS5HeKbYeyiVM1em8fYXpzA+HUv/fVhq7NokO006qWhIJDUkUho0PZ+DTNPCZQRm7y2eI4indPg8ZjqqNQkvlu/cu6GoZ08Wefg9oq2OrFBqbKbOwUenxvDZ+etwiTxmY6mCAblqB7gyf3frHgEzKOmShLQ93rChsSrXZ6xOiuke8PCuLrx7cgQfnhpFJK5gJqxhZDKGj06NwaDUtnLNcwSiwOGdL0YAmJPz9e1+XJuIIpQxaWfjB4NRmGLf+dt66tMK4MVw4swY/utPZ3LmlZ1NXty4sQl9HQGMTsYRS6nwymI6SFaplHBWarWyYQ72CsFa9aWUwqAUoZgKjgAcT0ApQEFB5lLDRYHHsVNj6OsIgBCC/uEQDh0fQkLRMBtRFhQ8u3VLM75zbx8aGnwIheKO+xBiRu29brFkZdNCk/ZS98teWchpYULMl2y591AKZwdn8Pt3+3PugaXGrj2y06STitnSw9AptCIEB9NPEJ0TTtJ0U7WY0pKc60du78bNm5sXvJbfI8Hjyh0O8qXGZuocZAawZqIpzEZTqPej4OSiWgGuzN89W4thJmLe13QEeOmdS+B5gjvri0uZZzCAhbsHnBuaxftfjSCWnEs/pWYwXDNyA+L1ftkWzJqYjePS8Cwa/C5bFwE2fjAY+Snlnb//th50tfgWPKe5oDWMIyeu2rZbSuEUwKHjQ9i3uzuntabAE9T55EWrhLNSq5UPKwpYIcxGk9B1A5pOkVJ0GBlp0ISY/TMJmVcxDcUUjE7GQSnFsVNjMCgQjS+sJi4KpsBSvnoRAlMJsTnoht8jldU2xJq0F6LBL6O7deEXITC/stDglyEJHPi5Fxs/1zc0e6JfyrmLZT7DwPn3tVJjS3GOGCsTJ42BcEwFNWhRav726mmknWzdoAjHVJgqCwvTGJBx1w3tBfcReILGoMvRuQbmA1iZMSObzkFWAIvjCEDN71uIagS4Mn93Ry2GjPsyKHDkBLNHRulY3QN2rG+06YxYz59umAFw69kzn0f7OUSHrKpYQgMBQTiu5jyX5vM6hCujYZwamMLgWIQ9u4w1TynvfFUz8M4XwwvajaYbeOmd/hznWuAJmurcabs1KHDs1JjtfG6Jz1ETX+z3coLNJ1cGbAW7xlE1HdGEBl1H2tic0qAtMlVMYykVo5NxhGIKFFWDUkSfP8OgmAonMTwVRbDOLpImCRwC3sX371uono0jwN5bu0qqM8lcWTh9ZRrHTo3lCM6Ue+5isDIMCp222qmxjNogW2PAqrnOcZxLgZrn0TTThgWBg2EYcJAbAGBml0gij5HrMRBCclLYALM+zFdEy5Ds1FhL54DnuXQKnoUV4LKU+516AlcjwAXYf/d8WgyZ9zUVTuLycAgNDhkuDEapWM9fMqWlA+B2nQUTU4eUQtV0iMLcZN0w0uO6rhs5/bSTKQ3nZxL4zz+dSW9nqaKMtU6x7/xESoPAc+mFp45m58yleFLFi0cu4MpoxLZdFjnUZymFA/MLWetafQh6JMhS7ni32O+VDzafrH2Yg12jpBQdsaQKZa5Wur3Jg6BXQiim5KZBz8FxXE4fvlhKRUrRMRNVipvcz62WxeLzNSqEmCtO+Va5yqGYerZSsVYWetr8WN8eWNLalUrWlTNWNtl/43RAzMEAifNmcCRr1YvY/3+XxCOZogBHc5xscU61VFF1/OHYgO3zoFfC3d9sxy1bmtOT+2LIDGB9PTCFj06NOTrPhBAEPCJmoinHQGC1AlyA/XcvFITM/CwUU5iDzagIkYQC3TDSWSoGzXWuCZDO+rKeQ4EnSGXFvjMzXTLTXjOfXZYqyljrLPTOt1Z4dd1Iz41jKefsqslQAs8dPI+pbKVwl1CwD31K09AUyHW+FwObT64OmINdY6QUHdGECjVr1kwIwZ4dbTh0fAiiwIPjzBWs+R3MnrXWSyDolRD0iXjzs2uYCttfGAWZE1XyesxHwyUJcEv8oletnVionq1Wz+1EJevKGSub7L9xeuDNlQfIi5VqbbXjslp1cRxn2jlHEE+qOc41ARD0ilBUHeG4GYzLdKQjcQWHTwwh6JNLnpRbASwA+Oz89bz7uWQB9TBrTBPKvOdQ7RW3zN+90GQnu18pg1EJZIGHYZjPF6W5gS8CM1hNQUEN0wHnOdOusp9XKxMtO+01ez/WdpKxlin0zs9Mn878zCvnBlQHRsN48fCFHPGzOp+1sJRnUYsA7Q3eijrXAJtPrhaYg10DUEqRnFux1goodm/oDGLf7m4cOzWGlKohHFMAivSkW55L1SSgaKl343/97quiWxFY8DyHxoALva0BNNe5ERMItAUUxxdD5qR9JZ07G6uufCaaP62nWqmxjNoiWxhMEnnwPAeq6Y4r1vm2EY5A4Dgzgu6R8Ojt3Xjz82GE46qZdu5glqLAQRR4TIdT4Ahnc655zpzIUyxuUr5QT2AA6Gjy4n8+tQNXJ2JL1l4k874yU9UzyRRkawy40NcZxOyss5Ajg1Esmm7A7xUR9EqYDieRPWTOO9eAYZj/jsZVJBUDAY8Ilyykn1ee59LlTZlpr07dMACWKspYu+R759ud6/lxMOiV0N5kL3384sJ1vPzeZVvWiMhz+OHejfiyfxpToUSOhgJgjqdNQVdV7K6YMZbNJ2sfJnK2jBiUIpZUcT2URCimFHSuLTZ0BvHjhzfjRw9sxgM3r8O6Zh8aAnLauXZLPACCd0+O5DjXPE9QKNDGc0DAI2LvrV1oDLocB3OGM/NiUPkjndVKjWXUFk7CYAGvCMIRm0bC/AHmYE2ImS7aEJDREHChMehCa4MHAY+IB2/tQmeLH3fe0A7DMDDjMPAKPOD3ilB1AwY14PMIGZ8Rx17wlfp+mVjPOsdxjmJQ1SLzvqxU9ezUekuQjSPAQ7uYPTIWj9W3GiC4dUszpsO5tkmIudrMzdm4ae8Eum5gJmrWbQe85vMa8MzrIqTTXvN0w7BgqaKMtUj2O9/vFmBrgEmQHgc5AuzZ0ZYjSvi7d/ptzrXfLeJ/PL4dO/oa8eCurhxdHWucFnhStTldsWMsG79qG/6nP/3pT5f7JqpFMqnC7ZaQTKoFa/KWGt0wEEuoCMUUpFTDMTpWCEII/F4JvW0B3Ly5GV3Nfqxr8cLQKc4OzmA2Zh9sJYHDrq3NEDiSViPO/jlEgaCzyYcfPrgZN21sAs9zNfnb1TLNdW60NXowMZs0W7TM0eCX8die9aumTs7rLawAXw61aqvl0lznRku9B6NTMSQUHcLcqhRHCDwyb6aQ0vk+15LIo7nOjeY6FwSBhzAXja/3Sbj3pnVY3x4AYNZeHzs1hkRW0aYkELhdIkSeg1viwXEEsiikJwNOA/GGzgBa6j0528v5fhbL/axn3peqU4g8B1Wn4DiCOp+U7on62J712NHXuKqeOSeYrRaGUoqh8SiuXY8ikdIL1lrmIxxXkVJ16IaB1z8axPWsGk6BAwwAPAFEkUdjnQseWYSiza+0qTpFb5sfd32zA4pmpG3KoBSKZqSf3Xzctq0Vdb7K/61rBY4jq+aZywez1fKw3vnDk1GkFAM8R6DqdG6eLEIWzRrq+3d2pltqqZqB373Tj4/PjNvO1Vrvxt98ezta6j3gOILO1gB8Mo/x6QRSqg4yN143BlxVH+dqdYxdCGar87AU8SVE0w3EkhqSKa18NeEsCCEwQHH4xFWMTuWmOm7trsONG5vwVf8UkqoBSTIn7y6RR3eLD5LII+gTsbGzDtvXN+Rtz8Uoju29Ddhz0zqcPDuG2WhqSVJjGbWFNWnXDQPf3tMLAIgmVfjdErpavLg6EUM4nkI0riKe1EA4oK89mE41y9QNqPdLiM850ylVxy8OnMNsdD6AJvAELXUu6AagzWky8HPPGkfMwS7fs7fY+q2l1jko9758LnPlz/ob1MI9Mpafs4MzixbCjCdV9F8LIZpUcPzMBC5eC6U/4wjBw7u6oBsGPjs/AZ7n4JEFiCIPTTcgS26zt71hBoAev2s9etsCeHhXl+3Z/cOxK44ZK5n3zFJFGWuZvo4AfvjAJgxfjyGWUuGZC0bFFS2ne0Y0oeKXhy9gcNyuFL65K4gfPrgpJ5C1oTOInlY/ZiIpGJQu6RhSq2MsoziYg11lDEqRTOlIpLQc4bLFklJ1HD1xFcdOj+WsgvvdIh67sxduicfhE2Y/PUIIpIyazGuTMTxyew9u3twMmaWDVwxCCHrbA1WtXWfUJoUm7ZYDbf43f92WtV8ipSE0l42i6Qb++8gFXLseS+/HcwT1PhmE4yALBILBgVIgpRmIJ8y2JC7e+RVfqUn5UuoclEKt3hejNjg7OOPYJrIUZe5Tl6dw8JMhzMYUROIKInG7OvF37+vDzk3NuHhtFmeuzIDnCUhWzmdmGZaV9ZT97D5U4ZaWDMZqIp5UEYmroEDe9lsWE7MJPH/gXE5t823bW/HYnl7nEi7M1W43Fj53tWBj2cqFOdhVQtPNNPCkoldstTqTc0Mz+MMHA7bVLItdW1uw/7ZuuCQeLx6+kLdZPQhw4uw4bt/eWoU7ZDDWFpWYtFuomm6KGMIM0r30Tn/W6hjQ3uhxtG1hrl99JKY6ppWySTljLWPVXuYbF4tR5j49MI3fvm3aejyp5TjXN29uxs5NzQCAgFsynesF7C1fRkk1WloyGCsdSinCMcWWPl2I/pEQfnn4ApIZ+xMAj97RY6vNzoQQ/P/s3VmQHNd5L/j/ycyqrL16A7rRABobsREgxZ0Ud0okQVKkJMqSbV1a4lXYoxszd+yY8MPo2k+KcPhBVoQcN+JOyDO2ZVPLlayN0pVEEdwk7iQIUlxAYl8aSy/ovfYlM888ZGV1ZS3dVdXV3dXd/58jTKG6KrtQyFOZ3znf+T50hX01A2+iuTDAbjEnsK530Dcqnsrh16+dwwdnJit+tq7Dj0fvtNPMAGBoLFlcASslACiq3fZnKpFjBVKiBWrFTbvDLBQxuzSWRCKTw9vHx/HBmQnXc+65dhOOnp9yPebsDxNCwKfPFj1cylZZRO3u/Ghizuq8wNyVuaWUePrNQVjSziKbLusc4dc1pDJ5SGnXANi3vRMvve9bUEVgpooSzZJSYiqeRa7OLMG3j1/Gky+dhVWS6unRFPzpJ67A3q1dVV+jKQrWdQSQiKeZjUhNYYDdInbhMgPpBvZXSykxPJ5CMpuv2CdSzpISh49dxlNvDCKXL2s9owjcfe1G3HVNv6tfdTKbLz8MFEUUKy46WIGUaGEWetPukFLi8LExvPTeEGZqpJ4+cPMANnQHXAG2oggICZSWzfbpGh68ZQCRgM6bcqKCeq93tZ53dHAKU4kcDMPCZMxd0MzrUdAR8iKWyuPyZBr7d9h1Te4tpHlXuzeoN6OEqaJE9r3wdJ3BtSUlnn3rAl58d8j1eCTgwZce2IONPdXTvjVVoDvqK7bLI2oGA+wFkFIib1hIZ42GU8FPX5rBa0dGXCvM0aAXt+7vK1Y6dFyeTuOHz53A6GS64ji9XX588d5dWN/hr/hZUJ9t61G6ulWOzeqJFmahN+2A/X3y1rHL+M3r52BJIJnOVwTXV23vwp0f68dQyV5sRQE0VYFhVnYkiAR03pQTlaj3elfteemsgYlYBqYlMRHLuMabpgp0hX0Qwm65JxQUi4Y6ad4vvHPRdc1nRglRfaSUSGdNJDN5V1utWvKGhZ/+/lRFtueG7gC+fGA3ojWq7ns1BR1h3dXWkqgZDLAbZFoWsjkL2byJnGE23GILsIPrg4fOV6STziRzOHjoPA7cNIAdG6MwTAsvvjuE3/3hUkW5eyGASNALTRGIJ3NVA+wNPQFEg17E0zkowg6uS6uWej1qyyuQOhWUuWJGa8lCbtqB2ZS3F98dgiXdBc4cfl1DvtDaZ0NPAB1BL+LpfM39YawuTFRpoDeErrDecMp2Lm/XRfCqKiYLQbZDUQS6Ir5C1X57Mjta1spl75ZO7N/ehcmUgaGRGAK6tuTXR16faSVytk0ZZn033Il0Ht87eBwXLidcj+8e6MCffmIndG/1or4+r9pUqz6iahhg1ymbN5HKGMjmF7a3WkqJ146MzLlX87UjI1AE8ItXzmJsOlPxHJ9XRTTkhaookLCfv70/UvGloKoKDtw0gF++cgaprIFYMg+zpJK5piq45creln2ZtKLtCdFK1OxNO2B/J0wncjg3HMdMModszqxoy6N71WLq6fB4Cpt6Qzhw8wB+8fKZBaWdEq1FV23vxsG3zkMRwlXJG6g+dkzLwnQiC9OSePmDIeRL0lMFgK6IDk1VXH1yq411IQSu2NSB7qBnyfd18vpMK1HesDCVyNbdU3l0KoXvPn284hr68X19+NTHt9RcmQ74NEQCzOak1mGAPQfLksjkDKQyBowWNUwfHk9VLTxW+jsHR+M4OjhV8TNFANGQDn+hgFHesFejxw0TQ+NJbFw3e0H3ago6QjrWd/gxPJHEr1495wquVVVBOODBoaOjGOgNL/gC28oKykQrjRCiuM/SkqjIFKkV8DrBdTZvIpnNI5c3K/d1agrCfg25vAlFEUjnDHRH7LGtqQrTTpcJVwNXHleQKYHpwriJBD3weTV0hXVctb0bpmVhcCReDJKn4zlYEvjtm4P46Jz72twZ0eHV1GJwrSqi7Sa3eH2mlaD0OzWga+iK+JBtYPvlqYsz+J/PVVYKv/3qDXjg5oGaYzLk9yDk91T9GVGzGGCXkVIil7eQzhkNDex6VSs85vzeTM7ETCLnqnRYypLAdCKLbM6EaUlY1mzA/L9ePYv7b7RTywM+DWG/B0IISClx4sI0ejp8yBkWLEtCVQQ8mgIhREPVjWtpZQVlopVq75ZO3LS3F0+/eR7prFF83K9reODmgYob2NLg2i54mLT3dZY8x0n/nilpx/fye0Poiviwd0tnW6SdrkVcDVx5yoNMn65B96rIFbZd7N7cgctTKbz43mxBpK6wjlv29WHz+hB+9epZvP7hqOuYukeBgH0T76xct9s5wOszrQSl36mWJWFasmZdomreOjqKX75y1nWeCwF0hnWcHorh+8+cqHqscMCDoI/BNbUeS+TBvgBlcyZmEllcnk5jKpFdtP7VpYXHHIZpYTKWxVQ8WzO4nn2vQCprIGe4U9UzORMHD53H6GQKkcDsHhKnurEQArpHhV/X4PWorgupU924WY1UUCZarY4OTuHQ0VFEQ150RX3oCOvojvoQDXlx6OioKyvFKuy5zuZNnL40g3976hiePXzRVdNBCEAICVnyoKapyORN/PT3p4rHE0Jgx8YowgEP4mm77Z5spjgE1cUJ1Mq/85zVwGrZR7S8agWZznURAF55f7ji33RsJoNfvXoWP3vxVEVwHfR70B31Q1UV3HxlL77y4F78n5+7qq2Ca4DXZ2p/znfqRCwD07SK9Q2cukSnL83UfK1VaJv35Mvu4FpRBHqiPvi8WtVjCdiFhRlc02JZsyvYzkp1Jmcgk2+uWFkznMJjM8kcpJRIZgzEk7ma+ygVAVTbqiWl/XcQQkBRFHhUBYoi8NJ7Q7h6R3cxgG5FdeNWvZbtwGi1Kr2BL71pd5SuEkkJTMYzMEyJ05dm8NQbgxibTldURpUSkJZdjRgAhCIQCXgqMk8+OjeJ3/3hCEYnk8XvMa6mLg6uBq5M8wWZTn2SvGEV92RbloRlSeTyJt4+Pu56vs+rIhLwFP/32eEYPvXxLW35b87rM7Uz5zvVLKxal9+LO3WJqtUZyhkmfvLCaXx4zl0p3KMq6IroUFX3GqJzrB0bI+gI+WoWOyNqhTW3gp03LMRSOYwVVqrTuaULrgH75vvW/X0wTBPjMxnEqgTXnWEdmjLbVkut8a8kJQABhAMatELKd/lM9EKrG7fytWwHRqtVvatEgyPxYjVUKSVeeX8Y4zMZV3VUAUDT7BsJszCRpmkqOkM6fLrmOt6L7w7hxy+cwsRMuuJ3cTW19bgauDLNFTzm8maxPokzySWlfbNvmBYmymoieDQFnWEdQghoqqh63W0nvD5TOzs/miheA2vdi88kcxgeT7kei6Vy+OdffVQRXPu8Kro7fBXBdemxkimDwTUtujURYJuWhVQmj4mZDCZiGaQyRs0ViMWWM0ycuDCNsemMqxIpYAfUd1/Tj+t397hm6pQaQbYQQEdQR8DncT2/9GbCqW48l4W281mK30HUzupZ/ZFSYmgiiXzhZv7i5QTOjcQrvge6oj5EAl6oioAigIDPg2jQ4wquneO9emR4zpoNzx2+wHTxFuJq4Mo0V/BYWp1YVey6JYZpr15PlvW6VgvtuEqDa0e7/pvz+kztSkqJ0alkXX2tS+sXjUym8O0nj+DSWNL1nH3bOtEZ1qHUyCQRsPvVp/NG1Z8TtdKqDrDTWQPj02lcnkojlsoXb2yXy8mL0/jvP3kfL78/XDFTt3dLJ/7bY9fh/psG0BX2Vby2WpAdCXoR8Hsq0mZKbyac6sY1OhO0pJ3PUvwOonY23+qPsyLm89hBsiUlDr51oaLtX2dYh+5RYRX2oUkJpDIGJmNZjE6mEE/lkM7a7QKd1oFzaeeVtZWIq4Er0+b1Qfg8KjJZA7myMee07VFVBZoqCuNOFrdxOIQAuqM+qEplcA207785r8/UjvKGnR2iKfWtJDv1i05cmMb/+8sPXZ0zFAF8+vatuOeaTcKzJskAACAASURBVDXPYyEAtTBu23Ws0uqyqvdgTyeyiKrLnwaSSOfx1OuDePfUeMXPuqM+fPaObdjRP1vZ8Ood3XjqjfPI5tw3z4oQcEqvCQGEqvTsqzYTvXdLJz5/9xWLWvV2KX4HUbuaqw+2lBKmKREJerGhJwApJX7z2iDODMVcz+sIeeHXNWTzBpIZA0IAKGwDsSyJvGkhmzcLK9sCmqYgXEdrkXZdWVuJFtLvnJaHU514OpHFVMJuz6WqSrE1l9ejQlMVhPwaLGmPtelEDrl8WWZJxAetEITnCx05nDZ87f5vzusztQun9lAynYeEuy5RLdHCtfONj0bw61fPuTJQdY+KL967E7s2d0BKWfVYTgs9IUTbj1VaPVZ1gL3cpJR458QYnnrD3bYHsIPlO6/pxz3XboRHcy9NK4qCOz+2Ac8evoDyDdqqApiWfTNePlM310z03i2d2DPQsah9W5fidxC1o/I+2A6rEFwrArh1fx+EEHjhnYt4/cMR1+vDAQ8ChWqmybRRrL1gWhLSkq5jmpaEogn4vaodMAggXGWyrXhszta3TK1/ZwdXA9tLaWsun66hE0AsZRc0m4pn0RkG+ruDuOXKXrx+ZBiGZU+Il1+vr7miG+MzGeQME1Nxo7hnGwA0VcEtV/a2/b85r8+03DI5A/FU3pUS7tQlOnjofM3v1Fv29eKpNwbx6gfu62ZHyIsvP7AHfV2BmsdSFEBVlOKx+P1MS4UB9iIZn0njFy+frVilAuxVkM/esb34pVDN7Vf3AwBeem/YtZId9Hlw3e51mEnkGp6JFkJgS1+4ob+HlBKDI/G6L8jN/A6i1WDPQAfuuLofrx4ZRipjQFOVil6eb340iucOX3S9TtcUCEjkDdOuEF64M1AUgZBPQyxtoHxPSdjvQSjgRSprIp7MI1RjJZuz9a3H1cCVoVrF99Le15Yl0RHU8V8f3Y9U1kTI78FTbwwinsq7jnPD7nX43F07cPjYZTz95nlXcK2qCsIBDw4dHcVAb7jt/+15fablYJgWYskcctVa4gDYsTGKAzcN4LUjI67V52jQixv3rMcbH45WFOzctC6ILx3YXTG5XHqseDoPtbA3gt/PtNQYYLeYYVp45f1hvPDORdf+LcBOZTlw82bctLe3ZhGGUrdf3Y9b9/fhg9MTSOYM9HcFcdPe9VAUBVLKRZ+Jfv/UGH72/ElXFVV+SRFVctJQJ+PZ4n5rTZW4ac963Lh3PYQQ+OD0OH75ylnX6xRhp5tmDQtIGdAUAQjAo9ltgIQikMqasAr54gICQtirZgAQCXowFc8il7egqvVntNDCcDWw/dWq+F7aRi+TN3Hy4gyiIR0QwOUpdzX+G/asw6N3bEfQp+HscAw9Hb5icK4qAp5C9w62ZyOqZEmJRMrOCJmvjNmOjVFs749geDyFZDaPgFdDIp3Hr14/h8mYexzv29qFL3xiB7xa9S2gOzZGce3OHoxNZ/j9TMuGAXYLnR+N48mXzmC07CINAFdu7cQjt21DNNhYuqamqbjnuk3F3pyOxZ6J/ujcJH724hnkDXdBGKf9z+fvvoJBNhHcaahS2tWH7dVr4PDxy+iO+jA0nsTTb56vfLGUUFUBRUpIFHaESImwX4NP14qpqvYkfElngcKsvM+roSssEPR7kCnJdOFE2OLjamB7q6f2gGVJXJ5OI5M38YNnTrhSV3dtjuIzt29HwOfBZCyLyXi2ao97h1NQsBXnxFJMoBMtpnTWQDyVa6hjjxAC/euCOH1pBk+9OYjB0YSryj8A3PmxDbj/poE5K4VHgnY9ky1989coIVosDLBbIJMz8MyhC3jzo9GKWbpI0ItP37YVV27tavi4Xk1BNOQt7h9ZKlJKPHOodnsfztYT2UrTUJ391qUsCfzm9XMYnUpXncG3AIhCsSTnhsG0gHjagE/XioF0KVVVXBNuPl3Ff/nc1YjH0phOZHlDToT5aw9YhUwTSOCJ3x5DJjc7mbyhO4AvfnIXArqGSMCDC5fjdf3OVhQULM2GcXDCjFaK+dLB53P60gx+8fIZTMayFdfMjpAXOzd1zBlcR0Ne+LwMbWj58SxcoA/PTuJXr51DrLxqIYBb9vXhvhs3NTXYAz4N4SotuJaCnVqXKaahVtPK2Xqiler8aAITsQwsKWFVuZ8wTKsi7bScKd39EoWwX5c3LHg1BaqqzO77FHZaeKnuiA87NkYxHfTAaPKmhmi1qaeyf9jvwTOHL2A6MXv9jgS9+PKB3Qj5PcViokvVnq00G6YUM8doJUhm8kik8vOmg9cipcSvXzuHibKUcCGArrAPulfFa0dGsL0/UnFvzOCa2g3PxCbNJHP41atn8dG5qYqf9XUF8Oid27B5fePBZ2l6y3Kpdxae7X9orZtOZov9qsuZpoXxaXdwrQi7Xlnp00u6cRWeIxD0eRDQNRiWRCTgwVQiC1WZbS1Uerz7buQ+a6JytSq+SylhmBICEumsgUtjyeLPdI+Kxx/Yje6ID51hvTiulqI9W7WibKWYOUbtaqGr1oC9XePHvztVscVSVQS6Ir5it52ZZA7D4yn0rwsWnyME0BHSa27fIFoODLAbZEmJQx+N4uChC8jm3fuTNVXgE9dtwh0f29BUWrcigM6wDk+Nwg1LZalm64lWsmzOhGVWD64tSxZWtmcfE8LeO11e/FA6/6/kntmnq3js/l0QEIincxifzuCDMxNV00ab2X5CtBaUV3x3ChBGAh4oinBNkCsC+OK9O7GxJ4iOsO7anrEU7dlqFWUrxcwxajcLXbUG7Gvpj144iePnp12PezQFXRFfsRJ48XdmZyv9K4rd23qujEui5cAAuwEjkyn84uUzOD+aqPjZ9v4IPnvHNvRE/U0du52+JOzZeh9iqdor1Ivd/odFXqhdOZVRU1kDfd0BRINeV2sRS9rBdXkgrSquGNrFrndg/1RVFfR1BbClN+w65++6pr/lY4LjjFY7p+L74Egcw5NJ6JqGM8MzeOoNd9HBz9y+Dbs3d6AjVP06XN6Gz6mD0Kr90cwco5XEkhIziVzFQlOjZhJZfPfgcQxPpFyP+7yqK4ukVFC3t0lpikBnRF/yOkVE9WCAXYe8YeF371zES+8NwypbrvLrGj718S24dmdPzRtTKWWx9UBQ92BDT8D13Hq+JJwb4Vgqi2TaQNDvQbjQ+zaRyVfcHDv9q88MxSAhsaM/Wpz1nuuG2vk9OzdF8fqHo6hSY6nu2fpmb97rKfLCwICWmpQSpy7OYHQ6hYB3dhzfur8PBw+dhyWBXN7ATDKPfFmqnKqIYnCtKnYhs1KmBGBZUBQF0aC36viqVbXafl/TGBqJIaBrVcdCtfFydHAKv3r1HKYSWSiKgFdT0B3xzRksNDLuOEapVRo5lyzLwqGjlzEey6An4sONe9bh4lgKI1MpeFUVpy/N4LeH3MF1f7cfkYAH0/EsUpk8zg7Hi9fNgd4QXnpvGK+8P4SJeBZWYZz6vSpuv7ofd13T35LzmpljtFIYpoXpeBZGIyXCy0gp8d6pCfzqtXPFbhmOkN+DcKB6DaJo0IsNPQFoqkBX2Fe1EChRO2jrAHt0dBR///d/jzfeeAO6ruOhhx7CX//1X0PX9SV7D3ZFw7OuXtCOa67owUMf34KQv3YrgNOXZvDakRHXClc06MWt+/uwY2MUXk1BR0if80vCCTiHxpOIpfJ2wSO7XS6Ukn2ZThAKAE++dAaXxpPF4kiqqqAz7EVA9yBfcndfGriWBrZOoaVkOg+frhb3fdY7W99sJdR6irwAYJVVWlIfnp3EwUODmIznkDdMWJZEJODFPddtRED3oK87iA/PTCCTN6vvx7YkTNjBtSIEhIqKvdumBWgqEPLX/7V8dHAKz799EbFUDoZpQcrKsVBtLBqGhfGZtOv3q6qCbM6sWUypkTHNSsjUKo2cSwcPncfTb54v3rBbUuI7Tx1FUNegaQpiybzr+ucYmkjjiYMn7AllIaCg0ApP2OM1lzcrrknxVB5Tr51Fb1egJef0UuzzJlqobN7ETCLbUPutcqcvzeDgofO4NJZ01yMRwO1XbcDZ4VjNrRi37u+DV1PRGdFrVhMnagfq17/+9a8v95uoRkqJP//zP4eqqvjWt76Fu+++G//6r/+Ky5cv4/bbb6/rGGOTSfh8HmSz+ao3vXNJZfL45Svn8NQbgxWza51hHV+8dyfu/Fh/RX/qUs6XSGn7D8D+gjozNIO+7iB29EfmDa5/+vtTmIxlMZXIQlp2n13DlDClhJQS2bwJASCZMfD28TG8fWLMvnku+YYyTQuxVB6xZA5ej1JMgUvnTBwdnEQmZ+LZwxeQytrvVQhA96rwehRICdxyZR/uv2Ez7rtxM9Z1zJ0G77xn51gO53et7wxUPYaUEj96/mTF64o/B3DiwhQ+PDvZ8LGXiqII+P1eZDL5iv6Nq0Uw2PoJrkwm37af2/unJ/CT353CVCKLmUQO6ayBbN7EdDKLd0+O44Mzk7g0HkfekFX3oZXeA0iJYksuTbV/oAj7z50hHV0RHyyJus5lZ5ylcwYURRSza0rHwvhMpmIsZrIGRqdSME0JO56YzXrJ5E1oioKx6TRu2ru++LNGxnSz43+pcaw2ZynHaiPn0sFD5/Hky2eKlfSdNlyWBWTzFtJZsyIDrZxEoQihnK00bpjVx7WU9rX87HAM91y7sa5V7LnOOSEEIkEvjg5OVv19igAevnVbW4ydpcax2pxWjlUpJZIZA/FkbkH7rU9dnMbPXjyDsWn3opUQdkeM267agCs2RjE2nXaln0eDXtxz7Ubs3dK5JMH1WjjnFsNa+NzqHattu4J95swZvPvuu3j11VfR09MDAPirv/orfOMb38DXvva1Rfu9Ukq8d3oCv3ntHJIZd2CtCOC2qzbgkzdsgneeQmRSSrx2ZKT2LJ8QeOPDEdywe92cx3ju8AWYlkQslQeci75zkyALK2OWxGQ8C01ViqtYqoJiynnxNYXnx5I5VyViSwJPv3ke0UJLEvfbFPBodlrdgzcP1JUW3mwl1PmKvEgpcWk8jY6Qt+rEBqusUqsl0jkcPHQe6Zxht+IrnNf2zbv9v1NZo1gJvJrye3pFEegO65hK5FC61VP3qsXzdr5zuXScVTvVLQk8+9Z5QIiKsTidyBXfkyklhJwNsiGBWCoPPZYpFlNqZEwDYCVkaolGzjspJZ5+87xrENaq7l/X70bluK3+HoGRyTTODcewrT/a3C8rUV6UzcHsD1pO2ZyJeDpXUVekHqVbJH2aip+/dNaV0QnYW6i6Iz5omoLXjozgz+7fhe39kYqtlbpHtQsQ8tpBK0DbBtjr1q3Dv/zLvxSDa0ciUVlgrBZnZVhVFQDztw+YiGXw5EtncPLCTMXPNq0P4o/u2oH+nmCVV1a6NJZELJWrevOrqvaK1VQii0sTSWzti1Q9xrnhGKYSWeRNC6Zlp4UXv94K7X4gC6WRRKFQknPjbDlVi92vAQDDlMgbZjFIzeVNpHMGAqZWbHPg7BgVEICQ877X8vc81/dfrWOlssacr8sZ9udgSVnzefW+z8WiFiImtQ2K1a0k7rG6/JwCLqcvzSCWzCGZKky2FSLp8izTem87RGHcGqa0V9MK57GmKPB6FNd5Pde5XDrOyseqY3Q6DQG4JqNyebP4XVJ878IdpJuWhbxpIZU1oGlKQ2MaEk2P/6XGsdqcpRqrjZx3Q2NJpHNG8bx2VqGXgpQS75wcx86B+YPfes65q3Z0Y//2LgyOxBFP5REOeioKHq41HKvNWehYTWcNJNOz2ypUtbFz8PSlGbzy/jBmkjlYlsT4TKaiPolXU9AVna0UHkvlMDqdwsaeEDb3zW6H8GgqupYwLZznXHP4uc1q2wA7EongjjvuKP7Zsix8//vfxy233FL3MUIhn+u/tZiWheffuoBfvXymYvDrXhWfvmM77rl+c0PFFC5OpCtaC4hCWqirqJiiorOzetB+9nISmqoglzdnb6KLPX0qld9QWJYFVVFrvEYU08RzeQui8BvKq6faX6hi3vda/p7nU+1Y/X35OV/rfA5eTZ3zefW8z8UWiay9NL6FcD6vdvjc8oaJiZkMdL8XUlFhWE7WSGEcNJEgpwj3CDTlbGAMAB012vPVOperjbPSsQrY46V0nNuPWYXvn9l3I6SozFwBsLEvgs7OYENjGqj8Dqn13OUeo452OOdWkqUaq42cd8nCNcxhyeb78TZFEQ2dz/V8dl1d3GtdjmO1Mc2O1XTWztiSqopAqLm2sccHJ3Hw0AXIwlbGasF1wKehO1JZKVwKFdFooPhnj6qgp8O/LAXNeM41h59bGwfY5b75zW/io48+wk9/+tO6X5NIZBAO+5FIZIrFvspdvJzAz148jaHxVMXP9m7pxGfv3IaOkI54PN3Q+xWWCbMst01TnZUv6Xre1FSy+jFM0075xuxNvXRWqKrc45dP7EnYK3FSVAsIJIziZyIL/4fiYwICqipgmrL4u+d6r+XveT7VjtUV0BAJeDEZrywo5/x9VEVAVcScv6Oe97lYVFVBJOJHLJauec6tdIsRGMViaUSjgWX/3NJZAzPJXKFtln0uGaaJ0gEnm1gaU1Wl2IMXAFRhjzpNURAOeuD1KFXP6Vrncuk4qzZWAae1tiw7bmHfdcnfSIrKKYNo0IvOgIapqWRDYxoSTY//pcax2pylGquNnHdBj2Kf+9K+5i3l3j8BYKAnWNf5vBbOucWwFj63dhirpmUhlswjkzPmfe6cJHDw9XMwTAu5vImJmWxF/QNVEegIeu0tIGU/E9LEzIx9T+5R7V7Yzp+Xylo45xbDWvjc6h2rKyLA/uY3v4knnngC//iP/4hdu3bV/TrnImuaFsyyvSPZvInn3rqA1z4cqVj5Dfs9ePi2rdi/rQtCiIrX1qO3M4BIYLY/rlZYXSr9XV1hHRu7g8WiLOU29gTRGdIxEctAVRSYpoU54mt7FlDIkjtnOxgoxt2FRThNtfdVO+/Fo6nwezV4VGX2/Qnn9lwWKxPP9V7L3/N8lVBrHeuT12+qWkUcAHRNQX9P0E5XqvFPUu/7XGymaS37e1hJSsfqcnxuliURS+UqChL2dgYQ8XsRS5TuGZtrx3UlUaj4L4SA5lGwpTeMh24ZwFNv2Hu7hRBV01nnOpdd46xsrBbfe4cfEAJTJWPRo6lQVaVYAApwZZUDsFegP/XxrYXvPdnQmAawoPG/HDhWG7NUY7WR866/K4DvHTxeUTdlKfh1DdfvXtfQZ8Fzrjn83BrTyFhNZQzE07mWbK0YGktiulAQdDqerbhaqsLO6sqbFjzCvUIeDXrR2xGAaUpoikAk4IVlLe2kWSmec83h5wa0fZL83/3d3+Hf/u3f8M1vfhMHDhxoyTGPnZ/Cf//Je3j1SGVwfdPe9fi//vhjuGp794L2PDn9cZVCQFt+rHp6SQshcO8Nm6EqApGAx27NJQRUUZoMB0DM9tlVFQFFmV3NFhDF1zjPiwTdfTQVATxw80BFSnsj77X8PdfK5JnvWE6Rl66wu0pfV1jHF+7ZiUfv3N70sYmqyeZMjMcyFcE1YJ/Pn7huo6tHvagRXGsKUC2jtTiuBNAR0vHp27fhqh09+PTt25oec/WMs/tuHMB9VZ4TCXqgFDJBPJri+h2aquCR27biyq1dDf0u570udPwTORo5l45fmIGmte6cEoXjz3dEj6rg4Vu3QlHa/laKqCrDtDAZyyCWak1wDQCJTA6JVB5TZcG1EEAk4IFS2MtdHjQ7bbiEsK9PnZG5W9gStbO2bdMFAP/jf/wP/Pu//zu+9a1v4aGHHmr49eVtuuKpHH7+4mk8+9bFipvpdR1+/Nn9u3DLvj54tNZcLHs7A9jaF8HoZArpkt/XFdbx8K3b6qoIuq7Dj/WdAYxNp2EYFvKF1XRVFXaqaiFoVoSwe12HdAR9HuQNO7Xc+XLSNBXrOnxY1xlwFYlw3sst+/qwvjOA4Ykk0jmzUCBNoDOs41Mf39pQ9VLnPTvHavTvva7Dj5v2rse2DRHs2BjBzXt7i+3BFnrsxcYWBc1ZjjZdliUxk8whkZ67jV9XxAdVFRgcScCyLFSblA35NTi5IqIwOw/Yk2vO2Ny8PoQ/+cTO4jk637m8Z6AD50cTuDiWQDprIhp0V/l3Xj86mUI2P9uCqHQsVPsdWiHlriPkRcDnge5R4fOq6O8JFr8DyzUy7tp9jDo4VpuzlGO1nnNJSonvP3MchmkHxNl89VWTsF9Dbp4VFUUAQrEnpFVVgaoK+LwqdI9qZ3wU6hKqhZW1R27bigM3DdT991kL59xiWAuf23KM1VQmj+lkrmI740KYloVnDl3ExTF3QWJVEejp8MOna9AUgbwp4dPV4uS104Zrx8YoVEWgK6K7JraX2lo45xbDWvjc6h2rQjazoXAJnD59Go888gi++tWv4rHHHnP9bN262q2tSn106jKi0QCmppM49OEofvtmZU9qVRG4+9qNuOua/roKqtTLqynFdgJSSpwfTSCeziHs92KgN9TwCo5zjFgqi2TaQNDvwfh0Gs+9fQGmhYrVKAGJO67utwMHIbF9QxRb+sIAMOd7cX5PKmvYRY4CWlMp8qXHWsjfezmOvRCapqCz096Pt1rTY9atC7f8mFNTySX93NJZA/FUrnYbvSo+PDuB/3jhVEWrEk0FoiEdukeDz6Ng5+YOXLdrHTRF4MxwDAIC2zdGalYCrnYuHzs/XXerHlUVmEwZGBqJIaBrVcdCtd8BzP1dUE0j465dx6iDY7U5Sz1WgbnPpWODU/j+syeKfdyn41nXhJmmCkSDHmiqCkDa274sCdO0kMlbsEwLmqpgXacPX7p/N6QEzg7Hi9fNgd4QLlxOIpbMYnA0DglgXdSeBG505XotnHOLYS18bks5Vg3TQiyZm3fCqVGZnIH/+exJnLrk7sTj1exJ3dLV6EjAg09etwmpnFFswyWEgKIIdIX1lt6PN2MtnHOLYS18bvWO1bbdg/3888/DNE18+9vfxre//W3Xz44fP173cUYmknji1x/aF8wyWzeE8dk7tmN9R2ur3ekeFR0lPaWFEMXgtlQjN6Czx3Afp6872HDPzGrvpfz3lA6SRvabVn/PrbeYx6bVq9Ze6/nkDBPPHb7oCq4FgK6IDqHYk2g37VmPG/euRzRorwwDqKs3bvm5fHRwqmodgsl4Fj/9/Sl8/u4rXGNbCIErNnWgO+ipeUGrNV4aHUONjDuOUWqVWudSMpPH2Ewa2ZyBeCpfETAoAuiO+mAW9nAG/B7Xz0uPaPeUV7B1Q7hi3DrX3qt2uNuGEq00rdxrXWoylsF3Dx7H5Sl3QWC/rrnuhwF7XN521QZsXO+ulK8ItEVwTdQKbRtgf/WrX8VXv/rVBR3j2bcu4Pd/uFSx4uTzqnjwli24fve6lvfU83tVRMpSOas5OjiFZ946j0tjSRiFGfSN64K4/8aBhlIo927pLKaStutKEVE7yOZMzKRyDactmZaFHz57EqNlNw5dER9072yBluMXpnHHxzYUg+tmSCnx3OELNVfWLQk8d/gC9gx0cIzTmpbK2EH1VCyLmWQWZpU5M0WBPekkRM2tX1JK5AwLliVx6tI0r5+0KjkVwrP5xiaX63HhchzfPXgCyXTe9fh1u9Yhlckjlpp9PBr04tb9fdix0T2JpQigM+xjcE2rRtsG2K3w3OGLFY9dtb0bD9+6BeGAt8orFibo0+o67tHBKfzLrz+y2wGV3ElPxrM4P5rAXzx8ZUNBNleKiGqzpEQ8lUc623iFYUtK/PzFMzh+Ydr1eGdYdwXXABBL5jCTyKEz7JvzmHNlrpwfTcxZNRmY/Z7gmKe1KpUxCkWZJI6en4IlRUV/elWxi3wmMgYG1gWRq7LVKZM1EEvli+1kXnjnEj46NzVnBhjRSpPOGpiMZVq+ag0AH5yZwE9+5946pSoCn797Bz52RQ+klBgeTyGZzbtSwUsJYV9TW1X/iKgdrOoAu1RHyIvP3L4Nuwdaf9EUAMIBLwK++T9OKSV+8OwJTCeyFZnX0pKYTmTxg2dP4O/+/CbOohMtULOr1oA9Vp9+4zz+cHLc9XjApxWLDJaOUVUVSGTy5YdxOTo4NeeWjng6N8erZ9X7PKLVpnRFbHg8heHxVMX4ttsAOZWKLdyyvw8fnJ7AyFQaliWhKAKWaWE6mSteh1VVgdej1tyKQbTSGKaFiZk0phPZlgfXUkq8+O4QnnnrguvxgE/Dl+7fXZwAFkKgf13tvsECdmtHj6bWfA7RSrTqA2xR2Ovxyes3Qfe0fgArhdY73jqPfW44hpHJVO1tzRIYmUzh3EgM2zbMv3+TiCo1u9e61EvvDeGVD4ZdjykCyOdNzORNKIqCkF+D7tXsNnlCIOyvncFSz97quV5fqt7nEa0m5emmR85NIJZyTzYpYrZ7hqoqiIa8SGdNJNL2Kp5z7TUsCQWF5wq7fZ2DWzFoNRifySASaW2NIcAO3H/58lm8fWLM9XhP1IfHH9yD7sjcWVwOgcbun9u9cCZRqVUdYO/a3IE/+uROdPibr4Q9F00R6GiwIMPh42NVV9NKvyKkJfH2sbGGA2x++RA1VyG83OFjl3HwkHtm3u41P3tQy7IQS+UQFQJBvwddYb1YnbtcvXur/+uj+9EV1udME5/r9xCtVslMHvGS4Pr8aBwvv+eeAPPrKoI+DVLawbVf15DJGXjtyDA8morOsI5YMm+3sbQkTACKarej9Hndt0PcikEr3WI0CUpnDfzg2RM4MxRzPb69P4LH7tsFv15/WBEJeiu2WtUyX/YXUbtZ1QH2nz+8F9FoADMzqZYf26sp6AjprrYD9RiZTFZ9XMIdZGfyje0X5ZcPrXVOX+uFFnH56Nwknnz5jOsxv67Cr6v2DX7pPYsEEuk8Qn4N996wueaEVr17qy9cTuLeGzZXXekG7NW5uX4P0WpUHlxPzNgVi0v793o99jVZLCkxTQAAIABJREFUCAEh7AkxAMhkTURDdsaHz6vB59UQT+YQS+UgIKAqSs3sNm7FIJo1Ecvgid8ew/hMxvX49bvW4TN3bGtosSka9NYdjDfaWYOoHazqAHux1FspvNzRwSlcvFw9wAZKgmwB7OjvaOi4zpdPaUXU4byJn/zuJL5wz05++dCqlskZiCUXtmoNAGeGYvjR8ydd+9XstnvOjbtAImXAsixIaZdVElJi37Zu7BmoPWYb2Vu9f1s3Pn/3FW0zYcbMGFpO5cF1Mp3Dv/z6I6Qys5PQmirQFfYVz0tVEcgbFrJ5ExISmZwJVRHFVFTdq0JJ2881TQt5w6qaprqQrRi1es8TrUSDI3F875njrnEHAAdu2ow7P9bf0DVhvuDaGTuxVBaJVB4vvHMJmZxZdYxyOwe1KwbYDQr5PQj5G2/D46SIBnwalBhqBgISQFDXcPOV6xs6riUrK6ICdprcky+dxp4/u55fPrTqtLL1yNB4Et87eNxVDXVdhx+qagfWTlGzoF9DNm8ilzMgoADSTikfGk/WDIAb3VvdLu33mBlDy6k8uD5+fgo//t0ppLOz411RBG6/qg+jUxnMJHPImyam4vYkmGlJmKbdRUBVBDyaikjQA59Xg6oqxWulWeWCvJCtGLXGzYGbB3BbZ+2CT0Tt6L1T4/jp70+7xommCnzhnitw1fbuho4VCcwdXDtjZ2g8iVgqj7xhwrRkxfgtxe0c1I5YE79OAvasWzPBNVCSIioEoiEdtW6TNQV4+NatUJT6/mmc42ayBqYSWVdwDdiz8+cvJ/Diu0NNvW+idpXJGZiYySwouJZSYmgsibePX8Z3fnPUdaz1HX7cur8X+byJZDqHyVgWM/EsZhJZJNMG8ubsHjdFEcV0taODUxW/Z6A3hK6wPud7Kb+hd9rv7d/WjS194WUJrn/6+1MVqe1z/T2JWiWRng2upZR488MR/PD5k67gGgAEJN748DK29oVw2/4+KELA71VhlaahSDuIzhsmpuJZZHKGXdSsMKTUsq1eC9mKMde4+fELp/D+qbEaryRqL1JKvPDORfzHC6dcwXXQp+EvHr6y4eA65PfM2W3HGTtD48nZ+1mJquO3HLdzULvhCnYdGq0UXk3p4I8E7VWqWDJX/NISsG/Sb7tqAw7cNNDQcaWUdmXVOSqTv3pkGHdd01gaD1E7sqREPJlDegEVwgHg9KUZvHZkBJPxDManM+4bCL+GSNCLQ0cvI5bKIW/YP1MVwJnDErAv+oo6m3paK11NCLGi9lbXW5SNaXm0GBLpPBJpO7g+fWkGrx4ZwckL0xUrzapit+MyLQu/+8MQ+rv90D0qYsk8BAQACec/zk26IgRiyTzWd/rRGbb3aJf2311Ihsb840biVy+fwf/+mX0NH5toKRmmhSdfOlPRpnJdhx+PP7AbXXVWCnf4veqcC1TO2DGtsvtZ5/JSNn7LV7HZWYPaDQPseSiKQFeDlcKrKR/8kaAXkYAHyYwBw7SgqQqCPg13X7ux4ePmDKti5bpcKmMwhYZWvIX0tS51+tIMDh46D8OUmJjJum7chQA8qkAqWzlLXhpcO/9DAK6e2LXS1fZu6WyrvdVzqbcoG79TqNXKg+uDh85jOpGtmsZdWh3UMCxcGk+jM+wtXg+FEFAFYDqr2RKQ0s7syuVNBHQNX75/NwI+T0u2YtQzbsan0xgcjWNTD/dkU3tKZfL4/rMncG447nr8io1RfPHenQ1VCgfsosDOwlItztgpv5916hI5k2Sl49eZ2GZnDWpHDLDnoBXad6h1pmvPxUkRdV18C+19HM18SQz0hhDUNUzO8RxVVeD1qEyhoRWrVavWgB0Mv3ZkBKYlMRnLwCi9mAtAUxSksxb8ukS+kKJWunI9+2Q7tVRKVBRJqjXW2mVv9XwaKcpG1CrxVA7JQhElZ5ymsgYS6epdNUxpFxkUwp7psm+83QPV6fRhSmnfoENCQCDg0/C5O3e0dGLLyShzCo0qioBXUyrGdzyZB3pa9muJWmZ8Jo0nnj6OibJK4TfuWY9P37614fthVRHFIqFzca4l5ZPn5ZNkzvh1ntdu2V9EDgbYNfi8KqJNVAqvpTRFNJMzZy++hZvyZr8khLDTyn/0wsnqKeIC9l4zMIWGVqZWrVo7hsdTmE5ki7PlpSIBD1IZA5YlYZhWyUVcQFHti7xlAaoqoJSM1fLVtbnGmrO3up01WpSNaKES6XwxuAbscTo+k8bUPCvCEvb4hASkkFUvg4oiIOz4GpGA3Xv3sXt3YeuGSEv/DuPTGYxNZyoKjUYCHvhKVv3CweZquRAtprPDMXz/mRNIl2RvCQAHbh7AHVdvaPj+VBFAZ7i+drbOtaTac0snyUQhZcXJLm237C8iBwPsKoI+DeHA4tw4qorAdCJXvACrqoKN64J49I7tTX9J3HVNP147MoJL48nKC3uh4iJTaGilsSyJeKo1q9alEpkcphM5ZMuO2xnWUXptNwuTYKU0RUFeVm7HKC2StBrGWtWMmzKr4e9J7aE0LdwxOp3CRCzraplXVeHnmqZASgndoyCTUyq2TQkhoKkKwkEvusJ6yye5jg5O4eX3K4uJmqaFqUQWnQD8Pg09HX5s6Q3DNFszYUjUCn84MYafv3TGNVnsURV84RNXYP+2roaPJwrBdb3bK51rzkQs46rw71AUAU1R0BHWEdQ1PHb/LmzpXfrin0T1YhXxEgL27PZiBNdOdcS8KbGuw4euqA8dYR0dIS8MY2EBhBACj965HX1dfnRHfegM6+iO+rC+0w+fV2MKDa04mZyB8Vim5cE1ALx3csI1Qw/M9uUsDahVRcCjKsWK/qU9dkvHkqoqxSJJq2WsORk3tRYeVsvfk5ZfMlMZXGdyBl54+5Ira6XWuSgUOz08EvBg0/oQfF4VkYAHFa06Ctlci3HulhY3K61OPvsEIJbKQwB45I7tHDfUNqSUePbwBfykrA1XyO/B//bIlc0F17ALA3u0+gsDO9ccVRE1x2805IXfq+Jzd+3A1r4IxxG1NQbYBc4XwlwtBJpVXllUCAHdo8Kva/B6VEgIPHf4QrHlTzOcAkp9XQH4CscF7FWmz999BVNoaEWwLInpRBbTidalhJd66b0h/OGUuypqOOAp1kLwaCoUxQ6qNdXeOxnya7CkhGFJmJYFRdipaaqqFG/sReGx1TTWnO+U8vZiq+3vScunvM81YPe2/+FzJzERm90DKgTQHfUjEvS47rsF7PTwjpAXAZ+GR+/Yji/csxP9PUF0hgpjFPYkWGdYR393cFHO3dLiZj6vZtduqbJyd9e1G3H1Feta+ruJmpU3LPzHC6fwu3cuuR7v7fTj/3h0PzatbzxDSQDoCOvQm+i641xzlnr8Ei0Gpohjdp9II7NtjViqirwrpYASUTXprIGx6TTyxtwV8Zv19vHLePrN867Hgj6tonVIOOABYBdOyuYMxFM5WHK257Vl2SmfA+vDuHV/H3o6fKt2rPE7hRZLtbRwKSV++co5nLw443q8K+yDR1Pg0ezssngybxcQV+zXZHMW7rm2t3jj7ZyzsZTdsz7o9yASWLxzt7zYn8+rwefVkMu7662si/pb/ruJmpFI5/GDZ05gcNRdKXznJrtSeHkbrHqFA96mgmtH6TVnqcYv0WJY8wF2q9pwzWUpK/KuhAJKROWm41l4DQlrAVkcczl6bhI/f+mM67Ht/RF4NcXuuVkQDXpx6/4+AMCzb53HaCJrZ55IexVNEQJCANIC4qksersCq342nd8p1Gql1cJLvfjuEA4fu+x67K5r+nF5Ko2ZZA7ZvIF01oDuVRHwaYUtHHbweujoKAZ6w9i7pbPknF2a87ZWsT9vWaDB4mbUDi5Pp/Hd3x6rWPi5+cpePHzrVldNkUb4CuNyoZZ6/BIthjUdYKuKQFekNW245sKKvERzS+cMeBfp/D87HMMPnz/pKpa0c1MUXzqwG6oiMDyeQjKbR1D3YENPAEIISCkR8nugqSpMy4KAHViXiqUMPPvWeewZ6OCs+gJJKblKvkbEkrmqPebfOzWOZ9664Hrs3hs24RPXbYKUEkNjSfyv185CUxXoHrXi/LAk8NzhC8syHustCrillwEDLa/Tl2bwg2dPIFNS30QAePCWLbjtqr6mx46miHl7XROtJWs2wNZUga6wr672AQvFirxEy2N4IonvPn0cRknF3s3rQ3jsvl3FrJX+dcGK141MpDAZz0JK6WrHVco0LYxOpRe8tWOtOzo4hecOX3B9P7L9yuo0k8hWLVx4djiGn/7+tOux63atwz3XbgRgr2jZE1+YM3W1FVutmlHahrNa6QgWBaR28Pbxy3jypbOuTDGPpuBPPnEFrtzaeDEzhxD2vuta10qitWhNFjnzagq6IksTXAOsyEu0HCZjGfz7U8eQzc/e0K/r8OPxB3ZXpG6Ws6Scvz0Q7FZepVs7pJQYHInjyNkJDI7EF1S4cC1wuiuUTz5OxrP46e9P4ejg1DK9M2olKe3ihdWC67HpNL7/zHFXBeMdGyP47B3bXNfEdN6o65rdiq1WzWBRQGpXlpQ4eOg8fvbiGVdwHQl48NVP71tQcA3YBYIXc5sl0Uq05lawdY+KjpB3yYNZ5+LLlRqixRdP5fCd3xxFPO3eX/2Vh/Yg4Jt7H6TuUdET9dd1M68qori1gyuxjSnvrlBuOVN+qXXs4DrnmuhyJNJ5PPHbY0hnZ3+2vtPvyjBx9HUE6joPlnOrFYsCUrvJ5U388NmTeP/0hOvxDd0BfPnAbkRDeo1X1icc8CyoqBnRarWmAmy/riG6jHtEePElWnzprIF/LyvgEtA1fOVTe9Exz82EIuxAvCPkRW9XANOJHEyzelVzVVXQ2+nHQG+ouBJbHiw6K7Fcwaq0VN0VaPlIKTEVzyJXpTNAzjDxvYPHXedA2O/Bf35wT0UaeNCnobfTvyK2WrEoILWLRCqPf/rlhzg7FHM9vntzB/70kzuhexcWGPu8KoLzTFgTrVVrJqcj4Fve4NrhXHz3b+vGlr7wkgTXTFultSJvWPjeM8cxPJEqPubVFDz+4B6s75i/RU4k6IWi2Ps977ths/2dUW2ICiAa9OC+GwcAoK6VWI47t6XsrkBLz5ojuLYsiR+/cAoXLieKj3k1BV9+cE/FJJimCIT8Hm61ImrQ//PzDyqC64/v68OfHdi94OCaRc2I5rYmVrDDAS98azSFhWmrtNpIKatW/jYtiR89fxLnhmf7eqqKwGP378Lm9aF5jxHweVwrZ3u3dOJLB3bjyZfP4NJYsriSraoKNvYE8OidO7B3SycGR+LFgmg5w5rte6spxZt9rsRWYneF1cuSEtM1gmsAePrN8/jo3Oz+eiGAP/3kTmzscRccFACiJVu6uNWKqH6lY0QI4FMf31psQ7kwErFkHiNTKWZiEtWw6gPsaNCLfFbAqHGhX82YtkqrzelLM3jtyAhmkrOrmtGgFx/f14v3Tk+4imIJAF+45wrs3NQx7zE6Ql48dMsWRIPuYi/2to7rMDgSx5mhGCAktm+IurJP4ukcMlkDsVTelU6uqgoiAQ98ulZ8Hs1id4XVyZISU7Es8jW2Vrx+ZASvfDDseuyRW7diT5VrUcCnwaO5J8e51YqoMV5NwZ/euxN7BhZ+v3f60gzeOnbZdf3kBBdRpVUdYEeCXoQCXkxl8/M/eZVhASFabU5fmsHBQ+crzumZZA4//t1pJNLucf7I7Vtx9Y7uuo6RSOfxsxdPQwhRcZMghMDWDRFs3RCp+r7GpzOYSmSBsmOapoWpRBadAHy6xpXYMmxttPrMF1wfG5zCr18/53rs9qs34JZ9latqmmqnhlfDfc5E9ekI63j8gd3o7Qws+FinL83g2cPnIYR7dykXbYgqreo92Gu5+EIjBYSI2p2UEq8dGakaiCVS+Yrg+pPXb8ItV7pv2msdw9lz3cxeaSkl3j8zAVWp8VUqgVgqj86QlyuxVbC10eoxX3B9aSyBHz5/0tX+bt+2Ljxw80DFcwWAaFDn5ArRAuzcFMV/+/KN6C/betEMKSXe/Gi0Irh2sNYIkduqXsFey1hAiFaT4fGUKyXNkcrkEUu5H7/lyl584rqNdR1DCHuftqPRvdLnRxOYimcRCXowFa9cxQYA07Jw9Y4eBgs1MOV35ZsvuJ6KZ/Hdp48jX7JVa/P6EP74niugVPl3Dvo98Girev6faNH9xSNXIhrWMTOTmv/J85iYybjaXlbDWiNEsxhgr1IsIESrSbLKNo9M1sB0wh0wb9sQxsO3ba0anFU7hlqlJHEjk07Oc31eDZ1hIJassg876EFPh6/uY65FTPlduZyCZrWC63TWwBNPH3PdnHeFdXzpwO6qQbRHVWqmhhPR0vNqCmS12eMquGhDZGOAvUqxgBCtJkHdfcOdzZsV57buUfHATQNVV8SqHUMtpIaXa2TSqfS5Pq8Gn1dDLm/OVhIvdC/gRBatRvNVCzdMCz949gQuT6WLj/l1Df/5wT1Vg2inajgRtQdNEegI64in6qtlxGsdkY05WKsUe4bSarKhJ1DsY583TEzGMq6fezQFW/vC2LS+9oRR6TGEsPdel2t00smZyCrl9ajw6VoxuOZEFq1G8wXXUkr84uUzdvX9AlUR+NKBXeip0ZM+HPBAU3lbQtQOFGEXSVOEqHqtK8drHdEsXslWMRYQotVCCIFb9/fBsixMzGRdhZI0VaAn6sPtV2+Yc8LIOYYiqqeGNzPpxIksWovkPME1ALzwziW8c2Lc9djn796BrX3Vq/HrHhWBNVyYlKidCAF0hvXihBevdUSNYYr4KscCQrRarO/0I5kxYJVE14oisLUvgruu6ceOjdF5j7FjYxR/dPcOvPTukCvFfCF9PJ2JrOcOX2jZMYnalSUlxqczyObNms9558QYnn/7ouuxAzdtxseu6Kn6fFURTA0naiMdQb1qD3pe64jqwwB7DWABIVrpMjkDT/z2mGsfmO5R8Ed37sC+7V11Txj5dQ0f29GDq7d3t3TSiRNZtFZMxbLwB2unip4emsGTL51xPXbjnvW482P9NV/TEfLWrJ1AREsrHPBA96pVf8ZrHVF9GGATUVvLGxa+d/A4hiZmW414NAVfeWgvBnrrnzhSFYFwwE5BXYxJJ05k0VqQM0xU30ENjE6l8INnTsAsaTa/c1MUn769emV/AAj6tIqVMiJaHn5dQ3CerRq81hHNj3uwiahtmZbEf7xwEmeH48XHFCHw2H27GgquAa6SES2meCqHJ357DJncbOp4X1cAX7x3J1Sl+q2Gpgq25CJqE15NQSTA8UjUCgywiagtSSnxy5fP4KNzU8XHBIAv3LMDuzZ3NHQsrpIRLZ5c3sR3Dx539aWPBL14/IHd8HmrJ8oJANGgztRSojagKAIdIY5HolZhgE1EbengoQs4fHzM9djDt26tWSipFq6SES0ey5L4jxdO4dJYsviY16Pg8Qd2IxqqvVc7FPDAo/EWhGi5CQCdIW/V1pVE1Bxe3Yio7bzy/jBeem/I9dgnrtuIj+/va+g4AuCsPNEi+s0bgzg6OJtlogjgP927Cxu6gzVfo3vUefd5EtHSiAS9zPAiajEG2ETUVt45MYan3hh0PXbzlb345PWbGj5WKOAp9vEkotZ69YNhvH5kxPXYZ27fNucWDkURiAbZkouoHQR0DX6d9Y6JWo13nkTUNo6em8LPXzztemz/9i48cmvtKsS1eDWFq2REi+TImQk89bp7Iuyua/px497eOV8XDTIVlagdeDWl2FmDiFqLATYRtYVTF6bx/WeOo6TDD67YGMUf33NFwzfkigCiIa6SES2Gs0Mz+NHzp1AyVHH1jm7cd+PmOV8X9GnQPUxFJVpuLGpGtLiYF0JEy254Ion/75cfwTBnb9k3rgvisft2NZXiHQ54a7YGIqLmTcQy+PaTR5A3rOJjW/rC+KO7dszZBs+jKiw2SNQG7KJmOjNJiBYR70CJaNn966+PIpU1in/uifrw+AN7oHsbX+3yeVXuKSNaJP/2m2OIp/LFP/dEffjS/bvmrAguYGeUcLWMaPnZRc14+0+0mDjCiGjZld6wR4JefOWhvU2tdimKQIQFlIgWzdh0uvi/Az4Njz+4B4F5ah2w2CBRewj6WNSMaCnwikdEbcOvq/jKg3vQGa7dP3cu0aB3zjRVImoNTRX48oHd6I745nweiw0StQfdoyIc4AQ00VJggE1EbcHrUfCVh/aityvQ1OsDLKBEtCQEgD/55E4M9Ibnfp4AM0qI2oCmCBb+JFpCzBMhomXn9Sj4L49ejU3dfpimnP8FZTRFIMwCSkRL4nP3XIGrd3TPO1bDfi9Tw4mWmSLs4JrZXURLh1c+Ilp2//d/uhb7tnc39Vq7gBLbjRAthS8d2IV7bxqY93m6R0XAxzl8ouXWEdY50UW0xDjiiGjZLWRfWNDvYUVUoiWyf3v3vJNZirDrIRDR8ooGvdw6RbQMeFdKRCuWV2NvXaJ2Ew2yxy7RcvPrGkIsaka0LBhgE9GKxAJKRO0n4NOa6l9PRK3FLBKi5cMAm4hWpEiABZSI2olHVVhskKhNsC4J0fLh3SkRrTi6R4VfZwElonYhBBANeXlTT0REax4DbCJaUezUcK6SEbWTaJAZJURERAADbCJaYcJ+L1SFX11E7SLg0+DzMqOEiIgIYIBNRCuIV1PYW5eojXDfNRERkRsDbCJaEVg1nKi9cN81ERFRJQbYRLQihP3c40nUTljJn4iIqFJbXxmz2Sz+9m//FjfccANuv/12fOc731nut0REy4Cp4UTtxe/VWMmfiIioira+Ov7DP/wDjhw5gieeeAJDQ0P42te+hv7+fjzwwAPL/daIaIk4aahE1B5URSAS9MKy5HK/FSIiorbTtgF2KpXCT37yE/zzP/8z9u3bh3379uHkyZP4wQ9+wACbaA2JBFg1nKiddIR0pFNZBthERERVtG2AfezYMRiGgWuvvbb42PXXX49/+qd/gmVZUOq44VYUu/CKyj1iDXM+M352jeHn1hz3WLWKj/u9GsIsbDYnnnPN4efWnJDfA5+uIZfNL/dbWXF4zjWHn1tzeA/cPJ5zzeHnNqttA+yxsTF0dnbC6529ue7p6UE2m8X09DS6urrmPUYk4nf9lxrHz645/NwaEwr5XP8F7DTU9Z2B4k0CzY3nXHP4uTVmY18UAD+3heBn1xx+bo3hPfDC8bNrDj+3Ng6w0+m0K7gGUPxzLper6xixWBrRaACxWBqmac3/AipSVQWRiJ+fXYPWwufW2Rls+TETiQzCYT8SiUzxc+uO+DAzk2r571pt1sI5txjWwue2WGOV19XmrIVzbjGshc9tMcYq74GbtxbOucWwFj63esdq2wbYuq5XBNLOn30+X7WXVHD2h5mmBcNYnf/Qi42fXXP4uTWmdKyapkTQp0ERgp9hA3jONYefW2N4XV04fnbN4efWGI7VheNn1xx+bm3cpqu3txdTU1MwDKP42NjYGHw+HyKRyDK+MyJaTJoqEPJ7lvttEBERERE1rG0D7L1790LTNLz77rvFx95++21cddVVdRU4I6KVRwiBjpAOIbjvmoiIiIhWnraNVP1+Pz772c/i61//Ot5//30899xz+M53voMvf/nLy/3WiGiRhAMeaKw+SUREREQrVNvuwQaAv/mbv8HXv/51PP744wiFQvjLv/xL3H///cv9tohoEfi8KhSN+66JiIiIaOVq6wDb7/fjG9/4Br7xjW8s91shokWkCIGOsA8xVg0nIiIiohWMuZhEtOw6QjpU9rsmIiIiohWOATYRLTvdqy73WyAiIiIiWjAG2EREREREREQtwACbiIiIiIiIqAUYYBMRERERERG1AANsIiIiIiIiohZggE1ERERERETUAgywiYiIiIiIiFqAATYRERERERFRCzDAJiIiIiIiImoBBthERERERERELcAAm4iIiIiIiKgFGGATERERERERtQADbCIiIiIiIqIWYIBNRERERERE1AIMsImIiIiIiIhagAE2ERERERERUQswwCYiIiIiIiJqAQbYRERERERERC3AAJuIiIiIiIioBYSUUi73myAiIiIiIiJa6biCTURERERERNQCDLCJiIiIiIiIWoABNhEREREREVELMMAmIiIiIiIiagEG2EREREREREQtwACbiIiIiIiIqAUYYBMRERERERG1AANsIiIiIiIiohZggE1ERERERETUAqs2wM5ms/9/e/cfU1X9x3H8dQ0NvU4DsWK18YcMkkUXumatYcurzswWBbG1lsRqmiullUsIM3DNfngXkZBj1Ghmv5ZJLMaWDmctV+mAAtFhQYulrnZxGAsRZ/d8/3DejQI53HPy3nO/z8fGH/fcw+V9DzzZPveee6/Kysq0YMEC5eTkqL6+PtIjRaU//vhDxcXFWrhwoRYtWqRXX31VIyMjkqTffvtNRUVFysrK0r333quDBw9GeNrotWbNGpWWloYuHzt2TAUFBfJ4PMrPz1dXV1cEp4tutGoOrdqDVsNHq+bQqj1oNXy0ag6tWkenY4vZBfa2bdvU1dWlnTt3qry8XDU1Nfryyy8jPVZUMQxDxcXFGh4e1ocffqg333xTBw4cUFVVlQzD0NNPP62kpCTt2bNHubm5WrdunU6dOhXpsaNOc3Ozvv7669Dls2fPas2aNVqwYIEaGhqUnZ2tJ598UmfPno3glNGLVidGq/agVWtodWK0ag9atYZWJ0ar1tHpZRgxaGhoyMjMzDS+//770La3337bePTRRyM4VfTp6ekx0tLSjEAgENrW1NRk5OTkGN9++62RlZVlDA0Nha577LHHjO3bt0di1Kg1MDBg3HXXXUZ+fr5RUlJiGIZh7N692/D5fEYwGDQMwzCCwaCxbNkyY8+ePZEcNSrRqjm0ah2tWkOr5tCqdbRqDa2aQ6vW0OnlxeQz2N3d3bpw4YKys7ND27xerzo6OhTT1gkdAAAIhElEQVQMBiM4WXSZO3eu3n33XSUlJY3a/tdff6mjo0MZGRmaMWNGaLvX69WPP/54pceMaq+//rpyc3OVmpoa2tbR0SGv1yuXyyVJcrlcuvXWWzl2Y6BVc2jVOlq1hlbNoVXraNUaWjWHVq2h08uLyQV2IBBQQkKCpk2bFtqWlJSkkZERnTlzJoKTRZdZs2Zp0aJFocvBYFAffPCB7rjjDgUCAV177bWj9p8zZ45+//33Kz1m1Pruu+/U2tqqp556atR2jp15tGoOrVpDq9bRqjm0ag2tWker5tBq+Oh0YjG5wB4eHh71j0VS6PL58+cjMZIj+P1+HTt2TM8+++y4x5Djd9HIyIjKy8v10ksvKT4+ftR1HDvzaDU8tGoerdqDVsNDq+bRqj1oNTy0ag6dmhOTC+yrr776X7/MS5f/+ceAi/x+v3bu3Cm/36+0tLRxjyHH76KamhrdfPPNox79vIRjZx6tTh6tTg6t2oNWJ49WJ4dW7UGrk0er5tGpOXGRHuC/cN1112lgYEAXLlxQXNzFuxgIBBQfH69Zs2ZFeLro8/LLL+vjjz+W3+/X8uXLJV08hj09PaP26+/v/9epH/+vmpub1d/fH3qN06V/KHv37tV9992n/v7+Uftz7MZGq5NDq5NHq/ag1cmh1cmjVXvQ6uTQ6uTQqTkx+Qz2/PnzFRcXN+pF9W1tbcrMzNSUKTF5l8NWU1OjTz75RJWVlVq5cmVou8fj0dGjR3Xu3LnQtra2Nnk8nkiMGXV27dqlpqYmNTY2qrGxUT6fTz6fT42NjfJ4PPrhhx9kGIakix8F0d7ezrEbA62aR6vhoVV70Kp5tBoeWrUHrZpHq5NHp+bEZGnTp0/XAw88oIqKCnV2dqqlpUX19fUqLCyM9GhRpbe3Vzt27NDq1avl9XoVCARCXwsXLlRycrJeeOEF/fzzz6qrq1NnZ6ceeuihSI8dFW644QalpKSEvtxut9xut1JSUnTPPfdocHBQW7duVU9Pj7Zu3arh4WGtWLEi0mNHHVo1h1bDR6v2oFVzaDV8tGoPWjWHVsNDp+a4jEsPM8SY4eFhVVRUaN++fZo5c6aeeOIJFRUVRXqsqFJXV6c33nhjzOuOHz+uvr4+bdq0SR0dHUpJSVFZWZnuvPPOKzylM5SWlkqSXnvtNUlSZ2enysvL1dvbq/T0dG3ZskUZGRmRHDFq0erEaNU+tBo+Wp0YrdqHVsNHqxOjVXvQ6dhidoENAAAAAMCVFJOniAMAAAAAcKWxwAYAAAAAwAYssAEAAAAAsAELbAAAAAAAbMACGwAAAAAAG7DABgAAAADABiywAQAAAACwAQtsAAAAAABswAIb4zp16pSam5tN73/gwAH19PSY3n/VqlUqLS21bf9Dhw4pPT1dJ06ckCT5fD5VV1dLkhoaGpSenm76ZwFOQquAM9Aq4Ay0CitYYGNcJSUl+uabb0zte/LkSa1du1anT5/+j6caX3Z2tg4ePKjk5OSIzQBEAq0CzkCrgDPQKqyIi/QAiA2GYUR6BE2bNk1z586N9BhAVKNVwBloFXAGWsU/8Qw2xrRq1SodPnxYn3/+uXw+n86dO6eqqiotWbJEmZmZys3N1d69eyVJJ06c0JIlSyRJhYWFoVNSWlpaVFBQoKysLGVmZiovL8/0o4HjGRoa0oYNG+TxeJSTk6Pt27crGAxK+vfpMcD/A1oFnIFWAWegVVjFAhtjqq6uVnZ2tlasWKHPPvtMzz33nBobG7V582Z98cUXWrp0qZ555hm1tLQoOTlZu3fvDn3f448/rq6uLq1fv14rV65UU1OTPv30UyUmJmrjxo06f/582HPt27dPCQkJamho0MaNG/Xee+/p/ffft+tuA45Dq4Az0CrgDLQKqzhFHGO65pprNHXqVMXHx2tgYED79+9XbW2t7r77bknS+vXr1d3drdraWi1dulSJiYmSpNmzZ8vtduuqq67S5s2b9cgjj4Rus7CwUKtXr9bp06fDfo1IRkaGXnzxRUnSvHnz1Nvbq/r6ehUVFVm6v4BT0SrgDLQKOAOtwioW2JjQ8ePHJUler3fU9ttuu02VlZVjfs/8+fM1e/Zs1dXV6ZdfflFfX5+6u7slSX///XfYs/xzhltuuUW1tbUaHBwM+zaBWEGrgDPQKuAMtIpwcIo4wmYYhuLixn6M5vDhw1q+fLmOHDmim266SevWrZPf77f8M6dMGf0nGwwG5XK5NHXqVMu3DcQqWgWcgVYBZ6BVXA7PYGNClz47r62tTYsXLw5tb21tVWpqqiTJ5XKN+p76+nrdfvvtoTd7kKRdu3ZJsvZui0ePHh11ua2tTTfeeKOmT58e9m0CsYJWAWegVcAZaBXhYIGNcbndbp08eVJut1uLFy/Wli1b5HK5lJKSoubmZu3fv19VVVWSpBkzZkiSfvrpJ2VkZCg5OVktLS1qbW3V9ddfr0OHDumtt96SJEtv8NDe3i6/36+8vDy1t7fro48+UkVFheX7CjgZrQLOQKuAM9AqrGCBjXE9/PDDKikp0f3336+vvvpKlZWV2rRpkwYHB5WWlqbq6motW7ZMkpSQkKD8/Hxt27ZNfX19Ki4uVn9/v9auXStJSk1N1SuvvKLnn39eR44c0bx588KaqaCgQL/++qsefPBBJSYmasOGDcrLy7PtPgNORKuAM9Aq4Ay0CitcRjR8OjoAAAAAAA7Hm5wBAAAAAGADThFHxL3zzjvasWPHZfcpKytTQUHBFZoIwFhoFXAGWgWcgVZjE6eII+L+/PNPnTlz5rL7zJkzRzNnzrxCEwEYC60CzkCrgDPQamxigQ0AAAAAgA14DTYAAAAAADZggQ0AAAAAgA1YYAMAAAAAYAMW2AAAAAAA2IAFNgAAAAAANmCBDQAAAACADVhgAwAAAABgg/8BjssPBptRMe0AAAAASUVORK5CYII=",
"text/plain": [
"PyPlot.Figure(PyObject <matplotlib.figure.Figure object at 0x322be5da0>)"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"lmplot(x=\"total_bill\", y=\"tip\", col=\"day\", data=tips,\n",
" aspect=.5);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### If Seaborn is working, let's keep exploring:\n",
"\n",
"* [Distributions](http://seaborn.pydata.org/tutorial/distributions.html#distribution-tutorial)\n",
"* [Categorical Variables](http://seaborn.pydata.org/tutorial/categorical.html#categorical-tutorial)"
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Julia 0.5.1",
"language": "julia",
"name": "julia-0.5"
},
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "0.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
karlstroetmann/Artificial-Intelligence | Python/5 Linear Regression/Linear-Regression-Rounding.ipynb | 1 | 8114 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%%HTML\n",
"<style>\n",
".container { width:100% }\n",
"</style>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Linear Regression: Rounding and Subclassing"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this notebook we investigate the influence of <em style=\"color:blue;\">rounding</em> and <em style=\"color:blue;\">subclassing</em> on linear regression. To begin, we import all the libraries we need."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"import sklearn.linear_model as lm"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We will work with artificially generated data. The independent variable `X` is a `numpy` array \n",
"of $\\texttt{N}=400$ random numbers that have a <em style=\"color:blue;\">normal</em> distribution with \n",
"mean $\\mu = 10$ and standard deviation $1$. The data is created from random numbers.\n",
"In order to be able to reproduce our results, we use the method `numpy.random.seed`. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"np.random.seed(1)\n",
"N = 400 \n",
"𝜇 = 10\n",
"X = np.random.randn(N) + 𝜇"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The dependent variable `Y` is created by adding some noise to the independent variable `X`. This noise is \n",
"<em style=\"color:blue;\">normally</em> distributed with mean $0$ and standard deviation $0.5$."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"noise = 0.5 * np.random.randn(len(X))\n",
"Y = X + noise"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We build a linear model for `X` and `Y`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model = lm.LinearRegression()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In order to use **SciKit-Learn** we have to reshape the array X into a matrix."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"X = np.reshape(X, (len(X), 1))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We train the model and compute its score."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"M = model.fit(X, Y)\n",
"M.score(X, Y)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In order to plot the data together with the linear model, we extract the coefficients."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"ϑ0 = M.intercept_\n",
"ϑ1 = M.coef_[0]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We plot `Y` versus `X` and the linear regression line."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"xMax = np.max(X) + 0.2\n",
"xMin = np.min(X) - 0.2\n",
"%matplotlib inline\n",
"plt.figure(figsize=(15, 10))\n",
"sns.set(style='darkgrid')\n",
"plt.scatter(X, Y, c='b') # 'b' is blue color\n",
"plt.xlabel('X values')\n",
"plt.ylabel('true values + noise')\n",
"plt.title('Influence of rounding on explained variance')\n",
"plt.show(plt.plot([xMin, xMax], [ϑ0 + ϑ1 * xMin, ϑ0 + ϑ1 * xMax], c='r'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As we want to study the effect of <em style=\"color:blue;\">rounding</em>, the values of the dependent variable `X` are rounded to the nearest integer. To this end, the values are transformed to another unit, rounded and then transformed back to the original unkit. This way we can investigate how the performance of linear regression degrades if the precision of the measurements of the independent variable is low."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"X = np.round(X * 0.8) / 0.8"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We create a new <em style=\"color:blue;\">linear model</em>, fit it to the data and compute its score."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model = lm.LinearRegression()\n",
"M = model.fit(X, Y)\n",
"M.score(X, Y)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can see that the performance of the linear model has degraded considerably."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"ϑ0 = M.intercept_\n",
"ϑ1 = M.coef_[0]\n",
"xMax = max(X) + 0.2\n",
"xMin = min(X) - 0.2\n",
"plt.figure(figsize=(12, 10))\n",
"sns.set(style='darkgrid')\n",
"plt.scatter(X, Y, c='b')\n",
"plt.plot([xMin, xMax], [ϑ0 + ϑ1 * xMin, ϑ0 + ϑ1 * xMax], c='r')\n",
"plt.xlabel('rounded X values')\n",
"plt.ylabel('true X values + noise')\n",
"plt.title('Influence of rounding on explained variance')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, we investigate the effect of <em style=\"color:blue;\">subclassing</em>. We will only keep those values such that $X > 11$. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"X.shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"selectorX = (X > 11)\n",
"selectorY = np.reshape(selectorX, (N,))\n",
"XS = X[selectorX]\n",
"XS = np.reshape(XS, (len(XS), 1))\n",
"YS = Y[selectorY]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Again, we fit a linear model."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"model = lm.LinearRegression()\n",
"M = model.fit(XS, YS)\n",
"M.score(XS, YS)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We see that the performance of linear regression has degraded considerably. Let's plot this."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"ϑ0 = M.intercept_\n",
"ϑ1 = M.coef_[0]\n",
"xMax = max(XS) + 0.2\n",
"xMin = min(XS) - 0.2\n",
"plt.figure(figsize=(12, 10))\n",
"sns.set(style='darkgrid')\n",
"plt.scatter(XS, YS, c='b')\n",
"plt.plot([xMin, xMax], [ϑ0 + ϑ1 * xMin, ϑ0 + ϑ1 * xMax], c='r')\n",
"plt.xlabel('rounded X values')\n",
"plt.ylabel('true X values + noise')\n",
"plt.title('Influence of subclassing on explained variance')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.10.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-2.0 |
hrayatnia/SciPy | ipython gallery/CS1001.py-master/recitation4.ipynb | 2 | 61199 | {
"metadata": {
"name": "recitation4"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# CS1001.py\n",
"\n",
"## Extended Introduction to Computer Science with Python, Tel-Aviv University, Spring 2013\n",
"\n",
"# Recitation 4 - 4-8.4.2013\n",
"\n",
"## Last update: 4.4.2013"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Reminder - `Big O` notation\n",
"Let $f(x)$ and $g(x)$ be two function. Then \n",
"$$\n",
"f(x) = O(g(x)) \\; as \\; x \\to \\infty \n",
"$$\n",
"If and only if there exist $M \\ge 0 \\;$ and $x_{0}\\in \\mathbb{R}$ such that\n",
"$$\n",
"|f(x)| \\le M|g(x)| \\; \\forall x>x_{0}\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Time complexity hierarchy\n",
"\n",
"The most common time complexities we encounter are (*c > 1* is a real constant, *n >1 * is the size of the input):\n",
"\n",
"* Constant - $O(1)$\n",
"* Logarithmic - $O(log(n))$\n",
"* Root/fractional - $O(n^{1/c})$\n",
"* Linear - $O(n)$\n",
"* Loglinear - $O(n log(n))$\n",
"* Polynomial - $O(n^{c})$\n",
"* Exponential - $O(c^{n})$\n",
"* Factorial - $O(n!)$\n",
"\n",
"See also this list on [Wikipedia](http://en.wikipedia.org/wiki/Time_complexity#Table_of_common_time_complexities).\n",
"\n",
"## Size of the input\n",
"\n",
"* For a numerical input (factorization, prime numbers) the size of the input is the number of bits of the numerical input\n",
"* For a list/vector input, the size is the number of elements\n",
"* For a matrix?\n",
"\n",
"## Examples\n",
"\n",
"### Constant, Linear, Loglinear, Polynomial"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from math import log\n",
"\n",
"domain = range(1,100)\n",
"const = [10 for x in domain]\n",
"lin = [x for x in domain]\n",
"loglin = [x * log(x) for x in domain]\n",
"poly = [x ** 2 for x in domain]\n",
"\n",
"# these lines are the plotting directives\n",
"fig = figure(figsize=(16,6))\n",
"ax = subplot(1,3,1)\n",
"ax.plot(domain,const)\n",
"ax.plot(domain,lin)\n",
"ax.legend([\"const\",\"lin\"],loc=2);\n",
"ax = subplot(1,3,2)\n",
"ax.plot(domain,lin)\n",
"ax.plot(domain,loglin)\n",
"ax.legend([\"lin\",\"loglin\"],loc=2);\n",
"ax = subplot(1,3,3)\n",
"ax.plot(domain,loglin)\n",
"ax.plot(domain,poly)\n",
"ax.legend([\"loglin\",\"poly\"],loc=2);"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA6kAAAFtCAYAAADlOSw4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlYVeXaBvB7I4gz4gQCKqUoouI8ZCc1TTNLlEEURXAC\nk0rjlKXlPA9fmWmYJscUQybnITVJHDBAUHEWVBQExBAHZBT2+v7oyDEDZdjsd6/F/bsurws37LXu\nF3dP77PeNagkSZJAREREREREpAP0RAcgIiIiIiIieoZNKhEREREREekMNqlERERERESkM9ikEhER\nERERkc5gk0pEREREREQ6g00qERERERER6YyXNqkTJkyAiYkJOnToUPRaRkYGBg4ciNatW2PQoEF4\n+PBh0feWLl0KKysrWFtb4/Dhw5WXmohIwywtLWFra4vOnTujR48eAFjviEi3aWqeFhMTgw4dOsDK\nygrTpk0rej0vLw8jR46ElZUVevXqhdu3b2tnYERU5b20SR0/fjwOHjz4t9eWLVuGgQMHIi4uDgMG\nDMCyZcsAAJcvX0ZgYCAuX76MgwcPwsvLC2q1uvKSExFpkEqlQlhYGM6ePYuoqCgArHdEpNsqOk+T\nJAkAMGXKFPj6+iI+Ph7x8fFF2/T19UXDhg0RHx8Pb29vfPnll9odIBFVWS9tUt966y0YGxv/7bU9\ne/bA3d0dAODu7o5du3YBAHbv3g0XFxcYGBjA0tISrVq1KproERHJwbMJ2zOsd0Skyyo6T4uMjERq\naioyMzOLziBxc3Mres/z23J0dERoaKi2hkZEVVyZr0lNS0uDiYkJAMDExARpaWkAgJSUFFhYWBT9\nnIWFBZKTkzUUk4iocqlUKrzzzjvo1q0bfvrpJwCsd0QkP2WtWy++bm5uXlTPkpOT0axZMwCAvr4+\njIyMkJGRoa2hEFEVpl+RN6tUKqhUqpd+vzSvEREB/1zJ1Kbw8HA0bdoUf/75JwYOHAhra+u/fZ/1\njog0RVu17lV1S5P7ISJ6UUVqXZlXUk1MTHD37l0AQGpqKpo0aQLgryNvSUlJRT93584dmJubF7sN\nSZIU9Wfu3LnCM3A8HJPc/4jWtGlTAEDjxo1hb2+PqKgo1juFf+aUOCaljUeJY6psZalbFhYWMDc3\nx507d/7x+rP3JCYmAgAKCgrw6NEjNGjQoNj9iv698jNXtcaktPEocUwVVeYm1c7ODps3bwYAbN68\nGcOHDy96PSAgAPn5+UhISEB8fHzR9Q1ERMW5+eCm6AgAgOzsbGRmZgIAsrKycPjwYXTo0IH1johk\np6x1y9TUFPXq1UNkZCQkSYKfnx+GDRv2j22FhIRgwIABYgZFRFXOS0/3dXFxwbFjx5Ceno5mzZph\nwYIFmDFjBpydneHr6wtLS0sEBQUBAGxsbODs7AwbGxvo6+vDx8eHp38QUYm2XdiGBccX4MKUC9DX\nq9CVBxWWlpYGe3t7AH+tFowZMwaDBg1Ct27dWO+ISGdpap7m4+ODcePGIScnB0OGDMHgwYMBABMn\nTsTYsWNhZWWFhg0bIiAgQNhYiahqUUmaWI8tyw5VKo0sAeuSsLAw9OvXT3QMjVHaeACOSddcSLuA\n/lv648jYI+ho2hGAMmuD0sYk589cSZQ2JqWNB1DemJRWFwDljUlpnzlAeWNS2ngA5Y2ponWBTSoR\nadXD3Ifo/lN3zO07F662rkWvK7E2KHFMRFQxSqwLShwTEVWMYprUBg0a4MGDB9qMIlvGxsa8BTzJ\nklpSwz7QHs2NmmPNe2v+9j0lTnJY78qPdY6UirWOnsdaR0ohSRL6/twX/o7+sKhnUeFaJ/ZCsOc8\nePBAcUW7svDaN5KrJSeWID07HcEjgkVHEYr17tVY54jkj7Xu1VjrSCmO3T6GjJwMmNct/mkHZaUz\nTSoRKdvB6wexLnodTnucRvVq1UXHISIiIiIN2RCzAZ5dPTV24KXMj6AhIiqrhAcJcN/ljm2O22BW\n10x0HCIiIiLSkPTsdByIP/C3e41UFJtUIqpUOU9z4BDkgJn/mok+LfqIjkNEREREGrQldgvs2tih\nQc0GGtsmm1QiqjSSJGHK/imwbmSNaT2niY5Dr2BpaYnQ0FAsXboUHh4eouMQEVWKZ7WuIsaNG4fZ\ns2cDAE6cOAFra2tNRCOSHUmS8NOZn+DZ1VOj2+U1qTrm1q1beP3111FQUAA9PR5DIHlbH7Me0SnR\niJgUwZtDyIBKpYJKpcLMmTNFRyEiqjTPap2mtvHWW2/h6tWrmohGJDsnE09CBRXebPamRrfLJlVH\n8W54JHcRdyIw5+gchE8IR53qdUTHISIi0ijO1Yj+WpDQ5A2TnuFSXSklJSXBwcEBTZo0QaNGjfDJ\nJ59AkiQsWrQIlpaWMDExgbu7Ox4/fgzgrxVRPT09bNmyBS1atEDjxo2xZMmSou1FRUWhW7duMDIy\ngqmpKT7//HMAQJ8+f12zV79+fdStWxeRkZHaHyxRBaU9ScOI4BHYaLcRVg2tRMehMpAkCfPmzcPY\nsWMBvLqWERHJVX5+Pj799FOYm5vD3Nwc3t7eyM/PL/r+ihUrYGZmBgsLC2zcuBF6enq4efPmP7YT\nFhaGZs2aFf3d0tIS33zzDTp27Ij69etj1KhRyMvL08qYiLTpfvZ97I/fD7eObhrfNpvUUigsLMQH\nH3yA1157Dbdv30ZKSgpGjRqFTZs2YfPmzQgLC8PNmzfx5MkTfPzxx397b3h4OOLi4hAaGooFCxbg\n2rVrAIBp06bB29sbjx49ws2bNzFixAgAf13XAACPHj1CZmYmevbsqd3BElVQgboAo7aPgntHd9i1\nsRMdh8qhuKOhL9YyntpGRHL2bKEhKioKsbGxiI2NRVRUFBYtWgQAOHjwIFatWoXQ0FDEx8cjLCys\n1NtWqVQIDg7GoUOHkJCQgPPnz+Pnn3+unIEQCbQ5djOGth6q0RsmPcMmtRSioqKQmpqKlStXombN\nmqhevTrefPNN/PLLL/jss89gaWmJ2rVrY+nSpQgICIBarS5679y5c2FoaAhbW1t07NgRsbGxAIDq\n1asjPj4e6enpqFWrVlEzylNHSO5mhs5E9WrVMb/ffNFRSINKqmVERHLl7++POXPmoFGjRmjUqBHm\nzp0LPz8/AEBQUBAmTJiAtm3bombNmpg/v2z/T5s6dSpMTU1hbGyMoUOH4ty5c5UxBCJhJEnChpgN\nmNx1cqVsX1ZNqkqlmT9llZSUhBYtWvzjRkapqalo0aJF0d+bN2+OgoICpKWlFb1mampa9HWtWrXw\n5MkTAICvry/i4uLQtm1b9OjRA/v37y97MCIdE3wpGCGXQ+Dv4I9qetVEx5EtUbXuZV6sZVlZWZrd\nARFVOaJrXUpKyj/mcSkpKQD+muM9fwqvhYVFmbb9fM2sWbNm0fyPSCmO3T6GanrV0LtZ70rZvqxu\nnCRqkbFZs2ZITExEYWEhqlX738TbzMwMt27dKvp7YmIi9PX1YWJigsTExJdus1WrVvD39wcAbN++\nHU5OTsjIyOAdUEm2rvx5BV4HvHDI9RAa1mooOo6s8YQKIqoKRNe6Z/O4tm3bAvhrHmdubg4AaNq0\nKZKSkop+9vmvnyntnI1zO1Ki9THrMbnr5Er7fMtqJVWUnj17omnTppgxYways7ORm5uL8PBwuLi4\nYNWqVbh16xaePHmCr776CqNGjSrVo2O2bt2KP//8EwBgZGQElUoFPT09NG7cGHp6erhx40ZlD4tI\nYx7nPYZ9oD1WvLMCXZp2ER2HKqg0lx3w0gQikjsXFxcsWrQI6enpSE9Px4IFC+Dq6goAcHZ2xqZN\nm3D16lVkZ2dj4cKFf3uvJEmlroOsl6Q0f2b9iV/jf8VY27GVtg82qaWgp6eHvXv34vr162jevDma\nNWuG4OBgTJgwAWPHjkWfPn3w+uuvo1atWlizZk3R+152ZOHQoUNo37496tatC29vbwQEBMDQ0BC1\natXC119/jTfffBPGxsaIiorSxhCJyk2SJIzfPR59LftifOfxouNQBT179t/z9au4WsaVASKSM5VK\nhVmzZqFbt26wtbWFra0tunXrhlmzZgEABg8ejKlTp+Ltt99G69at8cYbbwAADA0Ni97/qjr5/PdY\nM0lJfj73M+zb2sO4pnGl7UMlafnwjkqlKvaIUkmv0z/xd0W6ZPnJ5dhxdQeOjzsOQ33Dcm9HiZ9r\n1rvy4++IlEqJn+2qUOuuXLmCDh06ID8/v1RnzJWWkn5HVDWoJTVar2mNXxx+QU+Lkp9CUtHPNldS\niajcQm+G4rvI7xAyIqRCDSoREZGu2blzJ/Ly8vDgwQN8+eWXsLOz02iDSiRHoTdDUdewLnqY96jU\n/fC/NCIql8RHiXDd6YpfHH5BM6Nmr34DERGRjGzYsAEmJiZo1aoVDAwMsG7dOtGRiIT7MeZHfNj1\nw0o/hZ2n+8oQf1ckWm5BLvps6gMnGyd88eYXGtmmEj/XrHflx98RKZUSP9usdeXH3xHJSUpmCtr7\ntMftT2+jrmHdl/4sT/clIq2b+utUNDdqjum9p4uOQkRERERa4HvGFyPbj3xlg6oJsnpOKhGJ53vG\nFycSTyBqUhTvVkhERERUBRSoC7DhzAbsddmrlf2xSSWiUotOicaM0Bk4Pu64Vo6iEREREZF4++P2\no1m9Zuhk2kkr++PpvkRUKunZ6XAKcsKP7/+Ito3bio5DRERERFriE+2DKd2maG1/bFKJ6JUK1YUY\nvX00RrYfCUcbR9FxiIhk5fCNw1BLatExiIjK5XrGdZxJPYMR7UZobZ9sUkvB0tISoaGhWLp0KTw8\nPETHIdK62Udno1AqxOL+i0VHoUr0rNZVxLhx4zB79mwAwIkTJ2Btba2JaESytePKDkzZPwXZT7NF\nR6EK0tPTw82bN0XHINK69THrMb7TeNTQr6G1ffKa1FJQqVRQqVSYOXOm6ChEWrfr6i78cuEXRHtE\nQ1+PJUPJntU6TW3jrbfewtWrVzURjUiWUjNT4bXfCztH7kSd6nVExyEiKrPcglz8fO5nREyM0Op+\nOeMkohLF3Y+D515P7Bu9D41rNxYdh2SCz/wj+uu/gwl7JmByt8l4o9kbouMQEZVL8KVgdG3aFS0b\ntNTqfnm6bylJkoR58+Zh7NixAIBbt25BT08PW7ZsQYsWLdC4cWMsWbJEcEoizXmS/wQOgQ5Y1H8R\nepj3EB2HtCg/Px+ffvopzM3NYW5uDm9vb+Tn5xd9f8WKFTAzM4OFhQU2btxY4ilwYWFhaNasWdHf\nLS0t8c0336Bjx46oX78+Ro0ahby8PK2MiUjbfE774H72fcx6a5boKPQCS0tLLFu2DO3atUODBg0w\nYcKEolr0008/wcrKCg0bNsSwYcOQmpr6j/efPn0apqamfzsgt2PHDnTqpJ27nhJpk0+0D7y6e2l9\nv2xSy6C40+DCw8MRFxeH0NBQLFiwgKe2kSJIkoRJeyahp0VPeHThddhViSRJWLRoEaKiohAbG4vY\n2FhERUVh0aJFAICDBw9i1apVCA0NRXx8PMLCwkq9bZVKheDgYBw6dAgJCQk4f/48fv7558oZCJFA\nV/68gnnH5mGrw1YYVDMQHYeK4e/vj8OHD+PGjRuIi4vDokWL8Pvvv+Orr75CcHAwUlNT0aJFC4wa\nNeof7+3evTsaNmyIQ4cOFb3m5+cHd3d3bQ6BqNKdST2DlMwUvG/1vtb3zSa1gubOnQtDQ0PY2tqi\nY8eOiI2NFR2JqMK+i/gO1zOu44chP1T4GkWSH39/f8yZMweNGjVCo0aNMHfuXPj5+QEAgoKCMGHC\nBLRt2xY1a9bE/Pnzy7TtqVOnwtTUFMbGxhg6dCjOnTtXGUMgEia/MB+uO12xuP9itG7YWnQcKoZK\npcLHH38Mc3NzGBsb4+uvv8a2bdvg7++PiRMnolOnTqhevTqWLl2KP/74A4mJif/YhpubG7Zu3QoA\nyMjIwOHDhzF69GhtD4WoUq2LXocPu36IanrVtL5vWV2TqpqvmcmyNFdz10uZmpoWfV2rVi1kZWVp\nbNtEIhy7dQzLw5cjYlKEVu/iRv8jutalpKSgRYsWRX9v3rw5UlJSAACpqano0eN/p39bWFiUadvP\n18yaNWsWbZdIKeaFzYN5XXOehVIKImvd85ciPKtxKSkp6NKlS9HrtWvXRsOGDZGcnIzmzZv/7f1j\nxoxBu3btkJ2djaCgIPTp0wcmJiblHwSRjnmQ8wAhl0Nw7eNrQvYvqyZVk80lEf1T8uNkuGx3wRb7\nLbCsbyk6TpUlutaZmZnh1q1baNu2LQAgMTER5ubmAICmTZsiKSmp6Gef//qZ0q6+c5WelOb47eP4\n+dzPOPfhOX6+S0FkrXt+dTQxMRFmZmYwMzPD7du3i17PysrC/fv3i+rf8ywsLNCrVy/s2LEDW7du\nhZeX9q/ZI6pMm2M3Y4jVEDSp3UTI/nm6bxmU5o6VvKslyVV+YT6cgp3wcY+PMajlINFxSCAXFxcs\nWrQI6enpSE9Px4IFC+Dq6goAcHZ2xqZNm3D16lVkZ2dj4cKFf3uvJEmlroOsl6Qkj3IfwW2nG34a\n+pOwSR2VjiRJ8PHxQXJyMjIyMrB48WKMGjUKLi4u2LRpE2JjY5GXl4evvvoKvXr1+scq6jNubm5Y\nvnw5Ll68CAcHBy2PgqjyqCU11kWvg1c3cQdf2KSW0rNn/z1/ZLS4o6Q8ckpy5X3IGya1TTDjXzNE\nRyGBVCoVZs2ahW7dusHW1ha2trbo1q0bZs366w6lgwcPxtSpU/H222+jdevWeOONvx6tYWhoWPT+\nV9XJ57/HmklK8fGvH2OI1RC831r7NxihslGpVBg9ejQGDRqEli1bwsrKCrNmzcKAAQOwcOFCODo6\nwszMDAkJCQgICPjb+57n4OCAxMRE2Nvbo0YNXh5DyhF6MxQ19Gugd7PewjKoJC0fylapVMUePS/p\ndfon/q5I07bEbsGi44tw2uM0jGoYCcmgxM91Vah3V65cQYcOHZCfnw89Pc0d91TS74iUL+BiAOaF\nzcOZyWdQy6DWS39WiZ9tudW61157Db6+vujfv3+Ft2VlZYX169eXe1u6+juiqm1YwDB8YPUBPLqW\n/9r6in62uZJKVMWdTT2Lzw5/hh0jdwhrUEledu7ciby8PDx48ABffvkl7OzsNNqgEslJ0qMkTP11\nKrY6bH1lg0rKsmPHDqhUKo00u0S64tbDWziZeBKjO4i9WzVnFURVWEZOBhyDHLH2vbVo36S96Dgk\nExs2bICJiQlatWoFAwMDrFu3TnQkIiEK1YVw2+UG717e6GbWTXQc0qJ+/frBy8sLP/zwg+goRBr1\nY/SPcO/ojtrVawvNwdN9ZYi/K9IEtaTGB/4fwLqRNb5991vRcRT5uWa9Kz/+jkgOVoavxN64vTjq\nfrTUzxFU4mebta78+DsiXZJbkIvmq5ojfEI4rBpaVWhbFf1sy+oRNESkOfOPzUfW0ywsf2e56ChE\nRLJz7u45rDy1Eqc9Tgt50D0RkaYFXgxEV7OuFW5QNUFnmlRjY2Pe5bGUjI2NRUcgmdsXtw++Z3wR\n7RkNg2oGouMQEclK9tNsjN4+GqveXYUW9VuIjkNEVGGSJGHt6bWY23eu6CgAdKhJzcjIEB2BqEq4\nkXEDE/dMxM6RO2Fax1R0HCIi2fnity/QybQTxtiOER2FiEgjopKjkJGTgfdavSc6CgAdalKJqPJl\nP82GQ5AD5vSZI/TZV0REcnUg/gD2xu1F7IexoqMQEWnMmqg18OrmpTOXL7BJJaoiJEmC515PdDTp\nCK/uXqLjVGm8vOHVeFkD6aJ7Wfcwac8kbHPchvo16ouOo/NY616NtY50QdqTNOyP3481760RHaUI\nm1SiKmJt1FpcvHcRpyae4qRBMF7eQCQ/kiRh4p6JcO/kjr6WfUXHkQXWOiJ52BCzASNsRsC4pu4c\nNGGTSlQFnEw8iYXHFyJiUgQfNk9EVA7rY9YjJTMF2523i45CRKQxTwuf4seYH/HrmF9FR/kbNqlE\nCpeamYqRISPx8/Cf8brx66LjEBHJztX0q5h9dDZOjD+B6tWqi45DRKQxO6/uRKsGrWBrYis6yt/o\niQ5ARJXnaeFTOIc4w7OLJ4ZYDREdh4hIdvIL8zFmxxgsfHshrBtZi45DRKRR30d+j6k9poqO8Q9s\nUokUbPpv01HPsB5m950tOgoRkSzNOToH5nXNMbnrZNFRiIg06kzqGSQ+SsQw62Gio/wDT/clUqht\nF7Zhb9xeRHtEQ0/F41FERGUVdisMfuf9cG7yOd5wjogUZ03UGnh194K+nu61hLqXiIgq7ELaBUw9\nOBVHxh7RqTu1ERHJxYOcB3Db6QZfO180rt1YdBwiIo26l3UPu67uQvwn8aKjFIvLK0QK8zD3IRyC\nHLDq3VXoaNpRdBwiItmRJAmT902GfVt7DG41WHQcIiKN+ynmJzi0dUCjWo1ERykWV1KJFEQtqeG2\n0w2DWw2Gq62r6DhERLK0JXYLrqRfwRb7LaKjEBFp3NPCp1gXvQ77Ru8THaVEbFKJFGTJiSW4n3Mf\nIc4hoqMQEcnSjYwb+Py3z/G72++ooV9DdBwiIo3bfmU7WjZoiU6mnURHKRGbVCKFOHT9ENZFr8Np\nj9N8jh8RUTkUqAvgutMVs96ahQ4mHUTHISKqFKsjV2N67+miY7wUm1QiBUh4kAC3XW4IHhEMs7pm\nouMQEcnSwuMLYWRohE96fiI6ChFRpYhKjkJqZiqGtdG9x848j00qkczlPM2BY5AjZv5rJvq06CM6\nDhGRLJ1MPIkNMRtwxvMMH9tFRIq1OnI1Pu7xMarpVRMd5aVUkiRJWt2hSgUt75JIsSRJwoQ9E5Bb\nkAt/B39ZP8dPibVBiWMiUqKHuQ/ReX1nfD/4ewxtM7RS96XEuqDEMREpUUpmCtr5tMPNqTcr/RGF\nFa0L5T5UuHTpUrRr1w4dOnTA6NGjkZeXh4yMDAwcOBCtW7fGoEGD8PDhw3IHI6JX2xCzAdEp0dg4\ndKOsG1RdUVhYiM6dO2Po0L8mqS+raUuXLoWVlRWsra1x+PBhUZGJSAM+OvARBrcaXOkNqjaVdZ5W\nUk2LiYlBhw4dYGVlhWnTpokYChFpyLrodXBp71LpDaomlKtJvXXrFn766SecOXMGFy5cQGFhIQIC\nArBs2TIMHDgQcXFxGDBgAJYtW6bpvET0X5F3IjH76GzscN6B2tVri46jCKtXr4aNjU1Rw19STbt8\n+TICAwNx+fJlHDx4EF5eXlCr1SKjE1E5bT2/FWdTz+KbQd+IjqIxZZ2nFVfTnq2ATJkyBb6+voiP\nj0d8fDwOHjwocmhEVE65BbnYELMB03rK42BTuZrUevXqwcDAANnZ2SgoKEB2djbMzMywZ88euLu7\nAwDc3d2xa9cujYYlor/cy7qHEcEjsNFuI6waWomOowh37tzBgQMHMGnSpKLJWUk1bffu3XBxcYGB\ngQEsLS3RqlUrREVFCctOROVz88FNeB/yhr+jP2oZ1BIdR2PKOk8rrqZFRkYiNTUVmZmZ6NGjBwDA\nzc2Nczsimfrl/C/oZtYNbRq1ER2lVMrVpDZo0ACfffYZmjdvDjMzM9SvXx8DBw5EWloaTExMAAAm\nJiZIS0vTaFgi+usRCaNCRsGtoxvs2tiJjqMY3t7eWLlyJfT0/lcWS6ppKSkpsLCwKPo5CwsLJCcn\nazcwEVVIgboArjtcMePNGTr9rMDyKOs8raSa9uLr5ubmrHVEMiRJEr6L/A6f9vxUdJRSK9fdfW/c\nuIHvvvsOt27dgpGREUaMGIGtW7f+7WdUKlWJ18jNmzev6Ot+/fqhX79+5YlBVCV9FfoVDKoZYH6/\n+aKjVEhYWBjCwsJExwAA7Nu3D02aNEHnzp1LzPSymvbs+8VhvSPSTYuOL0Lt6rXh/YZ3pe5HRK2r\n6DytPFjriHTX7wm/Qy2p8c7r71TaPjRd68rVpEZHR6N3795o2LAhAMDBwQF//PEHTE1NcffuXZia\nmiI1NRVNmjQp9v3PFzIiKr2QyyEIvhyMaI9onb91+Ku8OImZP19c033q1Cns2bMHBw4cQG5uLh4/\nfoyxY8fCxMSk2Jpmbm6OpKSkovffuXMH5ubmxW6b9Y5I94QnhuPH6B9xZnLlP25GRK0r6zytuJpm\nYWEBc3Nz3Llz52+vs9YRyc+zVdTKvMmmpmtduSqztbU1IiIikJOTA0mScOTIEdjY2GDo0KHYvHkz\nAGDz5s0YPnx4hcIR0f9c+fMKpuyfgu3O29GwVkPRcRRlyZIlSEpKQkJCAgICAtC/f3/4+fnBzs6u\n2JpmZ2eHgIAA5OfnIyEhAfHx8UXXbBGRbnuU+wiuO12xYegGmNU1Ex2nUpR1nlZSTTM1NUW9evUQ\nGRkJSZLg5+fHuR2RzMTdj0PknUiMsR0jOkqZlGsltWPHjnBzc0O3bt2gp6eHLl26wNPTE5mZmXB2\ndoavry8sLS0RFBSk6bxEVdLjvMewD7TH8neWo0vTLqLjKN6zI40zZswotqbZ2NjA2dkZNjY20NfX\nh4+PDx8BRCQDkiTB64AX3mv1nqKv6S/rPO1lNc3Hxwfjxo1DTk4OhgwZgsGDB4scGhGV0erI1fDs\n6im7m8OpJC0/fZkPfCYqG0mS4BTshEa1GmH9B+tFx6k0SqwNShwTkZz5xfph6cmliPaMFjZhU2Jd\nUOKYiJQgIycDLb9victel9G0blOt7ruidaFcK6lEpD0rwlfgzuM78HfwFx2FiEi2bj64iX8f/jeO\njD0iuxUFIqLy2BCzAXZt7LTeoGoCm1QiHRZ6MxTfRX6H0x6nYahvKDoOEZEsPS18itHbR+Prt75G\nR9OOouMQEVW6/MJ8rI1ai32j94mOUi6Ve0s7Iiq3xEeJcN3pCn8Hf1jUs3j1G4iIqFgLji9A/Rr1\nMbXnVNFRiIi0IvhSMFo3bC3b50BzJZVIB+UV5MEpyAn/7vVvvP3a26LjEBHJ1rFbx7DxzEacnXy2\n0h83Q0SkCyRJwrcR32Je33mio5QbqzWRDvrk10/Qon4LfN77c9FRiIhk60HOA4zdORa+dr4wrWMq\nOg4RkVaoCc8/AAAgAElEQVQcv30cWflZeL/1+6KjlBtXUol0jO8ZX5xMPInISZF8rAkRUTlJkgTP\nfZ6wb2uPIVZDRMchItKab/74Bt69vGV99gibVCIdEp0SjZmhM3F8/HHUNawrOg4RkWz95+x/cC39\nGvzs/URHISLSmmvp1xBxJwIBTgGio1QIm1QiHZGenQ6nICese38drBtZi45DRCRb19Kv4csjX+LY\nuGOooV9DdBwiIq1ZFbEKH3b7UPaP2mKTSqQDCtWFGL19NEa2HwlHG0fRcYiIZCuvIA8u212w8O2F\naNekneg4RERak56djsBLgbj60VXRUSpMvicqEynInLA5KJQKsbj/YtFRiIhkbdbRWWhu1BwfdvtQ\ndBQiIq1ad3odHNo6wKSOiegoFcaVVCLBdl/dDb9YP0R7RkNfj/9JEhGV1+EbhxFwMQBnJ5/ljeeI\nqErJLcjFD6d/wO/uv4uOohGcERMJFHc/Dh57PbBv9D40qd1EdBwiItm6l3UP43ePh5+9HxrVaiQ6\nDhGRVvnF+qGbWTfYNLYRHUUj2KQSCfIk/wnsA+2xqP8i9DDvIToOEZFsSZKE8bvHw62jG/q/1l90\nHCIirVJLanzzxzf48YMfRUfRGF6TSiSAJEmYuGciepr3hEcXD9FxiIhkbU3UGvyZ9ScW9FsgOgoR\nkdbti9uHOtXroG+LvqKjaAxXUokEWBWxCtczruPk+JO8boqIqAJi78Zi4fGFiJgYAYNqBqLjEBFp\n3f+d+j983vtzRc0p2aQSadmxW8ewPHw5IidFoqZBTdFxiIhkKys/C6O2j8Kqd1ehZYOWouMQEWld\n5J1IJD5KhJONk+goGsXTfYm0KPlxMly2u8DP3g+W9S1FxyEikjXvQ97oZtYNrrauoqMQEQmx8tRK\nePfyVtwTIpQ1GiIdll+YD6dgJ3zc42MMajlIdBwiIlkLuRyC0IRQnJ18VnQUIiIhrmdcx7Hbx/Dz\n8J9FR9E4NqlEWuJ9yBsmtU0w418zREchIpK1xEeJ+OjAR9jrshf1DOuJjkNEJMQ3f3yDyV0no071\nOqKjaBybVCIt2BK7Bb/d+A2nPU5DT8Wz7ImIyqtAXYAxO8bg373+zcd3EVGVdS/rHgIuBuDqR1dF\nR6kUbFKJKtm5u+fw2eHPcNT9KIxqGImOQ0Qka4uPL0YN/RqY/uZ00VGIiIT54fQPcG7nDJM6JqKj\nVAo2qUSVKCMnA45Bjlj73lq0b9JedBwiIlk7cfsEfoz5EWc8z/CsFCKqsrLys+Bz2gfhE8JFR6k0\nrPBElUQtqeG6wxXD2gzDyPYjRcchIpK1jJwMuO50xcahG9G0blPRcYiIhNl4ZiP6tOiD1g1bi45S\nabiSSlRJ5h+bj6ynWVj+znLRUYiIZE2SJHjs9YC9tT3eb/2+6DhERMI8LXyKbyO+RfCIYNFRKhWb\nVKJKsC9uH3zP+CLaMxoG1QxExyEikrUNMRtwI+MG/B38RUchIhIq8FIgXjd+XfE3jmOTSqRh1zOu\nY8LuCdg1ahdM65iKjkNEJGuX7l3CrKOzcGL8CRjqG4qOQ0QkjCRJWBG+AisGrhAdpdLxmlQiDcp+\nmg3HIEfM7TsXvZv1Fh2HiEjWcp7mYNT2UVj+znJYN7IWHYeISKhfr/8KPZUe3m35rugolU4lSZKk\n1R2qVNDyLom0QpIkjN05FiqVCluGb4FKpRIdSVaUWBuUOCYibfLa74WMnAxsc9ymmJqqxLqgxDER\n6aI+m/pgSrcpcOngIjrKK1W0LvB0XyINWRu1FhfvXcSpiacUM5kiIhJl55WdOHj9IM5OPsuaSkRV\nXnhiOJIzkzGi3QjRUbSCTSqRBoQnhmPRiUU4NeEUahnUEh2HiEjWEh8l4sP9H2L3qN0wqmEkOg4R\nkXDLwpdheu/p0NerGu0br0klqqDUzFQ4hzhj07BNaNmgpeg4RESyVqAuwJgdY+Ddyxu9LHqJjkNE\nJNyFtAuITonGuE7jREfRGjapRBXwtPApRoaMhGcXTwyxGiI6DhGR7C08vhA19Gvgize/EB2FiEgn\nLA9fjmk9p6GGfg3RUbSmaqwXE1WS6b9NRz3Depjdd7boKEREsnfs1jFsiNmAM55noKficXQiooQH\nCfj1+q9YO2St6ChaxSaVqJy2XdiGvXF7Ee0RzckUEVEF3c++D9edrtg0bBOa1m0qOg4RkU5YeWol\nJnedjPo16ouOolVsUonK4ULaBUw9OBWhbqEwrmksOg4RkaxJkoTxu8djZLuRGNxqsOg4REQ6ITUz\nFQEXA3D146uio2gdm1SiMnqY+xAOQQ5Y9e4q2JrYio5DRCR7a6LWIPVJKkKcQ0RHISLSGasiVsHV\n1hVNajcRHUXrVJKWn77MBz6TnKklNYYHDEeL+i2w5r01ouMoihJrgxLHRKRpZ1PPYtDWQYiYGFEl\n7pCuxLqgxDERifYg5wFarWmFs5PPorlRc9FxyqyidYErqURlsOTEEtzPuc+j/UREGvAk/wlGbR+F\n7wd/XyUaVCKi0lobtRZ2bexk2aBqAldSiUrp0PVDmLBnAk57nIZZXTPRcRRHibVBiWMi0qRxu8ah\nml41+Nr5io6iNUqsC0ocE5FIT/Kf4PXVr+PE+BNo06iN6DjlwpVUIi249fAW3He5I2hEEBtUIiIN\n8Iv1Q2RyJKI9okVHISLSKeuj1+Pt196WbYOqCWxSiV4h52kOHAIdMONfM9CnRR/RcYiIZC/ufhz+\nffjfCHULRe3qtUXHISLSGbkFufg24lscGH1AdBSh+HBHopeQJAleB7zQplEbTOs5TXQcIiLZyyvI\nw8iQkVjQbwHvkE5E9IJNZzehS9Mu6GjaUXQUobiSSvQS62PW43TyaURMioBKpRIdh4hI9qb/Nh2v\n1X8NH3b7UHQUIiKd8rTwKZaHL0eAU4DoKMKxSSUqQcSdCMw+OhvhE8JRp3od0XGIiGRv99Xd2HNt\nD85OPssDf0REL/jlwi9o2aAleln0Eh1FODapRMW4l3UPI4JHYOPQjWjdsLXoOEREspf0KAme+zyx\nc+ROGNc0Fh2HiEinFKoLseTEEmwYukF0FJ3Aa1KJXlCgLsDIkJFw6+iGYdbDRMchIpK9AnUBRu8Y\nDe9e3ujdrLfoOEREOifwUiBM6pigb4u+oqPoBK6kEr1gZuhMVK9WHQv6LRAdhYhIEeaFzUNN/Zr4\n4s0vREchItI5akmNxScW49tB3/JSiP9ik0r0nOBLwQi5HIJoj2hU06smOg4RkewduXkEm85twhnP\nM9BT8QQuIqIX7byyE7UNamNQy0Gio+gMNqlE/3XlzyvwOuCFQ66H0LBWQ9FxiIhkL+1JGtx3uWPL\n8C0wqWMiOg4Rkc6RJAmLTizCgn4LuIr6HB7SJALwOO8x7APtseKdFejStIvoOEREsqeW1HDb5Ybx\nncZjwOsDRMchItJJe+P2AgA+aP2B4CS6hU0qVXmSJGH87vHoZ9kP4zuPFx2HiEgRlp9cjuyn2ZjX\nb57oKEREOkmSJCw4tgBz+szhKuoLeLovVXkrwlcg+XEy/B38RUchIlKE8MRwrI5cjWjPaOjrcapB\nRFScA/EHkF+Yz6dJFIP/56AqLfRmKL6L/A5Rk6JgqG8oOg4Rkexl5GRg9I7R+GnoT7CoZyE6DhGR\nTpIkCQuOL8CcvnN4U7lisEmlKivxUSLG7BgDf0d/NDNqJjoOEZHsPbt8wqGtA4a2GSo6DhGRzjp0\n4xCe5D+BQ1sH0VF0EptUqpJyC3LhGOSIz974DP1f6y86DhGRInwf+T1SM1MRPCJYdBQiIp0lSRLm\nH5uP2X1mcxW1BGxSqUqa+utUtDBqgc97fy46ChGRIkSnRGPxicWInBSJ6tWqi45DRKSzDt84jMd5\njzHCZoToKDqLTSpVOb5nfHEi8QSiJkXxTmpERBrwKPcRRoWMgs/7PnjN+DXRcYiIdJYkSZh3bB7m\n9JmDanrVRMfRWWxSqUqJTonGjNAZODH+BOoa1hUdh4hI9iRJguc+T7zb6l042TiJjkNEpNOeraKy\nXr5cuU+CfvjwIZycnNC2bVvY2NggMjISGRkZGDhwIFq3bo1Bgwbh4cOHmsxKVCHp2elwCnLCj+//\nCOtG1qLjkA7Jzc1Fz5490alTJ9jY2GDmzJkA8NKatnTpUlhZWcHa2hqHDx8WFZ1IuPUx63Et/Rq+\nGfSN6Cj0nLLO00qqaTExMejQoQOsrKwwbdo0EUMhUgyuopZeuZvUadOmYciQIbhy5QrOnz8Pa2tr\nLFu2DAMHDkRcXBwGDBiAZcuWaTIrUbkVqgvhst0FI9uPhKONo+g4pGNq1KiBo0eP4ty5czh//jyO\nHj2KkydPlljTLl++jMDAQFy+fBkHDx6El5cX1Gq14FEQaV/s3VjMPjobQSOCUEO/hug49JyyzNOK\nq2mSJAEApkyZAl9fX8THxyM+Ph4HDx4UOSwiWTt04xBXUUupXE3qo0ePcOLECUyYMAEAoK+vDyMj\nI+zZswfu7u4AAHd3d+zatUtzSYkqYPbR2VBLaizuv1h0FNJRtWrVAgDk5+ejsLAQxsbGJda03bt3\nw8XFBQYGBrC0tESrVq0QFRUlLDuRCJl5mRgRPALfvfsdWjdsLToOPaes87TialpkZCRSU1ORmZmJ\nHj16AADc3Nw4tyMqJ0mSMDdsLub2nctV1FIoV5OakJCAxo0bY/z48ejSpQs8PDyQlZWFtLQ0mJiY\nAABMTEyQlpam0bBE5bH76m5sPb8V2xy3QV+Pl2FT8dRqNTp16gQTExO8/fbbaNeuXYk1LSUlBRYW\nFkXvtbCwQHJyspDcRCJIkoQP93+IPi36YIztGNFx6AVlnaeVVNNefN3c3Jy1jqicDsQfQPbTbK6i\nllK5ZuwFBQU4c+YM1q5di+7du+PTTz/9x6m9KpWqxDunzps3r+jrfv36oV+/fuWJQfRKcffj4LHX\nA/tG70OT2k1Ex6HnhIWFISwsTHSMInp6ejh37hwePXqEd999F0ePHv3b919W0559vzisd6RE/zn7\nH5xPO4/ISZGio+g8EbWuovO08mCtIyrZs1XUeX3nKfa5qJqudeVqUi0sLGBhYYHu3bsDAJycnLB0\n6VKYmpri7t27MDU1RWpqKpo0Kb4peL6QEVWWJ/lPYB9oj0X9F6GHeQ/RcegFL05i5s+fLy7Mc4yM\njPD+++8jJiYGJiYmxdY0c3NzJCUlFb3nzp07MDc3L3Z7rHekNBfvXcSM0Bk4Pu44ahnUEh1H54mo\ndWWdpxVX0ywsLGBubo47d+787XXWOqKy2xu3FwXqAti3tRcdpdJoutaVq5U3NTVFs2bNEBcXBwA4\ncuQI2rVrh6FDh2Lz5s0AgM2bN2P48OEVCkdUXpIkYdKeSehl0QseXTxExyEdl56eXnSXy5ycHPz2\n22/o3Lkz7Ozsiq1pdnZ2CAgIQH5+PhISEhAfH190zRaRkj3Jf4IRwSPwzaBv0LZxW9FxqARlnaeV\nVNNMTU1Rr149REZGQpIk+Pn5cW5HVEZqSf3XKmo/5a6iVoZyX6C3Zs0ajBkzBvn5+WjZsiU2bdqE\nwsJCODs7w9fXF5aWlggKCtJkVqJS+y7iO8RnxOPk+JMaPZ2JlCk1NRXu7u5Qq9VQq9UYO3YsBgwY\ngM6dOxdb02xsbODs7AwbGxvo6+vDx8eHnzNSPEmSMGX/FLxh8QbcOrqJjkOvUJZ52stqmo+PD8aN\nG4ecnBwMGTIEgwcPFjksItnZeWUnqqmqYVibYaKjyIpKenaPcW3tUKWClndJVcyxW8cwMmQkIiZF\nwLK+peg4VEpKrA1KHBNVXf85+x98+8e3iPKI4mm+FaDEuqDEMRFpQqG6ELY/2uL/Bv4f3rN6T3Qc\nrapoXeCtTklRkh8nw2W7C7bYb2GDSkSkIRfvXcSXR77EsXHH2KASEZVS4KVAGBkaYXArnoFQVmxS\nSTHyC/MxIngEPur+EQa1HCQ6DhGRIjx/HapNYxvRcYiIZKFAXYB5YfOw7v11vCSoHHj1LinGvw/9\nG41rN8bMt2aKjkJEpAiSJMFrvxevQyUiKiO/WD+Y1TVD/9f6i44iS1xJJUXYErsFh28cxmmP07xz\nGhGRhmw6twkxqTGImhQlOgoRkWzkFeRh/rH5+MXhF66ilhObVJK9c3fP4bPDn+Go+1EY1TASHYeI\nSBEupF0oug61dvXaouMQEcnGxjMbYdPYBm82f1N0FNlik0qylpGTAYdAB6x5bw3aN2kvOg4RkSLw\nOlQiovLJfpqNJSeXYK/LXtFRZI3nRZJsqSU1XHe4Ypj1MIxqP0p0HCIiRZAkCR/u+xBvNn+T16ES\nEZXRD1E/4A2LN9ClaRfRUWSNK6kkW/OPzUfW0yyseGeF6ChERIqx8cxGnLt7DlEevA6ViKgsHuU+\nwspTKxE2Lkx0FNljk0qytD9uP3zP+CLaMxoG1QxExyEiUoTYu7H46vevcGL8CT4PlYiojL6N+Bbv\nWb3HyyQ0gE0qyc6NjBuYsGcCdo7cCdM6pqLjEBEpwuO8xxgRPAKrB6+GdSNr0XGIiGTlz6w/sTZq\nLWI8Y0RHUQSVJEmSVneoUkHLuyQFyX6ajTd834BnF0981OMj0XFIg5RYG5Q4JlImSZLgst0FRjWM\nsP6D9aLjKJoS64ISx0RUVt6HvFGgLsCa99aIjqITKloXuJJKsiFJEjz3eqKjSUd4dfcSHYeISDHW\nRa/DtfvX8MfEP0RHISKSncRHidgSuwWXvC6JjqIYbFJJNn44/QMu3ruIUxNP8cHIREQaEpMSg3lh\n83Bq4inU0K8hOg4RkezMPzYfk7tO5mVoGsQmlWQhPDEcC48vxB8T/+DNPIiINORh7kM4hzjD530f\ntGrQSnQcIiLZufLnFey9thdxn8SJjqIofE4q6by7T+5iZMhIbBq2Ca8bvy46DhGRIkiShPG7x2OI\n1RA42TiJjkNEJEtf//41pveejvo16ouOoihcSSWd9rTwKZyDneHRxQNDrIaIjkNEpBirIlYh+XEy\nAhwDREchIpKliDsROJ1yGr84/CI6iuKwSSWdNv236ahrWBez+84WHYWISDFOJZ3C8vDliJwUCUN9\nQ9FxiIhkR5IkzDgyA3P7zkVNg5qi4ygOm1TSWdsubMPeuL2I9oiGnopnphMRaUJ6djpGhYzCxqEb\nYVnfUnQcIiJZOnTjEO4+uYtxncaJjqJIbFJJJ11Iu4CpB6fiyNgjMK5pLDoOEZEiqCU1XHe4wqWD\nC4a2GSo6DhGRLBWqC/HlkS+xdMBS6OuxnaoMXJ4infMw9yEcghyw6t1V6GjaUXQcIiLFWHJiCbKf\nZmNx/8WioxARyZb/BX/UNqiN4dbDRUdRLLb+pFPUkhpuO90wuNVguNq6io5DRKQYvyf8Dp/TPoj2\njOaRfyKicsotyMXso7PhZ+8HlUolOo5i8f9SpFOWnFiC+zn3EeIcIjoKEZFipGSmwHWHK/zs/WBW\n10x0HCIi2fI57QNbE1u81eIt0VEUjU0q6YyD1w8WHeWvXq266DhERIpQoC7AqJBR8OruhQGvDxAd\nh4hIth7kPMCyk8tw1P2o6CiKxyaVdELCgwS473JH8IhgHuUnItKgr3//GrWr18ZXb30lOgoRkawt\nPbkUw62Ho12TdqKjKB6bVBIu52kOHIMcMfNfM9GnRR/RcYiIFGPPtT0IuBiAGM8YPsqLiKgCbj+8\nDd+zvrg45aLoKFWCSpIkSas7VKmg5V2SDpMkCRP2TEBuQS78Hfx5AXoVpsTaoMQxkXzcfHATvTb2\nwh6XPehl0Ut0HPovJdYFJY6J6EVjd47F68avY36/+aKjyEJF6wJXUkmo9THrEZ0SjYiJEWxQiYg0\nJLcgF05BTpjdZzYbVCKiCjqTegZHbh5B3MdxoqNUGWxSSZjIO5GYc3QOwieEo3b12qLjEBEpxrSD\n02DV0Aof9/hYdBQiIlmTJAmfH/4cc/rMQV3DuqLjVBlsUkmIe1n3MCJ4BDbabYRVQyvRcYiIFGNL\n7BYcu3UMpz1O8wwVIqIKOhB/AHef3IVHVw/RUaoUNqmkdQXqAowMGQm3jm6wa2MnOg4RkWJcSLuA\nzw5/hjD3MB7xJyKqoAJ1Aab/Nh0rB66Evh7bJm3irf5I62aGzoRhNUNeeE5EpEGPch/BMcgR3737\nHR+PQESkARvPbETTuk0xxGqI6ChVDg8JkFaFXA5ByOUQRHtEo5peNdFxiIgU4dmd0ge8PgBjbMeI\njkNEJHuP8x5j/rH5ODD6AC+dEIBNKmnNlT+vYMr+KTjkeggNazUUHYeISDG+/eNbJD1Kgr+Dv+go\nRESKsPTkUgxuNRidm3YWHaVKYpNKWvE47zHsA+2x4p0V6NK0i+g4RESKceL2Caw4tQJRk6JgqG8o\nOg4RkezdengLG2I24MKUC6KjVFm8JpUqnSRJGL97PPpZ9sP4zuNFxyEiUoy7T+7CZbsLfh72M1rU\nbyE6DhGRIswMnYlpPafBrK6Z6ChVFldSqdKtCF/B09CIiDSsQF2AUSGjMKHzBLxn9Z7oOEREivBH\n0h84mXgSG4duFB2lSmOTSpUq9GYovov8jqehERFp2Ne/fw1DfUPM7TtXdBQiIkVQS2p4H/LG4v6L\nUbt6bdFxqjQ2qVRpEh8lwnWnK35x+AXNjJqJjkNEpBi7ru5CwMUAxHjG8E7pREQa4n/BH2pJDVdb\nV9FRqjw2qVQpcgty4RTkBO9e3uj/Wn/RcYiIFCP+fjw893pi3+h9aFSrkeg4RESKkJWfhZmhMxHo\nFAg9FW/bIxr/BahSTP11KpobNcf03tNFRyEiUoys/Cw4BDlgwdsL0MO8h+g4RESKseLUCrzV/C30\nbtZbdBQCV1KpEvie8cWJxBOImhTFhx8TEWmIJEmYvG8yOpt2xuSuk0XHISJSjMRHiVgbtRZnJ58V\nHYX+i00qaVRMSgxmhs7E8fHHUdewrug4RESK4XPaB+fTziNiUgQPABIRadAXv32Bj3t8jOZGzUVH\nof9ik0oak56dDscgR6x7fx2sG1mLjkNEpBgRdyIw/9h8nJp4CrUMaomOQ0SkGMdvH8cfd/7Af4b9\nR3QUeg6vSSWNKFQXYvT20RjZfiQcbRxFxyEiUox7WfcwIngENtptRKsGrUTHISJSjEJ1Iab+OhUr\n3lnBA4A6hk0qacScsDkolAqxuP9i0VGIiBSjQF0Al+0ucOvoBrs2dqLjEBEpysYzG1HPsB6c2zmL\njkIv4Om+VGG7r+6GX6wfoj2joa/HjxQRkabM+n0W9FR6WNBvgegoRESK8iDnAeaGzcWvY37ldf46\niB0FVUjc/Th47PXAvtH70KR2E9FxiIgUY8eVHdh2cRtiPGNQTa+a6DhERIoyJ2wO7Nvao3PTzqKj\nUDHYpFK5Pcl/AvtAeyzqv4jP6yMi0qBr6dfw4b4PsX/0fjSq1Uh0HCIiRTmfdh6BFwNx5aMroqNQ\nCXhNKpWLJEmYuGciepr3hEcXD9FxiIgUIzMvE/aB9ljcfzG6m3cXHYeISFEkScInv36C+f3mo2Gt\nhqLjUAm4kkrlsipiFa5nXMfJ8Sd5Hj8RkYY8OwDYu1lveHTlAUAiIk0LvBSIx3mP4dnVU3QUegk2\nqVRmYbfCsCJ8BSImRaCmQU3RcYiIFOPbP75FwsMEnBh/QnQUIiLFyczLxPTfpmOb4zZe66/j2KRS\nmSQ/Tsbo7aOxxX4LLOtbio5DRKQYRxOOYuWplYicFIka+jVExyEiUpyFxxei/2v98a/m/xIdhV6B\nTSqVWn5hPpyCnfBR948wqOUg0XGIiBQj6VESRu8Yja0OW9GifgvRcYiIFOfKn1ew6dwmXJxyUXQU\nKgXeOIlKzfuQN0xqm2DmWzNFRyEiUoy8gjw4BTvh056f4p3X3xEdh4hIcZ7dLGnWW7NgUsdEdBwq\nBa6kUqlsid2CIzePIGpSFPRUPLZBRKQpUw9ORbN6zfDFm1+IjkJEpEhBl4JwL+sePurxkegoVEps\nUumVzt09h88Of4aj7kdhVMNIdBwiIsXYeGYjjt8+jshJkbxTOhFRJcjMy8Rnhz9DgFMA9PXY+sgF\n/6XopTJyMuAY5Ii1761F+ybtRcchIlKMqOQofBX6FY6PP456hvVExyEiUqR5x+ZhUMtBvFmSzLBJ\npRKpJTVcd7hiWJthGNl+pOg4RESKcS/rHkYEj8CGoRtg3chadBwiIkW6kHYBfrF+uOR1SXQUKqMK\nXVxYWFiIzp07Y+jQoQCAjIwMDBw4EK1bt8agQYPw8OFDjYQkMeYfm4+sp1lY/s5y0VGIKlVSUhLe\nfvtttGvXDu3bt8f3338P4OU1benSpbCysoK1tTUOHz4sKjrJUIG6ACNDRmKs7VgMtx4uOg4pVFnm\naCXVs5iYGHTo0AFWVlaYNm2a1sdAVBFqSY0p+6dgwdsL0Lh2Y9FxqIwq1KSuXr0aNjY2RdfRLFu2\nDAMHDkRcXBwGDBiAZcuWaSQkad++uH34z9n/IMgpCAbVDETHIapUBgYGWLVqFS5duoSIiAj88MMP\nuHLlSok17fLlywgMDMTly5dx8OBBeHl5Qa1WCx4FycUXv32BGvo1ML/ffNFRSMFKO0crrp5JkgQA\nmDJlCnx9fREfH4/4+HgcPHhQ2HiIymrT2U0oUBfAs6un6ChUDuVuUu/cuYMDBw5g0qRJRcVsz549\ncHd3BwC4u7tj165dmklJWnUj4wYm7pmIQKdA3qabqgRTU1N06tQJAFCnTh20bdsWycnJJda03bt3\nw8XFBQYGBrC0tESrVq0QFRUlLD/Jh/8Ff+y5tgf+Dv6opldNdBxSqLLM0YqrZ5GRkUhNTUVmZiZ6\n9OgBAHBzc+O8jmTjz6w/8dXvX+HHD37kUylkqtz/at7e3li5ciX09P63ibS0NJiY/NXUmJiYIC0t\nreIJSauyn2bDIcgBc/rMQe9mvUXHIdK6W7du4ezZs+jZs2eJNS0lJQUWFhZF77GwsEBycrKQvCQf\nsRof65QAACAASURBVHdjMe3gNOwYuQPGNY1FxyEFK8scraR69uLr5ubmrHMkG18c+QJjOoxBJ9NO\noqNQOZXrxkn79u1DkyZN0LlzZ4SFhRX7MyqVqsTb6c+bN6/o6379+qFfv37liUEaJkkSPPd6oqNJ\nR3h19xIdhxQuLCysxPohypMnT+Do6IjVq1ejbt26f/vey2ras+8Xh/WOAOB+9n3YB9pjzXtrYGti\nKzoOaZG2a11F52jlxVpHuuLYrWM4cvMILntdFh2lStF0rStXk3rq1Cns2bMHBw4cQG5uLh4/foyx\nY8fCxMQEd+/ehampKVJTU9GkSZNi3/98ISPdsTZqLS7eu4hTE0/xeX1U6V6cxMyfL/b6vKdPn8LR\n0RFjx47F8OF/3cympJpmbm6OpKSkovfeuXMH5ubmxW6X9Y4K1YVw2e4CRxtHjGo/SnQc0jJt17qy\nztGKq2cWFhYwNzfHnTt3/vZ6SXUOYK0j3ZBXkIfJ+ybj+8Hfo65h3Ve/gTRG07WuXKf7LlmyBElJ\nSUhISEBAQAD69+8PPz8/2NnZYfPmzQCAzZs3F030SPeFJ4Zj0YlF2O68HbUMaomOQ6RVkiRh4sSJ\nsLGxwaefflr0ekk1zc7ODgEBAcjPz0dCQgLi4+OLrtsietHXv38NtaTG0gFLRUehKqCsc7SS6pmp\nqSnq1auHyMhISJIEPz8/zutI5y07uQzWjaxh39ZedBSqII08J/XZqtuMGTPg7OwMX19fWFpaIigo\nSBObp0qWmpkK5xBnbBq2CS0btBQdh0jrwsPDsXXrVtja2qJz584A/nokQ0k1zcbGBs7OzrCxsYG+\nvj58fHx49gEVK+hSEAIvBeK0x2no6/HR5KR9r5qjvaye+fj4YNy4ccjJycGQIUMwePBgYeMgepVr\n6dewJmoNzk4+KzoKaYBKenbbN23tUKWClndJL/G08Cn6b+mPd157B3P7zRUdh6owJdYGJY6JSu9C\n2gX039Ifh10Po3PTzqLjkI5QYl1Q4phIXiRJQv8t/TGszTB82uvTV7+BKl1F6wLvyVzFTf9tOuoZ\n1sPsvrNFRyEiUoyMnAzYB9pj9eDVbFCJiCrZpnObkJmXiU96fCI6CmkIzz2qwrZd2Ia9cXsR7RHN\nZ0gREWnIsxslDbMehtEdRouOQ0SkaHef3MWMIzNweOxhPn9aQdikVlEX/r+9Ow+P8er/B/5OxBqx\nkyB2sUSsRVtrlqpSgghCRWyhtE9L+3hKV1W1VL+1VVu1tHaJfQ8imyUrscdORRBLREQiy8z9+2N+\nMaiQZTJn7jPv13XNlcnQzPtc5eP+zDn3OYmn8EnAJwj0DuR5fUREBjTlwBRotBrMfme26ChERNL7\nNOBTjGw9kmeiSoZNqhlKfpIMD38PzO0+Fy3tWoqOQ0QkjXWn1mHj2Y3cKImIyAh2XtiJozeP4u8+\nf4uOQgbGf0HNjFbRwmerD95r+B6GthgqOg4RkTRib8U+XaFSuUxl0XGIiKSWkpGC8bvG468+f6F0\n8dKi45CBsUk1MzMPzsTdx3exYcAG0VGIiKRx9/Fd9PPrh197/MoVKkRERjA5cDK6N+wOt/puoqNQ\nEWCTakb2XtqL32J+Q7RvNEoUKyE6DhGRFLI0WRi4cSAGNx+MQU6DRMchIpJe2D9h2H5+O06PPy06\nChURNqlm4lryNfhs9YH/AH/UsKkhOg4RkTQ+3/c5SluVxnSX6aKjEBFJLz0rHaO3j8ainotQoVQF\n0XGoiLBJNQPpWenw8PPAFx2/QJc6XUTHISKSxvLY5dh7eS8iR0fy6AMiIiOYGjoVrexaoU+TPqKj\nUBFikyo5RVEwfvd4NKrcCBPemiA6DhGRNCJuRGBy4GSEDg/lp/lEREYQlRCFFcdX4OS4k6KjUBFj\nkyq5xUcXIzohGhGjI2BhYSE6DhGRFG4+uglPf08sc1+GplWbio5DRCS9jOwMjNg2AvPem4dq1tVE\nx6EixiZVYpE3IvFt8Lc4NPIQypYoKzoOEZEUnmQ/QT+/fhjXdhx6N+4tOg4RkVn4IewHNKrcCIOa\ncYM6c8AmVVJ3Ht+B5wZPLOm9BI0qNxIdh4hICoqiYMyOMahTvg6+7Pyl6DhERGbh6M2jWHJsCY6P\nPc6VgWaCTaqEsrXZGLRxEIa1HMabyomIDGhexDycTDyJwyMP80KJiMgIMrIz4LPVB7+8+wuq21QX\nHYeMhE2qhKYcmIISxUpgmvM00VGIiKSx7/I+/HTkJ4SPCod1CWvRcYiIzMK0sGlwqOyAIc2HiI5C\nRsQmVTIbz27EhjMbEDMmhschEBEZyMX7F+G9xRsbBmxA3Qp1RcchIjIL0QnRWHpsKU58eIKrV8wM\nm1SJxN2Nw7hd47B36F5UKVNFdBwiIik8fPIQ7uvd8YPLDzxrmojISNKz0uGz1Qfzus+DXVk70XHI\nyCxFByDDSMlIQT+/fvjpnZ/Qpnob0XGIiKSg0WrwweYP4FrPFWPeGCM6DhGR2fg6+Gs4VXOCl5OX\n6CgkAGdSJaAoCkZsGwHnus4Y0XqE6DhERNL4MuhLPM56jHnd54mOQkRkNkKvhWLdqXU4Oe4kl/ma\nKTapEphzZA4SUhKw1mOt6ChERNJYfXI1NpzZgCjfKBQvVlx0HCIis/Ao4xFGbBuBxb0W8/Y1M2ah\nKIpi1De0sICR31JqB64cwNAtQxHtGw37cvai4xAVmIy1QcYxmYuohCi8v/Z9BPsEw6mak+g4JBEZ\n64KMYyJxfHf4QqPVYHmf5aKjUCEUti5wJlXFrj+8jqFbhmKNxxo2qEREBnIj5QY8/DywzH0ZG1Qi\nIiPafn47Aq8E4sSHJ0RHIcHYpKrUk+wn8PT3xGdvfQbXeq6i4xARSSEtKw191/fFx+0/hntjd9Fx\niIjMxp3HdzB251j4e/qjXMlyouOQYFzuq1JjdoxBUnoSNgzYwBvKSQoy1gYZxyQzRVEwZPMQFLMo\nhlX9VrG2UpGQsS7IOCYyLkVR0M+vH5pUaYJZ78wSHYcMgMt9zdCyY8tw8PpBRI2O4kUUEZGBTA+b\njisPriDEJ4S1lYjIiJYeW4p/Hv4DP08/0VHIRLBJVZmYmzGYfGAywoaHwaakjeg4RERS2HR2E5Yc\nW4LI0ZEoXby06DhERGbjwv0LmHJgCsJGhKGkVUnRcchEsElVkXtp99Dfvz/+eP8PNK3aVHQcIiIp\nxN6KxYe7PsTeoXtR3aa66DhERGYjS5OFoZuHYqrzVDhWdRQdh0yIpegAlDcarQaDNw2Gl5MX+jv2\nFx2HiEgKtx7dQp/1ffBbz9/Qpnob0XGIiMzK96Hfo0qZKvio3Ueio5CJ4UyqSnwT/A00Wg1+dP1R\ndBQiIimkZ6Wjr19f+LbxxYBmA0THISIyK6HXQrE8djlix8ZyHwD6FzapKrD13FasPrkaMWNiYGXJ\n/2VERIWlKApGbR+F+hXr4+suX4uOQ0RkVpLSk+C9xRvL+yyHbVlb0XHIBLHjMXHn753HmB1jsHPI\nTlSzriY6DhGRFKaHTcelpEsIHR7KT/CJiIxIURT47vCFp6Mn3mv4nug4ZKLYpJqw1MxUePh7YLrr\ndLSv2V50HCIiKfif8edOvkREgvx59E9ceXAFaz3Wio5CJsxCMfLpyzzwOW8URYHXJi+ULVEWS3sv\n5Sf9JD0Za4OMY1K76IRo9FzbE/uG7kPr6q1FxyEzJGNdkHFMVDROJZ6C60pXHBpxCI2rNBYdh4pQ\nYesCZ1JN1NyIubicdBmHRh5ig0pEZADxD+PR168vlvRewgaViMjIHmc+xqCNg/Bzt5/ZoNJrcSbV\nBIVeC8WgjYMQOToSdSrUER2HyChkrA0yjkmtUjNT0fmvzhjsNBj/6/g/0XHIjMlYF2QcExme7w5f\nPMl+gpV9V3ICxgxwJlUyCSkJGLxpMFb2W8kGlYjIALSKFkM3D0Vru9aY1GGS6DhERGZn7am1CL0W\niqNjjrJBpTxhk2pCMjWZ8NzgiY/bf4x3G7wrOg4RkRQmB07GgycP4D/AnxdHRERGduH+BXwa8CkC\nvQNhU9JGdBxSCTapJmTi3omwtbbF5E6TRUchIpLC0mNLseXcFkSMikCJYiVExyEiMitPsp9g4IaB\n+MHlB7S0ayk6DqkIm1QTserEKuy/vB/RvtGwtLAUHYeISPWCrgbhq6CvEDY8DJXLVBYdh4jI7Hyy\n5xM0qdIEY98YKzoKqQybVBNw/PZxfLbvMwT7BKN8qfKi4xARqd75e+cxeNNgrOu/jrtIEhEJsOrE\nKoT+E4oY3xjeakH5xiZVsKT0JPT374+FPRbCqZqT6DhERKp3L+0e3l/7Pma5zYJrPVfRcYiIzM6Z\nO2fw2b7PEDQsiPehUoFwXalAOTtOujd2h5eTl+g4RESql5Gdgb7r+2JAswEY0XqE6DhERGbnUcYj\neG7wxJxuc9DctrnoOKRSPCdVoO9CvkPw1WAcGHYAxYsVFx2HSCgZa4OMYzJliqJg6JahyMjOgP8A\nf97fTyZJxrog45ioYBRFgdcmL5QrWQ5Lei8RHYcE4jmpKrXzwk4sO7YMMWNi2KASERnA1NCpuJx0\nGcE+wWxQiYgEmB85H5eSLuHwyMOio5DKsUkV4HLSZYzcNhJbvbbCrqyd6DhERKq38sRKrDqxCuGj\nwlG6eGnRcYiIzM6h64cw89BMRIyKQCmrUqLjkMqxSTWytKw0ePh74Nuu36JDrQ6i4xARqV7otVD8\nd99/ETI8BLZlbUXHISIyOzcf3cSgjYPwd5+/Ua9iPdFxSAK8J9WIFEWB9xZvWFhYYGXfldyOm+gZ\nMtYGGcdkas7dO4euf3fFWo+1cKvvJjoO0WvJWBdkHBPlXaYmEy4rXNCjYQ983eVr0XHIRPCeVBVZ\nFL0Ip++cxpFRR9igEhEV0p3Hd/D+2vcx+53ZbFCJiASZEDABVctUxZedvxQdhSTCJtVIDl8/jB/C\nfsCRkUdQpngZ0XGIiFQtPSsdfdb3wZDmQzC81XDRcYiIzNLy2OUIuhqEKN8oblhHBsXlvkZwO/U2\n2v7ZFn/2/hM9HXqKjkNkkmSsDTKOyRRotBoM3DgQpa1KY1W/VVyZQqoiY12QcUz0euHx4eizvg8O\njjiIxlUai45DJobLfU1cliYLAzcMhG8bXzaoREQGMGn/JNxPu4+9Q/eyQSUiEiAhJQGeGzzxV5+/\n2KBSkWCTWsT+F/g/2JS0wTddvxEdhYhI9RZGLsSeS3twZOQRlLQqKToOEZHZeZL9BP39++Ojdh/h\n/Ubvi45DkmKTWoTWnVqH7ee3I8Y3huv0iYgKadu5bZh1eBYOjTiEiqUrio5DRGR2FEWB7w5f1KtY\nD1M6TREdhyTGJrWInEo8hU8CPkGgdyAvpoiICinyRiRG7xiNPR/s4Rl8RESC/HT4J8TdjUPYiDDe\nbkFFik1qEUh+kgwPfw/M7T4XLe1aio5DRKRql5Iuoa9fX/zV5y+0rdFWdBwiIrO04/wOLIxaiMjR\nkTypgoocm1QD0ypaDNsyDN0bdMfQFkNFxyEiUrW7j++ix5oemNp1Kno16iU6DhGRWTpx+wRGbR+F\nHYN3oGa5mqLjkBlgk2pgMw7OwP30+9g4cKPoKEREqpaWlQb39e4Y4DgAY9uOFR2HiMgs3Xp0C+7r\n3fFrz1/xpv2bouOQmWCTakABlwLwe8zviPaNRoliJUTHISJSLY1WgyGbhqBhpYb40fVH0XGIiMxS\nWlYa+vr1xejWozGw2UDRcciMFGjL2fj4eLi4uKBZs2ZwcnLCggULAABJSUno1q0bGjVqhHfffRfJ\nyckGDWvKrj64Cp+tPljXfx1q2NQQHYeI8mHkyJGwtbVF8+bNn772qno2c+ZMODg4oEmTJti3b5+I\nyFJTFAX/2fMfpGamYpn7Mm7OQZRPBblOy62uHT16FM2bN4eDgwM+/fRTo4+FxMm5hc2hkgO+7vK1\n6DhkZgrUpBYvXhxz587FmTNnEBERgUWLFiEuLg6zZs1Ct27dcOHCBbi5uWHWrFmGzmuS0rPS0d+/\nP6Z0moIudbqIjkNE+TRixAgEBAQ891pu9ezs2bPw8/PD2bNnERAQgPHjx0Or1YqILa1Zh2bhSPwR\nbB60matSiAogv9dpL6triqIAAMaNG4dly5bh4sWLuHjx4r9qJclrcuBk3E27yw8LSYgCNal2dnZo\n1aoVAKBs2bJo2rQpEhISsH37dvj4+AAAfHx8sHXrVsMlNVGKomD87vFoXKUxPn2TnzASqVHnzp1R\nseLzR0XlVs+2bduGwYMHo3jx4qhbty4aNmyIqKgoo2eW1aoTq7D46GLs/mA3ypUsJzoOkSrl9zrt\nZXUtMjISt27dwqNHj9C+fXsAwLBhw8zi2o6AxTGLse38NmwZtAUlrUqKjkNmqEBN6rOuXbuG2NhY\nvPnmm0hMTIStrS0AwNbWFomJiYUOaOoWH12MmJsxWNp7KT9lIpJIbvXs5s2bsLe3f/r77O3tkZCQ\nICSjbPZe2ov/7v8v9nywh7dNkFQyM8W9d16u03Kray++XrNmTdY7M7Dzwk5MDZ2KXUN2oVLpSqLj\nkJkq1MZJqamp6N+/P+bPnw8bG5vnfs3CwiLXpm3q1KlPnzs7O8PZ2bkwMYSJvBGJb4O/xeGRh2Fd\nwlp0HCJVCQkJQUhIiOgYefKqepbz67mRpd4VtZibMfDe4o0tg7agadWmouMQFUpGBhAVBQQFAVu2\nhOD8+RB8/jlgZeTtKgt6nVYQrHVyiE6IxshtI7Fj8A40rNRQdBxSEUNf1xW4XGZlZaF///7w9vZG\n3759Aeg+lbt9+zbs7Oxw69YtVKtW7aX/7bOFTK3uPL6DARsGYKn7UjhUdhAdh0h1XryI+f7778WF\neYnc6lnNmjURHx//9PfduHEDNWvmfmacDPWuqF1Ougz3de74s/ef6Fi7o+g4RPmWnQ3ExOia0uBg\nICICaNwYcHEBZs50RqdOzsjpEY1V6/JznfayumZvb4+aNWvixo0bz72eW71jrVO/y0mX0Wd9Hyx1\nX8qjZijfDH1dV6DlvoqiYNSoUXB0dMSECROevu7u7o4VK1YAAFasWPG0KMomW5sNr41eGNZyGNwb\nu4uOQ0RFILd65u7ujvXr1yMzMxNXr17FxYsXn96vRfmXmJqI7qu7Y6rzVPRtIue/GSQfjQY4ehSY\nMwfo2ROoXBn48EPg7l3gP/8B4uN1TeucOUCPHsALk5hFLr/XabnVNTs7O5QrVw6RkZFQFAWrVq2S\n9trO3N15fAfdV3fHN12+4bUtmQQLJWf7tnw4dOgQunTpghYtWjxdKjJz5ky0b98eAwcOxPXr11G3\nbl34+/ujQoUKz7+hhQUK8JYmZdL+STiZeBK7h+xGMctiouMQSUFkbRg8eDBCQ0Nx79492NraYtq0\naejTp0+u9WzGjBlYvnw5rKysMH/+fHTv3v2lP1eGeleUHmU8gvMKZ7g3csd3zt+JjkOUK60WOH1a\nN0saHAyEhgI1auhmSl1cgK5dgSpV8vazjFEXCnKdlltdO3r0KIYPH4709HT07Nnz6XE2xh4TFZ1H\nGY/gssIFPR16YprLNNFxSBKFrQsFalILQ+2FbOPZjZi0fxJifGNQuUxl0XGIpKH22vAyMo7JUDKy\nM/D+2vfRoFID/PH+H9x4jkyKogDnzumX74aGAhUq6JtSFxfAzq5gP1vGuiDjmMxFpiYTvdf1Ru3y\ntfFnrz9Zi8lg2KQaUdzdOHT5uwv2Dt2LNtXbiI5DJBU114bcyDgmQ9BoNRiyeQiytdnw9/TnihQS\nTlGAy5f1M6XBwUDJkrpm1NVV9/WZTW4LRca6IOOYzEFOLc7IzsDGgRthZWnknb1IaoWtC/zTmEcp\nGSno59cPP73zExtUIqICUhQFE/ZOQGJqIgKGBrBBJWH++UffkAYF6Zb0urgAbm7Ajz8C9eqJTkhU\ndBRFwUe7P8Kdx3ew54M9bFDJ5HAmNQ8URYHnBk9ULVMVf/T6Q3QcIimpsTa8joxjKqxpodOwOW4z\nQoeHonyp8qLjkBm5efP5mdJHj/RLd11dAQcHwBgrHWWsCzKOSXZfBX2FvZf2IsgnCOVKlhMdhyTE\nmVQj+OnwT7iRcgNrPdaKjkJEpFq/R/+OlSdW4tDIQ2xQqcjduQOEhOhnSu/d021w5OICTJwIODoa\npyklMjU/Hf4Jm+M2I2x4GBtUMllsUl/jwJUDmBc5D1Gjo1DSqqToOEREquR/xh/TD07HwREHYVe2\ngDvOEL1CUpJug6OcmdL4eKBzZ11TOnYs0KIFYFmgg/eI5PFHzB/4I+YPHBxxEFWtq4qOQ5QrNqmv\ncP3hdXyw+QOs7b8WtcrXEh2HiEiV9l3eh493f4z93vtRv2J90XFIEikpQFiYvim9dAno0EHXlC5f\nDrRuDVjxKofoqVUnVmF62HSEjQhDzXI1RccheiXek5qLJ9lP0PmvzhjoOBCTOk4SHYdIemqpDfkh\n45jyK+JGBHqv640tg7agU+1OouOQij1+DBw+rF++e+YM0L69fvfddu2AEiVEp3w9GeuCjGOSjd9p\nP0zcOxEHhh1A06pNRcchM8AjaIrImB1jkJSehA0DNvDMKCIjUEttyA8Zx5Qfp++chttKN/zV5y/0\ndOgpOg6pzJMnQHi4/qzS48d1s6M5Gx299RZQqpTolPknY12QcUwy2XpuKz7c+SH2ee9DC9sWouOQ\nmeDGSUVg2bFlOHj9IKJGR7FBJSIqgCsPruC91e9hbve5bFApTzIzgago/fLdqCjAyUnXkH73nW4p\nr7W16JRE6rLj/A6M3TkWu4fsZoNKqsKZ1BfE3IxBjzU9cHDEQTSp0kR0HCKzYeq1oSBkHFNe3Hx0\nE53/6oz/vv1fjGs3TnQcMlHZ2cDRo/rlu+HhQKNG+mNhunQBbGxEpzQ8GeuCjGOSwc4LOzFq+yjs\nHLwT7Wq2Ex2HzAyX+xrQvbR7aPtnW/zfu/+H/o79RcchMiumXBsKSsYxvc79tPvo+ndXfND8A0zp\nPEV0HDIhGg1w4oR+pvTgQaBOHf3y3S5dgIoVRacsejLWBRnHpHa7LuzCyO0jsWPwDrSv2V50HDJD\nbFINRKPVoMeaHmhdvTVmvzNbdBwis2OqtaEwZBzTq6RkpOCdle/ApZ4LZrnN4u0SZk6r1W1ulDNT\nGhYG2NrqZ0qdnYGqZngChox1QcYxqdn289vhu8OXDSoJxSbVQL4K+goRNyKwd+heWFnyVl0iYzPV\n2lAYMo4pN+lZ6XhvzXtwrOqI33r+xgbVDCkKcP68vikNCQHKl3++Ka1RQ3RK8WSsCzKOSa02x23G\n+F3jsWvILrxR4w3RcciMsUk1gG3ntuGTgE8Q4xvDg42JBDHF2lBYMo7pZTI1mejn1w8VS1XEyn4r\nYWlhKToSGYGiAFeu6JfvBgcDxYvrm1JXV6AWjxj/FxnrgoxjUqN1p9Zh4t6JCBgagFZ2rUTHITPH\nJrWQLty/gE7LO2HnkJ1cEkEkkKnVBkOQcUwvytZmw2ujF7SKFv4D/LkSRXLXrz/flGZl6ZtSFxeg\nfn2Ak+ivJmNdkHFMarM8djm+Cf4Ge4fuhVM1J9FxiHgETWGkZqain18//ODyAxtUIqJ80ipajNw2\nEqmZqdjmtY0NqoRu3Xq+KX34ULds18UFmDwZaNyYTSmRaAsiF+D/wv8PIT4hcKjsIDoOkUGY7Uyq\noijw2uQF6+LWWOa+jPdPEQlmKrXBkGQcUw5FUfDhrg9x7t457PlgD8oULyM6EhnA3bu6e0lzmtLE\nRKBrV/1MabNmgCVXcxeKjHVBxjGpgaIo+CHsB6w6uQr7vfejboW6oiMRPcWZ1AKaGzEXl5Iu4dCI\nQ2xQiYjyQVEUTNg7AScTT2Lf0H1sUFXswQPdrrtBQbqm9J9/gM6ddQ2pry/QogVQrJjolET0Iq2i\nxWd7P0PItRAcGnEItmVtRUciMiizbFJDroVg9uHZiBwdidLFS4uOQ0SkGoqi4MugL3Ho+iEcGHYA\nNiVtREeifEhJ0Z1PmjNTeuEC8Pbbuk2OliwB3ngDsDLLKwMi9cjSZGHk9pG4+uAqQoaHoEKpCqIj\nERmc2f1TlJCSgCGbhmBVv1VcFkFElE/fh36PnRd2ItgnmBdGKpCWBhw+rD8W5vRpoF073Uzp/PlA\n+/ZAiRKiUxJRXqVmpmLAhgGwsrTCPm+uZCF5mdU9qZmaTHT9uyt6OfTCV12+EpKBiF5OxnuaZBvT\nj2E/Ys2pNQgZHoJq1tVEx6GXePIEiIjQL9+NjQVatdLfU/r220BpLiASSra6AMg5JlN05/Ed9F7X\nG07VnLC412JuVkcmjUfQ5MNHuz/CjZQb2DJoC8/xIzIxMl7kyDSmOYfnYMmxJQgdHorqNtVFx6H/\nLzMTiI7WL9+NjNRtbpRzTmnHjoC1teiU9CyZ6kIOGcdkai7ev4gea3rAy8kLP7j8wP1UyORx46Q8\nWnliJfZf3o9o32g2qERE+TA3fC7+PPYngn2C2aAKlp0NHDumb0qPHAEaNtQ1pRMn6jY9Kl9edEoi\nMqTw+PCnRyb6vuErOg6RUZjFTOrx28fRbVU3BPsE84BjIhMl4yfxMoxpQeQCzI+cjxCfENQqX0t0\nHLOj1QInTuib0oMHgVq19Mt3u3YFKlUSnZLyQ4a68CIZx2Qq/E774eM9H2NF3xXo6dBTdByiPONM\n6mskpSehv39//NrjVzaoRET5sDByIeZGzGWDakSKApw5o29KQ0OBqlV1Dam3N7BsGVCNtwMTSU9R\nFMw4OAOLjy5GoHcgWtq1FB2JyKiknknVKlr0WtsLTao0wS/dfzHKexJRwcj4Sbyax7QwciF+ifgF\nwT7B3Am9CCkKcPGifvfdkBCgbFn9TKmLC1CjhuiUZEhqrgu5kXFMIj3JfgLfHb6IuxuH7YO3o4YN\niwCpD2dSX2Fa6DQ8znqM2e/MFh2FiEg1FkQuwNyIuWxQi4CiAFev6mdKg4MBS0vdJkc9egA/+64i\n2AAAF5BJREFU/QTUqSM6JRGJcjv1Nvqu74s6FeogbEQYj5ghsyXtTOquC7vw4a4PEeMbA9uytkX+\nfkRUODJ+Eq/GMc0Nn4uFUQsR7BOMOhXYLRnCjRv6mdLgYN0xMa6u+pnSBg0AbtRpPtRYF15HxjGJ\nEHMzBh5+HhjdZjS+6fINd/AlVVP1ETRF9nev4mVgVAfAbwsQ36GI3oSIDCGnAsl4kaO2Mc05PAeL\njy5GkE8QapevLTqOat2+rVu2m9OUPngAODvrG9MmTdiUmjO11YW8kHFMxrbi+ApM2j8Jf/b+E32b\n9BUdh6jQVN2kFoW0rDS8vextjGkzBh+1/6jI3oeIDEvGixw1jWnGwRn4+/jfCPIJgn05e9FxVOXe\nPd0GRzmzpbdu6XbdzZkpdXLSLeklAtRVF/JKxjEZS6YmE5/v+xwBlwKwddBWNKvWTHQkIoNgk/oM\nRVEwbOswWMACK/qu4DIJIhWR8SJHDWNSFAXfhXyHjWc34sCwAzwHNQ+Sk4GwMH1Teu0a0LGjvilt\n3RooVkx0SjJVaqgL+SXjmIzhRsoNDNwwEFXKVMHKfitRoVQF0ZGIDIYbJz1jUfQinEw8ifBR4WxQ\niYheQ1EUfBH4BQIuBSBkeAiqWfNsk5d59Ag4dEjflJ4/D7z1lq4hXbwYeOMNoHhx0SmJSE32X96P\nYVuH4T/t/4PJnSbD0oLLLYieJc1M6uHrh+Hh74EjI4+gQaUGBv/5RFS0ZPwk3pTHpFW0+GTPJwi/\nEY59Q/ehcpnKoiOZjLQ04MgR/e67J08Cbdvq7ylt3x4oWVJ0SlIrU64LBSXjmIqKRqvBtLBpWHJ0\nCVb1WwW3+m6iIxEVCc6kQrdd96CNg/BXn7/YoBIRvYZGq8HoHaNx8f5FBA0LQvlS5UVHEiojA4iM\n1G90dPQo0LKlriGdPh14+22gdGnRKYlI7RJSEuC9xRsAcGzsMdiVtROciMh0qX4mNUuTBbeVbnCr\n54bvnL8z2M8lIuOS8ZN4UxxTpiYT3lu8cT/tPrZ5bYN1CWvRkYwuKwuIjtbPlEZG6nbczZkp7dQJ\nKFtWdEqSlSnWhcKScUyGtuP8Dvju8MVH7T7Cl52/RDFL3rhOcjP7jZMmBEzAxaSL2DF4B9fzE6mY\njBc5pjamtKw09Pfvj5LFSmK953qUsiolOpJRaDTAsWP6pvTwYd3ZpDkbHXXpApQ378lkMiJTqwuG\nIOOYDCUtKw2T9k/Crgu7sMZjDTrW7ig6EpFRmPVy33Wn1mHHhR2I8Y1hg0pE9AoPnzxEr3W9UK9C\nPSzvsxxWlqou/6+k1eruI81pSg8eBGrU0M2U+voCq1cDlXkLLhEVsZibMRi6eSja1miL4x8e5+69\nRPmg2pnUU4mn4LrSFYHegWhp19IAyYhIJBk/iTeVMd1OvY33Vr+HLnW6YN5786T7UE9RgLg4/T2l\noaG6JjRnptTZGbC1FZ2SSMdU6oIhyTimwsjSZOHHgz/it+jfsKDHAng5eYmORGR0ZjmTmvwkGR7+\nHpjbfS4bVCKiV7jy4AreXfUufFr64OsuX0txPJeiAJcu6WdKg4N1Gxu5ugL9+gHz5wP29qJTEpE5\nOpV4Cj5bfWBX1g6xY2NRs1xN0ZGIVEl1M6laRYu+6/uiToU6WNhjoQGTEZFIMn4SL3pMsbdi0Wtd\nL3zV+SuMbzdeWA5DuHZNP1MaEqJrVF1c9Jsd1a0rOCBRHomuC0VBxjHlV6YmEzMOzsCi6EWY6TYT\no1qPkuJDQaKCMruZ1BkHZ+B++n1sHLhRdBQiIpMVdDUIXhu98Nv7v8HT0VN0nHxLSNDPkgYFAenp\n+uW7334LNGwI8PqPiExBeHw4fHf4on7F+jg+9jhnT4kMQFVN6t5Le/F7zO+I9o1GiWIlRMchIjJJ\n60+vx6cBn2LDgA3oWrer6Dh5cufO801pUhLQtauuKf38c6BpUzalRGRakp8k48sDX2Lrua34pfsv\nGNRsEGdPiQxENU3qteRr8Nnqgw0DNqCGTQ3RcYiITI6iKJhzZA5+jfoVgd6BaG7bXHSkXN2/r9vg\nKKcpTUjQHQXj6gqMGwc0bw5YyrW/ExFJQlEUrD65Gl8EfgH3xu44+9FZ7txLZGCqaFLTs9Lh4eeB\nyZ0mo3OdzqLjEBGZnGxtNiYETMDB6wdxZNQR2JczrZ2DHj4EwsL0TemVK0DHjrqZ0hUrgNatgWI8\n256ITNyJ2yfw8Z6PkZ6Vji2DtuBN+zdFRyKSkslvnKQoCkZuH4kn2U+w1mMtl1EQSUrGjTeMNaZH\nGY/gtckLmZpMbBywEeVLlS/y93yd1FTg0CF9UxoXB7z1lv6+0nbtgOLFRackMj7WOnW68/gOvgn+\nBlvPbcU052kY3WY0ilnykzWi3Ei/cdLio4sRczMGEaMi2KASEb0g/mE8eq3rhbfs38KvPX5F8WJi\nOr/0dODIEf19pSdOAG+8oWtIf/5Z16CWLCkkGhFRgaVnpWNB5AL8HP4zvFt44/zH57m0l8gITLpJ\njbgRgW+Dv8XhkYdhXcJadBwiIpMSeSMSHv4emPjWRHz+9udG/SAvIwOIitLPlMbEAC1a6JrS778H\nOnQAypQxWhwiIoPK1mZj9cnV+Db4W7Sr2Q6HRx5Go8qNRMciMhqNBkhO1m1k+LLH/fsv/z42Fqhd\nu/Dvb7LLfRNTE9F2SVss6rkI7o3djZCMiESScblYUY5pzck1mLh3Ipa5L0Pvxr2L5D2elZWla0Rz\nZkojIoDGjfVnlXbqBNjYFHkMItVjrTNtWkWLzXGb8U3wN6hSpgpmuc1Cx9odRcciKrDMTODBA90j\nt4bzxUbzwQMgJQUoVw6oVAmoWBGoXFn/NbfnlSrpHpaWha8LJtmkZmuz0W1VN3Ss1RHTXacbKRkR\niSTTRU6OohiTRqvBl0FfYsOZDdg+eDucqjkZ9Oc/fR8NcPy4fqb08GGgXj39PaVdugAVuOKNKN9Y\n60yTVtFi27lt+D70e1hZWmG663R0b9Cdt5qRSVAUIC1N30w+23C+rvlMT9f9e/1iQ/lsY1mx4vPN\naOXKQPnyhdvQUMomddL+STiZeBK7h+zmTelEZkKGi5wXGXpMSelJGLxpMLK12fDz9EOVMlUM9rO1\nWuD0aX1TGhYGVK+unynt2hWoYri3IzJbrHWmJVubjY1nN2LmoZmwsrTC1K5T0atRLzanVCSys5+f\n1XyxwXzx9We/Fiv28obyZc+f/WpjI+ZIN+ma1I1nN2LS/kmI8Y1B5TKVjZiMiERS80VObgw5pthb\nsfDc4Im+Tfpi9juzYWVZuC0FFAU4d07flIaG6j5pdXXVNabOzoCdnUGiE9EzWOtMQ1pWGlYcX4Gf\nw39GDZsamNxxMno69GRzSq+l1eqOVctpNl+c1XxZE5rzNT1dN0OZM5P5YkOZ2/OKFYFSpUSPPH+k\nalLj7sahy99dEPBBAN6o8YYxYxGRYGq8yHkdQ4xJURQsi12GKQemYGGPhfBy8irgzwEuX9bfUxoc\nrNttN2em1NkZqFWrUFGJKA9Y68RKSEnA7zG/Y/HRxehYqyP+2+G/6FS7k+hYZGRare6ey2ebyheb\ny9x+7dEjoGxZfZP57OPFxtJUZjVFkOYImpSMFPTz64fZ78xmg0pEBCA1MxUf7f4I0QnRCBsehqZV\nm+brv//nH31DGhSk+0fZxQVwcwOmTwfq1y+i4EREJkRRFIT9E4ZF0YsQeCUQQ5oPwZGRR+BQ2UF0\nNCqE7Gzd7rPJyf9uJl/22rOPlJTcG80KFXQNZZ06L29CK1Qo3L2alDcmMZOqKAo8N3iiSpkqWNxr\nsTHjEJGJUNMn8XlVmDEdv30cgzYOQsdaHbGgxwKULVH2tf/NzZvPz5Q+eqSfKXVxARwcAK5kIxKL\ntc547jy+g5UnVmLpsaWwtLDE+HbjMazlMJQrWU50NIJuhc/jx883ms9+ffG1F19PS9Mtnc1pLF9s\nNF/1ffnygJXJTNXJSYrlvj8d/gmb4jYhbHgYSlrxtHcic2SqFzmFUZAxaRUt5kXMw6xDszD/vfkY\n3Hxwrr/3zh0gJETflN69q9vgKGcH3mbN2JQSmRrWuqKVnpWOXRd3YeWJlQj7Jwx9mvTBmDZj0KFW\nB95vamCKAjx5om8cn30821C+6tdKlNA3kM9+fdVrOd+b09JZNVJ9k3rgygEM3TIUUaOjUKs8b4gi\nMlemdJFjKPkd07Xkaxi+dTi0ihZ/9/0b9Ss+vx43KUm3wVFOUxofrzuf1NVV92jRgv9gE5k61jrD\ny8jOQOCVQPid8cOOCzvQpnobDGsxDB5NPWBTkgc450ZRgNRUfcP48OHzX198/rJHsWL62cxnZzVz\ne/5sw1mhgq5JJTmpukm9/vA63lz6JtZ4rIFrPVdjxiAiEyP6Iqco5HVMGq0Gv0X/hu9Dv8cXHb/A\nZ29/hmKWxZCSojsKJqcpvXQJ6NBBP1Papg2XKxGpjTnXOkNKSk/C3kt7sf3Cduy5uAfNbZtjgOMA\nDHAcgOo21Y2aRYScczMfPnz5I6fBfNX3jx4BpUvrmsicpjHn+ctee7bhzHlNbTvOkvGotkl9kv0E\nXf7qggGOAzCp4yRjRiAiE2SuF24nbp/A2J1jUdKqJOa5/Ym7cY0RFKRrSs+cAdq312921K4dULy4\nkcITUZEw11pXWNnabEQnRGP/lf3Yd3kfTiaehHNdZ/Rq1At9GveBbVnbIn1/Q8rO1m3c8+wjp3nM\nef7say/+Ws5zKyt945jzKFfu368923i++JwfdFJRMbkmNSAgABMmTIBGo8Ho0aPxxRdfPP+G/z/w\nX7F/Yfel3fD39Ff9PQIhISFwdnYWHcNgZBsPwDGpgRov3PJa717mzuM7+HL/N9h8divefvIDkoNG\n48RxS7Rpo58pfest0/qUWrY/c4B8Y5JtPIB8YzK3WldQjzIeIeZmDMJvhCPsnzCE3whH3Qp10a1+\nN3Sr3w1d63ZFKauiKZAv+zOXc/9lSopuBvLZrzmPF79/2ePhQ93PsbHRNZTPNpcvfn3211/8feXL\n52+prGx/j2QbDyDfmEzqCBqNRoOPP/4YgYGBqFmzJtq1awd3d3c0bfrvYxOGtxqOD1p8oPoGFZDv\nD5Vs4wE4JjK8/NS7HJmZwP7D9zEnbB6OZP0O5fgwtEw+hxadK8L1O91SXmtrIw4in2T8MyfbmGQb\nDyDnmNSkILUuPxRFQeLjRJy9exYnbp9A7O1YxN6OxZUHV9DKrhXesn8L49qOwxqPNahcpnI+fq6u\nGUxN1TWPqan65znf5zx/8XHiRAiqVXN++n1OA2plpWsubWx0TWJOo1munP65jQ3QoIH++YsNp42N\n7ugTY1/+yvb3SLbxAHKOqTAM2qRGRUWhYcOGqFu3LgDAy8sL27Zte2khs7CwQIlivFuaiNQpr/Xu\n+nVgzRoF26KO4ZhmFbTNV8ER/fH7G1EY8L/6KMeTEIjIhOXn2u5lNFoN7qbdRWJqIm6l3kL8w3jE\np8TjyoMruHj/Ei7cvwALWKJh+WaoX9YJ9Ut3Qcean8LWvjky00sg7SaQcAlY/lh3XMmLj9TUf3/N\neV6ihO6Dv5zGMOfrs89zms7q1fXPra2BceP03+c8uMkPkfEYtElNSEhArVr6HXrt7e0RGRlpyLcg\nIjIJea13By6EY076CJRsn4VPWw7BfzrGonb52saMSkRUYHmtdbuj4uDtNx4ai3RkW6Qhu1gKsq2S\noSmWimKZlWCZbguLx3bAw9rQPqiF7LvvwiplPEqnN0QZVMX9MhZIKw1ctdZt5mNtDZQpo3vkPLe2\nBqpWBerU0TWY1ta6R87znAY053lB77c8fVq3soWIxDHoPambNm1CQEAAlixZAgBYvXo1IiMjsXDh\nQv0bSrC8l4iKhpru02K9I6KCYq0jInNgMvek1qxZE/Hx8U+/j4+Ph729/XO/R02FmYgoN6x3RGQO\nWOuISASDHvvetm1bXLx4EdeuXUNmZib8/Pzg7u5uyLcgIjIJrHdEZA5Y64hIBIPOpFpZWeHXX39F\n9+7dodFoMGrUKIPt/kZEZEpY74jIHLDWEZEIBp1JBYAePXrg/PnzuHTpEqZMmfLcrwUEBKBJkyZw\ncHDA7NmzDf3WRS4+Ph4uLi5o1qwZnJycsGDBAgBAUlISunXrhkaNGuHdd99FcnKy4KT5p9Fo0Lp1\na/Tu3RuAuseUnJwMT09PNG3aFI6OjoiMjFT1eABg5syZaNasGZo3b44hQ4YgIyNDVWMaOXIkbG1t\n0bx586evvSr/zJkz4eDggCZNmmDfvn0iIudJbvWOtc50sdaZNrXXOkDOeidrrQPkrXcy1TpAvnrH\nWvf6WmfwJjU3OedsBQQE4OzZs1i3bh3i4uKM9fYGUbx4ccydOxdnzpxBREQEFi1ahLi4OMyaNQvd\nunXDhQsX4ObmhlmzZomOmm/z58+Ho6Pj080P1DymTz/9FD179kRcXBxOnjyJJk2aqHo8165dw5Il\nS3Ds2DGcOnUKGo0G69evV9WYRowYgYCAgOdeyy3/2bNn4efnh7NnzyIgIADjx4+HVqsVEbtAWOtM\nG2ud6ZKh1gHmU+9kqHWAvPVOploHyFXvWOvyWOsUIzly5IjSvXv3p9/PnDlTmTlzprHevkj06dNH\n2b9/v9K4cWPl9u3biqIoyq1bt5TGjRsLTpY/8fHxipubmxIUFKT06tVLURRFtWNKTk5W6tWr96/X\n1ToeRVGU+/fvK40aNVKSkpKUrKwspVevXsq+fftUN6arV68qTk5OT7/PLf+MGTOUWbNmPf193bt3\nV8LDw40bthBY60wXa51pk6XWKYp51DsZa52iyFHvZKp1iiJfvWOty1utM9pM6svO2UpISDDW2xvc\ntWvXEBsbizfffBOJiYmwtbUFANja2iIxMVFwuvyZOHEi5syZA0tL/R8HtY7p6tWrqFq1KkaMGIE2\nbdrA19cXjx8/Vu14AKBSpUr4/PPPUbt2bdSoUQMVKlRAt27dVD0mIPc/Yzdv3nxu50i11QrWOtPF\nWmfaZK11gJz1TrZaB8hT72SqdYB89Y61Lm/1wmhNqkxnaKWmpqJ///6YP38+bGxsnvs1CwsLVY11\n586dqFatGlq3bp3rFvJqGlN2djaOHTuG8ePH49ixY7C2tv7Xcgk1jQcALl++jHnz5uHatWu4efMm\nUlNTsXr16ud+j9rG9KLX5VfT2NSU9XVY60wXa516yVLv1JIzr2Spd7LVOkC+esdap//1VzFak5qX\nc7bUICsrC/3794e3tzf69u0LQPdJwe3btwEAt27dQrVq1URGzJcjR45g+/btqFevHgYPHoygoCB4\ne3urdkz29vawt7dHu3btAACenp44duwY7OzsVDkeAIiJiUGHDh1QuXJlWFlZwcPDA+Hh4aoeE5D7\n35sXa8WNGzdQs2ZNIRkLgrXONLHWmT5Zax0gZ72TpdYBctU72WodIF+9Y63LW60zWpMqwzlbiqJg\n1KhRcHR0xIQJE56+7u7ujhUrVgAAVqxY8bTAqcGMGTMQHx+Pq1evYv369XB1dcWqVatUOyY7OzvU\nqlULFy5cAAAEBgaiWbNm6N27tyrHAwBNmjRBREQE0tPToSgKAgMD4ejoqOoxAbn/vXF3d8f69euR\nmZmJq1ev4uLFi2jfvr3IqPnCWmeaWOtMn6y1DpCz3slQ6wD56p1stQ6Qr96x1uWx1hnu1tnX2717\nt9KoUSOlQYMGyowZM4z51gZx8OBBxcLCQmnZsqXSqlUrpVWrVsqePXuU+/fvK25uboqDg4PSrVs3\n5cGDB6KjFkhISIjSu3dvRVEUVY/p+PHjStu2bZUWLVoo/fr1U5KTk1U9HkVRlNmzZyuOjo6Kk5OT\nMmzYMCUzM1NVY/Ly8lKqV6+uFC9eXLG3t1eWL1/+yvw//vij0qBBA6Vx48ZKQECAwOQFw1pn2ljr\nTJfaa52imFe9U3utUxS5650stU5R5Kt3rHWvr3UWipLLgnUiIiIiIiIiIzPacl8iIiIiIiKi12GT\nSkRERERERCaDTSoRERERERGZDDapREREREREZDLYpBIREREREZHJYJNKREREREREJuP/AeAtgiCH\nJjDWAAAAAElFTkSuQmCC\n"
}
],
"prompt_number": 35
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercises\n",
"### Transitivity\n",
"\n",
"If\n",
"$\n",
"f(n)=O(g(n))\\;\n",
"$\n",
"and \n",
"$ \n",
"g(n) = O(h(n))\\;\n",
"$\n",
"then\n",
"$\n",
"f = O(h(n))\\;\n",
"$\n",
"? \n",
"\n",
"### Symmetry\n",
"\n",
"If $f=O(g)\\;$ then $g=O(f)$? Or $g \\ne O(f)$?\n",
"\n",
"\n",
"### Series Loops\n",
"\n",
"Let $f_1 = O(g_1)\\;$ and $f_2=O(g_2)$.\n",
"\n",
"Show that $f_1 + f_2 = O(g_1 + g_2)$.\n",
"\n",
"This relates to two consecutive loops:\n",
"\n",
"\n",
" for i in range(len(list1)):\n",
" print i\n",
" for i in range(len(list2)):\n",
" print i\n",
"\n",
"### Parallel Loops\n",
"\n",
"Show that $f_1 \\cdot f_2 = O(g_1 \\cdot g_2)$.\n",
"\n",
"This relates to independent nested loops:\n",
"\n",
" for i in range(len(list1)):\n",
" print i\n",
" for j in range(len(list2)):\n",
" print j\n",
"### Maximum\n",
"\n",
"Show that $f_1 + f_2 + ... + f_k = O(f_{max})$. That is, in a finite constant sum of functions, the dominate function defines the growth rate.\n",
"\n",
"A private case is that of a polynomial.\n",
"\n",
"### Dependent nested loops\n",
"\n",
"For exmaple,\n",
"\n",
" for i in range(len(list1)):\n",
" for j in range(i):\n",
" print i, j\n",
"\n",
"Prove:\n",
"\n",
"* $\\sum_{i=1}^{n}{i} = O(n^2)$ - the arithmetic series\n",
"* $\\sum_{i=1}^{n}{2^i} = O(2^n)$ - the geometric series"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Primality testing"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### [Fermat's little theorem](http://en.wikipedia.org/wiki/Fermat's_little_theorem)\n",
"\n",
"If $p$ is a prime $a$ is a natural number such that $1\\le a < p\\;$, then $a^{p-1} = 1 \\; (mod \\; p)$.\n",
"\n",
"### Probabilistic test with Fermat's little theorem\n",
"\n",
"We can use this to create a primality test for *p*."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from random import randrange\n",
"def is_prime(p):\n",
" \"\"\"probabilistic test for p's compositeness\"\"\"\n",
" for i in range(100):\n",
" a = randrange(1, p - 1) # a is a random integer in [1..p-1]\n",
" if pow(a, p - 1, p) != 1: # this takes O(n^3) = O((log2 p)^3)\n",
" return False\n",
" return True # we get here if no compositeness witness was found"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 39
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"is_prime(11)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 4,
"text": [
"True"
]
}
],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"is_prime(190125101)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 5,
"text": [
"True"
]
}
],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Notes\n",
"\n",
"* `pow(a,b,c)` is equivalent to $a^b \\; mod \\; c$, only it is more efficient by use of *iterated squaring*. \n",
"* The *False Positive* rate - the probablity the function returns `True` when it should return `False` - is less than $0.25^{100}$ (Miller-Rabin)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Testing the prime number theorem\n",
"\n",
"\n",
"#### The theorem\n",
"Define by $\\pi(x)$ the number of prime numbersless than or equal to $x$. Then the [prime number theorem](http://en.wikipedia.org/wiki/Prime_number_theorem) states that \n",
"\n",
"$$\n",
"\\pi(x) \\thicksim \\frac{x}{log(x)}\n",
"$$\n",
"\n",
"for large $x$.\n",
"\n",
"Now, assuming the primes are uniformaly distributed, the probability that a randomly sampled number between $1$ and $x$ is prime is $\\frac{\\pi(x)}{x} \\thicksim \\frac{1}{log(x)}$.\n",
"\n",
"Since the number of bits in $x$, $n$, is $O(log(x))\\;$ this translates to $O(1/n)$.\n",
"\n",
"Now, the probability that a number with exactly $n$ bits is prime is roughly half of the probability that a number of $n$ or less bits is prime, and this doesn't change the order of magnitude, and we can say that\n",
"> A number with *n* bits is prime with a probability of $O(1/n)$.\n",
"\n",
"We'd like to check this, but for large *n* there are too many ($2^{n-1}$) numbers to check. So we will use *sampling*."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def prob_prime(n):\n",
" \"\"\"evaluate the probability of an n-bit long integer to be prime\"\"\"\n",
" count = 0\n",
" sample_size = 10 ** 5\n",
" for i in range(sample_size):\n",
" p = randrange(2 ** (n - 1), 2 ** n - 1)\n",
" count += is_prime(p)\n",
" return count / sample_size"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 34
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"prob_prime(20)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 36,
"text": [
"0.07423"
]
}
],
"prompt_number": 36
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"1 / 20"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 37,
"text": [
"0.05"
]
}
],
"prompt_number": 37
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The relative error is therefore small:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"(0.07423 - 0.05) / 0.05"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 40,
"text": [
"0.48460000000000003"
]
}
],
"prompt_number": 40
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Diffie-Hellman\n",
"\n",
"A Khan Academy video that illustrates the Diffie-Hellman key exchange:\n",
"\n",
"<iframe width=\"420\" height=\"315\" src=\"http://www.youtube.com/embed/YEBfamv-_do#t=6m19s\" frameborder=\"0\" allowfullscreen></iframe>\n",
"\n",
"See the paper [New directions in cryptography](http://www.cs.tau.ac.il/~bchor/diffie-hellman.pdf)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is the protocol:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def DH_exchange(p):\n",
" \"\"\" generates a shared DH key \"\"\"\n",
" g = randrange(1,p-1)\n",
" a = randrange(1,p-1) # Alice's secret\n",
" b = randrange(1,p-1) # Bob's secret\n",
" x = pow(g,a,p) \n",
" y = pow(g,b,p)\n",
" key_A = pow(y,a,p)\n",
" key_B = pow(x,b,p)\n",
" return g, a, b, x, y, key_A, key_B"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 20
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"DH_exchange(190125101)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 44,
"text": [
"(130721310, 61963609, 1775050, 132736567, 143446917, 74182194, 74182194)"
]
}
],
"prompt_number": 44
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"DH_exchange(833648000993161193752610727299)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 45,
"text": [
"(225405422835827732918401478004,\n",
" 153883981994400043514132897779,\n",
" 556710940458985113442266962618,\n",
" 620358857758647613746179753310,\n",
" 479744267228387852844588852918,\n",
" 610421506532174772126394293202,\n",
" 610421506532174772126394293202)"
]
}
],
"prompt_number": 45
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let's try and break it:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def crack_DH(p, g, x):\n",
" \"\"\"find secret \"a\" that satisfies g**a%p == x\n",
" Not feasible for large p\"\"\"\n",
" for a in range(1,p-1):\n",
" if a % 100000 == 0: \n",
" print(\"Iteration\",a) # progress bar\n",
" if pow(g,a,p) == x:\n",
" return a\n",
" return None"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 19
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that because `pow(a,b,c)` is not [injective](http://en.wikipedia.org/wiki/Injective_function) (in contrast to what might have been said in class...) this may return the wrong answer.\n",
"\n",
"To test the protocol, we first need a function that finds primes:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def find_prime(n):\n",
" \"\"\" find random n-bit long prime (no leading zeros: 2**(n-1)<= N < 2**n )\"\"\"\n",
" while True: #here we're optimistic, but actually we have a good reason to be:\n",
" # after O(1/n) iterations we expect to find a prime and halt\n",
" candidate = randrange(2**(n - 1), 2**n)\n",
" if is_prime(candidate):\n",
" return candidate"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 14
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"find_prime(10)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 15,
"text": [
"991"
]
}
],
"prompt_number": 15
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"find_prime(100)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 16,
"text": [
"1115065337204017303367921856997"
]
}
],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"find_prime(256)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 17,
"text": [
"59817822415413480116679649593332822338590599807236481764232916509620304609287"
]
}
],
"prompt_number": 17
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can now run the DH protocol and try to break it.\n",
"\n",
"We will start with a 10-bit prime:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from math import log\n",
"p = find_prime(10)\n",
"print(p,log(p,2))\n",
"g,a,b,x,y,key_A,key_B = DH_exchange(p)\n",
"print('g',g,'a',a,'b',b,'x',x,'y',y,'key_A',key_A,'key_B',key_B)\n",
"print('a',crack_DH(p,g,x))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"971 9.923327485419193\n",
"g 813 a 150 b 234 x 371 y 196 key_A 939 key_B 939\n",
"a 150\n"
]
}
],
"prompt_number": 27
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Running with a 16-bit prime:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"p = find_prime(16)\n",
"print(p,log(p,2))\n",
"g,a,b,x,y,key_A,key_B = DH_exchange(p)\n",
"print('g',g,'a',a,'b',b,'x',x,'y',y,'key_A',key_A,'key_B',key_B)\n",
"print('a',crack_DH(p,g,x))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"47809 15.54499460932774\n",
"g 42852 a 42613 b 27757 x 26351 y 21063 key_A 21555 key_B 21555\n",
"a 117\n"
]
}
],
"prompt_number": 28
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"p = find_prime(128)\n",
"print(p,log(p,2))\n",
"g,a,b,x,y,key_A,key_B = DH_exchange(p)\n",
"print('g',g,'a',a,'b',b,'x',x,'y',y,'key_A',key_A,'key_B',key_B)\n",
"print('a',crack_DH(p,g,x))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"232058770554614453837871524801758451143 127.44775783025453\n",
"g 159913793420381443650379750802964420717 a 116795875092692988667366016317257384027 b 173352797834467896747096128107523563976 x 224894493378616747082831720370075484037 y 202527828205657594721613336077418916066 key_A 6312501138165008035876819356018294783 key_B 6312501138165008035876819356018294783\n",
"Iteration"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" 100000\n",
"Iteration"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" 200000\n",
"Iteration"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" 300000\n",
"Iteration"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" 400000\n",
"Iteration"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" 500000\n",
"Iteration"
]
}
],
"prompt_number": "*"
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Fin\n",
"This notebook is part of the [Extended introduction to computer science](http://tau-cs1001-py.wikidot.com/) course at Tel-Aviv University.\n",
"\n",
"The notebook was written using Python 3.2 and IPython 0.13.1.\n",
"\n",
"The code is available at <https://raw.github.com/yoavram/CS1001.py/master/recitation4.ipynb>.\n",
"\n",
"The notebook can be viewed online at <http://nbviewer.ipython.org/urls/raw.github.com/yoavram/CS1001.py/master/recitation4.ipynb>.\n",
"\n",
"This work is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/)."
]
}
],
"metadata": {}
}
]
} | bsd-3-clause |
crazyhottommy/scripts-general-use | Shell/Awk_anotates_vcf_with_bed.ipynb | 1 | 6384 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Using Awk to join two files based on several columns\n",
"I was reading a thread on stackoverflow and found this [post](http://stackoverflow.com/questions/13258604/join-two-files-using-awk) very interesting.\n",
"I will go through the problem and the awk solution. Again, Awk is awesome!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I created some dummy files. \n",
"file_a is a tab-delimited bed file with 5 colums:"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"chr1\t123\taa\tb\tc\td\r\n",
"chr1\t234\ta\tb\tc\td\r\n",
"chr1\t345\taa\tb\tc\td\r\n",
"chr1\t456\ta\tb\tc\td\r\n"
]
}
],
"source": [
"cat file_a.bed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"file_b is the file that contain additional infomation, which we want to add to file_a:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"xxxx\tabcd\tchr1\t123\taa\tc\td\te\r\n",
"yyyy\tdefg\tchr1\t345\taa\te\tf\tg\r\n"
]
}
],
"source": [
"cat file_b.bed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"we want to annotate file_a based on the fact that columns 3,4,5 in file_b are the same as columns 1,2,3 in file_a. \n",
"To do this, we are going to use Awk associated array.\n",
"see a [link](http://www.thegeekstuff.com/2010/03/awk-arrays-explained-with-5-practical-examples/)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let me execute the awk one-liner first and then explain what's going on here:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"chr1\t123\taa\tb\tc\txxxx\tabcd\r\n",
"chr1\t234\ta\tb\tc\t\r\n",
"chr1\t345\taa\tb\tc\tyyyy\tdefg\r\n",
"chr1\t456\ta\tb\tc\t\r\n"
]
}
],
"source": [
"awk 'NR==FNR{a[$3,$4,$5]=$1OFS$2;next}{$6=a[$1,$2,$3];print}' OFS='\\t' \\\n",
"file_b.bed file_a.bed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"we annotated file_a using file_b. Aka, we added first two columns from file_b to file_a. \n",
"There are several things happening here: \n",
"we see built-in variables in awk: **NR** and **FNR**. NR is the line number of the \n",
"current processing line. \n",
"when awk read in multiple files, awk NR variable will give the total number of records \n",
"relative to **all** the input file. Awk FNR will give you number of records for **each** inpu \n",
"file. see a link \n",
"[here](http://www.thegeekstuff.com/2010/01/8-powerful-awk-built-in-variables-fs-ofs-rs-ors-nr-nf-filename-fnr/) \n",
"for all the built-in variables in awk. \n",
"Let's deomonstrate the difference between NR and FNR:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"file_a.bed 1\r\n",
"file_a.bed 2\r\n",
"file_a.bed 3\r\n",
"file_a.bed 4\r\n",
"file_b.bed 5\r\n",
"file_b.bed 6\r\n"
]
}
],
"source": [
"awk '{print FILENAME, NR}' file_a.bed file_b.bed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"FILENAME is another built-in variable for the input file name of awk. \n",
"There are 4 lines in file_a and 2 lines in file_b, and NR increments for the total lines. \n",
"compare with FNR:"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"file_a.bed 1\r\n",
"file_a.bed 2\r\n",
"file_a.bed 3\r\n",
"file_a.bed 4\r\n",
"file_b.bed 1\r\n",
"file_b.bed 2\r\n"
]
}
],
"source": [
"awk '{print FILENAME, FNR}' file_a.bed file_b.bed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now, awk prints out the line numbers in respect to each file."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"From the awk code, we are reading file_b first. **NR==FNR** means when NR equals to FNR \n",
"(this is true only for file_b) do the following: `{a[$3,$4,$5]=$1OFS$2;next}`. \n",
"We **created an associated array** named **a** using columns 3,4,5 in file_b as keys and \n",
"the columns 1 and 2: `$1\"\\t\"$2` as values. we set OFS=\"\\t\" in the end of the command. \n",
"**next** means to proceed for the next line, rather than execute the following { } code block."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"when awk reads in the second file (file_a.bed), NR==FNR is not true, awk \n",
"exectues the second { } code block:\n",
"`{$6=a[$1,$2,$3];print}` \n",
"we look up the associated array *a* we created from file_b.bed using \n",
"the first three columns in file_a.bed as keys, and assign column 6 to \n",
"the looked-up values and print it out the whole line."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Conclusion: Awk is very powerful in text wrangling. Once get used to the \n",
"syntax, you can do fairly complicated formatting in an awk one-liner. \n",
"I strongly recommand you to learn it."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Bash",
"language": "bash",
"name": "bash"
},
"language_info": {
"codemirror_mode": "shell",
"file_extension": ".sh",
"mimetype": "text/x-sh",
"name": "bash"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
Enucatl/machine-learning-aging-brains | local_postprocessing/show_dataset.ipynb | 1 | 1080225 | null | mit |
betatim/BlackBox | examples/bayesian-optimization.ipynb | 3 | 220897 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Bayesian optimization with `skopt`\n",
"\n",
"Gilles Louppe, Manoj Kumar July 2016."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"np.random.seed(123)\n",
"\n",
"%matplotlib inline\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem statement\n",
"\n",
"We are interested in solving $$x^* = \\arg \\min_x f(x)$$ under the constraints that\n",
"\n",
"- $f$ is a black box for which no closed form is known (nor its gradients);\n",
"- $f$ is expensive to evaluate;\n",
"- and evaluations of $y = f(x)$ may be noisy.\n",
"\n",
"**Disclaimer.** If you do not have these constraints, then there is certainly a better optimization algorithm than Bayesian optimization."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Bayesian optimization loop\n",
"\n",
"For $t=1:T$:\n",
"\n",
"1. Given observations $(x_i, y_i=f(x_i))$ for $i=1:t$, build a probabilistic model for the objective $f$. Integrate out all possible true functions, using Gaussian process regression.\n",
" \n",
"2. optimize a cheap acquisition/utility function $u$ based on the posterior distribution for sampling the next point.\n",
" $$x_{t+1} = \\arg \\min_x u(x)$$\n",
" Exploit uncertainty to balance exploration against exploitation.\n",
" \n",
"3. Sample the next observation $y_{t+1}$ at $x_{t+1}$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Acquisition functions\n",
"\n",
"Acquisition functions $\\text{u}(x)$ specify which sample $x$ should be tried next:\n",
"\n",
"- Expected improvement (default): $-\\text{EI}(x) = -\\mathbb{E} [f(x) - f(x_t^+)] $;\n",
"- Lower confidence bound: $\\text{LCB}(x) = \\mu_{GP}(x) + \\kappa \\sigma_{GP}(x)$;\n",
"- Probability of improvement: $-\\text{PI}(x) = -P(f(x) \\geq f(x_t^+) + \\kappa) $;\n",
"\n",
"where $x_t^+$ is the best point observed so far.\n",
"\n",
"In most cases, acquisition functions provide knobs (e.g., $\\kappa$) for\n",
"controlling the exploration-exploitation trade-off.\n",
"- Search in regions where $\\mu_{GP}(x)$ is high (exploitation)\n",
"- Probe regions where uncertainty $\\sigma_{GP}(x)$ is high (exploration)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Toy example\n",
"\n",
"Let assume the following noisy function $f$:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"noise_level = 0.1\n",
"\n",
"def f(x, noise_level=noise_level):\n",
" return np.sin(5 * x[0]) * (1 - np.tanh(x[0] ** 2)) + np.random.randn() * noise_level"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Note.** In `skopt`, functions $f$ are assumed to take as input a 1D vector $x$ represented as an array-like and to return a scalar $f(x)$."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAAEACAYAAABVtcpZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXmYFOW1/7+nZ59hFmZgGNYZQMDdMeJ2UaaNRpEYAX9G\n4xaJicuNyVWv+UWTmLg9uYkm4eqNmogxRiVxV4ICiRBtEL2ILCOgwyoDzDAsMvsMMDPd7/3j7Zqu\n6q7eqqu7qrrP53n6mX6r3q4681Z3nXrPOe85JIQAwzAMk5m4rBaAYRiGsQ5WAgzDMBkMKwGGYZgM\nhpUAwzBMBsNKgGEYJoNhJcAwDJPBmKIEiOhZIjpARBvD7K8jonYiWu9/3WfGeRmGYZjEyDbpOM8B\n+D2AFyL0WSmEuNyk8zEMwzAmYMpMQAixCkBblG5kxrkYhmEY80ilT+BcIqonosVEdGIKz8swDMOE\nwSxzUDTWARgnhOgloksBLAQwOUXnZhiGYcKQEiUghOhWvV9KRE8RUbkQojW4LxFxMiOGYZg4EUIY\nMrmbaQ4ihLH7E9EI1fuzAJCeAlAQQtj6df/991suA8vJcrKcLKfySgRTZgJE9DcAbgAVRLQHwP0A\ncgEIIcR8AFcS0b8D6AdwBMDVZpzXKhobG60WISZYTnNhOc2F5bQHpigBIcS1UfY/CeBJM87FMAzD\nmAevGDbA3LlzrRYhJlhOc2E5zYXltAeUqD3JbIhI2E0mhmEYO0NEEDZwDGcMHo/HahFiguU0l2TK\nWVNTAyLiF78ivmpqakz/7qVqnQDDMBHYvXt3wlEeTPpDZH7iBTYHMYwNICJWAkxUwn1P/NvZHMQw\nDMPEBysBA7AN21xYToaxDlYCDMPYmsWLF+Oqq64y5Vjnn38+XnghUsZ761i4cCGuv/76lJ+XlYAB\n3G631SLEBMtpLk6R00yKi4tRUlKCkpISZGVlobCwcHDbSy+9lBIZ7rvvPvzkJz9JybmsZPbs2diw\nYQMaGhpSel5WAgzDhKWrqwudnZ3o7OxEdXU1Fi9ePLjtmmuuCenv9XpNPf/q1avR19eH008/3dTj\n2pWrr74a8+fPT+k5WQkYwCm2YZbTXJwiZ7LQS1b285//HN/61rdw7bXXorS0FH/9619xww034KGH\nHhrs869//Qvjx48fbDc3N+OKK65AZWUlJk6ciKeeeirsOZcuXYq6urrB9s6dO+FyaW9bahPPs88+\nC7fbjf/8z//E0KFDcdxxx2HZsmW6x963bx9OOeUUPP7444PHeeCBBzBt2jSUlJRg5syZaG9vH+z/\n1ltv4eSTT0Z5eTkuuugibNu2DQDwpz/9CVdcccVgv/Hjx+O6664bbI8aNQqff/45vF4vXC4X5s+f\nj0mTJqGiogJ33HGHRia3243FixeHHY9kwEqAYZiEUGzZHR0dYW33Sny7EAKXXXYZzj77bLS0tGDZ\nsmX47W9/i/fff1/3c5s2bcKUKVN0jxWO//3f/8Vpp52G1tZW3Hnnnfjud78b0mfnzp2oq6vD3Xff\nrbkRv/TSS3jxxRdx8OBBdHd3Y968eQCAhoYGfPvb38aTTz6JQ4cO4cILL8Tll18Or9eLuro6fPDB\nBwCApqYmAMCHH34IANi2bRsGBgZw4omBOlpLly7Fhg0bsH79eixYsADvvffe4L4TTjgBO3fuxNGj\nRyP+j2bCSsAATrENs5zmYqmcDzwAEIW+Hngg9v7h+ibIeeedh5kzZwIA8vPzI/b96KOP0NXVhXvu\nuQdZWVmYMGECbrrpJrz88su6/dvb21FcXByXPBMnTsSNN94IIsKNN96IpqYmtLYGMtdv2rQJF154\nIX7961+H5AX67ne/iwkTJiA/Px/f/OY3UV9fDwB45ZVXMGvWLNTV1SErKwv33nsvOjo68PHHH2PS\npEnIzc3F5s2bsWLFCsycORPDhg3DF198gZUrV2L69Omac/z0pz/FkCFDUF1dDbfbPXgOQPpghBCa\nGUiy4RXDDOMEHnggvpt4vP0TYOzYsTH33bNnD3bv3o3y8nIAcmbg8/lwwQUX6PYfOnQourq64pKn\nqqpq8H1hYSEAoLu7e/CcCxYswJQpUzBnzpyon+3ulvWw9u3bh+rq6sF9RIQxY8agubkZAFBXV4f3\n338fmzdvxkUXXYSCggJ4PB6sWLFCY84CgBEjRuieA5A+GCJCWVlZXP9zIvBMwABOsQ2znObiFDlT\nTbB5pqioCL29vYPtlpaWwfdjx47F5MmT0draitbWVrS1taGjowMLFy7UPfapp546aHtXjg1AYy7Z\nv39/XPI+/PDDKCkpwXXXXRfzKu1Ro0Zh9+7dg20hBJqamjB69GgAwPTp0+HxeLBq1SrU1dVh+vTp\nWLFiBVauXBmiBCLR0NCA4447LuqMykxYCTAMYyq1tbVYvHgx2tvb0dLSgt///veD+84991zk5uZi\n3rx5OHbsGLxeLzZv3oz169frHmvmzJka5VtVVYWqqiosWLAAPp8P8+fP19ycYyE3NxdvvPEG2tra\nYk4TfdVVV2HRokVYuXIlBgYG8Oijj6KkpARnn302ADkTWL58OYQQqKysxPTp07Fo0SJ0d3fj1FNP\njVm2FStW4NJLL43r/0kUVgIGYBu2ubCcziDW5GVz587F8ccfj+rqasycOVMTSpqVlYUlS5ZgzZo1\nqKmpQWVlJW677bawJp8zzzwT+fn52LBhw+C2Z555Br/85S8xfPhwfPHFFzjnnHNillt5n5OTg4UL\nF6K5uRk333xz1P/vxBNPxPPPP4/bbrsNlZWVePfdd7Fo0SJkZWUBkA7dgoKCQft/WVkZxo8fj/PP\nPz+sLHrtl19+GbfcckvE/8dsOIEcw9gATiAXnqVLl+K5557Dq6++arUoSWXhwoV4/fXXsWDBgrB9\nkpFAjpWAATwejyOeCllOc0mmnKwEmFjgLKIMwzCMqfBMgGFsAM8EmFjgmQDDMAxjKqwEDOCUeHGW\n01ycIifDxAMrAYZhmAyGfQIMYwNqamriXvTEZB7V1dVobGwM2c4hogzjVPr6gH37gLY2wOcDioqA\nkSOB0lKrJWMcBDuGU4xTbMMsp7mYLmd3N9DQABw+LBUAAPT0ADt2AHv3Gj5sxo5nknCKnEbhLKIM\nYwVHjsibfbhKXAcPyr9xZOhkGCOYYg4iomcBXAbggBBCN1sSEf0PgEsB9ACYK4SoD9OPzUFMeuP1\nyhnAsWPR+9bUABUVSReJcTZ2MAc9B+CScDuJ6FIAE4UQkwDcCuCPJp2XYZxHc3NsCgAA9uyJvS/D\nGMAUJSCEWAWgLUKXWQBe8Pf9GEApEY2I0N/WOMVGyHKaiyly9vYChw7F3t/nk4ogDjJqPFOAU+Q0\nSqocw6MBqD1dzf5tDJNZGHH4dnbK6CGGSQKmhYgSUTWAt/V8AkT0NoBfCSE+8reXA/ixECKkkgT7\nBJi0pbMT2L7d2Gfz8oCTTpK1ghkmiER8AqmKDmoGoA5zGOPfpsvcuXNRU1MDQBZnqK2tHUzhq0zN\nuM1tx7VbWuBZu1a2p06V++NpHz4Mz+bN9vl/uG1ZW3mvt3AsXsycCdRAzgRO0dk3E8DtQoivE9E5\nAB4TQuiWA3LCTMDD+e9NJSPk7OkBtmxJTIAYZwMZMZ4pxAlyWj4TIKK/AXADqCCiPQDuB5ALQAgh\n5gshlhDRTCLaARki+h0zzsswjkGJ+0+EY8ekb6C8PPFjMYwfThvBMMlmYADYuBEw43tdWAiccELi\nx2HSCjusE2AYJhxffmmOAgBkiGl3tznHYhiwEjCE2jljZ1hOczEs5+HDpsoRzbSU9uOZYpwip1FY\nCTBMMunuBo4ejd7vN78BvvpV4PvfB1aujNy3vR3o7zdHPibjYZ8AwySTPXtiWyHc2yuVxbp1wNNP\nAyeeCNx3H5Cbq99/9GigqspcWRnHwj4BhrEjQsS+0rewUEb9fO1rwIIFMsvoQw+F7//ll+bIyGQ8\nrAQM4BQbIctpLnHL2dkpI4PiJT8f+NWvgFtuCd/n2DGgq0t3V9qOp0U4RU6jsBJgmGShNwvw+aSZ\np7U18mezs4Fx4yL3MdvhzGQk7BNgmGQghFwbEDwTWLgQWLQI+NOfAFeCz2AuF3DaaYkfh3E87BNg\nGLvR3R2qADo6gKeeAu65x5wbt88nI4UYJgFYCRjAKTZCltNc4pJT7+a8YAFQVwdMmRL/yYXQDzXV\nMSul5XhaiFPkNAorAYZJBsFKoKsLePNNYO5cY8d75x3gwQdDtxt1PjOMH/YJMIzZHDkCfP65dtuW\nLcC//gXcfrvxY15+OfDMM7LusJrqamDYMGPHZdKCRHwCrAQYxmxaWoB9+8w/7vz5wP79wC9+od1e\nXAxMnmz++RjHwI7hFOMUGyHLaS4xy9nRkRwBrroK8HiAAwe027u6NGkk0m48LcYpchqFlQDDmMnA\ngCwgkwzKyoCvfx145ZXQfRwlxBiEzUEMYyatrcCuXck7flMTsGYNcMUV2u1sEspoLK8sxjCMn87O\n5B5/zBj5CkZZl5DNP2kmPtgcZACn2AhZTnOJSU61EvB6ZUhoJB+ByyWzgR5/vKwfXFMjcwfFixCD\nJqG0Gk8b4BQ5jcKPDQxjFkeOaPP8b9gA9PUBpaX6/fPygOOO09708/NlNtE9e+LPFNrWxqGiTNyw\nT4BhzOLAAWmzV/iv/wJGjdJfIJaTI5/+w9ULAGKvRaBAJHMJZWXF/hkmLeAQUYaxA+rUzgMDwHvv\nARdfHNqPCJgwIbICAGQW0ZKS8Pu9Xpk/SEGI5IWnMmkLKwEDOMVGyHKaS0Q5hdAqgTVrgLFj5Uwg\nmBEjgCFDYjtpTU14Z++PfgR8/LF2W3t7eoynjXCKnEZhJcAwZtDTo30q37oVuOii0H55ecDIkbEf\nNydHPxoIAM45B1iyRLuto0MqJIaJEfYJMIwZ6KWKEEKaftRMmAAMHRr/8bdulWGgatrbgdmzgcWL\ngaKiwPbjjgvvjGbSEvYJMIzV6JV6DFYAhYXGFACgPxsoKwPOOEP6HtTw6mEmDlgJGMApNkKW01zC\nyilEbKki4jEDBVNUJG/6wVx6KbB0qWaTZ/ly4+dJIY6/7mkCKwGGSZTubq0/QI+8PP2beDzoKZHz\nzpOOY3VNgWTmL2LSDvYJMEyixJI6etw4YPjwxM+1fXtsqSmqqoDRoxM/H+MI2CfAMFai9gds2iRv\n1GpcLrkK2AyqqmLrx34BJkZMUQJENIOIthDRNiK6R2d/HRG1E9F6/+s+M85rFU6xEbKc5qIrZ7A/\n4IUXgG3btH0qKsxbxVtcDBQUROziWbtW1iM+dsyccyYJR1/3NCLh3EFE5ALwBIALAewD8AkR/V0I\nsSWo60ohxOWJno9JAl1dMr68t1euQs3OlouZysulLZsJj3p9wMAAsHYtcE/Qc1BFhbnnrKwEdu+O\n3q+9XS5MY5gIJOwTIKJzANwvhLjU374XgBBCPKLqUwfgR0KIb8RwPPYJpIr2dqC5WT416kEkE5KN\nHs35aMKxf78cQwD49FPgkUeAv/0tsL+gADjxRHPP6fMBGzdKhR2JIUOAKVPMPTdjS6z2CYwGsFfV\nbvJvC+ZcIqonosVEZPKvgomL/n5gxw5g587wCgCQpo5Dh2SRdJubFixDvYBr9Wrg7LO1+83yBagJ\n52N4/HGtL6CnRxs1xDA6pCqV9DoA44QQvUR0KYCFAMKWQZo7dy5qamoAAGVlZaitrYXb7QYQsM9Z\n2a6vr8edd95pG3nCtdW2zMH9S5YA+/bBffrpsr12rdw/dWrkttcLTJ4Mz+rVpsvr6PH0eACvV47X\n6tXwfPWrwNq1gfHbtAnYssV8ec46Czh0SHu9mprgefFF1JeX487rrgOEgGfxYqC01BbjF9wOO542\na9vx+6m8b2xsRKKYZQ56QAgxw98OMQfpfGYXgDOEEK06+2xvDvJ4PIMXxc6EyHnoELB3r/HcMrm5\nwAknmF69yrHj2dsLNDQE2gsXysVbih8l2eaYhgYpg8I77wArVsBz9dWDSghlZcDEicmTIQEce91t\nSCLmIDOUQBaArZCO4RYAawBcI4RoUPUZIYQ44H9/FoBXhRA1YY5neyXgSJqbpf06UYqLgUmTQlMi\nZCIHD0qlGo6xY6UTN1Xnb28HZs0C/vnPQKEal0vWGHBxNHg6Y6lPQAjhBfADAO8C+AzAy0KIBiK6\nlYhu8Xe7kog2E9EGAI8BuDrR8zJxsGePOQoAkJFEZh3L6QQndAsm0RXC0Sgv1yrjsjJZqEadXtrn\n089rxDB+THk8EEL8QwgxRQgxSQjxa/+2p4UQ8/3vnxRCnCyEOF0I8W9CiI8jH9HeqO1ydsbj8chQ\nwniqU8VCS4sspWgSjhpPNZGUQFFR9KIxiZKdHVp0pq4Ontdf126z6cIxx173NIPniOnM/v3x16mN\nBSHk7CKTOXZMW084mGTPAhSCo4QuuwyYM0e7zaZKgLEHnDsoXYm3Pq0Rxo9PTgikEzh8GIgUmXHS\nSdoC8snC55PrE6IlsJsyJfZqZozjsHqdAGM39u5NvgIApLM5UxW2OlXEk08CH3wQaOflpUYBANLh\nG8usg2cDTBhYCRjA1jbC5mYZNYJAjH/S6OsbPFci2Ho8VWjkVPsD3ntPGwWU6qpeQYVqdK+7DZWA\nI697GsJKIJ1oaUl95M6BA9FNEemG1xtwjH/5JdDWJsNmFVKtBEpLo6f1OHbMVGc+kz6wTyBdUOew\nSTXJjoe3Gx0dMu0GALz7rozL/93vZNvlAmprU7+OYtcuoFW19nJgQCooderpUaMSq27G2Bb2CWQ6\nyVAAn3win3Bj4cCBzPINqP0B69bJOr8KxcXWLKQLrl28YQPw4x9rt8V6PZmMgpWAAWxlI4ygACL6\nBIQAVqwA1qzR3792LXDFFcCjj2pTE+jR16d9Co0TW41nBAblVPsD6uu1SiA4bj9VlJQMrgr2rF0L\nnH66/F4cOBDoc+SIrRIBOu66pymsBJzMvn3GZgD79wN33gk88UT4dAL//u/Am2/KG8d118lMopEw\nwUHsCIKLyDz3nLX+AAWXS3vu7Gxg2jSp6NXY0EHMWAv7BJyK0XUAK1YAv/wlcPXVwLe/DeTkRP+M\nYvN+7LHIufEzIRY9OGmcmtxc4JRTUiuPmrY24IsvAu333gNefx146qnAtqIimVqCSSsS8QmkKpU0\nYxY+n3QCGnmie/VV4Pnngd/8RiYVi5VLLpE392imjkOH0l8JREoVYZUpSKG0VM4IlGitc88FHnxQ\nFqZXZOvpkea7ZKe0YBwDm4MMYJmNsL9f1q+NUQGE+AROPRX485/jUwAK06YBY8ZE7tPWZqiIiVNs\nrh6PR2sKCsZqJeByAcXFgeteUADccIOMZlJjEwexo657GsMzAafQ1SVnAJHy1UQj2WYAIWQ6hXSu\naxtpJlBcnDo5whEcJfS974X2aWtL72vExAX7BOyOEIFFYE4Yl/x8mTcnHenvl7V9AWliIQrc+JNR\nS9gIAwMyl1A0TjmFTUJpBK8TSFd6e2VUTktL/Aog2QpDCP1ww6NHI5tMnIx6FvDWW8DTTwfaVpuC\nFLKzY/PLJBDSy6QXrAQMkHQb4cCATAK3ZUv0GH09vF7g/vvh+fOfzZdN4fXXgd/+Vn9fnOmrnWJz\n9SxfHmh8+qnWt2IHU5Afz2efRe9kAyWQ8uvu88kHl95eaV7t7JT+ks5O2e7pkSHRfX3yN2SVnCmG\nfQJ2or9fxtsfOqT5EsaF1ws89JC8Ec+YYa58ai6+WD4JX3utTCmtpq1NppJIt5KGSu4dIaRZ6J57\nZJvIXlFRschy5IictaUq22mq6evT3tiPHo0/aIFI5mTatUum28jODrxycuQ+9basLPlyWOlVe/oE\n9BYeqQdWea/+q37vcgW2uVyBdlZW4L1dEEJ+WQ8fljfPRK6Hzwc8/LA0Hz32WPJ/4C++KFfMKnlz\n1EyYEOqkdDJCyFQMQshqbbffLgu7A0BhIXDCCdbKF8znn2sTxj3zDHD22TJCTKGqChg9OvWyJYtj\nx+TvqL3d2mR5ijJwuQJ/lffB9ySlDQTaevc3NTr3L6qoSLN1AsmuWqVWCMoFUzS5WrPrvRJFCPkF\n7ekJTEmNPvWr8fnkIrDmZuDxx1PzhHfVVcArrwCbNoUukjp8OL2UQE9PQEFv3GhbU9AgpaWhN8Ll\ny7VKoLU1PZSAUve6s9NqSSRerzm/6RRhTyWQbIQwFM8OAMjOhmf9erj/7d8CCkSt7dVaWgj5ZRgY\nkK9jx+Q0NRmzrwMH5I/gscdkpArkOgH31Knmn0shL0+uOn7uOWDePO2+zk75P8egOD0eD9xud3Jk\nNIuensB4er3AeecF9tlMCXg8HrjPPFObVtztBu6+G7jrrsB3VDGZWCR/wte9pwdoaooctmsCSf8d\nWUxmKoFEGBiQP54kf/HiZuRIuRI41Vx+uVRqQoQqwPZ2YNiw1MuUDNTXe/Zs7T47+QMUioqk3VpZ\nV3LccfL6bNsm03soHD5sOyUWlYEBefM/fNhqSdICe/oEkl0Ri9GSkyPNB4WFcjYzMCCfsjo6EisY\nU1wMTJ5snpxWsnGj/kI9O/oDFHbv1kZq/fd/S3lvvTWwzeWSJqJoRWnsQkeHrO1sdCafptDUqbxO\ngDFAQQEwcaK051dXA8OHAxUVcjXphAlyeyLFYrq6ElvhbBeOHQv/f9hxFqAQXHv4gguAVau023w+\n26SRiIgQMmx6xw5WACbDSsAASa/dG42jR4EYYpfDyulyyTxAJ5wgbxThoqWys2Wo56RJxp8UY8hz\nZPs4bP/iN93xtKESGBxPVY0BAFKpqzOKKhjJRmsCMV93JWeWRenKLf+9JxlWAk6jvR34/veBf/3L\nmIM5L0/mEBoxIvZQ2ZISaUc2Eh3lhKfMaNg9X1A4iLQrmbOy9OXt7TW2KDEVHDkiF03azQeXRrBP\nwEk0NsoIj+nTgR/+MP7FWCUl0sxj9Km+p0c+kYXzEwwM6CeQO/XU2OoW2JWGBnmTHBiQ6SKuvFLe\nYJ2QJ+nwYfm9icawYdIkaCe6uoCdOx0VbmkV7BPIBDwe4OabZWrgO+6IXwFUVMgIkUQcgEVFwLhx\n4fevWgX8/Oeh251czcrnC8Tbb90KvPFGYAZlQ1NQCKWlsc34WlvtZWtvbwe2b2cFkAJYCRgg5TbC\nI0eAv/xFRncEhydGYFDOykqgpsacldIVFfKlx7Rpcol9U5N2exSTkK19AqpFYp533tEutrKpEtCM\nZ6wJ5Xy+lPsGwl731lZZIc0mVgr2CcQAEc0goi1EtI2I7gnT53+IaDsR1RNRrRnnzRgKCuSCrJNP\njv+zI0ZI566ZjB2rb97JyZH5ipR0Cgrd3fZ6yowHtS16507tSmGbKoEQgqOEvF5g9erQfocOWX/j\nbW2VDxJWy5FBJKwEiMgF4AkAlwA4CcA1RHR8UJ9LAUwUQkwCcCuAPyZ6XiuxZPWggad499e/Hr0a\nmBGyssIrlm98QyoBtd9AiNDqVipsvVpYUQJCwL13b0AJ5ORIJ7sNCRlPdQF6QH6XHnxQW48YkFE4\nKVyAFSKnogCSSX9/5Cy3OmHN6bxaGDBnxfBZALYLIXYDABG9DGAWgC2qPrMAvAAAQoiPiaiUiEYI\nIQ6YcP704csv5Q30+usTz1NUWZkcBaAwdKh0NAfna5k8Wd50PvlEJixTaGsLb0ayM0pthJYWqdiU\nXDtOmQUAUlkVFAR8Gy4X8LWvAcuWaReOATLVREVF6pMstrXF5sCOByGA+fPlDK6xUaZWOXpUzoze\nflu/qM6cOVIRKJlhS0rk3z//Wf83uXy53F9crH2ZkWcsRZgh6WgAe1XtJkjFEKlPs3+bvhJ4/31t\nhr1Ro+SipmAOHpT2Z3Xf3FwZ6ZDEdAWm5hLxeoH164ElS6Tz95JL5Bc1kZvM8OHA2LHJz8kzZozM\nVhnMzTeH/sC6uuRNVMehbdvcQUeOBByTubnwzJ4Nt3JzLCqyTq4o6I5nWZk2odzFFwO/+AVwyy3a\nG76SiTMF6T4G5WxvT44JSLmRX3ihTHdeVSVv0JEU3PLlUg4lNUxXFzyffAK33k3d65WKtKtL++rt\nBT78MPS77vNJv15RkTYpZW6uTMaod/wPPgj8L+r73LRpxsclCFuqq7m//S1q/FPtMpcLteeeC/fd\ndwMIOGncU6cCmzbB88wzcqpeVAT4fPC0twNnnAG3P0pF0/+11+B5/HGgoADuoUNlUW6vV/b/4Q9D\n+x86BM+qVUBREdzTpgGFhfCsW4f6rVsHlYCmf7zt116D5w9/AEpL4Z4zB7jjDnh27AC2bDF+/O3b\nga4uuP1RPIrzTbkpmNouKIBn2zags1Mrz5AhcJ9+eqh8HR3w+Esfqo9XX1+fHPkSbXd3a+U/88xA\n21+v2VbyIsJ4nnUW0NISkP+MM+T+114DJkzQXr9PP4X7O98BiJIv7+LFQHNzQB4jv6ddu+T/V10d\nut+fJ8ntT18S1/Hz8uDZtQv1fX2Q0gbtz8qC55vf1P+8XwFo+vt88AwMAPv3wz18uExK2Nws9/uV\ngKa/EPC88IK8v5WVyXZ7u1QCeXnwrFuHxn37kCgJrxMgonMAPCCEmOFv3wtACCEeUfX5I4D3hRCv\n+NtbANTpmYOSuk5gYCCQxrm7e1DTo7JSm1RL4R//AF54IVB9qK9PTg+vuw6YOze0/+bNMq2yMqY+\nnzz+qafqa+6tW+U0PVLYZTyUl4cWeEk2x44Bn30W21OcFfIlQmOjvo3c5QJqa+1VlyIWNm2S32GF\n554D9u0Dfvaz0L5jxiS/GH1Xl0wDYTQ/1ZYtMm16UxPw058C555rrnwOIpF1AmbMBD4BcBwRVQNo\nAfAtANcE9VkE4HYAr/iVRrsl/oDs7IDNLhZmzNBW5+rrk8ognL2vu1vm8wcCN4iSkvCmAz3FY5Sh\nQ2UYaKrJy5PnjqVcYUdHaLZROxNulWpRkXP+BzVlZdrUC9/4hnxw0aOlRSrtZC3y6+42rgDa2+XN\n/6OPpOlx9mxH2eDtRsLRQUIIL4AfAHgXwGcAXhZCNBDRrUR0i7/PEgC7iGgHgKcBfD/R81qC39/g\n2bFDf/+rieJPAAAYe0lEQVQ55wA/+pF83X23fN18s3xqTCZlZfIJO+jGlLL4+6qq2Pp5vfLpLwhb\nrhPo75ezHBWD8eI29gcAEcYzuMjPsGGyzoAeXm/oeg+z6O4Gtm+HZ82a+D87MADcdJO09b/xhly9\nnWQFkO7rBEwZPSHEPwBMCdr2dFD7B2aciwli6FBdBZBSCgpkRFCEMNBBOjq0+WzsSqRcNU6KDFIz\nZIi2xkA0WlvlbCA4xDQREjUBZWcDzz6bXlXrLIZzBzmZ8nLzVgInSmenXOav5vPP5UrnRx8NbMvN\nDS1FaUf27g2YTh59FLjiCpl2A5BrBZxqftizJ76VwdnZwIknmmMW6uiQaxMSqVHB6MK5gzKRykrr\nZwBqSkpC6xpPmACsWaN1rvb12TdjpRplJuD1AosXB0Im8/OdqwCA0NXD0RgYMCeFw5dfynh9VgC2\ng5WAASy3EY4eHVMqiJTb2oML0OTnA+efL9NeqwlKKGc7n4DXG1BUO3dKBVBWJq+7zf0BQJTxDLeQ\nqacnvJmou9v4Sl6lGMzu3SGKJOrvaNUquajLYiz/vScZVgJOwuWST9exOmJTTXl56AKZCy8E3ntP\nuy0W34GVKKuEAVlW0on5gsJBpD8buO8+uVAqHG1t8c8Ijh0zXgzm7beBhx92VkixQ2GfgFPIy5MK\noLDQakkiE1zX9uhRuQr673/X3nxOOUV/2b4daG6W6RMAmRr7jDMC2VtPOinU7OU09Pw3Ho/03/zl\nL5E/W1gob8yRxsDnkzd+JdVGvPz1r8DLLwO//701Yc8OhH0C6c7QobIUpN0VABCabkAxCW3Zot1u\n59mAOjLo008DIb5ZWc5XAIC+Sej88+XT/saNkT/b2ysd/o2NgVQggPzb0yMV6KZN8q8RBfDSS8Cr\nrwLPPMMKIEWwEjBAymyE2dnyqctgNTBLbO1FRaE3yocflmso1Kj8ArbyCSg3M4U//nGw4pbns88s\nEio+oo4nUWiIZVaWTFz43HPRTyCEdPZv2wZs2BB4bdkiZ1Axpg0P+R11dABLlwJPP20rkyf7BJjU\nQySTwJ10krSzO43g2YBeBFNXlz2rRqmKyACQyQsV+dNhFqCgF2f/jW/Ip/xgU1E0zIr4KS0Fnn8+\n+QrA5QokblNeOTlSEdol2i6FsE/ATihPaCNHOvuG09+vzaEUjgkT7LfoZ98+acvWY/JkexeWj5fg\nXEKAzOBbXS2vjZMhkosYi4qkGTUvT76ys6OXZvX55APKwIB8eb3yO6209V4Wh75anTvIfCJFYKhv\nLEIE2sp79cvn0/axK7m5Mof7sGH2dZbGQ06OvFkG1xoIpr3dfkog3EphIkeEh8ZFeXnAAa5wwQXW\nyGIGLpecTSi1LozW03a55CueBXJCBBSG+qUoFJ9P+wq+P6lfyvHUf4Pfm4g9lYCZidWAwICrX8EX\nS9H86icA9UtFwvUEXC75dFJcLL+0Sbq5WJqnv6IiuhLwJ5TzrFhhj3oCQmj9AWry8+FZudIeckYh\n5uuupwRSiGfJErhnzkz8QLm5co3KsGHGb/wRiGk8iaTSSFbCvSRiTyVgNkTyy2H0CyKEVjm0tMgp\ns7JNUSqKslHOqRSAyM6WX47cXGnmyctLf9tjWZn839XT5HXrpMLz5+IPl1DOMrq7A/IeOSKvl/Kd\nGTLEWLy7nSkokA8jVqzgXrIE+N3vZFSSURNbTo702VhRCS2NsKdPwGYyMQb54gsZdqiwYIFcR6DO\nXz98uHn1FBJF7Q94+mmppL7vT3g7frwznfTROHhQruhNJe+8AzzxBPDUU8Z8D0TyyX/UqOj2/QyB\niHidAGNDgm+abjewYoU2KshO6wXUs5JPP5XFgBTSzR+gUF4e/im6rU0WVjKTRYuAJ58E/vAHYwqg\noEDOJMeMYQVgEjyKBrBVXHsELJeztFRrghszRk7dN20KbOvrg2fp0tTLFox6fcDAgCy2omQ7zcmR\n5fysHs8YiUvO7OzwSeWEAObNA+rrTZELS5bIdRd/+AMwfnz88ffDh0sFkOJFk0657kZhJcAkD708\nNcpsQE2k3P2poqsrEH2xfbuMVVfy6KfrLEAhXFH58nLg/vuBn/xEmwrEKFOmSCUQ70pgl0t+Ztw4\nfvpPAuwTYJJLR4csIqKwZYu8qbz5pnYR1kknWSOfQlMTcMBf8fSll6Q/Q/FdpKLertVs3hxSSW2Q\nP/1JZvR88snUK8TsbFnHId0VcYKwT4CxL8Hx2lOmAD/4gTbm+ehR+bISdThrZydw5pmBdibcgIYP\nD7/vppsC1+3IkdTJlJcnzT+ZMP4WwkrAAE6xEdpCTiJteUIimV5aNa33rF0bUmMgpfT3a29ut94K\nXHyxfE80aIO2xXjGgCE5hw0Lb2pxuYB77wWuuUbemKNx9CiwbFnUbhF9AoWFUgHEcr4k45TrbhRW\nAkzyiWVVsDqUNNVEWtRWWJgZduisLOm0DweRVIzhxsLnkwnlnn4amDULePfd0JQUsVJUJFN0OLmC\nm4NgnwCTfHw+GXIZLb+KVTUGdu2SRdX1GDFC+gQygaNHASOZUu+6S5YRHTFCZou98krjuYeGDJE+\ngCSs/E1nEvEJsKplko/LJX0D0Uw+bW3WOGAjzQQyyR6dny+jueI1zT30kHxqLyhI7PxDhgCTJmXG\nzMtG8GgbwCk2QlvJqWcS8te0HbQNW2ES6umJnP9elczQVuMZgYTkHDky/s8UFxtSABqfQFGRnAHY\nUAE45bobxX4jzqQnpaXalan9/cBll2lX6fb0GLcjG0W9YvnLL4GPPgq08/IcmRAsIQoLtY78VJ1z\n0iQ2AVkE+wSY1LF9u9b0ctddsv7wjBmBbaNHp7aqVENDIIHawoUyyd3DD8t2RUVmljjs7ZXjkgoK\nCtgJbAK8ToBxBsGrh+vqZIFzNak0CfX3azNorlsni8orZJI/QE1hYeRIIbPIz5czAFYAlsJKwABO\nsRHaTs5gJXD++cDq1fCsXh3Y1tubuoVjalOQEKFKIKi4ke3GMwymyJnsDJ15efC0tDjC3OaU624U\nVgJM6sjJ0T5dV1QAEyfKVBJqwoVrmo161tHUJP8q4aBZWYlHuziZ3FypCJJBXh6bgGxEQj4BIhoK\n4BUA1QAaAVwlhAjJDUxEjQA6APgA9AshzopwTPYJpDP79wPNzYH2a6/JG+4VVwS25eUBJ5+cXDm8\nXrl2QfmuBfsDSktltEomI4RU0GYWncnPlwrAATMAJ2GlT+BeAMuFEFMAvAfgJ2H6+QC4hRCnR1IA\nTAYQbBL65je1CgCQicySnVnUX9pykJoaYM6cQDtSnetMgUgW0zHLLKQ4gVkB2IpEr+4sAM/73z8P\nYHaYfmTCuWyDU2yEtpRTKa+pQjeHzOHDyZUj2AFdWwt85SuBto4SsOV46mCqnPn5spRqohQXyyR0\nKgWQkeNpQxK9MVcKIQ4AgBBiP4DKMP0EgGVE9AkR3ZzgORmnE66IiZq2tuhpJozi9UauaOZyZW5k\nkB7l5Yn5B4YN43UANiaqZ4aIlgFQr+UnyJv6fTrdwxnzpwkhWohoOKQyaBBCrAp3zrlz56LGH59d\nVlaG2tpauN1uAAGtbHVbwS7y6LXdbret5BlsHzkCd6V8XgieBSht99SpQFsbPP4qZKaev6MDbr8D\nWHM+pV1QAPfpp4d83rbjqdNWMP34ixbJtnq8wrVdLnj27AG6uuD2zyZ4PM2Tx+PxoLGxEYmSqGO4\nAdLWf4CIqgC8L4Q4Icpn7gfQJYSYF2Y/O4bTHSGAjRsjp2sApElmyhTzz79tm3alcjAjRyYvMsbp\ntLUBu3dr60TrUVYGjB1rTULADMRKx/AiAHP9728E8PfgDkRUSERD/O+LAFwMYHOC57WU4KcDu2Jb\nOYNqDHjWrpWVrYLl7e42v4hJX19kBQCEdQrbdjyDSKqcQ4fKyK2qqlAHb1aWNB0df7wM/Y2iAHg8\n7UGigbqPAHiViG4CsBvAVQBARCMBPCOEuAzSlPQWEQn/+f4qhHg3wfMyTqe0VOv87e0Fnn1W1iBW\nc/CgOY5JhWCH84cfysL3t90m20QcGRSN7GyZ3mP0aKlUBwakArBBARgmfjh3EGMNPh9QXx8I0xwY\nAGbOlIpg7NhAP5dL1hkwa2HRpk3aJHWPPCJNPzfcINtFRfJJlmEcBOcOYpyHy19jQCE7W5adfDdo\nkujzAYcOmXPO9vbQLKWrV8tCKAo8C2AyDFYCBnCKjdD2cvpDRQcjhC6+WL827cGD5oSLBiuT3btl\nniL1yuDi4rAft/14+mE5zcUpchqFlQBjHcF56087Taaa3rVLu31gQOb6T4Te3tAKYitWANOnB+oc\nsD+AyUDYJ8BYy5YtspiMws6d+qGFOTkyKsVl8Lnliy9CVwnffjtw7bXAtGmyXVgInBAxwplhbEki\nPgFWAoy1BCeUi8SoUcbKHx45Anz+eej2vj6pVBSnc1WVjHhhGIfBjuEU4xQboSPkLCvTzx2kx/79\nxspPKmmig8nN1UYdRfAHAA4ZT7CcZuMUOY3CSoCxlvz82FeV+nzAnj3xHb+9PdQXoAf7A5gMhc1B\njPU0N8un/FiprpZJyaIxMCDNQP390fsmK0UFw6QANgcxzkYvq2hXF7B3r37/vXu1zmQ9hJBRRrEo\nAEC7ZoFhMghWAgZwio3QMXJ+8kloHpoPP5SrefXw+YAdO8JXvBJCrgEIZwZatSq0jnEUfwDgoPFk\nOU3FKXIahZUAYw+GDtW23W6goSG8mWhgANi6VS4kU5sPjx4Ftm8PX5Tm8GHgvqAs6FlZXD+AyVjY\nJ8DYg64umeJZzSOPyGL03/te5M8qReG93uhZR196SfoJlFrCgDRHTZxoTG6GsQHsE2Ccz5AhoUni\n5swB3noret0Brze2tNNCyOPNmqXdzv4AJoNhJWAAp9gIHSUnUaiDePJkYMwYYPlyc06kFLI54wzt\n9uD0FZHkdAAsp7k4RU6jmJSfl2FMYOjQ0BxBP/yheWmkFy6UswtSzZrjWafAMGkI+wQY+xBr2Umj\nrF0rM4aqZxwjRsjZBsM4GPYJMOkBUWiUkJlMnRpqcorRFMQw6QorAQM4xUboSDmTqQSCycqKK1WE\nI8fTxrCc9oCVAGMviotDF44li9JSrX+AYTIQ9gkw9qOpCThwIHT7l1/KPEOnnWbOeSZMSO3Mg2GS\nBPsEmPSivFx/e1MTcO+9ck1ArPzzn3IhWjBEvD6AYcBKwBBOsRE6Vs7CQrkCOJjaWlkF7PHHYzvw\nZ58B8+Zp00oolJRIn0AictoUltNcnCKnUVgJMPakokJ/+513AuvXA2++Gfnz3d0yR9Ddd+s/8bMZ\niGEAsE+AsSv9/cCmTfpP8Xv2yHxCDz0EnHNO6P6jR4G77gLGjwd+/OPQ/UTSrxDnTIBh7Ar7BJj0\nIycnfAz/uHHAo4/KdNLBdHYCt94KDB8uZwF6lJayAmAYP6wEDOAUG6Hj5YxUPay2Frj++tDtQ4YA\n110HPPhg+Bt9OFNTFBw/njaD5bQHrAQY+1JaGn9eH5cLuPji8PH/2dm8SphhVLBPgLE3+/fLtQFm\nUVkJjB1r3vEYxgZY5hMgoiuJaDMReYnoKxH6zSCiLUS0jYjuSeScTIYxbJh8ujfzeAzDDJLor2sT\ngDkAVoTrQEQuAE8AuATASQCuIaLjEzyvpTjFRpgWcmZnG7bhhzBkiP76gxhJi/G0ESynPUhICQgh\ntgohtgOINA05C8B2IcRuIUQ/gJcBzIrQn2G0jBhhTo6fysrEj8EwaYYpPgEieh/A3UKI9Tr7/h+A\nS4QQt/jb1wM4SwjxH2GOxT4BJpRdu4DWVuOfz80FTj6ZE8YxaUkiPoGoJZuIaBmAEepNAASAnwkh\n3jZyUoaJm5EjgbY2/cVjsVBVxQqAYXSIqgSEEF9L8BzNAMap2mP828Iyd+5c1NTUAADKyspQW1sL\nt9sNIGCfs7JdX1+PO++80zbyhGurbZl2kCdcO+bxrKiA5x//kO2pU+X+tWujt3Ny4P7KVxKWN+3G\n0+I2j6fxtvK+sbERiWKmOehHQoh1OvuyAGwFcCGAFgBrAFwjhGgIcyzbm4M8Hs/gRbEzaSfnwACw\neTPg9cZ3gpoaU5zLaTeeFsNymkci5qCElAARzQbwewDDALQDqBdCXEpEIwE8I4S4zN9vBoDHIR3R\nzwohfh3hmLZXAoyFHDokcwfFSlERcLyjg9EYJiqWKYFkwEqAicr27TJHUDRcLqkAEggLZRgnwAnk\nUozaLmdn0lbO8eNjSycxdqypCiBtx9MiWE57wEqAcR7Z2cCkSZFrEVdV8epghokBNgcxzqWvD9i9\nW2saysoCxoxhBcBkFOwTYDKb3l6gp0cqAK4VwGQg7BNIMU6xEWaMnIWFsohMeXlSFUDGjGeKYDnt\nASsBhmGYDIbNQQzDMA6HzUEMwzCMIVgJGMApNkKW01xYTnNhOe0BKwGGYZgMhn0CDMMwDod9AgzD\nMIwhWAkYwCk2QpbTXFhOc2E57QErAYZhmAyGfQIMwzAOh30CDMMwjCFYCRjAKTZCltNcWE5zYTnt\nASsBhmGYDIZ9AgzDMA6HfQIMwzCMIVgJGMApNkKW01xYTnNhOe0BKwGGYZgMhn0CDMMwDod9AgzD\nMIwhWAkYwCk2QpbTXFhOc2E57QErAYZhmAyGfQIMwzAOh30CDMMwjCESUgJEdCURbSYiLxF9JUK/\nRiL6lIg2ENGaRM5pB5xiI2Q5zYXlNBeW0x4kOhPYBGAOgBVR+vkAuIUQpwshzkrwnJZTX19vtQgx\nwXKaC8tpLiynPchO5MNCiK0AQETRbFGENDI9tbe3Wy1CTLCc5sJymgvLaQ9SdWMWAJYR0SdEdHOK\nzskwDMNEIepMgIiWARih3gR5U/+ZEOLtGM8zTQjRQkTDIZVBgxBiVfzi2oPGxkarRYgJltNcWE5z\nYTntgSkhokT0PoC7hRDrY+h7P4AuIcS8MPs5PpRhGCZOjIaIJuQTCEJXACIqBOASQnQTURGAiwE8\nGO4gRv8RhmEYJn4SDRGdTUR7AZwD4B0iWurfPpKI3vF3GwFgFRFtALAawNtCiHcTOS/DMAxjDrZb\nMcwwDMOkDkvDNonoUSJqIKJ6InqDiErC9JtBRFuIaBsR3WOBnI5YFBeHnFaP51AiepeIthLRP4mo\nNEw/S8YzlvEhov8hou3+725tqmSLVUYiqiOidiJa73/dl2oZ/XI8S0QHiGhjhD6WjqVfhohy2mE8\niWgMEb1HRJ8R0SYi+o8w/eIbTyGEZS8AF0H6CwDg1wB+pdPHBWAHgGoAOQDqARyfYjmnAJgE4D0A\nX4nQ7wsAQy0cz6hy2mQ8HwHwY//7ewD82i7jGcv4ALgUwGL/+7MBrLahjHUAFlnxPQyS4zwAtQA2\nhtlv6VjGIafl4wmgCkCt//0QAFvN+G5aOhMQQiwXQvj8zdUAxuh0OwvAdiHEbiFEP4CXAcxKlYyA\nXBQnhNiOMM5vFZYuiotRTsvH03++5/3vnwcwO0w/K8YzlvGZBeAFABBCfAyglIhGIHXEeg0tD7IQ\nMhS8LUIXq8cS/nNHkxOweDyFEPuFEPX+990AGgCMDuoW93jaaRXvTQCW6mwfDWCvqt2E0H/cLjhh\nUZwdxrNSCHEAkF9sAJVh+lkxnrGMT3CfZp0+ySTWa3iu3ySwmIhOTI1ocWP1WMaDbcaTiGogZy4f\nB+2KezzNDBHVJZbFZkT0MwD9Qoi/JVuecDhlUZxJciadCHLq2VLDRSek1SLDFLMOwDghRC8RXQpg\nIYDJFsvkZGwznkQ0BMDrAO7wzwgSIulKQAjxtUj7iWgugJkAvhqmSzOAcar2GP82U4kmZ4zHaPH/\nPUREb0FO2029aZkgp+Xj6XfAjRBCHCCiKgAHwxwj6eOpQyzj0wxgbJQ+ySSqjOqbgxBiKRE9RUTl\nQojWFMkYK1aPZUzYZTyJKBtSAbwohPi7Tpe4x9Pq6KAZAP4/gMuFEMfCdPsEwHFEVE1EuQC+BWBR\nqmTUIeyiOL+GhmpR3OZUChYsUpjtdhjPRQDm+t/fCCDky2zheMYyPosAfNsv2zkA2hXzVoqIKqPa\nDkxEZ0GGg1ulAAjhv49Wj6WasHLaaDz/DOBzIcTjYfbHP54We7u3A9gNYL3/9ZR/+0gA76j6zYD0\nhG8HcK8Fcs6GtLMdAdACYGmwnADGQ0ZpbIBMsW1LOW0ynuUAlvtleBdAmZ3GU298ANwK4BZVnycg\nI3Q+RYSIMatkBHA7pNLcAOAjAGenWka/HH8DsA/AMQB7AHzHbmMZi5x2GE8A0wB4Vb+L9f7vQULj\nyYvFGIZhMhg7RQcxDMMwKYaVAMMwTAbDSoBhGCaDYSXAMAyTwbASYBiGyWBYCTAMw2QwrAQYhmEy\nGFYCDMMwGcz/AUL9kM1evLNfAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f704dc05588>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot f(x) + contours\n",
"x = np.linspace(-2, 2, 400).reshape(-1, 1)\n",
"fx = [f(x_i, noise_level=0.0) for x_i in x]\n",
"plt.plot(x, fx, \"r--\", label=\"True (unknown)\")\n",
"plt.fill(np.concatenate([x, x[::-1]]),\n",
" np.concatenate(([fx_i - 1.9600 * noise_level for fx_i in fx], \n",
" [fx_i + 1.9600 * noise_level for fx_i in fx[::-1]])),\n",
" alpha=.2, fc=\"r\", ec=\"None\")\n",
"plt.legend()\n",
"plt.grid()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bayesian optimization based on gaussian process regression is implemented in `skopt.gp_minimize` and can be carried out as follows:"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from skopt import gp_minimize\n",
"\n",
"res = gp_minimize(f, # the function to minimize\n",
" [(-2.0, 2.0)], # the bounds on each dimension of x\n",
" acq_func=\"EI\", # the acquisition function\n",
" n_calls=15, # the number of evaluations of f \n",
" n_random_starts=5, # the number of random initialization points\n",
" noise=0.1**2, # the noise level (optional)\n",
" random_state=123) # the random seed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Accordingly, the approximated minimum is found to be:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'x^*=-0.3143, f(x^*)=-0.8533'"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"\"x^*=%.4f, f(x^*)=%.4f\" % (res.x[0], res.fun)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For further inspection of the results, attributes of the `res` named tuple provide the following information:\n",
"\n",
"- `x` [float]: location of the minimum.\n",
"- `fun` [float]: function value at the minimum.\n",
"- `models`: surrogate models used for each iteration.\n",
"- `x_iters` [array]: location of function evaluation for each\n",
" iteration.\n",
"- `func_vals` [array]: function value for each iteration.\n",
"- `space` [Space]: the optimization space.\n",
"- `specs` [dict]: parameters passed to the function."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" fun: -0.85334081261963912\n",
" func_vals: array([-0.16593485, 0.28782384, 0.07394852, 0.68845217, -0.33531023,\n",
" -0.02492362, -0.18834878, -0.0666829 , 0.00322918, 0.09743466,\n",
" 0.01277742, -0.28339062, -0.82439528, -0.85334081, -0.80310607])\n",
" models: [GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f7068616cf0>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f7068616e10>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f7068616e58>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b42d0>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b4120>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b41f8>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b4048>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b4240>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b4090>), GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f70685b4438>)]\n",
" random_state: <mtrand.RandomState object at 0x7f7068616ca8>\n",
" space: Space([Real(low=-2.0, high=2.0, prior=uniform, transform=identity)])\n",
" specs: {'function': 'base_minimize', 'args': {'kappa': 1.96, 'xi': 0.01, 'n_calls': 15, 'n_points': 10000, 'n_random_starts': 5, 'dimensions': [(-2.0, 2.0)], 'acq_optimizer': 'lbfgs', 'acq_func': 'EI', 'n_jobs': 1, 'func': <function f at 0x7f704dbe6f28>, 'random_state': 123, 'n_restarts_optimizer': 5, 'verbose': False, 'callback': None, 'base_estimator': GaussianProcessRegressor(alpha=0.0, copy_X_train=True,\n",
" kernel=1**2 * Matern(length_scale=1, nu=2.5),\n",
" n_restarts_optimizer=2, noise=0.010000000000000002,\n",
" normalize_y=True, optimizer='fmin_l_bfgs_b',\n",
" random_state=<mtrand.RandomState object at 0x7f706864f900>), 'y0': None, 'x0': None}}\n",
" x: [-0.31431138440563028]\n",
" x_iters: [[0.78587674239144656], [-0.85544266019848214], [-1.0925941857431876], [0.20525907633156493], [0.87787587914225229], [1.0930078275284332], [-1.5825827673513784], [-1.8740230637856115], [2.0], [1.5920603878809236], [-1.3948575246313792], [0.91055125680324844], [-0.38405568667841866], [-0.31431138440563028], [-0.30894059737550278]]\n"
]
}
],
"source": [
"print(res)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Together these attributes can be used to visually inspect the results of the minimization, such as the convergence trace or the acquisition function at the last iteration:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZQAAAEbCAYAAAD9I3KtAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYFOW5/vHvzSKLCDPsm4BLVI7BoMYtokEBV1wTF2IS\nJ4s5MSYSPecXOcaEeOIxYhb1nJhEoxFi1KgkLkENEGFco6LSiIJoXABBRvZFUASe3x9Vje3QPTPd\nVE9V9Tyf65qLruq3q+8poN+u96l6S2aGc845t7NaxR3AOedcZfAOxTnnXCS8Q3HOORcJ71Ccc85F\nwjsU55xzkfAOxTnnXCS8Q3HOfYKkgZK2SfLPB1cU/wfjUkXSlyTNkrRe0hJJD0k6Mu5cFahJF6hJ\nGi/pj+UO49LBOxSXGpIuBX4FXAX0BAYANwKnxJkrl6TWcWdwLi7eobhUkNQZuBL4jpk9YGabzGyr\nmT1sZuPCNrtIuj48cnlH0nWS2obPfV7SYkmXSqoL29SEzx0q6V1Jynm/MyTNCR9L0jhJ/5K0XNKf\nJVWFz2WHh74uaSHwaLj+q5LeDttfIektSccWsb2vSloo6T1Jl+fkaiXp8vC1a8OjtX7hc/tJmiZp\npaT5ks5qYH/OlHS1pGfD7dyXzZCnbR9JD4TbfU3SN8P1xwOXA+eER4yzS/m7dZXDOxSXFkcA7YD7\nG2hzBXAocADwmfDxFTnP9wZ2A/oC3wRulNTFzJ4DNgDH5rQdA/wpfHwxcCpwVPja1cBv6r330cB+\nwPGSBhMcOY0B+gBdwtdlNWV7RwKfAkYCP5a0b7j+P4BzgBPMrAvwdWCjpI7AtDBzd+Dc8Pfbr/Du\n4itATbhftgL/V6Dd3cCisN1ZwNWShpvZVOBq4G4z283MDmzgvVxLYGb+4z+J/wG+BCxtpM2/gONz\nlo8D3gwffx54H2iV83wdcGj4+KfAreHj3Qg6mP7h8jzgmJzX9QE2E3whG0jwYTww5/kfAXfkLHcA\nPgSOLWJ7fXKefxY4O3z8KjA6z+9+NvBYvXW/A35UYF/NBK7OWR4cZlROhlbA7sBHQMectlcDfwgf\njwf+GPe/D/9Jxk+bonsg5+KxEuguqZWZbSvQpi/BN+mshXzyyGBlvdduBDqFj+8EnpL0beBM4AUz\neyd8biBwn6Tsa0XwIdsrZ1vv5DzuCyzOLpjZJkkrc55vyvbqCuTcHXiTHQ0EDpe0KmebrYHb87TN\nWpzzeCHQluDoJlcfYJWZbazX9uAGtutaKB/ycmnxT4Jv0Kc30GYJwQdr1kBgaVM2bmbzCT4oTyIY\nqroz5+lFwIlm1jX8qTazXc3s3dxN5Dx+F+ifXZDUAehW5PYKWQzsVWB9bb1tdjazixrY1u45jwcS\nHCWtqNdmKdBV0q456wYQ7Gto4tlgrmXwDsWlgpmtIxheuVHSaZI6SGoj6URJ14TN/gxcIam7pO4E\nQ08NfUOv705gLEFt496c9TcR1A0GAEjqIenUnOfFJ00GTpF0eHhSwE/qPV/s9nLdAvxU0t7ha4dI\nqgamAPtI+nK4X9pK+mwjNZQvh4X8jgQnPNxrZtkOQgDhUdrTwM8ktZN0APANPt6vdcCg3BMaXMvl\nHYpLDTP7FXApQaH9PYJv+t/h40L9VcDzwEvAnPDx/zS0yXrLfyYorj9qZqty1t8APABMk7SW4AP2\n0ELbMbN5wPcIitlLgXVh3g9L2V695V8B9+S89hagg5ltIKgZnRu+51LgGmCXBn7/24FJYdtdCDrT\nfO85BtgjbPcXgrrMzPC5ewk6n5WSnm/gvVwLoI+/kCRD+G3rboJD8LcJipFr87S7FRgN1JnZAc0a\n0rkihMNFa4C9zWxh3HkgOG0YuN3M/hB3Flc5kniEMg74h5ntC8wA/qtAu9uA45stlXNFkDQ6HJbb\nFfgl8FJSOhPnyiWJHcppBIfhhH/mLcKa2ZME5+87l0SnEQwRvUNQRD833jg7SNbQhKsISRzyWmVm\nXQst12s7EPibD3k551z8YrkORdJ0PnnOvQi+MV2Rp3myejznnHN5xdKhmNmoQs+F8yz1MrM6Sb0J\nzo4pmSTvkJxzrgRmVtTp4EmsoTxIML8QwPkEp1cWIho+Zx9Ix/Qy48ePjz1DpeRMQ0bP6TmT/lOK\nJHYoE4BRkhYAIwjOpc/OeDol20jSnQTn7+8jaZGkr8WSNiJvv/123BGaJA0505ARPGfUPGf8EjeX\nlwUXlI3Ms/5dgutOsstfas5czjnnGpbEI5QWqaamJu4ITZKGnGnICJ4zap4zfok7bThqkqzSf0fn\nnIuaJKwCivItUm1tbdwRmiQNOdOQETxn1Dxn/LxDcc45Fwkf8nLOObcDH/JyzjkXG+9QEiIt46pp\nyJmGjOA5o+Y54+cdinPOuUh4DcU559wOvIbinHMuNt6hJERaxlXTkDMNGcFzRs1zxi9xc3kl2dK6\ntfz+ridZsXoD3as7ccGYYfTt1SWSbWZmP8tjmfcj3WbSczrnKovXUJpoad1aLrnyHpbUrd2+rl+v\nLvzqx2eV/MG6tG4tl/73vand5nXjz/ZOxbkKVUoNxTuUJrry+oeY/sT8CBJVjlFHDWb890+OO4Zz\nrgy8KF9GK1ZvKOv21y5/o6zbj0puzpVl3ielSssYteeMlueMn9dQmqh7dae863fmW3qho560bLNb\ngX3inGuZ/AiliS4YM4x+9eoF/Xp14YIxwyLZZpcee0W+zSTnLKfhw4fHHaFJPGe0PGf8vIZShOyZ\nTitXb6BbxGdPpWGbv/vT49Q+8xrbthk/u+w0jjr0Uzu1TedccnlRPo+0XClfW1ubim8uY8ddzwuv\nb+G4owfz47HJLMinZV96zmh5zmhVRFFeUrWkaZIWSJoqaYev1pL6S5oh6RVJcyVdHEfWlujzh+1N\n61bi0acWsHzl+rjjOOcSJHFHKJImACvN7FpJlwHVZjauXpveQG8zy0jqBLwAnGZmr+bZXiqOUNLk\nx7/8GzOeXsCXzziUb3/56LjjOOfKoCKOUIDTgEnh40nA6fUbmNkyM8uEjzcA84F+zZawhTv7lIMB\neGD6S2z6YHPMaZxzSZHEDqWnmdVB0HEAPRtqLGkQMBR4tuzJyigt56bX1tby6X368ul9+7J+wwc8\nUvtK3JF2kKZ9mQaeM1ppyVmKWK5DkTQd6JW7CjDgijzNC45XhcNdk4Gx4ZFKXjU1NQwaNAiAqqoq\nhg4dur0olv3LjXs5Kyl5Ci1nMhkAzh59MC8vWMqvb7qTql3WcOyxxyQiX21tLZlMJjH7qxKWfX+2\njP1ZW1vLxIkTAbZ/XhYriTWU+cBwM6sLayUzzWxwnnZtgCnAI2Z2QwPb8xpKGWzZuo1zL7qFZcvX\ncc24Mxh2yF5xR3LORahSaigPAjXh4/OBBwq0+wMwr6HOxJVPm9at+OJJBwFwz5TnY07jnEuCJHYo\nE4BRkhYAI4BrACT1kTQlfHwkcB5wrKTZkl6UdEJsiSOQPfRMutyco0cMoUP7trz48mJef+u9+ELV\nk8Z9mWSeM1ppyVmKxHUoZrbKzEaa2b5mdpyZrQnXv2tmo8PHT5lZazMbamYHmtlBZvb3eJO3PJ12\nbccpIw8A4G4/SnGuxUtcDSVqXkMpr6V1azj3u7fSqpWY/LtvFZxE0zmXLpVSQ3Ep0rdXFUcdsjdb\ntmzjr49k4o7jnIuRdygJkZZx1Xw5zzn1swA8MG0OH374UTMn2lGa92USec5opSVnKbxDcTttyL59\nGbx3b9au38TfH5sXdxznXEy8huIiMf2J+Vx5/UMM7NeV26//Gq1aFTX06pxLGK+huNgcc8Q+9Oy2\nGwuXrOLZzFtxx3HOxcA7lIRIy7hqoZxt2rTmCycdCMA9U15oxkQ7Svu+TBrPGa205CyFdyguMqeM\nPID27dowa85C3li4PO44zrlm5jUUF6nrbnmUvzwym5OP/TT/dVGqJy9wrkXzGoqL3VknH4QE0x6f\nz6o178cdxznXjLxDSYi0jKs2lrN/n2qO/OxefLRlK/dNjedCx0rZl0nhOaOVlpyl8A7FRe6cU4IL\nHe/7e4YPN2+JOY1zrrl4DcVFzsz4xv+7ndfeeo9xFx7P6JFD4o7knCuS11BcIkji7NHBfefvnvI8\n3qE71zJ4h5IQaRlXbWrOEUfuR7fqXXlr8Uqef2lheUPVU2n7Mm6eM1ppyVkK71BcWbRt25ovnBhc\n6Pjnv/m9UpxrCbyG4spm7fpNnPmtm/hw8xZuv76GPXbvHnck51wTeQ3FJUqX3Tpw4vD9Abhnyosx\np3HOlZt3KAmRlnHVYnNmi/NTH5/HmnUby5BoR5W6L+PiOaOVlpylSFyHIqla0jRJCyRNldQlT5t2\nkp6VNFvSXEnj48jqGjegX1c+d/CebN68hfunzYk7jnOujBJXQ5E0AVhpZtdKugyoNrNxedp1NLON\nkloDTwEXm9lzedp5DSVmz7+0kO9feS9dqzoy+XffYpe2beKO5JxrRKXUUE4DJoWPJwGn52tkZtnx\nk3ZAG8B7jYQ6eMgA9hrYg1VrNvLok6/GHcc5VyZJ7FB6mlkdgJktA3rmaySplaTZwDJgupnNasaM\nkUvLuGopOSVxzvYLHV8o+4WOlbwv4+A5o5WWnKWIZexB0nSgV+4qgiOMK/I0z/vpY2bbgAMldQbu\nl/RvZpb3huY1NTUMGjQIgKqqKoYOHcrw4cOBj/9y417OSkqeQsuZTKak1488ahi/u+NxXpj1DDff\n1p5///o5ZcubyWQSs78qYdn3Z8vYn7W1tUycOBFg++dlsZJYQ5kPDDezOkm9gZlmNriR1/wIeN/M\nfpXnOa+hJMRt9zzNrXc/zecO3pNrLz8z7jjOuQZUSg3lQaAmfHw+8ED9BpK6Z8/+ktQBGAX44HzC\nnX78UHZp25qnX3iTRUtWxR3HORexJHYoE4BRkhYAI4BrACT1kTQlbNMHmCkpAzwLTDWzh2NJG5Hs\noWfS7UzO6i4dOf7z/wbAPQ+V777zLWFfNifPGa205CxF4joUM1tlZiPNbF8zO87M1oTr3zWz0eHj\nuWZ2kJkNNbMDzOx/4k3tmuqsk4Pi/CMzX2Hd+k0xp3HORSlxNZSoeQ0leS796WSey7zNv593FF85\n87C44zjn8qiUGoqrcNlTiP/yyGw++mhrzGmcc1HxI5SEqK2t3X4qX5JFkdPMOPeiW1hSt5aB/buy\nzx69uGDMMPr22mGWnaIsrVvL7+96kszsZxl64GGRbnPF6g10r+7kOVtIznJKy//1Uo5QfA4M1+ze\nfW8d72/aDMDCd1ax8J1VzHttKdeNP7vkD4KldWu55Mp7WFK3lrXLl7N8w/xIt5nlOSs/pyudH6G4\nZnfl9Q8x/Yn5O6yv7tKBgf27lbTNhe+sZPXaHYv8vs2Wuc1RRw1m/PdPLmmbLlDWIxRJZwF/N7P1\nkq4ADgKuMjO/0YUryorVG/KuX712E6vXvhPpe/k2W+Y2Vxb4N+bKq5ghrx+Z2b2ShgEjgZ8DvwX8\nNJ0IpGVcNYqc3as75V1/8JABnP/Fw0va5qTJz/DC3EUArF3+Bl167BXpNj1nunJ2K/BvLAnS8n+9\nFMV0KNnTcU4GbjazhyRdVYZMrsJdMGYY815b+omx9H69unDZhceXPO7du0eXHcbnfZstd5sXjBlW\n0vbczmlyDSW8Sn0JwTQnBwGbgOfM7DPli7fzvIaSTNkzc1au3kC3iM/28W22vG3+51WTWbR0NXsP\n6sHVPzjdC/IRKKWGUkyH0hE4AZhrZq9L6gMMMbNpxUdtPt6hOFf57p+a4Rc3/4OTjtmfy797Ytxx\nKkJZL2w0s41m9lczez1cfjfpnUmapGV+nzTkTENG8JxRGtC3K2uXv8GipavjjtKoNOzPUjVaQ5G0\nnuCeJPl6KjOzzpGncs65Igzo1xXAZ7GOmV+H4pxLPTPj+K/8Hxs3bWbKbd+hqnPHuCOlXlmGvCSt\nl7Su0E/pcZ1zLhqSGNC3GoCFfpQSm0Y7FDPbzcw6F/ppjpAtQVrGVdOQMw0ZwXNGbevG4OLIxUuS\nXUdJy/4shc827JyrCL26B99vFy31I5S4FFVDkVQNfApon11nZo+XIVdkvIbiXMsw4+kF/PiXf2PY\nIXtxzbgz4o6TeuWey+ubwFigP5ABDgf+CRxbzBs651w5DOgbnOnlNZT4FDPkNRY4BFhoZscABwJr\nypKqBUrLuGoacqYhI3jOqL352hyk4Mr5LVuSe+O2tOzPUhTToXxgZh8ASGpnZq8C+0YdSFK1pGmS\nFkiaKqngHAqSWkl6UdKDUedwzqXLLru0oVf3zmzduo2lOXN7ueZTzNQr9wFfA75PMMy1GmhrZidF\nGkiaAKw0s2slXQZUm9m4Am0vAQ4GOpvZqQXaeA3FuRbi0p9O5rnM21wz7nSGHbJ33HFSrdxTr5xh\nZmvM7CfAj4BbgdOKi9gkpwGTwseTgNPzNZLUHzgJuKUMGZxzKeR1lHg1uUORNElSFYCZPQY8AdxU\nhkw9zawufJ9lQM8C7a4D/h/BtDCpl5Zx1TTkTENG8JxRq62tZUC/4OLGJE/Bkpb9WYpi7odygJlt\nL8Kb2WpJB5byppKmA71yVxF0DFfkab5DhyHpZKDOzDKShpN/nrHtampqGDRoEABVVVUMHTp0+w1u\nsn+5cS9nJSVPoeVMJpOoPPmWM5lMovKkfTlN+3P5kgXhJJH9EpEnTfuztraWiRMnAmz/vCxWMTWU\nOcBwM1sdLncFHjOzISW9c+H3mR++T52k3sBMMxtcr83VwJeBLUAHYDfgr2b21Tzb8xqKcy3E8pXr\nOeNbN1HVuQNTbrso7jipVtYaCvBL4J+Sfirpp8DTwLXFvFkTPQjUhI/PBx6o38DMLjezAWa2J3Au\nMCNfZ+Kca1m6d+1Eh/ZtWbNuE2vXb4o7TotTTFH+j8CZQF34c6aZ3V6GTBOAUZIWACOAawAk9Qnv\nGlmRsoeeSZeGnGnICJ4zarW1tUhi977Jnso+LfuzFMXUUDCzecC8MmXJvscqYGSe9e8Co/Osfwx4\nrJyZnHPpMaBvNa+9WceipasYsl+/uOO0KH4/FOdcRbntnqe59e6nOe/0Q7nwK0fHHSe1yl1Dcc65\nxPO7N8an5A5F0pGS9ogyTEuWlnHVNORMQ0bwnFHL5sxe3JjUaezTsj9LUVQNRdIVwN7ARuBhYChw\nYxlyOedcSfr3qQJgSd0atmzdRpvWPhDTXIq9H8oZZnafpM4E055sMLNEn3nlNRTnWp4v/PtN1K1Y\nz13/9w12D28N7IrTHDUUk3SIma0zsz8nvTNxzrVM2TqKz+nVvIrtUIYD50maIukeSd8tQ6YWKS3j\nqmnImYaM4DmjlpszyXWUtOzPUhRVQwHuBTCzpyR1APaPPpJzzu2cAeEw1+IEdiiVzK9Dcc5VnFlz\nFnLJf9/LZwb358arzo07Tir5dSjOOQfbp7FfuGRlzElaFu9QEiIt46ppyJmGjOA5o5abs0fX3Wjf\nrg1r1m1i3YYP4guVR1r2Zyma1KEosHu5wzjnXBRatVKiC/OVqpj7ocyN+t4nzcFrKM61TON/NYVH\nn3qVH373BE485tNxx0mdctdQXpR0SJGZnHMuFh/XUfwIpbkU06EcBjwj6Q1JL0maK+mlcgVradIy\nrpqGnGnICJ4zavVzfjzktTqGNIWlZX+WopjrUI4vWwrnnIvYQJ91uNkVU0MRcB6wp5n9t6QBQG8z\ne66cAXeW11Cca5k2fbCZUef9L23btGb6nWN9ksgilbuG8hvgCGBMuLwen2nYOZdQHdrvQs9uu/HR\nlq0se29t3HFahKJqKGZ2EfABgJmtBnYpS6oWKC3jqmnImYaM4Dmjli9ndqbhJJ06nJb9WYpiOpSP\nJLUGDEBSD2Bb1IEkVUuaJmmBpKmSuhRo97akOZJmS0r0sJtzLh4f11GSVZivVMXUUM4DzgEOAiYB\nXwR+ZGb3RBpImgCsNLNrJV0GVJvZuDzt3gQODo+UGtqe11Cca6EmP/wi1986g1NGHsBlFx4Xd5xU\nKaWG0uSzvMzsDkkvACMAAaeb2fwiMzbFacDnw8eTgFpghw4lzOBVNudcQdlTh33W4ebR5A9kSRPM\n7FUzu9HMfm1m88Ojiaj1NLM6ADNbBvQs0M6A6ZJmSbqgDDmaVVrGVdOQMw0ZwXNGLV/OAV5DaVbF\nXIcyCris3roT86xrlKTpQK/cVQQdxBV5mhcarzrSzN4NaznTJc03syfzNaypqWHQoEEAVFVVMXTo\nUIYPHw58/Jcb93JWUvIUWs5kMonKk285k8kkKk/al9O8P+e9/CIbV78NDGL9+x/wwqxnYs+X1P1Z\nW1vLxIkTAbZ/Xhar0RqKpAuB7wB7Am/kPLUb8JSZfbmkdy78fvOB4WZWJ6k3MNPMBjfymvHAejP7\nVZ7nvIbiXAtW8x+T+Nfby7npZ+ex/z594o6TGuW6DuUkYDTQGjgl5+fgqDuT0INATfj4fOCB+g0k\ndZTUKXy8K3Ac8HIZsjjnUs5nHW4+TelQ9gI+AhYA6wguaFwPIKlrGTJNAEZJWkBwAsA14Xv1kTQl\nbNMLeFLSbOAZ4G9mNq0MWZpN9tAz6dKQMw0ZwXNGrVDO7XWUhEzBkpb9WYqm1FB+BzwK7AG8QFDv\nyDKCobDImNkqYGSe9e8SHClhZm8BQ6N8X+dcZRrQvxvgZ3o1h2KuQ/mtmV1Y5jyR8xqKcy3bq28s\n45s/+BN77N6N26//WtxxUqPc16FcKKka+BTQPmf948W8oXPONadsDWXJsjVs3bqN1j5JZNkUcx3K\nN4HHganAleGfPylPrJYnLeOqaciZhozgOaNWKGfHDrvQvWsnNn+0lWXL1zVvqDzSsj9LUUxXPRY4\nBFhoZscABwJrypLKOecitH1OL6+jlFUxNZRZZnaIpAzBzMMfSnrFzPYvb8Sd4zUU59wvbp7O/VPn\n8L2a4ZxzymfjjpMKZa2hAO9IqgLuJ7gyfTWwsJg3c865OCT1dsCVpslDXmZ2hpmtMbOfAD8CbgVO\nL1ewliYt46ppyJmGjOA5o9ZQzgEJuh1wWvZnKYo5QtnOzB6LOohzzpWL11CaR5NrKGnlNRTn3LZt\nxsjzbmDz5i1Mvf177NqxXdyREq/c95R3zrlUatVK7N67CvCjlHLyDiUh0jKumoacacgInjNqjeUc\nkJDbAadlf5aiSTUUSW2As4AjwlW7AluBjcBLwJ1m9kFZEjrnXAQGeB2l7JpyP5RDgKOA6WY2N8/z\newEnA3OSWKz3GopzDmDqY/P46f8+zPAj9uGq/zw17jiJV67rUD7Id+OqLDN7A/hfSXtK2sXMNhcT\nwDnnmsOAfsE09osTcOpwpWq0hpJ7VCJpD0ntC7R70zuT0qVlXDUNOdOQETxn1BqtoYQXNy5etoZt\n2+IbtUjL/ixFsUX5/wQOB5B0lKRh0Udyzrno7dqxHd2qd2Xz5i3UrYh/kshKVNR1KJLOJ7jB1mNm\n9pak083s/rKli4DXUJxzWd/78d3MfmUxv7jiCxx+4B5xx0m05rgOZXdgM3CppBmAz7LmnEuNJE3B\nUomK7VDeBCab2fcITiP2ySEjkpZx1TTkTENG8JxRa0rOJEzBkpb9WYpiO5S7gU+Hj/cEekcbByRV\nS5omaYGkqZK6FGjXRdK9kuZLekXSYVFncc5Vlt37hmd6+azDZdFgDUVSO6CTma1sdEPS7ma2eKcD\nSROAlWZ2raTLgGozG5en3USCWs5t4YWXHc1sh0qb11Ccc1lLlq3hnItuoXvXTtz/+2/HHSfRIq+h\nmNmHwBGSxkjqUOBNqyR9CxhYzBs34DRgUvh4EnmmyJfUGTjKzG4Lc27J15k451yu3j06s0vb1qxY\ntYGNm/wqh6g15TqUKcBM4BJJ10v6naRbJN0k6TrgG8DdZvZkRJl6mlld+N7LgJ552uwBrJB0m6QX\nJd1cqMNLi7SMq6YhZxoygueMWlNytm7div59gmGvuOooadmfpWj0SnlJpwEZM7s6qjeVNB3olbsK\nMOCKPM3zjVe1AQ4CLjKz5yVdD4wDxud7v5qaGgYNGgRAVVUVQ4cOZfjw4cDHf7lxL2clJU+h5Uwm\nk6g8+ZYzmUyi8qR9udL2p216B2jPoqWrWbb41WZ//6Tuz9raWiZOnAiw/fOyWE2Zy+s64I7wg/tU\nM3uwpHdqaiBpPjDczOok9QZmmtngem16Af80sz3D5WHAZWZ2Sp7teQ3FObfdTXc8we1/fZaaLx7O\nN8f4tdmFlGsurweBH4ZTrrSXtA8wF3jZzJaUkLMp71cDTADOBx6o3yDsbBZL2sfMXgNGAPPKkMU5\nV2E+nnXYz/SKWlNqKDPD+8mfCPwNmAXsRdDJ3C/p15L2jTDTBGCUpAUEHcU1AJL6SJqS0+5i4A5J\nGeAzQGRDcnHIHnomXRpypiEjeM6oNTVn3NeipGV/lqKoe8rnzDq8fZp6SecApwALoghkZquAkXnW\nvwuMzlmeAxwSxXs651qO7ZNELl3Ntm1Gq1ZFjeq4BuzUPeUl7Qf8G/CRmf0tslQR8hqKc66+U7/x\nG1at2cjk315A7555r51u8cpVQ8l9g9HAqeHrBBxkZp8pZhvOORe3AX27smrNRhYtXe0dSoSKnXrl\n08DPgSuBnwD3RB2opUrLuGoacqYhI3jOqBWTM87bAadlf5aiqCMUYA7wppltBZD0XPSRnHOuvLJ1\nFJ91OFrF3g/lKWBXYBXBkNdgM4t8gsgoeQ3FOVff0y+8wQ+uvo+Dhwzghp+cHXecRCp7DQW42swe\nynnDE4p8vXPOxW5gv26AzzoctaJqKLmdSej9CLO0aGkZV01DzjRkBM8ZtWJy9u7RmbZtWvPeyvVs\n+qB5J4lMy/4sRaMdiqT7JPWQNErSbEkzwp+ZwORmyOicc5Fq3boV/XpXAX6UEqWmzOW1r5ktkPQp\nwMzsXznPlX1ur53lNRTnXD6XX/sAjz/7OuO/fzKjjhrc+AtamLLUUMxsQfjn6+H0J+cA7cKnTyWY\ne8s551Il7ilYKlGx16H8AOhMcIZX9sdFIC3jqmnImYaM4DmjVmzOAeHtgBctad4hr7Tsz1IUe5bX\ndDN7OLsDgsrmAAASMElEQVQgyWf4dc6l0u5+hBK5Yq9D+RrwRaCO4OjkQDMbWqZskfAainMun3Ub\nPuCk839N+3ZtmPansT5JZD3NcR1KL+D7QPY8uy8X+XrnnEuEzp3aU92lI6vXbmT5qvX06t457kip\nV2wNJTv1ykIzWwj41CsRScu4ahpypiEjeM6olZLz4ylYmq+Okpb9WYpiO5QrgBdyrkO5vQyZnHOu\nWQzoly3Mr4w5SWUotoZycv2pV8zs72VJFhGvoTjnCrnzgVn85o+P8YUTD+SSb46IO06ilFJD2amp\nV5LemTjnXEP8WpRoFTvk5cokLeOqaciZhozgOaO2czWU5utQ0rI/S5G4DkVStaRpkhZImipph9up\nSdonnFfsxfDPtZIujiOvcy69+vTqQps2rahb0fyTRFainbqnfDlImgCsNLNrJV0GVJvZuAbatwLe\nAQ4zs8V5nvcainOuoPMu/gMLl6zitl98lU/t0TPuOIlR9hpKMzkNmBQ+ngSc3kj7kcAb+ToT55xr\nTJy3A640SexQeppZHYCZLQMa+8pwDnBX2VOVWVrGVdOQMw0ZwXNGrdSczV1HScv+LEWxV8pHQtJ0\ngqvut68CjOA6l/oKjldJaksw43HBITGAmpoaBg0aBEBVVRVDhw5l+PDhwMd/uXEvZyUlT6HlTCaT\nqDz5ljOZTKLypH250vfnmuVvArBwyaoWvT9ra2uZOHEiwPbPy2IlsYYyHxhuZnWSegMzzSzvzQok\nnQp8x8wK3orYayjOuYbMfXUJF/7wLvbZsxd/+PlX4o6TGJVSQ3kQqAkfnw880EDbMVTAcJdzLj7Z\nGsripavwL587J4kdygRglKQFwAjgGoDw5l5Tso0kdSQoyP81lpQRyx56Jl0acqYhI3jOqJWas8tu\nHajq3IFNH3zEilUbog2VR1r2ZyliqaE0xMxWEXQU9de/C4zOWd4I9GjGaM65CrV7366sWbeEhUtW\n0aPbbnHHSa3E1VCi5jUU51xjfnbj33loxstcesEIzjzhwLjjJEKl1FCcc65ZbZ/Tq5lvB1xpvENJ\niLSMq6YhZxoygueM2s7kbM6LG9OyP0vhHYpzrsWLY5LISuQ1FOdci7dly1ZGfOkGtm3bxj/uGEu7\ndm3jjhQ7r6E451wJ2rRpTb9eVZjB4nfXxB0ntbxDSYi0jKumIWcaMoLnjNrO5tx+O+Ay11HSsj9L\n4R2Kc87hdZQoeA3FOeeAKY/O5ZrfTOW4owfz47Enxx0ndl5Dcc65Em0/ddiPUErmHUpCpGVcNQ05\n05ARPGfUdrqG0jdbQ1ld1kki07I/S+EdinPOAVWdO9K5U3s2btrMytXvxx0nlbyG4pxzoQsvv5O5\nC5byvz85m4OGDIg7Tqy8huKcczthd7+//E7xDiUh0jKumoacacgInjNqUeTMraOUS1r2Zym8Q3HO\nuVD2WpSFS1bGnCSdvIbinHOhhe+s5Lyxt9GnZxfu/e0FcceJlddQnHNuJ/TtVUXrVmLZ8rV8uHlL\n3HFSJ3EdiqRqSdMkLZA0VVKXAu0ukfSypJck3SFpl+bOGqW0jKumIWcaMoLnjFoUOdu2bU2fcJLI\nJcvKU0dJy/4sReI6FGAc8A8z2xeYAfxX/QaS+gLfAw4yswOANsC5zZrSOVeRsoX5hX7FfNESV0OR\n9CrweTOrk9QbqDWz/eq16Qv8ExgKrAfuA24ws3/k2Z7XUJxzTXbjpFruevB5LhgzjPO/eHjccWJT\nKTWUnmZWB2Bmy4Ce9RuY2VLgl8AiYAmwJl9n4pxzxWrO2wFXmlg6FEnTw9pH9mdu+OepeZrvcHgh\nqQo4DRgI9AU6SfpSmWOXVVrGVdOQMw0ZwXNGLaqc26exL1OHkpb9WYo2cbypmY0q9JykOkm9coa8\n3svTbCTwppmtCl/zV+BzwJ35tllTU8OgQYMAqKqqYujQoQwfPhz4+C837uWspOQptJzJZBKVJ99y\nJpNJVJ60L7e0/bl+wyYgmHV45syZSGoR+7O2tpaJEycCbP+8LFYSaygTgFVmNkHSZUC1mY2r1+ZQ\n4FbgEOBD4DZglpndmGd7XkNxzjWZmXFSzY2s3/ABD9xyId2qd407UiwqpYYyARglaQEwArgGQFIf\nSVMAzOw5YDIwG5gDCLg5nrjOuUoiKWcKFq+jFCNxHYqZrTKzkWa2r5kdZ2ZrwvXvmtnonHZXmtlg\nMzvAzM43s4/iS73zsoeeSZeGnGnICJ4zalHm/HgKlug7lLTsz1IkrkNxzrm4VXXpAMCkyf/kyusf\nYmnd2pgTpUPiaihR8xqKc64YS+vW8u3L72DVmo3b1/Xr1YXrxp9N3155J+6oSJVSQ3HOudj8/q4n\nP9GZACypW8tNf3o8pkTp4R1KQqRlXDUNOdOQETxn1KLKuWL1hrzrZz7zGr+4eTqv/mvZTt1zPi37\nsxSxXIfinHNJ1b26U97127YZ90+dw/1T57DXwB6MHjGE444eTJfdOjRzwuTyGopzzuVYWreWS668\nhyU5hfh+vbow9hsjmDXnbaY+No91Gz4AoG2b1hx92N6MHjGEg4cMpFWrokoOiVZKDcU7FOecq2dp\n3Vp+f9eTrFy9gW7VnbhgzLDtBfnNH23hief+xUMzXmbWnLfJfrz06r4bJx37aU4+5tP07pn+4r13\nKHmkpUOpra3dPh1CkqUhZxoygueMWhw5ly1fxyMzX+bhmS/z7nvrAJDgswcMZPSIIQw7ZG/a7fLJ\nykJa9mcpHYrXUJxzrkS9e3Tma2d/jvO/eAQvvryIKY/O5fFnX2fWnIXMmrOQzp3ac9zRgzl5xBB2\n7dCO39/1JJnZz/JY5v1PHPWUKnsktWL1BrrXO5KKgx+hOOdchNat38T0J+YzZcbLvP7Wx3Pbtm3T\nmo+2bN2+3L1rJ8Z+/Vh6dMt/EkBjlq/cwA1/mMGKVR+flRbl9TI+5JWHdyjOubi89mYdUx6dy4PT\nX2LL1m3N8p6jjhrM+O+fvNPb8SGvFEvLuGoacqYhI3jOqCUx5z579uLSPXvx5qIVZOa9A8Da5W/Q\npcdeAHTs0JZB/buXtO2331nBxk07TmG4ssB1NM3BOxTnnCuzHt12y7v+yM/uXfLRxJXXP8T0J+bv\nsL5bgetomoMPeTnnXJkVurZlZ+od5dhmLq+h5OEdinMuCRq6tiVJ28zyDiWPtHQoSRz/zScNOdOQ\nETxn1DxntHy2Yeecc7HxIxTnnHM78CMU55xzsUlchyKpWtI0SQskTZWUt8IkaaykueHPxc2dM2pp\nuUdCGnKmISN4zqh5zvglrkMBxgH/MLN9gRnAf9VvIGl/4BvAZ4GhwGhJezZryohlMpm4IzRJGnKm\nISN4zqh5zvglsUM5DZgUPp4EnJ6nzWDgWTP70My2Ao8DZzZTvrJYs2ZN3BGaJA0505ARPGfUPGf8\nktih9DSzOgAzWwb0zNPmZeCocHisI3ASsHszZnTOOVdPLFOvSJoO9MpdBRhwRZ7mO5yiZWavSpoA\nTAc2ALOBrfXbpcnbb78dd4QmSUPONGQEzxk1zxm/xJ02LGk+MNzM6iT1Bmaa2eBGXvM/wGIz+12e\n55L1CzrnXEpUwmzDDwI1wATgfOCBfI0k9TCz5ZIGAGcAh+drV+wOcc45V5okHqF0Be4hqIksBM42\nszWS+gC/N7PRYbvHga7AR8AlZlYbU2TnnHMksENxzjmXTkk8yysSkk6Q9Kqk1yRdFneefCT1lzRD\n0itpuEBTUitJL0p6MO4shUjqIuleSfPD/XpY3JnykXSJpJclvSTpDkm7xJ0JQNKtkuokvZSzrkkX\nGzenAjmvDf/eM5L+IqlznBnDTDvkzHnuPyRtC0dlYlMoo6TvhftzrqRrmrKtiuxQJLUCfg0cD+wP\njJG0X7yp8toCXGpm+wNHABclNGfWWGBe3CEacQPwcHgix2eAHe9AFDNJfYHvAQeZ2QEEtcxz4021\n3W0E/29yNXqxcQzy5ZwG7G9mQ4HXSW5OJPUHRhEM68dth4yShgOnAEPMbAjwi6ZsqCI7FOBQ4HUz\nW2hmHwF/JrhgMlHMbJmZZcLHGwg+/PrFmyq/8D/AScAtcWcpJPxGepSZ3QZgZlvMbF3MsQppDewq\nqQ3QEVgacx4AzOxJYHW91U252LhZ5ctpZv8ws+yN258B+jd7sHoK7E+A64D/18xx8iqQ8ULgGjPb\nErZZ0ZRtVWqH0g9YnLP8Dgn9oM6SNIhgGpln401SUPY/QJKLbnsAKyTdFg7N3SypQ9yh6jOzpcAv\ngUXAEmCNmf0j3lQNasrFxknzdeCRuEPkI+lUgssc5sadpQH7AEdLekbSTEmfbcqLKrVDSRVJnYDJ\nwNjwSCVRJJ0M1IVHUwp/kqgNcBBwo5kdBGwkGK5JFElVBN/6BwJ9gU6SvhRvqqIk+UsFkn4IfGRm\nd8adpb7wC87lwPjc1THFaUgboNrMDgd+QHDmbaMqtUNZAgzIWe4frkuccMhjMnC7meW95iYBjgRO\nlfQmcBdwjKQ/xpwpn3cIvvk9Hy5PJuhgkmYk8KaZrQrnovsr8LmYMzWkTlIvgPBi4/dizlOQpBqC\nodmkdtB7AYOAOZLeIvhsekFS0o76FhP8u8TMZgHbJHVr7EWV2qHMAvaWNDA8e+Zcggsmk+gPwDwz\nuyHuIIWY2eVmNsDM9iTYlzPM7Ktx56ovHJZZLGmfcNUIknkSwSLgcEntJYkgZ5JOHqh/FJq92Bga\nuNg4Bp/IKekEgmHZU83sw9hS7Wh7TjN72cx6m9meZrYHwZegA80s7k66/t/5/cCxAOH/p7ZmtrKx\njVRkhxJ+6/suwVkfrwB/NrMk/YcFQNKRwHnAsZJmh+P+J8SdK+UuBu6QlCE4y+vqmPPswMyeIzh6\nmg3MIfiPfHOsoUKS7gSeBvaRtEjS14BrgFGSFhB0fk06hbScCuT8P6ATMD38v/SbWENSMGcuI+Yh\nrwIZ/wDsKWkucCfQpC+QfmGjc865SFTkEYpzzrnm5x2Kc865SHiH4pxzLhLeoTjnnIuEdyjOOeci\n4R2Kc865SHiH4pxzLhLeoTjnnIuEdyiu4oQ3Lfp5zvJ/SPpxBNsdGF45XHaSLpY0T9LtO7md9fke\nO1cO3qG4SvQhcGaZ7oS3U1NLhHN3NcWFwEgz+8rOvB+fzOvTYriy8g7FVaItBHNjXZq7sv4RRvbI\nJVw/P7yPygJJf5I0QtKT4XLuvSDahs/Pk3SPpPbhts6T9Gw4h9Rvsx1HuO1XJU0K37t/vUyXhrdY\nfUnhLaAl/RbYE3hE0tj6v5ykr0qaE87/Nilcd5+kWeG2vpnbPM/rO0qaEr7+JUlnFbV3nSugTdwB\nnCsDA24E5kqakOe5fPYGvmBm8yQ9D4wxs2HhzZB+CJwRttsX+JqZPSPpVuA7kh4GzgE+Z2ZbJd1I\nMOnnn3K2/ZVwGvDtJB1EMHvvIQR3cHxW0mNmdqGk44HhZra63mv+jeB+GkeY2erw3iqEmdaEHdws\nSX+p/9ocJwBLzGx0uM3d6r3HkcBZQC1Bh7S/mV1VYFvObedHKK4ihTcqmwTs8A2/gDfNLDvV/SvA\no+HjuQQ3wspaZGbPhI//BBxFMAPvwQQf5LMJpv3eM+c1C+t3JqFhwH1m9oGZvU9w/4mjwucK3cjs\nWODebGdhZmvC9d8PZ1jO3vr2Uw38rnMJZg/+maRhZlaotrLEzO4j6BCda5R3KK6S3QB8g+Ce7RAM\nhbXOeb59zuPc+2dsy1nexieP5Osf4WTvYT7RzA4yswPNbLCZ/XdOm/dLCd9Ukj5P0NEcZmZDgQyf\n/N0+wcxeJ7jx2FzgKklX1Hv+KWBvM5slqTPBnS+da5R3KK4SZW9mtJrg1qXZmkId0ENStaR2wOj6\nr2loe6GBkg4LH38JeBKYAXxRUg+AcPsDCrw+1xPA6eGNtnYlGFZ7vJHfbQZwVvaEA0nVQBdgtZl9\nKGk/4PCGfg9JfYBN4S1yf069u1oquE1tthM5CXg4HAZzrkFeQ3GVKPco4pfARYCZ2RZJPyW4o+c7\nfPIuiQ2dDZW7/CpwkaTbCIbGfmtmH4Tf8qdJagVsDt9zUYHtBSvNZkuaGOYx4GYze6mR18yT9D/A\nY5K2ENyk69+Bb0t6BVgA/LOR32sI8HNJ28KsF9Z7m/35uGPbQDDk90q+PM7l8htsOeeci4QPeTnn\nnIuEdyjOOeci4R2Kc865SHiH4pxzLhLeoTjnnIuEdyjOOeci4R2Kc865SHiH4pxzLhL/H0uzVCps\nouakAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f704dbfe0b8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from skopt.plots import plot_convergence\n",
"plot_convergence(res);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us now visually examine\n",
"\n",
"1. The approximation of the fit gp model to the original function.\n",
"2. The acquistion values that determine the next point to be queried."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfEAAAMuCAYAAAAJxTquAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4VNXd+D9nZjLZ94WQhQTCvihqQKQquFXUKlrrUuCt\n6K9iqRbFulcL1JXXVgVrRa1v1YpV21r3HQkWQSUoixCWQEhCQvZ1sk5mzu+PM0kmyUySySyZJPfz\nPPMk995z7/fcO/fO957z3YSUEg0NDQ0NDY2hh26wO6ChoaGhoaExMDQlrqGhoaGhMUTRlLiGhoaG\nhsYQRVPiGhoaGhoaQxRNiWtoaGhoaAxRNCWuoaGhoaExRPGIEhdCvCiEKBVC7HGyfZ4QokYI8Z3t\nc78n5GpoaAwMIcQCIcQBIcQhIcTdDrZPEkJsE0I0CyFud2VfDQ0N3yE8EScuhDgTMAGvSClPcrB9\nHvBbKeVlbgvT0NBwCyGEDjgEnAcUAzuAa6WUB+zaxAFpwOVAtZTyif7uq6Gh4Ts8MhKXUm4Fqvto\nJjwhS0NDw21mA4ellPlSSjPwOrDQvoGUskJKuRNoc3VfDQ0N3+FLm/gZQohdQogPhBBTfShXQ0Oj\nK8lAod3ycds6b++roaHhYQw+krMTGCOlbBRCXAS8DUz0kWwNDQ0NDY1hiU+UuJTSZPf/R0KIvwgh\nYqSUVd3bCiG0ZO4aGv1ASjlQE1URMMZuOcW2zqP7as+yhkb/Gejz7MnpdIETu7cQYpTd/7NRDnU9\nFHg7UkqvfjZv3jwsZAync9Gul2sfN9kBjBdCpAkhjMC1wLu9tLd/rl3adzhc6+F03wyncxlO18sd\nPDISF0K8BswHYoUQBcAqwAhIKeXzwM+EEMsBM9AEXOMJuRoaGq4jpbQIIW4BPkW9yL8opcwRQtyE\n7Zm1vXhnA+GAVQhxKzBVSmlytO8gnYqGxojHIyFmnkQIIf2tTxqDQ3p6Ovn5+YPdDb8hLS2NY8eO\nASCEQA58Ot0naM/yyEZ7fnvHU8+zpsQ1/BbbjT3Y3fAb7K+HpsQ1/B3t+e0dTz3PIzLtalZW1rCQ\n4Ss5w0WGxvBDe878U472PPuOEanENUYebW1trFu3josuuoi1a9fy2WefubT/q6++SmFhYa9t8vPz\nWbdunTvd7MInn3xCdna2x46noTGUefnll7nrrrtYt24dF154IeD4uWxra2Pt2rWD0cVBwVdx4n7F\n/Pnzh4UMX8kZdBmrV8OaNT3Xr1qltvUDg8HArbfeSm1tLcuXL2fRokWUlZVhMpk444wzkFKya9cu\nIiIiOHDgAPX19dx9991ERkYCsH//fpYsWcLKlSt58sknWbduHZdffjkrVqzgqquuYv/+/fzqV7/C\nYrHwpz/9ibPOOou//e1vnHXWWXzxxRc899xzPProo8TGxlJdXc0555xDWVkZmzdvZsGCBXz55Zdc\neOGF/Pvf/yYuLo4zzzyTCy+8kPvuu4/MzEyXr+dIQXvO/FOOvQwxgEliZ7PwQgiEEKSkpACwb98+\nlixZwoYNGxg3bhwffvghTzzxBM3NzbS1tWEwDH8Vp43ENfyf1avVU939008Fbk97SMf48eNZvHgx\nwcHBWK3WDtvUu+++S3JyMnFxceTl5XXs19raCqgfkfbjAIwbN44lS5bQ1NSElJKXX36ZyZMnM3v2\nbIKCgli0aBEzZsyguLiY6upqli9fTlVVFXPmzGH79u0kJyezc+dO9Ho9QgjOO+88br31Vr766isA\nWlpa3LhwGhqDj6NHt6+PMxYvXsyKFSuIiIgAOp/LZcuWcdttt3HDDTeg0+kYNWoUBQUFvji9QWdE\nKvHhZBMaLufiq+vVroR1OnXrn3rqqbz22mt89NFHCCFYuHAhVVVVhISEMGZMZ04To9EIwEknncSz\nzz7Ljh07OkYF7ccVQvD//t//o6CggE8++aTLNiklMTEx/OUvfyE2NhYhBGVlZZx22mmUlpYya9as\nLv1rf0kICgrywVUZumjPmX/K8ZaMjRs3sm7dOvbsUQUzAwMDAXj00Ud54403+Otf/0pLSwslJSVd\nnt9hjS+C5V0MepfeZvPmzcNChq/kDJYMX9wL/eXVV1+VBQUFPpX58ccfy+zs7I5l++th+3/Qn9fe\nPsPlWfaVnOF2Lr74/h09l2azWf7v//6v12W7i6eeZy3ETMNv0UJUuqKFmGkMJbTnt3c89TwPf6u/\nhoaGhobfkJeXzwMPvERRkZXkZB0PPriUsWPTBrtbQxbNJj6EZfhKznCRoTH80J4z/5TjTEZeXj4X\nXPA0GzfeQVbWGjZuvIMLLniavDwts9tAGZFKXENDQ0PD9zzwwEscObIGCLWtCeXIkTU88MBLve73\n8ssvc9VVVwGwcuXKPuX0p423ePPNN3us27JlC++8845X5I3I6XQt5nNkytAYfmjPmX/KcSajqMhK\npwJvJ5TiYmufx5w+fToffPBBRwTH/fffz6hRo2hra+OKK67g5ZdfJiwsjAsuuID9+/fz5ptvcvXV\nVwPw+eef89VXX3XkaMjKyuqS7+HNN9/EaDRSU1PD0qVLuf3227nhhhvIysri8ccfZ/Xq1axcuZLI\nyEi2bNnCa6+9xqmnnsro0aMJCwtj27Zt1NXVcccdd/D1119z9dVXc/7557N48WLKy8uJiYnhhx9+\nYMqUKUycONGNK9sTbSSuodGNw4cP91i3Z88eLWZbQ8NNkpN1QEO3tQ0kJfWtiq644go++ugjWltb\nqaysZN++fURGRlJTU0N6enpH2OZJJ53EtGnTOhQ4wHvvvcf999/PggULgJ6hnJs2bSI6OpqWlhZa\nW1s566yzuOSSS7j00kt59dVXAToSPwHMnTuXm266iS1btvDhhx9y//3389Of/pQvv/yyo82MGTO4\n/vrrOXHiBBMnTuTcc8/1uAKHEarENfuWD2RUV0NeHhQXQ1ubd2R4gba2No4fP95j/YwZM/ymjxqd\njPjnzE/lOJPx4INLychYRacibyAjYxUPPri01+O1K93f/OY3fPDBB8TGxnLyySfT1NTEtGnT2Llz\nJ9HR0YwdO5bt27cTGRnJyy+/3LH/T37yEx566KGOfBDd8z38+Mc/pqGhgYyMDIxGY0ceibPPPpsX\nX3yRG264oUt/vvzyS9auXduh7B9++GHeeust5s2b16PPQghSU1P5/PPPycnxQtXegcam2X+AF4FS\nYE8vbdYDh4FdwMxe2nkgAq93tJhPL8soKJAyO7vzs2ePlM3NLstovxdWbV4lWU2Pz6rNq1zqVlNT\nk/z73/8u33jjDVlXV9ex3mq1dvy/detWWVJSIqWUcv/+/fKZZ56RTz/9tKytrZWvv/66S/I8DVqc\neA9G9HPmx3J6ixM/evSYXLx4tTznnN/LxYtXy6NHj3m9P+1s2bJFvvPOO/1uv2nTJvnwww93WZeV\nleXSMZzhqefZI3HiQogzARPwipTyJAfbLwJukVJeIoQ4HVgnpZzj5FjSE33S6B9SSprbmmlua8Zs\nNWOxWhBCYNQbCQkIIcjgYsaw8nJwlO4wKAimTAFd/yd/PB1nunnzZmJjY9m8eTOXXHIJVVVVlJSU\ncM455/Dss88SGxtLaGgo11xzDUIIrFYrTz/9NCtWrEAIwauvvsqSJUs81h9X0eLENYYSWpx47/hV\nnLiUcqsQordAv4XAK7a23wghIoUQo6SUpZ6Qr+EajeZG6lrqqG+px9RqwiqdO5UEGYJICE0gLiSu\nY3rIKa2t4GAqGoDmZigqgtRUN3ruHtu3b2fWrFk0Nzfzn//8h9tuu4333nsPq9XK6NGjmTBhAjU1\nNZhMJsLDw3nppZdoaWnhm2++Yc6cOR2pVzU0NDT8BV/ZxJMB+3pxRbZ1g8JIs29JKalrqaOgtoA9\npXvIKc+hqK6Iupa6XhU4QHNbM2999Bb7y/fTaG7sXVBxMVh7OV55OTQ1Odzki+sVGRnJBRdcwN13\n301mZia5ubkEBATw7rvvctZZZzFnzhxmz57Nrl27ALjhhhu46667mDNnDvX19SQlJXm9jxqu4U/P\n2VCQ4Ss5WVlZpKWlddQU0D49P2lpnklw45chZkuXLiU9PR2AqKgoZs6c2RGy0H4DurO8a9cujx7P\n0XI73jp++3K7wum+fd68edS31vPhZx9iajVxypxTAMjepupTZ87N7PfywX0HyZybyYGKAxzfc5yI\nwIie/TnjDKiqIstW/3q+rXxml2UpyXrrLUhO7vf18iQ333xzx//nnHMOAFOmTOnSJiYmpsOpxZ7S\n0lLOPPNMj/fJVZYuXeqR4wghFgBPoV7kX5RS9ijALIRYD1yE8kJaKqXcZVu/Evh/gBXYC1wvpWz1\nSMc0hg3Hjh3z6vGzsrJ8Ei7nKzkDxWO5023T6e85sYlvADZLKd+wLR8A5jmaTtfsaO7RZG6isqmS\nqqYqzBazV2SkRaURFxLXdWVhIZSV9e8AU6dCcHCfzTSbWlc8ZUMTQuiAQ8B5QDGwA7hWSnnAro1D\nPxYhRBKwFZgspWwVQrwBfCClfMWBHO1Z1tDoB+48z56cThe2jyPeBX4BIISYA9Ro9nDPIaWkqqmK\nAxUH2F++n1JTqdcUOEB+TT7VTdWdK6xWqKzs/wFKta9+kJkNHJZS5kspzcDrKL8Ve7r4sQCRQohR\ntm16IFQIYQBCUC8CGhoag4BHlLgQ4jVgGzBRCFEghLheCHGTEGIZgJTyQyBPCJELPAf82hNyB8pw\nsW9JKXn7o7f5oewH8qrzaGjtnkTBM7RPsdtzrOZYp7yqKrBYujYoK4OPPoI9e6D7aKyqqkfsuBaD\n7VO6+6gcp6ePikM/FillMfAnoMC2rkZK+bkX+9orw82O7AuGy7kMp+vlDp7yTl/Ujza3eEKWhqKu\npY7C2kJKG0pJtfje49sqreRW5TIlfgrG7qPwvXvhtttg1iw4dAgZH0/LQ2sQMTEE6o1KqVdUQGKi\nz/ut4R5CiCjUKD0NqAX+JYRYJKV8bXB7pqExMtHqiQ8xLFYLhXWFVDa6MH3tRYKknknFLRh0du+D\nUkJtLS3hIZQ0lRO04QXCv93NwXW/Rx8aRmJgLPHhiYgZM3o9tlObeFsbrFwJOTkq9vzJJ8Hglz6a\nHsWDNvE5wGop5QLb8j2oZBNr7do49GMBzgIulFLeaFv/P8Dpjl7ShRDyuuuu86qTqrasLQ/F5ays\nLF566SUA0tPTWbNmzcCfZ39TmJoSd05zWzO5Vbm0tPlRDu+qSkIq6hgfmkqATZFbpZWSlkpKWiqV\n0pGSmC+2UTXv9A5lG24IIeOU89BHRDo9tFMl/pvfwLPPqil8vR5+/WtYv77Xbp44cYL169czevRo\nysvLqaurY926dQM/726sWbOGlStXEhER0aXwgifxoBLXAwdRjm0ngG+Bn0spc+zaXAzcbHNsmwM8\nZXNsm43K0DgLaAH+BuyQUj7jQI72LGto9AN/cWzzGFVNVdQ211LfUk+juZGWthYsVkvfO/aToWiv\nqW+p50DFgR4K3JG92tP0KqOunkZLM/vqj5DfeIL8xhPsrc/lRHNFpwIWgqrzftRltFzf1sihvOyO\n79Wl65WT02mDt1hg//4+d3nmmWe4//77WbFiBXPnzuX111/nhRde4Pbbb6euro6bbrqJ5557jrKy\nMh5//HHWrVvHmjVryM/P58orr+SDDz7gt7/9LQB/+MMfqK6uZt26ddx///1s376dw4cP89prr1Fb\nW8v27dvZt28fv/vd73jggQfYv38/y5cv57XXXuOXv/wlbW1tLF++nOeee46jR4/2/7yB2uZaqpqq\nXNqnO1JKC3AL8CmwD3hdSpnTHz8WKeW3wL+A74HdKGfW593qkBsMJ7uodi7+J8OXcgaKX85B5lXn\nOVwvhMCgM2DUGwnQBRBoCCRQH0iQIYggQxAB+gAf99Q31DbXcqT6iP+FW7W1dSRvsUgrFa01Lu3e\nWF1KXvVRxsdOcE3ulCmQldU5Ep86tc9d7EexUkqEENx4441s2LCBsrIypk6dSmVlJWazmU2bNrFo\n0SJKS0u7VDRqaWlh8+bNNDY2EhgYiBCCMWPGsGnTJiZOnMiiRYuIiIgA4KOPPmLFihVIKXn11VcJ\nCgpi0aJFlJeXU1JSwqxZsygrK6O5udmlU8+tynXtWjlBSvkxMKnbuue6LTv0Y5FSrgHWeKQjGhoa\nbuGXStwZUkrMFrPT8KkAfQChAaGEB4YTERjhNO+3LwL3PSWjvqWeo9VHnSrw9qQs3sSpDJOp419j\ncSmtSaMct3OGxUptRRElgeGuXa8nnwQh1Ah86lR44ok+d1m+fDkPPvggSUlJVFRUMH/+fJ5//nly\ncnK46qqr0Ov11NfXU1pa6rSi0cKFC5k7dy5PP/00ZWVl1NTUkJiYiNVqZdKkSWzYsIFly5YhhODi\niy9m/fr16HQ6Fi9ezPPPq8GqEAKLxYLJZMJisZCXl8fUfryEaDjGV0k4htJvhj/IGS4yfClnoPil\nTTy7yDNTxIGGQKKDookNiXW9kIcf0NzWzIGKAx41JXiU48ehvp7gw8cY//un2PvqE6B30UITGYFI\nTmFK3BSCA7omgNGSvXRFCEH7s5GZnKkVQNHQGCYMO5u4p2hpa6HEVMK+sn0crjxMXUsdMDTsNRar\nhdyq3D4V+KDZxKWEBjUSj393E+WXnttvBR657TuCDx9TC/X1SKuFf374Tw/1VmMkMZzsotq5+J8M\nX8oZKMNaidtT11LH4crDHKw4SHOba3bIweBYzTH/8kLvTlMjWCWitZXo/35LYFEJE+58jNSnX+l0\nOtM5frE0llaQ+Pr7asEqwdRAk7nJbYctDQ0NjZHGsJ5O742E0ASSI5LRCf97jylvKKeg1kFNbn+i\nvAwqKon6cgcpf/k7xqpahNWK1Okov/zHFK69F0JClfNbWSnU1nXsqmtoYsaSlex/4VHMcdEQGQFJ\nyRj1RqYnTO8oeZqenk5+fv5gnaHfkZSaxLtfvwto0+kaGsMJd6bTh5RjmycpayijrqWOcdHjethi\nB5OWthaO1zmpye1PmFTK1ZhNX2ENCUZUqFzqwmolqKRcKXBQYWVJySB0UKO8162hwVSfOYuYTdso\nveYS5SAnJa2WVsoby0kITQC8XwXJXcwWMwW1BdQ0u+aVr6GhoeEp/G8Y6gPabbztjmO1zbUelzFQ\nO8qxmmN91vi2Z1Bs4pY2sIVGNUzOoH76RKTNg9uiEzROGtfzIImJENTpXFj14zOJ/ey/yrZusZK9\neSsAJaYSl87fVTxl36prqWN/+X6HCtwX34mGYjjZRbVz8T8ZvpQzUEakErenPQd4RWPFYHeF8oZy\nTK2mvhsOIlJKvsrdjMWmaEt/fimFty6l/LLzKD91Mq+fHcOcqdv4+vjXXXcUAkaP7lg0TZuArrmV\n4FzbdHmjijc3W8x+k1LWGSWmEg5XHqbN2tZ3Yw0NDQ0vMmJt4o5IjUztmMr1NWaLmX3l+/w3nAwo\nri/mD1v+QLWpnKcn305CYEzXBuPGQmAQ2wq38cjWR5iXNo+Vc1Z2zat+ohhq1MyHsbiM1lFxyqvd\nYIAJKulLoCGQ6QnTfXVa/UZKSUFtgV+88Gk2cQ2N4cOgh5gJIRYIIQ4IIQ4JIe52sH2eEKJGCPGd\n7XO/J+R6msLawkH7gS6oLfBrBf718a9Z+s5S5qbOZWPmoz0VeHg4BKrp8rmpc3n9ytc5VnOM3376\nW1otrZ3t4uLVqBxoTUroDEuzy/7W0tbid3ZmKSV5NXl+ocA1NDQ02nFbiQshdMCfgQuBacDPhRCT\nHTT9Ukp5qu3zkLty3aE3m6WnHJVcsaPUNNcMWKa37a9WaeUPL/+B1VtW8+h5j/KLaYswmB28bMRE\nd1kMM4axbsE6Lhp/EQE6u3S4AQEQEd5j9+xdOWCq71guNZV67BzsGah9K68mj+qm6n611WzivmM4\n2UW1c/E/Gb6UM1A8MRKfDRyWUuZLKc3A66h6w93x66m/dqSU5FXn0Whu9J6Q1lY16rRaVWnR2kLv\nyXITKSVNbU28cvkrnDb6NBUf3p1AY6c3uh0GnYEF4xd0hIx1EBPrWFh9pxI3tZpoMje503WPUVBb\n0G8FrqGhoeFL3LaJCyGuRNUXXmZbXgLMllKusGszD/g3cBwoAu6UUjosPTWYNnF7jHojU+KndLXn\nuoOUUFEBpaXQYkviotORH9hERYQBdHrPyPE2JSVQXc24VU9RePP/YE6IhYR4iI1z7Tj5xzqc2bow\nPgMCjADEh8YzJnKM+312g1JTqV+G/Gk2cQ2N4cNQiBPfCYyRUjYKIS4C3gYmOmu86rZVJKUmARAW\nEcakaZM6inC0T1X6Yvlo9VGK9hQhhHCvEHxrK/NTU6Gxkaxsdfz5mZnUtNTy8RefQYCezIUXQ0CA\nT89vQMtf7UBfWc3Ju3Mwx0arafCUOjLPinPteNPGQ2MT2bty0NebmD1lPOa4aLK/2ArhEWTOzaSq\nqYrc73LRCZ1713+Ay3Utdbz98dt+cf0Bdm7fSXFhMRoaGhrteGIkPgdYLaVcYFu+B5BSyrW97JMH\nnCal7JFn0xcj8ext2f2u/jU6fDRJ4Ukuy8jKylKKob4ejhzpTEVqo9nSwgHTsY5QLQKNkJ7u8ojc\nlXPpizZrGw2tDUQGRTqWYbXAwUNEb9pG9JffcnTNbRAaAmPS+i2jxFRCq6WVMREpcPgwWKwk/e1f\nbC88QdrvfwMhwZCW3tE+LSqNuBAXR/m90PG99EGrpZWc8pwBhZF58jtxhjYSV/T3+xwKcrRz8T8Z\nvpIz2N7pO4DxQog0IYQRuBZ4t1sHR9n9Pxv18jAkEmWfqD/RUTjFZWpqbIqqqwJvsjRzqKGgU4ED\ntLRC8Qk3euoepaZSlr2/jI17NzpvZJv+jvh+H/WnTFPrwlX97LiQOFIiUvqs6f718a+5+/O7aba0\nduxbffYswvYeUCaHpmaVTMbGYHmD51XnaXHgGhoafo9H4sSFEAuAdaiXghellI8JIW5CjcifF0Lc\nDCwHzEATsFJK+Y2TY/mFTdyeAH0AU+OnumYfr66GvDylmGxYpIXylmpOtFRgdXbdk5MgItLxNi+x\nvXA7q7es5trp13Ldydc5zydfXgblFUxfcju5j9xBc1oyTJhAUvQYRoerRC4tbS3kVOQ4DZeTUnLf\nF/cRERjBvaeugPwCkJLp//Nbjqy+labxaSopTFRUxz7TEqb5tJRsiamEoroin8kbCNpIXENj+DDo\nNnEp5cfApG7rnrP7/xngGU/IGgzMFjN51XlMiJ3Qvx1qaroo8CZLM2Ut1VSZa50r73ZKy1TMtQ8K\ns5haTaz/Zj1fFX7FI+c9orzPe6OxEWNZJaLNQvOYJAgOJjw0ukOBg0rUkhKRQn6N48IlQgh+d9bv\nWPKfJWSl7GB+QAqYzdScmUnUV9lKidfXd1HiFY0VpESkeOSc+6LJ3ERxvWZ31tDQGBqMyLSrA4nj\nrWup61/scm0tHD1K1o4dtFnbyGssYn99HhWtNX0rcFBJTyr7b2lwJyb5/UPvY5VW3vjZG70q8Oxt\n2SCt0NRM66g49r34GAiBCA9z6D0eFxJHSECI0+OFGcNYPW81j259lOpAZVL4ZFQcUVt3qgaNDUqe\njaqmKjw1ousr5jO/Nt9tWUMhTryvBE22NuuFEIeFELuEEDPt1kcKIf4phMgRQuwTQpzuu553ZTjF\nCmvn4n8yfClnoIzYKmYDoai+iFBjKGHGMMcN6uqUE5uUNFtb2W/KwzwQu2pVpUqe4uWws2umXdMz\nhtsZzc0dMwvWMKWg4+LTnU5zJ4UnkVuV6/RwMxNnsnDSQnY15nEOY2hKT6Zu1gz1EmMwqMpmNpu5\n2WKmvrWeiMAIF87OdcoaymhobfCqDH/ALkHTeUAxsEMI8Y6U8oBdm4uADCnlBJuS3gDMsW1eB3wo\npbxKCGEAnL+xaWhoeBUtd7qLBOgDmBI3pacDV7sCt1qpM5s40ni8x8g76Ggh8e9vImzvIfRNTTSn\nJnFk9a3IQGNPQQOJvXaCVVqRUqJ356WgsgLKyjsWRUAAM370014d2faX7+9fwpbcXDCbu66z1Rhv\nJyY4hrHRY13udn8ZCrnr7XHHJm6LKFklpbzIttwjokQIsQHYLKV8w7acA8xH+bR8L6XM6IcczSau\nodEPBts7fURhtpjJrcrt+mNfW6sUkdVKrdlErgMFnvTim0y8Zy3mqAiaxiRhjonCGmBAGpwo1qrq\nLk5xrtJqaeW7E9/xp+1/4tJ/XMr249sHfCxAeY3bERfTtyf6qNBRvW7vwEEa1vYa4+3UNNd4tUTp\n8brjQ0aBe4BkwD5N4HHbut7aFNnWjQUqhBB/s9VBeF4IEezV3mpo9EFeXj5LlqzhnHNWsWTJGvLy\nHPvkDEdG5HS6u3G8jeZGDlcdJiM6g4CaOsjPBykpb6mmsLkUKSXZu3LInDmlY5+6zBmUXn0JSS/9\nm5j/7kBYrVh1gobHH+HRK2KZGTGRn40+v1NIWxvU1/FZ+bdsyttEVFAUUUFRhBnDCDOGMSV+CpNi\nJ/U4l8+OfMare1/lSPUR0qPSmZc2j/UL1jMu2kGN736SvS2bzPjOqWwhBImj+hyIERMcQ1F9EWaL\nufeG4eFkb/qqy/XCYoWGBghTpgurtFLdVE1siJOUrf3EUcynqdVEVZPnIh59ESc+iBiAU4GbpZTZ\nQoingHuAVY4aL126lPT0dACioqKYOXOmRxPz7Nq1i9tuu81jx3O2bG8X9Vaioaeeesrj18fRcvdz\nGurXKy1tLBdc8DRHjpwHBAOz+PrrVTz4YCajRyf65fXKysripZdeAuh4PgbKiJxO99SPrKGiiri6\nNgJ0BqrNdZjaOqeOuyvxdjLueISoXTkdy3smR/PvB37GqRGTSAnuNnINCaYwSk9ORU5HkRRTqwlT\nq4m5qXM5f9z5Pc7lcOVh6lvrmRI3heAAzwyQsr/8msz4SALKKjHHRBITEsPYMy5Wtus+OFF/ol/e\n3tlvvkPmjG5J/KIiYXRnop2IwIj+Rwg4wZESP1BxwKO2cH9P9tKfBE0OptMPAPNsm7dLKcfZ1p8J\n3C2lvNSHVlTBAAAgAElEQVSBHC3Zi5/J8JUcX8pYsmQNGzfeAdjXb2hg8eI/8uqrDt8tByTHm7gz\nnT4ilbjbtLWputgm13/4I598lvQPt2GQYNXpqLjsPApv+UXHdl1TM9ZgO2exjHFgDPRErwdObQ0U\nn2DKsvvIX3kD6fMuI3jGqf3a1Wwxs7dsb98e3yUlbMndxOSwdEa1lznV62DCxI7SpUIIZiTM6HMa\n3xWqmqrIq87z2PF8hZtKXA8cRDm2nQC+BX4upcyxa3MxarR9iU3pPyWlnGPbtgW4UUp5SAixCgiR\nUjoqQazZxDW8zrx5q/jyyzU91p9zziq++KLnen9Es4n7kpoaOHqkVwWuc1TYw0btimVULbyAulOm\nKQW+fHHnfqZGpl1/FwEVdlO7NX5QV7uxCZ2pkcDiMgyTpxIcFd/vXQP0AUQHRffdMDyMww0FPHz4\nRTLuWYu+zqSm1E2mjiZSSqqbPVdNTErp90ldvIGU0gLcAnwK7ANel1LmCCFuEkIss7X5EMgTQuQC\nzwG/tjvECmCjEGIXcDLwiE9PQEPDjooKHdD997iB0aNHhnobGWfZDZfjeKWEulrIOwonTijl4oTQ\nfYeYdsPdfP/VTscN9HoKb/kFhx+/R43A9Z2ObdawEKrOm8vov7/d2b62rlcHN1/EJGdvyyYsJ5fG\niWMZFTZKJaNxgfjQvpV+9q4DLE27jApzLRvT64n8epfaUFfbpV1lY6VLsrtjb+cqayij1dLa905t\nbWo2oqREVV/LzYWDByAnR30OHIBDB1WK3byjZL/9ARQdV+3Ly6G6Sp2HyaRKuba2KG98q8Ut50V3\nkFJ+LKWcJKWcIKV8zLbuOSnl83ZtbpFSjpdSniyl/M5u/W4p5Swp5Uwp5U+llLWOZPiC4RQrrJ2L\n6zIaG6GwcCkxMavoVOQN6PWrSEpa6jE5/ox/Orbl5vasPt4ezywEINRfAeh0KruZTqi/ep2Kr9br\nlILU60FvUH8N+v5nQmtrUzW/TSYw1UNb357LoT8cImP1Uxy7+1eYdBb+deJzrkw8r/+x2EDJNT9h\n2vV3UXrVxbSkJKp+NDZAqJPYdG9jtUCrmdB9h2meMYX4gDCXlXiYMYzggODew80EGMIjWT3hRn5j\neoh5/90GPz5TXX+rpSNmvtHcSHNbs9tpWC1WCyWmkt4b1dep9LkNfdSWlxIsErDa7psWqKvvfR97\n2u9lITrvz/Z17f9raGj04K9/hZSUNFau/A0bN/6RqiorMTE6Tj/9N2zYkMY990Cse76wfo9/2sQ/\n/7v3BOiETanr1AuATof6tZS2H2OLGiX1Mtp2RNjeg4xbs468e5azebyBNYef54zok7gr4xcYhGvx\n2Ykb3yGooJhj9y5XK7rFTPuUBhMUFDLhzkcRi5cQfvHlMKWnw15fVDRWOE3F2kFdLRQV89fDb3Bs\n24c8dPVzEBzUI5f6QCvL2VNUV+RciTeYbHXf+zFKHyQyz/8fLXe6xojn7LNh4kRYuLDntoceglNP\nhWef9X2/XEWzibuCVSol3dyiqnKZGmyj7QY14mpucV2B7znAuDXr2HfPL1kds5sHDj3L3RnXcd/4\n63sq8NAQlcglMRGio9XLRDfKFl5A5Le7CSi32cZNpi5pSH2Kzb4vw8IIO+X0jpAvV4kJjuk72UxY\nGAjB0owrCQgOxbzTViOnm1+Au1PqZouZsoaynhusFigugoJCv1bgGhoa0NgI2dlw1lmOt193Hfz9\n71A0zN1e/FKJl7ZUUWs20Wo1eyxntj3ZdiFeHkFKPr/nWi6Rf6fGbOIfpzxMUEE3j/LgYBg7VtXe\njo1TCjwxEcaP75HsxBoWQv5t13dOp3Zz8OpyLt62iTc3kb0rh5bHHkJERro8ld6OTuh6rQuevS1b\nTZmHhmDQGfhz4BWM+87mNd7UBC2dyWZaLa3Ut7gwXW1HVlYWJ0wneiaOaWlWRWtqB1h21g6P3192\ntMkRk5CmX2h2ZP+U4wsZa9dmMXo0xMQ43p6aCjNnwsMPuydHs4kPgOt3r6bJ0kKztRWLtLAoeQG3\njV3Uo112TQ5f1+whwhBGpCGMqIBw4o1RJAclEBngIxuyxUL0lzs4I/84H40eg/m2G7s4qwEQFwtx\n8Y5tmzo9JKeA7kSXEWfNvG41JerqOnKJ+wwpoakJvU5HnNE2nT3AkThAQmgCZQ1lvb+YhYWBqYGK\ni89B2s9SVNeolx4blU2VhAe6/kLRamntWaPcZFKOaFbfT/1apBW9Az+NVquZ3+5/kmpzPfWWRhot\nTTRamtGh479z/+rzfmpo+Bs7d8Lkyb23+dnPYNUqWLt2wOMPv8eT9cSforOe+FoHbdYDF6FcCJdK\nKXc5OVYXm3ibtGCVVoy6nrHBOaY8tlfvpa7NRK3ZRLW5nvLWas6Pm831qZc5bF/YVMqowBhGBcYS\nZ4xy2V7dndSnXyH+vU0IqxWp01FuH/ctBIxOhMhOe25UUBTRwdFYrBZKG0ppaWtRG6SEwgLnTlQ6\noYw/PihR2kFLMxzNIykontFBcRAUBNOmuXXII1VHqGnuJWzObFaOjd3RCZgwocPBTSd0nDTqJJfz\nwR+tPkp1k12YWm0NnCjxupe4lJL8phMcaijgcEMBhxsKyWssosJcy5Y5z/WoVS+lZFv1HqIDwgk3\nhBKiDyJUH0SgzogQQrOJa4x4TjkFzj0X+srDct99sGgR3HuvT7o1IAa1nrgHKiL13kGhByeKdkrY\nWKaE9b8oRmlLFZsqvqW0tYrSliqqzXXEBkSybMxPWZg4r0f73IZCchuP02RpptpcT2FTCYdrjnB1\n2iVcNupsAIIKihFWNTUrrFaC8ovbTxqSkzte/3RCR1pUGjHBnXM/sSGxHKk6Ql1LnWqflKxi0B3Z\n5K1S2e19+TrZ2IRe6EgItMV5uzEKb2dU2KjelXhAgHpZaO6aqx2rVDMVMbG2RStVTVX9Cl9rx9Rq\n6qrAq6tVGJiPWHP4BWIDIpkQOoaFo+YxLjSZ0YFxPRQ4qIf6RzEn+6xvGhpDCYsFDh6EFSv6bnvZ\nZfDMM3DXXT0nSYcDnhjWzQYOSynzpZRm4HWgu6/gQuAVACnlN0CkEKKf1TE8x/zY01g7ZQW3yGv4\naPZ6tp7xV/560gOcFTPTYfsf6o+wpXInP9QfobGmnHO3nWDDxnp+Etz549o8JgmpU5dR6nQ0pyWB\nEGQfL+9QuHqdngmxE7oocFCKPSMmg1CjLV2gwQDxCc5PoL6nvdarNvGmRhICY/jvzu/VsgeUeJgx\nrPN87ehyHt1eVFqsrbxV8gWyorLLiLm8sRxXOF53vFPOABR42O4cEv75IalPv0L6YxsYt+opMh54\nkpCDRwE1et5Vd4hN2TsACD58jJCcXAKLSjHUmfjbtN/xx6m3cVPaTzknLpO04NEOZ5g0+o9mR/ZP\nOd6WsWsXBARkEdePQo+nn67GSG++OTBZI8Em7qgi0uw+2rRXRCp1dMCUZzcidSoWXOp0NEybQO0Z\nPdN8Bh/JJ3TfYaxBQViDA7EGBWIJDqI1PgbzqL6/XYPOoKaJnXBlSCbX7w8k5otthOYcoeKScyh5\n9C6sIZ05yQt/vRgEBOUX05yWROGvl6gReJVyRAvQBzAhZoLTPOY6oSMjOoOcihxVKCQ6GmqqlZe8\nDX19A5bw0M7KXj6KG9Y3tTDqaCWHcnMhM9MjShwgMSyRI1VHnDcID1NJUtr7gY5/nfiCAGHg0vh4\ndY2AJnMTplaT8/rudlQ2VnbmR6+pGdAIPOTwMYzlVbQkj6ItLARrcBBSJzgRZeDt4+/zTskW9ELH\nla3nARC95RsivtuHoc6EvqERfUMTMsBA7kO3U39KT7NE4sZ3CCo8gTTokQZV4U4KQfll59OSOtrl\n/mpoDFe2bu3iItMrQsAFF8CTT8LPf+7dfg0GfunYdsveg6SGhYCEiAAD48NDmWJT4u2ev5kzp6A3\nNfL9t3sQrWbODg5E39zCVxVVmKZPYtzKG3q0j/n8Kw689i7JQYGMHZ2AJTSY/zY00TghnSnX/qRH\n+7iPsti1NRvTjElMvP8WZFBgl+0A2XsPkX3mLDJvmWIbgZdCbROZczMJM4ZRuLuQKn1Vn5VtTj3j\nVA5XHlYjxaYmMpPUy8Wez7aS/Pw/iH3zz2Cxkr15KwQFdymwYV9wo32k6fby7Jkk6iL47//9GUaN\nUtPcgYEeq+STMC2BJnOTc/mjoqDVzHfbvyck9xirrriRW/atJbgohKj0yWT+aBYA73z8DskRyb3K\ns1gtxE+zTbs3mMj+6IvO76/797krB5BkzpzaY3vZzy7qslzSUsmjn/+N7zYd4PzM01k9cRmtR80Q\nol6yin95De/aH19KvtuxB2mVnNb+3dltN02bwJfNLQiLhTMS49G1Wdh+vIT63HzaKmvYuTuH4hLX\nZh+GO74oGOIrOdq59J/du2Hy5P7LWLAA/vUv+P57ZUt3BV99LwPFbcc2dyoiSSl7jMS9mezFUF1L\nYHEp+oamjpGRvqGRxow06jNnuC8gaTRERqkRfvho4kPiXcrWVlhb2Bm/nJen7MJSMu2Gu8m7axmN\nU8Z3hqZ5mYCGJqbXBqL7+SJ44AE480wYN/Bypt2pbqrmaPVR5w3KSqGyCp2pkRmLV/LDK3/k2drP\n2F+fx5NnP4xI6LTGTImfQkhAiNND5dfkK4/0ulooPuHciU1K4t/5nKhtOzn8v/f0eQ7HGov5pHw7\n1yT9mKgA37q+ao5tGiOZOXNg9mw1wu4vzz4LkZHwj394r18DZbCTvewAxgsh0oQQRuBa4N1ubd4F\nfgEdSr/GkQL3Nm3RkTRMm8gXRiPV55xBxU/OpfSan7ivwIWA5CSCYhNJi0pjxqgZ7N+x3yUFDpAc\nkdyZTjQ2puPYVfNPJybLlvikvmt8tLds4kmEozM1QHExWSYThPa0Y7tDdHB0FxNDj/OwhdNZw0Ko\nm30yMVlfc33KZZS1VvFBzjtdHN+O1x13KqemuaaLAs/+fr/DdobqWsbf8zixn2+lYMV1/TqH9JAk\nbkq7socC92acuEZXNDuyf8rxtoy8PLBaXZOxcCG89x5UVfXd1h5/t4m7rcQ9UBFpaCMEuuQUUlOn\nMy1hGnEhcegGGAamEzrSo9KV8g+PUFPYQPX8OURv+Qasttzc3T23PUxIQAhxbUbYu1elWNXrPWYP\nt6fX1KnBwR3nX3HhWcR+/CUBQs+qCcvYV39EZVazqsQn9S31PWO/UTbzYzXHVAGSomKnI/DgowVM\nvmU1jZPGcmDd72lJ6Wp/llLSZPHuNdfQ0Ogf9fXKL3WUi67RSUkqrnz9eu/0a7AYebnTPYlehy51\nDONTTh5Q4hFnFNcXc6L+BFRUdDh4Tf3lveTfupSGGZMgLg7i+x9a5SqToscTtj8X/vIXteKWW1Tq\nIy841B2sOIip1XE2OkpLoKoarFamXX8Xx+5cRsP0iZ3bQ0NUWiahQyd0jIseR2RQJAANrQ0cqcrF\nXHxcPfFOMBaXMnnFGgpv/h+qzzmjx/aK1hoezv0/RgfGcVfGLxwcYXDQptM1Rir//S9cey1s2OD6\nvjt2wAsvqFSsOj/KVzrY0+kjk6BAGDuW9KRpHlXgAKPDRisbb1RUh+Isu+LH6BtsVcBMA0s52h/i\nQuIIa08bPmsW/PjHEBLiNY/41MhU5xsjbBnqdDrKrriQUW993HV7XT2pK37PhKtuIvl3j5FbdoCD\nFQc5VHmIA/nZmI8c6lWBA7SOTuDA06sdKvDPyr9h0fe/Y3xIKreNHYZurRoaQ5DduwfuFnTaaWA0\nDjzczB8ZkUrcbZtlTDSkpxMXmUR0cLTDJu7YUYQQjI0eiy7A2DGNXXHJOdTNscWzN7eAWWlaT9rE\nA/QBpESkdOZpnzULxo8na88ej8noTkhACAmhCY7PIzikY0q98sKzOLGoa/qB1L9sJP7tT4nYtpP4\nl/9F6j2PYCrIpf7AblXExC5Mr50e370QtI7uGptfY67n3gN/5rmCt3hi6u3cnH6VS/Hcmk3cd2h2\nZP+U400Zhw9DQgLs3eu6DJ0Ozj9fhZv1F3+3iftliJnfEhIMCaMgOBij3qgUnpcIMgSRGplKfn1d\nD2c2QCnaaCeZ/wdIelS6SmPaXV6w4xh3T5EckUyAMyUZEQ6VVViDg2gan9ZlU49seQeO9Dny7g/v\nlG4hwRjDqgnLCNIbOzcIAcYA9WKh71abXlpVpj2rBYwGVbu+HzXoNTQ0XCM3170AnfZws127lJVw\nqOOfNvGv3+pcYd8/KUG2r7PV/7a2/7V4p4CFTqjRcHQ0hHR6aGfEZBAVFNXLjp7hWHUelXu+7qkQ\nQkNURTQPkRCaoKa2rVZ1d9tf95NPVtnkvIip1cShykM9i6M026qLOSD16VeIe+9zdFaJVaejwj5v\nvTMsFtdyLwYalZNhWJhKB+uKWaH9vrTYPm0W231qU/jSqv63SvW/o/vb/lh2ZM79mWYT1xiRzJgB\nl14KZ/S0gPWbDRtUYsjXX/dcv9xhUHOne4XUMQPf12rpHBFZreqH02IBS1vXH1OLpfNHtP13RidU\ngY0AAwQGQXCQzR7c1eoQERjhEwUOMCYqjaaYPBrLirtuaGxS56R3/ysMNYZ2ziq0Z4VrJzDQ6woc\nVDrWpPAkiuq6Ff8NClL+Bw6mxgt/vRgrkuM5X1M4OpTkX/2c3tRzxLe7SXrlLQ6sX9W3V0toiHIg\nDHEjtE4I9f144DvyNO4WLbLVTMgGjkspe1Yb0tDwEsXFyp/VHRYuhJUrobISYmM906/BYvjZxHV6\nW3axIGVTDQ9XDmKxcWoqfHQS2YWlkJ4OY8dBxnhV03v8eBiXodYnp6gf8NCwHgpcCNG7M5YNT9lR\ndELH+LRTe9pkpQSTyW2buFFvJCM6ozOmvftUeliYz2xoiWGJxIY4eKIiIx3vpNdT9JvraP3zOh6+\nPIY1R17EbG1z2DTyq52k/+/z/PuCszoUeI25nv313RLOGAyQkqJmOQaowL1e491N7IoWXQhMA34u\nhJjcrU1H0SLgJlTRIntuBRwH3fsQzY7sn3K8JaOxUVVlTkwcmE28ndGjYepUeOKJvtv6u018+Clx\nL5MQmtCZkMVHBEREMSE6A4NOT+TX3xPz6Va1od5JaFY/MegMTIidQIDe7gWhvh6OHYM1a9Syh5O8\n9EVaZFqPQjFERnadxm5rI/XPr6CvV7nQA3VGnpp6O/WWRm7d90cqWrtWSYvO+oa0p/5G7iN30JSW\njNnaxuvFn3D1d/ewrdrOaS8iHDLGDd/Cw524VbRICJECXAxohc01fMqhQ2pM5onJwUsvVeFmZrP7\nxxpMRqQSt8877goB+gBGh/WvEIWn8+0GxSUyMXQMIsBI/Pub1MoGE5kOCsP0B4POwMTYiV1fSCwW\naGiA775T/wOEhfk013K7Z35imJ3nit6giqJ0dN6A1OkY+/AzCLMaeQfrg/jjlNuYETGej8u3dzQd\n9cb7pDy7kcOP3cmRMeH8EHeEn+68k23Ve3hm+t38cszlqmFCvJqBcbE+uSMGen/5EEdFi5L7aFNk\n1+ZJ4E46DVGDhpZv3D/leEvGwYN0VC6bMcM9Gaecol4Inn2293b+njvd/4x1fkxKRIry3h4MoqMJ\nLi0l5UcXYXjwaQyVNbTFRg2oxniQIYjxMeMJNAR23VBnK3Xa7rap13vdM90ZyRHJRARGUFhXSJO5\nSTkW1nVO9R9fdi0Zf3iacavXcezeX2EJC0UvdCxPuYLUv2wkqOAxmsck0ZSWxIGnV2FOiOWhH9aS\nYIzh0cm3MD08Qx1IZ6vjPvxH3x5BCHEJUCql3CWEmA/06oyzdOlS0tPTAYiKimLmzJluF8/Rlkfu\n8qefQmysWm6fTm9X5gNZPu00ePzx+fz617B1q+/OJysri5deegmg4/kYKP7pnV7kXZuifdWv/hIe\nGM7E2Il9N7SRlZXl+Te4vXuhtRXrffdSOWM8BRfNJTs3n8xLF/T7EDHBMYyJHOP4ZSQ/X2WJW7gQ\nnnpKeaVPmOCdc+lGbzLqW+qpaa7BlLOLlsZ6LNIWVmZuI+XZV4na9h2lV11M2ZULSH36FeLf24Sw\nWpE6HeXdPNazd+V0VCxDJ5SHjDvOaw4YyP3lKpnJmQP2ZnWnaBHKFr4EaAOCgXDgLSllj7AAX3in\n++Le9JUc7Vz65qab4MQJuPFGpYTdHY1LCbfeCvfdp47pCF9cLy1jm5fRCR1pkZ4L5xowtjrauvnn\nEL99NxmhKRib25xX5bIjOCCY8THjGRs91vlsQl0dlJUpD/X0dK/kSx8I4YHhpEamMmXCXGZGTuKU\nyElMD89gQvQ4LHfdScEf7kC0KsNWj9jx/GLHB9UJGDPG4wp8iDDgokVSyvuklGOklONs+33hSIFr\naHiDwkLPepMLAVdcAY880mlBHGqMyJG4q6REpDAqzMVs+97AZFJGIZMJLrkEPvwQQkOpTYmjOlBi\najXR0qZCsYQQGPVGwo3hRAdHExEY0fuxm5pg/3745BP49FP4059g4kT/mmaWEvbtg5aWbqslxc3l\nlLRU9jkSBzoVeLDz8qX+jjsjcegIMVtHZ4jZY0KIm1Aj8udtbf4MLECFmF0vpfyu2zHmAb91FmKm\nxYlreJpTTlGZoM8803PHlBJWrIA774Sbb/bccV3BnZG4psT7IMwYxqS4SYPdjU5271aVzEpLO8v4\nxMTA2LGAUmhWaUUndK6VQi0pUVUB2tqUh3pMjLKL6/xssqayUnnPO6C8pZoCUxGpz24kKL+Y5rQk\nCpcv7prcxUtT6L7GXSXuCzQlruFpkpPht7+FCRM8e9yvv4a//lX9tAyGG9CgTacLIaKFEJ8KIQ4K\nIT4RQjgM6BVCHBNC7BZCfC+E+NYdmZ6gv3G8Bp2BsdFjByTDa7GFUbYkMzYFnpWdDTU1KmkN6mbQ\n6/Qu1zKntlb9NRjUtH1wcIcC96u40thYp09ZfGA0o0LiKbzlFxx+/B41ArdX4EKQXVTudQXu73Hi\nwwkttto/5XhDhpSqFnj72MWdOPHuzJmj8rE/8kjPbcM9Tvwe4HMp5STgC+BeJ+2swHwp5SlSytlu\nyvQZY6PHYrTPne0PRDnIFGe1KkU+UNraOouetOMn9nCHjHGe0S85KIFQgwMlL4RK4hI0ON72Ghoa\n7lFRoRS5tyx8112nao2XlHjn+N7Cren0do9VKWWpECIRyJJSTnbQLg/IlFJW9uOYfjGd7jd28O5I\nqULAbCPvDiIjVda5gVBRoTzT7Rk3rsORzi85flyZFBzQbGlhvymvMw+7zqbAQ/34xcRFtOl0jZHG\nt9/CZZepBC3e4okn1E/p2297T4YjBtM7PUFKWQogpSwBEpy0k8BnQogdQggnjvz+Q2JYon8qcFAj\nSkdpSOvqBp56yFHlL38eiYMyjjl5JQ/SBzI60JYRwmBQKVSHkQLX0BiJHDvmeCLSk/zyl7Bli/IZ\nHir0mexFCPEZYK/RBEop3++gubPX7h9JKU8IIeJRyjxHSrnVmcxVt60iKTUJgLCIMCZNm9QRd9tu\nb3Rn+eC+gyy+cbHD7Ue/P0p9aD3J81VyqoEG9Lev80rCgLo65ier/j311FPMPOMM5p9+OlRWknXg\ngGvH+/xzOHqU+aecAuXlZBUWgtHI/NNO62i/a9cubrvtNs/131PXKyODrNdeg8ZG5meq7y8rW32f\n8047jWqjhf8ePQbltR3f78YXNnr8fuq+3Nv9NdBlgJ3bd1Jc6CRkboSixVb7pxxvyCgo6KrEPREn\n3p2ICFi0CH71KxUIFBzsu+9loLg7nZ6DsnW3T6dvllJO6WOfVUC9lNJh6vnBSvYihCA1IpX40HiP\nyPDqF2+xKC91Kcn62c+Yf8cdyjMjMBCmT3ftWKWlamr60CG4+274z39UXsO0zrh4v37opVSx7WVl\n0Nqq1oWFQUICDaFGDlQc6NLcF4lY/D3Zi6/Qkr34nwxfyfGGjFtvVT9Tv/61WvaGEgf1k/L738NJ\nJ8Err/h/shd3lfhaoEpKuVYIcTcQLaW8p1ubEEAnpTQJIUKBT4E1UspPnRzT5zbxIEMQ6VHphBqH\nUNjRoUMqFOyVV1QGhN/9Tq0fP9551S9H7Nunana/9JJS6HffrRK9DMX6fBaLMjfYhcUV1BZQ3lA+\niJ3yDpoS1xhp/PSnqjL0Ndd4X1ZVlSpV+txzcNVV3pc3mDbxtcAFQoiDwHnAY7YOjRZCvG9rMwrY\nKoT4HvgaeM+ZAvc1ep2e5IhkpsZPHVoKHDrnlc49Vxlx2tMNOXH2cojJpBQ4wJdfwtlnq//9KcGL\nK+j1PeLak8OT/S/CQENDw2VOnOgsfuJtYmJUitdly+Do0b7bDyZuKXEpZZWU8nwp5SQp5Y+llDW2\n9SeklD+x/Z8npZxpCy+bIaV8zBMdd4cfvv2B1MhUZiTMIDEs0fWY6n7g9dhCmxLPKimB+Hj4/nu1\nvr5eVSLrD+0Kv7oajhyB004Do1F97BiqcaWgXtTSo9I7ln0Rw63FifsOLbbaP+V4Q0Zpqfqpa8eT\nceKOmDsX5s+HefOyekTg+hN+lo7L8+h1ekICQogLiSMtKo3pCdNJi0ojITRh8CqSeQKjsTPpyQUX\nqHSp7RQV9b1/U1NnbPnWrTB7tjrmUB2F90J4YLj/RhtoaGj0i4oKSEzsu50nWboUQkPh8sv9N7e6\nX6ZdbW1rRSI7Uoi2/+/ob5d9EeiEDp3QYdAZMOgMQ1tR90VxsZpjKiuDL76Aa6/t3JaR0Xs8Rm5u\nZ5a2999XzmDz56v0rTExXu32YCCl5FDlIUyt/vlKrRM6AvQBBOgCOu5d+3tYL/TohA69Tv0NNYZq\nNnGNEUNzs/qJ+te/uiZh9AVNTXDvvSpv+z//qdxuPM2wy53ub33yWxobISfH8baAAJg6VcVJd6e6\n2rmh56ST1L7DkDZrGwcqDnQUifE1ep2eIEMQwYZgAg2BBBmCMOqNGPVGDLo+oz274M5D7yu0Z1nD\nU83WneEAACAASURBVBw6BKefrvx4B4P6erj/fjVh+Y9/eF6Ra6VIXWSo2oR6EBJC1p49jreZzZCX\n17NMaXNzz+xs7QQFOVTgw+V6GXQGivcWe93RLXtbNjqhIzwwnMSwRDJiMpieMJ2ZiTOZHDeZtKg0\nEsMSiQqKIiQgxGUFrtGJZkf2TzmellFQ0DPoxts2cXs54eHwhz+orHEXXqjGT/7CiFTiw4reMqvV\n1amMBQ0NyqBTXa2WnRl3IvooVzoMMOqNTIqbRJAhyKPH1QkdEYERJEckMyZyDDMTZzIxdiLJEclE\nBUURaAj0qDwNjZGEIyXuayIj4dFHVSHFWbPUGMkf0KbThzoNDXDgQN/t+oOrMeZDGKu0UlhbSEVj\nxYCPERIQQkRgBBGBEYQZw7wS5eAMbTpdYyTx4IPw6adw112D3RM1Bvq//1NRuevXwy9+4f4x3Xme\ntXm8oU5oqPIqb89WZrWqjyNbeG/odMPSM90ZOqEjLSqNuJA4Skwl1LbU0pfCCQ4IJswYRrgxnPDA\ncG0aXEPDRxQVeT9ven/R6+HGG5Wj2+23w2uvwbPPKp/gwWBETqcPRZtQr3Lsq4098gi8+27fO7a1\nwYoVymMD1LS8zvHtMOyulx2hxlAyYjI4edTJjI8Z31G9blTYKJLCk0iLSmNS3CRmJs5kavxUxkSO\nITo4ulcF7u/1h4cTmh3ZP+V4WkZxcc+gGV/axB2RmQl//rNycjvpJLj5ZhUo5GtGpBIfdtgr8Z/8\nBP72t74rmn3xhZqKbx99+8tr7iCh1+mJDIpkVNgoUiJSSIlIYXT4aOJC4ggzhg3vUEUNDT+npMQ/\nM0GHhqpc7o88oipEjxunYst37/ZdHzSb+HDhhx+gxRY6tWKFSjdkHzduT1ubSkB8xx1wxhlq3YwZ\nPTK1afgv7trEhRALgKdQL/IvSinXOmizHrgIaACWSil3CSFSgFdQ6ZStwAtSyvVOZGjPsoZHGDtW\npUB1tb6Trzl+XNWQ+uYbSE2Fq69WP7WTJvW+nxYnrtGZ+AVUDPiyZSqgMd5BVbY33lAj8Q0b1FxQ\nSAhM6bX4nIaf4dZDL4QOOISqd1AM7ACulVIesGtzEXCLlPISIcTpwDop5RxbtcJEm0IPA3YCC+33\ntTtGv59li0V5/ZaXd76LGo0qQ1dsrHcSbGgMHSIj4Y9/9H3GtoHS2qoc3779Vo2vYmLgRz+Cs85S\n5S4mTux6T2tx4i4yFG1Cfcqxn2saN06V3rn/fuXkZs+xY/D88yoFUftdZD8d35sML6LZA33KbOCw\nlDJfSmkGXgcWdmuzEDXiRkr5DRAphBglpSyRUu6yrTcBOUCyM0HffacSAr7wgoqzvflmuPJK9WM2\nZQokJSmLjtGoqt+efTZcdJH6zJsHKSkqu/C0aXD99fD5511TH2j3jX/K8aSM1lZl+es+nT7YNvHe\nMBrh/PPhvvtUgpobblAvp88/rxLGhIere/ryy1Ubd9Dca4cLgYHKOa09U/8vf6leA7s7q9XUqBp7\n6emd6/pQ4hrDjmSg0G75OEqx99amyLauo0yeECIdmAl840zQRRep9APh4Z2fqCiYOVONTqKj1Sgr\nKsp5QEV1tUpMuHs3LFqkjrdmDSxe3P8T1hi6FBSon7ahmkjSYIBTT1WfdsrLVc2p/HxVhNId3K0n\n/jNgNTAFmCWl/M5Juz7tb3Ztten0gVJZqUbarhAaCpMne6U7Gt7Dzen0K4ELpZTLbMtLgNlSyhV2\nbd4DHpVSbrMtfw7c1f6M26bSs4AHpZTvOJEjzz33OhIS0gEIDY1i3LiZzJgxH+gc4biybLVCWdl8\nXn8dxozJ4oEHYOFCtb199Dd/vrY8nJat1vnccAMsW6aW3bl//GV5794sNm16CYDg4HQ++GDN4NjE\nhRCTUM4tzwF3OFLi/bG/dWuvKfGBYrXC3r3Kca2/pKX5rkivhsdwU4nPAVZLKRfYlu8BpP3LtRBi\nA7BZSvmGbfkAME9KWSqEMADvAx9JKdf1Ike++653nuXGRhXeU1Cg3DsyMrwiRsMPeOklePJJeOih\nwe6JdygqguXLB8kmLqU8KKU8DPQmvD/2N58y1GxC/Zaj07mmkHW6fk2lD9vrNYRluMkOYLwQIk0I\nYQSuBbonF3gX+AV0KP0aKWX7VPr/Aft7U+DeJiQE7rwT0tKymDvX+ykwh9N9M9TOpajIcSJJf7aJ\n+xJfOLY5sr85dYTRcJOEhP678sbG+r6un8agI6W0ALcAnwL7gNellDlCiJuEEMtsbT4E8v4/e2ce\nH1dVNv7vMzPZ96RN2iZt032DUqBAWYSyyKK+oD9RgSIWVFAERERB5WXR1wVXQEVBQeR9WVTcKIKy\nhn1poCltaZsuadpm37eZZLbz++NMkkkyk0xmJpPJ5Hw/n/kk595z73PuzJ157jnPJiJ70SttXwYQ\nkZOBDcAZIrJFRN7zmctijgicey6sW6eLUnTHZ5VZQ4TU1EyLsg5hM+Zyuog8h44JHdgEKOA7SqlN\nvj4vAV8Pspw+pv1tWH+znB4phw6NnTpIRLtHppjCHFORqZI7faKW0/1RSi+1FhXBpk0TLs4QYz7+\nca3EP/WpyR7JxBDpcvqY3ulKqQ+Hc2I/aoB5fu0S37agbNy4kVKf93Rubi5r1qyZdOeKKdV2u1k/\nYwZ4PJSVl+v9a9fq/f3tc86BlJT4GK9pj9nu///AeB0XpwEiOuDiuuu0/XTjxskekSGa1NXpqFlD\nYKKS7MU3E79RKfVugH1WYDfasa0OeAe4WCm1M8i5JnwmXlZWNvAjOZVljCqnsVHPyANhtcLKlSFn\naJsW79cUk2Fm4ppt28oGvH/Ly3VVqd27tVUpmiTKfRMrOdGUsXChjpg98sih2/0/+4lkouVMqmOb\niHxcRA4B64CnROQZ3/bZIvIUBLe/RSLXEAKFhcENSSUlJsWqIeFYu1an5bzhhskeiSGatLRE/6Es\nkTBpVxMZjwf27NHpjvqZNQuKjV/hVMfMxAPT3AzXXguvvqpLRRqmNg6Hnov8+c/jr648VZjUmbgh\nzrFadeb9+fO118/SpUaBGxKaGTO0x/rXvjbZIzFEg717R8/mZ5imSnyqxUlGJEdE/7KVlAyWHY22\njCgQN+/XFJFh0ASK4f3Up2DLFnjzzejJSaT7Zipdy549wUuQmjhxzbRU4gaDIXFJT9fFJ265ZbJH\nYoiUfft0jn1DcIxN3GCYghib+Oh0d+tqvGVlcOyxkzIEQxS4+modZHPllZM9konD2MQNBoNhGJmZ\num7zrbdO9kgMkVBVZTzTx2JaKvGpZBOKBzmJIiNWcoxNPHaMZq+88EI9E9+zJ3I5iXTfTKVrOXhQ\n15wPhLGJa6alEjcYDIlPbi6ceCJ873uTPRJDuNTVBVfiBo2xiRsMUxBjEw+Nmhq48Ua9LDtz5qQO\nxTBOuru1U9uf/pTYIWbGJm4wGAxBKC7WWdx+9KPJHolhvFRU6AevRFbg0WBaKvGpZBOKBzmJIiNW\ncoxNPHaEYq/85CfhgQfAbg9fTiLdN1PlWrZsgdmzg+83NnHNtFTiBoNh+rB8Ocydq4ujGKYOW7YY\ne3goGJu4wTAFMTbx8fHWW/Dgg3D4sM5GbIh/Vq+G886DU06Z7JFMLMYmbjAYDGNwwgmQlgZ/+MNk\nj2R0+vrg4Ye1CWDhQl38IyNDx0qfdBLcfDPs2jXZo5x4enuhsnJk+VHDSKalEp8qNqF4kZMoMmIl\nx9jEY0eo9koRuOACHW7mco1fzkR/pl1dcMklZRQVwXe/CxYLXH45/OIX8Nvf6hSyxx4Lr70Gxx0H\na9bAI4+A1zt+WVPhO7Bpk7aH5+QE72Ns4ppI64lfKCLbRcQjIseM0u+AiGwVkS0i8k4kMg0GQ+SI\nyLkisktEKkXkpiB97hGRPSJSISJrxnNsPHL66ZCSEl+e6k6nHk9pKbz9Nnz721pxX3aZVtSFhTre\nfcECOPtsuOkmeOghvbJw0016+69+Fd6DSTzzxz/CMUE1isGfiGziIrIM8AL3ATcqpd4L0m8/cKxS\nqi2EcxqbuMEwBpHYxEXEAlQCZwK1wGbgIqXULr8+5wHXKKU+KiInAHcrpdaFcqzfOeLGJt7P7t1w\nxx3w+uva5jpZeL3aY/6OO/Qyf7/SHg9K6brpf/+7jqm+4Qa47jpITZ2YMceKt9+GM8+EX/96ehQ/\nidQmHlEEnlJqN4CIjCVcmKZL9wZDHHI8sEcpVQ0gIo8DFwD+ivgC4GEApdTbIpIjIkXAghCOjVuW\nLdPL6h/5iE7JunhxbOXb7dou/5OfaCV88cXwoQ/p5f7xIgKnnqpfb7+tZ6933gkbN8IXvgArVkR9\n+OPC64Vt27RT4Xvvwfbt0Nys34OkJG3vLyzUkQNz5+qSo/v36/dnw4bpocCjQazC6BXwnIh4gPuV\nUr+LkdyAlJWVsX79+ikvI1ZyEkVGrOTE6loioBg45Nc+jFbsY/UpDvHYmLFtWxlHHrl+XMd85jPa\ngeyYY+DSS7XDWE6OnsGKaOUKQ/9u3VrG6tXrB9rD+/TT3+63Vbvd0NgIBw5oRbt5M5SUaMe1U0/V\ntu9IrqWfE07Qr23b4N//hvvv10pxzRq94jBnDsyYoZXnzp1lrFmzHptt8Fr8X/1jD7RveL/+/z0e\nbdc/dEhf61tvlVFbu560NK2gi4v1+z1jhnbUc7mgowNaWqCpSSvvnh6t2G+8EY46auxrjuT9Gg+x\nkhMuYypxEXkOKPLfhFbK31FKbQpRzslKqToRmYlW5juVUq+NIjPE0xoMhhgR1pfy/PPj+7v8m9/o\nVyzZvVu/fv7ziZXT3Q3V1fDPf06snNFwOKC1FbZuDf2YF16YuPEkImMqcaXUhyMVopSq8/1tEpG/\no5/cAyrxeI99NRgSgBpgnl+7xLdteJ+5Afokh3AsYL7LBkMsiKadOuAXVkTSRSTT938GcDawPYpy\nDQbD+NgMLBaR+SKSDFwEPDmsz5PAZQAisg5oV0o1hHiswWCIEZGGmH1cRA4B64CnROQZ3/bZIvKU\nr1sR8JqIbAHeAjYppZ6NRK7BYAgfpZQHuAZ4FtgBPK6U2ikiV4nIlb4+TwNVIrIXHX1y9WjHTsJl\nGAwG4jDtqsFgMBgMhtAwYV8Gg8FgMExRjBI3GAwGg2GKYpS4wWAwGAxTFKPEDQaDwWCYohglbjAY\nDAbDFMUocYPBYDAYpihGiRsMBoPBMEUxStxgMBgMhimKUeIGg8FgMExRjBI3GAwGg2GKYpS4wWAw\nGAxTFKPEDQaDwWCYohglbjAYDAbDFMUocYPBYDAYpihGiRsMBoPBMEUxStxgMBgMhimKUeIGg8Fg\nMExRjBI3GAwGg2GKEhUlLiIPiEiDiLwfZP9pItIuIu/5XrdEQ67BYAgPETlXRHaJSKWI3BRg/zIR\neUNEekXkhvEcazAYYocopSI/icgpQDfwsFJqdYD9pwFfV0qdH7Ewg8EQESJiASqBM4FaYDNwkVJq\nl1+fGcB84ONAm1Lq56EeazAYYkdUZuJKqdeAtjG6STRkGQyGiDke2KOUqlZKuYDHgQv8OyilmpVS\n7wLu8R5rMBhiRyxt4ieKSIWI/EtEVsZQrsFgGEoxcMivfdi3baKPNRgMUcYWIznvAvOUUnYROQ/4\nB7A0UEcRiXx932CYBiil4np1y3yXDYbQCff7HBMlrpTq9vv/GRG5V0TylVKtQfrHYlgGw5RFJCL9\nXQPM82uX+LZF/VjzXTYYxiaS73M0l9OFIHZvESny+/94tENdQAUeC8rKyhJCRqzkJIqMWMmJ1bVE\nwGZgsYjMF5Fk4CLgyVH6+3+vx3vshGLum/iUkygyYiknXKIyExeRR4H1QIGIHARuA5IBpZS6H7hQ\nRL4MuAAH8JloyDUYDONHKeURkWuAZ9EP8g8opXaKyFX4vrO+B+9yIAvwishXgZVKqe5Ax07SpRgM\n056ohJhFExFR8TYmgyHeEJEpYRM332WDYWwi+T6bjG0Gg8FgMExRpqUSN/aa6SkjVnLi3YaWSJj7\nJj7lJIqMWMoJl2mpxA0Gg8FgSASMTdxgmIIYm7jBkDgYm7jBYDAYDNOQaanEjb1mesqIlZx4t6El\nEua+iU85iSIjlnLCZVoqcYPBYDAYEgFjEzcYpiDGJm4wJA7GJm4wGAwGwzRkWipxY6+ZnjJiJSfe\nbWiJhLlv4lNOosiIpZxwmZZK3GAwGAyGRMDYxA2GKYixiRsMiYOxiRviE/MDbjAYDBNKVJS4iDwg\nIg0i8v4ofe4RkT0iUiEia6IhN1yMvWaCZbhcsHcvvPcebNsGbW3RlxEmcfl+GcLG3DfxKSdRZMRS\nTrhEayb+B+CcYDtF5DxgkVJqCXAV8NsoyTXEGx4PVFZCR4duO52wfz+0tEzuuAwGgyEBiZpNXETm\nA5uUUqsD7Pst8JJS6k++9k5gvVKqIUBfY0ebyuzfH3jmLQIrVkBaWuzHlIAYm7jBkDhMBZt4MXDI\nr13j22ZIJDo7gy+dKwXV1bEdj8FgMCQ409KxzdhrJkjG4cOj7+/pCbqsPi3fL0PEmPsmPuUkioxY\nygkXW4zk1ABz/dolvm0B2bhxI6WlpQDk5uayZs0a1q9fDwy+oZG0Kyoqonq+QO1+Jur8/e2KiooJ\nPX/I79fRR4PDQVl5uW6vXav3D28/+SSUlrL+9NOHHN/PtHm/wrifysrKOHDgANFARM4F7kI/yD+g\nlLozQJ97gPOAHmCjUqrCt/1rwOcBL7ANuFwp5YzKwAwGw7iIpk28FG0TPzLAvo8AX1FKfVRE1gF3\nKaXWBTmPsaNNRfbs0cvpobBgAeTnT+x4EpxIbGgiYgEqgTOBWmAzcJFSapdfn/OAa3zf2ROAu5VS\n60RkDvAasFwp5RSRPwH/Uko9HECO+S4bDCEQyfc5KjNxEXkUWA8UiMhB4DYgGVBKqfuVUk+LyEdE\nZC/6qf7yaMg1TDzdzm46+zpxepwIQnpSOvlp+Vgt1sFOfX2hK3CAhgajxCeX44E9SqlqABF5HLgA\n2OXX5wLgYQCl1NsikiMiRb59ViBDRLxAOvpBwGAwTAJRsYkrpS5RSs1RSqUopeYppf6glLpPKXW/\nX59rlFKLlVJHKaXei4bccDH2mtHxKi8N3Q1sa9jG7ubdbPrPJlrsLTTbmznYcZDtjdtpdbQOHtDc\nPPQEfX3wyCPwla/AD36Ad99enF4XA7Myu13bxyf4OgKRSJ99BAx3ND3MSEfTgM6oSqla4GfAQd+2\ndqXU8xM41lEx9018ykkUGbGUEy6xsokbpgBe5aWpp4n67nrcXnfQfm6vm6q2KnrdvczJmgOtrUM7\nVFXBtm24P/Npuj7YQuaVX+TgDZ+n85S15CVlUZxaSHJTE2RkTPAVGaKNiOSiZ+nzgQ7gCRG5RCn1\naKD+ieDfEqt2LPw1/Jns653O71dZWRkPPfQQwMD3I1xM7nQDSima7c3Uddfh8rjGdexsSzZzakYu\npXe77ey31+DyuknfvZ9Ft93FB7//IZ7MDKxioTSzhNy1p4BlWgZIREyENvF1wO1KqXN97ZvRpq87\n/foMz+2wCzgN+BBwjlLqi77tnwVOUEpdE0CO+S4bDCEwFeLEDXFIv/Le0bSDgx0Hx63AAerqKqnr\nHbqc3ubsZE/PQVy+2bx92UJ2PHAnnkw98/YoL/u6DtJSuy/yizCEw2ZgsYjMF5Fk4CLgyWF9ngQu\ngwGl3+5LznQQWCciqSIiaOe4nbEbusFg8GdaKvHpbq9xeVzUddWxrXEb1e3V9Ln7Ru1f/kZ58J1d\n3dT2NrG/5zBtzk6q7XXst9fgHTYD82aMzNRWfXg77b3tYV9HOCTSZx8uSikPcA3wLLADeFwptVNE\nrhKRK319ngaqfM6o9wFX+7a/AzwBbAG2AgLcP1JKbDD3TXzKSRQZsZQTLsYmPk1wepx09nXS5mij\ny9lFVJY5e3t1sROgzdVFm6trXIernh6qmipZMXtEpl7DBKOU+jewbNi2+4a1RyyR+7bfAdwxcaMz\nGAyhYmziCYRSCrfXjcvros/dR5+nD4fLQY+rZ8zZdlg0NUFzM+JyM+vRf1J36SfAOs7FnVlFpBUW\ns3zGciwyLReGwsLkTjcYEodJjxM3TDxKKXpcPdhddnrdvTg9TtxeN26vG6/y4vF68CpvbAfV3Q1A\n3itvk7lt9/gUuFK6KEpHJ468fGq7ainJLpmggRoMBkNiMi2nPlPJXuP0ODnUcYj3G95nd/NuDnUc\noqmniY7eDnqcPbz+yuu4PK4JVeABbeJut15OBwqeeZmm888K+Xxz/vAEBc+8rBsOB7hcPP3c09hd\n9mgMd1Sm0mdvGJtEsouaa4k/GbGUEy5xORNv6mkC9BIDgCADbUFG/LWIZeBltVixinXg2KlMfXc9\ndV11sZ9hh0KPnoUnNbaQvvcgWVt2MHPTi/TOm8OhqzdAWipkZGqbuW/G3k/X6mWU/PYxWs47Tc/G\nu7WNvrq9mhUzV0zG1UQNj9dDr7uX9t523F73wAqJQqGUQhF4ebn/HgeG3Lv+24fvMxgMhri0iZfX\njOINHSIWsZBkTSLJkkSyNZkUWwpptjTSk9JJsaVEYaQTh1d52d+2n47ejskeSnBqa6Cjk6I/PUX+\nf14l7XA94vWiLBaaPnUeh352u1bQoBX+4cPg9d1rSrHqips48PUv0HPEUkhPg/mlAJTmllKQXjAp\nlxQOXuWlvbedjt4Oup3dOD2xqQOytnitsYkbDAmCsYkHwKu82rmLkQ5dSdYkspKzyEvLIyclJ65m\nN17lZW/rXrr6xufpHXN69NJ3/otvolKSEa9eLRCvl9TDjYMKHPSMvLgEDvmyeIrQfPaHKHj+da3E\n7Q69PG+zUdNVQ15aXtw7uXm8Huq762myN+HxeiZ7OAaDYZoS37+UE8Sbr75Jq6OVfa37eL/hfeq6\n6qL+QxyuHeVA+4FxKfBRY7ijxAgZfb1a6QL7bv8q7ctL8Vi00vZaLfQuXTjyJJmZkJ830Gw98yTy\nXn4HceqZa/mLrwE6hr3fnDIRRMO+1d7bzvbG7dR31we8b2LxmRg0iWQXNdcSfzJiKSdcpqUS98ft\ndVPbVcv2xu202FsmdSz13fW0OdomdQwhYdezcI/ycp/7LY449m2eODmP91bk8sC6FK48ozvwcTNn\ngk0v/rgKC+g44ShSDjf4zukY6FbfXR+ffgBAXVcd+1r3jZpb3mAwGGJFwtrEwyUvLY/S3NKYL+fa\nXXZ2Ne+KThKWiebwYejqwuV1c2/1X7hw9pkUZ8yCxYtxo1O5zsqcFfjYtlaobxi5XQSWLQXf+z43\nZy6FGYUTeBHjp7arlrquuskeBmBs4gZDIjHpudNF5FwR2SUilSJyU4D9p4lIu4i853vdEg25E0Gb\no41dzbvCyiMeLkopDrQfmBoKHMCuy4gmWWx8dcHFFKcWQl4eWKzYLLbgChwgN29gNj4EpYZ4sTd0\nN8TV+9Fsb44bBW4wGAz9RKzERcQC/Ao4B1gFXCwiywN0fUUpdYzv9T+Ryo2EsWyWDpeDypbKiBT5\neOwodd11OFyOsTsGIOY28b5e8Axb6hbRyjkURIbYxgdkVOyErkFfAKfHOZBXPZqEY9+yu+wc7DgY\ncn9jE48diWQXNdcSfzJiKSdcojETPx7Yo5SqVkq5gMfR9YaHE9dLf8Ppdfeyt3Vv9D2Pu7uhrk4v\nSbe00NvXQ313fXRlTCQ+e3hybeOgMs/IgKSkUQ8bMqvOzQVLgNuhu1vPyH009jRGPNxIUUpR1VYV\nV6sCBoPB0E/ENnER+SS6vvCVvvalwPFKqev8+pwG/BU4DNQA31BKfRDkfJNqEx9Obmoui/IXRX4i\nux0OHoSeniGbdzsO012Yq72345yK+gqW9mWQ3u1k9aeuYedvvoersABKiiErO+hxT1U+xd7WvVy/\n7vrBjXW10B4gDn7+PEjPGGiumLmC9KT0aF7GuIgnO7g/xiZuMCQOUyFO/F1gnlLKLiLnAf8Algbr\nfNv1tzFn7hwAMrMzWbZqGWtPWgsMLlXGqv38i8+zNWMr/++8/wcMLq2sX78+9HZrK+tLS0Epysr1\n+devXUtDXwtlb7+j5X3kDMjJjfn1hdrOXJrJjc/dyFe8F7K4ycuqzAxchQWUb9sFrT2sPTn48VnO\nLJ6rfY51JeuwHdS33NqjV0F7B+UVO8nctovjVi6h69gjKH/pdcjLHzh+0382UZRZNL73O0ptp8fJ\nv579F17lnfT3H+DdN9+l9lAtBoPB0E80ZuLrgNuVUuf62jcDSil15yjHVAHHKqVaA+yb8Jl4+Rvl\nAz+SoSAiLJ+xfFwzwrKyMtafdppOcNI0Mu6509XNXvvhwWVaET0LTRvfrHO81xIOL7z4Aj+v/zlf\nW3stZ3nmU/iXp0mpbeTQVzdCbg7MnjPmOTbXbObWslt57JOPkZuaqzfu3wd9TgqeKWPbs68x5xe3\n6GX5xYsHjrNarKwuWh21aIGysrIBhT0WB9oPhBV2GIvPxMzENeP5PONdjrmW+JMRKzmT7Z2+GVgs\nIvNFJBm4CHhy2ACL/P4/Hv3wMEKBxyth2UWVgqoqXA11NDvbaehroc3ZSZe7h9repqEKvL9/TS3E\nWfavXncv926+l08s/wRnFa4DIHvLDrqOXqU7+JbRk6xJzMyYGVTZHld8HOctPo/vvfK9wevOyQGg\n48RjSK+sQvqcOtd6X+/AcR6vZ1Ji53vdvZOeN8BgMBjGIipx4iJyLnA3+qHgAaXUj0TkKvSM/H4R\n+QrwZcAFOICvKaXeDnKuuLKJ+zMrcxbF2cVjd/Qp8OaGKg456vGO5z3Oz4OiUUK0YohXefnOi9/B\nZrHx3fXfRerrkKYWjvrkl9n2f7/Ak5sFS5dhsVhZMXMFqbZU2hxt7G/bH/B8To+Tz/3jc1y6+lI+\nuuSjWmHv3QvA0hu+T8OF59Fx0jE6KcyMGQPHZSZnsmzGsphccz9VbVW0OuL3OdPMxA2GxGHSsqN3\nVgAAIABJREFUbeJKqX8Dy4Ztu8/v/18Dv46GrMmkoaeB/LR80pLSgndSCg4coKl+PwcdYXidt7Xr\nmOvkyS/S4lVeluQvYcORG3R+ebsdW0cXrWechCc7UzvjiVCUWUSqLRXQyXKy7FkBU8cmW5P58Vk/\nJjvF5wSXlKSLn9gdtH1oLbmvl2sl3tU1RIn3FxZJtibH5LqdHidtvVMgc57BYJj2TMu0q+HG8Sql\nqO6oHr1TdTXdjYf5+1svhSUDpaAx9NzhExmTbLPYuOLoK9j2zjadK93pwjUjj4PXX647ZGZiEcuI\nzGqzM2cHPefcnLnkpOYMbsjWCv253Bxy39wCHo+uU+4aGqMfraXtUGI+I000MxXixMdK0OTrc4+I\n7BGRChFZ47c9R0T+IiI7RWSHiJwQu5EPJZFihc21xJ+MWMoJl2mpxCOhx9kTPH65uhpPcyNV9lqC\n6gC3m7Q9B8h8fxe21iDJTLq6htiF4wJHgGQ0GZkUpBdgswxd0MlKyRp9tWJIZ63E3Xk57P7Zt8Hi\nuyW7Ood0i9XStsfrocWR2LbwUBI0+aJIFimllgBXAb/123038LRSagVwFLAzJgM3GAwjMLnTw8Ai\nFlYVrhq6vFtdDc3NHLDX0uIcGf9s6bYz+9F/MuOZl3EV5OLJyCCppZUdD9yJSgmwTJyTDXNCsL/H\nisYGaPFTpKmpsGBB0Djuxp5GDnUcCu3c1QeGFEABhtQY72flzJWhPxyEybjGPYlEYhP3RZTcppQ6\nz9ceEVEiIr8FXlJK/cnX3gmsR/u0bFFKjZk8wdjEDYbQmGzv9GmHV3kHvdV9Tmw0N9Pm7AyowAFK\nf3I/1i47O391O11HrcSbnETHCWtQNmtgIZ1dA+U+Y0V5bTmdfZ2Bdw5XspkZpCelBw27y0/LD6lO\nu9vrxpUZQDH31xj3Ixaz8YksgxpHFAP+TyqHfdtG61Pj27YAaBaRP/jqINwvIhP7ZGUwGIISq2Qv\ncUU04ni7nd0cbK1ifqsHOjuxe3qpdgxm9iqv2MnaNSsG2lXfuRqVnMzcXz7MzE0vIF4vmVt34sJD\n/bVXjBSgFLS1aU/tCb4WgCc+eIL737ufe869Z9DxrF/G6+WsLRiWUS4jg4L0gqDns1lsZKdk09Eb\n+KGmn19v/jU2JZxQVTLk/QL0knpe/kCzrbcttOiAURgt5rOrr4ted+RmjFjEiU8iNuAY4CtKqXIR\nuQu4GbgtUOeNGzdSWloKQG5uLmvWrIlqYp6Kigquv/76qJ0vWNvfLjpRiYbuuuuuqL8/gdrDr8m8\nX6O3h19TtN6fhx56CGDg+xEu03I5PSo/ss4+OHyYDI+VVEsyba7OIaFkw5V4P3O/fgeFW/cOtF9c\nKJx/eSofKTyJmxZtHNrZZtOJT0aZ0UZ6LU6Pk7vfvpu3Dr/FXefcxdycuSNlvPQ6a2flU/B0GV3H\nrMI5pxBZtpzVs44aYQ/3Z7Rws35a7C1c8rdLuMJ7AZ857vShOwMsqUeahnU0Jb6vdV9Uiq7Ee7KX\nUBI0BVhO3wWc5tv9plJqoW/7KcBNSqn/CiDHJHuJMxmxkpMoMmIlxyynj5OIf2Db2/USep+THreD\nFmfHiFjwQAocwF06D4+v+IeyWFh15Fn8Y+1P+eSsMxGni7wyv/B5t3tErvVoXktlSyWX/eMyGnsa\n+cMFfwiowAHWHrUclKL4oSf0CkF6OtmpOaMqcICc1JwxM60VpBdw88k385jtGewePQtOrmvUciZg\nST3Yl9HpcdLRN/qqQahMgVn4mAmafO3LYEDptyulGpRSDcAhEelPm3wmELAOQiyIxY94rOSYa4k/\nGbGUEy7TUomHjcOhnbDq6sAbZIahFHkvvqlDpQJQd/VltJx/Fp1Hr6Lp/DM5fPUG8pKyWZwxF7xe\n5jz4Z7Le3T7Q//mdT/Ny9cu4vdG3j5cdKOPSIy8dGrsdCLuD5LomlFhwzpoJ6enkp+UH7+/DIpbB\nFKujcPqC01kzaw2/2P8IKMWyG35A6kFfjvDOoYp1IsqTgnZoC2nW6HLqeupdndDRrl+dHTqiwN4z\nGB6nvGOfa5JQSnmAa4BngR3A40qpnSJylYhc6evzNFAlInuB+4Cr/U5xHfCIiFSgvdN/ENMLMBgM\nA8SnTdxhD7BRBpeVBf2/WPRfi9//ITCu5U6ldInM9jboHn1WjFIU3/842e/t4MW0FFaecAQplmGe\n51Yrh665LPDhqSnUXv4pih/4M7uOWQUiWPr6+L+t/8v3X/0+5yw6hzNKz+DIoiMHZsGRLN1eeeyV\nIfUrf+Ndzq5vpHvVEj2mjKyQlDNoB7dQZs9n2s7m55138m7nLkpOOZbcVzdTP78YOjohf9D23ufu\nw+6yh72kHmhpzOP10GxvDnyAy6WVdE+PfogL9vDmx4ApxSJgtYHVCjarDp+z+P4XC1gt+q9F/O5n\n/O7z/vs5+onZxkrQ5GtfE+TYrcBxUR9UGCTSkqq5lviTEUs54RKfSvzAGAlVgiGifxj9fyyt/S+/\nH9O+Xj1j6v8R7f+N9Co9g3a5tM3b0atnV54QZlVKUXLfY2Ru3UnlT27m5fJN/LDizzx69PexSRAP\n9AC0nXY8sx5/itxXy2k/9TjOKFjLGas+xiFLN0/vfZqfvvlTartq+eun/xp0NqyUosvZRWNPI5Ut\nlRzuPByywh6BywkeD5k79tBzxFKwWsjNnRVyQZLslGxsFtuYKwlptjR+f+pPye/20n4ylNz3KPWX\nflx/Tn29kJI60LfN0RbV8qSNPY0j68Y7HNDcrB/gwsWrwOsakbjGYDAYokV8OrY9/7+TPYzxoRQl\nv3mEzO2VbP/hDfyo8a9s7azkJyu+Smn62BW+hpP9VgXFD/6Znfd9Xz+YDHPwarG3BPUMP/nBk/Eo\nDynWFGZmzGRx3mKWz1jOpasvHdOGHZCOdqitY+UXvsWBb3wR+7FHsvioM4ZmXRuD6vbq4DNdfxx2\n/QDn8bD609ey697v4iyaAQX5UDhQQ4cUWwpHFB4x/msJgMvjYkfTjkEl7nbrmPiOIKF2ccLasz5r\ncqcbDAnCpOdOn+7M/MezZO7Yw/Pf28i3q37OnNSZPHTU7WTYhoXPpqbqAicZmXoVoLdPL9O3D7X7\ndh6/mpL7HyN9937syxdpBy+XS+cah1FDu1647AUsYolennGHdjar23A+9kXzSMrMGd1+HoD8tPzQ\nlHhaul4pATpOPJrc18pp/OS5WqHOLBxYXo50Sd2f6o7qQQXe3Q11teCOr0pyBoPBEIxp6dhWXhHF\nLJEeD6lVh+lLttD4i//hYwUn8cNl17Bz+4HBPhaBWbNgwQLIydWhY2KBtDRdi7ukRPcZ6G9h913/\nrRV4P12BZ4bD83Sn2lKjWyjEYae8Yidtp58INht5eXNCSuLiT1ZKFknWpFH7DFxHZhYALR8+BU+6\nbwnd7YbuoQVVwvVS94/9PNRxaDCOvalJ134fRYErpehxOzjc28gHXft5v3NP4Gup2MmenoPst9dw\n0FFPXW8zTX1ttLk6I8rJbhiJ/+c51eWYa4k/GbGUEy5RmYn7SpHexWAp0jsD9LkHOA/oATYqpSqC\nne/SLf+NRSxYxYJFLJxZcByXFJ87ot9rrRU82fAKVrGQakkh1ZpMqiWZY3KW86H8o0f073T34PD0\n4fRGz0Y5995HmPnvVxCvl89bhOZZjRy6xk/JJSVpJZ2aGvwkWVlQXAKHD9OfdN2TPSy5SmfXEAev\nmOD16NWCfixCwYzAYWhjkZ+WT0N3w9gdMzOhvZ3uo1awe1kBqreRktRCnfgma3AFoM3RRkl2SVhj\ncXvdHGg/oBW4Unr2PcryuVd5+cL7/8M++2G8ykteUhbZtkxsFisPrr41gH+A4tbdv8WlPLiVW//1\nunErD8+fcO+I8yulWPfG5VgQLGLBJhYs6Hv/+RPuHfdDk8FgmD5EbBP3FVOoRMeL1qJjUC9SSu3y\n63MecI1S6qO+ikd3K6XWBTmfevjvd+DFi0d58SrFjORc5qYVjeh7yNHA7p4DuJWXPo+TXq+TXm8f\nSzPmcWLe6hH9n2x4hd9UP0GHqxsRyLFlkpuUxSdmnc6nZp81on9TXxud7h4yrKm4lIc+r5NGZxsz\nk3NZkjEPgCXf+BHZW3YMHNN59Cr2/ORm3UhJhrnzBpbBAYoyi5idOZsuZxdVbVV4/UORWppHr2C2\nePGQc004Pd1wcDDzZlp2PiuP+0hYp3K4HHzQFEI4sfJCZSV4FX+ufY4nG17hwaNuJdmSBAsXDHFw\nW1qwlKyUrHGNw+6ys691H06PU8s6fHjsqAPgg679FKcWkpOUOWbf8aKUwqM8ePDiVfq+9ygvXrzk\nJQU2XRibuMGQOEy2Tfx4YI9Sqto3mMeBC4Bdfn0uAB4GUEq97StlWORLHDGClVkLQxI8N60ooHIP\nxvlFp3J+0akopejzOml3d9Pu6iLTFti2+mb7Nh4+/C8cnl6SLDaSlIWSdi8fXX3hgBLvnTeHrK07\nEa8XZbHQO9/nyJaaAvPmaa94HzMzZg7MHnNTc5mfO5+qtqpBgQUzoKs7cMUw0EvKeWPHZ0eNYfnS\nZ+SHN/MFSEtKIy0pDYcryLX1IxbtM9DVxadmn8Xmjg/4RdWj3LToc9Daqs0PPlocLeNS4t3Obva0\n7NEPTsqrl897BsMZu90O2t1deuY/jBH3pNeLxdGHKC+etFQd+RAmIoJNbMZBxWAwjJto2MQjKaYw\nKby7dRep1hRmpRSwPLM04I82aKX/xLF38p9Fd/D2jpPZfWcPT+xazdnZg0v1h67eQNP5Zw4kbzn0\n5Q2Qkkx5TdMQBZ6RnMHc7KFL0flp+SPjrWfNCj7wzpFLvhNau7pXK9zyip2ICPkF4StxgBnpM4Lu\nG3IdWXq2KyLcuuQLvNH2Ps82vaWXvP3CtdocbSNDw4LgcDnY27qXd15/J6AC39V9gA1bvsNzTW8F\nPcfsP/6NFV/8Nmv+64scc85GVl90HUde8jWy/ZLzwKDPRdGf/sXcux9izh+eoPAvT1PwdBm5L7+N\nrS1wZjhxucEbv0li4pFEsouaa4k/GbGUEy5x+fB/1Ce+hLLo5C3KaqHl3NOovfzCEf3yXnqTwr/+\nB29aCt7UVLypKXjSUuhceyTtpx4/or+tvRNrVw/Wrm6kz4lKTho1QUz22xUU/v1ZMnbto239Oip/\n9h165w979hievCUlGebNh/q2wS4WKwtyFwS0bc7NmUtHX8egw1NqKuTmDHisWzu6yCl/n9YzT9Yz\nY497yMPBhKEUOBzMeOpFcg8cIu/4E7BlhR5WFoj8tHwOdx4e27krM1N/LkqRZcvgzuXXcs32H7M0\nYz6lzTkwezagbdUtjhYKMwI/hPXj8XrY17ZPK3yFXkLv7GLuvY+QerCW/UVJfPXEvXxj2UbOmnFC\n0PO0n3ws7Scdg3P2TDzpaYO1z4NgX1KKNzUZW2c3yc1tWKtrsPY46JtThDtv5Hu56NZfkLP5fZTF\ngkqyoaxWlAj77rie7iBpfA0Gw/QmGtqgBpjn1y7xbRveZ+4YfQb4f8cewZyZBfpHPC2VZUtL6Z/7\n9s9y1q5ZQdealbzW2Y30uTixuBBrbx9vVx7A2dzGqgD9s995nz0P/plSRy9rnHpG92JyEm0fOo6F\nN35xRH9vehpPrVyC/eNnc8y6NSP2j2gnJ1Fe0wz1bQNZ1MrfKKc4u5g1Z+vjh1e2eePVN2jsbmTR\nMYsG+uN2s7YwF5SifHslC37+IPknHYs3LZXyF16DzMwhWdr8s7b1z2gjbh9zBHi8vP/863hWL2dm\nzmywWiOq3GOz2NhVvouuvq6x5ZfMhB47FS+/zcx/Ps813/w0O7v30/xyO8yexdrTTgLgqf88xYK8\nBZx++ulB5dd01rB8rc7/TlMT5QcP8olXNzNz0wu87PXiBl6xHI/j5BMof287KXVNHPnR00d8vo7F\n83V778HAnz9DIx+6jlnFSz5FP2R/j4P+T8//+L0//AblFR+A18txK5dgcbsp37Ybj8cDFTt5d+tO\nauunRanUkEmk/NnmWuJPRizlhEs0HNuswG60Y1sd8A5wsVJqp1+fj6BLF37UV0zhrtEc22KV7EWc\nTqw9DpTVOtIbfLwkJ+kZ+DDHs7k5c8ecKbq9brY1bBvq5FZXOzAbX/ytn9By9ik6zCszE+aG5yE+\nLtpaoa6e1Z++lgP3/pAlJ31U2/gjpKuvi8qWytDk1zeA18sRn/06++64Hsfi+XrfsOQ383PnB12q\nb+hu4HCnz+u/pkbnOCewQ+LBr26k9M77cOXnsP+O68O+xlhgHNsMhsRhUquYRaGYQszpn/2o5GTc\neTkTosC3vLWFhXkLx1TgoGtvj+iX71dHe/0Jg9XN7D1DimtMmE3cbie5rhFltfBBs10/PESBrJQs\n0pLSRmwfcR394WQWCy0fPoWCZ1/1G5tDK3kfNZ01AdO6dvV1UdNVM+iF3tU18Nn3zpujTTboanLK\namHZV79L6xknsv+26yK6xqjmITCMSiLZRc21xJ+MWMoJl6gYVyMppjDlSU3FNr+UwpxiUm06/Mlm\nsdGZ10leWl7IpynKLKLJ3jToqJWSChnp0GOn/eRjmfvr/8PS48CbkaZDorLGF1o1buwOMrfvwX7E\nMrKTMiEjI2qnLswopLp9jPz4NpuecdsdtJx9Csuvu4Oaz38aleJLZNPQqP0H0tJxe93sa93HkoIl\nAzHbPc4e9rXtQ7ldWoEP87Q/dPUGEEitrsFi7yX1YC17fnwTjkXzo3adBoPBMNGY3OmRkJmJbe58\nlheuJMWWEvHpartqqeuqG9zQ1QmHtevAov/+OW2nHk/rh0/Rjm+zx5+TPWRcTti7j7l3P0TqoqVk\nX/4lWD0y7j5cvMrLtoZtY5dXbW3RyhpYdMvP6DjxGJp9tmpAp66dO1ena0VnqytIL8DpcdJsb0bZ\ne6CmdtQCJMm1Dcy7+48cuPmqgM5m8YpZTjcYEofJjhOffojAjBkwYwYLChZFRYEDFGUUDa2olZml\nZ6RuNzVXfEp7RIPO8a1UyKVXx41dh17VXfs5jkwrjeosHHSd8cKMQmq7akfvmJU9oMQb/9+5zPjX\nSwNKfGd3FX8//Dz33pVCWl0TvSuWcOi7X6fG7atQ19oSUhET55wi9t75zYivyWAwGCYDkzt9vKSm\nwPz5MGMG+Wn5QYuBhGNHsVqszMr0ixMXgRx9/t4Fc3EV+Zy33J6BmusTYhP3KfFZGUVY0tIp27o1\n6iIKMwqxWgYTpAS8jqQkvaQOdB29kqpbvjKwa2F6MR9/dAszNj1H9jsVzPzfvzL3+tugcjdUVQVU\n4BWdlfztzRejfi3DMTbx2JFIdlFzLfEnI5ZywsXMxEMlOUlnVMvJARFEhOLs6OerKcwopKmnSacF\nBcjNhZYAxT66uyE9ujPkAex2ki1JzEz22fTTRjqiRUr/A0tNZ9BIQ012jrZnD1t1SLEkc05PEVav\n9jYXr5fUA4eD1n6v623mpp33sMFzXngDTk6C9HRITtYPF1arL05cAKWTtHi9Wn51rS6f6vHoBy6P\nR8f3ezyh1aY3GAyGEIlPm/jOFwY3+I9P9beV/qsUeH1t/x9Rr+/H0uMZ/D8cbDbIzNDLusO8swsz\nCpmbMzGhXq2O1qHpWKuq9BKxP8lJsGhx9IW7XLB3LwvS55CfrB9YOProCVm69yov2xu34/KMUpDG\n44Y9e4feBz7m/vJhCjY9j9Wr8FqE5vPPGpp4x0eHq5svbfsBHys8havaFtF95LIRfQKSlAR5uZCd\nDUlRrAzXf08qr75/le/eHX5/w8j738faVWcZm7jBkCAknk08O8oORkoNmw35ZkgDP6K+HxqLgMWq\nf7xTUoIWG7GIZeiyd5TJT8unqaeJbme33pCTPVKJO13Q1zukIEhUsPeQaUvTChy0PXyCbO8WsVCS\nXTL0gWU4Vpt+gOrqGrGr38O8vfJ93sztZsWXLmZ4BvN2VxfXbP8x63KO4FuPHiSlsYI9P755INta\nTlImBUk5dHnsNPX5suzZbFA4U9+HE3HtFqt+TSKRVh70FT4qBw4rpc6PzagNBsNwpodNXET/MKek\nQnoG5dsqIS9Pl/acMQNmztSvghl6e2bmqNXCZmbMHLM+dqR2lHk58wbTtPo/1CiF9JcH7eqOuk1c\n7A7mWwt0fW2AjIwJtQn1+xWMeh25uSM2idM5kPK2656fMuM738dqG/qZ9HmdXL71Dk7MWcUvHm8l\npbmdxz/90SEKfFF6CXnJ2cxLm8WijBIkLw8WLdR138NU4BOazz4K+BTwr4BzgFXAxSKyfFif84BF\nSqklwFXAb4ed5qtACGXpJpZEsouaa4k/GbGUEy7TQ4lHkRHOZxNEWlIaszN1jnBsNh0zDhT+/VlK\nfve43h5gdhopxd5MUnfshm98Q2+IUpKX0ZifO3+Ik9sIMjL0e9CP283Kq24h8/3BQnmzUkbWWk+x\nJPPLxV/lZw83YOtxsPd/bkAl62Vxq1iYnzZ78EHJaiV3xdEsXHnypM+SY8BA5UGllAvorzzoz5DK\ng0COiBQBiEgJ8BHg97EbssFgCER82sRr4ncmU5xdHBMlDrrOdGVLpV5Wb2uD+npSq2tYctOdbHvs\nbj1TjGKN8RxJZXFtL/z+99px7vrrdXx4DGqYt/e2s691X/AOTU3Q3DzQzCrfxoIf30flnTfRuyC4\nb8Lib/8Ud1YG1V//gi5442NuWhGFKb6seCkp+n1M1aaJxp5GDnUcCnS6uGFt8dqwbWgi8kngHKXU\nlb72pcDxSqnr/PpsAn6olHrD134e+KZS6j0R+QvwfSAH+Hqw5XRjEzcYQiPxbOJxSrI1OaQ0qtFC\nRFiYt5CdzTtxZWVBfT298+bgTU0hvbIK+7KFOiFM/shZ6HhJtaWywJsP1MLWrfDJT47qFxBtclNz\nKcku0XnOA5GXBy0tA/4LXWuP5NBVl7D0Gz/i4HUbaf/QWv1Q4/EMVCfrnTeH6msvwzVr5pCl8RR/\nz/v0dFiyZMhMvzCjkF53L009ptjIcETko0CDUqpCRNaj3fODsnHjRkpLSwHIzc1lzZo1YRXPMW3T\nTqR2WVkZDz30EMDA9yNcpuVM3L/q13hYmLcw5FSqZWVlUat+0+PsobKlEu+B/WB3UPy7x1E2G7WX\nX0j5rn2s/cTHIjp/kjWJ5TOWk1x1EFpb4Ywz4J//hIULYcGCqF5LMPpljDoLrq0ZEf+dsaOS+b94\nEHdONpU/+zZzf/kwMze9gHi9KItF13j381gvr9jJp046UzvuZWbqGbh15PK5Uop9bfvo6A1c+3s0\nwr2/xkOEM/F1wO1KqXN97ZsB5e/cJiK/BV5SSv3J194FnIa2hV8KuIE0IAv4m1JqRFhALGbisbg3\nYyXHXEv8yYiVnEktgDJdyEnNGVcu9GiSkZzBovxFWLK1g1f7yceS+/q7emevE9xjpC8dhWRrMssK\nlpFsSdI29j17oLBQO5PFwB4+nMKMQpYWLB3IQz8E34pDqjWZwpQ85qfPJm/tKVT/4S6qr79c7ztY\ni3h1SKF4vaRWD80Kl2ZNHlTgS5YEVOAwuAqSkTxBsfiTy2ZgsYjMF5Fk4CLgyWF9ngQugwGl366U\nalBKfVspNU8ptdB33IuBFLjBYIgN03ImPl6sFisrZ64k2RrFWOEw6O5uZd/m/+B2u1h8y8/Y/9/X\n4k1LhVlFkJc/9gmGkZGcwaK8RdrTvrNTK/DNm/Vy+he+ACtXTkiil1BQStHZ10mXswuXx4XVYiXN\nlkb24UZSuntH9G92tnPIUU/xPX8MOhMXEZZnlpKeXTCqAvfH4/VQ2VKJ3WWP+jVGQiQzcRgIMbub\nwRCzH4nIVegZ+f2+Pr8CzkWHmF2ulHpv2DlOw9jEDYaIiWQmbpR4CCzKX0Ru6sgwp8nAuX0rVS17\n6Xb7VeVKS4Nx2FVEhKKMIuZkzRn0zj50CBobBztZrbBmTXQGHU0cDvggcGST3dPLvs5qin79EKnV\ntfTOn8OhL28YUNazUgooLiiFpUtDUuD9eLwe9rbuHYzbjwMiVeKxwChxgyE0Jm05XUTyRORZEdkt\nIv8RkYBZWkTkgIhsFZEtIvJOJDKjwXjieOdkzQlLgU9UbGFyQSHLMkuZnz6bZEuSztPtcIxaqcuf\nvLQ8Vs5cSXF28aACB2hvH9rRr+hJLOIkQ5aRlqZj+wOQbk1lRc4iOq7/Mnt+crOegfuUdU5SJnPy\n5lFWWzsuBQ56JWZpwVIK0kNzIIz3OPFEIhb3ZqzkmGuJPxmxlBMukdrEbwaeV0otA14EvhWknxdY\nr5Q6Wil1fIQyY0ZRZhGzs2ZP9jCG4kt8MiM5lyOyFjEndQZ5SVnYunsCdhcRMpIzmJM1hyMKj2Bh\n3sKR9ma7HZzOodsmwR4eMsXFQb3mbRYbSzLnUZo+m0xbGmnWFOakzmTRjKXIsmXjVuD9iAiluaUs\nyFuAzWKCOgwGQ3wQ0XJ6v8eqUqpBRGYBZUqp5QH6VQFrlVItIZxz0pfTRYTirGKKMosmdRxB2b4d\n+vqGbktNxbl8CS6PC4/yYBELNouNFGvK0Bl3IGpqoL5+6LZly+Jbkffb8ENhFC/0cHB73dR11dFs\nb8arJqegiVlONxgSh8mMEy9USjUAKKXqRSRYELUCnhMRD3C/Uup3EcqdMNKS0piXM4/M5DhWYLm5\n0NAwdFtvL8kOJ8nhKN62tqFtER0/Hc9kZ8PcudqWPxoFBbp0bBRzoNssNubmzGV21mya7c20Olpx\nuBxjH2gwGAxRZkwlLiLPAf5TUl/tRW4J0D3YY/fJSqk6EZmJVuY7lVKvBZN52/W3MWfuHAAyszNZ\ntmrZQNxtv70xkvbuHbvZ8MUNQ/avX7+emRkz2frWVhqlMeKA/v5tE5IwwOFgfaF+Xrrr6qtZ8+lP\n6/3NzZSVl4/vfM88AwcPsn7VKvjLXyjzeaSvP+aYgf4VFRVcf/310Rt/tN6vwkLK3nzf3XxZAAAg\nAElEQVQTGhsHx9t//evWQUkJZdu2wYEDA8ffddddUUs4YrPY2FWuU7+e9KGT6Orr4vkXn6eiooKL\nvnARbq87KvdrP++++S61h4aGzE13EilW2FxL/MmIpZxwiXQ5fSfa1t2/nP6SUmrFGMfcBnQppX4e\nZL/a2bQT/3Ep37NB/zb/9vD/h/cZOC+CRSxYxMJ7b77HKaeeQoothYykDDKTM8csaDJeJvSDVwre\nfx/cbsquvJL1H/kIfPzjurDH6tXjWzY+eFCnNH39dXjoIfjd72DWLG139hH3X0inU6dkdTj0e5CV\nBfn5A4VOoiYnRPpleJUXp8eJ2+seeHmVF4/Xg1d5USj91+/eDXav+28DWDpjqVlOJ7F+yM21xJ+M\nWMmZtBAzEbkTaFVK3SkiNwF5Sqmbh/VJByxKqW4RyQCeBe5QSj0b5JzGjhYKBw7oNKTPPQdPPgm/\n/KXeXlyslXAoeL36YcDjgTvvhKIi2LhRx1BnZ0/UyA1RIJIvfaww32WDITQmM2PbncCHRWQ3cCbw\nI9+AZovIU74+RcBrIrIFeAvYFEyBG8ZBf3nOk0/WirjTl460sXGwPvpYtLRoBa4UvPIKfOhD2nYc\nzw5tBoPBYBggIiWulGpVSp2llFqmlDpbKdXu216nlPqY7/8qpdQaX3jZkUqpH0Vj4JGQEDGM2dlg\nsVD2wQdw3HHQL8/lGlLta1T6k7vs2aMLgCxcqB3ahi1DJ8T7FUM58R5XmkiY+yY+5SSKjFjKCReT\nO32q0m/7BTj3XHjmmcF9dXV6qXw0Wluh15e+9JVX4NRT9Sy8/5wGg8FgiHviMu1qvI0pbmluhupq\n7djV1qZt2v0UFUFJSeDjvF7YsWMwwcuBA3omXlJi7OFTBGMTNxgSB1PFbLqSm6tnz8nJQxU46KXy\nrq7Axx0+PDRDW2mpVuAWi7GHGwwGwxRiWirxhLHX2GyU7dgReJ9SsH+/TqnqT0ODDikLREZG0LCs\niSaR7FvxbkNLJMx9E59yEkVGLOWEi0kCPdUZbebsdsOuXbpgSGoqdHQMerEHIidg/RqDwWAwxCnG\nJj7Vcbl0iFk0mMT64YbxYWziBkPiYGzi05mkpKGz8a1bRxYzCYZ/v6Qko8ANBoNhijEtlXjC2Wvy\n8gY3vPwy/PGPYx/Y2goXXwzd3bo9ylJ6wr1fCSDDoDH3TXzKSRQZsZQTLtNSiScc/kr80kvh2Wd1\nrPhoPPYYfPjDg7P4/gxwBoPBYJgyGJt4olBZORhSdu+9OozsBz8I3Le5GT7zGXjkEZ1n3WKBo44K\n6JluiE8itYmLyLnAXegH+QeUUncG6HMPcB7QA2xUSlWISAnwMDqdshf4nVLqniAyzHfZYAgBYxM3\n6LrZ/VxxhU7m8lqAaq9KwU9+oque9RdK8aVwNUwPRMQC/Ao4B1gFXCwiy4f1OQ9YpJRaAlwF/Na3\nyw3coJRaBZwIfGX4sQaDIXZMy1/uhLTX5OUNKuLUVLj1Vj0jH55+9YUXoKoKrrxycJv/cvxoMiaQ\nRLJvxbsNDTge2KOUqlZKuYDHgQuG9bkAPeNGKfU2kCMiRUqpeqVUhW97N7ATKGaSMPdNfMpJFBmx\nlBMuJk48UbBYdA3t/uInxx6r64MPn2GfeCIsXw4pKYPHGXv4dKMYOOTXPoxW7KP1qfFta+jfICKl\nwBrg7YkYpMFgGJtI64lfCNwOrACOU0q9F6TfmPY3v77GjhYuPT06uct4yM+HBQsmZjyGCSMSG5qI\nfBI4Ryl1pa99KXC8Uuo6vz6bgB8qpd7wtZ8Hvtn/HReRTKAM+J5S6p9B5KjPfe5zlJaWApCbm8ua\nNWtYv349MDjDMW3Tnm7tsrIyHnroIQBKS0u54447wv8+R6jEl6GdW+4DbgykxH32t0p0vfFaYDNw\nkVIqoLYxSjxCdu4cmWp1NJYuNZXLpiARKvF1wO1KqXN97ZsB5f9wLSK/BV5SSv3J194FnKaUahAR\nG/AU8IxS6u5R5JjvssEQApPm2KaU2q2U2gOMJjwU+1tMSWh7zfBCKKORmhqSAk/o92uKyoiQzcBi\nEZkvIsnARcCTw/o8CVwGA0q/XSnVv5T+IPDBaAo8Vpj7Jj7lJIqMWMoJl1g4tgWyv02aI0zCk5en\nq5qFQmHhxI7FEJcopTzANcCzwA7gcaXUThG5SkSu9PV5GqgSkb3olbYvA4jIycAG4AwR2SIi7/nM\nZQaDYRIYczldRJ5Dx4QObAIU8B2l1CZfn5eArwdZTh/T/jasv7GjRdru6GC9r5Z4WXm53r927dD2\niSfCEUdQ9sorkz9e0x6z3f//gQMHAPjjH/9ocqcbDAlCROaxaHzJxlDiY9rfhvU3X/xoMJZtfO5c\nMxOfwpgCKAZD4hAvyV6CDSAU+1tMmRb2mnnzQIJ8JOnpMHNm5DKiyKS/X1NMxnSjqqqaSy+9g9NP\nv41LL72DqqpqwNw38SonUWTEUk64RBQnLiIfB34JzACeEpEKpdR5IjIbnY7xY0opj4j029/6Q8x2\nRjxyw+hkZEBJCRw6NHS71apDyoIpeIMhzqiqqubDH/4l+/bdAWQAPbz11m0899y1kz00g2HSMbnT\nE53GRqip0ZnbUlK0As/ImOxRGSJkqiynV1UpnE6GvPr6Bv/2v3p7weHQf/tfDod+/fvfd7B//41o\nBd5PD0uW/JRrrrmNU06Bo482z6WGqUsk32eTsS3RKSzUedWdTh1SZn7pDDHkqKP04o/VCjbb4P/D\n2zbbyFdSkn51dHgZqsABMmhp8fLHP8Ltt+vn04svhltu0fmLDIaJxOWCPXv0q7YW6uv1fKmlRVd3\nttv1y+HQD6kuF7jd4PEMvrzewf8jYVoq8bKysgHv36ksI2Q5ViukpU2sjAiJq/drCsiYKvzf/0V+\nDrvdwssv9zB8Jn7kkRbOPruMI45Yz/bt8Pe/w8KF8LOfwec/H7lcfxLpvkmUa4nl+5Wfv56nn4aX\nX9a1perrdRXnggJdPyozU//NytJ1pdLS9Jyp/5WcPPJhtf8BtqkJbr45/PFNSyVuMBimDhs2bGT3\n7tuorx+0ic+adRsbNlxLU1MVInDkkfpVUQE33QSvvw6//70pzmcIn4YG+OlP4X//V8+oly3TZSeu\nvhpKS6NnlXQ6Izve2MQNhinIVLGJP/lkdL7L9fXVPPLIQ7S2esnPt7Bhw0ZmzZofsG9bG3znO3DG\nGboGkLEgTX2qq/Xr1FMnXlZzM9x4IzzxhH4w/PCH4Zhj9Kx5IqipgS9/eZLjxKOJUeIGw9hMNyU+\nXtra9BLl1VdrO7lh6lJVpZVoXx/84Adw/fUTJ+vBB7UCX7kSPvtZmDNn4mT1E6kSn5aLTSaGcXrK\niJWceI8rTSS2bSsLuD0vTyvxO+/UdsxISaT7Zqpdyze+AccfD//939qJsacn+jKcTrjkEvjmN+Gr\nX9UmmX4FHuweixempRI3GAyJz4IFsGEDXHqpDlkzTD3a2+Hpp+HTn4YjjtBOY9FwlvSnqwvWr4ct\nW+AXv9Cz/qmEWU43GKYgZjk9NJSCb38bzjoL7rprUocSMh4PPP88vPIKVFbqUKTCQq1cPvEJmDFj\nskcYO379a/jNb+CHP9Ttf/5TZ5R+/fXonL+3F045RftNfOtbOqQx1pjldIPBYAiCCHzlK9pTffv2\nyR7N6NjtcOutera5cSO88YYORUpLg4MH4e67dcmDM8+EV1+d7NHGhscfh3XrBttnnAHvvac9xyPF\n49EzfIdDP+hNhgKPBtNSiU81m9Bky0kUGbGSY2zisSMUe2VJiZ6Jf/nL4cuZ6M900yYoKSnjb3/T\njlv33Qc33KDttJ/5DHzpS3o2+vvf62Q2//VfcP75OtHIeJkq34G2Nigv10vd/WRl6VCvxx6LXMbX\nvw7vvqsdH22jBFsbm7jBYDBMMpdcArt2wV//OtkjGYrXq72hP/tZPcv84Q9h9ergYXHZ2XDZZXqZ\nubtbe1FH20YcLzz6KCxaBDk5Q7evXQt/+1tk5/7Nb3T44e2360QtUxljEzcYpiDGJj5+nn1W21T3\n7YuPpdO+Pj3L3rxZK5NZs8Z/jvJyuOceuOACPXtPSYn6MCeNdeu0M9sFFwzd3tqqV1UaG8NTwM8/\nr30LbrlFPwRNNsYmbjAYDCFw1lk6y1a/k9Rk0tKiHaoqK3VWsHAUOOhZ6V136QeBY47RDyiJwIED\nsG2bTrQynPx8XWn5L38Z/3l379Z28C9+MT4UeDSYlkp8qtiE4kVOosiIlRxjE48d47FXWixw+eVa\nadbXj09OND/TvXvhuOP0rPn73x+cTYZre83P1+dZujS0peZYfwfefReuvBJOPBGOPVYr0cceG73w\nx91368p06emB9x97LPzqV2WBdwahtRXOOUc/GJx+eujHJbRNXEQuFJHtIuIRkaDRdSJyQES2isgW\nEXknEpkGgyFyRORcEdklIpUiclOQPveIyB4RqRCRNeM5Nl5ZsUIruq98ZXLkv/aaXiY++midWGQ0\nh6rxYLXCFVdoB7grroDrrtNVsyaTt97SnvSnnaZn1scfr+3+SulkKqWl2hQwfJw1NfDAA3rJOxjn\nnqsLkRw8GNpY7HYtu7RU5w5IJCKyiYvIMsAL3AfcqJR6L0i//cCxSqm2EM5pbOIGwxhEYhMXEQtQ\nCZwJ1AKbgYuUUrv8+pwHXKOU+qiInADcrZRaF8qxfueIK5t4P21tcO21/H/2zjw8rqpu/J8zk0z2\nfWm2tumSllJoC8ZS9oJAW0BAfqBsQvF9ZbMCogiK0uIKKFJkeSmIAgoCKrIre0AESkPpnjZpm6Zp\ns+/JZCaznd8fZ5JMkkkymZlMJpPzeZ48mXPvufd7751753vP+W489RRccEFoZEqpFNZPfqKc2Fat\nGj9ZdXXwm9+o6llPPKFG/aFk0yYVc71xoxr1XnzxUNu1lCqE7m9/U74B3/++Utptbf3pTtesGVnO\nb36jcps//PDI/drb1Qjc4VDXf7xyoPvLhNrEpZR7pJQVwGjCRaCyNBpN0FgKVEgpq6SUduA5YJD7\nEOcDTwNIKTcCKUKIaT5uG9akpamc6ldeCS+9NP7yPvgAjjtOpYD9yU/GV4GDsq/fc49ScKefDmef\nDW++GXjd6pEwm9UU+YknqtF3Sgo8/rgyX3hzPhNC9b3/fjUy/uMf1fGedpoaLfsSDnjxxfD002p2\nwxtSwiuvqP32JnMJNwUeDEJVilQCbwshnMBjUsrHQyTXK5FW6zYSzkVfr5CSD1R7tA+hlPNoffJ9\n3DZkbN9ewtFHLx/zdiecoJTa1VerH/fRSks2NpaQleWbHClVJrCmJjWN7HAop7rbblN1pYfD33Px\nRlQUXHKJGoG+/LI6z44OdZ4xMSXk5i7HZOov1do7+SnlwM+e5zS4j5QqZWlNDRw6BPn5SjHfeCPs\n21dCQsLo5yKEcvA76aSxn2NnZwlXXbWclStV7HhWlrq+Nps617171f4vvFC9OPlbzS6Y38t4MKoS\nF0K8DUzzXIRSyndIKV/1Uc6JUspaIUQWSpmXSSmHeX9SU4UajSas8OuhPO+88H+W29pUDPl48sIL\n6m+i2blz/Pa9f7/6+/Ofx0/GcGz2ashVPPqo+otURlXiUkovTv5jQ0pZ6/7fKIT4J+rN3asSD/fY\nV40mAjgMzPBoF7iXDe4z3Usfkw/bAvpZ1mhCQTDt1F4fWCFEvBAi0f05ATgLCPMsxhpNRLMJmCuE\nmCmEMAGXAK8M6vMKcCWAEGIZ0CalrPdxW41GEyICDTG7QAhRDSwDXhNC/Mu9PFcI8Zq72zTgIyHE\nF8CnwKtSyrcCkavRaPxHSukE1gBvATuB56SUZUKIa4UQ17j7vAFUCiH2oqJPbhhp2wk4DY1GQxim\nXdVoNBqNRuMbOuxLo9FoNJpJilbiGo1Go9FMUrQS12g0Go1mkqKVuEaj0Wg0kxStxDUajUajmaRo\nJa7RaDQazSRFK3GNRqPRaCYpWolrNBqNRjNJ0Upco9FoNJpJilbiGo1Go9FMUrQS12g0Go1mkqKV\nuEaj0Wg0kxStxDUajUajmaRoJa7RaDQazSRFK3GNRqPRaCYpWolrNBqNRjNJ0Upco9FoNJpJSlCU\nuBDiCSFEvRBi2zDrTxVCtAkhNrv/fhIMuRqNxj+EECuFELuFEOVCiNu8rJ8vhPhYCGEVQtwylm01\nGk3oEFLKwHcixElAF/C0lHKRl/WnAt+XUp4XsDCNRhMQQggDUA58BagBNgGXSCl3e/TJBGYCFwCt\nUsrf+bqtRqMJHUEZiUspPwJaR+kmgiFLo9EEzFKgQkpZJaW0A88B53t2kFI2SSk/Bxxj3Vaj0YSO\nUNrEjxdCbBFCvC6EODKEcjUazUDygWqP9iH3svHeVqPRBJmoEMn5HJghpewWQqwCXgLmhUi2RqPR\naDQRSUiUuJSyy+Pzv4QQjwgh0qWULYP7CiECN9JrNFMAKaW/JqrDwAyPdoF7WVC31c+yRuM7/j7P\nwVTigmHs3kKIaVLKevfnpSiHuiEKvJdgONtpNJGMEAG5mGwC5gohZgK1wCXApSOJ83db/SxrNKMT\nyPMcrBCzZ4GPgXlCiINCiKuFENcKIa5xd7lICLFDCPEFsB74RjDk+ktJSUlEyAiVnEiRESo5oToX\nf5FSOoE1wFvATuA5KWWZ5zMrhJgmhKgGvgfc4X6uE4fbdmLORN834SonUmSEUo6/BGUkLqW8bJT1\nDwMPB0OWRqMJHCnlv4H5g5Zt8PhcD0z3dVuNRjMxBCVOPJgIIWS4HZNGE24IIQKxiYcE/SxrNL4R\nyPOs065qNBqNRjNJmZJKXNtrpqaMUMkJdxtaJKHvm/CUEykyQinHX6akEtdoNBqNJhLQNnGNZhKi\nbeIaTeSgbeIajUaj0UxBpqQS1/aaqSkjVHLC3YYWSej7JjzlRIqMUMrxlympxDUajUajiQS0TVyj\nmYRom7hGEzlom7hGo9FoNFOQKanEtb1masoIlZxwt6FFEvq+CU85kSIjlHL8ZUoqcY1Go9FoIgFt\nE9doJiHaJq7RRA7aJq4JP2w2aGqCzs6JPhKNRqOJWIJVT/wJIUS9EGLbCH1+L4SoEEJsEUIsCYZc\nf9H2mnGW0doKO3dCVRWUl8PeveByBVeGn4Tl9dL4jb5vwlNOpMgIpRx/CdZI/E/AiuFWCiFWAXOk\nlEXAtcCjQZKrCTe6uqCycqDSbm9XyzQajUYTVIJmExdCzARelVIu8rLuUeB9KeXz7nYZsFxKWe+l\nr7ajTVZcLjUCt9m8r58xA7KyQntMEYq2iWs0kcNksInnA9Ue7cPuZZpIor5+eAUOcPgwOByhOx6N\nRqOJcMLSsW316tWsW7eOdevWsX79+gE2iZKSkoDb69evD+r+vLV7l43X/nsZj+vj1/VyOqG+npLS\nUkpKS/vXe7adTkpefFFfLz/vp3Xr1rF69WpWr15NoAghVgohdgshyoUQtw3Tx6sfixDie0KIHUKI\nbUKIZ4QQpoAPyE88r9Vkl6PPJfxkhFKO30gpg/IHzAS2DbPuUeAbHu3dwLRh+srx5v33348IGaGS\n45OM2lopS0tH/9u8WUqbzT8ZQSBsrleAuJ8Tf59VA7DX/cxGA1uAIwb1WQW87v58HPCp+3MesB8w\nudvPA1cOI2fcr4O+b8JTTqTICJWcQJ7nYNrEC1E28aO9rDsb+I6U8hwhxDJgvZRy2TD7kcE6Jk0I\n2b595Kl0T3JzIS9vfI8nwgnEhuZ+BtdKKVe527ejfkTu8ejj1Y8FMAKfAEuATuCfwANSyne8yNHP\nskbjAxNuExdCPAt8DMwTQhwUQlwthLhWCHENgJTyDaBSCLEX2ADcEAy5mtDgki667d1027txupxD\nO7S3D1XgUqo4cW+KvbFx1JAzzbgy2EflEEN9VLz6sUgpa4D7gIPuZW3eFLhGowkNQVHiUsrLpJR5\nUsoYKeUMKeWfpJQbpJSPefRZI6WcK6VcLKXcHAy5/qLtNaMjpaTF0kJ5czl/ePEPlDWWUdZYxtb6\nrexv3U+Po6e/c3PzwI0rKuDyy+GSS2DlSnjsMWUz78XhULHkITiPwUTSdz8RCCFSgfNRU/F5QKIQ\n4rKJOh5934SnnEiREUo5/hI10QegCS+klDRbmqntrMXmtPUt81zfamml3drOzNSZpJtS1Ejck4IC\nuOEGOPFE2qr3EvuzX2Kv3EPnnbeRYUolxmhSo/SMjFCemqafw8AMj3aBe9ngPtO99DkD2C+lbAEQ\nQrwInAA8603Q6tWrKSwsBCA1NZUlS5awfPlyoP/HMZD2li1bgrq/iWxv2bIlJPJ6mejzncrXq6Sk\nhCeffBKg7/nwF507XdNHu7WdQx2HsDqsPm9T4IxnWkP3kOVWZw8HLLWYHRZEj40ZDz1N9bWXIZMS\nyI3JJDc2ExYuhNjYYJ7ClCFAm7gR2AN8BagFPgMulVKWefTx6scihFgKPAF8GehBJXraJKV82Isc\n/SxrND4Q0PMcbg+ZfvBDT7e9m0Mdh+js8SPP+aFD5NhM5Mdl9y1qtXVQZanFKYe3e6dGJzF7TjEi\nX6cL8IdAk70IIVYCD6BMak9IKe8WQlyLcnB7zN3nIWAlYAau7jWDCSHWApcAduAL4H+llHYvMvSz\nrNH4wIQ7tk02tL1GYbFb2N+6n7LGshEVeOnHpd5XSBeYu6jraWZ31wFqrU3sNVezv/vwiAocoM3e\nyf7q/lT7k+F6hZOMQJFS/ltKOV9KWSSlvNu9zCc/FinlXVLKBVLKRVLKq7wp8FCh75vwlBMpMkIp\nx1+0TXwK0tHTQYO5gXZr++idR6LLDC410jLbzJgdljFt3mZu5lBdOQU58wI7Do1Go5mi6On0KYLZ\nZqbN2kartXWgZ3kg1NZCWxvRTS0U3f4bdm34JRjHOLmTnsbsI04gLS4tOMc0RdC50zWayCGQ51mP\nxCMMh8uBzWmjx9GD1WHFbDdjtplxuMYhZ3lXFwCZr71P5+IjfFbgprpGXKZoHOmp0NFJVXsViaZE\noo3RwT9GjUajiWC0TXwSyei2d9PU3cShjkNUtlZS3lzOUy89xY6GHWyt28rm2s1srdtKWWMZ+1v3\nU9NZQ7u1PWAF7tUmbrWqeG+Xi4y3/4OxvYuiW+9m+oNPD4wJ90LWq++S88IbquFw4DR38sLrLwR0\njL4yWb97jXciyS6qzyX8ZIRSjr/okXiY0+Pood5cT6ul1asytjqswZseHwtmNQpP2FmBodtK+oef\nIVwukraWgRBUr/seJCWB3aYytPX0Z25rPO8MFlz3U2quuhBXXCx0dNBl66LV0qqn1TUajWYMaJt4\nmOKSLmo6a2gwNxCW1+NgFZi7mbH+TyR9voPY2oa+VR3LjqXiH4/193U54WA1WPod3+bccR+tpx5H\ny1knQXQ0zJ2LyWhiYfZCDCLyJogGf4dCBGbO1jZxjSZy0DbxCMPmtLG3ZS8W+9i8vUOGdEG3Orao\ntg66jppHTH0TwuVCGg1YFxQN7G8wqixulfvBoabam886iazX31dK3G4HqxVbLNR31ZOblBvqMwoI\nl3TRZevCbDNjcViwOW04XA4cLgcu6Rr2JaxXkQvEkM8CMaTP4O00Go0m8oY8PhDO9poeRw97mvb4\nrMCHjeEOIkNkdHerAifA/nU3sf/736LxvK/Q8aWjaLzyIjWVPpioKMjJ6Wu2H38M8RVVRDe2KBnv\n/ReAenP9+DjhuQnmd99l62J/63621m2lormCms4aWi2tfFDyAT2OHpwu54izKL2lBF3ShdPlxOly\n4nA5sDvt2Jy2PgfFXifF3r+wfbmbACLJLqrPJfxkhFKOv+iReBjhcDmoaKnoy1ketnSrNKvt9i7u\n3vckC5PmcMWaK2H6dEhMHH67pGSIb4FuC9JkouqWbyF7Pdotap9Ol5P6rnryk8M3k5vNaeNg+8HA\n4+w1Go0mQIJiE3encFxPfwrHewatPxV4GdjvXvSilPIXw+xLdtu6iYuOC/i4JhNSSsqby+mydU30\noYzOgQMcaq1izY57ODn9GL4z82JiE1Jg1qy+Lk3dTexo2MHywuUDt7V0w4Eq7/udOweiTRiEgaOn\nHU2UIfzeMdut7VS2VXovyRpCivOLtU1co4kQJtQmLoQwAA+hiinUAJuEEC9LKXcP6vqhlPI8X/a5\nq3EXGfEZ5CflT5nY4cOdhyeHApcuDrcd5Lrtv+KqgnO5OPcMtTwjfUC3jp4O7v7v3dicNs6ac1b/\nirh4iI/rs6kPoLMT0jNwSRcN5gbykvLG8UTGTnN3MwfaDkz0YWg0Gk0fwbCJLwUqpJRV7hzKz6Hq\nDQ9mTG8Zzd3N7GzcSauldfTOYyTc7DUdPR3Ud9X7JSfUNvGOtnq+u/1evpl/Tr8CjzKqqXIPZqfN\n5sGVD3Lvx/eyq3HXwB2mDy1BWrqlTClxNw3mBlyj5F/3B3+/+zZrm88KPBTfiUYRSXZRfS7hJyOU\ncvwlGEo8H6j2aB9yLxvM8UKILUKI14UQR/qyY6fLyf7W/RzqOBSEwwwDLBaoqoIdO2DrVtizB0dz\n46Qa3TnNXVyWv4LvfuwgqtVtE05OBi8e00UZRdxx0h3c+vatA1/GkpLA5GWGxWIFp3Jqc7qcNHc3\nj8cpjBmL3UJla+VEH4ZGo9EMIWCbuBDi/wErpJTXuNtXAEullDd69EkEXFLKbiHEKuABKaXXqhdC\nCFl6eOhIJi0ujVmpsyZneI2UcPgwNDT0eXX3stdcTXucgLx8r4ow7Kg6gKG5lUUXr2Hb3x5SyVpm\nzRqxLvgDGx/gYPtBfnvmb/u/v+YmaGjs7+R0qbStebmQkgpAbFQsC7MXjufZjIpLuihrLBtTjfVQ\noG3iGk3kMNFx4oeBGR7tAveyPqSUXR6f/yWEeEQIkS6lbPG2w7U3ryVvurKHJiYnMn/hfIpPKEYg\nqNqqnKKWL18O9E91hG37nXegpoblC5UyKilVLyjLi4upszbx7qZNABSfvBQKClGx69YAACAASURB\nVPqmYotPKAYIr7aUlH6ymYSyvcydV4grLpbSXRXQah5x++NcxzG7cDYSyecff67WL10CjU2UfrGL\njDc/YNnMAuovOZfSkk8gK4viE4qxOqy8/tbrJJgSJuz7+8cb/6DF0jLh1x/g808+p6a6Bo1Go+kl\nGCNxI7AH5dhWC3wGXCqlLPPoM01KWe/+vBR4QUpZOMz+vI7Ee8lJzAk4/KikpKTvR3q8KCkpYfnx\nx0N5OdiGhow19rRy0FI3cGFmJmRljUlO6celfT/440WfDLdnef6GZ3EmxFN3xQV+HXMf1dXQ1UXS\n5zvY99DTZP/pXjAImDcP3FnbUmNTmZM+J2jnMpbv3mK3UNZUNuaMeaH4TvRIXBGKZzlUcvS5hJ+M\nUMmZ0JG4lNIphFgDvEV/iFmZEOJatVo+BlwkhLgesAMW4Bv+yqvrqiM+Oj78c2zbbLBnD93WTlpt\nHTikE6MwYBAGuhzddDq6h27T3KzsxSNMTYeadms7TukOp3LHhydv3sXBG69Uy5KTAEgwJZAZn0lt\nZ63vce6pKdDVRefiIzA1tRLd2II9Kx3M3X3x5u097did9gmJUjjUcSg8U95qNBqNm7DMnT7SSBzA\naDByZNaRmIymEB3VGLFaobycwx2HqesZo3NWXBwUFo7LYY0Vu9POta9fy4VHXMi5886F6mqMh2s5\n+pvfZ8uLj6hQsTkq5/mRWUdiNBjHNnqVLqioAKeLwns2YJ4/m8YLzoTUVMjtT72an5xPTmLOCDsK\nPh09HVQ0V4RU5ljQI3GNJnIIZCQ+KdOuOl3OcfXo7nH00GhupMHcQGdP5+gbDNi4B8rLqe6oHrsC\nB+XB3hEemcB++8lvSYtN4+yis9UCSzfSFM2+dTepNKru0XJ+cj5GgxGAuOg4suJHn16XUqopc/c+\nWk/6Eqn/db+8dXUOcABs6m4K4ln5Rk1nZNuehRArhRC7hRDlQojbhunzeyFEhTuqZInH8hQhxN+E\nEGVCiJ1CiONCd+QajcaTSanEATp7Ov3+cR8u7s/hclDZWsmOhh0cbD9IdXs15c3l7GzY6Zsyt9mg\nvJxmcyNvbPzYr2MDVOlOH0cw4xWT/PzO5/m89nPuWn4Xmz/ZDD1WcLpwxcXSeazbYzwxkdioWNLj\nBiZ6yUnMGTGKoKazhutev05NuyenAPBedDQGq03VKHc4wdqfDKbH0RO0RDi+xHx29HRgtpn9lhHu\nceIeCZpWAAuBS4UQRwzqswqYI6UsAq4FHvVY/QDwhpRyAbAYKGOCiKRYYX0u4ScjlHL8ZdIqcYDD\nHYeDVizD5rSxu2k3LZahDvNWh5Xy5vKRR2duBW61dA51WHMj7A5SP/yMgof/zMzfPM60519DeHF6\nw2aHzg5/TyVg3qt8jye3PMkDKx4g0eTOhT44w5pBQHwC2QnZQ7aPNkaTFju8z0JuYi6JpkQe3/w4\nJCSA0YA0mdjz4Fo1wgfoGHj+oYwZr+2sDZmsCcKXBE3nA08DSCk3AilCiGlCiGTgZCnln9zrHFLK\nibtZNZopzqS0iXuSlZDFjJQZo3ccAYfLwe6m3fQ4ekbtmxmfyczUmQMXuqfQZU8Pu7sO0O0cGlOc\n+p9NTH/kL1jzshF2J1GdXTjjYtnz+zv7FZcnsbEDcpGHCikld5bcyeVHX84RmR6Ds9oaaPOY5k9M\nxDizkEXTFnmt/93Z00l5c/mwcpq7m7nsxcv47Zm/5WhnOrQP0gPuGuO9GA1GFk9bPO55Asw2M7ub\nBmcMDj8CsYn7mNvhVeDXUsqP3e13gB8CTuAxYBdqFF4K3CSlHJJHV9vENRrfmHI2cU+aupsCTsRR\n2VrpkwLvlbe/dX+/45bFAnv2gM3GYWuDVwUOEFPbQOWPb8BaOJ3E3fuIq64lYW8V0x991rsgq7Wv\nslcoEULw89N+PlCBQ59neh+JCaTFpnlV4ABJMUnERMUMKycjPoNbT7iVtR+sxRrnxUHRblfX1o3T\n5aTN2ubzefhLXZf3WRRNH1HAscDDUspjgW7g9ok9JI1m6hJ+ZaLGiJSSms4aZqfN9nkbz7i/+q56\nOnrGNhvYamnF4XIw25hJ1IGD4HTS2NNKfU//VHzpljKKlyzoa9d//RwAcp/+J8KlcoILl4vYqhGm\n6FtaID9+xGMJSZz4fzZSnDkwNzoJKqRsJDLiMkY0QZwx+wxKDpTwcNlTnFo9m+JFCwZ26OxQ3vpu\nWiwtAYcWjhTz2ePoCcqLQii+kwAZNUGTuz19mD7VUsre6bK/A14d4wBWr15NoTvaIjU1lSVLlgQ1\nMc+WLVu4+eabg7a/4dqedtHxSiy0fv36oF8fb+3B56Sv18jtwecUrOvz5JNPAvQ9H/4y6afTezky\n60ify5f2/pD3OHrY1bjLv0IbTU1ENbeQGpWEXTpotw90vBqsxF3SxUctWyh46Gku+KiZaAkug4Gm\n875C9ZorvcsQAormgnH4d62QKPF3/kNxfiZzfvo7ar/5NboXziP2iKNGTYlqc9rYXr99xD4dPR1U\nd1Rj+eQgxUWFA1cOmlIXQrB42uI+T3h/GEmJV7dX02Bu8HvfvYR7shcfEzSdDXxHSnmOEGIZsF5K\nucy97gPg21LKciHEWiBeSjlEketkL+EnI1RyIkVGqOQEMp0eMUrcn8xee1v20m4dYziXrQdqa72X\n0hyG8q4qfrn3jzikk2/mrOCqv1WQXN2AdWYe1ddfDkallIxdZhwP/I47v5bGhflnsiR5HiJnmteq\nX8HA5rTxt11/46IFF4049U1DPaKugcVfu45tzz+IKz+HvHnF5CblDr+Nmz1Ne3zzLO9oh8M1ICW5\nf3mJum+cizRFQ+FMVb7UzczUmaPOAPiDw+Vge/32camcNh4EGicuhFiJ8jLvTdB096AETQghHgJW\nAmbgainlZvfyxcAfgGhgv3vdkAdJ28Q1Gt+Y6NzpYUGbtQ2L3eLzaLyjp2NsCtxuVxnV2tpGDP+K\nam2n8J4NVP7oepwpKpvZ5o49fC3nNM6bdgoGYaD+xpPxVnjUmZhApoxn6f4efmF5AqMwcGHBWZyz\n7EqSYpJ8P1YfKGssY90H6yhILuC8eeeNrMQtFuIrDtCTn4MrIQ7i48mI9+3FIj0u3TclnpjYVwAm\nuXQ75vmz6Vi6WDm8eSjxVkvruCjxRnPjyArcbldhb9YecNhVGFxvfyFUzLvRAAaDmjkxGlWJVmPv\nX5RaP4wPQaiRUv4bmD9o2YZB7TXDbLsV+PL4HZ1Go/GV8FTitV5CfHq9koX7sxCqYRDqh1MYqOvZ\nzaz02f0/nFFR6m+QR3NJSQnZC4eGRg3B6VAOXe0d0NU1aux2VGs7837wa1pPWcrGymqKl6iKq5fk\nneXDSSvM37yEO275Jec/eS+fOav5R927PPrXr3LnqXdy+qzTh/Qf69Tt4Y7DbPh8A58e/pTvLfse\nK+esHNnj21305OzySrqOKgIgKXWaz9ny0uLSqO6oHjWDW+mnX1BckAXmblpPKib1o1KlxDs7YNq0\nvu+w09YZUBpWb1NjTpeTerOX1yqHQ720dbRDj4+pZBlqShmAEP3K3mDsv3977+W+exu1rHcbjVci\naUpVn0v4yQilHH8JTyXe5p9zUauoI6/RSsxgBeOp0KOi6Di4l6QUc/+PqBBKQUuU4rY71LT5GH64\no1ralAJffhy1V14IW/zLf2GdmU/7smPI+du/KP7WxRSnLqAl0YAha5pf+/NkT/Mern/9er6x8Bu8\neOKL/THgIx6QFSQk7qyg9ZSlEB1NeorvKVCjDFGkxKT45jCWlATmbhpPWMLRN73OwZuuVsu7utQ6\nlCNjq7XVa3y6v9Sb63G6nP0LnA5obBp11sUvpFSjeJyoUgIajUbjP+FpE3/nz35vn2lKZWb88LZa\nKSU7O/fR4wreD2hUcxvzbv01Lacfz46vLyfTlDp8Z4OA+Hg1+urx/qJgqm1gwXfWsv2Z+1W97kEO\nXp789P2fkhWfRUFyAYmmRExGE1aHlRVzVgwZYbukC6vDSnz0yB7vA2hphvoGjrriFvbc92Oc84tY\ndMzKMTmXtVpa2d+6f/SOdjsfffZ3njn8L959qIOaNavpOnq+UuAFBX3dEkwJQ0Pg/GSIc2NbGzTU\nq/rmYUzxGd/UudM1mghhSseJD6bZ3o5tBAXdZGsLqgIHSNm4hbqvLON7x7fxw7IHvE8dGw2QM02V\n2Zw+A/ILYPYcmDkDTAOnhm252TStOBlTvTutrN3uNWZcSsmpM08lwZTAzsadvH/gfV7e8zIfHvyw\nv/KYBwZhGJsCh75Y7R1P3ot9Wiap6blj9g5PiU3xbZvoaI7P/TIuJD87J4nUj3pzqXepqW03ZpvZ\n57j+kZBSUtlWqRS4ywmHDylTTpgrcI1Go+kl4pS4lHLYwiMu6aK2p4lSP6e6veJ0IsvLqf/oX3zj\nL9v4/RG3IIQYKCM+TinstPShjk3xCapq2aDyo4evvQxrYf/oc3AaUlBvb6l1qfzPMf/DT0/5Kb/+\nyq+5f8X9/Or0XxFlCJKlpNuizsWdVS4jY/ooGwzFIAwjpmGF/nzjxqQUfjHvep7MOswbZxSqlVJC\n+8DpeG/pcX2hN1bTJV3sb92vcqTb7VBVBR1jLHYzDEG9vzQj4hnLO9nl6HMJPxmhlOMvQVHigVRE\nGg+abG1YnUNHanU9zdiDlGsd1AuD677fUvD6f1hWYeFr/21mweP/HNgpNQVmzOxTgkIIkmKSBo5M\njVEwY7qaNh+OICmYMWG3DRgBR5tiSU4evUKZNwYXSRmWpCSyYtJYe8S13N76PC02dwRB60D7dLPF\n/1zqNqeN8uZyZafvscKBA8rr3AsO6WSvuZoPmzfzUl0J1RZvcQWwvWMvH7Vs4fP2Mg5aajnQXUtD\nT8uIs0IajUYTKAHbxN0VkcpRiSNqgE3AJVLK3R59VgFr3IkjjgMe6E0c4WV/AdnEe0mOSqAosT8p\nldXZQ1lXJa5AbXROl5oaB6osteR876ecsLdfAXQcs5CK37izUGakQ3a/Q1pMVAxz0+cSGxXbp0gG\nTAtbLEqhDMegmOlxpzd2203utDnkHXW837vb0bDDt2nwvXvBbuehA8/TYu/gzqJvq+UF+ZDUnzlu\nfuZ835zzPOiydbGvZZ8qnGOxQPVBr9PnHzZv5rmat9jeuZesmDSmx04jPTqFr+edwYLEoTntnzr0\nGp+3l2Fx9mB2WrE6e+h2WfnxnKs5JePYIf0fPvACOzv3E2UwYhRGooSRaBHFFfmrODJpaPbB1+o/\nospSgxACAwb+8D8vaZu4RhMhTHSceF9FJPfB9FZE8qwiMaAikrse8TQppfdhTRDocJipszaRE5uJ\nUzrZ3304MAXudJHxzkfkPPsKux++C2diAjPjcilYeDJy/3sIlwtpMGCdmaf6Z2ZAVr8HdZQhiqL0\nor54bJPRxJy0Oexu2t3vVBUXB+lp0NLq/Rg6O0OrxAcltMnIKBimo2+Mloa1j6REaGnluhn/D4vL\nQ+k3NQ9Q4k3dTWNS4u3Wdva17lM+CyMocACTIZqLc8/g3gU3khilrrmh20LM4Xpi6jZhNFswWCwI\nl6TthGO5quBcrio4d+BOnM6+RD6DWZl1Al9KWYBDOgf8pZtSvPaPNZqIM8biki5caJu9RqNRBEOJ\n5wPVHu1DKMU+Up/D7mVelXjKJ5uRwgAGgTQYsGVn0DMjb0g/Y3snUR1duGJjcMXF4IyNGVAR7LC1\nkTZHFzaXfcA0+ohxvIOIam4j/f1PyH75HezpKSqJS2JC/8necAVCCGKravozsGWkU1pxkGK3EhdC\nMCd9zpCEKnHRceQk5gxUbFlZyv7tGOqYRkfngJE9jHOKT0s3Uc1tbCqr4NTly4lJCSxzXEb88Ep8\nwHkkJUFLK1GGKJI8bftWq3JyS1SKu9XSSkFygU/2/y5bF/tb97Ppv5soPvYoOFDJ9Af/TOzBGqwz\n8qi+4fIBCndZ2tFD9jHj908Rt+8gttwsHInxKnJACAyDpuJ77685d64naesunElJOBLjcSbE4UyI\np2b1/2NOUSFzEga+FCVv3EJ0605klBEZFaX+CzAfWcQZmQMfqccYZLaZokRSrLA+l/CTEUo5/hKW\nceLFf32A+VExzO+MZYHdxOzixcxd802g32moeMkCUkq3UfH48wibndOcLowWK+8LaDtlKTPv+A4A\nH5Ru7uufuLWMHa+/T63ZQmZ1Dc6EeD6ub8Kelc6iM04csv9pz73G1r/+kwdOTMN102y+W/wdtd7j\nJaB0ezmlJ32Z4jXu9r5q6OivZFb6cSk5iTkcu1JNqQ5Oil9WWsaB1gMsXrZY9f/0C+jspHiGisXe\n9s5/yXr1XXIfuBPsdkpLPgaTqU/h7dm5Rx2vu93rIBZwe9kxYO1h36PPcLizi8yVF0JcXEBJ/01G\nE7tLd9Nl6xoiz/N6IaE4OxkcTkq37CKqrYMly5X1pfTNEsjNofiEYlzSxcv/fpmM+IwR5duddrIX\nZuOSLvZs3QmHDvG1ko1kvfouH7hcyC27WCiges2VA75/GHg/HLj9Ou/r27vofY0q3VLGnr1VFC9Z\nwL5f3MLmTdswmi0sm5GL0WyhdMceLPWNHOPOE++5v9jqWjZ/vh0cTk5JSkA4nHzU1knTipPpyc/h\n861l1NQ1otFoNL0Ewya+DFgnpVzpbt+Oyr98j0efR4H3pZTPu9u7gVO9TacLIeQfX7yTT1q38VbT\nRhwuB2vnXcOxKT7EBUuJsDtASmTM0Ixi8Xv2k+z+UTWau/v+tx9/LI3nnzGgr8Vp5cWqf/F047ss\nSi7i29MvYF7izCH7HEBqKuQOjFGfkTKDrISRncFaLC1UtlZ6nIcL9u5TTmVOJ4u+8V12/34dtrxs\nyMxUo/XxxtwFB6uZd/PPabzqImaddxVi3ryAd9tmbWNfy77RO7rrl0c3NLPg+p+y/a8PqFzqAHm5\nkKJi8aMMURyVfdSwIWwu6WJP0x667d3Kie3gQXA4Kbr1bpK/2NnXr9eXIa7iAGkflVJz9UUBn+t4\nouPENZrIYaJt4puAuUKImaiKSJcAlw7q8wrwHeB5t9JvG8kevii5iEXJRVwz40L2mKvINvlYflKI\n/h96L3TPn033/NFLlj57+N88deg1liTP46GjfkhRwoxRtxmswE1GEzNTZ5IckzzCRor0uHTquuqw\n2N02aGFQTnH1DWA00nbSl0n7YCP1l34VujpDo8S7LQibnfi9VcQvLkYkjs2BbDhSYlIwGU3YnKNk\nw0tKhrZ27NkZWGYVkPLpFhpOWsJHLVs4PWqZmlI3RuFwOajrqiM/Od/rbqraqoYocADrjDwStu7C\n6JK4DALrjFym/fVVpv3jXxz+9iVBOVeNRqMZbwIOMZNSOoE1wFvATuA5KWWZEOJaIcQ17j5vAJVC\niL3ABuAGX/YthOCIxEKvzj5SSq9hZL4wWhxvclQCDx91G/csuNE3BZ6ehsjLIzkmmZzEHOamz6Vp\nV5NPCryXvKRBNv/UVJXdDWhZvoz0ko1qubVHxTX3nsvHY6/45hOWbuL3HqCnIIed+2r77NCBIoTw\nOjMx5DwS4vuiAJrPOpmMNz/E4uxhfeWzvFP3MdT059evN9ereO9B1HTWqHhyi6VPgfd+9y9d9iX+\nsDSK+sVzaFq1HFNtIymbtlL28M9oXnFKQOeo48RDRyTFCutzCT8ZoZTjL0GJE5dS/ltKOV9KWSSl\nvNu9bENvSUN3e42Ucq6UcnFvScNAKDcf5NxN3+PhA3+jsWcYb24/OXfaycxN8DGpSVYW8QWzWZi1\nkKKMIvKT80mJTRm5qIgXUmNTB2ZTMxj7poy7jp5PVFs7MYfciqtrnGPG3d7biTvKcS46GqMwQkLC\n6Nv5SFZ8FobRqnkJQ9+LQ9vJXyaxbC9Zjd3cs+BG7t77FAcaylV6VNQL3d6WvXT2qOviki4Oth+k\ntrNWFVA5WDXAUfBAdy0/2vsIrh98n/of3UTSzgrsWemU33s79mnBr5Cm0Wg048Wkzp1ebann2Zp/\n8++Gjzkl41guy1vJ/NHs1m52dx3gs7adXFlwjn8HahCQl4cpNZMFWQuCkiGt3drO3pa9/Qt6rLBf\n2coLHvkLllkFNK9arkapM3w7T7+wdMOBKrJefZecWYswnbkCjjwyqCKq26tpMDeM3KmzEw4dAiD/\n8ecQdgeHbriCl+pKeLbm3zy5eB3xmbkDqpyZjCYcLgcuhw0aGr0W07m17AFOTFvMBTnLEdYeUj/e\nTOtpyyZVtTBtE9doIodAbOKTWon30m7v4p917/N87dv8cPaVnJY5NOTKJV0ctNTxn5YveKfpM5rs\n7VyUczpXFZw7+qhwMLGxkJ8HphiKMorGNG0+Gnua9gysv33ggJoOdrncJStRymZekRqtjwfNTdDQ\nSIYphcL4PGWDn+GDWWEM2J12tjdsH7lEqXRBRQU4XUQ3NJPy2Vaazj0dKSU/q/gDDoeNP72bSFx1\nHdZ5s6m+80Z1TbrN0N4+bAy4zWXHZPCvlGm4oJW4RhM5TPkCKCnRiaye/lVeKf4dJ6Yv7l/hdDL9\nwacpuvVudq9dw03b7qHa2sBpncW8XHwfV08/b2wK3GiAadkq17kphpTYlGEVuL92lCEOWqnuimgG\nj+OUUsVLM0428e5uhBDkxqip5ZIvvgi6iGhjNFnx/bZxr+chDH0lSO3ZGTSdq+qpCyG4bc5V3PzP\nWrJefY/kzTvIeuE1pv/4HjVyb2kdVoGXbikLXIELofIRmKLVX3S0art9GLRNPHREkl1Un0v4yQil\nHH8JyzjxvmnNMb7FRw+a0p7+yDNkvfouwuXicoOBFdlfUbHAXWVEiTGMYqOilDJNT1N5zt3kJ3n3\niA6ERFMiqbGp/fW3k5Ogvg5cg65FZycke8/uFRBue3imKbW/LntcXPDlADmJOTR1N/VnrPNGsvJS\nH0ys0cTRbYkYXGpb4XIRW+VDNjh/iI9T9vm4ODANTCg0BCmhqQNmz1IZ25xOZY93OlWdcpdLvWC4\nnOo7lS61zCUB6a5r765tr0exGo1mFMJzOv3wMKNL6e2HzqU+u6T6Yez7gXRR9K0fkvzZlr7NO750\nFBW/+4n7x3SE844yQkyM+tFOSFCpTgfZS9Pi0pidNnq4mj/0OHrY2bizf6r58KGhBVAMAubND74d\n12LBWHWQhUlz1EtRVBQsXjz6dn5S21k7cipWKVUudcfQwjXTH3y67yVNGgw0nqde0obuQiKEwFTX\nSM6zr3Dw5qsHzmx4w2iAtDRITRu5ME0o8XhWiwu+HNB0uhBiJbAeNRv3hGdeB48+vwdWAWZgtZRy\ni8c6A1AKHJJSnjeMDD2drtH4wETHiYcOIQABPp6qdeE8kj7fhnC6kEYD1kULYe5ctVLK/tEQ7h8a\nYVA/3j5Msecm5o7ax19iomKYljCNuq46tSA5ZagSd0kwm4MW+tVHt5nc2Mz+WY1g738Q0xKn0Wxp\nHr4wihCQkgzNQ0uPVt9wOQgGprz1wCld/PnQ67TYO/hRzBkU3fpr6r9+zgAFnhOTQYYphS6nhcPW\nBhwup5pxycoaP58DfwnSC5tbAT+ER9EiIcTLXooWzZFSFrmLFj0KeBYtugnYBQTPIUSj0YyZiLCJ\nD0f1ultovPJiOk76Mo1XXkz1uu8BbvurEGpqPDoaok3qLyrKJwWeEptCXPTIU8yB2lFyk3L7c60n\nJvbFTMftP0jCLrcHe2dn0G3i8T0usjslPP+8WpCQMK42IYMwUJhaOPJ59PoF9OJykfqfTYCges2V\nVPzmdqrXXIlDSH68+2H+WP0Kfzj4Epd/8RM+bt3K1RzDvB/8irrLzuNfHjXac2MzyY/LJtYYQ6Yp\nlSPS52OaUwTTcgJS4OMWux88+ooWSSntQG/RIk8GFC0CUoQQ0wCEEAXA2cAfQnfI3okku6g+l/CT\nEUo5/hLRSpyoKKp/cSsVz/8f1b+4dWRb5hgYz1F4LwZhYGaKO4xMiD4Hr7jKanL++qpaHuR4cQEU\nkor44gv49FO1cJxH4qD8AEasN26KUXbpXqQk+6W3yXvy7wO6GYSBVdkn0G7vwuy0cPOsS/kLF3Hq\n7Y9w+OqL+hzjABKi4voc9wBISSHmqMXMK1gSlHDBMMdb0aLBDh7DFS0CuB+4lb4pLI1GM1FMLpt4\nGJAck0xRRlHI5PXFU3d1QXU1xk4zR19+M9uef1BV0QpijfHpxjSyD7XCvfdCTg5cdRUsWTK6/TgI\n9CZs6ejp8N5hUG3zqNZ25t/0M5pWLaf+knP7p5qdTqY/8kxfdTKDuZvW04+nY2m/XV8IwYLEQuKM\nsWpBdjZM70/uY7aZKW8uH9nhboIpzi/2P65UiP8HrJBSXuNuXwEslVLe6NHnVeDXUsqP3e13gB8C\nucAqKeUaIcRy4PtSyq8OI0fbxDUaH5g6NvEwYEh61HGmILkAs92MOUGC0YAzKQHzEXNI/nwHbScV\nq7KlQVDi6XHpZHe7vdG3bIHbb4f4+JAocOgv11rRXDEwTr6XpGSIauhzcHOkpVD+uzuYe8d9JO4s\np/aKr9F9xOwBEQlJW8toPO8rAxQ4QKYptV+B5+UNKVqTYEqgMLWQ/a37x+Vcw4DDgGfgf4F72eA+\n0730uQg4TwhxNhAHJAkhnpZSDvUoBFavXk1hYSEAqampLFmyxK8KeLqt25HULikp4cknnwToez78\nZUqOxP2twZ0am8qc9Dk+9S0JYg1au9PO7qbd2A4dgLZ2sl5+m4Td+zlw27WU7iin+OLB5syxkWhK\npCijCMPuPdDQAKtWwXvvQUEBFBQE9VyGo1eGS7qoaqtSOc8H09QEjQNLcQqbnex/vkni9j3s+8X3\nh61O1ssX2/aw+qRz1ZR5QYHK9jYMdV11HO4YrNtGZ1xrvLsJcCRuBPagHNtqgc+AS6WUZR59zga+\nI6U8x120aL2Uctmg/ZyKGolPmHd6KO7NUMnR5xJ+MkIlR4/EhyEtLo28a4kd/QAAIABJREFUpDws\ndgsH2w/icA0NU/IVIcSwlbLGm2hjNHPT51Le0YajrZ22448l78kX+2OQLRa/Y7kTTAnMTZ+LweGE\n7m7Ytg0WLFAOfyGwhw/GIAzMSpvVV9ltwKg8PY34djNJIpakqARiDSZcuGi/Ko8qWwu4nFhn5JG0\ntawv7Mw6c+DMSZYp1ScFDiqO3ea00WiOrBreUkqnEKK3aFFviFmZEOJatVo+JqV8QwhxtrtokRm4\neiKPWaPReCdiR+KDR80Wu4U9zXtwupwjbDU82QnZTE/xsSjKOGHpMVPxyWvYnXbS3v+UthOPRZpM\nKiRqWs6Y95cck8zstNmqFndTE1RVQU2NGo0vWQKLFk14jLTT5aTH2YNAEBMVg6G2Dmprh/RzuBwc\ntNTRam1j+v89MzDszKg8zVOjk5iTUAD5+crm7yOVrZXeZwYmkEBG4qFC28Q1Gt+YsNzpQog04Hlg\nJnAA+LqUckh6LSHEAaAdcAF2KeXSEfYZsBKPjYplQdaCISlV26xt7GvZN+b9RRujWZi1UCm7CcZe\nsZv9NTvpclj6F0ZFQdHYnO1yEnPIS8rrr7a2b9/AYiExMXDUUUE44iDjdMKOHV6TvwA09rRyyFqP\na9B9HWeMYX7iTIx5BcoOPgaklFS1V9Hc3ez3YQcbrcQ1mshhInOn3w68I6WcD7wH/GiYfi5guZTy\nmJEUeDAQQjArbZbXnOipsankJOaMOY53ZsrMMSvw8YotjE7PYl7CTArisjEKg8rT7XCooh8+kGBK\n4IjMI8hPzu9X4C6XcpDzxGMqPaxiPo1GNRU+DFkxaSxInEVqdBJCCIQQpJuSmZcwA2NeASXl5WM+\nNiEEhamF5CT6NnqfBHHiEUOoYnjD6hmYBHIiRUYo5fhLoDbx84FT3Z+fAkpQin0wghDFpBckFwys\nyz2I/OR8Ek2+23qnJU4jJXYccpT7S0oKwmBgWkwGGdEp7DMdIsYQTU97B8R7r/ltEAaSY5LJSsjy\nXrClo0Mpck8mwB7uMxkZ0NIy9MXDTawxhjkJBUgpkUj1Qpebq0bgfijxXvKT84mLjuNg+0G/zTIa\njUYTTAKdTm+RUqYP1/ZYvh9oA5zAY1LKx0fYp9/T6b56j7uki/Lmcsy2kUevY/FGDynl5aoAigdW\nHJjnz8YmHTilE4Eg2hhNXFQcCaaEkau1VVYqpejJwoWq5Gq4YrfD7t1gs43cTwg1cs/ODppom9PG\nwfaDtFuHFmYJFXo6XaOJHMbVO10I8Tbg6cYrUJmafuKl+3BP7IlSylohRBbwthCiTEr50ZiPdgTi\nouMoTC30qa9BGChKL2J/6/5hk4tkxGf0Z0wLN1JS+pW4wwFGI7EiitgeA2SMMZucyzXQFg7Kxh7O\nChyUw11RkXqhsdu994mKglmzVCW0IGIympibPpeOng5qO2u9x7VrNBpNCBh1iltKeaaUcpHH39Hu\n/68A9R75lHOAhmH2Uev+3wj8E5W7eVjW3ryWDfdtYMN9G3jm8WcG2BhLPy4d0t62cRtF6UUYDUZK\nSkoG2DC8tdevX4/RYKQoo4jqrdVs27itb/2Oz3ZQs72GwtRChBA+7c9bu3eZv9uP2N66ta+9/vzz\nKXnpJdVoahr7/l57jZLPPoO6OvjWtygpLaVk584B/devXx/c4w/W9YqNpaS+npLdu/vXl5ZSsnmz\nKmCycCElmzcP2H79+vVBO/7kmGRqd9TSuKuR7IRsTEYTpR+X8szjz/T193a/+tMu/biUDfdtYO3N\na1l781o0ikiyi+pzCT8ZoZTjL4FOp98DtEgp7xFC3AakSSlvH9QnHjBIKbuEEAmo2NS7pJRvDbPP\nMU2nx0XHMTd9Lqbe2tc+UOIleL/XxhksD3RvMoLKrl1gsVDyox+xfPp0uOEGtXzBApVpzVcqKpRt\n+aWXYONG+PWvVQpSj+nncT+XYMjo6VHx8gaDKh9r9P49jve5WB1W3nznTZYsW4LFYcHqsI6L/VxP\npytCcW+GSo4+l/CTESo5Exlilg68gErPWIUKMWsTQuQCj0spzxVCzEKNviVq+v4ZKeXdI+zTZyWe\nGZ/J9JTpI9t7I5WaGhUvvWMHrF0Lf/+7sv9mZICvafx6etT2ALfcAmeeqbK1HXmk38ljNENxupzY\nnDYcLgd2lx2ny4lTOnG6nLika8CfRPY55PX+B/pqy/e2F2Yv1Epco4kQJixjm5SyBTjDy/Ja4Fz3\n50pgSSByPBFCkBKTQk5iDgkm797YU4LUVKXEFy4EqxX274c5c5SDWl4emHyYmWhwWz+sVvj8c/Uy\nYDRqBR5kjAYjcQZ9TTUaTfAJyyFsTmIOWQlZZMZnkhmfSXZCNgXJBRRlFLF42mLmpM8JSIFHhL0m\nPh5MJko+/xy+8hV4y22dkNJrRrMhOBwqSxvApk0wf75ymHOXPPUkIq5XCOWEuw0tktD3TXjKiRQZ\noZTjL2GZO32icpRPOlLc8evnnAPPP9+/vLlZ2bRHGlHX1vbHhu/eDaecoj57UeIajUajCU/CMnd6\nuB1T2NLRoRzTvJGQoEbXwouZxWKBsjI1au/F5VJOYdoePikIxIYWKvSzrNH4xkSmXdVMJElJw3ph\nYzYr57fBOJ0qucvgH1eDQcVeawWu0Wg0k4YpqcQjxl4jxIAY6SHU1cGhQ/3T5jYb7N2rRuLeGCYp\nSsRcrxDJCXcbWiSh75vwlBMpMkIpx1/C0iauGQOj5Tivr1c2cpNJKe+RpjeDnNlMo9FoNOOLtolP\ndqSErVvVNHmgLF6sUpVqwh5tE9doIgdtE5/KCNHvpQ7wxz/Cp5/6tu3TTyvbOShHOK3ANRqNZlIx\nJZV4xNlr0tL6F+TmwmOPjTxtDrB9O/zjH/2FTlKGL7cacdcrAmRMRiorq7jiirs47bS1XHHFXVRW\nVgW8T33fhKecSJERSjn+MiWVeMSRktLvpX7WWarC2X//O/I2GzbAN7/Zv90ISlwTeQghVgohdgsh\nyt11D7z1+b0QokIIsUUIscS9rEAI8Z4QYqcQYrsQ4kZf5FVWVnHmmQ/yzDM/oKTkLp555geceeaD\nQVHkGs1URtvEI4Wqqv4MbB9+CPffD889BzExQ/tu3Ai/+pXKtx4drZzejj46tMerCYiACiYIYQDK\nga8ANcAm4BIp5W6PPquANVLKc4QQxwEPSCmXuasV5kgptwghEoHPgfM9t/XYR9+zfOmld/Hccz8A\nPDMtmrn88t/yl7/oqmyaqY22iWtU4ZNeTjlF1dp+6KGh/bq64Je/hB/8QClwGDgdr5kKLAUqpJRV\nUko78Bxw/qA+5wNPA0gpNwIpQohpUso6KeUW9/IuoAwYNsXirl2wejW88IKLgQocIIF333UFxSdT\no5mqTEklHpH2msTEgaPuO+5QI+zeGPFePv0UTjgBTj65f9koSjwir9cklxEg+UC1R/sQQxXx4D6H\nB/cRQhSiihttHE7Q0qVw+DAce6wBMA9aa6ary8CFF47uwjEc+r4JTzmRIiOUcvxlSirxiCUzs/9z\nSgp897sqE5snZ5wBt3mYQGNilGe6RjMG3FPpfwduco/IvfL443DjjXDNNavJyVlLvyI3k5Ozll/+\ncjWbNsE994TiqDWayCPQeuIXAeuABcCXpZSbh+m3EliPeml4Qko57COrbeIB4HDAtm1jG9bk5SmP\nds2kIkCb+DJgnZRypbt9OyA9n0shxKPA+1LK593t3cCpUsp6IUQU8BrwLynlAyPIkaeffhXZ2YUA\nuFwu9uw5iMs1k/R0A8XF80lPzyEmZjnr1sEf/1hCVhYsX74c6B8B6bZuR1q7pKSEJ598EoDCwkLu\nuusu/5/nAJX4fMAFbAB+4E2J++JEM6i/VuKBUFmpaor7ytFH+1Z7XBNWBKjEjcAe1DNZC3wGXCql\nLPPoczbwHbdj2zJgvZRymXvd00CTlPKWUeTIV17x7Vm+7z71Pvnss/6ckUYzuZkwxzYp5R4pZQUw\nknBfnGhCSkTba6ZN833j1FSfFHhEX69JKiMQpJROYA3wFrATeE5KWSaEuFYIcY27zxtApRBiL+ol\n/XoAIcSJwOXA6UKIL4QQm90zbQHxzW/Cyy+rLMFjQd834SknUmSEUo6/hCJFlzcnmqUhkDs1iY9X\n9vD29tH7ZmeP//FowhIp5b+B+YOWbRjUXuNlu/8Cw5TO85/sbDjqKPjd77R9XKMZC6MqcSHE24Dn\n8E4AErhDSvnqeBzU6tWrKSwsBCA1NZUlS5YE3S7RSzjZSfxp9y4bsN5qZXlWlmqXlqr+xcUD28uX\nQ1KSvl7jJM9TVrD2V1JSwoEDB4hUzj0XHnkE7r5bZRP2Bc/vdTwJhRx9LuEnwx85FgtUV6sCkvX1\najzV2QkdHSrCt7MTurtVUUmrFez2wI4vKMlehBDvA98fxiY+qhPNoP7aJh4MPJO/eOOII7RX+iRm\nshRA8dUmDsof89vfhmeeUUEUGk04c/AgvPcelJbCnj3KHamuTinxpCRVFDIxEeLiVBBQ719srPof\nHa3+urvhhRfCI9nLcAewCZgrhJgphDABlwCvBFHumJkS9pqCguHt3dnZY1LgU+J6TTIZkYgQKq78\nT3/yfZvB13rnTrjgArjwQigr876NP0TSfRMp5xLq6+V0wmuvKf+NvDw1Drr3Xti7FwoL4cor4cEH\n4cUX4c9/hocfVqahdevgRz+CW26B73wH/ud/4Ior4BvfUPfpaacFdnwB2cSFEBcADwKZwGtCiC1S\nylVCiFzgcSnluVJKpxCi14mmN8QsiI+XxitGI8ydC+XlKvSsl6QkpeA1mjDktNPgF79QOYoMYxxi\nVFSoHEYnnaRu+RNPVLmN5s0bn2PVTA06OuDHP4YnnlCFHo85RuU+OOKI/tITE4nOnR7p2GwqZZbV\nqhzecnLG/uuoCTsicTod1JT6//6vKrDnmVTQF045RQVcfPvbqv3HP8KBA2q6Mxx+bDWTC7tdjaR/\n8xuVxfr882HxYt/9NXzl8GG4/vrwmE7XhCMmE8yaBQsWqDkgrcA1YYwQykv9738f23Zvvqmq615x\nRf+yK6+E5mb4wx+Ce4yayGfHDli0CJ56Sk2Fr10LS5YEX4EHgyn5ix6J9hotI3zkaJt4YCxdqpSy\nL/Re6/vugxUrlBNRL1FRcMklqt5PoEVWIum+iZRzGS8ZTz2lykssWgS//S24XOMjJ1hMSSWu0WjC\nl+JiFVxx6JBv/Vta4KOPYKWXlDMnnaRGTzoTnMYX7r5b2btvvVXN6kyGiUttE9doJiGRahPv5c47\n4aqr4OabR+/74IMqvvzee72vf+kl5bX+6ad+HYpmirB2rarefOedMHt26ORqm7hGo4k4Fi2CN97w\nre9f/6pG3MOxYoWycQYz5EwTWfzf/8Hvf68iI0KpwIPBlFTik9leMxFyIkVGqORom3jgnHACfPLJ\nwOhIb/z97yV88cXIsbZxccrOfv/9/h/PRNw3UkJtrcr+1dMzfnLGg2DK6O6GM89UoV379wdfxmuv\nqerMP/qR9+jb7duDI2e8mJJKXKPRhDd5eSrj1Ycfjtzv7bdV+E9S0sj9zj5bebwHmuIyFLz1Fqxa\nBenpalS4YIG6FkceCT//ObS1TfQRhpbvfQ8aGlSOqq9/fWyVlkejslJFMVx3nbrOkxFtE9doJiGR\nbhMHNb25YIH6Pxxf+hIsW+bdqW0wN96oPNUvu8zvQxpX9u1T2by2b4fTT1ezCwUFyjHPbFbx7u++\nq2Lfb79dOV9NBserQOjshPx8Nc2dnw/XXqvS8q5YEfi+7Xb48pdh+nS45prA9+cv2iau0WgikuJi\nNSodjkOHYNculeTFF04+GTZsGL3fRPDii+qFJCFB2WevvFIpl9645IQEOPVU+NnPlPJ+5BHlB1BT\nM7HHPd48+qhS3rNmqZQXp5468kvdWLjpJpXn/FvfCs7+JoopqcQnm01oouVEioxQydE28eBw7LEq\n1Kyuzvv6p56CGTNKiI/3bX9nnQWbNqmRz1gZz+/0vvvg6qvh3HNLuO66gbHu3jj6aFWyNTFROQCO\nZnIYzGR6Bh5/XJkWejn3XHj/fWhsDEzGiy+qsMMf/lDlExgJbRPXaDQaP4iNVXnPX3jB+/rnnlMK\nzVdSUpTSe+SR4BxfMPjVr9RU8V13KZu3r5hM8N3vwqWXKsX2zDPjd4wTxXvvqUKMnjMtmZkwf75K\nqesv1dUqte911yk7+2RH28Q1mknIVLCJA7z6KmzbNjTGu6xM2TOffFKVdfSVzz5TI/iqqolPoXnX\nXfDAA2qKfOZM//ezebMamd92myrUESl89auqVOfVVw9c/u678M47KmxwrLhcyociMxOuvz44xxko\n2iau0WgiltNOU0q8unrg8vXr4bjjxqbAQdnZe3p8j0EfL3760/645EAUOCizw89/rq7Jt7+tFNVk\np7dW91e/OnTdySerl7CdO8e+39tuU/n0//d/Az/GcCEgJS6EuEgIsUMI4RRCHDtCvwNCiK1CiC+E\nEJ8FIjMYTCabUDjIiRQZoZIzGWziQoiVQojdQohyIcRtw/T5vRCiQgixRQixZCzbBovERFU56ne/\n61/W3Q3PPw/nnDN2e6XBoGzjP//52I4jmN/pD3+oHLZ+8QvlvNZLILbXWbNUxrp331We+t3dw/cN\n5TPgcin784oVkJurQuVmzVIRAp98Mvz2t93WP2IejMmkXsZ+/OOSMR3TP/+pHBt/8AM1wveVSLeJ\nbwe+BnwwSj8XsFxKeYyUcmmAMjUaTQAIIQzAQ8AKYCFwqRDiiEF9VgFzpJRFwLXAo75uG2wuukjV\ncq6qUu3bblOj16Ii//Z33nmwZ8/Inu/jgculpnCfflopcG+JRQIhI0Pl/m5qUp7uE5mhzuWCP/9Z\n2fmvvx6yspRX/f33qzC6jg7lsHbssarsrKcF9c03VQKWyy8ffv/nnadyBLS2+nY8GzeqNL7f/W7w\nr/tEExSbuBDifeD7UsrNw6yvBIqllM0+7EvbxDWaUQjEJi6EWAaslVKucrdvB6SU8h6PPo8C70sp\nn3e3y4DlwKzRtvXYR8A28V6eeELFSRcXwwcfqDrPubn+7++NN5Si2L1bhW+NN/+fvfMOj6O6Gvd7\nd9W7Lau6yUXuNgYMOECCP0IzhECA/AKhOeWDAKYk1BAIEAiQkAIEEghfAoFAICGNHkoQzQlYgLEx\nLpJt2bJ679vv74+76rvSane1Wq3P+zzzrGbmzpw7szs6c+9p1dUmUUl1Ndx0k1Fq44XbbTyvX37Z\nJEq58UbjJBgJnE7jc3DXXSZ864wz4LjjfNdz7zVrvPyyMYt8/vNm28svm3jwY44ZWdYdd5iXgN/8\nZuR2r7xiqtmdc45J+hNthGoTH8W5Pmxo4DWllBv4rdb6kQjJFQRhONOBgVbm/cDQGTJfbaYHeGzY\n+eY3oajIxIb/9KeQnx/a+U4+GT75xNjVH3rIpGVNSAhLVwEzEm1uNolbnnnGKNUjjjB9H6sdf6xY\nrXD++eaaHn0UHnwQzjyzf+Sbnx9cHzye4YvbbVLDfvKJUb7PP2+mzE891fgzjJSMJjERvvIVM6ou\nLTUx/1armU2YNWv0/nzjG2ZWJisLLr3UZPmzWEyfGhrMOR991JgYvv1tWLNm7Nc8GRh1Ol0p9ZpS\navOAZYv304fLgV+O0lofApwMXKaUGqFcwfgTS3bRWLkWuV9Rz4T6cisFX/yimRIdqMBDsVdedx0s\nWmRGi8nJxk6akOB7iYsr8bvP1xIfbxTR+edDebnxQL/iipGVZ7htrwsXGoV4/fXGUey662DZMkhO\nLiE+nr5lYL8TE83Sew1xcUYxKmUUbEICpKSYNLdZWWZG4fDD4Qc/MKlRr77aONjl5pYEnE3OajUv\nON/4hklyE4gCB2huLuHWW830++LFpr8Wi+n/vHnmfjudJgIgFAUe7TbxUUfiWuvjQxWita7xfjYo\npf6OeXN/1197NdGxH4IQ21QBA/9VzvBuG9pmpo82CQEc28eXvzx5nuXRvLrd7rGdr6fHTJVWVZnR\nYDQxWmEZf2g9/D7Y7dDWBmVl8OKLofctVDwec+8rKszywgsT3aPxJZzT6T6fVqVUCmDRWncqpVKB\nE4Db/J0k2mNfBSEG2AjMV0rNBmqAs4FzhrR5DrgMeMZrQ2/VWtcppRoDOBaQZ1kQIkGoIWanK6Uq\ngdXAC0qpl73bC5RSve8/ecC7SqmPgf8Cz2utI+wXKghCL1prN7AeeBXYCjyttd6mlLpYKXWRt81L\nwB6lVDnwMHDpSMdOwGUIgkAUZmwTBEEQBCEwJGObIAiCIExSRIkLgiAIwiRFlLggCIIgTFJEiQuC\nIAjCJEWUuCAIgiBMUkSJC4IgCMIkRZS4IAiCIExSRIkLgiAIwiRFlLggCIIgTFJEiQuCIAjCJEWU\nuCAIgiBMUkSJC4IgCMIkRZS4IAiCIExSRIkLgiAIwiRFlLggCIIgTFJEiQuCIAjCJEWUuCAIgiBM\nUkSJC4IgCMIkJSxKXCn1O6VUnVJqs5/9xyilWpVSH3mXm8IhVxCE4FBKnaSU2q6U2qmUut7H/oVK\nqQ1KKZtS6ntjOVYQhMihtNahn0Spo4FO4HGt9Qof+48BrtZafzlkYYIghIRSygLsBL4IVAMbgbO1\n1tsHtJkGzAZOB1q01r8I9FhBECJHWEbiWut3gZZRmqlwyBIEIWQOB8q01nu11k7gaeC0gQ201o1a\n6w8B11iPFQQhckTSJv45pdQmpdSLSqklEZQrCMJgpgOVA9b3e7eN97GCIISZuAjJ+RCYpbXuVkqt\nBf4BLPDVUCkV+vy+IBwAaK2jenZLnmVBCJxgn+eIKHGtdeeAv19WSv1aKTVVa93sp30kuiUIkxal\nQtLfVcCsAeszvNvCfqw8y4IwOqE8z+GcTlf4sXsrpfIG/H04xqHOpwKPBCUlJTEhI1JyYkVGpORE\n6lpCYCMwXyk1WymVAJwNPDdC+4HP9ViPHVfkdxOdcmJFRiTlBEtYRuJKqaeANUC2UmofcAuQAGit\n9W+Bs5RSlwBOoAf4WjjkCoIwdrTWbqXUeuBVzIv877TW25RSF+N9Zr0v3qVAOuBRSl0JLNFad/o6\ndoIuRRAOeMISYhZOlFI62vokCNGGUmpS2MTlWRaE0QnleZaMbYIgCIIwSTkglbjYaw5MGZGSE+02\ntFhCfjfRKSdWZERSTrAckEpcEARBEGIBsYkLwiREbOKCEDuITVwQBEEQDkAOSCUu9poDU0ak5ES7\nDS2WkN9NdMqJFRmRlBMsB6QSFwRBEIRYQGzigjAJEZu4IMQOYhMXBEEQhAOQA1KJi73mwJQRKTnR\nbkOLJeR3E51yYkVGJOUEywGpxAVBEAQhFhCbuCBMQsQmLgixg9jEBUEQBOEA5IBU4mKvGWcZWkNd\nHezYARUVYLeHX0aQROX9EoJGfjfRKSdWZERSTrCERYkrpX6nlKpTSm0eoc39SqkypdQmpdTKcMgV\nopTdu2H/fujshKYm2LYNursnuleCIAgxR1hs4kqpo4FO4HGt9Qof+9cC67XWpyiljgDu01qv9nMu\nsaNNZmpqoLp6+Pb4eFiyBOLiIt+nGERs4oIQO0y4TVxr/S7QMkKT04DHvW3fBzKVUnnhkC1EETab\nUeK+cDqhsjKy/REEQYhxImUTnw4M/A9e5d02IYi9ZpxkVFUZe7g/mpvNFHsoMkIkqu6XEDLyu4lO\nObEiI5JygiUq5zbXrVtHUVERAFlZWaxcuZI1a9YA/Tc0lPVNmzaF9Xy+1nsZr/P3rm/atGlczx/w\n/TriCGhtpaS01KyvWmX2D13/+99h5ky5X0H8nkpKSqioqCAcKKVOAu7FvMj/Tmv9Ex9t7gfWAl3A\nOq31Ju/27wLfAjzAFuAbWmtHWDomCMKYCFucuFJqNvC8H5v4Q8CbWutnvOvbgWO01nU+2oodbTJS\nUWGc2AJh4UJISxvX7sQ6odjQlFIWYCfwRaAa2AicrbXePqCNTz8WpVQh8C6wSGvtUEo9A7yotX7c\nhxx5lgUhACbcJt7bD+/ii+eACwCUUquBVl8KXJikuFzQMpJLxBDq5KufYA4HyrTWe7XWTuBpjN/K\nQEbyY7ECqUqpOCAF8yIgCMIEEK4Qs6eADcACpdQ+pdQ3lFIXK6UuAtBavwTsUUqVAw8Dl4ZDbrCI\nvSbMMpqbweMZvG37dnj0UXj11eFx4m1t4Bg8+3pA3a+JZ6iPyn6G+6j49GPRWlcDPwf2ebe1aq1f\nH8e+joj8bqJTTqzIiKScYAmLTVxr/fUA2qwPhywhsjjdTjrsHdR31WNRFpLjkklNSB3caOg0+pYt\ncN11cOKJ8MEH8Mgj8POfw6xZZr/W0NgIhYWRuQghbCilsjCj9NlAG/CsUurrWuunfLWPBf+WSK1H\nwl9jIBN9vQfy/SopKeGxxx4D6Hs+gkVypwvD8GgPzT3NNHY30uXoGrY/wZpAQXoB01KmmbCyrVuH\nn8TpNLHhAH/5Czz+ODz1FKSnm23x8bB8OaioDnWOWkK0ia8GbtVan+RdvwHQA53b/PmxAJ8HTtRa\n/693+/nAEb5e0uVZFoTACOV5jkrvdGFi8GgP9V311HXW4fK4/LZzuB3sbd1Lc08zc2xJxPtq5FXg\ndrcD2+lrSSiaQVJqar/ThNMJHR2QkRHuyxBGZyMw3+uMWgOcDZwzpM1zwGXAMwP9WJRS+4DVSqkk\nwI5xjtsYua4LgjAQyZ0+iWWES45He6jrrGNL3Raq2quGKfDSDaU+j+uwd7Bt74e0OwfHfmutaXK0\n8lnHbj7t2EV5VyWfFWexubOcWlsjfaOzAdPwk+l+RYOMUNBau4H1wKvAVuBprfW2QPxYtNYfAM8C\nHwOfYJxZfxv5qzDI7yY65cSKjEjKCRYZiR/AaK1p6G6gtrMWp9s59hM4nTh7uiiji8z4NDLiUnF6\nXDQ723F4hp/P5XFTZWug1dXJ/JQZxLW2Goc4ywH5LjmhaK1fARa8eyJaAAAgAElEQVQO2fbwkHWf\nfixa69uA28avd4IgBIrYxA9A3B43Dd0N1HfVB6e8e2lphto60Jq0T7bTuWJhwAo5yZrAgtTZxM8r\nhqlTg+/DAYrkTheE2CFa4sSFKKfT0cne1r1srttMVXtVaAoc+lKopm3Zwex7fz+mQ21uB+VdlXia\nA0wQIwiCIAzjgFTiB4q9xuVx0WprZV/bPrbUbWFH4w4auxvxaI/fY3zh0yauPdBlyovmPP9v6k87\nPuBRePa/3iZt0za63TYqaraB2x0V92syyRAM8ruJTjmxIiOScoJFbOKTHK01DrcDh9uB3WXH7rZj\nc9nodnZjd9lHP0GwdHWD1li6e8h4fxPupASKr70b26xCKi89F6xWSEww2dzcQ14aNOT/+QXKVy6m\nxdFOQ+2u8eunIAhCDCM28UmEy+Oiw95Bl7OLHmcPdrcdh9vBhNyvulpobmHqq+9S8PhfSaxvRnk8\naIuFhq+cQOXPboaERG9ilwZo7J82Vw4Hy79+FdvvvwVHYR6WjAyWHHwiiXGJkb+OSYrYxAUhdpA4\n8RhGa02LrYXG7kY67B0T3Z1+ukwSmOw33sOTlITypl1VHg9JtY1GgYNJ5pKTCyiTpQ3QCQk0H3sk\n2a+9R82FZ+Dp7GBfSwXFOQt9SRIEQRD8IDbxKJbRZmtja8NW9rTs8avA/cVwh5NhMlwusJvc503H\nHUXnsgVorz1cWy3YFswbfpKcHEhN6VttOv5osl9714zUPZp/v/wyLT1jKKISJJPluxcCI5bsonIt\n0ScjknKCRUbiUYjWmn1t+2jsbpzorvimqz+5S+0Xj+C9FfEc1L2bIzoysC1bTOWt3/V9XEEB7NoN\nWtMzfzaepARSyiroXjAHerrZ376fzKRMLGpyv1t6tIceZw8ujwu3duPRHjzaM8jsoZRCefPX9f49\n0icw6G9BEAQQm3jU4fK42NW8i05H5+iNJ4qaamht462mj7hn9+MUJubw+eyDOf+YyyE+YeRj6+ug\nqRkAS1cPntRksz3OCvOLmZ45g/y0/HG+gPBid9lps7f1+SuEHLoXAKumrxKbuCDECBNuE1dKnQTc\ni5me/93AQgre/ccA/wR2ezf9TWt9RzhkxxIuj4udTTvpcfZMdFdGxN3ZyQN7/sTrjR9wa/HFrMpa\nDJkZoytwgOxsU3vco/sVOIDLDT3d1FpryUnJwWqxjt8FhIl2ezu1nbXR5asgCMIBRcjzlkopC/AA\ncCKwFDhHKbXIR9O3tdaHeJcJVeDRaK/xaA/lzeVjVuARt4k7nWxs2MRnnXt4YuWPjAIHmJo97DiX\nx8Ube94YvNEaB5lZw2Vs2gYdHbg9bmo7a8PZ/UGE47t3uB2UN5dT1lTmU4FH4jsRDLFkF5VriT4Z\nkZQTLOEYiR8OlGmt9wIopZ7G1BvePqRdVE/9RQyPB7q7we2G5GRISEBrze6W3T7LfkYd3V2snrKc\nwzKX9I+Wk5LMMoQOewcPfPAAHfYOTl90ev+OqVPMaHwonZ2QBw3dDeSn5UflaLzd3s6elj0jVnkT\nBEGIFCHbxJVSZ2LqC1/kXT8POFxrfcWANscAfwX2A1XAtVrrz/ycLzbtaG431NZCQ4P5u5fMTCqz\nFPWO1onr21ioqYHWVhZd+kN233IFjrxpkJ8PU6b4bF7RWsH/Pv+//PS4n3JwwcH9Oyr3QaePl5a5\ncyAxicL0QgrSC8bpIoKjuaeZitaKiYnLH4LYxAUhdphwm3gAfAjM0lp3K6XWAv8AFvhrvG7dOoqK\nigDIyspi5cqVrFmzBuif2phU6z09rJkxAxwOSkrNVOuaVasA+Psr/6De1caq006CxKS+qdhVR5r9\nUbf+3gfE1zezor4RR85USj/ZBk3trDr6CJ/tGz9r5Nz0c7npzZt48ownKf+o3OxfvgA6uyjdtI2E\n2noOW7YA+4wCSv/9HmRmsvro1eSl5fH2W2+P//cTwPrK1SupaK1g43sbJ+T+A3z4nw+prqxGEASh\nl3CMxFcDt2qtT/Ku3wDooc5tQ47ZAxyqtW72sW/c395LSkr6/kmPu4zmZqioMPHQQ2h2tLGn2/tP\nOS4OioogPn5Mcko3lPb9wx8vNryzgSM/f6SJDy8rI/vlt8j46FP2/OAySEuDmTNHPce9/72XyvZK\nfnb8z0yYlNZQXgYuN/lPPcfGz8qZecf3zLT8nDkAzMycSW5qblivJZjvvtvZzY7GHQHnnI/EdyIj\ncUMknuVIyZFriT4ZkZIz0VXMNgLzlVKzlVIJwNnAc0M6mDfg78MxLw/DFHjM0dAAe/b4VOD19mYq\nemr6N7hcUF0Vwc4Fxsaqjfz4nR8bG3CPKXiS/vFW2g9eahpkpAd0nssOu4y5U+bicJskMSgFGRkA\ntHzhMFI/22n8BWw2cJoQrfqu+vBeTBC4PW52Ne8ac9EYQRCESBCWOHFviNl99IeY3a2UuhgzIv+t\nUuoy4BLACfQA39Vav+/nXLFhR6uvh8rKvlWXx4XN46DbbaPJ0Ua32+b7uPw8mBId9bXLm8u55MVL\nuPu4uzm04FCTL72pmRVfu5zt9/0QR2EeFM8HaxzZKdlkJmZS21lLt7M7MAE9PWaWAljy7RvY+71v\n0bWkeJCNff7U+WQmZY7TFY7OnpY9NPdE3/umjMQFIXaYcJu41voVYOGQbQ8P+PtB4MFwyJoUNDT0\nKfBGRyv19mZ63AFWFGtoMCNU68Qm06vvqueqf13F1Z+72ihwgO4eEuqbcKWn4SjIhZTkPgVelFUE\nQHpiOtsatvWPuEciORkS4sHhpPWoVWS9U2qUeGdHnxKv76qfMCXeZmuLSgUuCILQy+TObxkk4xr3\n19gI+/bxRukH7Ozcy97umsAVOJiynU1No7fzMh4xyZ2OTq565SrOWnwWJ80/ycjQHrDbceRN47NH\n7jQN09KIt8YzM6PfJh5niWNW5qzAhWUYBf2v3Gyy3is1poeubvAYD/52e3tYS6oG+t17tId9bfuC\nkjEZ4sSVUicppbYrpXYqpa730+Z+pVSZUmqTUmrlgO2ZSqm/KKW2KaW2KqWOiFzPBxNLscJyLdEn\nI5JyguWAVOLjRlMT7N2LW7vZ31NPh2uEaeWRphlbWoyNfILYVLuJQwsP5cKDLuzf2NPT32dvsRPS\n0ihMLxwWz52ZlElaQlpgwrw2dfv0POrPOMmE32kNHf1JVBq6G4K+lmCp7awNbDZhEhJIgiZvFMk8\nrXUxcDHw0IDd9wEvaa0XAwcB2yLScUEQhiG500fA6XZitVgDK8jR1AQVFXi0h7KufXS6hmRe05qM\njZvJee510rbsxNrTQ8/sGWx/4FZ0oo90pdOyvSU8o4TGRjPV30t8PAkLl7Asd5nPohzt9nbKmsr8\nnq7V1soDHzzADUffQFzF3r6qaH2kp8OMGYAZ3a/IWxGx4h8Ot4Ot9Vuj2pktFJu4N6LkFq31Wu/6\nsIgSpdRDwJta62e869uANRiflo+11j5K1Q2TEzXPsiBEMxNuE48lbC4bNR01tNnbcHundJPikshO\nyfaf07uxEfbuBaCiu3q4Agdm/fL3pH26k9r/dzLOKZkk1tTjyJ6CjvOTlaylBaZNg2ip6NUzZFYh\nLY38tHy/ijUjMYOU+BS/Tm4ZiRlUdVTxx81/ZN30U8A+pGJbV6eZwlcWXB4XLbYWpiZHxuGvuqM6\nqhV4GJgOVA5Y34/JvDhSmyrvNjfQqJR6FDMKLwWu1FpHd8J/QYhRDkgl7i/ur76rnv3t+4dl5LK5\nbFS1V1HbWUtheiE5KTn9yqumBqpNrHdlTy0tTjMNXLppG6tWLu4/9xknUnn5hcx46Cmm/esdlMeD\ntljwpKdSuf6C4Z10e6CtHbKG5xkfSCRikks3lLJq2uBQsrj0DLJThudLH0huai4VrRU+91mUhZu/\ncDMX/OMCvpB/BM1D7hcebdKwppswtMbuxrAo8dFiPm0uG03dgfsk+CIS38kEEgccAlymtS5VSt0L\n3ADc4qvxeCdu2rRpE1dddVXYzudvfaBddLwSC917770RSWw19Jrkfo28PvSawnV/HnvsMYC+5yNY\nDsjpdF//yPe376eusy6g45PikpieVkBWXRs0N+PWbip76mhytPW1GarEeym+9i4yPu7PONt+8FLK\n7rnBj6D+xCf+CFVhbG/cjs1lY2X+Sr9tSt/awKrcKaTs3INtej6e1GTyD/kC06eM7MDm0R621G0Z\nMc/4s589y3M7n+Myx1c4YvmQujkZ6TB9Rt/qstxlJMYlBnZhfhhNie9q3kWrLbQUuNGe7CWQBE0+\nptO3A8d4d/9Haz3Xu/1o4Hqt9ak+5EiylyiTESk5sSIjUnImOtlL2BnvsJ6hX0h1R3XAChzA1tXK\nro/fYHPF+2zvrGBze9kgBQ4MU+Cdrh5+X/kczybtwen9qtwWhW124aB28fVNtDk7zWyAzWaWEQhW\nWWitefazZ1n/8vpRldaqg5YAMOeu35BYU49KTiYnY/Sa3xZlGXW0fubiM0mLT2Nb4f6BnTOfnd4p\ndS9NPaGNkGH4dz+Qbmd3yAocgv9OIsioCZq86xdAn9Jv1VrXaa3rgEqlVG/a5C8CPusgRIJI/BOP\nlBy5luiTEUk5wRKV0+n72/eTmZgZkSpWLT0t1HTUjN4QjEJpbDJObFrjBJw+RpnxdY0486b1rZd3\nVXLJp3exOmsFR15zHc2PbyB5XzW22YVUXnJuXztLZzeLL72ZU24sYqduZG3OkaxNXMv0uf5HycGw\nt3Uvd717F13OLv7v1P/ri/H2S0831rYO4pta6Zkzk6wp+SRYA6gdDuSk5Iz4gqSU4uYv3MwHFe+a\nDVqz+Ds3UXbXtbimZhkvdW8YWlN3E4XphX7PFSpV7WPImOd2mSl/MNnnLMr4L0TI+S4UtNZupdR6\n4FX6EzRtG5igSWv9klLqZKVUOdAFfGPAKa4AnlRKxQO7h+wTBCGCROVI3Ol2Ut0xfoUeem0TNpfN\nr812EG4XNDVC+S7jxDbCFGHme6UsXn8rH7/3Yd+2opRCHlp2I7cv/A6LMuez//ILKLvnBmMLt/a/\nqHjSUqg/4yT+9FIytxZfRJOzlQvf/i7feu5b/HXbX31OS481Jvn3H/+ebz73Tb4w+ws8dtpjoytw\noPS9jaRtLaNz8XywWsjNGf2YXhLjEklPHDk1a0F6AdPb50CcFZTCNms6WRs+Mjvb2vvaOdwO2mxt\nfs4SGP5iPjvsHbTb233uo6fHfO+VlVBeDtu3w84y83d5OZSVwY6d3u07KH32nyYTXWUl1FRDfZ35\n/bS0QHubcdrr6Qa7DZwOE07odpmXxAiZt7TWr2itF2qti7XWd3u3Pay1/u2ANuu11vO11gdprT8a\nsP0TrfVhWuuVWusztNahfSkhEEuxwnIt0ScjknKCJSpH4mzbRoPaztS0IlLjks223hGOUoMXi2Xw\nYrX2L3Fxvhet0Vqzp2WPby9kj9uEPNl6zJRuV3dA/1yz3i1l1r2PUn7nNbi7+6fB45SVeakzRjiy\nn/qvnMCyC6/h8LpTWV68ju/NOY8N1v1saNyEVYU+M3HkzCM5Y/EZZCWN7DDXh9sFTjdpW3fStayY\npLhE0qeOrURoTkoOHfaOkRspTDGV1jZajj6UaS+/ReOXjoWuLtMHbwa7pp6mccngtr99/+AN2mOU\nbksLOJyBn8jtAafbKP5Q6fvNh34qQRBik6h0bCt9/QkAkqwJLE6bE1ic9hipdjRR42zxToN6q2pp\nbZKNuMceXpT19kZm/eoPlN15DT3FRSH1Lecfr5FRupldd1xtNgyImR7K7pbd/OnTP5GVlEVKfAou\nj4tuZzfZydmct+K8kPoBmOns/ftZeOXtVF94BlnHf4nclUeN6RRaazbXbR7RwW2gLEuPjRVfu5wt\nT92LOy0V8nJhqrGtK6VYkbeCOEv43j8buxvZ27q3f0NrKzTUg8vt/6AJZtVx50vudEGIEWLOsa0X\nm9vBnu7qYSFfodLjtlHb02CqZdkdYLObT4czOAX+jlHgG+74Dle5X6DZ4Wd20aIgKxOmF5rynbk5\nJnf4EBrXHkPq9l0k7vfa6rs6+9KQDiUtIY2F2QtJikuiw96By+MiMzGTeVNGzcURGDYzouyePwvb\nkmKys0cvOzoUpRTTUqaN3jAtFSwKT3ISHQctJvP9TWZ7W//91FqHHAI2EKfb2T8Kdzph314TNhjF\nClwQBKGXqFbiAK3ODm8GtG4cHicdri6qbQ2Ude7js47d7OzcS729OeDkHFpr/rzh9bC+GNhm5PPU\nbWfx1bbfUpRcQGZ8OqWbhmSizEiHefOhoNA4aqWlQfY0mDsPpk4Z3MfEBHb/8ApcmSZGGs/gNKQD\n2ffJPs5achbfOvhbXHHEFVyy6hLWrVzH52Z+LjwX191N6aZtVF5+IVMy87BmBDeVPZoSL91QahzD\nUlL5uG0H1xzrImmPV7na7IOmpxu7G/2cZXQG2re01uxu2W2S+nR1QsUeYzoJkWHfvTBuxJJdVK4l\n+mREUk6whGVO0luK9F76PV1/4qPN/cBajKfrOq31pkDP3+HqZkfn3hH319mbKUopID0udcRz1dgb\nsYUxJ7bH5aTx6d9TVLGH14sPwvnd0wdnWVMK8vL6qnINQynIyweL1ThPeelcMSRmur0DMgO0Y4eL\n3jA3LzkJU8zLRxAkxiWSkZjh33msl/R0ilNncUtaDcvPOIGje7e3tpiqZxiHxE5HZ+D52f1Q0VpB\np6PT2L3r6iLmVCYIghAuQraJe4sp7MTEi1ZjYlDP1lpvH9BmLbBea32Kt+LRfVrr1X7O12cTD6Iv\nzEzKIyfRt8LsdHWzs2tf2Ebhbu2h4rbv8pX3monXoC0WGr78xf4MbBZlbNmp/comIzGD9MR0397Q\nVfuNsvaFUrCg2Cj7SDGg3ndmfBrzpy2AJUuCPl2rrZVdzbtGbuR2wc4yPmzbxg92/Jo/rrydaQlZ\n5vq9tcsBpiZPZc6UkRPh+ENrzZ7WPbT0tAzPCe+DvT01VPbUUWNvpMvVQ7fHhtaadTNO7Xe8HEBZ\n1z6SLImkx6WQZk0Oq/2+F7GJC0LsMNG50w8HyrTWe72deRo4Ddg+oM1pwOMAWuv3vaUM87yJI8KG\n1pp9PbU4PE6mJw8uHuLwONndXRWaAteatE930rnclE63KgtHtmUQr01yGuXxkLTXGxpntRi7d3KK\n2acURVlFfalD89PyqeusG+wVXVAA3T2+K5hpbxrSIKezg2JAvvTchCnGwS4EMhMzSbAmjFwdzBoH\nKckcymJOyzuGH+58iAeWXocFCzS3QE4OAC22Fma4ZxBvHe5TMBJuj5vy5nIzAm+oN3H/o3Bn+aMk\nqDjyk6aRbk0hxZqExWLB4icm/Oe7/0itvYkOVzedrm4SLPGkWJP4y6E/IcPHTNFv9j6LR3uIU3Ek\nWOKIV3HEW+I5Pf8YEi3D4/E/aN06pmsWBCF2CYdN3FcxhemjtKny0SZs1NqbKO+qxO5VFl2uHnZ2\n7u1LzDJmm6XWpH2yjeJr72LWfY9h7ezq25UwtxhtMbdRWywmA5vVQmlVU58CtygLxVOLh+X+zkvL\nIzd1wMuGxQr5ef774WOUPq61q7126C1bysmITwt6Kr0XpRQ5qTk+9w26Du/Lwv/O+gpOj4vH979o\ntre29GVw01qPuUSp0+3kieeeGJMCB3h4+Y38atl13FO9jJ++5OSuR/Zw9y+3cPD6H7P44ptI27Jj\nUPtvu7/CP1b9nA/iLmW7+xLeTbqUZzMvYmpdO9a2jmHOk1Pi00m2JgGaLncP9Y4WKnqq/c7u/6Xm\n9TFddywTS3ZRuZbokxFJOcESlXHic2+7H+3NgqUtFtpXraD5hKOHtUvdsoPM9zfhSUrEk5yEJykR\nd3ISttmFtM2bTZuzkziLFZcfz+7RSKyqI+udjUz99wZalYOWU0+mce0xgxK0VF56LihI2uvNwHbZ\neWYE3mgUbpwljvlT55Oa4NtWPyNjBp2Ozv5qX+kZkNJsRuQAbg+J1XXYZxYMquwVEbp7SP9wC7m7\nG+HzhKzEwcSM13TUjOyImJ4OdfXEKSt3LLyUdlen2e5yQ3OzcQgEGroayE/LDygE0el2sqNpB3aX\n3Uyh19Uz89dPkrSvGtusQt668Bi22So5JXf476wXi9OJI28anQctxpWWgic5CW2x4Cjw/WKSXLGf\ntE93ktfeibWr27v0sPum9XQcuqyv3dmFJwIw48EnSNm1Fx0X510eRCtFzQVfoWfe7L729yy+klWc\nP+o1C4IQ+4TDJh50MQVf0+lKKX3SinksyJxqanAnxjN/6QKWffk4oH8UvWrlYpLLKtj63OtYHE6O\nzkjDarOzobqe7oVzKL7onGHtc/75Gjv+8Dc8SYkclT0Fd2oybzlddC5fwMJ1Zw1rn/1yCW9+8AF/\nLnbwn7n7eergO6ncVte3f2h7LIrS6kZITGLVkatIikuiaksVCdaEESvb2F12cpbmoLU2I1K7nVX5\nZtS++bX3mPngE0z566+9I/xGSEnuy8/dO4IN+/phK6B8F9Xf/xlp85fwP9//PixfHpZKPnWddcw/\nZP7I8gumgs3Ox+99SPrHnzF/vVFapVu2Q2Ehq44+AoC9n+xlavLUEeW5PW7yl+Vjc9kofeUNaGnj\nK+9sJOf5N3jL48GtoPyIeKovX0dhTQ7K6eTQw1YM/37HeT2pYj8ffvgpyu1m9azpWFwu/runkp45\nM3CnpfHhJ9uorjWzDy++9q7YxAUhRgjFJh4OJW4FdmAc22qAD4BztNbbBrQ5GVO68BSv0r93JMe2\nzDvSmBqfwdFTV3L8lFWc8MQGkvfVYJtVaEa+1uCcu5TDQVzb4FGRtasbe0Eu3YsGx1W3OTv5Y9VL\n/K32TU7IWc03Z3zZr8McMMiJzaIs5KXlBTxKBPpKnfaxb29fuNPi79zE/ovPoePgpSbOvGD88of3\n0dYK1TUc9M3vE/eTe+CII0atqBYodpedrQ1bR/ZPaGiAxkaUzc6Kc67ks0fuxDnNa47IyjL+A4DV\nYmVZ7jK/zmNuj5udTTvNTEdzE9TVA1B87d1kfNxvW65ZMZeau2+i8A9/Je3Tney474dhudbxQhzb\nBCF2mNBkL1prN9BbTGEr8HRvMQWl1EXeNi8Be7zFFB4GLh3pnK8e8SC3LriYeEscrp/fw7Tn3yDj\n463kPP8GM3/zZPB9TUjAmTOVd1s76Fq6gPbDD6Llfz43TIF/2LaNMz68lhZnB39ceTvXz7swIAWe\nkDGVGRkzWJ63nJ0f7hxTprmC9ILBZTan9lf/al6zmikl75uVzs5BoVDjZhPv7iG5vQdrcyslLS1h\nmUrvJTEukSlJg+/nsOvIMHZxnZRIy9GHMfX1Df37Wluh2/gluD3uwdnWBuDRHsqby40CbzJT6L0j\nX9usQtwW88x4LIr43HwWrb+FxKo6dt12VUjXJ3HikSOW7KJyLdEnI5JygiUsNnGt9SvAwiHbHh6y\nvj7Q81mVhaXpc1maPpdiWzlWj6l0OMj7exxZkDqLPxx0KzOSR3Ay68XrhV6YO5/8tHxUkFWsLMrC\nzIyZlDeXmw1paZCYAHYHLccczqL1t7Lvcm/omq2nz2lu3OjpZsbOGtTy5SYnferI8fdjpSC9YOSS\ns4lJJpudw0nTiZ+n6GePUPf/TgaLhUZHK9Oq4szMQFwcrbZWqjuqB1U4c7gd7G7ZTZejy1uAZLCs\n8u98lX81/pfjO3JJTMskc+MWqr9xFo2n/M+kqEQmCIIAUZ47HWDmrx4n5/k3UB7PoDhsm9vO9dt/\nxRenHc6x2YeR5iNedzR6rz1YxUt8PMycwZz8xcM8z4NlV/Ou/prWLc1Qa2zwi9bfQvWFZ9J+2ArI\nngq5AbxgBIvbRfKufSz5/fNGeV98MRx0UNiV256WPSMr8l4Pcq1Z/J2bqfrW/2PzsmlcvOVOHjvo\nVgqypsOsWX2x4+mJ6WQlZWF32WnqacLttEN1jZm98IFHe0iqaWDRVbez+weX0XnQYp/tohGZTheE\n2GGi48THlWHe397621Zl5ct5x/By/Xv8YveTfG7Kck7OPYrPZS0fNblGo6OVfzdu5O+1b3LlnHNY\nPWX52DuWmgLTp5OfOSNsChxgZuZM2u3txns7MxPq68Gjqf3al/AkemOGOzrGV4l39zAjKRfWrjUz\nAikp4zI6LUwvpMXW4t82np5hlLhS1J15Irn/eJWiw6/h/BmncM22e/nd0hspvvJ3JNU2YFs0n8pb\nv2eqpWlt8q03NPiOufdiURYchXl8+vuf4kkb55kNQRCEcSDqR+KB0Obs5PXGD3i54T1mJuVxy4KL\nzA63uy+MqKoglbu/PIVNXbvYubWSYw49hNPyjmFV5uKxVUmzKJNwZGo2yfHJLJ622OdIvqSkpM9D\neqwMSgJTXTWopnYfc+dAYhKlG0r7PLvDRVZLN/Ns/UqtZM8e1px1Vlhl9FLZVkl9V73/69i9C+wO\nlMOJtbML19QstNbcsvNhvvX0Tk5/rwlL7yzNWWup/N63jbnBTwGT0k3b+jzDx4tIyJCRuCGU5yza\n5Mi1RJ+MSMmJ6ZF4IGTGp3FmwbGcWXDsoHKXM3/9ZN9UfOoninWOeWz7zploj2b1wiBG35kZkJNr\nptGB2Zmzg5+KH4Hc1FxabC3GnpuV5VuJd3Yau3GYsSgLM3UGMGAEmxR+Ob0UpheOPKWengH2RnRC\nPK6pJne8Uoqbi7+NtXY9Fo+JN1ceD0llFX6nztucnWTGh+icFx9v/BTi4iHOOjheX3tMEhePG5KT\nzD1zu81MQJS9KAuCEDtE50i89PkBWwb0r7fmt/b+jQaPx6x73KbaV++n1sPCiNoPXkrZPTeMrUPx\n8cZTesoUiO9PgZmdkk1RVlEQVxgYNpeNbQ3bzLR6ebkpkzmQ5GQoCr/8mWmF5JYNcR5cuTLosL5A\naO5pZk/LHt87nQ4o951vveD+35P7/JvE+cpbP4CK7mou+/mOToMAACAASURBVPQn/GLJ91hMztim\nztNSzYtEWhrEBfnOqz1mZsDtNr/PXmXv0WZf76ev33ffOQY/p6sOO01G4oIQI8TeSNwbAxwSHje2\n5YtJ37wN5fagrRZsi+fDtGnmn6nbNfifJxgvbIvFO+JKNIoyIXHYqS3KwvT0ccsaC0BSXBLTM6ZT\n2VZpZgCGpgjt8eZYD1ax+CA9MZ1czxAHweTkcVXgYIqZtPS09Dv0DSQ+wfRhQCnSXmouu5A4S9ww\nf4mBlDSV8uPy33Nl0dc58p0Kcv/+MNseusN8z14sSnn15gCFk5UJ2dk+v/8xoywQb+mbwYkGQq08\n6C18VArs11p/OTK9FgRhKFFfTzxoLFYqb7+Ghgu+SvvRh9FwwVepvOv7kJND6e79MH2GSY86azbM\nLjLLzFlme26eKfvp5x94flr+qIU3whFbmJuaS1ZSFmRk+G7Q0RG2OPF4azxzsuYMr1uemhqROMmK\nTRUkWIcX+wCMg58vrFYq119A2T03mBH4gJeNl+vf4/JPf8ov9/yJXy75Huvet1H4+N955qsn9ylw\ni1LMSSnk4MxFHJRRzIzkXCxJ3hmOgsKgFfi45rMPA14F/ABwIrAUOEcptWhIm7XAPK11MXAx8NCQ\n01wJfBaB7o5ILMUKy7VEn4xIygmWqFbi8dZ45k6Zy8EFB7Nw2kJS4sfoQRwXR+Ud11L2zG+ovOPa\nsIxa463x5KWNo2f4EIqyikhKzTK2WGDKm/8h99mXzc5OP2VLx4hSirlT5poXk44O2LEDrrzS7Axj\nkpeRsFqszJs6z7eTYWaGcSjsxeVi7q33Ed/g35a+uaOME3JW85dD7ubYf5WR/+cX2fGLG3HkmCQ6\nSimKU2cxNcG8IFiVlbxZS1h02FoS0iJYKW5i6Ks8qLV2Ar2VBwcyqPIgkKmUygNQSs0ATgb+L3Jd\nFgTBF9FpE68qJSkuiQXZCwaNeD3aw67mXcPrcEeQOVPmhDWkLBDsLjvbt72Nq76OtC07mPnAE2x7\n+I6w1RgvyioiOyXb2N03b4annzZ2+JtugqVLx9WxbSjt9nZ2Ne8aXiClpsZkavOS9/QLTHn7A3be\n8308qf5zBMz49R/JKN1C2V3X4syb1rd9dkqBqVMOZmQ+ezZMNd+r0+2krLmMHufwKfxoYdX0VcHn\nWlbqTOBErfVF3vXzgMO11lcMaPM8cJfWeoN3/XXgOq31R0qpvwA/BjKBq/1Np4tNXBACI+Zs4gnW\nhGEKHIwtet7UeZQ3l5t44AiTlpAWcQUOJk1p8exD2NnwLzqXFBPf1ExCbQOO/JyQa4zPypxlFDj0\nT6V/8gkcdZSZuYigAgfISMygOLuYXc27BkUaMGXKICVe97VTSKxtYMF1d7P7h5fj6FXQA8IKbbMK\naT9kKdUXnDHImW1qQka/ArdaYf78QTMO8dZ4FmQvoKyprL+6nACAUuoUoE5rvUkptQYY8R/PunXr\nKPI6YGZlZbFy5cqQiufIuqzHwnpJSQmPPfYYQN/zESxRORLvcfaQFOdfeXi0h7KmMlMXOgiCia1W\nSrF42mKS4wPLDDcesYXdn5RS3lxO4U9/Q8/cWdSfcSKlOytYddraMZ9LKcXszNn9ChygosKU6Tz5\nZHjkETMKnz9/QmI+nW4nle2VtPS09DfaW9FfohVAa/KeeZH8Z16kce0XqLroHL8Z/nrZvHknF3z+\nS1iV1bykLFhgHOd84Pa4KWsuM6F+Y2A8YveHEuJIPOjKgxhb+HmYGMRkIB34m9Z6WFiAxIlHn4xI\nyYkVGZGSM6EFUMaDkRQ4mBF5cXaxcfryQ5wljuyUbArSC0hPTA+5T/lp+QEr8PEiZVoBi9KKsH3+\nc2S996HZaOsxHvZjoHekOUiBA7S3Q1WV8dafPj1i9nBf9PpDLM1dSmF6IVlJWaTmzSQ1LpmMuFSm\nJmSQnZiF7fyz2fHInfQUzQQgaV81amDs+N7+cDmLUhQk5RgFHh8PCxf6VeBg7PTFU4vD8vuJMjYC\n85VSs5VSCcDZwHND2jwHXAB9Sr9Va12ntb5Raz1Laz3Xe9y/fSlwQRAiQ1SOxMfSp6buJmo7a7G5\nbACkJqQyLWUaU5OnDnKSarW1UtFagdvjO5PXSKTEp7Bo2qJxSewyJrq7Yds2dE8P+kunsOXJX+BK\nSoTphQFPqU9LmcaMjBlYh9rRvefm9dfh3/+GO+80Sm4CFblPPvtsWLiZ1poWZzvVtgZy7/ud35H4\n3JTpTEnIMCPwhQsDNhVordnTumfwrMAEE8pIHPpCzO6jP8TsbqXUxZgR+W+9bR4ATsKEmH1Da/3R\nkHMcg9jEBSFkJrSeeLgJ9sF3e9xYlGVERdvj7KGsuQyn2+m3zVCsFiuLpy0eXCZ0ItmyBRwOsNtx\nxFuotzfTlOTBVeg/tt6iLExNnkpeWp7/WY6aGqj2jlpdLjNSXblyUDx1VNDaCrt8J3/RWlPf3YDl\n3ntJrKjqix23xsUzO7mgX4GPMIU+EtUd1dR01IR4AeEhVCUeCUSJC0JgTNh0ulJqilLqVaXUDqXU\nv5RSPoeDSqkKpdQnSqmPlVIfhCLTH1aLddSRcnJ8MoumLWLz+5sDOqdFWZg3ZV5QCnzcYguzvCaE\nxEQSLPGUb61khSpg4ZT5zMiYQU5qDtkp2eSk5jA9YzrF2cUclH8Qs7Nmj2ymGOA0RlycKXriVeBR\nFfOZleV3dkApRV5qLtk33oHzwftwXH0VM9IKWJo+zyhwq5WSmpqgFDiYFLHzp84ftcBOtMeJxxKR\niuGNqmdgEsiJFRmRlBMsoXqn3wC8rrX+qVLqeuD73m1D8QBrtNYTPh+ZYE1gVuYs0hPTR/Rwt1qs\nzJsyL/rsoVlZprLZABSQ1uUkbVqQ8esOh5lOH0i0TaMPZNYsM/XvZ5RnURayE4b4S1itUFw8+GUl\nCDKTMlmau5TKtsqRc74LgiBEgJCm03s9VrXWdUqpfKBEa73IR7s9wCqtddOwkwxvG7EpuLrOOmo6\na4bZydMT05mdOTt6ptAHorWJ5R5aYjM93UwTB0N9PVRWDt42b17/qD8aqa01TniBEBdnFHhKeMuN\ndjo6qe6onpBwR5lOF4TYYSLjxHO11nUAWutapVSun3YaeE0p5QZ+q7V+JES5YSEvLY+c1BzabG3Y\nXDYsykJ6YvrYM8NFEqVMGtKmIe9DHR1gt5uc72OlxccESTSPxAHy883sga++DyQpycSBB3NfRiEt\nIY0F2QvocnRR31VPq611eJIaQRCEcWRUJa6Ueg0YOE+rMEr5Jh/N/b12H6W1rlFK5WCU+Tat9bv+\nZI53gohNmzZx1VVXAfD2W2+HfD5f673bxiVhQEcHawoLAbj3jjtYeeyxrDnySGhqomTnzrGd79VX\nYc8e1qxcCZ99RonDAYmJrDn0UJ/3a7wSIAR1v+bMoeT996G9nTWrTFx2SamxR69ZtQqysynZvRsa\nGvqOv/fee8ct4YhHe3jx1RfZ+NFGvvrNr+JwO/rs471x48GuA3z4nw+prhxSYe4AJ5ZiheVaok9G\nJOUES6jT6dswtu7e6fQ3tdaLRznmFqBDa/0LP/tjIkHEuMrweGDTJtCakq9/nTUXXQRr1hiP8uXL\nzWg9UHq90j/9FG6/HZ55BnJyjN3ZS9Tfr5YWYxLo6THOeOnpkJsLqanhlRMgvTKcbifdzm56XD3Y\nXXbsbjsOtwOn2xnyiF2m0w2x9I9criX6ZERKzoSFmCmlfgI0a61/4nVsm6K1vmFImxTAorXuVEql\nAq8Ct2mtX/VzTrGjBUJ5ObS1GaW7dSv86Edm+5w5fTnAA6I3ZO3hh40SvOoqmDvXpDkVxg2P9uDy\nuHB5XLg9bjzag1ubT4/2oLU2n2i01oM+AWZnzRYlLggxwkTaxH8C/Fkp9U1gL/D/vB0qAB7RWn8J\nMxX/d6WU9sp70p8CF8ZAVpZR4sceCw89ZBRxQgLU1QWuxNvazHEAb78NV19t/o52e3gMYFEWEqwJ\n/suvCoIgBEBIceJa62at9XFa64Va6xO01q3e7TVeBY7Weo/WeqXW+mCt9XKt9d3h6HgoxEQMo7fG\ndsnevWbk/IE3/L6726RPDYS6uv7P2lpYscI4gsUPLjwTE/crgnKiPa40lpDfTXTKiRUZkZQTLFGW\njksImPj4fpvvCSfAK6/07wsk9Kqzs79q2TvvwJFHmlCs9CiLixcEQRD8EjNpVw9IemOlW1uhtBSO\nO65/X1ERZGf7PZQdO4wiBygpMVPoq1aJPXySEIoNLVLIsywIgSG50w9UbDbj1OYLqxWWLDF28qE0\nNMC+fb6PO+ggMyIXohpR4oIQO8RcKdLxJmbsNUlJlGz2kwfe7TaFQtxDqrZ1dsL+/b6PSUnxqcBj\n5n5FSE6029BiCfndRKecWJERSTnBIkOuyc5INuze8qLTpxuHtfZ2ExPu8ROjnJExPn0UBEEQxgWZ\nTp/s9PSYGtvhYMECcWybJMh0uiDEDjKdfiCTnDw4L3h3t1HsgTDwH6zVKvHhgiAIk4wDUonHnL1m\nYHKXe+6BZ58d/UC7Hc4+u99DPT3db7rWmLtfMSBDMMjvJjrlxIqMSMoJlgNSicccA0PCzj0Xnnhi\neH3wobz0EuTl9Y++o7nsqCAIguATsYnHCp991j+NfuONJk78oot8t7XZ4Mwz4e67TcEUkNCySUao\nNnGl1EnAvZgX+d9prX/io839wFqgC1intd6klJoBPI5Jp+zBpFe+348MeZYFIQDEJi4MnlK/4gpT\nGKWiwnfbxx+HxYv7FXhamijwAwillAV4ADgRWAqco5RaNKTNWmCe1roYuBh4yLvLBXxPa70U+Bxw\n2dBjBUGIHAekEo9Je81AJZ6fDxdfDDfdNDycbMsWYzO/7rr+baNkaIvJ+zXJZYTI4UCZ1nqv1toJ\nPA2cNqTNaZgRN1rr94FMpVSe1rpWa73Ju70T2AZMj1zXByO/m+iUEysyIiknWGT4FSskJJg4797i\nJ1/9KhxyiKmvPZDUVLjlFlNvuxdJs3qgMR2oHLC+H6PYR2pT5d1W17tBKVUErATeH49OCoIwOqHW\nEz8LuBVYDBymtf7IT7tR7W8D2oodLVhaW02WtrGQkQHFxePTH2HcCCnXslJnAidqrS/yrp8HHK61\nvmJAm+eBu7TWG7zrrwPX9T7jSqk0oAS4XWv9Tz9y9IUXXkhRUREAWVlZrFy5kjVr1gD9IxxZl/UD\nbb2kpITHHnsMgKKiIm677baJyZ2ulFqIcW55GLjGlxL32t92Al8EqoGNwNla6+1+zilKPFi0hk8/\n7a8RHghz5gRef1yIGkJU4quBW7XWJ3nXbwD0wJdrpdRDwJta62e869uBY7TWdUqpOOAF4GWt9X0j\nyJFnWRACYMIc27TWO7TWZcBIwgOxv0WUmLXXKAU5OYEfHBcXUGhZzN6vSSwjRDYC85VSs5VSCcDZ\nwHND2jwHXAB9Sr9Va907lf574LORFHikkN9NdMqJFRmRlBMskXBs82V/mzBHmJgnJ8dkXwuEadOG\n28yFmEdr7QbWA68CW4GntdbblFIXK6Uu8rZ5CdijlCrHzLRdAqCUOgo4FzhWKfWxUuojr7lMEIQJ\nYNTpdKXUa5iY0L5NgAZ+oLV+3tvmTeBqP9Ppo9rfhrSXKbhQqa6GmpqR2yhlQszi4yPTJyGsSO50\nQYgdQnmeR/VO11ofH8yJB1AFzBqwPsO7zS/r1q0TZ5hQ1t1u1kybBi4XJaWlZv+qVWZ/7/rJJ0N8\nfHT0V9ZHXe/9u8Jf7L8gCJOOPXv2cvPNj4V2Eq11yAvwJnCon31WoByYDSQAm4DFI5xLjzdvvvlm\nTMgYUU5jo9alpb6XTZu0djpDlxFGJvx+TTIZ3uckLM/veC2x8ixHSo5cS/TJGE85u3dX6HnzrtbQ\nGdLzHFKcuFLqdOBXwDTgBaXUJq31WqVUASYd45e01m6lVK/9rTfEbFsocoUAyM42MePNzcP3zZ4t\nGdoEQRDGiZYW2LoV9u41ls36evPZ2GhqTnV1QXn5Y3R03AakhiRLcqfHMlrD7t0mfhyMHXzmzLF5\nsAtRidjEBWHicbvhww/hnXfg/feN4q6qMvWncnJM8E96ulkyM01ajtRUSEmBP//5FioqbvOeaRxt\n4sIkRimYN8+MyG028wtKSproXgmCIExabDZ46in429/g3XfNpGZREcydC6efbv7OzR098Of99y1U\nVHQR6kj8gIwvOuBiGDMyzK8qSAV+wN2vSSBDMMjvJjrlxIqMgXK2boULLjD/Su+6y4yub78dHn3U\nZLI+/3xYvdqUrggkcvfcc9eRn38Lpkhg8MhIXBAEQRD8sH8/nHYavPEGHHkk/PjHZrQdKvn5s/nR\njy7nkUd+xsaNwZ9HbOKCMAkRm7ggjC8uF9x6K9x3Hxx1FHz96+NTK6qqCi65RGzigiAI7NsHv/2t\nSVr4ne9AQcFE90iYjOzaZezbNhvccYexd0crYhOfxDIiJSdWZERKjtjEI8fAe/2f/8CKFfDvf8Mr\nr5iEhBs2hF/OeCHPQHTI+Oc/YdUq4xN8zz3Q1TU+csKFjMQFQZj0VFXBl74E55wDJ59str34Ipx6\nKnz8McyaNfLxggDwm9/A9dfDpZeaKfTJgNjEBWESIjbxwZx4oonZvfLKwdt/8xuTJiFcI3Ihdrnj\nDvjZz+DGG2Hx4sjJDdUmfkBOpwuCEDu8/DJs3Aj/+7/D933zm8a++Yc/RL5fwuThpz+Fn//cKPJI\nKvBwcEAq8clsr5kIObEiI1JyxCYeOd58s4TrrzdOSCkpw/cnJsI3vmGmSLu7g5cTS7+bWLmWcMl4\n8EETNnbrrSYj9VC2bAmPnPHigFTigiDEBm++afJSn3qq/zZHHWUSdNx2m/820UZHB7z2mjEHPPgg\n/OMfo1cXjlXeegsOPRSOOw4qK8N77scfh+9/H266Kbo90EdCbOKCMAkRmzh4PLBggbGHn3TSyG3L\ny01WrR07ojfsTGv461/h/vuNeSAnxyxKGbt+VZVJMnLeecb2n5Y20T0ef7ZvhyOOgDPOMOGDVVWw\neTMkJIR+7ueeg3PPheuug5UrQz9fsEicuCAIByT/93/gdMIJJ4zedv58OPhguPZa+OMfx79vY+W/\n/4Vvf9tUuTrxRGPfz8oa3MZuN+2eftqEPl16Kfzwh7FbDsHtNglWjjvOKHGPB264Aa65xrzohMJb\nb5mXocsvn1gFHg4OyOn0yWSviQY5sSIjUnLEJj7+9PQYG+aRR5YElKca4MILTQzwli1jlzde32lX\nF1x8MRx/PBQUlPDQQ3DWWcMVOBj7/jHHwJ13wg9+YK5l/nyj1MfCZHkGbr/dlPQ87zyzbrGYGYhH\nH4VPPw1exkcfGR+Kdevgc58bvX1M28SVUmcppT5VSrmVUoeM0K5CKfWJUupjpdQHocgUBCF0lFIn\nKaW2K6V2KqWu99PmfqVUmVJqk1Jq5ViODZYnn4TPfx6WLjUFJfwp3CuuMFPNy5cHfu6cHKMsv/Md\nM3U90bz0EixcaJLU/OIX8D//YzLNBcKiRaYIx9e+ZkaTRx1lppljhf/+13iLX3mlqRLWy/TpZqbi\nW98K7jt8//3+kf3xx4evvxNJSDZxpdRCwAM8DFyjtf7IT7vdwKFa65YAzik2cUEYhVBs4kopC7AT\n+CJQDWwEztZabx/QZi2wXmt9ilLqCOA+rfXqQI4dcA69e7dmzpzR+9TYaJR2aakpNpGf31+n+ZRT\nzPRxb8KW3lCgn//cKOaxYLfDVVeZl4DrrhvbseGipgYuu8xkljv/fKNMVAjeDXY7/OlP8OqrRjnd\nc49x5IsWWluN/fnFF024X2ensefPn2+qfh17rHkZ670Hb7wBX/2qWb70peHns9vNi8vttxsTRKD8\n+c9w0UWDEwJFAxNqE9da7wBQatSfoOIAnboXhCjkcKBMa70XQCn1NHAaMFARnwY8DqC1fl8plamU\nygPmBHBsH6tXw7PPmtG1P/78Z1i/3owuf/UrSPWWVz7iCDPSfPJJWLIEli0z06vNzcYWPFYFDmZK\n+qqr4Ec/grw8M8UeKerrTTzyI4/AIYfAAw9AZmbo501MNFPDa9fCY48ZL+vTToPvftd4dYfyghAM\nWhuHtL/8BV54wcymzJhhUuKuWWMUeGcn7N0LTzxhvguXy4yyu7qMZ/6555oRty8SE40J4nvfMy8C\na9aM3J/aWrj6ajPzcdll5jcZS0TKsU0Dryml3MBvtdaPREiuT0pKSlgz2jc/CWRESk6syIiUnEhd\nSwhMBwYG6+zHKPbR2kwP8Ng+Tj/djKQXLzZKOTfXTBnb7cbb+L33jFK+4ALf/4yzs82o+WtfM9PF\n6enGQS0x0ezfsqWE5ct9HDgCCxcaB7fvftc4xx17LEybZjye/Sm8HTtKWLjQtxytjRNW76fbbZyw\nXC5wOMx1fvghfPaZcaK6+WbTh6EEcy0Dycsz8fBVVSYk7fjjzX1atszc/9xco0D37TPX4uta/V2/\nx9N/jb1/93663eb7rK42UQCbN0NPj7mWww4zU+IZGSP3vbra9Ds5GYqL+79ff5iQsxJOPXUNa9aY\nl6L0dIiPN0VLurvNS9PHH5v+rFoFv/yl+T2NlVC/l3FHaz3iArwGbB6wbPF+njqgzZvAISOco8D7\nmQNsAo4eoa2WRRZZRl9Ge3ZHeMbOxLxM966fB9w/pM3zwJED1l8HDgnkWHmWZZFl7Euwz/OoI3Gt\ndcjmf611jfezQSn1d8yb+7t+2kZ17KsgxABVwMCSIDO824a2memjTUIAxwLyLAtCJAinndrnA6uU\nSlFKpXn/TgVOAD4No1xBEMbGRmC+Umq2UioBOBt4bkib54ALAJRSq4FWrXVdgMcKghAhQg0xO10p\nVQmsBl5QSr3s3V6glHrB2ywPeFcp9THwX+B5rfWrocgVBCF4tNZuYD3wKrAVeFprvU0pdbFS6iJv\nm5eAPUqpckz0yaUjHTsBlyEIAlGYdlUQBEEQhMCQsC9BEARBmKSIEhcEQRCESYoocUEQBEGYpIgS\nFwRBEIRJiihxQRAEQZikiBIXBEEQhEmKKHFBEARBmKSIEhcEQRCESYoocUEQBEGYpIgSFwRBEIRJ\niihxQRAEQZikiBIXBEEQhEmKKHFBEARBmKSIEhcEQRCESYoocUEQBEGYpIgSFwRBEIRJiihxQRAE\nQZikiBIXBEEQhElKWJS4Uup3Sqk6pdT/Z++8w+MqzsX9frur3iXLkrFsy90Ggw04Bi7FTughtJCE\nmuA04NJCQgj8EhJjQgiEEEy5tARiSEggN+HSe0CEjmUQGPciWc2yet+Vtszvj1n1XWm1u1qtVvM+\njx7tOWfO+WbOntnvzHxlPvdzfKWINIvIJ96/G8Mh12AwBIeInCIi20Rkh4hc7+P4QhF5X0QcIvKT\n0ZxrMBgihyilQr+IyDFAO/C4UuoQH8dXAtcqpc4IWZjBYAgJEbEAO4DjgWpgA3CeUmpbvzJTgFnA\nWUCTUuoPgZ5rMBgiR1hG4kqpd4GmEYpJOGQZDIaQWQHsVErtVUo5gSeBM/sXUErVK6U2Aq7Rnmsw\nGCJHJG3iR4lIiYi8KCIHRlCuwWAYyHSgot92pXffWJ9rMBjCjC1CcjYCM5VSnSJyKvAMsMBXQREJ\nfX7fYJgEKKWienbL9GWDIXCC7c8RGYkrpdqVUp3ezy8DcSKSPUz5Mf1bs2ZNTMiIpbaY+zW6vxCp\nAmb22y7w7gv7ubFwr2PpuYmltsTS/QqFcCpxwY/dW0Ty+n1egXaoawyj7FFRVlYWEzIiJSdWZERK\nTqTaEgIbgHkiMktE4oHzgOeGKd+/X4/23DHFPDfRKSdWZERSTrCEZTpdRP4GrAJyRKQcWAPEA0op\n9TDwDRH5b8AJ2IFzwyHXYDCMHqWUW0SuBF5Dv8g/opTaKiKX4u2z3hfvYiAN8IjIj4ADlVLtvs4d\np6YYDIZITEeMclpBjTVvvfVWTMiIlJxYkREpOZGQ4e0n495fh/uLlb4cKTmmLdEnI1JyQunPYYkT\nDycioqKtTgZDtCEiqAng2Gb6ssEwMqH050mZdrWoqCgmZERKTqzIiJScSLXFYJ6baJUTKzIiKSdY\nJqUSNxgMBoMhFjDT6QbDBMRMpxsMsYOZTjcYDAaDYRIyKZW4sddMThmRkhPtNrRYwjw30SknVmRE\nUk6wTEolbjAYDAZDLGBs4gbDBMTYxA2G2MHYxA0Gg8FgmIRMSiVu7DWTU0ak5ES7DS2WMM9NdMqJ\nFRmRlBMsk1KJGwwGg8EQCxibuMEwATE2cYMhdjA2cUN00tUFHs9418JgMBhilrAocRF5RET2i8jn\nw5S5R0R2ikiJiCwLh9xgMfaaMZbhcMCWLfDFF/DZZ7B/f/hlBElU3i9D0JjnJjrlxIqMSMoJlnCN\nxP8MnOzvoIicCsxVSs0HLgUeDJNcQ7TR3Q07doDdrrc9HqishJqa8a2XwWAwxCBhs4mLyCzgeaXU\nIT6OPQi8pZR6yru9FVillBoyRDN2tAnOjh3Q1ub72MKFkJoa2frEKMYmbjDEDhPBJj4dqOi3XeXd\nZ4glGhv9K3CAvXvB/KgbDAZD2JiUjm3GXjMGMpSC6urhyzgcUFcXvIwwEDX3yxAWzHMTnXJiRUYk\n5QSLLUJyqoAZ/bYLvPt8snr1agoLCwHIzMxk2bJlrFq1Cui7oaFsl5SUhPV6vrZ7GKvr92yXlJSM\n6fUDvl+HHAJdXRQVF+vt5cv18cHbzz8Ps2ez6itfGXB+D5PmfgXxPBUVFVFWVkY4EJFTgHXoF/lH\nlFK3+yhzD3Aq0AGsVkqVePf/GPg+4AE2Ad9VSnWHpWIGg2FUhNMmXoi2iR/s49hXgSuUUqeJyJHA\nOqXUkX6uY+xoE5Ft26CjI7CyM2dCbu7Y1ifGCcWGJiIWYAdwPFANbADOU0pt61fmVOBKb589Arhb\nKXWkiBwAvAssUkp1i8hTwItKqcd9yDF92WAIgFD6XGY+HwAAIABJREFUc1hG4iLyN2AVkCMi5cAa\nIB5QSqmHlVIvichXRWQX+q3+u+GQa4gS7PbAFThAba1R4uPLCmCnUmovgIg8CZwJbOtX5kzgcQCl\n1EcikiEied5jViBFRDxAMvpFwGAwjANhsYkrpS5QSh2glEpQSs1USv1ZKfWQUurhfmWuVErNU0ot\nVUp9Eg65wWLsNWGWUV8/cLu5Ge68E845B66+GrxT6r04HEMc4CbV/Rp/BjuaVjLU0dSnM6pSqhq4\nEyj37mtWSr0xhnUdFvPcRKecWJERSTnBEimbuCFWUUp7pfentRWsVrj9dti+HW68EX74Q63Ue6ir\ng7S0yNbVEDIikokepc8CWoB/isgFSqm/+SofC/4tkdqOhL9Gf8a7vZP5fhUVFbF+/XqA3v4RLCZ3\nuiE0Wlth587hy1RVwTXXwKOP9iluETjkELCZ98hgCNEmfiRwk1LqFO/2DWjT1+39ygzO7bANWAkc\nC5yslPqhd/+3gSOUUlf6kGP6ssEQAONuEzfENl2uLhrtjbR3t+P0OLFZbKTFpzEleQpxTU0jX2D6\ndPj73wcq7J4R/NSpY1dxgz82APO8CZr2AecB5w8q8xxwBfCUV+k3K6X2e31ejhSRRKAL7Ry3IXJV\nNxgM/TFx4hNYxljLcbgc7Gnaw/pn1lPdVk1rVyt2p522rjaq26r5Yv8mqvftwKOGLnLS5e6m2lHH\nzvZydraXU+VspMs9KAqp3zR8LNyvSMoIBaWUG7gSeA3YDDyplNoqIpeKyCXeMi8BpV5n1IeAy737\nPwb+CXwKfAYI8PBQKZHBPDfRKSdWZERSTrCYkbhhCB7lobqtmtqOWoabDvXYO9jXsZ8GSyN5Cdmk\nWJPo9jhpdLbS7BzouNbq6mB/dyNT47OYnjgVEdEe7V1dkJAw1k0yDEIp9QqwcNC+hwZtD5ki9+5f\nC6wdu9oZDIZAMTZxwwBaHC2Ut5TTPXjU7Iva/dDQiMXuYMb//IW9P/4+WEee3Em1JTEvZQZWseqp\n9vz8MNR8cmFypxsMscNEyJ1uiHKcbid7mvawq3FXYAocoL0dgOx/v4+ttT0gBQ7Q3t3BjqbduJV7\nqGe7wWAwGAJmUipxY6/pQylFbUctm+s202T37aRW/H7x0J1OJ3RpZT/llbep+9rxAcssePBvpD79\nArs7KlGdnTpd6wS5X9Eiw6Axz010yokVGZGUEyyTUokbNE32JjbXbaaipQK3xz26k70Z2hIqa4iv\nqSfjw0+Yf91tzLj3cXC7ITkJpuZCVhZYBs4SNa06kqnPvkFbVzsVjv0QiIe7wWAwGIZgbOKTDI/y\n0NDZQG1HLQ6XI/gLVVVCaxvTHnuazPc2klRWiXg8KIuFunO/RsXvf9VXtssB5eXg8r4oKMWiy39F\n1fe/Rdvyg5mdM5fsZUeF1rBJhrGJGwyxg7GJG4bF7XHTZG+itKmUz2o+o7ylPDQFDtDZCUDme8Wo\nOCvi0WFm4vGQWLFvYNmERCiYoRO8AIjQcNKx5LzxHgDljaV029tDq4/BYDBMQialEp+o9hqlFC6P\niy5XFw6XA4fLwWv/fg27006ns5P27nZau1pp6GxgX9s+SptK2VK3hZKaEvY07aHR3ugzpnskhtjE\nHY7eUfX2u39Fx6K5KIt+lJTVgmP+nKEXSUqCnJzezaYvH0nGB59i6bTjVh6e+udjo65XMEzU797g\nm1iyi5q2RJ+MSMoJFhMnHsW4PC6aHc20drXS6eyk2909JG67tKmUnLocP1cYIzr6Rs2epER2X3Yu\niJC4rx7HgQuouOnHvs+bMgVaW6DbiSsznfqvfYW4+ia6ZibR2dZAfWc9U5KnRKgRBoPBMPExNvEo\nxO1xs699H3UddUGNnMecinJo78DlcfFIxbO8VPseTx+5Duv8BX1T5v5oaYbqfUP3i2BdsJAlByzD\nZjHvliNhbOIGQ+ww7jZxETlFRLaJyA4Rud7H8ZUi0iwin3j/bgyH3FikrauNzXWb2d++PzoVuFJg\nt9Pu6uSKzb9jc/seHj7kRqw5OUMUuMvjGnp+egbEx/m8rrutharWqjGquMFgMMQeIStxEbEA9wEn\nAwcB54vIIh9F/6OUOsz7d0uockMhWu019Z317GzcidPtDPgcnzHcYWaADIeDjq4Ortp8B3OSp3PX\ngdeSl5gDmZkDzul2d3PB0xfwRe0XAy8mAtlDp/+LS7ZCWzv1nfXYnfaxaAYQ/u/e6XbSZG+iuq2a\nsuYydjXu4q/P/pVdjbvY07SHipYK9rfvp8XRMqrv1RAYsWQXNW2JPhmRlBMs4Zi3XAHsVErtBRCR\nJ9HrDW8bVC6qp/4iglI6JrqtTcdS9zh7xcezv30/la2V413DEVGdHVy/7V4O7ErnugXnglggLRWs\nAx+leGs8V6+4mp++/lMeO/Mx8lLz+g5mZkBdLbgHzTR0tIPyUNlayfyc+RFoTXAopWiwaxt+R3fH\nkOMdzg5aHC0+z02wJZCRkEF2UjYp8SljXVWDwRDjhGwTF5Fz0OsLX+LdvghYoZS6ul+ZlcC/gEqg\nCrhOKbXFz/Vi047W0qJjpbsHpTS1WKjLSaTc1jk+9RotFRVsqtzI+avvZNuf78CVlQEzZ0BKqs/i\n60vW82bZm/zp9D8Rb43vO7C/Bhp9JHmZMQNSU1mQs4C0hLQxakTwtHa1Ut5STperK+RrJcclMy1t\nGpmJmSMXHoSxiRsMscNEWE98IzBTKdUpIqcCzwAL/BVevXo1hYWFAGRmZrJs2TJWrVoF9E1tTJjt\nt96CujpWzZ2rt4v11PSq5csBeO79t9jnaGD5ScdBzpTeqevl/6WPR932B8Uk7anEnTsFV1YGxZu2\nQ2MHy4/2XX5JxxLeKX+HB4sf5Oojru47fvgSaGyiuGQrGR+X8KVFc2k+bgXFb70POdmkrkplYcLC\n8f/++m1XtVbxwmsvhO1+djo7eeqFp0iOS+Zbp32LBFuCX/k9n8vKyjAYDIYewjESPxK4SSl1inf7\nBkAppW4f5pxS4HCl1JDVLyLx9l5UVNT7IzmmMo47Dvbs0aNwHzR1t1Jqr+4LGysogLTRjT6L3y/u\nVRBjRa+MLgfsKSX/iWextbRReflFOq3qCKuQNdmbuOj/LuKRMx4hP7Vf2dJScDjIevMDtjz9KtPu\nuwlsNpivp9Ln58wnPSE9rG0J5rtXSlHWXEajPbDFWoL5TixioTCzkKykrIDKm5G4JhJ9OVJyTFui\nT0ak5Iy3d/oGYJ6IzBKReOA84LlBFczr93kF+uUhtpev8nhg506fCtyjPFQ76tjTWTUw7rtmH7h8\neHRHC53a4Szt0820HrZE70sf+aUjKymLf37znwMVOGjbONByxDKSSsuxdNh1++1aTk17TfjqHgLl\nLeUBK/Bg8SgPe5r2RE2bDQbDxCAsceIicgpwN/ql4BGl1G0icil6RP6wiFwB/DfgBOzAj5VSH/m5\n1sS3o/Uo8PZ23MpNk7MNu9uBW3lwKTcdbjsufwuOZKTDAdMjW99hcHlcbKvfxpKpS6C6CqmtZ+k3\nruDzp+7Bk54K8+aDCOkJ6WQlZbG/fX/gKV1dLti1C5Ri3s/voOHEY2j68lEwJQdypwKwaMqicXUA\nGw+Hw+np04e+8AzCjMQNhthh3G3iSqlXgIWD9j3U7/P/AP8TDllRj8ejFVN7O43dLZTba3CPJt67\npRWysrXnehRw78f3Utpcyt0n34102rF22qk59zQ8yUmQkgIipManMi97HiJCRkIGW+q2+I4RH4zN\nBinJ0N5B89HLyXx3o1bibW29Snx/x37mxPtI4xoBOro7qGqLfNx6VWsVNovNZK8zGAwjYnKnhxOl\nYPduaGvj6ff/TWln9egUeA91tQEXHcs48ee2P8d/9v6HcxLPQVwucDpxZWVQc9FZukBaGiJCYWYh\n4k30EmeNoyC9IHAhadrm/XpGKumffKFH513d0K29v5vsTWHxBO8h0O/eozyUNpcOSXMbCOH4Tspb\nymnvHrtFYUZK0OQtc4+I7BSREhFZ1m9/hoj8r4hsFZHNInLEmFV0BGIpVti0JfpkRFJOsExKJR4o\no/oB71Hgra3UdzdT1+3bmc3W1ELGexvJfuM9krft0ecNpqMT7OMbclZSU8K9H9/LH076g57OHlwf\nEUhJYUryFBJsCQMO5STnkGhLHPb62+q36fublgoiuFNT+eKx3+vROUBrW2/Zus66sLRpNOxr2xfW\nl4fRopRiT9OeMUkQE0iCJm8UyVyl1HzgUuDBfofvBl5SSi0GlgJbw15Jg8EQECZ3+iC6XF3UtNfQ\n0qUzbFnEQlpCGlOSp/iP5/V4er3Q212d7OgoH/ICELe/noI/Pkl68SY6DpyHOyWFuLoGdv7uelR8\n/NBrpqVpb/VxoKq1iu8//31+edwvOXrG0Xrn4Lju5CSkcDZLpi4ZGP/tpaGzgbLmMp/Xd3vcnP/0\n+Xxv2fc4Zd4pvbnYB5CYCLNnA2C1WDkk7xAsEpl3TofLwZa6LUGNwsNNekK6z8Q3odjQvBEla5RS\np3q3h0SUiMiDwFtKqae821uBVWiflk+VUnMDkGNs4gZDAIy3d3rMUNdRx5a6LdR31veOgDzKQ4uj\nhd2Nu9lWv21oSlC3W9vAW1ro9jjZ3Vnp88e/4E9PYS8sYNNf7qRrWh625lbsc2ehrFbflWlrA2e3\n72NjTL29nh8e9sM+BQ69num9pKSSlZjlU4EDZCdlE2f1kSMdrZTXrlzLHz78A3Uddb1T6gNwOHrb\n7/a4aehsCKotwVDZ6vs7HA9au1qp7QjcvBIg04GKftuV3n3Dlany7psN1IvIn73rIDwsItHhwGEw\nTEIm5XJRvuL+qlqrRgzv6ejuYGv9Vg5IO4C8lDzE6dRT6J2duDwudnaU93qdF5dsZfmyxb3nlv78\nchBhxr2Pk/v8vxGPh7TPtoJAxZXf8S2wqQmm5vk+5mUs4sSX5i1lad7SPhnvbWB5zqBQspQUpqZM\n9XsNEWFK8hT2tflYsQxYnLuYcxafw2/e+Q13nXAHGwfdLwBaWyFHO3fVddaRm5IbXIP6MVLMZ2tX\nq9+UqYES7u+kqrWK9IT0EU0UEcIGHAZcoZQqFpF1wA3AGl+FxzpxU0lJCddcc03Yrudvu79ddKwS\nC61bty4iia0Gt8ncr+G3B7cpXPdn/fr1AL39I1iicjrd5XZhtfgZoYaBwT/k+9r2Ud1WPaprJDkV\n0+ocpCgbnW4HFfb9dHv67JeDlXgPM6+9mdzPdvZutx56EDvvuMG3EJu1N4TLHxFJ9vLWuyzPzyH/\niWdpOm4FXYXTSTnoUBblDm1ff5xuJ5tqN/kd1TrdTi5+9mLOPehcpm+xsnzRoBnaflPqEJ5ws5GU\n+Na6rXQ6Q/NHGIvvJDkumUVTFvU6EIZhOn3YBE0+ptO3ASu9hz9QSs3x7j8GuF4pdboPOSbZS5TJ\niJScWJERKTkh9edoVOIVLRWj83AOgWZHM7sbdwd+glJQXw8NDb6d0vzwcfNm1lc+z/ee3MH3P3Ji\nU+C2CA1nnNA7ErfYHeQ+/2/2f/OrfYp7+gF6+c7xpL4e9u9n6TeuYMvDt+KcPZPCJceQkzx0NbLB\n7G7cTbOj2e/xXY27WFO0hsdXrcO6vx6UIvXzbbQfskjfg3lzIU5P2eck51CYWRiuVg2h0d5IaVPp\nmF0/VPJT85merme9Q1TiVmA7cDywD/gYOF8ptbVfma+iR9uneZX+OqXUkd5jbwM/VErtEJE1QLJS\nytcSxMYmbjAEQMzZxGs7asd0Ocoeut3dfp2vfNLWCnt2a6Xm78fJ7SbvyRcQR59nc7urk7tL/87X\nph7LIWvup/HME2k99CCtwP/7wt5ynvg4sv/9Ph++83c+aPpcj2D9pGwNF2/vfZuXd708fCG7ncSK\nfbiTk3BOycKamhZwetCRYp3nZc/jsbMew5rW96Iy665HSd7hVaYtrb37m+xNuP0lyQkRpdTIszFu\nF3R2QEszNDbo56C+HhrqoalR729r05783V26fBiVWE17TVgyxyml3MCVwGvAZuBJpdRWEblURC7x\nlnkJKBWRXcBDwOX9LnE18ISIlKC9028NuVIGgyEoonIkXrz136TYklmUvaD/gb7Rac9ni6Xvv8UC\nVmvf52HomR7Z0bCDtq62Ycvicmnl3dSk45eHw+1m9m0PYWtt48lvnMrhXzqk95BSqncqdDjSP/6c\nDS//kZtOT8Op3Jx3wImcdtRqkpJ8pzcNduq2vbud+zfcz9t73+a242/j4LyD/ZYt/sf/cXJFDWmf\nb6PshsuYuuQIZuQFtlSoUopNtZtGDJUqfr+Y5dOywdHF9D8+hbJaqP7eNyEhHub0TbPPyJgxrC1+\nJPxNjfnNzGbv1C8SHe3QHVi41xBTis3qfTatYPU+p2LRn8UCFu/zLN7nuecx6f+89+xCmJ46jfyC\nRSZjG7E1pWraEn0yIiVn3DO2hZ2qajqA2to2piZkj/58Ef1DabP5/mtpobZ6J22dNX0/nADKAy43\nuJxaYdvt2ks6ENxuZv/2Aaztney6+ceorQOn6ANR4ACtXzqY05/M46j9R/PaUfk8Wf0qD/zjTE5f\neAZXrrgSmyW0r8zlcfHyrpd5oPgB/qvgv/jb1/9GRuIw0/XdXeBWpG7eQftB88FmJTdnRsDyRnJw\nG0BqGji6aDrmcArv+KNW4j3fgzeDXX1nfUhK3Bcuj4t97YPq19aqR9mOMMSKu9z6LwwooJLoX3fe\nYDBEhugcib/xFwAsIixMLSTZGl6v3G6Pk81tu/GEq+0uF7NvfQCr3cEHv/gOOSm5w8c0i+hRmJ8f\n9tRN25l1x8NsXn8HWCxUqRbedu/hgoMvCLmqP3/z5zR2NnLZ8stYlr9s5BOam2HfPg66+Dp2r7ka\n2+HLWXjYiaOS2e3uZtP+TSMXdDj0ymYeDwdfcA07fncDXTMPGLJSWrjzqZc2lfZNU3d3wb59Q0Pq\noozlJ3zbjMQNhhgh9kbiXjxKsaujggUpM0m09mUFa3d10uJsx+HpxioWMmypZMUHvmRlhX1/+BQ4\nMPX/XsPq6OLP16zk5s1ruevAa1mS5iMXRmoq5GRDUrJW5C6XnqYf5CTXvmQBrsx0kneW0blwDtMl\ngwsWnuNT9q7GXWyt38q01Gm9cdsuj4ukuCSfi2jceOyNJMclB944b6a2sut+iKNwOrNHMQrvId4a\nT3pCOq1drcMXTEzEZRXeqPuIgqMPI+vdYmouOANaWyBvqp41QY/Gw6XEG+2NfQq8qQlq94PHKB6D\nwTAxiErHtv44PS62tpdS2llFWWc1m1p3sb19LzVdDTQ722jobmFPZxVb20rpco+cHKWpu5U3Nnwc\nvgq63cRV1VDZWknqfQ/zhwU/YknaXIpL+mWitFlhxgz9l5zSN31vs0FuLsyapcv0IML2P/yCzoX9\nFv5o9W27/+SDT/io8iMe2vgQ1//7eq565Sque+M6Xtr5ks/yo1LgAHY7xSVb6ViyAJstjqwpo1fi\nMLKDW0++cVdyIo9WPMufVqbjmHmAPuj26JhxL432xqAd3PrHfrZ3t7O3ea9+gdpXDTU1YVHgA757\nw5jS//uc6HJMW6JPRiTlBEtYRuLepUjX0bcU6e0+ytwDnAp0AKuVUiWBXt+jFI3dw4/iOt0OtnWU\nMS95Bik23wmkXB4XFY79gYoNiLR7HiLnpQ/IV7DYItQ/8REVV/Zb0C0xAQpmQJzv7GWAtvcWzIDy\nvX1KxDboq2lrhSlDFeGcrDl867++FYaW+MDtGuDMl5uYgySP8iXAS2ZiJjaLbcTVzRKzpvDbhVdy\n6aZbmXfo/2Nez4GmZsjQaW89ykOjvTGk5C/NjmZKm0rxuJ1QWanz1RsMBsMEI2SbuHcxhR3omNNq\nYANwnlJqW78ypwJXemNOjwDu7ok59XG9Xpt4MFhEmJcygzTb0OnW3R2VNDtH8EYfLZdfzuE7+q45\nIHlLcpIefXsT14gI01KnkZaQRmtXKzXtNQMToXjtz36ZOwfiE/wfDzft7VChM2+KCAdPP5S4hQcG\nfblAsuKhFOzcwYv7/sOfyp/h8WVr+77LwsJeB7ekuCQOzA2uLr3JfdwuKK8Y1nnRrTzUdNXT2N1K\no7MVp3ICwozEPBamzgpKfjgwNnGDIXYYb5v4CmCnUmqvtzJPAmcC2/qVORN4HEAp9ZF3KcM8pVR4\nh8X02dFnJ08nM64vLKvKXhuyAk+orCH/qRcov+LbqEStTAsWH4Ha9Sbi8aAsFhyzvFPAKclagXvt\nuFaLlXnZ80iNTwUgNT6VJFsSe5r29AnIzNQj7sGLgfTQ1gY5EVTi/VYuy7SlEpceWGy4P3JTckdW\n4iKQmsppU49hc9sefrX9Qe488MfaUbChoXdRGLvTTltXG2kJvkPvfKGUoqy5TNvA3S4oLx/R+/zZ\n/UU8WvEcOXEZZMWlE2+JA5eLYxMWsDTOgihFV36uXl8deLL6NR7a+y/SbSmkx6WSZksm3ZbCqpzl\nnJJ71JDrNzvbsLu7SLelkGxNHDmKwe1mxv1PBNxmg8EQ24RDiftaTGHFCGV6FlPwqcQtdgfKGwOu\nrP1iwQPEoxS7OyrJic8g1ZZMi7N9gAL3lxLVH0k7y5j6zOtkfvAJNeeeNqAulZdfhIiQuLcax6wD\ndPKW5CSKK2pZPlOP1KwWK/Oz5w9xxspKyiLfmT9QseXnw24/S5S2tvXmEu9ty1imXe3sBKUo/mwb\nFx1zqnbMC4F4azyZiZk+M7gNaEdaGrS08pPZF/BQ+dN0ebpJsibql5guByToaIWa9pqAlbhSit1N\nu/n3m/9m+RHLAlLgAGfnfZmv538FgBn3Pk72G+8hyoM7pRx38rsgQvmV36Hd+zx9c9oJTNs3hbkH\nTifhH0/T2VhDY7qL6bKRaZZq3ClJNB+3gu48/T0WNWzkjxXP0ObqoNvdTZoliXRbCuflrOLcvONB\nBE9ivA6ZBNLueZCclz8KqM2TgViKFTZtiT4ZkZQTLFHpnX7XmZcwGwGlyFSKwqMPZ+ZavchBj9PQ\n8mWLmfLCm+x49B+o+HiOyUjHk5hAkdNJ+yGLmH/ZBTR0t/Dqxx/2lo+vrqXk3Q2U1jdxdE4m7tRk\nPtq9F2WL61Xq/a+f9eYH7PjTkxRn2nnp66n8+rs3squyFbbs6iu/aQfFx3yJ5Vd6t7fuHuBJ/emH\nnzI9bTrLTtThXIOT4u/YuIO9LXs5eIVOtlK84XNoamT5HO1AVvL2x6R/+gVzrvkeOBwU/+cjsFl7\nFd72zdt1fb3bPQ5iIW8fdTg4HOy561HqGlpI+fI5kJIS8iIA24u3U9FaMUReD8XvF4PysDwnHZvF\nxhHNB7O5eQ/Ll+mp8+JX34IpuSz/r+W0drXyyhuvkGhLHFH+rKWzaHG0sP2LbbCvhuULC5lx/xNs\n2LyTrrxs3vrubL5ZcDJbvyjT7fd+vxs/29a7XXPuaTx32EG4U5KHPi/e+n/62XYqS2tZefhhJB77\nNUo+/ITUDjtLsjOho5MNW3fRkp7KIScfB0BBTR5r4y5l+ZcWc8DvHuCdzzbRZm3jBF6goPk5ilxu\nqr73TezzCtn42VYa3/2cVOM9bzAYvITDJh70Ygq+ptNFRH3vkTM4InMJh6TNJ04JM+5/gsTyahwz\nD6Di8gt7RyXS1Y2trR2LowuLvQurowuL3YFzShb2OTOH1DXz3WJyn30da4cda0en989O7VknUXXp\n+QPKupWH97a8zMOtRbgT4vjujDM4fsoKrMPFfycmwqyZvTbwBFsCc7PmkhQ3/EqN7d3tbK/f3rfD\n5YLdu8CjsHTaOeS8H7Hpibtwp6VAfh5kBZEAZ7TY7VBWxtxf3EncmWeTcva3YNGisFx6S92WkdPq\nVlRAeztxtQ3Mvfkett17U59Xf+EsHaYHZCRmMC97nv/roJcW3d++HzxubQO32wesJucS+L9jc8j5\nf7eQ5bKR+vk2Wo8IIIZ+HOipt8XjMTZxgyFGGG+b+AZgnojMQi+mcB5w/qAyzwFXAE95lX7zcPZw\npRR3l/6dSkctf3k9nUPfqcHiUUOW7lQJ8ThHkdGt+ZjlNB/jY+rZ7Rmw+UnLNn6z61HSbMlcsuB8\njs0+dGRbZT8FbhELuSm5HJB2wPBJX7ykxqeSk5zTt2a2zaY9sZua8CQn0XrYQWS+W0zDqSv1lHJE\nlHgneDykbdmJde0RkBK+5Cr5qfkjLzSSlgbt7Thzs7F0OkjZvJOOJd40vDU1UDgbRGhxtNDsaCYz\nMdPnZWo7avsUeIVW4ACJ5dWIR3/vNgUnteWxb3s1s29/iNbDDopaJV5x+YU6Leszr493VQwGQxQQ\ncpx4GBZTGMIVhd/i8WU389Shv2VxncLinT4Uj4fEvaNbMtQXQ+J4rQNvQ058BtfPvZg/H7KG43IO\nG1mBJyUhs2aRmZzD7KzZLM1fyq5PdgWkwHsoSC8YuPxqTp+iblp1JFlFXjtop10rpJ62DJqODhud\netET0tIpKisL2R7en56kNP0Z0o601N4c+Q0nHUvOa+8AOtue227XKVG9lLeU+8zN3tDZQEVLRZ8X\neqe997tvKsjB2ZNt12LB0uVk7tp7qLjsfMp//L2Q2jemceJWq//15ychsRQrbNoSfTIiKSdYwpLs\nRSn1ilJqoVJqvlLqNu++h5RSD/crc6VSap5SaqlS6pNArpubkEXG/IO1kxsM9P4GGrrHZoWvWUnT\nWJF5UGD5zlNTSJgzn8V5S5ibPZfspOxRKe8ebBYbB6T1tY24+F7F2XLEUlK27cbW3Kod3trbR339\nUWPvJHtLKdZlh+rtMCpxEWFa2rThC1lt2sMfaDzhaLLe2YClvZP7yv7B/5T9QyvxNu2s6HQ72dGw\no3eK3qM8VLdV6xXqnN2wd2/vCLyHO8/M5Z2vzKV12WIcBflYHV1s/Z+1tBw9tmuzGwwGQziJ6tzp\ngA6peeCJgd7fVistzna+vvE6FqUWcvrUYzkfCedmAAAgAElEQVQu57BR5Vjf1VHBv2re5NxpJ1KY\nfMDIJ/giK4v4A2awKHcxcdZhkrkEiFKKrfVb++zFHe16BAnMvuU+2pYdSP3XvgLpaTB9DNdb7+6C\n3XtY8sjzJBTOhfPPh4P9r3IWDEopNtdtpss1jId4U5OeOgdm/+Z+OhbOZseZx/Ddz9ayuuB0zpy2\nSq+3ntaXcjfRlojT49QZ3Vpb9PmDzCU98gHiaxuY9sSzVP73hXiSwpujfywxceIGQ+wQik08+pX4\nMHR5uilq2MiLte/yWetOjso6mLPzv8wRmUuGlFVKUeHYz/tNn/Nq3QfUdDVwet6xnDftJLLjh1nF\nyxcWgfx8JDOLBTkLemO/w8EQJ7ddu8DpJK62AXdKMp6UJD39P3/BgCUqw0pTExkN7cxLmaFH/jk5\nMHt22MU02huHt427XbBzFyhF8rY95Lz6Hyp+tJqyzmou2fQbfjvvcs7620YSq/fjWDSPil9fp+9N\nR6de7zvKFzEJBaPEDYbYIRQlHvW504cjwRLPyblHcc9B1/Hs8js5MvNg9jn6bKW43cy493HmX3cb\n9ttv4fKS37CjYy/HtR7K81+6i8tnfXP0Cjw1BebMgYxMcpNz/SrwYO0oqfGpA/OMZ2qHLefUHK3A\nQY8sO3VCmLGwiYvdTkGid7lPEYpKAs6QOyqyk7J7c7n7bEe/KfXORXOo+NFqAAqTD+CWhZcjd93J\nlOffIH3D5+Q+8QwzrvkVbN+h06j6UeCRyGtucqdHjliyi5q2RJ+MSMoJlqiMEw+GzLg0zspfNWDf\njPuf6A0jOtpioSTleCqv+g7FHVuxidX3hfyRnKRzl6dopR1njRtoww4jBekFtHS1aGetjAyoqxta\nqK29ty7hZponecCqcT2pTseCmRkz2Va/zX+B9HSfGexWZB5ETnseFo9eW3skp8cOl91vTv0RsQgk\nJ0NiEiTE6zz4VmvfWvRK6bXo3R7tdFhVq0MBXW5wu/WMgrvns7eMjyn+QEkNth0GgyHmiM7p9F3/\n6dvRv35KgerZp/R/jxr6I+rRn+df/kvSN/atYz0gr/nIFdFhYykp2gadMNBeWphZSE5yTvANHYEW\nRwu7Gnfpjb1lQ0eWNhvMnx92uckeK4tqXH1OfRYLLFs2dlP3aO/yug4fLyqgv9cdO3yuLjbj3seZ\n0hMzbbFQd8bxQzy3lVLcU/YkVY467ph7GZnvbqTpK0PTn/okKQmys3S4WxDOiiOiPPpZ9Xif38HP\nNwx5/qcm5zIjrQDJyDDT6QZDjDDeceLhJym4lbIG4zhkMWklmxG3B2W14Fh2IMyb2zdC6vkR7fmd\nsYhO1BJn0wuN+FFcyXHJY6rAQScxmZoyldqOWh0zPliJu1za4zqMo2SLWJhtzUGktm9nSsqYKnDQ\nMw+tXa2+ndzE0puGdTA9MdMDnB77UdvVyG27H6PZ2cq6uVcy95frcKcm07TqiN7UucnWRLLj0+n2\nOGnobsGtPHrlubw8vWzsWCIWbcMPcFIoMzGTGdk+1qkPRnSIKw96Fz4qBiqVUmeEpVIGg2HURL1N\nPCkuifzU/FEtdNFDxU0/oe4736T1mC9R951vUnHTtRAXT/Gnm3XIVFq6VpCZ3r/0DL0/IXFYxVWQ\nPrJneDjsKAXpBTrfek/MNCCOLmyN3tzj7W1htYnPzJhJot2pXw42b9Y7+6VaHSssYqHy80r/oXmZ\nQxO52JpaemOmd95xgx6BezP5vVr3AVd+8TvO+/TnzE+ZwcPzfsLhNz2EKyud/z1tVa8Cz45PZ1Fq\nIXkJOcxIyueg9LmkTi/UiWRCUOBj4aeQYEugMLMwLNfyKuD7gJOBg4DzRWTRoDKnAnOVUvOBS4EH\nB13mR8CWsFQoBGLJLmraEn0yIiknWKJaieen5nNg7oFMT5/OgpwFzMwYmkp1WGw2Km65jp1PPUDF\nLdcNXaM7CDITM4N6oQgGEWFu1lzi4pN6M6blvlTE9Ef/VxdoC9+yqvmp+Xp2oa0NSkrg7rv1gTDG\nhw9Hoi3Rv5JKToH4fiF8LhcLr/k1me9s8Fl8euJUvjXtBJ5ZfidXZZzEQT+/i+78XMquu6Q3JW6K\nLYnCpAP6zAbx8cQtXsKChUeTPcazLKNFRJiTNWdgMqDQ6F15UCnlBHpWHuzPgJUHgQwRyfPWpwD4\nKvCncFXIYDAER3TaxKuKOSDtAJ8JQeo66ihvKR+HmukR44G5B5Jgi+ByoOhlN3fs+RhXZQXxNXUs\nunINnz91n56KDcMa41OSpzArc5YegW/ZAg88oM0MV1wBS5eG5eUnUOo769nbvHfogcYG2N83zZ+8\nfQ/zfv579vzqKtqX+l+Rbv7PbqNj4Ryqv/uN3hG4RYQDU+eQ0JM1LiUF5s0b0M5h7fQRZkbGDKam\nTB2wL6S4UpFzgJOVUpd4ty8CViilru5X5nngt0qp973bbwA/U0p9IiL/C/wGyACu9TedbmziBkNg\nxJxNPC81z29Gr9yUXJweJ/va9kW4Vnq0GmkFDtqkMH/WYeys3kd3fi7OnCxSt+yk/eCFIa8xnpuS\n2zfD0eq1O5eUwMUXa8e+CCpw0C8UNouNsuYynbClhx4vfa+DW+fCOZTeeAVzbr6XmvNPp+6ME1Dx\ncb3rbfcsmLP7l1fiSRs4m1CQmNenwNPTYe7cIUvdzsyYiUUsOu/6OJKVlDVEgY8nInIasF8pVSIi\nq9CZ3P2yevVqCgsLAcjMzGTZsmVBr4Bnts12rGwXFRWxfv16gN7+ESxRORIPpE6BjpS8bzgD9gWz\nBndSXBKLpywOLBUrY7MGbde2zeyu2ULmo3/HandQedkFFG/ZzfJzvjbqa4kIBekFAxXEjh3Q2AjH\nHw8vvQSFhTBr1pi0ZTCDZTjdTqraqmi0N/Z9f/v2QfPAtcgTqvYz477HiWtsZutDvxmwOpkvj/Vt\nX5Rx4TGn6o3MTB3zP8x3WtNeQ1Vr1ajaEq413pPjklk4ZaFPX4EQR+JBrzyItoVfBLiAJCANeFop\nNSSheyRG4pF4NiMlx7Ql+mRESk7MjcQDYWbGTKxipaa9ZsgxEWFK8hTyUvJIsCVgd9qpbK2ktWuo\nh3MgWMTC7MzZASvwsSJhSh6L2jvZ/+Uvk/mLW6i89Hzo7tb5wePiR76Al6S4JAozC3sTrQB6+ry9\nHbZtg4ICbQuPkD3cF3HWOAozCylIL6Ctq40udxcqIQfrjl3EYSXeEodVLLgWzqL1roNoaNTx4v1X\nJxscOx5nsZHfs+pdAAoc9OxLvDWevc178ajgY7tHS7w1nnnZ84LKwx8Aoaw8+HPvHyKyEj2dblZk\nMRjGiQk7Eu+hrauNmvYaOp2dWC1WMhIyyEvNG7JKFvRbV3qUzMqcNTCL2njhcsFnn4FSOG+9hfJL\nzqU5zg1TcyFn5Pol2BK0A1tSztAXkuZm2L0bPv9cp3r9+tfhoIP0lHo0UVqqZwsG4VEe9jnqibvz\nLnKfGzoSt4qFBamzdH79jAw9hT6Kl7JOZyd7mvYMn+s9TCTYEliQs8DnM9xDKG/u3vNPAe6mL8Ts\nNhG5FD0if9hb5j7gFHSI2XcHL1zUT4kbm7jBEAIxlzt9LOs02unRvNS8gELKIsb27QNWMetyd9Nk\n66Z11jTsTjsuj6v3mEUsJNoSSUtIIzMxc/gc73v3DljeE5tNO7VFG11dOvzNzzPi6OrAceftWEr3\n9saOJ8QlMielQCvw9HTtxBbErIrb46aqrWpMHd5S4lN0RMIIC+qEqsQjgVHiBkNgjFvudBHJEpHX\nRGS7iLwqIj4TkYtImYh8JiKfisjHocgMlfzUfCo/rwxoajwUBT5msYWDYqY/+PRz8lUqC1JmsjR/\nKYdOO5Sl+UtZlr+MQ6cdyuLcxRSkF4y8SEvLoGVd+02lR1XMZ4I3EYsfEhNSyPz5zSQ8+EdsP7uB\n+emFHJQ2VyvwtDSKKiqCTl5jtViZmTGTxbmLSU9I91sumDhxESE/NZ+FOQvDsiLeZCFSMbxR1Qcm\ngJxYkRFJOcESqsHtBuANpdRC4E3g//kp5wFWKaUOVUqtCFFmyGQkZrBoyiKS4nxnO7NarL322KjD\nR+ITABoaAD36tllso4spbm8Hp3PgvnG0h4/ItGlamQ9DgjWe7PgM0uNS9QtbzwjcErqNOTkumfk5\n8zkw90ByU3KxWYJ3LRERspKyevMhjLffhcFgmFiENJ3e47GqlNovIvlAkVJqkY9ypcBypVRDANeM\n6BRck72JZkcz3e5urBYrafFp5CTnhPTDPOZs2aJjuvsTHx/8mt8VFVBbO3DfokW9CWaiko4ObVoI\n5FnJytJLqY6RglRK0eHsoK2rjQ5nB3annW53t9/ycdY4UuJSSE9IJzMxM6iRt5lONxhih/H0Tp/q\n9VhFKVUjIv4CWhXwuoi4gYeVUn8MUW7YyErKIispa7yrMToyMoYq8e5uHeed7n+a1y9NTQO3LRa9\nalc0k5KiFXNp6fCKfNo0OGBsVpvrQURIjU8dYLJQSuH0OHF73Chvcn6rWImzxo2Vx7nBYJiEjKjE\nReR1oL8RUtBK+UYfxf39mh6tlNonIrloZb5VKfWuP5ljnSCipKSEa665JmzX87Xds29Mrm+3s2qq\nfl9at3o1yy64gFUnnQT19RR98snorvfSS1BRwaqFC+HhhylauRKSk1l16KHRf7+ysih67z2oqemr\nb7G2R6865hiYOZOijRthx47e89etWzfmCUd67le8NZ6id8J3f4qKiigrK8PQRyzFCpu2RJ+MSMoJ\nGqVU0H/AViDP+zkf2BrAOWuAnwxzXI01b7311sSX8dlnShUXq7eOPFKpn/5UqeJipTZuVKq7e3TX\n2bNHn/u73yl1xBH6c3X1gCJRf79cLqXq6pQqL1eqslKplpaxkRMgkZDh7Sch9d+x/ouVvhwpOaYt\n0ScjUnJC6c+h2sRvBxqVUreLyPVAllLqhkFlkgGLUqpdRFKA14C1SqnX/FxThVKnSUN5uU5D+s47\n8Pjj8EevhWI008dut44L93hg7VpYsADOP1//T4vMIi+G4DA2cYMhdhi3EDPgduBEEdkOHA/c5q3Q\nNBF5wVsmD3hXRD4FPgSe96fADaOgx0v9iCN0cpaeGO+6Oq2UA6G+Xpf1eOC99+DYY7XzVzQ7tBkM\nBoOhl5CUuFKqUSl1glJqoVLqJKVUs3f/PqXU17yfS5VSy5QOLztYKXVbOCoeCjERw5iWBlYrRZ9/\nDkcfDW++qfe7XEM9zX2hVF+5zZv1S0FPutVBYVgxcb8iKCfa40pjCfPcRKecWJERSTnBYtxkJyo9\nsc8Ap57ap8QBamq0Mh+Oujrt0Q7wn//Accfpz2Ya3WAwGCYMky7takzR2KhDrNxunaylf57zKVNg\n1izf57lcevTdo+ibm/U1cnJg4cLoTvRiAIxN3GCIJSblKmYGdLy4CFit+q8/9fV6pJ7lIwa+vHzg\nSL3Hvm6xGHu4wWAwTCAm5XR6zNhrrFaKtm71f7ysbGhO9IqKocldekhL85nVLGbuV4TkRLsNLZYw\nz010yokVGZGUEyxmJD7RGW7q2+PRnusZGXqqvbV1aKa3/gST7c1gMBgM44axiU90XC4d6x2OexaN\n64cbfGJs4gZD7DCeceKG8cZmG+hRXlSkp9EDYdMm7dAGelUwo8ANBoNhQjEplXjM2Wv6O6/t3g2P\nPDLyifv2wTXXQFeX3s7wuRR8n4wxJpbsW9FuQ4slzHMTnXJiRUYk5QTLpFTiMUdWVp9D2rnnwocf\nwp49w5/z2GNwxhl9q5UNo8QNsYeInCIi20Rkhzdlsq8y94jIThEpEZFl3n0FIvKmiGwWkU0icnVk\na24wGPpjbOKxwu7dOt4b4K9/1Yr83nt9r6FdUQGrV8O//qXDy6xWWLp0zNbbNoSfUGxoImIBdqBT\nJVcDG4DzlFLb+pU5FbhSKXWaiBwB3K2UOlJE8oF8pVSJiKQCG4Ez+5/b7xqmLxsMAWBs4gbIzu77\nfN550NAAL744tJzHA7/5DXznO33x4T3x5obJwgpgp1Jqr1LKCTwJnDmozJnA4wBKqY+ADBHJU0rV\nKKVKvPvb0SsZTo9c1Q0GQ38mpRKPSXtNZqZ2cgP9/+ab4bnnhi6G8uqrOt3qRRf17fOVEMaXjDEk\nluxb0W5DQyvdin7blQxVxIPLVA0uIyKFwDLgo7DXMEDMcxOdcmJFRiTlBIuJE48VRPRovGdRk/nz\n4aGHho6wTzgBjjqqL8Ob1Wrs4YZR451K/yfwI++I3GAwjAOhrif+DeAmYDHwJaXUJ37KnQKsQ4/8\nH1FK3T7MNY0dLVjsdtiyZXTn5ObCzJljUx/DmBGiTfxI4Cal1Cne7RsA1b9fisiDwFtKqae829uA\nlUqp/SJiA14AXlZK3T2MHHXxxRdTWFgIQGZmJsuWLWPVqlVA3wjHbJvtybZdVFTE+vXrASgsLGTt\n2rXB9+cQlfhCwAM8BPzUlxIPxIlmUHmjxENhxw5oawu8/KJFJl/6BCREJW4FtqP75D7gY+B8pdTW\nfmW+ClzhdWw7ElinlDrSe+xxoF4p9ZMR5Ji+bDAEwLg5timltiuldgLDCQ/EiSaixLS9ZurUwE9O\nTg5Igcf0/ZqgMkJBKeUGrgReAzYDTyqltorIpSJyibfMS0CpiOxCv6T/N4CIHA1cCHxFRD4VkU+8\nM23jgnluolNOrMiIpJxgiYRN3JcTzYoIyJ2cZGZCUtLwOdJ7GI3CN8QUSqlXgIWD9j00aPtKH+e9\nB1gH7zcYDOPDiEpcRF4H8vrvAhTwC6XU82NRqdWrV4+5Ha2HaLKTBLPds2/A8fZ2Vk2bpreLi3X5\n5csHbh99NGRnm/s1RvL6ywrX9YqKiigLNKXuJKH/9zrR5Zi2RJ+MSMoJlrAkexGRt4Br/djER3Si\nGVTe2NHCwUi28dmzB8aWGyYUZgEUgyF2iJZkL/4qsAGYJyKzRCQeOA94LoxyR82ksNfMnAkWP19v\nWtqoFPikuF8TTIZBY56b6JQTKzIiKSdYQlLiInKWiFQARwIviMjL3v3TROQF8O9EE1q1DSOSmAiz\nZg3dHxenR+EGg8FgmPCY3OmxTnOzzpXe3Q2pqVBYqJcdNUxozHS6wRA7hBQyGm2dzHT8McLt7svS\nZpjwGCVuMMQO0WITnzBMSntNCAp8Ut6vKJdh0JjnJjrlxIqMSMoJlkmpxA0Gg8FgiAXMdLrBMAEx\n0+kGQ2QpLd3LL3+5nqoqD9OnW/j1r1cze7YP5+EgMDZxg2GSYZS4wRA5Skv3cuKJ97J791ogBehg\n7tw1vP76VWFR5MYmPkqMvWZyyoiUnGi3ocUS/e+1UnD33XDYYXDMMfDii2MjZ6wwfSD6ZHR1wa23\nFnHyyev7KXCAFHbvXsu5566npWXMqzEsk1KJGwyG2EIpuPhiuO02OO44mD8fLrwQbrppvGtmmIhs\n3aqfpylTYN06qK/30KfAe0hh82YPBQXwgx9AU9N41NRMpxsMExIznT6QO+6AP/xB/8/I0PsqKuDG\nG+F3v9M/sgbDSOzfD9dcA88/D0cdBWedpZNf3nnnWt5++6cMVOQdrFz5e849dw3r18OePfDoo3D6\n6aOXa6bTDQbDpGXnTrj5Zrj22j4FDjBjht73k5/opQQMhuFYvx4WLoSqKrjvPrj6aq3AAS68cDX5\n+WuADm/pDvLz13DhhaspKNAvi6tXwwUX6JfGSDIplXis2GsiJSdWZERKjrGJR46ioiKuugqOPVb/\nAA/mkEPgy1/WP7ChTArE0nMz0dqycyeccAKcdhrs2xd+GQ4HfOtb8NOfwo9/DNddBzk5fcc3bSoi\nP38WN998FStX/p6DD17DypW/5+abryI/v8+p7bjj4JZbtEnnllvCUrWAiMR64gaDwTAmbNwIH34I\nDzzgv8y3vw1XXQV/+hP88IeRq1sodHVBcTGUl+uMyfn5sHSp/j+ZaG3VL2FLl0JHB5x0EpSUhC/5\nZE0NnHxyn1Nkerr/svn5s7j22jXDXm/OHD0r9Ktf6Vmhq64KTz2Hw9jEDYYJiLGJ6x/eJUtgxQr4\n+teHL/vxx3D//XpUF60r8HZ3a5vq44/rl5PsbMjK0gqrrU0rnLw8bae9/HLfMw+xxg9+AJ9+qh0U\nXS49Wr7oIli7NvRrb9oEp5wCBx6o76ctjEPa7du1Mn/qKTj11JHLmzhxg2GSYZS4HlnfdBPce29g\nP8C33grz5sFf/jJmVQoKt1s75d15J6SkwPHHw8qVQ0eFLhd89hm8+SZ88okOo7v1Vh1SF4ts3Kjv\nw7p1+uUFtG/D2rX6ZaxnXzAUFcHZZ8PXvqan0seCt9+GRx6B99+HxYuHLztujm0i8g0R+UJE3CLi\n91ESkTIR+UxEPhWRj0ORGQ4mmk1ovOXEioxIyZkINnEROUVEtonIDhG53k+Ze0Rkp4iUiMiy0Zwb\nLKWlcMMNcNll2kPY3ztAW5t2JjruuKKAR1CXXgrPPgvvvDP6eo3Vd/rGG/oH/oEH4OSTi1i3Tns3\n+5rWtdng8MO1zfahh/RqwytXakW0fXvgMidCH/B4tB/D6acPVNYLFsCyZfCznwUv46mn9HW/853A\nFPimTcHJWblSj/RPPhnq6oK6RECE6ti2CTgbeHuEch5glVLqUKXUihBlhkxJSUlMyIiUnFiRESk5\nkWpLsIiIBbgPOBk4CDhfRBYNKnMqMFcpNR+4FHgw0HOD5a67tCPaO+/o8LDvfx+OPNK3Z/n3v6+9\nz5OTA7/XOTlwzjlaOXR2jq5u4f5Oq6v1tPg3vqF/7O+6C+LiApeRnq7vwYMP6u3DD9e2/+rqkc8d\njz6gFHzxBfzrX/DXv+qRcHu7//Ovv15/R+eeO/TYxRfD00/Dyy+Pvh2//z1ccomOWDjhhMDO2bMn\n+Pt1/vk6Z8Hxx2ub/lgQkhJXSm1XSu0ERpoGkFBlhZPm5uaYkBEpObEiI1JyItWWEFgB7FRK7VVK\nOYEngTMHlTkTeBxAKfURkCEieQGe28szz4xcme5uHZrz299qh6CekfgDD8C0aVpB/frX4HRqT+If\n/lBPVf7oR9DRMbp7ffbZ2uHovPP0aC9QwvWdOhywZg0sWqRnE+67D844AyyW0bcFtDK/9FLtlFVZ\nqe3kV10FjY3+z4lUH3A69WzKt78NBQVw9NHwi19o7+2LLtKJVJYu1XHZr7wCDQ16mvwHP4A//1nb\nv305sE2dCieeCH/5i5YRWH30S9Pvf6/v//LlgbclmO+lBxH9fcTHa6e8sVDkkVKsCnhdRDaIyATx\nDzUYYpbpQEW/7UrvvkDKBHJuLxdfrJ2GamqGHlNK23cPP1zbeu+8Uyu3HuLj9WjzV7/So7e0NK2A\n339fK4L+MeGBIqKVw6ZN8NWvBjZyDRWltHPWtdfC9Onwz39qRXLNNcG1wRdTp+rR5a23woYNepbi\ntNP0fRvLqdzB7NmjX77+/netpC+7TL9QXHWVdti74w79svbAA1pRn3gibN6sX0QKCrRy3bJFt6Og\nwL+ciy7SL39nn60VtD8qK/W9nj0bamu178H8+eFv93BYrfrFtLtbv7S8+mpo4Y6DGdGaJCKvA/1d\nCAStlH+hlHo+QDlHK6X2iUguWplvVUq9O/rqhoeysrKYkBEpObEiI1JyItWWCBOU081tt8Fjj0Fh\nofa2Tk/Xo06XS/+o2mzabnjOOf6d0xYt0iOo5mb9g5iW1nestrZs1HVKS9NK4o9/1CFB06drZRof\n7/+c3bvLeOUV/8c9Hv3nduv/Lpf+392ts4DFxcHBB+sXiCVLfF8jmLYMprBQj3Zra+G113S88g9+\nAAkJkJsLyclQWVnGiy/2jXKV6lMqPZ8D2e7/19EB9fX6JWnePOjuLuPWW/uSpfgiNVWbElauHH07\n4+Jg8eIyGht12F1BgW6b1arvucOhn5fOTjjoIP0CtXTp6OVAeL6XhAT45S/1zNSFF+pnIz9f3wMJ\n0T01LN7pIvIWcK1S6pMAyq4B2pRSf/Bz3LimGwwBEHRIisiRwE1KqVO82zfoy6nb+5V5EHhLKfWU\nd3sbsBKYPdK5/a5h+rLBECDB9udwJnvxWQERSQYsSql2EUkBTgL8RvlFe9iMwRADbADmicgsYB9w\nHnD+oDLPAVcAT3mVfrNSar+I1AdwLmD6ssEQCUINMTtLRCqAI4EXRORl7/5pIvKCt1ge8K6IfAp8\nCDyvlHotFLkGgyF4lFJu4ErgNWAz8KRSaquIXCoil3jLvASUisgu4CHg8uHOHYdmGAwGojDZi8Fg\nMBgMhsAY17AvEfmdiGz1JpP4l4j4zFwbanKJSCSlGYWMUNuSJSKvich2EXlVRHz6twbTllASgIyi\n/sPKEJGVItIsIp94/24MQsYjIrJfRD4fpkyo7RhWRpjaUSAib4rIZhHZJCJXj0VbwkUk+nMk+vIo\n5YTSlgndlwORE2o/iERfDkROVPdnpdS4/QEnoO3lALcBv/VRxgLsAmYBcUAJsGiUchYC84E3gcOG\nKbcHyAqyLSPKCFNbbgd+5v18PXBbONoSSN2AU4EXvZ+PAD4cZd0DkbESeC7E5+oYYBnwuZ/jIbUj\nQBnhaEc+sMz7ORXYHu7vJJx/kejPkejLgcoJQ1smbF8ehZyQ+kEk+nKAcqK2P4/rSFwp9YZSqifl\nwoeAr8jAUSWX8CNnzJPSBCgj5LZ4yz/m/fwYcJafcqNtSygJQMIpo6fuQaN0+GLTMEVCbUcgMiD0\ndtQopUq8n9uBrQyNyQ65LeEiEv05En15FHJC7c8TuS8HKqen/kERib4coByI0v4cNVnUgO8BL/vY\nP6rkEiEy1klpwtGWqUqp/aAfCmCqn3KjbUswCUCqfJQJVQbAUd6ppBdF5MBRXD/Yeoy2HYEStnaI\nSCF6pPDRoEORastoGe/+HIkEU6G2ZSL35UDlwNj250g+/1HZn8d8PXEJIFmMiPwCcCql/jaWcgJg\n2KQ0YZIxIsPI8WWH8eeZGFUJdkbBRmeNX9cAAAJISURBVGCmUqpTdP7uZ4AF41ynYAhbO0QkFfgn\n8CPvG/y4EYn+HIm+HEY5wzLJ+zKY/jyEcPfnMVfiSqkThzsuIquBrwJf8VOkCuif96fAu29UcgJB\nKbXP+79ORP4PPV30br/jocoIuS1e54s8pWN284FaX+VGakuQdasCZoxU/1Bk9H+olVIvi8j9IpKt\nlBomG/SoCbUdIxKudoiIDd3h/6KUetZHkTFvS38i0Z8j0ZfDJCektkzwvhyQnAj054g8/9Hcn8fb\nO/0U4DrgDKVUl59ivYkpRCQenVziuVDE+qlLsvcNCelLSvNFOGUQnrY8B6z2fr4YGPIgBNmWQOr2\nHPAd73V7E4CMou4jyuhv/xGRFegwyGA6vOD/ewi1HSPKCGM7HgW2KKXu9nM8XG0JmXHoz5Hoy37l\nEHpbJnJfDkhOmPpBJPrysHKiuj+P5Pk2ln/ATmAv8In3737v/mnAC/3KnYL25NsJ3BCEnLPQdgY7\nOsvUy4PloNNJlgCf/v/27hgFYSCIAug/gngZC09j44k8g4cQa0tB8AQW3sFCsEiKFCJR1+DAe5Au\n5O8kDNMsm3S/WH0rZ0xGo1rmSfb9M3ZJZq1qeba2dL+hXA/u2aTbkXrKi93Bn2akOyXs3K/9kGTx\nQcY2yTXJLcklyeoHdbzMaFTHMsl98C2P/ftrWkura4p+nqKXx+Y0qKV0L4/J+bYPpujlMTn/3M8O\newGAov5pdzoA8AZDHACKMsQBoChDHACKMsQBoChDHACKMsQBoChDHACKegCrVgjtwvNXBwAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f703f887d68>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from skopt.acquisition import gaussian_ei\n",
"\n",
"plt.rcParams[\"figure.figsize\"] = (8, 14)\n",
"\n",
"x = np.linspace(-2, 2, 400).reshape(-1, 1)\n",
"x_gp = res.space.transform(x.tolist())\n",
"fx = np.array([f(x_i, noise_level=0.0) for x_i in x])\n",
"\n",
"# Plot the 5 iterations following the 5 random points\n",
"for n_iter in range(5):\n",
" gp = res.models[n_iter]\n",
" curr_x_iters = res.x_iters[:5+n_iter]\n",
" curr_func_vals = res.func_vals[:5+n_iter]\n",
"\n",
" # Plot true function.\n",
" plt.subplot(5, 2, 2*n_iter+1)\n",
" plt.plot(x, fx, \"r--\", label=\"True (unknown)\")\n",
" plt.fill(np.concatenate([x, x[::-1]]),\n",
" np.concatenate([fx - 1.9600 * noise_level, \n",
" fx[::-1] + 1.9600 * noise_level]),\n",
" alpha=.2, fc=\"r\", ec=\"None\")\n",
"\n",
" # Plot GP(x) + contours\n",
" y_pred, sigma = gp.predict(x_gp, return_std=True)\n",
" plt.plot(x, y_pred, \"g--\", label=r\"$\\mu_{GP}(x)$\")\n",
" plt.fill(np.concatenate([x, x[::-1]]),\n",
" np.concatenate([y_pred - 1.9600 * sigma, \n",
" (y_pred + 1.9600 * sigma)[::-1]]),\n",
" alpha=.2, fc=\"g\", ec=\"None\")\n",
"\n",
" # Plot sampled points\n",
" plt.plot(curr_x_iters, curr_func_vals,\n",
" \"r.\", markersize=8, label=\"Observations\")\n",
" \n",
" # Adjust plot layout\n",
" plt.grid()\n",
"\n",
" if n_iter == 0:\n",
" plt.legend(loc=\"best\", prop={'size': 6}, numpoints=1)\n",
" \n",
" if n_iter != 4:\n",
" plt.tick_params(axis='x', which='both', bottom='off', \n",
" top='off', labelbottom='off') \n",
"\n",
" # Plot EI(x)\n",
" plt.subplot(5, 2, 2*n_iter+2)\n",
" acq = gaussian_ei(x_gp, gp, y_opt=np.min(curr_func_vals))\n",
" plt.plot(x, acq, \"b\", label=\"EI(x)\")\n",
" plt.fill_between(x.ravel(), -2.0, acq.ravel(), alpha=0.3, color='blue')\n",
" \n",
" next_x = res.x_iters[5+n_iter]\n",
" next_acq = gaussian_ei(res.space.transform([next_x]), gp, y_opt=np.min(curr_func_vals))\n",
" plt.plot(next_x, next_acq, \"bo\", markersize=6, label=\"Next query point\")\n",
" \n",
" # Adjust plot layout\n",
" plt.ylim(0, 0.1)\n",
" plt.grid()\n",
" \n",
" if n_iter == 0:\n",
" plt.legend(loc=\"best\", prop={'size': 6}, numpoints=1)\n",
" \n",
" if n_iter != 4:\n",
" plt.tick_params(axis='x', which='both', bottom='off', \n",
" top='off', labelbottom='off') \n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The first column shows the following:\n",
"\n",
"1. The true function.\n",
"2. The approximation to the original function by the gaussian process model\n",
"3. How sure the GP is about the function.\n",
"\n",
"The second column shows the acquisition function values after every surrogate model is fit. It is possible that we do not choose the global minimum but a local minimum depending on the minimizer used to minimize the acquisition function.\n",
"\n",
"At the points closer to the points previously evaluated at, the variance dips to zero. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, as we increase the number of points, the GP model approaches the actual function. The final few points are clustered around the minimum because the GP does not gain anything more by further exploration:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAAEMCAYAAAAidwoiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4VNXd+D9nZrLvBAIhQIKArAIC7oq4IIhWa1uLXajU\ntta2/rTrW636SluXVtvSVru4VrHV1tq6VV8XFFyrEhGBACGE7Ps2+z5zfn/cyWQms08myUTu53ny\nwL333HPP3Dtzv+d8VyGlREVFRUXl2EQz3gNQUVFRURk/VCGgoqKicgyjCgEVFRWVYxhVCKioqKgc\nw6hCQEVFReUYRhUCKioqKscwqhBQUVFROYZRhYCKiorKMYwqBFRUkkQIMXu8x6CiMlJUIaCikgQ+\nAXBKCvqZJYTYmIIhjStCiNVCiGwhRJYQ4qzxHo9K/OjGewAqY48QohxYJqV8aRzHcCmwGPAA7VLK\nx6K0/RRQCMwBeqWUfww4tgzYJKX8YZjzTgTWSSl/EaufJLhGSvnjeBtHuudSymYhxHlCiEVSygMj\nGE/SJPEsZgBZQLOU8t++Q48ClUA38M1h7UPueYqfhcoIEGruoGMLIcRSlBnsdOAdKeX2cRhDIbBD\nSrnSt/1f4GIpZV+YtkVAJ1AMOIFeYIWUskkI8X3gTEAvpbxq2HkCeB74QEr5s2j9xDnm7wJTgCbg\nPWC1lPLeOM+Nes+FEFnAVinlt+PpL5Uk+CxmAFdIKX/l234QuF5KaRFCfB14CeiQUnp8x8Pec0Af\nbn+8z0IltajqoGMP4fsj4N+xZjVQE7D9MXBOuIZSSgOwSkrpkMqMRYtv3FLK3wDPRrjGZ4Ed8fQT\nC9+LcqPvWm8DnwrsO54uiHLPpZQOIFMIkZ9An6ki7meBIgTPF0Jk+LbNKC9xAJeUsnVQAEDkez6S\nZ6GSelR10DGGlPJjIUQXimri1eHHhRDHAd8AJEM/zMH/S+A9KeVzIxzGDJTZ4CB6YF6UMdf4xnYW\n8KaUsjFa50KIUsCLMsPMS7afAE4BPpJSfuA7/w7gjjjPjXnPfXwMnA68EvA50upZSCk/EkJogGoh\nxP3AK1JKl+/wyb7VVylQNziuSPd8BM9CJcWoQuAThhDiEhTd7lnAPmA9cJuUsnawjZSyE2U5HoKU\n8ihw4ygPswSwB2w7gaizYCHEF4DLgO/H0f9npJQPCCGuHGE/CCFOAb4LtAkhPi2lfAbIlQF61JHe\ncx/tKC9fvxBI02fxC+AG4G6U+zLIg1LKjwCEEHuEEG/4ZvwR73miz0JldFCFwCcIIcQs4ICU8ogQ\n4mcoP1g90DxG1/8fIHv4bpRZ66MBOl8TMCmgTQ7RX5BIKZ8QQvwH+EgIcV4k/bEQ4mTg/ZH2E9D+\nfSGEDfjd4OyVADVqCu+5Hjg+wXPCksBzgASehRBiHnC2lPICIcT5wMNCiH1Syv+irGQGGQDW4FPV\nRbrniT4LldFBFQKfIKSUzQBCiDLAKKXUAy8k0scwFUTQIWKoIKSUd8V5mXpgVcB2KbA7wng2ADdJ\nKc+QUpp8apXPAb+O0PcpQI4Q4kLgDCDbN1N3J9hPIAuBQM8d9+B/UnHPfeQAlsAdyT6LBJ4DJPAs\ngEuAf/qusd230jrTN84NwJd87fIBT6RnJ4Q4GG4/8T0LlRSjCoFPEEKIBSiueycCb/r2XSyl/E+8\nfYyRCuIN4JcB2ytQVAyDL76GAHWLF58R1qdznomicgnEb1SUUt7j3ynErcou+ZwQYn2Yfvb6tucC\n9YEqnoA+yoCeYce6hBB5Pq+YEd9zH5MYNgNPw2dxFDgB2O/bzkZZdXmA+3zn5AGTgddRjM7hnp0m\nwn6VcUB1Ef0EIYS4DmUW1gEsAP4LtEkpd43rwMIghPgyUIXyAj8qpfybb/9u4GuD+mXfvm+hTFgq\nUYyOgy+ca4HPo7xEHgF+I6U0+Y5djvIClcCdUsqnovRzELgugqH8U8BpUsqfBOy7CuXluCNV91wI\n8SsUN9G2RM5LBQk+i+uBXJRVi15Kuc23/0so3kNVwBNSyvd9+yPd87D7VcaelAgBIcRDwMVAl5Ry\naZjjZ6PoB4/6dv1bSnnbiC+sopICfB4vZ0spdwTsW4GiiukHnpRSfhxwrAT4oZTyphSO4UEp5ddT\n1Z+KSrykKk7gL8C6GG3elFKu8P2pAkAlnfgcSgBYIF6gFegLFAAAUsoBoM/nijpihBAnAZFcR1VU\nRpWU2ASklG8LISpjNFODQVTSlReklLbAHVLKPcCeKOf8FmWlMCI1hhBCC5wrpfxlzMYqKqPAWEYM\nn+bzH35BCLFoDK+rohIVKaUldquQc7wp0mNPAX6fgn5UVJJirLyDPgRmSSmtPte9Z4jgEy2EUC3V\nKsccipOMikrySCmT+hKNyUpASmmWUlp9//8/IEMIMSlK+7T+u/XWW8d9DOo41XGq41THOfg3ElIp\nBAKTZAUfEGJqwP9PRvFK6k/htceUxsbG8R5CXKjjTC3qOFOLOs70ICXqICHE4yhh4qVCiGbgViAT\nJVDnfpQowW8BLsCGkpFRRUVFRWWcSbtgMSGETLcxDWfnzp2sWbNmvIcRE3WcqUUdZ3SqqqpoalLT\n/4wFlZWVQSsUIQQySZuAKgRUVFRSgu9FNN7DOCYYfq9HIgTUojJJsHPnzvEeQlyo40wt6jhVPomo\nQkBFRUXlGEZVB6moqKSEsVAHGY1GLr30UgA++ugjVqxYwezZs3nooYeS7lNKyebNm3n00UfjPmfT\npk3cfvvtzJo1K+nrxsO///1vhBBcdtllQftTqQ5SU0mrqKhMGAoLC9mxQ8nzt3r1al5//fUR9/nK\nK69w+umnj7if0eDSSy9l48aNIUIglajqoCSYKDpXdZypRR1nenLLLbfw9a9/nXXr1vHUU0/x05/+\nFICHHnqIxx9/HIBbb72Vc845h7Vr19La2hp0/vPPP8+5554LwFlnneXff8455wDKrP873/kOZ555\nJnfcEVxaevv27Vx55ZV4PB5OPfVUvvGNb7BixQpee+01AB555BFOO+00Vq9eTU1NDXv37uWGG24A\noLy8nJqaGrZv387WrVt56KGHuPzyy7nooov8qx2tVotGo8FkMqX6tvlRhYCKikrq2bIFhAj927Il\nvvaR2kVg4cKFvPzyy5SUlISk4NizZw99fX3s2LGDrVu38otf/CLoeF1dHVVVVUBw+o7A/2/YsIG3\n336b559/3r9v+/btbNu2jUceeQStVkt/fz933XUXzzzzDPfddx9ut5v77ruPd999l0ceeYSbbrqJ\npUuXsn//furr61m+fDnvvPMO77zzDmeccQaguNm+8MILlJaWcvDgQUBxB62t9ZerTjmqOigJJoKv\nOKjjTDXqOBNgy5bEXuSJth/GypUrgeAX96DO/ODBg7z22mv+2f6MGTOCzo2UtylQ575kyRIAcnJy\n/Pt+/vOfs2PHDv/5U6dOpaSkhMLCQgwGA93d3cyePRshBMcddxwDAwMA6HQ63njjDa677jqeffZZ\nurq6uOmmm9i3b5//OhUVFej1+qTvRyKoKwEVFZUJSeBLWqNRXmVFRUV0dHQAsG+fUrFy/vz5bNiw\ngddff53XX3+dv/zlL0H9zJs3zx94VVxcTGdnJ11dXfT09PjbDL7oA6/56KOP8o1vfCPsy1pKyZQp\nU2hoaMDj8VBfX09JSQkAJ554In/+8585++yzsdlsuN1udDpd0HUCr9XY2Mjxx4fNt5kSVCGQBBNF\n56qOM7Wo40wvBl+YgS/OE088kYaGBi666CL6+voAWLFiBcXFxZx77rmcf/75bNu2Laifiy66yK/D\nv/rqq9mwYQO33347kydPDuk/8JpVVVVs3bqVL33pS9hstpAVRUZGBldffTVnnnkmmzdv5uc//zkA\nZ5xxBlJKcnNzKS8v98/+w302j8eD1+ulsLAw+RsVA9VFNAnU9AGpRR1nahmvcU7UiOFkXETHirFw\nEVWFgIqKSkqYqEJgIqKmjVBRUVFRSQmqEEiCiaJzVceZWtRxqnwSUYWAioqKyjGMahNQUVFJCapN\nYOxQbQIqKioqKilBFQJJMFF0ruo4U4s6TpVPIqoQUFFROSYwm8188MEHIfuPHDlCW1vbOIwoPVBt\nAioqKikh3W0Cjz76KFdeeWXYY3/961/58pe/PMYjSh7VJqCioqKSAF6vF4vFEvF4Tk5OUK6gYwlV\nCCTBRNG5quNMLeo442fLzi2In4qQvy07t8TVPlK7Qf73f/8XgF/+8peYTCaeeeYZtm/fzj333ENX\nVxcAP/zhD3n11Ve57bbb2L9/PzNnzgSgtbWV1157jZ/85CfceOONdHR0MHfuXPbu3Zuyzz+RUFNJ\nq6iopJwta7awZc2WUWvvcDgAaGlp4b///S8VFRWcdNJJGI1Gpk6dCkBZWRlr165l7969GAwG8vPz\nASWx23nnnceLL77Iz372M/Ly8rBarRw6dCju63+SUFcCSTARkoiBOs5UM+rjTJE+faLcz2Rpamqi\noqICUFJIP/nkk5x00kkArF+/3t/OYDCwd+9eLr74YkpKSvzqoNzcXA4cOMCCBQv8aaCNRiPFxcVj\n/EnSA1UIqKiMJ04nNDbCRx/B7t1w6BAYDOM9qrTmvffeo7GxkRdffJGSkhIqKysBqK2t5cEHHwSU\nFMwlJSUsXbqU+fPns2DBApqbmwGlGMzHH3+M3W73V+w6cOAAJ5988vh8oHFGVQclgZpSOLUcs+M0\nm6G+HtzuoX0WCxw5AmVl4NNhJ8pEuZ/JsmfPHu6++260Wi0bNmzg3Xff5bnnnqOgoIDFixcD8Nxz\nzwWdo9PpyM3NBeCuu+4K6dPr9fqLvhxrqEJARWU8sNmUl73HE/54d7fyb5KC4JOMTqdDq9X6t08/\n/fSQNsPz7wNcfPHF7Nq1y686GuTw4cNccMEFqR/oBEGNE1BRGWs8Hjh4EHzGzahUVUFp6agPKRWk\ne5zAJ4m0ixMQQjwkhOgSQkT0sRJC/F4IUSeE2COEWJ6K66qoTEja2uITAADNzfG3VVFJglQZhv8C\nrIt0UAhxITBHSjkP+Cbw5xRdd1xIBz/seFDHmVpSMk6rFRIJSvJ6FUGQABPlfqqkBykRAlLKt4GB\nKE0uBbb52r4PFAkhpqbi2ioqE4qWlsTPMRphINrPS0UleVJmExBCVALPSymXhjn2PHCnlPJd3/Z2\n4H+klLvDtFVtAiqfTIxGqKtL7tysLFi8GERSat8xQbUJjB2ptAmkpXfQ5s2bqaqqAqC4uJjly5f7\nXd4Gl7rqtro94bY7OthZXa1sr1qlHE9ku6+Pnfv3p8/nCbMdE7sdHn5YiYlYsQKuugqys+M7VyWI\nLVu20NjYOOJ+xmol8Gdgh5TyH77tQ8DZUsquMG3TfiUwUfyw1XGmlhGN02JRAsFGQpyrgfG6nzFX\nAm+9Bd/4hrIa8npBq4W5c+GBB+CssxK61ssvv8ztt9+OTqdjxYoV3HXXXZx99tm89dZbI/wU8fHG\nG29QWVlJVVUVL7/8Ml6vlwsvvHBMrg1p6B00OA7fXzieA74CIIQ4FdCHEwAqKp9YBv3+R4LDMXFt\nA3a7IgBqaxUBAIqrbG0tXH21cjxO+vr6uOOOO3jllVd4/fXXmTJlCg888ABihKqyRCafO3fupL6+\nHoB169aNqQBINSlZCQghHgfWAKVAF3ArkAlIKeX9vjb3AusBC/DVcPYAX7u0XwmoqCSE2w1798aV\nG8jhcdLp6MPotuCRHrI0mZRkFDAlqwSt0EJuLixcOAaDTpyoK4E//hH+3/8bEgCBaLXw+9/Dt78d\n13W2bduGy+Xia1/7GqAkk7v00ksxGo3Mnz+fmpoatmzZwoYNG9i8eTNNTU1oNBpee+016uvr+fa3\nv43T6WTt2rX85Cc/4atf/Sr5+fkcPnyY2bNn873vfY/58+dz7733Mm3aNAoKCvjFL36BxWLhuuuu\nY+PGjRx//PEUFxdz/vnns2TJEjweD1dddRXXX389e/bsoaioiL/97W/09/ezadMmysrKaGpq4tln\nn8Vms7Fp0yZycnJYu3YtN9xww4jv9bjbBKSUX4yjzbWpuJaKyoSjtzcuAdDvNNBk68Ab0NbqsWP1\n2Oly9jMrexoloKSb8GXEnDDs3h1eAICyIvjoo7i76ujoYOnSIa1zVlYWTqeTnp4e/vnPf1JSUsIF\nF1zABRdcQFtbGzt27PC3vemmm3j44YepqKjgi1/8or+i2Jlnnsk999zDq6++ylNPPcVNN93Eiy++\nyL/+9S+EEKxbtw6Px8PZZ5/Nl7/8ZTZv3sxZZ53Fueeey6OPPgpAdXU1VquVN954g8cff5w//elP\nbNy4EYvFwlNPPcUTTzzBU089RUFBAddccw1f+cpXkriRqUdNIJcEE8UPWx1nakl6nH19MZv0OvU0\nWNuDBEAgbq+Ho9Y2Wm1dMVVLaXk/V6xQZvzh0GqV43FSXl4eVA7S4XCQkZFBaWkpFRUV5ObmotPp\n0Ol0XHnllWzatIlbbrkFKSW1tbVs2rSJc845h9raWtrb2wFYuXIlAOeeey47duygp6eHgoICcnJy\n2LVrF2vXruW8887j4MGDEcdVX1/PCt/nWLlypV9dtGjRIgCmT5+OwWDg8ssv5+OPP2bTpk289NJL\ncX/u0UIVAioqo4nZHFPfbXSZ8d59F8suu4Z5P/oFRf8NqykFoMvRT0N7DdLpTPVIR5errlKMwOGY\nNw+++tW4u7rwwgt57LHHsNlsAGzdupXLLruM/v5+2tvbsVqteDwepJRcccUVPPbYY3R3d7Nr1y4W\nLFjAE088wY4dO6iurmaVzwtLo1FehVqtlqqqKu6++25//qG7776bhx56iO3bt/vTTWdkZOAOTPwH\nzJkzh2qfN1d1dTVz5swJGbuUkoyMDH7961/z8MMP+4vjjCdp6SKa7kwETxZQx5lqkhpnf3/Uwy6v\nmwZbO96rLqfji5dQ8PEhKh74ByVvfEDT97+GzMwI7dJhQDR9TNW8k8L0mKb3Mztb8QK6+mrFO8jj\nUVYA8+bB/fcn5CY6ZcoUbrzxRtatW4dWq+XEE0/kRz/6Edu2bWPLli3s2bOHW2+9FaPRyCWXXILH\n46GoqIilS5dy22238dWvfhWHw0FmZiZPPfVUiEH5s5/9LBs3bqSjowNQktFdcsklLF++3C8E1qxZ\nw09+8hM++OADZs2aBcCqVavIyclh9erVFBYW8vjjjzMwMBDS/7PPPsu9997rtw2MN2oCORWV0UJK\nxSA8bMYYSJ25GaM7uPatcDiZfeef8GZm0PiTCMbSzAymLTuTisKKVI54RMQVLDYYJ/DRR3DiiWqc\nQJKkq4voMUNa6lzDoI4ztSQ8TqMxqgDodepDBACAzMrk6M3foeMrn4nct9NFZ3c9fdZQe0Na38/s\nbMUL6IEHlH9VATDuqEJARSVFeLweDHYDBrsBt9cd3qff64Wbb8bZ20WLrTNyZzodjhnTol/QYKDJ\n0ITFGSpIVFTiRVUHqaikgE5zJx2mDrxScYMUwJSmXqZn+Pz7B3nmGeRzz1H725uxeEeYIloj4Pjj\nydRls2jKIrSaCN43Y4SaO2jsSLs4ARWVY5lGfWOIWkZaLXRbe9Br9FTmTKMwIx8MBuQf/0j73beM\nXAAAeCWYTDgLNTTqG5kzKdQbZSyprKwccdSuSnwM1lVOBao6KAnSWucagDrO1BJunG3GtrB6eUwm\nAJxeF3WWFg6bmzA+ch/601fQWTk58YtLibCHERwGIwB6u55ea2/EcY4FjY2NSCnj/tuxY0dC7cfr\nLx3HmYrEcYOoQkBFJUmMDiOd5gh6fZM5aNOq7yH32Rdp3ZhcjpnSV96i6lcPhB6wWMCjGJ9bja04\nPRMsfkBl3FFtAioqSeDxejjQcyD8S9dhh6MNQbty6hopefMD2r/2+aSup7HZWbLp+9RuvQXHzPLg\ng+Xl4PNfL8gq4PjS45O6hsrERXURVVEZYzrMHZFn3cNWAQC2eVVJCwAAb042PZecz7R//Cf0oNEw\ndGmHKbx6SkUlAqoQSIKJrMNORybaOB1uB92WKPl7zKFCIBV0X7qW4nc+JKNnWBSyxRoUj/D0S08r\nLqppzkR77p9UVCGgopIg7ab2yK6QHjf4ctqkGk9RAX1rz6TsmVdCD/oM0aCoqlqNraMyBpVPHqpN\nQEUlARxuB/u790duYDRAW3vIbuF0UvrSm+TWNWKdV0Xf+tXIzMyEr5/Z3kXh7hp6Lz43+EBeLswK\ndhtcMHkBeZl5CV9DZeIxEpuAKgRUVBKgSd/kd8UMS0c76A1Bu/L2HqJy68Nkt3YipERqNNgrptL0\nvauwLF2QmoEJAfPmgnYo9CcvM48Fk1PUv0paoxqGx5iJoiNUx5latr+2nT5bDKOrOSCFg8fL/G//\nL1W/fpCclg6Eb3IjvF5yWjqo3Powwu2CyaVQVQVzjoPp5ZCV+AoBKf0G6ep3lXTGFqeFflv0LKbj\nyUR57hNlnMmiCgEVlTgxOAzR0yI47EEG2vx9tWT068lqD29Ezm7rovSDGphSBjk5kJkFRcUw+zi/\ny2dCmIwhu9qMbf5UFioq4VDVQSoqcSClZF/3PlweV+RG/X3QNfTCn/Xbv5BzuIH8ww0RT+n54qdp\nvvvm8Ac7OxMrLC8EHD8PhuUQmlE4g6n5U+PvR2XCoaqDVFRGGb1dH10AgOKqOYjbTfFbuzCctgKp\nCf8zk1oN1iXzI/c3bRrkRzHserzBdXulDOue2mnuxOP1RB+7yjGLKgSSYKLoCNVxpo5ea69f1x4W\nKcE6ZA8o3H0Ax/SpdG3cgL0i/CzcXjWTvo2XRL9w+XTQhc8OOmfLbyn8cJinkskUMk631x09rmGc\nmAjPHSbOOJNFFQIqKjFwepwYHaH69iDsNiWrp4/cI40MnH0yMjOTpu9dhW1muX9FILUabHMqabr7\nZmR2VvR+dTooKwt7yLjyBCZtfyd4p9kMYbSp3ZZudTWgEhbVJqCiEoMOUwftplDf/yB6e6GnJ3if\nlIqenoA4gY5erCcuoW/jJcjsLMxOM/mZ+bEH0dQI1uAgNK3BxJKv/JB9T/wWb27O0IGZMyE/tM+K\nwgqm5ccoVKMyIVFtAioqo0hcbpbWMNW9fAKgWn+QBzpfpPfzF9P825/Se+XlyOws2k3tfO6fn+NI\n/5HY/ZeFqpQ8RQWYly2g5K1dwQcCoocD6TJ3qZ5CKiGoQiAJJoqOUB3nyLG6rNjddoDINgEpI6aK\naLN3c2PtPSwvPB4mB9cRmF4wne+f+n2+8+J3YguCnBwoKAjZ3Xf+GUx67d2gfdVvfRC2C7fXnVbJ\n5cbiuUsp6bf1c6T/CHu79vJRx0fUdNfQYmjxP9dYpPP3MxWoQkBFJQpxrQJs1iB7wCBur5uba//E\n5hmfYlXZsrAv8QvmXMD1p1zPD175ASZH+Bm8n8mhxWgMJy9DarXgCdD3ezwRhVKXpSv6NT5BWF1W\nDvYepGGgAYPdgMvjwiu92N12ui3dHOg5QIuh5ZhfHak2ARWVKOzt2hvbNTScPQB4sPkZ9prq+O2i\nH6Apnw4lJRG7uPvdu+kyd3H32rujl2hsaQ6OSo7E5FIlCC0McybNoTg7iWC0CYTerqdhoCGuF3xe\nZh5zJ81Fp5m41XZVm4CKyihgdppjCwAIsgfkHThCztFmehwDPNH+MjfO+SoarRaKCqN28d1TvotG\no4k9Uy8tjWfoEe0CQFq6i6YSvV3P0YGjcc/wLU4Ltb21EyL99miQEiEghFgvhDgkhDgshPhxmONn\nCyH0Qojdvr8IIZITg4miI1THOTIGbMHRumFtAsPsAVOffIGc+mYyNDpumnsV5dmTlVQQmvC+/oNk\naDO46/y7Ynvv5OZBDLfS6j0HweEEV/iiNyaHCZtrdNJdJ8JoPHeL00LDQEP09B5hsLvt1PfXhz0v\nXb+fqWLEQkAIoQHuBdYBi4EvCCHCpS58U0q5wvd320ivq5JCTCZobYXDh+HgQairg44OcIQpbH4M\nobfrYzcKjA/weCjYcwDjyiUUZxRw7uSTlP1FRakdWMmk+NpFWQ30WEPVVxMdj9eT0ApgOGanmRZj\nS4pHFZ10UH2P2CYghDgVuFVKeaFv+wZASil/GdDmbOCHUspPxdGfahMYK/R6aGsDewQvCSEUY2RF\nBWijz2Q/aVicFg71HordsK8XupUXal7NYWb9/lEO3nf70PHsLCUhXCqRXkVQe2K87HJzoLIq7CGt\nRsvSqUvRiE+ORrhhoCElWVNH22ZidprpNHdicpjwSi/ZumxKc0spyytL+nmMt02gAggUn62+fcM5\nTQixRwjxghBiUQquq5IsLhccOQL19ZEFACiqjp4eOHQIg6Hb72ZX011Dm7HtEx2BGtcqAIICuAqr\n92NcuST4eGF0W0BSCA0Uhq4uKu57Aq0hYPZvsyuVzsLg8XrSOs10ohjshpR9nmZD86h9t1uNrdT2\n1mKwG/wrFrvbTpuxjYM9B+N2W00lY2UO/xCYJaW0CiEuBJ4Bjo/UePPmzVRVVQFQXFzM8uXLWbNm\nDTCknxvP7T179vDd7343bcYTaTtQl7nk5CX0Wnt5b/tO8vpNXHbSanQaHTurFT33mlWrlPOHbb9W\n/QFd9j7mL58LlbOort4HwKrTV9Fv66d9XztZuqxP3P2csmgKMGQHWHX6qiCbwKrTlftT/d9q8EhW\nLV9IYfU+nj7rJKx7DrJq+ULleE096BqH2gf0F217yclLONJ/BPsRe/j2K5bAwICi/wdWLV9IVkc3\nB//5IruKi/jS59aDlFS//jbk5Ye9Xq+1l/0f7B+3+x34/RxJf1JKpiwOfV4j2S5eW8ysolkp/X42\n6ht5efvLEa9vd9v563N/ZWbhTNadvy5qf4P/b2xsZKSkSh20RUq53rcdog4Kc04DsFJKGSK6J4I6\naOfOnf6Hks7s3LmTs88+m0Z9ozJLGhiAri6QEp1Gy3G5FRToImepdHnd1FmasXl8toGMDJhdFVS9\nSqvRMr90PjkZOWH7iHec6XQ/I5WQrH632v/jBZRVVMNQmujsF1/l/VOms6x0sbIjijomFvX99Vzz\nwjX88/KsW7zTAAAgAElEQVR/RlZNNDQEreQmvfIWxe/u5slPX+AXQhQUwIwZEa+zaMqiET27kZCq\n595l7hqVmsqD9yYV42wzttFp7oyrbaY2kwWTF5ChzYi7//FWB+0C5gohKoUQmcAVwHPDBjg14P8n\nowifCbsWTacXVjTWrFlDq7FVEQA93Up+ep+AdXs91Fla6Hcawp5r9zg4ZG4cEgCgqJHa2vx9gKJW\nqB+oH9HyOd3uZyRVUJAAACVILIC/r8hgW1dAEfgRqILmTJrD+cedzwO7H4jcqDhYJWQ4ZTmFu/dz\n0oIAG4TFrNgQIhCzUtookorn7vF64n65JsqgkXik4zTYDQmN0elx0qCPXIMi1YxYCEgpPcC1wCtA\nDfB3KeVBIcQ3hRBX+5p9TgixXwjxEfBbYONIr6sSG71dr/iEd3ZCb+iPXUpJg7WdDntvkJeC0WWm\n1tKE0xvGR95ihb7gvhxuB82G5pSPf7wwOMILxhCswULg3507uGzaOUM78kMjhBPh6hVX89KRlyLf\n28JCf34iUHIJWefNpnB3zVAbrwyuczCMflt/WnioJEu3pXvU/PtNDlPs7LExcHvdNOobk7p2l3ls\nortT4hogpXxJSjlfSjlPSvkL3777pJT3+/7/BynlEinliVLK06WU76fiuuPFRPAb9ng9/OvFfymu\nnjGqU7XbezhgPkqzrZPD5ibqLC24o83se3uVUooB9Nv6k/7BpNP99Hg9mJ2hhVkgTJxAgFH4kLmR\nfpeB00qWKjtychT1WQA6jY6p+VPjjkwtySnhy0u/zL277g3fQKuDvGB1nv70FdQ8/1pwuyiuoi6P\na8QvumQZ6XP3Su+oB761m9pHNM4WQ0vSQqrd1I7TEz7WI5V8cvzDVILoNHfi7ulW3EDjwO5x0uMY\nwOSOPGv0I6WyuhhGi6FlQs8qAUxOU3yfweUMqif8TOdOPj11DdpBF7+C0FTO80rnMaNwBnMnzY17\nPF9Y8gVqumsiJ5gbFoncd8FZ9Fy0JriNOXpOoonqJdRj6Rn1KF+L0xJxUhALk8M0onvrld5RsXUM\nR80d9AnE6XFSs3c73v5R/nFXTA9xVZxVNIspeVNG97qjSJO+iV5rb+yGBj20dwBg9di5eNd3+fuJ\nd1CW5QvkmnOcUjjeR2luKVXFVf7tRn1j3Bk9+239TMqJECAmvUqQX5gEdkFUVUJObthDGqFh2bRl\nEypmQErJ/u79YzJTzsvMY8HkcPGv0TnQcyAlkdnzJ8+PWXNivA3DKmlG5+Hdoy8AQAmSGiawO82d\nE3o1ELdqxDakDpv+6L/5pfe8IQGQmREkAADK8oKTuZXnl8c9pogCAJSYgTDZSUOIohLySm/8cRFp\ngt6uHxMBAMpqIGaG12H0WftSlpqjzdiWkn4ioQqBJEilDnsw33nDQAP1/fUjLgPobG6gt6MewO9D\nPmq4XDAQLGycHmfCHifpYhOwuWxRXyxBNoEAz6CKt/awuuzkoWPDqnrlZuSSmxE8C8/SZVGQNTLD\nsZ+CYJVQ2OceRQjA+KiERvLcxzLtRfW71Ql590gpY1eiSwCz0zyqdhtVCIwjLo+L2r5af7i73q6n\nxdBCTU9NwjMPADo66Gw+MLYz8b7+EBfEsfJqSDVx/9C8HrArrrO6Pj06vRHbcTOHjg8TAiU54VNI\nT84NrQ+QFPn5oI3xU3a6Qoz5gRgdxgkTAW5325P7fYwAo8OIxRlHCm8UAZXqVUqHqSOl/QWSlkIg\n3dUJqfBvHhQA4b5YLo+Luv66kCyWUensxNXaTJ9zaFnvDxgaTdzuEOOz3W1PaOaSLnECscbsjxMI\n8Aoq2HsI8wnzwVdEHo1QMn0GUJIdXggUZxenRg8vRJDgWbV8IbjdZHQNs22YIhs4pZRjrhJK9rn3\nWMY2+d3gc49nNeCV3lGJWzA7zUkbqGORlkJgPANYxgIpJfUD9TjckbN0Silp0DfE9zLt7IS2Nroc\nfXhTJEALPqpBp4/zRd7XH2IbmGg566WU8f/IAlJHF3x8ENOyAGGbmxfku5+tyyZLFz71s0ZoKMpO\nLMPojoYd3PtBGJfRYSqhgn21zPnZPcFtTNGf54A9gUnHOOGV3nF7P+jt+ph6/h5LT3w1KJJgtFbY\naSkE0l2dMFIddrupPa6lpZSSowNHo3/xfALA7XXT4xyW/z6aTUBKit7dTcHuGoTTyeTntjPr1w8y\n+bntCKeTgj0HWbz5R8y8ZxsaW4ykVi4XGIMDrIwOY9xL4nSwCZid5pgpiP02AZ89wOK2kV1TGywE\n8oNXAYVZ0aOGE81WuXTqUp4+9HSo62B+nrIKQXnuphPmk9XeTUZPgK7f7ohYYwDGXiWUzHPX2/Vj\nrrYKtAV1mCOrZUYzehmUzx5t4pgsaSkE7G47BnucUZsTDIvTklCd16hpGdrblTQOQGcCq4CMrl7m\n3vRrKh78B1kNrSz85s3MumcbU/7vDWbd+xgLv3kzhpVLqHnkbjR2BwuvuZmcusbonfYHCyApZVoV\nNY9F3OqrgCIyD7c+xw9uODGqPSCWECjKKopeTnIYpbmlfPGEL4auBoQm+No6HYZTllH87ofB7aIY\niKWU8UdLjxNxue+OIgO2Aayu8LE0HeaOUY9bGI0a0WkpBCC9C2KPRIfdbGhO2ObhcDtCc4k0NyvR\nwIDT66LbGbqUD2cTKHp3Nwu/cyvmxfM4dM8Wyv7zGjktHQjfmITXS05LB5VbH8aTm03Tj75B++bP\nMu/Gu8mtPRp5kHZ7SC6deJft6WATMDljGxpXnb5KKbTjlXill5d7/st5004fsgdkZEBGpr+9ECKm\nB5BWo43pAz6cL53wJfZ172Nv197gA75cRYPPXX/GSorfGSYEjNE/51jaBRJ97g63Y8wNwhCaM6rF\nEFp4ZrB4/WjTZ+1L+UoobYVAupTASyW91t6Is4hYGOwGRQXg9Sp1AAIKmzfb4vPNn/Lsq8y651Hq\nf3o9nV+6lEmvvUN2a/jla3ZbF6UvvQnAwDmn0fg/V+MOEwUbxLD0FA63Y9SMWanE4/XE/1x8gu6A\nuYFsTRZz8wJWAcNSOORl5MVl+C3KSswukK3L5lurvsVv3/tt8HPPz/erhACMq04g71A9WlOA6tFm\nU9R3EQjMc59upIut0Ow0B6msvdKbVEnLZPBKb8pXQ2krBCB9jYvJ6DI9Xs+Igz669G20f/x2kDdO\nl6MPgytCrpthNgHzonkc+v2tWBYrpRxy6xr9K4DhCK+X3CNN/m3jyctwTi8L23aokSmkiEk8/ufj\nbROIN1VE9bvVflXQ6727OKd0WFbRYfaAeOMAEjUOA1w490KWT1uOzR0wURIayM3zP3dvTjadn78I\nnXHY9yOKgdgrvWOWSyjR5z5e6sVwtaVbja3+6mB1fXVJT+6SodvSnVKBk9ZCoN/WP2F8l2PRae4c\nmb7QaoGGBjr6m6kzN9Pr1NNk7aDVFr+gtM2rwjVlKPrUOq8KqQn/FZAaDda5lYmNUUowBOuUB2wD\nae/ym5CKwWpDSsnrfbs4b7CG8CC5wQFhBZnxCYFsXTaZ2szYDQPQarRcd8p1IUFoFAZfs/PLn8ZR\nMTW4TRqphOLF5DCNWYRwvLQZ2zjcd3jMV7tOjzOlnlxpLQRGY+mTChLVZTo9zuRXNYMlHptb/AnL\njG4LTdYOep3Rf6yR4gTMvtlj3/rV2Ie/IHzYK6bSt3514uMdFjPg9rpj6tvH2yYQjz0AYNXJy8Hl\nwuKxsSxnNotkQLBXdlZQsR0hBHmZkQv2DCeZ1UBY8vNjx4fEoRIaC8GdyHMfz/dASB2JNCCVHpRp\nLQRgbMPDR4s2Y1tyela7HRobldTNif4ow7R3ed3c2/gPNu25BbfXjczMpOl7V2GbWe5fEXg0cHiy\nhleuPg+ZGWV2KiXCGWZm5nAG+dEDiQW9jTFurzt+25PPHpCvy+XP+6uYvu3poWPD7AG5GbkJBYLF\n8iKKG61OqWgWC2NkLyC3151WthyP15OWq5PxxOqypsyDMu2FgMPtSDt30UR0mWanOfG8LB43dHUq\nAiBaIfiI53up+uV9HHr8Wf+uHscA39x3B/WWVh5YerM/p71l6QIO3ncbzdduomfDGlqvvZLXf/dd\nrtI8xzv9H0e8xJTnXmPmH/4a/uCw1YDero86sxxPm0AiL7vqt4bKYOTvr/PbVoCQKOFEPX4KMgsS\nchWNRvWhKF5cgxij6/3HwlU03ufeZ+tLjbFaepU4CbtdUa9azGA2K/9aLcrkxWFXVkkBauhwNoF0\nIFX5icaq0PyI6LH2JLVctrvtuL1usnXZcRfySCVSysQqbrndSkK2gQHwJPml93ip+tUDZPTpsZx3\nOgAN1jaurbmby6au4aqZl4TMUGVmJr2XnO/fPgn4Vc53+cHBrfx+8Y9YmD875DL955zK4m3/pvsz\n67BXVgQfNBlh2lTFUMnQzDJlCdNSSEL2AF++IKQk70AdzdddqWwLETL7TlQIaDVa8jLykp6Btxpb\nOdJ/hDVVayKmjA7C7gCnIyTb6SB6u54ZhZFrE48lSamCXC7fi92uvNidTnAnaF8UQsnJ1NEOTY3K\nKkurBZ0WdDrFNThwn0YDGm1QxPhoYnVZ6bX2jjgHVXoKgWGuhgYGsDuzydZlKzsGb3LgvwH/t3rs\nNJtasbhtoBEIjZZJOZOYWVKFVpcx4ocUry6zzdQWW9UgpfJlNRgUg91IdLFeL5W/eZCMnj6O3PYD\nVmZn4fA6ub7mV3xr1ue4eOqZcXe1tHAed86/lmlZpWGPewrz6dp4ERUPPUn9z7437KBXmWEFpDLQ\n2/URhcB42gTifulKyapFc0FKsto68WZlDhnZs7KUH38AiQoBULyJkhUCbq+b2966jTklc1i1+lRo\nODoktIDyx57GuHIJlkXzhk4yGGBKeI8vh9uBzWUb1SL08Tz3hFzFXU7QG5QiOvYURNZKCW4PqxbN\nC8oXFROtTxhoxNC/QqPsF77/awbfWWLIrVcE7BvcZmjTT8D7q9VUQ27xnGQ/IZCuQiBM1aruAQez\ncqbFPLXfaaDR1hGkfpBAH2DR7mFe3izFE0Prk9xarU+S64b+jfYXJ73W3vDGGymVgCObzbcktSQ/\n6w/E66Vy68NkdfRw5PYfILOVGV6WJpNHl/+UkozEdc6rihdFPd796bVMeeZV8g4cwbJoWLUsvSFI\nCBgcBmYyk3QiofgAu80voPNrhqmC8kLTRCez8izMKkw6W2RVcRVfP/Hr3PrGrTxw8QNo8/NDXoQl\nb3wwTAgYIwoBUJ7ZaAqBeIjLocJqUepem+PL8jnqeLyp+U3Hcymgtm1k1cfS3iYwSJ9TH9PFst9p\noMHaHlH/bPc4qbM04/G6FdWL02fENJsVPXZfH3R1KakYmpqUoKzaWqipgY8/hg8/hI8/Zudf/qLs\nP3IEGhqU6N3WVmhvx9naRHPdLpqOfKh49XR1QnsbtDRD/RHlvIYGRdAZTSn7smT29KM1WThy+w/w\n5igrpkF/8WQEQDzIzEy6Nl7EtCeeDz1osQTFDDjcDuzu8PaN8bIJJDTrttl45YP32Hr0cfB4MZy6\nbOjYCO0Bg+Rl5KEdtqJIhM8v/jyZmkzu/OudIUXulejh6uCV5qDKJAKjbYyN9dztbnv0Mdhsipqm\nqXlUBcCo1+UYISNNGpmeK4EweKWkw9HLzAirAZPbQqMt9izK7nFy1NLGvPxZyQ1kUHiYlReI0+ui\n32nA4rFj89hxeEcng2AsnFMnc3TL9WN+3d71ZytLLSmD1WxSKqmLi4cSpOnteqblx17NjRUJCQGr\njd3GQzhLXPRtWBN8bIT2gEGEEBRkFiT98tUIDVvWbOELv/4Clxov5QRdtt+t2DZ7JggNOfXN2ALj\nPwyGECE2iMVpweVxkaHNSGo8IyVicKXHDd3dympTZcRMmJUAQI9TjyNMwIjd46De0hq3b7PRbaHL\nkXz04ZpVq5BS0mLrZL+pnjZ7D3qXadwEQCAttiEVVNz1BHQ65WU9bRpML4epZUrQkSZYGRnu/sqs\nTHo+vTa8nSVMZtFwjJdNINGVQF1ZC+eWDgsQy84OsQfkZcQfHzCckRrPp+VPY8vmLTQZmoITygkR\nIZeQMcgTZjijuRqI9txNDlP4a5vNcPTomAqAcL+jcJl3JyoTSghIKWm0Bat7HB4ndZYWPAm6kLXZ\ne7B7kjMeeaWXOksz3Y70iYaVUvKHxif58aF74r8X2VkwYwbMnQvl5VBSAkXFMKkUKnz7Jw0VRLmx\n9l72GGrjH5TF6p+JgvLSTZcIcK/0YnHFqUJwOem19nLU0srJxYuDjw1bBWg12hHp0VMRL3B25dlc\nfPzFIbWHB85YSdH7e4Ibe2XUCOLx8M/3eD006huDd0qpqFZbWhL38kkxeXsPhc28m7f30LiOK1km\nlBAAJdq13tqK2W2lz6nnkKURZxIzcCklTXGoj8Kd9/jbL2Fyj12ukOEIh5Pine/7ZyJFz7zET2v+\nwPv6Gv645Mdofa6ZEXWZGqHM9qtmKy+KSN5SWh1MnQazZoJWw5klJ3JP05OJCb6A1MVSyrDRueNh\nE7C6rPF/DpuNnX3VLOitIlMzTDUyLFXESFYBkFwKieH4/drz8oJWc5ZF86i768ehJwxEDuYzOU2j\nJrjDPXev9FI/UB+cIsLthuamkHTlY0Xg70g4nVRufThi5t2JuCKYMDaBQAwuc8SkaYlgdtvocQww\nJSt8+b9wtNt7sHiSCOBKEVqDieN/cDuZ3X1obQ6ElBQL+GNZDgM/ug5XRgx1QmaGMvvPyo7/onn5\nUFnJhZzFY20v8Gb/R5xduiK+c01GZYXhw+gwJlxIZTRI1B6ws283KwoXhB4bLgQSSBURicKswtSk\nSRBCeXaDglirwZMfZnx2u/KXHfqdGCw7WZob3lU4lbg8LuoH6oMLLjns0NIaNc3FWFL60psxM+8G\nxtxMBCbcSiDVtNm7407sZnSZ6XT0jU3t3jBkNbez4PqfkdmnR2e1+2ciGRJmdtmY97ttQTORkHHm\n58Hs2YkJAP/Fs9HOrOT/zd7IH5qeDK9y8niCK1lBiEoonF1gPGwCidoD7ljwHa48bT1Tnt0+5GGT\nlRmULwhGvhKAkdsFgnLd+NJ/x1QRRlkNjJZKKPC5Gx1GDvQcCBYAVovipTfOAiDwdxQr866mtm6s\nhpUyjnkh4JFeWuyxkzG5ve64vI9Gi6J3qpn//duwHD8brTm8KiqwBkAIxUUwY2aIETMhcnI4Y9F6\ninT5vND9dugY39vD7Dv/FHpegErI4XaMSom8RIk/SMwLDgeFujyKj3Yw+T+vD6nPwkTmpmolkDLy\n8xlwmbhi942026Pk4TIaQtKAD2JwGEbVltNt6aaury54MmYyKUkTx8jfPhC39HDY3MS/O1/nZ3UP\n8PndN/C+fj8QPfOuW8BvMqvZ8MF1QQ4a6c4xLwQA+p1GjDHUS822Tly+L2k0v+HR8BrQ2OxMe+I/\nHLntB3izMuOuAeAf56QSKJ8eUfdfmlvK4rLFzCyaGTN/jSgu4foTvk6mCNUkGk9eRnZzG5ntwwJ8\nhuWvH74aGGubgM1li/+lZhsKEtv3yltYFgcEWw0zCqcqPYlOowtNEZ0AQblutDpKiqfy2fJzuXb/\nXfQ7I3jVeCUMhJ/xj1bZyZ07d9Jt6Q6t1GU0KLE64+B08UDz05z73jXcWPsHPjbWsTB/Nlc4LmCl\nTxUYLfOua0Y5X77mj9y/9GbKs8Onchjt8pPJkBKbgBBiPfBbFKHykJTyl2Ha/B64ELAAm6WUe4a3\nGU+abJ0s1FaF/RH3OfUMuGLnmMnbe4jKrQ+T3dqJkBL58luUPf0KTd+7CsvSMPrkGFg9duoszVQb\nDtJwbRm3LZiD9XAD8uW3EN7QGVLYGgClk6As/JcWYFLOJKqKqwDlJebyuGIWy16yYDVLMmYEqXkA\nZIaO/nNPp/SVt+jY/NmAD2JTZpk+1YnJaWJK3pSo1xhN4vYKgqB0ATmNLZgvXDN0bBTsAYMUZhWm\nrlBJQQFXTF/HgMvEdTW/4s+LbqB8/1FMK08IbjcwAKWlYScL/bZ+JuVMCtk/EsxOcwQBkJrEaAAD\nLiMtti76XUYGXEYGXCYGXEZWFi1gzfCiQMCnpq5m4/QLKNQNPcvqroP+98Jg5t3KrQ+T3daF8HqR\nGg32iqk0fe8qyMpiBuGjsAdcRi6r/hErixZwWslSzihZFlFYxItwOiOv/uPtY6QujkIIDXAYOA9o\nB3YBV0gpDwW0uRC4Vkp5kRDiFOB3UspTI/Qnq7c/NqIxJUuhLo+5ecGzYavHTq25MWZUnnA6WfjN\nm8lpCVUZ2WaWc/C+2/BmZNDtHKDJ1oHBZWbtlFNC2nqkl2v23UG7oxe9y8TsnOmsKFrAGZOWcXLR\nYjQuV8zr+FNAxxAAWbosFk1ZFJRQTkrJvu59uDwx9LAmI7SGBvPk1Dcx55at7P/rb4Zq74ISf1Ck\nGIR1Gh3Lpi0LOXesaNQ3xl+lqsUXjSolJ1xxPbVbb1YqrOl0MG9eUNNZRbNSJtxMDhOH+w6npC9c\nTjhSj5SSO+sfocXWyfY722m584bQ5H/l5UEBfoMIIVg6dWnKEjG6PC5qemqCV2QJCoAexwD7TEdo\nsLUzJ3cGa0pXhrR5pnMnz3TtpCSjkJKMAiZp8in1ZLG0fDmLC44Laa81W/BmZSEzon/OwZdv7pEm\nrHMr6Vu/OnrqdR96l4n3BvbxzsBe3tPvJVeTzbqy0/h25eVxf+5BAiedGimRUiaVFC0VT/RkoE5K\n2QQghPg7cCkQ6DR7KbANQEr5vhCiSAgxVUqZVoozo9vCUWsbVbnlaIUWo8vMUWtbXGHZ0bwGMts6\n2P7wzfx8mYEsTQaVOeWUZBRwzuRV6MSQjl7Xr2fqy29xzbrLmJo7hfKsyX53z0FizUT8X8RJJVEF\nAEBlUWVIRlEhBFPzpir1jKNRUAj5+pBwfducSjyF+RR8dADTyiVDB4wmvxBwe91YXdYRqTxGQiJG\n4QPdNczNriC/W4/wenGW+17yYXL2p3IlkJ+Zj1ajTY0uPiMTsrMQdgc/nnMlWw7fx451+Zy08z06\nrvxscNu+XigqClkNSCnpt/VTlhejxGicNBmagj+byQjtHUMv17pGrPOqQl6u7fYe/t7+Cjv7qrF4\n7JxQMJc5eTPI04ZxdpCSb73cx/cbJ5Hd0k5m9yE0Difuwnz2/e1ThPtVL77yR+hMFqRG4MnLxZOf\nhyc/l0O/uyUod9hg5t3iNz/Ak5tDztFWPPm5ePJzcefnRswzVpxRwPqy01lfdjpe6VUmhO7wK9MG\naxs1pqNMz57C9OwpTMks8b8PAl1VR0oqhEAFELima0URDNHatPn2hRUCxW9XIwX+bHuOaVOwV4Wm\ntc3o7ServRuEQAolG583IwPXpGLcpcm5IepdJvYazWQIXcQI4Oo9B0M8b6J5DWi9sL5/EitX3ULx\ncBdOj5eCvQeZtP0dit/5kP5zTuOkrPPxZkcOOBqsARBxJlJSAlOnUf1udcSqSKW5pRG9UCbnTqbd\n1B47h3tZGZgbQna3b7oMmTnMn95qUYysvi+xyWHyC4GdO3eOmYeQ2+uO2zBtt+j51sd38OyqX5Ob\nkcE/L1rDfL9ROPj5aISGHF3qkq2NJIVE2OeeXwB2B1qh4efzv0WurGfSnX+m4yufCX7hO11KKokw\nq4Fea29KhIDersdgNwyN02SCtnbyPj4YU51q9zrJ1Wbzm0XfZ07ujOg2LKG8yAdWn4R91nScZZPx\n5OdGzSK8919/VAomuVxoLTa0Ziu7d9ewONxL3eNl0s730Jqtvj8LOpMVjd3ORy88FLwSBvB6mfHn\nx/Hk5iB1WqROxzSdFpmho+fS40O6Nzkt7K57g+cw0ooRPXbKKeAL2uVc01MZcdKZKGkZJ3DzHx6j\nMkt5oRVpNMw+6QTmfevLwJCxc9XyheQdqKf2sacRUnJWXg54vLxtNGNatoDjfvD1kPZTnt1O3f1P\n4M3O4sySQjx5eez0eDAvW8C8b1wR0j6jd4Dd7+/Bm5vDiacsw5uTTfXHh6g90uQXAoPtJ8+rQr78\nFm/4dPVrfJ9lJyCF4Lglq3BlFISM5/AjT9FTkE/uReew/+ov8H5DK9Q1hvQfbrv3kvOHtn0CoPpI\nM5RaWDVNydEzaCQcfClUv1uNVqNl86c3K+PzGWUHX8KD25XLKum39Yc937+dlc37h49iMfZx7qqT\nhsaXl8uqE+aHjt9spnqfouIoOreIqUxl586d7NmzJ+T6o7X90vaXaDO2hf88w7b/2/AWMzrLOFLT\nSvHyhZiWLx76PJ+uCmp/zjnnIIRI6XgLswrZ/vr2iOOLtF1bUxt6fMUS6O0dGv+yBSCg5rnt2Cpn\nBH+/9h9m1ecuASGC+re5bPzfq/9HTkZO0p9vx44dNOobWXrKUuV6r78F3T2ctHAOlVsf5n3fzHYN\niqPD+y0dOO78E1MevRuZmUn/YSOrWMTcypn+8WY3t7FyxWIcM8pDfi8vzlWe06o5lUOfj/C/p+Hb\n7sxM3mtqp9blZjBOPKi9VsOTl6wNc75klUYT2t7r5Q23B013L2dMnoSw2ni3Q/HYqrx0bUj7pfnH\nMeVJL5DHmYVTsQkvz9oG0IpGPsoY4C9S0sjISYVN4FRgi5RyvW/7BkAGGoeFEH8Gdkgp/+HbPgSc\nHU4dFMsmEGu5GBW3G63dgcZqVyS3xYrOYsU5eVJwUi0fJa+9y7QnX0BntKA1mdG43LgLcun63Aa6\nrrg4ZFyLNv+I7O7QKmKOyZOo2XZ3yDhzjjThzc7CMSNFSdWKCmF6RcxmM4tmxpzRGewGjvQfidnX\n8wee5vWDL7J10fcTGp9Wo2X5tOWxz0kxbca2mIbvQW558Ycsza7k8vJhwT8aAcfPD5pRTsufRkVh\n7HufCE6Pk31d+1LX4ZEjQT730x5/jsyuXpq/d1Vo26llSvqQYUzKmcTsktAiQ/HSZe4aUjVaLUoa\nCLAhiHwAACAASURBVK9UPOru2RZ2NS01Gpqv3RQShJVT18iM+58gq72b5u9+FeNJS5Me10Rj8nPb\nmXXvY34HEQHjahPYBcwVQlQCHcAVwBeGtXkO+A7wD5/Q0CdjDxix941Ohydfhyc/D1dZ7AjIgfNO\nZ8BXnQtAOF1ozRakNtTX/kPbUX56kY0nn8ol02RVHgrgLsyn44qLwgqqcIInaQoLFDfQGORl5sW1\npC/MKoxLJ732+Av5/a57abZ1xq73YDb7s40O5vIfa7tAvPYAl8fFO127uO7Ez4QezMkJUSmk0h4w\nSKY2k2xddsQU3AlTkB+UeqF33WryDimCvs3eTUV2wPeitxcKi0J02wP2ASo8FUmltvB4PUMC2Gb1\nCwCIHYQV6PqsNZiYcf/fKfrgY9q/chm9G9YotUCOIfrWr6bs6VdSYhMYcZyAlNIDXAu8AtQAf5dS\nHhRCfFMIcbWvzYtAgxDiCHAf8O1Er5MOOTtkZgbuScWKyiaA7b3v8+NDv+eCDf+Pmn/cQ/N1V9Kz\nYQ3N113Jvr//jr5PXzC6AysoUGbYw15Mw2ujCiGoLIpP8Agh4krvkK3L5tPzL+Ef7a/E7tTjDcpf\nP1jacaziBKSUcbtd7mp5j6qc6UEpRfxxFzlhjMIpiBQORzJlVSPWxC0MDkJzlxZjOGMVXunlhkP3\n8khLQF0Ijxe6Q+dpUsrwxZLioMvSpfjJ26zQ3Ez17gP+Y9GCsIJcn91uFlz3Mzx5Oez/y130fuq8\nURcA6VhPYNBBxDazPOJ9i5eU2ASklC8B84ftu2/Y9rXx9ndz7R+xeRwIBNnaTE4tXsrm9+1pmbPj\n8baX+Gvbi9y7+MfMz69EwtiOozC8AAhHRUFFQhkui7OL43KlvPyEL3DFPz/PNZWfpUAX42VoNiv5\nbFBm5VOJ7sGUSmxuW9wFy/OljitnXBz+YE5oJbHRyrlflFWU9Es3hByf18qw+A6N0PCbhd/jG/tu\nI1ubxRXTfZMWg1FZDeQH10fosfYwNX9qQqsBt9etVAkLUAEFEm1ma6+YSt/61cqGTkft727BXTw6\nhZImEoEOIvz+0aT7ScuI4dNLlnFR2ZlsKDuDM0qWMTt3ekLLxdFm0Aj0p6aneLpzBw8t/V/m56dQ\ntRMvgzr2CAIg0EOkJKeEqfmJvXALswpjRhADlOWVcfr0U3m2KzhoJbf2KMf99PfBjU1D6phB1cxY\neQYF5aWJwdLc2f4keTPv2UZ2Q8uQR1hOsDviaK0CYMhVNBEieYQBIemlB5mSVcKfltzIX9te5NnO\nN4YOdLSHBgVKSbspsYCuLnMXHqMhSAAEetjJzEzqr7+So2UZuH1vJanRYJtZHuz6DGMuAMYrV1g8\nDLqqjoS09A7aUHZGyD7rvKMRI2XdAhpnFY65RDujZBlfnL6eoozkKkmNiEmKG2g8FGYV+qOCE0Ej\nNBRmFWKwx04ZsHnV1+k8EhwEbquaQcHuGnQDBtwlPrWGy+XPWOn2uke9mHkgiWYOBcDjpfTVt2n/\nymXKdrikcaNgDxhECEFhViEDthSlUS7Ij5gsrjx7Mn9Y8mOu2Xcn2dpM1k05Tcnd39YKsyqDJht9\n1j4m506Oq4qay+Oiu60WOjqipoJ4eEoz+3+8mPsbl5JX35xQEJZK8qTlSiAc0XJ29E4t4DPlb/Lt\nfb9gt2H0CzsM6giXFs4bHwFQNgWmTkMIQWluKeUF5ZTklIREc3743w+Zlj+NuZPmhgSFxUu8yczm\nTprLmfPOC9onszIxnLqckjc/CG4ckFDO7DSPmU0g7nQRXo8iqFBSRbhKi/EU+dx7w9gDki0nGS+J\npt6OaBMApZSkLnRlobHaEC43lTnl3LP4R+RrA1ReVptSJ3sYjfrG2Oo1KWk/XI23vT1EAAzXtW8s\nX8vNi79N36Vraf7+13CWTWbSjvei9z8GpKNNIJVMGCEQzhAyuFzU/891/PO0rawvO517G59MqsjM\nhEAjYEYFlE5Gq9Eyv3Q+VcVVTC+YznElx7Fs2jIWTlnI7JLZzJk0hzklc6gorIhLpROJoqwEDJNF\nhSElKQdWn0zxW7uC25mHZuThisyMBokEiWEbyheUV1OHOTBp3DB7QKqDxMJRlFU0omcYhBAhRegB\nZt/5J0refB+AuXkzOWPSsLQeRpOyIgis6ud20GxojnwthwPLgT30ttfHNTSdRkee716WvvwmVb9+\nENus2B5v44FWaJifX8mJRfMpiVXDI80ZcZxAqok7TiDBnB0jpdepZ3LmOBZDycxQSj76Cn/MK52X\n2pTDUdjfvT/+F2hHB+iHolyFw8myy69l32O/xlMU8GOZOxcyMsjQZrB06uj7d8cb9wBATzf0Kgbx\nqjv/hGn5QvoGE8fNOQ4ys/xN8zPzmT95fphOUktdX13EGs0JYzEraZoDKHrnQ6Y98Ty1926JeJpw\nOind/l9yWzuxLl9M38ZLkNlZoTmTvF7o7ka2t3PQWI8twTKuZU/9H2VPv0LdL/4Hx8zyhM4dK+bk\nzfBH/3ull4PmBuxh6p+PFavO3zSucQJjSrKGELPbSr4uPp/0wIA0y9xK7j3BxqO9r/LUil/G3UdK\nKSxQEnv5DIRT8qaMmQAAZSba7e6O3RCUdAMBQkBmZaI/dTm5dY2YVgVkrTSboaQEl8eFw+0gS5cV\nprPUEa8q6P4P76fKnccFhYpROL/mMB1fulQ5qNUECQAYfVXQIMXZxakTAoMqoYBavYZTT2Tmn/5G\n3oE6LIvmhZwSEqPz1IuUPfgETXffRMtpAo2EUpGrPPveXnC7abZ2JC4A/v0yZc9up3brzXHF8owH\nhbq8oPQvGqFhVs40DpujrIrSmAmjDhopPz50D9/Z/0veHdgbtcrS8CLSFfdu4zs3PcO/NV/0C4Ax\n0xHqtFAxXVkB+ASAVqNlekF8S+RU6doTEjg5OVi0niCVXOON3woWAADmITXQS9tfGukQYxKPUVhK\nyQt1L1CpHUrve/hXP/HPRqsPHA05ZzSNwoEkYheIahMARSVUMOyZajV0Xb7h/7d35lFyXeWB/32v\n9rWrel/V3ZJa3ZIsIWN5A48RtgMCAzYJSybJASWZODt4QsBw4ATmDJMASYYECARmkthkkpAECDEG\nvGGLTd7atmRLtLW39q2lbvW+3/njVXdXdW2vql51Vbnv75w+qld133ufbr1637vfSuO/fDd5+PQ0\njX/5t8k5OsdO0n7vp+ClffQ/8wgnX9zN5JkTTE6NcXz8DAPTmeseffOpHzI4s6TYHMOjVP9wDwf/\n4mNlpQCW/95bfMnJliFngFApHhBtYNUogb/a9CHeVHsTf3viW7z9uXv5Yv+/0juU+OWmSkhzKei8\nNMP2v/mPlWsiLWIWgVu71ozTjqMp2GRbOV+rhDyhnGzSnzz8NR4beGbpjVT7jo2bDljM+P1iYyVJ\n7NCVQ6AUG/xti+9NN9Ytye9JNjuu1ErA5XDZe65wsh17YOetBA4ew3cs8Ym25uEfEzqbOl/Ee+YC\nNd83Q0ovTQ1yYOQYB0aOcWU686rlyvRVvnzi3zk6tuRwngsHeeVLn2KmobAa+1kxxHzAcrmW/pxO\nc6WX5ToPOwP4U1UshYJ7A5SKijMH5YvLcHJX4xu4q/ENHBk7xSOXnubb559ge2QpBthqE+mixQ2L\nmD/O2tokswOYN4Jc6tXbFX9viEHAFbAcYvm2nrv5eu//4c76W9IPUgrGxiAUZssNW9KPswGrncSe\nOP4EtzW+Lq3C2/6GxBYYdnUSs0rUF7X0HWTME1jAHzBvfnG1hJTHzckP7Eoqi+I/3I8jjeswnxyd\neTXPpw5/jV+66baE3595QBsd4B6PGc3l9Zo+NZfbvPlni5RT82bG9NwszM2xvTXWQGlujvpAKxh+\nczv+b36eUExBjM/ZVOZjhShPJZCiVvsi8RejUktvKBX7i3t/fj5ue4n1gTbWB9pYjl0JaRFXiDp3\nhBk1y9nJgezRSi6XWcM9EjFfp6Ep2JR3qGehhD1hy0rgls5b+dzPPsPhsZN0BdakHzgyAqEwk7OT\nzM7PFu2GatUf8MTxJ/iT7ntSfyiSFB66UqagBaLeaHInrkKoCi86wBcYuiVZgYzHKuRa7maXhW+c\nfZTh2TF+e02KukyFYIiZ3RwOQyCQfz9tMcBpJNVN8jg9VNVvTr2PUjA7S/1oI/1Xjpur3Pn5ZX/K\nVDDzC/eq+eR7loq7n0GK+10yEXdh0UnlqQTaO+w9noqf/LgvZW7e/LJi/45v22zpYk/VT2CBek+U\ntrhCalXOIIfGTiY6yAwxn078AfOiTRF7vhy3w02tP7flpp11+sOesOUsUafh5O71b+fb55/gvnW7\n0g+MFZTrfep51r9tfV51cqxgJVP40tgl5tQcm90tpOw24nHT+9QLCU/ZK2UKWsDlcBHyhBZrLqUj\nUx+JBMLJSiAVlks6WGDf8CH+4fSD/MPWT/LzHz7D1l9ITgzNGZfLTJ6MRPK/8WdgYT7r/BlW4SLg\nclEdaeb01MCK9RJuCDbQGk7utZILq8MnIGJeHE6nuST0eM1472DQtLlHo1BTy+X/9qtMdiavEAAm\nO9u4/Hvvh452qKszo3Ua6qG2JnYBVhGqbaKtqce8GKNRqK7GWd9I17rrcTe3QmurGWK4odtUdHV1\nlhQAQHOo2b5Y8TwIuAM5lS+4e+u7eeTS0wlL4+C+PnyH+5cGxRWUyymbN0esHLsuUMe/v/V+jFiU\nnTExacq3gC/Z6bfSSgCwt8+vx7sYcpyJVDk684akLOmQjReHD/HJrnvY+rMjtH7l/+EYzaHf83Kc\nTvN3uG6dWfa6CApgAUMMSw9hIpLzw1q++F1+WkKFly8vzzyBM1miG4pI4JkXaf/wp/H2n0Lm5lEO\ng8mONk78+ScYu/HatPs5DAeb6zanLSQ2Nj3GwcsHyWe+vU4vm+o2lVQJABwbPJZT+YKv/+SLvDn0\nWho85o2r/t+/j/fUOU7+0W8uDYpGobGxaPH2c/Nz7D2/N/tAgEuXzPBGoOmBbyNzc5z9jVjv15bm\nBCd9qfokz83P8dKFlywXwsvK4BU4b61AndUcnWw9P6of/Qktf/dvHP5cih7HmDfSZk8tIWeAKzNX\nuTg1uHyA+eBVV5fdvm8TNf4ay6VXbO8DkYbu2u7FBxERWT15AsVm7MZr6Xv0n6n51wfx7z/I+DXd\ni0kxmWgLt2WsJBlwB2gNt+Zl020NZ2mjt0KE3KGclMD7tu2C00tlt4dev52eD/wPTn7w181IDFjM\nHh6fGUcpZfv/03KpCEgocx3cf4gLv7Rz6bNlK7ZSrALAfNiIeCNcmUhuXpQX4TBcuJjS3uwcGib0\n/P7FnhpWcnSy9fyoefjHNP/DN9MqAIAOXxPVblPhBpw+PIabUxMxReX1mH0zLKxg7CSXp3u3w02V\nt8pSza18iXgjtl2DFWkO8jq9RU0uUl4PA+9/Nyf//BMMvP/dSQpgeRx22BOmxp89rrk+UJ9zHZgq\nb1XetnK7a/LknKAWDC7d7IHp5npmqqsI9MVl7s7M0PvkHubVfG43bItYrhyq5mEiZrqamyPwylHG\nNq03t2NmxPjvvVRKAMh6rWXNE4jH4TSLyqVCKTOB7OWDlg6VredHzcM/ovn+b3LoLz7GZHtLynyb\nGnfVogJYoN5TbWbrR6PQ0bHiCuDlZ1/O+fu2oxdzJqzmClmh4pRAQ7CBzfWb2Vy32V77aJ44DAft\nEevRER2RDssKzGE4WFOVIbpmhfE4PbkpX5Gk0sVDr7+OyM+eTxw3Ycbw51Lq2SqWFcvY+OLTsP/o\nSaYbapgLx374JSgal4mwJ5xXZ6+0pGgqDzAbraL/I/ew9tN/g/Ny5sSv7138Kfv/6fN4MoRYu89d\nTEi+W45DDFq9KW6ehkHbxhtxt6xZMfNPPBFP7uViwp4wXmdxlFXUF7W18m5FKYGQJ7ToCRcR2iPt\nK1aGOJ74yIs1VWty+kE6DAfrq9dbcrLmeuzlFKNOfyjXcLRlmalDr7uOyJ7nE8wP23vMnrXFcA5n\nUywD4wP86MSPkkxBo5s3LA2KhSwvfO+GGCveFnM5mfJFLEUGxRMImnH0KRi+4TVcevttrPvkX2GM\np0/qu967jhueOoWRIcTaNTic0E97eYRdk7c2OUzY6YQNGzBq60ryQGSIwdvf/Pa89i3WaqApaG89\npYpRAiKSdBEYYtAWTh3NsxLUBeryWo14nV66qrsyKoLGYGNZrHSWk7NJKBAAh7FYqmNifTtnfvO9\niTboqWmYnrJdCSzkH2TisWOPsbt/t5m4FsMxMsbItk1Lg1LkB5TaR1Prr7VXhmg07Ufnf+UdTKxv\np+u+z5lRU8sIvPQKOz74ebqPpbeBZ8sncBsu6tzLZPB4oKfHvIYwTaO5mlMLpcZfk3NTn/h97c59\niXgjtj/4VowSqPHVpFxehTyhosWXp6N3Ty9RX7QgBRRwB+ip7Un6QkWElnALLeHCQ7+KUac/5Mlx\nJSDCgdlz/M7Lf7q4PXTr9RDXF7V3bx+MjDA7P2tfU3WsmZd+eOyH3L5mB0wu5XGce/8vMvjGmxbl\nXbBBL9jac14NFQGn4Uz7kJCTT2CBSCSpDPgihsHJD+7i4i++mfllpTMS/AAZDp8qnyDeJ9DoqUlM\nhPT7TQXgSTQ/rnSQRJ2/Lu/fkSFGThn+VmgK2V9VtSKUgIhk/M/bESubiyw1/hrWRtcWfDF6nV42\n1m5kbXQtDcEGmkPNbK7bTGPQWsewUuA0nDlnyna3bOP05EWOjGWIjBo2E6DsXA1kO9bA+ABHB49y\nQ1WGMiBeb5IdupT+gHhsNTcYDqjK8JQtYirGZU3NM5VaAVBC1nwCj+FKLNMeCMCGDUkZu2D6pYrt\ndF0g5AkV/NRdH6i3Lcu/yltVFDNkRSiBqDea0Tbuc/mKskwUEfwuP1XeKmr8NbSGW7mm/hre9dZ3\n2XqOqC9Ka7iVplCTrVFPxerdm+uTsDMc5h2Nt/If559M+fn2bRvNTl4zM7YqgWxO4Sf7n+SWNbfg\nnsxQ1iOuhMn2121HRFa8XEQ6/C5/SvNczj6BBarTm4TSypCh1ArA6MYu+r76aca29iR9tuATaPbW\nLT1QBYPQ1QWO9CaYlSqi2BAwOxkW8jtyGk7bVgN2RgTFUxFKwMqTsd3LpLpAHVsbtrKxbiPrq9fT\nEemgIdhgb1RGhZKzX0AM7up8Kw9feipz442RYduUwNz8HBMzmauTPnH8CW7vvD3BH5DEcn+AK1Cy\n+k2psHXV6PakbUSfjvGuDlQaM5IyDK7c8bqMGcV+h3cpJNSCAgAzuKIYZpF4vE6vbWbmxmBjwddM\n1BctWjBC+VzNabC6JEv3VJQPLeEW1lStSfu0sVI9cQulWHIG3cGcL+rmxvVsCnbyxOWlVpMyYzpt\nF23DwyNMzU4xM1d4e1AroaHv3fxebqrZltBcJYm4chG9e3pz94kUmZAnlCRTXj6BBWpTJ0U5xKDG\nXUW9J7rYAhIWen+nVkTZ6gr17u2jzRfrGx4ImN3mDGvXVZ2/rmghmJCoXAv9HTkNJw3B1P3RrSAi\nRTV5l70SWFiSWcGOp4Naf21Z2+TLARHJ/WYYDPLeljcxNGPa/mVmli2/cm9i7ZiJCdtMQlaOsaNj\nB944U5Dz8hDhZ19aGuB2Jdmly8EpvBxbzQRer/lEHkedJ8qW8Ho6/M20+RrpCXbQE+wg4PRl7P2d\nra5QlStoNmry+y2tAOIREdqqihMZ6HF6bI/Maww25m1FaAw2FjU5tqxrB3mcHq6pvyan/Q9dPpS1\nymI6fC4fPbU9ZbXcL1cujV3K3GQ8FadOQtxNf90n/pIrb7x5sSwBAPV11K/ZVPAP3PJ1cPy46Y8A\nar6/m9C+Pvo/9rvmZ5Eqs0RBDEMMtjVuK3l4aCpyreuUkclJOH7czMXxNVKTobf25ekhzk4OMDM5\nllPvb6/DzcZgJ4Y/vRPYCkevHGVoMnMiW650RDosVQDIlaHJIY5eOZrTPl6nl411G7Pek161tYPy\niQJoCbXwytQrOe8nInREOrQCsEheprdgKEEJDL3OzB5OUALDI4xM56fEF1BKWcs+np1dVAAAoX19\njLwmLlLIW375AeloDbdydfKqPYXlvF4kEmHtTDChl24qatwRql1VXPWNMvSuOs7Pjmftn+E0HKzz\nt2L4YiuAPBUAQFtVG8NTw7YV1PO5fEXLz4l4I1T7qi3XfVqpe1LZ3vEchoMaX+7aOOAOEPXlHuXQ\nGGy07HhZ7T4ByKOEBCQ5Ha/efC3h5/fzfG9cxcXJSSbGhix1AkvH+My4tZvCaJzJSClC+/oYjVcC\ny5obvfxM8StD5ovb4V40CxXkE8C8+XSuv56Ix5pjVESIuEJ0+JvZEl7PNaF1tPkaCDqTfXkBp4+e\nQAdef5jd585lbKJkhfj/tx20hFqSFL2dv6M1VWss+zJaw60rEolWtkqgxpd/pl5LqCUn7el3+W1P\nxV4NVFm8SSzidCZE28xGq5jsaMV/pD9x3NXCooSy7buYkDay1AfXc/YiAFPNsdWnwzDr7cdR6lIR\n2WgINtiSw9AR6SBa1QDN+d1cPQ439Z5quoMdvCbcxbpAK+3+JrqD7fQEO/D4QwWZgJZTH6i35WYZ\n8UaKnnjqMBx01XRl9Q80BBtWLB+iICUgIlEReVREDorIIyKScgZFpF9E9onIiyLyrJVjFzIBHqfH\nspPYEIPOaGdOy/xixd/bTbHlzOsHs6xi5ZXbbua/BJf9gIevFmQSyrTvlYkr3PWNu5idnTKLxsUI\nLpiCFq6DZU1kHIaDnXfspNzpjHZy0y03ZR+Yho5Ix5I5pL7edNoWgNNwEnGFqHVHTCew1wvd3eB2\n23Z9igidkc68HxrB/H7T+aHs/h25HW66a7tTKi4RoTXcWnC3sFwodCXwUeBxpVQ38ATwsTTj5oEd\nSqlrlVI3ZDtoxBsp2BveELD2VJTL8kyTSD6hogsmofv6vsDpiQtcuusOBt52W+KY6RlGBtNnoWYj\n00rg8WOPs715O87xyYT6RZNtTQzc+calgctMQSF3qGz9AfG4HW7WVa/L+XsRETqjnYkOURHo7LQc\ntpkVn89cARRoAkqFx+mhvSq3XsfxFFqsMVfcDjc9tT2sja6l2ldN2BOmMdjI5rrNBYWT5kOh3+5d\nwAOx1w8Ad6cZJ7mcy45JEBHWRtdm/GKbQ815RQFon4CJIUbuoaJuD7hdNHhq+M6F3QAp68qPD5zP\nyy8wPjOecb9Hjj7CznU7F8tULDC2pZvR+KzWZU/AIU+oYr733j29OSkCp+Gkq7ortUPU64X2/G+u\ni4RC5gogTgHYPZ9RXzSvMPFshSCL+b1HfVE6o5101XTREm4paihoOgpVAvVKqQsASqnzQDobjgIe\nE5HnROS3sh3UrtosLoeL7trulEXa2qraip51uBrI2S8AEArxzsYdfPfCT9JX+RwZZiSPzkyZwkLP\nj56nf6ifm5qvT3QKL8eQpMigvP6fJSTsCdNd2511lRvyhNhYtzGzMq+uzts/AJgJaDnmAeRLc6g5\nJ1NylbeqpJWIy4GsnhkReQyIfzQXzJv6J1IMT5d08Hql1DkRqcNUBn1KqZ+mO+euXbvo6OgAIBKJ\nsG3btkW73IJWtrq95yd7UEqx9catjE6P8tye5wh7wrz29tfmdbzlTwX57r8S2zt27Cj6+fY+vZdj\ng8cW69UsRKZk3J6aYntjC22+Bu7/yUNsq1rqLbywKti+bSPDF0+xt/+lnOR57IePMTYzlvL8jxx9\nhC3jW9j35NNsb2tIOt/ittfN9u6exf3dDjfXvfO6FZlPu7bBdGRfPHCRockhurd3MzEzQe+eXkSE\n2954G3X+Ol58+kXOctb68R980Nzebs7v7t7e9NuGwe6TJ2FkhB2x1cRKXZ/d13VzduRsxuux2ldN\n/95+Tsvpivu9L7zu7++nUApKFhORPkxb/wURaQSeVEplKMkIIvJJYEQp9b/TfK7KLYFNk5m+S32M\nz4xnH7iAUnDkMA+d+RGPDjzFFzZ/OOUwT7CKa2603tBDKcXe83vThod+7fmvcUPLDWybjiY4hZOo\nrTWbmMeoC5SmoYndzKt55ubncBrO/P0bg4Nw4gTMZTHVRSLQ1gbu0tXaGp0e5fTw6aScEZfDRUuo\npSgJYaWikGSxQs1BDwK7Yq/fD/zn8gEi4heRYOx1AHgTsL/A85aUSrENr5ScOUcJiUAwyB21N3Bx\napA9L+zD33eEqp8lxrdPjV5lasR6Nujo9GjG/IB7rruHbTWbMysASHIKLyTGVfr3boiBy+EqzMEd\njcI110BjY7KD1+EwTUc9PbBuXVYFUOz5DLqD9NT2sKluE+2RdtZUrWFDzQa21G/JSQFUyveeL4Uq\ngc8CvyAiB4Hbgc8AiEiTiDwUG9MA/FREXgSeBr6rlHq0wPNqyoi8yngHg3gdbv7l2v+F23DjmJii\n6Z8eTBp29Yz1NPurUxZ8CFcTx4Sf3UfT/d9aekMkwSksImVZL6ikOJ3Q0gJbt8KWLbBxo6kYtm0z\no4kC5VFqewGfy0etv5a6QB0hT2VEea0kZVk7qNxk0mTn5QsvM52pTPRy1DwcPLQUpjk3x9b3foCD\nf/0nTLUsuaDC7hBdN99pKbHowMUD2TuTHTkCM0tlDdq+cD/TjXVceM+d5hs+H8T8UWA6TjfUbECj\nKWdKaQ7SaIA8VgNiJD4xOhwM3no90d1PJwwbmRll7kL2nIGp2ansCmBkJEEBAISf38/w9i1Lb/gr\nOypIo8kVrQTyoFJshCspZ14moVji2EKEzuAbbya6+5mEIUoprp49BvOZawENTlqooDmUOMZz+hzG\n5DQTnXEhgv5EU0a8v0N/7/ai5SwPtBLQ2ELQHcy95d+yuvWjm7twjoziPXEm4f3BiUEYGMh4qHTl\nhEenR/nI4x9hfmI8oYIpQORnL3D15muXSkWIJKwEPE6PzibXvOrRPgGNbZwYOsHAeOabdRL9KYW2\nuQAAEDRJREFU/TAxQe/QzzkzeYn3Tq5jqrkB5V6KPBERtlZvxLl1W8oSBpOzkxy4eCDl4b/d922e\nOv0Uf77pg0lZwl33fZYLv7ST4RteY77h9ZqOzRgNwYYVreGi0eSL9gloyoJ8SngvFJQLOH3831Pf\nYby9OUEBgGkSujw+ABcupDzE5fHLaQ//4KEHuWvtW5IUAMCR//lHDF8X17RoWSG7vExcGk2FoZVA\nHlSKjXCl5Qy5Q7mbhEIhevf2sTHYSdgZ4Omh1Ckkl6YGUefOwXRiBNK8mufS+KWU+xy9cpQLoxe4\nydmZ8nPldiWWMogLDXUazqTyJfp7txctZ3mglYDGNkQk99WA2wNuU3G8u+kOvnH2kZTDpuZnuDI1\nCCcTW1peHLuYtmDct/q+xds73mxWDM0ufIIS0KsAzWpB+wQ0tjI6PcrBgYO57XTpIgxcZmp+mrt6\nP8QXN3+YrkBymQaX4WRTsBNn5zqorWV6bpoDFw+kzBKem5/jPd98D1/Z9BHqHRZaYfp90N6xuLm+\nen3RG4xoNHahfQKasiHoDuZelz1ohop6DDe/3PxmHrn0FI7RMTxnEn0AM/OzHBk/zVT/USaGBjh8\n+XDaMhEOMfi3m/7CmgIACCyZfhyGI78eyhpNBaKVQB5Uio2wVHLmWpir98UDixnBv9q8k99vfw/h\nZ1+i7QsPJI0dm51g/9XD/HzfY0yOpqkrpBScP4djLLUZKPzMXmRqWXZzINEUlKq0gP7e7UXLWR5o\nJaCxnRpfHtUZw+ZqwBWrcDn0+usIHDqO60KakNPZOTjRD4NXEjqEMT0Fp07CUOo6Qs7Bq3T+6VcS\n93EYCf0DMjUY0WhebWifgKYoHBw4mFuz+PExOJHo9G37wv3MVEc4/2vpGtbFcBjg8ZhZxZNTGYfW\nf/sR/AeP0f+x3116MxSCVjMfwGk42dqwVRcZ01QU2iegKTtq/bW57eDzgzOx89TAnW+k7ntPwmya\n7mMLzM3D+ERWBYBS1H7/SQbesiPx/bgaRlFfVCsAzapCK4E8qBQbYSnljPqiOAxr7QR79/TGegwk\nlmyeWNfOZHM90R8/Z+k4k3PT3HvgLxmaSd1iMvDzw8jMHKOv6Un8IK58RSZTlv7e7UXLWR7kmNmj\n0VjDEIMaXw0Xxy5a3ykcgqElZ+/5qcv8+ruGeaAm9apCpqepefjH+A/3M97VwWc2XcFtuIi4Utf/\nr/3+bgbu3LFUKwjA415sjuJ1egm4y6sWvkZTbLRPQFM0MtX0SUms7SSzS8lff/zzv2KNr5EPdP5y\nwtDAS6/Q/vm/x3v6PKIU84ZwpBouf/gPcF93Q8rDB/f2MdHZylxVnJKoqYZ6s39BS7iFxmCjdXk1\nmjKhEJ+AVgKaonL48mGGp4at73D+vNnHNsbgzDC/9dyf8JXj13DdeRjv6uDKbTfT84f/A9+pc0m7\nT7Q10ffVT6Os9rZtXwP+ACLClvotuByu7PtoNGWGdgyvMJViIywHORuCDVnH9O6J6y0cTjTltPad\nZe9XhTvu/xF1P/gRa770j2ze9RG8p5MVAID3zAVqHv6xNeEchumQxmwek00BlMN8WkHLaS+VIme+\naCWgKSphTxify5d94AL+wGLimExP0/75v6fqzADO2OJQ5udxDw0jaRaLMj+P/8gJa+cKBhf9A3WB\nOusyajSvIrQ5SFN0BicGOTZ4zPoOFy/A5SvUPvg4a774dSTF9aCAVGtfJcLJP3wfA++4I/t5Wlsg\nFMbr9LK5frN1+TSaMkObgzRlTdQXza1DV9gs3OY/3J9SAUBqBQCgHAZXbrt56dxPmnWIkg8gi/kB\n9YF667JpNK8ytBLIg0qxEZaTnM2h5rSfJfgEwOzw5fUw3tWBStFJDMyVQCpkdo7qJ54CwP/KMdq+\n/E+pBwcCYDhwGk7LtY7KaT4zoeW0l0qRM1+0EtCsCFFfNLcY/KoqLu+8lcmW1I7ldCsBAfxHTmCM\nTdD5Z1/m1O/9GnOhFOeNOaDrAnUYon8GmtWL9gloVoyceg3MzsKRIwT29Zn5AGcuIPPzKMNgNuDD\nOTKW2idgGJz6nV8h8tQLTK5p4dQfvi95kAhs6MLhdLOlfovlzGaNplzReQKaiqF/qD9jT+AETp+G\nkZGlzOAjJxhf386V225m0z0fx3Mx+TiTLY3MBbxMrmmh/8P3mGGgy4kVjGsKNWU0U2k0lYJ2DK8w\nlWIjLEc528JtSfH4ST6BBSJmi0fldjPwjjs4+Ue/ycA77mA+GOD4R3+HibamRZ+BMgwm2pro/++/\nwYV330n/fb+dWgEAVFXhNJw0BLLnMMRTjvOZCi2nvVSKnPmiawdpVhSH4aAj0sHhy4ezDw4Gzbo+\nMzNJH41t7aHvq59OWCFc3nkryu0mRSzQEk4HBIO0hFu0GUijQZuDNCXi7MhZzo2kzvpN4PIAXLxk\n34mrowTb1tNd223fMTWaEqPNQZqKoznUbC00MxIBw776/ka0mvZIu23H02gqnYKUgIi8S0T2i8ic\niLw2w7idIvKKiBwSkfsKOWc5UCk2wnKXs72qnbpAXXqfAIDDCVURe07o97GmfkNuiWtxlPt8LqDl\ntJdKkTNfCvUJvAy8E/hqugEiYgBfAm4HzgLPich/KqVeKfDcmgpHRFhTtYamUBMuh4uZuWTbv4gQ\nbu6kaspLwOHFKQ7m1Tzjc5MMzoxwdXYUq+bDhpZuy4lhGs1qwRafgIg8CXxIKfVCis9uAj6plHpL\nbPujgFJKfTbNsbRPYBWilOLq1FVGp0eZV/M4DScBV4CQJ2Qmcx0/DleuJO03NTfNuakBLk+nbiy/\nQGOokZbrb09sKKPRvEooxCewEtFBLcCpuO3TQOquH5pVi4gQ8UaIeNOYfpqazD4Dyx4QPA43Hf5m\nGjzVnJ+6zODMSMLKwGO4aPU1EOncrBWARpOCrEpARB4D4gOqBbMay8eVUt8thlC7du2io6MDgEgk\nwrZt29ixYwewZJ8r5fbevXu59957y0aedNvxtsxykCfdtuX5rKlh98MPm9vbt5uf9/Yubnf6WzjW\n+yxTc9PcfO1WPA43z764nwHXGDtufEPB8r7q5rPE23o+899eeN3f30+hrJQ56FNKqZ2x7Yo3B+3e\nvXvxSylnXnVyzs7C/v0wN5d9bDwdHVBTuC/gVTefJUbLaR8lLxsRUwJ/rJR6PsVnDuAgpmP4HPAs\n8F+VUn1pjlX2SkBTQi5dgpMnrY8PBKCnp3jyaDRlQMnyBETkbhE5BdwEPCQiP4i93yQiDwEopeaA\nPwAeBQ4A30inADSarNTVQThsbaxhQLvOCdBoMlGQElBKfUcp1aaU8imlmhYigJRS55RSb4sb97BS\nqlsp1aWU+kyhQpeaeLtcOfOqlbOzE9wWGsm3tYEvh9aWWXjVzmeJ0HKWBzpjWFN5OJ3Q1WXWFUpH\nYyPU1q6cTBpNhaJrB2kql+lpOHEChoeX3nM4oLVVKwDNqqLkjmE70UpAkzPj4zA2ZiqAqirzX41m\nFaELyK0wlWIjXDVy+v2mw7i6uqgKYNXM5wqh5SwPtBLQaDSaVYw2B2k0Gk2Fo81BGo1Go8kLrQTy\noFJshFpOe9Fy2ouWszzQSkCj0WhWMdonoNFoNBWO9gloNBqNJi+0EsiDSrERajntRctpL1rO8kAr\nAY1Go1nFaJ+ARqPRVDjaJ6DRaDSavNBKIA8qxUao5bQXLae9aDnLA60ENBqNZhWjfQIajUZT4Wif\ngEaj0WjyQiuBPKgUG6GW0160nPai5SwPtBLQaDSaVYz2CWg0Gk2Fo30CGo1Go8kLrQTyoFJshFpO\ne9Fy2ouWszzQSkCj0WhWMdonoNFoNBWO9gloNBqNJi+0EsiDSrERajntRctpL1rO8qAgJSAi7xKR\n/SIyJyKvzTCuX0T2iciLIvJsIecsB/bu3VtqESyh5bQXLae9aDnLA2eB+78MvBP4apZx88AOpdRg\ngecrC4aGhkotgiW0nPai5bQXLWd5UJASUEodBBCRbA4JQZueNBqNpuxYqRuzAh4TkedE5LdW6JxF\no7+/v9QiWELLaS9aTnvRcpYHWUNEReQxoCH+Lcyb+seVUt+NjXkS+JBS6oU0x2hSSp0TkTrgMeAP\nlFI/TTNWx4dqNBpNjuQbIprVHKSU+oV8DrzsGOdi/14Skf8AbgBSKoF8/yMajUajyR07zUEpb94i\n4heRYOx1AHgTsN/G82o0Go0mTwoNEb1bRE4BNwEPicgPYu83ichDsWENwE9F5EXgaeC7SqlHCzmv\nRqPRaOyh7MpGaDQajWblKGnYpoh8TkT6RGSviHxLRMJpxu0UkVdE5JCI3FcCOSsiKS4HOUs9n1ER\neVREDorIIyJSlWZcSebTyvyIyBdE5HDs2t22UrJZlVFE3iAiQyLyQuzvEystY0yOvxORCyLyUoYx\nJZ3LmAwZ5SyH+RSRVhF5QkQOiMjLIvKBNONym0+lVMn+gDsAI/b6M8CfpRhjAEeAdsAF7AV6VljO\nbqALeAJ4bYZxx4BoCeczq5xlMp+fBT4Se30f8JlymU8r8wO8Bfhe7PWNwNNlKOMbgAdLcR0uk+MW\nYBvwUprPSzqXOchZ8vkEGoFtsddB4KAd12ZJVwJKqceVUvOxzaeB1hTDbgAOK6VOKKVmgG8Ad62U\njGAmxSmlDpPG+R1HSZPiLMpZ8vmMne+B2OsHgLvTjCvFfFqZn7uArwMopZ4BqkSkgZXD6ndY8kg7\nZYaCZ6oUUOq5JHbubHJCiedTKXVeKbU39noU6ANalg3LeT7LKYv3N4AfpHi/BTgVt32a5P94uVAJ\nSXHlMJ/1SqkLYF7YQH2acaWYTyvzs3zMmRRjionV7/DmmEngeyKyaWVEy5lSz2UulM18ikgH5srl\nmWUf5TyfhdYOyorFZLOPAzNKqX8utjzpsCKnBV6v4pLiRKRPpUmKK7GcRSeDnKlsqemiE4o+n69i\nngfWKKXGReQtwHeADSWWqZIpm/mMhdx/E/hgbEVQEEVXAipLspmI7ALeCtyWZsgZYE3cdmvsPVvJ\nJqfFY1hOiivgHIXKWfL5jDngGpRSF0SkEbiY5hhFn88UWJmfM0BbljHFJKuM8TcHpdQPROTLIlKt\nlLqyQjJapdRzaYlymU8RcWIqgH9USv1niiE5z2epo4N2Ah8G3qGUmkoz7DlgvYi0i4gb+GXgwZWS\nMQWVkhSXzn5ZDvP5ILAr9vr9QNLFXML5tDI/DwLvi8l2EzC0YN5aIbLKGG8HFpEbMMPBS6UAhPTX\nY6nnMp60cpbRfP498HOl1F+n+Tz3+Syxt/swcAJ4Ifb35dj7TcBDceN2YnrCDwMfLYGcd2Pa2SaA\nc8APlssJdGJGabyIWWK7LOUsk/msBh6PyfAoECmn+Uw1P8BvA/fEjfkSZoTOPjJEjJVKRuD3MZXm\ni8Ae4MaVljEmxz8DZ4Ep4CTw6+U2l1bkLIf5BF4PzMX9Ll6IXQcFzadOFtNoNJpVTDlFB2k0Go1m\nhdFKQKPRaFYxWgloNBrNKkYrAY1Go1nFaCWg0Wg0qxitBDQajWYVo5WARqPRrGL+P/wor8NIO7qG\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f706856a438>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.rcParams[\"figure.figsize\"] = (6, 4)\n",
"\n",
"# Plot f(x) + contours\n",
"x = np.linspace(-2, 2, 400).reshape(-1, 1)\n",
"x_gp = res.space.transform(x.tolist())\n",
"\n",
"fx = [f(x_i, noise_level=0.0) for x_i in x]\n",
"plt.plot(x, fx, \"r--\", label=\"True (unknown)\")\n",
"plt.fill(np.concatenate([x, x[::-1]]),\n",
" np.concatenate(([fx_i - 1.9600 * noise_level for fx_i in fx], \n",
" [fx_i + 1.9600 * noise_level for fx_i in fx[::-1]])),\n",
" alpha=.2, fc=\"r\", ec=\"None\")\n",
"\n",
"# Plot GP(x) + contours\n",
"gp = res.models[-1]\n",
"y_pred, sigma = gp.predict(x_gp, return_std=True)\n",
"\n",
"plt.plot(x, y_pred, \"g--\", label=r\"$\\mu_{GP}(x)$\")\n",
"plt.fill(np.concatenate([x, x[::-1]]),\n",
" np.concatenate([y_pred - 1.9600 * sigma, \n",
" (y_pred + 1.9600 * sigma)[::-1]]),\n",
" alpha=.2, fc=\"g\", ec=\"None\")\n",
"\n",
"# Plot sampled points\n",
"plt.plot(res.x_iters, \n",
" res.func_vals, \n",
" \"r.\", markersize=15, label=\"Observations\")\n",
"\n",
"plt.title(r\"$x^* = %.4f, f(x^*) = %.4f$\" % (res.x[0], res.fun))\n",
"plt.legend(loc=\"best\", prop={'size': 8}, numpoints=1)\n",
"plt.grid()\n",
"\n",
"plt.show()"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
juliusf/ipython-notebooks | erlangk-1,k CDF.ipynb | 1 | 25845 | {
"metadata": {
"name": "",
"signature": "sha256:ee5d0399412b6a5f8e72f81524eb11c4c3e1af0c8d5850634cc2f00b96b5390a"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sympy import init_session\n",
"init_session()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"IPython console for SymPy 0.7.6 (Python 2.7.6-64-bit) (ground types: python)\n",
"\n",
"These commands were executed:\n",
">>> from __future__ import division\n",
">>> from sympy import *\n",
">>> x, y, z, t = symbols('x y z t')\n",
">>> k, m, n = symbols('k m n', integer=True)\n",
">>> f, g, h = symbols('f g h', cls=Function)\n",
">>> init_printing()\n",
"\n",
"Documentation can be found at http://www.sympy.org\n"
]
}
],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"p,mu,x,k = symbols('p,mu,x,k')"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"f = p * mu * ( ( (mu * x)** (k -2)) / factorial(k - 2) ) * exp(-mu*x) + (1 -p) * mu * ( ( (mu *x )** (k -1)) / factorial(k -1) ) * exp(-mu*x)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"f"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$\\frac{\\mu p \\left(\\mu x\\right)^{k - 2}}{\\left(k - 2\\right)!} e^{- \\mu x} + \\frac{\\mu \\left(\\mu x\\right)^{k - 1}}{\\left(k - 1\\right)!} \\left(- p + 1\\right) e^{- \\mu x}$$"
],
"metadata": {},
"output_type": "pyout",
"png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAA3BAMAAAAReEuxAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMu92q4ndmc0QVCK7\nRGaiMfZFAAAINklEQVRoBb1ZfYwTRRR/vXbbbrfXNpAY9A85RA2RINW7C16MUCAQ/Ag0OeVDE20E\nhXASiyBoJKEmCicRaPgQEzDdxAQDYq4S9S/0GhNj9Ag0Gkj8R4oaD4PBXkTgjpDzzcxud2babbt7\nd7ykO+/93sfs252Pt1OAhvRwsmKibHuzwrtnuICegvswTjz9xYr1c7CkwrtnrICezSn3YZx45rIV\n6x6Ymq8IrhkuYCjlOoojx/OW9Szot16KBTvkuIC3K4cVng7rJvusl2KBDjku4O3KYc9n3Mtf7fB+\na5lzASckB09J6PUiStdjFqSkLb457m7BLEJicQEnJIdTQpfgi4Fn+o8AodNIPwAMiurGklYQbeYD\nC3iCBMzChOTwntglZMBbmOQxwdZkK/dSTLReG8yK2iAIASciB29S7BI6IRy/QzHBKcdPSPdkauza\nTkmBHfABQ22SfhzElrwUZB8E876HTHD26KjJNtnOlOzUNj6gtuVqXDIYu8gt3SxYUB9T0NaU7L5L\nBsZD9rSBNwHnBiZ34DBZgREZoLY/+XM3gPOFCCMgTQIguwp1Z/z+jq878aGTHsadlBT405BcrCsF\ngDMYngEH4c/4OoBIxl2HywHWome4hBfKq8nIan8G4BIC407BNOR0TX8HImWA9RieArAKXsh+iotq\nyl2HO0EdQU+/jhfKK1llOJQHOOouXn2vnA59WRVGQBkGmIW2FIAsvE/8PJiYC8IEQhgOWopAkkFe\nhWCBBJpKLuNNWAG9AdA6DOE2lgMDAP4lPbnMAW86kEF3koPJR+Mk4ITksAXgJY1MglyajSUGgGcI\nnx1ULyzkRhpSACdZMs/GkslPjeHLhfMNfV0YvALaiEImwW/YA5nTDDjmLUOX6zntL0C/nmRzmvGh\n7DzwYg8TMafVaxC4eRdEC55peP9P4/ClQOtIuKyVAAJpRJ1TLgXbP9dxjUvg/KL8Bf0sfIOBtjoP\n1tAjdL07juv2hXNz8miLb5oB6sKuzisIBIt1I6gpeAKUOZOxlBOo7/V2L+4udCgy/kD7/udLiOwW\n7CqCWN5WYIu5aLEG9wH4dOje2BEDX4ZCy+kV/HnwZRjLrid5oZrH7WMIunyZDZJqiSn3gPgJrrWZ\nGqHVCoIoC1iJ+mIyeAmiMW92CX6dt8SpbieziKRNwPAgD7MO+ZJaGWLBkmwy3QSwWK/wBFNYd6ba\nbOXy1sRZe4os0xkRA1gE/eCBPQj30/zohkSMBgzAcFAzBiM3xgeFvxgpAETzhlo1GG3ItA/nLZ5g\nH5oKsZXLW6Y9zJojm0kOlonx7bEB/kb4Jv7YWnf0hvF8TomLX9i8Oxat6prL+lblcc2PMU3IiGKt\nyFrB4onNQFUICsysCX9soF6Swz7JRB2GRYdx//JIOABZizi6zPG12L5s//HD5eWQZEozB86UrEUW\nRWo/EzHPirmQQ1Cv4JQJDWsjx/qVVOXjRlQ3kNRuuoYRqy2b5i5VF55rzzKXGjk0iMXUtLw1LI0K\nmkhCDszmYPtbhl1gbfsfpQOPdXcZsrPmfF4znjutETlntzmES1YQo4ImgJADLoG4VvfAl0SD5Ndp\n4+6iPQCHYswVx6RAbnPg7sesoElcIQdaQZ/U1Y1Gj9yBkXAPTQm+B9v/Mgw9GdHDbQ4tRVyxXib0\ntllBk8BCDrT6XPD7XGPYwhSr61GnVI4mLG+eU3p7d8zo7U0jFnUQtIz2JAeTjAoaVvb2vtjbS/ct\nui7RHK6aVmNso0nbAG7fAzeWzAqa9CG8B7p2/WfbtTNFC+YQr+3iNgd+TgdZBU06EHKgc/o+PJ6q\n3bUz1JuBQ/naLm5zUBJWPKOCJoCQQyCNyCOgmmur5eGGmzO3ZOPmNgd+jzMqaNKDkUNgwbWlRgXt\n3XTFpmsKe0p22uqy185SzsG2oqZnx1yUHos3KmgCmO+BKhtU0NQGT4uP3E857qJtPY3leQx3lASH\n2rKtJUGFFbX6bUqAiECK1PnYrrE0WN6aRFciJvxqYqRtUEFTU6zR8RRFogOg3KJlb39Z0jQjkpvF\nKSqRdpbAWJpx555WbVmpoCUv2wqas6OnxeRISKDHAe6hZS9+UDonUi5HdclP/X4Z5oDd4UdvhfCN\nGVSpoE3AaK0sJQUnktNi3F4kwsG1LEbK3mhG0jQjzkSjC3jDEs1DSG0DuMHhYnnLKUz2ssnUacl3\nhJKRDfZmSQ5BHVoSsqqxTFebldV2JAfYBXBvtWpsCDnLDSYjr8XkMK9myckvHsk6JlotvwuD0yRP\nmgP2t1bCxyyewQi5X1b9VJQiteL2jltkOCnhTYjhEo6ZWwc/miXZ0hwuAXwn4WMW12OEvsnVYfwF\nenDsK1WrGiF+HV2H4lVmNIejALhxjS+Rh7V9N42p7iBV8LoYFbbhFUtGRcfWIZFqNHADL0hGZU15\nmgOeuz5LpXG8kBxWf5GRI3oTiGAOXpaRrK4rkxz8jy6psjFzqPxFVmXhEsCxpA6pI5rk/gloeXJa\n58lKiiZEMpZysZyel2xpDrgO3inhYxZxTkfK6i3plMCTBm/e7Z9BZE7/A7liUro5mgPO6XEnPC32\nFWBIyuGrZ1YspgfH+zLOe1QSAE/hgWLNHLaCOsN5yPoe+G7xuQ3GRau9o6PXcN8oNlnzic44BPHP\ngMgmEYXNs9eU6NkxV/NJJi5FPC22pWbK3lrOPbVAhmlt9jrXGjwttqVmyt5azoO1QIYp0gu3t3Si\nGbA1VjO2qvqKOrWmzdlx/XgNtfgNZEN1bsXGw4C1gq3e/onZujShkE6LOY/LHO+Mta2oI3Vmn7Mu\n0Pp/ikdJsezYWDcAAAAASUVORK5CYII=\n",
"prompt_number": 5,
"text": [
" k - 2 -\u03bc\u22c5x k - 1 -\u03bc\u22c5x\n",
"\u03bc\u22c5p\u22c5(\u03bc\u22c5x) \u22c5\u212f \u03bc\u22c5(\u03bc\u22c5x) \u22c5(-p + 1)\u22c5\u212f \n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500 + \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" (k - 2)! (k - 1)! "
]
}
],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"F = integrate(f,x)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"F"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$\\frac{k \\left(- p + 1\\right) \\Gamma{\\left(k \\right)} \\gamma\\left(k, \\mu x\\right)}{\\left(k - 1\\right)! \\Gamma{\\left(k + 1 \\right)}} + \\frac{\\mu p}{\\left(k - 2\\right)!} \\left(\\frac{k \\Gamma{\\left(k - 1 \\right)}}{\\mu \\Gamma{\\left(k \\right)}} \\gamma\\left(k - 1, \\mu x\\right) - \\frac{\\Gamma{\\left(k - 1 \\right)}}{\\mu \\Gamma{\\left(k \\right)}} \\gamma\\left(k - 1, \\mu x\\right)\\right)$$"
],
"metadata": {},
"output_type": "pyout",
"png": "iVBORw0KGgoAAAANSUhEUgAAAvkAAAAyBAMAAAA0ItkVAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAELvv3c2ZVESJZjJ2\nIqu2f7MxAAAOX0lEQVR4Ac1bb2hk1RU/k8xMMjPJJihCFWumLAjdshiktgv1z2Cri6BuLMZaCjLU\nrbTQuiPux8pOab9oWzKC2lqiTmuTDxXZlEILIs34pbBU16AgxVJNrX6oWs2K27Xd6vb8uX/Offe9\nmTdJNnph3z333N+5597fvHnvzi93AT7ppdL+pM9wM/O7aDNBH0PMQx9DzrOfcnwukeOpRDtqPhF4\nal1pVle0O3OQMFiH9Lcr61H/tueIMiiHXaZyiRmuO+oe5FgSwDmfl3qy3jfgJoBdxHPt9TPvvHZV\nB+AFAAl9S8XhIIXdDeVwJge7Vn7j7mnEcqI/Hvjond3/AcjIYSeYf+h+yHiZAbqEs9LrDjpzNUaQ\nQiq3SEUDZpcXTmDfHPXX3gOgGxJXK6El8ppCg5SathXUHBx48jQK+xjFc1ytAzyK46fm8BPMM+xg\nTLRMHTJ5Cc1Be4a2C1+UkFNSHUsboLAm3nPuJPYZUvsIrTpMdLDiULYExoiplmmEVer4ISSlNdJk\nJydaXQcYkVlEOdQEU0bZhCtaphqjcPG7yL5et+rMa97NwHHiFcsVUoXXsZ5pTxDqXGrwtJowip+L\nhBZmDQYrGmQBZ5ZSODjF3991hAeTRMR+OSuHn2D/AfP2RssMAp/Hael1B535GsUO4SpzjB5vcJW4\nhOyXWtjN02rBj9A0oV9zQTzIg64ZGBwcePI0rmWQJCL2xyAjB7O/uRyp84iXqWHEPvh166689tiH\nhCx1qrevIJNNH3bv3qeP0/C42B5X+DWje58xPC0A2giaUDQPvzcNdxnA12H5SxJVm4WJdSg8+6+f\nLIYJzKAa5XPqzipP0SQi9qMcFu0naD1bq+Nl6vGYfaJgC4VvrJkf3P/DNj5Qu36gzuutSp2bIfvV\nOXSaae1B04QuQfXKB+rQk0EKH5z/qX0cDJUGFJtwPvy6dw0AB4s/vArK59S9xTq3JJGwTxNVOSya\n2c/MYVH563iZOpbZX9Ke4e2jdIMfeZoDiy0XP9m6Daob3AzZH2ug00xrP5om9DC8AvDtsTUAGmTs\ndA+7uJSaMNOC++Gx6XvQ3zDeZMUolVP3r7a5JYmE/UQOi2b2M3NYVP46XqaOZfYPa8/w9kwPYw7d\nyoGjbYDzvkLlGwXcy1TkXRyyX6OPxEyLbm8Tugq/xAdCBR00SPkkXqQg9fjWnIavUpODTUdQMUrl\n1J23S0MSCfs6h5kwgZj9zBx6zHx2vMzCzcTONSsUz+yv5hspC1Waw57rX6ErE2dxuMUYmUVC5+dv\nvmx+vkluvzg1LRPKs6j8GFHETPG5NyiAClL/Lar/R5dMZgRlchJSlSvFlkSefZXDgv0ErWdrdbxM\nPd52sD+B77TC6cKpSRxYPXnoeT3T5GThvc/bDTOt/T6Utj9Q6eCFBplZmWmtcTAcBLgOx66dhgJu\nTxvijK6C8jkVoPZfbpg5CvuJHBbN7GfmsKj8dbxMHcvs87q1dzh7Em/K6kbhA3pojHR9LD6JH5/m\nZsh+4q1rQ5cIWunhhQY5CjNt+iSwXA2Tpypw18QGPNPnrSson1Ni+Uq3BxaTSNhP5GAAXpj9s/LW\ntcu0mahm9nnd2jukfSmKN3U4TexrNWuqXjN7xpD9chOB9BMcC/7kt6F3UHsXfVw0yGswtdIpnMRW\n4X0of/iH8VMjG5NdfB800ZVSBAU+p8LQ8w+LSbRap4bLQQ1fmP2sHB6W24qXqUOZfV639g5p7+bb\ndbmHYfpLu3Dvn9ZkJMt++R/vv4n7+zZqXAfPXEyd+LXDu3C5h+at+I9+hMoge6D6XYAD+GGM/Xux\nd6xXePuZY7/BPgpOK4ICn1OBRuvckEQvHXjve9ikiUoO7jMXP0HvrXW9PcB6ItmfskwFufOqG7tm\n3c6bqbw6hDWqK2I9Zkim1g22E+ABZ1r2xfGi8+Mj3oVOzpKb2feDjGP3rjmFBx2s/Qblc6pO8/ZR\nHjTVRMMOSOR4waqwIeymsMmtXSspTnL5ZUYAWbd1ZyivqdrlWxJ0tG2DAZa9eYszx7vORGNRNapN\n2+AnPtzHTTdIFZujPQuhWgdrv0H5nKpzoaca1nQ5rMPXYQ6iOR6WxVAfYqzgRlG9fpnKKaas27rT\nlVcWQy3E1SWxVnvOAyN4t0opsKJoW74uBFPcazvOY+MRvrpBLsDmq/qGssGftmG2FlR6ziMti1K1\ny6F8Ytoc0proYB0tRcTQKPRY5DEOt8wIIOu2bhpgKjldEUMtxNU8M9wdNp2H/mhhyuGTPWsGdbhs\n/F5LkfnRUvkvH+LsYhXsyGzw96XfXwWVnvP5FY9zlp+ocxnD5pCmV2EDHL+eAw81MhVYt8woJPxc\nrsD+hekIxK/npLcwy56pddXxsrJTzScDL+1jqFTXpJZr5iA2OGJfRyftQ8HYtndgDgHSx2pUWBtJ\ndTr7meqoXaYegu1w3bQXgAcjkGxNI7eoo1P1qONsO7aB/QFTNHqrVmF1hGM/nwKrQ1PssQOfgTG8\n5StN7PTqrkO6e/93AMcBLjz+l2M9EYjxvTjnYDtlDMX+u7iuYYvVW3Fbio9WEXD1GI79SgOKgxVY\nHZpiP/7Pq2EC/fQbMEV59fc+7umuhUKnen0ROV/ikUYbXO3kZTj2NzEzq7fCfgw2KqwexrFfauZR\nYHVobE+uQ7l9D/pJ/1DqrkO6e/8WwI1FZbpygrRgUUeLs3Bm5wpPidmfGpx0g9DvyioGoz3C6a2w\nD4ONCqvlScd+rMAqyTTHDClndRqg08FEo238yWPUXTWMu/eR+rETKHeV6ggGUUeR/R0tD87Pf3l+\nPt6DZ03iEC5uE4X1VmbfqLB6DMd+PgVWh6bbP19BP7Gforw69pH68hzipnp4sew3yN7RMtSTR/8W\nH2KWrLfSk8cKuDrWsX8wlwKrQ9Pth8mdobw69sv4kumsIe8rgHcUbcfwE2twtZOXodhP3e8Pnq38\nCsW3bpo86djPp8AOzrZIkJFuoO66KPvcL9bh1VZnbPp5mED2zVuXvgw7W4ZiXyshQ0yT9VatwupY\nYn8G151PgdWRGfbfyZ+hvNK9z3rvTAMO/bW10LoE6NfKHTxU+n6/1uXOlMsTCd9TibZrJoGuAyz7\nmaHVFQ8+0vZ2imXG0BGMKvMVv954Ry73uOEuLIYW8RPIp8C6ODIsMeHqmtQ13khTXoHF0AN4tx/5\nzrMTi3DRsxf+ootoVoUDpQGdpuCP68Luhm25GkUrlgJvhK2cqDTsp0uCL33zc3I+srjOaRd6Lrsy\novRvqU4yhf0+8iT8NK8CS8NFZzpDRbRJmH7KK+m9bzDIXCZn2dAqm+9GmgE3w4liD0pOnsF3R33T\nJyrvk2FTJcHCOjzW5vORr24wbKYp6MQ1mb6U6Jcc1fRgxnbxnddjy1wWdSNpR2c65xRivMuNZeVK\nmFVsX659Rh1N1RBZgZtqaTja7qAkPi+B/sYXnag06qUDJgYIm6mSID6vR/EAVgcfzA2GZ/wWT6Y3\nmqHL8IhYe50jaRS6GQpsEiht/htvXR1dpdnbUlljK1T4bCfXF6D6eFp7jDqauqMjbTBFruO9AkmB\nJ4V9/HpfEQDNM0VkrEzN0MwiDDVO3ILtwr/Az+K2eI5dIxumJ6yIfZ3eaIYO1BErW56ku1F2fSam\nD3eIYPab6uiqXl1FhshWXqEb/uUQwNwW5rekmYKpeFqxXMfskxR4pbAfnagM2M/UDCXJeAPrKEfp\nBLFP5yNH1xnndofcchdiP0gvmqHrN0amPJkEAjwZu5SH2ddHV9NW97IK6G9adfTSNNhD5IzlOmai\n0iSxiJ88ka4XsE/APoW74xz4qwV3IziBooTXkn8cEaWQ2A/S85TJt91FdFBzuoSyyNHVAavLNws6\nURKXPehKkeuY/So+ET5r2adfGAoYsE/APiUR6pEL+NRYwpcKVlTwexYUVgrNh6/GwIizUyr4E7Vp\nj+8RMSKaDlhdvrmY4zIJ8H5sp8h1zP5YA+BNy35C1wvYJ2Cfkgj1yKvRRAVwV1dch3wPW6wUGvbV\nGKIZJrDb0SyxDmrufSJGRNMBq8uXeaSRhtuHzhS5jtmvbQD8zLI/2vZAjAnYJ2CfokO1JFiuYxAq\ngJWWBC+0pTZXUQoN+2oM0QwD6PY0RAc17BMxIpoOWF2+3FO9NBwlSZHrHPt/1uxboFIvHTBtcOMj\n5myohh2nBnI5sSLeYlNqczVKoTz31RhnjX3RQRX7IppuC/tHp4O1mcZ+rNVhTAthUscbAL+17Cd0\nveDeJ2Cfkgi1yLEm/I33gjUzsyq+hFUp42MYlUJhX43B2zSF2zbzIOug/sljRNMBq8uX/rZU2B70\nqsOYFsPsm9eNLH+kGwAD9ge8lxKhNsfvAZ6zCqD4vmC7uC6yUqjeumaeSwFqGxuigxr2kRgjmg5Y\nXa4JjH+YCnsUvXwYM+xl9stNKFyG936d+irrATBgH4H9SiLUQCeve/jOBiuA584ZF371VZlhpTBO\nf4fCbKdpzphGZzoHrC7XFEaaqTD6Gvc7KHkjpJ+oNOynnaiM8tBXN85Rwr/VYcet+E5YNyG46VBF\nlMI4PUaclSI6aHyms9Teejr+b+DxMP20wRcD+A1By9777AyBAY4bYWjQPzmrmqFA8obqUbJiEBFA\nttjYZb+CPI4nZtDqcqQ1/w08Qlabkcs5Fp1FxnLQuk+3QqDuETsMDfqNAmh8wVb+8gDoxggjAszW\nGqM9He+JGbQ6HZVhZzx4nAiUEhYelFRHP5PYBDDZjT9m12Kf8ZwX9JTXfTP8IvgxwgiP37IVnET1\nxAxcXY7Ev8rCZGuDCc6ydb0EMM6UHWoVQBvztjWSSqE/ebrXQ7bXSuxkLTEDVzd4FuPBM03js7XB\nJzUM7UxdLwlMxPULrSa+FeV2HGw8Jn0yIhO/1Q5LzODVDcx00TRB/g/oIxrhxmkAqwAAAABJRU5E\nrkJggg==\n",
"prompt_number": 12,
"text": [
" \u239bk\u22c5\u0393(k - 1)\u22c5\u03b3(k - 1, \u03bc\u22c5x) \u0393(k - 1)\u22c5\u03b3(k - 1, \n",
" \u03bc\u22c5p\u22c5\u239c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500 - \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
"k\u22c5(-p + 1)\u22c5\u0393(k)\u22c5\u03b3(k, \u03bc\u22c5x) \u239d \u03bc\u22c5\u0393(k) \u03bc\u22c5\u0393(k) \n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500 + \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" (k - 1)!\u22c5\u0393(k + 1) (k - 2)! \n",
"\n",
"\u03bc\u22c5x)\u239e\n",
"\u2500\u2500\u2500\u2500\u239f\n",
" \u23a0\n",
"\u2500\u2500\u2500\u2500\u2500\n",
" "
]
}
],
"prompt_number": 12
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Check if F is correct by deriving F, then subtract that from the original function"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"diff(F,x)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$\\frac{k \\mu \\left(\\mu x\\right)^{k - 1} e^{- \\mu x} \\Gamma{\\left(k \\right)}}{\\left(k - 1\\right)! \\Gamma{\\left(k + 1 \\right)}} \\left(- p + 1\\right) + \\frac{\\mu p}{\\left(k - 2\\right)!} \\left(\\frac{k e^{- \\mu x}}{\\Gamma{\\left(k \\right)}} \\left(\\mu x\\right)^{k - 2} \\Gamma{\\left(k - 1 \\right)} - \\frac{\\left(\\mu x\\right)^{k - 2}}{\\Gamma{\\left(k \\right)}} e^{- \\mu x} \\Gamma{\\left(k - 1 \\right)}\\right)$$"
],
"metadata": {},
"output_type": "pyout",
"png": "iVBORw0KGgoAAAANSUhEUgAAAz4AAAA/BAMAAADTUQDTAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAELvv3c2ZVESJZjJ2\nIqu2f7MxAAAOyElEQVR4Ad1cfYxcVRU/b3dmd+drdwJC5A+YlSYYiU3XALEo2IkKhQToYtiK+NER\nK4kB6UKI+Idml0BMICYdEGpMVjp+UBMRGVOJCWncASOxsLYTajRKdJePaviQLhXalUrXc+73fffN\nvPt2dpZdTrLzzj33fL1z5t13329eC7CWKdtYy9m3z/077aeN2d9V1SA3rNjVwNy2GpIwcshfqAaZ\n67+s+CUxPQ1fs9Sk1MzdXJbsajgWPr4asjBzuEwNfgiHFb8kJtjoa1YqKs3+smJXAZNqrIIkzBSC\nN9ToSphuqsGSmDt97e/S7ldXfx7Qia0ObqCs8tgIs5NqsCSmb9TTbFfugNRcVf0pLMi0VssxU9k3\np3KZ0MuOkiVhguOe2td9U61wq6o/PcOeJ7Biaumf3aFXuCs6Dfs9TwfH6kpxVfVnQuelEnx3maEb\ndfxMRfNL40qNCLtczRI+DJC76IMAt56NVAS3P++DwXGYuvGArtXjwgGadpfGot27GUXrdSp1KwV7\nnxyHfqrUBwD2dOofMuxaPOV8y9Gz1ggG65Af3puTQrc/D8FQPV88nJr87ZaTr6/7L0BhGIJ1ZTRA\n065S7m3mPpQ/gMqoq9EB3ErBk7kRedID1QHJLjWPAj/BrZb91dYIYBR6Gr/OSGH/iOTk8WWYhRxc\nh8PpYYAHAdJF/KvQ9Ch9dI8G57lvO38AnVH3YpNnt1Lw4Vy5KoI+dvutWIjOiC8Q1jYhL/1Lz/sh\n3Rx8RowK20825IRY8S6DH6PkHfybngPoAdiP7NA4fjCOjl2i0hx3rPJ3MupSYO42olLwRXitLoJu\nWlzsOPzBJroY0DsOHPWSyKRTzYHL4xPZy2dCbh5XQOpPH8DFqLSzSJoxpqTSCT06yazt/AGMjDrx\nHmubtFKxDl2FUhVlmVFzwngW5eL0uDnt8P1vFI7fMpsp4wpI/ekH9ojGHxxjTB1fCQUbuL6dP6ag\nM0roMJl60kol88600yN4SFezX6lDbgTyczjahX+cD2b+/d0pbF8FJWE6Y+brQtR36cwva2f9YeoJ\n3h+h/znYg9BYpGnYVfvxXoADMHDfczPPu3pvcRHPPzIj12YZJX6V6ihg5gSal+64985JyJQhVcHR\nufjH+TPgp41LALLW5YWzSANXwl85Byl9edH1g3egGi4xC2e8f2O0KakkoPsBLoXM4Ga4zzEawL0i\nEcs/OiOu4HwuD8rsVSkndiJB//9QfWIf2eCOq0Sl3qz4e2F38du4XJRREqJD48GNQqSQBXn9UMP6\nTzRoOspUmPketgKiHH9Jz8GjjkVmgYtY/tEZOTZCsCwos1elWmXgJw+Oot6Oa0kZm8PwIvzaC74I\nn6GJ3Dx92vTiL54uCsljemZ6jvjeSdwlvIUf0aYk9ydsTv8bUMTt4G4ZUBmnxb6G5R+dkdK1meVB\nmb0qZQdOPDoPLa74xyh+YnO+SuYUVfJ0dUX25yRNOKT7k/rjYZqNaq1j1VaAzSEUF7eD6xy9oTIX\nsfyjM3JsuGBAWOKoA5TZq1ItMvAVH2lCcCI4XgDYDnA5Htj6JvjcCQjwXlN2nYmVPzTB+0PrW6le\nGm9Gm4ZsYoZ9eFesNuF+CI45mrPDTMTzj87IseGC5UGZaX2LrVSLDHzFu2uQnQ8WcHP8SSgcJ5SA\n7nqcvyU/D7gri9ofXAiQd0Pw/vTUAG8WpclqtKlr1k6SGobZ8SpshexHHLWJChPx/KMzcmy4YHlQ\nZq9KtcjAV/xoFQaH4UQGgjeh753foBkCNJwfON4zX6jhvaTiOvs9BHJ/bUxOD9MgMwfwAmJy2J8o\nU1Lxp1IZdjw3Dkdhb90xOthgIp5/dEaODRcsD8rsVSkjg6AM/4LMU/teNWRx7M452g/vaUD/sanG\n/gaq34XbLsYHrz2x/+coSE/iR4jyN9FMiP685Sg1baBMF2H2JmSl6eMhTWf4sCMRgomvzeSnYGBh\nKuLrsKPGlHj+kRmx+UQoc8tMs+73w6tS4jzogAvRCXhicFRvHiE23OyocDAomVQTFM/mDgkN78OV\nSlOYIqDdjq5ug3QfZob4PBZBGyYjhK7IB2V2oHfbDSG+7rc+aaUGq4V5qKdrAP7hhkZEJr0NwWQr\noHgmmhIT3gf9u4cwpdNrTc/SNnm0xfxFTM7R8LDKtmZYEjnG9luEoVyUmZZmXK8oUzdYYQOJLSc0\n8K6U+EEoNZnFKEOUtXe4oXmKhDRb50eA9QaPsmBUTvgeeygDImm6nw/tz0BonXIz9YernGmr4E9J\nhG+w57HwDI43FSOEjihfDYkwlIsy09bGgt4No+CcIxjJ8ZO4UqXi4L1NmIY6f5L3CtdLxSHCxVTQ\nswaPIlVtOR97VMuZNL04yqS/IaR5SuFUNviWEKkD3cvwfrjlC0piMH7wfW/TMCGWhwoJqT99JvRu\nzR/E/gQjlogGCSs1UZy9/cz5+6HK++MVLvWOE5X2bAY9YvCe7N+EnjDlRQ7b2v3hSLfTn7CRNfbr\nj/7iCeNIUJ36Y0HvViTqD3zWEtEgYaW23/T0K8Frd8+gM+9wEf1x0uhUkKloD3ev33eAThar0WAH\nXDjo+uE63eiPH8pMBRNZcOidhopYf8hRcgqmnmoKK3qeFeQdLs0XeGnXlSM9sEqqvjSeGWYDuz+4\n90RK1J/A7/o5F/3i/i9VgTZ4PPtCW9A7y1F+sP48JEeJjnc1C1VuYIB+/uHSC4miLUnZ+AWiMP4l\nxCuYF7s//WUSJuvPf5ifuA/61uKWDOHfNni8KJgBvVtuWX+W9Cp+4aNwep37yrGvIOf59eMRrmcB\nFrtJ1IveSYDTPk30+QCOi5eGQusbR1J5fzzyobMMRH/aqFP0jfjHsfk2eLzoD2UqoHeZMVoDsP5M\nEyfOg9g2cdUUDH5s5kekHCLen/hwgP3pOlEakvBdgZ4RXHDGxq65YGysQmJ2/8H+PDA29qmxsa1S\nM/boub5Rf2LxeKM/Anq3wuv+WGKPwdBcpJLuT0y4leiPsb7RnaBUYSnb6xvf4yVa38Dv/rMZo23n\n2HxrPF70hzIV0LtVVtYfZyNoqbQYDFUjJ3h/PMKtxP2np6ZzxDvBT4psaPdnCfsDz/7Q/iAWjxf9\noUwF9K5TRo71Z0n7g17sT8PyxQa8Px7hVmL/RoC2pKHhHL43QmT3p69Csm5cP34oMwEuuOzOKeid\nhopYf25QwwRMfhROb7r63uFSof11LKAqY3kr2r/S7bxbPg7I/vS9+OYruMOaJMeyPyHIWcbE48MG\nH4HvSENDDZeleDzehd6NOHDzpqtqANeaoihelCRbNyefehpNw+QfLvR8itBMsK4cdsdgw1dRelUC\n5NVwogFt/CFUkuwPHx9iB9kfhJydl6qhcMPZdfZKd2qO22zhCyUOci8tvv7CJlxKpOGgrlEilNnI\nlMfQn4URzVucA0ZTpfwoPlzvvOWpPX5bwDuyN/Jq+N2jeb09G6hpKcAUG9wjRFfjUWsK4VlAL+yM\nIpQrct5QFzPYoKN8cVKGqCbIG2UmfSNTaS+PmYbkwsdwSdJhhZbj+HBD4lyFC4KRh8ZD/hR+i7+r\nshupg7wK3FkphhxInBSfWdSr0raKRLq5lEHFjubzAOcxoLtU5mo7dKK5kyga5hgzM+R4ONNLgsfr\nTHkI4/M0g7dZutmbJWHp2yotRvHh5LkKBxfjcWfR8Ub3R8Jv8YVNSqYvDPTKdYltdFygVwHacNtb\nDcc5CexECXIOv1QNcD7AkTqhz0Oj3MfBBj/iJ+sP/nClDFFNUhKUWWcqrdVxveLCTLgkbgHCFnIc\nH45vJKQ+ewp5QI70kfpD+O0nWiCvVn8igF4JaGuPIe4Ra0xPGhnRBD2xrUj9QfS5d44LJ6pqkvVn\nnP0wwg0NkDoRytwy0yy2vgVRfyzsGyvlSbHhJtC3pkwF+Tb47aW8P1g9W9Huzy7tcGkcOeAvVYfs\ncUeAkVMVLqa6CGL94e+Oc0OWoJzt8pHnYZSk4wLohI01AoX0wCRendYqyLHrB5/PPiT7E1K0+7Ok\nBzkz3rk44C+Fm1Jc8/AlN3yQ7RHXTUlfYqI/2hDVVox4f4ySdFwAnfqOuuaBvesuXp02xbw/iN++\nIvtDyIShaPcHFTujzWjOXwq3/aSGMWoZBmtcnJpX06I/2hDVVox4f4ySdFwAnfo2zSLXO9kev/2+\n7I+piHZ2fxjQa/lNONiI+vylcAiuIdz7Ev4tuh7luXnI4JeDqE8/W4v+aENUWzHi/TFK0nEBdOpv\nahY5itEOUH3G7I9UNHFnthB2nB6Vmb8UbmWXn8MhFj7PuwX9b6tpoz/c8N3pjyhJxwXQ53VMscTQ\nNdoOv/2V7E9I0b5+lgT0mnlsxrsgfynclMI3oNCktx9zRS4u0EMPJ72+CUNUWzHi149Rko4LoFLP\ns4c5NeypxeK3PJmQot2fjm+PeJsXL4WrzJDJVSDfpP2BovMVJ/qjDU01pdUlxilJxwVQiQ7OK5aY\nGPw2uACvn+EIRbs/N5BGJ/QgvlDKXgq3nPzpB7tewptOBU6VLdrdlAqE7yBpQ1RbMXJK0nEBVOq9\n8lS5hFYF8eq0UkFG4bdXQTTyKvujFE3r5DyuD3iB7mnYltsWF/FumZ4EiY/CbFVoFLYvnkO90oao\ntlLkluTaZQu9s2G7igdUhb6tKPvDJgsjts/kI4ScW9IhYyZdNgbEakNTLaTUraEqSecFUCkeKSqW\nMXvsoTmy8Vtb8Z7WiuaML5+ttNacMqayeoPNpdrQVDMsusmqktiV6iikvX0L45SWaxu/tQHNNorW\nlO9gfUtFG+h2/tGcNLTVWnpb1glVErtSncRwvoDxgKoI5624pPTwZ7YWpIrA5neHLn/1PxbZai18\nLbNYlUR+STr3nx4N+4gFVKWBt6I0SHIMQc6G6SMGj8/TVWuo34i21UJK3RqKkmSbyxZgZ33ZXL0r\njrL06vZ7mLau9XO7fK2fQNv88T8XWOPU6f9gvLpPv7e2uvOLzy5bjtdZuxqvr93UZeb/lMx78Nhf\nXvsnZbxnsPZPJnQGh5ZvIxjyvHLDYI3vQNtV6u9s8v/d4khJ24KeEAAAAABJRU5ErkJggg==\n",
"prompt_number": 7,
"text": [
" \u239b k - 2 -\u03bc\u22c5x k\n",
" \u239ck\u22c5(\u03bc\u22c5x) \u22c5\u212f \u22c5\u0393(k - 1) (\u03bc\u22c5x) \n",
" k - 1 -\u03bc\u22c5x \u03bc\u22c5p\u22c5\u239c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500 - \u2500\u2500\u2500\u2500\u2500\u2500\n",
"k\u22c5\u03bc\u22c5(\u03bc\u22c5x) \u22c5(-p + 1)\u22c5\u212f \u22c5\u0393(k) \u239d \u0393(k) \n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500 + \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" (k - 1)!\u22c5\u0393(k + 1) (k - 2)! \n",
"\n",
" - 2 -\u03bc\u22c5x \u239e\n",
" \u22c5\u212f \u22c5\u0393(k - 1)\u239f\n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u239f\n",
" \u0393(k) \u23a0\n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" "
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"eq = diff(F,x) - f\n",
"simplify(eq)t"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$0$$"
],
"metadata": {},
"output_type": "pyout",
"png": "iVBORw0KGgoAAAANSUhEUgAAAAoAAAAOBAMAAADkjZCYAAAAMFBMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEJmJdjLNVN0iZu+7\nq0QgoRR7AAAAVklEQVQIHWNgEDJRZWBgSGeQmMDAtYGBOYGB5wID+0cG/gsMfN8Z5BUY+L4wzDdg\nYP0MJeUNQCL8Cgzs3xk4DjBwfWRg2cDAlMDA0M4gHcDAIOxylQEA9FISlFfRJtkAAAAASUVORK5C\nYII=\n",
"prompt_number": 8,
"text": [
"0"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"simplify(F)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"latex": [
"$$\\frac{k}{k!} \\left(k p \\gamma\\left(k - 1, \\mu x\\right) - p \\gamma\\left(k, \\mu x\\right) - p \\gamma\\left(k - 1, \\mu x\\right) + \\gamma\\left(k, \\mu x\\right)\\right)$$"
],
"metadata": {},
"output_type": "pyout",
"png": "iVBORw0KGgoAAAANSUhEUgAAAhYAAAArCAMAAAAT4jG7AAAAM1BMVEX///8AAAAAAAAAAAAAAAAA\nAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADxgEwMAAAAEHRSTlMAELvv3c2ZVESJ\nZjJ2Iqtw02/hOAAABY5JREFUeAHtW+mWtCoMBHfcPt7/aS9bAIVGgvcwc6bxxzRiTFUKRCAOIfKg\nXT+oQvvTFPAVGCf/rJWbAkoBPjchmgJ3BRZO71XtvCnAxqZBUyBQYGSErFO/BRdaxRcrQPlCGV36\n5Ys1aKEHCsx824PKVvHtCkx8bAPFt3eCMP5hP8426Qx1+e4ayjdCxc7F8d0ytOivCqxc7H/zhYjl\nSDuaAqDA2YmSGDFatwBF2q9QoFvFn3UKFiObrM8+cNaZbtd3WyloTrXxcmQo4lQc+SPaIQeR7Owq\nynrM3ms/3/QLFCfdQhXxskUo4PQi8ic0oJ2XXUVYHx0iBfNmhYTgZB/bWngYEfCc3kSeRtthqpGV\nXc23pt10IrqFdWwbLrtgb82KwLi1N2XDWEN76zMeTgTrGKDow6LR3vDMBFwSAjfBr7vil3oDnZdd\nRVnviG5Be58UqoziBJ6r4SFECDjNwTwQ6OvfV5EHaL7vBb7Xysqu4qwRihAyln4KguNkY6+FhxHh\nzumhW7yM/I5mpREFBt9ruezqwrpj2/dTzBfngXdy2jibuWPE2nd2K0cU2dSgsJ/SkgqMY9mZfiSs\n65sTfVrKqTZeSD4UIZ/TrVugWuMZJaW4WrXKNnLZVUbOQTy6rCNrf7JBLlRgMItYh0LYmlARwtTg\nNMi+SGWWf9jJoOc+a3IKVMqpNp6N3RZCEfI5XbsFrjWeUVKKyw4gD5ddPWYyyqd55Yd6qKeFzDD1\nCa3VzR/+hIoQtdyRO/Ci24kRiInZh3E+w9ss5qyYU228kHwoQj6nS7dAtsYzSkpx+PjCZVdFa+lm\n4//0q4O5fdHQWulAx8Eeo9uBCBXRHWJWU1HpfFR7JsrHJrbm1RFzVsBJ+1KRVMGL0ZYcAhFyNFDk\nxbMKo7Q8X3NbQ92cgSIU58FhkKGh/eyqXpR0sDZgi23pmLVxFPkJFBFjkoxtsu8L7uK23SLiSFSV\ncaqNF+EeiJDFiY3yGHr1A9M/5T2zNTJQUoqb18Ilu6peS5QDGwY7G4TErCNSmKpAETLpqQUzWdxN\nZGjEJEOZ22l13F8Zp9p4Ee6BCAhOl9HC+M5sjQyUlOJmEnnJrqrX0trr5hITAPdIx6wjUpiqQBGi\n5q+HGNlFTxOrm12+OHaNk5oACasyTrXxIloEIiA4RbtFXmtkoKQUZ2paSS7ZVS7e+Jv7EFiuVM0R\ns4Zr4a9RhHJ4aVAuR4uJH9ss3goz6US3OEyiboLBKfQjazCcLGAlvDhjU3sXAcMp1i2SrYGKPKW4\nGUnUMGCyqwtf2D7B4kM0ows7Yu0u3krT2fPhlI0+wG7nzCe272L7VfR4eu473dkK6dv094Q4TgBY\nC+8WuXcaioDhFOsW6dbARJ5UfHDtb8LRK14Xm0eEhNbO7nNpMRiJTwYPmODGvSA5GcBqeHHS19oC\nTg/dItYa+Shace//kgf94tCsV7/VVZV6jbuQFnieZVVo7Qw/l8BD796Ld2NvAnO/JM+RnAxgNbwY\n5XtdAaeL9NrfpSrSGvkooDhIe3DYIlBI3W240CteFxS7XL9bO7vPJWq4HmrhEbWjMP2IXlWfoPpX\nHjgZwGp4PrVP5dectOP/LXKruNraEc71pMfS159y2FOx8T5eHmq3PJU2N2t7W6pgegVJrIjSvQ3L\nyQBWw0sFD9fecjJ+HlojHwUUd5lzuzLQULAWgADSvzjrtC97db2MSLY6t4DmVBsvJ5AiTsWRWzSX\nOe/9uUUO42bzdxVwmXOVwPy7gbbIEAp4mfPu+oJCOGmmf00Blzknao/pr8XX4ilSwGXOCSv9Pq4I\nuN30mxXwMue7TZT/ZsKNWwUF/Mz55nJfFZAbxC9W4JI5/8U8G7WqCniZc9qnd5qr8mpgP6qAnzm/\npMp+lFUD/1EF/gOD5j6EwdkoZAAAAABJRU5ErkJggg==\n",
"prompt_number": 9,
"text": [
"k\u22c5(k\u22c5p\u22c5\u03b3(k - 1, \u03bc\u22c5x) - p\u22c5\u03b3(k, \u03bc\u22c5x) - p\u22c5\u03b3(k - 1, \u03bc\u22c5x) + \u03b3(k, \u03bc\u22c5x))\n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" k! "
]
}
],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | apache-2.0 |
merryjman/astronomy | Motion.ipynb | 1 | 59232 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Motion Analysis\n",
"In this example, you'll analyze the 1-D motion of an object. Don't be afraid to run code without knowing what every line does. A great way to learn is to:\n",
"- run some code\n",
"- see what it does\n",
"- edit it\n",
"- see what changed\n",
"\n",
"Programmers often begin with a working program, then edit/modify it to do what they want. "
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# First, we'll \"import\" the software packages needed.\n",
"import pandas as pd\n",
"import numpy as np\n",
"%matplotlib inline\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"inline_rc = dict(mpl.rcParams)\n",
"\n",
"# Starting a line with a hashtag tells the program not to read the line.\n",
"# That way we can write \"comments\" to humans trying to figure out what the code does.\n",
"# Blank lines don't do anything either, but they can make the code easier to read."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Raw data"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>time (s)</th>\n",
" <th>position (m)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" time (s) position (m)\n",
"0 0 0\n",
"1 1 2\n",
"2 2 4\n",
"3 3 6"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Whenever you type \"something =\" it defines a new variable, \"something\", \n",
"# and sets it equal to whatever follows the equals sign. That could be a number, \n",
"# another variable, or in this case an entire table of numbers.\n",
"\n",
"# enter raw data\n",
"data = pd.DataFrame.from_items([\n",
" ('time (s)', [0,1,2,3]), \n",
" ('position (m)', [0,2,4,6])\n",
" ])\n",
"# display data table\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Plotting the data"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x7f720f688e10>"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAggAAAGHCAYAAADV8qrzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xl8VNX5x/HPM4CyqICg2P4qoEAVRdQEBVwAFUWpIm7U\nIFBABK0KooKIVXAtooiixa1aoGjUureIKCpWZZMgKrIkQQhW3JBFZCc5vz/OBCbJJCRhkjuT+b5f\nr3mRnDlz55nrtPPke8+9Y845RERERCKFgi5ARERE4o8aBBERESlCDYKIiIgUoQZBREREilCDICIi\nIkWoQRAREZEi1CCIiIhIEWoQREREpAg1CCIiIlKEGgQRkXIys45mlmdmHYKuRSTW1CCIxIiZHWlm\nT5rZCjPbamYbzexjMxtsZjUDru08MxtVSc/V3sxGmdlBZXjMBWY2y8x+MLPN4X34opl1qchaY6TA\n9erNrKuZTTOzNWa23szeMbPWQRUnUl5qEERiwMz+AHwJXAq8CVwHjABygLHAw8FVB0BX4I5Keq5T\nws9VrzSTzexm4A0gD7gPuAF4GWgO/LGCaqxI/wa2A3fiX08r4B0zaxBoVSJlVD3oAkQSnZk1BdKB\nlcCZzrkfI+5+3MxuB/4QQGmRLB6fy8yqAX8BZjjnzotyf8NYFlZJ2jnnPs3/xcwWATOAc/DvE5GE\noARBZN/dAtQBrizUHADgnPvaOfdo/u9mVs3MbjezbDPbZmYrzexeM9sv8nFmtsrM3jSzU81sXviw\nxQoz611oXvVwpJ8ZnrPWzD4ys7PC9/8D+HP457zwLTfi8Teb2Sfhx20xswVmdknh1xF+3AQzu9DM\nvgzXvjjyMED4MMbY8K+r8p/LzBoXs+8aAgcBs6Pd6ZxbG7Ht/OP9PczsPjP7zsx+NbM3zOx3Uept\na2Zvm9mG8GGLWWZ2SpR5vzWzZ83s+4jX1C/KvP8zs9fDz/mDmT0E7E+hhiiyOQjbHv53P0QSiOnr\nnkX2jZl9A2xzzrUo5fxJQB/gJWAW0Bb4E/Cac+6SiHkrgW1AXeAZYA3QHzgROM45tzQ871784Yyn\ngE/xH7htgM+dcw+YWVvgLqAz0IvwB5pz7vnw41fjI/4l+A+xy4GTgfOdc9Mj6skDPgcOASYCm4DB\nwGFAY+fcejNrBdwa3sYNwM/hh7/mnNsaZV8Y8CvwFdDFObe+hP3WEfgAfygnD5gEHAoMxR/KOcE5\ntz0890zgLWAB/nBFHtAPaAmc5pxbEJ53KJAB5Ib331rgPOBC4Abn3ITwvJrh1/474BHgO6B3eH8d\nB5zhnPtvlJr3B94Dfg/83jm3objXJxJ3nHO66aZbOW/AgfgPn1dLOb91eP4ThcbH4j+kOkaMrQyP\nnRIx1hDYCoyNGPsMeHMvz/sokFvMffsX+r0a8AXwbqHxvPBzN40YOy48/ueIsZvCdTcu5T4ZHZ6/\nCZiGbzBOjDKvY/i5VgO1I8YvDY9fFzG2HJhW+HUCK4C3I8b+DvwPqFdo7vPAuvx9AwwJ13hxxJya\nQGZ4vEOUequFX88WfFMS+PtVN93KctMhBpF9k79Sf1Mp53fFr3ofX2h8HP4v+8JrFZY453bH785H\n7suBIyPmbACONbPmpS06kgv/1Q1gZvWA+sBHQEqU6e8651ZFPPZL4JdC9ZT1+UcDPYGF+OP09wAZ\nZpZhZkdHechk59yWiMe/jP+Lvmv4NZwItADSzaxB/g3fzL0HRJ6SeDF+UWG1QnPfwS+yzN8H5wHf\nOedejXjebfjUoTijgS5AT+fcx6XaGSJxRIsURfbNL+F/Dyzl/Cb4v3azIwedcz+Y2Ybw/ZFWR9nG\nevyHeL47gNeBTDNbDLwN/DP84b1XZnY+cBtwAv6v7Hx5UaZ/U4p6ysw59yLwopkdgD/k0he4AnjT\nzFo553ZETM+OsolsoGn45/xGaUoxT5dnZnXxhwfqAQOBQdHKwh/CAP/fJdrzLi/mOcAfznnXOfd6\nCXNE4pYaBJF94JzbZGZr8KeylemhpZyXW8z47oVxzrmPzKwZ/rj5OcCVwFAzG+Sce7akjZvZ6fj1\nB7OAa/B/ie/Er3VIK089+8I59yv+r/z3zGwXfq1GW3yiUVr5yehN+HUD0fyKP1wDMBWYXMy8L8rw\nvIU1wO9PkYSkBkFk3/0HuMrM2jrn5u1lbg7+A6wFEX99hhfL1QvfX2bOL36bDEw2s9r4D9TRQH6D\nUFxDcjF+XUEX59yuiHquLE8de3muslqAbxB+U2g82mLQ5uxpBlaE/93knHu/uI2b2U/4Q0PVSpoX\nlgMcG2U82iGQfE/i14eIJCStQRDZd2PxC9H+Hv6gL8DMmpnZ4PCvb+H/2r6h0LSb8B+s08r65GZ2\ncOTv4ePz2RQ8XLA5PLfw1Q1zw8+7+4+F8HUdLixrHYWfi1JcKMnMaplZu2Lu7hr+t3CM3yd8KCJ/\nG5fhm4i3wkMZ+CbhZjOrE+U5GwI45/KAV4BLzKzIh3+hazC8Bfw28vTPcCN2VQkv7+/A3hoPkbil\nBEFkHznnvjaznsALwFIzmwIsxh/jPhW/yv4f4blfmNlkYKCZ1Qc+xEfoffBnQnxYjhKWmNks/Afj\nOuCk8HNOiJiTgW9MHjWzGfgzGl7ENyQ3AjPM7HmgEf6aCVn4My7KI/+57jOzF/CHLN50UU5zBGoD\ns81sLn7txDf4xqI7cBr+9MjChwnWAR+Hr+9wGP4Mg0z8BzLOOWdmA/Af6l+F530L/B9wBrCRPQ3Q\nCKATMM/Mnsaf6nkwkAqcyZ7DEE/jr475TzNrw57THPOboWiW4k/F7F/CHJH4FfRpFLrpVlVuQDPg\nCfxfr1vxH0Sf4D9Y9ouYF8JfPTAbf52DVcDdQI1C2/saeCPK83wAvBfx+63AHPw1B/KvKXALPjqP\nfM6Hge+BXUSc8ohfELgMn4J8hW9WRlHotEh82vBIlHq+Bp4pNDYSv8ByJyWc8og/FbA//i/5r8M1\nbMIfXhgKVI+Y2zG8rR74Mx2+C7/eN4DfRdl2a+BfwI/h7X6Nv5Jhp0LzGuKbqVXh/x7f4s9i6F9o\n3u+A18L1/YA/8+Rsij/NMbfwftFNt0S66UJJIpIQIi6UdKmLON1QRCqG1iCIiIhIEWoQREREpAg1\nCCKSSHRMVKSSaA2CiIiIFKEEQURERIpIuOsghL9IpQt7TkkSERGR0qmJ/96SGc65n0uamHANAr45\neC7oIkRERBLYFfivNS9WIjYIqwCmTp1Ky5YtY7rhoUOHMn584W/hFdC+KY72S3TaL9Fpv0Sn/RJd\nReyXpUuX0qtXLwh/lpYkERuEbQAtW7YkJSXa19WXX926dWO+zapC+yY67ZfotF+i036JTvslugre\nL3s9RK9FiiIiIlKEGgQREREpQg2CiIiIFKEGIUJaWlrQJcQt7ZvotF+i036JTvslOu2X6ILeLwl3\nJUUzSwEyMjIySly8sXr1atauXVt5hYlEaNiwIY0bNw66DBGRAhYuXEhqaipAqnNuYUlzE/Eshr1a\nvXo1LVu2ZMuWLUGXIkmqdu3aLF26VE2CiCSsuGgQzOy3wP3AeUBtIAvot7fupjhr165ly5YtFXKt\nBJG9yT/PeO3atWoQRCRhBd4gmFk94BPgPfxVEtcCLYD1+7rtirhWgoiISEXLzMxkxYoVNG/enBYt\nWgRSQ+ANAjACWO2cGxAxlhNUMSIiIkFZt24dPXv2ZsaMt3aPdenSlfT0qdSvX79Sa4mHsxguABaY\n2Utm9oOZLTSzAXt9lIiISBXTs2dvZs6cC0wFVgNTmTlzLmlpvSq9lnhoEI4ErgGWA+cAjwMTzKx3\noFWJiIhUoszMTGbMeIvc3An471I6HLiC3NxHmDHjLbKysiq1nng4xBAC5jvnbg///rmZtQKuBv5Z\n3IOGDh1K3bp1C4ylpaUFft6oiIhIeaxYsQKoA3QrdE9HALKzs8u0HiE9PZ309PQCYxs3biz14+Oh\nQfgOWFpobClwcUkPGj9+vBYgxqFJkybRv39/Vq1atXsFf6dOnQiFQrz//vsA5OTkcMQRRzBp0iT6\n9OkTZLkiInFj7dpWwBdArUL3fAhA8+bNy7S9aH80R1wHYa/i4RDDJ8BRhcaOQgsVizVnzhzuvPNO\nfvnll6BLKcLMMLMiY9HmiYgIbN4M118PffocTv36WwiF2uHXIHwDTKVatSF06dK10s9miIcGYTzQ\nzsxuNbNmZtYTGAA8FnBdcWv27NncddddbNiwIehSyqVJkyZs3bqV3r21zEREktuHH0Lr1vDMM/Dw\nw5CV9X+cfXYjoDfQGOhN587tSE+fWum1BX6IwTm3wMwuAsYAtwMrgSHOuReCrSx+lfby2M45duzY\nwf7771/BFZXdfvvtF3QJIiKB2bwZRoyAxx6D006Dt98GHxDU5+23p5GVlUV2dnag10GIhwQB59xb\nzrnWzrnazrljnXPPBl1TvLrzzjsZPnw4AE2bNiUUClGtWjVycnIIhUIMHjyY559/nlatWlGzZk1m\nzJgB+Gbh4YcfplWrVtSqVYvDDjuMq6++ukgK0bRpU7p168Ynn3xC27ZtqVWrFs2aNeOf/yy6XnTJ\nkiWceeaZ1K5dm8MPP5x7772XvLy8vb6G/FqnTJmye6xv374ceOCBrFmzhu7du3PggQdy6KGHMmzY\nsCINUWlfi4hIPCqcGnz4YX5zsEeLFi0477zzAmsOIA4SBCmbSy65hMzMTF544QUeeeQRGjRogJlx\nyCGHAPDee+/x0ksvcd1119GwYUOaNm0KwMCBA5kyZQr9+/dnyJAhrFy5kkcffZRFixbxySefUK1a\nNcCvDcjKyuKyyy7jyiuvpG/fvjz77LP069ePNm3a7L509Q8//ECnTp3Iy8tj5MiR1K5dm6eeeoqa\nNWuW63WZGXl5eXTp0oV27doxbtw4Zs6cyUMPPUTz5s0ZNGjQ7rmlfS0iIvFk82a49VZ49NHCqUGc\ncs4l1A1IAVxGRoYrTkZGhtvbnET24IMPulAo5HJycgqMm5mrXr26W7ZsWYHxjz76yJmZe+GFFwqM\nv/POO87MXHp6+u6xpk2bulAo5D755JPdYz/99JOrWbOmGzZs2O6xG264wYVCIbdgwYLdY2vXrnX1\n6tUrUlunTp3cGWecsfv3VatWOTNzkydP3j3Wt29fFwqF3L333lugxpSUFHfSSSeV67UEpaq//0Sk\n7D780Lkjj3SuVi3nxo93bteuYOrI//8nIMXt5fM26ROELVtg2bKKf56jj4batSv+eTp16sRRRxU8\nKeTll1+mXr16nHXWWfz888+7x0888UQOOOAAPvjgAy6//PLd48cccwynnHLK7t8bNmzIUUcdxddf\nf717bPr06bRr167A6TINGjTgiiuu4PHHHy93/ZFJAcDpp5/O1Kl7FueU9bWIiARp82YYORImTIBT\nT02A1CBC0jcIy5ZBKU8J3ScZGVAZl23IP6QQKSsriw0bNnDooYcWuc/M+PHHHwuMRfsGwvr167N+\n/Z7vz8rJyaFdu3ZF5hVuTsqiZs2aNGjQoMTnLetrEREJyn//C/37w7ffwkMPweDBkEhHQJO+QTj6\naP/hXRnPUxlq1Sp8gQ3Iy8ujUaNGPP/881HPgMhfv5CvuGP40R4bS6VZO1DW1yIiUtnyU4NHH4VT\nToHp0xMnNYiU9A1C7dqV85d9LJX1IkPNmjXjvffe45RTTonZKY9NmjSJel3wZRV8vKYiXouISKx8\n9BH06+dTg3HjEi81iBQXpzlK2dSpUweg1Kf19ejRg127dnHXXXcVuS83N7dM1+bO17VrV+bOncuC\nBQt2j/300088//zzZd5WWVTEaxER2VdbtsANN0DHjtCoEXz+OQwdmrjNAShBSEipqak45xg5ciSX\nX345NWrU4IILLih2focOHRg0aBBjxoxh0aJFnHPOOdSoUYPMzExefvllJkyYwMUXl/jVF0UMHz6c\nf/7zn3Tp0oUhQ4ZQu3Ztnn76aZo2bcoXX3yxry+xWBXxWkRE9kVkavDggzBkSGI3BvnUICSgNm3a\ncM899/DEE08wY8YMnHOsWLEi6vcg5Hv88cdp06YNTz75JLfddhvVq1enadOm9OnTh1NPPXX3vJK2\nETl+2GGHMWvWLK6//nruv/9+GjRowDXXXMNhhx3GgAEDSnxstN+LG4s2XtrXIiJSkbZs2XOGQvv2\nMG0a7MM67bhjFb3wLNbMLAXIyMjIKPbbHPO/raqkOSIVRe8/karv4499avC//8G99yZOahDxbY6p\nzrmFJc3VGgQREZFS2rLFry3o0AEOOQQWLYIbb0yM5qCsdIhBRESkFD7+2F/X4Jtv4IEH/KLEqtgY\n5FOCICIiUoLI1KBhQ58a3HRT1W4OQAmCiIhIsT75xK81SJbUIJISBBERkUK2bPFrC04/HRo0SJ7U\nIJISBBERkQj5qcHq1TB2bOJf8Ki8lCCIiIjgU4ObbiqYGtx8c3I2B6AEQUREhNmzoW9fnxrcf3/V\nPXWxLJQgiIhI0tq61acGp522JzUYNkzNAShBEBGRJDV7tl9rkJOj1CAaJQgiIpJUtm71awtOOw3q\n14fPPlNqEI0aBCmVUCgU9SuWo2natCn9+/ev4IqKN3bsWI455piYbrN9+/bccsstMd2miFS+2bPh\nhBPgscdgzBh/xkLLlkFXFZ/UIEipFP6Wxzlz5nDnnXfyyy+/FJkbCoWK/WbGirZp0ybGjh3LiBEj\nYrrdW265hb/97W/8+OOPMd2uiFSOyNSgXj2fGgwfrtSgJFqDIKWydetWqlff83aZPXs2d911F/36\n9eOggw4qMHf58uWEQsH0ns888wy5ublcfvnlMd3uhRdeyEEHHcTEiRMZPXp0TLctIhVrzhy/1mDV\nKp8a3HgjVNen314pQZBS2W+//Qp86Jf0NeE1atSgWkBt+aRJk+jWrRv77bdfTLdrZlx66aVMmTIl\nptsVkYqzdatfW3DaaVC37p7UQM1B6ahBKKWtW7fyyCOPcNppHWnf/jTGjBkTNV6vaKNHjyYUCrF8\n+XJ69OhB3bp1adiwITfccAPbt28vMDc3N5e7776b5s2bU7NmTY444ghuu+02duzYUWDeggUL6NKl\nC4cccgi1a9fmyCOP5MorrywwJ3INwp133snw4cMBv94gFApRrVo1Vq9evXus8BqElStXctlll9Gg\nQQPq1KlD+/bteeuttwrM+fDDDwmFQvzrX//i3nvv5fDDD6dWrVp07tyZFStW7HXfrFq1ii+++ILO\nnTsXGM/JySEUCvHQQw8xceJEmjVrRp06dejSpQvffvstAHfffTeHH344tWvXpnv37mzYsKHI9s8+\n+2xycnL4/PPP91qLiARr7lw48USYMAHuu09rDcojqfso5xxz587l22+/5fjjj6dFixZR523bto0z\nzzybefPm4VxXYD/mzx/NlCnPM3v2f6lXr16l1Zx/bL9Hjx4cccQRjBkzhrlz5zJhwgQ2bNjApEmT\nds+98sormTJlCj169ODmm29m3rx5/PWvf2XZsmW88sorAPz000906dKFQw89lFtvvZV69eqxatUq\nXn311WJruPjii8nMzOSFF17gkUceoUGDBgAccsghBWrM9+OPP9K+fXu2bdvGkCFDOPjgg5k8eTLd\nunXjlVde4cILLywwf8yYMVSrVo1hw4axceNG7r//fnr16sWcOXNK3DezZ8/GzEhJSYl6/9SpU9m5\ncyeDBw9m3bp13H///Vx22WWceeaZfPjhh4wYMYLs7GwmTJjAzTffzN///vcCj09NTcU5xyeffMLx\nxx9fYi0iEoytW+GOO+Chh6BNG58axHjNcvJwziXUDUgBXEZGhitORkaG29ucrKwsd8wxrR2w+3bR\nRZe4X3/9tcjciRMnOrOQgzkOXPj2lQuFark777wz6vY3b97snnnmGTdo0CB32223ueXLlxdbS1mM\nHj3amZm76KKLCoxfe+21LhQKuS+//NI559znn3/uzMwNGjSowLxhw4a5UCjkZs2a5Zxz7vXXX3eh\nUMgtXLiwxOc1swKv9cEHH3ShUMjl5OQUmdu0aVPXr1+/3b/fcMMNLhQKudmzZ+8e+/XXX92RRx7p\njjzyyN1js2bNcmbmjj32WLdr167d4xMmTHChUMh99dVXJdZ4++23u1Ao5DZv3lxgfNWqVc7MXKNG\njdymTZt2j48cOdKZmTvxxBNdbm7u7vGePXu6mjVruh07dhR5jv33399de+21JdZRmvefiMTenDnO\nHX20c/vt59yYMc7t3Bl0RfEn//+fgBS3l8/bpDzEkJuby7nnns/y5duA94C1wD948823GTLkhiLz\nX3vtDeBsoF3E6DHk5V3CK6+8UWT+mjVrOO64E7nyygE888xcxoyZSMuWLfnHP/4Rk/rNjGuvvbbA\n2PXXX49zbndsP23aNMyMoUOHFph300034Zxj2rRpANSrVw/nHG+++Sa7du2KSX2FTZ8+nZNPPpn2\n7dvvHqtTpw4DBw5k1apVLFmypMD8/v37F1jDcPrpp+Oc4+uvvy7xeX7++WeqV69O7dq1o97fo0cP\nDjjggN2/t23bFoDevXsXWF/Rtm1bduzYsfvwQ6T69euzdu3aEusQkcq1bZtfW3DqqXDggT41uOUW\nrTXYV0nZILz77rusWLGc3Nx/AmcCDYC+5ObezuTJU6Iefy6LIUNuICfnV+Ardu1aRG7uGvLy+jFw\n4CDWrFkTg1cAzZs3L/B7s2bNCIVCrFq1CoDVq1cTCoWKzGvUqBH16tUjJycHgI4dO3LppZdy1113\n0bBhQ7p3786kSZOKrFPYFzk5ORx11FFFxluGDwjm15Lv8MMPL/B7/fr1AVi/fv0+1VF4u3Xr1gXg\nd7/7XdTxaM/nnAvsFE4RKSp/rcEjj8C99/rrHOiQQmwkZYOwcuVK/Es/qdA9p7Br1w6+++67AqMX\nXXQh8C4wN2J0CaHQK1xyScHj51u2bOG1114jN/dmIH9FTE1gHHl5fgFeRSjuQ6s0H2YvvfQSc+bM\n4frrr2fNmjX079+fNm3asGXLlliXWSrFnQHhSjhzAqBBgwbs2rWLzZs3l2m7ZXm+DRs20LBhwxLr\nEJGKt22bTwnyU4OFC2HECKUGsZSUDcLRRx8N5AEfFrrnPWrWrF3kL8p+/frRtm17zE4HLgQuJRRK\n4aijmjNkyJACc7dt20Zu7i7gsELbPpBQqA6bNm2KyWvIysoq8Ht2djZ5eXkcccQRADRp0oS8vLwi\n83788Uc2bNhAkyZNCoyffPLJ3H333cyfP5/nnnuOxYsX88ILLxT7/GX5K7pJkyYsX768yPjSpUt3\n3x8L/r9rfgMYe2vWrGHHjh27kw8RCca8eT41ePjhPanBsccGXVXVk5QNQseOHWndOoXq1XsBLwBL\ngbGY3cc11wziwAMPLDC/Zs2avP/+u4wf/yCnnrqBdu2+57777mTu3I93x9H56tevT8uWx2H2LL4J\nyfc6u3ato1OnTvtcv3OOv/3tbwXGJkyYgJlx7rnnAtC1a1ecczz88MMF5o0bNw4z4/zzzweIejgl\nf4V+4dMmI9WpU6fYxxfWtWtX5s+fz7x583aPbd68maeeeoojjjgiZpdFbt++Pc45FixYEJPtFZaR\nkYGZccopp1TI9kWkZPmpwSmnwAEHKDWoaEm5W0OhENOn/5srrujDrFlpAFSvXoMBAwYwZsyYqI+p\nVasWQ4YMKZIYFGZmjB17H926dSMUOp28vMuALEKhZ+jS5Q+ceuqpMXkNK1eu5MILL+Tcc89l9uzZ\nPPfcc/Tq1YvjjjsOgNatW/OnP/2Jp556ivXr19OxY0fmzZvHlClTuPjii+nQoQMAkydPZuLEiVx0\n0UU0a9aMTZs28fTTT1O3bl26du1a7PPnn/I3cuRILr/8cmrUqEG3bt2oVatWkbkjRowgPT2dc889\nl8GDB3PwwQczadIkcnJySjydsqyOOOIIWrVqxcyZM+nbt+8+bSva4YV33nmHxo0bc8IJJ+zTtkWk\n7ObPh759YcUKuOcefwEkNQYVK2l3729/+1s++GAm2dnZrFmzhpYtW+4+j39fnX/++cyYMYPRo+/m\n009HcPDBDRk4cDgjR46MyQI3M+PFF1/k9ttv59Zbb6V69eoMHjyYsWPHFpj3zDPP0KxZMyZNmsTr\nr7/OYYcdxm233cYdd9yxe07Hjh359NNPefHFF/nhhx+oW7cubdu25fnnny8Q/Rf+LoY2bdpwzz33\n8MQTTzBjxgzy8vJYuXIljRs3LjL30EMPZc6cOdxyyy089thjbNu2jdatW/Of//xnd+IR+TzFvebS\n6N+/P6NGjWL79u3sv//+xdZf1udzzvHqq69y1VVXlaoOEYmNbdtg9Gh44AFISYGMDGjVKuiqksTe\nzoOs6BswCp/FR96WlDA/JtdBSFSjR492oVDI/fzzz0GXEpc2btzoGjZs6J599tmYbve1115zderU\ncd9///1e51bl959IZZo3z7mWLZ2rUcO5e+/VdQ1iIRGvg7AYaIRf2XcYcFqw5UiiOuiggxg2bBgP\nPPBATLc7duxYrr/+eho1ahTT7YpIUdu2+bUF7dtD7dp+rcHIkTqkUNniZXfvcs79FHQRUjUMHz58\n93dFxMrs2bNjuj0RiW7+fP/Ni1lZcPfd+nKlIMVLgtDCzL41sxVmNtXMDt/7Q0REpKrYvh1uvdWn\nBrVqKTWIB/HQIMwF+gJdgKuBI4D/mlmdIIuKV6NGjSI3N5eDDz446FJERGLi00/9AsRx4+Cuu2DO\nHC1EjAeB92bOuRkRvy42s/lADtADiM2XF4iISNzZvt2foTB2rL/w0cKFagziSeANQmHOuY1mlgk0\nL2ne0KFDi1ykKC0tjbS0tIosT0REYuDTT/11DbKyfGowfDjUqBF0VVVLeno66enpBcY2btxY6sfH\nXYNgZgfgm4MpJc0bP348KSkplVOUiIjExPbtcOedPjU4/nh/XYPw9d0kxqL90bxw4UJSU1NL9fjA\n1yCY2QNm1sHMmpjZKcBrwE4gfS8PFRGRBJK/1uDBB/2hhblz1RzEs3hIEH4HPI//zuWfgI+Bds65\nn/d1w/lsnFBsAAAgAElEQVRfBiRSmfS+Eylo+3Z/GOH++31qsGABtG4ddFWyN4E3CM65mC8aaNiw\nIbVr16ZXr16x3rRIqdSuXVtfCy2Cbwb69oXMTJ8a3HKL1hokisAbhIrQuHFjli5dytq1a4MuRZJU\nw4YNady4cdBliAQmMjVo3VqpQSKqkg0C+CZB/wctIlL5MjJ8arB8OYwa5S+brNQg8QS+SFFERKqG\n7dvhL3+Btm19Q7BgAdx+u5qDRFVlEwQREak8Sg2qHiUIIiJSbtu3+5SgbVv/vQlKDaoOJQgiIlIu\n+anBsmVwxx3+y5bUGFQdShBERKRMduwomhrccYeag6pGCYKIiJTawoU+NVi61DcJI0eqMaiqlCCI\niMhe5acGJ58M1ar51GDUKDUHVZkSBBERKVHh1ODWW2G//YKuSiqaEgQREYlqxw6/tuDkkyEU8l+2\nNGqUmoNkoQRBRESK+OwznxosWeIvfjRypBqDZKMEQUREdtuxw6cEJ58MZj41GD1azUEyUoIgIiJA\nwdTgttuUGiQ7JQgiIkkuMjUAmD9fqYEoQRARSWqLFvnU4KuvfGJw221qDMRTgiAikoR27PApwUkn\ngXM+NbjzTjUHsocSBBGRJKPUQEpDCYKISJLYscOnBCedBHl5Sg2kZEoQRESSQH5qsHixTw3+8hc1\nBlIyJQgiIlXYzp1FU4O77lJzIHunBEFEpIr6/HOfGnz5pf/+hNtvV2MgpacEQUSkislPDdq0gdxc\nnxrcfbeaAykbJQgiIlWIUgOJFSUIIiJVwM6dfm1BmzawaxfMm6fUQPaNEgQRkQT3xRc+NfjiCxgx\nwqcG++8fdFWS6JQgiIgkqJ07fUrQpo3/ee5cuOceNQcSG0oQREQSkFIDqWhKEEREEkhkarBjh1ID\nqThKEEREEsSXX/rU4PPP4ZZb4I471BhIxVGCICIS53bu9ClBaips3+5Tg3vvVXMgFUsJgohIHFNq\nIEFRgiAiEod27vQpQWoqbNum1EAqnxIEEZE4k58aLFrkU4NRo9QYSOVTgiAiEid27SqaGtx3n5oD\nCYYSBBGROLB4sU8NPvtMqYHEh7hLEMxshJnlmdlDQdciIlLR8lODlBTYulWpgcSPuEoQzOwkYCDw\nedC1iIhUtMjUYPhwnxrUrBl0VSJe3CQIZnYAMBUYAGwIuBwRkZjKzMxk+vTpZGVlsWuXTwlSU2HL\nFpgzB/76VzUHEl/iKUH4G/Bv59z7ZnZ70MWIiMTCunXr6NmzNzNmvBUeOYaDDnqNX39twbBhxujR\nagwkPsVFgmBmlwMnALcGXYuISCz17NmbmTPnAs8B64Ev+OUXx0kn3cSYMWoOJH4F3iCY2e+Ah4Er\nnHM7g65HRCRWMjMzmTHjLXJzJwM9gXpANSCDefPGk5WVFWyBIiWIh0MMqcAhwEIzs/BYNaCDmV0H\n7O+cc4UfNHToUOrWrVtgLC0tjbS0tIquV0SkVDIzvwZGAH8odM/pAGRnZ9OiRYvKLkuSRHp6Ounp\n6QXGNm7cWOrHW5TP3kplZnWAJoWGJwFLgTHOuaWF5qcAGRkZGaSkpFROkSIiZbRkCVx++Ta+/LIG\nsAw4NuLeqUBvMjMz1SBIpVq4cCGpqakAqc65hSXNDfwQg3Nus3NuSeQN2Az8XLg5EBGJd7t2wZgx\ncOKJsHNnTdq2HUa1ah3wTcE3wFSqVRtCly5d1RxIXCvTIQYzCwEd8flYE6A28BPwGTDTOfdNjOoK\nNtYQESmHJUv8dQ0yMuDmm+HOO2Hr1ttJS1vOjBm9d8/r3Lkr6elTgytUpBRK1SCYWS3gJuAa4GBg\nEbAG2Ao0B7oDT5vZO8Bdzrm5+1KUc+7MfXm8iEhl2rULxo3zX8V85JHwySfQrp2/r2bN+rz99jSy\nsrLIzs6mefPmSg4kIZQ2QcgE5gBXAe9GO9vAzJrgl+m+YGb3Oueejl2ZIiLxackS6NcPFiyAm26C\nu+6KfupiixYt1BhIQiltg3DO3tYDOOdygL+a2YNA432uTEQkjkWmBkccUTA1EKkKSrVIsSyLBZ1z\nO51zK8pfkohIfFu6FE49FUaOhCFD/HcpqDmQqqZc10Ews5pAa+BQCjUZzrk3Y1CXiEjcyU8NRo2C\npk3h44+hffugqxKpGGVuEMzsXGAK0DDK3Q5/kSMRkSpl6VK/1mD+/D1rDWrVCroqkYpTnusgPAr8\nC/iNcy5U6KbmQESqlNxcGDvWX9dg/Xq/1uCBB9QcSNVXngahEfCQc+6HWBcjIhJPli3zaw1GjIDr\nr4dFi3RIQZJHeRqEl4FOMa5DRCRu5Ob6lOCEE5QaSPIqzyLF64B/mdnpwJdAgWsiOOcmxKIwEZEg\nLFvmr4Y4fz7ceCPcfbcaA0lO5WkQ0oBzgG34JCHyssgOUIMgIgknNxceeghuvx2aNPFnKJxyStBV\niQSnPA3CvcAo/Dct5sW4HhGRSrdsmT9DYd48GDoU7rlHqYFIedYg7Ae8qOZARBJdbi48+KBfa7Bu\nnU8Nxo1TcyAC5WsQJgN/jHUhIiKVadkyOO00GD4crr3Wn6GgQwoie5TnEEM1YLiZdQG+oOgixRtj\nUZiISEXIzYXx4+Evf4HGjeGjj/ypjCJSUHkahOOAz8I/typ0n0NEJE4tX+7XGsydCzfc4Nca1K4d\ndFUi8anMDYJz7oyKKEREpKLk5sLDD/vU4PDD4b//9YcXRKR4ZV6DYGZ1zezgKOMHm9lBsSlLRCQ2\nli+HDh1g2DC45hq/1kDNgcjelWeR4gtAjyjjPcL3iYgELjfXn5Fwwgnw448+NXjoIR1SECmt8jQI\nbYEPoozPCt8nIhKozMw9qcHVV8Pnnys1ECmr8jQI++OvhVBYDUBnD4tIYPKvhnj88XtSg/HjlRqI\nlEd5GoT5wMAo41cDGftWjohI+eSnBjffrNRAJBbKc5rjX4CZZnY88F547CzgJPx3NIiIVJrcXJgw\nAUaOhN/9Dj78EE4/PeiqRBJfmRME59wnQHvgG/zCxAuAbKC1c+6j2JYnIlK8zEzo2BFuugkGDfKp\ngZoDkdgoT4KAc24RcEWMaxERKZXI1OD//k+pgUhFKFWCYGZ1yrLRss4XESmtrKyCqcEXX6g5EKkI\npT3EkG1mI8zsN8VNMO9sM5sODI5NeSIiXv53KLRuDd9/D7Nm+asj6gwFkYpR2kMMnYD7gNFm9jmw\nAFgDbAPqA8fg1yXsAv4KPBnzSkUkaWVlQf/+/uuYBw+G++6DOsopRSpUqRoE59xy4BIzawxcBpwO\nnIK/7sFa/Jc3XQVMd87lVlCtIpJk8vL2rDX4zW/8WoMOHYKuSiQ5lGmRonNuNTAufBMRqTDZ2f6b\nFz/+GK6/Hv76V6UGIpWpPBdKEhGpMHl58Mgjfq3BmjV+rcGECWoORCqbGgQRiRvZ2f4MhRtugAED\n/BkKHTsGXZVIclKDICKBU2ogEn/UIIhIoLKzoVMnnxpceaVSA5F4oQZBRAKRf4ZC69bwv//BBx/A\no48qNRCJF+W61LKZ1QNOBg6lUJPhnJsSg7pEpApbscJf1+C//4XrrvNnKBxwQNBViUikMjcIZnYB\n8BxwAPAL4CLudoAaBBGJKi8P/vY3GDECGjXyqUGnTkFXJSLRlOcQwzjgWeAA51w951z9iNvBZd2Y\nmV1tZp+b2cbwbbaZnVuOukQkjq1YAWec4a+E2K+fX2ug5kAkfpWnQfg/YIJzbkuMavgGuAVIAVKB\n94E3zKxljLYvIgHKy/NrC1q3hm++gfffh8ce0yEFkXhXngZhBtAmVgU456Y55952zq1wzmU75/4C\n/Aq0i9VziEgwVqyAM88smBqccUbQVYlIaZRnkeI04AEzOwb4EtgZeadz7s3yFmNmIaAHUBuYU97t\niEiwItcaHHqoTw3UGIgklvI0CE+H/70jyn0OqFbWDZpZK3xDUBPYBFzknFtWjtpEJGBff+3PUPjw\nQ/jzn+H++3U4QSQRlblBcM5VxLUTlgHHA3WBS4EpZtZBTYJI4sjLg4kT4ZZbfGrw3nv+8IKIJKZy\nXQch1pxzu4Cvw79+ZmYnA0OAa4p7zNChQ6lbt26BsbS0NNLS0iqsThGJTqmBSPxJT08nPT29wNjG\njRtL/Xhzzu19VuEHmXUEbgbyzzRYAjzgnPuozBuLvv33gBznXP8o96UAGRkZGaSkpMTi6USknPLy\n4PHHfWpwyCHwzDNKDUTi2cKFC0lNTQVIdc4tLGlumQ8XmFkvYCawBZgQvm0F3jOznuXY3n1mdrqZ\nNTGzVmb2V6AjMLWs2xKRyvP113DWWf5KiH36+DMU1ByIVB3lOcRwGzDcOTc+YmyCmd0I3A48X8bt\nHQpMBn4DbAS+AM5xzr1fjtpEpIJFpgYNG2qtgUhVVZ4G4Ujg31HG3wTuK+vGnHMDylGDiARg5Uq/\n1mDWLLj6ahg7Fg48MOiqRKQilOeMhG+As6KMdw7fJyJVTP4ZCscd55uEmTN9iqDmQKTqKk+CMA5/\nSOEEYHZ47FSgL/7MAxGpQlauhCuv9F+spNRAJHmU5zoIj5vZ98BN+KseAiwF/uiceyOWxYlIcPLy\n4IknYPhwv9Zg5ky/KFFEkkO5roPgnHsNeC3GtYhInIhMDQYNggceUGogkmwq4qqIIpKg8s9QOO44\n/0VL777rUwQ1ByLJp1QJgpmtA37vnFtrZuvx37kQlXPu4FgVJyKVZ9Uqnxq8/75SAxEp/SGGofgv\nUcr/ueyXXxSRuJSXB08+CcOGQYMGPjXo3DnoqkQkaKVqEJxzkyN+nlRh1YhIpYpMDQYO9KnBQQcF\nXZWIxIPyXGo518wOjTLewMxyY1OWiFQk5/zaguOOg6wseOcdnyKoORCRfOVZpGjFjO8P7NiHWkSk\nEuTkwNlnwzXXQM+esHix/11EJFKpT3M0s8HhHx0wwMx+jbi7GtABWBbD2kQkhpyDp56Cm2+G+vV9\naqDGQESKU5brIAwN/2vA1UDk4YQdwKrwuIjEmZwcv9bgvffgqqvgwQd1OEFESlbqBsE5dwSAmX0A\nXOycW19hVYlITBRODWbMgHPOCboqEUkEZV6D4Jw7Q82BSPzLyfHNwNVXQ1qaX2ug5kBESqu0F0p6\nCLjdObc5/HOxnHM3xqQyESkXpQYiEgulPcRwIlAj4ufi6AJKIgHKyYEBA/wXKw0Y4Nca1K0bdFUi\nkohKe6GkM6L9LCLxwTl4+mmfGtStC2+/DV26BF2ViCSyff6yJjM7yMy6m9nRsShIRMpm9WrfDAwa\nBD16+LUGag5EZF+V50qKL5nZdeGfawELgJeAL83skhjXJyLFyE8NWrWCpUth+nT4+991SEFEYqM8\nCUIH4KPwzxfhr4tQDxgM/CVGdYlICfJTg4ED96QG554bdFUiUpWUp0GoC6wL/3wu8IpzbgswDWgR\nq8JEpCilBiJSWcrTIHwDtDezOvgG4Z3weH1gW6wKE5GCVq/2KcHAgXDZZUoNRKRileVSy/keBp4D\nfgVygFnh8Q7Al7EpS0TyOQfPPAM33ugvj/zWW3DeeUFXJSJVXZkbBOfcRDObDxwOvOucywvf9TVa\ngyASU9984787YcYM6N8fxo2DevWCrkpEkkF5EgSccwuABRbmvGkxrk0kaTkHzz7rU4MDD1RqICKV\nr1zXQTCzPmb2JbAV2GpmX5hZ79iWJpKcvvnGNwMDBsAll/i1BmoORKSylTlBMLMbgbuBx4BPwsOn\nAU+YWUPn3PgY1ieSNAqnBtOmQdeuQVclIsmqPIcYrgeucc5NiRh708y+AkYDahBEyuibb/zZCW+/\nDf36wUMPaa2BiASrPA3Cb4DZUcZnh+8TkVKKTA0OOECpgYjEj/KsQcgGekQZ/yOQtW/liCSP//3P\nNwMDBsDFF8NXX6k5EJH4UZ4EYRTwopl1YM8ahFOBs4jeOIhIBOfgH/+AoUN9avCf/8Af/hB0VSIi\nBZU5QXDOvQK0BdYC3cO3tcDJzrnXYlueSNWSnxpceaVPDRYvVnMgIvGpvNdByAB6xbgWkSrLOZg0\nyacGdeooNRCR+FfqBMHMQmY23Mw+MbNPzWxM+OueRaQE//ufbwb694fu3ZUaiEhiKMshhtuA+4BN\nwLfAEOBvFVGUSFWQv9agVStYtMinBpMmQf36QVcmIrJ3ZWkQ+gB/ds6d65zrDlwAXGFm5boao0hV\n9u23cP75PjW48EJ/hoJSAxFJJGX5cG8MTM//xTk3E3DAb/elADO71czmm9kvZvaDmb1mZr/fl22K\nBCV/rcGxx8Jnn8G//w2TJys1EJHEU5YGoTqwrdDYTqDGPtZwOvAo/syIzuHtvaP1DRLvMjMzmT59\nOllZ/vIf+alBv357UoPzzw+4SBGRcirLWQwGTDKz7RFjNfHfwbA5f8A5d3FZCnDOFbg0jJn1BX4E\nUoGPy7Itkcqwbt06evbszYwZb+0ea9XqIVavHkKdOiHefBMuuCDAAkVEYqAsDcLkKGNTY1VIhHr4\nQxfrKmDbIvusZ8/ezJw5F//2PwNwLF78f/z2t++xePFZOpwgIlVCqRsE51y/iiwEwMwMeBj42Dm3\npKKfT6SsMjMzw8nBVOCKiHs+YM2azqxdm0n9+i0Cqk5EJHbKdaGkCjQROAZ/6eYSDR06lLp16xYY\nS0tLIy0trYJKE4EVK1bgv5Os8JG05gBkZ2fTooUaBBEJXnp6Ounp6QXGNm7cWOrHx02DYGaPAV2B\n051z3+1t/vjx40lJSan4wkTCnIMvvjgR+CrKvR8C0Lx580qtSUSkONH+aF64cCGpqamlenxcXMMg\n3BxcCJzhnFsddD0iha1Z4xcejhhxGL/5zWeEQq3whxm+AaZSrdoQunTpqvRARKqMwBsEM5uIP5jb\nE9hsZo3Ct5oBlyaCczBlir+uQUYGvPEGfPXViZx99tFAb/zlQXrTuXM70tMrYs2uiEgw4uEQw9X4\nsxZmFRrvB0yp9GpEwtasgUGD/CWSe/WCRx6Bgw8GqM/bb08jKyuL7OxsmjdvruRARKqcwBsE51zg\nKYZIJOdg6lQYPBhq1vSpQbduRee1aNFCjYGIVFn6cBaJsGaNbwb69PHfnfDVV9GbAxGRqi7wBEEk\nHkSmBvvvD6+/7i+XLCKSrJQgSNL77jvfDPTpA127+tRAzYGIJDslCJK0CqcGr70G3bsHXZWISHxQ\ngiBJ6bvvfDMQmRqoORAR2UMJgiQV5+C553xqsN9+Sg1ERIqjBEGSRn5q0Ls3nHuuUgMRkZIoQZAq\nzzl4/nm4/nqoUQNefRUuuijoqkRE4psSBKnSvv/epwS9evnUYMkSNQciIqWhBEGqpMKpwSuvwMWF\nv6FZRESKpQRBqpzvv/cpQa9e0KWLX2ug5kBEpGyUIEiV4Rykp/vUoHp1pQYiIvtCCYJUCd9/75uB\nK66Ac85RaiAisq+UIEhCcw5eeAGuuw6qVVNqICISK0oQJGHlpwY9e8LZZ/szFNQciIjEhhIESTiF\nU4OXX4ZLLgm6KhGRqkUJgiSUH37wzUDPntC5s19roOZARCT2lCBIQiicGvzrX3DppUFXJSJSdSlB\nkLj3ww++GYhMDdQciIhULCUIErecgxdf9KlBKKTUQESkMilBkLiUnxqkpcGZZyo1EBGpbEoQJK44\nBy+9BNdeC2b+58suC7oqEZHkowRB4saPP/qU4PLLfWqwZImaAxGRoChBkMApNRARiT9KECRQP/7o\nm4HLL4czzvBrDdQciIgETwmCBCY/NQB/tkKPHsHWIyIieyhBkEqXnxr88Y/QsaNPDdQciIjEFyUI\nUqnyU4P8axyoMRARiU9KEKRSFE4NlixRcyAiEs+UIEiF+9e/4M9/3vN9Cj16+LMVREQkfilBkArz\n00++GejRAzp08GsN/vhHNQciIolACYJUCKUGIiKJTQmCxNRPP/mUQKmBiEhiU4IgMfPyyz41yMuD\n9HQ1BiIiiUwJguyz/NTgssvgtNN8anD55WoOREQSmRIE2SevvALXXAO5ufD882oMRESqirhIEMzs\ndDN708y+NbM8M+sWdE1SsrVrfWpw6aU+NViyBNLS1ByIiFQVcdEgAHWARcCfARdwLbIXr7wCxxwD\nM2f61OCVV6BRo6CrEhGRWIqLQwzOubeBtwHM9DdovFq7Fq67zl8iuXt3ePxxOOywoKsSEZGKEBcN\ngsS/V1/1aw127YLnntPhBBGRqi5eDjFInFq71jcDl1wC7dv7MxR69lRzICJS1SVsgjB06FDq1q1b\nYCwtLY20tLSAKqp68lODnTuVGoiIJJr09HTS09MLjG3cuLHUjzfn4mtNoJnlAd2dc28Wc38KkJGR\nkUFKSkrlFpck1q6F66/3l0i+8EJ44gmtNRARqQoWLlxIamoqQKpzbmFJcxM2QZCK8dprcPXVPjWY\nOlWHE0REklVcrEEwszpmdryZnRAeOjL8++GBFpZEfv7ZNwMXXwzt2vm1BldcoeZARCRZxUuC0Ab4\nAH8NBAeMC49PBvoHVVSyiEwN/vlPNQYiIhInDYJz7kPiJM1IJj//7NcapKfDBRfAk0/Cb34TdFUi\nIhIP4qJBkMr3+us+NdixQ6mBiIgUpb/ak8zPP/tm4KKL4OST/VqDXr3UHIiISEFKEJLIG2/AoEGw\nfTtMmaLGQEREiqcEIQnkpwbdu/vUYMkS6N1bzYGIiBRPCUIVp9RARETKQwlCFbVunW8GuneHk07y\naw2UGoiISGkpQaiCIlODyZPVGIiISNkpQahC1q3zzUD37tCmjU8N+vRRcyAiImWnBKGKePNNnxps\n26bUQERE9p0ShASXnxpceCGkpsLixUoNRERk3ylBSGD//jcMHAhbt8KkSWoMREQkdpQgJKD1630z\n0K0bpKT4tQZ/+pOaAxERiR0lCAnm3//2aw22bIF//EONgYiIVAwlCAkiMjU48USfGvTtq+ZAREQq\nhhKEBPCf//i1BkoNRESksihBiGPr1/tm4IIL4IQTlBqIiEjlUYIQp6ZN86nB5s3w7LNqDEREpHIp\nQYgz+anB+efD8cf76xr066fmQEREKpcShDiSnxr8+qtSAxERCZYShDiwfr1vBs4/H1q39msNlBqI\niEiQlCAELDI1eOYZNQYiIhIflCAEZMMG3wzkpwaLF0P//moOREQkPihBCMBbb8FVVyk1EBGR+KUE\noRLlpwZ/+AMcd5xSAxERiV9KECrJW2/5tQabNsHf/67GQERE4psShAoWmRq0auVTgyuvVHMgIiLx\nTQlCBZo+3a81+OUXePppNQYiIpI4lCBUgA0b/CGErl3h2GN9ajBggJoDERFJHEoQYkypgYiIVAVK\nEGJkwwbfDHTtCscco9RAREQSmxKEGHj7bd8M/PILPPWUGgMREUl8ShD2wcaNPjU477w9qcFVV6k5\nEBGRxKcEoZxmzPBJwcaNSg1ERKTqUYJQRhs3+mbg3HPh6KOVGoiISNWkBKEM8lODDRvgySfVGIiI\nSNUVNwmCmV1rZivNbKuZzTWzk4KuKd/Gjb4ZiEwNBg5UcyAiIlVXXDQIZvZHYBwwCjgR+ByYYWYN\nAy0Mnxq0agUvvOBTg3fegSZNgq5KRESkYsVFgwAMBZ50zk1xzi0Drga2AP0rq4DMzEymT59OVlYW\n4E9ZVGogIiLJKvA1CGZWA0gF7ssfc845M5sJtK/o51+3bh09e/Zmxoy3do+lpt7G99/fxcaNIZ54\nQo2BiIgkn8AbBKAhUA34odD4D8BRFf3kPXv2ZubMucBUoCOwjYyM5hx88CK+/PIEmjat6ApERETi\nTzw0CIHJzMwMJwdTgSsi7pnHunXt2LkzE2gRTHEiIiIBiocGYS2QCzQqNN4I+L64Bw0dOpS6desW\nGEtLSyMtLa3UT7xixYrwTx0K3fNbALKzs2nRQg2CiIgknvT0dNLT0wuMbdy4sdSPN+dcrGsqMzOb\nC8xzzg0J/27AamCCc+6BQnNTgIyMjAxSUlL26XkzMzM56qijKJogTAV6k5mZqQZBRESqjIULF5Ka\nmgqQ6pxbWNLceDmL4SHgKjPrY2ZHA08AtYFJFfmkv//97+nSpSvVqg3GNwXfAFOpVm0IXbp0VXMg\nIiJJKx4OMeCceyl8zYO78IcWFgFdnHM/VfRzp6dPJS2tFzNm9N491rlzV9LTp1b0U4uIiMStuGgQ\nAJxzE4GJlf289evX5+23p5GVlUV2djbNmzdXciAiIkkvbhqEoLVo0UKNgYiISFi8rEEQERGROKIG\nQURERIpQgyAiIiJFqEGIUPiCErKH9k102i/Rab9Ep/0SnfZLdEHvFzUIEYL+jxHPtG+i036JTvsl\nOu2X6LRfogt6v6hBEBERkSLUIIiIiEgRahBERESkiES8UFJNgKVLl8Z8wxs3bmThwhK/uyJpad9E\np/0SnfZLdNov0Wm/RFcR+yXis7Pm3ubGxbc5loWZ9QSeC7oOERGRBHaFc+75kiYkYoPQAOgCrAK2\nBVuNiIhIQqkJNAVmOOd+LmliwjUIIiIiUvG0SFFERESKUIMgIiIiRahBEBERkSLUIIiIiEgRSdUg\nmNm1ZrbSzLaa2VwzO2kv8zuZWYaZbTOzTDP7U2XVWpnKsl/MrKOZ5RW65ZrZoZVZc0Uzs9PN7E0z\n+zb8GruV4jFV/v1S1v2SRO+XW81svpn9YmY/mNlrZvb7UjyuSr9nyrNfkuE9Y2ZXm9nnZrYxfJtt\nZufu5TGV/l5JmgbBzP4IjANGAScCnwMzzKxhMfObAv8B3gOOBx4B/m5mZ1dGvZWlrPslzAEtgMPC\nt984536s6ForWR1gEfBn/OstUbK8XyjjfglLhvfL6cCjQFugM1ADeMfMahX3gCR5z5R5v4RV9ffM\nN8AtQAqQCrwPvGFmLaNNDuy94pxLihswF3gk4ncD/gcML2b+/cAXhcbSgbeCfi0B75eOQC5wUNC1\nV+I+ygO67WVOUrxfyrFfku79En7dDcP757QS5iTje6Y0+yVZ3zM/A/3i6b2SFAmCmdXAd2nv5Y85\nv+hi1DcAAAYpSURBVIdnAu2LeVi78P2RZpQwP+GUc7+AbyIWmdkaM3vHzE6p2EoTQpV/v+yDZHy/\n1MP/FbyuhDnJ+J4pzX6BJHrPmFnIzC4HagNzipkWyHslKRoEfNdaDfih0PgP+PgqmsOKmX+Qme0f\n2/ICU5798h0wCLgEuBgflc0ysxMqqsgEkQzvl/JIuveLmRnwMPCxc25JCVOT6j1Thv2SFO8ZM2tl\nZpuA7cBE4CLn3LJipgfyXknEL2uSADnnMoHMiKG5ZtYMGApUqQVWsu+S9P0yETgGODXoQuJMqfZL\nEr1nluHXE9QFLgWmmFmHEpqESpcsCcJa/DGtRoXGGwHfF/OY74uZ/4tzbntsywtMefZLNPOB5rEq\nKkElw/slVqrs+8XMHgO6Ap2cc9/tZXrSvGfKuF+iqXLvGefcLufc1865z5xzt+EXiA8pZnog75Wk\naBCcczuBDOCs/LFw3HUWMLuYh82JnB92DsUfI0o45dwv0ZyAjwWTWZV/v8RQlXy/hD8ELwTOcM6t\nLsVDkuI9U479Ek2VfM8UEgKKO1wQzHsl6JWblbhCtAewBegDHA08iV81ekj4/r8CkyPmNwU24VeP\nHoU/rWsH0Dno1xLwfhkCdAOaAcfijynuxP9lEPjrieF+qYOP/07Ar7q+Ifz74Un+finrfkmW98tE\nYD3+tL5GEbeaEXPuS7b3TDn3S5V/z4Rf8+lAE6BV+H83u4Azw/fHxf+/BL6jKvk/yp/xXxO9Fd95\ntYm47x/A+4Xmd8D/hb0VyAJ6B/0agt4vwLDwvtgM/IQ/A6JD0K+hAvbJ/7d3N6FWlHEcx78/EssI\noQSrRWZFEb0RYkJkSLQQc+WmhMJ0VQntW0Roi8AQQaJdBQk3IqOoiLCiNoWLIHdib2ovmG8kimlo\n13+LM0dOZ+4999666oXz/cCzmOfMc+Y5cwfmd595ZmZZcwIc7StvDPPxMtX9MkTHy1j7ZBRY07PO\n0B0z/2W/DMMxA7wG7G3+7geBT7vhYCYdK77uWZIktQzFHARJkjQ1BgRJktRiQJAkSS0GBEmS1GJA\nkCRJLQYESZLUYkCQJEktBgRJktRiQJAkSS0GBEkAJFmWZDTJ3Eu0/YeT7G5eGDbRusuT7LoY/ZKG\nlQFBGgJJzjUn/3NjlNEkLwBfA9dX1YlL1M1NwIs1iee/V9UO4EySxy98t6Th5LsYpCGQZH7P4mpg\nI3Ab0P1v/WRVnbroHWskWQp8CFxXVWcm2WY9sLaqllzQzklDyhEEaQhU1eFuAY53qupIT/2p5hLD\nue4lhiRPJjmWZGWSPUn+TPJOkjnNZ/uS/JFka+9lgSSzk2xO8luSk0l2Jlk2QRcfAz7rDQdJ7kny\nRZITSY4n+SbJop42HwGLk9w0fXtKUtesS90BSTNK/5DilcCzwKPAXOD9phwDVgA3A+8BXwHbmzav\nArc3bX4HVgGfJLm7qn4aZ7sPAiN9dSPAt8BTdF4bfC9w9nxHq35Ncqhpu2+qP1TSYAYESYPMAp6u\nqv0ASd4FngDmV9VpYE+SL4GHgO1JFgBrgRuq6mDzHVuSrADWAc+Ps50bgQN9dQuAl6vqh2Z5rHBx\noGkraZoZECQNcqobDhqHgP1NOOit685xuAu4DPi+726E2cDRAduZA/zVV7cFeD3JGuBzYHtV7e1b\n5zSdUQ5J08yAIGmQs33LNU5ddz7TVcDfwCI6lwV6nRywnaPA1f/60qqNSUaAlcAjwIYkq6vqg57V\nrgGOTPQjJE2dkxQlTadddEYQrq2qvX3l8ATt7uivrKofq2prVS2nM/dhXfezJJcDtzRtJU0zA4Kk\nXhM+pGiQZr7AW8C2JKuSLEyyJMlzzTyE8ewAlp7vRHJFkleaOysWJHkAuA/Y3dPmfjqXJXb+nz5L\nGpsBQVKv6XgwylpgG7AZ2EPnLofFwC8D2owAdya5tVkeBeYBbwLfAW8DHwMbetqsBkaqqn/ugqRp\n4IOSJM0ISTYBc6vqmUmsO49O+FhcVT9f8M5JQ8gRBEkzxUvAZE/2C4H1hgPpwnEEQZIktTiCIEmS\nWgwIkiSpxYAgSZJaDAiSJKnFgCBJkloMCJIkqcWAIEmSWgwIkiSpxYAgSZJa/gEkJfV4XXwJ0QAA\nAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7211bb92b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# set variables = data['column label']\n",
"time = data['time (s)']\n",
"pos = data['position (m)']\n",
"\n",
"# Uncomment the next line to make it look like a graph from xkcd.com\n",
"# plt.xkcd()\n",
"# to make normal-looking plots again execute:\n",
"# mpl.rcParams.update(inline_rc)\n",
"\n",
"# this makes a scatterplot of the data\n",
"# plt.scatter(x values, y values)\n",
"plt.scatter(time, pos)\n",
"plt.title(\"Constant Speed?\")\n",
"plt.xlabel(\"Time (s)\")\n",
"plt.ylabel(\"Position (cm)\")\n",
"plt.autoscale(tight=True)\n",
"\n",
"# calculate a trendline equation\n",
"# np.polyfit( x values, y values, polynomial order)\n",
"trend = np.polyfit(time, pos, 1)\n",
"\n",
"# plot trendline\n",
"# plt.plot(x values, y values, other parameters)\n",
"plt.plot(time, np.poly1d(trend)(time), label='trendline')\n",
"plt.legend(loc='upper left')"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 2., 0.])"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# display the trendline's coefficients (slope, y-int)\n",
"trend"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Calculate and plot velocity"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>time (s)</th>\n",
" <th>position (m)</th>\n",
" <th>velocity (m/s)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>4</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td></td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" time (s) position (m) velocity (m/s)\n",
"0 0 0 \n",
"1 1 2 \n",
"2 2 4 \n",
"3 3 6 "
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# create a new empty column\n",
"data['velocity (m/s)'] = ''\n",
"data"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>time (s)</th>\n",
" <th>position (m)</th>\n",
" <th>velocity (m/s)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>4</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" time (s) position (m) velocity (m/s)\n",
"0 0 0 2.0\n",
"1 1 2 2.0\n",
"2 2 4 2.0\n",
"3 3 6 NaN"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# np.diff() calculates the difference between a value and the one after it\n",
"vel = np.diff(pos) / np.diff(time)\n",
"\n",
"# fill the velocity column with values from the formula\n",
"data['velocity (m/s)'] = pd.DataFrame.from_items([('', vel)])\n",
"\n",
"# display the data table\n",
"data"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>time (s)</th>\n",
" <th>velocity (m/s)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" time (s) velocity (m/s)\n",
"0 0 2.0\n",
"1 1 2.0\n",
"2 2 2.0"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# That last velocity value will cause problems for further coding\n",
"# Make a new table using only rows 0 through 2\n",
"data2 = data.loc[0:2,['time (s)', 'velocity (m/s)']]\n",
"data2"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x7f720f6c0978>"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAicAAAGHCAYAAABrpPKuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XmYFNXZxuHf28M6qICMgCiLigqIG4OIIgqiohDBHUcR\ncTdqNCTGxCVuiUbNJwombomKC6BoxBVFIYC4EgZxY99dWEQEVECBeb8/qmbs6dm6m56Zwnnu6+oL\n+vSpqremKfqZqnOqzd0RERERiYpYdRcgIiIiEk/hRERERCJF4UREREQiReFEREREIkXhRERERCJF\n4UREREQiReFEREREIkXhRERERCJF4UREREQiReFERGQ7ZGZHmVmBmR1Z3bWIZJrCicgvgJntaWYP\nmdlCM9toZuvM7G0zu9LM6lVzbSeY2U1VtK3DzOwmM9sphWVONLPJZrbSzH4If4bPmFnvyqw1Q4p9\n/4iZ9TGzV83sKzP71szeMLMDqqs4kXQpnIhs58ysL/AJcBrwEnAF8CdgKXAXcG/1VQdAH+DGKtrW\n4eG2GiXT2cyuBl4ECoDbgd8CzwFtgQGVVGNlehn4EbiFYH86Am+YWZNqrUokRbWquwARSZ+ZtQFG\nA4uBo919VdzLD5jZn4G+1VBaPIvitswsC7gBGO/uJ5Tyek4mC6siXd39f4VPzGwmMB44juDfich2\nQWdORLZvfwQaABckBBMA3H2Ru99X+NzMsszsz2a2wMw2mdliM7vNzOrEL2dmS8zsJTPrZmYfhJeK\nFprZOQn9aoWXUeaFfVab2VQz6xW+/hhwWfj3gvCxNW75q83snXC5DWY23cxOTdyPcLnhZtbfzD4J\na/80/tJLeOnorvDpksJtmVmrMn52OcBOwLulvejuq+PWXTi+4wwzu93MlpvZ92b2opntXkq9h5rZ\n62a2NrxUNNnMDi+lXwsze9TMVsTt03ml9NvNzF4It7nSzIYCdUkIY/HBJPRj+GcdRLYj5u4V9xKR\nSDKzz4FN7r53kv1HAIOAMcBk4FDgXGCsu58a128xsAloCDwCfAWcDxwM7O/us8N+txFcQnoY+B/B\nh31n4CN3/7uZHQrcChwDDCT8MHX3UeHyywguq8wi+AA9E+gC/MrdX4urpwD4CNgFuB/4DrgSaA60\ncvdvzawjcG24jt8C34SLj3X3jaX8LAz4HvgM6O3u35bzczsKmERw+awAGAE0BYYQXD47yN1/DPse\nDYwDphNcIioAzgPaA0e4+/SwX1MgH9ga/vxWAycA/YHfuvvwsF+9cN93B4YBy4Fzwp/X/kBPd3+r\nlJrrAhOBfYB93H1tWfsnEjnuroceemyHD2BHgg++55Psf0DY/8GE9rsIPiCPimtbHLYdHteWA2wE\n7opr+xB4qYLt3gdsLeO1ugnPs4CPgTcT2gvCbbeJa9s/bL8sru33Yd2tkvyZ3Bz2/w54lSDcHFxK\nv6PCbS0DsuPaTwvbr4hrmwu8mrifwELg9bi2fwNfAI0S+o4C1hT+bICrwhpPietTD5gXth9ZSr1Z\n4f5sIAhE1f7vVQ89Unnoso7I9qtwRsp3SfbvQzC7456E9rsJzmgkjk2Z5e5Flzw8uMwxF9gzrs9a\nYD8za5ts0fE8PNsAYGaNgMbAVKBTKd3fdPclcct+AqxPqCfV7d8MnAXMIBiX8Vcg38zyzaxdKYs8\n7u4b4pZ/juBMRp9wHw4G9gZGm1mTwgdBkJwIxE/7PYVgAGtWQt83CAb0Fv4MTgCWu/vzcdvdRHC2\npSw3A72Bs9z97aR+GCIRogGxItuv9eGfOybZvzXBb/kL4hvdfaWZrQ1fj7eslHV8SxAgCt0IvADM\nM7NPgdeBJ8PgUCEz+xVwPXAQwdmFQgWldP88iXpS5u7PAM+Y2Q4El7kGA2cDL5lZR3f/Ka77glJW\nsQBoE/69MKQ9UcbmCsysIcElmUbAxcAlpZVFcNkIgveltO3OLWMbEFxCe9PdXyinj0hkKZyIbKfc\n/Tsz+4pgumhKiybZb2sZ7UWDMN19qpntRTBO4jjgAmCImV3i7o+Wt3Iz604w3mQy8GuCMxCbCca2\n5KVTz7Zw9+8Jzm5MNLMtBGNzDiU4k5OswrPRvycYJ1Ka7wkukQE8BTxeRr+PU9huoiYEP0+R7ZLC\nicj27RXgIjM71N0/qKDvUoIPz72J+607HJjZKHw9ZR4MtHwceNzMsgk+zG8GCsNJWWHoFIJxJL3d\nfUtcPRekU0cF20rVdIJwsmtCe2kDj9vycxBZGP75nbv/t6yVm9nXBJfjssrrF1oK7FdKe2mXnQo9\nRDAeSGS7pDEnItu3uwgGPf47DBnFmNleZnZl+HQcwVmG3yZ0+z3Bh/qrqW7czHaOfx6Ox1hA8Us0\nP4R9E+/aujXcbtEvSeF9W/qnWkfitkjiJmxmVt/Mupbxcp/wz8RLJ4PCyz+F6zidIMCMC5vyCQLK\n1WbWoJRt5gC4ewHwH+BUMysRPBLusTIOaBE/xToMgReVs3v/BioKPSKRpTMnItsxd19kZmcBTwOz\nzewJ4FOCMQ3dCGaTPBb2/djMHgcuNrPGwBSCyxaDCGb8TEmjhFlmNpngQ3kNcEi4zeFxffIJQtF9\nZjaeYObOMwRh6HfAeDMbBTQjuCfKfIKZReko3NbtZvY0wWWil7yUqcRANvCumb1PMFbmc4JQcxJw\nBMEU5MRLM2uAt8P7tzQnmEkzjyAM4O5uZhcSBIrPwn5fArsBPYF1/By+/gT0AD4ws38RTKfeGcgF\njubnSz//Irjr75Nm1pmfpxIXBrHSzCaY7nx+OX1Eoqu6pwvpoYce2/4A9gIeJPitfSPBh+A7BB9q\ndeL6xQjuirqA4D4mS4C/ALUT1rcIeLGU7UwCJsY9vxZ4j+CeIoX3DPkjweWK+G3eC6wAthA3rZhg\n8OkcgrM/nxEEpZtImHpMcJZlWCn1LAIeSWi7jmAw72bKmVZMMN32fIIzGIvCGr4juKQzBKgV1/eo\ncF1nEMzoWR7u74vA7qWs+wDgWWBVuN5FBHdo7ZHQL4cgyC0J348vCWbrnJ/Qb3dgbFjfSoIZVsdS\n9lTirYk/Fz302J4eugmbiEgF4m7CdprHTekVkcqhMSciIiISKQonIiIiEikKJyIiydE1cJEqojEn\nIiIiEik6c5ICM8s2s07hPQZEREQkSal8huo+J6k5iGB65tlmNqe6ixEREdmOtANGEtyD6d3yOiqc\npKZN+OfI6ixCRERkO9YGhZOMWgLw1FNP0b59+4yvfMiQIdxzT+K32UuU6D2KPr1H0af3KPoq4z2a\nPXs2AwcOhPCztDwKJ6nZBNC+fXs6deqU8ZU3bNiwUtYrmaP3KPr0HkWf3qPoq+T3aFNFHTQgVkRE\nRCJF4UREREQiReFEREREIkXhJELy8vKquwSpgN6j6NN7FH16j6Kvut8j3SE2BWbWCcjPz8/XYC4R\nEZEUzJgxg9zcXIBcd59RXt9qP3NiZtea2TQzW29mK81srJntk8RyPcws38w2mdk8Mzs34fUOZvac\nmS02swIzu7KM9Vwe9tloZu+b2SGZ2jcRERFJXbWHE6A7cB9wKHAMUBt4w8zql7WAmbUBXgEmAgcC\nw4B/m9mxcd2ygYXAH4HlZaxnAHA3cBNwMPARMN7McrZpj0RERCRt1X6fE3fvE//czAYDq4Bc4O0y\nFvs1sMjdrwmfzzWzI4AhwJvheqcD08N13lnGeoYAD7n7E2G/S4G+wPnAXWnukoiIiGyDKJw5SdSI\n4KvJ15TTpyswIaFtPHBYshsxs9oEAWhiYZsHA3AmpLIeERERyaxIhRMzM+Be4G13n1VO1+bAyoS2\nlcBOZlY3yc3lAFllrKd5kusQERGRDKv2yzoJ7gc6EHxjoYiIiNRAkQknZvYPoA/Q3d1LHcAaZwXQ\nLKGtGbDe3X9McpOrga1lrGdFeQsOGTKEhg0bFmvLy8ur9nnhIiIiUTB69GhGjx5drG3dunVJLx+J\ncBIGk/7AUe6+LIlF3gNOSGg7LmxPirtvNrN8oBfwUliHhc+Hl7fsPffco/uciIiIlKG0X9jj7nNS\noWoPJ2Z2P5AH9AN+MLPCMxnr3H1T2Od2YDd3L7yXyYPA5eEsnEcJAsVpBGdeCtdbm+ASkQF1gN3M\n7EDge3dfGHYbCowIQ8o0gtk72cCIStpdERERqUC1hxPgUoLZOZMT2s8Dngj/vivQsvAFd19iZn2B\ne4ArgS+AC9w9fgZPC+DDcN0AV4ePKcDR4XrGhPc0uZXgcs5MoLe7f52pnRMREZHUVHs4cfcKZwy5\n+3mltL1FMBW4rGWWksRsJHe/n2AgroiIiERApKYSi4iIiCiciIiISKQonIiIiEikKJyIiIhIpCic\niIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyI\niIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiI\niEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiI\nSKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhI\npCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEik\nKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQo\nnIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikVHs4MbNrzWya\nma03s5VmNtbM9kliuR5mlm9mm8xsnpmdW0qf081stpltNLOPzOyEhNdvMrOChMesTO6fiIiIpKba\nwwnQHbgPOBQ4BqgNvGFm9ctawMzaAK8AE4EDgWHAv83s2Lg+hwOjgH8BBwEvAi+YWYeE1X0KNAOa\nh48jMrFTIiIikp5a1V2Au/eJf25mg4FVQC7wdhmL/RpY5O7XhM/nmtkRwBDgzbDtSuA1dx8aPr8x\nDC9XAJfFrWuLu3+9zTsiIiIiGRGFMyeJGgEOrCmnT1dgQkLbeOCwuOeHJdEHYG8z+9LMFprZU2bW\nMo2aRUREJEMiFU7MzIB7gbfdvbyxH82BlQltK4GdzKxuBX2axz1/HxgM9AYuBfYA3jKzBmntgIiI\niGyzar+sk+B+oAPQrSo25u7j455+ambTgKXAGcBjZS03ZMgQGjZsWKwtLy+PvLy8SqlTRERkezJ6\n9GhGjx5drG3dunVJLx+ZcGJm/wD6AN3dfXkF3VcQDGKN1wxY7+4/VtBnRVkrdfd1ZjYPaFvexu+5\n5x46depUQYkiIiI1U2m/sM+YMYPc3Nyklo/EZZ0wmPQHerr7siQWeQ/oldB2XNheXp9jE/ok1rED\nQTCpKByJiIhIJan2cGJm9wNnA2cBP5hZs/BRL67P7Wb2eNxiDwJ7mtmdZravmV0GnAYMjeszDDje\nzH4X9rmZYAbQP+LW+3czO9LMWodTj8cCm4Hi56JERESkylR7OCEYiLoTMBn4Ku5xRlyfXYGiWTTu\nvgToS3BflJkEU4gvcPcJcX3eIwg8F4d9TgH6Jwy03Z3gXihzgKeBr4Gu7v5NJndQREREklftY07c\nvcKA5O7nldL2FsGZkPKW+w/wn3Je1whWERGRiInCmRMRERGRIgonIiIiEikKJyIiIhIpCiciIiIS\nKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIp\nCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIpCiciIiISKQonIiIiEikK\nJyIiIhIpCiciIiISKQonIiIiEikKJyIiIhIptdJZyMyygKZANvC1u6/PaFUiIiJSYyV95sTMGpjZ\nRWY2EVgPfAHMA741s4Vm9oCZHVxZhYqIiEjNkFQ4MbMrgSXAr4G3gTOAzsB+QHfgTmAHYIqZvWJm\ne1VKtSIiIvKLl+xlne7AMe7+URmvvws8bGb1gAuBnsDCDNQnIiIiNUxS4cTdT0+y3ybgH9tUkYiI\niNRomq0jIiIikZLybB0zqwtcRnDppikJAcfdu2SmNBEREamJ0plK/G/gBGAs8DHgGa1IREREarR0\nwkk/4FfuPjXTxYiIiIikM+bkK2BtpgsRERERgfTCyR+AO8xst0wXIyIiIpJOOHkPqA8sM7NvzWxV\n/CPD9YmIiEgNk86Yk9FAK+BGYCUaECsiIiIZlE44OQLo5u4fZroYERERkXQu68wDame6EBERERFI\nL5xcDdxtZkeYWUMzy45/ZLpAERERqVnSuazzRvjnlDJez0qzFhEREZG0wsmxGa9CREREJJRyOHH3\niZVRiIiIiAgkOeYk1Ruumdmu6ZUjIiIiNV2yA2JnmNk/zezgsjqY2Q5mdp6ZfQSckZnyREREpKZJ\n9rJOR+AGYIqZrQfyCb5jZxPQGOgAHAB8AvzZ3V+qhFpFRESkBkjqzIm7f+3uVwG7Ekwl/hzYHdgf\nqAf8B+jq7ocomIiIiMi2SGlArLv/ADwdPkREREQyLp2bsImIiIhUGoUTERERiRSFExEREYkUhRMR\nERGJlJTDiZnVr4xCRERERCC9MycrzexhM+ua8WpERESkxksnnJwPtACmmtksM7vazJpluC4RERGp\noVIOJ+7+nLv/CmgJjCAIK5+b2Qtm1s/MsjJco4iIiNQgaQ+IdfcV7n6Xu3cAfg8cD4wFvjCzGzU2\nRURERNKR0h1i45nZLsA5wHlAW+AF4BGC29r/ATicILCIiIiIJC3lcGJm/QgCSR9gPvBv4Al3XxPX\nZyowK1NFioiISM2RzmWdkcAaoIe7d3T3e+ODSehL4M5kVmZm15rZNDNbb2YrzWysme2TxHI9zCzf\nzDaZ2TwzO7eUPqeb2Wwz22hmH5nZCaX0udzMFod93jezQ5KpW0RERCpHOuFkV3e/wN3fK6uDu290\n9z8nub7uwH3AocAxQG3gjfLGrJhZG+AVYCJwIDAM+LeZHRvX53BgFPAv4CDgReAFM+sQ12cAcDdw\nE3Aw8BEw3sxykqxdREREMiydcLImHG9SjJntbGY/pboyd+/j7k+6+2x3/wQYDLQCcstZ7NfAIne/\nxt3nuvs/geeAIXF9rgRec/ehYZ8bgRnAFXF9hgAPufsT7j4HuBTYQDADqUrNmzeP1157jfnz51f1\npkV+MXQciWy7KBxH6YSTWoCV0l4PKNi2cgBoBDjBpaOydAUmJLSNBw6Le35YeX3MrDZBAJpY+KK7\ne7jMYVSRNWvWcPzxfdl3333p06cP++yzD8cf35dvv/22qkoQ2e7pOBLZdlE6jpIOJ2Z2mZldRhAc\nBhc+Dx+/AYYDc7elGDMz4F7gbXcvb0Btc2BlQttKYCczq1tBn+bh33OArAr6VLqzzjqHCRPeB54C\nlgFPMWHC++TlDayqEkS2ezqORLZdlI6jVGbrXBv+acBVFD9L8hOwhOByy7a4H+gAdNvG9WwX5s2b\nx/jx4wj+IZwdtp7N1q2NGT/+Bl54YRmtWrWqxgpFom/p0qWMH78ceJJgEiHoOBJJTdnHkTN+/DnM\nnz+fvffeu8rqSTqcuHtLKJom3M/dM3qex8z+QfAT6e7uyyvovgJIvGV+M2C9u/9YQZ8V4d9XA1sr\n6FOqIUOG0LBhw2JteXl55OXlVVB2cQsXLgz/dmTCK32APpx8ckqrE6mhWhMMJ0uk40gkeWUdR0cB\nsGDBgpTCyejRoxk9enSxtnXr1iW9fMr3OXH37qkuU5EwmPQHjnL3ZUks8h6QOC34uLA9vk8vgstN\nhY4t7OPum80sP+zzUliHlbJMCffccw+dOnVKoszy7bXXXuHf3uLnMycA44AbGDv2Bf3GJ1KBpUuX\ncsopJwN/5eff+EDHkUjyyj6OpgDQtm3blNZX2i/sM2bMIDe3vLkuP0sqnJjZXcAt7v5D+Pcyufs1\nSW3553XfD+QB/YAf4r5EcJ27bwr73A7s5u6F9zJ5ELjczO4EHiUIFKdR/Cc6DJhsZr8DXg23kQtc\nFNdnKDAiDCnTCGbvZBN8Z1Cl22effejduw8TJlzJ1q1OkFCnkJV1Fccc05WTTtJ/qCIV6dSpNb17\n78qECeewdeswdByJpK7846hPlV7SAcDdK3wAU4FGcX8v6/FWMutLWHcBweWVxMeguD6PAf9NWO5I\nIB/YSHCn2nNKWfepwJywz8dA71L6XEYwXmYjwVmVzuXU2gnw/Px8z5Q1a9Z47959nGCgsQPeu3cf\nX7NmTca2IfJLp+NIZNtV9nGUn59fuN5OXkE2MA8+dCUJZtYJyM/Pz8/IZZ148+fPZ8GCBbRt27bq\nE6rIL4SOI5FtV1nHUdxlnVx3L22AS5F0vltnB6CWu69NaG8EbHH371Ndp8Dee++t/0xFtpGOI5Ft\nF4XjKJ2bsI0Bziql/Szg6W0rR0RERGq6dMJJV+C/pbRPCl8TERERSVs64aQupV8OyiKY6SIiIiKS\ntnTCyXTgwlLaL6b0O7iIiIiIJC3lAbHADcCbZnYAP39pXi/gcKB3pgoTERGRminlMyfuPpXgu29W\nA4OA04EvgIPcfUpmyxMREZGaJp0zJ7h7PnBGhmsRERERSS+cmFkMOBFoHzZ9Brzq7gVlLyUiIiJS\nsXRuwrYnwXfVtCG4bTzA3sAiM/uVuy/OXHkiIiJS06QzW2c4sAxo5e4HuPsBBN+1/CUVfJuviIiI\nSEXSuazTAzjc3b8ubHD3VWb2B+DtTBUmIiIiNVM6Z042U/rN1rLD10RERETSlk44eRV42MxyCxvM\nrDPwIPBKpgoTERGRmimdcPIb4HPgf2a20cw2Ah8QjEO5KpPFiYiISM2T8pgTd/8W6Gtm7YF2YfNs\nd5+T0cpERESkRkrrPicA7j4bmJ3BWkRERESSCydmdleyK3T3a9IvR0RERGq6ZM+cHJZkP0+3EBER\nERFIMpy4e/fKLkREREQE0putA4CZtTGzXmZWL5MFiYiISM2Wcjgxs53NbDywCHgDaBG2jzCz/8tw\nfSIiIlLDpHPmZGi43J7Ahrj2p4ETMlGUiIiI1FzpTCXuDZzg7kvMLL59HsEXAIqIiIikLZ0zJzsC\n35fS3hj4advKERERkZounXDyNjAw7rlbcArlamBSRqoSERGRGiudyzp/AP4bfvFfHeBvwH5AM6Bb\nBmsTERGRGijlMyfu/gmwDzCd4BuKdw7/PNjd52e2PBEREalpkj5zYmYd3f1TKPryv1sqrSoRERGp\nsVI5c/KxmX1gZheZ2Y6VVpGIiIjUaKmEk6OAz4C7geVm9riZ6bb2IiIiklFJhxN3n+ru5wO7Ar8B\n2gBTzGyemf3RzJpXUo0iIiJSg6QzIPYHd3/M3Y8iGBj7LHA5sMzMXsp0gSIiIlKzpP3FfwDuvgC4\nHfgr8B3QNxNFiYiISM2Vzn1OADCzI4HzgVOBAmAM8EiG6hIREZEaKqVwYmYtgMHhoy3wLnAlMMbd\nf8h0cSIiIlLzpHKfk9eAY4DVwBPAo+4+t7IKExERkZoplTMnm4HTgFfcfWsl1SMiIiI1XNLhxN37\nVWYhIiIiIrCNs3VEREREMk3hRERERCJF4UREREQiReFEREREIkXhRERERCJF4UREREQiReFERERE\nIkXhRERERCJF4UREREQiReFEREREIkXhRERERCJF4UREREQiReFEREREIkXhRERERCJF4UREREQi\nReFEREREIkXhRERERCJF4UREREQiReFEREREIkXhRERERCIlEuHEzLqb2Utm9qWZFZhZvySWudzM\nZpnZBjObbWbnJLxey8xuNLMFZrbRzD40s94JfW4Ktxf/mJXp/RMREZHk1aruAkINgJnAI8DzFXU2\ns18DtwEXAtOBQ4F/mdkad3817HYbcFbYZy5wPDDWzA5z94/iVvcp0Auw8PmWbd8dERERSVckwom7\nvw68DmBmVkF3gIHAQ+7+XPh8iZkdAvwReDWuz1/cfXz4/EEzOwb4PTAobl1b3P3rbd0HERERyYxI\nXNZJQ11gU0LbJqCLmWXF9fkxoc9G4IiEtr3Dy0kLzewpM2uZ+XJFREQkWdtrOBkPXGhmnQDMrDNw\nAVAbyInr8zsza2uBY4FTgF3j1vM+MBjoDVwK7AG8ZWYNqmQvREREpITtNZz8BXgNeM/MNgNjgRHh\nawXhn1cB84E5BGdQhgOPxr2Ou4939/+4+6fu/ibQB2gMnFEVOyEiIiIlRWLMSarcfRPBmZNLgGbA\ncuAS4LvC8SPuvho4xczqAE3cfbmZ3QEsKme968xsHtC2vO0PGTKEhg0bFmvLy8sjLy9vW3ZLRETk\nF2H06NGMHj26WNu6deuSXt7cPdM1bRMzKwBOcveXUlxuMvC5u59Txuu1gVnA0+7+5zL67AAsA250\n93+U8nonID8/P59OnTqlUp6IiEiNNmPGDHJzcwFy3X1GeX0jceYkHOPRlp+n8+5pZgcCa9z9czP7\nG9DC3c8N++8NdAE+AHYGfgfsR9wsHDPrAuxGMEV5d+CmcP1/j+vzd+BlYGnY9xZgM1A87omIiEiV\niUQ4AToDkwAPH3eH7Y8D5wPNgfhZNFkEU4L3IQgTk4DD3X1ZXJ96wF8JBrl+TzDFeKC7r4/rszsw\nCmgCfA28DXR1928yuXMiIiKSvEiEE3efQjmDc939vITnc4Byr6u4+1sEZ1PK66NBIiIiIhGzvc7W\nERERkV8ohRMRERGJFIUTERERiRSFExEREYkUhRMRERGJFIUTERERiRSFExEREYkUhRMRERGJFIUT\nERERiRSFExEREYkUhRMRERGJFIUTERERiRSFExEREYmUSHwr8S/NsmXLWL16dXWXIZK0nJwcWrVq\nVd1liIgACicZt2zZMtq3b8+GDRuquxSRpGVnZzN79mwFFBGJBIWTDFu9ejUbNmzgqaeeon379tVd\njkiFZs+bI79BAAAchklEQVSezcCBA1m9erXCiYhEgsJJJWnfvj2dOnWq7jJERES2OxoQKyIiIpGi\ncCIiIiKRonAiIiIikaJwIiIiIpGicCK/GCNGjCAWi7Fs2bKith49enD00UcXPV+6dCmxWIwnnnii\nOkoUEZEkKJxISt577z1uueUW1q9fX92llGBmmFmJttL6iYhIdCmcSEreffddbr31VtauXVvdpaSl\ndevWbNy4kXPOOae6SxERkTIonEhK3D3pfj/++GMlV5OeOnXq6OyJiEiEKZxI0m655RauueYaANq0\naUMsFiMrK6toHMeVV17JqFGj6NixI/Xq1WP8+PFAEFTuvfdeOnbsSP369WnevDmXXnppibMvbdq0\noV+/frzzzjsceuih1K9fn7322osnn3yyRC2zZs3i6KOPJjs7m5YtW3LbbbdRUFBQ4T6UNuZk8ODB\n7Ljjjnz11VecdNJJ7LjjjjRt2pQ//OEPJcJYsvsiIiLp0x1iJWmnnnoq8+bN4+mnn2bYsGE0adIE\nM2OXXXYBYOLEiYwZM4YrrriCnJwc2rRpA8DFF1/ME088wfnnn89VV13F4sWLue+++5g5cybvvPMO\nWVlZQDAWZP78+Zx++ulccMEFDB48mEcffZTzzjuPzp07F30dwMqVK+nRowcFBQVcd911ZGdn8/DD\nD1OvXr209svMKCgooHfv3nTt2pW7776bCRMmMHToUNq2bcsll1xS1DfZfRERkfQpnFSjDRtgzpzK\n3067dpCdve3r6dixI506deLpp5+mf//+Jb6HZd68eXz66afsu+++RW1vv/02jzzyCKNHj2bAgAFF\n7T179qR37948++yznHnmmcXWMXXqVA4//HAATj/9dFq2bMljjz3GXXfdBcAdd9zBN998w7Rp08jN\nzQXg3HPPpW3btmnv26ZNm8jLy+O6664DghCSm5vLI488UhROUt0XERFJj8JJNZozB8LP1kqVnw9V\n8TU/PXr0KBZMAJ577jkaNWpEr169+Oabb4raDz74YHbYYQcmTZpU7AO9Q4cORcEEICcnh3333ZdF\nixYVtb322mt07dq1KJgANGnShLPPPpsHHngg7frjz5AAdO/enaeeeirtfRERkfQonFSjdu2C4FAV\n26kKhZdx4s2fP5+1a9fStGnTEq+ZGatWrSrWVtq34jZu3Jhvv/226PnSpUvp2rVriX6JwSgV9erV\no0mTJuVuN9V9ERGR9CicVKPs7Ko5o1FV6tevX6KtoKCAZs2aMWrUqFJn+hSOVylU1piNZGcJpSuZ\nsSKp7ouIiKRH4URSkuoU3L322ouJEydy+OGHU7du3YzU0Lp1a+bPn1+ifU4lD+CpjH0REZGSNJVY\nUtKgQQOApKfOnnHGGWzZsoVbb721xGtbt25l3bp1KdfQp08f3n//faZPn17U9vXXXzNq1KiU15WK\nytgXEREpSWdOJCW5ubm4O9dddx1nnnkmtWvX5sQTTyyz/5FHHskll1zCHXfcwcyZMznuuOOoXbs2\n8+bN47nnnmP48OGccsopKdVwzTXX8OSTT9K7d2+uuuoqsrOz+de//kWbNm34+OOPt3UXy1QZ+yIi\nIiUpnEhKOnfuzF//+lcefPBBxo8fj7uzcOHCUr/XptADDzxA586deeihh7j++uupVasWbdq0YdCg\nQXTr1q2oX3nriG9v3rw5kydP5je/+Q133nknTZo04de//jXNmzfnwgsvLHfZ0p6X1VZae7L7IiIi\n6bPKHmj4S2JmnYD8/Px8OpUxknXGjBnk5uZSXh+RKNG/WRGpCoX/1wC57j6jvL4acyIiIiKRonAi\nIiIikaJwIiIiIpGicCIiIiKRonAiIiIikaJwIiIiIpGicCIiIiKRonAiIiIikaJwIiIiIpGicCIi\nIiKRonAiIiIikaJwItVmypQpxGIx3nrrrUpZ/4gRI4jFYixbtqxS1p9o2rRp1K1bl88//7xKtlee\n2bNnU7t2bWbNmlXdpYiIpEzhRKpVWd8GnKl1l/atwo8//nilbO+GG27g7LPPpmXLlhlf99q1a6ld\nuzbPPfdcUv3bt29P3759ufHGGzNei4hIZVM4kV+sQYMGsXHjRlq1alXUdv/991dKOJk5cyYTJkzg\n0ksvzfi6AV5//XVisRjHHXdc0stceumljB07lsWLF1dKTSIilUXhZDuyatUqli9fjrtXdynbBTOj\nTp06VbKtxx57jNatW9OlS5dKWf9rr71Gt27d2GmnnZJe5phjjqFRo0aVdqZIRKSyKJxsB2bMmMFh\nhx1Bs2bNaNGiBQcd1LnSxmmU5T//+Q+xWIypU6eWeO2hhx4iFosVG98wd+5cTjvtNJo0aUL9+vU5\n5JBDePnll5Pa1rPPPkvnzp3Jzs5ml1124ZxzzuGrr74q0W/u3LmcccYZNG3alOzsbNq1a8cNN9xQ\n9HrimJM99tiDzz77jMmTJxOLxYjFYhx99NEsXryYWCzGsGHDSmzj3XffJRaL8cwzz5Rb84svvsjR\nRx9dor1Nmzb069ePKVOmcMghh5Cdnc0BBxzAlClTAHj++ec54IADqF+/Pp07d2bmzJkl1uHuvP76\n6/Tt27eo7c0336R79+40btyYHXfckXbt2nH99dcXW65WrVr06NGDF198sdzaRUSiRuGkmnz22Wf8\n7ne/Y8CAAdx+++2sWrWq1H5Lly7lqKOO5n//+wF4CniGTz+tx7HH9uaTTz6psnr79u3LDjvswJgx\nY0q8NmbMGDp27EiHDh2AYN+6du3K3Llzufbaaxk6dCg77LADJ510UoUflCNGjGDAgAHUrl2bO+64\ng4svvpjnn3+e7t27s379+qJ+H3/8MV26dGHy5MlccsklDB8+nJNPPplXXnmlqE/imJNhw4ax++67\n0759e0aOHMlTTz3F9ddfzx577EG3bt0YOXJkiXpGjhzJTjvtRP/+/cus+auvvmLZsmV06tSpxGtm\nxvz58zn77LPp168fd9xxB99++y39+vVj1KhR/P73v2fQoEHceuutLFy4kAEDBpRYx7Rp01i9ejV9\n+vQBYNasWZx44ols3ryZv/zlLwwdOpT+/fvz7rvvllg2NzeXTz/9lO+//77M+kVEIsfd9UjyAXQC\nPD8/38uSn5/vFfV58sknPRaLea1azTwW6+mxWH1v3DjHP/744xJ9r776as/K2tlhrYOHj41eq1Yb\nHzTo3FLXP3XqVD/22ON9xx0b+5577uN33HGH//TTT2XWk6yzzjrLmzdv7gUFBUVtK1as8KysLL/t\nttuK2nr16uUHHXSQb968udjy3bp183333bfo+eTJkz0Wi/mUKVPc3X3z5s3erFkzP/DAA/3HH38s\n6vfqq6+6mfnNN99c1HbkkUd6w4YN/Ysvviiz3hEjRngsFvOlS5cWtXXs2NF79uxZou/DDz/ssVjM\n586dW9S2efNm32WXXfz8888v9+cyceJENzN/9dVXS7zWpk0bj8Vi/sEHHxS1vfHGG25m3qBBg2L1\nF9ZQ+PModOONN/oee+xR9Pzee+/1WCzma9asKbcud/fRo0d7LBbz//3vf2X2SebfrIjItir8vwbo\n5BV83urMSRX79ttvufDCiykoOJstW5ZRUPBfCgqWsH79rlx4YcnBlNOm5bN1ay+gYVxrPbZs6cv7\n708v0f+NN96gR4+e/Pe/K/nuu6tZtOhwrr32Bs4886xtHqsyYMAAVq1axeTJk4vann32WdydM844\no2j/Jk2axOmnn866dev45ptvih7HHXcc8+fPZ/ny5aWuf/r06axatYrLLrus2FiRPn360K5dO159\n9VUAVq9ezdSpU7ngggvYbbfdtmmfCp1xxhnUrVu32NmT119/nW+++YaBAweWu+w333yDmdG4ceNS\nX+/QoUOxsSiHHnooAL169SpW/6GHHoq7s2jRomLLjxs3rtglnUaNGgEwduzYCt/TwppWr15dbj8R\nkShROKlir7zyCj/+uBH4O1D4AdyUrVuvZ9q0d0vcI6NFi+bUqjWbIGz+LBabRYsWzYu1uTtXX/0n\nCgq6sXXrNOA64DHcn+D555/jgw8+2Kbajz/+eHbaaadi4y/GjBnDQQcdRNu2bQFYsGAB7s6f//xn\ndtlll2KPm2++GaDcS1hmxj777FPitXbt2rF06VKAog/v/fbbb5v2J17Dhg058cQTGTVqVFHbyJEj\n2W233ejZs2dS6ygrKMTPFgKKBrXuvvvuJWqAIOAVWrlyJTNmzOBXv/pVUduAAQPo1q0bF110Ec2a\nNSMvL68oJJZVU2VO2RYRyTSFkyq2ceNGwIDEWReN4l7/2UUXXciWLZ8C1wLfARuBOykomMSll15U\nrO/atWv55JMPcb8IqBX3ygCyshoxYcKEbaq9Tp06nHTSSYwdO5aCggK+/PJL3nnnHc4888yiPgUF\nBQBcffXVTJgwocTjzTffLAoyUTNo0CAWLVrE+++/z/fff8/LL7/MWWedVeFyTZo0wd2LhYp4WVlZ\nKbXHh4xx48ZRv359evToUdRWr1493nrrLSZMmMCgQYP45JNPGDBgAMcdd1yJgFJYU05OToX7ISIS\nFbUq7iKZ1KtXL4KzIA8AvwtbC4D7adlyD/baa69i/Y8++mjuuOMOrrvuOtyHYhajoOBH/vCHPxRd\nSilUp04dYrEYBQVrErb6A+6baNCgwTbXP2DAAJ544gkmTpzIZ599BlCsjj333BOA2rVrlzp7pTyt\nW7fG3Zk7d26xD2MIZua0bt262DY+/fTTlOsv7wzC8ccfT05ODiNHjqRLly5s3Lixwks6EJzVASrl\nfiLjxo2jZ8+e1K1bt8RrPXv2pGfPnvzf//0ff/vb37jhhhuYNGlSsZ974Uyk0s5GiYhElc6cVLG9\n9tqLK674DfB7zE4BbiUrqytmL3P33XeW+tv0H//4R5YsWcJ9993DPffcxfz587nrrrtKfNA2aNCA\nE0/sT1bW34HCD8rNBGddNnP66advc/3HHHMMjRs35umnn2bMmDF06dKlKDQA7LLLLvTo0YOHHnqI\nFStWlFi+vLEPnTt3pmnTpjz44INs3ry5qP21115j9uzZRZc2cnJyOPLII3n00UdTvlV8gwYNWLt2\nbamvZWVlkZeXxzPPPMOIESPYf//96dixY4XrbNGiBS1btmT69JJjgLbFli1bePPNN4td0gFKPUNz\n4IEH4u78+OOPxdrz8/PZb7/92HHHHTNam4hIZdKZk2owbNi9dOy4H//850N88cU7HHzwgVx33Zvh\nWZXStWzZkssvvzyJdd9Dfn4Pvvxyb2KxQzFbxJYtK7jvvn+WGOOQjlq1anHKKafw9NNPs2HDBu6+\n++4Sff75z3/SvXt39t9/fy666CL23HNPVq5cyXvvvceXX37Jhx9+WNQ3/jJErVq1uPPOOzn//PM5\n8sgjycvLY8WKFQwfPpw999yT3/72t0V9hw8fTvfu3enUqRMXX3wxe+yxB4sXL2bcuHHF1p8oNzeX\nBx98kNtuu422bdvStGnTYmNKBg0axPDhw5k8eTJ33XVX0j+X/v3788ILLyTdPxlTp07lu+++K5pC\nXOjWW2/lrbfeom/fvrRu3ZqVK1fywAMP0KpVK4444oiiflu2bGHKlClcccUVGa1LRKTSVTSdpyoe\nQHfgJeBLgmsc/ZJY5nJgFrABmA2ck/B6LeBGYAHBQI0Pgd5lrGdx2Od94JBytpmRqcSVbd26dX7f\nfff5wIEDfciQIf7RRx9ldP0TJkwIp0LX8i+//LLUPosXL/bBgwd7ixYtvG7dut6yZUvv16+fjx07\ntqhP4lTiQs8++6zn5uZ6/fr1PScnxwcNGuRfffVViW3MmjXLTz31VN955509Ozvb27dvX2y6cWlT\niVeuXOknnniiN2zY0GOxWKnTijt27Oi1atUqdZtl+fDDDz0Wi/k777xTrH2PPfbwfv36legfi8X8\nyiuvLNa2ZMkSj8ViPnToUHcPppF37NixxLKTJk3yk08+2XfffXevV6+e77777j5w4EBfsGBBsX6v\nvfaax2IxX7hwYbm1R+HfrIj88qUylbjag4kHH/rHA7cC/YGtFYUT4NfAWuA0oA0wAFgP9I3rcyfw\nOdA77HNpGGQOjOszANgEDALaAQ8Ba4CcMra7XYQT2TYHH3ywH3PMMSkv16tXLz/nnHMyVkeHDh38\nT3/6U9rL9+/f30899dQK++nfrIhUhe3uPifu/rq73+juLxJMZanIQOAhd3/O3Ze4+zPAw8AfE/rc\n5u7jwz4PAuOA38f1GRKu5wl3n8PPAeb8TOyXbH+mT5/OzJkzOffcc1Ne9vbbb2fMmDEpj4MpzebN\nmznzzDMZPHhwWsvPmTOHcePG8Ze//GWbaxERqWrb65iTugRnPOJtArqYWZa7bw37/JjQZyNwBICZ\n1QZygdsLX3R3N7MJwGGVVbhE02effcb06dMZOnQou+22W4mZUMno0qULmzYl/rNMT+3atfnzn/+c\n9vLt2rXjp59+ykgtIiJVLRJnTtIwHrjQzDoBmFln4AKgNpAT1+d3ZtbWAscCpwC7hq/nAFnAyoR1\nrwSaIzXKc889xwUXXMDWrVsZPXp0lX2bsYiIlLS9njn5C9AMeM/MYsAKYARwDcGAWoCrCC71zAnb\nFgKPkoFLNkOGDCm6m2ehvLw88vLytnXVUk1uuukmbrrppuouQ0TkF2H06NGMHj26WNu6deuSXn67\nDCfuvongzMklBCFlOXAJ8J27fx32WQ2cYmZ1gCbuvtzM7gAKv7hkNcHg22YJq29GEHbKdM8995T6\nDbQiIiJS+i/sM2bMIDc3N6nlt9fLOgC4+1Z3/8rdHTgTeLmUPj+FwaQ2cCrwQti+GcgHim4uYsFd\nzXoBJb97XkRERKpEJM6cmFkDoC0/z9TZ08wOBNa4++dm9jeghbufG/bfG+gCfADsTHAf+P0IpgQX\nrrMLsBswE9gduClc/9/jNj0UGGFm+cA0gtk72QSXiERERKQaRCKcAJ2BSQTznx0ovO3o4wRjRJoD\nLeP6ZxFMCd6H4P7sk4DD3X1ZXJ96wF+BPYDvgVeBge6+vrCDu48xsxyCe6w0IwgyvQsvDYmIiEjV\ni0Q4cfcplHOJyd3PS3g+h+CGaOWt8y2CsykVbft+4P7kKk3e7NmzM71KkUqhf6siEjWRCCe/JDk5\nOWRnZyf1bbYiUZGdnU1OTk7FHUVEqoDCSYa1atWK2bNnl/vtuyJRk5OTQ6tWraq7DBERQOGkUrRq\n1Ur/0YuIiKRpu55K/EuTeMMaiR69R9Gn9yj69B5FX3W/RwonEVLd/xikYnqPok/vUfTpPYq+6n6P\nFE5EREQkUhROREREJFIUTkRERCRSNFsnNfWg8m5atW7dOmbMmFEp65bM0HsUfXqPok/vUfRVxnsU\n99lZr6K+FnxnniTDzA4H3qnuOkRERLZj3dy93C/YVThJgZllA+2quw4REZHt2Bx331BeB4UTERER\niRQNiBUREZFIUTgRERGRSFE4ERERkUhROBEREZFIUTipQmZ2uZktNrONZva+mR1SQf8eZpZvZpvM\nbJ6ZnVtVtdZUqbxHZnaUmRUkPLaaWdOqrLmmMLPuZvaSmX0Z/qz7JbGMjqEqlOp7pGOo6pnZtWY2\nzczWm9lKMxtrZvsksVyVHksKJ1XEzAYAdwM3AQcDHwHjzSynjP5tgFeAicCBwDDg32Z2bFXUWxOl\n+h6FHNgbaB4+dnX3VZVdaw3VAJgJXEbwcy+XjqFqkdJ7FNIxVLW6A/cBhwLHALWBN8ysflkLVMex\npKnEVcTM3gc+cPerwucGfA4Md/e7Sul/J3CCux8Q1zYaaOjufaqo7BoljffoKOC/QGN3X1+lxdZw\nZlYAnOTuL5XTR8dQNUryPdIxVM3CX75WAUe6+9tl9KnyY0lnTqqAmdUGcglSJwAepMIJwGFlLNY1\nfD3e+HL6yzZI8z0CMGCmmX1lZm+EdxGWaNAxtH3QMVS9GhGcvVpTTp8qP5YUTqpGDpAFrExoX0lw\nGrM0zcvov5OZ1c1seUJ679Fy4BLgVOAUgrMsk83soMoqUlKiYyj6dAxVo/Ds8L3A2+4+q5yuVX4s\n6Yv/RNLk7vOAeXFN75vZXsAQQAMvRSqgY6ja3Q90ALpVdyGJdOakaqwGtgLNEtqbASvKWGZFGf3X\nu/uPmS1PSO89Ks00oG2mipJtomNo+6RjqAqY2T+APkAPd19eQfcqP5YUTqqAu28G8oFehW3h6bRe\nQFnfzPhefP/QcWG7ZFia71FpDiI4VS3VT8fQ9knHUCULg0l/oKe7L0tikSo/lnRZp+oMBUaYWT7B\nbwZDgGxgBICZ/Q1o4e6FpzIfBC4PR0k/SvAP4zSCpCuVI6X3yMyuAhYDnwH1gIuAnoCmqlYCM2tA\n8Bu1hU17mtmBwBp3/1zHUPVL9T3SMVT1zOx+IA/oB/xgZoVnRNa5+6awz+3AbtV5LCmcVBF3HxNO\n2bqV4HTYTKC3u38ddmkOtIzrv8TM+gL3AFcCXwAXuHviiGnJkFTfI6AOwX1RWgAbgI+BXu7+VtVV\nXaN0BiYRzCxwgp89wOPA+egYioKU3iN0DFWHSwnem8kJ7ecBT4R/35VqPpZ0nxMRERGJFI05ERER\nkUhROBEREZFIUTgRERGRSFE4ERERkUhROBEREZFIUTgRERGRSFE4ERERkUhROBEREZFIUTgRERGR\nSFE4EZFqZWZHmdlWM9upmrbfy8xmhV/0WFHf3mb2YVXUJVKTKZyISKUxs4IweBSU8thqZjcC7wC7\nuvv6airzTuBWT+K7PNx9PPCTmZ1d+WWJ1Fz6bh0RqTRm1jTu6ZnALcA+/Pyttd+7+4YqLyxkZkcA\nLwHN3f2nJJe5DBjs7l0qtTiRGkxnTkSk0rj7qsIHsC5o8q/j2jeEl3UKCi/rmNm5ZvatmfU1szlm\n9oOZjTGz+uFri81sjZkNi78UY2Z1zOz/zOwLM/vezN4zs6MqKHEA8GZ8MDGzA8zsv2a23szWmdn/\nzKxT3DIvA53NbI/M/aREJF6t6i5ARITgK9zjZQO/Ac4AdgLGho9vgROAPYHngbeBZ8Nl/gm0C5dZ\nDpwMvGZm+7v7wjK22x0YmdA2EpgBXAIUAAcBm4sKdf/czFaGyy5OdUdFpGIKJyISRbWAS919CYCZ\nPQcMBJq6+0ZgjplNAnoCz5pZK2Aw0NLdV4TrGGpmJwDnATeUsZ3WwFcJba2Au9x9fvi8tGDzVbis\niFQChRMRiaINhcEktBJYEgaT+LbCMS0dgSxgXsKsmzrA6nK2Ux/YlNA2FHjEzAYBE4Bn3X1RQp+N\nBGd3RKQSKJyISBRtTnjuZbQVjpvbAdgCdCK4FBPv+3K2sxpoXGyl7reY2UigL9AHuNnMznT3F+O6\n7Qx8XdFOiEh6NCBWRH4JPiQ4c9LM3RclPFZVsFyHxEZ3X+Duw9y9N8FYl/MKXzOzusBe4bIiUgkU\nTkQkCiq8AVp5wvEho4AnzOxkM2tjZl3M7E/huJOyjAeOKCrCrJ6Z3RfOIGplZt2AQ4BZccscRnAp\n6L1tqVlEyqZwIiJRkIkbLg0GngD+D5hDMJunM7CsnGVGAvuZ2d7h861AE+BxYC7wNPAqcHPcMmcC\nI909cayK/H87d2yDUAwEUXDdAAkNUARNQSFIlEklR0ADP+BLK3kmvsDh0waGP/EJG7C1tdY7yWVm\nHgdur/mFz31mPqc/DjZlOQF290pyNDRuSZ7CBM5lOQEAqlhOAIAq4gQAqCJOAIAq4gQAqCJOAIAq\n4gQAqCJOAIAq4gQAqCJOAIAqX2NXJqOUOEqiAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f720f6c0780>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# set new variables to plot\n",
"time2 = data2['time (s)']\n",
"vel2 = data2['velocity (m/s)']\n",
"\n",
"\n",
"# plot data just like before\n",
"plt.scatter(time2, vel2)\n",
"plt.title(\"Constant Speed?\")\n",
"plt.xlabel(\"Time (s)\")\n",
"plt.ylabel(\"Velocity (m)\")\n",
"plt.autoscale(tight=True)\n",
"\n",
"# calculate trendline equation like before\n",
"trend2 = np.polyfit(time2, vel2, 1)\n",
"\n",
"# plot trendline like before\n",
"plt.plot(time2, np.poly1d(trend2)(time2), label='trendline')\n",
"plt.legend(loc='lower left')"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 1.98602732e-16, 2.00000000e+00])"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# display the trendline's coefficients (slope, y-int)\n",
"trend2"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# Part Two\n",
"Choose one of the following:\n",
"- Mess with the data: edit the original raw data to add more data points and vary them slightly to make it appear like realistic measurements of constant speed motion.\n",
"- Constant a: edit/add to the raw data to represent an object moving with constant acceleration.\n",
"- More math: create new cells below and add an \"acceleration\" collumn to the data table, then plot it."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
hall1467/wikidata_usage_tracking | jupyter_notebooks/misalignment/longitudinal_results/.ipynb_checkpoints/correlation_between_used_entity_edit_types_and_views-checkpoint.ipynb | 1 | 4866 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"library(dplyr)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"used_entity_edit_types_and_views <- read.table(\"../../../results/sql_queries/wikidata_page_revisions_with_timestamp_editors/entity_edit_type_and_views.tsv\", header=TRUE, sep=\"\\t\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"colnames(used_entity_edit_types_and_views) <- c('entity_id','bot_edits', 'semi_automated_edits', 'human_edits', 'anon_edits', 'all_edits', 'page_views')"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
" entity_id bot_edits semi_automated_edits human_edits \n",
" P10 : 1 Min. : 0.00 Min. : 0.00 Min. : 0.000 \n",
" P1000 : 1 1st Qu.: 3.00 1st Qu.: 0.00 1st Qu.: 0.000 \n",
" P1001 : 1 Median : 8.00 Median : 1.00 Median : 0.000 \n",
" P1002 : 1 Mean : 12.95 Mean : 3.04 Mean : 1.817 \n",
" P1003 : 1 3rd Qu.: 18.00 3rd Qu.: 4.00 3rd Qu.: 1.000 \n",
" P1004 : 1 Max. :4165.00 Max. :6439.00 Max. :13600.000 \n",
" (Other):22229590 \n",
" anon_edits all_edits NA \n",
" Min. : 0.000 Min. : 1.00 Min. :0.000e+00 \n",
" 1st Qu.: 0.000 1st Qu.: 6.00 1st Qu.:1.300e+01 \n",
" Median : 0.000 Median : 13.00 Median :1.360e+02 \n",
" Mean : 0.071 Mean : 17.88 Mean :3.000e+04 \n",
" 3rd Qu.: 0.000 3rd Qu.: 23.00 3rd Qu.:9.980e+02 \n",
" Max. :6094.000 Max. :21863.00 Max. :1.253e+10 \n",
" "
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"summary(used_entity_edit_types_and_views)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"0.0593649614434352"
],
"text/latex": [
"0.0593649614434352"
],
"text/markdown": [
"0.0593649614434352"
],
"text/plain": [
"[1] 0.05936496"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"cor(used_entity_edit_types_and_views$bot_edits, used_entity_edit_types_and_views$page_views, method=\"spearman\")"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"used_entity_edit_types_and_views_each_month_has_some_edits <-filter(used_entity_edit_types_and_views, used_entity_edit_types_and_views$bot_edits > 0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "ERROR",
"evalue": "Error in used_entity_edit_types_and_views_each_month_has_some_edits$page_views: $ operator is invalid for atomic vectors\n",
"output_type": "error",
"traceback": [
"Error in used_entity_edit_types_and_views_each_month_has_some_edits$page_views: $ operator is invalid for atomic vectors\nTraceback:\n",
"1. cor(used_entity_edit_types_and_views_each_month_has_some_edits$bot_edits, \n . used_entity_edit_types_and_views_each_month_has_some_edits$page_views, \n . method = \"spearman\")",
"2. is.data.frame(y)"
]
}
],
"source": [
"cor(used_entity_edit_types_and_views_each_month_has_some_edits$bot_edits, used_entity_edit_types_and_views_each_month_has_some_edits$page_views, method=\"spearman\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "R [r]",
"language": "R",
"name": "R [r]"
},
"language_info": {
"codemirror_mode": "r",
"file_extension": ".r",
"mimetype": "text/x-r-source",
"name": "R",
"pygments_lexer": "r",
"version": "3.3.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
obulpathi/datascience | scikit/Chapter 1/Regression.ipynb | 1 | 4703 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Regression\n",
"============"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load the boston dataset:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn.datasets import load_boston\n",
"boston = load_boston()\n",
"boston.keys()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"print(boston.DESCR)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"boston.data.shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"boston.target.shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"boston.target"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn.cross_validation import train_test_split\n",
"X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Learning a Regressor\n",
"==========="
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn.linear_model import Ridge\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"ridge = Ridge()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"ridge.fit(X_train, y_train)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"pred_test = ridge.predict(X_test)\n",
"pred_test"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"R2 score:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"ridge.score(X_test, y_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"MSE:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn.metrics import mean_squared_error\n",
"mean_squared_error(y_test, pred_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Random Forest Regression\n",
"----------------------------"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from sklearn.ensemble import RandomForestRegressor"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"rf = RandomForestRegressor()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"rf.fit(X_train, y_train)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"rf.score(X_test, y_test)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mean_squared_error(y_test, rf.predict(X_test))"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
udaypandit/black_scholes | Lessons.and.Assignments/1D.Wave.Bar/1D.WaveBar.ipynb | 2 | 68747 | {
"metadata": {
"name": "",
"signature": "sha256:20be003d6a962dab4e4013fd31c9809caff293074ee6020df0358bac08325235"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 6,
"metadata": {},
"source": [
"Content under Creative Commons Attribution license CC-BY 4.0, code under MIT license (c) 2014 F.J.Gonzales. Portions of the code adopted from the #numericalmooc materials, also under CC-BY."
]
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"The French Connec... eh solution"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Solving the 1-D wave equation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Welcome to this bonus notebook that ties into the second module of [\"Practical Numerical Methods with Python\"](http://openedx.seas.gwu.edu/courses/GW/MAE6286/2014_fall/about).\n",
"\n",
"In the first notebook of the second module, we were introduced to the numerical solutions of *partial differential equations (PDEs)*. The equation used in that notebook was the 1-D linear convection equation, AKA *the advection equation*.\n",
"\n",
"However, in this notebook we will explore the 1-D wave equation shown below:\n",
"\n",
"\\begin{equation}\\frac{\\partial^2 u}{\\partial t^2}= c^2 \\frac{\\partial^2 u}{\\partial x^2}.\n",
"\\end{equation}\n",
"\n",
"The wave equation is second order in both spatial and temporal dimensions."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If the initial displacement $\\ f(x)$ and a velocity $\\ g(x)$ are specified for the wave equation, then the solution of the system is:\n",
"\\begin{equation}\\ u(x,t) = \\frac{1}{2}[f(x-ct)+f(x+ct)]+\\frac{1}{2c}\\int{g(\\tau){\\partial \\tau}}\\end{equation}\n",
"This solution is known as the d'Alembert solution for the 1-D wave equation."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For this notebook we will focus on the special case where the initial velocity is zero, $g(x)=0$\n",
"and the solution is simplified to the equation below:\n",
"\\begin{equation}\\ u(x,t)=\\frac{1}{2}[f(x-ct)+f(x+ct)]\\end{equation}\n"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"The Guitar pick example"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A classical example of the 1-D wave equation is when simulating the motion of a guitar string after it is plucked."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "heading",
"level": 6,
"metadata": {},
"source": [
"Image credit: G. Everstine, 2012 (Fig. 14, page 23)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As the figure above shows, the original triangular displacement splits into two waves traveling in opposite directions. One can also see that each of the travelling waves is half the height of the original function, which corresponds to d'Alembert's solution shown previously."
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Wave motion for a bar"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we have established the solution for the 1-D wave equation, we will use this to simulate the longitudinal wave motion on a finite length bar. "
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Problem Description"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's say we have a bar of finite length as shown below. The length is $10 \\rm{m}$ in the $x$ direction. As can be seen, the system ends with a dashpot, also known as a damper; this dashpot is an important part of this problem because we will see how this will create a non-reflecting boundary condition. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "heading",
"level": 6,
"metadata": {},
"source": [
"Image credit: G. Everstine, 2012 (Fig. 22 in page 30)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In addition to the problem description, the initial displacement $f(x)$ is defined below:\n",
"\\begin{equation}\n",
"u(x,0)=\\begin{cases}2-2(x-5)^2 & \\text{where } 4\\leq x \\leq 6,\\\\\n",
"0 & \\text{everywhere else in } (0, 10)\n",
"\\end{cases}\n",
"\\end{equation}"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Discretizing the equation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since the 1-D wave equation is second order in time and space, we will discretize the equation using central difference for both dimensions. Below is the discretized equation:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\\begin{equation}\\frac{u_i^{n+1}-2u_i^n+u_i^{n-1}}{c^2\\Delta t^2} = \\frac{u_{i+1}^n - 2u_i^n+u_{i-1}^n}{\\Delta x^2} \\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Solving for the unknown in the discretized equation we get the following:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\\begin{equation}\\ u_i^{n+1}=-u_i^{n-1}+2u_i^n+C^2(u_{i+1}^n-2u_i^{n}+u_{i-1}^n) \\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this equation $C= c\\frac{\\Delta t}{\\Delta x}$, which equates to the CFL number."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In addition to discretizing the wave equation, we also want to take a look at our boundary conditions. On the left-hand-side boundary, the bar is fixed, which would correlate with a Dirichlet boundary where the displacement is $u=0$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The right-hand-side boundary is more tricky and that is where the idea of the nonreflecting boundary condition comes into play."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If we look at a simplified version of d'Alembert's solution, $f(x-ct)+f(x+ct),$ we can see that the first term represents the wave that is moving towards the right boundary while the latter term represents the wave that bounces away from the right boundary. In the bar we are analyzing, the dashpot at the right-hand-side means that the second return wave term would go to zero."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Differentiating the first term of D'Alembert's solution in terms of space and time would result in the following PDEs:\n",
"\\begin{equation}\\frac{\\partial u}{\\partial x}= f^\\prime,\\frac{\\partial u}{\\partial t}= -cf^\\prime\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Rearranging the above equations gives the boundary condition we have to enforce on the right-hand side:\n",
"\n",
"\\begin{equation}\\frac{\\partial u}{\\partial x}=-\\frac{1}{c}\\frac{\\partial u}{\\partial t}\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Discretizing our non-reflecting boundary:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\\begin{equation}\\frac{u_i^n-u_{i-1}^n}{\\Delta x} = \\frac{-1}{c}\\frac{u_i^{n+1}-u_i^n}{\\Delta t}\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"and isolating for the end boundary:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\\begin{equation}u_i^n= -\\frac{\\Delta x}{c\\Delta t}(u_i^{n+1}-u_i^n)+u_{i-1}^n\\end{equation}"
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Lets rev up some code!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The first thing we always do is to import the necessary libraries for this problem. In this case we will use bothy Numpy and Sympy. We will also use Matplotlib for plotting our displacement."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import numpy as np\n",
"import sympy as sp\n",
"from sympy.utilities.lambdify import lambdify\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"from matplotlib import rcParams\n",
"rcParams['font.family'] = 'serif'\n",
"rcParams['font.size'] = 16"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We then create the initial condition for the bar."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# initial conditions and parameters\n",
"nx= 50\n",
"x= sp.symbols('x')\n",
"func= 2-2*(x-5)**2\n",
"init_func= lambdify((x), func)\n",
"x_array= np.linspace(0,10,nx+1)\n",
"u_initial= np.asarray([init_func(x0) for x0 in x_array])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lets plot the initial function so we can start off on the right foot."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.plot(x_array, u_initial, color='#003366', ls='--', lw=3)\n",
"plt.xlim(0,10)\n",
"plt.ylim(0,3)\n",
"plt.xlabel('x')\n",
"plt.ylabel('Displacement')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 3,
"text": [
"<matplotlib.text.Text at 0x109111d10>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEhCAYAAACz9e1lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VOXZ//HPRQCRTTbZXAgosqioj9iKQBtstZVi3bdH\nbbVWbe2jXfTn1laxPnVp7aZV61KLXV7aWrGotW6VaAUsahVQQB+BgBIUwyL7kuT6/XFOwjBMkjnJ\nyZzJzPf9es1rJvc595krgcyV+9ybuTsiIiJxapd0ACIiUniUXEREJHZKLiIiEjslFxERiZ2Si4iI\nxE7JRUREYqfkIiIisUskuZjZfmZ2m5m9Fj7eMbOXzGxiFnU7mNmNZrbAzOaZ2QwzG5uLuEVEJDtJ\ntVyOA84ATnf30cBw4GXgcTP7TBN17wBOA8a5+8HAA8CzZnZIawYsIiLZsyRm6JvZiUAvd38gpWwP\nYA3wc3e/ooF6w4D5wAXuPiWl/C2gwt0ntWrgIiKSlfZJvKm7/y1D8R7h88eNVD0JMGB6Wvl04GIz\n6+zum2IIUUREWiAvOvTNbC/gTuD18Lkho4AaYFla+RKCRDmyVQIUEZFIEk0uYcf+e8D7BC2Sk9x9\nQyNV+gCbfNd7eevC596tEKaIiESUaHJx90Xuvj/BLbH/A+Zo5JeISNuXF7fF3H29u38X+Ai4q5FT\nq4AuZmZp5d3D51WtEZ+IiESTSIe+mXVy9y0ZDr0FnGJmHdx9e4bjc4AzgX3Yud9lMLCdYCRZpvfT\npjUiIhG5e/of8llLquXytJkdmaG8FPikLrGYWb+0VspjgAMT0upNAJ5tbKSYuxf94/rrr088hnx5\n6Gehn4V+Fo0/Wiqp5OLADWbWC8AClwGjgdvDsrFAJSmjx9z9XeBe4Boz6x2edz5By+X7Of0ORESk\nQYncFiNIBF8HXjSzaqATQX/K2e7+UHjOeoJJlZVpdS8FrgdmmNl2gpFix7r73JxELiIiTUpqEuVM\nYGYT58wlGHqcXl4N/DB8SARlZWVJh5A39LPYQT+LHfSziE8iy7/kmpl5MXyfIiJxMTO8DXboi4hI\nAVNyERGR2Cm5iIhI7JRcREQkdkouIiISOyUXERGJnZKLiIjETslFRERip+QiIiKxU3IREZHYKbmI\niEjslFxERCR2Si4iIhI7JRcREYmdkouIiMROyUVERGKn5CIiIrFTchERkdgpuYiISOyUXEREJHZK\nLiIiEjslFxERiZ2Si4iIxK59Em9qZocC3wLGAtVACfA8cKO7VzVRtwJYk+HQ5e7+QsyhiohIM5i7\n5/5NzRYC84CvuPtmMxsI/JOgJXWIu29ppO4Sdx8c8f08ie9TRKStMjPc3ZpbP6nbYrXAVe6+GcDd\nK4GfAkOBiQnFJCIiMUnkthgwyt2r08pWhM89ch2MiIjEK5GWS4bEAnAA4MBLTdU3s1vNbIaZvWNm\nz5jZ8bEHKSIizZYXo8XMrAS4ALjf3d9r4vSVwOvuPhY4EJgGTDOzb7VymCIikqVEOvR3CcJsMvAl\n4DN1/TAR6z8JjAf6uvvWDMfVoS8iEkFb7dCvZ2bnA6cCxzUnsYRmA92AkbEFJiIizZZUhz4AZnYu\n8D3g6Kbmt4TndwJK3H1j2qGa8LmkobqTJ0+uf11WVkZZWVnUcEVEClZ5eTnl5eWxXS+x22Jmdg5w\nFfA5d18Zlk0CBrj7feHX/YCVdfe0zOw84Eh3/0bataYCXwT6uPumDO+l22IiIhG0ydtiZnY2cB8w\nBTjWzM4Jk83xwMDwnLFAJXBnWvWzzGx0yrXOAE4AfpIpsYiISO4ldVvsdqAjwcTJVA7cEL7eQLDM\nS2XK8aeAvYG7zKwDwZyY1cDF7n5/q0YsIiJZy4vRYq1Nt8VERKJpk7fFRESksCm5iIhI7JRcREQk\ndkouIiISOyUXERGJnZKLiIjETslFRERip+QiIiKxU3IREZHYKbmIiEjslFxERCR2Si4iIhI7JRcR\nEYmdkouIiMSuxcnFzHYzswa3FxYRkeKTdXIxs182cOg4YIOZXRBPSCIi0tZlvVmYmb3h7oc1cGwo\n8Dd3PzDO4OKizcJERKLJl83CNgOdYrqWiIi0cY0mFzO73sxqzawWOKTudfoDWAbMzUnEIiKS9xq9\nLWZmZUBZ+OXFwG+A9GbSdmAJ8Ki7b40/xJbTbTERkWhaelssSp/L79z9/Oa+UZKUXEREoslZcski\nkDHuPiuWi8VMyUVEJJp86dAHuCvGa4mISBsWZZ7LXmb2JzNbbmbVGTr1R7VinCIi0oa0j3Du74B9\nganAGqA27fjFcQUlIiJtW5TkMgIY7u4bMx00s17ZXsjMDgW+BYwFqoES4HngRnevaqJuB+A64NSw\n7jrgSnefke37i4hI64rS5/JuQ4klNDnCtR4GegCHu/so4BjgWGCGmTU1GfMO4DRgnLsfDDwAPGtm\nh0R4fxERaUVRkstPzWyymfVo4PjzEa5VC1zl7psB3L0S+CkwFJjYUCUzGwZcCNzi7qvCur8lmGfz\n4wjvLyIirSjKbbG7gZ7AD83sY2ATwYRKD58HRLjWKHevTitbET43lLwATgrfa3pa+XTgYjPr7O6b\nIsQhIiKtIEpy6Q48xq4z9Oscn+2FMiQWgAMIEtVLjVQdBdQQLDeTagnB9zISeC3bOEREpHVESS7v\nNzZD38zSWxNZC/eDuQC4393fa+TUPsCmDDMi14XPvZsbg0gubdtezdQX3qBn984ce+RIzJo9V00k\nL2WdXNz90CaOT2hBHD8EtgLfacE1RNqEdRs2c/KVv+GfsxcCcNFJ47nzqrNo31577knhiNJyAcDM\nSoHPAl3d/U4zGwksaO76KmZ2PsGw4rK6Dv5GVAFdbNf1XLqHz6saqjh58uT612VlZZSVlTUnXJEW\nu2fqS/WJBeDex/7FiqpPePjmC+ncqWOCkUkxKy8vp7y8PLbrRVm4sj1wD3AeQb/Lh+4+0MweAA4B\nvtDUHJUM1zwXuBL4nLuvzOL8q4CbgVJ3X5ZSfgdwEdAzU4e+1haTfFJTU8uZ197HX//5n53Kf3DB\nRG785gkJRSWys1yuLXYDMB64BPgMYSvB3b9GMG/l5ihvbGbnkJZYzGySmV2Yck4/2/lm9GMEnf7p\nt+AmAM9qpJi0BSUl7fjDj77GtJ9dwtXnfRGAsYfsx7XnH5dwZCLxidJyeY9g4uKH4df12x6HCeA/\nDW2DnOFaZwP3Az8APko5NB6odPcbzGwswcixe9z9kpS6dxMkk7Huviq8rfZrYIy7Z9ywTC0XyWe/\nf3IWk8aPotceXZIORaReS1suUfpcqusSSzp3dzPrHOFatwMdCSZO7nQpghYSwAaCNcwq0865FLie\nYDb/doKRYsc2lFhEkjTliZl8ccyB9O+zR4PnfGXSmBxGJJIbUVoubwMXuvvM8OvUlsunCIYR5+XK\nyGq5SBJeX7CU0efexGHD9uHFe6+gW5emVjYSyR+57HP5FfCCmf3ezL4B7GFm55jZbcCzwM+bG4RI\nIbrvsZcBeOOd97nqjqmR6i5fuYZbpjzNX57TnGBpm6LMc7k3XFfseuCcsPj3wEbgenefEn94Im3T\n5i3bePjZV+u/PusLR2Rdd1r5m5x85W+orXWOGFnK6ceMbo0QRVpVpHku7v4TM7sHGEMwW74KmOnu\n6xqvKVJcpr04h082BNO29tt7T8Ydun/WdccfNpT2JSVsq63m1fkVvL2okgP3G9haoYq0isjbHLv7\nJ+7+tLv/MXxeB2Bmp8cfnkjbNOXJmfWvz5s0JtLyLr326MIJn92xg8SDT86KNTaRXIicXMysfbjl\n8b4pj0EEt8tEip67c+RBQ9inX0/MrFmjwc5LqfOHp16huromzhBFWl2U0WIjgHuBo8i8MrK7e14u\njqTRYpKE2tpa/rNwGaNHlkauW11dwz5fupoPVwV3nP9593c5+ojhMUco0rCWjhaLklxeAbYD0whm\n56dXvMHdBzU3kNak5CJt0c2/+wcfrlrHeZPGcOiwfbRysuRULpPLIuAAd8/YPjeza939puYG0pqU\nXEREosnlPJe3mzhfA/JFRASI1nI5APge8CTwHsE2x/WHgb+7+0GxRxgDtVwkF2prazEz3b6SgpDL\nlktvYCLwODAfqEh5LAFGNDcIkULwl+de56AzbuCnv3+GFVWfJB2OSKKiTKK8iyCJ/ApYTYYO/biC\nEmmLpjw5k/mLV3Dl7VPZuq2aH3z9S7Fef2HFhyxZXsVxY/PyBoHITqIklx7A6EY69DWFWIrW8pVr\neO7fCwCaPbelIR98tIbTrr6HV+YtoX/v7rz/91u0JbLkvSi3xeY1cb469KVo/eGpf1NbGzTmJ4w+\ngH3794rt2v17d6eiMtjB+8NV63j2lfmxXVuktURdFfnBcLfI4Rlm6GtVZClK7r7TEi3nTToq1uu3\nb1/CuROPrP96ipaDkTYgSnJ5DjgTdeiL7OTjNetp1y4YVNO1826cfHRWG7JG8tWU22zTXpzD6k82\nxv4eInGK0ufyAfBDMi/9AurQlyLVt1d33vrz9by+YCnvLP2ILrvvFvt7HLjfQI4YWcqr8yvYtr2a\nh599lUtOK4v9fUTiEiW5POPuDzZ00MwOjCEekTbJzBg9srRZ64hl66uTjmTlmvV8ddKRTNSIMclz\nWU+ibMs0iVIKwbbt1bQvaUe7dpEXMxeJLJeTKDGzjmb2VTP7nZn9KSw73cxKmxuAiGSnY4f2SizS\nZmR9W8zM+gP/JOi4rwZWhof2AX5pZhPd/c34QxQRkbYmyp9BtwELCZLLbsDHAO7+M+C/gR/HHp1I\nnnvo6dnMX1xJbW1t0qGI5JUoC1cuJlhyvzr8+g13Pyzl+GvuPrp1wmwZ9blIa6hau4E9P385AP16\nd2f5U7dSUqLbVlIYctnnUlOXWBrQJ+qbm9kAM3vazPRnn7Q5s+Yuqn89ZK8+OUssz8x6m6vvmMpn\nL7qNpStW5eQ9RaKKMhT5IzO7wt1vSz9gZhcTTKTMmpmdTHCrbRu7LoLZVN0KYE2GQ5e7+wtRriXS\nXDPnLq5/PebgITl739v+8BzPzw7WMZs5ZxGDBvTO2XuLZCvKn1rXAjeZ2RIzewjYy8zuN7PXCJaG\nuTbie18OHA28QsMTMxvi7n5YhocSi+TMrJTkctSo/XL2vkcdsiORzZq3uJEzRZKTdXJx95eACcBy\n4HSC22DnEWwaVubuURc8GufuFRHriOSF7dU1zH57R2N9zKjctVxSE9nMlFtzIvkkym0x3H0GMM7M\nOgO9gNXuvqmJag1dSz3s0mZt3rKNS8+YwMy5i6lau4GBe/bI2Xt/+qDB9a/ffPcDNm7e2ipLzoi0\nRJR5Lu2ArgR5YT3hNsdmNtTd/6+V4mssnluBcQQtqArg1+7+RK7jkOLUvevu3HrZKQA5H4bco1tn\nDhwykLcXV1JTU8tr85fy2cMPyGkMIk2J0nL5JnAHsBQYnFJ+X5h4TnL3XA1dWQm87u5XmVl74CJg\nmpld6u535igGEYBEZs1fce4xbK+u4ahR+zFicP+cv79IU6LMc3kJ+Ku7355WXgJcDQx19/MiB2A2\nBfiKu7foN9TMngTGA33dfWvaMd2FExGJoKXzXKK0XLqnJxYAd68xs5uAN5obRExmAxOBkZlimTx5\ncv3rsrIyysrKchWXiEjeKy8vp7y8PLbrRWm5LHL3BsdbNnW8kXpTiNByMbNOQIm7b0wr/z5wI/Ap\nd38t7ZhaLiIiEeRyhv4yM/ufBoK4BFjW3CBoZBKlmfUzs9Rv8EzgZxlOPRzYQrBLpkirueuRcv7f\nr/7KY9PfYM067QgpkkmU22LfB6ab2aXAa8BqoCcwGiglmAPTXBmzo5mNBV4C7gEuSTl0lpndX9dC\nMbMzgBOAG5s7NFokW3/8x7/DCZTP8fjPL+H4zxySaDzuztr1m+jZvUuicYikyjq5uPtMMysDfkLQ\nejCgFpgJnOfur0R5YzO7CziOYCixm9kSghbMMHffHp62nmCZl8qUqk8BewN3mVkHoAdBorvY3e+P\nEoNIVFu3bef1BTsa6WNyODM/3QcfreGy2x5m5tzF9O3ZjbkPX5dYLCLpok6inAWMj2kS5SVZnDOX\ntAUx3X0l8L/hQySn/rNwGdu2B+u3Dt23L316dE0slh7ddmfai3OorXVWrl7PJxs2s0fX3ROLRyRV\ns4b/uvsmd/8gNbGEI8ZECtrMhNYTy6Rr504cMnRvILg1NvutSGvHirSqSC2XcLLkaIJJlKnrTRjB\nhmFRF68UaVNmztmxllcuV0JuyFGj9uONd94HgnXGjjlyZMIRiQSiLP8yEHgCOKypc0UK1c3/cxIT\nxx7ErHmLKcuDJVfGjBrCnY+UA1ohWfJLlJbLbcCLwNnAowQTFg3oD1wFvBx7dCJ55oBB/ThgUD8u\nOHFc0qEAO27NlZS0o7pGe+5J/ogyiXIucKi712bY4rgj8JS7f76V4mwRTaKUQuXuvPzme/zX8H21\nMrLEKpfLv2xz97o/jdqbWbu6r919m5nt3dwgRKR5zIzxhw1NOgyRXUQZLVZjZgeFrxcBt5pZj/Dx\nI6Ak/vBERKQtitJymQb8y8w+DdwKTCfYqrjOxXEGJpJPamtrMTN2XolIRBqSdZ/LLhXNDgHOIBiS\n/Pd83r9efS7SUtNfe4czrrmPMQcP4aQJh3Le8UclHZJIq8pln8tO3H0OMCclkD7uXtXc64nks1lz\nF/HxmvU8/tIc+vXulpfJZe36TbwybzGlA/swvFQbiEmy4txC79kYryWSV16dv7T+dT5Mnkx38+/+\nQc8J3+W4y+7goWdmJx2OSMMtFzObTiNL4aefDmjIihSs+YtX1L8+9IB9Eowks4F79qh/nRqrSFIa\na7mMJkga7bJ4qJdTCta27dUsWv4xENyHHpaHt5xGpMS0YMmHCUYiEmisz+U9d896jxYzS3qbY5FW\nsXh5FTXh7PdBA3rRuVPHhCPaVWofy7vLPqK6uob27TU7QJLTWHKZGPFaX2pJICL5anhpfz4p/yUL\nKz7kkw2bkw4no+5dd2evvj1YvnIt26trWPTBx3nZwpLi0WBycfeMN27N7HPAkcBAgk28Zrn7C+5e\nmel8kULQvevufOqgwUmH0ahDhu5Nt86dGDG4P7Uaei8Ji7K22J7AVGBshsMvAyfn61BkzXORYuDu\nmuQpsWnpPJcoQ5HvBroCpwP7A70JRoidCXQPj4tIQpRYJJ9EabmsAoa4+ycZjvUgGADQZ9eayVPL\nRUQkmly2XCoyJRYAd18LaI9VKThbt21n05ZtSYch0uZESS7/NrNjMh0ws2OB8rSyR1sQl0heeH72\nQrqOv4zBX76Wa379WNLhiLQZUdYWWwc8amYzgLfDr7sDBwGjgPvN7LrwXAPyb/ElkYgWLFmBu1NR\nuSpvhyGnqlq7gbfeW86Cig/57H8NZeSQgUmHJEUqSnK5Mnz+QvhI94O0r9XJIW1e6lIqI9rAvJFr\nfv0Y9/8t2HH8F987TclFEhPlttgcd2+X7QOY29QFzWyAmT1tZtr8W/LSgoqU5DJ4QIKRZEfLwEi+\niJJcrmv6lOzPN7OTgRlAKRFbOWbWwcxuNLMFZjbPzGaYWab5NyLN5u47fUCPHNIGkktKAkxNjCK5\nlnVycfcn0svMrKeZHWpmu2VzfprLgaOBV4i+8OUdwGnAOHc/GHgAeDbcwEwkFp9s2Ez3Lp0A6N6l\nEwP67JFwRE0bMVgtF8kPUea5nAh8G3jE3e8ys6OAfwDdgBXAse7+dtZvHE4+MbMpwFfCW2nZ1BsG\nzAcucPcpKeVvEQyXnpShjua5SLOt37iF9z9a3Sb6L2pra+n2mW/XD5/++Pmf0adH14SjkrYolztR\nXgzMJlgCBuAXwBrgfIIlYW4GvpztxVrwaX8SQUtnelr5dOBiM+vs7puaeW2RXXTr0qlNJBaAdu3a\nMWn8wdTUOCMG90d/VElSoiSXAe5+HICZDQWOAM5196lm9hgwrzUCzGAUUAMsSytfQvD9jARey1Es\nInnnzzdflHQIIpE69FNHdJ1BOO8F6lsh22OMqzF9gE0ZWj7rwufeOYpDREQaEKXlst7M/pughXAp\n8LC7bwEws/0B7UwkIiJAtORyNfAUsAfwEXATgJldQzDya0rcwTWgCuhiu/bSdw+fV2WqNHny5PrX\nZWVllJWVtVZ8UgA2b9nG/CUrGF7any677zIYUqTglJeXU15eHtv1sh4tBmBm3YBhwEJ33xCWHUxw\nK2qeu2f8YG/imlOINlrsKoLBA6Xuviyl/A7gIqBneoe+RotJVDPnLGLsBT8B4AtjRvL0Hd9OOCKR\n3Mrlqsi4+3p3f60usYRl89y9HDihuUHQyCRKM+tnO29U8Vh4/oS0UycAz2qkmMRhwZIdExD36Lp7\ngpE0z+y3lnDnX6bzP7c+xMIKzXeR3Mv6tpiZ7dvYYYJbYw80M46M2TGcdf8ScA9wCYC7v2tm9wLX\nmNmT7r7KzM4HBgP/3cz3F9nJgpQP5JFtYNmXdLc++AxTp78BwKcOLGV4G1gXTQpLo8nFzF4Flrr7\nqUBFE9eKuoTLXcBxBKO/3MyWhNcY5u51I8/WE8ylqUyrfilwPTDDzLYTjBQ71t2bXM9MJBupLZe2\nsKZYuhGD+9fPBFugloskoKmWy8sEnfcAHwA/pOGlWm6I8sbufkkW58wlSD7p5dVhLD+M8p4i2Ur9\nQG6LySV10mdqohTJlUaTi7t/N+XLx939wYbONbMjYotKJEG1tbWMKO1Pba3zwco1HLBv36RDikyr\nI0vSshotZma7AxcAXwQGhcVLCYYm/9bdt7ZahDHQaDFprk1bttG5U8ekw4hs05ZtdB1/Ge5OSUk7\nNv7rdnbr2CHpsKQNafW1xcKFIp8i6DCvIZhHYsAIYCLwPTOb6O7vNjcIkXzVFhMLBHF/45TPsGfP\nrowoHYD+tpJca7TlYmZdgDnAWoL9Waa7++bwWGfgGOBHQGfgUHff2OoRN4NaLiIi0bT2PJeLCUZq\njXH3p+oSC4C7b3L3acCngY/Dc0VERJpMLicC304ZGryLcH2xywiWwhcREWkyuezp7m80dRF3f40M\nQ4ZF2prq6hp+/+QsXn27gvUbtyQdjkib1VSHfpRRYPpNlDZv0Qcf89XJUwDYu19P3v/7LckGJNJG\nNZVc1AsuRSV18uTwQW1/yZQpT8zk1fkVLFjyIQ9c9xVKB+oGg+RGU8nlEDOroeFZ+RAkIEOJSArA\nzsu+FEJymcWL/wlmCby1qFLJRXKmqeSyBnicxpNLneNbHo5IslJns7fFZV/SjRwyoD65LFiygknj\nRyUckRSLppLLMnc/P5sLmVmTHf8i+W7+kh1rpI4ogJWEtQyMJKWp5HJshGtFOVckL00cezB9e3Zn\nQcWKgmi5pH4PCyq0gKXkTqSdKNsqzdCXYrV85Rr2nng1EGx6tmb6L9h57z2RzFp9bTERabsG7tmD\nG7/xZQ4Y1K8gWmLSdqjlIiIiu2jttcVEREQiU3IREZHYqc9FJHTv1Jfo1LEDpQN786kDB9NpN22u\nJdJc6nMRCe35+cupWrsBgA+euoW9+vZMOCKR5Gi0mEgMNmzaUp9YOrQvYUCfPRKOKD6rP9nI5b98\nhIrKVdS68+K9VyQdkhQBJRcRYOmK1fWvBw3oTbt2hdMd2Wm3Dkx5YhYA7UvaUVNTS0lJ4Xx/kp/0\nP0wEqFixqv516YDeCUYSv86dOtK3VzcAqmtqqfx4bcIRSTFQchEBKiqr6l+XDiys5AI7J8zURCrS\nWhJLLmbW18z+ZGYLw8cjZrZXlnUrzOyNDI+jWztuKUyHHLAP3zv785w84TDGHDwk6XBil5owKyqV\nXKT1JdLnYmYdgeeAhcDIsPgBYLqZHebuG5u4hLv7Ya0ZoxSXcYfuz7hD9086jFajlovkWiJDkc3s\nQuAeYIi7V4Rl/YDlwNXuflsT9Ze4++AI76ehyFLU5r23nIrKKkoH9mHwwN507dwp6ZAkz7V0KHJS\nyeVpYFh6gjCzucBGdx/TRH0lFxGRVtRW1xYbBSzJUF4BHJzNBczsVjObYWbvmNkzZqadMEVE8kRS\nyaUPsD5D+Tqgs5nt1kT9lcDr7j4WOBCYBkwzs2/FG6aIiDRHUpMoW3SPyt0/nfK6GrjLzCYCN5nZ\n/e6+taUBSvH4z8JlPPL865QO6M3hI/Zl9MjSpEMSafOSSi5VQLcM5d0J+lyakxxmAxMJRp+90YLY\npMjMmruIW6Y8DcDXTxyn5CISg6SSy1xgeIbywcC8xiqaWSegJMNw5ZrwuSRTvcmTJ9e/Lisro6ys\nLMtQpdAV8uz8VLc//AIPPTObispV/OSyUzj3S0cmHZLkkfLycsrLy2O7XlLJZSpwj5kNcvelUD8U\neThwdeqJYfnKlOFeZwJHAt9Iu+bhwBZgfqY3TE0uIqlSJxUW4uz8OstXruGVecE4Gs11kXTpf3Tf\ncMMNLbpeUh36UwhaKLeaWYmZtQNuARYDd9edZGZjgUrgzrT6Z5nZ6JTzzgBOAH7i7ptaOXYpMMXS\ncikd2Kf+tWbpS2tLpOXi7tvN7BjgFwQtDSdINkenJYf1wBqCBFPnKWBvgk78DkAPYDVwsbvfn4v4\npbAUS8tl51n6VY2cKdJyiS257+4rgbObOGcuwbDl9Hr/Gz5EWsTduelbJ1JRuYqlH64qqH1c0ml9\nMckl7eciRc3MuPCk8UmHkRODUlouH6xcq31dpFVpm2ORIvLCqwvZp19P9unXi067dUg6HMljbXJt\nsVxTchERiaatri0mIiIFTMlFRERipw59KWpX/PKv1NTUUjqwN+dOPJJee3RJOiSRgqDkIkXtwSdn\nUbV2AwCnfu6/gOJJLpu2bKNzp45JhyEFSslFitaGTVvqE0uH9iUFPcelzvKVa5j0nTupWLGKXt07\ns2jaj5MOSQqUkosUraUrVte/HjSgN+3aFX4XZM/uXXjz3feBILlqrou0Fv2vkqJVLGuKpercqSN9\newW7XVTX1FL58dqEI5JCpeQiRauicsf6WoW8pli6ndcY0zIw0jp0W0yK1hePOojf33A+FStWcdiw\nfZIOJ2e5HAl6AAAJuklEQVRKB/Zm9tsVQLDG2PjDhiYbkBQkJRcpWvvtvSf77b1n0mHkXF3LpX1J\nO1avS99zTyQeWv5FpMh8WPUJ1TW1DOizhzrzpUFaWywLSi4iItFobTEREck7Si4iIhI7dehLUXrx\n9Xe55cGnKR3Qmwmjh3H6MaOTDkmkoCi5SFF6a9Fynp75NhBMJizG5OLufLRqHV12341uXTolHY4U\nGN0Wk6JUjLPzU333Z3+h87hLGfDFK/lb+ZtJhyMFSMlFilJFZUpyKaLZ+XU6dihhy9btgGbpS+tQ\ncpGiVOwtl9KBfepfpyZakbgouUhRKvaWy87ri1U1cqZI86hDX4rSU7+6lIoVq6iorCqKfVzSpSZU\ntVykNSSWXMysL/AL4PCwaB7wHXdfnkXdDsB1wKlANbAOuNLdZ7RSuFJgjjiwlCMOLE06jMQMClsu\nnTt1pHuX3XF3zJo9GVtkF4ks/2JmHYFXgYXAWWHxA8BRwGHu3uhqemb2G6AMGOvuq8zsAuB24Ch3\nn5PhfC3/IpKmau0Geu/RRUlFMmqTa4uZ2YXAPcAQd68Iy/oBy4Gr3f22RuoOA+YDF7j7lJTyt4AK\nd5+UoY6Si4hIBG11bbFTgKV1iQXA3T8iSBqnNFH3JMCA6Wnl04FjzaxzjHGKiEgzJJVcRgFLMpRX\nAAdnUbcGWJZWvoSgD2lkS4MrVOXl5UmHkDf0s9hBP4sd9LOIT1LJpQ+wPkP5OqCzme3WRN1NGe5z\nrQufi29caZb0ixM48fK7OO/ymzj/him8/+HqpMNJnP5f7KCfRXySSi7qAJHEzJiziKUrVjHliVm0\na1fcndnV1TWsXb+JN995P+lQpMAkNRS5CuiWobw7sNHdtzZRt4vt2kvfPXzWoH1p0MbNW6lauwGA\nDu1LinKOS5333l/J8FOvp+b92Tz+XgcWT/tx0iFJAUlqtNg/gOHuPjitfB6w3t2PaqTuVcDNQKm7\nL0spvwO4COjp7pvS6qilJCISUUtGiyXVcpkK3GNmg9x9KdQPRR4OXJ16Yli+MqWV8hhwEzABeDDl\n1AnAs+mJBVr2AxIRkeiS6nOZQjAj/1YzKzGzdsAtwGLg7rqTzGwsUAncWVfm7u8C9wLXmFnv8Lzz\ngcHA93P1DYiISMMSSS7uvh04hmBI8fzw0RU4Oq3lsR5YQ5BgUl0KPALMCG+lfR041t3ntnbsIiLS\ntET6XETygZn9CxhLWv+dSLEwswHA7wj+OI+1sVGQS+6bWV8z+5OZLQwfj5jZXknHlQQzO9TM7jOz\n+WY218zeNrNfmVmfpmsXLjM7hSCxFO1fV2Z2ipm9ZGavmdkiM3vVzM5JOq5cM7PRZvaPlN+R2WZ2\nRtJxtTYzOxmYAZTSyO+BmXU1s1+Hn6Vvm9kzZtbkZPWCSy7hopjPsWO2/khgIzDdzLokGVtCHgZ6\nAIe7+yiC25HHEtxSLMqN08P/I7cATxEsJVR0zOy7wI3Aue4+GhgGvAscnWhgOWZmpcA/gZXAQeHv\nyG+Bh8zsxARDy4XLCf69X6Hx34NHCFZGOdTdDwT+DZSb2cDGLl5wyQX4KsESMle5e6271wJXAUOA\nbyYaWTJqCX4WmwHcvRL4KTAUmJhkYAn6FsEvyKtJB5KE8AP1ZuDSutGa7l4NXEHK4JkiMZFgzt3P\nw88K3P0eghU/zkwysBwYl7q+YyZmdgzwBeA6d98SFt8IlADXNla3EJNLSxbFLESj3H1xWtmK8LlH\nroNJmpn1IvgQvYYibbUA5xLsg/RCaqG7r3D315MJKTHV4XOHugIL9iAoAbYnElGOZLlU/CnANuDl\nlHrbCW6nNfp5WojJpSWLYhac8C/SdAcQ3GN9Kcfh5IPrgD+4ezGvd3IU8AEw0cymh30NM83sa0kH\nloCHCPaV+oGZdQmnRVxLkFh+lmhk+WEUUJnhc6QC6NdY320hbnPc5KKYTSwvU9DMrAS4ALjf3d9L\nOp5cMrOhwGkEk3WL2T7hYzJwgrtXhp27fzaz/u5+U6LR5ZC7rzezzxHMvasCNgCrgS+5+5tJxpYn\nGvs8hWCh4KpMFQux5VK0o3+y9ENgK/CdpANJwK3Aze6e6ZelmHQCdge+H/bB4e5TgWnAtWa2e5LB\n5VK4+eCrBHc7err7ngSt2+fN7KxGK0ujCjG5tGRRzIIWrmRwKnBcXQd/sTCz8cCBwG8yHc5xOElb\nT/BHWPpf5m8CnYEROY8oOTcSfDZ8u67D2t3/DDwD3G1mHRqrXAQa+zyFRhYKLsTkMpdgKZh0gwmW\nnClKZnYu8D2CVRAyNmML3OcJOmlfNbM3zOwN4OLw2FNh2ReTCy+nFhIk1PTf/5rwuRA/FxpyMPBB\nhj86/4/gA7Q05xHll7nAXmaW3oUyGPiwsc+SQvxPNBUYZGaD6gpSFsV8NLGoEhROjLsS+Jy7rwzL\nJpnZhclGljvufr277+/uh9U92NGKOS4sezrJGHPo8fB5VFr5QcAm4O3chpOoj4CBYV9kqkEEw/g/\nzn1IiWioO+FRgpF0Y+sKwnliY2ni87QQk8sUslgUs1iY2dnAfQQ/l2PN7Jww2RwPNDoJqghY2nOx\n+DNBP8P1ZtYdwMzGEQwt/XGR3TK9g6CF8qO6AjObAJwE/NHd1yYVWI5l/B1w9+cIbhHemNIX932C\n0XSNDvwoyLXFzKwv8AtgNEFGngd8x92XJxpYAsxsFcF8lvT/PA7c4O4/2rVWYQtnXv+C4OfSnWBh\n1O3uPiTRwHLIzHoSDHD4ArCZYJDH7e7+20QDS4CZHUuw1Ud/gnkvtQR/jP26gaH8BcHM7gKOIxgR\n1hlYRvC5MCycy1J3XheC/yt1iw2/T/B5uqDR6xdichERkWQV4m0xERFJmJKLiIjETslFRERip+Qi\nIiKxU3IREZHYKbmIiEjslFxERCR2Si4iIhI7JRcREYmdkouIiMROyUVERGKn5CIiIrFTchHJITP7\nk5l9Yma1ZvZsWHanma0xs8Vm9rWkYxSJg1ZFFskxMzsV+AvwFXf/o5ntBTwBjHP3TclGJxIPJReR\nBJjZo8BngZHAA8Av3f35ZKMSiY+Si0gCwq235wNVwMvufkHCIYnESn0uIglw948IttYdCkxPOByR\n2KnlIpIAM2sHvAjsBuwLjHT31clGJRIftVxEkvFtYCZwItAJuD3ZcETipZaLSI6Z2X7AI8AYd99q\nZhcDdwPHu/vfk41OJB5quYjkkJn9GPgX0A+om9PyTcCBP5nZX5KKTSROarmIiEjs1HIREZHYKbmI\niEjslFxERCR2Si4iIhI7JRcREYmdkouIiMROyUVERGKn5CIiIrFTchERkdgpuYiISOz+P+W+bkmY\nAeRLAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x109040690>"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can define a function to solve for the displacement."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def barsolver(u_init, T, C, nx):\n",
" ''' Returns the displacement of the wave equation for a bar.\n",
" \n",
" Parameters\n",
" ----------\n",
" u_init: array of float\n",
" initial displacement of bar\n",
" T: integer\n",
" final time for calculation\n",
" C: integer\n",
" CFL number for stability\n",
" nx: integer\n",
" number of gridsteps\n",
" \n",
" Returns\n",
" -------\n",
" u: array of float\n",
" final displacement of bar wave motion\n",
" ''' \n",
" #initial parameters\n",
" c= 2\n",
" C2= C**2\n",
" dx= 10./nx\n",
" dt = C*dx/c\n",
" nt= int(round(T/dt))\n",
" \n",
"\n",
" #create arrays\n",
" u= np.zeros(nx+1) #array holding u for u[n+1]\n",
" u_1= np.zeros(nx+1) #array holding u for u[n]\n",
" u_2= np.zeros(nx+1) #array holding u for u[n-1]\n",
" \n",
" u_1[4/dx:6/dx+1]= u_init[4/dx:6/dx+1]\n",
" \n",
" # Loop for first time step\n",
" n = 0\n",
" for i in range(1, nx):\n",
" u[i] = u_1[i] + 0.5*C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1])\n",
" # Enforce boundary conditions \n",
" u[0] = 0; u[-1] = -dx/(c*dt)*(u[i]-u_1[i])+u[-2]\n",
"\n",
" # Switch variables before next step\n",
" u_2[:], u_1[:] = u_1, u\n",
" \n",
" # Loops for subsequent time steps\n",
" for n in range(1, nt):\n",
" for i in range(1, nx):\n",
" u[i] = - u_2[i] + 2*u_1[i] + C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1]) \n",
"\n",
" # Enforce boundary conditions\n",
" u[0] = 0; u[-1] = -dx/(c*dt)*(u[i]-u_1[i])+u[-2]\n",
" \n",
" # Switch variables before next step\n",
" u_2[:], u_1[:] = u_1, u\n",
" \n",
" return u"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lets run the solver for $t=0$ and plot the displacement."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"u_ans= barsolver(u_initial,0,1,50)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.plot(x_array,u_ans)\n",
"plt.xlim(0,10)\n",
"plt.ylim(-3,3)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 6,
"text": [
"(-3, 3)"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAELCAYAAADeNe2OAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFodJREFUeJzt3X2UXHWd5/H3NxINAhmQKAjMJKA8qBhh4czI47SADKDo\nakYUBdlxyapwQCQsMPhAlKOIDCKsisLiwix7eDpERNCIDjQo7AAiEiA8qBB5kmAQFgbCU/LdP241\nxKbT6erUrVvVv/frnDrd3Kq6v2+Krk//+nt/91ZkJpKkckxqugBJUncZ/JJUGINfkgpj8EtSYQx+\nSSqMwS9JhTH4Jakwa3R6hxHxJuDTwEBr0zrAYuBrmfnjTo8nSWpPHTP+vYEPA/tl5vbAVsAvgcsi\nYtcaxpMktaGO4H8QOD4z7wXI6tTgk1pjva+G8SRJbeh4qyczLx1h81+1vv6p0+NJktoTdV+rJyI2\nBr4LbAi8KzP/o9YBJUmjqm1VT0S8KSJ+BzwABPABQ1+Smldb8Gfm7zPzzVRtnt8Ct0bETnWNJ0ka\nm9pbPS8NFLEQeCEz39GVASVJI6pjHf+UzHx2hLtuB2ZFxOTMfGGFx/uBAJI0DpkZ43leHa2e+RHx\nzhG2zwD+34qhPyQzvWVy/PHHN15Dr9x8LXwtfC1Gv62OOoI/gS9FxOsAonI4sD1weg3jSZLa0PFW\nD/A54GDgmoh4EZgCLAE+lpnn1zCeJKkNdZzAdT1wfaf3W4KBgYGmS+gZvhYv87V4ma9FZ3RtVc9K\nC4jIpmuQpH4TEWQPHdyVJPUwg1+SCmPwS1JhDH5JKozBL0mFMfglqTAGvyQVxuCXpMIY/JJUGINf\nkgpj8EtSYQx+SSqMwS9JhTH4JakwBr8kFcbgl6TCGPySVBiDX5IKY/BLUmEMfkkqjMEvSYUx+CWp\nMAa/JBWm48EfEdtExFkRsTAiFkTEHRFxWkRM6/RYkqT2RWZ2docRdwG3AR/PzKURsRHwb1S/ZN6R\nmc8Oe3x2ugZJmugigsyM8Ty3jlbPcuCYzFwKkJkPAycDmwP71DCeJKkNa9Swz5mZ+eKwbX9sfV23\nhvEkSW3o+Ix/hNAH2AJI4NpOjydJak/He/yvGCDiVcAtwP/NzE+OcL89fklqU6/1+If7AvAccEQX\nxpIkrUIdPf6XRMQ/Af8IDAwd7JUkNau24I+IA4Ejgd0yc8loj507d+5L3w8MDDAwMFBXWZLUlwYH\nBxkcHOzIvmrp8UfEAcAxwO6Z+Whr23uBN2bmWcMea49fktq0Oj3+js/4I+JjwFnA54E9I16qaxfg\n4U6PJ3Xa00/DuefCjTfCJz4Bu+wCMa63l9Sb6jhz9zGq9frD3yoJfCkzvzzs8c741RMeegi+9S04\n6yzYdVfYcUc480yYOhWOPBI+9CGYPLnpKqXK6sz4a1/OucoCDH417Ne/hlNPhSuugAMPhMMPhze9\nqbpv+fJq+6mnwm9/C4cdBrNnw3rrNVuz1OvLOaWe9Oyz8J73wPvfDzNnwr33wmmnvRz6AJMmwb77\nwlVXwWWXwe23V/effXZzdUuryxm/inXoofDII3DBBe21cO65B3beGS6/HP72b+urTxqNM36pTRdd\nBPPnw/e/337ffost4LvfhQ9/GB5/vJ76pDo541dxfvc72GGHKvi32278+/nMZ+D++2HePFf9qPuc\n8Utj9OyzsN9+cPzxqxf6AF//Ojz4IJx+emdqk7rFGb+KcuihsHgxXHxxZ2bp994L73yn/X51nzN+\naQyG+vpnn9251sxmm9nvV/9xxq8idKqvvzL2+9VtzvilUXSyr78y9vvVT5zxa8I79thqxt+pvv7K\nDPX7r7kG3vKW+saRwEs2SCv1xBNVH37BAthkk/rHO+EEWLTIM3tVP4NfWomTT4Zbb4XzzuvOeEuW\nwOabw513woYbdmdMlcngl0bw/PPVdXUuuwy23bZ743760zBtWjX7l+riwV1pBBddVM2+uxn6AJ/9\nLHzve/DMM90dVxorg18TUiaccgocdVT3x95ii+pa/uec0/2xpbEw+DUhXX01PPcc7LVXM+PPmVNd\nw3/ZsmbGl0Zj8GtCOuWU6lOzJjX0E77zztWHtfzoR82ML43Gg7uacBYuhN12q5ZVTpnSXB0XXlh9\nlOMvftFcDZq4PLgrreAb34BDDmk29AFmzYIHHoAbbmi2Dmk4Z/yaUBYvhq22qj4fd9q0pquBb34T\nrr++WmEkdZLr+KWWL34R/vQnOOOMpiupPPUUzJgBv/oVbLpp09VoIjH4Jap18zNmwC9/WS2p7BVH\nH12dTPbNbzZdiSYSg1+imuXPnw8//GHTlfylBx+EmTOri7itu27T1Wii8OCuirdsWbVufs6cpit5\npU02gX32gTPPbLoSqVJr8EfEGyNifkQsr3Mc6corYepU2GWXpisZ2Zw51dLO5b4T1ANqC/6I+CBw\nHTADsJejWl18MRxwQO9++tW228Laa8ONNzZdiVTvjH8OsBvw70CPvh01Ebz4YnUFzg98oOlKRvfB\nD1YfzSg1rc7g3zkzF9W4fwmAa6+tlkpOn950JaObNasKftcyqGm1Bb9LddQt8+ZVs+let8021UHo\n225ruhKVzlU96mvLl/dP8EdUdV5ySdOVqHQGv/raDTdUV8HccsumKxkb+/zqBQa/+tq8eVXvvF/s\nsEP1ubz33NN0JSrZGk0XADB37tyXvh8YGGBgYKCxWtQ/Mqu2ST/NoCdNqlYfzZsHxx7bdDXqJ4OD\ngwwODnZkX7VfsiEizgE+npkj/nXhJRs0Xr/5TdU6+f3ve3f9/kh+/nM47jjX9Gv19MMlG0x2ddzQ\nQd1+Cn2Av//76pfV/fc3XYlK1a3g77O3pvpBv/X3h0yeDO97H1x6adOVqFR1XrLhOxFxHzALyIi4\nLyLujYjJdY2pctx9N/z5z/B3f9d0JePjsk41ycsyqy+deGJ1ueNvf7vpSsbn2Wdhww2rX2AbbNB0\nNepH/dDjlzqqX9s8Q6ZMgb32qq4xJHWbwa++84c/wH33wa67Nl3J6rHdo6YY/Oo7P/hBdXB0jZ44\nC2X89t67+iD2J55ouhKVxuBX3+mXa/OsyjrrwMAAXH5505WoNAa/+srixbBgAeyxR9OVdMbQpZql\nbjL41VcuvbRqkUyZ0nQlnbHvvtWZvE8/3XQlKonBr74yUdo8Q173uupchPnzm65EJTH41Tduvx1u\nvrma8U8k++8Pp5/uB7Grewx+9YVly+Dgg+ErX6k+tHwiOeggWLoUzj676UpUCs/cVV847bSqzXP1\n1dWljSeaBQtg993h1ltho42arkb9YHXO3DX41fMWLYLtt6/WvG+xRdPV1OcLX4A77nCVj8bGSzZo\nwsqET30K5syZ2KEP8PnPw513Gvyqn8GvnnbeefDII3DUUU1XUr/XvAbOOgsOOwwef7zpajSR2epR\nz3r0UXj72+GKK6pWTykOPRSef776JSCtjD1+TUgf/ShsvDGcfHLTlXTXk0/C1lvDuefCu97VdDXq\nVasT/H1+mStNVFdcATfcALfd1nQl3Td1KnznOzB7dvXvX3PNpivSROOMXz3nqaeqGe/3v18tcSzV\nRz4C06fDSSc1XYl6ka0eTShHHFGFf+knNA0d47jySnjHO5quRr3G4NeE8cADVcjdfTe8/vVNV9O8\n006rTlrzg9k1nMGvCeOQQ6rr1NveqCxdCm9+c3XN/m23bboa9RKDXxOCs/2RnX46XHWVs379JYNf\nE4Kz/ZE569dIDH71PWf7o3PWr+EMfvU9Z/ujc9av4Xou+CPiDcCpwHatTbcBR2TmQyM81uAvnLP9\nsXHWrxX11NU5I+LVwM+ozgp+a+v2NHB1RKzV6fHU/048sTpL1dAf3ezZcNNNcMstTVeiftfxGX9E\nzAa+B2yWmYta2zYAHgKOzcx/GfZ4Z/wFc7bfHmf9GtJTrZ6ImA9smZmbDtu+AHg6M3cYtt3gL5i9\n/fbY69eQXgv+h4G7MnO3YdsvA3bLzLWHbTf4C+Vsf3yc9Qt6rMcPTAOeGmH7k8BrI+I1NYypPmRv\nf3zs9Wt11XFZ5ran7z/6UQ1VqKctXQoXXFDN9tWeNdeEY46Bo4+Gww9vuhr1ozqCfwmwzgjbp1L1\n+J8bfsecOXNf+n799QeYNm2ghrLUa04+2dn+eM2eDTffDGee2XQl6pYlSwZ57LHBjuyrjh7/T4Ct\nRji4exvwVGbuOGy7PX5JalOv9fjnAdMjYvrQhtZyzq2AS2oYT5LUhjpm/JOBXwF3Ah+j6vmfDewI\nbJuZzwx7vDN+SWpTT834M/MF4N3AMmBh67Y21VLOZ0Z7riSpfl6kTZL6UE/N+CVJvc3gl6TCGPyS\nVBiDX5IKY/BLUmEMfkkqjMEvSYUx+CWpMAa/JBXG4Jekwhj8klQYg1+SCmPwS1JhDH5JKozBL0mF\nMfglqTAGvyQVxuCXpMIY/JJUGINfkgpj8EtSYQx+SSqMwS9Jhakt+CNiUkQcHRHPRcRBdY0jSWrP\nGnXsNCL+BvhXYC1gMpB1jCNJal8twQ8cAZwBPAJcXdMYkqRxqCv4j8rM5RExUNP+JUnjVEuPPzOX\n17FfSdLqc1WPJBXG4Jekwqwy+CNij4hYPobbVd0oWJK0esZycPc6YKsxPO6Z8RYxd+7cl74fGBhg\nYGBgvLuSpAlpcHCQwcHBjuwrMutbYt9a1XMV8F8y819X8pisswZJmogigsyM8TzXHr8kFaZbwT+u\n30qSpM6rJfgjYreIuA84n+pyDf8SEfdFxP51jCdJGrtae/xjKsAevyS1zR6/JGnMDH5JKozBL0mF\nMfglqTAGvyQVxuCXpMIY/JJUGINfkgpj8EtSYQx+SSqMwS9JhTH4JakwBr8kFcbgl6TCGPySVBiD\nX5IKY/BLUmEMfkkqjMEvSYUx+CWpMAa/JBXG4Jekwhj8klQYg1+SCtPx4I+I9SLiqIi4KSJuj4iF\nEfHTiNip02NJktpXx4z/k8AxwEGZuTWwNbAQuCYi3l3DeJKkNtQR/AmckZkLATJzOXAssAw4rIbx\nJEltiMzs7A4jJsFLgb/i9sXA3Zm567Dt2ekaJGmiiwgyM8bz3DU6XczwwIeq7w+sDwx2ejxJUnu6\ntarnYGAxcGqXxpMkrcQqgz8i9oiI5WO4XbWS57+N6mDv/pn5eKf/AZKk9oyl1XMdsNUYHvfM8A0R\n8TfAZcDBmXltm7VJkmqwyuDPzKXAPe3uOCL+GrgS+O+Zeeloj507d+5L3w8MDDAwMNDucJI0oQ0O\nDjI4ONiRfXV8VQ/8Reh/LjPnrbD9h5n5/mGPdVWPJLWpp1b1RMQmwNXALcCaEXHACnfP7PR4kqT2\ndDz4gSOBzVq3WcPuW1TDeJKkNtTS6mmrAFs9ktS21Wn1eHVOSSqMwS9JhTH4JakwBr8kFcbgl6TC\nGPySVBiDX5IKY/BLUmEMfkkqjMEvSYUx+CWpMAa/JBXG4Jekwhj8klQYg1+SCmPwS1JhDH5JKozB\nL0mFMfglqTAGvyQVxuCXpMIY/JJUGINfkgpj8EtSYdbo5M4iYhJwGPBeYH1gcmuMi4CvZuZznRxP\nktS+yMzO7SxibeBJ4FOZeWZr23bANcD5mTl7hOdkJ2uQpBJEBJkZ43puh4N/TeDczNxv2PYfALtm\n5vojPMfgl6Q2rU7wd7TVk5lLgf1GuOuvgEc7OZYkaXxqPbgbEa+OiEOA/wR8ps6xJoLBwcGmS+gZ\nvhYv87V4ma9FZ9QW/BFxAfAE8M/AxzPzyrrGmij8oX6Zr8XLfC1e5mvRGaMGf0TsERHLx3C7avhz\nM/MjwFrAJ4FzI+LrNf0bJEltWFWP/zpgqzHs55mRNraO2v44Ik4CvhoRF2Tmr9usUZLUQZ1e1fMq\nYFJmvjBs+z7A5cDszDx72H0u6ZGkceiJVT3AgcA7gU8N2z6j9fWx4U8Yb+GSpPGp4+DuRyNix6H/\niIi3UR3gvRv4SQ3jSZLa0OlWzxuA/wa8D3g18CogqNo8J2fmK2b8kqTu6mjwS50SEb8AdgJmZOb9\nTdcjdVtEvBH4X8CemdnR7kwjV+eMiDdExP+JiLtat4sjYuMmamlSRGwTEWdFxMKIWBARd0TEaREx\nrenamhQRs6hCv+hZSUTMiohrI+JXEfH7iLgpIg5ouq5ui4jtI+InK7xPboyIDzddV50i4oNUqypn\nMMr7ICLWjohvtXL0joj4aUS8dVX773rwR8SrgZ9RHVh+a+v2NHB1RKzV7XoadgGwLrBdZs4E3g3s\nCVwXEVMarawhrZ+PrwE/pmoTFikiPgucAByYmdsDWwL3ALs1WliXRcQM4N+oLvmydet9cjZwfkT8\n5wZLq9scqv/X/87o74OLgZnANpn5NuAGYDAiNhpt503M+A8C3g4ck5nLM3M5cAywGfDpBupp0nKq\n12EpQGY+DJwMbA7s02RhDTqU6of3pqYLaUor7E4EDsvMPwBk5ovAUcC3m6usEfsA6wDfaGUFmfk9\nqqsAf6TJwmq2c2YuGu0BEfFu4B+AL2bms63NJ1AdWz1utOc2EfyzgD+s+I/KzMXAwtZ9JZmZmfcO\n2/bH1td1u11M0yLidVTh9s8UPNunWhb9IvAXZ8Rn5h8z8+ZmSmrMi62vk4c2RERQhdsLIz5jAhjj\nJYtnAc8Dv1zheS9QtYhGzdImgn8mcN8I2xdR/SVQjNYsbrgtqHp613a5nF7wReB/Z+YDTRfSsB2B\nB4F9IuLqVm/7+oj4RNOFNeB84C7g8xGxVuvDno6jCv1TGq2seTOBh0fIkUXABqMdK+z0CVxjMQ14\naoTtTwKvjYjXlPpJXa0zn/8r8D8z83dN19NNEbE58CHGdomQie6vW7e5wPsz8+HWwb4LI2LDzPxq\no9V1UWY+FRG7A+cAS4D/AP4MvCczf9NkbT1gtCyF6lMQl4z0xCZm/EWv1FiFLwDPAUc0XUgDTgJO\nzMyRfpBLMwVYE/hc67gPmTkP+CFwXOsDj4oQEVtSHe+5D1gvM19P9ZfhzyNi/0aL62NNBP8SqoM1\nw00Fni54tv9PwD8Cew8d7C1FROwCvA347kh3d7mcXvAU1QRp+Iz2N8Brgbd0vaLmnECVDZ8ZOoCZ\nmRcCPwXOiIjJoz15ghstS2GES+QMaSL4FwCbjrB9U+C2LtfSEyLiQOBIYLfMHPFPswluD6qDdTdF\nxC0RcQvV5byhurrrLRGxV3Pldd1dVL/whr8/l7W+NnL+TUPeDjw4woTwt1QBN6PrFfWOBcDGETG8\nZb8p8MhoWdLED9A8YHpETB/aEBEbUPV2L2mgnka1Tsg5Gtg9Mx9tbXtvRLzig+knqsw8PjPfnJnb\nDt14efa/d2vb/CZr7LLLWl9nDtu+NdUl0O/objmNWgxs1Dr+taLpVMuh/9T9krpuZe3xS6hWO+00\ntKF1HsxOrCJLmwj+c6hm9idFxKtaR+m/BtwLnNFAPY2JiI8BZ1G9JntGxAGtXwT7AqOegFGAGPa1\nJBdS9bWPj4ipABGxM9USva8U1gr8H1Qz+y8PbYiIdwEfAM7LzCeaKqyLRnwPZObPqFpeJ6xw3Odz\nVCueRl0A0Mi1eloXczsV2J7qt9ltwBGZ+VDXi2lQRDxGtV5/+P/YBL6UmV9+5bMmttbZmKdSvS5T\ngYeBFzJzs0YL67KIWI/qgPc/AEupDvqfPvzzLEoQEXsCxwIbUq3rX041WfrWSpZE972I+A6wN9XK\nndcC91PlwpYrft5J62oHJ1Gd9b8MeIAqS+8cdf9epE2SylLSQSJJEga/JBXH4Jekwhj8klQYg1+S\nCmPwS1JhDH5JKozBL0mFMfglqTAGvyQV5v8DEX50NJchjEUAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x109138c50>"
]
}
],
"prompt_number": 6
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As we expected, the displacement is equal to the initial parabola."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"u_ans= barsolver(u_initial,2,1,50) #solving at t= 2"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.plot(x_array,u_ans)\n",
"plt.xlim(0,10)\n",
"plt.ylim(-2,2)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 8,
"text": [
"(-2, 2)"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAY0AAAELCAYAAAAlTtoUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH8VJREFUeJzt3Xu4HFWZ7/HvjyRcAkQ5RDCoE0C5HJAI6qgQ0E6AiBwQ\nFQNyExFQUZmDwgOIohszDkFgVBAYQTlRxxt5QLmMXE1ajjkgDCcxMSGChwSUABFkSEII5PKeP6oa\nms6+VO9d1dW7+/d5nn4qWV1V/dJk17vXu1atUkRgZmaWxSZlB2BmZsOHk4aZmWXmpGFmZpk5aZiZ\nWWZOGmZmlpmThpmZZeakYWZmmeWeNCTtLekaSYskzZe0UNJ3JI3NcOwoSdMkPShpgaQ5kibmHaOZ\nmQ2O8r65T9JiYAHw8Yh4QdIOwG9IEtTbImJNP8f+G1ABJkbEM5JOBi4D9ouIP+QaqJmZNa2I8tQG\n4JyIeAEgIpYBFwO7AIf2dZCk3YBTgekR8Ux67A+AJcA3CojTzMyaVETSmBARjzS0PZFuX9vPcR8G\nBMxuaJ8NTJE0Oqf4zMxskHJPGhGxrpfmXYEA7u7n0AnAeuCxhvYlwEhgj1wCNDOzQSt89pSkEcDJ\nwPcj4s/97DoWWB0bD7KsSLfbFhGfmZll14opt+cDLwJntOCzzMysQCOLPLmkk4CPApXawHg/nga2\nlKSG3saYdPtMETGamVl2hSUNSScAXwQmR8TTGQ75A/Ax4E28elxjJ2AtsKiXz/DDQMzMBiEiNJjj\nCilPSToeOBs4MCKWp22HSTq1bp/tJdUH/UuSwfJJDaebBNwREat7+6yI8CuCr33ta6XH0C4vfxf+\nLvxd9P8aiiLuCD8OuAaYQTJV9vg0iRwO7JDuMxFYBlxROy4iHgKuBr4kadt0v5NIehpfzjtOMzNr\nXhHlqcuATUlu6KsXwAXpn1cBz5IkjnqnA18D5khaSzJzakpEzC8gTjMza1LuSSMiBpwaG8mSIBut\nRRXJPR7npy9rQqVSKTuEtuHv4hX+Ll7h7yIfua891UobT7QyM7OBSCLaaSDczMw6k5OGmZll5qRh\nZmaZOWmYmVlmThpmZpaZk4aZmWXmpGFmZpk5aZiZWWZOGmZmlpmThpmZZeakYWZmmTlpmJlZZk4a\nZmaWWWFJQ9I4SbdJ2lDUZ5iZWWsV8oxwSR8BLgFeInn4UjPHLiV5QFOjMyNi1tCjMzOzwSokaQBn\nApOBHmDXJo+NiNgn94jMzGzIikoa+0dESIN6xoeZmbWpQsY0/Dg9M7PO1JazpyRdJGmOpD9Jul3S\n4WXHZGZm7Zk0lgMPRMREYE/gRuBGSZ8rNywzM1ORlSRJM4CPR8SQkpOkW4ADgO0i4sW6dlfCzMya\nJImIGNSgczv2NHpzH7A1sEfZgZiZdbOiZk8NiqTNgRER8XzDW+vT7YjGY3p6el7+c6VSoVKpFBWe\nmdmwVK1WqVaruZyrFeWpEyJio4t9+v72wPJajUnSJ4D3RMRnGva7ATgEGBsRq+vaXZ4yM2tSu5en\neg1M0kRgGXBFw1vHSHpn3X5HA0cA36xPGGZm1npFLSNyJfABYCwQkpaQLCeyW0SsTXdbSbJcyLK6\nQ38NvBG4UtIo4LXA34FPR8T3i4jVzMyyK7Q8VTSXp8zMmtfu5SkzM+sQThpmZpaZk4aZmWXmpGFm\nZpk5aZiZWWZOGmZmlpmThpmZZeakYWZmmTlpmJlZZk4aZmaWmZOGmZll5qRhZmaZOWmYmVlmThpm\nZpZZYUlD0jhJt0naUNRnmJlZaxWSNCR9BJgD7Ejy8KVmjh0laZqkByUtkDQnfcqfmZmVrKiexpnA\nZOBe+njcaz8uB6YC+0fEXsC1wB2S3pZviGZm1qyiksb+EbG02YMk7QacCkyPiGcAIuIHwBLgG7lG\naGZmTSskaQzhGawfJumZzG5onw1MkTR6SIGZmdmQtNvsqQnAeuCxhvYlwEhgj5ZHZGZmL2u3pDEW\nWN1LT2VFut22xfGYmVmddksaw87zz8Ogi3Fm1lWef77sCIZuZNkBNHga2FKSGnobY9LtM40H9PT0\nvPznSqVCpVIpMj4AnnwSrr8errsO7rkH3vxmmDo1eb31raBm54uZWcf6859h5szktWAB7LMPHHUU\nfPSjsOOOrYmhWq1SrVZzOZcGP2ad4eTSDODjEZGpRyPpHOBCYMeIeKyu/XLgU8A2EbG6rn0IY+7N\neeKJJFHMnAnz58NhhyVJ4uCDk79fd13y3pZbOoGYdbtaorjuuuTaceSRyTVh333h7ruT9375S9hp\np9YnEABJRMSgrk6tSBonRMSIPt7fHlheu/JL2hV4EPhkRPywbr8/Aksi4vCG4wtPGuvXw2mnJf+T\na4liyhTYfPON942A3//+ld8qxo2Dm2+G7bYrNEQzaxOrViUJYN48+MhHkoRwwAEwopcr4Nq1UK0m\nieVXv0r2++lPe7+25K3dk0avPY30Lu+7ge9FxGfr2q8CJgETI+IZSScB3wX2jYj5DecoNGmsXw8n\nnQSPPw433ZT0IrKKgPPPhxtvhN/8xonDrNOtWgWHHgq77grf+17viaIvL70EJ5wAzz2XJJCiE8dQ\nkkZRy4hcKWkJcCQQkpZIekTSqLrdVgLPAssaDj8dmAnMkbQAOAWY0pgwilafMG6+ubmEAUlZato0\n+NCH4MADYfnyYuI0s/LVJ4yrr24uYQBsuin85Cfwmtck14w1a4qJMw+F9jSKVlRPozFhjB7CLYUR\n8NWvJr89uMdh1nkaE8YmQ/hVfN06OO644nscbdfTGM7yTBiQ9Di+/nX3OMw6UZ4JA2DkyPbvcThp\n1Mk7YdQ4cZh1nrwTRk27Jw4njVRRCaPGicOscxSVMGraOXF4TCN16aXJvOk77sg/YdSLgHPPTW7y\n+Y//8H0cZsPRKafAiy/CD3+Yf8Kot25dMs1/552Ta1Re2nbKbdHyShrLlsGECcnd3bvskkNgA3jp\nJdh7b7jwQjjiiOI/z8zyc++9yc16ixYlPYGiLV+e3Cg8a1ayzYOTxhAde2xyZ+Y3WvjEjlmz4OST\nYeHCYns2Zpaf9evhXe+CL3wBjj++dZ97xRXJDcOzZ+dTnfDsqSGoVmHOHDjvvNZ+7uTJ8O53w/Tp\nrf1cMxu8a65J7tk67rjWfu5nPgMrVsDPf97az+1NV/c01q5NykTTpiW3/LfaX/+afP6998Jb3tL6\nzzez7P72N9hzz+R+q732av3n33NPskTJgw/CmDED798fl6cG6dJL4c474dZbyxuQvvjipMvpQXGz\n9nbKKbD11vCtb5UXwyc/CdtsM/RBcSeNQWj14HdfPChu1v5aPfjdl7wGxZ00BqGMwe++eFDcrH2V\nNfjdlzwGxT0Q3qSyBr/74kFxs/ZV1uB3X8oeFO+6nkbZg9998aC4Wfspe/C7L0MdFHd5qgntMPjd\nFw+Km7WXdhj87stQBsWdNDJ67rnkdvx77knWjGk3L72UDM5fcUWyPpWZlWfhwuTn8E9/Knfwuy/L\nl8Mee8ADD8D48c0d23ZjGpK2k/QTSYvT10xJb8h47FJJc3t5TR5qXDNmJI9qbceEAcmDWM46C77z\nnbIjMbPLL4fPfrY9EwYkz+Y58US48srWfm7uPQ1JmwL3A4uBY9Lma4H9gH0i4vkBjl8SETtl/KzM\nPY0NG2C33ZIFxvbbL9MhpVi9Ovmt4d574c1vLjsas+707LNJVeLBB+H1ry87mr498kgys+uxx5qb\nedluPY0Tgb2AcyJiQ0RsAM4BdgZOK+DzMrnttuQ3hn33LSuCbEaPTmqVV1xRdiRm3evaa+Gww9o7\nYUCS2PbbL1lGvVWK6GncBuzW2FuQNB94PiL6vWwX1dM45JDk3oyPfzzT7qV69FF4+9uT7VZblR2N\nWXdZvz6ZwXjddfCP/1h2NAO76y744hfhD3/IPoGm3XoaE4AlvbQvJemBDEjSRZLmSPqTpNslHT6U\ngBYvhrlz4eijh3KW1hk/Ht73Pvjxj8uOxKz73HILbL/98EgYkAzWr1sHv/1taz6viKQxFljZS/sK\nYLSkzQY4fjnwQERMBPYEbgRulPS5wQb03e/Cpz4Fmw30yW3kn/4JLrsseWiTmbXOZZclP3/DhQSn\nn57E3ZLPK6A89SJwW0Qc0dD+78CxwBYR8WKT57wFOADYrv7YLOWp555LlgtZsADekGn+VnuIgLe9\nLZmDffDBZUdj1h0WLkx+3pYuTWYzDherViUVigcegB13HHj/oZSnRg7moAE8DWzdS/sYkjGNphJG\n6j7gUGAPYG79Gz09PS//uVKpUKlUXnXgjBnw/vcPr4QByW8Ptd6Gk4ZZa1x+ebJMx3BKGJCMfX7i\nE8n0229+c+P3q9Uq1Wo1l88qoqdxK7B7LwPhC4CVEdHnhFdJmwMjGqflSvoyMA14V0T8Z117vz2N\n4TLNti+efmvWOsNlmm1fmpl+224D4TcA4yW9fI+ipO2B3YHr63eUtL30qvH+jwG93RT/DmANsKiZ\nQIbLNNu+ePqtWesMl2m2fWnV9NsiksYMYAFwkaQRkjYBpgOPAFfVdpI0EVgGNF4Sj5H0zrr9jgaO\nAL4ZEaubCaQ2oDWc13H67GeTntKqVWVHYta51q9PJswMpwHw3rRiAk3uSSMi1gIHA+tJegaLgK2A\nyQ0X/ZXAsySJo+bXwMXAlenSIUuAs4FPR0RPM3EsXgzz5g2fabZ9GT8eKhX40Y/KjsSsc91yS9LD\nGC7TbPty4IFJAsxp+KJXHbtg4ec/n6wAOW1ai4MqQLUKp52WPDVsOPeazNrVgQcmD0I79tiyIxm6\nq65KVvK+4Ya+9/Eqtw2G6zTbvnj6rVlxhus0275kmX7bbgPhpRuu02z7Upt+69VvzfI3XKfZ9qU2\n/baoCTQd2dPYZ5/koSkNt2wMa6tXww47wEMPJUsim9nQrVkD48YlvY0ddig7mvw89BC8973w+OMw\nYsTG77unUefhh+HJJ+GAA8qOJF+jR8Ohh/ZfpzSz5txxR/Lgs05KGJA8M2jcOPjd7/I/d8cljZkz\n4cgje8+uw93UqcnKm2aWj5kz4aijyo6iGEVdLzquPLXPPvDtbyerxHaaF15Ifntwicps6GqlqeF6\nB/hAHn44qbj0VqJyeSpVK03tv3/ZkRRjiy1cojLLS6001YkJA2CXXYopUXVU0ujk0lSNS1Rm+ejk\n0lRNEdeLjipPdXJpqsYlKrOh6/TSVE1fJSqXp+j80lSNS1RmQ9fppamaIkpUHZM0uqE0VeMSldnQ\ndENpqibv60XHlKe6oTRV4xKV2eB1S2mqprcSVdeXp7qlNFXjEpXZ4HVLaaom7xJVRySNbipN1Uyd\nmvx3m1lzZs5Mfn66SZ4lqo4oT3VTaarGJSqz5tVKU4sWJdtu0ViiarvylKTtJP1E0uL0NVNSpjVn\nJY2SNE3Sg5IWSJqTPuWvV91WmqpxicqsebXSVDclDMi3RJV70pC0KXAnMBLYI309D8yWtGWGU1wO\nTAX2j4i9gGuBOyS9rbedu7E0VeMSlVlzurE0VZNXiSr38pSkU4HvATtHxNK0bXvgceDciLikn2N3\nI3k87MkRMaOu/Y/A0og4rGH/2Hvv6LrSVI1LVGbZdWtpqqa+RDVyZHuVp44EHq0lDICIeIokGRw5\nwLEfBgTMbmifDUyRNLrxgG4sTdW4RGWWXbeWpmryKlEVkTQmAEt6aV8K7JXh2PXAYw3tS3il3PUq\n3VqaqnGJyiybbi5N1eRRoioiaYwFVvbSvgIYLWmzAY5d3cvj+Fak220bD+j2fwSHHJI8C3j58rIj\nMWtfa9bALbckv2R2s6lT4frrh3aOkfmE8iotncPbraWpmlqJ6qKLOuvxtmZ5mj+/u0tTNbUS1VNP\nDf4cRSSNp4Gte2kfAzwfES8OcOyW2vjpSmPS7TONB0yb1vPynyuVCpUuvHKeeSZccEEyIG5mvfvK\nV8qOoDzVapVqtQrAG98I8+YN/lxFzJ66Fdg9InZqaF8ArIyI/fo59hzgQmDHiHisrv1y4FPANhGx\nuq69l0qWmZn1p91u7rsBGC9pfK0hnXK7O/Cqapqk7SXVB/5LkvLWpIZzTgLuqE8YZmbWekUkjRnA\nAuAiSSMkbQJMBx4BrqrtlN7lvQy4otYWEQ8BVwNfkrRtut9JwE7AlwuI1czMmpB70oiItcDBJFNn\nF6WvrYDJDT2FlcCzJImj3unATGBOWtI6BZgSEfPzjtXMzJrTEQsWmplZdu02pmFmZh3KScPMzDJz\n0jAzs8ycNMzMLDMnDTMzy8xJw8zMMnPSMDOzzJw0zMwsMycNMzPLzEnDzMwyc9IwM7PMnDTMzCwz\nJw0zM8vMScPMzDJz0jAzs8wKSRqSzpC0UNIfJD0g6YiMx/VIelTS3IbXt4uI08zMmjMy7xNKOhc4\nE3hXRCyRdBDwa0kfjIjbBjg8gPMj4kd5x2VmZkOXa09D0muB84ErImIJQETcBdwBXJL1NHnGZGZm\n+cm7PHUIsAUwu6F9NrCHpN1y/jwzM2uhvJPGhHS7pKG99ve9MpzjEEl3SZqfjodcIGmL/EI0M7PB\nyntMY2y6XdnQviLdbjvA8auBVcCnI2KFpL2B64GDJb03ItblF6qZmTWr356GpIMkbcjwmpVHMBFx\ncUScGhEr0r/PA84B3gMclcdnmJnZ4A3U05gD7J7hPKvT7dPpdmvg2br3x6TbZ7KH9rL70u27gZ82\nvtnT0/PynyuVCpVKZRAfYWbWuarVKtVqNZdzKSJyORGApKOBnwGViLi7rv1M4GJg94h4qJ/jXxcR\nf2toewPwF+DKiPh8w3uRZ/xmZt1AEhExqJmqeQ+E30bS65jU0D4JWFifMCSNlvSahv0eldQY0zvS\n7f/NNVIzM2tarkkjIp4DpgGfk7QTJOMiwBTgrIbd5wIPN8yM2hy4oJY4JI0HpgOL6aU0ZWZmrZX7\nHeERcZGkNcAtktYB64GPRsTtDbsuA14C6mdEHQccC8yTNAIYDdxKcpf4mrxjNTOz5uQ6ptFqHtMw\nM2teO41pmJlZB3PSMDOzzJw0zMwsMycNMzPLzEnDzMwyc9IwM7PMnDTMzCwzJw0zM8vMScPMzDJz\n0jAzs8ycNMzMLDMnDTMzy8xJw8zMMnPSMDOzzApJGpI2kXS2pBclnVjEZ5iZWevlnjQk/QMwC5gK\njAKaeuCFpCmS7pM0X9KDks6VNKh1383MLF+5P7kPOAO4CngSmN3MgZL2B24GpkbETZLeCPweGAOc\nl3egZmbWnCLKU2dFxC+AwfQOLgLuiYibACLir8C3gDMljcsxRjMzG4Tck0ZEbBjMcWlS2JeNeyez\nScpcHxxiaGZmNkTtNHtqr3S7pKF9ScP7ZmZWknZKGmPT7cqG9hXpdtsWxmJmZr3oN2lIOkjShgyv\nWa0K2MzMyjPQ7Kk5wO4ZzrM6h1ieTrdbN7SPSbfP9HZQT0/Py3+uVCpUKpUcQjEz6xzVapVqtZrL\nuRTR1G0U2U8sVUju1/hERPwow/7jgMeBnoj4el37O4D7gc9ExNUNx0RR8ZuZdSpJRMSg7n8rbUxD\n0mhJr6n9PSKeAO4BJjXsOglYS3L/hpmZlagVSaOvbDYXeFjSFnVtZwP7STocIL257wzgkjSpmJlZ\niXIvT0maDPwA2BzYDvg7sAo4LyJ+VrffbJIZU2+PiLV17VOAfwY2AzYFfhgR0/v4LJenzMyaNJTy\nVGFjGq3gpGFm1rxhOaZhZmbDj5OGmZll5qRhZmaZOWmYmVlmThpmZpaZk4aZmWXmpGFmZpk5aZiZ\nWWZOGmZmlpmThpmZZeakYWZmmTlpmJlZZk4aZmaWWSFJQ9Imks6W9KKkE4v4DDMza72BnhHeNEn/\nAPwI2BIYBWReu1xSD3ASyTM46v02Is7IK0YzMxuc3JMGyZP2rgKeBGY3eWwA52d5priZmbVeEUnj\nrIjYIKkyyOMH9WAQMzMrXu5jGhGxIe9zmplZe2jH2VOHSLpL0nxJD0i6QNIWZQdlZmbFlKeGYjWw\nCvh0RKyQtDdwPXCwpPdGxLpywzMz62799jQkHSRpQ4bXrDyCiYiLI+LUiFiR/n0ecA7wHuCoPD7D\nzMwGb6Cexhxg9wznWZ1DLH25L92+G/hpgZ9jZmYD6DdpRMQLwEMtigVJr4uIvzU0r0+3I3o7pqen\n5+U/VyoVKpVKIbGZmQ1X1WqVarWay7kUkfneu+ZOnEy5nQV8orf7LiSNBkZFxHN1bauBrepnYEn6\nIPAr4JSIuLbhHFFU/GZmnUoSETGo2xtaMXuqr8DmAg83zIzaHLhA0iYAksYD04HFuDRlZla63JOG\npMmSlgA/I7nD+xJJSyQd07DrMuApoH5G1HHA3sA8SQuBavo6ICLW5B2rmZk1p7DyVCu4PGVm1rx2\nL0+ZmVmHcNIwM7PMnDTMzCwzJw0zM8vMScPMzDJz0jAzs8ycNMzMLDMnDTMzy8xJw8zMMnPSMDOz\nzJw0zMwsMycNMzPLzEnDzMwyc9IwM7PMnDTMzCyzXJOGpG0knSXpfkl/lLRI0u2SJjZxjimS7pM0\nX9KDks6VNKh1383MLF8jcz7fp4EzgfdFxKL0sa2XAr+V9IGIuLO/gyXtD9wMTI2ImyS9Efg9MAY4\nL+dYzcysSbk+uU/SOcCWEfHVurbNgBXA7RHxwQGOnwOsjYhKXdtZwDeAHSPiiYb9/eQ+M7MmtdOT\n+y4GeuobIuJF4L+A1/Z3oKRxwL7A7Ia3ZgOjgH4TjpmZFS/XpBERGyJiQ32bpG2AbYHqAIfvlW6X\nNLQvaXjfelGtVssOoW34u3iFv4tX+LvIRytmT50CPAV8a4D9xqbblQ3tK9LttnkG1Wn8A/EKfxev\n8HfxCn8X+eg3aUg6SNKGDK9ZfRy/J3AOcExEPFvEf4CZmbXOQLOn5gC7ZzjP6sYGSf8A3AScEhF3\nZzjH0+l264b2Men2mQznMDOzAuU6e+rlk0pvAu4EzouIGzIeMw54HOiJiK/Xtb8DuB/4TERc3XCM\np06ZmQ3CYGdP5X2fRi1h3EFDwpB0Y0QcUff30cCoiHgOICKekHQPMAn4et0pJwFrSe7feJXB/keb\nmdng5Jo00pvxZgNzgS0kHV/39oSG3ecC20gaHxEvpG1nA7MkHR4RN6fnOwO4pPEeDTMza728b+77\nV5KLfG+WRsTOdfvOJpkx9faIWFvXPgX4Z2AzYFPghxExPbcgzcxs0AoZ0zArm6T/DUwkWUngsbLj\nMWuldIz4fwFTIiLXWyuG3Sq3kraT9BNJi9PXTElvKDuuVpO0t6Rr0kUh50taKOk7ksYOfHRnk3Qk\nScLo2t+IJB0p6W5J/ynp/6WLiB4/8JGdRdI7Jd1a93Nyn6Sjy46rSJI+QjLzdUf6+RmQtJWk76bX\n0YXp4rJ7DHT+YZU0JG1KMitrJLBH+noemC1pyzJjK8HPSZZmeUdETAAOBqYAcyRtXmpkJUr/jUwH\nfg105UQJSV8ApgEnRMQ7gd2Ah4DJpQbWYpJ2BH4DLAfemv6c/AD4maQPlRha0c4k+X99L/3/DMwk\nGWveOyL2JFkctipph/5OPqySBnAiyXIi59QtWXIOsDNwWqmRtd4Gku/hBYCIWEay9tcuwKFlBlay\nz5H847+/7EDKkF4oLwROj4hHASJiHXAWcEV5kZXiUJL7vv61trxRRHyPZJWJj5UZWMH2j4il/e0g\n6WDg/cBXI2JN2jwNGMEAK4oPt6RxJPBo/RcSEU8Bi9L3usmEiHikoa02w6zfxSE7laT/RnJx/BJd\n2ssATgDWAa9apSEinoiIB8oJqTTr0u2oWkP6bJ4RJNP4O1LGpb+PBF4Cfld33FqSsla/19LhljQm\nsPGChgBL6bIFDdPfHhvtSlLDzHIHfif6KvDjiPhL2YGUaD/gr8Chkmantfz/I+mTZQdWgp8Bi4Gv\nSNoyfb7PeSQJ49JSIyvfBGBZL9eRpcD2/Y2N5n5zX8HGsvGChpB0N0dL2ixdir3rSBoBnAx8PyL+\nXHY8rSZpF2Aq2Za96WRvSl89wBERsSwdGP2FpNdHxL+UGl0LRcRKSQcCM0iWKVoF/B34HxExr8zY\n2kB/11JIFoh9upf3h11Po2tnw2RwPvAifd8n0+kuAi6MiN5+ELrJ5sAWwJfTcS7SlRluBM6TtEWZ\nwbWSpN1IxraWANtExOtIeqN3STqm1OCGseGWNJ5m4wUNIVnU8Pku7mWcBHwU+EDd3fVdQ9IBwJ7A\nv/X2dovDKdtKkl+uGn+TngeMBv57yyMqzzSSa8P/rA32RsQvgNuBqySN6u/gDtfftRT6WSB2uCWN\n+cBOvbTvBCxocSxtQdIJwBeByRHRa3eyCxxEMrh5v6S5kuaSPK8e4Ndp2yHlhddSi0kSZePP9vp0\nO9x+5odiL+Cvvfwy+TDJxXHHlkfUPuYDb5DUOESxE/Bkf9eS4fYP6AZgvKTxtQZJ25PUsa8vLaqS\npDdrnQ0cGBHL07bDJJ1abmStFRFfi4i3RMQ+tRev9Do+kLbdVmaMLXRTum1c6+2tJI8wWNjacEr1\nFLBDOt5XbzzJlPW/tT6kluurpH89yayyibWG9B6niQxwLR1uSWMGSY/iIkkj0tkQ04FHgKvKDKzV\nJB0HXEPynUyRdHyaRA4H+r05p0uoYdstfkFSx/+apDEAkvYnmUb5jS4rX15O0qOof9TCJODDwL9H\nxH+VFVgL9frvPyLuJCnTTasb5/oyycyyfidLDLu1pyRtR/Lo2HeSZNEFwBkR8XipgbWYpGdI7sdo\n/EcRwAX1zyTpJumdvt8i+W7GAMuAtfWLZXY6SduQTAx4P/ACyQSJyyLiB6UGVoJ0AdRzgdeT3Lex\ngeQXre/2MW192JN0JfABkhlSo4HHSK4LuzUsDrslyb+Tg0nKl38huZY+2O/5h1vSMDOz8gy38pSZ\nmZXIScPMzDJz0jAzs8ycNMzMLDMnDTMzy8xJw8zMMnPSMDOzzJw0zMwsMycNMzPLzEnDzMwy+/+U\neOdjbouBlAAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x1092a5350>"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"u_ans= barsolver(u_initial,4,1,50) #solving at t= 4 "
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.plot(x_array,u_ans)\n",
"plt.xlim(0,10)\n",
"plt.ylim(-2,2)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 10,
"text": [
"(-2, 2)"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAY0AAAELCAYAAAAlTtoUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHJxJREFUeJzt3X+8VXWd7/HXW0QFkpEL6WAl0kPDINHSGZ0g25Ay6vhj\n0jR/VqakM8ZkgyOmlzjmNOJkmRo6Y+q1spxytGvNw/yRnD3dSKW8GgSZze2gGaZBORD4Az2f+8da\nB7abwzlrH9baa5+z38/HYz/W4bv3WvvjFvb7rO/3u75LEYGZmVkWO5RdgJmZDR4ODTMzy8yhYWZm\nmTk0zMwsM4eGmZll5tAwM7PMHBpmZpZZ7qEh6UBJX5a0UtIySSskXSNpXIZ9h0u6XNLPJS2XtETS\ntLxrNDOzgVHeF/dJegJYDnwoIl6UtCfwIElAHRARL/Wx778AFWBaRKyVdDZwLfDuiPhproWamVnD\niuie6gbmRcSLABGxGvgcsC9w9LZ2kjQJmA0sjIi16b43A13AZwuo08zMGlREaEyNiF/VtT2bbnfr\nY7/3AwI669o7gVmSRuZUn5mZDVDuoRERr/bS/DYggB/0setU4DXg6br2LmBHYHIuBZqZ2YAVPntK\n0jDgbOCmiPivPl46DtgYWw+yrEu3Y4uoz8zMsmvGlNv5wMvABU14LzMzK9CORR5c0lnAB4BKz8B4\nH9YAoySp7mxjdLpdW0SNZmaWXWGhIelM4O+BmRGxJsMuPwVOAd7C68c1JgKbgJW9vIdvBmJmNgAR\noYHsV0j3lKQzgIuA90XE82nbMZJm17xmD0m1RX+bZLB8Rt3hZgD3R8TG3t4rIvyIYMGCBaXX0CoP\nfxb+LPxZ9P3YHkVcEX468GXgVpKpsmekIXIssGf6mmnAamBRz34R8SRwI/ApSWPT151FcqZxad51\nmplZ44ronroW2Inkgr5aAVyW/vxH4A8kwVFrDrAAWCJpE8nMqVkRsayAOs3MrEG5h0ZE9Ds1NpIl\nQbZaiyqSazzmpw9rQKVSKbuEluHPYgt/Flv4s8hH7mtPNdPWE63MzKw/kohWGgg3M7OhyaFhZmaZ\nOTTMzCwzh4aZmWXm0DAzs8wcGmZmlplDw8zMMnNomJlZZg4NMzPLzKFhZmaZOTTMzCwzh4aZmWXm\n0DAzs8wKCw1J4yXdK6m7qPcwM7PmKuQe4ZJOAK4CXiG5+VIj+64iuUFTvbkRsXj7qzMzs4EqJDSA\nucBMoAN4W4P7RkS8M/eKzMxsuxUVGtMjIqQB3ePDzMxaVCFjGr6dnpnZ0NSSs6ckXSlpiaRfSLpP\n0rFl12RmZq0ZGs8Dj0bENGAKcDdwt6Tzyy3LzMxUZE+SpFuBD0XEdoWTpP8A3gPsHhEv17S7J8zM\nrEGSiIgBDTq34plGb5YCuwKTyy7EzKydFTV7akAk7QIMi4gNdU+9lm6H1e/T0dGx+edKpUKlUimq\nPDOzQalarVKtVnM5VjO6p86MiK2+7NPn9wCe7+ljkvQR4NCIOK/udXcBRwLjImJjTbu7p8zMGtTq\n3VO9FiZpGrAaWFT31KmSDq553QeB44F/rg0MMzNrvqKWEbkeOAoYB4SkLpLlRCZFxKb0ZetJlgtZ\nXbPrPcCbgeslDQd2A34PnBsRNxVRq5mZZVdo91TR3D1lZta4Vu+eMjOzIcKhYWZmmTk0zMwsM4eG\nmZll5tAwM7PMHBpmZpaZQ8PMzDJzaJiZWWYODTMzy8yhYWZmmTk0zMwsM4eGmZll5tAwM7PMHBpm\nZpZZYaEhabykeyV1F/UeZmbWXIWEhqQTgCXA3iQ3X2pk3+GSLpf0c0nLJS1J7/JnZmYlK+pMYy4w\nE3iYbdzutQ/XAScB0yNif+AW4H5JB+RbopmZNaqo0JgeEasa3UnSJGA2sDAi1gJExM1AF/DZXCs0\nM7OGFRIa23EP1veTnJl01rV3ArMkjdyuwszMbLu02uypqcBrwNN17V3AjsDkpldkZmabtVpojAM2\n9nKmsi7djm1yPWZmVqPVQsPMzFrYjmUXUGcNMEqS6s42RqfbtfU7dHR0bP65UqlQqVSKrM/MbNCp\nVqtUq9VcjqWBj1lnOLh0K/ChiMh0RiNpHnAFsHdEPF3Tfh3wMWBMRGysad+OMXczs/YkiYho9HII\noDndU9v8Vpe0h6Tawr+dvn5G3UtnAPfXBoaZmTVfM0Kj1zRLr/JeDSzqaYuIJ4EbgU9JGpu+7ixg\nInBp8aWamVlfChnTkHQ9cBTJbKiQ1EVyBjEpIjalL1sP/IEkOGrNARYASyRtIpk5NSsilhVRq5mZ\nZVfomEbRPKZhZta4Vh/TMDOzIcKhYWZmmTk0zMwsM4eGmZll5tAwM7PMHBpmZpaZQ8PMzDJzaJiZ\nWWYODTMzy8yhYWZmmTk0zMwsM4eGmZll5tAwM7PMHBpmZpaZQ8PMzDIr6iZMuwNXAwelTcuBCyLi\nNxn2XUVyc6Z6cyNicW5FmplZw3IPDUk7AQ8ATwCT0+ZbgE5J74yIDf0cIiLinXnXZWZm26+I7qkP\nA/sD8yKiOyK6gXnAW4G/KeD9zMysSYoIjROBpyJiVU9DRDwHrEyfMzOzQaqI0JgKdPXSvorkDKRf\nkq6UtETSLyTdJ+nYPAs0M7OBKSI0xgHre2lfB4yUtHM/+z8PPBoR04ApwN3A3ZLOz7dMMzNrVBGh\nEdu1c8QhEfGt9OdXI+J64B7gnzIEjpmZFaiIKbdrgF17aR8NbIiIlwdwzKXA0SSzsR6rfaKjo2Pz\nz5VKhUqlMoDDm5kNXdVqlWq1msuxFLFdJwZbH1D6HrBfREysa18OrI+Id/ex7y7AsPppuZIuBS4H\n/jwiflLTHnnXb2Y21EkiIjSQfYvonroLmCBpQk+DpD2A/YA7a18oaQ9JtYWfAny+l2MeBLxEMgPL\nzMxKUkRo3EpyBfiVkoZJ2gFYCPwKuKHnRZKmAauBRXX7nyrp4JrXfRA4HvjniNhYQL1mZpZR7mMa\nEbFJ0hEky4isJBkYXw7MrPvSX0+yXMjqmrZ7gDcD10saDuwG/B44NyJuyrtWMzNrTO5jGs3kMQ0z\ns8a12piGmZkNUQ4NMzPLzKFhZmaZOTTMzCwzh4aZmWXm0DAzs8wcGmZmlplDw8zMMnNomJlZZg4N\nMzPLzKFhZmaZOTTMzCwzh4aZmWXm0DAzs8wcGmZmllkhoSFpd0lfl/RE+rhD0psy7jtc0uWSfi5p\nuaQl6V3+zMysZLmHhqSdgAdI7go4OX1sADoljcpwiOuAk4DpEbE/cAtwv6QD8q7VzMwak/ud+yTN\nBv4VeGtErErb9gB+A1wcEVf1se8kklvEnh0Rt9a0/wxYFRHH1L3ed+4zM2tQq92570TgqZ7AAIiI\n50jC4MR+9n0/IKCzrr0TmCVpZI51mplZg4oIjalAVy/tq4D9M+z7GvB0XXsXW7q7zMysJEWExjhg\nfS/t64CRknbuZ9+NvfQ5rUu3Y3Ooz8zMBmjHAo7Z1EGG7363me/Wug4+GMaPL7uK8m3YAIsXl12F\n2dBVRGisAXbtpX00sCEiXu5n31HaeoR7dLpdW7/D3Lkdm38eO7bCuHGVRusd9F54AXbaCR58sOxK\nyjd/fvI57LVX2ZWYtY41a6qsXVvN5VhFzJ76HrBfREysa18OrI+Id/ex7zzgCmDviHi6pv064GPA\nmIjYWNPu2VPAiy8mZxlPPgm77152NeXp7oYJE+Dee2HKlLKrMWtdrTZ76i5ggqQJPQ3plNv9gDtr\nXyhpD0m1hX+bpHtrRt0xZwD31waGbTFiBBx9NNx1V9mVlOuRR2D0aAeGWZGKCI1bgeXAlZKGSdoB\nWAj8Crih50XpVd6rgUU9bRHxJHAj8ClJY9PXnQVMBC4toNYh46ST4I47yq6iXN/6VvI5mFlxcg+N\niNgEHEEydXZl+ngDMLPuTGE98AeS4Kg1B7gDWJJ2aZ0DzIqIZXnXOpQceSQ8+ig8/3zZlZSjuxv+\n/d8dGmZFy31Mo5k8pvF6p50Ghx0G551XdiXN99BDcM45sGJF2ZWYtb5WG9OwkrRzF5W7psyaw2ca\nQ0i7zqLyrCmzxvhMw4D2nUXlWVNmzePQGGLasYvKXVNmzePuqSGm3bqo3DVl1jh3T9lmI0bAUUe1\nTxeVu6bMmsuhMQSdfHL7dFG5a8qsudw9NQS1SxeVu6bMBsbdU/Y67dJF5a4ps+ZzaAxR7dBF5a4p\ns+Zz99QQNdS7qNw1ZTZw7p6yrQz1Lip3TZmVw6ExhA3lLip3TZmVw91TQ9hQ7aJy15TZ9nH3lPVq\nxAg49li47bayK8lXZyeMGePAMCtDIaEh6QJJKyT9VNKjko7PuF+HpKckPVb3+GIRdbaD88+HRYvg\ntdfKriQ/110HH/942VWYtacd8z6gpIuBucCfR0SXpMOBeyQdFxH39rN7APMj4qt519WuDjkExo6F\ne+5JzjoGu64u+OEP4etfL7sSs/aU65mGpN2A+cCiiOgCiIjvA/cDV2U9TJ41tTsJ5syBa68tu5J8\nLFoEZ50Fo0aVXYlZe8q7e+pIYATQWdfeCUyWNCnn97MMTj4Zli+HlSvLrmT7bNgAt96adLmZWTny\nDo2p6barrr3nz/tnOMaRkr4vaVk6HnKZpBH5ldh+dt4Zzj0XvvSlsivZPrfdBu95D+y9d9mVmLWv\nvENjXLpdX9e+Lt2O7Wf/jcAfgRMiYipwNnAG8KCk3Mdf2sl558Htt8MLL5RdycBEJF1sc+aUXYlZ\ne+szNCQdLqk7w2NxHsVExOciYnZErEv//DgwDzgUODmP92hX48cnV4jfckvZlQzM4sXJ+MyMGWVX\nYtbe+vvtfQmwX4bjbEy3a9LtrsAfap4fnW7XZi9ts6Xp9hDgG/VPdnR0bP65UqlQqVQG8Bbt4e/+\nDk4/HT7xCRg2rOxqGnPddUn98jQJs4ZVq1Wq1Woux8r1inBJHwRuByoR8YOa9rnA54D9IuLJPvZ/\nY0T8rq7tTcCvgesj4uN1z/mK8AZEJFNw588fXNNvu7rgz/4MnnrKs6bM8tBKV4TfS3LWUd+JMANY\nURsYkkZK+pO61z0lqb6mg9Lt/8210jYkJb+tD7bpt55ma9Y6cl97StI8kov7Dqm9uA84NiLuq3nd\nL4AxwISIeDFt6wY+CyyIiG5JE4Dvpbu8KyJeqnsvn2k06OWXk3WbFi+GyZPLrqZ/GzYk9f7kJ541\nZZaX7TnTyH1GUkRcKekl4D8kvQq8BnygNjBSq4FXgFdr2k4HTgMelzQMGEkSGvPrA8MGpnb67fXX\nl11N/267DaZPd2CYtQqvctuGnn02Ocvo6oLddiu7mm2LgHe8IxkEnzmz7GrMho5WGtOwQWD8eDj6\n6Naffutptmatx6HRpubMSbqoNm0qu5Jt++IXPc3WrNU4NNrUIYfAvvu27tIiDz4IP/sZnHlm2ZWY\nWS2PabSxX/wCpk1LFjMcP77sarZ45RU44ABYuBCOz3QnFjNrhMc0bEAmTYLZs+Ef/qHsSl7vmmtg\n4kQ47riyKzGzej7TaHMbNsDb3w5f+xq8971lVwPPPAMHHggPPwz77FN2NWZDk880bMBGjYKrr05u\nn9oKg+IXXgh/+7cODLNW5dAwTjghGdMoe1D8wQfhkUfg4ovLrcPMts3dUwYkg+LTp8OyZeUMir/y\nStItdcUVHvw2K5q7p2y7TZoE55xT3qD4NdckS4V48NustflMwzbrGRS/7TY47LDmva8Hv82ay2ca\nloueQfHzz2/uoLgHv80GD4eGvU7PoPg11zTn/R54wIPfZoNJ7kuj2+AmJUumH3YY7LknnHZace+1\ndGly+9lvfANGjizufcwsP4WcaUjaQdJFkl6W9OEi3sOKs88+yRnAhRcmX+hFWLoUjjkmWWn38MOL\neQ8zy1/uZxqS9gK+CowChgMNjVRLmgX8I7BLuv9XgCs94t1cU6YkwXHEEcmf8zzjqA2MY47J77hm\nVrwiuqcuAG4Afgt0NrKjpOnAd4GTIuI7kt4MPAKMBi7Ju1DrWxHB4cAwG9yK6J66MCK+CQxkOteV\nwEMR8R2AiHgGuBqYK6mF1mFtHz3BkUdXlQPDbPDLPTQionsg+6Wh8BdsfXbSSdJN5cu+SpJHcDgw\nzIaGVpo9tX+67apr76p73kpQ21X18MNwyilw6KGwQz+/dqxYAXfckczIcmCYDX6tdJ3GuHS7vq59\nXbod28RarBdTpsBDD8HYsfCxj8Fee8EnPwk/+hF015xfrlgBHR3J6488EtatSwLHgWE2+PUZGpIO\nl9Sd4bG4WQVbuSZMgAULklux3n8/7LbblgD56EdfHxQ33QRPPQVf+EJyJz4zG/z6655aAuyX4Tgb\nc6hlTbrdta59dLpd29tOHR0dm3+uVCpUKpUcSrEsJk9OAmTBAli5MjmbmD07uf94f91WZtY81WqV\narWay7EKW7BQUgVYDHwkIr6a4fXjgd8AHRHxmZr2g4AfA+dFxI11+/jyDTOzBg3KBQsljZT0Jz1/\njohngYeAGXUvnQFsIrl+w8zMStSM0NhWmj0G/FLSiJq2i4B3SzoWIL247wLgqjRUzMysRLl3T0ma\nCdxMsgzI7sDvgT8Cl0TE7TWv6ySZMfWuiNhU096zjMjOwE7AVyJi4Tbey91TZmYN2p7uKd+Eycys\nzQzKMQ0zMxt8HBpmZpaZQ8PMzDJzaJiZWWYODTMzy8yhYWZmmTk0zMwsM4eGmZll5tAwM7PMHBpm\nZpaZQ8PMzDJzaJiZWWYODTMzy6yQ0JC0g6SLJL0s6cNFvIeZmTVff/cIb5ikvYCvAqOA4UDmtcsl\ndQBnkdyDo9Z/RsQFedVoZmYDk3tokNxp7wbgt0Bng/sGMD/LPcXNzKz5igiNCyOiW1JlgPsP6MYg\nZmZWvNzHNCKiO+9jmplZa2jF2VNHSvq+pGWSHpV0maQRZRdlZmbFdE9tj43AH4FzI2KdpAOBO4Ej\nJB0WEa+WW56ZWXvr80xD0uGSujM8FudRTER8LiJmR8S69M+PA/OAQ4GT83gPMzMbuP7ONJYA+2U4\nzsYcatmWpen2EOAbBb6PmZn1o8/QiIgXgSebVAuS3hgRv6trfi3dDuttn46Ojs0/VyoVKpVKIbWZ\nmQ1W1WqVarWay7EUkfnau8YOnEy5XQx8pLfrLiSNBIZHxH/XtG0E3lA7A0vSccD/Bs6JiFvqjhFF\n1W9mNlRJIiIGdHlDM2ZPbauwx4Bf1s2M2gW4TNIOAJImAAuBJ3DXlJlZ6XIPDUkzJXUBt5Nc4X2V\npC5Jp9a9dDXwHFA7I+p04EDgcUkrgGr6eE9EvJR3rWZm1pjCuqeawd1TZmaNa/XuKTMzGyIcGmZm\nlplDw8zMMnNomJlZZg4NMzPLzKFhZmaZOTTMzCwzh4aZmWXm0DAzs8wcGmZmlplDw8zMMnNomJlZ\nZg4NMzPLzKFhZmaZOTTMzCyzXEND0hhJF0r6saSfSVop6T5J0xo4xixJSyUtk/RzSRdLGtC672Zm\nlq8dcz7eucBc4L0RsTK9bevngf+UdFREPNDXzpKmA98FToqI70h6M/AIMBq4JOdazcysQbneuU/S\nPGBURHy6pm1nYB1wX0Qc18/+S4BNEVGpabsQ+Cywd0Q8W/d637nPzKxBrXTnvs8BHbUNEfEy8AKw\nW187ShoP/AXQWfdUJzAc6DNwzMyseLmGRkR0R0R3bZukMcBYoNrP7vun26669q66560X1Wq17BJa\nhj+LLfxZbOHPIh/NmD11DvAccHU/rxuXbtfXta9Lt2PzLGqo8T+ILfxZbOHPYgt/FvnoMzQkHS6p\nO8Nj8Tb2nwLMA06NiD8U8R9gZmbN09/sqSXAfhmOs7G+QdJewHeAcyLiBxmOsSbd7lrXPjrdrs1w\nDDMzK1Cus6c2H1R6C/AAcElE3JVxn/HAb4COiPhMTftBwI+B8yLixrp9PHXKzGwABjp7Ku/rNHoC\n437qAkPS3RFxfM2fRwLDI+K/ASLiWUkPATOAz9QccgawieT6jdcZ6H+0mZkNTK6hkV6M1wk8BoyQ\ndEbN01PrXv4YMEbShIh4MW27CFgs6diI+G56vAuAq+qv0TAzs+bL++K+L5B8yfdmVUS8tea1nSQz\npt4VEZtq2mcB/wjsDOwEfCUiFuZWpJmZDVghYxpmZZP0f4BpJCsJPF12PWbNlI4R/y9gVkTkemnF\noFvlVtLukr4u6Yn0cYekN5VdV7NJOlDSl9NFIZdJWiHpGknj+t97aJN0IklgtO1vRJJOlPQDST+R\n9P/SRUTP6H/PoUXSwZK+V/PvZKmkD5ZdV5EknUAy83Vv+vg3IOkNkr6Ufo+uSBeXndzf8QdVaEja\niWRW1o7A5PSxAeiUNKrM2krwbyRLsxwUEVOBI4BZwBJJu5RaWYnSvyMLgXuAtpwoIemTwOXAmRFx\nMDAJeBKYWWphTSZpb+BB4HngHem/k5uB2yX9dYmlFW0uyf/rh+n738AdJGPNB0bEFJLFYauS9uzr\n4IMqNIAPkywnMq9myZJ5wFuBvym1subrJvkcXgSIiNUka3/tCxxdZmElO5/kL/+Pyy6kDOkX5RXA\nnIh4CiAiXgUuBBaVV1kpjia57usLPcsbRcS/kqwycUqZhRVsekSs6usFko4A/hL4dES8lDZfDgyj\nnxXFB1tonAg8VfuBRMRzwMr0uXYyNSJ+VdfWM8Osz8UhhypJ/4Pky/FTtOlZBnAm8CrwulUaIuLZ\niHi0nJJK82q6Hd7TkN6bZxjJNP4hKePS3ycCrwA/rNlvE0m3Vp/fpYMtNKay9YKGAKtoswUN098e\n672NpA8zyxX4Q9Gnga9FxK/LLqRE7waeAY6W1Jn25f9I0kfLLqwEtwNPAP9T0qj0/j6XkATG50ut\nrHxTgdW9fI+sAvboa2w094v7CjaOrRc0hOR0c6SkndOl2NuOpGHA2cBNEfFfZdfTbJL2BU4i27I3\nQ9lb0kcHcHxErE4HRr8p6U8j4p9Kra6JImK9pPcBt5IsU/RH4PfAX0XE42XW1gL6+i6FZIHYNb08\nP+jONNp2NkwG84GX2fZ1MkPdlcAVEdHbP4R2sgswArg0HeciXZnhbuASSSPKLK6ZJE0iGdvqAsZE\nxBtJzka/L+nUUosbxAZbaKxh6wUNIVnUcEMbn2WcBXwAOKrm6vq2Iek9wBTgX3p7usnllG09yS9X\n9b9JPw6MBN7e9IrKcznJd8MnegZ7I+KbwH3ADZKG97XzENfXdyn0sUDsYAuNZcDEXtonAsubXEtL\nkHQm8PfAzIjo9XSyDRxOMrj5Y0mPSXqM5H71APekbUeWV15TPUESlPX/tl9Lt4Pt3/z22B94ppdf\nJn9J8uW4d9Mrah3LgDdJqh+imAj8tq/vksH2F+guYIKkCT0NkvYg6ce+s7SqSpJerHUR8L6IeD5t\nO0bS7HIra66IWBAR+0TEO3sebDnrOCptu7fMGpvoO+m2fq23d5DcwmBFc8sp1XPAnul4X60JJFPW\nf9f8kppuW136d5LMKpvW05Be4zSNfr5LB1to3EpyRnGlpGHpbIiFwK+AG8osrNkknQ58meQzmSXp\njDREjgX6vDinTahu2y6+SdKPv0DSaABJ00mmUX62zbovryM5o6i91cIM4P3AbRHxQlmFNVGvf/8j\n4gGSbrrLa8a5LiWZWdbnZIlBt/aUpN1Jbh17MEmKLgcuiIjflFpYk0laS3I9Rv1figAuq70nSTtJ\nr/S9muSzGQ2sBjbVLpY51EkaQzIx4C+BF0kmSFwbETeXWlgJ0gVQLwb+lOS6jW6SX7S+tI1p64Oe\npOuBo0hmSI0Enib5XphUtzjsKJK/J0eQdF/+muS79Od9Hn+whYaZmZVnsHVPmZlZiRwaZmaWmUPD\nzMwyc2iYmVlmDg0zM8vMoWFmZpk5NMzMLDOHhpmZZebQMDOzzBwaZmaW2f8HPB7w67ZNCTYAAAAA\nSUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x10911dad0>"
]
}
],
"prompt_number": 10
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As we can see from the plots, the wave moving in the right direction has been absorbed while the left moving wave has flipped over and is now moving in the right direction."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Our code has expressed correctly the non-reflecting boundary!"
]
},
{
"cell_type": "heading",
"level": 5,
"metadata": {},
"source": [
"Now your turn"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What do you think will happen as more time passes?\n",
"\n",
"You will need to plot the displacement for t= 6, 8, 10 and check if what you expected was correct."
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Reference"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Barba, Lorena A., et al. \"MAE 6286 Practical Numerical Methods with Python,\" GW Open edX, The George Washingtion University, 2014. http://openedx.seas.gwu.edu/courses/GW/MAE6286/2014_fall/about .\n",
"\n",
"* Chapra, Steven C and Canale, Raymond P., \"Numerical Methods for Engineers,\" McGraw-Hill Education, Inc., New York, 2010.\n",
"\n",
"* Everstine, Gordon C. \"Analytical Solution of Partial Differential Equations,\" George Washington University, 2012. [PDF](http://gwu.geverstine.com/pdenum.pdf) \n",
"\n",
"* Fitzpatrick, Richard. \"Introduction: Wave Equation,\" University of Texas, 2006. [Wave Equation](http://farside.ph.utexas.edu/teaching/329/lectures/node89.html).\n",
"\n",
"* Strauss, Walter A., \"Partial Differential Equations: An Introduction,\" Wiley, Inc., New York, 2008. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"###### The cell bellow loads the style of the notebook"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from IPython.core.display import HTML\n",
"css_file = '../../styles/numericalmoocstyle.css'\n",
"HTML(open(css_file, \"r\").read())"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<link href='http://fonts.googleapis.com/css?family=Alegreya+Sans:100,300,400,500,700,800,900,100italic,300italic,400italic,500italic,700italic,800italic,900italic' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=Arvo:400,700,400italic' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=PT+Mono' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=Shadows+Into+Light' rel='stylesheet' type='text/css'>\n",
"<link href='http://fonts.googleapis.com/css?family=Nixie+One' rel='stylesheet' type='text/css'>\n",
"<style>\n",
"\n",
"@font-face {\n",
" font-family: \"Computer Modern\";\n",
" src: url('http://mirrors.ctan.org/fonts/cm-unicode/fonts/otf/cmunss.otf');\n",
"}\n",
"\n",
"#notebook_panel { /* main background */\n",
" background: rgb(245,245,245);\n",
"}\n",
"\n",
"div.cell { /* set cell width */\n",
" width: 750px;\n",
"}\n",
"\n",
"div #notebook { /* centre the content */\n",
" background: #fff; /* white background for content */\n",
" width: 1000px;\n",
" margin: auto;\n",
" padding-left: 0em;\n",
"}\n",
"\n",
"#notebook li { /* More space between bullet points */\n",
"margin-top:0.8em;\n",
"}\n",
"\n",
"/* draw border around running cells */\n",
"div.cell.border-box-sizing.code_cell.running { \n",
" border: 1px solid #111;\n",
"}\n",
"\n",
"/* Put a solid color box around each cell and its output, visually linking them*/\n",
"div.cell.code_cell {\n",
" background-color: rgb(256,256,256); \n",
" border-radius: 0px; \n",
" padding: 0.5em;\n",
" margin-left:1em;\n",
" margin-top: 1em;\n",
"}\n",
"\n",
"div.text_cell_render{\n",
" font-family: 'Alegreya Sans' sans-serif;\n",
" line-height: 140%;\n",
" font-size: 125%;\n",
" font-weight: 400;\n",
" width:600px;\n",
" margin-left:auto;\n",
" margin-right:auto;\n",
"}\n",
"\n",
"\n",
"/* Formatting for header cells */\n",
".text_cell_render h1 {\n",
" font-family: 'Nixie One', serif;\n",
" font-style:regular;\n",
" font-weight: 400; \n",
" font-size: 45pt;\n",
" line-height: 100%;\n",
" color: rgb(0,51,102);\n",
" margin-bottom: 0.5em;\n",
" margin-top: 0.5em;\n",
" display: block;\n",
"}\t\n",
".text_cell_render h2 {\n",
" font-family: 'Nixie One', serif;\n",
" font-weight: 400;\n",
" font-size: 30pt;\n",
" line-height: 100%;\n",
" color: rgb(0,51,102);\n",
" margin-bottom: 0.1em;\n",
" margin-top: 0.3em;\n",
" display: block;\n",
"}\t\n",
"\n",
".text_cell_render h3 {\n",
" font-family: 'Nixie One', serif;\n",
" margin-top:16px;\n",
"\tfont-size: 22pt;\n",
" font-weight: 600;\n",
" margin-bottom: 3px;\n",
" font-style: regular;\n",
" color: rgb(102,102,0);\n",
"}\n",
"\n",
".text_cell_render h4 { /*Use this for captions*/\n",
" font-family: 'Nixie One', serif;\n",
" font-size: 14pt;\n",
" text-align: center;\n",
" margin-top: 0em;\n",
" margin-bottom: 2em;\n",
" font-style: regular;\n",
"}\n",
"\n",
".text_cell_render h5 { /*Use this for small titles*/\n",
" font-family: 'Nixie One', sans-serif;\n",
" font-weight: 400;\n",
" font-size: 16pt;\n",
" color: rgb(163,0,0);\n",
" font-style: italic;\n",
" margin-bottom: .1em;\n",
" margin-top: 0.8em;\n",
" display: block;\n",
"}\n",
"\n",
".text_cell_render h6 { /*use this for copyright note*/\n",
" font-family: 'PT Mono', sans-serif;\n",
" font-weight: 300;\n",
" font-size: 9pt;\n",
" line-height: 100%;\n",
" color: grey;\n",
" margin-bottom: 1px;\n",
" margin-top: 1px;\n",
"}\n",
"\n",
".CodeMirror{\n",
" font-family: \"PT Mono\";\n",
" font-size: 90%;\n",
"}\n",
"\n",
"</style>\n",
"<script>\n",
" MathJax.Hub.Config({\n",
" TeX: {\n",
" extensions: [\"AMSmath.js\"],\n",
" equationNumbers: { autoNumber: \"AMS\", useLabelIds: true}\n",
" },\n",
" tex2jax: {\n",
" inlineMath: [ ['$','$'], [\"\\\\(\",\"\\\\)\"] ],\n",
" displayMath: [ ['$$','$$'], [\"\\\\[\",\"\\\\]\"] ]\n",
" },\n",
" displayAlign: 'center', // Change this to 'center' to center equations.\n",
" \"HTML-CSS\": {\n",
" styles: {'.MathJax_Display': {\"margin\": 4}}\n",
" }\n",
" });\n",
"</script>\n"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 1,
"text": [
"<IPython.core.display.HTML at 0x1038969d0>"
]
}
],
"prompt_number": 1
}
],
"metadata": {}
}
]
} | mit |
c4fcm/oped-gender-report | data_acquisition/Byline Statistics with Social Media.ipynb | 1 | 16265 | {
"metadata": {
"name": "",
"signature": "sha256:344d17e1cfd39d844498fa1b1e92f6247d7852b40fc3ff82fc636bd82d8549c0"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"#TODO: words written by men and women\n",
"\n",
"import csv\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import pylab as P\n",
"import os\n",
"\n",
"lines = []\n",
"\n",
"#CHOOSE A FOLDER FROM ABOVE\n",
"#folder = \"./test_results/30bf9fd5bb824eb49e89c8a828276348c0b1570c/\"\n",
"folder = \"./annual_data/\"\n",
"\n",
"files = [\"[2013-08-01T00:00:00Z TO 2013-09-01T00:00:00Z].csv\",\n",
"\"[2013-09-01T00:00:00Z TO 2013-10-01T00:00:00Z].csv\",\n",
"\"[2013-10-01T00:00:00Z TO 2013-11-01T00:00:00Z].csv\",\n",
"\"[2013-11-01T00:00:00Z TO 2013-12-01T00:00:00Z].csv\",\n",
"\"[2013-12-01T00:00:00Z TO 2014-01-01T00:00:00Z].csv\",\n",
"\"[2014-01-01T00:00:00Z TO 2014-02-01T00:00:00Z].csv\",\n",
"\"[2014-02-01T00:00:00Z TO 2014-03-01T00:00:00Z].csv\",\n",
"\"[2014-03-01T00:00:00Z TO 2014-04-01T00:00:00Z].csv\",\n",
"\"[2014-04-01T00:00:00Z TO 2014-05-01T00:00:00Z].csv\",\n",
"\"[2014-05-01T00:00:00Z TO 2014-06-01T00:00:00Z].csv\",\n",
"\"[2014-06-01T00:00:00Z TO 2014-07-01T00:00:00Z].csv\",\n",
"\"[2014-07-01T00:00:00Z TO 2014-08-01T00:00:00Z].csv\"]\n",
"\n",
"top = 0\n",
"for filename in files:\n",
" #with open (os.path.join(folder,\"month_06_2014.csv\")) as f:\n",
" with open (os.path.join(folder,files[0])) as f:\n",
" reader = csv.DictReader(f)\n",
" for i, row in enumerate(reader):\n",
" lines.append(row)\n",
" lines.pop(top)\n",
" top = len(lines)\n",
"\n",
"lines[0].keys()"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import requests\n",
"import json\n",
"\n",
"# reduces social media metrics to a single number\n",
"# highly reductionist, as you might expect\n",
"class SocialMedia:\n",
" def facebook(self, url):\n",
" #res = requests.get(\"http://graph.facebook.com/\" + url)\n",
" res = requests.get(\"https://graph.facebook.com/fql?q=SELECT%20like_count,%20total_count,%20share_count,%20click_count,%20comment_count%20FROM%20link_stat%20WHERE%20url%20=%20%22{0}%22\".format(url.replace(\"http://\",\"\")))\n",
" j = json.loads(res.text)\n",
" if 'data' in j.keys() and len(j['data'])>0:\n",
" return j['data'][0]['total_count']\n",
" return None\n",
"\n",
" def twitter(self, url):\n",
" res = requests.get(\"http://urls.api.twitter.com/1/urls/count.json?url=\" + url)\n",
" j = json.loads(res.text)\n",
" if 'count' in j.keys():\n",
" return j['count']\n",
" return None\n",
"\n",
" def reddit(self, url):\n",
" reddit_url = \"http://buttons.reddit.com/button_info.json?url={0}\".format(url)\n",
" res = requests.get(reddit_url)\n",
" #import pdb; pdb.set_trace()\n",
" j = json.loads(res.text)\n",
" if not \"data\" in j:\n",
" print \"REDDIT ERROR WITH {0}\".format(reddit_url)\n",
" return None\n",
" #return {\"ups\":\"0\", \"num_comments\":\"0\"}\n",
" else:\n",
" data = j['data']\n",
" if \"children\" in data and len(data[\"children\"]) > 0 and \"data\" in data[\"children\"][0]:\n",
" child = data[\"children\"][0]\n",
" return child['data']['ups'] + child['data']['num_comments']\n",
" #return {\"ups\":child[\"data\"][\"ups\"],\"num_comments\":child[\"data\"][\"num_comments\"]}\n",
" #return {\"ups\":\"0\", \"num_comments\":\"0\"}\n",
" return None\n",
"\n",
"sm = SocialMedia()\n",
"print \"Facebook: {0}\".format(sm.facebook(\"http://civic.mit.edu\"))\n",
"print \"Twitter: {0}\".format(sm.twitter(\"http://civic.mit.edu\"))\n",
"print \"Reddit: {0}\".format(sm.reddit(\"http://civic.mit.edu\"))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Facebook: 268\n",
"Twitter: 221\n",
"Reddit: None"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#SUMMARIZE SECTION IDENTIFICATION\n",
"MEDIA= {\n",
" '1': \"new york times\",\n",
" '2': \"washington post\",\n",
" '6':\"la times\",\n",
" '7': \"new york post\",\n",
" '1150': \"wall street journal\",\n",
" '1757': \"salon\",\n",
" '1707': \"daily beast\",\n",
" '1750': \"telegraph\",\n",
" '314' : \"huffington post\",\n",
"\"27502\":\"huffington post\" #assuming these are the same for now\n",
"}\n",
"\n",
"media = {}\n",
"\n",
"for line in lines:\n",
" mediakey = MEDIA[line['media_id']]\n",
" section = line['section']\n",
" if(not mediakey in media):\n",
" media[mediakey] = {}\n",
" if(not section in media[mediakey]):\n",
" media[mediakey][section] = 0\n",
" media[mediakey][section] += 1\n",
" \n",
" \n",
"for key in media.keys():\n",
" articles = 0\n",
" for section in media[key].keys():\n",
" articles += media[key][section]\n",
" print \"{0}: {1} sections, {2} articles\".format(key,len(media[key]),articles)\n",
" for section in media[key].keys():\n",
" if(section.lower().find(\"opinion\")>=0):\n",
" print \" {0}: {1}\".format(section,media[key][section])\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"salon: 1 sections, 1152 articles\n",
"huffington post: 1 sections, 149832 articles\n",
"washington post: 12 sections, 12144 articles\n",
" opinion: 3516\n",
"la times: 65 sections, 50772 articles\n",
" news/opinion: 1344\n",
" news/opinion/commentary: 720\n",
" OpinionLa: 1392\n",
"new york post: 6 sections, 58500 articles\n",
" Opinion: 12\n",
"new york times: 82 sections, 77100 articles\n",
" opinion/global: 120\n",
" opinion/sunday: 1056\n",
" Opinion: 252\n",
" opinion: 4596\n",
"wall street journal: 5 sections, 51180 articles\n"
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# GROUP BYLINES BY MEDIA ORGANISATION\n",
"# AND SUMMARIZE\n",
"sm = SocialMedia()\n",
"media_people = {}\n",
"mpop = {}\n",
"\n",
"from byline_gender import BylineGender\n",
"import time\n",
"b = BylineGender()\n",
" \n",
"#for key in media.keys():\n",
"# articles = 0\n",
"# for section in media[key].keys():\n",
"# articles += media[key][section]\n",
"# print \"{0}: {1} sections, {2} articles\".format(key,len(media[key]),articles)\n",
"# for section in media[key].keys():\n",
"# if(section.lower().find(\"opinion\")>=0):\n",
"# print \" {0}: {1}\".format(section,media[key][section])\n",
"\n",
"sections = []\n",
"for line in lines:\n",
" if(line['section'].lower().find(\"opinion\")>=0):\n",
" section = line['section']\n",
" mediakey = MEDIA[line['media_id']]\n",
" byline_text = line['byline'] \n",
" \n",
" #just for our social media analysis:\n",
" if not mediakey is \"la times\":\n",
" continue\n",
" \n",
" social_media = [sm.facebook(line['url']),sm.twitter(line['url'])]\n",
" smcount = sum([y for y in social_media if not y is None])\n",
" sys.stdout.write(smcount+\".\")\n",
" time.sleep(0.25)\n",
" \n",
" if not section in sections:\n",
" sections.append(section)\n",
" for byline in b.get_full_names(byline_text):\n",
" if(not mediakey in media_people):\n",
" media_people[mediakey] = {}\n",
" mpop[mediakey] = {}\n",
" if(not byline in media_people[mediakey]):\n",
" media_people[mediakey][byline] = 0\n",
" mpop[mediakey][byline] = 0\n",
" media_people[mediakey][byline] += 1\n",
" mpop[mediakey][byline] += smcount\n",
" \n",
"print \"---\"\n",
"print sections\n",
"for key in media_people.keys():\n",
" print \"{0}: {1} bylines\".format(key,len(media_people[key]))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'SocialMedia' is not defined",
"output_type": "pyerr",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[1;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-1-7ae5f380e6ad>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[0;32m 1\u001b[0m \u001b[1;31m# GROUP BYLINES BY MEDIA ORGANISATION\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 2\u001b[0m \u001b[1;31m# AND SUMMARIZE\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m----> 3\u001b[1;33m \u001b[0msm\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mSocialMedia\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[0;32m 4\u001b[0m \u001b[0mmedia_people\u001b[0m \u001b[1;33m=\u001b[0m \u001b[1;33m{\u001b[0m\u001b[1;33m}\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 5\u001b[0m \u001b[0mmpop\u001b[0m \u001b[1;33m=\u001b[0m \u001b[1;33m{\u001b[0m\u001b[1;33m}\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n",
"\u001b[1;31mNameError\u001b[0m: name 'SocialMedia' is not defined"
]
}
],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"for key in sort(media_people.keys()):\n",
" print \"{0}: {1} bylines\".format(key,len(media_people[key]))\n",
" values = media_people[key].values()\n",
" plt.hist(values, max(values))\n",
" plt.xlabel(\"Articles Published in {0}\".format(key))\n",
" plt.ylabel('Number of Authors', fontsize= 20)\n",
" plt.show()"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from byline_gender import BylineGender\n",
"b = BylineGender()\n",
"b.load_name_org_online()\n",
"unknown = []\n",
"known = []\n",
"\n",
"for org in sort(media_people.keys()):\n",
" print \"{0}: {1} bylines\".format(org,len(media_people[org]))\n",
" vals = {\"female\":{},\"male\":{},\"unknown\":{}}\n",
" for name in media_people[org].keys():\n",
" #gender = b.single_name_gender(name)\n",
" gender = b.org_name_gender(org,name)\n",
" if(not gender in [\"ignore\"]):\n",
" vals[gender][name]=media_people[org][name]\n",
" if gender is \"unknown\":\n",
" unknown.append(name)\n",
" else:\n",
" known.append(name) \n",
" m = 0\n",
" for v in vals.values():\n",
" if(len(v) > 0 and max(v)>m):\n",
" m = max(v)\n",
" \n",
" h = []\n",
" labels = []\n",
" for v in sort(vals.keys()):\n",
" labels.append(v)\n",
" h.append(vals[v].values())\n",
" if(len(h[-1]) == 0):\n",
" h[-1]=[0]\n",
" plt.figure() \n",
" n,bins,patches = plt.hist(h)\n",
" plt.xlabel(\"Articles Published in {0}\".format(key))\n",
" plt.ylabel('Number of Authors', fontsize= 20)\n",
" legend(patches, labels)\n",
" plt.show()\n",
"\n",
"print \"UNKNOWN BYLINES: {0}\".format(len(unknown))\n",
"print \"GUESSED BYLINES: {0}\".format(len(known))"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#OUTPUT TO BYLINE FILE\n",
"\n",
"#f = open('org_people_upload.csv', 'w')\n",
"#for org in sort(media_people.keys()):\n",
"# for name in media_people[org].keys():\n",
"# f.write(','.join([org.replace(\" \",\"+\"),name.replace(\" \",\"+\"),b.org_name_gender(org,name),str(media_people[org][name])])+ \"\\n\")\n",
"#f.close()"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def pct(a,b):\n",
" return 100*(float(a)/float(b))\n",
"\n",
"for org in sort(media_people.keys()):\n",
" print \"{0}: {1} bylines\".format(org,len(media_people[org]))\n",
" article_count = {\"female\":0,\"male\":0,\"unknown\":0}\n",
" people_count = {\"female\":0,\"male\":0,\"unknown\":0}\n",
" \n",
" total = 0\n",
" people_total = 0\n",
" for name in media_people[org].keys():\n",
" #gender = b.single_name_gender(name)\n",
" gender = b.org_name_gender(org,name)\n",
" if(not gender in [\"ignore\"]):\n",
" article_count[gender]+= media_people[org][name]\n",
" people_count[gender] += 1\n",
" people_total += 1\n",
" total += media_people[org][name] \n",
"\n",
" #ARTICLE COUNT CHART\n",
" P.figure(1, figsize=(6,6))\n",
" labels = 'female', 'male', 'unknown'\n",
" fracs = [pct(article_count['female'],total), pct(article_count['male'],total), pct(article_count['unknown'],total)]\n",
" explode=(0.06, 0, 0)\n",
" P.pie(fracs, explode=explode, labels=labels,\n",
" autopct='%1.1f%%', shadow=True)\n",
" P.title('Author Gender per Article in {0} across {1} authors and {2} articles'.format(org,len(media_people[org]), total), bbox={'facecolor':'0.8', 'pad':5})\n",
" P.show()\n",
" \n",
" #PEOPLE COUNT CHART\n",
" P.figure(1, figsize=(6,6))\n",
" labels = 'female', 'male', 'unknown'\n",
" fracs = [pct(people_count['female'],people_total), pct(people_count['male'],people_total), pct(people_count['unknown'],people_total)]\n",
" explode=(0.06, 0, 0)\n",
" P.pie(fracs, explode=explode, labels=labels,\n",
" autopct='%1.1f%%', shadow=True)\n",
" P.title('Unique Author Gender in {0} across {1} authors and {2} articles'.format(org,len(media_people[org]), total), bbox={'facecolor':'0.8', 'pad':5})\n",
" P.show()\n",
" \n",
" \n"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | mit |
tommyod/KDEpy | sandbox/Testing.ipynb | 1 | 309006 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Imports and setup"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"from KDEpy import KDE"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"from scipy.stats import norm, lognorm\n",
"from functools import reduce\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"np.random.seed(123)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Synthetic data sets"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"# Data from https://projecteuclid.org/download/pdfview_1/euclid.aos/1281964340\n",
"N = norm\n",
"datasets = [[(0.5, N(loc=0, scale=(1/10))), (0.5, N(loc=5, scale=1))],\n",
" [(0.5, N(loc=0, scale=1))] + [(1/10, N(loc=(k/2 - 1), scale=1/10)) for k in range(5)],\n",
" [(1/8, N(loc=3*((2/3)**k - 1), scale=(2/3)**(k))) for k in range(8)],\n",
" [(49/100, N(loc=-1, scale=(2/3))), (49/100, N(loc=1, scale=(2/3)))]\n",
" + [(1/350, N(loc=(k-3)/2, scale=(1/100))) for k in range(7)],\n",
" [(2/7, N(loc=(12*k - 15)/7, scale=(2/7))) for k in range(3)] +\n",
" [(1/21, N(loc=(2*k)/7, scale=(1/21))) for k in range(8, 11)],\n",
" [(46/100, N(loc=(2*k - 1), scale=(2/3))) for k in range(2)] +\n",
" [(1/300, N(loc=-(k/2), scale=(1/100))) for k in range(1, 4)] +\n",
" [(7/300, N(loc=(k/2), scale=(7/100))) for k in range(1, 4)],\n",
" [(0.5, N(loc=-2, scale=(1/2))), (0.5, N(loc=2, scale=0.5))],\n",
" [(3/4, N(loc=0, scale=1)), (1/4, N(loc=3/2, scale=1/3))],\n",
" [(1, lognorm(loc=0, scale=1, s=1))],\n",
" [(0.5, N(loc=0, scale=1))] +\n",
" [(2**(1-k)/31, N(loc=(k + 0.5), scale=(2**(-k)/10))) for k in range(-2, 3)]]\n",
"\n",
"# The sum of the fractions equal 1 in every dataset\n",
"assert np.all([np.allclose(sum([frac for (frac, d) in data]), 1) for data in datasets])"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsgAAAPoCAYAAADDcAj0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzs3Xl4W+WV+PHvkSxb8r4m3pI4+wKkIYRAoUCAhAKlpEOZAt07UxjaMrQwpaUbpUxhuv1KF+jQUijttEDpAqQ0lLKFfQtJWLLvidd4XyXZst7fH1dyZFuyJUuyHet8nicPkXSl97Udro+Ozj1HjDEopZRSSimlLLaJ3oBSSimllFKTiQbISimllFJKhdAAWSmllFJKqRAaICullFJKKRVCA2SllFJKKaVCaICslFJKKaVUCA2QlVJKKaWUCqEBspo0ROSAiLhFpFNE2kTkZRG5WkSi+ncqIlUiYkQkLdl7HbLuKhGpHuWYs0XkWRFpF5ED47Q1pZSKyhQ//94gIu8Gvrb9InLDeO1PHbs0QFaTzQeNMTnALOB7wFeBeyZ2SwnRDdwL6IlZKTVZTdXzrwCfBAqA84FrROTyid2Smuw0QFaTkjGm3RizDrgM+JSIHA8gIh8Qkc0i0iEih0Xk5pCnPR/4b5uIdInIe0Vkrog8IyLNItIkIn8Qkfxwa4rldhE5Esj0vh2yboaI/EhEDolIg4jcJSIuEckCHgfKA2t2iUh5mK/ndWPM/wH7EvddUkqpxJuC598fGGM2GWN8xpidwKPA6Qn7hqkpSQNkNakZY14HqoEzAnd1Y2UC8oEPAJ8TkQ8FHjsz8N98Y0y2MeYVrMzB/wDlwGJgBnBzhOXOC7zGgsDrXwY0Bx77fuD+ZcA8oAK4yRjTDVwA1AbWzDbG1Mb7dSul1ESbiudfEZHA17M1mu+BSl0aIKtjQS1QCGCM2WCMeccY4zfGvA08AJwV6YnGmD3GmCeNMV5jTCPw4xGO7wNygEWAGGO2G2PqAifUK4HrjDEtxphO4DZAP6JTSk11U+38ezNW7PObMT5fpYhxLaZXaowqgBYAETkFqzbueCAdyAD+FOmJIjIN+BlWxiAH68TYGu5YY8wzInIHcCcwU0QeBr4MOIFM4E3rXG29NGCP9wtTSqlJbsqcf0XkGqwM+BnGGG+sz1epRTPIalITkZOxTtAvBu66H1gHzDDG5AF3YZ0sAUyYl/ifwP1LjTG5wMdDjh/GGPMzY8xJwHFYH+ndADQBbuA4Y0x+4E+eMSZ7hHWVUuqYNpXOvyLyb8CNwLnGmBG7XigFGiCrSUpEckXkIuBB4PfGmHcCD+UALcYYj4isBD4a8rRGwA/MCbkvB+jCunCkghG6SIjIySJyiog4sGrtPEC/McYP3A3cHsiIICIVIvL+wFMbgCIRyRvhtW0i4gQc1k1xikh6lN8OpZQaN1Pw/PsxrLKMNcYYvVBaRUUDZDXZ/E1EOoHDwDewatY+E/L454FbAsfcBDwUfMAY0wPcCrwkVh/PU4HvAMuBduDvwF9HWDsX60TcChzEukDkR4HHvgrsAV4VkQ7gKWBhYN0dWLV4+wLrDruKGuviEzewHpgZ+Ps/o/mGKKXUOJmq59/vAkXAGyHdLu6K8nuiUpQYo58OK6WUUkopFaQZZKWUUkoppUJogKyUUkoppVQIDZCVUkoppZQKoQGyUkoppZRSISbloJDi4mJTVVU10dtQSqmkefPNN5uMMSUTvY9Qeu5VSk110Z57J2WAXFVVxcaNGyd6G0oplTQicnCi9zCUnnuVUlNdtOdeLbFQSimllFIqhAbISimllFJKhRhzgCwiM0TkWRHZLiJbReSLYY4REfmZiOwRkbdFZHl821VKKQUgIueLyM7A+fXGCMd8RES2Bc7R94/3HpVS6lgVTw2yD/gvY8wmEckB3hSRJ40x20KOuQCYH/hzCvC/gf8qpY4RfX19VFdX4/F4JnorxySn00llZSUOhyNhrykiduBOYA1QjTVCd13o+VdE5gNfA043xrSKyLSEbUAplXR67o1PvOfeMQfIxpg6oC7w904R2Q5UAKEB8lrgd8aaZ/2qiOSLSFnguZNCX7+fmlY3VcVZE70VpSal6upqcnJyqKqqQkQmejvHFGMMzc3NVFdXM3v27ES+9EpgjzFmH4CIPIh1vg09/14J3GmMaQ3s5UgiN6BSW127G0EozXNO9FamLD33jl0izr0JqUEWkSrgROC1IQ9VAIdDblcH7gv3GleJyEYR2djY2JiIbUXlsl++wqofbeBAU/e4ranUscTj8VBUVKQn6DEQEYqKipKRAYrm3LoAWCAiL4nIqyJyfoQ9Tsi5Vx27djd0ct7tz3PmD59ly+G2id7OlKXn3rFLxLk37gBZRLKBvwBfMsZ0DH04zFNMuNcxxvzKGLPCGLOipGR8WoN6+vrZdMj6n/uNAy3jsqZSxyI9QY9dkr530Zxb07DK21YBVwC/FpH8YU+agHOvOrbd9dw+Oj0+en1+bn9y10RvZ0rTc+/Yxfu9iytAFhEHVnD8B2PMX8McUg3MCLldCdTGs2Yi7Ws8mjXerO+ClVLHjmjOrdXAo8aYPmPMfmAnVsCs1Jh5ff2sf6eOK1bO5POr5vLiniba3X0TvS2lEi6eLhYC3ANsN8b8OMJh64BPBrpZnAq0T6b6491HOgHIzkhjf6OWWCg12TQ3N7Ns2TKWLVtGaWkpFRUVA7d7e3sTts5TTz1FXl4ey5YtY/Hixdx6662D7j/xxBNZsGABZ511FuvXrx943je/+c1Be/rGN76RsD2N4g1gvojMFpF04HKs822oR4CzAUSkGKvkYt94bVBNTZsOtuHu6+ecRdM4d/E0+v2GF3Zrac5UlOrn33i6WJwOfAJ4R0S2BO77OjATwBhzF7AeuBDYA/QAn4ljvYQ70NQDwKlzCgdlk5VSk0NRURFbtlinl5tvvpns7Gy+/OUvDzrGGIMxBpstvoqxs88+m0ceeYSuri6WLl3KRRddNOh+gE2bNvEv//Iv/O53v+Oss84C4IYbbuBLX/pSXGvHyhjjE5FrgCcAO3CvMWariNwCbDTGrAs8dp6IbAP6gRuMMc3julE15by+vwUROGVOIZkOO06HjTcPtnLR0vKJ3ppKsFQ//475KzLGvGiMEWPMUmPMssCf9caYuwLBMcbyBWPMXGPMCcaYSTXDtLHLQ36mg5mFWTR0aBsVpY4Ve/bs4fjjj+fqq69m+fLlHD58mPz8o+W1Dz74IJ/97GcBaGho4JJLLmHFihWsXLmSV199dcTXzs7OZvny5ezdu3fYY8uXL+cb3/gGd9xxR2K/oDEInG8XBM6vtwbuuykQHAfPv9cbY5YEzr8PTuyOVTI8t6uRtXe+xJ82Hh794ATYUd9BVVEWuU4HaXYbJ1Tk8dY4lSg+/k4da378HOvemjSVmikpVc6/8WSQj3nNXb0UZ2cwPTeD7t5+Oj195DgT16tUqanmO3/byrbaodfixmdJeS7f/uBxMT9v27Zt/OY3v+Guu+7C5/NFPO7aa6/lK1/5CqeeeioHDhzgoosu4t133414fGNjI6+//jq33norhw8PDzqWL1/Oz3/+84HbP/zhD7nvvvsA+NGPfsTq1atj/lqUGgtPXz9ffHAzbT19bK/r4LR5xVTku5K65o76ThZOzxm4/Z7KfP7v1YP0+w12W/IuKGt39/GVv7xNp8fHV/78FmfNLyEvM3V+X0+mcy+kxvk3pQPkpi4vxdnpTM+1+jg2dHg1QFbqGDF37lxOPvnkUY976qmn2Llz58Dt1tZW3G43LtfgQOLZZ5/lxBNPxGaz8a1vfYuFCxeGPUFbbd2PmogSC6UAntreQFtPH9+75ARu/Os7/O2tWq4+a27S1nP39nOguZu1y46WU8yfno3X56e2zc2Mwsykrf34O3V0enwDX+sjW2r41GlVSVtPjSwVzr8pHiD3clx5LtNyMwA40ulh3rTsCd6VUpPXWLMNyZCVdXS4j81mG3TiDO19aYzh9ddfJz09fcTXC611G8nmzZtZvHjxGHasVGI9s/0IRVnp/OuKGdz/+iH+ubU+qQHyroZOjIFFpbkD980tsX5n7mnsSmqA/PSOI1Tku7js5Bn88vl9PL+rMaUC5Ml07oXUOP8mZFDIscrKIGdQkGn94Np7tFWNUscim81GQUEBu3fvxu/38/DDDw88tnr1au68886B28GLTsZiy5Yt3HbbbXzhC1+Ia79KJcJr+1s4ZU4hdpvw3rlFvFPTjqevP2nr7ai3PuJfXHa0xGJOIEDee6QraesaY3jjQAvvm1eMiHD6vCJe3deMr9+ftDVV9Kbq+TdlA2Svr59Oj4/i7HTyA3VMbdrLUalj1ve//33OP/98zj33XCorKwfuv/POO3nppZdYunQpS5Ys4e67747pdYMf/S1cuJBrr72WX/ziFwNXUCs1URo6PNS0uVkxqxCAFbMK6es3vF3dnrQ1d9Z34XLYmVFwNFNcmJVOQaaDvUnsBFXb7qGtp4/jK/MAOGlWAd29/UldU8VmKp5/U7bEItjYPD8znXyXlUFu0wyyUpPWzTffPPD3efPmDctEXHbZZVx22WXDnldSUsKf//znEV979erVYS/uWL16Ne3tkQOO7373u6PsWqnk2Flv9fFfXGaVO7wnEDxuq21n5ezCpKx5sLmbWUWZ2IZcjDe3JJu9jcnLIG+tsf4fPK7c+lpPqLC+1ndr2llYmhPxeSpxUvH8m7IZ5I5AgJzrcuB02EhPs9HmTlzja6WUUipZdjVYAfKC6VaJQ0lOBnkuB7uSWOpwuLWHmWHqjOeWZLMvmQFybQc2gcWB2ufZxdlkptt5tzZ52XKlUjZADmaQ81wORIR8l0NrkJVSSh0Tdjd0UZSVTlG2dZG5iDB/WjZ7GpITqBpjONQSPkCeU5JFU1dv0n6Hbq3tYE5JNq50OwB2mzCnJIv9TVpioZInZQPkDrfVty/XaVWZ5Gc6tMRCKaXUMWHXkU7mTx/cdWn+9Bx2Hekc1gorERq7vHj6/GE7VQSD5sOtPQlfF6yykSVluYPuqyrSAFklV8oGyO0hJRYA+a50LbFQSik16Rlj2NPQxYLpg+tv50/Lpq2nj6auxP8uO9ziBgibQa4osHra1rS5E75uT6+P2nbPQClJ0JziLA639NDr004WKjlSNkDu8BwtsQArUNYMslJKqcmurt1Dp9fH/CF9+4MB8+5AfXIiHW6xssPhMsjB6X01rYkPkA82W+tWFWcNun92SRZ+A4dakpO1ViplA+RgrVRuYHJejjON7t7I4xKVUkqpkTR2emns9CZ9nQOB0oLgkI6gYMnF7iRcqBcMRCsLho+yLsxKx+WwU53EAHlW4ZAAudj6WsejzKKlu1fLOVJQ6gbI7j5cDjvpada3ICvDTrc3eQ3WlVJjl519NBBYv3498+fP59ChQ9x8881UVFSwbNky5s+fzyWXXMK2bdsGjl21ahULFy5k2bJlLFu2jEsvvXQitq9SwI76Ds74wTO87/vPsK22I6lrBQPRodncaTkZuBz2pGRVD7X0MD03A6fDPuwxEaGiwEVNW+LXPdhsBaYziwZ/rbOLrIB5f1PyumcAHGru4awfPMt5tz/Hq/uak7rWZJTK596UDZA7PT5ynEfbQGdnOOjyaAZZqcns6aef5j//8z/5xz/+wcyZMwG47rrr2LJlC7t37+ayyy7jnHPOobGxceA5f/jDH9iyZQtbtmwZtR+nUmP1kyd34+nz09vv5ydP7UrqWodbe7AJlOY5B90vIlQWuAbKIRKpptVNZUHkUdKVBa6k1CAfbOmhINMxUA4ZlJfpoCgrPemZ3Tue3U2n14fPb/jZ07uTutZklorn3pQNkLt7fWRnhAbIdnr7/Vrwr9Qk9cILL3DllVfy97//nblz54Y95rLLLuO8887j/vvvH+fdjT8ROV9EdorIHhG5MczjnxaRRhHZEvjz2YnYZyro8vp4ZucRPn1aFf92+mw27GwcuBA8Gapb3ZTluXDYh/8Kn1GYyeEklDrUd3goGxKQh6rIdyWpxKKbWUVZYR+bWZQ5UIKRDH39fv7xbj0fXl7JdasX8PLeZho6PElbb7JK1XNvyk7S6+ntJzPj6EdFWYFgudvrIz0tfaK2pdTk9viNUP9OYl+z9AS44HsjHuL1elm7di0bNmxg0aJFIx67fPlyduzYMXD7Yx/7GC6XVTe5Zs0afvjDH8a/5wkmInbgTmANUA28ISLrjDHbhhz6R2PMNeO+wRTzxoEWen1+zlsyHbtNuOfF/by+v4U1S6YnZb3q1p6wtcAAMwpcvLG/BWMMIhL2mFgZY6htc7N68bSIx1QWZNLW00e31zfw+zQRDjb3cNKsgrCPVeS7eLcmecNCNh9qo8PjY82SaVQWZPLjJ3fxyt5mPnRiRdLWjEjPveMudTPIXh+Z6aEZZOvvXV4ts1BqsnE4HJx22mncc889ox47tAds6Md8x9oJegQrgT3GmH3GmF7gQWDtBO8pZW080ILdJiybmc97ZuSTnmbjjQMtSVuveoRyhxmFmXR6fQnNYLf19OH1+SnLCx+Uw9FWb4nMIvf6/NS2uZkVpnMGWAFybbsHvz/xfZ8BNh60foYrZxexuCyXPJeDV/amVh1yKp97UzqDXJx9NFOsAbJSURgl25AsNpuNhx56iNWrV3Pbbbfx9a9/PeKxmzdvZsWKFeO4uwlRARwOuV0NnBLmuA+LyJnALuA6Y8zhoQeIyFXAVcBAbaGKzeZDbSwpyx1IupxQkcfmQ61JWcvr66e+wxMxgxwMnA+3uMnPTMynobXtVtA7comF9Vhdu5uFpTkRj4tFXbsbv4HKCAFyeb6LXp+f5u5eSnIyErJmqM2H2phTnEVhlvV9XFqZxztJzFiPSM+94y51M8i9PjJDPgYKLbFQSk0+mZmZPPbYY/zhD3+ImM34y1/+wj//+U+uuOKKcd7duAv32fnQNNrfgCpjzFLgKeC34V7IGPMrY8wKY8yKkpKSBG9z6jPGsL2ug+PKj056W1iaw66GrqRMtKtr82BM+HZrADMKrfsTOdWuvt2qux16UWCo0kB2ua49cTW6tW3Wa5VHyFyXB/ov1ybh4kCArTXtnFCZN3D7uPI8dh/pTLlrlVL13Ju6GWRvP1npw2uQOzVAVmrSKiws5B//+AdnnnkmxcXFANx+++38/ve/p7u7m+OPP55nnnmG0EAvtA6uuLiYp556akL2nmDVwIyQ25VAbegBxpjQz4LvBr4/DvtKOUc6vbT29LE4ZBTywuk53O8+RGOnl2m5kYPKsQiWMIxUYgEktJNFMOgNBqThTM/JwCZQl8BgtS6Yuc4P/z2sCAmQ3zMjP2HrgtUKtrbdw6LSoz/X48pz6es37D7SyXHleSM8e+pJxXNvygbI3b2Da5CDLd80g6zU5NPVdbTX6YwZM9i/fz8Aa9eu5eabb474vA0bNiR5ZxPmDWC+iMwGaoDLgY+GHiAiZcaYusDNi4Ht47vF1LCz3ppaF1pWEJxot7OhM+EBcjBbWhEhWM11Wi3REplBrmt3Y7cJxdmRyxjS7Dam5TgTmkEeCMwjZJAHJvglIYMc/LkuKjv6cw0OZtnf1J0yAXIqn3tTssTCGENPbz9ZEbpYKKXUZGaM8QHXAE9gBb4PGWO2isgtInJx4LBrRWSriLwFXAt8emJ2O7UdCAyymBMyCnlBYKJdMMhKpPpAm7FpuZGD1fJ8F3VtiQ1Up+dkYLeN3BWjNC+xAXJtm5uCTAeu9OHDSQByXWlkpdsHSjESaU9gGmHwzQ5AVbGVnT+gU/VSQkpmkL0+P/1+M7iLReDvnTosRCl1DDDGrAfWD7nvppC/fw342njvK9UcbO7B5bAPukisKDuD4uwMdjUkJ0AuzEoPO9EuqCLfmdBuEvXtHspGKK8IKs93siOBbwrq2j0jds4QEcrzXUmpQT7Q3E16mo2ykE8AMtPTmJ6bwf6m5PVeVpNHSmaQe3qtkdKDa5Ctv+u4aaWGS8bFRqlCv3dTmzXIInNYz+GFpdnsbEj8GOT6dg/TRynbSHTQWNfuGfECvaCyPBf17Z6E/ZuvbXNTHqH+OKg8PzkT/A40dTOrMBPbkKx5VVHWwKcG40HPH2MX7/cuJQPkYBlFaDPzNLsNp8NGd69mkJUK5XQ6aW5u1hP1GBhjaG5uxulMbB2qmjwONPcwq2j4BXNVRVkcSkIgVd8+8kQ7sILGDo8vIW1LjTHUtbsHZVIjKctz0tPbT4c7Mb9HR8sgg5W1TmRZR9CBCBP8ZhdnjVuJhZ57xy4R596ULLEYyCAPmfaTnZGmJRZKDVFZWUl1dTWNjY0TvZVjktPppLKycqK3oZLA7zccaunh3EXDJ8zNLMyktaePDk8fuU5HwtZs6PCM2rEh2G2irs3N/Onx9SRu6+nD0+ePqsQiGMzWtrvJy4zva+7ptYadROpgETQ910lzt5den5/0tMTk/Px+w8HmHs5aMLztYVVxFs3dvQn/uYaj5974xHvujStAFpF7gYuAI8aY48M8vgp4FNgfuOuvxphb4lkzEYJZ4swhhf/ZGWl6kZ5SQzgcDmbPnj3R21Bq0qnv8NDr8zMzTAZ5Zki7tUR1PPD6+mnu7h01gxwc2lGTgAA5mJ0dbU042o6trt09qO1d+Bd+GzZ8zxqfnJYBzlw4/lJY8W/gcI7aA3lgzTwnxsCRTk/E1nexauj04PX5w2aQqwL3HWjqZmllYlvLDaXn3okV79ut+4DzRznmBWPMssCfCQ+OIXyJRfC2BshKKaWiEaxFrQoTSB3tR5y4+tgjHV4ASqOoQQYS0t2hvsPaf3Q1yMEAeYR1jYEXb4dfnQWHXoaZp0JpIL/2xNfg7rPhyPajPZBHWTc4oKQ+gWUW+5si/1yDnSwONuuFelNdXBlkY8zzIlKVmK2Mn+CFeEMzyFkZaTooRCmlVFSCwzhmhhmFnIyBHcEWb9NHCRqn5Tix2yQhF+rFkkEOrhuxxZwx8OS34OWfw3GXwEW3gyskC7v7SXjkc/Crs8lY8g1gzojDSeDom4VE1iEHg99gMByqIsnT+9TkMR4X6b1XRN4SkcdF5LhIB4nIVSKyUUQ2JrvepidQYpGVPrwGWTPISimlolHX7kGEsF0l8lzWwI5DSZhoN1qwarcJpbnOhARx9e0e7DZhWs7oAbLdJkzPyaC2PcK6L95uBccnXwmX3js4OAaYvwaufgkqV7Dy7W/yH2l/G7VjRzCz3dCRuAC5urUHu03CXiCY43SQk5GmAXIKSHaAvAmYZYx5D/Bz4JFIBxpjfmWMWWGMWRE6qjAZugMX6WVmaA2yUkqpsWno8FCUlRHx4rAZha6EBsgNgQB5tKARrO4OiWh/VtfuYVoUQ0KCSvOc4csdNv4Gnv6OVWd8wQ9AIrxeznT4xCNsyTuXr6U9QPqme0ZcL9eZRma6PcEDSjyU5jojfs3l+S5qk9A5Q00uSQ2QjTEdxpiuwN/XAw4RKU7mmtHo8YbPIGdlpCWkLY5SSqmpz+oPHHmi3czCzISOfK7v8OBy2Ml1jl4daQVxickgR1N/HFSW7xocrPq88MQ34LEvwbw18C93gW2U0MOexk9y/otX00+F9TfA9sciHioikYPyMappc0cc5Q3Wmw/NIE99SQ2QRaRUAt3TRWRlYL3mZK4ZjWAG2eUYmkG266AQpZRSUalv94x4wdyMgkyqW9z4/YnpYxvsgTx0KEk45fnW0I54165rd496UeCgdfOs4NEYA60H4d73wyt3WGUVl/0e7NG1Rjvc3sf9ld+GipPgL5+FurciHlua6xy4qC8R6trdI7aXS9b0PjW5xBUgi8gDwCvAQhGpFpF/F5GrReTqwCGXAu+KyFvAz4DLzSToeN3j9ZGZbh82ISczPQ13Xz/9CTqZKaWUmroaOkaealdR4KK3309Ttzch69WPsl6o8nwXff2Gpq6xr20NCYkxg5znwuvz097SBL+5EJr3WYHxB34EjuheJ7hucUE+XPEAZBbCAx+FriNhjy/Nc9LQkZjvcb/fUN/uGfHiwPJ8F609fQPXM6mpKa4A2RhzhTGmzBjjMMZUGmPuMcbcZYy5K/D4HcaY44wx7zHGnGqMeTkx245Pd28/menDP6IKdrVw92kWWSmlVGSevn5ae/pGzK4Ge/gmot0axFbuENoLeaw6vT56evuj6mARFDzWPHEjdNbBJx6GxR+Mad0Ot7Vueb4TsqfB5fdDTzP88ePQN/zrKctz0tDhSUhyq6nLS1+/GSVAtr7GRP1c1eSUkqOme3p9ZA25QA8gM9AXWd8VKqWUGslAT+IRgseKAivIqmmN/+N4v99wpDO2DDLEF8QF63pLRxnWEaos38Ua20YKdv0ZzvgvqDwp5nVrB3ogB9YtXwYf+gUcfg1+fyl42gcdX5rnwuc3NMeRLR9YO/CGonyEn2vwjU8iyzrU5JOSAXK3N3wGOSuQQe7ROmSllFIjCAZHIwXI5Qnsmdvc3Utfv4k6m5uItWPpgRxUkd7NbY5f05KzEM68YYzrBgLk0Drg4y+BD98Dh1+F314M3q6Bh4JZ/PqWDtj3HGx5AI7sGNPaAxP8RimxgMS88VGTV0oGyD29voFgOFQwaO7WDLJSapITkfNFZKeI7BGRG0c47lIRMSKyYjz3N9UFh3aMVGKR57J65iai3Vqwz2+0GeRcp4PsaNY2Bryd4PcPe6g++CYg2ov0jKF4w9fIo5tHZt8EaenRPW+IiGOmT7gULvuDNZ76oU9a+wbKcjM43/Y6Cx48DX53MTxyNfziFFj3n9AbWxeRYHA+UoA8PQnDSdTkE9ckvWNVd28/ea7hV9IGa5B7ejWDrJSavETEDtwJrAGqgTdEZJ0xZtuQ43KAa4HXxn+XU1tDlFPtyvNdVCcg03i03CGGjhKjtSPb+og12a7tEGSVwNLL4PQvQbY1i6Auhr7LALz6v8j2R7nX8XF29lVGvc+h6trdpNmEkpwwLfQWnm9N4HvsS3DX++C91zB/55Pclf4EzY5FOD/0UyheAJv/D176GTTuhI8+NHwoSQQ1bW6y0kdupZeeZqM4OyOhw0nU5JOaGWRv+AxysC5ZA2Sl1CSlKP00AAAgAElEQVS3EthjjNlnjOkFHgTWhjnuv4EfAPqbPMHq271kptvJyRg5z1RRkJiWYNFkrIeK2AvZ74fHvwp/+hS4CuDcb8PMU+HV/4Vfngm1m6012z0UZ0cehDJI7WYr2F50Ec8WXR5faUebVWsdcTjJSZ+CTz0GjixY/2XSD73A//R/jF8vvgcWfQCK58OaW+Ajv4WaTfDgx6A/uk+Ga9vclOe7Rm2lV5qXMfAzUVNTagbIEbtYBC7S02EhSqnJrQI4HHK7OnDfABE5EZhhjIk8ZcE67ioR2SgiGxsbGxO/0ymqocPqgTxaIJWoiXYNHR5sAsXZ0ZctWP16hwRxvl54+Cp47S449fPw2WfgjOutVmxXbQCbHe67CPa/QF2g7/Ko+tzw1/+wstAX/5xp+dlxBY+17e7R1606HT73Elz9IvLFt/h79qXUdfQNPmbJWlh7Bxx8ETbcFtXade0eykYorwgqzXUldDiJmnxSMkDu7vWRHaaLRdZADbJmkJVSk1q4qGygx5WI2IDbgf8a7YWMMb8yxqwwxqwoKSlJ4Bantmh7ElfkZ9Lu7ot7Smt9u4eSnAzS7NH/2q7Id9HS3Yunr9/KGm9/DH59LrzzJ1h9M7z/NrCHJIvKlsK//xPyKuH3H2ZW0/PRlXQ8fQs07YS1d0JmIeV5TuraPYx17EG0QSoiUHoCZE+jLM8ZPih/z+Vw4sfhxdvh0KujvmRtm3ugRd5INIM89aVkgNzj7R9o6RYqc6DEQjPISqlJrRqYEXK7EqgNuZ0DHA9sEJEDwKnAOr1QL3Hqo8yuHu2ZG18Wub5j5Kl9I6195OB2KzD+48esC9su/Q287zorwBwqtxw+vR6mL+FbPbdxfv8G60K+SPZtgFd/YU3Km3cuYHW96PX5ae7ujWm/YLWzq2vzjDjqOZzSvBEyuud/D/JmwKNfgP6+8Mdg9bZu6uodfnFguPVynbT19FlvPtSUlHIBcq/PT2+/P0IXC61BVkodE94A5ovIbBFJBy4H1gUfNMa0G2OKjTFVxpgq4FXgYmPMxonZ7tTi9xtril4UAXJlsBdynAHyaFP7winPczFXaih76EJo2Qcfuguu2Wi1TBtJVhE9V/yVN/0L+PDB/4Y7VsAzt0Jnw+Dj3G3wyOehaJ5V8xsQ7Js8lhKExi4vvf3+qLK4oUpzMyJnrTNy4IIfQPMe2PS7iK8R3G9UJRZxfI3q2JByXSzcgeA3XA2yM82OiNYgK6UmN2OMT0SuAZ4A7MC9xpitInILsNEYs27kV1DxaO7uxec3UWV0E9Uzt77dw6lzimJ6TmV6F/c5foBP0nBc9RQUzol+PU86n+y9kT+esp8TO5+D539olSnMPw/SMqCvx+oQ0VkP//4kpGcOPDc0a358RV5Mew6+kQgOWYlWaWDEdVtPHwVZYeq0F7wfZr4Xnvu+VXaRnjXskIEhIdGUWAR7L3d4qCoe/lrq2JdyAXKwx3G4SXo2m5DpsGsNslJq0jPGrAfWD7nvpgjHrhqPPaWKWHoST8txkmaTuEos3L39dHh8MbV4w++n7J9X45EOHl74Kz4aQ3AMVkDeiwPP0k/C3Ougea91Yd+ep63SjPRsq1b53JuGTcsrG5g0F3t2NfhGoiI/c5QjBwuWu9R3eMIHyCKw+jtw73lWt44zvzx87WBwHlUGObCeZpCnrJQLkIP1xeEyyGCNm9YaZKWUUpHE0pPYbhNK8+LrZDGWFm+8/ktsh17mR2lfoLN/Nh+Ncc26oV9j0Vy48IdRPbcoKx2HXcYWIMeQxQ0VfLNS3+5hcVlu+INmngILPwAv/RRO+jRkFQ96eNjXPILSkIBcTU0pV4PcHRgjHS6DDFYdstYgK6WUiiTWgLUiP75eyAMBebQB8s5/wD+/CQvOZ3PhheF7IY+25liC8gBb4E1B3RjWrW1zk+tMI8c5fJjXSIIZ5FGD8tXfht5uePbWsGsXZ2eQkRY+PgiVnZFGTkaaZpCnsNQLkEfLIKenDQTRSiml1FD17R7skSa9hVFR4IqrBrm+w3puNBcFsvtJawxz6VK45G7KCzKH90KOQl27mzyXA1eYC9qjUZbnom4M69a0uqkoiK28AqAkJwObHB2PHfnAhbDySnjzPqh/d9BDte2emC4OnJ7n1AB5Cku5ALknmEGOECBnpdu1xEIppVRE9R0eSrIzIk96G6Ii30V9h4e+fv/Y1mv3AqNkc42xLqK7/yNQsgA+/hdw5g5kr2PtSVzd6h7owDEWZXnOMWWua6LsQzyUw26jJCfK3sSrbgRnvpVlD1Hb5h6on45GaW6E3stqSki5AHkggxypxCIjTS/SU0opFVG0Ld6CKvJd+M3Ri/vGsl5ORhpZkcZa93bDnz8DT91sTY/7tycgsxCA8jwnXp+flhh7EscfILto6PDg98cWmFsB8tjWLc11Rlf37Cqwpgfuexaqrc6HxpiBMdNRr6cZ5Ckt9QLkUTLImQ47bs0gK6WUiqC+3UNpbnTlFRB/q7e21mYuzdwEr/3S+tO46+jwjsNvwN3nwNZHrOl4l/5mUAuz4NqxlFkYY6hu7aFyDKUOR9d10tdvaOr2Rv2cDk8fnR5fzC3egmIKWE/6jBUoP/8ja223j57e/pguDizNddLY5cU3xk8G1OSWul0sImaQ7VqDrJRSKqL6Dg+nzY2+J3Ew4Iu55MDvhzfu5vv7v0UGXng85LGCKsgsgppN1vS7T/wV5p4z7CUGgvM2NydURteTuLm7F0+fP64McrAcpK7Nw7Sc6ILO4BuIWLK4ocryXLy8pzm6gzOy4dTPWxfr1b9DjX9WzGuX5jnp9xuaunpja8Gnjgkpm0HOdIQPkLPStc2bUkqp8Lq9Pjo9vphKLIKji6POIPf74PW74adL4fGvsNF2HHdU3QE37IMvvQMX/ghKTwBHJrzvS/D5V8MGx3C0p28sXTSqA/uML4Mcey/k2hj6EIczPddJp9dHV7TDvlZeCek58ML/C2kvF1sNMmirt6kqJTPIGWk20uzh3xtkZuigEKWUUuGNpf2ZK91OUVY6NaOVORgDOx6Dp2+Bpl0w8zT613yXT97v4OqyuZBVBBRZgd3KK6NaOz/TgcthjzFA7gFgRmF8F+kBMbV6i2VQx0hr1rd7mDcte/QnuApg5WfhxZ/QXvBZgJiy5oOGhcyIfb9qcku9DHKvL/KFDkCmI41en19ripRSSg3TEMMwiVDl+a6Rh4UcfBnuWQN//LgVKF/2e/jMeppnnk+/f2z9iAFEhLL82DpKVLfGF6gCFGalk55miymDXNPqJt1uozg7+vruUGOabnfylSA2yvc8gNNhoyjcFL5R14tvjLianFIvg+ztJ3OEvo7BASI9ff3kRsgyK6WUSk1jHaBRke9iT2PX8Af8/fDkTfDKHZBTDhf/HN7zUbCnDVovmrHWI609avY6xOGWHvIzHTEP6wglIpTHOEHwQHM3Mwpd2KJsnzfUWLLW5FXAogtZunMdVXlrEYl+7cJMa2JgfUf0FyKqY0fKRYDdvT6yR8ogB7pb9OiFekoppYYYCJDHkkFuHdKP2O+Hv33RCo5X/Dv855uw/JMDwTEcrcsd64VrYNVA18VYgxxP9jhoZlEWB5u7oz7+YHMPs4uzRj8wgtBx0zE5+Uqy/R1ckv56TE+z2YTpuU7NIE9RKRcg9/RGl0Hu1gv1lFJKDdHQ7iHHmRZxGmskFQUu3H39tPX0WXf4++Hv18Hm/4MzvwIX/RjSh18Ud/SCuTgC5HwXRzq9ePqiS/wcaO6mKo5ANWh2USYHmnqiGlLi9xsONHczq2js6zoddgoyHbFfNDf7TPZRyQXux2JeU4eFTF0pFyB3e0euQXYFultoBlkppdRQ9R2eMdUDB6fD1bS5rS4Vf/q0Ne74fdfD2V+P+LyaNjdZ6XbyXGMvd6gqtgLvQy09ox7b6/NzuKWHOQkIkKuKs+jy+mjqGn1IiRXA++MOzEvzXDFnkHv6+rmv71xmuLdbbfNiWk+HhUxVKRcgj55BDpRYaAZZKTWJicj5IrJTRPaIyI1hHr9aRN4RkS0i8qKILJmIfU419e2eMfW8rci3gtTqlh74+/WwfR28/zZY/W0Yoe61ptVNRYErptrYoeYUWx0d9oWrgR7iUEsPfgNzShITIIOVkR5N8JiqorG3lgOrDjmWCwPBKmN5uP8MfHYXbLwnpucGM8ixjvJWk19cAbKI3CsiR0Tk3QiPi4j8LHACf1tElsezXiJ09/oiTtEDBoLnHm31ppSapETEDtwJXAAsAa4IEwDfb4w5wRizDPgB8ONx3uaUNNYMcnBCm3Pnw7Dpt1bm+L1fGPV58YxeDpodCHb3No4eqO5vso6ZXRxFm7TR1g2USwRfcyQHmoIBcnyB+fQxlDxUt7rpJJPWuR+Cd/4C7taon1ua58TT56fDrUm1qSbeDPJ9wPkjPH4BMD/w5yrgf+NcL2493v6IU/TgaAZZa5CVUpPYSmCPMWafMaYXeBBYG3qAMaYj5GYWoCmuOPn6/TR2eseUQS7MSqfM0cUp22+DypPh7G9E9byaNveYRy8HZWekUZrrZF8UAXIwyzw7zkAVrLrpNJsMBL8jOdDcg8MucV2MCFYGuaW7N+p6azha5y0rrwSfG17/ddTPDf5bqOvQC/WmmrgCZGPM80DLCIesBX5nLK8C+SJSFs+a8Yo6g6w1yEqpyasCOBxyuzpw3yAi8gUR2YuVQb423AuJyFUislFENjY2NiZls1NFU1cvfjO2lmsiwledj5De3w1r7xzUqSKSbq+Ptp6+gfKMeMwpyWJvFCUW+5u6KcpKJy9z7DXPQWl2GzMKM6Mqsdjf1MWMwkzsY2zxFhQMWI/E0Hqtps2Nwy4UzlkOCz8AL/0UupuiW2+snTPUpJfsGuSoTuIwPifpfr/B0+cf8erjgTZvmkFWSk1e4aKIYRliY8ydxpi5wFeBb4Z7IWPMr4wxK4wxK0pKShK8zallrD2QATiynQ/2/YN/OC+AkoVRPWVgslycGWSwAuR9jV2j1srua+qOq9XasHWLs9hzZPTAfGd9J4tKc+JeL/iziWUwSk2rm/L8QP/l1d+Gvm545rvRrTeW4STqmJDsADmqkziMz0k6GPRmjVBiEcwg67hppdQkVs3g4baVQO0Ixz8IfCipO0oBwX63MZdYBPode+w5/Ljvw1E/rSYBE+2C5hRn0+Hx0dwduaOEMYY9R7qYWxJ//XHQorIc9jV24/VF/p3a0+vjYEsPC6fnxr1esB1esGwiGtWtPUe/xyUL4ZTPwZu/gcOj90WelhMIkLXV25ST7AA51pN4UgUvvBspg5yRZsNuE80gK6UmszeA+SIyW0TSgcuBdaEHiMj8kJsfAHaP4/6mpNrANLqY62TfvBcOv8bLc69jb7cz6vrYYFu2GYXxB8gLplvZ2Z31nRGPaejw0tLdy5Ly+APVoMVlufj8ht0NkbPIuxq6MAYWJiCDXFmQiU2IaUDJsAshz/465FZaQ1z6+0Z8bnqaNRq7QQPkKSfZAfI64JOBbhanAu3GmLokrxlRt3f0DLKIkJlup1trkJVSk5QxxgdcAzwBbAceMsZsFZFbROTiwGHXiMhWEdkCXA98aoK2O2XUtrlxOmwUxFKf290MT90Cs8+ic+GlA68Tjf1N3WSl2ynJzhjLdgc5LhD0vlvTHvGYbXXWY4kMkBeVWq+1Y4TAfGd9R+DY+APk9DQbFQUuDjaP3vMZrOx1Q4eXWaHt5TKy4cIfwpFt8PLPR32N0ryMmFvLqckvtlFAQ4jIA8AqoFhEqoFvAw4AY8xdwHrgQmAP0AN8Jp714hVNBtl63I5bSyyUUpOYMWY91jk29L6bQv7+xXHf1BRX2+6mPC/GnsQb/gd6u+CCH1DeZQVhNW1u5kRRxhCcaBdPD+Sggqx0KvJdvFvbEfGYrTXWY4vLEhcgzy7OIiPNxva6yOvuqO/E5bAzszD+ixEBZhVGP+L6QFNPYJ9Dfh6LLoTFF1s/v/nnQenxEV+jNNcZU0mHOjbEFSAbY64Y5XEDjN7ocZwMZJBHGBRiPZ6mbd6UUkoNUtvmia28onEnbLwXVnwGpi2iIs0KxqINpg40dXNced5YthrWceW5bK0dKYPcQVVRJtkjTJuNld0mLCzNGTlArutkwfRs6yK5BJhVlMljb0f3YXWwR3Nw2uAgF90Ov3gV/noVXPUspIXP5JfmOdl4MPreyerYkFKT9AYyyKP8z5+ZYddBIUoppQapbXMPDPwYlTHw+FchPQtWfQ2wapfT7bao+gL39fupbnWHD9zG6PiKPPY3ddPlDZ8A2lbXkdDyiqAlZblsre3A7x9+jb6v38/b1W28Z0Z+wtarKsqi3d1HW8/oI66PTvAL07kjqxjW3gFHtsKzt0Z8jdJcJ209fTH1XlaTX0oFyMGs8GgZ5Mz0tIFss1JKKdXr89PY5aUsL8oM8ta/wr5n4ZxvWoEWVjZ1dnF0/YhrWt34/IZZCRjYEXR8RS7GwNYwdciNnV4ONvdwQkXiAtWgFVWFtLv72NkwvA55e10n3b39rKgqTNh6wXriaOqQ9zV2Mz03Y2BI2DAL3g/LP2nVIh9+I+whpYF/E3qh3tSSWgFyIOgdNYOcrhlkpZRSRzV0eDAmypZrLfvgseug/EQ4+bODHpo7LSu6kc/NwZHPiQuQl88swCbw8t7mYY+9ss+677S5RQlbL+iU2Vbw+9q+4eu+fsCaNXZyVUHC1gu+qYhmQMmB5ij6Pp93K+SUw6Ofh77h5THB3st6od7UklIBclegM0X2KBfpZaWnaZs3pZRSA4JDO0atQfZ2wYMfA7HBv94HtsGfWM4tyeZg88h9gYGBMoxB3RXilJ+ZzgmV+by4Z/iUuJf3NJHjTOP4isTVPAfNKMykIt/Fq/uGD97deKCFygJX9Jn5KMwqslq9RTOgZH80g1GcubD259C0K2ypRbAvtmaQp5aUCpCjafMGmkFWSik1WF1gSEjZSDXIxsC6a6BxB1x6LxRUDTtk3rRs/Gb0j/93NXSR53IkpMVbqDPmFbPlcBsdnsH9fV/e28ypc4riHvUcySmzC3n9QMugOuR+v+H1/S2sTGB5BYDTYaeqOGvEns8Ard29tHT3Rpeln3sOnPQZePkOqHtr0EPBAFkzyFNLSgXIXV4fToeNNPvIX3ZWhtYgK6WUOmpgSEikTKffD//8Jmx9GM79thVQhRGcUrd3lOzmjvoOFpXmJKTFW6j3zS+m3294ec/Rcoe9jV0caunh9CSUVwSduaCElu5eNh062u3hzYOtNHf3cs7iaQlfb1FpTtia51DbB/ovR3lh4prvgCsfnr5l0N3ZGWlkZ6TpuOkpJuUC5OyM0Ru8uzSDrJRSKkRNm5vCrHRc4S7y7u2BP30KXrkDVl4Fp0duQR3MVo708b/fb9hZ35nQfsRBJ80qoCgrnUe31Azc9+jmGkTgghPKEr5e0LmLp5GeZuORkHUf2VKD02Fj1cLEB8gLpudwqKVnxHLJ7XVWAB3199mZB++7DvY8BQdeGvRQaZ5TSyymmNQKkD0+skcprwCry4XPb+j1+cdhV0oppSa7ujY3ZXlhyivaa+C3F8H2v8H7b4MLfgAjZH2zMtKYVZTJthH6Ale3uunp7U/IZLmhHHYblyyv4MltDRxs7qan18fvXzvEqgUlTM+NsoXdGOQ4HXxwaTl/3VRDc5eXpi4vj2yu4aKl5Qntuxy0qDQHYxhxxPWOug6Ks9MpyYmhjGXlVZBTBk9/xyqpCSjNdWqJxRSTUgFyt9c3vJVLnwd6Wgb9Qw9O2tML9ZRSSkGEISHbH4O7TocjO+Cy38N7vzBicBx0QkUeb1dHHtgx8NF/EjLIAFeeMYc0u3D9Q29x/R/foqW7l2vOmZeUtUJ9btUcen1+rnvoLa5/6C16fX4+t2puUtZaMN16czFSmcX2+o7Ys/QOF5z1FTj8Gux+cuDu0jynllhMMSkVIHd6fUffqXq74PEb4Xsz4Qez4c5T4OArwNGL+Lq1zEIppVKeMcYaEhLMIPv98NR34I8fg/xZ8B/Pw+KLon69pZV51LS5aekOP8hiR10nIrBg+ujjqMdiWq6T7394KW9Xt/GPrfVcv2YBJ81K7IVy4cyblsO3LlrCC7sbeWF3Izd9cMlATXaizSrKwuWwh+35DNaAkl0NXWMrYznxE9YFmM/cYv1bACoLXDR0enRYyBSS+M81JrFur8/qV9jbDb9bCzVvwrKPQclCaxzofR+AD/+azPRTB45XSimV2tp6+uj0+phRmGkFRH+/Ht78DZz0aaukIsII4kiCwzjeqWnnrAUlwx7fcriVuSXZA59mJsPaZRWcOqcIb5+fmQlsJTeaT51Wxeol0xGiaJkXB7tNWDYjnzcPhR8BvftIF70+P4vLxlDGYndY0xEf/g9rIMwJlzKrKBNjrPKYedOSE/Sr8ZVSGeRub6AG+eGroXYTfOR38KE74fRrrQxA5cnwyOco7dkJEHEcp1JKqdRxsMVqyTarKAte+JEVHL/vOrjoJzEHx2BNtAN4p7pt2GP9fsPGA62snJ38jO70XOe4BsdBFfmupAbHQSuqCthW2xH2d/nr+62ezCvGmjk/4V+hbJk1EObIDmYWWhdfHmoZfTiJOjakVIDc5fVxiudF2L4OzvkWLLn46IPOXKuGzJnPko3fxIafTo8GyEopleoOBiayHdfxojUoYullViu3MbZgy3E6mFuSxcaDw7Ob2+s66PT6BqbPqbFbUVWI38CWQ8PfiLy2v5mKfJf1qcBY2OxWzJDmhAcupyrTqj+OZry1OjakVIDs9bq5qO7nULoUTrt2+AHZJfD+W8lqfpfL7c/SpQGyUmqSEpHzRWSniOwRkRvDPH69iGwTkbdF5GkRmTUR+5wKDjb3UCotlD37JWt89Ad/OubgOOiM+SW8srd5WM3qa4HM5nhkkKe6E2fmIwIbDw6e4GeM4bV9LZwyJ87vcf4MuPwP0FFD4d+vJC/daIA8haRMgOzr97PW/wy5vUdgzS1gj1DbdfyH8ZadzOfTHqWrR/+hK6UmHxGxA3cCFwBLgCtEZMmQwzYDK4wxS4E/Az8Y311OHQeauvix616kvw8+fI/VySBOqxaW4PX5eXVf86D7X9nbzMzCzISOXk5VuU4Hx5fn8cLuwaO1dx/porm7l1NnJ2AwyoyV8MGfIQde4BbnAxxq0bhhqkiZALnb7eVzaetoyHsPzFkV+UAR+k+/jkppYtrBv4/X9pRSKhYrgT3GmH3GmF7gQWBt6AHGmGeNMcHf1q8CleO8xyljbs0jnObfZE1SK0pMW7JT5xSRkWZjw87Ggfu6vT5e2N3IOYsSPzgjVZ27eBqbDrVypPNoC7YntzUAcPr84sQssuwKOPXzrO19jPn1GjdMFSkTIPfteJwKaWbPvM+M+tGYc/EF7PDPYMmh34/T7pRSKiYVwOGQ29WB+yL5d+DxcA+IyFUislFENjY2NoY7JLW1V/Opjl+xN3MZnHxlwl7W6bBzxvxiHn+3jr5+q1XY4+/W4/X5uTCJE+1SzQdOKMMYeHRzLWCVVzyyuYblM/OpSOSFgmtu4VDOiVznvgP/4Y2Je101YVImQHa+9TvqTQHtM1aPeqzNbuMvsobp3Tuh7u1x2J1SSsUk3Lt8E+Y+ROTjwArgh+EeN8b8yhizwhizoqRkeMuxlOb343v4c4jp55UTvgO2xP7KvPzkmTR0ePnbW7X0+w2/fmEf86dlc3JVQULXSWXzp+ewYlYB9718AE9fPxt2NrL7SBdXrJyZ2IXsDt5ceTuNJh/zwOXQdnj056hJLTUC5I46sg5v4KH+s8jKjG6U5vMZZ+ETB2z5Q5I3p5RSMasGZoTcrgRqhx4kIquBbwAXG2O847S3qeOVn5N24Hm+6/s4xTMWJfzlz1k0jaWVeXz379v5zwc2saO+ky+uno/EeQGgGuz6NQuoaXPz+T9s4usPv0NVUSYXLytP+DozZ87iM303YPrccP9HwBN5WqKa/FIjQN7xGILh0f7TrT7IUfA7C9iSeTq8/Ufw6e8VpdSk8gYwX0Rmi0g6cDmwLvQAETkR+CVWcHxkAvZ4bKvdDE//N9Wl5/JA/zksLB3DQIlR2GzCTy5bhsthZ/079fzb6bP5gJZXJNxp84r58nkLeG5XIz6/4edXLCcjLbpYIBbzSnLYYyp5fMkPoWkXPPQp6O9L+DpqfKTGJL1tj9KZM5e9ngqyMxxRPSXHmcZT/jWsaNoAOx+H4z6U3D0qpVSUjDE+EbkGeAKwA/caY7aKyC3ARmPMOqySimzgT4GM5CFjzMURX1Qd1eeBv1wJWSU8VHYDGdVtzBxrv9xRzCnJ5rkbVtHt7ScvM7rfTyp215wzn0+eVoXLYcdhT05uMC/TwbScDDb0HccHL/oJrLvGmrr4wZ/F3RZQjb+pHyB3N8PBlzg897PQCFlRZpBznA5e6z4BMoth26MaICulJhVjzHpg/ZD7bgr5++gXXKjwnvseNO+Gj/+Vt563M29aNnZb8gKcNLuNvMzU+EB3IuU6k/8GZP70bPYc6YSPfAJaD1iTFwuq4Iz/SvraKrGm/v+RO/8Oxs+uwnMAyIkyg5ztTKPda2DRB2D3P62MglJKqamtdgu89DNY9nGYdy67GjpZMD3x5RVqapo/LYfdR7owxsA534TjL4Wnb4F3/zrRW1MxmvoB8rZ1kD+LQ+lW78poM8i5zjQ6vT5YfDH0dsH+55K5S6WUUhPNGFh/A2QWwfu/S4enj7p2D/OnZ0/0ztQxYv70bHp6+6ludVtlFR/6Bcw4BR69Bhp3TvT2VAymdoDsaYd9G2DxB+nw+HA57KRFWXuU43TQ6emD2WdCRi5sXzf6k5RSSh27tj4M1a/Dud8CVwE76zsBWKgZZBWl48rzAHi3JtDBIi0D/vU+a/riQ5+C3u6J25yKydQOkHc9Af4+WLjUx7sAACAASURBVLKWdncf+TFcAJGdkYanz0+fpMGC98OO9dDvS+JmlVJKTRifF566GaYfD8s+BsCWQ20ALK3Mn8CNqWPJ4rIcHHZhS3Xb0Ttzy+HDd0PjdtjwPxO3ORWTuAJkETlfRHaKyB4RuTHM458WkUYR2RL489l41ovZtkchpwwqVtDm7iPPFX2AnOO0rl/s8vhg4QXgbrHa/iillJp6XvsltB2E874LNqsUb8vhNioLXJTkZEzw5tSxIiPNzuKyXN4+PKQH8txz4KRPwyu/0AFkx4gxB8giYgfuBC4AlgBXiMiSMIf+0RizLPDn12NdL2Y+L+x9BhZeCDYb7T2xZZBzAle7dnp8MHsVILDv2eTsVSml1MTpbobnfwTzz4O5Zw/cveVwG8tmaPZYxWZpZR7v1rTj9w8Zbrn6Zqu+/W9fBL9/IramYhBPBnklsMcYs88Y0ws8CKxNzLYS4PDr0NcD86xOR+0xZpCzM6wMcqe3D7KKoGwp7NUAWSmlppznvmddjL3mvwfuOtLpoabNrQGyitnSynw6vT72NXUNfsBVAOf9N9Rugq3a1WKyiydArgBCh41XB+4b6sMi8raI/FlEZoR5HAARuUpENorIxsbGxji2FbD3GbClQdX7AGhz95LvSo/66bmBEotOT6DueM4q6+INb1fE5yillDrGNO6CN+6xPv6ednSc9KaDVg3piTM1QFaxOWlWAQCv7W8Z/uAJH7Hq3J/5Lvh6x3lnKhbxBMjhuqYP+TyBvwFVxpilwFPAbyO9mDHmV8aYFcaYFSUlJXFsK2Dv01C5Epy5ALTFWGKRG8g2t7sDYyLnnA1+Hxx8Kf69KaWUmhyevAkcmbDqa4PufmF3I9kZaZxQoQGyis2c4izK85y8sKtp+IM2G5z7bWjdD5sihkRqEognQK4GQjPClUBt6AHGmGZjjDdw827gpDjWi153E9S9ZRXFA56+frw+/0DQG42CLCvb3NYTeIc381SwZ1ht45RSSh379j8Pux6HM66H7KOJGWMMG3Y2ctrcItLTpnazJ5V4IsIZ80t4eW8Tvv4wtcbz18DM98ILP7aul1KTUjz/578BzBeR2SKSDlwODGoWLCJlITcvBrbHsV70gkHsPCtADmaBY8kgF2ZaAXJLdyCD7HDBrPdqHbJSSk0Vz9wKuZVw6ucG3b23sZuaNjdnLUzAp5kqJZ2xoJgOj4+3a9qHPygCZ30VOmth8+/Hf3MqKmMOkI0xPuAa4AmswPchY8xWEblFRC4OHHatiGwVkbeAa4FPx7vhqOx9xiqGL1sGWOUVQEw1yK50O06HjdaekBqhOWdbfQw76hK6XaWUUuPs4Ctw+FU4/VorARLi6e0NAJw5XwNkNTbvm1dMmk144t368AfMWQWVJ8OLt2st8iQV12dHxpj1xpgFxpi5xphbA/fdZIxZF/j714wxxxlj3mOMOdsYsyMRmx5lU1aAPGfVQC/LYJlELF0swMoit3SHBsirrP9qmYVSSh3bXrzdarl14icG3W2M4S+bqjlxZj4zCjMnaHPqWJefmc6qhdN4ZEsN/UPbvYGVRT7zK9B+GN5+cPw3qEY19YqrjmyHzrqB+mMYW4kFWHXIraEBculSKzO9/7mEbFUppdQEqH8Xdj8Bp3wO0gcHwW9Xt7OroYt/PSli0yWlonLJ8goaOry8tCfMxXpg1SKXLYMX/p9O6p2Epl6AvPcZ679zjjZ7bwsEyDFnkLPSaQktsbDZYPZZVgbZhHlHqJRS4ySKSaZnisgmEfGJyKUTscdJ66WfQno2rBw+3PV3rxzE6bBx0XvKwjxRqeids2gahVnp/Oal/eEPEIGzvgKtB+DdP4/r3tTopmaAXLwA8o+++2/vGWMGOXNIBhmsMovOOmjaHedGlVJqbKKcZHoI67qP+8d3d5Nc6wF49y9W32NXwaCH9hzp4uHN1XzslFnkOmP7faHUUP+fvfMOj6u4Gvd7Vr1LltxluWEbd7mAAQPGlMRUkwokISSBEAjBBn6EFD6CyZeQAqGTEAJ8CQmBhBoTTDPNVIN7wb3LstV73935/TF7pdVq1cuupfM+zz67996ZuefOnZ177pkzZ2KjIrjqtLG8s6OADYdKgyeadB4MnQ6r7gKvp28FVNqkfynIDbU2TvH4s5rtLq2pJ8IljavjdZRBCdEUBVOQQf2QFUUJJe2uZGqM2W+M2QTomrb+fPQQiAtOvq7ZbmMMv1mxjdioCK49Y3yIhFP6G98+eQxp8VH88uWtbfgi3wxFu2Hri30voNIq/UtBPvgRuGub+R9D0zLTIsHWNmmdtPhoKmrdNPjHMRw0FlJHq4KsKEoo6ehKpu3S46uYhjOVBbD+7zDzUkge0ezQU6sP8tb2fG46ZyIZiTEhElDpbyTGRPKLC6ew7mApf3p3d/BEky+CwcfDqrvBq++z4UL/UpD3vA2uKBgzv9nu4qr6TrtXAAxKsHmahXoDa0Xe/7461SuKEio6spJph+jxVUzDmdWP2IUZ5i9ttvuNrUdZtnwrp03I4Hvzx4ZIOKW/cnH2SC6cOYK739jJc2tzWiZwueD0H9swstuWtzyuhIR+piC/Y1e8i05otruwop7BXbAIOKvplTiLhTiMOwPqyiF3fRcFVRRF6RbtrmSqBFBbDp/9BSZfCBkTAPB4DY+u2sO1T61j6sgU/vjN2bhcnRtpVJT2EBHu+uoM5h+Xzs3PbuQPb+xoPjINMPVLdv7Uih9bP3kl5HTOKTecqTgKeVvg7GUtDhVU1jF1RHKni2xaTS/Agjx2gf3e+y6MOqHT5SqKonSTxpVMgcPYlUy/EVqRwpw1j0NtGZx6IwBrD5Rwx8tb2ZRTxqKpw7j76zM7PU9FUTpKbFQEj19xAre9tIUH397N61uPcvuFUzllfLp1/3RFwCX/gMe/AH+9EOZcYUc76irsinsl++08K1ckJA+3Lhmj51uDXbTG6+4N+k9v4PgEB/gfAxRW1HXJp6zRghzoYpGQbmMi73sPFvy40+UqiqJ0B2OMW0SclUwjgCeclUyBNcaY5SJyAvAikAZcKCJ3GGOmhlDs0FG0B977PWbiF/moJos/PvYJH+4uYnBSDPdfms1FM0d0eo6KonSW2KgI7vraTL44dRi3L9/KNx9bzeysVH54xnEsPH4IEYMnweUvwr+vgLf/FxAbjjBxiJ3/FJ1gXTvLc2Df+/DxQxCTbK3P834AQwfm37u36D8K8p63IT7Dhkvxo6beQ0Wdm8FJnVeQB/kU5KLKupYHxy2A1X+G+qoWLh2Koii9jTFmBbAiYN8v/H5/hnW9GNjUV+F+9nt4jIvLD1/Cp4+tZnBSDD8/73i+OW80CWo1VvqYs6cM5dQJGTy75hCPvLeXq55cQ2ZaHN+cN5qvz51K+g2boKEaIuOsf3IwGmrtUumb/m0/6/4GY0+H2VfAyDmQNsZGyFC6TP/oGbxeqyCPX9iiMRX6lNuuKMgZiTFEuIS88mAK8hnw0YNw8GM47uwuCK0oiqL0FsYY1u3PJ/75y5lYsZHrGm7CPWgYfzhzNOfPGE5sVESoRVQGMLFREVx+8hguOSGLNz4/yt8/PsDvXtvOvW/uZNG0YXxtbianjI+n1VYaFWv1kHFnwBd+BeuehE8fheevtMdjku1I94SzYdL5MHhiX1xWv6J/KMgAlzwFUXEtdueV1wIwpAsKcoRLGJwYw5Gy2pYHs06GiGjr2qEKsqIoSlhwqLiaF9cfZsXa3dxc8TvmRKznxVE/4abzfsSULsxFUZTeJDrSxQUzRnDBjBHszKvgH58c4KX1h1m+MZfhKbF8efZIvjI7k3GDE1svJH4QnHoDnPwjyNsMuRvsnKycz2DlMvsZOccurT5lMURG99XlHdP0DwXZ5YKseUEP5fqU2xGpLZXnjjAsJbZRyW5GdAKMmqfxkBVFUTqLMVBdBPWVdiKScWb0ix0W9rrt/qg4SBxqV7xrY7i4oraBVzcf5fl1OazeV8xgSnkm6V7GRuyh9ot386WTv98316Uo3WDi0CR+uXgaPz9vMiu35fHc2hz+9O4eHn5nD3NGp/HVOZmcN204Ka2FrY2IhBGz7Meh7LANHffZY/DCVda3+exl1m9ZXTDapH8oyG2QW1oDwPCU2C7lH54Sy678yuAHxy2At38FVYWQkNFVERVFUfo3JfttGM5Dq611q/SA9bHsKNFJMHK2DeN5/PkwbAbVDR7e3VHAK5uPsPLzPOrcXsZlJPDrU6O4ZMedRNYWw2VPEztpUa9dlqL0BrFREY1W5bzyWl5af5hn1+bwsxc284v/bOG0CYM5f/pwzpk6tP0l0VNGwknXwok/gF1vWAX5ue/aOVSLH4aM4/rmoo5B+r2CfKS0hqTYSJLaa0StMCwlllU7CzDGtJzlfNzZVkHe/l+Y853uC6sc+xTtgV1vQlW+tX5lTIIxp9ohsD6itsFDcVU9xVX1VNd7qG3wUNNgv+sarKXO5RIiXOASIdLlIiEmguS4KJJjI0mOjSI5Lkp9NJXuUV1sV63b/Bwc3WT3xWdA5lwbbSg1C2KSIDLGhrgyBjD2OyLKurA1VENFnl2GN+czzKq7kfd+x9GoUTxXN49P3eM5GDeFr889ji9nDyO74j3klRshIga+84pVqhXlGGZociw/WDCeq08fx+bDZfx30xFe2XSEt7fnE/2Ci9MnZnDBjBGcNXlI23qOywWTFsGEc2DDP+HN2+CR+daafOIPWp8MOIDp9wpyblktI7voXgGQmRZPVb2HkuqGxqgWjQzPtoG9N/5LFeSBTMVR2PICbH4WctfZfRIBxmN/u6Jg2pfhjJ/CoHHdOpXb4yW3tJZDJdUcKq72fdeQU1JNYaVViivremaFx8SYSIYmxzAsJZahybEMT4kla1A8YzMSGZuRQEZidM+Hxio/AlUFdnjd22BnYicN16HAY4XyXNj/gZ00vfVFcNfCyLl2EtHEcyF9fKfvZX55Le/syOet4nw2ufew0Luar/IxP3I9B9FgvC5k/yjYfBQ8dbZf/vrfbNtRlH6CiDAjM5UZman87NzjWX+olFc2HWHF5iOs3JZPdISLk8enc/bkIZw5eWjreo8rAmZfbhXl5UvgtZ/CgQ/h4j/ZF1alkX6vIB8qriYzresK8uhBNgD3gaKqlgqyCMy4xA5ZlOzXDnkgUV1sRw42Pwf7VgHGzhg+539h6sWQMsoqB0c3w5bnYe3f7PfsK2Dhz9t1yfF6DYdKqtlxtIJd+ZXsOFrBzrwK9hZUUe+3AlOESxiRGktmajyzslIZlBBNRmIM6QnRpCVEkxgTSWyUi9ioCGKjIoiJdPnKB48xeLz2U1nnpry2gYpaNxW1DZTVNJBfXkdeeS1Hy2v5ZE8ReRV1eLxNqxknxkQyNiOBcYMTmDw82fdJYkhSJ9yZSg7Yetz/ARxeB5VHW6ZJGgEzvm5fQgfpMsBhR+562PoS7F5pJwYBxKTAzMvgxKth6JROFef1GrbklvHWtnze3p7P5sNlgHV3+8LcqZw3/WyyxwyCujI4sgHZ/yEU74XkETAiG6ZcbJUARemniAizs9KYnZXGredNZv2hElZsPspb2/K47T9bue0/Wzl+WBJnTx7KWZOHMCMzlYjAFSKThsE3/gUfP2ytyY+dDZf+077EKgCIMab9VH3M3LlzzZo1a7pdjtdrmPyL17jilDH8/LzJXSpjV14F59y7ivsvzWZx9siWCUoPwX3TYOGtsOCWbkqshDVlObDtZdj+Chz4yFqIB42D6V+DaV9tO4xOxVFYdTeseQJiEu2Q1vSvNebJL69l/aFSNhwqZcPBUjbllFJV72nMPjI1jolDE5k4LIlxGQmMGhTPqLR4hqfEEhnRN0NjjvV6X1EV+woq2VdYxd7CKvbkVzZOhgUbHnHy8CSmjEhmZmYq2aNSGZ4S22Rt9jTAhqfspJGjm+2+9OPsLOsRsyElEyJj7ZBf4S7ru7rrDZtuxiV2JbR+ELJIRNYaY+aGWg5/utT3vnm7XbBg1Ek2pNT4M2HotE4pqQeLqvloTyEf7ini4z2FFFbWIwKzs9I48/ghnHn8EI4flqSLeShKGxhj2FtYxVvb8nhrWz5rDpTg8RpS4qI4eVw6849LZ/5xGYzNSGj+X9r7Ljz7XftMu+C+fj+Br6N9b79WkA+X1jD/t2/zmy9P57ITs7pURm2Dh8m/eI0bzprI0rMnBE/01wus8nT9OvXj6Y/seQc+vN8XscTAkCkw6Tw7WWjErM51JPnb8bxxG67dbyIY8qIyWe09noN1CRSaFHYyGvfQGUzKGsHUEclMHJbEhMEJJMVEdr1t1ZZB6UG7qA0AAklDITnTznruAUqr69l2pIJtR8rZdqScz4+UsyuvstHaPTgphtmZSXwt+iPmH36CuMqDMHymfUk4/vz2XU/Kc+Gjh+wLhrvGyj76FN9nPmRMOOY69H6jIFcVWn/h2I6FUDPGkFNSw7qDJXy0u4gP9xSSU2InUw9OimH++HQWTBrMgolDWo7aKYrSYUqr61m1q5APdxXywe5CDvsFLThlfAbzxg1izug0xmUkIKUH4N/fhiMbYfSp1uA39vRjrl/tCB3te/u1i8XeAht9Ykx611e6i42KIGtQPDvzKlpPNOc7Njj3rjesE7zSPyjeC/+90SrGySNhwU/sUH8nhqC8XsO+oio2HLTW4fWHSth+5LukeRdzbsSnnOvazEJZQ0JUBS7HZ7kYKHHBBt+kJYeULN8Q8mKroEfHBz9p/jbr/3ngI8jbCjXFwdO5oiB1lJ04FZcGcakQnw5pY+01Dj7ezoDuAKnx0Zw8Pp2Tx6c37qt3e9l2pJwNB4txbX2BM/Y/ziiTyxbvGO7x/JiDlaeSfTiNWRERZI8qY9LQpNat4ckjYNGdMH8pfP4fOPiRvS+b/22Px2dY15aTf6RuGH1NO+5CtQ0ethwuY93BEtYdKGXdwRLyK+ziS8mxkZw8Pp3vnzaO+celM35wolqJFaWHSI2P5qKZI7ho5giMMRwsruaD3YV8tLuIt7bn8fy6HADS4qOYMzqNORMeZVHWG4zZ8gDy5EXWbXD+Uuu21EPGlGOJfm1BfnTVHu5csZ31t51DWjcsET/4+xp25Vfy9v87I3gCTwPcP9MOE1+xvMvnUcKIdU/Cqz8FVyQs/BnM/Z6dbd8OJVX1PkXYcZcoobzWTppLiI5g5ijrcpA9KpXsrNQmf12vF6oLbQisoxvtMqLism/v4rJxYot2w4GPoSIXouJh1IlWoY1NsZ+GGtj3PuRvBcRat4dNs+0yNcumcc5VkWtfAEr2W3/qmhKoLbXWQP/wWymjbDjDSefZxXGi4m09dESJaaixyuwH90HBNhgyhapTbmFt3Hw25JTZ+jlUSnFVPQBxURFMz0xhVlYqs0alMSsrlaHJbfgzG2OjhjjK8ufLbT3N+padEJk8on0ZQ0i/sSD7UVXnZvvRcj7PtaMIzneDxz5nsgbFM2d0GrOzUpmVlcbk4cktfSMVRel1vF7D3sJK1h4oYc3+EtYeLGFvgR1ljHc1cHXKZ3zDs5wh9QdxRyXB6FOIPG6hXblv8PHHtGVZXSyA659ez7oDJXz40zO7Vc69b+7kwbd3sfWORcRFt+JX98G9drWaaz60SolybOKug1dvgbV/hbEL4OI/Wp/YINQ2ePj8SDkbD5Wy0afs7S+yyqVLbND3WVmOQpzGcUMSu68MeL1w4AM7KSp3vXWfqC2zym1EtJ3BP/Vi+8afNLTz5RsDlb6wWke32NnNe9+FuvKmNDHJVnFOGgaJQ+xCDskjIW20dXWoKYHNz1s/49pSG+llwU9g6pdbuIk4Vo0Nh0pZf9C+WHyeW9aoUI1IiSXbpzBnZ6UyfWRK6+Hnyo/Ah/fBZ4/bF5sTr4Lsb8KQrs0/6G36i4L82pYjvLzpCNtyy9lXVIXzSEmNj2LK8GSmZ6YwJyuNWVlpDO7CiqaKovQNxVX1rDtQwrqDJWzNLefzw6VMr1nNWa71zHdtYYwrD4CK6CEUD5tP5Ki5ZGROICZjjA1S0AEjUjigCjJwxl3vMGlYEn++vHvPoLe35/G9v67h6e+f1GwIuRk1JXDPFJh0Lnz1iW6dTwkRZYfh2e9Azqdw6k1w5v80TjTyeA17CirZ4FOGN+WUse1IOW5fVIchSTGNVuFZo9KYkZlCQkwfDkk5/+PeeKt311tFOW+rjcxRmQ9lh6wiXZlvJyB6G5rncUXC5AthzndhzGmd8p92XjzWO24pB0safVQjXcLxw5OswjwqlVlZqS0nnJTst/HJNz+H9RmfCtnfsK4pScPDZqiwvyjI96/cxbNrDzF1RDJThqcwZUQyU0ckN5+YqSjKMUl+eS1bc8vZmlvGkf07Sc37kCnVa5jv2kKqVDWm8+CiJCaTiuTjcKWOIjE+jqSEOKKjY+1IZ+JQa1BJGGw/Ivb5UZnn+xRAfQXUV9v5MvWVdkVNoHGFTXHZVYyj4u135lxr0e4kA15Bdibo3XbBFK48tXs+iWU1DWT/8o22J+qBfSivuguuesveOOXYoKHWzsJ//x4A6i98iB2DzmqcbLbtSDlbDpc1RpVIiolkemYKM0elNkZpGNbFlRr7BY57SPFea3mOiLGRDBJaeZnsAgUVdY3KsvOS4tyPlLgoZmRaxWzyMBtubtzgBKKqC+wSqxufgcNOfyLWZzZ5pB0ZSB5hfw+ZYperd9xQ+oD+oiB7vQZX4MiIMU0va4Evb4HH/JXowO226GrezuRzjvl/O78Dt8H+F1yulvkcAssSaT1Pa3Xo9Tbti4iAhgaIjGxK73ZDVFRTGo/HpvOX0cnrlGtMkwzOefyv35HR67XbTpnOd2A6/zKdPP7b/tfr8TTl8b8+/zpwzuN222t1tr3e5tfhv+3URWRkkwz+53DuYWttwLm3zscp1/lEduBFO1h9+m93Jb9Tj/5p2iqvI+29k/+lOreH/QWV5BzYS3HubmoK9hFVspvBNfsYaw4xREqJxEMkHqLE02o5QZEIiE60c2wionzTcJx691gXwLpK+/ukH8Ki33SufFRB5plPD/LTFzbz+g2nM2lY94NfX/TQB7hEeOm6+a0nqquAB2bbSULfe/2Y9tEZCDS4PRStfYGUVcuIq8phY+Jp3M3lfFSc1BjvNz46gknDkpg+MoWZmanMHJXKuIyElgqB0qd4vIbd+ZVNCnNOGbvzKxpdM6IjXBw3JLExNnN27FHGV28k1VOCVB6F8sN2xKA818bTBUBg2HQbFWPsaXYFxF5UmLurIIvIIuB+IAJ4zBjz24DjMcCTwBygCLjEGLO/rTJ7ZPRu2TIoLYV774U77oCSErs/LQ1uvx1uvBFSU+0+J52jDDnHli3r+Dk6k7cz+Zy0KSlQVgb33ANZWVbp+vrXYdMmmDkT/vUvqK6GxESbLiUFhg61SurBg03KaWYmfPGLTWXddBOsXw/l5ZCcDLNmNe13zunU02uvwbx5sGEDbN8OVVVNSlt1NaSn23319Vb5GzkS9u+35zxyBIYNg8OHbZ7kZKirg1NOsd8nngirVtlzZmfD6tWwaFHT/XFkvPBC+Mtf7O+6OltWVBRMnw6HDllZ8vOt8paRAUOGwAUXwMsvQ3S0TRMdDYMGNV3vunWwdi1MmwYnnWRlePRRKC6GmBhbpxUVViFuaLDXlpBgrzU+HuLi7PfFF8Mjj1il9f/9PytjYiL84Q9WxoQEe+9OOsnWYVkZxMba6/Rvk04bWLYMHnvMXk9Dg5X76qvh2WehqMi2gZQUWz9ttTXnvt13n913ww1N9duRNh6Y/6STbJu6+mr732qv3XekvXf1vxQEYwyl1Q0c9FvE6nBxOaWFR6krPYKrqoD4hhIypAwXhnyTSgGplEcMwpuQQUxCKgnxCaQlRJO2eT1ptZUM+spFpCZEkxYfRcofHyApKZ6kH99IUpQhOgK7Ym0nGdhRLIzhxfWHGZuRwMShifbP5XQmbnfTG7TzNgtNb6lRUU1vh2633e9yce604fzute0cLKgga3ArCndMkh2Wf3kJfPJHOPm6vrvmgUIn33QbPF6OltWSU1LDoeJq9hRUsqegioa87VxR+Thnutax3TuKO9y3cqBhDpOHJ/PDGcmNC1+MTovDFeFnWTHGOhj7txunU/F4mltyAq0rTv5g1+OfJpjlKTBPW3UTaM0Kdi7nPM5+Z5+/9SfQUhbM6tXB+9BYFw6OZcc/f6AMzv/WSefUuctFhEuYNDSRScOSuPSEUSBCg8fLnvwKth+pYNtR+1m1q6BxpjZkERM5xi5ukpHA2PEJjBucyLhkL6Nrd5BauAbXwY+s//nqP1lLxsjZMM43MSVzbnMfu85YO3sYEYkAHgbOAXKAz0RkuTHmc79kVwIlxpjjRORS4HfAJb0qmDH2YXv//U3384EH7PeSJVZBeOAB+9v/2L332ofy/ffD0qXtt3/nHJ3J25l8/mmzs61S9e67VskEePBBqxw78oNV5MAqrEeOtDz/4cNWsdywAd57z35nZEBhof1etappv3NOp55Wr7af9HSroAWSn9/yXNdfD7m5dvvIEbv94YdWuQT45BOrUK9ebbcdGcAqzSL2+hwZt2+H2trm56mrg2AvVLm59hOYJzbWKnjOuWJj7fFPP7WfQYOscgxWMa2sbFm2s6+qyn5iY5vuQ3093HWXLdOxcNfV2Xtz9Kg9h38dzpvX1CadNgBWBudeO+U+9FBzOWprW/ZjDsbYF0Pnvjk4cs6b134bD8xvjJUfYPlyq9jfdFPr7b4j7R269l9qBRGxym1CNDNHpQZNU1XnJr/CLkKVV15LQUUdR8tqKa6qp7i6npLqBvYXVVPiHkRF1FBYvrUpc8xJUA/8+i0AvnPKGJZdNLXD8nWWblmQe8OCAd20YixbxsYPN7J4zlXc8sVJ/HDZlfDBB00P167gcnFkwjROX/wrvr5lJb/e+h/7dh4MrxeeNKzGEwAAIABJREFUvcIuKLH4ITujXukZAt50q+saKPzpLyhISqfg69+ioLKOo2U1HC6p4XBpDTnF1RRVVBFp3MRQz3Ap5uTInXw5+hOmerZTb6LYPnUpnhOvYdyQFFJ+fkvwN+uUFHj9dXtvGxqs9WPHDtt5jB1rrUL33msfjCefDHPmwN13w/Dh1rrxpS81twT5/+fq6yEvz5adlWWVQ8fK1JpV67XX7G9jbEcL8MILtrMePRrOPdceW74cLrqouaVhwwbbsQdaJdavtw+n3FzbIS5dCk88YWW48srgVq/AsluzOIwZYx9kR4/ah9Ztt9n6GTIEDhyw+UeNsg/5yZNt+cuWwW9+Yx9wp54KCxfCf/5jyzj+eHjnnabryc5u01pZmJLBbhPH3iov+848n73L32RfdAoH49NxS5OSH+X1MDwjiawUFydH72eOZwPHVa4hvWwLYrx4TSTmuDOIGO9TmH/7F0hN67SVxaE7FmQRORlYZoz5om/7ZwDGmN/4pXndl+ZjEYkEjgKDTRudfo9YkJ324Dx0A1m61N4vaJnOOdbeQznYOTqStzP52ruOznD99U0KZyCOMhyIfz05SlxXcJRQf/wV0UCWLGnqGzp7/enpcOml8PDDradp7Xo7myaQ666z1vzCws7lg5ZtwBi778EHg6ePibGKeltuFsYEv29O/XakjQfLH1g3bbX7jrT3rv6XehtjaLjxJkr/8ldK45Iojkum7GuXUfHNb/tWfHUzLTOFhZOGdLroXnex8FkwduJnwQAu87dgiMgPgRnGmGt8FowvGWPatWB0uZM2hoIbbuEbVWMpiUvmXdaQ+MxTXfvDBBIVxe0LvseTs8/nT289zKLVrzS3iPlTXw3PXGZn/2d/0y4t3EokhIGKMYY6t5faBg81DR7qqiupK8untqKQuvJi3FWFeKuKcdfV4K6vwVNfizf3EO7qCtwJCXgiBfE2EIWbaNwkUEOKVJEi1aRINbFST7RpwEWQF6OMiXAoGR5+B65a0vKtOfDhHdghBT5wZsyww63QZLVw0jjfgRaztnDOF6wj68iD8vrrrXVm40Zb1tq1TZYG/2tZssSW6f8QmDkTTj+95T6nLH+rV2DZwTpVj8cO7zpWsiNHICmpqW4qKmx+//NNn27TOf/b6GirOG/c2FLGQEubv7XS2Q78/d57sHEjDa4IDl3/Y/Zv3cvhwgpyJ0zj8MWXkltWy+HSGvLKa/EaSKaKk1yfM9+1hVNdWxjvstbBUncC281khl/+B0Yfn93+fQ2gmwryV4FFxpirfNuXA/OMMT/yS7PFlybHt73Hl6YwoKyrgasBsrKy5hw4cKArIjUn0E/SH39/0MB0/sc6e46O5u1MvrauozP4jX60IHB0JZhc3ZGjoaHJJ9mhNctnd8/rdtv0beVp7Xo7myYQr9d+OuIbHCxvsBek1q7D8ftuj2BldKeNQ8u6aa+8jrT37vwPe5NekqsvXCxOBHYbY/b6TvgMsBjwH+JbDCzz/X4OeEhEpC0LRlcwxvDEh/vZeriM11LOwhNbz/89cxuJBzf13EkaGrjlvb+xPmsq15x9PfMe+5TZo9NIiYsiITqihU+qa8I9zDQPMmnjP2DTs+zNvJjSpIkYcRq28RkSnaF7MJhm276L8+2n0fJo/H77MuJ3BAOIMc3SGUAwGGN8302yNsnhf+6m8o0BrwGv14vX2DK8xuD12t8eY++BPQ5e4/UdB2O8uD0Gt9eL2+PF7TV4PR4GmWKGUcxwKWKEFDFc/GLvtnYLoiNpiIrE6wZvvYDHILHxSFo6rphkIhKGEZWQiis2xTr4R8baIfHIWDtxLH6QjR2cMsoWWOdTgJ0350AFz1GUAy0ogdYYRzn2V5z9v/2VbmhfwQ2mHIP97Vh22irDUTYd5dHpTJcutVbgG2+0+f3LcJT8jRuDK6KOXNCkHAeWHcziEBFhrb6Okuw8qJ26cravvx7ef9+WuXlz8zLq65tkgiYZnetxFHR/nGvzr3uRZumivB7G3f9bxjl19cx/m3XGDR5v4xBgYcXpFD3xd179OIL61LkMHlrB2JGVzIjeQVFoHiTBThrYr3YkDcaYR4FHwRonui2ZY5FqjRtvbP4SGuxYRy3Inc3bmXztXUdnWLq0dbnmzAm+37+ebrih6+dOCuISOKQNq9sNNzS3IHeGoUOtBbktWrvezqYJ5PrrrQW5KwS2AceC3BqJiR23IAfi1G9HLciBBNZNW+2+I+29q/+l3iYM5OqOBbnHLBi+Y92yYpz++3eoafBw2nEZXLtgHBOG987kmtqaOv66+hAvrjvMrvwKvO1U30gKuD7yRb4S8X7nZ3P2Y6ojU6mKHUpN3HBq44fRED8ck5BBVGI6MUnpxCZnEJ+SQUJiEhFRcTbGrzPzuafeKLvyZt0WwSw1geV2tLyesGq1ZmnoiFXC2efzwe9w2W3J4v8wCawr/5n1HaWt6wkmV1vp/GfSt0aw9mK8jaEAO0u/dLHwH67tqFXfeYkJHMVpq/0Hpu1I3s7k80/rvAw6IykOgdsdwSkrcDTGf1QmmA+yU4et+SAHEhEB11zT3NXhuuusD7LzohsdbV8+HRwZoLlLiLM/mKtGewTmcbZbK7Mt14/OnsMZzfOfdwHN6zBYO4S23Ssc2nKzCBztC/ZfaEtJDpbff7SvI6N3HWnv0LX/Um/T1f94B+kLC3KPWTCg+1aMFUtPIzEmsvW3rh4idtRIrjl6lGsWjMfrNdS6PVTVefB/5gQKb8ylFLnrcNWWAl4MBkEAsXOgnGoSQKRprhaCjSMqziHE8ZkUaIwxKmLT0pTfv3ynQGe/s89+tVa+/60LsGK2us9vfzv74l0RtLJQcuv05BtlV9+s2yKYpca/XOh422zLqtXRMoJZGhwLciCzZrXcN3u2tSB3tOzW7oPjZuFPYF0tXWotyJ3BuZ6bbmo7TWvWSn/mzLEPnNaU5LbaS2j4DJggImOBw8ClwDcC0iwHrgA+Br4KvN3To3ctELG+6M5D7I47mpQDxy/cSQPNH3ZOXaamtv1/DjxHR/N2Jp9/2pQUWLAgeBSLJUs6H8XCKau9KBYLFjTV07x5nY9i8eCD8OKLTVEsHnzQ5nGiWJx0UutRLAYNaro//TmKRWCbdNrAoEG2DtuKYhEb27oFWcSW7dw3xyIPtn7T0tpv48Hyr15t29RFF9l6bqvdd7S9d+W/1Nt09T/e0xjfkHlnP8DJwOt+2z8DfhaQ5nXgZN/vSKAQn9W6rc+cOXNMl/B6jVmyxBj71zXmRz8yJiOjabs7n6iopt8ZGca43V2TUekaXq8xS5fa+l+6NPh2T5blvy87u3lbiI1tvj1jRtPviIjmaZzvJUuat822Ps75Aq8rsH239rn+emNmzmwqy+MJfi1Llti0/nlnzgy+zz+v858KLDvYfXC7m9JnZBjT0NC8bhoaWp5v+vTm/9vo6CYZAmV0ZAqsX//twN/+ZflvO9fTm23PD2CN6WL/a7NzHnYeyB7gVt++XwIX+X7HAs8Cu4FPgXHtldnlvjeQwHYbuB3sd7Dtjp6jM3k7k8855v/t8QTf9npte/ff538sWFnGNLW51o47v/3TezxNz6D6+ubnqq9vnq+hoXlZ/nmdcv1lCHZ/nOPOOZwynW9nv3P9/mX610Ww6/XP4399/uU653Gu1dkOvA7/bWNsOn8Z/M/RVjt09jl15X+dznZHCFafnW3jgfkD+6j2yutIe+/O/7A36SW5Otr3dseCHH4WjGBvXZs29UgUC4YPt29tTzxh30Y7O4FA6R49+UbZ2TfrlBRrzWgrisW+fR2LYuGE93FoLYqFYz0KtGo57RtsOcGiWAwaBIsX2/SBloYNG4JbJZwoFuvWNZ3TiWKxeDGccUbwKBbtWTEiIuz/BZqiWNx8c1MUi8hIO2z2wgutR7GYN89GsXDKSE21eVyu5v7aHbVWLlxoh8cXLLDp1q2z9ywlJbgFOVysGQEYY1YAKwL2/cLvdy3wtb6WC2jZbrtyrDPn6EzezuTzG6Vr/A6U33/beS4E5murTJcr+P7W6imwjTquSk4af9clkZZWTv/8bZ0zmIzOt1Om8+2k838utnZ9gduBz9Jg8jnnca7N2Q6s78BtJ11gnQVut3afutM+g6XvifydLbMj6bsrZ28RYrm6G+btPOA+bJi3J4wxvxaRX2K18+UiEgv8HZgFFAOXGt+kvrboET84K6D97oE4yI3xbJ2VepTQYEzzP0ngdk+X5exz2lSwduMc1zjIweWCHo+D3OJ6AuvXfzvY78CVtAKvJxg92faA/rKSnqIoyrFEnywUErYWjGBWLIdgk6haIzq6ZbmqHIeWnnyj7MybdWtWH/90rVlTOmIx64pVq739rVlJOmqVCCZ3W9ffFoH/m0CrVjAZ2rIsBZMpmBwdtcJ1ZNJjuFpZFEVRlB6nBwI8KoqiKIqiKEr/QRVkRVEURVEURfFDFWRFURRFURRF8aNbk/R6CxEpAA704SkzsCHowg2Vq+OEo0ygcnWWcJSrt2QabYwZ3Avldple7HvD8b72Fnqt/RO91v5Dh/resFSQ+xoRWRNus8lB5eoM4SgTqFydJRzlCkeZjjUGUh3qtfZP9FoHHupioSiKoiiKoih+qIKsKIqiKIqiKH6ogmx5NNQCtILK1XHCUSZQuTpLOMoVjjIdawykOtRr7Z/otQ4w1AdZURRFURRFUfxQC7KiKIqiKIqi+KEKsqIoiqIoiqL4MeAVZBFZJCI7RGS3iPw01PIAiMgTIpIvIltCLYuDiIwSkXdEZJuIbBWRpaGWCUBEYkXkUxHZ6JPrjlDL5CAiESKyXkT+G2pZ/BGR/SKyWUQ2iMiaUMsDICKpIvKciGz3tbGTw0CmSb46cj7lInJDqOU6FhGRu3z3dpOIvCgiqaGWqTcRka/5+iOviPTLcFnh+OzsDcLxedxbhOtzPlQMaB9kEYkAdgLnADnAZ8BlxpjPQyzX6UAl8KQxZlooZXEQkeHAcGPMOhFJAtYCF4dBXQmQYIypFJEo4ANgqTHmk1DKBSAiNwFzgWRjzAWhlsdBRPYDc40xYRMIXkT+BrxvjHlMRKKBeGNMaajlcvD1FYeBecaYvlzEqF8gIl8A3jbGuEXkdwDGmJ+EWKxeQ0QmA17gz8DNxpiweBHtKcL12dkbhOPzuLcI1+d8qBjoFuQTgd3GmL3GmHrgGWBxiGXCGLMKKA61HP4YY44YY9b5flcA24CRoZUKjKXStxnl+4T8rU9EMoHzgcdCLUu4IyLJwOnA4wDGmPpwUo59nAXsUeW4axhj3jDGuH2bnwCZoZSntzHGbDPG7Ai1HL1IWD47e4NwfB73FuH6nA8VA11BHgkc8tvOYQA3ho4iImOAWcDq0Epi8bkybADygTeNMeEg133ALVgrUrhhgDdEZK2IXB1qYYBxQAHwfz6XlMdEJCHUQgVwKfB0qIXoJ3wPeDXUQijdQp+d/Zxwe86HgoGuIEuQfSG3PoYzIpIIPA/cYIwpD7U8AMYYjzEmG2uVOlFEQjoMJiIXAPnGmLWhlKMN5htjZgPnAtf5hhBDSSQwG/iTMWYWUAWEjU+jz+XjIuDZUMsSzojIShHZEuSz2C/NrYAbeCp0kvYMHbnefow+O/sx4ficDwWRoRYgxOQAo/y2M4HcEMkS9vh8fJ8HnjLGvBBqeQIxxpSKyLvAIiCUEyrmAxeJyHlALJAsIv8wxnwrhDI1YozJ9X3ni8iL2OHSVSEUKQfI8bP8P0cYKcjYF4l1xpi8UAsSzhhjzm7ruIhcAVwAnGX6weSX9q63n6PPzn5KuD/n+5KBbkH+DJggImN9VqJLgeUhliks8U2GexzYZoy5J9TyOIjIYGdGvIjEAWcD20MpkzHmZ8aYTGPMGGybejtclGMRSfBNvsDnxvAFQvsygTHmKHBIRCb5dp0FhNOkkMtQ94puISKLgJ8AFxljqkMtj9Jt9NnZDwnX53yoGNAKsm/SyI+A17HO6P82xmwNrVQgIk8DHwOTRCRHRK4MtUxYq+jlwJl+Ya/OC7VQwHDgHRHZhO203zTGhFVYtTBjKPCBiGwEPgVeMca8FmKZAK4HnvLdx2zgzhDLA4CIxGNn6g9oS0oP8BCQBLzp6zseCbVAvYmIfElEcoCTgVdE5PVQy9SThOuzszcI0+dxbxGuz/mQMKDDvCmKoiiKoihKIAPagqwoiqIoiqIogaiCrCiKoiiKoih+qIKsKIqiKIqiKH6ogqwoiqIoiqIofqiCrCiKoiiKoih+qIKsKIqiKIqiKH6ogqwoiqIoiqIofqiCrCiKoiiKoih+qIKsKIqiKIqiKH6ogqwoiqIoiqIofqiCrCiKoiiKoih+qIKsKIqiKIqiKH6ogqwoiqIoiqIofqiCrIQNIrJfRGpEpEJESkXkIxG5RkQ61E5FZIyIGBGJ7G1ZA857hojktJPmBhHZKyLlIpIrIvf2tZyKoiit0Z/7X7+00SKyvaPplYGNKshKuHGhMSYJGA38FvgJ8HhoReoRXgZmG2OSgWnATGBJaEVSFEVpRn/tfx1+DOSHWgjl2EAVZCUsMcaUGWOWA5cAV4jINAAROV9E1vsssYdEZJlftlW+71IRqRSRk0VkvIi8LSJFIlIoIk+JSGqwc4rlXhHJF5EyEdnkd94YEblbRA6KSJ6IPCIicSKSALwKjPCds1JERgS5nj3GmFLnVIAXOK4n6kpRFKUn6W/9r6+MscC3gN/0SCUp/R5VkJWwxhjzKZADnObbVQV8G0gFzgeuFZGLfcdO932nGmMSjTEfY5XR3wAjgMnAKGBZK6f7gq+Mib7yLwGKfMd+59ufjVVsRwK/MMZUAecCub5zJhpjcoMVLiLfEJFyoBBrQf5zJ6pCURSlT+lP/S/wIPBzoKbDFaAMaFRBVo4FcoFBAMaYd40xm40xXmPMJuBpYEFrGY0xu40xbxpj6owxBcA9baRvAJKA4wExxmwzxhwREQG+D9xojCk2xlQAdwKXduYijDH/9LlYTAQeAfI6k19RFCUEHPP9r4h8CYg0xrzY0TyKopOElGOBkUAxgIjMw/rGTQOigRjg2dYyisgQ4AGsBSQJ+1JYEiytMeZtEXkIeBjIEpEXgZuBWCAeWGv7als0ENGVizHG7BKRrcAfgS93pQxFUZQ+4pjuf31uGL8HzutIekVxUAuyEtaIyAnYDvoD365/AsuBUcaYFKwl1uk1TZAifuPbP8Nnvf2WX/oWGGMeMMbMAaZiLb0/xrpE1ABTjTGpvk+KMSaxjfO2RyQwvgv5FEVR+oR+0v9OAMYA74vIUeAFYLiIHBWRMe3kVQYwqiArYYmIJIvIBcAzwD+MMZt9h5KAYmNMrYicCHzDL1sBdvLbOL99SUAlduLISGyH29o5TxCReSIShfW1qwU8xhgv8BfgXp9FBBEZKSJf9GXNA9JFJKWNsq/yyzsF+BnwVocqQ1EUpQ/pZ/3vFqzvc7bvc5UvTzZwqAPVoQxQVEFWwo2XRaQC23HdivVZ+67f8R8Cv/Sl+QXwb+eAMaYa+DXwodg4nicBdwCzgTLgFaz1oDWSsR1xCXAAO0Hkbt+xnwC7gU98E+1WApN8592O9cXb6ztvsFnU84HNIlIFrPB9ft6hGlEURekb+l3/a4xxG2OOOh+su4jXt+3pXPUoAwkxpiujw4qiKIqiKIrSP1ELsqIoiqIoiqL4oQqyoiiKoiiKovihCrKiKIqiKIqi+KEKsqIoiqIoiqL4EZYLhWRkZJgxY8aEWgxFUZReY+3atYXGmMGhlsMf7XsVRenvdLTvDUsFecyYMaxZsybUYiiKovQaInIg1DIEon2voij9nY72vepioSiKoiiKoih+qIKsKIqiKIqiKH6ogqwoiqIoiqIofoSlD7KiKOFDQ0MDOTk51NbWhlqUY5LY2FgyMzOJiooKtSiKohxDaN/bPbrb9w5YBXlPQSW/fPlzrj1jPCeNSw+1OIoStuTk5JCUlMSYMWMQkVCLc0xhjKGoqIicnBzGjh0banGUMMTt8XLVk2u4buFxnDBmUKjFUcII7Xu7Tk/0vQPWxeK+lbt4b2cBj67aG2pRFCWsqa2tJT09XTvoLiAipKen94oFSEQWicgOEdktIj9tI91XRcSIyNweF0LpNvkVdby7o4Dr/7k+1KIoYYb2vV2nJ/reAasgb8opBeCD3YXUuT0hlkZRwhvtoLtOb9SdiEQADwPnAlOAy0RkSpB0ScASYHWPC6H0CMb37fZ6QyqHEp5o39t1ult3A1JBLqtp4EBRNccPS6Le7WVfYVWoRVIURekMJwK7jTF7jTH1wDPA4iDp/hf4PaBOjGFKbYM10DR4TDsplWON0up6dhytCLUYShcZkAryfp9CfP704QDszKsMpTiKorRCUVER2dnZZGdnM2zYMEaOHNm4XV9f32PnWblyJSkpKWRnZzN58mR+/etfN9s/a9YsJk6cyIIFC1ixYkVjvv/5n/9pJtOtt97aYzK1w0jgkN92jm9fIyIyCxhljPlvWwWJyNUiskZE1hQUFPS8pEqbOAqyx6sKcn+itsFD9i/f5Iv3rQq1KF1moPe/A3KS3tFya0w55bh07ntL2JWnb3iKEo6kp6ezYcMGAJYtW0ZiYiI333xzszTGGIwxuFzde99fuHAhL730EpWVlcyYMYMLLrig2X6AdevW8aUvfYknn3ySBQsWAPDjH/+YG264oVvn7gLBxg4bNSwRcQH3At9pryBjzKPAowBz585VLa2PqW2wrhXqYtG/OFJ27A/aDPT+d0AqyHk+BXnUoHhGpsZxoKg6xBIpyrHBHS9v5fPc8h4tc8qIZG6/cGqn8uzevZuLL76YU089ldWrV/PSSy8xc+ZMSkvt3IJnnnmGlStX8thjj5GXl8e1117LwYMHcblcPPDAA5x00kmtlp2YmMjs2bPZs2cPycnJzY7Nnj2bW2+9lYceeqixgw4ROcAov+1MINdvOwmYBrzr88MbBiwXkYuMMbqWdBjhzIFRC3L/wn9ukzGm2/6w4dL3wsDpfweki0VeeS0RLiE9IYaRqXEcLq0JtUiKonSSzz//nCuvvJL169czcuTIVtMtWbKEW265hTVr1vDvf/+bq666qs1yCwoK+PTTT5k6NfiDY/bs2Wzfvr1x+6677moc4lu5cmXXLqbzfAZMEJGxIhINXAosdw4aY8qMMRnGmDHGmDHAJ4Aqx2FInc+CrD7I/Yt6d9OIgLsfvvwMhP53QFqQj5bVMSQphgiXMCI1jo/2FIZaJEU5JuiKtaG3GD9+PCeccEK76VauXMmOHTsat0tKSqipqSEuLq5ZunfeeYdZs2bhcrm47bbbmDRpEocOHQosDmOaP+xC4WJhjHGLyI+A14EI4AljzFYR+SWwxhizvO0SlHDB8UFW+hf+CnK920tURPfskeHU98LA6H8HpIKcX1HLkKQYAEamxZFXXkuDp/sNWFGUviMhIaHxt8vlatZx+se+NMbw6aefEh0d3WZ5/r5ubbF+/XomT57cBYl7FmPMCmBFwL5ftJL2jL6QSek8tRpmtF/iryDXub0kxIRQmF5gIPS/A1IjLK1uIC3B3qzM1Di8Bo72A4d6RRmouFwu0tLS2LVrF16vlxdffLHx2Nlnn83DDz/cuO1MOukKGzZs4M477+S6667rlryK4uBM0lP6F3We5hbk/kx/7X8HpoJcU09qnF2be0SqNfOrH7KiHNv87ne/Y9GiRZx11llkZmY27n/44Yf58MMPmTFjBlOmTOEvf/lLp8p1hv4mTZrEkiVL+OMf/xjqCXpKP6KuoflkLqV/EOhi0d/pj/2vtPeHFJEngAuAfGPMtCDHvwn8xLdZCVxrjNnoO7YfqAA8gNsY06GlTufOnWvWrOm9uSTTl73OV2ZnsuyiqewrrGLh3e/yh6/N5CtzMtvPrCgDjG3btoWFS8GxTLA6FJG1He0T+4re7nuVljzy3h5++6qddLTzV+cSHTkg7Vb9juUbc1nytF0+fOVNp3PckKROl6F9b/fpTt/bkX/iX4FFbRzfBywwxszArtr0aMDxhcaY7HB5ELg9Xipq3aTGWwvy8JRYQC3IiqIoSt/jP0mv3tP/LY0DhUAfZOXYo10F2RizCihu4/hHxpgS3+Yn2HicYUt5rRug0cUiNiqCjMQYclVBVhRFUfoYfx/kOo1o0W8YaC4W/ZGeHsu5EnjVb9sAb4jIWhG5uofP1SVKq+3yiKnxTTMqR6ZpLGRFURSl7/G3IKulsf9Q79b7eqzTY2HeRGQhVkE+1W/3fGNMrogMAd4Uke0+i3Sw/FcDVwNkZWX1lFgtKK1pACDF52IBMCIllp263LSiKIrSx/ivuKaWxv5D/QCKYtFf6RELsojMAB4DFhtjipz9xphc33c+8CJwYmtlGGMeNcbMNcbMHTx4cE+IFZSyap+CHOenIKfGcaSsVmcQK4qiKH1KXUNofFVf33qUE369spmCrvQc6mJx7NNtBVlEsoAXgMuNMTv99ieISJLzG/gCsKW75+suFXXWBzk5tsl4Pjwllup6D2U+67KiKIqi9AW1IbIg//LlzymoqCO/vK7PzhlKNueU4e3DJZ/9X3Z08uWxSbsKsog8DXwMTBKRHBG5UkSuEZFrfEl+AaQDfxSRDSLixAgaCnwgIhuBT4FXjDGv9cI1dIpK3yS9xJjmFmSA3FJdLERRwpHExMTG3ytWrGDChAkcPHiQZcuWMXLkSLKzs5kwYQJf/vKX+fzzzxvTnnHGGUyaNIns7Gyys7P56le/GgrxFaVVmk3S60Nrrtc3YjoQBk4/2FXIhQ99wFOrD/TZOfuLBXkg973t+iAbYy5r5/hVwFVB9u8FZnZdtN6hss5aiZP8LMhNCnINU0Ykh0QuRVHa56233uL666/njTfeaJyrcOONN3LzzTcD8K9//YszzzyTzZs347hqPfXUU8ydGxZRJhW7nkiSAAAgAElEQVSlBaGapOcoyANhqeutuWUAHCiq7rNz1rlD8+LTWwzEvrfHJukdK1TWuhGB+OiIxn0jfLGQj5RpJAtFaZNXfwpHN/dsmcOmw7m/bTfZ+++/z/e//31WrFjB+PHjg6a55JJLeOWVV/jnP//J0qVLe1ZORekFahs8JMZEUlnn7lNLo+NtUDsAQsuV+OYepSVEt5Oy5+jxSXra9/Y5A05BLq91kxgTiYg07stIjCEqQjisLhaKEpbU1dWxePFi3n33XY4//vg2086ePZvt27c3bn/zm98kLs6OEp1zzjncddddvSqrMkA5ugV2vmZ9Fgq2gwgcfwFMWWx/t0Kd20tyrFWQ+9LS6ExKr6nv/wpyWY0N75oY03cqT73bS1JMJBV17mM6zNtA7nsHnIJcWecmKeBP4nIJw1Ji1YKsKO3RAWtDbxAVFcUpp5zC448/zv33399m2sBoNMf6MJ8S5ng98OpP4LO/NO1LGgEY2PwsjJwLX7wTsuYFzV7b4CE5Lorcsto+drGw3zUDwIJc6rMgu/t4kl5SrFWQe2SSnva9fc6AW/S9stZNUmxUi/0jUuJ0NT1FCVNcLhf//ve/+eyzz7jzzjvbTLt+/XomT57cR5IpAxpj4OUlVjk+8Qdwyz74+RG46XO4cSssfhjKcuCJL9gh8iAz4mobvCT7nkkh8UFuOHatmx3FUZD70oWl3u0hwWeMO5breCD3vQNPQa5zkxjb0nA+IjVOo1goShgTHx/Pf//7X5566ikef/zxoGmef/553njjDS67rM25xYrSM2z6F6z/B5z2/+C830P8IIiOty4VrgiY9S1Ysg5OvBpW/wnevK1FEXVua0G2v/tQQfY6CnL/tyA7rit96cJSXe8hPiaS+OgIaurdfXbe3mCg9r0DzsWios5NalxLC/LwlFiOltfi8RoiXK37iymKEjoGDRrEa6+9xumnn05GRgYA9957L//4xz+oqqpi2rRpvP322/gvNuTvB5eRkcHKlStDIrsS/tz+ny3szKvk6atPaj9xdTGsuAWyToaFt7aeLjoBzv29dcX46EFIHmmtzS5rn6pt8DYuXNWXFk4zEFws8j6HvK2MqatkAxl9+gJSVecmMSaC+OhIqvrQz9vt8VLr9va4v/VA7HsHnIJcWdtApi+smz8jUuPweA0FFXUM80W1UBQlPKisrGz8PWrUKPbt2wfA4sWLWbZsWav53n333V6WTOlP/O3jTsTJff8PUFcO599jrcVtIQKLfgPlh+G1n8LWl+D8P8CwaT4fZPso7tNJer7vfmlBrq+Gt/8XPvkTYLgHuDUmic8OXwXm9jYnTfYU1fUeMhJjSIyJoLqu7yzIB4qqqap3M21ECq4eMPYN5L53wLlYVNd7SIhp2ZmNSLVKca5O1FMURRnQBE42akFFHnz6F5h5GQyd0rFCI2Pg0qfhooegaBc8egbuve/j9ppGH+S+tCB7fC4W/c6CnL8N/nwafPJHOOEquPZjfhVzE1u9Y1h06F549RZrze9lKutsxKz46Egq6/qujh0reYOu3tdtBpyCXFXnJj46uA8ywOESVZAVRVEGMmU1DW0nWPMEeOrg9Js7V7DLBbMvh+s+g7QxRDz7bUZJHnHREURFSJ+6ADgKcm1/CvO2+y14/AtQVwHfXg7n3w1Dp/CqnMYVDT/h3fRL4dNHYUUn71sXqKpzEx8TQUJMBNV96IMcGWGtxqogd58BpyDXNHiaLRLikJkWD8DB4r5baUdRjhXatagpraJ1d+xRWFnX+kF3Hax5HCYugvTgiya0S0I6fONfGOPlL1H3kCh1xEZG9FlMYo/XNIYeqz2GY/Q2I3c9PH0ZpGbB99+GcQsaD9V7vBhcvJBxDZxyvX3BWf9Ur4pTVWejWHTXB7mz/Uekz62i3qP9Tnf73gGlINe7vTR4TGPoFX8SYyIZnBTDgaKqEEimKOFLbGwsRUVFquh1AWMMRUVFxMbqvIZjifyKNhTkjc9AVQGcdG33TpI+nuJzH2GC5PCF9dcxPK6B0ur67pXZQfxdOfrFQiG1ZfCvb0PCYPj2fyAls9lh53rr3B44axmMng+v/9xOtOwF6t1e6j1eEqMjrQW5iz7IXel7HQV5oFuQe6LvHVCT9Jxhjrio4BMqxqTHs79QLciK4k9mZiY5OTkUFBSEWpRjktjYWDIzM9tPqIQNhZWtKKpeD3z0AAyfCWMXBE/TCcpGnMbtDdfzYOkfeZ4fkLt3DGy4DmZc2hjlojfwnwzYL3yQX/85lOfA996AhIwWh5sUZC9ERMJ5d8Mjp8Lbv4IL7ulxcRxdw7EgV3fxJaQrfW9xVT3V9R6qYiIpjm8ZsWsg0d2+d4ApyLaRBpukBzAmPYH3dqoSoCj+REVFMXbs2FCLoSi9jkvsCnNVrVn8drwKRbvhq//XI5EQqurcvOI9ie+cPgfvmr8yuHYfvHQtvH8PjF9o4ydnTOj2eQLx93U+lpdBBmDnGzYW9ak3wqgTgiZx3EnqnAU7hk6BE66Ezx6Dud+FYdN7VKTKOkdBjiAxJpKqLvogd6Xvvepva1i5LY/LTsziN1/uP4t2hIIB5WLhvNUFm6QHMCYjgfyKutY7R0VRlDBBRBaJyA4R2S0iPw1y/BoR2SwiG0TkAxHpYLgFpdVoEqsfgZQsmHxRj5zHWb01buJCnh1zB9+KuBsufgRSR8G6v8OfT7exlve93yPnc6jzW9mt7li2IJccgJeugcGT4YyfBU3i8ZrGCYnNwuid8TOITYXXfhZ0hcPuUFXnGOPsQiF9qVM419iXEVH6KwNKQXYabbBJemAtyAD71Q9ZUZQwRkQigIeBc4EpwGVBFOB/GmOmG2Oygd8DPT+W3E8JGo84byvsf99aHiN6ZvD1sG/11pGpcaQnRFNY7cbMvBQuf9GuwDduIax7Ev52Abx5e48pcrV+19fXFuS1B0rYcbSi+wUd2WTrxeuGS5+yYfSCUN+atTx+EJx5q72n217uvjx+NFmQI0mIiaTBY/osxrVzjfUD3Ae5JxhQCrLjYtG6BdlGsjhQpH7IiqKENScCu40xe40x9cAzwGL/BMaYcr/NBJrWhlDaIaj1bf0/ICIaZn+7x85zuKSG+OgIUuOjGJQQTb3b2xTxIHkEXPZP+Ml+mPNd+PA+637haScEXQdoZkHuw8VJAL7yp4/44n2ruldIzhqfcuyFbz7fZjQR/3vZ4r7O/o61Pr/xPzY6SQ/hvACMSotnWLKdJNZXeoVzjfV9fF/7Ix1SkEXkCRHJF5EtrRwXEXnAN9S3SURm+x27QkR2+T5X9JTgXaHJcb5tC/K+QrUgK4oS1owEDvlt5/j2NUNErhORPVgL8pJgBYnI1SKyRkTWDOSJmMYYfCPxLa2qXg9seR4mfMFaHnvofHsKKhmRGoeIMNr3/Ln3zZ28vT2Pg0XV1jUgKhYuuBfO+DlsfNqGMqvv3jOqLoQW5G5RVwGv3wp/PR/iBsH3Xm3V77gxi6fpWmsDlcaISFh0J5Qe8K2613WKq+r5dF8x//rsIH9etYfhKbGMH5zACWNse3l3R363yu8oTQuF6Ptwd+noONFfgYeAJ1s5fi4wwfeZB/wJmCcig4DbgblY68VaEVlujCnpjtBdpaq+bReLhJhIRqbGsTOvB4Z/FEVReo9gM8RaPBGNMQ8DD4vIN4D/AVoYKYwxjwKPAsydO3fAPlXr2rI07lsFlXkw/WvdOocxho/3FvHyxiO8tyOf3LJafnD6OADOmTKUhZMG8/gH+3j8A7ucb0yki9lZaXxh6lAWzVrC8KSh8N8b4W8XwjeetfGUu4Bzrcmxkc2syWHN4XXw3Heh9KCN8nH27ZA0rN1szr2MdAk19UGudfyZMPFcWHU3TL0Y0sZ0SBxjDJtyyvjvplze31XIdj+3kagI4SeLjkdEGDUojnGDE7hzxXZe2XyUMycN4eJZIxpfiHoa9UHuOTqkIBtjVonImDaSLAaeNDZY3ycikioiw4EzgDeNMcUAIvImsAh4ujtCd5WadibpAUwaltQz/lGKoii9Rw4wym87E8htI/0zWMOF0gr+PpstrKqbn4PoJJj4xS6VXef28K/PDvHXD/ezt7CKxJhI5h+Xzg3nTOQrs20YqgiX8H/fPZHS6nr2FFSyO7+SnXmVrNpZwB0vf87//vf/s3fncVFV7wPHP4cZGPYdEVlcQUUFVNz3fS3NLTU1f6VmZXt92/fF9s0ss7Rs0VLTMsu0TMvc933HDVFBFNlhlvP744IOCgIyMAjn/XrNC2funTsPzDjzzLnPec4+ekU25ZEun9Hwv4cQs3vD0C+hVvMbigfA08WxQkssTDdaF7vtG/jtcXCvAf+3DMLalviu+Ymit6vj5RzgGn2nwswuMG803L0CDO5FHi/HZGbh1ni+XX+CA2fTcNI5EFvHhyf6NKRJLU/qB7gT6OmMk147QS+E4IeJbZm36RSrDiby4cpDfLjyEF0iApjUqR7tG1zblq4s8r/wqAS57GzV5q2o030lOg1YUS7PLL1OghwR6MGaw0kYzRYcddWqRFtRlJvHZiBcCFEXOA2MBEZb7yCECJdSHs67OgA4jFKkgnW5VsmFKQf2L4HGt4CjS6mOKaXklx0JvLviIPEXs2ge5s17w6MZEBWEcxH9+L1dnWhZ25eWta+UcsQlpbNgazw/bDpJ370ejAt+neczp+I4qzcM+UIb+byB39XT2ZHU7LLXNJdUWnYpuzlICX+9CGs/gnpdYejsUo+a53/x8XJx5EJGLlJKxNUt+nzrwrDZ8P1wrSvG8G+u6UNttkjmbTrJ9FVHOHMpm2bBXrx+W1NuaRqA587ZsHcx7EwEz2DwawDtH4SACABqeDrzUM9wHuoZztlL2czbdJJ5m04y+suNdI4I4Ol+jWgc5Fm6v00R8l+7OWqSXpnZKgMs6nRfiU4DQsXUwV1eKKSIEguARjU9MJolcUmqDllRlMpJSmkCpgDLgf3AfCnlXiHEK0KI/B5kU4QQe4UQO4BHKaS8Qrmi4Aiy1ajqiXWQkwqRgwq5V9FOXchk7KxNPPzjDrxdHfnmrtYsurc9Q1uGFJkcF6VegDtP9m3E+qd78PKtTfj9Uh1iL77BMacI5MK74MT6Uh0vP4nycnGs0BrkUifjq97QkuPYu2DMohsqKbkyguyERV6n5rpBT+j1qtbR4t+3C2zaeuICt0z7j+d+3kOwtwvf3t2aJVM6cEeML54/DIYVz2p9sUPbgNBpyfJn7eCfd7T6dSs1vZx5pFcE//6vG8/2b8zOUykMnPYf7y4/aJPR/FxVYmEzthpBLup0XzxamYX17asLO0BF1MFl5ppx1InLpz4K07CmBwAHzqZe/reiKEplI6X8Hfj9qttesPr3QxUe1E3Muh9wgSTqyF9a94q6nUp8rEXb4nl28R50DoLXBjdldOswHBzKvrCIs6OOO9vXYXhsCJ+tPsqQfx7hF8dnCZg7FucpaxEegSU6TrYxv8RCX6F9kEs1grzlKy1RbTEO+r93wysLXk6QXbRV5bJyzUV/QWl3P5zbA6vfBGdvsgOjeXOrA19vOU+QlzPTR7egf7Oa2gh0bgbMHal11BjyJURZ1aenJ8EfT8Kq12DHdxDcEgKbQqMB4FsPdI44O+qY2Lkew2NDeO23/Xyy6ggr9p1l+ugWhAfeeO6Ro7pY2IytRpCXAOPyulm0BS5JKc+gjW70FkL4CCF8gN55t9lFZq75uvXHAPUC3NA5CFWHrCiKUo1YjyAXGH07+jeEtQOn4idVZRvNPL1oN4/O30lUiBcrHunMmLa1bZIcW3N10vNY74bMf7APH/m+ANmXOPzpCC6lZ5Xo/lcm6TlWaL/c1KwSjiCfWA+/P66N6g78sEzLbudajZYDZF7vC4EQ0P8dqNEY/ngS5zl9eW53XxaG/cRf90YxICpIS46NWVo3kZPrYMjMgskxgHsADJ2llW34R2hJ9MqXYXpreDcC/nwBLh4HtJHtd4dH89X4VlzIyGXQ9LUs3XW96QRFk1KqPsg2VNI2b/OA9UBDIUS8EOLuvFWaJuft8jsQBxwBvgDuA8ibnPcqWr3cZuCV/Al79pCRYyqyg0U+g15HeA139p1Jve5+iqIoStVRaA3ypdOQuA8a9Cj2/pcyjYybtYl5m05yb9f6fD+hDbW8S1ezXFrhgR68M2U06yOfIyJrB0s+uI+tJ4r/iC04Sc+CtPFKckUpUYnFpdMwfyx419aSTIfSlaNcLb8W18s1fwT5+qPY0smdLyO/pr/xTf6nf4rkhrcTm7QYt5lt4MDvcHY3zO6rdTYZ/Bk0G1b4gYSApkPhjgXw8C54cLu2f50OsO4TmBZbYIGSbo1qsPSBTjQO8mTK3O28t+JgqZ8X66TYaKq2DWlspqRdLEYVs10C9xexbTYwu/Sh2V6m0VxsggzQLNiLvw8kFl7MryiKolQ5Bdu85Y0yHv1b+9mg53Xvezoli/GzN3EiOZNpo5pzS3St8grzGg4Ogu63P8T5eQcYe3Au98ysS9dB4xnVOqzI+1hP0pNS65nrpC//zzrrEguLRV47si4lLH0YcjNh/G/g4l3mx8z/Xb1dnIArC4YVJivXzJM/7WLJzgT6NW3Ns0OjtJHns1Ng8WT4IS8VcguA27/VJm6WlG897RIzOu9LwDiYf6fWiaTpEECrT/5hUlueW7yHaX9rkwGnDmlW4oYBBV7DagS5zGxVg3xTyMwx4WYo/leOCvFiwdZ4Ei5lE1zOIwCKoiiK/eXX5bo56a4kGkf+Ao8gqHH1Kt5XHElM544vN5CZa2bOXa1pV//GehOXlf+wDzDN2sf75z6n16LaHDjTkucHRqIvJLnKMVnQOYjLi2blmMzXnZtjK9YJXI7Jcu2E+f1L4PAK6DMVAhra5DHzl30O9NSWoi4qQT51IZN7vt3K/rOpPNGnIfd1rX9lgKxmU5i4EnYvgIzzWl10WRaM8QqGcT9rXTN+mgB6Z2jUHwBHnQNvDm1GkLczH/51mJTMXKbf0QKDvvjBvay8383Z0UFN0rOBatXHLCPXjEsJZg83C9G+te6OTynvkBRFUZRKID9B9nJx1JILswniVkH9Htrp8kLEJaUz6osNmC2wYHI7uyXHADg6ox/xFa6OMM//K75df4w7v9rEpULqfrOMZgx6Bwx5SXFFdbKwTtqyr64FlhJWvwUBjaD1JJs9ZnpeWUeNvAQ5q5Aa5N3xl7jt07WcupjJ7DtbcX+3BteePdYboPkY6PiwbVZTNHjA6PkQFA0LxkPc6subhBA83DOCVwY14a/9idz//bYSJbz5yb+Pq5NKkG2gWiXIWbnmEo0gN6rpgd5BsCv+UgVEpSiKothbdv7EtfzWZwnbIPsSNOhe6P4nkjMY/cVGLBbJvIltaFTTNn1sy8S3HqL/O9RO387PMVvYdOwCI2as5+yl7AK7Jafn4OfudHlUsqISZOvHuWbZ56MrIXGv1j9YZ7uT2/llHTU8nIEro6z51hxOYuTM9Rj0Ohbf14FujWrY7LGL5ewJY37S+ibPG6WdsbAyrl2dy0nyfSVIkjPyRsu9XLTJlxVVW15VVasEOSO3+El6oLXSaVjTg92nVYKsKIpSHWTnXpm4lmuyaMmKcIB63a7Z98ylLEbN3ECOycz3E9uUqS2XzUWPgia3EXXoE1a23IBXyl5GT1/JkcQrnZnOXcqgiWsqnuZkgApr9VZwBPmqZG/dNK2cpYzLeV8tPceEs6MDns55XSysEuRfdpzmrq83E+rryqL72tOgRtEr6JUbV1+t3MI7DL4bCksfBfOVUf8rSfI5nli4E4ul6KQ3f3TcO29CoqpDLptqVoNcskl6oNUhL9tzVk3UUxRFqQbyRzS9XBw5kZwBR1Zq/WuvOp2emm3k/77aTGq2iR8mta0cI8fWhIBbPoacdMJ2fcR8Adm5Tuz4tCGu0d2oZT7NjDMr8CIN/oCfneoh4z+EgC7lHpr1QhgFFsU4s1MrMej5MuidbPqYqdkm3A2Ol+ud8xcM+3JNHK/9tp82dX2ZOS72chs4u3CvAZNWw9+vwfpPtBZww2ZfnqQ4rl0d0nNMvP3HQQI9nXmmf+NCD5M/gpw/ITHXZClR7bJSuGo1gpyZayq2D3K+ZsHepGQaib9Ysr6SiqIoys3LugbZ2XgJTm/V6o+t5JosTP52K0cS05kxpiVNg73sEWrxnD1hzEJ4eA+M+BZj9Fj8HdKotfNjco78w9+yBUtrP8mp2KfwF6nUXTJEq/81l++y00WOIK/7BJzcoeV4mz9mWrYRT2c9vm5OuBv0HDybxhu/7+e13/bTr2lN5tzV2r7JcT5HF+jzOtw6DY79AzM6QsKOy5vv7VKfce1qM/PfOGb9d6zQQ+SXj/i45Y0gqzrkMqleI8i5pRtBBth+KoVQX9fyDEtRFEWxs6xcLZnwc3ci2rgD9LJAezcpJU/9tIt1R5N5f0Q0HcP97RVqyXmHgncoHpG3ktMrhyGz17ItIRMQPFO/EU0ja3Lrf/VZWv9nwla/AXsXweBPtZHzcpBT2CS9lFOw5ydoe69N2rpdLT3HhLuzHp2DIDrUi+83ngRgbNvavHRrE3Q2XsSlzFqM07qmzL8Tvr0N7loOAREIIXjxliYkpeXw6tJ9hPq40LtJzQJ3zS8f8cofQVYlFmVSbUaQc00WTBZZokl6oE3Uc3HUse3ExXKOTFEURbG3bJMZJ50D/m4GOrED6ewNwS0ub/9yzTEWbT/No70iGNIixI6R3hh/dwPf3NOZHo0CCfAw0KauHzU8DaTixtLwV2DkPG355K8HFuioYEuFdrHY8Jn2s83kQu5RdmnZJjyctc/9bg21CXhP9GnIK4MqYXKcLyQW7lyiLZIyfxwYtUmWOgfBB7fHEB3ixSM/7uDQuYIr/uaXj/i7awny1RMSldKpNgly/gunJG3eAPQ6B2JCvdmqEmRFUZQqL9toxuDogJeLns66XWSFdr68ituaw0lMXbaf/s1q8kD3BnaO9Ma5G/TMGt+Kzc/2JDrUG1cnPe4GPUlpOVof3gkrwacO/DgOko/a/PGtRzRzTBbISoFtc7QV57xDbf54AOnZJtzzBsbu6lCXA6/2LbyNW2XjVx9umwFJ++HvVy/f7Oyo4/Oxsbga9Ez8ZgspmbmXt+WPINfw1Dp25PeAVm5MNUqQtRdOSUssAFrW9mHfmdTLybWiKIpSNWUbzTg76gg1HiNQpHChZidAa+c2Ze52IgI9eGdYdOVPrEopwMNAYlqOdsUjEEbNAwcHWPh/Wi9oG8oxmS+3lM42mmHbN5CbDu2n2PRx8hnNFk6nZF1u8ebgIHAu4SBZpdCgJ7S4UxtlTzxw+eaaXs7MGNOSMynZPDBvO6a8Lx4ZudrfN38EOT1b5S5lUf0S5BKWWICWIJstkp2nVLs3RVGUqizbaMHFUUdI8loATvu3IyPHxKRvtgIwc2xsiUv0biYhPi7sPJWCMX9016cODHhf6yyx+UubPlauyXJ5QlxOrhm2fg1h7bTFMsrB1hMXSc8x0aHBTVAvXpQeL4DBHZY+UmASZcvaPrw2uClrDp/nzWVa8pyVa8LFUXe5pZ0aQS6bapQgay8U11J8e2wepk0Y2HZSlVkoiqJUZdoIsgN+Z//jgCWUc/jx9KLdHE5M45PRzQnzq5qTtce1q0P8xSyeW7wHc36P3Sa3aaOXq16HLNt9/uWYLJeTN6+kjXDhqDZCWg7OpWbz1E+78HTW06GBHVc4LCs3f+j3NpxcB78/DpYrZSojWoUyvn0dvvzvGIu2xZORa8bVSX/5i5xKkMumGiXIpS+x8HZ1okENd7Ycv1BeYSmKoiiVQJbRjLc+F5czm/jHEsVHfx1iyc4EHuvdkE7hAfYOr9z0bFyDB7o34Mctp3joh+3aRDohtJ7EOalaCzYbyTFZ8HTRkre6pxaDwQsiB9ns+PmOn89g2Ix1JKXl8NX/tcbDuRK0cSuL6JHQ8RFtxP3HMWC6Unf87IDGtK3ny1OLdrPuyHlqehku11xnqAS5TKpNgpx1AyUWALG1fdh2MuW6q9coiqIoN7dso5kWlr0Ii5F/LVEcTcqgZ+Ma3Nulvr1DK1dCCB7r3ZCn+zVi6a4zTP5uq/Z5WbOpNpK8cYbNRpFz80aQDeRSJ2k1RN4CTrYdmd9z+hLDZqwjPdvE9xPb0rK2j02Pbzc9XoS+b8LB3+DXhyBvGWlHnQPTR7cgwN3A8eRMOtT3v9y1I00lyGVSbRLkjPwSi1KMIAO0qO3DpSwjcefTyyMsRVEUpRLINlpoadwKjq6MGDKcno1r8N7wGBwqayswG7unS33euK0Zqw4mMuqLDSSn50Cnx7RJdFu/tslj5JgsuDrp6a7biZM5Q+teYUPrjp5n5MwNGPQ6FkxuT0yo7fsq240QWq/ork/Dzrmw/bvLm/zcDXw+tiX1/N0YGFULg94BnYNQk/TKqNokyPklFiVt85Yv/9vnluOqDllRFKWqSs7IITpnK9TpxKDY+nx5Zyu8XG/yU/OlNLpNGDPGtGT/mVSGfraOE471oG4X2Ph5gdP6NyrXZMagd2CQfj3peh+o09kGUWuW7T7D+NmbqeXtzMJ729GghrvNjl2pdP4f1OkEfzwNF09cvrlpsBd/P96VZiFeCCFwN+hViUUZlShBFkL0FUIcFEIcEUI8Vcj2D4QQO/Iuh4QQKVbbzFbbltgy+NLIL7Eo7Szkev5u+Lk5sfGYqkNWFEWpioxmC/qUE9QwnoYGPYq/QxXWp0lN5k5sQ0qWkSGfriMu/P8g7QzsXVzmY+eYLHiIbLqKbezx6ga6sncFkVLy+T9HuW/uNpqFeDH/nnYEebmU+biVloMDDJoOSPjl/gKT9qy5G/SqxKKMik2QhRA6YDrQD4gERgkhIq33kVI+IqWMkVLGANOARVabs/K3SSlvtWHspXKjJRZCCDqG+7Pm8HlVh6woiqcins8AACAASURBVFIFnUnJpoPYqV2xWl66umpZ25ef7m2Pi5OO/ssMpHnUh/XTLte93qhck4WYzHU4k8sWj+5ljjPXZOF/C3cxddkB+jcN4ru72+Dt6lTm41Z6PrWhzxtwfI220EohvF0dtQVglBtWkhHk1sARKWWclDIX+AG43rTTUcA8WwRnS1l5DbQN+tJXlXQKD+B8eg4HzqYVv7OiKIpyUzl1MZMuDjvJdg8F33r2DqdSqB/gzuL7OtC0ljevXugOZ3djjvunTMfMMVlonvo3icKPg46Ny3Ss8+k5jPlyIwu2xvNQj3CmjWqOSykHwG5qLcZBWHutFV926jWbo0O92XEy5UrrPqXUSpItBgOnrK7H5912DSFEbaAu8LfVzc5CiC1CiA1CiME3HGkZZeaacXPS39AqSJ3CtSbjaw4n2TosRVEUxc5W7ztNe4e9WOr3gCq2Ul5ZBHgYmDuxLS4tRpIkPdm94HUuZtxYLbLFInHIvkiDtI2scepMVhnO/m+MS2bAx2vYEZ/CRyNjeKRXRLWZTHmZENDnNchIgrUfXbO5VR0f0nJMbD2h5k/dqJIkyIW96or6SjISWCilNFvdFialjAVGAx8KIQrtmSOEmJSXSG9JSrJ9IpqZa7rhb5eBns5EBLqz5vB5G0elKIqi2NOhc2kc3LQCN5GDa+Pe9g6n0nHSO/Dy0FjORIwhJnsTkz+cy3838FmYmm2kl8NmdNLEOteu5JjMxd/pKmaLZPqqI4z6YgOuTnp+vq8Dg2IKHa+rHoJbQrPhsP4TuBRfYFOPxoEEehp4/uc9Wm9rpdRKkiDHA6FW10OAhCL2HclV5RVSyoS8n3HAaqB5YXeUUs6UUsZKKWMDAmzflD0z11zq+mNrncID2HT8wuXJfoqiKPZUgsnTjwoh9gkhdgkhVuad4VOsGM0WHpu/k8GOG5B6V61jg1KoqMGPYdEZGMdSxszayGtL95Xq8/BippFbHNaT7hZGgnNDso2l+yw9kpjO8BnreGf5QQZE1eLXBzoSWcuztL9G1dPjBa02fNUbBW72dHZk6pBmHDyXxid/H7ZTcDe3kiTIm4FwIURdIYQTWhJ8TTcKIURDwAdYb3WbjxDCkPdvf6ADsM8WgZdWRo62BOON6hIRQK7JososFEWxu5JMnga2A7FSyihgIfB2xUZZ+X22+iiHTidxi24DIvJWMFTR1mC24OaPQ8xo+lv+5Z6W7nz53zF6ffAPf+07V6K7pyVrZSznaw/E2UlHVgkT5ByTmemrjtD/4zXEnc/gw9tj+HhkzOXV4qo97zBodTfs/AEuxBXY1L1RIENaBDN99VH2nL5kpwBvXsUmyFJKEzAFWA7sB+ZLKfcKIV4RQlh3pRgF/CBlgWmujYEtQoidwCrgTSmlXRLkLKOp5CPIx9bAL1Ngeht4vwl8PZAOp2cT6pLLb7vPlG+giqIoxSt28rSUcpWUMjPv6ga0s39Knr0Jl/h45WGernsUR1M6xIyyd0iVX7v7EeYcnvZfy7yJbXFx1DHhmy3c9fVm9iVcO1HMmuHgEnRCktVwMAEeBs5eun6HBYtFsnRXAj3f/4d3lh+ke8MarHikM4ObB9/QXKIqrf2D4KCHNe9fs+nFgU3wd3fi0fk7bqispTorUUsHKeXvUsoIKWV9KeXrebe9IKVcYrXPS1LKp6663zopZTMpZXTez1m2Db/kSlRikXYOvh8OcwbC3p/Bpw7U6Qg5aej+mcoyh4dI3vdPqU8NKYqi2FiJJ0/nuRtYVtiG8p7/URnlmrTSCh83J+5wWQeeITZdtKLK8g+HiH6w+Uvahbny24OdeKpfIzYfv0D/j9cw+dutbIxLRhbSDs7v2FIOWEJxDWlKbT83zqfnkF5In95so5n5W07R+8N/mTJ3O25Oer67uw0zxrakhodzRfyWNx/PIIgZDbsXQGbBNRu8XB15c0gUh86l89FfqtSiNKrNOYrMHDM1PAxF73BiHSwYr7VL6f0atJoIjlb/Gc/swmHuOGamvsH2dY1o16VvucesKIpShBJPnhZCjAFigUILbKWUM4GZALGxsdWiJ9S0vw9z4Gwa3wwPw3HpKuj4iLYAg1K89lPg6wGw43ucWk1gcpf6jGodxqz/jvHV2mP8sfcsDWq4c0tULXo0rkGTWp6IS/H4X9zObPMI7nF1oo6fGwAnkzOJrOVJZq6JTccu8Mees/y2+wxp2SYaB3ny0cgYBkbVQlfdOlTciFYTYOtXsGOu9hxZ6daoBiNiQ5jxz1F6N6lZtZbgLkfVJ0E2moquQd7zEyyerNXyjF0MgU2u3ScoCqcJf3D2g040XPMgtNoArr7lG7SiKErhSjR5WgjRE3gW6CKlVKsGADtPpfDp6qMMbRFC5+xVIC0QrcorSqx2BwhtCytfgYb9wbMWXi6OPNorgnu71GfprgR+3HyKD1ce4oO/DuHprOd/nssZA2xw7cITznpq+7kC8PCP23Fx1LE3IRWTReLqpKNv05oMbRFC+/p+qpSiNGo2hdA2sGU2tL3vmi98zw2M5L/D53ls/g5+e7ATzo7VqGf0Dao2X5mzcs2Ft3nbvRAW3qW1S7n7z8KT4zx6r5osbfgG7sbz5Pz+dDlGqyiKcl3FTp4WQjQHPgdulVIm2iHGSifbaOaxBTsJcDfwwsDGsHMehLTSSgeUkhECBn8KZiMsfbTAJhcnHcNjQ1l4b3s2P9uTd4dHc0tUTbpnLGO3aMi9t/VCCEFkkCcjYkPIzDXj7qxnQqd6fHt3a7Y+14v3R8TQoYG/So5vROzdcOEoHFt9zSZPZ0feGhbF0aQM3v/zUMXHdhOqNiPIGTlm3K5OkBO2a2uZ1+4AY34Cx+LXb+/StQ+z9/Zn8p4foM0ECG1VThEriqIUTkppEkLkT57WAbPzJ08DW/Lmh7wDuAML8pKNk1LKW4s8aDXwwV+HOJKYzpy7WuN1cQ8k7oMB105sUorhVx+6PAl/vQhxq6Fe12t28Xc3MKxlCMMc18OuBGoNm02zyEAAHBwEbw+LrtCQq4XIQbD8GdgwA+pfu5R3p/AARrcJ44s1cfSODCS2jjoLfj3VYgTZYpFkGc24WJdYZKXAD2PALQCGzylRcgzQOMiTNUHjSRY+yD+fL/Pa9IqiKDeiuMnTUsqeUspAKWVM3qVaJ8dbT1zki3/jGNU6jC4RAbBtDuhdoNkwe4d2c2qTV5a44rmiPwdz0uHPFyAoGiJvq9j4qiNHZ2g9EQ4vh6TCR4mf6d+YYG8XHl+wU63rUIxqkSBn57U2KdDFYsVzkJYAI+aAe+kWJhnarhEf5g5CnFwPR/8u/g6KoiiK3WTlmnl8wU6CvFx4dkBjyEnTyuuaDgFnL3uHd3NydIauz8DZ3bD/mqURNP++rX3O9n9XTYKsKK0mgM4AGz4tdLO7Qc/bw6I4npzJW38cqODgbi7V4hWbkXNVgnx8LWz/Fto/oNUel1L/ZkGsMPQhWRcAq15Xo8iKoiiV2DvLD3LsfAbvDI/SFpjY8xPkpkPL8fYO7ebWbDjUaALzx8GMTvDni5Ce1yowYTus/xRixkBoa/vGWZ24+UP0SK2+PiO50F3a1/fnzna1+XrdcTbEFb6PUk0S5PzTCK5OerCYYdmTWt/LLteszloizo46RrVvwNvZg+H0Vjj0hy3DVRRFUWxkY1wyX607xp3tatO+vr9249Y5UCNSm6Cn3DidHkZ+D63v0bo6rfsYPmgCH8XAzK7g6gc9X7JzkNVQ2/vAlK11tCjCk/0aUdvPlScW7iSjkH7USjVJkDON2pPv6qTT6s7O7Yber4KT6w0fc1y7Ovzm0IXzTsHw9+tgsdgqXEVRFMUGMnJMPL5wJ2G+rjzZr5F245ldkLANWtypdWRQysa3LvR/G8b9Avdv0pY9DoqGbs/CPf+UuoRRsYEajaBBL9g0E4zZhe7i6qTnnWHRxF/MYuqy/RUc4M2hWiTI+SUWHqTDylehdkdoUrYJA75uTgyNrcvUzEFawl1UDZaiKIpiF1OX7Sf+YhbvDo++0gd/00xtcl7UCPsGVxX5h0Pfqdrcni7/A4+a9o6o+mr/AGQkwtavi9yldV1f7upQl+82nGTN4eqximZpVIsEOb/EInzvNMhOgX5v2mTkYEKneiyxdCDJuQ6sekMr31AURVHs7r/D5/luw0nu7lCXVvntrDKSteV4o0eqhZ6Uqq1uZ+3y79vaCsFFeKJPQ+oFuPG/hbu4lGWswAArv2qRIGfmmggX8QQe/E6blFGzmU2OG+rrSv+oYF7PvA3OH9RmRSuKoih2dSnLyBMLd1IvwI3H+zS8smHrV1ptZpvJ9gtOUSqCENDrFchMhrUfFbmbs6OO90fEkJiWw8u/7q3AACu/apIgm3lSPw+Loxt0e86mx36gezi/GltyzjUcVk/VVhdSFEVR7OblX/eSmJbDByNiriypazbC5llQr5tWo6koVV2t5tB0GKyfDqlnitwtJtSb+7vWZ9G20/yx52wFBli5VYsE2eXcNnrqtpPZ6n5w87PpsRvUcOfWmFBeShsMF49prVUURVEUu/hjz1kWbTvN/d0aEB3qfWXDwWVaT94299gvOEWpaD2eB4sJVr9x3d2mdA+nSS1Pnl28m/PpORUUXOVWLRLkpgc/5rz0xNK6fN4YH+wRzgpzc067RcI/bxc5a1RRFEUpP+fTc3h28W6aBnvyQPcGBTdu/Qo8g7XZ/YpSXfjU0RYP2f4dJBa9MIiT3oH3R8SQlm3imUW7kWp9h2qQIJ9YT/DFTXxmugVX9/JZMamuvxu3NQ/hmdTb4NIpWDetXB5HURRFKZyUkqcX7SYtx8T7I2Jw1Fl9vF08rq162mKc1rtXUaqTzk+AkzusfPm6uzWs6cHjfSJYse8ci7adrqDgKq8SJchCiL5CiINCiCNCiGtW1xBCjBdCJAkhduRdJlhtu1MIcTjvcqctgy+RtR+RqfdiIb0KvmHa2IPdw/nP3JQ9Xl1hzbuQfLTcHktRFEUp6Kdtp/lz3zme6N2QiECPghu3zgHhAM3H2ic4RbEnNz/o8BAc/B3iVl9317s71qN1HV9eWrKXhJSsiomvkio2YxRC6IDpQD8gEhglhIgsZNcfpZQxeZcv8+7rC7wItAFaAy8KIXxsFn1xkg7CoWVs9B8KTm7l+lBhfq7c0SaMSYlDMesM8NPdYMot18dUFEVR4HRKFi8v2av1de1Yt+BGs1E7vRzRF7yC7ROgothbuyngUxd+ewxMRdcY6xwE7w6PxiwlTyzcicVSfUstSjKk2ho4IqWMk1LmAj8Ag0p4/D7An1LKC1LKi8CfQN8bC/UGrPsY9C6s9hqsraJXzh7pGUGGc02muT+krUNfzOkMRVEUpWwsFskTC3ZikZL3hkejc7iqx/3en7UFE1qOt0t8ilIpODrDgHch+Qis/fi6u4b5ufLcgEjWHknm2w0nKijAyqckCXIwcMrqenzebVcbKoTYJYRYKIQILeV9bS/zAuxaADGjSDS7424o/7ozHzcnHu4ZzoenG3G83mhY/wkcWl7uj6soilJdzfrvGOuOJvPcwEhCfV0LbrSY4Z+3oEYTNTlPURr0hMjBsOY9SDl13V1HtQ6la8MApi7bz5HEtAoKsHIpSYJc2JJzV4+5/wrUkVJGAX8Bc0pxX21HISYJIbYIIbYkJdlgycNd88GcA7F3kZZtwt25YiZmjG1bm2bBXow+MRBTQBNYfA+c3FAhj60oilKd7I6/xNvLD9C3SU1GtgotZIeFkHwYuj4JDlV/TrqiFKv3a9rPP5+/7m5CCN4eGoWrk54H5u0g21j9VgouyTtGPGD9zhMCJFjvIKVMllLmF7V8AbQs6X2tjjFTShkrpYwNCAgoSexFk1Jbf7xWC6jZjLQcEx7OjmU7ZgnpdQ68PSyKpGzBG+7PgIsPfD0AVjwH6Wqtc0VRFFvIyDHx4A/b8XMz8ObQZghx1XiM2aSNHgc2hUa32CdIRalsvEOh48OwdzEcX3vdXWt4OvPu8Cj2n0nlrT+KbhFXVZUkQd4MhAsh6gohnICRwBLrHYQQQVZXbwX25/17OdBbCOGTNzmvd95t5St+MyTth5Za04y0bCMeFVBika9xkCcPdA9n9n7B4thvIXokrPsEPmgCP98PZ3dXWCyKoihV0cu/7uV4cgYf3B6Dt6vTtTvs+hEuHIWuT6vRY0Wx1v5BrSf4iue0AcXr6N4okPHt6/DV2uOsOpBYQQFWDsW+a0gpTcAUtMR2PzBfSrlXCPGKEOLWvN0eFELsFULsBB4Exufd9wLwKlqSvRl4Je+28rV1Dji6QdOhAKRnmyqkBtna/d0a0KGBH0/9fop9rabC/Zug+RjYuwhmdIRvBsOpTRUak6IoSlWwdFcC87fEc3/XBrSrX8jqqFkX4a8XIbglNBpQ8QEqSmXm5ArdnoWEbbDv52J3f6pfIxrV9ODxBTtJTK0+C6GV6Gu1lPJ3KWWElLK+lPL1vNtekFIuyfv301LKJlLKaCllNynlAav7zpZSNsi7fFU+v4aV7FQtCW02FAxaL8z0HBMeFVSDnE/nIPhoZHO8XR2ZMGczZ53CYOD78Og+6PmSNoo8qxf8cAdciKvQ2BRFUW5W8RczeXrRbmJCvXmoZ/i1O0gJfzytTdQe+CFcXXqhKIp2ZrtGJKx8RWuFeB3OjjqmjWpORq6JxxZUn9ZvVe+8076fwZgJzccBYDJbyMw1V9gkPWv+7gZmj2/FpSwj47/aRGq2UatJ7vgIPLQTuj0HR1fBJ621Ux3Zlyo8RkVRlJtFrsnCA/O2IyV8PLJ54Ys/bfoCds7TVg8Liqr4IBXlZuCg0wbrLsRpc7aKER7owfMDI1lz+Dyf/1s9BvWqXoK8Yy74hUNILAAZOdrMy4ouscjXpJYXM8a25EhiOpO+2UJWbt5MUIM7dHkCHtgKUbdrNcrTWsK+X+wSp6IoSmU3ddl+tp9M4a2hUYT5uV67w+ltsPwZiOgHXZ6s+AAV5WYS3htqd9Ams2anFrv76NZhDIgK4p3lB9gQl1wBAdpX1UqQL8TByfUQM+ryabW0HO3UgWcFdbEoTKfwAN4bEc3GYxe4e87mK0kygGcQDJ4Ok1ZpRfPzx8HiyWo0WVEUxcrSXQl8tfY4/9ehDgOigq7dITsVFt4F7oEw+FM1MU9RiiME9HoFMpNh7u3F5h1CCN4aGkUdfzemzN1e5euRq9Y7yM4fAAFRIy/flJZtArBLiYW1QTHBvD8img1xydz19WYyc00Fd6jVHCb8pY167JoPn7aHuH/sE6yiKEolcjQpnScX7qJFmDdP92t87Q7ZqTB/LKScgKFfgqtvxQepKDejkFjt/8ypjVq5596fr9vZwt2gZ8aYlmTkmJgybzsms6UCg61YVSdBtli0urN6XcHrymJ96TlaIlrRk/QKc1vzEN4fEcPGY8ncOXsTl7KuKozXOUK3Z+DuFaA3wDeD4M8Xii2gVxSl+hFC9BVCHBRCHBFCPFXI9s5CiG1CCJMQYpg9YrSFzFwT9363FYOjjk9Gt8BJf9XHVsIOmNkFjq2BQdOhdjv7BKooN6umQ2HCn+AeAAvuhJ/uBmNWkbtHBHowdUgzNh27wDvLD1ZgoBWr6iTIJ9ZCykmIGV3g5rRsLbm0Vw3y1QY3D+bjUc3ZcSqF2z9fX/gpipBYmLxG6+O89iOYNwpy0is+WEVRKiUhhA6YDvQDIoFRQojIq3Y7idZyc27FRmc7Ukqe/Gk3hxPT+fD2GGp5uxTcYds3WjcgYzbc+es17/+KopRQcEuYuBq6Pwd7FsF3QyE3s8jdBzcPZkzbMD7/N45lu89UXJwVqOokyDvngZMHNBpY4Ob8EovKMIKcb2BULb4a35qTFzIZ8tk6jp3PuHYnJze45SOtTdHRlTBnoNbbU1EUBVoDR6SUcVLKXOAHYJD1DlLK41LKXcBNew50+qoj/Lozgcd7N6RzxFUrrK55D5Y8oE0ymvwf1OlgnyAVparQ6bXuL0O/hBPrYMH4657Bfn5gJM3DvHl0/k72JlS9eVNVI0E2G+Hg79BkkNYA28qVEgv7TdIrTMdwf+ZNbEtmrplhn61jV3xK4TvG/h+MnAvn9molFypJVhQFgoFTVtfj824rNSHEJCHEFiHElqSkJJsEZwvL957l3RWHGBxTi/u61i+4cfOXWv/WZsPhjoXgVshiIYqi3Jhmw7R1Gw4v11rQFsGg1/H52JZ4uzoycc4WktJyKjDI8lc1EmSdI0zZCl2fuWbT5Ul6laTEwlp0qDcLJrfD2VHHiM/Xs3RXQuE7NuwHt38PiftVkqwoCkBhq1/cUPd+KeVMKWWslDI2ICCg+DtUgP1nUnnkxx1Eh3jx5tAoRP5iHxYzrP8Ufntca+U2+DNt1EtRFNuKvQva3AsbZ8CB34rcrYaHM1+Mi+VippF7vt1Cjslc5L43m6qRIIM2guB17QBKerYJBwGuTjo7BFW8+gHu/DKlA01reTFl7nbeX3Gw8FVqInpfSZJn9dF+KopSXcUDoVbXQ4AivmHfXJLTc5gwZwseznpmjovF2VGn1Rhv/06bjLf8aQjvBcO/0gZHFEUpH71ehqAY+Pk+SDtb5G5Ng714b0Q0206m8PSi3cjrdMG4mVSdBLkIadlG3A36KyMQlZC/u4HvJ7ZheMsQPv77CHd+tYnEtEIm70X01k4nZl2Amd20D4wq8kJUFKVUNgPhQoi6QggnYCSwxM4xlVlmrom75mzhfHoOM8fGEuhh0Fb5+rAZ/HK/Nmlo2GwYPR8cXYo9nqIoZaA3wNBZWkeL5c9ed9f+zYJ4pGcEi7adZtrfRyoowPJV9RPkHFOlqz8ujEGv4+1hUbw2uCmbjl2g/0drWH0w8dod63XRJqSExGofGIsnqw4XilLNSClNwBRgObAfmC+l3CuEeEUIcSuAEKKVECIeGA58LoTYa7+Ii2cyW3hg7nZ2x6cwbWQU0Yaz8P1w+PUh8GsA437RVh5tOvTyQlCKopQz/wbQ8RHYsxCO/n3dXR/s0YAhzYN5/89D/LDpZAUFWH5EZRwKj42NlVu2bLHJsSZ9s4WTFzL54+HONjleRTh0Lo0H5m7n4Lk0hrYI4Zn+jfBzNxTcyWKGf9+B1W+CfziMnKe9kBVFuSkIIbZKKWPtHYc1W773loaUkrfnLcd534+MCjhGjdR9YM4BvYu20lerCWplPEWxF2M2fNYOhA7uW3/d0iaj2cLdc7bw3+EkZo6NpWdkYAUGWjIlfe+t8u84admmSjlB73oiAj34ZUoH7utan192nKbH+/8wd+PJgivWOOig61Nw5xJtmchZveDkBvsFrSiKciPOH+botFt58tDtPKD/mRquOmg9UVv0Y8omaDNJJceKYk+OztDnDUg+rJU8XW9XnQOf3dGCpsFeTJm3ja0nLlRMjOWgyr/rpGQZ8Xat/CUWV3N21PG/vo34/aFORNTw4JnFu+n94b/8tutMwUl8dTvD3X+Ciw/MuRX2/GS/oBVFUUrq9DZYfC/m6W0ITN7MnwH/h3hkD0xcCX1eh+ZjwDvM3lEqigIQ0RfqdILVUyH7+j2P3Qx6Zo9vRU1PZ8Z/tbnoNraVXNVPkDNz8XJxsncYNywi0IMf72nL52NboncQ3D93GwOn/cdvu85gzk+U/eprSXKt5rDwLljwf9edcaooimIXUsKRv2B2P/iiG8Y9i/nW2IO3wr+n+70fIArpRKQoSiUgBPR+TTtj/d8Hxe6uNR9oi5eLI2NnbWLP6ZtvIZESJchCiL5CiINCiCNCiKcK2f6oEGKfEGKXEGKlEKK21TazEGJH3qXCZ1mnZBrxuQlHkK0JIejTpCbLHurMB7dHk5lr4v652+j27mq+WX+crFyz1ubuziVaL+gDS+GT1lozfUvV6UmoKMpNLPkofHubtoRtygk2RTxOi4xpbG78NC+N6obOQU28U5RKrVYMRI2E9dPh8F/F7h7s7cK8iW1xc9IxdtZGDpxNrYAgbafYBFkIoQOmA/2ASGCUECLyqt22A7FSyihgIfC21bYsKWVM3uVWG8VdItlGM1lGMz5uN+8IsjWdg+C25iGsfKwrM8a0wM/diRd+2Uv7N1fy7vKDJKRboOuTcO96qBUNvz0GM7vC8f/sHbqiKNWVlLDtG/isPZzeCv3eZlaLxYzY1YJ2kXX5cGQMel2VP5mpKFVD36kQ0AjmjYQVz0PW9csnQn1dmTepLQa9jtFfbLypRpJL8q7UGjgipYyTUuYCPwCDrHeQUq6SUmbmXd2A1rTe7lIytTXEb8Ya5OvROQj6Ng1i0b3tWTi5HbF1fJm++ggd3/qbSd9sYc1FLyxjftH6F2ZegK8HwA93QNIhe4euKEp1YjbCkge0S1hb5P2beCelC6/+cYQBzYL4ZHQLHFVyrCg3D1dfreVis+Gwbhq811DLL9Z+DIeWQ0byNXep7efGvEltcXHUMXLmBjbEXbtPZVSS9g7BwCmr6/FAm+vsfzewzOq6sxBiC2AC3pRS/lzqKG9QSlYuAD6uVWME+WpCCGLr+BJbx5dTFzKZu+kkP24+xYp956jn78YdbVsy7O71eO34XKsZOvg7RI+GHi+AR+VrvaIoShWSmwkLxsPh5dD5CSydn+LFpQf4dsMJRrYK5fXbmqmyCkW5Gbn6wm2fQdt7Yfu3sH+pVtqZzz8CgluCT10IioI6Hanr78HCe9sx5suN3Dl7E9NHt6iULeCslSRBLuwdrNDmyUKIMUAs0MXq5jApZYIQoh7wtxBit5TyaCH3nQRMAggLs83M5YsZVXMEuTChvq482bcRD/UIZ9meM3y7/gSvLt3HW3840KdJT0bdcgttT3+Nw5bZcGgZ3PIxNB5o77AVRamKcjO0WuNTG2HgB2RF3cljP+7g991nuadzPZ7q16hSr26qKEoJBEVB0DvQ/x3tbHXifu3//MkNELca0uZp+znooWE/glpNmfmmQAAAIABJREFUZME97Rj/9Wbu+W4rrw9uysjWlbdTTUkS5Hgg1Op6CJBw9U5CiJ7As0AXKWVO/u1SyoS8n3FCiNVAc+CaBFlKOROYCVqz+pL/CkW7mFm1R5AL4+yo47bmIdzWPIQ9py8xf8spftmRwK87jQR69mRCZGfGnnkd5x/vgBbjoM9UMLjbO2xFUaoKUy7MH6d9UA6dxbmw/kycuZ7dpy/xbP/GTOhUVyXHilLVuPpCnQ7aJZ8xC+I3a6UXO+bC/l/xrdOJHwa+yOS//Xlq0W4OJ6bzTP/GlfJsUkmKvzYD4UKIukIIJ2AkUKAbhRCiOfA5cKuUMtHqdh8hhCHv3/5AB2CfrYIvzvl0LU8P8DAUs2fV1DTYi1cGNWXTsz20xt21vHhzKzSL/x/znIYit32L6YNmyBXPw6nNYLEUf1BFUZSiWCzwy31aK7dbPmKPTw8GfbKWo4npfDE2lomd66nkWFGqC0cXba2GPq/DYweg3zuQuB/Xr3vxte833N/Kk1n/HWPCnM2kZRvtHe01ih1BllKahBBTgOWADpgtpdwrhHgF2CKlXAK8A7gDC/Le/E7mdaxoDHwuhLCgJeNvSikrLEFOSsvBQVSvEeTCGPQ6+jULol+zIJLScli25wy/7glkwbEoJpuX0H3ddPTrPibTLRRd7HgMsWNVjbKiKKW35l3YvQDZ/QXmGbvy8mfr8Hc3sPDe9jQO8rR3dIqi2IveoK2KGT0S/nkLh40zeMJxCcPqdWRNnJFf3vOie/s21GoQAzWbaav32ZmQ0ibVDDYVGxsrt2zZUubjPL1oF3/uS2TLcz1tEFXVcyEjl7/2nWPNrsO4nfiTwayircN+TOg45tcZU/RY6rQagIuL/V+oilLVCCG2Silj7R2HtTK99x7+E74fjrHJMB4z3seSXWfoFO7PB7fH4O9ePc/iKYpShKRDsOo1OL0NU1Yq5KahRzuLLfXOiLC2ENFP65bh5mfThy7pe29JapBvWklpOdW2vKIkfN2cGNEqlBGtQsk1dWXbyYvM2rUZ34M/0OX8n/j+vYoLKz1Y7dKJc2EDCWjSldi6fgR6qoRZURQryUfhpwlk+jZi6PHhHLxwhsd7R3Bf1wY4VMLaQkVR7CwgAkZ8A2iJ6PnUDN6cu5zUk7sY6X2KLql70P3xJKx4Fhr2h46PQHCLCg2xaifI6bn4u1fv8oqSctI70LaeH23r9QX6kpKaxq5Nv+C4fzHdk1diOPQ7Zw/6sNkSQaaTPx4eXvh4++AXGERQeCzudVpop1AURaleko8ivx5IttFCvzOTyPXUM3diLG3r2XbUR1GUqsvf0423J93GZ/9EMenPQ3i7juLDXno6pv+Z10puCTToCb1egcAmFRJT1U6QU7OpH6DepG+Et6cH3j3HQM8xkJOO6cAynLcvotO53Tjm7MGQkoUuxQLHgY2QgQsHPNqSVPc2vKP60TTUF3dDlX55KYoCJP71EU7p6YzKfpr2rVrxTP9GeDhX/daaiqLYloOD4P5uDejWsAZPLNzJmF9TGdBsKC9NeJiA/d/Cuo9hRidoPRG6PQPOXuUaT5XNYExmC2dTswn2drF3KDc/gzv66OF4Rw+/cpuUXErL4NDRw5w/shn3U6tpmrqGlrtWkbDTl9nmLmzx6o13SGMaB3kSWcuTxkEe1PBQ5RmKUpV873UP6xzb8szoXnQKD7B3OIqi3OQia3ny8/0dmPlvHB/9dZjVBxOZ0n0Qd907FsO/b8DGz7XFSQZNg/rdyy2OKjtJL/5iJh3fWsXUIc0YVYkbUVcpplxSdy3BuHkOvmfWIJAcEyEsMbbmO1MPkvDB391A4yAPImt5EhmkXer6u6FXy80q1UxVmaSXYzJjNEt1xkhRFJs7dj6D13/bz1/7zxHm68pT/RrR1ysehyX3QeRg6P5sqY9Z7SfpJaRkA6gR5Iqkd8KzxTBoMQwuxcP+pdQ9sJQHjy/mAadfORLYn8Vuw/n3goGv/jtOrlmbseqkd6Cevxv1a7jTIMD98s96AW44O+rs/EspinI9Br0OlRsrilIe6vq78eWdsaw5nMQrv+7jvu+30TjIk0e7LaBnZFChSz3bSpV9W0tIyQKglkqQ7cMrBNpOhraTEclHERs+I2L7tzx5ZglPRvTB1GUYR307se+8if1n0jiSmM6e05dYtvsMlryTGkJAiI8L9QPcqevvRpivK7X9XAnzdSXEx1Ulz4qiKIpSDXQKD2DZQ51YsjOBj1ceZuLcvYxqncbUIc3K7TGrbIJ8IjkTIdQIcqXgVx8GvAtdnoSNM2DHXPSH/qChoxsNG/XntqbDoHd30DuRbTRzPDmDI4npHE3M4EhSOkcS09l07AKZueYChw30NFDb141QXy1pDvV1IdjbhWAfFwI9nXFUZRuKoiiKUiXodQ4MaRHCrdG1+HlHAnX93cr38cr16HZ0NCmdYG8XXJzUKGOl4R4APZ6Hbs/CyXWweyHs+xl2LwAXH2gyBOc299CoZkMa1Sy46paUkuSMXE5eyOTUhUxOJGdy8oJ2WXvkPD+lZhfY30FAoKcztbxd8i7OBHu7UMtLux7s7YKni14te6soiqIoNxG9zoFhLUPK/3HK/RHs5GhSOvUD3O0dhlIYBweo01G79Hsb4lZpyfKO72HLLAjvDa0maLNTdVq7KCEE/u4G/N0NtAjzueaQ2UYz8RezOHMpi4SULE6nZJOQov17d3wKy/dkX655zufmpLNKoF0I9namppcLQV7O1PRypqYuDbesBEhNgMxkyLqYd0nRfmach4wkMGaBcND6QHvUBM9a4B8BgU0hMBK8QrV6EUVRFEVRbgpVMkE2WyRxSRm0rutr71CU4uidIKKPdsmYCltmw6aZMHeENqrc+BZoMgTqdAJd0S9XZ0cdDWq406BG4V+KLBZtBDo/aT6dkkVCfhJ9KYv40/EEZx2gmTiGp8NR3BzicBMXrzmOSThidPLCYvACtwAc/Rvj6OKOkIAxE9LPwYl1sOvHK3cyeEKNxlrCXCsGPGqBwR3cA8E7DBzUWQ5FURRFqUyqZIJ8JDGdLKOZprXKt4m0YmNu/tDlf9DhITj6N+xZpF22fQNuAVqyHNIaajQC/4bg5FriQzs4CAI8DAR4GIgO8YLzhyBuDWStA9N2MJ+AvEUXszzrct6zA2sNEZyUgRzN9SQuw5XDaY7EZ0hkVsHRYGdHB2p6aqPOQV4uBAY5E+Zmor48Sa3cY/imH8bl4gEcdi/QRsit6Z210eaARlqCnZsBFhNIizZ6rjNoPy0mbaTaYgKLWdtuTQjtNmkBJ3dw9dP+nr71IaChdnyPmmokW6kYUhZ8reVfL+r2692nsPsXdbzSxJL/byh43Xp7/mNcLf92630tFu3smBDav6UEne7K/S2Wa48rpXYf69usH/N6cV4dc/5xLHnvDYVdz48hP9ar/46FPXZhj3e958L671XY9aJc/TyZzdrfL/93sFhAr7+yLf93Kur5yT+mg9VclPzfuyTXzeZrt+U/n9Z/r/zHsX4s67/h1a+Tq7dfHXdhr5Orfy9r1o9t/VrLj9X6+ba+z9XHKsv/sZIo7jVd1H2Keh1WgCqZIG8/qY38xYR52zkS5YboDdCwn3YxZsHhFVqivGOeNsIMgACfOuBbF1z9tWTQ1e9KYph/m7MXpJyE84ch+QgkH4aTGyH9rHYYrzBtfffYu7SfQdG4OHsRCoQCHa4KzWi2kJSWw5lL2Zy9lM2ZS1mcS82+fH3TsQucS83GlN+Kgzp5l174uepp6n6ROi6ZBBmMhOgvEmqOp2bWEbzi1oLBHZ3BHb2jE0LoIDcTzBfBbLySLOsN2oeEsJ6AmP8GqdP+LrnpcHYXpCdCTuqV3Vz9oGazvEuU9tMv/Loj80rlJYToC3wE6IAvpZRvXrXdAHwDtASSgdullMfLPbCXXoKUFPjggysfsI88Ajt2QEzMtbd7571PF3Yf621eXnDpErz/Pjz66JXr3t7aY5Ymlvzj/vEHtGkDH36oXW/bFvbu1bYPHard75FHYONGiI/X9hk6VNu+fDlkZUFyshaHszPUrQsuLnDgAKSng78/DB4MP/0ECQnaNg8PCAuDEye0+wYGQmgo9OmjHWfHDsjOLhjXww9rMfTtW/Bv9fLLsGwZ5ObCrbdq2z7/XPtdJ026ch3AYABfXzh3DpKStOciPl7bNzBQu+3uu7XfC2D9+tI/F/mxgxa/9d8PtPgLe66ufp66dIF9++C+++Cff2DzZi3Ja9UKunaFd9+FnBwtCfT11bZlZoK7uxZvfiJtsWh/h5dfhhdfhCVLtL9TcdfnzNGev/r14fRp7Tn88UdwdYWaNbXXSJMmsGGD9jjt2sHx43DPPVr8F/POPu7cqf09jh/XYhoyRPtb7NmjvQ50Ou25b90aNm3SnqNDh7Tbr379Ffb3e+kl+PJLCAjQ4k5J0Z63vXuhZUto0QK2b4fU1Cu/p/XzmX+s/L//jfwfK4mXXrr2/5r1a7okr4nC4i5nVfKTceOxC/i4OlLXr3xnOCoVwNEFIgdpF7MJLsRB4j5IOqD9TDmlJb6ZF7TE8HqEDnxq8//snXd4HNXVuN+7u+rNliVX2cgdF2zZxjbdFNMCwUBIDCGNFEICGMhHviSQEEogAQJ8of0ICSWhhBKaAdMM2FTbYFvu3ZYtuaj3tu3+/rg72tFqq3allVb3fZ59dmfmzp0zZc+cOXPOuRx1Aow7FcYtUEZ2JOJYLR0xy4EwwjkMA7qisZ2qpnYqG9upbBzCxqZ2PqxW0+3OriVqrBbBkIxk8rNSGJKZQm5OErkZKeRmJDE4I5nc9GT17fkMSkvyP9CKlCpGunI7VGyDI5vUZ/XfwWVXbWypUDAXxi5Qx2PUsZ09DZo+iRDCCjwCnAmUAV8JIZZKKbeamv0EqJVSThBCXArcDSzuUcGkVDe1v/1NTRs3+L/9TRlk/uYvWaLmPfhg8GVFRcoAW7nSa2wXF8N11wX2iAWSZckStXz1aq/xIaUyUgCam9U2V65URo4ZsyxmmpqgqkoZbDU1al5FhXe/QBlxLS3KSDU4dEh92trUtoy+DbnMx2bePLWfDz7o9RwaMhvTRt9LlyoD0ZhOTYUDB7x9mgeEOXxYfb/2GmzapH5ff70yZiI5FzNneo/X6tVdj9/8+f69gubzdN99yjiuqoJHH1UGaUuLWvbVV8q4bFVlXDvtH6jz5svSpXDLLerbOGehphsb1TmsrlbTjzyivlNSvMdwzRp17QnhPVdvvAGnnAIPPaSmfa8TYz549+nQIe/6eXlqv43jHOz4SalkPHhQfcrKvOsax+rTTzv3+cc/KsP3b3/z/m/Ae/wj/Y+Fg5TqgcH8XzP2z3efzOsE+u9GI0vksss+95kzZ47sLk6XW8687T15wwvru92Hpp9ib5GyrlTKg+ul3LVcyuL/SLnqMSm3L5OycqeUjvZ4S9gJt9stG1rtck9Fo1y1p0q+teGQfOqzvfKed7fJX79cLH/05Gp5wUOfypPu/lBOu+VdedRv3gr4mXHre/LUez+WFz3ymfzJ02vkr18ulnct2yofW7FbvrBmv3xn0yH5+e5KueVgvSyrqpfNpRulu/g/Ur7zWyn/34lS/jFbfe6dJOXbN0q57zMpXa54H6KEBvhadlNHAscD75mmfwf8zqfNe8Dxnt82oArP6KmBPtHo3g7cbimvu84w19TnuuvU9eRvvtsdeJ1Ay3zbRCqL0e+SJV37nDnT/7auvVZ9/C2L1cc4Tv7kWrIk9PGIxWfJkq7bD/dcBJLdLH+45ykvL/p9KSqKbjrQx981Eui6iVbmYMfP7Q7vmvTt0/d/E81/LFydEOyajvS/GyXh6t6EG2r6/S1HuPKZtfz9+3M4e9rwGEum0cSPdqeL2mYHNc12alvsnb+b7VR3TDuobVbzfSt3mLFZBDlpSeSkJTEqpZUT2MAJ7Z8xtXk1SdJOfdpoSgq/Q83Eb5M+aCiD0pM72qcmWXSJvCiJZqhpIcQlwDlSyp96pr8PzJdSXmNqs9nTpswzvcfTpsqnryuBKwHGjBkzZ//+/d3an05I2TV+0/B6+ZsfbB1/y/y1iVSWQP2aY199twU9+4Yl0HEyL4PAxyNWMkD3z0V3z5Xvek6nN1Siu/iey0inw+03knW70zcEPn7hXAu+ffrrK5r/WDiEuqbDWSdGssR0qOloYt2EEL9DvepzAUuklO9FsB8R4XS5eeij3YzMSeWMyfnq4IL6NpImbDZ1sTidallysnc5eJMsLBbVxvgNatpi8Qa/+wvw9010kLJzwD14L1YjkN7oxzdBwNi2WT6jf2Mb4QTfB0sO8H1AMiecmJMQAiV1GM925uQEY7/8bS+QnJEkEXR3OpK+QrXzdxz9/ZlD7VME8qTYrAzPsTI8J7Xr+n6uRSkEze1O6lsd1LU6qG910NDi/W186lodNLSm8U7rSfzHPR+7bOA4xyouc3/E/G330b71Qd50H8/tzrPZIscCyrjOTLWRlWojMyWJrBTPb/M8z2/zdGaKjezUpI52/WIwl0iuq97DnwC+3o5w2iClfBx4HJRzImrJpFSvQ83ccIM3rtF3/gMPeH+Hu8y3TbD/VbB+r7++6zqzZ/vv67rr/M+PJcZx8re/RsiD0a6n8HdMwj0XgWQ3+v2//wusZ33XGx4DB9ecOdFNB8LfNRLouomUQDL4O35Shndd+vbp+7/xd/wDte0OUvq/riK9JmIhSwSENJCjiXUTQkwFLgWmASOB5UKISVLKzkOixYDmdid/eGMzmw7W83DSbmwn3awOcFmZigMzDOL0dG/sj8Hgwd6geoCMDGXgNTZ6ExsaGlSMmRBw8skqXmzzZtUuO1sZKJWVqm1hoUrAaGxU20pKUtsoLFTxS5WVypix2eDGG+HNN1UfDQ0qKL6kRMUUTZ2qkgNqa1Ugfmurkv8nP1H9vfOOCsBPTVUJA1KqxIXk5M7GrBEEHyhQ/pVX1O9vfUvNv/VWFY+VnAznnqv6WbpUyThrVucA/ieeUMf20CG4/XZYtgz27VOyr1jhPxDfN/jeN1nC+GP4SyIIFLAfSUB/uG2DJRv5JtGYkzT8JYDEQp5AnHqqSqRYu9b7oDVnDqK2lszhw8mcP59R4SZGeHC7L6Cxzcnhsk0kr3+KC3e9wiXWT6gYPItteWexK30W+xlBk91FY5uDxjYnRxraaKxw0tTupLHNgcMV2tZKsVlIT7aSnmwjLdnq+W2aTlLTack2MpKtnjY2zzxv+xSblWSbhRSbhRSblRSbpWPaZvUck7Y6FZPdVAHNFaqOdVsD2BuhvUnFsLc3qm+nHaQLyg6A0wEjh6Mqhwg4Uq6SJguOUt/n3afK+PUuZag8UoMC4FCANmVCCBuQA9T0qFTGtWvECppjB424Rt/5xsPmgw8GX2bEQ5q/zTGK/h6oA8liPNAaMaFGTPJDD3WO+TTH1JrjR/3FIBuYY5BTU71Ja6GYObPzcTLkMvbfiDs2YpDNMhvrSwkbN3pldLu90+HIcswx3tjQJUs6xyCHcy5WrAh8/Ix+/Rl55vN0333KOK6qUvGzw4ere62xD2lpne/XwTBk+/prOPbY8KcPHPCeQzMpKeoea+zTtdd6z8eGDWp/g8UghyIvr3P7YMfPMI6NbZljjY1j1dbm7bOoSN0jjBhk6PzQY45BDvc/Fg6GcWy+roz9CfeaMP93o5ElQsLxIM8Ddksp9wIIIV4AFgFmA3kRcKvn93+Bh4V6/7oIeEFK2Q7sE0Ls9vT3ZWzEV7Q5XCy8fyWH69u4YeFEzn/z/c7B4GZ8jWPo+mczB/q3tSnjz0BK1Xd7u3deY6P3d0WF+phxOLrOd7nU/DvvVErMuJhnzFDbdzqVYjt40JsoYMj/0EOqnaH4mpoC7y8oQ87tDh4ob/yWUgX2G3/SefPgs8/UdF4efPKJV4HPnKnkA/X0fPLJKjEAVJLFkiXw8MNeGQwFaw6+v//+zskRoZIIoGvAvtsdfkC/lOG1DdbOXxKNOUnDN+HD3z5FKk8g3G5v9vicOUoBzpnjPV+RJEaYsFgEOelJ5EyaDZNmQ9ufYP1zDP3qHwzddTcLQJXeO+pEmHISjJ6vqoYI9eZAIml3uGi2u2hud9Lc7qSpzUGz3Ulzu4umNgctdmVMt9rdtDpctDvstDpctDpctLW4qXY4KHO4abW7aHO4cPqEiwgfZ2iycDJSVDFaVFLQ8alilKgij3qShP/ncjtJtFnSabek0WZJx25Jx2VJRgorOAchG5rUlvJHYKmswFabhHVwNtYmgZU2kpvt5AU+Qz3FV8BEIcRY4CDKEfFdnzZLgR+i9O0lwEeyp2PqhFAPdsZNTQjvTdhsHJvnG9URQi3LyVHVDcwP6AsWqDb+ruNgshj9zp/f+UF39erwq1ikpMS+isWpp6rj5CuXIVtubudjddttSkebq1iUl6t9NU9DeFUsLrpIOWHAa7REci4M2Y1j61uFYfBg/284fc/T1Kmdq1ikp3e/isUFF6h2xvEIZ/pf/1JyhKpiYejt1auVg2TRIrWeYQRu2KCOQ6yqWJiPnxBq30eNCr+KhcXS+XwafRnHP9L/WDgIoeQOdE2He034k7uHCRmDHE2sG8poXiWlfNYz/wngHSnlf4NtszsxyM+s2s+0kdlqlDXfJ5b+gvGEJ6X3CToUvk+NvhheAMPo83dczE/BwWTz9yS8ZIn/TO9AMkDnp8NA/Zv/GIHWMbcJtdxMuG0DtTNeI/oeL/PTfjj7FKk8gfB4jDtty/CK/OpXXeX0PR+RICXU7oOSz7yfhoOR99PDuIWVppTh1KeMoD55OPW2XBosg6mzDKJGDKKGbKpkDnXudFpcArtL4nS5cbokDrf6drrcONwSZ0MjTrsDh8WK02LD6VMW77VfnsAsP6M7hiKaGGTP+t8A/g8V+vaklPJOIcTtqASUpUKIVOAZYBbKc3yp4egIRDT5H50IFpoUKFwlnGWBvrsji/EbuoZKmY0Qf/dIc3iZbxiaELoOsu9xMk8Hwvc86TrI4R0/87bN15qugxyQcHVvOAbyt4GzfQzkeVLKa01ttnjamA3kecDtwJc+BvIyKeUrfrYT20QR3z9Gf8D8h3S5wktQCJXI4BvU7u+4hJN8EixxwLgRhCuDPzm6k0QQat+CBfSH2zZQO3/HMVTCRyzkCYQ57tvYtqEwI02MiAQpobYEDq1XIQy++qTLdvzcEGK13JIEOQVqdMKsEbGr7+xzDKXLhVOijGi3m7Qkq/8yeyGI1kDuCWJmIGs0Gk0fJZZJetHEuoWzLgAxTRQxPKX9DeMVueFBDodQ7cxB8IGOi1HLMZRsgfpfuTJ8GcDrMQ3WfzhJBOY2oZabCbdtoHaBElF8kzRC7VOk8gTC8CD7btvwIPsSLDEiUoRQg7Xkjo2+r76In3MjfvUrkh54wJNgqIcJ12g0moQkVB04lBG9FxiLGox3AzDNp83VwGOe35cCL3l+T/O0T/GsvxewhtpmVLU4A9Xbi+UnJSV2fVks6js1VX3PmNG5/uOQIf7XmzEj/G0sWdK1PqW/WpegaiqaayZec4132pDLmDbXfZw5U7U1pvPyOk/7q+Fp1M00+isq6lwr1V/tTWOebx/Blgeq9xisbbB25uPjexxnzpTS6Qy9T5HKEwh/x8/3fPmTM1j9SY0i2nMTAqKog9xTn5jUQdZoNJo+TLi6N6QHWUrpFEJcgyo6b8S6bTHHugFPAM94kvBqPEYynnYvoRL6nMDVsgcqWHTCHBAuZc9UsZg/v2erWNTXq2D7UFUsUlLCq2IxeLCaDhQo76+KBah+hgzxJi/4q2JRVaWO7bp1qorF3LneKhYPPqi26xuI7xt8b06OCJVE4C9g32IJP6A/3OD/YO38JdGYkzR8Ez4C7VMk8gTCYlHnwYhft1i8iXq1tSrJJNzECE1n+kiiiEaj0Wh6n4QbKKQD835Jqesg+x4X30B537a6DnLwdv6Oo/k4hLtP3ZHdH4GSTQKdb23chU+05yYAOgZZo9Foep+YDhTSL/H10pmNB5uta2KbvyQz3zZJSZ379F3HPB3sBmr0a7Q3ZDPL6NuXP/n8zQ914w5mPJvxTewyZ1r7fvse63COg+983+35Wy+U7OHuWyRtA7XzN787+xSpPIEIdb66269GH0ONRqMZgPSzMg8ajUaj0Wg0Gk3Pog1kjUaj0Wg0Go3GRJ+MQRZCVAL7o+giDwhjlI1+RSLuEyTmfiXiPkFi7lc89+koKWV+nLbtlxjo3liTiNdcIPS+JiZ6X/seYenePmkgR4sQ4uu+lvwSLYm4T5CY+5WI+wSJuV+JuE+JxEA6P3pfExO9r/0XHWKh0Wg0Go1Go9GY0AayRqPRaDQajUZjIlEN5MfjLUAPkIj7BIm5X4m4T5CY+5WI+5RIDKTzo/c1MdH72k9JyBhkjUaj0Wg0Go2muySqB1mj0Wg0Go1Go+kW2kDWaDQajUaj0WhMJKyBLIS4QwixUQhRLIR4XwgxMt4yRYsQ4l4hxHbPfr0mhBgUb5ligRDi20KILUIItxCiX5eIEUKcI4TYIYTYLYT4bbzliQVCiCeFEBVCiM3xliVWCCFGCyE+FkJs81x718VbJk1XElXn+SOR9GAgElE/BiIR9WYgElWfJqyBDNwrpZwhpSwC3gJuibdAMeADYLqUcgawE/hdnOWJFZuBi4FP4i1INAghrMAjwLnAVOAyIcTU+EoVE54Gzom3EDHGCfyPlHIKcBxwdYKcq0QjUXWePxJCDwYigfVjIJ4m8fRmIBJSnyasgSylbDBNZgD9PhtRSvm+lNLpmVwFFMRTnlghpdwmpdwRbzliwDxgt5Ryr5TSDrwALIqzTFEjpfwEqIm3HLFESnlYSrnO87sR2AaMiq9UGl8SVef5I4H0YCASUj8GIhH1ZiASVZ8mrIEMIIS4UwhRClxOYniQzfwYeCeEXFWIAAAgAElEQVTeQmg6MQooNU2XkQBKItERQhQCs4DV8ZVEEwKt8/o3Wj8OABJJn9riLUA0CCGWA8P9LLpZSvmGlPJm4GYhxO+Aa4A/9qqA3SDUPnna3Ix6pfFcb8oWDeHsVwIg/Mzr928uEhkhRCbwCnC9z1snTS+RqDrPHwNEDwZC68cEJ9H0ab82kKWUC8Ns+jzwNv3AQA61T0KIHwLnA2fIflTEOoJz1Z8pA0abpguAQ3GSRRMCIUQSSpk/J6V8Nd7yDFQSVef5Y4DowUBo/ZjAJKI+TdgQCyHERNPkBcD2eMkSK4QQ5wC/AS6QUrbEWx5NF74CJgohxgohkoFLgaVxlknjByGEAJ4Atkkp74+3PBr/aJ2XUGj9mKAkqj5N2JH0hBCvAJMBN7AfuEpKeTC+UkWHEGI3kAJUe2atklJeFUeRYoIQ4iLgISAfqAOKpZRnx1eq7iGE+Abwf4AVeFJKeWecRYoaIcR/gFOBPKAc+KOU8om4ChUlQoiTgE+BTSgdAXCTlHJZ/KTS+JKoOs8fiaQHA5GI+jEQiag3A5Go+jRhDWSNRqPRaDQajaY7JGyIhUaj0Wg0Go1G0x20gazRaDQajUaj0ZjQBrJGo9FoNBqNRmNCG8gajUaj0Wg0Go0JbSBrNBqNRqPRaDQmtIGs0Wg0Go1Go9GY0AayRqPRaDQajUZjQhvIGo1Go9FoNBqNCW0gazQajUaj0Wg0JrSBrNFoNBqNRqPRmNAGskaj0Wg0Go1GY0IbyBqNRqPRaDQajQltIGs0Go1Go9FoNCa0gazpMwghSoQQrUKIRiFEnRDiCyHEVUKIsK5TIUShEEIKIWw9LavPdk8VQpSFaHOrEMIhhGgyfcb1lowajUYTjETWv552s4UQn3h0b7kQ4rrekE/Tf9EGsqav8U0pZRZwFPAX4DfAE/EVKWa8KKXMNH32xlsgjUajMZGQ+lcIkQe8C/wdGAJMAN6Pq1CaPo82kDV9EillvZRyKbAY+KEQYjqAEOI8IcR6IUSDEKJUCHGrabVPPN91Hi/B8UKI8UKIj4QQ1UKIKiHEc0KIQf62KRQPCCEqhBD1QoiNpu2mCCH+KoQ44PE+PCaESBNCZADvACNNnuGRPXZgNBqNpodJQP37K+A9KeVzUsp2KWWjlHJbjA6XJkHRBrKmTyOlXAOUASd7ZjUDPwAGAecBvxBCXOhZdorne5DHQ/slIIA/AyOBKcBo4NYAmzvL08ckT/+LgWrPsrs984tQ3odRwC1SymbgXOCQyTN8KED/3xRC1AghtgghfhHBYdBoNJpeJ4H073FAjSdspEII8aYQYkxkR0Mz0NAGsqY/cAjIBZBSrpBSbpJSuqWUG4H/AAsCrSil3C2l/MDjNagE7g/S3gFkAUcDQkq5TUp5WAghgJ8BN0gpa6SUjcBdwKUR7MNLqBtEvqevW4QQl0Wwvkaj0cSDRNC/BcAPgeuAMcA+j+waTUB6NZheo+kmo4AaACHEfFRs3HQgGUgBXg60ohBiKPAgygOShXoorPXXVkr5kRDiYeARYIwQ4jXgRiAVSAfWKl2tugas4e6AlHKrafILIcTfgEvQSlqj0fRt+r3+BVqB16SUX3nkug2oEkLkSCnrI+hHM4DQHmRNn0YIMReloD/zzHoeWAqMllLmAI+hlCWA9NPFnz3zZ0gps4Hvmdp3QUr5oJRyDjAN9Urv10AVSsFOk1IO8nxypJSZQbYbChlMDo1Go4k3CaR/N/q0M35rHawJiDaQNX0SIUS2EOJ84AXgWSnlJs+iLKBGStkmhJgHfNe0WiXgBszl07KAJlTiyCiUwg20zblCiPlCiCRUrF0b4JJSuoF/AA94PCIIIUYJIc72rFoODBFC5ATpe5EQYrAnEWUesAR4I8zDodFoNL1Goulf4CngIiFEkaf/PwCfSSnrwjgcmgGKNpA1fY03hRCNQClwMypm7QrT8l8Ct3va3IKK7QVAStkC3Al8LlQdz+OA24DZQD3wNvBqkG1noxRxLbAflSDyV8+y3wC7gVVCiAZgOTDZs93tqFCJvZ7t+suivtSzfiPwb+BuKeW/wjoiGo1G0zskpP6VUn4E3OSRoQKV6Pdd33YajRkhZXfeDms0Go1Go9FoNImJ9iBrNBqNRqPRaDQmtIGs0Wg0Go1Go9GY0AayRqPRaDQajUZjQhvIGo1Go9FoNBqNiT45UEheXp4sLCyMtxgajUbTY6xdu7ZKSpkfbznMaN2r0WgSnXB1b580kAsLC/n666/jLYZGo9H0GEKI/fGWwRetezUaTaITru7VIRYajUaj0Wg0Go0JbSBrNBqNRqPRaDQmojKQhRDnCCF2CCF2CyF+G6TdJUIIKYQ4NprtaTQajUaj0Wg0PU23Y5CFEFbgEeBMoAz4SgixVEq51addFrAEWB2NoBqNJj44HA7Kyspoa2uLtyj9ktTUVAoKCkhKSoq3KBqNph+hdW90RKt7o0nSmwfsllLuBRBCvAAsArb6tLsDuAe4MYpt9Uta7E4+2VlFflYys8cMRggRb5H6JTuONLK7oonjxuUyJDMl3uL0S9ocLj7dVUVWqo35Y3MjuhbLysrIysqisLAwbtewlJKmdicZKTYsEchgd7oASLZZe0q0oEgpqa6upqysjLFjx8ZFBk3/RkrJqr01HDcusv+tpu/y+e4q0pKtzB4zOGi7vqB7+yux0L3RGMijgFLTdBkw39xACDELGC2lfEsIEdRAFkJcCVwJMGbMmCjE6huUVDVz+T9Xc7CuFYBvzS7gnktmYLXoizwSHvpwF/d9sBOA7FQbT/xoLnMLc+MsVf/icH0rl/9zNXsrmwE4e9owHv7ubJKs4UVYtbW1xV1BN7Q52V/dzIicNPKzwn9I2n6kEYAZBYPCXqfd4eJwfRsFg9OwhXmMAiGEYMiQIVRWVkbVj2bg8ubGwyz5z3ru/tYxLJ7b/++NA51Pd1Xy/SfWAPCfnx3H8eOHBGzbF3RvfyUWujca7e/vjMmOhUJYgAeA/wmnMynl41LKY6WUx+bn96nSoBHjdLm59j/rabE7eeqKuVxz2gReWVfGYyv3xFu0fsUnOyu574OdXFg0kpd+fjx5WSlc+e+vqWxsj7do/Qa3W3L1c+uoaGjn79+fw2/OOZr3tpRz73s7Iuon3gq6sc0BgFvKEC39IyNYr77NQUObg0N1sXmt2VPHTueADAz2V6kH2wM1LXGWRBMLHlu5h6wUGzlpSTy6YnfI9vHWvf2ZaI9dNAZyGTDaNF0AHDJNZwHTgRVCiBLgOGDpQFDS//pyP5sO1nPHhdM5bfJQ/uesSZw7fTgPfbSLqiZt3IVDm8PF717dxPj8DP7yrRnMG5vL49+fQ1O7k799uDPe4vUb3tp0mHUH6rj1gmmcPW04vzh1PJfNG80/P91LiefG2x+wO91AZAay2+1t63JHYFh7mtpd7vDX6WVMOSDnAlOBy4QQU/200zkg/RyX55qPJLRI0zepbGzniz3VXHHSWL47fwxf7Kmmttkeb7E0AYjGQP4KmCiEGCuESAYuBZYaC6WU9VLKPClloZSyEFgFXCClTOgq9Hanm8dW7uHECUM475gRgHqKufHsybQ73fzj071xlrB/sLT4EAfrWrn1gmmkJqn40QlDs7hkTgEvfV1GRYNOWgiF0+Xmvvd3cPTwLC6eNapj/g0LJ2GzWni8H1yL1dXVFBUVcd5pJ3D67MnMOno8RUVFFBUVYbcHv7E4TAZuuzO4sbt8+XJycnIoKirixLlF/OPBv+KWsmP+rFmzmDRpEgsWLGDZsmUd6/3+979n1KhRHTLdfPPN0e1w+HTkgEgp7YCRA+KLkQOi/zD9FOPZTnsS+z+r91UjJZxx9FAWThmGyy1Ztbc63mIFxNC/RUVFDB8+vJOuC6V/I8Gsf6dMmcKdd97ZaX689G+3Y5CllE4hxDXAe4AVeFJKuUUIcTvwtZRyafAeEpN3Nh+msrGdey6Z0Umhjc/P5PwZI3n2y/1cd8ZE0pP75CCGfQIpJU9+vo+jh2dx0oS8TsuuWjCeF78q5akvSvjNOUfHScL+wae7qthf3cKjl8/GYop9H5qdyiVzCvjv12XcsHBSRDG9vc2QIUMoLi5m+5EG/nbPXQzOyeauP97UqY2UEiklFkvn532zB9gZhjf4tNNO4/XXX2f7gQoWnjyPM846l0zTfIB169Zx0UUX8e9//5sFCxYA8Otf/5rrr78+yj2NmJjlgCRa/keiYYQHWbWB3O9ZtbeazBQb00Zm45aQYrPwVUkt53qcaX0NQ/8C3HrrrWRmZnLjjZ1VSSD9GymGnm1qamLGjBmcf/75neZD7+vfqPZISrlMSjlJSjleSnmnZ94t/oxjKeWpie49Bnh21X7G5mWwYGLXOOrvzR9Ds93FB1vL4yBZ/2HdgVq2H2nkihO7JiccNSSDBZPyeWP9wU6v0DVdeXltKbkZySycMqzLsitOKMTucvPWxkN+1ux7uN3Gtzrnu3fvZvr06Vx11VXMnj2b0tJSBg3yJuK98MILXH3VzwGorqzg8ku/w7HHHsu8efNYtWpV0G2lpGcwZfpMSkq6ethnz57NzTffzMMPPxyjPes2McsBSaT8j0TECA/S+d39nw2l9cwcnYPNaiHZZmFmwSDWHaiNt1gRE47+/elPfwpAeXk5F198cdj6NzMzk9mzZ7NnT9ecrd7Wv9qNGUOO1LfxVUktN541qZPHzmBuYS6jBqXx2vqDLCoa5acHDcDbG4+QbLNw3oyRfpdfOGsU171QzFclNcwfFzgDeCBT12Lng63l/OD4QpJtXZ+DJw7LYsqIbJZuOMQVJ4ZfAue2N7ew9VBDLEVl6shs/vjNaQGXSyk74jBdphjkrVu38tRTT/HYY4/hdDq7rOf22It/ueW33HDDrzjn9FMoKSnh/PPPZ/PmzQG3V1FRwebitVz7v79H2uu6LJ89ezYPPfRQx/S9997L008/DcBf//pXFi5cGHyHY0MkOSAAw1E5IAkf5pZoGH4Af/cUTf/B7nSz40gjV5xU2DFvyogsXl5bhtstQ57feOjeYITSvwZLlizhf//3fznuuOPC0r+VlZWsWbOGO++8k9LS0i7Le1P/agM5hry7+TAA50z3/7rEYhFcOGskj63cS02zndyM5N4Ur1/gdkve2XyYBZPyyUzxf3meOXUY6clW3thwSBvIAfhoewUOl2RRkf+HDIALZo7k7ne3U1rTwujc9F6ULjKk9L5mNr8zGD9+PHPnzg2yovpa/dkKbty/h996bkC1tbW0traSlpbWqfnHH3/MrFmzsLskV173awrHT+TwljV+5On85iJOIRYdOSDAQVQOyHeNhVLKeqAjPkkIsQK4URvH/Y+Oa7+bFVw0fYOd5Y3YXW6mj8zpmHf0iGxa7C7KalsZM6Tv6mB/hNS/HpYvX86OHd6qSaH0r8Vi4Q9/+AOTJ0/2ayD3pv7VBnIMeWfzESYNy2TC0MyAbc6eNpxHPt7DJzsruXCW9iL7UlxWx+H6Nv73nMkB26Qn2zh1cj4fbatAXih18ooflm8rZ2hWSidl7Mv5M0Zw97vbWb6tPGwvcne9DdFgeI2FUMayQUZGRsdvi8XSSXG2tbV1tJVS8vaHn3BUfuBjAd5Yty2H6pFSVcxw09UoWb9+PVOmTIlij6JH54AMHJweF7I9RKKppm+zu6IJgMnDszrmGb+3H2kIaSDHQ/cGI5T+NZBSsmbNGpKTgzsEzbHGwehN/RtdVLWmg4Y2B1+V1HDW1OFB200fmUNeZjIf76joJcn6Fyt2VGIRcPrkrnGzZk6dNJQjDW0dA0FovNidbj7ZWcUZU4YFfW03OjedcfkZrNjRtwex8MZgKgvZX6k3i8XC4MGD2bVrF263m9deew2Jeng6/uRTeerxxzraGkkngXBLOgZRcfvYJMXFxdx1111cffXVUe5V9OgckIFBm0ONBtneh8sOakKzu6IJq0VQOMRrWE4apgzkHf38PuZP/xosXLiQRx55pGM6lP4NRm/rX20gx4gv91TjlnDyxLyg7SwWwSmT8lm5szKy2qwDhE93VTKjYBA56cHHTl8wWSUT9XXjLh58VVJDU7uTM44eGrLtgkn5rNpb3XET7ou4fbL4A9VCvvvuuznnnHM444wzKCgoQEq1zi1/vo81q1cxY8YMpk6dyj/+8Y+A2zIyspOs3m0Zr/4mT57MkiVLePTRRzsyqDWanqbVMJAd2kDuz+yuaOKo3PROOSGZKTZG56axvbx/G8jQVf8aPPLII3z++edh6V9/xFP/6hCLGPH57irSk63MCjG2OsCpk4fy6rqDbCyrC6v9QKG+1cGG0jquOW1CyLbDslOZMiKbFTsq+MWp43tBuv7DF3uqsFoExwUZwtRgwaR8nvq8hFV7qzl1cmiDOh4YD5I3/u731LbYkW6YMGFCF0/E4sWLWbx4ccd0aU0Lze1O8vLzefTJZynMyyAQCxcuZOHChR3bsnk87wtOO4P6+vqA6/3pT3/q9n5pNOHQ4UHWIRb9mt2VTYz3E345eVh2v/Ag33rrrR2/w9G/Bvn5+fz3v/8N2rehf/3Nj6f+1R7kGPHZrirmj831WzHAl+M9iWWr99X0tFj9ii/3VOGWcJKfEnn+OGnCENaX1vVp72c8+HJPNTMKcgImOZqZP3YISVbBl324WL3xosUwWsMdTc8tVWa4RYiI1gGwGiEWOjFKE2da7Uq/6Rjk/ovD5aakqtlvftLEYZnsr27uNLCRpm+gDeQYUN7Qxt6qZk6cEDy8wiA/K4Xx+Rms7sNGSTxYva+G1CQLRaMHhW4MzBs7BLvTzcaywE+YA43mdicby+o7HsJCkZZsZUbBINb04Ye1joESrJEZyC63xCIEVkv4BrKxLa8xHqm0Gk1s6QixcGpHQH/lQE0LTrdkQn5XA3l8fiYOl6S0piUOkmmCoQ3kGLBuvyr0fWxhbtjrzBs7hK9LanUcsol1+2uZWTAoLC88wNxCFZ6iHzS8fL2/FqdbclwE5e/mFuayqay+w1PV1+jqQQ5/PYtQn3CdM0bfVs+2dGktTbxp9cQe6xCL/otRwcKfB9mYZ7TR9B20gRwD1u6vJcVmYeqI7LDXOW5cLo3tTrYdjm3h7/5Kq93FlkMNzDkq/JjsQenJHD08izUlfdf72dusLanBIgjvOLbWwbJfc+22y7jT8nc27ew6clFfoCPswRJZ2INbKg+yRYiwDV239iBr+hjtjviEWKzcWRnWEO39nS/2VPHgh7t6NFTPMH7H5XfNgzDm7als7rHta7qHNpBjwLoDtcwoyAnb8wnKa2esq4GNZXU43TIiAxnUcVy7X3viDdaX1jFpWBYZoeKPS9fAw3Phq3+SkjuaC62fMW7ZYmjrew9sXcMeIotBFiICr7PbMMYj25ZG01MYsam9GWKxam81P3xyDf+3fFevbTMelFQ1891/rOb+D3Zy25tbe2w7eyqaGJ6dSlZq1+pM2alJDM1KYU+l9iD3NbSBHCXtThebDzYwO8JqFCNyUsnPSqG4tOtQtgORtZ4HhUirehSNHkSL3aWVC8q421AaRmWUulJ47tuQkgk/+xjbj5byh8w/kttSAsv/2CuyRoJv2INvbeJg66kQC4H0M+BHqG0Jwvc8azQ9hd3V+yEWVU3tAAmvV5/+ooRkm4WFU4bxytoyqj37HWt2VzZ5wyvcLji8ATb9F7a9BSWfMSkvNeGPdX9EG8hRsvlgA3aXO2LDTgjBzIJBbNAGMqDij8flZ0Q8/PZMT0KfftCAfdXNNLQ5mRUsyVFKWHotuBxw+X9hZBEA7sIFvCTORq79F1T3rVALt5QcN7mgw0B+7913mDhxIgcOHODWW29l1KhRFBUVMXHiRC6++GK2blWeICkl3/nmOZw8dybfOvMkioqKuOSSS0JuC/CEZugQC038MUIrejPEwhKi5ngiIKVk+bZyTpmYz/ULJ2J3ufloe+wH8JL7PuWcyie5ru3/KcfEPWPh76fAKz+BFy+Hp8/jvtprcFXs7JMP5JmZ3rjpZcuWhaV7AU499VQmT55MUVFRWLq3L6IN5CgxEvRmHxVe5QUzRaNz2FPZTEObI9Zi9SuklKzdX8ucbtSEHpeXQVaKjY1l2kBef0Adg6IxQa7F4udh78dw1u0wxFs/euboQdzX+k2kNQk+ubenRY0I455hEbD6s5X89sYbePfddxkzZgwAN9xwA8XFxezatYvFixdz+umnU1lZ2bHeo/94ipfe+5T169eHrMfpNm1LRFAeTqPpKRwudQ128SDXlcJ/LoM7hsL909T/tiU2+RjGAJyJfPnvq2qmrLaVUyfnM21kNsOzU2M78FRzNfz3J4h/nc9VvMoxDSug/iBMXQQXPQ6/XAU//wQu/ic5rjqelb+jofiN2G0/xnz44Ydce+21Yeleg+eee47i4mKKi4tD6t6+iDaQo2TdgVpG56YxNCs14nUN7+emAV6mbH91C7UtDmZHGH8MamTCYwpy2FA6sI8hQHFpLZkpNsb7KSUEKK/xyr/AqDkw58edFs0syKGSQRwYczFsflUl8PURDCP1s88+47bfXMdzL7/G+PH+B4dZvHgxZ511Fs8991zHesZg2+Hc7A0PjvB4kBPZQND0D/x6kHe+B4+dCPs+hWOvgPzJ8NGfVF7BiruhZm+UW038JFXjrePcwlyEEMwbmxu7nKD6MnhiIWx9g/0zrmdq+5OsW/w1/PILuOAhmLkYhk6BETNhxrfZ8I032CdHkP3Gj1TYRR/j008/5Wc/+xlvv/12SN37/PPP97J0PYceSS9KNh2sD7tury8zRnnDA8KtoZyIbD6kjNtjRuV0a/0ZBYN44rO9tDlcpCZZYylav6K4tI4ZBTkdoQhd2PwK1B2Ac+8BS+dn46OHZ5NstfBx2llc4XoetrwKx/64ax/v/BaObIqt4MOPgXP/EnCxlOCwt3PRhRfy+ItLGT9xctDuZs+ezfbt2zkdEAJ++bMrsCWnkJJk5awzz+TeewN7yM0hFtqDrOkLGIZxR5LegdXw4veUgfXtpyF3nJp/eCO8fzOs+LN6EJ79Azjt95AZ3sBLZrzXfeJe/8WldaQnWztig4tGD2LphkOUN7QxLDtyh1cHjlZ45mJoroIrlvHxgXza2Oq3BrJBwdhJnG6/hc+H3Ufeqz+DK5bByFmdG8VB9wK0t7ezaNEiVqxYwdFHHx20raF7DS6//HLS0tIAODOE7u2LaA9yFNS12CmrbWXayO4ZdjnpSYzLyxjw8bObDzaQZBVMGpbVrfWLRufgcMkBXTKvzeFi++HGwA9rbjd8ej8MnQYTz+6yONlmYcqILN6rGQZDp6pQjD6CW0pstiROOOEEXn/h2ZAJd75xfI898TQvvfcpX69dF1JBm0MsdAyyJt5IKTsn6VXuhBcug5wC+P7rXuMYYMQM+OGbcMMWmPdzWP8s/PMMFYoRIYYxnsjX/7bDDUwdkd3hUDBC04xQtW7z4e1QtQO+8y8YPY89lc1kpdrIz0oJuMqI7FQsSWn866i/QPoQeOkHYI/dwCFuJO0uV7eqPSUlKd37xBNPhGzrq3vNIRb9zTgG7UGOii2HlEE2fVT49Y99mTl6EJ/vroqVSP2SLYfqmTw8K6IyeWaMUJWwKjgkKDuONOJ0S2YUBHhY2/2BUtoX/7OL99hg5uhBvLK2DPcZF2P5+E/QeASyhnduFMLb0BNICRaLhZdeeokTTjmNv/31Hv5yR+BqG+vXr2fW7Dkd00KEP+iHlCAQnhALXcVC05m6Fjt/fX8Hvz9vaq+8rTLijwGSnU3w7MUgLCrBNj3AwFQ5o9T/dMa34d8XwbPfgp+vhKS0sLfb7hmcJJGv/31VzZx+9NCO6akjskmyCopL6zhn+vAgawahciesfky9fRt/OqBqII/Pz+zQQ/6wWATjh2awoS4ZLnoMnj4PPrkHRi32Nuqm7pVSUlLVTFO7E6sQTBqeRZI1/HutoXsXLlzIXXfdxU033RSw7fr16zn22GO7JWdfRHuQo2CLJzSgux5kgOmjcqhobKeisS1WYvUrpJRsPljP9CiO4fBsVTJv48GBG4dsPKwFvBa/fhIyhsK0CwP2MaNgEM12F6V5p6gZuz6ItZjdwnjdm56ezqP/epHXXn4xoDfjlVde4f333+c7iy8FVCSlEXESjvNEIjHuY5HUT9YMDO59bwfPrjrAG8UHe2V7hvc42WrhGvkfFdt66X86JdgGZNQc+PZT6sF4+a0RbddICEzU67+xzUFVk52xed6wh9QkK1NGZFNcGkUc8sq/gC0NTvUakXvMJd6CMD4/kz0VTVB4EhRdDl88pPJGoqTN4aKp3UluRjIuKalrsUfcR3p6Om+99RbPPfdcSN172WWXRStyn0F7kKNg88EGRg1Ki7g0mZkpI1RYwbbDjd1K9OvvHKpvo7bFwbRuxh+D8hBOGZHNtsONMZSsf7H1cD1ZqTYKBvvxEtWXwa734cTrwdq1UL3BtJHqTUixfRRHZY+CXe/B7O/3lMhhY75J5+bm8u+XX+fSC84mL0/F7T/wwAM8++yzNDc3M336dD766CPy8vKoLm8EIbjyxz/EmpRCss3K0Pw8li9fHnRbhoFsEQJnuEWXNQOCVs9oa8G8gbHE4TFU56eU8D3XB7jn/hTL6LnhdzDhDBVusfoxmHR2h1czFN4Qi8S0kEuqVPjC2Lz0TvOPGZXD0uJDSCkjP8e1JSrB+aQbOuK+G9ocVDS2B06cNjE+P5M3ig/RaneRduYdsGMZtNZ4Xmt1/3qra3UghGB4diqtDhf1rU7yuxHNmJuby7vvvsspp5wSVPfm53tj3s0xyHl5wXVvX0QbyFGw+VB9h1HRhaYK5bUr+1q9qp50Npy4BFI7G4LG8NTbDjewYFLkyRT9nc0er+/0QMcxTKaMyOLLPVU4XO6IXh8lClsPqXg6v0p93TNKyc75YS55RMoAACAASURBVNA+xudnkmQVbDvSxKKJZ8Gml2PiwYgWt5Rs2V8OKMNkxMhR7Nu3D4BFixZx6623dlnHMGTefvcDhEVQUtXMhPxM0kOMMCg9w1ODZ4CRxLQPNN3E6Ql5SLL2joFsd7mx4uIW/k4Fg8g++SbSQ6/WmTNvU6UdX/sF/OANGBo80Qq8iYGJev3vrVKDchTmdR76eerIbJ5bfYCy2lZG50Z4pNc/p77n/qRj1h7PENPj/Qwx7YthRO+tamLayCFw5h3Q3q5K92UMiUwWE41tTjKSrdisFjJTbFQ12nG71Sij4dDU5B3AZPTo0SF1r8GKFSu6LXNfYeBZEjGiud3Jvqpmpps9n20N8N7Nqgj4A9NhxV+UcZw2CD79KzxwDLz/B2U8exiUnsyInNQBm2C25WA9VovyAHfB7YJ2z59TSpVoFkBjTx2RjcMlB+RoRC63ZNvhRqb6e8hwOWHdv5XnaHBh0H6SbRYmDM1S1+L408DeBAfX9YzQEWB2oIQb9tCpXJtnXji+YN9tJXIMpiZyjDcKtgBx/LHG7nRznmU1E937uMPxfdqtoT2RXUhKU9UupBuePAvKQw+pbIRYGMNcJxqGB/mo3M6GqxGiZoSshY3bpRKbx5+uEig97KlsBggvxGJoRqd1KLocbKnQcBDczsjk8eB0uWlzuMj0OAYyUmxIJC327vU30NAGcjfZdrgBKU0Jek47PHMRrHpUeYlnfQ+uXQu/+Ax+9BZcuRImnA5fPgyPzIOytR19qfCAgWkgbz7UwIT8zK4JLxtfhnvGwZ9HwaPHw5+Gwu2D4f6pfmNjp5g88QONkupmWh2ujrcRndj9ATQeUrVSw2DK8Cy2H2mAwpM9nX8SQ0m7R2evbniFpwy7VojIkvTcUiI8NWB1DLLGF3PSXG9gd7n5nu0DjlhHsMw9r/vDTQ+bBj9drgyuFy6D1uBxtsZ22npx9L7epKS6mRE5qaQld77vTB6WhUXA1kjvI3s/hoayLiFpuyuaSLKKsLzRhUMyEMLrdcZiUc416YKW6sjk8dDieZOWnqwM5DTPfTZRz2us0QZyNzH+QFNHeDzIn9wDB7+GS55UpXbOv79zIsXIIvUU/8vVkJKt6lh6lNSUEVnsqWymzXMxDyS2H27g6BE+AVEHVsHrv4C8iXDy/3gfOBb8VmVuP78YNrzYaZVxeRkk2ywDMg45aILeppchPQ8mnRNWX1NGZFPe0E6NzIRhx8A+ZSDH05PqxuTVJbzKEr5DRqt5obclpTepL1ZVLLQXOnFwunp32GdRvoV5lh18knMBEkt02x18FCx+VpV9+/COoE3bPfei9gS9J+2ramZsXtewh7RkK+PyM9kaqQd5/bOQlguTv9Fp9tbDDUwYGl7ViNQkK6MHp3d+C2pNRialq5rK3dAjrXZ1/tKS1fZtFoHNIgaMrRGt7tUGcjfZcaSRnLQkhmWnqMEXPr0fZl4G0y4KvmL+JFUfsbkC3v0doIwSl1uyu2JghQc0tDk4VN/G5OEmA7nhsKoBOWi0KmV0xi3w43fh/AfgtN/BFe9A4Ynw2pWw7c2O1WxWC5OGZQ5ID/LWQ6qOdJfXeI42NeLW0ecFTc4z08kTP/YUKF1DanIy1dXVcTP0zB7k8EMs6GgfUZk3vO2FCC8sI7gckurqalJTB14CbiLidAcY9rmHyNn8b9pkEhuGnOfZbpSGzeh5MO9KlR9zaH3AZsb+tSaoIVVS3dwl/thgaqRvdFtqYPvbMGMx2Ly1jqWUbDkYJE/JD+PzM7whFkBqairVjhSksx3aI7+3tdpdpNisWD0hQUIIUpKstDkS34McC90bVZKeEOIc4G+AFfinlPIvPsuvAq4GXEATcKWUMnQAVD9gZ3kjk4Z5ahuueVzNPP334a08chYc90tVxuXkG5kyQtVc3Hq4oXNMc4Kzq1w9EEwa6jGQ7c3w4uUq7vgHb6jXS76kZsN3X1Z1Il+9UoWu5E8CYMrwbD7eUdF1nQRn6+EGJg71U0d67woVRzz1grD78lZVaeDEsSfDqkco4BBljRYqKytjKHX4HKlrpTHFRn1aEtVN7bjcEkd1cKXXandR3WyHuhQEUN7QjqM6qeNVYyAqG9sBcFSn0NDqoKHNia0h/Pqx/khNTaWgoCB0Q02fx0jSi9pQDYe2BgbtfpVXXcdjzRwCNMXGMD/td2pUzWW/hh+/77cuekeIRQIayLXNdupaHIwdEsBAHpnN0g2HqGuxMyg9jApVG18Clx1mXd5pdnlDO9XN9ogS0MfnZ/LFnmpcbonVIigoKKCs9ACVFdVwuBkyIhtx90h9G8k2C+5a737UtdhpsbtwVEen1/oD0erebhvIQggr8AhwJlAGfCWEWOpjAD8vpXzM0/4C4H4gvHe9fRgpJTvLmzh/xghlzK39N0xd1Ck4PyQnXKsM688eoPCCh0lNsgw47+fOchUOMXl4lkpyePH7yqux+Fk1jGogklLh0ufgkfnw5nXwo7fBYuHoEdm8vLaMisa2AVUyb+eRRk4Y7yfLeftbkJIDhaeE3deQzBTys1JUqMrcE0BYSDrwKWNPC1wcvieRUnLeTcv45akTuPHsyfzi2bXsrmjig1/NCrre6+sPcv3SYj76nwVkpNj45l0fcudF07l85lFB17vp0c/JTLHxzE+KeOTj3dz73g6233HOgB7CXOPFYR7VrqfZ+CJWZwvPuM7kJE+SVUy2m5oDZ94Or18F65/xW93GeADo7Zjr3mBftfLQBvMgg3I8nDA+hEEqpTqGI4rUsM0mOsZJiMDpNWFoJu1ON4fqVBWNpKQkxo4bD7ufhi8fgV9tg6xhYfVV3dTOuf9azk3fOJorj/WGez6zaj9/eGMzX/z2dEYOSnwjORqiCbGYB+yWUu6VUtqBF4BF5gZSSrPFl0GCDOxe0dhOfatDGXbFz0N7vfIIR0LmUBVXu+llrO11TB4+8BL1dhxpJD3ZyqhBabDyHtjzIZx3vwoJCEXWcDjrDjjwBaz5O+D1fm4fQHHI9a0OjjS0MWm4Txy3lLB7uapGYYusTndH0mhqjnrbsfvDGEocGU63xC0hxeMdT7FZOgZPCIZxg09JsnasG078ZrvDTYrN2rEt1Vfiv47UhIfDCLHo6VfUUsKaf9CQO4ONcjyZqYaBHCOP7sxLVSLuezerEEEfjP9Kb8Va9yYlVcpA9heDDN4ws7DikA8XQ/lmv/XiNx9sQAj8V2gKwMRhSo93SRKc/QOVrLfh+bD72mSUUPUx0Cd7trGjfODcJ7tLNAbyKMA8yHuZZ14nhBBXCyH2APcASwJ1JoS4UgjxtRDi63i9yg2XHUfUhTUxPwNW/z8omAuRFG83mPU9cLXDlteYOiKLbYcbB1RCz66KRiYOzcRStV0lOc64NOxqCwDM+j5MOhfe/z0cWNWppvRAYZdHyU0a5hN/XLENGg/DhIUR9zllRBa7K5qUt2zSOXBwbafShL2JcYM2wkeSbZawjBPDqE2xWToM3nAMXbvL7TXGPV7jvmokCCHOEULsEELsFkL81s/yq4QQm4QQxUKIz4QQU+MhZyJhJK3ZXT0celDyGVTt4MB4NSpZlseDHLNrUQhY9DAg4fVfqhKaJoz/SjgPo/2NkqpmLALGBKgskZ+VwtCslPAqWWx+FSxJMP1bXRZtOljH2LyMjhJr4TBtZDY2ixruuhN5E2HMCd6a9mGwOYCBbOSq7BlgOU/dIRoD2V+V6S5nTkr5iJRyPPAbIGCQrpTycSnlsVLKY80jsfRFjNCAac1fQs1eOO4X3etoRBHkHw0bXmDKiGzqWx0crh84Q07vONLEpGFZsPJuSMqAc/4cWQdCqHHrc0bDyz9ikLV9wNWU3umJ45441MeDvNszYtGEMyLuc8rwbOwuN3srmz3VL6RK9osDvgZyis0a1k3bbjKQjXXDM6xdXgPZaumY19cwhbidC0wFLvNjAD8vpTxGSlmEclDc38tiJhwtdqO6Qw8bjl88CGmDOTBSRSR6Pcgx3O7gQjj7Lij5tOMtnIGxf3anO+GcNvuqWxg1OK1rzoaJqSOzQ3uQpVTJeWNPhrTBnRa53JLV+2qYV5gbkWwdw10fqOu6cPb3oWYP7P8irL42HayncEg62amdE7QHpyeRmWKjrLY1ItkGItEYyGXAaNN0AXAoSPsXgAuj2F6fYWd5I3mZyWRveAKyC2DKotAr+UMImPEdKF3NMVnqtY/hnU50aprtVDW1c1xmOWx5Heb/XJVwi5S0QXDx48pbuvrvA27I6Z3ljWQYYSpmdi+HoVMhe2TEfXaqZDH8GHWN73w3FuJGTLtfD3Jog9W8ntUiSLKKsAxdu9PtNcaT+nSIxYANcYsnvRKDvP+LjqHhm13KuMlJS+qZ7c7+AUw4U5V9qz/YMdv8X3EmWDHwfVVNFAZI0DOYOiKb3RVNwXVG1U5lsPqUdgMVntHY5uR4f7khISgaPYiNZXW4fI/71EWqROz6Z8LqZ/NB/0n/Qqi6zAdqWiKWbaARjYH8FTBRCDFWCJEMXAosNTcQQkw0TZ4H7Ipie32GneVNzM9rh70r1VOdNYpiIJ4/1+SGLzx9DwzjztjPkw8/BcmZcPzV3e9s9DwVavHFgxwzRLC3qilhR4DyZWd5IxOGZXUeNtTeDAe+7Jb3GGBcfgZJVqFi1IRQw6Tv+UiVjetlvJ5gb1xwOEaCYUQnW72e57DWMxvIEXie40DMQtz6U3hbvPEayD30VkFKWH4bZI2AeVdS16KGeh+erR6AY16XWAg4768qvvV97wte83+lr4YYdQcpJSVVLYwLEH9sMHVkNk637Ki05Jftb6tvPwbyl3urADh+XOQG8szRg2i2u7qWfU3OgGMuUQ6lVj8eZhM1zXYO1rVyTIAEwTG5adpADoNuG8hSSidwDfAesA14SUq5RQhxu6diBcA1QogtQohi4FdA13TZfoaUkl3ljVxgXQVIOObb0XWYfzQMOor0kuXkZ6V0vDJPdHaWNzKKSvJL34W5P+6e99jMKTdCWz2nOj7B4ZLsr24OvU4CsLO8iUm+9Y/3f6nKDo3vnoGcZLUwNi+jI76ZyeeCo0W9iu1ljFhPswfZ6ZZdvSs+tDtVLLFR0zjZZgnbg5xiCudQMvRJAyFmIW79Kbwt3vR48trO96B0FSz4DSSnU9NiJ8kqKMhVBrJhMMeUwYVw4nWw5VWVb0DiGshVTXaa2p0BK1gYmCtZBGT72yqJOafLcylf7qlmXH4GQ7Mjr6Y0e4wqb/pVSY2fhT8AZyts/m/QPowEvcAGcjqlNS24E+ztQKyJaqAQKeUyKeUkKeV4KeWdnnm3SCmXen5fJ6WcJqUsklKeJqXcEguh48nBulaa7S6ObfxQ/TnMo+V1ByFUnOfeFUwbmsSuioHjQf5J6oeAgLk/i77DUXNg6FQmH1nq6T/xHzSMMJXJvhUsSleBsCrPejeZOCzLewwLT1Yx4jveiULa7tERKmH1MVpD3LTbTYauWi/85D6zMQ59djSxARviFk8crh4cKMTtgg9vg9zxKoEbVbN3cHoyWSk20pKslDf00Fuc46+B9CHw4e1A5/9XIr2NKwlR4s2gcEgG6clWtngMzS40HlEj5/qpuFTf4uDz3dUsmNS9h82xeRkUDE5jxQ4/b3NGFMGw6bDhhaB9bCpTHuZAJebG5KbT7nRT2dTeLRkHCnokvQjZWd7IWHGYIQ1bYfolsel0wkJwtnFaegm7ypsGxFPdnsO1XCJWII4+T42aFy1CwKzvkV6xnomWsgERqmLso1EaqIPS1TB8unol100mDc2itLZFDVWalKrKxe16v1vDnUZDRzWKpM5GazgGcrLNW7s4nNAMp8uNyy37S5m3ARviFk96NAZ57VNQsVUNOOUZ+bK62U5uRjJCCIZlp1De2EMGTWo2nHyjGlxo7wranS7vA2LfvP67xT6jxFuIGGSLRVA0ehBrSmr9NzCcBZO7GsjvbD6M3eXmolldPcvhIITgtMlD+Xx3Vde3XkbeUtlXUL0nYB/FpfWMy8/oiF33ZbSngocOswiONpAjZMeRJi6wfIFEwPSLY9PpmONAWJjt3kKrw8XBusTOLpVSklv+BdmyAYouD71CuBzzbUBwWca64LFjCYLfEm8uJxxcB6PnR9X3pGGZqpSyEQc3dgHUl6pPL9IRg2z1iQsOES5hrkah1rOGXMcIpUj2CbHoiwbCQA1xiydutzQNNR3jtwp1pfDe72H86TDV6+g3PMgAQ7NTe86DDHDsj1VC7vLbaHe4OkrLJZIHeV9VMzaLoGBw6AEyThg/hG2HG6hptndduP1tGDzW74BWr60/yLi8jIDhDeFw2tH5tDpcrNnnJ8xi+iWAgE0v+11XSklxaR1FBX5GovVglLg7UK0N5GBoAzlCdh1p4KKkVYjCk7pVIcAvqdkwoojCpnVA4ifqVTa2c7rrU9pt2eqGECsyh8KY41govkr4Ywiq0HtWqo3h5ji3iq1qeOkoDWTDK91xHMccp74PrIqq30jxVwcZQhutdqe7w+sMygMdyutsLg1nrGOe39cYiCFu8cQcix7zxM33b1bf33yw09DPNS12cjOVgTwsO5WKnjSQk1LVMNSH1rHAtZosT2m5PhqD3y1KqpoZk5uOzRra9DEqUKzeW915QXsj7FupwitE51SAtftrWL2vhu/MHd2R/9Adjh+XR3qylaXFfqKmckZB4UlqiGs/b/QO17dR1dTOzNGBDeRRg9MQQnuQQ6EN5AhxHiqmkIN+C4NHReFJZFZtIJX2hI+f3XmoirMsa6krPCfiUd5CcvT5jLHvwVG1r88aNrFiZ7mqI91JEZeuVt8F3Ri4xkThkHSSrRZ2GjHxw6ZBcpaqjtGLeAf8iCzsQcUgRxZi0aWkXB+ug6zpfcye1JgajXtXwNY34OT/6Qg3szvdrNxZSVlNKyNz1APw2LwM9te0cNUza7lr2TaeWbWfLYfqYxuSN+NSZN4krrO8SHaK0isOZ+KE/O2rag4Zf2wwo2AQ6clWvtjjYyDvXq6SoH3ij6WU3PPuDvIyk/nB8cGHtA9FWrKVRUWjeHPjIer9JWbO+I4qMXdwXZdFGzyDjAQzkFNsVkZkp1KqDeSgaAM5Alxuycy65biETdUkjCWFJyFcdk7PLPVWD0hQGnd8QpZoJfWYGB9DgCnnA3CGWNORkJGIGNVUuoygV/YVZA6HQWOi6t9mtTAuP8MbqmLxJP3F2YMc7rDR5mQ7tV7oMm9dSsr17TrIml7GSNCDGHqQXQ545zcwuBDX8dewcmclVz+/jlm3v88Pn1xDZqqNn5w0DoCrFozj4lkF7Kxo5OkvSvjD65s578HPmHXHB9zwYjErd1bijNZwt9pwLLiJiZaDnCHVw3aPjxrYS7jdkv3VLSFrIBskWS0cP24IH22v6DxYyva3VUKjz1u6Jz8vYfW+Gq5bOIn05ChKv3q4fP4Y2hxuXl7rJ6xtygVgTYGNL3ZZ9PX+WpJtFqaMyOq6ngldCzk00Z/FAcSB6ibOFV9Qnn8iI6MtS+bLqGMBOCXjAM8meCWLzAMf004SOVNiGF5hMLiQ1typnF31NTvLG9VIfQlIZVM7tS2OrvtXuloZslG83jOYOCyL9QdMSSpjjoeP/wSttV1GjuopfMu8eeOCQ8QgO3xjkC3UtfqJJTSv4/S/rUR/E6EJD7MHOWZvFdb8Ayq388mcB7npgS8pq21lcHoSi2aNYsGkfE4YP4Qsz0ho6ck27vvOTEAZe4fqW/m6pJbPd1fx3pYjvLb+ICNzUvnJyeO4dO5oMiIY4thM69hzOeweyjdalvIA07EniAe5vLGNVoeLsXn+h5j2xzeOGcGH2ytYd6CWOUflQnsTbF+m6hFbvG+o3tl0mD8v28aZU4fxvfnROScMpo/K4bhxuTzy8W6+PWc0OemmhLu0Qao+/eZX4Ow7O5I6AT7bVcW8wtxOb9D8MSY3nZU7dd3zYGgPcgRUblnBSFGD4/+zd97hUZXZH//caemF9EICIYSSQAq9N1GxYUfUtbuWtbu7rvvbXXd1i6vbXLuuXWxYsBcUpHeEAAmQAoGENEhIz2Ta/f3xZkISZiZtarif5/GJmbn3vidkMnPueb/ne9KdLK8ACIqEIcPJUhVTVD24nSxS6jZxwC8TdL1/o+oLmoyLmCQVUFZ6xCXX9wasld0uCXJjFZwsGZC9W2dGxQRTdrKV5jaTeMCqQy7d5pTr94b+VpAN5m42b9qebd7aummQdb1sCFQ4M7C+5iTJSbsKDRUYV/+VLaocrt8YSVSwH89dM4Et/3cWf7t0POdmxHUkx91RqSSGDgnkkpxE/nFlFtt/v5AXrp3A0IhA/vxlPrOeWM2bm0r61WDXJsNb5nNIa9tHplQ8aDTIxdViRzG1u2+8A84dF0ewn4a3N7d/luz/HIzNkH0NIHaVn11dyF3v/kRWUjj/WpI1IO1xd/5wYTp1rUb+sfLA6U9mLYWWE2KIUztVDXoOVjUyKy2qx2snRwRS3dgmnIoUbKIkyH0g4MAntMh+RE10kZ1owgSS9QfQGy2UnhycWx/yyRKGmssoj5rlsjW0GYtRSTIhJStdtoanKehwsOiUIJe2yx+SpjllDWujXoeTReJEUGnFKFw3YT9p7SHZNXbVIOvUfdcge/kkPQU3Y002g/00A06Qq+qaOPTcpRgNRl4OvJ3Xb5rCil/M4ILM+B4rf7bw06g5b3w8y2+fzie/mMHY+FD++Hkei55ax7o+VgnbjBaWm+fRog7ll5oPMQ6SHZRDJ8T72Mjo3ifIwX4arp6SxOe55ew7Vg+73xXuFUlT2V/RwNKXN/PPlQVckJnA27dMIdTODU1/yUgI4+aZKSzbcpTPdh/r+uTIsyEgoosn8oZCMcFvdm8S5EhRoCobpLmGM1AS5N4iyww9sZ5tmhyCQvpv3+KQxIkEtVYQTd2gbdQ7mf8jAOaUOa5bJDaDak08abVrXLeGhymoamRIoJao4E5Njke3gsYf4rOcskZau765w8lCFwhx46Fsh1Ou3xtOryD3dlBIP2zeuiXjGpWEylnVQgWfx6pBDvHTDEh2s2p/Fe/892FGtO1nY8afeOmBq5g/OsZplccJyUN459ap/O/6SVhkuP61bTz0US4N+t5N4WszWWgkkK1Db2Kueg8hFRudEpenKa5uIthPQ3SIX5/Ou2v+SCKD/fjjW99AyXoOD72IBz/M5YKn11NY3cS/rszi6aXZTtEd2+I3i8YwefgQfvVhLj/kV516QqMTVrMHvxbSD2D1gWqignWMjQvt8bqKF3LPKAlyb6kpZojpOKVhztm+tkniRAAyVcWD1qasrWgdtXIwcanZrltEkiiJXkC2KZe2JjtG7z5OQVUTaac5WGyBhAlOcwYZFiGcLAqrO92sDZ0E5bvE1C830H2SXq8ryN0n6Wl7X0G2nidJEn4a9aDZYlYYGB0VZH9Nv2Q3ZovM49/s59G3vuIX8nKahp/D2VfeibYXlmN9RZIkzk6P5dv7Z/OLeal8tLOMc/+zjo1FJ3o81/qzFSYvpUyOYvTef7p9QJArKD7eTGp0UJ9vRMIDdbx6wyQWGtcAcP2OFL7dV8mNM1JY86t5XD5xqFNlFd3RaVS8cv1k0uNDufOdnXyR28n6LeNSMOmhcCX1LUa+31/FhZkJqFQ9x5OsJMg9oiTIvcRcLCqfrUmzXbdIfCZIamYGHB20ThZBFVvZZhlLWpyLqvDt6Eeej04yc2LXFy5dxxPIskxBVSOjO8sr2pqgIheSB+Z/3Bmrk0WXm7XESUKDV73faes4onvS2ttBIaf5IPdi1HRHtVrdSZqhUXnrqGkFN2PoJLEwmmXMfegTaTGYuGPZTl5aW8zrkcvw89MRfNl/ndJM6wg/jZqHFo1hxS9mEuSn4WevbuWpHwocxm79mwsMCuJp06WE1+VByXqXxukOio83kdoHeUVnMhPDuD18O3XRk3ny1ovZ9ruFPHJROuGBTrYptUNYoJa3bplKdlI497y3i3+vPCj6lJKnQ1A07P+cZVuPYDBZWDKpd5NpI4N0BOrUlNYO7sFkA0FJkHtJy8HVHJMjiR52+uQcp6ELgpixTNIeHpwSi/oyQvXHyNeNtzsC01lEjZlFtRwuLHkGGZUNehr1pq4Wb0Xfg8UEqWc5da1RsSFdpxIOFW4rHHOPzMJgsqBTqzoqNH0ZNd3VB7lniYX1+dMSa0VioQAdWtzgdp1pb2UW1Q16lry0mVX7q3h9yjFSm3YiLXzUeYOmekFWUjif3z2TS7MTeeqHQm58fRs1TbbHVltvJEP8NXxmnoleOwS2vuS2WF1Bc5uJinp9nxr0unBsJ6raIsKnX8/01EiC++kQMhDCArQsu3UqSyYN5enVRdz85nYqGoUfs6XgO179MZ+zxsSQntCzvALELkOyYvXmECVB7g0WC35lG9lkzmBUL7Q9AyJxAmnGgxQfb+xThcInKNsOQF3UBJcvNSImhB8sE4muWAvGwXWHbL15SutcQc7/TFQShs1w6lqjYoM5VtdKk9XJImKEsHhzkw7ZcJqfcW8lFuYu5+k0KiwyDn1iDd3kHNA7aYbCmYG1gmwdwdwbmUV5XStLXtrMoePNvPqzTOYffQ5iMmDija4M1SZWm7jHLxvP1sO1XPjMBtF41g3rzxXsp6ENHQeHtutcT5a4OWLnUXxcvGemRvfOA/k0ct8T/R3Onn/QR/w0ap64PJPHLs5gy6Ea5jz5I08cHY3K2MJc9V7+tDijT9dLighUhoU4QEmQe0PlHnSGejbJ4/q9RdNrEiYQYG4k1lw56O7sLBV7McpqAhLHuXwtf62a3UGz0FlaxaSqQURhdwcLQwsUrISxF3Xx5nQG1iS8Q/IjSUJmcWynU9exR/dmu95UkGVZFoNC1H1LrDvkHNquzX2KD7ICnNIgB/n1rlG0tLaFJS9tpqbZwLJbpzK//BWoEjpF1AAAIABJREFUOwLn/sXpf6e9RZIkrp6SzCd3ihvpK1/czHd5lV2OqWkSfuGJQwIA2BV7OSDB9lfcGqszyStvAGBsfD8KXKY24Tc85gLwd600sDdIksT104ez8v65XDt1GOsMY2hWhfBoWlFH411vsVaQ5UGgMXcFSoLcGw6vBaAsbBL+Whe/sbU36mVLg69RT1+6myI5gdSEni1onEFTwnSaCIL9X7plPXdxsLKRqGA/IoLa9W/Fq4Qu2AXVjVEdCXI3mUX1ftA3OH297pxeQe55UIjJIiPL4K/tW2Jtq4Is7OEUDbICHQMzgv2ExMLRzVZpbQtXvbSZRr2Jd2+dxoSar2HjUzDhBkh1wYCkPjIuMYzP7prJqNhg7li2kxfXFnckSZUNegCGRwbhp1FRbomA9MXw01tg8M3ppHnl9YT4azoa0/pEwXdiOFLWNc4PbAAkRwbyp8UZfPXAAoIyFxN6ZBWYHA9DOu0aEYG0Gs2caOrbeWcKSoLcGw6tpUQaSkT8wOar94qYscgafzJVxYOuUU9VtYd8ebjbptulxkWwypyFfPBrMJvcsqY7KKhu6qo/zv9M+GEOc763dHJEIH4aFYXV3Rr1kIWbhYsxmLsmyFq10CI7SnS7+xlD58Ta0XlWDXIn7bIisVBop7OLBdi/STvR1MZ1r26l2WDm3Z9PZbx+B3xxL4yYB+f/003R9kxMqD8f3D6d88fH8/dvDvDQR3swmi1U1Itpfv5aNUMCdZxsNsDUO0BfL6QGPsi+Yw2kx4f2z21i9zsQHCt+f97K2MXQVt9RzOstipOFY5QEuSdMBuSjm1lrSu/qGuAq1FqkuEwma0sGV6NeUzX++uPkW4aR1t9GiT6SFhvCt+bJSK21cHSzW9Z0NRaLTFHnEdpmExSuhNHngdr5jSNqlURqdHDX12JCjvhasdvp63XH0E0qIazXHCetVteJLoNC+llBVpr0FKwYu2mQ9TZcURr1Rm54bRuVDXpeu3EyGdIRWH49RI+BJW87zYLRWfhr1TyzNId7F4zkw51l3PzGdgqrmogLE/KKIUE6TrYYIWmq2N3c/DxYfOvvwWyROVDZQEZCP+QRJ0tEBTnnOpe8vzqN1PmgCxHFkj5glWQoOmTbKAlyT5RtRzK2sNGcwag491Q+SZzIGA5RVFnnnvXcQeUeAKqDRxPkpg7gUbHBrLVkYVbp4MDgkFkcq2ul2WA+lSCXbReVnbRzXLbmqNjgrrsZQZEQnuyWCnJbN7s26DlptTZT2W7usy+XaDNZkKRTVWpxDbWSICsAp1eQu/tj641mfv7WDg5WNvLCtROY2LQGll0O/uFw7Yfg7+IG736iUkk8eM5onrwik83FNWw9XEt8mD8AQwK1nGwxiN6D6XdDbTEUfOPhiPvGoeNN6I0WMnrp7tCFHa+Jn33STc4PzJlo/GDUucK1qQ+7pUPbdeZKBdk2SoLcE4fXIqNiiyXdbdIAEifgJ7ehPnHQYde9T1G5V3yNcX2DnpWUqCDaVAEcDpsmdMiDoBHBKnXokFgUrgRJLSoILiItNoTyej2NnSdxJeS4R2LRrYIMPSetVpsqW819DhPrbpZy1msoPsgKcGqHwWrx1dlXW5ZlfvVhLlsO1fLPK8Yz/9A/4cMbISgKfvaxWy3d+suSSUm8cdMUFo6N5dqpyQBCYtHSrk8duxjCkmHTMx6Msu/sKhWFpvFD+1hBNurhp7dh9PkQNtQFkTmZ9IuhtRYOr+n1Kf5aNXGh/kqCbAclQe6JQ2upCBpDqzqY4ZH9tIjpKwnCBm0sRRwZJC9cS3kupXI0QxPd90Hhp1EzPDKQ9Zqp0FDmloTO1Zxm8Vb4vTCLd2F3tVUS02WiXkKO2H5sqXXZunB6kx5YK8j2k1ZrZa+rD3LvXCxsraW4WCgANLWJ15y1Obbza/DZ1UV8uaeC356TyiWH/gTbXhYV1zs2QMwYT4TbL2alRfHKDZM4a2wsAEOCtNS1tN8YqzUw/S4hVyvxnfHTm4triAzS9V3al7dCJJxTfu6awJxN2jnC6nPLC306LTkikCM1vtl86WqUBNkRbU1wbAe7NJmkRAWd9uHpMiJGYNaFCieLysHRqGcq30O+ZVjX5jI3MCo2hBXN40WVdRDILAoqG4kL9ReDVhrKoWovpJ3t0jVHt0uLurwW3aRDFjZvXZ1jemqcs1b2uvsgQ8/Nfd1davwUiYVCO416IxqV1DHkSN++s/Dtvkr+9X0Bl2UncFv9U7DvI1j4KJz7V4/ZuTmLiEAddS0Gmq0+6BNvgKAYWPt3zwbWS2RZZnNxDdNTI/veoLf9fxA1ClLmuiY4Z6P1h6m3Q9EPp3Zse0FqTBDFx5UE2RZKguyII5vAYuJ7/Rj3ySsAVCpIyCFTdYiDg8HJwtCMtu5Qe4OeG/8dEcnd3pMazMkzBoXdW0F1I2md5RUgtGcuJGlIIP5aVdfXYnyW+Oriqrztqq5jb+ION4o+2sO1mcw25BxKk56CoFFvIsRfQ1y7PvdYnZ79FQ08uHw32UnhPJG0ESn3PZj3W5h1v4ejdQ5zR8dgkeH1jYfFA9oAmHkfHF4HR7y/8fnwiWYqG/RMT43s24nHfhJe75Nvdfk4cKcy+Vaxm/jpndBQ0atTUqODqW02UNusWL11R0mQHXF4LbLaj2/q3WdNZkU9dCJjVKUcrjjh1nVdQlUeEjL5DGekmxwsrIyODUGWoTLhLDhxEE4UunV9Z2K2yBRWNTEmrpO8IixJdMi7EJVKYlRsSFdf7oAhYqqeixPk7jZv0HPSarBp89a7CrLthkBFg6wADXojoQFaIoN0hPpr2FFSy61v7iDUX8sbsxvR/vAHGHMhzHnI06E6jQnJ4ZyTHss/Vxbw9KpC4ZU86Waxlb/2CU+H1yMbisTn5/QRfUyQt78C2iDIWuqCqFxIwBC47BWoKYYXZ0HhDz2eYh2/bZ02qHAKJUF2xKG1NMVMoA1dxzaz20iciAYzloo97l3XFbQ7WDSGj3X9oJVuWJ1HdgXOFA/s/8Kt6zuTIzXNtJks4mbN1CYmBKad7ZYKx+jYEA5WdnsDTciBchdLLIwW/NQ2klYHjXMdE/H6OKK6zWjps5xD4czBWkGWJInEIYF8s6+SE01tvHHxEMK/vg1i0uHSl8QO4CBBkiSeu3YCl+Yk8u/vC/j9p/swqf1hxr1w6Ee3TdTsL5/vLmdUbDApUX3oH2o9KSbnZS7xisl5fWbUOXDbGuHd/M7l8MF1sOYJqD5g8/CR7dOBi6uVBLk7g+cv2dk010DVXg6HTAJwjwdyZxJFo150Q36H1s1nqdhDPSFExKe4fenhkUI7ntsQLBI6H9YhWyu4o+NCRKOMocml9m6dGR0XwommNmqa2k49mJAD9aXQdNxl6xrMfbd5O5Ug980HuftYa+s1DCaLMopVgUa9kZD2KXpTUyIAeOryMYxZcyeoNLD0XfBz7w6ZO9CqVfzryixunzuCd7Ye5aY3ttMw7mfCd3fz854Ozy5Ha1rYceQkl+Qk9k1/vO8TMOmF3tpXiR4NP18F034hdvnWPA7PT4PlN0Dlvi6HJoYH4KdRUVTdJCbxle0U/wYbnoKvfgVf3Ae7lglXjzOMASXIkiQtkiTpoCRJRZIkPWzj+QclScqXJGmPJEmrJElywyg6J9FulbJdysRfq+rfiMqBEJqA3j+acVKxz299WCr2ss+SzKg49/uAqlUSaTHBHKxqEtufx3ZCY6Xb43AGByubkCSEjrvwe1DrIGWOW9a27qB00SG7oVHPls1bbzXIfZ2kZzBZbCTI7Yn1YLFbVOg3Da0mQgOExdvD540h94/ncF7FC3D8AFz+CgzxnY+3vqJSSfz2vLH8/bLxbC6u4fJX99KYfjXkfwr1xzwdnk0+2lkKwMXZiX07cfc7EJMB8dkuiMqNaANg0ePwwD74dTHM/iUUrYIXZ8J/s+DHv0FjJSqVxOgoP8YXPgf/HAmvLICPboIf/gh7lkPep/DZXfDMRJ9yL3EG/U6QJUlSA88B5wHpwNWSJKV3O2wXMEmW5UzgI+DJ/q7ndop/BP8w1jQNZVRsCCqV+4X6pvgJZEnFXbWfvobZBNV55FuGub8K346QBzRA6gLxQMkGj8QxUAqqGhkWEUiATi2mOw2fBTr3WA9af3cHOztZxGUCkkt1yDZt3rSOdcG2JBanKsiOz/M7zcWiZ2mGwplBo95IiL+oIPtr1YSd3AfbXhJjmK3vLYOcpVOSeeuWKVQ3tnH1nmxk2SIs7byMuhYDr28s4ez0WBLDA3p/YvUBUUTJvsa3mvN6IigSzvoD3L8HFv0dIlKFhvzf6fDWxbzSfDcX1y8Tjh1Xvgl3boKHS+G3R+E3JXD958Il463FsPXlQTFToDcMpII8BSiSZfmQLMsG4H3g4s4HyLL8oyzLViPfLYAPuG0jfvmH1kDKHPZXtbi9Qc9KwLBJpKoqKCnrXTeqV1JTiMrcRp5luPsmEXZjdFwIVQ1t1IWNBb9QKFnvkTgGyoHKBvFarD0ENYWQ5lr3is5Eh/gRHqjterPmHwpRaS5LkGVZtm3zpu5dk16fNciOKshemCAP6h08L8SqQQbEZ8S3vxXNavN/59nA3MyM1ChW/GIGzYGJfGuejGHrq8j6Bk+H1YXn1xTTZDDxy3NG9e3EXW8LuYyvNef1lsAImHYnXPcJ3PMTzLgHWmowB0Zzo+EhTl74KmRcArEZpyY/ShKMmAs/Xw0jF8I3v4bvfndGJMkDSZATgdJO35e1P2aPWwC7MyolSbpNkqQdkiTtOH7cdZrGXlFTBPWlNCXO5kRT2ynXADejHjoRAGOpdzdCOKTdj7FQleK+QSvdsCbmBcdbYdgMn6wg641mSmpahNTB2pnsYv/jzkiS1F6J77ab4cKJekazjEUG/+4a5J58kJ2oQe7NBD5PMOh38LyM0toWGttMDB3SLrU78KXoA5j/O68dIe1KRkQHs+IXM9gafy06UyOfvv7EKa9kD7O5uIb/rT/EkolJjOmLrM9kgNz3YfR5YgLiYCcyFc5+FO7YQPGFH7PGkk1euYMbHf8wWPqe2DHZ8hysetR9sXqIgSTItvYfbN5SSJL0M2AS8A97F5Nl+WVZlifJsjwpOjp6AGE5geIfATgYLBr0PFVBtmo8Q2p7b/rtdVTkYkCLKnoUag/IVKCzPKBByBJqinrtEektHDrejNkii9di4UqxRRaZ6tYYRseFUFDV1LVhLSEHGitc8u95ys/49OEdjhLdjgpyp8Rao5JQSf1wsbBql72vUXbw7uB5Id/lib6FBWNihGzsh0fFEImc6zwcmecID9TxyO3Xcyx0AlMq3+fSZ9edfgPtZg5UNvCLd3aSEhnEIxd1v1/sgcLvoOUE5FzvmuC8mHGJ4kZi77F6xweqVEKiMelm2PAf4Y5h8a7igTMZSIJcBiR1+n4oUN79IEmSFgK/AxbLstzW/XmvpHg1DElhb7PoVHa7xZuVwAjqApJIaTtIo97omRgGSuVeiqRk0uLCPRZCfJg/If4a0WA2fJZ40MeqyFZpw9hIjZCIuMm9ojOjYkNoajNxrK711IMubNSzJrOnVZB78CbuaNLr1NwnSRI6jcphs529UdOdY/EinLaD51W7d15IaW0LT/1QyNSUCGEXtnuZkDgt/JMYv3wGo1JJJC66n0TpBGOat3PRMxt4fk0RJg80tW4qOsHSl7eg06h47cbJBPn18XezaxmEJMDIs1wToBcTHqgjKSKAfeU9JMggJBfn/xPGL4E1f4MPrgVDS8/n+SADSZC3A2mSJKVIkqQDlgKfdz5AkqQc4CVEclw9gLXch8kgEpDUBRysaiI8UEtMiJ/HwtFHZ5GpKqagygedLGQZS8Ueco3JHtMfwyl5QEFlk2gs8wvzOR3ygcpGtGqJ4S25woJo5EK3x2CVGnXRIceNB0klJk85Gau9YfeqrnVQiD3rtTaTBa1aOq2x1k+j7sE/2YbNm9ZrNchO28Hzqt07L8NktnD/B7uRgH9emQWGZvjxcUiaCqPP93R43sGo8yAwin+k7uassTE8+e1BLn9xM/mOtuudiN5o5vGv9/OzV7cSHezH8tunM7wvvscALbViRHPmlT4/Hry/jE8MY19PFWQrKjVc9jIsegIOfgOvnCWGkwwy+p0gy7JsAu4GvgP2A8tlWc6TJOkxSZIWtx/2DyAY+FCSpN2SJH1u53LeQ9l24S+buoCD7U1RfZ7h7kT8hk0mQarlSMkhj8XQbxqOodKfJE8e7rkqfDuj4kI4WNWILKkgeZrQD/oQBVWNpEYHozm6UTSRDJvu9hjS2qUqBzpvo+qCxICEsm1OX6/NhlQCRFVXloVG2Ra2rOGAXlWQu6+lU/dsD+chBu8Onhfx7I9F7Dxykr9cOo6kiEDY8gI0VcLZjw0ul4OBoNFB9tX4Fa/k+UuSeObqHEprW7jgmfX89pM9HG90zctOlmW+3VfBuU+t46V1h7hqcjIr7prJsP70uuR/ChYTjLvC+YH6CFlDwzlS00J1Yy/9jiUJpt0BP/sImqrg9fMHXZI8IB9kWZa/lmV5lCzLqbIs/7X9sUdkWf68/f8XyrIcK8tydvt/ix1f0QsoXg2SGnn4LAo6j/X1EGGpUwFoO7Ldo3H0i/YGPU9avFkZHRtCfauRqoY2GDoZThSAvpd3y17AwcpGoT8+vB4SJ7rN3q0zYQFaEsL8KeiuMxw+C45uFbsvTsReBdn6vb1kt81kPs2uTZynos1o+xxZltt9kE+fpGe9ppcxOHfwvIidR2p5elUhl+UkCi9dfQNselpUjpOneTo87yL7WrCYkPZ9wkVZCfz4y3ncPDOFD3eUMf+fa/j7Nwd6n3j1gMUis/pAFVe8uJk7lv2En0bFslum8vhl4wnuq6zCyt6PhaY8brxTYvRFZqSKxsTNxTV9O3HkQrjxK3GD8e4S8XcySFAm6XXn0I8wdDLlbX40tZk816DXjiohCzMq/KpzPRpHv6jYgwWJMt0I4sP8PRpKl0EX7VMKXenf60wa9UaO1bUyLkolYrbqqD3AqLiQrhVkEPGYWqHcuTILuxVka9JqRy5ha+AHtCfIdpJqa7Jtz+bNXmLtKQbtDp6X0Kg3ct/7u0kcEsCjF2eIB7e/Im6q5z7k2eC8kZixQr6W+x4AYYFa/nBhOisfmMPc0dG8vK6YWU/8yAMf7GZj0Qkslr5bhFU36PnfukOc+9Q6bn5jB5X1ev526Xi+vnc2s9IG4DrRUA5HNsK4y8/oXYH0hFBC/TVsKupjggzi97/kLag9DF/e7/zgPMSZ3WHQndaTQks572HheIAHG/Ss6AKp8h9BXFM+six7VO7RZyr3UKlOICkq2uNxW290CiobmTupvbHs2E4YMc9jMfUWq/58sqoAZDMMn+2xWEbHhrCpqAaj2YLWKmMYNlN8LVnv1MqaNSn1765BVjtunLPVbAeg06jtJrq2houI7x1Xqz2JLMtfA193e+yRTv/vfqH6IOGRz/KoqNez/PbpYjiIoQU2PwepZ51qTFXoStZS+O7/4PhBMeoYYQf33DUTOHyimVc3HOKz3eWs2HWMyCAdM0dGMW1EJKPjgkmNDibUX9vRN2AwWSg72ULx8WZ2l55kY1ENe8rqsMiQlRTOf67K4sLMhFPvQQNh70eALBLkMxi1SmLaiEg2HTrRvwsMnwlzfyMa98YvgdGLnBugB1AS5M6UbARkSJnDwcMiKfF0BRmgMWI86cdWcqJRT3RoH6YCeRi5Yjd7zMM8f5MBRATpiA7xE9XPwBHCJs0FjWWuwNoUl9qyG1RaSJrisVhGx4VgMFs4UtPMyJj232tgBMSOh6LVMOfXTltLb7V5s1dBtpcgG+1XkO3KMozWavXpDYFiLa+TWCi4iM92H2PFrmPcvzCNicOGiAd3viEswGb/0qOxeTXjroCVvxdewgv/2OWplKgg/nLJeH5/QTrf51ex+kA16wtP8HnuKdm8JEGgVo3RLHf5O1WrJLKTwrlnQRqLsxNIjQ52XsxmE2z7HyRPF0OPznBmpUWxMr+KouomRsb049951gOQtwK++iWkzAFdoPODdCNKgtyZkvWgCYDESRRsySc+zJ+wAK2no0KVPJXw8hX8VLiH6IlTPR1O72iuQaov4yfjbI/rj62MiQs55cCQONFnnCwOVjYSqFMTUrnFY/pjK6M6Nep1JMgA6RfDj3+Bk0dgiHMGtnUkrXaquvaSVoPZXgVZZVeWccpz2TckFgquoexkC7//dB8Thw3h7vkjxYONVbDm72K3adgMT4bn3YTEipHbez+EBX8Qnrnd8NequSgrgYuyEpBlmbKTrRRUNXL4RDMNehNNehM6jYpgPzVxYQGkRgeRFhtyura4er+w6jTpIXqsSMY0ur7HfOALqD8Kix7v5w89uDgnPY4/fp7Hl3vKuX9hH6cQgvgdXPhveP082PhfmP9b5wfpRpQEuTOH14ktYo2O/RUNXlE9BogcOwe2QHPRRvCVBLndF3evPIIFXlBBBpHcvbP1CGaLjHroJNi7XOjPQhM8HZpD8ssbyInVIJXvgtkPejSWkTHBqCQhVSGz0xNZV4kEec8HTtNoWpNWf233Jj3H1mu2xlNbz2uyM+3LvsSifS0vlFgoOBezRebBD3KRZfjPkmw01u377/8gNPbn/+uM1qj2isyl8MmtcGh1j1aUkiSRFBEo3EF6S0MFfPkAFHSz9A6JFxKPnOt6P0CppRZW/RkiR4rpeQrEhfkzZXgEX+SWc99Zaf2TRg6bARmXwcanIOdnEJ7U8zleitKkZ6XpOFTnQ8oc2kxmiqqbyEjwjhGiQ5LGUkcIfhU+5GRRIZoK8yzDSPeSf8fRcSHojRZKappFJRaEDtmLsVhk8isaODfkcLv+2HMNeiCS1eFRQezv3qgXniy00bvfcdpkJXsV5J7GPzts0rOnQbZXrdaquzyvMHh5cW0x20pqeeziDJIj25O2w+vFTd/M+yBqpGcD9AXGXgShQ2H1X8COT3m/Kd0OL88VhawFf4D798FvjojxxzFjYePT8OwkWH59uySmVpxnNsHJEqGN3voSLLsCnsqEJ0dA3RG48D9nrPexLS7KSqD4eDP7jg3AjeLsxwBJ3Fz6MEqCbMW63Z4yh4LKJkwWmYyEMM/G1I6kUnEoIIP4hj2eDqX3VOzmuDae8IgYQv09L1MBOm548sobIHac8BP28gS59GQLTW0mJpMn9MdDPac/tpIeH2p7CMCkm8QHUdH3TlnHfgXZcdJqr0nPT6N2aA3X+dpWTjUEKhrkwUxuaR3/+b6ACzPjuTSnfSChxQzfPAThwxTtcW/R+sP8/xNuO3s+cN51930Mb1wA2gD4+SqY8ytRmQwIhzHnw3Ur4MH9MOMecVPzxX3w73R4eR48ngj/zYLnpojf58kSMehlzq/h5u+EPEOhg4uyEgjSqXl94+H+XyQ8CWbdL/TIPja1tjOKxMJKyXrQhUB8Nnk7ReOAt1SQARqjJjChdAttDdX4hcZ4OhzHWMxwdCt7Lale9W+YFhOCVi2RV17P4qwEUXWo8G77vLz2RHRY4y7h3+wFTQ8ZCWF8uaeCuhYD4YGddH9jF4utzq0vwahzB7yO3q4G2XHSaq9JT+dgRLU9iYVWLSFJXjkoRMFJNLeZuP+D3cSE+PHXS8af2lbe+6HYVbzidZGYKfSOrKWigvvVr0RDccSIns+p3AebnxWN8qZWiEyDEXMhPgvyPoU970PSNFj6LgRF2r5GSKyoXC58VHjwb3lBfJ14E8Smi4JI0tTeSzDOUMICtFw5KYllW47w0KIxxPXXonXGvWJ89ze/gdvW+uRYdqWCbOXwOqGdUWvIK28g2E9Dcl+0US5GmyKaQyr2rvVwJL3gyCZoqmRFaw7p8d6TIOs0KkbHhZyqfsZniQTZ2VuBTiS/vIEQVRsBJ/YKGx0vYFyi+J2eVkVWa2HSzVC8yikTlexVdXsa/yya9GxrkO3rlm17LkuS5PA8Bd/nL1/lU1LTzL+vyiYssH23y2SAH/8mvH3TL/FsgL6GSg1XvCqa9FbcKQom9ijZCMsuhxdnQv7nkDQZRi0Cc5tojHxvKRz4EqbdBTd8bj857owkQXwmXPoC3LkBzvs7TLgesq9RkuNecsusFACeXl3Y/4voAuHcv0LVPtj5upMicy9KggxC+F9TBCnCXza/ooH0+NAOT0ZvIDF9OgZZTUvxJk+H0jN7l2PWBPK9ZSIZid6TIANkxIt587IsQ3w2tNRAfZmnw7JLXnk9i4ZUIMlmUf3wAqzSo33lNiYRTrheVGqc8IaoN1pQSaKK25lTLhb29MRmBxVk++d0vnaX89T2z1Pwbb7dV8l720q5Y24q00Z0Sr62PC/0qWf90aYbg0IPhCfDor9D6RZho9adtkYhg3jjfFGkWPAHeDAPrngNLn4Wfr4aHjp0Sjqx6G+g8XP/z3GGkhQRyHXTh/H+tqMc7N5v0hfGLoaUubD6z9DcT39lD6L85YOYngeQMhezRWZ/RYPXNJZZSYqJZD8jCKza4elQHGNqg/zPOBw9Hz1+XqPjtpKRGMrJFiMV9XqRIINXyyzyKxqYF9iuBbM2FnqYiCAdCWH+HfKPLoTEwZgLxNaasXVA61jdKLp3UvfkTWwwO/BBdlB1th5z2nlataJBHoRUNeh5+JM9jE8M44HOllbHdoomszEXwsizPBegr5N1NYw8G1Y9ClX54rHjBaKq/K8xsPNN0fx4/16hKQ4Y0vX8wAhhG+fvXZ/FZwr3nZVGiL+Wv3wlhpT1C0mC854UN0Qb/uPcAN2AkiADFK2CoBiIHUdJTTMtBrNXaWcBVCqJ0qBxJDTvF9t/3krRD6CvZ412LlHBOmJCvOuu35qw55U3QNw4kNQdlnTexommNqoa2hgnFwhNXmCEp0PqID1BVOJtMvnnYirlAJt02kwW/LW2E13r8zbPMzrwQXYU3wRiAAAgAElEQVRwjri2bWmG4mIxuLBYZH71YS5tRgtPLc0+9Xo5vA7eXAzBsbD4GcXWbSBIEix+GvxC4e1L4Yv74YUZsP8LyLhENNud/Zii7/ZSwgN13L8wjfWFJ/hsd3nPJ9gjZgxkXgXbXxWe4j6EkiBbzFC8WlQKVKqOqpi3VZABmmMnocOIucyLnRf2LIfAKD5rGMXY+FCPj5juztj4ECQJkdxpA8RIVC+tIAuNr0xC417RoOdFjEsM5dCJZloMNnyFh88S+u5Nzw7I8k1vtO9nDI58kC12zlNjtsiYbDhZ2NMgW9drU3yQBxWvbTzM+sIT/OHC9FOT2Y5sEhZgYUlwy0qvuiH1WUIT4GcfC9nVT29C5hK4dxdc/JzX7Igp2Of66cOZOGwIf/w8j6oGff8vNOfXYDYIb2QfQkmQK3ZDa22HqXleeT1atURajHcMt+iMf5qwo6nLX+XhSOzQ1ggF32JOv4QDx1u9Tl4BEKjTkBodfEoeEJ8N5bu9slEvr7yBJKkabVutaF7xIjISwpBl2F9hQ2YhSTD9HqgpFAMD+kmbyWInYbWvQZZl2eEkPbA99MPeJD1xnlqpIA8i8ssbePLbg5ydHsvVU9qHGNQdhQ+uE/ZUN30NYYmeDXIwETdOyCh+VwWXPA/B0Z6OSKGXqFUS/7giE73RzP99srf/UovIVOFusuM1aKx0bpAuREmQi1YBEoyYD4g3z1GxITY/YD3NqJTh5FuGYTm0ztOh2KbgOzDpORJ3Lkaz7HUyFSsZCaHkWRvM4rOguRoajnk2KBvkVzSwMPiI+MYLK8iAbR0yQPpioSnc/W6/19AbzfjbqARbm/ZsjY22Z9fW+TFbya71PNv+yfbt4RR8i1aDmfs/2EVYoJYnLs8UO1x1R+GdJWA2wtXvK5VjV6BS9W8UtILHGREdzEOLxrDqQDXvby/t/4Xm/Er8jfmQFtn7skB3U/QDJORAUCSyLJNf3uC1id3ImGC2ks6Qml1gHMB2h6vI/wyC49hhGQ14p0wFRIJcUa+nttnQ4VxCcf8rna4i71g9swNKQBsE0WM9HU4X4kL9iQjS2dcha/xg/JWw/0torevXGvYqyFbrNVsVZIfNdg4qz9ak2ToYpOt5iovFYOGxL/MoqGriX1dmERGkE0MMXp4nRs5f9TZEpXk6RAUFr+OmGcOZNTKKR7/Io6i6n64WESOE1d6O18Xfmw9wZifIjVVQth3SzgHgWF0rNc0GxiV6nzQAQKtWURo2GY1sEHF7E4ZmKPwexl7I7mMNhPhrSIkM8nRUNhlntSk7Vg8x6RCaCAe+8nBUXalvMXLoRDPjLAcgcYLXmaxLktReiXcwjjT7GuFnmv9pv9ZoM1psVpDBftJqb2Q00NHwp7dZeTajUUlobCXIWrXigzwI+CK3nPe2lXLnvFTmpEUJ+7G3LobASGErNmKup0NUUPBKVCqJfy/JIlCn4e53d9l8D+0Vc34NstlnqshndoK8/3OQLaKjFthdKipd2UnhnozKIdLwGZhlCfmQlw0MKfxeTEBKv5jc0jqyhoZ7lY90ZzLab4D2lNUJvWzWUiEPqT3k4chOkVtWRyB6opsLvcb/uDvjEsM4WNlo/80yPhsiR8Lej/p1fb3JbLOCDFbrNUda4tMT64D2kdWtdqQZtpJqUHyQBwNHapr57Sd7mZAczoMzo+CT2+DrXwkbslt/gKiRng5RQcGriQn1519XZnGgspG/f3OgfxcZMgyyrxWTFr14/oCVMztBzvsUoseIkcNAbmkdOo2KMXHeKQ0AGDs8ib1yCvrCNZ4OpSv5n0FgFPqEqRyobCQryTur8CBGaaZGB3XcEDH556LLeutLng2sE7mldWSrisWAkORpng7HJtlJ4Zgssv0qsiTBuCvENnZDRZ+vb29kNFiT1tMTXWuyHttyAD6+FZ4cAU8Mh+XXE3dyBxIWuxVkP62darVW0SD7MgaThXve24VKghcW+qF9dT7krYC5D4vRxf7e+16loOBNzB8Twy2zUnhjUwk/5PfTsm3Or0RT/Pp/Ozc4F3DmJsiNlXBkI2Rc2vHQ7tI6xiWEemWDnpXspHA2WzLwq9olZA3egNkkmh1HLWJfRTNmi0x20pCez/Mg2UlD2HW0TnTlhsbDuMvEcAu9HU2tm8ktq+PskBLxjZc16FnJad9p2XX0pP2Dxl0OyCIh6SP6HpPW06u6ppqjPK19hrk/XgGFKyHtXDG4pGQDOat/xia/ewnNWyZes50wOKggK6OmfZsnvj3AnrJ63ppeSeyHFwkf+Zu/hfm/VabkKSj0kYcWjSYjIZRff5RLeV0/hkGFJ0POtbDrba/XIp+57w77vwBkSBfyCqPZwt5j9WR5sbwCYERUELs0mahkExzd7OlwBMd2QFs9pC3sqMp6cwUZICc5nJpmA2Un2//Ap98FhibY8oJnA0NYle0urWOapkg05wV452syJtSfxPAAdpU6aMKLHgVx42Ff32UWjirIfhp1VxeLllrIW8HIFYs4W7WToxm/ENZSl74gPFfv20PJ3KcolaNJ3fp7eH4afHoXfP9H+OY3TKn+iKGqGjtrKRILX2XV/ipe21DMG8NXkr35XtFzcNsaGDrJ06EpKPgkfho1z1ydg9Esc9e7P/WveDDrATGDYtMzzg/QiZy5CXLeCpF8xIwBaNdSWrxafwxCLG9JnIIRDRT/6OlwBIXfi4l0I+azu7SOxPAAYkL8PR2VQ6y/547kLj4L0i+Gjf/1+F3tsbpWGpuaSNPniqEbXkx2cji7j/bgUjHuCjG+t/Zwn65tb+AHQKBOTavBBAe/gf8tgCdT4MMb0QfGc67hCY5P+XXXrXO/YPRjL2eJ4RF2TH8OgqKEg83m52DXMq6ofpr3W2+HLx84bRfhtGRcwScorW3hkeWbeTfkGeZVviG0jzd+JXaMFBQU+s2I6GCevCKTXUfr+NvX+/t+gSHD232RX4em406Pz1mcmQlyQ4WYmtRJXpFbJj7kc7xcGgAwdlg8Wy1jsBR+7+lQBEU/QNIUCAgnt6zO66vHAGPiQvDXqrrKAxY+ChYTrPqz5wIDckvrmaI6gMas73BY8VZyksI5VtdKtaMpS+MuE1/7WEVuM5ptjppGlplt2syfq34B7y0V1eMFv4drP2LTWR9xVI7F34Y0QzhiSByNnie22H91EB45Ab8t49cJb/K1/wWieeSVhV2SeaWC7HvojWYee+sL3pR/xzTTDlj0hNhJ0Hr3jbuCgq9w/vh4bp4p9Mhf5PajqDTrQTDpYcvzzg/OSZyZCXLeJ4B86oMb2H20joggHUkR3j8XPjspnB/NWahOHIS6ARh3O4OmajGNcORZnGhqo7S21eur8AAatYrMxPBTjXoAESkw7U7IfRfKd3kstp+OnuQsTS6yxt/rK8g5yd0q8bYIT4bk6ZD7QZ8mFtqsIDfXwLLLub/mMXSWNlj8LNy9XdgHpZ1Nq1kcbytBDtDZcbGQJI7IsSwbchfc8IV4Tb+5uGMnwU+jwmC29H+KlIJbkWWZ5z/4jCdPPkiyrgnpuk9g2h2iaVRBQcFp/Pb8MUwcNoSHP95DUXVT306OGgljL4Idr0JbH891EwNKkCVJWiRJ0kFJkookSXrYxvNzJEn6SZIkkyRJVwxkLaeyZ7mwoOpkCr/jyElyksLFZCUvJzspnDWWbPFNkYeryNYBGyPPZvvhWgAmDvONSVTZyeHkHWvo6lAw+5cQGAXf/c5j46e3H65hkXY30vDZoAv0SAy9JSMhDI1K4idHjXoAWVeL0dPHdvbqumaLGBndpYJcVwr/mw8lG/go5l5u8H8aJlwHam3HIa0G8bsMsFVBttq8GU6XS7QazCKBHj4Lrv9UjJ9/dwkYW9FpVMgyGM1KguwLfL5mM9cWPoDGLwDdHT/CiHmeDklBYVCiVat49poc/LRq7ly2k+Y2U88ndWbmfULStutt1wQ4QPqdIEuSpAaeA84D0oGrJUlK73bYUeBGoP/zZp3NiUJR8cxc0vFQdaOewyeamTrCNxK7yGA/iEzjhDoWCn/wbDCH10NABMRlsq2kFn+tivFeOmilO5OGDcFgtpBb2klz6h8mutuPbPTIdL2mNhP+lTuIM1cITbSX469Vk5EYxs6SHhLkjEtA4w+57/XquoaOkdHtiW5LrRjq0FoHN33N9pgrabLxXmytDttOkNtHTduQS7QazQS2V5hJyIErXoPKvfDVL/FrHx6iV6zevJ59BUVkrrmJYJWJwJs/E9O7FBQUXEZ8WABPL82h6HgTv/l4T9922oZOEruLm58/zVnIGxhIBXkKUCTL8iFZlg3A+0CXT3RZlktkWd4DeI+Ab9cy0VA27vKOh7YfFh/uU1IiPRVVn5maGsUqUyby4bXCtshTlKyHYTNApWJ7SS05SUO82iavM5OHixuibYe7uRfkXAfBcbDpabfH9NORk1wurcGkCeqikfdmpqVEkFtWZ7My24F/mLBb2/sRmNp6vOapgR8q0e388S1QXwrXLoehkwjQqW1Xgq0Jsu70BFmnVqGSHFSQtZ2mFY46F+Y8BLvfYXyVsKjr9/QoF+GzO3guoqa2BvV7S0iQajEvfR91XIanQ1JQOCOYlRbFQ+eO4cs9FTy/prhvJ8+4F+qP9nviqisZSCaTCHQWwJa1P+a9mI2w+10YtQhC4joe3na4hgCtmowE7x0Q0p2pKRH8YByPZGiC0q2eCaLuKNQdgeGzadQbyS9vYHKKb1ThAYYE6RgTF8LWdmlIBxo/oVk8tAYq9rg1pt3FpVyo3owl/RLwC3br2v1l6ogIjGbZsR8yQNY1oK8TUwt7oKU9iQ3UqWHri6Kaf96THUNTAnRqmxPx9IZOiXU3JEnCX6u2mei2GEwE6LqdM+9hSF3A5AN/J1MqdnwD4GZ8dgfPRbTpWzj24uWkWQ5Tec6LhI6e7emQFBTOKO6YO4JLshP4x3cHWZlX2fsTRy2CyDRRkPKyPo+BJMi2xLr9/ukkSbpNkqQdkiTtOH7cRbYf+Z9BczVMuL7Lw1sP1zJx2BC0at+ofIKofm6yZGCRNMJFwhOUbBRfh89i55GTWGSRuPsSU1Ii2HnkJEZzt02OiTeBLtjtPo26A58RJLWhm3yjW9cdCJOGR6CSYEv3G43ujJgnKvO9kFm0GMR2W6SpClb/RQz8mHhjx/MBWjVGs3za701vshCgVdvtJQjQ2k6shcRC0/VBlRoufxWDfzTP6/5LW71X2RH55g6eC5DNJvKfv5ZMwy72TvwLw2Zc3vNJCgoKTkWSJP5+eSZZQ8N44IPdHKi0M2G1OyoVzLgbKnLFjrQXMZCMsAxI6vT9UKDfBrKyLL8sy/IkWZYnRUdHDyAsOzQdh29+A3GZMHJhx8P1LUYOVjUyxccSu4TwACIiIijyy4DiVZ4JomQDBAyBmHS2l9SiUUkdrga+wtSUSFoMZvYd6zZBLyAccn4m/LKbbQ+QcDZtJjNT6r7muP8wr52eZ4tQfy3pCaGnS1W6o9ZA5pViwl3zCYeHNreZAZmcvY8BElzwzy4uBFaNcfdqcKvBjjVcO6KC3DVftFhk9EaLTd0ygRHsn/0s0dQR+8PdQu7hHThtB88txQlXYTZR+NK15DSsZv3we8hZfJenI1JQOGPx16p56bpJBPlpuPXNHdQ291L+mbkUgqJho/tljY4YSIK8HUiTJClFkiQdsBT43DlhORlZhi/ug7ZGuOxl8UHdzvaSWmT5lB7Vl5iaEsl3bRmimaixn3PRB8KRDTBsJqhUbDlUS0Zi2OlVOC9ncorwvT5NZgEw4QawGHvdWDZQDu7dyQSpgJq0JT5nSTU1JZJdR+u6OoLYIvta4TW9+x2HhzUbTFys2khUxTrhcRye3OX5Dsu2brKHVqPZdqLb6bxWY9dmEEe6ZQBLfA5/Mt1AWPl6WPcPh3G7Eaft4Lm8OOEqDM1UvraUUdXf8kXUrcy6wbP+5QoKChAX5s/L10+iurGNn7+1o3e9G1p/mHK7cOWqynd9kL2k3wmyLMsm4G7gO2A/sFyW5TxJkh6TJGkxgCRJkyVJKgOuBF6SJCnPGUH3mY3/hYNfwVmPQMzYLk9tKDqBv1blc5VPEHKGb/XjxDfudlyoOwonS2D4LBr0RnaX1jFrpO80OVqJCfFnRHQQm4ttVD9j00Ul96c33aKNatv+JkZZTcLcm1y+lrOZmhJBm8nS81S9mLEwfLaYYHfgK8j7FA58DfXHuhxmrK/mj9q3aI7Jgam3n3YZaxLcXS7RajTb9EC2EqRTt1enu54DnHKx6L6WTs175gWUJ10I6/8FtYcc/4zuwak7eD7HyRJaX1hAdNkPvBp8G2ff/qRPWHQqKJwJZCeF89RV2fx09CT3vb8Ls6UXn5+TbwFtkHiP9RIGJLqVZflrWZZHybKcKsvyX9sfe0SW5c/b/3+7LMtDZVkOkmU5UpZl97cVF/8IP/xJOAJMP337bV3BcaamRDr8UPVW5oyKJl9OpkUb4X4dsjUhHzGfTUU1mC0yc9J8qPrUiTlp0Ww9XGP7TnfC9XCiwPWNkGYjaRVf8pPfFEKjvLvX1RZTR0SiVkmsL3QsnQDg3L+CoRnevwY+vAHevxr+kw7LLofqA2DUM3rrwwSh58SCfwstcDfsDf1objMR5Gd/FyPIT3OaV6cj72SAIJ0GkMgd+0tQaeH7R3r+GV2P7+zgOZtjOzG9fBaGk2X80u8RFt/+F598/1ZQGMycPz6eRy5M57u8Kh79Iq9n+7fACJh6G+z7GI4fdE+QPeA7XWn9oakaPrkNokaJMaPdKgyltS0cOtHMnFG+mdjFhvozOi6MbdpJQtdpdDDu19kUrYLQRIgezbrC4wTp1EwY5v1jum0xd1Q0eqOFbbZkFhmXiWa9HiQBA6V531eEy3VUpF7p0nVcRViAlgnJ4awpqO754PgsuH8v3Loa7tgIt66Ceb+Fsh3w4iz4byZxVWv5s+k6dPFjbV7Cmsy2GGwlyPaTpUCdhqZuCbL1GvYkFtbKco0qEmY/APu/EPp7D+JTO3jOpGwn8usXUKVXc5Pqr9x32+1Eh/h5OioFBQUb3DQzhdvnjOCtzUd4cW0vdt6m3wPaQFj7pOuD6wWDN0GWZVhxB7Q1wJVvgC7otEOs1a65o6LcHJzzmDs6mjcbJoqf011VZLMJDq2F1AXIiCr89NQon3IB6cy0EZHoNCrWFthoUPILhtHnQ/7nLvWbbtr8OlVyOElTFrtsDVczd1Q0+441UN3Yixu1wAgYOhHixgmz+HkPwz07YfwVEDWKb7JfYJn5bLuadmvS2tJNLtHUZibYQQU52E99WlLdk8QisP16rQYzTL8bQhJg9V89bknkEzt4zqShHMt7V1NlDuEa82M8evOlpESd/r6uoKDgPfxm0Rguzk7giW8PsHxHqeODgyJhyq3tVeQC9wToAN/MaHrD3g+Fu8PZfxZaUhusKzhOQpg/qdG+4Tdri7lp0awzpWPwixAvKndwbCe01UPqAkpqWig72erTNxkBOjVTUyJYc9BO9XPc5cK/11U674YKoivX8bk0j6xk39NxW5k3OgaA9QW9kFnYIigKLn0RbvySwhDh4mEvaQ32F0lr92pwc5vJYYJsS2JhtZTrMiikE9ZqdbPBBNoAmP0gHN0Eh9f14odScAqGFszvLqWtpYFbDL/mb9cvZPxQ35jYqaBwJqNSSfzjiixmp0Xxm4/38NnuY45PmHGveJ9d5/kq8uBMkFtPwnf/B4kThfDbBkazhY3FJ5gzKtqnmzsmDh+Cn07HTyHzRdOTOyzJileBpIIR81jbnlTO9lH9sZV5o2MoPt5MaW3L6U+mLgD/cJfdgFh2v4sKC6VJl6Hx0So8QHp8KFHBfqyxVYnvI80GEzqNyu6uRIifFrCdIDvSIAf7nS6xaNKL70P8bZ+nVkn4a1WnHDNyrhNV5DWPe7yKfEZgsWD65A6kyj3cY7ibe66+iJkjffeGXEHhTEOnUfHydZOYMjyCB5fn8s3eCvsHB0XBZO+oIvvup7EjfnwcWmrhwqdsNvgAbDlUQ6PexPwxMW4Ozrn4adTMHBnFM/WzwdwGu952/aKF30PCBAiM4Nu8StJighnu41udc9t16D/aqiJrdJC+WNyAGGwk0ANBljHseIutljHkTJjo3Gu7GZVKYs6oKNYVHD998EofaWkzE2SnegydKsh6Y5fHm3qoIAfqNLSZLJg6xdfYniD3dF5ze6UZrX97FXkzHF7b48+iMDCMqx9Hc+AznjBdw6VX3cKicfGeDklBQaGPBOjUvHbjZLKTwrnnvV38kO/AmnbGvaDx97it5uBLkGsPw47XYMJ1EJ9p97Bv9lUSqFN3JEa+zHnj4tjYGENj/HTY/qprhxmcPALlP8HYCznR1Ma2w7WcNy6u5/O8nJExwYyMCearPXbubMddAcZmKPjWuQsf2YR/QwkfWeazYEysc6/tAc5Jj6O+1ciWQwPbyWg2mBx6aluT2c7VYKPZQpvJ0oOLhVUucepvpLE9ybZXQQYh9eiid+6oIv9dqSK7EP3uj9BueJIPzXMZd8XvuCBTSY4VFHyVID8Nr980mfSEUO58Z6f9z9vgaLH7v+8jjzpaDL4Eec3joNLA3IftHmK2yKzMq2T+mJhBYQ901thYtGqJ7wIvgvqjzk/iOpP/mfiafgkr86qwyAyais754+PZVlJru8ls+CwxJnnvR05dU971Fs0EUDf8PMICtE69tieYNzqaIJ2arx1tofWCRr3JYcKq06jw06ho7JQgW7XFPUksOh8Lp5LsYAfrhfpradB3kmZ0qSIrWmRX0FC8DenTO9luGY3/Jf/lomzfsz9UUFDoSqi/lrdvmUrW0HDuee8nlm+307g34z7QhcDXv/ZYEWJwJcjV+2HPcph2B4TaT9q2l9RyoskwKCqfICy2ZqdF83TZKOTQobDpWdctlrcC4rMhIoVv9lUwLDKQsfEhrlvPjVwwPh5Zhu/2VZ7+pEotmvUKVwqNuzPQNyDv+5TPTNNZkJninGt6GH+tmrPGxvLtvsoBySzqW4093jCE+Gs69MNwKtENcSSVaH/O2pgHIhkXCbf9m+XQAA0N3eQc5FwHF/0Xkqc5jFOh7xw/tBvzsis4LofSfMkbXDRxcPx9KCgoiJzlrVumMHNkFA99vIfXNhw+/aDgaDjrD0LG5i4Dgm4MrgR5w1PCQ2/GvQ4P+3ZfJX4aFfNH+7b+uDPnj4/naL2BY2NvER32RzY7f5GTJUJekXEpJ5sNbC6uYdG4OJ9ucuzMqNhgUqOD+Mpe9TPzSjF62lpFHyj7PkZl1rPcMo+z031fXmHlgsx4TrYYbU8n7CUNvUiQuzfcWSfkOa4giyS4sVNi3dhmItRB9RggxF9LQ2u3BFnrDxNvBI3iw+tMjuZvQfXWxZgsEicufZ95E2y7ECkoKPgugToNr9wwiXMzYnnsy3z+9vV+LN0n7k26GRJyhOmCvt7tMQ6eBLnuqLB2m3ij8Fi1g8Fk4fPcchaMiXH4QeprnD02Fp1axZv6ORAYCRv+7fxFrIlhxiV8uvsYJovMxVmDZ9tTkiQuyExg2+FaKupbTz8gPhsiR8KeD52ynvzT2xRLyYSPnEZU8OBJsuaOEjKLL3L7P/m4vtVIaE8Jsp0KsqNBIdaku7NcQsg5HK8V6q/tklQruID6Y5R+8Evil5+PBYm6Kz8mO3uyp6NSUFBwEX4aNc9dM4Hrpg3j5XWHuPOdnafcgkDs3F7wbzH07fs/uj2+wZMgb3pWWI/ZGCfdmR/2V1HbbOCqyUluCsw9hAVqWTQujg9yazBOvl1IASr3OneRvBWQMAE5fBgfbC8lc2gY6Qmhzl3Dw1wxYSgWGT6wpYuSJMi+Bo5sGHjjQFU+UvlO3jXM4arJyQO7lpfhr1VzQWY8X+2t6GiA6yu9kVgE+2m6aJDrW8UgF0fnhQfqAKhrOTX0pVFvdOhgAe0Si+4VZAXncKIQecUdmJ/KJCH/VdZq52C8bT1p4yZ5OjIFBQUXo1GreOziDP5wYTor86u46uXNVDV06gNKnAAz7oadr0PBSrfGNjgSZFOb0KhkLoEwxxXN97eXkhDm7/O+vbZYOiWJBr2JbwMuBG0QbHrGeRevyIXyXTDuMvaU1XOgspElkwbXTQZAcmQgs9Oi+GB7Kebu2z0AOdeDWgfbXxnYQruWYULDj34LOGvs4JFXWLlm6jBaDGY+2933KrLRbKHFYO6FBrmr7OFks/j/Ie1JsC3C269Z13LqvKYeGgKhvYLcZrL9mlDoH3VHYcUdyM9NwbhnBW8Zz+L3yW8z/VcfkZAw+N5bFBQUbCNJErfMSuF/102iqLqJC57ewKbiTgOnFvwBYjLgs7ugvsxtcQ2OBFnjB3dvF/+IDig72cL6wuNcOSkJtWpw6GY7M31EJMMjA3l7dwNMvEHcNDjrxbThKfALhQnX8/72Uvy1KhZnJzjn2l7GNVOSqajXs7bAhidycDRkXAa734O2xv4tYDJgyX2f7y0TmT9hLDrN4Pgz7EzW0DDGxofy7tajyH3sQK5vT3p7SpAjAnWc7FQJtv6/owQ5zEaC3KA39pwgt5/XpMgsBo7FAtv+B89Nw5K3go91i5ne+h9OzH6Mv9504aCSvikoKPSehemxrPjFTEIDNPzsla0892OR0CVr/ODy/4FJD6+dB7WH3BLP4PlkDoxw6FwB8PbmI0jAlZOGuicmNyNJ/8/eecdHVWUP/HsnvYckECABEnon9CJSbKCiWBd7Yy1rAd21/mysu7qurmtFXfuqKGJjUREUKTaQLr23hBZI723u74+XIZPJtCSTTGZyvp/PfGbee7ecd997Z849795zFVeO6MzqA9nsSr3GCI2y6rXGF5y1F7bNh2E3kV0VxpcbMrhgYEeiXYzb9FXO6ptIQmQI7688aD/BiJuhvAB+n9uwCjbPw1SSxSeV47lyhCuGwdoAACAASURBVH8Nr7CglOKqkZ3ZdjSfDem59crrroHcJiKY7KLyUwZ4bnEFJuU8nnFggImokEByS2oM6+yicuJdjAG3TOKrE8lCqB9FJ+GDi2DhvRyPHcTZ5c/xVOU1/OvGs7hvUm9Mfui4EATBfXq1j2LBnWM5b0AHnl28k5v+u4bM/FJI7AfXL4DyQsNIztze5LL4j4HsgrziCj5cdZApAzuS3Cbc2+I0GVeM6ExUSCAvrC2FfhfDuvegpH4GSh1+fRlMQTDqT3yw8iClFWZuHtfVI/K2RIICTNx4WgrLd55gc4admbNJQ42ZtavfrH98xoO/ohc9xCZ6ENTzLLq3i/SM0C2QiwcnER0ayGvL99Yrn2V8cEy4cwM5PiKYiip9anJeTnE5seHBLo2smPAg8qo9yFVmbRjIEY69zmDf8yzUk6O/wxsT0YdW8WHbPzMy/Q7iO3Zj4YzT/SqikCAIjSMyJJCXrxzME1P7sXJvFmc//yMLfj+C7pAGNy40Er17njHsswlpNQbyf1ceoKi8ij9N6OZtUZqUmLAgrh+TwrdbjnGo9x+N3ta69xpeYMFx2PgRpF1FQVA87/26nzN6t6Nnon/EPnbEdaO7EBMWxEtLd9c9qBSMvA1O7jQ86+6ydT68fxF5AfH8qfRObh7fw3MCt0AiQwK5aWwq3287zrYj+W7ny8wvAyAxKtRpujbVRm12kWFQ5xZXEOvCqAaIDQ8it9pLnVtcjlnj0kBOiDI8zCcLy1yWL9hh71L0O5MpLivnavNfeeLoCO6f3JuPbh5J+xjn11kQhNaHUorrRqewcObppCZEMOPjDdzx0XoyQ1Phpm8hOLLhb3HdpFUYyAWlFbz7y37O7N2OPh38K+qCPW4am0pYUADPbg6F1PHGMIsKO2HL3GH1G1BVDmPu4s0f95FTXMHdZ/m3YQfGBLDp1cbdlsN2vMgDLofE/vDNve6N8978GXx6A5Ud0pha8iip3fswItVxOEJ/4cYxqUSFBPLKMjsdDQdYZjAnRjsf9mAxarOqDeSc4nKn448ttAkPPpXH8u1qiEXb6uMnCsRArjc7FmKeM4102jM+9zFK2g5k4Yyx3D6hO4EBreIvSBCEBtKtbSSf3Taa+yf3Ysm2TM54bgVvbYWK6Utg0lNNWner0E6zl+0lp7iCGWf6v2EHEBcRzPSxqXz1+xG29rgNCo/Bytn1L6i8CNa+Db3P52hgR976eT/nD+jAwORYzwvdArl+TAptwoN4fMHWugHMTQFw2btGBJVProUKO8tTW9jxDXxxC3Q5jRc7PMPBklDum9SraYVvIcSEB3HjaSks3HyMdQez3cpzvKCMoADl0ti1eJBzLMZuoeuhEgDtokKNMW3VecC1B7lttQf5hHiQ3cdcRcmy56iaew2bKjtxVcUj3H7BGD67bQzd2/n3GyhBEDxHYICJ2yd0Z/E94xiW0oa/f7Od89/ewcr9jRw+6gK/N5D3nyzinZ/3c8mQJAZ1ah2GHcDtE7qT3CaMmasiMPc6H35+HvIdrBDniN8/NpZVHn0nsxZsxaw1D57bu2kEboHEhAXxf+f1Yd3BHD5ZaycuctuecPHrxuqCPzxhv5C9S+HTG6DjYHaf9Rav/XKEy4Ymt6p78dbx3egYE8rDX26h0o3lp4/nl9IuKtTlWGKL0ZpZUIbWmsO5JXSMDXNZfsfYUI7nl1JZZSaryDB4XXmQQ4MCiAoNFA+ymxQe28ORFyYStuIJFlcNZcHAV/nfvVO48bRUv4wgJAhC05OaEMG7NwznjWuHUlxexY+7TzRpfX5tIJvNmvs/+52QIBMPTG49hh1AWHAAT0ztx57MQt4LvwmqKuC7h90vwGyGla9C0lC+zEpm8dbjzDyzJ53i/HeCoz0uG5rMiNQ4/rFwO0dy7QxT6TMFhv8RVs2G/T/WPnbwV/j4KkjoSdkV87j7yz1EhQbyUCvqZICx9PNjF/Rjx7EC3vllv8v0x/NLTxm/zmgfHUqgSZGeXUx+aSWFZZUkuWEgt48JxawNb7DlmraPdj0Otm1UiHiQXZCXdYyf338cXh9LZN4u3mz7ECm3fcZjl41y2QkRBEFwhVKKc/q1Z8mfxzPjjKYdFeDXBvKry/ew5kAOj1/Qj0Q3/gD9jTN6J3LpkGT+tqqMA31uMeIir3/fvcy7FkH2Xo70nc7D87cyIiWOm09PbVqBWyBKKZ6+ZABmDXd8tJ6yyqq6ic5+AuK6wZd/qlkv/ve58OFlEJOMvuYL/v7DUbYeyeeZywa1SkNhUr9EzumbyLOLd7L+UI7TtPtPFNEl3nVHLMCkSGoTRnpOySlDN6mNawO5Q/WksKN5pRzIKqZNeJDLiBkA7aJCOJbnZChNK+bg5p9Y9+IVhL7Un7H7XiA9tDdHrljCzXc8SN+kGG+LJwiCnxEaFEBYcECT1uG3BvLSHcd57vtdTE3ryKVDnK+u58/87aJ+9EqM4qJNIynoOBYW3AWfTYdiF+NBV75CZVQSf1jRloiQQF68Mq3VTqjp2jaSZy4byIZDudw9d2PdYQLBEXDJG1BwFD64BOZeDV/eCh0GwfVf8Z/1hXyw6iC3jOvK2X39b9U8d1BK8exlg2gfE8rtH64ns8C+oVlQWsGRvFK3o6R0ahPOoexiDucYBrJ7QyyMNOnZxRzMKqJzfIRbdaUmRLD/ZJFbaVsTa16/jS6fT6F39lLWx5/Pvsu+o8+Dy+ndp7+3RRMEQWgwfmnxrNqXxe1z1tO3QzT/uGQASrXeMW/hwYH896YRREZEMO7w7RwceLcRmuzVUbBzkf04vofXw8FfeLX4bPLKNO/dOJwOMa4ND3/mvAEdeHRKX77dcozbPlxHUZnNimrJw2DqbGP53N3fw8SHqbpuAf9amc/T3+7ggkEdebCVDfOxJSY8iNeuHkpeSQVXv/mb3ZBpuzMLAejhZnzozvHhHDhZxNYj+SgFXdu6Nna7JkQSHGBi25F8DpwsJsUNb7UlX3ZR+ak4zYJBSP8L+bH7/ZTN3M7oGf+la/+R3hZJEASh0fidgbzg9yNc9/ZqkmLD+O9NIwgPlmVLE6NDmXfraNrFRjFhzQje7P0WVaFx8PE0eH0srHnLiFgBlJZXkP7ZQxTqML5QZzL31lH06yivSAGmj03lb1P7sXRHJue99BMrdp2ovYxy2pVw3254+Bi7ev+Jq99ZyyvL9jBtWCee/8MgWSUM6J8Uwzs3DCc9p5hp/1nJvhOFtY6vO5BzKp07DO4US15JBfPWptO9baRbqzsGB5ro1T6K77cf53BuCX3dDP2YmmAY33tPiBfZmoFjz2PcNQ8TFxfvbVEEQRA8ht9YjwWlFfzj2x189NshRqTE8Z9rhtDGeqyn1sYCD9aYzcY+y35z9atz630WA8g2r6W8qiowWfUzqqqM/QEBNccsZWhdk9ZaHstvpYzfttvW9VuOOfp2QMfYML64fQx//2Y7T64+xOzgh3m44wbOLF5I3Dd/oey7J9gQcyahJ7eSxk4+TLiLT2+Y5NZkKbvtay23vXMym2u3m6N2tqS3tKVtfkt627qt287S7pZt27zWZds7FyuuHZ1Cz8Qo7vtsE9e/s5o+HaI5u28i3dtFnpow9uPuE/yyJ4vo0ECeuXQglw9LdvwWw1671fdaW+5bS3ta7kHLOVvns74HLfe/bTpL2ooKCAysSW/ZVqqmDS15bLedMLpbPP+9cQS3fbiOC17+mVkX9uPSIckoBd9uOUqfDtF0jAm1/3bD5vxHdzOMssO5JVwxvJPrNqyWc2jnWN6rXkp8XM+29q9FVZXxHFcf651oeLU3ZeQytHOsy/MUBEEQfBel7f0JuZtZqcnAi0AA8JbW+mmb4yHA+8BQIAuYprU+4KrcYcOG6bVr17otR0l5FWc/v4IjuSVMH5vKX1Z/SmheDjz/fM2f4z33QGwszJplZJowAXbsgGnT4IUXjDQdO0J2NgweDKtWGenuvht++w0mT67JO2sW5ObCl1/CyZNw442wdi0cOgTHjhlpkpOhuBi6doWNG43yg4MNI+Kmm2D5csjKMvbn5UG/fkYdixZBebmRdvJkox5L/WBsx8QYef79b/jzn2u2rc/PCduO5PPuL/v5bttx8krKGap28cfAhZxtWkdOUCL5Q2+n2+S73DcALO1h3d6jRxvHJk2Ct9+GhAQYP96QcdEiWL8eQkOhb18j3UHDWKFz59qGVmgorFxptEm7dpCSAqWlsHWrYex07Gi0teX6WGSJiYHFi41yysrgwguNNnr3XSgpgaFDjXJnzYLZs416/vhHePzxuveKHcoqq/hsXQafrs1gU0Yu1mGSuyZEMDUtietGdzkVq9ftdrPUDe5d6wkTjHuve3ejTWfNgtdeM84xIQHat4cDB4x7sbISIiIgNRWOHDHudaWgbVtITDSuQUoK/PorBAUZ7duuHdx2GzzyCISFGTJ26gRt2sAFF0B+Pjz3HAwbBtHRxrPj5n14JLeEmXM3sOZADj0TI+l54iBfm+N5LOAgN/3wPowcaTyHSsGIEbB6tXE/WZ//rFn8pSiJRWGd+OqusXRNiHDchjExsGABXHAB6QXlnBMyhqFVuXwQvs+41a2vxfjxsG0b3H67sZ2TAytWMG7CffQc3JO3Nsxx+zwdoZRap7Ue1oj8Hte/9dW9DnHW8fNEfttOELjVwa2T3l4n2lVn1LZj76gTa41tJxKMDlhgYE05lZXGc2fBuoNmqdvWcWIth6OOriNnhGW/JZ+lPmeOGUftbb1ti3X91p10R+W4U7btOdlzclg7A2zPwbYtLHVY2tiyba+zbZ3Xtg6bTvWp8qzP2bIvIKCm3S33gdlct0zruh1dD0f3nr12dJTOtq1tz8VaBkv722sve21nOTdXTrH6PPeNwF3d22APslIqAJgNnA1kAGuUUgu01tuskk0HcrTW3ZVSVwD/BKY1tE5HhAUHMH1sKmmdYhncKRa+z4EXXzQOPv+88Yf54oswc2bNhc7NhePH4aWXjHTLlxvbYPwRz5xpXAjL8ZEjay5obq5RXmioYazNtrMIR3p13NysrJp9ldXjVi1lWrN6tWHUbN5cs6+0FDZtqqnfkjctzTC6V6wwvi3blvNzcQP17RjNs5cP4hmtycgpIa/kdCJDboWYYNoGBtK2vn9klvYAo70tnQrLORw+bHx+/x0GDTK+AQoLjfO2xnINLAwaZBjHAJmZxscaS9kjRxoPoEUWS5tYpzt5smb7t9+M9vroo5prlJNjyP7SSy7bMiQwgKtHduHqkV0oLq/kcE4JFVWa9jGhxLmxWIXddrPcpzNmGPtcXeuqKqOMoiKjTYcMqX2eoaE118FCSUntdgDjOlg6KMePG0auxSudmWl0BP/+95p9+flG+owMo6w5c4zvhAT48Ue378OOsWF8csto5m88zAcrD/JDVSyXblnCdUdWwMYNtWW3/C4rqzn/6uv9rxf/yl9n/pnIhEnO2zAhwZAzI4NOJ0+yatgootb+hppxV01aMAz+bduMtK++CldeCS+/DMDEPtv5eFsUx9/+gMTp13pMYdeXlqR/6+Cs4+dOh8JVfuvjf/2r8dyC0Wlz1cGdNcvooI8caaTJzTU6YQcPwq231nSk8vJqnjeLHI8/bnSwLrzQqNcilyWddWd2zBijPsv9cc458NVXRt7Fi43ObEAA3HefUVZyMhw9anwfOgSPPWZ0dPv2NZ79xx+H//zH6MBOmmTIrTV88YVRT0KCUX9pqfGMhIQYToO33zae6cRESEoyOprz5hnPtaVzfOutNU6LsDDDeTBokP02hZr2e+EFY9ueE8nChAlGm6xbB088YXTKf/rJuGZTp9auY/RoQ6dceqnzsq3LNJmMtnruOUO+jOpVTUeNMtrxlltqXyvr+8JyL0DN/fC//xltp1TtzjjUvSc7dTJ08OHDNXJYrtnEifDWW4bDTGuIi4MrroDXXzfsgMBAw1kRGWnomREjjDxvvGFsh4Yajjel4PPPjTwpKUY72F4PW0fKmDFGnaNG1W5bqDkn23SW/2bL9Vi2rLaDIDsbPv3UuGenTzeeg6go2LULunQxyrA8T7/9Zsjv6tmxyLRypevnvCF6xBNorRv0AUYDi622HwIeskmzGBhd/TsQOEm119rZZ+jQobpRmM1az5xpMYWNz8yZxn4LVVVaDxpUOw1onZZWd9+MGbXz2iu/MR97ddqr31m9tufXnNiTa8YM4+PonBISXLfLjBnGdbrrLvfax91rExfn/HhztaWz+9Tda+3oPm6qz+23a11Z6fiebUzbuftcWdfR0DZ0J62de/RgTKLufu+Xesp9H+k5qw7o77Ye0zlFZQ06XWCt1i1L/3pU91ra1na7Mfmrqmq2bXWM9ba9uszm2ultn5v4eOPbcm9bvi31Wu+3lsM2vb3n0XIv2d5ToaFa33FHzXZAgNZlZbXTV1TULtPRs2eR3/IZONC9Z7pNm9rbAwbYb9MZM2rrYnvtb/sfa9021nmt28G2XGdl25ZZWVm7rDvvrF2W7bWyft5t/59s28/S5vbuK9s6rOWIj3f9n2W59pbfwcHu6XHb62H5bXsPOmpbR+mst++8s/b9d+ed9u9la/lty3D17Ni7to6e84boERe4q3tdJnCYES7DeK1n2b4WeMUmzRYg2Wp7L5DgoLxbgLXA2s6dOzfq5LXWRgNaXzx7DVpVVfcGtLfPXl7b8hvzsVeno/od1est49iRXBYl5OicKitdt4u1EeRu+7iT3lXdzdmWzu5Td6+1q/vHkx9rw7wp2s6d58rV9XanDd1J6+A+WdRjlB76t+90lwe+1l0e+FqvO5jdoFNtpIHsUf1r+TTaQNbaPQdFY/K76vg4q8ueYeSoDOs/acvH1rBwlK4hn4CA2tu2xnRDO8K2hl9DPs4MS6hrHFuwNo5cfRw5VZwZ3o7aytG1sn3eXd0LzjrQd93lnhxN8amPE8BZ2zr7NPRcLI4tV8+OPZncdX40kuYwkC+3o6Bftkmz1Y6CjndVtniQHdQvHmTn7ePutREPcsM/rdyDbPlUzZypD2UV6k3pubqorKJBp9tIA9lj+tfjzgmt3XNQNCa/s46PO15qV/eYo865bcfQ3U68O5/y8trbth20hnaE3XFGuNsejs7VWZu7K7cjp4o7zi175+joWtXnXnB23haPtqfb2hPXw922bYr7pj7PTn2fcw/9LzeHgdwyh1i484rP1qiYMaPu66i77rL/GsC6PNtXDI39WL/agtoyOXudYv06o7mNZHvt6+w1Zn2NOXfT2/Za3enZ33VXbe+Kq1e0Td1u9l4dO7vWlZW122fQoNrn6a7nyNWr2QEDtDaZarYtr2RtXxtbvhvSdtbn7+ya2766q08b2spp2W973a1flyYk1O6gDRrksXvEL4dYaC0e5IZ+xIMsHuSGXA/xINcbd3VvY8K8rQF6KKVSgcPAFcBVNmkWANcDKzFeCS6tFq7pUMoYxD1zZs3g7uefN47FxtbMwoyNNSYuOIpiYZk8Bcag8zZtaibjWMpviigWYWG1o1hMmFBTPxj1xsQYs+ytIxtYIkQ094Qhe+39wgs1k6omTaqZwGWRMSSkflEsgoNdR7Fo08bIZ5ElJsaoR2vHUSxefNHIZ4liYZnQYDmnpmxLV/cpuL7WAQHGd0SE/SgWkZHGfldRLCIjoVs3x1EsLr7YmBBjiWIRHW1MzHAWxaK+bWfdHjExxvVwFMXCcv7W19udNrSKYkF+fu22tKS1lNO3b+1JKjNmGJOlYmON+7s57hHntEz9q3XtSdHWk0+hpn0bmt/yHNhOxISabUd1aV0zCRdqTxgGiI83dHJamlGGZWLszJlGvUOH1kzIW7euRg7bCbS25ULNBFHLt4XQUGPS0+zZNVEDiouNCXWW9EePGs+XpUzbCci28lsYONCY5G29zx5t2tRMdAQYMKBmsrh1m1rMlOoJq7Xa39KmlmcDDP1h3Wann16T17odZswwyrWevO6obK1rl7l2rRGpx1LWnXca9b/8sv1rBTU6wvpesNd+gwbVnLdFFss9OXNmzbnYyhEfD1ddVXPcEZZJ/mD8x/XpU/e+scX2eljkstwTtveGbds6Sme9feedMHduzf13xRXwyis1aS3Xzlp+6zJeesmYrO3s2bnnntrP7QsvOH7OG6JHPERjw7ydB7yAEWboHa31k0qpJzCs8wVKqVDgA2AwkA1cobXe56pcj4QashhYjrahVcVBbnLstTc4PicfjYPscZzdp+5eax+Lg+xWezjSS/bOvz5taCunvbQW7IU5svf8NhAPhHnzuP71iO6VKBYSxcKCRLEw0koUixYVxcJd3dsoA7mp8FgsTkEQhBZKYw3kpkDiILvRGZU4yHWPWW/bInGQa5+zxEGuK5Ptebq73UCaPA6yIAiCINjF3psgT+a33q5vXfbyuvq2YGu4uJvPOq/lWKDV369StY1jqG0c29bt6JytjSjLtm05luO25dnKYy+Pq2P2sK3HURvZK8dR2bbXwd45NqR8R9fXXlp7dVjL4ajtnbW7bf3O6rb97ezec5beUR2252J93CJnfdrLWVpH+xqrRxqJg6shCIIgCIIgCK0TMZAFQRAEQRAEwQoxkAVBEARBEATBCjGQBUEQBEEQBMEKMZAFQRAEQRAEwQoxkAVBEARBEATBCjGQBUEQBEEQBMGKFrlQiFLqBHDQzeQJwEmXqVouviy/L8sOvi2/L8sOvi2/p2TvorVu64FyPEY9dW9LwJfvo/rQWs4TWs+5ynl6D7d0b4s0kOuDUmptS1uNqj74svy+LDv4tvy+LDv4tvy+LLu/0VquRWs5T2g95yrn2fKRIRaCIAiCIAiCYIUYyIIgCIIgCIJghT8YyG94W4BG4svy+7Ls4Nvy+7Ls4Nvy+7Ls/kZruRat5Tyh9ZyrnGcLx+fHIAuCIAiCIAiCJ/EHD7IgCIIgCIIgeAwxkAVBEARBEATBCr8wkJVSf1NKbVJKbVRKfaeU6uhtmdxFKfWsUmpHtfxfKqVivS1TfVBKXa6U2qqUMiulfCKUi1JqslJqp1Jqj1LqQW/LUx+UUu8opTKVUlu8LUt9UUp1UkotU0ptr75nZnpbpvqglApVSq1WSv1eLf9fvS2T4Ps61F18UdfWB1/Wy/XBl3V4ffB1fQ9+YiADz2qtB2qt04Cvgce8LVA9+B7or7UeCOwCHvKyPPVlC3AJ8KO3BXEHpVQAMBs4F+gLXKmU6utdqerFe8BkbwvRQCqBv2it+wCjgDt8rO3LgDO01oOANGCyUmqUl2USfF+HuotP6dr64Ad6uT68h+/q8Prg6/rePwxkrXW+1WYE4DMzD7XW32mtK6s3VwHJ3pSnvmitt2utd3pbjnowAtijtd6ntS4H5gJTvSyT22itfwSyvS1HQ9BaH9Var6/+XQBsB5K8K5X7aIPC6s2g6o/P6Bp/xdd1qLv4oK6tDz6tl+uDL+vw+uDr+h78xEAGUEo9qZRKB67GtzzI1twEfOttIfycJCDdajsDH3to/QGlVAowGPjNu5LUD6VUgFJqI5AJfK+19in5WwGiQ30T0ct+jK/q+0BvC+AuSqklQHs7hx7WWv9Pa/0w8LBS6iHgTuDxZhXQCa5kr07zMMYriTnNKZs7uCO/D6Hs7BMvYDOilIoEPgfutnn70+LRWlcBadXjXL9USvXXWvv1WMKWgK/rUHfxM11bH0Qv+ym+rO99xkDWWp/lZtKPgG9oQQayK9mVUtcDU4AzdQsMTF2PtvcFMoBOVtvJwBEvydLqUEoFYSjLOVrrL7wtT0PRWucqpZZjjCUUA7mJ8XUd6i5+pmvrg+hlP8TX9b1fDLFQSvWw2rwQ2OEtWeqLUmoy8ABwoda62NvytALWAD2UUqlKqWDgCmCBl2VqFSilFPA2sF1r/W9vy1NflFJtLRESlFJhwFn4kK7xV0SH+gWil/0MX9f34CcGMvC0UmqLUmoTcA7gS+FEXgGigO+rw9S97m2B6oNS6mKlVAYwGvhGKbXY2zI5o3oyz53AYoxJA/O01lu9K5X7KKU+BlYCvZRSGUqp6d6WqR6cBlwLnFF9r29USp3nbaHqQQdgWbWeWYMxBvlrL8sk+LgOdRdf07X1wdf1cn3wcR1eH3xd38tS04IgCIIgCIJgjb94kAVBEARBEATBI4iBLAiCIAiCIAhWiIEsCIIgCIIgCFaIgSwIgiAIgiAIVoiBLAiCIAiCIAhWiIEsCIIgCIIgCFaIgSwIgiAIgiAIVoiBLAiCIAiCIAhWiIEsCIIgCIIgCFaIgSwIgiAIgiAIVoiBLAiCIAiCIAhWiIEsCIIgCIIgCFaIgSwIgiAIgiAIVoiBLLQYlFIHlFIlSqkCpVSuUupXpdRtSim37lOlVIpSSiulAptaVpt6JyilMlyk+VYpVWj1KVdKbW4uGQVBEJzh5/o3RCn1ulLquFIqWyn1lVIqqblkFHwTMZCFlsYFWusooAvwNPAA8LZ3RWo8WutztdaRlg/wK/Cpt+USBEGwwi/1LzATGA0MBDoCucDLXpVIaPGIgSy0SLTWeVrrBcA04HqlVH8ApdT5SqkNSql8pVS6UmqWVbYfq79zq720o5VS3ZRSS5VSWUqpk0qpOUqpWHt1KoPnlVKZSqk8pdQmq3pDlFL/UkodqvZCvK6UClNKRQDfAh2tvMMdnZ2bUioFOB34oBFNJAiC0CT4of5NBRZrrY9rrUuBuUA/jzSW4LeIgSy0aLTWq4EMDIMSoAi4DogFzgf+pJS6qPrYuOrv2GpP7UpAAf/A8Br0AToBsxxUd051GT2ry58GZFUf+2f1/jSgO5AEPKa1LgLOBY5YeYiPuDit64CftNb7XbeAIAiCd/Aj/fs2cJpSqqNSKhy4GsOwFgSHiIEs+AJHgDgArfVyrfVmrbVZa70J+BgY7yij1nqP1vp7rXWZ1voE8G8n6SuAKKA3oLTW27XWJ4xQFgAAIABJREFUR5VSCrgZuEdrna21LgCeAq5o4PlcB7zXwLyCIAjNiT/o313AIeAwkI9hrD9Rj/xCK6RZB9MLQgNJArIBlFIjMcbG9QeCgRCcjOVVSrUDXsLwgERhdApz7KXVWi9VSr0CzAY6K6W+BO4FQoFwYJ2hq42igYD6nohSaizQHvisvnkFQRC8gD/o39eqy4nH8ILfj+FBHlmPMoRWhniQhRaNUmo4hoL+uXrXR8ACoJPWOgZ4HUNZAmg7Rfyjev9ArXU0cI1V+jporV/SWg/FGJ/WE7gPOAmUAP201rHVn5jqyXaO6nXE9cAXWuvCeuQRBEFodvxI/w4C3qv2QJdhTNAboZRKcCOv0EoRA1lokSilopVSUzAmU3yotbaERIsCsrXWpUqpEcBVVtlOAGagq9W+KKAQY+JIEobCdVTncKXUSKVUEIaXoRSo0lqbgTeB56s9IiilkpRSk6qzHgfilVIxLs4pDLgcGV4hCEILxg/17xrgOqVUTHX5t2OMWz7pRnMIrRQxkIWWxldKqQIgHXgYY8zajVbHbweeqE7zGDDPckBrXQw8CfyijDieo4C/AkOAPOAb4AsndUdjKOIc4CDGBJF/VR97ANgDrFJK5QNLgF7V9e7AGIu3r7peR1EsLqqWY5kb7SAIgtDc+Kv+vRfD4N6NYcifB1zsToMIrReldX3eDguCIAiCIAiCfyMeZEEQBEEQBEGwQgxkQRAEQRAEQbBCDGRBEARBEARBsEIMZEEQBEEQBEGwokUuFJKQkKBTUlK8LYYgCEKTsW7dupNa67belsMa0b2CIPg77ureFmkgp6SksHbtWm+LIQiC0GQopQ56WwZbRPcKguDvuKt7ZYiFIAiCIAiCIFjRKANZKTVZKbVTKbVHKfWgk3SXKaW0UmpYY+oTBEEQBEEQhKamwQayUioAmA2cC/QFrlRK9bWTLgqYAfzW0LoEQRAEQRAEoblozBjkEcAerfU+AKXUXGAqsM0m3d+AZzCWehQEwceoqKggIyOD0tJSb4vik4SGhpKcnExQUJC3RREEwYcQ3ds4Gqt7G2MgJ2Gs124hAxhpnUApNRjopLX+Winl1EBWSt0C3ALQuXPnRojl+xzOLeGtn/axbEcmOcUVpCZEcPHgJKYN70RoUIC3xRNaGRkZGURFRZGSkoJSymPl5pdWkF1YTklFFQDhwQHER4YQGdIi5w43CK01WVlZZGRkkJqa6m1xBMH/qSyHvUvh2CbY/yMc2Qipp8NFr0FYrLelqxdNpXtbA57QvY0Zg2zvaulTB5UyAc8Df3GnMK31G1rrYVrrYW3btqjIR83K/A2HOeffK5iz6hDd20UxZWAHzFrz+IKtTH3lF/aeKPS2iEIro7S0lPj4eI8paLNZcyi7mAMniyipqCIyJJDIkECKyqrYd6KQwzklmLV2XZAPoJQiPj5ePECC0NRUVcCSv8JzveDjabDsScg5AP2mwu7v4ZNrDOPZh/C07m1NeEL3NsZVkwF0stpOBo5YbUcB/YHl1Re3PbBAKXWh1lriCNnhg5UHePR/WxmRGsdzlw+iU1z4qWPLdmRy76e/M+0/K/n45lH0SIzynqBCq8OTxvH+rCKKyipJjA6lbVQIpuqyzWbN8fxSThSWUWk20yku/NQxX0b+3AShiTFXwWc3wfYF0OdCSLsauk2EwBDjeMrp8OWt8PPzMOEB78paT0R/NJzGtl1jPMhrgB5KqVSlVDBwBbDAclBrnae1TtBap2itU4BVgBjHDliy7TiPLdjKWX0S+WD6iFrGMcDE3u2Yd9toTEpx/TuryS7yrZ6wIGitycgppqisks5x4SRGh9YygE0mRYfYMDrGhpFXUsHRPPG6CoLgAq3h67sN43jSUzDtA+g1ucY4Bhh0BfS7BH56DrL3eU9WwadosIGsta4E7gQWA9uBeVrrrUqpJ5RSF3pKwNbAkdwS7pm3kf4dY3j5ysGEBNofZ9ytbSRvXz+ck0XlzJy7Ae0nr6GF1kFWUTm5JRW0jwklNjzYYbqEyBDaRoaQVVjGvvSjpKWlkZaWRvv27UlKSjq1XV7uuU7ikiVLiImJIS0tjT59+vDkk0/W2j948GB69uzJ+PHjWbhw4al8jzzySC2ZHn74YY/JJAiCG2ybD+vfh7F/htF3OE436SkIDIVPbzSGYwguycrKatX6t1GzYbTWC4GFNvsec5B2QmPq8le01jzw+SaqzJpXrhpMWLDzSXgDkmN4dEpfHp2/hU/WpHPFiNY9oVHwDcoqqjiWV0pUaBBtI0Ncpm8fE0pReRUlleGsWbeeoAATs2bNIjIyknvvrT3fV2uN1hqTqXHrHk2cOJH58+dTWFjIwIEDmTJlSq39AOvXr+fiiy/m/fffZ/z48QDcd9993H333Y2qWxCEBlBRAt89Con94YxHnKeN7gBTX4Z518HK2TBWnllXxMfHs3HjRoBWqX/9Z7q4j7J46zF+2n2SJ6b2o0t8hFt5rh7RmW82HeHJhds5p1974iIce+MEwZP89autbDuSX+98pRVVmLUmLDiwzuzevh2jefyCfrX2KaVIbhPG7sxCjuWV1hlytGfPHi666CLGjh3Lb7/9xvz58xk0aBC5ubkAzJ07lyVLlvDWW29x/Phx/vSnP3Ho0CFMJhMvvfQSo0aNcihrZGQkQ4YMYe/evURHR9c6NmTIEB5++GFeeeWVUwpaEAQvsf4DyEuHi14FkxsRnvpOhd5TYPnTxu8434ks01Dd6wx7utcdWov+laWmvUhZZRVPLdxBr8QorqqHJ9hkUvxtan+Kyip5ZemeJpRQEBpPlVlTZdYEBZjshr5BA0Un4eRuKMw0xhQCoUEBJEQGk1NcTkl5ZZ1s27ZtY/r06WzYsIGkpCSH9c+YMYP777+ftWvXMm/ePP74xz86lffEiROsXr2afv3s/3EMGTKEHTt2nNp+9tlnT73iW7JkidOyBUHwEFWVsPIVSB4BqePcz3fes2AKhHnXQklu08nn57QG/SseZC/y318PcCi7mA+mjyAwoH59lR6JUfxhWCc+WHWAG8ak0Dk+3HUmQWgk9fU2aK3ZnVmIWWt6JkbVTMrTGsyVUFZg/EnlpRt/WvmFYK6AaEPhtosKIaeonKN5pXXG3Hfr1o3hw4e7lGHJkiXs3Lnz1HZOTg4lJSWEhYXVSrds2TIGDx6MyWTi0UcfpVevXqSnp9sWV0cObw2xUEpNBl4EAoC3tNZPO0h3GfApMFwmSQt+w65vIfcgTHqyfvmiO8Ll78FHf4BFD8HFrzWJeJ6mIZ7epqQ16F8xkL1ESXkV/1mxj3E923J6j4bFfb7n7J7M33iYF5bs4t/T0jwsoSA0nvySCkorquhsCdlWUQq5h6CiqHbCyPYQ1d4wlAszISgSwmIIMJloFxXKkbwSKqrMtbJERNQMSTKZTLUUp3XsS601q1evJjjY+VAk67FuztiwYQN9+vRxma4pUUoFALOBszFCbq5RSi3QWm+zSRcFzAB+a34pBaEJ2f4VhMVBz3Prn7fHWXD6X+DHZ6DfRdBzkt1kZZVVVFRpv1q8yFO0Bv0rQyy8xLy16WQVlXPnxO4NLiMxOpSrR3bhf78fISOn2IPSCULj0VqTWVBGSGAAMWFBRqzS7L1QVQaRiYaXOKEntB9kTKBRCqKTITAMcvbB0U2Qm05cGASaTBSVVTmsy2Qy0aZNG3bv3o3ZbObLL788deyss85i9uzZp7Ytk04awsaNG3nqqae44w4ns+WbhxHAHq31Pq11OTAXmGon3d+AZwCJmSf4D1UVsGuxYdgGNNB4HXefoX++fQAqy2od2neikJveW8OAx7+j/+OL+cPrK9mckecBwf0Tf9W/YiB7gfJKM/9ZsZfhKW0YkRpXN8GBX2DDh1B4wmVZN41NRQHv/HzA43IKQmMoLKukpKKKtlHBRsD2gqNQVQ5tUo3XnJHtIDgCrGc/m0yQ0N0wnkNjoDgLU+Z2UoJyKK8yU1FpdljfP//5TyZPnsyZZ55JcnLyqf2zZ8/ml19+YeDAgfTt25c333yzXudhefXXq1cvZsyYwauvvtoSJuglAdbvHzOq951CKTUY6KS1/tpZQUqpW5RSa5VSa0+ccK1zBMHrHFoFpbnQ67yGlxEYDJOfhpz9sPadU7t/2XOS81/6mTUHsrl+TBfuOasn+04Wcelrv7J0x3EPCO+f+KP+VS0xlu6wYcP02rX+O1Ru/obD3P3JRt69YTgTe7erOaA1LP4/WPWqsR0WBzd8A4l9nZb35082smjrMX598Ayn8WUFoSFs3769Qa+09p0opKzSTK/2UZjKiyBrN0QkQEwn15ktVJZB4XEozuKEjqUkNNEnx9vba0Ol1Dqt9bCGlKeUuhyYpLX+Y/X2tcAIrfVd1dsmYClwg9b6gFJqOXCvqzHI/q57BT9h0UOw5m24fx+ERDaurLfOhuIsuHMtW44WcOlrv5ISH8H700eQGB0KQG5xOde+vZqdxwv43x2n0adDtItCPUNDda9QQ2N0r3iQvcAHqw7SNSGC8T1txh5v+dwwjkfcAn/8wVgJaM7lUHDMaXk3j+tKcXkV89bWHdAuCN6gtKKKwrJK4iOCMWmzMe44IBiiOtavoMAQiO0MYXEkqFxKS4rqjEVupWQA1j2NZOCI1XYU0B9YrpQ6AIwCFiilGmSQC0KLQWvY8Q10Hd944xhg+HTI3kvRrqX8ac464iKCmXPzyFPGMUBseDDv3Tic6NAg7p67kbJKx8O9BP9BDORmZuuRPNYdzOHqUV0wmayCXlkCnnccbLz2SR4GV30CJTnw0TQoL3JYZp8O0QxPacPHq9Mxm1veGwGh9ZFdVI5SijYRwUYHr6rMMHTdiVVqj+gkwESCyiVHllkHWAP0UEqlKqWCgSuABZaDWus8rXWC1jpFa50CrAIulCgWgs9zYocRvaJXAybn2aPvRRAWx75Fr3A4p4RXrhpMgp3FjOIjQ/jnpQPYebyAD1Ye9EzdQotGDORm5sNVhwgNMnHZkOTaB9a8DQVH4OwnaoyIDoPg8nfh2Cb44pZT8WHtcdXIzuw/WcTKfVlNKL0guMZs1uQUlxMTGkRQVQkUZUJ4PIRENbzQgEBURBxtVBH5RcWtfpl1rXUlcCewGNgOzNNab1VKPaGUutC70glCE7LjG+O7IdEr7BEUyonUqfTM+YnbRrRhaBc784KqObNPIqf3SOCVZXvIK5Hlqv0dMZCbkaKySv638TAXDupITHhQzYGyAvj539B1Qt2A5z0nGUbzjq+NIRgOOLd/B2LDg/jot0NNIrsguEtuSQVVZk18RKDh6TEFnYpr3Cgi2gGaaHMuBaV1Fw5pbWitF2qte2qtu2mtn6ze95jWeoGdtBPEeyz4BTu/hY5DjMg3HuK5E8MJUZXMbOc6wsIDk3uTW1zBh6vEi+zviIHcjCzacozi8ir+MMxmktKq14xJAmc8Zj/jqNsNhbDoIYcr/4QGBXDpkGQWbz1GtryCFrxITnE5IYEBhFflG5PsYjs1fGiFNYEhEBpDnCogt0iilglCq6PgOBxe27joFTb8suckc9NjORnVh5CN7zt9UwvQPymG03sk8N9fD1DuJKqO4PuIgdyMfLnhMJ3jwhnapU3NzuJs+PVlY3345KH2M5oCYMrzUHwSvri5TsxGC5cNTabSrPlm0xG7xwWhqSmvrKKorJLY8CBUYSYEhUGI52Z8q8hEAjETWJZDpVn+nAShVbHrW+O7t2cMZK01zyzeSceYUGIm3AEntsP+FS7zTR+bSmZBGd9slv9af0YM5GbiaF4Jv+w9ycWDk4yYsABlhcbY4rICmPiw8wI6psG5z8Du72Cx/bR9OkTTKzGKLzcc9rD0guAeucXGuLy4gNKaBUGUcpHLNZGR1bPVgyP4avkaxo09nW079zJr1iySkpJIS0ujR48eXHLJJWzbVrOY3IQJE+jVqxdpaWmkpaVx2WWXNVoWQRC8xPavjcm+7ZyHPnWX1fuz+T09lzvO6E7QwMshoi2set1lvvE929IlPpxP1vh/5KhTuhdYuHAhPXr04NChQ61C94qB3Ez8b+MRtIaLB1ePxczeD++dB3t/gCn/dhnrGIARN8OoO2DNm7DPfi/3osFJrD+Uy6EsWVlPaF601uQUVxARHEhQeR6oAGOxDw/yww8/cPcj/2DxnJdJiDPKvueee9i4cSO7d+9m2rRpnHHGGVgveDFnzhw2btzIxo0b+eyzzzwqjyAIzUTeYeP/csAfPNLpBiPkanRoIJcMToagUBh0Jez53oge5QSlFJcPTWbVvuxW81/7ww8/cNddd7Fo0SI6d+4M+L/ulQXGmwGtNV+sz2BolzakJERAXga8MwkqSuHKuQ7XgbfLmY/CrkXw2Y1wxqMw4PJasSCnpnXkn4t2MH/jYWac2aMJzkZo1Xz7IBzbbPeQWWuSyqsICTRBVTGYAiEw1G7aWrQfAOc+7TLZTz/9xM0338zCr78hNbaC3Mp8qmyGWUybNo1vvvmGjz76iJkzZ7p1SoIg+AAbPgRthiHXeqS4zPxSFm05xvVjUggLrp4j0fci+PUlYyJg2lVO818yJJnnvt/F5+szuOfsnh6RySlOdG+Dqa/uXbiQbt262U3jj7pXPMjNwLaj+ew6XljjPf76HmN4xfTF9TOOwRjTedUnEJMMX98NLw6Eo5tOHe4YG8aornHM33C41YfCEpqXyiozKAhUZkAbBrKHKCsrY+rUqcyfP5/effuiQ2OIoYjSiroB+4cMGcKOHTtObV999dWnXvPdd999HpNJEIRmQmvY+KER6alNikeK/Hh1OpVmzTWjutTsTBoC0cmw7X8u83eMDWNkahwLNx/1iDwtlVq6t3dvp2n9TfeKB7kZWLj5KAEmxXkDOsCBX4xxxGf/Ddo1cAnJhB5wywpI/w0+uwk+vR5u+wWCjSV4L0pL4sEvNrPlcD4Dkj37ilto5TjwNmit2XesgLCgACIDs4xXlO0HgPJMHzwoKIgxY8bw9ttv8+KLLxIQHgelOVRV1J2watsxnDNnDsOGyQJyguCzpP9mrMY58RGPFFdRZeaj1QcZ17MtqQkRNQeUgj4XwNp3oLz41H+qI87t34HHF2xlT2YB3ds1Is67O7jh6W0KbHWvM/xN94oHuYnRWrNw8zFGd40nLjwIlj0Jke2N8cSNQSnoPAoufh2y9xlLVFczuX97Ak2KhVv8u2crtByKy6uoqDITGx4EpfnGoiAeMo4BTCYT8+bNY82aNTz11FMQEokZE0HmsjpLT2/YsIE+fRrY+RQEoeWx+VMIDPNY9Iol245zPL+M66y9xxa6n2lMME5f5bKcyf3bA/Dt5mMekaslUkf3OsHfdK8YyE3MjmMF7D9ZxLkD2sO+ZXDwFzj9L8ZQCU+QOs6ICfnLi1BkrKIXGx7M6G7xLNpyTIZZCM1CXkkFSimiAirAXOHxyXkA4eHhfP3118yZM4e333kXQqMJoYIyq2EWn3/+Od999x1XXnmlx+sXBMELVFXA1i8N47gxq3Fa8f7KgyTFhjGxd7u6B7uMMRY32rvMZTmJ0aEM69KGhVv810AGG9379tt20/ij7pUhFk3Mt5uPYlJwTp9E+ORGiOkEQ6/3bCVnPg6vjYaf/gWT/wEYPduHv9zCzuMF9G7vuTi0gmCL1pq8kgqiQgIJKMs3dnow9rE1cXFxLFq0iHHjxpEQFYpJaV6f/RLzP/uEoqIi+vfvz9KlS2nbtu2pPFdffTVhYUaHNCEhgSVLljSJbILQ4ijOhm3zIX21MW+lXV/ofb6x6I6vsHepsZDWgMs9Utzu4wWs3JfF/ZN7EWCyEw0jOAI6jYR9y90qb3L/9vz9m+0czCqiS3yE6ww+Si3dm5AAwPPPP8+HH37ot7pXDOQmZuGWY4xIjaNt7u9weJ2x4IenlVO73pB2Nax+E0beCm1SOKdvex6Zv4WFm4+JgSw0KSUVxvCK9tGhUJgDwZEQEOQ6Yz0oLCw89btTp07s378fzFVcOLYfd/z5fmISUwgOrLta3/Llyz0qhyD4BOlr4KsZkFkdlzainWFk6ipIHADXzYeIBO/K6C6bP4WwNtDtTI8U9+GqgwQHmJhmu6KtNd0mwNK/Q85BaGNnGIYV5/Q1DOSlOzK58bRUj8jYkrCre4GpU6cya9Ysh/n8QffKEIsmZPfxAvZkFnL+gA6waa4xhspDveA6TPw/Y8W9pX8HoG1UCMNT4lgk45CFJsYyvCI6sMIYuxfWxnUmT2AKQAdHEUMxeSUVzVOnILR0Tu6GDy6C8kI4668w/Xu4dxf83xH4wweQtRs+vQGqKr0tqWvKCmHHN9DvYggMbnRxhWWVfL7+MOcP7EB8pBNH1aArjTjua95yWWbn+HC6JkSwfOcJl2kF30IM5CZkUfW4pEm92sCWL4xXWx4aQ1WH6I4w6najt33wVwDO7d+eXccL2Xui0EVmQWgYluEVkSGBBJTmAgpCY5utflNYDMGqkpLiomarUxBaLFrDV3cbb3Bu/BbG3g2dRhiTuoNCoe+FxlvMAz/Bkse9La1rdi6EimKPOZa+3HCYwrJKrh3t3CtMTDL0mQLr3zeiWbhgfK+2rNqXZTfspOC7iIHchCzdmcmg5BjaHf8RSnNh0BVNW+G4e41lOL+aCZXlp2bYLvLzCQRC0+NosmdZpZnySjPRoYFGaLeQKAhoxpFb1ZMBgysL6kSzaCnIRFmh2dg2Hw7+bCwiFZNsP03aVTD8Zlj5Cnz3CJS34M7l5k+NeTudRjW6KK01H648SP+kaAZ3cqMTP/I24397i+sV4Cb0akdZpZmV+7IaLactoj8aTmPbrlEGslJqslJqp1Jqj1LqQTvHb1NKbVZKbVRK/ayU8swC6j5AdlE5G9NzjVmyGz40xoB1ndi0lQZHwLnPwsld8PtHdIgJY0BSDEt3ZDZtvYJfExoaSlZWll1lU1BqvKaNDigzolc01/AKCwFBmAPDiKaY/NKWN8xCa01WVhahoW6sKCgIjaG8GL571BhjPPQG52knPQUDp8GvL8N75xuT+ayprBtfvNkpOgl7foABl4Gp8b681fuz2Xm8gOtGpaDcWaq682ho1w9Wv2F45p0wMjWOkEATKzw8zMKZ7hWc4wnd22BXj1IqAJgNnA1kAGuUUgu01tuskn2ktX69Ov2FwL+ByQ2W1of4cdcJtIYpUXvg50VGgPPm8Kz1nARJQ+Gn5yDtas7s044Xf9hNVmGZ8zFXguCA5ORkMjIyOHGirvI/WVBGldbsySyFsgLIDQZ1vHkFLM2D0jyyj5QSF+mh8IkeJDQ0lORkB948QfAUv74Eeelw8X+M+SjOCAyGS96AfpfAvOvgxUHQczLEdoKdiyBzq/E/csmbEG9/aeEmZ+uXxqRCDw2veH/VQWLCgrhgUEf3MihlrFfw9d1GFJDOIx0mDQ0KYHS3eFbs8qyB7Ez3Cq5prO5tjMU2Atijtd4HoJSaC0wFThnIWut8q/QRQKvpBi3dkUliRADd1v3VGPYw5s7mqVgpGHc/fDwNNs3jrD5TeGHJbpbtPMFlQ+VPWqg/QUFBpKbWnZ1dWFbJhU98x02npfDQ7hshvjtc4/p1pMfJWAtv/YG7zTN5+tHHCQ1yYRwIgr+Rmw4/v2BMZks5zf18vSbDTd/Cmndg5zdQkmvEAR4zAzbOgf9eALf9DOFxTSe7IzZ/anhwE/s1uqjM/FIWbznGDWNSCAuuh34YcDks/j+jLZwYyABjuyewfOd2juaV0CHGMx11R7pXaB4a894iCUi32s6o3lcLpdQdSqm9wDPADEeFKaVuUUqtVUqt9fXeUpVZs2LXCR5ouxKVuQ3OedJzC4O4Q89J0H4g/PQv+rUPJzE6hKU7mtmrJ/g9P+8+SUWV5rzEXMjZ77FVrupNhzQqgqI5Xa/j170nvSODIHiTJbMADWc/Uf+8SUPhotlw7x548CDcuBDO+Rtc/RkUZhrh4pr7FX/OAWN56QGXeaS4j1enU2nWXGNv5TxnhERCnwth63yoKHGadHS3eABW7vX8OGTBOzTGQLY3iKfOU6S1nq217gY8ADhcSF1r/YbWepjWeph1oGlfZGN6DqaSLKZkvQup44213ZsTpWD8A5C9D7XlC87onciPu05SXtkyJzEJvsnynZlEhQbSv+BnY0cvLxnIAYGYBlzCeabV/Lp5l3dkEARvkXsItn5hTCqL7dzwcgICa6+AmTQEznwUtn8F6//beDnrw+bqN1EeMJArqsx8tPog43q2JSWhAQt5pF0JZXmw81unyfq0jyY2PEgMZD+iMQZyBmAdaTsZOOIk/VzgokbU5zMs3ZHJPUFfEFRZCOf+0zBYm5te50Fif/jxWc7sGU9hWSWr92e7zicIbqC1ZtnOTMb1aEvAzm8geThEtfeaPAGj/kSwqiJt+3MyoUVoXax91/ge/kfPlz36LsPJ8+2DkJfh+fLtobUxvKLzmMYZ/NUs2Xac4/llXFdf77GFlNMhsj1s+dxpMpNJMTI1rkkiWQjeoTEG8hqgh1IqVSkVDFwBLLBOoJTqYbV5PrC7EfX5DFu2beXKgGWowddAuz7eEcJkgnH3QdZuxpX/SEigiSXbZZiF4Bm2Hc3neH4Z53auhKMbvec9ttCuNzu738QU8zL2r/veu7IIQnNRVQkbPoCe5xoT7DyNyQRTXwFzpTHxuzk4thlO7PDY8Ir3Vx4kKTbMiCjVEEwBxtju3d8ZE4KdMLprPBk5JaRnu46dLLR8Gmwga60rgTuBxcB2YJ7WeqtS6onqiBUAdyqltiqlNgJ/Bq5vtMQtnGN5pZyV9REmhWGgepM+F0KHQQQvfZyzuobyw47j4l0TPIJl1ajxrDN29D7fi9IYtDv/EU7oGAJ/ftbboghC85C+CopOwMA/NF0dsZ1hyLWw/oPm8SJv/hRMgYZR2ki2H81n5b4srh3dhQBTI97k9r/+/FV7AAAgAElEQVQUqsphx0KnyUZ3M5bvFi+yf9Co4IJa64Va655a625a6yer9z2mtV5Q/Xum1rqf1jpNaz1Ra73VE0K3ZH7adoipAb9Q2OPCpunR1weTCaa8AEWZzGAu6dkl7MmUVfWExrN0RyYDk2OISl8BsV0goae3RSKhTSwLIy+lc+5qSF/jbXGaHIlDL7BjIQQEQ/czm7ae0+42vMjrP2jaesxmYyhD97M9Ejnj3V/2ExYUwBXDG/lfnDwMYjq7HGbRMzGS+IhgVsk4ZL9AVtLzMDkbFxCtSogeeZ23RTFIGgIjbqHnoU/oqdJZsl0WDREaR05RORsO5XBGjzbGkrXdz/TOOHs7lKbdQI6OpGzp094WpUmxikN/LtAXuNKOAfyR1nqA1joNI4rQv5tZTKEp0doIzZY63ljBsilp0wW6TjDCnZmbcLL3wV8g/7BHhldkFZYxf+MRLhmSRGx4cOMKUwr6XwL7lkGRY+NXKcWorvGs3CeLe/gDYiB7kPJKMz2PfUNeUFtU6uneFqeG8Q+ggsK4P2oxP8g4ZKGR/Lj7BGYN58cegvJC6NbE3qt6MK5/Km9XnkvI/iVw9Hdvi9OUnIpDr7Uux5gEPdU6QWuOQ98qyNxmhEPzQHhFrTVZhWVsO5LPz7tPsmLXCX7cdYJNGbkcyS2hyqyNYRZ56bB/eaPrc8jmTyEowiNzGj767RDllWZuPC2l8XKBMczCXAnbFzhNNqpbPEfzSjkk45B9nmZY2q31sHH7LsaykYxu04lxtZJRcxIeB0OuZ+LqN3j80MXkFg9rfI9aaLUs33mCuIhguuX/CioAWlBnsHf7KGZEXMjtlQsJ//FfMK2JXwl7D3tx6OusZKCUugNj/kcwcIa9gpRStwC3AHTu3PioAUIzsW0BoKD3lHpnNZs1mw/nsXRHJusP5bApI4+8EsdLtYcHB9A/MY7/BkSRv+ItYjqP9/yCPJVlsG0+9JkCweGNKqq80swHq4zQbt3beci73n4AxPcwhlkMu9FhshEpxtCQNQdy6BLfgLByQotBDGQPUrLyTQKVmcTTb/C2KHUZdRsBv73GVNPPrNh1JlPT6qzpIgguqTJrlu/MZGKvdpj2/QCdRtSOnepllFIM75PK+xsncdv2L4wlYjuN8LZYTYHbceiB2UqpqzDi0NeZKK21fgN4A2DYsGHiZfYVti+AzqMh0v3oDAezivhkTTqfr8/geH4ZJgW920dzbv/29EiMokNMKPERwQQGKLSGnOIKMgtK2ZNZyNYj+XxeMZrLDn7HmCe+YsKAFC4bmszorvEoTwyx2jTPiBKRdlWji/p8fQaZBWX863IPrkKnlOFFXvFPKDjmMKxlj3aRRIcGsvZAtqxe6+OIgewpygoZeuRj1oWNZmhSf29LU5c2KejkkVycsZLZOzLFQBYaxO8ZueQUV3BOagAs/B0mOlz7x2uc0asdM387nxvjfiVk/u1w6woI9jtPTkPi0L/WpBIJzUfmdmOIxWT3xtpvysjllaV7+G7bcUwKJvZqxwOTOzChVzviItx/m1i++3aC53zHPV0zeGZrGF+sP0zv9lHcNr4bUwZ2IDCggaM2zWb49WXDS5s6vmFlVFNZZebV5XsYlBzD6T0SGlVWHfpfAiueNlbWG3Wb3SQmk2JYShxrD+Z4tm6h2ZExyB4ia+X7RFLE0f7/z955h0dxnH/8s3engnpHAoQKCAnRkSgCbHq1DbiXuNtxXAC3xHacOHbi5BenOO5xizvuNsaADcamY6roTQIhhJAECCTU25X5/TE6qwv1PUnzeZ597m52dvZ7e7O7782+8771nzSOgDbkGqJIJyN5l/QpUyiayfqkbAwaXGI4KAv61/vUXlfG9ffHbHLn8z5/hJwUWFUnwENXQMWh785s+g84ucGQaxutlp5Twj0fJjL31Z/ZlprDoin92fLEVN65fRRXjezTLOMYwDlyArh6c4vvEXb+cRr/umYoVpvgoc/3Mvn59Szbl9WyyWkpP8L5ZBi3qNUTfr/dm8Wp3FIWTIlqm5Ht6gRGQ88hF41mERfmS0p2EReKK9p2/4oORRnIbYEQGHe+zT5bJINHT9NbTcMMmo9AY4L5Z/aeytNbjaITsjY5m7gwX9xPbYAevhAyXG9JdXBzNjE20p/3T4fCJY/A7g+rUtd2EVQc+m7M+RQ4+BWMugvc6x8hLa2w8u8fkpn2wgY2p5zn0ekD+PmJKTwyI5pgb9eW79voBFEz4OgqXI1wbXwoPzx0KW/fGo+HixOLPt3Dlf/dwq7mjp5ueQW8+rQ69nGFxcYra48RE+zJtIEtTAxyMQZfBRk7ZIrvBhhV6Yfc7OOgcCiUgdwWZO3GpziV1T3mEB7oobeahvEIwtp7NNMMu1mXpMK9KZpHdkEZBzMLmDQgEI6vhcjJMsuUAzIlOpDUc8WcHPoghI6F5Q9CznG9ZbUpKg59NyXxHTk5NmFhvav3pF/gspc38eq6FC4bEsLaRyexcGoUnq5ObbP/6NlQch4yZKxxg0FjemxPViycwD+vGUpWXilXv76FPy49QGFZwxP/fiFztwwXOfY+aYC3gk+2nyQtp4THZkW3/eixncFXyddD3zRYZWgfb5yMGjtP5raPBkWHoAzkNsC8/2sqhBERc4XeUi6KKfYyBhvSOHj4oN5SFJ2M9Udl9rxZgTlQdLb9kxO0Anta2bVHc+GadwAN1vxFX1EKRWsxl8G+T2XmSs+eNVZZrDaeX53M1a9vocxs5ZO7x/DC9cNbN2JcH/2nyUx3yTWzyhkNGtfFh7Lut5O4a0IEn2xPZ/p/NvLj4YuEFt3yCrh4wcjW5Q4oKDPz0ppjjOvnz+Todho9BvANh97xjbpZuDoZGdLbm8Q0NYLcmVEGcmux2bAeWMJG21ASBvfTW83FqYwv2ff8Bs4WlOksRtGZWJeUTbCXK5F5W2SBA8U/rk2YvzuRge6sSz4H3n1gzG/g8Ldw9rDe0hSKlpO0AkovQFxNb5nzReXc/M52XlmbwvwRvVn18KWM69/GE9TsuHrLpzLH19W72t3FxFOXx7Lk/vH4uDnx6w8TWfTpnvr9cS+kydBucbeDq1erZL344zEulJh5cs7A9hs9tjP4ahln/XxKg1VGhftxICOfMrO1fbUo2g1lILeW03twLTnNT1oCoyNanxqz3QmIotynn3KzUDQLs9XGpmPnmRwTiHZsNQQPBa8QvWU1yuToILal5lBSYYGEB2Qki43/1FuWQtFydr0vU7tHTPqlaE/6BS5/eTN70vN4/tph/Oe64Xi1lTtFQ0ROhDMHGs0qNzzUh+ULJ/DI9AGsPHia6S9sYNXBMzUr7XgbNAOMad3k9t3pF3hvywluGRvG4N4dEHZy0HxAg0NLGqwSF+ZLhdXGgcz89tejaBeUgdxKxLGfsKFRHjEVF5Nj+mPWxjn2chKMR9h6OFVvKYpOQmLaBYrKLUyLcIFT2+VEHQdnSkwQFRYbP6fkyGQ5o++R4Zm6mC+yopuQc1z66o68BQzy1v3d/tNc/+Y2nEwaS+4fx9UdFXc3chIgIG1jo9WcjAYWTY1i2YIJBHu7cu/iXSz8dA+5xRXSXWTvxzLRiXfLw46Wma08/tV+QrxceXx2TIvbaRZevSBsvJz820DUjrgwXwDlZtGJUQZyKylL+pEDtghGxQ7QW0qT0WLm4IQFp9Q1lFvU4x/FxVmXnI2TUWM8+0DYOoWBPCrcD3dnI+uSK5+UjL5Hjlbtek9fYQpFS9jzkZycN/xmhBD8b1MqD3yym2Gh3ix7YAKDenVgwp5eI8HZE1I3NKn6wBAvvrl/PL+dMYBVB08z44UN7Fv9gXQXib+zxTKEEDz5zQGOZRfx96uH4uHSgakdhlwjQ9Nl7a53tb+HC5GB7iSmqYl6nRVlILeG0jxczu5mo20ok6ID9VbTdPqMosLFj0vFTnaeUP9uFRdnXVI2YyL8cT3+A7gFQJ94vSVdFGeTgQlRAaxLypaxWb1C5OSmPR/L0SuForNgNcPeT2DATKwewfx5+WH++t0R5gwJ5qO7xuDbzHjGrcZogvDxcKJpBjLI0eQFU6JYvlCOJudu+5hzTr3IDRrbYhnv/ZzGkt2ZPDxtABMHdPA9ePDVMhb17g8brDIqTCYMsam8A50SZSC3hrRNGISVNJ+x9PLpobeapmMwYoiZzWTDXjYcydRbjcLBOZVbwrHsIiZH+cCxH2HALIcN71abKTFBnM4vI/lsoSwYdReU5sqJQQpFZ2H/51B0FuvI23n0i728vyWNuyZE8OqNI3F10ulcjJwEuamNxgOuj5hgL765awiXmg7zbdlIpr+wkZUHTjd791/sPMWz3x1mRmxPFk7p3+ztW42rl4zbfOArqCiut0p8uC/5pWaOnyvqYHGKtkAZyK2g4th6SoQLwbET9JbSbEyxV+CplZJ3uP6ZyAqFHXt4t9leJ6A8H2Lm6Kyo6UyqDPe01j4hNWIi+PeHROVmoegkWC2w6XlE8DAWJQawdG8Wv5sZzVOXx2IwtHO0hsawp4RuoptFdZxS12IUZmZcdRe9fHpw38e7uev9nRzIuPiENrPVxj9WJfHY1/u5JCqQl28cod9xGHYjVBTJgYN6iK9MGLJT+SF3SpSB3ArKj61npy2aiQNbPsFANyInYTa4MqRoM2nn6//3q1CAdK8I83cj5PRaMLlWTtDpHPT0cmVQL6+qiC2aBiNuhlPb5OiXQuHobH8DclN5Q1zFdwfO8OScGB6YrMOIaW2CBoJ7ULPcLH4h6TtwD6TvsIl8c/84npgdw860XK54dTO3vruD5fuyKCq31NikzGxlxf4sLn95M6+vP86No0P5363x+o2gA4SNky5nh7+td3W4vxsBHs4kqoQhnZIO9GjvYhRl41mYwm7jTSzs66O3mubj1ANz2EQmH9/NT0lnuWNCpN6KFA5ImdnKluPnuSE+FO3oSpk9z9ldb1nNYkpMEK+tSyG/xIy3mxMMuQ5++jPs/wImPaG3PIWiYfIzEGv/yj63cfzjZH+eviKWO8ZH6K1Komky3FvqBhnJoamxhy0VcGw1xM4DgxETcO/EfvxqTF8+2JLG4m3pLPx0j2w+wB2vHk5UWGwcP1dEmdlGuL8bb98az/TYnhfdVbtjMMLAK+S1xFwKTjVdLTVNIy7MV0Wy6KSoEeQWYkuV4W3MfS/BZOych9EtdiahhnMcPlj/LFyFYltqDmVmG5eH5Elfw+jZektqNpOig7AJ2HBMuorg3RsiLpWT9axNSIWrUOiE+PEZLFYrCy5czzNXDHIc49hOxEQozobsI03f5vhaKC+Q4d2q4enqxIIpUfz8xBQ+/fVYHpo6gP5BHni4mAjwcOGm0WF8cOdo1jw6yTGMYzux88BcDClr6l0dH+ZHem4J2YVqYnBnQ40gt5ALh9fgJHoQNXSc3lJaTmWqYK/MjRSXz8e9I0PkKDoF65KycXUyMKx4C6DJCXqdjOGhPvi5O7MuKZu5w3rJwoQH4JPrZOisVoSZUijaC5G+De3gl7xumc+NMyZwu6MZx1DlbnViA/SMbdo2uz+UrhkNpKo3GjQS+vmT0M+/TSS2O+EToIefdLMYeHmd1XHhMh7yrrQLzB7i2MmVFDXpnEOfDoAxbRM7bAO5JKYTd3jfcEo9I5jAXrYcbzgjkqJ7IoRgXfI5xvcLwCltPYQMA08HGrlpIkaDxsQBgWw4eg6rPdxS1AwIHQMb/gmWcn0FKhS1sVo48/lDnBG+mMc+yP2T+umtqH58QsEvElLXN61+4Rk4ugqG3wTGds7211EYnWT4yOSV9V5LBvfyxsVkIPGkcrPobCgDuSUUnMan7BTpXiMJ8HDRW02rcI6ZzljDETYePqW3FIWDkXq+mPTcEqZFecKpHdLfsJMyKTqQ3OIK9mXkyQJNg4mPQeHpBifYKBR6sevDxwgpPsL68Id45LIRaE3179WDiImQ9rOMtnEx9iwGYYWRt7a/ro4kdh5UFMLxulGhnE0GhvXxUQZyJ0QZyC2g8Kj0P3brf4nOSlqPMWo6PbQK8pM3yGQKCkUl9sgP09xTwWaWfrudlIkDAjFosN4ezQIgcooM+bb9Tf2EKRTVEYKDX/6VuJPvsMV7Dtfd9qBjG8cg3SwqChvMKPcLNpt0rwi/BPwddES8pURcCs4ekPx9vavjwn05lJlPaYXKXNuZUAZyC8g+tI5i4UJsXOeLf1yH8AlYDK7El24l6Uyh3moUDsS65GwG9PQg8Nx2MDhB3wS9JbUYHzdnRvb1ZW1yNQPZYJDppzMT4cwB/cQpFCDdKj5bwOBD/2Kr6yXE3fc/feMcN5WISwHt4m4WJ9ZD3kmIu739NXU0JhfoNwWO/iD/CNRiVLgvFpuoeoKl6BQoA7kFuGZu54AhhsF9OskkgsZwdsPSbxqzjTtYd6T52YwUXZOicgs7TuQyOSZIzjrvM6rThXerzeSYIA5mFpBdUG02+eBrwGCS2bAUCr0QgvyvFxGcvJjPna8kduHXuLh2kvPNzQ+Ch1w8Ycj+L8DVu070ii5D9GwoOgNn9tVZNbKvnKiXmKbiIXcmWmUga5o2S9O0ZE3TUjRNqxNQVNO0RzRNO6xp2n5N09ZomhbWmv05ApaiXEIqTnAhML5z/LtvAq7DriJQy+fMAZVVTyHZfOw8ZqtgRqiAM/sharreklrNlBiZVW998rmqQnd/Gdv54BIZy1Wh0IGCn9/G+/DHvKddybh7/4u3eyeb2xI5CU5tbzDlMpZymRwk5gpwcu1IZR1H1AxAg+RVdVb5uDkTFeSh/JA7GS02kDVNMwKvAbOBWOBGTdNqx3nZA8QLIYYCXwH/bOn+HIXUPWswIPCJ7rwTluoQNROzwYWo8z+RV1KhtxqFA7AuKRtPFxPDynbKggEz9RXUBsQEexLi7VqVdtrOkGsgPx0yduojTNGtKc7NwrDmGbaKwcTf+QKhfm56S2o+/SbLeQont9S/3h77eNCVHaurI3EPgNDRcHRlvavjw33ZffICNpv6I95ZaM0I8mggRQiRKoSoAD4D5lWvIIRYJ4Qoqfy4DejTiv05BLmH11MhjAwePVlvKW2HiwdFfacwy7CDDcln9Faj0BmbTbA2OZtLowMxHf8RvHpDUBNjnDowmqYxKTqIzSnnqbBU8xOMni19rI8s10+coltitQl2vvc7nG1laJf9iyGhvnpLahl9E2Qa+uNr619/6Btw9enUkXCaxIBZcHofFGTVWRUX5kdBmYVj2UU6CFO0hNYYyL2B6rHBMirLGuIuoP6/VoCmafdompaoaVriuXPnGqqmO8FnN3DMdTCenl56S2lTvEbfRKCWT97OL/WWotCZg1n5nCssZ3q0DxxfLx8dOvpM+iYyOTqQonJLTV9AV2850ShphXKzUHQor6/4mYSCVZwIvZKxoztx0imnHhA2rn4D2VwGSd/LlMxdJfZxQ9gzjR6t62YRH1bph3xS+SF3FlpjINd3x6z37qJp2s1APPCvhhoTQrwlhIgXQsQHBga2Qlb7cfr4AcJtpygI63zZxC6GMeYyzjiHMTnrLawVpXrLUejImiPZGDSY0uOEDN8UNUNvSW3G+P4BOBsNdd0sYi6D3FQ4l6SPMEW3Y+meTIw73sBJszHgyif1ltN6+k2R509erZj6R5bL68jgq/XR1ZEExoBPWL1+yGH+bgR4uLArTfkhdxZaYyBnAKHVPvcB6jxX0DRtGvAHYK4QolOnrMrcJme690nogie6wciJUU/RlzOcWdnpXcUVrWBtUjYj+/ridWotGJ271GNRdxcTYyL9WJdcj4GMBkdW6KKrJXTHSdJdhb2n8vjn1xu5w2k1xM5D6wpxgQdeAZoBEt+tKhMCtr8us+1FdJ3rSINomhxFPrEBKkpqrdKID/NlpxpB7jS0xkDeCURpmhahaZozcAOwrHoFTdNGAG8ijePsetroVHifXM1RQz9CI6L1ltIuxI6fzyrbaAL3vQEl6iTujpwtKONAZj5TBgbBsdUQPqHTh3erzeToII6fKyY9p9oNzDNYhrJL6hx+yN11knRX4Ex+Gfd8mMjvXJfiolkxTH1Kb0ltg284RM+BXe9BUba8h6z/O2TugvEPybjj3YHoOWApg5Qf66yKD/flVG5pzVCTCoelxT1WCGEBFgA/AEeAL4QQhzRN+4umaXMrq/0L8AC+1DRtr6ZpyxpozuEpycmgX/kRskKm6i2l3fB2c+KnwNtxtpXAjrf0lqPQAXv2vFm9yuD80S7lXmHHHu5tbdLZmitiLpMTbPLSdVDVbLrlJOnOTpnZyj0fJRJQns58649ocbd3raxy4xZBWT78Owr+GQEb/gFDroPhv9JbWccRNh7cA+XExFrE/eKHrNwsOgOt+ksnhPheCDFACNFPCPG3yrI/CSGWVb6fJoToKYQYXrnMbbxFx+Xkpk8waAKfkVfpLaVdiRwyhh+tcdi2vSEnVyi6FWuSsunt04OICz/Lgi5oIIcHuBMR4M665FqTgQdeIV+T6k8X62C06SRpRfsjhOB3X+3nQGY+7/ZdjWZyhUsf01tW29J3DNy7GaY+DdOfhTt/gKvfBqNJb2Udh9EEA+fKrHq14kIP6uWNi8lAovJD7hR0k2cerccr6QsOE8Gg4WP0ltKuTIkJ4n3rDAxlF+BIpx3wV7SAMrOVzcfOM3VgENqxH8GvX9ca3arG5OggtqbmUFJhqSr07weBA2U0C8enzSZJd5YIQp2d/64/zvJ9Wfx9vJHgjJWQcD949tRbVtvTcxBc8giMXwR9x+qtRh8GzQdziXRTq4azycCwUB92KT/kToEykJuALWs/vcuOcTDwCpyMXfuQRff0JM0jjmxTr5qTLRRdnm2pOZSarUzr7wlpm7pEcpCGmBITRIXFxtbjOTVXxFwGJ3+G4pz6N3Qc2mySdGeIINTZWX3oDP/6IZn5w3txffnX4OQOY+/XW5aivfjFzWJpnVWjwn05lFVAaYVVB2GK5tC1rb02ImfL+5QLE25x1+stpd3RNI2JA4P5sGIypG+F7CN6S1J0EGuTsunhZGSsdlhOMukC6aUbYlSEL27Oxrrh3gZeDsLWYDYsB6LbTZLurCSdKeChz/cyrI83z033Rzv4NcTfAW5+ektTtBcGI8TOq9fNIj7MD4tNsPdUnk7iFE1FGcgXw1KBe9LXrLGNZNyQAXqr6RCmRAfxScUl2AzOsOt9veUoOgAhBGuOZMs4wak/yhGusPF6y2o3XExGJvQPYF1SNqJ6cpCQ4eDVx+HDvXW3SdKdldziCn79YSIeLibeujUe14Ofg7DCqLv1lqZobwZdCZbSOm4WI/v6ommwM025WTg6ykC+GMdW42bJY3/AZfi5O+utpkMY19+fIpMPh30mwr5PwawSh3R1DmYWkJlXyszYIDj2I0ROApOL3rLalckxQWTll3H0bLXUr5om3SxS19UZ+XE0utMk6c6I2WrjgY93c7agnLdujaenhzPs+UhmbfSL0Fueor3pmyDTax+taSB7uzkR3dOT7Scc3o2r26MM5ItQvOMDzgofeo64TG8pHYabs4mxkf68UzJRhuypJ1yNomvxw6EzGA0aM4LyIT+9S7tX2JkcbQ/3Vk/SEEtZ/WlzFYom8rfvjrA1NYe/XzmE4aE+0mUt7ySMuEVvaYqOwGCU2QVTfgKbrcaqhH7+JKZdoNyi/JAdGWUgN0ZRNj3S1vCN9RKmD2ksglLXY0p0IN/kRWD2iYQ9i/WWo2hnfjh0htHhfnif3iwL+nfdeN92gr1diQ3x+iX28y+EjZMjPw7uZqFwXD7fmc77W9K4e0IEV8dVhp8+shyMLjKRhKJ7EDUdirPh7IEaxQmR/pRbbOxNV37IjowykBtj/xcYhJW9/nPo4+umt5oOZUpMT0DjgN9MOLkFCk7rLUnRThw/V8Sx7CJmDQ6G4+tkeDefvnrL6hAmxwSyK/0CeSUVVYVGJxn/OeXHOiM/CsXF2HUylz8uPcglUQE8MTtGFgohDeT+U8HFQ1+Bio6j/zT5eqxmVr0xEf5oGmxLVX7IjowykBtCCMy7PmKPrT+Dho7SW02H09ffjaggDz4sHAkIOFw3XI2ia/DDoTMAzIjxhbTN0G+yzoo6jumxwVhtgp+O1BpFjpoOJTmQtUcfYYpOyen8Un7z0W56+/Tg1RtHYrKHBc3aDQUZVcloFN0DjyAIGSbdLKrh7eZEbIgXW1PP6yRM0RSUgdwQZ/bjlJPEV9ZL5chaN2T2kBC+zXDHHDgYDn6ttxxFO/HDwTMM6+NNSMFBMBdDZPcxkIf18aa3Tw++P1DrCUm/qYAmR5EViiZQZrbym492UVph4e1b4/F2c6paeWQ5GEwwYJZ+AhX60H86nNoBpTXdKRIi/dmdnkeZWfkhOyrKQG6IA19hwchBnyn0D+qej8QuGxKCEHDAdypk7IQLJ/WWpGhjTueXsi8jn5mDg2XkBs0IEZfoLavD0DSN2YOD2XTsHAVl5qoV7v7QO67Oo1GFoj6EEPx+yQEOZObz4g0jiOrpWX0lHF4G4RNU7OPuSP9pMrRf2qYaxQn9/Kmw2NidrtJOOyrKQK4Pmw3bwSVstA0lYXAUmlZfVteuz4CeHkQGuvNe3khpOG2sN1OtohOz+tBZAGYOCoaUNdIodPXWWVXHMmdoCGar4KfDZ2uuiJoBmbugWD0GVTTO25tS+WZPJo9OH8D02Frpo0/vhdzjMOgqfcQp9KVPPDh7yutrNUZF+GHQYFvtbJ4Kh0EZyPWRsRNDQQbLLAnd1r0C5OjaZUNC+O6UEyWj7pcxPPd9rrcsRRvy/YHTRAV50M+YLf0ko2frLanDGd7HhxBv17puFlHTAKHCvSkaZX1yNs+tTOKyISE8MLl/3QoHvgKDE8SqMNTdEqOTjH19fI18mlCJl6sTg3t7q4l6DowykOvj8LeYcSLJewLD+nSv0bTazBkSgk3AUt/bIZRWg+IAACAASURBVGwCLF8EOcf1lqVoA87kl7EjLZcrhvWq/OOjwdCun069NgaDxuzBIWw8ep7C6m4WISPALaBOJiyFwk7quSIWfrqH6GAv/nXt0LpPG21WOX8jagb08NVHpEJ/+k2GvPQ6986ESH/2nLpAaYXyQ3ZElIFcGyGwHl7GRutgpg7v123dK+zEBHsSEeDOd4fOw9X/k3E8lz9Y45+wonOyYn8WQsAVQ4NlxsTIieDdveJ927lsaDAVVhtrqkezMBik/2DKT2A1N7yxoluSV1LBXR8k4mQ08NYtcbg5m+pWOvkzFJ6GIdd0vECF4xA1Q74eXVWjeGw/f8xWQeJJNYrsiCgDuTan92IsOMUq2yjmDuuexkJ1NE1jzpBgtqXmkmPwg2lPy8kGR5bpLU3RSpbvy2JIb28iivbIDF/Df6W3JN0YEepLsJcr39V2s4idC6UXIHWDPsIUDkmFxca9i3eReaGUt2+NI9SvgTj5B74EZw8VvaK74xsGQbF1DOTR4X44Gw1sOqbmOTgiykCuzeFlWDGQ6ncp0cGeF6/fDZgzJASrTbDy4BmIux0ComHtX+XjQ0WnJO18Mfsy8rliWAjs/ghcvLt1jFaDQWP2kGA2JJ8jv7TaaHH/aXLS4oEv9ROncCiEEPxx6QG2pebyz2uGEhfWQGQKcxkc/hZiLgfn7pVoSlEPA2bJpFulVVEr3F1MjIrwZX1ydiMbKvRCGcjVEQLzoWVstQ5k8ogYvdU4DLEhXkQFebB0T6bMLz/lj3D+KOz7TG9pihayfF8WAFcMcJdPA4ZeC049dFalL/OH96bCaqs5Wc/kArHzIGkFVJToJ07hMLy5MZUvEjNYNDWK+SMaecq4/XUoy4eRt3ScOIXjEj1Hhns7VjNpyMQBgRw9W0RWXqlOwhQNoQzk6pz8GacLKaywJXD50F56q3EYNE3jypG9STx5gZM5xXKksddIWP93sJTrLU/RApbvz2JUuC8h6cvBUgYj1E18aB9vIgPd+WZ3Zs0Vg6+BiqI6j0cV3Y9VB8/wj1VJXD40hIenRTVcsSgbNj4PA2bL+McKRe84cA+EoytrFE+KDgJg49FzeqhSNIIykKuz5RXyNS+OB88hPMBdbzUOxfzhvdE0+GZPJmgaTP0T5J+CXR/oLU3RTJLOFHD0bBFzh/WSIah6DoZew/WWpTuapnHViN7sSMvlVG610eLwCeARLI+VottyMDOfhz/fy7A+Pvz72mGNT+Be9zewlMKMZztOoMKxMRggaqYcQa426TcqyIMQb1fWJysD2dFQBrKdc0fh6CreM09j5vAIvdU4HL18epAQ6c83ezIRQkDkJOg7Dja/oEaROxnf7MnEaNCYE2mEU9thoIrPamfecPnIfOmeaqPIBiMMvlqGeytRs827I5l5pdz1wU783J15+9Z4XJ2MDVc+ewh2fwij7oaARkaZFd2P6FlQng/pW38p0jSNiQMC+TnlPGarTUdxitooA9nO1lcxay58YpvRuF9ZN+bKEb05mVPC7vQ8OYo88TEozII9i/WWpmgiFquNJbszmRwdhH/GGkBAzGV6y3IYQv3cGB3hV/VH0M6Im8Fmhi0v6ydOoQt5JRXc9u4OSiqsvHv7KAI9XRquLAT88Adw8YKJj3ecSEXnIHKyDJWaXNvNIpDCcgt70vN0EqaoD2UgAxRlI/Z9xjImMiwmigCPRi6A3ZjZQ0JwdTLwzZ4MWRA5SfpVbX0NbOqfb2dg47FznCss59r4PpD0HfiGQ89BestyKK4a0ZvUyigfv9AzFoZcC9vegILTDW+s6FKUma3c9UEi6TklvH1r/MUjGyWvhNR1MOkJcGsguoWi++LiIbPqJa+skUtgXP8AjAaNdSqahUOhDGSATf8Bm5lXy2ZybVwfvdU4LB4uJmYOCmb5vtOUW6xyFDnhAcg9riYwdRK+2JlBgIczUyJcIXW9DEHVzZPh1Gb2kBCcTQaW7M6ouWLyH8BmgQ3/0EeYokOx2gSLPt3D7vQLvHjDcMZG+je+QX4GfPsABA2C+Ls6RqSi8xE9Cy6ckJGgKvFydWJspB+rD53RUZiiNspAvnASEt9hs8csCt3DmBwTpLcih+bqkX3ILzWz+tBZWTBwHniHylFkhUOTU1TOmqSzzB/eG6fUtWCtkAayogbePZyYOSiYpXsyKTNXi/XtFwEjb4W9H0PhWf0EKtodIQR/+vYgqw+f5enLY5kzJKTxDSwV8NWd8py67gMwOXeMUEXnw540ppabxaxBwRw/V0xKdqEOohT10SoDWdO0WZqmJWualqJp2hP1rL9U07TdmqZZNE1zzFyb6/+O0Aw8kXOZNByM6j9DY0zoH0CoXw8+2Z4uC4wmGHMvnNwMWXv0FadolKV7szBbBdfGh0r3CrcACB2ttyyH5MbRoRSUWVixv5Y7RcIDcgb6zv/pI0zRIby6NoWPt6dz78R+3D7+IpO2LRWwbIGc8Dr3ZTUxT9E43n0geGgdA3nGoGBAhhJUOAYttgY1TTMCrwGzgVjgRk3TYmtVSwduBz5p6X7albOHYN9n7A25nkybL9eNCtVbkcNjMGjcOLovW1NzOH6uSBaOvAWcPdUosgMjhODTHekMC/Uh2s8IR3+AmDkyQoOiDgmR/kQGuPPJ9pM1V/j3g+jZkPgOmFVg/67IB1vSeP7Ho1w5ojePzYxuuKIQsOdjeGko7P8cJj4ho50oFBcjejZk7IDinF+Kenq5MrKvD6uUm4XD0Jrh0tFAihAiVQhRAXwGzKteQQiRJoTYDzjmDK41zyJcvfh99lTGRPgxoKdKLd0Uro0LxWTQ+NQ+iuzqLR89H/pG+uEpHI6tx3NIyS7ilrFhkPw9VBTCkOv0luWwaJrGTWP6sjs9jyOnC2quHHs/lOTA/i/0EadoN77YeYqnlx1iemxP/nnNUAyGevzzhYCMXfDBFfDt/eDVG278TE7MUyiawoBZIGwydGQ1Zg0O5mBmQc047ArdaI2B3Bs4Ve1zRmVZi9A07R5N0xI1TUs8d64DAmaf3ApHV3I86i6S8k3cNi68/ffZRQj0dGHm4GC+2p1R5aM55jfyhN/xlr7iFPXy4daT+Lo5cfnQEJki3DsUwsbrLcuhuXpkH5xNhip3IjvhEyAoFna9r4suO13Cxc2BWLYvi8eX7OeSqABevWlE/e52uSekYfy/KXB6P1zxEtz1oxwRVJNdFU0lZLhMPlQrq97MSjeLH9QoskPQGgO5vquBqKesSQgh3hJCxAsh4gMDA1shq0k7g5+eAY9gnrswmZ5eLkyP7dm+++xi/Gp0X/JKzFU+mr5hEDsPEt+H8iJdtSlqkpVXyurDZ7h+VF9cy3Pg+FoZssyg/O0bw9fdmTmDg/lmTyaFZVWZr9A0GHkbZO2GMwd00dYlXNwciB8Pn+WRz/cyKtyPt26Jx8VU6XpUegFO7ZQuSdvfhLcnw5n9MOs5eGg/xN2uziNF8zEYZDSLlDU1Em2F+bszMMSLlcoP2SFozZmdAVR32u0DZLVOTgeRvBJObeN8/CP8lFLITaPD1OS8ZpLQz58BPT3436bUqoQKCQtkliCVOMSh+GR7OgL41Zi+cOBLEFYYdoPesjoFd4yPoKjcwuc7T9VcMfQ6MDpD4rv6COsKLm4OwvrkbB74eDfjQ2y8P9NEj4JU+YTxkxvgH+HwzjT45DpY+Rj4hMGv18HY+6CHj97SFZ2Z6DlQUQQnNtUovmJYCLtOXiA9R7lZ6E1rrMKdQJSmaRGapjkDNwDL2kZWO2Kzwpq/gH9//ps/FpNB48bRanJec9E0jbsnRJJ0ppCfUyonGvSJh9AxsO01NYHJQSgzW/l0RzpTY4II9XGVBl3veAhsZPKR4heGhfowOtyP935Ow1I9Daybn8yut/tDmaa+42kzF7cOd29zIH46dIYlH73G965/4IOcX+H2/jR4NR7emyWjUlzyKNz4Ody9Fh7cD/eslxM1FYrWEjERnD3g8NIaxfOH90bT4Jvq6e4VutBiA1kIYQEWAD8AR4AvhBCHNE37i6ZpcwE0TRulaVoGcC3wpqZph9pCdKs4uATOHaFw3BN8kpjF/BG9CfJy1VtVp2TeiF4EeLjw9qbUqsLJT0JeOqz9q37CFL/wZeIpcoor+PUlkZC6FnJSpL+4osncdUkEmXmldWeXT3oSYueDSZfMm23m4tah7m0OxOo9KVg+v4WXTS8S4WOEaX+Wk+3m/RfmvQYPH4Kpf5KPwvvESTcy5WesaCucXOX148BXUHz+l+JePj0YG+HPkj0ZNdPdKzqcVvkVCCG+F0IMEEL0E0L8rbLsT0KIZZXvdwoh+ggh3IUQ/kIIfXPa2myw+T8QGMPbOUMoM9u4d2KkrpI6My4mI7clhLHh6DmOnq0Mbh45SWaR2voapP2sp7xuj8Vq482NqYzs68PoUDf5p8U9SF6UFU1m2sCehPu78famEzVvWB6BcM070nDqeDqvi5sDsCLxKD7f/IrphkTKJj+N8YFtMOEhOdluxK/k0wFnN71lKro64x8ESxlsfbVG8VUje3Myp4Td6Xk6CVNAd8ukd+wHyD5M+ZhFfLA1nRmxPekfpEK7tYabx4bh6mTgzQ3VRpGn/0UaDUvvUxP2dOS7A6fJuFDKfZP6o33/O5nI5fIXVJavZmI0aNw1IYJ9p/LYlpqrtxw7ndPFzQH4cssRgpbdQpzhKOZ5b+E68REVD1yhD4EDYNCVcgJoXpXH1OwhIfRwMvJF7bkPig6l+xjIQsCm/4B3XxYXx5NfaubeScqXrLX4ujtz0+gwlu7N5MT5Ylno4gHzX5euFj8+pa/AbooQgtfXHycqyIOpTodgz0cw4REYqFJLt4Rr40MJ8nThhZ+OOsRjz07r4qYjQgi++vozRq66kjjDUazz38J1xLV6y1J0d6Y9I+2TH37/S5GHi4l5w3vx7b5M8kvNDW6qaF+6j4F88mfI2EHFmAd4fdMpxkb6MbKvr96qugT3TorEyajxyppjVYVh42Ra3sR3pY+VokP54dBZks4U8sD4Xhi+fxj8+8PEx/WW1WlxdTJy/6R+7DiRy9bjORffoAPodC5uOmItK2TnK7dwzYHf4OMC4palOA9XxrHCAfANg0t/C0eWw7Gffim+eWwYZWYbX+9Sybf0ovsYyJv+A+6BvFsygfNF5fx2hprF31YEebpya0I4S/dmVqWfBpjyFPRNgCX3yCx7ig7BahP8e3Uy/QLdmZu/GC6kweUvykkhihZzw+i+BHu5OswosqJplJ8+wvnnxxCfs4LtIbfg97tdmPpN1FuWQlHFuIVyEOP73/4SF3lwb2+Gh/qwePtJdb3Rie5hIGftheNrKI27h9c2ZzI1Joj4cD+9VXUp7rk0EheTkZd+qjaK7OQKv/oS+oyCr++WCSoU7c6S3RmkZBfx5zFg2PqKnHAUcYnesjo9rk5GHpjcj51pF9h07PzFN1DozrmURErfmomxopDV8W8x5jevojm76y1LoaiJyQVm/wMunJChIyu5ZWwYqeeKWX+0e4VfdBS6h4G8+QVw8eKN4ikUlVv47Uw1etzWBHi4cOeEcJbty2LvqWozb108pZEcGAOf36pb5rHuQpnZyos/HWNEbw/GH3kWevjC9Gf1ltVluG5UKH18e/B/3x+pGRdZ4XAcSVyH8+J5lNmMHJvzBbOuuE5vSQpFw/SbCn3HwcZ/QYWcz3PFsF6EeLvy+vrjOovrnnR9A/l8Chz+loLBt/LG9nPMHdaLgSFeeqvqktw3qT+Bni48s+wQNlu1R0KuXnDTF9JY/vg6yFcB0NuL97ekkZlXyguhG9EyE2VKXDf1tKStcDEZeXLOQJLOFPKZmmHusGz4YQmhy2+gSHOn5OYVJIxJ0FuSQtE4mibjbhdlw9e/hrJ8nE0G7r4kkh0nctl10mEi6HQbur6BvPFfYHLhmXMTMRo0Hp8Vo7eiLouHi4nHZkaz91Qe3+6rZQR794abv5KpNT++Bsry9RHZhcnKK+Wln46xIDyL8P0vwqCrYMg1esvqcsweHMzoCD/+8+NRNcPcwSgzW/nggzcZs+Ue8pyCcL/3JyKjuu3cREVnIyxBulocXQVvTICsvdw4OhRfNydeXZuit7puR9c2kA9/C/s/I63/LSw5ambR1Ch6+fTQW1WX5uqRfRjax5vnViZRWFbLeOg5CK7/CM4fhS/vAKtFH5FdlL8sP0x/0nkk5xkIGCBjHqvMX22Opmn86fJYLpRU8OJPuqSZVtTD8XNFPPviK9yQ+iQX3PvR88G1+PTsq7cshaJ5jPkN3LlKhn57/zLcMrfw60sjWZd8ju2pjhFBp7vQdQ3kCydh2UJsISO54+R0+gd5cOf4CL1VdXkMBo1n5g4iu7Ccv69MqlshchJc9h84vgZW/6Gj5XVZ1idns+PQUT52fwGDiwf86ivo4aO3rC7L4N7e3DS6Lx9sSeNAhnoaojdL92Tyx1fe5Y/Ff6PCtz8hC1fh5Nl90mYruhiho+Gu1eAdCouv4a7eWQR7ufJ/K5NURIsOpGsayFYzfH0XCMHLvk9w4oKFZ+cNxtnUNb+uozGyry93T4jgk+3pbK5vtn/cbTD2Adj+BhxWyb9aS36Jmd9/vZ/X3d/C05ILN34iXVoU7cpjs2L41ZgwQnxU+Dy9yCkq54GPd/PnzzfyquklnLx74Xn3Cjk5VaHozHj1gju+B99wXL6+mWcSDOw7lcfy/af1VtZt6HoWoxCw6veQsZND8c/y4m4Ld46PIKGfv97KuhWPzogmMsCdx7/eT1F5Pa4U0/8MvUbA8kVQkNXxArsQT317kFklyxhj3Y0282/QO05vSd0C7x5OPDt/MAEeLnpL6ZZ8f+A0M17YyE+HT7O010f4aQWYbvgQPNTIsaKL4OYn5+6YejBz3yLGhBh4dsVh8kvU3IeOoOsZyOufg51vUxp/P7fv6MOAnh48NkuFdetoXJ2M/OvaoZzOL+X3Sw7UfSxkdIKr/ieDoi9bKP/YKJrNt3szSdm/hT84fQpRMyH+Lr0lKRTtytmCMh74ZDf3f7ybXj492DzhIGG5P6PN/D8IGaa3PIWibfHpCzd8jFaQxVve75NbXM5zq47orapb0LUM5F0fwIbnsA27iV+fnkd+iZkXrx+Bq5NRb2XdkrgwP347M5rl+7L4YEta3QoB/WHq05DyExz8usP1dXaSzxTyjyVbeK/HSxg9AmDea2pSnqLLUmGx8dbG40z593p+PHSWR6cP4JsrDATu+AfEzodRd+stUaFoH/rEw7Rn8E5bxWtRe/h0xynWJWfrrarL03UM5ANfwYqHod9U/ma8l83Hc/jrlYOJ7aViHuvJvZf2Y9rAnvz1uyMkptUTx3H0r6WrxbKF8jdUNInc4gru+WAbzxtfIUi7gHb9YvVoWdFl2Xj0HLNf2sj/fZ9EQj9/fnzkUhaOdML01e3gEwpzX1Z/DhVdm4QF0G8KM0+/zqU9y3jk871k5ZXqrapL0zUM5IpiWP1HCB3Dl/3+xjtbMrhzfATXxYfqrazbYzBoPH/dMPr49uDuDxNJyS6sVcEIN34GwUPlxMoVj4C5TB+xnYRyi5UFi3fwYPHLJIh9aHP+DX2U37Gi67En/QK/+t82bn13Bxab4N3b4/nfbaMIc7fIpEOWcrjxc3D11luqQtG+aBpc/iKaELzhvZgKi5X7P95NaYVVb2Vdlq5hIDu7w+3fsXzYazy+PJWJAwJ5co5KCOIoePdw4sM7x+BkNHDLOzvq/uv1DIbbV8D4ByHxHXh/DhSp3PP1UWGx8eBH27gt42muMmyESU/KqCAKRRfiyOkCfv1hIlf+dwtJpwv50+WxrH74UqbE9ASbFb66E3KPw/WLIUhd6xXdBN8wmPoUbulrWTzuLPsy8lj46R6V9r6d6BoGMrAyy42Hvk5iVLgfb9wch8nYZb5al6Cvvxsf3DGaojILN729jVO5JTUrGJ1g+l/ghk/g7GF4ZxrkntBHrINittr43SdbuDn1d8w0JsKsf8Ckx/WWpVC0CUIIthw/z23v7mD2S5vYlprDb2cMYONjk7lzQgQupsq5JFtflfMW5vwLIi7RV7RC0dGMvgd6DmbEkX/z7JxIfjpylt9+uQ+zMpLbnC5hRZZUWHjq20MMD/Xh3dtH0cNZTcpzRGJ7efH+naPJLa7g6te3kHSmoG6lmMvg9u+grAA+mAt56R0v1AEpKDNz37sbuTHlt4wzHoH5b8DYe/WWpVC0mjKzlW/3ZjL31Z+56e3tHMrK59HpA9j02GQWTInC3cVUVfn0PljzLAycC3F36CdaodALg1Gmo84/xc3Wb/ndzGiW7s3ivsW7KalQ2WnbEs0Rs7LEx8eLxMTEZm1z9Gwhwd6ueLk6tZMqRVuRfKaQW9/dTkmFlX9fO4yZg4LrVsraCx/OlQH/71gpg6Z3U07llvDA+5v4fd4zjDEkYbjqLRh6rd6yFK1E07RdQoh4vXVUpyXX3paSkl3IpztO8fXuDPJKzEQEuPPrSyK5amTv+iMPmUvhzYlQlg/3b5UxYhWK7sqXt0PySrh/Gx8la/xp2SGie3ryxs1xhAe4663OoWnqtbfLGMiKzkXGhRLuW7ybA5n5/PqSCH47M7rqEeovlRLhw/kyK9wdK7vlDfHbvZm8v/R7/slL9Ncy0a58E4Zep7csRRvQHQ3kM/llrNifxYr9p9l7Kg8no8aM2GBuGB3K+H4BGAyNRKL4/jHY8SbcvAT6T203jQpFpyDvFLw+Dlx94JZv2JDrzYOf7aHCYuPRGdHcPi4cY2PnUzdGGcgKh6fcYuWvK47w0baT9A/y4G/zBzMmslbGwxObYPHVEDIUbv1WTsjsBpzOL+WvKw7jd/hDnnL6GKObD8ar3lSGQReiOxjIQgiOnytmfXI2qw+dZefJXISAQb28mDe8F1fH9MC/+DgUnYWyPDkBz9ld3vT9+4NfpHykvO2/MlLRmPtg9nNtpk+h6NRk7ZX3R4DrF5PlPZw/fHOAdcnnGNzbi9/OiGbigEA0FQKxBspAVnQa1iVl89S3B8m4UMplQ0N4eFoU/YM8qyocWQFf3CJvltFzIHIi9E3oksZyfv4F1v+whJyDaxmlHWaIloqt/zQM899QcY67GF3GQM7cBZm7oSQHSnKoKC3ifEEJ2QWlpBfYOF3uTKFww8XTn/5hocSFehJ0bhukroPC0423bTCBiyeUXoABs+Da98GpR4u/n0LR5TifAh9dCfnpED0HkbCAlTlB/O3HU2TmlTIs1Ic7xoUza3Cw4ydNK86B80fhwgkoyobic1BeIP84W81gdAYXD3lNcA+E3nEyiUozUQayolNRWmHlv+tTeGfzCUrNVmYNCubmsWEkRPrLx65HVsD2NyB9G9jMYHCCsHEwaL6csOMeoPdXaDlF2Zzf/hnFe5fQq2A/TpoVs+aEredQXEbeKNNHG7rEfFpFNbqKgVy0/Ek8dr0GQCHuFAoXbBgQGPAymXEXJZhs5TU36uELkZPlDS5oIHj3kaPGBhOYi6H4POSkwNlDUHJe/jGOnqOSgSgU9VFeCNtehy2vSIMSED5hnHKN5pvcvqwq7EeWSwQzB/di6sCeXBIVgJuz6SKNtjNWs7yfp2+DjB3yj3ZJTs06JlcZ49zoLJ8kWc1QXlT5HQWMvR9m/b3Zu+7eBrIQ8kLa0Gtj29ix2aqMktrHSAi5zl5u/2x/b/9ss1W91zSwWuWrXQvUfG//bH+1WMBkqmrXZquqX71NAKNRllss4ORUtY3VWtVG7e9ls9XcZ3Xddp21j2ft+tU/126/vs8NUbmP3OIK3t6Uyqfb08krNdPXz41Zg4OZEduTEX19MVpKIH0rpG6ApO9kLFTNAFEzIP5O6D9NnkgOjrCaOZu4FOv2/xGcuwMjNpJtoaQHTCAqYS7hI6aCyaWBjWv11cb6dUPb1f7t6uvvtdfVPo8sFtnv7NTuW/Y+aj8n7G3by222uvXs5dXPL6j6bF/s/d1+DlTXV7vPVT8Hqp+f9R0T+3t7m/bjYD8Xm3ItaSJdxUD+5zc/8+X2NMwuPgwNC2R0uC/x4X6M6Osj5xUIAdYKKM2TI8E2MwTFts152txzofa1tr7P9bXXWLl92+rtN6bJ3j9r93Obrapf19ZsMNS8f1Rvx97na1+zG7pPWSxV5XYd9vZMprr3lfqOQ+3vb9dur1tdT/VrQH33ldq/TfXvZ9dUXaO9Dft3MJvlPc++H3vd2t/dvl19x7/6cajdf2ofv+rXP/vxAnnMjA306drXUHvdll5PGuqPpRcg7Wc4d0T+ucxIhPxTAOSZAlhlGcl3FSNJNAxhcB8/Rob5EtfXl6F9fOjp5dL+rhjlRXJiYfL3kLIGyvNleWCMHAkOGgQBA8AvAjx6Vj0lrv1dhZDGtKa1aHCsQwxkTdNmAS8BRuB/Qojnaq13AT4E4oAc4HohRNrF2m2VgfzMM5CXB97ekJ8P//kPPPJI1WcfH1mnvm1eeEEe8KefhmXLYO5c+fnCBdi2DTIzoXdvKC+X6/Lz4auvZOe/5x5Zd+VKqKiA3FzIyQFnZ4iKAhcXOHJEbqNp4Osr9200QkAApKTI8kGD5OuRI7Kd3/1Onlg5OfDGG/KkDAiAG26A/fvh0CHZprs7lJbKE++JJ+DZZ2HRIrmNu7v8fpMmybq7dsGUKbLs9Gm53W23webNUrevL7i6wqxZ8lg8/DDs3QtlZTBmDLz4otT+0EOwfbus98wzNdu3X3Di4uSxX7/+4r+Z/fgLQdnDj/K9ZwRLI8aw9fh5zFaBl6uJuDB58x3Uy4uoIA96laWgHVoCez6G4mzw7gsJ98PI28DZrWV9qB0oLDNz5HQhyelZ+B76iPjsrwjmPJnCnw2u0zANv5aJ4y+hp5dr4w3Vc6x4+OH6+3VD2/35z7JPg/ythajb32uv8/KCESOqzqf33oPiYggKgtBQ2S8+/VSeG0LIvjJiVW2aFAAAIABJREFUBMyeLff72WeQnS371T33yP6UnAxnz8q+Ehcn+3t2tuxDBoNsy9kZ+vWDefNkO2+8IdtPSICRI8HTU2oyGGQ/LymR51pEhPwuhw9LLQkJss/n5sKmTbJPrltXdeyg6vhERMjvFhEh2502DZ5/Xn7XK69s/FrSDFprILfH9bcl196088UUV1iICfbC+Jc/t6x/toTmngvPPAOrVsn3Y8bI7R5+WF7DQPbN4cPrtrd3b8PlF7smNnRvyc0FPz9ITITx4yEjQ7bl7g7z58u2vv5a7isoCFJT5bW/f384fx569YK0NHmOjBgBR49C377yPgUwdiykp8OAAVXnZEWFbKekWgz6YcNg3z7ZNsh2+/WT95+8PHm/O3Gi5nGofm8dN06eY87OcP/98toydizs3CmNx/vuk9/9oYfgiy9k2d13y33V/u0SEmT51q0weTJs2SLPv6AgeaxOn5bXB7tub2/YvRuKiuRxe/RR2eZrr8n7YK9eUidUGaienlBQII1qISAwULY/dy689ZZsy9tbarr6anl/z8+X25vN8lhXVMCBA7Ksd2/5fZ56CoKDpY60tJr9zn5fvOIKuW9PT3kdi42V7TX3etLcfp+XDmmbIXklImUNmrmYAqcAVpum8HpBAsetPQHwdDURFeTBgJ6ehPm709u3B7195BLk6dL4BNrGEAJObYc9H8HBb+QTIvdAGDATBsyG8PHyiVJbfNcm0uRrrxCiRQvyonwciAScgX1AbK069wNvVL6/Afi8KW3HxcWJFmGzCfHgg/L/xfDh9b8++KCsV982Dz4ohNVac5uFC6uPW1UtAQE1Pw8bJsSCBVWfXV1rrq/9+WKL0Vi13QMP1F/HxaXqvbNzzW1raykvr/pew4bJpb42q+tctEgu1Y9f7XL7Z4ul5nGrfRyt1ov/Zvbfptbn/NIKsXRPhnj8q31i6vPrRdjjK35ZBj61Usx+caO4+92fxeJ3XhIZz18qxNNeouxv4SLl67+IXUdPiaTTBSI9p1iczS8VOUXloqC0QpRWWITVaqtfU70ybaLCYhVFZWaRU1QuTueVipPni8XRMwXiQEae2HzsnFixL0ss3pYmXl17TDy7/JC4b3GiuOKVTWLkX1aL2Me/FM89eY/I+VMvIZ72EkeemyjWLX1XnDib17L+3cCxuuh29f129r5Qu79XX2fv7/bf1N4/L7Y01M9qnz8XW/z96+/7TT2vXF1rnhPVv2v1Y7JgQV1t9u9qf23oWtJMgETRhOthfUt7XX9bfO0VouX9syP2ZbPV7Pf19U3759rt1f69a5c3dF5ZrQ3fW+z9tqF+3dD94GLnxsKFNc/h2n1Z0y5+rlTX4O9fdd7UvpfWPn7+/vXfL2vXW7iw6ljZj2n1Y7dgQcPXjcauCUOHNu1acLHv3Nxl4cIqLQEB8l5op/pvbv8t7L+9/bU515PWnmMVpUIcXibEx9cJ8YyPEE97ibw3LxM/LP9M/HHJfnHdG1vEiL+srnGPDXt8hej/5Hci4f9+Epe9vFHc8s528dBne8Szyw+J19YdE59sPym+3Zsp1h45K3acyBGHs/JFek6xuFBQJMy7PxHitbFCPO0lxF9DhFh6vxBpWxq2B9ryuzZCU6+9LR5B1jQtAXhGCDGz8vPvKw3uv1er80Nlna2appmAM0CguMhOWzWCLIT8h/HSS3XXPfhg1T+Ri20zfLj8x9wUmlO3Obi6ylGF1rZRWFj1mCourvlaH3xQjhY8/DC8/HLNdYsWydET+6Or2u0PH141otwQ9R3/hn4rIK+kguQzhaScK+LY2SLSc0s4k1/G2YIycoorGKUlscC0lInG/RSIHuQLD6wYqN7p7K1qmqh6X1NUtbr1d1d7uVajbtWryQAGg4ZR03CzFeNkK6U8fCou055s0cQCKat5x6rR7arTWB9uaF1j/TMgQI50tQf+/vKJSlNpTKf92EHjx6eh7VrxSLI1I8jtdf1tE/e2lvTPjtiXEHIks/Y1DOR17IUX5NOR2u3Zn5rUV36xa2Jr7y1Npb4223I/DR2HhvD1rXoSVR37sYG6x2XRIvla3+/TGQgIgDNn6rpZNOW+25xzpK3OsYIs+eR1x1vy6WvIcBh+E5hcKbNYyS+p4EJxBXmlZvJKyikss1BSbqak3EpxhYXicssv2ftq3ws9KeVG01r6aOc5KvqwmMtZaxyP1ckdF5MBF5MRFydD1XuTAZNRw2QwYDRomAwahspX49YtmPbtxSBsmGxWjCNHYJo+DYPBwIi+PkyODmr6d66k3V0sNE27BpglhLi78vMtwBghxIJqdQ5W1smo/Hy8sk6dO6emafcA9wD07ds37uTJky3SBcgOVJ9BZvdfaso2jfkT1aY5dZuD3beqtW3U9kFurtbavs/1rWuo/eq+nI1Ru+3GfqtGKLdYySsxU1hmxnpyO57JX2KtKMVmsSCEDWvl336bENiEVvlarYEa+9SqvUhD11B54la9N2DUNJxMBpxNBlyMBpxMRkz2x1H29owuMOyGlhvG1WnpsWrovIDG+3BD6xrrn9X959ua5rbdmM7qx66x49PYdi2klQZym11/2/TaC212LrfLvi52b2iovaaW16ehNfeWplJfm225n8a+b300dI42dr5V9x1uDuXl0q1Kb2rPyajOxe67zT1H2vIcM5fB/s/g55flnJ424qzPcHb0uo0jnmOpsEK5xUa5xSpfzdXeW2yUma1YrAKrEFhtAovNhrX653PnsRqMWDUDFjd3rDZZfvu4cJ6ZO6jZ2jrCxeJapN+b/fMtwCu16hwC+lT7fBzwv1jbbfaYr/bS0LB8fdtUf3x2saU5dZuzNNcto6E2zGb5Pas/7mnOYn88WPsRJcgy+zGtr/3G3CsaO/5t/Ui2q9DSY9XYeXGxPtzQusb6Z3NdKJqz1H602przyH7sLnZ8GtquFdA6F4t2uf626torRMeey83dV31uFtWvY9VdImpf+xoqv9g1sbX3lqYu9bXZlvtp6Dg0tPj6NnycGzrfarupdLaltnuFnabcd5tzjrTXOWa1CpGXUbXkZ1YuWXIpOF25nJFL4dnKJVsuRecql/NClOS2TksTvqvNZmuWm2R1mnrtvWiFBjeEBOCHap9/D/y+Vp0fgITK9ybgPJWj1o0tygcZ5YPcVid9V0L5INft+93XB7ldrr/KB7me9pQPcs3vq3yQ636fzuKD3JlwAB/k1jwD3QlEaZoWAWQiJ4HcVKvOMuA2YCtwDbC2Ulz7oGlyduODD8qZoRMn1oxiMXGiXF/9UUT1bew+PHPnynX2Wf2LFl08isW8ebLu6NHtE8ViwYLGo1j0qAyeXz2KBchtXFykDm/vKp/gKVPkTODGolj4+spZ15om/afGjKk5YxvkjG1fX/k9qrdvMMhXexSLhh6b1Xf87T6htX+r7k5Lj1Xt7f785yp/P1/fqr5bvb/XXteaKBYTJ7Z9FIvRo5sXxWLUKOm7vHBhVRSLl/6fvTsPj7K8Gj/+PZNM9p0ACQQIS9iFgIAiKqhoXXCpWsWl2tq3vrZVu2jf1tpaa6t1+2ltpbV1rxtq3RU3qrig7PtuWBOWELLvyczcvz+eCQxhss5MZsn5XBcXmXmeeZ5DgDtn7jn3uR+xXtfSxaLl+/POO9bj9rpYeBtLelZoj7+B/r/c1Xu1jLknnGA9bquLhbfrrVnT9vPtjYkt/7a8/WzxZxeLceOOdLFoqUtdutQ/XSySkqya4KioI98Hz5+t3rpYLF3afheLjAzrXp7fl7/85cjfw1//anWxsNu71sXioousjhE93cUiI8Max1q6WHiWUthsR34uttfForPjSW/6eRkCf1Zf27ydC/wFa0X1U8aYu0XkLqzs/G0RiQOeAyYBZcBcY8yOjq6rfZDdv/fCPshtPlZHdPd75Xle67877YN89Ndh0Ac5EOOvXzZp6sn/y129V+ux1ttjb9dr7/mW13pev72YtA+y9++Lt3FH+yB715t+Xgbgz9q7NwpRSqkQFykbhSilVDjp7NjbxeWiSimllFJKRTZNkJVSSimllPKgCbJSSimllFIeNEFWSimllFLKgybISimllFJKedAEWSmllFJKKQ+aICullFJKKeUhJPsgi0gJsNvPl83E2mo13IRr3BC+sYdr3BC+sffGuIcYY/r6MxhfBWjs9Yfe+O8j2MI1do27Z4Vj3J0ae0MyQQ4EEVkRak35OyNc44bwjT1c44bwjV3jVu0J1+9zuMYN4Ru7xt2zwjXuztASC6WUUkoppTxogqyUUkoppZSH3pQg/yvYAXRTuMYN4Rt7uMYN4Ru7xq3aE67f53CNG8I3do27Z4Vr3B3qNTXISimllFJKdUZvmkFWSimllFKqQ5ogK6WUUkop5aFXJcgi8kcRWScia0TkIxEZEOyYOkNEHhCRLe7Y3xCRtGDH1Bki8h0R2SgiLhEJizYwInK2iGwVkQIR+XWw4+kMEXlKRA6KyIZgx9JVIjJIRD4Vkc3ufys/DXZMnSEicSKyTETWuuP+Q7BjinQ6DvaMcBwDITzHQR3/QluvSpCBB4wxE4wx+cC7wB3BDqiTPgbGG2MmANuA24IcT2dtAC4GPg92IJ0hIlHAPOAcYCxwhYiMDW5UnfIMcHawg+gmB3CLMWYMcCLwkzD5njcCpxtjJgL5wNkicmKQY4p0Og4GWBiPgRCe46COfyGsVyXIxpgqj4eJQFisUDTGfGSMcbgfLgFyghlPZxljNhtjtgY7ji6YBhQYY3YYY5qA+cCFQY6pQ8aYz4GyYMfRHcaY/caYVe6vq4HNwMDgRtUxY6lxP7S7f4XFeBKudBzsEWE5BkJ4joM6/oW2XpUgA4jI3SJSCFxF+Mwge7oOeD/YQUSogUChx+MiwmCwihQikgtMApYGN5LOEZEoEVkDHAQ+NsaERdwRQsfBwNAxMEh0/As90cEOwN9EZCGQ5eXQ7caYt4wxtwO3i8htwI3A73s0wDZ0FLf7nNuxPpJ5oSdja09n4g4j4uW5iHtXHIpEJAl4DfhZq096QpYxxgnku2th3xCR8caYsKl/DEU6DgadjoFBoONfaIq4BNkYM7uTp74IvEeIJMgdxS0i1wJzgDNMCDWv7sL3OxwUAYM8HucA+4IUS68hInasHw4vGGNeD3Y8XWWMqRCRRVj1jxH1A6Kn6TgYdDoG9jAd/0JXryqxEJE8j4cXAFuCFUtXiMjZwK+AC4wxdcGOJ4ItB/JEZKiIxABzgbeDHFNEExEBngQ2G2MeCnY8nSUifVu6KIhIPDCbMBlPwpWOgz1Cx8AepONfaOtVCTJwr4hsEJF1wFlAWLRUAR4FkoGP3S3qHgt2QJ0hIt8WkSJgOvCeiHwY7Jja414AdCPwIdZiiVeMMRuDG1XHROQl4GtglIgUicgPgh1TF8wAvguc7v63vUZEzg12UJ2QDXzqHkuWY9XgvRvkmCKdjoMBFq5jIITtOKjjXwjTraaVUkoppZTy0NtmkJVSSimllGqXJshKKaWUUkp50ARZKaWUUkopD5ogK6WUUkop5UETZKWUUkoppTxogqyUUkoppZQHTZCVUkoppZTyoAmyUkoppZRSHjRBVkoppZRSyoMmyEoppZRSSnnQBFkppZRSSikPmiArpZRSSinlQRNkpZRSSimlPGiCrEKGiOwSkXoRqRaRChH5SkRuEJFO/TsVkVwRMSISHehYW913logUdXBOmog8KyIH3b/u7KHwlFLqGBE+3p4mIp+KSKWI7PJyPNd9vE5EtojI7IAFrMKWJsgq1JxvjEkGhgD3Ar8CngxuSH7xMJAA5ALTgO+KyPeDGpFSqreL1PG2FngK+GUbx18CVgN9gNuB/4hI3x6KTYUJTZBVSDLGVBpj3gYuB64VkfEAInKeiKwWkSoRKWw1E/u5+/cKEakRkekiMlxEPhGRUhE5JCIviEiat3uK5WH3DG+liKzzuG+siDwoIntEpFhEHhOReBFJBN4HBrjvWSMiA7xc/nzgfmNMnTFmF9YPoev88b1SSilfRNp4a4xZZox5Dtjh5b4jgcnA740x9caY14D1wCXd/f6pyKQJsgppxphlQBFwivupWuAaIA04D/iRiFzkPnaq+/c0Y0ySMeZrQIA/AwOAMcAg4M42bneW+xoj3de/HCh1H7vP/Xw+MAIYCNxhjKkFzgH2ue+ZZIzZ18b1pdXX4zv8BiilVA+JsPG2LeOAHcaYao/n1rqfV+owTZBVONgHZAAYYxYZY9YbY1zGmHVYH5XNbOuFxpgCY8zHxphGY0wJ8FA75zcDycBoQIwxm40x+0VEgB8CPzfGlLkH1nuAuV34M3wA/FpEkkVkBNbscUIXXq+UUj0hEsbb9iQBla2eq3THotRhPVpcr1Q3DQTKAETkBKxaufFADBALvNrWC0WkH/BXrBmRZKw3heXezjXGfCIijwLzgMEi8gZwKxCHlcyutMZu69JAVBf+DDcDfwO+wZoleQm4oguvV0qpnhAJ4217aoCUVs+lANVezlW9mM4gq5AmIlOxBuwv3U+9CLwNDDLGpAKPcaR0wXi5xJ/dz08wxqQAV3N0qcNRjDF/NcYcj/Vx20isRR6HgHpgnDEmzf0r1RiT1M59W1+3zBhzlTEmyxgzDuv/3rKOXqeUUj0lUsbbDmwEhomI54zxRPfzSh2mCbIKSSKSIiJzgPnA88aY9e5DyUCZMaZBRKYBV3q8rARwAcM8nkvGmjGoEJGBtL2qGRGZKiIniIgdq/auAXAaY1zA48DD7hkSRGSgiHzL/dJioI+IpLZz7eEi0kdEokTkHOB64E+d/HYopVTAROB4axOROMBuPZQ4EYkBMMZsA9YAv3c//21gAvBah98o1atogqxCzTsiUg0UYrXfeQjwbIf2Y+Au9zl3AK+0HDDG1AF3A4vF6ut5IvAHrBXLlcB7wOvt3DsFa2AuB3ZjlUI86D72K6AAWCIiVcBCYJT7vluwSiZ2uO/rrYvF8VgrpauxZlmuMsbojIVSKpgidbw9FWsWegEw2P31Rx7H5wJT3Pe+F7jUXTOt1GFijK+fViillFJKKRU5dAZZKaWUUkopD5ogK6WUUkop5UETZKWUUkoppTxogqyUUkoppZSHkNwoJDMz0+Tm5gY7DKWUCpiVK1ceMsb0DXYcnnTsVUpFus6OvSGZIOfm5rJixYpgh6GUUgEjIruDHUNrOvYqpSJdZ8deLbFQSimllFLKgybISimllFJKedAEWSmllFJKKQ8hWYOslAodzc3NFBUV0dDQEOxQwlJcXBw5OTnY7fZgh6KUCiM69vrG17G39yTIJVvhwHo47tJgR6JUWCkqKiI5OZnc3FxEJNjhhBVjDKWlpRQVFTF06NBgh6OUTxxOF++t38++igbOHp/F0MzEYIcU0XTs7T5/jL29I0Gur4B506yv49NgxOzgxqNUGGloaNABuptEhD59+lBSUhLsUJTySaPDyfefXs5X20sBePjjbfzj6smcMaZ/kCOLXDr2dp8/xt7eUYO8/b9Hvl7+VPDiUCpM6QDdffq9U5HgoY+38dX2Uu69+DiW3HYGo7OTufml1RSW1QU7tIim40f3+fq9i+gEedehWk5/cBGfv/8yJj4dpvzASpab9D+0Ukop1Rkb9lbyr893cMW0QcydNpis1Dj+ftVknMbw0Mfbgh2eT4wxNDQ7gx2GCkERnSD/8/Pt7DhUS2b1Fg4kjYO8M8HRAPvXBjs0pVQnlJaWkp+fT35+PllZWQwcOPDw46amJr/dZ+HChaSmppKfn8+YMWO4++67j3p+0qRJjBw5kpkzZ7JgwYLDr/vtb397VEy3336732JSKlT847PtJMVE8+tzxhx+Lic9ge+dNJQ31+xly4GqIEbXfS6X4YbnVzL5jx/zxTdaBtVabx9/I7YG2RjDBxsOcMnEvuRt3cs7tSdwcXa+dXD/GhgyPbgBKqU61KdPH9asWQPAnXfeSVJSErfeeutR5xhjMMZgs/n2fv+0007jzTffpKamhgkTJjBnzpyjngdYtWoV3/72t/n3v//NzJkzAfjlL3/Jz372M5/urVSo2l1ay/vr93P9qcNJjT+6G8CPZg7n2a928exXu/jzxROCFGH3ff5NCR9uLAbgzwu2cPLNmVrS4KG3j78RO4O8t6Ke8rpmZvWpwI6DTyv7URHdB5KzYd/qYIenlPJBQUEB48eP54YbbmDy5MkUFhaSlpZ2+Pj8+fP5n//5HwCKi4u5+OKLmTJlCtOmTWPJkiXtXjspKYnJkyezffv2Y45NnjyZ22+/nUcffdS/fyClQtT85YWICN+fkXvMsdQEO3MmZPP2mn3UNjp6Pjgfvb5qL30SY7hjzlg27a9ia3F1sEMKC71l/I3YGeQNe62PfMbFHQJgh2sAS3aUcvaASZogK9VNf3hnI5v2+ffj1LEDUvj9+eO6/LpNmzbx9NNP89hjj+FwtP3D+eabb+b//u//OPHEE9m1axdz5sxhw4YNbZ5fUlLCsmXLuPvuuyksLDzm+OTJk/nb3/52+PEDDzzAM888A8CDDz7I7NnaJUdFBpfL8NbqvZyal0n/lDiv58ydNphXVxbxztp9zJ02uIcj7D5jDF9tP8QpeZmcNa4/d727ia8KShmdlRLs0LwKpbEXesf4G7EJ8vaSGgByXPsBOGjPZnFBKWdn58PW96GxGmKTgxmiUsoHw4cPZ+rUqR2et3DhQrZu3Xr4cXl5OfX19cTHxx913qeffsqkSZOw2Wz87ne/Y9SoUV4HaGPMUY+1xEJFqqU7y9hX2cCvzhnd5jmTB6cxNDOR99bvD6sEueBgDYdqmjhpeCY56QkMzkhg6c5SrjtZ+5V3Rm8YfyM2Qd5XUU96gp2Yqt2QkMm4vjks3n4Izp8EGNi/DnJnBDtMpcJKd2cbAiEx8cgmBTab7aiB03PnKWMMy5YtIyYmpt3reda6tWf16tWMGTOmw/OUCncL1u8n3h7FmWPb7nUsIpw9PovHP99BRV0TaQnt/z8LFev3VgKQP9gqDZg4KI3Ve8qDGVK7Qmnshd4x/kZ0DfLA9Hgo2wEZwzhxWB92lNRSnjbWOkHLLJSKGDabjfT0dL755htcLhdvvPHG4WOzZ89m3rx5hx+3LDrpjjVr1nDPPffwk5/8xKd4lQp1xhg+2XKQGSMySYhpfy7tnPFZOFyGjzcV91B0vtu4r4o4u41h7t0Ax2anUFReT2V9c5AjCz+ROv5GbIK8r6KeAanxULYTMoYyIScVgHUVsZCSowmyUhHmvvvu4+yzz+aMM84gJyfn8PPz5s1j8eLFTJgwgbFjx/L444936botH/2NGjWKm2++mb///e+HV1ArFam2Fdewt6KeM8b06/Dc4wamMiA1LqwS5C0HqhjVP5noKCsNGpNtlVxu2R+eLeuCLRLHX2ldz9GlF4ucDTwCRAFPGGPu9XLOZcCdgAHWGmOu7Oi6U6ZMMStWrOh2XADjf/8hcyf15bdrTodZv6bqxFuYcOdH3HrWSG48eCcc3Aw3r/LpHkr1Bps3b9aSAh95+x6KyEpjzJTuXrMz46/7vEuBV4Gpxph2B1Z/jL0qMvx9UQH3f7CVJbedQVaq9wV6nm57fR3vrt3P6jvOPJx0hrKZD3zKxJw0/nrFJAAKy+o45f5Pue+S47h8amjUUuvY6ztfxt5u/ysWkShgHnAOMBa4QkTGtjonD7gNmGGMGQf0yEqW+iYnNY0OhttLAQMZw0iJszMsM5F1RZUwIB/KtkNDZU+Eo5RSftWZ8dd9XjJwM7C0ZyNU4e7TLQcZNyClU8kxwCl5faludLC2qCLAkfnO6TLsq6gnJ/3IQrHs1DjsUcKuUt1pV1l8eZs3DSgwxuwwxjQB84ELW53zQ2CeMaYcwBhz0If7dVp5nbXDy0DXAeuJ9FwAJuSkuhNk6x2j7qinlApTnRl/Af4I3A80eDmmlFcVdU2s3F3OGaM7Lq9ocdLwPojA59sOBTAy/yiuaqDZachJTzj8XHSUjUHpCewurQ1iZCqU+JIgDwQ8e3AUuZ/zNBIYKSKLRWSJ+yPBgCurtRLkPqbUeiLFCuu4nDQOVDVQkuyebtc6ZKVUeOpw/BWRScAgY8y77V1IRK4XkRUisqKkRLfbVbBkRykuA6eO7Nvp16QlxDAhJ40vC0I/QS4qrwc4agYZYEifBHYd0hlkZfElQfa2H2PrguZoIA+YBVwBPCEiaa1fBP4dpFsS5DRnqRVmkvUueGy21QB8c2UMpA3WBFkpFa7aHX9FxAY8DNzS0YWMMf8yxkwxxkzp27fzCZGKXF9vLyXeHsWEHK8/rtt0al4maworQr4TRFG5lQQfmyAnsru09pheu6p38iVBLgIGeTzOAfZ5OectY0yzMWYnsBUrYT6GPwfplhKL5OZSSOwLUdb+8aOz3KtUD1RZZRZFK0H/Iyilwk9H428yMB5YJCK7gBOBt0Wk24sCVe+xZEcZU3LTiYnuWopw8ohMnC7Dkh2lAYrMP1pmkAe2SpBz+yRQ2+Sk1D3Jpno3XxLk5UCeiAwVkRhgLvB2q3PeBE4DEJFMrJKLHT7cs1NaZpDjGg5C8pEG5+mJMWSlxLFlfzUMmwWVe6xuFkopFV7aHX+NMZXGmExjTK4xJhdYAlzQURcLpUprGtlaXM304X26/Nr8wWnERNtYtrMsAJH5T2FZHf1TYomNjjrq+SHunshah6zAhwTZGOMAbgQ+BDYDrxhjNorIXSJygfu0D4FSEdkEfAr80hgT8LeW5bVN2ATsdcWQnH3UsdHZyWw+UA2jzgNbNLx3i3azUCrEJSUlHf56wYIF5OXlsWfPHu68804GDhxIfn4+eXl5XHzxxWzatOnwubNmzWLUqFHk5+eTn5/PpZdeGozw/a6T469SXbZkh5Xcnjis6wlybHQUkwalsXxXaCfIReX1Ry3QazEkw3pO65CP6M1jr09bTRtjFgALWj0IA0EYAAAgAElEQVR3h8fXBviF+1ePqaxvJik2Gqk+YLV08zA6K4XFBTtoTuiL/eJ/wevXwwe/gYvmtXE1pVSo+O9//8tNN93ERx99xODBVq/Sn//859x6660AvPzyy5x++umsX7+ellKtF154gSlTIq+yoKPxt9Xzs3oiJhX+luwoJTEmiuMGprZ90sEt8OVDcGADiA3GzIGpP4TEPkwbmsG8TwuoaXSQFOtTihEwRRV1TB6cfszzA9KskosDVdr0pbXeOPaGfjfvbqhudJAWa4PakmNmkMdkJ9PsNGwvqYHxl8Dx34f1r0BtaNdMKdXbffHFF/zwhz/kvffeY/jw4V7PufzyyznrrLN48cUXezg6pSLD1ztKmZKbgb2tzT72rYEnzoCtH1iL3ePTYNG98NgMOFTAtKEZuAys2l3es4F3ksPpYn9FwzEL9ADi7FGkJ9jZV1EfhMhCV28de0Pz7Z2PahocDIqtgUYDSf2POjY6y+pksWV/tfX1pKth+ePwzYeQ3+Emf0r1bu//Gg6s9+81s46Dc7xuAndYY2MjF154IYsWLWL06NHtnjt58mS2bNly+PFVV11FfLz1w/DMM8/kgQce8D1mpSLQweoGCg7WcOnxOd5PaKiEF74D8Rlw3QeQ6u4suH8tPHcxvHotk69dSJRNWLazrEtt4nrKgaoGHC7DIC8lFgDZqfEcqAzBGWQde3tcRM4g1zQ6GGR37+bTagZ5WN9EYqJsbD7g3m89eyIkD4CtC1BKhSa73c5JJ53Ek08+2eG5rVs0vfDCC6xZs4Y1a9aE3QCtVE9a6q4/nt5W/fFXj0LtQbj830eSY7B+jp7/CBRvIHHFo4wfkMKyEK1DPtIDua0EOY79oZggB0lvHnsjcga5usHBAJt74V1y1lHH7FE2RvRLsjpZAIjAqLNh3SvgaITo2B6OVqkw0sFsQ6DYbDZeeeUVZs+ezT333MNvfvObNs9dvXp1WNe9KRUsS3da9cfjBqQce7D2ECz5O4y96MhutJ7GzIFx34ZF9/HtvL9xz8Y0Gh3OYzpFBFtbm4S0yEqNY3VhCG6XrWNvj4vYGeR+tpYZ5Kxjjo/OTrZ6IbcYeTY01UDh0h6KUCnVVQkJCbz77ru88MILbc5mvPbaa3z00UdcccUVPRydUuFv2c4yjs/NINpb/fGXD0NzHZx2e9sXOO8hSBvM1dtvYZxzK+uKQq9DVFF5HSKQnRbn9Xh2ahxltU00NDt7OLLQ1VvH3oidQe6T5J4hTsg85viYrBReX7WXstomMhJjYODx1oED62HoqT0YqVKqKzIyMvjggw849dRTycy0/m8//PDDPP/889TW1jJ+/Hg++eQTPDcb8qyDy8zMZOHChUGJXalQVl7bxLbiGi7MH3jswcq9sOxxmHgF9B3Z9kUSMuB77yJPncPTzffz+tbpTM09IXBBd0NReT39k+PanNnOTnV3sqhsINfdF1n1zrE3IhPkmsZm0kw1xCRDdMwxx0dnH9lR76ThmZCYCUlZVssapVTIqampOfz1oEGD2LlzJwAXXnghd955Z5uvW7RoUYAjUyoytPQunjY049iDnz8AxgUzf9XxhVIGEHXVqyTOm07eugfhW6/6OVLfFJbVtVleAdYMMsB+TZCB3j32RlyJRbPTRUOzi2RXlfVu1gvPThaH9R8HxX5eIaqUUkqFgWU7y4iJtjEhp1X/47IdsPo5OP57kD6kcxfrO5Kv+l7GKbUf4dy3zu+x+qKovJ5BGd4X6IFVgwxwoEpbvfV2EZcg1zY6AEhqJ0HumxxLZlLM0XXIWeOhZCs4m3siTKWUUipkLNtVxqRBaceWHiy6F2x2OPXWLl2vesqNVJt4ahbe78cofeNwujhQ5b0HcouWEot9FdrJoreLuAS5xp0gxzsqrV6NbRidlcKWA54zyOPB2QSHvgl0iEqFndbte1Tn6fdOhbqaRgcb9lZyQuvyioObrQ5PJ1zvdcF7eybmDeV552xSdrxrTT6FgP2VDThdpt0EOT4mirQEe8j0Qtbxo/t8/d5FXILcsvI0rrkCEtreS350VjJbDlTjcLqsJ/qPs34/uKnN1yjVG8XFxVFaWqoDdTcYYygtLSUuzvuKeaVCwcrd5bgMTBva6mfm4kcgJhFm/KzL18xJj+fthItpsMXDx7/3U6S+6agHcouslNDohaxjb/f5Y+yNuEV6dU1WghzbXNFmiQXAmOwUmhwudh6qJa9/MqTnWgcq9vRAlEqFj5ycHIqKiigpKQl2KGEpLi6OnJw2diZTKgQs21lKtE2YPCTtyJO1pbDhdZj83XZ/lrZFRBgxdChPFXybn2x7AXZ+HvQuUYXldUDbPZBbDEiLD4kaZB17fePr2BtxCXJ9kxM7DqKba9qdQR7rboS+aX+VlSDHJEJcGlTt7alQlQoLdrudoUOHBjsMpVSALNtZxviBqSTEeKQEq58DZyNM/Z9uX3dqbjp3rz2T/+27iOiPfgs/XAS24H1wXVRej02O1Bm3JSs1jrUhsFmIjr3BFXElFnXNTtJwtyWJT2/zvOF9k7BHCZs9O1mk5lj9HpVSSqleoKHZydrCVvXHLieseBKGnAz9xnT72lNzM2gkhtV5N8P+tbD+FT9E3H1F5XVkpcQRE91+6pOdEkepbhbS60VcgtzQ5CRdWjYJaXsGOSbaxoh+yWza79HJImWAziArpZTqNdYUVtDkdB3d/7hgoVVuOK37s8cAI/snkxwXzRvN063tqf97FziafIy4mxyNTN/zL15w/hKeOhu++H9QvBFcrmNO7e9u9XawqrGno1QhJOIS5LomJ+ktM8gd1E2NzU5h81EJ8kBNkJVSSgVEQ7OT2kZHSC26WrazDBGYMsTj5+Wyx63Ns0bP8enaUTbh+CHpLN9dYW1RXbUXNr/tY8Td0FAFz57Pd2peoDkmFRwNVrL+j5Pg/qHw4uWw6jloqgWObBZyoCr4C/VU8EReDXKzk7SWGeR22rwBjMlO5rVVRZRUN9I3OdZKkOtKobkB7LrqXCmllG/2VdTz9OKdfLixmD1l1iKxtAQ7M0ZkcvUJQzhxWAYiErT4lu4sZVT/ZFIT7NYTZTusGeSZv4Iou8/Xn5qbwaKtWynPPoP0jGGw7F9w3KU+X7fTjIF3bsYUreCm5psZln81vzhrlFVOufMz2P0V7PoCtn0AH/4Gpnyf7LE3AuGbIDc0O4mJsmGzBe/fVSSIuBnk+iYnGZ0osQBrBhk4Mouc6t6DXmeRlVJK+cDlMjz++Q5Oe3ARTy/eRV6/JG45cyS/Pmc0Z47pz1cFh7ji8SVc98xy9lcGp2NCQ7OT5bvKmTEi88iTK54CsVk75/nB1FxromrFnkqYdj0ULoVdX/rl2p2y4knY+AYV03/Nu84TyWnZRS91IORfCRc+Cjevge9/AHlnweJHGPbiDP5m/yuN+zb2XJx+0tDsZPTvPuCeBZuDHUrYi7wEubnzJRZjWifIKQOs3zVBVkop1U2NDic3zV/N3Qs2M3NkXxb9chZPfm8qN52Rxw0zh/PAdyby9W1ncPu5Y1i6s4w5f/2Sr7Yf6vE4V+4up8nh4uSWBLmmBFY8A2MvgJRsv9xjQk4qMVE2Vuwqg8nXWp/Ufni719pfvzuwHj74DYw4k81Dvwe00eJNBIZMh0ufhGveQobNZKZtHZcsvdwqxeiJWP3kgw0HAHjiy51BjiT8RVyCXNfkJDOqBqLjwd5+K5f0xBiyU+M8EmR3v7yqfQGOUimlVCRyugw/fWkN763bz23njOaf3z3e68YUcfYofnjqMN6+cQZpCXaueXIZ76/f36OxfllwiGibWAv0nM3w2nVWfe5pt/vtHnH2KCbkpLJ8VxnEJMAZd8D+NbDxdb/dwytHE7xxg9XN6tuPUVRhLbgb1MEmIQybhVzyBNck/ZOlyWdai/kWPxzYWP1ojUd7usq65iBGEv4iLkFuaHaSaauBxMyOT8aaRd7Uega5sihA0SmllIpUxhh+++YGPth4gN/NGcv/zhzeYX3xiH7JvPmTGeQPSuPGl1bz7rqem6BZXHCIyYPTSYyJgvd+YW3mccHfIDPPr/eZkpvB+r2VVtu04y6DfuNg0Z/B6fDrfY7y1SNQvAHO/wskZlJYXodNrB7HnZGQ1o8H42+G8ZfAJ3+CwmWBi9WP9lYcKddp2RhFdU/EJch1TQ4ypbrD+uMWY7NT2F5Sa/3HjUmwFvZpiYVSKsSJyNkislVECkTk116O3yAi60VkjYh8KSJjgxFnb/KflUW8tGwPP5o1nB+c3PkNHpLj7Dx73TQmD07jFy+vZcmO0gBGaamoa2L93kqr/njJP2DVv+GUWyD/Cr/fa9rQdJqdxprdtNng9NuhtCBwfZHrymDxX60uHKPOAaxNQrJT47FHdS7tyUqJ40BVI5z/iNXR48PbrQV/IW5veT0ZiTEAHKwOz0WGoSLiEuT6ZpfVB7mTCfKY7BScLkPBQXfdcupAnUFWSoU0EYkC5gHnAGOBK7wkwC8aY44zxuQD9wMP9XCYvUrBwWrueGsj04f14dazRnX59Ymx0TxxzVQG90ng+n+vYHtJTQCiPOKr7aUYA2f2OQgLfw+jzoXTfhuQex0/OAMRWLqjzHpi1LnQfzwsfiQw9b1f/RUaq+G03xx+qqi8rsMtpj31T42juKoBlz0JZv0KipZZnS5C3L7KeiYNsrYML9Y+zj6JuAS5yeEkncoulFgkA7BpX0sni0G6m55SKtRNAwqMMTuMMU3AfOBCzxOMMR5N3kkEQn/6K0w5XYZbXl1HfEwUf5mbT1Q322ulJth5+ntTiY6y8aPnV1LXFLgShE+3HKRPnGHM17+EuDSrtCJA20CnJtgZNyDlyEJEEZjxUyjZ4v+ks6YElv7TKo3oP+7w00Xl9V5rwduSlRKHw2UorW2C/KshY5hVFhLCs8h1TQ4q6pqZOCgNESgO0zZ1oSICE2QXKabzM8hD+iSSEBPlUYc8EKp0BlkpFdIGAoUej4vczx1FRH4iItuxZpBv9nYhEbleRFaIyIqSkpKABBvpXli6m7WFFfz+/LH0T/Gth/6gjAT+dsUkCg7WcNvr6wOyqYjTZfhky0HuzXgPObjRSo47OanUXTOGZ7JqT/mRpH/cxVbS+d8/+LcWeck8aK6HWUeqjpocLg5UNXRpBrmlVrm4qgGiouHkX1jbZX/zsf9i9bPSGmuXwqzUOPokxuoMso8iLkHG0UiCqe90ghxlE0ZnJbNxX6X1ROpAaKi0Pp5RSqnQ5G2K8phMyhgzzxgzHPgV4PXzc2PMv4wxU4wxU/r27evnMCPfwaoGHvhgK6fkZXLBxAF+ueaMEZn84syRvLVmH88v2e2Xa3paU1hObt16ZpfNh8nXwKiz/X6P1k4akUmz07B8V7n1RFQ0nPUnaxZ5xZP+uUl9BSx7AsZddNRCw30V9RjTRou3NmS53+jsr3TPwk6cC6mD4fP7Q3YWubzOSpAzEmLomxxLidYg+yTiEuTYJvd/vk4myAATctLYuK8Kp8tYJRagZRZKqVBWBAzyeJwDtNf+YD5wUUAj6qUeXriNBoeTP1443q874v141ghOG9WXP767+cgEjp98sqGIh2Iew6QOgm/d49drt2Vqbjr2KOGrAo9+z6POhWGz4JO7oeag7zf5+lFoqrYWG3po2cFwUEYXSixabzcdZYeTfwZFy61uHyGorNZKkNMT7aTF26ms1zZvvoi4BDmu2d0DsEsJcip1TU5roV6K+1NKXainlApdy4E8ERkqIjHAXOBtzxNExLNX13nANz0YX6/wTXE1Ly8v5OoTh5CbmejXa9tswoPfmUh6op2bXlpNbaP/yhCS1j3NECnGdsFfIDbZb9dtT0JMNJMGp7PYc0MUETj3QWiug4/v8O0G1Qfg63lW7XHWcUcdakmQh/TpfIKcmRRLlE0orvSYhc2/CpKz4cvQXO9a4e57nJ4QQ1qC/fBj1T0RlyAnOtwJchfqqSbkpAKwrqgCUls2C9EEWSkVmowxDuBG4ENgM/CKMWajiNwlIhe4T7tRRDaKyBrgF8C1QQo3Yt33wRYSY6K56XT/9g1u0Scplr9cPoldh2q54y3/bHu8Y/ce5ja8wt4+02H46X65ZmfNGJ7Jxn1Vh2c6AasU4qSbYO1LsPur7l24sgheudba7MTLJid7yuqIibbRP7nz9eFRNqFvUuyREgsAexxM/QHsWARlO7oXawAdnkF2J8g6g+ybyEuQnV2fQR6WmURSbDTriiqtd4di0xILpVRIM8YsMMaMNMYMN8bc7X7uDmPM2+6vf2qMGWeMyTfGnGaM8U+GpQBrQmXh5oP878xhh/vOBsL04X246fQ8XltVxOurfJy4MYbmt39KIvXEndszpRWeZo7qizHw+bZWi0FPvdUqb3zvFivJ7SxjYNnjMO8EOLAOLnkc+gw/5rTdpbUMSo/H1sXuIlnuVm9Hyb8aJMrqGx1iKuqasAmkxNtJibdTUd8ckEWevUXEJchJTnetVkLnZ5BtNmH8wBRrBjkq2kqSK/YEKEKllFLhbt6nBaTERXPtSbkBv9dNp49g2tAMfvvmBnb40B/ZrH+VUaWf8GbaNfQZPtmPEXbOhIGpZCbF8N8treqNYxLhnPvg4CZYcKu1TXRnLLrXOj9nCvz4axj3ba+n7S6tY0ifrpfAWJuFtEqQU7Jh5Nmw+vnOx9lDyuqaSI23E2UT0uJjaHK4aGgOQJ/pXiLiEuRkZwUuBOLTuvS6iTlpbN5fTZPDBelDoXxXYAJUSikV1rYVV/PhxmK+d1IuyXH2gN8vOsrGI3PziY22cdNLq2l0OLt+kbIdON/5OStdeUSf/DP/B9kJNptw2qh+fLb1IM3OVonbqHOt3sgrn4EXLoXGDt4IrHsVPrsXJl4J330T0nO9nmaMYU9ZHYO7sECvRVZq3NE1yC2O/x7UlsC297t8zUCqrHeQlmB9mpGWYP27rKgPrSQ+nPiUIHe01anHeZeKiBGRKb7crzOSXVXUR6WCLapLrzsuJ5Ump4utB6ohIxfKdwYmQKWUUmFt3qcFJMRE8f0Znd9O2lfZqfE8+J2JbNxXxZ8XbOnai5sb4JVraXQKv7X9jHMmDur4NQFyxpj+VDU4WLm7/OgDInDmXXDRY7DrS3juImvLaG8Kl8FbP4EhM6ytoNvpHlJa20Rdk7NLC/Ra9E+Jo7rRQU3rBZIjzoCUHFj5bJevGUjVDc0kx0UDkBZvJchah9x93U6QO7nVKSKSjNWgfml379UVKaaSOntql183MceacV5bVGHNINcUQ1Otv8NTSikVxvaU1vHO2n1cfeIQ0gNYe+zNGWP6c92MoTzz1S4+3lTc+Rd+eBscWMdPG2/glGnHEx/TtQkkfzo5L5OYKBuftC6zaJF/BVz2b2tTjmfmQO2ho49X7IH5V0LKALjsOYhu/+9gd6nVwaI7M8jZLa3eWs8i26Jg8ndh+ych9WlzdYPjcIKc6k6QtZNF9/kyg9zhVqduf8TaxalHOlZnmnJqY7q+I1BOejzpCXarDjnDPStQprPISimljnj2613YRLiuB2ePPf3qnFGMH5jCL/+zln0V9R2/YP1/YMVTLO5/FZ+ayVx9wpDAB9mOpNhoThiWwUcbD7S9gGzMHLjyFSjbDq9+78jCvcYaeOkKq/b3ypchsePF+DsPWRNd3WnD17Ir4jEJMsCkq62Z61XPdfm6gVLd0ExyrJUYt5T+VDcEbrvynhSMxYa+JMgdbnUqIpOAQcaYd324T5dkUk59NxJkEWFCTprVySLdPfBpmYVSSim32kYHrywv5Nzjsg9vJNHTYqOjePSKyTQ7XPx0/mocrWt5PZXvgnd+RmP2VH5YdA6XTs5hcDdKDfxtzoRsdpXWsX5vOxugDD/NKp/Y9QW8cg18+md4/DRrId93noa+ozp1r28OVhMTZWNIN2aQB6ZZO+95fSOSmgMjzrQW6/lzq2wfVNUfmUFu+b26IfxnkJ9bspuhty04ttQlwHxJkNvd6lREbMDDwC1ezjv2YiLXi8gKEVlRUlLS8Qu8cDic9KOC+tjubZc6cVAa24qrqUkcbD2hM8hKKaXcXl9VRHWjg+/NyA1qHLmZidxz8XEs31XO797a2Pbs2js/xYhwV8zPcRDNzbMD06+5q84el409Snh7TXubP2Jt73zWn+Cbj+Gz+yA+A77zjFUD3EkFxTUM65tIdFTX052s1DhEoKitmfpJV0HNAdi9uMvXDgSrBrllBtlKkKsioAb5d29uAOBQdWOP3teXBLmjrU6TgfHAIhHZBZwIvN3WQj1jzL+MMVOMMVP69u1egttcV0WcNNMQ173XT81Nx2VgdYmBuDSdQVZKKQWAy2V4+qtdTMxJZdKgrnVJCoQL8wfy41nDeWnZHu56d9OxSfKORbBjEetG/IgXtsLPzxx5eEY02FIT7Mwc2Y931u3D6ergo/OTboJfFsCvdsEPPoSx3io527btYDUj+iV1K86YaBtZKXEUldd5P2HEbIiOgy3vdev6/uR0GWqbnB4zyJFVYgFQ2xQ+M8jtbnVqjKk0xmQaY3KNMbnAEuACY8wKnyJuh6NyPwBN8d1LkCcNTscmsHxXOWQM0xlkpZRSAHxRcIgdJbV8f8ZQpJ2uCT3pl98axXUzhvL04l385MVVVNR5tPT69B4aErK5cs1YpuVm8MNTglMz3ZYL8gdQXNXIsp1tdKrwFJ/W5datAHVNDorK68nr1/3ttHPS49lb3sYMckyitRvhlvesTUuCqMadCKe4F+fFRNuIs9uo7uGyBH/zfONX19SN9oY+iO7uC40xDhFp2eo0CniqZatTYEXLbk49yVllJcjN3UyQk2KjGZOdwopdZdZCvb0r/RmeUkqpMPXM4p30TY7l3OOygx3KYSLC7+aMISs1lnvf38LX20u5eHIOk2Ub5xUu5Z7ma8nt34fHr53SrRKDQJo9ph9JsdG8sqKQ6cM7v/NtV+woqcUYGNm/ezPIYNUhr2jdks7T6PNg6wJrJ7/sid2+j6+q3LXGLTPI1tf2sK9BbnQcqbEPpxrkDrc6bXXurEDOHgO4qg8A4Ijv1+1rTM3NYE1hBc60XKgo7Nq2l0oppSJOYVkdn24t4cppg4mJ9vJj0xW83cpEhOtPHc57N5/ClNwM/v31LsySv1NFIinTr+W1H510uOVXKEmIieaSyQN5b91+DtUEprZ0W3E1AHk+JMg56Qnsr2xoezHkyLNBbEEvs2gppUg5KkGOpirMSyw8E+S6xp6dQQ6tt5Q+Mu4E2ZXUv9vXmJKbTl2Tk322LDBO3XJaKaV6uVdXFiECl01ttcHG1vfhnzPhrnR4aBy881OrN25rxsDur2HpP2HTW1C63e8xjslO4fFrprD+52M5L3o5SdN/wK1zjifOHryexx357vRcmpwu5i8LzM/Z9XsribPbyO3GNtMtBqbH43QZittaIJaYCYNOhC0Lun0Pf6g+PIN85M2QNYMc7gnykaS4todnkLtdYhGKpKaYBmOH2K5vFNJiypAMANbVZlgrEMt3Qp/h/glQKaVUWHG6DP9ZUcgpeX2PLHIzBj67HxbdA31GwCm3wKFtsP41a6vkKT+AE26AdfOhci/sXQGlBUdfeMSZcPG/ICHDf8E21hD37o0gNuSE6/133QAZ0S+JU/IyeX7JHv535nDsfi4DWVNYwXEDU30qL8lJt/7Oi8rq2l7kOPJbsPD3ULXP2sAkCFoSYc8Si5S46LDvYtHYfGQGOZwW6YUcW+1BDpo0Ynx4x5yVGkdOejxflLo/ktGFekop1Wt9WXCIfZUNXD7FPXvsdFgzxYvugYlXwI+XwBl3wOXPw//tsLourHgS5k2FxY9Y3SRSc+CCR+GWrXD9ZzD7Ttj5GTxzHtR0r63pMWpLre2Zd38FF/0D0oK3nXRXfO+kXA5UNfDm6r1+vW6Tw8XGfVXk+9hxpCUpLmproR5A3pnW7wULfbqXL6q8ziBHR0ANss4g+4WttpiDpGOP8m2F8dTcDD755iAmOg4JoW0klVJK9axXVhSSnmBn9th+0FRn7ez2zYdwyq1w+m+t3dRaRMdYfXuHzYKDW2DctyF14NEXTM6CAfkwYBK8eDk8cQZ86x5rsVdnu2M4HbDtA9jztbXtMcDGN6C6GC57Fsac74c/ec84fXQ/jhuYyl8/+YaLJg302yzy5v1VNDlc5A9K9+k6A9PjsQnsLmuj1RtAv7GQMhC++QgmX+PT/brL+wxy+JdYNBw1gxwmXSxCUXT9IQ6ZVFK8LaLogim56byxei/NA4YQozPISinVK5XXNvHxxmKuOnEwsVE2eOPHVhJ03kMw9Qdtv3DEbOtXe4bNgu++Ce/+DF6+CgZMhiEnwbTrIb2N7aDrK2D547D8KajeZ/XgNS7rV/9xcOnTkON1q4GQJSL84syRfP+Z5Tz39W6uO9k/7ejWFFYAkD/Ytxnk2OgoctITDm9Z7ZWI9fe94XVrYX9Uzy+KrPbaxSI67BPkYM4gR1SJRXRDKWUmmRgf34FOH2a1nCmOztbNQpRSqpd6Y/VempwuLp86yNrJbeMbVnlEe8lxVwyZDjcshnMftGaClz0Oj06Br/9+bGeMPUvgb8fDJ3+CfqPh8hfgtr3wuxL4bQn87+dhlxy3mDWqL6fkZfLwx9s4WN3gl2t+vb2U7NQ4BvhhS/DczER2tZcgA+SdBU3V1t9TEFQ3OIiJthEbfaTENDnOTn2zk+b2tiMPcUfVIGsXi25yuYhurKCUFO9teLpgaGYiA1Lj2NqYadUgB7kBuFJKqZ5ljOGVFYVMzElldPECWPRnmHglzPipf28UFQ3Tfgj/sxBuXm3NRH54G9w7GP4xA978CXx4Ozx7PsSlWjXM330DxsyxXgtgC+8f5SLCHy4YR6PDxW9eX9/21tmd1Ohw8sU3JZw+up9fNnUZlpnIzkO17cc1bCbYomH7f32+X3dUNWPW9toAACAASURBVDhIiTt65rplNrkmjGeRPdu81TfrDHL3NFRgM05rBtnHBFlEODkvk2WVqeCoB3f7OKWUUr3DuqJKthyo5sZhB+CtG2HoqXD+I52vE+6O1IEw90W49CmYONfqiLD5Hfj6URh1rpVED8gP3P2DaFjfJH51zmgWbj7I04t3+XStpTvKqG1ycsaY7u+J4GloZiI1jQ5K2uvXHJsMOVNhx2d+uWdXVTc0H9UDGY4s2KsK44V6LSUWNrEWXvakyKlBrj0EQKlJ8UuR/4wRmby+KhNisMosUkJn9ySllFKB9fKKQsbY9zN77V2QMQwue85ahBdoIjD+EusXQHMD1JaETVcKX3z/pFyW7CjlT+9tYlBGAmeO7d6eBgs3FxNnt3HS8Ey/xJWbafVR3llSS7/kdko2hs60SnHqyyHet8WBXVXd4Diq/hiOzCCHcx1yyyK9lHj7UbPJPSFyZpDrrAS5HN9rkMFKkHcb97tPXainlFK9Rn2Tk6I1n/By7N1IdAxc9SrE+7bYq9vscb0iOQaw2YRH5uYzfmAqP3p+JW+v3dflazQ0O3l77T7OGN3fb5ukDHMnyLtKO6hDHjYTMLDrS7/ctyuqG5qPavEGHC65iIQZ5JQ4TZC7r64UgDLjew0yQGZSLMn9h+FCdDc9pZTqDSqLYNVzHHrmKp7kD8TEJ8O177TdVUL5XUJMNM//zwlMHpLOT+ev5v4PtnTpo/XXVhVRUdfMVScM9ltMA9LiiYm2UXCwpv0TB04Be0JQyiwidQa5JSlOjovu8RKLyEmQD5dY+GcGGeDEvCxKTBqO8t1+uZ5SSvmLiJwtIltFpEBEfu3l+C9EZJOIrBOR/4qIZnneHFgP7/8KHp0KD4+Dt28k6cAS3refQeyPP4N+Y4IdYa+TEmfn39dN47LjB/H3Rds5/29f8smW4g4X71XWNfOXhd8weXAa04f38Vs8UTZhZP8kthyobv/E6BgYMsPaBKaHVTU0H5Mgt8wgh3WC3FJioTPIPnCXWJSRgt0PM8gAJ+f1pchkUl2sJRZKqdAhIlHAPOAcYCxwhYiMbXXaamCKMWYC8B/g/p6NMsQ5HfD+r+Gxk2Hls5A6CM66m6K5/2VS3aMUzvgz0sN1pOqIOHsU9106gSeumUJ9s5PrnlnBOY98wVNf7uSQl8VytY0OfvziSsprm7jrwvF+6V7haWx2Cpv2VXXcYWPYTGvb8aqul4f4wppB9t7FIpx302totkosrBlk3Sike2pLaYpKpAm732aQp+VmsJC+DNPd9JRSoWUaUGCM2QEgIvOBC4FNLScYYz71OH8JcHWPRhjKXC547Qew6U1rY47TfnN4UdULH2zBJsKlx+cEOUgFMHtsf2aO6strK4t4cdke7np3E398bxNjs1MYNyCFrNR4ymob+XBjMaU1jTxw6UTGD0z1exxjslN4ZUURJdWN9EvpYKEewM7PrU4kPcDhdFHX5DxmBjnJ/biqPoxnkB0ubAKJsdE9PoMcOQly3SHq7NYiCl+3mm4RHxNFVPpgkiuXYpwOJCpyvl1KqbA2ECj0eFwEnNDO+T8A3vd2QESuB64HGDzYf3WbIW3Rn63k+My7jupr7HC6eG1lEaeN6kf/9pIg1aPsUTbmThvM3GmD2Xqgmo83HWBxQSmfbi2hpLqRhJgoThqeyQ0zhzElNyMgMYzJTgFg0/6q9hPk/uMhoQ/sWNRjCXKNe4e51n2Q7VE24u1RYT2D3OhwEmePIjbapm3euq32EHXRacRE2fz60Uq/QXlEVzrZtn07I0eO8tt1lVLKB94GOa+f/YrI1cAUYKa348aYfwH/ApgyZUrk74pUtBK+eNDa9OOkm486tGhrCQerG7lsau/oGhGORmUlMyormRtPzwPA6TJE2QLYm9rNM0GeNaqd/so2Gww7DQoWWp9U9MAmLi01xq1nkAFS4sN7u+mGZhex0TZio21ag9xtdYeoiUrzSwcLT3kjrbK+NRvW+fW6SinlgyLAM4vLAY4pehSR2cDtwAXGmHZ2OeglXE54+yZIzoZz7jtm049XVhSSmRTL6aP9s8GECryeSI4BUuPt5KTHs2FvZccn551l9a7evybwgXGkjVvrGuSW56obw3sGOTY6ipggzCBHToJcW0pNVJrfyitapGYPB2DPjq1+va5SSvlgOZAnIkNFJAaYC7zteYKITAL+iZUcHwxCjKFn7Xw4uBG+dQ/EpRx1qKS6kU+2HOSSyQP9stmUijxTczNYvqu844V6I2YDAt981CNxtcwQt95JD6xZ5XCeQW50uIi124iNjjrcE7mnRM4ocO79LEmb4/cZZFKthRqu8t3sr6z377WVUqobjDEO4EbgQ2Az8IoxZqOI3CUiF7hPewBIAl4VkTUi8nYbl+sdHE2w6F4YMAnGXnjM4ddXFeFwGb4zRcsrlHfThmZQUt3IzkMdbBiS2AdypsC2D3skrqr69meQW46Ho8ZmF3HuGWSXsdYJ9JTISZDHnE9B7Fj/v/OPScQZl0GOHGLhpmL/XlsppbrJGLPAGDPSGDPcGHO3+7k7jDFvu7+ebYzpb4zJd/+6oP0rRriNr0PlHjjt9mNKK4wxvLyikClD0hnRLylIAapQN22otQBw2c6yjk/O+xbsWwU1gf/wpsKdAKcleEuQw3sGucHhJNZuOzz52aQJcvc0OV3+n0EGbOmDGRFbzvsbDvj92koppQLMGPjqUeg7xv3x99FW7i5nR0mtLs5T7RqWmUhmUgxLO5Ugn2n9XrAwsEFhbZAC3hPklLhoqsI4QW70WKTX8rinRFaC7HD5rQeyJ0kbzPCYcr7eUcqByga/X18ppVQAbXkXitfD9J8cM3sMMH95IYkxUZx3XHYQglPhQkSYMSKTz7aVdPxRf/ZESMrqkTrkivomomxCUqyXLhZx9oho86YzyD5qDtAMMmmDSW8+gDGGd9f17O44SimlfOBohA9vh35jYeIVxxyuamjm3XX7uCB/IIleEgylPJ0zPouy2qaOyyxEIG82FHwCzsAmqOV1zaTF2722uE2OszbY6OkOEP7S6GiZQY6yHusMcvc0OQMzg0zqIGyOBk4ZAG+u2ev/6yullAqM5U9AxW741t3gZbOnt9fso6HZxVwtr1CdMHNkP+LtUSzYsL/jk/O+BY2VULgsoDFV1jV7La+AIwv3wnUWuaH5SJs3gCZnz3WyiKgEudlhAtOeJ80aOC8dbtiwt4qCgzX+v4dSSin/qi+Hz+6H4WfA8NO9njJ/+R7GZKcwIcf/2xOryBMfE8XpY/rx3rr9NDR3kKwNmwVRMbDprYDGVFHfRFpCjNdjLZuHhGsd8pEZZCu3a9AZ5O5pDFSJRaqVIM/q34BN4C2dRVZKqdD3xf+DhkprS2kvNuytZMPeKq6YNsivO7CqyHbNiUMor2vmtVVF7Z8YlwJjzod186E5cG1iK9wlFt6E+wyy1QdZa5B91uRwBWgGeTAAqU0HOGl4Jm+s3ovLFfk7siqlVNgq3w1L/wn5V0LWeK+nzF++h9hoGxdOHNjDwalwNm1oBhNyUnnii500d5SwHf99603axjcCFk9FXTOpbZZYWDPI4drqrbHZqV0s/KHZ6Tr8TfSr+DSITYGKPVw2dRBF5fV8UXDI//dRSinlH58/AGKD037j9XBdk4O3Vu/jvOOy20wulPJGRLjp9Dx2Hqrl2a92tX9y7snQdzQsfsTa6jwAKuqaSIv3XmKREuYzyA2Hd9LTGWSfWDPIAfqYLHUQVBRy9rgs+iTG8MKS3YG5j1JKKd9U7bO2lZ703cO7oba2YP0BqhsdzJ02uIeDU5Fg9ph+nD66Hw99vI3tJe2sSxKBWbdByRZY97Lf42hyuKhtcpLewQxyONYgG2NocrisRXpRVheLnuzGEVEJcsDavIG1UK+ykJhoG5dNHcTCzcW69bRSSoWiJX8H44KTbmzzlPnL9jCsbyJTc9N7MDAVKUSEP100nnh7FNf/ewUVdU1tnzz2QmuL84V/sBaO+lFlO7vogecMcvglyI3uZDjObiPW7i6xcGgXi25pcgQyQR4MFYUAXDltMAaYv6wwMPdSSinVPfUVsOJpGH8xpOd6PaXgYDUrdpczd6ouzlPdNyAtnnlXTaawrJ4rHl/KoZpG7yeKwJyHoa4UXv4uONpJpruost66VmobXSySWmaQ68OvxKKl3tiaQXaXWOgMcvcEbJEeWCUWjZVQX8GgjARmjuzL/OV7Oi7QV0op1XPWvQJNNTC97dnj577eTUyUjUsmey+/UKqzThzWhyeuncLOQzV857Gv+aa42vuJAybBBX+DXV/AOzdb25/7QXnLNtNtdLGIsgmJMVFhOoNszRbHRnvOIGuC3C1NgS6xAKi0Zo2vmT6E4qpG3lvXiWbhSimlAs8YWPUsZOfDgHyvp1Q3NPOflUXMmZhNn6TYHg5QRaJTR/bl+R+cQHVDMxfOW8w7a9vYcTf/Cpj1G1j7Enx2n1/uXVHXfokFWK3ewnGRXksyHBttC78ZZBE5W0S2ikiBiPzay/FfiMgmEVknIv8VkSG+3K89xpjA7aQHkOpeyOEus5g1sh8j+yfxj0XbMX56J6iUUsoH+1ZD8QaYfE2bp7yxei+1TU6unZ7bc3GpiDclN4N3/3975x0fVZU98O+dkkwSUoDQO0jvRYqoCMiKoqBYViyrrt2Vqv52Xde6a3dV7GDviIgKKiIqigtIlV6lh5oASSB9Zu7vjzuPeXmZSZ+SeL+f5DOv3HLunffenHveueeOP4vOTZIY//Fv3Dt7HbmFAay2Q/4Pel0NPz0Oaz6qcr2G73PdIC4WAElxjhptQXY57cQ67cWOhYNKa5NCCDvwMnA+0AUYJ4ToYkn2G9BPStkDmAU8Vdn6ysLjlUhJ6BRkXyxkw4JsswluG9KOrYdPsHDrkdDUqdFoNJrys/o9cMRB98sCnpZS8u6S3fRskULPFilhFk5T22mc7OLjmwdy+zntmLFiHxe+8D/WpWUWTyQEXPg8tBkCc8bDzp+Kn887rpam3rdCxU8ug6M5PgU5IbiCnOhycqKg5lmQ84tqrgW5P/C7lHKnlLIQmAGMMSeQUi6UUub6dn8FQubwZcTGc4bKxSIhVT14M/eeOnRRz6Y0S4nj1Z92hKZOjUaj0ZSPwlzY8Bl0vRhcgZeNXrLjKDvSc7huUMheZmr+4MQ4bPx9ZCc+umkgeUUexr6yhJcX/o7HvLiYIwb+/D6kdoAPL4dPr4f598FbI+GpdvDmCHjzXLX96Q1wfHfQ+g5n55MQY6dOrCNomkRXzbYgxzrtOO0CIWqOD3IzwBzGIc13LBg3AvOCnRRC3CKEWCmEWJmenl5hYYrc6uILmQVZCBVP06QgO+02bj6rDSt2H2fZzqOhqVej0Wg0ZbN5LhRkQ+9rgiZ5d8lu6ifEcEH3JmEUTPNHZFC7+nw78WzO69aYp+dvZdzrv7I/0xQa1pUMf5kD3S5VFuNl08BTBIMnwlWfwrhPoP8tsP07eHlg0JX4jmQX0CjJVaosiS5njY5i4XLYEEIQY7eF1YIcfMhRNoFi4wR0xhVCXAP0A4YEK0xKOR2YDtCvX78KO/UWeNRII2ST9OBULGQzfz69JS//tIOn52/l09sG6ZBBGo1GEwnWfKDCurUaHPD03qO5fL/5MLcNaYfL58+o0YSS5HgnL43rzbCODXngyw2MfH4Rj17SndE9m6oEdRrAJa+pba8HbJbrsuNIGHQHzLpRWZkLTpTwrz9yIp+GSaVPNq25FmSfi4Xvfo1x2GqMBTkNaGHabw6UmLophDgXuA8YLaUMEiSw6hijipBZkOHUanpm4mLsTDq3PSv3HOf7zdoXWaPRaMLOwXWwa5GyHgcxUrzxv504bDauO6N1eGXT/KERQnBp3+bMm3g27RvWYcLHvzHh49/IyrVYdK3KsUFyc/jLl9BuOMydCNu+K3b6cLksyDVTQc4v8od5U5/2GqMgrwDaCyHaCCFigCuBOeYEQojewDSUchxS7bHI43OxCKkFuSXkZihfNxNX9GtB29QEnvp2S3E/I41Go9GEnoWPqVfWp98c8PTRkwXMXLmPS3o3K1OZ0GhCQcv68cy8dRB3jejAN+sPct7zi/jf9ozyZXa64Ir3oFFXmH3zKUOdlJLD2fk0TCzdgpzkclLo8ZJXGL4IENWBOcyb8VkjJulJKd3AncB8YDMwU0q5UQjxiBBitC/Z00Ad4FMhxBohxJwgxVUZo9NCtlAImCJZpBU77LTbuOe8jmw/cpJZq/TqehqNRhM20lbCtnlwxniICxyZ4t2le8gv8nLz2W3DLJxG48dhtzF+eHs+v2MwCbF2rnlzGQ/N2Vg+xTW2Dlz+rnLFmH0zeD0cOVFAgdtLi3rxpWZt4Iv3HXSlvyjFHOYNlIJcI8K8AUgpv5FSdpBStpNSPuo79oCUco5v+1wpZSMpZS/f/+jSS6w8xop2IbUgJ/s8SkwT9QxGdmtMn5YpPPXt1tLXZNdoNJpqoBxx6M8WQqwWQriFEIHjntV0ivLgm7shvj4MuD1gktxCN+8t3c2ILo04rWGd8Mqn0QSge/Nkvp5wFtef0Zp3luzmwhd/KRkOLhD128Go/8LepfDLf9lzVL3NblU/odRsqYkqBFx6DVOQzWHeQOl3NcKCHG0UnLIgh3CS3KnV9EoqyEII/nNxdzLzinhq/tbQyaDRaP7wlDMO/V7geqDqqxFEI1LC3ElqcZCLXlAWtgDMXLGPzNwibhuircea6MHltPPQ6K58cOMAcgtVOLgXftiO21OGAtjjCuh+Bfz0OPlblD9yqzItyMqtKONEzVKQzWHewLAgawW5woTFgpzYBGyOEhP1DLo0TeL6M1rz0bK9rN57PHRyaDSaPzrliUO/W0q5DgjfL0o4WfcJrJsB59wLnS8MmKTQ7eX1X3bRt1Vd+raqF2YBNZqyObN9Kt9OPJtRPZrw7IJtXPbaUnZl5ATPIARc9Dw06MzAFZMYYV9Ns7pxpdZRUy3IBdqCXD2EJYqFzQ5JzUqEejMzeUQHGie5+Ofs9WH1ldFoNH8oKhqHPihVjUEfEY7thK/vgpZnwNn3BE32ycp97M/MY8Lw9mEUTqOpGMnxTqZe2ZsXx/VmV0YOF0z9hfd/3YOUQSb9xyTAtbPZ72jO685ncP7wABTlBy2/foLPB/lEzXL/LHB7sdvEqbllKopFDfFBjiZOKcihtCCDmqgXwAfZoE6sg8fGdmPLoRP897ttoZVFo9H8USl3HPqykFJOl1L2k1L2a9CgQRXFCgOeIvjsJmWwGDs9aHis/CIPL//4O31b1eXs9qlhFlKjqTgX9WzK/Eln0691Xe7/YgPXv72CA+bFRUzIOo242v0QS+uNgSUvwqtnwKEN/gTuQnAri3GMw0bdeCdHTgRXoqOR/CLPKesxKLcUwy85HNQaBTksLhYQMBaylWGdGnH1gJa8/stOluwoZxgXjUajKT/likNfK1n4GOxfpfyOU1oETTZj+V4OZeczZUQHvYCTpsbQONnFe3/tzyNjurJ81zH+9Nwi3v91D15LCNkd6TkcyBXsHPBvuPYLKMpVS1S/fwm80BsebQz/aQiPt4T3x3JL7PccO1az9JECt7eYghwXYz8VGzkc1BoFudAThjBvoCzIJw6q0Vkp3DeqM23qJ3DXzLUcy7GklRL2LFUr47x2Fkw7G14fBnt/DZ3cGo2mNlFmHPpaya5F8L/noPe10PXioMnyCj28/NMOBrSpxxnt6odRQI2m6ggh+Mug1nw3+Wx6tUjh/i82cOXrvxbzTZ63/iAAwzs1gnZD4eaF0H4EnDwCjbvDmZNh6L+g21jI2sftedN4et/VsOgZ9RamBlDg9hDr8L8hinPayA1jLOfaoyCHwwcZfBYLCdn7S00WH+Ng6pW9OZpTyJ0frfbPTJVSrYbz9kj4/QeIqQMJDSFrP3xyDeQcDa38Go2mxlOeOPRCiNOFEGnA5cA0IcTGyElcDRTmwpd/g3ptYeQTpSadtmgH6ScKuPu8jtp6rKmxtKgXz/s39uepy3qw5WA2I59fxBPztrD49wzeWryLM09LpXGyb+GbpCZqMZHbF6vP4ffDkHvUhL47VzC94xssk53hx3/D60MhPfpdQPOLvLicJguy006etiBXnMJwulhAqRP1DLo3T+bRi7uxZMdRnvx2izr4v+dg9bsqqP2UTfDXeXDNLLjmM8jLhHn/F0LhNRpNbaEccehXSCmbSykTpJT1pZRdIytxFVn0tJr/MfrFoCHdAA5l5TPt551c0L0xp7fWkSs0NRshBFf0a8H3U4Ywsltjpi3awdVvLMPjldx/oTWyY3BszftyY8EUci55F7IPwpvnws6fQyh51cktdBMf4zi174rRCnKlKAqrBZlSJ+qZubxfC64b1IrXf9nF3F9WwsJHoeslMOLfEJvoT9i4G5x1F2yYBdsXhEBwjUajqaEc2awmIvW6GloPLjXp0/O34vFK/jGyc5iE02hCT8MkF1Ov7M2ie4Yy7dq+fH/XEDo2Tiw7ow9jtb3t9c6Bm39UYWs/uDSq9Y3cQg/xMX4Xi3ing0K3F4+3UvORK0ytUZBP+SCH2oKc1BwQZU7UM/OvC7twVvtUdn33MtLrgeEPqliGVs6aAqkd1cpQHnf1yazRaDQ1lZNHlPtZXAqMeKTUpOvSMvlsdRo3DG5Ny/qlL56g0dREWtSL57yujWmY6KpQvg6NlDK97fAJqNsK/jofGnVR99auX0IhapXJKfQQH+u3IMfFKP0uXBP1ao+CHC4LsiNGjbzK4WJh4LTbeHVcd651/MjPshcrspODlB0Lwx+A47th69fVI69Go9HUVApOKCtX9gG44n1ICB6uze3xcu/s9TRIjOVvw04Lo5AaTfTTsl48sQ4b2w+fUAfiUuCaz6Fua/jkaji6I6LyBSKv0E1CjHmSntoOl5tF7VGQPcrkHtKlpg1SWpTbxcKgzo5vqCszmRc3muvfWs6ynUEm43U8X12wS1+pupwajUZTUynKg5l/gcMb1aSjVoNKTf7W4l1sPJDNw6O7kuRyhklIjaZmYLcJ2jeqw6aD2f6DCfXhqpkg7DDjKjUgjSJyCjzEmRRkl6EghymSRe1RkN1eYuy28MxYTq64gszy6VCvLVNuv43GyS6uf3sFi38PEJPQZocBt8G+X1WsT41Go/kj4fXAmo/g5QGw40e4aKoKX1UK+47l8uyCbZzbuRHnd2scJkE1mppF35Z1+W1v5ql1IwDlbnH5O5CxXUXYCrZ6XwTILXSTEGN2sVAKsnaxqCBFHm/oI1gYpLRUYd7K6yd8YA3sWwan30Sj5Hhm3DKIlvXiuf7t5cxenVYyfa+rISYRfn2teuXWaDSaaObIZph+DnxxO8TVhWs/hz7XlprF45Xc/ela7ELwyJiuOqybRhOE/m3qk1voYV1aZvETbYfA0H/Chs9g9XuRES4A1kl62sWikhS6veFxrwBIbQ9et/IVLg8rXgdnPPS6CoAGibHMvHUQp7eux5SZa3l2wbbia667ktSPwsbZyvdOo9Foajur3lHKcfYBuPRNtfBBu2FlZntl4e8s23WMh8d0o2lKXMjF1GhqKme2TyXGYWPu2oMBTk6BtufAvL+rgWqE8XglBW5vsTBvcdrFonIUusNoQW7QUX2mbyk7be4xWD8LelyhLCI+kuOdvHNDf67o15wXftjO7R+sJivPtLpN/1vUq8YVb1Sz8BqNRhNFeL2w4AH1erfVYLhjKXS/DGxlP89X7TnO8z9sZ3TPplzap1kYhNVoai7JcU7+1KURn61KK7nCr80Gl0xXMcY/vV4tzBNBcgvVG/piFmTfdq62IFeMIo839MtMG6R2UJ/lUZB/+wDc+XD6zSVOxThsPHlpD/41qjPfbz7MqBd+4be9x9XJem2g0yhY+XbEL1SNRqMJCVLCN3fB4qnQ70Y1YahOw3JlPXIin/EfraZJsov/XNJNu1ZoNOVg4vD25BV5mPzJmpKW2MRGMHY6pG+N+KJlxpLS8bElFWRtQa4gBeH0QY5NhJRWcGh96emkhJVvQctBaiGQAAghuOmstnx6m5qhfflrS3l2wTYK3B4YeDvkHVN+QRqNRlObkBK+vVc9I8+cDKP+C3ZH2flQk3RufX8Vx3ILee2avjpqhUZTTto3SuSRMd1YtD2di19ezC/b04u7eLYbpu7H395Xb78jhKEgmyfpJfru8xP5RQHzVDe1RkEu8kWxCBvN+sCB1aWnObAaju9Sk+7KoHfLunw94Swu7NGEF37YzqgX/scqOquFQ1a9Uz0yazQaTbSwfDosexUG3B588aQASCm5d/Z6ftubyXNX9KJbsyBx5TUaTUCuGtCSt68/nZMFbq59czmXv7aUbzcc9K9QN/Q+aDFQuT1FKD5yToFysTCHeUuOUwpyZq5WkCtEYTgtyABN+6hQbycOBU+zYTbYnND5wnIVmRzn5Pkre/P2DaeTW+Dm0td+5XP7CNi/smxrtUaj0dQUdv6krMcdR8F5j1VIOX547iY+/20/d43owPndm4RWTo2mlnJOx4b8ePcQHrqoC4ey87ntg9UMeXohb/yyk+wiCZe+ATYHzLoB3AVhl+94rvKRrhsfc+pYQowdh00Un68VQmqNglzkCbMFud1Q9bltfuDzXg9s/EK9rjBNzisPQzs25LspQ7j9nHY8vr8XBdLJqtnPkRWmUZNGo9GEjON7YOZ1ai7H2GnlmowHSjl+fN4W3lmym5vObMOderU8jaZKxDrsXD+4DT/fM5TXrulL05Q4/vP1ZgY+9gP/+OE4O858Gg6uhQUPhl02YxJhvQS/giyEIDnOSaZWkCuGCvMWxuY06gbJLWHrN4HPb/kKstNOhXarKHViHfx9ZCe+uPtC1qUMpcPhb/jTE3N57JvNHM7Or4LgGo1GEyG8HhXj2OuBcR+p+RzlwO3x8sCXG5m+aO8zpQAAHthJREFUaCd/GdSK+0Z11pPyNJpqwm4TjOzWmJm3DuKr8WcyqnsTvlxzgOFfJfB5zEWw7FVOrvg4rDJlnFQKcmqdmGLHk+OdYTMW1ioFOawuFkKoKBM7FkLByeLnpIT/PQ9120Dni6pUTdOUOE7/830kijwebLCIN37ZyVlPLuT/Zq0tGexbo9FoopmlL8OexXD+k1Cvbbmy5Ba6ue2DVbz/6x5uPbstD12kFwPRaEJFt2bJPH15T5bfN5zHx3bng6SbWObthPOr8Tw67T2+XLP/lH9wKDmWU4DdJkpMwE2Oc2oXi4pS6JHhtSADdBkNngLY+Hnx41vnqQl6gyeopaOrStNe0PkiLsiaweIbmnJ5v+bMXXuQ0S8t5sIXf+GjZXu1+4VGo4luDm+EH/8NnS4s95u1LYeyGf3SYn7ccoR/X9yNey/ojM2mlWONJtQkupyM69+Sz+48h7rXf0KOqyG3HbyfJ2b8QN//LOCOD1fxzfqDIVOWj+UUUjc+psT9nhLnJDOvMEiu6qX2KMhuD7HhtCCDCt/WqBv8/CTkZKhj7gKY/09o0Al6l75EaoW44BmITaTJd7fw6Ki2LLtvOI+M6YrbI/nn5+vp9+gCbnp3ZdhGdxqNRlNuco/BZzeDKxkumlrmpDyPV/Lukt2MeWkxmblFvPfXAVw7sFWYhNVoNGY6tG1NvRtnUy/Gw4Lmr3N1n4Ys33WcOz5cTe9HFnDtm8t4Z/Eu9h2rvjUbMk4WlnCvAGVBDlcUi/IFnawBFHlkeF0sQD3kR78Ib52nZmRf+josm6ZCu10zG+zVGJszsbEq/70x8POTJI14hL8Mas21A1uxLi2Lr9Yd4Kt1B/l+82FiHTYGtq3POR0bMLRjQ1qnJhQvK3Ofij2atgIKcyArTVm6u10Kw/4FTr1cq0ajqSbSt8LH4yBrH1z5MSSklpp8XVom93+xgbVpWQzp0IBnLu9Jg8TYMAmr0WgC0rATYuw06sy4ivubv8U/732RFXuO8+OWI/yw+TAPzd3EQ3M3cVrDOpx5WioD29ZjQJv61E0oqeSWh4NZeQHv+yYpcRxadxC3x4sjxF4DtUZBVpP0IvDqrVkfGDwJFj0FTXvDomeg/Z/gtOHVX1fbc6D3NbDkJWjWF7qMQQhBzxYp9GyRwr3nd2bV3uPMW3+IlVt3cmLey2z/di+rYpvQNNlFo0Qnje3ZxO/9CTyF0KQnxNeHhp2h8CQsfQn2/qpWs3LnwdoZyl8wPhW6Xw7tR5Q7HJNGo/mD4fVAfhbkZ4K7EDK2qcUGti+A+Hpw3VxoOTBo9i2Hspn6/XbmbThEg8RYXhjXm4t6NNH+xhpNtNBpFAz5O/z8JPaGnRh4xngGtq3PPy/ozO6MHH7ccoSFW4/wyYp9vLNkt8rSOJGBbeszoE09erZIoUmyq8x7urDIzYFDRzi/X13I2O47KsBmp2NSEV6vh7TjeSWNf9WMKLaCSpTQr18/uXLlygrl+e93W2nfKJHRPZuGSKpSKMqD14fDkY3gcMEtP0PDTqGpK/cYvH8JHFwD/W+F+qepZanzsyAnXb3CTN8Kaz5C5maQmdCW+Jw0Cr2CIuzk4mKjvQtLWt9By7ad6No0iS5Nk5Qj/KY5MPtmEDbVJqRyITl5WJV92rkw+iVICkHs0WM74bcPYf8q8Lohtb1SyludUf11aTRRgBBilZSyX6TlMFOZZy8LH1cLfuRnlTxXpzH0vR76/VUtY2uhyONlwabDfLhsD4t/P0pirIMbzmzDTWe10avjaTTRiNcLs66HTV/CGRPUm+cGncDpUvpJ+laKsg5y8MBe9hzJZM/RXLYfd3PYnUi6TCY3oTnNm7eiV7NEBiSl08G7m8SsrYisvWpticx9yLzjCErXTYucSTgH3gzDH6hwE8r77K01CnLEyT2mYiK3HKgU1lDiLoA5E2DdjMDnhR3aDlEXTtPeICUer2TL4ROs3H2cFbuPsWL3MQ5n+4N/t6wXT9emSZxTZx+Dsr4mPrUliadfRWzDdsoatOptFQvRZoful8GQf1SPouwpgoWPweKpar9xdzXIOLQeinKgw/kw5mVIqF/1ujSaKKLWKMibvoTdiyEuRcV8dyWDPQbqNISWZ5RYPjq/yMOSHRnM33CY7zcf5mhOIc1S4rjy9BZcO6gVKfGVeyWr0WjChKcIvpoEv32g9oVd3fu5GeXKXogTKSWxQs2XysdJhqMJOXFNIaUFW0+4WJ8huWNkH+omJflySfC6yck+xuvfrWJYKyc9Bo2EbmMrLL5WkP8IFOaoEHMZW9XFmdhUWXsTG6tXmmVw5EQ+Gw9ks+lANhsPZLHxQDZ7jvqd7G0CmteNp22DBNqm1qFLzBEGHXyXJvu+RtidMHY6otOoqsk/8zr4fYFajnvY/X6luyhPLUX746NQpxFc92W5w0JpNDWBWqMgW5HylCuW1yvZn5nL1kMnWbX3OCt2HWNdWhaFHi91Yh2c07EBY/s0Y0iHhtjLG53CKN/49HjAbvfve72lLz5i/OYZZRj5jH3zOUt7Suyb6wtWf6D6wJ/HSGPet6Y3yvN6/XlBtd1mKyl7ILmN9HZTZKWiInA4AstmtMOow9pOazvM34XXW/w7Mso2zlnbaO1/83mjLeZ+MPrCvG9um7mfzHmt2+b+83r9Mlq/t2AEOme9Pq39aOQz+qgiLkSBrkWrHEa5xnHrNVWZOoLlO7ZTLSRyeKNaVTi1g3LZTGwCCQ2UVRmgMFcpzycOQeYeOL6HAi/sdrRlo7cVK0/UZeuRPLYdOsEJX5CB8cNO464/dQwoz8WvLCE7r4hvJp6Fy1nxSGFaQdZUipMFbnal57Az4yQ70nPYmX6Snek57MrIIa/IA0ArcYgXnC/RXezi2bjxrG94EY2TXKQmxtCgTiypibH+z8RYEmMdJX2OPG6YcZVSji98Tr2GDcT+1fDBWIipAzcuCI17h0ZTXnKOwuH1anAnbJDcQrk5GT8EFaCqCrIQYiQwFbADb0gpn7CcjwXeA/oCR4E/Syl3l1ZmZZ69Jwvc7D+ex4GsPA6+/ykH873sP/0sdqSfZPuRk+QWqueGwybo3jyZ01vXY7BvEk+so4I/bg89BJmZkJwMWVnw22+waRPcfjtkZ0NSEsydq87/9FPg/N9+CwMGQEqK2i4oAJcLzjtPlb1smdrPz4d9+5Ri8+c/qx/qZctgzx7IzYUuXSA2VtW7ciXcdVfJ+gPVt2ePkuWWW1QbZs1SSk2HDkqW/v2VQpCSAvPnw+7dcOut8PPPsGULNG4MY8aoMl55BWJioH176NlTHatbFx58ECZPVmU89JA63ro15OTAoUNKCRwyBH75BeLjlezHj8PMmXDyJPTtq9p19Kj6NxStrl2hsBCOHFHnQaXt3RtWr4bNm6FzZ9i+HVq0UP138qTK6/VCv36wbZvKd+KEUhjbtSve/599ps5feik8/7zaHjgQ9u5Vffbww6p9c+bA6NFqf8gQ/3WwaJEqB9Tn6NGqncePQ6NGSv6kJHXt5OSo79AYABQWQlyc+m43bFADiAYNoHlz9R0KAb/+qsoWAkaO9PdvoOszOVnJeewYZGSocs84Qx2fOxfS0+Gmm4qXUda1/9xz/u9j0CB1bulSdezBB2HaNDXoufRSlXbyZHXdQkl5y1OH9ToKIVJKDmcXIAQ0SnIFlefbxNbc7m7P2N7N+e8VPStcT3mfvbVmkh6gLma7XT3Q3G7/yBDUMWMwEBOjzuXmqgvJPOo0bhTzKNvjAaez+GgWSloJrEqgeYRrjGiNNEYdxqjVOhJ2OEpaFwLVY94vy4IQ6Lyx70tbJ9ZB9+bJdG+WVCytlJLjJwvYn1XA/sxcVmcMpM7qSUzJfpFZ6Qd5+8B5bMtNwOMtOeCKcdhITYghOT6G5DgHKXExjMuazpCM+fzU/l7SioaSsu4AybEOkuJjSIh1UCfWQbxTkNCkN/Zrv4C3L4BPr4PrvgKHfgWrCSP5WbD6fVjzkZpnYOWGeWH3lRdC2IGXgRFAGrBCCDFHSrnJlOxG4LiU8jQhxJXAk8Cfq1uWZ+ZvPTUhB1pjs3lotHoHbU9rxhW5u2j//Rw6DB1Atyf+RVxsFX5ypFQ/llOnQq9esGaNX5F9+mn1mZqqFJFevQJbco8fV8rCsmVKoVy71n8+P9+/bz33wgsl5Vm2zF9f48bq01y/x1O8vh49YN06f/5XXlHKp4HbrfIayoxZhi+/VPIfPqz+pYQDB1R6UPUaMk6YAJMmqf2JE/3KaU6OX9YDB2DxYnUuJwdmz1YKobltBQX+31ODFStK9sPGjUopNb6LJUtUnkOHSqZdvLi4BRn8bTT3v7nPpYTly9X2nDnwwAPqc80adez++5VynJEBr74KTZv6+zk1FV58UW3Xr+8fnNSvrxR0gLy84vKcPOmvD1RfHThQ/JjBgAHFLcbW69O4Hox+XLlS/RvHQSnPpVlpjT4wygalME6a5L9WJk1Sx778Ul0fRv/9/HPxPjXLW546Jk9W+8Z1FOIJs0IIGie7ypRn5MSJTL/5Sjo3TQpeWHXIUxULcigsGFBJC7LLpW7oUNK/v/rSNvl+g+66S41eA42yzjlHjSBXrYJhw9T2gQPqZuzYUVkF4uPVA9LrVXlbtIC0NHWBDx6s2iOl+kxJgYULi9djHl09/LB6GENgC4LZkmGMyo0bzOVSN3RZI1PziF1KmDweUpYD28DuRA6ezLE+fyM9X5BxopD0k/lknCgk42QBGScLycorIiuvkNOyl/N47oN87D2Xewv/Wma3u5w2LnYs5wn5LJ/GjmVGys0kxDpIiLETH+PA5bThctqJdfg/T207bcQ67Lh8n8XT2HE6BE67DafNhsPu27YLPXNeo+7LVW8pH/nco9CsH+x3wckEmPJPNZk0cy+88T2kNKywhaUqFmQhxCDgISnleb79ewGklI+b0sz3pVkqhHAAh4AGspSHfmWevWv3ZbL3WC5NU1w0SXLR8OH7cEx93p9g4kT/s6WqGM9a40czEL16qeduIDcLKf3KYzAmTPD/GAdLN2GC+gx03lx/eeoz8hgKnxWrsl5erP3u8fgVeQOrAlxRKitbaYwfrz4NxdbA2kfWfbPSWV2U9r1MmKB+S61GqLKuTzPjx6u05XV9sJYd6DoM9p0Ekrc8dVTn/VtRQiRPyF0sfBaMbZgsGMA4swVDCHEH0ENKeZvPgnGJlLJMC0aFH9JFReq1SFVu9MrQo4d6TTNlin+U9dxz6kvt21fdWD16qAdloJvMsFYHwnquZ0/1GsmwCjz7rL9e601i3jfSmh/21vTGDWXIb36gGz8WRnuMh7+5zfePV0rEhllqNusV70GDjoHblXMUXh2kfKZv+Yl8YsjKKSDrwkvI2p1GVpfu5Dz5DLkPPEzO4QxyWrYh94abOFnoYdSepxiYOZfHU59ghehObqGbnAIPBW4P+UVeCtweijzV4zJktwmcdnFKcXbYbcTYfds2Q5EurlQ7bDbsNoFNCOw2TNsCuxDYbCqvzbdvTms9diqdKa9d+Mr0HVPuawIB2Hz7tgDHbYKgaTHyYM4LAiNfGfkD1K1cSX1l+frTGHAITO5xvjRmjHoCpT11/lTiwMeD5je55fnPB0mbk07M3Nux7/wRT6sz8Qx/GJr0hnvuRrz4Iowfj3jmGcTdd2GbOhVRiYd2FRXky4CRUsqbfPvXAgOklHea0mzwpUnz7e/wpcmwlHULcAtAy5Yt++4xrGyVJZCvaHX+uFrLt2L29axMfrP/bLB0Vl/g0uovqz4jjz2Iu0lp50ojUL8bbycNCgvVG9XKUlnZSiNY31rrsu673cXbVh2U1r5g13V5vu+yyghGoHsLgvtiV6auUN+/FSUE8oTDxaI/8LuUcqevwhnAGMD8im8M8JBvexbwkhBClGbBqBROp7LMhlNJNl6XGRei+QdSCKVEGkplMIIpx4HOrV1bXIkVQn1CydGqodya0xpW4xdeKD7aNBRgQ+E1yjIr0UZ6YzQdqM2XvQk9x8Hnt8Irg9QkQa8HpMfnRuJR+94isDngms/AGYcLcKXE02jRPNVfCz5R/0Z9Mz/z3xyFr8G0zdx37F/gSlLlOIS6io23MoBE4vtTczJ84WKk7xi+Y6f2MbxNpGnbfM5Xnhtwm8/766FYOeb8/sKsF70sfpqSKTSBkEG2q5MUcnAD97tv5KOtw2DrYeBbcJ0L95yrEv3rW3CNYPakZPo8+1C4f0QCVWbtjvKkQUo5HZgOyjhRJakMi4+ZyZOr34JcGn37lm1BLg3jdXVp9ZRWhrn+8tRn5AlGnz5l5w+Etd8NC7KZuCouClVZ2Upj4sTAx619ZN23tq06KO17mTQpuAW5vEycWHELslUGK8G+k0DylqeO6rx/K0qE5amKBbnaLBi+c1W3YhQVVW00XBGso7RAoxqrL3N1YK2nLCtHWWmDWUvKMzIN1Obsg7DiDcg7BsKuwsIJu88f3A7CpkLQtT0nsLxWC4FV3qM71CqA7nwVaqYWYij2Xt+96fUp6F78Cr9VSefUOX8ZSFlsACAtyro0bZ86e2pg4X8uGPL48xYvF1N66/Hi7So+eihtwGA+G1AhtmS2HpeWBIHyFavBMigqssexqcklHE9oW3zQY7TzX/cjfdf+5V+/SZOUeCpKbXGxOIX5dagxeLbuV+VHzVy+1QfZ+DT7AFuVZKu7g/VVtHm/vK4DRn3Wz169lK/plCn++qw+yPXrF/dBtroIWOWR0p+/R4/iPsjmsq1vEJ97Tj1bzX7SBw4UNyh161bcBzk2NrAPciCMdhjfQWl5SntrGqjPJ0xQ7TbcLYx+7dfP/0ZzxQpo0sTfNqsPstFH5v629n1lMbstBLo+rT7IBma5yuNmEejeCvSmt0+f4Ne0Vd7y1FGd929FCaE84bAgV5sFA6rBimG4WYSL3r2L71tHNV5v6aPPymKup6zRqjVtoNGmYS2ZMqXkcSvW9gQaySU1geH3l789BoH6K5AlqH47OO/RipdfgxC+/zAvnK6xEHButHHPLf3Ef+yhRpGwsKwA2gsh2gD7gSuBqyxp5gDXAUuBy4Afq/3tnRkj8kKgt1wpKVXvH3P5ycnK5ay0KBbWwbUQan7GgAH+qBKGImhEURgyxD8vY8CAqkWxsNtL1udyVSyKhcul5quMGaMmXDVqFDiKRd26fsXYmINilCGEkiXBt+qYEcVi8GB/FIuxY2Ho0MpFsejatfqiWAwZEjiKxbJlKorF6NFK9tGj1fHRo5VbRZcuxaNYGBE9MjNh3Dh/FIt27ao3ikXduibfrADXZ3miWNSrV/a9Eejeev55/yQ9Q+kdM0Z9v8GiWJjlLU8d1Xn/VpRokEdKWal/YBAw37R/L3CvJc18YJBv2wFk4LNal/bft29fWSEKC6W026X0GcrC9t+jh5Qej5QTJ6r9iROl9HrVsV69/GmMbeu/zRa8bOu5nj2lnDDBX4+53gkT/Oes+0baYOeNss3yW9Oa29OrV+A2V4VA5Vv3NZpI4/WWvO6rcB8AK2Uln78qOxeg5oHsAO7zHXsEGO3bdgGfAr8Dy4G2ZZVZ4WdvIKz9UNXnQ7DyjU+3u/h+Wc8Lr7d4GR5P8X3rtnE+0L65vmD1B6rPnMc4Zt63pjcw5zXaHkh2szxmjL4yKCwMLpvxadRhfBrtt7bDXL45jfFpPmf8B+v/QG2x9qt139w2q2zBtouK/PW73Wrf/J1Yv/tg8pmxXp/WfjQfr+i9Eejesh6zXp9lyVueOiJJCOQp77O3Khbk6LFgOJ1qxBRq/2NrFIuLL1YjT+uoRgg1QjRe8w0bprarGsXCGCWmpKh6zaOrhx8ObkGw2YpbMoxROfitJWWNTM0j9kBtrgo2W/H+stn8PtyBLEEaTSSIBouGCSnlN8A3lmMPmLbzgcvDKhSU7Ifq7hezxQ78blnGflnPC7M8xvM62DnrsUD75sUfAtVfnvpKq8t8zFq22SWtPP1udflzmpbzDlaXkcfaz4HaYaSx9klpbQjW/9Y0wfrdwNw28zlzXuu2eVKftW8qe91a22ztx0AyVrTsYPuByq1oO0J9/1aUCMpT1TBvFwDPo8K8vSWlfFQI8QhKO58jhHAB7wO9gWPAldI3qa80Ku0Hp+MgF68jUFrreWO/rLTW9gRrc1Wwll/WilgaTSQo7R6sALV2JT2NRqOJYsKyUEjUWTCM0bDNVnxkHIw6dcpXrjV0TKAfw7JGcsFGu4EUQKO+0kbqgfbLGmlVJW8gWat7JGctXyvHmmgk2iwsGo1Go6l2tAai0Wg0Go1Go9GY0AqyRqPRaDQajUZjQivIGo1Go9FoNBqNCa0gazQajUaj0Wg0JrSCrNFoNBqNRqPRmKhSmLdQIYRIB/ZUMFsqaiGSaEHLUzrRJE80yQJanrKIJnmqIksrKWWD6hSmqpTx7I2mfq8ualubdHuin9rWpprYnnI9e6NSQa4MQoiV0RRTVMtTOtEkTzTJAlqesogmeaJJllBTG9ta29qk2xP91LY21bb2mNEuFhqNRqPRaDQajQmtIGs0Go1Go9FoNCZqk4I8PdICWNDylE40yRNNsoCWpyyiSZ5okiXU1Ma21rY26fZEP7WtTbWtPaeoNT7IGo1Go9FoNBpNdVCbLMgajUaj0Wg0Gk2V0QqyRqPRaDQajUZjolYoyEKIkUKIrUKI34UQ/4iwLC2EEAuFEJuFEBuFEBMjKY9PJrsQ4jchxFdRIEuKEGKWEGKLr48GRVieyb7vaYMQ4mMhhCvM9b8lhDgihNhgOlZPCLFACLHd91k3wvI87fu+1gkhPhdCpERKFtO5u4UQUgiRGg5ZSpNHCDHe9/zZKIR4KlzyRAIhxL9918EaIcR3QoimkZapKkTq2g4lQojLfdeiVwhRY8NvRdPvenVQ2vOsJhKNuk51U+MVZCGEHXgZOB/oAowTQnSJoEhu4C4pZWdgIPC3CMsDMBHYHGEZDKYC30opOwE9iaBcQohmwASgn5SyG2AHrgyzGO8AIy3H/gH8IKVsD/zg24+kPAuAblLKHsA24N4IyoIQogUwAtgbJjmCyiOEGAqMAXpIKbsCz4RZpnDztJSyh5SyF/AV8ECkBaoikbq2Q8kGYCywKNKCVJYo/F2vDt4hwPOsBhONuk61UuMVZKA/8LuUcqeUshCYgfrBighSyoNSytW+7RMoBbBZpOQRQjQHRgFvREoGkyxJwNnAmwBSykIpZWZkpcIBxAkhHEA8cCCclUspFwHHLIfHAO/6tt8FLo6kPFLK76SUbt/ur0DzSMni4zng/4CwzjAOIs/twBNSygJfmiPhlCncSCmzTbsJhPk7qG4idW2HEinlZinl1kjLUUWi6ne9OijleVYjiTZdJxTUBgW5GbDPtJ9GlHxJQojWQG9gWQTFeB6lTHgjKINBWyAdeNvn8vGGECIhUsJIKfejLH57gYNAlpTyu0jJY6KRlPIgqIcQ0DDC8pj5KzAvUpULIUYD+6WUayMlg4UOwFlCiGVCiJ+FEKdHWqBQI4R4VAixD7iamm9BNhPRa1tTjKj9XdeUJEp0nWqnNijIIsCxiFs1hBB1gM+ASRarSzhluBA4IqVcFYn6A+AA+gCvSil7AzmE132gGD7f3jFAG6ApkCCEuCZS8kQ7Qoj7UK/VPoxQ/fHAfUSXUuYA6qJeMd4DzBRCBHom1RiEEN/7fPKt/2MApJT3SSlboK6DOyMrbdmU1R5fmohe2xWlPG2q4UTl77qmJNGg64QKR6QFqAbSgBam/eaE+TW5FSGEE3XBfCilnB1BUQYDo4UQFwAuIEkI8YGUMlJKYBqQJqU0RpmziKCCDJwL7JJSpgMIIWYDZwAfRFAmgMNCiCZSyoNCiCZAxF/bCyGuAy4EhsvIBU9vhxrMrPXpoM2B1UKI/lLKQxGSKQ2Y7euT5UIIL5CKelNSI5FSnlvOpB8BXwMPhlCcKlNWe6Lk2q4QFfiOaipR97uuKUkU6TohoTZYkFcA7YUQbYQQMahJVnMiJYzPevQmsFlK+Wyk5ACQUt4rpWwupWyN6pcfI6gc41Ni9gkhOvoODQc2RUoelGvFQCFEvO97G050TGacA1zn274O+DKCsiCEGAn8HRgtpcyNlBxSyvVSyoZSyta+azoN6BNB5RjgC2AYgBCiAxADZERQnpAihGhv2h0NbImULNVBtFzbmhJE1e+6piTRpOuEihqvIPsmWNwJzEcpNzOllBsjKNJg4FpgmC8U0hqfBVejGA98KIRYB/QCHouUID5L9ixgNbAedT+EddlMIcTHwFKgoxAiTQhxI/AEMEIIsR0VreGJCMvzEpAILPBdz69FUJaIEUSet4C2vtBNM4DraooVspI84XuVvw74EypCTk0mItd2KBFCXCKESAMGAV8LIeZHWqaKEoW/61Um2p5n1UCt13X0UtMajUaj0Wg0Go2JGm9B1mg0Go1Go9FoqhOtIGs0Go1Go9FoNCa0gqzRaDQajUaj0ZjQCrJGo9FoNBqNRmNCK8gajUaj0Wg0Go0JrSBrNBqNRqPRaDQmtIKs0Wg0Go1Go9GY+H94FgkpJb+fRgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 720x1008 with 10 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Number of points\n",
"n = 100\n",
"\n",
"plt.figure(figsize = (10, 14))\n",
"for i, data in enumerate(datasets, 1):\n",
" \n",
" # Sample the PDFs, then get x and y for true values\n",
" samples = np.concatenate(tuple(d.rvs(int(n*frac)) for frac, d in data), axis = 0)\n",
" x = np.linspace(np.min(samples)-0.1, np.max(samples)+0.1, num=2**9)\n",
" y_true = reduce(np.add, (frac * d.pdf(x) for frac, d in data))\n",
" y_kde = KDE('epa', bw = 0.2).fit(samples).evaluate_sorted(x)\n",
" \n",
" plt.subplot(5, 2, i)\n",
" plt.title(f'Data set {i}')\n",
" plt.scatter(samples, np.zeros_like(samples), marker='x', color='red')\n",
" plt.plot(x, y_true, label='True PDF')\n",
" plt.plot(x, y_kde, label='KDE')\n",
" plt.legend(loc='upper right')\n",
" plt.tight_layout()\n",
" \n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"-------------"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Cross validation"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXd4lFXah+8zNb0nhCT03os0EQUVESvFjnVtq6Ku67e6urrqFl1d3XXXFXtXVFARAVEQBVGQKjWh14RAei8zmZnz/fHOhARSJplJZjJz7uviksx73vM+iWR+85ynCSklCoVCoVD4GzpfG6BQKBQKRUMogVIoFAqFX6IESqFQKBR+iRIohUKhUPglSqAUCoVC4ZcogVIoFAqFX6IESqFQKBR+iRIoRVAhhDgshKgSQpQJIYqFEGuFEHcJIdz6XRBCdBdCSCGEoa1tPeW5k4QQWc2sOVcIsVIIUSKEONzA9e7O65VCiN1CiMltZrBC4QWUQCmCkcuklJFAN+BZ4I/A2741yStUAO8ADzVy/RNgCxAPPAZ8LoRIbCfbFIoWowRKEbRIKUuklIuAa4CbhRCDAYQQlwghtgghSoUQmUKIp+rcttr532IhRLkQ4kwhRC8hxA9CiAIhRL4QYq4QIqahZwqNF4UQuU5PZ3ud55qFEC8IIY4KIXKEEK8JIUKFEOHAN0CK85nlQoiUBr6fDVLKD4GDDTy3LzASeFJKWSWl/ALYAVzR2p+fQtHWKIFSBD1Syg1AFnC286UK4CYgBrgEuFsIMd157Rznf2OklBFSyl8AAfwDSAEGAF2Apxp53BTnHn2d+18DFDivPed8fTjQG0gFnpBSVgAXAdnOZ0ZIKbNb+G0OAg5KKcvqvLbN+bpC4ZcogVIoNLKBOAAp5Sop5Q4ppUNKuR3taGxiYzdKKfdLKb+TUlqklHnAv5tYXwNEAv0BIaXcJaU8LoQQwB3A76WUhU4heQa41kvfXwRQcsprJU5bFAq/pF0DvQqFH5MKFAIIIcaixaYGAybADHzW2I1CiCTgJTQPLBLtg19RQ2ullD8IIV4G5gBdhRBfAn8AQoAwYLOmVdrWgN7Tb8xJORB1ymtRQFkDaxUKv0B5UIqgRwgxGk2gfna+9DGwCOgipYwGXkMTC4CG2v//w/n6UCllFHBDnfWnIaV8SUp5BtrxWl+0pIZ8oAoYJKWMcf6JllJGNPHclpAO9BRC1PWYhjlfVyj8EiVQiqBFCBElhLgU+BT4SEq5w3kpEiiUUlYLIcYAs+rclgc4gJ51XotE81CKhRCpNJ5FhxBitBBirBDCiBbrqgbsUkoH8CbwotMjQwiRKoS40HlrDhAvhIhuYm+dECIEMGpfihAhhAlASrkX2Ao86Xx9BjAU+KLZH5RC4SOUQCmCkcVCiDIgEy3d+t/Ab+pcvwf4q3PNE8B81wUpZSXwNLDGWUc1DvgLWoZcCfA1sKCJZ0ehCVERcAQtQeIF57U/AvuBdUKIUmAF0M/53N1osbCDzueelsWHlnxRBSwFujr/vrzO9WuBUc5nPwtc6YyZKRR+iVADCxUKhULhjygPSqFQKBR+iRIohUKhUPglSqAUCoVC4ZcogVIoFAqFX+KzQt2EhATZvXt3Xz1eoVAoFD5i8+bN+VLKZhsV+0ygunfvzqZNm3z1eIVCoVD4CCHEEXfWqSM+hUKhUPglSqAUCoVC4ZcogVIoFAqFX6K6mSsUCkUj1NTUkJWVRXV1ta9N6ZCEhISQlpaG0Whs1f1KoBQKhaIRsrKyiIyMpHv37tQZg6JwAyklBQUFZGVl0aNHj1btoY74FAqFohGqq6uJj49X4tQKhBDEx8d75H0qgVIoFIomUOLUejz92SmBUigUCoVfogRKoWiEJduzuf39jTzx1U5yS1WQXNH+FBQUMHz4cIYPH05ycjKpqam1X1utVq89Z8WKFURHRzN8+HAGDBjA008/Xe/1ESNG0LdvXyZOnMjSpUtr73v88cfr2fTYY495zSZQSRIKRYO89uMBnv1mN6kxoazem88Pu3NZcPd4kqJCfG2aIoiIj49n69atADz11FNERETwhz/8od4aKSVSSnQ6z/yNc889l4ULF1JeXs7QoUO59NJL670O8OuvvzJjxgw++OADJk6cCMBDDz3EAw884NGzG0N5UArFKWzNLOaf3+7mkqGd+fGhSXx+95nkl1t4dMEO1IBPhT+wf/9+Bg8ezF133cXIkSPJzMwkJiam9vqnn37K7bffDkBOTg4zZ85k1KhRjBkzhnXr1jW5d0REBCNHjuTAgQOnXRs5ciSPPfYYL7/8sne/oUZQHpRCcQpPf51BfISZ564YikGvY2haDA9e0Jdnlu5m7YECzuqd4GsTFT7gL4vTycgu9eqeA1OiePKyQa26NyMjg3fffZfXXnsNm83W6Lr777+fhx9+mHHjxnH48GEuvfRSdu7c2ej6vLw8NmzYwNNPP01mZuZp10eOHMn//ve/2q+ff/553nvvPQBeeOEFJk+e3KrvpyGUQCkUddiWWczGw0U8edlAIswnfz1uOrM77645zJyV+5VAKfyCXr16MXr06GbXrVixgj179tR+XVRURFVVFaGhofXWrVy5khEjRqDT6fjzn/9Mv379GhSoU08R2vKITwmUQlGHj9YdIdSo54oz0uq9HmLUM2tMV/713V4yCyvpEhfmIwvbj3UHCzhaUMlVo9JUqjW02tNpK8LDw2v/rtPp6glH3dojKSUbNmzAZDI1uV/dWFNTbNmyhQEDBrTC4pajYlAKhZOSyhoWbctm+ohUokJOb81yxRlpCAGfbc7ygXXty/7ccq59Yx0Pf7Gdt3465GtzFM2g0+mIjY1l3759OBwOvvzyy9prkydPZs6cObVfu5IuWsPWrVt55plnmD17tkf2uosSKIXCyTc7j2OxOZg1pmuD11NiQpnQO4EvNmfhcAR2ssRnmzIx6AQ9EsL5eMNRlRzSAXjuueeYOnUq559/PmlpJ08A5syZw5o1axg6dCgDBw7kzTffbNG+rqO/fv36cf/99/PKK6/UZvC1NcJX//BGjRol1cBChT9x63sb2ZtTxk8Pn9vokdbCLcd4YN5WvrxnPCO6xrazhe2DlJJJL6yiW3w4Fw9O5pEFO/j6/gkMSon2tWntzq5du9rtOCtQaehnKITYLKUc1dy9yoNSKIAKi42f9+dzwcBOTcZbJvVLRCfgh9257Whd+3KitJojBZWc1y+xNiHk16PFPrZKEYwogVIogNV787DaHEwZmNzkupgwE2d0iw1ogdqeVQLAsC4xpMWGkhBhYlumEihF+6MESqEAVuzKJTrUyOjuzR/bnds/ifTsUk6UBGb7ox1ZJRh0ggGdoxBCMCwtRgmUwicogVIEPVJK1h7IZ0LvBAz65n8lzu/fCYCVewLTi9qZXULvpAhCjHoA+neO5GB+BVabw8eWKYINJVCKoOdwQSXHS6o5s1e8W+v7doogKdLMLwcK2tgy33Agr5w+nSJrv+6VGIHdITlaWOlDqxTBiBIoRdCz9kA+gNsCJYRgTI84NhwqDLj06+oaO1lFVfRMOFkE2jMxAoCDeeW+MksRpCiBUgQ9vxwooFOUud6bcnOM7RnPidLqgPMqjhRUIiX0TKwrUNrfD+ZX+MqsoCYiIqL270uXLqVPnz4cPXqUp556qnbURZ8+fZg5cyYZGRm1aydNmkS/fv1qR2FceeWVvjDfI1SrI0VQI6Vk3cECzu6T2KJ2PuN6xAGw/mAh3eLdFzZ/x+Ul9Uo8+aYYFWIkIcLMoTwlUL7k+++/57777mP58uV07aoVk//+97+vHb8xb948zjvvPHbs2EFiYiIAc+fOZdSoZsuN/BblQSmCmsMFleSXWxnjFBx36Z0UQVy4iXWHAisOlVmkeYRd4+v3GkyLDeVYcZUvTFIAP/30E3fccQdff/01vXr1anDNNddcw5QpU/j444/b2bq2Q3lQiqBmy9EiAEa2sCuEEIIx3ePYdLioLczyGdnF1USGGE7rRZgWG8rOYyU+sspP+OYROLHDu3smD4GLnm1yicViYdq0aaxatYr+/fs3uXbkyJHs3r279uvrr7++tmv5BRdcwPPPP++5ze2IWx6UEGKqEGKPEGK/EOKRJtZdKYSQQoiO61MqgootR4uJMBvonRTR/OJTGNE1hqOFlRRWeG/0tq85VlxFakzoaa+nxoaSXVwd8D0I/RGj0cj48eN5++23m117atLO3Llz2bp1K1u3bu1w4gRueFBCCD0wB7gAyAI2CiEWSSkzTlkXCdwPrG8LQxWKtmBLZhHDukSj17V8nMSwLtoE022ZxZzbP8nbpvmE7OIqUhoQqLTYMKx2B3nlFjoF69j7ZjydtkKn0zF//nwmT57MM888w5/+9KdG127ZsqVDx5xOxR0PagywX0p5UEppBT4FpjWw7m/AP4HALK9XBBxVVju7jpcxokvrmr4OSY1GJ7QR8YGCJlCnC1CaU7QyAyxrsaMQFhbGkiVLmDt3bqOe1BdffMHy5cu57rrr2tm6tsOdGFQqUHesYhYwtu4CIcQIoIuUcokQ4g+NbSSEuBO4E6jNQlEofMX2rGLsDsmIrjGtuj/cbKBPUiTbsgJDoCqtNooqaxr0oDo7RetEqfr86Svi4uL49ttvOeecc0hI0Jr4vvjii3z00UdUVFQwePBgfvjhh9oMPqgfg0pISGDFihU+sb21uCNQDZ191B50CiF0wIvALc1tJKV8A3gDtHEb7pmoULQNW5yez/AurRMogGFdovkuIwcpZYefOptdrIlPQzGoTpGaQOWWWtrVJgWUl58skO7SpQuHDmkDJKdNm8ZTTz3V6H2rVq1qY8vaHneO+LKALnW+TgOy63wdCQwGVgkhDgPjgEUqUULh72w5WkT3+DDiI8yt3mN4l1iKKmsComDXlUbekAcVE2bEpNeRU6Y8KEX74Y5AbQT6CCF6CCFMwLXAItdFKWWJlDJBStldStkdWAdcLqVU0wgVfouUkl+PFns8dHBYF22IXyDEobKbECghBImRZvKUB6VoR5oVKCmlDbgXWAbsAuZLKdOFEH8VQlze1gYqFG3BidJq8sosHh3vAfTtFEmIUce2zI5fI5RdXIVOQKfIhj3KTlHmoPSgAq3fYnvi6c/OrUJdKeVSYOkprz3RyNpJHlmkULQDO4+VAjA41bMx5ka9jsEp0WzN7PgFu8eKq0iOCml05EhSZAj7g6xhbEhICAUFBcTHx3f4GGN7I6WkoKCAkJDWlyWoThKKoGTnsRJ0AgZ0jmx+cTMMSYvmkw1HsTtkq+qp/IXs4io6N3C856JTlLm283uwkJaWRlZWFnl5eb42pUMSEhJCWlpaq+9XAqUIStKzS+iVGEGYyfNfgUEp0VTXODh4yhyljkZumYX+yY3bnxQVQmm1jeoae+0ww0DHaDTSo0cPX5sRtKhmsYqgZOexUo+P91wMSokCION4qVf28xV5pRaSIhs/jklyxqZUqrmivVACpQg68sosnCitrhUWT+mdFIHJoCM9u+MKVJXVTpnFRmIjCRJAbYujYEyUUPgGJVCKoCM9W8u485YHZdTr6NcpsnbfjkhemeYVuSVQqpuEop1QAqUIOlyezkAveVCgHfOlZ5d22JTkXKdXlNSEQKkjPkV7owRKEXTsPFZC9/iw02YeecLAlCiKK2s4XtIxvQuXB9VUDEp1k1C0N0qgFEHHzuwSBnnpeM+FK57VUeNQuW4c8aluEor2RgmUIqgoqawhs7CKIV4WqP7JUQhBh41D5ZZVo9cJ4sJNTa5LiDSTH0ADGhX+jRIoRVBRmyCR4l2BCjcb6JEQ3mE9qLwyC/HhpmYLjRPCTRSUKw9K0T4ogVIEFTudAuWtFPO6DEqJJqODClRumYWkqOa7useFmygoVx6Uon1QAqUIKnYeKyU1JpTYZo6yWsPAzlEcK66iuLLjvYHnNlOk6yI+wkxBhaXDZisqOhZKoBRBxc7sEganet97gjodJTqgF5VXbiHRjblYCREmauyS0mpbO1ilCHaUQCmChnKLjUP5FV6PP7noqC2P7A5JQbl7R3zxEZrnWagSJRTtgBIoRdCw63gpUnqvg8SpxEeYSY4K6XCJEgXlFhyy6SJdF/Hh5tp7FIq2RgmUImjYeaztEiRcDEyJ6nBHfO7UQLlweVD5KlFC0Q4ogVIEHlJCZSFUFIC9pvblHcdKSIo0kxTV+gFqzTEoJYr9eeVU19jb7Bne5mQfPjeSJFweVIXyoBRtj5oHpQgM7DWwaxHsXACHVoPF6cXozZAyAgZfwaGsrgxOjW9TMwZ2jsLukOzNKWNommfj5NsLd/rwuXAV8qpUc0V7oARK0bGx22Djm7DmJSjLhqhUGDwTEvqCzgDFR+HQj/DNQ7wlI9mScA/YR4C+bf7pD3ImYKRnl3YYgXKnk7kLk0FHVIhBxaAU7YISKEXHJXMjLPk95OyA7mfDpS9CnymgO/3kevfmlRR/9SiTDz4Hry2CaXMg7Qyvm5QWG0qk2dCh4lC5ZRaiQgxuT8lNiDBToLL4FO2AikEpOh5lObD4d/D2BVBZAFd/CDcvhn5TGxQngA3WHlxrfZzCS98Bazm8cyFsft/rpul0ggGdozpUT77cUotb3pOL+AjVTULRPigPStFxKD0Ov7wMm94BmwXG3QPnPgrmyGZv3XmshPhwM7FnXAIDz4UFd8Di+6GqECb83qtmDkyJYv6mTOwO2WxvO38gr9y9LhIu4sJNHMqvaEOLFAoNJVAK/6emGlb9A9a9Ag47DLkSJv4R4nu5vcWOY6UMSo1GCAFhcXDdp/DlXbDiKS3r7+wHvWbuwJQoKq12jhRU0DMxwmv7thW5ZdWM7Brr9vr4CDObDhe1oUUKhYYSKIV/k78f5t0Aebtg+PVwzkMQ16NFW1TX2NmXU8Z5/RNPvqg3wsw3tL9//xfNI5v4x0aPCFtC3dlQ/i5QUkryytxrc+QiIdxEYaW1w3iIio6LEiiF/7J3GXxxuyYmN3wBvSe3bpucMmwOeXqLI50eZryu7f/js5CbDtNfA7NnotInKRKjXpBxvJTLhqV4tFdbU2axUV3jcKvNkYv4CDNSQlGllYQWCJtC0VJUkoTC/5ASVj8PH18Dsd3hzlWtFifQCnShkRZHegNMfxUufAZ2fw1vT4HCQ61+Fmip2L2TIjtEy6OWpJi7cHWTUIkSirZGCZTCv7CUw/yb4Ie/a7GmW5dBTFePttx5rJToUCNpsaENLxACzpyteWmlx+DNc+Hgjx49c1AHaXmU6xzf3pIkCdVNQtFeKIFSuEWV1c7K3bl8uO4Ic9cfYcOhQmx2h3cfUnAA3poMu5fAlL/DzDfBFObxtjuPaSM2hGgmXtLrPLjjB4joBB/OgLUva0kZrWBg5yjyyy3klla36v72Iq9ceVAK/0XFoBRNUlRh5eWV+5m7/gjVNfUFKTHSzC3ju3PbhB5uF3k2yr4V8MWtIHRwwwLoda5n+zmx2hzsOVHGb87q7t4N8b3g9hWw4Lew/DHY+jFM+Rv0Pr9Fz61NlDhe2qa9/zzFJaDutDlyEV/b7kh5UIq2RXlQikbZfKSQqf9dzbtrDnHJkBQ+um0sG/50PmseOY9Xrx/J4JQonl+2h6n/Wd364ywp4ecXYe6VEN1Fizd5SZxAS5Cw2h0MasmIDXMkXDsXrnpfK+r9aCZ8MA2OrnN7iwEdZHhhXrkFk15HdKjR7XtiwkzoBAHfTWL9wQLu/mgzNd4+KVC4jfKgFA2yIiOHu+duJiUmlEX3TjgtwSA1JpSLhnTm5335/N9nW5n56hr+d91ILhjYyf2HWCvgq9mQ/iUMmqG1HzKFe/X72JpZDMDwlvbFEwIGTYd+F8GGN2HNf7TuEyNv1hIqmsn0iwox0iUu1P8FytlFotnjzzrodYK4cFNAj9yosTu45g3tA8mBvHL6J7fdiBZF4ygPSnEaP+3L4+65mxnYOYpFs08Xp7pM6JPAkvvOpl9yFHd/tJlvdhx37yGFh7SMufSFMPkpuPJdr4sTaAIVH26iS1wjCRLNYTDD+Hvhd9th/P2w5UN4ZyqUZDV766DO0X4/XTevvGVtjlzEh5vJD+AjviMFJztl7M8t96ElwY0SKEU9jhRUMHvur/RMiOCDW8cSHdb80U9ipJmPbhvDsC4x/O7TrWw6XNj0DQdWaplyJZlww+daq6EWfIJvCVuOFjG8S0yLPIQGMYVpsajrP4fiI/DmeZC1uclbBqZEcSi/gnKLzbNntyEt7cPnIj7CFNBj34+XnExuUQLlO5RAKWqx2hzc/dGvCCF486ZRbomTi8gQI2/dNIrU2FDu/HAzRwsqG1646V0tphORDHes9Ki+qTlKqmo4kFfBiK5eHHvR+3y47TswhMB7F2vFxI3gSpTY7cdelNaHrzUCZQ7oJAklUP6BEihFLS99v4+M46W8cNUwusa3PL07NtzEO7eMxu6Q3PHBpvpTZaWEVc/Ckgeg1/laplwLeum1hu1ZzvhTF/f7zLlFUn8tHT2xP3w6S4uhNcDAOi2P/BGrzUFhhbWVR3yB3dH8hFOgxvSII7OoysfWBC9KoBQApGeX8OqPB7jyjLSWJTqcQo+EcP577XD25JTx7De7T15Y9azW8HXYLLjuE4/bCbnDlqPFCAFDu7Qgg89dwhPg5kWQNho+vxU2vn3akuSoEGLDjH47esNVaNuSIl0XCREmZ5ukjjPaviWcKK0mLtxEclQIxZWBK8T+jhIoBVJK/ro4g6gQA3++ZKDH+03ql8StZ/XgvbWH+WF3jvbm/eOzWrPX6a9ove/aga2ZxfROjCAqpI2eFxKt1Wz1vgC+fhB++ne9y0IIBqdGs/OYf3pQri4SrYtBafcEahzqREl17QeMogD9HjsCbgmUEGKqEGKPEGK/EOKRBq7fJYTYIYTYKoT4WQjh+bucot1Ylp7D+kOFPDilX4viTk3x8NR+9E+O5Jv5byK//j/oOxUue6nNkiFORUrJ1sxihndp47HrpjC49mMYcpXWFX3jW/UuD02LZk9OGVVW//M0cstcHlTrjvggcLtJ5JZV0ynKTEyYidJqm/e7pijcolmBEkLogTnARcBA4LoGBOhjKeUQKeVw4J/Av1F0CCw2O88s3UXfThFcN7qL1/YNMep5+Twjf7P/h6Nhg7Q0cn37ld0dLayksMLKiBbMOWo1roazfS+Cr/8A2z+rvTQsLQa7Q5Jx3P+O+VyNYlvSydyFy4PKD9B+fCVVNcSEmYh1fmArrqrxsUXBiTse1Bhgv5TyoJTSCnwKTKu7QEpZ9wwjHJDeM1HRlszfmMnRwkoeu2QgBr0XT3yrS+m9ajZWUzQzC2ezMbt9e9K5Bup5NYOvKfRGuOpd6HYWfPlb2LscgGFOD25rpv8JVG6Z9v/E1fy1JSQEeD++ksoaokIMxDo9RRWH8g3uvCOlApl1vs5yvlYPIcRsIcQBNA/q/oY2EkLcKYTYJITYlJeX1xp7FV7EanPw2o8HOaNbLOf0SfDexlLC4t9B0SGM17xHSEwyjy7YgcXWfsdcGw4VEh1qpF+n5sfBew1jqJYA0mkQfHYzZG2mU1QIyVEhtRmF/kRemYW4cBMmQ8s/mLg8qEBMNXc4JGUWG9GhRmLDNIEqqlQelC9w519mQ0GD0zwkKeUcKWUv4I/A4w1tJKV8Q0o5Sko5KjExsaElinZk4ZZjHCuu4t7zenteyFqX7fMgfQGc+xihvc/m79MHsz+3nLd+8mzOUktYf6iA0d3j0LX3xNeQKK2YNzwR5l4BOekMTYtmW6b/CVRuCyfp1iXcpMds0AVkP74yiw0pIaquQAXg99kRcEegsoC6wYk0ILuJ9Z8C0z0xStH22OwO5qzaz5DUaCb19eKHhZIsWPowdBmndYgAzu2fxIWDOjFn5X5y2mH8RE5pNYcLKhnbI67Nn9UgkZ3gpq+0Yt4PpnNOfAmHCyr97pgor8zSqvgTaBmKCRGB2e6o1Blvigo1EuOKQSkPyie4I1AbgT5CiB5CCBNwLbCo7gIhRJ86X14C7POeiYq24JudJzhSUMnsc73oPUkJX90LDhvMeFUbqe7ksYsHYrNLnvt2dxMbeIf1h7RWS2N7+kigAOJ6wE2LQDq4MuM+Eilme5Z/xaFyS6tblWLuIj4iMIt1S5wCFV1HoIr87MNFsNCsQEkpbcC9wDJgFzBfSpkuhPirEOJy57J7hRDpQoitwIPAzW1mscIrvL/2MN3iw5jiQVHuaWx+Fw6uhCl/hbie9S51jQ/j1gk9WPDrsdoO423F+oMFhJv0DOzs4w7UiX3h+s8wW4t4y/QCGUdO+NaeOtgdkpwyCynRrWyii7ObRABm8ZVWOz2oECPhJi3ztMKP+ykGMm5FR6WUS6WUfaWUvaSUTztfe0JKucj5999JKQdJKYdLKc+VUqa3pdEKz9h5rIRNR4q4cVw378Voio7A8j9Dz0kw6rYGl8w+txcJEWb+ujgdKdsu0fPn/fmM6xnv3azE1pI6EnHF2wzRHWL41ic1L9MPyCuzYHdIkqNbP0xR68cXeJ5FaR0PSqcTRJgNlFv8r44tGPCD32BFe/Pe2sOEmfRcNcpLdU8OByy6FxBw+f8aLcaNDDHy0IV9+fVoMYu2NRXGbD1HCio4UlDJ2d7MSvSU/hezLPFWxlV8j1z3qq+tAeB4idZfrrNHAqUd8bXlhw1fUFqleUtRoZr3FG7WU25RMShfoAQqyCgot7BoWzYzR6a2aIpqk/z6HhxarY2jiOna5NIrz+jCoJQonv1md5t0V1i9VytfOMebiR9eoGTU/Syzj4Llj2s/Kx/jaobqiQeVGGHGandQWh1Yx191Y1AAEWYDFcqD8glKoIKMzzdnYbU5uPnM7t7ZsDgTlj8BPSbCGbc0u1yvEzx52SCOl1Tz+uoD3rGhDj/uzSctNpQeCd4ffugJo3sm8H81d1EW1hU+vQEyN/rUHtc4CY9iULXFuoEVhypzxptc8acIs6H2NUX7ogQqiJBSMn9TJmd0i6WPNwpYpdTGZ0g7XO5+n70xPeK4ZEhnXvvxANnF3htlYLHZ+eVAPuf0TfRuXZcX6JkQjik8hv+m/BPC4uDD6XDkF5/Zc7xora97AAAgAElEQVSkCrNBV5ul1hpcHSgCrRaq0mIj3KSvjc9GhBgor1ZHfL5ACVQQ8evRIg7kVXCNt2JPuxbD/hVw/pMQ271Ftz56cX+kpP5IDg9Zu7+ACqudyQOSvLantxBCMKpbLCuyjfCbpRDZWRvceOgnn9hzvKSaztEhHgl5oHpQFVYbYeaTfSPVEZ/vUAIVRMzbmEmYSc/FQzt7vpndBt//FRL6wejbW3x7WmwYv53Yi0XbstnY3Ih4N/lm53EizQbO6u1HCRJ1GN09jiMFleQSB7d8rcXr5l4Jh9e0uy0nSqo9ij8BJLgaxgZYJl+FxU5EHYEKNxsoV0d8PkEJVJBQbrGxZPtxLh3aud4vX6vZOhcK9sH5T7S6S/ldE3vSOTqEvyxOx+7wLBPMZnfwXUYO5w1IwmzQN3+DDxjt7Gyx8XCR1m3CJVKfXAc57VuZoXlQrY8/AbVtgAIt1bzSaiPMdPLfUKQSKJ+hBCpIWLrjOJVWO1d743ivpkqbkJs2Bvpf0uptwkwGHrmoPzuPlfL55szmb2iC9YcKKaqs4aLByR7t05YMSokixKg76TGGJ2gDD01h2uj4qvbp12d3SHJKqz1KMQcwGXREhxoDrli33GKrTZCAkx5UoKXTdwSUQAUJi7Zm0zUujDO6eWE+0vrXoSwbJj/l8QDCy4elMKpbLM8v20OJB/3OPt+cRaTZwMS+/hd/cmHU6xjRJZYNh+ocacZ0gave13oYfjW7XQp5C8ot2BzSY4GCwGx3VGm1E24+6UFFhBiwOyQWmxpa2N4ogQoCckurWXsgn2nDUzzPbqsqgp//rY05736Wx7YJIXjq8kEUVdbwj292tWqPksoalu44zrQRKYSa/PN4z8WEPglkHC+tHRYIQNexMPkvsHsJrH+tzW3Irq2B8uyIDyAh3ExeoCVJWE5PkgAoC7B6r+Z466eD/LTPt2ORlEAFAUu2H8chYdrwFM83+/k/UF0Kk5/0fC8ng1OjuX1CDz7dmMm6gwUtvv+rbcew2BxcO7rpImF/wNXhYs3+/PoXzpytTeRd8RQUeL8+rC5HCysB6BLnuUAlRpnri20AUGGxE17ng45LoIKtH9/fv97FjW9v8KkNSqCCgK+2ZTMoJYreSR7WPpVma5/wh1wFyUO8Y5yTByb3pWtcGI8u2NGiDhN2h+T9tYcZkhrN4NRor9rUFgxOiSYu3FTb8aIWIeDSF0FvhkX3a+2j2ohMp0B1jQvzeK+kSDO57TBCpT2psNoIr+NBuRImKtug84miaZRABTiH8yvYllnsHe9p1bPgsMN5j3m+1ymEmvQ8O3MIhwsqeHLRTrfvW7I9mwN5FdwzqZfXbWoLdDrBhN4JrN6Xj+PUzMWoznDh3+HIz1pn+DbiSEEFCRFmwkyeZ3MmRYZQYbUHTJablJKKU5IkXD+nSmtgfI/uYLP7R7xNCVSAs2hbNkLAZcM8FKj8fbDlIxh1a4uLct1lfO8EZk/qzfxNWSz4NavZ9Ta7g5e+30f/5EguHOS/2XuncnafBPLLLew+UXb6xRE3am2jvntSS5xoA44WVtIt3nPvCTQPCggYL8pic+CQ1POgXAkTFUHkQVXWnPxefZm9qAQqgJFSsnDrMcZ0j/O45oXv/wrGUDjnIe8Y1wgPTO7DmO5xPPblTnY0M+Dv9dUHOZBXwYMX9G3/0e4e4Gpku7qhALQQWtsoaYfFD7RJVl9mYZVXjvcAOkVpmYC5ARKHcsWZ6mbxhRqdHlSAeInuUDfeVuTDacJKoAKY3SfKOJhXweWeHu8d+QV2LYLx90NE23YJN+h1/G/WCOLCTdz87gb25TTgZaDNtPrPir1cOrQzUzqQ9wTam3r/5MjT41AuYrtrBdD7v4Mdn3n12RabnewS7wmUa2R84AiU5jmEmU73oIIpBlW3tVOOD71jJVABzPL0HISAKQM9eAOXEpY/pvWOG3+v94xrgk5RIXx0+1j0OsHMV9by7c4T9Y4Z0rNL+M17G4kPN/O3aYPbxSZvM6lfEhsOFTZe+zXmTkgdBd/8ESryG17TCo4VVSGldxIkIPCO+CqccaaIOh5UMMag6npQvvzwoQQqgFmecYIzusaS6HwTaRUZC+HYZjjvcTC13wiLHgnhLJx9Ft0Swrjro81c8epa/rV8Dw98uoXpc9Zg0Ak+vG0MseGmdrPJm0wdnIzNIVmxK6fhBTo9THsZLGWw7E9ee+4RZwaft2JQ0aFGTAZdwKSau0SoIQ8qmGJQFXXEuC3mtrmLEqgAJauokvTsUqYM6tT6Tew1WuwpaSAMu857xrlJakwoX9w9nr9NH0xptY3//bCfH/fmce3oriy5b4J3Rob4iKGp0XSODuHb9BONL0oaAGc/CNvnwb4VXnmuN1PMQSu0TowwB8wRn2u0e90YVIghuI/4LDbffd9e6Bqq8EdWZGifzC/w5Hjv1/eh8CDMmq99ovcBZoOeG8d148Zx3XA4JELgd7OeWoNOJ7hwUDKfbDiqpTU31sD37P+D9IVaG6TfrtaazHrAkYJKQow6z7zqU+gUZfZpnMKbVNYmSZz8/6HTCcJM+qBKkqh7nGn1YYsn5UEFKMszcuiTFNH6ybKWclj1HHQ7C/pM8a5xrUSnEwEhTi4uHtIZi83B8owmvCiDGa58ByylMP8msHnW925vThm9kyK8+nNMigwJIA+q/jRdF2EmQ3Ad8dXxoKw+rIlSAhWAFFdaWX+o0LPjvXWvQEWu1iMugETBnxjVLZa02FC+2Hys6YXJg+Hy/0HmOvj2jx49c8+JMvp1ivJoj1NJigqcbhKuY7xTPdpws56qIE2SsNQogVJ4kR9252J3yNZn71UUwJqXoP+l0GW0d41T1KLTCWaOTGPNgXyyi6uaXjzkSjjrAdj0jvanFRRWWMkts9A/2buxu6RIM6XVNqprOr6HUVGbJFH/SDvUqA8uD6ruEZ/yoBTeZHl6DslRIQxpbW+6FU9CTYVWi6NoU64YmYqU8OWWZrwo0P5/9L4Alj4ER9a2+Fm7T5QC0M/LAuUq1g2EOFSFxYZeJzAb6r81hpsNQZdmbnL+DFQMSuE1qmvsrN6Xx+SBSa3rrrBvBWz5EM76HST2876Binp0iw/nzJ7xzF13pPn+Zzo9XPEWxHSDeTdCccuGPO5xtlbytgeVGqN1KTnWnBfYAXB1Mj81Rhdm0teLywQ61TUOwk169DqhBErhPdbsz6fSam/d8V5VMSy6DxIHwKRHvW+cokFundCD7JJqlqU3UhNVl9AYuO5TsFvhnalwfJvbz9lzoozYMKNXM/gAUpwClV3c8T2oSmvDGZVhJr1P64Hamxq7A5NBh0mv82mauRKoAGN5eg6RZgPjesa3/OZvHobyHJj+ipY9pmgXzuufRNe4MN5Zc8i9GxL7wi1LAKmJVMZXbt22+0QZ/ZIjvZ4JmeyczNtsHK0DUGGxnxZ/Ai2rryKIjvisdgdGvQ6zUac8KIV3sDs7E5zbP6n2/Nhttn+mFYRO/COkjmwbAxUNotcJbpvQg81Hilh76iDDxug8DO5YCZ0GaennP/6zycayNruDvTll9E/2bgYfQIhRT0KEOTAEymqrHVBYlzCzPqgKdWvsEpNe86BUkoTCK/x6tIiCCmvL08uLjsDXD0KXcVphqKLduWZ0FzpHh/Cv7/a6P94gshPcvASGXgsrn9ZEqhH25JRRabUzomuMlyyuT2pMSIDEoGwNzskKNwVXkoTVZseo12Ey6FSaucI7fJeRg1EvmNi3BR3H7TZYcKf295lvgF41F/EFIUY9s8/tzeYjRazYlev+jcYQmP4qDJsFq56BX+Y0uOzXo8UAjOwa6w1zTyMlJjQwPCiLvcEYVKhJT3WNA/upQyYDlBq7xGjQshktyoNSeIqUkmXpJxjfK4HIEKP7N/78b60A9JJ/QWy3tjNQ0SxXj+pCn6QI/rI4vWUBeZ1OK+QdcLnWWHbz+6ct2XS4kMRIM2mxHs4Fa4TUmFCyi6t9OtzOG1RabY3GoFzXg4EaZwzKZNCrGJTCc/bllnOkoLJlx3vZW7Ux7kOugqFXt51xCrcwGXT8bfpgsoqq+M/3e1t2s96gpaD3ngyLfwc7Pq+95HBI1uzPZ3yv+DZrFZUSE0pVjZ1iHw638wbljXhQYUE2E8pqc9Qe8SmBUnjMcmdX7AsGuClQNgssvBsikuDi59vQMkVLGNcznmtHd+GN1Qf5eV8L50AZzHD1h1r/xAV3ak1m0bL38sutTOid0AYWa6QESC1UpdVWbxaUC5dXFSwCVWN3YNLrMKs0c4U3WJ6Rw4iuMSQ5q/qb5cfnIDcDLnsJQtsmLqFoHU9cNpBeiRE8MG8rWUWVLbvZFAaz5kHaaPjiNkhfyHcZ2uDKFsUmW0hqbS1UxxUoh0NSabU3mCTheq0iSDqa19glJoNKM1d4geMlVWzPKuGCgW56Tznp8PN/YPgN0Nc/OpUrThJmMvDq9SOx2uzc/M4Giipa2MHcHAHXfwapZ8Bnt2Dc9DpjWvLhpRWkxGh7d2QPqtLZS7ChNPOTMajg8aCMeqHSzBWe45r95Fb3CClh6cMQEgVT/tbGlilaS59Okbx50ygyi6q45o1fOFHSwi4NIVFw40JKupzHPdVv8pL1ccjb0zbGAnHhJsJNeo4UtNDj8yNc3lFYQ0d8tTGo4PCgrHYVg1J4ieUZOfRMDKd3UkTzi3d+AUd+hvOfhLC4tjdO0WrG9oznvd+MJru4mmlzfmbDocKWbWAK44mwx3nccRdJVQfh1bNg5TNQ4/2WREIIeiSGcyi/wut7txcugWqwUDdYY1AGHRZ/FyghxFQhxB4hxH4hxCMNXH9QCJEhhNguhPheCKHylduJkqoafjlQ4J73VF0Cyx+HzsNh5E1tb5zCY8b3SmD+b88k1Kjn2jd+4alF6ZRWu5cpl5FdyqLtxwkfdwvi3k0waIYWe3xlLGybBw7vvtn2SIjo4AKl/TwaK9TV1gSHB1Vjkx3DgxJC6IE5wEXAQOA6IcTAU5ZtAUZJKYcCnwONl7QrvMqqPbnYHNK99PIVf4GyE3DJv302wl3RcgamRLH4vgnMGtuV9385zHkvrOLVVQcoqWpcqCosNh6cv5X4cBN3T+oFEYlwxZtw40IwRcKXd2oeVcaiJlsktYQeCeFkFVX6NOvLE2qn6TaRxVcVADOv3KHG7sBoEP4vUMAYYL+U8qCU0gp8Ckyru0BKuVJK6Tp8XgekeddMRWMsz8ghMdLM8LRmWtgc+QU2vQ3j7oa0M9rHOIXXiAwx8vfpQ1g0ewL9kiN57tvdjP/H9zw4bysrMnJqvSopJTuPlTDrrfXsyy3nhauGERNmOrlRr3Pht6vhqvdA2mH+jfDGRNj3ncdC1TMhHIeEzMKOGYdyxZdOHfcOdbP4gkOgapvFGvQ+PeJzp69NKlB38EwWMLaJ9bcB3zR0QQhxJ3AnQNeuXd00UdEYFpudVbtzuXx4atOznyzlsPAuiOkK5z7WfgYqvM6QtGjm3j6OncdKeH/tYZaln2CBc9hhXLiJGruDsmobkWYDc2aNZFK/pNM30em0477+l8GO+bDqHzD3Suh6ptZRpNOgVtnWIyEcgIN5FfRO8u7MqfbgpAd1+ttiiFGHEEGUJGHTYlA6H8+DckegGnrna/CjlhDiBmAUMLGh61LKN4A3AEaNGtWxe6L4AWsPFFBhtTd/vLfiSa0h7C1LtBRkRYdncGo0z181jKdnDGHDoUK2HC0ip0xLfhiUEs1Fg5Pre04NoTfA8Fkw+EptSOXKp+H1c2DCg1rTYGPL0tK7OwWqo8ahXAkQDR3xCSG0kRtB4kG5Wh3pdAKr3YGUss26kDSFOwKVBXSp83UakH3qIiHEZOAxYKKU0uId8xRNsTw9h3CTnvG9mpj9dOAH2PgWjJsN3Se0n3GKdsFk0DGhTwIT+njQJcJggtG3wcDpWi+/1f+E9C/h8peg23i3t4kONRIfbuqwAlXRhAcFzqGFNYHvQdkdEocEo16HQa+Jks0hMerbX6DciUFtBPoIIXoIIUzAtcCiuguEECOA14HLpZQtaMWsaC0O5+ynSf2TMBsaSXioLISv7oWEvnD+n9vXQEXHIzweZr4ONywAuwXevQgWzobyPLe36JEQzsG8jipQziw+Y8O/T8Ey9r3GWZhrNIhaUarxUbFuswIlpbQB9wLLgF3AfClluhDir0KIy53LngcigM+EEFuFEIsa2U7hJbZmFZNXZmFKY90jpISvZkN5Lsx4DYxt08VaEYD0Ph/uWQdnPaANsXz5DNjwpltp6b2TItibW9Yhu5pXWG2EGHUY9A2/LYYFyUwoV+cIk16H0fmzqLH55v+nW3VQUsqlUsq+UspeUsqnna89IaVc5Pz7ZCllJynlcOefy5veUeEpy9NzMOhEw0FwgF9ehj1LtW4RqSprT9FCTOFwwV/g7rWQMgKW/gHemtxsN4pBqdEUV9Z0yJZHFRZbgxl8LsKDZKpujTMpwmQ4KVC+anekOkl0UJZnnODMXvFEhzYw+ylzA6x4CgZcBmPvanfbFAFEYl+tduqKt6HoMLx2Nqx5qVFvanCKNlI+Pbu0HY30DhUWW6PxJ9A8qIpgECi75i0ZnSPfQQmUogXszy3nYF5Fw8d7lYXw2W8gKhUufxl8kHmjCDCEgCFXwuz10OcC+O7PWnzqxI7TlvZPjkInIP1YiQ8M9YwKq73BYYUuwkx6KoOgk0RtDEqvw2hwxqB8lGquBKoDsjxDm/00+VSBcjjgy7ugIlcrxAxtpnhXoWgJEUlwzUcw4w3I2w2vTdDS0tf+D/L3g8NOqElP76QIdnZQD6qhPnwutBhU4HtQ1lqBEidjUD7yoNxJM1f4Gd9l5DA0LZrO0ackPvz0AuxbBhc9D6kjfWOcIrARAoZdo03u3fk5bP1Y6++4/HHQmyCuJ/+yJ/DL0VTYdQIikrWmxHqTFtcKidEKhf2QCqu94SNzJ1oMKng8KFehLvjuiE8JVAcjt7SaLUeL+cOUvvUv7PlGK7Qceg2MucM3ximCh/B4GPtb7U/RYTi0Ggr2Q8EBuhxNZ5B9Dcyb18CNQhuQGd8LuoyFHudA97O1QYs+psJiIzWm8eLkUJM+OGJQtpMxKH1tmrlvsviUQHUwvtvlnP00qE738oID2ojvzsPgsv+quJOifYntrv1xcuBIITe/+j2vXxzDWckSqoq0uiprhRYjrcyH3F2w4Q0t21Rv1jIFu46FHhOh5ySfNDOutNga7GTuItxkwGpzYLM7Gk1FDwRqj/gMOgw639ZBKYHqYCxPz6F7fBh9XLOfrBUw70btF/qaj1S9k8LnDE2LQZoi+aYwmbPOGdL4wppqOLJG63aSuR5+eQXW/Fc7Fhxxvdb9JLyJLileprzZGJRzJlSNnagAFqiaOjEog85VB6UEStEMZdU1rD2Qz2/O6qH1xZISFv8OcjPghi+0ZrAKhY8x6nWM7RnPmv0FzSwM0YqCe5+vfV1TBfuWw9ZP4Kd/w/rX4czZMOH3bf7BS0pJZTNZfK4U9EqLnaiQxmNVHR1Xc1iTXofe6UFZVJq5ojlW7cmjxi65wJW9t+FN2PGZ1qHc9UuuUPgB43vFcyi/guyWFOwaQ2HgNJj1qdbJos8F2oDFV8+Cwz+3nbGAxebA5pDN1EFp4lUR4IkS9dLM9b71oJRAdSCWpZ8gIcLEyK6xcHQ9LHsU+k7VOk8rFH6Eq3ntmv35rdsgqb9WKnHTV9rcqvcuhR//qZVStAG1ncybrIPSxKsqwBMl6gqUyeBKM/fjVkcK31NdY2fl7lwuGJiMvjIPPrsZorvAjNf9Nm1XEbz06xRJUqSZFc6knlbTc5LWbmno1VqW6qfXafPNvIyrk3lYEx6US7wCfey71SlGJoPv66DUO1sHYe2BfCqsdi4ckAAL7tAyo675UBXjKvwSIQSXDk1h5e48SiobH03vFqZw7YPYRc9rk38/uBwqmolvtRDXsV1TSRKhriSJQPegamNQ+tpu5qrVkaJJvt15gkizgQk5H8LBVXDRPyG5iQwphcLHzByZitXu4Osdxz3fTAgYe6eWqZqTDu9OhbITnu/rpLy66VlQda8FTQzKIOoc8SmBUjSCze7gu4wc7uh2HMOP/4AhV8HIm3xtlkLRJINSouidFMGXW7K8t2n/i7V5VSXH4IPpWl2VFyhzClRUiBtp5oHuQdWNQakkCUVzbDhciKgs4M7cpyG2B1z6oirGVfg9QgiuHpXGxsNFbM0s9t7G3c+C6z6BwoPw4QywlHm8ZWm1dgwZ1VSrI5MrzTywPShrnW7matyGolm+25HFS6Y5mGtKtMwmc6SvTVIo3GLW2G7EhBn53/f7vLtxz4lw9QdaR/UvbndrmGJTlFZpAhXZhAcVWptmHhweVL2BhSqLT9EQDruDkdv/wgTdDsQl/4LOQ31tkkLhNhFmA7dP6MH3u3O960UB9JsKFz0He7+F757waKvS2iO+xj0os0ErXA34NHNb3W7mziQJdcSnaIgTS5/hMscP7Op7D4y80dfmKBQt5ubx3UmKNPPIF9u9H2wfcweMvkPr6ffrB63eprS6BpNBR4ix8TooIQRhJn1QJEkIAXqdQAhNpFSShOJ00heSsvl5vrKfRcq0v/jaGoWiVUSGGPnb9MHsPlHGnJX7vf+Aqc9Cr/NgyYNweE2rtiitsjWZIOFCG1oY2B6U1S4x6nVaOzW0WJQSKEV9jm1GfnkXO3T9+arbo0SHm3xtkULRai4clMz04Sn89/t9rNyT693N9Qa48l2to/q8G6DwUIu3KKuucau/XrjJQGVNgAuUzVGbvQcugVIxKIWLkmPwySxqQhO4pfJ3nDdYNYFVdHz+MXMo/ZOjuP/jLez09kj40BiYNQ+kAz6+Bqpbtn9ptY3IJjL4XISZA3/se43dURt7AjAZdCqLT+HEUg6fXAPWCj7t/TyFIpopp452Vyg6IKEmPW/dPIqoUCM3vr2evTmep4fXI76XVshbeAA+uwXs7guJ5kG5c8RnCIoYlLGOB2XS61SShAItVXbBnZCTjrzqXT44EMbo7nEkRTU+5VOh6EikxoQy9/axGPU6Zr25nl3HS737gB5na3WCB36Ab/+ojaRxg9Iq9474wkz6gC/UtZ4iUCpJQqH9In3zR9jzNUx9jj2RY9mfW85lw1J8bZlC4VW6J4Tz8R3jMOoFV7/+C+sPerevHiNvgvH3w8a3YO1Lbt1SUmUjKrR5DyrcZAj4ZrE1donZcGoMSglUcLPmP7DxTRh/H4y9k8XbstHrBBcNTm7+XoWig9E7KYLP7x5PYqSZG9/ZwPJ07/XVA2DyX2DQTK0+avv8JpdKKSmutBIT1nwiUoTZQEWAZ/HV2E71oHRYbSpJInjZMhdWPAWDr4TJf0VKyeJtxxnfK56ECLOvrVMo2oTUmFA+v2s8AzpHcddHm/lkw1Hvba7TwYzXoPvZsPAercFyI5RbbNgckjg3BCoyxFDbFilQqbE7MBpOJkkYDcqDCl72LoNF92lzb6a/Cjod27NKOFpYyWVD1fGeIrCJCzfx8e1jObtPIo8u2MHzy3Yj3YwbNYvBrCVNJPSFT2+AzI0NLiuq0AQn1o1SjqhQI5VWu8/esNuDU2NQJhWDClKOb9OyjZKHaL9IBu0XZPG2bIx6wYWD1PGeIvAJNxt46+ZRXDu6C3NWHuD387Z6L2ssNAZu+BzC4+G9S2Dz+6clThRWWgGIC28+ScLVq881niMQOTWLT8WggpGyHPhkFoTGwaz5tQ1gHQ7Jku3Hmdg3keiw5n9hFIpAwKjX8Y+ZQ/jDlL4s3JrNze9soKTKS0dpUSlwx0roOhYW368NPCw4UHu5qEITqFg3jvhcmX6BfMxXY5f1CnVNBpVmHlzYLFrFe1UhXPcxRJ6sc9p8tIgTpdUqe08RdAghuPe8Prx4zTA2HSnkylfXklVU6Z3Nw+Lgxq/gkn9D9jZ45Uz48XmwWSmqbIFAOYt5ywLeg6oTg9LrakdwtDdKoNobKWHx7yBrgxZz6jys3uXF27IJMeqYPEAV5yqCkxkj0nj/1jGcKK1mxitrvdd1QqeD0bfBvRug30Ww8u/w+tkYj20A3ItBuY74Sr3l3fkhVtvphbrqiC9YWPs/2PYJTPoTDJpe71KN3cHSHcc5r39Sk6OnFYpAZ3yvBL64ezwmvY6rX//Fu/37IpPh6ve1o3VrBZdt/g1/Nn5ElKF5rygYjvisdgdGgyrUDT72LtPqMgZOh4kPn3Z59d488sutzBiR5gPjFAr/om+nSBbcM54eCeHc/v4mPl7vxTR0gL4Xwj3r+CVuBrfplyJeORN2LWmy+0StBxXgR3ynNYtVMagAJ3c3fH6bNnBw+qsNjmz/fHMW8eEmJvVL9IGBCoX/0SkqhHm/PZMJvRP405deTkMHMEfweuQ9PBb5dy0tfd718OF0yG94LIgrBhXIR3w1Nlk/BmVQMajAprJQawBrCoNrP9H+ewpFFVa+35XLtOGp9c5/FYpgJ8Js4O2bR3HdmJNp6Bab97o5nCipJidhHNy1Bi56Ho5tgVfPhB/+DjVVp9kCwZAkoWJQwYHdBp/dDKXH4dqPITq1wWWLt2djtTu44oyGrysUwYxBr+OZGUN46MJ+J9PQK73jxeSUVtMpKkSbKzX2Trh3IwyaAaufh5fHwMa3oaYa0KbMRoYYvJcC74ecVqir0swDmB/+BodWw2X/gbRRjS77YnMW/ZMjGZQS3Y7GKRQdByEEs8/tzX+vHc7mI0Vc8ZrnaejVNXaKKmtIrjsxILITzHwDbl4MEYnw9YPwnyHw84tQXUpcuKk2NT0QsdocmI0dKElCCDFVCLFHCLFfCPFIA9fPEUL8KoSwCSGu9L6ZHZRdS7QmsKNuheGzGl22L6eMbVklXHmGSo5QKJpj2vBUPrh1LDleSEPPLbUA0Cm6gZE2Pc6B27/XhKrTIK1f5nNgASMAAB2kSURBVIuDuVd+gq00p9XP9GeklFhsDsynJEnYHBKHo/3jUM0KlBBCD8wBLgIGAtcJIQaesuwocAvwsbcN7LAUHICFd0PKCJj6bJNLP/81C71OMG24Ot5TKNzhzF7x9dLQf9jdOsE4Uaod3SU3NnNNCE2oblqodaPoNYkrKufz7+wbtR6aB34Ae+Ac97km55qN+trXXMd9NY7296Lc8aDGAPullAellFbgU2Ba3QVSysNSyu1A4HZQbAnWSph/E+j0cPUHWnZQY0ttDr7YnMW5/ZJIjFSdyxUKd+nbKZIv7xlPr8QIbn9/E2/9dLDFGX6H8ysA6BZ/euLSaaSOhKs/4LleH7Bcfzbs+Bw+nAEv9NE6pu/5VusS04FxxZrqzoNypZzX+CCTzx2BSgUy63yd5XxN0RBSwpLfQ046zHwLYro2uXxZ+gnyy63cMK7pdQqF4nSSokKY99txTBmYzN+/3sWfvtzZonjJgbxyTHodabFuCJQTe2xv/lhzJzx0AK6ZC32maMf5n1wD/+ylTcU+vq01347PsTgFynRKoS7gk1ood9oVnF6wA62SUiHEncCdAF27Bugb8qa3YfunMOlR6DO52eVz1x8hLTaUc/qo2ieFojWEmQy8cv1IXli+h1dWHeBIQQWvXD/SrQGEB/Iq6J4Qhl7X0Ntcw8SGm6i02qkWZkIGXAoDLgWbVUuG2rUI0r+E7fOg92RtcGLyYE++vXbF0oAH5eoq4YtECXc8qCygS52v04Ds1jxMSvmGlHKUlHJUYmIAviEfXKWNbe8zBc45vVPEqezPLWfdwUJmje2KrgW/IAqFoj46neDhqf3511XD2Hi4kBmvrOVgXnmz9x3ML6dnQkSLnhXn7NlXL5PPYNI+kF7+Evx+J5z/JBzbDK+fDUsehAovj7VvI04e8Z0eg7L4wINyR6A2An2EED2EECbgWmBR25rVAcnbC/Nugvg+cMXbWmPKZvh4/VGMesHVo7o0u1ahUDTPFWek8fEd4yipqmHGK2tZeyC/0bVl1TUczq+gb3Jki54R6xyDU1jRSKp5SDSc/SDc9yuMvgM2vwcvnwG/fgA+SDRoCa4C6LpHfGZ/9qCklDbgXmAZsAuYL6VMF0L8VQhxOYAQYrQQIgu4CnhdCJHelkb7HRUF8PHVoDfCrHkQEtXsLdU1dj7fnMnUwZ3VWHeFwouM7h7HwnvOIjHSzE1vb2h0lPymI0U4JIztEdei/V2/r3llzSREhMXBxf+Eu9dA4gAt6++9i+HEjhY9rz2x1DRwxOfnSRJIKZdKKftKKXtJKZ92vvaElHKR8+8bpZRpUspwKWW8lHJQWxrtV9gsWv+u0my47hOI7ebWbYu2ZlNabeP6sQEai1MofEjX+DAW3DOe8b0TeHTBDv705Y7T2iOtO1iAQScY2TW2RXt3cqaku2qomiVpANzyNVz+MuTthtfOhi9uh8KDLXpue1CbZt7AEZ9felCKJpASvroXjv4CM16DLmPcvE3y9s+H6J8c2eJPbwqFwj2iQoy8c/Mo7prYi4/XH+Xq19eRXaz11rPaHHz56zHG904g1KRvZqf6JEVpHpSrhsotdDoYeSPcvwUmPKBl/b08WpsNV2e6r69xeVANZfFZfSBQauhQa3E4YNmfYMd8OO/PMHim27eu3pfPnpwy/nXVMEQDXc0VCoV3MOh1PHJRf4Z3ieYPn21nyourufOcnhwvqSa3zMJzV3Rv8Z5mg564cFPLBMpFaCxMfgrG3gWrX9DiU5vfg+Sh0P8S6DtVG2Lqo/cFl5fZYB2Un6aZK07FYYdF98PWj2DcPXD2/7Xo9jdXH6RTlFmNdVco2ompgzszoHMUf1uSwb+/2wvAjeO6tXq0TaeoEHJbI1AuIpPhkhdgwu8hfQFkLIJVz8Kqf0BMN83bGn49RLXve4S1oToo59+VB9URsFlhwR2QsRAmPgKTHmnRp52M7FJ+3p/Pw1P71ftHoFAo2pZu8eG8dfNoMgsrsTsk3RPCW71Xpyhz6zyoU4lOhfH3aX/K82DfMq2G6v/bO/P4qorrgX8ne0IkC0SWEBJBRBYhQICAZXGpxg3ciwparYpYgVDbX2ttK0Xtx1qrorXu1qqAuxa1CrggaAk7KJiAECAQDBJIWAJZXjK/PyaXvDxekpfk5t2X5Hw/n/vJu+/OO3POzNx7cmfOzHz+AHzxF+g3wfwD3G1Q8/PyAa/zoBwcgxIH1Rhc5fDWz2HLR3DBgzD6rkaLeOGrXKLCgrlhhG/BFIIg2EtSvO+rRtRFt5gIvt3T9EVqvRKdAEMmm+Ngrun6W/Mv889wnwvgnHuhe6q9eXpwoouv1lp81WNQrgCN4hMw0Xpv3mic08WPNMk57S0+zsINe7k2LYmY6rkUgiC0PnrGd+BASTlHSltoodj4XvDTOZD5rRnj3rMGnhtnov+KdrZMnrh18QWfPA/KiS4+cVC+4CqDN6bA1o/hkr/DiNuaJObppdtRCm4dc5rNCgqC4E9O62zewnYWNm8/qgaJjIWxv4aZG0xXX/aH8GQafPw7KKl7EnJTOdHFF+ruoMzbVGmFfbsY+4o4qIaoKIXXbzB9w5c+BsNvbZKYvcXHeWP1bq5JS2rUwpSCIAQe1vjVjgMl/skwIgbO+5MJU0+9HlY9C3NTza6/5fbp4G0MygrDFwcVaFSUwuvXw7YlcNlcs/FgE3l66XY0mjvH97ZRQUEQnCClk3FQ1nYdfqNjN7Pe351Z0GucCaZ4YqgZq6p0NVt8mZcuvsjq8ajj5eKgAoeK4/D6dWZDsglPwrCfN1lUfvXb09XD5O1JENoCEaHB9IiLZEvBEWcUSOgLk+bBLYvM6jUfZsI/0yH7A7OAQBMpc1USFhJUa35mhOWg5A0qQKgohQXXwfYvYOI/YOiNzRL398VbQMFd555uk4KCIDjN4B6xbNhd7KwSPdONk5o030x3eWMyvHQh5GU1SVy5q6pW9x5AcJAiLCRIHFRAUOmCd34BuV/AxKdMyGcz2Lz3EO+tz+fms1NIjI20SUlBEJwmNSmW/OLjDS8a29IoZVahmLYCLnsCivOMk1pwHRTtapSoMi8OCiAqLJhS6eJzGK3N2lg5H0LGX2HIDc0W+dDHOcREhnLneHl7EoS2xJCesQCs3nnQYU2qCQ6BYTeZbT7O+5PZQPGfo2D1Cz5v81FaUVlroViLyNBgeYNyFK1h8R/M8kXjfgfpdzRb5Oc5+1j+fSF3nXM6MZEy70kQ2hKpSbHERYWyeHOB06rUJizKhKTfucIsYP3R3fDKBJ/mTx0rqyTKy+K5xkHJPCjn+HourPgHjJhqli9qJqUVldy3cDO9Ezpw46iU5usnCEJAERIcxPn9uvBZ9o8cLWt+BJ3txPaEKe+ZIK8fNsIzY82af/VQUu6iQ/jJCwxFhAZzvNz/NoqDAvjmLfj0Phh4FWQ8ZMtKwv9cup3dB49z/+UDZc09QWijTE5P5kiZi1dXNG6sx28oZYK87vgKOvWGN6fAx781y7Z5oaTMRbQXBxUZJl18zrBjObw/DZJ/Apc/7dNW7Q2Ru/8ozyzdzoTB3Rndu7MNSgqCEIgMTorl/H6nMvezrWzKt3ltPjuJSzbRfiPvgJXPmCAKLwEUJWWVdAivo4tPgiT8zI/ZZpWITr1h0msQ0vyt1yurNL9+ayMRoUH84ZJ+NigpCEIg8+AVZxEfFcZ1z2eRlXvAaXXqJiQMLvorXPsKHNgGz46FLZ/USnK0rJ4uPhmD8iPFefDaVRAaCTe8ZTYSs4Hnl+eyLq+YORMHcmr11tCCILRdunSM4K1po0mIDue657OYvXBzYI5JWfSfCFO/NGNUC34GH2Se2NW3pNxFhzDvXXyy1JG/OLIPXpkI5Udh8tumomwgp+Awjy7eSsaArkxMlc0IBaG9kBgbycLpP+GmUSn8e8VOznlkKQtW5eFyYAVwn4jvBb9YYoLC1r8GTw6D+ZM4q3wDHbxG8QVJF59fOF4Er15hnNQNb0PXs2wRe7TMxZ3z1hETFcoDVwyUrdwFoZ0RHR7C7AkDeHfaaHrGR3HPu99y8RPL+TxnH7oZyw+1GKERcPHDMGsTjP0Nes8qXg15kFs3T4avn4D9W04smyTzoPxB2VGYdw0c+N6sY5U0whaxWmvuefdbdhaW8MSkIXSObv5YliAIrZMhPeN4+45RPH3DUMpdVdzy8homPZfFykAdnzqlK5x7L8VTN/CbittRQSGw5I/w1AiYOwg+upsBJVnoihbeWsQLyinPnpaWptesWeO/DEsK4c2bIG8FXPtv6HeZbaJf/GoH93/4Hb+5sC+/PEdWjBAEwVBRWcX8lXn844tt7D9Sxtmnd2LW+WeQlhLvtGonsfvgMcY8/AUPXz2Ia08Htn0K3y+B3KVQUUK5Dia0+0DUuN/BmRc3Ky+l1FqtdVpD6drHlu95WfDWzXDsAFzxrK3Oacl3+3jgo++4oH8Xpo2TrTQEQaghNDiIm0ancG1aEvNW7uKZL7dz9TMrGNOnM9PP7cPwlLiAGQ4oqZ6IGx0eArHdIO1mc7jK+Pijd9ix+mNuCysmNCTMbzq1bQelNfzvSfh0tgmEuHUJdBtsm/hv9hQzY8F6zkqMYe6kIQQFBUZDEwQhsIgMC+bWMb24YWQyr2UZR3XtsytITYpl6theXDCgK8EOPz9KqiMPTwozDwmntOdYHl4RQ8al4+iVEO03ndqugzp2EN6/02zT3m+C2TYjIsY28d/tPcyUF1cR3yGMF25MO7HrpCAIQl1EhgVz29heTE5P5u21u3nhqx1Mm7eOlE5R/GJML64amkiUlzBvf3C0zARBeIvii40yb01Fxyr8qlPbdFB71sJbP4cjP5hVyUdOtWX5IoucgsNMfnElUWHBvH57usx3EgShUUSGBTNlVArXj0xm8eYCnl2Wyx/f38TDn+Rw1dAeTE7vyemnnuJXnYqPmeWPYqNOXtg63nJQJd6XSGop2paDqqyArKfhszlwSjeztEePYbZmsWrHQW7992oiw4KZf1s6SfGyQ64gCE0jOEhx0VndyBjYlbW7ingtaxfzV+bx8v92MvK0eCanJ/PT/l1O7GrbkhQcKgWga8zJ+9bFnXiDEgfVNHK/NIsg7s+GvpeYLr0oeyNlPvxmL796cyM94iJ55ZYRsn27IAi2oJQiLSWetJR4/nhpGW+u2cP8VbuYvmA9HSNCuGRQN64Y0qNFgyp+OFRKdHiI18Vi4zqYtypxUI3lx2xY+hB89z7EJsOkBdD3Ilu79FyVVfz1kxyeX76DYclxPH9jGvEd/BfJIghC+6FTdDjTxvdm6thefL29kPfW5fP++r0sWLWbHnGRXDEkkYmp3W3vAtx3uJSuMd6HK6LDQwgNVjIG5TOF28xksi3/hdAoGP97OHuGWVvPRnYUlnD3mxtYl1fMjaOS+cMl/WX7DEEQWpygIMWYPgmM6ZPA/Ze7WLS5gPfW5/PUF9t48vNt9ErowIUDunLhgK4MSoxpdhTxD4dK6VrHeLpSitioMBmD8pmgINi9yux+O3Kq7d155a4qXv7fDh5dspWw4CDmTkplYmqirXkIgiD4QofwEK4c2oMrh/Zg3+FSFm8uYNHmfTy/LJenl26na8cIftq/C+POSCC9dyev3XQNse9wKaefXvf2QPFRYRwUB+Uj8b3gV9lmCXkb0Vrzec6PPPBRNjsKSzjvzFP5y5Vn0UUi9QRBCAC6dIxgyqgUpoxK4dCxCj7L2ceizQW8vXYPr2btIiRIMTQ5jrF9OjOmTwIDE2ManGNVUuZi3+FSusfW3QOVGBfJrgP+Xe6o9ToosNU5VVVpPs3ex9Nfbmd9XjG9Ezrwr5uHc07fU23LQxAEwU5iokJPvFmVuSpZu6uI5d8Xsvz7/TyyeCuPLN7KKeEhDE2OY3hKHMOS40lNij1p3ubX2wqp0pDeq+6eqDO7nsKyrfspc1USHuKfeZ+t20HZQOHRMt5fn8+CVXls319Cz/goHrh8ID8bnkRosIw1CYLQOggPCWZ0786M7t2Z32acSeHRMr7eVsiqHQdZs7OIRxZvBSAkSDGge0cGJMYwoHtH+nY5hXkr84gODyEtuR4H1a0jrirN9h9L6N+9o19sapcOat/hUj7L/pFPs/exbOt+XFWa1KRY5k5K5ZKzuhEijkkQhFZO5+hwJqYmnhg7Lz5Wzrq8IlbvLGJ9XhEfbtzL/JV5J9L/X0bfegPA+nczUYM5BYfFQdlJ4dEy1uwsYu2ug2TlHuTb/EOA2WTs5rPNQo59uvh31rYgCII/iY0K49wzu3DumV0AM96+p+g4WwqO0Ck6jCE9699VPKVTB355Tm/O8OOzss1st6G15mBJOflFx8gtPEZOwRG27jvCloLD5BebGdJhIUGk9ohlXN8Ezut3Kn27nNL4SW9a155jZZWf53fNmYflLtOzfrQ2EYye6aqqzF/rN546WJ+96VafTVVVJj/ru6oqCA6u+WzlaZ17080699TdOte6Rq71O/drnvKtNJWVEBJSI8uSUVcZuNvnbofnby27POvAXf+q6p1S3fXxVl/u31v6eJNpXXP/61l+7ueNwbNePPNyLxdPXdzz9Gxjntfcf+t5Xl9deLPbW1nVZ7+d96VnW62qMufu7cWS7S1fJ1Ynr6sN+lL23mTUlcYmbN1uQymVAcwFgoEXtNYPeVwPB14BhgEHgJ9prXc2VunGsKOwhOeW5ZJffJz8omPsLS6tteNjaLCid0I0ww7sYEq4i+G3XcvAxJjmDe7Nng3FxfDYYzUVP2qUubZiRc13s2ZBbKxJ35Q8PvkERo40MoqLjcx33zXXO3eGiRNNusxMWLkSCgqgrAyuuQbi4qCoCJYtg9xc6NcP0tPN9/fdd7Ju9dkUHg6HD8OaNXD22bB7N5SXQ//+MH48/Oc/EBEBGRnmdwsXwoQJRk5RkZFh5ZuUZBxKfj7MmQMHD8Ly5SZdRUWN3NRU80B4+2044wwYMsTou3QpHDoEl10GixdDXp757fDhxvb1642c7t2NnrNmwRtvwLFj0LEjJLpNEVi/3ugydCjs3WvsP34coqNNmX7wAYSGmgfUhRfCokXw3XfQuzesXQt//rOxvaDA2D9xopG7cSMMHmzqZM8euOoq831srKnTzZth4EAjs7gYsrKMHbffbmyLiTF/N2yA0lLTBh5/3Miw6jojo3Htavx4I3PtWlPuRUWmXIqKTNsICzP1lZ5uvu/b15S5pw6zZ9fUd0SEsdOqX6vuO3Y0v+3Y0ZThZZeZ9mPZ5XlPWG3Puv7oozB6tCk7lwuSk819NWuWKSulvNtv5305eza88IK5z9atM3X93HNG/ogRph1adRERYdqre77NufebSl3PjFWrTFurr+xb8llmB1rreg+MU9oO9ALCgI1Af480dwLPVH+eBLzRkNxhw4bp5rApv1gPmbNYX/rEcj31lTV6zsJN+sVfPaI/6ZOuczJ/r8vKXVrPnGn+F5o5U+uqqmblp6uqTpY3Y4b1v5b57C1NY/Nwl5maWvPZ/Rg8uHa6Tp1qX/P2mxkzan5j6daQTZbczp1ry+rcWetBg2rOp0+v0TU11Zy753vXXbVtcr/uLjsi4uR8LBmWXZ66BAV5Lx9vZeDL4Snfsw4GD64t3z19Xfl6fu95bslwL0Nv9ebeznyhsrJGlmebqeuw6txdR/fy99TPve4tOzz/Wtfd7wn3tueuY0Nl52m/nfel528HDapta3x87euWbpZMO583vtLQM6Ohsm+pZ1kDAGu0rt9HaJN7gw5qFLDI7fwe4B6PNIuAUdWfQ4BCqrsP6zqa66C84l6o1mFn4XqT7/kAaW6eno2loWPGDK1drrqdmefhqZuvNvly1KeD+4OsMYelr/vDtjHH9OlNs8WzPNydbFMPXxznzJnGVm86N8Y5WTSl3OrToSl1763d1dX2GqoHb/bbeV/6ev/NmGHKqCWfN77SkM6+lr3dz7J68NVBNTgGpZS6GsjQWt9afT4FGKm1vsstzabqNHuqz7dXpyn0kHU7cDtAz549h+3atauxL3wNo3VN3zHUHk9oKflgb56eedSHlZf7mIov6evLz5tNvlBZWbcOnv34vuKur682ev4eGm+L3TKg/vJxz8vqXvHMr6ntqrHlVp8OddGQbXXp3pS27g0770tfdKqrjOx+3vhKfTr7WvYt8SyrA1/HoHxpGd608/RqvqRBa/2c1jpNa52WkJDgQ9aNRGvTZ+rOrFnm+5aSn5lpDrvy1PpkefWRmWkeDsN83FbEUzdfbfKF+nSYOdN3Hd2x9K2qatrvZ85smi3uZGbCjBnNkwFmzKshZs0ytnrTOTOz8e2qKeVWnw510VAe3u4Jb22vPuqy38770tf7LzPTlFFLPm98pSGdfS17u59ldtDQKxatpYvPW5+pjEF5f32XMai6DxmDOllHGYMyh4xB2QY+dvH5EsW3GuijlDoNyMcEQVzvkWYhcBOwArga+LxaCf+hlIk2mTmzJjLlscfMtdjY5r+mepP/+OMmmgfM5+bmqZSJiho5siYiZ+xY02y8RfFBTRRfaGhNFN/YsXVH8Vl2WLrVZ1NDUXxKmUim+HgTvQc1UXzWG4eV73vvmTc9K5ps+vSaKL6wsIaj+GJjzTVfovjWrWt6FN+0aSdH8YWHnxzFBzVRfNdX3w4bNxq7vUXxhYfXjuIbN857FN+4cSaCzmoDVhSfVddxcb63q6AgIzM1tabcZ8zwPYrPXQervVlRfO71a9V9fVF848bVbnfu95N13ZcoPk/77bwvLfmJibWj+AoKTBsZOLCmPqwovpZ63vhKfc8MK4qvvrJvqWeZXeb54keUUhcDj2Mi+l7SWj+olJqD8YILlVIRwKvAEOAgMElrnVufTLvnQZ1A65aN4/cmH+zN012mZ/1oLfOgrDQyD8o3ZB6U9zR14dlWZR6U7er6OgbVZibqCoIgCK0DO4MkBEEQBMHviIMSBEEQAhJxUIIgCEJAIg5KEARBCEjEQQmCIAgBiTgoQRAEISARByUIgiAEJOKgBEEQhIBEHJQgCIIQkIiDEgRBEAIScVCCIAhCQOLYWnxKqf2ArzsWdsZs4dFeEfvbr/3t2XYQ+9uq/cla6wY3BXTMQTUGpdQaXxYWbKuI/e3X/vZsO4j97d1+6eITBEEQAhJxUIIgCEJA0loc1HNOK+AwYn/7pT3bDmJ/u7a/VYxBCYIgCO2P1vIGJQiCILQzxEEJgiAIAUmrcVBKqfuVUt8opTYopRYrpbo7rZM/UUr9TSmVU10G7ymlYp3WyV8opa5RSm1WSlUppdpNyK1SKkMptUUptU0p9Tun9fEnSqmXlFI/KqU2Oa2LEyilkpRSXyilsqvb/kyndXKCVuOggL9prQdprVOBD4E/Oa2Qn1kCDNRaDwK2Avc4rI8/2QRcCSxzWhF/oZQKBp4CLgL6A9cppfo7q5VfeRnIcFoJB3EBd2ut+wHpwC/bWf0DrchBaa0Pu512ANpVdIfWerHW2lV9mgX0cFIff6K1ztZab3FaDz8zAtimtc7VWpcDrwMTHdbJb2itlwEHndbDKbTWP2it11V/PgJkA4nOauV/QpxWoDEopR4EbgQOAec4rI6T3AK84bQSQouSCOx2O98DjHRIF8FBlFIpwBBgpbOa+J+AclBKqU+Brl4u3au1/o/W+l7gXqXUPcBdwH1+VbCFacj+6jT3Yl7/5/lTt5bGF9vbGcrLd+2q10AApVQ08A6Q6dGL1C4IKAeltT7fx6TzgY9oYw6qIfuVUjcBlwLn6TY2ga0Rdd9e2AMkuZ33APY6pIvgAEqpUIxzmqe1ftdpfZyg1YxBKaX6uJ1OAHKc0sUJlFIZwG+BCVrrY07rI7Q4q4E+SqnTlFJhwCRgocM6CX5CKaWAF4FsrfWjTuvjFK1mJQml1DtAX6AKs03HHVrrfGe18h9KqW1AOHCg+qssrfUdDqrkN5RSVwBPAglAMbBBa32hs1q1PEqpi4HHgWDgJa31gw6r5DeUUguA8ZjtJvYB92mtX3RUKT+ilPoJsBz4FvPMA/i91vq/zmnlf1qNgxIEQRDaF62mi08QBEFoX4iDEgRBEAIScVCCIAhCQCIOShAEQQhIxEEJgiAIAYk4KEEQBCEgEQclCIIgBCT/DxgL99bv9INaAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"data = datasets[-1]\n",
"np.random.seed(123)\n",
"n = 100\n",
"\n",
"# Sample the PDFs, then get x and y for true values\n",
"samples = np.concatenate(tuple(d.rvs(int(n*frac)) for frac, d in data), axis = 0)\n",
"x = np.linspace(np.min(samples)-0.1, np.max(samples)+0.1, num=2**9)\n",
"y_true = reduce(np.add, (frac * d.pdf(x) for frac, d in data))\n",
"kde = KDE('epa', bw = 0.4).fit(samples)\n",
"y_kde = kde.evaluate_sorted(x)\n",
"\n",
"\n",
"plt.title(f'Data set {i}')\n",
"plt.scatter(samples, np.zeros_like(samples), marker='x', color='red')\n",
"plt.plot(x, y_true, label='True PDF')\n",
"plt.plot(x, y_kde, label='KDE')\n",
"plt.legend(loc='upper right')\n",
"plt.tight_layout()"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl8VOW5wPHfM1nJSkggCQESNhd2JGziEndcKlpFsS5oVVxqa+ttb21rtaXqrdrqrVfaSpWqVETEDRXFjXFBtrATEAhbCAlrIJCELDPz3j9mJkySmcwkZCGc5/v55MPMOe85531jnGfeXYwxKKWUUrb2zoBSSqmTgwYEpZRSgAYEpZRSHhoQlFJKARoQlFJKeWhAUEopBWhAUEop5aEBQSmlFKABQSmllEd4e2egKVJSUkxWVlazri0vLyc2NrZlM9QBWLHcViwzWLPcWubQrFix4oAxpmuwdB0qIGRlZZGbm9usa+12Ozk5OS2boQ7AiuW2YpnBmuXWModGRHaGkk6bjJRSSgEaEJRSSnloQFBKKQVoQFBKKeWhAUEppRSgAUEppZSHBgSllFKABQNC/r4yvtt6oL2zoZRSJx3LBYR/2Lfy33PXtnc2lFLqpGO5gFDlcFJ6rKa9s6GUUicdywUEp8tQVuXAGNPeWVFKqZOK5QKCw2UwBiqqne2dFaWUOqlYLiA4Xe6aQVmVo51zopRSJxfLBoSjlRoQlFLKl2UDgtYQlFKqLssFBIfLBUCZ1hCUUqoOywWE4zUEHXqqlFK+LBcQHNqHoJRSflkuIGgfglJK+We5gOBwegKC1hCUUqoOywUErSEopZR/lgsI3lFGRzUgKKVUHZYLCLU1BG0yUkqpOkIKCCIyXkQ2iUi+iDzs5/x5IrJSRBwicn29c04RWe35medzvLeILBWRLSLypohEnnhxgnNok5FSSvkVNCCISBgwDbgcGADcJCID6iUrAG4HZvm5xTFjzDDPz9U+x58CnjPG9AcOAXc2I/9NpjUEpZTyL5Qawigg3xizzRhTDcwGJvgmMMbsMMasBVyhPFREBLgQmOs59CpwTci5PgG18xC0hqCUUnWEh5AmA9jl874QGN2EZ0SLSC7gAP5sjHkPSAYOG2O8n8qFnuc0ICJTgCkAqamp2O32Jjz6uLKyMux2O5WVVQAcOHy02ffqSLzlthIrlhmsWW4tc8sKJSCIn2NN2V2mlzGmSET6AF+KyDrgSKj3NMZMB6YDZGdnm5ycnCY8+ji73U5OTg5iXwA1DhwSTnPv1ZF4y20lViwzWLPcWuaWFUqTUSHQ0+d9D6Ao1AcYY4o8/24D7MBw4ADQWUS8AalJ9zwRvvMQdNc0pZQ6LpSAsBzo7xkVFAlMAuYFuQYAEUkSkSjP6xRgHLDBuD+JFwLeEUmTgfebmvnm8PYh1DgNVY6QujyUUsoSggYETzv/A8ACYCMwxxiTJyJTReRqABEZKSKFwETgRRHJ81x+JpArImtwB4A/G2M2eM79GnhIRPJx9ym83JIFC8TpMiREuysmOvRUKaWOC6UPAWPMfGB+vWOP+rxejrvZp/513wGDA9xzG+4RTG3GGIPDZegcE8mRSgdllQ5S4qLaMgtKKXXSstRMZU9rEZ1jIgCtISillC9LBQTvOkaJndwBQfdEUEqp4ywVELwjjDrHuFfJ0BqCUkodZ6mA4B1h1Lm2hqDbaCqllJelAoLT6a0haB+CUkrVZ6mA4K0haB+CUko1ZKmA4O1DiIkMJyJMtIaglFI+LBUQvKOMwsOEuKhwXQJbKaV8WCogeGsI4TYhLjpcawhKKeXDUgHB24cQZhPioiK0D0EppXxYKiAcryHYiI8Kp6xKh50qpZSXpQKCw+lTQ9AmI6WUqsNSAaFOH4J2KiulVB2WCgjeUUZhYVpDUEqp+iwVEHxrCPFR4dqprJRSPiwVEOqOMgqnyuGiWndNU0opwGIBwXeUUZxn17RybTZSSinAYgGhfg0BdIE7pZTyslRAcHqXrrAJ8Z4agvYjKKWUm6UCQp15CFG6BLZSSvmyVECo7UPwDDsFdLayUkp5hBQQRGS8iGwSkXwRedjP+fNEZKWIOETkep/jw0RksYjkichaEbnR59wrIrJdRFZ7foa1TJECc9SbmAbaZKSUUl7hwRKISBgwDbgEKASWi8g8Y8wGn2QFwO3AL+tdXgHcZozZIiLdgRUissAYc9hz/lfGmLknWohQOWs7lW3ERIYB2mSklFJeQQMCMArIN8ZsAxCR2cAEoDYgGGN2eM7VGdRvjNns87pIRPYBXYHDtAN/NQRdvkIppdxCCQgZwC6f94XA6KY+SERGAZHAVp/DT4jIo8AXwMPGmCo/100BpgCkpqZit9ub+mgAysrKyCvcCMCypUvoEi0IsH7zVuxmV+MXd2BlZWXN/p11VFYsM1iz3FrmlhVKQBA/x0xTHiIi6cBMYLIxxluL+A2wB3eQmA78Gpja4EHGTPecJzs72+Tk5DTl0bXsdjv9uvaG9es5d9zZdEuIJu6rBSSnZpCTM7BZ9+wI7HY7zf2ddVRWLDNYs9xa5pYVSqdyIdDT530PoCjUB4hIAvAR8IgxZon3uDGm2LhVAf/G3TTVqpw+E9MAz54I2mSklFIQWkBYDvQXkd4iEglMAuaFcnNP+neB14wxb9U7l+75V4BrgPVNyXhzeOchhNvcxY6L1iWwlVLKK2hAMMY4gAeABcBGYI4xJk9EporI1QAiMlJECoGJwIsikue5/AbgPOB2P8NLXxeRdcA6IAV4vEVL5kdtDSHMXUOI0xqCUkrVCqUPAWPMfGB+vWOP+rxejrspqf51/wH+E+CeFzYppy3Ad5QRQFx0BKXHdGKaUkqB5WYqezbI8fYhRIdTVqkBQSmlwGIBoXa1U9FOZaWUqs9SAcHpMtgEbJ4aQlJsJCXl1dQ4dZMcpZSyVEBwuEztCCOA01PjqXEatu0vb8dcKaXUycFSAcHlMvjEA85MTwBgY/GRdsqRUkqdPCwVEOrXEPp0jSUyzKYBQSmlsFhAcLpM7QgjgIgwG/1T49igAUEppawVEBwuV+0cBK8z0xO0hqCUUlgsINSvIQAMSE/gQFk1+45WtlOulFLq5GCpgOBwGr81BICNxUfbI0tKKXXSsFRAcLpM7TpGXgN0pJFSSgEWCwj1RxkBJMZE0D0xWgOCUsryLBUQ/PUhgHYsK6UUWCwg+BtlBO6AsHV/OZU1znbIlVJKnRwsFRAaqyE4XYb8fWXtkCullDo5WCoguPsQGgaEAd3dHcsbirTZSCllXZYKCIFqCJldYoiJDNMZy0opS7NUQHDPQ2hYZJtNOD0tXjuWlVKWZqmAEKiGAMdHGhlj2jhXSil1crBUQHC4XISH+Q8IfVJiOVLp0D2WlVKWZamA0FgNIS0xGoC9R6raMktKKXXSCCkgiMh4EdkkIvki8rCf8+eJyEoRcYjI9fXOTRaRLZ6fyT7HR4jIOs89nxcR/5/ULSjQKCOAtAR3QNhzRBe5U0pZU9CAICJhwDTgcmAAcJOIDKiXrAC4HZhV79ouwGPAaGAU8JiIJHlO/wOYAvT3/IxvdilC1FgNIdUTEPaWakBQSllTKDWEUUC+MWabMaYamA1M8E1gjNlhjFkL1N+t/jLgM2NMiTHmEPAZMF5E0oEEY8xi4+7FfQ245kQLE4y/tYy8uiVEAbBXawhKKYsKDyFNBrDL530h7m/8ofB3bYbnp9DP8QZEZArumgSpqanY7fYQH11XWVkZR8tsHAw7FvAecRGw8vtt2MN2N+sZJ6OysrJm/846KiuWGaxZbi1zywolIPhrYwl1bGaga0O+pzFmOjAdIDs72+Tk5IT46LrsdjuR0S66p3UhJ2eY3zQ9Vn9NWFwncnJGNusZJyO73U5zf2cdlRXLDNYst5a5ZYXSZFQI9PR53wMoCvH+ga4t9Lxuzj2bzekM3IcA7pFGOspIKWVVoQSE5UB/EektIpHAJGBeiPdfAFwqIkmezuRLgQXGmGLgqIiM8Ywuug14vxn5bxKHywSchwCQGh+to4yUUpYVNCAYYxzAA7g/3DcCc4wxeSIyVUSuBhCRkSJSCEwEXhSRPM+1JcCfcAeV5cBUzzGA+4CXgHxgK/Bxi5bMj8ZGGQGkJkZzoKwKh7N+37hSSp36QulDwBgzH5hf79ijPq+XU7cJyDfdDGCGn+O5wKCmZPZENTbKCCA1IQpjYH9ZFemJndowZ0op1f50prKP2slpOhdBKWVBlgoIgXZM86qdnKYdy0opC7JUQAjah1AbELSGoJSyHksFhMbWMgJIjo0k3CY60kgpZUmWCQguYzAGwhrpVLbZhG7xUVpDUEpZkoUCgvvfxuYhgHvoqQYEpZQVWSYgOD0BobE+BHCPNNJRRkopK7JMQKitIQQJCKkJ0ezTUUZKKQuyTEDwTj4OVkNITYjmaJWD8ipHi+fh7RWFrCw41OL3VUqplmCZgBB6DcG9L4J3pNHRyhpmfLudnQfLTzgPf/ggj3/Yt57wfZRSqjVYJiA4jTsiNDbKCI7PVvZ2LL+yaAdTP9zA+c/YufXlpXy+YS/GhLr693FlVQ6OVjrYsvdok69VSqm2YJmAEHINIfF4QDDG8M6q3Qzr2ZlfXHwaW/aWcddrubz0zfYmP9/bUb2zpILKGmeTr1dKqdZmmYAQ6igj3+UrVu06zPYD5fxodC8evLg/3/76AsYPTOPPn3zPd1sPNOn5xaXHADAG8veVNb0ASinVyiwTEEKdhxAXFU5cVDh7Sit5e0Uh0RE2Lh+U5rnWxl9uGEpWcgw/nbWKosPHQn5+sc9Q1s3abKSUOgmFtPz1qSDUGgK4O5Z3lVSwfEcJlw1MIz46ovZcXFQ4L96azTXTFjFlZi7ZmV1YW3iY/H1lPH/TcHJO7+b3nt4mo3CbsHlv3RpC0eFjuIyhR1JMM0unlFInzno1hJACQjRfbd7PkUoH153VcJuHft3i+MvEoeQVHeHN5bsIswkiwuxluwLes7i0kpS4SPp2jWvQsfyTWSt56M01TSuQUkq1MOvUEFyhjTIC90gjh8uQmhDFuH4pftOMH5TG8t9dTOdOEYSH2fjDvDzeWFZAWZWDuKiGv9bi0mOkJ3YiMzmGNYWHa4+XHqthza7DdI6JbGbJlFKqZWgNwY9uno7la4ZnNNrElBIXRXiY+1d45ZB0qhwuvti412/aPaWVpCVGc1pqPLtKjtVOfFu2vQSXgZLyao5W1jSlSEop1aIsExCa0oeQmexuy/fXXBTIiF5JpCZE8dHaYr/ni0srSU+M5rTUOOD4SKNF+cdHK+08WBHy85RSqqVZJiA0pYZw7fAMPvzpOZyWGh/y/W024YrB6dg372/wTb+i2kHpsRrSEzvV3tM70mjx1oN0jXfPjt5VogFBKdV+LBMQmlJDiI4IY1BGYpOfcdWQdKodLr7YuK/Oce+Q0/TEaDKTY4kMt7F571H2H61i096jTBzhrons1ICglGpHIQUEERkvIptEJF9EHvZzPkpE3vScXyoiWZ7jN4vIap8fl4gM85yze+7pPed/vGYLcXmWmwg2D+FEDO+ZRHpiNB/WazbyDjlNS4wmzCb07RrH5r1lLNl2EIDLBqaRFBOhTUZKqXYVNCCISBgwDbgcGADcJCID6iW7EzhkjOkHPAc8BWCMed0YM8wYMwy4FdhhjFntc93N3vPGmH20ouM1hNarFHmbjb6u12zkW0MAOD3VPfT0u60HiY8OZ2D3BHolx1JQcuIL6CmlVHOF8uk4Csg3xmwzxlQDs4EJ9dJMAF71vJ4LXCQi9b+K3wS8cSKZPRFN6UM4EVcOSafa6eJzn9FGxZ4Zzd5lMfqnxlNUWsmX3+9ldO9kwsNsZHaJ0RqCUqpdhTIPIQPwnXFVCIwOlMYY4xCRUiAZ8F3w50YaBpJ/i4gTeBt43PhZRlREpgBTAFJTU7Hb7SFkuaHyikpAWLVyBQe2tF4twRhDfAS8/W0eSaX5AKz4vor4SFiy6BsAqve7h5zuPVLFRd0PYbfbMWXV7D5Uw+dfLmzRoFVWVhby72zVPgfdY22kxnbsrqWmlPlUYsVya5lbVigBwd+nU/0P7kbTiMhooMIYs97n/M3GmN0iEo87INwKvNbgJsZMB6YDZGdnm5ycnBCy3NCyNz4HqhgzaiT9mzB6qDnG7spl896jePP62o7l9EqpJCfnXAB6HyznbyvtANw2fjRnpCWwP24XH2xdS98ho+idEtvo/StrnBQdPkafrnFB82K32xl37nnMXlbA1cMySOwU4TfdFxv38rdPcrl6aHeev3J4wPv9Z8lOyqsc3HN+36DPbi92u53m/p10ZFYst5a5ZYXyVbAQ6OnzvgdQFCiNiIQDiUCJz/lJ1GsuMsbs9vx7FJiFu2mq1Xj7EGyt3GQEMDKrCzsOVrDvqLvvoOiwe5ayV8+kGKIjbCTHRnK6JzhlJruDQLCNeIpLj3HdP77j4me/YtOe0BbJ+78v8/n9+3m8let/aY1dJRU8NMe9dMaKnYF3dNu6v4w/fpDHXz/dTOkxnUSn1KkmlICwHOgvIr1FJBL3h/u8emnmAZM9r68HvvQ2/4iIDZiIu+8Bz7FwEUnxvI4ArgLW04pqRxm1QUDIzkoCIHeH+8N1z5HK2g5lcAelcX1TuGJwOt6uFu9kuIJGhp6uKjjE1S8sYufBCqIjwnhhYX7QvOQfcvLCl1sAWLKtpMH5KoeTB2atxGUMk8dmsvvwsdrNgXwZY/jDvDxEhGqni0/W+5+Ap5TquIIGBGOMA3gAWABsBOYYY/JEZKqIXO1J9jKQLCL5wEOA79DU84BCY8w2n2NRwAIRWQusBnYD/zrh0jTC1YR5CCdqUEYi0RE2lu8o4Vi1k8MVNaT5BASAl28fyZ+uGVT7vlt8FNERNr8dyy6XYebiHdw4fQmdIsJ49/6zuW1sFh+uLWp0b4WyKgcvrq2ie+dOXDUknWXbD9au6eT1P/O/Z01hKc9cP5RrPTOzV/qpJXyyfg/fbDnAby8/gz4psby7aned88YYNhYf4f3Vu3lmwfc8++mmZu0sp5RqPyEtbmeMmQ/Mr3fsUZ/XlbhrAf6utQNj6h0rB0Y0Ma8nxFk7yqj1O0wjwmwM75nE8h0ltRvjpNcLCPWJCL38jDT6fs8RfvPOOlYVHObc/in8bdJwusRGcte5vXn1ux38fWE+z944zO89p36Qx4FjhjmTh1F0+Bgfri1mY/GR2kl3xaXHeOW7Hdw2NpPxg9KodriICrexYuchLh+cXnufimoHf/pwA2ekxXPLmEyOVDp49rPN7D58jIzO7qawR9/PY+aSnZ6yuDcCGt4riQvOaNXpJUqpFtSxh5M0QVvWEABG9u7ChqIjtd/gffsQAunVpe5chHdWFnLV89+y82AFz94wlNd+PIouse5VUVPiorh5dC/eW72bHQca9jt8vXk/c3ILubJPBCOzujC6dzJA7WQ4gPnr9gBw+9lZAESG2xjaozMrCurWEP6+cCtFpZX86ZpBhIfZuGZYBgDzVru7kpZtL2Hmkp3cmN2TBT8/j7w/XkZG5068sDD/hGoJxhhmLS3QJT2UaiOWCQjONpqH4DUyKwmXgfnr3G3twWoI4O5HKCipwBhDjdPF059sYmBGIl88dD4/PKsH9ad2TDmvDxFhNv5ur9uXUON0MfXDDWQlxzChn3tUUVpiNL1TYuv0I8xfV8wZafF1RiudlZnE+t2ltfs+H6t28up3O7hySDojs7oA0Cs5hhGZSby7qpBqh4vfvruOjM6deOzqAZyeFk9MZDhTzuvDip2HWLa9Yb+FV7Bg8e6q3fz23XU899nmoL87pdSJs0xAqK0htOLSFb6G90rCJvDZBvcEtfp9CP706hJDZY2LfUermL+umD1HKvnZhf1IivW/V0K3hGhuGtWLd1burvPNf+bineTvK+ORKwcQ4RMAx/TpUtuPUFx6jBU7D3HVkPQ69xyRmUSN07B+dykAH64t4miVg8ljs+qku2Z4Bpv3lvFfb60hf18Zj18ziJjI4y2QN47sSUpcJNPsW/3mffHWg2Q//jmfb/C/XPj+o1VM/XADIjB/fXGzlgYvLj1G/j7drlSpUFkmIDjbcJQRuLfaHNg9kfJqJ11iI4mOCAt6TS/PSKOdByuY8e12+qTEckGALTm9HryoP1kpsdz5ynJWFhziYFkVz32+mXP7p3DRmXWvHdMnmSOVDjYWH6ltLrpicN2AMLxXZ+D48NM3lhXQt2ssIz0jp7yuGpxOuE34YE0RVw5Ob9BXEB0Rxo/P6c3Xm/ezrrC0zrnKGie/eWctB8ureXD2Kr97TP/hgzwqqpw8c/1QKmtcDdaHCmb1rsNc/rdvmPDCInY3Ye9rpazMMgHB5XL/21Z9CHB8+GlaQvDaAUBmF3dAeG/1btYUlnLHuKyg8yaSYiN5/a7RpMRHMXnGMn751hoqqp08etWABk1Mvv0I/pqLwN03kZUcw4qdh9i05ygrCw5z06heDe6VFBvJhWd0Iz4qnEd/UH9pK7dbx2QSHx3eoElr2sJ8dhys4K8ThxITFc5dr+ZyqLy69vyCvD18tLaYn13Uj+vOyqB/tzjmBJhD4c+Gg05+9K8lxEWF4zLw23fW6YgnpUJgmYDQlqOMvEZ52txD6T8A6JEUg01g9rICEqLD+WGIG/SkJkTz+l2jSYiOYOGm/dw6JtPvbGxvP8L7q4v8Nhd5nZWZxMqCQ7yxrIDIMFvAjYKeum4IH/7snNo1muqLj47g9rOz+Hj9Hh59fz3lVQ627D3KP7/ayg+HZ3DdiB68eOsI9pRWct/rK5j+9VZ++dYafv32Ws5Ii+ee8/siItyQ3ZNVBYdDav75YuNens2tpGdSDO/cdza/uux0vtq8n3dW7g56rVJWZ5mA4O1DaMMKAiO8NYQQA0JkuI30xE64DNw0uhexfvZmDqRHUgyz7h7NXef05heXnBYw3Zg+XVjn6R+o31xUm+/MJA6UVfPGsgLGD0oL2IeRFBtZO8M6kJ9c0I87xmUxc8lOxv/tax6cvZq4qHB+d+WZAJzVK4knrh3Ekm0lPDn/e77avJ/BGYk8f9NwIjzbk3q3Mn0rt7DRZzmcLh55bz3d42y8ec8YuiVEM/nsLEZkJjH1ww3sP1rV6PUt6ZP1xazZdTh4QqVOIpYJCE7j7j9ouAhr6+kWH80vLz2Nidk9gyf2yEyOIcwmDTpxQ7s2lkeuGhBwvSJw9yMAfpuLvEZkugNZlcPFTaN6NTkfvqIjwnjsBwN5c8pYbCJsKD7Cb684k+S4qNo0E7N78t3DF7Lq95ew/HcXM/PO0XV2q+saH8UFp3fj7ZW7qXG6Aj5r4ab9FJdWMqFfBJ1j3EEszCY8dd0QjtU4eWjOavb5mYXd0g6VV/OTWauY+OJiFuTtafXnKdVSQv8K2sG5TNv2H3g9cGH/JqW/85zejB+URvfOwectNMeYPsmE24Srh3UPmKZ/t3jio8JJiY9iTJ8uLfLcUb278MmD57F612G/9wxW3huye/D5xr384s3V1DhdFJdWct1ZPZjsmUMB8PrSnaQmRDGsa90O/H7d4vj9lWfyxw82cO7TC7l1TCb3nN+3duvSlvbphj04XYbMLjHc958VPHntYCadYGBVqi1YJiA4jWmzEUYn4qIzU1v1/qkJ0Xzy83MbbeoJswmPXzuIbvHRLVqj6hQZxti+yc269oIzupGVHMMXG/eRkdQJp8vwxEcbGdcvhX7d4thVUsFXm/fzswv7E2arv/Yi3Do2i/NP68bzX25hxqLtzF1ZyNx7x9KvW8uvfPvRuj307NKJD356Dve/vpKH31nHkcoappx38q4QqxRYqMmovWoIJ6N+3eJr2+cDmTAso9kf3q0hIszGl/+Vw4apl/H5Q+cz556xREfY+O2763C5DLOWFWATabSJq1dyDH+ZOJRPfn4e4Tbh9n8vb/F+hcMV1XyXf4ArBqcTGxXOS5OzuXJIOk/O/75JI6Waq7LGyTMLvm+TpjF16rFMQHAaCA/yIahObjafPqCu8VH89oozWba9hNeXFTBn+S4uOqNbSB34p6XG8/LkkRwoq+Ku13I5Vu1ssTx+umEvDpfhSk+HfUSYjeduGMa5/VP4zTvr+GKj/4l4gbyxrIAxT37BgbLQAtcbywqYtnArf/xwQ5PzrpRlPiFdLq0hnGpuyO7JqKwuPPb+eg6WV3PzmMyQrx3aszPPTxrO2sLDTJmZy4K8Pew9Uokxht2Hj/H5hr28sayAsipHk/I0f10xPZI6MdizgCC4R4/945YRDEhP4CezVjJ3RSG5O0rYur+MKkfgYOR0GaYtzGfPkUqe/uT7oM92uAz/+nobkeE2Plpb3OiyIV67Sir4yevuPClloT6EtpulrNqGzSY8+cNBXP63b8hIjObcfilNuv7SgWlMnTCIqR/k8c0W926v0RE2KmuOj2R64ct8nvzhYM4/rWvQ+5VW1LAo/wB3jOvdoO8lLiqcf98xkon/XMwv31pTezwlLorfX3UmVw/t3uCazzbsofDQMYb0SGRObiE/Gp3JsJ6dAz5/cZGDotJq/nHzWUz9cAN//CCPeQ+c4/eLkDGGN5bt4omPNlBe7WT7gXKuHxHavBd16rJMQNA+hFNTv27x/POWESR0imjWbni3jslk4oge5BUdYW3hYQpKKujTNY4B6fHUOA2/e3cdk2cs44bsHjxy1QASogMP6f1s415qnCbg/I6UuCg+fvBc8veVcbC8mgNHq3h18Q4enL2aObm7+NOEQXWGAs/4dgc9kjox887RXPLsVzz2/nrevX+c33I6XYaPttcwID3BvZS508WDs1czd8UubhzZi8oaJ99uOcDmfUcpOFhBXtER1u0uZVy/ZPqkxDFzyU4OlFWREtc6I69Ux2CZgNBRRhmppjvRkVnREWGMyEyqnX/h66OfncvzX2zhxa+3sSj/IP87aVjtqq9eFdUO9h2p4t1VhWR07sTQHokN7uP7rEE+zUnXDM9g1tKdPL1gExNeWMTrd49mSI/OrCssZdmOEh658kwSO0XwmyvO4BdvruEtzwd8fZ/m7WFPueGRCe7Z3VcP7c5ri3fyzIJNLNt+iE/z9nDU0/wdNaydAAAVgUlEQVSVEhdJry4xPHHtIH40qhdrC0uZuWQn3209yNVDAw9HVqc+ywQErSGo5oiOCOO/x5/BxQNS+fns1dz44mLuPq8PcZHhrCw4xOpdhzlUcXwl1nvO79OkobphNuHWsVlceGYqN764mFtfXsbsKWOYsWg7sZFh3DDSPanxmmEZvL6kgMc/2sjqXYcZ1rMzA9IT6RRpQ0SYZs8nNUa4fJC7diIiPPaDAVwzbRGf5u1h/KA0fjC0O2dlJhFXbwb8oIxEEjtF8O2W/XUCwn+W7GT7gXIevLh/ozUjdeqwTEBw9yFYpg9dtbCzeiUx/8Fz+cO8PF78yr0b7GmpcVw6II3MlBhS46NJTYiuXdCwqTI6d+KNu8cw8Z+LueWlpRyprOHm0Zm1H8QiwtPXD2Hqhxv4aG0xbyxrOIT1jkGRdb70DOnRma9+dQFd46MaXW03zCac3TeZb7ccwBiDiHC0sob/mb+R8monH64t4olrBnPxgKbVxLz3CqTG6eKVRTu4fHAaPZJimnRv1TosExBcpu32QlCnpriocP4ycSj35/QlOTaKxJiW/dbcs4t7PaobXlyCw2W4Y1xWnfN9usbxyh2jcLkM2w+Ws2XvUWqcBpcxRIXbiNzfcCRSzy6hfdCO65fCx+v3sP1AOX26xvHeqt2UVzt5/JpB/GfJTu56LZfLBqZyX06/Rju2vWYtLeCvn27i7zefxeg+/uezLMjbwxPzNzJ7eQHv3D+u0SVXVNuwTEBwz0PQgKBOXKA1oFrq3u/efzbbDpQHnE1uswl9u8bRt14+7PZNzX7uOZ4RWovyD9A7JZaZS3YyOCORm0f34obsnrz41Vamf7ONBXl7yc5M4roRPUhPjCYlLoqeSTF1guMXG/fyyHvrEBHufi2XufedXWdtKq//LNlJcmwkBSUV3P/6Cl65Y1TQCZOqdYUUEERkPPA3IAx4yRjz53rno4DXgBHAQeBGY8wOEckCNgLev9Qlxph7PdeMAF4BOgHzgQdNKy5a73JRZ/cwpU5WPbvEhPzNvqVkJsfQI6kT3+Yf4LTUeDbvLePp64YgIkSGCz+9qD93nNObt3J3MWPRdn7zzrraayPDbNw8phc/uaAfRYeP8cCsVQzsnsizNwzl5peWMnnGMt65/+w6+4rn7ytjybYS/nv86e5FIN9aw6Pv5/HktYPqNDM5nC5++dYa1u4uxSaCTWBYz8785IJ+QVfaVU0XNCCISBgwDbgEKASWi8g8Y4zvVMg7gUPGmH4iMgl4CrjRc26rMWaYn1v/A5gCLMEdEMYDHze7JEE4jaGTBgSl/BIRzumXwkfrirGJkBAdzg/qjTiKiwrnjnG9uW1sFrtKKjhYXsX+o9Us/H4fry3eyZvLdxEVbqNLbCQv355Nt/hoXrljFDe8uJjbZyxnzr1ja5uFXl+6k4gw914XKXFRbNtfxt/tW+mdElNnzadpC7fy3uoiLjqjG9ERYVQ5XLy/uoi3V+7mh8MzGB0XePVb1XSh1BBGAfnGmG0AIjIbmAD4BoQJwB88r+cCL0gjvUkikg4kGGMWe96/BlxDKwYEHWWkVOPG9Uth9vJdfLx+D3ee05tOkf47osNsQlZKLFkp7m/o4welcc/5fXj2s82sKjjMqz8eSbd49xIiA7on8OKtI7j938u4d+YKXvnxSFwueHtFIeMHpdfOe/jlpaez82AFT87/nozOMVw5JJ1VBYd4/sstXDOsO/87aXjt8/cdqeSfX23j9aU7+TLccElOTcD+B6fLUOVw1tnvWwUWSoNdBuA7pKHQc8xvGmOMAygFvD1JvUVklYh8JSLn+qT3nSvv754tSkcZKdW4cT4zvW8e3bTluvt0jeOFH53FoocvbLCC7Lh+KTx9/RAWbzvIr+eu5YM1RRypdHCLzzNsNuGvNwwlOzOJX8xZzVeb9/OLN1eTlhDNHycMqnO/bgnRPPqDAbx5z1gOVxl++27DLVLLqxy8smg7OX9ZyLg/f0lxad19tRdu2scP/u/bJq8tdaoLJWz6+1pdv60/UJpioJcx5qCnz+A9ERkY4j3dNxaZgrtpidTUVOx2ewhZbqjG4aT08KFmX99RlZWVaZktoiXKfVqSjU7hQkFeLgUtky0AkoAf9o/gndVFzF9XRPc4oWLnWuwFdT8Kbu9reHy/YfKMZQjw61HRrFq6KOB9r+hl+GBtMWmug5zbI4Iqp2HBjhoW7KihvAb6Jtoor3Jx9/Sv+K/sKESEQ5UuHll0jGMOuPPVXMZ2D+PmM6KIizyel2qnYddRF3srDENSwuqca46SShcOF3SLOfEvpa359x1KQCgEfLf86gHUX3Dem6ZQRMKBRKDE00lcBWCMWSEiW4HTPOl9F07xd088100HpgNkZ2ebnJycELLsx3cf0y0lmZyckc27voOy2+00+3fWQVmxzNAy5R59thMRGp230Fznn2+IencdbyzbxZQLzuSCcb39phsyooKb/rWE60f04N5GtoMFcJmF7A+L5o3NpaRn9uWl77az50gNlwxI5d7z+zAiswszF+/g9+/nUdipDz8a1YtbXlqKi2o+fnAc89cVM21hPusOVtMtPoqIMBtOY9h+oAKnZ9/dLrGRPHz5GUwc0aNZ+4NUOZxc8uzX7D9axcu3Z3N236atuVVfa/59hxIQlgP9RaQ3sBuYBPyoXpp5wGRgMXA98KUxxohIV9yBwSkifYD+wDZjTImIHBWRMcBS4Dbg/1qmSP5pH4JSwQXqN2gJIsKfJgzi0oFpjS5E2Cs5hm9/fUFIH742EZ67cRjj//cbHv9oI0N6uPfjHtX7+PIit4zJ5NMNe3nyo41s2nOExdsO8vR1Qzg9LZ7T0+K5bGAaM5fsoKzKSY3DhcsYxg9MY1BGIl1iI3n6k+/577lrmZtbyL05fTinX1ciw20YY8jdeYj3V+/mikHpnB2gTDO+3UFBSQXdE6O549/L+ddt2ZwXwmKJ7SFoQDDGOETkAWAB7mGnM4wxeSIyFcg1xswDXgZmikg+UII7aACcB0wVEQfgBO41xnjX5L2P48NOP6YVO5TBs5aRzkNQql2Fh9m44PRuQdM15Zt4emInXvvxKIoOH+OygWkNFv/zzvK+7Lmv+c+SAq4cks7E7OMNFAO6J/A/PxwS8P5z7hnLWyt28dQnm/jxK7kkdorggtO7snZ3Kdv2lwPw3daDfP6L8xs8e9/RSl74cgsXn9mNp64bws0vLeWuV3N5ZuIQrhic3mDeRZXDSeGhYxSUVOByGS44vVuzFm1srpC63o0x83EPDfU99qjP60pgop/r3gbeDnDPXGCQv3Otwb0fgnYqK3UqGtqzM0MbmUGdntiJv94wjFlLd/LktYObFHBsNuHGkb24dngPvtmyn4/WFvPF9/vo1y2OZ67vi8sYfv32Oj7buJfLBqbVufYvCzZR7XTxuysHkBwXxRt3j+G2Gct4cPZqHpuXx8VnpnJaahwbPKvPbj9QjsunN/Wcfin8ZeLQkDZ+agmWGYul+yEoZW2XDEjlkiaux+QrMtzGRWemNlhd1+F0MW3hVv5u38qlA1Jrg8363aW8taKQu87pTW/PEN2k2Ejeuncs9k37WZC3hwV5e5i7wkFqQhSDMxK5cnA6mcmxZCbH8P2eozzx0UbG/+1r/ufawVweYFn1lmSZgKB9CEqp1hAeZuPu8/rw+/fWs2RbCWP7JlNSXs2v5q6lS0wkP72of5300RFhjB+U5t63wuGirMpBl9jIBvfNzurC2X2T+fmbq7nv9ZW8c//ZnNWreYsnhsoybShaQ1BKtZaJI3qQEhfJP7/ayp7SSm58cTHb9pfxlxuGNrp0eKRnZncgfbrG8fZ9ZzPtR2e1ejAACwUElzFaQ1BKtYroiDDuGNebrzbvZ8K0bykureTVH48KqQM9mIgwG1cOaf3mIrBQQNAaglKqNd0yJpO4qHCqHS5m3T2aMQGW/T6ZWawPwTLxTynVxhI7RTD3vrEkREfQvXOn4BechCwTEHQ/BKVUazsjLaG9s3BCLPOV2T0PQQOCUkoFYpmAoH0ISinVOEsEBJfLYNAaglJKNcYSAcHpWStdawhKKRWYNQKCZ3EQHWWklFKBWeIT0uHSGoJSSgVjiYDgdHprCBoQlFIqEEsEBIfLBeg8BKWUaowlAsLxPgQNCEopFYglAoL2ISilVHCWCAg6ykgppYKzxCekozYgtHNGlFLqJGaJj0inp1NZawhKKRWYJT4htQ9BKaWCCykgiMh4EdkkIvki8rCf81Ei8qbn/FIRyfIcv0REVojIOs+/F/pcY/fcc7Xn58S3FgrAofMQlFIqqKD7IYhIGDANuAQoBJaLyDxjzAafZHcCh4wx/URkEvAUcCNwAPiBMaZIRAYBC4AMn+tuNsbktlBZAnJqDUEppYIKpYYwCsg3xmwzxlQDs4EJ9dJMAF71vJ4LXCQiYoxZZYwp8hzPA6JFJKolMt4U3sXttIaglFKBhRIQMoBdPu8Lqfstv04aY4wDKAXqbyh6HbDKGFPlc+zfnuai34tIq31aH68hWKLLRCmlmiWULTT9fVCbpqQRkYG4m5Eu9Tl/szFmt4jEA28DtwKvNXi4yBRgCkBqaip2uz2ELNe18aATgHVr1+DYHdbk6zuysrKyZv3OOjIrlhmsWW4tc8sKJSAUAj193vcAigKkKRSRcCARKAEQkR7Au8Btxpit3guMMbs9/x4VkVm4m6YaBARjzHRgOkB2drbJyckJqWC+wrccgOVLyR4xnJFZXZp8fUdmt9tpzu+sI7NimcGa5dYyt6xQ2lCWA/1FpLeIRAKTgHn10swDJnteXw98aYwxItIZ+Aj4jTFmkTexiISLSIrndQRwFbD+xIoSmKN2HoL2ISilVCBBA4KnT+AB3COENgJzjDF5IjJVRK72JHsZSBaRfOAhwDs09QGgH/D7esNLo4AFIrIWWA3sBv7VkgXzpaOMlFIquFCajDDGzAfm1zv2qM/rSmCin+seBx4PcNsRoWfzxDh0tVOllArKEsNudJSRUkoFZ4lPSK0hKKVUcJYICN7F7bQPQSmlArNEQNC1jJRSKjhLBITaPgTdU1kppQKyREDQPgSllArOEgFBRxkppVRwlviE1BqCUkoFZ4mAoKOMlFIqOEsEBK0hKKVUcJYICE6nrmWklFLBWCIgaA1BKaWCs0RAcLoMNoFW3JRNKaU6PEsEBIcnICillArMEgHB6XKhk5SVUqpxlggIWkNQSqngLBEQnC6jNQSllArCEgHBXUPQiKCUUo2xREBwOrWGoJRSwVgiIGgfglJKBWeJgOB0uQizREmVUqr5QvqYFJHxIrJJRPJF5GE/56NE5E3P+aUikuVz7jee45tE5LJQ79mStIaglFLBBQ0IIhIGTAMuBwYAN4nIgHrJ7gQOGWP6Ac8BT3muHQBMAgYC44G/i0hYiPdsMTrKSCmlggulhjAKyDfGbDPGVAOzgQn10kwAXvW8ngtcJO51IiYAs40xVcaY7UC+536h3LPF6CgjpZQKLpSAkAHs8nlf6DnmN40xxgGUAsmNXBvKPVuM1hCUUiq48BDS+PsoNSGmCXTcXyCqf0/3jUWmAFMAUlNTsdvtATMaSBdnNWEJzmZd29GVlZVZrtxWLDNYs9xa5pYVSkAoBHr6vO8BFAVIUygi4UAiUBLk2mD3BMAYMx2YDpCdnW1ycnJCyHJdOTlgt9tpzrUdnRXLbcUygzXLrWVuWaE0GS0H+otIbxGJxN1JPK9emnnAZM/r64EvjTHGc3ySZxRSb6A/sCzEeyqllGpDQWsIxhiHiDwALADCgBnGmDwRmQrkGmPmAS8DM0UkH3fNYJLn2jwRmQNsABzAT4wxTgB/92z54imllApVKE1GGGPmA/PrHXvU53UlMDHAtU8AT4RyT6WUUu1H5+8qpZQCNCAopZTy0ICglFIK0ICglFLKQwOCUkopAMQ9XaBjEJH9wM5mXp4CHGjB7HQUViy3FcsM1iy3ljk0mcaYrsESdaiAcCJEJNcYk93e+WhrViy3FcsM1iy3lrllaZORUkopQAOCUkopDysFhOntnYF2YsVyW7HMYM1ya5lbkGX6EJRSSjXOSjUEpZRSjTjlAoKIjBeRTSKSLyIP+zkfJSJves4vFZGsts9lywqhzA+JyAYRWSsiX4hIZnvks6UFK7dPuutFxIhIhx+NEkqZReQGz3/vPBGZ1dZ5bA0h/I33EpGFIrLK83d+RXvksyWJyAwR2Sci6wOcFxF53vM7WSsiZ53wQ40xp8wP7qW0twJ9gEhgDTCgXpr7gX96Xk8C3mzvfLdBmS8AYjyv7+voZQ613J508cDXwBIgu73z3Qb/rfsDq4Akz/tu7Z3vNir3dOA+z+sBwI72zncLlPs84CxgfYDzVwAf496Zcgyw9ESfearVEEYB+caYbcaYamA2MKFemgnAq57Xc4GLRKQj77gctMzGmIXGmArP2yW4d6jr6EL5bw3wJ+BpoLItM9dKQinz3cA0Y8whAGPMvjbOY2sIpdwGSPC8TiTADowdiTHma9z7ywQyAXjNuC0BOotI+ok881QLCBnALp/3hZ5jftMYYxxAKZDcJrlrHaGU2deduL9VdHRByy0iw4GexpgP2zJjrSiU/9anAaeJyCIRWSIi49ssd60nlHL/AbhFRApx77Py07bJWrtq6v/7QYW0QU4H4u+bfv1hVKGk6UhCLo+I3AJkA+e3ao7aRqPlFhEb8Bxwe1tlqA2E8t86HHezUQ7umuA3IjLIGHO4lfPWmkIp903AK8aYv4rIWNw7OA4yxrhaP3vtpsU/y061GkIh0NPnfQ8aVh1r04hIOO7qZWPVspNdKGVGRC4GfgdcbYypaqO8taZg5Y4HBgF2EdmBu411XgfvWA717/t9Y0yNMWY7sAl3gOjIQin3ncAcAGPMYiAa95o/p7KQ/t9vilMtICwH+otIbxGJxN1pPK9emnnAZM/r64EvjaeHpoMKWmZP08mLuIPBqdCmDEHKbYwpNcakGGOyjDFZuPtOrjbG5LZPdltEKH/f7+EeRICIpOBuQtrWprlseaGUuwC4CEBEzsQdEPa3aS7b3jzgNs9oozFAqTGm+ERueEo1GRljHCLyALAA98iEGcaYPBGZCuQaY+YBL+OuTubjrhlMar8cn7gQy/wMEAe85ek/LzDGXN1umW4BIZb7lBJimRcAl4rIBsAJ/MoYc7D9cn3iQiz3fwH/EpFf4G42ub2Df9FDRN7A3fSX4ukbeQyIADDG/BN3X8kVQD5QAdxxws/s4L8zpZRSLeRUazJSSinVTBoQlFJKARoQlFJKeWhAUEopBWhAUEop5aEBQSmlFKABQSmllIcGBKWUUgD8P4kUUxCLMOBFAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"good, bws = [], []\n",
"for bw in range(100):\n",
" bw = (bw + 0.000000001) / 100\n",
" kde = KDE('epa', bw = bw).fit(samples)\n",
" more_samples = np.concatenate(tuple(d.rvs(int(n*frac)) for frac, d in data), axis = 0)\n",
" goodness = kde.evaluate_sorted(more_samples)**2\n",
"\n",
" #print(bw, np.mean(goodness))\n",
" \n",
" good.append(np.mean(goodness))\n",
" bws.append(bw)\n",
" \n",
" \n",
" \n",
" \n",
"plt.plot(bws, good)\n",
"plt.grid(True)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x18d5fe00da0>]"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAD8CAYAAACb4nSYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAF4NJREFUeJzt3X2MXNV9xvHvExtDEhIgsIqCX7DTOBVug0DZGLVp6UsMOG1kEwkUo0R1VCSLNlYpKFKcUgF1FCkvVVJaERVLWEqjJA6BVlqpRoQEaBulDl4TXmITJ4sT8NZRcGLIi0iha//6x9y1h2GWubs794zPmecjrTx35t6Zc733PnvmnHPPVURgZmbD4VWDLoCZmaXj0DczGyIOfTOzIeLQNzMbIg59M7Mh4tA3MxsiDn0zsyHi0DczGyK1Ql/SWkn7JU1I2tLl9WslPS7pEUnflLSq7bWPVtvtl3R5PwtvZmazo15X5EpaAHwfuBSYBHYDV0fEvrZ1Xh8Rv6gerwP+MiLWVuH/ZWA1cC7wdeCtEXF0ps8755xzYvny5fPaKTOzYbNnz56fRsRIr/UW1niv1cBERBwAkLQDWA8cD/3pwK+8Fpj+S7Ie2BERLwA/lDRRvd9/z/Rhy5cvZ3x8vEaxzMxsmqSn6qxXJ/QXAwfblieBi7t84IeAG4BFwB+3bburY9vFdQpmZmb9V6dNX12ee1mbUETcFhG/AXwE+NvZbCtpk6RxSeOHDx+uUSQzM5uLOqE/CSxtW14CHHqF9XcAV8xm24jYFhGjETE6MtKzScrMzOaoTujvBlZKWiFpEbABGGtfQdLKtsU/BX5QPR4DNkg6VdIKYCXw0PyLbWZmc9GzTT8ipiRtBu4FFgDbI2KvpK3AeESMAZslrQH+D3gW2Fhtu1fSnbQ6faeAD73SyB0zM2tWzyGbqY2OjoZH75iZzY6kPREx2ms9X5FrZjZE6gzZtEwc/uULfPmhp5k6emzQRTGbtbNPP5U/+53zkLoN+rN+cegX5J7v/pjP3Pd9AHzeWE6mW5nXrHoji8989WALUziHfkGmjrbOnEdvuowzXnPKgEtjVt9deyb58Fcf5ejRk6uPsURu0y+ITxfLXfgobpxDvyDHR2K5accyM33InmSDCYvk0C+Q2/MtNz5m03HoF8jnj+VmOvRd0W+eQ78gx1t3XG2yzKiqqpxsF4uWyKFfEHeCWe58BDfPoV8Q9+Naro437zj1G+fQL8j0+eLWHcuXU79pDv0CyXV9y4z7odJx6BfkREfuYMthNlsep5+OQ78g7si1XHnIZjoO/YK4lmS58zHcPId+gdy8Y7k5Pk7fdf3GOfQLMn1hiztyLTeuqKTj0C+QTyDLjTty03HoF8QXZ1mufHFWOg79gpy4OMuxb7lxm34qDv2CuJZkufMx3DyHfkGma0mu51tu/OU0HYd+QXxFruXKh2w6tUJf0lpJ+yVNSNrS5fUbJO2T9Jikb0g6r+21o5IeqX7G+ll4685t+pab6WPWzTvNW9hrBUkLgNuAS4FJYLeksYjY17bad4DRiHhe0l8AnwLeV73264i4sM/lti58vliujg/Z9FHcuDo1/dXAREQciIgXgR3A+vYVIuKBiHi+WtwFLOlvMa2WCDftWJY8ZDOdOqG/GDjYtjxZPTeTa4B72pZPkzQuaZekK+ZQRqvJ54vlzsdw83o279C9j6Xr70bSB4BR4A/anl4WEYckvRm4X9LjEfFkx3abgE0Ay5Ytq1Vwe7kId4hZnk7U9B37TatT058ElrYtLwEOda4kaQ1wI7AuIl6Yfj4iDlX/HgAeBC7q3DYitkXEaESMjoyMzGoH7IQg3IlrWfJ8UenUCf3dwEpJKyQtAjYALxmFI+ki4HZagf9M2/NnSTq1enwO8E6gvQPY+synjmXJ8+kn07N5JyKmJG0G7gUWANsjYq+krcB4RIwBnwZOB75a1TSfjoh1wPnA7ZKO0foD84mOUT/WRxEeo2958oRr6dRp0ycidgI7O567qe3xmhm2+xbwtvkU0OoL/DXZ8nSiWdKp3zRfkVsQ15Isdz6Gm+fQL0jg4TuWJ9fz03Hol8SZb5lyX1Q6Dv3C+OSxHB2/R66r+o1z6BfEHbmWK1+clY5DvyDhuXcsU27TT8ehXxBXkix3Poab59AvSKt5xyxDPnCTcegXpHVFrs8ey498Y/RkHPqFceRbjnxBbjoO/YL44izLlTM/HYd+QTyfvuXK98hNx6FvZicNt+k3z6FfkNY4fdf1LT8+bNNx6BfGJ4/lyPPpp+PQL4jH6Vuu5DtnJePQL4jH6Vu+pjtyHftNc+gXJAjX9C1Lrumn49AviCtJlj0fw41z6BckcEeu5cmHbToO/eL49LH8HL84y1X9xjn0C9LqyB10Kcxmz0M203HoF8UduZanE3fOGmw5hoFDvyCu6VuuTkytbE2rFfqS1kraL2lC0pYur98gaZ+kxyR9Q9J5ba9tlPSD6mdjPwtvL+Vakpn10jP0JS0AbgPeDawCrpa0qmO17wCjEXEBcBfwqWrbNwA3AxcDq4GbJZ3Vv+Jbu9Y4fVf1LT++MXo6dWr6q4GJiDgQES8CO4D17StExAMR8Xy1uAtYUj2+HLgvIo5ExLPAfcDa/hTdunHzjuXMkd+8OqG/GDjYtjxZPTeTa4B7ZrOtpE2SxiWNHz58uEaRrBvPp2+5ckduOnVCv1uOdP3VSPoAMAp8ejbbRsS2iBiNiNGRkZEaRbJuWhdnOfYtP/K9s5KpE/qTwNK25SXAoc6VJK0BbgTWRcQLs9nW+sO1JMudj+Hm1Qn93cBKSSskLQI2AGPtK0i6CLidVuA/0/bSvcBlks6qOnAvq56zBvhqRsuVv6Cms7DXChExJWkzrbBeAGyPiL2StgLjETFGqznndOCrVfPC0xGxLiKOSPoYrT8cAFsj4kgje2LgcfqWKc+ymU7P0AeIiJ3Azo7nbmp7vOYVtt0ObJ9rAW12HPqWo+MXZzn1G+crcgvSunOWU9/yc6Km79RvmkO/IK0bow+6FGaz5wnX0nHoF8Tni+XOx3DzHPoF8cVZlit/Q03HoV8QX5xl+fKN0VNx6BfGkW85cl0lHYd+QcLtO5Ypd+Sm49AvSGvIpll+fI/cdBz6JfH5YplzTb95Dv2CBOGOXMuSj9p0HPoFcZO+5crz6afj0C+MK/qWI98YPR2HfkFaNX2nvuXH98hNx6FfkFab/qBLYTZ3jvzmOfQL4kqSmfXi0C+IM99yJd8iNxmHfkEiPPeO5ckXZ6Xj0C+MI99y5GkY0nHoF8UduZYn3yM3HYd+QcI3RrdM+R656Tj0C+Lzxcx6cegXJCJ8cZZlyTdGT8ehX5DWnbMGXQqz2XNHbjq1Ql/SWkn7JU1I2tLl9UskPSxpStKVHa8dlfRI9TPWr4Jbd858y5I7cpNZ2GsFSQuA24BLgUlgt6SxiNjXttrTwAeBD3d5i19HxIV9KKv1EK7qW6aON0u6qt+4nqEPrAYmIuIAgKQdwHrgeOhHxI+q1441UEaryXfOslx5yGY6dZp3FgMH25Ynq+fqOk3SuKRdkq6YVelsVjxDoZn1Uqem363yOJt0WRYRhyS9Gbhf0uMR8eRLPkDaBGwCWLZs2Sze2jq5dcdy5I7cdOrU9CeBpW3LS4BDdT8gIg5V/x4AHgQu6rLOtogYjYjRkZGRum9tHXznLMvV8bl3nPqNqxP6u4GVklZIWgRsAGqNwpF0lqRTq8fnAO+krS/A+s8TrlmOPMlmOj1DPyKmgM3AvcATwJ0RsVfSVknrACS9Q9IkcBVwu6S91ebnA+OSHgUeAD7RMerH+igI1/QtS75Hbjp12vSJiJ3Azo7nbmp7vJtWs0/ndt8C3jbPMlpNnnvHcuUrydPxFbkFcS3JcudDuHkO/YK0mndcY7IM+cboyTj0S+PMtwy5WTIdh35BPGTTcuVx+uk49AviqXcsV75HbjoO/ZKER0FYnnzUpuPQL4hrSZY7N+80z6FfEI/Tt1x5ls10HPqFcehbjnxj9HQc+gVpzafv1Lf8+B656Tj0CxIRrulb1lzTb55DvyA+XyxXrqyk49AviGtJZtaLQ78grYuzXGWy/JzoyHXNpWkO/cI48i1Hnk8/HYd+SdyRa5nynbPScegXpDVk0yw/J+6RO+CCDAGHfkF8wphZLw79ggThjlzL0onmHddcmubQL4jn07dcuSM3HYd+YVzRtxydmE/fmubQL0irluTUt4y5qt84h35BfOcsy5mP3TQc+gXx1YyWOx/BzasV+pLWStovaULSli6vXyLpYUlTkq7seG2jpB9UPxv7VXDrzpUly5Vw604KPUNf0gLgNuDdwCrgakmrOlZ7Gvgg8KWObd8A3AxcDKwGbpZ01vyLbd34zlmWM0kesplAnZr+amAiIg5ExIvADmB9+woR8aOIeAw41rHt5cB9EXEkIp4F7gPW9qHcNgPfRMVy5Zp+GnVCfzFwsG15snqujvlsa7PUujhr0KUwmxvJbfop1An9bjFS93dTa1tJmySNSxo/fPhwzbe2Tm7esZz5W2oadUJ/EljatrwEOFTz/WttGxHbImI0IkZHRkZqvrV1ci3JcufmnebVCf3dwEpJKyQtAjYAYzXf/17gMklnVR24l1XPWQMiwrUly5c8904KPUM/IqaAzbTC+gngzojYK2mrpHUAkt4haRK4Crhd0t5q2yPAx2j94dgNbK2eswb4glzLmcBfVxNYWGeliNgJ7Ox47qa2x7tpNd1023Y7sH0eZbRZcOZbrtyRm4avyC1J+B65li8hX1WegEO/IL5zluXM9ZU0HPoFcS3JcudDuHkO/YJ4lk3LmXCbfgoO/YL4zlmWM0mu6Sfg0C+MO3ItV62avlO/aQ79ggThmr7lywdvEg79goSH71jGPMtmGg79gviEMbNeHPqF8dw7lqtWR65rLk1z6BckwvPpW748DUMaDv3COPMtV27TT8OhXxBfnGU583DjNBz6BWldnOUTx/LkcfppOPQL4hPGcufmneY59Avie+RaztyRm4ZDvyBu07e8ee6dFBz6xXHqW57k+yUm4dAviJt3LGc+dNNw6BfFE65ZviR35Kbg0C+ITxjLnY/h5jn0C+KOXMuZkIcdJ+DQL4wvzrJcuXknDYd+QTzhmuXM98hNo1boS1orab+kCUlburx+qqSvVK9/W9Ly6vnlkn4t6ZHq55/7W3xr53uoWM48904aC3utIGkBcBtwKTAJ7JY0FhH72la7Bng2It4iaQPwSeB91WtPRsSFfS63ddEasukTx/Ll5p3m1anprwYmIuJARLwI7ADWd6yzHvh89fgu4F1y+iTnG1BY7tyR27w6ob8YONi2PFk913WdiJgCfg6cXb22QtJ3JP2HpN/v9gGSNkkalzR++PDhWe2AneDTxXImN+onUSf0u9XYO381M63zY2BZRFwE3AB8SdLrX7ZixLaIGI2I0ZGRkRpFspn4+5XlyhOupVEn9CeBpW3LS4BDM60jaSFwBnAkIl6IiJ8BRMQe4EngrfMttM3A8+lbxnzsplEn9HcDKyWtkLQI2ACMdawzBmysHl8J3B8RIWmk6ghG0puBlcCB/hTdOvniLMtZa5y+6/pN6zl6JyKmJG0G7gUWANsjYq+krcB4RIwBdwBfkDQBHKH1hwHgEmCrpCngKHBtRBxpYkesGqc/6EKYzZGb9NPoGfoAEbET2Nnx3E1tj/8XuKrLdncDd8+zjFaTTxjLnSv6zfMVuQXx1MqWM0muuCTg0C+ML4+wXAm36afg0C9IeD59y5kP3iQc+gUJT75jGXNHbhoO/YL4hLHs+SBunEO/JL44yzLW6sh16jfNoV+QwPPpW75aHbmDLkX5HPqFceZbrnznrDQc+gXxOH3LmZsm03DoF6Q1eMcnjuWpNcumq/pNc+gXxBe2WO58CDfPoV8Qz7JpuXPmN8+hX5AId+RaviS5pp+AQ780rupbpnzkpuHQL4xPHMtVq77iqn7THPqFmO7EdUXfcuVx+mk49Avhk8VK4MO4eQ79QkyfLB6nb7kS8rDjBBz6hXDzjuWudXGWNc2hXxhnvuXKx24aDv1CHG/e8ZljufI4/SQc+oWYPll8j1zLle+clYZDvxCeqMpK4I7c5tUKfUlrJe2XNCFpS5fXT5X0ler1b0ta3vbaR6vn90u6vH9Ft3Y+VxrW+R/s//C+85fUNHqGvqQFwG3Au4FVwNWSVnWsdg3wbES8Bfgs8Mlq21XABuC3gLXA56r3s4b4xGnALbfA9defCPqI1vIttwyyVMXxnbPSqFPTXw1MRMSBiHgR2AGs71hnPfD56vFdwLvUalxeD+yIiBci4ofARPV+1hCP0++zCHjuObj11hPBf/31reXnnnNK9ZH7o9JYWGOdxcDBtuVJ4OKZ1omIKUk/B86unt/Vse3iOZf2FTz3/Iu893PfauKts3DM4/SbIcFnP9t6fOutrR+A665rPe//8L55lWD8qSP80d8/OOiiDMz5b3odn3v/2xv9jDqh3+2o7qzezLROnW2RtAnYBLBs2bIaRXq5Ba8Sb1t8xpy2LcXbl53FmvPfOOhilGc6+KcDHxz4Ddj4u8v52t6fDLoYA7X87Nc0/hl1Qn8SWNq2vAQ4NMM6k5IWAmcAR2puS0RsA7YBjI6Ozun78utOO4V/vPqiuWxq9sqmm3TaXX+9g7/P3nPBubzngnMHXYzi1WnT3w2slLRC0iJaHbNjHeuMARurx1cC90dr7NUYsKEa3bMCWAk81J+imyXQ3oZ/3XVw7Fjr3/Y2frOM9KzpV230m4F7gQXA9ojYK2krMB4RY8AdwBckTdCq4W+ott0r6U5gHzAFfCgijja0L2b9J8GZZ760DX+6jf/MM13Tt+zoZLsYYnR0NMbHxwddDLOXinhpwHcumw2YpD0RMdprPV+Ra1ZHZ8A78C1TDn0zsyHi0DczGyIOfTOzIeLQNzMbIg59M7Mh4tA3MxsiDn0zsyHi0DczGyIOfTOzIeLQNzMbIg59M7Mh4tA3MxsiDn0zsyFy0k2tLOkw8NQ83uIc4Kd9Ks4glbIf4H05WZWyL6XsB8xvX86LiJFeK510oT9fksbrzCl9sitlP8D7crIqZV9K2Q9Isy9u3jEzGyIOfTOzIVJi6G8bdAH6pJT9AO/LyaqUfSllPyDBvhTXpm9mZjMrsaZvZmYzKC70JX1M0mOSHpH0NUnnDrpMcyXp05K+V+3Pv0k6c9BlmitJV0naK+mYpOxGWkhaK2m/pAlJWwZdnvmQtF3SM5K+O+iyzIekpZIekPREdWxdN+gyzZWk0yQ9JOnRal/+rrHPKq15R9LrI+IX1eO/AlZFxLUDLtacSLoMuD8ipiR9EiAiPjLgYs2JpPOBY8DtwIcjYnzARapN0gLg+8ClwCSwG7g6IvYNtGBzJOkS4FfAv0TEbw+6PHMl6U3AmyLiYUmvA/YAV+T4e5Ek4LUR8StJpwDfBK6LiF39/qziavrTgV95LZDtX7WI+FpETFWLu4AlgyzPfETEExGxf9DlmKPVwEREHIiIF4EdwPoBl2nOIuI/gSODLsd8RcSPI+Lh6vEvgSeAxYMt1dxEy6+qxVOqn0ayq7jQB5D0cUkHgfcDNw26PH3y58A9gy7EkFoMHGxbniTTcCmVpOXARcC3B1uSuZO0QNIjwDPAfRHRyL5kGfqSvi7pu11+1gNExI0RsRT4IrB5sKV9Zb32pVrnRmCK1v6ctOrsS6bU5blsv0GWRtLpwN3AX3d8089KRByNiAtpfaNfLamRpreFTbxp0yJiTc1VvwT8O3Bzg8WZl177Imkj8B7gXXGSd8DM4veSm0lgadvyEuDQgMpibar277uBL0bEvw66PP0QEc9JehBYC/S9sz3Lmv4rkbSybXEd8L1BlWW+JK0FPgKsi4jnB12eIbYbWClphaRFwAZgbMBlGnpV5+cdwBMR8ZlBl2c+JI1Mj86T9GpgDQ1lV4mjd+4GfpPWSJGngGsj4n8GW6q5kTQBnAr8rHpqV8Yjkd4L/BMwAjwHPBIRlw+2VPVJ+hPgH4AFwPaI+PiAizRnkr4M/CGtGR1/AtwcEXcMtFBzIOn3gP8CHqd1vgP8TUTsHFyp5kbSBcDnaR1frwLujIitjXxWaaFvZmYzK655x8zMZubQNzMbIg59M7Mh4tA3MxsiDn0zsyHi0DczGyIOfTOzIeLQNzMbIv8PpCk2riZHRNsAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"np.random.seed(123)\n",
"data = np.array([0])\n",
"\n",
"x = np.linspace(-3, 3, num=500)\n",
"y_kde = KDE('box', bw = 1).fit(data).evaluate_sorted(x)\n",
"\n",
"plt.scatter(data, np.zeros_like(data), marker='x', color='red')\n",
"plt.plot(x, y_kde, label='KDE')"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(-1.7320508075688774, 1.7320508075688774)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAD8CAYAAACb4nSYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAFyZJREFUeJzt3X2MHVd9xvHvk3XsUNKEQLYIbG9swBRMQYlYHCHaUDVOYtrKm0qJcAqtUSNZabFKhZAwTZWoRki8SBQJBRFLsZQiwISkrVaqIxMg0CIw2XVIAnYwLIbEW9PG4PCm0KTr/PrHnV1fbu76zr7MuXvOPh9plTtzZ+6eiWeePfecM2cUEZiZ2fJwTr8LYGZm6Tj0zcyWEYe+mdky4tA3M1tGHPpmZsuIQ9/MbBlx6JuZLSMOfTOzZaRW6EvaIumopAlJu7q8f5Okb0t6SNLXJG1se+991X5HJV2zmIU3M7O5Ua87ciUNAN8DrgImgTHghog40rbNBRHxi+r1VuBvImJLFf6fBTYBLwW+CLwyIk7P9vsuvvjiWLdu3YIOysxsuTl06NBPImKw13YranzWJmAiIo4BSNoHjAAzoT8d+JXnA9N/SUaAfRHxNPBDSRPV531jtl+2bt06xsfHaxTLzMymSXqsznZ1Qn81cLxteRK4vMsvfCfwbmAl8Edt+x7s2Hd1l313ADsAhoaG6pTbzMzmoU6bvrqse06bUETcFhEvB94L/MMc990TEcMRMTw42PPbiZmZzVOd0J8E1rYtrwFOnGX7fcC189zXzMwaVCf0x4ANktZLWglsA0bbN5C0oW3xT4DvV69HgW2SVklaD2wAHlh4sc3MbD56tulHxJSkncABYADYGxGHJe0GxiNiFNgpaTPwf8CTwPZq38OS7qLV6TsFvPNsI3fMzKxZPYdspjY8PBwevWNmNjeSDkXEcK/tfEeumdkyUmfIpmXi5C+f5rMPPM7U6Wf7XRSzOXvR+av4yzdegtRt0J8tFod+Qe79zo/56H3fA8DXjeVkupV588YXs/oFz+tvYQrn0C/I1OnWlfPwLVdz4W+d2+fSmNV396FJ3vP5hzl9emn1MZbIbfoF8eViuQufxY1z6JfITTuWGZ+y6Tj0CzI9/Nbt+Zab6XN2iY0gL5JDv0DOfMvNTOj3txjLgkO/IK4lWe6W2s2iJXLoF2S6E8zjnC03qr6fOvKb59AvkCPfcuN6SjoO/YJMfzP2BWS5cutO8xz6BZm+XuS6vmXmTJOkU79pDv2CuJZkufM53DyHfkHOdOT2uSBmc+R6fjoOfTPrO1dU0nHoF8QduZarmSGbruo3zqFfIHfkWm7O3JHr1G+aQ78gvpvRcudTuHkO/YK4ecdy5VM2HYd+gXwBWW48y2Y6Dv2CzNyc5aq+ZWd67h2nftMc+gWZad7pbzHM5sw1/XQc+gVxLcnMenHoF8QduZYrn7Lp1Ap9SVskHZU0IWlXl/ffLemIpEckfUnSJW3vnZb0UPUzupiFt+7cpm+5mT5n3bzTvBW9NpA0ANwGXAVMAmOSRiPiSNtm3wKGI+IpSX8NfBh4a/XeryPi0kUut3Xh68VydWbuHZ/FTatT098ETETEsYh4BtgHjLRvEBH3R8RT1eJBYM3iFtNqiXDTjmXJHbnp1An91cDxtuXJat1sbgTubVs+T9K4pIOSrp1HGa0mXy+WO5/DzevZvEP3Ppau/zaS3g4MA29uWz0UESckvQz4sqRvR8QPOvbbAewAGBoaqlVw684VfcuRv6GmU6emPwmsbVteA5zo3EjSZuBmYGtEPD29PiJOVP89BnwFuKxz34jYExHDETE8ODg4pwOwMyLciWt5OjPLpuv6TasT+mPABknrJa0EtgG/MQpH0mXA7bQC/4m29RdJWlW9vhh4E9DeAWyLKAjX9C1PM7NsWtN6Nu9ExJSkncABYADYGxGHJe0GxiNiFPgIcD7w+aqm+XhEbAVeDdwu6Vlaf2A+2DHqxxaRK0mWO5/DzavTpk9E7Af2d6y7pe315ln2+zrw2oUU0OoL3DZqefJpm47vyC2MH6BiOTrTF+WqftMc+gWJwFUmy9JM5DvzG+fQL4g7ci1XckduMg79kviKscy5pt88h35B3JFruXJfVDoO/cL44rEcnZl7x1X9pjn0CxKecM0y5bE76Tj0CxLhwTuWKc+ymYxDvyC+Xix3nk+/eQ79gnjCNcuV+6LScegXxpeO5cg35Kbj0C9I4EZ9y5MzPx2HfkHckWu58oPR03Hom9mS4Y7c5jn0C9Iap++6vuXHp206Dv3C+OKxHHmWzXQc+gXxzMqWK8+ymY5DvyAep2/58oPRU3HoF8SdYGbWi0O/IB6yably8046Dv3CuHXHcjRz2jr1G+fQL0jrenHqW35mbs5y6jfOoV8Q94FZ7nwON8+hXxQ/RMXy5NM2HYd+YXzxWI7kh6gkUyv0JW2RdFTShKRdXd5/t6Qjkh6R9CVJl7S9t13S96uf7YtZePtNrXH6/S6F2dxNz6fvzG9ez9CXNADcBrwF2AjcIGljx2bfAoYj4nXA3cCHq31fCNwKXA5sAm6VdNHiFd/atYZsOvUtP34wejp1avqbgImIOBYRzwD7gJH2DSLi/oh4qlo8CKypXl8D3BcRpyLiSeA+YMviFN06eeSD5c5ncPPqhP5q4Hjb8mS1bjY3AvfOc19bADfvmFkvK2ps0y1Guv5BlvR2YBh481z2lbQD2AEwNDRUo0g2G2e+5cgduenUqelPAmvbltcAJzo3krQZuBnYGhFPz2XfiNgTEcMRMTw4OFi37NYh8IRrlif5gYnJ1An9MWCDpPWSVgLbgNH2DSRdBtxOK/CfaHvrAHC1pIuqDtyrq3XWANeSLFeu6afTs3knIqYk7aQV1gPA3og4LGk3MB4Ro8BHgPOBz1c1zccjYmtEnJL0flp/OAB2R8SpRo7E3JFrZj3VadMnIvYD+zvW3dL2evNZ9t0L7J1vAW0O3JFrmfIsm+n4jtzCOPQtRzM3Zzn1G+fQL0jrcYlOfcvPmZq+U79pDv2CRHjCNcuTH4yejkO/IL5ezKwXh35B/LhEy5U7ctNx6BfGN2dZnqY7ch37TXPoF6TVkWuWH9dV0nHoFyTcvmOZckduOg79gvh6MbNeHPolcUXfMjXdF+Vx+s1z6BfGHbmWIzfvpOPQL0gQrulbljzLZjoO/YL4yVmWK08fko5DvyCuJVnufAo3z6FfGNeYLEdnmncc+01z6Bck8IRrljdHfvMc+gVxJclyJT8iNxmHfkF8vZhZLw79grRG77h9x/Ljm7PScegXxpFvOfLNWek49IvijlzLk+fTT8ehXxDfnGW58oPR03HoF8TXi5n14tAvSET45izL0pnmHVddmubQL4ybdyxH7shNx6FfED8u0bLljtxkaoW+pC2SjkqakLSry/tXSHpQ0pSk6zreOy3poepndLEKbs8Vgav6lqWZZklX9Ru3otcGkgaA24CrgElgTNJoRBxp2+xx4B3Ae7p8xK8j4tJFKKv14MvFzHrpGfrAJmAiIo4BSNoHjAAzoR8RP6ree7aBMlpNrY5cs/x4nH46dZp3VgPH25Ynq3V1nSdpXNJBSdd220DSjmqb8ZMnT87ho62TW3csR+7ITadO6HeLkbn80wxFxDDw58DHJL38OR8WsScihiNieHBwcA4fbZ2c+Zajmbl3nPqNqxP6k8DatuU1wIm6vyAiTlT/PQZ8BbhsDuWzOfCEa5Yrn7Xp1An9MWCDpPWSVgLbgFqjcCRdJGlV9fpi4E209QXY4vKNLZY7n8HN6xn6ETEF7AQOAI8Cd0XEYUm7JW0FkPQGSZPA9cDtkg5Xu78aGJf0MHA/8MGOUT+2iCJcY7I8ySM2k6kzeoeI2A/s71h3S9vrMVrNPp37fR147QLLaHPg1h3L0cyEa30ux3LgO3IL0qrpO/UtQ34wejIO/YIEbt+xPPkbajoO/YK4kmRmvTj0C+MKk+XIN2el49AviOdbs1z5wejpOPRL4o5cy5Rr+uk49AviWpKZ9eLQL4gfjG658iyb6Tj0C+PQtxzN3Jzl1G+cQ78grcclOvUtP34wejoO/YJEhGv6ZnZWDv2CuI5kuXPzTvMc+gXxBWO58jfUdBz6hfFDVCxHZzpyXXNpmkO/IK2OXLP8eD79dBz6JXFHrmXKp206Dv2CuJJkufM53DyHfkH8uETL1cyEa079xjn0C+OOXMvRzIRrrus3zqFfkCBc07csuSM3HYd+QTzhmuXK31DTcegXxLUky51P4eY59AvSumBcY7KMuebSOId+Yfwt2XIluaafgkO/IBHuyLV8+dxNo1boS9oi6aikCUm7urx/haQHJU1Juq7jve2Svl/9bF+sglt3rulbriS5dSeBnqEvaQC4DXgLsBG4QdLGjs0eB94BfKZj3xcCtwKXA5uAWyVdtPBiWze+YCx3HqffvDo1/U3AREQci4hngH3ASPsGEfGjiHgEeLZj32uA+yLiVEQ8CdwHbFmEctss/OQsy5VwxSWFOqG/GjjetjxZrauj1r6SdkgalzR+8uTJmh9tnQJPuGb5ckduGnVCv1uM1P23qbVvROyJiOGIGB4cHKz50dbJN2dZzvwtNY06oT8JrG1bXgOcqPn5C9nX5si1JMudm3eaVyf0x4ANktZLWglsA0Zrfv4B4GpJF1UduFdX66wBrSGbri1ZpuSO3BR6hn5ETAE7aYX1o8BdEXFY0m5JWwEkvUHSJHA9cLukw9W+p4D30/rDMQbsrtZZU5z5limBv64msKLORhGxH9jfse6WttdjtJpuuu27F9i7gDJaTX5couXMHblp+I7ckoRnK7R8uWkyDYd+QVxLstyFe3Ib59AviOfesZxJHr2TgkO/MG7dsVwJf1tNwaFfEHfkWs484VoaDv2ChDtyLWM+c9Nw6BfEN7ZY7nwON8+hX5AI15YsY+7ITcKhXxqnvmXKp24aDv2CtGr6vnQsT+6PSsOhXxhfN5ar1jh9t+80zaFfEF8wljufwc1z6BfE4/QtZ35cYhoO/cK4ecdyJclDNhNw6BfEHbmWM5+5aTj0C+IHo1vOPOFaGg79gviCsdz5FG6eQ78ggdv0LWeecC0Fh35xnPqWJ/khuUk49AvSmmWz36Uwmx+fumk49IviJ2dZvtyRm4ZDvyC+YCx3Poeb59AvjJt3LFfCN2el4NAvSGsaBqe+5ckVljQc+gWJ8M1Zli/PvZNGrdCXtEXSUUkTknZ1eX+VpM9V739T0rpq/TpJv5b0UPXzycUtvrXz9WK58zncvBW9NpA0ANwGXAVMAmOSRiPiSNtmNwJPRsQrJG0DPgS8tXrvBxFx6SKX27rw4xItZ5JvzkqhTk1/EzAREcci4hlgHzDSsc0IcGf1+m7gSvkxOH3h/+2WM3fkNq9O6K8GjrctT1brum4TEVPAz4EXVe+tl/QtSV+V9AcLLK+dhR+iYjlzfSWNns07dG8x6EyX2bb5MTAUET+V9Hrg3yS9JiJ+8Rs7SzuAHQBDQ0M1imTdeO4dy5mEG/UTqFPTnwTWti2vAU7Mto2kFcCFwKmIeDoifgoQEYeAHwCv7PwFEbEnIoYjYnhwcHDuR2EtvmAscz6Fm1cn9MeADZLWS1oJbANGO7YZBbZXr68DvhwRIWmw6ghG0suADcCxxSm6dfI4fcuZkJsoE+jZvBMRU5J2AgeAAWBvRByWtBsYj4hR4A7gU5ImgFO0/jAAXAHsljQFnAZuiohTTRyItbh5x3IluaafQp02fSJiP7C/Y90tba//F7i+y373APcssIxWU4QnXLN8+dxNw3fkFsQduZYzj9NPw6FfEF8wljufws1z6Bek9WB0V/UtT625dxz7TXPoF8aRb9nyyZuEQ78g0RqzaZYl35uVhkO/IB6nbzmTx2wm4dAviS8Yy5wnXGueQ78grY7cfpfCbH78EJU0HPqFceZbrlxhScOhX5AIXziWr9bcO/0uRfkc+gVxR67lrNWP69RvmkO/IL6xxXLnU7h5Dv3CuHnHcubMb55DvyC+N8ty5ilE0nDoFyQ8zaZlzEM203Dom9kS4tRvmkO/ENOduK7nW64k1/RTcOgXxq07liufu2k49AsxXUPyOH3LlZAbdxJw6Bdi+mJxbcly1Wrecew3zaFfCF8sVgKfxc1z6Bdipqbf11KYzZ+HbKbh0C+Mm3csWz55k3DoF2KmI9cXjmXKj0tMw6FfCM9OaLlzR24atUJf0hZJRyVNSNrV5f1Vkj5Xvf9NSeva3ntftf6opGsWr+jWzteKmdXRM/QlDQC3AW8BNgI3SNrYsdmNwJMR8Qrgn4APVftuBLYBrwG2AJ+oPs8a4tYdy5U7ctOoU9PfBExExLGIeAbYB4x0bDMC3Fm9vhu4Uq3G5RFgX0Q8HRE/BCaqz7OG+OYsy5X7o9JYUWOb1cDxtuVJ4PLZtomIKUk/B15UrT/Yse/qeZf2LH721DNc/8lvNPHRWXh2eu4dXzeWKQGHHnuSqz761X4XpW9e9ZIL+PgNlzX6O+qEfrcY6fwSNts2dfZF0g5gB8DQ0FCNIj3XOeeIDS8+f177lmLjSy/kylf9Tr+LYTYvf/HGSzhw+L/7XYy+WnvR8xr/HXVCfxJY27a8BjgxyzaTklYAFwKnau5LROwB9gAMDw/Pq1XvgvPO5RNve/18djWzJWDk0tWMXNpIQ4C1qdOmPwZskLRe0kpaHbOjHduMAtur19cBX47W2KtRYFs1umc9sAF4YHGKbmZmc9Wzpl+10e8EDgADwN6IOCxpNzAeEaPAHcCnJE3QquFvq/Y9LOku4AgwBbwzIk43dCxmZtaDltrNEMPDwzE+Pt7vYpiZZUXSoYgY7rWd78g1M1tGHPpmZsuIQ9/MbBlx6JuZLSMOfTOzZWTJjd6RdBJ4bAEfcTHwk0UqTj+VchzgY1mqSjmWUo4DFnYsl0TEYK+NllzoL5Sk8TrDlpa6Uo4DfCxLVSnHUspxQJpjcfOOmdky4tA3M1tGSgz9Pf0uwCIp5TjAx7JUlXIspRwHJDiW4tr0zcxsdiXW9M3MbBbFhb6k90t6RNJDkr4g6aX9LtN8SfqIpO9Wx/Ovkl7Q7zLNl6TrJR2W9Kyk7EZaSNoi6aikCUm7+l2ehZC0V9ITkr7T77IshKS1ku6X9Gh1br2r32WaL0nnSXpA0sPVsfxjY7+rtOYdSRdExC+q138LbIyIm/pcrHmRdDWtZxNMSfoQQES8t8/FmhdJrwaeBW4H3hMR2UylKmkA+B5wFa0HA40BN0TEkb4WbJ4kXQH8CvjniPi9fpdnviS9BHhJRDwo6beBQ8C1Of67VM8Uf35E/ErSucDXgHdFxMEeu85ZcTX96cCvPJ8uj2fMRUR8ISKmqsWDtJ48lqWIeDQijva7HPO0CZiIiGMR8QywDxjpc5nmLSL+g9ZzL7IWET+OiAer178EHqWhZ3A3LVp+VS2eW/00kl3FhT6ApA9IOg68Dbil3+VZJH8F3NvvQixTq4HjbcuTZBoupZK0DrgM+GZ/SzJ/kgYkPQQ8AdwXEY0cS5ahL+mLkr7T5WcEICJujoi1wKeBnf0t7dn1OpZqm5tpPXns0/0raW91jiVT6rIu22+QpZF0PnAP8Hcd3/SzEhGnI+JSWt/oN0lqpOmtzoPRl5yI2Fxz088A/w7c2mBxFqTXsUjaDvwpcGUs8Q6YOfy75GYSWNu2vAY40aeyWJuq/fse4NMR8S/9Ls9iiIifSfoKsAVY9M72LGv6ZyNpQ9viVuC7/SrLQknaArwX2BoRT/W7PMvYGLBB0npJK2k9A3q0z2Va9qrOzzuARyPio/0uz0JIGpwenSfpecBmGsquEkfv3AP8Lq2RIo8BN0XEf/W3VPNTPWh+FfDTatXBjEci/RnwcWAQ+BnwUERc099S1Sfpj4GPAQPA3oj4QJ+LNG+SPgv8Ia0ZHf8HuDUi7uhroeZB0u8D/wl8m9b1DvD3EbG/f6WaH0mvA+6kdX6dA9wVEbsb+V2lhb6Zmc2uuOYdMzObnUPfzGwZceibmS0jDn0zs2XEoW9mtow49M3MlhGHvpnZMuLQNzNbRv4fhg/0IuWtXBoAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"g = KDE._available_kernels['box']\n",
"plt.plot(x, g(x, bw = 1))\n",
"g.support"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x18d60053cc0>]"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl4VOX5xvHvM9kDISEkIWQjhCUh7BAQUFFEWUTBXXCvC66tP5da2qq1Lq2tba2tWKXU4oYiVhEFRVQUWSUIhJAAhjULkEBIWJKQ7f39kaGNMZAJTObM8nyui4tZXmZuJuTm5D3vOUeMMSillPIuNqsDKKWUcj4td6WU8kJa7kop5YW03JVSygtpuSullBfScldKKS+k5a6UUl5Iy10ppbyQlrtSSnkhf6veOCoqyiQnJ1v19kop5ZHWrVt3wBgT3dI4y8o9OTmZzMxMq95eKaU8kojsdmScTssopZQX0nJXSikvpOWulFJeSMtdKaW8kJa7Ukp5IS13pZTyQlruSinlhSxb565UWymvrGHL3sPsOniMQxU1VNXUERLgR8fQQLpFtyM1NowOwQFWx1SqTWm5K6+w++Ax5q8v4vPc/WwuKqf+FJcGtgn0T4hgTFoMVwxJID4ixHVBlXIRseoC2RkZGUaPUFVnau2uUl5amsfSrSUAZHTtyNk9ohiUFEFKVHuiwgIJ8vejqqaO0mPVfF98hI355Xy9rYQN+WWIwAWpMfx0TE8GJkZY/LdRqmUiss4Yk9HiOC135YnySyt46uMcPsvZT2S7QG4ekcxVGa3bCs8vrWBeZj6vr95NWUUNY9M789gl6SRGhrZhcqXOjJa78kr19YZXlu3gr59vwybCfRf04NazuxES6Hfar3n0eC2vrdzFi1/mUW8Mj4xP49azkxERJyZXyjm03JXXKT5SxYNzN7I87wDj+8Tym0npdAl33nx5UVklj83P5ostxYxOjea5qwcQ1T7Iaa+vlDM4Wu66FFJ5hA35ZVz8wnIyd5fy7BX9+McNg51a7ABxESHMujmDJyf3YcX2g1zyt+XkFB126nso5Spa7srtLcnZz5SZqwgJtPHhvecwZVhSm02ZiAg3jUjmg3tGIgJXv7ySpVuL2+S9lGpLWu7Krc1du4c738gktXMY7999NqmxYS553z5x4Xxwz9l07dSO21/LZP76Qpe8r1LOouWu3Na8zHymv7+Jc3pG8/a04USHuXb+OzY8mHfvGsHQ5I48+O4GPtygBa88h5a7cksfrC/gkf9kcU6PKGbeOITQQGuOt2sf5M+rtwwlIzmSB+Zu4OOsIktyKNVaWu7K7Xy1tZiH52UxIqUT/7wpg+CA01/m6Ayhgf78+5ahDOnakQfmbmD1joOW5lHKEVruyq3k7j3MfXPW06tzGDPdoNhPaBfkz6ybhpIUGcq01zPJKz5idSSlTknLXbmN4sNV3Dp7Le2C/Hj1lgzaB7nXqY/CQwOY/ZNhBPrbuOXfazl49LjVkZQ6qRbLXUReFZFiEck+yfPXi0iW/ddKERng/JjK29XU1XPvnO8oq6jh1VuGOn0Nu7MkRoYy6+ahFB85zv/N3UDdqc5QppSFHNlynw2MP8XzO4HzjDH9gaeAmU7IpXzMHz/dwtpdh3j2yn70iQu3Os4pDUyM4MlJffjm+wO88Pk2q+Mo1awWy90YswwoPcXzK40xh+x3VwMJTsqmfMSn2fv45zc7uXF4VyYPjLc6jkOuHZrI1UMS+NuXeSzdogc5Kffj7Dn324BPnPyayovtLa/kkfc2MiAhnEcv6W11HIeJCE9d1pe02DAenreRAzr/rtyM08pdREbTUO6/OMWYaSKSKSKZJSUlznpr5aHq6w0/n5dFbb3hhSmDCPJ3j5UxjgoO8OOFKYM4cryW6f/JwqqT8CnVHKeUu4j0B2YBk40xJ10EbIyZaYzJMMZkREdHO+OtlQd7fdUulucd4NcTe5Mc1c7qOKclNTaMR8al8nluMXPX5lsdR6n/OuNyF5Ek4H3gRmOM7l1SDtlecpTff7KF0anRXDcsyeo4Z+TWs7sxsnsnnvw4h/zSCqvjKAU4thTybWAVkCoiBSJym4jcJSJ32Yc8DnQCXhKRDSKiJ2lXp2SM4VfvbyLI38Yfruzv8RfFsNmE565uWAH82IfZOj2j3EKLR4kYY6a28PztwO1OS6S83rzMAtbsLOX3V/QjpkOw1XGcIj4ihIfHpvLkxzl8lLWXSQPirI6kfJweoapc6sDR4zyzKJehyR25NiPR6jhOdfPIZPonhPPkR5spq6i2Oo7ycVruyqV+tzCXiupafn9FP2w2z56OacrPJvz+in4cqqjhj4u3Wh1H+Tgtd+Uy3+05xPvrC7nj3BR6xLjmohuu1icunBuHd+Xtb/ewuajc6jjKh2m5K5cwxvDkRzlEhwVxz+geVsdpUw9c2IuIkAB+uyBHd64qy2i5K5f4cEMRG/LLeGRcqtud7dHZwkMDeHhcKt/uKmXhpr1Wx1E+SstdtbmK6lqe/WQLfeM7cOVg3zj10JShSfTu0oHfL9pCVU2d1XGUD9JyV23u5a+2s+9wFY9f0sfrdqKejJ9NeGxibwrLKnlz9W6r4ygf5N0/HyuXKz5cxYb8MrIKytl54BhF5ZVszC/jsoFxDOsWaXU8lxrZI4pze0YxY2ke1wxNpENwgNWRlA/RcldnbOu+IyzctJclOfvJ3XsYaNhyTYoMJS4imJtHJvPzcakWp7TGI+PSuPTF5cxatoMHx/rmZ6CsoeWuTkt1bT0LNhYxZ81uvttThk0go2sk0yekMTS5I+ldwgkJ9KyzPLaFfgnhTOzfhVnLd3LjiGSiw4KsjqR8hJa7apXq2nrmrcvnpaXbKSyrJCW6HY9O7M3lg+Lp1F6LqzkPXdSLT7P3MWNpHk9M6mN1HOUjtNyVw5ZuKebJj3PYeeAYg5IiePryvpzfK9rjT/zV1lKi23NNRiJvrdnNtFEpxEW45/VhlXfR1TKqRfvKq7j9tbX8ZPZaRODfPxnK+3ePZHRqjBa7g+67oAfGwCtfb7c6ivIRuuWuTsoYw4KNRTw2P5vqunp+dXEat4zsRqC/bhO0VnxECFcOTuDttfnce0EPYsK842yYyn3pd6lqVlVNHQ/N28j972ygR0x7Prl/FNNGdddiPwP3jO5ObV09/1y2w+ooygfod6r6kfzSCq78x0re/66Qn43pybt3jqCbh14Gz5107dSOyQPjeXP1HkqP6SmBVdvSclc/sGr7QSa9uJw9pRX86+YMHryoF/5++s/EWe4d3Z2q2jr+tVy33lXb0u9a9V+LNu3l5le/pVP7IBbcdw5jene2OpLX6RETxsV9u/Dayt0crqqxOo7yYlruCoA3V+/m3jnf0S8hnPfu0mmYtnTXed05eryWud/mWx1FeTEtd8VLX+Xx6PxsLkiN4c3bziIiNNDqSF6tX0I4Z3WL5N8rdlJbV291HOWltNx93D+X7eCPn25l8sA4XrlxiJ4ywEXuODeFovIqFmXvszqK8lItlruIvCoixSKSfZLnRUT+JiJ5IpIlIoOdH1O1hdkrdvLMolwm9uvCn68eoDtOXeiCtBhSotox65sderUm1SYc+W6eDYw/xfMTgJ72X9OAf5x5LNXW5q7dwxMf5TA2vTN/nTJQi93FbDbh1nO6kVVQztpdh6yOo7xQi9/RxphlQOkphkwGXjcNVgMRItLFWQGV8y3dWsyvPshmVK9o/n7dIAK02C1x5eAEOoYGMOsbXRapnM8Z39XxQOPd/gX2x5Qbyi4s5963viMtNoyXrh9MkL/OsVslJNCPG4Z3ZUnufnYfPGZ1HOVlnFHuzZ05qtlJRBGZJiKZIpJZUlLihLdWrVFYVsmts9cSERLAq7cM9foLVXuC68/qik2EOWv2WB1FeRlnlHsBkNjofgJQ1NxAY8xMY0yGMSYjOjraCW+tHFVZXcftr2VSWV3Hv38yjM4d9MRV7iA2PJix6Z2Zm5mvF9JWTuWMcl8A3GRfNTMcKDfG7HXC6yonMcbwy/ez2LLvMH+7bhCpsWFWR1KN3Di8K2UVNSzM0m8b5TyOLIV8G1gFpIpIgYjcJiJ3ichd9iGLgB1AHvBP4J42S6tOy+yVu5i/oYgHL+zF6NQYq+OoJkZ070RKdDveWL3b6ijKi7Q46WqMmdrC8wa412mJlFN9u7OUZxbmcmHvztw7uofVcVQzRIQbh3fltx/lkF1YTt/4cKsjKS+ga+C8WOmxau6b8x2JkaH85doB2Gx61SR3dcXgBEIC/HhTt96Vk2i5eyljDI+8l0VZRQ0vXjeIDsEBVkdSpxAeEsBlg+KYv6GQ8ko9W6Q6c1ruXurN1bv5PHc/v5iQRp84/THfE1x/VleqaupZsKHQ6ijKC2i5e6Gt+47w9MJczk+N5tazk62OoxzUNz6c9C4dmJuppwJWZ07L3ctU19Zz/zvrCQsO4E9XD0BE59k9ybVDE8kuPMzmonKroygPp+XuZV5cmseWfUd49op+RLUPsjqOaqXJA+MI9Lfx7lrdeldnRsvdi2QXlvPS0jyuGBTPhel6iTxPFBEayLg+sczfUKRHrKozouXuJapr63l43kYi2wXym0v7WB1HnYFrMxIpr6zhs5z9VkdRHkzL3UvMsE/H/O7yfoSH6rJHTzayeyfiI0J0akadES13L5BXfISXvspj8sA4nY7xAjabcHVGAsvzDpBfWmF1HOWhtNw9nDGGR+dnExLgx2OXpFsdRznJlYMTAPhQ17yr06Tl7uE+3FDE6h2lPDI+TVfHeJHEyFCGJUfywfpCvcaqOi1a7h6svLKGpxfmMCAxguuGJVkdRznZ5YPj2V5yjE2FuuZdtZ6Wuwf70+KtlB6r5pnL+upJwbzQxX27EOhn44P1OjWjWk/L3UNlFZTx5prd3DQiWU8R66XCQwO4IC2GjzYWUVtXb3Uc5WG03D2QMYbffpRDp3ZBPDS2l9VxVBu6fHA8B45W803eAaujKA+j5e6BFm7ay7rdh/j5uF6E6al8vdr5qdGEhwQwX6dmVCtpuXuYqpo6nv1kC2mxYVw1JLHlP6A8WpC/H5f078Lizfs4erzW6jjKg2i5e5jZK3dRcKiSRyem46c7UX3CZYPiqaqpZ0nOPqujKA+i5e5BDhw9zowv8xiTFsM5PaOsjqNcZEhSR7qEB7Mwa6/VUZQH0XL3IH/9fBsVNXX88uLeVkdRLmSzCRf368KybQf0EnzKYQ6Vu4iMF5GtIpInItObeT5JRJaKyHoRyRKRi50f1bflFR9lzpo93HBWEj1i2lsdR7nYxP5dqK6r53M9U6RyUIvlLiJ+wAxgApAOTBWRpicxeRR41xgzCJgCvOTsoL7u+SXbCAnw42djelodRVlgUGIE8REhfJxVZHUU5SEc2XIfBuQZY3YYY6qBd4DJTcYYoIP9djig/wKdKLuwnIWb9nLbOd3opOeP8UkiwsT+Xfjm+wOUV+jUjGqZI+UeDzQ+sXSB/bHGngBuEJECYBHwU6ekUwD8+bOthIcEcPuoFKujKAtN7NeF2nrDYl01oxzgSLk3t96u6WnqpgKzjTEJwMXAGyLyo9cWkWkikikimSUlJa1P64Myd5WydGsJd53XnQ56wJJP658QTmJkCB/rqhnlAEfKvQBofLRMAj+edrkNeBfAGLMKCAZ+tFbPGDPTGJNhjMmIjo4+vcQ+xBjDc4u3EtU+iJtHdrU6jrKYiDCxXxwr8g5w6Fi11XGUm3Ok3NcCPUWkm4gE0rDDdEGTMXuAMQAi0puGctdN8zO0PO8Aa3aW8tMLehAa6G91HOUGLunfhbp6w+LNOjWjTq3FcjfG1AL3AYuBXBpWxWwWkSdFZJJ92EPAHSKyEXgbuMXoFQbOiDGGP322jfiIEKYM09MMqAZ94jqQ3ClUp2ZUixzaHDTGLKJhR2njxx5vdDsHONu50Xzb8rwDbMwv43eX9yPI38/qOMpNnFg18/LXOyg9Vk1ku0CrIyk3pUeouqm/f5FHl/BgrhzSdGGS8nUT+jZMzei5ZtSpaLm7oTU7DvLtrlLuHJWiW+3qR/rEdSAxMoRPsrXc1clpubuhv3+ZR1T7IKbodVFVM0SECX27sCJPzzWjTk7L3c18t+cQy/MOMG1UN4IDdKtdNW9C31hq6gxf5Oq5ZlTztNzdzItf5hERGsD1Z+m6dnVyAxMjiAsPZtEmnZpRzdNydyPZheV8uaWY287uRrsgXdeuTk5EGNc3lmXfl+gVmlSztNzdyCvLdtA+yJ+bRiZbHUV5gIv7daG6tp4vtxRbHUW5IS13N5FfWsGiTXu57qwkwkP0HDKqZUOSOhIdFsSn2XpAk/oxLXc38eqKnQjwk7OTrY6iPITNJozvE8vSLSVUVtdZHUe5GS13N1BeUcPctflMGhBHl/AQq+MoDzKhbyyVNXV8vU2nZtQPabm7gbe+3U1FdR23n6vna1etM6xbJNFhQfzj6x3U1evpnNT/aLlb7HhtHbNX7OLcnlGkx3Vo+Q8o1Yi/n41HJ/ZmY34Z/16x0+o4yo1ouVtswYYiio8cZ5peZUmdpkkD4hiTFsOfPtvKnoMVVsdRbkLL3ULGGP75zQ7SYsM4p8ePrm2ilENEhKcv74u/zcb097PQs20r0HK31PK8A2zbf5Q7zk1BpLmrGSrlmC7hIfzy4jRWbj/I3LX5Lf8B5fW03C302spdRLUP5JIBXayOorzA1KFJDOsWybOfbqFUL8Pn87TcLbLnYAVfbCnmumFJelpf5RQ2m/DU5L4cqarlj59usTqOspiWu0VeX7ULPxGuH64nCFPOkxobxq1nJ/PO2ny+23PI6jjKQlruFqioruXdzHzG942lc4dgq+MoL3P/hb3o3CGIxz/M1rXvPkzL3QIfrC/kcFUtt+gJwlQbaB/kz6MT08kuPMycNbutjqMsouXuYsYYXlu5iz5xHRjStaPVcZSXuqR/F0akdOIvS7bp1Zp8lEPlLiLjRWSriOSJyPSTjLlGRHJEZLOIzHFuTO+xavtBtu0/yi0jk3X5o2ozIsKjl/SmrLKGGUvzrI6jLNBiuYuIHzADmACkA1NFJL3JmJ7AL4GzjTF9gP9rg6xe4bVVu4hsF8ilA+KsjqK8XJ+4cK4anMDsFbvIL9UjV32NI1vuw4A8Y8wOY0w18A4wucmYO4AZxphDAMYYPUVdM/YfruLz3GKuzkjQ66Mql3h4XCp+NuFZXRrpcxwp93ig8SFvBfbHGusF9BKRFSKyWkTGN/dCIjJNRDJFJLOkpOT0Enuwd9fmU1dvmDo0yeooykd07hDMtFEpLMzay7rdujTSlzhS7s1NDDddX+UP9ATOB6YCs0Qk4kd/yJiZxpgMY0xGdHR0a7N6tLp6wztr8zmnRxTJUe2sjqN8yJ3npRATFsTTC3P0vDM+xJFyLwASG91PAIqaGfOhMabGGLMT2EpD2Su7Zd+XUFhWydRhutWuXCs00J+Hx6ayfk8ZCzfpJfl8hSPlvhboKSLdRCQQmAIsaDJmPjAaQESiaJim2eHMoJ5uzpo9RLUP5KL0zlZHUT7oyiEJpMWG8YdPt3C8Vi/J5wtaLHdjTC1wH7AYyAXeNcZsFpEnRWSSfdhi4KCI5ABLgZ8bYw62VWhPs6+8ii+3FHPVkEQC/fXQAuV6fjbh1xN7k19ayesr9cAmX+DvyCBjzCJgUZPHHm902wAP2n+pJt7NtO9IHZbY8mCl2si5PaM5PzWav3/5PVcNSaBju0CrI6k2pJuRbayu3jDXviO1ayfdkaqs9csJvTl6vJZ73vqO2St28u3OUg5X6RGs3sihLXd1+pZta9iR+uuJva2OohSpsWE8PC6VWd/sZNWO/82cpsWGMbJ7FCO7d2JYSiQdggMsTKmcQcu9jc35tmFH6oW9dUeqcg/3nN+Du8/rTvGR4+QUHWZTYTlrdh7krTW7eXXFTvxtwsgeUUzsF8tF6bFE6vSNR9Jyb0PFhxt2pN5xboruSFVuRUTo3CGYzh2CGZ0WA/SkqqaO9XvK+GprMZ9k7+MX/9nErz7I5tyeUUwdlsSYtBj8/fTfsafQcm9DH6wvpK7ecE1GgtVRlGpRcIAfI7p3YkT3TkyfkMbmosMs2rSX/3xXwJ1vrKNzhyCuyUjkxuFdidHrELg9seqItYyMDJOZmWnJe7uCMYaxzy+jQ0gA/7l7pNVxlDpttXX1LN1awpw1u/lqWwkBNhtXDkngzlEperS1BURknTEmo6VxuuXeRrIKyvm++Ci/v6Kf1VGUOiP+fjYuSu/MRemd2XOwgleWbWfeugLmrt3DxP5xPHhRL7ppybsdnUBrI++tKyDI38bE/l2sjqKU0yR1CuWZy/ux/BejmTaqO1/k7ueiv3zNY/OzKTly3Op4qhEt9zZQVVPHgo1FjO8bq0vKlFeKCQtm+oQ0vv75aKYMS2TOt3s477ml/P2L7/X0Bm5Cy70NfJFbTHllDVcN0R2pyrtFhwXx9GX9WPLAKM7tGcWfl2xjwl+/YWXeAauj+Twt9zbw3rp8uoQHM7J7lNVRlHKJlOj2vHJjBrN/MpQ6Y7hu1hruf2c9B47qVI1VtNydrPhwFV9vK+GKwfH42fQaqcq3nJ8aw+L/G8XPxvTkk037GPf8MhZv3md1LJ+k5e5k768vpN7AlYN1Skb5puAAPx68qBcf/fQcYsODufONdTz07kY9h42Labk7kTGG99YVMKRrR1Ki21sdRylLpcaG8cE9Z/OzC3owf0MhE/76jV7qz4W03J0oq6CcvOKjuiNVKbtAfxsPjk3lP3ePxM8mXPvKKmZ9s0Mv9+cCWu5O9MH6QgL9bVzcT9e2K9XYwMQIPvrpOYzpHcPTC3OZ9sY6yit0mqYtabk7SW1dPR9n7eWC1BjCQ3Rtu1JNhYcE8PINQ3j8knSWbilm0ozl5BUfsTqW19Jyd5KV2w9y4OhxLhsUZ3UUpdyWiHDrOd2Ye+cIjh2v4/IZK1m6tdjqWF5Jy91JPtxQRFiwP+enxlgdRSm3N6RrRxbcdzZJnUK5bfZanYdvA1ruTlBVU8fizfuY0DeW4AA/q+Mo5RHiIkKYd9cIxvWJ5emFuTw6P5u6ei14Z9Fyd4Ivcos5eryWyQPjrY6ilEcJDfRnxnWDufv87ry1Zg/3vLWOqho9N40zOFTuIjJeRLaKSJ6ITD/FuKtExIhIi+ca9iYfbigkJiyI4SmdrI6ilMex2YRfjE/jiUvT+SxnPzf+a42upHGCFstdRPyAGcAEIB2YKiLpzYwLA34GrHF2SHdWXlHDV1tLuHRAnJ5uQKkzcMvZ3fj71EFszC/n6ldWUny4yupIHs2RLfdhQJ4xZocxphp4B5jczLingD8CPvUV+SR7L9V19VymUzJKnbFL+scx+9ahFByqZMrM1ewr96k6cSpHyj0eyG90v8D+2H+JyCAg0Rjz8aleSESmiUimiGSWlJS0Oqw7mr+hkJSodvSN72B1FKW8wsjuUbx+6zCKjxzn2pmrKCyrtDqSR3Kk3Juba/jvLm0RsQHPAw+19ELGmJnGmAxjTEZ0dLTjKd3U3vJK1uwsZfLAeER0SkYpZ8lIjuSN24ZReqyaa15exZ6DFVZH8jiOlHsBkNjofgJQ1Oh+GNAX+EpEdgHDgQW+sFP14417MQYmDdQDl5RytkFJHZlz+3COVddy7cxV7D54zOpIHsWRcl8L9BSRbiISCEwBFpx40hhTboyJMsYkG2OSgdXAJGNMZpskdiMfZxXRLz5cLw6sVBvplxDOnNuHU1lTx/Wz1rC3XKdoHNViuRtjaoH7gMVALvCuMWaziDwpIpPaOqC7yi+tYGNBuV4AW6k2lh7XgddvHUZZRQ03zFrDQb26k0McWudujFlkjOlljOlujHnG/tjjxpgFzYw93xe22hdt2gvARD0DpFJtrn9CBK/eMpTCskpuevVbyit1HXxL9AjV07Rw0176J4STGBlqdRSlfMKwbpG8fMMQtu0/wq2z11JRXWt1JLem5X4a8ksryCoo1612pVzs/NQY/jZlEOv3HOKet76jtq7e6khuS8v9NJyYktGLcijlehP6deGZy/vx1dYSHp2frWeTPAl/qwN4ooWb9jJAp2SUsszUYUkUHqrkxaV5JEaGcu/oHlZHcju65d5KJ6ZkdKtdKWs9NLYXlw+K57nFW/lgfYHVcdyObrm30kKdklHKLYgIf7iyP/vKq3jkvSw6hwUzskeU1bHchm65t9IinZJRym0E+tt4+cYhdItqx11vrmPnAT2K9QQt91bYc9C+SkYPXFLKbYSHBPCvm4fiZxNuf20th6t0DTxoubfKouyGKZkJfbXclXIniZGhvHT9EHYfrOD/3tmgl+tDy71VdEpGKfc1onsnfnNpOl9uKeZPn221Oo7ltNwdVFRWSVZBOeN1q10pt3XD8K5MHZbEP77azocbCq2OYyktdwd9nrsfgLF9OlucRCl1MiLCbyf1YVhyJI+8l0VO0WGrI1lGy91BS3L2kxLdju7R7a2OopQ6hUB/Gy/dMJiI0ADueWudz+5g1XJ3QHllDau2H2RseqzVUZRSDohqH8SL1w0m/1Alj8zL8slTFGi5O+CrrcXU1hudklHKgwxNjmT6+DQ+3byPfy3faXUcl9Nyd8BnOfuJDgtiYEKE1VGUUq1w+7ndGJvemWc/2cK63aVWx3EpLfcWHK+t46stxVzYuzM2m14EWylPIiI8d/UA4iJCuPet9T51FSct9xas3H6QY9V1OiWjlIcKDwngpesHU1pRzc/f8535dy33FizJ2U+7QD9Gdu9kdRSl1GnqGx/Oryak8eWWYl5ftdvqOC6h5X4K9fWGJTn7OT81hiB/P6vjKKXOwM0jk7kgLYZnFuWyZZ/3r393qNxFZLyIbBWRPBGZ3szzD4pIjohkicgXItLV+VFdb0NBGSVHjuuUjFJeQER47qr+hIcE8LO311NVU2d1pDbVYrmLiB8wA5gApANTRSS9ybD1QIYxpj/wHvBHZwe1wpKc/fjbhPNTY6yOopRygk7tg/jz1QPYtv8ov1uUa3WcNuXIlvswIM8Ys8MYUw28A0xuPMAYs9QYU2G/uxpIcG5Ma3y2eR/DUzoRHhJgdRSllJOM6hUOhqR2AAAMtUlEQVTNHed24/VVu/k8Z7/VcdqMI+UeD+Q3ul9gf+xkbgM+OZNQ7mB7yVG2lxzTKRmlvNDD41LpE9eB6e9nUXqs2uo4bcKRcm9ucXeza4lE5AYgA3juJM9PE5FMEcksKSlxPKUFltj/R7+wt5a7Ut4myN+Pv1wzkMOVtTw6f5NXLo90pNwLgMRG9xOAoqaDRORC4NfAJGNMs0cKGGNmGmMyjDEZ0dHRp5PXZT7bvI9+8eHERYRYHUUp1QZSY8N44KJeLNq0j4+y9lodx+kcKfe1QE8R6SYigcAUYEHjASIyCHiFhmIvdn5M1yo+XMX6/DLGputWu1LebNqoFAYlRfDY/GyKD1dZHcepWix3Y0wtcB+wGMgF3jXGbBaRJ0Vkkn3Yc0B7YJ6IbBCRBSd5OY/weW4xxsBFOt+ulFfzswl/vnoAx2vrmP6+d03P+DsyyBizCFjU5LHHG92+0Mm5LLUkZx9JkaGkdg6zOopSqo2lRLfnF+PT+O1HOczLLOCaoYkt/yEPoEeoNnH0eC0r8g4yNr0zInqiMKV8wc0jkhmeEsmTH+ewr9w7pme03Jv4emsJ1XX1XKTz7Ur5DJtN+MOV/amtr+fR+dleMT2j5d7Ekpx9RLYLZEjXjlZHUUq5UNdO7Xjwol58nrufRZv2WR3njGm5N1JTV8+XW4oZkxaDv59+NEr5mlvP7ka/+HB+syCbsgrPPrhJG6yR11bu4nBVLRP7d7E6ilLKAv5+Np69sh+HKmp4ZqFnn3tGy92usKySvyzZxgVpMZzXy70PsFJKtZ0+ceFMG5XCvHUFLP/+gNVxTpuWO2CM4bH52RgDT07uo6tklPJx94/pSbeodvzqg01UVnvmqYG13IFPsvfx5ZZiHhrbi4SOoVbHUUpZLDjAj99f0Y89pRW8uPR7q+OcFp8v96PHa/ntR5vpE9eBW0YmWx1HKeUmhqd04opB8cxctoPtJUetjtNqPl/uf/vie/YfPs7Tl/XVFTJKqR/45cW9CQ7w4/EPPW/tu0+32bb9R3h1+U6mDE1kUJKua1dK/VB0WBA/H5fKiryDfOxhZ4702XI/sRO1fbA/j4xPszqOUspNXX9WV/rGd+Cpj3M4UlVjdRyH+Wy5f7ihiDU7S3lkXBqR7QKtjqOUclN+NuHpy/pRcvQ4f/3cc3au+mS5H66q4emFuQxIjGCKl5wBTinVdgYmRjB1WBKzV+4id+9hq+M4xCfL/fkl2zh47DhPTe6DzaZr2pVSLXtkXCrhIQE8Oj+b+nr337nqc+Weu/cwr63cxfVnJdE/IcLqOEopDxERGsj0CWms232IBRt/dKVRt+NT5W6M4YkFmwkPCeDhsalWx1FKeZirBifQPyGcZz/ZQkV1rdVxTsmnyn3x5v2s2VnKg2NTiQjVnahKqdax2YTHL0ln3+EqXv56h9VxTslnyv14bR2/W5RLr87tmao7UZVSpykjOZJLB8TxytfbKSyrtDrOSflMuc9esYs9pRU8dkm6HomqlDoj0yekIQLPfrLF6ign5RMtV3LkOH//Mo8Le8dwbk89na9S6szER4QwbVR3PtpYROauUqvjNMuhcheR8SKyVUTyRGR6M88Hichc+/NrRCTZ2UHPxF+WbKOqpo5fXdzb6ijerem5N1o6F0drx6uW6WfqMnedl0Jsh2B++1GOWy6NbLHcRcQPmAFMANKBqSKS3mTYbcAhY0wP4HngD84Oerpyig4zd+0ebh6ZTEp0e6vjeK8nnoAHHvhfmRjTcP+JJ5wzXrVMP1OXCg30Z/qENDYVlvPedwVWx/kRR7bchwF5xpgdxphq4B1gcpMxk4HX7LffA8aIG1zxwhjDUx/nEB4SwM8u6Gl1HO9lDJSVwQsv/K9cHnig4X5ZWfNbk60Zr1qmn6klJg+MY1BSBM8t3srR4+61NNLfgTHxQH6j+wXAWScbY4ypFZFyoBPg9GtUfZG7n199sIl601De9QbqjaG+3mBO3Lb/bgxU19Xz1OQ+hIcGODuKOkEEnn++4fYLLzT8Arj//obHm/4/39rxqmX6mVpCRHjsknSueGklI373BaFBfggtf9Y3jujKvaN7tG22ls5RLCJXA+OMMbfb798IDDPG/LTRmM32MQX2+9vtYw42ea1pwDSApKSkIbt372514KyCMuas2YOIYBOw2X9vuG9/zCaI/bnYDsFcf1aSrpBxBWPA1uhzrq8/dam0drxqmX6mlvhoYxFrd5VyvKbeofHnp0YzoV+X03ovEVlnjMloaZwjW+4FQOOF4QlA02NvT4wpEBF/IBz40S5kY8xMYCZARkbGaf2c2D8hQk8b4I5OTAM09sADJ99qbO141TL9TC1z6YA4Lh0QZ3WMH3Bkc3Yt0FNEuolIIDAFWNBkzALgZvvtq4AvjaddtkSdvsbzu/ff37C1eP/9P5z/PZPxqmX6maomWtxyt8+h3wcsBvyAV40xm0XkSSDTGLMA+Bfwhojk0bDFPqUtQys3IwIRET+c3z0x/xsR0fyce2vGq5bpZ6qaaHHOva1kZGSYzMxMS95btRFjflgiTe+f6XjVMv1MvZ6jc+66l1E5T3Nb6M4cr1qmn6my03JXSikvpOWulFJeSMtdKaW8kJa7Ukp5IS13pZTyQlruSinlhSxb5y4iJUDrTy7jHFG0wUnNnEwzOo8n5PSEjOAZOT0hI5x+zq7GmBavOmRZuVtJRDIdOQjASprReTwhpydkBM/I6QkZoe1z6rSMUkp5IS13pZTyQr5a7jOtDuAAzeg8npDTEzKCZ+T0hIzQxjl9cs5dKaW8na9uuSullFfziXIXkUgRWSIi39t/79jMmIEiskpENotIlohc66Js40Vkq4jkicj0Zp4PEpG59ufXiEiyK3K1MuODIpJj/9y+EJGurs7oSM5G464SESMiLl9R4UhGEbnG/nluFpE57pZRRJJEZKmIrLd/zS+2IOOrIlIsItkneV5E5G/2v0OWiAx2dUZ7jpZyXm/PlyUiK0VkgNPe3Bjj9b+APwLT7benA39oZkwvoKf9dhywF4ho41x+wHYgBQgENgLpTcbcA7xsvz0FmOviz86RjKOBUPvtu12d0dGc9nFhwDJgNZDhbhmBnsB6oKP9fowbZpwJ3G2/nQ7ssuDrPQoYDGSf5PmLgU8AAYYDa1yd0cGcIxt9rSc4M6dPbLkDk4HX7LdfAy5rOsAYs80Y8739dhFQDLR4oMAZGgbkGWN2GGOqgXfsWRtrnP09YIyIS0/S3WJGY8xSY0yF/e5qGq6z62qOfJYAT9Hwn32VK8PZOZLxDmCGMeYQgDGm2A0zGqCD/XY4P76mcpszxiyjmes0NzIZeN00WA1EiMjpXZH6DLSU0xiz8sTXGid/7/hKuXc2xuwFsP8ec6rBIjKMhq2W7W2cKx7Ib3S/wP5Ys2OMMbVAOdCpjXM1+/52zWVs7DYatphcrcWcIjIISDTGfOzKYI048ln2AnqJyAoRWS0i412WroEjGZ8AbhCRAmAR8FPXRGuV1v67dQdO/d5p8RqqnkJEPgdim3nq1618nS7AG8DNxph6Z2Q71ds181jT5UuOjGlLDr+/iNwAZADntWmi5p0yp4jYgOeBW1wVqBmOfJb+NEzNnE/DVtw3ItLXGFPWxtlOcCTjVGC2MebPIjKChusn93XB90trWP190yoiMpqGcj/HWa/pNeVujLnwZM+JyH4R6WKM2Wsv72Z/1BWRDsBC4FH7j3JtrQBIbHQ/gR//iHtiTIGI+NPwY/Cpfhx1NkcyIiIX0vAf6XnGmOMuytZYSznDgL7AV/ZZrVhggYhMMsa46mK+jn69VxtjaoCdIrKVhrJf65qIDmW8DRgPYIxZJSLBNJwnxdVTSKfi0L9bdyAi/YFZwARjzEFnva6vTMssAG62374Z+LDpABEJBD6gYZ5unotyrQV6ikg3+/tPsWdtrHH2q4AvjX3vi7tktE93vAJMsmCO+IRT5jTGlBtjoowxycaYZBrmN11Z7C1mtJtPww5qRCSKhmmaHW6WcQ8wxp6xNxAMlLgwoyMWADfZV80MB8pPTM26ExFJAt4HbjTGbHPqi1uxB9nVv2iYo/4C+N7+e6T98Qxglv32DUANsKHRr4EuyHYxsI2G+f1f2x97kobigYZvnHlAHvAtkGLB59dSxs+B/Y0+twUWfZ1PmbPJ2K9w8WoZBz9LAf4C5ACbgClumDEdWEHDSpoNwFgLMr5Nw4q2Ghq20m8D7gLuavQ5zrD/HTZZ8bV2MOcs4FCj751MZ723HqGqlFJeyFemZZRSyqdouSullBfScldKKS+k5a6UUl5Iy10ppbyQlrtSSnkhLXellPJCWu5KKeWF/h+oggI92CT7xAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"np.random.seed(123)\n",
"data = np.random.random(3)\n",
"\n",
"x = np.linspace(data.min()-0.5, data.max()+0.5, num=500)\n",
"y_kde = KDE('epa', bw = 0.2).fit(data).evaluate_sorted(x)\n",
"\n",
"plt.scatter(data, np.zeros_like(data), marker='x', color='red')\n",
"plt.plot(x, y_kde, label='KDE')"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"ename": "TypeError",
"evalue": "evaluate_sorted() got an unexpected keyword argument 'weights'",
"output_type": "error",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[1;31mTypeError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-11-c842b4596a56>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[1;32m----> 1\u001b[1;33m \u001b[0my_kde\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mKDE\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;34m'epa'\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mbw\u001b[0m \u001b[1;33m=\u001b[0m \u001b[1;36m0.2\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mfit\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mdata\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mevaluate_sorted\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mx\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mweights\u001b[0m\u001b[1;33m=\u001b[0m\u001b[1;33m[\u001b[0m\u001b[1;36m3\u001b[0m\u001b[1;33m,\u001b[0m \u001b[1;36m1\u001b[0m\u001b[1;33m,\u001b[0m \u001b[1;36m1\u001b[0m\u001b[1;33m]\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[0;32m 2\u001b[0m \u001b[0mplt\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mscatter\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mdata\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mnp\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mzeros_like\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mdata\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mmarker\u001b[0m\u001b[1;33m=\u001b[0m\u001b[1;34m'x'\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mcolor\u001b[0m\u001b[1;33m=\u001b[0m\u001b[1;34m'red'\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 3\u001b[0m \u001b[0mplt\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mplot\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mx\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_kde\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mlabel\u001b[0m\u001b[1;33m=\u001b[0m\u001b[1;34m'KDE'\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n",
"\u001b[1;31mTypeError\u001b[0m: evaluate_sorted() got an unexpected keyword argument 'weights'"
]
}
],
"source": [
"y_kde = KDE('epa', bw = 0.2).fit(data).evaluate_sorted(x, weights=[3, 1, 1])\n",
"plt.scatter(data, np.zeros_like(data), marker='x', color='red')\n",
"plt.plot(x, y_kde, label='KDE')"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [],
"source": [
"from scipy.spatial import cKDTree, KDTree"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {},
"outputs": [],
"source": [
"list_of_points = np.array([0, 1, 3, 8, 17]).reshape(-1, 1)\n",
"tree = KDTree(list_of_points, 1)"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([list([0, 1, 2, 3]), list([3])], dtype=object)"
]
},
"execution_count": 62,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ans = tree.query_ball_point(np.array([4, 10]).reshape(-1, 1), 4)\n",
"\n",
"ans"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[0, 1, 2, 3]"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ans[0]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%load_ext autoreload"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%autoreload 2"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from KDEpy import KDE\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"np.random.seed(123)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import KDEpy\n",
"\n",
"\n",
"np.random.seed(123)\n",
"data = np.random.rand(5)\n",
"\n",
"kde = KDE(kernel = 'gaussian', bw = 1)\n",
"kde.fit(data)\n",
"x = np.linspace(-1, 2, num=500)\n",
"y = kde.evaluate_sorted(x)\n",
"\n",
"plt.plot(x, y)\n",
"plt.scatter(data, np.zeros_like(data) + 0.1, marker='x', color='red')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"data = np.random.rand(5)\n",
"\n",
"kde = KDEpy.KDE(kernel = 'gaussian', bw = 1)\n",
"kde.fit(data)\n",
"x = np.linspace(-1, 2, num=500)\n",
"y = kde.evaluate_sorted(x)\n",
"\n",
"plt.plot(x, y)\n",
"plt.scatter(data, np.zeros_like(data) + 0.1, marker='x', color='red')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"y"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"np.random.seed(123)\n",
"n = 2**16\n",
"print(n)\n",
"data = np.concatenate([np.random.randn(n), np.random.randn(n) + 5])*15\n",
"\n",
"\n",
"#data = np.array([0, 0.1, 0.2, 0.3, 0.4, 2, 3, 4])\n",
"\n",
"kde = KDEpy.KDE(kernel = 'gaussian', bw = 0.6)\n",
"kde.fit(data)\n",
"\n",
"x = np.linspace(np.min(data)-1, np.max(data)+1, num = 2**10)\n",
"#weights = np.array([1, 2, 3, 4, 3, 2, 1, 0])\n",
"weights = None #np.arange(len(data)) + 1\n",
"#x = np.linspace(-2, 2+5, num = 5+5)\n",
"\n",
"y = kde.evaluate_sorted(x, weights = weights)\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plt.plot(x, y)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"kde = KDEpy.KDE('box', bw = 2)\n",
"kde.fit(np.array([0, 0, 0,0.5, 1, 2, 3, 1]))\n",
"x = np.linspace(-1,10, num=500)#np.array([0])\n",
"y = kde.evaluate_naive(x)\n",
"#assert np.allclose(y, np.array([1.]))\n",
"\n",
"plt.plot(x, y)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"kde = KDEpy.KDE('box', bw = 2)\n",
"kde.fit(np.log(np.array([0, 0, 0,0.5, 1, 2, 3, 1]) + 0.0001))\n",
"x = np.linspace(0,10, num=500)#np.array([0])\n",
"y = np.exp(kde.evaluate_naive(np.log(x + 0.0001)))\n",
"#assert np.allclose(y, np.array([1.]))\n",
"\n",
"plt.plot(x, y)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Tests against scipy"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from scipy import stats\n",
"from scipy.stats import gaussian_kde\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"bw = 0.01\n",
"n = 3\n",
"\n",
"\n",
"data = np.array([0, 0.1, 1])\n",
"x = np.linspace(-1, 1, n)\n",
"density_estimate = gaussian_kde(dataset = data, bw_method = bw/np.asarray(data).std(ddof=1))\n",
"y = density_estimate.evaluate(x)\n",
"y"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from KDEpy import KDE"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"KDE(kernel='gaussian', bw=bw).fit(data).evaluate_naive(x)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"gaussian = KDE._available_kernels['gaussian']"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"x = np.linspace(0, gaussian.var*10, num = 3)\n",
"\n",
"gaussian(x)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"i = np.searchsorted(gaussian(x), 10e-10, side='left', sorter=np.arange(len(x))[::-1])\n",
"i"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"np.insert(gaussian(x), i+1, 10e-10)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"np.diff(np.insert(gaussian(x), i+1, 10e-10))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"------------"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"tolerance = 10e-10\n",
"x_samples = np.linspace(-gaussian.var*10, 0, num = 50000)\n",
"sampled_func = gaussian(x_samples) - tolerance\n",
"\n",
"to_search = sampled_func\n",
"#to_search"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"i = np.searchsorted(to_search, 0, side='right')\n",
"print(i)\n",
"print(x_samples[i])\n",
"print(gaussian(x_samples[i-1]))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"inserted = np.insert(to_search, i, 0)\n",
"inserted"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"np.all(np.diff(inserted) >= 0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"np.argsort(np.array([10, 8, 6, 2]))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.5"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
mfkaptan/ipythomic | src/ipythomic_demo.ipynb | 1 | 1871 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Basic example of real time data visualization in IPython notebook"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from ipythomic import MicrophoneWidget"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Be sure that your microphone works! Don't have a microphone? Try redirecting your speakers to your microphone!\n",
"mic = MicrophoneWidget()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mic # Display the Widget"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Change display by clicking Lines or Bars"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Change attributes from Python and it updates in JavaScript."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mic.thickness = 15"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mic.background = 200"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-2.0 |
yugangzhang/CHX_Pipelines | 2018_2/XPCS_Setup_2018_V9.ipynb | 1 | 1466400 | null | bsd-3-clause |
myfunprograms/deep_learning | project1/files/dlnd-your-first-neural-network.ipynb | 1 | 1321029 | null | gpl-3.0 |
XinyiGong/pymks | notebooks/cahn_hilliard.ipynb | 2 | 237753 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#Cahn-Hilliard Example\n",
"\n",
"This example demonstrates how to use PyMKS to solve the Cahn-Hilliard equation. The first section provides some background information about the Cahn-Hilliard equation as well as details about calibrating and validating the MKS model. The example demonstrates how to generate sample data, calibrate the influence coefficients and then pick an appropriate number of local states when state space is continuous. The MKS model and a spectral solution of the Cahn-Hilliard equation are compared on a larger test microstructure over multiple time steps."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Cahn-Hilliard Equation\n",
"\n",
"The Cahn-Hilliard equation is used to simulate microstructure evolution during spinodial decomposition and has the following form,\n",
"\n",
"$$ \\dot{\\phi} = \\nabla^2 \\left( \\phi^3 - \\phi \\right) - \\gamma \\nabla^4 \\phi $$\n",
"\n",
"where $\\phi$ is a conserved ordered parameter and $\\sqrt{\\gamma}$ represents the width of the interface. In this example, the Cahn-Hilliard equation is solved using a semi-implicit spectral scheme with periodic boundary conditions, see [Chang and Rutenberg](http://dx.doi.org/10.1103/PhysRevE.72.055701) for more details."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"%load_ext autoreload\n",
"%autoreload 2\n",
"\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Modeling with MKS\n",
"\n",
"In this example the MKS equation will be used to predict microstructure at the next time step using \n",
"\n",
"$$p[s, 1] = \\sum_{r=0}^{S-1} \\alpha[l, r, 1] \\sum_{l=0}^{L-1} m[l, s - r, 0] + ...$$\n",
"\n",
"where $p[s, n + 1]$ is the concentration field at location $s$ and at time $n + 1$, $r$ is the convolution dummy variable and $l$ indicates the local states varable. $\\alpha[l, r, n]$ are the influence coefficients and $m[l, r, 0]$ the microstructure function given to the model. $S$ is the total discretized volume and $L$ is the total number of local states `n_states` choosen to use.\n",
"\n",
"The model will march forward in time by recussively replacing discretizing $p[s, n]$ and substituing it back for $m[l, s - r, n]$.\n",
"\n",
"###Calibration Datasets\n",
"\n",
"Unlike the elastostatic examples, the microstructure (concentration field) for this simulation doesn't have discrete phases. The microstructure is a continuous field that can have a range of values which can change over time, therefore the first order influence coefficients cannot be calibrated with delta microstructures. Instead a large number of simulations with random initial conditions are used to calibrate the first order influence coefficients using linear regression.\n",
"\n",
"The function `make_cahn_hilliard` from `pymks.datasets` provides an interface to generate calibration datasets for the influence coefficients. To use `make_cahn_hilliard`, we need to set the number of samples we want to use to calibrate the influence coefficients using `n_samples`, the size of the simulation domain using `size` and the time step using `dt`."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import pymks\n",
"from pymks.datasets import make_cahn_hilliard\n",
"\n",
"n = 41\n",
"n_samples = 400\n",
"dt = 1e-2\n",
"np.random.seed(99)\n",
"X, y = make_cahn_hilliard(n_samples=n_samples, size=(n, n), dt=dt)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The function `make_cahnHilliard` generates `n_samples` number of random microstructures, `X`, and the associated updated microstructures, `y`, after one time step `y`. The following cell plots one of these microstructures along with its update."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAoAAAAEsCAYAAABT+wIrAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzsnXlYVHX7xm9gYIZtQDZBQRHRUFzTSMVQyyUT9zSxzPqp\n",
"Zfb2Zqa+r5VLLmmrmhllWImlgaJp5pJpuORCkmjuGyooqIjszAzM8PvDi3nFeZ7D4kbT87kurgvu\n",
"meecM2ebh3POfX9tysrKyiAIgiAIgiD8Y7B90AsgCIIgCIIg3F+kARQEQRAEQfiHIQ2gIAiCIAjC\n",
"PwxpAAVBEARBEP5hSAMoCIIgCILwD0MaQEEQBEEQhH8Yqge9ALWJ+Ph4bNmyBUuXLn1gy3Do0CFc\n",
"unQJTz31VJXeX1JSgk2bNmH37t3IyMgAAPj7+yM8PBw9e/aEg4PDvVzce8qZM2dw8OBBDBky5K5N\n",
"s7S0FGvWrEFYWBgCAwPN+tWrV/Haa6/hP//5Dx5++OG7Nj9BSExMxC+//IL09HTY2NigUaNGiIyM\n",
"RPv27as9rcuXL2P37t2IjIyEk5PTPVjams1j37592LJlC86fPw+DwQAvLy+0a9cOffv2RZ06de7J\n",
"ct4PcnNzsWXLFnTr1g3e3t53bbq//vor3Nzc8Mgjj1TQX331VXTs2BHPPffcXZuXIHBIA3gbNjY2\n",
"D3T+hw4dwv79+6vUABoMBsyePRtpaWno06cPQkJCAAAnT57EunXrYGtrW+VGsjZy5swZrF69+q43\n",
"gAkJCahbt26FBtDDwwNz5sxBvXr17tq8BOGrr77C9u3b0atXL0RFRcFoNOL333/Hhx9+iOHDh6N/\n",
"//7Vml5GRgYSEhLw+OOP37MGsLrziI2NxcaNG9GtWzf07dsXjo6OSEtLw9atW3H16lVMnDjxnizn\n",
"/SA3NxcJCQlo0aLFXW8AGzRoYNEATpo0Ca6urndtPoKghDSAt/F3ysX+4YcfkJqairlz58Lf39+s\n",
"t2jRAr169cLly5cf4NLdP8rKylBaWgp7e/tq1dyKSqVCcHDw3V404R9MUlISfv31V4wZMwbdu3c3\n",
"623atIG7uztWrlyJVq1aoVGjRtWe9v04T1VlHgcOHMDPP/+MV155BV27djXrzZo1Q/fu3XH48OF7\n",
"uIS1C4PBcMd3XG79p1QQ7jU2MhLI/7j9FvDRo0cxc+ZMTJ8+HZs3b0ZKSgrc3NzQt29f9OzZ01y3\n",
"ePFipKenY+DAgVixYgWuXbuGxo0b46WXXjI3ZtwtxvLauXPnIj4+HgkJCRWWqUuXLhg3bpzFsur1\n",
"eowePRo9e/bEiBEjKv1s58+fR2xsLE6fPg2VSoW2bdti5MiRcHNzq7B848ePx19//YU9e/bA0dER\n",
"3bp1w5AhQypcGb1w4QJWrlyJkydPwmg0wt/fH8OGDUOrVq0AAAUFBfj+++9x4MABFBUVISgoCCNH\n",
"jqzQYD3zzDMYOXIkcnJysH37dtjY2KBDhw4YOXIkVCoVEhMTER0dXeEzNG/eHNOnTzdvp0mTJmHZ\n",
"smW4ePEixo4di7CwMHz33Xf466+/cP36dbi5uaFt27YYPnw4HB0dzfO9ncWLF8NkMllsH5PJhNWr\n",
"V+O3335DXl4efH19MXDgQHTu3Nli+0VFRSE2NhZXrlxBo0aNKmx74Z/Ju+++i+zsbCxYsMDizkJR\n",
"URFeffVVhIWF4ZVXXgFw8/Zfhw4dKhzP5cdBbGwszpw5g5kzZ1aYjre3Nz777DPz+9577z0sW7YM\n",
"586dg6enJ5599lmEhYWZ338n8+A+o06nw9y5cytdH3l5eYiNjcXBgwdhMBgQHByMESNGICgoyGL5\n",
"6tSpgw0bNkCv16N169Z46aWXKlyNzM/Px8qVK5GcnIyCggJ4e3ujZ8+e5jseJpMJ69evx7Zt25Cd\n",
"nQ0vLy8MGjQIXbp0MU9jxowZ0Gq1CAsLQ1xcHPLy8hASEoKXX34ZHh4e5nPi7cTFxZm/G9566y1s\n",
"3rwZR48eRadOnTB27Fj89NNP2LNnDzIyMmBvb4/g4GCMHDkSvr6+5vkeP368wjTHjRuHLl26kNtn\n",
"z549SEhIQGZmJrRaLbp06YKhQ4fC1ta2wvb78MMPsWzZMpw6dQpeXl6IioqqsO0F4XbkCmAV+PLL\n",
"L9GlSxf06NEDu3fvxtKlSxEUFGRuaGxsbHDt2jUsX74czzzzDBwcHBAfH485c+bg008/rfKVqe7d\n",
"uyMzMxNHjx7FpEmTAABarZZ877lz52AwGNCmTZtKp5uXl4cZM2YgICAAr7/+OoqLi7FixQrMnj0b\n",
"c+fOhUr1v93gu+++Q4cOHfDmm2/ir7/+QkJCAgICAtCxY0cAwKVLlzB16lTUr18fY8aMgaurK86e\n",
"PYvs7GwAN59JnDVrFoqKijBixAhotVr88ssvmDVrFhYuXAh3d3fzvDZs2IAWLVrg3//+N86fP4+V\n",
"K1fC29sb/fr1w8MPP4zIyEhs2LABc+bMAQBzEwfc/G978eLF6N+/P+rVqwd3d3fo9XoYjUY888wz\n",
"cHd3R1ZWFtasWYNPPvkEb7/9NgBg2rRpmDlzJgYPHmxu9Nzd3c3LfytxcXFYv349hgwZguDgYOzb\n",
"tw+LFi2CjY0NwsPDAdzc9llZWfjuu+8wePBg2NvbY/ny5Zg/fz4+/vjjSreNYJ0YjUacOnUKvXr1\n",
"Ih8rcXJyQmhoqEUjoPQISlBQEEaMGIHly5dj4sSJqFOnToVjFwAWLFiAXr16YdCgQdi2bRvmz5+P\n",
"efPmoWHDhndtHuWUlpbi1KlT6Nu3Lzu9W/nwww9x9epVjBgxAq6urli/fj3effddvP/+++bmCAD2\n",
"7t2Lhg0bYuzYscjKykJsbCxWrFiB0aNHA7h57M+YMQP5+fl4+umnUb9+fWRkZODKlSvmaXz99dfY\n",
"uXMnnn76aQQFBeHQoUOIjo6Gq6ur+bi3sbHB6dOncePGDYwcORIGgwHffPMNvvzyS0yZMgUeHh54\n",
"7bXXsGjRIowaNapCo1rOF198gW7duiEyMtJ8nr9+/Tp69eoFb29v6HQ6/PLLL5g6dSoWLlwIJycn\n",
"jB49Gh9//DHq1q2Lp59+GgBQt25dcvscOnQICxcuRJcuXfD888/jwoULiIuLQ35+PsaMGVNhWT79\n",
"9FN0794d/fv3x6ZNm7BgwQJ89tln8PDwqNL2Ef55SANYBcLDwzFo0CAAN69CJScnIykpydwAlpWV\n",
"IT8/H5MnT0bTpk0B3DyRvvbaa0hMTESPHj2qNB8PDw+4u7tX6XZkecPi5eVV6XR/+ukn2NjY4O23\n",
"34ZGowEA+Pn54e2338b+/fvNzUz55yv/77Nly5ZISUnB/v37zQ3gqlWr4OzsjJkzZ5pPeC1btjTX\n",
"79q1C2lpafjkk0/MJ/VWrVrh9ddfx4YNGyo83Ozj42O+utmqVSucPHkS+/fvR79+/aDVas3P3FDr\n",
"wmAwYOTIkRYP0r/00kvm341GI7y9vTF9+nRcv34dnp6eaNy4MYCbJ1yldVxQUICNGzdi8ODB5m3f\n",
"qlUrXL9+HatWrTKvs7KyMhQUFGDWrFnmz1tWVoaPPvoIly9flmcK/6Hk5+ejtLRU8bkxLy8vpKSk\n",
"VHmajo6O8PPzAwA0atSIPPafeOIJREZGAgBat26NCRMmYO3atRg/fvxdm0c5BQUFKC0trdI5KCUl\n",
"BadOncKMGTPQrFkzADcfVXn11Vexfv36CsetSqXCpEmTzFe40tPTsWfPHnMDuGPHDqSnp+ODDz4w\n",
"N7ahoaHm+szMTGzduhWvvvoqIiIizPO6ceMGVq1aZW4Ay8rKoNPpMGXKFPPVxZycHCxbtgwlJSWw\n",
"t7dHgwYNANw01lHni44dO2Lo0KEVtBdeeMH8u8lkQsuWLTFmzBgcOHAAERER8Pf3h0ajgVarrfQ8\n",
"Hx8fj9DQUPN5snXr1gCAFStWYPDgwRWau8jISPNt+KCgIIwZMwbJyclV/v4R/nlIA1gFyg86ALCz\n",
"s4Ofn5/FFSM3Nzdz8wfcPLkHBQXhzJkz9/QArIpp5cyZM2jdurW5+QNuNlXe3t44efJkhQbw1s8K\n",
"APXr18f169fNfx89ehQRERHsVc3Dhw8jKCgIPj4+MBqNZr1Zs2Y4e/ZshfeW3zK+dV7nzp2r9POU\n",
"07ZtWwtt586d2LBhAzIzM6HX68365cuX4enpWeVpX7x4EQaDwdz4ltOxY0dER0cjPz/f/LC2j49P\n",
"hSsY9evXB3CzSZcGULif3HrLz8bGBu3bt8e+ffvu6Tyreg5yc3MzN38AoFar8fDDD+PkyZMV3hsa\n",
"Gmpu/oCbzVdubi5MJhNsbW1x5MgRBAUFVbiqeSt//fUXbG1t8cgjj1Q4B7Vo0QK///47ysrKzMvc\n",
"uHHjCreWbz12b70qx0ElBpw6dQpxcXE4f/48CgoKzHp5SkNVMZlMSE1NrdBQAjfPQd9//z1OnTqF\n",
"Dh06mPVbz6cuLi7QarXknQ1BKEcawCrg7Oxc4W87OzsYDIYKGnWr1tXVFTk5Ofdkmcr/88vKyqrQ\n",
"fFDk5OSY/5O9FTc3twonKAAWrj+VSoWSkhLz3wUFBYqxDvn5+Th9+jSioqIsXrt9OW9fryqVymK9\n",
"cri4uMDOzq6ClpSUhMWLF6Nnz54YPnw4XFxccOPGDXz00UcVPkNVKN9u5c9IllN+C7ugoMDcAFLr\n",
"DECVP4tgfbi6ukKlUuHatWvse65du1atf0qqwu3nIa1Wixs3btzVeZTj4uIClUqFrKysSt9748YN\n",
"8hxJnYOo8wJw8/EStVqNgoKCCo+S3E5+fj5MJpNF43TrspSfP7ljt6rni9vPD1lZWZgzZw6aNGmC\n",
"l156yXwLfe7cudU+B+Xl5cFoNFp81vJ5VmW9VXeewj8LaQDvErm5uRZaXl6eufEqd4eVlpZWeE9h\n",
"YWGN5te4cWOo1WqkpKSgRYsWiu+tU6cOuXw5OTnmW6JVxcXFRfG/SldXV/Pth9upjku3JuzduxdN\n",
"mjTBqFGjzNqxY8dqNK3yk25eXh5cXFzMenljeKsmCLdjZ2eHpk2b4s8//8SIESNIE8ixY8fw6KOP\n",
"mjUHBweL88PtX/KVcfv+mpubW+Eftrsxj3JUKhVCQkKQkpJCmqtuhTsH5ebmVvtYcnV1RWZmJvu6\n",
"i4sLbG1tMXv2bPLqJPdcdU24ffopKSkwGAyYPHmy+ZxvNBprtI61Wi3s7Ows1lv533IOEu4UGQmk\n",
"BlAnlby8PJw6dcr8d1ZWFlJTU83PeJQfzOnp6eb36HQ6i9sfVf2vzcHBAd27dzcHzN5OYWGheXmC\n",
"g4Nx6NAh6HQ68+tnzpxBVlaWOTuwqrRs2RJ79+5ll7FFixbIzMw03wK/9ScgIKBa86ruf+MlJSUW\n",
"D6zv2rWrRtNs0KABHBwcsGfPngr63r17Ua9ePcnqEirlqaeeQkZGBrZt22bx2o8//gidTocnn3zS\n",
"rHl4eFgcy7fHqFR2dXn//v3m300mEw4cOFDhObO7MY9beeqpp3Du3Dns2LHD4jWTyWR+xrFJkybI\n",
"y8urYHrR6/X4888/q30OatGiBVJTU3Hx4kX2dZPJhMLCQotzUFBQkPnzVeXWdXXPQQaDATY2NhVu\n",
"Ye/duxcmk8liupWtX1tbWwQFBWHv3r0V9L1798LGxqbCI0eCUBPkCmANoJJzXF1dsWjRogouYHd3\n",
"d/NDuba2tmjfvj1+/vlneHt7w8nJCRs2bIBara4wnfLnXRITExEQEFDBDHE7w4YNw9mzZzF16lT0\n",
"6dMHDz30EADg9OnT2LJlCwYMGICmTZsiMjISW7duxZw5c9C/f3+zC7hBgwYVrkBUhaeffhpTpkzB\n",
"9OnTERkZCRcXF5w/fx6urq7o1q0bunTpgq1bt2LGjBno27cvfHx8kJ+fjzNnzqBOnTro06dPledV\n",
"/jzOxo0bERoaCicnJ8Vn6lq1aoWlS5dizZo1CA4OxsGDB3HkyJEK71GpVPDx8cGePXvg7+8Pe3t7\n",
"8lkiFxcX9OnTB2vWrIGdnR2CgoKwf/9+pKSk4PXXX6/yZxD+uTzyyCPo0aMHli5divT0dDz88MMw\n",
"mUzYs2cPduzYgeHDh1fIfQsLC8PXX3+NtWvXonHjxti3b59Fs1a+/2/duhWdOnWCWq2u8HjH9u3b\n",
"oVKpEBAQgG3btuHKlSsVDCB3Yx630q5dO/Tp0wdffPEFTp48ifbt20Oj0eDSpUvYunUrfHx80KZN\n",
"G7Ru3RpNmzbFggULzI9n/PTTTygpKUG/fv2qtV67dOmCLVu2YPbs2RgyZAj8/Pxw9epVZGZmYvjw\n",
"4ahXrx569OiBhQsXol+/fggKCkJJSQnS0tKQkZGBsWPHAqhazqGXlxccHByQmJgIR0dH2NnZKd41\n",
"KW8+P//8c3Tr1g1paWnYsGEDnJycKsyvXr16OHToEA4dOgQXFxfUrVuXvKI3dOhQzJkzB59//jk6\n",
"deqEixcvIi4uDt27dxd3r3DHSAN4CzY2NlX6r5B6j7e3NwYOHIjvv/8eWVlZaNy4McaPH1/hitSo\n",
"UaPw5ZdfIiYmBi4uLhg0aBBOnjyJtLQ083s6duyII0eO4Pvvv0deXh6bAwjcvAo4depUbNq0Cbt2\n",
"7cK6desAAAEBAejfv7/ZfKLVajF9+nTExsZi4cKF5hzAF154weI5uso+a7169TBr1ix8//33+PLL\n",
"LwHcbFrLn/mzt7c3Z/XFx8cjNzcXbm5uCA4OrjST6vb136xZM/Tt2xcbN27EihUrzDmA1HIBN2N0\n",
"rly5gk2bNsFgMKB169Z4/fXXzREw5YwZMwbLly/HrFmzUFpaisWLF5PLU5619csvvyA3Nxd+fn54\n",
"7bXX0KlTJ3b9CMKtjB49GsHBwdi6dSu2bdtmvqozefJktGvXrsJ7b91/S0pK0KVLFwwaNAhfffWV\n",
"+T3e3t4YMWIENm3ahM2bN8PT07NCRt/48ePx7bff4ocffoCXlxfeeOONCk3m3ZjH7Tz//PN46KGH\n",
"sHnzZnz66acwGAzw8fFB+/btK0TETJo0CbGxsfj2229RUlKCJk2aYPr06VUyW9xK+Tnm+++/R3x8\n",
"PIqKiuDj44NevXpVWO/16tXDtm3bEB8fD0dHRwQEBKBbt27m91Tl2HVwcMDLL7+MVatWYcaMGTAa\n",
"jYiLi2Pf36BBA4wbNw6rVq1CUlISAgMDMWHCBMyfP7/C/AYPHoysrCzMnz8fxcXF5hzA2ylPUFiz\n",
"Zg12795tzqG93XksCDVBgqDvAreGOQuCINxvbg1zvv2ugiAIAoU8AygIgiAIgvAPQxrAu4DcBhQE\n",
"QRAE4e+E3AIWBEEQBEG4j2zevBmJiYlIS0tDeHg4+6w/cHPY1PXr10Ov16NDhw4YM2YMO0RjdZAr\n",
"gIIgCIIgCPcRDw8PDB48uIIxiSIlJQXr1q3DtGnT8Pnnn+Pq1auIj4+/K8sgDaAgCIIgCMJ9JCws\n",
"DI888kilgd47duzAE088AX9/fzg7O2Pw4MFITEy8K8tQ6TXEtae/IPWXw/9D6rN/nc5O6woz6kV2\n",
"/CG2JimMXjn6j/eSOgCs2f4Bqa87e4rUAeC5QDqMtFTN98iutvTq69fvLbbm3W/fIHXDaX44paNu\n",
"RlJfnPIHW5N7yzi4t7KizwC25vCPf5J6RJfWpA4AA5M2kXp9Fz4ouf6P50k9+2l+YHTTF8mk3qQJ\n",
"Hy599GgqqZ8dHsTWqGzp7d20Dp+51TvNgdRPt+QPbBPz5EWfoCZsTSsVvU5N7hpSB4CIH5aR+ice\n",
"/DZdUHqe1B1V9EguXeu2wzsRY9npVZWMwg0Wmkrh+drsW4LNb6W0zETqAODmQDtk7ZjtDgCu9vT2\n",
"zdHT8weAfCbk11Hhto0zM1KOu5rfvqWGUlJ3cFA4tTPrNFtXzJZcLS4i9TzmPAMAtsx8nBRGBOKe\n",
"SCpUCGJ2caC3T4ArP+KHI3Pt4+pVfuhOjYaej1rryNYcunaF1K8rrGs7G3rZPDT8flBiovd5g5H+\n",
"7gD47aO0v7kzy+DGbAMA0DKudKV9p7iU3q8baPuzNdZKenp6hQi1hg0bIjc3FwUFBXc8GoxcARQE\n",
"QRAEQaiF6HS6CmNWOzo6mvU7RYKgBUEQBEEQ7jK3PqsXGhqK0NDQak9Do9GguPh/V4yLiorM+p0i\n",
"DaAgCIIgCFZN/S8H3tf5XXp57V0ZsSUgIADnz59Hhw4dAAAXLlyAm5vbHd/+BeQWsCAIgiAIVo6t\n",
"jc19/akMk8kEg8EAk8kEk8mEkpISmIhnOSMiIrB9+3akp6ejoKAACQkJ6Nq1611ZJ5VeAXyqAf3A\n",
"/Nk02ob8392/sdPycXQi9V+20g/4A0DLJ/qS+uQlb7I1C/9MIvUbCg/eDgx+iNTVhfzDxzNO7Cf1\n",
"Zv/pydb8Z+c2Un8hlH8ov3DzaVJ/tpQ3WnzpST+E3t63PlvziT/9ecpKr7M1TwXSxo2Udy0f6C/H\n",
"4b896Pks2MnWfP/ju6R+rZjfpsXn6eWeeJY3zzT39CL15CsZbE1hIf0A9luP9iJ1AODCN1efOs7W\n",
"HDddI/W6iXlsTdHb9P72rm8KW/PBetrE9Nm/lpK6KsIXiGAnV2Uog4S+lH+I3d6O/v/VXuH/Ws6E\n",
"oVN4WL64lD4HGEx8TU0oZQwQnNkFANQqeizvEuYh+ppiZEwG3MP6AKBmxhkvYAwyAG+O4gwyAODj\n",
"6EzqKsZMAQC2zGteXm5sDWesyS3hP49DJWOtU5TUYL/SMuYmW4U+hGtSOFMNAPg50985pcX8OijK\n",
"o8/RXu78FaxSZn+7E6rSlN1PVq9ejYSEBPPfu3btwpAhQ9C1a1fz+NGenp5o06YN+vXrh3fffRcG\n",
"gwEdOnS4a2NByy1gQRAEQRCsGhvUrgZw6NChbCMXGxtb4e/IyEhERkbe9WWQBlAQBEEQBKtG6Wro\n",
"PxVpAAVBEARBsGpq2y3g2oA0gIIgCIIgWDXSAFoiDaAgCIIgCFaNNICWVNoATthFuwiHPNSc1LXb\n",
"LrLTGv1WFKm/c7gzW9MtfjmpN2vFD+f1XwPtdHVihrICgPgV9Ofs8Cj9OQGg2EC7A1eNWMLWfPTx\n",
"OFJPWrqbrZn30cuk/kky7XYGgEFF3qT+VzI/HN6/3ehhyBac52uGFtJDpA2d8xJbY2BcgGmfPM/W\n",
"TN65ndQb/ZHN1tTzox29J6auZWtWH/2a1Lv/vIqt2fkQ7cD77pF/sTWvrnyN1NNW8I74R8bQVtuc\n",
"ItodDADpGQmkXr/uILamSR1PUr927Qap5+fTQzzeDZSe2/HQ0ENwlSg4ejk0Cm5Ne1v6NRNn5Qag\n",
"tqNdjErOVBPrDVeaD30Kd1AY2o4bKi9fwc2qZ9ap0pcqt2xKNXoj7SrmhhMDAFfGtWqvsA64odNK\n",
"FYLR9IwbvEhhmDpu2Dul4dYKme3AOaQBwF1Drx9nFe/oVRqWkMOB2XY6Bbd+KfOagfn+BAAHB/67\n",
"uqbUNhNIbUCuAAqCIAiCYNXIFUBLpAEUBEEQBMGqkQbQEmkABUEQBEGwaqQBtEQaQEEQBEEQrBrJ\n",
"AbREGkBBEARBEKwaG7kCaIE0gIIgCIIgWDW24gK2oNIGcOXQz0nd+cfxpL5zOz/IfOvnw0n9k+T9\n",
"bE3qG+tIvcsne9makBm9ST0slR9g2ja8Aal/dukYW9MujdYTptNxHQDw1CB6HXR/4mG2ZurvO0i9\n",
"b+OmbM2CP+l1euw8b9fnbPkHkcnWNA2hI0P2rPyVrek7qS+pa3R6tubSfHod/P5MY7bGxymL1Ft9\n",
"Npit+fXaJVLnYo8A4EjWVVIP/fxZtmbtmytIPSrqCbZm72V62SJ7t2Rr7Jl4k17L/4+taeiiJXXn\n",
"iXRck4MvHR9UXaiIFKMNf8xyMRaKUStMlIZa4cvBxOS9qJj4EYAfzL64lI45AfgvKGcmSkQJk5Ff\n",
"bw4qep8wMsushFohPodbbqW4G277KG1TLu5FaT7c9uEicgDgUkE+qefodGyNilk2rQMfa+PORN7Y\n",
"KcTacJE7Pk5ObE1BQTGpOznxy2bLfR4tPx+uRgnuOHG6g3QYeQbQErkCKAiCIAiCVSMNoCXSAAqC\n",
"IAiCYNVIA2iJNICCIAiCIFg1YgKxRBpAQRAEQRCsGjGBWCINoCAIgiAIVk1tzAEsKChAdHQ0Dh8+\n",
"DK1Wi6ioKHTuTJvtVq9ejW3btqG4uBiNGjXCqFGj4O/vf0fzr7QBfDHh36TOOZ8+Xfs2O62fv/yF\n",
"1Ef0512Mj6x/lNTT0q6xNQOfpF24Z06nszU79bRj9AW3RmwN3Gh5t09btuT8cXoZunalXdUA4PnR\n",
"k6TuouBCdGAGsF+zdidbU/dftEO5cwntkAaAxscKSf3IoBC2JkzrTerbDbTLFQD27TtO6h1f4t3T\n",
"lxnX3rQOj7E1r/WaTupjXopkaz5+hX5tR9p5tibgg2dI/dcPt7A1La7Q+6JrSChbA8ZVeSAzgy0J\n",
"bT6S1BP2zid1tbEuP/9qoDfyDlkKxpxbI9cs54gE+MHs3d1d2BrOxWhvxzsiNYyTk3M7A4CJcbNm\n",
"36D3faUaLw9XtoZzx5YouI05h3BhKZ02AABujAPWz5lf1yZm+yi5Tzl3fLGe3wcLDAZSL1L4PB4a\n",
"R1IPcOXXNVfDOaQB3vGs09HLDADZ2XmknpvLO7u5fV6tVjjmbOhlU3Kq34vbtbXxGcCYmBjY29sj\n",
"JiYGqampmDdvHgIDAy0auwMHDmDr1q2YNWsWvLy88MMPP2DRokV4//3372j+1fdnC4IgCIIg/I2w\n",
"tbG5rz+VodPpkJSUhGHDhkGtViMkJATt27fHzp2WF2nS0tIQEhICHx8f2Nra4rHHHkN6On9Bq8rr\n",
"5I6nIAiCIAiCUIuxsbG5rz+VkZGRATs7O/j6+pq1wMBApKVZBgy3bNkSp06dQkZGBkpLS7Fjxw60\n",
"bcvfaawq8gygIAiCIAhWTW0zgeh0Ojg6Vrzdr9FooCMerwsODkaXLl0wfvx42NrawsvLC1OnTr3j\n",
"ZZAGUBAEQRAEq+ZBPAMYHx9v/j00NBShof97Xluj0aC4uOKzx0VFRdBoNBbT2bx5M44cOYLo6Gi4\n",
"u7tj586dmDlzJj755BM4KHgBKkMaQEEQBEEQrJoH0QAOHTqUfc3Pzw9GoxGZmZnm28AXLlxAQECA\n",
"xXtTUlLCnYjrAAAgAElEQVQQHh4ODw8PAEDXrl2xbNkypKenIygoqMbLJ88ACoIgCIJg1dS2ZwA1\n",
"Gg3CwsIQFxcHvV6PEydOIDk5GRERlikmDRo0wN69e5GbmwuTyYSdO3fCaDRWeH6wRuukrEzBWw7g\n",
"Qu6PpP7tAlovNdKWfAAIHtqe1H+euZatmfXFa6RedpWOHwGAuPjtpL6mIW/XXxJCR6BcqsP3yPNH\n",
"f07qF58LZmv6pNDrZ+zYfmxNz56TSP3EiWVszYjn55J612n8fPxdtaS+4exptiZzPh0rc/DgGbbm\n",
"7S1vkfrVhENsTZ0BLUh9bLM2bM3585mkvqP0OlvDJBZgcud32Jru3duR+hMzBrA1nerR+U0hdTzZ\n",
"mpdepC3/A6c/zdbEvRVH6m9O5P8z9a/vRepXHejYBqcyPzT368pOr6qUGLdV6/3cf/RK/+lzcS8O\n",
"DtW/GaIUM6JnYlOUYmC46CYutkVpGS5evMLW5OfT68DNzZmt8feno5sKS/hzan4JHUFSovAd4a62\n",
"vP0FADcyb7A1eXlFpO7j487W+PjUIfUzOfx8MgsLSN2o8BXqzsTaNPOkjzEASD9Pbzsujgjg41lK\n",
"Svia/Hx6vdkqBOZx83Fw4GNgNJrq36Lkjkc7uyeqPa1y+v74So1ra8JPA6Irfc/tOYDDhw9HeHg4\n",
"srKyMGHCBMyfPx+enp7Q6/X45ptvkJycDIPBAD8/P0RFRaF169Z3tIxyC1gQBEEQBKumtplAAMDF\n",
"xQWTJlle4PHy8kJsbKz5b7VajbFjx971+UsDKAiCIAiCVVMbg6AfNNIACoIgCIJg1UgDaIk0gIIg\n",
"CIIgWDX3Yni5vzvSAAqCIAiCYNXIFUBLKm0AN/9AuzzjGtBOsq4Bgey0+utoR9SsP3mXqWcZvYjt\n",
"dtIuZACov/kkqfeYO5CtKS6mHWvjh7zH1ry/ZRqpuzjQnxMA2vR2I/WIiH+zNUeOfE3qDi70oOEA\n",
"kB3VlNQNv55lay73oN3LUwJ5p+2XzS+SuocH7SgGgEVDFpD6jh2fsjXxV+jlHrZ1HVvjrKKdaQsf\n",
"78XWvP7iR6TesiWftdSnTwdS97vEDyw/7W16HZw9d5mt+WADnfz+3MPj2Zp9e2mnuntD3m28d/Of\n",
"pB4S0oDUVWoD4MdOrsrk5Vi6LLWM6xAA9Iyb1FHFn9ZYt69KwdHLuC9dVbRrFwBKSmlnKOf0BXiX\n",
"Zwl4l6kN40C1s+Pno9fT57rcXLYETk70Oc29jitbo2aWgdtuAFCmp4+ZrCx+4Thnt9IVHy9v2iGs\n",
"M/LHLLfcJgUXsB3j0lbaD7jvIs61C/DrQMmpzrl9XRS+VwwGev1otbyDnHMBc8sMAHl5dMpH3bps\n",
"SaXURhPIg0auAAqCIAiCYNUopNv8Y5EGUBAEQRAEq0ZuAVsiDaAgCIIgCFaNmEAskQZQEARBEASr\n",
"Rq4AWiINoCAIgiAIVo00gJZIAygIgiAIglUjLmBLKm0Ap0//ltSPHV9W7Zmd1uWR+ob9C9mandkZ\n",
"pK5SiDno3ftRUu9q68PWXPelYw4aNeLzLabu2UHqLvb84Nd5M7aT+qxZo9iaQmac7QDXp9iaFYfp\n",
"SJU5H89na9o8TEfU4Cgd9QIAW7ceIPU//1zC1kya9AWp7y26xtYcyKTjUT4JDWdrPrpwmNRn7d3F\n",
"1rR4gx5sXHMjm62Z/+ZqUv/6m/+wNa7j6H3042at2JrAYnqff+edEWzNyIPbSN35KL+PTmxHx9q0\n",
"a/4SqUdFRWHZsp7s9KpKDhEDozjIPBNNUlhSwtaUwkTqxTo6ekMJlULEBhcNorRsXHxNoY6Py+Bw\n",
"deWjPPLzNaTOxYIAQFGRntSdnOhpKeHMxIIAQE4hPR+l/UCrpbeD0jooLqXjTFQ2/Db10NDTKy7l\n",
"tyl31clg4qNwPD3pCC0uvgfgI4ScnPj1xkUiqdX89uGWrYRfbTAy+7xKIUYpL4+OvLmjGBi5AmiB\n",
"XAEUBEEQBMGqEROIJdIACoIgCIJg1UgOoCXSAAqCIAiCYNXILWBLpAEUBEEQBMGqEROIJdIACoIg\n",
"CIJg1dTGK4AFBQWIjo7G4cOHodVqERUVhc6dO5PvvXLlCr755hscP34cKpUK3bp1w3PPPXdH86+0\n",
"AXR4tyupL/lyPakHDmjDTqu5pxf9gsKGeTNxK6nXW3aKrem56r+kfibnBlvjzCxChw7N2ZqAYtpV\n",
"3GdwV7ZmvCvtolowZxVb8+uvyaT+9vZpbE1wHQ9S79u3I1vzbOO29Hz0+9iaXbsWkXrDhs+wNQdO\n",
"0w7yTefPsjUhzL6jU3Bv7su4ROpKTj/v5SdI/XIG7wLuHU0fhL5167A1G3vE0PMf+SRb88GCcfS0\n",
"ju1maxo70suQMnEtW2PY8Aipf/fdO6Ret24IO63qQLkClQaM5waZVzrRG420C1gJzp2r5P7kXKZK\n",
"GEy0Y9NEG4oBACWMm1StoR3SAODrS58blNa1VutE6krO4ZIS3unKoWGcu8HB9dkabrnd3V3YGn0Z\n",
"vR/4ufA13BWkQoX9wIFxipsM1V83Xl5MSgNoBz0AFBXp2BobG3pdq9W8c7hMxXweBVezK5OKUaDn\n",
"9zel/aqm1EYTSExMDOzt7RETE4PU1FTMmzcPgYGB8Pf3r/C+0tJSzJ49G08++SQmTJgAW1tbXL5M\n",
"J2NUBwXztiAIgiAIwt8fWxub+/pTGTqdDklJSRg2bBjUajVCQkLQvn177Ny50+K9iYmJ8PDwQJ8+\n",
"feDg4ACVSoUGDRrc8TqRW8CCIAiCIFg1te0WcEZGBuzs7ODr62vWAgMDcfToUYv3njp1Ct7e3pg7\n",
"dy7OnDmDBg0a4MUXX7zjJlCuAAqCIAiCYNXYwua+/lSGTqeDo2PF2/AajQY6neVt++zsbPz+++/o\n",
"3bs3lixZgrZt2+LDDz9EaQ0eNbkVuQIoCIIgCIJV8yByAOPj482/h4aGIjQ01Py3RqNBcXHF5yCL\n",
"ioqg0ViOruPg4IBmzZqhTZubHot+/fphzZo1uHz58h1dBZQGUBAEQRAEq+ZBmECGDh3Kvubn5wej\n",
"0YjMzEzzbeALFy4gICDA4r0NGzbEyZMnzX+XMUNNVhe5BSwIgiAIglVT20wgGo0GYWFhiIuLg16v\n",
"x4kTJ5CcnIyIiAiL9z722GM4ffo0/vrrL5hMJvz888/QarWoX593x1eFSq8AXv7XOlJ/4QYdA3Mg\n",
"8TA7LYM7HT9wLjeLrWn1cyapz45+g63xVTmTupstb1WfdzqF1F+f0J+t2Z52ntSPXOc/j7+WtvIf\n",
"f4WPz3mj7yBSHxoxma35akJ7UvfbRMecAMCUt+k4kwO/ZbA1+3OvkHpGxhq2ZtoeS5cTAAwPCSV1\n",
"AOgQNJLUj/V+lK0pPUTHyuw7TEewAEDHj14mddOEMLZmx5t0hM/ABb6kDgB2TJzC5rb8Ibmq/hBS\n",
"b75oMFsTcZGez7+W8vuOypmOwhg+eQap9+s3CF26DGOnV1UMhuo9z5KVlUvqSnEZdg78QPccXKSL\n",
"zsifT7jXShRqDApRGhxsRIxBz9a4O1veYgKAekzUCwCUltLLprLn91cq1gdQjsi5oadjS5Sim+xd\n",
"6cibQhM/HzcHuubSJf7crdfTkVPc5wQAlRO9runQlptw+69SpItJKSuIgYt70ev5WBsPO/qzclFJ\n",
"AGAw0NNTuiJny8Tn3Am1zQQCAKNHj0Z0dDRGjx4NrVaLMWPGwN/fH1lZWZgwYQLmz58PT09P1KtX\n",
"D6+99hq++uor5ObmIigoCJMnT4Ydsz2qitwCFgRBEATBqqmNI4G4uLhg0qRJFrqXlxdiY2MraGFh\n",
"YQgL4y9E1ARpAAVBEARBsGpq4xXAB400gIIgCIIgWDW1cSSQB400gIIgCIIgWDUPIgamtiMNoCAI\n",
"giAIVo3cArak0gZw+o4ZpH4y+TSpz5y5jJ3Wq9/Qg9mfifuDrXn22R6k/kPuRbbGp4R2cmXr+MGn\n",
"92VcIvU3Mnm/1tNNm5H669u3sDWTfZqT+tJXP2FrUrs8QerRn49na37//Qip53/AO0aLjLRr7t+F\n",
"vJu1Y31/Um/89edszcKuvUh96sufsTX/+hfthH788bZszZEj50i9vvcAtub4pThS33Upja1ZQAR3\n",
"AkCqJ1uC48fo42T9+t/Zmn8zA75/EPE4W/PtLNqh7O7OD3rvH0i7EF99dSCpBwfz26A6+Pi4W2ic\n",
"0xcA8vKKSN1oNLE1rq6OpO7kQusAUFhCuxj1zPEC8DldKgV3o9qOPh0rOWBNoOfjrKIdngD/RZhf\n",
"yrs/HWxpt6HJxK9rI/OaSSHDzIFZP9w2AIA8Az0fdzXt9AWAggL6uyCHOcYAoKSE3t5K60CtpufT\n",
"sGFdtqaYcYOXafiv68BA+hydmZnN1nCuYu5zAoCJObZslZzQjFNcyUHu60snhtwJtdEE8qCRK4CC\n",
"IAiCIFg1cgXQEmkABUEQBEGwasQEYok0gIIgCIIgWDVyBdASaQAFQRAEQbBqpAG0RBpAQRAEQRCs\n",
"GmkALZEGUBAEQRAEq+bujy7896fSBtDJgY4TiPtuO6n/3//1Zqc1d/BHpL51K60DQOT2H0k9JjiS\n",
"rSk6eZXUDx9OZ2vecKhP6nvL+BiKjc99TeodO4ayNZ7NtPR8LvDxOR/8sZfUX1Q3YGuW+Nwg9dGJ\n",
"fGRBXqM8Uo/zzmdr/s+Gtv/Xd+ZjRp4KbETqb/T2ZmvaZDiQ+sW6fPxA//bdSX327O/Ymjp29Hzy\n",
"DXq2JqFbP1L/o/A6W7Pw0wRSNz4ZxNZw/Hk1k31tfWv6v16dFx+J1HtfKqnvDKanZeI3W7Wwd7KM\n",
"7XBRiGfhYmCuX+ePWUdHevsWKkSgcHEmXGwLADiq6de4OBUlHFX8fLirGqUK0ST5JQZSz9bRsSA3\n",
"50PrSp/H28mJ1JVibUrL6OV2VIi1sa9JDbPY3P4BAGo1PT2VUgQK85rSfn21iN6vucgfgI84UYp7\n",
"cnCg9yuTiZ8PtyNkFdPLrISdQiRSCbP/8mutcsQEYolcARQEQRAEwaqRW8CWSAMoCIIgCIJVIw2g\n",
"JdIACoIgCIJg1UgDaIk0gIIgCIIgWDUyFJwl0gAKgiAIgiDcZwoKChAdHY3Dhw9Dq9UiKioKnTt3\n",
"VqyZOXMmjh49ipUrV8JWwUhTFSptANsV0gPd/xRBW/8y45PZafXo0Y7UdxbQrl0AWNXpKVLfez2L\n",
"rUlzoF2rA7rxg9afPk07hJMUPo/nKx1I/UAMX/PmpGdIvU2rUWxNk/f6kPp7hcfZGs7HtW/vMbbm\n",
"4oVrpD5nxlC2Zve2g6TeZCvvTD3e4iKpj7jEO9biV/9G6idnxbI1/RNeIfWrV9eyNYez6H1xaNPm\n",
"bM35fNp1+s7viWzN4lefJPXHG/0fW9Mjjt5Hlrz4BVtzdM8iUl8es4mt2deCdsSGqeuReiMXd3Za\n",
"1aGYcOJ6eLmx7y8ooJ3MRUW8Y5tDydFra0O7ZpXQMNNTcvRyKDl6WRdwGe/kLGNe0xtL2Rp9qZHU\n",
"XR141yznEM7LK2Rr6mid2dc4SpllU6wx0jVK7lwOrcIyazT0+snW8S58zu2rdAWrxER/Hmc1/f0N\n",
"8A7lUoULZXpmvSnBuX2LS/n9jXPe3wm10QUcExMDe3t7xMTEIDU1FfPmzUNgYCD8/f3J9+/atQvG\n",
"GmwDDonGEQRBEATBqrG1sbmvP5Wh0+mQlJSEYcOGQa1WIyQkBO3bt8fOnTvJ9xcVFWH16tV47rnn\n",
"7to6kVvAgiAIgiBYNVyW5YMiIyMDdnZ28PX1NWuBgYE4evQo+f4VK1agV69ecHPj74pUF7kCKAiC\n",
"IAiCVVMbrwA6OlZ85ECj0UBHBLKfPXsWp0+fxpNP0o8O1RS5AigIgiAIglXzIFzA8fHx5t9DQ0MR\n",
"Gvq/UcI0Gg2Kiys+C1pUVASNpuJzmyaTCTExMRg5cuQdmz5uRxpAQRAEQRCsmgdhAhk6lDdQ+vn5\n",
"wWg0IjMz03wb+MKFCwgICKjwvuLiYpw7dw4LFiwAcLMhBICxY8diwoQJCAkJqfHySQMoCIIgCIJV\n",
"U9uCoDUaDcLCwhAXF4exY8ciNTUVycnJmD17doX3OTs7Y8mSJea/s7Ky8NZbb+H999+Hq6vrHS1D\n",
"pQ1g5/AWpF4Y9yepP9qkPjutoCA/Uk94O46taT2TjsXYevEcW/NkNm3LL3yCjyxwvGQ5ED0ArA3m\n",
"Lde9f6HjTE4MDmRrZu7bTeqff/4GW7NLTcfapC9LYmtM3eiYnh496CgPAPj5532k3tanLlvj0J2e\n",
"XhOF/eD11xeTeuv/9mRrenV5ltRbFdLrBgBOvbuF1Cc483EzHJPDOrGvDe08kdRnz+GjfXZ8u4PU\n",
"my3l/2NM6D+E1L9o2JiteWPHVlLf8xkfhbPrz2hS92AiJYqK7lYMjGUshEEhDqJePS9Sz8qiY3kA\n",
"wGCgoyc87OhIDACwZ+JMavJQuVKkCxfdolFYtnwDHVFTSETqlGNi5sPFtgCAWk1/VSgtGzt/Ex9R\n",
"U1ho+fwTANjZ8be+uBgYLoIFAEqYyTm685Euzvb2pG4y8tv0hp7+PNx2AwB7Zp062vNf10oxRhyF\n",
"JvpYKCzh9x0uukWl0Fx5OTrRNfb8NlWKJKopta0BBIDRo0cjOjoao0ePhlarxZgxY+Dv74+srCxM\n",
"mDAB8+fPh6enZwXjh15/M+bKzc3t3ucACoIgCIIg/J2pjQ2gi4sLJk2aZKF7eXkhNpbOuPXx8UFc\n",
"HH/RrDpIAygIgiAIglVjI0PBWSANoCAIgiAIVk1tywGsDUgDKAiCIAiCVVMbbwE/aKQBFARBEATB\n",
"qpEG0JJKG8Cuq74j9dbePqT+5rSu/LTil5P6I660SwgA3j2XTOov2geQOgCM19M1zV+hnZcA8Mmy\n",
"N0k9Tt+ArUnMpx29Hw0bxNYEL6UdsGUhtNsaAEZ6NSH10d1S2Zqux2hn3JoQfiD2EUO7kLqjwoAx\n",
"SfuOk7qXFz9cTd1/047a0jLeTZeWTzs7l/Xux9asvMq4Vut4sjVXi+n14+pAu8QBoMUH9DL06tWB\n",
"rflp/R5Svx59gK1JepxOgR/WLJTUASA504PUZx+g90MA+GEp7Z4+ePAUqbdvH4Fx49qx06sqlENW\n",
"pzDwuaMjffry96cd8ADvEOacpADg6kC7SQtLeCcnB+f0BfhbVAYD78rklq3ExH8ezlmtVdjHuWVz\n",
"VNHOWIB3umrdeKct9yWttA4cHOj9QK9wPskz6EldKSvOUUXPR6fj9wNXJ3qdlig4h7nzIOfAVULP\n",
"7wYoYLZPtq6Y1AGglHFwc+sGAAzMvuhqz7u0OSf0nSANoCVyBVAQBEEQBKtGTCCWSAMoCIIgCIJV\n",
"I1cALZEGUBAEQRAEq0YaQEukARQEQRAEwaqRGBhLpAEUBEEQBMGqkSuAlkgDKAiCIAiCVaPk8P6n\n",
"UmkDOD+YjrKo4+FK6km//cVO6+OuPUi9WTc+FiAs7BVS75c4i61586I/qRunP8rW/Bz7G6lvqs9b\n",
"/D/rG0Hqfr58DEyXLq1J3T33CltzbVgwqRs/TWJr5v1xgtR/v0CPLwgAg39aTervL1/C1uyJjCL1\n",
"UaM+ZGvy84tI/cO1/DZ1q0Pvb0pDYU+d+jWpP/QQH+0TvfptUo/8kR97cWXn3qQ+bcpXbE3qU/VJ\n",
"vW3/RmzNmZxsUlcrRCZ8dpDeR74NpyNlAACd6YilZkzchZ+fFz+taqCmoiQUoi9KmIgYKk6mMrKz\n",
"89jXvLzdSd1g4td7cSkdW+KkEH2hsqH35gKdjq3JySkgda2WP6e6O9LxSFw8DAA4MIPOmxRibXL0\n",
"9HIXMutGaT4uTNwNANgy7k6Twr5jb0tvO3s7hTMKE4HCRQspoRRVlG+k149eIRIpT0/H2mQV85Eu\n",
"XIyR0ny4c41axR8L3H6txL24XcvtJ/9k5AqgIAiCIAhWjdwCtkQaQEEQBEEQrBppAC2RBlAQBEEQ\n",
"BKtGGkBLpAEUBEEQBMGqEROIJdIACoIgCIJg1VTfinLvKSgoQHR0NA4fPgytVouoqCh07tzZ4n2J\n",
"iYnYvHkzMjIy4OTkhPDwcAwfPhy2jGmqqlTaAD57eDupTw7rSOr5vvwC/fH2ClJXcmU+9BDtSPR3\n",
"1bI1S+rT7q/hWr6m4bBwUl/7zDy2xn1jf1J/Z+rzbE1iQ9phdVxhIPbh7rQLcdCC59iab9xol+mi\n",
"47xL227eXlKfqvB5Dh48Q+qur4SxNVdybpD68vO0cxkAXnCh3dNp+bx7c+bMF0l97dpdbM30cZ+R\n",
"+sGN+9ga12vPkPquhx3ZmlbudUj9g3aPsTWDfl1H6v9+mF/XPw8cRuqxyzazNS8M6UbqBU2bkXqZ\n",
"wZOdVnUwEi7UYgUnpwm0K9NF4ViyZeyFRUW827+0hF4GannL0TFOSrUdX1Oso92fpaW8K9NgoJfN\n",
"YOCdtirGsemgYL0sLaOXm3OfAkCugV6nrgpOaO4qTbaCE7qwhP+sHI6U4xyAs619taelRF5eIalf\n",
"vMjvB5xDuAR8TbaOdvvmGfjtozcy+46Rnw/nAnZX085yAFAz7lt9MX/MqR35faSm1MZbwDExMbC3\n",
"t0dMTAxSU1Mxb948BAYGwt+/YpKJwWDACy+8gCZNmiA3NxcffPAB1q9fjwEDBtzR/GtjUywIgiAI\n",
"gnDXsLWxua8/laHT6ZCUlIRhw4ZBrVYjJCQE7du3x86dOy3e27NnT4SEhMDOzg4eHh7o3LkzTp48\n",
"ecfrRG4BC4IgCIJg1dS2K4AZGRmws7ODr6+vWQsMDMTRo0crrT127BgCAui7o9VBrgAKgiAIgmDV\n",
"2NjY3NefytDpdHB0rPiYkEajgU7hcQcA2L59O1JTU9GvX787Wh+AXAEUBEEQBMHKeRAjgcTHx5t/\n",
"Dw0NRWhoqPlvjUaD4ttGaikqKoJGwz9PmZSUhJUrV2LatGlwcXG54+WTBlAQBEEQBKvmQdwCHjp0\n",
"KPuan58fjEYjMjMzzbeBL1y4wN7aTUlJwZIlSzBlypS7cvsXkFvAgiAIgiBYObXNBKLRaBAWFoa4\n",
"uDjo9XqcOHECycnJiIiIsHjvkSNH8Omnn2LixIlo3LjxXVsnNmVlCqN5A8jXbyH117bT+nPNW7LT\n",
"usFY1RcdPMDW2H35J6lfuHCFrfll64ek3uO3H9maP58bTeoL5q5ka9I7eZF629N8dMXljOukPuGN\n",
"p9makJCRpB72KB3LAQDFz4eSutKO+UY7Ok5kYp/ZbI3jW3RsyZRH6VgdACjcc4HUlQZVTz2fSep/\n",
"hruxNQn96HWaVURHMwDAR28uJfWU7vS2BoDYVo+T+npdBlvzSA4dVfKbUz5bE16fjkuKO3GErXmv\n",
"Mx3pEt6c3t8B4MyFH0h9787DpO7u3hjt2t1ZHAEAFBh+sdAyFbYVF2PhphADU9fJmdRzsvn1zsWm\n",
"qF34WzVcLIdSXAYMdNxLCRNDAwA5OQWkzsXdAIAdE+Vhb0/rAODuRUdoncvJYWu4eBZ3hVtcXDzL\n",
"NcX9gF5vWoX9wMuRjmhS2j4qJnNN6bzFvcbtUwAQHExHeCkdCznMc2PcMQIAOQoRPhzeTk6kHszE\n",
"WgHA5YvXqj0fDw9XUndzi6z2tMo5kb26xrU1IcSD/04v5/YcwOHDhyM8PBxZWVmYMGEC5s+fD09P\n",
"T7z77rs4ceIE7O3/F1PUrFkzTJky5Y6WUW4BC4IgCIJg1dTGkUBcXFwwadIkC93LywuxsbHmv6dP\n",
"n35P5i8NoCAIgiAIVs2DMIHUdqQBFARBEATBqqltOYC1AWkABUEQBEGwaqQBtEQaQEEQBEEQrBpp\n",
"AC2p1AXcpk0wqXODjUct5d2FqXm0Y6wsjh/6ZHsH2nW06PEn2Zo/YneRuv/gtmxN0qfbSH3Bgn+x\n",
"NTk5tHPw+ZHvsTXa1zqRemkM7XYGeCdZwNtPsDVN63iS+rHrvCMrusdTpJ5ZwDskFx9KJvVDV3mX\n",
"tr8r7Sh8oXlrtkb3ZzqpNw9txNZMO0u7y3MX7mFrevd+lNTPtqGXGQDsmBPLwm492Zo5s5eT+tam\n",
"bAmW9e5P6jPHf8HW3OgfROqD83j3tIYZiL1ZN9pZrjb54qG6XdjpVZWCgk0WWqk9f9K+xOyXKhs+\n",
"3SrQjf7cJsaBCwBGo4nUlQasz2Zcma4OfI2acZnm5RWxNQUFtNtYCZ3OQOru7nywrJ0r7ajNKKRd\n",
"yABQwrhzne35dcCRo+dHRygupb+LnFT8fHydaTe4nzO/DoqLaNdscTHvpr18OYteNifebcy5gDln\n",
"OcAbHDiHNABcYbado8qe1AGggZY+fopyeYfymTOX2Nc4fH09SL1hw2HVnlY5F/PX17i2JjRwvfOR\n",
"Ou41cgVQEARBEASrRkwglkgDKAiCIAiCVaMQjfmPRRpAQRAEQRCsGnkG0BJpAAVBEARBsGqkAbRE\n",
"GkBBEARBEKya2jgSyINGGkBBEARBEKwauQJoSaUNYJdPhpD6ix50vER8Ph3XAQCXmdiG2eP4geQP\n",
"vPg+qY+bSUe9AECdOd1JfYm3D1uTOZqO/7hcwkcw1KtDD1id/2JLtsY3/gSpB7ai1ycAnO5IW+KH\n",
"NG3O1qTE7ib1jgNasDVRfd4h9XeWvc7WGH84QuqdnuMjd96PeJzUp/6+g60ZEP4Qqa9aspWtWfHW\n",
"s6Te5NV4tmbDlg9IvX1rPt6ox6LhpB7e6VW2Zu/ez0ldfWAfW7P7Uhqp943syNYsWrCW1JfZ8YPR\n",
"nzt3mdR/TFpA6pUkSVUZe3vLZSoFHcECAA629GewU3jam3MC5uTxMRYcdho+LsMEep3kG+gIlpvT\n",
"o6NW7O3507SLiyOpK8XDODrS8/Hy4qOBbjAxLL5OdJwKAOiYCBKNwr7H1dgzETkAUMjEwKjt+PVW\n",
"k6tBhYX0Oi1i4mEAwGSq/rGRk0PHs3goxPRw27uOC799uGNBpXD8GArp/eD8+Uy25to1OsaMOt7L\n",
"UYokqiniArZErgAKgiAIgmDVyBVAS6QBFARBEATBqpEYGEukARQEQRAEwaoRE4gl0gAKgiAIgmDV\n",
"yHO9LoAAACAASURBVC1gS6QBFARBEATBqqmNJpCCggJER0fj8OHD0Gq1iIqKQufOncn3btiwAevX\n",
"r4der0eHDh0wZswYqFR31sJVWm36kXatZk+kXZlTmnVip/WfCdGkHjv4AluzbNkUUl+5chtbMzjk\n",
"MVJ3U/MDcNsxA8ifuZHN1rw4Yhqpt20RyNa8+9UE+oU83kmWfukaqY/az7tm53ZqRep+drSjGAB6\n",
"xf2X1Bu48e7Atotph7BNMe3MAwBndS9S33j2K7am9Ox1Uldyn2nU9GDwX3zBbAMAjswBFbN1Nlsz\n",
"6pcNpG7K4Z2ls2cvJ/XJ/4liazZePEfqoS15B/mAAfTJhHP6AsDkyc+Q+nOP08di79798OGHXdnp\n",
"VRXKMVlSxg9m72RPu3CdGR0AVApuUg6DoZTUldysDsx8THfJMV0ZNXFRGgz8MevmQDuHla6qcJ/V\n",
"YOKd3QDtklYx52cAcNfQ53UlF3AJ4zZGDbZPTVzaDg7V/+LOU3CqX72aQ+qc4xsA/Op5krqeWzcA\n",
"Sgz095RKxR8Lzs709lFab/eC2ngFMCYmBvb29oiJiUFqairmzZuHwMBA+Pv7V3hfSkoK1q1bh+nT\n",
"p6NOnTr46KOPEB8fj+HD6QSKqlL9s6EgCIIgCMLfCFsbm/v6Uxk6nQ5JSUkYNmwY1Go1QkJC0L59\n",
"e+zcudPivTt27MATTzwBf39/ODs7Y/DgwUhMTLzzdXLHUxAEQRAEQajF2NjY3NefysjIyICdnR18\n",
"fX3NWmBgINLSLPNe09PT0bBhQ/PfDRs2RG5uLgoK6MzIqiLPAAqCIAiCYNXUtlvAOp0Ojo4VHxHQ\n",
"aDTQ6SzDtnU6HZycnMx/l9fpdDq4uNQ8NFsaQEEQBEEQrJv79PytGRsgPv5/o06FhoYiNDTU/LdG\n",
"o0FxccURXIqKiqAhnmm9/b1FRUVm/U6QBlAQBEEQBKumJsPy3Ql2dsDQoUPZ1/38/GA0GpGZmWm+\n",
"DXzhwgUEBARYvDcgIADnz59Hhw4dzO9zc3O7o6t/gDwDKAiCIAiClWMyme7rT2VoNBqEhYUhLi4O\n",
"er0eJ06cQHJyMiIiIizeGxERge3btyM9PR0FBQVISEhA165d73id2JRVMpL75YKfSL1rHB1jMSKD\n",
"70jXNqAt/hcn0PMAgEeX0LEYNz7axda88MUoUg90dWdrJg2YQ+onT1o+kFlOeOzzpL6632C2Zu3p\n",
"k6S+KfUMW/NxGzrWpmvX8WzN2bMrSD09P5+tmfvfpaTeZBQf7bPyxFFSf9VYj61p8kQoqb+719L9\n",
"VE7/4BBSf1jHXwIffYLeRxqv5bcpF1mw4Ks32JoenegoHFuFsYeuXLlB6snJS9iaw3o66uHyb6fY\n",
"mhON6SicN9t1YGuOXKdjh24Qz6YAgI+qIR4L6s1Or6qUGC2jnbJ09CD3AKBmYliUYmB0BfRn4KJe\n",
"AECvp+NR6tf3Ymtu6On5aBSiSbjPoxQdw8XaKNVwz0Ll5PAPlOt09Llbo6H3L6XXlGryDfR8Ssv4\n",
"L9Q6TLyX0pcw94pSTFBhIb1N7ez4moICev9VOjdwkSr5+fyxkJ9fROqurk6kDgB1/ehIsMLS6scB\n",
"ZWfnsTVZWbmkrhQd4+GhJfU6dfqyNZWh12+tcW1NUKt7VPqe23MAhw8fjvDwcGRlZWHChAmYP38+\n",
"PD1vxvVs2LAB69atg8FguH85gIIgCIIgCH9nqnJV7n7j4uKCSZMmWeheXl6IjY2toEVGRiIyMvKu\n",
"zl8aQEEQBEEQrJr7/Qzg3wFpAAVBEARBsGpq4xXAB400gIIgCIIgWDVyBdASaQAFQRAEQbBq5Aqg\n",
"JZW6gD9bTDscXbo2JvWpu39jpzU8lXZrdRzVla3xvEK7wjb8tIetOZdKD3R/IrI+W7PyqQGkHp3y\n",
"J1vTLo1eddOmfc3WzPj5LVKPn/g9W/NNwnRSX/LRarYmMrIjqZ8/n8nWeIQ1JPVnO7zJ1iQe/YrU\n",
"A1xc2Ro3J9ox+uKLT7I1/gHepN50aHu2Rn2cdtqu09A6AIR60c7OR4t4N12qJ+3oS//xMFvj9GQT\n",
"Uj+SRTtwAWBh5+6k3vdnfj9Qf0Mvg9qBd8pGRtIO4REjepG6Xl8H7u5h7PSqCuUCzi+hj3+Ad/vm\n",
"ZfNu1qIi2smpdHXAyYl2Pnp5ubE1OQY9PR+F0y23CEquZnvGgap0scOoo12enJMUAAwGukbJ0evs\n",
"7Ejqake+xoTqX6WxZb7X8/IK2RolByqHHePSVnIBc+tHZzTyNcx8uG0AAEVF9P7mouXPW1eL6e2t\n",
"1BJwQ5z5OvLzuXz5erWmBQCenrQL2NGRPgdVhevX19e4tiZ4eva7r/OrCXIFUBAEQRAEq0auAFoi\n",
"DaAgCIIgCFaNPANoiTSAgiAIgiBYNXIF0BJpAAVBEARBsGrkCqAl0gAKgiAIgmDVyBVAS6QBFARB\n",
"EATBqpErgJZU2gCebkbbuwdpaZt2va9PsNM64UsPPr2w5WtsjYMDvYhBnw1ka0pC/Ehd+8Uhtiar\n",
"G20vb+TGRz10rF+P1Bdvn8PWPOpH1+xvWJetWTz3B1Kf8M5wtmbwTwmkPuQaH89y+Tq9rRt+yI8/\n",
"uHbJZlJv/vQjbM3/jXqK1JM78+va/xytr5y8gq3518LRpK6dz0f7bAynBy6PYwapB4AfWtH7YvHL\n",
"vmxNgCt9/IR9/w1bM+RpOg7I+EIoWzNu0RhSN6TQUUkAEBREHz8/XjhN6n72gejqzk6uytgSsRDO\n",
"NnxcR2Z6Fqnn5PAxMKWldPyGkxMdUQUA9ep50tNSiCxxcaDjPwoU9qNCJvKmuJSP/+BiUxxVfHSM\n",
"jyMdz1JcTEeJAICtLR3ZwUW93HyNXqfZumK2hovJcVfz28eWSWFRq5UiaujpFRTwy8atH+476uay\n",
"0eutRGHfKWEiYpTigLRu9DLkMnFESvNRiuIpLi0ldZUNH4XDxSUpret7gVwBtESuAAqCIAiCYNXI\n",
"FUBLpAEUBEEQBMGqkSuAlkgDKAiCIAiCVSNXAC2RBlAQBEEQBKtGrgBaIg2gIAiCIAhWzd/xCmBB\n",
"QQGio6Nx+PBhaLVaREVFoXPnzuR7ExMTsXnzZmRkZMDJyQnh4eEYPnw4bDmXFKrQAJYwXXPc3LWk\n",
"HhMzmZ3WDXd6QbJ2N2FrvmrdldRnnTvI1mR/tofUHSY+xta8OfA9Us8Z25KtKQ6lHVHrz9FuSQC4\n",
"Ukg7FE9Fj2drfjx9itRnv8U7Rpe8Qg9EXS+Qdxs/sZp21K4ZMIStOZVND/TtcDGfrXns9Z6k3klh\n",
"EPKrIfR6mzzqcbYmbRe9HbKv8y7Rjf3GknrWtRy2pnNruqZXzPNsTbeAQFLf9Qxfs7zlX6T+a1oq\n",
"W1PflXZ9H2tOO/IBoHe3/5B6eOcWtN7pCXSdyDvFq0r29TwLLSuLdmUDQF5eYbXn4eBAOyk5tyYA\n",
"6HS0O5ebFgCoVLR72UPDu2YNzLk2R6djawoY57C9rYKjF/Rn9WHcmgC/HYyMkxQASpnPw31OAFAR\n",
"TnCA/x4CAEcV/TWmduRdwIUltLPaxYXfPtx+oOQ659zl7u4ubA3nVM+5wZ9TtVpnUq+j4J52sKX3\n",
"0Rw9v78Vg/7OKyzl3e2uTvR2UDrmrhPnAgDw92dLKuXveAUwJiYG9vb2iImJQWpqKubNm4fAwED4\n",
"EyvCYDDghRdeQJMmTZCbm4sPPvgA69evx4ABA9jp862hIAiCIAiCFWAyld3XnztFp9MhKSkJw4YN\n",
"g1qtRkhICNq3b4+dO3eS7+/ZsydCQkJgZ2cHDw8PdO7cGSdPnlSchzSAgiAIgiAItYiMjAzY2dnB\n",
"1/d/ebKBgYFIS0urUv2xY8cQEBCg+B55BlAQBEEQBKvm73YLWKfTwfG20HaNRgOdwiMh5Wzfvh2p\n",
"qakYN26c4vukARQEQRAEwap5ECaQ+Ph48++hoaEIDf3fqE0zZszA8ePHybqQkBC8+OKLKC6uOFpK\n",
"UVERNBr+uU4ASEpKwsqVKzFt2jS4uPDPmgLSAAqCIAiCYOU8iCuAQ4cOZV+bMWOGYq1Op4PRaERm\n",
"Zqb5NvCFCxcUb+umpKRgyZIlmDJlSqW3fwF5BlAQBEEQBCvn72YC0Wg0CAsLQ1xcHPR6PU6cOIHk\n",
"5GRERESQ7z9y5Ag+/fRTTJw4EY0bN67SPCq9Aqj++SypN20ZROrvvBPDTuv334+Q+kMP8Z3q0Nwd\n",
"pD52LB1zAgDbx4WR+sA8fsT6A+F0xIVXhpat8VfR9v9fooazNYevXSH1d3YnsjWvtX2E1OMuZLI1\n",
"GzfuJ/U//jjB1iz+eBSphzV9ga154w06Ikbpv60pU+h9pMN3I9iaXoH0Dj3x6XlsTZ8+HUi908Re\n",
"bE1qIR0/MOVfC9ia4OB6pP5Jlx5sTeOAZ0i9Xj0vtmbhwn+R+ug+A9maiPjl1V62wPn0sbW4P/Pf\n",
"rMGTnVZ1uHjR8thQGjCei8tQyr0yGOgYC6X9NTubjt+wt+dPn3o9HYuhVvPRJH5+dDSPg8LnMRXR\n",
"XzTFJfTnBPiYD2d7PtbG0VHNvsZhQvW/BG2ZGBguUgYADCZmP2DibgDAjlmnBgMdDwPwcS/cfgjw\n",
"MTBKNdw+r3Qs1GTZuOiY+r58RJSjjt7nlaJ9bJhtykUlAUBxMR9jVFP+bs8AAsDo0aMRHR2N0aNH\n",
"Q6vVYsyYMeYImKysLEyYMAHz58+Hp6cnEhISUFxcjPfe+1+kXbNmzTBlyhR2+nILWBAEQRAEq+bv\n",
"GATt4uKCSZMmka95eXkhNjbW/Pf06dOrPX1pAAVBEARBsGr+jlcA7zXSAAqCIAiCYNX8Ha8A3muk\n",
"ARQEQRAEwaqRK4CWSAMoCIIgCIJVI1cALam0AXzq9adIPXrCN6SesGYmO623f08k9WMf/crWfLlu\n",
"GqkP3/AjW3Ny6CpSX1/K/wew8I/3Sb2uE+2UAoDtCzeResPHm7E1687QY/O52PMuu47NaHdur69H\n",
"sjUj2tNW8QMP8U6/OUm/k7rtdHpaAHA2iHZJZxTyA6QPWvsKqXtvucTWLPz/9u49Oqr62gP4NzPJ\n",
"zOQ1hCSGZyAg1UBEUDGiQUSp7xZFFIErRRBasBVtKipaNSgKiIoLrbQSBanK2zdKry/AVm9TaBFE\n",
"EHkYgzxjSCCZRx6T+4dXrjr7ewARNcP3s5ZryZ7Z55w558zML785e5/fTTXjS5c+wLdt83Yzvq/E\n",
"jgPAM9V2FfDY6b+mOR63XVH4u18/THPYh9Ef5/+B5pzZoZMZ79fvDpozilRCzxr/LM1p+PgzM952\n",
"6DNmfMiQIXjmmTPp8g4Vq9BlWBWjx8M/1lhVpFN1LqsM3bmz4rBznKq8AwG78tGfxD8baurs9XyX\n",
"Ctj6Rv756Eqwc1jVLgBUkDsWBOt5pW01eV9EGvmXt9dtV5OmOTTMTXbZ50g5qfgGgHDY3u46h4pr\n",
"Vrnr9yfRHKfHmO3by804O6cAwOOxvwucqo39Pvt94iKfgQAQqLHPA6f3D6tqPhKaAYymGUARERGJ\n",
"aZoBjKYBoIiIiMQ0zQBG0wBQREREYppmAKNpACgiIiIxTTOA0TQAFBERkZimGcBoGgCKiIhITNMM\n",
"YLSDDgBvvWKSGR8z5jL7+e++TZe1/gG73cvEp35Pc1q77FL+5rPX0ZyZT9xsr399Kc35bP4qM37c\n",
"8LNpzh8fGGXHSbsbAGj2N3sb8q+/gOZkv3a7GU/28NYVnzXYpfezLvgFzbm83x/NeM3/8H2duNhu\n",
"eTM+/yyaM/eBF8x40cO/oTl1l9ktUJxuGs5aCWRlpdGcfwbsNjBON7bfHQyY8ZtvvprmLFy4zIyf\n",
"5uHbVvzRGjPu1FpkW7dmZtzdsSvNyZxeZcZvWWafH3l+3vbocFgtWlirFwBIT081405/6ftIG4tQ\n",
"qJbmVFTY54RTDms349TegrX/SHJoA5PmtT8f032JNCfcYLctqWuwtxkAvsvkCWvdkhzPP7fYtlXV\n",
"8vc5a0Xj1AqHcdrX1dV22xSnz6Aa0gLFqdVKUpJ9TFNS+DFNT7fbcblc/HyLj7fb5zi1UXK57H1a\n",
"6zC4Ysurq+PnG9u2I6EZwGiaARQREZGYphnAaBoAioiISEzTDGA0DQBFREQkpmkGMJoGgCIiIhLT\n",
"NAMYTQNAERERiWlNcQawuroaM2bMwJo1a+D3+zF48GD06tXroHn33HMP1q1bh7lz58JF7v0NHMIA\n",
"cPbs28x4SZxdGXd3+xPosgq2PWfGH1tdQnOuamxhxttlZ9Gc/v3tyt3+V/ehOTeOecRe/wm8wnF3\n",
"wK7+PL1FK5pTvPwVM/75Nvtm3gDw2KxxZvzpGfayAKDfDf3N+OUvL6Q5/uvzzfiY2y6kOee1zzHj\n",
"DQ43bz9h2Jlm/JTOw2lO8TK7Gr2ZQ7Xjrnf+Y8YvG3oezSm51z5H75v0Fs3BmFPN8NUndKEpZWX2\n",
"cfjlL8fTnBueGmPnjO9Hcx5a+T9m/MFzfk5zRpQ9b8b/0s1+na664+iyDodV+ZeWlkKfz6oi2U3u\n",
"ASAp2a6wZDesB3hFr9N6WIVwOFxHcyoq9ptxpw9wVjnsULSORFI5vL+OVzUzTpXDnjh7u1nVLgDU\n",
"RezHPC5eFRpHludUuc8GA243Xw+rIHcaWNTU2NW+n322m+awY9q2LX+ftW6dcVjLAvh5FZ/AhwWs\n",
"2rfBaXBFZt4aHb4jamvtavAj0RRnAIuLi5GQkIDi4mJs3boVkydPRk5ODtq2bUtz3n33XTQ4vC+/\n",
"jn+yiIiIiMSASCTyg/53pEKhEEpKSjBo0CB4vV7k5uaiR48eWLFiBc0JBAJYtGgRrrnmmkNah34C\n",
"FhERkZjW1GYAd+zYAbfbjZYtWx6I5eTkYN063pf3ueeew4UXXohmzez+r9+mAaCIiIjEtKZ2DWAo\n",
"FEJi4jcvc/H5fAiF7MtVNm/ejE8++QQjRoxAeTm/pOzrNAAUERGRmPZjzAAuWLDgwP/n5eUhLy/v\n",
"wL+Lioqwfv16My83NxfDhw9HMPjNa0gDgQB8vuhreCORCIqLizFs2DDHa4a/TQNAERERiWk/xgzg\n",
"wIED6WNFRUWOuaFQCA0NDdi5c+eBn4FLS0uRnZ0d9dxgMIgtW7bgkUe+LGb96rWOHj0ahYWFyM3N\n",
"NdehAaCIiIjEtKZ2DaDP50N+fj7mz5+P0aNHY+vWrVi1ahUmTpwY9dzk5GQ88cQTB/5dXl6O22+/\n",
"HVOmTEFqqn3PdOAQBoDXXjvZjNfdeLoZ75vS0owDQJ9HBpnx33c4mebcs+FfZnzq1NE0Z8GnH5vx\n",
"izt0ojkffLDZjPftW0hzAgH7JuDduvP1FP51rBlv43CQPOTG2AUFXWnO6DdfM+N7H3yX5iS2stsM\n",
"jH38Rprz+KY1ZnxoF35MO+22/xK7on9vnpPW3IyX7NhOcxYuXG7GX375PZozcOC5ZnzVSvucAoCH\n",
"Ku22Mpv2VdKc5un28c4Yx/dBfss2Zvzxe+fRnNcnXWfG3Q38w7DDvReZ8T7d7Pdcv379MX16AV3e\n",
"oaqsjL5xfWYmv5jZ67XbctQn8DYj5UG7LYfXw9t/sPYbrNULAFRX2+uxXuNXWLuZfftqaA6b1cjK\n",
"st8vAFBVa39uhcn6AcBFdmmCQ9uUZJf99cJeJwCkJNnH1E2uewJ4K5qIQ5uR+AR7u50GCawNjNNP\n",
"boGAvd11dXwfWO2QAOfzzZdit/bxkLZHAG/dwlq9AICHtNypdxhbVTqcv8wXX9ht5o5EU7sGEABG\n",
"jhyJGTNmYOTIkfD7/Rg1atSBFjDl5eUoLCzEtGnTkJGR8Y3Cj3D4y/d4s2bNjqwPoIiIiEhT1tRm\n",
"AAEgJSUF48bZfYAzMzMxZ84c87GsrCzMnz//oMvXAFBERERiWlOcATzaNAAUERGRmNYUZwCPNg0A\n",
"RUREJKZpBjCaBoAiIiIS0zQDGO2gA8AWLexqsuVjFpvxklm8Avad4FYzPuGUs2jOZ/vtaqD8M8bQ\n",
"nElL7zLjbnJzcgB4+x/TzfijDy6kOR92s2+0/cJ1f6U5Ex76jRl/cOX7NGfo6y+Z8REndaM55++2\n",
"q79ebZlJc846q4sZX75sNc35cMEyM150Ha+Ara61q9kCZ/KKz3eet/fPhx34KTxmzGVmvOCqnjSn\n",
"5EW76vz+SaNoTlxP+8bcG+7k5861NXZl3K/qW9CcQNleM759+x6a89hD9jZMmTKX5lx8Sb4Zv+MO\n",
"+/6S2dm8Gv1wWJWzO3dW0OdnZaWZ8X0RXmEZrLdvMp8cSaA5zVLsim0XK40FkJKSaMZbtkynOYzT\n",
"empr7ddT+x32QbC+jm8D7G1Id/P3H6v2dapmddXa62npT6Y55cGAGa9r4DM+9Qn2YMCpQplV56al\n",
"pdAcp8cYv9/+XvE77ANW8by/nu9rlhPvUD3t89iV0LWkshzg3TJYhTQANJDK7iOhGcBomgEUERGR\n",
"mKYZwGgaAIqIiEhM0wxgNA0ARUREJKZpBjCaBoAiIiIS0zQDGE0DQBEREYlpmgGMpgGgiIiIxDTN\n",
"AEY76ACwUyf7BvRXX32uGb/77tl0WcPm2DeTv/VfK2jOfw8YbMY/yj2T5rzx+kozvmcYb7Fx8aLn\n",
"zHiEd01B+h3vmPHU+8+nOXeMfdyM/2HKtTSnZv4aMz7gis40Z9DHdpueNx8bS3Me3vgfM3559+40\n",
"Z/XqTWa8S87xNOfiDvZjVWHeFqB/75vt+IxhNOf++58x4yceV01zJnU/zYy/WLuT5hSQNiEDrzqP\n",
"5pQs/ciM+268hOb8buU/zPiDD4+kOa99ah+fpwY8SHN6t802459/ssOM+3wt6bIOh9U6xePhH1Ee\n",
"j926JRjkLSlq6uxWJ4nxfD2sXUZdHW9VkZBot5wq27+f5gTq7JYdKaT1BgAkxtv7oFmEt7zyuu12\n",
"Jh6Hm8az/VYRim7d85V0n90KJ4W0OQGAcNDeB1aLoK+kJdktr5yESGuSqiq7PRMAJCfb62EtfwAg\n",
"NdV+rWxZALCftMmqcmi14nVox8MEyDENObRg2Ue2we/x0pzWrTPMuNOAzKlV0HelGcBomgEUERGR\n",
"mKYZwGgaAIqIiEhM0wxgNA0ARUREJKZpBjCaBoAiIiIS0zQDGE0DQBEREYlpTXEGsLq6GjNmzMCa\n",
"NWvg9/sxePBg9OrViz5/165dmDVrFtavX4/4+Hice+65uOYa+x7uwCEMAO+/f5QZP/HEoWb8ztfG\n",
"02Wtr/jCjP+p70U0Z+cO+2bwqe34TdWf+MurZvz+++yqUAD4rGyhGT97Mc/x3Xa2GX/tF1fQnHFv\n",
"PmLGnSqvCs7qasaTq/jN24d0tnO2NvJquqtz88x47Q5eudi9eyczflZ2e5oz78m/mfHbb59Jc7w+\n",
"u9rxoy/20JzZs28z438m5wcA7Jpyhhl/4/0tNKfzFrtirWPfLjRny/F2Zeekofb5AQDPvjbRjF/+\n",
"kn3uAsCVZXa1oXsQr9zduWW3Gd+4cZsZb9EiBSeeSBd3yNq2PS4q1ry5XWENAAHY7xlWseqk1uHL\n",
"gS0vwc2rZhvIbMO+MK/k/Lzafp/Fu+JoThtSge5U0RsXZy/P7ZDDHguSilWAVwin+XgFrJfsU6eq\n",
"0Ei9fR445VRU2PvaaZCQmkqqmh2qgFm17+5AgOYE6+3zLdWhGjwQsV9rsL6e5tST1xpu4DnsMadz\n",
"J0Iq7Fu35i026skxPRJNcQawuLgYCQkJKC4uxtatWzF58mTk5OSgbdu2Uc+tr6/HxIkTcdFFF6Gw\n",
"sBAulwvbt293XD4/aiIiIiIxIBKJ/KD/HalQKISSkhIMGjQIXq8Xubm56NGjB1assNvmLVu2DOnp\n",
"6bj00kvh8XgQHx+Pdu3aOa5DPwGLiIhITGtqM4A7duyA2+1Gy5b//2tNTk4O1q1bZz5/48aNOO64\n",
"4zBp0iRs2rQJ7dq1w/Dhwx0HgRoAioiISEz7Ma4BXLBgwYH/z8vLQ16efZmVJRQKITHxm5cX+Hw+\n",
"hEL2DRMqKiqwbt063HrrrejatSuWLFmCqVOnYtq0aYgnP8NrACgiIiIx7ceYARw4cCB9rKioCOvX\n",
"rzcfy83NxfDhwxEMfvM62kAgAB+5htbj8aBz587o/n937urXrx+ef/55bN++nc4CagAoIiIiMe2n\n",
"VgVcVFTk+HgoFEJDQwN27tx54Gfg0tJSZGfbt+ps3749Pv744wP/biS3sPw6FYGIiIhITItEGn/Q\n",
"/46Uz+dDfn4+5s+fj3A4jA0bNmDVqlXo3bu3+fyzzz4bn3zyCdauXYtIJIIlS5bA7/ejTZs2dB0H\n",
"nQE8/fTRZvysPw82404tGEp2fG7GK0lJPgAM/cdSM947m1/YmJRk35jad//Pac7EVe+Z8SGdT6I5\n",
"8zbYF2M+te4DmlPaz97uu/6xjOZcm9/NXs/2jTSn40a7zUBNS358Tmxut9YZNWYSzSkt3WXGX/1F\n",
"Ps15t739l9hnn82nOcw//2lPoQNAfIJ9epf15+eOi7TI6JIR3aLkKz17nm7Gj09Lozlj3nrdfuA3\n",
"J9OcJVs3mfGnLupHc9bssY8Pe50A8HKN3TogeXu5Gfd6q+myDod103gvab0BAGX795nxhkb+l747\n",
"zv6bt5JcVwPwliqsBQsA7AzUmPGaOt6ahLX/cDpWYdI+yqmtTXK83VLp+7av1m554/R6slP9h70e\n",
"j8d+PS6H1iSsRYxTDluPz8fbs1SRfVDvcI4muN1m3OvmX9esDct3aW/kAj8+ieRaMiesFU2EvE4A\n",
"aNeuxWGv52B+ajOAh2LkyJGYMWMGRo4cCb/fj1GjRh1oAVNeXo7CwkJMmzYNGRkZaN26NW644QbM\n",
"nDkTVVVV6NixI2655Ra4HfazfgIWERGRmNbUqoABICUlBePGjTMfy8zMxJw5c74Ry8/PR34+n3z5\n",
"Ng0ARUREJKY1xRnAo00DQBEREYlpTXEG8GjTAFBERERimmYAo2kAKCIiIjFNM4DRDjoA7N+/lxk/\n",
"+YRcM94pza4kBYALfHZlz+JFy2lO8zak6aGLV7Z88MEWM77hvLtpzsOfrjXj3bNamnEAaOaxDyWm\n",
"IAAAEJxJREFUq42vbt6er+fiKWY80WcvCwAKbrQr/eY/+RrNmfDKeDM+9V/v05zuWfbxmTRpFM15\n",
"7PMNZvzMZ2fRnImJJ5rx++5/huZU9I2++TXgXIl5U+dTzXiXp/9Gc3pfafdYmnUL37Y9/o5mvHDS\n",
"VJqzb619jt70wh9ozt+3lZnxm8+8g+ZMfdCu4h92/eU057ekQjkx1a6CvNS3H7wO+dClpCVHxfYE\n",
"7Gp2AIjA/kD3k/clAERIb6zKMK8C3k8qd1kFLgAkJ9j7KtXDK0aD9fZnXbxDZWqr5BQznh7P1xMI\n",
"2JWpaWn2sgAg3GBXcrJKXwDYX2vvt3qHL2JWzcoqsQEgXGsvL9Ghy1l8vP394fdHn4MHuOzqWFbl\n",
"CgDxpOo8NYEfH1ZpGw7yCvLqoP0+Sfcn0RwvqQ516h+X5rXPUSfs/bMvzM+dRvL+4T0BDk4zgNE0\n",
"AygiIiIxTTOA0TQAFBERkZimGcBoGgCKiIhITNMMYDQNAEVERCSmaQYwmgaAIiIiEtM0AxhNA0AR\n",
"ERGJaZoBjBbX6FTzDV4u/+ulN5vxLVV76bL+K5BpxrOy0mjOvMadZvyN0q00Z0y308z4qgd4+49n\n",
"5t9lxq9+9Xma4/fa7SbG+I+nOYGA3W7izjufojn7R59sxh9p04PmjNj6nhnvd/wJNKfD6ioz3vrS\n",
"k2hOx2b2sctNakZzrhxQZMbvnj2W5syb9IIZb9WKtx366BS7Rcw9BefwnBUfmfH3m/MWDHGvbzLj\n",
"7L0DABMmDDfj48fPpDkRcgP54bdcSXM2Vdrvx+v78NYx7adeasav2G43YTj++FNw+eW/pss7VBWh\n",
"6PYzFSHenqWBfKCzFiwAECKtW/aGgjSHtcto5+fneLKLtPIgxxAAdtRU08cY9v7bvYt/Dns89rYl\n",
"pPAWH7tJm5FPqyppDmsdk+7jzTxSSJsc1nIL4J/DTjmhkP1+bmjgxych0T6vyoP83HHF2a1jWKsX\n",
"gLeOQS1vO7R/v318fD7eboY95iLtbgA+i1Zfz7eNnW+V9XU0h23CcUn2Z9OhOP98/n15NLzxxsof\n",
"dH3fhWYARUREJKZpBjCaBoAiIiIS03QNYDQNAEVERCSmaQYwmgaAIiIiEtM0AxhNA0ARERGJaU1x\n",
"BrC6uhozZszAmjVr4Pf7MXjwYPTq1Ys+f9GiRXjrrbcQDAbRoUMHXHfddWjbti19/kEHgH3nXWfG\n",
"P/xijxn3PrmGLqv+4aFmvGJtOc0ZWmBXwE7rcwHNuaqfXeHY9SRenTt00EQzflYPXjXr+Xl7Mz7z\n",
"sVdpzrPPvmnGR7xWSHO8pGKse9ef0Zzs8g/NeM/W/GT4y55dZrz+3yU0Z+WvnjHju2uW0JwWhfYJ\n",
"nN+qNc15dI9d1ei9qgvNaUNuIF+2fx/N6dLbXl5nmgHcSPZb6Z1Lac45I88z4+PvGUZzEkh14N8+\n",
"3UJzRuTb1fpDh55Pc047+VQzPhP/NuN90+pwOV3aoQvWR1eN+kgFLgB4ScWotZyvsKYHCeRcAQCv\n",
"237/OVVy7qussbctyKvJ22b4zbjLw/dBoMauknaqZk1Pt9ez3aEKOVDHt5th+63e4Yu4jmw3q6YF\n",
"gJo6u5q0jlR8A0BmYpIZZ9XBABAmla6s2hkAGsisE6tgBwA3ORe9Dl0FWCcNl8N5zThV9NbW2vun\n",
"spKfO0lJdjV2qt8+BgBQVRumj31XTXEGsLi4GAkJCSguLsbWrVsxefJk5OTkmIO6lStX4o033sC9\n",
"996LzMxMzJs3D48++iimTJlCl3/4Z4eIiIhIExKJRH7Q/45UKBRCSUkJBg0aBK/Xi9zcXPTo0QMr\n",
"Vqwwn19WVobc3FxkZWXB5XLh7LPPxrZt2xzXoQGgiIiIxLRIpPEH/e9I7dixA263Gy1btjwQy8nJ\n",
"QVlZmfn8rl27YuPGjdixYwfq6+uxfPlynHLKKY7r0DWAIiIiEtN+jGsAFyxYcOD/8/LykJeXd8i5\n",
"oVAIiYnfbJru8/kQIs3xO3XqhHPOOQc33XQTXC4XMjMzceeddzquQwNAERERiWk/xjWAAwcOpI8V\n",
"FRVh/fr15mO5ubkYPnw4gt+6y0wgEIDPZ9+xZ+nSpfjwww8xY8YMpKWlYcWKFbjnnnvw8MMPw0Ou\n",
"l9YAUERERGLaT60KuKioyPHxUCiEhoYG7Ny588DPwKWlpcjOzjafv3r1ahQUFCA9/cvbo/bp0wdP\n",
"P/00tm3bho4dO5o5ugZQRERE5CfE5/MhPz8f8+fPRzgcxoYNG7Bq1Sr07t3bfH67du3w/vvvo6qq\n",
"CpFIBCtWrEBDQ8M3riH8trhG1hfh/2yvfsWMj/mvyWa8Zct0uqxf3WVPh7ZJSaU5zch05+0r3qY5\n",
"HtI6Ii8jk+a8OH6h/QDvPoCTbrVbaXxevZ/m9Nxs/xWSlpZCc6qr7ZuNrz6eT+Cen2OP+Pu260Bz\n",
"ih990Yxn/7IrzcEHdguUQBd+HmysrDDjvar4zeh79+5mxidPnktzTupqv9aFSfb6AeDUNfa+Zjc0\n",
"B4AnMyvN+G+785uPsxvY/7xZK5rz9OcbzfjSm+fTnLlz7WtAWrTgx2dPrb0PmvsSzXg4mIbmqUd+\n",
"o/Vgvd0iiT/fbv+xJxCgOaxlSMThY5C133D63PKQziC7dvFzj3E6Vl5vghkPBOzrhADA708247sd\n",
"9lt5yH7su7QziSftjADeUiXBxVug1EXstiVJCfbPXgCQnWofO4/Deti5UxGy3y8AsJ+0z2Etcpw4\n",
"7Wv2eeJ1aKPEjoNTyx13g/0+cWqf43LZy0tK4p/3Lre9bW6X3T7rUHTtan8nHi1r1/L2XIfq230A\n",
"hwwZgoKCAgBAeXk5CgsLMW3aNGRkZCAcDmPWrFlYtWoVamtr0apVKwwePBjdutnfnYB+AhYREZEY\n",
"91P7CfhQpKSkYNy4ceZjmZmZmDNnzoF/e71ejB49+rCWrwGgiIiIxLSm2Aj6aNMAUERERGJaU5wB\n",
"PNo0ABQREZGYphnAaBoAioiISEzTDGC0gw4AbxrxkBl/+unbzPiN779Dl8WqY5d+upnmLP5kgxkf\n",
"e8rpNKfmzU1mvHk7u1IKAC6ZOMCMv3TrPJrTtdSuPtvXkleffXii/VfI7087leZc/erzZvy9PtfS\n",
"nFHX2jeA7jd7PM3Zu9e+oXfZdn4/wct6nmjGhy19meb8qe9FZnzt3/9Fc3JySHXsxcfTnHBzu3ry\n",
"93uPozk7rrLfEg+ufJ/m3JBnn4u1b/MqsBqffY5s7mff1B0ALvG2MOOp04fSnGZZzcz4Ux99QHMm\n",
"/sKu8D/nHLua7Iwz+mDs2COvAo433hpBUuEJAF8E7erLfQ43kg/V21Wm8aRiFQBSXfax8jlUcia4\n",
"7crHrKzmNKe8vMqM793Luwqw7gFOFZa1ZJ+yaloASI63q42TE+y4k3qHius9Afv4VIZ5VXM9+WJ3\n",
"qhxuILNBoUa+D6rIecWqgwGgrsFeXrCOlIkDaIS9bW6H6unE+MOfy6mos/epx+G9kEIaCqf6k2gO\n",
"e29VVtrfNwAfrGVk0JSD0gxgNM0AioiISEzTDGA0DQBFREQkpmkGMJoGgCIiIhLTNAMYTQNAERER\n",
"iWmaAYymAaCIiIjENM0ARtMAUERERGKaZgCjHXQAuL1/jhmv89il3QNP7EyXtaumxoxnp/ppzvXV\n",
"duuLctICAgA+WrXRjF85ym4/AgBPrv2PGV+yxG6JAQAFBb8z426HG3D379/LjJc28pYht51RYMbP\n",
"XfgMzenXJceMf0FK/wHgggvtVh7vJNjtKQBgb9g+Dv++ZgTNmVzynhm/JD+X5tz3qX18nNofjD3V\n",
"bs/S+59zzDgA/CrhZDOe/UIpzdncuq0Z/+2I82lOn66/MeNx8Z/RHHZj957v8ONz3V+6mvHBnU+i\n",
"OTnvTjLj46+w3wvZ2V/QZR2Omkh0awynFhuhBruVRi1pvQEAHrIP032JNIe1voiLs1u9AECYzDa4\n",
"fbxtSmam3bJn9+69NGfnzgoznpLCXw9bj9N7KUT2qduhZUgD2QcRhzYwbJ865bhIDos7rcfFUxBP\n",
"2rBESNsWwPn8ZRJJy52GRj6DxVrUsG0GgD1B+/vYqd1MqxS77VCjw/Fhr4e1MDpaNAMYTTOAIiIi\n",
"EtM0AxhNA0ARERGJaZoBjKYBoIiIiMQ0zQBG0wBQREREYlpTnAFcunQpli1bhrKyMhQUFOD66693\n",
"fP6rr76Kl19+GeFwGD179sSoUaMQ73BtL7/aU0RERCQGRCKNP+h/34f09HQMGDAA55577kGfu3r1\n",
"arz00ku466678Pjjj2P37t1YsGCBY85BZwBfvHygGU9OsCvjzm3XgS7rufVrzXhmIr+R9N5Eez3u\n",
"1bzycPr0G8z4+S8tpDnP9rArNk+fO5vm/GmaXQV88skdac7cuW+Z8VColub8rNqu2tt37zKa03vm\n",
"zWZ8KqnABYDsVHs99515D82Z+Z+Hzfhf139IcwratDPjz01+meas/PsHZjw7264SB4BfflFuxtcM\n",
"G0VzZv75FTM+e9atNOffVfZ6nCoXb3r+92b8la2baM61ed3M+NIWPOfBNSVm/MK4TJrT59SfmXHf\n",
"OLsaPaHV8XRZh8OqmHSqLmQVjl43/1hLTrArEv0e72HnBOt5hee+sF2V6XX4azzVa3/WpafzLgnV\n",
"1XYVfkMDn+0Ih+3tTvTyCmV2LrPXCQDBertKO96hcthHjl11HP98ZNW+7LgBgIvsn8rKaprDqlaD\n",
"pMoVAKpd9nY7Vao7nVcMWx47BgAQJlX0Tu+fiiDvIsGwSvFQmG8b2+42R1A43BRnAPPz8wEAmzdv\n",
"RkWFXfH/leXLl6Nv375o2/bLrhQDBgzA9OnTMWTIEJqjn4BFREQkpsX6NYDbtm07MGAEgPbt26Oq\n",
"qgrV1dVIIe17NAAUERGRmNYUZwAPRygUQlLS//+ampiYeCCuAaCIiIgck5wuizhavn4NXl5eHvLy\n",
"8g78u6ioCOvXrzfzcnNzMWHChMNal8/nQ/BrN8gIBAIH4owGgCIiIiLfs4ED7RoK4MsB4PcpOzsb\n",
"n376KXr27AkAKC0tRbNmzejsH6AqYBEREZGfnEgkgtraWkQiEUQiEdTV1dGfsnv37o23334b27Zt\n",
"Q3V1NRYvXow+ffo4Lv+gM4CNEfspkQY77nSZpTfOnopMiOMVeF5vshmPc/EKosZGuyor3ZNKc+Li\n",
"SAWeh1fgud3264mQfQbw15OQwO/d6XLZ+ycjg1dysm1LbuQV1z6XvQ1ZWVk0hx3TRIc/LdjxTiVV\n",
"yAB/rWlp6TQnnhxvdu4CgM9n/7XkdEzdIPeKJechACSSfd3c4Rxl+9qfwP/CS3Lbx9tNlgXw18q2\n",
"LSmeL+uwRIz95XTfWPKYq9HhHrCN5HPL4fjSzzqH9YB8SH+39Tj9dMWrSel62DY4vC8a2fVTDpsW\n",
"R/ZPXOPhzzuw95jTeszz6auHyD5g3x1OOU7rcTWSLhYOx80Fh/PqMMWD35e+gTwW7zAsYK/nu+1r\n",
"h9FC5PvbB03ZokWLsHjx4gP/fvfdd3HVVVfhyiuvRHl5OQoLCzFt2jRkZGSge/fu6NevHyZMmIDa\n",
"2lr07NnTcQYSAOIaHY+CiIiIiMQa/QQsIiIicozRAFBERETkGKMBoIiIiMgxRgNAERERkWOMBoAi\n",
"IiIixxgNAEVERESOMRoAioiIiBxjNAAUEREROcZoACgiIiJyjPlflfia3xDU3KgAAAAASUVORK5C\n",
"YII=\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7fcae1720c50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from pymks.tools import draw_concentrations\n",
"\n",
"draw_concentrations((X[0], y[0]), labels=('Input Concentration', 'Output Concentration'))\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Calibrate Influence Coefficients\n",
"\n",
"As mentioned above, the microstructures (concentration fields) does not have discrete phases. This leaves the number of local states in local state space as a free hyper parameter. In previous work it has been shown that as you increase the number of local states, the accuracy of MKS model increases (see [Fast et al.](http://dx.doi.org/10.1016/j.actamat.2010.10.008)), but as the number of local states increases, the difference in accuracy decreases. Some work needs to be done in order to find the practical number of local states that we will use. \n",
"\n",
"### Optimizing the Number of Local States\n",
"\n",
"Let's split the calibrate dataset into testing and training datasets. The function `train_test_split` for the machine learning python module [`sklearn`](http://scikit-learn.org/stable/) provides a convenient interface to do this. 80% of the dataset will be used for training and the remaining 20% will be used for testing by setting `test_size` equal to 0.2. The state of the random number generator used to make the split can be set using `random_state`. "
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import sklearn\n",
"from sklearn.cross_validation import train_test_split\n",
"\n",
"split_shape = (X.shape[0],) + (np.product(X.shape[1:]),)\n",
"X_train, X_test, y_train, y_test = train_test_split(X.reshape(split_shape), y.reshape(split_shape),\n",
" test_size=0.5, random_state=3)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We are now going to calibrate the influence coefficients while varying the number of local states from 2 up to 20. Each of these models will then predict the evolution of the concentration fields. Mean square error will be used to compared the results with the testing dataset to evaluate how the MKS model's performance changes as we change the number of local states. \n",
"\n",
"First we need to import the class `MKSLocalizationModel` from `pymks`."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from pymks import MKSLocalizationModel\n",
"from pymks.bases import PrimitiveBasis\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next we will calibrate the influence coefficients while varying the number of local states and compute the mean squared error. The following demonstrates how to use Scikit-learn's `GridSearchCV` to optimize `n_states` as a hyperparameter. Of course, the best fit is always with a larger value of `n_states`. Increasing this parameter does not overfit the data."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"GridSearchCV(cv=5,\n",
" estimator=MKSLocalizationModel(basis=<pymks.bases.primitive.PrimitiveBasis object at 0x7fcaf83d0f50>,\n",
" n_states=2),\n",
" fit_params={'size': (41, 41)}, iid=True, loss_func=None, n_jobs=1,\n",
" param_grid={'n_states': array([ 2, 3, 4, 5, 6, 7, 8, 9, 10])},\n",
" pre_dispatch='2*n_jobs', refit=True, score_func=None, scoring=None,\n",
" verbose=0)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from sklearn.grid_search import GridSearchCV\n",
"\n",
"parameters_to_tune = {'n_states': np.arange(2, 11)}\n",
"prim_basis = PrimitiveBasis(2, [-1, 1])\n",
"model = MKSLocalizationModel(prim_basis)\n",
"gs = GridSearchCV(model, parameters_to_tune, cv=5, fit_params={'size': (n, n)})\n",
"gs.fit(X_train, y_train)\n"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"MKSLocalizationModel(basis=<pymks.bases.primitive.PrimitiveBasis object at 0x7fcacee46e50>,\n",
" n_states=10)\n",
"0.99999908222\n"
]
}
],
"source": [
"print(gs.best_estimator_)\n",
"print(gs.score(X_test, y_test))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAawAAAEnCAYAAAD1v3e3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzs3XtAVGX++PH3MAMMd7mIqCCkUiiWmoqYqGx2WW3rW6lk\n",
"dtsu7lZmu9/a6re7pdluW1sZ25rad0Pt4u4GYoVZVpsFmpuieCO85AUQVO4CjjAMM3N+fwCjI6MM\n",
"ODAz8nm1LXPOec4znzPafDjnuakURVEQQgghXJyHswMQQggh7CEJSwghhFuQhCWEEMItSMISQgjh\n",
"FiRhCSGEcAuSsIQQQrgFSVhCCCHcgsbZAfQGpaWlrFixgsLCQgIDA7n33ntJSEiwWba5uZl//vOf\n",
"/PDDDxgMBiZOnMiDDz6IWq3uVF2ZmZmsWbOGF154gREjRjjsWoxGI2+99RZHjx6lqqqKhQsXMnz4\n",
"cIfVL4QQFyJ3WA6UkZHBmjVrrPaZTCZef/11xo4dy6pVq/jVr37FkiVLOHnypM06Pv30UwoLC3nz\n",
"zTd56623KCwsZO3atZ2qq6ysjK1btxIcHNwt1zls2DDmz59Pnz59uqV+IYSwRRKWA6lUqnb7jh8/\n",
"zqlTp7jllltQqVSMGDGCuLg4Nm3aZLOOnTt3Mm3aNPz8/AgMDGTatGl89913napr5cqV3HPPPZa7\n",
"sjbNzc188MEHPP7448ydO5d3330Xg8HQqWvUaDRMnz6duLg4PDzkr48QoufIN44TmM1mSkpKLnj8\n",
"3NmyFEWhpqaGxsZGu+r64Ycf8PT0ZPTo0e3K/vOf/6SsrIzXX3+dJUuWUFNTQ2Zm5iVciRBC9BxJ\n",
"WA5ka1rGAQMGEBQUxLp16zAajezZs4f9+/df8M5m5MiRfPHFF9TX11NbW8uGDRsAaGpq6rCuxsZG\n",
"PvroIx588EGbsW3cuJEHHngAPz8/tFotd9xxB//9738d+AkIIUT3kU4Xl+jVV1/l4MGDAJbE8cUX\n",
"XwAQFxfHc889xzPPPMPKlSvJyspiyJAhTJgwAU9PT5v13XnnnTQ0NPDss8/i6enJ1KlTKSoqsrQX\n",
"XayuNWvWMGnSJMLCwiz1tSXR+vp6DAYD/+///T+rY23HKyoqmD9//gWv89e//jXXX399lz4jIYRw\n",
"BJXM1u44a9asQaVSMXPmzIuWe/7550lOTuaGG27osM5vvvmGnJwc/vSnP3VY17PPPkt1dbWl7aq+\n",
"vh5fX19uv/12br31Vu6//37+/ve/O6wzxmOPPcb8+fOll6AQokfIHZYDXSj3Hzt2jIiICBRF4auv\n",
"vqKuro7k5GSbZWtqagAIDg7m0KFDrF27lscee8yuuhYsWIDJZLLE8vvf/54HHniA0aNHo1KpmDp1\n",
"Ku+99x4PP/wwgYGB1NTUUFJSwsiRIzt1nc3NzZZrNRqNGAwGvLy8OlWHEEJ0liSsS1RQUEB8fDzQ\n",
"0kvQVk/BTZs2sXHjRkwmE8OGDeP5559Ho2n56KuqqnjqqadITU0lNDSU8vJy3n77berr6wkLC+Oe\n",
"e+7hmmuusasuf39/q/f18PDA39+fw4cPEx8fzz333ENmZiZ//OMfqa+vJyQkhJtvvrnTCeu3v/0t\n",
"VVVVALz88ssALF261OpRZFec+1m6MonTsSROx3KHOLscoyIuSXp6urND6JA7xKgoEqejSZyOJXE6\n",
"TldjlF6CQggh3IIkLCGEEG5BegkKIYRwC9LpwgFOnDjh7BAuKiAggNOnTzs7jA5JnI4lcTqWxOk4\n",
"AwYM6NJ58khQCCGEW5CEJYQQwi04/ZGgTqdj+fLl7N27l8DAQO6++26SkpJsll2/fj3r1q2jqamJ\n",
"xMRE5s6daxmD1FE9+fn5rFixgurqaoYOHcq8efOsxg0dPXqU999/n8LCQry9vbnjjjuYPn169168\n",
"EEIIuzn9DistLQ1PT0/S0tKYP38+aWlplJaWtiu3e/dusrKyWLBgAcuWLaOiooKMjAy76qmvr2fx\n",
"4sXMnj2bVatWMWTIEFJTUy3n1tfX88orr3DjjTeycuVKlixZ0unBtEIIIbqXUxOWXq8nNzeX2bNn\n",
"4+3tTVxcHGPHjrW5VlROTg5Tp04lMjISPz8/ZsyYQXZ2tl315ObmEhUVRWJiIhqNhlmzZlFcXGzp\n",
"LLF+/XpGjhxJUlISGo0GrVbLwIEDe+xzEEII0TGnPhI8efIkarWaiIgIy76YmBgKCgralS0tLbVa\n",
"Cj46Opq6ujp0Oh2VlZUXraekpITo6GjLMW9vbyIiIigtLWXAgAEcPnyYQYMG8cILL1BWVsbQoUN5\n",
"+OGHL3mqISGE+9u4OZsPvsjArAYPE9w/PYWpk5KdHVY77hBnW4z/ef/TLp3v1ISl1+vx8fGx2qfV\n",
"atHr9TbL+vr6WrbbztPr9R3Wo9frCQoKsjru4+NjWRSxurqawsJCXnjhBaKioli9ejVvvfXWBWdI\n",
"F0JcOnf5gv3LmqXU3xhu2feXNUsBXCrWbzZ/xysZy6i/6WycL2cspclsYPJ1kwBQUDArCgotywop\n",
"rfsUyz4wo4CiYObsPgVz68+z55lb93FOncB59beWVVreKXdrLu9/nk7Tz7v+9MqpCUur1bZbSbeh\n",
"oQGtVtth2YaGBsv+C9XTlsR8fHws5W0d9/LyIiEhgcGDBwMwa9YsHn74YRobG9slwoKCAqs7wJSU\n",
"FAICAjp13T3Ny8vL5WMEidPRXDnOr7K/4dW1y6mdevYpxqtrl+Pj68PNyR0vu6MoCkbFRLPZhNFs\n",
"tPrZbDZiPO9ns2Ki2WRsPadtv/U5bduWcxUT/85che6cZAVQf2M4L2b8nc1BJZgVMyZFQVHMmBQz\n",
"ZkVp3dfylX/+vrbXtrbNKJjMZ1+bW4+b2o63leWc92g9Xp+1j8D/sV7m5/RN4fzv6lcIrM9yzB/a\n",
"JTo/xnP7IMTHx9s1Ga5TE1b//v0xmUyUlZVZHucVFxcTFRXVrmxUVBRFRUUkJiZaygUFBeHv749G\n",
"o7FZT2RkJACRkZHk5ORY6tLr9ZSXl1uOn/u4sCO2PlhXH6TnDgMJQeJ0FGfcuSiKgsFspMGo54yx\n",
"iQaj/uxrk54GYxNnjC0/G4x6Mld9SOPN/a3qqJ0axvy0RQzTfduSPJSziaMlmbTsa/vZE+obqwkk\n",
"vN3+iqZaPi/e2iMx2MWj/SoR0LJig4/aGxXgoVIBLStKeKBCpQJV2z+qtp9YbbeVAxUerftorcvq\n",
"PMBD5dFytK3+1n0tu1Ts8Sq0ii0lJaXTl+n0O6yEhATS09N59NFHKSwsJC8vjz//+c/tyk6ePJll\n",
"y5aRlJREnz59WLt2rWUdqI7qSUhIYPXq1Wzbto3Ro0eTmZlJTEyMZbR1cnIyixcvZtq0aURGRpKZ\n",
"mUlcXFy7uyshXF1nHmEZzSYaTU2WBHPm3CTT7rV1wjlj1NNgst5nUsx2x1lvqCWQ/u3260x6Dta3\n",
"7yVsi1rlgUalRuOhxtNDjVqlxtNDg0bVsq3xUOOpUqPx0LRsW8pq0Kg80Hhozilz9lyN5VwN/9pY\n",
"xSkb7z3UfwDzR/8SD5UKD5VHy7+0vW75clerWr621SoPVK3b7cu1/uTseR4qD9ScPUelUqHGw6ru\n",
"s+Vbfj743yfYZyPO8aFxvDf9Tbv/XLrTA58ftRljZzh9LsHzx0/NmTOHiRMntlsnClp682VlZWEw\n",
"GDoch9VWT5v8/HxWrlxJZWUlsbGx7cZhff3113z88cc0NTUxbNgwHnnkEUJCQuy6BpmayTEkzktT\n",
"a9Dx8B/mc2yKb7tjyhdFXDU7yZKUGoxNNJmbHfr+GpUaX403vhotfpafWut9ai2+Gi3/XrqKmqnt\n",
"//uK3tTIn//4YmvS0FglJEsiat3X9tt7d7L1C0Dg1xX8IWWeS7VhuUOc58Z4/NefdKkOpyesy4Ek\n",
"LMeQODt2xqinRFfBsTMVHDtTyTFdecvPMxWcbm6g/rP9BN46rN15tvarULUmk5ZE4qfxxtdTi5/6\n",
"3CSjbZeEfDXerftbX7eW91J72n0d7vAF22bj5mw+3LAGk4eC2qzivmmzXC5GcI8422L8+j1JWE4j\n",
"CcsxJM4WepOB0jNVlJxpSUwlZyop1pVTcqaS6qb6C57nq/HmdNZ+1LcMbncsKqeBl59fZEk2fhot\n",
"WrWXzRWye4o7fMGeS/5+Ok5XJ791+tRMQvRGRrOJ4w1VlLTeHR3TVVBypoLiMxVUNNZaugmfz8tD\n",
"Q6RfXwb5hTPIP7zlp184UX59CfUO5Fv/HJt3LvNS5jGsz6Ceujy7TJ2UzNRJyW7xBStcgyQsIbqJ\n",
"WTFT3njqnMd3FRw7U84xXQUnGmswX6CTglrlwQDfMEsyGuQfTpRfONF+4YT79Llo203bHYrVnYsL\n",
"PmYToiskYQlhJ1vdxa9PmkJ1U/05d0lnH9+VNFTSbDbarEuFigifEAb59WWQfz+i/PoS7deSmAb4\n",
"hqLxUHc5TrlzEZcrSVhC2MFWJ4HffPAy2h1pqIYGXfC8EO8Aov36WR7fRfn1ZZB/OJG+ffHuRCcF\n",
"IYQkLCHs8o/PVlslKwCf266kft0+Bg6LaH181++cdqW+RPr1xd9TxvIJ4SiSsIS4CF1zIysPfcme\n",
"2kICiGt3fGToEDJ+/oYTIhOi95GEJYQNRrOJT49t4Z0D66lrPoNitt1BwtfDu4cjE6L3koQlxHl+\n",
"qNhHasFaCnVlAIwMGczEmVNY/cWadt3F70uZ56wwheh1JGEJ0arwdBmpBWv5obJlxrP+PiH8Zvgd\n",
"XN9/NCqVikF+4dJdXAgnkoQler3aJh3/d3A9Hx/bglkx46v25uErp3HXFclWPfmku7gQziUJS/Ra\n",
"zWYj6YXZpP20gTNGPR6ouDM6iV9f9QtCvF1zHSkhejNJWKLXURSF7LI9vLXvY443VAMwPiyO38bP\n",
"YGhg1+Y4E0J0P0lYolc5WFfC4h/XsKvmCACD/MJ5Kn4G14XHO3UiWCFExyRhiV6hUl/L0v3r+KI0\n",
"FwWFQE9ffn3VLdwZPemSpkESQvQcSVjisqY3GvjwyDd8cOQ/6E0GNCo1KVdM5uHY6QR6tV/oUAjh\n",
"uiRhicuSWTHz5fEdvL3/Uyr1dQBM7ncNvxl+B4P8wzs4WwjhiiRhicvOnpojLP4xk/11xwCIDRjI\n",
"UyNmMjbsSidHJoS4FJKwxGXjREM1b+37mG9P7gYgxCuAecNu45aoRNQXWUNKCOEeJGEJt6drbmTV\n",
"oa/4d+F3NJuNeHlouGfIVH459CZ8NVpnhyeEcBBJWMJtmRQznxZv4Z2D66k16AC4acAY5g+7nQjf\n",
"ECdHJ4RwNElYwi1tqzzAmz+u4WjrBLXxfaL53YhZjAi+wsmRCSG6iyQs4VaKdOW8+WOmZYLaftpg\n",
"nhx+OzcOGCMDf4W4zEnCEm6h1qDj/w6s55NjWzApZnzUXvwy9mbmDL4erdrL2eEJIXqAJCzh0prN\n",
"RjIKc0j7aQM6YyMqVNwalcjjcbcRpg1ydnhCiB4kCUu4JEVRyCnby9/2fczxhioArg2N5en4mVwZ\n",
"FOnk6IQQziAJSzjdxs3ZfPBFBmY1eJjghuTr2exfwq6awwBE+obxv/EzmNTvammnEqIXk4QlnGrj\n",
"5mz+smap1dLzWzOW4h0fTuiwKB65chopV0zB00P+qgrR28m3gHCqD77IsEpWAIG3D8f36zI+fWIR\n",
"QV5+TopMCOFqZL4a4VTNmGzuH+gfJslKCGFFEpZwKk9sr0XlpZKbfyGENZf4VtDpdCxfvpy9e/cS\n",
"GBjI3XffTVJSks2y69evZ926dTQ1NZGYmMjcuXPRaDR21ZOfn8+KFSuorq5m6NChzJs3j7CwMAAy\n",
"MjL45JNP8PT0BEClUvH6668THi5LUXSn+6en8MJHqTT//GzPv8CvK7gvZZ4ToxJCuCKXSFhpaWl4\n",
"enqSlpZGYWEhr776KjExMURGWndf3r17N1lZWSxcuJDg4GDeeOMNMjIymDNnTof11NfXs3jxYh59\n",
"9FHGjh3LRx99RGpqKi+//DLQkqAmTpzIE0880ePX35tNnZTMJ8Wb+c+6bxno35dBPn25L2UeUycl\n",
"Ozs0IYSLcfojQb1eT25uLrNnz8bb25u4uDjGjh3Lpk2b2pXNyclh6tSpREZG4ufnx4wZM8jOzrar\n",
"ntzcXKKiokhMTESj0TBr1iyKi4s5ceIE0DLuR1GUHrtucVZlpIrA24az7C+pvPeXpZKshBA2OT1h\n",
"nTx5ErVaTUREhGVfTEwMJSUl7cqWlpYSHR1t2Y6Ojqaurg6dTtdhPSUlJVbnent7ExERQWlpKdBy\n",
"h5WXl8dDDz3E008/zddff+3waxXtnWo6zdHTJ/Hy0DAydIizwxFCuDCnPxLU6/X4+PhY7dNqtej1\n",
"eptlfX19Ldtt5+n1+g7r0ev1BAVZT+Xj4+NDY2MjABMmTODGG28kKCiIQ4cOsXjxYvz8/Jg4ceKl\n",
"X6S4oJ3VhwC4JngwXmpPmmj/5y6EEOACCUur1VqSRpuGhga02vYL751ftqGhwbL/QvW0JTEfHx9L\n",
"eVvHz20vu/LKK5k2bRpbt25tl7AKCgooKCiwbKekpBAQEGD39TqDl5eXy8a4p74IgIkDr3bpOM8l\n",
"cTqWxOlY7hJnRkaG5XV8fDzx8fEdnuP0hNW/f39MJhNlZWWWx3nFxcVERUW1KxsVFUVRURGJiYmW\n",
"ckFBQfj7+6PRaGzW05aIIiMjycnJsdSl1+spLy9v17GjI7Y+2NOnT3eqjp4WEBDgsjH+cPJHAK4O\n",
"iMZgMLhsnOdy5c/zXBKnY0mcjhMQEEBKSkqnz3N6G5ZWqyUhIYH09HSampo4cOAAeXl5TJ48uV3Z\n",
"yZMn8+2331JaWopOp2Pt2rUkJyfbVU9CQgIlJSVs27YNg8FAZmYmMTExDBgwAIDt27ej0+lQFIXD\n",
"hw+zYcMGxo0b12OfQ29Upa+jSFeOVu3J8D7RHZ8ghOjVVIoLdI07f/zUnDlzmDhxIlVVVTz11FOk\n",
"pqYSGhoKtIzDysrKwmAwdDgOq62eNvn5+axcuZLKykpiY2OtxmG99dZb7N27l+bmZkJDQ7n55pv5\n",
"+c9/blf8bT0NXZWr/sb19fE8/rhzJQlhV7F0wpMuG+f5JE7Hkjgdyx3ibLtR6CyXSFjuThJW1/xl\n",
"z7/45NgWHo+7jQdjb3bZOM8ncTqWxOlY7hBnVxOW0x8Jit5rR/VPAIwJjXVyJEIIdyAJSzhFpb6W\n",
"kjOVaNVe0n4lhLCLJCzhFHlVLeOvRoUMQeNhewJcIYQ4lyQs4RQ7qg4CMC7sKidHIoRwF5KwhFPs\n",
"aJ3hQtqvhBD2koQlelxZ4ymON1Thq/bmqqD2A8SFEMIWSViix+2saukdOCp0qLRfCSHsJglL9Ljt\n",
"rd3Zx4Zd6eRIhBDuRBKW6HF5rXdYY0MlYQkh7HfByW8XLVrU5UoXLlzY5XPF5e1kQzUnG2vw1/hw\n",
"ZVDnJh4WQvRuF0xY+/bt68k4RC/RNrvF6NAhqFVygy+EsN8FE1Z6errVdnNzM6mpqZSUlDBjxgzi\n",
"4+MJCgqitraWffv2sXbtWgYNGsT//u//dnvQwn3tsDwOlPFXQojOsXs9rLVr13LkyBEWL16Mv7+/\n",
"ZX94eDjh4eGMHTuWp59+mszMTGbPnt0twQr3piiKZYaLMWEy/koI0Tl2P5P5/vvvGT9+vFWyOpe/\n",
"vz/jx4/n+++/d1hw4vJyvKGacv0pAjQ+xAYOdHY4Qgg3Y3fCOnXqFJ6enhcto9FoOHXq1CUHJS5P\n",
"eZb2q1g8pP1KCNFJdn9rhISEsGPHDoxGo83jzc3N7Nixg5CQEIcFJy4vZ+cPlO7sQojOszthTZky\n",
"hbKyMhYtWsS+ffswm80AmM1mCgoKeOmllygvL2fKlCndFqxwX4qisKO1/UoGDAshusLuThe33347\n",
"R48eJS8vj0WLFuHh4YG/vz86nc6SvMaMGcPtt9/ebcEK91VyppKqpjoCPX0ZHNDf2eEIIdyQ3QlL\n",
"o9HwzDPPsGXLFr777jsKCws5ffo0vr6+DB48mOTkZJKSkrozVuHG8s6ZnV3ar4QQXWF3wgJQqVQk\n",
"JSVJYhKdtr21/WqsrH8lhOgi+VVXdLuW8Vcy4a0Q4tJ06g4LoKioiO+//57jx4/T1NTEggULAKio\n",
"qODw4cNcc801FxyrJXqnYl05NYbTBHv5c4V/hLPDEUK4qU4lrI8++ohPPvnE5jGz2cxbb73FAw88\n",
"wPTp0x0SnLg8tLVfXRsai0qlcnI0Qgh3ZfcjwS1btvDJJ58wcuRI/vrXv7brDRgREcHgwYPJy8tz\n",
"eJDCvW23jL+S9ishRNfZnbA2bNhAv379eOaZZ4iJiUGtbr9S7MCBAykrK3NogMK9KYpi1UNQCCG6\n",
"yu6EdezYMUaNGnXR6ZlCQkKora11SGDi8lCoK6PWoCPEK4Bo/37ODkcI4cbsTliKonTY/lBbW9vh\n",
"fIOid2lbTmRM2JXSfiWEuCR2J6yIiAh++umnCx43m80cPHiQqKgohwQmLg/SfiWEcBS7E9Z1113H\n",
"0aNHWbdunc3jn3zyCWVlZUycONFhwQn3ZlbM7JT2KyGEg9jdrX369Ols3bqVf/7zn2zdutWy/4MP\n",
"PmD//v0cPXqU2NhYbrjhhm4JVLifo6dPUt/cQJh3EFF+fZ0djhDCzdmdsLy9vVmwYAHvvfcemzdv\n",
"RlEUAD7//HNUKhWTJk3i4YcfRqPp9FhkcZnaYZndQsZfCSEuXaeyi5+fH/PmzeP+++/nyJEjlslv\n",
"Y2NjCQwM7FIAOp2O5cuXs3fvXgIDA7n77rsvOFfh+vXrWbduHU1NTSQmJjJ37lxLguyonvz8fFas\n",
"WEF1dTVDhw5l3rx5hIWFWdVvNBp55pln0Ov1LF++vEvXI87KlfkDhRAOZHcb1rx580hLSwMgICCA\n",
"UaNGMWnSJMaMGdPlZAWQlpaGp6cnaWlpzJ8/n7S0NEpLS9uV2717N1lZWSxYsIBly5ZRUVFBRkaG\n",
"XfXU19ezePFiZs+ezapVqxgyZAipqant3mPdunWXdC3iLLNiZnf1YQDGhMr8gUKIS2d3wqqvr8fX\n",
"19ehb67X68nNzWX27Nl4e3sTFxfH2LFj2bRpU7uyOTk5TJ06lcjISPz8/JgxYwbZ2dl21ZObm0tU\n",
"VBSJiYloNBpmzZpFcXExJ06csNRfUVHB5s2bueOOOxx6jb3VofrjnDY2Eq7tw0DfUGeHI4S4DNid\n",
"sKKioigvL3fom588eRK1Wk1ExNkJUWNiYigpKWlXtrS0lOjoaMt2dHQ0dXV16HS6DuspKSmxOtfb\n",
"25uIiAir91m5ciVz5syRcWQOsuOc2dml/UoI4Qh2J6zp06ezY8cOioqKHPbmer0eHx8fq31arRa9\n",
"Xm+z7Ll3eG3n6fX6Dus5/9y289uO5+bmoigK48aNu/SLEsC561/J40AhhGPY3ekiJCSEa665hgUL\n",
"FnDDDTcwdOhQ+vTpY7Ps8OHD7apTq9XS2Nhota+hoQGtVtth2YaGBsv+C9XTlsR8fHws5c8/rtfr\n",
"Wb16NX/4wx/sirmgoICCggLLdkpKCgEBAXad6yxeXl49GqPJbGbPqaMATIm+lgA/+967p+PsKonT\n",
"sSROx3KXOM/tgxAfH098fHyH59idsBYtWmR5/fnnn1+0bHp6ul119u/fH5PJRFlZmeVxXnFxsc3Z\n",
"MqKioigqKiIxMdFSLigoCH9/fzQajc16IiMjAYiMjCQnJ8dSl16vp7y8nMjISMrKyqisrLSs62U0\n",
"GmloaOBXv/oVf/nLX9r1JLT1wZ4+fdqu63WWgICAHo1xf+0xdM2N9PcJIdDsbfd793ScXSVxOpbE\n",
"6VjuEGdAQAApKSmdPs/uhDVjxgy7ynWmvUKr1ZKQkEB6ejqPPvoohYWF5OXl8ec//7ld2cmTJ7Ns\n",
"2TKSkpLo06cPa9euJTk52a56EhISWL16Ndu2bWP06NFkZmYSExPDgAEDMJvNvPPOO5b3OXjwICtW\n",
"rOC1115zi99SXFHb48BrZXYLIYQD2Z2wupIN7fHII4+wfPlyHnnkEQIDA5k7dy6RkZFUVVXx1FNP\n",
"kZqaSmhoKKNGjeK2225j0aJFGAwGEhMTrWK6UD0AgYGBPP3006xcuZIlS5YQGxvLb3/7WwA8PDwI\n",
"Cgqy1OPn59dun+icHa0JK0HGXwkhHEiltE1ZIbrs3O7xrqgnHxEYzSamfvkMDaYm1t/wZ/r5BNt9\n",
"rjs8ygCJ09EkTsdyhzgHDBjQpfPs7iUohD0O1pXQYGpioG9op5KVEEJ0pFNTM5nNZrZu3crevXup\n",
"qamhubnZZrmFCxc6JDjhfra3jr+6Vma3EEI4mN0Jq7m5mb/85S/s27evO+MRbm67tF8JIbqJ3Y8E\n",
"s7Ky2LdvH3feeScrVqwAYObMmbzzzjs8+eSThIaGct111/Hvf/+724IVrs1oNrG3dfzVmDDpISiE\n",
"cCy7E9YPP/xATEwMd911F/7+/kBLF/bg4GAmTpzIwoUL2blzJ+vXr++2YIVr21dbjN5kINI3jL5a\n",
"24PKhRCiq+xOWOXl5cTFxVntMxqNltf9+vVj9OjRVgN0Re8i0zEJIbqT3QlLrVZbTQyr1Wqpr6+3\n",
"KhMWFubwCXKF+2ib8HactF8JIbqB3QkrJCSEmpoay/aAAQM4dOiQVZni4mLL40LRuzSbjeSfKgRg\n",
"jNxhCSG6gd0JKy4ujp9++smyPW7cOI4dO8by5cvZuXMnH3zwAXv37rV74ltxedlXW0yTuZlBfuGE\n",
"essimEIIx7O7W/vEiROprq6moqKC8PBwy3Ij2dnZloUUIyIiuOeee7orVuHCciul/UoI0b3sTlgj\n",
"RoxgxIgRlm2tVstLL73Ejh07KCsrIzw8nDFjxuDt7d0tgQrX1tbhYlyotF8JIbpHp2a6aHeyRmNZ\n",
"7kP0XgZTMwW1RYCMvxJCdB+ZS1Bcsh9rizCYjcT4RxDsLUuyCCG6h913WNnZ2XavdTVlypQuByTc\n",
"z/a29itZ/0oI0Y3sTljLly+3u1JJWL2Lpf0qLK6DkkII0XV2J6zHHnvM5v4zZ85w5MgRtmzZwvjx\n",
"47n22msdFpxwfU2mZvbVHUOFimvDhjo7HCHEZczuhNW2HP2F/OxnP+OVV15h2rRplxqTcCP5pwpp\n",
"NhsZHNC2vnG3AAAgAElEQVSfPl4yaFwI0X0c1uni6quvZtSoUWRkZDiqSuEGcisPANJ+JYTofg7t\n",
"Jdi/f3+OHDniyCqFi5P2KyFET3Fowjp+/LjdPQmF+9MbDRyoK2lpv5I7LCFEN7ukgcMAZrOZqqoq\n",
"Nm7cyK5duxg1apQj4hJuYE/NEYyKiaEBAwn08nV2OEKIy5zdCeuuu+7qsIy/vz/33XffJQUk3Me2\n",
"qtb2K5ndQgjRA+xOWMOGDbO5X6VS4efnR2xsLD/72c8IDJSZunuLvOqW5WVk/SshRE+wO2G9+OKL\n",
"3RiGcDcNRj0H60rwkPYrIUQPkbkERZfsrj6CSTETGzgQf08fZ4cjhOgFJGGJLslt7c4+Ru6uhBA9\n",
"xO5HgsuWLevymzz++ONdPle4przqltWnE/rK+CshRM+wO2Hl5OR0+U0kYV1ezhj1/FR/HA+VB6NC\n",
"Zf5AIUTPsDth/f3vf+f999/nwIEDTJs2jeHDh9OnTx9qa2spKChgw4YNDB8+nAceeKA74xUuYGfV\n",
"IcyKmbigKPw0WmeHI4ToJexOWNu3b2f//v389a9/JTw83LJ/4MCBxMfHk5yczHPPPUdubi6/+MUv\n",
"uiVY4Rq2W9qvrnRyJEKI3sTuThcbN25kwoQJVsnqXOHh4UyYMIGNGzc6LDjhmtrGX42X9ishRA+y\n",
"+w6roqKCcePGXbSMr68vFRUVnQpAp9OxfPly9u7dS2BgIHfffTdJSUk2y65fv55169bR1NREYmIi\n",
"c+fORaPR2FVPfn4+K1asoLq6mqFDhzJv3jzCwsIs9X711VfU19fj5eXF6NGjefDBB/Hxke7a59M1\n",
"N3K4/jhqlQejQoY4OxwhRC9i9x1WQEAAe/bsueBxRVHYu3cvAQEBnQogLS0NT09P0tLSmD9/Pmlp\n",
"aZSWlrYrt3v3brKysliwYAHLli2joqLCaimTi9VTX1/P4sWLmT17NqtWrWLIkCGkpqZazh03bhyv\n",
"vPIK77//PqmpqVRVVfHxxx936jp6i7zqQ5hRuCooCh+Nt7PDEUL0InYnrAkTJlBUVMSbb77Z7i6q\n",
"vLyc1NRUiouLue666+x+c71eT25uLrNnz8bb25u4uDjGjh3Lpk2b2pXNyclh6tSpREZG4ufnx4wZ\n",
"M8jOzrarntzcXKKiokhMTESj0TBr1iyKi4s5ceIEAP369cPfv2XxQUVRUKlUBAcH230dvcnZ9a+k\n",
"/UoI0bPsfiSYkpLCgQMH2LZtG9u3byckJISgoCDq6uqorq5GURSGDBnCrFmz7H7zkydPolariYiI\n",
"sOyLiYmhoKCgXdnS0lISEhIs29HR0dTV1aHT6aisrLxoPSUlJURHR1uOeXt7ExERQUlJCQMGDADg\n",
"+++/591330Wv13Pdddcxffp0u6+jN9nZ2n6V0FfmDxRC9Cy7E5aPjw8vvfQSn332GdnZ2ZSXl1NV\n",
"VQVAREQEycnJ3HrrrZY2JXvo9fp27URarRa9Xm+zrK/v2SUs2s7T6/Ud1qPX6wkKCmp3Pee+T1JS\n",
"EklJSZSVlfHmm2+yfv166e14njrDGY6cPolGpWZksLRfCSF6VqfWw/L09OTOO+/kzjvvpLGxkYaG\n",
"Bnx9fbvcOUGr1dLY2Gi1r6GhAa22/die88s2NDRY9l+onra4fHx8LOVtHT9XREQEt99+O59++qnN\n",
"hFVQUGB1B5iSktLpdrue5uXl5ZAYtx47iIJCfEgMfYNDHRCZNUfF2d0kTseSOB3LXeI8tw9CfHw8\n",
"8fHxHZ7T5QUcfXx8LrkXXf/+/TGZTJSVlVke5xUXFxMVFdWubFRUFEVFRSQmJlrKBQUF4e/vj0aj\n",
"sVlPZGQkAJGRkVYzdej1esrLyy3Hz2c0GvH2tt2hwNYHe/r06U5eec8KCAhwSIzZJbsAGB08pFuu\n",
"2VFxdjeJ07EkTsdyhzgDAgJISUnp9Hl2d7rQ6XSUlpZiMBis9n/77be89tpr/O1vf+PQoUOdenOt\n",
"VktCQgLp6ek0NTVx4MAB8vLymDx5cruykydP5ttvv6W0tBSdTsfatWtJTk62q56EhARKSkrYtm0b\n",
"BoOBzMxMYmJiLO1XGzdupL6+HmhpK8vKymL8+PGdupbewNJ+FSbjr4QQPU+lKIpiT8F3332XzZs3\n",
"k5aWhpeXFwAbNmzgvffes5Tx9PTk1VdfveCdiy3nj5+aM2cOEydOpKqqiqeeeorU1FRCQ1seP61f\n",
"v56srCwMBkOH47Da6mmTn5/PypUrqaysJDY21moc1rJly9i1axdNTU0EBwdz/fXXc9ttt6FSqey6\n",
"hrbehq7KEb9x1Rp03PjVc3h6aPju52/grfZ0UHRnucNvhiBxOprE6VjuEGfbzUJn2Z2wfve73xEe\n",
"Hs6zzz5r2ff444+jKAq/+c1vqK2tZcmSJSQlJfHYY491KRh31RsS1jfHd/L7nSsYGTyYtKSnHRSZ\n",
"NXf4Dw0kTkeTOB3LHeLsasKyuw2rpqaGESNGWLZLS0uprq5mzpw5xMW1PCL673//y4EDB7oUiHBt\n",
"26pa/lxl/SshhLPY3YZlMBgsjwIBS2K6+uqrLfsiIiKorq52YHjCVeyyjL+S9ishhHPYnbCCg4M5\n",
"fvy4ZXvPnj34+PgQExNj2afT6aySmrg81DSdpvhMBV4eGq4OvsLZ4Qgheim7HwmOGDGC7OxsNmzY\n",
"gKenJzt27GD8+PF4eJzNeRUVFZYOEuLy0bacSHyfGLy6obOFEELYw+6Edfvtt7Nt2zZLr0CtVms1\n",
"DVNDQwMHDhywdDUXl4+2+QOl/UoI4Ux2J6x+/fqxePFitm7dikqlYuzYsZZu4QBlZWXccMMNF1wa\n",
"RLivXTWHAWm/EkI4V6dmuggODmbatGk2jw0ePJjBgwc7JCjhOqr0dZScqcTbw5MRwTHODkcI0YvZ\n",
"3enifEVFRVbTHYnLU25r+9WI4Bg8Pbo8k5cQQlyyLies3Nxcli1b5shYhAva3tp+da20XwkhnKzL\n",
"CUv0DrtqjgAwXtqvhBBOJglLXFBF4ymON1Tho/Yivk+Ms8MRQvRykrDEBW2raHkcOCI4Bo2H2snR\n",
"CCF6uy4nLD8/P6tu7eLys726pcOFtF8JIVxBl7t93XLLLdxyyy3t9tfX1xMYGHhJQQnXsLu1/Sqx\n",
"7zAnRyKEEA58JHjmzBn+9a9/8cQTTziqSuFEZQ01nGyswVftTVzQIGeHI4QQ9t1hVVRUcPToUTw9\n",
"PYmNjbW6gzIYDKxfv57PPvuMhoYGmfz2MrGtcj8g7VdCCNfRYcJasWIFX3/9tWXby8uLhx9+mOTk\n",
"ZAoKCli6dCnV1dVoNBqmTZvGHXfc0a0Bi57RNuHt2LArnRyJEEK0uGjCys7O5uuvv0alUllWiDx+\n",
"/Dj/+Mc/8PT0ZNmyZZjNZm688UbuvPNOQkJCeiRo0f3a2q8SpP1KCOEiLpqwcnJyUKvVLFy4kKuu\n",
"ugqAffv28ac//YklS5YQGhrKc889x6BB0sZxOSk9U0m5vhY/jZa4oChnhyOEEEAHnS6Ki4tJSEiw\n",
"JCuA4cOHk5CQgKIoPProo5KsLkNty4lcHXwFapUM1RNCuIaLfhs1NDQQERHRbn/bvnMTmbh8bK/6\n",
"CYAxodJ+JYRwHRdNWIqioNG0f2qoVrf0GpMegZcfRVHY0zb+KlzmDxRCuI4uPe9RqVSOjkO4iNIz\n",
"lVQ21RHg6cOVgZHODkcIISw67Na+Zs0a1qxZY/PYXXfdZXN/enr6pUUlnGZr6/ira4IH4yHtV0II\n",
"FyLfSMLKjuq29iuZP1AI4Voueocld0q9i6IolvFX42X8lRDCxcgdlrAo0pVT03SaQE9fhgYOcHY4\n",
"QghhRRKWsGibP3BkiLRfCSFcj3wrCYs8GX8lhHBhkrAE0Dr+6tRRAMb3lfFXQgjXIwlLAHDk9ElO\n",
"GXT08fJnSIC0XwkhXE+XVxx2JJ1Ox/Lly9m7dy+BgYHcfffdJCUl2Sy7fv161q1bR1NTE4mJicyd\n",
"O9cyG0dH9eTn57NixQqqq6sZOnQo8+bNIywsDIB169aRk5NDVVUVAQEB3HTTTdx2223df/EuYmvF\n",
"PgBGBg+WgeFCCJfkEndYaWlpeHp6kpaWxvz580lLS6O0tLRdud27d5OVlcWCBQtYtmwZFRUVZGRk\n",
"2FVPfX09ixcvZvbs2axatYohQ4aQmppqVf/8+fNZtWoVf/jDH/jqq6/473//270X7kJ21RwGYIys\n",
"fyWEcFFOT1h6vZ7c3Fxmz56Nt7c3cXFxjB07lk2bNrUrm5OTw9SpU4mMjMTPz48ZM2aQnZ1tVz25\n",
"ublERUWRmJiIRqNh1qxZFBcXc+LECQBuu+02YmJi8PDwYMCAAYwdO5YDBw702OfgTIqisLdG2q+E\n",
"EK7N6Qnr5MmTqNVqq1nhY2JiKCkpaVe2tLSU6Ohoy3Z0dDR1dXXodLoO6ykpKbE619vbm4iICJvv\n",
"oygK+/fv7zVLpxyqP05t8xlCvAK4wr/97PxCCOEKnJ6w9Ho9Pj4+Vvu0Wi16vd5mWV9fX8t223l6\n",
"vb7Des4/t+18W+/TNndicnJy5y/IDW2tODv+StqvhBCuyumdLrRaLY2NjVb7Ghoa0Gq1HZZtaGiw\n",
"7L9QPW1JzMfHx1Le1vE2X375JZs3b2bRokU2l1YpKCigoKDAsp2SkkJAQIA9l+o0Xl5eF41xb30R\n",
"ANcNuNqp19JRnK5C4nQsidOx3CXOc/sfxMfHEx8f3+E5Tk9Y/fv3x2QyUVZWZnmcV1xcTFRU+6XZ\n",
"o6KiKCoqIjEx0VIuKCgIf39/NBqNzXoiI1uWyIiMjCQnJ8dSl16vp7y83HIc4NtvvyUrK4tFixYR\n",
"EhJiM15bH+zp06cv4RPofgEBAReM0ayY2VnZMmB4ZOAVTr2Wi8XpSiROx5I4Hcsd4gwICCAlJaXT\n",
"5zn9kaBWqyUhIYH09HSampo4cOAAeXl5TJ48uV3ZyZMn8+2331JaWopOp2Pt2rWWx3Yd1ZOQkEBJ\n",
"SQnbtm3DYDCQmZlJTEwMAwa0jDnavHkzH330Ec8//zzh4eE9dv3OdrCuhNPNDYR5BxLj38/Z4Qgh\n",
"xAWpFEVRnB3E+eOn5syZw8SJE6mqquKpp54iNTWV0NBQoGUcVlZWFgaDocNxWG31tMnPz2flypVU\n",
"VlYSGxtrNQ7riSeeoKamxuox4OTJk3nkkUc6jL+tp6GruthvXO8d+oqlB9Yxtf8oXh07t4cjs+YO\n",
"vxmCxOloEqdjuUOcbTcKneUSCcvduXPCenLr2/xQuZ9nRqSQcsWUHo7Mmjv8hwYSp6NJnI7lDnF2\n",
"NWE5/ZGgcB6T2UT+qSIAEmX9KyGEi5OE1YvtrytBZ2wkXNuHQf69p91OCOGeJGH1Ypb1r4IHOzkS\n",
"IYTomCSsXmxXdcv8gdeGxjo5EiGE6JgkrF7KaDbxY20RAOOl/UoI4QYkYfVSBaeKOGPU008bTJR/\n",
"X2eHI4QQHZKE1Uttq2qZiX5UyBAnRyKEEPaRhNVLnW2/GurkSIQQwj6SsHohg6mZgtpiQMZfCSHc\n",
"hySsXujHU0U0mpro7xPCAL8wZ4cjhBB2kYTVC+VK+5UQwg1JwuqFdtUcAWT8lRDCvUjC6mUMpmb2\n",
"SfuVEMINScLqZXbXHEFvMjDQN4wIX9uLVAohhCuShNXLbK86CMCoEJk/UAjhXiRh9TJ7WtuvxoRe\n",
"6eRIhBCicyRh9SJ6k4F9tccAGN83zsnRCCFE50jC6kV2VR+mydxMlF9fwn2CnR2OEEJ0iiSsXmSH\n",
"pf1Kxl8JIdyPJKxeZHfNUQCuDZHxV0II9yMJq5doaNZzoK6l/SoxXMZfCSHcjySsXmJnzWEMZiPR\n",
"/v0I0wY5OxwhhOg0SVi9xM6qnwAYFSzjr4QQ7kkSVi8h8wcKIdydJKxe4LShgQN1JahQMV7mDxRC\n",
"uCmNswO4HFTr61ChouV/KgBUKhUeeKBqfa1StRzxwAMPy/bZsiqsz3Wk3Ir9GBUTV/hHEKoNdGjd\n",
"QgjRUyRhOcATC59h1s3/w6TrJp7dqbT+UBRa/gGUlp8t/9+anM4WBaV1uyX3oUKF6pwkCNbJ7fwk\n",
"CeChakmT5ybJbeX7ARgp8wcKIdyYJCwHOJzkyd8/WQlgnbTA6k4KB904nU16yjnZru2gqV2S3FV5\n",
"CJD5A4UQ7k0SloOcuSmCpVnvUx+lwUvtiZeHpvXf1tfqlteeHhq8z3nt5aFB46F2aCxtSXLzf7eQ\n",
"/uUn7KktBLOZJv9KiHToWwkhRI+RhOVApY1VLD2wrtPneag82iU4T7UGbw8Nnq3b3uqzr1sSYGs5\n",
"Dw3eHp54qlv2e7cmwp92/si6bzZgnBZFAC0T3f79k1X4a3yZOinZwVcuhBDdTxKWA4V7BfGzgeMw\n",
"mI00mZtpNhkxmI0YzM2tP40YTC2vm8/ZNitm9CYDepPBYbHUf7GPwP8Zbr3vxnA+3LBGEpYQwi25\n",
"RMLS6XQsX76cvXv3EhgYyN13301SUpLNsuvXr2fdunU0NTWRmJjI3Llz0Wg0dtWTn5/PihUrqK6u\n",
"ZujQocybN4+wsDAAfvzxR9auXUthYSF+fn4sXbq0U9fg91UZT975CJOGT+y48DkURcGkmM8mtvOS\n",
"XLOpJfmdn+RsJcCmc87Z7F1s8/0MirFT8QkhhKtwiYSVlpaGp6cnaWlpFBYW8uqrrxITE0NkpHWD\n",
"y+7du8nKymLhwoUEBwfzxhtvkJGRwZw5czqsp76+nsWLF/Poo48yduxYPvroI1JTU3n55ZcB0Gq1\n",
"XH/99TQ1NfHJJ590Kv7YLUZm3vlQuw4X9lCpVGhUajQeanzx7vT5F/Kk/y4O29jvpXKJP3IhhOg0\n",
"pw8c1uv15ObmMnv2bLy9vYmLi2Ps2LFs2rSpXdmcnBymTp1KZGQkfn5+zJgxg+zsbLvqyc3NJSoq\n",
"isTERDQaDbNmzaK4uJgTJ04AMHToUCZNmkR4eHinr2HJi68x5bokSydARVFQFAWzYsasmDGZzRjN\n",
"JprNJowmE0aTmWZTy3az2WQ51vKvEaPZhMlswqSYMbXWoSjndwe8uFk3/w9+X5dZ7Qv8uoL7ps3q\n",
"9PUJIYQrcPqv2ydPnkStVhMREWHZFxMTQ0FBQbuypaWlJCQkWLajo6Opq6tDp9NRWVl50XpKSkqI\n",
"jo62HPP29iYiIoKSkhIGDBhwSdcQ2snJZNu6nUNrF3Wl7XXLT7PZjJmzXdPbEqACmDG3K9/Su/2c\n",
"ruxA0oTrUBSFzP+sQ/FQoUXDfSnzpP1KCOG2nJ6w9Ho9Pj4+Vvu0Wi16vd5mWV9fX8t223l6vb7D\n",
"evR6PUFB1onFx8fH5vt0N6uxWdB+fJaD7ntnTP0FM6b+goCAAE6fPu2YSoUQwkmcnrC0Wi2NjY1W\n",
"+xoaGtBqtR2WbWhosOy/UD1tSczHx8dS3tZxexUUFFjd/aWkpBAQENCpOnqal5eXy8cIEqejSZyO\n",
"JXE6VkZGhuV1fHw88fHxHZ7j9ITVv39/TCYTZWVllsd5xcXFREVFtSsbFRVFUVERiYmJlnJBQUH4\n",
"+/uj0Whs1tPWcSMyMpKcnBxLXXq9nvLy8nYdOzpi64N19bsXd7nDkjgdS+J0LInTcQICAkhJSen0\n",
"eU7vdKHVaklISCA9PZ2mpiYOHDhAXl4ekydPbld28uTJfPvtt5SWlqLT6Vi7di3Jycl21ZOQkEBJ\n",
"SQnbtm3DYDCQmZlJTEyMpf1KURQMBgMmkwmA5uZmjEbpAi6EEK5CpXS2+1k3OH/81Jw5c5g4cSJV\n",
"VVU89dRTpKamEhoaCrSMw8rKysJgMHQ4Dqutnjb5+fmsXLmSyspKYmNjrcZhFRQU8NJLL1nFNXz4\n",
"cBYuXNhh/G09DV2VO/zGBRKno0mcjiVxOk5XO7q5RMJyd5KwHEPidCyJ07EkTsfpasJy+iNBIYQQ\n",
"wh6SsIQQQrgFSVhCCCHcgiQsIYQQbkE6XQghhHALcod1ic4dre2q3CFGkDgdTeJ0LInTcboaoyQs\n",
"IYQQbkESlhBCCLegfvHFF190dhDuritraPU0d4gRJE5HkzgdS+J0nK7EKJ0uhBBCuAV5JCiEEMIt\n",
"SMISQgjhFiRhCSGEcAtOX8DRHRmNRt59911+/PFHdDod/fr1Y86cOYwaNcrZobXz97//nR9//JGm\n",
"piYCAgK4/vrrufPOO50dlk0nT57kd7/7HYmJicyfP9/Z4bTz4osvcujQIdRqNQChoaGkpqY6OSrb\n",
"tmzZQmZmJlVVVfTp04d58+YRFxfn7LAs7rvvPlQqlWXbYDBw00038dBDDzkxKtuqq6t59913+emn\n",
"n9BoNCQmJvLLX/4SDw/X+n2/tLSUFStWUFhYSGBgIPfeey8JCQlOjenLL78kOzubkpISJk6cyOOP\n",
"P245lp+fz4oVK6iurmbo0KFWyz1dkCI6Ta/XKxkZGUplZaWiKIqSl5en3H///UpFRYWTI2vv2LFj\n",
"SlNTk6IoinL8+HHlkUceUXbt2uXkqGz705/+pCxYsEBZsmSJs0Ox6cUXX1Q2btzo7DA6tGfPHuXx\n",
"xx9XDh06pCiKotTU1CjV1dVOjurCGhsblfvuu0/Zv3+/s0Ox6fXXX1eWLl2qNDc3K6dOnVKefvpp\n",
"5YsvvnB2WFaMRqPy5JNPKuvXr1fMZrOSn5+v3HvvvcqJEyecGte2bduU3Nxc5d1331WWLl1q2V9X\n",
"V6c88MADyg8//KA0NzcrH374ofKHP/yhw/pc61cEN+Ht7c2sWbMsvw1ce+21hIeHU1hY6OTI2ouK\n",
"isLLy8uyrVarCQwMdGJEtm3ZsgU/Pz9GjBiBIh1XL0lGRgYzZ85k6NChAAQHBxMSEuLkqC5s69at\n",
"BAUFudQd4LlKSkq47rrr0Gg09OnTh1GjRlFSUuLssKwcP36cU6dOccstt6BSqRgxYgRxcXFs2rTJ\n",
"qXElJCQwbtw4/P39rfbn5uYSFRVFYmIiGo2GWbNmUVxc3OHagpKwHKC2tpYTJ04QGRnp7FBsSktL\n",
"47777uOpp57izjvvZPDgwc4OyUpDQwMZGRk88MADLp+s/vWvf/Hwww/zwgsvsG/fPmeH047ZbObo\n",
"0aPU1dXx5JNP8thjj7Fy5UoMBoOzQ7ugnJwcpkyZ4uwwLmjkyJF8//33GAwGampq2LVrF6NHj3Z2\n",
"WB0ym80ul1jblJSUEB0dbdn29vYmIiKiw3glYV0io9HIkiVLSE5O7vIqmt3tkUce4YMPPuCFF14g\n",
"PT2dw4cPOzskK+np6UydOpWQkBCrdg1Xc8899/D222/zf//3f9xwww389a9/pby83NlhWamtrcVk\n",
"MrFt2zZeeuklXnvtNQoLC/n444+dHZpNlZWV7N+/36UTVkpKCiUlJTzwwAM89thjDBkyhHHjxjk7\n",
"LCsDBgwgKCiIdevWYTQa2bNnD/v373fZX1Samprw9fW12ufj44Ner7/oeZKwLoHZbObtt9/G09OT\n",
"hx9+2NnhXJRKpSI+Pp7ExES+//57Z4djUVRUxI8//sj06dMBXPoOa+jQoWi1WjQaDVOmTOGqq65i\n",
"165dzg7LStvj32nTptGnTx8CAgL4xS9+4XJxttm0aRPDhg2jb9++zg7FJkVRePnll0lMTOTDDz9k\n",
"xYoV6HQ6Vq9e7ezQrGg0Gp555hl27tzJr3/9az7//HMmTJjgso+CtVotDQ0NVvsaGhrw8fG56HnS\n",
"S7CLFEXhnXfeob6+nt///vcu12PoQkwmEwEBAc4Ow2Lfvn1UVFRYeg/p9XrMZjPHjx/n1VdfdXJ0\n",
"7sff399lv6Rs2bRpE3fccYezw7ig06dPc/ToURYsWIBGo8Hf35/k5GTS09O59957nR2elUGDBnHu\n",
"THvPP/88ycnJTovnYiIjI8nJybFs6/V6ysvLO2xWcY9vWRf07rvvcvz4cZ599lk8PT2dHY5N9fX1\n",
"bNmyxZIEdu/ezQ8//MDYsWOdHZrFDTfcwNtvv83rr7/Oa6+9xo033si1117LH//4R2eHZqWhoYHd\n",
"u3djMBgwmUxs3ryZ/fv3u+RQhp/97Gds2LCB+vp6dDodn3/+OWPGjHF2WO0cPHiQmpoaEhMTnR3K\n",
"BQUEBNCnTx++/vprzGYzZ86cIScnx6r9xVUcO3YMg8FAU1MT69ato66uzukJy2w2YzAYMJvNmM1m\n",
"mpubMZvNJCQkUFJSwrZt2zAYDGRmZhITE9Nhs4rMJdgFlZWVPPHEE3h6elrdWf3qV78iKSnJiZFZ\n",
"q6+v580336S4uBhFUejfvz8zZsxwqYR1vjVr1lBeXs4TTzzh7FCs1NfX88orr3DixAk8PDwYOHAg\n",
"d911F1dffbWzQ2vHZDKxatUqtmzZgqenJ9dddx333nsvGo1rPVD5xz/+gcFgcLk/6/MdOnSIDz/8\n",
"kJKSEjw8PLj66qt56KGHXK637erVq9m4cSMmk4lhw4bx0EMP0a9fP6fGlJGRwdq1a632zZo1i5kz\n",
"Z5Kfn8/KlSuprKwkNjbWrnFYkrCEEEK4BXkkKIQQwi1IwhJCCOEWJGEJIYRwC5KwhBBCuAVJWEII\n",
"IdyCJCwhhBBuQRKWEEIIt+BaIwmF6GYvvvgi+/fvJz093dmhOMzJkydZvXo1P/30E/X19fj6+rJq\n",
"1Spnh9UtLsc/P2E/SVi9yF133QVwyf+xt9UTFhbG3/72N5tTU82bN4+qqir+/e9/u808i+7IbDbz\n",
"+uuvU15ezuTJkwkNDbVrqjBH/V1wB3v37uWrr77i8OHDnD59Gm9vbwIDA4mOjmbYsGFMmzbNUrai\n",
"ooL58+czZcoUq9VxL8W8efMAWLp0qUPq680kYYkuq6qq4vPPP+f22293dii9VkVFBcePH2fq1Kn8\n",
"6le/cnY4Lufjjz8mPT0dtVrNqFGjGDBgAB4eHpSVlbF//362bdvGzTffbPmlqruWt3HlZXPciSQs\n",
"0SV+fn6oVCqysrKYOnWqS80A35vU1NQALasKC2uVlZVkZGTg6+vLSy+9RFRUlNVxRVHIz8+3egIg\n",
"M9W5NklYoku8vb259dZbef/991mzZg0PPfRQh+cUFBTw0ksvMXPmTGbNmtXuuK1HJ9nZ2SxfvpzH\n",
"Hg/coqMAAA4ISURBVHuMkJAQMjMzKSoqwtPTkzFjxvDLX/4SX19fjh49Snp6Oj/99BMmk4kRI0bw\n",
"4IMPXnCdJaPRSGZmJps3b6a2tpaQkBCmTJnC7bffbnOS2OPHj/Ppp5/y448/UldXh5+fH1dffTUz\n",
"Z85sN8P00qVL2bRpE0uWLCEvL4+NGzdSVlZGbGwsCxcu7PBzOnr0KB9//DEHDhygsbGRPn36MHr0\n",
"aGbOnEmfPn0s5doe6wFkZmaSmZkJcMHPt6uam5v5/PPP2bx5MxUVFXh4eBATE8PPf/5zJkyYYPOc\n",
"w4cP89lnn3HgwAF0Oh3+/v4MGjSI66+/3uqc7OxsduzYQVFREbW1tajVagYNGsRNN93EpEmTLinu\n",
"Q4cOoSgK8fHx7ZIVtNz1XHPNNZbtcydqzcnJsVr+4rHHHiM5ORmj0cg333zDrl27KCkpoa6uDm9v\n",
"b6644gpuvfVWq9n72/6+tzn3z+v8R46d+ftVW1vLunXryMvLo6amBo1GQ1BQEFdeeSUzZ84kPDz8\n",
"Ej411yYJS3TZzTffzJdffsk333zD9OnTiYiIsOu8iz0eudCxHTt2sHPnTsaMGcNNN93EwYMHycnJ\n",
"oby8nDlz5vCnP/2J+Ph4pk6dSnFxMXl5eZSXl/PGG2/YrPPNN9/kyJEjTJgwAbVazfbt21mzZg1H\n",
"jhzhueeesyq7e/du3njjDcxmM2PGjCEiIoLq6mq2bdvGzp07WbhwIVdccUW791i1ahUHDhzg2muv\n",
"5dprr7WrLS8vL4/FixejUqkYP348ffv25ejRo/znP/9hx44dvPTSS5YvpJkzZ1JZWUlOTg7Dhw8n\n",
"Pj4egOHDh3f4PvYyGo28/PLL7N+/n4EDB3LzzTfT1NTE1q1b+dvf/kZRURF333231TnffPMNaWlp\n",
"qNVqxo4dS//+/amtreXo0aN8/fXXVgkrLS2NqKgohg8fTnBwMKdPn2bXrl28/fbbnDhxwupLvrPa\n",
"ZlMvLy/HbDZ3+PmPGDGChoYGNmzYQExMjNWqwm1/vjqdjvfee4+rrrqKkSNHEhgYyKlTp8jLy+OV\n",
"V17h17/+Nddffz0A4eHhzJw5ky+++AKAW265xVJfTEyM5XVn/n41NTXxwgsvUFFRwTXXXMO4ceNQ\n",
"FIXKykp27NhBYmKiJCwhbFGr1cyZM4fU1FRWr17N7373u257r7y8PBYsWMCwYcOAsyvB5ufn88or\n",
"r/Doo49aLe3yzjvv8N1335GXl2dzOZUTJ06QmppqWaZ79uzZLFq0iJ07d7Jp0yYmT54MtHxBvfXW\n",
"W2i1WhYtWsTAgQMtdZSUlPDHP/6Rd955h7/+9a/t3qOoqIjXXnvN7tV09Xo9S5cuRVEUFixYQFxc\n",
"nOVYVlYW//rXv3j33Xcta4XNmjWLgoICcnJyiI+PZ+bMmXa9T2d89tln7N+/n9GjR/Pss89avvRn\n",
"zZrF73//ez799FPGjBnDlVdeCUBpaSkrVqzAz8+PRYsWtVuQr+0RZps333yz3Res0WjklVde4dNP\n",
"P+XGG2/s8oKUsbGxhIWFcezYMRYtWkRycjKxsbGWdqzzDR8+nL59+7Jhwwaio6Ntfp7+/v4sW7as\n",
"XUwNDQ288MILrF69mqSkJLy8vOjbty+zZs0iOzsblUpls77O/v3Kz8+noqKCW265hfvvv9+qLpPJ\n",
"RHNzc5c+K3ch3bfEJUlMTOTKK69k+/btHDhwoNveZ+LEiZZkBS13Ym1JJSYmpt06ZG3HioqKbNY3\n",
"Y8YMS7IC8PT0ZM6cOQB89913lv2bNm2ioaGBlJQUqy8TgKioqP/f3rmGNPmFAfy3mene1mUryNJk\n",
"mJZRll1M7UtZZGE3wupDUBQVVERQUUIXlMIgDD8EURAE0ZVqFllQkWVlRbhqM2tl2iyNvDTz0rSb\n",
"8/9B3uHcazrN+K/O79M4z3vOefbu7DznOec55zBz5kxKS0spLy/3qGPhwoVeXf2en5+Pw+EgPj7e\n",
"zVgBLFiwgCFDhlBQUMCnT5+6XGZPuXPnDiqVipUrV7p18gMGDCA5ORmAnJwcV7p80WFycrLi7bHt\n",
"O3olb6BPnz4kJibidDopLCzstu4BAQGkpKRgMBh49eoVR48eZdu2baxcuZK0tDRu3rzJz58/3fJ0\n",
"tobVp08fRQMqSRIJCQk4HA5KSkq6rGNX29eHDx/cZEqRoH5+fgQGBna5bl9EeFgCN6qqqsjNzXVL\n",
"U6lUv1wTWbFiBXv27OHkyZOkp6f3il4jR470SJPXc8LCwjxkcqfSfkQvozRtNnr0aFQqlZuRKyoq\n",
"AloN3/nz5z3yfPz4EWhdg2jfQYeHhyvW3RE2mw1onZpqj1qtZsyYMdy/f5/S0tJOL7r7HTQ1NVFZ\n",
"WYler1e8CVbWs+37evPmDUCXb2L+9OmTa+3Gbrfz/ft3N3lHv19XCQ0N5cCBA7x9+5bCwkJKS0sp\n",
"KirCarVitVq5desWqamp9OvXr8tllpWVceXKFaxWK7W1tR5ezefPn7tcVlfbV3l5OcHBwYwdOxa9\n",
"Xs/ly5ex2WxER0cTGRmJwWD4J7aPCIMlcKO6utrjhlDglwZr1KhRxMbG8vjxYx4+fMi0adN+u15t\n",
"vSEZPz+/DmXyn7f9CFpm4MCBiuX179+fhoYGV5r8ua0XocS3b9880toGSHSFxsZGoOOIPzldfq63\n",
"6Uwf+fu11cfhcACenpQSlZWV7Ny5E4fDwZgxY4iOjkaSJNRqNVVVVdy9e7fD389bwsLC3AY2xcXF\n",
"HD58mHfv3nHhwgVWrVrVpXKKiorYu3cvLS0tjBs3jpiYGDQaDWq1GpvNhslk8mpaztv2pdFoSE9P\n",
"5/z585hMJiwWCwD9+/cnMTGR5ORk1//ib0QYLIEbY8eO7dZm0uXLl2MymTh79ixTp05VfEYOfmhu\n",
"blaUOxwOtFqt13V3h7q6OgYPHuyW1tzcTENDAxqNxpUmG8OMjAxCQ0O9qsPbvTdyXbW1tYpyeeSu\n",
"ZKB7g870kdPb6iN7KjU1NYpeWVuuXr3Kly9f2LhxI9OnT3eT5eXluUXp/W7Cw8NZs2YN+/bt48WL\n",
"F13Ol5WVxY8fP0hNTfXw0i9duoTJZPJKj+60L71ez/r164FWz6uwsJAbN25gNBppaWnpUaDK/52/\n",
"34cU/BGCgoJITEykqqqK69evKz4jGyOlNZiKigqampp6Vce2KHVSr169oqWlxS3iTw4msFqtva6T\n",
"XK+Sbs3Nza41QqWIxN5Ao9EwdOhQ7HY7FRUVHnJ5famtPhEREQA8e/as0/LlMmNjYz1kL1++7JbO\n",
"3qC03iN75k6nUzFPRUUFWq1WcUq5I53VanWH5fW0fYWEhDB37lx2794N4LXB9DWEwRL8NpYsWYIk\n",
"SWRlZfH161cPeXBwMBqNBpPJRH19vSv9+/fvf/zsO6PR6Jq+knU4c+YMADNmzHClJyQkIEkSFy9e\n",
"pLi42KMcp9Pp1Qj9V8TExKDVannw4IFrLUjm2rVrVFdXM378eA/PsDdJSEgA4OTJk26dbn19vWvq\n",
"WH4GIDExEbVajdFoVAxEsdvtrs9ywEX792c2m7l9+3aPdS8uLiY3N9djXQxap4ovX74M4BbM86tB\n",
"lazzly9feP/+vVv67du3KSgoUMyj1Wqpq6tT1MPb9lVeXq7o8cppffv2VdThb0FMCf6DdHSmmUql\n",
"Yu3atd1u9FqtlsWLF3P69GlFuZ+fH0lJSRiNRnbs2EFMTAzNzc08f/4cvV6PTqf7YycNhISEsHXr\n",
"VuLi4lz7sKqqqpg0aZIrwlD+Ttu2bSMjI4Ndu3YRFRXlCq6w2+0UFRXhcDg4depUj3UKDAxkw4YN\n",
"ZGZmkpaWRlxcHIMHD8Zms1FQUMCgQYNYt25dj+tpS2dtYcGCBZjNZkwmE9u3b2fixImufVj19fUs\n",
"WrSI0aNHu/KFhISwdu1ajh07RkpKClOmTCEoKIiGhgZKSkqQJMm1eXrOnDnk5uaSmZlJXFwcOp2O\n",
"srIyzGYz8fHxPHr0qEffraamhiNHjnD8+HEiIyMJDg7G39+f2tpazGYzdXV1BAUFuYWbBwYGEhER\n",
"gdVq5dChQwwbNgy1Wk1MTAyhoaEkJSVhsVjYs2cP8fHxSJJESUkJr1+/dq3jticqKoq3b9+yf/9+\n",
"IiMj8ff3x2AwMHnyZK/bl8Vi4dSpU4waNYphw4YxYMAAampqyM/PR61Ws3Dhwh69s/87wmD9g9y7\n",
"d69D2apVq3o0SktKSuLmzZtUV1crypctW0bfvn3JyckhJycHnU7HtGnTWLp0KVu2bOn1M9fk8rds\n",
"2cLFixfJy8vj8+fP6PV6li5dqngu4rhx4zh48CDZ2dlYLBasViv+/v7odDqioqKIi4tTrKM7TJky\n",
"hX379nHp0iUsFguNjY3odDpmz57tcdLF76CztiBJErt37+bq1avk5eVx/fp1/Pz8MBgMrF69WjHA\n",
"ZtasWYwYMYLs7GxevnxJfn6+67BZeVMttEbwpaamcu7cOZ4+fYrT6cRgMLB9+3YkSVI0WN682/Hj\n",
"x7N582YsFgs2m42SkhIaGxuRJInhw4czb9485s6dS0BAgFu+TZs2ceLECSwWCw8ePABaD3oODQ0l\n",
"OjqalJQUjEYjjx49Qq1WEx4eTlpaGhUVFYoGKzk5mcbGRp48ecLr169xOp1Mnz6dyZMnA961r+jo\n",
"aOx2O1arFZPJRFNTEzqdjgkTJjB//nzXFOPfiqpFHJ4lEAgEAh9ArGEJBAKBwCcQBksgEAgEPoEw\n",
"WAKBQCDwCYTBEggEAoFPIAyWQCAQCHwCYbAEAoFA4BMIgyUQCAQCn0AYLIFAIBD4BMJgCQQCgcAn\n",
"EAZLIBAIBD7Bf+R2ifblbJkxAAAAAElFTkSuQmCC\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7fcacecc5490>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from pymks.tools import draw_gridscores\n",
"\n",
"draw_gridscores(gs.grid_scores_, 'n_states',\n",
" score_label='R-squared', param_label='L-Number of Local States')\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As expected the accuracy of the MKS model monotonically increases as we increase n_states, but accuracy doesn't improve significantly as n_states gets larger than signal digits. \n",
"\n",
"In order to save on computation costs let's set calibrate the influence coefficients with `n_states` equal to 6, but realize that if we need slightly more accuracy the value can be increased."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model = MKSLocalizationModel(basis=PrimitiveBasis(6, [-1, 1]))\n",
"model.fit(X, y)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here are the first 4 influence coefficients. "
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABOAAAAEjCAYAAACb/37NAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzt3X9Y1HW+//8HMMigOKQgEQ05ubo7RbbWssRRvmhbm53d\n",
"6mozPUG5ZYK1etxaXdtv++OIp+3orrp8j9qyZ8Nata1grXPV1Z7v9m2zYNe22LXjYgZtJiKIqGih\n",
"Iw4Iw/ePPk6NvN8MIyBv39xv18V1yWte85oXg/NkePCaeUZ1d3d3CwAAAAAAAMCgiB7qDQAAAAAA\n",
"AAB2RgAHAAAAAAAADCICOAAAAAAAAGAQEcABAAAAAAAAg4gADgAAAAAAABhEBHAAAAAAAADAICKA\n",
"AwAAAAAAAAaRY6g3cEZ5ebleffVVbdy4MaLrbd26Va+99po++eQTTZ8+XQsXLtQTTzyhxsZGrVy5\n",
"cpB2O7Tefvttvfrqq9q3b586OjqUnJysr3zlK7r11ls1ZsyYAb89o/vYaFySGhoa+ny/D+b36a23\n",
"3lJHR4dmzJgx4GvDHqg5fUfNCY+ag3CoOX1HzQmPmoPeUG/6jnoTHvUGGDiWCeAkKSoqKqL5H330\n",
"kX73u98pLy9PGRkZSkxMHKSdWcfmzZv1P//zP7r++ut16623Kj4+Xg0NDXrttdd0+PBhff/73x/Q\n",
"2zO7j83GOzo6+rz2nXfeqdOnTw/ofs/4y1/+Ip/PNyA/KN577z0988wziouL04oVK/q1lt/v1zPP\n",
"PKO0tDQ1NzfrS1/6kqZNm9bvPeLcUHPCo+b0jVVrjiR1dnbqxRdfVGpqqnJzc/u9Hs4dNSc8ak7f\n",
"WLXmtLS06NVXX1V3d7f27dunG2+8UdnZ2f3eIyJHvQmPetM3Vq03jY2NqqqqUlRUlBoaGnTttdcq\n",
"Jyen33sEBpOlArju7u6I5h84cECSNHPmTMXHxw/Glizlb3/7m37/+9/rO9/5TkgBvOKKK3TjjTeq\n",
"urp6wG/T7D4eiPv+4osv7v8Gz4OrrrpKGRkZcjj6/3A5E7594xvfUCAQ0Pe+9z2lp6frsssuG4Cd\n",
"IlLUnN5Rc4bGQNacN998U/v379eOHTt0xx13DMDu0B/UnN5Rc4bGQNWcQCCgF198UfPnz1dMTIwO\n",
"Hz6spUuXyuVy6corrxyg3aKvqDe9o94MjYF8jvPEE0/o3nvvldfrVVNTk773ve/poosu0lVXXTUA\n",
"OwUGh6UCuM87c4w2Ly9Pmzdv1qFDh3T55ZdrwYIFcrvdeuKJJ1RZWSlJuu+++yRJy5cvN/wBX1RU\n",
"JJfLpSVLlgTHdu/erX//93/X2rVr5Xa7JUk1NTV6/vnntXfvXo0YMUJZWVm699575XQ6+7yvM95/\n",
"/3397ne/00cffaTo6Ghdfvnluvfee+XxePp8W2f7/e9/rwkTJhj+9SE6OlpTpkwJGXvrrbf0wgsv\n",
"qLm5WS6XS9OnT9ecOXMUHf3ZW//1tg+z+/iNN94wHT/76HNv94PRUemB+B488cQTqqqqkiT9y7/8\n",
"iyRp9uzZuvPOO9XQ0KDNmzfro48+0unTp5WcnKybb75ZM2fONL3fJam2tlZ33nlnr3PCaW9vV0VF\n",
"hdauXSvps+/Zn//8Z+Xn5/drbfQfNacnak7fvgdWrTmSgt+7urq6fq+FgUXN6Yma07fvgVVrTnNz\n",
"s/bu3avW1laNHTtWKSkpmjBhgl5//XUCuCFGvemJetO374FV680ZdXV18nq9Sk5OlvTpaUICOFiZ\n",
"ZQO4qKgotbS06JlnntGsWbMUGxurLVu2qLi4WGvXrtWdd96p5ORkvfjii1q+fLlGjBihSy+91HSt\n",
"cGpra/XYY48pKytLS5cu1fHjx/Xss8/q5MmTIT9gwu1L+vSH0E9/+lNdddVV+td//VfFxcXpgw8+\n",
"0LFjx+TxePp8W5/X2dmpf/zjH7r11lv7dP/9/e9/13/+539q+vTp+va3v636+nqVlZXpxIkTKiws\n",
"7NPXbHYfJyUlGY6/8cYbIXswuh9qa2uD98NgfQ/uvPNOHT16VG1tbSooKJAkjR07VpL0s5/9TG63\n",
"W9/97nflcDjU1NSkU6dO9Xpftre3a9++ffrSl77Up/veTFNTkzo6OjRu3LjgWFJSkv7617/2a10M\n",
"DGpOKGrOhV9zYG3UnFDUnAu/5jidTh05ckQff/xxcD+jR4+Wz+fr17roP+pNKOrNhV9vJIWEjS0t\n",
"LZKkL3zhC/1eFxhMlg3guru75fP59Nhjjyk1NTU4tmbNGjU1NSktLS141PYLX/iC4uLiel0rnGef\n",
"fVZer1cPP/xwcGzs2LF67LHH1NDQoPT09D7v69lnn5XH49GPfvSj4Fpf/vKX+3RbjY2NIX/xOcPn\n",
"86mzszOY7odTXl6ujIyM4Bt7nrn9Z599VrNmzdLYsWP7tA+j+zg+Pr5P9324+8Fo/kB9D0aNGqXu\n",
"7m5NnDgxuNbx48d15MgR/eAHPwiu1Ze/kHz44Ye65JJLNHLkyLBze9Pa2iqHwxHyxMXpdOqTTz7p\n",
"17oYGNScUNScC7/mwNqoOaGoORd+zRk7dmzIm/53d3ervr5eN9xwQ7/WRf9Rb0JRby78enO2N954\n",
"QzNmzOD0GyzPsgGcJKWkpAQLgaTgX2KOHTumtLS0Abud9vZ2ffjhh5o3b566urqC416vVzExMdq7\n",
"d2+wsITb19ixY7Vnzx7NmzfvnG7ro48+MvxBcUZf/uoUCARUV1cXPMZ8xj/90z/pt7/9rf7xj3/o\n",
"mmuuCfs197aPcPx+f6/3w9kG8ntg9n8jISFBSUlJ+vWvf61//ud/7vMbzNbW1srr9Rp+jU8//XTY\n",
"JyJut1u33XabfD6fRowYEXKZw+FQW1tb2D3g/KDm9ETN+dSFWHNgfdScnqg5n7JDzfnrX/+q6Oho\n",
"ffOb3wy7Bww+6k1P1JtPXcj1Zv/+/dq5c6cOHDigBx54IOztA0PN0gHc2cn4mTdrjKQjTF+cPHlS\n",
"gUBAGzduNGzXffTo0T7v6+TJk5Jk2rY60ts6IyEhQQ6HI3i8tjfHjx9XV1eXLrroopDxM0XR5/OF\n",
"3Udfbqc34e4Ho/kD9T0wEx0drR//+Md67rnnVFJSoo6ODnm9Xs2bN8/w6PYZH3zwQbAd+Oc5nU59\n",
"5zvf6e3L6jH/bO3t7T1COQwdas5nqDkXfs2B9VFzPkPNsVfNOXHihF588UX94Ac/UGxs7DmtgYFF\n",
"vfkM9cY+9eayyy7TZZddpmuvvVZLly7Vj3/8415vHxhqlg7gBsqIESPU2dkZMnamkEmfFZ05c+bo\n",
"mmuu6XH9vhY7SRo1apSioqL08ccfG15+rrflcDjk9Xq1c+fO4BtgmnG5XIqJiVFra2vI+JnPExIS\n",
"wu7jzGv7z1W4++FsA/k96E1aWpqWLl2qQCCg999/X7/97W+1cuVK/dd//Zfh/EAgoA8//HBA/qIy\n",
"ZswY+f3+kLH29vY+H3/HhYOa8ylqztDWHAwf1JxPUXOsUXO6urr09NNP67vf/e6AnqyCNVBvPkW9\n",
"sUa9OcPtdmvMmDHatGmTli9fPuDrwzp8Pp9KSkpUXV0tl8ulvLw85eTkGM595ZVX9PLLL6u9vV3Z\n",
"2dkqLCwMBszh1tm1a5c2btyoo0ePauLEiVq0aNGA/N4+LAK4sWPHqqamJmTs73//e/DfTqdTX/zi\n",
"F3XgwAHNmjWrX7fldDo1adIkVVRU6Oabbza8/Fxv6xvf+IZ+/vOfq6KiosdfDgKBgKqrqzVlyhRF\n",
"R0drwoQJ+stf/qKvf/3rwTl/+ctfFBUVpS9+8YsD+jUbCXc/GM0fyP04HI6wf7W56qqr9M1vflPr\n",
"16/XyZMnNWrUqB7z6uvrFR8fr+TkZO3evVsZGRnByyI9Kj1+/HiNGDEieKRekg4ePMibhdoQNedT\n",
"1JzPDEXNwfBBzfkUNeczQ1lztm7dqjvuuCMYvlVWVio3NzfSLxEWRb35FPXmM0NRb2pra7VmzRr9\n",
"8Ic/1IQJE4L75K197K+0tFSxsbEqLS1VXV2dVq1aJY/H0+Nl3jt37tRLL72k5cuXa8yYMVqzZo3K\n",
"y8uVn58fdp3jx49r7dq1evDBB5WZmannn39excXFevzxx/u9/2ERwGVlZemNN97Qpk2bdM0112j3\n",
"7t0hPygk6e6779Zjjz2mDRs26LrrrlN8fLxaWlr07rvvKi8vT5dcckmfby8/P1+PPfaY/uM//kM3\n",
"3nijRowYoX/84x+aOHGirr322nO+ra985Sv65je/qV/96lf64IMPlJmZKafTqQMHDui1115TSkpK\n",
"sGX2nDlz9Pjjj+uXv/ylpk6dqv3796usrEw33nhjMPwZyK/5XO6Hsw3kfi699FL97W9/01//+leN\n",
"HTtWY8eO1fHjx7VlyxZNnTpVKSkpOnnypF566SV5PB7DHxLSpwHZpEmTdOzYsR7NEiI9Ku1wOPTV\n",
"r35VVVVVuvnmm9XR0aHq6mr98Ic/7PMauDBQc6g5Vqg5n9fd3d2nN87GhYmaQ82xSs159dVXgy/t\n",
"a2lpUSAQ0JEjRyJaA9ZGvaHeWKHexMXFacSIEcG3+Dlx4oT279+vuXPn9nkNXHj8fr+qqqr0i1/8\n",
"QnFxcfJ6vcrMzFRlZWUwWDujoqJCN9xwQzCYmzVrltatW6f8/Pyw61RVVSk9PV3Z2dmSpNmzZ2v+\n",
"/PnBxiT9YZkALioqKuSNMPvyppi9rfV51157rfLy8vTqq69q27Zt+upXv6r77rtPq1evDs7xer1a\n",
"sWKFysvLtWHDBgUCAY0bN05TpkwJeUPJvuzriiuu0I9//GOVlZVp/fr1cjgcuvzyy3XddddFdFtG\n",
"vv3tb+tLX/qS/vCHP2jdunXq6OhQSkqKMjMzQ1ppX3311XrooYf04osv6s9//rMSExN16623as6c\n",
"ORF/zX119n0T7n44e/5Afg9mzpypffv2qaSkRCdPntTs2bN100036aKLLtJ///d/69ixYxo1apSu\n",
"uuoq3X333abrXHnllfrzn/+sbdu26Vvf+lYkd4eh++67T0899ZQ6OzvV1NSkuXPnhrwJKs4fag41\n",
"ZzjUnO3bt+t///d/tWfPHn388cfas2ePbr311mDHNZw/1Bxqjt1rTmNjo37zm98oEAiEjM+fP79f\n",
"6yJy1Bvqjd3rzeWXX6558+bprbfeUmdnpxobGzV37tw+nRC8UJ387o1DvYVBN2rdH3u9/ODBg4qJ\n",
"iQlpGuLxeLR79+4ecxsbG5WVlRX8fPz48WptbZXP59ORI0d6XaehoUHjx48PXhYXF6fU1FQ1NDT0\n",
"O4CL6uZP4gAAAAAAAJZ08qGvh590gRv1n6/1enlNTY2Ki4v161//Ojj2xz/+Udu3b+/x3n+LFy9W\n",
"QUGBvvzlL0uSOjs7dffdd+uJJ57QkSNHel2npKREiYmJIafqfvKTn+jGG280bCISCcucgAMAAAAA\n",
"AMBZ+nGS9UJSXl4e/HdGRkbIewU6nU6dOnUqZH5bW1vwpcifd/bcM+8P6HQ6TdeJj4+XJMXHx/d4\n",
"P8HPX94fBHAAAAAAAABWNUwCuM+/tPtsl1xyibq6utTc3Bx8+Wh9fb3hWzqlp6dr3759wfdxq6+v\n",
"V2JiohISEuRwOAzXOfN+cW63WxUVFcG1/H6/Dh061KPRw7mI7vcKAAAAAAAAGBzRUfb/CMPpdCor\n",
"K0tlZWVqb29XbW2tduzYYdhpOzc3V9u2bVNjY6N8Pp9eeOEFzZgxo0/rZGVlqaGhQe+88446Ojq0\n",
"detWeTyefr//m8R7wAEAAAAAAFjWye//81BvYdCNWvP/hp3j8/lUUlKi6upquVwu5efna9q0aWpp\n",
"adGSJUtUXFyspKQkSdIrr7yil156SR0dHcrOzlZhYaEcDkev65yxa9cuPfXUUzpy5IgmTZqkRYsW\n",
"KTk5ud9fIwEcAAAAAACARbUt+8ZQb2HQjVz9P0O9hUEX9j3gTj5s/24bwHARSLhIo3/6u6HeRq+o\n",
"OYB9dFz5Txqz4N+Hehu9ouYA9jHq/+m9g95Qo94A9nJea84weQ84u6MJAwAAAAAAgFURwNkCARwA\n",
"AAAAAIBVEcDZAgEcAAAAAACAVRHA2QIBHAAAAAAAgFVFE8DZAQEcAAAAAACAVXECzhYI4AAAAAAA\n",
"AKyKAM4WCOAAAAAAAACsigDOFgjgAAAAAAAArIoAzhYI4AAAAAAAAKyKAM4WCOAAAAAAAACsigDO\n",
"FgjgAAAAAAAALCoqmgDODgjgAAAAAAAArIr8zRYI4AAAAAAAAKyKl6DaAgEcAAAAAACAVRHA2QIB\n",
"HAAAAAAAgFURwNkCARwAAAAAAIBVEcDZAgEcAAAAAACAVRHA2QIBHAAAAAAAgFVFE8DZAQEcAAAA\n",
"AACAVXECzhYI4AAAAAAAAKyKAM4WCOAAAAAAAACsigDOFgjgAAAAAAAALCqKAK5PfD6fSkpKVF1d\n",
"LZfLpby8POXk5JjOf+WVV/Tyyy+rvb1d2dnZKiwslMPhUGdnp5588km999578vl8uvjii5Wfn68p\n",
"U6ZIkg4fPqzFixcrLi4uuNbtt9+uO+64o9f9EcABAAAAAABYFQFcn5SWlio2NlalpaWqq6vTqlWr\n",
"5PF45Ha7e8zduXOnXnrpJS1fvlxjxozRmjVrVF5ervz8fHV1dSk5OVkrVqxQcnKy3n33XRUXF2vN\n",
"mjUaN25ccI1NmzZFFI5GD8hXCQAAAAAAgIEXFWX/j37y+/2qqqrSXXfdpbi4OHm9XmVmZqqystJw\n",
"fkVFhW644Qa53W6NGjVKs2bN0ptvvilJiouL0+zZs5WcnCxJuvbaa5WSkqK6urqQNbq7uyPaIyfg\n",
"AAAAAAAArCqaE3DhHDx4UDExMUpNTQ2OeTwe7d6923B+Y2OjsrKygp+PHz9era2t8vl8SkhICJn7\n",
"ySefqKmpqcdJuoULFyoqKkqTJ0/W3LlzNXr06F73yAk4AAAAAAAAqxrq02kXyAm4+Pj4kDGn0ym/\n",
"3286f+TIkcHPz1z37PmdnZ1av369ZsyYobS0NEmSy+XSypUr9ctf/lKrVq2S3+/XunXrwu6RE3AA\n",
"AAAAAABWNUzeA668vDz474yMDGVkZAQ/LyoqUk1NjeH1vF6v5s2bp1OnToWMt7W1yel0Gl7H6XSG\n",
"zG9rawuOnxEIBLRhwwbFxsZq/vz5IdedMGGCJCkxMVH333+/HnjgAfn9ftPbkwjgAAAAAAAArGuY\n",
"BHBz5swxvayoqKjX6/r9fnV1dam5uTn4MtT6+nqlp6cbzk9PT9e+ffuUnZ0dnJuYmBh8+Wl3d7d+\n",
"9atf6fjx43r00UcVHR3+BaTh3hOOl6ACAAAAAABY1VC/PPQCeAmq0+lUVlaWysrK1N7ertraWu3Y\n",
"sUO5ubmG83Nzc7Vt2zY1NjbK5/PphRde0IwZM4KXP/nkkzpw4IAeeeQRxcbGhlx3z549ampqUiAQ\n",
"0IkTJ/T0008rIyOjx0tgz8YJOAAAAAAAAKsaJifg+qugoEAlJSUqKCiQy+VSYWFhsHFCS0uLlixZ\n",
"ouLiYiUlJWnKlCm67bbbtGLFCnV0dCg7Ozt4Au/IkSN6/fXXFRsbqwULFgTXX7BggXJycnTo0CE9\n",
"99xzam1t1ciRI3X11VfroYceCrs/AjgAAAAAAACrogtqnyQkJGjZsmWGlyUnJ2vz5s0hY7fccotu\n",
"ueWWHnPHjRunsrIy09uZNm2apk2bFvH+COAAAAAAAACsihNwtkAABwAAAAAAYFUEcLZAAAcAAAAA\n",
"AGBRUQRwtkAABwAAAAAAYFUEcLZAAAcAAAAAAGBVBHC2QAAHAAAAAABgVQRwtkAABwAAAAAAYFXR\n",
"BHB2QAAHAAAAAABgVZyAswUCOAAAAAAAAKsigLMFAjgAAAAAAACrIoCzBQI4AAAAAAAAqyKAswUC\n",
"OAAAAAAAAKsigLMFAjgAAAAAAACrIoCzBQI4AAAAAAAAq4omgLMDAjgAAAAAAACLiuIEnC0QwAEA\n",
"AAAAAFgVAZwtEMABAAAAAABYFfmbLRDAAQAAAAAAWBUn4GyBAA4AAAAAAMCqCOBsgQAOAAAAAADA\n",
"qgjgbIEADgAAAAAAwKqiCeDsgAAOAAAAAADAqjgBZwsEcAAAAAAAAFZFANcnPp9PJSUlqq6ulsvl\n",
"Ul5ennJyckznv/LKK3r55ZfV3t6u7OxsFRYWyuH4NCYrKirShx9+qJiYGElSUlKSiouLg9fdtWuX\n",
"Nm7cqKNHj2rixIlatGiRkpOTe90fARwAAAAAAIBVEcD1SWlpqWJjY1VaWqq6ujqtWrVKHo9Hbre7\n",
"x9ydO3fqpZde0vLlyzVmzBitWbNG5eXlys/PlyRFRUVp/vz5+trXvtbjusePH9fatWv14IMPKjMz\n",
"U88//7yKi4v1+OOP97q/6IH5MgEAAAAAADDgoqLs/9FPfr9fVVVVuuuuuxQXFyev16vMzExVVlYa\n",
"zq+oqNANN9wgt9utUaNGadasWXrzzTf7dFtVVVVKT09Xdna2HA6HZs+erfr6ejU1NfV6PQI4AAAA\n",
"AAAAi4qKirL9R38dPHhQMTExSk1NDY55PB41NDQYzm9sbNT48eODn48fP16tra3y+XzBsWeffVbz\n",
"58/XT37yE73//vvB8YaGhpDrxsXFKTU11fS2zuAlqAAAAAAAAFbFS1DD8vv9io+PDxlzOp3y+/2m\n",
"80eOHBn8/Mx1/X6/EhISdPfdd8vtdsvhcGj79u362c9+ptWrVyslJUXt7e1yuVwh68XHx5ve1hkE\n",
"cAAAAAAAAFYVPTwCuPLy8uC/MzIylJGREfy8qKhINTU1htfzer2aN2+eTp06FTLe1tYmp9NpeB2n\n",
"0xkyv62tLTguSRMnTgxeNn36dG3fvl3vvvuubr75ZjmdzuD8z1//7ADwbARwAAAAAAAAVjVMTsDN\n",
"mTPH9LKioqJer+v3+9XV1aXm5ubgy1Dr6+uVnp5uOD89PV379u1TdnZ2cG5iYqISEhLC7tPtdqui\n",
"oiLktg8dOmTY7OHzeA84AAAAAAAAqxrqBgkXQBMGp9OprKwslZWVqb29XbW1tdqxY4dyc3MN5+fm\n",
"5mrbtm1qbGyUz+fTCy+8oBkzZkj69DTbzp071dHRoa6uLv3pT39STU2NpkyZIknKyspSQ0OD3nnn\n",
"HXV0dGjr1q3yeDxKS0vrdY+cgAMAAAAAALCqYXICrr8KCgpUUlKigoICuVwuFRYWBk+ltbS0aMmS\n",
"JSouLlZSUpKmTJmi2267TStWrFBHR4eys7ODJ/A6OztVVlampqYmRUdH69JLL9UjjzwSPFnncrm0\n",
"dOlSPfXUU1q/fr0mTZqkhx9+OOz+COAAAAAAAACsigCuTxISErRs2TLDy5KTk7V58+aQsVtuuUW3\n",
"3HJLj7kul0srV67s9bYmT56s4uLiiPZHAAcAAAAAAGBVBHC2QAAHAAAAAABgVQRwtkAABwAAAAAA\n",
"YFXRBHB2QAAHAAAAAABgVZyAs4Xood4AAAAAAAAAYGecgAMAAAAAALAqTsDZAgEcAAAAAACARUUR\n",
"wNkCAdyFqLt7qHfQNxQJwB6oOQCsYChqEXUFAGAF/DyyBQI4AAAAAAAAqyKAswUCOAAAAAAAAKsi\n",
"gLMFAjgAAAAAAACriiaAswMCOAAAAAAAAKviBJwtEMABAAAAAABYFQGcLRDAWcFAdfUaqkaFZrUg\n",
"0q+LogKcHxdKV9NIUXOAC8uFUIuoK4C9XQh1SKK2gP8DNkEABwAAAAAAYFUEcLZAAAcAAAAAAGBV\n",
"BHC2QAAHAAAAAABgVQRwtkAABwAAAAAAYFFR0QRwdkAABwAAAAAAYFWcgLMFArjzKdIuOxdIU56I\n",
"9xlp11SKDXBuLvQOy5GKtFRQc4DzY6i6DJrd7GA+xKkrgDVdKN1OzVBbwPfaFgjgAAAAAAAArIoA\n",
"zhYI4AAAAAAAAKyKAM4WCOAAAAAAAACsivytT3w+n0pKSlRdXS2Xy6W8vDzl5OSYzn/llVf08ssv\n",
"q729XdnZ2SosLJTD8WlMNnfuXEV9Lvjs6OjQTTfdpPvvv1+HDx/W4sWLFRcXF7z89ttv1x133NHr\n",
"/gjgAAAAAAAArIoTcH1SWlqq2NhYlZaWqq6uTqtWrZLH45Hb7e4xd+fOnXrppZe0fPlyjRkzRmvW\n",
"rFF5ebny8/MlSVu2bAnO9fv9WrBggaZOnRqyxqZNm0JCunCiz/HrAgAAAAAAwGCLjrL/Rz/5/X5V\n",
"VVXprrvuUlxcnLxerzIzM1VZWWk4v6KiQjfccIPcbrdGjRqlWbNm6c033zSc+/bbbysxMVFerzdk\n",
"vDvCBi+cgBsMVut2avZ/2SypNdv/QO0z0q5kdP0BejdU3U4jfQhGWnPMmE0fio6HAD5jtS6DZk/m\n",
"h2KfPJcBzo/BfnwP1GN2wJ67UVuGDb6nYR08eFAxMTFKTU0Njnk8Hu3evdtwfmNjo7KysoKfjx8/\n",
"Xq2trfL5fEpISAiZW1FRoenTp/dYY+HChYqKitLkyZM1d+5cjR49utc9cgIOAAAAAADAqqKi7P/R\n",
"T36/X/Hx8SFjTqdTfr/fdP7IkSODn5+57tnzjxw5opqampAAzuVyaeXKlfrlL3+pVatWye/3a926\n",
"dWH3yAk4AAAAAAAAqxomJ+DKy8uD/87IyFBGRkbw86KiItXU1Bhez+v1at68eTp16lTIeFtbm5xO\n",
"p+F1nE5nyPy2trbg+OdVVlbqiiuu0Lhx40KuO2HCBElSYmKi7r//fj3wwAPy+/2mtycRwAEAAAAA\n",
"AFjXMAng5syZY3pZUVFRr9f1+/3q6upSc3Nz8GWo9fX1Sk9PN5yfnp6uffv2KTs7Ozg3MTGxx8tP\n",
"Kysr9a1vfatP+w/3nnC8BBUAAAAAAMCioqKibP/RX06nU1lZWSorK1N7e7tqa2u1Y8cO5ebmGs7P\n",
"zc3Vtm3b1NjYKJ/PpxdeeEEzZswImfPBBx/o2LFjwZDujD179qipqUmBQEAnTpzQ008/rYyMjB4v\n",
"gT0bJ+AAAAAAAACsagC6hA4HBQUFKikpUUFBgVwulwoLC+V2uyVJLS0tWrJkiYqLi5WUlKQpU6bo\n",
"tttu04oVK9TR0aHs7OweJ/AqKip03XXX9XhZ6aFDh/Tcc8+ptbVVI0eO1NVXX62HHnoo7P4I4M6n\n",
"gWrKY/aBRzYDAAAcGklEQVTgi4kxHneYjEfakbCzy3i8y2Q8MECdDak1wMAaqG6nZjUn2uRwtVnt\n",
"MqsVgYDxuFnNGajuqHQUA3o3VF0GzcbNak6kz3OMao5pZ3g6GAJDaqAegwNVbyJl9hxnoGoOtcV+\n",
"+N71SUJCgpYtW2Z4WXJysjZv3hwydsstt+iWW24xXW/BggWG49OmTdO0adMi3h8BHAAAAAAAgFUR\n",
"wNkCARwAAAAAAIBVEcDZAgEcAAAAAACAVRHA2QIBHAAAAAAAgFURwNkCARwAAAAAAIBVEcDZAgFc\n",
"fwx6FzCT8RGxxtNHxhuPjxoZ0TrqOG043H2yzXi87VRE60TcHdUM3X0w3ETcASvC9c0eOrEmNccZ\n",
"Zzx/pNNwOMph/COnu7PTeJ02v/F8f7vx/NMmNYfuqIA1mT12zDosmz3/iRthPN+k5sik5nS3d/Qc\n",
"NHsuY9qNeZCfGwLDzWB3OzXrahprXD/MnssoxmSdLuNup6bPfU6bjEfaNdUMz2UuXNF8j+yAAA4A\n",
"AAAAAMCqCEltgQAOAAAAAADAqgjgbIEADgAAAAAAwKoI4GyBAA4AAAAAAMCiogjgbIEADgAAAAAA\n",
"wKoI4GyBAG4wDFQDLJMuO2bdTqNTk43H3ZcYr5OYYDje3eozHA80HjQeb24xXsek648CJt19zETa\n",
"qRBA78weOyadB826nUYlXWQ4blaLzDoym3VYNqstOvqJ8TpmHcJMuxUaDwP4Pwa927tJMTLrdpo4\n",
"2nA8eozLeJ14447MOmXcYTnw8fEeY92tJ4zX8A9QR0IzdCoEBpbZY8es26lJ/TB7LmNWt0w7KZs8\n",
"9+mWcX0yXYfOy8MH9d8WCOAAAAAAAACsKpoAzg4I4AAAAAAAAKyKE3C2QAAHAAAAAABgVQRwtkAA\n",
"BwAAAAAAYFUEcLZAAAcAAAAAAGBVBHC2QABnBWaPJYdJR0KT7jtm3U5jb8g2HH/jrd2G49d/zXj+\n",
"6W1vG453nzDp4mPSZUydJl1QaeIDDK3oaOPxkcadwMy6nTqyrjYc73SnGs9vbDaeX1VtON5lVlv8\n",
"7cbjZl1QAQwtk5oTFTfCeLpJt9MY7wTj+ZelGY4H9jcZ76d2b8+5JnWl26wjoVk3ZgDnh1lIYVZv\n",
"HCZdUM1+37o0xXj+WOPO8N3HjDu3Bw4cNhzXaePfk7o7zTq6m/wCRXdU+yGAswUCOAAAAAAAAKsi\n",
"gLMFAjgAAAAAAACriiaAswMCOAAAAAAAAIuK4gScLRDAAQAAAAAAWBUBnC0QwAEAAAAAAFgVAVyf\n",
"+Hw+lZSUqLq6Wi6XS3l5ecrJyTGcu3//fm3ZskV79+6Vz+dTWVlZRGvt2rVLGzdu1NGjRzVx4kQt\n",
"WrRIycnGTerOIICzArMHk9n4iFjj6YkJhuPbtht3O/36TcsMx//42mrD8f/LZH2z/UT8ddGtBzg/\n",
"TDuEGY9H2iHs9KUXG47fd+8qw/FNm/5v4/V374loP91m741BzQHOD7OHVKSPTZPHuOJNOjKbdDt9\n",
"q/GY4fhUk/ld9QbdUc32EulznIDJncPvU8DQijHpAG/2+5ZJt1OzbsxdBt2VJUlHPo5sPwABXJ+U\n",
"lpYqNjZWpaWlqqur06pVq+TxeOR2u3vMdTgcmjp1qmbOnKnVq3tmIL2tdfz4ca1du1YPPvigMjMz\n",
"9fzzz6u4uFiPP/54r/vjEQ4AAAAAAGBVUVH2/+gnv9+vqqoq3XXXXYqLi5PX61VmZqYqKysN56el\n",
"pen66683DOfCrVVVVaX09HRlZ2fL4XBo9uzZqq+vV1OTwR/zPocADgAAAAAAwKqGOhy7AAK4gwcP\n",
"KiYmRqmpqcExj8ejhoaGAV+roaFB48ePD14WFxen1NTUsLfFS1ABAAAAAAAsqtv0fR7so78RnN/v\n",
"V3x8fMiY0+mU3+8f8LX8fr8SExNDLo+Pjw97WwRwAAAAAAAAFhUwey9RG4mJkcrLy4OfZ2RkKCMj\n",
"I/h5UVGRampqDK/r9Xo1b948nTp1KmS8ra1NTqfxe8j2xul0Gq51JpSLj49XW1ub6eVmCOAAAAAA\n",
"AAAsKhAIDPUWBl1MjDRnzhzTy4uKinq9vt/vV1dXl5qbm4MvHa2vr1d6enrEe7nkkksM1zrzfnFu\n",
"t1sVFRUht33o0CHD95P7PAI4KzDrxGc23nHaeHqrz3D8+huyDcdf+/+Mu51ePzXDcPz0629HtJ+I\n",
"vy4A54fZY9DkL2vdnZ3G4yfbDMdjDxwyHP/Nb35gOO5obDYc7zRZ32w/pl0GqTnA+WH22pFInw+Y\n",
"PcZPGb+sI7Df+A2Pzbqdms03XN9sL5F+TTSvA6ypyyTUMPt969gnxsuYdDs1m2/6+5PZfjDsDYcT\n",
"cP3ldDqVlZWlsrIyPfjgg6qrq9OOHTv005/+1PQ6HR0d6vw/P+tPn/70cRkbGxt2raysLD3zzDN6\n",
"5513dM0112jr1q3yeDxKSzN+7nEGARwAAAAAAIBFDYcTcAOhoKBAJSUlKigokMvlUmFhYfBUWktL\n",
"i5YsWaLi4mIlJSXp8OHDWrx4cfC699xzj8aNG6cNGzaEXcvlcmnp0qV66qmntH79ek2aNEkPP/xw\n",
"2P0RwAEAAAAAAFgUJ+D6JiEhQcuWLTO8LDk5WZs3bw5+npKSorKysnNaS5ImT56s4uLiiPZHAAcA\n",
"AAAAAGBRnICzBwI4AAAAAAAAi+IEnD0QwAEAAAAAAFgUJ+DsgQDOCszC7M4u4+kmnQEDjQeNlzHp\n",
"XpqbmGA4btbt1Gx9s/2Y7d/06wUwtMx+sLeZdB5sbjEc76yqNhyPHjXSeL5ZTTNZ32w/pvsHYE0m\n",
"j9nu9g7j6R8fN17HpPtgV30E3U5N1jfbC/UGsCjTTu8m9cas07HZc5MDh43nH/nYeNysm2rEnd5N\n",
"ag6d3ocNTsDZAwEcAAAAAACARXECzh4I4AAAAAAAACyKE3D2QAAHAAAAAABgUZyAswcCOAAAAAAA\n",
"AIviBJw9EMABAAAAAABYFCfg7IEAbjBEmYxHGlqbdMHpbjtlOG7WMbD7hEmX0hGxxuORdusx2Y+6\n",
"TLqgRsrs/gRwbsxqkcljttvfbjz/6CfGy5h0GIxyGP/IMe34ZdLt1HQ/ZjWHPxgC5ybK5AfwQHXd\n",
"M1vH7HlI6wnD8YBZTTCpOabPr4w6nprsZdA7D5rd9wDOjdlj9rRJPZBJx3WT+YqJNh7virD7qtn6\n",
"dDsd9jgBZw8EcAAAAAAAABbFCTh7IIADAAAAAACwKE7A2QMBHAAAAAAAgEVxAs4eCOAAAAAAAAAs\n",
"ihNw9kAABwAAAAAAYFGcgLMHArj+GPTuYCbjRl26JHWbddkx6UgY8f47TToMmnXxGeyQng5hGG4i\n",
"fcxG2pHZbPy0SUdCsycCJh0Ju6NNNmT2Fz2z9Qeq22mkJYSaAwwss9pl9hj3mzzPMetUGmnNNKo5\n",
"ZnPpSAicHwP1+1Ykj3vJvBuz2e9DkTK73cGuOTyXuWBxAs4eCOAAAAAAAAAsihNw9kAABwAAAAAA\n",
"YFGcgLMHAjgAAAAAAACL4gScPRDAAQAAAAAAWBQn4OyBAA4AAAAAAMCiOAFnDwRw51OkHQnNmHYq\n",
"NOlGatalNNKuQoPe1XSQ1wfsaqi6o5p1KjQbH7BOZpFNp7YAA2zQu8BH2AXQ7JeSwd7nQKAjIXBu\n",
"Brs76mB3Ix3sOkRtsR1OwNkDARwAAAAAAIBFcQKub3w+n0pKSlRdXS2Xy6W8vDzl5OQYzt2/f7+2\n",
"bNmivXv3yufzqaysLHhZZ2ennnzySb333nvy+Xy6+OKLlZ+frylTpkiSDh8+rMWLFysuLi54ndtv\n",
"v1133HFHr/sjgAMAAAAAAMAFrbS0VLGxsSotLVVdXZ1WrVolj8cjt9vdY67D4dDUqVM1c+ZMrV69\n",
"OuSyrq4uJScna8WKFUpOTta7776r4uJirVmzRuPGjQvO27Rpk6IiOHFKAAcAAAAAAGBRvAQ1PL/f\n",
"r6qqKv3iF79QXFycvF6vMjMzVVlZqfz8/B7z09LSlJaWpubm5h6XxcXFafbs2cHPr732WqWkpKiu\n",
"ri4kgOvu7iaAAwAAAAAAsANeghrewYMHFRMTo9TU1OCYx+PR7t27+732J598oqamph4n6RYuXKio\n",
"qChNnjxZc+fO1ejRo3tdhwAOAAAAAADAojgBF57f71d8fHzImNPplN/v79e6nZ2dWr9+vWbMmKG0\n",
"tDRJksvl0sqVK+XxeHTixAlt3LhR69at049+9KNe1yKAGwyD3ZEwUqadDYfoQRxpUx66+ADnx0B1\n",
"RzUz6B2/Bmodag5wTqzWddTsl5WheIhTV4DzY6i6NA8VasuwMVxOwJWXlwf/nZGRoYyMjODnRUVF\n",
"qqmpMbye1+vVvHnzdOrUqZDxtrY2OZ3Oc95PIBDQhg0bFBsbq/nz5wfHnU6nJkyYIElKTEzU/fff\n",
"rwceeEB+v7/X2yOAAwAAAAAAsKjhcgJuzpw5ppcVFRX1el2/36+uri41NzcHX4ZaX1+v9PT0c9pL\n",
"d3e3fvWrX+n48eN69NFHFR0d3afr9Cb8CgAAAAAAABgSgUDA9h/95XQ6lZWVpbKyMrW3t6u2tlY7\n",
"duxQbm6u6XU6OjrU2dkpSTp9+rROnz4dvOzJJ5/UgQMH9Mgjjyg2Njbkenv27FFTU5MCgYBOnDih\n",
"p59+WhkZGT1eAns2TsABAAAAAABY1HA5AddfBQUFKikpUUFBgVwulwoLC4ONE1paWrRkyRIVFxcr\n",
"KSlJhw8f1uLFi4PXveeeezRu3Dht2LBBR44c0euvv67Y2FgtWLAgOGfBggXKycnRoUOH9Nxzz6m1\n",
"tVUjR47U1VdfrYceeijs/gjgAAAAAAAALGq4vAdcfyUkJGjZsmWGlyUnJ2vz5s3Bz1NSUlRWVmY4\n",
"d9y4caaXSdK0adM0bdq0iPdHAAcAAAAAAGBRnICzBwK482mguqOaGarHJJ0HAWuK9DE1ULXoQkHN\n",
"Ac6PoeqOSrdTAGdYrUtzpKgtwx4n4OyBAA4AAAAAAMCiOAFnDwRwAAAAAAAAFsUJOHsggAMAAAAA\n",
"ALAoTsDZAwEcAAAAAACARXECzh4I4AAAAAAAACyKE3D2QABnBXbtVEi3HuDCQocwAOfTQD3/GUzU\n",
"FcDeeIzjAsEJOHsggAMAAAAAALAoTsDZAwEcAAAAAACARXECzh4I4AAAAAAAACyKE3D2QAAHAAAA\n",
"AABgUZyAswcCOAAAAAAAAIviBJw9EMBdiOjWA+B8ouYAsAJqEQBgmOIEnD0QwAEAAAAAAFgUJ+Ds\n",
"gQAOAAAAAADAojgBZw8EcAAAAAAAABbFCTh7IIADAAAAAACwKE7A2QMBHAAAAAAAgEVxAs4eCOAA\n",
"AAAAAAAsihNw9kAABwAAAAAAYFGcgLMHAjgAAAAAAACL4gScPRDAAQAAAAAAWBQn4PrG5/OppKRE\n",
"1dXVcrlcysvLU05OjuHc/fv3a8uWLdq7d698Pp/KyspCLi8qKtKHH36omJgYSVJSUpKKi4uDl+/a\n",
"tUsbN27U0aNHNXHiRC1atEjJycm97o8ADgAAAAAAwKI4Adc3paWlio2NVWlpqerq6rRq1Sp5PB65\n",
"3e4ecx0Oh6ZOnaqZM2dq9erVPS6PiorS/Pnz9bWvfa3HZcePH9fatWv14IMPKjMzU88//7yKi4v1\n",
"+OOP97q/6HP/0gAAAAAAADCYAoFu23/0l9/vV1VVle666y7FxcXJ6/UqMzNTlZWVhvPT0tJ0/fXX\n",
"G4Zz4VRVVSk9PV3Z2dlyOByaPXu26uvr1dTU1Ov1OAEHAAAAAABgUZyAC+/gwYOKiYlRampqcMzj\n",
"8Wj37t3nvOazzz6r3/72t0pLS1NeXp6uvPJKSVJDQ4PGjx8fnBcXF6fU1FQ1NDQoLS3NdD0COAAA\n",
"AAAAAIviPeDC8/v9io+PDxlzOp3y+/3ntN7dd98tt9sth8Oh7du362c/+5lWr16tlJQUtbe3y+Vy\n",
"hcyPj48Pe1sEcAAAAAAAABY1XE7AlZeXB/+dkZGhjIyM4OdFRUWqqakxvJ7X69W8efN06tSpkPG2\n",
"tjY5nc5z2svEiROD/54+fbq2b9+ud999VzfffLOcTqfa2tp63NbZAeDZCOAAAAAAAAAsaricgJsz\n",
"Z47pZUVFRb1e1+/3q6urS83NzcGXodbX1ys9PX0gtyhJcrvdqqioCLntQ4cOhX0/OZowAAAAAAAA\n",
"WFQgELD9R385nU5lZWWprKxM7e3tqq2t1Y4dO5Sbm2t6nY6ODnV2dkqSTp8+rdOnT0v69DTbzp07\n",
"1dHRoa6uLv3pT39STU2NpkyZIknKyspSQ0OD3nnnHXV0dGjr1q3yeDy9vv+bxAk4AAAAAAAAyxou\n",
"J+D6q6CgQCUlJSooKJDL5VJhYWHwVFpLS4uWLFmi4uJiJSUl6fDhw1q8eHHwuvfcc4/GjRunDRs2\n",
"qLOzU2VlZWpqalJ0dLQuvfRSPfLII8GTdS6XS0uXLtVTTz2l9evXa9KkSXr44YfD7o8ADgAAAAAA\n",
"wKKGy3vA9VdCQoKWLVtmeFlycrI2b94c/DwlJUVlZWWGc10ul1auXNnrbU2ePFnFxcUR7Y8ADgAA\n",
"AAAAwKI4AWcPBHAAAAAAAAAWxQk4eyCAAwAAAAAAsChOwNkDARwAAAAAAIBFcQLOHgjgAAAAAAAA\n",
"LIoTcPZAAAcAAAAAAGBRnICzBwI4AAAAAAAAi+IEnD0QwAEAAAAAAFgUJ+DsgQAOAAAAAADAojgB\n",
"Zw8EcAAAAAAAABbFCTh7IIADAAAAAACwKE7A2QMBHAAAAAAAgEVxAs4eCOAAAAAAAAAsihNw9kAA\n",
"BwAAAAAAYFGcgLMHAjgAAAAAAACL4gScPRDAAQAAAAAAWBQn4OyBAA4AAAAAAMCiOAFnDwRwAAAA\n",
"AAAAFsUJOHsggAMAAAAAALAoTsDZAwEcAAAAAACARXECzh4I4AAAAAAAACyKE3D2QAAHAAAAAABg\n",
"UZyAswcCOAAAAAAAAIviBFzf+Hw+lZSUqLq6Wi6XS3l5ecrJyTGcu3//fm3ZskV79+6Vz+dTWVlZ\n",
"yOVz585VVFRU8POOjg7ddNNNuv/++3X48GEtXrxYcXFxwctvv/123XHHHb3ujwAOAAAAAADAojgB\n",
"1zelpaWKjY1VaWmp6urqtGrVKnk8Hrnd7h5zHQ6Hpk6dqpkzZ2r16tU9Lt+yZUvw336/XwsWLNDU\n",
"qVND5mzatCkkpAuHAA4AAAAAAMCiOAEXnt/vV1VVlX7xi18oLi5OXq9XmZmZqqysVH5+fo/5aWlp\n",
"SktLU3Nzc9i13377bSUmJsrr9YaMd3d3E8ABAAAAAADYASfgwjt48KBiYmKUmpoaHPN4PNq9e3e/\n",
"166oqND06dN7jC9cuFBRUVGaPHmy5s6dq9GjR/e6DgEcAAAAAACARXECLjy/36/4+PiQMafTKb/f\n",
"3691jxw5opqaGi1cuDA45nK5tHLlSnk8Hp04cUIbN27UunXr9KMf/ajXtQjgAAAAAAAALGq4nIAr\n",
"Ly8P/jsjI0MZGRnBz4uKilRTU2N4Pa/Xq3nz5unUqVMh421tbXI6nf3aU2Vlpa644gqNGzcuOOZ0\n",
"OjVhwgRJUmJiou6//3498MAD8vv9vd4eARwAAAAAAIBFDZcTcHPmzDG9rKioqNfr+v1+dXV1qbm5\n",
"Ofgy1Pr6eqWnp/drT5WVlfrWt77Vp7nd3b1/n6L7tRMAAAAAAAAMmkAgYPuP/nI6ncrKylJZWZna\n",
"29tVW1urHTt2KDc31/Q6HR0d6uzslCSdPn1ap0+fDrn8gw8+0LFjx5SdnR0yvmfPHjU1NSkQCOjE\n",
"iRN6+umnlZGR0eMlsGfjBBwAAAAAAIBFDZcTcP1VUFCgkpISFRQUyOVyqbCwUG63W5LU0tKiJUuW\n",
"qLi4WElJSTp8+LAWL14cvO4999yjcePGacOGDcGxiooKXXfddT1eVnro0CE999xzam1t1ciRI3X1\n",
"1VfroYceCrs/AjgAAAAAAACLGi7vAddfCQkJWrZsmeFlycnJ2rx5c/DzlJQUlZWV9breggULDMen\n",
"TZumadOmRbw/AjgAAAAAAACL4gScPRDAAQAAAAAAWBQn4OyBAA4AAAAAAMCiOAFnDwRwAAAAAAAA\n",
"FsUJOHsggAMAAAAAALAoTsDZAwEcAAAAAACARXECzh4I4AAAAAAAACyKE3D2QAAHAAAAAABgUZyA\n",
"swcCOAAAAAAAAIviBJw9EMABAAAAAABYFCfg7CF6qDcAAAAAAAAA2Bkn4AAAAAAAACyKl6DaAwEc\n",
"AAAAAACARfESVHsggAMAAAAAALAoTsDZAwEcAAAAAACARXECzh4I4AAAAAAAACyKE3D2QAAHAAAA\n",
"AABgUZyAswcCOAAAAAAAAIviBJw9EMABAAAAAABYFCfg7IEADgAAAAAAwKI4AWcPYQO49q/efD72\n",
"AeA86B4RP9RbCIuaA9hH18Weod5CWNQcwD5GDfUGwqDeAPZyPmsOJ+DsIaq7u5soFQAAAAAAwIJG\n",
"jx451FsYdCdOtA31FgYdL0EFAAAAAACwKE7A9Y3P51NJSYmqq6vlcrmUl5ennJwcw7lvvvmm/vCH\n",
"P+jgwYMaOXKkpk2bpvz8fEVHR/dprV27dmnjxo06evSoJk6cqEWLFik5ObnX/RHAAQAAAAAAWBTv\n",
"Adc3paWlio2NVWlpqerq6rRq1Sp5PB653e4eczs6OnTfffdp0qRJam1t1c9//nO9/PLLuv3228Ou\n",
"dfz4ca1du1YPPvigMjMz9fzzz6u4uFiPP/54r/uLHpSvGgAAAAAAAP0WCARs/9Fffr9fVVVVuuuu\n",
"uxQXFyev16vMzExVVlYazr/pppvk9XoVExOjsWPHKicnRx988EGf1qqqqlJ6erqys7PlcDg0e/Zs\n",
"1dfXq6mpqdc9cgIOAAAAAADAojgBF97BgwcVExOj1NTU4JjH49Hu3bv7dP33339f6enpfVqroaFB\n",
"48ePD14WFxen1NRUNTQ0KC0tzfQ2COAAAAAAAAAsiveAC8/v9ys+Pj5kzOl0yu/3h73utm3bVFdX\n",
"p4ULF/ZpLb/fr8TExJDL4+Pjw94WARwAAAAAAIBFdXUNjwCuvLw8+O+MjAxlZGQEPy8qKlJNTY3h\n",
"9bxer+bNm6dTp06FjLe1tcnpdPZ6m1VVVXruuef0b//2b0pISJD0adhmtNaZUC4+Pl5tbW2ml5sh\n",
"gAMAAAAAAMCQmjNnjullRUVFvV7X7/erq6tLzc3NwZeO1tfXB19WamTnzp369a9/rUcffTRk3iWX\n",
"XGK41plmDm63WxUVFSG3fejQIcNmD59HEwYAAAAAAABcsJxOp7KyslRWVqb29nbV1tZqx44dys3N\n",
"NZz/3nvvad26dfr+97+vL3zhCxGtlZWVpYaGBr3zzjvq6OjQ1q1b5fF4en3/N0mK6u7u5t38AAAA\n",
"AAAAcMHy+XwqKSlRdXW1XC6X8vPzNW3aNElSS0uLlixZouLiYiUlJWnFihWqra1VbGxs8PpXXHGF\n",
"Hn300bBrSdKuXbv01FNP6ciRI5o0aZIWLVqk5OTkXvdHAAcAAAAAAAAMIl6CCgAAAAAAAAwiAjgA\n",
"AAAAAABgEBHAAQAAAAAAAIOIAA4AAAAAAAAYRARwAAAAAAAAwCAigAMAAAAAAAAGEQEcAAAAAAAA\n",
"MIgI4AAAAAAAAIBBRAAHAAAAAAAADKL/H8pT1AYeV1mOAAAAAElFTkSuQmCC\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7fcacee533d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from pymks.tools import draw_coeff\n",
"\n",
"draw_coeff(model.coeff[...,:4])\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Predict Microstructure Evolution\n",
"\n",
"With the calibrated influence coefficients, we are ready to predict the evolution of a concentration field. In order to do this, we need to have the Cahn-Hilliard simulation and the MKS model start with the same initial concentration `phi0` and evolve in time. In order to do the Cahn-Hilliard simulation we need an instance of the class `CahnHilliardSimulation`."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from pymks.datasets.cahn_hilliard_simulation import CahnHilliardSimulation\n",
"np.random.seed(191)\n",
"\n",
"phi0 = np.random.normal(0, 1e-9, (1, n, n))\n",
"ch_sim = CahnHilliardSimulation(dt=dt)\n",
"phi_sim = phi0.copy()\n",
"phi_pred = phi0.copy()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In order to move forward in time, we need to feed the concentration back into the Cahn-Hilliard simulation and the MKS model."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"time_steps = 10\n",
"\n",
"for ii in range(time_steps):\n",
" ch_sim.run(phi_sim)\n",
" phi_sim = ch_sim.response\n",
" phi_pred = model.predict(phi_pred)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's take a look at the concentration fields."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAn4AAAElCAYAAAB6ce/JAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt0VeWZP/Bvcm45uZyEJIRbuIjoRONdSlmCiNJ26ug4\n",
"tgitTG2romN17LQUbZ1ZKtSqVVtp1SkVcWxZq7Wm4LS2tnRZWYC31lEHuYgXEBTkGgK5n3t+f/Az\n",
"I83zfcM+HEKy/X7WYi3ynrOvZ+8nb96zn+ct6Orq6oKIiIiI+F7hsd4BEREREekb6viJiIiIfEyo\n",
"4yciIiLyMaGOn4iIiMjHhDp+IiIiIh8T6viJiIiIfEwEj/UOyKFWrlyJP/7xj9i1axcKCwtRU1OD\n",
"+vp6fPnLXwYA7NmzBzfeeCO+/e1v46yzzuqTfZo3bx5isRjmzJlz2Mvs2LEDzz//PC6++GIUFxd3\n",
"t69cuRILFy7EkiVLEIlEjsbuisgx1NDQgGXLlmHo0KH48Y9/3OP1r3/969i9ezcuu+wyzJgxAw0N\n",
"DfjTn/6ERx99tPs92WwWDz30EP7617/i29/+Nk477TTE43H85je/wUsvvYR9+/YhGo1ixIgRmDJl\n",
"Ci644IK+PESRAU0dv37kv//7v9HQ0IB/+qd/Qn19PVKpFDZv3oznn3++u+NXWVmJO++8E8OHD++z\n",
"/SooKPC8zM6dO7Fs2TJccMEFh3T8zjrrLNx5550Ih8P53EUR6UdCoRD27NmDd999F2PHju1u37Rp\n",
"E/bu3YtQKHRIXPno/7u6uvDwww/jL3/5C+bOnYvTTjsNAPDDH/4QW7duxfTp0zFq1CgcOHAAGzdu\n",
"xJo1a9TxE/FAHb9+ZPny5fj0pz+NL37xi91tZ511FmbMmNH9czAYxLhx4/p0v46kxvffLhuLxRCL\n",
"xY50l0SkH4tEIhg7dixeeOGFQzp+L774Ik455RS8++67h7z/o3Hi0UcfxerVq/HNb36z+1uNnTt3\n",
"Yu3atfjmN7+JiRMndr/3nHPOOcpHIuI/6vj1Ix0dHSgvL3e+x/qq94YbbsDEiRNRVlaGP/zhD0gm\n",
"k7jgggvw5S9/Ga+88gp+8YtfoKmpCaeeeiq+9rWvoaSkBAD/2vXD9V1xxRXmPnzwwQf49a9/jbfe\n",
"egttbW2oqanBtGnTcOGFF6KgoAAbNmzAvffeCwD413/9VwDA4MGD8dBDD5nbbGlpwZIlS/C///u/\n",
"SCaTGDduHK644opDfmF8uE+DBg3C73//eyQSCZx++um49tprDxlRFJH+4ZxzzsGvf/3r7jjS1dWF\n",
"l156CV/4whd6dPw+9LOf/Qx//vOf8fWvfx0TJkzobm9vbwcAVFRUHP0dF/E5JXf0I2PHjsXy5cux\n",
"atUqtLa2elr2xRdfxObNm3HDDTfgkksuwdNPP41HHnkEv/71r3H55ZfjmmuuwYYNG/DLX/7ysNbn\n",
"+np3//79GD58OK6++mrccsstmDZtGhoaGvDb3/62+zg+DPZz587FnXfeiblz59L13XfffVi3bh2u\n",
"uOIKfOMb30A2m8X8+fOxa9euQ9730ksvYcOGDbjuuuvwz//8z3jttdcO+3hEpO8UFBTgk5/8JJqb\n",
"m/Hmm28CADZu3IiWlpZDOnQf9fjjj+OPf/wjrrvuuh4jeSNGjEAkEsHPfvYzrF27Fslk8qgfg4hf\n",
"acSvH7n66qtx33334Sc/+QkAoLa2Fp/85Cfxj//4j4hGo85lw+Ew5syZg4KCApx++ul45ZVXsGLF\n",
"CjzwwAMYPHgwAGDr1q1YtWoVrrnmmiPaz1NOOQWnnHIKgIN/xf/d3/0d4vE4nn32WVx66aWIRqMY\n",
"NmwYAOC4445DdXU1XdeaNWvw9ttvY968eTjppJO613/DDTfgqaeewrXXXtv93mAwiJtuugmFhQf/\n",
"Xtm+fTtefPFFzJ49+4iOR0Tyr7i4GKeffjpeeOEF1NXV4cUXX8SZZ55pjtC3tbXhN7/5DS666CJM\n",
"nTq1x+vRaBT/8i//gocffhh33nknAoEATjjhBEyZMgXTpk3rg6MR8Q91/PqRUaNGYcGCBXj99dfx\n",
"+uuvY/369Vi2bBleeOEF3HPPPSgqKqLLnnzyyYeM0g0ZMgTt7e3dnT4AGDp0KFpaWpDJZBAIBHLe\n",
"z2Qyid/85jd47rnnsG/fPmQyme7Xstlsd8fscGzatAnl5eXdnT7g4PNBZ511Ft56661D3ltfX3/I\n",
"umtra9Hc3Ox5myJydH34zN4555yDn//85/jKV76Cv/zlL7jqqqvM90ejUdTW1mLFihWYMmUKxowZ\n",
"0+M9kyZN6v6jdv369Vi7di0WLVqE9evX49/+7d+O5uGI+Io6fv1MMBjE2WefjbPPPhsAsGLFCjz8\n",
"8MNYsWIF/uEf/oEu9+Fzex9dz9/+ZR0MHvy40+n0EXX8fvGLX2DFihWYMWMGxo4di+LiYvzP//wP\n",
"nnzySaRSKU9lWvbv328me5SXl6Otre2QNusYAXjepoj0jfHjx+Phhx/GL3/5SyQSCYwfP958XyAQ\n",
"wHe+8x3ceuutuPvuu3HHHXegpqamx/tKS0sxdepUTJ06FZlMBosWLcLKlStx6aWXYvTo0Uf7cKSf\n",
"WL58OVauXIlt27Zh0qRJuP766/t0/evWrcOjjz6Kffv2Ydy4cbjhhhuc32z1Nxom6ecuuOAClJaW\n",
"YseOHXlfdygUAnCwI/hRHz5IzfzlL3/BhRdeiEsuuQSnnHIKxo4dm/OI26BBg9Dc3Nyjvbm5GaWl\n",
"pTmtU0T6h6KiIpx99tn4wx/+gPHjxzvLOJWWluI//uM/UFhYiDvvvBMtLS3OdQcCAVx00UUAcFTi\n",
"o/RflZWVmD59Os4///w+X39LSwt++MMf4otf/CIee+wxHH/88ViwYMFR2Y+jRR2/fsTqALW0tKCj\n",
"o+OoZLNVVVUBOPis3IfeeecddHZ2HvK+v030SCaT3aNtwMGvd1988cVD3vPh6709hH3CCSegpaUF\n",
"Gzdu7G5LJBJ47bXXUFdX5+FoRKQ/+sxnPoPx48fj05/+dK/vra6uxn/8x3+gtbUVd911F+LxOAAg\n",
"Ho+bsWTnzp0A0Gs1BPGXCRMm4BOf+IQ5OPDqq6/ipptuwpVXXolbb70V77//fl7X//LLL2PkyJGY\n",
"OHEigsEgZsyYgffee29A/fGhr3r7kblz5+ITn/gETjvtNMRiMTQ2NuJ3v/sdIpEIzjvvvLxvb9y4\n",
"caisrMRjjz2GL3zhC2htbcXvfvc7RKPRQ+pq/W0tvtNOOw1/+tOfMHToUJSWluJPf/pTj1HDDwtM\n",
"P/PMMzjnnHMQiUQwatSoHvtw+umn48QTT8SPfvQjzJo1C6Wlpfjd736HVCqFSy65JO/HLCJ96+ST\n",
"T8bJJ5982O+vra3Fd77zHdxxxx247777cMstt+CDDz7Avffei/PPPx8nnngiIpEItm7diieffBJj\n",
"xozRH4kCANiyZQt++tOf4tvf/jaOP/54rF69Gvfccw9+/OMfHzJYcSS2bdt2yGMFkUgEQ4cOxbZt\n",
"2/p0YoUjoRG/fuSyyy7D3r178dhjj+HOO+/EE088gZEjR+Kuu+46JEnjcBzObBvBYBBz585FQUEB\n",
"7r//fjz99NOYPXs2SkpKaFV9ALjqqqtw0kkn4dFHH8XChQsxatQoXHrppYe8Z/Dgwbjiiivw8ssv\n",
"47bbbuuu62e56aabcOqpp+JnP/sZFixYgIKCAtx+++0YMmSIp2MWkWOvoKDA02w/1vtPPPFEfPOb\n",
"38Qbb7yBhx56CEOGDMG0adOwbt06/Od//ie+//3v489//jOmTZuG2267TcldAgD485//jE996lMY\n",
"N24cCgoKcN555yEUCuHtt9/O2zYSiUSP5+ej0Wj36PRAUNB1JNMyiIiIiBwDv/rVr9DU1NSdfHH3\n",
"3XfjjTfeOGR0L51O42tf+xrOOecczJs375DHij6qrq4O8+fPd64fOFhkPJ1OH1JG7Fvf+ha+8IUv\n",
"0BqV/Y2+6hUREZEBr6qqCp/73Ofw+c9/3nx93rx5R7yN2tparFq1qvvneDyO3bt3o7a29ojX3Vc0\n",
"Pi4iIiIDRjabRTKZRDabRTabRSqVQjabxac+9Sk888wz2LRpE7q6uhCPx/Haa695/hqWrR84mPix\n",
"bds2/PWvf0UymcTSpUsxZsyYAfN8H6CvekVERGQAaWhowLJlyw5pmzFjBi677DKsWbMGTzzxBHbt\n",
"2oVwOIy6ujp87Wtfc06A4GX9wME6fv/1X/+FvXv34oQTThhwdfzU8RMRERH5mNBXvSIiIiIfE70m\n",
"d/x20yKzvS1lF+ZtTiTI++12AEikM2Z7FnwwMlRoTzkWJbV6WDsARALec1wyXVmzvfNv6tl9KJmx\n",
"jxHoWSfvQ9FgyGyvikbpukaW9Zz+DADGVgyiyxTbu4y3395utm/duouua/fu/WZ7e3un2Q4A2ax9\n",
"/MEg+YyjfHq28vISs726mhd4HT68ymyvrbVL6BSTbQDAzvZWs31vRwddht0zqSy/ZpggKWvB7heX\n",
"LLkuPzX6Ss/r6s3vNj/So60lyWOG1zjDYgzA44zXGON6LZcYwz7/hCOWJEj8cYmQfa4mcaa21I4x\n",
"ADBuUKXZzmIM4D3OsBgD8DjDYgzgPc6wGAPwOOM1xgA8zrAYA/A40xcxBuD3TCEp75PO2r9HixDD\n",
"5NHTPe+bHB5l9YqIiIjvjHj4c326vQ/+5b/7dHu5UsdPREREfIeNNH7cqeMnIiIivqOOn00dPxER\n",
"EfGdAqjjZ+m147e15YDZvoc8RLo/bj9cuz/BCyiyhAiXooD9EGlxyE6IKAuF6brYw83BAv4Qa5ok\n",
"d7CHq10PZLOH6EPkGCsivB5REylU6XpQflyF/UD2WWefaLbX1FTQdW3bttds37evmS7T2mpfM4mE\n",
"nUCUdjyon0ymyPZb6DKZjP1ZJpP2ZzlsmP2gNgAcN8Ku5VQS5NdfE7lnWAJVZ9o+RgBIkmNJZOxj\n",
"cd17rUl7+0fDu809H9hnMQYA9nWSh9jJdd4XMQbgcYbFGMD7g++5JHe4EuXC5IF8FmeaOnksZ3Hm\n",
"xEH8nvEaZ1iMAXicYTEG8B5nWIw5uH07zniNMQCPMyzGADzOeI0xAI8zLMYAPM6wa5YlnZSRe8+r\n",
"QvX7TBrxExEREd/RV702dfxERETEd9Txs6njJyIiIr6jjp9NHT8RERHxHSV32NTxExEREd/pbyN+\n",
"y5cvx8qVK7Ft2zZMmjQJ119/PX3v0qVL8eyzz6KzsxPHHXccrr76atTW1uZlP3rt+L3fYmdJ7epo\n",
"N9t3t9vtBxxZvXGSCVTo6K2XkMy6WMSeZmeQIxOWZemxbDfAldXLplni2VtJkr3HMpJaSCYUAHSQ\n",
"LC3WDgDtKTt7i2VcHVfDpz87u8aeGm77dp6Jx6ZgYhl6Bw600XXF4yQTtpMv09lpHyeb/qmtjWcI\n",
"smVGjOBTM5WQafYaSeYqy9wGgJYuciweP2OAZ84eDVac2dHOPzM2NRWLM65M6ADJ3mfTr1UU8VhS\n",
"HrbjD4tXAJ/mimXiujKUWVZvisQYACggvxxZhnR7Dpmg7PoD+DU4erB9X7AYA/A445rmzWucYTEG\n",
"4HHGa4wBeJxxLcPijNcYA/B76YAjZrDPeT+JWSzGpEN8Wk4v+lvHr7KyEtOnT8frr7+OpKNqwiuv\n",
"vIJnnnkGd9xxB6qrq/GrX/0KDz74IO6555687IdG/ERERMR3+lvHb8KECQCAzZs3o6mpib5v27Zt\n",
"qKurQ01NDQDg3HPPxdNPP523/eCF6kREREQGqMKCvv2XL6eeeirefvtt7Ny5E+l0GqtWrcKZZ56Z\n",
"t/VrxE9ERER8hz3G0N+NGzcO5513Hr7xjW+gsLAQ1dXVuPXWW/O2fnX8RERExHdceQJHS0NDQ/f/\n",
"6+vrUV9f73kdy5cvx/r167Fw4UJUVFRg9erV+O53v4v7778f4TCfBepwqeMnIiIivnMsnvGbOXPm\n",
"Ea9jzZo1mDRpEiorD06nOnXqVPz85z/H9u3bMXbs2CNev57xExEREd8pLCjo03+9yWazSCaTyGaz\n",
"yGazSKVSyBoZ96NGjcJLL72E5uZmZLNZrF69GplMBkOHDs3Leel1xI9NlM7KtuwhZV7Y5N0ALzUQ\n",
"cUzUzE5yCZkkPdvFJyln6woU8n5xYZe9TKaQTaxOV4UMOf7OLCkNQ0rGAECKLMNKxrheY2UjOtI8\n",
"DX1UmV3qZezxw+kyRUXehq5dE5uzydhdJRBY2YaWFvtadpVzYaUeXPs8alSN2V5ZFDXbXaU5WKkN\n",
"dl10OMpsuMrG5JsVZ1iMAYA9nSTOkFITGcf9H3Lc55YSxyT1jCuWBMlrLGaFHetiUTbtuGbYtcFK\n",
"UKUyrvhjbyfuWIbFmTZyLY+K2aVJAB5nvMYYgN+zLMYAPM6wGOMqTcXLufD7ku2z1xgD8M+y1VGG\n",
"xGucYTEmkOXb8KK/ZfUuXboUy5Yt6/75ueeew4wZMzB16lTMmTMHCxYsQFVVFaZPn47HHnsMc+fO\n",
"RTKZxLBhw/Ctb30LxcXFedkPfdUrIiIivtPfkjtmzpxJvwpesmRJ9/8jkQiuu+66o7Yf6viJiIiI\n",
"7xyL5I6BQB0/ERER8Z181tbzE3X8RERExHf62zN+/YU6fiIiIuI76vjZeu34tZMMTpY9mCDZW66s\n",
"2gD5cNgk6QAQi9iTOFeSCdSHlJTSdVWQdUWDfGJ1djwse4lNeA7wybDbSPZUkmROAa7J0Plk3F3k\n",
"WFi2sSurL52118UmnAeA42rticU7Osgk4Y5MOKajg59/tp1me+5257qy5PgLHd85sIzDceNGmO3s\n",
"egF4oGNZnZ1pntXL7vGjodXYlmv7LLOd3ZcsxgA8zpSTuFAd5ZmQg4tLzHYWlwAgErC3z+7Ldsdn\n",
"Fg3a1+Z+xzXjNc7wGAO44gyT6bKvTRZ/XBnKDIsxQN/EGZYJHAjw65JVCGAxBgBCIbsSBosxY8cO\n",
"o+ti94WrM+U1zlj3PQCUFLquscPX35I7+guN+ImIiIjvKLnDpo6fiIiI+I6+6rWp4yciIiK+o46f\n",
"TR0/ERER8R0942dTx09ERER8R3X8bOr4iYiIiO8oucPWa8ePZY6zicVZCngkYKeZu5apdJRNGFFa\n",
"5ql9mKOcS3XUnviYlVkAeAkCNoH1ng4+4fzeTrsEQiNpP0AmtgZymySdlZphE8u7JpyPkM/SVZqn\n",
"ImKXuojF7NIY0SifcD0QsPctlXKUwGm3jz9Dzlkmw8spsLIJFRX8+mOTsbNyDq7zz8qZZEh70lEa\n",
"g11LR4NVuoTFGAAoCdmlliJBO864SjOxUisslowsi9F1sThTWcRjGds3FmOaE7ycEIsZux3xhy3T\n",
"QrbDSnYB/HpylbNi13Oo0P4sWYwB+HXBYgzgPc6wGAPwONPZacdsV2mWNClZFA47ypzF7N9lLMZ0\n",
"dvKSSexrUldpNhZn2O8fVrKHrccrPeNn04ifiIiI+I46fjZ1/ERERMR3lNxhU8dPREREfEcjfjZ1\n",
"/ERERMR3lNxhU8dPREREfEflXGy9dvyKSDZuLGxPYF4atjOhwiRDC+BZdcNK7Kw6ABgVszPrRsfK\n",
"zfZaRyYey7hjxw7wLKUDZDL0nW18wu/3W5rN9hKS7efKNuaZeGm6DMvSSqTtZVyTtLeS7D2W7Qzw\n",
"SeIHldqfSyTCs3pZxptrMvQukj2ZZRlnjqzGRMI+N6zdtR2GZcIBjuxdj1l1fc3K+ndlYrI4U0Tu\n",
"Dde6hpXambijyuxYcly53Q7wTOAqUjkA4HHGa4wBgA9aW832Qa0tdJltJBN2TwepKuDYforssysT\n",
"lMUZFhdcWc0szrB1Ad7jTJBkjufCVW2AZfUmkzyWs/WxGOPKUO5Ke6sQAPA4Y2Xt9wV91WvTiJ+I\n",
"iIj4jpI7bOr4iYiIiO/0txG/5cuXY+XKldi2bRsmTZqE66+/3nzfypUrsXz5cuzcuRPFxcWYNGkS\n",
"Zs2ahUJHbVMv1PETERER3+lvHb/KykpMnz4dr7/+OpKOxw+SySS++tWv4oQTTkBzczPuvfdePPXU\n",
"U7j00kvzsh/q+ImIiIjv9Les3gkTJgAANm/ejKamJvq+z3zmM93/r6ysxOTJk7Fhw4a87Yc6fiIi\n",
"IuI7/W3EL1dvvPEGRo4cmbf19drxY9m7xSQTrC+y6gBg3KBBZvtxsQqzvf0An6uy6YP9drsje6q4\n",
"2D4vo4dUmu01jqy+MpKhGA2ReY8dWWW72+3jdGXVZmFnXIUcWc1Mhsw9yeYdBfj8nkUl5Lw45upl\n",
"mXiuTGA2v24uc2Wyfctln9l+JeL8WmbZ26ksyfYjnz3gnl8732KRnvcTy9wFvMeZISX2fKwAMIbE\n",
"jLEVdvvx5XbsAXicYTEG4HHGa4wBeJwpN87vh2icIefYVe2AxZm04/5ncYY9mO/KEGXXuWtOaq9x\n",
"ht2XrmXa2+3flwUF/JmtEPsdm8P2vcYYAOgk13Jnmlco8BpnQuSZtWCeOmx+SO5YsWIFtmzZQp8H\n",
"zIVG/ERERMR3jkUdv4aGhu7/19fXo76+Pud1vfzyy3j88cdx2223oZQMkOVCHT8RERHxnWPxVe/M\n",
"mTPzsp41a9Zg0aJFuOWWW/L6NS+gjp+IiIj4UH9L7shms0in08hms8hms0ilUggEAj3KtKxfvx4P\n",
"PPAAbr75Zhx//PF53w91/ERERMR3+ltyx9KlS7Fs2bLun5977jnMmDEDU6dOxZw5c7BgwQJUVVVh\n",
"2bJl6OzsxF133dX93pNOOgm33HJLXvZDHT8RERHxnf6W3DFz5kz6VfCSJUu6/3/77bcf1f1Qx09E\n",
"RER8p7+N+PUXvXb8qkl5AFZShJZTKOblFI4rJ+UUSDsAFHbaJRDWvfaO2f7++3voug4caDPb2cTW\n",
"ABCL2cczfHiV2X7iifzhzJMqq832AEn1Z+0AL8HQFO+kyyTIxNpsO6z8DABEg/b2XfvMFJKULFdp\n",
"lrIye8L18nJ+/WXI8bNyLsXFvDRRRYWdeVVZGfO8DCuN4SrN00kmvE+TMjuuzyUatMtJHA1WnHGV\n",
"k2FxZliJfS5HxxyloSrs8ixeYwzA4wyLMQCPMyUl9rU8cuRguq7jjx9htp802I4xgPc4w+5xgMcZ\n",
"FmNc26FlrhzbDxV6L0HkNc6UltqfC8DvZfYZsxjj2n5lZZnn7bP29hQvzcLijOuzTGXs42TP2pWE\n",
"2Gecn9ijjp9NI34iIiLiO/0tuaO/UMdPREREfOdY1PEbCNTxExEREd/pb8kd/YU6fiIiIuI7esbP\n",
"po6fiIiI+I46frZeO35scnOWVTeUvH9UGc+qY5Oh73h/L13mzTffN9s3b95hr2vHPrqu9nae8cqw\n",
"LKm2Nu/rOvnkMWb7ceX2OesiE14DQJhkQpaR7CmAZ4Iyrqy6iiL7uighE44DQJhM1P231cy7t08m\n",
"Igd4tnV1Nb/+wmH7eLIkE7a4mE94X1Vlb2fwYJ6hPniwvczeZNxsb0/xrN44+SzZxPbhAM/qDRby\n",
"48w3K+ufxRgAGE7mrawts7OnWeYuwOMMizGbNn3A17Wj0WzPJS7QTExHvGLX7Mmh0XQZFn8ZFmMA\n",
"Hme8xhiAxxkWYwAeZ1iMAbzHmVjMrnQBAIMG2Rm3QVIFI0OyYAGgpMQ+Tlcsqamxr3MaYxJ2jAF4\n",
"nGExxoVVAQmRa4ll+3ql5A6bRvxERETEdzTiZ1PHT0RERHxHyR02dfxERETEd1TOxaaOn4iIiPiO\n",
"vuq1qeMnIiIivqPkDps6fiIiIuI7GvGz9drxG1Fqp6fXFNsp7aycwnExnoLOyiO89dY2usyWLTvN\n",
"9vff3222NzY203XF43baOkvBB/ik26zUx549B+i6KirsEhB1daPMdnaOAT7heSzMS3O4Juq2uEqA\n",
"lJI0fFcJBld5GAubvBzwPkk64J503eIq58LKxgwZwsuJZMiDKOxzSTmOhWHlFAKOki3hHCa8z9VI\n",
"45pmMQbwHmdcJVhYnNm82V5m+3ZeZord5yzGAECAlLTIZFg5IX4v7dmz32yvrLTjOACcGBtpto8o\n",
"s5dx/TJlccZrjAF4nCkO8tJQLM64YgyLDSzOsBjjUl5ul5lyYXGmspLH/6FDK812rzEGyC3OhMhn\n",
"VlpgHwv7jGOB/JSSUnKHTSN+IiIi4jsa8bOp4yciIiK+o46fTR0/ERER8R11/Gzq+ImIiIjv8KfR\n",
"j522tjYsXLgQa9euRSwWw+WXX47Jkyeb7929ezcee+wxbNy4EcFgEOeffz6+9KUvHfE+qOMnIiIi\n",
"vtMfkzsWL16MUCiExYsXY8uWLfj+97+PMWPGoLa29pD3pdNpfO9738NnP/tZzJkzB4WFhdixY0de\n",
"9qHXjt8YkiU3tMTOUmJZwFu37qLbYJm4e/fyTNjm5nazPZn0PoE0y94NkQm/e3vNkk5n6GsdHQmz\n",
"vamp1WyvcWSIMmVhngnbmbYzu7JddlZhwDHheVHAvqSKHecrQpZh2OTlAJBK2Rl3oRDfRiplXzOF\n",
"JBOuqMh7VjHL9gWAxs4Osz2Zta8Z19cXUZLxGCSfmWtdbML7o2F0rOf5GVbCsye9xhkWYwAeZ1pa\n",
"7M/FlaHLsMxdAIhE7GuTtbukUvY1w2IMABw40Ga2szjjqo3G4gyLMYD3OMNiDMDjDLsvXKJR+1hc\n",
"WbUsE5jFGBeW1evKKmbZ202JuNnOYgzAY4PrXLJlWPxhMaaowHsW9EAQj8fx8ssv4/7770ckEkFd\n",
"XR3Gjx+P1atXY9asWYe8d+XKlaisrMRFF13U3TZqlF3pwyuN+ImIiIjv9Ldn/Hbu3IlAIIChQ4d2\n",
"t40ZMwYbNmzo8d63334bgwcPxt13341NmzZh1KhRuPLKK/PS+euPX4GLiIiIHJHCgoI+/debeDyO\n",
"aPTQurFFRUWIx3uOyDY1NeGFF17AhRdeiEWLFuHMM8/Efffdh3Ta++jx39KIn4iIiPjOsRjxa2ho\n",
"6P5/fX096uvru38uKipCZ2fnIe/v6OhAkVF4PBwO46STTsIZZ5wBALjkkkvw5JNPYseOHUc86qeO\n",
"n4iIiPjOsZird+bMmfS1YcOGIZPJYNeuXd1f97733nsYObLn7DmjR4/GW2+91f1zF3kWNhf6qldE\n",
"RER8p6AnIVBiAAAgAElEQVSgoE//9aaoqAgTJkzAE088gUQigTfffBOvvvoqpkyZ0uO95557Lt55\n",
"5x2sW7cO2WwWTz/9NGKxGEaMGHHE56XXEb9xg+zMrijpM777rp1uvHNnE90GyypzZcJGInY2EMtq\n",
"KinxNh/rwW3w08Pmd2UZX2VlfN7RcNjeDjv+ZIJnyFXmMFdlKmNvJ0v+wCDJrgB4Jp5r3lc2vyPj\n",
"yqpln79rPl7XPL6WcJhntbFMvDg5xwA/z+ycsfmQASDiyB6138+vi1gkP/NlHo4TBvWcY5TFGIDH\n",
"mR079pntLMYAQDJp30/svnRldXqd9/ngduzriccYPu8umxPWNe+41zhTUcSvCzYnNIsxLuxrOtcv\n",
"WHbPuGJMIYlZbE5k17lkn5nXGAN4vy4AIElGhbzGGIDHmZCjqgPD4kw5iTGF2fxk9fa35A4AmD17\n",
"NhYuXIjZs2cjFovhmmuuQW1tLRobGzFnzhwsWLAAVVVVGD58OG688UY88sgjaG5uxtixY3HzzTc7\n",
"KwQcLn3VKyIiIr7jGqQ4VkpLS3HTTTf1aK+ursaSJUsOaZswYQImTJiQ931Qx09ERER8pz+O+PUH\n",
"6viJiIiI7xyL5I6BQB0/ERER8Z3+OGVbf6COn4iIiPiOvuq1qeMnIiIivqOOn63Xjl/b3laz/b19\n",
"zWZ7U5P9/paWdroNVk4gGuVlA1wlPSyuId9QyE6PzqVsBysBEIvxci6xmJ26zrbhwtLzgyGegp8N\n",
"5rEwZB5vNDZ5e5iU8gG8XxeA91ILrPwDwPc56dgGK4FRAftaKg17P8YwnSSdryvAakAcBVacYTEG\n",
"8B5nXKWh2D3LriXX58/iDIsxAI8zbPuuch4szrAY49oO4yoBwuJMLjGmr35pe40zfRFjAH6dsf39\n",
"/xsym73GGKBv4gyLMek03y8v1PGzacRPREREfKdAyR0mdfxERETEd/pjHb/+QB0/ERER8R191WtT\n",
"x09ERER8Rx0/mzp+IiIi4jvq+Nl67fitWbPJbG9v7zTbk8m02e7Kqo2Q7KmqKp6JxjLbWFYby9wD\n",
"eJYWm6T94Gv2PrMJvF0Te3tdxpXV5cz4Ytv3OOm2K0MtlxstTdaXJseScWw/l+Nn+xwg5yXo2D47\n",
"l0WOibXDZPtlQfsac2WoxuNJs731QIfZ3tjaSNe1b1+L2T558mfoMrmy4gyLMQCPM4wrE3PQoDKz\n",
"vbzcjj+uDH2vGcIAjzPs/ndVG8hn/GFc9xi7l1xxgcaTXO5lcv+xGAN4jzN9EWMAHmdc8ZrFGdae\n",
"DTrOC4kzLMYAQEdr3Gx/74AdZ1iMCYcrkI8papXcYdOIn4iIiPiORvxs6viJiIiI76jjZ1PHT0RE\n",
"RHxH5Vxs6viJiIiI72jEz6aOn4iIiPiOK6n040wdPxEREfGdQmX1mnrt+K1b967ZzlK9WWmCiopS\n",
"uo2SErsEQnV1OV2mtnaw2T50aKXZvj9hp5kDQEcqZba3Z3nZjHaQchJZuz2Y4in4hWmP5UQcf8Ww\n",
"ZVwTq4cCbDt2u2uSelbqwFUCIUXKFiTJ+U9l+OdC5vx2PuvBzlkROc9BR2kWVuqgo8Nx/XUkPC3D\n",
"3g8ALS3tZvuBA22e2l2vTZ5MF8mZFWdcZWu8xhlW/gkAhgwZZLZ7jTEAjzMsxgCuOENKbWT558/i\n",
"DIsxgPc44ypBwuIMizEHt0P2OY+loViMAbzHGRZjAB5nvMYYgMdZVzkV9lp7u31ddnbya6mtzS6n\n",
"xGIM4D3OsPaKiqF5Keeir3ptGvETERER3+mPHb+2tjYsXLgQa9euRSwWw+WXX47J5K/p3//+93jq\n",
"qaeQSCQwceJEXHPNNQgGj7zb5q1yr4iIiMgAUFhQ0Kf/DsfixYsRCoWwePFi3HjjjVi8eDG2b9/e\n",
"431r1qzBb3/7W9x22234yU9+gj179qChoSE/5yUvaxERERHpRwoKCvr0X2/i8ThefvllfPGLX0Qk\n",
"EkFdXR3Gjx+P1atX93jvqlWrMG3aNNTW1qKkpATTp0/HypUr83Je1PETERER3yns43+92blzJwKB\n",
"AIYOHdrdNmbMGGzbtq3He7dv347Ro0d3/zx69Gg0NzejrY0/l3249IyfiIiI+E5/e8YvHo8jGj00\n",
"0ayoqAjxeM/km3g8juLi/5sX/MPl4vE4Skt5suzh6LXj98YbW832UMieKJxl1eUysXhlpT15OgBU\n",
"11SY7ZsO7Dfbd7XzXnJL0s5scmWCMSGSiRUJ8FMdYRNrk4c42ftd23EuQ7YTJscScmQIM1nwVDiW\n",
"8ZvKkEnSHeuiungAiJCsQvZZsgw5ILfs2dbWDk/LsInNAWD//lazvanJXsa1X83N9n4dDVacYXEB\n",
"8B5nXOticcZrjAF4nGExBvAeZ9h1efA1Fkv48UeD9jljMSOXWMZijGsZlu2bi3QXP8de44yrQkGQ\n",
"jPuESAfE9VkmE3YmeC6Z+LnEJRZnWIwBeJxparKXaW21M4eHDydVMzw6Fh2/jz6HV19fj/r6+u6f\n",
"i4qK0Nl56DF3dHSgqKhnZZO/fW9HR0d3+5HSiJ+IiIj4zrHo+M2cOZO+NmzYMGQyGezatav76973\n",
"3nsPI0eO7PHekSNHYuvWrZg4cWL3+8rLy494tA/QM34iIiLiQ/0tuaOoqAgTJkzAE088gUQigTff\n",
"fBOvvvoqpkyZ0uO9U6ZMwYoVK7B9+3a0tbVh2bJlmDp1al7Oizp+IiIi4juFKOjTf4dj9uzZSCaT\n",
"mD17Nh588EFcc801qK2tRWNjI7785S9j3759AIAzzjgDl1xyCebPn48bbrgBQ4YMcY4meqGvekVE\n",
"RMR3+ltyBwCUlpbipptu6tFeXV2NJUuWHNJ28cUX4+KLL877PqjjJyIiIr7THzt+/UGvHb+tW3eZ\n",
"7cXFdmZJhsxv6MrQZd+Nu+bXbIzb2UA72+3soW2tjkwksq5EmmcWsX0Okwy1qDOrzX6NLeNaF8vQ\n",
"cy/DtuMt2w8AgiRLzfX8Qz5vTja/aMixz+z4E532vJeurLbGxmZP7QDPhNu7115m3z6+Lradffvs\n",
"fd6/n2cIu+YEzrd3393Zo624OELfnyUTplZV2fN7u64/FmdYjPmgjX/+21pJ9rRjrnBXnLHkkiHL\n",
"7uWDr3mNP/lbl2t9NNvXkQnLPmdXjGFZumwZV7ZxhGRPl5BjZDEG8J6hD3iPPyzGuLa/Zw/Pamfb\n",
"YdnDbD7gdJrf+1645mj/ONOIn4iIiPjO4SRcfByp4yciIiK+c7gJFx836viJiIiI7+gZP5s6fiIi\n",
"IuI76vjZ1PETERER31HHz6aOn4iIiPiOkjtsvXb89uw5YLbHYsVmOyvBkEjwtHVWAqbQkbbfSUog\n",
"tCbt7RyI83IKrJxLe8qeJNuFTpLuKCfCSgDkUk4ll3IuJSF7GdZeHAzz7Yfs7bgmdmfnhp3LUIBf\n",
"F0UeS+MAvNQAK5vgKs2SSwkWNoF5Lutiy7CyLa5J2vuynItVIiIWK6HvZyVY2D6zGAPwOOM1xgC8\n",
"bEtjZwddhm2HlRkJk/sCcMWSfJaT8l7OhcUS12sszrAYA/BjccXfAPn8WZxlMQbgx9/S0m62s3sf\n",
"yK00VD7LubA4k8syLM50dNj3SyzGS9Z4oeQOm0b8RERExHdUx8+mjp+IiIj4jp7xs6njJyIiIr6j\n",
"jp9NHT8RERHxHSV32NTxExEREd/RiJ+t145fPG5nsIXDZGL7hJ2hxtYDAMmkvUw67cjEi3jrs2Zh\n",
"Z8gBQDKTNdtTjkzANMm4S8A+loQjqyyctl9rLbTPWS4Zsq5MvNKwnT1XRtorIvxcMq6JzQtIJhzL\n",
"UCwL8aziTpLV+cFuOzsd4JOR55JVxzKBXdl7LOPNazsAtLfbGepsMnRX5i7LuDsarPgQDvNrlsWT\n",
"FMnEZzEG4HGGxRjXA+MsEzed5fdMgmT1shiTKuBxKZHxlqEMACGS1cqyh9l9CQAlJBO32JHVWx6x\n",
"K0HEwnZc7oL9foDHGRZjAJ6Jy+IMizEAjzNeYwyQW1WBfMYS9hqLMQCPGayd3ceJhPeKGhZl9do0\n",
"4iciIiK+oxE/mzp+IiIi4jsq52JTx09ERER8R8kdNnX8RERExHf0Va9NHT8RERHxnYGY3NHW1oaF\n",
"Cxdi7dq1iMViuPzyyzF58mT6/t27d+Oxxx7Dxo0bEQwGcf755+NLX/qScxvq+ImIiIjvDMQRv8WL\n",
"FyMUCmHx4sXYsmULvv/972PMmDGora3t8d50Oo3vfe97+OxnP4s5c+agsLAQO3bs6HUbvXb8giR1\n",
"n01s3tVlp+C7SrOw1G1XOYmKikFmOytBUuIoZ8ImCc+QYwEAeJxY3VUahr3GLtrOQl6agZVgiAYd\n",
"5Sxcx2kIOSaJZ6URXDcgW6Y8bJdtyOck5bks4yqBsH9//kogtLfbZSOSSV7qIJu1P0t2v7L7G3CX\n",
"U8k3az8KHU9mZ0l5FBZnXOWk2PlnMabEUU6IlQBpDfLtp7IkNrAYQ9cEJMnnnybtAJAg92aAlXkh\n",
"5acAIBG0jyXJjhE8NrA4w+K1a10sxgDe40w+Ywkr2XLwNbsEDIsxAI8zXmMMwOMMizGA9zjD23n5\n",
"Ly8GWscvHo/j5Zdfxv33349IJIK6ujqMHz8eq1evxqxZs3q8f+XKlaisrMRFF13U3TZq1Khet6MR\n",
"PxEREfGdgZbcsXPnTgQCAQwdOrS7bcyYMdiwYYP5/rfffhuDBw/G3XffjU2bNmHUqFG48sore+38\n",
"5adbLSIiItKPFBYU9Om/IxWPxxGNRg9pKyoqQjxuj9g2NTXhhRdewIUXXohFixbhzDPPxH333Ye0\n",
"o2A7oBE/ERER8SPy6NVRUwA0NDR0/1hfX4/6+vrun+fNm4eNGzeai9bV1eHKK69EZ+ehX9d3dHSg\n",
"qKjIXCYcDuOkk07CGWecAQC45JJL8OSTT2LHjh3OUT91/ERERMR32LPAR0sgAMycOZO+Pm/ePOfy\n",
"8XgcmUwGu3bt6v6697333sPIkSPN948ePRpvvfVW989dh9nR1Ve9IiIi4jvZbLZP/x2poqIiTJgw\n",
"AU888QQSiQTefPNNvPrqq5gyZYr5/nPPPRfvvPMO1q1bh2w2i6effhqxWAwjRoxwbqfXEb9YrJjs\n",
"oJ29lksmYCJhZ7y1tHTQZcYcN8xsH1QUNduroo7sJUfGGdNJspcSJEM347goWMYdm6Q97cgQdm2H\n",
"CQVY9pz38xIk5yWXrLpdu5o8tQPABx80mu27d/NlvGbiua5Llj3nymp3veYVuy8zGftacmX1ujJh\n",
"8y0WK+nRVlxsXxcAEA7b1xP7C9+VCc0+TxZjqqJ2jAGAAwkyGb3jnmXPBrUX2vtMs4DBKwSwagMA\n",
"zwQuJMvkM8YAQCLjrUICizGA9woBALBnz36zfceOfWY7izEAjzO5ZAiz69JV7SKZJOcyD52SD4Uc\n",
"WdUlJfa9wTL0WYwpLbX7HV719YhfPsyePRsLFy7E7NmzEYvFcM0113SXcmlsbMScOXOwYMECVFVV\n",
"Yfjw4bjxxhvxyCOPoLm5GWPHjsXNN9+MgON+A/RVr4iIiPhQPju8faW0tBQ33XST+Vp1dTWWLFly\n",
"SNuECRMwYcIET9tQx09ERER8ZyCO+PUFdfxERETEdwbiiF9fUMdPREREfEcjfjZ1/ERERMR3NOJn\n",
"67XjV1Njz1fJskZYVo8re5BlNba38+yltlY746k6amcDtSV5hiKbk9eVPdZK1teesjPxOh2VtFlW\n",
"G8uec2Xo5YJNiVoI+4VwgJ+XIpJVF3Nk1bU0t5vtLHt369ZddF3bt+8123fs4Jl4bDtsTt62Nj7v\n",
"LruWCwr4OYtE7HOWS+Y8W6a42C4A6sp27cus3pqaih5truzB0lI7zrC45MqcZp+n1xgD8DjjumfZ\n",
"/dScsCsRuGIJe43FGAAAywTmS+RVkNwb7LywGAPwOMNiDMCzd1mcYTHG9RrLHGbz8QI8e5dl7gI8\n",
"e5bFDBYvDi7jLS4BQEmJff6TSft+ZfGnujpGt+GFRvxsGvETERER39GIn00dPxEREfEdjfjZ1PET\n",
"ERER39GIn00dPxEREfEdjfjZ1PETERER39GIn00dPxEREfEdjfjZeu34DR9e5WmF0ahdNsKVAs4k\n",
"ErycBJvAumZ4pdnenuo5CfyH0uSvgoCjBEeo0C4bEWbtAX4snWl7OwlSgiJNys8AfML3iKOcTiRg\n",
"XwbREGl3lFMoC9mfc1mYf/6b3rdLILAyK65J0t9/fzdp30OX8VrOJZcyJ67rPxazy4OwEkislAnA\n",
"y7awMiddjmvJVQIl32prB3t6PzufrJyECysp4TXGAEBb0v4sWYwBeJxhMcZVmorFGRZjAO9xhsUY\n",
"gMcZV8xgcaaElPNhMQbgcYbFGMB7nNmyhZeT+uADb7GsqamFriufcaaiotRsZyVbXOtiMQbwHmdY\n",
"jGFl5LzSiJ9NI34iIiLiOxrxs6njJyIiIr6jET+bOn4iIiLiOxrxs/EHP0RERETEVzTiJyIiIr6j\n",
"r3ptvXb8WLZdJmMPoYZC3jMRc8n4ZRlPheRzLndklSai9r51gQ8Ts8y2YCHJ0Eu5MoTtrMJEgGTb\n",
"OS5mtl+urDo2sbnXdgCIRcgk6S18knSWPcva9+1rpuvas+cAabcnSQfym9WbSyauK7POEiLZjgDP\n",
"EGbbLyTXK9C3QdOKMyzGAN7jTF/EGACoINd/MsszpFmc8RpjAB5nWIwBvMcZV1YvizOuTFwWT0pD\n",
"drurQgCLM+xeBoB9++zMWhZnXPGHxZIdO+wMYdd+seuPxRgAiMXs6hXhMMmQLuPVLlicYTEG8B5n\n",
"WIyprs5XVq++6rVoxE9ERER8RyN+NnX8RERExHcG4ojf8uXLsXLlSmzbtg2TJk3C9ddfT9+7cuVK\n",
"LF++HDt37kRxcTEmTZqEWbNmOb/JAdTxExERER8aiCN+lZWVmD59Ol5//XUkHcXaASCZTOKrX/0q\n",
"TjjhBDQ3N+Pee+/FU089hUsvvdS5nDp+IiIi4jsDccRvwoQJAIDNmzejqcl+ZvRDn/nMZ7r/X1lZ\n",
"icmTJ2PDhg29bkMdPxEREfGdgTjidyTeeOMNjBw5stf3qeMnIiIivjMQR/xytWLFCmzZssX5TOCH\n",
"ci7nkkrZJQACAfuhQlc5BZYCzlLQAaCw0C4pwCZ9jgT4oZYE7e2kHGVL6H6RSgchVwkGMhl7IpM2\n",
"213XMtt+lBwjAJSTEhS0zILjvLCJ1Zv22xPeA7xsgdd212sdHQm6TFtbp9nOSkMkk/bnAvBSC64S\n",
"DOyaZQ/ouu4lVs5h0KAysz0S4ddFX7LiDIsxLtGofW7c5XTsc+A1xgA8zrAYA3iPM+weB3icYTEG\n",
"8B5nXNtnxz+oqIguQ8tGkbhU7CgNc+CAXWrFFTMSCW9xpqMjTtfFXuMxhsdFFmeCQf67hMWZdLrU\n",
"bA8E+IfJ4gyLMQBQUWFvx2s5pViswtP7mWMx4tfQ0ND9//r6etTX13f/PG/ePGzcuNFcrq6uDvPn\n",
"z89pmy+//DIef/xx3HbbbSgttT+Dj9KIn4iIiPjOsRjxmzlzJn1t3rx5ed/emjVrsGjRItxyyy2H\n",
"9TUvoI6fiIiI+NBAfMYvm80inU4jm80im80ilUohEAiY3wCtX78eDzzwAG6++WYcf/zxh70NdfxE\n",
"RETEdwbiM35Lly7FsmXLun9+7rnnMGPGDFx22WVobGzEnDlzsGDBAlRVVWHZsmXo7OzEXXfd1f3+\n",
"k046CbfccotzG+r4iYiIiO8MxBG/mTNn0q+Lq6ursWTJku6fb7/99py2oY6fiIiI+M5AHPHrC712\n",
"/IYOrTTbvZ5QV1Yjy7hzTQYdidhZQmw7mS7e82eTnrsygYuDHo/fkdXLtpMiE7tnu/i2+bHw888m\n",
"Pa8gmXgscxcAwiR70JUJybCsSle2d4Acp+v6Y6/1Nu2NF+xYXNthx1JSwrNA2T1TVRUz24uL+brY\n",
"9o+G4cOre7Tlcs2wz9KV1cvOmdcYA/B7Npf732uMcW3HFcu8xpnCAn4tR4P2dliMAXhVARZnihzX\n",
"ZT6vGdYecsQ/r+tyxYVcsFjCtuM6FhZnXL+XWfWAsjL7/mMxJhotp9vwYiCO+PUFjfiJiIiI72jE\n",
"z6aOn4iIiPiORvxs6viJiIiI72jEz6aOn4iIiPiORvxs6viJiIiI72jEz5b3rN5Mxu5hh0I8E6u4\n",
"2M4edWUPsSyhQjJXcDrF51ctIFlqIUf2WBT28QdJ9pRrrtxkxs5Ec2UiMwWwt19Esu1cr5WTOTRd\n",
"846yrDp2jgHvc0Ky+SABoKrKziprbbXn3QX4/JrsWFxzdeaSVcpeY9d4LnNlsvayMn6Pue7ZfKup\n",
"6Tk3Zy5Bm51/9/zG9jkoL7fPM4sxAJDN8jjDsDjjNcYAPM6wGAN4jzMsxgA8lrjij9c448rcZXEm\n",
"l7ni2T3DYgwAHDhgZ8+zucJdx8KWyaVChtcY41rGHX/t42dxhs0VHgrZ6/FKI342jfiJiIiI72jE\n",
"z6aOn4iIiPiORvxs6viJiIiI72jEz6aOn4iIiPiORvxs6viJiIiI72jEz6aOn4iIiPiORvxsvXb8\n",
"qqvtyZK99qRdk1GzydBdqeaspEVn2i6nkMnhAgg7JlYPFthp6FlStsB1urrIZOi5YOUMXMfCJnCP\n",
"kLIBbCJ2AMiS8gSu0iCsbEBlpV02IR5P0nUlkymzPZPh55hNbM5KQLS1dXpel6uci1XKBACqqux7\n",
"z1VOgb3GzqWrNEw43Hd/F1pxpq/KuXgtgdGesq8xgMcZVzkjdm96jTEAjzN9EWMAfiwsxgDe4wyL\n",
"MQCPM677j/2OSybt3yWuEizstUDAe5kZV9koht3PgwcPMttZjAGAykq7pIor/niNMyzGFBTwMlNe\n",
"aMTPphE/ERER8R2N+NnU8RMRERHf0YifTR0/ERER8R2N+NnU8RMRERHf0YifTR0/ERER8Z2BOOK3\n",
"fPlyrFy5Etu2bcOkSZNw/fXXO9+/dOlSPPvss+js7MRxxx2Hq6++GrW1tc5leu34sWwcryfUNbF0\n",
"OGxnrxUX25N3A0Aya2dPpXP4oIvIJOlg7QACJHutkExgXujIhHO9ZnFl1bHkabZfABAkx8I+Y1dW\n",
"G8uEy2Vi8UzG3j7LnHVtx5U9x7LHWcZbezvP6mXnrLi4iC7DtjNy5GCzfejQSs/rYpl4JSU825FN\n",
"oH40WPuXy1/rrHoAqxwAACUl9mdDY0xXfisEFJI4w+7zYIFjXR5jiWsZtn1HgQYaZ1iMAbzHGRZj\n",
"AH7/u7J6vcaZXH6Xsd+j1dX76bpY9QBXhQKvsWzEiCq6LhZncskEZuefncuuLv55eTEQR/wqKysx\n",
"ffp0vP7660gmeQULAHjllVfwzDPP4I477kB1dTV+9atf4cEHH8Q999zjXE4jfiIiIuI7A3HEb8KE\n",
"CQCAzZs3o6mpyfnebdu2oa6uDjU1NQCAc889F08//XSv2+B/homIiIgMUNlsV5/+62unnnoq3n77\n",
"bezcuRPpdBqrVq3CmWee2etyGvETERER3xmII35ejBs3Dueddx6+8Y1voLCwENXV1bj11lt7XU4d\n",
"PxEREfGdYzEK19DQ0P3/+vp61NfXd/88b948bNy40Vyurq4O8+fP97St5cuXY/369Vi4cCEqKiqw\n",
"evVqfPe738X999+PcJg/16yOn4iIiPjOsRjxmzlzJn1t3rx5ed3WmjVrMGnSJFRWHkzEmTp1Kn7+\n",
"859j+/btGDt2LF2u145fNGpn1rK5H9mJdmVisvn6XMuAZNyx7DFXVlmApKmFC3n2FpsTlmWcpXKY\n",
"35GdS9dfMSxDLZe5OllWXyDgyCok59L1WbKMW5bx5co2ZeuKxfjcjywTrampxWzv6EjQdbHz79pn\n",
"lnHL5vCtqbHn3QT4vKNsG65sZ1f2eL5ZWbf5vGbzmaHsigsgr7EY41ofiwuuuapZnHFl4nuNM+wa\n",
"B/omzrjmffc67zbA40w0ai/jWheLM+y+bGriWbUszrg+S7ZvXmPMwdfsOONahmUvs34E+4zTaV7R\n",
"w4uBmNWbzWaRTqeRzWaRzWaRSqUQCATMa3vUqFF46aWXcM4556CsrAzPP/88MpkMhg4d6tyGRvxE\n",
"RETEdwbiM35Lly7FsmXLun9+7rnnMGPGDFx22WVobGzEnDlzsGDBAlRVVWH69Ol47LHHMHfuXCST\n",
"SQwbNgzf+ta3UFzMBzoAdfxERETEhwbiiN/MmTPp18XV1dVYsmRJ98+RSATXXXed522o4yciIiK+\n",
"MxBH/PqCOn4iIiLiOwNxxK8vqOMnIiIivqMRP5s6fiIiIuI7GvGz9drx4+nWPKXc4up5p1Le1gXw\n",
"tH02SbhrfztIeYS97XG6TGennWrf0WEv45pYnO2b1zIvufI6GbmrnAF7zTVJOlvGazvAyylUVpbR\n",
"ZVjZAjZJuqucBvtsXBO7s3PDSiOw0gyudXktmQP07V/LoVDP/XDdM17LRiUSdvkl17rYuXHNc8nu\n",
"WRZjAB5nvMYYgJ8zV/zrqzjDhMN2qZ1c7n+v1z8AFBfbpUNyiWUszniNMQCPM67PhV2zXmMMwONM\n",
"WRnPGGUlcNh9yY6loCA/Y1Ia8bNpxE9ERER8RyN+NnX8RERExHc04mdTx09ERER8RyN+NnX8RERE\n",
"xHc04mdTx09ERER8RyN+tl47fmxC7mTSzpLjGWLePwDXZNxsfblMbM4yq1wZV+y1Y53Vm8t5Zplg\n",
"oZB9eZSUFNF1sUwwVyYqy4RjGWcsC+/gMiyrN0aXYefZ6zXu4sqe9ZrVmMzy7WfI558CuS4c15Ir\n",
"ezXfrMx+13lmnw27/l2xhPEaYwAeZ3KJJV5jDMDjDDtfAD9OFmfyHcvZ9c8yUV2xhL3myuoPBr3F\n",
"GRZjAKC6utxsz2e2tQs7zyyWsHMPAPGMvf2MI2YkyGsBEn/ChSRzPof71aIRP5tG/ERERMR3NOJn\n",
"U8dPREREfEcjfjZ1/ERERMR3NOJnU8dPREREfEcjfjZ1/ERERMR3NOJnU8dPREREfEcjfrZeO36p\n",
"lCspbqMAAA6VSURBVJ2G3tFhTyDOyhm4UtNZyZiuLt5bZ+UJOjvt7be3ey+n0NLS4XmZXI7fa9kW\n",
"97m0z1lXF78BCgrswh2RiH15uCcpt8umDB5cQZdhxxkI2Kn+rnIuaVI2IOEogZICKacTtEsKZB2l\n",
"WVipg2yX4/NnpUkS9vXnqnQQJJ9lNEhK84T45PUh2BsiH8sRseJMLhPYs3uDxRiAxxmvMQbgccZ1\n",
"LCzOeI0xAJBI2PvsiqVe4w+LMQe34/0XrddyLq7SLEOGVJrtrg6A1zjDYgwAdKbt35cpcv9nHTWT\n",
"0qTSivOzJHEu3Umuiw6+roIC+/4PF/Kd9hpnsshfyaCjuR6/0YifiIiI+I5G/Gzq+ImIiIjvDLQR\n",
"v3Q6jUceeQTr169HW1sbhgwZglmzZuGMM87oddnvfve72LBhAx5//HEUOkZlAXX8RERExIcG2ohf\n",
"JpNBdXU15s+fj+rqarz22mtYsGABfvCDH2Dw4MF0ueeeew4ZMtOKpS9nZRIRERHpE9lsV5/+O1KR\n",
"SAQzZsxAdXU1AOCss85CTU0NtmzZQpfp6OjA0qVL8aUvfemwt6MRPxEREfGdgTbi97cOHDiAHTt2\n",
"oLa2lr7nl7/8Jf7+7/8e5eX2PNGWXjt+7e32hOBeJxBnk1QffM3OOHJlr7LMus5OO9u4paWdrstr\n",
"Vh3AjzORsI/Tle3mdZJ013lh20+l+CTtLEsvFPKeVVtd3Wa2s+sI4FlqQZI9G43yTNTSCnvC9fY0\n",
"P/62JMkET5FrjGTuAUCCDLenHQEoy46fPKcRcaTVloXZuSkyW11Zvew6C/F53XNmXR+53H8szrAY\n",
"A/Dj7KsKASw2sexddo8DoF/3uH4BsvufrSuXc+mKWew+Ly62r9mqKv4Ljn1mrkxYtv2SEnv7xTFe\n",
"1YDFhpaE/Xup3RGXO0nMYjEG4HGmi2QiB0gVAIDHmfIIj/8szkSDdtBg92s6nUaRvSpPBtozfh+V\n",
"Tqfx4IMPYurUqRg+fLj5ns2bN+Odd97BVVddhcbGxsNet0b8RERExHeOxYhfQ0ND9//r6+tRX1/f\n",
"/fO8efOwceNGc7m6ujrMnz8fwMH9fuihhxAKhXD11Veb789ms1i8eDG+8pWv9JrM8bfU8RMRERHf\n",
"ORYjfjNnzqSvzZs3r9flu7q68NOf/hQtLS245ZZbaKeus7MT7777Ln70ox8B+L9O7nXXXYc5c+ag\n",
"rq6ObkMdPxEREfGdgfiM3yOPPIIPPvgAt956K0KO52pKSkqwaNGi7p8bGxvx7//+77jnnntQVsaL\n",
"nAPq+ImIiIgPDbRn/Pbu3Ytnn30WoVAI1157bXf7tddei8mTJ6OxsRFz5szBggULUFVVdUhCR+L/\n",
"P0daXl6uOn4iIiLy8TPQRvwGDx6MJ554gr5eXV2NJUuWmK/V1NQ4l/2oI5ir186q8zqHL8Dnl0wk\n",
"+DJeM+5yyaprb7ePBeBZsq55LL3KJauOnX/2eQH8s2HHUlTEM0Gbm+3z7MrqDgTsv07CYe9zBVdU\n",
"lNLXGJY91xS3z1lLkl8XLEsv4cgEZiJk3stY2JVVZytmc2U6sh27HJmY+Wbd665rlmXPsuuMxRi2\n",
"7YPbtz9n97y7dixxLcPiDLsvc5kP14WNirA4w84LALS2ep9fmB0PizNsG4C7egHjNc7EYsWet8Fi\n",
"zIEEv8bZa65M4JSHIr4AEHJUCGBxppDM4QvwOMPkMre2FwNtxK+vaMRPREREfGegjfj1FXX8RERE\n",
"xHc04mdTx09ERER8RyN+NnX8RERExHc04mdTx09ERER8RyN+NnX8RERExHc04mfrtePHeszshPL3\n",
"8563awJtr8ukUt4nKWfFDkMhnuoeCPCUdgubCNyFpbq7ysywZVpb+TlmpRZYu2uSelfZBiZASgoU\n",
"F9vlBFwlWyorY2Z7JOr9b5xUlpzLJD9GNhk7K+fgwiY2dy9jHycr8+Aq5+LtCj8yVjzJJWiz+9wV\n",
"Y7zGMlepiVz2mcUSVs7EFXtYLCss5Mt4jTOJhPfSRK7SXCxmsBI4uWzfNQNCWZldtoXFGRZjAB5n\n",
"WAmURIYfCyvb4ioB4zXOuGIM2+cSx7n0Wk4ml/5CPtb/cacRPxEREfEdjfjZ3PN6iIiIiIhvaMRP\n",
"REREfEdf9drU8RMRERHf0Ve9NnX8RERExHc04mfrteMXDtsZPNEomcCZZI+x9QA8q8yVIcrWx7Jn\n",
"o1E+eTSbdJztF8CPk2WoujKEWSYem1jelVW7e/cBsz2T4X/5sInNvWb7uhw40EZf27+/xWxvbGw2\n",
"2/futdsBoLq63Gwfc9wwusw+ktkWKPD+CGySZALHHdluXrPao2l+27JM5HSXHQBZOwBEc8hEz1U4\n",
"3POYWFarez32Z5lM8mxHth1rn1zbAIBIxH6to8OOlwCPMywuuCoEsH1m6wJ4nGlt7TDbc/lcXDGD\n",
"vZZM2hmvra3tdF2RiH38LHMXAPbssbN3q6rsWMJiDACMGjPU3q+AvV+hQv5Zsoz7pCOWJBy/syyF\n",
"jtz9RNo+/yzGAN7jTITcS2lHjPNCI342jfiJiIiI72jEz6aOn4iIiPiORvxs6viJiIiI72jEz6aO\n",
"n4iIiPiORvxs6viJiIiI72jEz6aOn4iIiPjOQBzxe+CBB7B+/XokEgmUlZXhggsuwOc//3n6/t//\n",
"/vd46qmnkEgkMHHiRFxzzTUIkjnbP9Rrx49NVM1S+llpAtfE5qychaucCisB0NFhT2DNSrYAvNSD\n",
"66JhJRVCIfuUsjIPAC8Nw8oZ7Ntnlz8BgMrKfWa7qwQDm/SdlYBoaeHlFJiMowQB+2xaWuxyEvv3\n",
"t9J1NTXZr9XUDKLLxMJ2qY2ysH3ODiT4bcPKNiQcx5/O41+lrAREitx/rv0qJyWbjgYrzriu2VTK\n",
"3m+vpXEAfv93dtoxprOTxxIWf9i9DPBRCRZjIhF+XlicYTEG4MfJSjDt3GnHGIB/ZizGuF5j97/r\n",
"WHIpDdbWZpfHYnGGxRiAx5mKSJG9rjgvzVUSsj/LtqSrnBMpp9IHMQYAMmQ7rMxMeXGx2Z5K8d+X\n",
"XgzEEb/Pfe5zuO666xAOh7Fjxw7cfvvtGDt2LM4444we712zZg1++9vf4vbbb8egQYPwgx/8AA0N\n",
"DZg1a5ZzG5qrV0RERHwnm+3q03/5MHLkSIQ/MugQCAQQi8XM965atQrTpk1DbW0tSkpKMH36dKxc\n",
"ubLXbeirXhEREfGdgTjiBwCLFy/GqlWrkEqlcNVVV2Hs2LHm+7Zv344JEyZ0/zx69Gg0Nzejra0N\n",
"paX2t7WAOn4iIiLiQwPxGT8AmD17Nq6++mq88cYbuP/++zF27FiMGzeux/vi8TiKP/J1eTQa7W5X\n",
"x09EREQ+Vo7FiF9DQ0P3/+vr61FfX9/987x587Bx40Zzubq6OsyfP7/754KCAtTX12PixIl4/vnn\n",
"zY5fUVEROjv/7znRjo6O7nYXdfxERETEd47FiN/MmTPpa/PmzfO8vkwmg7KyMvO1kSNHYuvWrZg4\n",
"cSIA4L333kN5eblztA84jI5fAZn0uqSITK5MethZ8A+AZQkVFvDsrTCZ3DpK0phdk7S7Mu7o9j1O\n",
"4B53ZE8yRQH7GJuaeFbv1q27zPZYzM6eAoDiYjt7s7jY/qth795mui6WPccmTwd4lh7L3GSZkwDP\n",
"RGxs5Ps8avQQs701ZR9Le4pfS64JzJlExr7+2DUeINnWLhkySbrrWJoK7IzDwfxSylkg2jMbtIxc\n",
"lwCPGWwyeFcmYhmJMyxDm92XAI8zfRFjgL6JMyzGADzOsBgD8Exgds8mEvxchkL2sbgygdlnxuIM\n",
"izEA3+faUTVme0uS30ydafs4XZn4BeRaZjEm6IglucQZllXcnrZjaVPc3t9sGhjMk9cP20B7xq+l\n",
"pQXr1q3D2WefjXA4jLVr1+Kll17Crbfear5/ypQp+MlPfoLJkyejoqICy5Ytw9SpU3vdjkb8RERE\n",
"xHcG4jN+zzzzDBYvXoyuri4MGzYMN954Y/fXvI2NjZgzZw4WLFiAqqoqnHHGGbjkkkswf/58JJNJ\n",
"TJw40Tni+CF1/ERERMR3BtqIXywWc34dXF1djSVLlhzSdvHFF+Piiy/2tB11/ERERMR3BuKIX19Q\n",
"x09ERER8Z6CN+PUVdfxERETEdzTiZ+u14/deK8msInPvsewhlqEE8EzIAvBMLJaNxLJ6WYYeAIQC\n",
"OWQvddh/SXSm7Qwxlu3kEiHZdtVRngl2yhnH28tUl9Nl2HzMrH3HDj5XJ8t46yLZlgDPUmQZeq4M\n",
"STaPsCurt7Q0arYPJ8fP5qMEeCZ6iGToAvzeYJmo7Bp3iZNttCT4vLPsXj4aWb1WnEk5shfZOWPt\n",
"ucxVGib3H7svD75mfzZ9EWMAHmdcWc3semJx5uTT7RgD8DgTi5XQZcrL7dd27Gg025ub7Tl8AT4n\n",
"uGveZxZ/WJxxzVXO4gyLMcPKedmNXK5Zdm16jTEAvy5c1Ta8xhm2X4EsMNiuYOKJRvxsGvETERER\n",
"39GIn00dPxEREfEdjfjZ1PETERER39GIn00dPxEREfEdjfjZ1PETERER38lk1PGz9NrxC2TtjKsg\n",
"ydLsgp1VlQXPxAwU2OtyZfUGyGthckjBLp6JF8jy7TBdJBsqTI6zEDlkFYLMO5m159AFgHSKvcaz\n",
"x4qKKs32igr7WFJ0G0BRkZ1xx84XAIRC9mdWVmZnwrFsYwAoKakg2+BZzV1ddvYiO5eFjvl4I+S6\n",
"LCnk86sGA+SeIecs4sgQjhaQ+V1hZzUGu/h+BbLeM1FzZcUZZya4xzgTLPD+lU8I9vGz+xLgcaYv\n",
"YgzA44xrrnQWM1mc4TEGYHEmGrVjDOCKM/b8vtEon6ubjfC45jf2GmdYjAF4nGExJpPm55LFGRZj\n",
"AKCkkNznHmMMwONMtICfyzDs11icYTEm0GV/JpIfBV2u38giIiIi4ht99ye9iIiIiBxT6viJiIiI\n",
"fEyo4yciIiLyMaGOn4iIiMjHhDp+IiIiIh8T6viJiIiIfEz8Pwu/jaZGtiSQAAAAAElFTkSuQmCC\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7fcacea16350>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from pymks.tools import draw_concentrations_compare\n",
"\n",
"draw_concentrations((phi_sim[0], phi_pred[0]), labels=('Simulation', 'MKS'))\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The MKS model was able to capture the microstructure evolution with 6 local states. \n",
"\n",
"##Resizing the Coefficients to use on Larger Systems \n",
"\n",
"Now let's try and predict a larger simulation by resizing the coefficients and provide a larger initial concentratio field."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"m = 3 * n\n",
"model.resize_coeff((m, m))\n",
"\n",
"phi0 = np.random.normal(0, 1e-9, (1, m, m))\n",
"phi_sim = phi0.copy()\n",
"phi_pred = phi0.copy()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once again we are going to march forward in time by feeding the concentration fields back into the Cahn-Hilliard simulation and the MKS model. "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for ii in range(1000):\n",
" ch_sim.run(phi_sim)\n",
" phi_sim = ch_sim.response\n",
" phi_pred = model.predict(phi_pred)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's take a look at the results."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAn4AAAElCAYAAAB6ce/JAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzsfWuUZVV57TzPenY1NA2CtoQgmsZGTZQQBxhFiXmZGBOE\n",
"qFeTGwWD8SY3EtCYXB+JwRf3hjxMCAaDYSQaWjEGY4JDZSBGNFz1AoLEB2JEBA229rOqzvP+2Guu\n",
"x1xrnXOqu6opyzV79Nh19tlnn73XXnud/c01v/nVhsPhEAUFBQUFBQUFBRse9Yf6AAoKCgoKCgoK\n",
"Cg4PyoNfQUFBQUFBQcH3CcqDX0FBQUFBQUHB9wnKg19BQUFBQUFBwfcJyoNfQUFBQUFBQcH3CcqD\n",
"X0FBQUFBQUHB9wmaD/UBFIS48cYb8a//+q944IEHUK/Xccwxx2DHjh34lV/5FQDAt771Lfzmb/4m\n",
"XvWqV+GJT3ziYTmm17/+9VhYWMCFF1448We+8Y1v4N/+7d/wcz/3c5idnbXrb7zxRlx++eW4+uqr\n",
"MTU1tRaHW1BQ8BBi586duPbaa3HsscfiT//0T6P3f+u3fgvf/OY38dznPhfnnHMOdu7ciQ996EN4\n",
"xzveYbcZDAZ429vehn//93/Hq171Kjz+8Y/H0tIS3v/+9+OTn/wkvv3tb2NmZgaPeMQj8NSnPhXP\n",
"eMYzDucpFhR8T6M8+K0j/OM//iN27tyJX/iFX8COHTvQ7XZx991349/+7d/sg9+WLVtwySWX4OEP\n",
"f/hhO65arbbiz9x///249tpr8YxnPCN48HviE5+ISy65BO12ezUPsaCgYB2h1WrhW9/6Fr7yla/g\n",
"xBNPtOu//OUv47/+67/QarWCccX/ezgc4oorrsCnPvUpXHTRRXj84x8PAPg//+f/4Ktf/SrOPvts\n",
"HH/88fjud7+Lu+66C7feemt58CsoWAHKg986wvXXX49nPvOZeN7znmfXPfGJT8Q555xjXzebTZx0\n",
"0kmH9bgOxeNbP7uwsICFhYVDPaSCgoJ1jKmpKZx44on4xCc+ETz43XzzzTjllFPwla98JdjeHyfe\n",
"8Y534KabbsIrXvEKO6tx//334/bbb8crXvEKPPnJT7bbnn766Wt8JgUFGw/lwW8d4cCBA9i8efPI\n",
"bVJTvS9/+cvx5Cc/GZs2bcK//Mu/oNPp4BnPeAZ+5Vd+BZ/+9Kfx93//99i1axce97jH4WUvexnm\n",
"5uYA5Kddub8XvehFyWO477778J73vAdf+MIXsG/fPhxzzDE466yz8DM/8zOo1Wq488478da3vhUA\n",
"8D/+x/8AABx99NF429velvzOPXv24Oqrr8b/+3//D51OByeddBJe9KIXBT8YPKYjjzwS//zP/4zl\n",
"5WU84QlPwEtf+tKAUSwoKFgfOP300/Ge97zHjiPD4RCf/OQn8cu//MvRgx/xzne+Ex/5yEfwW7/1\n",
"WzjttNPs+v379wMAjjjiiLU/8IKCDY6S3LGOcOKJJ+L666/Hxz72Mezdu3dFn7355ptx99134+Uv\n",
"fzme/exn44Mf/CD++q//Gu95z3vw/Oc/H+effz7uvPNOvOtd75pof6Omd7/zne/g4Q9/OF7ykpfg\n",
"1a9+Nc466yzs3LkT//RP/2TPg4P9RRddhEsuuQQXXXRRdn+XXnopPve5z+FFL3oRfvu3fxuDwQB/\n",
"8Ad/gAceeCDY7pOf/CTuvPNOXHDBBfhv/+2/4bOf/ezE51NQUHD4UKvV8GM/9mPYvXs3/uM//gMA\n",
"cNddd2HPnj3BA52Pd7/73fjXf/1XXHDBBRGT94hHPAJTU1N45zvfidtvvx2dTmfNz6GgYKOiMH7r\n",
"CC95yUtw6aWX4i//8i8BANu2bcOP/diP4ed//ucxMzMz8rPtdhsXXngharUanvCEJ+DTn/40brjh\n",
"BvzZn/0Zjj76aADAV7/6VXzsYx/D+eeff0jHecopp+CUU04BUEXxP/RDP4SlpSV89KMfxXOe8xzM\n",
"zMzguOOOAwD84A/+ILZu3Zrd16233oovfvGLeP3rX4+TTz7Z7v/lL385rrvuOrz0pS+12zabTVx8\n",
"8cWo16t45etf/zpuvvlmnHfeeYd0PgUFBauP2dlZPOEJT8AnPvEJbN++HTfffDN+5Ed+JMnQ79u3\n",
"D+9///vxrGc9C2eeeWb0/szMDH79138dV1xxBS655BI0Gg08+tGPxlOf+lScddZZh+FsCgo2DsqD\n",
"3zrC8ccfj8suuwy33XYbbrvtNtxxxx249tpr8YlPfAJvectbMD09nf3sYx/72ICle9jDHob9+/fb\n",
"hz4AOPbYY7Fnzx70+300Go2DPs5Op4P3v//9+PjHP45vf/vb6Pf79r3BYGAfzCbBl7/8ZWzevNk+\n",
"9AGVPuiJT3wivvCFLwTb7tixI9j3tm3bsHv37hV/Z0FBwdqCmr3TTz8df/u3f4tf/dVfxac+9Sm8\n",
"+MUvTm4/MzODbdu24YYbbsBTn/pUnHDCCdE2Z5xxhg1q77jjDtx+++14+9vfjjvuuAP/83/+z7U8\n",
"nYKCDYXy4LfO0Gw28aQnPQlPetKTAAA33HADrrjiCtxwww342Z/92eznqNvz96ORdbNZXe5er3dI\n",
"D35///d/jxtuuAHnnHMOTjzxRMzOzuL//t//i/e9733odrsrsmn5zne+k0z22Lx5M/bt2xesS50j\n",
"gBV/Z0FBweHBqaeeiiuuuALvete7sLy8jFNPPTW5XaPRwO/+7u/iNa95Dd70pjfhDW94A4455pho\n",
"u/n5eZx55pk488wz0e/38fa3vx033ngjnvOc5+AHfuAH1vp0Cr4HcP311+PGG2/EvffeizPOOAO/\n",
"8Ru/sar7//rXv453vOMduOeee7CwsIAXvvCFWfnCekWhSdY5nvGMZ2B+fh7f+MY3Vn3frVYLQPUg\n",
"6INC6hw+9alP4Wd+5mfw7Gc/G6eccgpOPPHEg2bcjjzySOzevTtav3v3bszPzx/UPgsKCtYHpqen\n",
"8aQnPQn/8i//glNPPXWkjdP8/Dx+//d/H/V6HZdccgn27Nkzct+NRgPPetazAGBNxseC701s2bIF\n",
"Z599Np7+9Kev+r77/T4uvfRSnHrqqbjqqqvw0pe+FH/+53+O+++/f9W/ay1RHvzWEVIPQHv27MGB\n",
"AwfWJJvtqKOOAlBFMMSXvvQlLC4uBttpoken07FsG1BN7958883BNnx/nAj70Y9+NPbs2YO77rrL\n",
"rlteXsZnP/tZbN++fQVnU1BQsB7xkz/5kzj11FPxzGc+c+y2W7duxe///u9j7969eOMb34ilpSUA\n",
"wNLSUnIs4Q/uODeEgu8fnHbaafjRH/3RJHHwmc98BhdffDF+7dd+Da95zWvwta99bUX7vu+++/Cd\n",
"73wHz3rWs1Cr1XDKKadg+/btuOmmm1br8A8LylTvOsJFF12EH/3RH8XjH/94LCws4MEHH8QHPvAB\n",
"TE1N4WlPe9qqf99JJ52ELVu24KqrrsIv//IvY+/evfjABz6AmZmZwFdLvfge//jH40Mf+hCOPfZY\n",
"zM/P40Mf+lDEGtJg+sMf/jBOP/10TE1N4fjjj4+O4QlPeAIe85jH4E/+5E/wghe8APPz8/jABz6A\n",
"breLZz/72at+zgUFBYcXj33sY/HYxz524u23bduG3/3d38Ub3vAGXHrppXj1q1+N++67D29961vx\n",
"9Kc/HY95zGMwNTWFr371q3jf+96HE044oQSJBWNxzz334K/+6q/wqle9Co961KNw00034S1veQv+\n",
"9E//NCAyVorBYIB77713FY907VEYv3WE5z73ufiv//ovXHXVVbjkkktwzTXX4JGPfCTe+MY3Bkka\n",
"k2CSahvNZhMXXXQRarUa/viP/xgf/OAHcd5552Fubi7rqg8AL37xi3HyySfjHe94By6//HIcf/zx\n",
"eM5znhNsc/TRR+NFL3oRbrnlFrz2ta+1vn4pXHzxxXjc4x6Hd77znbjssstQq9Xwute9Dg972MNW\n",
"dM4FBQUPPWq12oqq/aS2f8xjHoNXvOIV+PznP4+3ve1teNjDHoazzjoLn/vc5/AXf/EXePOb34yP\n",
"fOQjOOuss/Da1762JHcVjMVHPvIR/MRP/AROOukk1Go1PO1pT0Or1cIXv/jFiffx8Ic/HJs3b8Z1\n",
"112HXq+H2267DXfdddf3nL1QbXgoZRkKCgoKCgoKCtYZ/uEf/gG7du2yyR1vetOb8PnPfz5g93q9\n",
"Hl72spfh9NNPx+tf//pAcuRj+/bt+IM/+AMAwNe+9jX8zd/8De6991486lGPwqZNm9BqtXDBBRes\n",
"/UmtEspUb0FBQUFBQcGGxlFHHYVf/MVfxC/90i8l33/9618/0X6OP/74YNv/9b/+V9J7cj2j8OMF\n",
"BQUFBQUFGwKDwQCdTgeDwQCDwQDdbheDwQA/8RM/gQ9/+MP48pe/jOFwiKWlJXz2s5+1CUST4mtf\n",
"+xo6nQ6Wl5dx3XXXYffu3d9zD35lqregoKCgoKBgQ2Dnzp249tprg3XnnHMOnvvc5+LWW2/FNddc\n",
"gwceeADtdhvbt2/Hy172spHFERR/93d/h49+9KPo9/s4+eST8eIXv3hiPfpKPAa/+c1v4qqrrsJd\n",
"d92FZrOJpz/96XjhC1848XGOQnnwKygoKCgoKChYY9xyyy2o1Wq47bbb0Ol0sg9+vV4Pr3jFK/DT\n",
"P/3TeOYzn4l6vY5vfOMbSWeMg0HR+BUUFBQUFBQUrDFY4ePuu+/Grl27stvdeOON2LJlizUoB7Bq\n",
"D33ABA9+F3z4laibVPuGlzI/ZUp+zZgMmU3GkX2+VZXOOnK6Wh4xNR0sAWDL9Ez4ntm2u9gFAHz3\n",
"u1Wprr17DwAADhxYMstlu49Op9p2MAgJy3q9OtZ2u6pKMT1dHdfMTPUdmzbN2G0XFqoSYEccURk9\n",
"7jUp2d9drr5vd6f6vj3LZtlx389t93er41g0PnaLvep1dzCojs8QqlzWPdsC/t0y7TrdqNpyqsm2\n",
"rc5hzlTYmJXX/t9zreo8Z81rXhe7T3O9Bv2B/Wyv108uFWxTWiY0m67cG//mcsnU7e2a5XKf7dIz\n",
"r/vmddfug++5tuxOtN7/m+9x/8tmfc+0e99cj97Qnb89P1Tn1zTnx36ufZxtzDafb7kqBJtNybiF\n",
"tuln5n7Q1/NmOeNlljXN9y8uVn2KtY/Zt9n+LLM3NWWuf931JbbD3m61j32mf7LP7pY+rK8B16cP\n",
"dNmW1T55TdmGf/XMvDXPweLMa17i7odG1f7a/ze3XVm+I80YssVM0RwzW93LW2eq9UfPzJn1VdnC\n",
"o837/SXX77797cowfdeuvQCAPXuqijUcZ5aWqvbgfTEw5+/3f44zs7PVsc3Pm7HNjClbtiyY5SYA\n",
"wF6v3+9aqozSdy1W4w3HHV3qWMPrArhxpjcI+7UbW6pjnZa+POv1Xdu+pg+zX+tr7cP+/tiH2XYc\n",
"n9l23W44tjQa7reE/ZvtqmN33Wyr97o/DrBtuDzQC9tM25B9HHD3zH6z5H4PyLizJGNa1x9LE+MK\n",
"4MaWVmP8dWD7ut/M8Dd0i+3zZjkT/6byHmFf3rMn/A3tdMy4mBjr2f76m7l5c3XvzM5V38d++aAx\n",
"+n9w8YDdB9d926x7cKla7jI6uu+apY5TALDktesJc8fhb571hugYv1/wxS9+EUcffTTe9KY34ctf\n",
"/jKOP/54/Nqv/drhY/w6g74dRPxiO32zrm9+nDrmJug3ORANZRnfJAPwoaha32o1giU7YuqBw3Vc\n",
"GfDMtvSFcj+a5ke9ET+08KGMx8Ulb2wOrh3vRncPMOnBiIMD24fnGhwr+EBt2tcM0u7BL9w3fwgP\n",
"9NyD3/4ufxzDbTiY8+Flqhk+AAJA2/zdNIPPNNss48FlH2K9c+ma89tvHiD4wNcZDILXyzJo8rW/\n",
"rjfQvqMPz8nDCo65Wauu88CcW5375A8h4hrF/Alq2gc+fQA3D37N8OF6s1cfOPfjaB/a5YG87nXb\n",
"A0vhj2UumCEGA3PdGvHtO5RAg23YH7IPmx/iQT9439+G/V+vYe7HbTXQ9caZuh1bBsFy4KlSeKzD\n",
"YbqvDBG2A7cLHzjqZlnLvNZlOB4BceCTW/Izfa+93fiSCZJ6OsaYB3Hv4VEfygei3GlKEMNxYCYI\n",
"vNpmWa3bZB4e+JDEPr2va/p/xws8m+zXZtk2DzQz1bZttukEvn72/jfnsMi+ah7ilmTM9R+AF7u5\n",
"cZj9PbwPkgGg9D8GgHx41vGnWXP70HbXfdix3VwHNy74wWMYLPKB78jpcHmEWfqB0Cazn337qgev\n",
"vXurJR/4GMTwwY9BjN+X2c8HEkTwt1THhc4gbNvq72qdfUjuhYG4Hf/Na+7D37Y/HKzaWPOIK35x\n",
"VfYzKe779X9clf3s2rULd955J171qlfhcY97HD74wQ/i0ksvxWWXXXZIZtNEmeotKCgoKCgo2HCY\n",
"JOBYbezcudP+vWPHDuzYsWPF+2i32zj55JPxwz/8wwCAZz/72Xjf+963ajq/sQ9+/cEQw5qJquEa\n",
"kZEM2Z8c06ARuL+OUSo/6yLu0ZE34CJpqRRm1zOy18ibbGKwD2H4yNIpSxJMsQhzolG5mw4gW5Jg\n",
"/BhhmtecDmj3quWiYfzIEpEBXPanOluMcDmFyCkPfsYwf6TxPZaIU8z8XrJlbGa9aVLMG69/X6ac\n",
"uhoVSuS95J1DR5gPy+ZAo+j4uJqMUochk8cotW+otVYmIgeAhjlv7ouMn2v3cKrXyRriaZrc1C6Z\n",
"kYGJavclZAu5aNxnugE3bcYpsdR5K8OcY8L6XmTdE4bNskhyj68FeoOBZad07CD09UrAz8Z8b2qW\n",
"QMchYdESUgfOJPCa6LjD+6DjsSOOMQlZcd4rS/1wLCHTt9+bpuR7nUyb2dkaMn+9qi8ve6yBMosq\n",
"l3AsWrWc8/r9AcNcTYu0ZNzYkgLHFY7H/UHIMKl8JDVrsGTOhUuO3T0Zn1LQWQO2GcjSc9ZgGLO3\n",
"CmX62B4zlOaY8cCfNo+nemU5zSnfmPHbZ2RRnNol80fGT2Uk9ji9GSDH+KXvM65WFr2XYPyUWe3Z\n",
"bYdmu/A3N/jMYDCybVeCh+LB79xzzz3kffzAD/wAvvCFL9jXqz32Fh+/goKCgoKCgg2H2mH+Nw45\n",
"j0HFj//4j+NLX/oSPve5z2EwGOCDH/wgFhYW8IhHPGJV2mVFU70pndq4KFxZGyB+erX7qCnDp5G3\n",
"e05ldK5siK5X1iSlz6FOzWkYwmiRkYjPjsRM1ujo3eoaRzB/TbMto+SO0XKREXNLF7V1Bq3gveW+\n",
"iej71XpG8WSt2l6ER70Jo9OmZb5CBmQUIo2VMIBW+xlpzFKRXshGaeCpGhzAsXXtRrgN9TcDiW2o\n",
"q6wFrKHooBpkL6rXs5JAk2L8rBDevLdJEkH272fkXTF9jMSBmOljxK2skT1ealO9NtTIto40W+te\n",
"h8twnV6H8RrL1UQuSg8So+Q6at/gIBz3mfxJcJaA409ujEkxfqpLJvPXNpo3q+fz7t1u5r5einSx\n",
"ut6x5ZpM1RM2hufQNX1c9Vn+up6Mc93M8YRJFTKzIPdQm9pqjuGI72Htmz3Rb04yhlhtWS9so66y\n",
"14nLTxaSY0nDzBJMmZ/HWq3aZ5Ns+ojfPNX26ViiSR2bPMaPswWbbVKHJEgK07dr1x77WTJ9TOqg\n",
"xm95WROUwoQxvy+z/7fb1bY5lmko7F04axD+HthtpI/p2KLrVmusGcUwPxR473vfG3gMfvzjH8c5\n",
"55yDM888ExdeeCEuu+wyHHXUUXj4wx+O3/zN38Rf//VfY/fu3TjxxBPxyle+MmBoDwVF41dQUFBQ\n",
"UFCw4fBQTPWOwrnnnpudCr766quD16eddpq1f1ltrOjBT1kEYHx0nqI/c0ySZi9q5O2/z+ik72kE\n",
"gDjyzi39vxdNSrnqFAcS2fS8MKRvWULRLkiWHSPr/iAR4Rj2ge1KPZpGRcPM0v+7b7UTYTTMCJzR\n",
"eiqrl/oTa2di9ThyPczLVDSmGjLVabloPcGe9kNNX06npPY34ffz2M2+ZBtlhpre+y2NzsVOhzY6\n",
"myRT19fnMArnOmbtMiqnzYXaKlR/h9m8OXsLwulbHWtjNa3Za7e+BkBFvVaLrrPa6/h2UsyEb2b6\n",
"LvWadhyi5lPGi1HgWEJNpeqG/b+V4XNLw7ybrPdOgul2uqjwXol0s1av5mXVC/ulzLsdWzKMC5Cf\n",
"gXFuB+Fxdf1MTDOzoOMLM2E5xjQyzGzqe4n+MGTp4gz1uC2VDeTr1GwV4foM11TXzumD68nj86H6\n",
"wJZlPkMGlGPHqFkDm9U7HWr86uZ8H3ig8n+j7RngmD5q+6jp63bT9i2OqXaPAJwNY9/lZ6gLbNVi\n",
"TXEO+tu1Er1uNRZM/FUjsd7HvYcKhfErKCgoKCgo2HAoD35pjH3wq9ditgRwegfnRZdmHA6G+VM4\n",
"7U2sz1OWcFJfLR8DYalsVmOGAfQ/k4tscutT/kQ2Gh3U7RoA6CJtqJyCPR60wu8bNINz6w7c+bf6\n",
"jMrTTF9T2naUeFW1nBqlK/OX03b40CxeHp8v2+N7/Kw1qh6m96EROeAZaEsWrzPMTjN9mxJZvYy4\n",
"d++uInDV9KmfFhBH42rYPDOTjtZptAo4c1VlusiExdo3BMtwXZqdYXb/WqBZr1uWiAbOLZsZKVmW\n",
"8LMlQ9a6LbpVNy7Ri8zrd5nMQc3mpV/6JAbmumS/1JkAwM84VV2UaO6ExfPHEB27dHxR5q8+MJo/\n",
"b2yx95fRxY1i5fxz8r+X50K2nNclnkUIv3Pc/qvvGD2bAMQ6YWUHc7MI/jHa1zYzPp37OEon7JjO\n",
"0ITcOQOE5u8pjd+CYf6ONEwfmT1dkuUDnKZv//5qyfElN5ugxuOAY7izn410tcnmmQhJvTavw2Aw\n",
"8bPBOEyScPH9iML4FRQUFBQUFGw4FMYvjfLgV1BQUFBQULDhUB780hj74Neo15PTY7acDQXPnJ6y\n",
"omtdetO0mengnHFkysDZ/S12HWJFolPCQdm3jFGtHkbKkkaRtZUQG4lRNgbu+2vBa7VMaXj1vpg8\n",
"Uutz6j10tNZp1L73nZ0ahdAUYOt1QfKcJkFu+pZt6yd35LYlTU/Rdb3G6bN69FlFVH6JRrYiPgfi\n",
"mrxa9i43xdvzpmu/9a3vAHBTvVo6ibYKKSNV7fcuYaA6HhXf27rIS67OJadsXJmpcIotvrahVMNf\n",
"xz5rp0n5/Wvo+tmqN+xY4krmhdeDy+o9GpKH4nk3PWzaUJI//Gl1tntuypdQQ/mwVm86mYNLZ5WS\n",
"mKYdISVJHkfCCkXXpRLwRq33ocb6fZtUUi2bZrxITfHpfd2gBUo9/H1Qm51Rx0EMZVweZQVipTUY\n",
"3bZWNgKgbrZtNtIdXKc2VTYC5JM5dIrXjSXGusWf6jVTvINO1Xb33fcggHiKd+/e0LoFcMljtI1i\n",
"Uof2bTe2xO+zn1NCwqQmTvmqbCQl48r9/qkUzEkxvOnyobvPmt74fCgoD35pFMavoKCgoKCgYMNh\n",
"vfn4rReMffBr1xte+ZlR4urGyPUB4ydmnrbM1BirhbCgNCO4dHkrClU1SvdZwzgqTH9vKkqtWzYq\n",
"XNpIxuyzyYQNE8D0/S+RTslDq0lEmUquUWikS3aQx9mtxaacPFaygDnLhYNh/HJIsRrjWDs2VA3h\n",
"caaOKbICsQbPofh6KjCyNtG5sTaYa6aj87bZt5ql+uuU8RtXJL36OxReu6SOdvA++wHZpOVlV7qL\n",
"+203w/tNGfdmJvL21/Eetkw479fh2o2iM82mZU20VJ4uAWCuaUoUtnSb0EiY15tMn8/4qaktkZph\n",
"AEZbQuWWy5kyeIBjsnIzCmoGrNcOAPpSOrNhWBNlid2YUi392RudgckJ693Y4vZdlwQ0fi9nJbqD\n",
"yRjJUd9nX69CCb/Ug0BdmSz5XdJ7yY0p8axBjumzhs2S1NHy2uO7u9JJHLmkDo4xgBtfuHRWLOZ6\n",
"NMKxw08MI/ge90HWkMwfx6xmLd0+gGvfaPyRhEE+S/Q9Zs9P1Gtn2NeVYrWSRDYaCuNXUFBQUFBQ\n",
"sOGwkkDj+wljH/ymGg37JM5oBshrbKjL0ZI9vumuK+AtVgtWczN5JKf6Gy20TvYkVfatN+ZrIk2H\n",
"Fy7y2Bt9ZZKEPbDfFepnABexKmvVkAi0XQ/ZGV+fNq68WhSle/pAQ5ba41ANhz0H2fUkKfIHww7m\n",
"mMVRr2sR8zqO6WM/dW1oo/NmaNvCJSPrb+9mOaSY8YuZvrRhs1ok+FBtnxZU5/tTU2T8nMaPUfr8\n",
"wmxwvmp34ixTQobeX+cKq5t7x96fq1M4PQWf8ZuTQvazrXAZrCPzF7GDoY3GstFW+iypY/wMG9cP\n",
"S+b5Y4X/OixzNZrxWzR6rTTTHb7OstXmGnXr/eCcqs9Uy9YgvHZask11ab62qh31iVDTzW1TGkN3\n",
"LmacAdswzZ6lEBlIZxjQSQyU7euM9cioso/jmD29h6aDMcQwaRmdsJZwJHv3Tc+EeRzDx1kFWkVx\n",
"jAF8lq7q32T6CM6AqTmzz2qTBVT2UE2g4xKfcVtyqeONex3b7DQ87bb/rHEoKBq/NArjV1BQUFBQ\n",
"ULDhUB780hjP+DWbEXsCuKhzSiLtqUx2k/8Ez6f/pkRaS6LDGYxgAOPybmT4wqhcC68Hn8saBldL\n",
"ZZP8TDBGLn6moQ9+plsPI/FRpZJy0XlNGMcU40fWVPVALkqPj9Gau4rZsmKSm2c8Sxdun8oE09ea\n",
"NabmxEAcrauRb9QPm/F1c4xftY7Zug/u3g0gjrj1NRBr+nKMH9klv0+P0/Yp08TInBnC1f6rSJ89\n",
"1GXbh0tl4FvePd0y7HXP9K+BYa+70rfWAnOtdpRdTW0l9VC+2a2yslpOj/vgEZMdJXsBxLq/XFF6\n",
"1Qn7jB+ZFGX+7HeMKEofjzMhW8LZFGtCbMzZg3KD3GaQ/p4ou13GC38dmb+G1WGFZtipcXCcDtjq\n",
"qGVsSWXkEqpXzsGfxsu5KjTZA6Isf0+vLmXlyNppKUf2T74/7TGvkROAlHnk+HDft6oxRVm91DrO\n",
"LLjXoUkzxxbAjS/U4w1Nn6mZ85yaMscs2j6/ZJvqkDmm8P6wOmKzL8sIJ9pSZ2DYl/i8oMbi/jog\n",
"ZLUPBeVVZgebAAAgAElEQVTBL43C+BUUFBQUFBRsOJTkjjQm0vhpGRog1tDokvoHy7j43leMpKTY\n",
"vMtEIisyuabIaftyy5it0Ag/Kj8nmg6ftcyVF+NnbEH1Zphlm2MVgnOIltX76sXmf1+ciTaagfM/\n",
"Q+S0Nv3RgXdyX/lz4dKP+JHcRpm+VIa4Mnz2WjXDa5bTgAEuW5dRuWppVNOn2/nrlPFj1Ly8XEXL\n",
"w0TJPo3Kqe2LyyxV76v2pvqeXrDM6ZLcvRz7GU43Mr6B9XTZq9XEfLttGa5pYUvmWyHzB7iC9o7p\n",
"S+szD+wPr4fvfchro1mLXKouOO0nGs40sN9Pwp7HMwqGcTLtMByGswm8/7sNLzOZ5cwyLFluXPAz\n",
"g3OMXuTbNoFej8gdT2ocVB1yjgEkUi4HbpaE0zYm29mMMw2E5zBqDHHMc0teM1M31JUCTnPKfode\n",
"dZ4PPhgyfBxDJmH8dIaBY8z+/XFfprZPyz86z89W8D7HnJanm52bC3WwHEv4mp+dNjMSLlPX60s1\n",
"/c0Mx+POgF6secavjhpmVkvjV5I7kiiMX0FBQUFBQcGGQ/HxS2Psg99MsxVFRNX60KdI3fV1GWQE\n",
"M+PXRAX7F6uo3DF+kzOAucy7HPz3axkdTDOKWvKMh828ZWTDYuy2aDg/W22fYvw0gs5loKUi7nHa\n",
"OsUoH71clD5pZYHUsQ5ZhUTbOIgS0/tSpk9ZLH9drCkNo3btrx0vu3OXZOTmsuhyzJ//tzJLyvil\n",
"QJ1Yt2v0L6LtU6bPReS+j18YlbfpE8Y2kwo72qYA0DVVYJjNS/RMtt1aMn6b2k7j5wrZm+oGht1j\n",
"EfvqvXawjlVV6JfG68vropmKgGM0dLwZh9BPNNT/NcR/LMdWAfGMAjVj6utHzd3UIBxTgPje1e/R\n",
"+83NasTHkavuMgo6NtgqQ8Ow6kc0pnivyfTFFZTS407q+Cyzw/5M1lbOITUj0rRavvSYMSu/cZqp\n",
"669jf+OYkcvUVf1eahsdZ3SM8e9/1cVrv5yeNhm5ZrAl00em0N+fZvHq/aFMnz9rwFlBjittmS3r\n",
"NcPfcN8b2HeX8DP4DwVF45dGYfwKCgoKCgoKNhzKg18aYx/85lqtKMsMSNXRVI1f3nXfzvdLhKFa\n",
"gsEgHc2moJF2yrev2mdKYxVq+2zdRXpiJbLLbLYSMyEZtQ7jqBxYoQdVRuu2EgwzUXMvUTmAx26r\n",
"fTDLN8pITHyP6gItWylsqj2HmD1qaFSONFuh9XaBletxWMuSmXFAPls3x/zxs6MYP2X61JPP14l1\n",
"u0b3Mmib90IPSmbiucy9UM8H+Jl31ffOzk0D8DLnhcVuN0KWAwB6A8M4ChPeWgHje7CYb7UjVnZT\n",
"O2T6fMaPdU253GzeM5JafDfSXIYVVADXVppx7cYM3iuhF2jAuGf0f7mM1JQ+l/2Z9yP7P8ddN6aM\n",
"vw65GtWa3e2PKZotH2XmRjWF3Xs63pE17tgqTKaPmu5PzZ2vGx7ITIOroZ5mCVMzH7YWMP0DM5Uf\n",
"UmOq6l/jMYSZumF2+ZT32zJOw8cxJMcAAsB3vkM2MBx3mM27uJiuAgTktX2cLdD1OqYATuuqmntd\n",
"2vFYtKFA7Buq2j6OMUTqN6VeCzOmDwUluSONwvgVFBQUFBQUbDiU5I40JtD4OR+/lFP5rPoXydIy\n",
"gJ7Gr2kuxgHxC1JtgTrrp7zPFLn1yW2ZiSusCHUHQ8ks8v2KGOlO9cMsJce0jf5OH6lawKnXKUQa\n",
"mwyLx+PtePWQua5mwnF+X8ewU7xpRmXZRcyG1fpQ21etbpqmqyeYEB5zzFaEEWVK4xdr+kYzfdTW\n",
"+GzdpEwfP6t+WoBjlJhxR+1MqjYvkK73qq8ZlSsTnqo76zJTw7a0mj51zpclALQbrDJhPPBq+aoT\n",
"q41Nbcf4aTbvEVOh1g9wDB91VmRfyKDEFVTyWb2xTyiZv/C6OL/FWOPnXte9PXjrRT8M+D5xrJBS\n",
"rdfxdlTFlPw9E7LkyviFXnzhvghl+NwY4vU7c2zL/aqf04u1UevJPk1b0ykgcU78PjJ9Oa1fsu7v\n",
"gPpEzlKM1qWGteM5voS+fapT1980n63LMX3jlrt3O2cAp/9La/ty9XiBuA9zDLH1dTMOGv645NwE\n",
"BrI016UfXjN1wQBSY3Wo8dMqUX7f9sesuaLxW1MUxq+goKCgoKBgw2G9Pfhdf/31uPHGG3Hvvffi\n",
"jDPOwG/8xm8kt7vxxhtx/fXX4/7778fs7CzOOOMMvOAFLxibvDopyoNfQUFBQUFBwYbDetP4bdmy\n",
"BWeffTZuu+02dDqd7HadTgf//b//dzz60Y/G7t278da3vhXXXXcdnvOc56zKcazIzsW3ZNGkjfG2\n",
"Lu6znHbLUdexoWqq7A9F1ePOIIRPiTcNtd810wO0vBggnOKh9UG3HtsoDFqjBdc6LZEyHY0KiWd0\n",
"CYPENPJQkjbURsGJravlct2fpklP8dpp4344taIi7FHnzVNgogiPmeLu8HOj7WxU7N7yEhJaMj2j\n",
"U7/sW4uLYQm1VGIGl5zK5Wv9LEXWfskkNVVVQ1WditEi6v62eh/wGqutkX8/2H4gUzhaosuVUgqn\n",
"twCgPwyHg3r/8A2am1pta+GgJdpSdi4LYuCsU7zjpsmAvH2LTr2PQi6JjNDEMX9azO/HANAcMAFn\n",
"tHF9yjA3Z3Lekilevu/PUOdYESsXsWOK6Zdev1vsdc2ymtpdbFTL/d1wvNPp2s4ISyr3/WnT+z73\n",
"FSTZpL9HkUpgUdPhlpQ1VBmJSxBz9z/HjEmXbqzZb/dB6QjHEpUnaOJYqv9qP9Qp3lT505XCTh/X\n",
"w982wG9LJi6Z31jTt4dmjEmZwttksnojWwp1pVhvPn6nnXYaAODuu+/Grl27stv95E/+pP17y5Yt\n",
"eMpTnoI777xz1Y6jMH4FBQUFBQUFGw4bJbnj85//PB75yEeu2v4mSu7QNHeuB3wRvUn2EAEsP+Ob\n",
"TbJguqalU8TOJA9l/FaSuDEJosLljD7MaZIl6Zn1Uw0XnYwzTHUMH8LvSBQ453vjTi9lAh3ZKFBs\n",
"bSLwZROlMzJve8JsRulj7RtslJiPFscxf7Xhyq+d2rmkyk21NUo3/W1g2DFlehYXY+ZHt9H+mVuG\n",
"VgjdYBmXIazahwaqfl9ezShc96lMc0PE/Y0g2SBMVFIbobXUy8y3256NS9qcecFL7mBSh0vECRNy\n",
"tIQer7tvq5OzwOgbppNt6MpBhtYt4XtpO5fYHN59dkj2DUzAGZ3EoCxe9Rka5YbMt66HMMJkk6u3\n",
"0mPZfMsY7beN6fmAY4nr9/tNfz9glnvN9FVDztslbpjxquH6KxnEXP/KJ3d422QSQcYxf/7f1l7H\n",
"ln0MCw1wTOEMAJepdbmlsnipZCM1f+c4o6xdetwILYjsOUrfZcm20Iy8nlmOvu9TFkVxudPwWBuD\n",
"eJ/+Z1atZNs6m+o9GNxwww245557snrAg0Fh/AoKCgoKCgo2HB6KB7+dO3fav3fs2IEdO3Yc9L5u\n",
"ueUWvPvd78ZrX/tazM/Pr8bhAZjgwW+q0Yh0U0DeuDkybDZRCSMdwEXfzuQ2becSmy2HMV6FtB4n\n",
"J+oM92n0MNyWtgoDWpGYCCTBdCmT4hgVo51ilEjtXSLSJvuwHEVyaY0PGQlfg8RofM6wI/yk1dyY\n",
"Ja/d/p5jXt2xV69z1jAu0qbmxmOrMixgVGZpTBmmYFtlT6M29jROwqSS4ehIWTO1DArLnaVthHLL\n",
"1HVSzd5KWLxcFE520OrEGumIXP9OfkemhJevF+tbw+5G9B5wcEbik2KTx/jRxmW+HZoz+yWyFs14\n",
"oia3yvRNootSrKTsoxrHZz8jrJ2PhlrCRAxfyGpPB+UvQzaK571nqWJAlZ1OWQGpcTX729RUdT1o\n",
"KzQ7a67L/Iz97MxM9fc+cxw8F56S2kuR3SN7CLjxtzth/xpVdnLcbZcycFaLG9XFst17HTNeL4e/\n",
"W6l1uSXHfL0e/t/DYTjTlT2XBBOnvxE0cHavq2vKMpGNhv9b0kzuw41HaT1rij1V3WTP6lYNI12P\n",
"z63d8Bi/+veugfO55567Kvu59dZb8fa3vx2vfvWrV3WaFyiMX0FBQUFBQcEGxHqb6h0MBuj1ehgM\n",
"BhgMBuh2u2g0GtHD9B133IE/+7M/wytf+Uo86lGPWvXjmIDxa0ZlsQBgppVm+BiNWpPmpdg4VUtO\n",
"5Zg+jXhGBeJOYzN5mq/LTqpzRbWPXLmfRJTIffBclgyzsCejW/SZJrJ/WgQ7Pm/DAEjUVv1t2Nip\n",
"KiqfM6W6GJVPTRu2oEsdYf5GsJm3kincrLPMkikhNcizJqrDWQ3ksp+BPPOqbTmqbykrq4xejoH1\n",
"QXau32d0rBobLg0j7F1DXleNwnV9HImP15pFTsI8nkSx+t6AmXjmo8KspNiq1cJcq4VZKYlFhm/W\n",
"LHueplKNuJkRqUyfOgb4DIsyqZMyLH6767hjxx9mzCNs54E3a6FsRDOTocuyV5xF8LNJH9y/Nzhf\n",
"vqeZ6Kqj1hKCPtg3ObbMzk6bpcmuXpiz2x5xRDX9tMUs9ZzI9NE4nkbPy545NvWI1CdnZ2t0hW8k\n",
"P8JkPoWQpUovdTbhQC/UifptqOu45HEMh/EsAeBYfsBnXM33Ztg7qyNNFDTQ3whla/lal/5nWlbb\n",
"mWYAiUlmbdTQObedv81Uo4GZ2ipp/NZZcsd73/teXHvttfb1xz/+cZxzzjk488wzceGFF+Kyyy7D\n",
"UUcdhWuvvRaLi4t44xvfaLc9+eST8epXv3pVjqMwfgUFBQUFBQUbDuvNzuXcc8/NTgVfffXV9u/X\n",
"ve51a3ocE2n8WDB5KijZxnVa3ib0OtIMpdS6OAMyjIpcRO6Vd6mnIwj9jOogQqaH2cLV6xyjoYwQ\n",
"AOzrhNohy/iNyQRNZXEp85dj/DQSB2Kmb//+qeB7Nm2aBQBsnnUZkdH5CcPXMWXo2o2w3Fu3H+oY\n",
"q2MNs/bGYSXlv/SmTZVqypabYqk66UujWB1lzTTS5ZKMXMsrK6QaPxeVp8t+pVjbXDSuy5ZkWwJO\n",
"j6W6HM12tAXuZQn4zLc51lqY3buWjN9Ms2U1frNS9rFtrst3Pd/EnJZPs7aV4RpV9lEZDS3RNkpb\n",
"qSyVdjO+72f1IqNdpaZ6WrwoH9wXehX6f7OsIJlPLVmXa4/wfEOmif2Nswdc+nptV/au6jRbtiwA\n",
"cAyX+olaxs/7/iXzd7PeM0uj+TNjy3hVpsN4pm/Ue+H4orMIsa9s/FuSg73+0RgSa+x8Fs6HevIF\n",
"x55h/Mj0zcxUvw9zczPBctb7XeDf/C3hbwuPh8fH3wmdIQqOJ1NKsC0/276rADV+M80WplaJk1pv\n",
"U73rBYXxKygoKCgoKNhwWG+VO9YLxj74TTedxs/PJmuLt5/69VHTlvI8y/kT5TLuyNr4LJ9G2pN6\n",
"DqWQ03BpJi7PyT+H2F09ZCD4OsX45TLulKVSjZfP9GimHSM53Scj4U1ehMd11NbY6LxJh36TgSbZ\n",
"bvWhx7wmKpKMwqjtUq76wMFlk2ommlsf67Q0+tZ2brertpyeznMP1Ph1OtVn/ezt1HY+u8SI2kXl\n",
"1TVy2qpp2S6lzwlZwFz2tGZhj/Iz0/WNNRxEp5vNrDPAgf1xtRWtZqAejOM8QQGfHc14vUXeZ3mN\n",
"n8/cjILf3o4FNExfRstHPaN6FfrrWLlEfQxzlUtS/ZN9k0w2x5ZNm6oxhdo+f/ZGxyq22fxC9Zkl\n",
"8RHlzJDvBUimp9ELdcjR0lYOWjl0TPF/Jib1q1Q/2VFaT44pToNdnTf7I+/d4TA+G+6DfWpqyjBt\n",
"4gnqf5a6QG6rGj/+LmzePCtLp9dUFpDMn2P8zDlIlaiVaP3qw/A+8SsH+X7B7Yxbx0pRGL80CuNX\n",
"UFBQUFBQsOFQHvzSGPvg16jVnY+UxwQoC0iWINa+xZ5HeX+0dPSYew3EWj7VqXCZitYVms2pTF+K\n",
"rXN1G9PampwWyd+H6m7YHso4MIok4wM4Noj7PeKIXrAvQjUmgMuWdIxfyPQtmbq+1Pox0usOYtaC\n",
"zN9KNHxriZxeT1k8AJiZGa2xJHLaPwBYXmaGOq9lHJVXxxVG5v4xMdLmNVVt1czMlPlsPiOPDAOv\n",
"aX9F0bk9ymA9mb5cZt5qYLrRtHphjinqTZdmy9WvcbRTgI+B7cfheeX6Tsr7TPtCT9pdGVZ/6qkp\n",
"tafJ9LmxJRxTyOaR3QOAXbv2BOu43L37QLAPbcPU7Ir2TTLQZIdGfZbjsPZl6jQPmLGGlT78uu/8\n",
"fWH/ahmNccf4hvZqUtljhHMA21crKdn3R8wejJsWzGZwI77/OEZzTMnNAPhMsWorlZ1141OeJWTf\n",
"1GvIWQSytgsLs8EScOwft3HjUZgRvNv8xvP3oueNcTq+1KIZoep99U4E/NnDJprDVWL81llW73pB\n",
"YfwKCgoKCgoKNhwK45fG2Ae/VqPuHOS9SJd/kwXUDN1YtxY7lFMfMs4nLeWOrzoLZfp0PSOrMCNv\n",
"tJaDGjh3TnFmstZgZHTOSgLqN3bAy0yMa8T2zPeG7aGsgs/0zM2FzIe2pXrCUWsCAFu3bq7WMdIi\n",
"s9ELI3Bm4DWs1strQ6nmYf0NJSqPahn7WqdMVDaJtk8zy7jM6fV4Lf02dP2QGp7RLLLqZ4C4v69E\n",
"4zcp40etFZepjDzuizVTHfMX9unhiLrLvC00m9e/7quNVr1uq65wTFmyVTdC30/AseT6XuzXOL7e\n",
"tzJ8OT/F1D3E9mYf6ZCV0So4rH+c+CGylovWEzSs2coxwzF/++1nyfDt2rU3eO00f/vNPkItZFir\n",
"dxCcHzV+ZIlGMX25LFL22SO2bKqOXdwf2g3H3lqNn/gYckn/0OEIpo99VLP8c7rhlLY1B15D7Q++\n",
"u4Jm5LJ9dfZAxyWfxWbb6ezBuLrfQJ7xcz5+6TGFPoz+33SCcMxf9dklqTTVFXYbGF+ZSccSX+Pn\n",
"njPqyVq+B4OS3JFGYfwKCgoKCgoKNhzWm4/fekF58CsoKCgoKCjYcChTvWmMffCr12rWsLfpTfW4\n",
"8kLVcn83XRqJlHdYFDyc/tD1OfsEf3osNw0zbjm6pBttY9SwMzZw1qQVnbZVYbZOAQPA4mIouM5N\n",
"9aro2p9iVLsWpfx1esqfHqTZ87TZLwXXrUZ1TpxyIx2/3A+vOeCmYQbmmOmMkbNPSNm/aOH0cVO8\n",
"vmCef1Ng3JNpKyZCjDJY1Sk+Z40Strfa7/jTNLmEpdx3+QkCvDZq1KzTMrklEE/HMEHHCrAHYXJH\n",
"aiomZ2uRmy5bTTTrLomM/WtUm8ZlDtNTu7EZemy+TCmJjhWuP7RkGU/xdaS92f6uvXme3sFIc2p5\n",
"QS51bPETxHRcyU31qq2LP23u2qM6INffqz6lU4spKyJn/TIbfB+nD2ekCICf3MG/2xx3THJHs2ba\n",
"wRiJD+piRu6PISJLyBkI6/ujME4+4o/D46Z22U/Y/rxfffmQky2kp3i5b0pTfAmUylJypvD8XiZ1\n",
"0MIFcNeKSR4cX9pmfGJSB024bZ/3pnp1nKGkRMd4vS7+381aHfVVkpWU5I40CuNXUFBQUFBQsOFQ\n",
"GL80xj74NWt1y+758+XaoJoIwch7XAkdH7EJppZKct8Zi/ebsgyj87okHfh/2+jQfk/InqXgoq8w\n",
"8UPF5irQJssH5KNwTQxgpL20FCYo+McRJyCEtgJLS3G5pfn56nuPYGKA2QftNJYa1fHQWJWMTLfu\n",
"JeoMGEmHzMbAMn8w74vhdoLxOxhmSaNyJjE0G2RJqzZzjGjIJgMxo5Nj+OJrnLco0uicUHbJ/5ul\n",
"2HjNcoJsLvl+dWLV+Swbo1zH/IVMaG8Qtpd/PzA6zzN/WDM06vWxTJ/f72OmL8fw1bKvleGLmb1w\n",
"DFEjWwC27Fq3FzJ9HWE+LAZ176PVNi1jXcF3lPnja036qNZVfZHjCscZMoBq6JwqoUnYBBVJlHHG\n",
"zjHTxe9ZWKjGFc50KEs5JbMKU36ioLULCxlfJhCqJU4qUYaJIGSNWpJEoGOL38ejco+SkNMzy7Yw\n",
"fX4iHa+R3t/cNsfm+cxrrr9zDBn1W8q20O/XvutM4cMkHMAlc5C1nTHb7DWzeTTd5lJnEwCgPya5\n",
"g0iN9S6pp446VofxK8kdaRTGr6CgoKCgoGDDoTB+aUyk8dMi4tXfaR2cWmMQozVW4dP9OPPd1Lqs\n",
"Dsfsi3qEfuI4tIB6Thc4iRVMLmpL6cI0Ks7ZJjiNX76wOiN9njcjOi1an9KU0BCVEXZDomen8TOR\n",
"v1c6r1cPo+NBLYz4tPC5S+f3I73QxmEcA+hfwqFl+owVhtEF8Zry2J3dScgI+23CqFjte5QB0agd\n",
"SJmshmbgRIq9dhYMaYYpF6XXPdZQo/FIh2Puy/4wrcFJIafLWQs0azV7zQZ91euNL9IV2zvxWMP2\n",
"TjGt8WxB2P7Uiep6IG5vy7SyH1DjZNpw6JWH4yGy7063aA0TzkAQqT6VG2doBZKzhhml8dP2dkw4\n",
"zerdrAFnEGhknxvTFmZNG9bD2QPA3aNcturhciBmvimNn45VHFN036r18/czjvmrSxm2wcD1A2cb\n",
"FvaRcex16lrqbIEdW0fcB1rCNGdnldMRA2584bhCpo+m2wfMkn19WfSsgGP/OK5EvwMye5DUetdq\n",
"kf71YFEe/NIojF9BQUFBQUHBhkNJ7khj7INfzYvEU8hpaxSjjFMVGq0wikqZ3jL64jY2GjPbRVmN\n",
"fkaoRCPDehhZKgOQyipWNlDPM5dtCLhsuXw0mDadbTZ9I+mcliQsXaWGt9Xf4TpqWFg6qiXF0x0z\n",
"5xfWDlkJtnNDLq2yev4+cjqclWTeUYdTN9+/DFO6zmiqGqKBnPcYv8GginQ1E10zR3PvV/tIa1zH\n",
"lX+r/g6PTbV+ao7bM314f8/1A8s82WXIPPWtxk+ZP++YxjT3WutlnJHxSnTB4f3XkLJyeg/5TK9q\n",
"9nKsiGouOx7DsSRMH9kQMqw6xvQS2if2zalByM6oGf0oZwKOJfp6Er0k+6q2JceZuBye63f8m+OM\n",
"atk47rgxhebw/hgSZvpONcLZGTVuTunHOK64fYW6QVcWLhyHAG/8gTJ+1ZL3DK+7mnZX60Jj+HHj\n",
"QPr3IGT0JmH6FCtl/uredSCDx7KrOouw2OsG23Xsb6t3DhOUhgyO1zfy99jA1Rppio9fGoXxKygo\n",
"KCgoKNhwKMkdaazowS/lm4SMRij24vM8AJuNkZ/R6ES9kIA4WmdUztjIRiVW28fsxvh4eS79uolW\n",
"JPNM2TTAaVeUDcz5C+YYwZWA/n6paN35SIXbaMm8VGYkl+02NX7OTwnwsuzqYfF0/z0ix9JR06f7\n",
"qtaF0bpuq03mZ7cNVOPH46BOxlzT2kDYxERWn/XYmzb9rtYKttVzTbVlTpcziY8g+476x5FxWDbL\n",
"JdHYAF40LtmlzOrtCPOXOhyuU7b2cGAUu5u6d+L7K2Q4CBKAynxU69JeZ7qkxo8dcTHBtKrWz2r8\n",
"JLu9kWDruK5dD1mjmJGMZx7Uc9D1pXDczekGU8hlSjsddzxroTMbOdY8pfFryTqWirReiOZnqpHL\n",
"lIa7N235SRnDlfnz/eNy2mLbHuY3riuMnN8f2+LFOQ6TMmKp41kJ3IxIWLpx/yB2kGAmutXw9YTF\n",
"5vjTC1/7Wb05n9CVnEMdtYnKdU60r/Lgl0Rh/AoKCgoKCgo2HMqDXxoH/eDnstUquEgzjCj5ut/3\n",
"NU2qWQmj0ZwHkR9N6XvK9GmWnWP8Yr2EMjoatcy14mhOMy6Z3Ubmcf/+MHtUveEA523V7YZshGOH\n",
"Qu0Ns3trB+FqnvKV00jetkOGnWvWjRbQu8bMuLMaJs1izTjopzQ+qv/jtmREUkJdW7lD2AB+X3dy\n",
"eYyFTg8oS5jKSGuIPorvtTOsZQq87PTC2tup+gqZD2pp+HrJY/y0YsRytmIHgtep88zhcA2iOh6k\n",
"2Cpl1gNvvRGfJcsH+Nq9KfN6yrwOs6jn5qrXvB77PY0bMx1V/6TtTrQ9DaL6svG+m5oKv59LrZLh\n",
"r8stNYvd6nm92ROycTr+5sbnUdCqTKp1s7MJvj5OdH9k6XqD8OeJ48EoHz+OJdP00TMVQ/jafYfb\n",
"N4+pIfcuwd8O/tgNeuPZOo5L/dz9h5gZG2bYMkXqPsxNaUbVsTIMIOD6rPWi7IevdRxSvbC/f2W6\n",
"o+NNjOVrMb6U5I40CuNXUFBQUFBQsOGwHhm/ffv24fLLL8ftt9+OhYUFPP/5z8dTnvKU5Lbvfe97\n",
"8dGPfhSLi4v4wR/8QbzkJS/Btm3bDvkYVv3BT9k85/6e1vX5yGmclDXz/2ZWUi7zKOerBcTsEDVt\n",
"LlpH8L7veaSebnyPjN7cXNrPyj+HlB8c4CJrreDBdvF1TLHGJ60lHKUttJmPys5ZBi6MpnueF9mg\n",
"wegvZPQUyuaN0vgpAxi57idu5iiCtsyWeSnRdFDBJRF9j8IonWBDGD5lk1PHnstWtKyJ6FOtntHL\n",
"Lu3baD3U3biofGXnmDq+tYarZ5tm60J9ntGBdcPZAbZvxKbJLALgmD3ek2T2HNNWvY6zG53Wl+PN\n",
"/u5kjF+qrqk9RmZimnFwkxlTWFGBswp+vW/WXGVlDvr0cVtW51HmzR8PVH8a+xtW46+Oz9W6ydhA\n",
"jmXNNu/xmPHX7F62j84mpBi/diPcL/dBpo+1gmea5jfFm3FgxnFzxPgCuHuMd11YBapaOiaN96i+\n",
"lhkor+3V+y53r6bux1RFkty2/r6Hid/DgYw7/eh1vu73uIR8PZ7V0vLlsB6TO6688kq0Wi1ceeWV\n",
"uOeee/DmN78ZJ5xwQvRA9+lPfxof/vCH8YY3vAFbt27FP/zDP+DP//zP8Za3vOWQj2F16qIUFBQU\n",
"FBQUFKwj1GuH9/84LC0t4ZZbbsHznvc8TE1NYfv27Tj11FNx0003Rdvee++92L59O4455hjU63X8\n",
"+I//OL7+9a+vTrusyl4KCgoKCgoKCtYRWHnscP0fh/vvvx+NRgPHHnusXXfCCSfg3nvvjbZ93OMe\n",
"h3VIeJsAACAASURBVC9+8Yu4//770ev18LGPfQw/8iM/sirtMkHJtjHvR0JsNQGNp3hdwscgeK2i\n",
"4pxgGQCaRqStU7w6HZMrWQXEU72cpuRnOLWmRcIBN8WilijOKDk0NlXzXyBfzovGqToFnBKyq4h7\n",
"nJ2MJt8E3y9THU1JrnDTtP4+muaztK8I25TQUkn+PuIkknDqN1UyUJGb0tWpF06tpPqBTs+5qZf0\n",
"d/r3Rk2mdLVPWTmB2Bz570UGstLv1LomNU006RRv7jqF53f4pkn84xuX7AUAvV51D6gcQhOkRpV9\n",
"1CldfW3tW5jU0TNlz7ouQYtTvPulnFVX+hLb0rfg6Zh7NWd9wSnITZuqsYbTuPv3z9ttFxeXzXvG\n",
"dHeRpRlDuw7arrBN/XbIjTNqZ6NjDQC0WqHZdM6qS8/N71u8J6bUxmVo9j0Ip891X9U+wsQQjh0z\n",
"NrkjtHfxkzvsZzh22nsW5jjC66OSC//Y1EZM7ZXU/Ngfh3RsWslUb0OOOTf+jNoHkRsrclPRqfFR\n",
"j0PLPh62RLF1ltyxtLSEmZmZYN309DSWlpaibU866SQ87WlPw2//9m+jXq9j69ateM1rXrMqx1GS\n",
"OwoKCgoKCgo2HB6K5I6dO3fav3fs2IEdO3bY19PT01hcXAy2P3DgAKanp6P9XH/99bjjjjtw+eWX\n",
"44gjjsBNN92EP/zDP8Qf//Efo92ezC8yhxU9+KVEnHVh6zTCTpWbYTSe+4walqqRKTCe6cuVl+kH\n",
"5yCiZjJN/eo4+iLMDbZvV+zAEUfMB+epxqVxKa+EjYYwG0wE0UicNi60gQHy5aWc+XVo+hqWCkvf\n",
"FBqVMQK2RdMTiTqaoKDFuJXx85NAbAF1MY7OJUr4yLFiZPqczUnayLhaF9oWMPK2DFvCAkgRR9hI\n",
"nq97HbMVk0bDaVF1uG6YMVbX4w2LpCNa569fa9jSXBnWOmW+zP6uswiaADA1FY4pgGP21MaF99Lu\n",
"bOkql9wxKeNH+KXCusauRBmemjDcWw1DsGXLAoDQSH55uWOW4UwDzd6tjUqD7VB9JxlCIE78UMaP\n",
"7TI3J4wo/PEmHGdy5eX03IDYuHlKbFzqfc4ApMeW5D7UyLkZvm7732+ZvtH3n2XkEslVanbsDL37\n",
"5rUkHcr7/n57w5jR95G6T3OzM7EZfp4JPNj7PPW5XPlNPfZ0UYjVw0OR3HHuuedm3zvuuOPQ7/fx\n",
"wAMP2One//zP/8QjH/nIaNtbb70VZ5xxBrZs2QIAOPPMM/G3f/u3+PrXv44TTzzxkI6xaPwKCgoK\n",
"CgoKNhzWm8Zvenoap512Gq655hosLy/jP/7jP/CZz3wGT33qU6Ntjz/+eHzyk5/E7t27MRgMcNNN\n",
"N6Hf7wf6wIPFQU/1ql1CzPSFhsF+5JfXtoVaHtWWLKVKVNmIajQD2E3oRDSiUm2Zlr1KaS42R8xf\n",
"aGAamSQnGDctSaeMX06vBMRRuZq9KtPhfzZr/YJQh6YGp61EIDpOj+IYL3POHmsYRauZaDH5XRlD\n",
"VNXBdfqhxoaRefXeZEal2ud91ORYNeImE6HtAMRaRi1Vp/qYZDsY5Ji+3KCU0inm2n2t9TIROybj\n",
"AXV9QHyfsS+PG1t8nTCZPrVx0bGDbN4BYff8v3Xc0T5kz8lr8KV6OBuR0/rx/ti6ec60g6cTFEuo\n",
"XB/V89+/3zF+XXMO1AGSHaR+j0zfpk1z5rXTKOl4M2qGITieoGRaOKNAto4fJdMXzyb49xCN4TOM\n",
"n+j4fMZPZxoINWG26+0Y49qa11v7jHvdCV5riT9/H8osumIJ4bic0kla5pOl6eqhXtSym/VwXK7W\n",
"hbMTkzL/IWuY1vRZO6tIC53ez2rhoZjqHYfzzjsPl19+Oc477zwsLCzg/PPPx7Zt2/Dggw/iwgsv\n",
"xGWXXYajjjoKZ599Nq666ipcdNFF6HQ6OO644/A7v/M7mJ2dPeRjKBq/goKCgoKCgg2H9fjgNz8/\n",
"j4svvjhav3XrVlx99dX29dTUFC644II1OYZDfvAbSMTtskolEyrQq4UaMdWFqH7HZkh50dFShunT\n",
"SGtZCtp3PNZQ2RGNRpb7TfOZmPFjFMYI+whTZmnLlk1IIVX2SDWN+/aFZd0YzY9i/NTcWnVLcaF3\n",
"x5rkdDj2mEWXwYh46Bk412vMTNTPhvvQqLrlZRfHmj7zvRmGydf12ah4EOohVZ9H1laz64BYb8M+\n",
"o1l2mlUYnm8Y4WppukYvZCT8rOZ2Y5D+jETeej0mMT8dp9vx9zFOB7SWg+hgGGdX67jg6/OU2eP4\n",
"4pckBBybzn1wFgFwTB/N13umXzl2Rtm8cOn/fUDGnSXTh1Qf6vfplmSx6nik9wGv5datm6PzTmmH\n",
"/fO2usXdB8w5uyzC5WVzrH2WbgvHGZ1N2LTJMX5sOzfupF0G1E3A75cNmQVQ4/xWPd0uKZ2wNYHO\n",
"aPoc4+fG0JrcV+oQwBzunowx/njA3wgdQ9iXLFscGX57ek0WBRiE7G2OCU7rJKUdzPn2abRv+qNt\n",
"F/+nmKdjdxvOTuTGAX8MyWn7VGvIz6ScGuq1GrBKY03RsqVRGL+CgoKCgoKCDYf1WLljPWC8jx+c\n",
"aHE4IotQS7QNhyGrN6pkGD/L6JBRIwMQmzHlsYaMlJayWVTp7N6ux/T0NBqXSHK5EWq+Qs+ltO6P\n",
"zJ8flQOeXs7TtpHZVNZOGb9cSbfqs2Hms8vAS2v+fNaE7c5jiyJLMqA1ZvMiQsrjMPis1QeGWhM/\n",
"0mtKBJtjllS/V21sPiPlnfQzXDIy95lfjdLta9OHesJEpXRUNYloeU7dQegrZtlDj3HgsbUlW9pF\n",
"46PbxUeuZJ4itS+Nxm1G9pjrstpgn2rLuOCz1Y4Fr44tLkkW6ldTZR95b9CZgOxMPIakNX9AzOTY\n",
"8Yb+npKxG+jSjHsAxySnKU37o6UYl2OOOSLcRmYWcuMDS7wB+XEml93rl66k3k8zo52rQKj1S3Hm\n",
"HF/cOMO2SmyMtCaPTN60aPxaovVryn06CjrGd2syq+DPPMiswLJoirXvqObP39b2h0zf0bHVP1+O\n",
"N1ON3OxE6Lvq9yUOP3nWLjcD4TN+1TKn8VONc/D9E1yTgtVBYfwKCgoKCgoKNhzWo8ZvPWCCyh2j\n",
"G04Zn7xzu8dwSFQeaXjMdy5HOr1YD6H6rFiPE36262mAOtYhPoyobJZZv1p2bESeZ/xUj6HMn9Mv\n",
"+owfdUdpxi/n5+ezp6oTjKsRhN5kPmvC9uZxxFoSLsn8kQJy56DsV022dYyfYSDkdbVt2rePiDQ3\n",
"fuRNXz7z2e6EzJ/P3pJBZN9YtjqtkOl11xwReMzdQZhdp9nGNuL2dDHdTGTNzzSkPVJZvtlM3DH3\n",
"b1qfU72210OyCdcKg0ylFN4ffl9j31U92qTVgKp9VPtVXbBddtOMX6APjcYds01Gr+W3YbNOVsiw\n",
"ljKWrATHHlt5fbE9HEu6csZPNcXKlvqMH/+m7k99RflZtn8nwXxaLV8jZJR6tfBedtq2cPYAiLV9\n",
"bdG4gay9Ocf9XvUVvTbOZaE6dvbLzmC8Bll1qpwtWurrb1nIBPrvcRwax/j5OulsRrj5/qZlXNPb\n",
"+X87rXs4lqlTQZrxqyX35X5bw9kdn7UNfm9WS+NXHvySKIxfQUFBQUFBwYZDefBLYyLGb1Rkw+hc\n",
"tX7284w0gjA+XbHDMn1S77Ajuonqb8PKZLJ3VbeV8k1SvyR7dPVQhzAlWj/Ad9uvXufqGB4xHTJ/\n",
"PlunkTR1Mqy/Gfv5xbqNXLWTnK9fivGw+syMXk/1a/WE1jOOytMMn/pLAX5tzDHscoI1ce9Vy45h\n",
"UdTratS+GQVbx3xhBTtS5znlnxdnGgpLa+6hfp3f4Wm9kGbJx2XG+Rqf2IMvucto3z6iNhvhubXa\n",
"8Pc9FNYkldVLqG/ouNkEn/FeUm2nZOTqTIOONUCs6XOMH2uFh9V/fOg90hffyKx+dkRfPuaYI4Pz\n",
"JnuljB/r/lZ/V+NNTiepbehX7uD44rJ7075+3NfQY7gIO95ahwjDdNfT/ZDbT3kzD8rw8c7oSEUT\n",
"ra3ug8fYN24O7FM8l665d5frsT6O0MxsnRGyTGBCc06mj797WjFKx9b6wH3/oMYxrFpO6bkhbEuO\n",
"U34FITJ70+w79P6T8Sb2+4uawTF+mTEllZkczCysWlZvefBLoTB+BQUFBQUFBRsOJas3jbEPfn7D\n",
"pRpRtW12Lt9G4jHjp5lnNuNSaiBazVW/F6yv1oVVNZakVmKO6fMzg11kldGpmeMk4+Nr/HKMZ8ZO\n",
"yzGARzqfP62ny8iSEXjOz8+HanpUL6hsos/4qY/fgBUEMjoQnr0fJTZkG83QdY7x4WufvewZLZVW\n",
"e7HfIXqtaY9Vtv3PZAK2TVabjc4le+1gqH/t47kqJQBQt203+ntG6WLUVV+rEqSqf0zqgTjqOHSd\n",
"+ptpZYO1gm3nCfTDk/YZqzEbJGYNZCzhGOHqOw+S7/vrloTB0VmLfkIfanWh5p7oZc5bMYp5Zdtt\n",
"MeNMLjPX1/iNG2dGZUa7/bIKSqj143iUc0EAPBZKZhSULbJefFKFAnDZvDyHA/aczLi/zOoked9D\n",
"dabQmvIcw5q9mK1yDFr6Hhl3TYG8Xtx+1ixyKnrAMZ0Rs2d9DMOxZLrp1X0X70ObGS0egar9TY1l\n",
"Ch1LiFDj5/Y3XPkwnUSZ6k2jMH4FBQUFBQUFGw5rKU/5XkZ58CsoKCgoKCjYcCiMXxqTJXdM0HZW\n",
"IE9BtjVQ5TLxGZni5TRJX1LhORUbmC/LNlw6g95wn9b+xRfTZkS0hJuuDMX9gE/HI/lZd45mKSXe\n",
"AGB+tpoOObodlqjjNAynYLpdlqOKpylyhq06jcx987W/bc6Y2FLvw/B1uE34nqb+qzCYUzE8J/+8\n",
"cnYSKjL3p5qmbJkn00fMtWrUQxuDRmYaFYinLOw5aVH0EdOnOTGzCtJTU0INaTudWtHC87bQemKa\n",
"pCE362qIm1NC7NVGqm+xm+uYAgDttpEn2JJ96elJ9h1b9tGfppXp2U40loSv1Vg32Ickoun38TMp\n",
"q5aOTfgJx6FRkoIcVHJyxHw1tXuMtXuKp3r3768SPbpGcpGzj2Jb+mMIxxWWwqNxPO9R3rMcd0ed\n",
"k+3PdkypluNkI0BsgaXL1LijUBsXe1zmHJjA4u4/L0GtHt7vzshdEyHySWeTJkQ4+ysvMUPGBrbR\n",
"tBhYzzRbZtkMluG6lvmMJHnIeR+KfCYlG/PPd7hKSRkluSONwvgVFBQUFBQUbDiU5I40VlSyLQVr\n",
"sUE1Zi1k/tKRfJh6TsaNES+j5p4me3gJAV3ZJssARvvwxN1SkisyI6YVg0Tk/jlMItr14RMTtJPZ\n",
"1K6i4y1bFgC4iJPR6iTCZE3y0Og1VbKNKfPahso4jGJ81YgzigrNdqPK0FGATYG+GqqqUN+HFZFT\n",
"3G2u7zSTPEyky/J7LJPll0ezUbL5LMup9QzV2bZsdrX9KAPnpgrQha2YtqJq9/25KJzC6ymJ2q3I\n",
"3GcNM2XVNOLV/joJq3Q4pkv8Adr2O44T9g13/1l2IDOj4GYTwkQx//63Mw0y48D7QI27e/LaX9eX\n",
"fej3uX0kkgpGJD4E55pgnsexLjy+ze0q+YK2Uj5rTiZrnH2UltYEXPKGGkVz3ImSWxLjpY4vynzl\n",
"mD4eL+DsaRYXOWZ2gte5WQXAjZ39fiN6zz9vnqNNfvDYslYvvN+VJWtn2LNWImGQ7dGTRBE1uuZx\n",
"APHYMdfimNIKXnM532oHr/1tuQ81w3ZjfdjnRj1c6W/qpOPNYLBKjF958EuiMH4FBQUFBQUFGw7l\n",
"wS+NsQ9+zXot0hykYDVvCJm/1BM+Aypl+vi6L9FxSoPnWCqa7Ybf1xvoPhM6wWG4zmf0/PPtD0Lb\n",
"mdQ2Toch60cY6g6FNeQxz4gJqjJ+o8xHxzF//jmouewoHZKPVLm1pkSDfK1Mn9orjDsv/9x8bZGC\n",
"rMW0iYJ5Th1aFJhoviPFzP11vYExbhXdpjNQzrePZScaYcTPqJxM34w5h9mmY1w0WreRd6uZ3IfT\n",
"UbpOldMFKeIScg5qI/FQw7a/ee1b/9I2py6+D1r2Tft2z2Nz+tGsQTiW8LWas/dTzP+YpY5lPobW\n",
"Lind7tYiKWXj0wk1rFGpQtEWsx1mZl3/oxWLsmPjTLH9v3O2OVp+LKen9uHKPqbN3zmW+IyfG1dC\n",
"po+vObZQ4+ffw1qqTTXGy8vN4DtmjY7RN5B2FijK0odL3uMpM3j282bm98bpqA3j5zGOjuGr1s23\n",
"qmvK2SQulenzGb9Z8950RlPM9s9Zs/jQMpvRfTFiHPK/41BRHvzSKIxfQUFBQUFBwYZDrSR3JLEi\n",
"A+dJEDF/sh4YHxUPJDpWFs9flyuVpmxaKsKIGccw+ujzM/V8dKoMS0OyuhoSHdUCfU64r4FG5WR+\n",
"TETOQuO+BkV1OKmoHEibVat2aRzjM4nZL89bSyNxSaaPGYSpbaLvsGX/YraE7y0thQbWZO/Ias40\n",
"Qz1Xf+i3Q/q8rcFuRgMZbpvWI7lsunRWHRBH65pVx9eqcQqZV9H2kUVSjU2GEfO3PRgd4KFilBbY\n",
"buO/hzRLpn1YmSaf1bdZtBg9luRM2SdBzpTX/17HWlZn2DXl/sh4sURY05SHI6sMOBawLdn0WsJP\n",
"j8ef+bD9zWToch+p+w1wY4y/Py5pmD9ubEm1KZnMyNC8Ft7/ZO1CnXA4o8Dxha91jPHPzZVqS2cz\n",
"28zkJTHHT2jslumi0DOv+9VnujJ2sD18Zp5MPnWhuXKYZPx43fzv51hCho8zC+OYP38fufEmyqBP\n",
"aZ15DRv1YL1qXJP3gz/+rBrjtyq72XAojF9BQUFBQUHBhkOZ6k1jIh8/+/cI2lSjk1HZPMosKLO3\n",
"kog7YjQy266EtYi2NcFhr+aixMbQROf0ADNRGEs1NU3k21ANnF+UOtMphxIVdSUTzM9grJv3lOHp\n",
"2Kix2i7FeMTMavJwvOPNH3fEXtro0HxvL9TW+NH6qGi8OkcyECOYV2E6mZHWtdm91XK2FWsdc1oa\n",
"XqucBtRHpEdqhFG5snd+pD2dYQNtdi+zeaUPBWXvhC3VI7U+j8IE9/xsWns/pvU4a4k6ahE7z/Em\n",
"ee+OuZ+j2YRBeE9V76W3neRYo3UZjd0kPzw6G2E1v9blwGSkm77sexG2DBtIps1m1Utf0eMImU+O\n",
"GaE/pGUP9Rw8ZiyalRGGz7LpI/qQXmctA0kM5Br6/V9L9/F+0NfpMcaM2dQnGpbQekCa1+oNSK0f\n",
"4DF+fTJvFaOm2nN7zjZD19MJ9smWhp/RUo5kBkMPvtHZu5bpM9nddrsEa8ifF573nk6VMa2aT3su\n",
"/m9aRmNuPVitnjqR5c79DpNk4kGhPPilURi/goKCgoKCgg2H9fjgt2/fPlx++eW4/fbbsbCwgOc/\n",
"//l4ylOeMvIzf/iHf4g777wT7373u4MH7YPFRD5+o6BRSb6CRaxtyW6bed6fzAMot/7QO0BSH2j2\n",
"q15gZAC7jdA/cCkRrbvqDlWEpRE2/eQYTacqNuSOVds61HQhuY3uWyPymr9dpllddKjLkAkEXFSu\n",
"GhKXTSjH5V3kep1aHmb6hS77jISVeRil02NkPZXxYktB/fvaWY1fyO6Neo8soUbgSwlN5Dg9FiNu\n",
"zWAMMjTpX4gwGq+vkBFbLUTjwARfr9c30vp65zAuez2q5JLwLVNWTPtQd0DtL+8h74aRrx83A6Cs\n",
"GuBlr7NSiGGNWj2tnGOOfcR4zn1p1vgkPm06O5O7DikM2GYIs1mzvw+Jai1cp9+j7GCu0gvg7qe6\n",
"6JSdfrC6P8n4+Z6ovGc549NthV6QsUOAGWM8naCOMzxE9r+2zPykqm7MiXZPtXzz7fB10+sPBw4s\n",
"y/mG+sjcGOP7OtJzlW1Db0S6SnC9nfny9+mtG67SA9t6TO648sor0Wq1cOWVV+Kee+7Bm9/8Zpxw\n",
"wgnYtm1bcvuPf/zjkf70ULF2NZgKCgoKCgoKCh4iVCVnD9//cVhaWsItt9yC5z3veZiamsL27dtx\n",
"6qmn4qabbkpuf+DAAbz3ve/FC1/4wlVtlxVp/A6ldmQKWu920gg8tU6XWhuVrJWvsSNLZ3WJNX7/\n",
"wUcJkW/WIFz6HmCuJmi6nmNu331Pa5hzTx8Xifvv5drd6lMkIq8P430oXH3PcJmCi8o1Oue+qdOp\n",
"XvnnqjqcZjNk/pjlO/A0ddGxik8aWRL2D9ZsHY6gnGx2ZcbHT1m9qUS0ziWjcHqRuQzFsN7ouPsF\n",
"yPusaZsD+WjcmujnCc/DgoPRGq5kzMp5b5I1UO0bEGfVdush489+YI/Dk1jquKc1oSepjBDpA8ns\n",
"y/jD2uV2lqEfa7dpbemYxdHjUXAcmWzNSRwC2JqDWmYf5hxt1q94lvrrbBtOwFZmz0V0yY75C7V+\n",
"PuO3sDAHwGnm9LxtH+JsgmHJlhO143MzL+xrrPrjs4Vk8KgX3hT59VWvOcawVvMezwtRNYyqk5yk\n",
"ohL/5mc4/irYdmE/MNe/VotcQQ4W622q9/7770ej0cCxxx5r151wwgm48847k9u/613vwk/91E9h\n",
"8+bNq3ochfErKCgoKCgo2HCo1w7v/3FYWlrCzMxMsG56ehpLS0vRtnfffTe+9KUv4ad/+qdXqzks\n",
"JmL8VJ8AxFHJWup/UtmkGgVRMxFVkmDkbaITRrGAY3YIxj61zLmMqo1qo/RcxYQRvkV9u5RqI4bZ\n",
"61Djwc/5GiN7TKP1kil2b9KoXCNyXx4TZYKabVxUPnoJxFG6SkmU+fP1Dr0eGb+u7CtkBVgFI3Wu\n",
"ts+Y5RQzgftpnQ7h90etqhA5+Cvj50XrzHRjpL1HIm+tb5yqN2qPSViRHOMX1GwWKPPXU+ZvjbEa\n",
"Y8kkbKjq8sjK2LFEPTmlLjXgGN6uqbbAzNup6N4yDIdXKzh3nvo9bhkeLzBeg63ehFqlpPo+M/Nh\n",
"LjDHwWbGRy5djUm1lCMPy7I7AKLqKz2QrTOa5kGYka592f+b2tVu11wzYaV0LAnXyTllmb+4cgg1\n",
"bHOcYUB6rGB/WW5ytsfLkB6mtX3sl1rvN6Xxy2X37t9fPVg8+N39AFxt46UE4zdunFF/Q5579Xc4\n",
"rrD9NduX+2w2vd/gNXiEeCgYv507d9q/d+zYgR07dtjX09PTWFxcDLY/cOAApqeng3WDwQBXXnkl\n",
"fvVXf3VVkjkUJau3oKCgoKCgYMNhtUq/rQTnnntu9r3jjjsO/X4fDzzwgJ3u/c///E888pGPDLZb\n",
"XFzEV77yFfzJn/wJABeEXHDBBbjwwguxffv2QzrG8uBXUFBQUFBQsOEwjhE/3JiensZpp52Ga665\n",
"BhdccAHuuecefOYzn8Ef/dEfBdvNzc3h7W9/u3394IMP4vd+7/fwlre8BZs2bTrk45ioZJud6vMo\n",
"/nH2LQeDnLg5ZY7qjEnD15rUwencHq0qPGuQQUMEuGb/qULq/r4BN+3C1HraNXAfWsh6JZRzzsCa\n",
"0zS+uLw3RnE/Smw9blqG0zE6FeM7SNftNCCn0qvXuWmZ1DSNWjE4+5b0uflTD2rQ2myG0zGcYpg1\n",
"x2xtDLxzaPUpB+AUb2jYrKX8iMDWQ6YHtcA5p2KYBOBPsXx372KwTqd4KSrP2d1U5xlOqehUr07B\n",
"6Hb++bgi9WZbe1+unZzjcCGUi5hlZrxxYwgteqp+MeX1XZoeTzXCZAqdaq7XTPKRN1+uBtIuMS2U\n",
"rVAm0LJTfV7fFcPmXGKKwk9U0jHC2vfU7MbB+z50DMmVfdRz9M0p7LiqxsDm+2mcT8sa9uVez00x\n",
"uulJM9WaMRvW7f1tc+D7uWQPwE2d8r5ickXTJv/Q0N1YwvRZQjNfMlETEhsiI5n2bFTU/N1O7e4+\n",
"EBwfLVt0rKnOpxucb86omefoT/Eq1BJHk8oOF9ZbcgcAnHfeebj88stx3nnnYWFhAeeffz62bduG\n",
"Bx98EBdeeCEuu+wyHHXUUUFCx/Jydd02b958eHz8CgoKCgoKCgq+17AeH/zm5+dx8cUXR+u3bt2K\n",
"q6++OvmZY445Btdcc82qHcND+uDnWLEwwtHIuyYRePW3YdysjYJhmkRs3R+a9HJbSigsWeV/T1NM\n",
"mRWBjYMa9opxbzsqnVSL9qHR+aQImNcJt02V3xoXpdNE09l5xNGzE2Ib81PzGTKRLjoPI79Wy3W9\n",
"XFQ+GIQMFOHbOKgtiUbjLjqqIl4WWJ/xolVG0ryGvWaYZDNOhA/ESUVkZbgFrVn2Le8PXgPA8jIZ\n",
"vtC2RZk+2rgkj0VE1E0pzaYMH+8pf7vY7Ja00eEZPKP+N4IdWKl2x1qWJBIj1HSZ9y7tfNyYQsbN\n",
"9VeyL7lEKdvOZtlNMDwKl9xhGJ6mJAp5iUFuXfiemjBHiSreWJprS3vb1fLXITeG5AzkOfwEiYJ9\n",
"w5KyFCFC2xDAMWsAUGcpw+m2XTfKmBkA6vWOWZrr4N1LOXNcZbj0PuR96h8rPzM9XR3HnDlGJhcy\n",
"YYzsZSrZzn6/WJO16+G1HvRdXyJz960DewE4Zo/MH8cYjjt87TOfahPlDPTTiWL2OL3x2CXRxEb9\n",
"DwXW44PfekBh/AoKCgoKCgo2HB6K5I7vBRzyg9+kT9QhS2UFKAAcs1SXaNBqXcjeeZE2o3Jaodhy\n",
"N/VQczPKssRG44bZSJks+/CjZC2YTVZAy21pBB7oc8w6Z0kT6hRzjOBKDFU18vb1amNLI4kuxzKA\n",
"I7VejM5DlsKPznNg+TWCEaiWbBsFZf6Wl6lbCRkBP+KnBcScaFZy7ZPSnHL/ZOkOdJaD16rb8xm/\n",
"nEEzmQg/Kg+Ow+tL/X5ol6DbaCTujtvrD2NYk7XEIKE5OxQ4vbDdq3nta/xCRqVhrJ4a5vxVH+x0\n",
"fONZO8KWbiObnCi3Fh1zLT22qEUQkC/z57YNP6NMIBCz1Q0ZcCxbmtAE55i+np1hSWv9/B5dl3Gl\n",
"aS23emYf8SyNf+4AMDtb2WHEWtdwyfvAZ+tG2SOF+6wH5+Tflxy7yLCpFQy/l/rQuYyxsQ/dZ3Dw\n",
"LAAAIABJREFUR2epOuZdS9WsQcqKRZfU9uk4pHpF//sUubEjtshZ+dgR2pu5daPM8leCYlScRmH8\n",
"CgoKCgoKCjYcylRvGoftwS95AfhQb5kLwziY53QaiNpSQl4U0JOo3GltzLZj2BoAaBhdGhnF3iAd\n",
"pdrt6zHjZ8voMLKWcjpq2Ovrc/TYrT6QTKDViYU6nUmKpitSgVhWhxPttFpYLZRngh21N9LROc91\n",
"dnYKgJZdI1ulOrXxhsXROYk+jWxaTgtYbRNm2qoOjog1cF5/FIZRWbycfs9flzNO7ffDSFvbCYh1\n",
"N9yG0H2k+kmqFNbhwmA4zGpNJxm8s9twPTPi/e+sh+PMkOXVGmT+w3JrznDd7SXHTPB4qDXu1EMz\n",
"cH9/+plGRi+qYwwQM31jGUBmedfdPlRTmG3LhObPltZKaIj9c9RxIrXjOvu7aSua7ffryiryu92+\n",
"eN7z81VVBNWwkglvt3kfums4Lms+l0WZuv/tGZljdVrjUAM46h7T+1/HDI4x1OkBcXnHnDMAP8vZ\n",
"hElM4N16cz36ef2efpbtrowrlz577t//q+UWUh780iiMX0FBQUFBQcGGQ3nwS2PVH/wOqqEZwUkG\n",
"nEbk/USppCHSUfkkuixbYH3IMkajS3MFPoL0+GqE2b1aQNtF4mEEHmwjUXhLmD/V/qRMKS1rx2Pm\n",
"+glK6+UKrCtclq97v5n5rO7T6qSocZlzJWpcWaWuWZoC5st8PZ750+hcSzP1euF2foSuzF6OLVPG\n",
"z98H/6Y+j5F3jglMfdadX1prx6iZxxF6IY6OkPWctExeCrYtD4P31vAgo/xR90S4oWFxh37fNX8I\n",
"ST0wTN9QdMLUE6dYvlomQ7jb53gQjjGjzkUzb0dp/HRmgeOPjjdWY0zmK+FQMG7sTmW5M3tfVahD\n",
"Yee07GHqWluPP+Mb2lAGkPcdx2uPeeWx2fYwMwtTRktHzzkyYcvL7rNkAfU+zLHk1u+1H1/L1NgA\n",
"5O+zlMY2p/HN6YVT7ymzdzDlHunIoAyom3GI2UtdpyXzdGail8hq7g0HqzbmlOSONArjV1BQUFBQ\n",
"ULDhsN4qd6wXjH3wGxeJa5SoT9ij5EK1IbN5jcbDvM756IX6kfDQB5loXNk6P5uNflw2ks1o3VKs\n",
"gvVWEsZPo/IcAwi46Ntq/DLF4Jv1fBtrZE3NDSNxrbrgx6E8X2XrbPUBactUFQDV4/SolyRLYiPx\n",
"UAPU9zJ1XVRetQP1KlYH0ktHrf7fg0F4bC5K5ZIZwtwu74mXc65Xn6tRrF1Ot6d6ovAcRke5TifD\n",
"NQlPygmzGpnJ7Ot4clG5aqvWApWuJ1ynY0egCx1T5Se1f0DGEJ6muYzDergNmT+t8JNCzPiZ+6CR\n",
"HmP8Y9JzmXRsAfLjS3Y2IZHVqzMKeny2v3Ns8XWKfTkHM4b3ZR9ubIlZw9w4o23ZqYWMX9dj3Lrm\n",
"vDvN0CePushZM8NAd4FUxQrem7nxZlTWO9k/ZwkY+/Sl9jFqDNGxZCU6YT2XXMZuqnJPK5NwzHFB\n",
"xxK/ggfHcK7T1zarehBXLvEzwVerwkeZ6k2jMH4FBQUFBQUFGw7lwS+Ng37wyzF9Wv8ytz3gRdbm\n",
"LTKAVqgWERr+4RrmZExUrl54zOAFHONns3kzGXoagQJ+xt1ory3r49cIM/P8bWy9TfEVI+M3qvPG\n",
"Pn1hVit1eSnHfD1dZfpG6ZEI6nFYs7chNXv74l9GXU637kW6g7AWKfV/q6GPy0XYqXq/hDJ6qttR\n",
"5g+II+6cTifFJk6avVuvxywdwUg6l82Ye+2ze6rxSbJka4RJ2MSgzu6YKj8RWyizC9WXmmU6ET1y\n",
"E7DH6A1DWhPXavsG4dgyibYtp+1rScWG6WY8hkTjTjOcRXBMX5yxnpuVsfo8cw6szuOT5TFLOoZx\n",
"Fb0kMH6c0brsroKKu3DLHH/N/cZ2WG6Gr5UBBBwLmMvIz93LoY6vHqzTMUPvf2XzwnW95DbK+Pnf\n",
"n2P4xtXd9e9/VlNS38I4M7pi79hufhUmfW9qqm3WmwpOg5CtTfla9garyfitym42HArjV1BQUFBQ\n",
"ULDhUJI70igPfgUFBQUFBQUbDiW5I42xD35BqbXE03Nuinec2Dr1HmngOq0nyGQnpmJsGR85A/1e\n",
"a9JMgbBXkLs/dNSyj0h0zWli3wIhMx3TEtuSaVuyzUxFeNM0uWkYlkzStkxNE2kSBX1caLNCGwtO\n",
"xfYT03a6X52eypWw81ETk+m+SfboGkF2axAWKfcF6h3zfdNmCsdaYDRHT/0C8fRvvDTnOMibIquZ\n",
"aX5f45NMclPPqelhQq1oogQpmXrR6Vz/b7WvyL1OTfXaEkxSdou3x2pNv6TgTyfrYO3Kr8XJHQ2Z\n",
"BtR7xu3EfI93Dna/g5X9ONT78Trb/00/b4l8JDXVG49VKxtTgEmSOUIzaNsvE1YkhBXxm+Po1XRM\n",
"9xqA95e13AotTwid4vWnd/tip+U+A/N9XIZjettPlOtXx7rcCKd2x039Aq49aQEzM6ymJ9UUOZVU\n",
"YZtB7FtySV256dvUunHmy/5nx40zvB5OPhKdQtZ6hdO0HDs4jcvlzIwrx0mDfn2PV3aZx55I7vCN\n",
"uVetZFth/JIojF9BQUFBQUHBhkN58EvjoB/8lOnLJSJMUvjdpoerYawJyiaKyM2Z1PvCFlgmiskH\n",
"nhWKTWKYLDGkERhIN4J1Gmlr4sZUI3y/ei+dxOGiRx4frUhiw8xps99ehr0YsEg4I/5hnllRdkIZ\n",
"0UkE6hS1a0k7lq7q1kO7BQCYNskdXUbnhhXtDhidh8J13/w5FyUrHKvGNvaNU0Omb5z5qUbv/t+5\n",
"yHvUfcBjcgapoW1CzoqFkbj/9+TLVrQPljfLMX1raeQ8GA6jsUMZscB8PVNmLDf+2HvHT2pgWS3z\n",
"uo003Hkb8XuKeRxjBs97K2WJpIlivHeUxePraY+t0nvDzmyY+2Bpabk6nmRCQgjtZ+yHZHp8loxg\n",
"Uh3tnGps7zG2Ov4sQodWKGNMnvUaL3uzN2wzTYRpN3rB66ne+LJ3ygBO9Wn+zPvSWcEoeN/b880k\n",
"czgTZsfa5cqsjbObqb5n9O+sWjSl1rvxxfSziNmr2oOsnlu68Zh/870c08eZn5S90XA4XDXvqPLg\n",
"l0Zh/AoKCgoKCgo2HEpyRxoTPfipVUK1zuxA2KpRBpXEONuKprBnPeT1KIQ7NkZQ1ak16kwfr47D\n",
"Z+2U4XLnZs43U4YJyJdAytm3qNYGcJHcYnd84WzAtU/D17ZY9id03bRRsxgnN31tzVjT23BfGpHr\n",
"3/6+uoOwDR2rYfQ5A3cOVvdnrjtZQ0bgZBzVlBUApsSCwJUiq14zitZ+mRoQuI3aueSYvoOxlSFS\n",
"liyusHmotVF2TiPx1LrcMmL6vHawFjwTMLyrjeFwaI/FWqRkjI0Bx/TZWQJaQWQLyIesOeCPM9Sy\n",
"5Y6O/S3WdhG2jNcgZJ5y90d17OF5qS6PzLcyUT7zRq3e0oGK2RtXsmuSUl2q7eI+rEWHZ99hxwaO\n",
"s7z/c1pL+RzgxhXqr/vCOOeZP7fO6SONlq+fK6VpZhH6ifHHfLZLE2hb/s5YwBgWa9TYwfG4202I\n",
"6OAYwZRe2f4eZLSFOVuZal3YRo1GeE2J2Hw5njWgLo/XmyweZ1ocq1ct5+dn7D7YRj3ze7NMe6sB\n",
"GT8xNM+NLatl51KSO5IojF9BQUFBQUHBhkPx8UtjRQ9+fiPmdGnjNE7V3yZr1uyQEYw1jjXv50pI\n",
"jQZ1OIbhG4Y6uqDcUCaq0BJKmm0LxCWQcho/Ri5kiw4kCmtrUfBxGVl+e/T7YSFtRmlafq5fCyNy\n",
"/zxziLV+cRb0uOyryNi2Ts2fuw5kAWnMyrbrDLgMs36DMj+DsEi9n2EGxMxPionu98e0g7B2o0vH\n",
"Tcb0pQqbaxQ+juk7FMbPXcvYQPVwMHyjEJdZDPV8/jq9Frl7iPDZGl4bO85wNoDGzdQcWZPieBxS\n",
"Y/hBfTRLmtIp2ux+0QMrw9czDNC+AwfsPsjw6ZLjL1mjURowLcWlJrz6mVmPReLMRs+4LDCbuWu1\n",
"fuF5p1jknKaYszQ6lqXGLTJ+1JKp5m+5z7Y07KU3huoMA1/PmLGF30stIJkvv49p+3Jsr2eePLid\n",
"vw/Xh8M+nWP6lOVLIVdeLTWG5Ji8SZcAsGSOcblvMpF5fw5Dpq83wimijhpqpWTbmqIwfgUFBQUF\n",
"BQUbDuvxwW/fvn24/PLLcfvtt2NhYQHPf/7z8ZSnPCW57T//8z/juuuuw/LyMp785Cfj/PPPR7N5\n",
"6I9tE+1hlI/WOI+zVKSpmXZ2n5Ld2Be9jurYRsGyBowayZoN09qL8LPVkgyARuaAr+1LM3yLRnMz\n",
"ygMq11bR8QhL5LdDLpK30bo5LEZYvk6KGXhcVxvh7QU4zU0/wZqOy8Sj5k8LrgPOt4yRNrU+LE3V\n",
"t7qQsOyPf0xkBcj8+Zm/PtinUmxdSnd3qMj18ZROc1JNn2pvRm3DZVwcPfZTU2bFHnPi/l8LcP/W\n",
"p7BGnVZeH6tsSI5ptd/h7cPNRlRLtje/dzDBRAOz6KlDzpW309kDwN13mvFvxxJzXAf2L1XLA1wu\n",
"230o05fLANVxwmei4ize9GftuXjnQLanb5jOZeOxZ71IM5na/nDlxo7qNZm+njCAo/xEnQ5UNcVk\n",
"IDmrQMcAz0fUjAkcO3IuBo6d4/035c5BZrrYlzqdkE3lrI1+LgXVHI9yxiCo7cuNJZqx648hzNrN\n",
"MXoLC7MAgLm5GbOsPrvY8zKTyfT1mb0bavtGeYHmyi0eCtZjcseVV16JVquFK6+8Evfccw/e/OY3\n",
"44QTTsC2bduC7W699Vb80z/9E173utfhyCOPxP/+3/8bO3fuxAte8IJDPobV/6UrKCgoKCgoKHiI\n",
"Ua/VDuv/cVhaWsItt9yC5z3veZiamsL27dtx6qmn4qabboq2/djHPoazzjoL27Ztw9zcHM4++2zc\n",
"eOONq9IuYxm/6oTMxl6kF2c8dpPrU5USxmnYnMZPmIdERl72uMkqIvQma04UcZBxMDqRlAcfWTjz\n",
"urMc+jPlInA/i2tSlkIj8tC/KdThqPdb20R4fXPsXY9p4/lNmoGXYvXIGA2lkH2ONbLVWbzv6ht9\n",
"UM9E5z1zrOryr5E44LFUEDbY9OxY88f+GHtgsV3Z3o4JDDPktI2BOJs4Rx6qngpwUTmj8ZxDvovS\n",
"jb/YlDs3nifXqWM+o/KeaGyGCa0VYdkZeb0WqPnjDJm+Rsj0dUboY/learwB0vpYhTLqvD+G1B6b\n",
"vub3qJ6wlLmxjec0yhmA/nwcO5ThWw3Gz51rIrvZsEKqC1Qkvd/IKLGd++FsSVOZ70RXsuOL+KuS\n",
"reutgDVyutB+cFydhplV8Bh3ZvGSURznJ2jPoR1rbJ0ur2rDdjtc8rromA74Y0e6Uo8bM/JjTL7q\n",
"RnV8ZOnI4pHlA4DNm+eC9/5/e18battVnT32XvvjfNybG5KrjTbR1Fa4chEsSCgkWvunLVSkoIYq\n",
"YmsbIViEklaLhbY3Iv0EUyo0YEOl+VFJSPqjIARKSxp/FKSCWtO0WptKxFiIeXNz7zlnf6293x9r\n",
"PnOO+cw511rn3nNuco/jgcM6e+211/eae49nPOMZYPjC6+b9iRuf9pwbxcEqPJdFvz66tv6YVRbB\n",
"3yNHOM682qp6n3/+eamqSm655RY/7/bbb5enn346WfZ73/ue3HHHHf71G9/4Rrl48aJcvnxZTp06\n",
"dVX7YRo/g8FgMBgMJw6vNo3fbDaT7e3taN7W1pbMZrPssjs7O/41PjebzY7/h99gMAiaF11NWeg5\n",
"2KX1ywGRDfrvcrTeegDoLwqfOmj4fDTkGKYNuoJktk+VZ6ErQMw8aMbPO7C74y5V14HhY61fM69c\n",
"+SySVntiikreHEqeXDimsdKYoJuGj45JH7PMsHMM7n7SGSVnvAN9NR98G4d538BsRWBHVTFX+7ZV\n",
"meN6lDSmXcysXobB1XWaNWEdDrN2HK0z86fnYV0ccXNvTNZGRvvqo+TmveoaDJ7DwSBhh/C85fSx\n",
"eL7a+idroHJbjy18HZm17R5bmnebCdgKPq5myl59Ioodcx/ac1q+g4OY4bt06SA7v/k/9u/jc1XS\n",
"AOcY53D/5cdsnB+tMWYdKo6Px1Cu7m8bU1hTl/qIxsvlgGWXPuMTe4JqZ4C6ZXzJgb8nREROj+Nn\n",
"dWsrHu+9fpSef+h7RUSWyyq7TOjo02wv9/1Y6rPLY0WpYlekzPBh/tCt89KyudeQRZgrjd+c9Jkl\n",
"pwB//Y9BVx1v51hXn8Wjjz7q/z9//rycP3/ev97a2pKDg4No+f39fdnaSjXpvOy+q+bPLXtYGONn\n",
"MBgMBoPhxOGVKO64++67i++97nWvk7qu5Qc/+IFP9373u9+V2267LVn2tttuk//93/+Vn/mZn/HL\n",
"nTlz5qrZPpFeGr/w63yxDL/sS9q1Un/TPr162VdrPs8v16yXun2AlUQA4YVJzQS+QDmFT8m3j6sJ\n",
"EVXr/0vTUk/GPt5vJU0ZIu0+7OlotHRTp/VwuoxaMQ6+b+4QlXhOl4Nq5kIHkzYk0ToxSrCe0tqL\n",
"NbGx0PJA+9dVOdwHu6NYN6evA5g+aOu4iq5UVad1UsGDst23j/ufiqS+fSVNH6L1nAfX0EX8iMID\n",
"44cIPGU6ivD61XxF5nFgpDILeO64Y0ru+etyEUgZ8HANWSsW+jjH7MmQ7v/hRt27XlOWP65S9kAk\n",
"sGNdTN/e3oGbP4+W15/h8aeLAdVfiKjixX3I9zmzSLNZmfEbj9ibMM4mVJme7m09mUXSqt+c1i8Z\n",
"Z9YxK8cV622f5f1KOzjF+kWRcH3ByuN7kKvPwQTmrk8p4xDuy/i7tM0LtGsMYR1f83/M8Hk20F1T\n",
"Zvo841eH3wV+vMHYSec2ML/N6+L38RGNNa+2VO/W1pbccccd8sgjj8i9994rzz77rHz1q1+Vz3zm\n",
"M8my73znO+Wv/uqv5K677pIbb7xRHn/8cXnXu951JPthVb0Gg8FgMBhOHIYyuKZ/fXDPPffIYrGQ\n",
"e+65Rz73uc/JRz/6Ubn11lvlhRdekA9/+MPywx/+UERE3va2t8l73vMeuf/+++U3f/M35cd+7Mda\n",
"2cTDwFK9BoPBYDAYThxebYyfiMipU6fkE5/4RDL/7Nmz8vDDD0fz3v3ud8u73/3uI9+Hzh9+o8Ew\n",
"Sbno/0vFC12FCxrcqo3BqRcRLbyH9QtSKiQahfa6pQiAxbreqNntO6dRcvP6pn5xXppjaE+Dc3qw\n",
"T3FBWhASi4t1esIXraxjqxcu8sA02B0oWx+/L/ExcGqlrVn9mgpD2PrhauDTdG66O27SVDnzVb5X\n",
"eQrgWuZMcLtsRIKoOzx6h7VvQToJ6VwRkQNnrcDN0H3bqx52Cj61hWvVkYI7SlTDobc1wfXfO2hS\n",
"mm3PH8afrnEmPEPp+94CZFRHy3o7n4psNXSaUmLLGz+fTahbCsQwdgYblyZ9G1K/zfTyZaR8+xd3\n",
"cKqXU98iWp6TN8jHPYzzoos7cI9i+0gX+mu5Gsav3baQ8tX/+yI7ssgJ91+8X/pe5vHFjz9+bInl\n",
"JDm5SEnakKZ68X2hnn9v/dVshw2S2eYll+otyURKVkXaDLpU1MFjCMyX2bpFJKR4cQ1X7vD2F821\n",
"DfYtcYp3ocY8jD+l8R7P9nqTjiUD/T3co9FCH7waf/i9GmCMn8FgMBgMhhOHV2PnjlcDehk4L8i6\n",
"RSRl+lhUzFGKjma4jRWbqnJUmmuzxaXukIn6X/gtDb31sYlok9U4slsk7da0gWzesLmL8csXd7Qz\n",
"foiwc8albPZZVXFRh2/V5RiAiSoq8KbOrshjXKEQIG5Wjgh3tUbRR9gPRHDBwBlGtmBC8seWa9IO\n",
"xemmR/NxRiIQh4h44JqlD+L93Vasxc5Ovngj2QYZqoIhavsss7awb9CsCdg/2LdwEQeidXwGEfcs\n",
"ElXHram4NVupICYSqGOfi8se3yA6GVaeaQ9sXvwMaaYL93PuudLIFXWk78WMelL0QYyT3pJnidjG\n",
"hQtCwAyqcZCPgaelsUQbOKPQA+eK18njLx+zfo+LBgLDFxs758ZBZhgnZE49qZ3Ni2P3Joqtmjur\n",
"HRhaL4Yw248zDChMwjndaNbI/Zswf/geoAyEbv+GZ2VQx98HlZ+SzZBjLcfqnpu4Ajk8m7B3gUFy\n",
"uQgpZaCZ6Uu/6+Ll9DJ9bVyY3dPvgem7vHDFRMT0YerHGmWGX5fGDvoe5tZ1ImqMHgxlc0KLO14t\n",
"MMbPYDAYDAbDycMVOEBcFa6T35mdP/xWqzobVTPTV4r8wNbpKDpt0dbTSDUy3S2Y6nJ0DjIp88uf\n",
"m0Ijogt6DG5Ll2ocu6Jzfr+Pxo8ZT24ir+lrLBtYqFifBGY2WIaESw49yngda/3QcH3poth15Wwe\n",
"3G5uIm1NbLmS2Fq4y+Kb2Lc8iP49d3jc3i3X7m3oWjIN67weKLWKaM6HPoeIjkvG4SU2NafPKduI\n",
"5Fsp6e2nupwmSofGDJE3tDUzFWlDyweWFueKtZb+mHD86pCHmShcJOjUjrP90bgaytqdf2a2wPTl\n",
"NH54nnQLPo02bR/GnxILw9mEKwHr1NYZA+nSOMMMIJ7l2ATesTAHi+h1F+OnW4XxuQn3aNxmLGek\n",
"zeM99nG6DUPn2KJnOkI2IWx/6sYXWIBMKujEYtPlcRVfh4V+4cd/aUXQHA+SeRtiA/EsgdmC4f3M\n",
"MV5jzbhByzhEe8/mM2DxWdsXrkuOiY7H8snk8G33eAxhw+acncvcrX+PNH17riXbwTLW9vFYI1Ie\n",
"Z0pjS9SyTbU1XK+PZqzpyuIcNaorHyquKYzxMxgMBoPBcOLQVgh5HDgxP/xWq7rAeLEuJW/k3Kbx\n",
"QxslRJ9sdrtel6P1owQzGcFAs9wOqtQqqnReENUvlQl2qZ0SUNY+hnVw1ShH3qzx09cQUSE0fnUV\n",
"R3BTYvrWVcoeYV64lWJNnY/KUV096G/CjAg8MH1uCyoaDGbTcXQ+gh7Rva7qWJ9XqXOI9SI6Z3CT\n",
"dOj0NHtbahyPz7K2T1f1cms2vF45tu6AmD60RcoxfmmrpHh/Qp/32Ng2e7w0Pcpqa8ZkWMnl/aZq\n",
"tY+2rdSaDChp+zRLUjJ9Lj2PudnMqHZpinKtAnHvMPPH425g89JxmJm++Xzl1s3ZlPQgVk7UlTKP\n",
"yPRMsu/rZTDFmBlM8PNav7GqbgbDB8P2ehN/LW38uY33W7P2tdcht48vpQphkbITAcYfVK+O3Xg5\n",
"V88f9NF4RkfunFaTWGvXru1jbWW+MpuXF9GMX+wQwNW8p0/HjN9c7cclMH2rmPEDwzlbxeNPqYJX\n",
"RD8HcTV1eN/tt3oeK3XP1Ec01lxrxu96gTF+BoPBYDAYThyuNeN3vaCnxi9XzRVHn10tlDSGw7wO\n",
"qm/kHa8rXseqwHT0jchz28+xliXGj6Nirn7OsYZAzp9Jg7WPue2zpq80XyREiVP4ljl2YEqeb8wK\n",
"5SO8+FgQDcIDq06uT1hHF1sWtptuP3gLxpXHC/ILG7n9Q+X2XPmIecbXnQ9m/kIkHmvC2jy4AJxj\n",
"rurV7dY4SgeT5xm+Fb1GOyjl41dqlcT3PbRNQzA/6hTzM4Pzj2loFp891KuC1hKXmD6t8eti/Era\n",
"Pv1s8XhT0niWKkXb3guVpy2aVmJ/vMas5nEwdjXItfnicSdkXJgJbdOU8di9ya4zvu/jZVjzF5i+\n",
"2M9wqj1ZN5RZKI0Hq5iBXqrrhbELzH+pZSR7BIoE1qmkYS0xgFrbhudvTu0vUfkb/EMbzV0fbV+p\n",
"7WnOi5H9QeH1WarqRWUuWD6RMtN3sMLrmOkrtWUTUd6MFZ1/yiJop4DQ5q+SwfpoBhlj/PIwxs9g\n",
"MBgMBsOJgzF+eXT+8Fsslq0aP640Y+YLkZeOsCoXBXBkw5q2KwEivA1Faf599Zq9hUrgCLz5Px+V\n",
"hw4CtB8Utev1MivAzAMivBDFpxV53j9rEkfgHK3ra4gqVUSHQdPXX4fn9V9Od+ebcLvXXPmFc15n\n",
"WJMr0uX4KHzj1h97DwbNn1sHVf/m1jscxb56QUcZ3+M55sOvo1DVi4h8qvwUUfHG/nxg9uakrck5\n",
"5oP5XBUGutQ5P8+IZD+Dqmp3vMfB+M1mC1+Z2uWJKZKON3z+S9q+OqqqTZn83GeAHIvE44xnVjNa\n",
"ur7oYv70/uK5hpaPMy114omJ6l5V1VpgRcL2Cw4Kkj4LnGHYdowTmL/purn/63V6DhmeFfI6XlST\n",
"wu9P+8fF97/3r2y5v/12JGafSlkhMFuYai9AjHNg4ceO4Zw7LbH3D93KZxNE0s4opY4dALIHIip7\n",
"Qzph9gT1lbq+Ylcxfm7efkeHjj7avkHBTcAfK8bFQarxmwyHMjgiz1Bj/PIwxs9gMBgMBsOJgzF+\n",
"eVyxj1+p9yBrbliXIJJGeKU+pwwdgXPHisAaCb1uYTSwDDM+PaINjsJKUXlb5W6pvygzDfzZmHnM\n",
"6xBLkXjOixHXd+LYqE3VfltE3kvuXM1rROXN1EflVAEGZk5Hy6z7y2lGRNKemfy//iwzgIhWB07r\n",
"V63VvVTwgJuSC35JeyNSvoalql7NzHFkXdL44RzOvZ4vPYdB2+f2A3Z9m/jc5QLhxPuQzvfqGKPn\n",
"xWKZdOooeWHqebqyWiTVx7JDgB57ykwfa0vz1Z7xPMzBAOSeQ3cOxzRe8f+vJLrGuz77yePhhhhQ\n",
"dPKAc0Ctzn3J+407Z6Dbh2eeKjWW0fjiO3SQn2UbAvMXd+rgnr3pNU+3BwYQzyr8QwEwf7nK3KCT\n",
"dNX9hapenSEr+fiN3JheYvrwWkRr+mg8SrR98VgzkHQ8HlbxPYXDDJpr932h7i3fx3qz4dbvVwxj\n",
"/PIwxs9gMBgMBsOJgzF+eXT+8FuvN0nllkhaRYbXOS1bAx01xo74XZE3+/uJZDpVsMYO2i/ysdIM\n",
"EZYZbNoj3itBl27muNCXAdT/I8LEeZ4WRFxB86X7bMaRG5gNRLzhdcwAxowfRel0zdrFRO7tAAAg\n",
"AElEQVQqsgMLmN3lZJ01tIeK5cNng3+de8/JISGpBOOwle0k067xw36AzdPbRyTdVc3rdUQ9zmE4\n",
"Nmj74vPRyoRzn1nS+B0HFotVsWMFM39YPrdP8AYFAuPXrucTCWwhjzfwU2SPxGYeafygcXXvc2X8\n",
"SN2ofI9wFXUfMBs3QDWlr94tMdHDzGfi49YaMj2/Dd57k8YbjAOrIZwEWvRhCdPnxik8O1WsNRPR\n",
"lbbx8943m6DBmQVm/nLjEGuNofWr3HiDDMNA9dcWEZkqP88daNwmeWeMtqre0JlpHG2f++yC6Tsg\n",
"b75mHnUGIqYvaPviY9a3BZ+b0uvcdwm+QxaLlaxWK9nakquGMX55GONnMBgMBoPhxMEYvzzsh5/B\n",
"YDAYDIYTB2P88jhUy7bYiiSmoZniT094+OU9HOZTiSHVkk+BaGqb0xArT7U7in9TsErRr93qhptY\n",
"tMspj5Kh8pVArwvnKk3X4Hh5mqa8u8Cp37a2c96CAS3EXMp3QLT8XFvzIMXrUr5Ld229rQGlfrHO\n",
"OE0TXzukaXIiagYXJAzIhJWNjLEuLQHwFi8Spw3Z8mSz4fMR5Tjiz7qpT8vSfalTvWzI3JXibWuO\n",
"nqaykGqO7/E+4DTNcUbPOdsoTufqQo7cmCSSFop1mTOLtD1/zgLGpcPaRP3eggXn13228qL/ZjpR\n",
"gnwe3wCMEaXxUO9vSA/jMwO3P1hnvA4sN52GoR9jKc5daZrbfgksMUGxAWxddLEFP8OwVUEryZV7\n",
"7tikXEsdgvwhHktY6tF2DRlsI4WUbzUoHz9LKXDdl4UCMr1tmFtvkeVLn1QvjrdkCYU0Lt4/WKap\n",
"XqR2SyneLjlJ7j2AJTm4xlr6AAPn/dXiyCRRxvjlYYyfwWAwGAyGEwdj/PLo9cOPjTyb//NFBFcC\n",
"ZrJKjFuufD0YdsaMSmeTehEZFGwachGVns//54+pm5UribhTkXmZ+QzReJ4lZMTmr3FUjs+AacG6\n",
"UcyQa6w9RlQI8fYmjnAXVcxwBcYrNR/mogWOMA9jKF1iANl2QURkhc+wrw+Bi0zqPpG/xNvDMWnG\n",
"k5m+EGnnmT681uweGzeHKNwZ9hLjx0xoG9osiY4KucxCyYRcz+NxZ70G49XjXik833j+UvYmHmP0\n",
"PL43BvSZ9TA9376IwW0PzFsX0x+b/saf3Wzax2Fm8ZrPojAgLhBgixBMx+O07WNpvOHvDrDkG5X1\n",
"4WKisaumWpH1y2oUmzNHdkY07jMryO3WDmMg7/eT2421FOFsaHulsT6yF3LMZu3ulQExjshQYYyt\n",
"lRULZxIW3k4mtmgB08ftH/X/JaavZA7f1hSBC2XYKkrbuegisqNi6ozxy8MYP4PBYDAYDCcO1yPj\n",
"d/nyZXnwwQflG9/4htxwww3ygQ98QO66667Oz33605+Wp59+Wr74xS92yjF62Lkc/S/mUgTLzFZJ\n",
"a6KXXRCTFKLygh5Bm00y4+ctF2ItVxt716XD4ZZd0b6Q1USpzVdo95WeB14GbX/66AFZl8nLJtE6\n",
"GADNFjibgpUzffbMHrR8dRytL8mSQSQwXtD/MSvG0bpmutoY3eZ1SfOX6lKS6Jx0ObhfRp7x6342\n",
"fLRM9+dCPVdLirRhUFvS9DGL0fwfbxfvsY1LHzuLVwLr9SZjXxEzjW0tE7sYdmbR9WdSLVvMjq78\n",
"+W4+V2eYJr9fuCZu9nowjJaLNF0Jw5cfM0rPeO49YFBgo7FNzdp5Ta9r9wWNGaaYDyZQtxsMbGHM\n",
"EpZM6HPjoB/vkTUg02XWUfpMgLqXa3pGAtOe135H13AdPxvMbHVpAPW+82cSxh8fqdN1Yz+ge+uy\n",
"9cnZCpUYP9YNM7snklrgMNPHLHrb/nGmha16mPkTiZ/7H2XG76GHHpLxeCwPPfSQPPvss/Inf/In\n",
"cvvtt8utt95a/MyXv/zlKCPShVeHdbzBYDAYDAbDEQI+xNfq72oxm83kK1/5ivzKr/yKTKdTOXfu\n",
"nLz97W+Xp556qviZ/f19eeyxx+RDH/pQ7+10Mn6lFkNlHQoOPv6lrSM91qohgmVmi+frdbC2j5m+\n",
"kvZG75Vv6+X1N7kzkK9mK+kSmSXEPiPyiHWC+epmjuy53ZeO1lmXw6wgn8M2CjhX+SsSIj1UVeqK\n",
"aqwPOsDJMGY46iqOGtFmSTNegQWDuXF7NV/M+LXrANtMV/n41gPS/+Fcue0jql/3WGfKUsT3p67y\n",
"W3mNoztHa9Y65pk+3UKNmbzQXireH96/eF7xcF4R9KvIzV+DUmW8ZilKz7BvnVXQ9uWYVlzngR9n\n",
"YrZwvBlG83Pb4zEj1TrH44GISF03zz/Gl1KWojSWiKQM387O1E0bB10wgpivq07B/mFM4mMpOSJo\n",
"howzL2Nmz4Tv3WYa6+PidZQyQMwMZt9LdOLx90Pu2SkZFTPzh7ENHSNHal3IIKw2pD3l6vqcTtnv\n",
"c/Nel0MAZxea/+PKaB7D+DoMe4wXXQbOWTPs9aaXRvck4vnnn5eqquSWW27x826//XZ5+umni5/5\n",
"u7/7O/mFX/gFOXPmTO/tmMbPYDAYDAbDicP1luqdzWayvb0dzdva2pLZbJZd/jvf+Y58+9vfll//\n",
"9V+XF154ofd2On/4DQaDRMfW/F+qOM37R+U8+Erata75IqG91YoqQNMoLZ7qSJMZng1V3qX6vXD8\n",
"zFpyhFuK1vV54JuypO1hVg+vc/OYFUREnjuHrNEI++NYO8/8xX6DOS1Bib2Yutfbo2Z/EInWil4K\n",
"TF+hEpj1g9mqSncMHVo21p5ocHQuxPyt3X5yFWKfdWH/cscAFqCksWENYhvzCeBWhZZxQ/vB0Xy0\n",
"76StuhL/yKMAP1O6HVupIjcw3Xw/xtWvIrqqNs+Ko2oyYW81S8PPsJuiQHzDrIk63aMC05geS5mt\n",
"Y/2jbxG4zrOGuTEkMH1g+Bpmb3d3y82PGUC8Fgn6P7CCrPXrqvoVSdmfRL/pj3UdvdYASzis4nOa\n",
"MoAxI9bMi3W3/IyyTpCfD5HuKnI/pviEmPvOGWS+U7jNKNh7eob1NlnDuKTsQWD46mh57YVYqmJP\n",
"xoNDtBT0x3AFnzkKvBLFHY8++qj///z583L+/Hn/+sKFC/LMM89kP3fu3Dn5yEc+IgcHB9H8/f19\n",
"2cr0r1uv1/LQQw/Jr/7qr/by1tQwxs9gMBgMBsOJwyvB+N19993F9y5cuND62dlsJnVdyw9+8AOf\n",
"7v3ud78rt912W7LswcGB/M///I/8xV/8hYiEY7333nvlvvvuk3PnzhW30/nDr6qGWbaI5/EJVoVn\n",
"IhJH2oHRi3UhpSmi03Um0i7pb7gSDwGn1nYMWIfBrAlFqfpXdbmaN6/tA+IIJF/V18X45SryOJIv\n",
"VQJqzU3JrzC/r4Hxyj1MXQwM3sf+TdW9hGpeZvpYDxi8AlO2jK8/MzFd1b/Rsh3ROdicYUuFLEfl\n",
"bVWFrN1jj72a7uWcB1/ZMT/PfOd0gsyW8zmt+KE+QgyHg+R+ZCZOa0+5OpSZ9ZLGNfavi5+J0njA\n",
"XYFy2jLGYJNfl/7ssMo//yXNM55x3cGEn0XW57JXoH/+pkGnFzR8eYavxADqfQJrWKoybgN3+WCt\n",
"cen9NnSxpmcm4RhwbbgSNjB/G3odM4EiKRvI6/b3ySCeP9ykA1EXO8bPp0i4rxaUPViQPpo9UlfR\n",
"OJT/Hiy9PgyLV3pO9Hz9Hbru8FTtvd1Xm3C5A1tbW3LHHXfII488Ivfee688++yz8tWvflU+85nP\n",
"JMvu7u7K5z//ef/6hRdekN/7vd+TP/3TP5XTp0+3bseqeg0Gg8FgMJw4wBrmWv0dBe655x5ZLBZy\n",
"zz33yOc+9zn56Ec/6q1cXnjhBfnwhz8sP/zhD0VE5MyZM/4PP/bOnDkjo1E7p9fJ+E0mIx8lzudV\n",
"NF8krbgLGpN19DrHFkJ/VtKpcfSoIxzW9m0SlkKi+WuEWoOyLiPt4FHuTdnlPcgdTfi8xOs6nLZP\n",
"V9X1PXc5do99BP15SPzT4tf6mndpW5hxaOscgPtha9IcH1f5LipUqAVWYzKMK4K9HmcQM2zYWp9q\n",
"MY7OE2IP7E0fjR/dl+xFFi1T0PZ1Tfl/jeEgrxMckwZK/19i07k/9lFiNKqSTAC2t1zGz4NIuK+4\n",
"mjawY/E6OLvQLBM/K1jWjy3c3zXHtPLNgQxDMrZgml4nHkP4WcF+oqOO9tHb0FjVpRvmCl79PzN7\n",
"p05tR/OZGWz2zV0TdF1w52zGHpieJY89+zSY6VsslvQ67t2c6yQVjjufieFrro8fxwI2MOmoA+9Y\n",
"0gKKhN6zSVcRGiIS9iyXNSgMUZvk+U/Xm3ZByo8tOS9QXld23zJo63hSYgvbtjEaVVLXR8NJXW+M\n",
"n4jIqVOn5BOf+ET2vbNnz8rDDz+cfe+1r32tPPLII722YRo/g8FgMBgMJw7XW1XvtYL98DMYDAaD\n",
"wXDicD0yftcCPVK9Y5lMGop9eztQ2552phNbLvZIRdXc/LuUtvT2Cq7RtEiahvLi2k38PuCJY5We\n",
"y1HmIoF+xmf6mL/imOo6TvX6/a1TYXg5tRMfP1IRSFch5aKX6ZvqzYFTuLBrCakXLFcnx5C22Sqk\n",
"HAsFLPr/+Tx/H+yiqMW5no5UOyrYFFTuPaRfkHoZoaUc9o9Sn32QFHtgfluKo6PdVM6KhYs22IKF\n",
"38+laRPj2E1+HTWlhkTSFKdvnefui11lI3LUaMYZtARz4nrXUD7Xlm00qrPvcXqUjc1z7c64IGpB\n",
"14ytWNrSY52pvcw165JDJEVuGRYDzyGe4a4xRRdolIo4SqlevfU5ma93tTebONN6neLDvCA9iYs5\n",
"ZrNFsw2X6p3Pl+5YdZFLLEthcJGHTpezhIbP0WknPUH6unLFHyP1feDTv876CteUv6eArI1SsQAi\n",
"v5weQ0IqF8UdG3qdtznrs/0rAfaN2+CVTLL1Ms01OhpZiTF+eRjjZzAYDAaD4cTBGL88ehV3IBLS\n",
"VgElMS3bCYT3A0uTMnx5lsoXdeTa7FBRByJIFsAyBrp8nqNzbkmTtD0qW6GkVgx5JjS3/lI0ykJs\n",
"FiHH82KWjA1M29oMsXEqi6lz7eaAktVCjuEUSdkNffzhvlhFr6fT2k2bY9wdh2h97kTAFZkrV5v2\n",
"CFxf6y4LhtDu7xAsYcIWdbN1pcj+MCgxTMHGoZlfDdJnypu+DjGFnY4zP3bT6THUeOTGGR5L9P0H\n",
"SxMu7mDbEn52NNPDz13JuLnV7PoIWJLUbDo2jGcWU4+92Gc+VyW2EDYuYPVEUmbv9OntaP7K3fd7\n",
"jvqH3YlIYLpKLTIxrXBu3b01rcIY5g3RuVUbmVOD6ZvPYwZQH3/5+6fc9q40zqK4hG1uRqPmOsxV\n",
"5mGozklzoO7+9KbM+TEk1/6P76mcfRO/9lZDRSuo/H1aMrq/UpSyEoH5i7MIunUn2sltb09kuTya\n",
"7IIxfnkY42cwGAwGg+HEwRi/PHpp/Lr0EyIh4p5M8svqaI6jUGjXSjo1bs8mEiIn1vYdpU6B9z3X\n",
"si61ceHjLptA47PB1iav7ePm6Tk7F2894Bk4Z32wKV8zaOUQlY89WxJrKxnaQDYsE0fcJe1fjjUM\n",
"Gj8wnjHjF/RLzVQf/7bb18oZfoI9WK6JLcJ5cZvX5qslk9UutN1rJeuFPubLXWanOdawFLnj+cA1\n",
"RsQ9Aqun7tfROmb4Ksemjp0Ga+nZmuymrgrT6UR2dvieiZnmPhq/0JqtXT+s//c2Lkm7R4leA4dh\n",
"ftsQbKPyDF9q5JwO1/yclexLSpYtIoHZw3TixqM9x3weuLHkYNW81vdMsFGKxxk/LroxZuyOpXbT\n",
"yLjXLYu2jhUZW+PYvE6W7F5Egg6QmWA+Lzzm6s9y6zowilgn1oX3pxlD84Tp9897PD7VdI9Fn23R\n",
"8pbmM6OWfiZerg+4VRwD8wctrGUwiqbMg28tF8bpmWNNx8OJHBVPZ4xfHsb4GQwGg8FgOHEwxi+P\n",
"zh9+B6uVbLtIiM2aRVLGK2euKZJn/Ni4l5k+rgTSUSUbQCYMi6/MPZ7m0Gk1bx3tO1Bq7aaX5fNQ\n",
"Mkz12hPFZl1aNNEqdDclzY3fb12ZDKbPMTrQcAVmJzZ9BbSOpq7zmpou7Z8GzqHXWIHhXY2jdSDy\n",
"1tvf2dnE+4g7miQ3Cxw3PjpU+8G7hKi1RY9TQskg+mqY6D6fLY1vMHD2Wj53+60cQwqtn0gwfa0G\n",
"cfX0fLhy62qWOxXfDkeC3d2txCkgsHlpJTjYGK5iZdYMmjZm/vQyfryReOy4EmbvasYb1guHsaU8\n",
"TPN4w0bWnDXY3W1YPej4RALTh2rmF2dNk/iU8XMMmBp/cM8wkzRw52ECTR1YY8fqrVRnAYxDzMZB\n",
"y8fm1BgHtMYP/7Ppc0mLjnWLpAbZPM6UWCNtZI1syXqD9qLipm7cQ+OAlluqxPSVmL/YGUB6fYYx\n",
"EP19gGnMSrJTQBtSo/j4Ne4XmGJPhuFeGtdhXr3Of68cFsb45WGMn8FgMBgMhhMHY/zy6PzhN6tX\n",
"PhLTuhAA0RgiLURLzATlmK60mjP202Jtn76GpXZrRwFsZ0jN2+N2Z/lqXn4/vE7XUdL0cZN0hGJg\n",
"9w6UnyGYvrlvxl32SWpWFSI8VNrBRwsMHyrucE6hvcH+5VolMStXej/n94d7hSsUg7ZvknyGAebH\n",
"36MF5i98QP0P9q8n85dDuf1f50evGDm9Tvoc4HrHxxiqLpVeE+w99KL1gJY9HvZcpHnWcd9zlO7H\n",
"g5lut9Ze+csV8rlWXVzNu4Z/ZQdbErF6hVMyOMQ5Y10ej4/YT2cnF2kdu3wMeUwB46fHcowrl5bN\n",
"dN8xfWG8iZk/XdWb86UUCazxpEIlePNAgi3UzxQzfmiZxtcsrfpVLg/kRMDMn99WRq8NFwEeo/iZ\n",
"DmN92soTrOna3V7BE9N9xr0eOqa9jc8qsXZ8jnP6wKOE963tYP70eeJ9haYP1x2+qng9U/fSeIVM\n",
"w0A2q6PhpIzxy8MYP4PBYDAYDCcOxvjl0UvjlwMiRlREhYgz1lZwVVW8bBydsravpNuL5l2D68r6\n",
"IZFU2wisVtCpxZEGNDe5JvGlijswnvuLuYikWpvmf+dt5ZYNzblTllQk6DhEQlSOaHyKRu4VMa3u\n",
"vO+O4v1tjjfW4yHiLkXnJe1N85m4ig/nEMuW9HMauFYlzZ+/b/T+gQxzeje8U9JHHkd0ndtOvcm/\n",
"zqGrAtAzT0P49zmWJdL4OOa1wPRVhSrvo8D+ciFDR2mBPSkxYSKB0SmNM1zVylkFkfBMeh1Wgenp\n",
"A+9FdwhWFM/VKPEEZZ0itK757EIzL9ZBlrIHI3f8/28+85+9TIyff+2mQeuXVvWiKpM11T6b4PZr\n",
"240di9p5Ebb4iiIDwb6lgQFN78OSByl3NAG0jx8vwyxRyPjkq6/1/6iIXpJOdkn3R+gCVb7Xupi+\n",
"NmcA/gzGfV9dnGGk8Rm+hzcFD0K/bTUfFb5gggeO2yxlEyrlhTgarMKyBe34YWGMXx7G+BkMBoPB\n",
"YDhxMMYvj84ffvN61arxQVQWvNiaqJB9lDS4So81HKt1rFe7mgg8mX8VMiXNYiFiTHUgYK3atTfN\n",
"/83p56pdRNh+uoq1fdDgNPOa/2fQ2PlzF2ssgCjCcvvmGb9Vs4+Izkvn//Q4MH7Yd0TN7L2XahvT\n",
"Sjk+V3jN3U+AuGdy3ieRGR9ob4KvVvjMxlXcofcm+FR/vx9C69cXuerqusAwtpYCFlBiJVf+tKcR\n",
"NZi+EKXH+zEYLJPPHBUOVkpLPI57pQZ2PVRi4nnq6hAT+oI7v8dMr96+DG5Wt0esbJhKumwBJU/Q\n",
"CfVGbuu3XdL2ee2Ze/xedtkDsHl63sV5M728LDF+qcaP/TIBjDNbbmzZHjnt3SRfBSyiPP+gOd6K\n",
"x0Vm/ko+oyIpA8haP61Bxz2RVgDnq6yD5rLc73eE7ziM/0No266cgTqMV+1A4vuQmf9NhqEObCBt\n",
"13cf8SvPrlMkzdJxz+CFe14xxlSDcC/pZ2hoVb3HCmP8DAaDwWAwnDgY45fHFWv8GF7LsR3322zT\n",
"cjHz19Wz9Eq0VW1sZV89Tk7TkatObdDPV0v/P3I+fj7CXsWM334hAhdJo3Cu7i0xISLaY6tZH5g+\n",
"RKU1afxyOLPVsDIlr73Foorm5wDWBkF4VbVfZ818cIUdtF/MCiDyrgdxz1ARkbXEfY2H8Ibk+6MQ\n",
"8YqE87pJouD4Q+F2yWmcMGWNXzy/j+bPb4Ui77XfL8cyqVJmXeGrtzNwHOjgmDwxRWLGD8D9CM1r\n",
"3N+53a8tLMfdL8LzyRmGvuNL27jhWUE6V555yXivAcG3L89AtWn72CEAbCm8+fbd2HHRsXsvO3ZP\n",
"RDN+i+j1JTcN45DLLii2jHvBej2oZ/yafd5xLO6qpXcsWDF44iEDsYtOGdPGXzDXszzXC10kpy1O\n",
"NeecWQiV4fH3E59j3TmEq4nHqEQnTR+zxppd6/M8HxaDhNnDRobRJELBCaKckVAf9ekRXkf8GbxG\n",
"r3X93mg4kGpjjN9xwhg/g8FgMBgMJw7G+OVhP/wMBoPBYDCcOBjjl0fnD79lXXvR7VC54abFE054\n",
"i5J8iOpbTjyLc5EG4AbXbQBlnKTlrgBJg+0NigzSdCWnFvoWGehULwyiQxFHnOK9TEJsiK51qhf/\n",
"c6rXt1LqkeqFcTM+u6TiGr+/wlYEQZDtU0veyHvljpttFeLWfho+LZlp6yYSzqX+LLaXmt/GKV+c\n",
"95XbRrVRqR6yeFnXSIviuBu0tb/De5zyLSFX3MHiak7TcKo1fp03VeVnCAJtvra5fcN9wFYMx4GD\n",
"1TJJ9TL0s9O3mKxUSKZRbndHaTnfyk1du9Y9ls5jaraP4qbYriVn2MwoFXUgHevHEDd2IMWLdK6I\n",
"yP+bxfOwzMUk1Yv2kOE+wH3E9xmbws/82JKmejk9PB7GNlPb280UKf+Dg3l0zCLhnJVSvkCw/6nV\n",
"PCqA8yne5rgXi5Gbxulc3TKOpS7bY3wfDqNj9CnPI5ZNdMuWsB9xsQXGHJGQamcbmWAF5e52uua5\n",
"a4n3uuxdhnW+uGO86Scx64IxfnkY42cwGAwGg+HEwRi/PHrYudTZAglE/0MmAVyUhqhg1MP09UpE\n",
"1bzZIKqO15kaZnbDN5p2DCSiVy0MT/at0KINkSiKXvRt2JfpYwsGbeey59spOeYPRRVesN4sB0ak\n",
"GqYRHiLr3bGLWrlAJDEDTRk/GLbC3oUNVAMzFzMwIiEqw7Il5g/nVEfazJKwfQMXe3CRR/P/Ojou\n",
"ZnjYSDln78Lmznw/los80u1ypM3WC7nnsa+5tDfazVhDQLwNtjgwjmi3dHzFHfO6lmoIA1dx03Jh\n",
"1mGKyUTyFiBd54pNmYdgRwaqQKNQxMH7nLPigGE0Cm5KZvBc1BEXucRMF4q99ig7wKbMKOQQSZk+\n",
"mDu/XGD8dHFHycCZx5Y5GctrBFE/PhPbSqFl5GlnTXP5clzkIRJMrg8O8hZhjHhsybeK5CnYZR7b\n",
"mnlLt15itKjY5yiYvmxRRY/Ci2a5Zhq+l1WRm7u/J+52W+DwvOm7W65g76L3w49dZOeC+TzGNO/p\n",
"5/+oijuuP8bv8uXL8uCDD8o3vvENueGGG+QDH/iA3HXXXcXlH3vsMfmnf/onOTg4kJ/4iZ+Q3/iN\n",
"35Bbb721dRvHZ8VvMBgMBoPB8AphvV5f07+jwEMPPSTj8Vgeeugh+fjHPy4PPfSQfO9738su+2//\n",
"9m/yj//4j3L//ffL3/zN38ib3/xm+dznPte5jU7Gb7Ve+/z8QukiKrR8oshmiV/qiFLpl34OnZE3\n",
"NYvW8zgKX/vIqrCuTMSFaDVpEUdRutaUeCuIVX5LrO1DxBO3W0MLtjii9lF64bU2X2Vz1Zlb1yKj\n",
"pRFhtq7539u4QB84Thupi4ToTJtAV2SXcuO0YfxY8zedxsyMjpZxrlgfx8wft+fS60GknTB8o5gJ\n",
"ZK2fSND79dX6eajTsyaWri/zF60ZEhq33RHtB9gknP/1QD8PmLrtU1TO15I1OHqfwcpgivZui4L2\n",
"8iiwqGt/XMyO5FkSZ62B1mB4zjLaUZF2nZxfJrHcoGtIjG/zJj1fHYxOrqG9vxeRJfFsVX5dmsXC\n",
"uMJt1fD6UmEMubwMGr9LbPVCDCDWcbCKxxoRkWUdjzOhvV88trCNiz5PGIdg3AyGb3vh7HzG8fQU\n",
"MX8iZZNnbreWA8YXbhnJuj2MMfx+My/OWmCK8bHEYuvx+GrsknL2MCLhO4zHJT8+qQ94NnaNdnvN\n",
"S2b+PEOK7/boeaDtU4YhMH+0TYnHmWEPfX8fXG+M32w2k6985Svy2c9+VqbTqZw7d07e/va3y1NP\n",
"PSUf/OAHk+Wfe+45OXfunLz2ta8VEZF3vOMd8qUvfalzO8b4GQwGg8FgOHG43hi/559/Xqqqkltu\n",
"ucXPu/322+W5557LLv/Wt75VvvWtb8nzzz8vq9VK/uVf/kV++qd/unM7nYxfvVkHBkBpfGr3S3oz\n",
"JJaM2TN8JKNp6gKiQs9eqHBiXYjCPZNR0jhIGnEPKApCdDp0O79yqxpJqq0pVfMCYEmhvdPtjjiC\n",
"Tlq1kT6H54uECP6AmD9u3eb3T50XROW+EngdR+f+M6TbmSjNEbRWE9L0sNYPU1T76gppNsMusTa5\n",
"SJu1fcwK8jrXFHHq4ytF41zNmY2WOLBMIl+3v56JCx+AdmZD55l1shtfRZey6IEFjN9j09VktzMM\n",
"FLQ+/nlAC73h8TF+y/Xa64ahJRw55oHniwRdJj+b3gy+aLCegp0BvD6Jxxi6Ls1C7esO42CcRRBR\n",
"z5m7nTdgeEkvx1hkNHYYV0IWARmA9rFFJGQaeJy5VJivx7CF1+7F4y5YPDCCXs/otcY6a9AsO3VM\n",
"38U52rw149Elx/zBBHrXZROQVRAJjF9g/pplx+Nm35fL2GWhzg8xzT76MYS+ywpjSTwvHn+Go7iq\n",
"9zDgZ7hPu1FmDSv6DMYfjCX6+2HoXQXQXq2ZD+Zv5Z8/TwG6+coEvpBhYGCz+oO+HMsAACAASURB\n",
"VLMYw0bDtX++rxbXI+O3vb0dzdva2pLZbJZd/qd+6qfkZ3/2Z+W3fuu3ZDgcytmzZ+X3f//3O7dj\n",
"Vb0Gg8FgMBhOHF6Jqt5HH33U/3/+/Hk5f/68f33hwgV55plnsp87d+6cfOQjH5GDg4No/v7+vmy5\n",
"vtWMJ554Qr75zW/Kgw8+KDfeeKM89dRT8ulPf1o++9nPymQyyX5GpMcPv/Um1QXo/0t6OB/Z9dAt\n",
"JKwd6yE8E6IYv3Uclft1SRpZl+D1JqS1GRLzhwBnraiekh/TiqppSxG5/v9gGXvwcdTOjOB+xsdv\n",
"jzy25u4zqxbGByzdsoKWK/ZR5Go7ROnQ4jT/x0wfWMzpNG6wjikq43SFNEfjJS+8XPRWisZ5ygzQ\n",
"SFVG1kNiejuqOZMq3ww8W03n0ntfqWVHvsAu30YpVFW3e5Tp7QlXM17BAHglLRKvFOvNJmEYcT+G\n",
"qdJlOvYR+kzWWBa3o9kJ6K/AcII9JA0l2Cs8uTnPUD5X/Nr7mcU743YEL90xrFP9l16nZuTBqJUY\n",
"P2b4eL5I6gywn2j68mOM3i4fL8aIVea7QyQ4JTT/uwpttOhz01CZPIn2/Yxn/MKX4fZ2Mw9MX9pe\n",
"ze3nIZhgIHyGtcabzmXwFKat2uKxTiPRCR/iO5TvmdI9BFRKo8qaXmx36W631Ec0HVM4i4bxuZiB\n",
"2+S3fz0zfnfffXfxvQsXLrR+djabSV3X8oMf/MCne7/73e/Kbbfdll3+a1/7mtx5551y0003iYjI\n",
"u971Lvnbv/1b+d73vidvetObitsxjZ/BYDAYDIYTh+tN47e1tSV33HGHPPLIIzKfz+U///M/5atf\n",
"/aq8853vzC7/hje8Qf71X/9VLl68KOv1Wp566imp6zrSCOZw1aneEivQFnl0ReV+p7ymxk1UdDIq\n",
"6G6SKl/avej1gKJRtw7UzIYqz030Wh9DqVoKDERg/OJp8/8qmnovPpo/Kyyn/0c07D8Lxou6oejI\n",
"a+mYDV9xR6wJlg2O+rEbv0iowAODgNfTqtmPbWL8ZjNoblRl4DLPypU6eLRH2vl1MCO4pTzTSo3T\n",
"eT5X6moUq8jps54J1FpTXz0KxsdtP4n0wSZDC6MZeK7Ec/cZMX9tVd6lysBrAc34Je9J/ExheRHF\n",
"Cncyfem6cWp89bRj68Hogfnb4Lr4jITaVpdvIo0tmi30/n2eQcY0fyyeCY0Yv3hcYZaua4wR0frj\n",
"ZjrzWYM4A8HbEAnuATV96a2G6TUTCecabJ5IOoawr2lgIuOxDixf8388zsBFABo/MIA5xs/r8Xp4\n",
"zmrkvuj5PjuMb1/Q9MWv/bope5D7bMIodmj+NpKOIVXJ13QQCyNz+1Hz92BPf8HjwvWm8RMRueee\n",
"e+TBBx+Ue+65R2644Qb56Ec/6n35XnjhBbnvvvvkgQcekJtvvlne+973yhe+8AX5nd/5HVksFvK6\n",
"171Ofvu3f1t2dnZat2EaP4PBYDAYDCcO12PnjlOnTsknPvGJ7Htnz56Vhx9+2L+eTqdy7733Hnob\n",
"nT/8ourHLDsQswSJFxbppUTKF8NrbrAsRckj5R9XisL7djBolmmmKyG2MOxQsxwq05TuoKTRCE7l\n",
"jvFbx1H0TEfaFK0vvF6HK4FpubWO+Ndumv9MqZemiNIycVRO3TjA3gU2Idw27EV4sILbfjMf3ltB\n",
"cxP7bIkEvR9r/cCjlZg/Ddbd4B7z18P7/eU6B2Br+ajZV3dmOjf47XdE9hXdJ1qtl7jbV3F1XdhP\n",
"RPFxd4Dmf9xDrDmNq5hZixuvQ9z6Y21niT04ShyWCUg994gdKVR36yp8yG295yPGl2Hcx5R9/TSL\n",
"s6HxplTNGPTEGZaEGJbSmNJH48djxYzGAyyvPRnhPIApxhLu2Z3TWi6pqpePF8C5DfuZjiHMSiYV\n",
"yvT+TdtB4weGLzB+42jKbgKjUdg/3Ae4N7o8H/swfRhncJR8bds6SZW+w/p07hmQHp6fi9K9pben\n",
"q2tFQvaAmb9VRovK98qGNPelMYaP66iYweuR8bsWMMbPYDAYDAbDicP1yPhdC3T+8BvIwEcA2nvJ\n",
"67+IFUBkh1/2QT+Teh4xhsM4Kh8NmZFSfTZ9JOGiERdBlOyZOGrW+wxNBar6oPUZko/aIBNhMXz3\n",
"A+gF13FEvtSRNkXWSYTt/RNjDyytp8EyK2IDsI6aXkf7DYKjxrVz++p6pk7rKtr3OVUoi2jN0Liw\n",
"bDMN1XYxAygisljEXTZSv76y9qYU0eW6fIjoKmDF3hLTx2x1yTNS42p0cbjvBoMq2seVxPuzJDYv\n",
"dw+G/rrxMojOS9obvayv4vaRf549OEroKJ/3fUQdPfT/yXFSNTczvNq/raqIlYI35yYe26DtRZah\n",
"TdfHvbHD/LI+q28f8ZrGBRHNzjHzF/t5+q4867RnLo8va2Jpkvk9uipwFxgel3QXKGYawUZi30sZ\n",
"EH1lofEbj5txpdTJA9kFvj4aPvPUo3NKF7qemVZngMJ7vjvKIGXLRuSMEL6PC8x4hvEbV7E+3Y8D\n",
"5KeJ66S1f8wWrmj85edAM36V2te+z0QXjPHLwxg/g8FgMBgMJw7G+OVhP/wMBoPBYDCcOBjjl0fn\n",
"D79JVXn6WBdXwHSTCwEwhUEnp15EQvqF6XbQu6DjXZV/IroWERm50nNfcMGpFEq5tJlQM5gW98bO\n",
"UZa0kOoVpGNjwT7SKUuV4oAgekWpllxaum1/29C2jiFth9Mx2Ffe96WKopb0Huj/BaWtd1uKO7y4\n",
"fhTfM0NvV9IdtQXbljW9zqd89YAwrPLpEC76yBn3dqFLXC2SPgc4Z2hlhdZlSKlwqkVvB9fBp+8p\n",
"5QJh/iaTrhtQyhvPPWx8JlX/FNdhUQ0GiVF4IiNRD+CIxh+WB5SMu3X6rpTuC5KDWNTOEgCRIC1J\n",
"WlUW7J2ytjJdVjQ0LujiCqRS0ZoN9wSbYIf0bfcYguOrSHKDc62/BzD+lgoR+H7Pbd8fF6eHSa6y\n",
"5CIU9UxDQoJiDlxDlpZAVtL2g8BfZ5/yjafHhVCAhXMWf6dxAYe+b/BsVIXv5VEh1avB9yq+w3G+\n",
"J24cWjgJ0HiI6xDOC+4/voalojL9nYr7bDysovaoVwNj/PIwxs9gMBgMBsOJgzF+eXT+8BsPK9+O\n",
"a6wi/rEz8cU8RAdgAhFxo0VXrVTVSSNrEtNyJJ7YLYhI7YTWnhWAYW/hOHJ2C4kJrENi6Jth97qi\n",
"dC7MQCTUh3HkbQxICKuLbEIUHrOyNRuoXkXkw+yFFuzyvNoftxMIgzUZNmJrZvdERCp3L7GdAqZH\n",
"EbSl9h6KLavS4h0Rdf198Q/uhzKK6xCen9lHtx1cXy+QH8QMIAqEKs2Ag+FbozAjFvHj/hsPY8Yv\n",
"V+zEVgtgEzAOHAe2RiNvDI6xBPc0GEfdKrCigpOZG2cWi2YaGL82ET/ur3V2vn+WMvY9JTB7nhRO\n",
"HOJ7iMcHXDP9/AV2np4/GLcTs5u7H5klwtg+qePzPq7y7F6zjjiLg+eAM0NsEaSXZZTagHI2RURk\n",
"7Bm+fGaBGcDcfYEsATJO3EIyHZ9UcQU90FUVP8NXgiRbUGDkRdJMG54PvE6LPdLt+fNNY8O4htG/\n",
"ez1EkU085jTvxewsmOc+hs6hqGxgjN8xwxg/g8FgMBgMJw7G+OXR+cNvOqp8BKgjfkRyWxVadDnt\n",
"BAxFXQQO40yt8SvpbhBBaTZIA9GaiIr4vYlkM7+kKQnau5StSu8Njkow7W/FwHqcHMNSAkdnQfuA\n",
"qC5EQzjvq41rSVTY99WgHEExa8v2NX10Ify6xBLm9DKIjr2dhl9mE039Malw9UrMVhlJe8GCNZA3\n",
"Vu2xrpLdyGHOqdeLDeOIewJjVaUX9ZoeNw/3CpigMWn92FhV7ysAe4UJ2P1j1DhNqyppCThF+z9Y\n",
"cahWgbhX0QIQTN9iEY83bebfYHYAzjxgvGm7ZjyGMNOH5x8MXI7x78sK+ftCPeOs5WO9MCOXNcC5\n",
"ROu0Elvp15FhaVhLOCTWeErfIZNhei1HhWeHj9+/VucB1w7ZA2b6SlON0vdQYADLWr8uC5jDIBg4\n",
"5+eznk8knEM8o3hWAoubt13LIfnOrKD1c2webWOpsnlB6928l2r9yozfUDH8483RcFLG+OVhjJ/B\n",
"YDAYDIYTB2P88uj84bc9GvkobUtF3F73R23NwPTN500kjsgbkbhI+Vc4ojXWYXkGTEVppfZaJayJ\n",
"gRPJR+FtiHQpmcqqtu32Mc4Fs8J6ncXasXrr5pzXo5Q18OtCpD1YRZ/NRe987qae2Ym1VqwByrXZ\n",
"6YtcyyKOkhOdnNdila9T1bPi9DADAbfqEt+yLV22i+FrM1LtYo1LurHxOjwPS6e7GTu9DXSA4w4G\n",
"Koeu6t7jwLQapUwfsUR6/AkMXzMF84eWXNAUl/TEItrMO6/x9Qw0rmlLy7rkWpHGlTWwzbISfaYv\n",
"cqxh2hor1mvi2q0c8ztV57IexdkCvjPYbHdWh8/CVLk0llY+MxRfy51xyN7wdfds1bD8zDAC4xez\n",
"criGJSZQY43sEbGHQ86ADOP7Q89j5u9Q1dSe6SvoMt3h83jczHPX2etkSa9J2j8ej3IIjQSa/ZlC\n",
"r17F7f+WVc6MO85K5CrSGZrJrNZHM9YY45eHMX4Gg8FgMBhOHIzxy6Nb41eNkmit+d/9IncnlrU2\n",
"BwfNa0TescavoD8Z5atsh66FmNbkQH+zJFaQwW3OdDTFugOOnrkpfU6P0JdxzK0DEc56U0Xb93pJ\n",
"7Ne4rIvgil9EeHO0W4OvGar81PGzdmni9TjNdd72zAtprRRrgv8PE52L5Bk6jtrrGkwf3k+r6Y4S\n",
"iZazMGbkq7zjz/pqc9I6eW2qlO8lRqKXdFOtrRk7X8uxu+4rV4GJZVaF56Ct/VbJC+w4sDseq+rR\n",
"Znvbo+YZx/iDsUUkjDdh3FlFy5SqejW7XKzmHcWfbdNtpRWn7GsJRiytRGXWtU3/1IXgj4bX8X0X\n",
"GMF0yOd7lrXE0HGjPeNMa7oK9xdQ0bp4bBEROT1pKv53HQuYjDtgraqYtWpjYDmzEJjAlK0LbHDM\n",
"8LH2GN8/7EKgP8Nj1ArJAtLttrWM8+ssMH3BZzHV+DHTFzSVQ+xIs19Oew+GPAc+/i13faaOjVtW\n",
"qdbYt90rjD8lj1p9vNVwIIPaGL/jhDF+BoPBYDAYThyM8cujl8aPK3dFgqaPI2+u5kUEriOLkm9e\n",
"zmNNJERPeh1cccdIPYma1zrKDrqbUhTSVoHUTKuCdiupFCVmzu1ccyz+tI6yy3LnlLgizuluRojK\n",
"qUn7KB9xaQQdWqwTQeQN5oWnIo3/mkjqtVZR5RmOCdtvq7YEuLq3fRnW5+Qr8NrZG0xL171lPzqY\n",
"PmZGNXy3Cap2533GsWyN4uheROn/XIN1ROFckZf6yvU/prZKwKvF9mikGD/HMBDThzFG/8+MH8af\n",
"oN/LjyXNeyVtX5ylmLhuEL26HqC6l8aWwPzp8aef/ivpJNOmdfNjB147PzvvkRZXaouE8YTZODzn\n",
"GEswtmim2Vd6QlNZeEa46nRbafx23XZOOebv9DhmAFlPzu4DIuE687hSYvp0BqqqquxnSpXAzPzl\n",
"lvGetB3P25V0kgqdVMJ9UBWYPn6GSsy4SPe4E47f/R5wz8X2ZOo/AzbYM30j3B/9O8iMBkPZDMbF\n",
"9w8DY/zyMMbPYDAYDAbDiYMxfnn0YPzGPmrQ0QFH3CU/LbzWF6AUhXOVnddJeE+usH3MAxt2WJ2U\n",
"SOqEn/PJEslX8Pr/h/hsHI1xVR1Q6SitivU3wfUcLFEcJfuIvA4V0rNVExklTB/1zsXrOMLEscTH\n",
"hO1ueeav2cYOaXD0/9vkuRa8ueLz0ctXj1g5rurV75cqgPl1WnWn2IIOxqUrEtf7UdL04TWOX1e5\n",
"g6XgStQSEHnrY0f0PcF12MRM39RX6LV7tOWOL3RhOL6q3u3ROGFFS2OMSMoCsn+fHqs0cho/1vax\n",
"B2Db2BIqYeNqafav5E4GuWWTfQVLLtACx2xebt9CFS9XiMYeidF+uOcarOScWJuZnx+PLc1n4mrl\n",
"VeH5Lo0tIun4As3fqTFr/8bROrTWGC4SJQ0dP/clr1i9TKn7BzN/eh5XAq/cuFzqQtIGTk5gbGFd\n",
"t0jaIQWv+TkpPS/8f7RdYkuRbTs4cNdyaxL2w50zXEN//1PXl1WLq8BQBlKLafyOE8b4GQwGg8Fg\n",
"OHEwxi8P++FnMBgMBoPhxMEYvzw6f/htVVVWXA2quKu4oyv1IqJTefFF4s/m2r6NXPqzVNrP6du4\n",
"wTlZMRRSL5xyaZZBisVR/AW9NZvglopRRHSp+yjaP6RWMJ2p8+DTMus4HcMpXk7JZPfV2wTEqb0p\n",
"pXN3lTB7Z9RuwTAmmUAubd83KsvZuXARB6dyeD6bsIqoe4QsTvpYLiT7WDBu5hSvtibhc4PzUSqA\n",
"YcG6SEh1IQ3DaSlYMbApa59jZNPX48D2aOSPf+9gJiJhDOmT6mWj+K5zp4HPhBTf2K0D14OkKZlH\n",
"OLF1oTGFn+V42Xj9qYE2CjNyNkLumSVz9apD+qLB+8jpaVhm5QpU/LhCUoLSGBpaiOlmALGkBOML\n",
"pje44gG2e9Gpzsv0fVMq9gjPf/jsiL4F2cAZ6Ut+tnQLUU7/ruh8hGmc6txkpDddYHsX/T+skLj4\n",
"cn9/Hr1mSZZIeu789mhMDcc/itYpEtK+fM6m7jXW1dXQYHlEnNT1yPg98cQT8uSTT8pzzz0nd955\n",
"p3zsYx8rLvvkk0/KE088Ic8//7zs7OzInXfeKR/84Ac7Lc+M8TMYDAaDwXDicD0yfjfddJO8973v\n",
"la9//euyWCxal10sFvJrv/Zr8uY3v1kuXrwof/Znfyb/8A//IL/8y7/c+rnOH357e7PEmqX5P47G\n",
"u2xcosimEFFwUQfWmSvBx3oRUQxJXN+nVzZH3CV7hVD8EOaPKHLhCDtE4LGoWUepwUBZon1PLGgo\n",
"eoybYsfRePo6nq8Zz85G7t76oWy+GljAvAUDRNx7ew2LkzPWRVTO90UuOtfzm/di4TEzetx+K2fz\n",
"sqLCl3QabT57b6X2PfH8RQsDXipM6BJb62PAvMlkFR0vWzCAkfCWEEx3ZOBtltx16tkd71DY25sl\n",
"Zu88xuQMnNnGpatAZrNJReNcRMb3KKZtbD2Dizs2GRuLkGGIP8P3Vxhj3P7qAjF6RtlWSbfB0p/N\n",
"ZUjYaqPU5m+hxh82puasSTim/Pio952zBRhTdsZ5JhBjikjK/LYZd/PrIRUtgenzBVMTTGMWC89U\n",
"7j0U2+Ec8jTXQjQdj+MMTPIdp64hW32BNS9l5nIsOjN+XEyH84IxJHcesL4S81eyvdFYi0i9GolM\n",
"k7cOjeuR8bvjjjtEROQ73/mOvPjii63L/vzP/7z//6abbpK77rpLnn766c5tGONnMBgMBoPhxOF6\n",
"ZPyuBv/xH/8ht912W+dynT/85vNFEoGLdDN9zGLoC8CRBBv0Yh14P88SxWxI3/ZGbNXSZxlufN4G\n",
"NlstmdKKpK2wqo68fE36LD2Pm2MzO9jG+HUxf2xCrFv3pSbPMSsYmN+4RZBms1hnVorSuP2SiNbw\n",
"OWZ1zExX3oohYl6gbSLdDZuAhx3GfRDmM4/EjAqOKfcslZ6ZkubGbyPSKcGoNc/4lawphhkGmnVw\n",
"bDdz5kx2d64KepzBPVIaU/T/zPSlbB0sW8rPFtu3lM7/cBSzZiJlbTEjp+frMnAuZS3ito8x08da\n",
"W4w73MpLm/+yLhXg9lq5tmysGe3bEjBiq8j6iLMFPLbgu+fgYO7Xwd9HuHY8tuQ0nvwePzPMWoHN\n",
"AiOo561oPF741zwup5prZkcx/iTWNPQdE31mHT+rzJbv7zdMIFqqQhvcLBPrY7FdHhfS8xPOw3I5\n",
"cetttre9DeYvPy6VbHXW60p2d7NvHQrXI+N3pfjnf/5nefbZZ1s1gYAxfgaDwWAwGE4cXgnG79FH\n",
"H/X/nz9/Xs6fP+9fX7hwQZ555pns586dOyf333//FW3zK1/5inzxi1+UP/iDP5BTp051Lt/5w2+x\n",
"WGXbu3B1JkfrfVgLzGLGz7MyxJLk2stgXkkvxywdGyqLHM5Us4TEQJWqWhGtasaP2cAJ6XD6MD1s\n",
"iAn2yrfsoogzF62zpjAck5sm7cfUMbgocKvKM31cTcbV3vo4+zJ9Okpk41R+XdKW6EbzKzo3C2It\n",
"kspX3/A8rQzm24urC3PVhjgXJfaqrSIe4ONjPc5ikT8fWmPTZmrb7PvxRc8HBwt/ngMrmjeD18uU\n",
"zhVXRldVed9L68K1wpg2JR2pSLu5s8aVjC1pdW+qj0vM3QvMu9fPkcG6SK7iHvfmIJr65y/0mEz0\n",
"pqWq8ZLmT4MzIBhvcN1ffnlPRNJKVT2Px5dUT47tpvpYNm5mhq801cvuLZt9neOZrmNjfczPGV7z\n",
"uWEdOSPSelJ2jLMHgSWN2dJcpXxZW1xq3ZZmL3Bu8EyB8ePMg257p9nYzeaoWrZde8bv7rvvLr53\n",
"4cKFI9/e1772Nfn85z8vn/rUp3qleUWM8TMYDAaDwXACcT1q/NbrtaxWK1mv17Jer2W5XEpVVVm5\n",
"yje/+U35y7/8S/nkJz8pP/mTP9l7Gz0Yv2WWeShVILL3VY7NYW8l2MKt13HUUtLe6P+9nx8iiEL1\n",
"Wo7pA1gzUfeIzgcSR+GIzlChNqHWRKxXaf6P2bHLVPna5UkmUm5CjunOBF5Yk2i+SJktLB6z9+JK\n",
"9TnY58uXD6JjQoTJeq0+rYJYj5PThXDDcO8bNY0rzhBpeo+yqDI61uOEasaOQWOoI9T2c8ftCHPt\n",
"BzHvsFq/ZlfyXlvLZRyd+1aHmXOJ6Lukg2q7D68WdV0nbB2YtrYxhJl/fg3k7jHWEJeYPlw7bseo\n",
"/+cMQ1rl3b8imNfBDNBEXR+utGevzVN47t3+4fl8STE9pTZerPUCNOMJRrl0/zGznNOWAnO6znwd\n",
"mM0DQ67f4/Elre7FeKnnxfvWl+nb2Qllp9zWjhm+JbksoDI6pzlfb+J7BQxvH9aYzx2z5jhPOHea\n",
"8StlHAC+xhhTsU6RcG64Ij7cU837rL3W62+uR1jn1eB61Pg99thj8vjjj/vXX/7yl+X973+/vO99\n",
"75MXXnhB7rvvPnnggQfk5ptvlscff1wODg7kj/7oj/zyb3nLW+RTn/pU6zaM8TMYDAaDwXDicD0y\n",
"fnfffXcxXXz27Fl5+OGH/es//MM/vKJtdP7wW683SQTezI+jM2YD+Be/fr9UxcnRSkl7o//HPm07\n",
"RgN+Rl4v4qdx1CwSKl1DZA0dSj5az0X6YP4q2m7Q3uQr00SCDxX0Fqi46mo8r29mjpxLETdHaSKp\n",
"DiztdhFrX3wUqbbH+4br0cVe5fSaoQKTPbfybILed67A48o7nDHudCISonX2S2QG1DMdmcFk5T23\n",
"mvfGTkOUVvem7FVJy1piL3KVqsxe8fXGZ6Cd4Weu+Qye1fx1P06sVnVyHpgl1fsR3ov3LR2H+P1w\n",
"Pfhcle7hJLugNHacYRiQjyiPHTrzwFW7nHlgzztMtcYW7F+J6ZNVs88vvrwvIkEnp/VxGHcwr+TB\n",
"mrsPupi+rmmzjvh+Y/Azw98Pffe1tK1SlSoYvZ2dLXrdTFeKrTtYuQyH8+/DFMwfXnMnJc3ildji\n",
"0ZC12CmLhXEG1cKBJc2PKcz8Nf/H3zv8LLHGusSq9kFOwwet/3A4kMGgW9fcB9cj43ctYIyfwWAw\n",
"GAyGE4frkfG7FujB+K2P/eQhsmDWAoxULuJnbzHWwQTmL/bI04wfWMD1xjEbA2h54v3Luc2zxx3W\n",
"NaFKXdbgaLf5S5eaKBy6G468S30Vc56Ifl8poi35uDXzuPdkswxrvboicr1PzPBypWae8WqvXm5j\n",
"LYOrfqzLwTJDdwwcgeuqXszzfn5U7ez3x0XVm8x5ABs4dvcS1jXJVIIySnq1EpuqPun/42vF55Tv\n",
"k3a9YN5f8zhxpZF5uCfjc1M6vriDEDOKsf6ydB3GaoAYrVDFH+vv5nXMzsGzT48/4jMO8T5y390J\n",
"rVszfsgkTMlPE0zfSy9djqYvE/MnEsafS5eaKTM/bdXlpfGm1DkGDHxOp8uMUp9xB+j6juIshq4m\n",
"RdYg1fDFTN+pU9vNOtz+7a0CW7bvqnn3aAomkDMNfoxRtz3uA9aSsutAG/MHbKiqmscQZv6aebFO\n",
"spRhyI3DjHDtStNmXbFe1H9aelzyXjDGLw9j/AwGg8FgMJw4GOOXR68ffvh1rr2wEEmECGqYnY9p\n",
"3SNlz7/OS9FKs768dqEakaYP0TPpZPT/COCDjxJpu8jHrvmsi/SJ4YO2D1W88M0KVa5BW4NIG1NE\n",
"4Yi82WspVxGbskBu/6p8BK77KpZ6LnJUzn1w8TkNjspLD1wuAuur6cs5xZcq7kbuWEpaG834ccVd\n",
"V4/e1QbHOlLvxRqbyTCOynM9grvA2to2/RKeB81k5JD4rql7iT3Ojirq7oM2P0Gu3G/m5dkIjFFd\n",
"Wi+NErPH1aNgRHbGW/6zvhPGKtb4Ttx86IhDdiG9PiX/NowlrO2bqvMwJZ9QTF988WURCQwfM3+Y\n",
"6mVY/xcq8tsrZUXKrgI8toRODuEZLvVz5SwFjwuaLSplJ/h7iPvw6u0clum7vAhqZ2b69pauMwZV\n",
"++Y6KAGB4aNuIzQf2QS9WKlDin9/HWdgch2UunuF590For7nhSzFZJJqiq8FjPHLwxg/g8FgMBgM\n",
"Jw7G+OVhP/wMBoPBYDCcOBjjl0fnD7/RqEpsD0SCIJ3bq5Xmj1X1dik9CXAahxtPi5Qp5V2kFnwK\n",
"1tlrkFWHiEidSbuISLG90Eilo5DKKRV1YPuY//IMhRuhuAP/h1RvXOzBRR9s86KPv0S/c4pDp2lL\n",
"KV5OvbS12SlZwYT9yAu042KHdmF4qYWS/h9pGU7xss0CUi+zOpxDb4GQpHrj6z/0BRz4ZGoyimUW\n",
"a5ee2+RTTpze1iinydtb2zXrzRcslCwxRHJpe0699zcfvlLk0rhtSMebDrFVqAAAH49JREFU+DOh\n",
"YKxsSZOOVbFNSMnWRZSoHs83irhgAg75AFKxQYgf7hncK2jfxabwfgyhoo5J1DIx3j6Kx5Cu5bEF\n",
"Kd4XX7zk1xEKP/aiz+ztcbtFGPxqyY/bd6Sjx/EYMZ3GadS2Z5inXeNSXKgWF6bh+2bkil1wH/C6\n",
"9PYOm+JFWldE5JKbt79yLdHI1mXh5SSpjQvgxxcq7qictcmkosIQld7FI4OUd6mYjFO++rnoKibD\n",
"ukvfz/G8fj+4tFm8TuUPBkejMzHGLw9j/AwGg8FgMJw4GOOXR+cPP90jLlfOv1rlf5nPXQ2D9xHN\n",
"fLbropTsFvT6wH6hCbS3XHCR38SxOLV7XasIYFNo3I5oDO108sUdw2g7lWf+4vncJHuWaZUUbFyY\n",
"AYwj8Nw65vPmuBF5l+xdQnFHoF7ZxqAkwOZIWxeIlApBulo2adawxIZ1tVAS6c/08fy5Yo8RjaNV\n",
"HwuvmfFbwVB1kxZ3VK7t4Lh295u7x7Y9S7Fwx6jupUPY5oi0G+m2MXm5bWhmILDEZRH9cUGL/ZmJ\n",
"Q1GTZh77nqNgkdN/WbZ1wRiD507f/9vu/lugRd7aTSu0CHTrzIw1wwEY5nyLrglnD6rYFF7/j2Ky\n",
"F+co0IjHkhLzp/8vMX887pRaLIqUizva2p1h3vZ2w7jt7jbvTaeYP6HXdfRaY2srn3Hg7EE8hrQz\n",
"fZdcoQYsW8DuXV7mijvyjB8YYGSccowfvl/W7t7hTNOCitB020l8r42p2LILOVstzONGC2y71udH\n",
"VVdL0TJr216k1hfG+OVhjJ/BYDAYDIYTB2P88uj84afL3ttKv0tl9FqPxsgZM+eASCNnY8J2LvO5\n",
"a12020Rx9TqOvKeV0iOQlgvMXk1RWc7AGdF3YhfjDaSbz8y9PiZmD0TSSDplAGOdDmtu9P9gJ7q0\n",
"frFxahyNsx6nNNXszHKZ1+OwfQw3c8+5juC9ribpmi1gpo+NU/swfiVT1ZLGExF5tO9Yxt0Hy6G7\n",
"3m7d003MdOrrwPpIMGxsleTNyjNsV4ktZI0ns3la89l1zY5T67e1NUmYBNYW4xnX+xRe5/eN2Slu\n",
"Q6W3xxo/PKtV1Ww315R+WjsDZXdPLKHDcrYqbTYbuGd4HGI7F69XHlbR+yJB78f73D22BK0xGD5M\n",
"wfwxW8gGvyLlDANnC/gZBrsnInL6dMOw7exgrMRrN4b7sY23Fc4D7lW29wljSlkn3MX0QdPHr3Ma\n",
"P4wvYAdnBeNmfwyKTfeMHzFtmI/vLrR703p1/L/tNY2uReCAv5fLTGBJh70pWFLlxhwe3zjDw601\n",
"c1rL0aiS9Tpt6XYlMMYvD2P8DAaDwWAwnDgY45dH5w+/7e1pawUQosDDtNdhzWBJf9NWgYSoG9Fn\n",
"0HDE82F26rUVuhKKW3INEJXFkTg3TxcJzB5PR9RuabbJt4HS/4dIOp7CQBXR+sFBzATq44TWry44\n",
"ZV8J44eoHOvGfuloGceAebhWeM2sVQ7MNCEKxOtS5a6IZvgc40dVdfvEAM5gytvK+PF9EWs8maGJ\n",
"joVaBI5XqO5s1g1GFMy0Pn5m4ZbLUpupXOusrpZZpYpprfnsZ+B9HADbosFZhcUinDM8G8xsXA1K\n",
"LfPCWBOzaSLh3GD/a8e4rKAXbblXwniTZ4Gg8fNVvaT5Ewn32YoyIOm5i02o81rjfCUwZyD6MH4l\n",
"jR+eYZ35wJiFrEhpncwa6bEUn2E2qsT0gU0UOTzTdxiNH4ybF9TCEt89uSwSf++MV7G2c+myWEvF\n",
"XkPvN5y4MZKeezwfmLL2Wv/PRu78PrN48XdKfiyHTpPPf666u3ESSfWbhqODMX4Gg8FgMBhOHCzV\n",
"m0fnDz9o5UTybNVoFDNu0MOUNAYiccSo0eVfpn2FsD5EjtiP2SyOQnZGsc+VjrwTZqcGWxM3xQYq\n",
"dQxB2xdru4bEPBzmxmONUalZvD5/iNaZ8evS+okEdhT+XNDrcWsmVAxvNumx8HXGec95P2poBpCj\n",
"U0TnHCWynk//D6YPkfc+M4GFFkoiIRrn6w0MiIHJtXTzrKDbHu4VVFtie1suIs8xbYiOF4s4auZr\n",
"GTR/62ReyfuwSzepP4NqyS6PxqPEehjOp29WT/owzfiF8ebwrfAA1v+Fqkbok+OxjMcW/T+mU7BR\n",
"m3S8aY5NMSwrMMntmmLcSzgvOvOA/8H+cGVmXcevc+24SqwgXpf0grwekRzjF7st5HzemGkK4wCY\n",
"/3F2XTnwOFRiHDXD3MX0vewsKpjpu5Rp2bZPjN/MOwbkswkjxfgt12D83H7RfbDldKMYw6Afbv5f\n",
"R/NKjH/Q7aYZIM4adLG5yAzoKveQLWJvRJ5Oo9f6s6v1WjaDo+GkLNWbhzF+BoPBYDAYThyM8cuj\n",
"84efZlcqzRaRA3pg3vKRuI4SS0CknUbi0G+kPn6sk2PmDxEgmEvtTcQ+RUOnnRpiP4Q6GOim4MM8\n",
"w9eFPl5kpe4OcMyPvZfYc2yZLKPR1ug+3Y+YJYSbOs6xXh8zfVw9WfJxEglaEWahwDzhNTdCFwlM\n",
"H1fasfaPq3yXOloG49dRzR20gCmb41kqsBar5phmrspzSlG6rmYLur+Fe8/pxNy53GziCjdctzha\n",
"7+d92Mb48TxozxbwtXTnbudoCu4igFXRwDPmu+KMwvMCxiZUKx9e41fy7+PxpzS26O1iesNoV0RE\n",
"tkd5xi+HmjTFft2cTZDYT7INJW0tP8ttKLGEObaQx5vRqF2vp+/d4I/Y3FgYwzjz0YZS1iB4k8YM\n",
"k77vLy6ctrHA9L28iBm/Pho/n1lwzwy0nvjO8cykupbTTfx1jFsa1d0zdAEZYd1KpwydpBvLuLsJ\n",
"v27z0QPSTEPM9OEc6qwgM3s473heearpa5zDxbqW9aqSHbl6GOOXhzF+BoPBYDAYThyM8cuj84ef\n",
"1jHoXrUcjZcqAfv0JgVChXCho4a6iHWd1+GU/AQR+Wpfwi6wj5FG6XC44hNREk9FynqsrsrM9q4X\n",
"6OCQ1/rpCmp8BkxiiLCb1+yViMhb9+rM+aJp8H7xMYuknUI4kmSPPrB8ImWmz2tuUOW7jDU3WuMX\n",
"evSKm5J/H6rrSOOX8+BCFe94iKq+Kp66909PUm0dM32rVXyv4n7M+fnhPWY8Sh6IuerGoXtGfH9R\n",
"dL2B9tSdoONg/C4uFkU2ZEzdKUSCX5lmG0RSFj04AqTdCAJbxSx17DqAdYZKYt1fNK445Spf7Odm\n",
"k24fWErc1cGvmzrGsO9f838z5bEhHTu4+05a3d+3+06fsbzUzzXHqrKWONepSYPHEv1/aQwJmrPm\n",
"/o+yBjRmYExhps9r/TIav/0C4xeeIWZzm6nWja8K+r95FTsRzMkbsPk/9vabjtq/U4L2N4yDfL5D\n",
"pi2fTQg6veCrygwfPBpvuGEnmo8swv4iMP3e87CuZVBXclauHsb45WGMn8FgMBgMhhOH65Hxe+KJ\n",
"J+TJJ5+U5557Tu6880752Mc+1rr8//3f/8kXvvAFeeaZZ2Q0GsnP/dzPyYc+9KHWz3QzfkrHMMox\n",
"HI7xQ69KaFtyvlxA6Vc4z+dKsNhXiKvJwBaC6Wv2m6uKI88h6o2Y6HFQIesOuy14gC8Tpj7ycgwj\n",
"T0XaOlM4pssxDKGqEVW4qkcjudqnURvpFI+4MrOkIepiIHRVa6nyDhFg8MbKaPw4Wl8yA9juqyWi\n",
"Gb92jRVH5MOB0jriuN3zsEX9NBH55xz8+fiDfxzf42Bz00ppPr9d9xbO8Up5WR4s0dUE5yreVxz/\n",
"jyVbv3q8NJtlemPHjB/GFpFQxYh921Wsg0iOaUq7/4TqRafxdG9hmZI3oNYrM6ON5wH3PXcQanMV\n",
"wJCGMWRIGuNcNTnY2AnGX6qEBwOD/djbS1ka9Mbd29uKjg9T1tzlxu+0upe7PJS7PbDukJnFLhZT\n",
"/1+675lp0t9rl0mzd3GeZ/pKWkCRtGPQvI6f/9LYMlYsduLfh2xaHeuSeSoSngNsb0R+fmmVf9o5\n",
"o9SLl68D7jGc093d8F1/5kyjcQXDd+ONp9zr3eg8XaIxvfk/9DUebX50q3pvuukmee973ytf//rX\n",
"ZaFY5RxWq5V85jOfkV/8xV+U++67T4bDoXz/+9/v3IYxfgaDwWAwGE4crkfG74477hARke985zvy\n",
"4osvti775JNPyk033SS/9Eu/5Oe94Q1v6NyG/fAzGAwGg8Fw4nA9Mn6Hwbe+9S15zWteI3/8x38s\n",
"//3f/y1veMMb5CMf+Ujnj7/OH37aZiFX3OGbk7v0E1IPEDW3p3yRYmHjYqac4+X1PGC1gqFzQx2z\n",
"kWcwIw3UOtId4wqpPIj3m/c3rsjEp+UG6U0Eer5mqt2lLZCeQsolZ4Uwn8NAOW+bAEG4LqpgcHoE\n",
"hs4smNbCbKRW0KqNhd9s4AuqXwvDu9MxcVqmzUYE1wOXli1Y9qgBukh3ipdtXZDG1O2OkIZl4b03\n",
"bnYpl7TFXziXXNQxW8E4PLZZQIpyqW7gKaVdggVF3LaIU5MabLWAdbGtAlJ+SKPnUi0+1buKU0p9\n",
"rEmuFC/NZ2lRjR9jmmNbKlsPb1hM+3SabJvwTHE7RJFc2jFfENWGUvES3//cOrL5Py4E26D9Gm0f\n",
"72N5neKb10gZNp/F9d7d5XaPzTi+t9e0X0MKTiSMFViWx6GSGXzzmSq7bKmYi1ONeh6PQ+n8eAzR\n",
"spm0JVhcZADz95fmzfHn5CIlg+auFm56HXh2ZpzqpbEjyEfSe200cM+fu+8XtbNMw/ckFVuJKAnJ\n",
"Jv7OwjkrX4e0Xyqn9PmzoXAmLuAQCSlepHYxvUQFMzlrLoxFy/VapnI0LduuR8bvMHjxxRfl6aef\n",
"lt/93d+Vt771rfKlL31J/vzP/1weeOABGY3KP++M8TMYDAaDwXDi8Eowfo8++qj///z583L+/Hn/\n",
"+sKFC/LMM89kP3fu3Dm5//77D7WtyWQib3nLW+Rtb3ubiIi85z3vkb//+7+X73//+62sXzfjt5j7\n",
"0vOBEhujfdUSjIZj/kqN7rWYmFuwsQlxYALzRs4apfY9oaVb3FIuZz7szagds1MPIWbvtlHwkVxH\n",
"ZJEzkGaGs83yQUMzbszCIZJLTVDTdVZVvkyfIzuOvLWoOrw3pnXEBQsckWvGD2wUonJm6bgNW1tx\n",
"BzN9ZcZPMa8Fc9Vhwc4HovuFYj78c1Ao4lgUij1EAqPFrB1vtySgF0kF7zjfMMFOrXHiohf9v468\n",
"RUQW1HbqOPDi7MD/X2L85nVgeFYlqw/3WYw3eA6Wy7gNmYjIfI7nKGU9RHTBFNjzjK0TWV2AAcN1\n",
"AIsG5gNjjEgYZ+phvnjIF4yBGcw8w7hXK3ftTrvrDZE9jruURYjn5a9vOj6Ea4Xj62IHeUzRmaDU\n",
"Ymianc9TjBvNsvlWYGzfwq3VREQuL+NiDs4ilJi/eBzKt4TEfcpsNq69/goeDdwY4c7Zkp47TL11\n",
"izrX2I63XiI7MbZ14QyMBrfZ5HEJ5z1Ytez6ZfE/GGUUxLAVTu4c6sKY3eH1y/jdfffdxfcuXLhw\n",
"pNt64xvfKP/1X//lX3f9dgCOr/mmwWAwGAwGwyuE9XpzTf+OZp/XslgsZL1ey3q9luVyWfwB+453\n",
"vEO+/e1vy7//+7/Ler2WL33pS3LDDTfIj//4j7duo5PxuzifqwhcafxWaBwNqwXH9BV0UJUyrEU0\n",
"xsbAiMBTCwBE3tr0s91stdTKLW5RE7fPQvTMjM+yxUbBv3ZT1u2wKbA2nOXtwQqiy0g11sfEkdvB\n",
"QaNhgW5n6SIqMH46qofGj61XwOyVrEC09qwUlfN8br8Wm3428+Zed9bs+z6xdUHzl0aJrAfk6WyF\n",
"dkCxFlMk6Gw4Kgezt3bnxV8nZ5EzVrYqyzrW3WCK6DxE4vFrPQ8RNTPfAEfiOcaPtX3+viCmL5hh\n",
"q3O5jM8zG8WWWLajgNb4gemrSCerLXi6rHfG3rC9Of7xOG6Hp+fN52SbUmhlCHJU27zARgrWS7gO\n",
"aL+HawqmsVJt5/j599uXmL3hY9VjLGcJsOwZN84cxgSXdXkwdi492yLa8iVmFsM6Y0Y0ZxyO9YEt\n",
"8ubX21vRa55qbRlbi7B9y96KMwNp1gBm7/yMlMahPcUahowCGzfnx5b1BmNKOF/V2t2zuP/c/BUx\n",
"fF4Tqu6DNWn7sF3WaYcMTbO/uXZ4fN+X7LaCji80VwPTV7LC4TZ4MeMXsjHrqlwbcBhcjxq/xx57\n",
"TB5//HH/+stf/rK8//3vl/e9733ywgsvyH333ScPPPCA3HzzzfL6179ePv7xj8tf//Vfy8WLF+VN\n",
"b3qTfPKTn4yaPORgGj+DwWAwGAwnDtdjVe/dd99dTBefPXtWHn744WjeHXfc4S1g+qLzh59uRF0N\n",
"Mho/x3qwlgHwjJ9iJ06PYxYI0SKiEOhSEKWUdHwiZeava6r/DxWv8T4zciwNM38DxwYtHfOwIKZH\n",
"V3HtbjeR1GvGZ0QkbXvHJpu5iPvll/dFRGR/f+amTSRVMl/VWj9o/ICS1o91Ynr7iNwRYeM9fCZU\n",
"Gcaf1doSmAin7F07m5ebx1F5qcouNj8t3bOO+cM1dZ+FTktrbLxxt5u3IX1WeD7SbaKd08QxW1wh\n",
"7bdB+5lrWcXsDDN9lwpshl6WGb9rofFrGL/mf27V5nWZmeidsxEwZZ+6qurTYJPnYMSVSwEx6WDc\n",
"cUqY+cu1ksRnwJyUxhvombeVPpbHGWbtwHDyedfnYT6IGSZmfG5wz9trXnNj9phFyuNMeO6bdbz8\n",
"cvOMX7oUNH7IMLDWj1FqqSaSVuCePt0wSWfOxG2+SlP9P8YZ6La5ireN8QPjzWbMpXFortgy1vYt\n",
"fDVvjCFr/dbhe9Fff9Z2Fn67tFXZe4ZxGLfbazPSZ3TpMzHVGj+cOzB6YPpems2i+W2M33y1ks34\n",
"R5fxuxYwxs9gMBgMBsOJw/XI+F0LdLdsW2gfvxCdjF3T+dUIrYjiz6WaGxVhohWNi8rm89hrqE9T\n",
"8PSCwq+uWbYUccdegHE7p+GQGBbyz9JsXWCO8joczxo5LSQiwYNVOOWIEned5+HZsw3zx1VrzJ5p\n",
"xg1R1+XLTRReYvzAqsbHH3v7lby3sH2uFBVJmTz2duIKPRzDSDEfl6jClCPqEqsXLcsedNzQnJi+\n",
"hT4PhapdcdH4ehBrbljHmltHKRrnqD63LHQ5dd2h04hYm5hJKWn6WD+ZZT6I2ci1mTtqvDQL4ww0\n",
"b1vUqk0/8kPS4Y7JV3R7FT9bOf+4MM7ka9zC+IANx2OMSDfDl6uiZTDTB71oWiGergNM59zdK/Be\n",
"DFqzZl3Isrz+9TeLSN5HszTO4FlGdgFjjUjINLDWr6u6F/pBkcAoYrupFxy3/4qZQP0/3itlAPje\n",
"zi+bH4dwbmeZynz8H9jxfAYMaaU2to5b9WW+/tz8whu5ZallXo75ZaS6zJiZxbleqd24WND0vUTa\n",
"Piy3n9FJLta1jCWMS1cDY/zyMMbPYDAYDAbDiYMxfnl0a/yUO7nW6SGyTquW3IpJc4Mqu+azjvFz\n",
"jaRDx4iY+ePq3jYEPU6sy8HUR9XqRuDPYCtrqpTjrhwiOf1Tu8ZxvIoZCREVfbroFxHPrmNCf/zH\n",
"m5o8jrgvXgxVVJcuxVE4R+BtVXd1HUdDpapiXBf2cWr+z7MErAMBE4joMaft6NTpEasnkjJ40EV5\n",
"DyzWWGa0qMzG+LNCAXXbXcgM1GGicb9dr8txVa2FyixmZkXCeQUbMavzrCkzfZfU842qRmidZqRb\n",
"Yj3rUeKiziy4c4fOBb7qWrGkGGegO556dhDPEu6dmOnT57Siau1cZkGDx4vm/5gVBNPXx0+LKzEX\n",
"xPClurE0u5BqHJtjShgu16HhjHNXuOGm0LkDzzOe4eDP1owzL754SUREXn55T0Rijd/eXvM/xpmu\n",
"jkE5bRnrUlMNGTN+cVcIvYyv4k18+/KVuSI6GxOPN0t6lpZUqVtHOl3cow1KjB7GkDBOhPe8pthn\n",
"y2I/yzB11eBqgOo7/mDs4M5WzXvxZ9JqXui1m+sydJ992ekoRcLvBa7eZaYvaPzyldFbEuZfDYzx\n",
"y8MYP4PBYDAYDCcOxvjl0fnDT/t8wVdLJEQ4m00TFbD33Yg0N3PFNM1HMUsTdB9537pcRB76+BJb\n",
"QxF4iQHU8OuSmOlbEVsUVdN5Fiqvw0FVJ6IyRGmjDGuKaPTyqIlyTrmofHfZTE87Fu31FAGLpLqb\n",
"UnUv+gFr36a0qjnW+uE166N0tM5VvCXNH3eOyHnxBZaKz218/rWfG2v3Sj0rWVvXxshwNM5RNJ4D\n",
"fS2hy0mXia+/v5eZTmwBR+lgZrVebUWsdFkfma9UFFFVjWA+VjHzd5xVvbonOLIDW+vm+HLXCszW\n",
"tGJNZ1wBDBZtd9rcf7q/K/ek5vser7V/aPM61cn2ZRZyTPOKtH3MQHntE2UX9PpY6wjXhcvLuBvO\n",
"/jJl3G+YNs/qrbe+pnlNTB+YtTbGD+NN6JSSZz5xD+vrkLoW5P37WPun+w2DfboMJgnsdcERIKrI\n",
"XcXfR+HeiZk99tHLsXoYETbEuA3oexH371jpyr32HRkxp20d83z3vTFR7DWeGWTlMF3X+e+9UI2u\n",
"v1Pj54CvS+jR21yfi5nKXGZawfBdIuYPz3uO8Vuua9mvTON3nDDGz2AwGAwGw4mDMX552A8/g8Fg\n",
"MBgMJw7G+OXRnepdLpP0lUiZwgeVjTTdfAT6NmxqSRYbu6N2OxfQ0nGRR94otE8hSAlsrhtSME7k\n",
"qywAcHwHVHDA9i6citFt7wKF7ywoRnFaZncM012X8nWWDLuqZdqtLu1RSvXu7TWvc03qu4TouKZI\n",
"hXERjkhI2XDJP6d+01RjOJfeJoHSMEjbYj43LRdJU7ptNgm5Y9NgC6LKFyZV0XRSIV2j0vajOB0T\n",
"lqmidU1IoK3fw/bZNoX3NWdDMifrlZCmje/PNmucvYLlRclI+CiB1JyIyMSZwtcUrcfFZc2+bY/y\n",
"Nj6+UIIKImIxO7eGjFO8fdBVEALgGuoCFYwzvnjM3+/taXotdSiNw7j/MLbsjZ2cBEbeqqgHdkoQ\n",
"5t+41Tyzt99+i4iIvPTSZRHpl+plI+dSCzd9jllCwtZPqY1IM+aNlNSBjcnZvmhe56ciaXu1RB5S\n",
"KtTQrfsKRRWp7RDSuPFUJFwrpHinZGfk36f5IiJb7j1YIGGc2XetBFmSgMK+3L1eMvLnAjJvGbXS\n",
"qV53L7mplzEt4vsuXK9MqreuZW90VKleY/xyMMbPYDAYDAbDiYMxfnl0/vA7WK28YFWbMHOk6RmN\n",
"GobFzbIzZ1i8GIULsKAIVwZxq7LQQqls5BwilfyF5c/krGHYYuAAbZc2sVCeiwtEygzWkpkGMvvV\n",
"rClbMATGbxy9BvO374o+dsbKQNlZwey66OzsbtOaaQVLjoKtS/N/s+8lgXrJ9FNbYjDjh+nQMQ6I\n",
"vBFhcySu/1+QRQ7Od+1F8HFELtLN8CHSHhCbl6utwO3lhddVzOJxpA3rkOY9jsrjKSJyzx4qUTds\n",
"G7gwqcTmAOuMyD9lq1EwgHMbv9bMx5wF8Kt4meM0cNaZhXoYMy2wuYAlkojOJMRjyYKyCdwqUY8h\n",
"qVF8XETDY0gogkpZkmDBk7fL8KbcioEIVkTxeebCnD0yOI/Yqjp/TUJxXbPdSwuMJc09e3qSCvIv\n",
"T2I25oyz20Lbtze4YoqcgXNXq0hmXnLXge1DOIsABhBdzi4ptgiMEo5lRvcyF4rpe5ktnwDO1iRF\n",
"Xjp7s3FjoxtfMO4PfXFffD3A9O2OwliOoj5kdk5P8tNd975m/HhMQlFHMPCPr0ewNwvHXBrv+bqA\n",
"tfPjxTJnhu2YV5ruE9OXaxm5WNc+U3G1YMsyQ4POH363TF/jvyNHuorI3eC4gXfcDbdTuR8iQ3ez\n",
"DJqHdrwJ3m+DdXMDrVfNdDlspqGPLFK8GDSb9zebcDMMh3CIzw8oSEdiWlXN9geDsB/rdTOQLJfN\n",
"tMYPUfejdejS0+ONc7ZXbuL1oNl+5fZj7FJPq8E6mia9GtWXN/s0TYfux8IAU/fguctUoYJapc03\n",
"tfNTdMss3bR2P7jR/QHV1yLhHA7cMYTvsfwPv7DLuP465Y/tNOtfuh+t6G9bu/1bo4quxvshBTRy\n",
"13Xi9g3nVtx04M7xyFV6TdR9sON6lc7cMvOKvvjph0Hd8jvRe1CiIpfSZRi08eWpf/jtuvt+Z4B7\n",
"xQUz7t4ZrpvXfL1ERJbuHOKsrtwAyIMWfkwsXaXmUHWQwHnG+nGPjNx1n4p7xgbux/6wmQ5H4ctz\n",
"vGnmbbtzuRjGlbHH6eP3xt3XJal2VC3uuC+1HXW+T7sfJTeOXAXo0PWAHrjOMJtmKnWTHlwtm/d1\n",
"FeNggPQvKk2bZdbruZuP6xD/eNGBD37Q4UtxMtlyyzTTzaZJS65WbozRP97dvlQutT1198QOXSPc\n",
"91Mnb1kOw7OzHOavCUsLEHBsu3sZ47OIyJYLvCfunq3cvSq1u2dW7tl2y6mCWNls4Lzgnmvs8wjP\n",
"aJw2BXQQMxrhB8coWhfGrDC2NNdn4x6UteqCJDWeCTce05jtx5SW+37qltl19//pIdwG6Ic5gnwt\n",
"Oanj8T5xdaD+00jFb1dqDHE/sE6N4h+AN7jvrl13j0+lmVbqO1Xq5n/c5/gODd+PCHKaY6rcODlU\n",
"989ggOuA+9t9T/vvSfcMuQBs4O5f/OgVCffSKfedvho5z79JEyBMNwt3LI6QGIWxfKaCtVu2zorh\n",
"+DDY9HEaNRgMBoPBYDBc97jySgiDwWAwGAwGw3UF++FnMBgMBoPB8CMC++FnMBgMBoPB8CMC++Fn\n",
"MBgMBoPB8CMC++FnMBgMBoPB8CMC++FnMBgMBoPB8COC/w9E5sa7otVOqgAAAABJRU5ErkJggg==\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7fcaced94c90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from pymks.tools import draw_concentrations_compare\n",
"\n",
"draw_concentrations_compare((phi_sim[0], phi_pred[0]), labels=('Simulation', 'MKS'))\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The MKS model with resized influence coefficients was able to reasonably predict the structure evolution for a larger concentration field. "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
facundoq/dynamic-programming-tracker | Dynamic Programming Tracker.ipynb | 1 | 12611 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Dynamic Programming Tracker for Hands\n",
"Implementation of [Dreuw06 - Tracking Using Dynamic Programming\n",
"for Appearance-Based Sign Language Recognition](http://thomas.deselaers.de/publications/papers/dreuw_fg06.pdf)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Imports"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"\n",
"%load_ext autoreload\n",
"\n",
"%autoreload 2"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"import os\n",
"import numpy as np\n",
"import skimage.io\n",
"import skimage\n",
"from scipy import ndimage\n",
"from skimage.draw import circle_perimeter_aa,circle\n",
"from skimage import transform\n",
"\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib\n",
"import matplotlib.animation as anim\n",
"\n",
"from scipy.stats import multivariate_normal\n",
"import numba\n",
"import skvideo.io\n",
"import skvideo.datasets\n",
"\n",
"import itertools\n",
"\n",
"import scoring\n",
"import util\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Configuration\n"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Original video shape: (54, 368, 480, 3)\n",
"Resulting video shape: (20, 368, 480, 3)\n"
]
}
],
"source": [
"test_path='test_data/All_Blacks.5846.main_glosses.mb.r480x360.mp4'\n",
"#test_path='test_data/_1276_small_3.mov'\n",
"output_path='tmp/'\n",
"filename =os.path.basename(test_path)\n",
"tracked_video_path= os.path.join(output_path,filename)\n",
"debug_video_path=os.path.join(output_path,\"_debug\".join(os.path.splitext(filename)))\n",
"data = skvideo.io.ffprobe(test_path)['video']\n",
"rate = data['@r_frame_rate']\n",
"video = skvideo.io.vread(test_path)/255\n",
"\n",
"print(\"Original video shape: %s\" % str(video.shape))\n",
"video=video[0:20,:,:,:]\n",
"util.video_rgb_to_hsv(video)\n",
"\n",
"T,h,w,c=video.shape\n",
"\n",
"# new_size=(320,320)\n",
"# video_original=video\n",
"# video=np.zeros((T,new_size[0],new_size[1],c))\n",
"# for t in range(T):\n",
"# video[t,:,:,:] = transform.resize(video_original[t,:,:,:], new_size, order=1)\n",
"\n",
"T,h,w,c=video.shape\n",
"\n",
"print(\"Resulting video shape: %s\" % str(video.shape))"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(19, 368, 480)\n",
"Movement score treshold: 0.017744\n",
"Pixel score treshold: 0.024918\n",
"Optical flow treshold: 0.421541\n"
]
}
],
"source": [
"def jump_penalty_euclidean(p1,p2):\n",
" d=p1-p2\n",
" return np.sum(d**2)\n",
"def skin_config_asllvd():\n",
" mu_hsv=np.array([20.0,35.0,73.0])/255.0\n",
" #mu_rgb=np.array([176,134,112])\n",
" cov=np.array([0.3,0.5,10])\n",
" return mu_hsv,cov\n",
"def skin_config_boston():\n",
" mu_hsv=np.array([357,56.0,85.0])/255.0\n",
" #mu_rgb=np.array([176,134,112])\n",
" cov=np.array([0.3,0.7,15])\n",
" return mu_hsv,cov\n",
"\n",
"mu,cov=skin_config_asllvd()\n",
"#mu,cov=skin_config_boston()\n",
"\n",
"movement_weight=0.1\n",
"optical_flow_weight=0.4\n",
"scorers=[scoring.manhattan_movement_score,lambda video:scoring.skin_pixel_scorer(video,mu,cov),scoring.optical_flow_movement_score]\n",
"scorers_labels=['manhattan_movement','pixel','optical_flow']\n",
"scorers_weights=[movement_weight,1-movement_weight-optical_flow_weight,optical_flow_weight]\n",
"local_score,scores=scoring.calculate_local_score(video,scorers,scorers_weights)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Test model"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Calculating score for frame:\n",
"1/19 - 2/19 - 3/19 - 4/19 - 5/19 - 6/19 - 7/19 - 8/19 - 9/19 - 10/19 - 11/19 - 12/19 - 13/19 - 14/19 - 15/19 - 16/19 - 17/19 - 18/19 - 19/19 - Tracking coordinates\n",
"[[315 315 324 336 342 338 313 288 263 238 213 214 201 198 192 190 190 191\n",
" 197 202]\n",
" [183 179 184 184 194 219 235 243 251 255 250 251 256 254 257 262 262 264\n",
" 257 254]]\n"
]
}
],
"source": [
"class DPTracker: \n",
"\n",
" def __init__(self):\n",
" pass\n",
"\n",
" def backtrack_path(self,backtracking_path,score):\n",
" Tm,h,w,dim_indices=backtracking_path.shape\n",
" T=Tm+1\n",
" path=np.zeros((T,2),dtype=int) # 2 => (x,y)\n",
" best_index_last_frame = np.argmax(score[-1,:,:])\n",
" x,y= np.unravel_index(best_index_last_frame , score[-1,:,:].shape)\n",
" path[-1,:]=np.array([x,y])\n",
" for t in reversed(range(T-1)):\n",
" x,y= tuple(path[t+1,:])\n",
" path[t, :] = backtracking_path[t,x,y,:]\n",
" return path\n",
"\n",
" @numba.jit\n",
" def track(self,video,local_score,jump_penalty_matrix):\n",
" video = ndimage.gaussian_filter(video, sigma=(0, 2, 2, 0), order=0)\n",
" T,h,w,c=video.shape\n",
" self.backtracking_path=np.zeros((T-1,h,w,2),dtype=int) # 2 => (x,y) for T-1\n",
" self.score=np.zeros((T,h,w))\n",
" n=int((jump_penalty_matrix.shape[0]-1)/2)\n",
" n2=n+1\n",
" \n",
"\n",
" self.score[0,:,:]=local_score[0,:,:]\n",
" self.local_score =local_score\n",
" \n",
" initial_values=np.zeros((h,w,2))\n",
"\n",
" for i in range(h):\n",
" for j in range(w):\n",
" initial_values[i,j,:]=np.array([i,j])\n",
" self.backtracking_path[:,:,:,:]=initial_values\n",
" \n",
" print(\"Calculating score for frame:\")\n",
" for t in range(1,T):\n",
" print(\"%d/%d - \" % (t,T-1), end=\"\")\n",
" for i in range(n, h-n):\n",
" for j in range(n, w-n):\n",
" neighbourhood_score=self.score[t-1,i-n:i+n2,j-n:j+n2]\n",
" previous_score=neighbourhood_score-jump_penalty_matrix\n",
" \n",
" index=np.argmax(previous_score)\n",
" best_score=previous_score.flat[index]\n",
" relative_x,relative_y=np.unravel_index(index, jump_penalty_matrix.shape)\n",
" x = i + relative_x - n\n",
" y = j + relative_y - n\n",
" self.backtracking_path[t-1, i, j, 0] =x\n",
" self.backtracking_path[t-1, i, j, 1] =y\n",
" self.score[t,i,j]=self.local_score[t,i,j]+best_score #np.mean(previous_score)\n",
" self.path=self.backtrack_path(self.backtracking_path,self.score)\n",
" \n",
" return self.path\n",
"\n",
"def generate_jump_penalty_matrix(jump_penalty, neighbourhood):\n",
" n=neighbourhood*2+1\n",
" matrix=np.zeros((n,n))\n",
" center=np.array([neighbourhood,neighbourhood])\n",
" for i in range(n):\n",
" for j in range(n):\n",
" position=np.array([i,j])\n",
" matrix[i,j]=jump_penalty(center,position)\n",
" return matrix\n",
"\n",
"neighbourhood_size=25\n",
"jump_penalty_weight=0.0003\n",
"jump_penalty_matrix=jump_penalty_weight * generate_jump_penalty_matrix(jump_penalty_euclidean,neighbourhood_size)\n",
"\n",
"\n",
"tracker=DPTracker()\n",
"track_result=tracker.track(video,local_score,jump_penalty_matrix)\n",
"\n",
"print(\"Tracking coordinates\")\n",
"print(track_result.T)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Save output"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"\n",
"def draw_tracked(video,track_result):\n",
" T,h,w,c = video.shape\n",
" image_shape=(h,w)\n",
" radius=5\n",
" color=np.array([1.0,0,0])\n",
" for t in range(T):\n",
" x,y=tuple(track_result[t,:])\n",
" if (x-radius>=0) and (x+radius<h) and (y-radius>=0) and (y+radius<w):\n",
" rr,cc=circle(x,y,radius,shape=image_shape)\n",
" video[t,rr,cc,:]=color\n",
" return video\n",
"\n",
"\n",
"def generate_debug_video(video,scores,labels,output_path):\n",
"# FFMpegWriter= anim.writers['ffmpeg']\n",
" metadata=dict(title=\"Output\")\n",
"# writer=FFMpegWriter(fps=6,bitrate=16384*2,metadata=metadata)\n",
"\n",
" columns=int(np.ceil(len(scores)/2))+1\n",
" f,axes=plt.subplots(2,columns,dpi=100)\n",
" axes =list(itertools.chain.from_iterable(axes))\n",
" image_ax=axes[0]\n",
" f.set_size_inches(10,10, True)\n",
" T,h,w,c=video.shape\n",
" base_file,ext=os.path.splitext(output_path)\n",
" if not os.path.exists(base_file):\n",
" os.mkdir(base_file)\n",
"# with writer.saving(f,debug_video_path,T):\n",
" cbars=[]\n",
" ranges=[]\n",
" for s in range(len(scores)):\n",
" ranges.append( (0,np.max(scores[s])) )\n",
" for t in range(T):\n",
" plt.suptitle(\"Frame %d/%d\" % (t,T-1))\n",
" image_ax.cla()\n",
" plot=image_ax.imshow(video[t,:,:,:])\n",
" \n",
" for s in range(len(scores)):\n",
" ax=axes[s+1]\n",
" ax.cla()\n",
" ax.set_title(labels[s],fontsize=10)\n",
" \n",
" data=scores[s][t,:,:]\n",
" vmin,vmax=ranges[s]\n",
" plot=ax.imshow(data,cmap='gray',vmin=vmin,vmax=vmax) \n",
" if t==0:\n",
" cbar=f.colorbar(plot, ax=ax)\n",
" cbar.ax.tick_params(labelsize=10)\n",
" cbar_ticks = np.linspace(vmin,vmax, num=10, endpoint=True)\n",
" cbar.set_ticks(cbar_ticks)\n",
" cbars.append(cbar)\n",
"# plot.set_clim([data.min(), data.max()])\n",
"# cbar_ticks = np.linspace(data.min(), data.max(), num=10, endpoint=True)\n",
"# cbars[s].set_ticks(cbar_ticks) \n",
"# plot.autoscale()\n",
" a='%s/%03d.png' % (base_file,t)\n",
" plt.savefig(a)\n",
"# writer.grab_frame()\n",
"\n",
"tracked_video=np.copy(video)\n",
"util.video_hsv_to_rgb(tracked_video)\n",
"tracked_video=tracked_video/255.0\n",
"tracked_video=draw_tracked(tracked_video,track_result)\n",
"tracked_video=tracked_video.astype('short')\n",
"show_scores=[local_score,tracker.score]+scores\n",
"show_scores_label=['local','global']+scorers_labels\n",
"generate_debug_video(tracked_video, show_scores,show_scores_label,debug_video_path)\n",
"\n",
"# skvideo.io.vwrite(tracked_video_path, tracked_video, outputdict={\n",
"# '-vcodec': 'libx264',\n",
"# '-pix_fmt': 'yuv420p',\n",
"# '-r': rate,\n",
"# })\n",
"plt.close(\"all\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"score=tracker.local_score\n",
"plt.imshow(score[T-2,:,:])\n",
"plt.colorbar()\n",
"plt.figure()\n",
"plt.imshow(score[T-3,:,:])\n",
"plt.colorbar()\n",
"plt.figure()\n",
"plt.imshow(score[T-4,:,:])\n",
"plt.colorbar()\n",
"plt.figure()\n",
"plt.imshow(tracked_video[T-1,:,:,:])\n",
"plt.colorbar()\n",
"plt.figure()\n",
"mean_scores=np.sum(tracker.score,axis=(1,2))\n",
"print(mean_scores.shape)\n",
"plt.plot(mean_scores)\n",
"plt.show()\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| agpl-3.0 |
jakemathai/computer-vision | text_detect.ipynb | 1 | 1926 | {
"cells": [
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The image text says :\n",
"Jack & Jill\n",
"Jack and Jill\n",
"Went up the hill\n",
"To fetch a pail of watei\n",
"Jack fell down\n",
"And bioke his ciown\n",
"And Jill came tumbling after.\n",
"Up Jack got\n",
"And home did tiot\n",
"As fast as he could caper\n",
"Went to bed\n",
"And plasteed his head\n",
"And plastered his head\n",
"With vinegai and biown pa\n",
"www.Siyalla com\n",
"\n"
]
}
],
"source": [
"#This script detects text/OCR in within an image. Jack and Jill ...\n",
"\n",
"import argparse\n",
"import io\n",
"\n",
"from google.cloud import vision\n",
"\n",
"client = vision.Client()\n",
"image = client.image(source_uri='http://www.siyalla.com/kids/nursery_rhymes/jack-and-jill.jpg')\n",
"\n",
"texts = image.detect_text()\n",
"texts[0].locale\n",
"x=texts[0].description\n",
"\n",
"print \"The image text says :\"\n",
"print x"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12+"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
google/trax | trax/examples/trax_data_Explained.ipynb | 1 | 39539 | {
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"name": "trax.data Explained",
"provenance": [],
"collapsed_sections": [],
"toc_visible": true,
"authorship_tag": "ABX9TyMN9H/craeNOTmFImALz3Uk",
"include_colab_link": true
},
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
}
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "view-in-github",
"colab_type": "text"
},
"source": [
"<a href=\"https://colab.research.google.com/github/SauravMaheshkar/trax/blob/SauravMaheshkar-example-1/examples/trax_data_Explained.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>"
]
},
{
"cell_type": "code",
"metadata": {
"id": "6NWA5uxOmBVz"
},
"source": [
"#@title\n",
"# Copyright 2020 Google LLC.\n",
"\n",
"# Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
],
"execution_count": null,
"outputs": []
},
{
"cell_type": "code",
"metadata": {
"id": "u6IGlnMDLf6M"
},
"source": [
"## Install the Latest Version of Trax\n",
"!pip install --upgrade trax"
],
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "zOPgYEe2i7Cg"
},
"source": [
"Notebook Author: [@SauravMaheshkar](https://github.com/SauravMaheshkar)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "jtMr8yxvM2m3"
},
"source": [
"# Introduction"
]
},
{
"cell_type": "code",
"metadata": {
"id": "yD3A2vRGSDwy"
},
"source": [
"import trax"
],
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "v5VsWct1QjPz"
},
"source": [
"# Serial Fn"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "gEa5pT6FQuta"
},
"source": [
"In Trax, we use combinators to build input pipelines, much like building deep learning models. The `Serial` combinator applies layers serially using function composition and uses stack semantics to manage data. \n",
"\n",
"Trax has the following definition for a `Serial` combinator.\n",
"\n",
"> ```\n",
"def Serial(*fns):\n",
" def composed_fns(generator=None):\n",
" for f in fastmath.tree_flatten(fns):\n",
" generator = f(generator)\n",
" return generator\n",
" return composed_fns\n",
" ```\n",
"\n",
"The `Serial` function has the following structure:\n",
"\n",
"* It takes as **input** arbitrary number of functions\n",
"* Convert the structure into lists\n",
"* Iterate through the list and apply the functions Serially\n",
"\n",
"---\n",
"\n",
"The [`fastmath.tree_flatten()`](https://github.com/google/trax/blob/c38a5b1e4c5cfe13d156b3fc0bfdb83554c8f799/trax/fastmath/numpy.py#L195) function, takes a tree as a input and returns a flattened list. This way we can use various generator functions like Tokenize and Shuffle, and apply them serially by '*iterating*' through the list. \n",
"\n",
"Initially, we've defined `generator` to `None`. Thus, in the first iteration we have no input and thus the first step executes the first function in our tree structure. In the next iteration, the `generator` variable is updated to be the output of the next function in the list.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "1rkCvxscXtvk"
},
"source": [
"# Log Function"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "oodQFyHDYJHF"
},
"source": [
"> ```\n",
"def Log(n_steps_per_example=1, only_shapes=True):\n",
" def log(stream):\n",
" counter = 0\n",
" for example in stream:\n",
" item_to_log = example\n",
" if only_shapes:\n",
" item_to_log = fastmath.nested_map(shapes.signature, example)\n",
" if counter % n_steps_per_example == 0:\n",
" logging.info(str(item_to_log))\n",
" print(item_to_log)\n",
" counter += 1\n",
" yield example\n",
" return log\n",
"\n",
"Every Deep Learning Framework needs to have a logging component for efficient debugging. \n",
"\n",
"`trax.data.Log` generator uses the `absl` package for logging. It uses a [`fastmath.nested_map`](https://github.com/google/trax/blob/c38a5b1e4c5cfe13d156b3fc0bfdb83554c8f799/trax/fastmath/numpy.py#L80) function that maps a certain function recursively inside a object. In the case depicted below, the function maps the `shapes.signature` recursively inside the input stream, thus giving us the shapes of the various objects in our stream.\n",
"\n",
"--\n",
"\n",
"The following two cells show the difference between when we set the `only_shapes` variable to `False`"
]
},
{
"cell_type": "code",
"metadata": {
"id": "PqZZAYC4YlIt",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 663
},
"outputId": "aa36ceb1-65b1-4c65-83ae-c93d197759b7"
},
"source": [
"data_pipeline = trax.data.Serial(\n",
" trax.data.TFDS('imdb_reviews', keys=('text', 'label'), train=True),\n",
" trax.data.Tokenize(vocab_dir='gs://trax-ml/vocabs/', vocab_file='en_8k.subword', keys=[0]),\n",
" trax.data.Log(only_shapes=False)\n",
" )\n",
"example = data_pipeline()\n",
"print(next(example))"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"text": [
"(array([ 182, 31, 43, 5981, 67, 6322, 243, 3898, 22, 8, 2138,\n",
" 2, 36, 47, 66, 597, 300, 10, 34, 3986, 2613, 64,\n",
" 5281, 2367, 2, 46, 1902, 4713, 2942, 3461, 8, 4797, 55,\n",
" 1466, 1351, 409, 3, 121, 114, 1622, 5622, 66, 124, 4106,\n",
" 47, 1972, 10, 536, 8, 4533, 2, 124, 1466, 3207, 93,\n",
" 449, 90, 407, 4860, 76, 114, 3898, 22, 36, 6, 2339,\n",
" 5160, 275, 2395, 6293, 181, 8, 182, 3898, 22, 25, 43,\n",
" 402, 4423, 794, 995, 3040, 2420, 2128, 2, 5116, 2, 8,\n",
" 28, 180, 3166, 3171, 3839, 44, 80, 668, 232, 4, 1743,\n",
" 3661, 239, 3082, 4076, 80, 2067, 124, 2700, 35, 3854, 1052,\n",
" 221, 8, 6149, 5481, 4607, 12, 547, 2942, 75, 4445, 3054,\n",
" 29, 3, 7, 245, 5372, 1135, 75, 14, 3304, 2, 4935,\n",
" 1197, 39, 5281, 2367, 2, 31, 5032, 2528, 121, 12, 3166,\n",
" 3171, 5888, 5403, 2, 2305, 93, 10, 12, 3898, 22, 37,\n",
" 31, 3060, 2558, 2, 5, 345, 2715, 2213, 8, 139, 907,\n",
" 2133, 1051, 2390, 200, 37, 266, 55, 3898, 44, 461, 114,\n",
" 3, 4269, 1264, 617, 36, 6, 461, 3986, 2613, 64, 5281,\n",
" 2367, 2, 36, 6, 2730, 177, 8, 139, 449, 1120, 839,\n",
" 4198, 2, 340, 71, 21]), 0)\n",
"(array([ 182, 31, 43, 5981, 67, 6322, 243, 3898, 22, 8, 2138,\n",
" 2, 36, 47, 66, 597, 300, 10, 34, 3986, 2613, 64,\n",
" 5281, 2367, 2, 46, 1902, 4713, 2942, 3461, 8, 4797, 55,\n",
" 1466, 1351, 409, 3, 121, 114, 1622, 5622, 66, 124, 4106,\n",
" 47, 1972, 10, 536, 8, 4533, 2, 124, 1466, 3207, 93,\n",
" 449, 90, 407, 4860, 76, 114, 3898, 22, 36, 6, 2339,\n",
" 5160, 275, 2395, 6293, 181, 8, 182, 3898, 22, 25, 43,\n",
" 402, 4423, 794, 995, 3040, 2420, 2128, 2, 5116, 2, 8,\n",
" 28, 180, 3166, 3171, 3839, 44, 80, 668, 232, 4, 1743,\n",
" 3661, 239, 3082, 4076, 80, 2067, 124, 2700, 35, 3854, 1052,\n",
" 221, 8, 6149, 5481, 4607, 12, 547, 2942, 75, 4445, 3054,\n",
" 29, 3, 7, 245, 5372, 1135, 75, 14, 3304, 2, 4935,\n",
" 1197, 39, 5281, 2367, 2, 31, 5032, 2528, 121, 12, 3166,\n",
" 3171, 5888, 5403, 2, 2305, 93, 10, 12, 3898, 22, 37,\n",
" 31, 3060, 2558, 2, 5, 345, 2715, 2213, 8, 139, 907,\n",
" 2133, 1051, 2390, 200, 37, 266, 55, 3898, 44, 461, 114,\n",
" 3, 4269, 1264, 617, 36, 6, 461, 3986, 2613, 64, 5281,\n",
" 2367, 2, 36, 6, 2730, 177, 8, 139, 449, 1120, 839,\n",
" 4198, 2, 340, 71, 21]), 0)\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "uyqL-JMCaGn0",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 357
},
"outputId": "dfd51b28-159c-41b7-ba2a-39e95b1e3964"
},
"source": [
"data_pipeline = trax.data.Serial(\n",
" trax.data.TFDS('imdb_reviews', keys=('text', 'label'), train=True),\n",
" trax.data.Tokenize(vocab_dir='gs://trax-ml/vocabs/', vocab_file='en_8k.subword', keys=[0]),\n",
" trax.data.Log(only_shapes=True)\n",
" )\n",
"example = data_pipeline()\n",
"print(next(example))"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"text": [
"(ShapeDtype{shape:(203,), dtype:int64}, ShapeDtype{shape:(), dtype:int64})\n",
"(array([ 182, 31, 43, 5981, 67, 6322, 243, 3898, 22, 8, 2138,\n",
" 2, 36, 47, 66, 597, 300, 10, 34, 3986, 2613, 64,\n",
" 5281, 2367, 2, 46, 1902, 4713, 2942, 3461, 8, 4797, 55,\n",
" 1466, 1351, 409, 3, 121, 114, 1622, 5622, 66, 124, 4106,\n",
" 47, 1972, 10, 536, 8, 4533, 2, 124, 1466, 3207, 93,\n",
" 449, 90, 407, 4860, 76, 114, 3898, 22, 36, 6, 2339,\n",
" 5160, 275, 2395, 6293, 181, 8, 182, 3898, 22, 25, 43,\n",
" 402, 4423, 794, 995, 3040, 2420, 2128, 2, 5116, 2, 8,\n",
" 28, 180, 3166, 3171, 3839, 44, 80, 668, 232, 4, 1743,\n",
" 3661, 239, 3082, 4076, 80, 2067, 124, 2700, 35, 3854, 1052,\n",
" 221, 8, 6149, 5481, 4607, 12, 547, 2942, 75, 4445, 3054,\n",
" 29, 3, 7, 245, 5372, 1135, 75, 14, 3304, 2, 4935,\n",
" 1197, 39, 5281, 2367, 2, 31, 5032, 2528, 121, 12, 3166,\n",
" 3171, 5888, 5403, 2, 2305, 93, 10, 12, 3898, 22, 37,\n",
" 31, 3060, 2558, 2, 5, 345, 2715, 2213, 8, 139, 907,\n",
" 2133, 1051, 2390, 200, 37, 266, 55, 3898, 44, 461, 114,\n",
" 3, 4269, 1264, 617, 36, 6, 461, 3986, 2613, 64, 5281,\n",
" 2367, 2, 36, 6, 2730, 177, 8, 139, 449, 1120, 839,\n",
" 4198, 2, 340, 71, 21]), 0)\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Wy8L-e9qcRY4"
},
"source": [
"# Shuffling our datasets"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-cfg48KgcrlM"
},
"source": [
"Trax offers two generator functions to add shuffle functionality in our input pipelines. \n",
"\n",
"1. The `shuffle` function shuffles a given stream\n",
"2. The `Shuffle` function returns a shuffle function instead"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "4iD21oiycWf4"
},
"source": [
"## `shuffle`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "bVgN1yYAcaKM"
},
"source": [
"> ```\n",
"def shuffle(samples, queue_size):\n",
" if queue_size < 1:\n",
" raise ValueError(f'Arg queue_size ({queue_size}) is less than 1.')\n",
" if queue_size == 1:\n",
" logging.warning('Queue size of 1 results in no shuffling.')\n",
" queue = []\n",
" try:\n",
" queue.append(next(samples))\n",
" i = np.random.randint(queue_size)\n",
" yield queue[i]\n",
" queue[i] = sample\n",
" except StopIteration:\n",
" logging.warning(\n",
" 'Not enough samples (%d) to fill initial queue (size %d).',\n",
" len(queue), queue_size)\n",
" np.random.shuffle(queue)\n",
" for sample in queue:\n",
" yield sample\n",
"\n",
"\n",
"The `shuffle` function takes two inputs, the data stream and the queue size (minimum number of samples within which the shuffling takes place). Apart from the usual warnings, for negative and unity queue sizes, this generator function shuffles the given stream using [`np.random.randint()`](https://docs.python.org/3/library/random.html#random.randint) by randomly picks out integers using the `queue_size` as a range and then shuffle this new stream again using the [`np.random.shuffle()`](https://docs.python.org/3/library/random.html#random.shuffle)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "-kdz2fNIfn2l",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 105
},
"outputId": "110aa969-dab0-4e7a-e75f-41a6ab2fe0c4"
},
"source": [
"sentence = ['Sed ut perspiciatis unde omnis iste natus error sit voluptatem accusantium doloremque laudantium, totam rem aperiam, eaque ipsa quae ab illo inventore veritatis et quasi architecto beatae vitae dicta sunt explicabo. Nemo enim ipsam voluptatem quia voluptas sit aspernatur aut odit aut fugit, sed quia consequuntur magni dolores eos qui ratione voluptatem sequi nesciunt. Neque porro quisquam est, qui dolorem ipsum quia dolor sit amet, consectetur, adipisci velit, sed quia non numquam eius modi tempora incidunt ut labore et dolore magnam aliquam quaerat voluptatem. Ut enim ad minima veniam, quis nostrum exercitationem ullam corporis suscipit laboriosam, nisi ut aliquid ex ea commodi consequatur? Quis autem vel eum iure reprehenderit qui in ea voluptate velit esse quam nihil molestiae consequatur, vel illum qui dolorem eum fugiat quo voluptas nulla pariatur?',\n",
" 'But I must explain to you how all this mistaken idea of denouncing pleasure and praising pain was born and I will give you a complete account of the system, and expound the actual teachings of the great explorer of the truth, the master-builder of human happiness. No one rejects, dislikes, or avoids pleasure itself, because it is pleasure, but because those who do not know how to pursue pleasure rationally encounter consequences that are extremely painful. Nor again is there anyone who loves or pursues or desires to obtain pain of itself, because it is pain, but because occasionally circumstances occur in which toil and pain can procure him some great pleasure. To take a trivial example, which of us ever undertakes laborious physical exercise, except to obtain some advantage from it? But who has any right to find fault with a man who chooses to enjoy a pleasure that has no annoying consequences, or one who avoids a pain that produces no resultant pleasure?',\n",
" 'Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum',\n",
" 'At vero eos et accusamus et iusto odio dignissimos ducimus qui blanditiis praesentium voluptatum deleniti atque corrupti quos dolores et quas molestias excepturi sint occaecati cupiditate non provident, similique sunt in culpa qui officia deserunt mollitia animi, id est laborum et dolorum fuga. Et harum quidem rerum facilis est et expedita distinctio. Nam libero tempore, cum soluta nobis est eligendi optio cumque nihil impedit quo minus id quod maxime placeat facere possimus, omnis voluptas assumenda est, omnis dolor repellendus. Temporibus autem quibusdam et aut officiis debitis aut rerum necessitatibus saepe eveniet ut et voluptates repudiandae sint et molestiae non recusandae. Itaque earum rerum hic tenetur a sapiente delectus, ut aut reiciendis voluptatibus maiores alias consequatur aut perferendis doloribus asperiores repellat.']\n",
"\n",
"def sample_generator(x):\n",
" for i in x:\n",
" yield i\n",
"\n",
"example_shuffle = list(trax.data.inputs.shuffle(sample_generator(sentence), queue_size = 2))\n",
"example_shuffle"
],
"execution_count": null,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"['Sed ut perspiciatis unde omnis iste natus error sit voluptatem accusantium doloremque laudantium, totam rem aperiam, eaque ipsa quae ab illo inventore veritatis et quasi architecto beatae vitae dicta sunt explicabo. Nemo enim ipsam voluptatem quia voluptas sit aspernatur aut odit aut fugit, sed quia consequuntur magni dolores eos qui ratione voluptatem sequi nesciunt. Neque porro quisquam est, qui dolorem ipsum quia dolor sit amet, consectetur, adipisci velit, sed quia non numquam eius modi tempora incidunt ut labore et dolore magnam aliquam quaerat voluptatem. Ut enim ad minima veniam, quis nostrum exercitationem ullam corporis suscipit laboriosam, nisi ut aliquid ex ea commodi consequatur? Quis autem vel eum iure reprehenderit qui in ea voluptate velit esse quam nihil molestiae consequatur, vel illum qui dolorem eum fugiat quo voluptas nulla pariatur?',\n",
" 'Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum',\n",
" 'But I must explain to you how all this mistaken idea of denouncing pleasure and praising pain was born and I will give you a complete account of the system, and expound the actual teachings of the great explorer of the truth, the master-builder of human happiness. No one rejects, dislikes, or avoids pleasure itself, because it is pleasure, but because those who do not know how to pursue pleasure rationally encounter consequences that are extremely painful. Nor again is there anyone who loves or pursues or desires to obtain pain of itself, because it is pain, but because occasionally circumstances occur in which toil and pain can procure him some great pleasure. To take a trivial example, which of us ever undertakes laborious physical exercise, except to obtain some advantage from it? But who has any right to find fault with a man who chooses to enjoy a pleasure that has no annoying consequences, or one who avoids a pain that produces no resultant pleasure?',\n",
" 'At vero eos et accusamus et iusto odio dignissimos ducimus qui blanditiis praesentium voluptatum deleniti atque corrupti quos dolores et quas molestias excepturi sint occaecati cupiditate non provident, similique sunt in culpa qui officia deserunt mollitia animi, id est laborum et dolorum fuga. Et harum quidem rerum facilis est et expedita distinctio. Nam libero tempore, cum soluta nobis est eligendi optio cumque nihil impedit quo minus id quod maxime placeat facere possimus, omnis voluptas assumenda est, omnis dolor repellendus. Temporibus autem quibusdam et aut officiis debitis aut rerum necessitatibus saepe eveniet ut et voluptates repudiandae sint et molestiae non recusandae. Itaque earum rerum hic tenetur a sapiente delectus, ut aut reiciendis voluptatibus maiores alias consequatur aut perferendis doloribus asperiores repellat.']"
]
},
"metadata": {
"tags": []
},
"execution_count": 5
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "k-kTDkF-e7Vn"
},
"source": [
"## `Shuffle`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "I5Djvqw2e9Jg"
},
"source": [
"> ```\n",
"def Shuffle(queue_size=1024): \n",
" return lambda g: shuffle(g, queue_size)\n",
"\n",
"This function returns the aforementioned `shuffle` function and is mostly used in input pipelines.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "AA-Z4Sipkq98"
},
"source": [
"# Batch Generators"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "yzwONDulksbd"
},
"source": [
"## `batch`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-DCABkndkudF"
},
"source": [
"This function, creates batches for the input generator function.\n",
"\n",
"> ```\n",
"def batch(generator, batch_size):\n",
" if batch_size <= 0:\n",
" raise ValueError(f'Batch size must be positive, but is {batch_size}.')\n",
" buf = []\n",
" for example in generator:\n",
" buf.append(example) \n",
" if len(buf) == batch_size:\n",
" batched_example = tuple(np.stack(x) for x in zip(*buf))\n",
" yield batched_example\n",
" buf = []\n",
"\n",
"It keeps adding objects from the generator into a list until the size becomes equal to the `batch_size` and then creates batches using the `np.stack()` function.\n",
"\n",
"It also raises an error for non-positive batch_sizes.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "BZMKY6VUpD3M"
},
"source": [
"## `Batch`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "g6pYJHgOpIG4"
},
"source": [
"> ```\n",
" def Batch(batch_size): \n",
" return lambda g: batch(g, batch_size)\n",
"\n",
"This Function returns the aforementioned `batch` function with given batch size."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "cmQzaXw9vrbW"
},
"source": [
"# Pad to Maximum Dimensions"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "iL3MuKQIvt-Q"
},
"source": [
"This function is used to pad a tuple of tensors to a joint dimension and return their batch.\n",
"\n",
"For example, in this case a pair of tensors (1,2) and ( (3,4) , (5,6) ) is changed to (1,2,0) and ( (3,4) , (5,6) , 0)"
]
},
{
"cell_type": "code",
"metadata": {
"id": "lvbBDuq4p4qW",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 51
},
"outputId": "ed69c541-3219-4a23-cf73-4568e3e2882f"
},
"source": [
"import numpy as np\n",
"\n",
"tensors = np.array([(1.,2.),\n",
" ((3.,4.),(5.,6.))])\n",
"padded_tensors = trax.data.inputs.pad_to_max_dims(tensors=tensors, boundary=3)\n",
"padded_tensors"
],
"execution_count": null,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"array([[1.0, 2.0, 0],\n",
" [(3.0, 4.0), (5.0, 6.0), 0]], dtype=object)"
]
},
"metadata": {
"tags": []
},
"execution_count": 6
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "PDQQYCdLOkl1"
},
"source": [
"# Creating Buckets"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "RjGD3YKJWj58"
},
"source": [
"For training Recurrent Neural Networks, with large vocabulary a method called Bucketing is usually applied. \n",
"\n",
"The usual technique of using padding ensures that all occurences within a mini-batch are of the same length. But this reduces the inter-batch variability and intuitively puts similar sentences into the same batch therefore, reducing the overall robustness of the system. \n",
"\n",
"Thus, we use Bucketing where multiple buckets are created depending on the length of the sentences and these occurences are assigned to buckets on the basis of which bucket corresponds to it's length. We need to ensure that the bucket sizes are large for adding some variablity to the system."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "17z3ASA-OrSF"
},
"source": [
"## `bucket_by_length`\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "rf5trhANYpy5"
},
"source": [
"> ```\n",
"def bucket_by_length(generator, length_fn, boundaries, batch_sizes,strict_pad_on_len=False):\n",
" buckets = [[] for _ in range(len(batch_sizes))]\n",
" boundaries = boundaries + [math.inf] \n",
" for example in generator:\n",
" length = length_fn(example)\n",
" bucket_idx = min([i for i, b in enumerate(boundaries) if length <= b])\n",
" buckets[bucket_idx].append(example)\n",
" if len(buckets[bucket_idx]) == batch_sizes[bucket_idx]:\n",
" batched = zip(*buckets[bucket_idx])\n",
" boundary = boundaries[bucket_idx]\n",
" boundary = None if boundary == math.inf else boundary\n",
" padded_batch = tuple(\n",
" pad_to_max_dims(x, boundary, strict_pad_on_len) for x in batched)\n",
" yield padded_batch\n",
" buckets[bucket_idx] = []\n",
"\n",
"---\n",
"\n",
"This function can be summarised as:\n",
"\n",
"* Create buckets as per the lengths given in the `batch_sizes` array\n",
"\n",
"* Assign sentences into buckets if their length matches the bucket size\n",
"\n",
"* If padding is required, we use the `pad_to_max_dims` function\n",
"\n",
"---\n",
"\n",
"### Parameters\n",
"\n",
"1. **generator:** The input generator function\n",
"2. **length_fn:** A custom length function for determing the length of functions, not necessarily `len()`\n",
"3. **boundaries:** A python list containing corresponding bucket boundaries\n",
"4. **batch_sizes:** A python list containing batch sizes\n",
"5. **strict_pad_on_len:** – A python boolean variable (`True` or `False`). If set to true then the function pads on the length dimension, where dim[0] is strictly a multiple of boundary.\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "c0uQZaaPVyF_"
},
"source": [
"## `BucketByLength`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Qhh21q71aX3l"
},
"source": [
"> ```\n",
"def BucketByLength(boundaries, batch_sizes,length_keys=None, length_axis=0, strict_pad_on_len=False):\n",
" length_keys = length_keys or [0, 1]\n",
" length_fn = lambda x: _length_fn(x, length_axis, length_keys)\n",
" return lambda g: bucket_by_length(g, length_fn, boundaries, batch_sizes, strict_pad_on_len)\n",
"\n",
"---\n",
"\n",
"This function, is usually used inside input pipelines(*combinators*) and uses the afforementioned `bucket_by_length`. It applies a predefined `length_fn` which chooses the maximum shape on length_axis over length_keys.\n",
"\n",
"It's use is illustrated below"
]
},
{
"cell_type": "code",
"metadata": {
"id": "PFeqDQNsV0PV",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 153
},
"outputId": "ab9139c1-de56-4570-bcb6-731c1b475b12"
},
"source": [
"data_pipeline = trax.data.Serial(\n",
" trax.data.TFDS('imdb_reviews', keys=('text', 'label'), train=True),\n",
" trax.data.Tokenize(vocab_dir='gs://trax-ml/vocabs/', vocab_file='en_8k.subword', keys=[0]),\n",
" trax.data.BucketByLength(boundaries=[32, 128, 512, 2048],\n",
" batch_sizes=[512, 128, 32, 8, 1],\n",
" length_keys=[0]),\n",
" trax.data.Log(only_shapes=True)\n",
" )\n",
"example = data_pipeline()\n",
"print(next(example))"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"text": [
"(ShapeDtype{shape:(8, 2048), dtype:int64}, ShapeDtype{shape:(8,), dtype:int64})\n",
"(array([[ 155, 452, 29, ..., 0, 0, 0],\n",
" [ 182, 1989, 1826, ..., 0, 0, 0],\n",
" [1389, 2597, 5378, ..., 0, 0, 0],\n",
" ...,\n",
" [4846, 1008, 2, ..., 0, 0, 0],\n",
" [ 68, 12, 173, ..., 0, 0, 0],\n",
" [ 186, 3817, 2064, ..., 0, 0, 0]]), array([0, 1, 1, 1, 1, 0, 1, 0]))\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "9D0YdAT_ceSN"
},
"source": [
"# Filter by Length"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "YLvi4Wu-eFAF"
},
"source": [
"> ```\n",
"def FilterByLength(max_length,length_keys=None, length_axis=0):\n",
" length_keys = length_keys or [0, 1]\n",
" length_fn = lambda x: _length_fn(x, length_axis, length_keys)\n",
" def filtered(gen):\n",
" for example in gen:\n",
" if length_fn(example) <= max_length:\n",
" yield example\n",
" return filtered\n",
"\n",
"---\n",
"\n",
"This function used the same predefined `length_fn` to only include those instances which are less than the given `max_length` parameter.\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "qyueQ1z-cg2p",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 153
},
"outputId": "da007ab0-e719-4044-e6a4-6bba5f43131e"
},
"source": [
"Filtered = trax.data.Serial(\n",
" trax.data.TFDS('imdb_reviews', keys=('text', 'label'), train=True),\n",
" trax.data.Tokenize(vocab_dir='gs://trax-ml/vocabs/', vocab_file='en_8k.subword', keys=[0]),\n",
" trax.data.BucketByLength(boundaries=[32, 128, 512, 2048],\n",
" batch_sizes=[512, 128, 32, 8, 1],\n",
" length_keys=[0]),\n",
" trax.data.FilterByLength(max_length=2048, length_keys=[0]),\n",
" trax.data.Log(only_shapes=True)\n",
" )\n",
"filtered_example = Filtered()\n",
"print(next(filtered_example))"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"text": [
"(ShapeDtype{shape:(8, 2048), dtype:int64}, ShapeDtype{shape:(8,), dtype:int64})\n",
"(array([[ 155, 452, 29, ..., 0, 0, 0],\n",
" [ 182, 1989, 1826, ..., 0, 0, 0],\n",
" [1389, 2597, 5378, ..., 0, 0, 0],\n",
" ...,\n",
" [4846, 1008, 2, ..., 0, 0, 0],\n",
" [ 68, 12, 173, ..., 0, 0, 0],\n",
" [ 186, 3817, 2064, ..., 0, 0, 0]]), array([0, 1, 1, 1, 1, 0, 1, 0]))\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "1XRrJSsUeZX-"
},
"source": [
"# Adding Loss Weights"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "P3ySYhnpejy4"
},
"source": [
"## `add_loss_weights`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "QgaXAlhgeuQv"
},
"source": [
"> ```\n",
"def add_loss_weights(generator, id_to_mask=None):\n",
" for example in generator:\n",
" if len(example) > 3 or len(example) < 2:\n",
" assert id_to_mask is None, 'Cannot automatically mask this stream.'\n",
" yield example\n",
" else:\n",
" if len(example) == 2:\n",
" weights = np.ones_like(example[1]).astype(np.float32)\n",
" else:\n",
" weights = example[2].astype(np.float32)\n",
" mask = 1.0 - np.equal(example[1], id_to_mask).astype(np.float32)\n",
" weights *= mask\n",
" yield (example[0], example[1], weights)\n",
"\n",
"---\n",
"\n",
"This function essentially adds a loss mask (tensor of ones of the same shape) to the input stream. \n",
"\n",
"**Masking** is essentially a way to tell sequence-processing layers that certain timesteps in an input are missing, and thus should be skipped when processing the data.\n",
"\n",
"Thus, it adds 'weights' to the system. \n",
"\n",
"---\n",
"\n",
"### Parameters\n",
"\n",
"1. **generator:** The input data generator\n",
"2. **id_to_mask:** The value with which to mask. Can be used as `<PAD>` in NLP."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "hZPWc6a9hk_u"
},
"source": [
"```\n",
"\n",
"train_generator = trax.data.inputs.add_loss_weights(\n",
" data_generator(batch_size, x_train, y_train,vocab['<PAD>'], True),\n",
" id_to_mask=vocab['<PAD>'])\n",
"\n",
"\n",
"```\n",
"\n",
"For example, in this case I used the `add_loss_weights` function to add padding while implementing Named Entity Recogntion using the Reformer Architecture. You can read more about the project [here](https://www.kaggle.com/sauravmaheshkar/trax-ner-using-reformer)."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "GL31NErOgL3u"
},
"source": [
"## `AddLossWeights`"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "mBLf6iuXgPp2"
},
"source": [
"This function performs the afforementioned `add_loss_weights` to the data stream. \n",
"\n",
"> ```\n",
"def AddLossWeights(id_to_mask=None):\n",
" return lambda g: add_loss_weights(g,id_to_mask=id_to_mask)\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "Jwtt-k_2iHEy",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 173
},
"outputId": "52295b0e-ff9c-415e-9ba6-1d5c1359b508"
},
"source": [
"data_pipeline = trax.data.Serial(\n",
" trax.data.TFDS('imdb_reviews', keys=('text', 'label'), train=True),\n",
" trax.data.Tokenize(vocab_dir='gs://trax-ml/vocabs/', vocab_file='en_8k.subword', keys=[0]),\n",
" trax.data.Shuffle(),\n",
" trax.data.FilterByLength(max_length=2048, length_keys=[0]),\n",
" trax.data.BucketByLength(boundaries=[ 32, 128, 512, 2048],\n",
" batch_sizes=[512, 128, 32, 8, 1],\n",
" length_keys=[0]),\n",
" trax.data.AddLossWeights(),\n",
" trax.data.Log(only_shapes=True)\n",
" )\n",
"\n",
"example = data_pipeline()\n",
"print(next(example))"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"text": [
"(ShapeDtype{shape:(8, 2048), dtype:int64}, ShapeDtype{shape:(8,), dtype:int64}, ShapeDtype{shape:(8,), dtype:float32})\n",
"(array([[4176, 570, 636, ..., 0, 0, 0],\n",
" [3030, 2, 7, ..., 0, 0, 0],\n",
" [ 28, 3898, 22, ..., 0, 0, 0],\n",
" ...,\n",
" [ 139, 36, 76, ..., 0, 0, 0],\n",
" [2275, 2, 4198, ..., 0, 0, 0],\n",
" [ 182, 103, 151, ..., 0, 0, 0]]), array([0, 1, 1, 0, 0, 0, 1, 0]), array([1., 1., 1., 1., 1., 1., 1., 1.], dtype=float32))\n"
],
"name": "stdout"
}
]
}
]
} | apache-2.0 |
csaladenes/aviation | code/airport_dest_parser2.ipynb | 1 | 6636 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd, json, numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from bs4 import BeautifulSoup\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load airports of each country"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"L=json.loads(file('../json/L.json','r').read())\n",
"M=json.loads(file('../json/M.json','r').read())\n",
"N=json.loads(file('../json/N.json','r').read())"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import requests"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"AP={}\n",
"for c in M:\n",
" if c not in AP:AP[c]={}\n",
" for i in range(len(L[c])):\n",
" AP[c][N[c][i]]=L[c][i]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"record schedules for 2 weeks, then augment count with weekly flight numbers.\n",
"seasonal and seasonal charter will count as once per week for 3 months, so 12/52 per week. TGM separate, since its history is in the past."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"parse Departures"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"baseurl='https://www.airportia.com/'\n",
"import requests, urllib2"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def urlgetter(url):\n",
" s = requests.Session()\n",
" cookiesopen = s.get(url)\n",
" cookies=str(s.cookies)\n",
" fcookies=[[k[:k.find('=')],k[k.find('=')+1:k.find(' for ')]] for k in cookies[cookies.find('Cookie '):].split('Cookie ')[1:]]\n",
" #push token\n",
" opener = urllib2.build_opener()\n",
" for k in fcookies:\n",
" opener.addheaders.append(('Cookie', k[0]+'='+k[1]))\n",
" #read html\n",
" return s.get(url).content"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"good dates"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"SD={}\n",
"SC=json.loads(file('../json/SC2.json','r').read())"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"2 Turkmenistan\n",
"CRZ ASB KRW TAZ MYP\n",
"3 Lithuania\n",
"VNO KUN PLQ\n",
"4 FYR of Macedonia\n",
"OHD --W- 5 SKP\n"
]
}
],
"source": [
"for h in range(2,5):#len(AP.keys())):\n",
" c=AP.keys()[h]\n",
" #country not parsed yet\n",
" if c in SC:\n",
" if c not in SD:\n",
" SD[c]=[]\n",
" print h,c\n",
" airportialinks=AP[c]\n",
" sch={}\n",
" #all airports of country, where there is traffic\n",
" for i in airportialinks:\n",
" if i in SC[c]:\n",
" print i,\n",
" if i not in sch:sch[i]={}\n",
" url=baseurl+airportialinks[i]\n",
" m=urlgetter(url)\n",
" for d in range (3,7):\n",
" #date not parsed yet\n",
" if d not in sch[i]:\n",
" url=baseurl+airportialinks[i]+'departures/201704'+str(d)\n",
" m=urlgetter(url)\n",
" soup = BeautifulSoup(m, \"lxml\")\n",
" #if there are flights at all\n",
" if len(soup.findAll('table'))>0:\n",
" sch[i][d]=pd.read_html(m)[0] \n",
" else: print '--W-',d,\n",
" SD[c]=sch\n",
" print "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Save"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"cnc_path='../../universal/countries/'\n",
"cnc=pd.read_excel(cnc_path+'cnc.xlsx').set_index('Name')"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"MDF=pd.DataFrame()"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for c in SD:\n",
" sch=SD[c]\n",
" mdf=pd.DataFrame()\n",
" for i in sch:\n",
" for d in sch[i]:\n",
" df=sch[i][d].drop(sch[i][d].columns[3:],axis=1).drop(sch[i][d].columns[0],axis=1)\n",
" df['From']=i\n",
" df['Date']=d\n",
" mdf=pd.concat([mdf,df])\n",
" mdf=mdf.replace('Hahn','Frankfurt')\n",
" mdf=mdf.replace('Hahn HHN','Frankfurt HHN')\n",
" mdf['City']=[i[:i.rfind(' ')] for i in mdf['To']]\n",
" mdf['Airport']=[i[i.rfind(' ')+1:] for i in mdf['To']]\n",
" file('../countries/'+cnc.T.loc[c]['ISO2'].lower()+\"/json/mdf_dest.json\",'w').write(json.dumps(mdf.reset_index().to_json()))\n",
" MDF=pd.concat([MDF,mdf])"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"MDF.reset_index().to_json('../json/MDF.json')"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
AllenDowney/ThinkStats2 | solutions/chap08soln.ipynb | 1 | 51220 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Chapter 8\n",
"\n",
"Examples and Exercises from Think Stats, 2nd Edition\n",
"\n",
"http://thinkstats2.com\n",
"\n",
"Copyright 2016 Allen B. Downey\n",
"\n",
"MIT License: https://opensource.org/licenses/MIT\n"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"from os.path import basename, exists\n",
"\n",
"\n",
"def download(url):\n",
" filename = basename(url)\n",
" if not exists(filename):\n",
" from urllib.request import urlretrieve\n",
"\n",
" local, _ = urlretrieve(url, filename)\n",
" print(\"Downloaded \" + local)\n",
"\n",
"\n",
"download(\"https://github.com/AllenDowney/ThinkStats2/raw/master/code/thinkstats2.py\")\n",
"download(\"https://github.com/AllenDowney/ThinkStats2/raw/master/code/thinkplot.py\")"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"\n",
"import thinkstats2\n",
"import thinkplot"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## The estimation game\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Root mean squared error is one of several ways to summarize the average error of an estimation process."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def RMSE(estimates, actual):\n",
" \"\"\"Computes the root mean squared error of a sequence of estimates.\n",
"\n",
" estimate: sequence of numbers\n",
" actual: actual value\n",
"\n",
" returns: float RMSE\n",
" \"\"\"\n",
" e2 = [(estimate-actual)**2 for estimate in estimates]\n",
" mse = np.mean(e2)\n",
" return np.sqrt(mse)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following function simulates experiments where we try to estimate the mean of a population based on a sample with size `n=7`. We run `iters=1000` experiments and collect the mean and median of each sample."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Experiment 1\n",
"rmse xbar 0.36938349871245846\n",
"rmse median 0.465156358337244\n"
]
}
],
"source": [
"import random\n",
"\n",
"def Estimate1(n=7, iters=1000):\n",
" \"\"\"Evaluates RMSE of sample mean and median as estimators.\n",
"\n",
" n: sample size\n",
" iters: number of iterations\n",
" \"\"\"\n",
" mu = 0\n",
" sigma = 1\n",
"\n",
" means = []\n",
" medians = []\n",
" for _ in range(iters):\n",
" xs = [random.gauss(mu, sigma) for _ in range(n)]\n",
" xbar = np.mean(xs)\n",
" median = np.median(xs)\n",
" means.append(xbar)\n",
" medians.append(median)\n",
"\n",
" print('Experiment 1')\n",
" print('rmse xbar', RMSE(means, mu))\n",
" print('rmse median', RMSE(medians, mu))\n",
" \n",
"Estimate1()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using $\\bar{x}$ to estimate the mean works a little better than using the median; in the long run, it minimizes RMSE. But using the median is more robust in the presence of outliers or large errors.\n",
"\n",
"\n",
"## Estimating variance\n",
"\n",
"The obvious way to estimate the variance of a population is to compute the variance of the sample, $S^2$, but that turns out to be a biased estimator; that is, in the long run, the average error doesn't converge to 0.\n",
"\n",
"The following function computes the mean error for a collection of estimates."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"def MeanError(estimates, actual):\n",
" \"\"\"Computes the mean error of a sequence of estimates.\n",
"\n",
" estimate: sequence of numbers\n",
" actual: actual value\n",
"\n",
" returns: float mean error\n",
" \"\"\"\n",
" errors = [estimate-actual for estimate in estimates]\n",
" return np.mean(errors)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following function simulates experiments where we try to estimate the variance of a population based on a sample with size `n=7`. We run `iters=1000` experiments and two estimates for each sample, $S^2$ and $S_{n-1}^2$."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"mean error biased -0.12563818267874013\n",
"mean error unbiased 0.020088786874803213\n"
]
}
],
"source": [
"def Estimate2(n=7, iters=1000):\n",
" mu = 0\n",
" sigma = 1\n",
"\n",
" estimates1 = []\n",
" estimates2 = []\n",
" for _ in range(iters):\n",
" xs = [random.gauss(mu, sigma) for i in range(n)]\n",
" biased = np.var(xs)\n",
" unbiased = np.var(xs, ddof=1)\n",
" estimates1.append(biased)\n",
" estimates2.append(unbiased)\n",
"\n",
" print('mean error biased', MeanError(estimates1, sigma**2))\n",
" print('mean error unbiased', MeanError(estimates2, sigma**2))\n",
" \n",
"Estimate2()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The mean error for $S^2$ is non-zero, which suggests that it is biased. The mean error for $S_{n-1}^2$ is close to zero, and gets even smaller if we increase `iters`."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## The sampling distribution\n",
"\n",
"The following function simulates experiments where we estimate the mean of a population using $\\bar{x}$, and returns a list of estimates, one from each experiment."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"def SimulateSample(mu=90, sigma=7.5, n=9, iters=1000):\n",
" xbars = []\n",
" for j in range(iters):\n",
" xs = np.random.normal(mu, sigma, n)\n",
" xbar = np.mean(xs)\n",
" xbars.append(xbar)\n",
" return xbars\n",
"\n",
"xbars = SimulateSample()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here's the \"sampling distribution of the mean\" which shows how much we should expect $\\bar{x}$ to vary from one experiment to the next."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYcAAAEGCAYAAACO8lkDAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAh7klEQVR4nO3deXwU9f3H8dcn4Vbw4JIbqiAiosWIilrw6k8slSq0BfmpWGvqfd9Hq9Va6631QARKtR5VtEotVm2r7U8ryqGiQFEElIgKCAoEQg4+vz92qbuZ3YRAZmeP9/Px4JHMdya7b2Mm78zOznfM3REREUlUFHUAERHJPioHEREJUDmIiEiAykFERAJUDiIiEtAk6gAN1a5dO+/Zs2fUMUREcsrs2bNXuXv7rd0+58qhZ8+ezJo1K+oYIiI5xcw+bsj2ellJREQCVA4iIhKgchARkQCVg4iIBKgcREQkILRyMLPJZrbCzN5Ps97M7B4zW2Rmc81sYFhZRESkYcJ8K+sU4F7g4TTrhwG94/8OBB6IfxQRKUiVVdVUVdcExpd++iXlGytp2bwpPbu0pfUOLULPElo5uPu/zKxnHZuMAB722JzhM8xsZzPr5O6fhZVJRCQK68or+Hj5l9Rsjt0iYe26jSz7fA0tmjdlzdpyFi75go+Wrdyqx7r6Z8cysF/3MOMC0V4E1wVYlrBcFh8LlIOZlQKlAN27h/9NERFpqA0bK5m/+DMWLv6c5s2bUr5hE9NeebfRn2fHVs0b/TFTibIcLMVYyjsPufsEYAJASUmJ7k4kIpFZV17BuwvL+N0z/6Z3jw5U19Tw9oJl9X9hA7Rs0SwwZsCgAb3o3aNDoz5XOlGWQxnQLWG5K7A8oiwiIgC89Pp8nn55Dj06tU0anz0/OPvEzPeXNvjxB/TpCsDa8gqaFBfRv3dnqqs3YwYD+3Vnnz5dMEv1t3NmRVkO04BzzOwJYieiv9b5BhHJpFVr1nPPH/7Bss/XsHb9xsC6bbVT65YMPaAPxUVF7NymFUce1JcWzZtub9yMCq0czOxxYCjQzszKgF8ATQHcfTwwHTgWWARsAE4NK4uIiLuzcs16qqpr+PMr7/L6nI/YUFG5XY/Zq2s7Tjj62xQXFbFDy2bsvUfnrPirvzGE+W6lMfWsd+DssJ5fRAqTu/P5qrW88uZC3l+0nIVLPt+mx+nfuzPDhw5IGisuKqJvr91o1TJ4TiDf5NyU3SIi6Yw8f/w2f+1PTjiEfrt3ot0uO2bkOoJsp3IQkZy2YWMldz3895QnjNPZsVVz1m/YxHGH78sRB/Wl2267hJgwN6kcRCTnvPfBp1x3359p0qSY6hRXFCcackAf9undhX37dqXNDi1o0qQ4Qylzm8pBRLJexaYqnv3HOzz119lJ4+mK4d5rxtCp/U6ZiJa3VA4iktXWlVcw7qopW7XthScfxaH77xFuoAKhchCRrOPuXHffn3n/w7qvi+23eyeuPH0YzZoW6+WiRqZyEJGssWrNema+v5SJU19Lu813D+nHMYf2p0fnXTOYrPCoHEQkK5T+4hG+/Kq8zm2evKOU4mLdoywTVA4iEplNlVVcd9/zfLD0i7Tb/PrC4+nTs2MGUwmoHEQkAtXVNfz44ofSri8qKmLfPbtw9c+OzZvpKHKNykFEMuqau59jweL0c2yePWYoRxzUN4OJJBWVg4hkTF3TW1x75vfYr2+3tOsls1QOIhK6yqpqxlwyMeW6Oy7/IT06t025TqKjchCRUM2a9zG/nvBCYPwXZw1nwJ5dI0gkW0PlICKhufexV3jlzYWB8RvPG8Feu3eKIJFsLZWDiDS6Wye9yIy5S1Kvu2Qk3+rWPsOJpKFUDiLSaNydURc8mHJdcXERT95RmuFEsq1UDiLSKNydn/92Wsp1Rw/eizN+PCTDiWR7qBxEpFHcNvkl5n+UfP2CZknNXSoHEdlub7yzOHCO4bZLR9Gra7uIEsn2UjmIyDb7fNVazr7hscD4OScermLIcSoHEdkmW27VmcrhB+6Z4TTS2FQOItJgT/51Fn98YVZgvN/unbjhvBERJJLGpnIQka2ycvU6/vD8m7w2e1HK9X+8/XTdjS2PqBxEpF6PPf8WT788J+36p+8+I4NpJBNUDiKSlrvzy/v/wtwPylKu//7QAYw7fnCGU0kmqBxEJK10VztfcNKRHFbSO8NpJJNUDiKS0uPTZwbG2u/SmvHXjY0gjWSaykFEAqqra5j64uyksdNGHsKx39knokSSaUVRBxCR7JLq/s79du+kYigwKgcR+a8Pln4RKAZA1y4UoFDLwcyOMbOFZrbIzK5IsX4nM/uzmb1rZvPM7NQw84hIehWbqrjyzj8FxifecHIEaSRqoZWDmRUD9wHDgH7AGDPrV2uzs4H57r4vMBS43cyahZVJRFKrqqph7GWTAuM3X3Q8u7RpFUEiiVqYJ6QHAYvcfTGAmT0BjADmJ2zjQGszM2BHYDVQHWImEall5vtLufmhvwbGdWFbYQvzZaUuwLKE5bL4WKJ7gb2A5cB7wPnuvrn2A5lZqZnNMrNZK1euDCuvSMFx95TFMOWmcZkPI1klzHKwFGNea/l/gHeAzsB+wL1m1ibwRe4T3L3E3Uvat9e9Z0UaS6qL3G65eCStd2gRQRrJJmGWQxnQLWG5K7EjhESnAs94zCJgCdA3xEwiEnfS5ZMDY0/ffQa7d9cfYBJuOcwEeptZr/hJ5tFA7RvMfgIcCWBmHYE9gcUhZhIR4F+zPmBDRWXS2G+vHh1RGslGoZ2QdvdqMzsHeBEoBia7+zwzOyO+fjxwAzDFzN4j9jLU5e6+KqxMIgLryiu4+5F/JI1dVTqMzh12jiaQZKVQp89w9+nA9Fpj4xM+Xw58N8wMIvKNDz/+givuSL6WoUfntuy/d4+IEkm20hXSIgXi81VrA8UAcPtloyJII9lO5SBSAKqqajj7hscC40/dWUrsMiORZCoHkQIw+pLgfEmP3nIaRUX6FSCp6SdDJM9detvTgbFHbv4JLZo3jSCN5Ardz0Ekj7313lIWL0ueVeDx235Ks6ba9aVuOnIQyVMrVq/jNxOTp8Y49fjBKgbZKioHkTy0YvU6zrz+0aSxrh13YfjQARElklyjPyFE8szjf3mLqS/NCYzfdeWPIkgjuUpHDiJ5ZO36jSmLYepdP9NbVqVBVA4ieeTUq38fGJty0zgVgzSYXlYSyRNzF5YFxnTDHtlWKgeRHOfuPP/qe0x59t9J47phj2wPlYNIjkt1w56Obdvohj2yXXTOQSSHvfOfZSnHdW8G2V46chDJYTc88Jek5THfG8TIo7+tE9Cy3VQOIjnqslpzJg3s151R3x0YURrJN3pZSSQHuTsf1Zoz6eJxR0eURvKRykEkBz383Iyk5V+ee5xmWZVGpXIQyTFfrdvAtFfeTRrbe4/OEaWRfKVyEMkxp13zcNLyOSceHlESyWcqB5EcMunp1wJjhx+4ZwRJJN/p3UoiOaC6uoYfXxy81edTd5ZGkEYKgY4cRHLANfc8Fxg79jv9dQ9oCY1+skSyXGVVNR9+vCJpbECfrpw28tCIEkkh0MtKIlmsYlMVYy+blDR2w3kj6Ld7p4gSSaHQkYNIlnL3QDEAKgbJCJWDSJZKNdvqo7ecFkESKUR6WUkkC1VsqgqM/fH202nSpDiCNFKIdOQgkoVqv5x0y8UjVQySUSoHkSwz7qopgbHdu7fPfBApaKGWg5kdY2YLzWyRmV2RZpuhZvaOmc0zs3+GmUck2y1c8jnryiuSxh67VecZJPNCO+dgZsXAfcDRQBkw08ymufv8hG12Bu4HjnH3T8ysQ1h5RHLBVXc9m7R81pghNG+m2VYl88I8chgELHL3xe5eCTwBjKi1zYnAM+7+CYC7r0CkQP320VeSlju2bcORB+0VURopdGGWQxcg8Qa3ZfGxRH2AXczsVTObbWYnp3ogMys1s1lmNmvlypWpNhHJabdOepFX31qYNPabi0+IKI1IuOWQ6ia2Xmu5CbA/8D3gf4BrzaxP4IvcJ7h7ibuXtG+vE3OSX96cu4QZc5ckjX1vyD603qFFRIlEwr3OoQzolrDcFVieYptV7l4OlJvZv4B9gQ9CzCWSVW6Z9GLS8vAhAzj1hMERpRGJCfPIYSbQ28x6mVkzYDQwrdY2zwGHmVkTM2sFHAgsCDGTSFZZsXpd0vIubVqpGCQrhHbk4O7VZnYO8CJQDEx293lmdkZ8/Xh3X2BmfwXmApuBie7+fliZRLLNmdc/mrR87zVjIkoikizU6TPcfTowvdbY+FrLtwK3hplDJBvdOP4vgbEWzfW2VckOukJaJCJvL1iWtKyL3SSbqBxEIvDKm8lvWz3jx9/RxW6SVVQOIhm2YWMl9z6WfMHb0YP7RZRGJDWVg0iGnXTF5KTlIw/qG1ESkfRUDiIZtH7DpsDYWWOGZj6ISD1UDiIZdMqVv0tavu/aEyNKIlI3lYNIhjzwRHBG+t3atYkgiUj96iwHM5uS8PkpoacRyWN/eyP54v8/3n56RElE6lffkcO+CZ+fH2YQkXz29MtzkpZPHD5It/2UrFZfOdSeRVVEGqiyqprHnn8raWzk0QMjSiOydeqbPqOrmd1DbPrtLZ//l7ufF1oykTzxwv/NS1r+6ahDI0oisvXqK4dLEz6fFWYQkXz18HNvJC0PO6x/RElEtl6d5eDuv89UEJF8dO09zyUtDx8yIKIkIg1T71tZzewUM5tjZuXxf7PS3c5TRL7h7sz/6LOksXHHHxxRGpGGqfPIIV4CFwAXAXOInXsYCNxqZrj7w6EnFMlRoy54MGn5onFHY5bq7rki2ae+I4ezgOPd/RV3/9rdv3L3fwAj4+tEJIVxV00JjB3y7d0zH0RkG9VXDm3cfWntwfiYLu0USaH0F4+wrrwiaey6s78fURqRbVPfu5U2buM6kYL0o4smUFOzOWns5BEHs0+fLhElEtk29ZXDXmY2N8W4Ad8KIY9ITnJ3rrzzT4FiGD5kACOO2DfNV4lkr/rKYV+gI7Cs1ngPYHkoiURyUO2TzwBnjh7CUQfvFUEake1X3zmHO4G17v5x4j9gQ3ydSMFzD84yM+yw/ioGyWn1HTn0dPfAy0ruPsvMeoYTSSS33Db5paTls8YM4ciDVAyS2+o7cmhRx7qWjRlEJBetWrOeGXOXJI2pGCQf1FcOM80sMOm8mZ0GzA4nkkju+Nl1f0haPu9/j4goiUjjqu9lpQuAP5nZWL4pgxKgGXB8iLlEst6c+Z8ExoYc0CeCJCKNr76J974ABpvZ4cCWqST/Er9KWqRglW/cxK8enJ409vhtP40ojUjjq+/IAQB3fwV4JeQsIjnjtGuSpxXr2aUdzZpu1e4kkhPqnZVVRJJVbKqiqromaey2S0dGlEYkHCoHkQY676Ynkpan3DROs61K3lE5iDTQl1+VJy233qGud3yL5CaVg0gDLClblbT8q/N/EE0QkZCFWg5mdoyZLTSzRWZ2RR3bHWBmNWY2Ksw8ItvrklunJi336dkhoiQi4QqtHMysGLgPGAb0A8aYWb802/0GeDGsLCKN4bl/vJu03L3TrhQV6eBb8lOYP9mDgEXuvtjdK4EngBEptjsXeBpYEWIWke2yas16Hn7ujaSx2y/Tga7krzDLoQvJU32Xxcf+y8y6ELvSenxdD2RmpWY2y8xmrVy5stGDitSlsqo6ME3GIQP30FGD5LUwf7pTvbev9tzGdwGXu3tNim2/+SL3Ce5e4u4l7du3b6x8IltlzCUTA2MXnXJUBElEMifMSzrLgG4Jy10J3iCoBHgi/h7xdsCxZlbt7s+GmEtkq73wf+8Hxqbe9bMIkohkVpjlMBPobWa9gE+B0cCJiRu4e68tn5vZFOB5FYNkk4lTX0tannzjKbrgTQpCaOXg7tVmdg6xdyEVA5PdfZ6ZnRFfX+d5BpGojTw/+Ud0+JAB7NRatzGRwhDqTGHuPh2YXmssZSm4+7gws4g0xKW3PR0YO/WEwREkEYmG3m4hksLiZcnvitNNfKTQaI5hkVpqv5x0ZekwSvbuEVEakWjoyEEkwQ8veDAwpmKQQqRyEIm7/PZn2OzJl+L8+kLdDVcKk8pBhNgNfBZ9kjyDy1Wlw+jTs2NEiUSipXIQAcZeNilp+cThg9hfLydJAVM5SMGb9PRrgbGRRw+MIIlI9lA5SEH758wPmP6v5Cky7rj8hxGlEckeKgcpaPf84R9Jy7u1a0OPzm0jSiOSPXSdgxSsq+56Nmm5d48O3HzRCdGEEckyOnKQgvTItBksXPJ50piKQeQbOnKQgnL/46/y9xn/CYxfWTosgjQi2UvlIAXjzof/xmuzFwXG9+/XQ1dBi9SicpCCsGbthpTFcOLwQXrbqkgKKgfJe+7OT699OGls8Ld35+JxR0eUSCT76YS05L1RKSbTUzGI1E3lIHltY0VlYOyxW0+LIIlIblE5SF476fLJScu/PPc4mjdrGlEakdyhcpC8NWf+JyROwG3A3nt0jiqOSE5ROUheqqqq4VcPJt2+nIk3nhxRGpHco3KQvOPujL7koaSxHVo2Z+fWrSJKJJJ79FZWySuPTJvBs39/JzA+6QYdNYg0hMpB8sbI88enHH/gF2Np2rQ4w2lEcpvKQfLCzPeXphyfdOPJejlJZBuoHCTnvfT6fB588l9JY98fOoBxxw+OKJFI7tMJaclpmzdvDhRDyd49VAwi20nlIDntd3/6d2BM02+LbD+9rCQ56/yb/kjZF2uSxp6++4yI0ojkFx05SE66/r7nA8Vw5ughEaURyT86cpCck+4tq0cdvFeGk4jkr1CPHMzsGDNbaGaLzOyKFOvHmtnc+L9/m9m+YeaR3FZdXZOyGE49frBeThJpZKGVg5kVA/cBw4B+wBgz61drsyXAEHcfANwATAgrj+S+H1/8UGDs5BEHM3zogAjSiOS3MI8cBgGL3H2xu1cCTwAjEjdw93+7+5YXjmcAXUPMIzls7sKywNjY4Qcy4ggdbIqEIcxzDl2AZQnLZcCBdWx/GvBCqhVmVgqUAnTv3r2x8kmOcHeuv//5pLGJN5zMLm105bNIWMI8crAUY55iDDM7nFg5XJ5qvbtPcPcSdy9p3759I0aUXPCTa5Lv/9y/d2cVg0jIwjxyKAO6JSx3BZbX3sjMBgATgWHu/mWIeSQHfbbya9au35g0dv05x0WURqRwhHnkMBPobWa9zKwZMBqYlriBmXUHngFOcvcPQswiOWjz5s2cc+PjSWPXn/P9iNKIFJbQjhzcvdrMzgFeBIqBye4+z8zOiK8fD/wcaAvcb2YA1e5eElYmyS03TQiegurfu0sESUQKj7mnPA2QtUpKSnzWrFlRx5CQpbqeYepdPyP+R4SINJCZzW7IH9+aPkOyTqpiuPjUo1UMIhmkcpCscu09zwXGhg7ak8H77R5BGpHCpbmVJCusWL2OM69/NDB+0wU/YM9eu0WQSKSwqRwkcjeO/wtvL1gWGL/mjO+pGEQionKQyLg7oy54MOW6ww/ck2/v1S3lOhEJn8pBIvHuwjJ+WWtKjC2eurOUoiKdDhOJkspBMqqyqpoxl0xMue7csYczdNCeGU4kIqmoHCSj0hXDb68eTecOO2c2jIikpXKQjEl1/cKII/Zl7PADKS7Wy0gi2UTlIKFb/XU5p//8kcD4Q788iV132iGCRCJSH5WDhKamZjNjLp1ITc3mwLorTj9GxSCSxVQOEoqnXpzNE9Nnplz36wuPp0/PjhlOJCINoXKQRuPuvPfBp4G7tiV68o5SnV8QyQEqB2kUNTWb+dFFE9Kuv+G8EfTbvVMGE4nI9lA5yHarqqph9CUPpVw3fMgATj1hcIYTicj2UjnINqvYVMXYyyalXNejc1tKf3gYfb+luZFEcpHKQbbJhTc/ySefrU657p6rR9NFF7SJ5DSVg2y1qqoapr48h6kvzk67zSM3/4RWLZtlMJWIhEHlIGm5O2VffMVrsz/kvQ+Xs3DJ52m3fezW02jerGkG04lImFQOksTdeWL6TKa9MpfKqup6tz991GEcc9jeGUgmIpmkcpAk6e6vUNt3Snpz7tjDNbW2SJ5SOQgAb7yzmNt+91Kd2xw0oBc/OGo/9ujeATPLUDIRiYLKocCt37CJU678Xcp1Y743iKEH9KHdLjtmOJWIRE3lUIDWlVdQvrGSs294LO02V5YOo2TvHhlMJSLZROVQALZMmd28WVM2VVbVue0RB/blrDFD9LKRSIFTOeSpf7/zEfc//k82VlT+d6y+Yjhz9BCOOnivsKOJSA5QOeSRjRWVTHn2Df72xoIGfd0dl/+QHp3bhpRKRHKRyiHHuTsffryCK+/8U73bttmxJdef83067NqaFs11wZqIpKdyyFELl3zOQ1NfY0nZqjq326N7B0467kD69tqNJk2KM5RORHKdyiHLrSuv4ItVa5n26lzeWbCMJk2K+Hrdxnq/7rqzv88+fbpkIKGI5COVQ4atWrOeVWvW8+mKNSz6ZCWG8frbi+jUfieaFBezYvVavvyqnGZNm2zV9BWJWjRvyn3XjmHn1q1CSi8ihSLUcjCzY4C7gWJgorvfXGu9xdcfC2wAxrn7nDAz1Wf11+WsK69IGlu+4ms2VlSmfHvn2/9ZRutWzSkqiq37aNkqVq5eR/tdWwe2rWviug8/XpG0vLXF0LFtG84aM4T+vXWUICKNJ7RyMLNi4D7gaKAMmGlm09x9fsJmw4De8X8HAg/EPza619/+iBdfm0dlVfV/fxHXnhdo8+bNjfZ8q78ub7THAmjapJiq6hqOP3I/+vfpQq8u7dipdctGfQ4RkS3CPHIYBCxy98UAZvYEMAJILIcRwMPu7sAMM9vZzDq5+2eNGaSyqpr7H3+Vik3J7/NvzDJoqOLiIjru2pqd27Sid48OtGrZnN49OtCkOFZYndrvRKsWzSgqMpo11at/IpJZYf7W6QIsS1guI3hUkGqbLkBSOZhZKVAK0L179wYH2VhRFSiG+nTrtGvS8rLPVrN/vx603rFFYNsVX65l377daBl/e2hlVTUd27Vh1zY7BLZt2aIp3TvtqiuQRSSrhVkOqX77+TZsg7tPACYAlJSUBNbXp2WLpvx01KGs/qqcr9dv5KiD96LIjO6dd6Wo1i9pM6O4WNNQi0hhC7McyoBuCctdgeXbsM12a9a0CcMO69/YDysikrfC/BN5JtDbzHqZWTNgNDCt1jbTgJMt5iDg68Y+3yAiIg0X2pGDu1eb2TnAi8TeyjrZ3eeZ2Rnx9eOB6cTexrqI2FtZTw0rj4iIbL1Q3wbj7tOJFUDi2PiEzx04O8wMIiLScDrzKiIiASoHEREJUDmIiEiAykFERAIsdk44d5jZSuDjWsPtgLpvbBA9ZWwcuZARciOnMjaOXMm4g7u339ovyLlySMXMZrl7SdQ56qKMjSMXMkJu5FTGxpGvGfWykoiIBKgcREQkIF/KYULUAbaCMjaOXMgIuZFTGRtHXmbMi3MOIiLSuPLlyEFERBqRykFERAJyshzM7EIzm2dm75vZ42bWwsxuNbP/mNlcM/uTme2cbRkT1l1iZm5m7bIxo5mda2YL4+tuybaMZrafmc0ws3fMbJaZDYo44/nxfPPM7IL42K5m9rKZfRj/uEsWZsy2fSaQMWFdtuwzKTNm2T6T6v91w/cZd8+pf8RuI7oEaBlffhIYB3wXaBIf+w3wm2zLGP+8G7FpzD8G2mVbRuBw4G9A8/h4hyzM+BIwLD52LPBqhBn7A+8DrYjNcvw3oDdwC3BFfJsrIv55TJcxm/aZlBnj67Jln0n3fcymfSZdxgbvMzl55EDsP7qlmTUh9k1Y7u4vuXt1fP0MYneVi1IgY3z8TuAyUtwONQKpMp4J3OzumwDcfUWE+SB1RgfaxNfvRAh3D2yAvYAZ7r4h/vP3T+B4YATw+/g2vwd+EE08IE3GLNtn0n0fIXv2mXQZs2mfSZexwftMzpWDu38K3AZ8AnxG7O5xL9Xa7CfAC5nOtkW6jGZ2HPCpu78bVbYt6vg+9gEOM7M3zeyfZnZAFma8ALjVzJbF118ZVUZif6V9x8zamlkrYn+VdQM6evyuhvGPHbIwY6JI9xnSZMymfYb038es2WfqyHgBDdxncq4c4q/djgB6AZ2BHczsfxPWXw1UA49GkzBtxpOBq4GfR5UrUR3fxybALsBBwKXAk2ZmWZbxTOBCd+8GXAhMiiIfgLsvIPaSzMvAX4F3if38ZY36MmbDPlNHxqzZZ+rImDX7TB0ZG7zP5Fw5AEcBS9x9pbtXAc8AgwHM7BRgODDW4y+uZVHGU4n9knvXzJYSO4SfY2a7ZVHGwUAZ8IzHvAVsJjZpVzZlPCX+OcBTQKQnpN19krsPdPfvAKuBD4EvzKwTQPxjpC/PpcmYTftMqoxLya59Jt33MZv2mXQZG7zP5GI5fAIcZGat4u18JLDAzI4BLgeOc/cNkSZMnfEZd+/g7j3dvSexH6iB7v55FmVcADwLHAFgZn2AZkQ342S6jMuBIfFtjiD+iy4qZtYh/rE7cALwODCN2A5J/ONz0aSLSZUxy/aZVBkfzrJ9Jt3/62fJnn0mXcYG7zOh3kM6DO7+pplNBeYQO1x6m9il4fOA5sDL8SO6Ge5+RpZlzBp1ZHRgspm9D1QCp0T1F2UdGd8G7o6fpK4ASqPIl+BpM2sLVAFnu/saM7uZ2MsLpxEruR9GmjB1xnvJkn0mXcYIs6ST6vs4mSzZZ+rIeDoN3Gc0fYaIiATk4stKIiISMpWDiIgEqBxERCRA5SAiIgEqBxERCVA5SF4ws6vjs1DOjc88eWDIz/eqmWX1TeVFtkfOXecgUpuZHUzsKt+B7r4pPq1zs4hjieQ0HTlIPugErEqYFXOVuy8HMLOfm9nM+Pz2E7bMeRP/y/9OM/uXmS0wswPM7BmL3X/hxvg2PS12v4Pfx49IpsYnM0tiZt81szfMbI6ZPWVmO6bYpt7ni2/3v2b2Vvzo50EzK46PP2Cxefjnmdn1CdsvNbPr48/9npn1beTvrRQolYPkg5eIzeD5gZndb2ZDEtbd6+4HuHt/oCWxI4wtKuPzz4wnNr3F2cTmwx8Xv8IUYE9ggrsPANYCZyU+cfwo5RrgKHcfCMwCLkqTs87nM7O9gB8Dh7j7fkANMDb+tVe7ewkwABhiZgMSHndV/LkfAC6p97slshVUDpLz3H09sD+xKQFWAn80s3Hx1YdbbCrl94jNKbN3wpdOi398D5jn7p/Fjz4W882U1svc/fX4538ADq319AcB/YDXzewdYvMo9UgTtb7nOzL+3zEz/lhHAt+Kf82PzGwOsalD9o4/5xZbJlSbDfRM89wiDaJzDpIX3L0GeBV4NV4Ep5jZE8D9QIm7LzOz64AWCV+2Kf5xc8LnW5a37Bu155epvWzAy+4+Ziti1vd8Bvze3ZPm2jezXsSOCA6Iz5MzJc1/Rw3ap6WR6MhBcp6Z7WlmvROG9iN2S8ktv0BXxc8DjNqGh+8eP+ENMAZ4rdb6GcAhZrZHPEur+Myc2+LvwKiEWTV3NbMexO7gVQ58bWYdgWHb+PgiW01/ZUg+2BH4rZntTGz21kVAqbt/ZWYPEXsZZykwcxseewGxo5AHiU1z/EDiSndfGX8J63Ezax4fvgb4oKFP5O7zzewa4CUzK+KbWTVnmNnbxGYeXgy8XtfjiDQGzcoqkoaZ9QSej5/MFikoellJREQCdOQgIiIBOnIQEZEAlYOIiASoHEREJEDlICIiASoHEREJ+H9i4XOAu2U1cAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"cdf = thinkstats2.Cdf(xbars)\n",
"thinkplot.Cdf(cdf)\n",
"thinkplot.Config(xlabel='Sample mean',\n",
" ylabel='CDF')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The mean of the sample means is close to the actual value of $\\mu$."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"90.15936484024559"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.mean(xbars)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"An interval that contains 90% of the values in the sampling disrtribution is called a 90% confidence interval."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(85.94658544221595, 94.36667819207565)"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ci = cdf.Percentile(5), cdf.Percentile(95)\n",
"ci"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And the RMSE of the sample means is called the standard error."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2.544286153256379"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"stderr = RMSE(xbars, 90)\n",
"stderr"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Confidence intervals and standard errors quantify the variability in the estimate due to random sampling."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Estimating rates\n",
"\n",
"The following function simulates experiments where we try to estimate the mean of an exponential distribution using the mean and median of a sample. "
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rmse L 1.128569912777519\n",
"rmse Lm 1.6900702519369455\n",
"mean error L 0.36208572112105514\n",
"mean error Lm 0.476809799168978\n"
]
}
],
"source": [
"def Estimate3(n=7, iters=1000):\n",
" lam = 2\n",
"\n",
" means = []\n",
" medians = []\n",
" for _ in range(iters):\n",
" xs = np.random.exponential(1.0/lam, n)\n",
" L = 1 / np.mean(xs)\n",
" Lm = np.log(2) / thinkstats2.Median(xs)\n",
" means.append(L)\n",
" medians.append(Lm)\n",
"\n",
" print('rmse L', RMSE(means, lam))\n",
" print('rmse Lm', RMSE(medians, lam))\n",
" print('mean error L', MeanError(means, lam))\n",
" print('mean error Lm', MeanError(medians, lam))\n",
" \n",
"Estimate3()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The RMSE is smaller for the sample mean than for the sample median.\n",
"\n",
"But neither estimator is unbiased."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercises"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise:** Suppose you draw a sample with size n=10 from an exponential distribution with λ=2. Simulate this experiment 1000 times and plot the sampling distribution of the estimate L. Compute the standard error of the estimate and the 90% confidence interval.\n",
"\n",
"Repeat the experiment with a few different values of `n` and make a plot of standard error versus `n`.\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"standard error 0.8775230553742727\n",
"confidence interval (1.2428797428759237, 3.6613337571071947)\n"
]
},
{
"data": {
"text/plain": [
"0.8775230553742727"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEWCAYAAABrDZDcAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhYklEQVR4nO3de7xVdZ3G8c/DTe6gghdAxQuGZGB6QitNzTRvSY064yUvlZmTppmVzkw1zjTVdJ2ZUiMzU8sks0zMe+Wl1EowBQFFREAuylFEkfuB7/yxF4e99rlyzl5nnb338369zov1W2ux1rOOuL973X4/RQRmZla7euQdwMzM8uVCYGZW41wIzMxqnAuBmVmNcyEwM6txLgRmZjXOhcCqkqQrJf08md5d0luSenbBfs+V9Oei9luS9irTtv9V0nXJ9GhJIalXmbbdZb8j635cCKysJB0q6TFJb0haIelRSe/KM1NELIqIgRGxKYd9D4yI+a2tI+kISYvbsa2vR8R55cglaYGkDxRtO7ffkeWvLN8mzAAkDQZ+B/wzcCvQBzgMWJ9nrmogqVdENOSdw6qTzwisnPYFiIhbImJTRKyNiPsjYgaApL0l/VHSa5JelXSzpKFb/nLyLfULkmZIWi3pJ5J2lnSPpFWSfi9p+2TdLZdGzpe0VNIySZc1F6r0MoqkhyR9NTlbWSXpfknDitY/W9LCJOeXS789l2x7R0lTJb0p6W/A3iXLQ9I+yfTxkmYn+1wi6fOSBgD3ACOSSzNvSRqRXNq6TdLPJb0JnFt8uavIx5s7fkk3SPqvonbjWYeknwG7A3cm+/tiM7+jEclxrZA0T9Ini7Z1paRbJd2UHMssSXXN/X6sMrgQWDnNBTZJulHScVs+tIsI+AYwAtgP2A24smSdk4GjKRSVD1H4kPxXYBiFf68Xl6x/JDAGOAa4oqUP7GacAXwM2InCmcvnASSNA64BzgR2BYYAI1vZztXAumTdjyc/LfkJ8KmIGATsD/wxIlYDxwFLk0szAyNiabL+JOA2YChwcwvb3Objj4izgEXAh5L9fauZ1W4BFlP4b3UK8HVJRxUtPwmYkmSbClzV1n6t+3IhsLKJiDeBQ4EAfgzUJ98qd06Wz4uIByJifUTUA98DDi/ZzA8i4pWIWAL8CfhrRPw9ItYDtwPvLFn/PyJidUTMBH4KnN7OuD+NiLkRsZbCZawDkvmnAHdGxJ8jYgPwleR4mkhurJ4MfCXJ8AxwYyv73AiMkzQ4Il6PiCfbyPh4RPw2IjYnOZvT0eNvkaTdKPx3vDwi1kXEU8B1wFlFq/05Iu5O7in8DJjQ2f1aflwIrKwiYk5EnBsRoyh86x0B/C+ApJ0kTUkui7wJ/JzCN/1irxRNr22mPbBk/ZeKphcm+2uPl4um1xRtd0TxNiNiDfBaC9sYTuE+W2mGlpwMHA8slPSwpHe3kfGlNpaXrrMtx9+aEcCKiFhVsu3iM6PS31/fcj3BZF3PhcAyExHPAjdQKAhQuCwUwPiIGAx8lMLlos7YrWh6d2BpSyu20zJg1JaGpH7Aji2sWw80NJOhWRHxRERMonA56rcUzkSghTOOVuYXa+n4VwP9i5btsg3bXgrsIGlQybaXtCOPVSAXAisbSWMlXSZpVNLejcKlir8kqwwC3gJWShoJfKEMu/2ypP6S3k7hmv8vO7m924APSXqPpD7Af9BCsUoui/wGuDLJMA44p7l1JfWRdKakIRGxEXgT2PKo5ivAjpKGdCBvS8f/FHC8pB0k7QJ8tuTvvQI0+35DRLwEPAZ8Q1JfSeOBT9DyfQqrcC4EVk6rgIOBv0paTaEAPANseZrlP4ADgTeAuyh8iHbWw8A84A/AdyLi/s5sLCJmAZ+hcCN0GYVjWk7Lj8BeROGy0ssUzn5+2srmzwIWJJfFLqBwRrTlzOkWYL6klZK25fJOS8f/M+BpYAFwP00L5DeALyX7+3wz2z0dGE3h7OB24N8j4oFtyGUVRB6YxiqRpNHAi0DvLJ+vlzQQWAmMiYgXs9qPWZ58RmBWQtKHksstA4DvADMpfLM2q0ouBGZNTaJwSWQphWf0TwufOlsV86UhM7Ma5zMCM7MaV3EvgAwbNixGjx6ddwwzs4oyffr0VyNieHPLKq4QjB49mmnTpuUdw8ysokhq8a13XxoyM6txLgRmZjXOhcDMrMa5EJiZ1TgXAjOzGpdZIZB0vaTlkp5pYbkkfT8ZBm+GpAOzymJmZi3L8vHRGygMX3dTC8uPo/D6/hgKPVb+MPnTzIqsXbeBze4BoKYtWPIaq9duoN92vRk9ckcGDehb1u1nVggi4pGkh8iWTAJuSvpw+YukoZJ2jYhlWWVqj3nz5jVO77PPPjkmyU+l/A42bGxg/Yb2dzy6eXOwYGlLg4113PyX6pnx3BJ69hQr3ljDwqWvscuwwZ3ebgS88tqbZUho1eTfPnU8B45rcfyjDsnzhbKRpIfZW5zMa1IIJJ0PnA+w++7l/QVY/t5as56FS19Lfaiv27CRFxbV069vHxa//Dovv/oGOw4ZwJp1G5kxd3GOadvn5Vf9AW7ZGNh/u7JvM89C0NyoT82e/0bEtcC1AHV1dT5HriCrVq/j2RdfRhKbNwdzXlhGv7692RzBr+97cpsueTyfYc5K0K9vn7wjWI4ETBy/J2P22Kns286zECwmPd7qKDo/3qzl5PU31/C5b/6KTZs2s3rterYf3J/X31zTJfvu37cPUvuGPl69tjDQ2Ph9R7Wx5rZ56eUV7DVqOBPGjmLIwH4M234gQwb1K8u2Bw/sy4B+5f8WaLZFnoVgKnCRpCkUbhK/kff9Ads2S5av5M4Hn+aBx+Y0WdbRInDA2K3fDTZsbOCNVWs5ePyerNuwkaGD+zNi+FCgcHq86/AhDNt+YIf2Y2ZbZVYIJN0CHAEMk7QY+HegN0BETAbuBo6nMN7qGgoDb1s3t2nTZm69bzq33Td9m/5e/759GLvXLkQEi5at4PC6fenRQ/Tr24ejDhlb9qcgzKz9snxq6PQ2lgdwYVb7t/Jat34jv3t4Jrfc9bc21/3Cx49ht113oG+fXkhi+8H9233pxsy6XsV1Q21dJyJYsnwlF39tSpvrnnTkBE4+5sBMnmgws2y5EFgTEcFVv3yc5xbUM2DAgBbXO3vSuznpyPH+tm9W4VwILGXugle4+JtTW13nfXVjuOiMI+nZ011VmVUDFwJr9PEv3cgbq9a2uPwbl36EfUfv3IWJzKwruBAYt93/ZIs3gb92yYcZu9cuXZzIzLqSC0GNWr12Pdfd9mcemdb8+7q9e/Xke5edwBgXAbOq50JQY9Zv2MgZX/hJq+t87qOHsdeoHbookZnlzYWgxrRWBM758Ls56cgJqd5Hzaz6uRDUiA0bGzj989c1u+yUYw7k9BMmdnEiM+suXAhqQEQ0WwR++d1P0qtXzxwSmVl34gfBa8Apn/1Rk3lf+fSJLgJmBviMoKpFRLNF4Iavn+tO3syskc8IqtjNd/61ybzLzzvWRcDMUlwIqtjtf3gq1b707A8w8R2jc8liZt2XC0GVKh30/NKzP8ChB3XfgejNLD8uBFXq0//5i1T7vQfunVMSM+vuXAiq0K33Tmsyz11Fm1lLXAiqzIaNDfzynnQhuOU75+WUxswqgQtBlSl9cezTpx9On95+StjMWuZCUEUaGjY1mXfUIfvlkMTMKokLQRX5p8t+nGr/+D/PyimJmVUSF4IqtsOQlscbNjPbwoWgSsycuyTVvv6/zskpiZlVGheCKnHl1Xem2kMG9cspiZlVGheCCrdhYwMnXzI5NW/0yGE5pTGzSuRCUOEu++avmsz77hdPySGJmVUqF4IKt7T+jVT7M2cemVMSM6tUftOogn3p/+5Itb92yYcZu9cuOaUxs0rlM4IKNmf+slTbRcDMOsKFoELd8cenU+3Lzzs2pyRmVulcCCrQho0N3HTH46l5HnDGzDoq00Ig6VhJz0maJ+mKZpYPkXSnpKclzZL0sSzzVIvSjuU+9Y/vyymJmVWDzAqBpJ7A1cBxwDjgdEnjSla7EJgdEROAI4DvSuqTVaZqsGjZiibzjnlv6a/VzKz9sjwjmAjMi4j5EbEBmAJMKlkngEEqjJoyEFgBNGSYqeJd+t+3pto//Pczc0piZtUiy0IwEnipqL04mVfsKmA/YCkwE7gkIjaXbkjS+ZKmSZpWX1+fVd5ub84Ly5rM22mHQTkkMbNqkmUhaG5sxChpfxB4ChgBHABcJWlwk78UcW1E1EVE3fDhw8uds2J86fvp9wZ++d1P5pTEzKpJloVgMbBbUXsUhW/+xT4G/CYK5gEvAmMzzFSxItI1dNCAvvTq1TOnNGZWTbIsBE8AYyTtmdwAPg2YWrLOIuAoAEk7A28D5meYqWI9v3B5qj3Z9wbMrEwy62IiIhokXQTcB/QEro+IWZIuSJZPBr4K3CBpJoVLSZdHxKtZZapkP7r1T6l23+1655TEzKpNpn0NRcTdwN0l8yYXTS8FjskyQ7VYsGRrfdx1+JAck5hZtfGbxRXgydmLUu3Lzj06pyRmVo1cCLq5iOBrP0qdVLHnKA88Y2bl40LQzf3L/9yeag8a0DenJGZWrVwIujk/LWRmWXMh6MYeeGx2qv3lfz7BTwuZWdm5EHRTK1etYfIvH0nNO2Dsbi2sbWbWcS4E3dQV303fG/jQEeNzSmJm1c6FoJtq2LQp1T73I+/JKYmZVTsXgm7q9TfXNE5f/NH355jEzKqdC0E39J2fPpBqTxg7KqckZlYLXAi6ocefeiHVHjqof05JzKwWuBB0M9NnLUy1zzvl0JySmFmtcCHoZqY++HSqfdxh++eUxMxqhQtBNxIRPPP81rF7Ru28fY5pzKxWuBB0I7NLxiT2ZSEz6wouBN3ID37+YKr9jn1H5pTEzGqJC0E3Uv/6qsbpMXvslGMSM6slLgTdxJR7nki1P336EfkEMbOa40LQTfzq3ump9u677pBTEjOrNS4E3cALi+pT7WMPfXtOScysFrkQdAN/e2ZBqv3JUw/LJ4iZ1SQXgm7gtvu2XhbyuwNm1tVcCLoZDz5jZl3NhSBnDQ3pcQdOP+FdOSUxs1rlQpCzh6fNTbU9JrGZdTUXgpw9O/+VvCOYWY1zIcjZH//6bOP0xHeMzi+ImdUsF4IcRUSqPW7vETklMbNa5kKQo+KzAYAjJu6bUxIzq2UuBDn67e+fSrUHDeibTxAzq2mZFgJJx0p6TtI8SVe0sM4Rkp6SNEvSw1nm6W6W1r/ROP3+g8fmmMTMalmvrDYsqSdwNXA0sBh4QtLUiJhdtM5Q4Brg2IhYJKlm+l7evHlzqn3C4R6S0szykeUZwURgXkTMj4gNwBRgUsk6ZwC/iYhFABGxPMM83cqdD81Mtd3bqJnlJctCMBJ4qai9OJlXbF9ge0kPSZou6ezmNiTpfEnTJE2rr69vbpWKc9Mdj6faPXr4do2Z5SPLTx81My9K2r2Ag4ATgA8CX5bU5NGZiLg2Iuoiom748OHlT9rFml4WekdOSczMMrxHQOEMoLgHtVHA0mbWeTUiVgOrJT0CTADmUsXmLkhfATv1gwfllMTMLNszgieAMZL2lNQHOA2YWrLOHcBhknpJ6g8cDMzJMFO3cPvv/55q+7FRM8tTZmcEEdEg6SLgPqAncH1EzJJ0QbJ8ckTMkXQvMAPYDFwXEc9klam7mDZrYeP0brt4/AEzy1eWl4aIiLuBu0vmTS5pfxv4dpY5urOTjz4w7whmVuP8qEoXW7d+Y6p90Nv3yCmJmVmBC0EX+/ucl1Lt/v365JTEzKzAhaCLPfBY44vV9OrVM8ckZmYFLgRd7PmFWx8dPeBto3JMYmZW4ELQxdas29A4fcx7x+WYxMyswIWgC61euz7VHj1yx5ySmJlt5ULQhR76W/qF6R2HDswpiZnZVq0WAkk3FE2fk3maKrf8tVV5RzAza6KtM4IJRdOXZBmkFsxd+Erj9H577ZpjEjOzrdoqBKW9hVonzF2wtRAceuA+OSYxM9uqrS4mRkn6PoUupbdMN4qIizNLVmVKu54eufPQfIKYmZVoqxB8oWh6WpZBql3pjeK37+NLQ2bWPbRaCCLixq4KUu2uvuWhVNsjkplZd9Hmp5GkcyQ9KWl18jOtpSElrXkR6VstRx0yNqckZmZNtXpGkHzgfxb4HPAkhXsFBwLflkRE3JR5wirwp+nPp9oX/NP7ckpiZtZUW2cEnwY+EhEPRsQbEbEyIv4InJwss3a47rZHU21fFjKz7qStT6TBEbGgdGYyb3AWgapNRKS6ljhk/J45pjEza6qtQrC2g8ss8ejfX0i1TzthYk5JzMya19bjo/tJmtHMfAF7ZZCn6jz97OJU22MUm1l301YhmADsDLxUMn8PYGkmiarMvEVbxx941/6j8wtiZtaCti4N/Q/wZkQsLP4B1iTLrA2Llq1onH7XOzw+sZl1P20VgtER0eTSUERMA0ZnkqiKzH5hWao9YvjQfIKYmbWirULQt5Vl/coZpBp9+ft3pNpj99olpyRmZi1rqxA8IemTpTMlfQKYnk2k6rT3bsORlHcMM7Mm2rpZ/FngdklnsvWDvw7oA3wkw1wVb/mK9CA0X734pJySmJm1rq1O514B3iPpSGD/ZPZdydvF1orpsxam2tv16Z1TEjOz1rV1RgBARDwIPJhxlqpS3O30LsP8EraZdV/u9CYjy+rfaJweOrh/jknMzFrnQpCR4v6F/uED78wxiZlZ61wIMrBpU3pYyj1G7JhTEjOztrkQZGBp0WUhgB2HDsgpiZlZ2zItBJKOlfScpHmSrmhlvXdJ2iTplCzzdJU5RW8U992ut98fMLNuLbNCIKkncDVwHDAOOF3SuBbW+yZwX1ZZulrxo6Pr1m/MMYmZWduyPCOYCMyLiPkRsQGYAkxqZr3PAL8GljezrCI9++LLjdPvqxuTYxIzs7ZlWQhGku6+enEyr5GkkRTeUJ7c2oYknS9pmqRp9fX1ZQ9abm+t2frE0Nv3GZFjEjOztmVZCJq7MB4l7f8FLo+ITa1tKCKujYi6iKgbPnx4ufJ1ibft6Y7mzKx7a9ebxR20GNitqD2KpoPZ1AFTkpupw4DjJTVExG8zzJWpJctXptojdxqSTxAzs3bKshA8AYyRtCewBDgNOKN4hYhoHMld0g3A7yq5CAD8+Fd/SrV79PATumbWvWVWCCKiQdJFFJ4G6glcHxGzJF2QLG/1vkClmjl3Sd4RzMy2SZZnBETE3cDdJfOaLQARcW6WWfLw6dMPzzuCmVmbfN2ijF59/a1U+7CD/OiomXV/LgRldP+js1PtPr0zPeEyMysLF4IyWr+hIe8IZmbbzIWgjH738IzG6X86ri7HJGZm7edCkJHh2w/KO4KZWbu4EJRJRPql6f3HuGsJM6sMLgRlUvpG8bDtB+YTxMxsG7kQlMlNv/1Lqu0xCMysUrgQlMn02VvHINhhiEckM7PK4UKQgbNPOiTvCGZm7eZCUAYNDeletPfZY6eckpiZbTsXgjK49d7pqfauw931tJlVDheCMvj1A0/mHcHMrMNcCDqp9P2Bs3x/wMwqjAtBJ722cnWqfeLh78gpiZlZx7gQdFLpQDS9evXMKYmZWce4EHTS1b94sHHa/QuZWSVyIeikQQP7NU5vjs05JjEz6xgXgk568621jdPnfPg9OSYxM+sYF4JOKH1iaF+/SGZmFciFoBPmzH851R6+g+8RmFnlcSHohN89NKPtlczMujkXgk7464wXG6dH7jQ0vyBmZp3gQtBBpfcHTv3gQTklMTPrHBeCDnpk2vOp9nveuXdOSczMOseFoIN+OOXhVLtnT/8qzawy+dOrgzYWjUEwxo+NmlkFcyHogNdWvpVqX3LWUTklMTPrPBeCDvj6tfem2h6IxswqmQtBByxY8mreEczMyibTQiDpWEnPSZon6Ypmlp8paUby85ikCVnmKYfivoUAvviJD+aUxMysPDIrBJJ6AlcDxwHjgNMljStZ7UXg8IgYD3wVuDarPOXy7IuvpNoHj98zpyRmZuWR5RnBRGBeRMyPiA3AFGBS8QoR8VhEvJ40/wKMyjBPWcxbuDzvCGZmZZVlIRgJvFTUXpzMa8kngHuaWyDpfEnTJE2rr68vY8Rt98y8pY3Th0zYK8ckZmblkWUhUDPzopl5SDqSQiG4vLnlEXFtRNRFRN3w4cPLGHHbLat/o3F66KB+raxpZlYZemW47cXAbkXtUcDS0pUkjQeuA46LiNcyzFMWxTeL9x/T2gmOmVllyPKM4AlgjKQ9JfUBTgOmFq8gaXfgN8BZETE3wyyZGLXL9nlHMDPrtMzOCCKiQdJFwH1AT+D6iJgl6YJk+WTgK8COwDWSABoioi6rTJ21aVN6TOLh2w/MKYmZWflkeWmIiLgbuLtk3uSi6fOA87LMUE71r6e7lui7Xe+ckpiZlY/fLN4Gs+YtyTuCmVnZuRBsg2tu2dr19PaD++eYxMysfFwI2ql0RLJ37rd7TknMzMrLhaCdnn5ucar9iZPfm1MSM7PyciFop3seeSbV9o1iM6sWLgTtNG3WwsbpurfvkWMSM7PyciFohw0bG1LtieNH5xPEzCwDLgTt8MQzC1Pt9x88NqckZmbl50LQDnc9PDPVTt6CNjOrCi4E7fDciy83To/be9cck5iZlZ8LQRtWrV6Xan/4qAPyCWJmlhEXgjbc9Uj6stBBfmLIzKqMC0EbfnXv9LwjmJllyoWgFaXdSvhpITOrRi4Erfjxr/6cap910sE5JTEzy44LQSvue3RWqj14oMcoNrPq40LQgldXrk61LzrjyJySmJlly4WgBVdNeTzVPvxdY3JKYmaWLReCFpSeEfTo4V+VmVUnf7o1Y/6SFan2lRd+KKckZmbZcyFoxvd+9qdUe/8xI3JKYmaWPReCEtfcmr43sF2f3u5kzsyqmgtBkeUrVjF7/vLUvJu/9fGc0piZdQ0XgiK//f1Tqfak90/w2YCZVT0XgiKlL5CdPendOSUxM+s6LgSJl199M9U++8QDc0piZta1XAgSF371F6l23bhROSUxM+taLgTAzLlLmszr0cP3BsysNtR8Idi8eTNXXn1nat63Pnt8TmnMzLpezReCUy+9tsm8/n1755DEzCwfNV0ITr5kcpN5V10xKYckZmb5ybQQSDpW0nOS5km6opnlkvT9ZPkMSZk/qrN67Xruenhms0Xgxm98LOvdm5l1O72y2rCknsDVwNHAYuAJSVMjYnbRascBY5Kfg4EfJn+W3aN/f4Hv3fBAi8svOuNIBvbfLotdm5l1a1meEUwE5kXE/IjYAEwBSq+7TAJuioK/AEMl7VruIBs2NnDNLQ+1uPxz5x7NkQe/rdy7NTOrCJmdEQAjgZeK2otp+m2/uXVGAsuKV5J0PnA+wO67777NQdau28i69RubzD/x8PGc+5F3uxsJM6tpWRaC5j5dowPrEBHXAtcC1NXVNVneln59e3PeKYeyYuVqVq/dwCdPPdQf/mZmiSwLwWJgt6L2KGBpB9bptD69e3HcYfu3a9199tmn3LuvOP4dmNWWLO8RPAGMkbSnpD7AacDUknWmAmcnTw8dArwREctKN2RmZtnJ7IwgIhokXQTcB/QEro+IWZIuSJZPBu4GjgfmAWsAP79pZtbFsrw0RETcTeHDvnje5KLpAC7MMoOZmbWupt8sNjMzFwIzs5rnQmBmVuNcCMzMapwK92srh6R6YGHeObbRMODVvENkoBqPy8dUOarxuLI8pj0iYnhzCyquEFQiSdMioi7vHOVWjcflY6oc1XhceR2TLw2ZmdU4FwIzsxrnQtA1mo6HWR2q8bh8TJWjGo8rl2PyPQIzsxrnMwIzsxrnQmBmVuNcCDIkaTdJD0qaI2mWpEvyzlQuknpK+ruk3+WdpVwkDZV0m6Rnk/9m7847U2dJujT5t/eMpFsk9c07U0dIul7ScknPFM3bQdIDkp5P/tw+z4zbqoVj+nby72+GpNslDe2KLC4E2WoALouI/YBDgAsljcs5U7lcAszJO0SZ/R9wb0SMBSZQ4ccnaSRwMVAXEftT6A7+tHxTddgNwLEl864A/hARY4A/JO1KcgNNj+kBYP+IGA/MBf6lK4K4EGQoIpZFxJPJ9CoKHywj803VeZJGAScA1+WdpVwkDQbeB/wEICI2RMTKXEOVRy+gn6ReQH8yGAGwK0TEI8CKktmTgBuT6RuBD3dlps5q7pgi4v6IaEiaf6EwamPmXAi6iKTRwDuBv+YcpRz+F/gisDnnHOW0F1AP/DS55HWdpAF5h+qMiFgCfAdYBCyjMALg/fmmKqudt4xomPy5U855yu3jwD1dsSMXgi4gaSDwa+CzEfFm3nk6Q9KJwPKImJ53ljLrBRwI/DAi3gmspvIuNaQk18wnAXsCI4ABkj6abyprD0n/RuHS8s1dsT8XgoxJ6k2hCNwcEb/JO08ZvBc4SdICYArwfkk/zzdSWSwGFkfEljO22ygUhkr2AeDFiKiPiI3Ab4D35JypnF6RtCtA8ufynPOUhaRzgBOBM6OLXvRyIciQJFG45jwnIr6Xd55yiIh/iYhRETGawo3HP0ZExX/LjIiXgZckvS2ZdRQwO8dI5bAIOERS/+Tf4lFU+A3wElOBc5Lpc4A7csxSFpKOBS4HToqINV21XxeCbL0XOIvCt+ankp/j8w5lLfoMcLOkGcABwNfzjdM5ydnNbcCTwEwK/79XZLcMkm4BHgfeJmmxpE8A/w0cLel54OikXTFaOKargEHAA8nnxeRWN1KuLO5iwsystvmMwMysxrkQmJnVOBcCM7Ma50JgZlbjXAjMzGqcC4FZGySdK2lEUfu6cnQeKGm0pDM6ux2zznIhMGvbuRS6aAAgIs6LiHK8bDYacCGw3LkQWM2S9FFJf0te3PlRMsbCDUnf/TOTvvxPAeoovGj2lKR+kh6SVJds4y1J35Q0XdLvJU1Mls+XdFKyzmhJf5L0ZPKzpZuH/wYOS7Z7abL/b0t6IumP/lP5/Gas1viFMqtJkvYDvgX8Q0RslHQN8ApwaEQcnawzNCJWSnoI+HxETEvmN7YlBXB8RNwj6XZgAIUuuscBN0bEAZL6A5sjYp2kMcAtEVEn6YhkOycm2z0f2Cki/kvSdsCjwKkR8WIX/VqsRvXKO4BZTo4CDgKeKHTDQz/gXmAvST8A7gLa02XzhuTvQaEbh/VJYZlJ4dIPQG/gKkkHAJuAfVvY1jHA+OQsBGAIMAZwIbBMuRBYrRKFb+ypEaCS7n8/CFwI/COFPuFbs7Goh8jNwHqAiNicDAYDcCmFs40JFC7Hrmsl02ci4r5tPBazTvE9AqtVfwBOkbQTNI5/uwfQIyJ+DXyZrd1Qr6LQEVhHDQGWRcRmCp0Q9mxhu/cB/5x0XY6kfSt9cByrDD4jsJoUEbMlfQm4X1IPYCPwOeD2pA1bx4u9AZgsaS3QkQHtrwF+LelU4EEKg94AzAAaJD2d7OP/KFxOejLpNrqeCht+0SqTbxabmdU4XxoyM6txLgRmZjXOhcDMrMa5EJiZ1TgXAjOzGudCYGZW41wIzMxq3P8DLxVkw5Q4XBkAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Solution\n",
"\n",
"def SimulateSample(lam=2, n=10, iters=1000):\n",
" \"\"\"Sampling distribution of L as an estimator of exponential parameter.\n",
"\n",
" lam: parameter of an exponential distribution\n",
" n: sample size\n",
" iters: number of iterations\n",
" \"\"\"\n",
" def VertLine(x, y=1):\n",
" thinkplot.Plot([x, x], [0, y], color='0.8', linewidth=3)\n",
"\n",
" estimates = []\n",
" for _ in range(iters):\n",
" xs = np.random.exponential(1.0/lam, n)\n",
" lamhat = 1.0 / np.mean(xs)\n",
" estimates.append(lamhat)\n",
"\n",
" stderr = RMSE(estimates, lam)\n",
" print('standard error', stderr)\n",
"\n",
" cdf = thinkstats2.Cdf(estimates)\n",
" ci = cdf.Percentile(5), cdf.Percentile(95)\n",
" print('confidence interval', ci)\n",
" VertLine(ci[0])\n",
" VertLine(ci[1])\n",
"\n",
" # plot the CDF\n",
" thinkplot.Cdf(cdf)\n",
" thinkplot.Config(xlabel='estimate',\n",
" ylabel='CDF',\n",
" title='Sampling distribution')\n",
"\n",
" return stderr\n",
"\n",
"SimulateSample()"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [],
"source": [
"# Solution\n",
"\n",
"# My conclusions:\n",
"\n",
"# 1) With sample size 10:\n",
"\n",
"# standard error 0.762510819389\n",
"# confidence interval (1.2674054394352277, 3.5377353792673705)\n",
"\n",
"# 2) As sample size increases, standard error and the width of\n",
"# the CI decrease:\n",
"\n",
"# 10 0.90 (1.3, 3.9)\n",
"# 100 0.21 (1.7, 2.4)\n",
"# 1000 0.06 (1.9, 2.1)\n",
"\n",
"# All three confidence intervals contain the actual value, 2."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise:** In games like hockey and soccer, the time between goals is roughly exponential. So you could estimate a team’s goal-scoring rate by observing the number of goals they score in a game. This estimation process is a little different from sampling the time between goals, so let’s see how it works.\n",
"\n",
"Write a function that takes a goal-scoring rate, `lam`, in goals per game, and simulates a game by generating the time between goals until the total time exceeds 1 game, then returns the number of goals scored.\n",
"\n",
"Write another function that simulates many games, stores the estimates of `lam`, then computes their mean error and RMSE.\n",
"\n",
"Is this way of making an estimate biased?"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"def SimulateGame(lam):\n",
" \"\"\"Simulates a game and returns the estimated goal-scoring rate.\n",
"\n",
" lam: actual goal scoring rate in goals per game\n",
" \"\"\"\n",
" goals = 0\n",
" t = 0\n",
" while True:\n",
" time_between_goals = random.expovariate(lam)\n",
" t += time_between_goals\n",
" if t > 1:\n",
" break\n",
" goals += 1\n",
"\n",
" # estimated goal-scoring rate is the actual number of goals scored\n",
" L = goals\n",
" return L"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Experiment 4\n",
"rmse L 1.4145133438748465\n",
"mean error L 0.001306\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEGCAYAAAB/+QKOAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAATGUlEQVR4nO3df5BdZ33f8fcHqYbgQmljYahkV6YRUAVsQhdjaiaJSc3IJINoJhmsEsdJ8ajOWPyapuBM3MyUejrMkLYBbFA1xsGZ2vJ0wGo1QfhHIYnbYgfJlFiWwaCRId7IjuVA4ww02IJv/zhnyWX1rPautGfvrvV+zezs+fE8z/1qvd7PPeee85xUFZIkzfasSRcgSVqeDAhJUpMBIUlqMiAkSU0GhCSpafWkC1hMZ5xxRq1fv37SZUjSinHfffc9UVVrWvueUQGxfv169u3bN+kyJGnFSPKNufZ5ikmS1GRASJKaDAhJUpMBIUlqMiAkSU0GhCSpyYCQJDUZEJKkJgNCktT0jLqTernadu3OQca97potg40/M7akU5dHEJKkJgNCktRkQEiSmgwISVKTASFJajIgJElNBoQkqcmAkCQ1GRCSpCYDQpLUZEBIkpoMCElS06ABkWRTkoeSHExydWP/25Lc3399Psl5I/u+nmR/ki8l2TdknZKkYw02m2uSVcD1wMXANLA3ye6qenCk2cPAT1XVt5JcAuwAXjuy/6KqemKoGiVJcxvyCOJ84GBVHaqqp4Bbgc2jDarq81X1rX71XmDdgPVIkhZgyIBYCzwysj7db5vL24HPjKwXcGeS+5JsnatTkq1J9iXZd+TIkZMqWJL0N4Z8YFAa26rZMLmILiBeP7L5wqo6nOSFwF1JvlJVdx8zYNUOulNTTE1NNceXJC3ckEcQ08BZI+vrgMOzGyU5F7gB2FxVfzGzvaoO998fB3bRnbKSJC2RIQNiL7AhyTlJTgMuBXaPNkhyNnAbcFlVfXVk++lJnjezDLwReGDAWiVJswx2iqmqjibZBtwBrAJurKoDSa7s928Hfgv4UeCjSQCOVtUUcCawq9+2Grilqm4fqlZJ0rGG/AyCqtoD7Jm1bfvI8hXAFY1+h4DzZm+XJC0d76SWJDUZEJKkJgNCktRkQEiSmgwISVKTASFJajIgJElNBoQkqcmAkCQ1GRCSpCYDQpLUZEBIkpoMCElSkwEhSWoyICRJTQaEJKnJgJAkNRkQkqQmA0KS1GRASJKaDAhJUpMBIUlqMiAkSU0GhCSpyYCQJDUZEJKkJgNCktRkQEiSmgwISVLToAGRZFOSh5IcTHJ1Y//bktzff30+yXnj9pUkDWuwgEiyCrgeuATYCGxJsnFWs4eBn6qqc4F/B+xYQF9J0oCGPII4HzhYVYeq6ingVmDzaIOq+nxVfatfvRdYN25fSdKwhgyItcAjI+vT/ba5vB34zEL7JtmaZF+SfUeOHDmJciVJo4YMiDS2VbNhchFdQLxvoX2rakdVTVXV1Jo1a06oUEnSsVYPOPY0cNbI+jrg8OxGSc4FbgAuqaq/WEhfSdJwhjyC2AtsSHJOktOAS4Hdow2SnA3cBlxWVV9dSF9J0rAGO4KoqqNJtgF3AKuAG6vqQJIr+/3bgd8CfhT4aBKAo/3pombfoWqVJB1ryFNMVNUeYM+sbdtHlq8Arhi3ryRp6XgntSSpyYCQJDUZEJKkJgNCktRkQEiSmgwISVKTASFJajIgJElNBoQkqWnQO6n1zLDt2p2LPuZ112xZ9DElLS6PICRJTQaEJKnJgJAkNRkQkqQmA0KS1GRASJKaDAhJUpMBIUlqMiAkSU0GhCSpyYCQJDUZEJKkJgNCktRkQEiSmgwISVKTASFJajIgJElNBoQkqcmAkCQ1DRoQSTYleSjJwSRXN/a/PMk9Sb6b5Ndn7ft6kv1JvpRk35B1SpKOtXqogZOsAq4HLgamgb1JdlfVgyPNvgm8E3jLHMNcVFVPDFWjJGluxz2CSPKJkeXLFzj2+cDBqjpUVU8BtwKbRxtU1eNVtRd4eoFjS5IGNt8ppvNGlt+1wLHXAo+MrE/328ZVwJ1J7kuyda5GSbYm2Zdk35EjRxZYoiRpLvMFRJ3E2DnJ8S6sqlcDlwBXJfnJVqOq2lFVU1U1tWbNmhOpU5LUMN9nEOuSfJjuj/3M8g9U1TuP03caOGt0LODwuIVV1eH+++NJdtGdsrp73P6SpJMzX0D865HlhV5JtBfYkOQc4M+AS4F/Pk7HJKcDz6qqv+qX3wi8f4GvL0k6CccNiKq66UQHrqqjSbYBdwCrgBur6kCSK/v925O8iC54ng98P8m7gY3AGcCuJDM13lJVt59oLZKkhTtuQCTZfbz9VfXmefbvAfbM2rZ9ZPkxulNPsz3JD39ALklaYvOdYnod3ZVIO4E/pv3BsyTpGWi+gHgR3Y1uW+g+P/g0sLOqDgxdmCRpso57mWtVfa+qbq+qy4ELgIPAHyZ5x5JUJ0mamHmn2kjybOBn6Y4i1gMfBm4btixJ0qTN9yH1TcArgM8A/7aqHliSqiRJEzffEcRlwLeBlwLvSjJzJ3SAqqrnD1mcJGly5rsP4pR5XsS2a3cu+pjXXbNl0ceUpKUy3ymm5wBXAj8G3E93s9vRpShMkjRZ8x0h3ARMAfuBNwH/YfCKJEnLwnyfQWysqlcCJPk48IXhS5IkLQfzHUH84EE+nlqSpFPLfEcQ5yV5sl8O8CP9ulcxSdIz3HxXMa1aqkIkScvLKXMZqyRpYQwISVKTASFJajIgJElNBoQkqcmAkCQ1GRCSpCYDQpLUZEBIkpoMCElSkwEhSWoyICRJTQaEJKnJgJAkNRkQkqQmA0KS1DRoQCTZlOShJAeTXN3Y//Ik9yT5bpJfX0hfSdKwBguIJKuA64FLgI3AliQbZzX7JvBO4LdPoK8kaUBDHkGcDxysqkNV9RRwK7B5tEFVPV5Ve4GnF9pXkjSsIQNiLfDIyPp0v21R+ybZmmRfkn1Hjhw5oUIlSccaMiDS2FaL3beqdlTVVFVNrVmzZuziJEnHN2RATANnjayvAw4vQV9J0iIYMiD2AhuSnJPkNOBSYPcS9JUkLYLVQw1cVUeTbAPuAFYBN1bVgSRX9vu3J3kRsA94PvD9JO8GNlbVk62+Q9UqSTrWYAEBUFV7gD2ztm0fWX6M7vTRWH0lSUvHO6klSU0GhCSpadBTTNJ8tl27c9HHvO6aLYs+pnQq8ghCktRkQEiSmgwISVKTASFJajIgJElNBoQkqcmAkCQ1GRCSpCYDQpLUZEBIkpoMCElSkwEhSWoyICRJTQaEJKnJgJAkNRkQkqQmA0KS1GRASJKaDAhJUpMBIUlqMiAkSU0GhCSpyYCQJDUZEJKkJgNCktRkQEiSmgYNiCSbkjyU5GCSqxv7k+TD/f77k7x6ZN/Xk+xP8qUk+4asU5J0rNVDDZxkFXA9cDEwDexNsruqHhxpdgmwof96LfCx/vuMi6rqiaFqlCTNbcgjiPOBg1V1qKqeAm4FNs9qsxn4vercC7wgyYsHrEmSNKYhA2It8MjI+nS/bdw2BdyZ5L4kWwerUpLUNNgpJiCNbbWANhdW1eEkLwTuSvKVqrr7mBfpwmMrwNlnn30y9UqSRgx5BDENnDWyvg44PG6bqpr5/jiwi+6U1TGqakdVTVXV1Jo1axapdEnSkAGxF9iQ5JwkpwGXArtntdkN/HJ/NdMFwF9W1aNJTk/yPIAkpwNvBB4YsFZJ0iyDnWKqqqNJtgF3AKuAG6vqQJIr+/3bgT3Am4CDwHeAX+27nwnsSjJT4y1VdftQtUqSjjXkZxBU1R66EBjdtn1kuYCrGv0OAecNWZsk6fi8k1qS1GRASJKaDAhJUpMBIUlqMiAkSU2DXsUkTdq2a3cu+pjXXbNl0ceUliOPICRJTQaEJKnJgJAkNRkQkqQmA0KS1GRASJKaDAhJUpMBIUlqMiAkSU0GhCSpyYCQJDUZEJKkJgNCktRkQEiSmgwISVKTASFJajIgJElNPlFOOkFDPK0OfGKdlg+PICRJTQaEJKnJgJAkNRkQkqQmA0KS1GRASJKaBr3MNckm4EPAKuCGqvrArP3p978J+A7wK1X1xXH6Ss90Q1xG6yW0WojBjiCSrAKuBy4BNgJbkmyc1ewSYEP/tRX42AL6SpIGNOQRxPnAwao6BJDkVmAz8OBIm83A71VVAfcmeUGSFwPrx+gr6SR4hKL5pPvbPMDAyS8Am6rqin79MuC1VbVtpM3vAx+oqv/Vr38WeB9dQBy378gYW+mOPgBeBjw0yD/ob5wBPDHwawxpJddv7ZNh7ZOzFPX/g6pa09ox5BFEGttmp9Fcbcbp222s2gHsWFhpJy7JvqqaWqrXW2wruX5rnwxrn5xJ1z9kQEwDZ42srwMOj9nmtDH6SpIGNORlrnuBDUnOSXIacCmwe1ab3cAvp3MB8JdV9eiYfSVJAxrsCKKqjibZBtxBd6nqjVV1IMmV/f7twB66S1wP0l3m+qvH6ztUrQu0ZKezBrKS67f2ybD2yZlo/YN9SC1JWtm8k1qS1GRASJKaDIgFSLIpyUNJDia5etL1jCvJWUn+IMmXkxxI8q5J17RQSVYl+T/9vTMrSn8D6CeTfKX/b/C6Sdc0riTv6X9nHkiyM8lzJl3TXJLcmOTxJA+MbPt7Se5K8rX++9+dZI1zmaP2D/a/M/cn2ZXkBUtdlwExphU+/cdR4F9V1T8CLgCuWkG1z3gX8OVJF3GCPgTcXlUvB85jhfw7kqwF3glMVdUr6C4YuXSyVR3XJ4BNs7ZdDXy2qjYAn+3Xl6NPcGztdwGvqKpzga8Cv7HURRkQ4/vB1CFV9RQwM/3HsldVj85MglhVf0X3B2rtZKsaX5J1wM8CN0y6loVK8nzgJ4GPA1TVU1X1fyda1MKsBn4kyWrguSzj+5Gq6m7gm7M2bwZu6pdvAt6ylDWNq1V7Vd1ZVUf71Xvp7gdbUgbE+NYCj4ysT7OC/sjOSLIe+AngjydcykL8DvBe4PsTruNEvAQ4Avxuf4rshiSnT7qocVTVnwG/Dfwp8CjdfUp3TraqBTuzv7eK/vsLJ1zPifoXwGeW+kUNiPGNPf3HcpXkbwOfAt5dVU9Oup5xJPk54PGqum/StZyg1cCrgY9V1U8A32b5nub4If35+s3AOcDfB05P8kuTrerUk+Q36U4T37zUr21AjG+cqUOWrSR/iy4cbq6q2yZdzwJcCLw5ydfpTuu9Icl/mWxJCzINTFfVzBHbJ+kCYyX4p8DDVXWkqp4GbgP+yYRrWqg/72eIpv/++ITrWZAklwM/B7ytJnDTmgExvhU7/Uf/YKaPA1+uqv846XoWoqp+o6rWVdV6up/556pqxbyLrarHgEeSvKzf9DOsnGnr/xS4IMlz+9+hn2GFfMA+Yjdweb98OfDfJ1jLgvQPTXsf8Oaq+s4kajAgxtR/WDQz/ceXgf+6jKb/mM+FwGV0776/1H+9adJFnULeAdyc5H7gVcC/n2w54+mPej4JfBHYT/f3YtlOXZFkJ3AP8LIk00neDnwAuDjJ14CL+/VlZ47arwOeB9zV/z+7fcnrcqoNSVKLRxCSpCYDQpLUZEBIkpoMCElSkwEhSWoyIHTKSHJmkluSHEpyX5J7kvyzExxr/ejMm8tVkk8k+YVJ16GVyYDQKaG/0eu/AXdX1Uuq6h/T3Xi35BOgnax+ZmFpcAaEThVvAJ7qn4UOQFV9o6o+ApDkOUl+N8n+flK9i/rt65P8zyRf7L+OmWoiyY8n+UJ/M9P9STbM2r+qfyf/QD/+e/rtP5bkfyT5k37sf5jOB0favrVv+9P9Mz1uAfb3Y34wyd7+Nf9l3y5JrkvyYJJPs3Inp9MysHrSBUhL5Mfp7giey1UAVfXKJC8H7kzyUrq5ey6uqr/u//DvBKZm9b0S+FBV3dxPwzL7Hf6rgLX9MxUYefDLzcAHqmpXugfxPAv4+b79ecAZwN4kd/ftz6d7PsDDSbbSza76miTPBv53kjvpZup9GfBK4Ey6aT1uHOsnJM1iQOiUlOR64PV0RxWv6Zc/AlBVX0nyDeClwDeA65K8Cvhev222e4Df7J9bcVtVfW3W/kPAS5J8BPg0Xfg8jy40dvWv+dd9Xa8HdlbV9+gmmvsj4DXAk8AXqurhfsw3AueOfL7wd4ANdM+emOl/OMnnTvynpFOdp5h0qjjAyCyqVXUV3eRza/pNrencAd4D/DndO/op4LTZDarqFuDNwP8D7kjyhln7v9X3/0O6I5UbjvN6c22Hbqrw0XbvqKpX9V/njDyrwflztCgMCJ0qPgc8J8mvjWx77sjy3cDbAPpTS2cDD9G9M3+0qr5PN+HhMR8QJ3kJcKiqPkw3e+i5s/afATyrqj4F/Bvg1f3zOKaTvKVv8+wkz+3reGv/GcMauiOCLzT+PXcAv9ZP406Sl6Z7ENHdwKV9/xcDF439E5Jm8RSTTglVVf0f4/+U5L10T3n7Nt10ygAfBbYn2U/3cJZfqarvJvko8Kkkvwj8AT/8Ln7GW4FfSvI08Bjw/ln719I9UW7mDdnMs4UvA/5zkvcDTwO/COwCXgf8Cd2RwHur6rH+c5FRNwDrgS/2V2gdoXuc5i66D+T30z3H+I/G+wlJx3I2V0lSk6eYJElNBoQkqcmAkCQ1GRCSpCYDQpLUZEBIkpoMCElS0/8HacyPmjoI0GkAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Solution\n",
"\n",
"# The following function simulates many games, then uses the\n",
"# number of goals scored as an estimate of the true long-term\n",
"# goal-scoring rate.\n",
"\n",
"def Estimate6(lam=2, m=1000000):\n",
"\n",
" estimates = []\n",
" for i in range(m):\n",
" L = SimulateGame(lam)\n",
" estimates.append(L)\n",
"\n",
" print('Experiment 4')\n",
" print('rmse L', RMSE(estimates, lam))\n",
" print('mean error L', MeanError(estimates, lam))\n",
" \n",
" pmf = thinkstats2.Pmf(estimates)\n",
" thinkplot.Hist(pmf)\n",
" thinkplot.Config(xlabel='Goals scored', ylabel='PMF')\n",
" \n",
"Estimate6()"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [],
"source": [
"# Solution\n",
"\n",
"# My conclusions:\n",
"\n",
"# 1) RMSE for this way of estimating lambda is 1.4\n",
"\n",
"# 2) The mean error is small and decreases with m, so this estimator\n",
"# appears to be unbiased.\n",
"\n",
"# One note: If the time between goals is exponential, the distribution\n",
"# of goals scored in a game is Poisson.\n",
"\n",
"# See https://en.wikipedia.org/wiki/Poisson_distribution"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise:** In this chapter we used $\\bar{x}$ and median to estimate µ, and found that $\\bar{x}$ yields lower MSE. Also, we used $S^2$ and $S_{n-1}^2$ to estimate σ, and found that $S^2$ is biased and $S_{n-1}^2$ unbiased.\n",
"Run similar experiments to see if $\\bar{x}$ and median are biased estimates of µ. Also check whether $S^2$ or $S_{n-1}^2$ yields a lower MSE."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Experiment 1\n",
"mean error xbar 0.0006146708992637597\n",
"mean error median 0.0013680157776572379\n"
]
}
],
"source": [
"# Solution\n",
"\n",
"def Estimate4(n=7, iters=100000):\n",
" \"\"\"Mean error for xbar and median as estimators of population mean.\n",
"\n",
" n: sample size\n",
" iters: number of iterations\n",
" \"\"\"\n",
" mu = 0\n",
" sigma = 1\n",
"\n",
" means = []\n",
" medians = []\n",
" for _ in range(iters):\n",
" xs = [random.gauss(mu, sigma) for i in range(n)]\n",
" xbar = np.mean(xs)\n",
" median = np.median(xs)\n",
" means.append(xbar)\n",
" medians.append(median)\n",
"\n",
" print('Experiment 1')\n",
" print('mean error xbar', MeanError(means, mu))\n",
" print('mean error median', MeanError(medians, mu))\n",
" \n",
"Estimate4()"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Experiment 2\n",
"RMSE biased 0.5161459570059862\n",
"RMSE unbiased 0.578408257713436\n"
]
}
],
"source": [
"# Solution\n",
"\n",
"def Estimate5(n=7, iters=100000):\n",
" \"\"\"RMSE for biased and unbiased estimators of population variance.\n",
"\n",
" n: sample size\n",
" iters: number of iterations\n",
" \"\"\"\n",
" mu = 0\n",
" sigma = 1\n",
"\n",
" estimates1 = []\n",
" estimates2 = []\n",
" for _ in range(iters):\n",
" xs = [random.gauss(mu, sigma) for i in range(n)]\n",
" biased = np.var(xs)\n",
" unbiased = np.var(xs, ddof=1)\n",
" estimates1.append(biased)\n",
" estimates2.append(unbiased)\n",
"\n",
" print('Experiment 2')\n",
" print('RMSE biased', RMSE(estimates1, sigma**2))\n",
" print('RMSE unbiased', RMSE(estimates2, sigma**2))\n",
"\n",
"Estimate5()"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"# Solution\n",
"\n",
"# My conclusions:\n",
"\n",
"# 1) xbar and median yield lower mean error as m increases, so neither\n",
"# one is obviously biased, as far as we can tell from the experiment.\n",
"\n",
"# 2) The biased estimator of variance yields lower RMSE than the unbiased\n",
"# estimator, by about 10%. And the difference holds up as m increases."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
CyberCRI/dataanalysis-herocoli-redmetrics | v1.52/Tests/5.1 Game map analysis tests.ipynb | 1 | 15544 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 5.1 Game map analysis tests"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%run \"../Functions/5. Game map analysis.ipynb\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Function tests"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allTypes = rmdf152['type'].dropna().unique()\n",
"\n",
"types = [\"death\", \"reach\", \"add\", \"craft\", \"remove\", \"select\", \"selectmenu\"]\n",
"craftTypes = [\"add\", \"craft\", \"remove\", \"select\"]\n",
"gameTypes = [\"hint\", \"pickup\", \"newfurthest\", \"newownrecord\", \"configure\", \"end\", \"complete\", \"restart\", \"start\"]\n",
"webTypes = [\"gotostudy\", \"gotomooc\"]\n",
"adminTypes = [\"switchtogameversion\", \"switchfromgameversion\", \"webconfigure\"]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allTypes"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### WARNING: very long test"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allLocatedEventsDF = filterAndLocateEvents(allTypes)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"locatedEventsDF = filterAndLocateEvents(types)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"craftLocatedEventsDF = filterAndLocateEvents(craftTypes)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"gameLocatedEventsDF = filterAndLocateEvents(gameTypes)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"webLocatedEventsDF = filterAndLocateEvents(webTypes)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"adminLocatedEventsDF = filterAndLocateEvents(adminTypes)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"len(allLocatedEventsDF)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"print(\"minX=\" + str(min(allLocatedEventsDF['x'])))\n",
"print(\"maxX=\" + str(max(allLocatedEventsDF['x'])))\n",
"print(\"minY=\" + str(min(allLocatedEventsDF['y'])))\n",
"print(\"maxY=\" + str(max(allLocatedEventsDF['y'])))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"type(min(allLocatedEventsDF['x']))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"type(allLocatedEventsDF)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allLocatedEventsDF.columns"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"type(allLocatedEventsDF['x'].value_counts())"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allLocatedEventsDF['x'].value_counts().hist()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allLocatedEventsDF['bucket'] = pd.cut(allLocatedEventsDF['x'], 10)\n",
"allLocatedEventsDF.head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"newdf = allLocatedEventsDF[['bucket','x']].groupby('bucket').sum()\n",
"newdf.plot(kind='bar')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allLocatedEventsDF['bucket'] = pd.cut(allLocatedEventsDF['y'], 10)\n",
"newdf = allLocatedEventsDF[['bucket','y']].groupby('bucket').sum()\n",
"#newdf.plot(kind='bar', orientation='horizontal')\n",
"newdf.plot.barh()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Plots"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%run \"../Functions/5. Game map analysis.ipynb\""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"constants = getConstants()\n",
"constants"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"for event in allTypes:\n",
" plotLocatedEvents(allLocatedEventsDF, [event])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plotLocatedEvents(allLocatedEventsDF, ['end', 'configure', 'restart'])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plotLocatedEvents(allLocatedEventsDF, types)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plotLocatedEvents(allLocatedEventsDF, craftTypes)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plotLocatedEvents(allLocatedEventsDF, gameTypes)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plotLocatedEvents(allLocatedEventsDF, webTypes)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plotLocatedEvents(allLocatedEventsDF, adminTypes)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Tinkering"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### filterAndLocateEvents"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"rmdf152.columns"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#rmdf152['customData.chapter'].dropna().head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Filter columns"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"mapRelevantColumns = ['type', 'section', 'coordinates']\n",
"mapDF = rmdf152.loc[:,mapRelevantColumns]\n",
"len(mapDF)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"mapDF = mapDF.dropna()\n",
"len(mapDF)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Filter by event type"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"mapDF = mapDF[mapDF[\"type\"].isin(types)]\n",
"mapDF.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Filter by section"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"tutorial1DF = mapDF[(mapDF['section'].str.startswith('tutorial1'))]\n",
"#sandbox2DF = mapDF[(mapDF['section'].str.startswith('sandbox'))]\n",
"tutorial1DF.head(2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"len(tutorial1DF)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### [x,y] coordinates"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"tutorial1DF['x'] = tutorial1DF['coordinates']\n",
"tutorial1DF['y'] = tutorial1DF['coordinates']"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"tutorial1DF.head(2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"m = re.findall('-*\\d+', '[-259, -713]')\n",
"m"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"coordinates = re.findall('-*\\d+', tutorial1DF['coordinates'][10])\n",
"coordinates"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"subsetCount = 100\n",
"subset = tutorial1DF.head(subsetCount)\n",
"subset.index = range(0, subsetCount)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"f = FloatProgress(min=0, max=len(subset.index))\n",
"display(f)\n",
"\n",
"for index in subset.index:\n",
" coordinates = re.findall('-*\\d+', subset['coordinates'][index])\n",
" subset['x'][index] = coordinates[0]\n",
" subset['y'][index] = coordinates[1]\n",
" f.value += 1"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"subset.head(2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"types"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plt.figure(figsize=(15,15))\n",
"plt.axis('equal')\n",
"\n",
"# c = [\"black\", \"red\", \"blue\", \"green\"]\n",
"c = ['black', 'red', 'blue', 'green', 'orange', 'purple', 'brown', 'pink', 'olive', 'cyan', ]\n",
"# a = [ 0.3, 1, 1,1 ]\n",
"a = [ 0.3, 1, 1, 1, 1, 1, 1, 1, 1, 1, ]\n",
"\n",
"scatters = {}\n",
"\n",
"for i, t in enumerate(types):\n",
" pts = subset[subset[\"type\"] == t]\n",
" x = pts[\"x\"]\n",
" y = pts[\"y\"]\n",
"\n",
" scatters[t] = plt.plot(x, y, 'o', c=c[i], lw=0, alpha=a[i])\n",
"\n",
"plt.legend([ x[0] for x in scatters.values()], list(scatters.keys()))\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"_mapBackground = image.imread('../../images/map.png')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"type(_mapBackground)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"len(_mapBackground)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"len(_mapBackground[0])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"_mapBackground.shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#types = allTypes\n",
"subset = allLocatedEventsDF"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"allLocatedEventsDF[allLocatedEventsDF['type'] == 'complete'].head(5)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"scrolled": true
},
"outputs": [],
"source": [
"imgStartCoordinates = [833,432]\n",
"imgEndCoordinates = [1333,334]\n",
"constants = getConstants()\n",
" \n",
"print(getGraphPosition(imgStartCoordinates, constants))\n",
"print(getGraphPosition(imgEndCoordinates, constants))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# from image dimensions\n",
"print(getXGraphPosition(0, constants))\n",
"print(getXGraphPosition(1665, constants))\n",
"print(getYGraphPosition(890, constants))\n",
"print(getYGraphPosition(0, constants))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### getConstants tinkering"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"gameStartCoordinates = [-229,-608]\n",
"gameEndCoordinates = [450,-475]\n",
"\n",
"# only for '../../images/map.tutorial1.png'\n",
"imgStartCoordinates = [833,432]\n",
"imgEndCoordinates = [1333,334]\n",
"\n",
"scaleX = (gameStartCoordinates[0]-gameEndCoordinates[0])/(imgStartCoordinates[0]-imgEndCoordinates[0])\n",
"scaleY = (gameStartCoordinates[1]-gameEndCoordinates[1])/(imgStartCoordinates[1]-imgEndCoordinates[1])\n",
"\n",
"offsetX = gameStartCoordinates[0] - (imgStartCoordinates[0]*scaleX)\n",
"offsetY = gameStartCoordinates[1] - (imgStartCoordinates[1]*scaleY)\n",
"\n",
"newConstants = pd.Series([scaleX,scaleY,offsetX,offsetY], index=['scaleX', 'scaleY', 'offsetX', 'offsetY'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### plotLocatedEvents tinkering"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#constants = getConstants()\n",
"constants = newConstants\n",
"\n",
"plt.figure(figsize=(18,12))\n",
"\n",
"# background map image display\n",
"mapBackground = image.imread('../../images/map.tutorial1.png')\n",
"\n",
"# background image dimensions\n",
"minX = 0\n",
"maxX = mapBackground.shape[1]\n",
"minY = mapBackground.shape[0]\n",
"maxY = 0\n",
"\n",
"plt.imshow(mapBackground, aspect='auto', zorder=-1, \\\n",
" extent=(getXGraphPosition(minX,constants), \\\n",
" getXGraphPosition(maxX,constants), \\\n",
" getYGraphPosition(minY,constants), \\\n",
" getYGraphPosition(maxY,constants)), \\\n",
" alpha=0.5)\n",
"\n",
"\n",
"colors = ['black', 'red', 'blue', 'green', 'orange', 'purple', 'brown', 'pink', 'olive', 'cyan', ]\n",
"alphas = [ 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, ]\n",
"scatters = {}\n",
"\n",
"for i, t in enumerate(types):\n",
" pts = subset[subset['type'] == t]\n",
" x = pts['x']\n",
" y = pts['y']\n",
"\n",
" scatters[t] = plt.plot(x, y, 'o', c=colors[i], lw=0, alpha=alphas[i])\n",
"\n",
"plt.legend([ x[0] for x in scatters.values()], list(scatters.keys()))\n",
"\n",
"# graph dimensions and extrema on tutorial1\n",
"# minX=-1152\n",
"# maxX=539\n",
"# minY=-1161\n",
"# maxY=-100\n",
"plt.xlim([-1200, 600])\n",
"plt.ylim([-1220, -20])\n",
"\n",
"plt.show()"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python [conda env:python3]",
"language": "python",
"name": "conda-env-python3-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.4"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| cc0-1.0 |
ztianai/INFO370-Project | code/tianai & peter/FBI DATA.ipynb | 1 | 4832371 | null | mit |
zipeiyang/liupengyuan.github.io | chapter2/homework/computer/4-19/201411680496_task7.ipynb | 20 | 7828 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"练习一:自己定义一个reverse(s)函数,功能返回字符串s的倒序字符串。"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"飞\n",
"如\n",
"马\n",
"去\n",
"归\n",
"花\n",
"赏\n"
]
}
],
"source": [
"def reverse(s):\n",
" for i in range(0,len(s)):\n",
" j=len(s)-i-1\n",
" print (s[j]) \n",
" \n",
"def main():\n",
" text = '赏花归去马如飞'\n",
" reverse(text) \n",
"main()"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"练习二:写函数,根据给定符号和行数,打印相应直角三角形,等腰三角形及其他形式的三角形。"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"plz input line num: 7\n",
" \n",
" *\n",
" ***\n",
" *****\n",
" *******\n",
" *********\n",
" ***********\n",
"\n",
"* \n",
"* * \n",
"* * * \n",
"* * * * \n",
"* * * * * \n",
"* * * * * * \n",
"* * * * * * * \n"
]
}
],
"source": [
"def tri1(m,n):\n",
" for i in range(0, n):\n",
" for j in range(0,n-i): \n",
" print(' ',end='')\n",
" for k in range(0,2*i-1):\n",
" print (m,end='')\n",
" print()\n",
"def tri2(m,n):\n",
" for i in range(1,n+1):\n",
" for j in range(1,i+1):\n",
" print (m, end=' ')\n",
" print() \n",
"\n",
" \n",
"def main():\n",
" sym='*'\n",
" n=int(input('plz input line num: '))\n",
" tri1(sym,n) \n",
" print()\n",
" tri2(sym,n)\n",
"main() "
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"练习三:将任务4中的英语名词单数变复数的函数,尽可能的考虑多种情况,重新进行实现。"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"plz input a word: tomato\n",
"tomates\n",
"plz input a word: apple\n",
"apples\n",
"plz input a word: sandwich\n",
"sandwices\n",
"plz input a word: q\n",
"qs\n"
]
}
],
"source": [
"def plur(s):\n",
" l=len(s)\n",
" if (s.endswith('o') or s.endswith('ch') or s.endswith('sh') ): \n",
" print (s[0:l-1],end='')\n",
" print ('es')\n",
" else:\n",
" print (s[0:l],end='')\n",
" print ('s') \n",
" \n",
"def main():\n",
" s='st'\n",
" while(s != 'q'):\n",
" s=str(input('plz input a word: '))\n",
" plur(s)\n",
"main() "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"source": [
"练习四:写函数,根据给定符号,上底、下底、高,打印各种梯形。"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"plz input upper line: 4\n",
"plz input lower line: 8\n",
"plz input height: 4\n",
"****\n",
"*****\n",
"******\n",
"*******\n"
]
}
],
"source": [
"def trap(a,b,h):\n",
" x=(b-a)//h\n",
" for i in range(0,h):\n",
" for j in range(0,a):\n",
" print ('*',end='')\n",
" a+=x\n",
" print()\n",
"def main():\n",
" a=int(input('plz input upper line: '))\n",
" b=int(input('plz input lower line: '))\n",
" h=int(input('plz input height: '))\n",
" trap(a,b,h)\n",
"main()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"练习五:写函数,根据给定符号,打印各种菱形。"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"plz input line num: 5\n",
" \n",
" *\n",
" ***\n",
" *****\n",
" *******\n",
"*********\n",
" *******\n",
" *****\n",
" ***\n",
" *\n",
"\n"
]
}
],
"source": [
"def tri(m,n):\n",
" for i in range(0, n):\n",
" for j in range(0,n-i): \n",
" print(' ',end='')\n",
" for k in range(0,2*i-1):\n",
" print (m,end='')\n",
" print()\n",
" for i in range(n,0,-1):\n",
" for j in range(0,n-i): \n",
" print(' ',end='')\n",
" for k in range(0,2*i-1):\n",
" print (m,end='')\n",
" print()\n",
"def main():\n",
" sym='*'\n",
" n=int(input('plz input line num: '))\n",
" tri(sym,n) \n",
" print()\n",
"\n",
"main() \n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"练习六:与本小节任务基本相同,但要求打印回文字符倒三角形。"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"赏花归去马如飞飞如马去归花赏\n",
" 赏花归去马如飞如马去归花赏\n",
" 赏花归去马如如马去归花赏\n",
" 赏花归去马如马去归花赏\n",
" 赏花归去马马去归花赏\n",
" 赏花归去马去归花赏\n",
" 赏花归去去归花赏\n",
" 赏花归去归花赏\n",
" 赏花归归花赏\n",
" 赏花归花赏\n",
" 赏花花赏\n",
" 赏花赏\n",
" 赏赏\n"
]
}
],
"source": [
"def plalindrome(line):\n",
" for i in range( len(line)*2,1,-1):\n",
" if i == 1:\n",
" print(' '*(len(line)*2-1) +line[0])\n",
" elif i%2 == 1:\n",
" print(' '*(len(line)*2-i) + line[:i//2] + line[i//2] + line[i//2-1::-1])\n",
" else:\n",
" print(' '*(len(line)*2-i) + line[:i//2] + line[i//2-1::-1])\n",
"\n",
"def main():\n",
" text = '赏花归去马如飞'\n",
" plalindrome(text)\n",
"\n",
"main()"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
kootsoop/DSP.SE | Python/Twitter Posting.ipynb | 1 | 9025 | {
"cells": [
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"First pic found : /Users/kootsoop/Pictures/COVID-19-FORECAST-7-20-20.png\n",
"Second pic found : /Users/kootsoop/Pictures/COVID-19-FORECAST-HISTORY-7-20-20.png\n"
]
},
{
"data": {
"text/plain": [
"{'created_at': 'Tue Jul 21 15:42:22 +0000 2020',\n",
" 'id': 1285601015933407232,\n",
" 'id_str': '1285601015933407232',\n",
" 'text': '7-20-20: Forecast date for 200k deaths in the USA. #tracking200k https://t.co/adTbuy5kco',\n",
" 'truncated': False,\n",
" 'entities': {'hashtags': [{'text': 'tracking200k', 'indices': [51, 64]}],\n",
" 'symbols': [],\n",
" 'user_mentions': [],\n",
" 'urls': [],\n",
" 'media': [{'id': 1285601005380435968,\n",
" 'id_str': '1285601005380435968',\n",
" 'indices': [65, 88],\n",
" 'media_url': 'http://pbs.twimg.com/media/EddfTZCWAAA0ZTB.png',\n",
" 'media_url_https': 'https://pbs.twimg.com/media/EddfTZCWAAA0ZTB.png',\n",
" 'url': 'https://t.co/adTbuy5kco',\n",
" 'display_url': 'pic.twitter.com/adTbuy5kco',\n",
" 'expanded_url': 'https://twitter.com/kootsoop/status/1285601015933407232/photo/1',\n",
" 'type': 'photo',\n",
" 'sizes': {'medium': {'w': 1200, 'h': 1200, 'resize': 'fit'},\n",
" 'small': {'w': 680, 'h': 680, 'resize': 'fit'},\n",
" 'thumb': {'w': 150, 'h': 150, 'resize': 'crop'},\n",
" 'large': {'w': 1440, 'h': 1440, 'resize': 'fit'}}}]},\n",
" 'extended_entities': {'media': [{'id': 1285601005380435968,\n",
" 'id_str': '1285601005380435968',\n",
" 'indices': [65, 88],\n",
" 'media_url': 'http://pbs.twimg.com/media/EddfTZCWAAA0ZTB.png',\n",
" 'media_url_https': 'https://pbs.twimg.com/media/EddfTZCWAAA0ZTB.png',\n",
" 'url': 'https://t.co/adTbuy5kco',\n",
" 'display_url': 'pic.twitter.com/adTbuy5kco',\n",
" 'expanded_url': 'https://twitter.com/kootsoop/status/1285601015933407232/photo/1',\n",
" 'type': 'photo',\n",
" 'sizes': {'medium': {'w': 1200, 'h': 1200, 'resize': 'fit'},\n",
" 'small': {'w': 680, 'h': 680, 'resize': 'fit'},\n",
" 'thumb': {'w': 150, 'h': 150, 'resize': 'crop'},\n",
" 'large': {'w': 1440, 'h': 1440, 'resize': 'fit'}}},\n",
" {'id': 1285601008303902720,\n",
" 'id_str': '1285601008303902720',\n",
" 'indices': [65, 88],\n",
" 'media_url': 'http://pbs.twimg.com/media/EddfTj7WkAAqSfO.png',\n",
" 'media_url_https': 'https://pbs.twimg.com/media/EddfTj7WkAAqSfO.png',\n",
" 'url': 'https://t.co/adTbuy5kco',\n",
" 'display_url': 'pic.twitter.com/adTbuy5kco',\n",
" 'expanded_url': 'https://twitter.com/kootsoop/status/1285601015933407232/photo/1',\n",
" 'type': 'photo',\n",
" 'sizes': {'medium': {'w': 1200, 'h': 1200, 'resize': 'fit'},\n",
" 'small': {'w': 680, 'h': 680, 'resize': 'fit'},\n",
" 'thumb': {'w': 150, 'h': 150, 'resize': 'crop'},\n",
" 'large': {'w': 1440, 'h': 1440, 'resize': 'fit'}}}]},\n",
" 'source': '<a href=\"http://www.kootsoop.com\" rel=\"nofollow\">Pjkr</a>',\n",
" 'in_reply_to_status_id': None,\n",
" 'in_reply_to_status_id_str': None,\n",
" 'in_reply_to_user_id': None,\n",
" 'in_reply_to_user_id_str': None,\n",
" 'in_reply_to_screen_name': None,\n",
" 'user': {'id': 24472612,\n",
" 'id_str': '24472612',\n",
" 'name': 'Peter J. Kootsookos',\n",
" 'screen_name': 'kootsoop',\n",
" 'location': 'CT, USA',\n",
" 'description': 'Need to do FUN STUFF! Oz/Irish/US engineer, currently living in the USA. Married, one dog 🐶, one cat 🙀, two kids, and three passports. He/him.',\n",
" 'url': 'https://t.co/PZLkrwluOI',\n",
" 'entities': {'url': {'urls': [{'url': 'https://t.co/PZLkrwluOI',\n",
" 'expanded_url': 'https://kootsoop.com/',\n",
" 'display_url': 'kootsoop.com',\n",
" 'indices': [0, 23]}]},\n",
" 'description': {'urls': []}},\n",
" 'protected': False,\n",
" 'followers_count': 345,\n",
" 'friends_count': 1321,\n",
" 'listed_count': 28,\n",
" 'created_at': 'Sun Mar 15 02:26:51 +0000 2009',\n",
" 'favourites_count': 29751,\n",
" 'utc_offset': None,\n",
" 'time_zone': None,\n",
" 'geo_enabled': True,\n",
" 'verified': False,\n",
" 'statuses_count': 13924,\n",
" 'lang': None,\n",
" 'contributors_enabled': False,\n",
" 'is_translator': False,\n",
" 'is_translation_enabled': False,\n",
" 'profile_background_color': 'ABB8C2',\n",
" 'profile_background_image_url': 'http://abs.twimg.com/images/themes/theme18/bg.gif',\n",
" 'profile_background_image_url_https': 'https://abs.twimg.com/images/themes/theme18/bg.gif',\n",
" 'profile_background_tile': True,\n",
" 'profile_image_url': 'http://pbs.twimg.com/profile_images/1195087017882849281/Pma0Mbg__normal.jpg',\n",
" 'profile_image_url_https': 'https://pbs.twimg.com/profile_images/1195087017882849281/Pma0Mbg__normal.jpg',\n",
" 'profile_banner_url': 'https://pbs.twimg.com/profile_banners/24472612/1452297426',\n",
" 'profile_link_color': '4A913C',\n",
" 'profile_sidebar_border_color': '000000',\n",
" 'profile_sidebar_fill_color': 'F6F6F6',\n",
" 'profile_text_color': '333333',\n",
" 'profile_use_background_image': True,\n",
" 'has_extended_profile': True,\n",
" 'default_profile': False,\n",
" 'default_profile_image': False,\n",
" 'following': False,\n",
" 'follow_request_sent': False,\n",
" 'notifications': False,\n",
" 'translator_type': 'none'},\n",
" 'geo': None,\n",
" 'coordinates': None,\n",
" 'place': None,\n",
" 'contributors': None,\n",
" 'is_quote_status': False,\n",
" 'retweet_count': 0,\n",
" 'favorite_count': 0,\n",
" 'favorited': False,\n",
" 'retweeted': False,\n",
" 'possibly_sensitive': False,\n",
" 'lang': 'en'}"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import os\n",
"from dotenv import load_dotenv\n",
"from twython import Twython\n",
"from datetime import datetime, timedelta\n",
"import os.path\n",
"from os import path\n",
"\n",
"# Get file names\n",
"date = datetime.now() - timedelta(days = 1) \n",
"date_string = date.strftime('%-m-%-d-%y')\n",
"first_pic = '/Users/kootsoop/Pictures/COVID-19-FORECAST-' + date_string + '.png'\n",
"second_pic = '/Users/kootsoop/Pictures/COVID-19-FORECAST-HISTORY-' + date_string + '.png'\n",
"\n",
"load_dotenv(dotenv_path='/Users/kootsoop/.env')\n",
"\n",
"API_KEY = os.getenv('TWITTER_API_KEY')\n",
"API_SECRET_KEY = os.getenv('TWITTER_API_SECRET_KEY')\n",
"ACCESS_TOKEN=os.getenv('TWITTER_ACCESS_TOKEN')\n",
"ACCESS_TOKEN_SECRET=os.getenv('TWITTER_ACCESS_TOKEN_SECRET')\n",
"\n",
"twitter = Twython(API_KEY, API_SECRET_KEY, ACCESS_TOKEN, ACCESS_TOKEN_SECRET)\n",
"\n",
"image1_ids = ''\n",
"image2_ids = ''\n",
"\n",
"if path.exists(first_pic):\n",
" print('First pic found : ' + first_pic)\n",
" image1_open = open(first_pic, 'rb')\n",
" image1_ids = twitter.upload_media(media=image1_open)\n",
" \n",
"\n",
"if path.exists(second_pic):\n",
" print('Second pic found : ' + second_pic)\n",
" image2_open = open(second_pic, 'rb')\n",
" image2_ids = twitter.upload_media(media=image2_open)\n",
" \n",
"twitter.update_status(status=date_string + ': Forecast date for 200k deaths in the USA. #tracking200k',media_ids=[image1_ids['media_id'], image2_ids['media_id']])\n",
"\n",
"# page_access_token = os.getenv('FACEBOOK_ACCESS_TOKEN')\n",
"# graph = facebook.GraphAPI(page_access_token)\n",
"# graph.put_object(\"me\", \"feed\", message=\"Posting on my wall1!\")\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| mit |
JCardenasRdz/Insights-into-the-I-SPY-clinical-trial | 2-Inferential_Stats.ipynb | 1 | 112483 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h1><center> Inferential statistics on the I-SPY1 Clinical Trial</center></h1>"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/Julio/anaconda/lib/python3.5/site-packages/statsmodels/compat/pandas.py:56: FutureWarning: The pandas.core.datetools module is deprecated and will be removed in a future version. Please use the pandas.tseries module instead.\n",
" from pandas.core import datetools\n"
]
}
],
"source": [
"# import custom modules wrote by julio\n",
"import seaborn as sns\n",
"import pandas as pd\n",
"%matplotlib inline\n",
"#from capstone_01 import clean_data\n",
"from ispy1 import inferential_statistics\n",
"\n",
"# reload modules without restartign the kernel (makes development easier)\n",
"# import importlib\n",
"#importlib.reload(inferential_statistics);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 0. load clean data"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>SUBJECTID</th>\n",
" <th>age</th>\n",
" <th>White</th>\n",
" <th>ER+</th>\n",
" <th>PR+</th>\n",
" <th>HR+</th>\n",
" <th>Bilateral</th>\n",
" <th>Right_Breast</th>\n",
" <th>MRI_LD_Baseline</th>\n",
" <th>MRI_LD_1_3dAC</th>\n",
" <th>MRI_LD_Int_Reg</th>\n",
" <th>MRI_LD_PreSurg</th>\n",
" <th>Alive</th>\n",
" <th>Survival_length</th>\n",
" <th>RFS</th>\n",
" <th>RFS_code</th>\n",
" <th>PCR</th>\n",
" <th>RCB</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1001</td>\n",
" <td>38.73</td>\n",
" <td>Yes</td>\n",
" <td>Yes</td>\n",
" <td>No</td>\n",
" <td>Yes</td>\n",
" <td>No</td>\n",
" <td>No</td>\n",
" <td>88.0</td>\n",
" <td>78.0</td>\n",
" <td>30.0</td>\n",
" <td>14.0</td>\n",
" <td>No</td>\n",
" <td>1264</td>\n",
" <td>751</td>\n",
" <td>1</td>\n",
" <td>No</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1002</td>\n",
" <td>37.79</td>\n",
" <td>Yes</td>\n",
" <td>Yes</td>\n",
" <td>Yes</td>\n",
" <td>Yes</td>\n",
" <td>No</td>\n",
" <td>Yes</td>\n",
" <td>29.0</td>\n",
" <td>26.0</td>\n",
" <td>66.0</td>\n",
" <td>16.0</td>\n",
" <td>No</td>\n",
" <td>1155</td>\n",
" <td>1043</td>\n",
" <td>1</td>\n",
" <td>No</td>\n",
" <td>3.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" SUBJECTID age White ER+ PR+ HR+ Bilateral Right_Breast \\\n",
"0 1001 38.73 Yes Yes No Yes No No \n",
"1 1002 37.79 Yes Yes Yes Yes No Yes \n",
"\n",
" MRI_LD_Baseline MRI_LD_1_3dAC MRI_LD_Int_Reg MRI_LD_PreSurg Alive \\\n",
"0 88.0 78.0 30.0 14.0 No \n",
"1 29.0 26.0 66.0 16.0 No \n",
"\n",
" Survival_length RFS RFS_code PCR RCB \n",
"0 1264 751 1 No 2.0 \n",
"1 1155 1043 1 No 3.0 "
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df = pd.read_csv('./data/I-SPY_1_clean_data.csv')\n",
"df.head(2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 1. Inferential_statistics: Categorical vs Categorical (Chi-2 test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 1. 1 Effect of categorical predictors on Pathological complete response (`PCR`)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>ER+</th>\n",
" <th>Yes</th>\n",
" <th>No</th>\n",
" </tr>\n",
" <tr>\n",
" <th>PCR</th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>Yes</th>\n",
" <td>17.0</td>\n",
" <td>28.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>No</th>\n",
" <td>81.0</td>\n",
" <td>42.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"ER+ Yes No\n",
"PCR \n",
"Yes 17.0 28.0\n",
"No 81.0 42.0"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# example of contingency table\n",
"inferential_statistics.contingency_table('PCR', 'ER+',df)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>p-value</th>\n",
" <th>Relative_Risk</th>\n",
" <th>RR_lb</th>\n",
" <th>RR_ub</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>White</th>\n",
" <td>0.833629</td>\n",
" <td>0.8878</td>\n",
" <td>0.5076</td>\n",
" <td>1.5528</td>\n",
" </tr>\n",
" <tr>\n",
" <th>ER+</th>\n",
" <td>0.001988</td>\n",
" <td>0.4337</td>\n",
" <td>0.2582</td>\n",
" <td>0.7285</td>\n",
" </tr>\n",
" <tr>\n",
" <th>PR+</th>\n",
" <td>0.000198</td>\n",
" <td>0.3219</td>\n",
" <td>0.1707</td>\n",
" <td>0.6069</td>\n",
" </tr>\n",
" <tr>\n",
" <th>HR+</th>\n",
" <td>0.000307</td>\n",
" <td>0.3831</td>\n",
" <td>0.2286</td>\n",
" <td>0.6422</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Right_Breast</th>\n",
" <td>0.851883</td>\n",
" <td>1.0965</td>\n",
" <td>0.6649</td>\n",
" <td>1.8080</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" p-value Relative_Risk RR_lb RR_ub\n",
"White 0.833629 0.8878 0.5076 1.5528\n",
"ER+ 0.001988 0.4337 0.2582 0.7285\n",
"PR+ 0.000198 0.3219 0.1707 0.6069\n",
"HR+ 0.000307 0.3831 0.2286 0.6422\n",
"Right_Breast 0.851883 1.0965 0.6649 1.8080"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Perform chi-2 test on all categorical variables\n",
"predictors = ['White', 'ER+', 'PR+', 'HR+','Right_Breast']\n",
"outcome = 'PCR'\n",
"inferential_statistics.categorical_data(outcome, predictors, df)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h3><center> 1.1.2 Conclusion: Only `ER+` , `PR+`, and `HR+` have an effect on `PCR`</center></h3>\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 1. 2 Effect of categorical predictors on Survival (`Alive`)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>p-value</th>\n",
" <th>Relative_Risk</th>\n",
" <th>RR_lb</th>\n",
" <th>RR_ub</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>White</th>\n",
" <td>0.439359</td>\n",
" <td>1.0935</td>\n",
" <td>0.9032</td>\n",
" <td>1.3239</td>\n",
" </tr>\n",
" <tr>\n",
" <th>ER+</th>\n",
" <td>0.001135</td>\n",
" <td>1.3095</td>\n",
" <td>1.1025</td>\n",
" <td>1.5554</td>\n",
" </tr>\n",
" <tr>\n",
" <th>PR+</th>\n",
" <td>0.162557</td>\n",
" <td>1.1266</td>\n",
" <td>0.9739</td>\n",
" <td>1.3031</td>\n",
" </tr>\n",
" <tr>\n",
" <th>HR+</th>\n",
" <td>0.038917</td>\n",
" <td>1.1950</td>\n",
" <td>1.0094</td>\n",
" <td>1.4148</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Right_Breast</th>\n",
" <td>0.729139</td>\n",
" <td>0.9602</td>\n",
" <td>0.8287</td>\n",
" <td>1.1125</td>\n",
" </tr>\n",
" <tr>\n",
" <th>PCR</th>\n",
" <td>0.070860</td>\n",
" <td>1.1796</td>\n",
" <td>1.0333</td>\n",
" <td>1.3467</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" p-value Relative_Risk RR_lb RR_ub\n",
"White 0.439359 1.0935 0.9032 1.3239\n",
"ER+ 0.001135 1.3095 1.1025 1.5554\n",
"PR+ 0.162557 1.1266 0.9739 1.3031\n",
"HR+ 0.038917 1.1950 1.0094 1.4148\n",
"Right_Breast 0.729139 0.9602 0.8287 1.1125\n",
"PCR 0.070860 1.1796 1.0333 1.3467"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"predictors = ['White', 'ER+', 'PR+', 'HR+','Right_Breast','PCR']\n",
"outcome = 'Alive'\n",
"inferential_statistics.categorical_data(outcome, predictors, df)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h3><center> 1.2.2 Conclusion: Only `ER+` and `HR+` have an effect on `Alive`</center></h3>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 2. Inferential_statistics: Continous vs Categorical (ANOVA)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.1 Effect of Age on PCR "
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"---------------------------------------------\n",
" sum_sq df F PR(>F)\n",
"age 0.256505 1.0 1.302539 0.255394\n",
"Residual 32.689923 166.0 NaN NaN\n",
"---------------------------------------------\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAEFCAYAAAAPCDf9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAD69JREFUeJzt3X+QXWV9x/H3ZjdrEmcT02GZiloaRb/TZip0cHSqhey0\nIRIq0k6r7fSH8sNWMmk7IB0rktGp03QYEdJBB5HgELGdsUKLBUpoqjUY+sMOtkiD4UuVjDOtjrPS\nZLN1FzfZ3f5xbiC/dlkwz57Nfd6vmQz33HPPfb7JHD73meec5zk909PTSJLqsKjtAiRJ88fQl6SK\nGPqSVBFDX5IqYuhLUkX62i5gNsPDo95aJEkv0ODgQM9M++zpS1JFivX0I+JS4NLO5hLgHODngT8H\npoHdwMbMnCpVgyTpaMV6+pm5LTOHMnMI+Brwh8CHgE2ZeR7QA1xSqn1J0vGKD+9ExBuA1Zl5G3Au\n8FBn13Zgben2JUnPmY8LuR8E/qTzuiczD1+cHQVWzHbgypXL6OvrLVmbJFWlaOhHxMuAyMwvd946\ncvx+ANg/2/H79o2VKk3SArJ377cAWLXqNS1X0h0GBwdm3Fd6eOd84EtHbP9HRAx1Xq8HdhVuX9Ip\nYOfOL7Jz5xfbLqMKpYd3AnjqiO1rgK0R0Q/sAe4u3L6kBW7v3m/x7W/vffa1vf2yehby0spOzpK6\n3x13fOrZ0D/zzFVcdtl7W67o1OfkLEkSYOhLatnQ0NoTvlYZC3rtHUndb9Wq13Dmmauefa2yDH1J\nrbOHP38MfUmts4c/fxzTl6SKGPqSVBGHd+bBjh0P8Pjjj7VawzPPjAOwZMnSVusAWL369axbd1Hb\nZUhVsqdfiYmJCSYmJtouQ1LLnJFbiS1brgfg6qs/0HIlkkpzRq4kCTD0Jakqhr4kVcTQl6SKGPqS\nVBHv05cqthDmkMDCmUdSwxwSe/qSWuc8kvljT1+q2Lp1Fy2Inq3zSOaPPX1JqoihL0kVMfQlqSKG\nviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqIoS9JFTH0Jakihr4kVcTQl6SKGPqSVBFDX5IqYuhL\nUkUMfUmqiKEvSRUx9CWpIoa+JFXE0JekivSV/PKIuBZ4O9AP3AI8BGwDpoHdwMbMnCpZgyTpOcV6\n+hExBLwZeAuwBngVcBOwKTPPA3qAS0q1L0k6XsnhnbcC/wncA9wH3A+cS9PbB9gOrC3YviTpGCWH\nd04DzgTeBqwC7gUWZeZ0Z/8osGK2L1i5chl9fb0FS6xHb2/z+z44ONByJdLxPD/nT8nQfxp4IjMn\ngIyIZ2iGeA4bAPbP9gX79o0VLK8uk5PNpZPh4dGWK5GO5/l5cs3241lyeOdh4MKI6ImIM4CXAl/q\njPUDrAd2FWxfknSMYj39zLw/Is4H/o3mx2UjsBfYGhH9wB7g7lLtS5KOV/SWzcx8/wneXlOyTUnS\nzJycJUkVMfQlqSKGviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqIoS9JFTH0Jakihr4kVcTQl6SK\nGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUp+uSstn3605/kwIGRtstYEA7/O2zZcn3LlSwMy5ev4Ior\nNrRdhjTvujr0DxwYYeTACIuXLW27lNb19PUCMHZoouVK2ndwbLztEqTWdHXoAyxetpR4x8Vtl6EF\nJO+6r+0SpNY4pi9JFTH0Jakihr4kVcTQl6SKGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUx9CWpIoa+\nJFXE0JekinT9gmvSQuXS389x6e+jlVz629CXWnLgwAijoyOsWOHS3/39zdLfixa59PfISNmlvw19\nqUUrVizluusubLsMLSCbNz/I1FS573dMX5IqYuhLUkUMfUmqiKEvSRUpeiE3Iv4dONDZ3AtsBrYB\n08BuYGNmFrxkIUk6UrHQj4glQE9mDh3x3r3ApszcGRG3ApcA95SqQZJ0tJI9/bOBZRGxo9POB4Fz\ngYc6+7cD6zD0JWnelAz9MeBjwO3Aa2lCviczpzv7R4EVs33BypXL6OvrfdEF9PYugkMv+nB1sd7e\nRQwODrRew/T0839O9Sl5fpYM/SeBb3ZC/smIeJqmp3/YALB/ti/Yt2/sRypgctLLBTqxyckphodH\nW69hkbdS6AR+1PNzth+Mkqfc5cCNABFxBrAc2BERQ53964FdBduXJB2jZE//08C2iHiY5m6dy4Hv\nA1sjoh/YA9xdsH3Gx8c5eHCCvOu+ks3oFHNwbJzxxZNtlyG1Yk6hHxErgY8CrwHeAdwAXJOZ+2Y6\nJjMngN88wa41L6JOSdJJMNee/lZgB/BGmguw3wX+AvilQnWdFEuXLmV6cS/xjovbLkULSN51H0v7\n+tsuQ2rFXMf0V2XmbcBUZk5k5nXAKwvWJUkqYK6hfygiVtCMzRMRrwW8NUaSTjFzHd75MLAT+ImI\n+ALwczQXZiVJp5A5hX5mPhgRjwBvAnqB92bm94pWJkk66eZ6986Hjnnr7IgYB/Zk5t+d/LIkSSXM\ndUz/LJrJVPs7f9bS3Hr5uxHx0UK1SZJOsrmGfgBDmXlzZt4MXACclpm/DLy1WHWSpJNqrqG/kqOH\ngl5Cs3bOC/kOSVLL5nr3zieARyLifpoLueuBmyPiKuCxUsVJkk6uuYb+bcDLaO7T3w98Eng58Fng\nljKlSZJOtrmG/l8Dy2gu6O4Czgf+JTP/q1RhUrcbHx/n0KEJNm9+sO1StICMjIzT11duQcAXciH3\nF2iecvVRmjV4XlGqKElSGXPt6X8vM6cj4gng9Zl5Z0S8pGRhUrdbunQpixb1ct11F7ZdihaQzZsf\nZGqq3IKAcw39xyPi4zRj+X/ZeSjK4mJVSZKKmOvwzgbg85n5DZp1eF7OidfKlyQtYHNde2eSzqMN\nM/Ne4N6SRUmSynBilSRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqIoS9JFTH0Jakihr4kVcTQl6SK\nzHXBtVPWwbFx8q772i6jdZMTEwD09pdbve9UcXBsHJb776A6dXXoL1++ou0SFowDY+MALFtm2LG8\n33ND1erq0L/iig1tl7BgbNlyPQBXX/2BliuR1CbH9CWpIoa+JFXE0Jekihj6klQRQ1+SKmLoS1JF\nDH1JqkhX36cvLXQjI+Ns3vxg22W0bmysmTHu5MHmnBgYKPfvYOhLLTk8K3hqquVCFoCJiWbG+JIl\nhv7AQNkZ40VDPyJOB74GXAAcArYB08BuYGNmerqrWs4Yf44zxudPsTH9iFgMfAoY77x1E7ApM88D\neoBLSrUtSTqxkj39jwG3Atd2ts8FHuq83g6sA+6Z7QtWrlxGX19vsQJr0tvb/L4PDg60XIl0PM/P\n+VMk9CPiUmA4M/8+Ig6Hfk9mTndejwLPO2i1b99YifKqNDnZjKQND4+2XIl0PM/Pk2u2H89SPf3L\ngemIWAucA9wJnH7E/gFgf6G2JUkzKDKmn5nnZ+aazBwCHgXeBWyPiKHOR9YDu0q0LUma2XzesnkN\nsDUi+oE9wN3z2LYkiXkI/U5v/7A1pduTJM3MZRgkqSKGviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9\nSaqIoS9JFTH0Jakihr4kVcTQl6SKGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUx9CWpIoa+JFXE0Jek\nihj6klQRQ1+SKmLoS1JFDH1JqoihL0kVMfQlqSKGviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqI\noS9JFTH0Jakihr4kVcTQl6SKGPqSVJG+tguQ1J4dOx7g8ccfa7sMDhwYAWDLlutbrWP16tezbt1F\nrdZQmqEvqXX9/f1tl1ANQ1+q2Lp1F3V9z1ZHKxb6EdELbAUCmAauBJ4BtnW2dwMbM3OqVA2SpKOV\nvJB7MUBmvgXYBGwGbgI2ZeZ5QA9wScH2JUnHKNbTz8wvRMT9nc0zgf3AWuChznvbgXXAPTN9x8qV\ny+jr6y1VYlV6e5vf98HBgZYrkdSmomP6mXkoIj4D/Arwa8AFmTnd2T0KrJjt+H37xkqWV5XJyWYU\nbXh4tOVKJJU2W+eu+H36mflu4HU04/tLj9g1QNP7lyTNk2KhHxG/ExHXdjbHgCngkYgY6ry3HthV\nqn1J0vFKDu/8DXBHRHwFWAxcBewBtkZEf+f13QXblyQdo+SF3B8A7zzBrjWl2pQkzc61dySpIoa+\nJFXE0Jekihj6klQRQ1+SKmLoS1JFDH1JqoihL0kVMfQlqSI909PTz/+plgwPjy7c4l6AhfAc0sPP\nIF2+fNaFTedFDc8hldo0ODjQM9M+H5dYCZ9BKgns6UtS15mtp++YviRVxNCXpIoY+pJUEUNfkipi\n6EtSRQx9SaqIoS9JFTH0JakiC3pyliTp5LKnL0kVMfQlqSKGviRVxNCXpIoY+pJUEUNfkipi6EtS\nRQz9LhQRQxExEhGvOuK96yPi0hbLUuUi4u6IuPaI7YGIyIg4u826amPod68fAndExIxP0JHm2ZXA\nlRHx053tG4DbMvPrLdZUHZ+R273+keZHfSPwicNvRsQ1wG8Ah4CvZOYft1OeapOZ34+I3wduj4gP\nAq8GNkTEzwA3Az3A08DlQD/wVzTn8BLgysx8tJ3Ku4s9/e62Abg6Is7qbA8A7wTe3Pnz2oh4W1vF\nqT6ZeR/wBHAHcFlmTgNbgY2ZOQQ8ALwfeCPND8B6mo7LS1spuAsZ+l0sM58GrgI+w3M9pn/NzIOd\n/9l2AatbLFF1uhP4amb+T2f7p4BbImInTS//FcB24J+AvwU+Aky1UGdXMvS7XKdnlcClwDPAmyKi\nrzPWfz7wZIvlSdCcn+/q9PTfD9wPDAHfzcx1wJ8Cf9ZadV3GMf06XAX8IjAKfJ6mB7UIeBj4Qot1\nSdAMQ94ZEX3ANHAFzdDO5yJiA01OfaTF+rqKSytLUkUc3pGkihj6klQRQ1+SKmLoS1JFDH1Jqoi3\nbEpHiIifpJm78A2a2wf7ge/QzB7974h4F/AHwGKaTtPtmXlz59idwCuB/+t83XLgKeC3MvN78/jX\nkGZkT1863ncy85zM/NnMXA08Anw8In6PZs7D2zPzHJrJbb8dEVcccex7OseeA5wFHADeN99/AWkm\nhr70/L4CvA7YBLwvM78LkJn7gXcDu2c47qXAacD/zkeR0lw4vCPNIiIWA78OfBW4rPPfZ2XmnmMO\nuT0ifgCcThP2nwO2zEOp0pzY05eOd0ZEPBoRjwKP0Sz5+0edfc/3fIL3ZObZwK8CPwY8kJkT5UqV\nXhh7+tLxvtMZkz9KRDwFvIFmuOfwe2uA9Zn5gSM/m5n/HBE306wpc3ZmHipdtDQX9vSlubsBuDEi\nfhwgIk4DbgS+OcPnb6IZ179yfsqTnp+hL81RZt4KfBb4h4j4OvBlYFtm3j7D538IXAd8OCJWzF+l\n0sxcZVOSKmJPX5IqYuhLUkUMfUmqiKEvSRUx9CWpIoa+JFXE0Jekivw/yvWROKWcJ5AAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x113ce0898>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"predictor= ['age']\n",
"outcome = 'PCR'\n",
"anova_table, OLS = inferential_statistics.linear_models(df, outcome, predictor);\n",
"sns.boxplot(x= outcome, y=predictor[0], data=df, palette=\"Set3\");"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.2 Effect of Age on Survival "
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"---------------------------------------------\n",
" sum_sq df F PR(>F)\n",
"age 0.062227 1.0 0.399719 0.528104\n",
"Residual 25.842534 166.0 NaN NaN\n",
"---------------------------------------------\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAEFCAYAAAAPCDf9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAD2pJREFUeJzt3X+MZXV5x/H37J2d7q6dXScyJCKW2opPWioYMZJqgUmL\nq0tB2iimbarlR6jQNS2EhIoQmtpuQ9CwDTWIrISV0h/KKhYoS0moILZVi5UiFB5stf3DGjOS3dmp\nM3R2Z6d/nLtl9scMA8x3zuV+369kknvOmXvOw+7dz334nnO+Z2Bubg5JUh1WtV2AJGnlGPqSVBFD\nX5IqYuhLUkUMfUmqyGDbBSxmfHzSS4sk6QUaHR0eWGibnb4kVaRYpx8R5wHndRfXAG8CfgH4U2AO\neBzYnJn7S9UgSTpYsU4/M7dn5lhmjgHfAH4XuAa4OjNPBQaAc0odX5J0uOLDOxHxFuCEzLwZOBl4\nqLtpJ3BG6eNLkp6zEidyPwL8Yff1QGYeODk7CWxY7I0jI+sYHOyUrE2SqlI09CPilUBk5pe6q+aP\n3w8Duxd7/65dU6VKk6S+NTo6vOC20sM7pwEPzFv+ZkSMdV9vAh4ufHxJ0jylh3cC+M685cuBbREx\nBDwJ7Ch8fEnSPAO9PLWyN2dJZd1//7088cRjbZfBs89OA7BmzdpW6zjhhBPZuPHMVmtYDt6cJamn\nzczMMDMz03YZVbDTl9S6rVuvBeCyyz7cciX9wU5fkgQY+pJUFUNfkipi6EtSRQx9SaqIoS9JFTH0\nJakihr4kVcTQl6SKGPqSVBFDX5IqYuhLUkUMfUmqyEo8I7d6vTBnea/MVw79M2e59HJkp18J5yuX\nBHb6K2LjxjNb72ydr1wS2OlLUlUMfUmqiKEvSRUx9CWpIoa+JFXE0Jekihj6klQRQ1+SKmLoS1JF\nDH1JqoihL0kVMfQlqSKGviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqIoS9JFTH0Jakihr4kVWSw\n5M4j4krg3cAQcCPwELAdmAMeBzZn5v6SNUiSnlOs04+IMeBtwNuB04HXAtcDV2fmqcAAcE6p40uS\nDldyeOedwLeAO4G7gXuAk2m6fYCdwBkFjy9JOkTJ4Z2jgOOAs4DXAXcBqzJzrrt9Etiw2A5GRtYx\nONgpWGI9Op3m+310dLjlSqTD+flcOSVD/xngqcycATIinqUZ4jlgGNi92A527ZoqWF5dZmebUyfj\n45MtVyIdzs/n8lrsy7Pk8M5XgHdFxEBEHAO8AnigO9YPsAl4uODxJUmHKNbpZ+Y9EXEa8HWaL5fN\nwHeBbRExBDwJ7Ch1fEnS4YpespmZVxxh9ekljylJWpg3Z0lSRQx9SaqIoS9JFTH0Jakihr4kVcTQ\nl6SKGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUx9CWpIoa+JFXE0Jekihj6klQRQ1+SKmLoS1JFDH1J\nqoihL0kVMfQlqSKGviRVxNCXpIoY+pJUkcG2Cyjplls+yZ49E22X0RMO/Dls3Xpty5X0hvXrN3Dh\nhZe0XYa04vo69PfsmWBizwSr161tu5TWDQx2AJjaN9NyJe3bOzXddgmATcl8NiUHK9mU9HXoA6xe\nt5Y49+y2y1APyTvubrsEoAm6yckJNmywKRkaapqSVatsSiYmyjYlfR/6Ui/bsGEtV131rrbLUA/Z\nsuU+9u8vt39P5EpSRQx9SaqIoS9JFTH0Jakihr4kVcTQl6SKGPqSVBFDX5IqYuhLUkUMfUmqiKEv\nSRUx9CWpIkUnXIuIfwH2dBe/C2wBtgNzwOPA5swsOLWQJGm+YqEfEWuAgcwcm7fuLuDqzHwwIm4C\nzgHuLFWDJOlgJTv9k4B1EXF/9zgfAU4GHupu3wlsxNCXpBVTMvSngI8DnwaOpwn5gcyc626fBDYs\ntoORkXUMdp/49GJ0Oqtg34t+u/pYp7OK0dHh1muYm3v+31N9Sn4+S4b+08C/d0P+6Yh4hqbTP2AY\n2L3YDnbtmnpJBczOerpARzY7u5/x8cnWa1jlpRQ6gpf6+VzsC6Nk6F8AvBH4nYg4BlgP3B8RY5n5\nILAJ+FLB40s9bXp6mn37Ztiy5b62S1EPmZiYZnBwttj+S4b+LcD2iPgKzdU6FwA/BLZFxBDwJLCj\n4PElSYdYUuhHxAhwHfDTwLnAx4DLM3PXQu/JzBngN46w6fQXUafUd9auXcuqVR2fkauDNM/IHSq2\n/6WOKG4D/hl4Fc0J2O8Dt5cqSpJUxlJD/3WZeTOwPzNnMvMq4NiCdUmSClhq6O+LiA00Y/NExPGA\nl8ZI0svMUk/k/gHwIPATEfFF4OdpTsxKkl5GlhT6mXlfRDwCnAJ0gA9m5g+KViZJWnZLvXrnmkNW\nnRQR08CTmfm3y1+WJKmEpY7pv57mZqrd3Z8zaC69vCgiritUmyRpmS019AMYy8wbMvMG4B3AUZn5\nK8A7i1UnSVpWSw39EQ4eCvoxmrlzXsg+JEktW+rVO58AHomIe2hO5G4CboiIS4HHShUnSVpeSw39\nm4FX0lynvxv4JPBq4M+BG8uUJklabksN/c8D62hO6D4MnAb8U2Z+u1RhkqTl90JO5P4izVOurgPe\nCrymVFGSpDKWGvo/6D4M5SngxMz8b5qTuZKkl5GlDu88ERF/RjOW/xfdh6KsLlfW8pienmbv3hny\njrvbLkU9ZO/UNNOryz2kQuplS+30LwE+l5n/RjMPz6s58lz5kqQettS5d2ZpTuCSmXcBd5Usarms\nXbuWudUd4tyz2y5FPSTvuJu1g+UeUiH1Mm+skqSKGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUx9CWp\nIoa+JFXE0Jekihj6klQRQ1+SKmLoS1JFDH1JqoihL0kVMfQlqSKGviRVZKmPS5RUwMTENFu23Nd2\nGa2bmpoBYN06H24zMTHN8HC5PwdDX2rJ+vUbANi/v+VCesDMzDQAa9YY+sPDQ///2SjB0JdacuGF\nl7RdQs/YuvVaAC677MMtV9L/HNOXpIoY+pJUEUNfkipSdEw/Io4GvgG8A9gHbAfmgMeBzZnpKSxJ\nWkHFOv2IWA18CpjurroeuDozTwUGgHNKHVuSdGQlO/2PAzcBV3aXTwYe6r7eCWwE7lxsByMj6xgc\n7LzoAjqdVc3/X0iH6HRWMTo63HYZ6up0mv7Tv5PyioR+RJwHjGfm30XEgdAfyMy57utJ4HkvRN21\na+ol1TE76+iRjmx2dj/j45Ntl6GuA/9W/TtZHot9eZbq9C8A5iLiDOBNwG3A0fO2DwO7Cx1bkrSA\nImP6mXlaZp6emWPAo8AHgJ0RMdb9lU3AwyWOLUla2ErekXs5sC0ihoAngR0reGxJEisQ+t1u/4DT\nSx/vUHunpsk77l7pw/ac2ZlmQqvOkHOb7J2ahvX+OahOfT33TslJi15u9kw1V846iyGwvuyEVlIv\n6+vQd0Kr5zihlSRwGgZJqoqhL0kVMfQlqSKGviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqIoS9J\nFTH0Jakihr4kVcTQl6SKGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUx9CWpIoa+JFXE0Jekihj6klQR\nQ1+SKmLoS1JFDH1JqoihL0kVMfQlqSKGviRVxNCXpIoY+pJUEUNfkipi6EtSRQx9SaqIoS9JFTH0\nJakihr4kVcTQl6SKDJbacUR0gG1AAHPAxcCzwPbu8uPA5szcX6oGSdLBSnb6ZwNk5tuBq4EtwPXA\n1Zl5KjAAnFPw+JKkQxTr9DPzixFxT3fxOGA3cAbwUHfdTmAjcOdC+xgZWcfgYKdUiVXpdJrv99HR\n4ZYrkQ7n53PlFAt9gMzcFxGfAX4VeC/wjsyc626eBDYs9v5du6ZKlleV2dlmFG18fLLlSqTD+flc\nXot9eRY/kZuZvwW8gWZ8f+28TcM03b8kaYUUC/2IeH9EXNldnAL2A49ExFh33Sbg4VLHlyQdruTw\nzheAWyPiy8Bq4FLgSWBbRAx1X+8oeHxJ0iFKnsj9EfC+I2w6vdQxe9X999/LE0881moNe/ZMALB1\n67Wt1gFwwgknsnHjmW2XIVWp6Ilc9Y6hoaG2S5DUAwz9FbBx45l2tpJ6gtMwSFJFDH1JqoihL0kV\nMfQlqSKGviRVxNCXpIoY+pJUkYG5ubnn/62WjI9P9m5xUh/ohbvF4bk7xtevX3Ti3eL65W7x0dHh\ngYW2eXOWpNZ5x/jKsdOXpD6zWKfvmL4kVcTQl6SKGPqSVBFDX5IqYuhLUkUMfUmqiKEvSRUx9CWp\nIj19c5YkaXnZ6UtSRQx9SaqIoS9JFTH0Jakihr4kVcTQl6SKGPqSVBFDvw9FxFhETETEa+etuzYi\nzmuxLFUuInZExJXzlocjIiPipDbrqo2h37/+F7g1IhZ8go60wi4GLo6In+0ufwy4OTP/tcWaquMz\ncvvX39N8qW8GPnFgZURcDvwasA/4cmb+fjvlqTaZ+cOI+BDw6Yj4CPBTwCUR8UbgBmAAeAa4ABgC\nPkvzGV4DXJyZj7ZTeX+x0+9vlwCXRcTru8vDwPuAt3V/jo+Is9oqTvXJzLuBp4BbgfMzcw7YBmzO\nzDHgXuAK4K00XwCbaBqXV7RScB8y9PtYZj4DXAp8huc6pq9m5t7uP7aHgRNaLFF1ug34WmZ+r7v8\nM8CNEfEgTZf/GmAn8A/A3wAfBfa3UGdfMvT7XLezSuA84FnglIgY7I71nwY83WJ5EjSfzw90O/0r\ngHuAMeD7mbkR+GPgT1qrrs84pl+HS4FfAiaBz9F0UKuArwBfbLEuCZphyNsiYhCYAy6kGdr564i4\nhCanPtpifX3FqZUlqSIO70hSRQx9SaqIoS9JFTH0Jakihr4kVcRLNqUjiIifA74FvDczP99d9580\n14+fCLwlM69pqz7pxTL0pSM7H9hBM0nY5+dvyMy7gLvaKEp6qbxOXzpE9yah7wGnAv8InJKZ/zGv\n0z/w8wXgtzPzrO77PgS8AbiMZgbJMaADbM/MrSv4nyAtyDF96XC/DPxXZj5Nc8fyBxf4vZ3AmyNi\npLv868DtwEUAmflmmonDzomIU8uWLC2NoS8d7nzgr7qvPwucFxFDh/5SZu6l6fbfExHHAa/KzK8D\nZwDvjohHga8BxwJvXJHKpefhmL40T0QcDZwJvCUifo9mjvcR4D0LvOV24I+6v/OX3XUd4IrM/EJ3\nn0cBPypZt7RUdvrSwX4TeCAzj83Mn8zM44AtLDDEk5lfBY4B3k/zBQDNA2wuiojVEfHjNBPbnVK+\ndOn5GfrSwc4Hbjxk3Y00Y/NrFnjPZ4H/yczvdJdvAr4NfBN4BLg1Mx9c/lKlF86rdySpInb6klQR\nQ1+SKmLoS1JFDH1JqoihL0kVMfQlqSKGviRV5P8Ac/d4YyGeJ8sAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1142b6ef0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"predictor= ['age']\n",
"outcome = 'Alive'\n",
"anova_table, OLS = inferential_statistics.linear_models(df, outcome, predictor);\n",
"sns.boxplot(x= outcome, y=predictor[0], data=df, palette=\"Set3\");"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.3 Explore interactions between age, survival, and PCR"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAETCAYAAADah9Z7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH0JJREFUeJzt3XucVXW5x/HPzB5GZmQYKDC7SVj6lKQQcKT0IHTUOWJ5\nKbWLXQTRBC1PCCkISpEoZUqhogZ4wdPVCyaKCFYYUmqmhiA+llInk+MhwxlsBoe5nD9+a2AY5ibM\nmjXM7/t+vXgxe++193r22nt/17N/67Lz6uvrERGROORnXYCIiHQehb6ISEQU+iIiEVHoi4hERKEv\nIhIRhb6ISEQKsi4gBmb2F+B0d3+ylWlKgSXu/h+dUM+/AePdfYKZDQemuvvpKc+zHujv7v94C/fZ\nUWd6lcXFzCYAfdx9zh7cdzRwvbt/uMML231e1wP/cPdvNrl+LPADYCNQD+QB/wKmuPvvkmneDcwG\nhgF1wDbgSnf/RXL7KmAAUJ48bA7YD7jC3Ren+by6AoV+19EXOLKT5jUIeA9AsiJKNfD3wo46pWO4\n+01Z19ABVrv7JxsumNlJwD1m9l7C5+i3wAxgnLvXm9lgYKWZVbr7yuRu33D3uxo9xnBgjZktcfet\nnfdUOp9Cv5OZ2TZgDnA88C7gB+7+feBWoMjMniF0KIcSOpq3EzqRee5+S9Jt/YDQ3exPWFF8F/go\nUELofM5x9zVm1gu4DjgaqAHuBW4EZgGlZnYrcDtJ95Z827gBGELooh4ELnX3mpbqNrMDgcVAv+Qp\nPuDul7Xw9Gcn3Xs+MMPd70+WyXjg/OT614CvJs+vcZ1DCB/Uh83sc8BtQF93rzKzBcDTwELgO8Co\nZJk9DVzo7hVJ93c9cBDQA/ipu19pZu8DfgksA0YAbwOmu/vPmnntLgVOBXomy36Kuy8xs2LgpuQ1\neB14DsDdx7Y03xaWT8N8ehHeD4cQOtU/AOcBx9Co027ceZvZN4GPAe8E1gEjgU81fLs0s58CjwDv\nILxW9wHXuPvhye19CN3zwYT3y6VAIXAAcHsrr2lz9X+U8J7cL6lnpbuPb21Zm1lvwus3GNhEeL8+\n2s5Z/hI4EOhDeB896u53NNzo7n80s9MIr01LDia8595s7/PcV2lMv/PtR/jaejShw55jZj2BcUCV\nuw8hBPddhGGXYYQQm5J8mAA+DHze3QcDQwkh/DF3P4wQ4lOT6WYRAupDhNA8Gng/cDmhWxrXpLZ5\nhNA9HBhO+ABOaaPuc4GX3H0oIWgOSVYezWmY7ovA7WbW38xGAWcBI939I4SwuMfd/9akziXACcnj\nnABsAUaaWT7wCeCe5HnXAMOSZfMKYUUFcAdwS7I8jwSOM7PPJLcdDDzk7kcClyQ17MLMBgDHAaPc\n/QhgerJ8AS4jNFAfTKb5SKO7tjbflnwKKEneC//WqMa2DACGuvuZwC3A2KT2voSV9Y8bTbsS6JV0\nuACfBx4gBONk4Cx3H05YkU0zs360338Bl7v7COAw4GQzG9boeTS3rL8FVBGW4RmAtWdGZpYHfAVY\nlwwdDgfWNJ3O3Ve7+7ONrrrazJ4xs7+Y2auEZX6su1e/hee5T1LoZ+MXyf9PEcJ0/ya3H0oI51uS\nzv8RoIidYfI3d/8rQDKOOQM4z8y+RwjkXsl0xwGL3L3W3avdfZS7r2qlrjGEzrHe3d8kdK9j2qh7\nOXCamS0jdKNT3b2c5t2U1LyO0A1/jBDYHwB+mzzX7wJvM7O3Nbnvkka1jASuJQTZCOBFd/9f4JPA\nKcDTyWOdChxmZvsTVpzfTq5/jNB5D0kebzuh+2x4bk3nTbK8zwK+YGZzgAnsXM4nEpZznbtXEFa8\ntGO+LXkUGJSMPU8Fvu/uf27jPgCPuXtN8vctwGfMrJAQ6Esbvy7uXg8sIlkxEJqOhcn1JwHDzGwm\nYTnnsft7tDVnAX2Sb0bzgWJ2LquWlvVxwOLkvbeZ8Hq3ZGQS2E8D6wnfgE5Lbqujfbn2jUYr1f8B\nNrv70+16dvs4hX42qmDHBw/Ch6qxHPC6uw9p+EfouG5Nbn+jYUIz+wShQ4MQyjc1erwawjBNw7Tv\nNbO3t1JX0/dDPmFIosW63f33wEDgh8D7gCfM7KgWHr+20d95hADIAXc0ep5DCd3alsZ3TLq0QjM7\nGfgzsBQoA04G7k4mywH/1eixjiSsBHPJ/I5qsjwbhlmq3b0u+bth4+AuzGwoYay4N7CCMIzUeDk3\nvk/D82xrvs1y942EFeFVyfweNrPTm6mtsMldd7wvkpXUU4QV4ThgQTOzupWwYhhC2Li7KllRPU14\nHZ4CvkF4nXZbJq1YTVgRPk/4NvRyo/u3tKybPrcaWrY6WZ4fcffD3P3T7v5CcttjhGW8CzM7z8wu\nanp9soL5LHCOmZ3Rvqe3b1Podx01QC75uurANjP7IoSwJozTDmvmfscTurgbgd8TuttcctvDwFlm\nlm9m+xGGjEYl8+rRzGM9BFxgZnnJ9F8hDAO0KOl6L3P3ewlf69cTvqk0Z2xyn6GE8erHCQH6eTN7\nZzLNBMIYbcMyaVznEkLYrnD354FS4AvsDP2HgK+aWWEy7LMAuCrpvh8DLkrm34cwBHBKa8+tiWOA\nJ939WsI3r8bL+QFgXLKci4Ezgfo9na+ZTSQE8gp3vyR5Xh8GNgMHmdkByfvk1DZqXkAYQil29+aG\nPP5OeA1uJoynQ3hdehO2uSwlvF/2a/RcW5UMJQ0HLnH3e4B3E1Zgbd1/OTA+WYZ9eWuvTWM3A6PN\n7AvJMiIZWpoFPNvcHdz9JcLePnOTlV63ptDvOjYROqsNhA2ypxC6j7WEYLysuQ8uobMflUz3O+BF\nYGASet8CqoE/Erq3ZckH8XfAB82s6VfoCwkb7p5N/jnhw9Ca7wNDzGwd8CRhY+BPWpj24OQr+ULg\nc+7+T3d/iBDkK5PncCbw6eTbRNM6lxDGfBtWRCuBTcn4P8C3gb8kz/U5Quc4ObntTOCjZvYsIeh+\n4u4/auO5NfYToJ+ZPUfYsPoGYRiqhNCRbyMss4eB/wMq25qvmS1MdqFsajEhJJ8zsycJIfwDd3+O\nEGpPElYmm9qo+T7Ct69FrUyzgDBseHtyeS1wP/C8mT1F+Cb1HCG4dzCz4cmQ1S7cfQtheTyV1D6N\nsKL7QNNpm/gm4RvF84Rvcc0GdFvc/Z/AaMJwz7pkud9A2PW3tQbme4TXrN0brPdVeTq1ssjeSfYm\nqnD3ZcnK9m5Cl35jG/c7Hviwu8/tjDo7mpk94O6fyLoOeWvU6YvsvXXA9KTzXUfYa2hh63cBwu64\nrXXhXVayK+r8rOuQt06dvohIRNTpi4hERKEvIhKRLn0ahs2bt2rsSUTkLerfv6TF4yrU6YuIRCS1\nTt/CKVDHJhd7Eg49/3fCft31hL0cLmh0dJ6IiKQstU7f3W9z99HuPppwMMuFhBNozXD3kYQDZ/b0\nqDsREdkDqQ/vJGfxG+TuPyScRuCR5KYHCSdZEhGRTtIZG3IvJZwOAMIJuho2zm4lnDulRX37FlNQ\n0K5TfoiISDukGvrJCabM3X+dXNV4/L6E1n/UgC1bKlu7WUSkw2zc+CIAAwe+P+NK9l7//iUt3pb2\n8M4x7DxjIoTznI9O/h5DOAWriEjmVq16mFWrHs66jNSlPbxjwEuNLk8GFiQ/7LCBcKpfEZFMbdz4\nIn/968Ydf3eHbr8lXfrcOzo4S0Q6w6233rwj9AcMGMi4cedlXNHe0cFZIiICKPRFRBg9+rhm/+6O\nuvS5d0REOsPAge9nwICBO/7uzhT6IiJ0/w6/gUJfRITu3+E30Ji+iEhEFPoiIhHR8I6024oVy1i/\nfu1ePca2bVUA9OxZtMePMWjQEZSVnbhXdYjESp2+dKrq6mqqq6uzLkMkWjoiVzrV3LlzAJg0aWrG\nlYh0XzoiV0REAIW+iEhUFPoiIhFR6IuIREShLyISEe2nL7IP29tjJ3TcRHzU6YtETMdNxEedvsg+\nrKzsxL3qsnXcRHzU6YuIREShLyISEYW+iEhEFPoiIhHRhlwR6Ra0+2r7qNMXESGe3VfV6YtIt6Dd\nV9tHnb6ISETU6bdBPxEoaVm06EYqKsozraFh/g1dblZ69y5l/PiJmdYQC4V+J2gYJ9yb0Jfup6Ki\nnPKKcnoUZ/e+yCvIAVBZk91Y9vbKqszmHSOFfhv2dpwQ4hkrlLeuR3ERdsZJWZeRKb9zadYlREVj\n+iIiEVHoi4hERKEvIhIRhb6ISEQU+iIiEVHoi4hERKEvIhIRhb6ISEQU+iIiEVHoi4hEJNXTMJjZ\nNOBkoBCYDzwC3AbUA+uAC9y9Ls0aRERkp9Q6fTMbDRwFHA2MAt4LXAvMcPeRQB5wSlrzFxGR3aU5\nvPOfwLPAEmApcD8wjNDtAzwIHJfi/EVEpIk0h3f6AQOATwIDgfuAfHevT27fCpS29gB9+xZTkJz6\ndV+Wy4V1a//+JRlXkj0ti51yuXyoybqKriGXy8/8PRHLezPN0H8NeN7dqwE3s22EIZ4GJcDrrT3A\nli2VKZbXeWprw2aLzZu3ZlxJ9rQsdmpYFhKWRdbvie703mxtxZXm8M6jwAlmlmdm7wL2B36ZjPUD\njAFWpzh/ERFpIrVO393vN7NjgCcIK5cLgI3AAjMrBDYAd6U1fxER2V2qu2y6+8XNXD0qzXmKiEjL\ndHCWiEhEFPoiIhFR6IuIREShLyISEYW+iEhEFPoiIhFJdZdNEWlZVVUV27dX43cuzbqUTG2vrKKq\nR23WZURDnb6ISETU6YtkpKioiPoeOeyMk7IuJVN+51KKCgqzLiMaCv2ILFp0IxUV5ZnW0DD/uXPn\nZFZD796ljB8/MbP5i2RJoR+Riopytm4tp7S0KLMaCgvDqbLz86szmX95eVUm8xXpKhT6kSktLWL6\n9BOyLiMzs2cvp05nNJaIaUOuiEhEFPoiIhFR6IuIREShLyISEYW+iEhEFPoiIhFR6IuIREShLyIS\nEYW+iEhEFPoiIhFR6IuIREShLyISEYW+iEhEFPoiIhFR6IuIREShLyISEYW+iEhEFPoiIhFR6IuI\nREShLyISEf0wukiGtldW4XcuzWz+tdXVAOQKCzOrYXtlFfTObv6xUeiLZKR379KsS6CisgqA4uIM\nQ7d3YZdYFrFQ6ItkZPz4iVmXwNy5cwCYNGlqxpVIZ+n2ob9o0Y1UVJRnWkPD/Bs+YFlQJyUiEEHo\nV1SUU15RTo/iosxqyCvIAVBZU53J/LcnX+FFuio1Zzv17l2a6rfAbh/6AD2Ki7AzTsq6jMxkuaFQ\npD0qKsrZurWc0tLsmrPCwtCc5edn05wBlJen36BFEfoi0vWVlhYxffoJWZeRqdmzl1NXl+48Ug19\nM3sKqEgubgRmA7cB9cA64AJ3T/kpiohIg9RC38x6AnnuPrrRdfcBM9x9lZndBJwCLEmrBhER2VWa\nnf5goNjMViTzuRQYBjyS3P4gUIZCv9NUVVVRU1PN7NnLsy4lM+XlVRQU1GZdhkhm0gz9SuB7wELg\nEELI57l7fXL7VqDV/Qj79i2mINnzZU/lcvlQs1cP0S3kcvnk5+dlXUaXkJ+fR//+JVmX0SXkcuFM\nLFkvj1wun/r6tqeLQS6Xn+rrkWbovwD8OQn5F8zsNUKn36AEeL21B9iypXKvi6it1SYDCMthv/16\nUlSUH/XGsrChrJDNm7dmXUqHWLFiGevXr93j+zfspnjppdP3+DEGDTqCsrIT9/j+EN6f+ToTGBCW\nxd6+P1tbaaS5mM8GrgEws3cBvYEVZjY6uX0MsDrF+YtIGwoLCynM8Lw70vnS7PQXAbeZ2aOEvXXO\nBv4BLDCzQmADcFeK8xfp9srKTtzrLlvi0q7QN7O+wHeB9wNnAFcDk919S0v3cfdq4Mxmbhq1B3WK\niEgHaO/wzgLg98DbCRtgNwH/nVZRIiKSjvaG/kB3/yFQ5+7V7j4deE+KdYmISAraG/o1ZlZKGJvH\nzA4BtFuMiMg+pr0bcmcCq4CDzOxe4GOEDbMiIrIPaVfou/tyM3sSGAHkgPPc/dVUKxMRkQ7X3r13\nLm9y1WAzqwI2uPsDHV+WiIikob1j+h8gHEz1evLvOMKul+ea2XdTqk1ERDpYe0PfgNHuPs/d5wHH\nA/3c/VTgP1OrTkREOlR7Q78vuw4F7Uc4d85beQwREclYe/feuR540szuJ2zIHQPMM7OvA3t+ticR\nEelU7Q39HwJ9CPvpvw7cCLwTuAOYn05pIiLS0dob+ncDxYQNuquBY4Dfufuf0ipMREQ63lvZkPsf\nhF+5+i5wJPDutIoSEZF0tDf0X01+DOV54Ah3f4WwMVdERPYh7R3eWW9m1xHG8n+U/ChKj/TKEhGR\nNLS3058I/NzdnyOch+edNH+ufBER6cLae+6dWpKfNnT3+4D70ixKRETSoQOrREQikuZv5IqItEtV\nVRU1NdXMnr0861IyVV5eRUFBbarzUKcvIhIRdfoikrmioiLy83NMn35C1qVkavbs5dTVFaY6j24f\n+lVVVWzfXo3fuTTrUjKzvbKKqh61FBUVZV2KiGRMwzsiIhHp9p1+UVER9T1y2BknZV1KZvzOpRQV\nhK+M5eVVmW4sq6ysBqC4ON2vsC0pL6+ipCSbeYt0Bd0+9GWn3r1LAairy66G6uoqAHr2zCZ4S0oK\ndywHkRgp9CMyfvzErEtg7tw5AEyaNDXjSkTipDF9EZGIKPRFRCKi0BcRiYhCX0QkIgp9EZGIKPRF\nRCKi0BcRiYhCX0QkIgp9EZGIKPRFRCKi0BcRiYhCX0QkIgp9EZGIpHqWTTM7APgDcDxQA9wG1APr\ngAvcPcOT/IqIxCe1Tt/MegA3A1XJVdcCM9x9JJAHnJLWvEVEpHlpdvrfA24CpiWXhwGPJH8/CJQB\nS1p7gL59iykoyO1VEblcfviOEblcLp/+/UuyLiO8HtAlapGuI5fLp74+6yq6hrQ/q6mEvpmNBTa7\n+0Nm1hD6ee7e8LJuBdr8+aItWyr3upbaWo0gQVgOmzdvzbqMHa9HV6hFuo7a2jrytYUR6JjPamsr\njbQ6/bOBejM7DhgCLAYOaHR7CfB6SvMWEZEWpBL67n5Mw99mtgqYAFxtZqPdfRUwBvh1GvMWkX1T\neXkVs2cvz2z+lZXVABQXZ/P7zRCWQUlJuvPvzN/InQwsMLNCYANwVyfOW0S6sIYfq6/LcDS2ujrs\nc9KzZ3ahX1JSuGNZpCX10Hf30Y0ujkp7fiKy7xk/fmLWJTB37hwAJk2amnEl6erMTj8z2yur8DuX\nZjb/2urwtTFXmE0Hsb2yCnpn172ISNfR7UM/7a9K7VFRGb42ZjZW2Dv9r4wism/o9qGvr40iIjtp\nz1gRkYgo9EVEIqLQFxGJiEJfRCQiCn0RkYgo9EVEIqLQFxGJiEJfRCQiCn0RkYgo9EVEIqLQFxGJ\niEJfRCQiCn0RkYgo9EVEIqLQFxGJiEJfRCQiCn0RkYgo9EVEIqLQFxGJiEJfpBVXXTWLSy6ZBMCm\nTa9w0UVfA+Db3748y7JE9li3/2F0kT21bds2Xn75b/To0YNXX/3fXW677LJZGVUlsnfU6Yu04JFH\nfsXQocM59tgyHnjgvl1uO/PM03jhheeZOXMaADU1NZx99heoq6vjjjtuY+LEs5kw4WyeeOKxLEoX\naZFCX6QFy5c/QFnZGD7+8eNYuXI5dXV1u9x+6KEfZNOmTVRWVvL4479jxIij2LjxJdaufZr58xdx\n7bXXM3/+POrr6zN6BiK70/COSDM2b/4/nn9+A3PnXg1AZeW/+P3vd+/aR48+ltWrV/HYY79l3Lhz\n+NOf/sRf/rKRr33tPACqq9+kvLycPn36dGr9Ii1R6Is046GHlvHlL5/N5z//RQDWrFnNgw8u3W26\nsrIxzJkzi+3bazjooPexbds2Djvsw3zrW1dSU1PD7bcvoqSkpLPLF2mRhndEmrFixYMce+zxOy6P\nGPEx1q9fR03N9l2m69evH/X1cMwxo4Ew5DNw4MGcf/45nHvulyktLSWXy3Vm6SKtUqcv0ozFi3+2\ny+WCggKWLFm24/KPf3z3jr+vuWbeLtOOHXsOY8eek26BIntInb6ISEQU+iIiEVHoi4hERKEvIhIR\nhb6ISES09450azfePI+tb2ztsMcr6VXCxPMu7LDHE+lsCn3p1ra+sZWDTzuxwx7vpbuXtTnNU089\nybRpk1m8+Ge84x0HAnDjjdcxYMD7OPHEkzqsFtnVihXLWL9+7R7fv6KiHIC5c+fs8WMMGnQEZWUd\n935Lg4Z3RFLQo0chV145S+fd2YcUFhZSWFiYdRmpU6cvkoJhw4ZTV1fPPff8nNNO++yO63/yk//m\nl79cQS6XY/Dgj3D++Roq6ihlZSd2+S67K0gt9M0sBywADKgHJgDbgNuSy+uAC9y9rqXHENmXTZky\nlXPPPYsRI44CwknbfvWrldx00y3kcjmmT7+YNWtWc/TRIzOuVGKS5vDOSQDufjQwA5gNXAvMcPeR\nQB5wSorzF8lUaWkfLrxwMrNnz6S+vo7q6moGDTqcgoIC8vLyGDx4CBs3vph1mRKZ1Dp9d7/XzO5P\nLg4AXgeOAx5JrnsQKAOWtPQYffsWU1Cw75+sKpcL69b+/XW2xc5eFnn5eR3+eG3V3qdPMfvt14P+\n/Uv41Kc+wRNPPMry5Q9w/vnns2bNI/TtW0Qul2PDhmc59dRT9b6QTpXqmL6715jZ7cCngNOB4929\nYcvWVqC0tftv2VKZZnmdprY2jGBt3txxuw7uqzp7WfQq7tWuPW7aq6RXSZu1v/56JW++uX3HdOed\ndyFr1vyWurocI0d+nNNP/wz19fUcccRgBg8eofeFdLjWGonUN+S6+1lmdgnwOFDU6KYSQvcvkpos\n9qkfOnQ4Q4cO33F5//17cffd9++4/LnPfbHTaxJpkNqYvpl9ycymJRcrgTrgSTMbnVw3Blid1vxF\nRGR3aXb69wC3mtlvgB7A14ENwAIzK0z+vivF+YuISBNpbsj9F/CZZm4aldY807C3R/lBPEf6iUjX\np4OzOkEMR/mJyL5Bod8GHeUnIt2JQl+6tYUL5/FGB55ls1evEs45R6dOkH2XQl+6tTfe2MqMGcd3\n2ONdccXKNqeZMeNizD7El740DginXxg//kvMmjWHQw45tMNqEdkTOsumSAebMuVS7r33bjZufAmA\nG274ASef/GkFvnQJ6vRFOlifPn2YNOlivvOdK/jKV87nlVf+zpQp03jxxT/z/e9fTX19PaWlpUyb\nNpPt27czc+Y06urCuXm+8Y1pHHKIZf0UpBtT6Iuk4N///Rh+85tfc9VVs5g/fyF5eXl85ztXMG3a\n5QwceDD3338vP/rR7Rx++GB69y7lssu+xcaNG6mqqsq6dOnmFPoiKTnhhE/w5pvb6N//AAD++teN\nXHNNOFajtraG97znID760aN4+eX/YerUyRQUFHDWWeOzLFkioNAX6SQHHTSAGTNmceCBB7J27TO8\n9to/ePrpP/D2t/dj7twbWLduLTfffAPXXXdz1qVKN6bQl3bbF49O7tWrpF173LRXr157fhrkyZOn\nccUVl1NbW0teXh5Tp15GaWkpM2deypIld1FbW8u4ced2WK0izcnryr/huXnz1q5bXIQ6IvS3bQtj\n1j17FrUxZct0SgqR1vXvX9LiD0ko9EVEupnWQl/76YuIREShLyISEYW+iEhEFPoiIhFR6IuIRESh\nLyISEYW+iEhEFPoiIhHp0gdniYhIx1KnLyISEYW+iEhEFPoiIhFR6IuIREShLyISEYW+iEhEFPoi\nIhFR6HdDZjbazMrN7L2NrptjZmMzLEsiZ2Z3mdm0RpdLzMzNbHCWdcVGod99vQncamYt/oKOSCeb\nAEwws8OSy1cDP3T3P2ZYU3T0w+jd168IK/ULgOsbrjSzycDngBrgN+5+STblSWzc/R9m9lVgoZld\nChwMTDSzw4F5QB7wGnA2UAj8jPAe7glMcPdnsqm8e1Gn371NBCaZ2QeSyyXAZ4Cjkn+HmNknsypO\n4uPuS4HngVuBce5eDywALnD30cAy4GLgSMIKYAyhcdk/k4K7IYV+N+burwFfB25nZ8f0mLtvTz5s\nq4FBGZYocVoMPO7uf08ufwiYb2arCF3+u4EHgTXAL4BZQF0GdXZLCv1uLumsHBgLbANGmFlBMtZ/\nDPBChuWJQHh/fjnp9C8G7gdGA5vcvQy4Argys+q6GY3px+HrwLHAVuDnhA4qH3gUuDfDukQgDEMu\nNrMCoB4YTxja+amZTSTk1KwM6+tWdGplEZGIaHhHRCQiCn0RkYgo9EVEIqLQFxGJiEJfRCQi2mVT\npBEzex/h2IXnCLsPFgKvEI4efdnMvgx8DehBaJoWuvu85L6rgPcAbyQP1xt4CfiCu7/aiU9DpEXq\n9EV294q7D3H3j7j7IOBJ4Doz+wrhmIeT3X0I4eC2L5rZ+Eb3PSe57xDgA0AFcFFnPwGRlij0Rdr2\nG+BQYAZwkbtvAnD314GzgHUt3G9/oB/wz84oUqQ9NLwj0goz6wF8FngcGJf8v4O7b2hyl4Vm9i/g\nAELY/xSY2wmlirSLOn2R3b3LzJ4xs2eAtYRT/k5Jbmvr9wnOcffBwGnA24Bl7l6dXqkib406fZHd\nvZKMye/CzF4ChhOGexquGwWMcfepjad199+a2TzCOWUGu3tN2kWLtIc6fZH2uxq4xswOBDCzfsA1\nwJ9bmP5awrj+hM4pT6RtCn2RdnL3m4A7gJVm9kfg18Bt7r6whenfBKYDM82stPMqFWmZzrIpIhIR\ndfoiIhFR6IuIREShLyISEYW+iEhEFPoiIhFR6IuIREShLyISkf8H+Wug4GK2vogAAAAASUVORK5C\nYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x114382390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# create a boxplot to visualize this interaction\n",
"ax = sns.boxplot(x= 'PCR', y='age', hue ='Alive',data=df, palette=\"Set3\");\n",
"ax.set_title('Interactions between age, survival, and PCR');"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"---------------------------------------------\n",
" sum_sq df F PR(>F)\n",
"age 0.637369 1.0 3.674443 0.057611\n",
"Residual 20.988648 121.0 NaN NaN\n",
"---------------------------------------------\n"
]
}
],
"source": [
"# create dataframe only for patients with PCR = Yes\n",
"df_by_PCR = df.loc[df.PCR=='No',:]\n",
"df_by_PCR.head()\n",
"\n",
"# Anova age vs Alive\n",
"predictor= ['age']\n",
"outcome = 'Alive'\n",
"anova_table, OLS = inferential_statistics.linear_models(df_by_PCR, outcome, predictor);"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Effect Size</th>\n",
" </tr>\n",
" <tr>\n",
" <th>Predictor of Alive</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>age</th>\n",
" <td>-0.409422</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Effect Size\n",
"Predictor of Alive \n",
"age -0.409422"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# estimate the effect size\n",
"mri_features = ['age']\n",
"outcome = 'Alive'\n",
"# Effect Size\n",
"inferential_statistics.effect_size( df_by_PCR, mri_features, outcome)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Conclusion."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"1. `age` has an important effect on `Alive` for patients with `PCR` = Yes\n",
"2. To quantitify this effect a logistic regression is needed"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.4 Effect of MRI measurements on PCR ANOVA"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmIAAAJZCAYAAAAK61mIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmYXFWZ+PFv0iEkwRCDRhmVgYjyiiiCIOsAUSAsLig6\nyigwCLL9QAQXQNERHFCQJQI6oAmbjAvKooAgESEIuCAoIIivEgOOChogJNFspNO/P+7tUDSd7uqk\nq25V9/fzPHlyt7r3raru0+8599xzRnR1dSFJkqTmG1l1AJIkScOViZgkSVJFTMQkSZIqYiImSZJU\nERMxSZKkipiISZIkVWRU1QGo9UREFzApM5+o4LoPACdk5g099h0MfILiZ/Zm4JjMfKaXc3wMOBhY\nDswFDs/M2RGxAXAR8FKgAzgzMy8rX/Ne4NPlKZ4oX/OHmnO+EPgJcHBm3l1uexVwATAJGA1clJln\nl/s+DBwNLAYeAo7KzKciogM4B9ijfB9nZeaFvbzPd2Xm28v1m4A3AZ/PzLMG8nlKw1Gbl1+9HhcR\n44AZwJYUDSgnZOb3erz2c8B6mXl0uT4SOB14K7AC+ANF2TY3IsYCZwI7AusA0zPzzPJ1rwfOByYA\nneVr7ulxrauBv3Zfq2b7ZOAeYGpm3m35VR9bxNRq3txLIfY64BRgZyCAFwLH9XxhROwGHAJsn5lv\nAK4GLil3fwW4ody+K3B+RLwiIl4KXAi8NTM3L1/z5Zpz7g3cBbymx+UuBa7IzC2A7YHDI+ItEfFm\n4ARg13LfDcDXytccDrwaeB1F4XRsRGxTXme9iLiQogAc0X2RzNwDuLaeD05S5dak/OrruJOBf2Tm\npsDuwP9ExCvK170iIq4EPt7jlAcDWwFvzMzXAw8DZ5f7zgDWA7amKIuOiojtyoRvJvDFzNwS+G/g\nGz3iPB7YqZf4xwD/S1ExBSy/6mWLWBuKiCkUtZm/AK+kaHk5KDMf6nHcBOD/gE0y8/Fy288pftln\nUyQnLwBeBtwLvC8zl9S8/iDgPZn5tp7rETGa4pd5F4oWpl9T1N4W9IjhRGC/Xt7Grpn5ZJ1veR/g\n2sycW57zq8B5wBd7HPc4cGRNDHdTJEUA7+TZBOdfKVrMFmfmkxHx0rLWOQrYEKiN6xjgP4Fv9bjW\nRcAVAJk5PyIeLl/7IuDmzPxzedzVwIzy83oX8LXMXA7Mi4hvA/tTJHrvBR6jKEzfWufnIrUdy69V\nll99Hfcu4P0AmfmniJhJUWacQ1H5vJ2i9X1izfkeBD6RmUvL9bspEq4RwAHAmzKzE5hfViDnAVOB\n2TXJ5LXAnJrP483AnhSV19prQfF9XAqcVOfnopItYu3rjcDZZSvOJcDlPQ/IzPnANRR/7ImITYF/\nAW4CDgUuy8ztgVcBkxlYAnAiRTKzVdnK9FeKZvCeMZyemVv08q/eQgxgA4oCudufgVf0cq0HMvM2\ngIhYu4znu+W+FZnZGRGzgJ8BM7pjKJOwrcvzHkbRKtV9zj0z82e9XOuSzFxUXmtPYAfghxRJ1Vsi\nYsPy0A9S1BBf1Nf7yMwLM/MUij9K0lBn+TWw4/oqO07JzHMpbiPWxv6zzPwVQERMBP6LojycBIwH\ndouIWRFxL/COzHwa2AR4PCIuioi7gR9RNthExMuAc4EP9LxWRHwIWCszp/f/cagnW8Ta132ZeXu5\nfDHwlYh4US8FxHSKvkxnUSQFl2Tmiog4Adi9bGbehKJW+YIBXP9tFE3nu0cEFMnG33seNEg1yt4q\nDJ29bOu+5iTgSmA+8KnafZk5pdz/o4h4KDMvKbffDaxfJlU/iIhXlgVTnyLiPyma+9+TmY8Bj0XE\nKcA1EbGC4rt5Clg20PchDWGWXwM7brXLjojYGPgecAdFq9XLKFoBNwbeQpGYzYqIR4G1gL0pbrH+\nIiL2AW4oK5bfBo7NzMfKz6z7/G8EjqC4parVYCLWvpbXLI8o/3WWtZtuH8rMOyJiVNkX6f0ULTdQ\n3GobBXwH+AHF7boRPFdXj22ja5Y7gI9k5o0AEfECYEzPIDPzdHqpaQ7Qnyhqwt1eTlEjfJ6I2Jyi\nOf0a4ONl0zsR8R7gpsxcWHZW/R7wxrIz6esz86Yy3h9GxAKKQuqe3q5Rnm8ExR+H9wC7Zea95fbx\nwG2ZeVG5/lKKfhZPDeR9SEOc5dfAjuve93jNvtrPqlflrcQrKPp8nVVumws8A1yemSuAv0XE9RR9\nXX8H/C4zfwGQmd+PiBkULZiTgXPKJGx9oKPsF/YPYF3gp+W+lwHfiIhPZKb9w+pgIta+toiIzTPz\nforbaXeWLThb9HLsDIrbbfdn5p/KbXsAu2TmfRHxWmBbyj5PNeYCryt/2ZYDb6/ZdxNwdET8uNw3\nneIX8tDBeXvPcS3w/Yg4rYzpMIoa3nNE8STjrRT9Ii7usftIiprz58u+J/sAn6MofK+IiK0z8+Gy\n4BpF0d+iL+dSFFxbd/fpKL0M+HFEvLbsb/IZ4FuZ2RUR3wcOjojrKGrv+1HUJKXhxvJrYMd9v1w/\nsuykvydwal8XjYgdKCqk+2XmD7u3Z+aysgw6EPh4mYTuXp7vDuDsiNgqM++JiJ0pEtpfZ+YGNec+\nGXhxPvvU5LE1+x4BPlDeZVAdTMTa1+PAaRGxEUWT+gF9HHsZ8HngP2q2fYri9tlTwCLgNoq+FrVm\nltt/R9GR/FZg83Lff1O0CP2aonZ5L/Cx1X87q5aZ90fxaPYtFE3nv6DoaEtEvAM4IjP3puiYPw44\nJiKOKV++NDO3BQ4CvhoR95fbp2fmNeU5DgGuiuLx86eBt3f3/+pNFENhHA08SnGLs3vXuZl5SUSc\nDvwiisfH7yiPheIWy8bAfRS1869292mThhnLL55bfvV1HPBZ4IKIeLCM9xOZObufS59C0SJ4elkm\nAczJzHdRJJznRsRvy/N9MzOvLGN6J8VTmesAS4F9ax+C0OAb0dXVVXUMGqDyqaMvZ+brqo5lMEVF\n4/+0uoi4FHggHYdHQ4Dl1/Bi+dU/n5pUq7k1irG7xMoBXd9RdRyS6mL5VcPyqz62iEmSJFXEFjFJ\nkqSKmIhJkiRVpC2fmpw7d6H3U6VhZtKk8T3HiWpLll/S8NNX+WWLmCRJUkVMxCRJkipiIiZJklQR\nEzFJkqSKmIhJkiRVxERMkiSpIiZiUhuYM2c2c+b0N8ev1Nr8OZaery3HEZOGm1mzbgZg8uSNK45E\nWn3+HEvPZ4uY1OLmzJnNo4/O4dFH59iaoLblz7HUOxMxqcV1tyL0XJbaiT/HUu9MxCRpFSJi24iY\n1WPb+yPiZzXrh0bE3RHx84h4W9ODlNTWTMSkFjdlym69LquxIuJ4YAYwpmbblsAhwIhyfX3gGGBH\nYA/gCxGxdvOjbX3+HEu9s7O+1OImT96YDTecvHJZTTMb2Be4HCAiXgR8HjgWmF4esw1wZ2YuBZZG\nxMPA5sAvV3XSiRPHMWpURyPjbknz5o1bufzCF45j0qTxFUYjtQ4TMakN2ILQfJl5VURsBBARHcBF\nwEeBxTWHrQvMr1lfCEzo67zz5i0a3EDbxPe+d+1zlj/4wcMrjEZqrr4qHiZiUhuwJaxyWwGvBi6g\nuFX52oj4EnALUFvCjgeebn54ktqVfcQkqR+ZeVdmbpaZU4D9gN9m5rHAXcBOETEmIiYAmwIPVBhq\ny7KPmNQ7W8QkaTVl5uMRcR5wO0XF9qTMXFJxWC3Jvo5S70Z0dXVVHcOAzZ27sP2ClrRGJk0aP6Lq\nGAbDcC6/ugdyNRHTcNNX+WWLmCSpKUzApOezj5gkSVJFGtoiFhHbAmdk5pSI+DawfrlrI+Dnmblf\nRJwL/BvFY98A+2Tm/OefTZIkaWhpWCJWjkp9APBPgMzcr9w+EbgVOK48dCtgj8x8olGxSJIktaJG\n3prsHpW6p1OA8zPzsYgYSTE2z9ci4s6IOLiB8UiSJLWUhrWI1Y5K3S0iXgLsyrOtYesA5wPnAB3A\nrRFxd2be39e5h+sUIZIkaWhp9lOT7wG+mZmd5foi4NzMXAQQEbcAbwD6TMSG6xQh0nDm3ISShqJm\nPzW5G3BjzfomwJ0R0RERa1F02v9Vk2OSJEmqRLMTsQD+2L2SmQ8BlwM/B24Dvp6ZDzY5JkmSpEo4\nsr6ktuDI+pLaVV/llwO6SpIkVcRETJIkqSImYpIkSRUxEZMkSaqIiVgbmTNnNnPmzK46DEmSNEia\nPaCr1sCsWTcDMHnyxhVHIkmSBoMtYm1izpzZPProHB59dI6tYpIkDREmYm2iuzWs57IkSWpfJmKS\nJEkVMRFrE1Om7NbrsiRJal921m8TkydvzIYbTl65LEmDZebMG3jwwfsbfp0lSxYDMGbM2IZeZ7PN\nNmfq1L0beg1psJiItRFbwiS1s2XLlgGNT8SkduKk35LagpN+t79p004H4LjjTqw4Eqm5+iq/bBGT\npFWIiG2BMzJzSkRsAZwPdAJLgQMz828RcShwOLAcODUzr68uYkntxs76bcSR9aXmiYjjgRnAmHLT\nucCHM3MKcDVwQkSsDxwD7AjsAXwhItauIFxJbcpErI3MmnWzY4hJzTMb2Ldmfb/MvLdcHgUsAbYB\n7szMpZk5H3gY2Ly5YUpqZ96abBPdI+t3L/vkpNRYmXlVRGxUs/4YQETsABwN7EzRCja/5mULgQl9\nnXfixHGMGtUx6PG2g46Oou4/adL4iiORWoeJWJvoObK+iZjUfBHxPuAk4K2ZOTciFgC1WcV44Om+\nzjFv3qIGRtjaOjtXADB37sKKI5Gaq6/Kh4mYJNUhIvan6JQ/JTOfKjffBZwWEWOAtYFNgQcqClFS\nG7KPWJtwZH2pOhHRAZxH0eJ1dUTMiohTMvPxcvvtwC3ASZm5pMJQJbUZW8TahCPrS82XmY8A25Wr\n663imOnA9GbFJGloMRFrI7aESZI0tJiItRFbwiRJGlrsIyZJklQRW8QGycyZN/Dgg/c39BpLliwG\nmjNh7mabbc7UqXs3/DqSJA1ntoi1kWXLlrFs2bKqw5AkSYOkoS1iPSbM3RK4HvhDufuCzLxiqEyY\nO3Xq3g1vQZo27XQAjjvuxIZeR5IkNUfDErFywtwDgH+Wm7YCzsnMs2uO6Z4wd2uKiXXviIgfZebS\nRsUlSZLUKhrZItY9Ye7l5fpWQETEPhStYsdSM2EusDQiuifM/WUD45IkSWoJDUvEek6YSzEVyIzM\nvCciTgI+C9zLACfMheE7aa4T5kqSNLQ086nJazKzezLca4DzgZ8wwAlzYfhOmuuEuRrOrIBIGoqa\n+dTkTRGxTbm8K3APRSvZThExJiIm4IS5kiRpGGlmi9iRwPkR8QzwOHBYZi6IiO4Jc0fihLmSJGkY\naWgiVjthbmb+Ctixl2OcMFeSJA1LDugqSZJUERMxSZKkipiISZIkVcRETJIkqSImYpIkSRUxEZMk\nSaqIiZgkSVJFTMQkSZIqYiImSZJUERMxSZKkipiISZIkVaSZk35LUluJiG2BMzJzSkS8CrgU6AIe\nAI7KzBURcShwOLAcODUzr68sYEltxxYxSepFRBwPzADGlJvOAT6dmTsBI4B9ImJ94BhgR2AP4AsR\nsXYV8UpqTyZiktS72cC+NetbAbeVyzcCuwHbAHdm5tLMnA88DGze1CgltTVvTUpSLzLzqojYqGbT\niMzsKpcXAhOAdYH5Ncd0b1+liRPHMWpUx2CG2jY6Ooq6/6RJ4yuORGodJmKSVJ8VNcvjgaeBBeVy\nz+2rNG/eosGPrE10dhYf4dy5CyuORGquviof3pqUpPr8OiKmlMt7AbcDdwE7RcSYiJgAbErRkV+S\n6mKLmCTV52PA9IgYDTwEXJmZnRFxHkVSNhI4KTOXVBmkpPZiIiZJq5CZjwDblcu/B3bp5ZjpwPTm\nRiZpqKg7EYuIdYCNgd8A4zLznw2LSpIkNdzMmTfw4IP3N/w6S5YsBmDMmLENvc5mm23O1Kl7N/Qa\ng62uPmIRsStwH/B9YH3gkYiY2sjAJEnS0LBs2TKWLVtWdRgtqd4Wsc8D/wbcmJmPRcQuwLeAmQ2L\nTJIGQUQc2GNTF7AY+F1m2rFew9rUqXs3pQVp2rTTATjuuBMbfq12U+9TkyMz8/Hulcz8bYPikaTB\ntg9wMrBF+e8zwFHAJRFxXIVxSVLdLWJ/joi3AV0R8UKKQuxPjQtLkgbN+sAbM/NpgIg4GbgO2B64\nB5hWXWiShrt6W8QOBz4AbAD8kaJWeVijgpKkQTSJYsT7bouB9TJzOcVtSkmqTF0tYpn5d+A/GhyL\nJDXCVcAtEfEdisrnu4HvlX3HHqs0MknDXl2JWETsAZwKrAeM6N6ema/s53XbAmdk5pSI2AI4H+gE\nlgIHZubfIuJcigcBumus+5ST50rSGsvMT5ZdK3anKH/OyMwbI2I74P3VRidpuKu3j9j5wEcppu6o\nqyk/Io4HDgC6xxs7F/hwZt4bEYcDJ5Tn3ArYIzOfGEjgkjQA8yhGw78U2AYgM39eZUCSBPUnYk9k\n5vUDPPdsYF/g8nJ9v8zsvg0wClgSESOBVwNfi4iXAhdl5sUDvI4krVJEfAR4J/By4DvAVyPiosw8\nq9rIJKn+ROz2iDgH+CGwch61zPzJql6QmVdFxEY1648BRMQOwNHAzsA6FK1t5wAdwK0RcXdm9jnM\n78SJ4xg1qqPO0IeOjo7i2Yq+ZnGX9DwHAdsCv8jMpyLiTRSTdZuISapcvYnYNuX/W9Zs6wLeMpCL\nRcT7gJOAt2bm3IjoAM7NzEXl/luANwB9JmLz5i0ayGWHjM7OFQDMnbuwnyOloWcNKiCdmbksIrrX\nl1D0FZOkytX71OSb1/RCEbE/xTAYUzLzqXLzJsAVEbElxdNM/wZctqbXkqQat0XEWcA6EfFOiqF3\nbqk4JkkC+knEIuJrmXlYRNxKL530M7OuFrGy5es8ikFgry5rprdl5mcj4nLg58AzwNcz88EBvgdJ\n6ssngEMp5ss9ELgBuKDSiCSp1F+L2FfL/09enZNn5iPAduXqeqs45kzgzNU5vyT1JSJeACzNzK9S\nlmcRsTbFU9ufrzI2SYL+R9ZfJyJ2pmgN6+2fJLWkcpicp4C/RcQby23vA35PMVOIJFWuvxaxU/rY\nN+DO+tJQNHPmDTz4YJ/Pl6yxJUsWAzBmzNiGXgdgs802Z+rUvRt+nSY4HngTMBk4MSIWAXsCnwVm\nVBmYJHXrMxEbjE76ktbcsmXLgOYkYkPIPzPzPuC+iJgO/BjYJDMXVByXJK1U7xRHG1LUIDcCdgK+\nCRxc9gGThrWpU/dueAvStGmnA3DccSc29DpDTO0QFfOAAzLzmaqCkaTe9NdHrNtXKTrU/wP4G/At\n4OuNCkqSBkFtP9Z/mIRJakX1Duj64sycGRFnZGYXMD0ijmpkYJK0hl5dDhLdcxmof/gdSWqkehOx\nxRHxCsoaZkT8G7C0YVFJ0pp7W9UBSFJ/6k3EjgOuBzaOiHspxgT794ZFJUlrKDNv6++YiPhVZr6x\nGfFIUm/qneLo7nKi3E0oJud+yP4WkoaAEVUHIGl4q/epyW0o5oH8MkXL2JYRcURmXtXI4CSpwQY0\nMHVErEUxH+5GFE9lHgosBy4tz/UAcFRmrhjUKCUNWfU+NXkecA/wHmARsBXgc/SShpu9gVGZuQPw\nOeA04Bzg05m5E0UL2z4VxiepzdSbiI0s+1u8FbgqM/9E/f3LJGmo+D0wKiJGAusCz1BUTLv7o90I\n7FZRbJLaUL3J1KKI+BiwK3B0RHwEWNi4sCSpKQbaR+wfFLclfwe8mOLJzJ3LYX2gKBcn9HWCiRPH\nMWpUxwAvOzR0dBR1/0mTxlcciZrN737V6k3EPgAcAuybmfMi4mXAfzQuLEkaHBHxn5l5WY9tR2Xm\nV4AvDPB0xwE3ZeYnI2ID4BZgdM3+8cDTfZ1g3rxFA7zk0NHZWXSdmzvXevxwM9y/+74S0HqfmvxL\nRFwHvCAidgZ+COwBXDwoEUrSIIuIYyluHx5RTtPWbS3g/cBXMvM7AzztPIrbkQBPlef6dURMycxZ\nwF7ArWsUuKRhpd6nJi8DdqAYP+whYAvgTkzEJLWuhyn6b43gubcglwAHreY5pwEXR8TtFC1hnwLu\npphtZDRF+Xjl6gYsafip99bkzhRjiJ1P8QTlCIqhLCSpJWXm9cD1EfGdzHxokM75D+C9vezaZTDO\nL2n4qTcR+2tmPhMRDwGbZ+a3I8Ied5Lawb9GxNcpWvRXtoxl5iurC0mSCvUmYn+JiE8CNwNfjAiA\nFzQsKkkaPOcDH6UYbHVAA7hKUqPVm4gdArw1M38ZEVdTPDF5ZOPCkqRB80R5m1KSWk69T00uBL4d\nEetQdtLPzH82NDJJGhy3R8Q5FE97L+nemJk/qS4kSSr0mYhFxMYUU3j8jeIJyZspJv0eFRH/kZk/\naHyIkrRGtin/37JmWxfwlgpikaTn6K9F7GLgaoqRomcB+2fmDyJiK+ASwERMUkvLzDdXHYMkrUp/\nidjEzDwXICI+2N0Clpn3RMSKhkcnSaspIv6rr/2Z+blmxSJJq9JfIra8Znlej30mYpJa2UDnkZSk\npusvERsfETsBI3l2eqNuDl8hqWVl5in9HRMRJ2fmyU0IR5J61V8i9megu/n+L0BtwfaX/k4eEdsC\nZ2TmlIh4FXApRSfZB4CjMnNFRBwKHE7R+naqj5lLaqJ3ACdXHYSk4avPRKyeTq6rqlFGxPHAAUD3\nMBfnAJ/OzFkRcSGwT0T8DDgG2BoYA9wRET/KzKUDexuStFq8fSmpUiMH4RzvWMX22cC+NetbAbeV\nyzcCu1E8Vn5nZi7NzPkUk/RuPggxSVI9HGlfUqXqHVm/L73WKDPzqojYqPa4zOwu9BZSDImxLjC/\n5pju7X2aOHEco0Z1rF60bayjo8ibJ01yms/hxu9ekoamwUjE6q1R1j5lOR54GlhQLvfc3qd58xbV\nHdxQ0tlZfIRz5y6sOBI1m9+9SaikoWkwErF6/ToipmTmLGAv4FbgLuC0iBgDrA1sStGRX5Ka4bdV\nB9Cfiy66gAUL5vd/YBvofh/Tpp1ecSSDY911J3DIIU67rDXTzETsY8D0iBgNPARcmZmdEXEecDtF\nf7WTMnNJXyeRpHpFxGuADwGvARZTJF4XZeafADJz/wrDq8uCBfOZv2A+a40bW3Uoa2xE2aVk0fJl\nFUey5p5ZtLjqEDREDEYitsoaZWY+AmxXLv8e2KWXY6YD0wchDklaKSL2Ai4HrqCYjq2L4mGgX0bE\nezPztr5e30rWGjeW+Pe3Vx2GauR3r6s6BA0R/SZiQ6FGKWlY+hywR2beU7sxIi4FzgJ27u1FktRM\nfQ5fUdYo7wDGUtQofwxMoqhRPq91S5JayJieSRhAZt6FM4NIahH9tYhZo5TUrp6pOgBJ6k9/idgq\na5QRYY1SUivrniu3t7EOLb8ktYT+EjFrlJLaVe1cuT31O1euJDVDf4mYNUpJbameuXIlqWr9JWLW\nKCUNORGxIDPXrToOSeozEbNGKWmI6nWO3HpExCeBdwCjgf8BbgMupRin7AHgqMxcscoTSFKN1R7Q\ntZ1qlENlihCnB5EGTb1z5D5HREwBdgB2BMYBHwfOAT6dmbMi4kJgH+CaQYpT0hC3JiPrr3aNstmG\nyhQhTg8i1S8i/nUVu0aw+uXXHsBvKBKtdYFPAIdStIoB3AhMpY9EbOLEcYwqf5fr0dExEpavZrRq\nqI6OkU5GX6eOjmLYUj+v51uTRGy1apRVcYqQ1uL0IGqC2yjKqd6SridW85wvBjYE3gZMBq4FRmZm\nd3m4EJjQ1wnmzVs0oAt2dnqXs1V1dq5g7tyFVYfRFrp/jofr59VXAtpnItagGqUkNVxmTu7vmIg4\nLDO/NoDTPgn8LjOXARkRS4ANavaPB54eWKSShrP+WsQaUaOUpFZxBDCQROwO4CMRcQ7wL8A6wI8j\nYkpmzgL2Am4d9CglDVn9PTXZiBqlJLWKAbXsZ+b1EbEzcBfFXL1HAXOA6RExGngIuHLQo5Q0ZK1J\nH7FuA61RSlKrGHBf18w8vpfNuwxCLJKGoZGDcA77ikmSJK2GwUjE2urpSUmSpFYxGImYJLUrn3CU\nVKnB6CMmSS2n7FS/Spn5k8x8S7PikaTeDEYiZo1SUis6pY99XYBJmKTK9TegqzVKSW0pM9+8qn0R\nUf8cQ5LUQP21iFmjlNSWImIscCDwZGZeWbN9b+BMYLOqYpOkbv0N6GqNUm3toosuYMGC+VWHsca6\n38O0aadXHMngWHfdCRxyyJGNvsxlFPNCToiIlwDXAdOB7YEzGn1xSapHf7cmrVGqrS1YMJ+FC+cz\nYcLYqkNZI6NHF/WekSOXVRzJmps/f3GzLvUm4NXAesAPgOOBHwIHZObcZgUhSX3p79akNUq1vQkT\nxnLSSXtWHYZKp532Q1asaMqlns7M5cDfI2ID4P9l5tVNubIk1am/RMwapaR2VTvY9N9MwiS1ov4S\nsUGtUUbEQcBB5eoYYAuK1rXrgT+U2y/IzCtW9xqSVBpdllsjgY5yeeWUbJn5p8oik6RSf4nYoNYo\nM/NS4FKAiPgKcDGwFXBOZp69JueWpB7WAW4rl0f0WO4CXllFUJJUq79ErCE1yojYGtgsM4+KiAuK\nTbEPRavYsZm5cHXOK0k1Tu5jn3PkquUNlae+YWg9+T3YT333l4g1qkb5KZ4do+wuYEZm3hMRJwGf\nBT7e14snThzHqFH1j57R0TESlq9mpGqYjo6RTJo0vuHX6PJPbstpxncPXAL8HbgZ6H7ctLsi2QV8\nvdEBDIbFixfzzDPLyO9eV3UoqvHMosUsXquzodcYKk99w9B58rsRT333l4id3Me+1frzFhEvBCIz\nby03XZOZ3dMkXQOc39855s1bNKBrdnY25xEtDUxn5wrmzm1s42dn5wpGOrV9y1md7341Erc3Au8D\ndgfuA64Abs5MCwS1DZ/6bi2NeOq7v0SsETXKnYEf16zfFBEfzsy7gF2Be1bjnJL0HJl5L3Av8Mmy\nO8T7gM9HxN3AtzNzVpXx1Wvs2LF0rdVB/Pvbqw5FNfK71zF21Oiqw9AQ0F8i1ogaZQB/rFk/Ejg/\nIp4BHgc9R/RoAAAgAElEQVQOW4NzS9LzZObdwN0RsRNwOrA/8IJqo5Kk/qc4GvQaZWae2WP9V8CO\nAz3PQNjHovU0o3+FFBEjKFrh/x3Yi6I8O59icGpJqlx/LWIrWaOU1E7KJ7L3BH4NfAc4ITP/WW1U\nkvRc/SZiQ6FGaR+L1mP/CjXB4cCTwJblv89HxMqdmek4YpIq19+k39YoJbWryVUHIEn96a9FzBql\npLaUmY9WHYMk9ae/RMwapSRJUoP099SkNUpJqhERL6EY73B3ijk7LqUYV/EB4CgHjJU0EI45Lkl1\nioi1gK8C3fOcnAN8OjN3ohjsep+qYpPUnuoevkKSxFnAhcAny/WteHYO3huBqRRTta2Sc+UOHY2e\nM9W5clvTYH/vJmKSVIeIOAiYm5k3RUR3IjYiM7v/VC4EJvR3HufKHToaPV+uc+W2psGeK9dETJLq\nczDQFRG7AVtQzLX7kpr944GnqwhMUvsy15akOmTmzpm5S2ZOoRjY+kDgxoiYUh6yF3B7ReFJalO2\niEnS6vsYMD0iRgMPAVdWHI+kNmMiJkkDVLaKddulqjgktT9vTUqSJFXEFjENaYsXL2b58mWcdtoP\nqw5FpfnzFzNqVGfVYUhSS7BFTJIkqSK2iGlIGzt2LCNHdnDSSXtWHYpKp532Q1asGF11GJLUEmwR\nkyRJqoiJmCRJUkVMxCRJkipiIiZJklQREzFJkqSKmIhJkiRVxERMkiSpIiZikiRJFXFAV0mSWpBT\ntLWeRkzR1vRELCJ+BSwoV+cApwGXAl3AA8BRmbmi2XFJkiQ1W1MTsYgYA4zIzCk1264FPp2ZsyLi\nQmAf4JpmxiVJUqtxirbW04gp2prdIvYGYFxEzCyv/SlgK+C2cv+NwFRMxCRJ0jDQ7ERsEXAWMAN4\nNUXiNSIzu8r9C4EJ/Z1k4sRxjBrVUfdFOzpGwvKBB6vG6ugYyaRJ4xt+ja6u/o9TczXjux9Knlm0\nmPzudVWHscY6ly0DoGN0+0/6/syixbBu+78PVa/ZidjvgYfLxOv3EfEkRYtYt/HA0/2dZN68RQO6\naGenXc5aUWfnCubOXdjwa4z02eCWszrf/XBN3NZdt9+6adtYsGgxAOPGDYEEZt3RQ+q7UXWanYgd\nDLwe+H8R8TJgXWBmREzJzFnAXsCtTY5JklrWIYccWXUIg2batNMBOO64EyuORGodzU7ELgIujYg7\nKJ6SPBh4ApgeEaOBh4ArmxyThrj58xe3/ePfixYVt3SGQkvC/PmLGT++/d+HJA2GpiZimbkMeH8v\nu3ZpZhwaPrpvHaxo87vTy5YVt3TGjGn/BGb8eG/pSFK3YTOg61Do7GpH14EbKrd1vKUjSUPTsEjE\nhkrt246ukiQNLcMiEbNVRJIktaJhkYhJ0pqKiLWAi4GNgLWBU4Hf4hRtktaAIyxJUn32B57MzJ2A\nPYEvA+dQTNG2EzCCYoo2SaqbLWKSVJ/v8uzwOiMo5usY8BRtA50ZZCjp6Cjq/sN1cN6BcmaQ1jTY\nM4OYiElSHTLzHwARMZ4iIfs0cNZAp2gb6MwgQ0n3LCeNnlFjqHBmkNY02DOD+BVLUp0iYgOK2T8u\nz8xvArX9weqaok2SapmISVIdIuKlwEzghMy8uNz864iYUi7vBdxeRWyS2pe3JiWpPp8CJgKfiYjP\nlNs+ApznFG2SVpeJmCTVITM/QpF49eQUbZJWm7cmJUmSKmIiJkmSVBETMUmSpIrYR0ySpBY1f/5i\nTjvth1WHscYWLVoGwLhxoyuOZM3Mn7+Y8eMH9z2YiEmS1ILWXbcYH3jFEJi9dNmyxQCMGdPeidj4\n8aNXfi+DxURMkqQWdMghR1YdwqCZNu10AI477sSKI2k99hGTJEmqiImYJElSRUzEJEmSKmIiJkmS\nVBETMUmSpIqYiEmSJFXEREySJKkiJmKSJEkVMRGTJEmqSFNH1o+ItYCLgY2AtYFTgf8Drgf+UB52\nQWZe0cy4JEmSqtDsKY72B57MzAMiYj3gXuBzwDmZeXaTY5EkSapUsxOx7wJXlssjgOXAVkBExD4U\nrWLHZubCJsclSZLUdE1NxDLzHwARMZ4iIfs0xS3KGZl5T0ScBHwW+Hhf55k4cRyjRnU0OtyW09FR\ndOmbNGl8xZGo2fzuJWloanaLGBGxAXAN8D+Z+c2IeGFmPl3uvgY4v79zzJu3qJEhtqzOzhUAzJ1r\ng+Fw43dvEippaGrqU5MR8VJgJnBCZl5cbr4pIrYpl3cF7mlmTJIkSVVpdovYp4CJwGci4jPlto8C\n0yLiGeBx4LAmxyRJklSJZvcR+wjwkV527djMOCRJklqBA7pKkiRVpOmd9YeqmTNv4MEH72/oNRYs\nmA/AtGmnN/Q6AJtttjlTp+7d8OtI7S4iRgL/A7wBWAp8KDMfrjYqSe3CRKyNjB49uuoQ1AuT8GHv\nncCYzNw+IrYDzgb2qTimAWnGzzA07+fYn+H6+d1Xz0RskEydunfbfflqHybhLe3fgB8CZObPI2Lr\nvg5uxXEQx45da+VYdY209tprAzT8WmPHruVwJ3Xyu6/eiK6urqpjGLC5cxe2X9CS1sikSeNHVB1D\nbyJiBnBVZt5Yrv8JeGVmLu/teMsvafjpq/yys74krZkFQG0VfOSqkjBJ6slETJLWzJ3A3gBlH7Hf\nVBuOpHZiHzFJWjPXALtHxE+BEcAHK45HUhsxEZOkNZCZK4Ajqo5DUnvy1qQkSVJFTMQkSZIqYiIm\nSZJUERMxSZKkipiISZIkVaQtR9aXJEkaCmwRkyRJqoiJmCRJUkVMxCRJkipiIiZJklQREzFJkqSK\nmIhJkiRVxERMkiSpIiZiLSwipkTE/IjYoGbb6RFxUIVhqYEi4sqI+GTN+viIyIh4Q5VxSQNl+TX8\nWH6tHhOx1rcUuCQiRlQdiJriCOCIiHhtuX4m8LXMvK/CmKTVZfk1vFh+rYZRVQegft1CkTAfBXy5\ne2NEfAzYD1gO/CQzT6gmPA2mzHwiIo4GZkTEp4BXAkdGxOuB84ARwJPAwcBo4AqKn48xwBGZeW81\nkUu9svwaRiy/Vo8tYu3hSOC4iHhVuT4eeC+wQ/nv1RHxtqqC0+DKzOuA3wGXAB/MzC5gOnBUZk4B\nbgCOB7ahKNT2ovhDt04lAUt9s/waRiy/Bs5ErA1k5pPAscBlPFt7+HlmPlP+kN8ObFZhiBp8Xwd+\nkZl/Kdc3Bf4nImZR1CZfDtwI3Al8H/gcsKKCOKU+WX4NS5ZfA2Ai1ibKWkYCBwFLgG0jYlTZ92Jn\n4PcVhqfGS+DAskZ5PHA9MAV4LDOnAqcCn68sOqkPll/DnuVXH+wj1l6OBXYFFgLfoahNjATuAL5X\nYVxqvCOBr0fEKKALOISiWf/bEXEkxe/y5yqMT+qP5dfwZfnVhxFdXV1VxyBJkjQseWtSkiSpIiZi\nkiRJFTERkyRJqoiJmCRJUkVMxCRJkiri8BWqXERsRDGO0G8pHm0eDfyVYlTmP0fEgcCHgbUoKg8z\nMvO88rWzgFcA/yhPty7wR+ADmfm3Jr4NScOQ5ZfWlC1iahV/zcwtMnPLzNwMuBs4PyIOoxh/6B2Z\nuQXF4I/7R8QhNa/9UPnaLYBXAQuAjzb7DUgatiy/tNpMxNSqfgJsAnwa+GhmPgaQmU8D/wk8sIrX\nrQO8GHiqGUFKUi8sv1Q3b02q5UTEWsD7gF8AHyz/XykzH+rxkhkR8U/gJRQF2LeBaU0IVZKew/JL\nA2WLmFrFyyLi3oi4F7gfGAF8vNw3op/Xfigz3wC8G1gPuCEzlzUuVEl6DssvrTZbxNQq/lr2kXiO\niPgjsDVFU3/3tl2AvTLzxNpjM/OnEXEexZxmb8jM5Y0OWpKw/NIasEVMre5M4OyIWB8gIl4MnA08\nvIrjz6HoZ3FEc8KTpFWy/FK/TMTU0jLzQuBy4EcRcR9wK3BpZs5YxfFLgZOAz0bEhOZFKknPZfml\neozo6uqqOgZJkqRhyRYxSZKkipiISZIkVcRETJIkqSImYpIkSRUxEZMkSaqIiZgkSVJFTMQkSZIq\n4hRHep6I6AImZeYTFVz3AeCEzLyhx76DgU9Q/MzeDByTmc/0co4+j4uI0RTTjVyZmWeV294LfBZY\nDvwZ+H+Z+WjNa15YvubgzLy73DaWYtTsHSlGwp6emWeW+44GjgS6gNnAoZn59x5xXk0xLcrRvcT/\nrsx8e7l+E/Am4PPd8UrDQSuWQ6s4fjJwDzC1u3yo97iIuAp4A/CP8rBbM/O4iOgAPgO8g6J8uQH4\naGZ2RcS2wFfK7X8F9s/Mx8rzvRv4FLA28ChwYGY+GRGbAxeUr+kCPpWZN5av2Z+izOwCFlGUmc95\nH6sqr+oREW8FvlDGdD9wSGYuKPfNBf5Sc/iZwAuB44Almfm6gV6vHdkiplbz5l6SsNcBpwA7A8Gz\nv6isxnFfAjauec2rga8C+5UT754BXFmzf2/gLuA1Pc5zBsUEvVtTJEpHRcR2EbEVxWS/O5SFyB+A\n/+4R5/HATj22rRcRFwLnUzNJcGbuAVzb871KaqjnlUO9iYgxwP8Co1fzuO2BnTNzi/Jfd3n1EWAK\nRUVv8/K495UVySuBj2TmpuXyReU1tga+DLy7LHt+D5xWnu9/gTPL+TAPAL4TEaMjIiiSnz3LfacC\nV/eI/XnlVb0iYhJwSRlTAH8ETi/3BTCv5r1vkZnfyMyvAB9aneu1K1vE2lBETKH45fkL8EpgMXBQ\nZj7U47gJwP8Bm2Tm4+W2n1MkK7MpalUvAF4G3Au8LzOX1Lz+IOA9mfm2nutlgXAGsAvQAfyaoia1\noEcMJwL79fI2ds3MJ+t8y/sA12bm3PKcXwXOA744kOMi4gBgAvCDmte8AbgvM38DkJk/iYiNImKj\nzHwEOAb4T+BbNe9pBEVh9qbM7ATmR8SbKQqVpyPi1Zn5TFn4vhyYU/PaNwN7AhcCE2vieC/wGEUS\n99Y6PxepMsOwHOrNV4BLKaYlGtBxZQvZeODCiNiIorXsY5n5FHAg8PHMXFwe+25gGUWlb0Fm3lme\n5iLgSxHxImB/4KKy3AI4GXhRufxGoLNc3hh4ulxfCnyou0UNuBtYPyJGZ+ayVZVXEbEpcG55/g7g\nvMy8uJf3PRX4ZWb+oVy/ALgvIo4CdgA6I+LW8jxXAqeVZeqwYotY+3ojcHZmbk5R47i85wGZOR+4\nhuIXtPuX51+Am4BDgcsyc3vgVcBkBpYAnEhxK2+rsiXpr5Q1nR4xnN6jxtP9byCF3wYUBXm3PwOv\nGMhxEfF6ilrmYT1e82vgdRGxRXnc2ykKhX8p498zM3/W4zWTKArQ3SJiVkTcC7wjM58uX/NMRLyz\nvP7OFN8PEfEyisLrAzxbKFK+5sLMPIXij5nULoZTOfQcEfEhYK3MnL6ax72EovvE4cCWFLcnu5OZ\nTYDXRsSPI+J+iq4OT9GjjMvMZcBcigrfJsCoiPh+Oa/lV4CF5XHLy1hmU7R4nZGZnZn5SGb+oNw3\ngmLS8WvLJKzX8ioiRlEkTSdm5lYUSfDHI2K7Xt5+b2XyuhTl5yjgRxSJ3s7AHsCH+/oshypbxNrX\nfZl5e7l8MfCViHhRLwXLdIpayFnAB4FLMnNFRJwA7F42O29CURt9wQCu/zaKW3+7Fy3MjAb+3vOg\nQaqJ9lZh6K3W1OtxZY38cuD9mfnPMl4AMnN22S/rwohYG/g+cB9F7XNV1qKoBW4MvIUiMZsVEY9m\n5vfK834P+F5EHArcVP7x+TZwbGY+VhuD1MaGUzlUe743AkdQJBCrdVxm/gJ4V82xJwOPl618awHb\nAXtTvKfrKJKU5723Umf5mrcDu5bHfZHic39neb0uYOOyJe72iPhtZt5SXnsdiha7DYA9I2ItVl1e\nbUJR9l1cs30sRTL58x5xraqxp7NHYro0Is6huAPxpVW8ZsgyEWtfy2uWR5T/OsvWmW4fysw7ImJU\nRGwDvJ+iORiKW22jgO9Q3Kr7V2r6JpW6emyr7d/QQdFPobvD5wuAMT2DzMzT6aWGOkB/omyhKr2c\nomZV73F7UBTW3ywLjn+lKLjXpehD8XBmble+j1HAsdTcTuzFXOAZ4PLMXAH8LSKuB7aPiAeA9TPz\njvLYiyma9bemqO2fU8awPtAREWMyc1j1h9CQMpzKoVoHUrTs/LT8fX4Z8I2I+ERmXlvPccA8YGLN\n8SOAFRRJ1V+Bb2fmUook5bsUydz51JRxZcL0Yorbw38FflNz+/cS4JYysdsX+E5mrsjMORFxM0Xi\ndEtE/CtFovcQRd+4xRGxPasoryhayZ4u+5R1x/FSii4an6N4wACKvq2/B7at+TxeTtGF459lV5H7\nMvP+mvf/vAewhgMTsfa1RURsXv4QHwbcWd4a26KXY2dQ/ALfn5l/KrftAeySmfdFxGspflmu6PG6\nuRS37cZQFLhvr9l3E3B0RPy43Dedomn90MF5e89xLfD9iDitjOkw4Hv1HpeZ36Eo6AGIiEuBBzLz\nrDIZu7P8LP+PonP/HWU/jV6VzfbXUfbjKAv/3Sk6uv4L8K2I2CKLp70+UF7rToraZncMJwMvztV4\nCklqIcOpHFopM4+lqLABEBGPAB/IHk8b9nVcROwFnB8R3eXNJyie5u6MiCuB/csKXgdFy9+PgV8A\nL4qIHTLzp8DBwM/KvqlXAmdFxGllK9++FP2zlkXEqRStU98sbzm+GfhyRKwH3AZcWnaN6I77Z6yi\nvCoTuyURsX9m/m9EbAD8CnhnZv4X8F81r3sJcHYU/Wb/QNE6+P1y9+uAd5f930YDRwPfGMDXMGTY\nR6x9PQ6cFhG/oWh6PqCPYy+jKBhn1Gz7FHBNRNxN0WJzG0UfjVozy+2/A24HflOz77+BRyj6WP2W\nojbzsdV8L30qC/nPAbeUsXRSdNAlIt4RETf0d1wf515AUWjfGBEPUTyddFAdYR0KvDQifkvRyfaa\nzLyyvE1zGsWtynspboe8c0BvWGofw6YcGoiIuDeKpxhXqWzFO4+iIpgUt/u6K2afpvhsHwAepHja\n8EtZDMWzL0UH/QcpKnofLM93HcVtvdvKcmkHnu0T+y7giLJMuh74RJk0HknRCvmuMubuf92d/HuL\nexnFg1EfKvuvzQQ+U/MAQe2xfy/ju7IsX1/Ps9/PKRT93n5DMazFT3nuz8awMaKrq6vqGDRAUTyt\n9OUcYmOsREXjBrW62ha8qmORulkOqVGG6s/WqtgiplZzaxRjd4mVA7q+o98DJQ0my6GKRDG0xbBq\nGbNFTJIkqSK2iEmSJFXEREySJKkibTl8xdy5C72fKg0zkyaN7zm+VFuy/JKGn77KL1vEJEmSKtLQ\nFrGI2JZiTqsp5cBu0ykmDu0ADiynlzmUYq6t5cCpmXl9I2OSJElqFQ1rESvnDpvBs9NNfBH4Rmbu\nTDFY3WsiYn2KuaV2pBhh+QvlfH+SJElDXiNvTc6mGAG4247AK8o5rj4AzAK2oZgSY2lmzgceBjZv\nYEySJEkto2G3JjPzqojYqGbTRhSTfe4WEf8FnEAxIej8mmMWAhP6O/fEieMYNapjEKOVJElqvmY+\nNfkkxaTMUMz0fhpwNzC+5pjxwNP9nWjevEWDHpyk1jZp0vj+D5KkNtPMpybvALqnjNiZYiLTu4Cd\nImJMREwANqWY5FS9mDNnNnPmzK46DElaLZZh0vM1s0XsY8CMiDiS4nbk+zNzXkScB9xOkRSelJlL\nmhhTW5k162YAJk/euOJIJGngLMOk52toIpaZjwDblcuPArv3csx0imEt1Ic5c2bz6KNzVi5bkElq\nJ5ZhUu8c0LVNdNckey5LUjuwDJN6ZyImSZJUEROxNjFlym69LktSO7AMk3rXlpN+D0eTJ2/MhhtO\nXrksSe3EMkzqnYlYG7EWKamdWYZJz2ci1kasRUpqZ5Zh0vPZR0ySJKkiJmKSJEkVMRGTJEmqiH3E\nJGkVImJb4IzMnBIRWwDnA53AUuDAzPxbRBwKHA4sB07NzOuri1hSu7FFTJJ6ERHHAzOAMeWmc4EP\nZ+YU4GrghIhYHzgG2BHYA/hCRKxdQbiS2pSJmCT1bjawb836fpl5b7k8ClgCbAPcmZlLM3M+8DCw\neXPDlNTOvDXZRubMmQ34CLjUDJl5VURsVLP+GEBE7AAcDexM0Qo2v+ZlC4EJfZ134sRxjBrVMejx\nSmpPJmJtpHuiXBMxqRoR8T7gJOCtmTk3IhYA42sOGQ883dc55s1b1MAIJbWiSZPGr3KfiVibmDNn\nNo8+OmflssnY8GJraPUiYn+KTvlTMvOpcvNdwGkRMQZYG9gUeKCiECW1IROxNtHdGta97B/k4cXW\n0GpFRAdwHvAn4OqIALgtMz8bEecBt1P0uT0pM5dUF6mkdmMiJrU4W0Ork5mPANuVq+ut4pjpwPRm\nxSRpaDERGyQzZ97Agw/e37DzL1/+zMrlJ574O9Omnd6wawFsttnmTJ26d0OvofrYGipJQ5fDV7SJ\nUaPW6nVZktrFnDmzV/Z3lFSwRWyQTJ26d8NbkM48878BOO64Ext6HbWWKVN247LLpq9cltqVfR2l\n5zMRayO2hA1PkydvzIYbTl65LLUj+zpKvTMRk9qALWFqd/Z1lHpnIia1Af9oSdLQ1NDO+hGxbUTM\n6rHt/RHxs5r1QyPi7oj4eUS8rZHxSJKqUduqawuv9KyGtYhFxPHAAcA/a7ZtCRwCjCjX1weOAbYG\nxgB3RMSPMnNpo+KSJDWffR2l3jXy1uRsYF/gcoCIeBHweeBYnh38cBvgzjLxWhoRDwObA7/s68TD\nddLcjo6iAbOvOaskqVW95jWvrToEqeU0LBHLzKsiYiNYOT3IRcBHgcU1h60LzK9ZXwhM6O/cw3XS\n3M7OFQDMnbuw4kik5rMC0v5+97vfArD99jtVHInUOprVWX8r4NXABRS3IF8bEV8CbgFqS9fxwNNN\nikmS1CQOXyH1rimJWGbeBWwGULaSfTszjy37iJ0WEWOAtYFNgQeaEZMkqXkcvkLqXaVTHGXm48B5\nwO0UrWMnZeaSKmOSJElqloa2iGXmI8B2fW3LzOk823lfkjQEOVWX1DsHdJUkNZzDV0i9MxGTJDWF\nLWHS85mISZKawpYw6fkq7awvSZI0nJmISZIkVcRETJIkqSImYpIkSRUxEZMkSaqIiZgkSVJFTMQk\nSZIqYiImSZJUERMxSZKkipiISZIkVcRETJIkqSLONSlJqxAR2wJnZOaUiHgVcCnQBTwAHJWZKyLi\nUOBwYDlwamZeX1nAq2nmzBt48MH7G36dJUsWAzBmzNiGXmezzTZn6tS9G3oNabDYIiZJvYiI44EZ\nwJhy0znApzNzJ2AEsE9ErA8cA+wI7AH8//buPbyuukz0+DeXhqaYlqr1cpSBiPrq8Azi5TjKCETF\nCgzKnJmjeEbGEfECg46DOggWzqBYZRSpgz6IVhR0njkqKKMgIN6Kt6OoAyoIL4oRHy9HK5ak2EDa\nNOePtVPSkmTnsvZeeyffz/PkYe219l7rzYVf399v/db7e2dE7FVFvO1gdHSU0dHRqsOQWoojYpI0\ntTuAvwY+Xnv9VOD62vY1wFpgDPhmZt4H3BcRPwUOAr473UlXr15Bd3dXw4Kej5e+9DjguIZf56yz\nzgLgnHPOafi1pHZhIiZJU8jMT0fE/pN2dWTmeG17K7AKWAkMTXrPxP5pbdmyrcww28rY2E4ANm/e\nWnEkUnOtWdM37TFvTUrS7OyctN0H3A0M17b33C9Js2IiJkmzc2NEDNS2jwK+DtwAHBoRyyNiFfBE\nion8kjQr3pqUpNl5I7AxInqAW4HLM3MsIi6gSMo6gXWZeW+VQUpqLyZikjSNzPw58Iza9u3A4VO8\nZyOwsbmRSVosGpqI7VGD52DgfRRPGd0HvCwzf7sYavBIkiTNR8PmiE1Rg+ffgNdl5gDwGeDN1uCR\nJElLWSMn60/U4Jnwksy8qbbdDdwLPJ1aDZ7MHAImavBIkiQteg27NblnDZ7M/A1ARBwCvBY4jGIU\nbE41eKA1CyI2Q1dXkTfPVI9EkiS1j6ZO1o+I44B1wF9m5uaImFcNnqVaENFiiFrK7IBIWoyalohF\nxPEUk/IHMvMPtd03AOsjYjmwF9bgkSRJS0hTErGI6AIuAH4BfCYiAK7PzH+xBo8kSVqqGpqITa7B\nAzx4mvdYg0dt7brrruaWW37Y0Gvce+8IAMuX9zb0OgAHHngQa9ce3fDrSJJc4khqC6Ojo4yOjlYd\nhiSpZFbWlxZo7dqjGz6CtGHDuQCceurpDb2OJKm5HBGTJEmqiImYJElSRUzEJEmSKmIiJkmSVBET\nMUmSpIqYiEmSpIYaHLyDwcE7qg6jJVm+QpIkNdSmTV8CoL//gIojaT2OiEmSpIYZHLyDO+8c5M47\nBx0Vm4KJmCRJapiJ0bA9t1UwEZMkSapI3TliEXECcHNmfrf2+p3ATzLzI40OTpIWKiJetseucWAE\nuC0zb64gJGlJGRg4gksv3bhrW7ubcUQsIl4HnAQMT9p9DXByRJzcyMAkqSTHAmcDB9e+zgJOAT4a\nEadWGJe0JPT3H8B++/Wz3379TtafQr0RsROBwzJzVyKWmV+LiKOALwMfaGRwklSCRwBPycy7ASLi\nbOBK4JnA94EN1YUmLQ2OhE2v3hyxnZOTsAmZ+XtgZ2NCkqRSrQG2Tno9Ajw4M3dQ3KaU1GD9/Qc4\nGjaNeiNiOyLiYZn5u8k7I+LhQFfjwpKk0nwa+EpEfIqi8/k3wH/W5o79ptLIJC159RKx9wNX1+ZR\n3AB0AE8D3gN8qMGxSVIZzgSOAp4HjAH/mpnXRMQzgL+tNDJJS96MiVhmfiwilgP/Djy6tvtnwHmZ\n+cFGBydJJfhuZj4FuGryzsz8dkXxSNIudctXZOaHgA9FxEMo5oxtAYiIx2fm7Y0OUJIW6LcRcShw\nQ2bet5ATRcQy4FJgf4rRtVcBO4BLKOab3QyckpnOoZU0K7Mu6JqZdwFbI+K4iPgq8F+NC0uSSvM0\n4LrWYtIAABmuSURBVHpgJCJ21r7G5nmuo4HuzDwEeBuwHjgfODMzD6WYvnFsGUFLWhpmteh3RPQD\nrwFOAPYB3gG8uIFxSVIpMnNNiae7HeiOiE5gJbAdeAZFogdFncW1wBUlXlPSIjZjIhYR/4OioOtT\nKBqW44GNmfnWJsQmSQsWEf97qv2Z+bZ5nO4eituStwEPBY6hqLU4UQZjK7BqphOsXr2C7u6l+dB5\nV1dxE2bNmr6KI5FaR70RsU8DlwHPzMyfAkTErOc+RMSfUzyhNBARj2WKeRQR8SqK0bYdwNsz86pp\nTyhJc9cxaXsZcCTwnXme61TgC5l5RkTsC3wF6Jl0vA+4e6YTbNmybZ6Xbn9jY8U/H5s3b63zTmlx\nmanzUS8ROwh4OfCNiPg58H9m8RkAIuI04O+AP9Z2Tcyj2BQRFwHHRsT/Bf6RYg7H8tp1vrjQCbWS\nNGHPEfyIOAe4bp6n20JxOxLgDxSJ3Y0RMZCZmyjKZHx1nueWtATNOFk/M2/OzDcBjwLeCQwAD4+I\nz0fEX9Y59x3AX096/VR2n0dxBPB04JuZeV9mDgE/pUj+JKlRHgT8yTw/uwF4SkR8nWI07C0U61a+\ntdax7AEuLyVKSUvCrEa3MnMM+Czw2YhYQzHS9Q7g8zN85tMRsf+kXR1TzKNYCQxNek/d+RWwdOdY\nOL9i6fJ3P38RMcj9Sxl1Ujxw9O75nCsz72HqB5UOn190kpa6epP1D5vm0PdqX3MxeW7ZxDyK4dr2\nnvtntFTnWDi/Yunyd7+gJHRg0vY4cPdUa+hKUhXqjYhNzK14CPBY4JsURQwPAX4IPGsO15pqHsUN\nwPpa9f69gCdSTOSXpAWLiIdSJF5DtRH6/wncSHFbUZIqV2+O2LMz89nAL4GDMvN5mXkk8GcUj3HP\nxRvZYx5FZv4/4AJgYr7Fusy8d67fhCTtKSKeD9wCHBQRDwe+CzwZOKf2tLYkVW5Wc8SA/SbKV9T8\nAtiv3ocy8+cUxQ6pLYf0gHkUmbkR2DjLOCRptt4KPCszf1J7ivtHmXl8RKwAvo3tjqQWMNtE7PsR\ncSnwKYpRtL+lGMWSpFa1PDN/Utt+DvA5gMzcVquML0mVm20i9krgdRRV9ncCXwYubFRQklSCjojo\nAHop5rO+ESAi9q7tk6TKzbZ8xSjwnoj4PPCnwHczc0dDI5OkhbmCouxOF3BTZt4SEQdRLNZ9WaWR\nSVLNjMPzEfHciPhVRPwoIl4OfAl4CXB9RLygGQFK0nxk5tnAvwNfoFgTEuC5wE3AuorCkqTd1BsR\nexfF3IrHUPQsH5uZv4iIRwJXAVc2OD5JmrfM/BQUtyNro2H/BvTWilRLUuXqTVhdloVrgK9k5i8A\nMvM3FGusSVJLi4jnAD+g6Ew+HPh5RKytNipJKtRLxG6PiHMjorNWP4yIeEREvBe4tfHhSdKCvZNi\nsv7dtU7k4cxziSNJKlu9ROzvgW2ZOXl5oscD9wEnNiwqSSpPZ614NACZ+eMqg5GkyWacI5aZf6R4\nwmjyvq8BX5t4HRFXZeYxe35WklrELyPiGGA8IvYBTqEoSi2pSQYH7wCgv/+AiiNpPbOtIzaTR5Vw\nDklqlNdQTNLfF7iDYjm1V1cakbTEbNr0JcBEbCplJGLjJZxDkhrlHzPzf1UdhLRUDQ7ewZ13Du7a\nNhnbnct8SFrsXlCrsC+pAhOjYXtuq1DGiJgktbK7gNsi4r+AkYmdmfmK6kKSpEIZiZg9TUmt7NKq\nA5CWsoGBI7j00o27trW7MhIxGzlJLalWTf8eivVxfVJSqkB//wHst1//rm3tbsGJWGa+t4xAJKlM\nEXEKcA5wO/D4iHhVZn664rCkJcmRsOnNmIhFxEeZ4alI51hIamH/ADwhM38XEU8CLgJMxKQKOBI2\nvXojYl8H3gv8M3Bv48ORpNKMZubvADLzBxGxd9UBSdKe6lXW/0hEPB7oz8zTmxSTJJVhz9H8HZVE\nIUkzmM0csX8BDmt0IJJUsodExMume52ZH6sgJknaTd1ELDPvA7443fGIODszzy4zqLJdfPEHGB4e\nqjqMBZv4HjZsOLfiSMqxcuUqTjzx5KrD0OL1FeDZ07weB0zEJFWujPIVLwTOLuE8DTM8PMTQ8BDL\nVvRWHcqCdHR3AbBtx2jFkSzc9m0j9d8kLUBmnlDvPe3QkZQWAxf9nt6SKei6bEUv8aIXVB2GavKy\nK6sOQYI26EhKi4GLfk+vqYt+R8QyigKw+wNjwKsoJtBeUjvPzcApmbmzhLgkqZ626EhK7cxFv2fW\n7LUmjwa6M/OQiHgesB5YBpyZmZsi4iLgWOCKJsclaWmadUdyQkScQTGS1gNcCFyPnUlpWnsu+m0i\ntrtmJ2K3A90R0QmsBLYDz6BoyACuAdZSJxFbvXoF3bX5UrPR1dXpg+stqKurkzVr+qoOoy10dXUC\n+POqWEQMAIcAfwGsAN4EnI+dSUnzVEYi9uM5vPceituStwEPBY4BDsvMiV7pVmBVvZNs2bJtTgGO\njdk5bUVjYzvZvHlr1WG0hYm/4aX882qRJPT5wI8oEq2VFMWuX8UcO5PSUuKi3zOrm4hFxBOAVwJP\nAEYoEq+LJxbQzczj53C9U4EvZOYZEbEvxePkPZOO9wF3z+F8krQQc+lIQtGB3I+iE9kPfA7onEtn\ncq4j+ouJI7tL05o1B/Otbz0OgKc//eCKo2k99daaPAr4OPBJ4PMUcyAOAr4bES/OzOtn+vwUtlDc\njgT4A8X8sBsjYiAzNwFHAV+d4zklaUoldyQB7gJuy8xRICPiXmDfScfrdibnOqK/mDiyu3QdcsgA\nsHR/9zN1PuqNiL0NeH5mfn/yzoi4BDiPuVfc3wB8JCK+TjES9hbge8DGiOgBbgUun+M5JekBGtCR\nBPgG8PqIOB94JLA38GU7k9LMnKA/vXqJ2PI9kzCAzLwhIh4014tl5j3Ai6c4dPhczyVJdZTdkSQz\nr4qIw4AbgE7gFGAQO5OS5qleIra9znFJalWldiQnff60KXbbmZQ0L/USsb6IOJSpix7OuyGTpCaw\nIym1CJc4ml69ROyXFMP7U/lVybFIUpnsSEotwiWOpjdjIpaZz25WIJJUMjuSUgtwiaOZzbuga0QM\nZ+bKMoORpLLYkZRag0sczaxzAZ91sVxJbSkihquOQZJgYYnYnBfLlaQWYUdSapLJyxq5xNED1aus\n/yfTHOrAhkxt4OKLP8Dw8FDVYSzYxPewYcO5FUdSjpUrV3HiiSdXGYIdSalJ+vsPYK+9lu/a1u7q\nzRG7nqLBmirp+n354UjlGh4eYuvWIVat6q06lAXp6SnWJuzsHK04koUbGhppynXsSEqtYXDwDu67\n795d2yZju6v31GR/vRNExKsz80PlhSSVa9WqXtatO7LqMFSzfv217NzZlEvZkZRagJP1ZzbvpyYn\nOQkwEZPUUuxISmoHC5msP8Ehfknt6qSqA5AWOyfrz6yMETEnvUpqVy3fkVwsD5yAD50sVf39B7Df\nfv27trW7MhIxSWpXLd+RHB4eYmh4iGUr2vuBE4CO7uKhk2072v+hk+3bmvPQyWLhSNj0TMQkqcUt\nW9FLvOgFVYehSfKyK6sOoa04Eja9MuaI3V3COSRJ0iI1OHgHg4N3VB1GS6pX0PWwmY5n5tcy8znl\nhiRJTWNHUmqCiRIWjow9UL1bk2+d4dg4YBImqSXZkZRaw+DgHdx55+CubZOx3dUr6Prs6Y5FRFf5\n4UhSaexISi3Agq4zq3drshd4GXBXZl4+af/RwLuBAxsbXjlGRkbYvn3UyZUtZPu2EUaWjVUdhhYx\nO5KS2kG9W5OXAvsBqyLiYcCVwEbgmcC/Njg2SZq3xdKRlNrdwMARXHrpxl3b2l29ROy/A48DHgx8\nHjgNuBb4u8zc3ODYStPb28v4si4f/24hedmV9Hb3VB2GFjc7klILsKDrzOolYndn5g7gdxGxL/AP\nmfmZhVwwIs4AXgj0ABdSLMx7CcWcjZuBUzKzOUsCS1rMFkVHUloMHAmbXr06YpOrTv+2hCRsADgE\n+AvgcGBf4HzgzMw8lGK5kWMXcg1Jqrk7M3dk5u8o2po3ZOZJJmFS8/X3H+Bo2DTqjYj11EbCOoGu\n2vautdky8xdzvN7zgR8BVwArgX8GXkUxKgZwDbC2dlySFqLUjqQkNUK9RGxv7k+SOvbYHgceM8fr\nPZRizsYxQD/wOaAzMycazK3AqnonWb16Bd3ds3/oqaurE3bMMVI1XFdXJ2vW9DX8GuMtv5rg0tOM\n3z3ldyQlqXT1ErGzZzg2n3/e7gJuy8xRICPiXopbBhP6mEWl6y1bts3pomNjTjlrRWNjO9m8eWvD\nr9FZxkJeKtV8fvfzSNzK7khKUunqJWIfBX4HfAkYre2b6FGOAx+b4/W+Abw+Is4HHknRUH45IgYy\ncxNwFPDVOZ5TkqZy9gzHHCeV1BLqJWJPAY4Dngf8APgk8KX5PtWYmVfVlh25geJ2wSnAILAxInqA\nW4HLZziFJM1W2R1JadG57rqrueWWHzb8OvfeOwLA8uW9Db3OgQcexNq1Rzf0GmWrt8TRTcBNwBkR\n8TSKpOwdEfE94BO1Uaw5yczTpth9+FzPI0l1lNqRnFCrSfb92nl3YPkdqa7R0aIv1OhErB3VGxHb\nJTO/B3wvIg4FzgWOBx7UqMAkaSEa0ZGMiGXAB4GR2q6J8jubIuIiivI7PvWttrF27dFNGUHasOFc\nAE499fSGX6vd1E3EIqIDOAx4EcUcrpuA91FUqZaklldiR/I84CLgjNrrpzLH8js+9b14NOnp30Wh\nq6t4asqf1wPVW/T7A8CRwI3Ap4A3Z+YfmxGYJC1UmR3JiHg5sDkzv1BbIQSgY67ld3zqe/FoxpPf\ni8XE3/FS/XnNlIDWGxF7DUXJiSfXvt4REbsOZqaPf0tqSQ3oSL4CGI+II4CDKSb7P2zS8VmV35Gk\nyeolYv1NiUKSyldqRzIzD5vYjohNwEnAuy2/I2kh6j01eWezApGkkjWjI/lGLL8jaQFm/dSkJLWT\nRnYkM3Ng0kvL70iaNxd/kSRJqoiJmCRJUkW8NalFbWRkhB07Rlm//tqqQ1HN0NAI3d1jVYchSS3B\nETFJkqSKOCKmRa23t5fOzi7WrTuy6lBUs379tezc2VN1GJLUEhwRkyRJqoiJmCRJUkVMxCRJkipi\nIiZJklQREzFJkqSKmIhJkiRVxERMkiSpIiZikiRJFTERkyRJqoiJmCRJUkVc4kiSWtjIyAjbt4+S\nl11ZdSiaZPu2EUaWuXi9Fq6SRCwiHgZ8H3gesAO4BBgHbgZOycydZV9z+7aRtm/IxkZHAejqaf91\n+rZvG4GV7f99SJK0EE1PxCJiGfBBYKS263zgzMzcFBEXAccCV5R5zZUrV5V5usoMbyt+ZCtWLIIE\nZmXPovm9SI3U29vL+LIu4kUvqDoUTZKXXUlv9yJoi1W5KkbEzgMuAs6ovX4qcH1t+xpgLXUSsdWr\nV9Dd3TXrC55++mlzj7IFnXXWWQCcc845FUfSPrq6OhkfrzoK7amrq5M1a/qqDkOSKtfURCwiXg5s\nzswvRMREItaRmRP/VG4F6g6TbNmyrUERtraxseKO7ebNWyuOpH2Mje1k69YR1q+/tupQFmTbtuK2\n9GIYDR0aGqGvr2fOf8cmbpIWo2aPiL0CGI+II4CDgY8BD5t0vA+4u8kxaRGbuP25s/RZh801Olrc\nll6+vP0Tsb4+b0tL0oSmJmKZedjEdkRsAk4C3h0RA5m5CTgK+GozY9LiduKJJ1cdQik2bDgXgFNP\nPb3iSCRJZWqF8hVvBDZGRA9wK3B5xfFIkiQ1RWWJWGYOTHp5eFVxSJIkVcXK+pIkSRUxEZMkSaqI\niZgkSVJFWmGyviS1vNqqIB8B9gf2At4O/JgmLNEmafFyREySZud44K7MPBQ4Eng/9y/RdijQQbFE\nmyTNmomYJM3OZcBZte0OYAcPXKLtiAriktTGvDUpSbOQmfcAREQfRb3DM4Hz5rpE21zXyu3q6ixS\nPrUc10ydva6uYtzHn9cDmYhJ0ixFxL7AFcCFmfkfEfGuSYdntUTbXNfKnVhjVq1nbGyna//O0lJf\nK3mmBNRETJJmISIeDlwHvDYzv1zbfaNLtKlRLr74AwwPD1UdRikmvo+J5dra2cqVq0pdPs9ETJJm\n5y3AauCsiJiYK/Z64AKXaFMjDA8PsXXrEKtW9VYdyoL19BS34zs7RyuOZGGGhkZKP6eJmCTNQma+\nniLx2pNLtKlhVq3qZd26I6sOQzXr11/LzpJnC/jUpCRJUkVMxCRJkipiIiZJklQREzFJkqSKmIhJ\nkiRVxERMkiSpIiZikiRJFTERkyRJqoiJmCRJUkWsrC9JLW77thHysiurDmPBxkaL5W26enoqjmTh\ntm8bgZXt/32oeiZiktTCVq5cVXUIpRneVqzTt2LFIkhgVvYsqt+NqtPURCwilgEfAfYH9gLeDvwY\nuAQYB24GTsnMkldykqT2dOKJJ1cdQmk2bDgXgFNPPb3iSKTW0ew5YscDd2XmocCRwPuB84Eza/s6\ngGObHJMkSVIlmp2IXQacVdvuAHYATwWur+27BjiiyTFJkiRVoqm3JjPzHoCI6AMuB84EzsvM8dpb\ntgJ1b7qvXr2C7u6uhsXZqrq6irx5zZq+iiNRs/m7l6TFqemT9SNiX+AK4MLM/I+IeNekw33A3fXO\nsWXLtkaF19LGxoqpc5s3b604EjWbv3uTUEmLU1NvTUbEw4HrgDdn5kdqu2+MiIHa9lHA15sZkyRJ\nUlWaPSL2FmA1cFZETMwVez1wQUT0ALdS3LKUJEla9Jo9R+z1FInXng5vZhySJEmtwIKuJbnuuqu5\n5ZYfNvQaw8NDwP21eBrpwAMPYu3aoxt+HUmSljITsTbSswiWBZEkSfczESvJ2rVHO4IkSZLmpNkF\nXSVJklRjIiZJklQRb01KktSCRkZG2LFjlPXrr606FNUMDY3Q3T1W6jkdEZMkSaqII2KSJLWg3t5e\nOju7WLfuyKpDUc369deyc2e5FQwcEZMkSaqII2KStAAR0QlcCDwJuA94ZWb+tNqoJLULR8QkaWH+\nCliemc8ETgfeU3E8ktqII2LSArm81ZL3LOBagMz8dkQ8reJ45qwZf8PQvL/jxfQ3PDQ00tCnJrdt\nG2X79nKfAqzSsmVdrFjRuFVohoZG6Osr9/wmYlIbcHmrlrYSGJr0eiwiujNzx1RvXr16Bd3dXc2J\nbJZ6e5fR1dX4GyR77bUXQMOv1du7jDVr+hp6jWZ4yEMe3PCfVUfHTmBnQ6/RTB0d3XR0LG/Y+ffZ\nZzn77LNPqX9fHePj46WdrFk2b97afkFLWpA1a/o6qo5hKhFxPvDtzPxU7fUvM/PR073f9ktaemZq\nv5wjJkkL803gaICIeAbwo2rDkdROvDUpSQtzBfC8iPgW0AGcUHE8ktqIiZgkLUBm7gROqjoOSe3J\nW5OSJEkVMRGTJEmqiImYJElSRUzEJEmSKmIiJkmSVBETMUmSpIq0ZWV9SZKkxcARMUmSpIqYiEmS\nJFXEREySJKkiJmKSJEkVMRGTJEmqiImYJElSRUzEJEmSKmIi1sIiYiAihiJi30n7zo2Il1cYlhoo\nIi6PiDMmve6LiIyIJ1UZlzRXtl9Lj+3X/JiItb77gI9GREfVgagpTgJOiog/rb1+N/ChzPxBhTFJ\n82X7tbTYfs1Dd9UBqK6vUCTMpwDvn9gZEW8EXgLsAL6WmW+uJjyVKTN/HxGvBT4cEW8BHgOcHBF/\nBlwAdAB3Aa8AeoBPUvx9LAdOysybqolcmpLt1xJi+zU/joi1h5OBUyPisbXXfcCLgUNqX4+LiGOq\nCk7lyswrgduAjwInZOY4sBE4JTMHgKuB04CnUzRqR1H8Q7d3JQFLM7P9WkJsv+bORKwNZOZdwD8B\nl3J/7+Hbmbm99kf+deDACkNU+T4GfCczf1V7/UTgwojYRNGbfBRwDfBN4LPA24CdFcQpzcj2a0my\n/ZoDE7E2UetlJPBy4F7gzyOiuzb34jDg9grDU+Ml8LJaj/I04CpgAPhNZq4F3g68o7LopBnYfi15\ntl8zcI5Ye/kn4LnAVuBTFL2JTuAbwH9WGJca72TgYxHRDYwDJ1IM638iIk6m+H/5bRXGJ9Vj+7V0\n2X7NoGN8fLzqGCRJkpYkb01KkiRVxERMkiSpIiZikiRJFTERkyRJqoiJmCRJUkUsX6HKRcT+FHWE\nfkzxaHMP8GuKqsy/jIiXAa8DllF0Hj6cmRfUPrsJeDRwT+10K4GfAS/NzN828duQtATZfmmhHBFT\nq/h1Zh6cmU/OzAOB7wHvi4hXU9QfemFmHkxR/PH4iDhx0mdfWfvswcBjgWHgDc3+BiQtWbZfmjcT\nMbWqrwGPB84E3pCZvwHIzLuBvwdunuZzewMPBf7QjCAlaQq2X5o1b02q5UTEMuA44DvACbX/7pKZ\nt+7xkQ9HxB+Bh1E0YJ8ANjQhVEnaje2X5soRMbWK/xYRN0XETcAPgQ7gTbVjHXU++8rMfBLwN8CD\ngaszc7RxoUrSbmy/NG+OiKlV/Lo2R2I3EfEz4GkUQ/0T+w4HjsrM0ye/NzO/FREXUKxp9qTM3NHo\noCUJ2y8tgCNianXvBt4TEY8AiIiHAu8BfjrN+8+nmGdxUnPCk6Rp2X6pLhMxtbTMvAj4OPDFiPgB\n8FXgksz88DTvvw9YB/xLRKxqXqSStDvbL81Gx/j4eNUxSJIkLUmOiEmSJFXEREySJKkiJmKSJEkV\nMRGTJEmqiImYJElSRUzEJEmSKmIiJkmSVJH/D8kaVCsRcipxAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x114525a90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"R = inferential_statistics.anova_MRI('PCR', df);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Estimate the effect size **"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Effect Size</th>\n",
" </tr>\n",
" <tr>\n",
" <th>Predictor of PCR</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>MRI_LD_Baseline</th>\n",
" <td>0.191798</td>\n",
" </tr>\n",
" <tr>\n",
" <th>MRI_LD_1_3dAC</th>\n",
" <td>0.304774</td>\n",
" </tr>\n",
" <tr>\n",
" <th>MRI_LD_Int_Reg</th>\n",
" <td>0.502345</td>\n",
" </tr>\n",
" <tr>\n",
" <th>MRI_LD_PreSurg</th>\n",
" <td>0.590352</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Effect Size\n",
"Predictor of PCR \n",
"MRI_LD_Baseline 0.191798\n",
"MRI_LD_1_3dAC 0.304774\n",
"MRI_LD_Int_Reg 0.502345\n",
"MRI_LD_PreSurg 0.590352"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"mri_features = ['MRI_LD_Baseline', 'MRI_LD_1_3dAC', 'MRI_LD_Int_Reg', 'MRI_LD_PreSurg']\n",
"outcome = 'PCR'\n",
"# Effect Size\n",
"inferential_statistics.effect_size( df, mri_features, outcome)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.5 Effect of MRI measurements on Survival ANOVA"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmIAAAJZCAYAAAAK61mIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XuYXFWVsPE36RCSSBKjRh0vAxFhiWhEQVAUiIpBkRGH\nUUEFPy5yG1DBC6DoiAoIA4KCihpAEEcFuQkIEhGCwIAICgjiQjIBZhQ0YkgiuXf6++OcCkXb13RX\nnaru9/c8/eTUqVOnVld376y9zj57j+nq6kKSJEnNN7bqACRJkkYrEzFJkqSKmIhJkiRVxERMkiSp\nIiZikiRJFTERkyRJqsi4qgNQa4uILmB6Zv61gve9Fzg6M6/u9tz+wCcpfn+vAz6Smat7OEePx0XE\ni4FzgOcBHcApmXl+ROwMnFp3ionA5sA2mXlnRBwH7Al0AncCB2fmioh4JXAr8GDda/fMzIyIw4FD\ngS5gPnBgZv4lIp4FnAVsBTwJfCczz4yIw4AjgRWZ+Yr1+/Sk0WuEtlmTgLOBV1MUUI7OzMvL12wH\nfB14BvAnYO/MfLTunM8EfgHsn5l3lPumA98FNgbWAgdl5n+Xz70D+BKwIXAPcEBmLimf+3fgQxRt\n453lcyvr3mtGuX92Zt4REdcCrwVOzMz6tlV1rIiplb2phwbtFcDngR2BAJ5JkbgwiOO+Dlydma8C\n3gKcGREvyszrMnOr2hfwW+CkMgmbBewFvAZ4JTAF+HB5vu2B79e/tkzCtgY+AWxfJlV/AL5YvuZ0\n4O/Ay4HXAW+PiN0y8+sUDZ2k9tOoNus44O+ZuQXwVuAbEfGiiBgPXAx8tHzuYopOZu2cuwK3Ay/r\n9nZfB27KzJcDewM/iohJZYL2HeDfMjOA/wFOKs+1B0WbtzOwJUUytu77iIgJwPeA8bV9mbkLcEW/\nn9ooZ0WszZUJwinAH4GXAMuBfTPz/m7HTQX+F9g8Mx8r991G8Yc/n+IPcyPgBcBdFBWdFXWv3xd4\nd2bu1v1x2RicDOxEUWH6DUVPbkm3GI6hSGa6e0tmPj7Ab3l34IrMXFie81vAGcB/DuK4dwFjyuP+\nGVhD8bnVx7o3sEldvB3ABIrGp7Pcrn0+2wMviYjby8cnZealZQK3WdmjnQC8EFhQHrM1cHhmdgKd\nEfET4N3AVQP8HKS2ZJu1Xm3WvwLvB8jMRyJiLvBe4JfAksy8pTzHOcBXIuLZZXwfAf4f8IO672kc\nsBtwWHm+uyLiD8DbKNq3X2XmH8rDzwLuLiv1HwS+nJl/K89zCHVJF8XP4zzg2AF+LipZERsZXkPx\nBzKTojdzQfcDMnMxcBlF74eI2AL4J+Ba4EDg/Mx8PfBSYAbwjkG8/zEUyczWZZXpT5S9qG4xnNSt\nalT7GmiDBvBiisa55v+AFw3muMxcm5mdETGP4pLi2fUxlI30l4AjMnNN+ZqfAz8DHgEeo+itfqt8\nyZMUFbFtKRq9s8pqGGUS9q7y/Xek+PlA0YDuExEbRMRGwL9R/Dyk0cA2a3DH9fbc0/Zn5ipgIUWn\nj8x8W2be2u19ngOMrSV8fZ2v3D8FmEwxTOO5EfHTiLiHokr3BEBEfAjYIDPn9PB9qR9WxEaGuzPz\npnL7XODrdT2ienMoejinAvtRjEtaGxFHA2+NiKMo/theQNHTHKjdKBKTt0YEFL2kv3Q/aJh6lz11\nHjrX57jMnFWW4n8WEfdnZi1JejcwPzNvrh1bjt2YQfEfwSqK/zy+DHw4M/+97pz3R8RFwDspxkpQ\njuW4PCIOBK6NiJcCH6f4OfwGeJQiydu+v29eGiFsswZ3XG/P9VZM6en8fb3PQM63AcVl0d0prgac\nD5wQEd8FDqHoaGo9mIiNDGvqtseUX50RcVfd/g9l5s0RMS4itqUoc9f+4/8Bxe/CRcBPKC7XjeHp\nurrtqy9Jd1CMUbgGoKzwTOgeZGaeRA+9zkF6hKdXjl5I0Wsb8HER8W7g2sxcmpkLI+Jyih56LRHb\ns267Zg/gvzJzaXmObwNfi4gOit71GbXnKD6n1WXC9fy6hO5c4JvANIqBtUfVlfmP5umD/aWRzDZr\ncMfVnnus7rm7ur8mIjagqHj9sY94/lIeOy0zF3V7r8XAdt1iWJSZT0bEn4DL6gbufw/4j/K4KcB/\nl0ntC4D/iohPZqbjwwbARGxk2CoiZmbmPcBBwC2Z+QTFHXndnQ2cCdyTmY+U+3YBdsrMuyPi5RR/\niBd2e91C4BXlWKc1wL/UPXctcHhE/Lx8bg7FQPQDh+fbe5orgB9HxAllTAcBlw/yuEMpetEnluNQ\ndge+ABARYyh6dod1O9+vgT0i4gKK3uEewG3lJc53UvQQvxwRG1NcZnwzRQP5g4jYKos7uD4A3JuZ\nj0fExykar8Mj4nkUn9X7hvjZSO3CNmtwx/24fHxoRLyIYjzX8RSJ2LMjYvss7nrcH7i1/Cx7lJlr\nyjGpBwMnRcRMipuG5lHcKfnlcmzrHygqXT8uX3ox8N6ImEPR3r2LYjzZEcARtfNHxEPAB7K8Q1P9\nc4zYyPAYRYn4txR/HPv0cez5FI3d2XX7Pg1cFhF3UFRsbqQYd1Fvbrn/98BNFHcU1nwReIjiMtvv\nKHqhH1/P76VPZcP9BeD6MpZOikG3RMQ7I+Lq/o4D9gXeWI5zuAk4NzMvK597DrBRZnbvsZ5IMXbi\ndxS3dD+Lp77HD1Dc9fhb4BqKsWX3l5deTgDmlT39vSh+PlCMQXtRRNxbxnhcZv5qiB+P1C5ssxhU\nm/U5YKOIuI9iWotPZub8LKbA2INigP59FG3RfgMI69+BN5Ttz38B+2Tm4sz8S/n6iyPifoo7xGuf\nyzfK976zjG8jip+DhmhMV1dX1TFoCMo7kL6WI2zOqahoLqBWMFJ/phKM3N/v0dxm9SUizqO4EuA8\nYr2wIqZWdkMU8+CMGuVt4mf3e6CkVjTq2qy+RDGh6zurjqPVWRGTJEmqiBUxSZKkipiISZIkVaQt\np69YuHCp11OlUWb69Mnd54lqS7Zf0ujTV/tlRUySJKkiJmKSJEkVMRGTJEmqiImYJElSRUzEJEmS\nKmIiJkmSVBETMakNLFgwnwUL5lcdhiRpmLXlPGLSaDNv3nUAzJixacWRSJKGkxUxqcUtWDCfhx9e\nwMMPL7AqJkkjjBUxqcXVqmG1batiGm5z517Nfffd0/D3WbFiOQATJkxs6PtsueVMZs/etaHvIQ0X\nK2KS1IuI2C4i5nXb9/6IuLXu8YERcUdE3BYRuzU9yDayatUqVq1aVXUYqoDjXHtnRUxqcbNm7cz5\n589Zt63miIijgH2AJ+v2vRo4ABhTPn4+8BFgG2ACcHNE/CwzVzY/4vU3e/auTakgnX76SQAceeQx\nDX8vtRbHufbORExqcTNmbMrGG89Yt62mmQ/sAVwAEBHPBk4EjgDmlMdsC9xSJl4rI+JBYCbwq95O\nOm3aJMaN62hk3C2ro6O4CDN9+uSKI1EzPfDAAzz88AIAFi16lM0337ziiFqLiZjUBqyENV9mXhIR\nmwBERAdwDvAxYHndYVOAxXWPlwJT+zrvokXLhjfQNtLZuRaAhQuXVhyJmunyy6942vZ++x1cYTTV\n6KvzYSImtQErYZXbGtgMOIviEuTLI+IrwPVAfQs7GXii+eFJalcO1pekfmTm7Zm5ZWbOAvYCfpeZ\nRwC3AztExISImApsAdxbYahSy6mv6Fvd/0dWxCRpPWXmYxFxBnATRcf22MxcUXFYUktxnGvfTMQk\nqReZ+RDwur72ZeYcnhq8L6kHVsJ6ZyImSZIaykpY7xwjJkmSVJGGVsQiYjvg5MycFRE/BJ5fPrUJ\ncFtm7hURXwXeSHHbN8Dumbn4H88mSZI0sjQsEes+K3Vm7lXunwbcABxZHro1sEtm/rVRsUiSJLWi\nRl6arM1K3d3ngTMz89GIGEsxN8+3I+KWiNi/gfFIkiS1lIZVxOpnpa6JiOcCb+GpatgzgDOB04AO\n4IaIuCMz7+nr3KN5iRBJkjRyNPuuyXcD38/MzvLxMuCrmbkMICKuB14F9JmIjeYlQqTRyvUJJY1E\nzb5rcmfgmrrHmwO3RERHRGxAMWj/102OSZIkqRLNTsQC+J/ag8y8H7gAuA24EfhuZt7X5JgkSZIq\n0dBLkz3MQL1lD8ecApzSyDgkSZJakRO6SpIkVcRETJIkqSImYpIkSRUxEZMkSaqIiZjUBhYsmM+C\nBfOrDkOSNMyaPaGrpPUwb951AMyYsWnFkUiShpMVManFLVgwn4cfXsDDDy+wKiZJI4yJmNTiatWw\n7tuS1C4cXtE7L01KkqSGcnhF76yISS1u1qyde9yWpHbg8Iq+mYhJLW7GjE3ZeOMZbLzxDHuTktqO\nwyv65qVJqQ1YCZOkkcmKmNQGZszY1GqYpLbk8Iq+WRGTpF5ExHbAyZk5KyK2As4EOoGVwAcz888R\ncSBwMLAGOD4zr6ouYqn11IZX1Lb1dFbEpDbgrd/NFxFHAWcDE8pdXwU+nJmzgEuBoyPi+cBHgDcA\nuwBfiogNKwhXammzZu1sNawXVsSkNuCt35WYD+wBXFA+3iszHy23xwErgG2BWzJzJbAyIh4EZgK/\nanawUiuz7eqdiZjU4mq3fte2bdCaIzMviYhN6h4/ChAR2wOHAztSVMEW171sKTC1r/NOmzaJceM6\nhj3edtDRUVyEmT59csWRSK3DRExqcd1v/TYRq05E7AkcC7wjMxdGxBKgPquYDDzR1zkWLVrWwAhb\nW2fnWgAWLlxacSRSc/XV+TARk6QBiIi9KQblz8rMv5W7bwdOiIgJwIbAFsC9FYUoqQ05WF9qcd76\nXb2I6ADOoKh4XRoR8yLi85n5WLn/JuB64NjMXFFhqJLajBUxqcV563d1MvMh4HXlw2f1cswcYE6z\nYpI0spiISW3gZS97edUhSJIawEuTUhv4/e9/x+9//7uqw5AkDTMTManF1aavePjhBU7qKkkjjJcm\npRbn9BWSGmXu3Ku57757Gv4+K1YsB2DChIkNfZ8tt5zJ7Nm7NvQ9hpsVMUmS1FCrVq1i1apVVYfR\nkhpaEeu2YO6rgauAP5RPn5WZF7pgrtS3WbN25vzz56zblqThMnv2rk2pIJ1++kkAHHnkMQ1/r3bT\nsESsXDB3H+DJctfWwGmZ+eW6Y2oL5m5DsbDuzRHxs3LdNkk4fYUkjWSNrIh1XzB3ayAiYneKqtgR\nuGCuNCBWwiRpZGpYItZ9wVyKpUDOzsw7I+JY4HPAXQxywVwY3YvmanSaPn2rqkOQJDVAM++avCwz\na4vhXgacCfyCQS6YC6N70VxptOpr0VxJalfNvGvy2ojYttx+C3AnRZVsh4iYEBFTccFcSZI0ijSz\nInYocGZErAYeAw7KzCURUVswdywumCtJkkaRhiZi9QvmZuavgTf0cIwL5kqSpFHJCV0lSZIqYiIm\nSZJUERMxSZKkipiISZIkVcRETJIkqSImYpIkSRUxEZMkSaqIiZgkSVJFTMQkSZIqYiImSZJUkWau\nNTmizZ17Nffdd09D32PFiuUATJgwsaHvA7DlljOZPXvXhr+PJEmjmYlYG1m1ahXQnERMEkTEdsDJ\nmTkrIl4KnAd0AfcCh2Xm2og4EDgYWAMcn5lXVRawpLZjIjZMZs/eteEVpNNPPwmAI488pqHvIwki\n4ihgH+DJctdpwGcyc15EfBPYPSJuBT4CbANMAG6OiJ9l5spKgpbUdhwjJkk9mw/sUfd4a+DGcvsa\nYGdgW+CWzFyZmYuBB4GZTY1SUluzIiZJPcjMSyJik7pdYzKzq9xeCkwFpgCL646p7e/VtGmTGDeu\nYzhDbRsdHUXff/r0yRVHombzZ987EzFJGpi1dduTgSeAJeV29/29WrRo2fBH1iY6O4uPcOHCpRVH\nomYb7T/7vhJQL01K0sD8JiJmldtvB24Cbgd2iIgJETEV2IJiIL8kDYgVMUkamI8DcyJiPHA/cHFm\ndkbEGRRJ2Vjg2MxcUWWQktqLiZgk9SIzHwJeV24/AOzUwzFzgDnNjUzSSDHgRCwingFsCvwWmJSZ\nT/bzEkmSJPVhQGPEIuItwN3Aj4HnAw9FxOxGBiZJkjTSDbQidiLwRuCazHw0InYCfgDMbVhkUptw\neavWFhEf7LarC1gO/D4zHVgvqVIDvWtybGY+VnuQmb9rUDySerBq1ap1S1xp0HYHjgO2Kr8+CxwG\nfCcijqwwLkkacEXs/yJiN6ArIp5J0Yg90riwpPbh8lYt7/nAazLzCYCIOA64Eng9cCdwenWhSRrt\nBloROxj4APBi4H8oepUHNSooSRpG0ylmvK9ZDjwrM9dQXKaUpMoMqCKWmX8B3tfgWCSpES4Bro+I\niyg6n/8GXF6OHXu00sgkjXoDSsQiYhfgeOBZwJja/sx8ST+v2w44OTNnRcRWwJlAJ7AS+GBm/jki\nvkpxI0Ctx7p7uXiuJA1ZZn6qHFrxVor25+TMvCYiXge8v9roJI12Ax0jdibwMYqlOwZUyo+Io4B9\ngNp8Y18FPpyZd0XEwcDR5Tm3BnbJzL8OJnBJGoRFFLPhnwdsC5CZt1UZkCTBwBOxv2bmVYM893xg\nD+CC8vFemVm7DDAOWBERY4HNgG9HxPOAczLz3EG+jyT1KiI+CrwLeCFwEfCtiDgnM0+tNrKBOeec\ns1iyZGRcJKh9H7WbT9rdlClTOeCAQ6sOQ21uoInYTRFxGvBTYN06apn5i95ekJmXRMQmdY8fBYiI\n7YHDgR2BZ1BU204DOoAbIuKOzOxzUqZp0yYxblzHAEMfOTo6insr+lrFXSOTP/sh2RfYDvhlZv4t\nIl5LsVh3WyRiS5YsZvGSxWwwqfFzyDXamLLdXram/adiWb1sedUhaIQYaCK2bfnvq+v2dQFvHsyb\nRcSewLHAOzJzYUR0AF/NzGXl89cDrwL6TMQWLVo2mLcdMTo71wKwcOHSfo7USOPPfkhJaGdmroqI\n2uMVFGPF2sYGkyYS7/mXqsNQnfzRlVWHoBFioHdNvmmobxQRe1NMgzErM/9W7t4cuDAiXk1xN9Mb\ngfOH+l6SVOfGiDgVeEZEvIti6p3rK45JkoB+ErGI+HZmHhQRN9DDIP3MHFBFrKx8nUExCeylZc/0\nxsz8XERcANwGrAa+m5n3DfJ7kKS+fBI4kGK93A8CVwNnVRqRJJX6q4h9q/z3uPU5eWY+BLyufPis\nXo45BThlfc4vSX2JiI2AlZn5Lcr2LCI2pLhr+8QqY5Mk6H9m/WdExI4U1bCeviSpJZXT5PwN+HNE\nvKbctyfwAMVKIZJUuf4qYp/v47lBD9aXpCY6CngtMAM4JiKWAW8DPgecXWVgklTTZyI2HIP0Jaki\nT2bm3cDdETEH+DmweWYuqTguSVpnoEscbUzRg9wE2AH4PrB/OQZMklpR/RQVi4B9MnN1VcFIUk/6\nGyNW8y2KAfV/B/4M/AD4bqOCkqRhUD+O9e8mYZJa0UAndH1OZs6NiJMzswuYExGHNTIwSRqizcpJ\nortvAwOffkeSGmmgidjyiHgRZQ8zIt4IrGxYVJI0dLtVHYAk9WegidiRwFXAphFxF8WcYO9pWFSS\nNESZeWN/x0TErzPzNc2IR5J6MtAlju4oF8rdnGJx7vsdbyFpBBhTdQCSRreB3jW5LcU6kF+jqIy9\nOiIOycxLGhmcJDXYoCamjogNKNbD3YTirswDgTXAeeW57gUOy8y1wxqlpBFroHdNngHcCbwbWAZs\nDRzTqKAkqUXtCozLzO2BLwAnAKcBn8nMHSgqbLtXGJ+kNjPQRGxsOd7iHcAlmfkIAx9fJkkjxQPA\nuIgYC0wBVlN0TGvj0a4Bdq4oNkltaKDJ1LKI+DjwFuDwiPgosLRxYUlSUwx2jNjfKS5L/h54DsWd\nmTuW0/pA0S5O7esE06ZNYty4jgG/YUfH2OLip1pOR8dYpk+fXHUYbaGjo6j7+Hn9o4EmYh8ADgD2\nyMxFEfEC4H2NC0uShkdE/L/MPL/bvsMy8+vAlwZ5uiOBazPzUxHxYuB6YHzd85OBJ/o6waJFywb1\nhp2dDjdrVZ2da1m40JrEQNR+j0fr59VXAjrQuyb/GBFXAhtFxI7AT4FdgHOHJUJJGmYRcQTF5cND\nymXaajYA3g98PTMvGuRpF1FcjgT4W3mu30TErMycB7wduGFIgUsaVQZ61+T5wPYU84fdD2wF3IKJ\nmKTW9SDF+K0xPP0S5Apg3/U85+nAuRFxE0Ul7NPAHRSrjYynaB8vXt+AJY0+A700uSPFHGJnUtxB\nOYZiKgtJakmZeRVwVURclJn3D9M5/w68t4endhqO80safQaaiP0pM1dHxP3AzMz8YUQ44k5SO/jn\niPguRUV/XWUsM19SXUiSVBhoIvbHiPgUcB3wnxEBsFHDopKk4XMm8DGKyVYHNYGrJDXaQBOxA4B3\nZOavIuJSijsmD21cWJI0bP5aXqaUpJYz0LsmlwI/jIhnUA7Sz8wnGxqZJA2PmyLiNIq7vVfUdmbm\nL6oLSZIKfSZiEbEpxRIef6a4Q/I6ikW/x0XE+zLzJ40PUZKGZNvy31fX7esC3lxBLJL0NP1VxM4F\nLqWYKXoesHdm/iQitga+A5iISWppmfmmqmOQpN70l4hNy8yvAkTEfrUKWGbeGRFO9yypZUXEf/T1\nfGZ+oVmxSFJv+kvE6lc4W9TtORMxSa1ssOtISlLT9ZeITY6IHYCxPLW8UY3TV0hqWZn5+f6OiYjj\nMvO4JoQjST3qLxH7P6BWvv8jUN+w/bG/k0fEdsDJmTkrIl4KnEcxSPZe4LDMXBsRBwIHU1Tfjvc2\nc0lN9E7guKqDkDR69ZmIDWSQa289yog4CtgHqE1zcRrwmcycFxHfBHaPiFuBjwDbABOAmyPiZ5m5\ncnDfhiStFy9fSqrU2GE4xzt72T8f2KPu8dbAjeX2NcDOFLeV35KZKzNzMcUivTOHISZJGghn2pdU\nqYHOrN+XHnuUmXlJRGxSf1xm1hq9pRRTYkwBFtcdU9vfp2nTJjFuXMf6RdvGOjqKvHn6dJf5HG38\n2UvSyDQcidhAe5T1d1lOBp4AlpTb3ff3adGiZQMObiTp7Cw+woULl1YciZrNn71JqKSRaTguTQ7U\nbyJiVrn9duAm4HZgh4iYEBFTgS0oBvJLUjP8ruoAJI1uw1ERG6iPA3MiYjxwP3BxZnZGxBkUSdlY\n4NjMXNHXSSRpoCLiZcCHgJcByykSr3My8xGAzNy7wvAkaVgSsV57lJn5EPC6cvsBYKcejpkDzBmG\nOCRpnYh4O3ABcCHFcmxdFDcD/Soi3puZN/b1eklqhn4TMXuUktrUF4BdMvPO+p0RcR5wKrBjTy+S\npGbqc4xY2aO8GZhI0aP8OTCdokf5D9UtSWohE7onYQCZeTuuDCKpRfRXEbNHKaldra46AEnqT3+J\nWK89yoiwRympldXWyu1prkPbL0ktob9EzB6lpHZVv1Zud/2ulStJzdBfImaPUlJbGshauZJUtf4S\nsRHRozznnLNYsmRx/we2uNr3cPrpJ1UcyfCYMmUqBxxwaNVhaBSKiCWZOaXqOAZi+fLlrF69ivzR\nlVWHojqrly1n+QadVYehEaDPRGyk9CiXLFnM4iWL2WDSxKpDGZIx5fqay9asqjiSoVu9bHnVIWh0\n63GN3IGIiE8B7wTGA98AbgTOo5in7F7gsMxc2+sJJKnOek/o2k49SoANJk0k3vMvVYehkr17VWyg\na+Q+TblM2/bAG4BJwCeA04DPZOa8iPgmsDtw2TDFycSJE+naoMP2q8Xkj65k4rjxVYehEWAoM+uv\nd49SkhotIv65l6fGsP7t1y7AbykSrSnAJ4EDKapiANcAs+kjEZs2bRLjyur2QHR0jIU16xmtGqqj\nY6yL0Q9QR0cxbamf1z8aSiK2Xj1KSWqSGynaqZ6Srr+u5zmfA2wM7AbMAK4AxmZmrT1cCkzt6wSL\nFi0b1Bt2dnqVs1V1dq5l4cKlVYfRFmq/x6P18+orAe0zEWtQj1KSGi4zZ/R3TEQclJnfHsRpHwd+\nn5mrgIyIFcCL656fDDwxuEilno2UG81gZN1sNtw3mvVXEWtEj1KSWsUhwGASsZuBj0bEacA/Ac8A\nfh4RszJzHvB24IZhj1Kj0pIli1m6dDFTp7b3jWYA48cXl+PHjm3vm80WLx7+G836u2uyET1KSWoV\ng6rsZ+ZVEbEjcDvFWr2HAQuAORExHrgfuHjYo9SoNXXqRI499m1Vh6HSCSf8lLXDPFpgKGPEagbb\no5SaZqSU9kdSWR9aag65QY91zcyjeti90zDEImkUGo5EzLFialkjpbQ/Usr60JjSviS1q+FIxLx7\nUi3N0n5raURpX5La1diqA5CkCnmHo6RKDUdFTJJaTjmovleZ+YvMfHOz4pGkngxHImaPUlIr+nwf\nz3UBJmGSKtffhK4joke5fPlyVq9e5fqGLWT1suUs36Cz6jA0gmXmm3p7LiIGvsaQJDVQfxUxe5SS\n2lJETAQ+CDyemRfX7d8VOAXYsqrYJKmmvwldR0SPcuLEiXRt0EG851+qDkWl/NGVTBw3vuowNLKd\nT7Eu5NSIeC5wJTAHeD1wcpWBSVJNf5cm7VFKalevBTYDngX8BDgK+CmwT2YurDIwSarp79KkPUpJ\n7eqJzFwD/CUiXgz8e2ZeWnVQklSvv0TMHqWkdlU/2fSfTcIktaL+ErFh7VFGxL7AvuXDCcBWFNW1\nq4A/lPvPyswL1/c9JKk0vmy3xgId5fa6Jdky85HKIpOkUn+J2LD2KDPzPOA8gIj4OnAusDVwWmZ+\neSjnlqRungHcWG6P6bbdBbykiqAkqV5/iVhDepQRsQ2wZWYeFhFnFbtid4qq2BGZuXR9zitJdY7r\n4znXyJXUEvpLxBrVo/w0T81RdjtwdmbeGRHHAp8DPtHXi6dNm8S4cQOfPaOjYyysWc9I1TAdHWOZ\nPn1yw9+jy/9yW04zfvbAd4C/ANcBq8p9tY5kF/DdRgcgSf3pLxE7ro/n1uu/t4h4JhCZeUO567LM\nrC2TdBlwZn/nWLRo2aDes7Nz7aCOV3N0dq5l4cLGFj87O9cy1qXtW876/OzXI3F7DbAn8FbgbuBC\n4LrMtEHhU/F5AAAgAElEQVSQ1DL6S8Qa0aPcEfh53eNrI+LDmXk78BbgzvU4pyQ9TWbeBdwFfKoc\nDrEncGJE3AH8MDPnVRmfJEH/iVgjepQB/E/d40OBMyNiNfAYcNAQzi1J/yAz7wDuiIgdgJOAvYGN\nqo1Kkvpf4mjYe5SZeUq3x78G3jDY80hSfyJiDEUV/j3A2ynaszMpJqeWpMr1VxFbxx6lpHZS3pH9\nNuA3wEXA0Zn5ZLVRSdLT9ZuI2aOU1KYOBh4HXl1+nRgR657MTOcRk1S5/hb9tkcpqV3NqDoASepP\nfxUxe5SS2lJmPlx1DJLUn/4SMXuUkiRJDdLfXZP2KCWpTkQ8l2K+w7dSrNlxHsW8ivcChzlhrKTB\ncM5xSRqgiNgA+BawvNx1GvCZzNyBYrLr3auKTVJ7GvD0FZIkTgW+CXyqfLw1T63Bew0wm2Kptl65\nVu7I0eg1U10rtzUN98/dREwj2vLly1mzZhUnnPDTqkNRafHi5Ywb11l1GIMWEfsCCzPz2oioJWJj\nMrP2X+VSYGp/53Gt3JGj0evlulZuaxrutXJNxCRpYPYHuiJiZ2ArirV2n1v3/GTgiSoCk9S+TMQ0\nok2cOJGxYzs49ti3VR2KSiec8FPWrh1fdRiDlpk71rYjYh5wCHBKRMwql3t7O3BDNdFpJLKi33oa\nUdE3EZOk9fdxYE5EjAfuBy6uOB5JbcZETJIGKTNn1T3cqao4NLJZ0W89jajoOwxQkiSpIqOmIrZ6\n2XLyR+29TnnnqlUAdIxvv/E13a1ethymtP/3IUnSUIyKRGzKlH7vKG8LS5YVc0hOmjQCEpgp40fM\nz0VqtJHQkQQ7k1JPRkUidsABh1YdwrA4/fSTADjyyGMqjkRSs4ykDoudSekfjYpETJLa1UjpSIKd\nSaknDtaXJEmqiImYJElSRUzEJEmSKmIiJkmSVBETMUmSpIqYiEmSJFXEREySJKkiJmKSJEkVafqE\nrhHxa2BJ+XABcAJwHtAF3Asclplrmx2XJElSszU1EYuICcCYzJxVt+8K4DOZOS8ivgnsDlzWzLgk\nSZKq0OyK2KuASRExt3zvTwNbAzeWz18DzMZETJIkjQLNTsSWAacCZwObUSReYzKzq3x+KdDvKqrT\npk1i3LiOhgXZqjo6iiF906dPrjiS9tHRMZaurv6PU3N1dIz191iSaH4i9gDwYJl4PRARj1NUxGom\nA0/0d5JFi5Y1KLzW1tlZDJ1buHBpxZG0j87OtYz1lpSW09m5dtC/xyZukkaiZv8XtT/wZYCIeAEw\nBZgbEbPK598O3NTkmCRJkirR7IrYOcB5EXEzxV2S+wN/BeZExHjgfuDiJsckSZJUiaYmYpm5Cnh/\nD0/t1Mw4JEmSWoGjZyRJkipiIiZJklQREzFJkqSKNH2JI6nZFi9ezgkn/LTqMIZk2bJVAEyaNL7i\nSIZu8eLlTJ7cft9HRGwAnAtsAmwIHA/8DpdoUwONhPYLRk4b1oj2y0RMI9qUKcX8wGvb/L/GVauW\nAzBhQns3YgCTJ49f93NpM3sDj2fmPhHxLOCu8ssl2tQQI6X9gpHThjWi/TIR04h2wAGHVh3CsDj9\n9JMAOPLIYyqOZFT7EU9NrzMGWMN6LNE2WlcGAVcHGaxjjjmq6hCGzWc/+1kAvvjFL1YcSesxEZOk\nAcjMvwNExGSKhOwzwKmDXaJttK4MAq4OMpqN9p99X50PB+tL0gBFxIuBG4ALMvP7QP1FowEt0SZJ\n9UzEJGkAIuJ5wFzg6Mw8t9z9G5dokzQUXpqUpIH5NDAN+GxEfLbc91HgDJdok7S+TMQkaQAy86MU\niVd3LtEmab15aVKSJKkiJmKSJEkVMRGTJEmqiImYJElSRUzEJEmSKmIiJkmSVBETMUmSpIqYiEmS\nJFXEREySJKkiJmKSJEkVMRGTJEmqiGtNDpO5c6/mvvvuaeh7LFmyGIDTTz+poe8DsOWWM5k9e9eG\nv48kSaOZiVgbGT9+fNUhSJKkYWQiNkxmz97VCpIkSRoUx4hJkiRVpKkVsYjYADgX2ATYEDge+F/g\nKuAP5WFnZeaFzYxLkiSpCs2+NLk38Hhm7hMRzwLuAr4AnJaZX25yLJIkSZVqdiL2I+DicnsMsAbY\nGoiI2J2iKnZEZi5tclySJElN19RELDP/DhARkykSss9QXKI8OzPvjIhjgc8Bn+jrPNOmTWLcuI5G\nhyu1jI6OYjjn9OmTK45EkjScmn7XZES8GLgM+EZmfj8inpmZT5RPXwac2d85Fi1a1sgQpZbT2bkW\ngIULR2+x2CRU0kjU1LsmI+J5wFzg6Mw8t9x9bURsW26/BbizmTFJkiRVpdkVsU8D04DPRsRny30f\nA06PiNXAY8BBTY5JkiSpEs0eI/ZR4KM9PPWGZsYhSZLUCpzQVZIkqSIucSRJQxARY4FvAK8CVgIf\nyswHq41KUrsY09XVVXUMg7Zw4dL2C1oj1ty5V3Pfffc09D2WLFkMwJQpUxv6PgBbbjmzJddNnT59\n8piqY+hJROwBvDMz942I1wGfyszdezu+FduvZvwOQ/N+j1v1d7gV+bNvjr7aLytiUhsYP3581SGo\nd28EfgqQmbdFxDZ9HdyK8yBOnLjBurnqGmnDDTcEaPh7TZy4gdOdDJA/++pZEZPUFlq4InY2cElm\nXlM+fgR4SWau6el42y9p9Omr/XKwviQNzRKgvgs+trckTJK6MxGTpKG5BdgVoBwj9ttqw5HUThwj\nJklDcxnw1oj4b2AMsF/F8UhqIyZikjQEmbkWOKTqOCS1Jy9NSpIkVcRETJIkqSImYpIkSRUxEZMk\nSaqIiZgkSVJF2nJmfUmSpJHAipgkSVJFTMQkSZIqYiImSZJUERMxSZKkipiISZIkVcRETJIkqSIm\nYpIkSRUxEWthETErIhZHxIvr9p0UEftWGJYaKCIujohP1T2eHBEZEa+qMi5psGy/Rh/br/VjItb6\nVgLfiYgxVQeipjgEOCQiXl4+PgX4dmbeXWFM0vqy/RpdbL/Ww7iqA1C/rqdImA8DvlbbGREfB/YC\n1gC/yMyjqwlPwykz/xoRhwNnR8SngZcAh0bEK4EzgDHA48D+wHjgQorfjwnAIZl5VzWRSz2y/RpF\nbL/WjxWx9nAocGREvLR8PBl4L7B9+bVZROxWVXAaXpl5JfB74DvAfpnZBcwBDsvMWcDVwFHAthSN\n2tsp/qN7RiUBS32z/RpFbL8Gz0SsDWTm48ARwPk81Xu4LTNXl7/kNwFbVhiiht93gV9m5h/Lx1sA\n34iIeRS9yRcC1wC3AD8GvgCsrSBOqU+2X6OS7dcgmIi1ibKXkcC+wApgu4gYV4692BF4oMLw1HgJ\nfLDsUR4FXAXMAh7NzNnA8cCJlUUn9cH2a9Sz/eqDY8TayxHAW4ClwEUUvYmxwM3A5RXGpcY7FPhu\nRIwDuoADKMr6P4yIQyn+lr9QYXxSf2y/Ri/brz6M6erqqjoGSZKkUclLk5IkSRUxEZMkSaqIiZgk\nSVJFTMQkSZIqYiImSZJUEaevUMuIiFcAvwXenZmXlPseophvZiawTWb+R1XxSVJvbL+0vkzE1Er2\nAy6mWDj2kvonMvMK4IoqgpKkAbD90npxHjG1hHKivz8COwD/DWyXmfPrepS1r0uBgzJzt/J1hwOb\nA0cCp5THdADnZebpTfwWJI1Stl8aCseIqVW8A3g4Mx+gmGX74F6OuwZ4TURMKx+/D/gecCBAZr6G\nYjHZ3SNih8aGLEmA7ZeGwERMrWI/4Afl9oXAvhExvvtBmbmaolf5bxGxMfDszLwd2Bl4Z0TcBfwS\neBHwyqZELmm0s/3SenOMmCoXEc8FdgW2iYiPAmOAacC/9fKS7wFfLI/5frmvAzgqMy8tz/kc4MlG\nxi1Jtl8aKitiagV7Az/PzBdl5iaZuTFwAr2U9zPzNuAFwD4UjRrA9cCBEbFBRGxEsZDwdo0PXdIo\nZ/ulITERUyvYD/hGt33foBgrMaGX11wI/D0z/6d8/E3gD8BvgDuA72TmvOEPVZKexvZLQ+Jdk5Ik\nSRWxIiZJklQREzFJkqSKmIhJkiRVxERMkiSpIiZikiRJFTERkyRJqoiJmCRJUkVc4kj/ICK6gOmZ\n+dcK3vde4OjMvLrbc/sDn6T4nb0O+Ei5blv3c/R5XLn+2y+AizPz1HLfdsDXgWcAfwL2zsxHI2JD\n4AzgzcDfgSuB4zJzbUTMBM4qX9MFfDozr+kWy7uA72bmlPLxxPJ9XkvRCfolcFhmLo+INwGnABsA\ny8u4b4+Ia8vjT6zFK6l3I7H9iohJwNnAqynajqMz8/Jur90WuAl4YffvPSJOBzbLzN0i4pnAvG5v\n/Urgk5l5WkR8GXgP8LfyuczMPSOiAzgN2KWM79TM/GZ5ftuvIbAiplbzph4asVcAnwd2BAJ4JnBk\n9xcO8LivAJvWvWY8cDHw0czcotw+p3z608DGFI3U1sA/Af9ePvc94JTM3IpiqZKL6hf5jYjNgFN5\n+t/YsRQN2KuAmcBE4FPl6y4EDszMVwHHAxcAZOYuwBW9flqSWkmj2q/jKGbi3wJ4K/CNiHhR3Wuf\nQ9Ex/IeFxiPivRTLMAGQmU9k5la1L4r27mbgzPKQ7YG96o7Zs9x/MLAZ8AqK5OqIiNjW9mvorIi1\noYiYRdH7+CPwEooeyL6ZeX+346YC/wtsnpmPlftuo/hjn09RndmIYt2zu4A9M3NF3ev3Bd6dmbt1\nf1z+8Z0M7ESxYO1vKHpBS7rFcAywVw/fxlsy8/EBfsu7A1dk5sLynN+iqFT952COi4h9gKnAT+pe\n81pgSWbeUj4+B/hKRDybIvn6Ye0ziYjLKXqrXwNeA3SWr9kUeKL2uOy9fg/4GE8t6gtFJe6hzFxb\nHvcbYMvMXBURLyx7vmMofqYD/WyktmL7tV7t178C7wfIzEciYi7wXuC0iBhL0d58Gvhpt/i3AI4C\nvkBRyaLb8y8FPgO8tmx/NqSoun0iIjYFHgSOzMxHyhi+nZlrgEUR8UOKqwe3234NjRWx9vUa4MuZ\nORP4DmUPpF5mLgYuo+wNlX+U/wRcCxwInJ+ZrwdeCswA3jGI9z8GWANsXfaC/gSc1EMMJ9X3vuq+\nBvOH+mKKBrnm/4AXDea4iHgl8FHgoL5ek5mrgIXACykuHe4ZERuVDff7KT4/ysaIiJgPXAqcnJm1\nxOxb5dc99W+UmXMz84HydRsDRwA/Kp9bHRHPK2M+hX9spKWRxPZrcMf19dwXgNsz89r6k5WLh18A\n7Ass7SW2E4Azy0QLiqT2euBTwFbAbcCPywSr1xhsv4bGilj7ujszbyq3zwW+HhHP7qGBmENRsj6V\nYnHa75RjnI4G3hoRRwGbU/wBbjSI99+NonT+1oiAoiT+l+4HDVOPsqcOQ2cP+3o8ruxZXwC8PzOf\nLOPt6zW1858MnAjcCiyiKL/PrB2QmV3AphExA7gpIn4HvAxYk5nnRsQmPZ04Iram+A/ma5l5Vd35\n/gy8MCJeA/w8In5XS9ykEcb2a3DH9da2vQPYjh6qXRTV/TMz896I2Kb7kxHx4vJ1H6rty8wFwK51\nx5wKfBbYpL/vw/Zr/ZmIta81ddtjyq/OiLirbv+HMvPmiBhXDuR8P8X1f4AfUPz8L6K4VPfP5Tnq\ndXXbVz/+oINiXNU1sK73NaF7kJl5Ej30NAfpEcpKVOmFFD2vgR63C0Wj+/2y0f1nigZ4CjC3/jUR\nsQHwHIrLJs+i6LV/onxuT+DBsjq2B3BRZq7NzAURcR1FSX9PYFL5cxgPTCy3d83MP0XEXsA3gMMz\n8/vleacCb87MywAy89cRcTfF2DQbMo1Etl+DO6723GN1z90F7E9Rlfp1XQfzhog4FNgBiIg4kqIt\nmxoRV2dmLdF6N3BZZq6rlpU3Ib0qM+srlGOA1b3FZ/s1dCZi7WuriJiZmfdQXG67JTOfoCgnd3c2\nxUDMe+pK0LsAO2Xm3RHxcope1YXdXrcQeEVETKBoOP+l7rlrgcMj4uflc3Mo7iw8cHi+vae5gqI8\nfkIZ00HA5QM9LjMvomiwAYiI84B7M/PUMvF6dkRsn5n/TdGw3ZqZT0TEQcBuEbE7xd2RH6MYoL8q\nIo6n6CF+PyJeALyJosL15br32aR8n63Kx++mGPMxOzPvqIu7Ezg3Iv6SmbdExJYUlbVfDulTk1qX\n7dfgjvtx+fjQcpD+24DjM/Or9SeI4s7NN2Vx1+QL6vbvS914udJOFDcn1VsLnBERN5fVsUMpPvf/\ni4gfA/tHxJUU1ce9gEOw/Royx4i1r8eAEyLit8C7KO7c6835FA3c2XX7Pg1cFhF3AN8EbqQYa1Fv\nbrn/9xS3Rf+27rkvAg9RDHL9HUWv6ePr+b30qWysv0AxduH3PHXZkIh4Z0Rc3d9xfZx7NUV16ysR\ncR/wAYpLIFBcMllIcUv6HRQVsFrD9a/AIWUP/iqKW7/voG9foviczo6Iu8qvr2fm3yl+hl8pz3cu\nxWXUnnrN0khg+8Wg2q/PARuVbdR1FO3N/CGGthnFZ1Af673Ah4ErI+J+inbufeXTZ1HcJHE38Cvg\nnMy80fZr6MZ0dXVVHYMGqbzr6GuZ+YqqYxlOUdH8P62uvoJXdSzSUNl+jS62X/2zIqZWc0NE7Nr/\nYaNDFBMivrPqOCQNiO1XHduvgbEiJkmSVBErYpIkSRUxEZMkSapIW05fsXDhUq+nSqPM9OmTu88T\n1ZZsv6TRp6/2y4qYJElSRRpaEYuI7SjW4JsVEc+lmDRvGsWsxh/MzPkRcSDFqu5rKCaou6r3M0qS\nJI0cDauIlWuAnc1Ty0b8J/BfmbkjxWrvL4uI5wMfAd5AMVPyl6JY/V2SJGnEa+SlyfkUM5bXvAF4\nUbkm3weAecC2FEtbrMzMxcCD1C2qLEmSNJI17NJkZl5SrrVXswmwKDN3joj/AI6mWBB0cd0xS4Gp\n/Z172rRJjBvXMYzRSpIkNV8z75p8nGJRU4ArgRMo1u+bXHfMZOCJ/k60aNGyYQ9OUmubPn1y/wdJ\nUptp5l2TNwO1pR92BO4Dbgd2iIgJETEV2IJigWVJdRYsmM+CBUNd41eSqmEb1rtmVsQ+DpwdEYdS\nXI58f2YuiogzgJsoksJjM3NFE2OS2sK8edcBMGPGphVHIkmDZxvWu4YmYpn5EPC6cvth4K09HDOH\nYloLST1YsGA+Dz+8YN22DZmkdmIb1jcndJVaXK0n2X1bktqBbVjfTMQkSZIqYiImtbhZs3bucVuS\n2oFtWN/actFvaTSZMWNTNt54xrptSWontmF9MxGT2oC9SEntzDasdyZiUhuwFympndmG9c4xYpIk\nSRUxEZMkSaqIiZgkSVJFHCMmSb2IiO2AkzNzVkRsBZwJdAIrgQ9m5p8j4kDgYGANcHxmXlVdxJLa\njRUxSepBRBwFnA1MKHd9FfhwZs4CLgWOjojnAx8B3gDsAnwpIjasIFxJbcpETJJ6Nh/Yo+7xXpl5\nV7k9DlgBbAvckpkrM3Mx8CAws7lhSmpnXppsIwsWzAe8DVhqhsy8JCI2qXv8KEBEbA8cDuxIUQVb\nXPeypcDUvs47bdokxo3rGPZ4JbUnE7E2Ulss1URMqkZE7AkcC7wjMxdGxBJgct0hk4En+jrHokXL\nGhihpFY0ffrkXp8zEWsTCxbM5+GHF6zbNhkbXW699SYAXv/6HSqOZPSKiL0pBuXPysy/lbtvB06I\niAnAhsAWwL0VhSipDTlGrE3UqmHdtzU6zJv3c+bN+3nVYYxaEdEBnEFR8bo0IuZFxOcz87Fy/03A\n9cCxmbmiwlAltRkrYlKLu/XWm1i5csW6batizZOZDwGvKx8+q5dj5gBzmhWTpJHFilibqF8w1cVT\nR5f6SphVMUkaWayItYkZMzZl441nrNuWJKldeNd/70zE2oiVsNFp1qy3cO21P1m3LUntxrv+e+el\nyTYyY8am/hKPQq9//Q5suOEENtxwguPDJLWd2l3/Dz+8YF1lTE+xIia1ASthktpV97v+LSg8nYmY\n1AashEnSyNTQS5MRsV1EzOu27/0RcWvd4wMj4o6IuC0idmtkPFK7WrBgviV9SW3Ju/771rCKWEQc\nBewDPFm379XAAcCY8vHzgY8A2wATgJsj4meZubJRcUntyIGuktqVd/33rZGXJucDewAXAETEs4ET\ngSN4avLDbYFbysRrZUQ8CMwEftXXiV00V6PJAw88sG55q0WLHmXzzTevOCJJGhwrYb1rWCKWmZdE\nxCawbnmQc4CPAcvrDpsCLK57vBSY2t+5XTRXo8nll1/xtO399ju4wmiq09eiuZJam5Ww3jVrsP7W\nwGbAWRSXIF8eEV+hWJutvnWdDDzRpJgkSZIq1ZRELDNvB7YEKKtkP8zMI8oxYidExARgQ2AL4N5m\nxCS1i1mzdub88+es25aG29y5V3Pfffc0/H1WrCguiEyYMLGh77PlljOZPXvXhr6HNFwqnb4iMx+L\niDOAmyju4Dw2M1dUGZPUahzoqpFi1apVQOMTMamdjOnq6qo6hkFbuHBp+wUtDYHrtMH06ZPHVB3D\ncBjN7dfpp58EwJFHHlNxJFJz9dV+OaGr1AZGcwImSSOZa01KkiRVxERMkiSpIiZikiRJFTERkyRJ\nqoiJmCRJUkVMxCRJkipiIiZJklQREzFJkqSKOKGrNETNWKevWWv0gev0SVIzWRGT2sCqVavWrdMn\nSRo5rIhJQzR79q4NryC5Rp8kjUxWxCRJkipiIiZJklQRL01KUi8iYjvg5MycFREvBc4DuoB7gcMy\nc21EHAgcDKwBjs/MqyoLWFLbMREbJt45J40sEXEUsA/wZLnrNOAzmTkvIr4J7B4RtwIfAbYBJgA3\nR8TPMnNlJUFLajsmYm2kdtdcMxIxScwH9gAuKB9vDdxYbl8DzAY6gVvKxGtlRDwIzAR+1dtJp02b\nxLhxHQ0LupV1dBSjYaZPn1xxJFLrMBEbJt45J40smXlJRGxSt2tMZnaV20uBqcAUYHHdMbX9vVq0\naNlwhtlWOjvXArBw4dKKI5Gaq6/Oh4P1JWlg1tZtTwaeAJaU2933S9KAmIhJ0sD8JiJmldtvB24C\nbgd2iIgJETEV2IJiIL8kDYiXJiVpYD4OzImI8cD9wMWZ2RkRZ1AkZWOBYzNzRZVBSmovJmKS1IvM\nfAh4Xbn9ALBTD8fMAeY0NzJJI0VDE7Fuc/BsBZxJcZfRSuCDmfln5+CRJEmjVcPGiJVz8JxNMbcO\nwFeBD2fmLOBS4OiIeD7FHDxvAHYBvhQRGzYqJkmSpFbSyMH6tTl4avbKzLvK7XHACmBbyjl4MnMx\nUJuDR5IkacRr2KXJ7nPwZOajABGxPXA4sCNFFWxQc/DA6J0Q0ckQRy9/9pI0MjV1sP7/b+/+o+ys\nykOPfzMzGTLRmTRqoF6lgMv62HJFi96qtEBUiIAo916rtr3oBSNKmrY02iIItvgjShWJ9boQ5QrI\ndVnlh1RBQaoIor2KWFBAeVCrdenylohhkpCBSWbm/vGewSEmc+bHe84+Z+b7WWvWOuc957zvM5xh\n59n73fvZEfEq4CzgJZm5OSLmVINnsRZEtBji4uV3bxIqaWFqWyIWESdSTcpfnZm/bBy+FdgYEcuA\nfbAGjyRJWkTakohFRC/wAeAnwKcjAuDmzPw7a/BIkqTFqqWJ2NQaPMDj9vIea/BIkqRFyS2OJEmS\nCjERkyRJKsRETJIkqRATMUmSpEJMxCRJkgoxEZMkSSrEREySJKkQEzFJkqRCTMQkSZIKMRGTJEkq\npG2bfkuSpM5yww2f5+67v9Py6zz00AgAy5YNtPQ6Bx98CGvWHNfSa9TNETFJktRSo6OjjI6Olg6j\nIzUdEYuIk4G7MvObjefvBr6fmRe3OjhJmq+IeM1uhyaAEeCezLyrQEhSx1iz5ri2jCBt2nQuABs2\nnNHya3WbaUfEIuIvgFOBrVMOXwesi4h1rQxMkmpyAnAO8KzGz1uB9cAlEbGhYFyS1PTW5Frg6MzM\nyQOZ+RXgWKoETZI63W8Ch2bmGzPzjcBzqNq+5wMnlQxMkpolYuOZuXX3g5n5C2C8NSFJUq1WAdum\nPB8BHpeZu6huU0pSMc3miO2KiH0z876pByNiP6C3dWFJUm2uAm6MiMupOp8vB/6pMXfs50Ujk7To\nNUvEPgh8vjGP4lZgCdWw/vuAj7Q4Nkmqw9lU0ymOBsaAv8/M6yLiecCfFo1M0qI3bSKWmZdFxDLg\n48CTG4f/DTgvMz/c6uAkqQbfzMxDgWunHszMrxeKR5Ie0bR8RWZ+BPhIRDyeas7YFoCIeFpm3tvq\nACVpnv4jIg4Hbs3Mh+dzoohYCnwMOJBqdO0UYBdwKdV8s7uA9ZnpHFpJMzLjgq6ZeT+wLSJeFRFf\nBv61dWFJUm2eA9wMjETEeONnbI7nOg7oy8zDgLcDG4HzgbMz83Cq6Rsn1BG0pMVhRlscRcRBwBuA\nk4HfAN4FvLKFcUlSLTJzVY2nuxfoi4geYAjYCTyPKtGDqs7iGuDqGq8paQGbNhGLiP9GVS/sUKqG\n5UTgosx8Wxtik6R5i4i/3dPxzHz7HE63neq25D3AE4DjgSMyc7IMxjZgxXQnWLlyOX19i3PReW9v\ndRNm1arBwpGo3fzu967ZiNhVwBXA8zPzBwARMeO5DxHxXKoVSqsj4qnsYR5FRJxCNdq2C3hnZl67\n1xNK0uwtmfJ4KXAM8I05nmsD8IXMPDMi9gduBPqnvD4IPDDdCbZs2THHS3e/sbHqn4/Nm7c1eacW\nmsX+3U+XgDZLxA6hqjz91Yj4MfCPM/gMABFxOvBq4MHGocl5FDdFxIXACRHxf4G/pJrDsaxxnX+e\n74RaSZq0+wh+RLwDuGGOp9tCdTsS4JdUid3tEbE6M2+iKpPx5TmeW9IiNO1k/cy8KzP/GngS8G5g\nNbBfRHwuIl7S5Nw/BP77lOfP5tHzKI4Cfh/4WmY+nJnDwA+okj9JapXHAr81x89uAg6NiFuoRsPe\nQim6gG4AABamSURBVLVv5dsaHct+4MpaopS0KMxodCszx4DPAJ+JiFVUI13vAj43zWeuiogDpxxa\nsod5FEPA8JT3NJ1fAYt3joX32Bcvv/u5i4gf8autjHqoFhy9dy7nyszt7Hmh0pFzi07SYtdssv4R\ne3nptsbPbEydWzY5j2Jr4/Hux6e1WOdYLPZ77IuZ3/28ktDVUx5PAA/saQ9dSSqh2YjY5NyKxwNP\nBb5GVcTwMOA7wB/O4lp7mkdxK7CxUb1/H+B3qCbyS9K8RcQTqBKv4cYI/R8Bt1PdVpSk4prNEXtB\nZr4A+ClwSGYenZnHAM+gWsY9G29it3kUmfn/gA8Ak/MtzsrMh2b7S0jS7iLixcDdwCERsR/wTeD3\ngHc0VmtLUnEzmiMGHDBZvqLhJ8ABzT6UmT+mKnZIYzukX5tHkZkXARfNMA5Jmqm3AX+Ymd9vrOK+\nMzNPjIjlwNex3ZHUAWaaiH0rIj4GXE41ivanVKNYktSplmXm9xuPXwh8FiAzdzQq40tScTNNxF4H\n/AVVlf1x4EvABa0KSpJqsCQilgADVPNZ3wQQEY9pHJOk4mZavmIUeF9EfA74XeCbmbmrpZFJ0vxc\nTVV2pxe4IzPvjohDqDbrvqJoZJLUMO3wfES8KCJ+FhF3RsRJwBeBPwZujoiXtiNASZqLzDwH+Djw\nBao9IQFeBNwBnFUoLEl6lGYjYu+hmlvxFKqe5VMz8ycR8UTgWuCaFscnSXOWmZdDdTuyMRr2D8BA\no0i1JBXXbMLq0qxcB9yYmT8ByMyfU+2xJkkdLSJeCHybqjO5H/DjiFhTNipJqjRLxO6NiHMjoqdR\nP4yI+M2IeD/wvdaHJ0nz9m6qyfoPNDqRRzLHLY4kqW7NErH/CezIzKnbEz0NeBhY27KoJKk+PY3i\n0QBk5ndLBiNJU007RywzH6RaYTT12FeAr0w+j4hrM/P43T8rSR3ipxFxPDAREb8BrKcqSi1JxdVR\n1PBJNZxDklrlDcD/APYHfgg8C3h90YgkqWGmBV2nM1HDOSSpVf4yM/+kdBCStCdu8yFpoXtpo8K+\nJHWcOkbEJKmT3Q/cExH/CoxMHszM15YLaeY++tEPsXXrcOkwajH5e2zadG7hSOoxNLSCtWvXlQ5D\nXa6ORMyepqRO9rHSAczH1q3DDG8dZuny7t8ec0lfLwA7do0WjmT+du4Yaf4maQbqSMS6upGTtHA1\nqulvp9oft2tXSi5dPkC8wl3lOkle4cYyqse854hl5vvrCESS6hQR64GbgL8B7oiIl5eNSJJ+3bQj\nYhFxCdOsiuyWORaSFqU/A56emfdFxDOBC4GrCsckSY/S7NbkLcD7qXqUD7U+HEmqzWhm3geQmd+O\niMeUDkiSdtessv7FEfE04KDMPKNNMUlSHXYfzd9VJApJmsZMJuv/HXBEqwNppYWy/Nul39KsPD4i\nXrO355l5WYGYJOlRmiZimfkw8M97ez0izsnMc+oMqm4LZfm3S7+lWbkReMFenk8AJmKSiqujfMXL\ngHNqOE9Lufy7s7j0W62WmSc3e083dCQlLWx1bHFkQVdJ3eplpQOQtLi1ddPviFhKVQD2QGAMOIVq\nAu2ljfPcBazPzPEa4pKkZuxISiqq3XtNHgf0ZeZhEXE0sBFYCpydmTdFxIXACcDVbY5L0uI0447k\npIg4k2okrR+4ALgZO5OS5qjdidi9QF9E9ABDwE7geVQNGcB1wBqaJGIrVy6nrzFxfSZ6e3tcuN6B\nent7WLVqsHQYXaG3t5pF4H+vsiJiNXAY8AfAcuCvgfOxMylpjupIxL47i/dup7oteQ/wBOB44IjM\nnOyVbgNWNDvJli07ZhXg2Jid0040NjbO5s3bSofRFSb/hhfzf68OSUJfDNxJlWgNURW7PoVZdiYl\naVLTRCwing68Dng6MEKVeH10cgPdzDxxFtfbAHwhM8+MiP2plpP3T3l9EHhgFueTpPmYTUcSqg7k\nAVSdyIOAzwI9s+lMOqK/cDiqP3OO6u9ds70mjwX+D/Ap4HNUcyAOAb4ZEa/MzJun+/webKG6HQnw\nS6r5YbdHxOrMvAk4FvjyLM8pSXtUc0cS4H7gnswcBTIiHgL2n/J6086kI/oLh6P6M7fYR/WnS0Cb\njYi9HXhxZn5r6sGIuBQ4j9lX3N8EXBwRt1CNhL0FuA24KCL6ge8BV87ynJL0a1rQkQT4KnBaRJwP\nPBF4DPAlO5OS5qpZIrZs9yQMIDNvjYjHzvZimbkdeOUeXjpytueSpCbq7kiSmddGxBHArVR1GNcD\nP8LOpKQ5apaI7WzyutTR3Ge0M7Vpn9FaO5JTPn/6Hg7bmZQ0J80SscGIOJw9Fz2cc0MmtcvWrcNs\n2zbMihXdvc9of381ubunp/v3GR0ebts+o3YkJXW8ZonYT6mG9/fkZzXHIrXEihUDnHXWMaXDUMPG\njdcz3p7553YkJXW8aROxzHxBuwKRpJrZkZTU8eZc0DUitmbmUJ3BSFJd7EhK6gY98/ism+VK6koR\nsbV0DJIE80vEZr1ZriR1CDuSkjpCs8r6v7WXl5ZgQyape9mRlNQRms0Ru5mqwdpT0vWL+sORpHrY\nkZTUDZqtmjyo2Qki4vWZ+ZH6QpKkWtiRlNTx5rxqcopTARMxSR3FjqSkblBHItbxQ/wjIyPs3DlK\nXnFN6VDUsHPHCCNLx0qHIdmRlFTUfFZNTnLSq6Ru1fEdSUkLWx0jYh1vYGCAiaW9xCteWjoUNeQV\n1zDQ1186DMmOpKSi6hgRkyRJ0hzUkYg9UMM5JEmSFp1mBV2PmO71zPxKZr6w3pAkqW3sSEoqqtkc\nsbdN89oEYBImqSPZkZTUDZoVdH3B3l6LiN76w5Gk2tiRlNTxmt2aHABeA9yfmVdOOX4c8F7g4NaG\nJ0lzY0dSUjdodmvyY8ABwIqI2Be4BrgIeD7w9y2OTZLmzI6kpG7QLBH7L8BvA48DPgecDlwPvDoz\nN7c4NkmaDzuSkjpes0TsgczcBdwXEfsDf5aZn57PBSPiTOBlQD9wAdXGvJdSzdm4C1ifmePzuYYk\nYUdSUhdoVkdsatXp/6ghCVsNHAb8AXAksD9wPnB2Zh5Otd3ICfO5hiQ1PJCZuzLzPqq25o2ZeapJ\nmKRO0mxErL8xEtYD9DYeP7I3W2b+ZJbXezFwJ3A1MAT8DXAK1agYwHXAmsbrkjQftXYkJakVmiVi\nj+FXSdKS3R5PAE+Z5fWeQDVn43jgIOCzQE9mTjaY24AVzU6ycuVy+vpmvuipt7cHds0yUrVcb28P\nq1YNtvQaDz/8EKOjD7Nx4/UtvY5mbnh4hP7+8ZZ/99TfkZSk2jVLxM6Z5rW5bJZ7P3BPZo4CGREP\nUd0ymDTIDCpdb9myY1YXHRtzylknGhsbZ/PmbS29xvi4ezp3ovHxiVl/93NI3OruSEpS7ZolYpcA\n9wFfBEYbxyZ7lBPAZbO83leB0yLifOCJVA3llyJidWbeBBwLfHmW55T2amBggJ6eXs4665jSoahh\n48brGR/vb8elzpnmNTN0SR2hWSJ2KPAq4Gjg28CngC/OdVVjZl7b2HbkVqrbBeuBHwEXRUQ/8D3g\nymlOIUkzVXdHUpJq12yLozuAO4AzI+I5VEnZuyLiNuCTjVGsWcnM0/dw+MjZnkeSmqi1IzmpUZPs\nW43z7sLyO5LmodmI2CMy8zbgtog4HDgXOBF4bKsCk6T5aEVHMiKWAh8GRhqHJsvv3BQRF1KV33HV\nt2rx0Y9+iK1bh0uHUYvJ32PTpnMLRzJ/Q0MrWLt2XW3na5qIRcQS4AjgFVRzuO4A/hdVlWpJ6ng1\ndiTPAy4Ezmw8fzazLL/jqu+Fo9Urvx98cBvbtg2zYsVAy67RLv391d98T89ok3d2tuHhkdq/92ab\nfn8IOAa4HbgceHNmPljb1SWphersSEbEScDmzPxCY4cQgCWzLb8z21Xf27c/yM6do+QV9n07yc4d\nI2zfOdbSld9jY+OsWDHgYqMOsnHj9XNa8T9d4tZsROwNVCUnfq/x866IeOTFzHT5t6SO1IKO5GuB\niYg4CngW1WT/fae8PqPyO5I0VbNE7KC2RCFJ9au1I5mZR0w+joibgFOB97a6/M7AwAATS3uJV7y0\n7lNrHvKKaxjoa0sZFi1wzVZN/nu7ApGkmrWjI/kmLL8jaR5mvGqy2+3cMdL1cyzGRqtJjr393d8L\n27ljBIa6//dQ52plRzIzV095avkdSXO2KBKxoaGm82e7wtYd1Yr55csXQAIz1L9gvhdJkuZqUSRi\nddb7KGmy/sqGDWcUjkSSJNWhp3QAkiRJi5WJmCRJUiEmYpIkSYWYiEmSJBViIiZJklSIiZgkSVIh\nJmKSJEmFmIhJkiQVYiImSZJUiImYJElSISZikiRJhZiISZIkFWIiJkmSVIiJmCRJUiF9JS4aEfsC\n3wKOBnYBlwITwF3A+swcLxGXJElSO7V9RCwilgIfBkYah84Hzs7Mw4ElwAntjkmSJKmEEiNi5wEX\nAmc2nj8buLnx+DpgDXD1dCdYuXI5fX29LQuwU/X2VnnzqlWDhSPpHr29PUxMlI5Cu+vt7fHvWJJo\ncyIWEScBmzPzCxExmYgtyczJfyq3ASuanWfLlh0tirCzjY1Vd2w3b95WOJLuMTY2To8zITvO2Nj4\nrP+OTdwkLUTtHhF7LTAREUcBzwIuA/ad8vog8ECbY5IkSSqirWMFmXlEZh6ZmauBO4DXANdFxOrG\nW44FbmlnTJIkSaUUWTW5mzcBF0VEP/A94MrC8UiSJLVFsUSsMSo26chScWjhGx4eYePG60uHMS87\ndowCsHx5f+FI5m94eITBwe7/PSSpDp0wIia1zNBQtfZjvMsr042OVtVeli3r/gRmcLD/ke9FkhY7\nEzEtaGvXrisdQi02bToXgA0bzigciSSpTi7slyRJKsQRMUmagcauIBcDBwL7AO8EvotbtEmaB0fE\nJGlmTgTub2zHdgzwQdyiTdI8mYhJ0sxcAby18XgJsItf36LtqAJxSepi3pqUpBnIzO0AETFIVe/w\nbOC82W7RNtu9cnt7e6qUTx2n1XumulduZ6r7ezcRk6QZioj9gauBCzLzExHxnikvz2iLttnulTu5\nx6w6z1z2TJ2N7dsfZNeu0a6vg7iQDA+P0Nc3Vuteud6alKQZiIj9gBuAN2fmxY3Dt7tFm6T5cERM\nkmbmLcBK4K0RMTlX7DTgA27RplYYGBigp6eXs846pnQoati48XrGx+strG0iJkkzkJmnUSVeu3OL\nNklz5q1JSZKkQkzEJEmSCvHWpCR1uJ07RsgrrikdxryNjY4C0Nvf/ZvX79wxAkPd/3uoPBMxSepg\nQ0NNS5N1ja07RgBYvnwBJDBD/Qvqu1E5JmI1ueGGz3P33d9p6TW2bh0GYNOmc1t6HYCDDz6ENWuO\na/l1JE1v7dp1pUOozWTbtWHDGYUjkTqHiVgX6V8Aw/mSJOlXTMRqsmbNcY4gSZKkWXHVpCRJUiEm\nYpIkSYWYiEmSJBViIiZJklRIWyfrR8RS4GLgQGAf4J3Ad4FLgQngLmB9Zo63My5JkqQS2j0idiJw\nf2YeDhwDfBA4Hzi7cWwJcEKbY5IkSSqi3YnYFcBbG4+XALuAZwM3N45dBxzV5pgkSZKKaOutyczc\nDhARg8CVwNnAeZk50XjLNqDpnhErVy6nr6+3ZXFKnaa3t+ozrVo1WDgSSVKd2l7QNSL2B64GLsjM\nT0TEe6a8PAg80OwcW7bsaFV4UkcaG6umTW7evK1wJOWYhEpaiNp6azIi9gNuAN6cmRc3Dt8eEasb\nj48FbmlnTJIkSaW0e0TsLcBK4K0RMTlX7DTgAxHRD3yP6palJEnSgtfuOWKnUSVeuzuynXFIkiR1\nAgu6SpIkFWIiJkmSVIiJmCRJUiFtL18hSZJmZnh4hI0bry8dxrzt2DEKwPLl/YUjmZ/h4REGB+v9\nHUzEJEnqQENDVX3z8QWw+/Lo6AgAy5Z1dyI2ONj/yPdSFxMxSZI60Nq160qHUJtNm84FYMOGMwpH\n0nmcIyZJklSIiZgkSVIhJmKSJEmFOEdMkuYhInqAC4BnAg8Dr8vMH5SNSlK3cERMkubnvwLLMvP5\nwBnA+wrHI6mLLJmYmCgdw6xt3ryt+4LWgnXDDZ/n7ru/09JrbN06DFD7suk9OfjgQ1iz5riWX2e2\nVq0aXFI6hj2JiPOBWzPzk43nP8vMJ+3t/Z3YfrXjbxja93fcqX/Dncjvvj2ma7+8NSl1gf7+7q69\ns8ANAcNTno9FRF9m7trTm1euXE5fX297IpuhgYGl9Pa2/gbJPvvsA9Dyaw0MLGXVqsGWXmOh8Lsv\nzxExSV2hw0fEvp6Zlzee/zQzn7y399t+SYvPdO2Xc8QkaX6+BhwHEBHPA+4sG46kbuKtSUman6uB\noyPiX4AlwMmF45HURUzEJGkeMnMcOLV0HJK6k7cmJUmSCjERkyRJKsRETJIkqRATMUmSpEJMxCRJ\nkgoxEZMkSSqkKyvrS5IkLQSOiEmSJBViIiZJklSIiZgkSVIhJmKSJEmFmIhJkiQVYiImSZJUiImY\nJElSISZiHSwiVkfEcETsP+XYuRFxUsGw1EIRcWVEnDnl+WBEZEQ8s2Rc0mzZfi0+tl9zYyLW+R4G\nLomIJaUDUVucCpwaEb/beP5e4COZ+e2CMUlzZfu1uNh+zUFf6QDU1I1UCfN64IOTByPiTcAfA7uA\nr2Tmm8uEpzpl5i8i4s+B/x0RbwGeAqyLiGcAHwCWAPcDrwX6gU9R/X0sA07NzDvKRC7tke3XImL7\nNTeOiHWHdcCGiHhq4/kg8ErgsMbPb0fE8aWCU70y8xrgHuAS4OTMnAAuAtZn5mrg88DpwO9TNWrH\nUv1D95giAUvTs/1aRGy/Zs9ErAtk5v3AXwEf41e9h69n5s7GH/ktwMEFQ1T9LgO+kZk/azz/HeCC\niLiJqjf5JOA64GvAZ4C3A+MF4pSmZfu1KNl+zYKJWJdo9DISOAl4CHhuRPQ15l4cAdxbMDy1XgKv\nafQoTweuBVYDP8/MNcA7gXcVi06ahu3Xomf7NQ3niHWXvwJeBGwDLqfqTfQAXwX+qWBcar11wGUR\n0QdMAGuphvU/GRHrqP5ffnvB+KRmbL8WL9uvaSyZmJgoHYMkSdKi5K1JSZKkQkzEJEmSCjERkyRJ\nKsRETJIkqRATMUmSpEIsX6GOERH/GbgT+KPMvKpx7MdU9WYOAZ6TmX9bKj5J2hvbL82ViZg6ycnA\nlVQbx1419YXM/Czw2RJBSdIM2H5pTqwjpo7QKPT3M+Bw4F+A52bmD6f0KCd/Pg28PjOPb3zuz4Gn\nARuA9zbe0wtcmpmb2vgrSFqkbL80H84RU6d4CfDvmXkvVZXtN+zlfdcBh0bEysbzPwE+DpwCkJmH\nUm0me0JEHN7akCUJsP3SPJiIqVOcDPxj4/GngJMion/3N2XmTqpe5csj4gDg8Zl5K3AU8LKIuAP4\nBvBk4BltiVzSYmf7pTlzjpiKi4h9geOA50TEacASYCXw8r185OPAOxrv+UTjWC9wemZ+unHOJwAP\ntjJuSbL90nw5IqZOcCLwpcx8cmYemJkHABvZy/B+Zn4d+E/Aq6kaNYAbgVMiYmlEPJZqI+Hntj50\nSYuc7ZfmxURMneBk4ILdjl1ANVdi2V4+8ylge2b+W+P5hcD3gduB24BLMvOm+kOVpEex/dK8uGpS\nkiSpEEfEJEmSCjERkyRJKsRETJIkqRATMUmSpEJMxCRJkgoxEZMkSSrEREySJKmQ/w+26XQeaXGZ\nwgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1146327f0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"outcome = 'Alive'\n",
"R = inferential_statistics.anova_MRI(outcome, df);"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Effect Size</th>\n",
" </tr>\n",
" <tr>\n",
" <th>Predictor of Alive</th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>MRI_LD_Baseline</th>\n",
" <td>0.375046</td>\n",
" </tr>\n",
" <tr>\n",
" <th>MRI_LD_1_3dAC</th>\n",
" <td>0.357002</td>\n",
" </tr>\n",
" <tr>\n",
" <th>MRI_LD_Int_Reg</th>\n",
" <td>0.678682</td>\n",
" </tr>\n",
" <tr>\n",
" <th>MRI_LD_PreSurg</th>\n",
" <td>0.469548</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Effect Size\n",
"Predictor of Alive \n",
"MRI_LD_Baseline 0.375046\n",
"MRI_LD_1_3dAC 0.357002\n",
"MRI_LD_Int_Reg 0.678682\n",
"MRI_LD_PreSurg 0.469548"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"mri_features = ['MRI_LD_Baseline', 'MRI_LD_1_3dAC', 'MRI_LD_Int_Reg', 'MRI_LD_PreSurg']\n",
"outcome = 'Alive'\n",
"# Effect Size\n",
"inferential_statistics.effect_size( df, mri_features, outcome)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### stratify analysis by PCR"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Outcome = Alive | PCR = No\n",
"---------------------------------------------\n",
" sum_sq df F PR(>F)\n",
"MRI_LD_Baseline 0.081585 1.0 0.484431 0.487791\n",
"MRI_LD_1_3dAC 0.019421 1.0 0.115317 0.734774\n",
"MRI_LD_Int_Reg 0.423490 1.0 2.514580 0.115474\n",
"MRI_LD_PreSurg 0.143688 1.0 0.853186 0.357537\n",
"Residual 19.872834 118.0 NaN NaN\n",
"---------------------------------------------\n",
" Effect Size\n",
"Predictor of Alive \n",
"MRI_LD_Baseline 0.314555\n",
"MRI_LD_1_3dAC 0.362579\n",
"MRI_LD_Int_Reg 0.582373\n",
"MRI_LD_PreSurg 0.484103\n",
"\n",
"\n",
"\n",
"Outcome = Alive | PCR = Yes\n",
"---------------------------------------------\n",
" sum_sq df F PR(>F)\n",
"MRI_LD_Baseline 0.128853 1.0 1.966383 0.168546\n",
"MRI_LD_1_3dAC 0.240330 1.0 3.667597 0.062650\n",
"MRI_LD_Int_Reg 0.543712 1.0 8.297407 0.006352\n",
"MRI_LD_PreSurg 0.404720 1.0 6.176300 0.017228\n",
"Residual 2.621118 40.0 NaN NaN\n",
"---------------------------------------------\n",
" Effect Size\n",
"Predictor of Alive \n",
"MRI_LD_Baseline 0.597109\n",
"MRI_LD_1_3dAC 0.037712\n",
"MRI_LD_Int_Reg 0.804525\n",
"MRI_LD_PreSurg -0.234776\n",
"\n",
"\n",
"\n"
]
}
],
"source": [
"# predictors and outcomes\n",
"predictors= ['MRI_LD_Baseline', 'MRI_LD_1_3dAC', 'MRI_LD_Int_Reg', 'MRI_LD_PreSurg']\n",
"\n",
"# split data and run anova\n",
"PCR_outcomes = ['No','Yes']\n",
"\n",
"for out in PCR_outcomes:\n",
" df_by_PCR = df.loc[df.PCR == out,:]\n",
" print('Outcome = Alive' + ' | ' + 'PCR = ' + out)\n",
" # Anova\n",
" anova_table, OLS = inferential_statistics.linear_models(df_by_PCR, 'Alive', predictors);\n",
" # Effect Size\n",
" print(inferential_statistics.effect_size( df_by_PCR, predictors, 'Alive'))\n",
" print('\\n' * 2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Conclusion "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"1. The largest tumor dimension measured at baseline (`MRI_LD_Baseline`) is not a statistically different between patients who achieved complete pathological response (`PCR`)and those who did not. While all other MRI measurements are statistically different between `PCR = Yes`, and `PCR = No`\n",
"2. All MRI measurements of the tumor dimension are different between patients who are Alive at the end of the trial and those who did not. These results do not indicate anything about the size of these effects. An statistically significant effect is not always clinically significant\n",
"3. The estimated effect sizes are very small, and most likley not clinically significant\n"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"## 3. Inferential_statistics: Continous vs Categorical (ANOVA)"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
bzamecnik/ml | instrument-classification/analyze_instrument_ranges.ipynb | 2 | 158629 | {
"cells": [
{
"cell_type": "code",
"execution_count": 142,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"from music21.duration import Duration\n",
"from music21.instrument import Instrument\n",
"from music21.note import Note, Rest\n",
"from music21.stream import Stream\n",
"from music21.tempo import MetronomeMark\n",
"import numpy as np\n",
"import os\n",
"import scipy.io.wavfile\n",
"\n",
"from generate_audio_samples import make_instrument, write_midi\n",
"from midi2audio import FluidSynth"
]
},
{
"cell_type": "code",
"execution_count": 143,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"mpl.rc('figure', figsize=(20, 10))"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"midi_notes = np.arange(128)\n",
"instruments = np.arange(128)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def sweep_instrument(instrument_id, output_dir):\n",
" s = Stream()\n",
" duration = Duration(1.0)\n",
" s.append(make_instrument(instrument_id))\n",
" s.append(MetronomeMark(number=120))\n",
" for midi_number in midi_notes:\n",
" s.append(Note(midi=midi_number, duration=duration))\n",
" s.append(Rest(duration=duration))\n",
" os.makedirs(output_dir, exist_ok=True)\n",
" midi_file, audio_file = [\n",
" output_dir + '/instrument_{0:03d}.{1}'.format(instrument_id, ext)\n",
" for ext in ['midi', 'wav']]\n",
" write_midi(s, midi_file)\n",
" print('instrument:', audio_file)\n",
" FluidSynth().midi_to_audio(midi_file, audio_file)\n",
"\n",
"def sweep_instruments(output_dir):\n",
" for instrument_id in instruments:\n",
" sweep_instrument(instrument_id, output_dir)"
]
},
{
"cell_type": "code",
"execution_count": 120,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"instrument: data/working/instrument_ranges/instrument_000.wav\n",
"instrument: data/working/instrument_ranges/instrument_001.wav\n",
"instrument: data/working/instrument_ranges/instrument_002.wav\n",
"instrument: data/working/instrument_ranges/instrument_003.wav\n",
"instrument: data/working/instrument_ranges/instrument_004.wav\n",
"instrument: data/working/instrument_ranges/instrument_005.wav\n",
"instrument: data/working/instrument_ranges/instrument_006.wav\n",
"instrument: data/working/instrument_ranges/instrument_007.wav\n",
"instrument: data/working/instrument_ranges/instrument_008.wav\n",
"instrument: data/working/instrument_ranges/instrument_009.wav\n",
"instrument: data/working/instrument_ranges/instrument_010.wav\n",
"instrument: data/working/instrument_ranges/instrument_011.wav\n",
"instrument: data/working/instrument_ranges/instrument_012.wav\n",
"instrument: data/working/instrument_ranges/instrument_013.wav\n",
"instrument: data/working/instrument_ranges/instrument_014.wav\n",
"instrument: data/working/instrument_ranges/instrument_015.wav\n",
"instrument: data/working/instrument_ranges/instrument_016.wav\n",
"instrument: data/working/instrument_ranges/instrument_017.wav\n",
"instrument: data/working/instrument_ranges/instrument_018.wav\n",
"instrument: data/working/instrument_ranges/instrument_019.wav\n",
"instrument: data/working/instrument_ranges/instrument_020.wav\n",
"instrument: data/working/instrument_ranges/instrument_021.wav\n",
"instrument: data/working/instrument_ranges/instrument_022.wav\n",
"instrument: data/working/instrument_ranges/instrument_023.wav\n",
"instrument: data/working/instrument_ranges/instrument_024.wav\n",
"instrument: data/working/instrument_ranges/instrument_025.wav\n",
"instrument: data/working/instrument_ranges/instrument_026.wav\n",
"instrument: data/working/instrument_ranges/instrument_027.wav\n",
"instrument: data/working/instrument_ranges/instrument_028.wav\n",
"instrument: data/working/instrument_ranges/instrument_029.wav\n",
"instrument: data/working/instrument_ranges/instrument_030.wav\n",
"instrument: data/working/instrument_ranges/instrument_031.wav\n",
"instrument: data/working/instrument_ranges/instrument_032.wav\n",
"instrument: data/working/instrument_ranges/instrument_033.wav\n",
"instrument: data/working/instrument_ranges/instrument_034.wav\n",
"instrument: data/working/instrument_ranges/instrument_035.wav\n",
"instrument: data/working/instrument_ranges/instrument_036.wav\n",
"instrument: data/working/instrument_ranges/instrument_037.wav\n",
"instrument: data/working/instrument_ranges/instrument_038.wav\n",
"instrument: data/working/instrument_ranges/instrument_039.wav\n",
"instrument: data/working/instrument_ranges/instrument_040.wav\n",
"instrument: data/working/instrument_ranges/instrument_041.wav\n",
"instrument: data/working/instrument_ranges/instrument_042.wav\n",
"instrument: data/working/instrument_ranges/instrument_043.wav\n",
"instrument: data/working/instrument_ranges/instrument_044.wav\n",
"instrument: data/working/instrument_ranges/instrument_045.wav\n",
"instrument: data/working/instrument_ranges/instrument_046.wav\n",
"instrument: data/working/instrument_ranges/instrument_047.wav\n",
"instrument: data/working/instrument_ranges/instrument_048.wav\n",
"instrument: data/working/instrument_ranges/instrument_049.wav\n",
"instrument: data/working/instrument_ranges/instrument_050.wav\n",
"instrument: data/working/instrument_ranges/instrument_051.wav\n",
"instrument: data/working/instrument_ranges/instrument_052.wav\n",
"instrument: data/working/instrument_ranges/instrument_053.wav\n",
"instrument: data/working/instrument_ranges/instrument_054.wav\n",
"instrument: data/working/instrument_ranges/instrument_055.wav\n",
"instrument: data/working/instrument_ranges/instrument_056.wav\n",
"instrument: data/working/instrument_ranges/instrument_057.wav\n",
"instrument: data/working/instrument_ranges/instrument_058.wav\n",
"instrument: data/working/instrument_ranges/instrument_059.wav\n",
"instrument: data/working/instrument_ranges/instrument_060.wav\n",
"instrument: data/working/instrument_ranges/instrument_061.wav\n",
"instrument: data/working/instrument_ranges/instrument_062.wav\n",
"instrument: data/working/instrument_ranges/instrument_063.wav\n",
"instrument: data/working/instrument_ranges/instrument_064.wav\n",
"instrument: data/working/instrument_ranges/instrument_065.wav\n",
"instrument: data/working/instrument_ranges/instrument_066.wav\n",
"instrument: data/working/instrument_ranges/instrument_067.wav\n",
"instrument: data/working/instrument_ranges/instrument_068.wav\n",
"instrument: data/working/instrument_ranges/instrument_069.wav\n",
"instrument: data/working/instrument_ranges/instrument_070.wav\n",
"instrument: data/working/instrument_ranges/instrument_071.wav\n",
"instrument: data/working/instrument_ranges/instrument_072.wav\n",
"instrument: data/working/instrument_ranges/instrument_073.wav\n",
"instrument: data/working/instrument_ranges/instrument_074.wav\n",
"instrument: data/working/instrument_ranges/instrument_075.wav\n",
"instrument: data/working/instrument_ranges/instrument_076.wav\n",
"instrument: data/working/instrument_ranges/instrument_077.wav\n",
"instrument: data/working/instrument_ranges/instrument_078.wav\n",
"instrument: data/working/instrument_ranges/instrument_079.wav\n",
"instrument: data/working/instrument_ranges/instrument_080.wav\n",
"instrument: data/working/instrument_ranges/instrument_081.wav\n",
"instrument: data/working/instrument_ranges/instrument_082.wav\n",
"instrument: data/working/instrument_ranges/instrument_083.wav\n",
"instrument: data/working/instrument_ranges/instrument_084.wav\n",
"instrument: data/working/instrument_ranges/instrument_085.wav\n",
"instrument: data/working/instrument_ranges/instrument_086.wav\n",
"instrument: data/working/instrument_ranges/instrument_087.wav\n",
"instrument: data/working/instrument_ranges/instrument_088.wav\n",
"instrument: data/working/instrument_ranges/instrument_089.wav\n",
"instrument: data/working/instrument_ranges/instrument_090.wav\n",
"instrument: data/working/instrument_ranges/instrument_091.wav\n",
"instrument: data/working/instrument_ranges/instrument_092.wav\n",
"instrument: data/working/instrument_ranges/instrument_093.wav\n",
"instrument: data/working/instrument_ranges/instrument_094.wav\n",
"instrument: data/working/instrument_ranges/instrument_095.wav\n",
"instrument: data/working/instrument_ranges/instrument_096.wav\n",
"instrument: data/working/instrument_ranges/instrument_097.wav\n",
"instrument: data/working/instrument_ranges/instrument_098.wav\n",
"instrument: data/working/instrument_ranges/instrument_099.wav\n",
"instrument: data/working/instrument_ranges/instrument_100.wav\n",
"instrument: data/working/instrument_ranges/instrument_101.wav\n",
"instrument: data/working/instrument_ranges/instrument_102.wav\n",
"instrument: data/working/instrument_ranges/instrument_103.wav\n",
"instrument: data/working/instrument_ranges/instrument_104.wav\n",
"instrument: data/working/instrument_ranges/instrument_105.wav\n",
"instrument: data/working/instrument_ranges/instrument_106.wav\n",
"instrument: data/working/instrument_ranges/instrument_107.wav\n",
"instrument: data/working/instrument_ranges/instrument_108.wav\n",
"instrument: data/working/instrument_ranges/instrument_109.wav\n",
"instrument: data/working/instrument_ranges/instrument_110.wav\n",
"instrument: data/working/instrument_ranges/instrument_111.wav\n",
"instrument: data/working/instrument_ranges/instrument_112.wav\n",
"instrument: data/working/instrument_ranges/instrument_113.wav\n",
"instrument: data/working/instrument_ranges/instrument_114.wav\n",
"instrument: data/working/instrument_ranges/instrument_115.wav\n",
"instrument: data/working/instrument_ranges/instrument_116.wav\n",
"instrument: data/working/instrument_ranges/instrument_117.wav\n",
"instrument: data/working/instrument_ranges/instrument_118.wav\n",
"instrument: data/working/instrument_ranges/instrument_119.wav\n",
"instrument: data/working/instrument_ranges/instrument_120.wav\n",
"instrument: data/working/instrument_ranges/instrument_121.wav\n",
"instrument: data/working/instrument_ranges/instrument_122.wav\n",
"instrument: data/working/instrument_ranges/instrument_123.wav\n",
"instrument: data/working/instrument_ranges/instrument_124.wav\n",
"instrument: data/working/instrument_ranges/instrument_125.wav\n",
"instrument: data/working/instrument_ranges/instrument_126.wav\n",
"instrument: data/working/instrument_ranges/instrument_127.wav\n"
]
}
],
"source": [
"audio_dir = 'data/working/instrument-ranges'\n",
"sweep_instruments(audio_dir)"
]
},
{
"cell_type": "code",
"execution_count": 181,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def analyze_instrument_rms(i, audio_dir):\n",
" \"\"\"\n",
" Compute the RMS of each note in the synthesized signal for a single instrument.\n",
" \"\"\"\n",
" fs, x = scipy.io.wavfile.read('{0}/instrument_{1:03d}.wav'.format(audio_dir, i))\n",
" # convert from stereo to mono\n",
" x = x.mean(axis=1)\n",
" # cut the leading rest\n",
" x = x[fs // 2:]\n",
" # align the ending\n",
" x = x[:len(x) // fs * fs]\n",
" # split the notes\n",
" x_notes = x.reshape(-1, fs)\n",
" # RMS for each note\n",
" x_notes_rms = np.sqrt((x_notes**2).mean(axis=1))\n",
" return x_notes_rms"
]
},
{
"cell_type": "code",
"execution_count": 182,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABJAAAAJoCAYAAAA5wRtnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XecnWWd///XlUmDZOikEEIAaQlDc1kIJSGAIF1WaT9Y\ndFHBXUVklVURfyu40nZXXASxwwKrUmRFet9Qg/QySeg9oYUUJgGSTHJ9/7jOMZMwc+b0+5yZ1/Px\nyGPOnHLf10wOQ+73fD6fK8QYkSRJkiRJknoyIOsFSJIkSZIkqbEZIEmSJEmSJKkgAyRJkiRJkiQV\nZIAkSZIkSZKkggyQJEmSJEmSVJABkiRJkiRJkgoyQJIkSepGCGGLEMLjIYQFIYQTs15Pd0II40II\ny0MI/ptOkiTVlP/YkCRJ6t63gbtijGvGGC/MejEFxHqcJITwfyGEL9bjXJIkqfEYIEmSpH4vhBC6\nuXscML3M47VUtiJJkqTGYoAkSZLqLoTwcgjhuyGE6SGE90IIvw0hDO7y+PEhhOdDCHNCCNeGEEbl\n7j89hPDT3O2BIYSFIYRzc58PDSF8GEJYK/f5xBDC/SGEeblWtD26HP//Qgg/CiHcF0JYBGyyyvru\nBPYEfhZCeD+EsFkIYY0QwmUhhHdy6z+ty/O/kDvWeSGEOcAPuvmaQ+5rfiGE8G4I4YoQwtpdHr8q\nhPBmbr1TQwgTujw2NITw4xDCK7nH7wkhDMk/DPx9COHV3Nq+V+D7fkkI4cIQwg25r2taCGGTLo/v\nGkJ4KHeOv4QQdsnd/yNgEnBh7nX5v4OtQgi35f4OZ4YQDu/p3JIkqbkZIEmSpKwcDewDfALYEvg+\nQAhhL+As4DBgNPAacGXuNXcD+SDob4G3gMm5z3cFnokxzg8hjAFuAH4YY1wbOAW4JoSwbpfz/z3w\nZaAVeLXrwmKMewP3Al+LMa4RY3wBuDD33I2BKcDnQwjHdXnZzsALwAjgzG6+3pOAQ0hBzAbAPOBn\nXR6/Kfe9GAE8Bvyuy2M/BnYAJgLrkNrrlnd5fDdgc+BTwL+GELbs5vx5R5ICrrWAF/NrzYVZNwD/\nBawL/AS4MYSwdozx+7nvx4m578dJIYTVgduA/wHWA44iBW5bFTi3JElqUgZIkiQpKxfEGGfHGOeT\nQoz/L3f/0cBvY4xPxhiXAqcCu4QQNgKmAZvnwo7JwG+BMbkwYzIpYAI4BrgxxngrQIzxTuAR4IAu\n5//vGOMzMcblMcZlhRaaG1J9JPDdGOMHMcZXSaHOsV2eNivGeFHueIu7OcxXgNNijG/mvq4fAofl\nB2DHGP87d+z8Y9uFEFpz7XXHASfFGN+KyYO550GagXR6jHFJjPEp4ElguwJfzp9ijI/GGJeTQqrt\nc/cfCDwXY/x97mu4AngGOLiH4xwEvBxjvCy3pieB/wWsQpIkqQ8yQJIkSVl5o8vtV0lVOeQ+/rUi\nKMa4CHgPGBNj/IgUBE0hBUZTgQeA3UmVSfkAaRxwRAhhbu7PPFKVzqgu53y9hLWuBwwkVUN1XfOY\nEo43DvhTfk3ADGApMDKEMCCEcE6uvW0+8DIpGFov92cI8FKBY7/d5fYHwPACz32rh+eu9H3PWfVr\nXPXrmbjK9/hoVv4eS5KkPmJg1guQJEn91tgut8cBs3O3Z+c+ByCEMIzUUjUrd9c9wF6kypmHc59/\nmtTSdk/uOa8Dl8UYv1Lg/KXsXjaHFPaMI1Xl5Nc8q8tzejvea8AXY4zTVn0ghPD3pEqfvWKMr4UQ\n1iS1uIXcuT8itbc9XcKaSzUb+Nwq920E3Jy7verX9zowNcb46RquSZIkNQgrkCRJUla+FkIYE0JY\nB/gecEXu/j8Ax4UQts0Nij4LeDDGmK/+uRv4PDAjxthJqkL6Mqmd6r3cc/4HODiEsG+uumdoCGGP\nEEK+yqkkuXavq4AzQwjDQwjjgH8GLi/hML8Ezsq14hFCWD+EcEjusVZgMTAvF5idTS6wiTFG4BLg\nvBDC6NzXMzGEMCj32u52kCvHTaT2wKNCCC0hhCOB8aS5SJCqnDbt8vwbgC1CCH+fG2g+KISwozOQ\nJEnqmwyQJElSVn5PGsL8AvA8uWHOuXlF/z9pns4s0g5pR3V53QPAUHLtajHGGcCHrGhfI8b4BvAZ\nUjD1LqkV6xRW/NunmOqjVZ9zEqnl6yVSpdP/xBgvKeorTc4H/gzcFkJYkPs6dso9dhmpQmkW0J57\nrKtTSNVHD5Pa+c4p8LUU+tp6fCzGOJc01+gUUtXTKcCBufvz6z88t+Paf8UYFwL7kv5uZuf+nAMM\n/tjBJUlS0wvpl1o1Onj6reE9pH9IDAT+GGM8I4TwA+B44J3cU78XY7wl95pTgS8CncA3Yoy31WyB\nkiQpEyGEl4EvxRjvynotkiRJ6l1NZyDFGBeHEPaMMX4QQmgB7g8h5Pvoz4sxntf1+SGE8cARpHLp\nDYE7Qgibx1qmXJIkSZIkSSqo5i1sMcYPcjeHkAKrfBjUXb/+Z4ArYoydMcZXSOXsO3XzPEmS1Nz8\n5ZAkSVITqXmAlBv0+Dhpy9jbY4wP5x46MYTwRAjhN7mdRiBtE9t1C9xZ9Lx1rCRJalIxxk1tX5Mk\nSWoe9ahAWh5j3IHUkrZTCGECcBGwaYxxe1Kw9ONar0OSJEmSJEnlqekMpK5ijO+HEKYC+60y++jX\nwPW527OAsV0e2zB330pCCJa9S5IkSZIkVVmMsbuRQ7UNkEII6wFLY4wLQgirAfsA54QQRsUY38o9\n7bOk7WoBrgN+F0L4Cal1bTPgoe6O7VxtNavTTz+d008/PetlSGXx/atm5vtXzcr3rpqZ7181s/74\n/g2h2+wIqH0F0mjg0hDCAFK73JUxxptCCJeFELYHlgOvAF8BiDHOCCFcBcwAlgJfdQc2SZIkSZKk\nbNU0QIoxPg18spv7P1/gNWcDZ9dyXZIkSZIkSSpezYdoS1rZlClTsl6CVDbfv2pmvn/VrHzvqpn5\n/lUz8/27stCMHWIhBDvbJEmSJEmSqiiE0OMQbSuQJEmSJEmSVJABkiRJkiRJkgoyQJIkSZIkSVJB\nBkiSJEmSJEkqyABJkiRJkiRJBRkgSZIkSZIkqSADJEmSJEmSJBVkgCRJkiRJkqSCDJAkSZIkSZJU\nkAGSJEmSJEmSCjJAkiRJkiRJUkEGSJIkSZIkSSrIAEmSJEmSJEkFGSBJkiRJkiSpIAMkSZIkSZIk\nFWSAJEmSJEmSpIIMkCRJkiRJklSQAZIkSZIkSZIKMkCSJEmSJElSQQZIkiRJkiRJKsgASZIkSZIk\nSQUZIEmSJEmSJKkgAyRJkiRJkiQVZIAkSZIkSZKkggyQJEmSJEmSVJABkiRJkiRJkgoyQJIkSZIk\nSVJBBkiSJEmSJEkqyABJkiRJkiRJBRkgSZIkSZIkqSADJEmSJEmSJBVkgCRJkiRJkqSCDJAkSZIk\nSZJUkAGSJEmSJEmSCjJAkiRJkiRJUkEGSJIkSZIkSSrIAEmSJEmSJEkFGSBJkiRJkiSpIAMkSZIk\nSZIkFWSAJEmSJEmSpIIMkCRJkiRJklSQAZIkSZIkSZIKMkCSJEmSJElSQQZIamodHTBtWvooSZIk\nSZJqwwBJTaujA3bfHSZPhkmTDJEkSZIkSaoVAyQ1rfb29KezE2bMgOnTs16RJEmSJEl9kwGSmlZb\nG6y+OoQAAwfCpptmvSJJkiRJkvomAyQ1rRAgRrj9djjwQDjppPS5JEmSJEmqLgMkNa0774SJE2Hv\nveHyy+HVV+H007NelSRJkiRJfY8BkprWzTfD/vun20OHwrXXwmWXwe9+l+26JEmSJEnqa0Jswp6f\nEEJsxnWremKEcePg1lth/PgV97e3w157pTBp112zW58kSZIkSc0mhECMMXT3mBVIakozZsCAAbDV\nVivf39YGl14Khx0GL7+czdokSZIkSeprDJDUlG66CQ44IA3SXtX++8Opp8JBB8GCBfVfmyRJkiRJ\nfY0BkppS1/lH3fn612HPPeHII6Gzs37rkiRJkiSpL3IGkprO++/DmDHw1lswbFjPz+vsTFVI48bB\nP/xDam9rba3bMiVJkiRJaiqFZiAZIKnp/OlP8POfw2239f7cN96AzTZLYVJbG9x7ryGSJEmSJEnd\ncYi2+pT8/KNivP46LF0Ky5alwdvTp9d2bZIkSZIk9UUGSGoqMfY+/6irtjYYPTrt2DZhAmy9dW3X\nJ0mSJElSX2SApKby9NMwZAhssUVxz29thXPPhd13t31NkiRJkqRyGSCpqdx0U6o+Ct12ZHZvk01g\nyRLDI0mSJEmSymWApKZy883Fzz/KGzky7dgmSZIkSZLK4y5sahrz58PYsfD227D66sW/buFCGDEC\nFi0qrXJJkiRJkqT+xF3Y1CfccUeaZVRKeAQwfDi0tEBHR23WJUmSJElSX2eApKaRn39UDtvYJEmS\nJEkqnwGSmkKM5c0/yhs1KrW+SZIkSZKk0hkgqSk88URqRdtss/JeP2qUFUiSJEmSJJXLAElNoZLq\nI7CFTZIkSZKkShggqSlUMv8IbGGTJEmSJKkSBkhqePPmwVNPwR57lH8MW9gkSZIkSSpfTQOkEMKQ\nEMJfQgiPhxCeDiH8IHf/2iGE20IIz4YQbg0hrNnlNaeGEJ4PIcwMIexby/WpOdx2G0yaBKutVv4x\nbGGTJEmSJKl8NQ2QYoyLgT1jjDsA2wP7hxB2Ar4L3BFj3BK4CzgVIIQwATgCGA/sD1wUQgi1XKMa\nX6Xzj8AWNkmSJEmSKlHzFrYY4we5m0OAgUAEPgNcmrv/UuDQ3O1DgCtijJ0xxleA54Gdar1GNa7l\ny1OAVMn8I7CFTZIkSZKkStQ8QAohDAghPA68BdweY3wYGBljfBsgxvgWMCL39DHA611ePit3n/qp\nxx+HtdeGTTet7DgjRqQKpBirsy5JkiRJkvqTelQgLc+1sG0I7BRC2JpUhbTS02q9DjWnSndfyxs6\nFIYNSwO5JUmSJElSaQbW60QxxvdDCFOB/YC3QwgjY4xvhxBGAe/knjYLGNvlZRvm7vuY008//a+3\np0yZwpQpU2qwamWpowOuugp+9KPqHC/fxrbOOtU5niRJkiRJzWzq1KlMnTq1qOeGWMOenhDCesDS\nGOOCEMJqwK3AOcAewNwY47khhO8Aa8cYv5sbov07YGdS69rtwOZxlUWGEFa9S31MRwfssgtMnw7b\nbAP33w+trZUdc8oU+Nd/hb32qsoSJUmSJEnqU0IIxBi73cys1hVIo4FLQwgDSO1yV8YYbwohPAhc\nFUL4IvAqaec1YowzQghXATOApcBXTYr6p/Z2eOaZdPuZZ1KQNHFiZcd0JzZJkiRJkspT0wApxvg0\n8Mlu7p8LfKqH15wNnF3LdanxtbXB6NEwezZMmABbb135Md2JTZIkSZKk8tRtBpJUitZW+Mxn0q5p\n55xTefsawMiRBkiSJEmSJJWj5ruwSeV6+WXYd9/qhEdgC5skSZIkSeUyQFLDeu452HLL6h3PFjZJ\nkiRJkspjgKSGtGQJvP46bLpp9Y45cqQVSJIkSZIklcMASQ3pxRdh7FgYPLh6x7QCSZIkSZKk8hgg\nqSE9+2x129cA1l8f5syBZcuqe1xJkiRJkvo6AyQ1pFoESIMGwVprwXvvVfe4kiRJkiT1dQZIakjV\nHqCdZxubJEmSJEmlM0BSQ3r2Wdhii+of1wBJkiRJkqTSGSCpIdWihQ3ciU2SJEmSpHIYIKnhzJ0L\nixenaqFqswJJkiRJkqTSGSCp4eSrj0Ko/rENkCRJkiRJKp0BkhpOrQZogy1skiRJkiSVwwBJDadW\nA7TBCiRJkiRJksphgKSGU6sB2mCAJEmSJElSOQyQ1HBqGSDZwiZJkiRJUulCjDHrNZQshBCbcd3q\n3bJlMHw4zJkDw4bV5vhDh8IHH8CgQdU/viRJkiRJzSqEQIyx2y2trEBSQ3ntNVh//dqERwAtLen4\n77xTm+NLkiRJktQXGSCpodRygHaebWySJEmSJJXGAEkNpZbzj/IcpC1JkiRJUmkMkNRQDJAkSZIk\nSWo8BkhqKPUIkGxhkyRJkiSpNAZIaijPPWcFkiRJkiRJjcYASQ1j0SKYMwfGjq3teUaONECSJEmS\nJKkUBkhqGM89B5ttBi0ttT3PqFG2sEmSJEmSVAoDJDWMesw/AlvYJEmSJEkqlQGSGka9AiRb2CRJ\nkiRJKo0BkhpGPQZoA6y9Nnz4IXz0Ue3PJUmSJElSX2CApIbx7LOwxRa1P08IqQrJOUiSJEmSJBXH\nAEkNIcb6VSCBbWySJEmSJJXCAEkN4c03YejQ1F5WD+7EJkmSJElS8QyQ1BDqNUA7z53YJEmSJEkq\nngGSGkI929fAGUiSJEmSJJXCAEkNoV4DtPOsQJIkSZIkqXgGSGoItrBJkiRJktS4DJDUEOodINnC\nJkmSJElS8QyQlLnFi+GNN2DTTet3TiuQJEmSJEkqngGSMvfSS7DRRjB4cP3OaYAkSZIkSVLxDJCU\nuXoP0AYYPhyWL4eFC+t7XkmSJEmSmpEBkjJX7/lHACGkKiTnIEmSJEmS1DsDJGUuiwAJbGOTJEmS\nJKlYBkg11tEB06alj+peVgGSO7FJkiRJklQcA6Qa6uiAbbeF3XaD7baD99/PekWN6bnnrECSJEmS\nJKmRGSDV0H/8B7zyCsQIL78MO+4IV18Ny5ZlvbLGMXcuLF6cqoHqzQBJUjOxolWSJElZMkCqkQsu\ngIsvTpU1gwalSqQf/QjOOw8mTIBLLoGlS7NeZfby7Wsh1P/ctrBJahYdHbD77qmidffdDZEkSZJU\nfwZIVRYj/PCH8NOfwv33w8MPwz33wH33wRFHwAMPwC9+Ab//PWy2GVx4IbzzTv/9rXJW84/ACiRJ\nzaO9HWbMSP+PmTkTpk/PekWSJEnqbwyQqihG+Na34Jpr4N57Ydw4aG2FiRPTR0iVNnvuCbffntrZ\nbrkFxoyBSZPSn/4WIhkgSVLv2trSLx0ANt4Ytt460+VIkiSpHzJAqpLOTvjSl+DBB2Hq1BRO9Gan\nneC009LtZcvSb5T722+VsxqgDbawSWoera3w85+n2z/4wYpfSkiSJEn1YoBUBYsXw1FHwRtvpMqi\ntdcu/rVtbek3yQMHps/XX782a2xUzz4LW2yRzblHjkwVSDFmc35JKsWSJenju+9muw5JkiT1TwZI\nFejogLvuggMOSCHE9dfDsGGlHaO1NbW73Xtvan877rj+M1x72TJ48UXYfPNszr/66jBkCCxYkM35\nJakU8+alj6+9lu06JEmS1D8ZIJUpvyPO3nvD44/Db36Twohy5OcknXUWrLFGCpL6g1dfTRVXpYZu\n1WQbm6RmMX8+rLVW+tkpSZIk1ZsBUpna29MfgIULUytWpQYMgP/5H7j5Zrj88sqP1+iyHKCd5yBt\nSc1i3jzYdlsrkCRJkpQNA6QybbZZCnwGDoQJE6q3I85aa8G118I3vwmPPVadYzaqLAdo5xkgSWoW\n8+bBdtsZIEmSJCkbBkhl+t3vYN99V8wvquaOOFtvDRddBJ/9LMyZU73jNposB2jnNWILW0cHTJuW\nPkpS3vz5sNVW6eOHH2a9GkmSJPU3BkhlWLgQzjkHzj47zS6qxXbKhx+ednY76ijo7Kz+8RvB9Olp\nkHaWQUmjVSB1dMBuu8HkyTBpkiGSpBXmzYN114UNN0y7fkqSJEn1ZIBUhgsugClT0iyKWjrzzNQm\n973v1fY8WejogAcegG9/O9ugpNECpPxsrc5OmDEjhWySBClAWntt2Ggj29gkSZJUfwOzXkCzmT8f\nzjsP7ruv9udqaYE//AF23DHNWdpyS2hrq03FU73ddNOKyqp8UDJxYv3X0WgtbG1taVe6hQthgw2q\nN1tLUvPL78JmgCRJkqQsWIFUovPOg4MOqt/w53XXTTuzffnLfaut6YUXYJ11YNCg6g4hL1WjVSC1\ntsImm8B3vpNCpLlzs16RpEZhBZIkSZKy1LQVSB0d9a/EmTMHfvYzePTR+p53wACIMc0LyrJap5pu\nvx1+/vN0IbT11tlVVTVagASpyuCrX03h4dFHw913p93+JPVvXQOkBx/MejWSJEnqb5q2AmnixPpX\n4px7Lhx5JGy8cX3P29YG48en25tv3vxtTXPnwmOPwcEH124IebFGjIB334Xly7Nbw6rmzEnh0be+\nldrZfvjDrFckKWsxwoIFsOaaViBJkiQpG00bIM2YASedBO+/X5/zzZ4Nv/0tfP/79TlfV62taVv3\nQw6Bz362+Wcg3XxzGkK+2mpZrwQGD07fz0ZpFfvgg3ShuPrqqfLsssvg17+GqVOzXpmkLHV0pJ+Z\ngwYZIEmSJCkbTRsgjR8PixenWUQXXQRLl9b2fGedBccdlwYbZ6G1Ff7t3+Dii2HJkmzWUC3XX5+q\njxrFqFGNM0j7vfdS9VEI6fNRo9Lf+bHHpsck9U/59jWAsWNTgBRjtmuSJElS/9K0AdJf/gK//32q\nZrn22tTm9ac/1eYf1K+8knZD++53q3/sUmy7LWyxBVxzTbbrqMTSpXDrrWkQeaMYObJx5iC99x6s\nt97K9+2/PxxxBHzpS14wSv1Vfgc2gOHDU5XinDnZrkmSJEn9S9MGSPk2ru23h9tug5/+FH7wg7RL\n2Z13ppavas1I+rd/g3/6J1h//eocrxInnZS+1mZ1771pjtPo0VmvZIVGGqSdn3+0qrPOgtdfT4PH\nJfU/XSuQwDY2SZIk1V/TBkir+vSn4fHH065V++0Hu+9enS3vn3sOrrsOTjmlOuus1CGHwJtvwkMP\nZb2S8jRa+xqkCqRGamFbtQIJYMgQuOKKFJI+/XT91yUpWwZIkiRJylqfCZAAWlpghx3S7eXLob09\nbXlfidNPh5NPXtE6kLWWFjjxRLjggqxXUroYUxjXaAFSM1QgQarc+vGP4aijUuBVzSo7SY2tawsb\nGCBJkiSp/vpUgARpFtLWW8PAgenzARV8hQ8+CLfcAl/8YnXWVi1f+hLccEPjhB7FmjkzzUDabrus\nV7KyRgqQeqpAyjv22BXv8cmTq1NlJ6nxWYEkSZKkrPW5AKm1Nc3ZufdeuPBC+Pzny7vAnjcP9tkH\nFixIQ4wb6SJ97bXhyCPhF7/IeiWluf76NDw7v8NYo2ikFrZCFUiQvnfHH5+Cps5OmDGj8io7SY3P\nAEmSJElZ63MBEqQQaeJE+Md/TLOQTjihtN2rFi+GQw+FRYtSK1wjXqR//espQFq8OOuVFO/669MM\np0bTTBVIADvvDGPGpDBpwoRUjSSpb7OFTZIkSVnrkwFSVxdckFqnLrqouOcvWpRCjrXWSq1CgwY1\n5kX61lvDNtvA1VdnvZLizJmThj9PmZL1Sj6ukQKk3iqQIAWkjz+eqhF++csVOxJK6rusQJIkSVLW\n+nyAtNpq8Mc/whln9L5z2YIFaTe30aPhmmvg/vvhnntSO1wjXqSfdBKcf35p1VVZuekm2HtvGDo0\n65V83Hrrwdy5sGxZ1isprgIJYP31086AP/tZ7dckKXurBkijRqWfW81UhSpJkqTmVtMAKYSwYQjh\nrhDC9BDC0yGEr+fu/0EI4Y0QwmO5P/t1ec2pIYTnQwgzQwj7VmMdm22WKjWOOCJdoHdnzhzYa6+0\ni9vFF6ch3PlWuEYMjwAOOCBdQPzlL1mvpHeNuPta3sCBqeLs5puzn3VVTAVS3j/9E9x4o1UIUn+w\nagtbSwtssAG88UZ2a5IkSVL/UusKpE7gmzHGrYFdgBNDCFvlHjsvxvjJ3J9bAEII44EjgPHA/sBF\nIVRn5PLf/R0cdlgaqr18+cqPzZ4Ne+wB++0HP/1pZTu31VNLC5x4YqpCamSLF8Mdd8CBB2a9ku51\ndMDChek9kvWuZsVWIEG6mPziF+G882q7JknZW7UCCWxjkyRJUn3VNCqJMb4VY3wid3shMBMYk3u4\nu2DoM8AVMcbOGOMrwPPATtVaz9lnpza1c85Zcd/LL6fQ4Nhj4cwzG2+HsN4cdxzccgvMmpX1Snp2\n990wfjyMGJH1SrrX3p5Crqx3NVu8GJYsgeHDi3/NySfDZZf1XFknqW8wQJIkSVLW6lZrE0LYGNge\nyDdcnRhCeCKE8JsQwpq5+8YAr3d52SxWBE4VGzQIrrwyDda+8Ub4wx9SePStb8F3v1uts9TXWmvB\nMcekHdkaVaPuvpbX1gbrrJMqurIcmP7ee6l9rZQQc8wY+Oxn4cILa7cuqVl1dMC0adm3plbDqi1s\nYIAkSZKk+hpYj5OEEIYDfwS+EWNcGEK4CPhhjDGGEH4E/Bj4cinHPP300/96e8qUKUwpcnuvMWPS\nPKRDD00VJ2PHpuqjZnbiiakF77TTGm9IdYwpQLrhhqxX0rPW1lTJM306/OpX2c28mjOn+Pa1rv7l\nX1IQesopMGxY9dclNaOODth22zQjaOutG3czhGJ89FFqvV5ttZXv32gjeOSRbNYkSZKkvmHq1KlM\nnTq1qOfWPEAKIQwkhUeXxxj/DBBjfLfLU34NXJ+7PQsY2+WxDXP3fUzXAKlU66+/Yg7SW2+l4GDi\nxLIPl7mttkrDv//7v2G77VJFTaNcKLW3p4qarKp6irXllvD449l+3/IVSKXackvYffc0/P3rX6/+\nuqRm1N4Or7ySbudbU5v153y+fW3V6sSNNko7hkqSJEnlWrUg54wzzujxufVoYbsYmBFj/Ouo5xDC\nqC6PfxZoz92+DjgqhDA4hLAJsBnwULUX1NYG22yTWtqybFmqpi9/Gf75n2Hy5OwHQXeV332t0WdL\nbbzxiovNrJRbgQTwne/Aj38MS5dWd01Ssxo9On0cMKD5f87Pm/fx9jWAceNsYZMkSVL91DRACiHs\nBhwD7BVCeDyE8FgIYT/g30MIT4UQngD2AP4ZIMY4A7gKmAHcBHw1xhirva7W1tTOcM89zd3W0NXo\n0anNIetB0Ku6/voUIDW6RgiQyq1AAth5Z9hkkzTjSxI891wKridPbv6f8/Pnf3yANqQW7NdeS63C\nkiRJUq3VtIUtxng/0NLNQ7cUeM3ZwNk1W1ROa2vztjN0Z9ttU2vee+81zm/b334bnnkmzWdqdOut\nlwK4jo4sv4nKAAAgAElEQVTmm4GU953vwLe/nYaqN3rFl1RrDz8Mn/50CoabOTyC7ndgg/R1DR2a\nfu5X8rNDkiRJKkbddmFTbbW2plkYo0enyqpGuGC68UbYd18YPDjrlfQuhNQO8uqr2a1hzpzyK5Ag\nXSwPGAA331y9NUnN6pFH4OijU4C0ZEnWq6lMTy1s4E5skiRJqh8DpD5k991TWPPii1mvJGmW9rW8\nrNvYKq0iCCFVIJ17bvXWJGWhowOmTatsltvDD8Nuu6Vg+Pnnq7e2LPTUwgYGSJIkSaofA6Q+JAQ4\n/HD44x+zXklqB7vrLjjggKxXUrysA6RKK5AAjjgiXUxOm1adNUn11tEBO+2UNgMod0OAN9+EDz9M\nc8HGj4eZM6u/znrqqYUNDJAkSZJUPwZIfcxhh8HVV2c/VPWGG1Ig0wzta3kbb5xtC1s15pgMHAin\nnGIVkppXe3sagL1sWfkbAjzyCOy4YwrVJ0xIx2lmBkiSJElqBAZIfcyOO6Z5H08/nd0aOjrgH/8x\nXQiWW0GQhb5QgQRw3HFw//3whz80z/deymtrg2HD0u3NNy9vQ4B8gAR9I0CaP98ZSJIkScqeAVIf\nE0KqQsqyje2pp1I1zfLl5VcQZGHcuOaegZS3bBm0tMDf/31zBXgSpPBo4MAU/JxySnkbAjz8MPzt\n36bbfSFAsgJJkiRJjcAAqQ/Kuo1t6VIYMgQGDUoXb+VUEGQhywqkJUvggw9gjTUqP1Z7e3MGeBKk\n9rU114QvfzkFQaWKceUKpC23TEO0Ozuru856MkCSJElSIzBA6oN23hkWLcrut+533JFa2O65B+69\nt7wKgiyMGJG+b4sW1f/cc+em9rUQKj9WW9uK0G6jjZonwJMAHngAdt0VJk+Gu+8u/fWvv54q8MaM\nSZ+vvjpssAG89FJ111lPhVrYRo9O7a+LF9d3TZIkSep/DJD6oBDgc59LVUhZuPZaOPJImDixecIj\nSN+3ceOyGaRdrflHkL7n996bWtgOO6y5/g6kfIC0/fYwaxa8+25pr3/44RUDtPPGj2/uNrZCFUgt\nLSkgmzWrvmuSJElS/2OA1Ecdfng2c5BefDGFITvvXP9zV0NWc5CqNf8or7UVjjkGHnyweseU6iEf\nILW0pI/33lva6x95ZMX8o7wJE2DmzOqtsd4KBUhgG5skSZLqwwCpj5o4MbU91Pui6c9/hkMOgQFN\n+s7Kag5SNSuQ8nbbLV1Mf/RRdY+r/qujA6ZNq91g9rlzUwvaNtukz/fYo/Q2tnwFUlfNPEi7szPN\nRytUSWiAJEmSpHpo0st89WbAgNTGVu8qpGuvhc98pr7nrKasAqRqVyBBuuBsa7MKSdUxb16q0Js8\nuXa7+/3lL7DTTmkXNkjnuuee4l8fIzz6aN8KkBYsSMP1C4XyBkiSJEmqBwOkPuyww+obIL37Ljz5\nJOy9d/3OWW0bb9z8M5C6mjIFpk6t/nHVv8QIn/98CpE6O2u3u98DD8Auu6z4/G/+Bl54IZ23GC+8\nkMKWESNWvn/8eHjmmbQzYbPprX0NDJAkSZJUHwZIfdiuu8I776Rtsevhhhtgn31g6ND6nK8W+lIF\nEhggqTp+8IM0pHmLLdLn48fXZne//PyjvMGD0zy1++8v7vXdzT+CVI237rrZhMOVKrQDW54BkiRJ\nkurBAKkPa2mpbxvbn//c3O1rkN0Q7VpVIDkHSZX65S/hD3+AW25J76WNN4af/KT6u/t1dsJDD6X5\nbV2VMgepu/lHec3axmYFkiRJkhqFAVIfd9hhcPXVtT/PBx/AXXfBgQfW/ly1NHIkvP9++nrqqVYV\nSM5BUiWuvRbOOCOFRyNGpPfTUUfBnXdW/1xPPw1jx8I666x8fylzkHqqQIJUNdXXA6QY67MmSZIk\n9U8GSH3cpEkwe3aaDVJLt9+efvO/6sVfsxkwIF2M1bvVpVYVSGAbm8pz//1w/PFw3XXwiU+suP+Q\nQ9J91bZq+1rezjuneUu9De1etgwefzzNTerOhAn135WyGoppYVtjjTR4vNhZUZIkSVI5DJD6uJYW\n+Oxna9/Gdu21cOihtT1HvWQxSLtWFUhggKTSzZyZfm5cfvnHW8J22inNVnvppeqes6cAaehQ+OQn\nYdq0wq9/5hkYPbrnsKUvt7CBbWySJEmqPQOkfuDww2sbIC1blgZoN/v8o7ws5iDVsgLJOUgqxezZ\nsP/+8O//Dvvt9/HHW1rgoIPg+uure95p07oPkKC4OUiF5h/Biha2ZmvzMkCSJElSozBA6gcmT04X\nFtWuGMh74AEYMyYFL31BvXdi6+yEhQt7b1MpV2tr2jHLOUgqpKMjtaLuuy985SvwhS/0/Nxqt7G9\n+SYsWLBil7dVFRMgFZp/BKm9dtiwtJtcMymmhQ0MkCRJklR7Bkj9wMCBqb3smmtqc/y+1L4G9Q+Q\n5s5NF4gDavhf45Qpxe9kpf6noyNVqu27L7z1Fnzta4Wf/6lPpYqfas3cmTYNdtml5/8GdtkFnngC\nPvyw52P0VoEEzdnGVmwF0rhxBkiSJEmqLQOkfqJWbWwxwp//3Hfa16D+M5BqOf8ozzlIKqS9PQ2q\nhrQLYW8hy7BhqSrolluqc/4HHkghUaHzbbNNz1V0S5akr2GHHQqfpxl3YrOFTZIkSY3CAKmfmDIF\nXnyx+sHI9OmwdClsv311j5ulelcg1XL+Ud5uu6UKDecgqTttbek9OGBAqtLZeuveX1PNNraeBmh3\nNXky3HNP94+1t8Mmm8Dw4YWP0Yw7sZXSwlbv4f+SJEnqXwyQ+olBg+CAA+DHP+59O+xS5KuPQqje\nMbM2alT6rX+hdplqqkcF0hprpFDgL3+p/rE7OlILUjXfV6qv1tbUlva978G996bPe3PQQakCacmS\nys790Ufw5JOF5xdB4TlIvc0/yuvLLWxWIEmSJKnWDJD6iY4OuO8+uOACmDSpehf7fW3+EaQqjLFj\n63cxVo8KJKhNG1t+ds7kydV9X6n+FiyAnXcuLjwCGD0attyy56qgYj32GGy1Ve/VQ/kquu4Cq2Lm\nH0EKkKZPb66d2IoNkEaPhnffrTzQkyRJknpigNRPtLfD66+n29Onr5h3Uok33kg7u02aVPmxGk09\n29jqUYEEtQmQ2tvTn87OVNlRjfeVsjFnTunvw2q0sRXTvgaw5pppl7aHH/74Y8VWIK2/fgqI33mn\n9HVmIcbiW9gGDkwhUrPtMidJkqTmYYDUT7S1pRamAQPSb7OLmXHSm+uuS21xgwZVfqxGU89B2vWq\nQKrFHKQNNkgXuSEUPztHjamSAKmSip5p04oLkCBVuq3axvbhh/Dss7Dttr2/Pv8+bZY2toULYejQ\n4n/G2sYmSZKkWjJA6idaW9NskyuugOXLYfDgyo/Z13Zf62rcuL5XgVSLOUgPPpgu/ldbLQUJxbY/\nqfGUEyDlQ+mnny7vnDEWX4EEaQ7Sqi1zTz6ZdlcbOrS4YzTTTmzFtq/lGSBJkiSplgyQ+pHWVjj8\n8PSb+muvrexYCxakyoFPf7o6a2s09Wxhq1cFElS/je2mm+CYY2C//eDOO6t3XNXXkiXwwQepTawU\nIVTWxvbKKymA2mij4p6/++4pcOrsXHFfsfOP8pqpAmnevOLa1/IMkCRJklRLBkj90AknwK9/Xdkx\nbr45zT7qqxUnfXEGElQ3QFq+PL0P9t8fjjwSrryyOsdV/b33Xgoxy9lNsZIAKV99VOx511svVQc+\n/viK+4qdf5Q3YQLMnFnaOrMyf74VSJIkSWocBkj90N/9XWr7ePHF8o/Rl9vXoG/OQILqzkF69NG0\n7k02gQMPTBVp771X+XFVf+W0r+VNmgQvvACzZ5f+2lLa1/JWnYPU1yuQDJAkSZLUKAyQ+qEhQ+DY\nY+E3vynv9e+9BzfcAHvtVd11NZLRo9PXuXhx7c9Vzwqk/Bykhx6q/Fg335yGqAMMG5baGf/3fys/\nruqvkgBp0KDUwnjDDaW/9oEHYJddSntN1zlIHR0p6C1lePsGG6TB280QdtrCJkmSpEZigNRPHX88\n/Pd/w9Klpb2uoyO1iyxcCIcdlj7vi1paYMyY2l+MLVtWeptKparVxnbTTSsCJEhtbFddVd6xOjpS\nBVNffT81ukoCJCivja2jA557DnbYobTXTZ6cNgRYtgweeyzNdCtlJ8j8TmzN0MZWbgtbJbviSZIk\nST0xQOqnxo+HzTYrvWrg6adXzAaaMQOmT6/60hpGPeYgzZ+fBhe3tNT2PF1VI0B69910Ab777ivu\n23//1E707rulHaujI7Ug7bprOp4hUv1VGiDtv3+qClq0qPjXPPRQCo+GDCntXKNGwYgR0N6e5h+V\n0r6W1yw7sZXawrbmmmko+fz5tVuTJEmS+i8DpH7s+OPhV78q7TUvvACDB6ff+E+YUFrrSLOpxxyk\nes4/yqvGHKRbb4U991z54n/11VOQcM01pR2rvR2efz7d7uuhZKOqNEBac03YeWe47bbiXzNtWunz\nj/L22CPNQXr44dIGaOc1yxykUlvYwDY2SZIk1Y4BUj922GGpCqDYkGTePPjud+H661O1wb339t1d\n2KA+FUj1nH+Ut8Ya6QK6kjlIXecfdVVOG1sIqQJrwIAUpvXlULJRVRogQeltbOUM0M7LD9IutwKp\nr7awgQGSJEmSascAqR9bfXU4+mi4+OLinv/tb8Ohh8I++8DEiX07PIK0XXitA6QsKpCgsja2ZctS\nBdL++3/8sf32S3Np3nqr+OP95Cfwr/8KF1yQhpf39fdVI6pGgHTwwakldtmy3p+7fHmqQCp1gHbe\nHnvAHXfAO+/AlluW/vpmqkAyQJIkSVKjMEDq544/Hn77W+jsLPy8u++GW26Bs8+uz7oaQV+tQIJ0\nAV5ugPTQQ2knq7FjP/7Y0KFw0EHFt7HNnAn/93/wz/+c3ouvvgqzZpW3LpWvGgHSxhun98WDD/b+\n3GeeScHpyJHlnWvs2NTa9YlPwAcflP76jTZK4cz775d3/nqxhU2SJEmNxACpn9t227Tb2C239Pyc\njz6CE05IFSJrrlm/tWWtHgFSVhVIu++egqBy5iDddFP31Ud5pbSxnXkmnHwyDB+e5mrtv39528Gr\nMtUIkCC1sV19de876lXSvgbp2B0d8NRTMGlS6YPXBwyArbZq/Da2clrY1l8/VQE6jF6SJEnVZoAk\nTjgBfv3rnh8/66w0l+bQQ+u3pkawwQZpR7ElS2p3jqwqkNZYI7X+XHxx6ReaPc0/ytt337Rb3+zZ\nhY/z/POpFe7EE1fcd/DBacaW6qtaAdLee8MvfpFmFBUKdioNkNrb07GXLy9/8Hoz7MRWagtbRwec\nc05q7ysnWJMkSZIKMUASRx6ZhmJ31zo0fTr8/Odw4YX1X1fWBg5M1Vmvv167c2RVgdTRkb6ur3+9\ntAvNt96CF18sfPE/ZEiqRPnjHwsf66yzUni0xhor7ttvv9K3g1flqhUgDRoEixenltgnn4TPfQ5O\nPx1+97tU8TZvXnqv3XknbLdd+edpa0uhdiW7QTbDHKRSW9ja21dsiuCOhpIkSao2AyQxfDgccQRc\ncsnK9y9fnubS/Nu/pWqc/qjWg7SzqkBqb4e5c0uv4LjlFvjUp9KFeyFHHAFXXtnz4y+9lHbsOumk\nle9fa620q9YddxS3HlXugw/S4Othwyo/1rbbpj+DBsFmm6UAadmyVFX2T/+U5vOsvXaa0fOP/1h+\nhUxra9oFspLdIBs9QProo/S9W3314l+TD9YANtnEHQ0lSZJUXQZIAlIb229+kwKFvF/8Is0KOeGE\n7NaVtVrPQcqqAil/oRlCmplS7IVmb/OP8j71qTQouafqrXPOga9+tfv2HNvY6isfYoZQ+bFaW+G+\n+1Kw89hj8JWvpAD6iivg0UdTy2L+PDNnVlYh09pa2W6QEyY09gyk/PyjUv5e8sHaAQfA177mjoaS\nJEmqLgMkAfA3fwPrrAO3354+f+MN+MEP4Fe/SiFSf7XxxitaQmohqwqk/IX+73+fKh2KqQTp7Ezv\nj/326/25gwenmVlXX/3xx159Ne3SdvLJ3b/2kEPgxhtXDjNVO9VqX8srFOxss03lrWfVsskmqSWz\nUdslS51/lNfamgKkp5+u/pokSZLUv/XjaECrOv74FcO0v/719BvsCROyXVPW+moFEqQLzaOOSq1E\n3/pW78+fNi1ddBfbznjEEd3vxnbuuem91tPX/YlPpAvnRx4p7jyqTLUDpEKq0XpWLQMHwuabw7PP\nZreGQubPL23+UVd/+7fw8MOVnb+jo/fd9CRJktS/GCDpr44+OlWY/Mu/pNaSU0/NekXZq+UMpOXL\nU5XBOuvU5vjFOu00ePDB3ucO3XRT4d3XVrXXXmngdtfv36xZqZ3pm98s/Frb2OqnngESVN56Vk2N\nvBNbuRVIkAaUP/dcmm9Vjo4O2Gmn3nfTkyRJUv9igKS/GjAAWlrgP/8zhRu13L6+WdSyAmnBgjS4\nuLeB1LW2+upwwQWp4mzx4p6fV+z8o7xBg+Dv/m7lNrZ//3c47jgYMaLwaw8+OA3ZVu3VO0BqJI08\nSLuSAGnIkPS1PfFEea9vb08zzDo73c1NkiRJKxgg6a/a21f8pvm117xoANhwQ3j7bVi6tPrHzmr+\nUXcOOihVY/zHf3T/+KxZaS7WzjuXdtyubWxvvQWXXw6nnNL763bZBWbPru38KSUGSFmvonuVtLBB\nZW1sm22WhncPGJD9rCpJkiQ1DgMk/VV+Z65GGHDbKAYOhNGjU3hSbVnOP+rO+efDf/0XvPTSxx+7\n+WbYd9/0/SjFlCkpBHrxxVTZduyx6fvZm5aW1C53ww2lnU+l6+8B0vTpjTnrp5IKJKgsQJoxA2JM\nA+2znlUlSZKkxmGApL9qpAG3jaRWbWyNVIEEad7TKaekAeoxrvxYqfOP8gYOhM99LgVTv/oVfPWr\nxb/WOUj10Z8DpJEjU7jZiLN+sgyQ7r4bttgitbD5/wFJkiTlGSBpJY004LZR1GqQdqNVIEEabv3y\ny3DttSvuW7IE7rwTPv3p8o550EFw4YVpu/Qjjyz+In3ffeH++xvror4v6s8B0nPPpY+NOOun0ha2\n8eNTG+j8+aW/9u6706YKs2aVf35JkiT1PQZIUi/6SwUSwODBcNFF8I1vwMKF6b7774ctt+x98HVP\n1lwzzVNZvry0i/Q11kizkG67rbzzqjj9OUBqa4NPfCLdHj++sdp2K61AGjgQtt8eHn20tNctWQIP\nPZTCXgMkSZIkdWWAJPVi441rM8y5ESuQIM0t2mMP+OEP0+fltq/lbbcdbLttebO1DjnENrZa688B\nUmtrCljGj4fvfa+xKi8rDZCgvDa2Rx6BzTdPf+bNczdOSZIkrWCAJPWiP1Ug5f3nf8Ill6Sd+SoN\nkCqZrXXwwen8y5aVf371LMbGDTLrZY014PvfTzO6GkmlLWxQXoB0990pQG5pSTOiZs+ubA2SJEnq\nOwyQpF70pxlIeSNHwhlnrGhj2XLLyo5X7mytceNg1Cj4y1+Ke35HR2PuqNWoFi5MlWGrrZb1SrJ1\n2GHwzDPw1FNZr2SFrCqQ8gESwJgxtrFJkiRpBQMkqRcbbghvvpkG7VZTo7cOHX10Gqj9/vvpgjKr\nUObgg+G663p/3vvvp/a4RtxRq1E1+nuwXgYPhq99Dc4/P+uVrFCNAOkTn0gh4dtvF/f8zk544IH0\n3w8YIEmSJGllBkhSLwYPThU5b7xR3eO+917jViABzJwJS5emNqcsd6g6+ODe5yAtXJiqSF5/vTF3\n1GpUBkgrnHAC/O//wjvvZL2S1LK5cGFqr6tECLDjjsVXIT32WKr6y/9cMkCSJElSVwZIUhFqMUi7\n0S/e29pSRU85w6+raaedUtj20kvdPz5zJuy8cwr5Ro2CAQOyXW8zafT3YD2tt14KIX/5y6xXAgsW\npPBoQBX+D11KG1vX9jUwQJIkSdLKDJCkIlR7kHaMMHduY1cgVTL8upoGDIADD+y+CunKK1PL2je/\nCZdfDqefDvvsk+16m4kB0sq+8Q246CJYvDjbdVSjfS3PAEmSJEnVYoAkFaHag7Tffx+GDk3tcY2s\n3OHX1bbqHKQlS+Ckk9LW67fdBl/6Urp/ww1T4JT1epuFAdLK2trSn6uuynYd8+ZVvgNbXj5AirHw\n85Ytg/vuS4FsngGSJEmSujJAkopQ7QqkRp9/1Gj22Qceeii19rz+eqqSePVVePRR2GGHFc9bd930\nvVVxDJA+7uST4Sc/6T1wqaX586tXgTRmTGpD7a0F98knYfTo1Ara9bUGSM3NnSklSVI1GSBJRaj2\nDCQv3EszbBjsskuqNPqbv4FDD4U//enjVRrrrGOAVArfhx+3//5pgPV992W3hmq2sEFxbWyrtq9B\nCpBmz842TFP5Ojpg113dmVKSJFWPAZJUhPXWg2eeqd4/wK1AKk1HRxqWfc01abjwV7/a/YBhK5BK\nY4D0cQMGpFlI55+f3Rqq2cIG5QdIw4bBkCFpXpuaT3t72pHSnSklSVK1GCBJvejogGOPhTffhN12\nq06I5IV7adrb4a230u3XXuv5QmittdLfz7Jl9VtbM5szB9ZfP+tVNJ4vfAGmTq1u22opqtnCBr0H\nSMuXp8HzqwZIYBtbM2trgxEj0u3x492ZUpIkVc4ASepFe3uqfoH0sRq/xbUCqTRtbeniZ9AgmDCh\n5wuhlhZYc81UwaHeGWR2b/hwOO44uPDCbM5f7Ra2HXdM88J6ClanT0/tnxts8PHHNtzQAKlZtbbC\nMcek2xdc4OYCkiSpcgZIUi/y4cWAASmcqMZvcb1wL01ra6qQuOee9LHQhZBzkIrn+7BnJ54Il1yS\nzdyYarewrbtuqjR79tnuH++ufS3PCqTm1tmZdvt88MGsVyJJkvoCAySpF/nw4ve/T/8QHz688mNa\ngVS61laYOLH336I7B6k4y5en2TbrrJP1ShrTuHGw555w6aX1P3e1W9igcBubAVLftWgR7L033Hln\n1iuRJEl9gQGSVITWVjjyyBQePfFE5cez8qN21l3Xob/FWLAgvZ8HDcp6JY3r5JPTMO3ly+t73mq3\nsEHPAVKMqbJv8uTuX2eA1NwWLYIDD4QHHoDFi7NejSRJanYGSFIJDjoIbrih8uNYgVQ7ViAVxxCz\nd7vtlkK2886rbytbtVvYoOcA6ZlnYLXVUsVVdwyQmtuiRenvcKutbGOTJEmVM0CSSlCtAMmL99px\nBlJxfA/2buHCVM327W/DpEn1C5Fq0cL2yU/C00/DkiUr31+ofQ0MkJrdokUwbJhtbJIkqTpqGiCF\nEDYMIdwVQpgeQng6hHBS7v61Qwi3hRCeDSHcGkJYs8trTg0hPB9CmBlC2LeW65NKtfvu8Nxz8Pbb\nlR3HCqTasYWtOAZIvWtvh9mzU5vXjBnV2YGxGLVoYRs+HDbdNIVIXRkg9W1dA6Q77sh6NZIkqdnV\nugKpE/hmjHFrYBfgayGErYDvAnfEGLcE7gJOBQghTACOAMYD+wMXhRBCjdcoFW3wYNhnH7jppvKP\nEWO6eDdAqg1b2IpjgNS7/A6MIcDYsdXZgbE3MaYKpGq3sMHH29hi7D1AWn99eP995+c0q3yAtPvu\n8NRT6e9SkiSpXDUNkGKMb8UYn8jdXgjMBDYEPgPk97a5FDg0d/sQ4IoYY2eM8RXgeWCnWq5RKtVB\nB8H115f/+kWLYODANHdE1WcLW3EMkHqX34HxC1+Az32u9x0Aq2HRohRUDx5c/WOvGiC98AIMGJAq\nk3oyYACMGpUqsdR88gHSaqvBTjulgemSJEnlqtsMpBDCxsD2wIPAyBjj25BCJmBE7mljgNe7vGxW\n7j6pYRxwQJolUe5v5L1wry0rkIrz7ru+D4vR2grHHAPTptXnfLVoX8tbNUDKVx/1VudrG1vzygdI\n4BwkSZJUuboESCGE4cAfgW/kKpHiKk9Z9XOpYa23Xmptufvu8l7v/KPacgZScQwyi7fLLvD44/DB\nB7U/Vy12YMvbdttUdbRoUfq8t/a1PAOk5mWAJEmSqmlgrU8QQhhICo8ujzH+OXf32yGEkTHGt0MI\no4B3cvfPAsZ2efmGufs+5vTTT//r7SlTpjBlypQqr1zqWX43tn3LGPPuhXttWYFUHN+HxRs2DLbb\nLlUh7b13bc9Vix3Y8oYMSXOcHn88zcS55x74/vd7f50BUnOKMYWe+QBpxx3htdfgnXdgxIjCr5Uk\nSf3H1KlTmTp1alHPrXmABFwMzIgxnt/lvuuAfwDOBb4A/LnL/b8LIfyE1Lq2GfBQdwftGiBJ9XbQ\nQfCZz8D55/fe/rEqK5BqyxlIxTFAKs2UKTB1au0DpFq2sMGKNrYNN0xtuFts0ftrxoyBN96o3ZpU\nGx99BIMGQUtL+nzgQJg8Ge66C446Ktu1SZKkxrFqQc4ZZ5zR43Nr2sIWQtgNOAbYK4TweAjhsRDC\nfqTgaJ8QwrPA3sA5ADHGGcBVwAzgJuCrMUbb29Rw2tpg2bK0tXepvHCvreHDYenSdPGknvk+LE0+\nQKq1WrawQRqk/PDDxc8/AiuQmlXX9rU829gkSVIlalqBFGO8H2jp4eFP9fCas4Gza7YoqQpCWNHG\nVurW3lYg1VYIK+YgbbBB1qtpXAZIpdl11xVzkFZfvXbnqWULG6QKpDPPhKFDUzVKMQyQmlNPAdL5\n53f/fEmSpN7UbRc2qa/JB0il8sK99pyDVFhnJ7z/fm0rXfqarnOQytHRkV7b0VH4ebVuYdtqK3j7\nbbj55uIGaIMBUrPqLkDaeusUgr70UjZrkiRJzc0ASSrTnnvCU0+VHlRYgVR7zkEqbO7cFFK09FQf\nqm6V28bW0QG77ZYqfiZNKhwi1bqFraUFttkmhQhjx/b+fEgB0uzZaSizmkd3AVIItrFJkqTyGSBJ\nZRo6NIVIt9xS2uusQKq9fAubuud7sDzlBkjt7elPZ2eamzZ9es/PrXULW0cHPP98+rjHHr1XRAGs\ntsRljDgAACAASURBVFoKIubMqd26VH3dBUhggCRJkspngCRVoJw2NiuQas8WtsIMkMrTdQ5SKUaO\nXDGseostCs9Nq3ULW3t7OkeMvYdZXW24oW1szaZQgHTXXbB8ef3XJEmSmpsBklSBAw6AW29Nu34V\ny4v32rOFrTDfg+Updw7SddfB4YfDIYeknxmtrT0/t9YBUltbCrAGDYIJE4rfBMA5SM2npwBp3DhY\nY40UJkqSJJXCAEmqwAYbwKabwv33F/8aK5BqzwqkwgyQyldOG9ull8KXvww/+QlcfHFqU+vJ/Pm1\nnYHU2gr33gv33JM+FgqzujJAaj49BUhgG5skSSqPAZJUoVLa2D74ILWO1HIbcDkDqTcGSOUrNUB6\n6qn0/d5zzxQ2H3AA/OxnPT+/1hVIkEKjiROLD4/AAKkZGSBJkqRqM0CSKnTwwcUHSPnqo/w8FNWG\nFUiFGSCVr9Q5SJdeCsceu2LHu1NPhfPPTxf33alHgFQOA6TmUyhA2nPPVIFWSvu1JEmSAZJUoR12\ngPffTzsb9cYL9/pwBlJhvg/Ll5+D9OCDvT+3sxN+9zv4whdW3Dd+fNr97Je//PjzFy9OF/SNWKFo\ngNR8CgVI668Pm2wCDz9c3zVJkqTmZoAkVWjAADjwwOKqkN57zwv3erACqTADpMoU28Z2662w8caw\n5ZYr33/aafDjH8NHH618//z5qfqoESsUDZCaT6EACWxjkyRJpTNAkqqg2DlIr7+eZiB1dNR+Tf2Z\nM5AKM0CqTLEB0qWXrlx9lLf99qly8ZJLVr6/UdvXwACpGfUWIH3qUwZIkiSpNAZIUhXsvTc89BAs\nWPDxx2KEZ56Bc8+Fr30tXXhOmmSIVEvrrJMCpBizXkljMkCqzK67wmOPFZ6DNG9eqkA68sjuHz/t\ntPQzoesMmnnzarsDWyXWWy8FEh9+mPVKVKzeAqRJk+CRR3qexyVJkrQqAySpCoYPT7saXXhhCobm\nz4drroETTkgtLPvuC/ffD0uWwPLlMGMGTJ+e9ar7riFDYPBgQ7qeGCBVppg5SFdemf67X2ed7h/f\nZRfYbLM0Iykv38LWiEKA0aNh9uysV6Ji9RYgDR+eKuHuu69+a5IkSc3NAEmqgo4OmDkTvv99GDUK\nNtwQfv1rmDABbrkFXn01XSi2tcGgQen+rbfOetV9m21s3Vu8OM3eWWONrFfS3HprY+upfa2r006D\ns86CZcvS543cwga2sTWb3gIkcA6SJEkqjQGSVAXt7fD22+n2kiVw440pODr55LTrUgjQ2pq2Tb7n\nnvSxtTXbNfd1DtLu3nvvpe9NIw5qbiaFAqTnnoOXX4ZPf7r3Y6y/Plx9dfq8kVvYwACp2RggSZKk\najNAkqqgrS1VFA0alD5+8pPdP6+1NbW6GR7V3jrrGCB1x/a16ig0B+myy+Doo9PPg0JCSFWLZ56Z\nWlsbuYUNDJCaTTEB0s47p8Dz1ltt+ZUkSb0zQJKqwOqixmMFUvcMkKpj2DDYdtuPz0Favhwuv7z3\n9rW8/fZL87quv94WNlVXMQHS4sUpyDzwQDd3kCRJvTNAkqrE6qLG4gyk7hkgVU93bWxTp6YQaLvt\nijtGCGkW0pln2sKm6iomQGpvT1V0y5a5uYMkSeqdAZKkPskKpO4ZIFVPdwFSMcOzV3Xooeli/8Yb\nrUAqV0cHTJtmBU1XxQRI+fbrEGDkSDd3kCRJhRkgSeqTmmEGUhYXvQZI1bPqHKSFC+HPf07zj0ox\nYAB873tpEP+bbzZuCNKoAVJHR6r4mjzZNqyuigmQWlvhvvvgN79JVUgtLfVZmyRJak4GSJL6pEav\nQOr4f+zdeZzVdd3//8d7mGGTwyIIoqS4ojCioCUJKLlrmdqitliaXle/S81My+1qMb28UkvNMi1L\nTb3c2rXM3BJBpbRcB0QtxQVEXOEogsB8fn+8OV8GZpjtLJ/POfO4327nNjPnfM7n82I4MzfOk9f7\n9c7HAbaVftNrgFQ6AwasPQfpt7+Nf5cjRnT9XAceCH37wsknZzcE2WQTWLAgznnKkieeiLverVzp\nMqyC99+PH3v37vjYXA6+9CWYMgUuuaS8dUmSpOpmgCSpJmV9BlJTE8ydW/k3vQZIpdVyGVt3lq8V\nFF4LWQ5B+vaFQYPgtdfSrmRtK1fGJVgAY8e6DAs61320rnPPhQsvzHbwLkmS0mWAJKkmZb0DqbER\n+vePb3wr+abXAKm0CgHSCy/ETpiDDureeQqzaBoash2CZHEZ2/Tp8OUvw8CBcOONbmQA3QuQttkG\nDjsM/vd/y1OTJEmqfgZIkmpS1mcg5XIwfHisc8aMyr3pNUAqrcIcpCuuiG+++/Tp3nlyOZg5M74W\nZs7MbgiSxQDpttvi9/6QQ+Cee9KuJhu6EyABfPvb8MtfxkBUkiRpXQZIkmpS1pewJQksXBiX3yxe\nXLnrGiCV1oABsVvo+9+HT32quHPlcjBpUnbDI8hegLRwITz7bJzfc+ih8Ic/pF1RNnQ3QNp4Yzjh\nBPjWt0pfkyRJqn4GSJJq0uDBsGRJ3Fkoi95+G+rrYY891gxhrgQDpNLK52HePFixAr72tWwOvy6l\nrAVIt98Oe+8dl/7tuy88/HC2g+NK6W6ABHDKKXDnnfD446WtSZIkVT8DJEk1qVevOBPlrbfSrqRt\nCxbEN+OTJsHf/16Zay5dGjuf+vevzPV6gqamNYHFU09lc/h1KWUtQLrtNvjYx+Ln/fvDnnvCn/7U\nvXPl8zBrVm2EgMUESAMHwn//N5xxRmlrkiRJ1a9LAVIIoSGEMCGEMLxcBUlSqWR5kPaCBXFb9EmT\nKteBVOg+KuxYpeJVy/DrUslSgPT++3D33XDAAWvuO+SQ7i1jy+fjMrjdd4epU6s/RComQII4lHzu\nXLj33tLVJEmSql+7AVII4achhHGrPx8EPA5cCzwaQvhMBeqTpG7L8hyk+fPjm/FddoHHHotvhsvN\n5WulVy3Dr0slSwHSzJkwZkwcRl/wsY/FQdpLl3btXE1NsXts5cr4sdo7yYoNkHr3hnPPhdNOi12L\nkiRJ0HEH0tQkSQr/jDoaeCZJkh2AnYFTy1qZJBWpGjqQcjnYcsu4BXy5GSCVRzUMvy6VLAVILZev\nFQwdCjvvDHfd1bVzjRsXQ5MQYjfZdtuVrs40FBsgARx+eJwh95vflKYmSZJU/ToKkFr+n/g+wB8A\nkiRZWLaKJKlENtwwuwFSoQMJKreMzQBJxdpwQ1i2rOsdPuVw223w0Y+2vv/QQ+H3v+/auZqaYMSI\n2Em2885w9dWlqTEtpQiQ6urg/PPhzDPjkHhJkqSOAqS3QwgfCyFMACYDfwEIIdQD/cpdnCQVoxo6\nkMAASdUjhPi6TbsL6dln45yiCRNaP3bIIXGQ9sqVnT/fRRfBySfHOUhXXx2Xbz33XOnqrbRSBEgQ\nd7jbYgu49NLaGTAuSZK6r6MA6cvACcDVwEktOo/2Am4rZ2GSVKysz0BqGSBVYic2AySVQhaWsRW6\nj9oaCP+BD8Do0XFGUmc89xxMnw5HHx2/3nprOPXUOEi6Wuf/lCpAAvjWt+L3o1YGjEuSpO5rN0BK\nkuSZJEn2T5JkpyRJftni/juSJDml7NVJUhGy3oFUWMK23Xbw2msx4CknAySVQpYCpPU59NDO78Z2\nySVw7LEwYMCa+04+OYbPv/xlUWWmppQBUn09NDfHjq45c6p/wLgkSeq++vYeDCH8qL3HkyQ5sbTl\nSFLpZHUG0qpVsGgRbLxx/LquDj70odiF1N6b4mIZIKkU0g6Q8vm45LO9OUeHHAIHHgg//GHbXUoF\nb78N113Xeoh9fT1ceSXsuy8ccMCan9VqUcoAqbEx3pqaoG9f2Gab0pxXkiRVn46WsP1/wBRgAfAP\n4J/r3CQps7K6hG3RIhgyJO76VLDrruWfg2SApFJIO0C66y7Ybbe1O4bWNXYs9OkDjz7a/rl+/vMY\nNI0a1fqxnXaKnUlf+Upx9aahlAFSLgf33w/33ReXsB1/fAzBJUlSz9NRgDQSuALYDzgSaABuSZLk\nmiRJril3cZJUjKwuYWs5QLugEoO0DZBUCmkHSB0tX4PYdXTIIe13Ka1YAT/6EXzta+s/5tvfjt1J\nnV0OlxWlDJAghkhTpsBvfxsD8OOPr975UJIkqfs6moH0RpIkP02S5CPA0cBgYE4I4ciKVCdJRcjq\nEraWA7QLdt0VHn44zhopFwMklUKaAVJzc+cCJOh4DtKvfw1bbQU777z+Y/r2jV1KJ5wQl7tVi1IH\nSAV9+8Itt8A//wlnnln680uSpGzrqAMJgBDCROCrwOeB23H5mqQqkOUOpMIA7YJhw2CjjWDu3PJc\nM0ligDR0aHnOr55j1Kj0AqRHHonLP7faquNjd901vub/9a/WjyUJXHghnNKJ7UB23x0+/nH4xje6\nXm9ayhUgQexGuv32GCRdcEF5riFJkrKp3QAphHB2COGfwMnAfcAuSZIckyTJnIpUJ0lFGDAgLlNZ\ntiztStbW1hI2KO8ytnw+zoTp27c851fPMXIkvPpqebvl1qez3UcQh9MffHDbXUgzZ8afic6e67zz\n4I474N57O19rmsoZIEEMvO+8Ey6/PHZoSZKknqGjDqRvEpet7Qh8D3gkhPBECOHJEMIT7T9VktIV\nQjYHac+f37oDCco7SNvlayqV3r1h8OA4C6fS/vQn+NjHOn/8oYe2PQfpoovi7KO6TvVhw8CBcNll\ncMwxMUTK5ztfQxrKHSBB7ES76y446yy49lqYNSv73xdJklSc+g4e36IiVUhSmRTmILXV8ZOW9jqQ\nrriiPNc0QFIpFeYgVXJ7+4UL43K0yZM7/5yPfASOOCI+t1Drs8/CAw/A9dd37fp77AFvvQV77w07\n7BC7mHK5rp2jUioRIAFsvXWcJbX77vHrxsZsf18kSVJxOhqi/UJbN+AlYEplSpSk7sviHKT1dSCN\nHw/PPVee/8U3QFIppTFI+/bbYZ99oKGh88/p3RsOOABuvXXNfT/8Ifznf3Y9YGlqij+bzc0wZw7M\nnt2151dSpQIkiJ2eIcCqVdn/vkiSpOJ0NANpYAjhjBDCpSGEfUP0FeA54LDKlChJ3ZfFJWzr60Dq\n3Rt22gn+8Y/SX9MASaW06abw8suVvWZXl68VHHLImjlIb74JN9wQd1XrqsZG2GJ1X/bYsTBuXNfP\nUQmrVsXZb5Wad9bYGL8fANtvn93viyRJKl5Hq/+vA8YATwLHAvcCnwIOSZLk4DLXJklFy1oH0vLl\nsGTJ+sOccg3Sfv31uMubVAqV7kB6/324557YTdRVBxwA998ff+5+9rM4WHvkyK6fJ5eDm2+Os3+y\nvEzr3Xehf//YFVQJuVz8/uZycWe2rH5fJElS8TqagbRlkiQ7AIQQfgG8AmyWJEnG9jSSpLYVZiBl\nxYIF8c3r+ob3TpoE111X+uvagaRS2nRTmDGjctebOTN2t3QnBM3lYOrUGG78+MdxKVx3jR4dA5os\nhySVXL5WkMvFv5tVqyp7XUmSVFkddSCtKHySJMkq4GXDI0nVJGtL2Na3fK2gsBNbkpT2ugZIKqVK\ndyD96U/w0Y92//mHHgonnRTr3nLL7p9n8OA4B2nlyu6fo9zSCJAgfm/efrvy15UkSZXTUYC0Ywhh\nyepbHhhf+DyEsKQSBUpSMbK2hG19A7QLRo2C+nqYN6+01zVAUilVOkC67bbiAqSPfCQGyY8+GruR\nujuovq4OhgzJVii9LgMkSZJULh3twtYrSZKBq2+5JEnqW3w+sFJFSlJ3ZXEJW3sdSCGUZw6SAZJK\nqTBEe9as8uwa2NIjj8Bbb8FWW3X/HIsWxWC2FDuFDRsWf56yygBJkiSVS0cdSJJU1bLWgdRRgAQx\nQPr730t7XQMklVKvXvDOO7D77sV19HQkn4eDDoodP7vv3v3rNDbG3cEaGorfQc0AqW1DhsSgT5Ik\n1S4DJEk1LWszkDpawgZ2ICn7Zs+Oc7pWriy+o6c9TU0xdG1uLu46uVwcxD1jRvE7qBkgtc0OJEmS\nap8BkqSaVo0dSDvvDE8+CcuXl+aazc2xM2DDDUtzPqmxMXac9OpVfEdPewYMiNcoRedQLhfD2WJ3\nUDNAapsBkiRJtc8ASVJN23DD2IFU6l3NuqszHUj9+8OYMXHgbym8/XZ801xfX5rzSbkcnHMO7LVX\n8R097bntNjjqqNJ0DpXK0KEGSG0xQJIkqfYZIEmqaX36QO/e5R/02xlJ0rkOJCjtMrZ58+Ibyix8\nD1Q79t4bnn66vKHOjTfCF75Qms6hUrEDqW2DBzsDSZKkWmeAJKnmZWUO0pIlcZe1gZ3Yw7JUAVI+\nD4cdFnfMKuewY/U8224bw4r588tz/jlz4vLTKVPKc/7uMkBq25AhdiBJklTrDJAk1bwNN8zGHKTO\ndh9B6XZia2qC556Ln5dz2LF6nhBgt93ggQfKc/6bboLDD4e6jP1LxQCpbS5hkySp9mXsn2WSVHpZ\nGaTdlQBpm21ix9LChcVdc8mSOPuoFEOIpXVNnlyeAClJ4vK1z3ym9OculgFS2wyQJEmqfQZIkmpe\nVpawdWaAdkEI8KEPFdeF1NwM3/oWXH55toYQq3ZMngz331/68z7ySAyRdt659Ocu1rBh2Qik18cZ\nSJIkqVwMkCTVvGrsQILi5yD96lfxTfjRR2drCLFqx847w9y58M47pT1vofsohNKetxTsQGqbM5Ak\nSap9BkiSal5WZiB1pQMJYuhz//0wa1bXh18vXw5nnAE/+EH2ZsiodvTtCzvtVJp5XQXNzXDzzXDE\nEaU7ZykNHAjvvQfvv592JW1LK0Dq1w9Wroy/eyRJUm3ybYWkmletHUjbbw8PPgi77971HdQuvRTG\nj4c99uh6nVJXlHoO0gMPxG6WrM7rCiE7v1PaklaAFEJcxrZ4ceWvLUmSKsMASVLNy8oMpAULutaB\nNH9+7MZYubJrO6i98Qacdx6cf3736pS6otQBUlaHZ7eU5WVsaQVI4CBtSZJqnQGSpJqXlW6B+fO7\n1oHU2AhjxsTPN9mk8x0Z//M/cNhhsN12Xa9R6qrddouzulatKv5cK1fCb34Dhx9e/LnKyQCpbQ7S\nliSpthkgSap5WZiB1NwMCxfCyJGdf04uBw8/DNdeG98UzpzZ8XP+/W+47jr4zne6X6vUFRttFF/X\nTU3Fn+uee2DLLeMtywyQ2uYgbUmSapsBkqSal4UOpNdeg0GDoE+frj0vl4Mjj4Q//QmOOgruvbf9\n4884A04+GYYP73apUpeVahnbTTdld3h2SwZIbXMJmyRJtc0ASVLNy8IMpK4O0F7XrrvCr34Vl/bM\nmtX2MbNmxaVEJ53U/etI3VGKAGnZMrjllrj8MusMkNpmgCRJUm0zQJJU8wYPhiVLSjOjpbu6OkC7\nLdOmwTXXwCGHwGOPrf1YksApp8A550D//sVdR+qqUgRIt98OO+5YXNBaKVkNkJqb4b330vsd4Awk\nSZJqmwGSpJrXqxcMHJjuG5uuDtBenwMOgMsugwMPhKeeWnP/734X3zh+/vPFX0Pqqm23jZ0v8+d3\n/xw33ZT93dcKshogvfce9O0LdSn9684ZSJIk1TYDJEk9QtrL2IpdwtbSJz8J550H++4Lzz0H778P\np50G3/9+DMukSgsh7sbW3S6kd96Bv/wlvrarQVYDpDSXr4FL2CRJqnX1aRcgSZWQ9iDt+fNhl11K\nd74vfCG+WdxzT5g6Ne5atffepTu/1FWFZWzdmWF0660wZUr8Oa0GBkhtM0CSJKm22YEkqUfYcMN0\nA6RSdiAVfP7zsfvo//4PXngB8vnSnl/qismT4f77u/fcG2+sjt3XCgyQ2uYMJEmSaltZA6QQwpUh\nhFdDCE+0uO87IYSXQwiPrL7t3+KxM0IIz4YQngoh7FvO2iT1LFnoQCp2iPa6mprgtdfi588/D7Nn\nl/b8UlfsvDPMnRuXo3XFm2/CjBlw8MHlqascDJDaZgeSJEm1rdwdSFcD+7Vx/0VJkkxcffsLQAhh\ne+AwYHvgAOCyEEIoc32SeohamoFU0NgI48ZBQwOMHRs/l9LSty/stBP8/e9de97vfgf77BMH3VeL\n/v3jro5Ll6ZdydrSDpAcoi1JUm0ra4CUJMn9QFvNzG0FQwcDNyVJsjJJknnAs8CHyliepB4kzQ6k\n99+Pb6qGDy/teXM5mDkzdm/MnBm/ltI0ZUrXBmnn8/DTn8Ihh5SvpnIIIXYhpdnV2Ja0AyQ7kCRJ\nqm1pzUA6IYTwWAjhFyGEQavv2xR4qcUx81ffJ0lFS3MG0iuvwIgR5dlaO5eDSZMMj5QNhUHanZHP\nx9fuP/8JF1xQfTO8sriMLe0AadCgGCAlSXo1SJKk8kkjQLoM2DJJkp2AhcCFKdQgqYdJswOpHMvX\npCzabTf429/i8q6ONDXFmUkQP1bbDC8DpNb69o1B+XvvpVeDJEkqn/pKXzBJktdafPlz4I+rP58P\nfKDFY6NW39ems8466/99Pm3aNKZNm1ayGiXVnjRnIJVjgLaURcOGwciRMRzaccf2j33ttRg29OpV\nnTO8DJDaVpiD1L9/unVIkqTOmT59OtOnT+/UsZUIkAItZh6FEDZOkmTh6i8/ATSt/vxW4PoQwsXE\npWtbAw+t76QtAyRJ6kiaS9jsQFJPUljG1l6AlM/DiSfCTTfFcHXcuOpbhmmA1LbCHCR/50mSVB3W\nbcj57ne/u95jyxoghRBuAKYBQ0MILwLfAT4SQtgJaAbmAV8GSJJkTgjhV8AcYAVwXJK4il5SaaS9\nhM0OJPUUkyfDPffAccet/5hTT4W99oJPfrJydZWaQ7Tb5iBtSZJqV1kDpCRJPtvG3Ve3c/z3gO+V\nryJJPVXaS9i23z6da0uVNnkynH32+h+/5x7405/gyScrV1M5DBu2ZoZTVrz7buy2TNPgwfBWW/vv\nSpKkqpfWLmySVFEDBsD778Py5ZW/tkvY1JNsu20MMua3McUwn4djjoErrohBQzVzCVvb7ECSJKl2\nGSBJ6hFCSG8OkkO01ZOEEHdje+CB1o+deirsuScccEDl6yo1A6S2FYZoS5Kk2mOAJKnHSGsOkh1I\n6mkKg7RbKixdu+iidGoqNQOkttmBJElS7TJAktRjpDEHKZ+HVatg0KDKXldK0+TJcP/9a77O5+HY\nY+FnP6v+pWsFBkhtcwaSJEm1ywBJUo9Rqg6kfB5mzYofO1LoPgqh+OtK1WKXXeDpp+Gdd+LXp50G\n06bBgQemWlZJDR0aA6Qs7ReblQDJDiRJkmpTWXdhk6QsKcUMpHw+znd56ilobISZMyGXW//xCxY4\n/0g9T58+sNNO8Pe/x/D0j3+s/l3X1tWvH9TXx9BmwIC0q4myECA5A0mSpNplB5KkHqMUHUhNTTBn\nTlyWNmcOzJ7d/vHz5zv/SD3TLrvAVVfB0UfX1tK1lrK2jC0LAZIdSJIk1S47kCT1GKUIkEKIt7q6\n+D/t48a1f7wDtNUT5fNwyy0wb178OZk6Ne2KyqMQII0enXYlkQGSJEkqJzuQJPUYxS5hSxI480w4\n/3y4/npoboaGhvafM3++S9jU8zQ1wcsvx8/feafjTr1qZQdSaw7RliSpdhkgSeoxiu1A+v3v4bXX\n4KtfhSOOgJ13hptvbv85diCpJ2psjN15DQ0wdmzHnXrVKksBUpJkJ0CyA0mSpNpkgCSpxxg6FN58\ns3vPfe89OOUUuOSSODgX4MQT49ft7cLkEG31RLlcHDA/Y0bHg+arWZYCpOXL4++m+pSHEwweDIsX\nZ2t3OkmSVBoGSJJ6jGI6kC68ECZOhD33XHPf/vvH5TkPPLD+5zlEWz1VLgeTJtVueATZCpCy0H0E\nMcDq1y/+bpQkSbXFAElSj9HdGUgvvwwXXww/+MHa99fVwVe+Aj/6UdvPSxJ45RUYObLr15SUfUOH\nGiC1xTlIkiTVJgMkST1GYQlbV5dWnHoqHHccbLFF68e++EW4+2546aXWj73+OgwYEP83XlLtsQOp\nbc5BkiSpNhkgSeox+vSB3r27trTi/vvjDJfTT2/78YED4cgj4bLLWj/mAG2pthkgtW3IEAMkSZJq\nkQGSpB5lyBC46y7I5zs+dtWqOCj7ggvaf2P2la/AL34RB2235ABtqbYZILXNDiRJkmqTAZKkHiOf\nj2/2DjsMpk7tOES6+mro3x+OOKL947beGnbdFW64Ye37HaAt1TYDpLY5A0mSpNpkgCSpx2hqghUr\nYmfRE0/AVVetfx7S22/DN78ZB2SH0PG5TzwRLrlk7fPZgSTVtsLOjlnYsj5rAZIdSJIk1R4DJEk9\nRmNjvDU0wKhR8NOfws47w003wcqVax979tlw0EEwcWLnzr3PPjGcuu++NffZgSTVtt69Y5fi4sVp\nV2KAJEmSys8ASVKPkcvFgdgzZsDs2fF29tnwk5/AmDFw+eVxjtE//hG7k844o/PnDiF2If3oR2vu\nc4i2VPuGDYtdSGnLUoDkEG1JkmqTAZKkHiWXg0mT4se6OvjYx2KodO21cPvtsPnmMGVKnI/0iU90\nbth2wZFHxg6kefPi1y5hk2pfVuYgZSlAsgNJkqTaZIAkScDkyXDrrXDxxXEpWnMzzJkTu5Q6a8AA\nOOqo2NEELmGTegIDpNYcoi1JUm0yQJKkFj7+cdhhhzgnaexYGDeua88/4YS4e9vixfDmmzBiRHnq\nlJQNBkit2YEkSVJtqk+7AEnKksKcpNmzY3iUy3Xt+VtsEZfAff/7sNFG0KtXeeqUlA0GSK05A0mS\npNpkgCRJ6yjMSequE0+Ms5VGj44zlLoaQkmqHgZIrdmBJElSbXIJmySV2C67xBlKc+fC1KldG8Qt\nqboYILXmDCRJkmqTAZIkldjs2bByJSRJ1wdxS6ouBkitDRwI77wDq1alXYkkSSolAyRJKrHGxnjr\n7iBuSdUjKwHS0qXZCZDq6uLS3SVL0q5EkiSVkjOQJKnEih3ELal6ZCVAylIHEqwZpD1kSNqVds3g\n8wAAIABJREFUSJKkUrEDSZLKoDCI2/BIqm0GSG1zDpIkSbXHAEmSJKmbCp02ac/7yWKA5E5skiTV\nFgMkSZKkbqqvj0Oj0w5LDJAkSVK5GSBJkiQVYejQ9JexZS1AKnRmSZKk2mGAJEmSVIS05yCtXBmX\n0PXunV4N67IDSZKk2mOAJEmSVIS0A6R334X+/SGE9GpYl0O0JUmqPQZIkiRJRchCgJSl5WtgB5Ik\nSbXIAEmSJKkIBkitGSBJklR7DJAkSZKKYIDUmkO0JUmqPQZIkiRJRTBAas0ZSJIk1R4DJEmSpCIY\nILXmEjZJkmqPAZIkSVIRDJBaM0CSJKn2GCBJkiQVYdgweOON9K6fxQDJGUiSJNUeAyRJkqQi2IHU\n2gYbwLJlsGJF2pVIkqRSMUCSJEkqwuDBkM/DypXpXD+LAVIILmOTJKnWGCBJkiQVoa4uLtl68810\nrp/FAAkMkCRJqjUGSJIkSUVKcxmbAZIkSaoEAyRJkqQiGSC15iBtSZJqiwGSJElSkQyQWhs8GN56\nK+0qJElSqRggSZIkFckAqTWXsEmSVFsMkCRJkopkgNSaAZIkSbXFAEmSJKlIBkitOQNJkqTaYoAk\nSZJUJAOk1pyBJElSbTFAkiRJKtLQoQZI63IJmyRJtcUASZIkqUh2ILVmgCRJUm0xQJIkSSqSAVJr\nBkiSJNUWAyRJkqQiGSC15hBtSZJqiwGSJElSkQYOhGXLYPnyyl63uTlet1+/yl63MxyiLUlSbTFA\nkiRJKlIIcZD2G29U9rpLl8bwqC6D/6JzCZskSbUlg//ckCRJqj5pLGPL6vI1gL59IUlih5QkSap+\nBkiSJEklYIC0thCcg6TakM/DrFnxoyT1ZAZIkiRJJWCA1JpzkFTt8nkYMwamTIGpUw2RJPVsBkiS\nJEklYIDUmnOQVO1mzIBXXokD6+fMgdmz065IktJjgCRJklQCw4ZVfoi2AZJUXnfeGQfk19VBLgfj\nxqVdkSSlxwBJkiSpBOxAas0ZSKpmr74K110H998Pf/lLDJGefz7tqiQpPQZIkiRJJWCA1JozkFTN\nLrgAPvc52G472Gcf+M534JRT4u6CktQTGSBJkiSVgAFSay5hU7VauBCuvhrOOGPNfV/+Mrz0Etx+\ne3p1SVKaDJAkSZJKwACpNQMkVavzz4cjj4RNNllzX0ND7Er6+tdh5cr0apOktBggSZIklYABUmsG\nSGpLPg+zZsWPWfTKK3DNNXD66a0fO+gg2Hhj+MUvKl+XJKXNAEmSJKkEDJBac4i21vXqqzBmDEyd\nGm9ZDJHOOw+++EUYObL1YyHAhRfCd78LS5ZUvjZJSpMBkiRJUgn07w/NzbB0aeWumfUAySHaKlix\nAi6/HBob43yhVatg9ux4y5L58+POa6edtv5jJkyA/faLQZMk9SQGSJIkSSUQQuxCeuONyl2zGgIk\nO5B6tlWr4Prr405mf/gD/OY3MH481NfHx/v3T7e+dZ13HnzpS3GZWnvOPRd+9jN44YXK1CVJWVDW\nACmEcGUI4dUQwhMt7hsSQrgzhPB0COGOEMKgFo+dEUJ4NoTwVAhh33LWJkmSVGqVXsZmgKSsKcw3\nWrIEbr0VdtoJLr0UrrwS7rgD9tgDZs6Mt/POg89+NjvL2F5+GW64AU49teNjN90Ujj8ezjyz/HVJ\nUlaUuwPpamC/de47Hbg7SZIxwF+BMwBCCGOBw4DtgQOAy0IIocz1SZIklczQoQZILTkDqWfJ59fM\nNho5Mg6hPvdcePBBmDZtzXG5HEyaBCefDLvtFnc7a25Orez/53vfg2OOgeHDO3f8qafCvffCQw+V\nty5JyoqyBkhJktwPrLvy/WDgmtWfXwMcsvrzjwM3JUmyMkmSecCzwIfKWZ8kSVIpDRoU3yxXqqMi\n6wHSoEExQEqStCtRJTQ1xZlGq1bB8uXw85/Dxz8el3e2JYTYnfTGG3DWWRUttZWXXoKbboJvfKPz\nzxkwAM45B045xde4pJ4hjRlIw5MkeRUgSZKFQCHj3xR4qcVx81ffJ0mSlHn5PMyYAWefXbndpbIe\nIPXuHW/vvpt2JaqExsY4O6iuLn4+fnzHz+ndG377W7jmGvj1r8tf4/r87//Cf/wHbLRR15531FFx\nud4NN8Sle+393BeW92VlyZ4kdVV92gUA3crrz2rx3xTTpk1jWsu+WEmSpApraoo7jjU3w5w5sRNj\n0qTyXjPrARKsmYM0YEDalajccjk44oj4c3DxxfHrzhg+PA7Y3ndf2GabODepkl54AX71K3j66a4/\nt1evGBofdlj82d98czj//PjY0qXw3nvx41tvwS9+AYsWwbhxcQZUZ78/klRO06dPZ/r06Z06No0A\n6dUQwogkSV4NIWwMLFp9/3zgAy2OG7X6vjadlXafqyRJUguNjTBmTAyPtt8+vkkst2oKkEaNSrsS\nVcKCBXGL+66GIxMmxOVshx4aZwp1tROoLfl8DHYbG9dfTz4PX/1q7CQaNqx71xk+HFaujAHSc8/B\n978Pm2wSd5jr1y9+fOut+L2BygXMktQZ6zbkfPe7313vsZUIkMLqW8GtwFHA+cAXgVta3H99COFi\n4tK1rQFH0kmSpKqQy8Hf/gYTJ8KFF1amu6AaAqQhQ+KbZ/UMzz8PW2zRvecefjg88QR86lNw111x\neVt35fPwwQ/GrqLevWHbbWOYmcvBwIHxY58+cdlcoSvorLO693Pb2Ag77BCDobFjY+3rniefh3vu\ngYUL4zGVCJglqdTKOgMphHAD8CCwbQjhxRDC0cB5wD4hhKeBvVZ/TZIkc4BfAXOAPwPHJYnj6CRJ\nUvXI5eLQ4L/9rTLXq4YAqdCBpJ7h+edh9OjuP/+cc+Lw9f/6r+LmBT322Jolac3N8PWvw//8Dxx3\nHBx8cAyXQliza+Izz8SuoO7I5eKStBkz1r80rXBMv37w5z+7fE1SdQrVmNGEEMyWJElSJt1+O1xw\nQdzeu5ySBOrr4f334xyWrPr85+OSpiOPTLsSldt778XAcOnS4l6T8+fDVlvBihWxs6c784LOOSfO\nInr//djx09Y58vk48L7QOVSJuUQf/zh88pPwxS+W9zqS1F0hBJIkaXP/zDR2YZMkSapZU6fCww/H\nN9HltGwZNDRkOzwCO5B6knnzYLPNin9NvvgirFoVO4dmz+56Z9DTT8Mll8CDD3auK6i9Y0rtyCPh\n2mvLfx1JKgcDJEmSpBIaMCAOBL7//vJepxqWr0GcgZSlAMmt1Mtn3rzuzz9qqbExzgiqr4/LzEaO\n7Pxzm5vhmGPg29+G8ePjoOr2gqFcruNjSumgg+DRR2NIJknVxgBJkiSpxPbeG+6+u7zXqJYAafDg\n7AzRzufhwx+GKVPizRCptIoZoN1SoTNo5kz48pfjPKTm5s4999JL48cTTii+jnLo2xc+/Wm4/vq0\nK5GkrjNAkiRJKrG99oo7LpVTNQVIWelAamqCuXNjGFHYSl2lU6oACdZ0Bl10UQz6/vd/O37Oc8/B\n2WfDVVdBXYbf5XzhC3DddXGOmSRVkwz/apUkSapOu+4K//oXvPFG+a5hgNR1jY1xC3eI3zu3Ui+t\nUgZIBQ0NcPPNcPnlcNdd6z8uSeDYY+G002DbbUtbQ6ntthssXw7//GfalUhS1xggSZIklVhDQ1wi\nVc6d2GotQKrEbKIBA+ISoquvjrN1liwp37V6ouefh9GjS3/eTTaBG26IA6jXNzvoiiviz8TJJ5f+\n+qUWQuxCcpi2pGpjgCRJklQG5Z6DVC0B0pAhHc9Ayudhm21i6DZ1avlCpLlzY7j3xS/C5z4XQweV\nTjk6kAr22COGQ5/+dOzeaenFF+Gb34xL17K+K2HB5z8PN94I77+fdiWS1HkGSJIkSWVQ7jlI1RIg\ndaYD6ZZb4NVXyz+b6K67YJ99YgfIccfFAMk38KWxeHEMdjbaqHzX+MY3YjfSKaesuS9J4qDtr361\nupYkbrUVjBkDf/lL2pVIUucZIEmSJJVBY2NcIvXCC+U5f60ESEkS59tsumkMdjbaqHxBQCFAAhg7\nFrbfHn73u/Jcq6eZNy92H4VQvmuEAL/8JdxxR1zSBnEZ2MKFcfZRtSkM05akamGAJEmSVAZ1dbDn\nnuXrQqqWAGnQoBikrW8b9v/7P1i2LO6QdsUVcYlZ//6lr2PFCpgxI3aGFRx/PPzkJ6W/Vk9UzuVr\nLQ0aBL/9bew4uuUWOOkkuPTS+LqpNp/+NNx5Z8dLPCUpKwyQJEmSymSvvco3B6laAqReveLw6rYG\nVr/9Npx6Klx2WexUOvZYGDkyBgOl9re/wdZbw7Bha+47+ODYOfP446W/Xk9TqQAJYPx4+J//gUMO\nia+r448v7/D1chkyBPbbD371q7QrkaTOMUCSJEkqk733jh1ISVL6c1dLgATrX8b27W/DQQfBrruu\nue/kk+Gii0pfQ8vlawX19XF+jl1IxatkgAQxROrVq/xzs8rN3dgkVRMDJEmSpDIZPTp23zQ1lf7c\n1R4gPfoo3HwzfO97a99/6KHw8svw0EOlraGtAAngP/4Dfv3rjgd9q32VDpAaG+OtoSHOs6qmAdot\n7bcfPPss/OtfaVciSR0zQJIkSSqjQhdSqVVzgNTcHHdBO/dcGDp07WPr6+HEE+Hii0t3/bffjiHe\n5MmtHxsxAg44IA5nVvc9/3wMTCsll4OZM+Ncq5kz49fVqKEBPvOZOAtMkrLOAEmSJKmMyjUHqZoD\npKuvjsv6vvSlto8/5pi409ZLL5Xm+vfeC7vtBn37tv348cfHOUzrG/St9iVJ5TuQIIZGkyZVb3hU\nUFjGVo6lrpJUSgZIkiRJZbTnnrFDYsWK0p63mgKkIUPW7DT1xhtw5pkxsKlbz79EBw2CL34Rfvzj\n0lx/fcvXCnbbLe78dtddpbleT/P669CnT/x7U9dNnAj9+sEDD6RdiSS1zwBJkiSpjIYNgy23LP1M\nn2oKkFp2IJ15Zty+fOLE9p9z4olw1VXwzjvFX7+jACkEOOEEh2l3VxrdR7UkBIdpS6oOBkiSJEll\nVo45SNUYID30ENx6a9yCvSNbbAHTpsXlbsWYNy9u9b7DDu0f99nPwoMPxuPVNQZIxfvc5+A3v4Fl\ny9KuRJLWzwBJkiSpzMoxB6naAqQ33oD/+i84//z4dWecfDL88IewalX3r33XXTHAW99yuYL+/WMX\nyE9/2v1r9VQGSMUbNQrGj4cLL4R8Pu1qJKltBkiSJEllNnUqPPJIaZZjFVRTgNS3b9zlrE8fOPLI\nzj/vwx+OSwD/+MfuX7uj5Wst/dd/wZVX2gXSVQZIxcvn4bnn4Fvfir8vDJEkZZEBkiRJUpltsAHs\nvHMcpl0q1RIg5fOx6+jdd2MXUldCtBBiF9JFF3Xv2qtWxaWDnQ2Qttkm/j3dfHP3rtdTPf88jB6d\ndhXVrakJXnkl7sQ2Zw7Mnp12RZLUmgGSJElSBey1V2nnIFVLgNTUBC+/HD9//vmuvzH+5CfjXKJ/\n/KPr1370URgxAjbdtPPPOf54h2l31bx5diAVq7ERtt8+fr799jBuXLr1SFJbDJAkSZIqoNSDtKsl\nQGpsjG+GGxpg7NiuvzGur487sl18cdev3ZXlawUHHgivvhqXsrmMqGPNzfDii3YgFSuXgwceiD/T\nt94av5akrDFAkiRJqoAPfjDOOHntteLP9f778WPv3sWfq9xyubh0b8aM+LE7b4yPPRZuv31NJ1Nn\ndSdAWroUVqyI15w0yRCpIwsWwJAh0K9f2pVUv1wudsstXZp2JZLUNgMkSZKkCmhogN13h3vvLf5c\n1dJ9VJDLxTCmu10VgwfH4dsXXgizZnUu1Fm6FB5+GPbYo2vXampaE/LNmQM//3nX6+1JHKBdWsOH\nxw44ScoiAyRJkqQK2WsvuPvu4s9TbQFSKRxzDPz4xzGE68wuVTNmwIQJXQ+tWi6522qruHTuuOPi\n91ytGSCV1ogRBkiSsssASZIkqUL23jsuq+psF836vPoq1NX1rOVV774b5+2sXNm5Xaq6s3wN1l5y\n9+ij8OST8fs8cWLsaNLaDJBKywBJUpYZIEmSJFXIZpvFOT6d7aJpSz4Pn/50PE93z1GNGhvjLQQY\nMGDNjlXr090ACdZecjd4MFx3HZxzDnz0o3D22THEUmSAVFoGSJKyzABJkiSpQmbPhiSJAURTU9e3\ntAf4/vfjm3boXCdOrSjsUnXPPTE8+vrXY0dSWxYuhJdegl12Kd31DzssdiTNnBmDu8ceK76TrBbM\nm+cObKVkgCQpywyQJEmSKqTQRVNfH5eg3XwzrFrVueeuWBG3s7/+ehgzJs7oGTs2zuvpKXI5+MhH\n4C9/ieHZCSfEQG5dd98dj6uvL+31N90U7rgDDj00hlNTprhTmx1IpWWAJCnLDJAkSZIqpDBfZ+ZM\neOaZOF9n//3h9dfbf96iRXF+0r//Df/8Z5zFM2NGPE93dzarZrkc3H47PPIInHRS6xCpmOVrHamr\nix1IIcQOqDlz4BOfiH8XbYVZtWzFitjt9YEPpF1J7TBAkpRlBkiSJEkVVJivM3p07KSZOBE++MEY\nhrTl4Yfj43vsAX/8Y5zJ03JGT081cGD8/j34IHzjG2vCmyQpb4AEa+/U1tgYw71jj4Udd4Sf/nRN\nR1I+X9vL3F58EUaOjN8HlYYBkqQsM0CSJElKSX09nH8+XHAB7LcfXHvt2o//8pdw4IHwwx/G4c11\n/sttLYMHxyVl99wDZ54Zw6M5c6BPH9hqq/Jdt+VObQ8+CKedBnPnwsUXx/Bq883hP/8zBn/FDEzP\nOpevld6IEbHjsKd1s0mqDiVeGS5JkqSu+vSn4zyjQw+Fhx6Cb34zzvd5/HG47774mNq24YYxtNlz\nT+jdG/r1g/Hj4Z13ytuhVegCKwgB9tor3l5+Gb79bXj66fhYYdh5y+NrgQFS6W2wAfTqFQPHgQPT\nrkaS1maAJEmSlAHjxsXw6LOfjcOakyTe53yZjg0bFgdn7747/Otf8b6pU9ObETVqFFxySexQ+ve/\nYbvtanPYuQFSeRSWsRkgScoaG6ElSZIyYvBg+O//jt0sSRI7WGbPTruq6jB8OPzgB3Gw9apVa7p+\n0pLLwaOPxs6ogw6qzXlV8+bFWV4qLecgScoqAyRJkqQMGT8+DmZuaIhL12qxc6Vc9tgjfv+y8r3L\n5eCqq+BnP4sDp2uNHUjlYYAkKasMkCRJkjKk5YDmtJZgVassfu823xyOPz4O2q41BkjlYYAkKasM\nkCRJkjKmMKA5CwFItcni9+7UU+GBB2KoVSuWLoXFi2HkyLQrqT0GSJKyygBJkiRJKqMNNoALLoCv\nfjXOZ6oF8+bBZptBne8mSs4ASVJW+StfkiRJKrPDD49B0lVXpV1Jabh8rXwMkCRllQGSJEmSVGYh\nwCWXwLe+BW+/nXY1xTNAKp/hww2QJGWTAZIkSZJUARMnwkEHwdlnp11J8ebNM0AqFzuQJGWVAZIk\nSZJUIeeeC9ddB3Pnpl1JcZ5/HkaPTruK2mSAJCmrDJAkSZKkChk+HM44A772NUiStKvpPpewlc/A\ngbByJbz7btqVSNLaDJAkSZKkCjrhhBjA/PnPaVfSfQZI5ROCXUiSsskASZIkSaqg3r3h4otjF9L7\n76ddTde9/XbskBk6NO1KapcBkqQsMkCSJEmSKuyAA2DbbeGCC2DWLMjn066o8wrdRyGkXUntMkCS\nlEUGSJIkSVIKzjkHvvMdmDIFJkyAxYvTrqhz3IGt/AyQJGWRAZIkSZKUgmXLoK4Ompvh3/+GbbaJ\ny9r+9rdsD9h2/lH5jRgBixalXYUkrc0ASZIkSUpBYyOMGwcNDbDjjnDbbTBoEBx1VAxoTj0VZsyA\nBx/M1hK355+H0aPTrqK22YEkKYsMkCRJkqQU5HIwc2YMiWbOhA9+EM46C556Cm69NXYm7bMPTJ4M\nu+6anRDJDqTyM0CSlEUGSJIkSVJKcjmYNCl+LAgBxo+HT34yhkgQQ6VbbkmnxnUZIJWfAZKkLDJA\nkiRJkjKo5RK3zTaDk06Ce+9Nt6YkcYh2JRggScoiAyRJkiQpg1oucWtqgt/8Bo44Am68Mb2aFi2C\nfv3W7phS6RkgScqi+rQLkCRJktS2whI3gGnT4J574MADYf58OOWUuNytkuw+qowhQ2Dp0rhTX9++\naVcjSZEdSJIkSVKVaGyMu7Jdc01c0rZqVWWv7/yjyggBhg+PHV+SlBUGSJIkSVIVGTUqLm174om4\npO2112DWrMrs0maAVDkuY5OUNQZIkiRJUpUZPBj+8pe4S9sWW8Duu8PUqeUPkZ5/HkaPLu81FA0f\nboAkKVsMkCRJkqQq1KcPnHwyvPcerFwJTz4ZO5HKyQ6kyrEDSVLWGCBJkiRJVWr8eNhhB6ivh0GD\n4PDD4RvfgAULSn+tfB6eego22qj051ZrBkiSssYASZIkSapSuVychzRzJrzwAjz+OKxYEYdt/8d/\nwDPPdP5c+fzas5SSBN54A/7xD7juOhgzJu7+dvTRlZm31NMZIEnKmpAkSdo1dFkIIanGuiVJkqRK\neP11uPRS+MlPYNo0+MpXoFevOL8oSWDxYliyZM1t0SI499wYWAwYEAd1v/QS1NXFJWsDB8L998eZ\nSw0NMGMGTJqU9p+ytl1/Pfzxj3DTTWlXIqknCSGQJElo67H6ShcjSZIkqbyGDYOzzoKvfz0GSXvt\nFeck1dXF4cxDhsRQaODAuPRt2bIYHjU3w9KlcOqpcPDBcVg3xI6jqVNhzhwYOxbGjUv1j9cj2IEk\nKWsMkCRJkqQaNWAA7LHHmq979YLf/75199C6AdEnPhGXxxUUlsrNnh3Do5aPqTwMkCRljUvYJEmS\npBq2bjg0c2bbAVA+b0CUJYsWxb+v119PuxJJPUl7S9gMkCRJkqQaZzhUfVatgr5945LChoa0q5HU\nUxggSZIkSVKV2XhjeOQR2GSTtCuR1FO0FyDVVboYSZIkSVLHnIMkKUsMkCRJkiQpgwyQJGVJaruw\nhRDmAYuBZmBFkiQfCiEMAW4GNgfmAYclSbI4rRolSZIkKS0GSJKyJM0OpGZgWpIkE5Ik+dDq+04H\n7k6SZAzwV+CM1KqTJEmSpBQZIEnKkjQDpNDG9Q8Grln9+TXAIRWtSJIkSZIywgBJUpakGSAlwF0h\nhIdDCMeuvm9EkiSvAiRJshAYnlp1kiRJkpQiAyRJWZLaDCRgcpIkr4QQNgLuDCE8TQyVWlr3a0mS\nJEnqEQyQJGVJagFSkiSvrP74WgjhD8CHgFdDCCOSJHk1hLAxsGh9zz/rrLP+3+fTpk1j2rRp5S1Y\nkiRJkipo+HADJEnlNX36dKZPn96pY0OSVL7JJ4TQH6hLkuSdEMIGwJ3Ad4G9gDeTJDk/hHAaMCRJ\nktPbeH6SRt2SJEmSVCkLFsCECYZIkionhECSJKHNx1IKkLYAfk9colYPXJ8kyXkhhA2BXwEfAF4A\nDkuS5O02nm+AJEmSJKmmrVgB/frB8uXQq1fa1UjqCTIXIBXLAEmSJElSTzBsGMyeHechSVK5tRcg\npbkLmyRJkiSpHQ7SlpQVBkiSJEmSlFEGSJKywgBJkiRJkjJqxAhYtN69qSWpcgyQJEmSJCmj7ECS\nlBUGSJIkSZKUUQZIkrLCAEmSJEmSMsoASVJWGCBJkiRJUkYZIEnKCgMkSZIkScooAyRJWWGAJEmS\nJEkZZYAkKStCkiRp19BlIYSkGuuWJEmSpK5YvhxyOVi2DOr8739JZRZCIEmS0NZj/gqSJEmSpIzq\n0wc22ADeeivtSiT1dAZIkiRJkpRhLmOTlAUGSJIkSZKUYcOHGyBJSp8BkiRJkiRlmB1IkrLAAEmS\nJEmSMswASVIWGCBJkiRJUoYZIEnKAgMkSZIkScowAyRJWWCAJEmSJEkZZoAkKQsMkCRJkiQpwwyQ\nJGWBAZIkSZIkZdiIEbBoUdpVSOrpQpIkadfQZSGEpBrrliRJkqSuWroUNtwQ3nsPQki7Gkm1LIRA\nkiRt/qaxA0mSJEmSMqx/f2hogCVL0q5EUk9mgCRJkiRJGeccpPLL52HWrPixmGOkWlWfdgGSJEmS\npPYVAqRtt027ktqUz8P48fDCCzBwIOy/PwwaFLu/+vWLH+vq4LLL4t/DuHEwcybkcmlXLlWOHUiS\nJEmSlHF2IJVXUxPMmwdJAu+8A2PGwMSJsNlmsMEGsGwZPPEELFgAK1fCk0/CH/6QdtVSZdmBJEmS\nJEkZZ4BUXhtvHDuMevWCsWPh619v3V2Uz8PcuTBnDgwbBt/4Btx4I5x+Okyd6oBz1T47kCRJkiQp\n4wyQyuuvf4WPfxxmzFj/0rRcLj42YwY8/XTsWDr0UDjmGNhtN7jlFmhudk6SaldIkiTtGroshJBU\nY92SJEmS1B2XXw6PPQY/+1naldSmj30MPvc5+Mxnuv7cVavgd7+D886Ly9+WLoWFC2HrreGOO2DU\nqNjdVJDPxyVzjY3OUFL2hBBIkqTNfjoDJEmSJEnKuN/9Dq691rk75ZDPw6abwksvxcHZ3ZUk8OMf\nw0knxc8hDt9evhw23BCGDo3nf+qpGDTtsIODuJU97QVILmGTJEmSpIwbPtwlbOVy++0weXJx4RHE\nGUhHHx13c2togB13jJ1I770Xh27/5jfwhS/Au+/GpW5z5sDs2aX5M0iV4BBtSZIkSco4ZyCVz+9/\nH2cZlUJhTtLs2TBu3JruohEj4m2zzeCKK+Dxx2GLLeIxUrVwCZskSZIkZdySJTByZOxeUeksXx53\nYJs7NwY8lZDPw6c+BQcfDMcdV5lrSp3lEjZJkiRJqmK5XFz29M47aVdSW/7619gFVKnwCOLf5b77\nxtBKqiYGSJIkSZKUcSG4jK0cSrl8rSsmTIBHHqn8daViGCBJkiRJUhUwQCqtVavgllvSC5Aefzx2\nlUnVwgBJkiRJkqrAiBGwaFHaVdSOWbPi/KMtt6z8tYcMgWHD4NlnK39tqbsMkCRJkiSOCDaiAAAO\nrklEQVSpCtiBVFppLV8rmDgRHn00vetLXWWAJEmSJElVYPBg+Mc/4i5eKk6SpB8gOQdJ1cYASZIk\nSZIyLp+HG26AK6+EXXaBt99Ou6Lq9sQT8eP48enVYAeSqo0BkiRJkiRlXFNTnH+UJPDMMzBqFOy/\nP5xzTtyK/t1343H5fJzt016XUmeOqXWF7qMQ0qthwoQYICVJejVIXRGSKny1hhCSaqxbkiRJkroj\nn4epU2HOHBg7Fn73u9hF88AD8fb447DttvDyy/Dmm7DRRnDUUVBXBytXxtuKFbB0KfzhD7GDacst\nY5A0bFjaf7rK23FH+MlPYMqUdOvYeGN46CHYbLN065AKQggkSdJmtFpf6WIkSZIkSV2Ty8HMmTB7\nNowbF7/ecks45JD4+LJlcM01cNxxcWv4116D11+HLbaAhgaor48fX3wxhkfNzfCvf8VOpp13hg9/\nGHbbLX4cMCB2PDU2xuvUmueei8PIP/zhtCtZs4zNAEnVwA4kSZIkSaoB63YpzZzZOgBa95jbb4en\nnoqdSA8+GG/vvhs7lkaMgB/8IIYcW28dA6iW56nWkOnCC+Hpp+GKK9KuBP77v2O4993vpl2JFLXX\ngWSAJEmSJEk1Ip9fu0upq8c88ABMmxYDpLq62JW0cCG89FLsZtp++9j59Otfw4IFMYS6//7qCpGm\nTInBzQEHpF0J/Pa3sXPs1lvTrkSKDJAkSZIkSR1aXxfTsmXw7LOxW+nOO+Gqq9YMf/7c5+D442HX\nXWPolGWvvgrbbRdDsT590q4mLqfbffc4u0rKAgMkSZIkSVKndNTF1DJk2mKLOIfpttvi8O5DD4VP\nfCKGIsuWZW+Z2xVXwL33wo03pl1JlCQwZEjcWW/48LSrkQyQJEmSJEkl1FbI9Mwz8Pvfxx3inn02\n3rd4MYweDTfdFHeJGzgQQlj7PJUMmQ44AI4+Gg47rPzX6qyPfAROPx322y/tSiQDJEmSJElSBf3h\nD/DJT8bd3kKAD3wA3ngjfr7ppvE2YgTcc0/cLW7zzeHmm+OyuQ02WPtcHYVMnQ2hFi+Odcyfn52O\nKICTT47dR6efnnYlUvsBUn2li5EkSZIk1ba99oIddlh7ltKAAbBkSQxwXn4Z7rsvhkfNzTBvXgyc\nXnstBkibbx5vI0fGMGrhwhj+/OAHsNFG8VwbbBCXgH3603FXtXHj2t55ruDPf45L67IUHkHc5e6P\nf0y7CqljdiBJkiRJkkquK7OUWoZMixbBCy/E2333weWXr+lk2nVXaGiAd9+Fd96Jc5def33NOY84\nIi5Pmzy59Uyhww6Ly8SOOaa8f+6umj07zpEqLPuT0uQSNkmSJElS5nQnZGp5XMvHN9ss7gj30EMw\naxZsvDFMmRJv48bFWUNPPhkHf2fJypUwaBC88kqcESWlyQBJkiRJklSVOhMyrfv4qlVxLtLMmXHX\ntVtvjfeNH9/+Mre0TJoEF1wQl9hJaTJAkiRJkiT1SLNmxWBm5cq4/G3GjBjYZMlxx8GYMfDVr6Zd\niXq69gKkukoXI0mSJElSpTQ2xu6khoa4DG7cuLQram3CBHjkkbSrkNpngCRJkiRJqlm5XFy2NmNG\nNpevQdyJ7dFH065Cap9L2CRJkiRJStHy5TBkSNxVrm/ftKtRT+YSNkmSJEmSMqpPH9hmm7hLnJRV\nBkiSJEmSJKXMZWzKOgMkSZIkSZJS5iBtZZ0BkiRJkiRJKbMDSVnnEG1JkiRJklKWz8PGG8PixVBf\nn3Y16qkcoi1JkiRJUoblcjBqFMydm3YlUtsMkCRJkiRJyoAJE1zGpuwyQJIkSZIkKQMmTnSQtrLL\nAEmSJEmSpAywA0lZ5hBtSZIkSZIy4PXXYaut4K23oM52D6XAIdqSJEmSJGXcsGEwaBA8/3zalUit\nGSBJkiRJkpQREyY4B0nZZIAkSZIkSVJGTJzoHCRlkwGSJEmSJEkZYQeSssoASZIkSZKkjCh0ILlv\nlLImkwFSCGH/EMLcEMIzIYTT0q5HkiRJkqRK2HRTaG6GV15JuxJpbZkLkEIIdcClwH7AOOAzIYTt\n0q1KKp3p06enXYLUbb5+Vc18/apa+dpVNfP123UhwA47wA03QD6//uPyeZg1q/zHVOo6WazlJz+Z\nXlX1luL725769h9OxYeAZ5MkeQEghHATcDAwN9WqpBKZPn0606ZNS7sMqVt8/aqa+fpVtfK1q2rm\n67fr8nloaoL77oMrr4RrroHevWHFijW3t9+Gr30NXnwRNtsMzj8f+vdf+zxLl8JppxV3TCnOUc21\nzJs3nQsvnFY19Zbi+9ueLAZImwIvtfj6ZWKoJEmSJElSTWtqgjffjMvY5s6Fww+HgQOhoSHeeveO\nb/bnzYtzkubNg4svhiFD1j7PW28Vf0wpzlGLtdRyve3JYoAkSZIkSVKP1NgYb3PmwNixMHMm5HJr\nH5PPw9Spa465447yHFOp62S1liefjMsJq6XeUnx/H3+c9QpJxka7hxAmAWclSbL/6q9PB5IkSc5v\ncUy2ipYkSZIkSaoBSZKEtu7PYoDUC3ga2At4BXgI+EySJE+lWpgkSZIkSVIPlbklbEmSrAohnADc\nSdwl7krDI0mSJEmSpPRkrgNJkiRJkiRJ2VKXdgFdFULYP4QwN4TwTAihg03mpPSEEEaFEP4aQpgd\nQngyhHDi6vuHhBDuDCE8HUK4I4QwKO1apfUJIdSFEB4JIdy6+mtfv6oKIYRBIYRfhxCeWv17eFdf\nv6oWIYSvhRCaQghPhBCuDyH09vWrrAohXBlCeDWE8ESL+9b7eg0hnBFCeHb17+d906laWu9r94LV\nr83HQgi/DSEMbPFYj3/tVlWAFEKoAy4F9gPGAZ8JIWyXblXSeq0ETk6SZBzwYeD41a/X04G7kyQZ\nA/wVOCPFGqWOfBWY0+JrX7+qFpcAf06SZHtgR2Auvn5VBUIImwBfASYmSTKeOHLiM/j6VXZdTXx/\n1lKbr9cQwljgMGB74ADgshBCm8N6pQpo67V7JzAuSZKdgGfxtbuWqgqQgA8BzyZJ8kKSJCuAm4CD\nU65JalOSJAuTJHls9efvAE8Bo4iv2WtWH3YNcEg6FUrtCyGMAg4EftHibl+/yrzV/1s4NUmSqwGS\nJFmZJMlifP2qevQCNgjh/2/vbkMtq+o4jn9/OJqNFqGmZuVDSClETkNmKNjgTBAI900RjhHaE0EQ\nV5BeOL0Ygl4MiMakvSkzSHJkmihvNZSoIyniU04PKvhmKGduOGVqhYEO+u/FXoNnbvfse6/aPWfj\n9wMH9l53rXPW4f7Z3P1j7XWzBngrMI/1qylVVfcBzy1oHlevM8Bt7br8Z7ob9I+uxjylhRar3aq6\ns6peaacP0N2/gbULDC9Aejewf+T8QGuTplqSM4F1dBehU6rqIHQhE3Dy5GYm9fo28HVgdLM861dD\ncBbwTJIftkcwv5dkLdavBqCq/gpcBzxFFxz9s6ruxPrVsJw8pl4X3s/N4/2cptcXgN3t2NpleAGS\nNDhJjgd2AbNtJdLCnevdyV5TJ8mlwMG2iq5vea71q2m0BlgPfLeq1gMv0D1O4fVXUy/JO+hWb5wB\nnEa3EumzWL8aNutVg5LkG8Chqtox6blMk6EFSPPA6SPn72lt0lRqS893AbdU1e2t+WCSU9rPTwX+\nNqn5ST0uAmaS7AN2AJckuQV42vrVABwA9lfVI+38p3SBktdfDcEmYF9VPVtVLwM/Ay7E+tWwjKvX\neeC9I/28n9PUSXIl3TYOl480W7sML0B6GDg7yRlJjgEuA+YmPCepz83AE1W1faRtDriyHV8B3L5w\nkDRpVbWlqk6vqvfRXWvvrqrPAb/A+tWUa49N7E/y/ta0EXgcr78ahqeAjyU5tm3QupHunxlYv5pm\n4cgVy+PqdQ64rP1nwbOAs4GHVmuS0iKOqN0kn6TbwmGmql4c6WftAqka1mrC9gvdThd+/aCqtk14\nStKiklwE/Bb4E92y3QK20F1odtIl2H8BPlNVz09qntJSknwcuLqqZpKcgPWrAUhyHt0G8EcD+4DP\n021MbP1q6iXZShfeHwL2Al8C3ob1qymU5FZgA3AicBDYCvwc+AmL1GuSa4Av0tX3bFXdMYFpS+Nq\ndwtwDPCP1u2Bqvpq6/+mr93BBUiSJEmSJElaXUN7hE2SJEmSJEmrzABJkiRJkiRJvQyQJEmSJEmS\n1MsASZIkSZIkSb0MkCRJkiRJktTLAEmSJEmSJEm9DJAkSZKAJK8k+dHI+VFJ/p5krp1fkeQ77Xhr\nkgNJHk3yZJJdSc4dGbsnyfpFPmM2ybGr8X0kSZLeSAZIkiRJnReADyZ5Szv/BLC/p//1VbW+qj4A\n7ATuTnLiEp9xFbD29U9VkiRpdRkgSZIkvWo3cGk73gzsWM6gqtoJ/Aa4fFyfJF8DTgP2JLmrtW1O\n8sf22jbS999JvpXk90nuT/LO1n5SW+30YHtd+Jq+pSRJ0goZIEmSJHUKuA3Y3FYhfQh4cAXj9wLn\njH3zqhuAeWBDVW1M8i5gG7ABWAecn2SmdT8OuL+q1gH3Al9u7dvpVj5dAHwauGkF85MkSXrN1kx6\nApIkSdOiqh5Lcibd6qNfAVnB8OX0zUi/84E9VfUsQJIfAxcDc8BLVbW79fsdsKkdbwLOTXL4PY5P\nsraq/rOCeUqSJK2YAZIkSdKR5oBr6VYGnbSCcR8GHl7hZ40LnQ6NHL/Mq3+zBbigqg797xBJkqT/\nHx9hkyRJ6hwOc24GvllVjy+zP0k+Rbfp9q1LjPkX8PZ2/BBwcZITkhxFt+rpniXG3wHMjnzueUv0\nlyRJekMYIEmSJHUKoKrmq+rGZfS/KsmjSZ6k2zz7ksOPox1+r0V8H/h1kruq6mngGrrQaC/wSFX9\nconxs8BHkvwhyWPAV5YxT0mSpNctVeP+PpEkSZIkSZJcgSRJkiRJkqQlGCBJkiRJkiSplwGSJEmS\nJEmSehkgSZIkSZIkqZcBkiRJkiRJknoZIEmSJEmSJKmXAZIkSZIkSZJ6GSBJkiRJkiSp138Bn0vX\nmRuK4P8AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x115e8a080>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(analyze_instrument_rms(1, audio_dir), '.-')\n",
"plt.title('power for each note')\n",
"plt.xlabel('MIDI tone')\n",
"plt.ylabel('RMS')\n",
"plt.xlim(0,127);"
]
},
{
"cell_type": "code",
"execution_count": 183,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def analyze_rms_for_all_instruments(audio_dir):\n",
" \"\"\"\n",
" Compute a matrix of RMS for each instrument and note.\n",
" \"\"\"\n",
" return np.vstack([analyze_instrument_rms(i, audio_dir) for i in instruments])"
]
},
{
"cell_type": "code",
"execution_count": 184,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"x_rms_instruments_notes = analyze_rms_for_all_instruments(audio_dir)"
]
},
{
"cell_type": "code",
"execution_count": 185,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmIAAAKSCAYAAABxxLf/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXu4ZldV5vvOVEyFVMg9KUgCKUggAQKEuw0ItKDdig12\nKyrS54B41OeoiHr0iLS2xFu32mIr+rRXEHgUJdgIIg05BBJuzS0ETEISSLBCLqZI5Z4KqVCVef74\nviL7e9fYe4496/v22rvq93ueeqrm2vMy1phzrT1rrXeNUWqtAgAAAIC155CxDQAAAAA4WGEjBgAA\nADASbMQAAAAARoKNGAAAAMBIsBEDAAAAGAk2YgAAAAAjwUYMYIGUUu4vpbxlSXlTKeXmUsq7p+WX\nl1L+YPrvXymlXF9K+Wwp5apSyjtKKY9Z0vZDpZQnB2P8aSnlrA7bnlhK+Y6+M1sMpZRXl1IOH9uO\neWDzeVkp5QeW/OwvSym7Silblhz779P1cty0/J+m7T4/7eNpY5wHACwWNmIAi2WXpLNLKZun5W+T\ndN0K9V9fa31yrfVMSW+X9MFSyvErDVBr/dFa65Udtp0j6TujH5RSNnX0Nw9+WtIRPQ1HtHklXl9r\nfbKk75b0J0tsrJK+JOnFklRKKZL+taTrp+Vv1mRuzqm1PlHSC7Tyulkz1qmfATYsbMQAFs97Jb1w\n+u+XSnpbplGt9e2S3i/pB1eqt/RJWSnlrlLKr5dSPldK+Xgp5cTp8ZeUUi4tpVxSSrmwlPJNkn5V\n0vdNn7a8ZPoE5y2llI9Kesv0ad0blozzD6WU5ywZ57enT2zOL6U8bWrH1aWU75rWOWRa55NTe35k\nevy507rnlVKuKKW8dXr8VZJOlvShUsoF0/ZvKqX80/Sp0KuDc39TKeV/lFI+Iem3pnZ8vJRycSnl\no6WUR03rvbyU8nellP81fdr4W0v6+OHpsU9Mny7ue0J5wvSp5Cenf56ZmbeIWuvVmmzKj11y+G8k\nff/038+T9DFJe6blh0raWWvdM21/a631puD8PzR9knbJ1E9Pmx4/tpTyzqnfPl5KOXt6/J9KKUdN\n/72zlPIfp/9+cynl+Y05+3Ap5V2SLu/1AwAMYSMGsFiqJr9wXzp9KvYESZ9cRftLJK3mteMWSR+v\ntZ4j6SOSfmR6/JclfXut9UmSXlRr/bqk/yzpb6dP4M6b1nuMpG+ttb5sif3LjfOBWuvZku6W9GuS\nni/pP0z/LUk/LOn2WuszJD1d0o+WUk6b/uwcST8l6bGSTi+lPLPW+gZJN0h6Xq31+dM6p9RanzB9\nKvSmZWw5pdb6zbXWn5N0haRn11qfIulXJP2XJfWeKOklmszB95dSTimlPFTSL03te5Zmff37mjzR\neoak75X058uM32S6Uf5SrXXnksNfknRiKeUYDTfo50t6eCnlylLKH+3bAC/Dg6bz+hOS3jg9dq6k\nz0799p8kvXV6/KOSnlVKeZykayR9y/T4v5L0ca08Z0+S9Kpa66pfgwPA8hw6tgEABzq11stKKds0\n+WX7j5LKKpqvpq4k7a61vnf674s1eaUlTX4Bv7mU8nZJ/3OF9u+utd6XHOf86b8vlXRvrfX+Usql\nkvb94v52SY8vpbxkWj5K0qMkfV3Sp2qt/yJJpZTPSdqmyUag6IFz/rKkR5RSfl+Tp4r7xnPOW/Lv\nYzR5mvcoTTaRS+9xF9Ra756OefnUzhMlXVhrvWN6/LypjdLEd4+ZvjaUpCNLKUfUWu9peucBfraU\n8sppn//OflY1mYsf0GTT82Oannutddd08/Ytkr5V0t+UUl5Ta32Lhrxt2uYjpZQHl1KOlvRsTTbF\nqrV+qJRyXCnlSE3WwXMlXSvpjyX9SCnlZEm31lq/VkppzdlXVnHuAJCAJ2IAa8O7Jf2Okq8ll/Ak\nTZ7yZPn6kn/v1XQjUmv9cU2ejDxM0sWllGODttLk9dk+9mj2HrFURL90nPsl7Z6Os3TzUzR5gvKk\n6Z/Ta60fmP5sd2TnUmqtt2vyFOtCTTYpyz2RWmrzr0n6YK318ZpsfJbavHTM+83OiCLpGUvsf7hv\nwkopb5y+FnzPMn28fvrU8HslvbGUcpj9/O1Tm8+vlvi3TvhwrfV1kl4l6XuWGcOfWt6/zLlI0oc1\n2dw9W9KHJO2c2vaRJfWWm7OlfgaAOcFGDGCx7PsF+EZJ59ZaW/qab2wKSinfo4m4/687xps9WMoj\na62frrX+iqSvarIhu0uTJx7LsV3SOWXCwzR5arPiOPaz90v68VLKoVMbHlVKaQnx79xnU5l8pLCp\n1vpOTV6tPqnRVtO2N0z//UOJ+p+W9JxSytFTO5duds6X9A1dWinlid641vrK6Yblu1YapNb6D9Ox\nXmHHvyLptZL+x9LjpZRHl1LOWHLoHE2eYkV8/7TNsyXdUWu9S5ON1T791/Mk3VxrvbvWer2kEyQ9\nqta6XZMnZD+nyQZN6pszANgPeDUJsFiqJNVab5D0h4n6P11KeZkmGqzLNNFr3bq0r+XGaNT5nX3C\ndU1e0f1TKeU6Sa8ppXxWEy2VP5H5WClluybi7Cs0edXZGmfpz/5ck1eOn52+3vuqJl8PrmT/n0l6\nXynlBkk/I+lNpZRDpnVe02grTZ46vrmU8kuavAZe0cZa642llN+U9ClJt0q6UtId0zqvlvRHpZTP\nS9qkyWblx1fos8WvSforSX+61O5a65+5XZKOlPSG6WvGPZKulvSjy/R773QOD9UDm8/XafIE7vOa\nPMl6+ZL6n9AD/wn/iKTf1GRDJuXnDADmRLGn4QAABxWllC1TTdYmSe+U9Be11neNbVeGUsqHJP0/\ntdbPjm0LAPTBq0kAONh5XSnlEk0+OvjyRtmETeF/0gAbHJ6IAQAAAIwET8QAAAAARoKNGAAAAMBI\nsBEDAAAAGAk2YgAAAAAjwUYMAAAAYCTYiAEAAACMBBsxAAAAgJFgIwYAAAAwEmzEAAAAAEaCjRgA\nAADASLARAwAAABgJNmIAAAAAI8FGDAAAAGAk2IgBAAAAjAQbMQAAAICRYCMGAAAAMBJsxAAAAABG\ngo0YAAAAwEiwEQMAAAAYCTZiAAAAACPBRgwAAABgJNiIAQAAAIwEGzEAAACAkWAjBgAAADASbMQA\nAAAARoKNGAAAAMBIsBEDAAAAGAk2YgAAAAAjwUYMAAAAYCTYiAEAAACMBBsxAAAAgJFgIwYAAAAw\nEmzEAAAAAEaCjRgAAADASLARAwAAABgJNmIAAAAAI8FGDAAAAGAk2IgBAAAAjAQbMQAAAICRYCMG\nAAAAMBJsxAAAAABGgo0YAAAAwEiwEQMAAAAYCTZiAAAAACOxLjdipZR/W0q5spTyxVLKL4xtDwAA\nAMAiKLXWsW2YoZRyiKQvSnq+pBslfVrSD9RarxzVMAAAAIA5c+jYBgQ8XdKXaq3XSlIp5W8kvVjS\nNzZipZT1tXsEAAAAWIFaa4mOr8eN2CmSrltSvl6TzZnxkenfb5T0ys6hvqmjje8Bvx7U2dMoZ2x5\nUKMsDafPbbs1aHOXlVey7W2SXirpJDs+r3N2+71NtN/ea+VNVv5qYtwMD7byvYk2fj7HB3X2ndNf\nSnqFcn46vGGL/1ySvmblaBw/1poPabgW7rSyz480nCNvE/nWr4foVrWcvX8r6fuXaeNr16+RzDw7\nZyTGyaztmxN1WuslOufMGnN87H3z+n5J/6ajv+Xw6yxzzTvz+jXmY7vfbpvTOMtxgSYvgjK2ZJjH\n77eecdcrF0p63ojjn7vsT9bjRizJG6d/XzL986QRbQEAAADYx/bpnzbrcSN2g6SHLymfOj1m7HsK\n9kaxCQMAAID1w7bpn31ctGzN9bgR+7SkM0opp0n6F0k/oMn7MWPfI9Rzpv9uPb5eFJlXPq1XQBH+\naiPTpuexcvSacd8j7bOX6Sfj655H2t7GX2ll2mTGjfr1c8q8SmqNFfl2H4+fts/Y2zrHnjUorWzf\ncj9vvXKLxpnXumyxr9+zVhijZ7300Fo/mflYq9vzal4Hnj7nsXuu+VYfEd5vdH4Z2ckiecQaj3ew\nsW1sA5Zl3W3Eaq17Syk/Kel8TcJr/EWt9YrlW/A0bHE8fmwDDmCeOLYBBzCPG9uAA5hIDwfz4ZFj\nG3CAs21sA5Zl3W3EJKnW+j5JZ45tBwAAAMAiWZcBXQEAAAAOBtiIAQAAAIzEunw1meMJVm6JiHtO\ndV6i4nmIPo8IjrXiPh2XsCUjGu6JR5PB7ffYVxGtOh7nSpK2WvmooE7rnD32VdTGbYv81vJ/FC/O\nydRxW6I2XsfXS+Rr76dH7N5zzURz1iLjf+/3+qBNKyZbxrc7Em22WdljbEnDOHk99xZfy5FvW9dZ\n5pwz67Sn3577ssfRPC3Rh48b/Q7pOWeP5RjRuh9l5t1ty7Rx35LQZi3giRgAAADASLARAwAAABgJ\nNmIAAAAAI7GBNWLvs7LHt8loxHq0Tz0aqx5bvE4UgLCVazLKjea59TJ6C9ddZdpk9Amup+jRWPk5\nR7kmMzqHlr4uk1/T58O1adLwnPycozlzP93Y+HnUb6T5ucfKmeuhpSPL6Mp8Da4UVHglWhrDTB8Z\nW1qcEhxrXSPRPLuOLLP+nZ42vp4yzCsQbqSDW+3YPfk1g2QtTaLcvesJn+cejR6MAU/EAAAAAEaC\njRgAAADASLARAwAAABiJDawR8/fhK6Sj7GZRyYkzzCN2V0/cmIgottI8+m2xKI1DtOyPbbSJ5qOl\ncXPNz3L9tH7ek5zbdX0nBnV64jO5psfjMfWsW9eqSUPbtgV15nCNbLY+oqWxy+2LYvo5Hqtru5Uj\n/aDN2RaPfSVpV2PYZwTHPtlok8LXWLTmMno7j1m2PTG26xJd8xlp9Nz/Hrsr86vPr4co9li0dp2W\nLjSK4+b9Zq7NHs1kS898bWJc2F94IgYAAAAwEmzEAAAAAEaCjRgAAADASLARAwAAABiJUqsHxFz/\nlFKqnnH/7EHXGPZoxXv6iOq02kU6UT/m5cOT/bTsuNfKdwd1brLy7oxQ14XrJjTeHDRx7egWK0fn\nd7uVB+LlW4JGLiKOhNItMkm/nXl97NFK+BuJfX3sKHCm18nMswvVfd4zH1hst3IUhLf1IURU51GJ\nsf2c/CONSJzs9rk4PBPsN1o/jq/LVuJtaTj3kXjcbcn02xLeu4A+6jda//4RSUtgLg0TdvvvrGjN\nuf0u1s8EkvU60TrtCfLaE5DWzznyrfeTuf94v+7/nmC/EHOuaq3BFzg8EQMAAAAYDTZiAAAAACPB\nRgwAAABgJDauRkwfsqM9yXDXM5mAgy3tUESPbqmVkDzqN6NXcG3HPILj9gQ+XBTzWnOtZL6947SC\nOWaScbfWSlTHdU3zuge1tESSdLWVXfMWaaz8nDIaw5617P4/OajjWicnCjrq2iYXnN4ctGlph3qC\ng0btMm1a9Ph6HvMTEa25eQiWnUXZ72SuzUUFNd9otPz7c2jEAAAAANYbbMQAAAAARoKNGAAAAMBI\nbOCk30euwRjRO19/H763o9+MjiDz3j0TD6g1zrzaZOIBOV4nc849WsAejVtm3B6NXot5Jf3u4fhE\nvy2tUORHX++eDD3SNfk4HgBPGmrlfJyojcexcr1aFO+rlbQ58pPHoOq5hiL7fSyvE8VBa12L0fXg\n/bqvozZ+zpnYafdZOfKlx3pzzVsU08zxfqM4Yq6/cy1d5p4WXb+uO/Q6mTaLoqXtvWyN7Di44YkY\nAAAAwEiwEQMAAAAYCTZiAAAAACPBRgwAAABgJDawWD8Ssi7FBZDzCrTn8dgyGbwzP28JyhcVHDTy\ngSey9XKUZNoFtV4nSszbShgdiWNd6O3C3Sjgpff78KCO42O3AmlKuSC2PYl5Wx9CRPPhQunMRwBe\nZ1PDrojo45VWRvtIYO5E68f94ALszAc9mTXn9xq330XdUZseIv+3ErNHHz64fyN7nda1eVvQxtdP\ntBb8Pux1/D4SjeW2ZD5qyNw/Wx+9hLE4jeh69qDBmeToPlYm+HVLeB+1yZwTLBqeiAEAAACMBBsx\nAAAAgJFgIwYAAAAwEhs46ff/tqOtYIiRRsD1FD3v4aM6rtlpJW2O+s1oxFoamZ4E38uNtZSMtNBt\nc52E1A6gGI3jbdyXriGTckmbW9dBpGPy4KCZIKSeyNnPJwqC6XVOsXLkpxsSdRz3k2sDpeGa6gl6\n2ZNcPPLl6Vb2OYrWv9sbaZ3mgeu73P5MENiMLrFH5+pkAgJ7sN+IVuDSaCy/fnvOJxqndT1nAg+7\n/6MgsH4+dyfqOGcFx1q/Q6LrzK9XX3OR5rD1ezLy4zwSjmfuRz1BznuYV6J5kn4DAAAAbDjYiAEA\nAACMBBsxAAAAgJHYwBqxP7WjPXG2Wu+poz5b8XWWO7baNj36LtcVRDqCnnfzTqRjct2Vn08mAXBm\nDr2fVhLqiNb8RP32aOkymoYevVSP5jCiFWtpHlqQedGzbqOYVC7RcM1YpItrxQSLtDduS8YvrjmM\n5tXXv9vmGkSprTXL6PqcTJy0ExN1MjG1WveSjM4vE79vHhqkjPbMie4jrftCRn/Xg9t64xz6hAnn\nohEDAAAAWG+wEQMAAAAYCTZiAAAAACPBRgwAAABgJDZw0m8PatkjVOwRK7eS7kptofe8Eng7ngA7\n45MeQXm0bFzk3COazyxHFx57EMlIeOy2HJeokwmg2OojoifptwtoW0mos3XmIazPfOzTSh4eCb8z\nvvSxfc4ikbqfsycG90C4UvuDkGg99dyPorGd1pxFfrulUSeaw1Yi9oyo/ktBndZ1FtnfumZ6PuTI\nXA8912qGtfoIZlEBUGHe8EQMAAAAYCTYiAEAAACMBBsxAAAAgJHYwBox1xJkEna3+vD38JFeweOx\nRS7MBAx1Wkm+o3EWEVBUGibOdo1MdH4ePNODy0Zt/JwyAWndNtfFRXjC8SjopeNje+DPiIzGcB5B\nU30NZtZbr45stUTxCqPAqkvJ6Pp69IMZv3gd155KuQC6To+mJxOQ1s/R2zw8aONrt3WvkYZ+yCSE\nzwRxbvkuWgveJhPE2eesRyPmSb6jc3YiWzLJ0J2eILsteu4118zdChjCEzEAAACAkWAjBgAAADAS\nbMQAAAAARmIDa8TcdNemeGyfSJvQSji7qDgsexPHojotejVhjvvStRIRnnjXyz2x0zJx3DJz5nWu\nTNTpmfse/deikmSvVQyhRdmfoSc+31ixlXr81BP77Yo5jT0PMhrJRTGPGGCLiiOWYa1iT7bGXU9b\nhDHvNYuFJ2IAAAAAI8FGDAAAAGAk2IgBAAAAjAQbMQAAAICRWE9KvFViQToPffpsebNVj+Jxuvbv\nbiuHenkPKBq58PioYYOWiLhnqjLixowguEcE3SM2zYhj5yHQjtr4hxsZW7xOJtCnB+TM2DYP4W4m\nQGSPONnbZMZZRLBKqf0hh9S2N0rg7XUygWO9TcY2pyeZdY9APjMf81qnHtzUgy1nPtCZB2uZwHs9\nfSzRwm3NBMyG/YUnYgAAAAAjwUYMAAAAYCTYiAEAAACMRKm1jm3DqimlVOl+PzqHnt0XkW/8HXqU\n2LaVmDeilYg30qH4MbfXRW/SUKPhtkpDzUgmoGurj542PTqUjOYto71x32b0aj36KLc/42u3JRo3\no9fxtettXL8jtXVkkW9bfunRr2XGzsyZz3N0PbT67dFlRW3clqOCOu4rn8N5Bf5saSYjeq6ZedCj\nwcrMWY8uLqNL7Pl90LPm5uHrRek5D0bOVa013KjwRAwAAABgJNiIAQAAAIwEGzEAAACAkWAjBgAA\nADASGzig69VjGzBnXIyZEWTPgyjSbXSshWkQD3/MbNkD7ErD1efDRprWlpvuiGzzjxhujSoZHtgz\n0Fi6vX6ORyaGud3Ku6JKLrq9PtGxkxHeZz4QaYnBo49X/JiXbwvanNEYR+oLJtv6OCJadLc0+ozG\n9TXmwvvoo4xojpzWxxxRH75ePCh1Bj+fKPBt9HHBaokE5lutfIWV1+qjnuhDDvdD5Nt7rXy2lW8I\n2jg9H2H4dRbNj9eZV/BZv3csKqi2j+Pn0xNsOSLzIYRfe9G9MIYnYgAAAAAjwUYMAAAAYCTYiAEA\nAACMxAYO6Pp5O3qflV13Er0rPsXKJ1k5odmItE/+Knuv+zhKpNoK9Om2ZuhNoNujR3N7vRy933cR\nlWdZj9ZmK1huJtBhpIFzHUdGn+DBcVs+iPrt0TW5EC7Srvh6yQTX3DZb3BQ08Ska9JEJiJrRTvj1\nm1m3p1k5Omf397ZEv74OM3PWWpeRbT06Ji9HwkQP7OzrP/JtSy/Vkyg84sbGuBGnJ8bp0VRldEyr\n7UManpPrTdfqd3BPENjzFmTLwQgBXQEAAADWHWzEAAAAAEaCjRgAAADASGzgOGInN37+KCtHpxrp\nxpaS0Cvs7kmsGsUCasUzymhvnN6YMC2/uJ4qGquluZLamrDIty09RTSOa7l65iwSTLmfvJy5vNyW\njJ88dlFv/Ca312JF7Y3irbXWRibpt+tSojhKPVqhTOw9r+Nj9+iNIj/1JHruSX7e8q00PCePyxXR\nukYyMZ0y19mxVh6IEDW81/u95bCgjd9PexJ4+/lk5ie6Plpzn7lmMn16Pz33ltb1DYuAJ2IAAAAA\nI8FGDAAAAGAk2IgBAAAAjAQbMQAAAICR2MBi/fdYuZXAOKJHUOtEglQXT/cIReeRgDkTXDCTFNXF\n4T2BASMyASxb9JxPRpCasaUV9DKiRwzrgUpdHB6tWw/a2ROENLLV+/XgxNGHKB6cNeMnD0wanaMH\nA/U2NwdtfGxP0hwls3bfZXzpH3dk7gEuXI8+wvCPCzwIdSaBekZU735xgXwmaXO0fnx9XGtl94Ek\nXWlln6NoPvyceoJUZxKd+8dDBECF1cMTMQAAAICRGGUjVko5tZTywVLK5aWUS0spPzU9fmwp5fxS\nylWllPeXUo4ewz4AAACAtWCsJ2J7JP1srfVxkv6VpJ8opZwl6TWSPlBrPVPSByX94kj2AQAAACyc\nUTRitdabJN00/ffdpZQrJJ0q6cWSnjut9mZJF2qyOQvoCcq5WqLgoZkk066vcD1FpKNpBQfNtHHb\nouTKHhg2quP2ut4lCm7ao6+L+llKxv89gTLnlfS7B7cl069rVTJBPDM6oJYmLKN/9PUUBTd1WutW\nygWa9LHdL5mk8R4UNroe3JaMHtWvV19f0Rp0fVcUONnH9jZRoGvXlWU0Vp4o/EQrR4FXXd/l+q/l\nxlpKFLja/ZtJkp1Zh47r7Vq+lobz/JKgjq9vD6jrvy+k4bV3qpWvD9q0AjtHvm/p4N7Z6BPmwega\nsVLKNknnSPqEpK211h3SNzZrfmUAAAAAHDCM+tVkKeVISe+Q9OrpkzH/r84K//V595J/nynp7Lnb\nBwAAALB6tk//tBltI1ZKOVSTTdhba63vmh7eUUrZWmvdUUp5iIbfxi/hRYs3EgAAAGDVbJv+2cdF\ny9Yc84nYGyV9odb6+0uOvVvSKyT9lqSXS3pX0G5KpCXYX3rcEelD/EGev5uPdCitfiPbMrHS5oFr\nGDJ+ytjWiqnVE28twu2N1o5rdjIJyHuSfM9De+a2ZtZgRlfj5xjZ1lq7kfaplYw70j9mYne1YkVl\nkn5fY+WMZrJlR9RmHrEEs2M7rgPK6KdcK+SasQj3XbTmMnpNx/txWzKa1UyMvBX+378sPfH5XLOX\n0Xj6PSvSg/XoZ3sStcO8GWUjVkp5lqSXSbq0lHKJJlfaazXZgL29lPJKTZSe3zeGfQAAAABrwVhf\nTX5My38y94K1tAUAAABgLEb/ahIAAADgYIWNGAAAAMBIbOCk3z1JXFdLxj2RHS2RbdSvH2uVIzLC\n1wwu2PTAkhnheiYgrZ+Tt4n86IJgF7FGAlW3N7LFA1S6QDjq18ce63KKgmtmRLetpOXRObfOMboe\nWv1GH0/0JFTPzJnTCiostUX0kW2tjyM8QGrUb4T7130XjevrPUqs7bgg3u8tUXBT90MmIG0mObff\nFzIBjX1e/XwiP3kdTyKfOedPBXUAVoYnYgAAAAAjwUYMAAAAYCTYiAEAAACMxAbWiPVoqBYxboaS\n6MPrzCPJdG/g1ZbeqyeIaqQXcTJ1nFZQ2MiWyLd+Tj4frhfJsFYBdyM9WEb7tFb06L3mcT1ndHKR\n7qdFjxZtHuNKbX1adA21NG6ZgLSun4p0ZpmgqY7bn9GvueYtM8+ZRPOtsTOpj5+eqJNhvfxq/vjY\nBhwU8EQMAAAAYCTYiAEAAACMBBsxAAAAgJFYLy+iO/BYMj/Z+HmkV/DEqfPS9LiGxGP9ZGKguQ7i\niA477gmO9SSpdW1ERhOTSSDdk3C2pTeK5jCzFlp+iS6Vlh8yGhkfN3NJZuKXZXRAbr8neu6J6ZSJ\nMefjRom2M767utFvRm/k9FwfER53y9tk5iPCfeVtoliCrkfzpNM99CQ6zzAPbWzEPJJZL8q2iLVK\nvt06p/W+RVjLOVkcPBEDAAAAGAk2YgAAAAAjwUYMAAAAYCTYiAEAAACMRKm1lZx2/VFKqTrm/tmD\nWxuNIg3r4JgH8Uxwe3DsevOpx1iMhjneyid4OWjU0gO7HZJ0vZV3BbY4p1k5o1vfmei3FWc1Gqcn\n5utuK29O1FkzWsE2peHHH9c0+sjSE2i1JdbPjJM5554PNzyIbSTk9QXUSg4dkQnomgn+6bioPrpp\nub8zHyjssPKiRPW+fqK14f53X0YJ7FvBiaM2Ts/vOT/Htfxd2bo215NIfa0+LFhLFuHfX1atNdxk\n8EQMAAAAYCTYiAEAAACMBBsxAAAAgJFY79Halsdf11+V0Ro4LU1Jj04lapfQZOww7Y3LOtJjN8YZ\ntImCvhrX9rwvzwR0nQcdc7S7Z9nPK4it40mCIxGcr23XDnnwX2mo5YrquH23BnUcDwbqazvSNbXm\n6PTgWEsLJfXpZtwPbn8UXNYDP3udSOPmvnTNWBSgOaNBcomJtXliIEFxHavfWyL3e5sbbJzjg3F8\nOiK5nU/Rbr//BH7x2/Tef7YDjwgGcl/6uvU5lYbr1Ocwcz99Z1AHYGV4IgYAAAAwEmzEAAAAAEaC\njRgAAACwlIJRAAAgAElEQVTASGzcOGL63dmDb/2Z2bLHsYqkN0c2yhEugYkkMS2txPagjR/zeF8Z\n23ycjEbjmES/fo5Rv26f9xvZ7/26LiWScvnYPq9Rm1OtvC2o4+2838uCNtut7Gsukix5fLiMn7yN\n++3CoI2vn8gvPtaVVo5klkdb2ePQeTw8aejLWzJxuFyH5YnOl2u3lEyMs9a4GXrioG0Ljrm9kY6p\nFcctSpbu55TRuHm/Pb7MtMloPHvinrX0vpmk5U6mzX0JW3q0jeslCXiW9ZxkPeP/Rfj7p4kjBgAA\nALDeYCMGAAAAMBJsxAAAAABGgo0YAAAAwEhs3ICuLqb7IdPA9eQzzjDQ9UUfO7SCy0bGNBKOR01a\nmsM9Gdsi5b2LeTOBSt0YF7FGQthWmyjZr9vbEiJLQ3uPC+q0zrFHrJwR97YCjEb9XGvlaHFEQm/H\nz8kV/oEtt7jvTBzucTPDccJKHbgw3cuZAJy+XjIC4R6xtbe5tKNNRM+6dDJi/UUFQe75OALgwIIn\nYgAAAAAjwUYMAAAAYCTYiAEAAACMxAbWiJn+YE8j0XZG1uRsDo4NZEsNbZckHToHN/doxCLbBjqy\nKBm0HfM2UaBP91VPLL5MnvaBDujEjoFbgRsjIr1dYu4HtAIFZvSDiUTtKTyi6+Ot3BP0MrL/WCuf\n3OgjIooU6/ZttfL2RJsoAGqLjADV/eSaq0inmAnO6rjGyn0Q9ZNJqO70BF6N9Gute2FG89Y6n4ge\n+51onB5dYub3QWtO5hVwtGXbeXMaB1aCJ2IAAAAAI8FGDAAAAGAk2IgBAAAAjAQbMQAAAICRKLVG\nIuT1TSmlSve3aq2+44yG0utE7mvFb80I7728pWFXxL3BsYFYP6hzR8dYh1vZ7Y3O2dtk2GkO39XR\nx6bE2hh8ODAvsb734+VMn5lrtudriR2JOq3At5H9J62yj6gf/ygjomM+/OOb1Acj7v/Ml0A3W9l9\nIg0/wgjE46c0BOXRNbXTyne4/6OLsyXijs7Z+41uQN6PC+DvCtr4JHm/kU+8jQeCznwI4c6MbMvg\n59gTuLrlN2k4J5mPGnzOvPypoA30ca5qreFNiidiAAAAACPBRgwAAABgJNiIAQAAAIzEBg7oepGV\nWwmkE6c6kD0E2oOU9MbGyvQ7eDdvdVznEY3TRYctURuXbdzb6iMzTiZwaUewxL3RJHqATbfFg59K\nQ82IazA8kKkk3baCYVKsXXE/ZRJVn27lKLm7n5MnCg/kDEdbsN8ePaETSWRSWi0/745AvV2asJZ+\nJ7LFNGGR5nOXz33g/xtaOrhIP3irlRPz7Ofkusq9ka/92BFBHcdt+eNEG4ADC56IAQAAAIwEGzEA\nAACAkWAjBgAAADASGziOWKR5WUpPYud5JGOV2glZMzFsemJUOdHcuv2ZJLVOxk8Z//do3FyXldFL\nORn/Z/yU0cA4PifebxSrqCcmmPcbJZnuSSw8j2TEvjbWKoFxpk4mPpOTGcfpPef1Ysui7M/8PprX\nenF6rrMMLXsz+tl5sKjzy9CjGZ4H8zrnHtt87F8mjhgAAADAeoONGAAAAMBIsBEDAAAAGAk2YgAA\nAAAjsYEDut5o5bEEkWslBsyI3zPn0/OxwaLE1S0iW59mZRehZ87v6sRYZ1k5c87XJupsbYwbZW1u\nBYHN4EE9pTjxdMuW1lqI/DTW+oloifUtYG3IPIS7mX4z96yeDxQyrNW90QNzAxx88EQMAAAAYCTY\niAEAAACMBBsxAAAAgJHYwBqxv7LyDzbqR5mFo2OrJdJBuFszWolIj7NaMn1spGCIka0tHZZrsKJ+\nIj959mfXVM1rDj1gqNsWBbSMgrzOgx59nWd3z+C+9XOel65pHmtwUfqvDD73GV9vNI3YxgsgDrBo\neCIGAAAAMBJsxAAAAABGgo0YAAAAwEhsYI3Yz8+hj5a+YswkqYuamsw5RYmPW7i9PUnXM7Q0VpHt\nbkukI3N6NGKez/W0RJtMv6eu/OPjj+rr1uvs8gTqPYwZIyxDT9Lv1jlFzm6ty6iNH4v0VF4nk5x+\nLI1Y1AcaMQCHJ2IAAAAAI8FGDAAAAGAk2IgBAAAAjAQbMQAAAICR2MBifRdGOy4K9aCSET3BKnuS\n+c6LeQSfnFei8EWQSSDd24/TOsfoUvE15sm5b+gYJ4Odzy2JOuuaMT+KccZMaO/0BGedV0DXFr1+\nQqwP4PBEDAAAAGAk2IgBAAAAjAQbMQAAAICR2MAasUutvIhTGVP/lWFRgRrXi2YnstWDl3qdjO0P\nTtRxLcuOoI6PfUqi3x480GomWf2iLu1FJIOOkqXPY5yMLtTJ+G0e10dmDheV+NzX9qKu90xAWgDg\niRgAAADASLARAwAAABgJNmIAAAAAI7FxNWLHP322vAjpQW+f68kWp0c2k2Ie8YF6NHmZZMoZvVGr\nTiZReKbPnolsadqi2Gp+aR+RGMftjez3fk6ychTfz/u53spRvDWf1+gcXS/oSdYjX99j5eOt7LZJ\n0rVWfpCVo/m5y8oe7C06n8OsfGJQx8/Jx74saONz5LYdG7Rxbky08fmIEqj7seMafUhDf/scRW3c\nv66z9D6l4Tp1P0Vt/HyiOq02EW6Ln08mxmJmnNa4GaK13DN2i0XpsXvuyfON18cTMQAAAICRYCMG\nAAAAMBJsxAAAAABGgo0YAAAAwEiUWjdeEtZSStX3m91HauXyCUFHnuP7GCtn9HhRLEpvl2nT6iNT\nJ6MV9DpRnvNWnTA3us2H9xHZ1rI3+vndqyxHxzK2ZOxfbR9S0perJLMGM2s5Y7/349fM4YFY/15b\nGzu1clmSdgfHnKN9bB83aOP2e5to/eyyssdijXzrbQYfCQQfT3g/mZivTvQxjvfjvo3GGfRjc7gp\nmOeFfQjk+O+s6AORebTp4dwF9Qsbn3NVaw0XHk/EAAAAAEZi1I1YKeWQUspnSynvnpaPLaWcX0q5\nqpTy/lKK/58XAAAA4IBh7Cdir5b0hSXl10j6QK31TEkflPSLo1gFAAAAsAaMphErpZwq6U2SfkPS\nz9ZaX1RKuVLSc2utO0opD5F0Ya31rKBtlX7djs4jNm0UmK6HVuC5TADOjC2tc84EN80IgTJBCltj\nR7a2zjEjbMr4zc85CgA5jwCK7qeMb52ojQfkvLUxrhSfo+NBFz04aBSUsRU0Mkp87gFb3d7IJ36O\n0fm07I/wsd231wRtetaGByr188ncAzygaDRWTxBkJ3OfcHujOcsEdPV+M9eMB2PN+N/93cNjEuM4\nbuu8yAiCP7WgsWE+rE+N2O9J+nnNqii31lp3SFKt9SYN75IAAAAABwyjpDgqpbxQ0o5a6+dKKc9b\noeoKj+suWPLvR0h69FxsAwAAANg/tk//tBkr1+SzJL2olPKdmjybfnAp5a2SbiqlbF3yavKry3fx\n/DUxFAAAAGB1bJv+2cdFy9Yc5dVkrfW1tdaH11ofKekHJH2w1vp/SPoHSa+YVnu5pHeNYR8AAADA\nWjDWE7Hl+K+S3l5KeaWkayV93/JVj53DcC6+dB1d5J6My3pE/26LR0fM2JIRdGaiyTouqM0I153I\nFhdXewTOyNaWiDjC+8nMobeJbHF7/Rw9qnCEz3MkOHfRs0snb0u0iYTTPq9eJxP51tu4MF8azpmX\nI9/6ONGa80ik11o587HH1Y2fR2P3fPDiAVwza3BHcKy13jPrp/XBhdS+zqKPJ1yoHilL/AOEjLjd\nx/J7f2S/j525T/g5u23RPPs4COZh9Yy+Eau1XqTpM7ta662SXjCuRQAAAABrw9hxxAAAAAAOWtiI\nAQAAAIzE6K8m+3FdTCaYo9PSDUSx1zLJYnsyRreIpsptWcS4Ui4zdSvjbyYYYk+bnkzDmfNx3UlG\nbxRpVVq09EcRrrPx4KHSUHeV0eK4/ZlApa7XiXzbCpoaBS51f2d865q86KNrnzPXyZ0WtGnNSRQE\n1sfxpN8ZzVI0r47fA04P6lzS6CNa21E/S4nuLZn14+edydTu/VyZsMXpCfycuU94m8hvrQC08wok\nntEIr7ZN5r6Xmeee+3+mj+ja23jwRAwAAABgJNiIAQAAAIwEGzEAAACAkdjAGrEnWbmlAcgknc7E\nB/I6mcTITmSLa1Va5eWOLSXSyHgyXNeuSNJhVnbdQ0avE+l+nJY+ITq/VkytqI2fcyaZsmtvorh1\nbq/rFCP9QuuSy8THcx9sT9Tp0XpE699jW/XMmZNpE8XUWgSfXaNxFsUn59TPpXPqBwBa8EQMAAAA\nYCTYiAEAAACMBBsxAAAAgJFgIwYAAAAwEhtYrB8J0VfLok6/R6zvwQPvTrTpCQTo/UTJe71ftyWD\nC7CjQLgezDET6NDtd79FwvAbrdz6yEEaBkB1wX/ENiufnGjj6/jmoI77yT82iIIZZwIct/wd+cnb\nZPzigVYzgSa9zYmJNsdbOXN9e9DU6EMO90PPhwPeR7S2M4naW4ExM4FKM/Pcc2/MrIUWmXtaJnBp\nT6DSFhnffryjXzjY4YkYAAAAwEiwEQMAAAAYCTZiAAAAACNRaq1j27BqSilVh94/e9DlIXdYeUvQ\n0S1WPtrKUc7XjLTAJT1ejmj1mxk3I5243cruA0lD3YNrYjLBZY+YLUb2b7Ky2xvm827ZFulqfHBf\nLFG/mcS2fiwTxLaljzol0UdPAt1MP0c0fp7pI6MTymjEfD1lbHG9Y9SmNfZtiXH8nhmN05OM3s85\nujf7WD5OFBC4pRGLrhn3U2bO3N5FtcnQ6mdR19C1c+oXDjzOVa01EkvzRAwAAABgLNiIAQAAAIwE\nGzEAAACAkdi4ccT2fGq2vKMRH+veRNLjOxJxfHZ7P4FealdLg9ETHyiK99Vq05OQPMLPOZP028bZ\nE7TZ00rUHtHSu0Q+8TpfmcM4vW1avsvEx/NxonN2vdcZQR0X6bnGLTPPHm8tk1zc60T2uy2ZGE4u\n8sxoAW+wcubazMQEO8zKHhctwv3kvpWGfvE2Uby1Kxvj9uilIg3WPOKIrRWZ+0RvPy16fu3OSzsH\n6xGeiAEAAACMBBsxAAAAgJFgIwYAAAAwEmzEAAAAAEZi4wZ03WIBXVvBQKOAri0NcY/uOCKTM7sV\njDUKA7e50SYKSJuKM+lBUu9pDCQNTyAjom8RjeMCZnduZpwowm4rgGvkOD9n7zeaAK+TEcTPI8F9\nxDwEwPMKjNlircTK81qnmejKiyAjQl/UnK0nQfmiAsUC9EJAVwAAAIB1BxsxAAAAgJFgIwYAAAAw\nEhs3oOuuNzcqmA7ijp5gfb203BrYMggUm2hz7zwCEGb68ACW81o285iTTIZ1D9oZ6UVcU+KBMzO6\nmq0JW5xM4NLjOmzJ0FoLUXJ3912YNb7Rb88ajHC5hSe8zvT7YCtHmj33gwcuzWjEIl86mYCurbnP\nBL7NzHPPnGTWQovMuD1BnHvI3Od8zj4V1gJYCZ6IAQAAAIwEGzEAAACAkWAjBgAAADASG1cjNkii\n26MJmEcC7J5xoj5adSIdR0t3EmlXevRFUcJxp+XLaFy3PxOkrSceUCtpszS032OpRdoh1yidZeVM\novaMdsj7cY1Sxk/ROK0YZhnbnB5dTe9tyP1/spUz17fr+iKdkydQd3ri6kX4fPT4MpqzlkbMdXK9\nZGKnzeNXzlrpfXtsjXShUTxBgAfgiRgAAADASLARAwAAABgJNmIAAAAAI8FGDAAAAGAkNqxY/yfu\n//JM+V9MqHujHjpTPilInHydTp0pP1i7Zsr36bBBm7vsI4EHBxm992rTTPk2HT2o42zWfTPlTQOh\nqwf+lPZaMu7dZu/X6lBkfM/9s7bs/fpwCdx5rQmYr7YKURLzlk63R2MfrU7XvWZs227n06OB3plo\n47ZFGt3BsePb/fp3KW7/Me0uBn1Ex7ZZObL/dj/whNniGUEbn5PLWn1KOsHK5yRs8fPxbyckHfr8\n2SCpe661DyG2Dq95fcwE2J+x9eS2SkPNtteJztmP+dqWpLOt7Od4U9Dmc402GfvfZ+VXBG38Gomu\n+VOsfJGV/23QZruVfb1fH7Q5rTFOdD24b33cjOb+HU8ZHnN73S+RLT6P3ib6JqB1X4vujW6b17ng\n9UGj4e8i2D94IgYAAAAwEmzEAAAAAEaCjRgAAADASJRaPdnx+qeUUu8/1w7eaOXnW/mTQUfPsvJX\nrBxJuzxm5D8HdTz+5sOtHGknXMJ2h5X3Bm2cLVY+Kajj5xTYcsczZnUyn9s0K9D5WhA0cpMZ6Dq5\nPVaOONT68D4laadpqj6nJ82Ur9PDBm0+ZwKj3do8qHOPndPdu2aDXO667MShwa6JcX1FRmPl5UjH\n4Roe13Vsi9rMXtfHneMXiHTSptmgta6jjOb5Lgv+6SFVH6MvDNq4vz++95kz5dv+3oVDGvoh8stu\nK79w9pzPOvOSQZN/2T2rHT1x8+w5f3W3B3iV7rzgIbMHXNa3Z3gP3Xz2bTPl++6d9UH9S79YNbzm\nh6YM4826rim6zHwd7rLymUGb7Vb2+MaBFErXWPkhQR2//3w+0e/FVnYdYnSdnW7lC6x8qoY8zsp+\nb9wetMnovQYasdn1svVZw18iO655xOyB6+1Ki36H+LGMLtF5yKxtR50xFB3ev2d2kX3Xln8Y1Nlm\nzjrCghV/vM7eAyTpfdd+1+yBd1ng3hfeP2hz3qNnhXGXDmqsH35VUq3Vb5mSeCIGAAAAMBpsxAAA\nAABGgo0YAAAAwEhsWI2Y9MZGrZ7k1ovCk9RGtrUS2a73kG+tpOU9iZF7/BS1CWJDrZpo3FYy5ciW\nVqLtiFby7cg2T+ScSQDvtkXJoF2Q43MY3U/cvmFMvyHebybxvHNDR5tAr9Zcc5k59fM5LtFPdM7e\nj6+Na4M2XieTXDyTTLw1Tub6zdwnnEyi9nngYsBoHF/vfx/UWU+/i9aK1r4ilEotYJz1xK+iEQMA\nAABYb7ARAwAAABgJNmIAAAAAI8FGDAAAAGAk1rsCfAXGSjzaEu5KQ7e6Pi8jwvVxMuNmcOFoRlCe\nyXbr5+j2RmLfTB3nTiv7OojWhfvWMwJHuGj4nrDWLC0hsiQd2xgnwvvx+YiiSLofoizBPnZG4B/1\ns5Rorbi42seJxO6+FqL13xL0Pz1oY2NvsnW71yOXSkPRfyTod3ydum3Rdef+jtap22L2n/7cYZNr\nbO1uOmK2HAaLdhG0X9+RnzyCdPThwLZosNXxDCt/Mohc7TGb3bV7I5G3VTrF1twNfu1Kufvpwci8\nxPjrZZzFwhMxAAAAgJFgIwYAAAAwEmzEAAAAAEZiAwd0/aNGrYz2pkWk8fF30pFmxtt5QNFIC+W6\nGa8T2ZLR0bSINA2uL7o1YYvrgFq6IGlg/0CvEzQZaFOusHKkS3FbnhPUcZ2SlyNNTI/Gyuu4rzPz\nfJuVPQuyNMxQHAUQbemY/OdRnUyw1rOsfL2Vo4zervuJrhk/dqWVM3odt22YHH2YQdrXWKRx8/uC\nL+bovuFZsyONmJ+Tr5/HBG1c3+htIvtbaztqkwm02rovZwI/e53omnmslf33nN/Tgn6PtzV4S7S2\nbezNwXW22/1gvjszyEB+lbfx6y6y3/FrKGH/wLdR5nknus6830zQY9Mu6ktWju4B7u9MIGK/Z0V7\nILfXbYt+H/hYPmeHENAVAAAAYL3BRgwAAABgJNiIAQAAAIwEGzEAAACAkdjAYn0Tv242DZxL4o4O\nOjqmMdDO4JhrAaNYmg9p9BPpUe+wsseMjMZxPaRrfaO4k97P5UEd1ybfFNRp9et65kjz6fYfapN2\nezSQrVf35a6gic99FHO0Fdo4E9u0pXtd7thSItv8WPgRg+PXdSSWbQWgzQRLzIzjJ+0fAWRsy3x8\nc1+ijuMf0kS2+LHMRwAtsXuE99vzwVH0wU700cVqx3HbonF6gplm2vhYGeF3Dy1bMn7aPgc74MDk\n3H6xfinlgswxAAAAAFgdyz4HKKUcrsk3myeUUo7VA/89Pkq5HB8AAAAAsAIrvZD5MUk/LelkSRfr\ngY3YnZL+cMF2AQAAABzwNDVipZRX1VrfsEb2pJhoxH59Dj15wMR5JdZukcm17gHkMoE+XcOQSSwc\n0dKDzCtX/LwC0K62z8h+1514P9G4Lb/MS3vTw6KSD2f80iITdNHnI6qziLEj/VFrXk9MjOtCvyig\nq4v/EompB0TrZ5OVI1+2xsn4KVOnReY669Ho+RxmNG7zOJ+oXeYa79ELzkPj5n1ckmgDOZbXiDV/\no9Za31BKeaakbUvr11rfMjf7AAAAAA5CmhuxUspbNfmO7nN64L9sVRIbMQAAAID9IPOO6amSHls3\nYpwLAAAAgHVMZiN2mSaRsf5lwbaskpMbP8/oCPzd/TwShffSSpIa6Qp6tFo92qeemFSuS0kFv5oD\nmXmP6mTO0elJbNvSrmR0fU+zckZzEiWp9bE9SW10PXgi4UysMceTULseMqoTnOPxdsxlVzdEvrQ5\n2mrnHLlpS3BsKZGbdvsBX18Jv0WxD+9oJPA+OgjYd4f5YZP5Lbw0O9ocb+VbovhlrrvyeQ0mYJOd\nU9etxP0WEa3DpXiyeml4zfxezhyAJWR+k58g6QullE9pye2l1vqihVkFAAAAcBCQ2Yi9btFGAAAA\nAByMZL6avKiUcpqkR9VaP1BKOULD904AAAAAsEoyKY5+RNI7JP3J9NApkv5+kUYBAAAAHAxkXk3+\nhKSnS/qkJNVav1RKccXuCBzX+HlPMtmeYJoZF2YCrbaYV/DTHjF7JrhgS6juwXOl+QVMXEo0H5kA\nol7Hs3j1+DIS/87jowwLDnq0q6Q1TCK/xUXFGiZI32zl3cGH0ptMZD4QTkdzaH44xco7AuH6kVYn\nOMVBknjXeZ8Z+PJQO3aW9XFhMM4tVj7Gyp7wPrJlQHDO/rHBGYH/L/6dlbv1eY/oEbtn2rif5sVa\nfecDMBLNJ2KSdtda79tXKKUcqjjkMwAAAACsgsxG7KJSymslPaiU8m2SzpP0D4s1CwAAAODAJ7MR\ne42kmyVdqkki8PdK+qVFGgUAAABwMNBM+r0emST9/tM59NSju8okzG0lmI3GdYGI9xGN27K/J6ht\ndCyjsfJjXs4kLc8Em73Vyp5MOdKv+djHBnUcF6YsStfXo2XsSRQ+j3GkvkTzPXi/D07U6Uns7HLX\nGxt29eLXVHQ9uL3ROXtgUut381OGTXZ7YFXvN7oHtK75zNq4IajTauPXtzTUA0eBYp3WuszcJxLB\nZgdckKgDByfLJ/3OfDX5XaWUS0opt5ZS7iyl3FVKyVwJAAAAALACmU/+/ruk/yDpUvJNAgAAAMyP\njEbsOkmXzXsTVko5upRyXinlilLK5aWUZ5RSji2lnF9KuaqU8v5SSpRtDQAAAOCAIPNE7P+V9N5S\nykWazTX5+v0c+/clvbfW+pJpSIwtkl4r6QO11t8upfyCpF/U5GOBANd2tDQAGU1GhkwbH6tHR+N9\nHBbU8WOuM4vGcU1VFKTH41+1fJ0hejXuvnQ/Rb5221w/kkncHmnc3C/uy+htvJ+Tt8mQWactWsmK\npViv4/51+6MAWY77LQox6L5zv50etHF7M/HVPNhYNGe2dp9obT4fxCfc2ohXFjHIee+2BHHddIWV\no1iJfu25/yPc3xldpSUTH4z71aCNJxyPbPM15uNEbbyO2xu18bWb0Q96P64ljeYMlQ7sP5knYr+h\niUL0cE1Unvv+dFNKOUrSt9Ra3yRJtdY9tdY7JL1Y0pun1d4s6bv3ZxwAAACA9Uzmv98n11rPnvO4\nj5C0s5TyJklPlPQZST8taWutdYck1VpvWh8R/AEAAAAWQ2Yj9t5SyrfXWs+f87hPlvQTtdbPlFJ+\nT5NXkK5DW0GX9rYl/z5b0llzNA8AAACgl+3TP20yG7H/W9LPlVJ2ayIUKJJqrTV6YZ7leknX1Vo/\nMy3/nSYbsR2llK211h2llIcoFiJMeamV5xW/CAAAAGB/2Db9s4+Llq3Z3IjVWvdLD7ZMnztKKdeV\nUh5da/2ipOdLunz65xWSfkvSyyW9a/lezrByS6TdE9AyQyT8drd6kMIogKKL5r3fExO2uA8in/gx\nVxVn+o0E/v7wMmOL+9v9kglim5kztzdq42O5cDfKOu24KDp6s+7/t3BB8NVBm1Zi8OhDCBd6R+fs\ngua7G+NK7WCg0f+dfI25b68M2mTWQssvUb92HxiI84N1uqMVxDm4t+xtJbTPBDiO6ri9NveRiORi\nm+ct1mZX5v/jPu+3BXV8LUfr5xQr+5cP0X1im5Wvt3L0sUpL1RJdD9tni5vsmt9rPweYE80rsJTy\nnOh4rfXD+zn2T0n6q1LKN0n6sqQf0uSO/fZSyislXSvp+/ZzDAAAAIB1S+a/Qj+/5N+HS3q6pIsl\nfev+DFxr/bykpwU/esH+9AsAAACwUci8mvx3S8ullIdpEm0fAAAAAPaDVSf9LqUUSZfXWh+7GJNS\nNtQb758Nun+P6Su+ZrqBPYEW6j5tninfZTqIvUGb3RZE1ceJ8LH3Jh5ERmO36rhtfj7RsVt0wqDO\nNRZg82rT490X6CseZMmIj0gEmnT7N7mWK1ia1+192Ez5tqtOnq0QSaz8WOR+N9flUtHptOrcHmi3\n7rWTysSfbcVVPTU4druVI+3QQxptXIojScdY+RwrR7Z6Px+18s6gjR+L/L+tUY76dV/5Wvhc0Mb9\n4v0OL6Ghve7ryLfbGuNKQ//6+VwfrLnbfc1ZnWOCC83P8RorPyOw7TNWjvxyqI19g4393KDNJ6zN\nkYlrqCV/vDfwk/vBbb078bsyE8M2E/fZz8nbRGvD/e19uA8ybSJbfexonn2snjZOdN92+zL2Z2Ig\nt8aJ/N+a108esmzS74xG7A164FfiIZrcej/bagcAAAAAK5PRiC39f84eSW+rtX5sQfYAAAAAHDSs\nuBErpWyS9O211petkT0AAAAABw0rbsRqrXtLKaeVUg6rtd63VkZlOOUrs/FnLj/tzJny10wzFuu9\nZiNeOmgAACAASURBVDVi95nGysvZOj5Wj94r0rQN28xOn59PpF+72zRirq2bHJtt97U6+/L7vvtn\nx5GkYuaGL8INt3+TveDfE2jRvrbL7L3bRore/++2cqQp2WVl78d/nuk3Gmd3addxWmGs7ojGSdTx\nfl2jEbXxib3FypH/W3qvjGYjCl3nc+L2RnPmx3wpZ0LvuS3ROI77NjofHydKLu7z2gp/J0l32KT5\nXX9HcLV6aLSW5kca+iEK1eX+dq1WpPF0P/g1FGmLXMuY0Xzualybrq2Tctoh93dPGy9H9vu16Occ\nre1rW/1GujjvKNpGNJLTXxW18bhzmXEyN1Bn/QV/z7ya/LKkj5VS3q0ll1qt9fULswoAAADgICCz\nEbtm+ucQPRBeeXWfWgIAAADAgMxG7Au11vOWHiilvGRB9gAAAAAcNBySqPOLyWMAAAAAsAqWDeha\nSvkOSd+pSb7Hv13yo6MkPbbW+vTFmxdTSqnSO+yon0cmGXRLBR3h/UbCP6/jDx4jgaHb4v0e1bAr\nIrKtR9zoov95iR1bcxR9sBCpnFu4vZmk35lzbPkyI0j1cXvmJ0O01nvmsWVfz/UQJYfuoZUEPGIY\n9LjNVitHPvFzvNPKmes5quP93mDljP8tCHJ4TXkbv7/eFbRxX94T1PFk4W5vtBaOD46t1Ic0XO8Z\n//vYnsQ8SnTu8/HHQR0ASTq3K6DrjZrEEHuRJrkl93GXpJ+Zn3EAAAAAByfLbsSmSbk/X0r561rr\n1yWplHKspIfVWqP/GgAAAADAKshoxP6/UspRpZTjNElt9GellN9bsF0AAAAABzyZryaPrrXeWUr5\nvyS9pdb6K6WUf1q0YW1eYGV/v5/RHjjHWTnSmGT69WPu5oxGqaWridq4ViVzzq6diMbu0dE4GV1c\ny29RPxnfZrRQLX1RRofibTK+zdDSGGbWxq0d40a0/JJZ2+7rzDqN1qD7IaP59Dnxa3570MY1VN4m\n0tl6lux56fF8rt0vGS2g67sya2OblaMMxy5/GQaUHh47NzE2wIFN5onYoaWUh2oi2n/Pgu0BAAAA\nOGjIbMR+VdL7JV1da/10KeWRkr60WLMAAAAADnyaryanwVzPW1L+sqTvWaRRAAAAAAcDzY1YKeVE\nST+iiUjgG/Vrra9cnFkAAAAABz7LBnT9RoVSPi7pI5rEEvuGarXW+neLNW1Fm6p0vh11kbCLVjPf\nJTiZ4Jo9wSgj4XFL+B2JcFtBFyMRbivDfcRJHW2cnkCfET1BO33sjKg7c46twKQ9wvweMh81RMFx\nPQpN5mMPX7unWjm6n/g69GCa0UcNLih/fFDHx7o7qOOYr7aY8H7XpxJ9ONHaPsvK7tvMtZkR0Z+S\nqNPzgYWvl0wg5Uy/zn1Wnte9xcn06/14m95xvF3GT63fK/M65xa942SCmK92rJ57cuYjsej3wSL2\nDy/tCui6jyNqrb/QYQUAAAAArEBGrP+eUsp3LtwSAAAAgIOMzEbs1Zpsxr5WSrmzlHJXKSV6lwAA\nAAAAqyDz1eQ8onkuAA8oeFjj54vSiEWaGH/X7a+Fo357Ekg7rreI3rm3dBARGR1cS0+R0RH06L16\ndFlRwuKegJtuf9Rvi0zg2FabaH565tnPx5MeR3V2JPp1XPsU6decqxO2tBKqB+yK+nXcDz7ujUEb\nD+ia0a74vSQKmnpBcAwA8vTcpxfLsr/dSyln1VqvLKU8Ofp5rfWzizMLAAAA4MBnpccsPyvpRyX9\nbvCzKulbF2IRAAAAwEHCshuxWuuPTv/+12tnDgAAAMDBQ49wap3wYSu3TmVeMZ0yWo8et7bsG3Oq\nWsnFM0T298xJS0MV6YIy2qGWLZk4aBm8H08gHekXetaG64vuTdTxeY3icp1sZY9FFumafGy3d+VY\nhsv362OfaOWbgzbu/9OsfG3Qxu33PiIZrZ+jx+GK4n95v5F+7ZlW9jmL+vU1tjWo4/j3WFc0xpWG\nvrwhqONr2W2LvgNbxLUZXTN+n/B4d9E47od3NsYFGJL5ahIAAAAAFgAbMQAAAICRWOmryfBryX3w\n1SQAAADA/rGS8Cj6WnIffDUJAAAAsJ+s9NXkBvtachFxZzMC+UUldnYRaCRW7kma3TN25gMFt8Xn\noyega0ZQ6/1G47gtUQJjF3q7aD7j2682xpXagYajeXZ7PcBoJCJ2gXnUr/sq08YDlfqHD5ngsu6X\nSJSeSYx8tpX9fI4M2rj9rfUkDdfCPUGdFvMKIum+c79E4/hHDe6DjNjd60QfvPjHEVF+Y/evC/ov\nCtoAHNis+NullHK8pB+UdNb00BWS/rrW6qGxAQAAAGCVLCvWL6U8RtJlkp4i6YuSviTpaZIuK6Wc\ntVw7AAAAAMix0hOxX5P06lrr25ceLKV8j6TfkPQ9izQMAAAA4EBnpY3Y42ut3+sHa61/V0r5zQXa\nlCQTVLFFS98V6UVaQTClxQRfzWjRMsmgM8FZj7ByK7lyNLbrQyJNSUt7FgUUbenKEomeBwnio7G9\nfFLQxjVVj0+M7W08QGqURNvPqTU/0lB7E81ZSwsYfTjttri9nwraOB608/nDKluPt2EiXZZry1wL\nFSUtdzIBXb1OFHTUOdXKfr/yYKGS9DErR/c014B5OWrjfvEk61FAXbfX73vRevJ+ouvXx/54UAfg\n4GKlOGK7On8GAAAAAAlWenRzUinlZ4PjRcNPzAAAAABglay0EfszLf++788XYAsAAADAQUWpNZNw\nd31RSqnSr9jRRcXz6mEeCch7YpitVWLwyH7XDrXK0bGM/Zm4T47bG8WXcltce5OJT+Z1Ij+14jFl\nzifjJ7+uo6Tf3o+XozattRvFHnM9lOu9onhTGe1fS8cXxcdq6bsyGj3HNXsRrtkLNGJbz2ibMuCW\n2eKZxw+rXGXlo618R9SvrZ9NNkdRKD7PJR7Zv8XKvuTuCLSAJ5h/T7effzIYx+tc49dDsOa8zU63\nLfhdeYr1E12at1vZL6vdQZvBOFa+Kajjc+K+jgRF3q/bH0kmB/3+c1DJr19fDJ7sPWrjieajhPZ+\nXWV00nbNhNe3t/PrKrLf+3HbXqhaa3SzWzHF0R8s9zNJqrX+1Eo/BwAAAICVWem/1hevmRUAAAAA\nByErpTh681oaAgAAAHCwsdKryXev1LDW+qL5mwMAAABw8LCsWL+UcrOk6yS9TRM55IzIrNY6WnbW\nWKy/0VlPHxs4mQTMzlolTHfbMgF2I3Fmy5ZMYuRWsNmoTsaOVmJtV0lHdaJzziRydtw+D9AZCfy9\nX//IwZOlR20ioa7b72NHgloX67vA3xNiS8Ogu15nW9DG/XKllaM587URBRG+0cp+PlEQXr/Hex/R\nvEe+W0qUbtgD6Hog2ahfD8obiau9jc97pCjvCfzsmft8XUZr0H0bnXPr+s0Eu46uq3ngHy75ONH9\nyuv4WpeG9+FoXlv42NGaa93/o/v2ezpsmQfnrl6sL+khkr5N0ks1Sfz9j5LeVmu9fP4GAgAAABx8\nLBtZv9a6t9b6vlrryyV9syb/dbmwlPKTa2YdAAAAwAHMiu9JSimbJb1Qk6di2yT9gaR3Lt4sAAAA\ngAOflcT6b5F0tqT3Sjq31nrZmlmVYrXBSzOBMvd3jHn266+S1ypYa4RrAKLX3B7IMxNs1rURGc2Y\naw28nNEo9WToymgcMhorD/6Z0d+1Aq9GGo1MnVabiFY/UR/uuyjoq+PXa6QPaRFFFG3dByJNiWuQ\nfJ4zScBd7xX5MZPA2zVJvl4SGslNpnWKgrM2A2V6UExJm03LtTvSmfm9w4LYRr7cYsFvd3nQ123B\nOI63SQThPcX85C6RNDifTcE57/U5s/XjAVKlIPjqWBrizP0o+n3ga9k1kdE109L1BUGQB9d45n76\n7xvjSsP7jZ9Ppk10L4lZ6c77HzVZDq+W9FOlfMPZRVKttUZeAQAAAIAkK8URW1Y/BgAAAAD7D5st\nAAAAgJEYU3i0n6xW89VzqvNyT0bv1Xo/3qOxit5Ru17n7qCO4/FzMgmYMz93rZD7KRqn9UY8Ey8r\nE3fL/R3Z30psnok9lsF1J66LODVok9G0uU6jFTsq6tfPOUg6reut7OspEt/4PGc0GU4mma/PR+SD\nbVb22FfROL62PSZVtI5DsZbh67AVoyrgGNOe3RL50fr9N+aXjwYxznbZ9XtM0K1fetdam82BXw61\nOrs9CXigUfJE20damxuCNp4M3XVa0RLcYvqvSP6441eDgyuMAwcdPBEDAAAAGAk2YgAAAAAjwUYM\nAAAAYCTYiAEAAACMxAYW66/W9DDXZoOMeDaiZVsk/PZjmbHnkQg2Upe6yPxmK2c+HGiVpWFQRU9A\nG+GB9VqB96RhYMxEMMeBbyMRtAuwMwFdvU7moxM/J7clOp9MAEIf29tkEqi7n1zILg2TQWfmzMeO\nPrBwYb0nXI4E8X4f8D6uCNr4MRf4e8DOyBYnEsh7v9GHD/6BhX1sc2YQBPYqs28gDvf5kQb+/5j9\neFfiOrs9WAu3Nz62uTcKwnu2lS2B+lXbgjZ2X9vh8cifEIxt5dPMb7cHc3aHlXdFH3u8xMqPnS2G\nAV1bAWgjP3mbRyTabLeyf4Th9zhpeA/bFtS50Mo+75Gf3BYn+tCpFdC1l3kkLc/DEzEAAACAkWAj\nBgAAADASbMQAAAAARqLUGukb1jellCr9Vzs6D7nbWknmeoJ6rqWcrydBeitobSZ5rNfJaK4y69f1\nCJHeKGOv0wq6mznnVp9Rm4xGzLUSmWTcmSDCLa1EZL+vJ9clRnqjTEBdP+ZtoqTZ3iYRbNnzcw+S\nOPckhI/Ox+fssKDOfY1xIm2p2+dJ7zNBnTPJlF3jGfnFhVi+FqI2fv225l0a6lp9EiPfej8Z29yW\nyC/uO18LGa2v25bRQvnajhJt+zXiOrhIy+V+iPTXkfZ4KZH9rd870fXccz9yMoGfPcl9pN/0OfL7\n2kNVaw3F6jwRAwAAABgJNmIAAAAAI8FGDAAAAGAkNnAcsZa+ZT3Rir200cj4OqPxadWZV+wW93ek\niZnHpdBKwh7VydjR0hd5Em2pnZxbGupkMj7IxGAzjjY/eOylKN7XZivvDvr1+Eu7XHcSyDFON1vc\nlZ4sWpLuMK3HZtOqeBJqSQP/H2+23B6sjb0d/vcm7jdJ2hVpa5YS/dx96Zqf6B7mzuypE2ncPCZb\nRmPYsjfSlno/3kfmvhGdcysmWBQ/sSd2oM9ZRtfn4/h9Iooj5kT36ZM7+vG14fYnktMPbIl+7/h8\nRLT66dG4LQ9PxAAAAABGgo0YAAAAwEiwEQMAAAAYCTZiAAAAACOxgQO6/jc7Oq9knzMjBcd6RN09\nbXoE8fPChYouQI2E3y5szQjX3X4XoEZz6rZlxJluSyYYn18XmSTsPUm/M4LaVpsoQG1GrO+4aD4K\nyuj+zfRrbZrifQ31y5EIfTDVNmdHBtevj+V9HBOMc6b1e7X1G36HYm32Wpso0fPt1iZy/71hPMhG\nGyu7b8NYuXXlOpEmPXM7asVizXzTk9HH+zF3W7Se/IMQn6NIq++3hcw6dVs81mzUxseJ2jiZW9Z6\nJvPBzobiEAK6AgAAAKw32IgBAAAAjAQbMQAAAICR2MAasfvtaE8iXieT9Lih0YhoaRyk4ftw13pE\n2o+WJiPSW7h2IgpgudsD3m23cqRJOn7lKpH2xrUqXo40GW6K52INg/WZ9uz0oIqTiQHbymUd0RPb\n19u4VuLooI37JQz02agTaTJcmzLQskSBGzNCoFabCL9ePalxECh20K9r3KKgkT16O7fN+8gE7o3G\ncX2gBeTcGugfdwTdrJrM/bUVXFMaXiQerDXCA862gpBK7Xt59HvvEiv7+onOZx7CuHm1aemKI82t\nt/Gk8uclxoUc56IRAwAAAFhvsBEDAAAAGInRNmKllJ8ppVxWSvmnUspflVIOK6UcW0o5v5RyVSnl\n/aWU6KULAAAAwAHBKBuxUsrJkl4l6cm11ido8gL8pZJeI+kDtdYzJX1Q0i+OYR8AAADAWjCKWH+6\nEfvfks7RRHn5PyX9gaQ/lPTcWuuOUspDJF1Yaz0raF9fev+fzxx7nV43U77LBJ57gwh4u3WY1ZlP\ngNRNJrTM9OttnEM7ovPtCc75ayZcvz1Q0f+zts2Uv6DHzpTvHohnpU1m34NMNB/Z720OM3V41OY6\nPWymfHU9Y6Z81R2PHrTZfflxg2MD/KOF7Y2yJN1kZRf0Z4T43kckrPYPHx5i5TM05AQrbwvqRO2W\ncmXj55L01Nn7x1FnDk/gzsvsBH7XKnwu6Nd96R8WSNJTrfwyK7tvpeE8P9e0s38b3A/98j218fPl\nji0lutz9nG8PdL0nmH0+z1EbP2f/kOMHA1v+wsrXWvmFgZ8+YWMfGdQ528ofs/LLA1v+xsqD3wgB\n/uHPZ6wcrf3WnO0MjvlaiD5+8rl2H1wftPF+/BuHyFZfC77+ow+mfBwvR/cw90OmTqbfQWBnXz+Z\nD2kygd29n+gjB//wxz8QyXz44L8nn7O+xPq11hs1uR1/RdINku6otX5A0tZa645pnZsknTSGfQAA\nAABrwaJy5KxIKeUYSS+WdJom++DzSikv03ALvOzjuktf965v/Puk550pPW/+dgIAAACsnks0DIkS\nM8pGTNILJH251nqrJJVS3inpmZJ2lFK2Lnk1GQUlkiQ9/nUvXhtLAQAAAFbFk6Z/9vGXy9YcSyP2\ndE1UCE/TJGzkmyR9WtLDJd1aa/2tUsovSDq21vqaoH19ev3QzLHdFo1ys+mN/OeSdJ9pxFxTFWm7\n7qmzwQO/ttsTVUv37Jo99vV7DxvUGXBvFHFzqXGJQLL+3j16D+86lChQaet9fpgkuFHOJObtGScT\nK9R9FwVe9WOup4hiObqfMra4HsTHjbQrXiejPfNgrJlkyn7OTwnaeJ0brLwzuJ+Ypu3QZ8zqLfZs\nDwKvuqbHdXHS0C/XWPmYoS1bXhwJfR5g187hh9qbj5m9SHZfbZrDSBfkfvIk4K5hkqQrbZ1G/bof\nDq8r/1ySLvMk5bNtyrOHQZDrdst4fdlsmxN++LpBm52ff/iK40ga+mX7bHHzU4cBXnffPXvP3Xzk\n7MW4e+dQ/FSsTt1p92n3W9TmdvNBdK/0ayjoV0c2slXvCTJ43256o8y93d2QiZvsOj63NbLNXlSV\nw4d6qXp9w3fRZbjd69SVfy7FOtClRNeQ9xNdi35vcXujKfUk8d7vtcsn/R7liVit9VOllHdo8tzu\n69O//1QTddvbSymv1EQe+n1j2AcAAACwFoz1alK11nMlnWuHb9XktSUAAADAAQ+R9QEAAABGYrQn\nYvvLMfby91QT3zzY4n5sC14we53H6guzP68eO0R63Fe/PHtg2O0wFtSXrBzFTbI69Z9tmOCzBQ/t\n4/KjSCLgkU2i9N3PfoQd+M9Wfk7QyDULZv/yn10swXUEQ/erPmf2FftN3zqr6flf+o5Bm3fq38+U\nPRaZNFxPHl/tC7fMxlKTpD2fiZJKLyGKD+RXnGusojhiz7Cy6xeuCtqcNauvOPX/9EUoPVGfnylf\nY9nQr7zhMYM2zz7lo7Plp3xkpnyjHjpo8/e7Z/1/58W26iK9iMdEivxiGrBjf+zGmfJtF588aHLS\nltmF6PEG77l7qPncffmxsweudjsC23bN2vbwF81O0lc+duawjZ/jaUG/PtdnmORke6BR8jV2zGyb\nes3wnAe5uK+abbPzjcNraBB37qxADuO6MdPF7S7ma2lwHe32CyCId1efaue0va0Trdusjc9zRvN5\nQnDOx5j+19tk4tBtt3Kka/I2fk+OrrOdbq/ZeuFvB41MSxfU2FAM4pd14v72eH0rwBMxAAAAgJFg\nIwYAAAAwEmzEAAAAAEaCjRgAAADASIwS0HV/KaXUz9RZIbEn9b7Hklt78NaI+yxp531BEFhXJnri\n8GXbNWzxYLLeR5y0fLaO9xsl9N5h8vxIuH5VnRUS3/xlq7M7EKRuvn+2fPh9wzqOBwu814IYRsH4\nXEDrQTwziZ4j0W0mSOqgjfkhE7SwFbQ2E2w2E6hxECg2kcy6FRxRGiYs9gCimQDBh5vfIrHyZd6m\nZZiku+0coyDIz7Y6g0TbQb8eaNU/tomSULsvT7Vxrw9s22blSJDt68fHjj4QaSWDjoLAul98zW1L\ntInmtdVvT3DNCO/H/RbZ1mqTCTCdEdFnrl/3k/9KacSIDfuIaOXIvje4b2TsbwX4zvTRM+482vTS\nGmuFgK48EQMAAAAYCTZiAAAAACPBRgwAAABgJDZsQNenvury2QPbGg3m9X655133vOqsloz9kTbK\ndTIDTUbwmvtQ29MfbsKOzEpz7VCE2+K2RhqfQWLeoI77pemDoM1qf56lpTHJ+PamhG+f1RhHGuqL\nvM4wZ/YwGa7r/C4O2ri+JVqnp1r5UDvHaM5cm+X6KNemReOcYuVIi+PyzKNt3Oh8XAcUyXd9rj0Z\nvftWGq7lTEBR953Pe2S/H4uuMz8nn/tIr+b2RTosx+33deq6OWlor4/j8y5pIN29MKjj9me0dC3N\nahRE+Jut7Ov25cMF9fAnzkYIvqfOaqt3vtYSuUvSe6x8VaQj8+jEHlXYF640jGj8KCsPg1IPo357\nEOpbgzbbrXxSUOdJVv60le8M2mxrjLM8PBEDAAAAGAk2YgAAAAAjwUYMAAAAYCQ2bBwxnW12+/v9\nVjlTJxPTJqrjx7xNpKPxNq1y1G8m1pIT6VtcQ+JJdSP9gtvnGobINtdGeJtIO+G2bW+UpWGsscj/\nTkYj5nUyWrTWOWZ0fXut7NouaagPOSOo4/OY0Q75ObmsI1qnnrTc9UauOZGG8xitOZ/XbY1xpaEG\nyaUrjwva/ImVfd4j7VArAXC0Nk63cpTM/XlW9tzh0fXsujFPcvzcoM0nrHytlV8ctHG9V+QXX1N+\nXUXaJ1+Xvv6j5OiOz1mkRfNrZruVoyTOvt6jX6et3xmZeGt+D3ZbI3yew98PZrD76ZhAW+prO/L/\n7Y1+I1taGsPo3ui+zGi4Mxpbt6UViy/q1+2/iDhiAAAAAOsONmIAAAAAI8FGDAAAAGAk2IgBAAAA\njMSGFeu/8v43zBz7sL5lpnyCKSsP0zAJ9VctkNv1u2aTWx+9ZRgd9J69lkz83iDp972zkRkPO3y3\nldsJsTdtmlWk7t07TPrtY++xJNp79wxViJsObUcZdfvrTovImUkm60SBVl2o6zLG4SkPx26Vo2MZ\ncWwmUGwm+bDj/eyyck/y8QyRiN6F0a2PTKShINX7yATKdB9sD9p4vMdM0FFfPz0fr0QiXA+06rZE\ntrmw2z8QidaOi9Cj9e/Jnp+a6NfxOpk583UZrSf3XSS8b91+on5drN8SaEvtOYquZ7c3c99wegTl\nEe7vTLDclrg9Grd1jj3BZpcbq9XHoI3vTaJOPWu514kCx3qbKDir9+Nton5bfAtifQAAAID1Bhsx\nAAAAgJFgIwYAAAAwEhs26fcXy6NnyseGL/0f4N7gpbrrxh65xSJEBm9zH7zJkox6QmNJe7bMijvu\nM5HJpoEYRNprgpDDyqwYZO+m4VRt3jJbZ4/1sTeY3vs0qyu7a/eDB3V2326iBg8MGOmwWtqCSNPg\nQQkzmp5WMuLINtfVDN0/JBO4txWMNaOlyATlbWm3MsFyowCQrg3KzFmrjyhQps/JZ6wcyVRXvpzj\nsc6ycqR98mNejpJ+b7eyr7loHLd/m5UzOstMMnHvN1pzrrHya+icoI2fowfPfX7QJko47rj93ubs\nRL9+PWT85D6I5Ea+nnwOM/rTTIBvbxPZ0tKoRm38OsqM49KnwXUXXZxftXJ00rdZOdJhtfr1302Z\nE3Dt1jcFbbyO9xG1e5CVI794P56QfHl4IgYAAAAwEmzEAAAAAEaCjRgAAADASGxYjdjzdcFMebfp\nsM7Xt82Un6eLBn2cr2+fKT+6fHGmfNfgHbW0vcxmOD1dXx7U8XbX6JEz5UOD/e9xunWmvNmETZtK\nW9h0j2ZjnEX277Wxj9k8FOPceffW2QOuF4n0O61YOZF2paUri6QHHlvJtStR7KWeZNYuAfDk1pk2\nkabE9XbupyjKjMsVvI/ofPxY1K+fk+vIojhQfk5uS4Qnr/bk0NHacL3O8UEdj8HmMo6HBTqOp5jD\nd5ijvjsY533mPJ/3SCPml6snE4/OebuVI99us7In/c5o6zz2WDTPz7by+638vESbKKbZNitfYOUo\ngb3ff/y+EGnTXC/ousTomvE23m8m9tU/BnV8nfrYkUTJ597LgTa5GXssst9j5A1uYn8cNIpuhrA/\n8EQMAAAAYCTYiAEAAACMBBsxAAAAgJFgIwYAAAAwEhs26bf0X1q1rBydZ5h/cw64utrVmFGQuRaZ\n7yp6+s2QSXjqSulWQDxpeE6tPqKxW+WI4UcMbd9FilpX6vr5RH36OWbWRsu26Hxa40YcZeXonL0f\nD1oYjdMaO/r5PNZyxv5Wduuojc97ZGvrvrqoew8cvCzid/kfBMc8WCvkOJek3wAAAADrDTZiAAAA\nACPBRgwAAABgJDZsQFfpDCtvDWs9gOtfIlxrk9GpRP22kopG/frYrksJXi377Hkw0yhHaibh9UBr\n4JENM9obn48j1ORoK///7d179GZVfd/xz9cZBsSR2yjQAWVUrCAgiEZMtZGlxmsXSWrqkqRdWtvV\nWNtqekkD+ofadjWarMTaWlfbVaWJ9bK8lIqNVoJKrFjwBlGuIcogzIRBrsJQBmfY/eN5SH7P53xn\n9p4zz/M7z/nN+7UWi98+v3PZZ599zm/P83zPd2e90xNW7vG6ePZWSdpm5VpfkbqT1GYTuLZMHutq\nWWxb+obLLrTv5+iG7R6xcksGS6/bsd1NjrRr3/LUudv3kaxz/0O2YLuVT1LHE6xddnpySu8rUvfa\n+3X2Z5HU7RsnVPaZHbtlMuIzrOxtInXb5RgrtyTo9PM5J1nHH0DfSNbxrKm3WtnrJnXbyvvyf/qW\nSgAAIABJREFUjck23t7ettk943Xz42YdtxYnKnXP0Z+VWVxr7W9G9kzwuvh+s7rVJsk+Ndmmdlyp\n/ixseVbWYq3ntU0mO6eVWmKR2/GJGAAAwEAYiAEAAAyEgRgAAMBAxptH7KhHZxd6SICHt2QT29a+\n3s8m0PV1sq+SfSJql00S7GFLvs7GJEbMz8nrlk063TKB91brEzs9XiqLNajEgB2W1N9TOPnEzv57\nqVvfbd5/s5gAjyHxuJoWLfE6Hp/TEjtRi9GQ6jElWVyNHye7PtZ2r7NrlE2m7JNx+32WTdS+xfZ7\njf0+C/HxSY47kxNL2mn190nLkxCx7n1k+8gumU9M7bIJmJ1P/JxNYu5xcVlb+nPC19mSbOMTXvtx\nsnCvK628y8o+2bjUfbZk968v83bJwjd98nA/5+w4fh1b+qk/1ryvX9uwTcbr4sf240jJc87KLe3U\ncs5eN7/OWT/1ezO7z2p/S7O/TX4dW/4e+zm1/A30dbJQWOd/a72vZ/v189n2OPKIAQAALBsGYgAA\nAANhIAYAADAQBmIAAAADGW+w/glWbw+BawnA80C+lkC/jqz9smSNK7VMwOyV6TFJcN/8g52A5YY+\n8oQe9esz77Ff16a6+rLk3x+ei9LtyfZbS+rXMtF8S19w/lJAEojvQaxHJo292+p3iK3TklDXy1ng\nsS/zoOLbs3bylw2ye+oeKz+zXpda4PeDSV1232ALPII5S67p+/GHSZZ41ZPhNkQar7cXNXZnL5X4\nJM0tSYQ9ua8nhT092cbXyXgEcy3ZbMZfHsr4fXVnwzbeLrVEvlI98Wcmu/bOny1+nJZEpfPYpqWt\nM/NKrLosx/X9Zs/tWoJvJv0GAABYOgzEAAAABsJADAAAYCDjjRH711bv59tKX7fyi5MdedLCl1vZ\nE09K3YSJ2Xy/HvNicSgbT/9xZ5Pjn/DnM+WjLfjm8Uk80uEWa7DBsvE9kMSu/Lk2z5TvLd1Mtzuu\ne/rsgn9oK2Txdz5f7llWztrpSdZOW2brH+u6M5SX71j2zMtthcuT/vwdK5/ZMIG6xz79ILtPWgLu\njE9e/aDVJZuU3ePXPF5tfXI+ntw0SwBZS8y4JdnGExneZOUzk208IeqLrJyG2dg5ZuFSnvT4SdYO\nlyXbeFM9z8rZnPFH7ft+ThNl+n58nSwhZC3xp9Ttl7vshJ6X9FNPzOttmSWY9rp4fbP4O1+nJf7U\nE7p6Ym4pvya14/g5+jMrSwJb22/fmFuvSy1xabZfL2fPic6zxcre1lI9GfHd/z1ZWMtYjhwxYgAA\nAEuHgRgAAMBAGIgBAAAMhIEYAADAQMYbrO/BvB4M7gGqHkwuSVut7DkKfR9SN7C1G+ve3c6DM49P\n2rwWAJwdx5f5cbKg+loQqCTdbvGE37bfZ4HTXhcPFs/q7+d4orVLto0Ht99ov78l2cYD7T2oW+q2\nnQfIZ215n+3XA6dTfu39JYwkueYmW+Z1zYKt77byK5N1vP1rgdSS9Awre7t48L7UDcD2425NtvH9\n+HEl6apk2UrZOb+wcuwsQN772HVWzvqp83UObdgm63MepO0vPmT8eeTB4S3PCX/h5bUNx8l4kL+3\nbUsSXu///nup+/zxFwlaXv7wfWxNtqkF4mf8ONkz2Ovr6/R52cBf9JC6/bLzgkLyt8pfnsheNvBl\nferv27Qkaff9Zm1bq1tLXVr4Ntc9jmB9AACAZcNADAAAYCAMxAAAAAYy4hixi2xplrFypZZJOn3C\nWZ9UOFsn4xOlHmHlbJLgbOLdGj8nL2f7bJkE1ffTEMdU3Uef8+tjXv3Z95NlUKy1ZdbnPESgob6H\n2TYeB5HFNXWSnSbrdGL0rJzdUl59j6XLYilq9c1iP3yblpieLck6bqPHC1qFH04CXg6rBYh0r+EJ\nJ906U35oz+zE7BvWzSYvlqT11se2bfMLIp1wwmyAzmabNHtXEny2wyYTP8Qu0jP1p51t7rbGvd+y\nhf4Nfb6zzTV67kz5Kbqts85x2jFT/p7OmCk/qRPcKN1ngUxHWbDTLm3obHOyJR315NYPafZ6TPY7\nOzn6Dyzw2OshSU+0icE3JfV/jb5gdZsNpntGkiD1yddYh7e50ctTu6FG206f/dv0cZ0/U/5yJ2O5\ndLVds/vumr3Ou4+9urONdIWVV2tC77EjoSsAAMDSYSAGAAAwEAZiAAAAAxltjNhrH/3UzLLt+isz\n5dv0lJnyUaWbROXOR2ZjJzZseGSmvGePB8BID+2cjfs59LBHOut4yMhDO2fjEdav78acbDxyNibg\nUJvAO5v0+1BZfS1gJ4uDeKjMLntkVze+4idXWHCQT57cko/Gyxsbcnd5DqEs9slzBnmOs2yC4Gs9\nLihZx+Ow/CK2TNLckvfm4dj3Oll+HW9LP06Wx8on9N6SrOPhUC25fZwfO5u02fvLH1s5i//yumxJ\n1vH+4eeTbfN8K99h13lT0k+vsHW8j7XkEfM8htk5t0ya7cfa0rDNtVZuyYXo+7ncyr+YbOOy54RP\nLO8Twp+VbFPLH5Xdm1us7M+JrK/3yT3m+7k8WaeWqysLQdxaqUtWf2+nLL9ah//997joD7bsBE2I\nEQMAAFg6DMQAAAAGwkAMAABgIAzEAAAABjLaYH3po7bUk2d6BKQnVc20RFH6OlnSTtcnuWlLkjy/\ndh4HmNXNj51F93qQf7aO87Zqqb/XpZagtkV2XK9bS7v0UJu4XeoG2R5p5Wyb2uTu2TYtdcmCj1fK\nLrsf29fJchV7jlEPFs+O43VrmWjeZQHN2aTSNbVg8ezlj1oO2GyfXrcs2NqvY8sLFg/ac6Lz8kfD\nZPUP+wsv3YS0us8u9FHJOg/bOt5OGxu2cVlb+35224tX67MEzb5f22Z30lH92Nkk2S3HqtbFj72g\n4/h44OnZ208XW/mBZB10EawPAACwdBiIAQAADISBGAAAwEBagn+W02m/Ols+2X7/JSu/LNmHJ5Y8\n08pZjIYnyjwtWcfjWTyxYdbqHmfisR8tsSAtCUVb9nujlT2Z4M5kG491qsUSZcta4l/8nLZa+b7k\nQHs8GW43Ua/0qJW9Me9MtrH9duKaWuLVvG7ZNh7f6Oe4KdmmYZ1an6rFRkltyUHvs7iTux6yFbqT\nHrepTU6fxQJ6u3hs4E+SbbrJlGd1J+eWTW4tHWPl7Dr7cbLYG9+uJeazFr+Zze7u7eCJPrNt/Jyz\nuFyvn+8328br0iee09vW+6DUjY31duo7ubXX1/eTBbm1rFPbpkVtv359+h4H+8InYgAAAANhIAYA\nADAQBmIAAAADGXEeMY/p8e/877VyFldQy1uVxVtUJoeW1P0O3euSxaH4Nl6XLA7I1/EJyP24Uvc7\n/5ZYFY9v6ROvkLV/lnRqpe6k5d391uJ3snWy+JbacbK+4PutxR9lvC9kcU2+zGOHsnbyALAsfY3X\n/9jK77O6uOw4fo/4frN7qKXtKutkl8zDA32dLP7Rt5lDuqYmWShj7djZpOse6+qpuvocpy9PCZak\nDVsV2Tl71/W6Zn2jz7FWq//MxX9Llm2zcsvfA5BHDAAAYAkxEAMAABjIQgdiEfHhiNgREd9bsezo\niLg0Im6KiC9FxJErfndhRNwcETdExCsWWTcAAIChLfoTsYskvdKWXSDpslLKsyR9RdKFkhQRz5b0\nekmnSnq1pA9FRMMkaAAAAOO08GD9iDhJ0udLKc+Zlm+U9JJSyo6IOF7S5aWUUyLiAkmllPK+6Xpf\nlPTuUspVyT7LqY9+e2bZq/XFmfIZ5fsz5dc/9OlO3d56+Adnyh+56R/PlC865Q2dbZ5YZgOlf/kz\nf9hZ521/670z5ePKbDLQd2793c422582GxC/ocwG3j/528msx9+cLRZLqvqT87vBzHc/bjbo/+lf\n9WytUnlwdvx78Xmvmilv0t2dba7RWTPlMzTb/puS7LiHdl4umLVVWzrLdlvk6216ykz5y3p5Z5ur\nyjkz5Qce6c6AvW7d7Msfjzy8Yaa884pkZudsPtyVsoTAHtfq5Wxya08I7HH4L0628f1k8bQvnC2e\ncubVM+VdpTvZ8i2XWgbjjbPPj+NedEtnm8PLbHD+LX/w7NkVvp7Uzc8xa+uj7N9p59rvszyrfqxf\nsPLnkm38OvotkyWx9fY/3crXJtt4F8sS6vrLBT5ReNZ/vL7en7JJy30dl02e7sdpmczdZdt4O3jf\nyPp2LX68JcF0ra6Z7Li+385E58k2fuzaPualc5wFjQ9a2qllm3lYrba86nFLFax/bCllhySVUu7Q\nX76qdYKk21ast035O0AAAABrwjJMcdRryP3jd//nv/j58HOf1/3XMAAAwBB+cvnkvwZDDMR2RMRx\nK76afOx7u23SzPdMJ6qbsOQvPPndv2ZLvpiuBwAAsKqOOHfy32O2/au9rroaMWJbNIkRO2Nafp+k\ne0op74uI35R0dCnlgmmw/scknaPJV5J/JOmZJangJKHrh2xpy6zYbkyTl/aZ6LZlnN0y4Wwfq1Xf\nluAJX5YlJa1NnryooIaWhLQ1tSSrrVra3+tbm1A6U5usO5P1p0VMjLyogJGWuq5WINCYnnuLkt0z\n87gXh1SbXHy1jjuvY/t+swTgnty6lhhd6vfMalFr/70ndF3oJ2IR8XFNvjTcFBE/kvQuSe+V9OmI\neLOkWzV5U1KllOsj4lOSrtfkDN6aDcIAAADWioUOxEopv7KXX3VfbZus/1uSfmtxNQIAAFgeZNYH\nAAAYyDK8NdnTy6zsEzlvtfLJyT58nWdaeUeyjU+A3TIxtTXz+uRrYssB1gl5y3LN+DotYXJZbiLn\nOYRubfmG2M7Jcytlc5Z7fT2fUXY+ntPJy7cm23TynmWV6aObT21WnxifLF7B+5w5NOmD3sWyec79\n7vf2zvIo1Z4YWU4tX7bVyt1Udt1+mkVWdCZlbpho3rfxVfw+lLrtcL+vkN0ftTiU7LnhE8Afkaxj\nxzrUGiadRNuP7cdpuR+sr69Lttnj7ZBdND/2POKyfJ9S91ne0Ddqz23dk2zj+/lYss6dybJFGCr2\nb1HH9f1m7V+zmnF//duBT8QAAAAGwkAMAABgIAzEAAAABsJADAAAYCALT+i6CGlC13VvmS3vaQmc\n82DM2Pevs2UeLCtJ661NPdg3Daj1gFMPTMwCavskgPTgxT5JVB9K1vHgY0+klyXjS3Pb/aUsWL/z\nsoH334ZEmdnLEuus7M2yM7tPvB1qyWalevLVpG4eYN6pW6UdpTyI3l8AeYKVs37q7bSz4Ti1btqd\nW7w+ObqUvMBi1+iwpF2yCa5Xyl5m8X7oL4hsTPpG7cWHrG5e/43JOn4s78vZZNy32zad+ifH6UxG\nb/s4Ptnmrob29/r7i0HZS0m+TtMrZnZsn7w6ewYc5uvY773dsnWyfur3REvfrj3KWyaEb9ln7ZH1\npUuSjb7fsGN07T2hK5+IAQAADISBGAAAwEAYiAEAAAxkxAldf2a2eIgnFLVEey3xXrttH9n38P51\n+P1Z7JAn8PN4tSxRoy+zclb/LPnkSmm+Ua9vlgzxXit7NtAswaifox88q4wnQ7T4tYf7TMybNZRd\ntN3JOrutLp34qJaYw5bJZL3+3gbJOXtddvk+sjaxc/Q4G0m6r9aWLRO32znekV0zn5g363OuTyyj\n30MtsSte36xufRI11iZHbzmfPhMWt1wzr1vLfdbSBpX7ubdaIFafONeG58SqTcKeqbV3y3Wehyyp\nOeaNT8QAAAAGwkAMAABgIAzEAAAABsJADAAAYCAjDtb/2mzx4T1W7hNc6kGrfWdTrwXU9gj6zALM\nO/HvLfvtE3TuAZt9glaz43r7t9St/wz3+2cegbmLquu8goYXUb8TG9Zpeex4RtSWc/ZA+5Ztnmxl\nz1ibaXkpI0tgvJInbM5k+61lA+3TN7Kg+j59w7dpacs99VWq55T9vpboeTWfNYsI8l/UiwN+zllW\n7dVy8CSK5RMxAACAgTAQAwAAGAgDMQAAgIGMOEasloixT8K7eSXt7HNsvxS1cktdsoy0ferSEidQ\nO+eWOJRHrNwnRqA2qfbe+Dm3JKOs9ZcsRqaWNLJPQs6+t3GfuJla/bIJ4WvH7dO3s7q0TADvbrVy\ny3Xvkei20y/7xr/4OfpxWtrSHZ0s83bwZ0n2TJhHQtcsZszvI18nq4vXt8894tv0mWk70xL/6NfV\n54qe15/uPnF9Lrsf+sTX9YkZrsnatk/b9bnn2/GJGAAAwEAYiAEAAAyEgRgAAMBAopRs0urlFhFF\nxz06u9AnNe5M2txynv49fKIWrjColhiZPnEbLd+p94kR6zOxcB8tk657W3msU0vep9o+pW5b9okd\napk022XXpzZ5eJ/rnm3jk363TFTt68wrFrO2j5YYN48VquUMazWPCbz7TGad6RNj1RJnWYt1mle+\nwT5q9968YjFb9tsnhrAW0zaPODlpPrGlfe7necSwZvvpE+OWxQv6fjwW8M0qpaSDDD4RAwAAGAgD\nMQAAgIEwEAMAABgIAzEAAICBjDeh647/sZ8bzGlC7KUKzq/pmzRytSbW7mOoiWCXuU1ajG0C3b6J\neQ9Uy3U+2cotbesv0vgLDJksILh2rCy5aZ+JwheVTNP1eXGgz8sHLWr77Zsgu89LGLV9LJOWl5Ie\nXI2KJFbz5Q9/OaX9pSo+EQMAABgIAzEAAICBMBADAAAYyHhjxDrfx9YSS7ZMZtpnwtM+k4q2xAi0\nJMrsoyVuoyWppfP6ejmL+elzTn7d+0wOnSXgrMUNtFznPgk4a/tsMa8JaVv2423XkiDYr33t3pXq\nk2ZL3TgrXyc7Z9/mWCtniXs9AfAxVs7awOPI/szKz0y28fsu63Pe/lut/LSG/e6wckuyX++XW5Jt\ntlk5i5HZVFkn6/++zd1W7nPfZdfsBCt7O7XE0rX001pSZ6nblr5OFmPofaN2XKkex5Sdc8t95tvV\nngFSt36+j2wbP2fvC1ny7pZnrG/n9c+eE14Xr/8Fez0an4gBAAAMhIEYAADAQBiIAQAADGTEMWK3\nWnlRsTWrpRZvlJ1fn4m2+8Q+Zd+z99mvq+WK6jOBcdYm91b2IXXbqiUOohYH1yd+MMtVtNnKd1o5\nm0fW4xWytvZjbWyoi/PEes9I1vlB5TjZNfP4lmyd2gTS2TbHWdnjgr7fcBzvTxl/Pvn5ZMfx+mdx\nQLX77EeVemVanhPef/yaSt3nRHbP/NjKtbggSbq2Upes/lkMT83VVj6j4TieH87PT6qfY/ZM8Puq\n5V78csM6WEZ8IgYAADAQBmIAAAADYSAGAAAwEAZiAAAAA4lSPNhw+UVEkf6dLe0zqfE8kqa2bNNn\n8lsPEM4m860FK7fo8xJAn5ccWo4zj8lXs6D0lvbvkwyxpiVRaUtb9pno2YN7s+N4AmPvT/OaKNyf\nMb7fvu3U5wWRmqwPetJXXycLpK717SypsL8E4C81SN2AcQ/qbvHcyj6lbqLPlpdXPPHq7Q118f1m\nwe7eDi3JWWt9oeVZ423bMolzn2dYS1Lklr79yBz2sVqTi2f3c8uLGzW1RMTZsVvav+X57/3F++2v\nq5SSvVnFJ2IAAABDYSAGAAAwEAZiAAAAAxlxjJgn+Vum5KwAltONVvbYj5Z4kRbziq9ztdi5LPas\ndk596toSS7RabTAvtUSrfc9nteKu5tHePh7Ikgqjn/cQIwYAALBsGIgBAAAMhIEYAADAQEY86ff/\nWoVjLCrubFHNvkxxci3xFSPufgeFPjEnLRO1L5OW+J1F5Ltr0XLPtEwgvczt71arbZfJmK4PFoFP\nxAAAAAbCQAwAAGAgDMQAAAAGwkAMAABgIOONlv4P/3K2fLz9/korn5Ls48+sfJSVs7l877ByNi+v\nt+qDyToum7d5f34vdeub1d/rkq3juXJdFlvqbeey+vsyb7esbn7NfF7hljmQfW7i7Fhel+xO8Wt/\nl5V3Zgf3iYP9BI5LtjnGyouaNPvmhm1OsLInC80a14+z1cr3NGxzRLKOTxjtFynbr2/j+/UOlu3X\nzzmrW23S7Owm8m2yvuDH9m2yYPfDK9t43bJ1WrSc4zwmavfjZAlra5M/z+tFiNpxW7S8ZLVMSWzn\n0Q5ZXlP/g+DHztpgHi/StLT/vCYGz/GJGAAAwEAYiAEAAAyEgRgAAMBARjzp94eGrsZB7GBMuojl\nR2JMYPF8zHAw3Hct46R0Pu8VLmDSbwAAgGXDQAwAAGAgDMQAAAAGMt48YnrLvn+9zsp7ku94D7Wv\na3fZOuuSr3N9P33Wacl11Uuf2K0s19JDVm7J5+I8N0vW1Xwdzw+U5Xfp02X7TIbu59iSq8jLWTvV\n2rIl3sLbKcsD1aJ2HVvyQM3DomJMViv3UsuxlylX1KKsVuzoUDGqyxQLtUxxusvULm6Z2mnv+EQM\nAABgIAzEAAAABsJADAAAYCAMxAAAAAYy3mB9D7R3LWe2x/ZxqP1+Vy1Bm/YSeG8zSO/xIO4suNED\n5Ft4AHBLQLA3THaOPkmwBzxmweG+jjdM1lC+7IFknXnoE0w6jyDPeQWx+n68nfq22yKCbFczOHZM\n9fdZ5ZcpiHg1g62X5byXOcBcWp52yix729UsX0JaPhEDAAAYCAMxAACAgTAQAwAAGMh4Y8Revp/r\n726I93rY1vGwjmydB5N1Hnz8vsvZfnslee0zYXtDO3T26zFILclN/SRbEro+0cpZLJpv48fNYu1a\nYgC8fh4nd0xDXVp42zZcj05y4to+pbZrVpO1v18jq7/XNdOp/93JSltrG0l6spWPazi494WWJMI1\ntyTL7qzs94RkG+9jLXXx/r4jWWeTlf2cs6TOvh+/P05MtvG+kd13tRjV65NtvB22WDmr/0+s7Oec\ntX/NtmSZ7zc7Z+/fW6ycXTM/5yOs7G0tde9xb5fsGXaDlU+t7EPqnrO3tdStb0s71ZIgZ88wP7Yf\nN/u74/vJ7jNv35Y4b7/O7c8SPhEDAAAYCAMxAACAgTAQAwAAGAgDMQAAgIFEKX0CvocVEUX6N0NX\nYwmM912L8ckCL2vBpVib/L5rCUpHf2vtvhpT3xiy7Ydsp0Wc9xtUSknfzuITMQAAgIEsdCAWER+O\niB0R8b0Vy347Im6IiGsi4rMRccSK310YETdPf/+KRdYNAABgaIv+ROwiSa+0ZZdKOq2UcpakmyVd\nKEkR8WxJr9ckkcmrJX0oIlqSXgEAAIzSQr+ELaV8PSJOsmWXrSheKel105/Pk/TJUspuSVsj4mZJ\nL5B0Vb73n5t7fbuxHi3NM/yEoQcmm1zWvx9viYVa5klqXUtMz9iv61DG1A8WiXZYPdyrq+tg6Nur\ne45Dx4i9WdIXpj+fIOm2Fb/bpn7pjwEAAEZhsNcSIuKdkn5aSvlEvz18ZMXPz53+BwAAMLQb1J1C\nKjfIQCwi3iTpNZJeumLxNklPWVE+UfnkXlNvXkDNAAAADtSpmp278+K9rrkaA7HQipldI+JVkn5D\n0s+VUnatWO8SSR+LiPdr8pXkyZK+uffdZhMSo6426XFmXuvMwzLHJyxzrMpqtdvY4yrnVbfVyr+0\nzG2Z8byV2WTu+2u13unKcm6Orf3nYR7XbOzm2xcWOhCLiI9LOlfSpoj4kaR3SXqHpA2S/mj6UuSV\npZS3llKuj4hPSbpek78aby1jzDYLAADQaMSZ9b81dDVGauz/guMTsX6Wqd2WuZ3mVbfVeq4uc1tm\nFvGJ2GrhE7GJg/GcXZ++8A/IrA8AALBsGIgBAAAMZEyzj5pvDF2BfVhrk9Sulj6B3iPuws0Oxv7U\n57o+0coPzKMiWKiD8Wsu/1rrYGwDrMQnYgAAAANhIAYAADAQBmIAAAADGXGAzauGrsA+jLhZV9Va\nj41YppQR87LWr1lmLV7HlQ7Ga5pZ69c5w7XPHVyTfgMAABy0GIgBAAAMhIEYAADAQEYczLS/OYJa\ncjG1fC98dMM6986hLvOQXd4+MQG+n/+XrFM7p6wunk/n4f3cZ+txWs65z61Q22/Wn/w4vo+Wc15n\n5b7TxPh+WtrfZ+jokxPpsIZ1XLZfX+b7ndf0ObVrktWt1p/mdW/OQzbrymr9afB7pE9d5tX+89Dn\nGmbPiT7P00X0n5a69al/n2PP62/4463cp//Mt635RAwAAGAgDMQAAAAGwkAMAABgIAzEAAAABjLi\nYP3/PXQFAAAADgifiAEAAAyEgRgAAMBAGIgBAAAMZMQxYj8zdAXWsJaEfVj7sgSK9AUAmCc+EQMA\nABgIAzEAAICBMBADAAAYyIhjxH5+6Arsg0+EPJRFTSK8WnFCLZOxrtZEycsUGzXU5NCZIdulNikw\n12ximdqhZpn6thtTO2aWuW2lg7l918AnYpcPXYE17I+HrsAadsXQFVjD/u/QFVjDvjl0Bdaw7wxd\ngTXu6qErsFcMxLAPXxu6AmsYA7HFYSC2ON8augJrGAOxxWIgBgAAADPaGLGzz578f/t2afPmYeuy\nvOKAtp60bbaP1Rq/Z8fxZatVl3Vz3dv27aHNm+e7z4OP983J42z79nXavPmQ5PdDGvJaz+/Y27ev\n1+bNh81tf117FrjvA5Xl1Zuf7dsP0ebNhy/wCMvcttKiY9i2b9+gzZs3LvAI+67/d7+7999FKcsS\nWN4uIsZXaQAAcNAqpaT/OhzlQAwAAGAtIEYMAABgIAzEAAAABsJADAAAYCCjHYhFxKsi4saI+NOI\n+M2h6zNmEXFiRHwlIq6LiO9HxNumy4+OiEsj4qaI+FJEHDl0XccqIh4XEd+NiEumZdp2DiLiyIj4\ndETcMO2/59C28xMR/zQiro2I70XExyJiA+3bT0R8OCJ2RMT3Vizba1tGxIURcfO0b79imFqPw17a\n9renbXdNRHw2Io5Y8bulattRDsQi4nGSPijplZJOk3R+RJwybK1Gbbekf1ZKOU3Sz0r6R9P2vEDS\nZaWUZ0n6iqQLB6zj2L1d0vUryrTtfHxA0hdKKadKOlPSjaJt5yIiNkv6J5LOLqU8R5PlP4UCAAAF\nnklEQVT8IOeL9u3rIk3+Zq2UtmVEPFvS6yWdKunVkj4UEcuUj2XZZG17qaTTSilnSbpZS9y2oxyI\nSXqBpJtLKbeWUn4q6ZOSfmHgOo1WKeWOUso1058flHSDpBM1adPfn672+5J+cZgajltEnCjpNZL+\n64rFtO0Bmv4L96+XUi6SpFLK7lLK/aJt52mdpCdExHpJj5e0TbRvL6WUr0u61xbvrS3Pk/TJaZ/e\nqslA4gWrUc8xytq2lHJZKeXRafFKTf6mSUvYtmMdiJ0g6bYV5duny3CAImKLpLM06bjHlVJ2SJPB\nmqRjh6vZqL1f0m9odjZ42vbAPU3SXRFx0fRr3/8SEYeLtp2LUsp2Sb8r6UeaDMDuL6VcJtp3no7d\nS1v637ht4m/cgXizpC9Mf166th3rQAwLEBEbJX1G0tunn4x5kjmSzu2niHitpB3TTxz39fE3bbv/\n1ks6W9J/LKWcLWmnJl/10G/nICKO0uQTm5Mkbdbkk7FfFe27SLTlnEXEOyX9tJTyiaHrsjdjHYht\nk/TUFeUTp8vQ0/Srh89I+mgp5XPTxTsi4rjp74+XdOdQ9RuxF0k6LyJ+KOkTkl4aER+VdAdte8Bu\nl3RbKeXb0/JnNRmY0W/n4+WSflhKuaeUskfSxZL+mmjfedpbW26T9JQV6/E3roeIeJMmYSG/smLx\n0rXtWAdi35J0ckScFBEbJL1B0iUD12nsPiLp+lLKB1Ysu0TSm6Y/v1HS53wj7Fsp5R2llKeWUp6u\nST/9Sinl70j6vGjbAzL9Sue2iPir00Uvk3Sd6Lfz8iNJL4yIw6bBzC/T5IUT2re/0Own43try0sk\nvWH6lurTJJ0s6ZurVcmRmmnbiHiVJiEh55VSdq1Yb+nadrRTHE0b+QOaDCY/XEp578BVGq2IeJGk\nr0n6viYfjRdJ79Ckc35Kk3893Crp9aWU+4aq59hFxEsk/fNSynkRcYxo2wMWEWdq8hLEIZJ+KOnv\nahJgTtvOQUS8S5N/QPxU0tWS/r6kJ4r23W8R8XFJ50raJGmHpHdJ+p+SPq2kLSPiQkl/T5O2f3sp\n5dIBqj0Ke2nbd0jaIOnu6WpXllLeOl1/qdp2tAMxAACAsRvrV5MAAACjx0AMAABgIAzEAAAABsJA\nDAAAYCAMxAAAAAbCQAwAAGAgDMQAjE5EPBoRf7CivC4ifhwRl0zLb4yIfz/9+V0Rcft0PsqbIuIz\nEXHqim2/GhFnz6FOL4mInz3Q/QA4uDAQAzBGOyWdHhGHTss/r9mJfN3vlVLOLqU8S5NkpF+JiE1z\nrtO5mkwBBADNGIgBGKsvSHrt9OfzNZnLs6qU8ilJX9Ls/HMdEXFLRLw7Ir4TEX/y2FRKEXF0RFw8\nXfaNiDg9Ik6S9BZJvz795O1FEfGk6advV03/Y5AGoIOBGIAxKpI+Ken86adiz5F01X5sf7WkUxrW\nu7OU8jxJ/0nSv5gue4+k75ZSzpT0TkkfLaXcOl3n/dNP3q7QZAq23yulnCPplzWZigkAZqwfugIA\n0Ecp5dqI2KLJp2F/qNnJlGta1714+v/vSPql6c8vlvQ3p3X4akQcExEbk21fLunU6YTZkrQxIg4v\npTy0H/UEsMYxEAMwZpdI+h1N4rOetB/bPVfStxrW2zX9/x7t//MyJJ1TSvnpfm4H4CDCV5MAxuix\nT5k+Iuk9pZTrGtdXRLxOk+D+j/c89v+R9Len+zpX0l2llAclPSDpiBXrXSrp7SuOe2bP4wFYwxiI\nARijIkmllG2llA82rP9YEP1NmgTpv7SUcs/Kfe3tGIl3S3peRPyJpH8r6Y3T5Z+X9EuPBetLepuk\n50+D+q+V9GsN9QRwkIlS9vasAQAAwCLxiRgAAMBAGIgBAAAMhIEYAADAQBiIAQAADISBGAAAwEAY\niAEAAAyEgRgAAMBA/j8G65lMtbOjrAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x116792a20>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(x_rms_instruments_notes, interpolation='none')\n",
"plt.suptitle('MIDI instruments range - RMS power')\n",
"plt.xlabel('MIDI note')\n",
"plt.ylabel('MIDI instrument')\n",
"plt.savefig('data/working/instrument_ranges_rms.png');"
]
},
{
"cell_type": "code",
"execution_count": 186,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"np.save('data/working/instrument_ranges_rms.npy', x_rms_instruments_notes)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There's a peak at value around 1.0 which represents quiet."
]
},
{
"cell_type": "code",
"execution_count": 193,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABI8AAAJPCAYAAAD1zfSMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAG1tJREFUeJzt3W+s5Gd53+HvjS2EQlyLkOJV16SmIQZDSajVblIlqg5p\n5D9Vha1IQZAqhAASkk0TqS+KXanytkIifpGWImoqUhdMBbLcRJUdlWKDwKqoQuy0gEnW2Ju0Nt5t\nvDQNRaJSJJvcfXEGOKzP7TPnz845e/a6pJFmnnlm5hlbj87sR7/5TXV3AAAAAGAzL9jvBQAAAABw\ncIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBoy3hUVZdX1Wer6g+r6itV9auL8ZdU\n1QNV9VhV3V9Vl254zK1VdbKqHq2qazaMX11Vj1TV41X1/nPzlgAAAADYK8scefRskn/U3a9N8reT\n3FxVr05yS5LPdPerknw2ya1JUlWvSfKmJFcluT7JHVVVi+f6UJJ3dPeVSa6sqmv39N0AAAAAsKe2\njEfd/XR3f2lx/VtJHk1yeZIbkty1mHZXkhsX19+Y5O7ufra7n0hyMsmxqjqS5JLufngx72MbHgMA\nAADAAbStcx5V1RVJXp/kC0ku6+4zyXpgSvKyxbSjSZ7a8LDTi7GjSU5tGD+1GAMAAADggFo6HlXV\nDyb5rSS/tjgCqc+acvZtAAAAAM5zFy8zqaouzno4+vfdfe9i+ExVXdbdZxZfSfv6Yvx0kpdvePjl\ni7FpfLPXE6IAAAAA9lh319azvt9S8SjJv0tyorv/1Yax+5K8LcntSX45yb0bxj9eVf8y619Le2WS\nh7q7q+qbVXUsycNJ3prkA9MLdutHsGrHjx/P8ePH93sZcMGx92B/2Huwf+w/2B/f+z2z7dkyHlXV\nTyf5B0m+UlVfzPrX0/5J1qPRPVX19iRPZv0X1tLdJ6rqniQnkjyT5Kb+Xgm6OclHk7woySe7+1M7\nWjUAAAAAK7FlPOru/5rkouHunxse874k79tk/L8led12FggAAADA/tnWr60Bh9va2tp+LwEuSPYe\n7A97D/aP/QfnlzqI5xaqqj6I6wIAAAA4X1XVjk6Y7cgjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAA\nwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBI\nPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwC\nAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAA\nAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABg\nJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAOAQOXLkilTVcy47Vd29h8vb\nG1XVB3FdAAAAAAfdeijarKtUunvbFcmRRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADA\nSDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8\nAgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIA\nAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAA\nYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAk\nHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4B\nAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAA\nADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAw\nEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKP\nAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAA\nAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwGjLeFRVd1bVmap6ZMPYbVV1qqr+\n++Jy3Yb7bq2qk1X1aFVds2H86qp6pKoer6r37/1bAQAAAGCvLXPk0UeSXLvJ+L/o7qsXl08lSVVd\nleRNSa5Kcn2SO6qqFvM/lOQd3X1lkiurarPnBAAAAOAA2TIedffnk3xjk7tqk7Ebktzd3c929xNJ\nTiY5VlVHklzS3Q8v5n0syY07WzIAAAAAq7Kbcx69u6q+VFX/tqouXYwdTfLUhjmnF2NHk5zaMH5q\nMQYAAADAAXbxDh93R5J/3t1dVe9N8htJ3rl3y0qOHz/+3etra2tZW1vby6cHAAAAOOQeXFx2Z0fx\nqLv/94abv5nkdxbXTyd5+Yb7Ll+MTeOjjfEIAAAAgO1aW1y+45/t6FmW/dpaZcM5jhbnMPqOn0/y\nB4vr9yV5c1W9sKpekeSVSR7q7qeTfLOqji1OoP3WJPfuaMUAAAAArMyWRx5V1SeynqleWlVfS3Jb\nkjdU1euT/EWSJ5K8K0m6+0RV3ZPkRJJnktzU3b14qpuTfDTJi5J88ju/0AYAAADAwVXfazsHR1X1\nQVwXAAAAwEG3/qWvzbpKpbtrkzue125+bQ0AAACAQ048AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAA\nAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACM\nxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQj\nAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAA\nAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAA\nRuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbi\nEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEA\nAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAA\nACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj\n8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EI\nAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAA\nAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACA\nkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4\nBAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQA\nAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAA\nwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBI\nPAIAAABgtGU8qqo7q+pMVT2yYewlVfVAVT1WVfdX1aUb7ru1qk5W1aNVdc2G8aur6pGqeryq3r/3\nbwUAAACAvbbMkUcfSXLtWWO3JPlMd78qyWeT3JokVfWaJG9KclWS65PcUVW1eMyHkryju69McmVV\nnf2cAAAAABwwW8aj7v58km+cNXxDkrsW1+9KcuPi+huT3N3dz3b3E0lOJjlWVUeSXNLdDy/mfWzD\nYwAAAAA4oHZ6zqOXdfeZJOnup5O8bDF+NMlTG+adXowdTXJqw/ipxRgAAAAAB9henTC79+h5AAAA\nADhALt7h485U1WXdfWbxlbSvL8ZPJ3n5hnmXL8am8dHx48e/e31tbS1ra2s7XCoAAADAhejBxWV3\nqnvrg4aq6ookv9Pdr1vcvj3Jn3X37VX1niQv6e5bFifM/niSn8z619I+neTHurur6gtJfjXJw0n+\nU5IPdPenhtfrZdYFAAAAwPdb/+2yzbpKpbtrkzue15ZHHlXVJ5KsJXlpVX0tyW1Jfj3Jf6iqtyd5\nMuu/sJbuPlFV9yQ5keSZJDdtqEA3J/lokhcl+eQUjgAAAAA4OJY68mjVHHkEAAAAsDN7feTRXp0w\nGwAAAIBDSDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgE\nAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAA\nAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADA\nSDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8\nAgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIA\nAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAA\nYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAk\nHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4B\nAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAA\nADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAw\nEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKP\nAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAA\nAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAA\nGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJ\nRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcA\nAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAw2lU8qqonqurLVfXF\nqnpoMfaSqnqgqh6rqvur6tIN82+tqpNV9WhVXbPbxQMAAABwbu32yKO/SLLW3X+ju48txm5J8pnu\nflWSzya5NUmq6jVJ3pTkqiTXJ7mjqmqXrw8AAADAObTbeFSbPMcNSe5aXL8ryY2L629Mcnd3P9vd\nTyQ5meRYAAAAADiwdhuPOsmnq+rhqnrnYuyy7j6TJN39dJKXLcaPJnlqw2NPL8YAAAAAOKAu3uXj\nf7q7/6Sq/nKSB6rqsawHpY3Ovr2U48ePf/f62tpa1tbWdrpGAAAAgAvQg4vL7lT3jtrOc5+o6rYk\n30ryzqyfB+lMVR1J8rnuvqqqbknS3X37Yv6nktzW3b+3yXP1Xq0LAAAA4EKyforpzbpKpbu3ff7p\nHX9trap+oKp+cHH9xUmuSfKVJPcledti2i8nuXdx/b4kb66qF1bVK5K8MslDO319AAAAAM693Xxt\n7bIk/7GqevE8H+/uB6rq95PcU1VvT/Jk1n9hLd19oqruSXIiyTNJbnJ4EQAAAMDBtmdfW9tLvrYG\nAAAAsDMH5mtrAAAAABx+4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJ\nRwAAAACMxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcA\nAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAA\nAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACM\nxCMAAAAARuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQj\nAAAAAEbiEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAA\nAABG4hEAAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAA\nRuIRAAAAACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbi\nEQAAAAAj8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEA\nAAAAI/EIAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAA\nACPxCAAAAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj\n8QgAAACAkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EI\nAAAAgJF4BAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAACPxCAAA\nAICReAQAAADASDwCAAAAYCQeAQAAADASjwAAAAAYiUcAAAAAjMQjAAAAAEbiEQAAAAAj8QgAAACA\nkXgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG4hEAAAAAI/EIAAAAgJF4\nBAAAAMBIPAIAAABgJB4BAAAAMBKPAAAAABiJRwAAAACMxCMAAAAARuIRAAAAAKOVx6Oquq6qvlpV\nj1fVe1b9+gAAAAAsb6XxqKpekOSDSa5N8tokb6mqV69yDcDswQcf3O8lwAXJ3oP9Ye/B/rH/4Pyy\n6iOPjiU52d1PdvczSe5OcsOK1wAM/BGH/WHvwf6w92D/2H9wfll1PDqa5KkNt08txgAAAADOG0eO\nXJGqes7lyJErVjZ3mr/XDuwJs89+49dd98b9XhIAwJ6bPiBedNGLt/XBkXNrux/keX4X6n/Pzd73\nqvf6XvwDdrM1n8v3sdk6tvO8e/EP8XP1eudybbuduxfv+7D8f5qcOfNkkn7O5cyZp5/zvOdq7jx/\nb1X33j/p+GJVP5XkeHdft7h9S5Lu7tvPmre6RQEAAABcILp724cmrToeXZTksSR/N8mfJHkoyVu6\n+9GVLQIAAACApV28yhfr7m9X1buTPJD1r8zdKRwBAAAAHFwrPfIIAAAAgPPLvp0wu6quq6qvVtXj\nVfWeYc4HqupkVX2pql6/6jXCYbXV/quqX6yqLy8un6+q1+3HOuGwWeZv32Le36qqZ6rq51e5Pjis\nlvzcuVZVX6yqP6iqz616jXAYLfGZ8y9V1X2Lf+99paretg/LhEOnqu6sqjNV9cjzzNlWb9mXeFRV\nL0jywSTXJnltkrdU1avPmnN9kh/t7h9L8q4k/2blC4VDaJn9l+R/JPk73f0TSd6b5DdXu0o4fJbc\ne9+Z9+tJ7l/tCuFwWvJz56VJ/nWSv9/dfz3JL6x8oXDILPl37+Ykf9jdr0/yhiS/UVUrPbUKHFIf\nyfre29ROest+HXl0LMnJ7n6yu59JcneSG86ac0OSjyVJd/9ekkur6rLVLhMOpS33X3d/obu/ubj5\nhSRHV7xGOIyW+duXJP8wyW8l+foqFweH2DJ77xeT/HZ3n06S7v7TFa8RDqNl9l4nuWRx/ZIk/6e7\nn13hGuFQ6u7PJ/nG80zZdm/Zr3h0NMlTG26fynP/cXr2nNObzAG2b5n9t9E7k/znc7oiuDBsufeq\n6q8kubG7P5Rk2z+hCmxqmb97Vyb5oar6XFU9XFW/tLLVweG1zN77YJLXVNX/SvLlJL+2orXBhW7b\nvcUhgcCoqt6Q5FeS/Mx+rwUuEO9PsvGcEAISrMbFSa5O8rNJXpzkd6vqd7v7j/Z3WXDoXZvki939\ns1X1o0k+XVU/3t3f2u+FAd9vv+LR6SQ/suH25Yuxs+e8fIs5wPYts/9SVT+e5MNJruvu5zvkEVjO\nMnvvbya5u6oqyQ8nub6qnunu+1a0RjiMltl7p5L8aXf/eZI/r6r/kuQnkohHsHPL7L1fSfK+JOnu\nP66q/5nk1Ul+fyUrhAvXtnvLfn1t7eEkr6yqv1pVL0zy5iRnfzC+L8lbk6SqfirJ/+3uM6tdJhxK\nW+6/qvqRJL+d5Je6+4/3YY1wGG2597r7ry0ur8j6eY9uEo5g15b53Hlvkp+pqouq6geS/GSSR1e8\nTjhsltl7Tyb5uSRZnG/lyqz/cAuwe5X5KPZt95Z9OfKou79dVe9O8kDWA9ad3f1oVb1r/e7+cHd/\nsqr+XlX9UZL/l/UqDezSMvsvyT9N8kNJ7lgcAfFMdx/bv1XD+W/Jvfd9D1n5IuEQWvJz51er6v4k\njyT5dpIPd/eJfVw2nPeW/Lv33iQf3fBz4v+4u/9sn5YMh0ZVfSLJWpKXVtXXktyW5IXZRW+pbp9N\nAQAAANjcfn1tDQAAAIDzgHgEAAAAwEg8AgAAAGAkHgEAAAAwEo8AAAAAGIlHAAAAAIzEIwAAAABG\n4hEAAAAAo/8POjBT/U44iKAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1164ca978>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(x_rms_instruments_notes[x_rms_instruments_notes <= 1].flatten(), 200);"
]
},
{
"cell_type": "code",
"execution_count": 194,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABI4AAAJPCAYAAAAaD5+yAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3WGMpdd5H/b/Q621Mm2ZZatyb0MqGrtSJNEoahswlVYJ\nMqgTWnJQkkgA1UnQ2FXzoZFduUkRi8wXrj/FlBPYBgohSC0bG5cJQxtwTAeOSRHMfHAQS3ItRYpJ\ns9saXNNb75VipUoVASwZPv1wL6XZmTO7dzj3zp258/sBL3jn7Lnve+6ceZe7/33Oeau7AwAAAAB7\n3bLuAQAAAABwMgmOAAAAABgSHAEAAAAwJDgCAAAAYEhwBAAAAMCQ4AgAAACAoYWCo6r6a1X1r6rq\nc1X1aFW9sapur6qnqur5qnqyqm7b1f+hqrpcVc9V1b2rGz4AAAAAq1LdfeMOVX8kya8neVd3/39V\n9Y+S/GqSu5P8YXd/tKo+kuT27n6wqu5O8miS705yV5Knk7yjb3YhAAAAAE6URZeqvSHJN1XVuSTf\nmORqkvuTXJr/+qUkD8xf35fkse5+pbtfSHI5yT1LGzEAAAAAx+KmwVF3/99J/k6S38ssMPpydz+d\n5EJ3T+d9riW5Y/6WO5O8uOsUV+dtAAAAAJwiNw2Oquo/yKy66G1J/khmlUd/KcnepWeWogEAAABs\nkHML9PnTSX63u7+UJFX1S0n+yyTTqrrQ3dOqmiT5wrz/1SRv3fX+u+Zt16kqQRMAAADAknV3Letc\niwRHv5fkj1fVm5K8lOR7knw6yVeS/GCSR5L8QJJfnvd/IsmjVfWTmS1Re3uST41ObL/ss+PixYu5\nePHiuofBMTHfZ4v5PlvM99livs8W8322mO+zxXyfLVVLy4ySLBAcdfenquoXk3wmycvz//69JG9O\n8nhVfTDJlSQfmPd/tqoeT/LsvP+HPFENAAAA4PRZpOIo3f1jSX5sT/OXMlvGNur/t5L8raMNDQAA\nAIB1uunm2LAM29vb6x4Cx8h8ny3m+2wx32eL+T5bzPfZYr7PFvPNUdS6VpFVlRVsAAAAAEtUVUvd\nHFvFEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAA\ngCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAA\ngCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAA\ngCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAA\ngCHB0QpMJlupqn3HZLK17qEBAAAALKy6ez0Xrup1XXvVqirJ6LNVNvUzAwAAAOtXVenuWtb5VBwB\nAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwB\nAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwB\nAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwB\nAAAAMHTT4Kiq/lhVfaaqfmv+3y9X1Yer6vaqeqqqnq+qJ6vqtl3veaiqLlfVc1V172o/AgAAAACr\nUN29eOeqW5L8fpL3JPnhJH/Y3R+tqo8kub27H6yqu5M8muS7k9yV5Okk7+g9F6qqvU0bo6qSjD5b\nZVM/MwAAALB+VZXurmWd77BL1f50kv+ru19Mcn+SS/P2S0kemL++L8lj3f1Kd7+Q5HKSe5YwVgAA\nAACO0WGDo/8myT+Yv77Q3dMk6e5rSe6Yt9+Z5MVd77k6bwMAAADgFFk4OKqqb8ismugX5k1711xZ\ng7VEk8lWquq6YzLZWvewAAAAgDPk3CH6vj/J/97d/3r+9bSqLnT3tKomSb4wb7+a5K273nfXvG2f\nixcvfu319vZ2tre3DzGczTadXsneLG46XdoSRQAAAGAD7OzsZGdnZ2XnX3hz7Kr6h0l+rbsvzb9+\nJMmXuvuRAzbHfk9mS9Q+EZtjv/YrC2+OPT6HzbUBAACAgy17c+yFgqOqujXJlSTf1t3/77ztP0zy\neGbVRVeSfKC7/5/5rz2U5L9P8nKSH+nupwbnFBwd+hyCIwAAAOBgawmOVkFw9HrOITgCAAAADrbs\n4OiwT1UDAAAA4IwQHAEAAAAwJDgCAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEen\nyvlU1b5jMtla98AAAACADVTdvZ4LV/W6rr1qVZVk9Nkqi37m8TmOfl4AAABgc1VVuruWdT4VRwAA\nAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAA\nAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAA\nAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAA\nAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAA\nAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDgaM0mk61U1b4DAAAAYN2qu9dz4ape17VX\nbRb8jD5bZe9nvlHf/e2LnxcAAAA4e6oq3b20ihQVRwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABg\nSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABg\nSHAEAAAAwNBCwVFV3VZVv1BVz1XVb1fVe6rq9qp6qqqer6onq+q2Xf0fqqrL8/73rm74AAAAAKzK\nohVHP53kV7v73Un+8yS/k+TBJE939zuTPJPkoSSpqruTfCDJu5O8P8nHqqqWPXAAAAAAVuumwVFV\nfUuSP9ndP5ck3f1Kd385yf1JLs27XUrywPz1fUkem/d7IcnlJPcse+Cn0/lU1XUHAAAAwEm1SMXR\ntyb511X1c1X1W1X196rq1iQXunuaJN19Lckd8/53Jnlx1/uvztvIS0l6zwEAAABwMp1bsM93Jfmh\n7v7NqvrJzJap7U09Dp2CXLx48Wuvt7e3s729fdhTAAAAAJxZOzs72dnZWdn5q/vGeU9VXUjyL7r7\n2+Zf/4nMgqP/NMl2d0+rapLkn3X3u6vqwSTd3Y/M+/9akoe7+5N7zts3u/ZpNVuCNvpso/bl9N3U\n7yUAAACwuKpKdy9tb5ybLlWbL0d7sar+2Lzpe5L8dpInkvzgvO0Hkvzy/PUTSb6/qt5YVd+a5O1J\nPrWsAQMAAABwPBZZqpYkH07yaFV9Q5LfTfLfJXlDkser6oNJrmT2JLV097NV9XiSZ5O8nORDG1ta\nBAAAALDBbrpUbWUXtlTtBm2H77up30sAAABgcce+VA0AAACAs0lwBAAAAMCQ4AgAAACAIcERAAAA\nAEOCoyOaTLZSVdcdAAAAAJvAU9WOaPwENU9VAwAAAI6fp6oBAAAAcCwERwAAAAAMCY4AAAAAGBIc\nAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIc\nAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIc\nAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIc\nAQAAADAkONoI51NV1x2Tyda6BwUAAACcctXd67lwVa/r2stUVUn2fo5R20Htq+u7Cd9fAAAAYHFV\nle6uZZ1PxREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDg\nCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABgSHC0oMlkK1W1\n7wAAAADYVNXd67lwVa/r2q/HLCQajXfUfjL6nqbvLwAAAHB0VZXuXlqli4ojAAAAAIYERwAAAAAM\nCY4AAAAAGBIcAQAAADAkOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQwsFR1X1QlX9y6r6TFV9\nat52e1U9VVXPV9WTVXXbrv4PVdXlqnququ5d1eABAAAAWJ1FK45eTbLd3d/Z3ffM2x5M8nR3vzPJ\nM0keSpKqujvJB5K8O8n7k3ysqmq5wwYAAABg1RYNjmrQ9/4kl+avLyV5YP76viSPdfcr3f1CkstJ\n7skxmUy2UlX7jslk67iGAAAAALARFg2OOsknqurTVfVX5m0XunuaJN19Lckd8/Y7k7y4671X523H\nYjq9Mh/u9cesHQAAAIBFnVuw33u7+w+q6j9O8lRVPZ9ZIrPb3q8BAAAAOMUWCo66+w/m//1iVf3j\nzJaeTavqQndPq2qS5Avz7leTvHXX2++at+1z8eLFr73e3t7O9vb2YccPAAAAcGbt7OxkZ2dnZeev\n7hsXClXVrUlu6e6vVNU3JXkqyY8l+Z4kX+ruR6rqI0lu7+4H55tjP5rkPZktUftEknf0ngtV1d6m\n5XygqoyLnypHud6Nzru//WT0XcX3FwAAADi5qirdvbSHlC1ScXQhyS9VVc/7P9rdT1XVbyZ5vKo+\nmORKZk9SS3c/W1WPJ3k2yctJPrSShAgAAACAlbppxdHKLqziaOV95XUAAABwtiy74mjRp6oBAAAA\ncMYIjgAAAAAYEhwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAA\nAAydoeDofKrqumMy2Vr3oAAAAABOrOru9Vy4qldx7apKMjrvqL2y6BgOe96T0HddcwsAAACsR1Wl\nu2tZ5ztDFUcAAAAAHIbgCAAAAIAhwREAAAAAQ4KjjWUzcAAAAOBobI69wZtj2zAbAAAAzhabYwMA\nAABwLARHAAAAAAwJjgAAAAAYEhwBAAAAMHTGg6P9Tx7z9DEAAACAmTP/VLWD+u4dm6eqAQAAACed\np6oBAAAAcCwERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABg6Ny6B3AynZ8/RQ0AAADg7BIcDb2U\n8ePtAQAAAM4OS9UAAAAAGDrVwdFkspWquu4AAAAAYDmqe++SrGO6cFUf9dqzoGi0pGx0Xn2Tyrrm\nGwAAAFi9qkp3L62y5lRXHAEAAACwOoIjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABg\nSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABg\nSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAkOAIAAABg\nSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADC0cHBUVbdU\n1W9V1RPzr2+vqqeq6vmqerKqbtvV96GqulxVz1XVvasYOAAAAACrdZiKox9J8uyurx9M8nR3vzPJ\nM0keSpKqujvJB5K8O8n7k3ysqmo5wwUAAADguCwUHFXVXUm+L8nP7Gq+P8ml+etLSR6Yv74vyWPd\n/Up3v5DkcpJ7ljJaAAAAAI7NohVHP5nkbyTpXW0XunuaJN19Lckd8/Y7k7y4q9/VeRsAAAAAp8hN\ng6Oq+rNJpt392SQ3WnLWN/g1AAAAAE6Zcwv0eW+S+6rq+5J8Y5I3V9XPJ7lWVRe6e1pVkyRfmPe/\nmuStu95/17xtn4sXL37t9fb2dra3tw/9AQAAAADOqp2dnezs7Kzs/NW9eKFQVf2pJP9zd99XVR9N\n8ofd/UhVfSTJ7d394Hxz7EeTvCezJWqfSPKO3nOhqtrbdPjBV2V/odOo7aD2s9a3ctTvOQAAAHBy\nVVW6e2kPKVuk4uggP57k8ar6YJIrmT1JLd39bFU9ntkT2F5O8qEjJ0QAAAAAHLtDVRwt9cIqjtbQ\nV8URAAAAbLJlVxwt+lQ1AAAAAM6YExccTSZbqap9x2Syte6hAQAAAJwpJ26p2nj5WTJaZmWp2mH7\nWqoGAAAAm8xSNQAAAACOheAIAAAAgCHBEQAAAABD59Y9gMWdn+9pBAAAAMBxOEXB0UsZbwANAAAA\nwCpYqgYAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjhiaTLZSVfuOyWRr3UMDAAAA\njkl1733E/TFduKpH166qJKMxjdoXbdN35k1JXtr37gsX3pZr1164/t03mId1/cwAAAAAN1ZV6e5a\n1vnOLetEnAYvZRQGTadL+3kCAAAANoilagAAAAAMqTgiyfn50jQAAACArxMckfESNkESAAAAnHWW\nqgEAAAAwJDgCAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgS\nHAEAAAAwJDgCAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgS\nHAEAAAAwJDgCAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgS\nHAEAAAAwJDgCAAAAYEhwxCGdT1Vdd0wmW+seFAAAALAC59Y9AE6bl5L0dS3Taa1nKAAAAMBKqTgC\nAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgSHAEAAAAwJDgC\nAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADN00OKqq81X1yar6TFV9vqoe\nnrffXlVPVdXzVfVkVd226z0PVdXlqnququ5d5QcAAAAAYDWqu2/eqerW7v5qVb0hyT9P8uEkfz7J\nH3b3R6vqI0lu7+4Hq+ruJI8m+e4kdyV5Osk7es+Fqmpv02vtSUZjGrUv2qbvqq+1yM8RAAAAsFpV\nle6uZZ1voaVq3f3V+cvzSc5llhzcn+TSvP1Skgfmr+9L8lh3v9LdLyS5nOSeZQ0YAAAAgOOxUHBU\nVbdU1WeSXEvyie7+dJIL3T1Nku6+luSOefc7k7y46+1X520AAAAAnCKLVhy92t3fmdnSs3uq6tuz\nf72StUoAAAAAG+TcYTp397+tqp0k70syraoL3T2tqkmSL8y7XU3y1l1vu2vets/Fixe/9np7ezvb\n29uHGQ4AAADAmbazs5OdnZ2Vnf+mm2NX1VuSvNzdX66qb0zyZJIfT/Knknypux85YHPs92S2RO0T\nsTn2Celrc2wAAADYZMveHHuRiqP/JMmlqrols6Vt/6i7f7WqfiPJ41X1wSRXknwgSbr72ap6PMmz\nSV5O8qFhQgQAAADAiXbTiqOVXVjF0Rr6qjgCAACATbbsiqOFNscGAAAA4OwRHAEAAAAwJDgCAAAA\nYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgSHAEAAAAwJDgCAAAA\nYEhwBAAAAMCQ4IglOJ+q2ndMJlvrHhgAAABwBOfWPQA2wUtJel/rdFrHPxQAAABgaVQcAQAAADAk\nOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjVuh8quq6YzLZWvegAAAAgAWdW/cA2GQvJenr\nWqbTWs9QAAAAgENTcQQAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAAAAyt9alqf/Wv/k/r\nvDwAAAAAN7DW4Ojv/t23JPnmXS3PrGsoAAAAAOyx1uAo+R+SvGXX1y8n+ZU1jQUAAACA3exxBAAA\nAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgSHAEAAAAwJDgCAAAAYEhwBAAA\nAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgSHAEAAAAwJDgCAAAAYEhwBAAA\nAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgSHAEAAAAwJDgCAAAAYEhwBAAA\nAMCQ4AgAAACAIcERAAAAAEOCIwAAAACGBEcAAAAADAmOAAAAABgSHAEAAAAwJDgCAAAAYOimwVFV\n3VVVz1TVb1fV56vqw/P226vqqap6vqqerKrbdr3noaq6XFXPVdW9q/wAAAAAAKzGIhVHryT56939\n7Un+iyQ/VFXvSvJgkqe7+51JnknyUJJU1d1JPpDk3Unen+RjVVWrGDwAAAAAq3PT4Ki7r3X3Z+ev\nv5LkuSR3Jbk/yaV5t0tJHpi/vi/JY939Sne/kORyknuWPG4AAAAAVuxQexxV1VaS70jyG0kudPc0\nmYVLSe6Yd7szyYu73nZ13gYAAADAKXJu0Y5V9c1JfjHJj3T3V6qq93TZ+/UCPprk1vnr7cO/HQAA\nAOAM29nZyc7OzsrOX903z3uq6lySf5Lkn3b3T8/bnkuy3d3Tqpok+Wfd/e6qejBJd/cj836/luTh\n7v7knnN28sUkb9nV+hNJfjTjDKoG7Yu26XuSxrXIzxwAAABweFWV7l7aXtOLLlX72STPvhYazT2R\n5Afnr38gyS/vav/+qnpjVX1rkrcn+dQSxgoAAADAMbrpUrWqem+Sv5Tk81X1mcxKSP5mkkeSPF5V\nH0xyJbMnqaW7n62qx5M8m+TlJB9qJSYAAAAAp85CS9VWcmFL1dbQ92SMS44IAAAAq7GupWoAAAAA\nnDGCI47Z+VTVvmMy2Vr3wAAAAIA9brrHESzXSxkta5tOl1ZFBwAAACyJiiNOiP2VSKqQAAAAYL1U\nHHFC7K9EUoUEAAAA66XiCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAk\nOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYERwAAAAAMCY4AAAAAGBIcAQAAADAk\nOAIAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAAQ4IjAAAAAIYER5w6k8lWquq6YzLZWvewAAAAYOOc\nW/cA4LCm0ytJek9brWcwAAAAsMFUHAEAAAAwJDgCAAAAYEhwBAAAAMCQ4AgAAACAIcERAAAAAEOe\nqsYJdj5VnpYGAAAA6yI44gR7KUkP2oVJAAAAcBwsVQMAAABgSHAEAAAAwJDgCAAAAIAhwREAAAAA\nQ4IjAAAAAIYERwAAAAAMCY7YaJPJVqrqumMy2Vr3sAAAAOBUOLfuAcBynE9VHfBrfd1X0+lB/QAA\nAIDdBEdsiJeyNyCaERIBAADA62WpGgAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4\nAgAAAGBIcAQAAADAkOAIAAAAgCHBEQAAAABDgiMAAAAAhgRHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4\n4gw6n6rad0wmW+seGAAAAJwo59Y9ADh+LyXpfa3TaR3/UAAAAOAEU3EEAAAAwJDgCAAAAIAhwREc\n0mSyZY8kAAAAzoSbBkdV9fGqmlbV53a13V5VT1XV81X1ZFXdtuvXHqqqy1X1XFXdu6qBw7pMp1cy\n2yPp+mPWDgAAAJtjkYqjn0vyvXvaHkzydHe/M8kzSR5Kkqq6O8kHkrw7yfuTfKyq7DgMAAAAcArd\nNDjq7l9P8m/2NN+f5NL89aUkD8xf35fkse5+pbtfSHI5yT3LGSqs2nnLzwAAAGCXc6/zfXd09zRJ\nuvtaVd0xb78zyb/Y1e/qvA1OgZcyW3b2ddOpgjkAAADOrmVtjt037wIAAADAafJ6K46mVXWhu6dV\nNUnyhXn71SRv3dXvrnnbAT6a5Nb56+3XORQAAACAs2lnZyc7OzsrO39137xYqKq2kvxKd/9n868f\nSfKl7n6kqj6S5PbufnC+OfajSd6T2RK1TyR5Rw8uUlWdfDHJW3a1/kSSH824gKkG7Yu26Xuyx3Wy\n++798Z3t9z5+/yL3EwAAAKxKVaW7l7bvyk0rjqrqH2RWDvQfVdXvJXk4yY8n+YWq+mCSK5k9SS3d\n/WxVPZ7k2SQvJ/nQKDQCAAAA4ORbqOJoJRdWcbSGvid1XCe7r4ojAAAATotjrziCs+38PCgCAACA\ns0dwBDf0UsYVSwAAALD5bln3AOAsmky2UlXXHZPJ1rqHBQAAANdRcQRrMJ1eyd5KpulUJRMAAAAn\ni4ojAAAAAIYER7A05y0/AwAAYKNYqgZLs38jbcvPAAAAOM1UHAEAAAAwJDgCAAAAYEhwBCfcZLJl\n7yQAAADWQnAEJ9x0eiWzvZO+fkyn1/aFSQIlAAAAlk1wBCfG/qeyVR20ufZrG3HvDZSuLHw1lUwA\nAADcjKeqwUqdv0H4s9f+p7LNrObJbF+vZNrd5ilwAAAAfJ3gCFbqeMOgUVB1yy235tVXv7qi6wEA\nALDJBEewUfYHVa++WvvaZlQXAQAAcGP2OAIAAABgSHAEAAAAwJDgCNhl/GQ3T1sDAAA4m+xxBOwy\n3szb09YAAADOJhVHAAAAAAwJjgAAAAAYEhwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIAAAAgCHBEQAA\nAABDgiMAAAAAhgRHwFpMJlupqn3HZLK17qEBAAAwd27dAwDOpun0SpIetNfxDwYAAIAhFUcAAAAA\nDAmOgBPmvOVrAAAAJ4TgCFiq0d5Fhwt+XspsCdvXj9myNgAAAI6bPY6ApRrtXTSdvilV9i4CAAA4\nbQRHwDF4rYpoN0ESAADASWepGrCAde87tP/6B41htFTOPkkAAACvj4ojYAH7K4am0+OsGBpVLI3H\nMFoqd1Av04XCAAAKWklEQVRfAAAAbkxwBLxO50/AvkUnYQwAAACby1I14HXa//SzUaXP8Y/heB39\nKXIAAAAnl4ojgCMYP0VOFRQAALAZVBwBAAAAMCQ4AgAAAGBIcAQAAADAkOAIYAGjTbA90Q0AANh0\nNscGzqzJZGu+ufX1brnl1rz66lcH7xg9tU14BAAAbC7BEXBGnD+gQmh/GPTqqzVoFxABAABnj6Vq\nwBnxUmZh0O7jbDloud1ksrXuoQEAACeU4Ahg6c6vJKAZBT+HOedsWd7e8KyHy/WW4ajjBQAA1s9S\nNYCle6266XrT6Zv2LZc7aD+lCxfelmvXXtjz/teCn91tJ3cJ3WkbLwAAsJ+KI4Bjs3+53Cw0GlUB\nXTvSE9xG1T6rctaeOGfJHwAAZ4mKI4ATaVS1NApjDtr0Owu+/+hGlUWrvN66HfR5VVMBALCJBEcA\np9p4WdymhjYAAMDxslQN4Mzbv5n3QcuujnMJHAAAsH6CI4Azb//eSwc9aW38ZLb1s+8QAACshuAI\ngFNvHGgdHIAdF4EWAACnnT2OAGBFbKQNAMBpp+IIgIH9+x4tZz+j8XlHFTirqtYZndeeTgAAMKbi\nCICBVT2tbXzeUQXOqqp1Ruc96JzjMQiPAAA4OwRHAJwA51dUzbOq8677WgAAcDwsVQPgBNj/ZLeT\nfd7lX8tG2gAAnESCIwBOmf37JG2Ck/pkOHi9DrOfGABwcgmOADhlVlFFtKrNwFfjJFQnCQWO32n7\nno/C0IOC0NP22QDgME7Cn92OorpXU7ZfVe9L8lOZhVMf7+5H9vx6J19M8pZdrT+R5Edz8Iasow1K\nF2nT92SP67T1PanjOm19T+q4Tlvfkzqu09b3+Me19/+/s6Bq+X1XZTyG47v+WXTavufj8b4ps/B3\n5PR8NgA4jOP+s1tVpbuX9q+gK6k4qqpbkvwvSb43ybcn+QtV9a5VXIvTYmfdA+BY7ax7AHDCHWa5\n3dGW5h30L1xveMM3LfyvXqNzHHUMo+sfNIZVfYaT8K98qxrXcX7PDzrv2KhiUDh0Uuzs7Kx7CCfW\nSf095CjM99livjmKVS1VuyfJ5e6+0t0vJ3ksyf0ruhanws66B8Cx2ln3AOCEO8xyu8P03R8yHbR3\n0quvfnVf23R6bRgAXH+Oh28yhv1GYxhd/6ClTIf7DOOlUIdZNnUYR/3L5Hhc43kYGy+zXN73/OGb\nnuOg867CaS/1P+lO218sjzPMWdXvIet02uabozHfHMWqgqM7k7y46+vfn7cBACtz1P2fVIMkh6vW\nWTT4WV1VzibP2eJB6GG+50etVFtG5dZJDbr+9t/+qSN9H4+7kvAwwetRx3BUp+1nAVbNPXG6rHVz\n7De/+S/mW77lv/7acf78z65zOADAkSxjk/GjPjXvMGM4erXO2P4w5zircg7vpD6p8GiVeQd9z49a\nqXZw5db+wOIwQddh/rJ0mL9wHaYq59/9uy8f6fu4jO/NYaohx8Zh6lHHMDb+PWQUPB3myZnHvTx3\nVX1PquNcIryq+3pV1l3Fd6Pfjxcd72FC7cPcU2fdSjbHrqo/nuRid79v/vWDSXr3BtlVdVL+tAQA\nAACwMZa5OfaqgqM3JHk+yfck+YMkn0ryF7r7uaVfDAAAAICVOLeKk3b3v6+qH07yVGbL4T4uNAIA\nAAA4XVZScQQAAADA6beWzbGr6n1V9TtV9X9U1UfWMQaWr6peqKp/WVWfqapPzdtur6qnqur5qnqy\nqm7b1f+hqrpcVc9V1b3rGzmLqKqPV9W0qj63q+3Q81tV31VVn5vf/z913J+DxRww3w9X1e9X1W/N\nj/ft+jXzfUpV1V1V9UxV/XZVfb6qPjxvd39voMF8/4/zdvf3Bqqq81X1yfmfzT5fVQ/P293fG+gG\n8+3+3mBVdct8Xp+Yf+3+3mDz+f7Mrvk+nvu7u4/1yCys+j+TvC3JNyT5bJJ3Hfc4HCuZ299Ncvue\ntkeS/Oj89UeS/Pj89d1JPpPZcsmt+c9ErfszOG44v38iyXck+dxR5jfJJ5N89/z1ryb53nV/NsfC\n8/1wkr8+6Ptu8316jySTJN8xf/3Nme1R+C7392YeN5hv9/eGHklunf/3DUl+I8k97u/NPQ6Yb/f3\nBh9J/lqS/y3JE/Ov3d8bfAzm+1ju73VUHN2T5HJ3X+nul5M8luT+NYyD5avsr2K7P8ml+etLSR6Y\nv74vyWPd/Up3v5DkcmY/G5xQ3f3rSf7NnuZDzW9VTZK8ubs/Pe/393e9hxPkgPlOZvf5XvfHfJ9a\n3X2tuz87f/2VJM8luSvu7410wHzfOf9l9/cG6u6vzl+ez+wvEB3398Y6YL4T9/dGqqq7knxfkp/Z\n1ez+3lAHzHdyDPf3OoKjO5O8uOvr38/X/8DC6dZJPlFVn66qvzJvu9Dd02T2h9Ukd8zb9/4cXI2f\ng9PojkPO752Z3fOvcf+fPj9cVZ+tqp/ZVfpsvjdEVW1lVmn2Gzn879/m+5TZNd+fnDe5vzfQa8sa\nklxL8on5Xxbc3xvqgPlO3N+b6ieT/I18PSBM3N+bbDTfyTHc32vZ44iN9d7u/q7MUtAfqqo/mf0/\n1HZj32zmd7N9LMm3dfd3ZPYH0r+z5vGwRFX1zUl+McmPzCtR/P69wQbz7f7eUN39and/Z2aVhPdU\n1bfH/b2xBvN9d9zfG6mq/myS6byKdFRx8hr39wa4wXwfy/29juDoapI/uuvru+ZtnHLd/Qfz/34x\nyT/ObOnZtKouJMm8LO4L8+5Xk7x119v9HJxOh51f836KdfcXe74YOsn/mq8vLzXfp1xVncssRPj5\n7v7lebP7e0ON5tv9vfm6+98m2Unyvri/N97u+XZ/b6z3Jrmvqn43yT9M8l9V1c8nueb+3kij+f77\nx3V/ryM4+nSSt1fV26rqjUm+P8kTaxgHS1RVt87/9TJV9U1J7k3y+czm9gfn3X4gyWt/IXkiyfdX\n1Rur6luTvD3Jp4510LwelesT7kPN77xc9stVdU9VVZK/vOs9nDzXzff8Dx+v+XNJ/tX8tfk+/X42\nybPd/dO72tzfm2vffLu/N1NVveW1ZQtV9Y1J/kxm+1q5vzfQAfP9O+7vzdTdf7O7/2h3f1tmf6d+\nprv/2yS/Evf3xjlgvv/ycd3f55b6aRbQ3f++qn44yVOZBVcf7+7njnscLN2FJL9UVZ3Zz9Wj3f1U\nVf1mkser6oNJ/v/27tg2qyCIwug3ROREdEFOYpoggAKQoAMqsFwFECABuUUJ5EiODW0gsQQ/AcHa\nshPL2Od0sLqa1b4bzPtRPa9aa53NzOfqrPpVvf6nKeUWmpmP1VH1aGZ+dtjgf1x9uWa+b6p31cPq\ndK319SbPwdVckPezmXlS/a7Oq1cl7//dzDytXlbf/+7FWNXbDn9lue79Le9b7pK8X5jvO+lx9X5m\nHnR4d39aa53OzLfM9110Ud4fzPe9cpz5vk9ObmK+Z/lWBwAAAGDDcmwAAAAAthRHAAAAAGwpjgAA\nAADYUhwBAAAAsKU4AgAAAGBLcQQAAADAluIIAAAAgC3FEQAAAABbfwCU1S0NQY4rwgAAAABJRU5E\nrkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x116733588>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(x_rms_instruments_notes[x_rms_instruments_notes > 1].flatten(), 200);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The range of instruments split into quiet (black) and sounding (white) regions. We can limit the pitches to the sounding ones."
]
},
{
"cell_type": "code",
"execution_count": 197,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmIAAAKSCAYAAABxxLf/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xu4bHV93/HPZ/aJ8cpFjRpROTESRA1sSOMlmrgLShKT\nqo0JUZOUo9a0D1YhJq2gbdGmTap5YjCaXrxRsF4CWgMmRE7wsI+3eolwlHuw9iBgOYkhEDQtgTPf\n/jFrw+zZs2fPnj3fvX6/mffredbDrLVn9vqdzx72+u71+85ajggBAABg+3XaHgAAAMC8ohADAABo\nCYUYAABASyjEAAAAWkIhBgAA0BIKMQAAgJZQiAGJbHdtn9+3vmD7r2xf3Kyfavv3m8dn277F9hW2\nb7D9UdvH9L32ctsnDNnHu20/eYKxHWf7pyf7l+WwfbrtB7Y9jmkY+HlebfulfV/7b7a/a/shfdvO\nad4vD2/W39S87qvN9/jRNv4dAHJRiAG5vivpaba/t1l/vqSbRzz/7RFxQkQcLekCSXtsP2LUDiLi\nVyPi+gnGtijpBcO+YHthgu83DWdIevAkL2xxzKO8PSJOkPRiSf+1b4wh6UZJL5Ik25b0DyXd0qw/\nU72fzWJEHCfpeRr9vtk2heYMVItCDMh3iaSfaR6/TNKHx3lRRFwg6VJJLx/1vP4zZbbvsv3vbe+z\n/Xnb39ds/wXbV9m+0vay7e+R9O8kndKcbfmF5gzO+bY/K+n85mzdO/v28wnbP9G3n7c1Z2x22/7R\nZhxft/2zzXM6zXO+2Izn1c325zbPvdD2dbY/0Gx/raTHSrrc9qea159r+2vNWaHTh/zbz7X9n21/\nQdJbm3F83vZXbH/W9lHN8061/THbf9qcbXxr3/d4VbPtC83ZxZUzlI9szkp+sVl+bJyf2zAR8XX1\nivLD+zZ/RNIvNo+XJH1O0r3N+vdL+nZE3Nu8/vaIuG3Iv//y5kzalU1OP9psP9z2x5vcPm/7ac32\nr9k+pHn8bdu/3Dw+z/ZJG/zMPm37IknXTJoDgLUoxIBcod4B92XNWbFjJX1xE6+/UtJmph0fIunz\nEbEo6TOSXt1s/zeSTo6I4yW9MCLukfRvJf1hcwbuwuZ5x0g6MSJ+qW/86+3nsoh4mqTvSPpNSSdJ\n+rnmsSS9StIdEfEMSU+X9Ku2j2y+tijpdZKeIukHbf9YRLxT0q2SliLipOY5R0TEsc1ZoXPXGcsR\nEfHMiPgNSddJek5E/IiksyX9dt/zjpP0C+r9DH7R9hG2v1/Sv27G92ytzvod6p3Reoakn5f03nX2\nv6GmUL4xIr7dt/lGSd9n+zCtLdB3S3qC7ett/8FKAbyOBzU/19dIen+z7S2Srmhye5OkDzTbPyvp\n2bafKul/SfrxZvuzJH1eo39mx0t6bURsehocwPp2tD0AYNZFxNW2d6p3sP0TSd7EyzfzXEm6OyIu\naR5/Rb0pLal3AD7P9gWS/seI118cEX8/5n52N4+vkvT/IqJr+ypJKwfukyX9sO1faNYPkXSUpHsk\nfSki/o8k2d4naad6hYB1/7/5G5J+wPY71DuruLK/QRf2PT5MvbN5R6lXRPb/jvtURHyn2ec1zTi/\nT9JyRNzZbL+wGaPUy+6YZtpQkh5q+8ER8XcbpnO/19t+ZfM9/9HA10K9n8VL1St6/pmaf3tEfLcp\n3n5c0omSPmL7zIg4X2t9uHnNZ2w/zPahkp6jXlGsiLjc9sNtP1S998FzJd0k6b9IerXtx0q6PSL+\nr+2Nfmbf3MS/HcAYOCMGbI+LJf2OxpyW7HO8emd5xnVP3+ODagqRiDhNvTMjj5f0FduHD3mt1Js+\nW3GvVv+O6G+i799PV9LdzX76ix+rdwbl+Gb5wYi4rPna3cPG2S8i7lDvLNayekXKemek+sf8m5L2\nRMQPq1f49I+5f5/dgXEOY0nP6Bv/EwaLMNvvb6YF/3id7/H25qzhz0t6v+0HDHz9gmbMu2Pgxr/R\n8+mIeLOk10p6yTr7GDxr2V3n3yJJn1avuHuOpMslfbsZ22f6nrfez6w/ZwBTQiEG5Fo5AL5f0lsi\nYqP+mvuKAtsvUa+5/0MT7G/1RvuJEfHliDhb0l+qV5Ddpd4Zj/Xsl7Tonserd9Zm5H4GvnappNNs\n72jGcJTtjRrx/3ZlTO59SGEhIj6u3tTq8Ru8Vs1rb20ev2KM539Z0k/YPrQZZ3+xs1vSfX1pto8b\nfHFEvLIpWH521E4i4hPNvnYNbP+mpDdK+s/9223/kO0n9W1aVO8s1jC/2LzmOZLujIi71CusVvq/\nliT9VUR8JyJukfRISUdFxH71zpD9hnoFmjTZzwzAFjA1CeQKSYqIWyW9a4znn2H7l9TrwbpavX6t\n2/u/13r72OA5v7PSuK7eFN3XbN8s6UzbV6jXSzV4RuZztver15x9nXpTnRvtp/9r71VvyvGKZnrv\nL9X79OCo8b9H0idt3yrp1ySda7vTPOfMDV4r9c46nmf7X6s3DTxyjBHxLdu/JelLkm6XdL2kO5vn\nnC7pD2x/VdKCesXKaSO+50Z+U9IHJb27f9wR8Z7BcUl6qKR3NtOM90r6uqRfXef7/r/mZ7hD9xef\nb1bvDNxX1TuTdWrf87+g+/8I/4yk31KvIJPG/5kBmBIPnA0HgLli+yFNT9aCpI9Lel9EXNT2uMZh\n+3JJvx4RV7Q9FgCTYWoSwLx7s+0r1fvQwTdqKcIa/CUNVI4zYgAAAC3hjBgAAEBLKMQAAABaQiEG\nAADQEgoxAACAllCIAQAAtIRCDAAAoCUUYgAAAC2hEAMAAGgJhRgAAEBLKMQAAABaQiEGAADQEgox\nAACAllCIAQAAtIRCDAAAoCUUYgAAAC2hEAMAAGgJhRgAAEBLKMQAAABaQiEGAADQEgoxAACAllCI\nAQAAtIRCDAAAoCUUYgAAAC2hEAMAAGgJhRgAAEBLKMQAAABaQiEGAADQEgoxAACAllCIAQAAtIRC\nDAAAoCUUYgAAAC2hEAMAAGgJhRgAAEBLKMQAAABaQiEGAADQEgoxAACAllCIAQAAtIRCDAAAoCUU\nYgAAAC2hEAMAAGgJhRgAAEBLKMQAAABaQiEGAADQEgoxAACAlhRZiNn+KdvX2/4L229oezwAAAAZ\nHBFtj2EV2x1JfyHpJEnfkvRlSS+NiOtbHRgAAMCU7Wh7AEM8XdKNEXGTJNn+iKQXSbqvELNdVvUI\nAAAwQkR42PYSpyaPkHRz3/otzbZVIkIRoVNPPfW+xyzTXciWbGtcyJZsa1xKyLbb7a5asD1KPCM2\nll27dmnnzp3at2+fzjnnHC0uLmppaUmStLy8LEmsb3F9RSnjmaX12267TStKGM8srd92221aXl4u\nZjyssz7O+opSxrOyjm3QdgU+uEh6pqRP9q2fKekNA8+JFWeffXYgB9nmIds8ZJuHbPOUkG232121\nSGKZ4hLr1D0lTk1+WdKTbB9p+wGSXirp4vWeTNWeh2zzkG0ess1DtnnIdn4VNzUZEQdt/wtJu9Xr\nYXtfRFzX8rAAAACmrrhCTJIi4pOSjm57HAAAAJmKu47YOGxHjeMGAKBUg8fVTqfE7qV6RUWXrwAA\nAJgL1Rdigx/9xfSQbR6yzUO2ecg2D9nOr+oLMQAAgFrRIwYAAOgRS0aPGAAAQGGqL8SYV89DtnnI\nNg/Z5iHbPGQ7v6ovxAAAAGpFjxgAAKBHLBk9YgAAAIWpvhBjXj0P2eYh2zxkm4ds85Dt/Kq+EAMA\nAKgVPWIAAIAesWT0iAEAABSm+kKMefU8ZJuHbPOQbR6yzUO286v6QgwAAKBW9IgBAAB6xJLRIwYA\nAFCY6gsx5tXzkG0ess1DtnnINg/Zzq8dbQ8AAAC0z149c9btdlsayfQtLy9raWmptf2PmualRwwA\nAKzBcXZ6Op0OPWIAAAClqb4QY149D9nmIds8ZJuHbPOQba6S86VHDAAAcPmKltAjBgAAKMSS0SMG\nAABQmOoLsZLnfWtHtnnINg/Z5iHbPGQ7v6ovxAAAAGpFjxgAAFhj2AVdFxYWWhjJbKBHDAAAoDDV\nF2LMq+ch2zxkm4ds85BtHrKdX9UXYgAAALWiRwwAAIyFY+9kuNckAABAgaovxJhXz0O2ecg2D9nm\nIds8ZJur5HyrL8QAAABqRY8YAADgXpPJ6BEDAAAoTPWFWMnzvrUj2zxkm4ds85BtHrKdX9UXYgAA\nALWiRwwAANAjloweMQAAgMJUX4gxr56HbPOQbR6yzUO2ech2flVfiAEAANSKHjEAAECPWDJ6xAAA\nAApTfSHGvHoess1DtnnINg/Z5iHb+VV9IQYAAFAresQAAAA9YsnW6xHbsd0DAQAA5bFX1wndbrel\nkcyeUUVt9eUu8+p5yDYP2eYh2zxkm4dsc5Wcb/WFGAAAQK3oEQMAAGtwnJ2eTqfDdcQAAABKU30h\nVvK8b+3INg/Z5iHbPGSbp5ZsO50OywTLyEy36WcHAACAAfSIAQCANYYdZ7m22OToEQMAAChM9YVY\nLfPqNSLbPGSbh2zzkG2eErKNiFXLZnudMBlSBQAAaAk9YgAAgHtNJqNHDAAAoDDVF2IlzKvPKrLN\nQ7Z5yDYP2eYh2/m1o+0BAACA9tmrZ8663W5LI5m+5eVlLS0ttbb/UdO89IgBAIA1OM5OD/eaBAAA\nKFD1hRjz6nnINg/Z5iHbPGSbh2xzlZwvPWIAAIDLV7SEHjEAAEAhloweMQAAgMJUX4iVPO9bO7LN\nQ7Z5yDYP2eYh2/lVfSEGAABQK3rEAAAAPWLJ6BEDAAAoTPWFGPPqecg2D9nmIds8ZJuHbOdX9YUY\nAABAregRAwBgCoYdl+izwgp6xAAAAArTSiFm+3G299i+xvZVtl/XbD/c9m7bN9i+1PahG30v5tXz\nkG0ess1DtnnIFpi+ts6I3Svp9RHxVEnPkvQa20+WdKakyyLiaEl7JJ3V0vgAAADSFdEjZvuPJL2r\nWZ4bEQdsP0bSckQ8ecjz6REDABSvpmPV4FgXFhZaGslsKrZHzPZOSYuSviDp0RFxQJIi4jZJj2pv\nZAAAALl2tLlz2w+V9FFJp0fEd2wP/umw7p8Su3bt0s6dO7V//34tLi5qcXFRS0tLku7vY2B9a+sr\n20oZzyyt79u3T2eccUYx45ml9XPOOYffB0nrK49LGc8sra9sK2U8K+vI19rUpO0dkv5Y0p9GxDua\nbddJWuqbmrw8Io4Z8tr7piaXl5d5wyQh2zxkm4ds85Dt5o17jC0hW6Ymc603NdlmIXa+pG9HxOv7\ntr1V0u0R8Vbbb5B0eEScOeS19IgBADBF3GsyV1GFmO1nS/q0pKvUm34MSW+U9CVJF0h6vKSbJJ0S\nEXcMeT2FGAAAU0QhlquoZv2I+FxELETEYkQcHxEnRMQnI+L2iHheRBwdEScPK8IG9c+vY7rINg/Z\n5iHbPGSbh2znF+UuAABAS4q4jthmMTUJAMB0MTWZa72pyVYvXwEAQK0oXDAN1b9rmFfPQ7Z5yDYP\n2eYhW2D6qi/EAAAAakWPGAAAE2BqEptBjxgAAFNkrz6udrvdlkYyHVxZvx3Vl+/0LOQh2zxkm4ds\n85BtHrKdX9UXYgAAALWiRwwAgCmo/bjE1GQuesQAAEg02DNWm1nreSvJqA9yVD81ybx6HrLNQ7Z5\nyDYP2eYh21wl51t9IQYAAFAresQAAMAaHGenp9PprNsjxhkxAACAllRfiJU871s7ss1DtnnINg/Z\n5ikxW9szs+zdu7fV/Y9SfSEGAABQK3rEAAAAEtmmRwwAAKA01RdiJc6rzwqyzUO2ecg2D9muFhGr\nlrb7oFjKXUapvhADAACoFT1iAABMYPA4NOo2NgA9YgAAAIWpvhCjZyEP2eYh2zxkm4dsVxvsA+p2\nuxMve/bs2dLrWcrOd5TqCzEAAIBa0SMGAMAUcFzCerjXJAAAQIGqL8ToWchDtnnINg/Z5iHbPGSb\nq+R8d7Q9AADAfOByD8Ba9IgBALYFhRjmGT1iAAAAham+ECt53rd2ZJuHbPOQbR6yBaaPHjEAwLYY\nvPnxRhe6nCfLy8taWlpqdQyDU8cLCwstjWS+0CMGAGgFv8fLQiGWix4xAACAwlRfiNGzkIds85Bt\nHrLNQ7Z5yHZ+VV+IAQAA1IoeMQAAwHXektEjBgAAUJjqCzHm1fOQbR6yzUO2ecg2D9nOr+oLMQAA\ngFrRIwYAaAU9SZgn9IgBAAAUpvpCjHn1PGSbh2zzkG0esgWmr/pCDAAAoFb0iAEAisDvdcyqTqdD\njxgAAEBpqi/E6FnIQ7Z5yDYP2eYh2zxkm6vkfKsvxAAAAGpFjxgAoAj8XsesGtUjtmO7BwMAmE9c\nwBVYq/r/C0qe960d2eYh2zxkm4dsgemrvhADAACoFT1iAIBtwdQk5hnXEQMAAChM9YUYPQt5yDYP\n2eYh2zxkC0xf9YUYAABAregRAwBsC3rEMM/oEQMAAChM9YUYPQt5yDYP2eYh2zxkC0xf9YUYAABA\nregRAwBsC3rEMM/oEQMAAChM9YUYPQt5yDYP2eYh2zxkC0xf9YUYAABAregRAwBsC3rEMM/oEQMA\nAChM9YUYPQt5yDYP2eYh2zxkC0xf9YUYAABAregRAwBsC3rEMM/oEQMAAChM9YUYPQt5yDYP2eYh\n2zxbzdb2qqXb7bI0y549e1ofwywvbec7SvWFGAAAQK3oEQMAtILf45gXnU6HHjEAAIDSVF+I0Q+S\nh2zzkG0ess1DtnnINlfJ+e5oewAAgPlkD52pqQaX48A00CMGAMAEKMSwGUX2iNnu2L7C9sXN+uG2\nd9u+wfaltg9tc3wAAACZ2i7fT5d0bd/6mZIui4ijJe2RdNZG36Dked/akW0ess1DtnnIFpi+1gox\n24+T9AJJ7+3b/CJJ5zWPz5P04u0eFwAA45jmBWo3c8HRgwcPrllQr9Z6xGxfKOk/SDpU0q9HxAtt\n/01EHN73nNsj4uFDXkuPGACgKNt1XBq2n4WFhW3ZNya3Xo9YK5+atP0zkg5ExD7bSyOeuu67eteu\nXdq5c6ck6bDDDtPi4qKWlnrfauX0Oeuss84666zP2npErPk66tXKGTHbvyXplyXdK+lBkh4m6eOS\n/oGkpYg4YPsxki6PiGOGvP6+M2LLy8v3vSExXWSbh2zzkG0esh1tK8fTzWTLGbE6FfWpyYh4Y0Q8\nISKeKOmlkvZExK9I+oSkXc3TTpV0URvjAwAA2A6tX0fM9nN1f4/YwyVdIOnxkm6SdEpE3DHkNfSI\nAQBaxXXEsBnrnRFrvRCbBIUYAKBtFGLYjKKmJqeJRsU8ZJuHbPOQbR6yBaav+kIMAACgVkxNAgAw\nBRyX8szCJ0VndmoSAACgVtUXYvQs5CHbPGSbh2zzkG0esp1f1RdiAAAAtaJHDEBxuCwAgFlDjxgA\nAEBhqi/EmFfPQ7Z5yBYAIM1AIQYAAFAresQAFIceMQCzZr0esR3bPRAA2Ii9+vdVt9ttaSTA+Gbh\noqPYftX/mUmvTR6yzUO2ecg2D9kC01d9IQYAAFAresQAFI//31EDpiYxCj1iAKo12DMGlGCw8KLo\nwiSqn5qkZyEP2eYh2zxkm4dsgemrvhADAACoFT1iAABMgOvdYTPoEQMAYIpm7Xp39Ly1o/rynZ6F\nPGSbh2zzkG0ess1DtvOr+kIMAACgVvSIAQAwBbUfl5iazLVejxhnxAAAAFpSfSHGvHoess1DtnnI\nNg/ZjmZ74mXv3r1bev00lk6ns2rpdrtVLwcPHrxv+dSnPqWDBw9u23thcCyjVF+IAQAA1IoeMQAA\nsEbtx9k27/05eBas0+nQIwYAAFCa6gsxehbykG0ess1DtnnIdrSIWLO03fc1zZ6x2paFhYU1y3YZ\nHMvI527TmAAAADCAHjEAAKZg2HGJ+09iBT1iAAAAham+EKNnIQ/Z5iHbPGSbh2xHG9Zn1X8tq+28\njhXqUX0hBgAAUCt6xAAASDJ4PSnu3zi/6BEDAAAoTPWFGD0Lecg2D9nmIds8ZAtM3462BwAAwKwa\nvHzFejeAXl5e1tLS0jaMaGsG24KYat06esQAANgmtR+7KMQmR48YAABAYaovxOhZyEO2ecg2D9nm\nIds8ZDu/6BEDAGCb2ENnp+67AGzpBse4Xs9badruwRt1qyt6xAAAwEQ4Fo+n0+nQIwYAAFCa6gsx\n5tXzkG0ess1DtnnINg/Z5io5X3rEAACYgmHTdKN6gwCJHjEAAKaCQgyj0CMGAABQmOoLsZLnfWtH\ntnnINg/Z5iFbYPqqL8QAAABqRY8YAABTQI8YRqFHDAAAoDDVF2L0LOQh2zxkm4ds85AtMH3VF2IA\nAAC1okcMAIAkHKsgca9JAACAIlVfiNGzkIds85BtHrLNQ7Z5yDZXyflWX4gBAADUih4xAACScKyC\nNLpHbMd2DwYAgFkwWGRx8VZMYsN3je1PjbOtLSXP+9aObPOQbR6yzUO2wPSte0bM9gMlPVjSI20f\nLmnllNohko7YhrEBAADMtHV7xGyfLukMSY+VdKvuL8T+VtJ7IuJd2zLC4WOjRwwA0CqmJrEZ6/WI\nbdisb/u1EfHOlFFNiEIMAFCa2o9Lg+NfWFhoaSSzaeILukbEO23/mO2X2/4nK8v0hzgZehbykG0e\nss1DtnnINg/Zzq8NPzVp+wOSflDSPkkHm80h6fzEcQEAAMy8caYmr5P0lJLmApmaBACUpvbjElOT\nubZyHbGrJT1G0v+Z6ogAAKgYzfqYhnHeNY+UdK3tS21fvLJkD2xczKvnIds8ZJuHbPOQLTB945wR\ne3P2IAAAAObRWPeatH2kpKMi4jLbD5a0EBF3pY9u/fHQIwYAaBVTk9iMiS9fYfvVkj4q6b82m46Q\n9EfTGxoAAMB8Gqd8f42kZ6t3RX1FxI2SHpU5qM2gZyEP2eYh2zyznG1ErFpss7S4dDqdVQswiXHe\nOXdHxN+vrNjeod51xAAAALAF41xH7G2S7pD0TyS9VtJpkq6NiDflD2/dMdEjBmDu0JME1Gsr95rs\nSHqVpJPVu/H3pZLe22YlRCEGYB5RiAH1mrgQK1F/Iba8vKylpaV2BzSjyDYP2eaZp2y3+/f3PGU7\nDq5Ej83Yyqcmf9b2lbZvt/23tu+y/bfTHyIAAMB8GWdq8uuSfk7SVaXMBzI1CQD139uwdpwRw2ZM\nfEZM0s2Srp525WP7UNsX2r7O9jW2n2H7cNu7bd/Q3FLp0GnuEwAAoCTjFGL/StIlts+y/fqVZQr7\nfoekSyLiGEnHSbpe0pmSLouIoyXtkXTWRt9klq8Z1DayzUO2eeYp2+2+btbevXtbv3ZXScvgdcQO\nHjy4ZgE2Mk4h9h8k/Z2kB0p6WN8yMduHSPrxiDhXkiLi3oi4U9KLJJ3XPO08SS/eyn4AAABKNk6P\n2NUR8bSp7tQ+TtK7JV2r3tmwP5d0hqRbI+LwvufdHhEPH/J6esQAAEXpdrtrttE3hhXr9YjtGOO1\nl9g+OSJ2T3E8OySdIOk1EfHntn9PvWnJwepq3Wpr165d2rlzpyTpsMMO0+Li4n0fq16ZmmCdddZZ\nZ531NteBjYxzRuwuSQ+RdLeke9S7qGtExCET79R+tKT/GRFPbNafo14h9oOSliLigO3HSLq86SEb\nfD3XEdsGZJuHbPOQbR6yHY0zYhhl4k9NRsTDIqITEQ+KiEOa9YmLsOZ7HpB0s+0fajadJOkaSRdL\n2tVsO1XSRVvZDwAA22VYQz+wkXHOiP3EsO0R8ekt7bjXJ/ZeSd8j6RuSXiFpQdIFkh4v6SZJp0TE\nHUNeS48YAKAow45L3IYKK7Zyr8lP9K0+UNLTJX0lIk6c3vA2h0IMAFAaCjGMspWpyX/Utzxf0tMk\n/c20BziplcZITB/Z5iHbPGSbh2yB6RvnU5ODbpG0poEeAIB5NqwnbFgD/zB8ECJX2/mOOjM6ztTk\nO3X/ZSQ6khYl7Y+IX57WADeLqUkAQA04VkHqFWJbuY7Yn/c9vlfShyPic1MZGQAAwBwb2SNme0HS\nyRFxXrN8sLQijJ6FPGSbh2zzkG0ess1DtrlKznfkGbGIOGj7SNsPiIi/365BAQAwC8a9lhjXHctV\ncr7j9Iidr15z/sWSvruyPSLenju0kWOiRwwAAFTB9pZ6xP5Xs3QkPazZRhUEAACwReNcae7aiHhL\n/yLpuuyBjavked/akW0ess1DtnnINg/Z5io533EKsbPG3AYAAIBNWLdHzPZPS3qBpFMk/WHflw6R\n9JSIeHr+8IajRwwAUBpucYRRJukR+5Z61xB7oaSv9G2/S9KvTW9oAAAA82ndUj0ivhoR50l60sp1\nxNT75OTXI4J7Tc4Bss1DtnnINg/ZAtM3zjnTP7N9iO2HS7pC0nts/17yuAAAAGbeONcRuzIijrf9\nTyU9PiLOtv21iDh2e4Y4dEz0iAFA5QZ/j9NPhVm2Xo/YOO/6Hba/X72m/T+e6qgAAADm2DiF2L+T\ndKl6vWFftv1ESTfmDmt89CzkIds8ZJuHbPOQLTB9G15ZPyIulHRh3/o3JL0kc1AAAADzYJwese+T\n9GpJO9VXuEXEK1NHNnpM9IgBQOXoEcM82cq9Ji+S9BlJl0k6OM1BAQDml736uNTtdlsaCZBr1B8Z\n4/z58eCIeENEXBARH1tZpje8raFnIQ/Z5iHbPGSbh2zzkG2ukvMdpxD7Y9svSB8JAADAnBmnR+wu\nSQ+RdLekeyRZUkTEIfnDW3dM9IgBwIzh9zpmVafTWbdHbMNCrEQUYgBmHTeQBmbLpi/oavvJzX9P\nGLZkDXSzSp73rR3Z5iHbPGQLoCajPjX5ekm/Kul3h3wtJJ2YMiIAAIA5wdQkABSIqUlgtmzlOmIA\ngG02eI0tietslW5Y8bywsNDCSFCT6v+8oh8kD9nmIds8ZJuHbIHpq74QAwAAqNW6PWIbfTIyIq5I\nGdEY6BEDMI/4vVc2piYxyqavI2b78tHfL1r71CSFGIB5xO+9slGIYZSZvaDr8vKylpaW2h3QjCLb\nPGSbh2zzZGfLJ0Uxyyb61KTtR0h6uaQnN5uuk/ShiLh9usMDAACYP6OmJo+RtEfSpZKuVO8ek8dL\ner6kEyMAluUMAAAYFklEQVTi+u0a5JCxMTUJADOGM2KYZZP0iH1U0gURccHA9pdIenlEvGTqoxwT\nhRgAzB4KMcyyTd9rUtIPDxZhzTf6mKSnTWtgW8V1bfKQbR6yzUO2ebaabUSsWmyvWjqdzpoFmHWj\n3uXfnfBrAAAAGMOoqclbJL192JcknRERj88c2ChMTQJAfQZ/b3PGC/Nkkk9NvkfSw9b52nu3PCIA\nAIA5x3XEsC6yzUO2ecg2z7SzrfH4k4X3ba628+10Ops/I2b790d904h43VYHBgAAMM9G9YidOuqF\nEXFeyojGQI8YANSP3+OYF6POiFU/NQkAqBO/xzEvRhVi635kxfbFo5a84W4O1wzKQ7Z5yDYP2eYh\n2zxkm6vkfEd9avJZkm6W9GFJX1TvshUAAEyFzWFlxcpFbZFjJd8SL6EyqkdsQb37Sr5M0rGS/kTS\nhyPimu0b3nBMTQIAgM1qsxDb9NRkRByMiE9GxKmSninp65KWbf+LpDECAADMlZGloO3vtf1zkv67\npNdI+n1JH9+OgY2r5Hnf2pFtHrLNQ7Z5yDYP2eYqOd9R1xE7X72be18i6S0RcfW2jQoAAGDKBvvw\nut3utux31BToqB6xru6/uXf/kywpIuKQaQ1ws+gRAwAAW7VdtcREV9aPiPY/SgAAADDDqi+2Sp73\nrR3Z5iHbPGSbh2zzkG2ukvMddR0xAACwBSVetwpl4RZHAAAkoRDDik1fRwwAAAC5qi/ESp73rR3Z\n5iHbPGSbh2yB6au+EAMAAKgVPWIAAGwTjl3zadR1xDgjBgAA0JLqCzF6FvKQbR6yzUO2ecg2D9nm\nKjnf6gsxAACAWtEjBgAAkMg2PWIAAAClqb4QK3net3Zkm4ds85BtHrLNQ7a5Ss63+kIMAACgVvSI\nAQAAJKJHDAAAoEDVF2Ilz/vWjmzzkG0ess1DtnnINlfJ+VZfiAEAANSKHjEAAIBE9IgBAAAUqPpC\nrOR539qRbR6yzUO2ecg2D9nmKjnf6gsxAACAWtEjBgAAkGhUj9iO7R4MAAAoz+AJjk6HSbPtUH3K\nJc/71o5s85BtHrLNQ7Z5yHZ+VV+IAQAA1Kq1HjHbvybpVZK6kq6S9ApJD5H0h5KOlLRf0ikRceeQ\n19IjBgDAFDE1mauo64jZfqyk10o6ISKOVa9X7WWSzpR0WUQcLWmPpLPaGB8AAMB2aLPcXZD0ENs7\nJD1I0q2SXiTpvObr50l68UbfhHn1PGSbh2zzkG0ess1TQra2Vy3dbndmlj179rS6/1FaKcQi4luS\nflfSN9UrwO6MiMskPToiDjTPuU3So9oYHwAAwHZo5fIVtg9T7+zXkZLulHSh7V+SNNj4tW4j2K5d\nu7Rz505J0r59+7S4uKilpSVJ9/9lwTrrJa+vKGU8s7K+sq2U8czS+tLSUlHjYZ31UtdXHu/fv18b\naaVZ3/bPS/rJiHh1s/4rkp4p6URJSxFxwPZjJF0eEccMeT3N+gAAJOI4Oz2dTqesZn31piSfafuB\nti3pJEnXSrpY0q7mOadKumijb9RffWK6yDYP2eYh2zxkm6fEbAd7xmpe9u7d2+r+R2llajIivmT7\no5KulHRP8993S3qYpAtsv1LSTZJOaWN8AAAA24F7TQIAACQada/JtqYmAQAA5l71hViJ8+qzgmzz\nkG0ess1DtnlKzDYi1ixt93rVuoxSfSEGAABQK3rEAADAGsOOs9x/cnL0iAEAABSm+kKsxHn1WUG2\necg2D9nmIds8ZDu/WrmOGAAAKNuwJvONbmBdquW+2561YdSULj1iAABgLBx7J1PiLY4AAADmXvWF\nGPPqecg2D9nmIds8ZJuHbHOVnC89YgAAYCwbXZy0VONcWLUt9IgBAAAk4l6TAAAABaq+ECt53rd2\nZJuHbPOQbR6yzUO2uUrOt/pCDAAAoFb0iAEAACSiRwwAAKBA1RdiJc/71o5s85BtHrLNQ7Z5yDZX\nyflWX4gBAADUih4xAACARPSIAQAAFKj6Qqzked/akW0ess1DtnnINg/Z5io53+oLMQAAgFrRIwYA\nAJCIHjEAAIACVV+IlTzvWzuyzUO2ecg2D9nmIdtcJedbfSEGAABQK3rEAADARIYdizsdzvEMQ48Y\nAABAYaovxEqe960d2eYh2zxkm4ds85Dt/Kq+EAMAAKgVPWIAAGAi9IiNb70esR3bPRAAAFCnwcKL\nomvrqk+QefU8ZJuHbPOQbR6yzUO286v6QgwAAKBW9IgBAICxMDU5OXrEAADAltira4lut9vSSOoy\nqmCtvpRlXj0P2eYh2zxkm4ds85BtrpLzrb4QAwAAqBU9YgAAYCIci8fT6XToEQMAANM12DOGzat+\narLked/akW0ess1DtnnINg/Z5io53+oLMQAAgFrRIwYAAJDI9ro9YpwRAwAAaEn1hVjJ8761I9s8\nZJuHbPOQbR6yzVVyvtUXYgAAALWiRwwAACARPWIAAAAFqr4QK3net3Zkm4ds85BtHrLNU2u2EbFm\nsc0ysIxSfSEGAABQK3rEAADARIYdizsdzvEMQ48YAABAYaovxGqdV68B2eYh2zxkm4ds85Dt/NrR\n9gAAAECdhjWid7vdFkYy2vLyspaWllrb/6jpWnrEAADA1HB8XqvT6dAjBgAAUJrqCzHm1fOQbR6y\nzUO2ecg2D9nmKjlfesQAAMBEuHzF1tEjBgAAJkIhNj56xAAAAApTfSFW8rxv7cg2D9nmIds8ZJuH\nbOcXPWIAAGANph23Bz1iAABgDQqx6aJHDAAAoDDVF2LMq+ch2zxkm4ds85BtHrKdX9UXYgAAALWi\nRwwAAIxlnGPv4HMWFhayhlMVesQAAAAKU30hxrx6HrLNQ7Z5yDYP2eYh2/lVfSEGAABQK3rEAADA\nRLjW2PjoEQMAAChM9YUY8+p5yDYP2eYh2zxkm4ds51f1hRgAAECt6BEDAAAToUdsfPSIAQAAFKb6\nQox59Txkm4ds85BtHrLNQ7bzK7UQs/0+2wdsf61v2+G2d9u+wfaltg/t+9pZtm+0fZ3tkzPHBgAA\n0LbUHjHbz5H0HUnnR8Sxzba3SvrriHib7TdIOjwizrT9FEkflPSjkh4n6TJJRw1rBqNHDACA9tEj\nNr71esR2JO/0s7aPHNj8IknPbR6fJ2lZ0pmSXijpIxFxr6T9tm+U9HRJX8wcIwAAmIy9trbodrst\njKRso4rTNsrWR0XEAUmKiNskParZfoSkm/ued2uzbSTm1fOQbR6yzUO2ecg2D9nmKjnf1DNiY5po\njnHXrl3auXOn9u/fr3379mlxcVFLS0uS7g+c9a2tryhlPLO0vm/fvqLGM0vr+/btK2o8rLM+zvqK\nUsazlfWIKGo8/bZzf8vLy9q/f782kn4dsWZq8hN9PWLXSVqKiAO2HyPp8og4xvaZkiIi3to875OS\nzo6INVOT9IgBAFAmjs9rdTqdVq8j5mZZcbGkXc3jUyVd1Lf9pbYfYPsHJD1J0pe2YXwAAGBKbLMM\nLKOkFmK2PyTp85J+yPY3bb9C0n+U9HzbN0g6qVlXRFwr6QJJ10q6RNJp45z2GjztiOkh2zxkm4ds\n85BtHrLNVXK+2Z+afPk6X3reOs//bUm/nTciAACAcnCvSQAAgES227mOGAAAuN/gSQQuforq3wEl\nz/vWjmzzkG0ess1DtsD0VV+IAQAA1IoeMQAAtglTk/OrzeuIAQAAYIjqCzF6FvKQbR6yzUO2ech2\n6wYv9NntdtXtdrVnz577Hte0HDx4cM2Czam+EAMAAKgVPWIAALSk9mPZsPEvLCy0MJLy0SMGAABQ\nmOoLMXoW8pBtHrLNQ7Z5yHb6VnrF9u7d2/qNqce5UXWn01m1LCwsrFmwOdUXYgAAALWiRwwAAKwx\n7DjLdc8mR48YAABAYaovxOhZyEO2ecg2D9nmIds8ZDu/drQ9AAAAUJ5hDfvdbreFkWzd8vKylpaW\nWtv/qCldesQAAMBYOPZOptPp0CMGAABQmuoLMebV85BtHrLNQ7Z5yDYP2eYqOV96xAAAwFjWu9Br\n6UZdpLZt9IgBAAAksk2PGAAAQGmqL8RKnvetHdnmIds8ZJuHbPOQba6S862+EAMAAKgVPWIAAACJ\n6BEDAAAoUPWFWMnzvrUj2zxkm4ds85BtHrLNVXK+1RdiAAAAtaJHDAAAIBE9YgAAAAWqvhAred63\ndmSbh2zzkG0ess1DtrlKzrf6QgwAAKBW9IgBAAAkokcMAACgQNUXYiXP+9aObPOQbR6yzUO2ecg2\nV8n5Vl+IAQAA1IoeMQAAKjd4TOx0OM9SGnrEAAAAClN9IVbyvG/tyDYP2eYh2zxkm4ds51f1hRgA\nAECt6BEDAKBy9IiVb70esR3bPRAAADBd9upjfLfbbWkkGGZUYVx9ycy8eh6yzUO2ecg2D9nmIdtc\nJedbfSEGAABQK3rEAACYMRwjy9LpdOgRAwBgXgz2jI2Dhv92VJ9yyfO+tSPbPGSbh2zzkG0esp1f\n1RdiAAAAtaJHDAAAMDWZjHtNAgAAFKb6Qox59Txkm4ds85BtHrLNQ7bzq/pCDAAAoFb0iAEAAHrE\nktEjBgAAUJjqCzHm1fOQbR6yzUO2ecg2TwnZ2l61dLvdmVn27NnT6v5Hqb4QAwAAqBU9YgAAYA2O\ns9Mz6l6TnBEDAABoSfWFWAnz6rOKbPOQbR6yzUO2eUrMdrBnrOZl7969re5/lOoLMQAAgFrRIwYA\nAJDINj1iAAAApam+ECtxXn1WkG0ess1DtnnINg/Z5io53+oLMQAAgFrRIwYAAJCIHjEAAIACVV+I\nlTzvWzuyzUO2ecg2D9nmIdtcJedbfSEGAABQK3rEAAAAEtEjBgAAUKDqC7GS531rR7Z5yDYP2eYh\n2zxkm6vkfKsvxAAAAGpFjxgAAEAiesQAAAAKVH0hVvK8b+3INg/Z5iHbPGSbh2xzlZxv9YUYAABA\nregRAwAASESPGAAAQIFSCzHb77N9wPbX+ra9zfZ1tvfZ/pjtQ/q+dpbtG5uvnzzOPkqe960d2eYh\n2zxkm4ds85BtrpLzzT4jdq6knxzYtlvSUyNiUdKNks6SJNtPkXSKpGMk/bSk/2R76Gk8AACAWZDe\nI2b7SEmfiIhjh3ztxZJeEhG/YvtMSRERb22+9qeS3hwRXxzyOnrEAABAFUruEXulpEuax0dIurnv\na7c22wAAAGbSjrZ2bPtNku6JiA9P8vpdu3Zp586d2r9/vxYXF7W4uKilpSVJ988Fs7619ZVtpYxn\nltb37dunM844o5jxzNL6Oeecw++DpPWVx6WMZ5bWV7aVMp5ZW1/Ztp37W15e1v79+7WRVqYmbe+S\n9GpJJ0bE3c22wanJT0o6e6OpyeXl5fsCwHSRbR6yzUO2ecg2D9nmajvfUVOT21GI7VSvEPvhZv2n\nJP2upJ+IiL/ue95TJH1Q0jPUm5L8M0lHDWsGo0cMAADUYlQhljo1aftDkpYkPcL2NyWdLemNkh4g\n6c+aD0V+ISJOi4hrbV8g6VpJ90g6jWoLAADMsk7mN4+Il0fEYyPieyPiCRFxbkQcFRFHRsQJzXJa\n3/N/OyKeFBHHRMTucfbRPx+L6SLbPGSbh2zzkG0ess1Vcr6phRgAAADWx70mAQAAEpV8HTEAAIC5\nVX0hVvK8b+3INg/Z5iHbPGSbh2xzlZxv9YUYAABAregRAwAASESPGAAAQIGqL8RKnvetHdnmIds8\nZJuHbPOQba6S862+EAMAAKgVPWIAAACJ6BEDAAAoUPWFWMnzvrUj2zxkm4ds85BtHrLNVXK+1Rdi\nAAAAtaJHDAAAIBE9YgAAAAWqvhAred63dmSbh2zzkG0ess1DtrlKzrf6QgwAAKBW9IgBAAAkokcM\nAACgQNUXYiXP+9aObPOQbR6yzUO2ecg2V8n5Vl+IAQAA1IoeMQAAgET0iAEAABSo+kKs5Hnf2pFt\nHrLNQ7Z5yDYP2eYqOd/qC7F9+/a1PYSZRbZ5yDYP2eYh2zxkm6vkfKsvxO644462hzCzyDYP2eYh\n2zxkm4dsc5Wcb/WFGAAAQK2qL8T279/f9hBmFtnmIds8ZJuHbPOQba6S86328hVtjwEAAGBc612+\nospCDAAAYBZUPzUJAABQKwoxAACAllCIAQAAtKTaQsz2T9m+3vZf2H5D2+Opme3H2d5j+xrbV9l+\nXbP9cNu7bd9g+1Lbh7Y91lrZ7ti+wvbFzTrZToHtQ21faPu65v37DLKdHtu/Zvtq21+z/UHbDyDf\nydh+n+0Dtr/Wt23dLG2fZfvG5r19cjujrsM62b6tyW6f7Y/ZPqTva0VlW2UhZrsj6V2SflLSUyW9\nzPaT2x1V1e6V9PqIeKqkZ0l6TZPnmZIui4ijJe2RdFaLY6zd6ZKu7Vsn2+l4h6RLIuIYScdJul5k\nOxW2HyvptZJOiIhjJe2Q9DKR76TOVe+Y1W9olrafIukUScdI+mlJ/8n20E/cQdLwbHdLempELEq6\nUQVnW2UhJunpkm6MiJsi4h5JH5H0opbHVK2IuC0i9jWPvyPpOkmPUy/T85qnnSfpxe2MsG62Hyfp\nBZLe27eZbLeo+Qv3xyPiXEmKiHsj4k6R7TQtSHqI7R2SHiTpVpHvRCLis5L+ZmDzelm+UNJHmvf0\nfvUKiadvxzhrNCzbiLgsIrrN6hfUO6ZJBWZbayF2hKSb+9ZvabZhi2zvlLSo3hv30RFxQOoVa5Ie\n1d7IqvZ7kv6lpP5rxZDt1v2ApG/bPreZ9n237QeLbKciIr4l6XclfVO9AuzOiLhM5DtNj1ony8Fj\n3K3iGLcVr5R0SfO4uGxrLcSQwPZDJX1U0unNmbHBi8xx0blNsv0zkg40ZxxHnf4m283bIekESX8Q\nESdI+q56Uz28b6fA9mHqnbE5UtJj1Tsz9ksi30xkOWW23yTpnoj4cNtjWU+thditkp7Qt/64Zhsm\n1Ew9fFTSByLiombzAduPbr7+GEl/2db4KvZsSS+0/Q1JH5Z0ou0PSLqNbLfsFkk3R8SfN+sfU68w\n4307Hc+T9I2IuD0iDkr6uKQfE/lO03pZ3irp8X3P4xg3Adu71GsLeXnf5uKyrbUQ+7KkJ9k+0vYD\nJL1U0sUtj6l275d0bUS8o2/bxZJ2NY9PlXTR4IswWkS8MSKeEBFPVO99uicifkXSJ0S2W9JM6dxs\n+4eaTSdJuka8b6flm5KeafuBTTPzSep94IR8J2etPjO+XpYXS3pp8ynVH5D0JElf2q5BVmpVtrZ/\nSr2WkBdGxN19zysu22pvcdSE/A71isn3RcR/bHlI1bL9bEmflnSVeqfGQ9Ib1XtzXqDeXw83STol\nIu5oa5y1s/1cSb8eES+0/XCR7ZbZPk69D0F8j6RvSHqFeg3mZDsFts9W7w+IeyRdKemfSnqYyHfT\nbH9I0pKkR0g6IOlsSX8k6UINydL2WZJepV72p0fE7haGXYV1sn2jpAdI+uvmaV+IiNOa5xeVbbWF\nGAAAQO1qnZoEAACoHoUYAABASyjEAAAAWkIhBgAA0BIKMQAAgJZQiAEAALSEQgxAdWx3bZ/ft75g\n+69sX9ysn2r795vHZ9u+pbkf5Q22P2r7mL7XXm77hCmM6bm2n7XV7wNgvlCIAajRdyU9zfb3NuvP\n1+ob+Q56e0ScEBFHq3cx0j22HzHlMS2pdwsgABgbhRiAWl0i6Weaxy9T716eG4qICyRdqtX3n1vD\n9v+2/WbbX7H91ZVbKdk+3PbHm22ft/0020dK+ueSzmjOvD3b9iObs29fbBaKNABrUIgBqFFI+oik\nlzVnxY6V9MVNvP5KSU8e43l/GRE/Ium/SPqNZttbJF0REcdJepOkD0TETc1zfq858/Y59W7B9vaI\neIakn1fvVkwAsMqOtgcAAJOIiKtt71TvbNifaPXNlDcy7nM/3vz3K5L+cfP4OZJ+rhnD5bYfbvuh\nQ177PEnHNDfMlqSH2n5wRPzdJsYJYMZRiAGo2cWSfke9/qxHbuJ1x0v68hjPu7v570Ft/velJT0j\nIu7Z5OsAzBGmJgHUaOUs0/slvSUirhnz+bL9EvWa+z804b4/I+mXm++1JOnbEfEdSXdJOqTvebsl\nnd633+Mm3B+AGUYhBqBGIUkRcWtEvGuM56800d+gXpP+iRFxe//3Wm8fQ7xZ0o/Y/qqk35J0arP9\nE5L+8UqzvqTXSfoHTVP/1ZL+2RjjBDBnHLHe7xoAAABk4owYAABASyjEAAAAWkIhBgAA0BIKMQAA\ngJZQiAEAALSEQgwAAKAlFGIAAAAt+f+Ju6PNFoxgEAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x115a725c0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(x_rms_instruments_notes > 1, interpolation='none', cmap='gray')\n",
"plt.grid(True)\n",
"plt.suptitle('MIDI instruments range - RMS power')\n",
"plt.xlabel('MIDI note')\n",
"plt.ylabel('MIDI instrument')\n",
"plt.savefig('data/working/instrument_ranges_binary.png');"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.4"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
nanditav/15712-TensorFlow | tensorflow/examples/udacity/5_word2vec.ipynb | 20 | 316485 | {
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"version": "0.3.2",
"views": {},
"default_view": {},
"name": "5_word2vec.ipynb",
"provenance": []
}
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "D7tqLMoKF6uq",
"colab_type": "text"
},
"source": [
"Deep Learning\n",
"=============\n",
"\n",
"Assignment 5\n",
"------------\n",
"\n",
"The goal of this assignment is to train a Word2Vec skip-gram model over [Text8](http://mattmahoney.net/dc/textdata) data."
]
},
{
"cell_type": "code",
"metadata": {
"id": "0K1ZyLn04QZf",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
}
},
"cellView": "both"
},
"source": [
"# These are all the modules we'll be using later. Make sure you can import them\n",
"# before proceeding further.\n",
"%matplotlib inline\n",
"from __future__ import print_function\n",
"import collections\n",
"import math\n",
"import numpy as np\n",
"import os\n",
"import random\n",
"import tensorflow as tf\n",
"import zipfile\n",
"from matplotlib import pylab\n",
"from six.moves import range\n",
"from six.moves.urllib.request import urlretrieve\n",
"from sklearn.manifold import TSNE"
],
"outputs": [],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "aCjPJE944bkV",
"colab_type": "text"
},
"source": [
"Download the data from the source website if necessary."
]
},
{
"cell_type": "code",
"metadata": {
"id": "RJ-o3UBUFtCw",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 14640,
"status": "ok",
"timestamp": 1445964482948,
"user": {
"color": "#1FA15D",
"displayName": "Vincent Vanhoucke",
"isAnonymous": false,
"isMe": true,
"permissionId": "05076109866853157986",
"photoUrl": "//lh6.googleusercontent.com/-cCJa7dTDcgQ/AAAAAAAAAAI/AAAAAAAACgw/r2EZ_8oYer4/s50-c-k-no/photo.jpg",
"sessionId": "2f1ffade4c9f20de",
"userId": "102167687554210253930"
},
"user_tz": 420
},
"outputId": "c4ec222c-80b5-4298-e635-93ca9f79c3b7"
},
"source": [
"url = 'http://mattmahoney.net/dc/'\n",
"\n",
"def maybe_download(filename, expected_bytes):\n",
" \"\"\"Download a file if not present, and make sure it's the right size.\"\"\"\n",
" if not os.path.exists(filename):\n",
" filename, _ = urlretrieve(url + filename, filename)\n",
" statinfo = os.stat(filename)\n",
" if statinfo.st_size == expected_bytes:\n",
" print('Found and verified %s' % filename)\n",
" else:\n",
" print(statinfo.st_size)\n",
" raise Exception(\n",
" 'Failed to verify ' + filename + '. Can you get to it with a browser?')\n",
" return filename\n",
"\n",
"filename = maybe_download('text8.zip', 31344016)"
],
"outputs": [
{
"output_type": "stream",
"text": [
"Found and verified text8.zip\n"
],
"name": "stdout"
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "Zqz3XiqI4mZT",
"colab_type": "text"
},
"source": [
"Read the data into a string."
]
},
{
"cell_type": "code",
"metadata": {
"id": "Mvf09fjugFU_",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 28844,
"status": "ok",
"timestamp": 1445964497165,
"user": {
"color": "#1FA15D",
"displayName": "Vincent Vanhoucke",
"isAnonymous": false,
"isMe": true,
"permissionId": "05076109866853157986",
"photoUrl": "//lh6.googleusercontent.com/-cCJa7dTDcgQ/AAAAAAAAAAI/AAAAAAAACgw/r2EZ_8oYer4/s50-c-k-no/photo.jpg",
"sessionId": "2f1ffade4c9f20de",
"userId": "102167687554210253930"
},
"user_tz": 420
},
"outputId": "e3a928b4-1645-4fe8-be17-fcf47de5716d"
},
"source": [
"def read_data(filename):\n",
" \"\"\"Extract the first file enclosed in a zip file as a list of words\"\"\"\n",
" with zipfile.ZipFile(filename) as f:\n",
" data = tf.compat.as_str(f.read(f.namelist()[0])).split()\n",
" return data\n",
" \n",
"words = read_data(filename)\n",
"print('Data size %d' % len(words))"
],
"outputs": [
{
"output_type": "stream",
"text": [
"Data size 17005207\n"
],
"name": "stdout"
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "Zdw6i4F8glpp",
"colab_type": "text"
},
"source": [
"Build the dictionary and replace rare words with UNK token."
]
},
{
"cell_type": "code",
"metadata": {
"id": "gAL1EECXeZsD",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 28849,
"status": "ok",
"timestamp": 1445964497178,
"user": {
"color": "#1FA15D",
"displayName": "Vincent Vanhoucke",
"isAnonymous": false,
"isMe": true,
"permissionId": "05076109866853157986",
"photoUrl": "//lh6.googleusercontent.com/-cCJa7dTDcgQ/AAAAAAAAAAI/AAAAAAAACgw/r2EZ_8oYer4/s50-c-k-no/photo.jpg",
"sessionId": "2f1ffade4c9f20de",
"userId": "102167687554210253930"
},
"user_tz": 420
},
"outputId": "3fb4ecd1-df67-44b6-a2dc-2291730970b2"
},
"source": [
"vocabulary_size = 50000\n",
"\n",
"def build_dataset(words):\n",
" count = [['UNK', -1]]\n",
" count.extend(collections.Counter(words).most_common(vocabulary_size - 1))\n",
" dictionary = dict()\n",
" for word, _ in count:\n",
" dictionary[word] = len(dictionary)\n",
" data = list()\n",
" unk_count = 0\n",
" for word in words:\n",
" if word in dictionary:\n",
" index = dictionary[word]\n",
" else:\n",
" index = 0 # dictionary['UNK']\n",
" unk_count = unk_count + 1\n",
" data.append(index)\n",
" count[0][1] = unk_count\n",
" reverse_dictionary = dict(zip(dictionary.values(), dictionary.keys())) \n",
" return data, count, dictionary, reverse_dictionary\n",
"\n",
"data, count, dictionary, reverse_dictionary = build_dataset(words)\n",
"print('Most common words (+UNK)', count[:5])\n",
"print('Sample data', data[:10])\n",
"del words # Hint to reduce memory."
],
"outputs": [
{
"output_type": "stream",
"text": [
"Most common words (+UNK) [['UNK', 418391], ('the', 1061396), ('of', 593677), ('and', 416629), ('one', 411764)]\n",
"Sample data [5243, 3083, 12, 6, 195, 2, 3136, 46, 59, 156]\n"
],
"name": "stdout"
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "lFwoyygOmWsL",
"colab_type": "text"
},
"source": [
"Function to generate a training batch for the skip-gram model."
]
},
{
"cell_type": "code",
"metadata": {
"id": "w9APjA-zmfjV",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 113,
"status": "ok",
"timestamp": 1445964901989,
"user": {
"color": "#1FA15D",
"displayName": "Vincent Vanhoucke",
"isAnonymous": false,
"isMe": true,
"permissionId": "05076109866853157986",
"photoUrl": "//lh6.googleusercontent.com/-cCJa7dTDcgQ/AAAAAAAAAAI/AAAAAAAACgw/r2EZ_8oYer4/s50-c-k-no/photo.jpg",
"sessionId": "2f1ffade4c9f20de",
"userId": "102167687554210253930"
},
"user_tz": 420
},
"outputId": "67cccb02-cdaf-4e47-d489-43bcc8d57bb8"
},
"source": [
"data_index = 0\n",
"\n",
"def generate_batch(batch_size, num_skips, skip_window):\n",
" global data_index\n",
" assert batch_size % num_skips == 0\n",
" assert num_skips <= 2 * skip_window\n",
" batch = np.ndarray(shape=(batch_size), dtype=np.int32)\n",
" labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)\n",
" span = 2 * skip_window + 1 # [ skip_window target skip_window ]\n",
" buffer = collections.deque(maxlen=span)\n",
" for _ in range(span):\n",
" buffer.append(data[data_index])\n",
" data_index = (data_index + 1) % len(data)\n",
" for i in range(batch_size // num_skips):\n",
" target = skip_window # target label at the center of the buffer\n",
" targets_to_avoid = [ skip_window ]\n",
" for j in range(num_skips):\n",
" while target in targets_to_avoid:\n",
" target = random.randint(0, span - 1)\n",
" targets_to_avoid.append(target)\n",
" batch[i * num_skips + j] = buffer[skip_window]\n",
" labels[i * num_skips + j, 0] = buffer[target]\n",
" buffer.append(data[data_index])\n",
" data_index = (data_index + 1) % len(data)\n",
" return batch, labels\n",
"\n",
"print('data:', [reverse_dictionary[di] for di in data[:8]])\n",
"\n",
"for num_skips, skip_window in [(2, 1), (4, 2)]:\n",
" data_index = 0\n",
" batch, labels = generate_batch(batch_size=8, num_skips=num_skips, skip_window=skip_window)\n",
" print('\\nwith num_skips = %d and skip_window = %d:' % (num_skips, skip_window))\n",
" print(' batch:', [reverse_dictionary[bi] for bi in batch])\n",
" print(' labels:', [reverse_dictionary[li] for li in labels.reshape(8)])"
],
"outputs": [
{
"output_type": "stream",
"text": [
"data: ['anarchism', 'originated', 'as', 'a', 'term', 'of', 'abuse', 'first']\n",
"\n",
"with num_skips = 2 and skip_window = 1:\n",
" batch: ['originated', 'originated', 'as', 'as', 'a', 'a', 'term', 'term']\n",
" labels: ['as', 'anarchism', 'a', 'originated', 'term', 'as', 'a', 'of']\n",
"\n",
"with num_skips = 4 and skip_window = 2:\n",
" batch: ['as', 'as', 'as', 'as', 'a', 'a', 'a', 'a']\n",
" labels: ['anarchism', 'originated', 'term', 'a', 'as', 'of', 'originated', 'term']\n"
],
"name": "stdout"
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "Ofd1MbBuwiva",
"colab_type": "text"
},
"source": [
"Train a skip-gram model."
]
},
{
"cell_type": "code",
"metadata": {
"id": "8pQKsV4Vwlzy",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
}
},
"cellView": "both"
},
"source": [
"batch_size = 128\n",
"embedding_size = 128 # Dimension of the embedding vector.\n",
"skip_window = 1 # How many words to consider left and right.\n",
"num_skips = 2 # How many times to reuse an input to generate a label.\n",
"# We pick a random validation set to sample nearest neighbors. here we limit the\n",
"# validation samples to the words that have a low numeric ID, which by\n",
"# construction are also the most frequent. \n",
"valid_size = 16 # Random set of words to evaluate similarity on.\n",
"valid_window = 100 # Only pick dev samples in the head of the distribution.\n",
"valid_examples = np.array(random.sample(range(valid_window), valid_size))\n",
"num_sampled = 64 # Number of negative examples to sample.\n",
"\n",
"graph = tf.Graph()\n",
"\n",
"with graph.as_default(), tf.device('/cpu:0'):\n",
"\n",
" # Input data.\n",
" train_dataset = tf.placeholder(tf.int32, shape=[batch_size])\n",
" train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])\n",
" valid_dataset = tf.constant(valid_examples, dtype=tf.int32)\n",
" \n",
" # Variables.\n",
" embeddings = tf.Variable(\n",
" tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))\n",
" softmax_weights = tf.Variable(\n",
" tf.truncated_normal([vocabulary_size, embedding_size],\n",
" stddev=1.0 / math.sqrt(embedding_size)))\n",
" softmax_biases = tf.Variable(tf.zeros([vocabulary_size]))\n",
" \n",
" # Model.\n",
" # Look up embeddings for inputs.\n",
" embed = tf.nn.embedding_lookup(embeddings, train_dataset)\n",
" # Compute the softmax loss, using a sample of the negative labels each time.\n",
" loss = tf.reduce_mean(\n",
" tf.nn.sampled_softmax_loss(softmax_weights, softmax_biases, embed,\n",
" train_labels, num_sampled, vocabulary_size))\n",
"\n",
" # Optimizer.\n",
" # Note: The optimizer will optimize the softmax_weights AND the embeddings.\n",
" # This is because the embeddings are defined as a variable quantity and the\n",
" # optimizer's `minimize` method will by default modify all variable quantities \n",
" # that contribute to the tensor it is passed.\n",
" # See docs on `tf.train.Optimizer.minimize()` for more details.\n",
" optimizer = tf.train.AdagradOptimizer(1.0).minimize(loss)\n",
" \n",
" # Compute the similarity between minibatch examples and all embeddings.\n",
" # We use the cosine distance:\n",
" norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))\n",
" normalized_embeddings = embeddings / norm\n",
" valid_embeddings = tf.nn.embedding_lookup(\n",
" normalized_embeddings, valid_dataset)\n",
" similarity = tf.matmul(valid_embeddings, tf.transpose(normalized_embeddings))"
],
"outputs": [],
"execution_count": 0
},
{
"cell_type": "code",
"metadata": {
"id": "1bQFGceBxrWW",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 23
},
{
"item_id": 48
},
{
"item_id": 61
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 436189,
"status": "ok",
"timestamp": 1445965429787,
"user": {
"color": "#1FA15D",
"displayName": "Vincent Vanhoucke",
"isAnonymous": false,
"isMe": true,
"permissionId": "05076109866853157986",
"photoUrl": "//lh6.googleusercontent.com/-cCJa7dTDcgQ/AAAAAAAAAAI/AAAAAAAACgw/r2EZ_8oYer4/s50-c-k-no/photo.jpg",
"sessionId": "2f1ffade4c9f20de",
"userId": "102167687554210253930"
},
"user_tz": 420
},
"outputId": "5ebd6d9a-33c6-4bcd-bf6d-252b0b6055e4"
},
"source": [
"num_steps = 100001\n",
"\n",
"with tf.Session(graph=graph) as session:\n",
" tf.global_variables_initializer().run()\n",
" print('Initialized')\n",
" average_loss = 0\n",
" for step in range(num_steps):\n",
" batch_data, batch_labels = generate_batch(\n",
" batch_size, num_skips, skip_window)\n",
" feed_dict = {train_dataset : batch_data, train_labels : batch_labels}\n",
" _, l = session.run([optimizer, loss], feed_dict=feed_dict)\n",
" average_loss += l\n",
" if step % 2000 == 0:\n",
" if step > 0:\n",
" average_loss = average_loss / 2000\n",
" # The average loss is an estimate of the loss over the last 2000 batches.\n",
" print('Average loss at step %d: %f' % (step, average_loss))\n",
" average_loss = 0\n",
" # note that this is expensive (~20% slowdown if computed every 500 steps)\n",
" if step % 10000 == 0:\n",
" sim = similarity.eval()\n",
" for i in range(valid_size):\n",
" valid_word = reverse_dictionary[valid_examples[i]]\n",
" top_k = 8 # number of nearest neighbors\n",
" nearest = (-sim[i, :]).argsort()[1:top_k+1]\n",
" log = 'Nearest to %s:' % valid_word\n",
" for k in range(top_k):\n",
" close_word = reverse_dictionary[nearest[k]]\n",
" log = '%s %s,' % (log, close_word)\n",
" print(log)\n",
" final_embeddings = normalized_embeddings.eval()"
],
"outputs": [
{
"output_type": "stream",
"text": [
"Initialized\n",
"Average loss at step 0 : 8.58149623871\n",
"Nearest to been: unfavourably, marmara, ancestral, legal, bogart, glossaries, worst, rooms,\n",
"Nearest to time: conformist, strawberries, sindhi, waterfall, xia, nominates, psp, sensitivity,\n",
"Nearest to over: overlord, panda, golden, semigroup, rawlings, involved, shreveport, handling,\n",
"Nearest to not: hymenoptera, reintroducing, lamiaceae, because, davao, omnipotent, combustion, debilitating,\n",
"Nearest to three: catalog, koza, gn, braque, holstein, postgresql, luddite, justine,\n",
"Nearest to if: chilled, vince, fiddler, represented, sandinistas, happiness, lya, glands,\n",
"Nearest to there: coast, photosynthetic, kimmei, legally, inner, illyricum, formats, fullmetal,\n",
"Nearest to between: chuvash, prinz, suitability, wolfe, guideline, computability, diminutive, paulo,\n",
"Nearest to from: tanganyika, workshop, elphinstone, spearhead, resurrected, kevlar, shangri, loves,\n",
"Nearest to state: sextus, wuppertal, glaring, inches, unrounded, courageous, adler, connie,\n",
"Nearest to on: gino, phocas, rhine, jg, macrocosm, jackass, jays, theorie,\n",
"Nearest to and: standings, towed, reyes, willard, equality, juggling, wladislaus, faked,\n",
"Nearest to eight: gresham, dogg, moko, tennis, superseded, telegraphy, scramble, vinod,\n",
"Nearest to they: prisons, divisor, coder, ribeira, willingness, factional, nne, lotta,\n",
"Nearest to more: blues, fur, sterling, tangier, khwarizmi, discouraged, cal, deicide,\n",
"Nearest to other: enemies, bogged, brassicaceae, lascaux, dispense, alexandrians, crimea, dou,\n",
"Average loss at step 2000 : 4.39983723116\n",
"Average loss at step 4000 : 3.86921076906\n",
"Average loss at step 6000 : 3.72542127335\n",
"Average loss at step 8000 : 3.57835536212\n",
"Average loss at step 10000 : 3.61056993055\n",
"Nearest to been: glossaries, legal, unfavourably, be, hadad, wore, scarcity, were,\n",
"Nearest to time: strawberries, conformist, gleichschaltung, waterfall, molality, nominates, baal, dole,\n",
"Nearest to over: golden, semigroup, catus, motorways, brick, shehri, mussolini, overlord,\n",
"Nearest to not: hinayana, it, often, they, boots, also, noaa, lindsey,\n",
"Nearest to three: four, seven, six, five, nine, eight, two, zero,\n",
"Nearest to if: glands, euros, wallpaper, redefine, toho, confuse, unsound, shepherd,\n",
"Nearest to there: it, they, fullmetal, pace, legally, harpsichord, mma, bug,\n",
"Nearest to between: chuvash, wandering, from, kirsch, pursuant, eurocents, suitability, jackie,\n",
"Nearest to from: into, in, workshop, to, at, misogynist, elphinstone, spearhead,\n",
"Nearest to state: sextus, glaring, connie, adler, esoteric, didactic, handedness, presidents,\n",
"Nearest to on: in, at, for, ruminants, wakefulness, torrey, foley, gino,\n",
"Nearest to and: or, who, but, zelda, of, for, thirst, chisel,\n",
"Nearest to eight: nine, six, seven, five, four, three, zero, two,\n",
"Nearest to they: he, prisons, there, we, hydrate, it, not, cumbersome,\n",
"Nearest to more: skye, blues, trypomastigotes, deicide, most, readable, used, sterling,\n",
"Nearest to other: trochaic, hush, surveyors, joachim, differentiation, attackers, reverence, attestation,\n",
"Average loss at step 12000 : 3.66169466591\n",
"Average loss at step 14000 : 3.60342905837\n",
"Average loss at step 16000 : 3.57761328053\n",
"Average loss at step 18000 : 3.57667332476\n",
"Average loss at step 20000 : 3.53310145146\n",
"Nearest to been: be, become, was, hadad, unfavourably, were, wore, partido,\n",
"Nearest to time: gleichschaltung, strawberries, year, nominates, conformist, etch, admittedly, treasuries,\n",
"Nearest to over: golden, semigroup, motorways, rawlings, triangle, trey, ustawa, mattingly,\n",
"Nearest to not: they, boots, often, dieppe, still, hinayana, nearly, be,\n",
"Nearest to three: two, four, five, seven, eight, six, nine, one,\n",
"Nearest to if: wallpaper, euros, before, toho, unsound, so, bg, pfc,\n",
"Nearest to there: they, it, he, usually, which, we, not, transactions,\n",
"Nearest to between: from, with, about, near, reactance, eurocents, wandering, voltaire,\n",
"Nearest to from: into, workshop, by, between, in, on, elphinstone, under,\n",
"Nearest to state: glaring, esoteric, succeeding, sextus, vorarlberg, presidents, depends, connie,\n",
"Nearest to on: in, at, upon, during, from, janis, foley, nubian,\n",
"Nearest to and: or, thirst, but, where, s, who, pfaff, including,\n",
"Nearest to eight: nine, seven, six, five, four, three, zero, one,\n",
"Nearest to they: there, he, we, not, it, you, prisons, who,\n",
"Nearest to more: less, most, deicide, skye, trypomastigotes, interventionism, toed, drummond,\n",
"Nearest to other: such, joachim, hush, attackers, surveyors, trochaic, differentiation, reverence,\n",
"Average loss at step 22000 : 3.59519316927\n",
"Average loss at step 24000 : 3.55378576797\n",
"Average loss at step 26000 : 3.56455037558\n",
"Average loss at step 28000 : 3.5040882225\n",
"Average loss at step 30000 : 3.39208897972\n",
"Nearest to been: become, be, were, was, spotless, hadad, by, hausdorff,\n",
"Nearest to time: gleichschaltung, year, day, nominates, jesus, strawberries, way, admittedly,\n",
"Nearest to over: golden, semigroup, motorways, rawlings, interventionism, counternarcotics, adaption, brick,\n",
"Nearest to not: often, they, it, never, still, nor, boots, pki,\n",
"Nearest to three: four, six, two, eight, five, seven, nine, zero,\n",
"Nearest to if: when, before, so, should, toho, where, bg, wallpaper,\n",
"Nearest to there: they, it, which, usually, he, that, also, now,\n",
"Nearest to between: with, from, in, panasonic, presupposes, churchmen, hijacking, where,\n",
"Nearest to from: into, elphinstone, workshop, between, through, speculates, sosa, in,\n",
"Nearest to state: esoteric, glaring, presidents, vorarlberg, atmosphere, succeeding, lute, connie,\n",
"Nearest to on: upon, in, janis, during, torrey, against, infield, catalans,\n",
"Nearest to and: or, thirst, in, but, of, sobib, cleaves, including,\n",
"Nearest to eight: nine, six, four, seven, three, zero, five, one,\n",
"Nearest to they: we, there, he, you, it, these, who, i,\n",
"Nearest to more: less, most, deicide, faster, toed, very, skye, tonic,\n",
"Nearest to other: different, attackers, joachim, various, such, many, differentiation, these,\n",
"Average loss at step 32000 : 3.49501452419\n",
"Average loss at step 34000 : 3.48593705952\n",
"Average loss at step 36000 : 3.50112806576\n",
"Average loss at step"
],
"name": "stdout"
},
{
"output_type": "stream",
"text": [
" 38000 : 3.49244426501\n",
"Average loss at step 40000 : 3.3890105716\n",
"Nearest to been: become, be, were, was, jolie, hausdorff, spotless, had,\n",
"Nearest to time: year, way, gleichschaltung, period, day, stanislav, stage, outcome,\n",
"Nearest to over: through, semigroup, rawlings, golden, about, brick, on, motorways,\n",
"Nearest to not: they, radiated, never, pki, still, omnipotent, hinayana, really,\n",
"Nearest to three: four, six, five, two, seven, eight, one, nine,\n",
"Nearest to if: when, before, where, then, bg, because, can, should,\n",
"Nearest to there: they, it, he, usually, this, typically, still, often,\n",
"Nearest to between: with, in, from, about, against, churchmen, johansen, presupposes,\n",
"Nearest to from: into, through, elphinstone, in, workshop, between, suing, under,\n",
"Nearest to state: esoteric, presidents, atmosphere, vorarlberg, lute, succeeding, glaring, didactic,\n",
"Nearest to on: upon, at, in, during, unitarians, under, catalans, batavians,\n",
"Nearest to and: or, but, s, incapacitation, including, while, of, which,\n",
"Nearest to eight: nine, six, seven, four, five, three, one, two,\n",
"Nearest to they: we, he, there, you, she, i, not, it,\n",
"Nearest to more: less, most, deicide, toed, greater, faster, quite, longer,\n",
"Nearest to other: various, different, attackers, joachim, clutter, nz, trochaic, apulia,\n",
"Average loss at step 42000 : 3.45294014364\n",
"Average loss at step 44000 : 3.47660055941\n",
"Average loss at step 46000 : 3.47458503014\n",
"Average loss at step 48000 : 3.47261548793\n",
"Average loss at step 50000 : 3.45390708435\n",
"Nearest to been: become, be, had, was, were, hausdorff, prem, remained,\n",
"Nearest to time: way, year, period, stv, day, gleichschaltung, stage, outcome,\n",
"Nearest to over: through, golden, semigroup, about, brick, counternarcotics, theremin, mattingly,\n",
"Nearest to not: they, still, never, really, sometimes, it, kiwifruit, nearly,\n",
"Nearest to three: five, four, six, seven, two, eight, one, nine,\n",
"Nearest to if: when, before, where, because, connexion, though, so, whether,\n",
"Nearest to there: they, it, he, this, now, often, usually, still,\n",
"Nearest to between: with, from, fashioned, churchmen, panasonic, explores, within, racial,\n",
"Nearest to from: into, through, under, elphinstone, between, workshop, circumpolar, idiom,\n",
"Nearest to state: atmosphere, vorarlberg, esoteric, presidents, madhya, majority, moulin, bowmen,\n",
"Nearest to on: upon, in, catalans, tezuka, minotaurs, wakefulness, batavians, guglielmo,\n",
"Nearest to and: or, but, thirst, signifier, which, however, including, unattractive,\n",
"Nearest to eight: six, nine, seven, five, four, three, zero, two,\n",
"Nearest to they: we, there, he, you, it, she, these, not,\n",
"Nearest to more: less, most, quite, very, further, faster, toed, deicide,\n",
"Nearest to other: various, different, many, attackers, are, joachim, nihilo, reject,\n",
"Average loss at step 52000 : 3.43597227755\n",
"Average loss at step 54000 : 3.25126817495\n",
"Average loss at step 56000 : 3.35102432287\n",
"Average loss at step 58000 : 3.44654818082\n",
"Average loss at step 60000 : 3.4287913968\n",
"Nearest to been: become, be, was, prem, had, remained, hadad, stanislavsky,\n",
"Nearest to time: year, way, period, stv, barely, name, stage, restoring,\n",
"Nearest to over: about, through, golden, adaption, counternarcotics, up, mattingly, brick,\n",
"Nearest to not: still, never, nor, kiwifruit, they, nearly, therefore, rarely,\n",
"Nearest to three: two, five, four, six, seven, eight, one, nine,\n",
"Nearest to if: when, though, before, where, although, because, can, could,\n",
"Nearest to there: they, it, he, still, she, we, this, often,\n",
"Nearest to between: with, from, churchmen, among, ethical, within, vma, panasonic,\n",
"Nearest to from: through, into, under, during, between, in, suing, across,\n",
"Nearest to state: atmosphere, infringe, madhya, vorarlberg, government, bowmen, vargas, republic,\n",
"Nearest to on: upon, through, within, ridiculous, janis, in, under, over,\n",
"Nearest to and: or, while, including, but, of, like, whose, bannister,\n",
"Nearest to eight: nine, six, five, four, seven, zero, three, two,\n",
"Nearest to they: we, there, you, he, it, these, she, prisons,\n",
"Nearest to more: less, most, quite, further, toed, very, faster, rather,\n",
"Nearest to other: different, various, many, nihilo, these, amour, including, screenplays,\n",
"Average loss at step 62000 : 3.38358767056\n",
"Average loss at step 64000 : 3.41693099326\n",
"Average loss at step 66000 : 3.39588000977\n",
"Average loss at step 68000 : 3.35567189544\n",
"Average loss at step 70000 : 3.38878934443\n",
"Nearest to been: become, be, was, prem, remained, were, being, discounts,\n",
"Nearest to time: year, way, day, period, barely, ethos, stage, reason,\n",
"Nearest to over: about, through, fortunately, semigroup, theremin, off, loudest, up,\n",
"Nearest to not: still, nor, never, they, actually, nearly, unelected, therefore,\n",
"Nearest to three: five, two, four, six, seven, eight, nine, zero,\n",
"Nearest to if: when, though, before, where, because, then, after, since,\n",
"Nearest to there: they, it, he, often, she, we, usually, still,\n",
"Nearest to between: among, with, within, from, ethical, churchmen, racial, prentice,\n",
"Nearest to from: through, into, within, during, under, until, between, across,\n",
"Nearest to state: city, atmosphere, desks, surrounding, preservation, bohr, principal, republic,\n",
"Nearest to on: upon, tezuka, through, within, wakefulness, catalans, at, ingeborg,\n",
"Nearest to and: or, but, while, including, thirst, jerzy, massing, abadan,\n",
"Nearest to eight: seven, six, nine, five, four, three, two, zero,\n",
"Nearest to they: we, you, he, there, she, it, prisons, who,\n",
"Nearest to more: less, most, quite, very, faster, smaller, further, larger,\n",
"Nearest to other: various, different, some, screenplays, lab, many, including, debugging,\n",
"Average loss at step 72000 : 3.41103189731\n",
"Average loss at step 74000 : 3.44926435578\n",
"Average loss at step 76000 : 3.4423020488\n",
"Average loss at step 78000 : 3.41976813722\n",
"Average loss at step 80000 : 3.39511853886\n",
"Nearest to been: become, be, remained, was, grown, were, prem, already,"
],
"name": "stdout"
},
{
"output_type": "stream",
"text": [
"\n",
"Nearest to time: year, way, period, reason, barely, distance, stage, day,\n",
"Nearest to over: about, fortunately, through, semigroup, further, mattingly, rawlings, golden,\n",
"Nearest to not: still, they, nor, never, we, kiwifruit, noaa, really,\n",
"Nearest to three: five, two, seven, four, eight, six, nine, zero,\n",
"Nearest to if: when, where, though, before, since, because, although, follows,\n",
"Nearest to there: they, it, he, we, she, still, typically, actually,\n",
"Nearest to between: with, among, within, in, racial, around, from, serapeum,\n",
"Nearest to from: into, through, in, within, under, using, during, towards,\n",
"Nearest to state: city, atmosphere, ferro, vorarlberg, surrounding, republic, madhya, national,\n",
"Nearest to on: upon, poll, in, from, tezuka, janis, through, within,\n",
"Nearest to and: or, but, including, while, s, which, thirst, although,\n",
"Nearest to eight: nine, seven, six, five, four, three, zero, two,\n",
"Nearest to they: we, you, there, he, she, it, these, not,\n",
"Nearest to more: less, most, smaller, very, faster, quite, rather, larger,\n",
"Nearest to other: various, different, joachim, including, theos, smaller, individual, screenplays,\n",
"Average loss at step 82000 : 3.40933967865\n",
"Average loss at step 84000 : 3.41618054378\n",
"Average loss at step 86000 : 3.31485116804\n",
"Average loss at step 88000 : 3.37068593091\n",
"Average loss at step 90000 : 3.2785516749\n",
"Nearest to been: become, be, was, prem, remained, grown, recently, already,\n",
"Nearest to time: year, way, period, day, barely, battle, buds, name,\n",
"Nearest to over: through, about, fortunately, off, theremin, semigroup, extraterrestrial, mattingly,\n",
"Nearest to not: nor, still, never, otherwise, generally, separately, gown, hydrate,\n",
"Nearest to three: four, five, six, two, eight, seven, nine, zero,\n",
"Nearest to if: when, where, before, though, because, since, then, while,\n",
"Nearest to there: they, it, he, we, she, still, typically, fiorello,\n",
"Nearest to between: with, among, within, from, churchmen, prentice, racial, panasonic,\n",
"Nearest to from: through, into, across, during, towards, until, at, within,\n",
"Nearest to state: bohr, city, atmosphere, ferro, bowmen, republic, retaliation, vorarlberg,\n",
"Nearest to on: upon, in, tezuka, at, during, within, via, catalans,\n",
"Nearest to and: or, including, but, while, like, thirst, with, schuman,\n",
"Nearest to eight: seven, nine, six, five, four, three, zero, two,\n",
"Nearest to they: we, there, he, you, she, it, prisons, these,\n",
"Nearest to more: less, most, very, faster, larger, quite, smaller, better,\n",
"Nearest to other: different, various, tamara, prosthetic, including, individual, failing, restaurants,\n",
"Average loss at step 92000 : 3.40355363208\n",
"Average loss at step 94000 : 3.35647508007\n",
"Average loss at step 96000 : 3.34374570692\n",
"Average loss at step 98000 : 3.4230104093\n",
"Average loss at step 100000 : 3.36909827\n",
"Nearest to been: become, be, grown, was, being, already, remained, prem,\n",
"Nearest to time: way, year, day, period, years, days, mothersbaugh, separators,\n",
"Nearest to over: through, about, semigroup, further, fortunately, off, into, theremin,\n",
"Nearest to not: never, nor, still, dieppe, really, unelected, actually, now,\n",
"Nearest to three: four, two, five, seven, six, eight, nine, zero,\n",
"Nearest to if: when, though, where, before, is, abe, then, follows,\n",
"Nearest to there: they, it, he, we, still, she, typically, often,\n",
"Nearest to between: within, with, among, churchmen, around, explores, from, reactance,\n",
"Nearest to from: into, through, within, across, in, between, using, workshop,\n",
"Nearest to state: atmosphere, bohr, national, ferro, germ, desks, city, unpaid,\n",
"Nearest to on: upon, in, within, tezuka, janis, batavians, about, macrocosm,\n",
"Nearest to and: or, but, purview, thirst, sukkot, epr, including, honesty,\n",
"Nearest to eight: seven, nine, six, four, five, three, zero, one,\n",
"Nearest to they: we, there, you, he, she, prisons, it, these,\n",
"Nearest to more: less, most, very, quite, faster, larger, rather, smaller,\n",
"Nearest to other: various, different, tamara, theos, some, cope, many, others,\n"
],
"name": "stdout"
}
],
"execution_count": 0
},
{
"cell_type": "code",
"metadata": {
"id": "jjJXYA_XzV79",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
}
},
"cellView": "both"
},
"source": [
"num_points = 400\n",
"\n",
"tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)\n",
"two_d_embeddings = tsne.fit_transform(final_embeddings[1:num_points+1, :])"
],
"outputs": [],
"execution_count": 0
},
{
"cell_type": "code",
"metadata": {
"id": "o_e0D_UezcDe",
"colab_type": "code",
"colab": {
"autoexec": {
"startup": false,
"wait_interval": 0
},
"output_extras": [
{
"item_id": 1
}
]
},
"cellView": "both",
"executionInfo": {
"elapsed": 4763,
"status": "ok",
"timestamp": 1445965465525,
"user": {
"color": "#1FA15D",
"displayName": "Vincent Vanhoucke",
"isAnonymous": false,
"isMe": true,
"permissionId": "05076109866853157986",
"photoUrl": "//lh6.googleusercontent.com/-cCJa7dTDcgQ/AAAAAAAAAAI/AAAAAAAACgw/r2EZ_8oYer4/s50-c-k-no/photo.jpg",
"sessionId": "2f1ffade4c9f20de",
"userId": "102167687554210253930"
},
"user_tz": 420
},
"outputId": "df22e4a5-e8ec-4e5e-d384-c6cf37c68c34"
},
"source": [
"def plot(embeddings, labels):\n",
" assert embeddings.shape[0] >= len(labels), 'More labels than embeddings'\n",
" pylab.figure(figsize=(15,15)) # in inches\n",
" for i, label in enumerate(labels):\n",
" x, y = embeddings[i,:]\n",
" pylab.scatter(x, y)\n",
" pylab.annotate(label, xy=(x, y), xytext=(5, 2), textcoords='offset points',\n",
" ha='right', va='bottom')\n",
" pylab.show()\n",
"\n",
"words = [reverse_dictionary[i] for i in range(1, num_points+1)]\n",
"plot(two_d_embeddings, words)"
],
"outputs": [
{
"output_type": "display_data",
"metadata": {},
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3MAAANpCAYAAAChBGCHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdAldUfx/H3BdlbQEVzoyDukZaae5aZ5tbcIzUz9x5Z\njhwNNXMVztTExFHqT9Ny50hFc+ZKEVBwAbLh/v4gSXILChc/r3+69/Lc53yfewL8cM5zjsFoNBoR\nERERERERk2KW0QWIiIiIiIjI01OYExERERERMUEKcyIiIiIiIiZIYU5ERERERMQEKcyJiIiIiIiY\nIIU5ERERERERE5TmMBceHk7fvn1p2LAhb775JgEBAdy6dYvOnTtTv359unTpQnh4eHrUKiIiIiIi\nIv8wpHWfuaFDh/Lqq6/SvHlzEhISiI6OZvbs2bi4uNC9e3fmzZtHeHg4gwYNSq+aRUREREREXnpp\nGpmLiIjg4MGDNG/eHIBs2bLh4ODAtm3baNq0KQBNmzbll19+SXulIiIiIiIikiJbWt4cGBhI9uzZ\nGT58OKdOnaJ48eKMGDGC69ev4+bmBoCbmxvXr19Pl2JFREREREQkWZpG5hISEjhx4gRt2rTB398f\nGxsb5s2bl+oYg8GAwWBIU5EiIiIiIiKSWprCXK5cuciZMyelSpUCoH79+pw4cQI3NzdCQ0MBuHbt\nGtmzZ3/kedJ4256IiIiIiMhLJ03TLN3d3fHw8ODChQsULFiQvXv34unpiaenJ/7+/vTo0YM1a9ZQ\np06dR57HYDAQGhqRllIkE3N3d1D/ZmHq36xLfZu1qX+zLvVt1qb+zbrc3R2e+j1pCnMAo0ePZtCg\nQcTHx5MvXz4mTZpEYmIi/fr148cffyRPnjx89dVXaW1GRERERERE7pHmMOft7c2PP/543+sLFy5M\n66lFRERERETkIdK8abiIiIiIiIi8eApzIiIiIiIiJkhhTkRERERExAQpzImIiIiIiJgghTkRERER\nERETpDAnIiIiIiJighTmRERERERETJDCnIiIiIiIiAlSmBMRERERETFBCnMiIiIiIiImSGFORERE\nRETEBCnMiYiIiIiImCCFOREREREREROkMCciIiIiImKCFOZERERERERMkMKciIiIiIiICVKYExER\nERERMUEKcyIiIiIiIiZIYU5ERERERMQEKcyJiIiIiIiYIIU5ERERERERE6QwJyIiIiIiYoIU5kRE\nREREREyQwpyIiIiIiIgJUpgTERERERExQQpzIiIiIiIiJkhhTkRERERExAQpzImIiIiIiJgghTkR\nERERERETpDAnIiIiIiJighTmRERERERETJDCnIiIiIiIiAlSmBMRERERETFBCnMiIiIiIiImSGFO\nRERERETEBCnMiYiIiIiImCCFOREREREREROkMCciIiIiImKCFOZERERERERMkMKciIiIiIiICVKY\nExERERERMUEKcyIiIiIiIiZIYU5ERERERMQEKcyJiIiIiIiYIIU5ERERERERE6QwJyIiIiIiYoIU\n5kREREREREyQwpyIiIiIiIgJUpgTERERERExQQpzIiIiIiIiJkhhTkRERERExAQpzImIiIiIiJgg\nhTkRERERERETpDAnIiIiIiJighTmRERERERETJDCnIiIiIiIiAlSmBMRERERETFBCnMiIiIiIiIm\nSGFORERERETEBCnMiYiIiIiImCCFOREREREREROkMCciIiIiImKCFOZERERERERMkMKciIiIiIiI\nCVKYExERERERMUEKcyIiIiIiIiZIYU5ERERERMQEKcyJiIiIiIiYIIU5ERERERERE6QwJyIiIiIi\nYoIU5kREREREREyQwpyIiIiIiIgJUpgTERERERExQQpzIiIiIiIiJkhhTkRERERExAQpzImIiIiI\niJgghTkRERERERETpDAnIiIiIiJighTmRERERERETJDCnIiIiIiIiAlSmBMRERERETFBCnMiIiIi\nIiImSGFORERERETEBCnMiYiIiIiImCCFOREREREREROULaMLEBERkcxnxYqlbNiwHoBGjZpQrVoN\nBg78kFKlyvLnnwG4u+dg0qTPsbKy4sqVQL74Ygq3bt3E2tqaoUNHki9fgYy9ABGRl4BG5kRERCSV\nU6dOsnHjT8yfv4i5cxeyfr0/ERHhBAZeplmzlixZshJ7ewe2b98GwJQpE+jffzDffbeE3r0/4vPP\nJ2fwFYiIvBw0MiciIiKpHD16hGrVamJlZQ1A9eq1CAg4jIdHHjw9iwDg5eVNcHAQ0dHRHDt2lNGj\nh6a8Pz4+IUPqFhF52SjMiYiISCoGg+GBr1taWqQ8NjMzJykpDqMxCQcHBxYsWPaiyhMRkX9omqWI\niIikUrp0GXbs+I3Y2Biio6PZseNXSpcue99xRqMRW1s7cufOza+//pLy2tmzf73okkVEXkoamRMR\nEZFUihb15s03G9G9e0cA3n67KQ4OjveN2N19PmbMeKZN+4xFi3xJSEigTp16KdMxRUTk+TEYjUZj\nRhcBEBoakdElyHPi7u6g/s3C1L9Zl/o2a1P/Zl3q26xN/Zt1ubs7PPV7NM1SREREntnx4+eYP38j\nf/xxMqNLERF56SjMiYiIyDNZt24/LVpEM3JkC1q1smLhwu0ZXZKIyEtFYU5ERESeyeLFNwgLex0w\nEB5emqVLYzK6JBGRl4rCnIiIiDwTo9HwyOciIvJ8KcyJiIjIM2nd2gEXl0MA2NmdpkULLZItIvIi\n6aeuiIiIPJMWLSpToMAJ9u3zo2TJXFSvXiujSxIReakozImIiMgze/VVH1591SejyxAReSlpmqWI\niIiIiIgJUpgTERERERExQQpzIiIiIiIiJkhhTkRERERExAQpzImIiGSAyMhI/P1XZXQZIiJiwhTm\nREREMkBERDj+/n4ZXYaIiJgwbU0gIiKSAebMmcmVK4F07tyWIkW8qFatJlWrVmP48EE4OjoyfPgY\nfvppLUFBV+jRozcrVixlw4b1ADRq1ISWLdtk8BWIiEhG08iciIhIBujVqy958rzCggXLqFTpdY4e\nPQxAWNg1/v77IgBHjx6hbNlynDp1ko0bf2L+/EXMnbuQ9ev9+euv0xlYvYiIZAYKcyIiIhnAaDSm\nPC5VqgwBAUe4ePECBQsWxsUlO9evh3H8+DFKlCjN0aNHqFatJlZW1tjY2FC9ei0CAg5nYPUiIpIZ\naJqliIhIBnN3z0FkZAT79u2hdOmyhIeHs3XrFmxtbbGxscFgMKQ63mg03veaiIi8fDQyJyIikgFs\nbW2JiopKeV68eElWrlxOmTLlKF26DCtWLKVUqbIAlC5dhh07fiM2Nobo6Gh27vwt5WsiIvLy0sic\niIhIBnBycqZkydJ06NCK116rTKlSZThwYB958rxCzpy5iIgIp3Tp5MBWtKg3b77ZiO7dOwLw9ttN\nKVKkaEaWLyIimYDBeO+k/QwUGhqR0SXIc+Lu7qD+zcLUv1mX+jbzuHr1KsHBoXh7e2JtbZ0u51T/\nZl3q26xN/Zt1ubs7PPV7NM1SREQkE/P13U61apepV8+DRo02cflySEaXJCIimYTCnIiISCYVHx/P\nrFnx3LxZEyjA0aPt+eKLgxldloiIZBIKcyIiIplUXFwcUVH2qV6LibHMoGpERCSzUZgTERHJpOzs\n7Kha9W8gGgBHx8M0bOiUsUWJiEimodUsRUREMrHZs5tRvPhPhIVBzZq5qF27UkaXJCIimYTCnIiI\nSCaWLVs2+vVrkNFliIhIJqRpliIiIiIiIiZIYU5ERERERMQEKcyJiIjIA02ePJ6LFy9kdBkiIvIQ\numdOREREHmjo0FEZXYKIiDyCwpyIiMhLIDo6mjFjhhEaGkpSUiIfftgHBwc3vv76S6Kjo3FwcMBo\nNBIaGsrVq8GMGPEx/v5+tG79Ht98M4OkpCQGDRrGwoXfcvr0SfLnL8DkyV/i6upGnz49KF68JIcO\nHSQyMoJhw8ZQunSZjL5kEZEsT9MsRUREXgL79u3BzS0HCxcuY/HiH6hWrRrTp09lwoQpfPfdEgoX\n9uTatWssW7aKfPnyU6BAAQwGAwcO7KNBgzdp2/Y9xowZTrly5alf/03atGnPvHnfAGAwGEhKSmL+\n/EX07TuQBQvmZfDVioi8HBTmRETkpRcZGYm//yoADh06yJAh/TO4ovRXuHARDh7cx+zZMwkIOEJQ\nUBDnz5+jX7/edO7clj17dnPtWgizZ8+kWLES7N27G4CDB/dRu3Y9SpQoxZ07kSxZspBjx46yeLEv\noaGhKeevXr0mAF5e3oSEBGfINYqIvGw0zVJERF56ERHh+Pv70bRp84wuBUgOl1u2bKJp0+YcOnSQ\nFSu+Z8qUL9N0zrx58+Hr+z179+5i/vxveOONKhQsWJg5c3xTjomIiGDv3l34+a1g9+4d5MiREzCQ\nJ88rnDhxnGzZsuHunoMvvpiJq6tbqvNbWFgCYGZmTmJiYppqFRGRJ6OROREReenNmTOTK1cC6dy5\nLbNnzyA6OopRo4bSrl1zPvlk9Auv5264fBpJSUmP/HpYWBiWlpbUq9eQNm3ac/ToUW7dusWffx4D\nICQkhKCgK9Sr15BOnboRGxtLSEgwFSu+BsDGjeuwsrKmXr03mTx5AgkJCVy4cP7ZLlBERNKFRuZE\nROSl16tXXy5cOM+CBcs4fPgPhg8fyNKlfri6utGrV1eOHj1CqVIvbkGPe8NltmzZsLa2YdSooVy4\ncA4vr2KMGfMpAM2bv03t2vU4cGAf7dp1wMHBEV/fecTFxZEnzyuMGDEWGxsbTp06ycSJ47hy5TLm\n5ubkyZOXyZMncft2DNOnTyMyMpLIyAgSExNxdnYmWzYLGjZshJ/fcl59tRKHD//BX3/9xfTp3zB9\n+uf89dcZWrR4m65d36dgwUIPuALDC/usREReZgpzIiLy0jMajakeFytWHDc3dwA8PYsSEhL8QsPc\n48LlsWMBlCxZGoPBgJOTM76+S7l16xajRg1h+vRvsLKyZunShYwePYzg4CvcunWLZctW4eTkzNat\nm9m//3eKFy9OaGgEX3/98MVKPvpoIJA86jdt2nTs7R0eePzMmXNTHjs7O+Pntzb9PxQREbmPwpyI\niMh/3L3/C8Dc3OyF3wP2uHAZHBxMyZKlAahduy4Ax48f4+LF8/Ts2QWA+PgEwsKuMWHCVEaMGES/\nfr2B5GDm6ur+xLVs3nyETz4JJCzMHR+fv5k3rw5ubtn/aSOedet2YzQaady4CpaWlo85m4iIpCeF\nOREReaiFC79l8+aNODu7kCNHTry8itGmzXsZXVa6s7W1JSoqKqPLeKj7w2VCynMbG5uUxxUqVOLj\njycAMHXqRDZsWM/UqZNwcHAkVy4PgoKCuHPnDtHR0VSsWJEiRbyoVKlySp+2b9+SqVNnYDQmMWBA\nH4oXL8mmTfs5f96PhAQPdu0yMn7893z11TvEx8fToYMfW7e2BQysWLGM779/FysrqxfzoYiISPos\ngJKYmEiTJk3o2bMnALdu3aJz587Ur1+fLl26EB4enh7NiIgIEBwcRLt2zZk8eQLt27dkwIA+xMbG\npns7R48eZfv2bSxatIJp02Zw6tRJDFn0VignJ2dKlixNhw6tmD17RoZf57OESx+fEhw7FsCVK4EA\n9OnTH2dnF775Zj4RERE4O2dn0aLlJCUlYWZmxv79+++bOmq458KvXAnknXfe5fbtYSQkeNw9gtu3\nbQHw89vO1q0dAAfAnh07OrFs2fZnvWQREXkG6TIyt3jxYgoXLsydO3cAmDdvHpUrV6Z79+7MmzeP\nefPmMWjQoPRoSkREgMDAy4wbN4mhQ0cyZsxwtm/fRr16DdO1jUOHDvHGGzWwsLDAwsKCKlXe4J7Z\nf1nO2LHjH/h6//5DXnAlqcOllZUV2bO7PvY9Li4ujBz5MR9/PIK4uHgAEhISMDc3x9XVjbNnz/Dm\nm7UJD7+NmZkZc+fOZe/e3VStWo3mzd9m1ar1AMTGxtC3b09y5sxF9uyu5Mo1HisrX5KSbLh+/UMq\nVkwOfPHxRlL/M8Kc+PhHr6gpIiLpK81hLiQkhO3bt9OzZ08WLlwIwLZt21i6dCkATZs2pX379gpz\nIiLpyMMjD56eRYDkTZqDg4PSvQ2DwZDq3i3IwknuH7Nnb+P77+NJTDTn3XcTGDy4QYbV8iTh0s9v\nXaqvlStXgfnzF6c8b9GiMVFRUZiZGRgz5lPy5s1HixaNSUhIwMnJCTMzAxYWFhQpUpRDhw4SFxfH\nwYP7KVOmHBcunGPKlAnMmjWeRYv+4tKlq0RHf0rPnsv/OXcV/PwWs39/J8BAuXILadv2zXT/HERE\n5OHSPM1y4sSJDBkyBDOzf091/fp13NySNxN1c3Pj+vXraW1GRETuYWlpkfL4eW3SXK5cOXbv3klc\nXBxRUVHs2bMrw6cfPk8HDhxn6tTCnDnTnHPnmjJjxqts3Lgvo8t6qMGDP+LOnchHHnPt2jUaNVrP\n0aNedOz4FZcvhxAbG4u1tTUXLlzA1taO06dPUatWXVavXklwcBC7du2gcuU3SEpK4tixo0yaNI6g\noGVky7YVa+uklKmYtra2/PDDW3z88Y+MHbsKP7+G2Nvbv4hLFxGRf6RpZO7XX3/F1dUVHx8f9u17\n8C88g8GQag7+w7i7O6SlFMnk1L9Zm/r3xYqNtSNbNvOUz93e3gozs8R07wd395LUr1+XLl3a4ubm\nho9PMXLlcsuy/X3hQiiRkZVSnsfGFiAo6Gimvd6FC30f+XWj0UhiIoSFVSE21gczsxF07dqNhIQI\nmjdvxrFjx/D0LMTly5dZunQBwcHB5MuXj7//Pk/16q+zfPkinJwc+emn9Q9tw93dgbFjW6b3pUk6\nyKz/30r6UP/KXWkKc4cPH2bbtm1s376duLg4IiMjGTx4MK6uroSGhuLu7s61a9fInj37Y88VGhqR\nllIkE3N3d1D/ZmHq3xfvxo07JCYmpXzukZGxxMTEpXs/uLs70LhxS1q16khMTAx9+vSgdeuCWba/\ny5cvjIfHbwQH1wTA1XU/ZcrkzhTX+7//bWDVqh9ISIjHx6cEAwYMpVWrJvj6LsXR0emBq462aNGa\nhIT82Nntxs3tC8zNw8mevTEJCetZvdqf6OgoTpw4ycCBw6hVqw6jRw/D0tICOzt7rK2dWbhwBb16\ndWHlSn9q1qyD0Wjk3LmzKdN7JfPSz+WsTf2bdT1LSE9TmBswYAADBgwAYP/+/fj6+jJ16lSmTJmC\nv78/PXr0YM2aNdSpUyctzYiICBAXF8fhwydwdXVk0aIVKa+n91YBcXFx/PzzXlxd7dm2bTV//32B\nuLg4GjZsRJEiXunaVmZSuHBepk+/yXff+WE0GmjdOjvly7+a0WVx8eIFtm3bwpw5vpibm/P555PZ\nvHljyqyXkyePp6w6Gh8fT5cu7+HtXYxs2bLh6BhHeHgcly/74ez8A0lJSzAYzOjQoTO//76L3Lnz\nUqtW8u/omjVrM2bMCF55pRtjxqxn5Mh6jBkznmnTPmPRIl8SEhKoU6eewpyISCbyXPaZ69GjB/36\n9ePHH38kT548fPXVV8+jGRGRl0ZERAStWn1HaOgerl79mM6d/Tl/fjmffPIZBQsWSrd2YmJiaNvW\nn1272gLxNGhwmgULPsHc3Dzd2sjMatQoRY0apTK6jFT++GM/p0+folu39kDyfXDR0cnbFhiNRo4d\nC7hv1dG7ihZ1p2xZC+LjV1GqlBmbNsWwYsVaNmxYT6FChejZs1/Ksb/9FsOZM39w5owd27bFcePG\nMr7+uhmffz7jxV6wiIg8sXQLcxUrVqRixYoAODs7p6xsKSIiaTdjxg4OHhyJq+sM7O1/Y+3aS3Tv\nXjVdgxzAokW/sWtXZyB5gZVNm1qxfv0umjSpnq7tyNNp2LAR77//QarXWrRo/M+jh686ajAY6NKl\nBl5e3ty6dYuff/7moW0cOWIN2P3zzJJDh+wYMuQn4uKy8e67r1CtWon0uBQREUlH6bJpuIiIPF8x\nMeaAGdevf4Cd3W6yZbtMzZr10r2d+/cOsyImJiHd25HHu7s5/OHDh1i+fCkffvg+sbGxjB07An//\nVQB07tyOCxfOsWzZYjp0aMWZMyfZs2cX8fHxTJw4jtOnTzJu3Eh27Uq9mbednV3K3rB3ubqm3qQ8\nOPgKCxe2YdmyFvTuncDBg6ef7wWLiMhTU5gTETEB775bmNy5t2BufhODIQp7+zDy5Xsl3dtp1+51\nSpVaTPLoTgKvv76UJk2qpHs7mcXKlcuIjY3J6DIeKjDwMp06dWP06E/4668ztG37LgcP7vtnS4Lk\n1aI9PYvSrl1Hbt68yaBB/Shc2JOAgCNUqFARL69iDB48glmzpv9zncn32ZUtW4GzZ8/SuXNbtm37\nBYCxY1/l9dcX4e6+gcKF53DnzuspdVy79gb/+9+FDPgERETkUZ7LPXMiIpK+ypYtwqJF8PHH3cmf\n/zVKlnRm/vxvUm0gnR5cXJzx86vFkiWrcHKyokWLxlhbW6drG5mJn98K6td/EyurzHmNdzeH9/Qs\nQkhIEAkJCVy5EkjevPnw81tLixaNqV69FnZ2dlSqVJk5c2YSEhJCdHQ0S5cuxNzcnBkzPic+Pp7Y\n2Bj8/NYC4OjoyKpVq1KtiFegQG7Wrn2XuLg4LlzITf36iUSlDNZF4eqqv/+KiGQ2CnMiIiYiKOg0\nxYvnYfz4oSQlJdGzZxcOHTpIuXIV0rUdFxdn+vZtkOWWv46OjmbMmGGEhoaSlJRIzZp1CAsLpW/f\nnjg7uzB9+uyMLvE+928OH/vAY6ZMmcCpUye4du0anTt349dft/LxxxPImzcfAElJSQwe7M/Oneew\ns4ulf393unat9ZA2LfHyKkyfPv9jwYJQYmIcqFnzBN26NX8+FykiIs9MYU5ExEQ0bNiIhg0bAWBm\nZsa8eQsztiATs2/fHtzccjB16nQA7tyJZMOG9cycORdHR6cMri5txo4dz6lTJ5g1azrvvdeJO3fu\nsGrVipSR2wkTFrNkSUfAEYAxY36mWbNbwMNXKR00qD49e0YQGxtH9uwlU7ZCEBGRzENzJkREMrmp\nUzdRpcoWqlX7H99++1tGl2OyChcuwsGD+5g9eyYBAUews7PP6JIe6+kClCHl+E6dupGQkEDHjq1p\n374lBw78wt0gBxAUVIRLl4Iee0Z7ewdcXV0V5EREMimDMfV6xhkmK03lkdSy2lQtSU39+3z9/PM+\nevb0JDa2AAAODkdYtSqesmW9n3vbaenbjRt/YsWK7zEYDBQu7Mno0Z88cx11677Bli07n/n994qI\niGDv3l2sW+dP+fKvsmHDer77bonJj8w9zurVe+nXz5OYmOStLHx8fuDgwcZERmql0qxIP5ezNvVv\n1uXu7vDU79E0SxGRTOzMmZspQQ4gIqIkR4+ufiFh7lmdP3+OxYt9mTt3AY6OToSHh6fxjOkzKhQW\nFoaDgwP16jXEzs6en35ai61t8hL9WSXMHT78FzNmnCEmxoIGDazo2DF5f8B3332d69e3sm3bYWxt\n4xg4sDg2NjZERuofhCIipkxhTkQkE6tcOR8uLge5eTN5kZPcuX/L9Js3Hzp0gFq16qYEJEdHx8e8\n48U4f/4ss2ZNx8zMQLZsFgwaNJw//wxg4MAPcXfPkSkXQHmQNWt+ZO3aHwGIjIzEwyM37dt3Yt68\nbzhx4haRkaUICZnE3r2XWbmyHo0avc2BA/to164DBQoksXTpUj77zMiBA7Xo2PH9DL4aERFJC4U5\nEZFMrFIlHz777Hf8/FZhZmaka1cPChZM//3l0pPBYCCTzOBPpWLF16hY8TWMRmPKKJ2XlzfNmrXK\n6NKeSpMmzWjSpBkJCQl89FEv3nqrMYsW+dK2bS9atSqBi8tPuLgs4MaND4iNTcLJyRlf36WEhYXy\n/vud8fVdir29A0OHfsTOnb/xxhs1MvqSRETkGWkBFBGRTK5p09dYtqw+S5c2oGbN0mk6V3BwEB06\nPN/wUq7cq/z66y+Eh98GSPlvZhAREUHLlj9QqVIIlSvv5vvvd2d0Sc/sq6+mUb78qzg4OHLx4nl8\nfb+kUKH2ODquxcIiGIPhOtmyGahduy4AJ08ep1y5Cjg5OWNubs7bb7/NkSOHM/gqREQkLRTmREQk\nXRUsWIgOHbrQp08POnVqy9dff5XRJaWYMmU727d3JTKyMoGBTZg2LYbo6OiMLuupbdiwnmvXrtKl\nSw+MRiMVKlRiyZKVDBw4DHv7jtjbV6Br1w04ONhgY2MD3D9imhlHT0VE5OlomqWIyEvqypVARo8e\nypAho/D2Lpau5753TzyAFSuWsmHDegAaNWpCy5Zt0rW9J3X7tgX3/h3z5s1cREREpAQeU3Dq1ElW\nrFjKrFnfAuDjU4IvvpjMlSuBtGjxGo0aRRMWFkrevPlo0cI35X3e3sX56qtp3L59C3t7BzZs2EDj\nxtoIXETElCnMiYi8hC5dusjHH49k5MhxFC7smebzrVq1h3XrIrGwSKBPnyKULVsk5WunTp1k48af\nmD9/EUlJRnr06EjZsuUoUsTric6dnnuc1azpxLp1J4iK8gGSKF/+GO7upnXP3OrVK4mIiKBv3+TF\nS7y9fRg58mM+/ngEcXHxAPTo0Zu8efOlep+bmxs9e/ahb9+eGI1G6tSpTdWq1V54/SIikn60z5w8\nd9oPJWtT/5oGP78VrF37I/ny5ePYsWM4OjoyceI08ucv8ND3PGnf/vbbUbp1syM8vAwAhQqtYePG\ncri4uACwcuVyIiLC6do1OXx8++0cnJ2dad68ddov7Bn4+//Otm23cXSMY+jQ6plmtc0XTd+7WZf6\nNmtT/2Zd2mdOROQldvdvcw8ayVqzZhXTp88mPj6eAQP6kDOnBwEBhx8Z5p7U7t1BhIe3SHl+/nx1\nfv99Hw0bVnlgPUaj8YE1nj79N7NnHyc+PhvNmuWkVq20LfbyME2bvkbTps/l1JnW5s2HmTs3hPh4\ncxo3tqBbt5oZXZKIiKQDLYAiImLCgoODaNPmXcaPH0uHDq24du3qfcdMnTqRoKArDBz4IT//vBYL\nCwsmTpzXjaYmAAAgAElEQVTKpk0/s2XLpjTXkC+fNWZmoSnPnZ1PUKxY3pTnpUuXYceO34iNTV5s\nZOfO3yhVqmyqc9y6dYuuXU+ybFkr/Pya8eGHBg4ePJ3m2gQCA4MZPDiOnTtb8vvvzZgwwZv//e+P\njC5LRETSgUbmRERMXPJCJp/g4/PgzcQHDx7B/v2/M3PmXO7cucPOnduxtrZmypSv6N+/N7a2dlSp\n8sYzt//ee9U5eXINmzc7YmWVQI8eNhQoUCrl60WLevPmm43o3r0jAG+/3ZQiRYqmOseOHcc4c6ZB\nyvPQ0Cps3epHhQpPdl+dJNu1awcXL57nvfc68d13c7G1tcPK6hWSkrZjb59IZGR97O0Xs3OnB++9\nVyOjyxURkTRSmBMRMXE5c3o8NMjd6/btW5iZmbNgwTIA7O3tmT9/cZrbNxgMTJzYlAkTHjx9EqBV\nq3a0atXuoecoVCgXtrbniIoq8885b5Ejh0Waa3vZVK1aLWVRE4PBgMEA5cp5Ym29mjt3kvvm9u1u\nvPba2YwsU0RE0onCnIiIibOxsX7sMeHh0dSvf5bIyLxUqfIDCxY0xdr68e97Gg+6N27t2l1cu3aH\nd96pQM6cbg99b4kSRejXbwsLFvxNfLwN9epdoWPHd9O1vsfp1asLs2f7PvTrdeu+wZYtO19gRakF\nBwcxcOCHlChRimPHAvD29qFhw0YsWDCPmzdvMXbsp1y4cJ7Tp0/Sv/8QAIxGKFDgFcqVS+L8+d0Y\njZE4OMzD0/MTALZs2cTSpQsxGo28/npVevX6MOVaW7Row549u7CysuKzzz7HxSV7hl27iIg8mO6Z\nExHJ4kJCgrl924wbN2oQE1OerVs7M336tufaptFopF+/H+nZsyKjRjWnWbODnD8f+Mj39OtXlwMH\nqnLgQCm++qo5ZmYv9lfUo4JcsvTbIuFZXbkSSOvW77Fs2Y9cuvQ3W7duZvZsX/r0+YjFixc8dGQ0\nf353Ro0qxy+/1OWVV7JjMBi4evUqc+Z8zYwZc1iwYBmnTp1g587fAIiJiaFEiVIsXLiM0qXLsm6d\n/wu8ShEReVIKcyIiJu5x+7CFhd0iKeneiRgWREQ83x//gYGB+PuXIinJDTBw5kwLvvsu4LHvs7S0\nxM7O7rnW9jB16ybfNxgWFsYHH3Snc+e2dOjQiqNHj6QcM3PmF7Rv35KPPurNrVu3AOjTpwezZ8+k\ne/eOtGnzLgEBRx54/vTg4ZGHQoUKYzAYKFiwEBUqVASgYMHChIQEPfF5jEYjx44do2zZ8jg5OWNu\nbk7dug04cuQwABYWFlSuXBUAL69ihIQEp//FiIhIminMiYiYmIiIcE6dOk1UVBQeHrlZtGjFA4+7\ndu0aoaGhFC1amBw5OpKU5ASAq+teGjTI+8D3pJcHbWFqNGb8yNajJde3ZcsmKlV6nQULlrFw4XI8\nPZMXa4mJicbb24clS1ZStmw5FiyYl/wug4GkpCTmz19E374DU15/Hiwt/72P0MzMDAsLi5THiYmJ\n91/RIz7y+/8I8O89j+bm/4Z/MzPDA88tIiIZT2FORMSEbN58hJo1/6BaNUfq19/B4cN/3XeM0Wik\nf/9VVKp0lddeC2LUqJ9ZtKgO77+/gg4dVjF7dhJVqxZ/rnXmzZuXd94JwGC4ARjx9PyRrl1LPtc2\n04uPT3E2bFiPr+88zp07i62tLZAcmGrXrgdAvXoNU43YVa+evG+bl5d3phnFMhqNPCBTA8lBrlSp\nUhw5cojbt2+RmJjIL79spkyZci+2SBERSRMtgCIiYkK+/PIKly61BuD06aJMm7aC778vkuqY1at3\nsHx5Y5KSXAFYssSTGjUC+PTTRg88Z3BwEEOH9mfx4h/SrU6DwcCMGc2pXn0H169H8/bb5cidO0e6\nnf95Kl26LLNmzWfPnl1MnPgxrVq1o0GDt1Id89+Nzy0sLAEwMzN/rqNY/x1Ne9AU27uv3V3N8mHc\n3d3p2bMPffv2xGg0UrnyG6lWwnxUGyIikjkozImImJA7d6xSPY+KsrzvmKtXo1KCHEBiYg6CgyOe\ne23/ZTAYaN68+gtvN61CQkJwd3fn7bebEBcXy19/naZBg7dISkri119/oXbtemzZsum+jc+ft/9O\nqR0xYmyqr90N4w0bJof2Ll16PPDYmTPnpjyuU6c+derUT9XO7du3+PbbxSQmJmJubk6NGrWpUaN2\n+l6MiIikC02zFBExIVWrRmIw3ATA0jKQGjXun0fXqFEZChZcl/Lc03Mtb7316OlzSUlJTJ48gfbt\nWzJgQB9iY2PTt3ATcHcE6vDhg3Tu3JYuXdrx669badGiDQDW1jacOHGcDh1acfjwITp37vawMz1V\nu8HBQXTo0CotpaebefN+o3LlE1SunEiLFquIiHjxfwQQEZEnZzA+6C71DBAaql8YWZW7u4P6NwtT\n/75YRqORefO2cvFiEqVK2dKmTdUHHnfixAUWLjwFGOnWrQRFi+Z76DmDg4No3bop3323FE/PIowZ\nM5yqVavRrl1L9e0L8DymuT6J/37vhoff5vXX/yQ0tME/ryTRq9cPjBv34Om5knnp53LWpv7Nutzd\nHZ76PZpmKSJiQgwGA++/X+exx/n4FGTKlIJPfF4Pjzx4eibfe+fl5U1w8JMvc/8y+vvvYEaO3E9Q\nkB1Fitzm88/rY29vn+bzXrkSyOjRQ6lTpwHHjh0hJiaGwMDLtG7djtjYOH75ZRMWFpZMnTodR0fH\ndLiSf0VERBAefu99jWZERlo89HgREcl4mmYpIiL/WfL++S7ikRUMGbKPzZvf488/m+Lv34FRo35J\n8zkvXbrI6NFDGTlyHM7Ozly4cJ6JE6cxf/5i5s37Bjs7O3x9v6dEiZJs2vRzOlxFah4eualU6Q8g\nue+dnf+gfn33dG9HXi6DB3/EnTuRjzxm8WLfF1SNSNajMCciIvKULl26dyqMGZcvp21U7ubNmwwf\nPoixYydQuLAnAGXLVsDGxgZnZ2fs7R2oUiV5pclChTyfaoPwJ2VmZsbChY3o08ePjh1/ZNasKOrV\n01YFkjZTp07Hzu7R3x9Llix8McWIZEGaZikiIk+05L38q0CBcM6dM5K82EkCBQs+euThcezt7cmZ\n04OAgMPkz18Ag8Fw3wbhd58/bIPw9GBvb8+YMW89/kB5KURHRzNmzDBCQ0NJSkqkY8duODk58c03\n00lMTMTb24dBg4bzxx8H+PnndXz66WcAHDp0kBUrvmfKlC9p3vxtfH2X4ujoxP/+t4FVq34gISEe\nH58SDBw4jLlzZxEXF0vnzm0pVKgwo0d/msFXLWJaFOZERF5y/13yvk2b915Y2w/6x52ZWeafNPLF\nF1UZOXIpwcH2FCkSzqefNkzT+SwsLJg4cSoDBvTBxsbmkcdmknXL5CWwb98e3NxyMHXqdBYu/Jb5\n87/h6tUQXn21EmXLVuDYsQA6dWqDlZU1Fy6c4+zZ03h6ejF16iRy5MhBjx6diIgI54svpmA0JrF/\n/+/Y2zswfPgYpk6dyLvvvknFiq9jaWnFggXLmDbtM7p160BsbAw1atSma9f3AWje/G0aNmzE7t07\nSUxM4NNPPyNfvgIZ++GIZBKZ/zemiIg8F3fu3GH9+p0cOHAsQ9q/ePEC27ZtYc4cXxYsWIbBYMbm\nzRszpJan5eHhjq9vEzZurMOMGe8+NoA9jsFgwNramilTvmLlymXcuRP5n9HR1Jt4a+RUXoTChYtw\n8OA+xo8fy6ZNPzN27AS8vX24dOkSAMHBweTMmQtf36W89loVxo0bTUJCAqGh17CwsGDu3AU4OjoB\nEBh4GSsrawA++qg3CQkJNG78LufOncVoTAKgR4/efPvtYhYuXM6RI4c4f/4skPz/vLOzC76+S2nS\npDnLly/NgE9DJHPSyJyIyEvo2rXrtGu3nYCAd7G0DKFTp3WMH9/4hdbwxx/7OX36FN26tQcgNjYW\nV1fXx7wr67l3ZNTe3p758xffd4yf39qUxw0bNkrZGFzkecqbNx++vt/z5ZdTSEhI4Pffd2Nubk6V\nKm8QFxfLxYvnCAqyonPntkRFRXHz5g0OHz6Ik5MTderUT/VHh0KFPKlY8XUaNXqHgQP7smLFagCC\ngq5w4cJ5ALZt28y6dWtITEzk+vUwLly4QKFCyfeQVq9eC4CiRb3Zvn3bC/4kRDIvhTkRkZfQrFl7\nCQjoABiIi3NgyZLr9O59hdy587zQOho2bMT773/wQts0Fdu2HWXSpEvcvGlD+fI3mTHjbaysrDK6\nLHmJhIWF4eDggLe3D0lJifz55zFCQoLJk+cVHBwcMDMzo3v3njRv3prExERat27KunVryJ07D9bW\n1qnOVaRIUVavXkX16rWwtLQgPPw2UVHRmJmZYW5uxuXLl1ix4nu+/XYJ9vb2TJw4jri42JT3371n\n1Nz8+d0zKmKKNM1SRMTEzJnzNatX+6U8/+67uU897Sg+3px7p+7Fx9sRHR2TXiU+kfLlK/Lrr1u5\nefMmkLxpdUhIyAutIbNKSEhg1KhAAgLacOlSE/z92zFlypaMLuup1K37RkaXIGl0/vxZevTohL+/\nH7t27aBz5+707z+EzZs34u+/CltbW5ydXYDkhXl8fEqwb99ecuTIec9Zkn/O5MiRk+7dezF+/BgC\nAy/Tv38fbtwIA6BChUoMHPght2/fws7Ojhs3rvP773te9OWKmCSFORERE1O7dl22bfv3H/a//rqV\nOnXqPdU52rQpQt68d+9Pi6Zu3T0ULPjkm4ynhwIFCtK9ey8GDPiAjh3bpPrH3cvu9u3bXL36yj2v\nWBISYplh9Twb3ddn6ipWfI1Fi5azfPlq2rbtwIQJY/nss08pWtSL7t17Mm/eIjZu/JlOndrSvn0r\nChYsxObN2zE3N0+ZYunntxZLS0sMBgO1a9dl6tTp5M2bj+++W4KPTwkAGjR4k5Ur1/LGGzVo27YZ\n48aNplSp0g+pSveMitzLYMwky2KFhkZkdAnynLi7O6h/szD1b8Z4770WfPXVbG7evMEXX0xm9uzv\nnvocp0//zdq1J3F2NqNLl1pky5Z65n16922vXl2YPfvBmwPfu5S5JK9Y2ajRjxw40BkAc/MQPvlk\nH92710q3Np73927dutXYsmUHUVFRDB8+iIiIcBITE+jevRdVq1YnODiIQYP6UqpUWf78MwB39xxM\nmvQ5VlZWnDx5nM8++xQzMzMqVKjEvn17WLz4BzZsWM/p0yfp338IAEOG9KNNm/aULVueadM+49Sp\nE/ethLh37y6+/vorrK1tKFmyFEFBQUyZ8iXR0dF8+eUULlw4T2JiAl269KBq1eqcP3+OSZM+ISEh\nnqQkIxMmTOGVV/I+t8/peXjSvk1MTMTc3PyJzhkdHY2NjQ2ffjqGY8eOMmHCZIoU8Xqm+vbsOcGm\nTZdwdjbywQe1NH34Ken3btbl7u7w+IP+Q/fMiYiYoJo16/Dbb79w/fr1px6Vu8vLKz9DhuRP58oe\n7m6QMxqNLFmyg2PHYihUyIyePeu8sBpMhcFgYPbsKkyc+D3h4da89hp061Y3o8t6JlZWVkyaNBVb\nWztu3bpFz56dqVq1OpC8wuG4cZMYOnQkY8YMZ/v2bdSr15CJE8cxbNgYihcvwZw5Xz9iJObfUZoe\nPXrj6OhIYmIi/fr15ty5s7zySl6mTp3EN998S65cHnz88UjunmrxYl8qVKjIiBFjiYiIoEePjlSo\nUIl161bTokUb6tVrQEJCQqa8P+vu3+EfN0K1cOG3bN68EWdnF3LkyImXVzH27NlJkSJFOXo0gLp1\n61O6dDm+/jo53Do5OTNy5FhcXd24ciWQL76Ywq1bN7G2tsbOzo7Q0GsEBQVRpcobFCnixfz5swkN\nvcawYaOfeEuR3347Su/eBsLCWgBxHDq0gCVL2jzwWuLi4pgyZTOBgZYUL26gT586GpUT+Q+FORER\nE1SrVl0mTx7P7du3mDVrfkaX80Tq1n2DLVt20rlzf06cuILRaMHq1R0IDFxLs2avEB0dxahRQ7lw\n4RxeXsUYMyZ58+CXdY+pfPk8mDPnxa4w+jwYjUbmzPmagIAjmJkZCAsL5ebNGwB4eOTB07MIAF5e\n3gQHBxEZGUl0dDTFiydPwatbtwF79ux8bDv/XQnx4sXzJCUlkjt3HnLl8gCgTp36rFvnD8D+/b+z\ne/cOli9fAkB8fDxXr4ZQvHhJFi/2JTT0KtWr18o0o3LBwUEMGNCH4sVLcvr0SYoVK86pUycwGAx0\n6NCV2rXrcujQQXx95+Hq6kJAwFESExPp2fMDVq/2Y/v2bSmfw+XLlzAzM2PTpp/x9Z3PvHkLyZ+/\nACNHDuGDD7rj7p6D48f/pG3b9+jWrRfHj//JvHmzWLBgGRMnjqNy5arMmjWd6OhoRowY+1TXsX59\nMGFhzf95ZsnOnWW5ejUkpbZ7DRiwjpUr2wDW+Ptf586djQwb9mYaP0mRrEVhTkTEBBUsWIjo6Chy\n5MhJ9uymspy/ge3bt3HxYggXL27E3PwG+fI1Z9euzjRrBn/9dZqlS/1wdXWjV6+uHDsWQMmSpVPt\nMeXvv4rly5cydOiojL4YeUKbN2/k9u1b+PouxdzcnBYtGhMbGwf8u0IhgJmZOYmJsfe9/967QczN\nzUlK+vf53dUOg4KuPGAlxDjuv28v9Z0lEyZMJW/efKley5+/AMWLl2TPnp0MGvQRQ4aMoFy5Cs9y\n6enuypVARo/+hNDQa6xZ8yOLFq3g1q2bdOvWgTJlygJw9uxfzJq1iWXLVrJgwXxCQkL47rulfPjh\n+xw7dgQzM3Pefbclr79ehfPnz9KtW8d/Apw7YWFhxMfHM3/+Yt55pz6LFy9g166dGAwQH58AJPfH\nwoXf4eNTnCFDRj71NVhaxpPcD8l9Y2d3E1vb3A889vBhZ8D6n3ZdOXDA1O4bFXn+tACKiIiJWrRo\nBdOnz87oMh4rODiIDh1aAXD06BGcnEoABhITXYmOfhVr6wsYDAaKFSuOm5s7BoMBT8+iBAcHp5zj\n3j2mgoODMuIy5BnduXMHF5fsmJubc+jQQUJCgh95vL29Pba2tpw48ScAW7duTvlarly5OXv2NEaj\nkatXQzh58jgAUVFRWFvb3LcSYr58+QkKupLS5tatW1KmWVas+BqrVq1IOfeZM6eA5GCYO3cemjdv\nzRtvVOfcubPp80Gkg5w5PfDxKUFAwGHq1m2AwWDAxSU7ZcqU4+TJE/98H/ng5uaGuXk2HBwcqVTp\ndQCcnJwJD0++zyoqKor+/T9gxIjBAHh7F2PBgmU0bdqcdu06YGZmwMHBkXz58jNt2nQWLFjG0qUr\nAVLaOH36FOHh4U99DQMGvE758guBSzg47OH99++kbCz+Xy4uqVfYdXKKfur2RLI6jcyJiJgIo9HI\n6tU7CQmJon794nh6Zo7pX0/HQP36Obl504/Tp0tgb3+ZJk2qAmBh8e9f3ZP3kkpIea49pkzP3Xub\n6tVrwNChA+jYsTVeXsXIn7/gfcf89/mwYaOZPHkCZmYGypQpj52dPQClS5fBwyMP773Xgvz5C+Ll\nVQwAT88iFC3qRdu2zciRI1fKSohWVlYMHDiMgQM/xNrahmLFfFLa6NSpGzNmfE7Hjq1JSkoid+48\nTJ78Jdu2beF//9tAtmzZcHV1o0OHLs/3g3oKNjbJo1QGg4H/rl9397rufh+VKlWa+fNnAwaioqI4\nceJPbGxsAfj++0V07fo+FSu+RsuW73DjxnUAkpKSCA8Px87Onty5c3P16lUSEhIxGo2cO3c2ZUps\npUqvU7HiawwZ0o8vvvgaW1vbJ74Gd3dX1qx5m+PHz5AzZ3by5Cn50GNHjCjM8OHLCArKQ5EiFxk5\nsuITtyPyslCYExExEYMHr2bp0rdISnLH13cj8+dHU65c0Ywu64kkJiYSFxfLtm1bSEhIYM2aFVy8\neIEJE4Jo3boRFy6cz+gSJZ1t3rwdSB4RGjt2PAMHfghAYmICc+d+TcOGjbC1taV163cZO/ZTmjRp\nxpdfTqF7947Ex8fRvXtPqlatzqhRQ7lx4zoDB/blypVAqlWrkXI/5b0edu9WuXIV+P77VQB8/vlk\nvL19gOSgN3jwiJTjbt68we7df/DWW415771O6flRpLtSpcqydu1qGjZsxO3btwkIOEyfPv1SfR95\ne/vg5OTE2LHDyZXLAw+P3ERGRmIwGIiJicbNzR0LCwu8vLw5cuQQnTq1JSwslLJlywMwZsx4OnRo\nxaBBHwIG6tSplxLmDAYDNWrUJioqimHDBjBt2gwsLZ98CqSVlRXlyj08xN1VuXIxfv3Vi/Dw2zg5\nldXiJyIPoDAnImICwsNvs25dXpKS3AG4fLkhixevxMPDnoEDP8Tb24czZ05RoEAhRo8eh5WVdQZX\nnNqlS39jZWWFv/8GOnRoRadObXBxceGDD/rh4pKdixcv8GT/TtMeU8/Kz28Fa9f+iJeXN6NH3x+G\nnrcrVwIZP34Kw4ePoVu3DmzdupnZs33ZtWs7ixcvoECBgimrS/700zpGjx5GnjyvkC2bBYmJiXz6\n6SSyZbPgnXca0Lhx04cuTDJ58nhatWpHgQLJI4Dr1/uzceNPxMcn4OXlxTvvvHvfe7ZtC2DQoNsE\nBpYlb97DTJ3qRK1aD9vnLOPc/X+/evWaHD9+lE6dkleB7N37owd+H+XIkZOPPhpE/vwF6NKlHS4u\n2ZkxYw67dm1n9OihODg4Ur58BaKiopgxYw6+vvNSRtk8PHLj4ZGbKVOmkytXrpRz3hua33qrMW+9\n9eSL9AQHBzF0aH8WL/6BU6dOsGnTBvr1G/TAY+/druTuxuQicj+FORERE2AwGDAzS0r12t2VwC9f\nvsSIEWMpUaIUkyZ9wurVq2jT5r0MqPLh3NzcU/az6tdvMH5+K5g0aVrK18uWLZ8yIgCk7CMG4Oe3\nLuWxt3cxZsyY8wIqznrWrFnF9OmzcXNzT3ktISHhvv0FnxcPjzwUKlQYSF7Ap0KFiv88LkxISBCh\noddSrS7p6urGhAlTOXHiT44eDcDW1g5IXvTk8uW/HxjmkpKS7lscp2XLtrRs2faRtc2YcYXAwOT7\nOi9fzs3MmT9kujDn4ZGbRYv+vcevd++P6N37o1TH/Pf7KGfOXHz22SfExcXx5ptvp4w4Vq1aPWV7\niHt16dIj1fPFi39IeZyYmMjnn2/mr7+ykS9fLMOG1cfCwuK/p3hi3t4+KaOkIvLsFOZEREyAg4Mj\nLVtew9f3EnFxr1Co0Dq6dfMGkv/6XqJEKQDq138TP78VmSrM3bhxnRs3rtO370Ag+d6/Jxld+/HH\nPaxZE4GlZSK9exemfPln26BYYOrUiQQFXWHgwA+5ejWEKlWqERoagqtrDt5//wM+/XQM0dHJi0sM\nGDCEEiVKpSxz7+zsct92ESdPHmfGjM+Jjo7BwsKCGTPmYGlpyZw5X3PkyB9cv34do9GIk5Mznp5F\naNy4KWFhoXTs2AZnZxccHR2xsLBgwoSP8fEp/s/m1dm4ciWQrVt3p7Q9f/5sjh37N8j5+a0gLi6O\nL7+cyooV3zN9+mzq1n2Dd95pxsGD+xkwYAjz5n1Dnz798fYuxv79v+PrO4+4uDjy5HmFESPGYmNj\nw+zZM9m9eyfm5uZUrPgaMTGpQ0VMzLOHlMxk7NjxT3zsnj0n+PXXS3h4WNCpU8379o3r1WsSf/zx\nFwZDEnv3Fuf69RiOH59OixZt2LNnF1ZWVnz22ee4uGTnypVAxo0bRWxsDFWqVMPPbwVbtuxIdb57\nR94OH/6DGTM+B5L/cPX118nbrTxsuxIR+ZfCnIiIifjkk8ZUq7afS5f28+ab5ciVy53g4KBUwehJ\ng9Kz6tWrS8rm308qe3ZXkpKSUhar2LJlE6VLl3nke3bsOMawYTm4fbs+AH/+uZYNG9xwdTWVbRgy\nl8GDR7B//+/MnDmXVat+YM+eXfj5/cDt27HExsbw5ZezsLS05PLlS4wbN4pvv10MwNmzZ+7bLsLb\n24exY0fwySef4e1djKioKCwtLfnpp7XY29szfPhYRowYhI2NLRMnTsXOzp5Ro4bi4ODAokXL+fnn\ndfj6zqN27bqp/l+tWPE1/vrrTMrz06dPsnz5avbt28vcubM4diyAFi1aM2fOTD76aCBVqlQDICYm\nhuLFS9CnTz8gOQwYDAZu3brF4sX/Z+8+A5o6uwCO/zNI2MsFooKigoLgrnsWt7Yqjrq1asW6xf1q\nnbgHWndFcSuu2rp3XXWhOHHjYIlMIRAgyfshEkGw1bo6nt8ncnPHc29Sm3Ofc88JwN9/CUqlMevX\nr2HLlg20adOOkyePs3HjdgBSUpJJTT3F9evhpKc7oFA85csv/1tFdvbvv8SQIabExbUDErh6dQcL\nFngb3g8Le8idO7d58mQ7IKNgwUlcvnwfrTYNd3cP+vbtz5IlC9m9eyfdu3+Lv/8cOnToRMOGjdi1\na/ufHn/z5vUMHz4ad3cP0tLSDDN+r7cruXr1Ch4ef/xvhyD814hgThAE4R/kyy9zV3OLjo7i+vVr\nuLuXe6tA6X28ayAH+h/XxYo5snPnVmbMmIyTUwm+/tr7D7c5dSqcxMR2htcPH9bj7NkztGhR652P\nL7ySVQGxVq06LwtWqMnIyGT+/Jncu3cXqVTK06dPDOtntYsAXraLiMDU1Ix8+fLj6qoPzrOesbpw\n4Xfu37/Hrl3b0Wgy0Wq1PH36hCpVvuDu3VAKFCgE6GeP586dkSOQk0gk9OjRmw0b1tK9e0dUKhVK\npZL8+QsglUqxtrYhMjKScuWyUh9fbSuVSqlXr2Gu87xx4xphYQ/o109fjTIjI5Ny5TwwMzNHoVAy\nffpkatSoTc2atfH1bULRoqe4ceMM7u4WtG/f5MNd9H+AnTtjiYur9/KVNYcP26FWq1EqlQBcunQe\nne4pxYq1BUAiUWNsXJSMDCNq1ND/N+niUoaLF88BcOPGNWbMmAeAl1djFi/2/8PjlyvnycKF82jU\nqKibZbUAACAASURBVAl16zagQIGCQO7vX1RUpAjmBOE1IpgTBEH4h3vXQOl9eHnV5tChk++0jZ2d\nvaGa4NtydDRBKo0xFHyxsrpJmTJF3mkfwptlL5CzZcsG8uXLz/jxU9BoNDRoUMPwXu52EZo/LFQz\nbNhIHj9+RGxsLH379s+2rYyAgPWG16amptSt24Dffz+DlZUNgYGb0Wq1SKUSAgM3G1LwALy8mhAa\netPQqsLWNh/lynkY9qVQKN84G1258hdMnDgt1/KVKwO5ePE8x48fYceOrfj7L6VDh9w3CqZNm0jN\nmrVzBYvva9Wq5Ziamv1t0qGNjDJyvFYq03I9S9mkiRcnT5bhwYPCFC0aycyZbowYccHwvlQq+ctt\nQ7p06UGNGrU5e/YUPj7fMm/eopfjyv39EwQhJ9E0XBAE4R9OJpMxfvwU1q8PYurUmYa76R/H26dw\nqtVqZs3ay6hRB9m79+I7HaVTpzr07r2fYsV2UapUEOPGxeHs7PSOY/37yN44HWDjxnUEBKz4jCN6\n5dixw8TFxQGwf/8etFp9oZ3ExARu374F6J9vOn1aH8QXK+ZEbOxzQkNvAtC2bQvi4+OoWrU6O3Zs\nw9OzIseOHebmzeukpaWRlJSIu7uHofn3wYP78PSsAOgD/axjnDr1G5mZr3oLJieraN58J+XLn+bX\nXx8QHa0fo6mpKSkpKX94ThKJBDe3cly7FkJ4+FMAUlNTefLkMampqSQnv6B69ZoMHDiMe/fu/OF+\n3tW0aRM5fvwIgOFavmm/Pj5/3MNu7dqcM+F/tv5fNWCAG6VLBwHxWFhcoHdvqaFgEUClSlUJCbnI\n+vV1uXjRjW3b6mFnZ/7G/bm5lePYMf01OHz44BvXyxIe/pQSJZzp3Lk7rq5lefz4kahaKwhvSczM\nCYIg/AMdP36V48cjMDdP5F0CrE/pu+92sHdvD0BBUNB15sw5S5s21d9qW4lEwtSpXzNlysd9BvBz\n+TznlD2t8dVSR8fiXL58iR49OvHFF9UNjaWtrKwNqZTZyeVyJk+ezvz5s1Gr1cTFxZKRkUnLll8T\nGRnBlCnjSU1NZeDAfjg4OODqWpYhQ0YyffokNm5ch42NjaG8fatWrRk9eniuYwPcufOCq1e7AaDT\nXWbnzkf06KHfZvjwgRQoUBB//6VvvJbW1taMGzeRiRPHkp6un3nq27c/pqamjB49nPT0dEDHwIHD\nDNvs2/crmzdvQCKR4OxcEplMxpUrl9myZQOxsbH07z+IevUa5ijeATBv3kzKlHGjadMWHD9+hOTk\nZNauXU3nzt0wMzNnxYolaLVarK2tWbBA/3dY2APkciPat/+K9u2/wdu7Y65zWLduTY6m5X8lzflt\nuLo6sXevDWfOnMfZ2Z5SpRrkeN/JqTh9+vjw7bedSUhIxMTEhNmz/XOlymYZNGg4kyePZ9261VSt\nWg1zc/M818v6MyhoE8HBF4mJeUbx4s5Uq1aTa9dC3rJdiSD8t0l0WQn0n1lMzIvPPQThIylQwEJ8\nvv9i4vP99H7++Ry+vvlITKwAJNGhwzYWLWr3p9u9q7w+Wy+vOrmq0uUlOTmZypWvExfnZVjWtu12\nli5t9MHH+U+Qvb8WwKZN60lNVeUqBf8pZAUsRkYyHB1LIJPJMDU14/btmzkCluxjzh68JCYmMHHi\nOJ4/j8Hd3YMLF84RELCe6OgoRo8eTrlynty/f5fZsxdy9OhBjh07THp6BnXq1OPbb78jMjICX99B\neHhU4Pr1EAoUKMj06XNzzSh7eR0mJKS14XXFijvYv9/r9dP5YB48uM+4cSNYvnw1lpZWJCUl8eOP\n80lLS2Py5OmEhT1k9OhhbN68M8f12LfvV378cT5KpTEVKlTit9+OUbKkC6AlJiYGlUpFQMB6IiLC\nWb58MTY2Nly7FkKxYo7cvXuX7dt/oWPH1hQv7kxqqgqNRsPw4WM4c+Ykmzevp0QJZ0qUcGb8+CmG\nNGeVSsWYMb68eJGERpNJnz4+1KpV13Btv/iiKhcuXHzjtf2rOnf2fqv2Fmp1miGV9/DhAxw5cihH\nK5I38fObRI0atT54Wuu/jfj/7r9XgQIW77yNmJkTBEH4h/nllwQSE798+cqS48cLkZ6e/rKgxd+D\nsbEx5uYveJm9B+gwNVV/ziF9VjKZDK321b1TtTrts4zjwYP7rF0bwPLlq3F2LsL9++H8+ON84uJi\nWbo0wBCw/NGP6dWrV+LpWYEePXpz9uwpfv31Z44evcbUqc9QKp8RFVUcf/9uPH4cxtOnT2jduh2h\noTe5fTuUkJDLFCxYiKdPnzBp0nRGjRrHhAljOHHiKI0aNc1xHHf3JEJC1IASSMPD449TK9/GihVH\n2b1bg1yuoU+f/DRvXtnwXnDwBRo08MLS0goAS0tLAGrX1vdjc3IqbkhHff161qlTDw+PCtSsWYff\nfjuGhYUFs2bNZ8eOIJYtW4SdnT0REeE8eHCPdeu2snfvLxgZGXHv3j2srKyRy40oV84TH5+BaLVa\n0tLS8PQsz44dQaxevTHbEfVTVUqlkunTZ2NqakZCQgL9+vU09I17+vQJCxf6M2jQyDde278ir/YW\nERHh2NnZM3iwL3Pm+BEdHQVAs2at+PnnHcTGPkcikWBnZ59rBjL7LGjJkqX43/8mAXDlSjBz5/5I\nYmIKtrZfMnlyGzw8Sr73+AXh30oEc4IgCP8wSmXOYgXGxrmLFXwsb5seKJfLGTzYhBkzDhAbW5SK\nFS8wYkTtjzy6vy9b23wkJMSRlJSIsbEJZ86colq1Gn++4Qf2VwKW14WEXMbPTz/LUr16LSwsLFm6\nNJKIiEYUKbKWsLChzJ+/merV73LhwjnOnTtLWloaFhaWPH36hIIFC2Fv70DJkqUAcHFxJTIyItdx\nZs5sgaXlDsLCFDg7pzNmTPP3OvcDBy7i51cWlUp/3Hv3juHuHo6jowOg/27nlayUvTF21vsymRyd\nTmu4nrGxz4FX17NWLX3bhEKF9FUhs5Qp44adnT0Acvmr/RobG3PkyEGUSiW1a9ejVKnSf3guOp2O\nZct+JCTkClKphOfPY4iP139u9vYOuLq6EhPz4o3X9q/Iq73FkiU/oVAomDhxHO3bd8LDozxRUVH4\n+g5k/fogVq1azsWL51m0aDkpKcl06tSW1q3b8ehRmOGmgqWlFS9evDCc1/nztzh/fgtGRgmkpfkw\nZEgZDh50+mT/xgnCP434L0MQBOEfZsgQD65f38KtW7WxsrpHv37KXA1+35dOp0OlUuVYlpiYYPix\n+ja6dq1FixZxPH8ei6Nji7/VzOGnJpfL6dGjN336dKdAgYI4ORX/LM/N5RWwqFQqFi9ewNmzp7lz\nJxS1Og21Oo379+8RERHOt992RSKRYGGhT/9Rq9WMGeOLTqfDwaHIy++KEnv7YchkyRQr9jVPn8YR\nF1eBLl16oFAoCA29ydChI4mPj2fq1AnExETTp083Bg0ajlQqQ6PJPWurUCiYNKnFBzv3K1eeo1LV\nN7x+9qwa588fNARzFStWYexYXzp27PwyzTLxjfuys7MjLOwhVap8gVqt5tKli4aiLoAh8Chb1h2t\nVmsIqN4UkJiYmDBmzETu3buNn99EOnToTJMmbw5eDx7cR2JiAgEB65HJZLRr1wq1Oh0AheJVkPim\na/s+cre3gIsXz/Po0UPDOiqVitTUVCQSCTVq1EIul2NlZY2NjS1xcbG5bipkfbckEglSqSs6XT7S\n0/Mhkz3n3r1SPH8eYwiCBUHISQRzgiAI/zClShVjzx5bQkJu4+hoR5EiFf58o3cQHHyXUaNuEhFh\nR/Hi4fj7V8XKSsnAgd/xzTdd32lfNja22NjYftDx/VN5e3fMs8jFp5Q9YClQwMIQsDx//pw2bdrh\n7u5B3bpfsH37Vo4cOUihQnasWrWOn35axt69vwD6oL5OnfqMGvU/Jk36Hy9eJFGrlopDhzIBHVFR\ni+jVaytXr/7C06dPadasJQAxMc+YP382LVp8RUzMM6ZMmYWv70CaN//qk5y7h0c+jI3vk5bmDEDB\nguepUuXVDFjx4iXo1q0XAwb0RSqVUbq0C/B6wQ7934UK2VG//pds2bKJxMR4KlWqApArALSxsUGh\nUDBu3AiSk1NQqZKz7evVepmZGVhaWtKy5dekp6u5e/c2TZo0Ry6X5/lMWkpKCjY2tshkMoKDLxIV\nFfkBrtC7yd7eAnSsWBGYYxYzS/YZSKk0q71F3rOgAHZ2MuAFYIFEosPR8QH58n28ZyUF4Z9OBHOC\nIAj/QObm5tSsWemj7HvKlFBCQvT9r2JiYMqUDaxZ04pNm3Z8lOP9W92794S5c0NQqRR4eRnTpUud\nzz2kHAGLQmFEiRKlkEj0lSvd3fW92+RyI86d+53Hjx+h0Wjo2bMTKSnJpKenk5KSjEKhJDo6iq5d\n21OihDNyuRFjxjQhNHQLyclS5sy5TseOfWnbdjd16tQnMHAVarWaO3dCCQsL4/HjMCIiwhkzZhgq\nlYrMzIxPMkvZtGkVRo06xC+/hGBkpKF3b1ucnIq8tk4LmjZ982zgwYMnDH/37z+I/v0HsW/fr2za\ntI4tWzZy+fIl6tf/EjMzM8N6MpmcgIANBAdfZMsWfe+86tXrk5qaZgjounbtxZgxw5DL5Ziamhme\nH2vVqjU9enyDi4sr48dPMVynRo2aMGrUMLp374iLSxkcHYsbjvf6tfwU17ZKlWoEBW2mUyf9zZ67\nd+/8QaqoJI9Z0CTDrH+zZp7IZDs5f96CjIxMZs4snmeQKAiCngjmBEEQhBxiY01yvI6LM3nDmsKb\npKWl8d13l7l2rTMAx4/fwcLiHF999cVnHtmrgCWrIl5kZAQDB35neH/WrPls374VZ+dSLFuWsxR+\ncnIyUqmUefN+BPT9wZ48eYKVlTVFixakZ89xVKz4qqhImzbe2Nracvv2LYYOHUnz5l8yfPgEbGws\ncXJy/DQnnM3333vx/fcfdp9vGwBWrFiZChUq4eu7nY0bK5OZaU3Dhv1IT09/4z58fAbi4zMw176s\nrKxzfTZZAgM3G/7+8E3J825vMWSIL/PmzaR792/QaDSUL18RX9/RudbLktcsaFa7CplMysyZ+iqm\njRpNoUaN3O0xBEF4RQRzgiAIQg6enomEhmZVEUyiQoXPU3nxn+zhw0dcu/YqqElNLc3Zs1f56tNk\nFL6z6Ogorl+/hrt7OQ4d2o+bmzu//LLLsCwzM5MnTx5TvHgJLCwsCQm5gqdnefbv30OFCvoZYp1O\nx9Gjh6hYsTIhIVcwN7fA1PTVDFVaWhrp6fZ07HiS1NSG9Oz5K126lKJUKZfPddqf3Jkzl9m4sS6Z\nmfqZtCNHerBq1W58fJq8975TU1NZvvw46eng41MTC4u3f771bQUF/QyQq6WGlZU1kyZNz7X+6+tl\nteaAvIPg778fTGamxvA6+0yoIAh5E8GcIAiCkMPcuS3Jn38Hz56Z4+SUyrBhzT73kP5x7O0LUqjQ\nTaKjswIVFfZ/4/oNxYo5snPnVmbMmIyTUwm8vTtStWp1/P3nkJycjEaTSYcOnShevATjxk1kzpzp\npKWl4eBQxDCjIpFIUCgU9OrVGY1Gw5gxEwzLJRIJS5Yc49q1lRQs6Iel5WT27UtBo3Fl6tQZn/PU\nP6m4uBQyM/NnW6JEpXr/NMiMjAw6d/6ZU6d6AnJ27/6ZdetcKF7c4b33/alMnvwrGzYUIDNTQbNm\nR/H3b/vBCzsJwr+RaBoufHSiueW/m/h8/51WrVpOwYK2tGz54ZuR/1cEBf2Ov38cycnG1KwZy8KF\nbZDJZJ97WAbZ0yyzNzT/qwYO/I4BA4bi4uKa5/tTpux/rbl9JDt33v5oz37+HalUKtq23cOlSz0A\nKSVK7GLTJtf3DrqOHz9P+/buQCHDsqFDtzJmzPv1l/Px6cXSpXmnc35IZ85coX17O9LTS71cksDc\nuSfo2rXBRz/2P5H4/+6/l2gaLgiCIHwQn6Ns/r9Nu3bV8PbWodVq/1ZBXF4+9uedmJiIVhuDtfXP\nJCR8BWipWnUvlSt/uLzTXbu2Y2xs/Icl/T83U1NTNm1qxJIlW8nMlPLNN27vHMidPHmcokUdcXJ6\nVfTEzMwYmewFGk1WMKdBofjr9+qzKmh+ikAO4NGj56SnV822xJqYmPRPcmxB+KcTwZwgCIIAQGDg\nKvbv34ONjS0FCxaiQAGbzz2kfzyJRPK3D+Ts7QvnKJrxVy1atDzP5bGxcXTocIyrV/sBV3F0nEKr\nViUYPLgJSqXyvY8LoNFoOHBgzycLPt6HtbUVY8f+9YDzt9+OU7NmbZYvX8yzZ9Gkp6vx9u5Ihw53\nOH++LQkJbSlY8ABhYY5cv16UZcsWER0dxeDBvtSqVQeNRsOyZT9y5col0tMzaNOmHV991Ybg4Iv8\n9NMyLC0tefz4ERs3bsfLqzaHDp0EYP36NRw6tB+JREr16jX57rvv2b17J7/8spOMjEyKFCnC+PGT\nUSqNmTZtImZm5ty+fZPY2Fj69x9EvXoN33hOjRtXwsXlZ27fbg9AkSKHaNYs7xleQRByEsGcIAiC\nQGjoLY4ePcSaNZvQaDLp1asLlSt/2P51wn9TQMDvXL3aHX0lxPI8elSI2rVv5tmAPjU1lQkTRhMT\nE4NWq6F79944OBThxx/nk5qaipWVNePG/UC+fPkZMKAvpUu7EBJyBS+vxlSpUo1Nm9bzzTddCA9/\nyrx5s0hIiMfY2JhRo8ZRrJgTR48eZs2alUilMszNzfnxxxWf5Bps3LgWhUKBt3dHFi6cy/379/D3\nX8qlSxfYs2c3TZs2Z9WqFaSnpxueQzQxMWHp0kWcPn0SmUxG1arVqFu3PqdPn+TKlcuYmJgwY8Zc\n1Oo0+vbtgYNDUaTSNLp31zJt2lG8vBoxfvwoChQogIdHeaZNm0jjxk05c+Y0L14kMWrUOGrUqE3/\n/r2pWrUaAHfv3mbduq3ZGnTrZ2zPnj3N6dO/sWJFIEqlkqSkJADq1WtAq1b6ypMrVy7l119/pm3b\nDgDExcWydGkAYWEPGT162B8Gc7a2NgQGlmPp0s1oNDI6dXLC1dXp43wYgvAvI4I5QRAEgatXL1On\nTv2XMyVKatas88amvoLwrgoXHoBcHolEkk5CQkugJF5etWnd2puzZ0+TL19+evf2YcaMyTx79owJ\nE6ZQq1YdkpIS6datA7a2+dBotBQqVIgVK5bQuHEz7t69Q3R0FEZGRnTs2IV69arRr98AAIYNG4BM\nJkOhUGJv78DcuTNp2LAR/v5zsLd3oFixIgwbNuqTnb+nZ0U2b16Pt3dHQkNvkZmZSWZmJiEhl3F2\nLklgYAALFizB2NiY9evXsGXLBtq0acfJk8fZuHE7ACkpyZiZmVOrVh1q1qzNvXt3GTt2BOHhT5BI\npIwYMZbvv+9NRMQ9lEolFhYWZGRksHz5GnQ6HQ0a1CAuLo7SpUsTGnqLSZP+h5NTcVJSUnj69Aky\nmYwyZdyyBXKvXLx4nubNWxlmUrMC8fv377Fy5VJSUpJRqVL54ovqgH5GunbtugA4ORUnLi7uT69R\niRJFmD27yJ+uJwhCTqJMkCAIgkD2/lF6IpATPoxvv61OvnzuPH68jcePAyladC3ly5ciLS2NSpWq\nsm7dVkxNzVi1ahnTps3C1NSUmTOnEhJyhaCgTSQmJr68saDj4MF9PH36BIDUVBU+PoMMwU7Wd/jE\niWNERIRjZGSERAJ37twiNjaWevUavOyvVwC1Op19+379ZNfAxcWV27dvoVKloFAocHcvR2joLa5e\nvYJSqSQs7AE+Pr3o2bMT+/fvJTo6CjMzcxQKJdOnT+bEiWMolcaG/V25cplNm9axYMFitFotOp2W\nKVPGo9FoiI2N1V8NiQSpVEpw8EWkUikajYbq1WsAMGrUOLRaLT/+uIKtW3+mShV9/0Nj41c9Jb29\nWxpu6EgkEvK6t+PnN4nhw0cTGLiZXr36kJ6uNryXvdG3uDEkCB+PmJkTBEEQKF++AtOmTaJLlx5o\nNJmcPn2K4sU7fe5hCf8CtrY2tG0bh6lpfaRSCWq1mvBwfbCVNZPj7FwShUKBo2NxAgM307Ztc1au\nXEJCQryhOItUKiVfvvz06NEbAFNTMxwccs/kBAdfwNTULNdzgJcvX+LBg/vExj4nMTGRkJBgWrb8\nGktLq498BUAul2Nv78Devb9Qrpwnzs4lCQ6+QHj4U+ztHahc+QsmTpyWa7uVKwO5ePE8x48fYceO\nrfj7LwUgIyMdqVSKkZERJiamqFQqRo36HyNHDmX9+q0A6HTg4lKGSpWqvHytQ6fTUbVqdXbs2IZC\nocTMzJzHjx9RsGChXMfOXhSnSpUvWLNmJY0aNUGpNCYpKQlLS0tSU1XY2uYjMzOTAwf25rkfQRA+\nLhHMCYIgCJQu7UrDhl706PENNja2lC3r9rmH9LcTGRnB8OEDcXf34Nq1EFxdy9K0aQtWr15BfHwC\nP/wwhTJlxHV7XXDwRa5fv8q2bdtRKpUMHPgd6elqZLJXP0EkEglyuRHPnz/HwsICiUTKN990ZebM\nqVhaWjF8+Jgczcvj4+Py7EGm04GRkQJrayuOHTtM/fpfotPpuH//Hn5+kxg2bCTVq9di375f+fHH\n+Tx79uyTBHMAnp7l2bRpPWPH/kCJEs4sXDiPMmXK4uZWjnnzZhIe/hQHhyKkpqby/HkM+fMXIC0t\nlerVa1KunCcdOugrf5qampI/fwG0Wh1t2jQnNTUVY2MT0tPTSU1V4ec3iUePHpCc/IKrV0M4fvwI\nz5/HALBq1QocHIrg5laOkyeP07mzNzY2tigUCsLDnxIfH8fRo4dp0OBLQF/VslevLmg0mVSp8gXf\nftsNIyM51avXom/f/vTu3Y++fXtgbW2Nm5s7KpXKcL7Zg0FRHVcQPh4RzAmCIAgAdOvWi27dehle\ni15GuYWHP2Xq1FmMGTOB3r27ceTIQZYuDeDUqROsXbua6dPnfO4h/u2oVClYWFi8TCd8yI0b19+4\n7oMH91i82J+0tFTWrPmJFi2+5vr1EJYuXUhKSgppaSo6dOiMo2PxPLeXSPSzSJcvX2T37p0EBgag\nVqtp3LgpqakqduwIYunSRURGRlCokB0lS5bKcz8fg6dnBdatW427ezmUSmOUSiWenhWwtrZm3LiJ\nTJw4lvT0DAD69u2Pqakpo0cPJz09HdAxcOAwABo2bMS0aRNJS0tl6tSZuLiUoX//3vj5TUIul/P8\n+XN27NjB0KG+REVFIpFI8PbuyPLli+ndux9Nm7YA9NUply5dRXDwRc6d+515834E9M/mZRk4cCht\n27Zn585t3LkTapj1y/L11958/bV3rnPNaiSf5eDBEx/sOgqCkJMI5gRBEP7Drl9/wPjx14mONqNs\n2Xj8/ZtiZmb2uYf1t2Vv70CJEs4AFC9egsqVq77825moqIjPObS/rS++qMGuXdvp0qUdRYs64u5e\nDsg9WyORQNWq1ahatRqNGtVl5cpAdDodK1Ys4cyZk+h0OgoVsqdRo6bcuXObcuU8cjQoVygUdOzY\nBdBXZdy/fy9GRnLq129Ijx69sba2ZsOGdVhbW9O8eascs0ifQqVKVTh27Kzh9aZNOwx/V6xYmZUr\n1+baZuXKwFzLypXzZP78xQwY0NdQIXL8+MkEBW3i3r27jBo1DtAHVH5+kwzbWVvbULNmbcPrrEIn\nzs6lWLzYn6VLF1GjRm08Pcsb1qlbV9+0u3RpV06cOPqn5xgWFs66dVeRy7X061cTGxvrP91GEIT3\nI4I5QRCE/7DRo69x/rz+B/C9exqsrTcxZ86Ha+T8b6NQvCrqkPXMUtbfGo3mcw3rb83IyIg5cxbm\nWp59tqZXr755vieRSPjuu+/57rvvc7xfoUIlKlSo9Mb9denSgy5degDw/HkcPj47iYqywtW1F5Mm\nNUWhULzXOf0dZA+GdTodEok+7dTExCTXujduPCAhQUVg4DF8fFogl7/6+Ve0aDECAjZw9uwpVq5c\nQuXKVQ3PJWZ932WyP/9+P3kSRefON7h7tz2g48SJNWzfLm4OCcLHJoI5QRCE/yidTkd4uHm2JTIi\nInL/EBT+fsaM8TU0jG7X7htatWrNr7/uYsOGtZibW1CyZCkUCgVDh44kPj6euXOnEx0dBcCgQcMp\nV87zM5/Bp9O6dSC3b3sC6Zw+XQ2p9ADTprX83MN6b9HRUVy/fg1393IcOrQfDw9P7t69nWu9+/cj\nGDLEFLm8INOnV+fy5SBWrepoeD/rOcVGjZpiZmbOnj27/9J4tm27wt277V6+khAc3JF9+w7h7V3/\nL+1PEIS3I4I5QRCE/yiJREKpUgmEh+vQl3VX4eKS/rmH9beWOzXw8xR5GDNmApaWlqjVafTp050a\nNWoRGBhAQMAGTExMGDzYh1KlSgPg7z+H9u074eFRnqioKHx9B7J+fdAnG+vrIiMjGDVqKGvXbnnv\nfQUHX2Tz5g3MmjU/z/c3bz7N7dudAeeXSzYRGip77+N+bhKJhGLFHNm5cyszZkzGyakErVt7s337\n1lzrnj4dTXi4D9bW0RQpMoCrV02JiHiVbpn1nKJUKkEul+PrOzavI/7p99vMTAKkAfoWClJpHDY2\npu9xloIgvA0RzAmCIPyHLVpUlwkTNhATY4qbWyrjxjX73EP627K3L5yj3H32Ig+vv/exBQVt4uRJ\nfVrhs2fR7N+/hwoVKmFhYQFA/foNefLkMaBv+Pzo0UPDtiqVirS0NMDik433c7lwIZlXgRxAWayt\nj3yu4Xwwdnb2rF27BZksZ2AaFJRzVm3s2B8YN+5XQEdCQhcSErpgaXkChUJpWDfrOcXXZd+Xq2sZ\nFi5c9odj6tmzASdOBHLoUCPk8jS8vc/SoEHu4iiCIHxYIpgTBEH4DytUKD/Ll4tn5N6WTqdjzZrj\nPH6cTrVq+WncuNKfb/SBBQdf5NKlCyxfvtpQ6t/R0YlHj8KyjTP7TKGOFSsCczRx/qsOHNjL1Vgz\nsQAAIABJREFUtm1byMzMoGxZd4YNG0WTJvVo1+4bzpw5hVKpZMaMudjY2BIe/pRJk/6HWp1GzZp1\nCArazKFDv+XYX2RkBFOn/kBqaioAw4aNxN3dg+DgiwQErMDa2oaHD+/j4lKGCROmAPD772dYtGge\nSqUxHh7lc40xO3t7LZAK6NOHTUxuMHVqi/e+Dh/Sm67poUMnATh27DBnz55m7NgfmDZtIgqFgrt3\n7+DhUZ7GjZsye/Z01Go1Dg5FGDNmAhYWFnTt2hVHR2euXLmEWp2Ou/sTrl//DmPj+1SsuISxYzPQ\naDLp1asvtWrVzfE5xMa+4MWLlsjlxahX7wkREefy/BxeZ2RkxNq1Hbh8+QbGxgrc3LxFSwJB+ARy\nN2kRBEEQBCFPY8bsYvToWixe7E2/foVYv/63P98om8jICLp16/BeY8he6v/RozBu3LhOamoaV64E\n8+LFCzIzM3NUHqxSpRpBQa9mDfN6rupthIU95OjRQyxbFsDq1RuRSmUcPLiPtLQ03N09WLNmI56e\nFdi9eyegT+/s0KETgYGb39hM2tbWlvnzFxMQsJ5Jk/xYsOBVa4d79+4wZIgv69cHERERzrVrIajV\nambNmsasWQsICFhPXFwsfxQvDB78Jd7emyhadBdly27mxx/tsbe3/0vn/2d8fHr96Tpbt25ErU4z\nvH7TNdWnPeu9HhA9fx7D8uWrGTBgCFOn/sD33w8mMHATzs4lWb16BaCffX38+BGrV29k1KhxWFv/\nSt++k/n224307t2WlSsD8fdf9rINRJrhc+jVawQ3b44lKekUV660Zf36QoSGhub4HK5evWIYi5dX\n7Rxjk8lkVK7sgbu7qwjkBOETETNzgiAIgvCWjh61QKezBSAlpQz79t2kS5e32zYzM/ODjCGvUv8F\nCxaka9ee9OnTHUtLSxwdnTA11VcRHDLEl3nzZtK9+zdoNBrKl6+Ir+/odz7upUvnuX07lN69uwKQ\nnp6OjY0NRkZG1KhRCwAXlzJcvHgOgBs3rjFjxjwAvLwas3ixf659ZmRkMn/+TO7du4tUKuXp0yeG\n98qUcSN//gIAlCxZmsjICIyNjSlc2AEHhyIANGrU1BA85sXIyIglS9q9rPb4cYOLpUsD/nSdoKDN\nNG7cDKVS/1zZm65pdlqtzvC3RCKhfv0vkUgkJCcnk5ycjKdnBQCaNGnO+PH6z1WlUmFrmx/Q97eT\nSCSMHu3L4ME+3L9/k02b1gGQkZHBs2dR2NrmZ/78mfz+ezBWVrYoFI8ASEkpgY2NfY7PISoqMtuM\nqAjYBOFzE8GcIAiCILwlE5MM8uVbiEZjRUJCd5TKDJYvX4ytbT6ePYvm3LkzSCQSunX7loYNvQgO\nvshPPy3D0tKSx48fGRozg74B+fjxoxg58n+4upZ56zG8qdS/i0sZWrVqTWZmJuPGjaBOnXoAWFlZ\nM2nS9Pc+d4CmTVvkahOwadN6w99SqeSdWjRs2bKBfPnyM378FDQaDQ0a1DC8Z2T0qn3Aq9L4rwcP\nOt7Gp5gl8vKqzaFDJ9+YIhoUtJnnz2MYNKgf1tY2+PsvJSws7OX4pDg4FGHs2B8wMTFh9eqVLF26\niAsXzuHuXo5jxw5TqJAdp079xqVLFyhb1g1b2/xkZGTQr18v0tPVAKSnZ5CRkcHTp0+Jjn5Gz56d\n6NKlJ6mpqSxZog+mhwwZwZo1P5GYmIiDQ1GUSmO2bNnAnTu38fT05PDhh0gkKszND2BmFoWNjTmD\nB/fnxYskoqIiMTKS06hR049+PQVBeDsizVIQBEEQ3pKPjxUyWWEsLbfh7LyTAQNKcvToIQoWLMi9\ne3cIDNzMggVLWLLEn9jY54A+rXHIkBFs3LgdnU4ffDx+HMb48aMYN27SOwVyfyQgYAU9e3aie/eO\nFC5cBDc3T+bN28f8+ftITEx87/1XqlSVY8eOEB8fD0BSUiJRUZFvXN/NrRzHjumLjRw+fDDPdVSq\nFGxt8wGwf/8etFrtH47B0dGJyMgIwsOfAnDo0IF3Po+P51XAmFeKaLt2HcmfvwCLFi3H338pCQkJ\n3Lp1HaVSydy5i3BxcSUwcBVRUZFIpVK0Wi0//bTW8D2ytrahVq06VK1ajU2b1mNubo61tQ3fffc9\nAQEbKF7cmczMDIyMjHBwcKBQoUKsXr2R/PkLYGxsjJGREVWrVsPPbxLNmrUkMHATHh6eLFgwB5Uq\nBaXSGLlcR7NmVZBIoGjRSfTunYyVlQXTp88mIGA9derUe+NnKQjC5yFm5gRBEAThLXXsWIN69aIY\nPVrG4ME2qNWxlCrlwtWrV/DyaoJEIsHGxpby5Sty69ZNzMzMKFPGDTu7V89pxcfHM2aML35+c3B0\ndPpgY/v++8GGvxMTE2nb9jBXr3YHdBw4sJpt25phbm7+5h38CSen4vTp48OwYd+j1eowMjJi6NCR\nb2zPMGjQcCZPHs+6daupWrVajmNnrde6dTvGjRvJ/v17+eKL6piYmGZbJ/cYFAoFI0eOY+TIISiV\nxnh6ViAi4mme49VoNLmqPX4quVNEI3P19rtx4xpRUZEYG5vg7d0CrVaHqakptWvXw8LCkmPHDnP1\n6hVDsF+3bgNu375F4cJFuHTpPADffz+IsWNHoFanYWRkRL58+tRKiUSCVCqlV6/OaDQamjdvRVJS\nIj169GbLlg1s3LiODRsCsbcvzM2b1/n++8Hs3fsr8fFxfPll45cpumnUrl2WzZuDWbbsR0JCrvD8\neQwqVQrx8XHY2Nh+ugsqCMIbiWBOEARBEN6BnZ0dXbt248SJY8THx9K8eSsuXjxnmHXLkhWwGBvn\nbMRubm5OoUL2hIRc/qDBXHabN5/h6tVu6GeLJAQHdyco6Gd69mz0Xvtt2NCLhg29ciw7ePCE4e96\n9RpSr15DAAoUKMCKFWsAOHz4gKFVQvY2DkWKFCUwcJNhex+fgQBUrFiZihUrA/pqjzdv3uDq1Stc\nv36VYcNG8exZdI5qj35+k96p2uOAAX0pVcqFK1cuodFoGDNmAmXKuJGamsr8+bN4+PBBjmqP7yor\nRTQoaDNHjhzk3r07NGrUJNd6lSt/wcSJ03ItNzExYdWqdVhaWgFw5swpFAojxo79gdDQm5w/f/bl\ndT1I797f0bZtB6KiIhk48DvDPooVc2LyZH167b59v5KUlIhSqcTU1JSAgPXI5XIyMzP5+usmFClS\nlNq161KjRi3q1WuIj89AvLzqULFiZaKiIjl37gwBAeuRyWS0a9cKtVr0oxSEvwuRZikIgiAI76hu\n3fqcO3eG0NBbVKtWAw+PChw5cgitVkt8fDwhIZcpW9YtV4AH+mfe/Pxms3//Hg4d2v9RxmdsLAey\n/+BOw8Tk085ShYaG0qNHJ7p3/4Zdu7YzYMCQd95H9mqPP/20jjt3IvD1nZXjuv6Vao8SiQS1Oo3V\nqzcyfPhopk+fDMDatQFUrlw1V7XHv2rXrm3Url2Xr75qA4CpqSkpKSkAlC3rzrVrIYaU0eTkF4aA\n922lpKQYZgD37HnVF04mk+UYd/br5e7uwZEj+lTJgwf3GQqovC4jI5PmzQ+ycOEFXrzQz3IGB1/8\nw9RaQRA+PTEzJwiCIPyrZRWmeF/BwRfZvHkDs2bNRy6XU6lSFSwsLJFIJNStW58bN67So8c3SCQS\n+vcfjI2NLWFhD3OlC0okEoyNjZk1awFDh/bH1NSMmjVr53nMrVs38tVXbQzVD99Wp071OHAgkMOH\nvQEtTZrsoF2792uJ8K48PcuzZs3G99pH9mqPT54kkJhoyosXVciXT8eNGw9wcyuRY/23rfYI8OWX\njV+OswIpKSkkJydz/vzvnD79W65qj8WKOf3pWHOmm8Ls2X5ERIQTHx9Perqa3347RmJiIp07e1Oy\nZClWrAikQoVK9OnTnfR0NXK5EUOHjmDJkoXExDxjwIC+jBz5P9zdy6FSpTJkyPfodFoKFy5iOE6n\nTt2YNu0HAgNXUb16LbKe29uwYQPdu/cwFECRSCSG8Q0ZMpLp0yexceM6bGxsGDv2h1znsGvXWdLT\n5dy82RaptAGJiR3p3NkbN7dyODoWz/OcBUH4PEQwJwiCIOQQGnqL/fv3MG3aJFatWo6pqRnffPOW\n9fffko9PL5YuDSAqKpJr10Lw8sqdgvbhfPgfnFqtlhs3rjF16izDsv79B9O//+Ac61WoUIkKFV41\nFs+eYmhubs7KlWv/8Divl7J/fQxSad4JNvoGzu05fPg8UqmEhg07fLbnx95X06YtaNq0JTVrpqNW\n6wMzG5sANmy4jZ9fCdRqdY71jY3fLfDNkhWXTJs2m6JFixmWBwVtZuzYEbi4uDJ+fN4Ns+FVumn2\nFNHz539n1ap1rFq1HBsbW6ZPn0tw8EUWLdK3bLC3L0zhwg4sWfITCoWCCRPGULFiZaZPn4NOp0Ol\nSiEs7CHu7u74+c1BJpMxZ84MatfWp366u5dj06YdhjH06eMDgJWVVa7vVtOm+mbpdnZ2+PsvzTX+\n7EHdtWuJ3Lt3GQCt1ob79zcyadIlGjWqnuc5C4Lw+YhgThAEQcjB1bWMoejC+9x5z8zMRC7P+38z\nWT25IiLCOXTowEcO5vR0Oh1LlizMs31AXqXkAX7//QyLFs1DqTQ29NZ6+PABI0YMRiaTMXbsCNLS\nUpFIpBgbG6PT6ShWzJELF86RlpaGvb09CxYsoVAhO/r2/Z6wsOJIpR589ZWMHTsmvnMpey+v2nz1\nVVsuXjxPvXoNuH07lOnT9Y22L1z4nZ07t+PnNxsAuVxOkyY18r4Y/xCVKlVl9Ojh1KvXEJlMg1Sa\ngFSagkaTn9TUaLRaLb/9dgwzs9yFXczNzbGwsCQk5AqenuXZv3+PIbDW6XQcPXqIihUrExJyBXNz\nC8zMzKlatRrbtm1m6NCRANy5E8quXdvw919qSGf8I3l953U6HdeuhTBtmv5zqVixMomJiahUKUgk\nEmrVqoNCoX/GLjj4ouG7J5FIMDMzZ//+PTl60anVavLly/cXr+jbcXOzRKl8jFqtD2rz5TvPyZPh\nPHmSQs+eDd54E0EQhE9PBHOCIAj/cpGREYwaNZS1a7cAsHHjOtLSUrl8+RJly7oTHHyR5OQXjB49\nAU/P8kyfPpkjRw7h5laWGzdu0rVrD8LDnzJv3iyCgy9QurQrAwYMZcuW9URHRwH6yoXlynmyatVy\nIiKeEhERgZ2dPV279mT69ElkZmai1erw85uNg0MRQ+rjsmU/8vhxGD17dqJp0xb89ttxBg/2pVSp\n0gD4+HyLr+8YnJ1Lvvd1OHHiqKF9QEJCPL17d6N8ef1Mz717d1i/Poh8+fLj4/Mt166FULq0K7Nm\nTWPRouU4OBRhwoQxSCRQvHgJatasjY2NLXXq1Gf48IFYWFiyZs1GlixZyC+/7GLgwKHUqlUHb++W\nzJ8/m169BnL5spzY2BokJzcmNPQuJUq8KsOf1/HbtevI1q0bWbRouaEQRlpaGm5u7obnzzp39iYx\nMQErK2v27PmFFi2+eu/r9HeSVUFzxozJlC6dQHy8FdHRP2BsXJXHj7fj43MCV9cypKamGrbJfgNi\n3LiJzJkznbS0NEMft6x1FAqFodrjmDETAOjRozcLF86le/eOaLVaVCoVcXGxDB8+kKZNWxAScpmI\nCH3z8pEjx+HsXDLXd37QoGHMmuVHZGQEMTHPCA29CcCJE8c4cuQgmZkZJCUlodVq0Wq1nDlzkqNH\nDyGRSEhLS8vzOcu8+vt9TG3a1CAs7AAHDlwiNTWeiAhYvrw3kERwcBCLF7f/ZGMRBOGPiWBOEATh\nPyb7j12tVsvKlYGcPXua1atX0K/fQC5fvkT58hVZvHghdevW5cGDe8yadYmvv26LVquhd28fRo8e\nxrRps/DwKE9UVBS+vgNZvz4IgEePHhnSxhYsmE27dp1o1KgJmZmZ2RpK68fg4zOQTZvWM2vWfAAs\nLCzZt+8XSpUazuPHj8jIyPgggRzwp+0DcpaS1/9gL1zYAQcH/TNKjRo1ZffunQCGmZbTp3+jWbOW\n7Nv3KypVCsbGxmRkpNOkSXNkMhkFCxbi6tXLnD9/h7S0VzM7KlUptNpXP9rfppQ9gFQqNVSLBGjc\nuBkHDuyladOW3Lhx3TCr80/wtq0DslfQPH78ApGRT2natB/W1qNyrZs9VRCgVKnSLF++Os/9Nm7c\nnEGDhhteJye/ICzsCT4+g3K0UWjXrhWLFi1n1arluLiUMaRKTp06gdWr9c8EZv/OZ6VKtmvXEW/v\nlhQr5oiTUwl2797BunVbCQm5zPjxozl16jdiY2NJSUkxpEqOGzeCnTu30b79N2g0GtLSUg2zk+3b\nd8LGxoakpERUqlTs7Oz+9Nq9j2HDGjNsGAwatJ/Q0HYvl1py8GAJww2E1w0Y0JeBA4fh4uLKiBGD\nmThxGjodHDq0n9atvQF9gZoFC+YwderMdx7TtGkTqVmzdo7/BgThv04Ec4IgCP9hdevWB8DFxZWo\nqEiuXr2Mh0d5kpKSMDc3p1q1GoSGhhITE839+3dQKJTMmeNHYmIC8+e/el5MpVKRmpqaK23Mza0c\na9cGEBMTTd26DShSpGiO478+C1G//pcEBq6if//B7Nmzm2bNWn6wc5VIJG9sH5BVSh5AJpO+DDpf\nTzHNua1Op8tzn1nvAUil+mClenVXjI33kZKin40zM7uFTvdqZi738TPzPAeFQpkjGG/WrBWjRg1F\noVDQoMGXnyX9bc2anzh4cB/W1jYULFgIF5cy1KlTj3nzZpGQEI+xsTGjRo2jWDGnHK0DypXz5MWL\nJMPr+Pg4Ro8ez969vxAaepOyZd0NwdmcOTMIDb2JWp1GvXoNsbb+EgBv75Y0bdqC06dPotFkMmXK\nDIoUKUanTt4sWxaAtbU1Wq2WTp3asnz56jwDEIDjx68xcmQMYWHuODufY84ce2rWLGt4P69UybCw\nh2+RKinFzMwcZ+eSHD9+BC+vOkil+psJkZERWFpakpSUyIIFs6levRbDh49m9mw/9uz5GalUiq/v\nWNzc3HP095PL5QwfPuqjB3NZjIw0OV4rFKnI5UZ5rpv9uzl7tj+gzwzYuTPIEMzlz1/gLwVyWfsX\nRVcEIScRzAmCIPzLyWSyHLNA6emvCkZk/SiTSmV5BjD58uUnKSkBMzNzlErjl72vLGnR4ktWrAjE\nyCj3j7rsxTq8vJrg5laOM2dO4us7mJEjxxqKQ+TF2NiYypW/4OTJ4xw7dpiAgA1/9bRz8fCowM8/\n76Bp0xYkJiYSEnKZAQOG8PDhgzzXd3R0IjIygvDwpzg4FOHQoQM59nXw4D7q1m3AsGEDsLKywtTU\njLS0NOzsCnPkyEEaN25GcvILypRxw9m5GF9+ac2FC9tRKlVUrHib48c1eR43u6xS9llplq/Lnz8/\n+fPnJzAwAH//JX/twryHW7ducOLEUQIDN5ORkUGvXl1wcSnDrFl+jBgxhiJFinLjxnXmzp1pKLqR\n1TpAIpHg5zeJ5ORkli9fzalTJxg9ejjLlgVQvHgJevfuxt27dyhVqjR9+/bH0tISjUbDkCH9efDg\nHiVKlEQikWBtbUNAwHp27tzGpk3rGTXqfzRu3JSDB/fRvv03XLx4npIlS+cI5BYtWp7jPObPf0xY\nWEcA7t93ZsGCzTmCuSzZA/fsTbOzvvOZmZk51gsK+hnQf687dOicZ6pkz559OHfuDLt2bcfS0pLp\n0+fmeF+tVlOyZCmWLFmFiYlJru3/iqwiR0OG+L5xneDgiwQGriIiIoLSpbejVr9AoylEhw5NuHXr\nBkuW+KPRaHB1LYuv75hc/xZ4e7dk1ap1LFu2iPDwp/Ts2YkqVarRpk07RowYzLp1W9FoNCxduojz\n588ikUhp1ao1bdu2Z/XqlZw5cxK1Wo27uwcjR44z7DevmyeC8F8mgjlBEIR/OVvbfCQkxJGUlIix\nsQlnzpziiy+q57lu+fIV2LZtM8WKOZGcnMzp06dwdi7Fw4f3sbCwwNLSEp1Oh6urG0FBm+nUSV+U\nIetH9+siIsIpXNgBb++OREdHc//+vRzBnKmpGSpVSo5tWrb8mpEjh1C+fMUc6W5/Vdad/HdpHwCg\nUCgYOXIcI0cOQak0xtOzAhER+p5gvXr1Zfr0yRw7dgSFQkFaWio9enRCItEfZ+/eX9i4cR3JyS/o\n1asvACNHDmT06OGo1WsoXLg6Jiam2caY99hbtWrN8OEDKVCgIP7+S/OclfDyakJiYuJblc//0K5d\nC6F27XoYGRlhZGREzZq1SU9Xc/16COPHv0qDzMjQBznZWwdkyWrLULy4M7a2+ShRwvnl6xJERUVQ\nqlRpjh49yO7du9BoNMTGPufhw4eUKKFPv61btwEApUu7cuLEUQCaNWvJmDG+tG//DXv2/IydnT19\n+nQnMzODsmXdGTZsFE2a1KN1a2/Onj1NfLwUY2NX8uefg1weRWKifsZ6795fiIuLZfTo4UREhDNj\nxlQWLlxKcPBFYmKeYWpqRkREOCEhlwkJCebx40dUqlSF4cMHkpqqQq1Op0WLr6hatVqeqZImJsbI\n5XLq1m1A0aLFmDJlQo7re/nyXYYMucPdu2VwcjrJjBkO1Knj9t6fW/YiR38mKiqCuXNHExOj4bff\ndlGoUBR+fktZuHAZRYoUZerUHwypodllzaL5+Azi4cMHhpTUyMgIw+e/e/dOoqOjWLNmE1KplKSk\nJADatu1Az559AJgyZQKnT598Y/sOQfivE8GcIAjCv5xcLqdHj9706dOdAgUK4ujoBOSVsiShdGlX\nKlaszOHDB+nbty9ly7phbW3D5cuXyJcvPz16dCIzM5Patetw+/ZNunfXP9tTvnxFfH1Hv9zvqz0e\nPXqIAwf2IpfLyZcvP9269TIcG6BkyVLIZDJ69OhEs2Ytad/+G1xcXDE3N6d581Yf5Pyzl09/m/YB\nWZUMAb74ojobNmzLtU/9DMqcHMtUKhXPnkVjb18YpVKZaxsbG9scz2/5+AwEcpayf/34bdt2oG3b\nV/3hsp+LRqMhKiqS4OCLtGz5dR5n/inkTjPV6XSYm1sYfry/7vXWAVkzOlKpFIXi1eyOVCpFq9US\nERHO5s0b+OmndZibm+PnNynH7HLWNq/SY6FQITtsbW25dOkCV6+GULq0C8uWBSCTyZg7dyYHD+4j\nLS2NSpWq0r//YNq27UJy8hyePg3E1PQs+fOPAwYB+l5z//vfJJRKJZ06edOxYxusra1RKPSfsUQi\nISbmGYsWLcfOzp6NG9exZ8/PyOVypFIJP/+8ndq16+aZKqlQKPHzm2RIue3Xb2COazN79m1u3dIH\nSffueTJnzmbq1HEjNTWVCRNGExMTg1aroXv33lhZWRlmy8qX92TAAF+MjIy4desGCxfOJTU1DSMj\nI/z9lxIaetPQM/HmzessXDiP9HQ1SqWSMWN+oFgxR8MYChYsZLj5U7iwMWvW/EThwg6GlOmmTVuw\nY8fWXMFc9u/Dm1y6dJ6vv/Y2pAdbWloCEBx8gY0b16FWp5GUlESJEs4imBOENxDBnCAIwn+At3dH\nvL07vvF9a2trQ0rY6NHjGT16PAUKWBAT84L09HR8fAbmmVL5uqxZqCxduvSgS5ceudbLCkrkcnmO\nnlcZGRnEx8eh1WqpWrXa25za38KxY1cZOzaaR49KUrr0YRYudMHD48MUbslLRMQzevf+jefPNyOT\nSXF2bvDRjvVHPDw8mTXLj65de5KZmcmZMydp1aoNhQsX5tixw9Sv/yU6nY779+9RsmSpd96/vtea\nCmNjE8zMzIiLi+X338/kCL7fpGXLr5k8eTwlSjjnKO2fnp6OjY0NRkZGhiCladNaXL8ejonJTsqU\nUbBx46vZ4saNmxmK4HTo0AkLC0vat/8GL686L7dtQXR0FHZ29gDcvHktRw/AjIwMnj59gpubO506\ndcvVhiMgYP0bz+HFC2Wer8+dO0P+/AUNz6UlJyfTrVsHw2zZnDlT2blzG61be/PDD2OZPHkGrq5l\nUKlUuW40ODkVZ/HilchkMi5cOMeKFYtz9E/MfsMnK1BPSkrMsex9vL69Wq1m3rxZrFq1jgIFChIQ\nsIL09PT3OoYg/JuJYE74P3vnHRbF1cXhd5elSK8qikRABBVFECtW7L0XiNIixoLGFmvsBaMkdgVR\nEMUSNcZesNdYsUQFKwQQLKj0ust+f6xsqJaoMeab93l8dGbuvXPv7IL3zDnndwQEBARKRS6XM336\nHn77TQ+xWIaraw6TJnX8JPfKz89n9OidnD37J+XKHaBVq8/lafp7+PvH8vChwjNx504dFi7cQljY\npzPmFiy4wJUrnoAXAIsXb6VXL/k7iUMUFIIfNWrYB8/D1rYmTZs2x8NjAIaGRlhZVUNHR5vp0+fi\n77+A0NBgpFIpbdq0UxpzxedY+Li0a9WqWVO9ug1ubr0pX74ideqUVPl83bpY+GZz5s+fRc2adtja\n1iySryaTydiy5S8jSiwW07ChDa6u7QHYuLGoKmYBcrkcsbjkM9bQKJrLNnbsBOrXL/oyIiLiirKm\nYlLSS/z8zpGWpk6LFuX4+uvSvU5Nm+Zx5cozZLLyQDJNmiiMTCsra1auXMrq1ctp0qQZmpqaRbxl\nPXr0ICQkFCen+hgZGStDKjU1NUvcIy0tjTlzZvD4cRwikUiZ91fA06dPuHXrD+zsanPkyCFsbWuw\ne/dOZS7p4cMH3mhca2pqkpmZWeo1J6eG7N69E0dHJ1RUVEhNTVV+hrq6emRmZnLixFFcXNqWOb6A\nwP87gjEnICAgIFAq27efZu1aF6RShcdh1aqHNG58lRYt3u4VeV/Wrj3G1q29AV2MjIzYu/cpQ4c+\nJjQ06IuQIk9LKxo6mJFRMszy49/vL6MiJUUbqVT6Tt7Tj60G6Oo6CG/vIWRnZ+PrOwQbmxqYmlbi\np5+WlWhbvHRA4WNT00q0atUGN7feSmXMhIQE7t+/S0xMNGpq6mhpaTFx4jRevnyBj4/FVRY3AAAg\nAElEQVQH27fvARR5WH5+swgN3cqdO7fw85tHRkYaYrGY+vUbsmDBXK5du0LNmnZcuxZB48bO5ORk\ns3r1ciIirvD4cTytW7cjKiqSgIDl5ObmMGbMCO7du4tUKsXUNIjTp48TFxfHokVLAJDL8xk3bhQJ\nCfGkpCQTGxuDuXlVkpKes2iRH4aGhrx8+ZJ+/Vzp0qVHkZqKjx+bcf36KkDEoUMPUFU9T79+JQu8\nT5jQESOjE9y5k4elpZjhwxXqrlWqmBMcvInffz9LUNAq6tWr/7c/v7VrA3Byqo+fnz9PniQycuS3\nRa6bm3/Fb79tY8GC2VStakn//l9Tq1Ztpk2biEwmo0aNWvTo0afM8fX09Kld2x539/40auRMr159\nld/Brl17EBcXi4eHKxKJhG7detKrV1+6du2Bu3t/DA2NqFnTrsh4gpqlgEBRBGNOQEBAQKBUoqNT\nlIYcQHa2BQ8eRNCixce/V2KiDFDky8jlIrKyTIiOTvxipMgbN04jKioV0EUieULTpm9XqvwQWrZU\n59ixR2RnWwK5NGjw5I2GXGjoOg4d2o+BgaGyfMD27dvZtGkzeXlSzMzMmDZtNjKZDA8PN7Zs+RWJ\nREJGRjqenl+zZcuv/PbbDnbv3omKigpVq1owa9Z8ABYunEdMzCNyc3Pp2LEL1tY2f2tNZSljzp07\nk7FjJ2Bv78C6dYGEhKxh1KhxSKV5JCYmYGqqUA9t3bod2dlZjBw5mceP26CnF06lSnU4cGCvsvB4\nXFwspqaVcXZuTljYemWdxVmzfuDy5QuMGzeRdu06cvXqZebP92f//j0sX/4zR48eIj9fjrW1NQ8e\n3MfR0Ync3FzGjPmeZ8+esnZtgFKx08zMnLS0dLKyshCLxaxevZyOHbsoayqOGzeJhg1fUGCMZ2dX\n4+zZ6/QrpQ63SCRi8OCSIbRJSUno6OjQrl1HtLS02blzO0+eJCq9Zbt378bBoR7m5lV58SKJqKg7\n2NrWJDMzo4jaLEBGRoayxuH+/XtK3EtFRYVp04rWL6xXr36pSrOFVUILDG2AGTPmFmkXGrpVOfbI\nkWMYOXJMkes+PsPw8SnpOS7+MkBAQEAw5gQEBAQEyqBzZzuWLj1BYqJC2c/c/CDt2tX92+MdPLiP\nrVs3KUPnBg8eyvz5s0hJSUEul2BoqM/Ll4pwqgoVHuHg0JczZ/Yrc2qioiJZsWIxWVlZ6OnpM3Xq\nDIyMjImMvM2CBXMQi8U4OTXk4sXzbNjwCzKZjICAFVy/fpXc3Dx69epL9+69PvzBlIKfX3fMzI4Q\nEyOndm0NPDzaf5L7FODh0QJ19XNcuBBB+fJSxo0rOyw1KiqS48ePsH79FmQyKd7eA7G1rUHbtm1p\n2VKRvxUUtJp9+3bTu3d/HBwc+f33szRr1pKjR8Np2dIFiUTCpk2h7NixV2nkFVB8o/53KU0ZMzs7\ni/T0NOztHQDo0KEz06YphHZcXNpy7Fg4Awd6cvz4UebMWcCKFdvJzExDW/sKMpkh8fFxJCdfYcqU\nGezatYOqVS0wMDAkIGA5xsYm/P77Wc6ePcWIEd8RGXmbiIgrbNu2hS5depCXl8uBA3vIz8+nXLly\nTJkyk6ioO+zevZO7dyORy+UMGtQPfX199PUNSE1VhCdKpVIGDPhaKUrTrl0LtLS0ld9jXV1djIxu\n8VfkoRQDg7z3elaPHj1g5cqliMUiJBJVxo+fTHp6mtJb5uBQlx49+iCRSJg924/FixeRk5ODhoYG\nixevfP2SRDGWm5s78+bNIDR0HY0bN6VoeZLP8zIlJSWFn38+Q1aWKl26VKZ5c7u3dxIQ+D9FMOYE\nBAQEBErFzs6SlSufEha2HbFYzuDBVlSp8vcKFT969JANG4IJDAxBV1eP1NRU5s6dQadOXenQoTP7\n9+9BLA5CVTWVly//oEWLr9DW1gFQ5vEsWbKIH3/8GT09fY4dC2fNmlVMnjyd+fNnMWnSdGrVsiMg\nYIVy87lv3260tbUJCtpAbm4uw4cPpkGDRpiaVvpoz6gAsVjMyJHtPvq4b2LAAGcGlK1po+TmzWs0\nb97qtfCFOs7OzZHL4d69eyxa9BMZGelkZmYpxUC6du3B5s0baNasJQcP7mPixB8ARZ7WzJlTad68\nJc2atfwEKyq9AHtZuLi0Zdq0SbRo4YJIJKJyZTOysmTk5lYjLu4XACSSaJycPJR9ChdnB5g2bQ4v\nX75g06ZQpRImKBQy160LpGLFSsTHx+PpOZi5c6fTr58bcnk+8fFxGBgYsnHjL7i59Wbt2o2IxWLG\njfuVkydT+O23RCIi9jFjRpcSaypXrhxTp+qwcOF2UlL0qFfvTyZOfD/l1gYNGpUqEFTgLSsQLwJF\nXmNhFVUoquBqZ1ebLVt2Kq8VeMSKq6z+U+Tl5TFo0GEuXPACxOzbd46goDul1v0TEBAA8eeegICA\ngIDAv5emTe0ICOjAqlUdcXQsWUfuXYmIuIyLS1tl8WtdXV3u3PlDqezXvn0nkpL+JCioHZ07V8fE\nxEDZVy6XExsbQ3T0Q0aPHo6XlxsbNgTz/Plz0tMV4Wy1aine3Ldt20G5eb58+QKHDu3Hy8uNb7/1\nJDU1hfj4uL+9hi+X0j0rkydPZty4SYSGbsXb20cp91+7tj2JiYqSBzKZDAsLSwAWLVpCr159uXs3\nCh8f9yLGz8egTh17zp07Q25uLpmZmZw/fwYNjXLo6Ohy48Z1AA4d2q80QipXNkNFRcz69Wtp3Vph\nSHt5daRcuVg0NK4B+dSqtRMNjb/CTwsbVvr6iiLiNja2PH36tMR8/vjjBiNHjkFPTw97ewdSUlLI\nzs4GRDRt2pzKlSsTEXEFAwNDXr58werVW9m0qSu5uZVIS7MnKKgRJ09eUY5XuKZir14NOH++HVeu\n1CEsbECpwiT/JHK5nLCwU8yZc4jDh69+1rncvfuACxdaULBFTUpy5uDB2M86JwGBfzOCZ05AQEBA\n4JMjEpXudSnLE1NaZJeFhRUBAcFFzqWlpb1xvNJUBf/fqFvXgXnzZjFwoCcymZRz587QvXsvMjIy\nMDQ0QiqVcvjwAcqXr6Ds06FDJ2bPnoan52BA8VyfPn2Co6MTderU5dixcLKzs9DS+vCi7gWUpYw5\ndepM/P39yM7OpnJlsyJ5Uy4u7Vi9ehk+PsMBMDOriL//HObPn4hUmoOOjoScnGxl+8JKjQUeXLFY\nhfx8GWKxSolriu9TUbVNkQgkElWlYmdCwmNGjhyKnp41+fkFpTlE5Oaa8+efV99YU1FLS+ujPb8P\nYdasfQQGtkEmK4+WVhSzZp3G3b35Z5mLsbE+OjqJpKUVqMFK0db+tDmoAgJfMoIxJyAgICDwyXF0\nrM+UKeMZMODr12GWKdjZ1eHYsXDat+9EePhBZV6UXC6nsE0mEokwN69KcvIrpUS6VColLi4WCwtL\nNDU1uXPnFjVr2nHsWLiyX4MGjdm5cwcODk5IJBJiY/+kfPkKJYpWv4n09HSOHDlEz55lq/X9E6xb\nF6isbwYQGLgSQ0Mj8vJyOXHiKLm5eTRv3pJvvlEoEU6ePJ5nz56Sm5tD376utG7dFk9PVx4/jqdK\nFXO2bt1Ez549cXXtSW5uHuXKafDixQvl/dq27UBQ0GratlXk/slkMubMmU5GRjpyuZy+fQd8VEOu\ngNKUMa2tq5cIE/yr/UBcXQcWOdeoUUP27PkVUBhvPXp0IDU1hZ9+Ws7Ikd8qw0m//34qNja2JCcn\nIxaL2b59NxERVyhfvgKjR3/PkiX+hIcfVJ7X1zegR4/evHiRBKBU7HR378/ChUtJTc3l8uVw4uP9\nALCy2kWHDvXw8Ci9puK/ifBwzdflDyAjw5YDB+7g7v555lKxoikjR95i9epjZGQY4+x8ke+++7JK\nlQgI/JMIxpyAgICAwCfHwsISd3dvfH2HIBarUL26DaNHT8DPbxabN2/EwMBA6XEpLM5QgEQiYc6c\nH1m61J/09HRkMin9+7thYWHJpEnT+PHHeYjFIurWrac0Mrp27UFiYgLffDMQuVyOgYEh8+cveuc5\nS6VS0tJS+e237Z/dmOvcuRtTpnxPv36u5Ofnc/z4EYYMGcHVq5cICtpAfn4+kyaN48aNa9jbOzB5\n8nR0dXXJycnGx8eDFSuCcHf3plmz+gwePJRWrdogkUg5evQYmzcrDJ/CoiY3b16nVas2ymcpkUhY\ntWrtJ1/nx1LGLEAikeDpORgfHw9MTMrz1VdVAUpRSS3sfVP87e09BD+/2Xh4uFKuXDl++GFmob4l\n71W9ujlr1mSxceM2VFTk+PjUQE1Nwvff7yUlRYOmTdU/m7frbWhoFBVgUVOTltHyn2H06La4u78g\nPT0dM7P+ygLsAgICJRHJ3yfb+BNSkKgr8N+jcCK2wH8P4fP97/KlfLZZWVmUK6co2jxt2kQiIq5i\nYlK+hGKmvr4BU6ZMp0KFisybN7NI/bq2bZtx5MgZIiKusHZtALq6uvz5ZwzVq9ty9uwpzM2/on79\nRgwfPuqzrXPMmBEMHz6KFy9esG/fbkxNK3Hy5DG0tbVfP4dsBg3ypHPnbqxbF8iZMwqP0JMnCfz8\n8wpq1rSjRYuGnDx5AZFIhIFBObp374mNjS1NmjTD2bkZEomExYsXcvHiBfz9l2JmVoWwsDOcOpWF\nnl42kyc3xcjI8LM9gy8JuVxO797bOHv2G0CEmlo08+ff+UcMuvf92d227XdmzlQlKckOC4vzLF9u\nSoMGNT7hDAU+hC/ld7PA+2NiovPefQTPnICAgIDAF83582cJCwshKyuLpKTnTJmykGXLnrN/v5gz\nZ0YzbFg/evTozf79e1iyxB8/P/9S5Nb/Or5//y4bN26jYkVTnjxJJDr6ISEhm//ZRZVCly492L9/\nL69evaBz525cvXqZgQM9S5RbiIi4wtWrlwkMDEFdXZ2RI78lNzcXADU1deXaJRIJQUGhXLlyiZMn\nj7Fz5zaWLl3NmDETlGNt3XqOKVNsyM62AuQ8eBDMb7/1/SJq/30KQkNPcfZsDrq6CsPW2LhswzY5\n+RV//GFNwXcrN9eCCxciPlv44pvo168xTZsmEhl5A0fHuhgYCAa7gMCXguC3FhAQEBD4omndui0h\nIZvp06c//ft/zeLFzzh/fiAPH7qRkvKSkycVm+n27Tvxxx/X3zpejRq1qFhRUSz9nw5e8fUdQlRU\nZInzBw7s5fr1q1y8eJ6oqEgaNWpCw4aN2L9/D1lZWQA8f/6MV69ekZmZgY6ODurq6vz5Zwy3b98q\n9V6ZmZmkp6fRuLEzI0eO5cGDeyXanD2b8dqQAxBx40ZNkpKSPtp6vyQ2bTrDDz/UYvfu3mzc6Mbg\nwcfe+P3Q1tbB0PD566N8QIaBQc4/Mte/Q6VKprRu3VAw5AQEvjAEz5yAgICAwH+CAsXMhISiYSqJ\nieVKtFVRUSE/X7ERz8/PRyr9K2dIQ6Nk+38CmUxWSi7XX4jFYurVq4+Oji4ikYj69RsRExPD0KFe\nAGhqajJt2hwaNmzCrl2/MnBgX6pU+Qo7u9rKMQqPnZGRwYQJY1577eSMHDm2xD2NjHIBKQXbBWPj\nRHR1rT/amr8kfv89i5wci9dHIv74w5YXL15gbGxcQnCmW7eedOrkQpMmzkgky0lNdUVffwUmJr0Z\nNGgjRkbGDB48jICA5Tx79pRRo8bRtGlzfH2H8N1347G2VpQBGTbsG8aPn4yVVbWyJyYgIPB/jWDM\nCQgICAj8JyhQzLSy0iUuTo5YnEJ2tj36+hFAxyKKmRUrmnL3biQuLm04e/Z0Ecn6wmhqapKZmfnW\ne2/evAE1NTX69BnAsmU/8fDhA5YuXc3Vq5fZv38PjRs7Exa2HrlcTuPGTRk2bCSgyNXr3r03V65c\nYuzYCUXG3L9/D2Fh69HW1qFateqoqkq4ffsP5s5dqGzTt+8A+vYtWTnc339ZqfMMDz+l/LeJiQlB\nQaFvXNfEiS48eBBCRMRX6OklM3Gi0evi4/9/GBrmUNiwNTJKRFdXIdBSXHCmZUsXsrOz6datDT/9\nNJ+srCw6dFhC48bOjB49nilTvmfdugCWLl1NdPQj5s2bQdOmzencuRsHD+7F2nocsbF/kpeXJxhy\nAgICb0Qw5gQEBAQE/hMUKGZu3LieOnW2AGY4OjYjO/ssHh6uRRQzu3XryaRJ4/D0dKNhw8aUK/dX\n0ebCjjE9PX1q17bH3b0/jRo5lymAYm/vyNatYfTpM4CoqEikUilSqZQbN65RpYo5AQErCA4OQ1tb\nh7FjfTlz5iTNmrUkOzubWrXs8PUdXWS8pKQkgoPXEBwchpaWNj4+HiQkxNOtWy8qVzb7oOckl8vZ\nvv0UmZlyWra0oWrVSmW21dTUZNOmAWRmZqKhofHZVAWLC9Z8DiZNas2jRyFcu2aOnl4ykyaZoKam\nBsD27VuUgjPPnj0jLi4OsVhMy5atEYlEaGlpoaqqqiyLYGVVDTU1NVRUVLC0tCIxMRGAVq3aEBq6\njuHDv2P//j106tT18yxWQEDgi0Ew5gQEBAQE/jN07NiFjh27FDs7sEQ7AwPDIrXLCjxljo5OODo6\nFWk7Y8bct97XxsaWu3cjyczMQE1NDVvbGkRFRXLz5nWcnZvj6OiEnp4+oKjhdv36NZo1a6nc8BdG\nLpdz584tHBzqKft07tyVuLhYRoz47q1zeRNyuZzRo39l69buyOWGWFjsJTg4m1q1LN/YT1NT843X\nPyVvCz/9p9DU1CQsbABZWVloaGgo51O64ExOEbEZABWVv7ZcIpEIiUQVUITPymSKotgaGho4OTXk\nzJmTnDhxlODgTf/gCgUEBL5EBAEUAQEBAQGBQty8+YAffjjIrFn7ePny1Tv1kUgkmJpW5sCBvdSu\nbU+dOnWJiLjM48fxmJqaFhPKkCs3+cU3/AUUP/WxdFiePXvGnj22yOUKkYvo6K5s2FBS+ORTcPjw\nAXx8PPDycmPRovnk5+fj7+/H4MHuDBrUj3XrApVt+/TpyurVy/H2HsjJk8cAhSEaEXGFyZPHK9td\nvnyBKVO+/0fmX0C5cuWKfGaFBWdiYqLLFJx5V7p27cGSJf7UqFFLWXZCQEBAoCwEY05AQEBAQOA1\nkZExeHk9Zc2afqxcOQA3t2PvlDMHYG9fly1bwqhb1xF7ewd27fqV6tVtqFGjFtevR5CSkoxMJuPo\n0XDq1nUscxyRSETNmnZcvx5BamoKUqmUEyeOfpT1icVixOL8Yvf79IqdMTHRHD9+hICAYEJCNiMS\niQkPP8iQISNYu3YD69dv4fr1CB49evB6TiL09PQJDg6jdet2ynOOjk7ExsaQkpIMwP79e+nSpfsn\nn/+baNiwCTKZjIED+xIYuFIpOFPcSC95XPo1GxtbtLW16dy526ebtICAwH8GIcxSQEBA4F/I/fv3\nSEp6TuPGzp97Kv9X7N4dRVxc39dHIiIiunP27BXatWv81r729g5s3BiCnV1t1NU1UFdXx97eASMj\nY4YO9WXUqKHI5XKaNGlG06aKwtFlhQ4aGRnj7T2Eb7/1Qltbh+rVbT4ozDA/Px+xWIyJiQl9+pxh\n40YLpNKKWFvvZPBgu7897rty9eol7t6NYvDgQQDk5uZiZGTE8ePh7NmzC5lMxosXSURHR2NpqRD8\naN26baljtW/ficOHD9CxY1du377F9OlzPvn834SqqmqpgjOFxWaKH3t7Dylx7eHDP4mMjMPaujz5\n+fk0aNDo00xYQEDgP4VgzAkICAj8C7l//y5370a+lzEnlUqRSIRf6x+Cjg5ADqBQbFRTe4qJid47\n9a1Xrz4nTvyuPN6yZafy323atKdNm/Yl+hTf8C9fHsi6dYHcuHGNfv1c6dSpK4GBKzE0NCIvLxcf\nH3dyc/No3rwl33zzLUCpsvhQVClz3LiJ1K5tD8CCBT1p2fIC6ekRNG/uRIUKRu/6eD6Ijh278O23\nI5THCQmPGTvWl7VrN6Ktrc38+bPIzf2rDlu5ckVLRBSEqnbq1I2JE8egpqaGi0ubzybK8jHZsOEM\nc+fqI5MlU7HiTLy8/oWVxQUEBP6VCP/rCwgICJTCwYP72Lp1EyKRiGrVrBk8eCjz588iJSUFfX0D\npkyZToUKFZk3bybq6hrcv3+XV69eMmnSNA4c2EtU1B1q1rRTqie2bduMbt16cunSBQwNjZk1az76\n+vr4+g7B13cMtrY1SE5OxsfHnS1bdrJ2bQC5ubncvHmdQYO8adzYmcWLFxId/QiZTIq39xCaNm3B\ngQN7OXXqONnZ2eTn57N8eeBbVibwJnx8XDh/PoTjx5ujppaGh8cDHBz+2XC3jh27MGzYcB4+NKB1\na3OOHz/CkCEjuHr1EkFBG8jPz2fSpHHcuHENe3uHUmTxW6Orq1umUqZIJKJjx8aYmOjw/HnaP7Km\nevUaMGnSOPr1c8PAwIDU1BSePn2ChkY5tLS0ePnyBRcunMfBod5bxzI2NsbY2JjQ0GCWLl31D8z+\n03L27GnWrDlEcvJyjIyukpT0LWfPaiISBVK3riP16tVn27bNdO/eC3V1jc89XQEBgX8ZgjEnICAg\nUIxHjx6yYUMwgYEh6OrqkZqayty5M+jUqSsdOnRm//49LFnij5+fPwDp6WkEBoZw9uwpJk0aR0BA\nMBYWlgwe7M6DB/epVs2a7OxsbG1rMnLkWNavX0tIyBrGjJlQqkqfRCLBx2cYd+9GMnq0QtwhMHAl\nTk4NmDJlBmlpaQwZ4oGTU0NAEZIZGroVHZ2ixbIF3h81NTU2bnTlwYOHlCunQ5Uq/3ze0oIFvxMb\na0ZEhB1bt56mUaMKREXd4fLli3h5uQGQlZVNfHwc9vYObNoUSnj4QfT09Hn27Cnx8bHUrGlXqlLm\n56JqVQt8fIYxduwI8vPlqKqqMmbMBKpXt8HNrTfly1ekTh37N45R+OekbdsOpKSkYG5e9RPP/NPT\ntGlz8vJyAZDLFWvMy5MoPa8A27dvpX37Tu9lzBWE1goICPy3EYw5AQEBgWJERFzGxaUturqK8Dpd\nXV3u3PlDaby1b9+J1asVOTIikQhn52YAWFhYYWhohKWl1etjS548SaBaNWvEYrFSyKFdu45Mnfpm\nBT65XF5EAfHSpQucO3eaLVs2ApCXl8fTp08QiUQ4OTUQDLmPiFgspnp1689y7/T0dMLDzcjNHYCu\n7q/I5S/IzKyFXJ7PwIGedO/eq0j7All8LS0t1q/f/FoWX2EYlKWUWUB+fn6Z1z4FrVu3LZEHV6tW\n6fl627fvKXJc4OEu4ObN63Tt2uPjTvADWLcuEE1NLVxdi5bBuHHjGqNHD6dt2w5cvXoJNTUNxoz5\nnpCQNbx6lcyMGXOIjn6EhcUBYmObAKCunkD37pWUtfWSkp6TlPScUaOGoq9vwNKlq/H39yMqKpKc\nnGxatmytNPz69OlK69btuH79Cs7OLTh58jjBwWEAxMXFMmPGFOWxgIDAfwPBmBMQEBAohkgkKiYl\nr6C0c6AQQACFEaCmpqo8X7h+VPFxCjbZKioqyOWKTXXhfKHSmDdvEVWqmBc5d+fOrRK5RQJfFoVD\nei0sLFFXb4S6+jm0tBT5dKqqX9OwYQPmz5/NjRvXeP78GQkJj+nevReWllYkJT0jLS2Nr7/uQ3x8\nHPfv32Xz5o3K8X/++Udq1KhFx45dlJv9y5cv0rlzR/bvP/jFbPZlMhlz5x7k5Mk1qKlJGDjQ+4PG\nK/h5/hj16940Rl5eHgMGDGTy5OkMHuzOsWPhrF4dzNmzp9iwIYTmzVvSoIEFPXpc4fDh21hZGdOv\nnzPz5x9FJBLRp88AfvllM8uXBypfMA0ZMgJdXV1kMhmjRw/n0aMHWFpWU6qA7ty5k+fP07hy5RL3\n79/D2ro6Bw7sFRQyBQT+gwj+dwEBAYFiODrW58SJo6SmpgCQmpqCnV0djh0LByA8/CD29g7vNWZ+\nfr5SXv7IkUPUqaPob2paiaioOwDKeloAWlpaRSTxGzRoxI4dW5XH9+5FAWUbmAJfBgUhvcuXB7B+\n/WbGjJlAzZq/kZ3tTGpqF8TiuqSnH6F+/UZYWlpx+vQJUlKSMTQ0YsuWjTg5NaRKla/Iz8/H3Lwq\n9vYOypp0BQZGYUOjsOT/0KFD0dbW5v59RZ2599nsr1sXyJYtH8/oe5fx5s8/yMqV3bh9+wTXroUz\nevTp975PYmICrq69mDt3Bv36dWfhwnn4+Ljj4eGKp6crJ08eIzExATe33owf/x29enXmhx8mkpOT\nDSg8XwW/F6Ki7jBy5F+hkA8e3GPoUG8GDOjF3r27lOclElUsLa24du0qL1++wMmpAZmZmRw8uJ+L\nF88TFLSahIR4BgxoTrNm1bCyqvTWdRw/Ho6390C8vQcSHf2I6Oho5bXC3s8uXXpw4MBe8vPzOX78\nCG3bdnjvZyYgIPDvRjDmBAQEBIphYWGJu7s3vr5D8PR0Y8WKJYwePYEDB/bi4eFKePhBvvvur8LF\nxTfLpaGhUY47d27j7t6fa9ci8PIaDICr60B+++1XvL2/JiUlBVD0d3BwIibmEV5ebhw/fhRPz8FI\npVI8PAYUKbBcWs7d52LdukCuXLn0uafxRVFaSG9aWiwODsEYG++lSpWnSKV5ZGVlUatWbTw8vmHD\nhl8ICgrFyMiY9PQ0pkyZQZUq5vj5+bNsWQDVqilCRIsrZRbwMTb7H/s79y7j3bmjBmgV9ODePf2/\nda/Hj+Pp1asvtWvb8/DhA4KCNhASsonU1FRiYhRGUVxcLNWr29CsWQu0tLTYuXPHG+cpl8t5+PAB\ny5YFEBgYTEhIEC9eJJXoIxKJUFVVZf36tWhr62BmVgUfn2GYmJQv1ObN809IeMzWrZtYtiyA0NAt\nNGnStEwV0JYtXbhw4Rznz5/B1rYGurq67/ewBAQE/vUIYZYCAgICpdCxYxc6duxS5NzSpatLtCuc\ny2NqWonQ0K2lXgMYOXJMif7m5lUJDd2iPPbxGQYoNvVBQRuKtP3++ynvNM9PidoUXuUAACAASURB\nVEwmQ0VFpdRrhQUbBN6N0kJ6ZTIp+fky+vYdwIgR3xW5JpEUDeOVSouG8W7deo6tW2+TkfGU06dv\n0by5HTk5RcN3i2/2Q0LWUK+e01s3+6Gh6zh0aD8GBoaUL18BG5saPH4cz88/LyQ5+RUaGhpMnDgV\nQ0NjPD1d2bFjLwBZWVl8/XUftm/fw5MniSXaFxcxuX//LosW+ZGTk0PlymZMnjwdHR0dXr0KwMQk\nknLlriAS5aGpmY2n5zqSkp7z1VdVSUtLIzY2BiMjYzQ1tRCJwMSkAjExjwgJ2URCQgLz5s1ALpez\natUyIiNvk5eXR7Nm9dHW1iYjI4ONG9dz+PABxGIxu3f/ikgkRktLi0ePHpTIhyv+OTZr1gI1NTXU\n1NRwdHTizp1bSiO9OFevXsbXdzSRkbcAhfAOFOTKlmyvqalJRkYGurp6ZGRkvLMKqJqaGg0bNsbf\nfwGTJ08vc/4CAgJfLoJnTkBAQOAf4GN6MtauPUn79ofp0OEQmzad/VtjZGVl8f333+Hp6Ya7e3+O\nHTtCVFQkvr5D+OabQYwdO5Lnz58D4Os7hGXLfmLwYHc2bAimT5+uSgMkKyuLXr06I5VKmTdvpjJU\nNDLyNsOGeePp6YaPjwdZWVnIZDJWrlyqDGvbvXtnmfP7J0hMTMDdvf87tz94cB9JSUnK423bNivD\n76BoCN674uBQr0RIb6NGzvTo0UdpyBWEQRZQPCRRU1OTzMxMTp/+gx9+MOXSJTdSUzMYPfoF9+8/\n5OrVK2Xev/Bmv1OnskMso6IiOX78COvXb8Hff6kyNHjhwvmMGfM969ZtZPjw7/jppx/R1tbG2ro6\nERGK+54/f4aGDZugoqLCwoXzSrQvoOBHZO7cGYwY8R2hoVuwsqpGSMgaACwtDTE3v4lY7ImeXmXU\n1V+xfv1mevbsg0wmIy0tlXnzFpGc/ApDQyO6dOmBuro6ubk5SKVSlixZxMCBnqirq9OzZx/KldOk\nefNW1K3rSJcuPWjfvhO2tjXQ1zfAwMAQsViFNm3aMWHCVExMKgCKHNf8fMV3Pycn942frUgkLrKu\nv84rThQ24guHxJb2q6Jbt56MGzeS774bhrV1daUK6KxZ096qAtqmTQfEYrFQhFxA4D+K4JkTEBAQ\n+AcoK+TtTWRlZTF9+iSeP39Ofr4MD4/BLF7sT1xcc9TUbpOfr8HcuV7UqnWX9PSnbNgQjFSah66u\nHjNmzMXAwJDMzEyWLFnE3buRgAhvbx9atHAhLGw9UVGRmJiUp0oVc+ztHZg2bQILFvyMnp4+x46F\ns3jxYsaMmYxIJEIqlbJ2rcJTeO9eFNeuXcXR0Um5UZdIJMqQz7y8PGbMmMLs2Qt49OgBt2/fRE1N\njX37dqOtrU1Q0AZyc3MZPnwwDRo0wtT07TlCoDCWgoPDyvR2fGoOHNiLhYUVxsbGAISErCUnJ4dB\ng7xYtuwnXr58ASi8Lvv370FTU4uoqDtlKg5evnyRr7/2UIb0isUqVK9uw+jR4/n55x/x8HBFJpNR\nt64j48dPAhSGQfEXA3p6+tSubY+f3yTU1LqSmvo9aWkd0dZeyowZGtjY2LxxXW3adOD06ZNv3Ozf\nvHmN5s1boa6uDqjj7Nyc3Nwcbt26wbRpE5Xt8vKkALi4tOX48SM4Ojpx9Gg4vXv3IzMzkz/+uFlq\n+wIyMtJJT09X5qR26NCZadMUa1dRUWHePB8cHZ2Ii7Nm4MC+LF36ExkZGdjY1EAikdC4sTNyuRx3\ndy927tyGlVU1rl+/yuPH8URHP2Tt2gBycnLYsCEYFRUVIiNvU6FCRVq0aMW2bZtp0qQZv/22nRcv\nkl6LE8k5cuQQ9vZ1AahY0ZSoqDs0atSEU6f+ynGVy+WcPXuKQYO8yMrK5Nq1qwwbNpLc3FzMzKoo\n21WrVp0WLVyIjLzzWgDlFwCaNm0BgLf3EGXbEyeOKr37vXv3p3fvv148FPf6F1BcBRQUdexyc3P/\nNeHYpSGUURAQ+PsIxpyAgIDAv5SLF89jbFyeRYuWAoqNbl6ejOxsCxITF6Cjswsdnd1cvtyaAQOa\nsmbNegD27t3Fpk0b8PUdzfr1a9HR0VGGf6alpZGcnMylS7+jrq5O/foNSU9PY8OGYB49esjo0cMB\nxebK1LSici4FZRWg9I16AXK5nNjYPzEyMsbWtgbR0Q+RSFRRUVHh8uULPHz4QOm9y8jIID4+7p2N\nuU+xGZXJZMyePY1796KoWtWSadNmsXnzRs6fP0NOTg52dnWYMGEqJ04cJSoqktmzf0BdXZ1OnbqR\nlZVJWFgoV65cIi8vD7lcjlQq5caNa6iqqnLnzi3k8nxq17bn2rWrJRQHC6tGFg+VnTXLr8hxaOg6\njhw5VCTEsW9fV6ZNm0BenhQzMzO8vL5n3DgbqlZtTUzMYaTSZkycCHPnTlGOV9pm/+bN63Tu3O0t\nz7fkNblcjra2DiEhm0tcc3Zuzpo1q0hNTeXevSjq1atPZmYGOjqlt39fqlQxx8jIGEtLS0JDgzE3\n/wpQhJ6qqEiUirEFf2SyfCwsrOjXz43582cRGrqV4OA13Lt3lytXLjF37gwyMtKxsamBTCbD3Pwr\nYmNjCQ8/RL169enRow8AXl5DWLBgNmvXauPgUK+IR83KyppRo4aSnJyMl9dgjIyMSUxMKJYzp/jb\nw+Mbfv75R9zd+yMWq+DtPYTmzVu+9Zm/D1FR0cyaNZ3s7GT09P5efuHHYvLk8Tx79pTc3Bz69nWl\nW7eetG3bjO7de3PlyiXGjp1AYmICO3b8glSaR82adowbNwmxWIy//4JSX4oICAgoEIw5AQEBgX8p\nVlbWrFy5lNWrl9OkSTPs7euipiYBLAFIS+tMhQpzaNjwW549e8r06ZN4+fIFeXl5VKpUGVB4iWbP\n/ssw0NHR4dy5MyQmJmBoaMTRo4dJTk7mq6+qYmFhRUBAsLKtiYkOz5+nAQoBlwKcnZsTGLiSMWNG\ncO3aVeLjY/H09CE5+RWBgasASEp6rlTjTEp6zrhxo7h58xqNGjkzZ84CQKHquWLFYuRyOY0bN2XY\nsJHK82Fh60uc/xTExv7J5MnTsbOrg5/fbHbu3EHv3v3x8vIBYM6c6Zw7d4ZWrdqwc+d2fH3HYGNj\nC8Avv2wCwM/PnylTvkdNTY379+9x8eLvqKmp0aVLN/bt28PJk8eRSvOIjo7G0rIaQIl6a2+icIij\nTCbF23sgtrY1aNGilbLWWlDQalRUnjJ8eAb791egRo35fPONEzExz2nZ0qVEnqNMJmP58gPs2LEG\niSSTNWuCS7u1krp1HZg3bxYDB3oik0k5d+4M3bv3olKlSpw4cZRWrdogl8t58OA+1tbV0dTUxNa2\nJkuXLsLZuRkikQgtLe0S7R8+fKAUbJHLQUtLGx0dXW7cuI69fV0OHdqvzAeTy+XKlwinT59EW1uH\nrl17cvXqFe7diyI3N5fHj+MBOHz4AHXrOpKamoqOji6XLv3O8+fPOHXqGDVq1GTECB8qVjTF2ro6\nGRnp+PqO4ddff0Ff3wBQeAFVVSU0bdqcqVNnKp+DvX1dtmwpGR5c2KNWmMJ5tI6OTjg6OgGKvMXC\n476JzMxMJk8eT1paKjKZFB+fYTRt2oLExATGjx9FnToO3Lp1AxOT8vj5/YS6ujoBAdvx9w8gL0+b\nvLxGmJmdf6d7fSomT56Orq4uOTnZ+Ph40LKlC9nZ2dSqZYev72hiYqLZtCmUgACFx9TffwHh4Qfp\n0KEzQ4YML1KG4eHDB1hZVfus6xEQ+DchGHMCAgIC/1KqVDEnOHgTv/9+lqCgVdSrVx8NDTVGj37K\nwYM7AClZWVCnjjW+vkNwdR2Es3Mzrl27SnDwGuU4pZUvqF27LjNnzkNdXZ1z586wa9cO4uLiuHXr\nD+zsaiOVSnnw4AF6ehVK9NXU1MTY2JiEhAS6devJ2LETychIZ8GCOXh6DqZ/fzdcXXsRHf0IuVzO\n3btRhIRs4siRw6xcuYQnTxKRSCSsWLGENWvWY2xswtixvpw5c5IaNWoRELCC4OAwtLV1lOebNWv5\nSZ5x+fIVsLOrAyiKwW/fvhVTU1M2bdpAbm4OqampWFpaKQvDF89zKl++IgcO7KV2bXsePLjPjRvX\niIuLRUVFheXLF2Nu/hX6+vqoq2uUqTj4NkoLcZTLea3EuJqMjHQyM7No2LAxkydPoksXMzZv3oC7\n+xiGDvVm4sQfiownl8sZOnQ7u3e7AZ2oVOkI9+49wcmp7PDV6tVtad26LZ6erhgYGFKzZi1EIpg+\nfS7+/gsIDQ1GKpXSpk07rK2rAwqDdfr0ySxfHqgc5969e+zbt6dI+wJjTiRSFE1v3NiZVauWkp2d\nTeXKZsqQQpFIhJqaGt7eX5OWloZYrIKXlxuvXr3CxaUtzs7NmDZtItnZWaioqNCjRx82bAjGyakh\nO3b8gpaWFjdv3iA9PQ25XI6lZTVOnz5JQkI89+7dVd4DFN48FRWJUlF20CBvXFzavPNnVhY7d/7O\nlSspmJmJGTq0zTuFFqqrq+PntwhNTS2Sk5MZOtRLGZYZHx/HrFl+TJw4lenTJ3Pq1HHatevIypUr\nePz4J7KznTA2Xkhy8gdP/YPYvn0LZ84oQs2fPXtGXFwcYrGYli1bA3D16iXu3o1i8OBBAOTk5GBk\nZAQoyjDs2bMLmUzGixdJxMQ8Eow5AYFCCMacgICAwL+UpKQkdHR0aNeuI1pa2uzbtxsAHZ1X7Nnj\nyeHDBzhxwhGAzMwMjI1NAIVQRwH16zdk585tjBo1DlCEWdaqVRs/v9l4eX2NuroaKioquLt7Y2pa\nmaVL/UlPT0cmk/LNN960bFm6VH2bNh1YsmQRaWm1uHHjOtra2mhoqGNmZoZEImHOnAUsXryI58+f\nkZeXh6qqGj179mHr1jBGjRqKTCZ7HaanjYqKCm3bduD69WuIRCIcHOopw8IKzn8qY65wCFxBaN7P\nPy9k3bqNmJiUJzh4Dbm5uaW2B7Czs2PLljCmTJnB/v17OHBgL+XLl8fWtiZRUZGEhGzi1auXeHq6\nfcgsSz07f/5sFiz4CSurahw8uI9r164CULu2PYmJiUREXEEmk2FhYVmk39OnTwgPt6dA5j8hoS1b\nt27HyenNuXXu7t64u5cs1P3TT8tKbd+yZWtOny5aqkIsFpfavsCzlZiYwLlzp5W5ZAUkJiZw585t\ntLV1ycvLe12K4SdiY2NYtMiPq1cv8+RJIkuXBqCjo4Ov7xBWrVrKzZs3aN68JRKJBIlEFR0dbVas\nWMOCBXPQ1NRETU0NY2MTzM2/omvX7oAi5PVThPSuXXuC2bNrkZ1tBaQQHb2LRYt6vbWfXC4nIGAF\nN25cRywWkZT0nFevXgJgalpZaQzb2NiSmJhAeno6+fnZZGcrvICpqd0xMNhX5vifmoiIK1y9epnA\nwBDU1dUZOfJbcnNzUFNTL/KcO3bswrffjijSt6AMw9q1G9HW1mb+/FlFfh4FBAQENUsBAQGBfy2P\nHj1gyBBPvLzcWL9+LR4e3wAKg8zDw5UdO35h5MixgGIzPG3aRL75ZhD6+vrKTZKHxzekpaXh7t4f\nT083rl27ir6+PrNn+6GlpUl+vpy8PCkqKhKsrauzYsUa1q/fzMaN2+jbty8Ay5cHKkMLC+jTpz8H\nD56gcWNngoJWcerUcczMzGnRwgUAW9uaBAaG4OMzDBeXNmhoaCASiaha1ZLJk6czZsz3NGjQCC0t\n7dcjllX8XP5JhRuePn3CrVt/AAXF3BXKgLq6emRmZioLvUOBPHx6kWMrq+q8fPkCO7vaqKiooKam\nRqNGTbh+/RpffVUVN7feTJs2merV32wovYm6dR04ffokOTk5ZGZmcO7cGQCysjIwNDRCKpVy+PCB\nIn06dOjE7NnTSi0CrpDPzyh0Ro6qqrREu09JZmYm3303HG/vgXh4DODsWYXXJiBgOY8fx+Pl5caq\nVQqjb/PmDUyaNI6cnGzEYhEbN25DW1uHU6eOM3fuzFKVLwuL9ri7e9O0aXN8fb8jOHgTlSubAYq8\n0KCgUEaMGM20afMZNOggTZv+jKPjcZo1O8D27Rc+6pqPHs17bcgB6HHmzLsJ+YSHHyQlJZng4DBC\nQjZjYGCoVNJUUytcqkIFmUxRqkJbWwUTk98BUFePQ+/zaAYBKHMl1dXViYmJ5vbtWyXa1KvXgBMn\njvHq1StAoer65MkTMjMzS5RhEBAQKIrgmRMQEPi/4ODBfdSv30ipRPgl0KBBo1IVBr/+2r1EHlnT\npi2UoVeFKSs3x9HRqUQdu/ehuNdw164dvHz5gqioO9ja1iQzMwN1dQ1lWGJQ0AmOH5fy8uVTmjR5\nQrNmDVmyxJ+UlGS0tXU4ejScPn0GUKNGzVLPfwpEIhHm5l/x22/bWLBgNlWrWtKzZx+l8WtoaETN\nmnbK9p06dcXf3w8NDQ1Wrw6mW7eerF8fRJ06dVFX1wBg7doN6OrqYW1tS1hYCGpq6mRnZzFixCjl\nWKWJkLyJskIcBw8eypAhnujr61Orlp0yRxEUHs2goNW0bdu+xHiGhka4u//OmjVR5ORUplatPfj6\nNvw7j/BvU1bo4LBho4iOfqQUSbl06QLx8XEsWPATo0ePIC8vjxs3rmFjY8vjx/Gkp6eVqnwJRUV7\noGS4cYsWrQDYuTOOJ0/yuHBBExgHKF4wzJ59iDZtXmJgYPhR1qypmVfkWEvr3TxMGRkZGBgYoqKi\nQkTEFZ48SXxje21tbSpUMOabb2JISIgjNvYMiYnab+zzKWnYsAm7dv3KwIF9qVLlK+zsagNFvdxV\nq1rg4zOMsWNHkJ8vRyKRMG7cRGrWtFOWYShfvuJbyzAICPw/IhhzAgIC/xcUl5X/cvlwL9Xu3eeI\niUnDxaUatWv/vdyTR48esHLlUsRiERKJKuPHT0Yuz2fx4kXk5OSgoaHB4sUrEYlEPHz4hN27a5OT\nY0GlSuEsXhxN+/YuDB3qy6hRQ5HL5TRp0oymTZsDlHn+Y6y9MBUrmrJp044S5318himLtxemRQsX\npecRSsrFFzbSWrduW0Lk5NSpCB48eEbr1nWoWvXdFDwLKCvEsUBlsTg3b16nVas2hTyfRZk2rQtf\nfx3D7dtnaNmyFTo6Ou81nw+lrNDB4gbXpUsXuHz5IjdvXuf586eIRCLi4+MQi1VIT0974z0Ki/ZA\nyRBZVVVFoe6oKG1EonwgnwJDDuDpUysSEp5+NGNu7FhbHj7cRmRkPUxN7/Ldd2/+XVQw33btOjBx\n4lg8PAZgY1ODr76yKHNNBcd+fn5MmDAJkQjq12/EkyePPsoa/g6qqqr4+5cMrS1erqW0nxkouwyD\ngICAgg8y5hITE5kwYQIvX75EJBLRr18/3N3dSU5OZsyYMSQkJFC5cmWWLFmCrq7ux5qzgIDA/yGl\n1Vw7evQwfn7+AFy+fIHffvuVuXN/xM9vNnfvRiISiejcuRvly1dQysoXeFWiox+xYsVisrKy0NPT\nZ+rUGRgZGePrOwQbG1tu3LhOVlYmP/wwiw0bQoiOfkTr1m3x8RlW6lzeR53wQ9i+ffcH9Z8xYy9B\nQa2QSk1Zu/YMy5bdoFWr93/bXZbXMDAwpMhxx45dOHlSlZwcxQY0ISGAhIS7xMbG0aZNe9q0Kek5\natOmPS1auJCYmKDMA4QPX/s/wfbtv7NxYyoAbm7aDBjgDMDChQdZscKB7OxmVKkSzurVKTRoUOOj\n3lsul7NmzTHCw3eRlfWAwMA1b2zfsGFtLC2rftQ5vCuFQwdVVFTo27dbmUW4Bw70pEGDRkycOEaZ\nS7dlSxhaWtro6paufAlFPXGKENm/QktzcnKYPn0Sv/yyCyOjLF68ADAG7gOKHLRata5gadn6o63Z\nzs6KgwdNefgwhipV7JTKmWVRYOzo6ekXUZktTIFSJoCr60Dlv2vVqsX69X+VgBg+fNSHTP2zcPz4\nTVaufExOjoQOHcDX95/5HSsg8KXxQcacRCJhypQp1KhRg4yMDHr16oWzszO//vorTZo0wcfHhzVr\n1rBmzRrGjx//seYsICDwf0hpNdeCgwNJSVHUUNq/fy9dunTn/v17JCU9V276MjLS0dLS5tdftyll\n5aVSKUuWLOLHH/8qkL1mzSomT56OSCRCVVWNtWs3sH37ViZNGkdIyCZ0dHTp378H/fu7ERFxpcRc\nvgSkUim7d2shlZoC8PRpMzZt2v63jLn3wcxMBKQBCu9P5cr3MDV1KLP93bt/MmLETSIja2Fmdp45\nc4xp167uJ53jx+Datbv88IMRr14pwvuioq5hZXUHR0cbtm5VIztbYSTExXVg7dptH92YmzlzLwEB\nHZDLe6Ki8oywsONMnmz+3uMkJiYUMZxAUR7h0KH9jB79cf4vLyt0UFNTs0i4aMOGjQgKCqBOnbqI\nRCKeP3+GRKLIExOJREyZMhN/f78SypcF1wto3bodP/44jx07flGWxijg++/t8fVdS4UKSWhoHKdK\nlaqULy9hzJja76U6+i5oampSu3bNjzpmYY4cucrNm89p1coSR8fqn+w+n5qkpBeMH59KfLyihuXN\nm9FUqXKB7t3LLmwvIPD/ygcJoJiYmFCjhuI/Iy0tLaysrHj69CnHjx+nZ8+eAPTs2ZOjR4++aRgB\nAQGBt2JlZc2VKxdZvXo5N25cR0tLm/btO3H48AHS0tK4ffsWjRo1wdS0EgkJj1myZBEXL/6OpqaW\ncoyCN/WxsTFERysKZHt5ubFhQzDPnz9XtisI67O0tMLS0gpDQyNUVVWpVKkyz549K3UuXwIikQix\nOL/IueLHn4IRI9owcOCvWFjsws7uF2bN0kJXt2xFhh9//IObN93Iy7MnOron/v7xn3yOH4OLFx/x\n6tVfnqHkZAcuX/4TuVxOfrHHnJ//8UVdzp3TRC5XyLnLZOU5c0bto41ta1vjoxhyhUMHo6Ii8fAY\nwKFD+5Whg3p6+tSubY+7e39WrVpG/fqNaNu2AzNnTgFg+vRJZGVl4uo6EC8vH6ytqxMYGEJo6Bbm\nz1+EtrbiZ7G4aE/t2vaEhW0jODiMypXNmDVrPqqqqvz44zwWLZqBk5MtFy82ZPPmDhgb/0ZWVhih\noStIS1OEcvr6DiEqKhKA5ORk+vZVCMs8evQQHx8PvLzc8PBwLVLnruD8okXzyS/+BfgErF59DB+f\nSvz4Y1/69NEmOPjkJ7/np6Jv367Ex9dHReUppqajyM624ObNlM89LQGBfyUfLWcuPj6eyMhI6tSp\nw4sXL5R5KcbGxrxQxC8ICAgI/G2K11xzcmpAly49mDhxDGpqari4KGo26erqEhq6lYsXz7Nr168c\nP36EyZOnA39tJOVyShTILkxBLk2Bl64AkUiETCYrdS6enoM/8RP4cFRUVPj6axnLlt0lK8sac/ND\n+PhYvr3jByIWi/n5597v3D49vagRkpb2cb0jnwpHR3P09G6QklKgiPkHDg6KUg09emQSFPSYvLzK\nVKx4mkGDKn/0++vo5BQ51tb+cAn3x4/jmTZtIm3adOD69QgWLlzMunWBPH36hMTEBJ4+fUK/fq5K\nkZr169cSHn4QfX0DypevgI1NjSLhf+8SOjhjxlwA0tJSefXqJX37DqBv348jgpOdnc2aNSd58eIV\ncXGxzJw5X1mj7ezZU2zatIGxYydgb+/AunWBhISsYdSocYhEolJVVXfv/pW+fV1p164DUqkUmUxG\nTEw0x48fKbUA9qdk1y4ZmZkKb1x6ug07d97Cu2Sa5Wfj7NnTxMQ8YuBAz7e2VVFRoWLFazx50pbE\nxGWoqcVRo8aX8dJMQOCf5qMYcxkZGYwaNYqpU6cq34oVUNYvQAEBAYH3obh64v79ezA2NsbY2JjQ\n0GCWLl0FQEpKMhKJhBYtXKhSxZy5cxVhV4Vl5c3NvyI5+VWRAtlxcbEl6nGVhlwuL7P+25fAuHHt\nadz4Bvfv36J16zqYmVX83FMqQbNmIs6dUxg+kEHDhq8+95TeiQYNajFt2mk2b76HXC7C1VWDxo0V\nCqMzZ3bF0fEcf/55DhcXG2rV+vhG9LhxFjx5spPoaBuqVYtk/Hirt3d6A7GxMcycOZWpU2eRmprC\n9esRymtxcbEsXx5IRkY6bm696dmzL/fuRXHq1HFCQ7eSl5eHt/dAbG3/XijpvHn7CQszJC9Pnfbt\nj/6PvfMOqKn/4/jrdttLQ0h2KDREZkY/hOxRZBXx8JgP2VtWZh57RzYRHnvzGI+RyCoy00BG2rfu\n7f7+uE+XFIoQz3n9wznne77ne86593Y+5/P5vt8sXuySK4PtTyGVSunRYzdnzvRCVfU5Zcv6I5Mp\nXhzkRh0zJ6ysbP7N7D+nYcNGlChR8pMG2N8SVdWs2T+xWPbNj5kX6tVr8J6Y0acRiUTMmqXG4sUr\nSEzcQps2g9DWljJu3EgkEglRUZE0aOConAt4+fJFpSdkZrltfpfICggUVL46mEtPT2fIkCG0adOG\nJk2aAGBsbExsbCwmJia8ePECI6PPK0GZmHxfJS2B74twf39tvsf9vXs3hNGj56CiooKqqire3t6Y\nmOjRsWN7Nm7cSPXqCrnrV6+iGDVqnLKsadSokZiY6OHm1glf39loaWmxbds2li5dwvTp00lISEAm\nk+Hh4UHNmraoqYkxNNTGxEQPQ0MdNDRUleenpibGyEiHV6+ilGNRU1NjypQpP9VnvG3berlu+yPO\na+rUDpQseZIrV4IpVUrO2LHuiMXi7z6OL2H48JYMH57ztt69czZgz4lt27ahqalJu3btctU+MjIS\nP7/p3LixnaioaEqUaJmrh9mc7q9EosPbt3FMmDCKJUuWYG5uzqVLl5TfBV1dTZycGmNqaggYUrhw\nYUQiCQ8fhtG8eTOKF1f8zXdyaoyOjkaeP0MXLoSwcqUdqakKb76AADsaN75Av365v345cf58MGfO\nNAcUc+7S0ozYt+8B9epZoa+vzfPnCYjFKsrxpqTooKYmxsREDy0tDQoVEIHtwgAAIABJREFU0sTE\nRA+ZLAkVFREmJnp07epK/fq1OX36NGPGDMPb2xtdXU06duyAl5fXV403r/zxhynDhl0kNTUGE5NV\nqKtLWbz4FlOmTOHcuXP8+eefyGQyDA0NWb9+PXFxcYwbN47IyEi0tLSYOnUqFhYWLF68mOjoaCIj\nI4mJicHDw4MePRSB6bp16wgMDATAxcUFDw8PIiMj6dOnD3Z2dgQHB2NlZUX79u1ZsmQJb968Ye7c\nudjY2BAYGMjt27eZOHEiL1++ZPLkyURGKspSp0yZgp3du3m0IhF4eDjSuHF5+vc/wJw5nQgMDOTR\no/vs2bMHdXV1mjdvzu+/90FNTY2tW/3ZvHkjmpqarFq1in37Ahg4cGD2i/QL8TP9zRH4tnxVMCeX\nyxk/fjzm5ub07NlTub5Ro0bs3r2bvn37smfPHmWQ9yliYz8tMSzw82Jioifc31+Y73V/LSxsWbt2\nc5Z1sbEJnDv3D82bt1aOwdjYjJUr/bO1s7Orw8aNAQDEx6dhbGzGggXLs7Xz9V2m/H/ZspWYNm2u\nsu/MbUWKlMpxLL8aP/K7265dDTLjmNevkz/d+BdDJpPRuLGiJC+31//16ySkUhlJSTIMDIqSmCj9\nrHT/x+7v69dJaGvrULhwUU6fPo++fhHi4pKRSKTExiaQlCRBS0us3Fcuhxcv3pKUlEZiYqpyfXKy\nhMRESZ4/Q9evPyY19X2POH0ePkz46s+iVCpHVTUeqdIfXY5UmkJsbAKJiRJUVNTR0dHl+PGz2NpW\nZcuWHVhZVSU2NgFj4yJcvBhEsWJl2LVrLxkZcmJjE4iKisTMrATNm7fjwYMnBAffpEaNWqxbN5xW\nrVwwNDQkPv4tyckpFCv2bbPgTZvasmTJWdasWc+ffy7BxKQI8+fPZtOm7axevZxly9ZQrJgpCQmK\na7lgwXzKlq2At/dsgoODGD58BOvWbSEpSUJ4+IMsmVcnp9aEh98jIGAnq1atJyNDTt++HlSoUAVd\nXT0iIiLw9p7FsGFj6dPHncDAvSxevJpz586waNFSfHzmkZCQSkpKGrGxCUyaNAVr66pMmTKLjIwM\nUlKSs9xfuVzx2c/8XMfGJpCQkErVqvakpMhJSZFQsmRpbt26R0JCAuHh4bi4uAKQni7F2trml/xN\nzkR4rvp1+ZIg/auCuatXr/LXX39hYWGhfHvo5eVF3759GTp0KLt27VJaEwgICAjkN56e3dHW1mbI\nkI+kQvIZuVzO/v0XiI6Ox9m5KqVKmX6X434JP6NJ+q9ETEw0w4cPxtKyMvfuhVGmTDkmTvTm0aNH\nH7XEqFjRghs3QmjSpCnJycloaWnTpUt3wsPvMneuDxKJBDOzEowdOwk9PT3CwkLx8ZmKSCSiZs38\nNf1WU1Nj5sy5eHkNQktLC2Pjd5+jD73gFIiwsbFlzpyZ9OjRC6lUyoUL52jbtkOej92kSTUsLfcR\nFqZQMixe/CTNm1f40lNRUrlyRbp1C2TLFg3kcglaWnEMHPiu7O9T6phdunRn4sSx/PXXburUqUem\n5+HJk8c5evQgqqqqGBsXxt3dEz09vRwNsL91MAfw+nU0SUmvGDduOFKpDIlEwp07t7Czq0axYorf\nq0xPwZs3Q5gxYy4A1arZ8/btW5KTkxCJRNStWw9VVVUKFTLA0NCI169fcePGdRo0+B8aGpqAwncx\nJOQa9eo1xNTUjHLlFGW9ZcuWw96+5r//N+fZs+hs4wwODmLSpGmAYk5tbkWk1NXVlP9XUREjkylK\nSe3tazFlyow8Xy8BgV+Brwrm7O3tCQsLy3Hb+vXrv6ZrAQEBgc/i57fpux5v3Li9+Ps7IZUWZe3a\nA6xZk4SNzZeZbn9rfh2T9J+Xp08jGDduMlZWNvj4TGXXrh2cPXsaHx9fDAyyW2JIpVLWrNkAgJ/f\nKjKnm0+fPhkvr9HZRDl8fLzx8hqDrW1Vli1b+Nnx7NmzC01NzWxCHDlZEYhEIjQ1NZkz50+GDRuA\nh0cf5XgUc+Hf7f/2bRwSiQRLy8rUq9cADw83jIyMMTcvn20efW4wNDRg/Xprli3bjkymQufOpbCy\n+rr5f5nMnduBzp1vEReXSL16u9HUVAQm74u0fOiVCFCqVBn8/bcqlzNN5Xv06EmPHj2ztf+YAfb3\nwNm5FRMmjFFmbs6fP8uJE0dzbJtzYI7S/gEUwZZMJsumfyCXy5XrsgZZivLz9/fNy7HzgkgkokoV\na3x9ZyuzpCkpKbx8GUvJknm35RAQ+BnJNzVLAQEBgV+Z+Pi3BAaaIpUq3q4/ftyK9et34Ov7bYK5\ngmCS3rp1S7p16/1Nzu+/QJEiRbGysgGgWbMW+Pv78fDhA4YNGwBARkYGxsbvTNEbN26arY+kpEQS\nExOziXIkJmaur/pv/y25ePHCJ8fTrl3uFEVNTYsrzah1dXVZvVoRYGaKV3h69s3SXl1dAwMDhdVE\nly498PTsS2pq6r+frS8TQClXrgTz5pX4on0/h7291TfpFxSCcNu3n0NVVYSbmyPq6vlnD5Ebqlev\nyZgxwxkwoC+gRnz8W8zNyzN//ixiYqIxNS1OfPxb9PULYWNjx9Gjh+jZsw/BwUEYGBiira2DXC4n\nIeEt7u6d3wvwRdjaVmXGDG+6d/cgI0POqVPHcXZupQzKMr0IczfOGuzevZNOnbogk8lITU3Jkp17\nP3DM/P/HBPUMDAwYP34KU6aMIy0tHYC+fQcIwZzAfwYhmBMQEBAogBQEk/QuXdrTurUr+vr6P/JS\n/LS8/+Apl8vR0dH5pCWGpuY7wZLExAQCAwO4c+cWL1/GMmHCaCZO9GbgwN/IyJAxcOBvpKamKlX8\nEhLiefkylpSUFLS0tFi+fDHnz59FLBZTq1ZtBgz4g7VrV6KtrUOXLt0JCwuld+/pyGTyLCWaMpmM\nFSuWcP36VdLS0unQwZW2bTsQHByEn98qDAwMefToARYWlZg0aRoBAduIjY2lc+euiMW6lC9fjPj4\nl6SlpeHs3IoKFSy+3QUuYCQmJtKp00GCgjwAKfv3+7N5s6syS/U9KFOmLL/91h9PT0/S0qSoqqri\n5TWaUaPGM378SDIy5BgZGeHruwRPz774+EzFw6MLWlpaTJgwBcj83GYPmipWtKRFi1b89psHADVq\n1OLmzRs0adIMkUiEpWUlLC0rMXOm92eDsaFDRzBnzgwOHNiLiooKI0aMo0qVd0F2poXF+y8WnJ1b\n4ezcStlmzpwFyv9Xq2avfOkgIPBfQwjmBAQEBHKBvn4hOnaMYf36GKTSYpQuvZ+ePb9+Hs/HMDev\nwNKlC1m+fDF169bH1raq0iTd2bk1t2/fYtKkaSQmJipN0uvUqUfNmrWVfeRkkg7ZM0I5maQDlCxZ\nkufPnxWYYM7JqT7Hjp390cPINc+fP1PaXxw7dpgqVazYt29Pri0x4uLe0KlTVyIiIpBIUtm1K4DU\n1JR/Pxur6d69E8uWLWLlSj/Wrl3F4cP72b59Mx06uHL27Gm2bNkFoLTkeL880sfHm6lTvSld2iJL\nieb+/XuV2bi0tDQGDOij/Ezdv3+PTZsCMDYuTP/+vbl5M4TWrduxaNFqrl//i4wMQyIjT7JhgwG2\ntt/uu1FQ2bDhLEFBPQExoMrp093Yu/ckLi7/y/djfWxO5s2bN9i8eT0gx9KyEiNGjEVNTQ0Xl9Y0\nauTEpUsXSEh4J9yiq6tLr159cHRsDLz7jsXERHPunCKgmj17AdOmTSQlJQWAUaPGY2VlQ9++PYmI\neMy4cSNo2bINwcFBbNu2mTlzFhAf/5axY4cTHR2NpqYWDx7cx9m5FdHRUcyc6Z2jR+GX8PBhJMuX\nh5CRIaZLl7LY22d9efCz/WYICHwJX2faIiAgIPAfYsaMtqxaFcK0aTvZtcvim86XyzQmNzcvz+rV\ny1i/fg0tWrThyJFDnDhxJJtJup1ddfbs2cWsWdOUfXxokr5u3RbWrduCv/82fH0XK9t9yiQ90+Kh\nYPBzeZaWKlWa3bt30L27K4mJibi4uDFt2mxWrFhMz55d6dWrK7dv3/jo/rq6elhZ2TB+/BRiYqLx\n919DerqU4cMV3mdt2rTj4cP7tGjRmEOH9pGQkMjz58/Q0dFFXV0DH5+pnDlzSilYkUlmiaa9vT2g\nKNHM5MqVixw+fIBevbrSr19P4uPfEhn5FJFIRKVKVShc2ASRSET58hWJiYnh8uWbpKVpkXlvYmIa\nsW/fgxzPJzExkd27d37RtXRxaU18/Nsv2vdX5enTCDp0cGXTpgB0dHTYunUTM2d6M3XqLPbt24dM\nJlNeb5FIhJ6eHv7+2+jYsRMLF85Xrs9K9u+YkZERCxYsxc9vE97eM/nzT0Wpd//+g7GxsWPdui10\n6tQ1yz5r167EwqIS/v5b6ddvINOnTwIUnnuXLoVQpkxr5s5dxLp1qz86p+5zvH79hp49b+Lv78bG\nja707fuasLDHnz0fAYFfDSEzJyAgIJBLRCIRrVo5fJdjFRST9IJIcnIyY8eOICEhHplMym+/9ade\nvYZs2bIBdXV1XFzcWLRoPg8e3GfhwuVcvXqFAwf+UqrnfS/EYjETJ2Y9ZoUKFVmyZFW2tosXr8yy\n7Orahb//Pq3cZ9iwUezatYPw8LtKURszs5I0auSUo4rf6tX+BAVd5vTpEwQG7mDhwuXZ2mTyoRCF\nl9coatSonWVdcHBQlkBfLFZBJpNSpIghItH7D+MS9D6irJ2QEM/u3QG0b++SbZtUqigJ/BCZTIZY\nLM5xrlRBw929Pvv3r/+3zFKGo+MW2rbNfq75xYdzMtevX0Px4maUKFESUJQlBgbuoFOnLgA0adJM\n+e/ixb65Pk56upQFC2Zz/344KioqREY+BT4tYPKhUmZMTAxubu2JjIwhMbE2s2e7cfjwegoXLsSb\nN68pXPhdpcDBg/u4ezeUYcNGAXDkyEF27tyOVJrOw4cPOHnyAs2bO1K5cm2Sk6MpWXIX0dHLiIxs\nSkDASiIjvUlNTcHBIXcG5QICPztCMCcgICBQAHn48D5Lly5ERUWEqqoqI0aMA8DJqTlv376lVKky\nAMTGxjJzpjdyuSKD9vvvgwFo0aI18+b5KAVQpk2bzcKF80hMTEQmk9K5c9dswdyHKoUFFQ0NDXx8\n5qKtrUNcXBy//96LevUaYmtbjW3bNuHi4kZYWChSqRSpVEpIyDWqVq32RccaOfIPpkyZ8Unp9EGD\n+jJo0DAsLbOKfaSlpfHPP+epU+fLXgB8WKZpY2NLePhdbt9+xMaNMaSkpPDixZVsKn6FC5uQmppC\nnToOWFvb0rlzW0Dx8C2XK0RNdHX1uHr1KqVKVeTo0UPKY9asWYfAwJ3Y2dmjqqpKRMQTihQpCsCL\nF8/x8OiCSCQiLU1CqVKl2bRpFerqbyhduiOxsb9Tt+4btLTeZCmla9asBSdOHCUtTcLz589p3tyR\nFi1aU7p0WZYtW6hU8ty+fQ/z5vkQFHQFNTVVtLV1cHHpTJEixYiNfcGgQX3R1y/EkiWrkEgkzJ8/\ni7t3QxGLxQwaNIxq1ew5eHAf5879jUQiISoqkgYNHBkwYMgXXf+8oqurS0BAS7Zt24Oamgg3t46o\nqalx9uxpSpYsTZkyZfP1eB/OydTV1cuSvXxfbfJj+4rFYjIyFEFZRkYGUml6trbbt2/G2LgwEydO\nQyaT0ahR3VyN7/1gLyUlmebNf2PFCglyuS4gIiTEg5o11yGVZs3MvT/mx48fcfLkMVas8EMsFuPo\nWJujRw+RmpqKjY01u3aNQF9/N4UK7eD16y6EhR3C3b0LzZq1IDAwIFfjFBD42RGCOQEBAYECSM2a\ntbPMf8vkxo3rtG7dTrlcvnyFHC0aGjZsRMOGjZTLuckI2dlVx86uunJ548aNBdKYVi6Xs2LFEkJC\nrqOiIuLly1jevHmNhYUld++GkpychLq6OpaWlQgLC+XGjevKt/x5Pc6cOX9+NiuU03ZT0+K4u3ty\n8eKXB3OZZZqzZk2lTJlytG/vwo4dW/HyesqDB4qytqJFZYwc6YWamhhQqPhpa2szZsxw0tLSADmD\nB3spx5k51HHjJjN16lRksgxq1KitPIfWrdsRExNN797dkcvlGBoaMXPmXJ49iyEy8imBgfvR1y/E\n7NnTOXr0EAMHDsXOrjqbN29ER2caGzacZd261Tx9GqE0nXZza09iYiLTp89h7doVynLNnTu3IZPJ\n2LQpgNu3b/4ryjOZ8eNHUqpUaW7eDKFFizYMHtwXIyNjlixZhVisOM/AwABUVFTw999GRMRjhg0b\nxNatgYBibt/69VtQVVWja9eOuLq6YWJS5IvuQV7R0dGhd+9mWdb9/fdpHBzq53sw92Gwb2lZib17\nA4mKisTEpBJHjhzM8hLjxImjdO/ekxMnjiozesWKmXL3biiNGjXh3Lm/kb5zVFeSnJykvH6HDx9Q\nll5ra+uQnJyU49jeV8ocPXoYGRkZnDq1BS2tsqioSHjzxhOx+BlJSXGMGTMMNTU1hgwZjrW1bZZ+\nTp48yqVL/+DkVB8dHV1kMhkxMdGoqanRu7c7UVH72bkzA1XVqzRurM7jx9HKDGSzZs4sX744p+EJ\nCPxSCMGcgICAwE/CtzRJT09PZ8uW06SmyujUqTaGhgb5foz84ujRQ7x9G4ef3ybEYjGurm2QSNIw\nNFTF1NSMgwf3YW1ti7l5eYKDFZmr0qXL5KrvmJhovLwGUaWKNXfvhvL48SMOHDiOvn4h1q9fw9Gj\nhzAwMKRIkaJYWFRS+pOdOnWc+fNnkZiYwJgxk6hSxYo1a1aQlpbGjRvX6dHDk0aNmuTpPHMq0+ze\nfSS//95Yufz8uSfu7vqMHJk1gFi92j9bf+9bClhYWLJ3715lsJ6ZvRKJRPTrN5B+/QZm2Tc5OYnO\nnbuir6+wIBg9egKtWjmxYMEcAAoV0gfkSCSSbKbT+vqF0NTUomJFhThFpk1DTEw0IpGIsWOHK0V5\nAgK2EhZ2hxcvnvP2bRyRkRFYW9ty8OB+Dh8+oPTIu3kzBBeXzoDCA65YMVOePo1AJBJRvXpNtLV1\nAIW6Y0xMdJ6Duc+V7Do7t2Tt2lWkpaUpzcU/VBGtWbM2DRv+j/Pnz3L9+jX8/dcyffoczMzyx3Lh\nw2C/c+duVKlizcSJowE5FStWol27d2WeCQkJeHh0QV1dXVma26ZNe8aMGU7Pnl2pVasOWlrayvaZ\nAX779q6MHz+Kw4cPZmlTvnwFxGIxPXt2pUULhXJp5suCD5UyjY0L4+fnj5vbAF6+1AFeY239O4UK\nGTNrlkKVcsSIwWzaFJAlo3f69Elq1arL7Nm+BAYGsHz5Yjw9+7J1q+IF1qRJrahe/S8uXXrK1Kmd\naNkya7mygMB/ASGYExAQEPhJ+FYm6VKpFA+PAI4f9wDUCQjYyI4d/+Ps2WMEBV37oqzWtyQpKQlD\nQyPEYjHBwUE8exaj3GZrW5WtWzcxbtxkypUzZ9EiXypVqpyn/qOiIpk4cSqVK1vh6toGgNDQ25w5\ncxJ//22kp6fj6dk9S1llRkYGq1f7888/51m3bhV//rmM337rz927oQwdOvKLzjOnjF+FCsXR1b1H\nYqLCX05F5SVmZprZ2uU3IpFI+ZB94EAQhw69JjFRwqpVvhQvXixb+w9Np98n06ahWLHiFC9uppSY\nDw4OYs2aFVSsaMmQIcNZsmQBaWlpjBgxlrNnz/DyZSy9e/dg7dqNnxxrVgNr8ReJ+HyqZNfcvDz+\n/n78+ecyNDU12bRp/UdVRHV0dKlXrwEODvWzZMrzg5yC/erVa+DntxkTE71sWfVu3dzp339wlnWG\nhkZZTNIzt79vCVCiRMkshumZbVRVVbPNxczM7Ovr6ys9MQFcXdsgFosZMqQrx4+foVmzyyxd+gJd\nXRPGjlVkjpOTk5WKmZm8ePECiSSNN2/e/JtpW5Tl+w6K+cGZ5u/W1racOHGUpk2dOXr08EevnYDA\nr4SgZikgICDwH+fUqSCOH+8AqAMq3Ljhjp/fPz96WNnIDG6aNm1OWFgoHh5uHD58gNKl35Wv2dhU\n5fXrV1hZWWNoaISGhobScDu3FC1qSuXK7zyv5HI5N2+GUL++I2pqamhra+PgUD/LPg0bKuTnLSws\nlQ+bijlqHxeJ+BTvP0y/j7V1Rby8HlGy5G6KFduPu/sBunT59kIP1arV4NSp4+zde46hQw3YubMx\nr183wt19PunpinlW4eH3Prr/y5exREQ8Jjk5WWnTkJSUQEJCPKB4ofDo0QP09PRQUVEhJiaa27dv\nAYrgWl1dne7de2JgYMDz58+xta2qnOsXEfGE58+fUbp0mRyv95fcgw9Ldq2srJUluxoaGjx+/JD+\n/T3p1asrhw8f/KyK6Jd+Dj5F3kRhfvxk2MOHgwkMvM3bt2k0bVobkLNqlb9SZTcw8ABaWlpZzkss\nVqFPn9/x8hrI7797IpFIePXqVY4+dgB//DGCwMAAPDzcePky9qcQzhEQ+FqEzJyAgIDAL8DnysLq\n1HFg06b1yOVy6tSpp3y77uRUn6pV61Kq1J+8eDEVdfXHGBmt4syZdNTVv49yZ27JNBIuVMjgo8bb\n9vY1OXXqXSCaOY8qL2hp5ZTpEn3wQJ714TxT6VFFRfzFUuu5ITExETOzOC5fbk9s7AuWLPkTkajD\nNzteJmXLlsPd3ZMFC3woVMgQTc3KvHgxAZFoBO7unRGLValatRojRihsEz58hi5e3IyjRw+RkBDP\nqVPHadWqHZ6e/Vi+fBE9e3ZFJpPSsWNnZDIZoaG32bVrO1ZW1gAsW7aQ2NgX9O/fh1q1alOhQkVK\nly7DvHk+eHi4IRaLGT9+CqqqqlmMqTP5kgd6VdWPl+yampphb18rTyqi+R1UfCzY/xgBAXvz9fh5\nJTExlbFji6OiUgMNjet4ee2mRo3aBARso2vXHgCEh9+lQgWLLN8za2tb5PIM1q3bwu7dO1m2bBFV\nqlgpfwsAHB0bK33yTE2LZ/lt+O23/t/pDAUEfhxCMCcgICDwC/CpsrCSJUuxYsUS/Pw2oaurh5fX\nIM6ePU39+o6kpqbi7NyEFy9iiYoywtR0OAYGrqxf3xJv77GUK/dzmT9HRT1nzZqrZGRAr162lClj\n9tV9ikQibGxsmTNnJj169EIqlXLhwjnatv10EKWjo0NycvJXH/993pf3L1bMlOnTZ+dr/5/C2bkV\nISEifH07AopSxrQ0N5YsqYCxsbGy3ftz8wB8fZcwevSwbCWBQBYxH4B27Tpma5OTEqm6ujrjxk3O\ncYzOzq2Uy5klnF/Cx0p2q1Sxxtd3dq5VRBU2ITkLhfxXSEmRk5xcAV3dSECds2cNOXHCiz//nIuH\nRxdkMpnyZcD7Afkff4zA23sCmzf7U69ew08GxSdPhrBnzzM0NaX88Yc9ZmZFv9PZCQj8WIRgTkBA\nQOAX4FNKjg4ODahWzZ5ChRSiJk5Ozbl+/Rr16zuioqLC//7XhIYNM5g7dxl375qyeHEHdHV1adGi\nBaGhHy+dK2i8fv2Gbt0uc+dOF0DE8eMBBASoUbx43sQvsj4wKv5vaVmZevUa4OHhhpGRMebm5dHV\n/ZhdgWIfOzt7Nm1aT69eXb9IACUnVqxYTFRUJL16daVEiVI8efKIDRu2c/DgPs6ePU1qaiqRkU9x\nc+uGRJLG8eOHUVNTZ+7chejr6xMVFYmv7xzi4t6gp6eDl9cYpc1Fbhg6tDG3bq3j4kVLdHVfM2iQ\napZA7mPkJTPl53eaPXvSUFWV0aePCS1a2Odqv4sXb3Ht2lNq1CiDvX2lz+/wGWxt7di4cR1WVtZo\naGgqS3YNDAwYP34KU6aMIy1NUWL6KRXRxo2bMnv2DHbu3M60abPyTQDlZ8LC4g/u3DEgPr490J6K\nFbdjaGiEt7dPtrbvB+S5zbT9808oAweKefXKBZATHLyRv/5qhra2do7tBQR+JYRgTkBAQOAX4NNl\nYQr58Xe8859SV9dAJBIhFotxcLBGKn2pDFK+xTyfb8nevZe5c6czmcFUeLgLu3cHMHCgc677+LB8\n7f3ytC5deuDp2ZfU1FQGDeqLhYUiYHjf3qFQoUKsWOGHRCJBX1+f1as3fOVZZaV//yE8evSQdeu2\n8OxZDKNGDVVuy1wvkUjo3LktAwb8gZ/fZhYv9uXw4QN06tSFOXNmMHLkOEqUKEl09ENmz579SUPx\nD9HU1GTjRjfi4t6gpVVJKTzxKfJSEnjy5DWmTatAUpIlAOHhp6lcOZIyZT4dAPn7n2HatNLEx3fC\nwCCYqVPP4+b2dWXC1avX+GjJbrVq9jne25xURK2tbdm0acdXjeVnx8vLmnv3tnH7dk2KFLnPkCGG\nn93n9u1wbt9+SsOG1hQtavLJtseOPeHVK9d/l0TcuOHEtWuhODhU/+R+AgK/AoIAioCAgMAvQmZZ\nWNWq1bC1tWPPnl1UrGhBpUpVuH49mLdv45DJZBw/fjTH0rVKlay4fj2Y+Pi3SKVSDh/+udTgChfW\nQSR6/d6aBAwN1fOt/zlzZtCrV1d69+6Oo2MjKlSwyLI9Pj4eV9cd1KwZhYPD3wQEXMy3Y2fyfoD9\nYbBtZ2ePlpYWBgYG6Orq4eCgEEYpV648z55Fk5KSws2bN5g4cTS9enVl8uTJvHr1Ks9jEIlEGBoa\n5SqQyyvBwS+UgRzA8+d1uHQp7LP7bd2aSny8Yo5dXFw1tmxJzPex5YV//gmlY8cDODkdZ/Lkv366\nFyP5jYVFaQ4ebMSxYy84c6YinTrV+WT71atP07ZtBoMGNaNVqztcvhz6yfaGhgDvlDB1dSMwMyuc\nDyMXECj4CJk5AQEBgV+Ej5WFGRsX5vffBzFkyO/I5XLq1q1PvXqKB/33y98KFy6Mp2df+vXrha6u\nHjY2VnxDLY98p1UrBzp33smuXfbI5WJatbqAm1unfOt/8uTpn9zu43OGv//2BFRISIDZswNp2zYN\ndfX8Cyg/RVZJfhXlsoqKCjKZDLk8Az09Pdat2wKQo3z9j8bKygiT9TckAAAgAElEQVRNzQekppoD\nULhwENWrf8m8zR8XPKWmpjJy5BPu3XMD4MaN1xQrdoL+/b+8zDYxMZFjxw7Tvr3LR9s8exbDzZsh\nODk1/2RfMTHRjB49jA0btn/xeL4ELS0tbG2rfLadXC7Hz09CfLyivPbJk1asWLGdmjU/Xjrbv38T\nQkI2ceaMBRoaifTtm0qZMk75NnYBgYKMEMwJCAgI/CJ8qiysSZNmNGnSLNs+76vCAbRo0ZoWLVoD\nBfNh/1OIRCIWLnRhyJCHZGRIqVCh83eVJo+P1+D9gpe4uMIkJSWirm6Ub8fQ1tbOs6hKZlZIW1uH\n4sWLc+rUcf73vybI5XLu3w+nfPmCI3LTvHkNRo48xt69IaiqSunTx5Dy5W0+u1/Xrlrcv3+D+Hgb\nDAyu0q2b/ncYbc48exbDw4fvsrZyuRH37+fd6+593he++RjR0VEcO3bks8Hcz4BUKs6ynJ4u/khL\nBaqqqqxe3Zk3b16jqaklzJUT+E8hBHMCAgIC/2Ey3/gXK1aF06efYGqqjofH/34qf6ZDh/azbdtm\nRCIR5ubladTICX//tUil6ejrF2Ly5OkYGhpx7dpVFi2aDygCv6VL16ClpcWWLRs4deo4aWnpNGjg\nSO/e/b5oHI6Oeuzff4+UlIpABtWq3cPAoGo+nqnClsHa2hZ3986ULl1WeZ+yS/Jn9eHK3DZp0nTm\nzZuFv78fkIGjY5MCFcwBDB7sxODBn2/3Pu7uDbC0vM3VqzuoWbMs1avX/TaDywXFiplSvvxpwsIU\nQaiKykssLD4djHyO94VvatSohVwOly5dQCQS4e7em8aNnVixYgkREY/p1asrrq4uVKtWh2nTJimN\nuL28RmFl9fnA+EcjEolo2TKFVaueIZUWw8AgCBeXQrnaz8jo82I8AgK/GiJ5ASnk/pne/grkjZ/t\n7b5A3hDu789NTEw0Awf+TmjoLF69qoVI9IZu3fbg6+uS473N/JNRUIK9hw8fMH78SFauXIe+fiHi\n4+MRiUTo6ekBsG/fHp48ecygQUMZPXoYPXr0wsrKhtTUVNTU1Lh69QqnT59g1KjxZGRkMGbMcLp1\nc8+z0XgmAQH/cOZMAoUKSRgzxlE5joKI8N39dly5cpc5c+6TmKhO3bqpTJjQ6qu+M5liNxs2bOf0\n6RPs3RuIr+8S4uLe0KePO6tWrSci4glbt25izpwFmJjoERkZi0ikgrq6Ok+fRuDtPYE1azb8sDLL\nvCCXy9m58zyPHiVSv34p6tSp/KOHVKAQvru/LiYmef+bIWTmBAQEBP7DrFixmNjYWHR0fBCJ6iKT\nGXPhwjbc3XfSokVz3Nx6EhMTjZfXIKpUseb27ZukpaWRmJiISARSqRQHh/oYGRVm//49SKVSrK1t\nmTv3TzQ0NJkxYwoaGpqEh9/lzZvXjBkzkYMH9xEWdofKla2UXmGXL1/Ez28VaWlpmJmVYNy4yWhp\naX12/MHBV2jUyAl9fcWbe319fR48uM+kSWN4/foV6enpFC+u8JqztrZl0SJfmjZtTsOGjTAxKcLl\nyxe5cuUSvXp1BSAlRSHt/6XBnKtrHVxdP9/ueyOVSvH1PcajR2IqVJAzdKgwn+hbUqOGBQEBFp9v\nmEvef+9+48Z1nJyaK4VoqlatRmjoHXR0dLLsk54uZcGC2dy/H46KigpPn0bk23i+NSKRCFfXej96\nGAICPwWCmqWAgIDAf5j+/YegoWFIRMQekpProqb2hPT0AaxZs4Hbt28TEnINgKioSDp0cMXXdwmx\nsS9ITU1h2bK11KlTjzt3bvP27RuOHTvLtGmziI2NZf9+haS/SCQiMTGBlSvXMWSIF2PGDKdrV3c2\nbtzBgwf3CQ+/R1xcHBs2+LFw4TL8/DZhYWHJ9u2bczV+kUiUTSlwwYI5uLi44e+/jZEjxyGRSADo\n3r0nY8ZMRCKR0L9/byIiHivXr1u3hXXrtrBtWyAtW7bJp6tbcBg7dh/z5rVi166OzJrlxJQp+3/0\nkAS+kJw+8zll/bZv34yxcWH8/bexZs1G0tPTv9cQBQQEviNCMCcgICDwH0Yul2NsrEGFCjvR1j6J\nru5JTE0X0a9fTx49ekRk5FMAihY1pXJlKwCKFCmGqakZ5cqZY2lZCV1dXUxNzRgwoA/Lli0iJiaa\nR48eKY/h4FAfgLJlzTEyMqZcOXNEIhFly5bj2bNobt++yePHD/n9d0969erK4cMHef78Wa7GX61a\nDU6dOk58/FsA4uPfkpycROHCCl+qQ4feBS1RUZGUK2dOt24eWFpWJiLiCbVq1ebAgb+U84piY1/w\n5s2br7yqBY/gYD0gUxSiEEFBn896ChQc3he+sbGpyokTx8jIyODNmzeEhFyjcuUqaGlpk5ycpNwn\nOTlJOYfs8OEDZGR8nQiLgIBAwUQosxQQEBD4j6Ohoc6BA7WYOvU4Fhbt6NdPIQCSOS8jJiYaLa13\nnmJqaqqoqWXK3iuEHfbu3c3ChcvQ1tZmwIA+pKVJ3mv/TiL/Q/l8mUyGiooYe/taTJky47NjXbt2\nJdraOnTp0h2AsmXL4e7uyaBBfVFREVOxogWenn2ZOHE0enr6VK9uz7NnMQAEBGwlODgIkUiFcuXM\nqV3bAVVVVR4/fszvv/cCFA/NEydOw9Dw86bGPxMGBikfLKd+t2P/DHO0voSzZ09TsmRpypQp+82P\n9b7wTe3adSlfvjw9e3ZBJBIxYMAfGBoaoaenj1gspmfPrnTq5EL79q6MHz+Kw4cPUqtWHbS03ik8\nFpQ5rwICAl+PEMwJCAgI/IfJfONvYGCAm1tH1qxZQUqKO1paWjx//py3byWf7wRIS5NgZGRMYmIC\niYm5n5gvEomoUsUaX9/ZREVFYmZWgpSUFF6+jKVEiZLKNu+3/xBn51Y4O7fKsq5evYYAyGQyxGJF\nwDl06Mhs+6anp9OmTXtcXd0+O9bZs6fj5tad0qXLsGGDH+7unkDuPMB+NOPHWzJy5GYiIkpStuwT\nxo8v+KqGBZ2//z6Ng0P97xLMQXafwwED/siyrKqqysKFy4F3L2L8/bcqt/fvr5AINTUtjr//tm88\nWgEBge+FEMwJCAgI/If58I2/k1NzZZZKX1+PsWOnZJO9zy6DD02aNKVv355oa2tnM8n+VDB27tzf\nrF27EhUVFYYM6YeGhhYxMVFYW9vy5s1r5s5dxJEjBzh8+ACGhkYUKVIUCwuFeXBUVCS+vnOIi3uD\npqYmo0ePp1SpMsyYMQV1dXXCw+9hY1OVQYOG5njuvr5H2bBBjFSqRsuWL5k1q/1HMxYZGRmMHj1B\nubxx43plMJcbD7AfTbVqFTh2zJz4+LcUKlT1izIz69ev4ejRQxgYGCrvg719DebO9UEikWBmVoKx\nYyehp6dHWFgoPj5TEYlE1KxZ6xuc0ddz5MhBdu7cjlSaTuXKVgwfPgZf39mEhYUikaTi6NhYaVOx\nfPlizp8/i1gspmbN2jRs+D/Onz/L9evX8Pdfy/TpczAzK/GDzyhnNm8+x7p1ichkYtq1gz/+EMRv\nBAR+JQRrAoFvjiCh+2sj3N9fl299bxUP/N7Mn78YVVU1Bg/uy6RJ0+jduwcrVvhRubKVss2qVf7I\nZFI8PbvTrl1H3Ny688cf/Rk5chwlSpTk9u1brFq1lIULlzNjxhTi498ya5bvR4OWoKDb9Ox5grS0\nUsTF9aBIkYlYWQWzbds2rl69wv79ezl37m/atu1AUNBlvLxGsWrVMgYNGsapU8fZtm0T5cqZU7as\nOTKZjHPnzlCqVGlq1KjNgAFDcvSui4mJZsSIIdjY2HHrVggmJkXw8ZmPhobGN7vGnyIv9zc09DZz\n5sxg1Sp/0tPT8fTsTtu2HTh8+ABeXqOwtbVj7dqVJCUlMmTIcDw83PDyGoOtbVWWLVvIxYsXClSZ\n5ePHj1i+fBEzZ85DLBYzb94srKysqVu3Pvr6+shkMoYOHcDQoSMpXLgw/fv3ZsuWXQAkJSWio6PL\nzJneODjUp2HDRj/4bLKTeW9DQx/Qtm0qcXG1AdDUfMTKlQ9xdq75g0co8DUIf3d/XQRrAgEBAQGB\n78alS6EsXPiIlBRVmjRRYeDAJnna//r1YOLji+Dg8AhNzQTq1ClLSMi1LGIrN25co0GD//0b8Gjg\n4NAAgJSUFG7evMHEiaOV/aWnSwFF9u9//2vyyezTvXvRxMc3w9BwI3FxPVBXf0BSUipSqZQbN65T\ntWo1jh8/QpUqVsrMXmZGsn//wQQGBrBu3RZA4QH26NED5fLlyxeJjHzK6tUblN51ISHXKFKkKJGR\nT/H29mH06PFMmjSWM2dO0rSpc56u24/g5s0Q6td3RE1NDTU1NRwc6pOamkJiYoLSxqF585ZMnDiG\nxMREEhMTsbVVGKY3a9aSixcv/MjhZ+Pq1cvcvRtGnz49AEhLS8PY2JiTJ4/y1197kMlkvHr1kseP\nH1GmTFnU1TXw8ZlK3br1lYI+QDZVyYLG1asPiIt7p86amlqWO3eCcC74HzkBAYFcIgRzAgICAgJ5\nJiEhnj/+iObhw84ABAU9plixC3TsWDfXfVy4cI+wMCvevGkMwD//nKN69bgsYivwYUCmeHiWyzPQ\n09NTBlAfoqmpmeP6TBo3tsPM7Boy2W1EokTU1FKoWtWasLBQQkKuMXToSFRUVHB0bPzZ8/jwgf5j\n3nVFihTF1NSM8uUrAGBhYUlMTPRn+y8YZJfDzy0FNeBxdm5Fv34DlcvR0VF4eQ1izZqN6OoqMm9p\naRLEYjGrV/sTFHSZ06dPEBi4Qzk3raALidSrV5lixc7x7Nn/ANDXv0WNGmY/eFQCAgL5iWBNICAg\nICCQZ0JDH/LwYXXlskRShpCQvJX9qKmVQVf3DCJRKiJRMurqtzA0NM3SpmpVO/7++zQSiYTk5CTO\nnz8HgLa2DsWLF+fUqeOAImC4fz8818cuWrQwK1eWxchIjQYNJuPkZE7jxo4EB18hKipKmY350of1\nj3nXva/mee/eXRISfo5SKRsbW86fP0taWhrJyclcuHAWTU0t9PT0CQm5Dijk7+3sqqOrq4uurh43\nbijWHz166EcOPUeqV6/JqVMnlDYU8fFvef78GZqaWujo6PD69StlNjElRZGBrFPHgcGDvbh//x6g\nEA9KSkr66DEKAmXKlGDePBUcHQOoV28X3t4RNGhg/aOHJSAgkI8ImTkBAQEBgTxTvnxJihe/RXS0\nQnFSRSWWsmXVP7NXVtq1q8mJE28oVcoVAG3tilSvbs2+fe8CqIoVLWnc2ImePbtgaGhE5cpVlNsm\nTZrOvHmz8Pf3QyqV0qRJU2XWKzdBmI1NeTp1asKBA3/Rvv1kypUzZ9EiXypVqvzZfVVVVZFKpaiq\nqmbxAAOoVas2q1evoGlTZ7S0tIiNfYGqqlq2PkJD76Cjo/PZYxUELC0rU69eAzw83DAyMsbcvDx6\nerqMHz+FefN8SE1NxcysBOPGTQZg3LjJ/wqgQI0atQtcBqtMmbL89lt/vLwGkpEhR01NjWHDRlGx\nogVdu3akSJFi2NjYAgq/tjFjhpOWlgbIGTzYC4DGjZsye/YMdu7czrRps76bAEr//p4sX+730e0u\nLq3Zu3cPoFBxbdq0Gk2bftmxnJzqc+zY2S/b+V/27NmFpqYmzZu35ODBfdSsWYfChQt/VZ8CAgLv\nEARQBL45wkTdXxvh/v66fO7eHjx4lUWLnpOSoo6jYzJTprTO80P74cNX2b//FWpqaQwbVp1SpUw/\nv1M+cvXqFUaMGMLhw6fQ0NCkS5cOtG/vQqdOXWnatCFHj55Rth08uB+DBg3DwsLyX3XDv7GwsGTi\nxGl4e0/gwYNw7O1r8fTpE8LD7xEf/xZDQyN0dfVQV1dHIkklJiaGbdsCuXHjOt7eE9HR0aZo0WIs\nX+733YVQ8vrdTUlJQUtLi9TUVAYN6svo0eOpUMEiWzu5XK4UCSloQdx/AVfXNuzZs5v0dPFX9+Xk\n1IBjx/7Oh1EpGDy4HwMHDsXSslK+9flfRPi7++vyJQIoQjAn8M0RfnR+bYT7++vys93bK1duEhn5\nmiZNqqGnp/iDGBYWyuHDBxg6dMRH9wsPv8fLl7HUqePw1WM4ffoEly5dZPTo8YBC+XDEiCHMmuVL\noUIGnDhxlMuXLzJ27KQsweGPIK/319t7Ao8fPyQtLQ1n51Z0794zW5t79yIYOjSIBw/MKFXqGXPm\nVMbOrkI+jvrH8ezZS0aO/JsnT/QpUyaeuXMbUrSo8XcfR2a27OXLl0yePJbk5CRkMhkjRozFxqZq\nlmBu7NgRvHjxnLQ0Ca6uXWjTpr2yD1fXLly4cA4NDQ1mzZqPoaER0dFReHtPIDU1BQeHBgQEbMtz\nMHfo0H62bduMSCTC3Lw8ZmYl0NLSxtTUlBkzvDExMUFDQ4O+fQfw11978PGZB8CVKxfZvXsXM2fO\nzfdr9qvxs/02C+QeQc1SQEBAQOA/yZQp+1mzphppabZYWe1h48ZamJkVxdKy0mezAOHhd7l7NzRf\ngjlz8wosXbqQ5csXU7duffT0dHn48AEDB/YlKiqJtDQRGhradO4cBRRccZCc+NC0OiemT79OUJAH\nAG/ewPTpW9i169cI5saMOcuRI+6AiLAwOaqqG/Hza//Njjdy5B9MmTIDHR3dD7Yosp3Hjh2mVq06\nuLt7kpGRQWpqarY+xo6dhL6+PhJJKr/95oGjY2P09fVJTU3FysqGvn0HsGzZIv76azceHr1ZuHAe\nHTq40qxZCwIDA/I85ocPH7Bhgx8rV65DX78Q8fHx7Ny5DZEIHB0bs2vXjiwvMJYs+ZO3b+MoVMiA\nAwf20apV2zwfU0Dgv44ggCIgICAgUGBJSUlh5Mg/6NmzK+7unTlx4hhBQZfx9OyGh4cbPj5TiYmJ\nYdMmM0QiCSVL9iY+fgd9+vQlOTmZ4OAgRo0apuxr5kxvfvvNA0/Pbpw7dwapVMqaNSs4ceIYnp7d\nOHHiGG5uHYiLiwMUZuFubu15+zYuV+MtWbIUfn6bMTcvz+rVyzh9+iRly5qjodGV27fPEB5+hlu3\nDjFhQhBQ8NUQ88rr11pZll+90vpIy5+PqCg93qmriv5d/nbMnbswWyAnl8uVLwAqV67CwYP78PNb\nxYMH99HW1s7WR0DAVnr27Eq/fp68ePGcyMgIANTU1Khbtx4AFhaVePYsBoBbt27QpEkzAJo1y7t/\nQXDwFRo1ckJfvxAA+vr6PHnymNevXyvb7Nmzk6Cgy/8eowVHjhwkISGB27dvUbt27tVwsx733fdc\nQOC/hpCZExAQEMhHZDIZYvHXz1URUHDp0gUKFy7C3LkLAUhMTMTdvTOLFq2gRImSTJ8+mQMH9pKW\nVh9TUy9iYv5EIrHC0XFztjloGzb4YW9fk3HjJpOQkEDfvh7Y29fit9/6c/duKEOHjgQgIuIxR48e\nolOnLgQFXaZ8+YoUKmSQq/G+fPkSPT09mjZ1RkdHlz17dhIXF8fr169QBALpqKs/ISZGl5IltUlK\nSszPy/XDqV49lcuX4wF9IBU7u/gfPaR8o2zZeEJCMlC8B8+gbNm3+dZ3TuWQLi6t8fPbRFJSEl5e\ng6hSxZq7d0OVwZytrR1Ll67mwoVzzJw5hc6du9G8eUtln8HBQVy9eoWVK9ehoaHB4MH9/hVxAbH4\n3eOfiooImUyWZTw7dmxRBnWfYseOLbRt2wENDYUViEiU3cLiyZPHqKm9EwBq185FmZlr0aINo0cP\nQ11dnUaNmqCiIuQYBATyihDMCQgICOSB9evXcPToIQwMDClSpCgWFpW4cOEsFSpU5MaNkH8VFSuy\nbNlCZDIZlpaVGTFiLGpqasqHM339QoSF3WHp0oUsXryStWtXEh0dSVRUFHFxcXTr5k7r1u1+9KkW\nCD4sW9TW1qZ4cTNKlFCoaDo7tyIwcAcNG6Zz544xEokVJUocoWtXy2xB9eXLFzl//m+2bt0IQHp6\nOs+fP8uS7QBo2bINY8YMp1OnLhw4sJeWLVvnerwPH95n6dKFqKiIUFVVY8SIsaioqDBkyBhKlTqJ\nSJTBmzfuVKiQQosWrZk3zwdNTc0fIoDyLZg0qQV6eke4e1eF0qXTGT0699euoDN/vhNqapuIiNCl\ndOkEfHy+UCIyB7KXQzbKkrWNiopk4sSpVK5shZNTAwCePXuGiYkJrVu3Iy1NQnj43SzBXHJyEnp6\nemhoaPDkyWNu37712XFYW9ty4sRRAgK2IZVKc2wTExPNiBFDsLGx49ChfZw7dwYrK1siIp4QEfGY\np08jePAgnKlTfThx4hgPHoTz4sUzunbtSGpqCitXLqFNm/Y4Ojbm8eOHREZGsGDBXOrXb0h6erry\nt9LZuRXnz59FJpMybdosSpUqw507t1i0yJe0NAkaGhqMHTuZUqVKf+XVFxD4uRGCOQEBAYFcEhp6\nmzNnTuLvv4309HQ8PbtjYaGYj6Uo19uARCKhS5cOWTJHu3fvpFOnLp8sqXv48AErV64nJSWZXr26\nUadOvWzy3R+TCf+Vpb8zyxb/+eccq1cvo3r1Glm2ZwZhkyY1Y/To07i5BdCypQWVK5fNsb8ZM+ZS\nsmSpLOvu3Mn6kFukSFGMjIy4evUKoaF3mDJlZq7HW7NmbWrWrJ1t/e7dW5g06QiPHmlRr14y06Y1\nRVdXl4YNG+XYz6BBfRk0aNhPp/onFosZMaL5jx7GN0FPT4+lS7/NHLmAgK2cPatQTn3x4gVPnz7N\nsr1oUVMqV7YC3pXmXrsWxNatG/+1x9BhwgTvLPvUqlWXPXt20b27KyVLlsbK6p2/3Pu/Renp6Vy5\ncomePbsikaSyYsUSXrx4ztatG5FIFPPw5s3zISwsFIkklerVaxIZ+RQHh4aIRCLu3r3Lw4cPcXHp\nRJs27Zk/fzb//HMBZ+dG1KpVBzU1NRwcGjB+/BTOnDnJzJnePH0agb19TWbO9MbTsx+nTh1HU1Mr\ny2+lgYEhfn6b2L17J1u3bmL06AmUKVOWpUtXIxaLuXLlEqtWLWX69Dn5f0MEBH4ihGBOQEBAIJfc\nvBlC/fqOqKmp/fuAUl+5rXFjxVv6iIgnOWaOOnXq8tF+RSIR9eo1RF1dHXV1dapVsyc09Bb16zt+\n2DLH/du166j8/6FD+ylXrvwPCeYSExM5duww7du7EBwcxLZtm5kzZ8FX9flh2WJgYADPnsUQFRWJ\nmVkJjhw5iJ1ddcqWLYeqqpTWrUthaVmW5OQkZelXJjVr1mbnzm0MGzYKgHv3wqhY0TKbTxxA69bt\nmDp1Is7OrfJlXpumpiY+Pq1YtuwEkZFaHDlyg44dPz4/SCQS/XLz6QRyJudySEmWNlpa7z7LmXYZ\nzs6tcHZula2/gIC/MDDQIz09gXnzFuV4zPctN9TV1ald2yGLAmv37p3Q0NCgRo3adO/uSokSJVmy\nZBXdu7ty8+Z1Chc2oVGjxuzcuZVOnboQEnKNq1eD8PNbjYqKGD09PczMSlC8uBnq6ho4ONQnODiI\nAwf20bBhI6pXr8H06ZOJj3/Lhg1rady4KQ0bNmLYsEHK38rMFx0VK1py5sxJABISEpg2bTJRUU8R\niUQfzR5msnbtSrS1dejSpfsn2wkI/MwIwZyAgIBArsk+HyQTTc2chR7kcrnyoVwsFpORodhfIknL\n1nbLlg2oqyuMt/fv/4udO7ezcOFyrl69wv79ewFYtWpZNjnxzAcWU1NTwsJCmTp1grJ079GjhyxZ\nsoCUlBQKFTJg/PjJGBt/m0AvISGe3bsDaN/eJd/6/LBs0ctrFMnJyUycOBqZTEalSlVo184FVVVV\npk71YcGCuUgkEjQ1NVmwYOm/QZGir549+7Bo0Xw8PNzIyMigeHEzZs9egJ2dPZs2radXr650796L\nxo2dcHBowMyZ3rRokX9lgsOH72bLFldAl61bH/D27WmcnSsyfPhgLC0rc+9eGGXKlGPixKwZlnnz\nZhEWdgeJJBVHx8b07t0PUGSKFy2aT0pKKmpqaixatAJ1dXVWrFjC9etXSUtLp0MHV9q27ZBv5yCQ\n/7xfDvn48aNclUPmJ+bmFfD1nUvnzl4UKWLOpElugKK0c8IEb6ysbPj9d0/c3NoTF/eGxMTELGIr\nYrEKGRkZ3LwZgra2NkWKFOXx40c8fvwQU1OFb+SHLyZOnTpOZGQ86ekZFC9uSq9efXnwIJz3m6mr\nqyn7z5zTt2bNCuzta+DjM49nz2IYPLjfJ89NeCEi8F9ACOYEBAQEcomNjS1z5sykR49eSKVSLlw4\nS5s2igflzCCvVKnSxMREZ8kcVa1aDYBixUwJC7tD7dp1OXPmhLJfuVzOuXNnGDp0JFu3biQ8/B7G\nxsaA4s3zjRvXqVq1GsePH8lRTjwzYPlQ+lsqlfLnn3OZPfudx9mqVcsYO3bSN7k+K1YsJioqkl69\nuqKqqoqmphYTJozm0aMHWFhUYtKkaYDC+y2nADM8/C5z5/ogkUgwMyvB2LGTqFmzNhs2+FGxogU3\nboRw8eIFDh7cz9atu1BVVSUpKZEuXTqybVsglpaVWblyXZYx2dlVx86uOgAaGhqMHDku27j19fVZ\nvXoDoBCwCQq6QUzMU8qXr5iv83HOnzcEFOqEqanmHD9+HWdnePo0gnHjJmNlZcP/2TvzgBjzP46/\npmu6iwodEklFypH7vuW2ZLGI3NbNSm65rXWvYyMikZy5WbfcVO4rQqdC0TXVzPz+mF+jUVjk2n1e\n/3iO7/U8M43n83w+n/dnzhwfduzYptJvwIAhGBoaIpVKGTlyCJGRD7C2LsXUqRPw8ZmLg4Mj6enp\naGlpsXfvbvT19fH13UBWVhZDhvSjevWamJtbFNp1CBQu7w6HfGOIfEmjJClJQlTURNLScjAy2kqX\nLjMwMpJjamqGk5MzsbExxMfHYWdXjqioR5QpU5Z79+6ojCESiVBTU6NKlWr4+MyhU6fW2NiUYdCg\nYVy6dJG0tDQMDAyV7S9cuMb9+2uxtBzG1auehIU95ty5/TYq9kAAACAASURBVEoBFLlcztq1qwkL\nu4JEkoWmpuJxNS0tjVu3bhASspOXL18oX4qdPXuaa9fC6N27O1ZWVkye7JPPMy8g8G9FMOYEBAQE\n/iEODuWpW7c+Hh5dKVrUBFvbsujr66uExInFYiZMmJrPcwTQp88A5s71Yc0afSpXrqrsoyiua8eK\nFUu5c+c2w4eP4vTpk5QpY8udO7eJiAhj5Mjf8smJX758ocB15hqWT55E8ehRJCNHDgEUMvsmJmZf\n7P4MHjycR48esm5dIGFhV/D2HkNAQDAmJqYMHtyXa9fCKV/e6Z0G5syZUxk92gsXl8qsXbuadev+\nYvjwMcpwqjVrFAZXXFws586doV69hvz992EaNmxcKAqi2dnZ9OkTzKVLLzE23ouTU3MVz+rnoqcn\neWtf8SBarFhxnJycAYVUe3DwFpV2x44dJiRkF1KplOfPk4iKegiAiYmpMqcu11Ny6dJ5IiMfcOKE\n4mVBWloa0dFPBWPuO0ZTU7PAcMh16wLIzs7G3NwCf/8tBfQsHLZvDych4RfkcjEymQEyWQBGRmqA\n4nckLS0NLS2xUpHy2rVwdHS0kUiyUFNTVypkurhUJjT0FP369URf3wCZTEZcXCz6+voEBm4kJyeb\nYsWKk5WlS0aGBnK5AfHxszEzm8/s2c9p2rQmGhqKOTIzJTx8GIm//xYuXbrA+PGjef48CWfnSvz1\n159YW5eibduOHDy4//9zV+Hp0yfMm7cIX9+V7N27m06dfv5i90xA4HtCMOYEBAQEPoJu3Xri6TmA\nzMxMhg4dgIODYz7lyapVq+HntylfXxeXSmzevKPAcW1t7Zg0aTojRgxBLpdTsaILtrZluXr1EjEx\nMdjYlP6gnHguucaHXA6lS9uyapXfp17uR5E3BFUul+PoWAFTU4XxWLZsOeLj49DX1y/QwExLSyU1\nNRUXl8oAtGzZmsmTxyvHy81JBEU+W2DgBurVa8iBA3vx8ppUKOtft+4Yhw97ANq8fDmex49jOHbs\nIk2a1CgUQZJRo0yZOnUfsbFlqVAhjDFjVAUtgHzGY2xsDFu2bGLNmo3o6+sze/Z0srKyeJ99OXr0\nOKpVyy/CIvDjMGfOfjZsMCYnR0yLFn+zdGnnLybbL5XGY23dGblcHblck+TkrtSpc5Xdu7fRt29P\n1q7diJqaGteuhSOVyrCxKU27dh05efIopqamnDhxjOzsbPT19Zk/f7HSQ6+oxReDtrY2GzYEKfNo\nvbwmsXfvVIyNN5GYOIEnT3ZSp44f48e7c/ToEQCaN29B2bLlEIlEVK9ek0aNmnL79i2SkhIZOfI3\nqlRxxdDQkP79BwOgr6/P69ev8fDoSnp6BjVq1Poi90pA4HtEKOghICAg8BHMnz+LPn2607dvDxo2\nbIydnf1njbd790X8/e+zbNl9Jk3a/X+DL4BKlarg4lKZXbu2U65cufeOoZDWV2zr6r6pXWZtXYrk\n5JfcuHEdUChuPnr08LPW+zFoamopt/PmvZQubcu6dYGsWxeIv/8WFi5cxjtSEZXkzUmsWNGFuLg4\nrl69jFQqpXTpMoWy3rQ0OfAmNEsmK8rLlwphlM/xzuWKNLRvX52TJ505efI1+/c3xsHBBoCEhHjl\nZ3TkyEGcnV0AxeealpaGtrYOenp6vHjxnPPnzwJgbW3D8+dJ3LlzC1DkXUmlUqpXr8WOHduUcz55\n8pjMzMxPXvv3wODBnu8937lzW169Kpyab82a1ftwoy/MpUs3WLnShefPW5CS0pCtWzsTEHDii803\nffpAHBzakpAwlVevfqV/fyk9evSiVCkbbGxs6NHDnbJl7di+fR9z5y4kOfkl27dvRV1dg2LFihMY\nuB03tzbY2tqxbp0vGRmZjB07nk2bgnF1rabytyMSgY6ODt27N0BLK5JSpdywt69P/fqqnvWC6tUB\nZGVlsWrVJWrVklCr1k3WrFEIucyePZ0xY8bj778FT8/++QRkBAT+zQieOQEBAYGPYOrUmYU21vPn\nz5k0KYeEhFUAREY+Z9iw9bx48Rwnp4qIxdqIxWKlt0r1oUh1O3f37dplM2bMY8mSBaSmpiKV5vDz\nz90Lzfh5m4JUId/G2tpGaWA6OVUkJyeHp0+fULp0GQwMDImICMfFpRIHD+5T5roVRMuWrfDxmUzv\n3v1UjuetgXXjRgRmZsWYM+cPxowZpvSsJScn079/L4KDQ9i/fw+nT58gMzOTqKgo7OwukJTkiIHB\nXnR1k6lb9y/l2IcO7WfevBlIpVK8vafg6FiBjIwMFi2az6NHD5FKc/D0HEDdug3Yv38PJ08eIzMz\nE5lMxrJlqwEwMjLOV4Dc2roUO3duZe5cH2xsytCxY2dCQ08jEomwsytHuXL2dO/eiWLFSigNvYIE\nXxYvXkHbth2Ii4ulb98eyOVyihQpyuzZv3/U5/i9sXLl+z3LhZtP9u0FM6KinpGZWSnPESOePcsv\nmFRYaGlpsWFDV2JiotHRscHEpCpxcbGoq6szefIMlbbvii6oWbMZCxfeJDOzDi1bimnTpgGASoho\nlSquVKniCsDo0a3p0KECT548o1q1Cujp6amM5+xcmd27d+Dm1oaUlBQiIsIYOnQkQUFXSUhIJCvL\nkcTEyixevIMuXVLIyEinaFETcnJyOHRoP8WKFQd4p2CVgMC/CcGYExAQEPhGREY+JSGhvHJfLjch\nM9Oa48fPKY/lfXDKKyfesGETGjZsAoCn5wDl8QYNGqvULrOzK8fy5W8Mki+JkZExFSu60KvXz4jF\nYooWNcnXRkND450G5sSJ01iwYA6ZmZlYWloxYcLUd87VrFlLfH1X0qxZi3znoqOfMn36HLy8JjJl\nijcnTx57r9R/bp6fRCLB3b0dDRqIKF36ZzQ0rnHq1HG6dOmGXC5HIslk3bpAIiLCmDPHhw0bgtiw\nwQ9X1+pMmDCV169fM2CAB66uNQC4f/8e/v5bMDAweO99K+ihOdf4A955H94WfJHL5aSkJNO370AG\nDvz1vXP+SOTWV0xKSmLqVG+lF3LsWG+cnSuptPX2HsuzZwlkZUlwd+9Gu3YdlWO4u3dTUYJNSEhg\n+/Ygnjx5zMuXL5QvTYB8c40Z442Li+pcoPAK+vkFYGhoVGjX27RpFRwc9nLnjjsA5ubHaNnSrtDG\nLwiRSKQsp5L32D8hPT2dwYNvcfu2oqTAqVP3MTa+QIcONfK1vXs3ipUrbyKTqdOtmzUNG1YvcM4G\nDRpx8+Y1evdW1JwbMmQERYoURUvLkdTU4lhbd0Iu10QisefVKwf69RvEgAG9MTY2pkIFJ+VLpbwv\nugQE/q0IxpyAgIDAN6J8eVvKlj3PgweKhyht7UhcXY0/0OufExQUyvnzqRQvLmX06KbKsgdfknd5\nLnNru8G7DUw7u3L51ChB1bDJ5dq1cBo1aoqenn6+c+bmlpQtq3j4tbd3IC4u9r1rrlzZFR0dHXR0\ndDA0NGT27CGYmpqyb5+UyMj7gOKhsGlTheHo4lKZtLQ0UlNTuXjxPKGhp9i8eSOgEFFJSIhHJBLh\n6lr9g4Zc7tify/PnL+jf/2+uX7fFxOQZkycXo3Xrd3s2fywU9+fIkYPUqFGLXr08kclkBYaPentP\nwdDQEIkkk/79PWjYsAmGhoZkZmYWqAT76lUKP/3kTnT0UyIjHyjHyTuXXC4nIyOj4JV9AUuhSBFj\n1q934s8/t5CTozB6nJxsC32e9/ExoiuRkVHcvv3GKMvMtOPixXA6qKYSk5T0Ak/Pu9y/ryh9cPLk\ncTZtilS5trwvrIYMGcGQISNUxmjRwow9e0rz+PEAQEq9en5YWFjSoUNnOnTonC/nNO+LLgGBfyuC\nMScgICDwkUil0kJRT9TXN2D58lIsXryZzEwtmjfXpEOHRoWwQli37iRTppRHIikDSHjwIIA1a7oU\nytjfkjNnIli79i9evoxi+fJVBbbJrU8FoKamjlQq+X+NP0XO3tv5NKrt1ZT7ampq7xSZAZRv/GfN\n+p2SJa1Vzt26dQMdnYJrD+alsJQKZ806w5kznoCIlBSYM2czrVoVnhLn90D58hWYM8eHnJwc6tVr\niJ2dai5pXFws/ft7KEV3oqOfsnLlUqKjFQWm163zZdmyhTRr5kZ8vCLn8sKFcwwfPoYVK5YAIjIz\nM7h2LZySJa2ZPn0iO3YEY2BgwLhxE6lY0YWUlGSmTZtIUlIiTk7OXyyMr0wZK/74w+qLjF3YWFmV\noHjx2yQk5IZvv8LSMr8kw5EjV7l/v51yPy6uEYcPB3+Uodq8eRWWL7/KoUPbMDDIZuzYNqipqXH7\ndhReXuFERxtgZ5fC4sX1MDf/csq9AgLfE4IxJyAgIPAW69ev4fDhAxgbF6FYseLY2zty9uxp7OzK\nce1aBE2bNqds2XKsWLEEqVSKg0N5xo71RlNTUyXs6s6dW/z55xKWLVvN2rWriY2NJiYmhuTkZH75\npRdt23bA2rooBga7UVdP49QpKdWqFSkwnOtjOXlS8n9DDkDMpUtm5OTkoKHx4/7sr1t3kpkzy/D6\n9QaMjcM5deox3buX/HBHFEbT3bu3cXSsoJTt/xBvq3MeO3aEKlVciYgIR1/fAD09fapXr8m2bVuU\nnsd79+5QrpwDERFh3L59E4BTp05gbV0KG5vSH3nF/5yUFG3y5nu9fGlEVlYWYrH4i835tXFxqcyf\nf/py9uwZZs+exs8//0LLlq2V52/evE5mZgarV69DLBbz888dlMa4mpoavr7+nDsXysqVy1RUSUuU\nMKd9+05oaKizcaM/zs6VmDZtIlOmzCQ5+SVBQYFMnuzFrl0HWbfOFxeXyvTu3Y9z586wd+/ur34f\nvjeKFCmKj48GixcHkZ4upn79ZAYP7pivXenSxdDWfkRmpkI0SiR6QYkSH//9bN68Cs2bqx6bNCmC\n8+d7AhAdLWfKlE34+rb/+IsREPgB+XH/VxcQEBD4Aty+fZOTJ4/h77+F7OxsPD17YG+vePDLrXUm\nkUjo1u0nli5dhZVVSWbOnMrOndvo0qXbez0hDx9Gsnr1ejIy0unT5xdq1ar7j8O5PhZ9fdUQNEPD\n9ELxJn5LtmzJ5PVrRY5hcnIltmx5QPfu+du9/RmIRCK6devB5MnehITspFatuuQaPm/n0snlb4y4\nvOdEIhFaWlp4ev6iFEAB6N27H0uX/oGHR1dkMhkWFpbMm7dIZczTp09Qp069L2rM1a6txaFDT8jK\nsgakVKoU+68y5ADi4+MxMzOjbdsOZGVJuH//rooxl56ejpqaGmKxmMePo4iPj1PmweV+9+3tHUhO\nfqnsY2BgyNGjhwG4e/dNIeyLF88TFfUQkUhEWloqaWnpZGRkEBERxuzZCwCoVauuSiHs/zIdO9ag\nY8f8pTXyUrOmM4MHHyAgIJKcHDGtWj2hW7dOhTJ/QkJeARURz57pFsq4AgI/AoIxJyAgIJCH69cj\nqFevIZqammhqalKnzhup8txaZ0+ePMbCwlIpGODm1oYdO7bSpUu3d44rEomoW7cBWlpaaGlpUaWK\nK7dv3/hg6Nin4uVVncjI9dy44UyxYk8YO9bshw+5e3v5IlH+ELe3wxa7deuh3Pb336zczq1P5ebW\nhkqVqtCt209UqFARHR1tduwI5uzZ02RlZVO/fkMA5s9fzJQp45HJ5MjlcmJjY3FwKM8vv3TO54kF\nRfkELS0tbty4RmjoacLDw/D3X8vMmfOxtCz88Lm+fRuioXGSCxcuUaSIhAkT2hT6HAXxJQRA3ib3\nexsWdpnNmzeioaGBrq4ekyZNV2lXtWo15HI5PXq4U7JkKaWiYd4x1NTUkclkyuOlS9uyY0cwMTHR\n2NqWVbbLyclGKpWiqamJpaUVkyZNV4bNCgqJ7+ZDvzHe3m4MH56GTCbFwKD6e9t+DI6OKdy7JwXU\ngUwqVCicl2ICAj8CgjEnICAgoELB9Y1AtdZZXvK+jVbkZin6SyTvlxMXidQ+GDr2qZQsWYI9e9oT\nHx9H0aK10NX98d9U9+ihy8OHYSQnV8LE5DK9ehWeARETE83kyT6kpaVy/PhRfH03IJPJGD9+DBER\nYSQnv8TUtBi//64w1tLT0wDVh9f7959y40YSder8jYXFZapXF+Pk5EzduvWpU6eeisrol8DDowEe\nHl90iny8qx5YYZIriuHm1gY3t/xGanBwCAC6unqIxWJWrFiDtrYOw4YNpEQJc+LiYlm+3FfZXkdH\nhwkTpnL16mW0tbVZunQlW7YEkJaWxuLFKwCoU6c+dnb2dO+uCN27f/8eJUqY4+JShSNHDuLh0Zdz\n50J5/frVF732fyNvlyEoDBYvbomR0WZiY3Wws8ti0iS3Qp9DQOB7RSgaLiAgIJAHZ2cXQkNPk5WV\nRXp6OmfPnlaey31otbYuRVxcLDEx0YCi/lilSlUARf5NbiHnkyePqvQ9c+YkWVlZpKQkExZ2BUfH\n8sTHx2NsXIS2bTvQpk0H7t+/W2jXoqGhgZVVyX+FIQfQo0c9tmzJYcaMYIKC1OnUqVahjV28uDnl\nyztx4cJ5Ll26oCwM/+TJY6Kjn1KmTFkuX77AypXLiIgIR1c3/wPp8uWRpKQU5/79joSF1eLixafK\nc/8Gb05GRga//TaC3r2706vXzxw9egSAbduC8PTsgYdHV548iQLg1asUvL3H4OHRjYED+yiVIj08\nupKWlopcLqdVqyYcPLgPgBkzpnDp0oXPWp+Ghga9e/ejf38PRo8eSqlSNkD+UNq8uYW5h+vUqc/J\nk8dp3botw4atxtW1FXfv3sLDoxs9enRh925FiRBPz/5ERITRs2cXTp06QYkS5p+1ZoHCQU9PjwUL\n2hMY2Jzp09ugqan54U4CAv8SBM+cgICAQB4cHMpTt259PDy6UrSoCba2ZdHX11d5IBSLxUyYMJXJ\nk72QSqU4OlagQ4fOAPTpM4C5c31Ys0afypWrquRc2draMXz4IJKTk+nTpx8mJqYcOLD3vaFjPyJx\ncbF4eY1iw4agTx4jLOwKmpqaODk5qxyvUsWBKlUcPneJ+dDR0VZu9+jRm/btf8rXxs9vE+fOncHX\ndwWurtXp3buf0hMrk8lITMybo6ZOWtqbHMUfPcQV4MKFsyreybS0VFatWoaxcRH8/ALYuXMbmzcH\n4OU1ibVrV2Nv78icOX9w9eplZs6cwrp1gVSs6MK1a+EUL14CS0tLrl0Lp2XL1ty8eYNx4yZ89ho7\nd+5K585d33ne2NiY4GCFaEneItYlS1qjqdmBS5d6cumSNocOXWHx4k5Mn+6q0t/Q0IiFC5d/9joF\nBAQECgvBmBMQEBB4i27deuLpOYDMzEyGDh2Ag4MjbduqFk2qWrUafn6b8vV1camkUug7L7a2dvmM\ntXeFjv3XuXr1Mrq6evmMuS9NjRo18fVdRfPmbujo6JCY+AwNDU2kUikGBgY0b+6Gnp4++/YpQvty\nPbE1a9bG1PQySUm5RpuEIkUUuVm6urqkpaV91ev4Etja2vHnn0tYuXIZtWvXU6qu5oaPlivnwMmT\nxwBF7umsWb8DCqMpJSWF9PQ0nJ0rEx4eRokS5nTo0JmQkJ0kJSViYGCAWKxd8MRfgdevX3HmjC2g\nWENyclX27dtOq1Zv2oSEnOPu3RRq1LCgfv2v+70UEBAQeBeCMScgICDwFvPnzyIq6iFZWVm4ubXB\nzs6+UMbN65yZO3c/e/ZooaEhpW9fXXr1qvfujj8gUqkUH5/J3Lt3BxubMkyePJ1Hjx6xfPkiMjIy\nMDIyZuLEqZiYmBIcvIXdu3egrq5O6dJlGDRoKCEhO1BTU+fw4f2MHDmuUMo1vI9cz1m1ajWJiopi\n0KA+gMIQmzTJh5iYaP78cwlqaiI0NDQYO1bhRcrriW3SxJGjR69QqtQOzMzCcHCwARTCOfPmzWLb\ntiBmzJj7RQRQvgYlS1qreCerVq0GvKnTp66uWpcvf2ipiEqVKrNjx1YSEuIZMGAIp04d5/jxo8ow\n5W+FWKyNru4rXiqFLuVoa7/JeV2w4CBLllRHIimFoeF1fHxO0737v+tvVkBA4MdEMOYEBAQE3mLq\n1JmFPqan5wDl9s6doSxfXoesLMVD/YwZF6hWLRJHx39ePPd758mTx3h7T8HJyZk5c3zYvn0rp0+f\nYM6chRgbG3P06GH++msF3t5T2LTJn23b9qChoUFaWip6evq0b98JXV1dunbt8eHJPpO3FTDd3bvi\n7q4aqmdpaUX16jXz9X3bE+vllbvVjPT0dORyORUruhAQsPWz1zlv3kx+/vmX95Y4OH36BCVLfpma\ndklJSUrvpL6+AXv27HpnW2fnyhw+fIDevftx9epljI2LoKuri66uLsnJyUilOVhYWOLsXInNmzcy\nerTXO8f6GmhpaTF4sDoLFpwgObkUlSqdZsyYOsrzISHqSCSlAHj1qiK7dt0tsCyGwIc5cGAv1arV\nxNTUFPg6iqgCAv9mBAEUAQEBga/M/fuvlYYcQEqKC9euRX27BX0BihUrrgyRbNGiFRcunOfhw0hG\njRpCnz7d2bDBj8TEREARvjdt2kQOHz6AmtqbPLMfVTPk8eM42rbdQdWqETRtuodLlwpH1MbLa9IH\njbRTp04QFfWwUOZ7m4cPHzBgQG/69OnOunW+eHj0Ja+YCLzJK/X0HMDdu3fw8OjGX3+tYNKkacpW\nFSo4UbKkwjBydq7E8+dJODt/Wc/rP2HAgIacPm3F4cPxhIS4YWFRTHlOU1Om0lZdXfZ29/8cv/02\ngrS01I/qI5VK2b9/D0lJicpjX0MRVUDg34xI/p38BSUmvv7WSxD4QpiZGQif778Y4fP9eE6fvoGn\npw4pKYoHWCurQ+zZUwZLyxLfeGWqfOpnGxcXy7BhA9m2bQ8AV65cYvv2rbx48ZxVq/zytZfJZISH\nXyU09DQXLpzF338L/v5r0dHRVakT96l8qrdKEf65HXt7ByZPnvGP+/XtG8KePb8o92vWDCQkpG2+\ndnFxsYwZMwwHh/Iq4ajXr19jxYolSKVSHBzKM3asN5qamgwdOoBhw0Zjb+9As2b1cHfvxtmzZxCL\nxcyd+wfR0U/x8hqNnp4++vp6H6xpJ/zt/nMCAs7g41OE5OTKWFicYuFCHRo3dvnWy3onX/qzPXhw\nH9u2BSGV5lC+vBNjxoxn4cJ53LlzG4kkk4YNm9C370BA4Xlr0qQ5ly5doGvXX/j99zmYmZmhra3N\nihVr6dHDHTe3NoSGnkYqzWHGjLlYW9t8sbX/GxD+dv+9mJkZfHQfwTMnICAg8JWpV8+J2bMTaNx4\nGy1aBLN4seF3Z8h9LgkJ8dy4cR2AI0cOUr58BZKTXyqP5eTk8OjRQ+RyOQkJ8VSp4srgwcNITU0l\nIyMDXV1dZS23zyEnJ+eTvVW7dm1j8eIV/8iQy8nJUW6/eKFaj/D584LrEwI8ffqEn35yJyAgGD09\nPTZvDmD27On4+MzF338LUqmUnTu3AaqKmJmZmTg5ObN+fSAuLpUJCdlJxYou1K1bn6FDR7BuXeB3\nmZuXlPSCfv124uZ2hF9/3U5q6o8hDNOjR11CQrRZunQ/e/aU+q4NuS9FXFws3br9xPjxY1i4cB53\n795m8eIV3Lp1k9mzpzNgwK+sWbOBBg0ac+jQAR4+fEBg4AaeP0/i4MF91KlTj+bN3ShdugwSiYQy\nZcrSv38vZDKZUhG1Q4fObN4c8K0vVUDgh0LImRMQEBD4Bri718bd/VuvonB428NUooQFVlYlGTly\nCFpaWshkMkaOHEvr1u0ZOXIwMpkMHR0dBg8eRsmS1owbN5KYmBhAjplZMfT19alatTrDhw8iMHAj\nRYsWJTs7mypVXLlx4xqvX7+mePHivHjxnCJFiiKVSklPT8fQ0AiZTIpUKqNGjZpcuxZB/foNCQ09\nTXh4GP7+az/orcrl999nExsbw5gxw3Bza0NERBixsbFoa2szbtxEbG3LsnbtajZs8KN8eSeMjY15\n+vQJDg7lycm5TunSS0lMnIC29mV0dPYzYsQO6tdvQKdOP6vM83Y46vr1a7CwsMTKqiSgUDvdsWMr\nXbp0U+mnqalJ7dp1AbC3d+Ty5Tc12r6TgJsCGTPmBAcO9AJEXLkiRV19E0uXdvzWy/pHODjY4uDw\n78lr/RRiYqKpW7c+d+7cIisri2HDBpKRkU54+FWOHTtMSMguHj16iI6ODkeOHCIlJRlTUzOWLl3F\nokW/ExERBsCzZwn89JM75cs74e7erkBFVAEBgX+G4JkTEBAQEPhs8nqYTExMaNu2I0WKFKFHj94c\nPHgcV9fq7Nq1je3b93LkyGnKli2HkZExr1+/Ji0tjcDAbRw7dpY1azYCcOzYEUaN+o2jR88wZ84C\nkpISadOmHbVr18XWtiwtWrTG3z+Iv/7yp1+/QWhpadG//2A2bAjCyMiInJwc1qzZQK9enp/krfrt\ntwmYmpqxbNlq4uJisbd3xN9/MwMH/srMmVOU7eRyOUuWrGTOnD9o1KgpcXGx7NgRRMuWnbG0HE3j\nxlL27duFuroagYEb882T19sml8vR11cNsXmXYaau/uZdrJqaSEVF8nuuaRcVZcibPDt1Hj36+JAi\ngW9H8eLmlChhjptbG8zMirF8+V8EB+9BXV2dTZs2MHLkWBwcHKlbtz737t3h0qULJCY+w8trNE+e\nPCY6+ikAJiamlC/vpBz3XYqoAgICH0bwzAkICAgIfDZve5iCgzcD0KRJMwBu375JlSquGBkZA9Cs\nWUvCw8NQU1OnUqUqGBoa0bdvMNeuFcXUNA0joxOEhp5i8+aNZGdno6amhomJGRUqVCQ09DT79oWg\npaXJwYP7SU19TWxsDFu2bERf3wB1dXWaNGmusr5P9VbJ5fJ31kwTiUSoq6ujpaVFXFwsu3Zto0uX\n7jx9+oTY2GNADqmpF0lM7ERi4jOeP0+iT5/uVKtWkyFDhgNvwlGdnCpy5MhBHBwc2b17BzEx0Vha\nWnHo0H4qV676j9erra3zXde0s7Z+ze3buXtySpYUnY+NGwAAIABJREFU8n5+JHR0tKlatTrjx49B\nKlWIwLx6lULFii5cvnyRc+dCqVWrDtu2BWFnV44ePXoTELCe5ctXK9UqDx8+gKam5re8DAGBfxWC\nMScgICAg8Nm87WESiRSBHzo6OsrzqgaVqnE1a9ZR9uzpBWjw+DHY2/uyadNyrK1LKQVVSpWyoVQp\nG+RyOZs2bWDJkj+YNm0WjRs3Y+XKZURHP8XXdwUJCfFoa6vmqX2ut+qfGoMaGprs3r0dd/duzJs3\nE4lEgq/vSp4/T0IkUmPVKj+uX7+Gp+cvZGZmoqurx/btQUyfPpHs7GyCgnYhk0np2rUjpUuXwd7e\nkaCgQDp37opEImHRovlkZ2cjkWTy5EkU1tY27NgRzPPnSQwY0BsLC0sCAzcWWNOuIAn4jIwMpkwZ\nT2JiIjKZFA+PfhgZGRUowNK5c9vPFqqYN68O4E9MjCFlyqQwe3bTj+ov8O2xsSlN//6DmTFjMkOG\n9EdbW5uff/6F8+fPsnnzRsqXr4izswvm5pbs2xeCTKYw+hITn6GhoUmjRk1YsuQPPD1/YeXKtwWR\nRN+1Z1lA4HtECLMUEBAQEPhs3hY8cXZWFYhwcKhAePhVUlKSkUql/P33YSpXrkqFChUJD7/K06cZ\ngAZqaskApKc7ERQUqOwfHx/HjRvXiY2N4erVy7i5tUZLS4v4+HiePn3CmTMnKVvWjm7deirru+Wi\nq6v7Wd6q3JppQJ6aaXrvNPCcnJzZuNGPnJwcoqOf4O7elRYtWiMSiVQETv74YxkikQhHxwps2bIT\nLS0txGIxqalpODiU57ffJtCqVVulx1NHR4dJk6azdu1GVq70448/5gFgbFwEI6MiLFmykmnTZhEQ\nsBU/vwAVQ04qlRb4kHzhwllMTYuxfn0gGzYEUaNGrfcKsHyuUIWFRTE2bvyJY8easmZNJ4yNv//a\nYnFxsfTq9fOHGxbA1auXGTduVCGv6NuR+x1q0qQZZmbFWbHClzVrNtCsWQtMTExwcanMihW+zJw5\nn19/HUGzZi3R19dn2LCBTJkynoyMdGrUqI21dSn8/DYhFosJDg5RvmBwcHBk6dJV3/ISBQR+OATP\nnICAgIDAZ2NtXYqdO7cyd64PNjZl6NixM9u3vymUbWpqyqBBQxk+fBByuZzatetRt259AMaNm8jM\nmXMpVWonOTnFiYlZg7V1JSASD4+uZGVloaOjw86dW7l48TwSSRYWFhaYmJiyc2cw+/fv4cWLF+zc\nuY3ixUtQooS5iuHSpElz5s2bVaC36v0ovASengOYM8cHD49u/zeopinOFmAciUSKENIKFSrSvXtn\n1NTUyMrKAkAsFnP16mWlwElcXCwGBoZERFylS5duWFpa8fhxFHfu3KJr118IDw9DJpMikUjYvHkD\n169fY9CgPkgkWVhZWfH69Wt69x7A7duvgGSaN/+JNm3q4+XlDUCzZvVo374Tly9fZPTocco1SiSZ\nTJgwjrZtW2FrW54//1zCypXLqF27Hrq6uu8VYBGEKv67mJtb4O+/RbkfHLxb5Xzec7m4u3fF3b1r\nvuP+/lt4/vwFq1adQyZTo2dPF2xsLAp/0QIC/wEEY05AQEBA4LNRV1fPJ+EfHByist+0aQuaNm2R\nr2/NmrXZs2c38+cf4OpVDWrWDGDq1MaUKKHwhsTFxeLlNeqjar3lpWJFFwICtn644VvkfVidM2dB\nvvOengNUvFNFihSla9cexMREk5j4il9/nYSv7zwiIx/Qp08//v77EPr6Brx6lQIoHo69vCayc2cw\nAC4ulTl37gzq6hpUrVqdgwenIpPJadmyNceOHcHAwABLSytycnJYsWIN/v5r8fV9iLr6bRISJvP6\ndQf09VtTu/YJ6tVrSGZmJhUqODF06EjlGtPT05kyxRs3tza4u7uTmPgaP79NnDt3Bl/fFVStWk3l\nGhUhs2+M1v+qUIVUKsXHZ/I/qgd4/vxZli1biFisjbNzJUQixX3s1q0Tq1b5YWxsjEwmo3v3Tqxe\nvU6ZR/pvRiaTsXDhYW7dUsfCIpORI2vSrdspIiI8ABEHDwYTFKSOlVXxb71UAYEfDsGYExAQEBD4\nbD43z0UkEuHl1eqjxt+37yJhYS9wdDSgU6c6yuPJySnMnHmS58+1cXUVMWRI0y+Wh5N33Nzt8eOX\ncvfufeRydcTidExMzDA0NEJHR5fr1yOQSCQFCpy4uFRmxowptGrVFmNjY1JSUkhOfkmjRk3w9V1B\n8eIlSE1NxdW1Grdv3+LcuVCyshzR0DBDLtcH1DEwqEJ4eBj16jVETU2Nhg2bKNcnl8sZP34Mv/zS\ni2bNWgKQlJSEgYEBzZu7oaenz44dwcTHx6msr1KlKl/k3v1IPHnyGG/vKTg5OTNnjg+bNwcQErKT\npUtXYWVVkpkzp7Jz5zbat/+J+fNnsWzZaiwtrZgyReElFYlEtGjhxuHDB+jSpRuXL19UKrr+F5g1\naz/LlrUCjIBsLl/+g4iIUeQqm96/78727cGMGNHyWy5TQOCHRDDmBAQEBAQ+i7fDr77G+H/9dYyZ\nMyuQmdkELa1oHj06yNixigfBgQMPcfx4H0CNgwfjEYmOMmTIlxHaOHz4pMoaHz9+wsmTfcnMdEVD\nIxpLy/6sXLkJP79VlCtnz+TJPty4cY3Jk72QSqU4OlagQ4fOAMrC6i4ulQEoW9aOly9foKGhgbm5\nJc7OLhw+fIBTp05w5MhBsrNzsLe3JzJSBogwNLyGk5NYaVRqaYnzGZvOzi6cP39Wacw9fPiAqVO9\n0dc3wNi4CGPHepOa+rrA9b0pKaDY/lQD+f79eyQlJVKrVp0PN/5O+Kf1ACtXroqFhaUylLd5czdC\nQnYC0Lp1O8aPH0OXLt3Yt283rVu3/TYX8w2IiNBGYcgBaBIXZ42a2ktkshL/P5aBvr4g4yAg8CkI\nxpyAgICAwA/H3r1SMjPLApCVZcWBAxqMHQsSiYQbNyzI1feSSktw5crXK6Kdnp5BVpYBkADsB9IR\niRoREDBY2aZq1Wr4+W3K11cs1ubYsbPK/XHjJiq3XVwqsW9fCBMmTKVMGVv69u2Js3Mlhg/vR8+e\nx2nYMI7GjTU5ePABjRvnz1HKpV+/Qfj5+fLHH/OYO3cm1avXpF69htSuXVfFi1fQ+vKGneYKVeSK\nwHyMYXf//l3u3r39UcZcTk4OGhrf7pGloHqAueGyuccK5s3xYsWKU7RoUa5cucTt27eYNm32l1ru\nd0eRIqoCRNbWUL/+frZvr0VOjpiWLY/g4dHlG61OQODHRjDmBAQEBAR+OMTinLf2swHQ0tLC1DSZ\nxMTcMzJMTDK+2rrKlStLw4aBHDumD7gBezh/vg27dl2gQ4canzyui0tlNm5ch5NTRcRibcRiMWlp\nOmzceJXevfty6NBWAgNVhWXyG1iKfXt7B5YuXUitWkepVq0m6urqhIeHERS0iefPnzNkyHAaNmxC\neno63t5jSUh4RlJSBmZmzRg8uAl2diaMHj2UChUqcvfubX7/fSkBAeu5c+cWEkkmDRs2oW/fgYCi\nvuDSpX+QkZGJlpYWixYtZ82aVWRlZXHtWjg9e3pSq1YdFi2az6NHD5FKc/D0HEDdug3Yv38PJ08e\nIzMzE5lMxrJlqz/5/n0ub9cDPHv2NCYmply/fo2goE3o6OhQuXJVSpWyIS4uVhmmeuTIIUAhRnPk\nyGnatu2Aj89k3NzaIBKJOH36BCVLlsLGpvQ3u7avwdSpNUlMXM/9+8WxsHjO1KmOVK1qx8CBd8nK\nekmlSl1RUxM8cwICn4JgzAkICAh8BbZuDaR9+58Qi7ULZbyCaoZ9DPv37+Hu3duMGjXuw42/QwYP\ntuDBgwPExNSkWLEwBg0yBRQGzNSp1vj4BJKUZISTUzyTJn29PBx1dXV8fKpz/LgmOTklefx4DwBn\nztyiQ4dPH/fu3dv8+usIxGJtlixZQGKinKNH56CjE4al5Q4aN7YlPv4poaGn0NTUpG/fgcyZswBv\n77FK8ZZx47yZPNmbZ8/iCQraia2tFZGRMSxfvogXL56zcqUfUVGPGD9+NA0bNkEsFjNkyBi6d48l\nJqYm1tZdGTq0PkuXPiYmJprJk30oX94JgAEDhmBoaIhUKmXkyCFERj7A2roUU6dOwMdnLg4OjqSn\npyMWi+nffzB3795m5MjfAFi9+k9cXaszYcJUXr9+zYABHri6Kgzf+/fv4e+/BQMDg8/4VD4PkUiU\nT61VU1OTCROmsmjRPJVwVA0NDcaNm8i4cSMRi7VxcalMbGw0uYZ0nTr1mT17Oq1aKUIsT506QZ06\n9f71xpyVVXF27eqERCJBLBYrjzs5OXzDVQkI/DsQjDkBAQGBr0Bw8BZatGhVaMbcPwlrmzdvJj//\n/As2NqWRyWQf9eY7Li4WT8+x+PkFfrjxN6BxYxcOHkwkLOwizs5lsLAokeecM40aVSQ7OxstLa2v\nvjZzc3NKlIggLi631p4EM7PPU350canCli0BdO7clbCwq7x8qQtooKNzhcTEn5DLM1izZpbSmHr4\n8AFVq1Zj4cJ5vHjxggULThMaGoJYrEGDBlWVLwEMDQ0BqFevAaAoCP3ixQtAETq4YMFC1NSSsbL6\nCw2NZyQmOnHu3HaKFzdXGnIAx44dJiRkF1KplOfPk4iKegiAiYkpDg6OgKLeH8CyZYto0KCRsu/F\ni+cJDT3F5s0bAcjOziYhIR6RSISra/VvasgBlChhzqZN21SONWtWn6pVqzFr1u94eY1i/PjJZGZm\nMn36JB49ekipUqVJSkqkZcvW2Ns70KxZff76awXHj/+NXA4GBgZcvx5BaOhpwsPD8Pdfy8yZ8z+i\nbMaPSV5DTkBAoHAQjDkBAQGBQiYjI4MpU8aTmJiITCalUaOmJCUlMnz4IIyNFcWdFyyYw507t/OF\npXXu3BY3tzaEhp5GKs1hxoy5WFvbkJKSzLRpE0lKSsTJyVklR8fbeyzPniWQlSXB3b0b7dp1BODv\nvw+hp6evrDP29OkTAgLWo69vQNmy5ZQy8z8qxYub0bKlWYHnRCLRNzHkAAwMDPH21mDx4mBev9an\nZs0YRo3q+Flj2ts7cPfubdLT0xCLxWRllURb+8b/jbmJJCauxNNzh9KYevToEWXKlKVFi1ZMmLCI\nXbu8sLZeR1xcbySSE3h7y1TG19R8813I/W4dPnwATU0ZCQnzycx0oHTpxmhqPsHSUo/bt9+8lIiN\njWHLlk2sWbMRfX19Zs+eTlZWFgW9b3hX8fJZs36nZElrlWO3bt1AR0fnc27bV2XHjmCMjIwICNjK\nw4eR9OnTHYArV+6RkZHBrl3hiESp1K1bj5CQnXh49KVu3frUqVNPWb/veye3TMiGDUHfeikCAgL/\nRzDmBAQEBAqZCxfOYmpajN9/XwJAWloq+/fvYdmy1UqPyIABv6qEpT18+IAyZcoiEokwNi6Cn18A\nO3duY/PmALy8JrFunS8uLpXp3bsf586dYe/eN2IU3t5T0NTUZOLE31i8+HeCgjbh6TmQjIwMihQp\nyvr1gTRtWhd1dXWKFSuBSCTiwYN7VKjgRExMNNOnT0IiyaROnfoEB2/hyJFTKtcjlUpZtWo54eFX\nyMrK5qef3Gnf/qevd0N/QLp2rUWXLjKysrLQ1q772ePlKlru37+H6tVrkpWVxIULB9DSisLRcS8v\nX15l3brAPMaUBIBWrdqxcWNfDAxOkJrqRnp6LSQSX54+fUzx4s4qIh5vk5aWRrlyZRg69Dpbt+5D\nQyOGBg1W0qzZGIKCljBixGCWLFnJ5csXSUlJ5uzZ0/j7ryU6+ikvX76kWbOWPH+eRJMmdejY0Z2L\nF88zevQ4RCIRGRnpyuLlRYsWZcuWTTx7Fk9iYiIZGekMGPDre0RFvk+uX49QFlcvU8YWW1s7Xrx4\nyYgRmWhoaHL58maKFr1I+/YXiI+PVvb70a5TQEDg+0LINhUQEPhPM3ToAO7cuV2oY9ra2nH58gVW\nrlxGREQ4enr6+docO3YYT88eeHr24NGjhzx69Eh5LvctfblyDsTFxQIQERFGixaKOmy1atXFwMBQ\n2T44eDM9e3bhzp3baGlpMXHiNGrWrAWgLAKdmZmJg0N5Nm4MolKlKhgbF0Eul7NkyQJ+/rk7/v5b\nKFas4IK9e/fuRl9fH1/fDfj6+rNnzy7lugTejZqaGtrahRNWCwpFy82bA6hUqQp//DGI0qV34+ho\nwsKF1dDT00dPT48XL55z/vwbRUxTU1OMjAwoWnQFKSk/kZVVFh2dmkyaNJ727duzfPlioOB6ec2b\nt+TOndvcvLmejh1jsbCwoEQJRbioRCIhIyODnJwckpISKVHCnFmzpmFsXIS6desTFxfDuXNn8PGZ\ng0Qi4cSJo+jq6uLgUB6xWExU1CPatGmOlZUVM2fOJzY2mhs3riOV5mBjU5qaNWshEn16+YNvxduG\n2dWr94mKak7uu/MXL6pz61aSSsH1s2fPIJFkfs1lfhYymYx582bRs2cXRo8eikQiUfkdTU5Oxt29\nHaDIzfX2HsOoUb/i7t6O7duDCAzciKfnLwwc2IdXr14BEBKyk/79e9G7d3cmTRqnvB+zZk1j8eIF\nDB7sSZcu7Tlx4ui3uWgBge8YwTMnICDwn+ZLPDCWLGmNn98mzp07g6/vCqVBlUvBYWkS5fnc8Ed1\ndTWVh76C3uBfvXqZK1cuMW/eIsaPH41MJuPWrVuUL++Empqa8to0NDQwMysGgL29IxERYVhYWHDz\n5nXmzl0IQLNmLfjzzyX55rh06TyRkQ+UD1JpaWlERz/F3Nzic26TwEfytqKloaEBrVo1o2JFZ8qV\ns6d7904UK1YCZ2cXlX4DB/Zg0aJVFCkSjqHheSZN6oazc1nMzAxITHydb57c2nlGRsasWuWnPJ6T\nk0P37p0wMjLCycmZMmVsuXPnNteuhdOqVTvu3bvDxInTAMULgPDwMIYNG4W6ujrBwSHK76LiXxHj\nxk1Q1rsbPdqL0aOHUrt2PSwsSnHp0i0aNWqKm1ubL3AnvwwVK7pw7NjfVKniyqNHD3n48AGdOvVC\nX//NyyJ19QTMzMSAQqpfV1eXI0cOKcVt/ikfmwNbmDx9+oRp02bj5TWRKVO8OXny2Ht/Rx89esi6\ndYFIJBJ+/rk9Q4aMwM9vE8uWLeTgwX106dKNhg0bK8PDfX1Xsnfvbjp1+hmgQHEeAQGBNwjGnICA\nwH+CuLhYxowZhoNDee7du4ONTRkmT56u0mbBgrn55NWvXLnEtm1BSkXAS5fOs3PndmbP/p2LF8/j\n5/cXWVlZWFpaMWHCVHR0dOjYsRVNmjTn6tXLuLpW5969u+jq6pGWloahoRFpaWloa+uoeFIqV676\n3vW7uFThyJGDeHj05dy5UF6/VrzRTk9Pw8DAAFvbskyfPochQ/qyd+9OXr9WDZ/T0NAkPPwqr16l\nIJfLiI2NUQpT/BNGjx5HtWo1/3F7gcKnatVqHD9+Trm/efMO5faECVPf2e/69Qh+/dWT1q2bfdb8\neUM9K1Z0wda2LFevXiImJhpzc3Pu3s3r4ZZ/VPHy3BcgY8cuY+3abaSm1qJ06ccEBjajSBHjz1r3\nl6AgT2Z2dhY3b16jR48uZGdnoampRaVK5enZcz9//51J6dK9KVo0iitXpBgZGf+/rxopKcl07Nia\ncuXKsWrVunf+rnTu3JYmTZpz6dIFfvnFgyZNPu/z/FTMzS0pW9YOUORyfshLX7myKzo6Oujo6KCv\nb0CdOorSGWXKlCUy8j4AkZEP8PVdSVpaKunpGdSooYgsEIlEBYrzCAgIvEEIsxQQEPjP8PTpE376\nyZ2AgGD09PTYsUNVoW7AgCGsWbOB9es3Ex5+VakI+ORJFCkpyQDs27eHNm3ak5yczIYNfixZsgI/\nvwDs7R0IClIUWpZKczhy5CByuYywsCv07t2Pdu06MGbMMEaMGIydXTmlJ2X69Mn5PClvePO229Oz\nPxERYfTs2YVTp05QooQ5ADVq1EYqldK160/4+6/F2bkSTZq04N69u6ojiUR4eg5g4MA+rFmzCn19\nA0QiERUqVOT4cYXH7e+/Dxe4iurVa7FjxzZychS13Z48eUxm5o8TFvZfZevWUFq2bEdo6BWaN3cr\nlDHzhnq6uFRm167tlCtnj6NjBcLDr5KSkoxUKuXvvw9TqVKVd47Tr98gDAwM+eOPeQAkJSWRmJjI\noUMdeP58ONraj7lypQ9Ll54plHUXNrneS3NzC/z9twBQpUo1LCysCAjYir6+ATk52ZiYmFKqFIwb\nN57Dh2dw4MAegoP3oK9vwMOHDxgxYgzm5hbs2rWfVavWvfd3RSQSYWRkjJ9fwDcz5AAV4SQ1NXWk\nUinq6urIZIoogrxRBvnbqyn3RSKRMvJg9uzpjBkzHn//LXh69lcZoyBxHgEBgTcInjkBAYH/DMWK\nFcfJyRmAFi1aERy8ReX82/LqeRUBDx3aj5tbW27evMGUKTM4dy6UqKiHDBrkCUB2dg4VKyrGFou1\nWb78L4oXfyOXb2/voAwbgnd7UoKDQ5TbDg6OLF26CgBDQyMWLlxeYJ8FC5Zy8eJ5/vxzCWpqIk6d\nOs6YMeNJTX0TQicSiWjVqi2tWrXlxImjnD17hpEjfyM6+ik+PpPZuHEd1avXRF8/f35f27YdiIuL\npW/fHsjlcooUKcrs2b+/+0YLfHP+/PMIc+dWRSI5jkj0gmnT9jNrVvvPHreg4uUuLpUxMTFl0KCh\nDB8+CLn8nxUvHzlyLLNnT2fFiqW4ulZn4cL5mJmpI5MZ8OzZNEBEdvaP85hSqlQpzp49Ta9eXYmL\ni6FWrTo8eHCfa9fCGTnyN44f/5tdu3YQG5uCRJLKypW7mT9/tMoYN29ef+fvCvBNjbj3YW5uwd27\nt3F0rPBJeW0ZGekULWpCTk4Ohw7tf2f+roCAQH5+nF9JAQEBgc8k70OlXC5X2X9fHlurVu3w8hqF\nlpYWjRs3VeaquLrWYNq0WQXO9bUl1atXr0n16qphkMuWrQYgMDCUnBxv6tU7QqtWWXh7t1bmnZiZ\nmfHXX+sBRSmDp0+fAIqHsz179pCY+BqRSMTAgb8ycOCvX++CBD6LY8dESCSlAJDLi3LqlF6hjPu+\nUM+mTVvQtGmLfH1yvVi5BAe/UWLN+1Jj06ZgevYM4u+/+wBaWFoeonNn20JZ99fA0NAIZ+fK1KtX\nn5SUFJUwVLFYzJYtm9DQ+Inw8IEULz6JXbvKYGGR3xv+Pf2uFMTbxrlIJKJbtx5MnuxNSMhOatWq\nS67Bnj+XTjU8Nfdcv36DGDCgN8bGxlSo4ER6enqB8/1ogjgCAl8DwZgTEBD4z5CQEM+NG9dxcqrI\nkSMHcXZ2ITT0NHK5/L15bKamppiamuLvrwh/Aihf3omFC+cRExONpaUVGRkZJCUl5quV9a2JjHyM\nj48+L14ocpMePYrBzi6Uzp3rAHDnzh0WLZqPXC7HwMAAb+8pKv3XrDlBQIAEmUxEp04iRoz4Pj0D\nAqro6KiGuunqSt7R8tsSFRXL1KmXePZMFyenVFavbouf325SU6F9ezucnH4cYw7ehKFOmDCVMmVs\nWbp0IY6O5f//+6JNRIQ56uov0dM7RXp6Da5ckaKrq6vMp/0Svytv14YLDNxIZmYGBgaG7N69A3V1\ndWxsSjN9+uwPjpU3rBSgW7ceym1//83K7f79BwPg5tZGRcQmryGf91yHDp3p0KFzvvnejmB4+8WA\ngICAYMwJCAj8h7C2LsXOnVuZO9cHG5sydOzYmdDQ04hEIpU8toIUAZs1a0lKSgrW1jYAFClShIkT\npzFt2gSysrIBRc7d92bMXb8exYsXDZX7WVmW3L//RrrexaUS69cHFtj3woWbzJ1bilevFGFef/wR\nSfnyl2nWzPWLrvlH4F3Fk9euXY2LS2VcXasX2O/06ROULFkKG5vSX3R9o0bZERUVzL17VbCyus3I\nkeZfdL5PZdSoC4SG9gLgyhUJuro7mD79x1GwfJt3haGWLWtHuXIOREb+TokSu8nIqArIKVo0gwYN\nOjJmzDDMzIqxZMnKd/6uyGQypk6dwMuXL5HJpHh49MPS0orlyxeRkZGBkZExEydOxcTElK1btxIY\nuJns7BxMTEyRyd4Uic/1bm3a5M+2bXvQ0NAgLS31W9yud3L0aDhr1sQjlYpwdzfA3b32t16SgMB3\ni0j+nWSTFiSPLPDv4F3y1wL/Dn6Uz/ddD9//lIUL52Fv70jr1u0KPJ+c/BKZTEbRoiafs8xCJyEh\nkVat7vL0qUIAw8DgJmvWvKRRo3eJrrxh69YTDB3ahryhUZMmbWP48PyhdP81PvX7NGvWNOrUqfdR\n8uq5AhMfS1paGlFRTyhZ0kJZrD4v3/pvVyaTUbnyceLiOiiPNW++nYCA5t9sTV+aU6duMmXKQxIT\ni+LgEMeqVY0wM3v3b4ZcLufRo0doamoSGXmPCxfO4+U1EYC0tFTGjh3O3LkLMTIy5ujRw1y8eB5v\n7yloakrJzlZ8ZxYtms+JE8fYvfsgAJs3B5CRkc7NmzfQ0dGhfv2G1KvX8LsI4QR49Cia9u3jiY9v\nBICxcRj+/hJq1arwjVf2/fCt/3YFvhxmZgYf3UfwzAkICPxn+NR8C0/PHujq6jJ8+JgCz0+cuJut\nWy0ANdq1O86CBZ2+m9yO4sXNWLQogdWrt5KdrUa7djo0alT/H/Vt0qTi/9g784CcsjeOf963fZUt\nS0mpVKRIYxiyJcY2zNjXMBh+1rGHoiyhLNmXlLJkZDD2nRFZxhZmZEmJNor29X17f3+8ekkhS9b7\n+Wfee+65555z79Wc55zn+T5UqhRCQoK8ftmyF2nU6PPaefyUFCRPvnEjjIoV9fH0XIi3t6fCWFu1\nahlnzoSgpKREgwYNadasBWfOhHD16hUCAtYze/YCMjMz8PKSJ9Y2MDDExcUNHR0dRo4cSs2aFly7\nFkbjxg7s37+XoKA/FbsoAwb0YevWHa818rStySyMAAAgAElEQVS0tKhdu+TpJ96XtzVwxWIxRkap\nxMUVlORhZJRN164d8fPbVKwB+qXTtGltTpyoRU5OzhsTykulUoYO3caBAw1RUsqgc+co4uPPs2rV\nMn74wQEdHW3u3Ytg7Nj/AfLvsXz5igDcvn0bL6+FZGSkk56eVkgdsiAht7e3D1euXMLffx2enh60\naOGIm9vsdx7b+vVrqFvXjvr1v2PkyKGMHPn7W6U/KeDUqRvEx/+iOE5OrsfZs8GCMScg8AoEY05A\nQOCb4OVYj7fBz2/TK88dPHgOf/8WSCQGAGzebM0PP4TQpUvJDKaPQdOm1jRtav3W11laGrNw4X38\n/ILJz4eePXX57rsv390pPPwmBw/uY+zYCe/VzuuSJ6ekJBMScpItW/4E5LsoWlraNGnSlMaNHWjW\nrCUAzs49GTduMra29Vi/fg3+/msZPXo8IpEIiUSCr28gIDeUzp49jYNDc44ePUzz5i3fabfuc8Pb\n244ZMzbz+LEmtWql4ObWnn79fD91t0oVkUj0RkMOIDDwBHv29AG0kEjgzz8r4etrhrJyJuvWrcTO\nzh4TE9NCid0LmDJlCnPnLsTU1Iy9e/9i0aL5pKamoK6uQWjoab7/vhEJCfHY2dnj7e2Jjo4u48dP\nea9x/frrb4XG+K4LWnXr1qBMmaukpMhjltXVI7GyKvdefRMQ+JoRjDkBAQGB9+Dhw2QkkufxSPn5\nFYiPz/iEPfqwtG5tR+uvzOvN0tLqnXYMXuZ1yZO1tXVQVVXD09ODH35woHFjB8W5guiG9PR00tPT\nsbWtB8CPP7bH1fX5hNrR8fmD79ixM1u2BOLg0JwDB/YyefL09+5/aSCVSvHwcOX27XCMjWvg6urO\n9evXWLnSB6lUiqVlLSZMcEFFRYWLFy+wcqUPampSWrV6Xl5ATk42U6dOokWLlrRq9SOurpN5/Pix\nIl7sc5Xp/1CkpEiA5yqkMpmYpKRM+vVri5aWNrt2bSc5OVkh6iSRSHjwIBoTkxpkZj6X+j969BBm\nZuYMGeJMxYr6GBubKN5TVNQ9UlNTKVeuPLt2/UlIyN/k5uagpqaGi8sMjIyqs3//HkJCTpKdnc3D\nhw/o2bMPOTm5HD16EBUVVby8fNDV1S3iQiyTydi3bzcREXcUXg27d+/k/v1IRo0aV9yQAbC1rcm0\naX8TELAdqVRM5875tG0ruHYLCLwKwZgTEBAQeA86dKjP+vW7iYiQx/0YGe2jXTubN1wlUBpkZWXh\n5jal0IS/atWq+PgsJDs7GxUVFXx8VhEe/h9bt25mwQK5cMTixQuIjLyHVCph0KChNGnSjP3793D6\n9ClycnKIiXlI06bN+d//RhMXF8v//jeYrKws0tPT+OmnNkyf7s6OHcE8eZKEqqoaly79w44dwSgr\nK3P16mUSEuLZsWMbU6a4cvbsGa5evUxgoD/Dho0C4PLli/j5rUVNTZ2oqHt4eLgCoK6uUchVMykp\nkcuXLyKVSjExqfEpH/UriY6+j4uLG9bWNnh6ehAUtIndu3eydOlqDA2rMXv2DHbu3E6nTr8wd657\nkfLu3XsBkJmZiZubC23bdqBNm3acPHmMChX08fLyAfjsBDtKg06d6hAUtJvIyJ8AGRYWfhw+fJbj\nxzeirKzChAkuiMVifHy8SU9PRyqV0KNHb0xMajBmzJgiUv8FypDx8XEkJaUwcOAQVFRU6NbtJ9av\n34iysjI9e/ZFSUmJf/45z9q1K5g9ewEAkZH3WL58LYcOHWDt2pV06NCZChX0qVatGgcP7qN7915F\nduNEIhEtWzoRGOjHiBFj2bDBl5Mnj+Hu7vnGsQ8Y0IwBA0rjqQoIfH0IxpyAgIDAe1C5ckX8/U3x\n9d1Gfj4MGGCGiYnBp+7WN8n586FFJvwDB/bBw2MelpZWZGZmoqamVuiawEA/7O0bMHXqDNLS0hg6\n1Bl7++8BuHv3Nhs2bEFZWYXevbvQrVtPUlJSePz4EdOnu7N5cwDKysocO3YYA4NqVKhQkcTEx5ia\nmhMe/i9r1mxAW1uHwYP7k5aWQrly5WjevCVWVrWpU8cWd/fp6OjoEhFxl7t3b9O+/U9Ur27Mf//d\nICcnh/T0tEKumoGB6/HwcGXAgMEf98G+Bfr6lbC2li9mtGnTjg0bfKla1QBDw2qAXI5+x45t2NnZ\nF1vevXsvZDIZU6aMp0+f/jg5yVNqmJqas2KFjyJezNa27qcZ4EfExMSADRty2bRpG0pK+fzvf32p\nXPn3IvWWL19bpKxXr160alVUFdTb+xCrVlUhPb0ijRr9ycaN7RXn0tLSmDVrBjExDxCJREilUsW5\nevXsycvL49ChfWhr62BtbcODB9HUqGFGRMSdV45BQ0MDO7vvOHMmBFvbemzZEkiNGoXTTbxrfN3+\n/Xu4desmv/8+6a2uExD42hCMOQEBAYH3xNLSGG9v40/djW+elyf82tralC9fQTFJ1NTULHLNhQvn\nOHPmFEFBGwHIy8sjISEekUhE/foN0NSUu7kZG5sQFxdLVFQUmpqa2NrWIyhoI6am5tjbN2DlyqXk\n5GSTnp7OkydJ5Ofn06dPV0BEfr6UIUOGk5cnISbmIXv37kYsFgEiVq/2w919GlJpPnFxcUydOoPV\nq5dz5colNDW1CrlqtmnTnoAAP5ycPl+Xsxd3ZmQyGdraOqSmphQqK44Xy0UiETY2tpw7F6ow5qpV\nM8LPbzNnz55m3bqV2Ns3+KyN2g+FlZUJc+aUPI3F7t0X2Lz5CaqqKnTrpsNPPz1PkZGQkMDq1fqk\npclzTIaGmuHjsw2QP39f39XY23+Hp6c38fFxjBr1PAZOVVWF1auXERPzEKlUysaNfmhpabNz53Zi\nYh6QnJyMsrJ8ShkefpM7d27h4TGdSpWq0K1bT/7660/u349CVVW+mNK1a0ccHVvzzz/nyc3Nfaf4\nus9FZEpA4FMj/tQdEBAQEBD4Nrh8+SKTJhXdWfhQFEz4TU3NWLduJX//fbxE182Z44W//xb8/bew\nffseqlc3BuQT2ALEYiWkUikikQixWKwQ1BGLxaioqFCuXHlmz16AsbEJpqbmbNoUzPHjoRw/foaT\nJ8/Rp48zf/yxGTMzc06cCOXw4VNIJHmYm9dk3LjJ1KtXn7lzvdDW1kZJSUzfvs5YWdVi3boAmjd3\nJDQ0hIkTx9CiRSu0tLRL4/F9EBIS4rlx4zoAR44cxNLSiri4WGJiHgJw6NB+6tWrj5FR9WLLCxg8\neBg6OrosXDgfgMTERFRVVWndui29evXj1q3wjzyyz59r1+4wZYoWJ05049ChzkyZos21a893zVJT\nU8nIqPDCFWKysp6v6WdkZFChglwNc9++3UXaHz58NAYGhlSsqM+gQb9x584tnJx+xMmpLbGxMTx5\nkoRUKmXJEi9MTExxdZ1F+/YdOXnyGI8ePSIhIR5VVVU8PFxJTHzMuXNnWLXKl7Jlyyru4e09j8GD\n+9OvX3fWr1+jKL9581+GDx/EgAG9GTp0AJmZmYUWAEJDTzNs2KBCCwcCAt8KgjEnICAgIPBV8PKE\n/+bNf3nyJInw8P8AyMzMKOQ6BtCgQUO2b3+ucnr7ttxIKG4HSSQSUbOmBVlZ2Qqxk9zcXEU7+/fv\nUfz29V1VpM3MzAxFHsKDB/cVSuRcHAVxeeXKGfLvv7FERt7D2fnXkj+Qj4xIJMLIqDo7d26jb99u\npKen06NHH6ZOnYGr62ScnXuipKRE585dUVVVLbZ8/vzZSCQSAMaOnUBOTjYrVy7l3r27DB06gIED\ne7Nhg+8H35ULDt5K377daNu2JZs3BwByqf2goFcr2X5unDlzl8TEhorjxMTvOXPmruK4Ro0aNG58\nBpD/G9DXD6FDByNAHuvWu3d/Vq9ezqBBfZ59m/Kdr4JYuOf/JuS/raxqo6uri1gswsysJllZWTx+\n/JjIyAju3r2Nu/s0AgP9ePz4MS1btqJMmbI8eZLEL790o2JFfapXN2HHju2FxjB06P/w9Q1kw4Yg\nrl69TETEXfLy8pgxYypjxkxkw4YtLFmyEjU1NcXO3N9/n2Dz5gC8vZd+leksBATehOBmKSAgIPCN\nUJxAiIGBIcuXy4VAypTRY9q0GZQvX4GHDx8wceICHj9OQiwWM3v2fKpWNWDFCh/Onw9FJBLRv/+v\nODo6KQQ89PTKEhkZgYWFFW5uswA4dy6UZcsWoaamjo1N6cY53bt3lxUrfBCLRQqBCJksn8WLvRR5\nvRYvXvFsciq/ZsCAwSxduhBn557k5+dTtaoB8+cvfqW0uq6uLvr6+kybNpH8fBnJyU9p0cKRAQMG\nM2+eBw8fPuDUqRNkZWUVafPnn7sxbdokDh7cz/ffN0JD47nbZ3EeY5mZGYwaNYKoqCzy8rR5+tSV\nRYsusHjx55nrr3LlKmzevL1Ief363+Hnt7lE5S+rdBaIdoDcSC4tdu3ajo/PKsXOFHx5bnx16lRF\nSyucjAxLALS0wrG2fq60q6SkREBAR5YuDSYjQ4n27avTqJEVwcF/AWBtXYegoB2K+kOGDAfk8Yxt\n23ZQLGAEB//F5csXUVFRVZxbvHgBHTp0wsLCkhMnjhZJlzBp0u8YGFQlLy9HEVPp5NSG/fv3Fqp3\n/Phhdu/ehVQqJSkpkaioewDFukvLZDIuXbpIePhNFi9eUawbtYDAt4BgzAkICAh8IxQnEDJhwmjm\nzVtEmTJ6HDt2mLVrV+Li4oa7+3RGjvwftrbfk5eXR36+lJMnj3H37m0CAraSnPyUwYP7U7euXFb/\n7t3bbNoUTPnyFRg+/FeuXw+jZk1LFiyYw7JlazAwMMTNzaVYo+VD0aBBw2In/GvW+Bc6rlevvsKl\nT01NjYkTpxa5pmCSWsCCBYsVv4ODi7qgAcyYMee1/TM0rEZAQJDiePhwuZqlnZ09dnb2ivLRo8cT\nEXGP3NxcKlUayNGj3RTn9u49iZvbE8qW/fR5t+LiYhk/fhTW1jZcvx6GpWUt2rbtgJ/fWpKTk5kx\nYxahoafR1NSiV6++APTr1x0vr6WUKVOm0MLCgAFDaNmyVSExjHPnQlmzZgUJCSmAFr/9No5Onb7/\noGNwcnKgdeu2xMQ8pE+fbvz661BiYh6SnJzM5csXqV27Dr169WXkyKFYWFgSFnaVrKxMpk93JzDQ\nn8jIezg6OikMn09Jkya2TJ58nKCgf1FRUaJLFxEODi0L1dHS0sLFpf0rWng9mpqaZGZmvraOkZEx\nyclPuXHjOmZm5vj47OXo0dXUqVMbPb1yQJSirkxW2GCOjY1h69bN+PpuRFtbm7lz3Z/F0xV/L5FI\nhIGBAXFxsURH3/8g6UYEBL5EBGNOQEBA4BvhZYEQHR1t7t2LYOzY/yGVSklNTaVGDTPOnj1DRMQd\nWrVqxePHac9yf6lw/XoYeXm53L8fhbGxCXXr2nHz5n9oaWlhZVVbsathZlaTAwf2sn37H1StaoCB\ngSEArVu3ZffunZ/wCZQOoaFh3LwZR8uW1piYGL5XW9nZ2Tg77+TUqSaoqz/B2PhWofNKSnmfVbLw\nmJiHzJ69ABcXNwYP7s+xY4dZvdqP06f/JjDQH3PzmoXqyyfvsmIXFgrOi0Qinj59yoIFc9DQ+ImL\nF0cjFmczZkwMOTmhdO/+IRPXi5g4cSoXLpxj/fqNnDkTQnZ2Nrdu3eTnn7sqdntEIhEqKqr4+gYS\nHLyVKVPG4++/GR0dXXr06EyPHn3Q1dX9gP16N4YNa8mwYVCxog6PH6d90LbLlNGjTh1b+vfvgZqa\nmsJl+EWUlZWZNWs+ixcv4L//YsjIKMPTpxNITVWlUaMdpKQkK2IqT548ho2NLWfOhCCTycjIyEBd\nXQMtLS2ePEni3LnQZ/GVxiQlJRIe/h+WlrXIzMxATU0dmUxG5cpVGDFiDFOnTmLWrHmfbcoOAYHS\nRDDmBAQEBL4RXlYEtLOzx8TElNWr/YiLi2Xy5N9ZtGgZZ8+efmUbbdt2xNj4ubpewcq6svJzsRAl\nJTESSV4xVxevZPgl4+NzhMWLrcjMbIyBwVGWLk3GwcH6ndtbufIEJ04MBFTIyIC7d1UwMlpOdPRv\nqKo+oFevxM8qLqhKFQOF1LyJSQ3s7Rs8+21KfHxsEWNOjui1qQZkMhn//nsda2sbgoPrAKrk56uS\nmanL0aP/0b37hx+HRCJh+PBf6dPHmZCQv8nJyWbXrj9p3tyRmJiH3L17h6SkRK5fD6NDh5+oUcNU\nYcxUrWpAQkL8Z2HMlTYzZswutvzF9ADm5jXp128EnTrVAOSLG6mp0KpVAkZG8ezcuQ01NTVyc3P5\n+eeunDkTgkgkwty8JjVrWtC7dxf09StjY2MLyA1EDw/PV7hLizAyMmbGjFm4uk5hwYLFVK0qpIYR\n+LYQjDkBAQGBb4TExER0dHRo3botWlra7Nq1neRk+Up5cPCWZ65m8t0IZWUVevbsyZMnTzE3r4mL\nixs2NvWYN28WNWqYUblyFQ4fPoCGhib//HOOsmXLsW/fbjZt2kB6ejrVqxtjbFyDGzeuERPzEAMD\nQ44cOfSpH8EHRSaTERQkIzNT7t4VE+OEn9+29zLmMjLEwHPDOCenCh4e1XnyZDfVqpWnWbOiucM+\nJYUVP8XPdnHlv6VSKUpKSshkz4VeCgRj3pRqQCQSoaSkhI5OGklJBaUytLSyS31MjRs7cOvWTZo3\nd0RTU5MFC+ZQrZoR48dPQSKRsHChJxUq6Bfq65vEbL41dHQ0UVFJJU+xpiOlTJkydO8+kfPnn9Kw\nYROGD2+FkpISy5Y9V618MUbyRSwtaxVxl37RFdrc3IJNm7aVxlAEBD57BGNOQEBA4BuhOIEQsViM\nj483T58+JT8/n169+mJgUI3Jk39/NqFW5vTpEM6ePUPz5o74+Hgzc+ZU1NXVAahf3x5HRycCA/3w\n81uLn98mfH1X888/5zEzM2fSpGlMmjQWNTV1bG3rERv78BM/hQ+LVFpYFDo///2CAn/6qQZ//nmM\n2FhHIJ8GDQ7i6NipSLLzL4UqVapy5kwIALduhStENF5eWHhRCl8kElG7dh0WLpzHr79+z8qV+0hK\nKouNzS0mT25W6n0uUG2UyWTk5uZy48Y1xGKx4rtPTU0rZMwJFMXa2oLevXewebMyEkk5vv9+F3p6\neoweXZ2srFZAOnfvBrNkSdd3av/gwUv88UciSkoyfv1VLuQiIPCtIhhzAgIC3zzp6ekcOXKQn3/u\nyuXLF9m6dXMhwYuvhVcJhCxfvlbhZtmhQ2eF8MOmTYE8fpyGt/c8cnPlS+wGBoaMHPk7165dxcfH\nm/nz59Cv3wB+/rkbISEnKVNGj/Hjp7B9+1aio6Np0KBhIYXD+Pg4jhw5qEgG/SUjEon45ZdcVq6M\nJifHiIoVz9Knz/tN8m1tzfH1vcXOncGoqkoYO7bNZ23Ivaz4WHD86FECDx8+oFmzlhw8uI9+/bpT\nq5Y11apVB15eWFBmwoTCIjR6enpMmjSNKVPGYW1tiK5uGZYtW6NITF1a43hRxbTgv9raOhgZVWfk\nyN+xsLDkypVLbN365aQs+FR4ef1C9+7XSUm5j4NDZ3799W+yssyfndXm9OmyyGSyt1YNvXz5NuPG\nqZGYKDcEr1w5wF9/xWNoWPkDj+DjUvA3ODDwj0/dFYEvDMGYExAQ+OZJS0tl585gfv753VaJv0ZU\nVFQVv5WUxEilkkLnd+3ajrq6BgcPngAgJORkodxsf/8dzqVLiWzZcoxOnbJwde0IyBXrjhw59FUY\ncwAuLu2wtT3H3bvnad7cFBubd3exLMDe3gJ7e4sP0LvSpSBxegEvusjp61fC0LAaampqLFq0vMi1\nlStXLnZh4UWXu4YNf6BiRX1WrVpf6nGCK1asY/Lk32nbtgN169oxefLvDBo0FICzZ0/zyy/dsLCw\nRCaToaOjy/z5zxd7XuyzQGG++66O4remZm6hc5qaOe+U/uHUqUiFIQfw4EFrTpzYSb9+X7Yx97ZI\nJJJSW9wQ+LIQvgIBAYFvntWrlxET85CBA3ujrKyMuroG06dPLpIzLTz8ZrE52b4GSiI7XkBg4Hpi\nY2OQSCRs2yaPtevXbxAeHq6IRCL+/fc/7t1LJiurPioqAezencfVq+vZuHELq1cvJzo6ioEDe9O2\nbUe6d+9VyiMrfdq1K738Z18yUqkUDw9Xbt8Ox9i4Bq6u7ly/fo2VK32QSqVYWtZiwgQXVFRUuHjx\nAitX+pCXl0dmpi6amr9gZSVTLBDk5GQzdeokWrRoSYcOnT9YH180Jl71281tNt7e8wgI8OPJk1SS\nk2uTl9caJ6cM3N07fnH56D4V48ZZc/t2EP/99x2VKt1l9OiiapglwcREGxWVGPLy5EInWlo3sbJ6\nPxXZklCQisPSslaJvumuXTvSsqUT58+HoqqqxsyZczAwMGTOnJk0buxA8+aOgDw9xpEjIUXuNXv2\nDLKysgAYN24S1tY2XL58EV/f1VSoUI47d+4Wygso8O0iGHMCAgLfPMOHjyYy8h7+/lu4cuUSLi7j\nC+VMu3btKrVqWbNkiRfz5xfNyfY1UBLZ8QL69/+V27dvkZycjI6OXMGvQoUKmJnV5MSJY+jolCc9\nvRWammeIj19IdnY9unffjJqaGsOHjyIoaNNX6cYqUJjo6Pu4uLhhbW2Dp6cHQUGb2L17J0uXrsbQ\nsBqzZ89g587tdOr0C3PnurN06WpmzTrP1av/kZOTzaFDXbGxWUxmZiZubi60bduBNm3afdA+Hj78\nN1B4l/HF3zk5OYjFYry8lhATE0fr1gkkJcnj9qKiHmFhcYo+fUo/ju9rwNLSmAMHKnHvXhRVq1q9\nc67ETp0aExa2l7/+0kBZWUq/fmLs7Vt94N4Wz4MH0UydOuON33T37r0QiUTo6OgQELCVgwf34eOz\nkAULFhdj/BddDChXrhyLF69AVVWVBw+icXefjq9vIAB37txiyZJ9qKp+/eqpAiVDMOYEBAS+eV50\nD5TJZEVypsXHx6GtrU1kpDwnG0B+fj7ly1f8JP0tLUoiO/6iS9n27bsV4haJiYloa+syZsx46tVr\nSKdOEaSkVKNiRU/y8+tQv37DZ8qGX196AoHi0devhLW1DQBt2rRjwwZfqlY1wNCwGiBXI9yxYxt2\ndvaK8n//vUVq6i/o6W0hOdmZ3FyYMmU8ffr0/+iuufv3X8bdPYn4eEOsrc/Qu7cGSUnPjQapVJ97\n97I+ap++dDQ0NKhd+/3FStzcOjB9en6hGMePQUm/6QKPg1at2ij+u2zZohLfJy9PwuLF87l79w5i\nsZiHDx8ozllZ1cbAwOCD5xEU+HIRv7mKgICAwLdF0XgxKSDPneXvvwV//y0EBGxl0aJlJWpv+PBB\nwHPxj6+N8PBYmjaN4OBBNRYtukl+vozly8uhr7+MmjWb0bFjBitXziE6OqpE7W3btoWcnNKXoBco\nXV6cZMtkMrS1dQqdL86wr1ixsHGkpAQ2NracOxdaOp18DQsWxBEZ+QtZWQ34558BnDiRjInJ8xyM\n2tr/8f33gqrlp0IsFn90F9eSfNOv6lNBuZKSEvn58m8/Pz+/2Jycf/yxmfLlKxAQsBVf342KlB4A\n6uoa7z0Oga8LwZgTEBD45ilJvJiRkTHJyU+5ceM6IA8+j4y8V6L2V63yA56Lf3xN5Ofnc+2ahMTE\nVujohBIdbc/ChRdp1MgKNTUxQUH98fCYhqVlLaKj76OlpU1mZsZr2wwO3kp29rdrzK1fv4agoM9T\nLTEk5CRRUZElqpuQEK/493LkyEEsLa2Ii4slJkaenuLQof3Uq1cfI6PqivKZM60wMVmEsrImjRtv\nQE9PjcGDh6Gjo8vChfNLbVwvk5+fT0qKeqGynJwKLF9elbZtt+Lo+CceHpG0bm1XKvd3cnIotnzO\nnJmcPHmsVO4p8GZK8k3Xrfv8mzh27LDivwU7epUrV+HWrZsAnD59ComksLgUQGZmhsLV/eDBfUIe\nQ4HXIrhZCggIfPOUJF5MWVmZWbPm4+PjTXp6OlKphB49emNiUuON7RcEuL8s/mFv3wBPT3ckEgn5\n+TLmzFmgcNf5/BEpkiXn5akWKs/KkkvpSyQS+vfvgUwGKSnJxMY+RCKRIBKJGDCgN61atSEs7DKP\nHz8mP1+Ks/Ngnj5NIjHxMaNHD0NPryw+Pqs+zfA+IR9rt6Fgx/ltOHXqJI0bO2BsbPLaeiKRCCOj\n6uzcuY158zwwNq5Bjx59qF27Dq6uk5FKpVhZ1aZz564oKyszdeoMRfmPP9Zm7NgJqKur062bPE5o\n7NgJzJ3rzsqVS/nf/0a/03jfBrFYjL39E2JicgFVVFWjcXBQ5rvvLAkIsCz1+xcXRwV8dLdCgcKU\n9JsuIC0tDWfnXqiqqjJz5hwAfvrpZ6ZMGc+AAb35/vtGaGhoKuoXvNuff+7GtGmTOHhwfzF1PtJg\nBb4YRLLPJIBB8P39eqlYUUd4v18xwvt9M05OTTly5BRXrlwqJP6xZIkXtWrVoXXrH5FIJEil0o+e\nU6xAoc3a2obr18OwtKxF27Yd8PdfS1paKtOmuWNgYIinpwexsbGoq6szadI0TE3NSElJZubMaVy7\nFsGjRw5oal4gKWk2Xl4ZaGo+Yc6cmZiammFlVZv//W802to6tGrVBGVlFSpXrkKLFo74+a2lTx9n\nQkNPo6ysjJfXEoYOHcD69RtLXY7+cyIgYD0HD+6jbNly6OtXwsLCCnv77/Dy8iQnJwcDA0NcXNyQ\nSPKYMGEM69dv5M6d2wwa1Ic//9yLvn4levToTGDgVry956Glpc2pUyd48iQJAwNDzM0tsLCwIjQ0\nBHPzmly7FsbPP3fC1LRWsQqtu3fvZM+eneTlSTA0NMTV1YPbt28xefI4tLS00dbWYvbsBRgYlL6K\n4Idg/fo1aGpq0atX3xJfk5OTg4uLL8nJqjRvbkH//k2LKBF+CLZu3cT+/XsA6NChM92791L8zZDJ\nZCxevICLFy+gr18JFRUV2rf/6Y33F/HSUSIAACAASURBVP4uf3jeNg9ct24/fZC/YzKZjKioKJSU\nlDAyMgKE9/s1U7GizpsrvYTgZikgICBQAq5eDSco6ChxcY/euY2X185q167Dxo1+bN4cQHx83CdL\nDh0T85CePfuyZcufREff59ixw6xa5cekSZMIDPTHz28tFhZWBAQE8dtvI5g9W67g6e+/Dlvbehw8\nuId27bRRUYnF2zuZevUqcfz4EdTU1PH33wJAjx4DadKkI9nZ2WRlZbF48XJatnRCKpUSHX2f33+f\nhJ2dPbt37/wkz+BTEh5+k+PHj7BhQxDe3j6Eh/8HwOzZMxkxYgwBAUGYmprh77+WsmXLkZubQ2Zm\nBteuXcHSshZXr14hPj6OsmXLoaYmdw2MirpHmTJl8PXdSF5eHuHhNxX3k0gk+PoG0rdvX5Ys8WLO\nnAWsX7+R9u07snbtSgCaN2/JunWBbNiwherVTdi79y/q1LGlSZOmjBw5Bn//LaVqyGVkZLB9+wmO\nH7/wQURz3mU3S01Njdq1lXFy0qB//6bv3M7rCA+/yYEDe1m3LoA1azawZ89O7ty5pTh/6tQJHjyI\nZvPm7Uyf7sH169eEnblPyNs9+/d/T/n5+Qwb9gdNmsho0iSbceO2CyJSAkUQ3CwFBAQE3sCKFcdY\nuNCE9PQOGBkdZtWqJ3z33fu7Wjk5/Ujt2nUIDQ1hwoQxTJo0FTs7+w/Q47ejShUDatQwBcDEpAb2\n9g0AqFmzJnFxsSQkxDFnjhcAdnb2pKSkkJmZQVjYFebO9UZFRYX588fQrt1uWrSow9Gjh7h1K5zs\n7CwGDuzNgwexpKToc//+MczNbZBItElLS8PIqDoqKio0bdqcdetWUrZsObS1tT/6+D81165doWnT\nFs+MeTUaN25KdnYW6elp2NrWA+DHH9vj6joFAGtrW65dCyMs7Cr9+g3k/PlQQKaoKxKJKF++AjY2\ndTEzMyc5OZmOHZ/nZnN0bA3AvXv3XqnQGhFxl3XrVpGRkU5mZhbff99IcX1pTyafPHlKr17HuHKl\nB0pKT+jZ808WLery1kZMcbudMTEPWbRoAcnJT1FXV2fy5GkYGRlz+vQpAgP9kEjy0NUtw4wZs8nO\nzmb37h2IxUocOXKAMWMmAnD16hX++GMzSUlJ/O9/o99rl+7atavP3r3cCG/WrCVXr15RnL969QpO\nTj8iEomoUKEC9et//L8PAnJeTFlREoKD/3rve27ZcpydO3sAuuTlQVCQAa1ancXZuc17ty3w9SAY\ncwICAgKvQSaTERAgJT3dFoDo6PasWfPHOxlzmppahcQ/YmNjqFrVgK5de5KQkEBExN1PYsypqqoo\nfovFYlRU5MfymDgpYrHKKyfwrypv27YD27f/gb//Fnr1mklcXFlACZlMCZEohadPn6CpqYWSkjKt\nW7dFS0ubDRt8MTGpgaamJhkZGV+dm+WBA3v57ruGVKjwcqL5tzNS6tatR1jYFRIS4nFwaMamTRsQ\niUT88MNz0YwX00C8/I4K1PBkMhkmJqasXu1X5B5z57ozb94iTE3NOHBgL1euXHre21LeGVq9OpQr\nVwYAIqRSTbZt+54hQ25Tq5ZFidt4cbdTKpUwaFBfLCysWLBgLhMnujxLg3CDhQvn4+OzClvbeqxd\nuwGAPXt2sXlzICNHjqVTpy5oamrSs6fcPXPv3l08eZLEqlV+REVFMmXKuPcy5op7li8WiUSlbzwL\nfL48fZoHPM8nJ5VW4PHj9E/XIYHPEsHNUkBAQOA1yGQypFKlQmUvH7+JggmbmZk5SkpKDBjQm23b\ntnD8+BH69evOwIG9iYyM4Mcf23+wfn9IbG3rcfjwAQAuX76Inl5ZNDW1sLW1U6RaOHv2DGlpqYhE\nIurXb8CJE88V9+rXt0JD4zzVq3dEJJIgFlegfPkK3Lt3l5ycbAYO7M2GDeto3rwlIBcIGD9+FGPG\nDP/4gy1F9u/fQ2Li4yLldevW49Spk+TkyN0nz5wJQV1dAx0dXcLCrgJyRbt69eoD8vdx6NB+DA2r\nIRKJ0NXV5ezZM9jY1FW0Wb26MWfOhDyTNJcRGhqiOFdgHJiYmLxSoTUrK5Ny5cojkUg4dGi/4toC\nQ7s0kUrFvGjg5uWpk52d++oLiuHF3U5NTS0aN25Kbm4ON26E4eo6mYEDe+PtPZekpCQAHj1K4Pff\nR+Ds3JOgoI1ERT1Xqn3RlhKJRDg4yJOEGxub8OTJk3cfKGBrW/fZu5e7H586dUKxwyo/b8exY0fI\nz88nMTGRy5cvvaY1ga+Nzp3rYWq6S3FsZRVMx47ffcIeCXyOCDtzAgICAq9BLBbTvn0Gvr7xSCSV\nKV/+PN27F1W7fB2HD/8NyBUxX1Zn7Nt3wIfq6jvz8u7Ai8cikYiBA4fg6emBs3MvNDQ0mD59JgCD\nBg1h5sxp9OvXHWtrWypXrgLIJ7lDhgxn0yZ/nJ17oaysjKNjM27erMHTpzNYsWIZhobVMDSshoaG\nJv7+W7h1K4L9+w+Sl5dHly496NKlx0cb//vwsniFg0OzQiIJW7ZsJDs7ixo1TAkPv4mb2xQSEx9z\n4MAJRYxkzZqWODo6MWBAL8qWLUetWrURiWDatJl4e3uSnZ2NgYEhU6fOAOQ7usnJyQoJdFvbes+S\ntj93UTU0rEaTJk1xdu5JTk4OpqZmaGtrF1JDVFVVfaVC6+DBwxg6dAB6enrUrm2tSN3h6Nia+fPn\nsH37H8yaNa9U4ub69KnD/v07iIj4BcjGyekwtrY937KVojteBXnBCuI4X2Tx4gX06tWPxo0duHLl\nEn5+a1/ZcsHOdUGb70PNmpa0a9eBIUOcAejY8WfMzS0U76hZsxZcvvwPfft2o1KlytSpY/Ne9xP4\nsqhWrTIBATkEBv6BWCxj6FB7ypUr+6m7JfCZIahZCpQ6gurS18238H5lMhk7dpzh/v0MmjY1xt6+\n5O5exXHx4i2OH4/EwECd3r2bfbaCBh/r3S5ffpRFi4xITzfFwuIwvr61sLCoXur3fV/Cw2/i6enO\n2rUbyM+XMXSoM25us5g1y01hzAUFbXoWOziEUaN+o2fPvqxZs7zEinjFcfnyRbZu3axQRX0VWVlZ\naGhokJ2dzciRQ5k8eRrm5s+/3c/t3+6LaoH378cxb94KxOJcRKJkzM0tuHr1ElKpFBcXN6ysar+2\nrdu3w5kzR/5u5G6W/ejU6RdOnTpO9+69adGiFTKZjIiIu5iZmTNoUB8mT3bFwsKSuXPdiYuLZdmy\nNWzduomMjAx+/fU3QO5++sMPTRSulQWqk58bn9u7FfiwCO/36+Vd1CyFnTkBAQGBNyASiejSpckH\naevIkSuMGaNMYmI3xOIkwsJ2smDBLx+k7S+JHTvOsmdPGioqWYSGqpOeLnchvHWrOytWbGXp0s/f\nmHuTeEUBL66Zyt12pXh4uHL7djjGxjVwdXVny5aNhIaGkJOTg7W1DZMmTQPg4cMHeHl5kpKSjFgs\nZtaseYXavnnzX7y85jJ79gL09MoyZ84xEhPVqF9fmbi4Y0RFRZKbm0vbth0KGXIlJS0tjcmTjxAZ\nqUO1aul4ejanfPnS3xmoXr0KTZtakpWVyZUrl8jJycbffwthYVfw9PR4ozH8qt1ON7fZeHvPIyDA\nD4lEQqtWrZ8Zc0NxdZ2Mjo4u9evbEx8fB0Djxk2ZPn0yZ86cUgigvLxzXVpER8exefNVVFRk/Pab\nAzo6bz/JExAQ+PoRjDkBAQGBj8j27Y9JTOwCQH5+eQ4cqMDs2bmoqqq+4cqvh2PHrjJpUhVSU1sD\nWYjFRwqdz839Mv7XJBKJOHBgL40bN8XS0gqZTEZGRjr5+c+Nt5yc7CKT/+jo+7i4uGFtbYOnpwc7\ndmynS5ceDBw4BIBZs9w4cyaExo0dcHefTv/+A3FwaE5eXh75+VISEuIBuH49jCVLvJk3bxH6+pVw\ndt7GgQPOgDJ79sQxdaqUGTPmvNcYJ08+wvbt/QAxly7JkEgC8fP7+IsPrVrJ1ftsbeuRkZFBRkY6\nWlqvVz7t338Q/fsPKlK+cOHSImVNmjSjSZNmRcqrVTMiICAIkBvitWtbo6z8/PsscKH+0Dx8mEDv\n3mHcvt0dkHLy5AaCgzuioaFR4jYOHNjL1q2bEYlEmJmZM3jwMObOdSclJQU9vbJMnepGpUqVmTNn\nJmpq6ty5c4unT58wZYor+/fvITz8P2rVsla49zo5OfDTTz9z4cI5ypWrgLv7XPT09IrNSaimps6c\nOTPR0tLm1q3/Cil/zp49g2bNWuDg0BwAd/fpODo6Ffv8BQQE3owggCIgICDwEVFWlhY6VlHJQ0np\n7QRVvnRCQuJJTa3z7EiD/Pw4IAWA8uXP8csvFT9Z394GW9u6JCcnk5eXS1ZWFiEhJ2nY8AeSk5+Q\nmppCbm4uoaGnFfU1NTXJzMxAX78S1tby2Kc2bdpx7dpVLl/+hyFDnHF27snlyxeJirpHZmYGSUmJ\nikmvioqKYhfw/v1IvLzmsmDBYvT1K5Gfn8/Vq+UpWKOVSKpw4cL7R1FERenwfKogIjJS93XV3wsl\nJaVChnBubs4r635s1+Rduy7g4HAAO7vTDBmy7ZmwzPsRHLyVvn27MWuWa5Fz27Zd4fbtbs+OlLhw\noTuHD/9T4rbv3LlDYKAfy5atZsOGLYwePZ5FixbQrl1HAgKCaN36R5Ys8VbUT09PY80af0aPHseU\nKePp3bs/GzduIyLiLnfv3gEgOzsbS8tabNy4jXr17PD3l8cVFpeTsIAC5c8FC5awevVyADp06MT+\n/Xuf3TedGzeuF1JiFRAQeDu+jOVPAQEBga+E4cNrcvnyTiIi2qCldZsBA/Lfy5gbPnwQq1b5ER8f\nx/XrYTg5/fhO7XTt2hE/v03o6pYhOHgrf/31JzY2dZg0ye2d+/YqDAyUkRtv8tQDeno1GTZsFzk5\nWrRsacT339t98Hu+SFxcLOPHj8La2obr18OwtKxF27Yd8Pdfy9OnycyYMQsAH5+F5ObmoKamhovL\nDIyMqpOTk83cue5ERNzFyMiYMmXKMHv2DNTU1LCxqceSJd6oqqrRpUsHzMxqYmxsorhvu3YdWbHC\nh6SkRHJy5O3KZDJEIhGLFskTd1esqI+f39pnxkLxBktBHrm8vFxu3w6nUaMmiMViypXLIi6uoJYM\nPb2s935WhoZpXLwoe9YXGUZGpRenU65ceYUhrK6uQWjoaUV+u+PHj2BnZ09Y2FW0tXXQ1NQqtX68\nTEZGBh4eGTx8KBfl+euvHMzMdjF5crv3anfXru34+KyiQoWiixfq6gC5gHzHXix+Qpky6iVu+9y5\nc7Rs6aRI76Grq8t//13H01NuwLVq1YZVq+Q7lCKRiMaN5caUiYkp5cqVL5R3Mj4+FjMzc8RisSJH\nYevWbZk2Te52+qqchK9S/qxb146FC+eRnJzMyZNHadGiJWKxsLcgIPCuCMacgICAwEfE2tqUPXv0\n+PvvY5ibV8XGxum92lu1Sp4jLDY2hiNHDr2zMffiTkfBJNPKqkapBNn/+mtLbt7cwYkT5VBTy2X4\ncE2cnT+u615MzENmz16Ai4sbgwf359ixw6xa5cfp038TGOiPq6sHK1asQ0lJiX/+Oc/atSuYPXsB\nO3duR0NDk02bgomIuMugQX1YuzaASpUqM336JHx8VqKmps6mTRuQSCQMGDBYcc9mzVpSs6Yl3bt3\n4s6d21hb1+HIkYPY2Nhy48Y1dHXLkJmZyYkTR2nZ0glNTU0qVtQnJOQkDg7Nyc3NRSbLV6gyuri4\nMnbsCNTVNahXrz7TplXD3T2IR4/0sbK6z/TpLd/7Oc2f3xKpNJCoKF2qVUtj/vzS20FRVlZmwIDB\nDBniTMWK+lSvbqw4p6qqyqBBfRQCKMXxooDKh+TJkyQePTJ6oUSNR4/ebzfdy2susbExjB8/irZt\nOxAWdoXY2FjU1dWZNGkagwY1Z/fuocTGaqOiEkOVKjLu3XPg9Ol9xMXFkpAQz6hRv3P9+jX++ecc\nFSroM3/+IpSVlQkPv8nGjRtJT0/n5s3/mDZtBuXLVyAtLY1lyxZz48Y1HB0L/91RUVEhPT2dI0cO\nFsk7KZVKeZmCRQh4fU7CVyl//vhjew4d2sexY0eYNm3mez1LAYFvHcGYExAQEPjIVKhQni5dmn+Q\ntpycHDhyJITVq5cTHR3FwIG9adu2I/b2DfD0dEcikZCfL2PuXC8MDAw5dGg/27f/gUSSR61a1owf\nP0WxKi6TyQpNMrt370b79l0+SD9fRCwWs2hRV6RSKWKx+JOoeVapYlBo98HevsGz36bEx8eSnp7G\nrFluxMQ8QCQSKSa0YWFX6dZNLpNvamqGqak5AP/+e52oqHsMGyaP0crLk1Cnjg1btpzmjz8yUFKS\n0b9/WRo2NMLIqDo7d25j3jwPjI1r8PPPXUlLS6N//x6UK1eeWrWsFf10dfXAy2suvr5rUFFRwcPD\n81l6AShbthwLFixmwoTRTJ06g1atbGnZsg4ZGeno6DT4IM+pbFk91q//eIZ216496dr1eRoCiUTC\n+fNncXRsw+jR4z9aP16kSpWq1Kmzm0uX5Hn81NUjaNjw/dxNJ06cyoUL51i2bA3r16/BwsIKT8+F\nXL58kdmz3fD330KXLrU4evQIY8ZMpVGj+vj5rSUuLpalS1cTGXmP334bwNy53owcOZapUydy9uxp\nGjVqwpIlXsybN49JkybTooUja9euZMSIMWhraxMVdQ9f30D2799TKJ8dQFpaKocOHUBFpfipYX5+\nPidOHMXRsfWzRQj59S/nJNTXr/TG8bdr15HBg/tToULFQkb727Jt2xY6dfpF4X78vvUEBL5EBGNO\nQEBA4ItGbggNHz6KoKBNCrn6JUu86NatN61b/4hEIkEqlRIVFcnx40dYvdoPJSUlvL3ncfjwAUWy\ncpFIVGiSaWpqWKry129yL42Li2XChNHY2NTjxo0wKlbUx9NzIYmJj1m0aAHJyU9RV1dn8uRpGBhU\no2fPXwgO/ou0tDTat3dk2bK12NrWZcSIIUydOqNQTrSXdx8KdhAKdiJ8fVdjb/8dnp7exMXFMnr0\nsFf2s2DHwd7+e2bOfC44cvbsDfr31yQlxRaAW7fOsn17Fps3by/SxpAhwxkypGiSdEPDaoVyE2Zk\nZHD9ejT9+snrVqpUmY0btxUai45O6cW1fUzCwu4wdmw4aWkShg07h5eXMg0bWr72mvz8fObPn1Po\ne4mOjsLLy5OcnBwMDAxxcXFDR0eHkSOHYmFhSVjYVbKyMpk+3Z3AQH8iI+/h6OikeB/Hjh1GX387\ntrZ+qKgY0a1bN7p1a/FBxiiTybh+PYw5c7wAsLOzJyUlhczMDJSUlGjbth0//GAPyP99Nmz4A0pK\nStSoYYpMJlO4NJqamhEXF0d09H0iIyPw8PAgNzeXxYsXoKysjEwmw9DQiNTUVJyde1G2bFmFsElB\n26tXLyMhQe6nu3KlD3p65ThzJoTLly9y9+4d1NU1+O+/f5k/fw4go2JFfXbv3qnISRgfH4e5eU3C\nw2/y6FECKiqq+PquZuXKpYwePb7Qok3ZsuUwNq5B06bN3+v5BQdvpU2bdm800kpaT0DgS0Qw5gQE\nBAQ+Ia9yDVu/fg22tvUUO0Zv4uWUobVr1yEw0I/HjxNo1qwlhobVuHTpArduhTN4cD8AcnJyKF/+\n7RKgf2wePnyAu7snkydPw83Nhb//Ps6+fXuYONEFQ8Nq/PvvDRYunI+PzyqMjKoTGXmP2NiYZ5P0\ny1hZ1eLRo0dvldy6QJWyIJapICk4QN269Thy5CB2dvbcu3eXiIg7iEQiateuw6JF84mJeYiBgSFZ\nWVkcO3aVlJTnBtrjxw0JDd2OlVWNd3oW8fGP6ds3hGvXOqKu/pDfftvHtGnt36mtL4F5827x77+9\ngd4ALFgQxI4drzfmHjyIZubMuYW+l82bAxk3bhK2tvVYv34N/v5rFcaF3OAIJDh4K1OmjMfffzM6\nOrr06NGZHj368ORJEsePH8HPb6NiAaRKlcwPPtZXpfx92fhQVn6+6KCk9HwK93z3WIaJiSl//hlc\nZCFm1KjfGDduMhYWhZ9hgVFnYWFFZOQ9AgP/4MKFc5w8eYx9+46Sn5/PlCnjkUqljBr1O87Ov6Kr\nq0tOTjZDhjizfPk6OnfuioPDd/z22wi+/74RU6dOJCsrk4CArURG3mPOnBkcPvz3s53WMJSVRTx8\nGI2TU5sSP6OsrCzc3Kbw+PFj8vOltGjRisTEx4wePQw9vbL4+KzC29uT8PCb5ORk07y5I7/++hvB\nwVuL1Ltw4ZwiNtXAwJCpU2egoaHBqlXLOHMmBCUlJRo0aMiIEWNK3D8BgU+FYMwJCAgIfIYUJCl+\nV5ycfqR27TqEhoYwYcIYJk2aCkDbth347bcRH6KLH4UqVQwwM5O7MlpYWBIXF8uNG2G4uk5W1MnL\nkwBydcmwsMvExsbSt+9A9uzZSd26dlhZ1SrS7suunS8ei8VievXqz5w5MwgIWE+jRk0o2AHt3Lkr\nc+e607dvN6pXN8bSUt62np4e06bNZObMqeTm5gHQqNGPaGndIiPD4lmdy9jbv5shB7B06XmuXesP\niMjOLseGDUkMH55EuXKft0H+rqSmqhU6Tkl5867Ky99LTMxD0tPTFC6FP/7YHlfXKYr6TZo0BaBG\nDVNq1DBVPMuqVQ1ISIjn2rUrpb4AYmNTj8OHDzBgwGAuX76Inl5ZNDW1XmngvQ4jI2OSk59y9epV\nDAxMkUgkPHgQjYnJm7+7gvuFhJwkJORvrly5xMCBckM6KysbkJ8PDg4iJESekuHRowQePoymVi1r\nVFRUCu0UqqqqKnYR4+LiyM7Opn//nVy4UJlKlbwwNbVBQ0OzxGM7fz6UChX08fLyASAjI539+/ew\nbNkahdDL0KEj0NXVRSqVMnbs/7h37y7duvVk27YtinrJyckEBvoVim/944/N/PJLN0JCTrJly5+K\n9gUEvgQEY05AQEDgE1Oca5i3tyeNGzvQvLljiVaLNTW1yMzMUBzHxsZQtaoBXbv2JCEhgYiIu3z3\n3fdMmTKe7t17U7ZsWVJTU8jMzKJy5cofc7hvRWF3SCVSU5+gra2Dv/+WInVtbe3YuTOYpKREBg8e\nRlDQRq5cuVQkNqhKlaoEBGxVHL/obvbiuaCgHYryApc7NTU13N3nFttXOzt71q0LfKn0GH/+eQOx\nOJ/+/bWxtX335PN5eSq8qHCZk6NDTs6r5fs/Fi/HI02cOIaZM+e8Mg/c+vVr0NTUolevvq9tt2HD\nbC5efIJMVg5IpUGDN0+uX/5e0tNf7yasoiJXiyzYpSvgxTjJ0lsAESESiRg0aCienh44O/dCQ0OD\n6dNnKvrwcjjpi8dFFyTkIjKzZs3H29ubp09TkEol9OjRu0TGHIBMBqdOnSQ1NYW+fQfQqVPheMnL\nly9y6dI/rFnjj5qaGqNG/aZI0/DyTuGLu4hy1+UTnDw5EFAhMvInoqOjCA29QuPGJVOvNTU1Z8UK\nH1atWsYPPzhga1u3SJ3jxw+ze/cupFIpSUmJREZGUqOGWaE6r4pv1dLSRlVVDU9PD374wUGh8Ckg\n8LkjGHMCAgLfNC4uE3j0KIHc3By6devFTz/9/NH7UJxrmHwiJyIlJfm1q8UFEzozM3OUlJQYMKA3\n7dp1IDc3l0OH9qOsrEz58hXo338QOjo6DBkynHHjRpCfL0NZWZnx4ycXY8x9fEGSkqKlpUXVqgac\nOHGUFi1aIZPJuHv3DubmNalVqzazZrliYFANVVVVzMzM+euvHYqV/NIiPT0dL6+TpKaq0LJlOTp2\n/E5xbtgwR4a9OtzurejevTqHDx8nLq4lkEWrVleoXLnHh2n8HZFKpUXikd70vEsqeDN9egfKlTvK\nrVv5mJqKGDXqp7fun5aWNrq6uoSFXcXWti4HD+6jXr36JbpWJBJRv36DUlsACQ5+no+tIGXAiwwa\nNPS1xy8mLH/xnLa2NomJiZibW3L7djjnzp3FyelH7Ozs8faeS05ODtbWNkyaNA2AkSOHUrOmBVeu\nXOLx40ckJSWirKzMpUv/YG1tw5w5M58pZapw/34UERF3UVNT4/79KP7990aJx5uVJQKeG9tSaVme\nPr1Z4uurVTPCz28zZ8+eZt26ldSv/12h87GxMWzduhlf341oa2szd677K3MVvhzfWsC6dQFcvHiB\nkyePsWPHtkLxqgICnyuCMScgIPBN4+LiVij+o3nzlgqXnY9Fca6EBWhr67x2tbhgQqesrFxk4tG3\n74Ai93J0dCoiSw4QHLz7hd9/FTn/qSjOHdLNbRbe3vMICPBDIpHQqlVrzM1roqKiQqVKlaldW64G\naWtbj2PHjmBqalZc0x8EmUzGoEH7nu04KLF793Vksgv89NO7q0kW5PmzsLBkyhQ3JkwYQ2pqMv36\nDWLjRmP27QtGT0/EkCFdS10JtLjFDicnBzp16sLFixdo3rxlkXikF3MWHjiwl61bNyMSiTAzM2f6\ndPdC7cfEPCwiZmNkZAzI3/WIEW+XuqO472Xq1Jl4e3uSnZ2tiI8q7rriHqWxsUkJF0A+L6Kiopg8\n2ZXateswbNgIpkyZw++/D2HgwCEAzJrlxpkzITRu7IBIJEIikeDvvwV39+mcPXuG2rWtsbP7Dg+P\n6cTExDBx4ljmzvUiLi6WihX16du3G9WqVcfauo7insXtFL54rls3G3bs2ElExM9APg0abKdVq5Ib\n6ImJiejo6NC6dVu0tLTZu/cvNDW1yMjIQFe3DBkZGaira6ClpcWTJ0mcOxeqMNw1NTUV9WrVsi4S\n35qY+JgKFSqSnZ1Fo0aNqVPHlh49Or37CxAQ+IiIZO/ilF0KlKZimsCnpWJFHeH9fsV86e93/fo1\niviP+Pg4Fi5cpjAGPgYvC6AEBW0iKyuT+Pg4fvihCc2bO5KXl6dYLY6PjyuV1eLQ0KtERCTQunV9\nKlWqAHz57/Zj8OjRIxo0eExmHMSaCAAAIABJREFUZkNFWc+e21m6tOTCDi/Tp09XRTLpGzeu4+u7\niiVLVn6I7haiJO83NTX1JbGLtbT/P3vnGRDV0YXhZ5dd6tJEsGChWFBRhGCvUTEaNdEoAWzYWxJ7\nrLFHsKAGjYoSaSrYjd1YY8GosYFG8TN2moKKtKXsst+PlZUqFlCT3OfX3r0zc2fuXS5zZs55T5cO\nzJ3rzaefdgDA1fUL1q1br1kEyT1OTExk+vTvWbMmECMjY1JSUjA0NCQgYC36+vq4u/dlzJiRfP/9\nNI2Yzdq1K4XdkHckLi6WMWNG0LOnG8ePqzh40BYTk18xNi6HtXUkKpWS5ORkevVyo08fT777bjhD\nhozQuCN7ec3RvHsADh06yI0bf/Hdd+Pw8PgKf/8QjIzeTjH17t0YQkMj0dZWMWJEKwwNDV+77vnz\nZ1m50hexWO3COXHiVK5di2D79i2Ym1vg67saL685XL0agYVFRQwNZbRo0ZrOnbuyffvmfOUuXbrA\n6tXLNfGtw4aNws6uDlOmTHjhNqrCw6OfRun3Y0N4N/97MTd//b+JXISdOQEBgf8sRcV/ZGdnlfl1\n3yS5sVwuL/PVYm/v/axe7UhGRjNsbffyyy/W1Kv39kIdH4qnT5+xadNZ9PUl9OnTNl/C4rJCJpNh\nbHyNdI3AYQ6Ghq//G9q0aYNGLbNr1+48eHBPk+evY8fO7NnzK0lJzxg4sDc//rjojVQ5S4P8YheP\nefjwIWKxWDPRLw6VSsWlS3/Srp2LxsgrOHGXy+VcvRpZpJjNx8DduzEsWuTHw4eXMDWV0a1bdxQK\nBdraUnr1cmf58iXcvv03vr6ruXjxT/bt283MmfNwcWmFq6sHZ86cRkdHhwULlmBqWu61r6tQKJBI\nJMUevw4ikYjQ0A1cvLgELa0cVCoxmZnHsbQcwPz57holx1x0dfUK1c+lbdt2BAau5ZNPnLGzq1Oi\nIRcefoVbtx7RsaMjlStb5DtnbW3J9OmWbzSWXBo3bkrjxk3zfVe7th09e750NS5q1xWgZ0+3fOWK\njm9Vu1kKCPzTEIw5AQGB/yzp6WkYGhq+VfxHaVKcq5xIJCI9PS3favE334wt1WtnZGSwcaOMjIxa\nANy+3Z01azazfPk/y5h7/PgJbm6n+euvPkAGR46EEBzsVmIuu3dFX1+fCROk+PjsJSmpIp98coXJ\nkzu/Vt2oqBscOLAXf/9gcnJUDBvmycyZ8zh37g+N8l7duvb58geWBampqRw+fJAePXpx6dIFNm3a\nyKJFy4oRu8hEW1vntdw7RSLRKxUZVaocDA2LFrP50ERF3cPT8xQ5Obd58GAXn322kT17djJ58gw2\nb95Ir17uREXdQKFQoFAoiIi4TMOGaiGPjIwM7O0bMGzYKCZOHIOnpwflyplha1sDLS2tfLteLi6t\nOHxYncvtl1/8MDIy4v79e0yaNB1//9UYGRnx4MF9NmzYyurVK7hy5SJZWdl89ZUrX375FZcuXSAg\nYC0mJqbcvXub2rXrMHToSGJiYtDS0qJSpRloaaXz9Olg9PQuo6WlR3p6OsePH6Fdu5curHmfU65L\nYi7a2to0adIMH58FTJ0685X3bdGiA/z8syMZGc1ZtWo/a9c+p2HDmm/9HIpa+IqKusHBg/sYO3bi\nW7dbsP3PPx/N0aNp6OtnMmlSYywtS058LiDwsSD+0B0QEBAQ+FA0adIcpVJJ376u+Pn9nC/+o6zJ\nVbCcNGksZmblyczMJCYmmgsXzhMefoqYmGisrW0wMyuPlZU19vb10dHR5c6d26XaD6VSiVIpKfBd\n2RpAZUFQ0LkXhpwI0OPQoS84derie7l2//6tOHPmE86dM2T7dtfXdkGLjLxC69afoqOji56eHm3a\ntOPKlcv5yryPSIiUlGR27txa6Pu8ix337t0tdrGj4OQf1Iack1Mjjh8/QnLyc0DtspmLSqVWYK1c\nuTLHjx958Z1azOZjIDT0Bs+eGZCa2hGVypTDh9tRr15Drl+/xs2bN0hPT0NbWxt7+/pERd0gMvKK\nxk1RKpXSvHlL7ty5za1bN2nUqAlBQaGMGVOU8fHSKL516yZjx35PWNgOVCqV5jg0dDt79vyKTCbD\n3z8Ef/9g9uz5VRNb+/ff/2Ps2Ils2LCV2NgYbt68gY2NDVKpNjLZc+TyBjx/7o5EUo+//vqFCRO+\no27d/K7keY3z9u07Ehq6nkGD+hIbGwNAhw6dEIvFhXbG8pKVlcXGjTpkZNQEtLh3rxv+/qX7vgKw\ns6tTKoZcLsnJcqZMqc6uXT0JC/Ng8ODTZGdnl1r7AgJljbAzJyAg8J9DpVLx+PFjxGIxPj7LP0gf\nilKwzJsMOzh4B0OGTMLWdgAGBsloaalYsyaw1AUvDAwM6No1nvXrE8nJKU+lSsfp0+f9uvKVBoVv\niwKp9P0ZpTKZDJmsaCn+4ijqWZaxnkmR+PmtICYmmoEDeyORSNDV1eOHHyZz587fpKena8QubGxs\n8PX1ITMzg/Hjv2P69FmYmZWnatVqeHj0RCqV0Ly5WqBHLs8gLGw9CoWS7t07Y2ZWHkfHTzRucLnj\nnDnzx0JiNrliQB8SsVj54pPamJZIMpBIxIjFIipVsmT//j3Ur++ArW0NLl36k5iYaKpXtwJeSvRf\nuqRWg8zdHS7JyK9Tpx4VK1Yq8vjPP89y+/bf/P77UQDS0tKIjn6IRCKhTp16mgT3NWrU4vHjx0gk\nEkxNTfH3D2b//ks8f76Hr76aRoUKhXPkrVixJt9x/foObNiwJd93kZFX6NLli1e+f1QqVaGFoZyc\n0vtBx8REM2PGZDp06MSVK5dYtGgZ69at4dGjeOLiYnn0KJ6vv/agVy93AIKCfuHQoQOYmJhiYVGB\n2rXr4OHRl6ioG3h7z0UkEtG4cRPS0pSkp9dBJMrEwmI2T55cZMCAMCZMmIKTkzP79+/h1KnfycjI\nIDr6Ie7ufcjMzOLIkYNIpdosXuz71jGEAgKlgbAzJyAg8J9CpVIxZsw2mjRJoGnTGKZO/fW97H4U\n5FXJsN3cerJ69QaePROzfbsbZ86k4+TUBJFIRFxcLP37F5ajX7duDRcunH+rvixa1ANf37NMm7aV\n0NByNG9er1CZb78dRlSUWkb82LEj9O3rypgxI9/qemXBkCHNadgwCFAASXTrdoBmzRxLqPVhcXBo\nyMmTv5OZmYFcLufkyeOFcuLlZf/+PSxbtqjU+zFy5GgsLasQGBjKqFFjXuwITWTjxm1UrFiJSZOm\nM2/eAiQSKb6+qzl58jxdunRj7Vq1KMu1a1c5cuQUhw+fYtKkaWzduptff92Gs3Njtm7dxa5dvyGR\nSBg/Xh0bN2jQMNzd+5KU9Iw7d+KYNm0WQUGhbNiwhQEDhpTauLZsCSUzM+Ot6o4a1YwqVeKRyQ4j\nld7k668vEhl5GQcHJxwcGhIWtoGGDZ1wcHDk11+3U6tW7UJtqA2f/O8WLS0tcnLU3+Xk5KBQvNwB\nKhi3VvB4/PhJBAaGEhgYypYtu2jUqAkqlSpffjwtLTE5OUrNsVgspnfv9owc2blIQ+5VbNoUztCh\nh+natS/79+/B1dX9leV1dHT44ounaGk9AqBixd/p3fvt4uMK8uDBPWbMmMz06XOoU6duvnMPHz5g\n2bKV+PsHExjoj1Kp5MaNvzhx4hjBwZvw8VlOVNQNzQKCt/ccxo+fTFCQ2r1XIlEBmZiYbATEZGSM\nY9q0WcyfP1sTV3j37h28vHzw9w9h7dpVGBgYEBCwEXv7+hw8uK9Uxigg8LYIO3MCAgL/KTZv/p3N\nm7u/SEQMwcE2tG17js8+a1qsDPu7iBkUx6uSYfv4HOT4cVfN+ZQUS27dintle4MHD3/rvohEItzc\n2pRYJndVfu/eXUye/AP16zu89TVLG1NTE3bs6MT27buQybTp0cMNsfjjXq+sVcuOzz/vytChngB0\n69ajUILjvJL5ZZWGIO9ihkqlKrTTEx8fh0wm4+7d24wdOwpQGyJmZuoytrY1mT17Oq1bt6VVq7aA\nWnkwPPwkYWHrAcjOzubx43hN2oHw8OuMHfuY+/c/oXLlSLy99ejc+fWSR78OReW/exMsLMzYvbs/\nXl4J3Lw5goQEPbp160HNmrV4/jyJ9esDNa7POjo6GiP8++/HaNpwcmrE+vWBNGyolsdPTn5OxYqV\n2Lo1DCMjI9LT01EoXk/wpXHjZuzYsQ0QsXXrJr79diwWFkXHdRkbm7Bnzx4+/7yLRo7/Tdm58yxT\npliTnl4b6IGzcxD6+gYl1ps//0ucnU/z8GEaHTrUKhUhpWfPnjF16kS8vHyoXt2KS5cuaM6JRCKa\nN2+JRCLB2NgEU9NyPH36hKtXI2jVSi2CJJVKNSldUlJSSE1N1SQc/+yzLvzxRzjduq3n6tXf0NJq\nxJgxWtSrV5+KFSvx8OEDRCIRjo7O6Onpoaenh0xmSIsWrQGwsanB7dsfh2uwwH+XMjPmTp48iZeX\nFzk5OfTq1Ythw4aVXElAQECgjElIyNAYcgAKRUXi4s4CReecyytmsGrVcnbv3omn5+BS71feZNhV\nq+qhpfUYLa2nZGXZIZEkU7lydU3Z3Hi7a9ciMDe3wNt7CT4+3rRo0Yq2bdvTq1c3XFw6cfZsOGKx\nFpMmTcfPbwWxsTF4ePSje/eeJCYmMmvWVNLT01AqlUyYMBUHh4acP39Wo3RnY2PFhAnT0dNT7xCo\nVCoCA/25ejUCb++5tGzZmlGjxhQ3pPeOTCbD07NjmbQtl8uZOXMKCQkJ5OQo8fQcgqVlFX7+eRly\nuRxjYxOmT59FamoqP/44S6OKFxcXy5Qp4wkO3kRU1I1C5d3c+nDq1Alq1arNb7/tR6lUMHbs94wb\n9w2ZmZmYmZUvMrlxURTlViaTydi9ewfZ2QqqVKnCjBlz0dHRZf782ZiYGBIZeY3ExATEYjE//jiL\ny5cvanaOABITH7Nu3RqkUilaWhJWrVqHnp4eq1evIDz8FJ6eHjRq1ITmzVsSHn6KkJAA/PwCiY5+\noDEIPT2H4Oe3AhMTUwCioq4zY8ZM7t//DTOzFeTkPGDBgssEB4vo06c/3bp159KlC6xbtwYDAwOi\nox/i5OTMhAlTEIlEHD58kA0bglCpVDRr1pKRI78DKDH/3ZuiTjxdWB3R2bkxx4//oTnOjXFTqVT5\nEqZbW9swfPi3hIWtZ8CA3tSqVZuRI7/jzJnT/PzzTzRp0gw9PX1N+YJ52fIed+vWnbi4WBYv9iIp\n6RlLlizAy2txsfnxAL74ogcTJnynkeN/E06ffv7CkAMQERHhRGxsDNWqVX9lPZFIxFdftXplmTdF\nJpNRoUIlIiIua1xZ8yKR5F0YE6NUKoGC4jsqTf/yolKpEIlErFvnxpQp5+jV6xOcnQvniMy/+CbW\nHL+8noDAh6NMli2VSiXz5s3jl19+Yd++fezbt4/bt0s/CFZAQEDgTenatQFWVns1x7Vq/crnn6tX\nzrduDWPAgN4MHz5II8OeK2YAULt2HeLjX71D9roUlwx7797dHDjgR/36PahYcTVVquykbt1kbG1f\nxrE9fPiAnj2/Zv36Lchkhpw4cSzfzplIJKJChYoEBobSsKEjXl6z8fLyYc2aIAIC1gJw+PBBmjRp\nRmBgKEFBYdSsWYukpCRCQgLw9V1FQMAG6tWrx+bNG/P1ceDAodjZ1WHWrPkflSFX1pw7d4by5S0I\nCgolJGQzTZs2w9d3MfPnL2LduvUat8Pq1a1QKLI14hRHjx6iffuOKBQKfvqpcHlAk7T5l19CcHfv\ny7Vr6Zw7N5JjxxYSFVWOdevUz+xV7sDFuZW1afMp/v4hBAWFUr26NXv37tJcMyUlhTVrAhk2bBTx\n8XH07t2fadNmkZ6exq1b/yMpKYmoqBv06eNJUFAYAMuXLyU5+TknT/7OvHkLCAoKpXPnrjg5OTNy\n5HekpqZy+vQJKlWyxNm5seZeFRSUyMl5Of3Q1r6FltYI1qwJIDDQn8TExBdjus64cZPYsGErMTHR\nnDhxjMTEBPz8fmb5cj8CA0OJirrOqVO/A2oVyXr17AkKCmXAgCGUL2/OihVrSi1v3aZNG+jf343+\n/d3YsiWM+Pg4PDy+4scfZ9G/vxvz5m2mbdsOjBmzieTkZIKCfmH9+kBkMkOsrKyxtrbF1LQc1apV\nZ8CAwYwc+R1GRkasW7eGn3/+ifj4OB48uAeoXRafP3/OoEF9GDlyEA8fPmD48G+YMmUGDRt+gq/v\nagwMZDg6fsLChS+VTseNm0Tnzl0BtRx/aOj2txq/mZkCeJm6wNz8AeXKvbtHwtsglUrx8lrMwYP7\nOHz4YL5zRf9NiGjQwIHw8FNkZWWRnp7OmTOngdzYVkMiI68AcOjQAU0tR8dPOHLkNwAePLjPo0fx\nVK9uVYIi60eRqlngP06Z7MxFRkZSrVo1qlRRTz66dOnC0aNHsbW1LYvLCQgICLw21taWBARkEBy8\nBbFYxdCh9bGwMCtWhj1XzABALBaVyipspUqVCQ7epDn28Oir+bxkiVqQJS0tjYiIG9jYWFKxYocC\n9QvH2xWkZUu126SNTQ3kcrnGRUgqlZKWlkrduvXw9p6LQqGgVau21KxZi8uXL3Lv3h1GjBgEqKXj\n69QpOoH6f20SY2tbk5UrfVm9egXNm7fC0FDGnTtFux22a+fC0aOH6Nt3AMeOHWHevAU8eHCvWDdF\nUCsIgnoHcM2aRKTS/VhaJvDsWTYnTmgxsQTxvqLcylQquH37b/z9V5OWlkp6upwmTZpp6nz66acA\n2Ns3QE9Pj9mzp6Gjo4O+vj7x8bE8fvyI5ORkgoPXsXPnVmQyGeHhJ7l+/RqPHsWxePF8XF092LIl\njPT0NFQqFa6u7tSrV5/U1BQiIq7w9ddfoqOjQ0pKcr7+lisHOjr3UalEyOVN6NEjC2NjE5ycnLlx\n4xoymSF169ajUqXKAHTo8BmRkVeQSCQ4On6CsbEJAC4unbhy5TKtWrV9rfx3b0tRaSQcHZ1eiHLM\nZe/eh/j4uGBtHcbmzT2Ji1uNgcFZgoM3kZ2dzaBBfbGzqwNQaOHFxMSUgIAN7Ny5jbCwDUye/ANW\nVtasXOmPlpYWf/55jrVrV/LjjyXHS169eotz5/7ms88cqFq18luPd8KEDty6FcL581UwNExh3Dhj\nZLI3T2ZcGohEInR1dVm06CfGjRuFp+eQfK7HRe1M2tnVpWXL1nh6umvSQuQKFE2bNuuFAAo0atRU\n8yx69HDFx8cbT093tLS0mD59NhKJJN/zenHVfH0rK/dnAYHXpUyMuUePHlGp0ktFpgoVKhAZGVkW\nlxIQEBB4Y+ztbVm8OP/i0uvKsL8Pbt68z7Bh17hxowVmZreYPv02ffu21JwvGG+nVGYWaiOvG1De\n5Nm5bkEODo6sXOnPmTOn8fKajZtbHwwNjXB2bqJx6zM3NyQhIaXIPv7XJjBVq1YjIGAjf/xxGn//\nVTg5OWNtbYufX0Chsu3auTBjxhTatGmHSCTC0rIKt2//XWx5eCl2kZ6ejpbWfhITx5GW9il6eucp\nV+7Vub3UFJ3TzctrLgsWLMHWtgYHDuzl8uWX6RpyfxdisZiKFStpcnl5ec1BqVQiFmvRunXbIt08\ns7OzuXDhPL//fhRtbW1Wr16X73xgYCh//HGa3bt38sknjfjtt/0a983MzCwsLU3p2zeKnTv/wsxM\nwrRp37wciaiw01CuO1xhXn7/uvnv3oa8aSQA2rRpR0TEZSpUqETduvbMnx8LmOaOgHv3njJiROGY\nraJo06YdoI6hPHHiGKCO7Zo3bxYxMQ81O7clsW3bWWbMMOLJE1d8fC4xe3Y47u4t3mq8Ojo6BAa6\nIZfL0dHR+WDxp3kXvnJTMwC0bKmOWRs0KH8IT958dB4e/Rg0aBgZGRl8++0watdWG9O1a9tpxE8A\nRo0aDajz6RWVdLxz566a3U6ArVt3FXtOQOBDUCbG3Nu8TM3NP8yKj8D7QXi+/27+Dc+3S5eO7N+/\nC09PN6ytrXF0bIiJiT5isUgzPmNjfXR1pWU+3jFjorhxQ60c9+RJVfz8tjF2rAyRSERmpgESiZam\nDzKZDmKxEl1dKUZGepibGyIWizAzk2FiYohMpoOenramfO659PQUatashp1dP3R0xDx4cJfhw4fj\n67sYufwZ1apVIz09nbS0J1hZWSGVamFqqo+5uWG+z/8VHj9+jKWlGX36fE3lyuaEhYWRmppMTMxt\nGjZsSHZ2Nvfv36dGjRqYm9dBR0fKpk3BfPllN8zNDTE2rkdKyvMiy0ulWpiYqJ9d+fIyjIySiI9X\nKw+amQVgbq6Dubkhhoa6+Z5lXlq3bsasWbMYP3402dnZnDsXjpubGxkZ6dSqVR1DQ12OHz9ExYoV\nMTc3RFdXbciZmxsW+k3p6koxNtbH2dm50O/h8ePHWFhYIJdn8cUXnfj00xZ06NBBU1cdf7me69eN\nqFQJPDw8OHz4N6pXr0Zc3F1q1mzN+fOnkEq1GD78M7Ky/sfRo0cxMdElLS2NyMjL/PDDVO7cuUNU\n1HUyM59TuXJlTp8+jru7Ow0bNmTFiqVIJAqMjIw4efIY/fr1w9zcEJEo/7vI0FCGjk7pvJ8MDXVR\nKjM0benrayOT6WJoaIC5uSGWlgryKlcaGyvR13/5rPT0pMhkupp7n/dvtVIlU0xMDDEzkyEWq/u7\nZMl82rZtRd++fYmJidGM0cREHx0dSZFjCgtL48kTdSLwp08/YdOmnXz33buO/Z/7Nz5hwmxu375N\nZmYmPXr0oHlz53dqb9mygxw7loWRUSbz5jXHxqZ0lDrflv/S+1fg1ZSJMVehQgXi4l7GlcTHx1Oh\nQtGqS7kUt/or8M/nVav7Av98/inP99Sp36latTpWVtaAWmr/22/HaVyfALy8luark5qayi+/rCcu\n7hkSiQQnp+Y4OTUv8/EmJ+dfEEtNlfLo0XO0tLR4+jQNpTJH04fU1Ezk8kwyMrJJTpaTkJBCTo6K\nJ09Syc7WIjVVfS63fE4OPHmSSnj4KcLC1iORSNDXN+CHH+agVEqZMmUmo0ePISsrG4lEzKBBIzAw\nMCM7W8mzZ+kkJKTk+/xf4c8/I1i50hexWIREImXixKmIxWK8vReSmpqKUqnAza03xsbq/3WtW7dn\n9erl9Os3VHOfZs/2LrJ8draSpCS5pty0aWNZsGAYIEWlSuX5cz06dHDByMgYU9Ny9OrlyrNnScya\nNQ8AX98lZGVlkpSURMeOn2FhUQEdHT127PgVY2NTWrZsiYmJKZ9+2p70dPVzy8jIRiQSkZCQUug3\nlftbKvh7ABg2bBR2diqmTJnwQrZdxbffjtPUnT9/L/7+lpibr+DmTTEXLybh57eYjIwM5s6dq4nz\nUijU10tPz6J6dRs8PPqQlJRE//6DAF2SktKxs6vLjBmzXgigNKJhQ3XC6qFDR9GnT19UKhXNm7ei\nfv1GL64vyveb7NLlSwYOHPRWAiAFsbWtw/z5c/jqKw9yclQcPPgbM2bMRaFQkpCQwpQpzbh/P4iH\nD9Oxt9/G0KHNOHgwlK++6o1CoeDo0WN8+eVXmntf1N9qUlI62dnq9p48SUJXV/1uXb8+jJwcFQkJ\nKSQlpZOZqSjyby8rK78LeGZmzn/qb7QgU6bMznf8Lvdi/fqTTJ1an6ysagBERQWzb9+XmhyC75t/\nyv9dgTfnbYx0kaoMAh8UCgWdOnUiKCgICwsLXF1dWbp06Stj5oQf5b8X4aXz7+af8nznz5+tUXsE\n+O674Xzzzdh8xlxetm49h5eXnISEqjRocJmAgDZUrKiOcVIoFEgkZZfZZcuWM0yZUoXU1HpAMh4e\n2/H17VVm1yuOf8qz/bcSFxeLu3sPAgNDsba2YciQ/tSoUZOpU2dy+vQJ9u3b80KdUgctLS1Onz7J\nwYN7+eGHufTr9zUKRTYbN25DIpHSu3dPVq9eh7m5hab9sni+ffoc4vDhnppjS8tfuXSpXbEeOwEB\na9HT088XNwpw6dIFNm3ayKJFy4qs9yHYvHkj+/btBtRpJFq1asPkyePyxb+6un7BunXrMTIyJiBg\nLYcPH6RcOTNMTU1p2rQ5Xbt2x8trDi1atKJNm3b5ykdF3WDVKl+WL/fj2rWrzJ8/Cz09PZo1a8mh\nQwfZunUXly5dYPPmjflET3IJCTnJ3LnVSU62x9DwBtOm/c3gwW3f1+35VzNmzG+Ehb18B+vqXuDs\nWRmVK3+Y3Tnh3fzv5W2MuTKZjUgkEmbMmMHgwYM1qQkE8RMBAYG35U3yv8XFxeLtPZfnz59jYmLK\ntGkzefz4EeHhp7hy5TIhIQHMm7cQgOPHj7BkyQJSU1OYMmUmDg4NUSqVrF69grCw40gkMvT0+nDh\nwgCmTfNCVzcSIyMj7t+/R1jYjjIZq1wu588/N+PoeJ/U1GwcHdvh5TWuTK71JmzfHs7//pdCkyYV\nadeu4Yfuzr+e48cj8fW9ikplwq5dfzNunC3W1jYa2XRra1vi42NJTU1h3ryZxMQ8fPE3ksXgwWqx\nDZnMSJMbzMrKmri42HzG3Juye/cFli17TGqqDi1aPGPJkh6FdiYqVEgHcsgVy65UKbXE0IuiTr9K\ncv9V7N9/gXPnEqleXZuBAz8t1Rg6N7c+uLn1yfddXkMOYOvW3ZrPxcVs5Y3Lylvezq4Oy5f7AWBv\nXz/fO2bo0JEAODk54+RUtLtg//6tqVHjKhcvbqNtW1vq12/7FqN8e1JTUzl8+CA9evQiMTGRn35a\nzI8/LnyvfSgrKlVSABmAOmayYsUHlCtXuikYBATeljJbWm7Tpg1t2rw6Ca2AgIDA6/Am+d+WLVvM\n5593o1OnLuzbt5uffvLB29uHli1ba1bDc8nJycHfP5g//ggnMHAtP/20ir17d6Gnp0dS0iQSE9tR\ntaoHaWktyMjQ5uHDm6xfv4WKFSu9orfvRq4Efm6+qrS01NcSH1i3bg0ODo5F5kh6V7y99/Hzz63I\nzrZEJrvOnDkn6devdakXG+jbAAAgAElEQVRfJy9xcbFMnjwun6ABlO04PxaePXvKxInPiIvriqXl\nPpYsaUKVKuH5xGxyhWx++cUPZ+dGeHv7EB8fx3ffDWfjxm3s37+HmzdvaNoUi7XIycl56z4lJz9n\n1qw0YmLcALh/PxUbm4OMHv1ZvnJz5rTnyZNgbtwwxcIijXnz6r6y3YICFrk4On6Co+Mnb9THkJCT\nzJpVg7S0TxGJnvD337vw8ur+Rm2UJosWzefevTtkZWXRuXNXatasXXKlPMTHJzJ16iliYw2xtU1m\n0aKOGkXG4mjevD7Nm9f/IDs3KSnJ7Ny5lR49elG+fPl/jSEHMH68C/fuhXL+fDmMjTOYNKkSurpv\nnoxeQKAsKDs/IQEBAYFSYuvWME6dOgFQbP63CxfOAXD9+lW8vX0A+Oyzz1m9ermmnYJe5W3afPqi\nvp0mf9yff57l9u2/qVhxF3p6qxGL05DJztCwoQ7R0fXK1JCDwhL4Dg4vd8Fy+1/UbsPgwcPLrE8H\nDmiTna12J0pNrcvu3dfp16/MLvdKynKcHwvXr9/l4UMnJBK18ZWVVZWrV89ScO6oUqlIS0vVJOfO\ndQEsjneJqoiPf0xsbI0838iIiSlcztDQkODg9+8SDHDwYAZpaWqDSaUy49ixDysQMWvWj+9Uf+LE\nkxw61B8QcflyDlLpRnx9P5xxWhJ+fiuIiYlm4MDeVKlSjfv37xISspn9+/dw6tTvZGRkEB39EHf3\nPmRmZnHkyEGkUm0WL/bFyMiImJholi5dRFLSM3R1dZk8eTrVqllx7NgRgoL8EYu1kMlk/Pzz2vc+\nNm1tbfz8XF+hqiog8OEQjDkBAYGPmrfJ/1bcpLXgP2GpVPtFfa189cePn0SDBo4sXXqUxEQJLVoY\nYmVlzqZNpZNixc/vZywsKvDVV66AerdJX98AlSqH48ePoKury8OHD/D3X0Xt2nacOXOaevXqc/Pm\nDRYvXs66dX7cvHkDkUhEly5f8vXXHvliAi9cOM+qVb4olUrs7OoyceJUpFIpvXp1o3PnroSHn0Kp\nVDBv3gKqVbMqsb9SqbLA8dvv8LwJOTk5LFw4n2vXIjA3t8Dbewk+Pt6acfbq1Q0Xl06cPRuOWKzF\npEnT8fNbQWxsDB4e/ejevWfJF/kIqVPHiipVrhAf3wAAqTSGunUNuHMn/29YLBbj4dGf+fNnERy8\njmbNWpKbA6uo/FfvMgmtVq0q9eod4do1OwB0dO7i7Pxxqenp6ORPTK6rm1VMyX8G9+8b8zKnmZi7\ndw0+ZHdKZOTI0dy9e4fAwFDi4+OYNGms5lzu95mZmbi5fcmoUWMICNjIihVLOXhwH19/7cGiRfP5\n/vtpVKlSlb/+usaSJQvx9V1NcPAvLF26kvLly5OWlvoBR/jfS8ki8M/gwyQOERAQEHhN3jT/m719\nA44ePQTAoUMHcHBwBEBfX5+0tLQSr9e4cTN27NiGlpYWU6d+zpgxtfn8c8d3H0ge2rd34dixw5rj\n48ePYmJiQnT0Q7y9l7J2bTAKhYKmTZtz585tYmKi+eorV9av30JS0jMSExMICdlMcPAmunTpBryc\nvGdmZuLlNYe5cxcQHLwJpVLJzp3bNGVyExR3796LsLANr9XfoUONKFfuNJBK1aoHGDGiaqnej+J4\n+PABPXt+zfr1W5DJDDlx4lihhMsVKlQkMDCUhg0d8fKajZeXD2vWBBEQ8P5X70uLcuXMWLjQkEaN\nwjEzG8SYMadxd2/FtGmzNG7Cufm3cmOrAgI2MnToSE0OrM6duzJ27PeaNhctWkbDhk5v3SddXV1W\nrbLniy/C6NBhOzNnRuLq2vzdBlrKjB5dC1vbnUAs5csfZdQokw/dpXeiWrXneY5yqF79wxoyJZF3\nEa3ggpqjozN6enqYmJggkxnSooXaTdvGpgbx8bHI5XKuXo1kxozJDBzYGx8fL548eQJA/foOzJ8/\niz17fs236CYgIKBG2JkTEBD4qGnSpDm//rqdvn1dqVq1Ovb29YH8K6R5P48dOwlv7zmEhq7H1NRU\nIzbQvn1HFi6cz7Ztm5k3b0ERV1K30a1bd+LiYhk8WC19bmpaDi+vxW8tyFAUNWvWfmGUJfLs2VMM\nDQ25c+c2f/55josX/yQhIQGVKoe7d28zduz3REdHU7euPQCWllWIjY3hp58W06xZSxo3bqppV6VS\n8eDBfSpXtqRKFbXB1blzV3bs2MLXX3sARScoLgl39+Y0afKAq1dP0qSJHRUqmJfOjSiBSpUsqVGj\nJqB2hY2Liy1UpmVLdWy2jU0N5HI5enp66OnpIZVKSUtLxcDg1TFGHysuLg1xcXk7oZkdO8K5eTMF\nZ2cLXFze3oAriJ2dFb/8YlVq7ZU2jo41OXSoApGR/6NGjeolpkT62PHxacXUqeuJjTXExuY53t4d\nNede5XL9MaKtLdV8FovFmuPc2E+VKgdDQ0MCA0ML1Z04cSrXr1/jjz/CGTy4n0b9U0BAQI1gzAkI\nCHzUSKVSfHyWF/r+0KETms9t27bXpByoWLFikTml6td3YMOGLZrjFSvWaD6bmJhodjREIhHDh3/D\n8OHf5Kv/NoIMr+LTTzvw++9HePLkCe3buxAfH0/fvgP48suv8pWLi4tFT+9lsJQ6JmkT586d4ddf\nt3Ps2GGmTp2pOV9wclcwxiN3EqWlJX6jVW5r62pYW1d7ozG+K/kngFpkZ8uLLZNXHCT3+L+4ir9o\n0QGWL29OVlYVDAyimDXrBAMG/HfEyAwNjWjRovT+TovKR1malORyrVJl4+bWlsGDhxMXF8vQof01\nLtft2rmQkpLM6NETANi9eyf379/lu+/Gl0lfS0JfX5/09PQ3qpNrlOrrG1C5cmWOHz/Cp592QKVS\ncfv239SoUZOYGPViVt269pw9G87jx48FY05AIA+CMScgICBQDCqVipMnL/D4cQqdOzcuUUnuTWjX\nzoWFC3/k+fMkVq70JzR0FwEBIdSq1YA6dWqQkPAYiURaqN7z50lIJBLatGlH1arV+PHHlzLnIpGI\natWqExcXS0xMNJaWVfjtt/1FutclJiZw48ZfpTaeVxEXF8uECd9hb9+Aq1cjsLOrS+fOXQkMXKtJ\nfm1pWQVv77nExsaiq6vLwIFDAfXkNjY2moiIK+jrG2BjY0toaAgbNgSRmJjA9evXaNq0xTuJe3xM\nBAX9wqFDBzAxMcXCogK1a9dBJpOxe/cOsrMVVKlS5UVuOV3mz5+Njo4ut27d5Nmzp0yZMoM9e3ZQ\nqVIQGRkOPHrkze7df1G37lkCAtaSlZWFpWUVpk1T5y8TKJl32fl6nXyU7du74Ou7RGPMHT9+lD59\n+nP1agT+/iHk5OQwZcoEIiIuY2FRgZiYaGbMmEvduvbI5XIGDPDgm2/GoqWlxYEDe/j+++lv3d93\nxdjYhPr1Hejf343q1a3zuUPnv4/5vSpyz82c+SM+PgsIDg5AoVDQoUNHatSoyapVvkRHP0SlUuHs\n3FizWy8gIKBGMOYEBAQEimHSpJ1s3NgWhcICB4ethIa2xtzcrFTatra2QS5Px8KiAkuXniYgwBWZ\nzITBg8dhaSmhfHlTZsyYV2gilJCQgJfXHFQqtQjJiBHf5WtXW1ubadNmMWPGZJRKJXXq1KN791x1\nwaInVO+DmJhofvxxEVOnzmTIkP4cPXqI1asDOH36BCEhgVSooDZcvL2XcOnSBZYuXajJYXb//n26\nd+9JVlYWBw7spWvXL/H0HMxXX3XB13cJTZu2eOWE8Z/CjRt/ceLEMYKDN5Gdnc2gQep8cW3afEq3\nbmoVQ3//1ezdu4uePd0QiUSkpqawZk0gp0+fYMqUCejoDOLmzW+oVq0n2tpRiMXJhIRsw9d3FTo6\numzYEMTmzRsZMGDIBx7tu/M6iwRWVjYsW7aIu3fvoFQqGDRoGC1btnlthUWA337bz8KF81AqlUyd\nOpM6deohl8uLbffEiWNkZGSQk5PD7NnzmTlzKunpaSiVSiZMmJpPofZVLtcDB/YGQC5X99HCogIV\nKlTSuFzr6enh5NSI8PBTVK9uhUKhwMbmw+b0LUrBs3PnrnTu3FVznOsFUfBcpUqVWbKksBfG/PmL\ny6CnAgL/HgRjTkBAQKAI7t69y6ZNDVAoqgMQEdGPVas2M2tWl1K7RnDwJtLT03F2voRCUZmkJE+S\nkjxxctrCzz93zlculxo1ahIQUFi4JG8i4k8+aURAwMZCZfJOomxta1CxYqVCapEPHtxj8WJvMjMz\nsbGxYvz4aSgU2UycOIZ169Zz69b/GDSoD9u378XCogJff/0l69dvQUdH55VjrVTJUjPRzJv82sam\nBnFxsTx6FKeZtDk5OZOens6GDVvYtGkjLVu2pm/fAQDs2LGV338/yu+/H8XY2Jjnz5+TkZHxygnj\nP4WrVyNo1aotUqkUqVRKixatUKng9u2/8fdfTVpaKunpcpo0aaap06KFOnGxtbUt5cqZ0bNnbWbO\nPEVmphUVK+6hQwd99u69w4gRgwDIzlZQv36DDzK+sqCkRQIrK2ucnRszbdosUlJSGDbME2fnJsDr\nKSyqVCoyMzMIDAwlIuIy3t5zCQnZTEhIQLHt3rr1P4KDN2FoaEhY2AaaNGlG//6DUKlUyOWFXYXf\n1uUaoFu3LwkJCaB6dWu6dPmijO7yh+P8+WtERkbTunUdatWq/qG7IyDwUSIYcwICAgJFkJmpQKHI\n64omQqksfQFg9Y6SqsB3pe8yGBh4gl27MpFKlQwdWpH69Svw8OEDZs/2YvLk6cycOZUTJ46xcWMI\n48dPwsHBkbCwQAID1zJ69ASysjJJT08jMvIydnZ1uXLlMg0aOFCunFmJhhwUFkDIjW8TiUTk5CgR\ni6XFukrq6OSdwKpYuzZYUz8jIwMvr8PExOhQt24O48Z1fK0k6x8noiLvgZfXXBYsWIKtbQ0OHNjL\n5csXNefyJhHX1pbi6tqURo2iWbAggU6dHDA3Nyc+vgmzZ89/b6N4nxS3SGBtbUt8fCwJCY8JDz9J\nWNh6ALKzs3n0KB6RSKRRWNTT0yuksHj79i1A/fvs0EGdGN3BwZG0tDRSU1M5f/5sse06OzfG0FCd\ntqFu3Xp4e89FoVDQqlVbatasVWgMBV2ub9++hb+/Hx07dkZPT69Yl2t1+/Y8fvyY//3vJiEhm9/6\nPrq4tOLw4VNvXb8s8PM7xqJFtqSm9qJChZMsXfoUF5fSVRYWEPg38E/9jycgICBQptSqZUvHjicB\n9Uq6tfVu+vQpfREEPT09evVKQls7GlBRvfp+Bg2qUWK9N+Ho0cvMnVuDM2d6cuLE13z/fTZxcY8L\nqUXGxESTmpqiSefQo0cPrly5DIC9vQORkRFERFyhX7+BRERcIjLyCg0avJ3iYkEcHBw5dOgAoM4t\naGJi+kIIIr9x06hRU7ZufblTOXz4Ovz8XNmzpycLF7rg7b2/2GukpqZq0jRcunSBSZPGlUrfS4sG\nDRwIDz9FVlYW6enpnDmjnlzL5WmUK2eGQqHgt9+KH18uVlZVqFatAqamJtSrV5+rVyOIiYl+0Zac\nhw8flOk43ifFLRLkFcCZP38xgYGhBAaGsm3bHqpXtyqybkGFxeLI9eYtrt288YgODo6sXOmPubkF\nXl6zOXhwX6H28rpclytnRqNGTXFx6cSIEQPx9HRn5swpyOXpL65d2H24XbsONGjQ8B1jel/fLVml\nUr2XGNXQUAWpqfaAiEeP2hAY+KjMrykg8E9E2JkTEBAQKAKxWMy6dV8TFLSf5OQcevSoj7W1ZZlc\na86cbjRrdpb79//gs88aYGVVuVTbv3DhEWlprTXHcXHNuXx5UyG1yNTUlHz18k7YGjZ0JCLiMo8e\nxdOqVRs2bAhCJBLRvHmr1+rDqxJYi0QiBg4cirf3XFq1akS9evX54YfZmnN5q44dO5GlSxfi6emB\nUqnk7l0LIHccJly6VPwuYUpKMjt3bqVHj17FlvmQ2NnVpWXL1nh6ulOunBm2tjWQyWQMGTKCYcMG\nYGJiQr169vkUA4tL0ZGLiYkJ06fPZvbsaWRlqZNqDxs2iqpV368y6YeiceOmbNu2iXHjJgHwv/9F\nUauW3SuNkYL50o4dO4yTkzMREVeQyQwxMJC9drvx8fGYm5vTrVt3srKyuHXrJp06FXbVzutKDeDq\n6o6rq3uJ5QAiIyNwd+/zirvw+qSnpzN16kRSUpJRKhUMHTqSli3bEBcXy/jx32qUNBcvXs7Bg3sL\nifV4ePQlJiaapUsXkZT0DF1dXSZPnk61alZv3JecnILKvP+8OFgBgfeBYMwJCAgIFINEImHIkI4l\nFywFOnVqWnKht6RePVN0dO6RmWkFQPnyF7G3t+LEifzlDAxkGBkZERFxBQeHhuzatUuTjsHBwZE1\na1bi6PgJIpEIIyMj/vgjvJAAS1HkJrjOJW9836lTv7N2bRA6Orp4e/vQsqUzfn4BmvODBg3TfM7M\nzCQpKYkpU2Zqdj+6dduT71qmpoVjknLx81tBTEw0Awf2RiKRoKurxw8/TObu3dvUrl2HmTPnARAV\ndYOff16GXC7H2NiE6dNnYWZWnm+/HUbt2nZERFxBLk/nhx/mEBISyN27d2jf3oWhQ0eWeC9KwsOj\nH4MGDSMjI4Nvvx2GnV0datasnUfE5iV572Nx91ilUlGrlh1r1wb/Y3KSvQklLRIMGDAEX18fPD3d\nycnJoXJlSxYuXPbaCosikQhtbW0GDeqjEUABGDBgCMuXLymx3cuXLxAWth6JRIK+vgE//DCn1Mb+\n559XmDt3KnXq1MHJyblU2tTR0cHbezH6+gYkJSUxYsRATS7HvEqaxYn1ACxaNJ/vv59GlSpV+euv\nayxZsrDIdDEl0asXLF16h4wMG8zMzuPhYVoqYxQQ+LchGHMCAgL/KPbv38PNmzc0K+ICJdO1axNu\n3fqNPXsuIZUqGDLEhGrVqhc5EZ42bTY+Pt5kZGRgY2PFhAlqqfOKFSsBaNIcODg4kpiY+FquXa9K\ncLx16yY+++zzAnFxakJDQzh+/AhZWdnUrt2AQ4cacOuWNVZWQ6hcOR09PW2++KILcvkGnj37AwOD\ny6SnG7Jy5V2++WZMofZGjhytEb24fPkiU6dOYMOGrZiZlWfkyMFERl6hbl17fvppMQsXLsXY2ISj\nRw+xdu0qpk6diUgkQirV5pdfQti6dRNTpkwgMHAjhoZGuLl1x82tj0YB8W1ZtGg+9+7dISsri86d\nu1KzZu23buvy5Vt8//1fREdXwsYmmp9+akStWh92Ry4uLpbJk8dp4rtCQ9eTkSHH0NCIXbt2oKWl\nhZWVNXPmeBWrGJnLqxYJ8p77/vtphfrxugqLefNR5kVHR+e12i14XFqsXn2MxYurkpp6iMePj3Dp\n0v9wciocj/emqFQq/Px+JiLiCmKxiMTEBJ49ewqQT0mzKLEeULvxXr0ayYwZkzVtZmcr3qovY8e6\nUK/eBaKiLtCihQ1OTo3fcXQCAv9OBGNOQEDgH8W/cXfhfTBu3GeMKxAilnci7OHRV/N5zZpAAMzN\nDUlIeOl6uWPHy3iffv0G0q/fwGKvV9Atq06dety5c5vMzAzatm3P4MHD2bp1E4mJCYwePQITE1PN\n6v3atas4cuQ35PJ0QkI2Y2xsQseO7iQnP8DS8hFKZSqpqd3ZunUUfn4raNbsL8LDT9OmzafMmvUj\naWmpRfYp16h0cWnFwoXLqFOnHuXLmwNQo0Yt4uPjkMlk3L17m7FjRwGQk5ODmZm5po2WLXNFMmyx\nsVErSAJUrmzJo0fx72zMFSXt/rbMmxdFZGQ/AJ4+hR9/3EhIyMflXpn797xxYzDbtu1BIpFonl9x\nipG6uoUN/4+NR4+eEBR0DrEYhgxpjqmpSam1rVKpCAxUkJqqXli5e/cL/Pw2s3btuxtzhw4d4Pnz\nJAICNqClpYWr6xdkZmYBFFDSLCjWo3rRtxwMDQ0JDAx9574AuLg44+JSKk0JCPxrEYw5AQGB98pv\nv+1n27bNKBTZ1K1rz4QJU1i6dCFRUTfyTfRBnXdr+fIlyOUZaGtr89NPqwB1wusJE0YTExNN69Zt\nGTVq9Icc0n8CuVzO6NH7uHrVlHLl5MyYUYNmzexeWSevW1ZycjJGRkYolUrGjh3FnTt/4+rqzpYt\noaxYsQYjI2NNPXv7BmRlZbFnz68MGOBBuXJmZGREI5e7kJz8FVWq9CclZRMREc2RSrWJjY2latWq\naGtrc+LEcc0uQfGoDQipVFvzjZbWS9ELa2vbfK6eecmtk7tLp2lRJCInJ6eE675fnj7Nnxj82bOP\nN1G4rW1NZs+eTuvWbWnVqi1AkYqRjx/Hv1X81fvkyZOnuLuH89dfvQEVR44EsX1753cUKHlJTk4O\n2dla+b4rePy2pKWlYWpaDi0tLS5dukB8fFyR5Ro0cGDRIi/69RuIQqHgzJnTfPnlV+jrG1C5cmWO\nHz/Cp592QKVScfv230KibwGBMkQw5gQEBN4b9+7d5dixw/j5BaClpYWPzwIOHTrAsGHf5Jvo3779\nN9WqVWfWrGnMnbsAO7s6pKeno6Ojg0ql4tat/xEUFIpEIqV37564urpjbm5R5DXj4mKZOHE0DRo4\nFptPzdKyClOnztTIiQsUZv78I+za1ReQcucOTJ++kaNHa79ypzSvW9axY4fYvftXlEolT54kcvfu\nXWxsilbtbN68JZcuXaBduw4ATJ78A+3atUEmO4aBwUlycgyRSJ7j57cCqVRKq1Zt6NPHkwsXzvP7\n70fZsWNLkTE6+vr6+cRDVCoVK1f6cu7cGRITE8nJycHFpRPx8XEMHNgHS8sq3LnzN1WqVGXRop8A\niIy8wty5P7yYUCuYNGkcixYte9vbWqY0bJjM9esZgC6QjKNj8fGE7wstLS1ycl7u6GRmZgDg4+PL\n5csXCQ8/RUhIgGbXeP78xf84sZbNm8+9MOREgIjLl/uxY8du+vcvnfhbLS0tunRJZd26xyiVFpQr\nd55evcq9U5u5f8cdO3Zi8uTxeHq6U7t2HapXty5UBooX6wGYOfNHfHwWEBwcgEKhoEOHjoIxJyBQ\nhgjGnICAwHvj4sXz3LwZxZAhatevrKwszMzMCk307927A4CZWXlNUL2+vj6gnlB88klj9PUNALCy\nsiYuLrZYYw4gOvohc+Z4F5tPbd26NZp8agJFEx+vw0vVSIiLM0cul2ueS1HkumXFxsawadNGfvll\nPTKZDC+vOWRlZb7yek2aNGXJkoUaY1BXV4svv3Tj1q1satQwYPToTvzxRzgrV/pqlDibNWtB/foO\nuLl9WWSbxsYm1K/vwJEjv7F69XJyclQoFNkEB29iwYJ5HD16mAEDhjB48HAWL/YmOzsbsVjM/fv3\nuHo1gpycHNavD2Tt2iDi4mKZM+cHPmav38WLu2Fm9isPHkipXTuH8eNLP3brTSlXzoykpKckJz9H\nV1ePM2dO06RJMx49isfJyZkGDRpy9Ogh5HJ5sYqRHzv6+hIgE7URDZCKTFZyLsY3Yd68L7C3P8WD\nB+m0bl2Npk0bvVN7hw6p1ZCMjU2K3ZUuqKRZUKyndm31u7pSpcosWbL8nfojICDw+gjGnICAwHul\nc+euDB/+jeY4NjaG8eO/LTDRz3rlJLmgpH5J7m0l5VPr1KkLM2ZMeYdR/fuxt1exZ89TVCr1DkDt\n2rHo6zd7rbppaWno6uphYGDA06dPOHv2jEYlU19fn7S0tHxulqDOJ9egQUNOnfodT093RCIxOjrR\n9O/vzMqVvvTtuw4DAwMaNnQiOzuLSZPGkZWVhTp2R0Ry8vNCbYI6Ju306ZP4+4ewfPkSatSohUgk\nYurUmSgUM7lx4zoAtrY1CAzcCICPzwLi4mIZO3Yivr5LqFixEjk5Klxd+3LlynmgeKGMD4lUKmXG\njMIy+B+ShITHaGlJGDrUE3NzC6ysrFEqlcydO4O0tFRUKhWuru7IZDIGDBjCmDEj6dfva0Adl3jp\n0oWPLrl1Qfr0acuRI8EcOvQFoKBbtwN07+5WqtcQiUS4u7cuuWAZUlCsJzo6k8mT9yOXS2nfXsHE\niZ0/aP8EBP4rCMacgIDAe+OTTxozZcoEvv66N6ampiQnP+fRo/giJ/rVqlnx5EkiUVHXsbOrS3p6\nGjo6ukXmhyopgW1J+dQESmbMmI5kZh7g4kUp5cpl8MMPLUusk+uWVbNmLWrVqk3v3j2xsKhIgwYO\nmjJffNGDCRO+w9zcAl/f1ZodV1C7W4JapfD58ySWLl3IypXhKJVKnJwaMXHiFAIC1qKvr4+/f7Cm\nnqvrF6+V1FgkKijioI5Hio5+SEpKsua7l/F06vH4+PzG6tWVUalkVK8er4kHFHg9jI2NNWqWxZGa\nmkpiYgKJiQmsW7ceY2O1gIiLy4c1YF4HqVRKcLAbp05dRCrVolkzN8Ri8YfuVqmTV6wnKekZ7dtH\n8PCh2miNjIyhSpXTuLuX/J4QEBB4NwRjTkBA4L1hZWXN0KEjGT/+G3JyVEilUsaNm1TkRF8ikTB3\nrjfLli0mMzMTXV1dli1bWUR+qDdXuCyYT+3gwX2anSKBohGJREye/Plrl3+VbHxeevZ0o2fPl7sW\nue5eAG3btqdt2/aA2v1rzhzvQvWtrBrg77+cvXt3IxaL8PQcAsC2bZsJDz+FUqlg3rwFVKtmRXLy\nc7y955KRIWf48IG0a+fC0aOHiYuL5d69u4SHn3whrR5BSkoKAwf2pl+/QZprVatWnejohxw+LCYl\npTkVK27n2bNqLFt2klmzPrwL45vi6OjIoUMnC6ULKGtyd+L+978orKxsmDFjDlevRrJqlS9KpRID\ngwqcO/c5aWl/U778Y4YPH0yFChb51E7PnDmNjo4OCxYswdT03eLFygItLS3atv3vSOlHRd3j4UNH\nzXF2tiV//XXmA/ZIQOC/g2DMCQgIvFfat3ehffv8WtP16tkXWdbOrq5GJj+XgnmbXkd8oqR8apaW\nVYo1NgQ+PlQqFWtzuAAAACAASURBVPv3n2H9+rNcvFgBHR0HDA0b4e9fHWvrCvj5rcDExJSAgA3s\n3LmNsLANTJ78A+vWraF27TpcvHiB4cO/YcWKpTRq1IRff92OXJ7O1Kmz6NixE35+P3P06CGNvHpE\nxCVAnVusX7+BLFz4M4aGG8jIqA+IyMiQvqK3AgV58OA+U6fOxN6+Ad7ecwkL28Du3TtZvtyPKlWq\n0qrVEFJS0khKmoKx8SEMDNzw9VW7WmZkyLG3b8CwYaNYtWo5u3fvxNNz8AcekYCdnRVVq17h4cMq\nAEilsdSta1BCLQEBgdJAMOYEBAT+MRw5cpktWx4jkSgZMaImDRqUrJBWcIfI3b0PV69GkZiYxsqV\n/kgkwmvwn4RKpWLcuO1s2tSZnJwOSKVrKFfuFM+fm7B06U0CAkYC0KZNOwBq1bLjxIljgDrR8fz5\nixkwQL179/z5cwYMGIKurh5isZiOHTsB6h24XBdPIF+C+s8++5xNm5ScODEIC4v5SCQGdOtWtczH\nLZfLmTlzCgkJCeTkKPH0HMLq1ctxcenE2bPhiMVaTJo0HT+/FcTGxuDh0e//7J1nQBRXF4af3aU3\nqQpWigZUBLEX7L3Ghl0Ru35qbFHRWFGJXWygKFgRxa7BCPYSY0Ox90pTUEDqwrL7/diwiqAxStFk\nnl87s3PvnDtDmTPnnPfQqVNXUlNTcXefSFLSW7KyZAwZMiJH4+2ioHjxEtjbOwDK67lx43pKlixF\n6dLK6yiV1kRb+zIJCa4AJCe/awGhrq6uuje2thW5fPlCIVsvkBeGhkYsWmTEihU7SE9X1sz16iXU\nzAkIFAbCU4yAgMB3weXL9/jpJzViY7sBEBa2jwMHjCle3OSz51AoFPz88x62b69NZmZJGjUKYsuW\nzt9FE+KCpEWLBv9IVOLq1Suoq6urHsgLkydPnrBrlxNyuTkAmZkjefbMCF1dPSIjV+Pvr/y3ll0n\n+X7/OPh4faWm5rufgQ8juQqFgoMHz/HyZTJi8Qt0dI5TrdpmdHVL8tNPY6hXr1K+rjEvLlz4A1PT\n4ixa5AVASkoyPj4rKVHCHH//AFauXMr8+bPw8fFHKpXSv38POnXqiqamJp6ei9DR0SUhIYHhw92K\n3Jl7//oqFAr09PR5+zZRta9SpSSuXs3661gZ9eu/66Emkbx7bBGLRTnurUDR0rSpA02bFv7fBAGB\n/zr/vopcAQGBfyUnTjwhNraeavvx41acOhX+j+a4dOkGAQHOZGZWBEpz6pQb69adzF9Dv0v+Wc1h\nWNhlbty4XkC2fBqZLAu5/F1ao0QSi0Khjr6+Hj16dOH+/XsfHevg4ERIyGFAuQZDQyN0dHRzOXgf\n9qP7+ec9DB1ajWnTuuLnV45fflnA778fZvfuDTRs6EhhYGNTgcuXL+DtvZLw8Gvo6ip7emU7ZtbW\n5alcuQra2toYGhqirq6uUof08VmFq2svxo0bSVxcLPHxbwrF5o/x8mUMN2/eACA09Hfs7CoSHR1F\nZGQEADY2b3F21qJfv12UKCHGxSX/61nv3r3D8uWL831eAQEBgcJGiMwJCAh8F5QurYVYHIdcbgqA\nru4DfvihFHK5/LOV4uLjU5DJ3hdLUCet6PsoFzgBAZvR0NCgW7eerFixhEePHuLl5c2VK5c4dGg/\nkLeoxPHjx1m5cjUyWSYGBsWYOXMu6enpHDiwB7FYQkhIMGPHTsLRsWqhraVChfK0bbuDAwfKAXqY\nm3tTokQIRkZ6nD+vy4QJUz5oM/FOMGfgwKF4es7B1bUX2tra/PLLLOURIlGOVhhOTjXYunUjbm69\n6dixC7t22SGXlwDgwYOubNgQyK+/Fm4j6zJlyuLnt43z58/i67uG6tWVfcWyI5BisRh19fdVW8XI\nZDJOnTpMYmICfn5bkUgkuLh0RCrNKFTb30ckElG2bDn27t3Jr7/OwdLSmh49+lC5chWmT59MVlYW\nFStWxsvLHTU1NXbvTsihdvp+VO+fCh+9j51dRVUPy89BJpN9Vkp2TEw0N26E06JF6y+27XOZN28W\n9es3UIkECQgI/DcRnDkBAYFC5ciRYHbt2oFMlkmlSvbY2FQgJiaKkSN/AiA4+CD37t1h3LhJuY51\ndX3D4cMm6Ou7Y2tbm2XLXtK4cVPu3buLp6fyLfulS3+yd+9u5s9flOvcjRo5UavWXi5edAPEWFvv\nw8Ulb/GVfxOOjtUIDNxKt249uXv3DjKZDJlMxvXr16hatRpHjx7JU1SiRo0arFu3EYCDB/exbdtm\nRo0ay48/dkVHR4eePfsW+lpEIhFr17rQqNFREhIy6Ny5D6VLj89xTFDQftVnO7uKrFjhA4CBgYHq\n5+R9Bg4cmmPbwMAAX9/NgDKKBB9Gsgo/qSUuLg59fX1atmyDnp4+Bw/uy/H9x9JHU1JSMDIyRiKR\nEBZ2mZiY6MIw96OYm1uwbduuXPurV6+Jn9+2XPs/pXZqa1uRdevWMH/+bG7cCMfOrhJt2rTH338d\n8fEJzJzpAYCX1xIyMqRoamri7j6TsmXLERZ2mcDAbSxcuEylchoVFYWWlhaTJk3DxqY8GzasJSoq\ngqioKMzNLXJI8X+MqKhIQkOP/CNn7nMdxQ/JS9lXQEDgv4fgzAkICBQaT58+4fjxUHx8/JBIJCxZ\nsgBtbW1Onz6pcuaOHw/F1XVQrmMXL/6VJk008fCoS7NmmfTr144mTZoD0KdPNxITEyhWzJDffjtI\n+/Y/5nl+LS0ttm9vw5o1O8nMFNOzpz3W1qULbf1Fha2tHffu3SE1NQUNDQ3s7Cpy9+4dwsOvMnbs\nzx8VlYiOjsbDYx5v3rwmMzOTkiVLqeb8jDZuBYZEIqFfv/yNRhw+fIXff49DRyeDn392xtjYCFCK\ndXTqdJbt28ujUBhjbb0fN7fPj+jkF48fP2T1ai/EYhFqauq5IpC5H+yV2y1btmby5PG4uvbE1rYi\n5cpZ5RiT1+dvkVevXnPmzHUqVCiFg8MPqv2RkRHMnbsQd/cZDB7cn2PHQvD29uPs2VNs3uzP9Olz\nWL3aF4lEwqVLF1i3bjVz5y7MMXe2yqmn5xLCwi4zd+4MlZLps2fPWLNmPSdOHGXIEFfVi6W2bTuy\ncOE8fH03kZWVxdChrsye7YmPzyqeP3+Km1tv2rTpQLduPfD2Xsm1a1fIyMikSxcXfvyxC2Fhl1m/\n3gcDAwOePXvKpEnT2LBhLYaGRjx58ghb24rMmKF0RjduXM+5c6eRSqXY2zswadI0le2f009RQEDg\n343gzAkICBQaV65c5N69uwwe3A+AjIwMjIyMKFmyFLdu3aR06dI8e/aMKlUc2b17R45jpVIpJiYm\naGhoIBaLc6QWtWrVliNHgmnTpgO3bt1UPQTlhb6+PpMntyvYhX5jqKmpYWFRiuDgg1Sp4oiNTXnC\nwi4RGRmJpaXVR0Ul5s6dS7duvahfvwFXr17Bz29dUS2hQAkNvcZPPxmQkNAYUHDrlj979nRGTU0N\nkUjEsmVdcXY+TWxsKu3bO1GmjHmh21irVh1q1aqTY9/7EcgPW3a8/52Pj1+OcfHxb0hKektYWBix\nsUm5FF+/NcLDHzBs2AseP26Bnt49Jkw4xv/+p/z9t7AohbW1DQBWVtbUqFHrr882xMREkZychIfH\nDCIjXyASiZDJZLnmz1Y5BahWrQaJiYmkpqYgEolwdm5IVFRkrpdQL148w9m5Ib6+3kil6bRq1RZr\naxtGjBjN9u1bVS1T9u/fg56eHr6+m8nIyGDkyMGq+/jgwT22bNmJubkFYWGXefjwPlu3BmFiYsqI\nEYO4fv0aDg5V6dKlu0qB1cNjBufOnaF+/QYFe9EFBAS+GwRnTkBAoFBp06Y9w4b9L8e+3347wPHj\noZQrZ0mjRk0+eSyAhoZmjkhC27YdmTx5HBoaGjRt2vyza+j+Szg6VmX79q1MnToTa2sbVqxYSsWK\nn1ZhTE5OxtTUDIDDhw8ByjTYS5cuUKNGLTZsWIuOji69en1+uuU/Vc4sDI4efUlCQre/tkRculSb\n58+fqZwEkUhEt25FqwCZHygUCsaO3U1wsBUSSQZDhlxgwoQWfz+wiPH2fsDjx8pUy+RkJ/z9nzBi\nhBx4VzMIOesGxWKliun69T7UqFETT8/FxMREM3r0sDzP8SmV0w9fQkmlUoyNjXFzG8KgQf3Q1NRU\nta/4cJ5Ll/7k0aOHnDx5DFCmvUZEvEAikVCxYmXMzS1Ux1asWFn1+1a+/A/ExETj4FCVsLBLBARs\nQSpN5+3bt1hb2wjOnICAgArhiUdAQKDQqF69FidOHCM+Ph6At28TiYmJoWHDJpw5c5KjR4/QvHnL\nTx6bF6amppiamrJpkx/t2nUonMV8Zzg6OvHmzWvs7atgZGSMpqYmjo5OwMfT7UaNGsX06ZMZNKgf\nhoaGqlS+lJQUfv89mP379xAdHaU6PizsMpMmjfsbS769dL5ixWTAu4iNoWEUhoaGRWdQAbF9+0kC\nAzuRmNiYN29asny5I+fOXStqs/4WmUySYzszU4JcLv/bcQqFgpSUdy8kfvvtQJ7HfY7KqbIWLwB/\n/wACAnbj5jaEhIQE0tPTSEtLRSqVftSO8eMnqcbu3LmfmjVrA6ClpZ3jOHX1d/30sltqSKVSli5d\nyLx5C9m0KZAOHTqRkVF4AjbR0VH0798j1/4NG9Zy+fLFT47dsGEt27dvLSjTBAQE/kKIzAkICBQa\nlpZWDBkygvHj/4dcrkBNTY0JEyZjbm6OpaU1z549wc6u0t8em1d9T4sWrUlMTKRsWctCXtWXER0d\nxcSJY3BwcOLmzXDMzIrj6bmE58+fsmiRJ1KplFKlSuPuPgN9fX1GjRpK5cpVCAu7THJyElOmzPhH\nKpLVq9fkxInzqu3t2/eoPoeEnOLw4UMEBm5DJBJhY1Oec+fOEBCwET09PfT19enVqx+6unrs37+H\nqlWrMX78JPz81qGtrQMoa5e8vVfy/Pkz/ve/IUyePI2yZS2Jiopk9uxfSE9Po379hvl3AfORceOa\ncvOmH+fPV0Ff/zWjRyswNv78/oXfCy9fSlEojFTbUmkZnj4Np379IjTqM+jWzZRz5y7w+nVtxOJY\n2rRJVAmGfPi34P1tsVhMr179mTdvJps2baBuXWfef5mQfejfqZxWr16LKVMm0L17b4yMjHj7NpHU\n1FSWLVvIkCEjiIqKxNt7BePGTUJHR5fU1BTVOWrVqsuePbtwcqqBmpoaz58/o3jxEp+99mzHzcCg\nGKmpqZw4cZSmTYs+mjpoUN4Rzvf51uswBQT+LQjOnICAQKHSrFkLmjXL/TAikUjQ09OnX7/uuLj0\nomPHzvz66xxcXHrxxx9n/6r7KklqagrFihmqFOBiY2MZMWIgdevWp0OHTkWwoi8nIuIFs2d7Mnny\nNGbMcOfUqeNs27aZ8eMn4ejoxIYNa/H3X8eYMRMQiUTI5XJ8fTdx/vw5/P3XsXz5mnyx4/HjR2zc\nuJ6SJUsRHx/P3bt3qFatBo0aNSI09ChPnz7BzW0AERGjSU9/g4nJUZWs+/PnT+nTpxuxsa9o2LAJ\nRkbGuLoOYsmSBXh5eePltZguXVxo1aote/YE5Yu9+Y22tjbbtvUkLi4OHR0rdHV1i9qkAqFNGzu2\nbAkhIkIZ/a5Y8Tdatcr/Hm75TevW1TE2vsPJk0GUKaNFz57K3/MPa/2mTp2p+vz+d++/uBgyZASg\njPQXK6aMvn6OyumHL5YaNGiEuroGzZu3Qi6XM3z4QMLCLuPgUBWJRMKAAb1p27YDLi49iY6OYtCg\nvigUCoyMjJk/f1Gudhgfbmejr69Phw6d6N+/B8bGJlSqlFN9tzAcJrlczoIF83K8dFq82FPVFuH8\n+bOsWrUcLS1tqlRxICoqSlUz+PTpY0aPHsbLlzF0796Lbt16Fri9AgL/NUSKb0QKKTY2qahNECgg\nzMz0hfv7Lya/7u/bt28xMDBAKk1nyBBXVq1aR7t2zVmwYBn16jmzZs0KdHV1cXUdxPz5s3F2bsSR\nI4kEB99HW/s3TExM2Lt3xxdJfBcF0dFRjBs3isBA5YPmtm2byMjI4NCh/ezeraxPi4yMYPr0Kfj5\nbWX06GEMG/Y/7O0dePPmNSNHDiYwcG++2LJrVyDXroWhr1+MyZOVSnk3b17H338tcXGvycjI4Pnz\neKKiFiGRxGNk5IujY3Vq1dJnz54gVq/2ZcgQVzQ01FEoFJQsWYrMTBlbt+6kXbtmHDgQgkQiISUl\nmU6d2hIaejpf7Bb451y6dJeAgKeIxXKmTauDsbHx3w/6l3H27Cm8vVfi7j4Te/sqOb5bsSKU/ftB\nIpExaFAxevSoV0RWfh359Xc5OjqKnj07s2HDVsqXr8CMGe44Ozfk8uWL1K/fgDp16tOrVxfWrFmP\nubkFs2ZNIy0tlQULlv2VinmBlSvXkZKSTO/eXVV/CwS+DuG56t+LmZn+Px7zfTz1CAgI/OsJCtrO\nmTPKHlKvXr3ixYsXH5XM79ChE0uWLCMkZDUWFod4/nwHL16oc/LkVZo3r1lka/in5BRvkJCc/Ol/\nztk1NWKxRKU4mR+IRCIMDY24cOE83t4rqVevAb6+a6hVqwZnz/5BSkoKkIaGxkOyspTph2lp6iQm\nJmBgYICFhQX6+vr8/PNUDhzYq3orL/BpNm/2o3//gYV6zpo17ahZ0w747z4QOjs3wtk5t6BNcPBF\nFi92Ij1d2b5h5sw/cHJ6Snj4n+zfvxtbWzumT/+4Um5BolAoOHHiEi9fvqVt25oUK1as0M5tYVGK\n8uUrAMo2J9l1sgqFgufPn1KyZCmVkEvz5q04cED5kkkkElGvXgPU1NQoVswQIyNj4uPfqGoYBQQE\n8gdBAEVAQKDICQu7zJUrl1i71p+NGwOoUOEHMjKkH5XMr1LFkbi4ONTVnwFZZGSU/6v+53URrSB/\n0NXVw8DAgPBwpSjF77//hpNTwafBVatWkytXLuHl5Y2NTXl8fFby4sUzdu7cybx5C3Fyqo6amg4i\nUToAYnEGFStqqsbr6OhSsmRJrl9X2q1QKHj48AGgvFfHjoUAEBLye4Gv5Xtiy5aNRW3CN8vHhDcK\nklu33qgcOYA3b2pw5cpD9u3bxfLla4rMkQNwd99H374V+OmndnTqdJqoqFeFdu4PXzrlfJH0YZpn\nzmQvNbWcaqMyWf69hBIQEFAiROYEBASKnNTUFPT19dHU1OTp0yfcunXzb8e0bt2aN29GExs7HgBL\ny2Batfp8QZBvgbzEG6ZOncXixZ6kp6dTqlTpHHVAH4zONzusrKzp3NmFSZPGoqamjqGhISVKWHD3\n7m0mTRpH1apOqKtnUKPGTeTyGJKSMmnQoCL3798jKektkZERzJgxl+HDB5KWlka/fj1o3rwl5ctX\n4KefJjJ79i9s27YJZ+dG/1lRBHf3ibx69ZKMDCkuLr2IiookI0OKm1tvrK1titRR+KdER0cxYcJo\n7O0duHEjHDu7Sn+pPa4jPj6BmTOVa/HyWkJGhhRNTU3c3WdStmw5goMPcvRoCG/exJGeLqVhw8aM\nHDmGQ4f28/jxQ8aMmQDA0aNHeP06rlDXVb26OXp6t0lOVoowmZuf486dE0RFRTJhwmiaNWtJZGQE\njx8/IitLxsCBQ3F2bsTPP//E8OGjsbEpj5tbbxo1asqAAYNZv96HEiXMv7qWNyoqku3bbZHJygJw\n61YvvL134OGRf/0yv7RlSNmy5YiKiiQmJhpzcwv27dvN27dvAaGhuYBAYSE4cwICAkVO7dr12Ldv\nN337ulCmTDlVHcvHJPMBevXqye7dATRvnoGa2g4GD65QJM2cv5QPxRve79W2dq1/ruNXrPBRXQND\nQ8McTaHzg+zm4SKRshfWxInuXL58jgMHDnL37h2aNWuJubkFbm5DmD9fKcM+ZMgIHByqMmnSWDQ1\ntWjatAVRUREsWPAuzdLComSOptXZAhT/NdzdZ+SqCd29eyf+/gFFbdoXERkZwdy5C3F3n8Hgwf05\ndiwEb28/zp49xebN/kyfPofVq32RSCRcunSBdetWM3fuQgAePXpA+fIV8PRcQu/eXXFx6UmzZi3Z\nssWf//1vLBKJhJMnj6Gjo8ucOdO5f/8ulpbWTJ8+mydPnrBq1TLS0tIoVsyQadNmYmJiSkTECxYt\n8iQxMQGxWMzcuQswMjJmypQJJCW9JStLxpAhI3B2bkR0dBSTJ49j8+YdAAQEbCE9PY2BA4fStetc\nLl78A5FIxA8/lGXOHG+6deuAlZUNu3fvRF1dnbFjJ+LoWI2hQ12pUaM2jo5OhIdfxdzcHDU1NW7c\nuA7A9evX+PnnqV99rTMyMsnK0nxvj4isrPxOrPr4S5aPvYARiURoamoyYcIUJkwYjZaWNjo6Oqp0\n8Y+JuggICOQvgjMnICBQ5Kirq7N48Ypc+0NCTqk+N27cjMaNm6m2r1+/RrNmLfjll86FYmNRsXHj\nadavTyUjQ43WrVOZPbtDgUS3atWqQ61adXLsc3auSZ8+g3Idmx0tjIl5SVKSCC+vtZia5pTyj4h4\nyZQpfxARoY+19VuWLGmKkdG/r3fb55JXTej3woeRuHLlLDE2NmbRonnExydQpkwZKleugrv7BJ49\ne8arVzHcunWDPXuCePjwvirCNnBgXzp27ExWVha3bt1g2LABaGpqERMTTZUqxalWrSbnzp2hXDlL\nZDIZMTHRzJw5F3t7Bzw957B7907OnDmJp+dSDA0NOXYshHXr1uDuPoPZs3+hf383GjRoTGZmJnJ5\nFmpq6nh6LkJHR5eEhASGD3fLs1Yuu38iwIMH5zh27CBqamqkpCQDkJSURNWq1Xjx4jlSaTrTp0+h\nbFlLMjMzefUqBkdHJ3btCsTCoiR16zpz+fJFpNJ0oqOjKFOm7Fdf/3LlytGmzQ727y8P6GFpeZC+\nfW2/eL4Po8QdOyr/hq5cuZSLF//E2NiU2bPnY2hoSHJyEpqaWri69srVKqVECWWdnI1NeTIyMti0\nKZA2bZoA4ObWmz59Bqj6hgIq51lAQCB/EZw5AQGB74qQkDC8vPxITX3A2LGTi9qcAuX+/SfMm2dC\nYqIyncrX9yWVK5+hR4+i79e2f/9Fpk1T8OqVE2XKXGDpUiMaNXqnDDh58nlCQ/sDcPu2Ak3NLXh7\n/7sd74/xfk2opqYmo0cPIyPj402mv0Xej8S5uvYkPT1dFYlbtmwRCoUCe3sHxoyZwJgxw5kxw53B\ng4chl2cxatRYVq1azpo16zl69AgODo7IZFksXLiMSZPGqWqwOnT4kc2b/ShXzoqmTZuTnJyMvb0D\nAK1atWXTJj8eP37EuHEjAaVkvomJGampqbx+HUeDBo0B5cshUEcmk+Hjs4rw8GuIxSLi4mKJj3+T\n5/qyUwJtbCowa9Y0GjZsrJovI0NKUNB2VSqhiYkpHh6eqp6WMpmMu3fvULJkaWrWrE1iYgL79+/F\n1rZivlx7kUiEj48L9euHkpAg48cfq2BlVeqL5/swSty4cVPS09Ows6vE6NHj2bhxPf7+6xg3bhJz\n585k/PjJebZKyXaAjxwJJjb2FQMG9MbGpgImJuaEh9di/Hh1rKz2sHx57a+yV0BA4NMIAigCAgLf\nDdevP2DcOHUuXdrErVt/MHu2Nk+fRhW1WQXG7dsvSEx811cqK6sET56kFqFF7/D2juPVq+aAKS9e\ntGP16pyRpogIvfe2RB9sf3u0aNGgwOb+WE2ompoaMpmswM6bn1hYlMLa2gaRSETp0mVVzeKtrcuT\nmprKs2dPadWqLQBaWlpkZEjR1zegShVHli1bREpKMklJbxGLcz92ZDtSlSrZ8+rVK0JDf6d+/Zz1\nlQqFAl1dXaysbPD3D8DfP4BNmwJZunQlH4puZBMScpjExAT8/Lbi7x+AkZExUmkGEokEufzdGKk0\nXfV50aLldOniwr17dxkypL/K0Zw2bTbdu/emRo1a7Np1kLJlLbl//y6gvI9mZsU5ceIo9vYOODg4\nERi4lapVnb7iiudE2buuOWPHtv5qxygoaDsDBvRm2LCBqiixWCymWTNlFK1lyzZcv36NlJRkkpOT\ncXRUrqN163Zcu3Y113w//tgVM7PibN26k44dO3P5cjwXL/YjJqYj58+7MmvW5a+yV0BA4NMIzpyA\ngMB3w4kTj4iNfdf3KSKiOcePXy9CiwqW+vUrY2l5QrVtaHiVevW+jTfcUqlGju2MDPUc21ZWibx7\nyM7C2jq5cAz7YgquuKd27XpkZWXRt68La9euVtWEduzYmQEDeuHhMb3Azp1f5FQ0FKscLZFI9Jcz\nJlI5ZWKxGB0dHfz81nH8eCj16jVAoYARIwbx5s1rPrzW7zttTZs2x8GhKrq6urx8GcPNmzcACA39\nncqV7UlIiFftk8lkPHnyGB0dXczMinPmzEkAMjIykErTSUlJwcjIGIlEQljYZWJiogEwNjYhIeEN\nb98mkpGRwR9/nFWt4+XLGKpVq8GIEaNJTk4mLS0NTU1NDh7cw4ABg5HJZPTs2Zl+/bqzYcNald1V\nq1bDyMgYDQ0NHB2rEhcXq3KCYmKiCQ39tJJrXi8TgoMPsmyZss4wOTmZvXt3fXKOz+FjysHwzqlW\nKBR/m8otkUhQKOQAuaLMaWk5k75iY3W+2m4BAYGPI6RZCggIfDfY2BRDQyOCjIzSAOjo3KNixZJF\nbFXBYWZmwurV5nh77yAzU0Lnzvo0bPhtNDFu1SqD+/ejyMwsibb2I9q2zdkIeMmSpmhobCEqSg8r\nqyQ8PVsXmC1paWnMmDGF2NhY5PIsXF0H4+Ozkg0btmBgUIy7d2+zerUXK1euJTU1leXLF3Hv3h1A\nxMCBQ2nUSFnns27dGv744yyampr8+usSjIzyp6H2x2pCnZyqM2LE6Hw5R2Gio6PD6NHjVNvFixen\nevVahIQcZsCAwfz000RWrVqOn99WIiMjKFWqNJMmTeWXXyZjaWlFzZp1WLlyKUCunoTXr4fTs2cf\nRCIRZcuW1bCnbgAAIABJREFUY+/enfz66xwsLa3p1q0ntWrVxctrMcnJyWRlyejRozdWVtZMnz6H\nRYvms379WtTU1Jg7dwEtW7Zm8uTxuLr2xNa2IuXKKdsOqKmpMWDAYIYMccXMrDiWlsr9WVlZeHjM\nICUlGYVCgYtLT/T09Ni//wgrVixh6FBX5HI55cpZ5hD5ARg8eDiDBw8HwNTUjNOnL6q+i4qKJDT0\nCC1a5P4dkMlkqKmpkdfLhPcdqqSkt+zdG0Tnzt0++z5lO2fvz/OxKLFcLufkyWM0a9aS0NDfcXBw\nQldXD319ZasUR8eqOVqlWFiU5O7d29jZVeLkyWOq+XV1dTE0TAYyAXUgHXv7b/1FjoDA943gzAkI\nCHw3tG9fl+HDD7FvnxZisZw+fUTUrduiqM0qUN5v8vwtMWVKW6ysznD//jmcnIxp375pju9NTIxY\nt65wauQuXPgDU9PiLFrkBUBKSjI+PivzPHbjxvXo6+urlESTkpTKe+npadjbOzB06EjWrFnBgQN7\ncXXNLf7yNWzbdpZt21IA6NlTm/79i7728XPIysrKs43G+5/d3Ibg6TkHV9deaGtr88svswBlSl9Y\n2GVEIjHW1jbUqVMfyE4b7E2bNu24eVOfK1dEpKWtompVW6pVqwHAtm25I1EVKvzAqlXrcu0vXboM\nXl7eufa/r6T6Pt269aRbt5659q9Zsz7XvqNHQ7h58wYikRhbW1sGDx7OmDHDSUxMxNDQiKlTZxAb\nm8qYMXNJTdVHR+cpRkZyRo8eS+PGzfDxWcXz509xc+tNmzbt0dc34OTJY6SnpyOXy5k3bxFSqRRX\n115oaGggEomQyWTEx79RNev28VlJZGQEbm69qVmzDiNHjiEgYDMnThwlIyOThg0bM2jQMKKjoxg/\nfhTVq1cjPPw6ixevoESJdyq/H1MO1tLS5vbtW2zatAEjIxPmzJkPwLRpebdK6dWrL9Onu3PgwF7q\n1nUm2xl1cqqBmZk/1ao1R0enCY6Otkyd2j7PeyAgIJA/iBTfSCOQ2NikojZBoIAwM9MX7u+/mKK4\nv3m9cRbIf76X390XL54zfvwomjZtQb16DXB0rIqLS8c8I3ODBvVjzhxPSpUqnWOOpk3rcfz4HwAc\nOxbK5csXmDz5l3yz8fLlO/Tpk4lc/ozExN4YGFxn1qzLXL/+R67o1NcQHR3FxIljcHBw4ubNcMzM\niuPpuYS4uFiWLl1IQkI8WlpaTJ48jerVq7B3729s3uyHTJaJgUExZs6ci5GRMRs2rCUqKoKoqCjM\nzS2YOXNuvtn4PgsWBLNkSTtAWVNZqVJbDh1aj56efoGc75/w9u1bBg7cSlTUAbS1BzJzZmWqVi3D\n3Lkzadq0Oa1bt+O33w5w9uxp7txpwKNHNxGL04mOXkaHDstJSfmNwMC9XL16he3bt6ruc3DwQdav\n92HTpkD09fVZtmwh+/fv5eTJ81y6dIFVq5axaVMgu3btwNfXmyNHThITE82kSWNVipAXL/7JyZPH\nmDRpGnK5nClTJtCnT3+KFy9Bjx6d2LFjBxYWVp9aXr6hUCh4/Pgx6urqlC379eqdAn/P9/K3WeCf\nY2b2z//2CTVzAgIC3x3vK6kJCJQpUxY/v23Y2JTH13cN/v6+OUQupNKMHMfn9Q5TInmXqCIWi1TC\nF/nFlStPSUoqh6HhdgDevnXg/v3Yr5rzYzZGRLyga9fubNmyEz09fU6dOs7ChfMZN+5nNmzYwsiR\nP7FkyQIAHB2dWLduI35+22jWrCXbtm1WzfPs2TO8vLy/2pGLjX3N//63j+7dQ/DwOJTD7ocP1VA6\ncgpAQUzMWESib+PRZM6cE1y/bkF8vAs3bgxi1qzHGBgYcPv2DVXKZKtWbblx4xoxMXqAiOTk5oCI\nxMSyvHmjVM788OdNJBJRo0Yt9PWVD203boQjkSjTlJ2cqhMVFUm/fj3Yvn0z6elpxMe/yTXHxYt/\ncunSBdzcejNoUF+eP39GRIRShKhECQscHBwK8Mq8IysriyFDdtCggQRn5zR+/nmP0CxcQKCQEdIs\nBQQEBAS+a+Li4tDX16dlyzbo6upx6NB+VU1PnTr1OHXqXU1PzZq12bNnJ2PGTACUaZbZD9X5TWDg\nVoKDDwJQtWpdSpYMRl39OWXLdiIrqwJ2dpU5fz6cX36ZzJMnj7C1rciMGR4A3L17J8/m2KNGDeWH\nH2y5fj2c5s1bUry4ORs3+iIWS9DT02PatFlYWJRSpefZ2toRHR3FzZvhTJ/+rpVHZqZSRfPVq5fM\nmDGFN29ek5mZScmSSoEdkUiEs3NDNDRyCt38HT4+qyhevARdurgAsGHDWnbvvkd0dCYSyVuePJES\nF3cPL68JREdH8ezZEkqUOI+W1l0iI9dhZvYLMtnuXNevfftOdO/e65MNv4OCAtm/fw8SiQRLSytm\nz57/Rfctm7g4bSCNbCGf2Fh9lfrohw6Lre0bwsIUKBTqQBqVKkk5f/7jTo22tnae+0NCDiOXK1iz\nZj1nzpxk+fLFuV5GZNO37wB+/LELAIcPHyIwcBsBAVtISkokMjKSiRMn5UgFLVHCnHnzZqGpqcWD\nB/eIj3/DlCnTCQ4+yN27t6lUyV6VRtmiRQM6d+7G+fPnMDExZfDgEfj4rOTVq5eMGTMBZ+eGSKVS\nhg8fw82biZQsGUxs7BS2bWuKufkKXr+OQCqVEhkZQcOGjRk5csw/uPICAgL/BMGZExAQEBD4rnn8\n+CGrV3shFotQU1Nn4kR30tPT+fXXOaxfr4eTU3VVJNfVdRBLly6gf/8eiMUSBg4cSsOGjXPVgH0t\nd+/e4fDhQ/j6bkIuVzB0qCuurl0JCnqMsXFfevXSwc5Om82b77F1axAmJqaMGDGI69evUamSPcuX\nL2LBgqUUK5azOXZ2PdX69Zv/Wk9Pli5djampKSkpybx9+/YD5UkJb9++QU9PH3//gFx2Llu2kF69\n+lG/fgOuXr2Cn9+7ejRNTa1/vO5mzVrg5bVE5cydOHGUmJheREV1RaHQQyx+Q3h4e0DpTKenx1On\njgkPHw6iXr2TZGYqa8byun5OTtVypV++H6Xftm0Tu3blbPj9NTg5wbFjtlhYbCE+fgCVKsWSmpqC\nvb0Dx46F0KpVW0JCDuPo6MTkya3o1+8wCoU2Tk5vmD69DW3aLAJAR0eX1NQU1bwfOoIODk48fvwY\ngHv37qCtrY2+vj7Pnj1RjdPR0SE19V1bktq16+Dr60PLlm2Ijo7C39+XxYtXoK6uzsSJY/Dw8KBt\n2w6qVNDlyxfj6bkYgOTkJNau9efs2VNMmTIBHx8/rKysGTy4Pw8fPqB8+Qqkp6dTvXotRo78ialT\nf2bDBh+8vLx58uQx8+bNxNm5IXv2BJGZCc+e/Ya6+mNKlx7E06cHSExM4+HD+2zcGICamjq9e3fF\nxaUnZmbFv/qeCAgI5EZw5gQEBAQEvmtq1apDrVp1cu3fvn1Prn3a2tpMmzYr1/6QkFOqz40bN6Nx\n42ZfZdP169do2LCJyiFq1KgpxYopsLTUY/PmVoBSJr5ixcqYmpoBUL78D8TERKOnp8eTJ48YOzZn\nc+xssvuBAVSp4si8eTNp2rSFSpXzQ3R1dSlZshQnThylSZPmKBQKHj16iJlZNVJTU1TnP3z4kGrM\nl6bKVahgS0JCPHFxccTHv0Ff34DixUVkZCxFW/syCoUYufytqnl3iRIW+PqOUo13cfFFoVDkef3C\nw6/i7Nwo1zk/1fD7axgzpgUKRSinTtWgWLEOaGgYsGrVbcaOnYSn52wCArZgZGTE1KkzMTAwoHbt\nctSvX5VGjZRiQNlOZvnyFVSCL23bKgVQ3n9hMHDgUPbuDcLVtRfq6uqYmprh6tpTpSYJUKyYIVWq\nONK/fw/q1KnPyJFjePr0KcOHu5GYmIBIJP5LFVOp1nnt2jVmzfoVUKaCenuvUNlUv76yDYKVlQ3G\nxiZYW9v8tW1NTEwU5ctXQF1dndq16/51XcujoaGBRCLB2tqG6Ghli4cbN8Lp3bszDx4c4MmTjmRm\nlqRixXU4Olqjq5uFjo4uAJaWVkRHRwnOnIBAASE4cwICAgIC/1liY18zd+5Z3r7Vpm5dNYYObfr3\ngz6DvKJ7eQX81NXfpTFKJGJVPZmVlc1HlRi1tN6l6E2c6M7t2zc5f/4cgwb1Y/78RXkqT86Y4cHi\nxb+yaZMfMpmM5s1bUrduNQYOHMr06ZPR1zegevUaql5syojXP142AE2aNOfkyaO8fv2a5s1b8urV\na3buvEZKygAqVUokOXmjKnVQWzvv6N+Ha8juffZ3Db+vXQvj3LkzbN7sx6ZNgapatC9BJBIxdmxL\nxo5tCUzJ8V1eypnZKYrZZL8gUFNTy3V8mzbvFB4NDAw4derC39rzYe2ii0tPXFx6snv3Dl6/fq1K\nkd20KZAOHVp81CFXV1dGbsVica7+gdk/f+/XkIpEyoj3h8cAmJubsmmTKVu37uTatVimT6/Kmzev\nckWH5XL5365PQEDgy/g2qowFBAQEBAQKGYVCwZAhx9i+vQ+//daV2bOr4e9/6u8HfgaOjlU5ffok\nUmk6aWlpnD59gipVquZIlfsYZcta5tkcOy8iIyOoVMmeQYOGYWhoiEgkVrVdAKWEvJvbECwsSrJk\nyQo2bgxg69adDBgwGABn50bs3LlfJYyyYoUPoIwW9ezZ94vW3rRpC44eDeHkyWM0adIcU1M9fvzR\nnosXW/DTT5a8evXyk+NFIlGu63fmzEkcHJwwMjL+7Ibf6elpX2R/UbBo0WFatTpKx46HCQm5+o/G\nlitXnoCAfdSseZDOnfcRFnYLJycnjh0LAVClguY3jo5VCQk5jJ2dJUOHVkJLK4Pq1avl6UQKoigC\nAgWHEJkTEBAQEPhPkpAQz61b5cnukZWZWYZLly7h5vb1c//wgx1t27ZnyBBXADp06IytrV2OVLm6\ndevnGf1SU1PDw2NBns2xP2TNGi8iIl6gUCioUaOWSvjkSzh37jaHDr1ASyuT8eMbfbEwjJWVNWlp\nqRQvXgJjY5OPNu+GvCKYyu28rl+FCj8AfHbDb11dvS+yv7AJCjrH8uX1yMxUtst4/vww1au/xsTE\n5LPGr137ghcvJmFs7MeLF2ImT9YkOHg5EydOypEKms3n1Ifmju7m/q5zZxcWL/bE1bUnEomEadNm\noaamlqfasKA+LCBQcAh95gQKHKEfyr8b4f7+e/m331uZTEaDBkd59Mglew/DhgXh4fHfaHL8/v09\nf/4OgwdnEBvrDMipV8+PoKAuqpS8r6Vbtw74+W3FwKAYLVo0IDT0TL7M+29g1qzfWbPG5b09L9m1\n6xYNG9b8rPEdO4by559dVNt2dnu5c6fzv/p397/Ov/1v83+ZL+kzJ0TmBAQEBAT+k6ipqTFzZgnm\nzw8kPl4PJ6eXuLt/H45cbOxrAgMvoqkpxtW1MZqaml8136FDz4iNzXYoxJw/35CHDx9TsaLt1xuL\nMjKTlpaOh8cM0tPT6d+/B66ugylWrBhr1niRlZWFnV0lJk50R11dnW7dOtCiRWv+/PMcYrGESZOm\n4eOzkqioSHr16kenTl0BCAjYTGjoEaKiEjAwqMygQT1o3bp6vthcWDg4GKCp+RypVNlwu3TpK9jb\nV/rs8XZ2Kfz5ZwagAcixs3tbMIZ+BgqFgt9/P8+rV0l06FALY2OjIrNFQOC/guDMCQgICAj8Z2nd\n2olWraoik8nyLQpV0Lx69Zru3c9y+3YfIJPQUH8CAly+yn59/SxARvZjgZ7eS4yMSnzRXO7uE3n1\n6iUZGVJcXHrRsWNnAK5cuYipaXG0tLTZvHkHycnJ9O/fgxUrfChdugxz585k795ddO/eC5FIRIkS\n5vj7B7By5VLmz5+Fj48/UqmU/v170KlTVy5e/JMXL54TF9eJq1ddKVnyf0yYEIWamoTmzat+8bUo\nbLp0qcfz5yGEhl5BSyuT//2vJMbGn5diCTB3blvU1IJ4+FCLUqVS8fBo+feDCoiJE/cQENCKrCwz\n/P2D2LatJqVKfdnPkYCAwOchOHMCAgICAv9pRCLRd+PIAWzefPEvR04EaHDqVDeOHbtE69b1vnjO\nMWOacOWKP+fO1UVXN44RI15jbv5lDpG7+wwMDAyQStMZMsSVxo2VCqFWVtb4+/uSmZlBePg1dHR0\nKFmyFKVLlwGUCo979uyke/deAKo2BNbW5UlLS0NbWxttbW3U1dVJTk7m4sU/OX/+HDEx4ZQtewCx\nOI3k5BaEhr6kefMvvhRFglI188vGamhoMH9+x/w16At4/vw5QUH2ZGVZAHD7di98fALx8GhXxJYJ\nCPy7EZw5AQEBgSIkLS2NGTOmEBsbi1yehavrYEqVKs2qVctIS0ujWDFDpk2biYmJKZGRESxdupCE\nhHi0tLSYPHkaZctaFvUSBAoZZTsxOZAtuy9FQ+PLJfhB2ZQ6MNCFp0+fYmBQFjOzL09VDArazpkz\nSlXQV69e8eLFCwBKlSqNn982fvyxFb6+a6hePWdNWHb7gWyy5e3FYnEOZ1spjy8DoHv33nh4/MDr\n19neWybFiu36YtsFvpysrCyysnK+FJHLBeETAYGCRmhNICAgIFCEXLjwB6amxdm4MYDNm3dQp05d\nvLwWMW/eQjZs2EK7dh1Yt24NAAsXzmPcuJ9VMvJLliwoYusFioLBgxtQs+ZGIB14TYcOh2jc+PPE\nMj6FRCLBxsYGMzOzvz/4I4SFXebKlUusXevPxo0BVKjwAxkZUgBev37zV/NpNXr16sfNmzeIiYkm\nMjICgCNHgqlatVquOfPSaROJRNSuXYeTJ48xalQC5uaH0NcPpnHjVYwb93UN3wW+DEtLS9q3vwQo\na/ZsbPbRv3/lojVKQOA/gBCZExAQEChCbGwqsHq1F97eK6lXrwH6+no8fvyIsWNHAiCXyzExMSMt\nLY0bN64zffpk1djMTFlRmS1QhOjp6REU1J4DB35HT0+Ttm17IBZ//N1sXjVsLVo0oHfv3hw/fgIT\nE1MGDx6Bj89KXr16yZgxE3B2bohUKmXJkl+5d+8OEomEUaPGUa1aDYKDD3L27GmkUimRkRE0bNiY\nkSPHAHDq1HHu37/HqFFDKVHCnPDwdz3Tnj59zKxZU0lPT2PjxvVMnOhOcnIS06dPJisri4oVK9Op\nU7e/js4pn59T2l75uWbNOjx9+pRDh/xxdJSjqanF7Nnz0dbWJjk5mdDQ3+ncWTlfWNhlAgO3sXDh\nsvy5CQK5EIlEeHu70KDBceLjM+jUyYkyZcyL2iwBgX89gjMnICAgUISUKVMWP79tnD9/Fl/fNVSr\nVgMrKxt8fPxyHJeSkoy+vj7+/gFFZKnAt4SOjg49e346AhUUFMj+/buxtrZhw4YtOWrY0tPTqVu3\nLm5uI5g69Wc2bPDBy8ubJ08eM2/eTJydG7JnTxBisbIJ+fPnTxk3bhTbt+8B4OHD+2zcGICamjq9\ne3fFxaUnIpGIc+fOYG9fhdjYV4SFXcbExPQva0RUr16DJk2a0bJlI3x9N6ns9PPbloft+1Wf27Rp\nT5s27fP8zsWlJy4uPXONT0p6y969QSpn7mvJyspCIvm6VNb85syZk5QpU07Vay8/+Nq2EWKxmL59\nhciogEBhIjhzAgICAkVIXFwc+vr6tGzZBl1dPfbt20VCQgI3b97A3r4KMpmMFy+eY2VlTcmSJTlx\n4ihNmjRHoVDw6NHDr2oSLfDvZt++XXh5ebN//x4GDOgNvKthU1dXp0GDBsTGJmFjU/6v9EcJ1tY2\nREdHA3DjRjjduvUAoGxZS8zNLXjx4jkikYjq1Wuho6MLgKWlFdHRUSQkJODkVJ1p02YBsGtXIC9e\nPMfJqXoOBywk5NRXr00mk7F//1mkUhldujizb98ugoMPAtC+fSdu3bpBZGQEbm69qVmzNnXrOpOW\nlsovv0zmyZNH2NpWZMYMDwDu3r2TZ43qqFFD+eEHW65fD6dFi1b06NHnq+3OT06fPkn9+g3+kTMn\nk8lQU/vUo59Q4yYg8L0hOHMCAgICRcjjxw9ZvdoLsViEmpo6Eye6IxaL8fJaTHJyMllZMnr06I2V\nlTUzZsxl8eJf2bTJD5lMRvPmLQVnTgCAwMCtOZyZ58+fEhUVyciRgwARW7bsRFNTk9Gjh5GRIUUi\neffvXyRS/uxBtrhI1t+eL1ucRDlGQlZWFqIP/ACZLIuwsGdMmHCEOnUMcHGp+/ULRRklGzBgJyEh\nvQF1tm1bhLHxH6xfvxm5XMHQoa7MmOHBkyePVJHssLDLPHhwj61bgzAxMWXEiEFcv36NSpXsWb58\nEQsWLKVYMUOOHQth3bo1uLvPQCQSIZPJWL9+c77Y/XdER0cxceIYHBycuHkzHDOz4nh6LuHIkWAO\nHtxLZqaM0qVLM336HO7fv8e5c2e4du0qmzf74eGxAE/POYwaNQ47u4q8efMGF5euBAUdIDj4IKdO\nHSc9PR25XM7ChcuZMmUCSUlvycqSMWTICJVyqICAwPeH4MwJCAgIFCG1atWhVq06ufavWrUux3Zc\nXBxZWVksXuz1Qf2QQF6MGjWU0aPHY2trR7duHfDz24qBQbGiNqtAuHv3DocPH8LXd1MOZ+bChfMM\nHjyCY8dC0NTU5OnTJ9y6dfOz53V0rEpIyGGqVavB8+fPePkyhnLlLLl3706uY0UiERUrVmbFiqUk\nJSWhra2Nn18QkZENiI3tRlDQY5KTT+Hm9vVOw8GD5wgJ6QnoA/DgQWmaNi2HpqYWAI0aNeXatau5\nxlWsWBlTU6W4S/nyPxATE42enh5PnuSuUc2mWbPC7dkWEfGC2bM9mTx5GjNmuHPq1HEaN26q6tXn\n6+vNoUP76dq1B87ODalfvwGNGilbP+SuLXzHgwf32bQpEH19fbKysvD0XISOji4JCQkMH+4mOHMC\nAt8xgjMnICAg8I0zb95vbNxojlRqQNOmO/D17fpd9UUrCt5/qM0v51cul39SaKSouH79Gg0bNsnT\nmalWrQYhIYfp29eFMmXKYW9fBch9Td7fzP6uc2cXFi/2xNW1JxKJhGnTZqGmpvZRp8HU1Ix+/dwY\nMsQVAwMDEhNLIJcrHej0dGtOnLiKm9vXr1cmyyLn44sYuTyn4mVet1xdXUP1WSJ5F4HMq0Y1Gy0t\n7a819x9hYVFKFW23tbUjOjqKR48e4uvrTUpKMqmpadSu/S7CmZfSZ17UrFkbfX191Rgfn1WEh19D\nLBYRFxdLfPwbjIyM839BAgICBY7gzAkICAh8w9y8eZ+1ayuRnu4AQHBwJdatO8j//te6iC0rHAIC\nNqOhoUG3bj1ZsWIJjx49xMvLmytXLvHbbwdo06YdGzasIyMjg1KlSjN16ky0tXM/gO/atQMDA4N/\nPE+3bh1o1qwlly5doE+f/ujrG+Dn9/fnK0zycqyyd2loaLB48Ypc379ftzZw4NA8v9PQ0GDq1Jm5\nxn4oSPK+QmSLFq3p2LEzmZmZNGkygPT0Kqrv9PTSP3NFn6Zjx/oEBGzj7Fk3QIK5eRCJiWlIpenI\n5QpOnz7BtGmzCQzMLawCykjmtWtXsbOrxK1bN3ny5HGeNapFQe70VSnz58/h11+XYGNTnsOHD3H1\n6hXVMe/fe4lEgkIhByAjIyPHvFpaWqrPISGHSUxMwM9vKxKJhLZtmzJixCAqV7YH4KefRpKUlEif\nPgO4fPkCPXr0+Whd3tmzp3n69DF9+w746JqCgw9y794dxo2b9PkXQkBA4LP59l4xCggICAioiI5+\nQ3p6qff2aJGYWDDnGjFiYMFM/BFiYqIJDf39k8c4OlYjPPwaoHwIT0tLQyaTER5+FRub8ixa9CsL\nFizDz28rtrZ27NiR9wO8vb3DJ+fZtMmP5cvX5JpHJBJRrJghfn5bqV69Fps3++Hllfu4osTRsSqn\nT59EKk0nLS2N06dP4OjoVGjnT0tLY8KEfXTpEkrfvj/j6tqTAQN6Ua1aSYyMUlBTu07VqluYNKlG\nvpxPQ0ODgIDOzJ27n5kzd3HwoA9durgwZIgrw4YNoEOHztja2lGliiP9+/dgzZoVf0UTlePt7CpS\ntary+qipqVGnTj18fFYyYEBv3Nx6c+vW9Y+eWyYr/HYgaWmpGBubIJPJOHIkWLVfR0eHlJQU1baF\nRUnu3r0NwO+/f/z3KiUlBSMjYyQSCWFhl3n79i0zZ85l+nQP5HI5IpFSYbRZsxZMnvzLJwVWnJ0b\nftKRg/yLjAsICOSNEJkTEBAQ+IapV68Kjo6HCA/vD4iwsDhOu3Y2+Tb/+/23vL3zTjUrCGQyGVFR\nkYSGHqFFi49HGW1t7bh37w6pqSloaGhgZ1eRu3fvcP36NZydGxITE8Xo0UORSCRkZsqoUsUhz3nK\nl6/wyXmePn2scmY/nKdZsxYA3Lp1g6dPHzN8eN7HFRU//GBH27btGTLEFYAOHTpToYJtoZ1/8uTD\nBAb2QflI8SOdO29h7dquACQnJxMXF0upUu3yJTU4LS2NGTOmEBsbi1yehavrYKZN+5nRo8fTo0cf\nWrRoQGzsS/r1646JiSmTJv2Cj89KTp48xpgxEwDlz3x0dDTjxk0iOPgghoaGzJ49n7NnT7N5sx97\n9gRx9GgIc+Z4YmRkzIYNa4mKiiAqKgpzcwtmzpz71ev4GHk5PoMHD2Po0AEYGhpSubI9qampgLKe\nb8GCeezatYO5cxfQq1dfpk9358CBvTRr1pRsZcr302IDA7dy8OA+YmKiOXHiGLq6SkVSD48ZtGvX\nkYwMKXfv3mbgwD65RFX+/PMP1q1bg1wux9DQkOXL1+SIumVfP5ksEwODYsycOVdI3RQQKAQEZ05A\nQEDgG0ZXV5etWxuyYkUgmZnquLiUw9GxYBQss3tMhYVdxs9vHSYmRty5c5cmTZpjZWXN7t07yMjI\nYP78xZQqVZp582ahoaHBvXt3SUlJZvTo8dSr5/zJZtPZqnpZWVlkZmby7NkT3Nx606ZNBxo2bIyH\nxwwN72x0AAAgAElEQVTS0tIAGD9+Evb2Dujp6ePm1gd1dXWePXtCWNhlUlJSePz4EQqFApFIhIFB\nMby8vD+6NjU1NSwsShEcfJAqVRyxsSlPWNglIiMjsLAoRY0atZk1a16eY99Po/zUcUVJjx596NGj\nDzKZjPj4eORyOUFBBwrl3A8e6PPucULCgwfvhGb09PTQ09NTbW/YsBYdHV1SU1NwdHSiRo1ahIdf\nZdEiTzQ01PH29mP9eh/+/PMcdes6q5qRZ3Phwh+YmhZn0SIvQNl/cd++Xarv09PTqV69FiNH/vTR\n/nkAWVky9u7dhaampmqso6MT7u7zWL78KlFR4cyZs4BlyxYA8OzZM9asWY+GhgYFhYVFSTZtClRt\n9+rVV/X5XTP1d1Sp4sjWrTtz7Nu0aTsAZmb69OkzCHiXFpstlOPntzWHUM7UqT/j4+OHgUExKlWy\nZ/v2rarU2WxHMD4+noUL57FmzXrMzS1ISkpSfZ+No6MT69ZtBODgwX1s27aZUaPGfnZdX0GQ/fP2\n/rV8n4Lo1ScgUNgIzpyAgIBAEfO5kuQeHnPQ1NRi3rxZaGpq8eDBPeLj3zBlynSCgw9y9+5tKlWy\nV9U5Xbz4Z571XX/++QcrVy5FU1MLB4eq71ny7sHs4cMHrF79OxkZYlxcOtKhQ6f/s3eWAVFlbxx+\nhu6yQLBAKSXEVuze1V1XxVpFReVv69qFhaBgIq4oJuiCK3Z3d6CirphgEAoiHQIz/w8jIwgoKpj3\n+TQz99xzzo2B+877nt+PVav8CQraxNat/8qyHM+fR7N6tT/Pnj1l5MjBbNq0/b1m07lV9a5du5rn\nwTEjI53Fi/9GSUmJp0+fMGvWNFav9sfEpCoHDuxl1ix3bG3t6Ny5AzVqWOHsPIw9e3YxZcoMzMws\nSEtLIzY2hgoVKhZ4nm1sbAkM3MiUKTMwNjZh6dJFWFhYUr26FYsWeRAR8QxDQ6NC+7G0rFGkdl+L\n8+dDmTjxAc+eVcLE5Aze3jUxN69c4uMaGCQDEnLuH+n7gsl5+B8w4H+yzw4d2o+jY3/atGkPwO7d\n29m//3iBWSoTk2r8/bcXPj7eNGzYGBsb2zzBgqKiokwgpDD/PJBmhrdvD6JHj7cP+U+ehDN4sCvp\n6QqIRJmEhWlx4kQIIpEIe/sm+QK5qKhIJk78C3//f4t4pr4uuYVyrl69R1xcBUaODEQsTpO1KSjw\nkkgk3L59E1tbO/T1DQBkYiq5efHiOdOnTyIu7iWZmZmUL2+Yr82X5kMlnp/i1Scg8K0hBHMCAgIC\n3wAfI0kuEolITk5i5cp1nDlzkkmTxrJixVqqVDFm4EBH7t+/R5kyZWXru5SVVdi4cT3//vsPPXv2\nwdPTDW/vlRgaGjF9+uQClf8sLCwpXbo0MTFJGBlVkD0gGxubEBx8BZA+KLVoIS1BNDKqQPnyhjx+\nHP5es+natevmUdXLTWZmFosXe/DgwX3k5OR49uwpIH2AB2jUqDHKyiooKytTrlw5dHR00NHRwcNj\nDtnZUuEHZ+eh7wnmarJhwzpq1LCS9WNjUxMdHR2mTp3JzJlTeP06s9B+dHV1i9TuazF37gNCQ3sC\ncONGQ9zd/8Hfv3KJj+vu3pj09A2EhWlRsWIi7u55rTb8/NZw4MBedHX1KFu2HGZmFri7z6JhQ3uS\nk5M4fvwoly5d5MKFc6SmppCWloaT05/07t0fO7vaLFw4l+fPowEYOXIsa9f+w9y5s5k2bQKKiopk\nZmaSlJTEtGkTyMrKYtAgR0aOHItIJCI4+ApPnz4hKiqSlJRktmzZhLFxVR4/DiMpKYk1a1agra0D\ngIfHXJ49G0BKSldUVS9RqpQ3x49HUqkSMqXQ75mcwCY5OZmRI8OJi6tOdrYeenqX2bnzEn36tP7g\nvu9j8WJPevbsQ6NGjbl27Spr1/p+cJ+SoKD7bffuHezate2DXn1Xr17O5+n3I1x7gR8bIZgTEBAQ\n+Ab4WEnyRo0aA1JZdT29Uhgbm7x5b0x0dCQvXjwvcH3XkyePKV/eEENDIwDatGnPrl3b880nt4y7\nSCSSvReJRO81lf7QQ9/7lB///fcfSpUqjYuLK9nZ2bRo0RAAU1MzGjSwR0lJGYlEQrt2v2BubgmA\nsrIyS5Ysz+ch5+29UvY6p9ywVq06HD9+XvZ5TrYQpBL+q1blN4d+t1SxsHbfAvHxKu+8/zIqm/r6\npQkI+KPAbaGhdzh27DDr1weSnZ2Fk1NvzMwsAOm90qFDJ0JCbuTxS2vduonM7HvmzKl069YLa2tb\noqOjGT16CH5+mzAxqcqjRw+oVKkKqakpBAT406/fAC5evICrqyfjxo2Q/dDw9OkTvL1X0qqVPUuX\nLqJy5SpkZ4tRV9egQ4dObN8eRN++PYmOjkBV9RUpKaCjsw5l5dtcvfqE+/dVaNOmnex45s6djUgk\nom7deiV9aosVGxtb3NxmYW1dlwcPLKlYcT3R0Z5IJOsICUkqdD+RSET16lYsXDiPqKhIDAzKk5iY\ngJaWdp4fZFJTU2Q+fvv37ynx4ymIgu43c3MLmjZtTseOnYD3e/VpamoW+AOagMC3jBDMCQgI/NTk\nrBOLjY1hyZIFzJnjUaT2xc3HSpLniEnIycm9s6/UP0tOTr7A9V337997Z+RPX88ikUg4fvwI7dt3\nIDIygsjICCpVqpzHbNrHx5vbt28yc+YUTEyq8fTpY7ZtC6JzZwfU1TV49OgBgYEb6dmzN8HBl4mK\niuLixQsYGBggFouJiorE1XU6AI6O3fPJ7Oco+mlpaRMcfI9Fi+6TlqZEixYwbFjhmYZPOdbNm0/w\n8mU6v/1mh5FRuWLru7ioUyeR0NBUQA2RKI569TK+9pQICbn2prRPGVCmUaMmBbYrbF3VlSuXePw4\nTPY+KSmJQYMciY+PR15env79B/H330v4779bLF7sSUZGOpMnjyE1NZWsrCxEIhENG9pz//5dsrPF\nVKxYkV69+jJ/vhvq6hrs3r0DKytb3Nw8mTFjMqdOLUNHJxBIQE1NnZ07dzJq1BAuX75Iv34DmTt3\nFmPGTMLGxpbly71K4IyVHDlCOUuWuGFikk5s7AAyMiwAMZUrS/+G5Fb9zI2Ojg4TJkxl6tTxiMUS\n9PT0WLRoWR5xFScnZ1xcJqKpqUWtWrWJjo7K1eeXUbQs6H6TSCiyV1/+dvULGEVA4NtCCOYEBAR+\ncqQPGaVLl/lgIJe7/ZfgXUnysmWLFkDk/JJe0PquSpUqExUVKfv88OGDefZ7+7rwvnO2iUQiypXT\nZ9CgvqSkJDN+/GQUFRVlZtPdu/9BTMwLPD0XY2VlS8+enbG1rcmxY4fp3NkBE5OqxMe/Yu/eXURE\nPKVUqTIkJ6cgEkFY2COZOEVsbAxWVjYsX74633x+++0Pxo4dgZ5eKa5d68L9+z0AuHTpMWXLnsPB\noWGRztn7kEgkjBgRRFBQZyQSHTZs2Mn69emYmVX67L6LEw+P3yhXbg+PH8tjYSFi2LBfv/aU+Pzv\niwRfX798Sphr1/qiqqqGubkF3t4r6dChVaHtFBQUuXnzBv37D+TEiaPY2trRunU7zp49hUgkws3N\nEwBn52E8ffqUJUv+pl+/XmzbtheAyZOn4+IyieTkZJKTk7Gxka4zbdv2Vy5cOPeZx/dlyRHK2b8/\nmCVLokhL206TJgMZOlTqG1izZi1q1qwla587w12/fkPq18/7fcrtOWhv3xR7+6b5xnzXl7BkKfh+\nK6pXn7v7LObNW1RgOwGBbxXBZ05AQEAAqZiBo6O0nGbfvt1MmTKesWNH0qNHZ5Yvz2+6HB8fz+DB\nTpw/f5bY2FiGDRtE//69cHTsLvMz+xjeJ0k+ZMiAfAv08wZeeff181uLoqICU6fOZMqU8bRo0ZDB\ng51Ys2YFW7duZsKEqUyYMBonp97o6ZWSBWc5ZtF2drXx8HhrBO3tvRIzM3NA+rCXe1udOvVYvdqf\n2NgYGjSwB96aTXfp0o0//3Skbt0GqKqq0qHD71Svbk18/CtiY2MJC3tEtWpmbNy4GRUVVe7cuY2c\nnOhNwCgnMxnW1y+fJ5D7668JsofDLl26ExCwFWfnUdy/bydrk5FRiWvXEot49t9PZGQEu3bZIJHo\nAiIePuyEn9/tYum7OFFQUGDChPZ4eDTE0DBBtmZswoS/vtqcbG1rvvHAyyA1NYWzZ99mtYuiclin\nTn2Cgt4qPObPLBe1nSifUEpmZmaBfcnLy5OVlc0ff+yiUaMjTJ16ALFYnK/d11Rp/Fzat7fj4MFf\nOXWqFXPm/F5o5qwo3pM3blyjd+9uODn9SVzcS/76awfduh1i2rRd+czLi4tr165y69ZbP8AdO7Zy\n4MDeQu+3tLSUInn1FebpJyDwLSNk5gQEBAQK4MGDe6xfH4CCgiK9enXBwaEHZcqUBeDVqzgmThyD\ns/NQateuS2DgRurVa4CjoxMSiUQmrV9UPlaSPEetsqB9c2+zs6vNvHkLmTjxL/z8AmWCBPXqNeCf\nf97KuRfG+9bG5Sf/w+C7D4hSGwFo3rwVJ04c4eXLl7Rq1Ua2vXfvfvz+e+c8+0RFRaKqqiLbf/bs\nPZw9q4aGRhrjxpnQsKF0/VWlSoYYGt4gIsL4zdhxVKnyab5mmzZtZN++3QB06NAJMzNzDAxmkJJi\nj6rqNbKyyiEWN/ukvr8ESUmJbN8exB9/5L93vjSmpua0bNmafv16oqurh6Vlddm2wn6QyP169Ohx\nLFrkQd++PcnOzsbW1o5x4ya9aUeR21lb2+Dp6S77fl65cgkDA0MePw5j5sypzJzpxoEDe6lZsxbq\n6hrEx8sTHm5Genpt4uK8sLLSe2OzoElIyHWsraWlxJ9LUNAmdu7cipmZOS4urp/dX3FTFO/J3Gqk\nAwduZdcuR0COEycyyMoKYt683/O0z8rKQkHh8x4/g4OvoKamTo0aUp/HTp26yLa9e7+JRDBw4OAP\nevW5us4rtJ2AwLeMEMwJCAgIFECtWnVRU5Ma6lauXIXo6CjKlClLVlYmo0YNYezYSdjY1ATA0rI6\nc+fOJisri8aNm1GtmmmRxti/fw+bNv2DSCSiatVqDBw4GHf3WSQkJKCjo8uUKdMpV04fN7eZqKtr\ncPfuf7x8+ZKhQ0fSrFlLYmNjmTFjMqmpKWRnZzNu3GSsrW3p2rUja9duREtLm61bN/P06ROGDh2I\nRCLHvXv3uXjxLhDH/ft3SU1NRUdHBy+v5VSsWJlhwwYRFvaQjIwMTE1NmTbNlalTJ/DyZSwVK1bC\n2tqWo0cPsWTJcu7fv8exY4e5ezeU9PQ01qxZydmzp8nOzsLVdZ5McKF3776IxRJOnz6Bi4srCgoK\neHjMISEhnr//XgVAvXr1WbVqBW3atEdVVZWYmBcoKOQNxnx9j7F8eVskklIAPH++hSNHKqOqqoq2\ntg7u7posWbKJ1FRlmjRJZuDA39895R8kx4tr1So/mRdXzZquKClFExXVnhcvZmFq6oCVVcqHO/tK\nrFjhTUTEM/r374WCggIqKqpMmzaRsLCHmJlZMH26NGg4f/487u5zyc7OxtzcknHjpGWyPj7enD17\nGnl5eerWrc+wYaN49epVPlVJKyubIs3H0dEJR8fCMzy5f4CAtxliAG1tHWbNmptvHycn5zzvi9LO\n3r4Jhw8fYMECd0xMqlK/fkPMzCxZsGAuffv2lNl3iMVikpJ6UqbMfOTk0nj9uiKKim1kc5UKoEiz\ngZ+7FmzHji14efnIhEOgeIKd4uJd70kdHd0899Hu3TtkaqQXL54jNLQppUvPR139DADXr0tLNoOD\nr7B69Qq0tLR4/DicCROmsmbNSjQ1NXn48EGhXpYFGZGnp6eza9c25OTkOXRoH6NHT+DKlYsyP7kG\nDRpx5swpUlJSSE9P59dff0dTU5MjRw5RvboVwcFXSE5O4saN69jY2Mq8+pKSErGwsMbff9N7hZoE\nBL41vo2/FgICAgLfGPkFSaRZKgUFBczNLblw4ZwsmLOxqcnff6/i3LkzuLvPpHv3P2nX7v3rlR49\neoi//1pWrlyHlpY2iYmJzJkzg19+6Ui7dr+yd+8ulixZwNy5CwCIi3uJj89awsPDmDRpDM2ateTw\n4QOyjKBYLCY9PR14m9kIDb3DuXOnMTQ0olmzznh5zebVK0ceP66AgcEc1qzxo3JlY7p27cjcua64\nukqNvq2ta+LpuZhJk0YzZco4xo+fgpfXAoYOHcXEiX9hYFCe+fPdsbCwpH79hrIHUR0dXdau3cj2\n7VsIDNzIxInT+OWXDgwa1BeAjh3/kAW6aWmplC1bDj09aWBWp059wsPDGTy4PyAtf3Jxcc0jnnD/\nfrYskAMICzMnOjqKKlWk2bj27e1o3/6TLreM3F5cAE2btuDGjWsYGhoxcWIi0dFbyc6uR1ZW+ucN\nVIIMGTKSsLBHrFsXwLVrV5k8eSwbNwZRqlRphgwZwM2bNzA1NWfy5MksXrwcI6MKzJkzg+3bt9Cu\n3S+cPn2CgICtgNSUG8DLa0EeVclx40awcWPQ1zzMj+b33zsTGlqOiAh5wsN96d27P9WqmbJy5bp8\nbY2NVTl9ehPSjHMKDg5SVVMzM3PWrw+QtXvX1PxjmD/fncjICMaOHcHz59E0atSEyMgI9PUNGDVq\nHAsWuOcLntPS0li82JOwsEdv1BqdC1ynVnzk9p68l+c+Cgm5TseOnbh5860a6cWL80hJieLx413I\ny79EQ6M9L19Kv//3799lw4bN6OsbEBx8hQcP7hMQsAVNTa1CvSwLMyL//fcuqKmpyXwCr169JMvU\nzpkzgzFjJmJjU5M1a1aybp2vzKpCLBazapUf58+fZd06X5YsWQ7A/v3BTJ2awLNnplhYHOfvv82o\nUcOkBM+rgEDxIQRzAgICAh+FiMmTpzNt2gT++cePP//sS3R0NGXKlKFjx068fv2a+/fvfjCYCw6+\nTIsWrWWS+lpaWvz3301Z8Na27S/4+EjX6olEIho3lj6wVa5chbi4OOD9GUGJREJIyDXq1WvAkSOH\n8PX1JjGxI1lZZRGJ5BCLJbi6zkBBQZ709HRiY2O4c+c2pUqVpk2bdigoKNCmTRvc3NxYuHAejx+H\n4+npRlpaKq1bt2PVKh/KldPHxqYmVlbWLF7sKZP3NjU15+TJY8BbwYV3yV0amoODQw8cHHoU2tbM\nTAE5uVjE4tIAGBvfwcCg2XvP88dSWKZFSUmRDh0aARAYuJG0tG+3/Cr3Wi6JRIKFRXVZwF21qilR\nUZGoqKhiZGSEkVEFQCpSsW3bZrp06YaSkjJz586mYcPGMguMd1UlU1NTSU9PR0Xl+/Hg6t17DDEx\nYkSi1yQmdiYo6CEuLhYFtvX2bszMmf8QG6uOlVUakya1JzLyBfv2BVOhgi5t236+LcH48VO4dOkC\n3t4r2bLlX86dO8Py5atRUlLKZ8mQEzz7+6+ldu26TJkyg6SkJJyd+1K7dr0vch3evY+io6Oxts7b\npk6ddLKz9VBU3ImxcTwmJnW4c+c/1NXVsbCoLjMdl/ZnKfsxpzAvy/cZkRe0ZDElJUekRvpDW7t2\nv+LiMkm2vWnT5oA0KM9R2wRYvDiKZ8+kf3vu3DFnwYJA1q8XgjmB7wMhmBMQEPipKWitzvuktHO2\nzZzpzsSJY1BTU0dFRYXAwA0oKCigpqbOtGmzijRuQQIKhYkq5Fbpy2nz4YygCIkENDQ0EIuVUFB4\nTkaG2ZttCvj4rEZDQ5MJE/6iZ8/esixMzoOhWCxGUVGJdesCmDfPlapVqxEaegdra1uys7O4dSuE\nkSPHyOaTk82Ul5f7yPV2+fH03M/u3QrIy2fj5KSOo2NjBg5szvPnezlzRhlNzdeMG1e12B9i3y0N\nPXXqOC4uswv04vteyO0ZmHNtClrPKN0uz6pVfly5cokTJ46ybdtmvLx8KExV8nvi1au+PHnSSfY+\nJGRroW3Lly+Lr+/bMt07d8JwcnrEw4ddUFSMwslpF66uvxXLvHLOvb19E5SUpNeqoOA5LS2NS5cu\ncPbsKQIDNwCQmZnJixfRVKxYuVjm8j7y30dZ+dro6WkxfHhVfv21JQCurjdk95qKSt7SxaJ4WRa3\nEXnOGLmrLQCSk/P+HUlJUUJA4HtBCOYEBAR+anLW5+QWEnlXStvTc3G+9oqKiixa5C37/GOlt+3s\n6jBlyjh69PjzTZllAjVqWHP06CHatv2FQ4f2y35dLoy8GcGMPBlBkUiErW1Ndu7ciry8PG5u0xk+\n3InsbG0yM01QUVHi8uWLNG/eColEQmRkBPXrNyQu7qVsDd6xY8coV64cx48feVPutJyOHTthamqG\nvLw8GRkZqKmps337h8VUPoZdu87j7V2fjIyKALi6XqJ27QdYWlZl2rSSlTjP8eLKXRqqqamVL/j5\nUr5Zn4KamtoHhRsqVqxERESEzKLi4MF91KxZi7S0NNLT02jQoBFWVjZ07y4NaHLUInv16gPA0KED\nmT9/CRIJHD58QCa2Ehx8hU2b/snzncnBw2MO3bv/mU+Z9UtRunQKjx7lvJNQunTRs6urV4fy8GE3\nADIzDdm8WZ/x4xPymdV/DjmlvTnzKyx4dnObT4UKFYtt3OIgJyC1tq7Jzp3baN++AwkJCdy4cY3h\nw0cTFvboAz0UTGFG5O+qUErnAOrqGmhqasnWw+WI2nyIRo0SePAgAdBGWfkJzZsLYu8C3w9CMCcg\nICDwidy9G8a1aw9p2NCSihXLf9S+VaoY4+joxPDhzsjJyWNqasbo0ROYO3cWAQEb0NXVzSMMUVAG\n8dq1K+/NCJqamtOwoT1btvyLr+8iGjduxPXr52nXrgzJyc3Ys2cXfn5riYh4RqlSpfj1198wM7Ng\nzRpfNm36h1atWvLXX5NYsGAe0dGRxMS8IDk5GTk5OUxNzXj27Bl9+/YoYM3O55kE37uXIAvkABIS\nbLl+fQ+WllU/uc+PIXdpqEQi4fLlEAYNGicTpsitNvotoq2tg5WVDY6O3VFWVpaVsuVGSUkJd3d3\nXFwmkp2djYVFdTp16kp8fDyTJ499IykvYcSIMUDBapHq6hpERUUWWTlz4sRpxX2oH8Xs2RZMmbKR\nqChNTE1fMXNm0deavZswF4vlCrQrKC7eDZ7v379HtWqm1K1bny1bNslsO+7dC8XU1LzE5lEU78nc\n7Zo2bc7t2yH069cTkUjE0KGj0NXVIzw8LM/+hZmTv7utMCPyRo2aMG3aRM6ePcWoUePzzG/q1Jks\nWDCX9PR0mahNISPJXnl4dKJy5SM8fizBzk6DHj1aFX6wAgLfGCLJN2KUEhOT9LWnIFBClCmjKVzf\nH5if9foGBp5l1ixt4uLsKF/+DAsXKtGype3XnlaxUti1zcrKIj09DQ0NTeDtr/LFla06c+YW/fur\nkpAgPZ+GhofZtasSFSoYfGDP4kUikTB8eBBbtzZHLFahRYvd+Pt3lZXCfe+877sbEOCPkpISXbv2\nYOnShTx8+AAvLx+uXr3Mnj07uXUrhNWr/Vm0yIMzZ05RsWIl6tSpR4MG9qxd64u2tk4+9czhw50Z\nMWIMZmbmtG7dGAeHnpw7dwZlZWXmzVuIrq7eFznu7Oxs5OXlP2qf69fvM3BgFE+e/IqcXAy9e+9l\nwYIuH97xAzg4/M7q1X5s3bo5j6BHQkI8ixZ5EB4ensdqISMjg6VLF3LrVghisZjy5Q3z+D7m8LP+\nXf5ZEK7vj0uZMpofvY+QmRMQEBD4BNasSSIurh0AkZEt8fXd/MMFcwURGHiOhQuTSUrSoU6dhxgZ\nyXP0aCkUFTMZNEiV/v0/X1nP3r4Gc+acZevWLSgoiHF2NvzigRzAoUMX2LLlVyQSfQCOHevH+vW7\ncXZu+8Xn8qWxsbFj06aN3Lp1k5Mnr5CRocavv+6gQYNQbG3tuHUrBJFIlEc5E6Rllvfv382nnmll\nZZMn2E9PT6dGDWucnYeyfPlSdu3aTt++A77IsX1sIAdga1uNzZtV2b9/M/r66nTu3PnDOxWBoKCd\nQNGsFtLT03n27ClDhoyQ/ZAi8GHOn7/DiROPMTJSoXfvpt90ibSAwKcgBHMCAgICn0BWVt4HwszM\nj39A/N5ITk7CwyOTyEhpRuLQoSbAv4BUVMLd/QL29mFUq/b5a6K6d29E9+6f3c1nkZCQhkSSe02U\nEqmp30QxS4ljZmbO3bt3yMjQJTm5FKmpDXj2zIqkpH/o3bs7GzeuBwoW7MmvnhmVz5NOUVGRhg3t\n34xlwZUrF0v2gIoBY2Mjhg0z+ipj3779iOHD/+POHRsMDa/g6qrFL798eC3Yz87evZcZM0aDV68c\nEIlecvPmdjw9iycQFxD4VhBWeAoICAh8Ar/9JkZZ+TEAmpq36dz5+5Fo/1Ti4+OJjc39MKsIaMne\nJSRYEhr67IvPq6To0KE+tWoFAtK1Uaamm+nWze7rTuo9REVF0qtXF9zdZ9GzZ2dmzZrGpUsXGDzY\niR49OnPnzm3WrFlJYOBG2T59+nQjOlrqZbZ//x769u1Jv369mDfPFQMDQ5KS4hGLVVBTO0X58s5k\nZcV8UHyjKKqH8vJvf0uWkxN9tvrpj87Chbe5fbsnYrElT5/+xqJF0V97St8FO3a84tWrugBIJKU4\neFCXrKz896OAwPeMkJkTEBAQ+ATGjGlLtWoXCA29RJ06BjRr1uRrT6nEMTAoT82a27h40QYQoaJy\nCzm5RHKEE6tUOUGDBtbv7eN7Qk1NjX//bcvKlUFkZYno3duO8uXLfu1pvZeIiGfMmePJ5MnTGTjQ\nkaNHD7FixVrOnDmJv/+6PF6E8Had47sm9klJSQQFBXL9+jUkkrI8e/YPlSr9jpxcfJ4yxaIoZwp8\nPikpynnevyulL1AwCgp5AzclpUzk5IQ8hsCPhRDMCQgICHwiHTvWp2PHrz2LL4e8vDxr17bAwyOQ\nlBRlWrTQRF6+LDt2bEVRMYthw6pSunR+5cTvGS0tLcaP/+VrT6PIGBgYYmwsNTuuUsWY2rXrvvOR\nnUEAACAASURBVHltQnR0ZL5gTookn4m9pqYmNjY1EYtXU69eJV6+PEFsbHY+Vcfcypn16zeiQYNG\n71U9zKEgdVaBwmnWTI5z5568UXlNolGj+K89pe+CoUNNuX59Ow8ftkRT8x4DBigKwZzAD4cQzAkI\nCAgIFJkyZUqxYEHeCLaYtCAEioEc43YAOTk5mU+ZnJycTMVRInkrqS+1ICjYxL5WrTq0b/8rDRvW\np1mzlkAbWreWZqCDgnbJ2s2YMSfPfrl9vXIk9AG8vVfKXuf4NQI0a9byTf8ChTFkSCt0dc9w9eol\nKlYUMXRopw/vJICVVVX27SvFmTNnqFatPObmzb/2lAQEih3h5wkBAQEBAYH3MH78KFJSkklOTs5j\nkB4cfIUJE/76ijP7eAwMynP3bigAt2/fJioqEhBhZ1eH48ePkJiYAEBiYmKJjJ+QkMCkSbsYOvQQ\nmzadLZExflR69LBn/vy2jBjR5pMUOX9WdHV16dixMebmJl97KgICJYKQmRMQEBAQEHgP8+d7AVKB\nka1bNwHwxx9duX//Lnfu3P6icwkOvsKmTf/g6ZnfWwzylyy+W87YtGkLDhzYS58+3bCzq0mFCpWA\ngk3sc8yWi6skUiKR4OR0gNOnnQA59u69h5zcObp1a/jJfQoICAj87Aim4QIljmBu+WMjXN8fl5/l\n2n6MQfbp09LywK5du1O6dBnWr1+DnV3tfAbZuRGLxcW2TudDwdzH8KWvb2xsLHXrRpGc/DZ469Zt\nK8uWtflic/hZ+Fm+uz8rwvX9cfkU03ChzFJAQEBA4KfGxsaOGzeuAxAaeoe0tDSysrIICbmOra3U\niiDHIFtRUQmRSMTlyxfZsWMrKSnJvH6dAcDFi+cJCZH207VrR3x8vHFy6s3x40c4fPgAffv2wNGx\nOz4+3rKxW7duLHt9/PgR3N1nAVJVSmfnfvTt2wNf3+WytWoAaWmpTJs2kT//7Mrs2S4lck7S09MZ\nP34nf/xxmBEjthdL2aWmpia6us9zfZKNru7rz+5XQEBA4GdGCOYEBAQEBH5qcgyyU1NTUFJSokYN\nK0JD73DjxjVsbGrK2kkkEvT09DA0NGLdugCsrW0Ri8VMmDCVjRuDkJeX4/Jlqfm1SCRCW1uHtWs3\nYmNTkxUrlrF06QrWrQsgNPQ/Tp8+8abXgksYvbwW0L17L/z8NlG2bLk8871//y6jR49j48YgIiMj\nZAFkcTJ16n78/Lpz9mxn/v23N3/9dfiz+1RWVmbSJE0qVdqKtvYJmjdfy8SJzT5/sgICAgI/McKa\nOQEBAQGBnxoFBQUMDAzZt283VlY2mJhUJTj4MhEREVSuXKXQ/apUMUZLS5vSpcsAoKOjS1zcS9n2\nli1bA3Dnzm3s7Gqjra0DQOvW7bh+/RqNGzcrtO/bt28yb96iN+3b8vffXrJtFhbVZWNWrWpKdHQU\n1ta2n3bwhXDvngZSU3gAOe7f1y6Wfh0c6tGpUyYpKcloa9sJtgSfyKZNG9m3bzcAHTp0okmTZowZ\nMxxzc0vu3QvFzMyUCRNcUFZWITT0DsuWLSYtLQ1tbR2mTp1BqVKlGT7cmerVrQgOvkJychKTJk3H\nxqZ47yMBAYGSRwjmBAQEBAR+emxsbAkM3Mj//jecVat8SEtLw8LCkoCADSQlJbFz5zb2799DZGQE\nKiqqgDRIS09PA8DNbSYvX8Zy6tQJLl++SFpaGqqqqojFYnbu3MbNmzeIjY1BQUGBcuX0ZX3kDmYy\nMjKKNFdFRSXZa3l5qeVAcVO+fAogISdzaGiYXGx9KyoqoqOjW2z9/WyEht5h//49rFrlh1gswdm5\nLzVr2vH06ROmTJlBjRrWLF48l23btuDg0IMlS+bj4bEIbW0djh49hK/vciZPno5IJEIsFrNqlR/n\nz59l3TpflixZ/rUPT0BA4CMRyiwFBAQEvnOioiJxdOz+tafxXRMf/4rnz6M5evQg8vLyKCsrY2NT\nUxZsbdmyCX//f7G3b0p6ehrLly8lPDxMtn9qaiqJiUnY2zfB03MJSUnSNWYnTx4jMzMTTU0tRo0a\nx61bN7l584ZsLZ6enh6PH4cjFos5deq4rL/q1a04fvwoAEeOHPrg/IOCNtG7twOursWzhs7NrQlt\n2/pTteoOmjXbwNy5dYulX4HPJyTkOk2aNEdZWQVVVVWaNm3B9evXKFu2HDVqWAPw22+/ERJynSdP\nHhMW9pDRo4fSv38v/P3XEhMTI+uraVOp75qZmTnR0VFf5XgEBAQ+DyEzJyAgICDwQ9G6dWMOHz5N\nbGwMS5YsYM4cD/bt283du3fymFjn5urVy+zYsZ/MzEwmTvyLwMBtAAQGbqRbt57cvn2LmTOn0rRp\nc+Tl5Th//gzh4WHo6+sD0gybiooy1ta2VK5cBbFYaswdEnKDdu1+RVFRkRkzJpOdnY2hYQXs7aWC\nJoMHD2fChNFoa+tgYWFJWpo00zdy5Fhmz3Zhw4Z11K1bHw0NDdlcC6pM3LFjC15ePrLyS4CsrCwU\nFD7t33zp0nps2CC4wX+LFFSaKhLl/Vwikbx5L6FKFRNWrFhbYF85WV45OfkSyfAKCAiUPEIwJyAg\nIPADIBaL8fBw49atG5QpU5a5cxdy8OA+du/eTmZmFkZGRri4zEZZWYVjx46wfv0q5OTk0dDQYNky\n3689/WJG+lBbunQZ5szxkH7ynrVZ8+e7ExkZwdixI4iKikJZWVm2LSDAj9at2zN27ESGD3cmPPwR\nERHPsLdvRlhYGLGxCYwfPxYVFQU0NDQJCblBQIA/IpEIZWUVRCKIi3tJcPBVFBQUUVRUwM6uFiAt\nzVRSUkJbWwdra1uGDx8tG7dMmTL4+q4H4MiRgzx9+gQAO7va2NnVlrX7668Jeeb//Hk0jRo1ITIy\nAn19A/73v2G4u88iISEBHR1dpkyZTrly+ri5zURHR5OQkFu8ehXHpEku7Nu3m9DQ/7C0rCHzmBMo\neUJD73DgwF5Gjx5XpPY2Nra4uc2id+++iMUSTp06jovLbLy8FnLr1k1q1LBiz5492NjYUrFiZeLj\nX8k+z8rK4unTJ1SpYlzCRyUgIPClEMosBQQEBH4Anj59Qpcu3diwYTMaGpqcPHmMZs1asGqVP+vX\nB1CpUhX27NkJgJ/fahYt+pv16wPw8Fj0lWdecuQuP81tqXru3BkGD3YiISGeS5cu8PDhAyQSMDAw\npHNnB9LSUklMTOD169ekpqYikUiIjY0hNjaGiROnoaWlzblzVojFirx40ZnTp38hOTmVly9jZddA\nJBJx8uQxrKxsCAjwZ/Toccyfv4TMzCx27dohm0tsbAwrV67LE8gBhIaG0q9fL/r27cmOHVtl2x8/\njmTDhoPcuHFP1nb8+CmULl0Gb++VdOvWi/DwMLy8fJgxYw6LFnnyyy8d8fMLpE2bdixZskC2X1JS\nEitXrmPkyDFMmjSWXr0c2bBhMw8fPuD+/XsIfBnMzS2KHMgBmJqa88svHRg0qC//+18/Onb8A01N\nLSpWrMT27Zvp3duBpKQkOnXqioKCAq6uHqxY4U2/fr3o378Xt2+HFNLzlxGjGT7cmdDQO19kLAGB\nnwEhMycgICDwA2BgYEjVqtUA6fqXqKhIHj58wKpVPqSkJJOamka9eg0AsLKywc1tBi1atJatmflZ\nOHnyOJs3B7BgwVKysrLw91+Ll9dyevfuRtWqVQkJuUGdOvUYNKgvZcqURVFRiezsbJYuXYicnBzz\n57tjbl6Xdev6UrXqMkDEo0edqFTJD11dPdk1kJOTIyoqEgeHniQlJeHo2ANFRQUkEkhNTQGk2cLm\nzVsVmDW0sbFl/fqAd+Z+k9GjU4iI6ISW1k0mTTrJwIFNZdtzAtbGjZuipCQtn/vvv5vMnSsN4Nq2\n/QUfn6W5xm4GQJUqJujplcLY2OTNe2OioyOpVs20mM76j09UVCRjx46gRg1rbt68gbm5Je3bd2Dd\nOl9evYpnxgypmbyX10Jev85AWVmZyZNnULFipTxG8GvWrOT582iioiJ5/jyabt160rVrj3zjde/+\nJ927/5lnfHl5eVxcpOPkNpWuVs20wOy7t/dK2WsdHR2CgnYWy7nIuQ8Ly4aLRCJBxVRAoBgRgjkB\nAQGBHwAlJUXZa+n6lwzc3Wczb95CTEyqsn//Hq5duwrAuHGT+e+/W5w/f5YBA/qwZs0GtLSKR3r+\nW+bq1SuEht5h8eK/UVNT4+zZ04SHP2LwYCdiYl5w9OgR1NTUqF+/IXPnLgSgR48/6NXLEYlEzMSJ\nf+Hv/y8nTlzG3z8GUCAmZhqQRv36v3Lt2jbZWM7Ow94oXUrQ0dFl166DJCTE4+zcL8/6JRUVlSLP\nf/XqCCIiHABITKyJn99DBg7M305ZOW+fubOSuVFUlN4zcnJy79w/JaOQCTBkiBM+PgWv3/reiYh4\nxpw5nkyePJ2BAx05evQQPj5rOXPmJP7+63Bxmc3ff69CXl6ey5cv4uv7N3PmeObr5+nTJ3h7ryQl\nJZlevbrwxx8OyMvLf3D8DwVI69ev5tCh/WhpaRMZmU1mZkVMTKqgqHiVxMREVFRUmDhxKhUrVsbN\nbSbq6hrcvfsfL1++ZOjQkTRr1hKAgAB/jh8/wuvXmTRp0owBA/5HVFQkY8YMp3p1K+7evcP8+UvZ\nuHE9oaH/kZGRTrNmLRkw4H+fdmIFBATei1BmKSAgIPCDkpaWip5eKbKysjh4cJ/s84iIZ1ha1mDA\ngP+ho6PDixcvvuIsvwwikQhDQ0PS0lJ58uSx7PPateuxbl0AZcqUZcWKNXTv3ou7d0MBuHs3lKio\nyHx9NW1amz//PIpEIkJO7jbt22+ga9cGedqIxdlcunSfxYtPk5qaSteuHRk2zJm+fQfw8uXLfH0W\nhezsvA/rWVkffsCvUcOao0elapiHDu3PY4L+NfhRAzmQZseNjU0QiURUqWJM7dpSBdAqVUyIjo4k\nOTmJadMm4ujYnWXLFhMW9ihfHyKRiIYN7VFQUEBbWwddXT1evYorwtjl8fPbVOj2O3duc/LkMfz8\nNiGRtCY6OplHj6w5ezaYlJSarFmzgaFDR7FwoYdsn7i4l/j4rMXTcwkrViwD4NKlCzx79pRVq/xZ\nt+4f7t4N5caNa4D070rnzg5s2LAZfX19nJ2Hsnq1P+vXB3L9ejAPHz74qPMpICBQNITMnICAgMAP\nQEG/yg8c+D+cnfuho6ND9eo1SE1NBWD5ci+ePXuKRCKhdu26stLAHxmJRIK+vgHDho1iypQJuLrO\nw9KyBosWeRAR8QwQkZ6egYlJNQ4c2EufPt2wtKxBhQqVZH3knGORSMSCBV2YO/c/goOHY2Jig6Ji\nM9l2iURCUFAIoaGWxMU5YGAAlSptJjs7nYCADbRq1UZ2zj+m3MzBQZsrV64SH18LZeUndOr0OtfW\nt/3k7nL06AnMnTuLgIAN6Orq5hE2yT32u/MoqTK4HKXR4OArrF3ri46OLmFhDzEzs2D6dNcSGfNL\n8W52M3fmMzs7m9WrV1C7dh3mzl1AdHQUI0YUnKlSUMjbT1bW52dJb968QePGzVBUVOThwzIkJ7dA\nJMpAVfU6oaGP6d//GACZmVmA9Po3biwt4a1cuQpxcdKA8tKlC1y+fJH+/XsBkJaWzrNnTylbthzl\nyhlgaVlDNuaxY4fYtWsH2dnZvHwZS3h4GCYmVT/7WAQEBPIiBHMCAgICH8GnlonlXhdTVNasWYma\nmjo9e/Z+b7t3f5XP3b5Tp6752ru5zS/yHL5HCgpSctbpVKxYmRkzXHFxmYSn52KmTp3JzJlTUFNT\nY8KE0Tg7D2XRomUF9vtu5mPyZJcCt0dHRxEcPIj09DoAREU5oKsrYsGCtoDU0y409C5jx07Ko5z5\nIf74oz76+rc5fz6IatW06djxF9m2nPVOTk7OefbR19fHy8snX19TpsyQratKTX1N375/kZycjIaG\nRgkrWb69Ng8e3GPjxiBKlSrNkCEDCAm5jrW1bQmO/fWQSCSkpCTLrCP27t1VaLuSQSTr28AgmchI\nADFisSbGxgNYt65Tvj1ygtF359W7dz9+/z2vbUVUVCSqqm/LeyMjI9i06R9Wr96AhoYG7u6zeP06\no3gPSUBAABCCOQEBAYGPojjLxD7kfVbc2ZGnT6M5ePA6lSrp0br1j2sCfejQSSBvkNu+fQfat+8A\nQLVqZmzcuBmA8uUNWbXKv1jHV1FRQUXlGenpOZ9IUFTMBCAo6AKzZ2fz4kUVrKwO4utrh7GxUZH7\nbtCgOg0aVC+2uS5bdoRFiwxJTrbB0vII69fXpHJlw2Lr/32Ymprj4TGHmJgYXryI5ujRQwQHX+Hs\n2VNkZGRQo4Y1EyZMBaQKiGZm5ty4cZ20tFSmTZuFv/86wsIe0bJlawYNGgLAwYP72LLlX7KyMrG0\nrMHYsZOQk/syK0rel92Uk5OjZ09H3Nxm4Oe3hgYN7Ckomyr90aH452ZtbYOnpzt9+vTHxcUGZ+fl\nZGQ0QFVVmQ4dpJk/iUTCw4cP3pupr1evPqtWraBNm/aoqqoSE/MiTyYxh5SUFFRUVFFXVycu7iUX\nLpyjZs1axX9gAgICQjAnICAg8DEUpUzszp3bLF26kLS0dBQVFfNlRnIybjo6OgD06dON+fOXoq+v\nj5/fGg4c2Iuurh5ly5bDzMwCkK5HWbTIk/j4V3mECopKSMh9BgyI4PHjrigpPWXgwN3MnNmxeE7K\nd0ZmZiZz5hzg4UNlKlRIZ/r01qiqqhZb/7q6ejg5vWT58uukpxthbb2PUaPskUgkLF4cx/PnUruE\nkBAzFiwIYPnyogdzxUlGRgarVsmRnCwN7P/7rydeXptYvPjLBHMpKSkYGlZg/nwvFi/2pEoVY1q0\naEO/flJVF1fX6Zw9e5pGjRojEolQVFRi9Wp/goI2MWnSWNat+wdNTS26d+9E9+5/Ehf3kmPHDrNi\nxVrk5eVZsGAehw7tp127X0v8WN7NjufObubelmNGD8gC0Nzege9mVv39/y2W+ZmbW2Jv34S+fXug\np1cKe3tb6tevSa1a/2PBgnns2bOVrKysQkuAc17XqVOf8PBwBg/uD4CamhouLq75FCqrVTPF1NSM\nXr26ULasPtbWNsVyHAICAvkRgjkBAQGBjyJvmdjChctwc5vBpUsX6Nz5V6ysbLh27Sq6unpkZGQw\natRYHj16yKJFnsTEPGfIECdMTc1RU1N/26NIxNWrl9m8+R+ys7MZPnw0fn5rOHnyGOHhj+jUqQue\nnm6MHz8FI6MK3L59i4ULPQosnyuMNWse8PhxNwBev65IUJAuEyakoqamVnyn5jth6tS9rF/vAKgA\nmSQl/cOyZV2KdYxJk9rz++/3iYi4RoMGbVBXVyc7O5uUlLxKk6mpRS+zLG4yMzNJT1fP89nr1/mz\nLCWFmpo6V65cxMfHm9jYGMzNLQkOvkxAwAYyMtJJTEzE2NiERo0aA2Bv3wQAY2MTjI2ldgogza4+\nfx5NSMg17t4NZeDAPoA0WC1VqtQXO55PRSKR4OGxj1OnlNDQyGDcuKrUrWte7OP07NkHJydn0tPT\n32Q6LTAwKM/ChUvztX231DYn2w3g4NADB4f8dgnvliEXVq6b2xJBQEDg8xGCOQEBAYFPxMKiOnp6\nekREPKNp0xY0atSYDRvWI5FI8PML5MyZk2zeHIiLy2xGjx7H5s2BODj0wMtrAb/++rtsHUpKSjI7\ndmyhVau2JCYmEhi4EW/vlfj6+vDkSTgbN67n5s0QXFwmysbOESooKhKJ6J33ciW4PqdgPmW94enT\nJ6hQoRKVK1cptnncvq2BNJADUOT27ZKxZbCwqIaFxduSNXl5eeztXxIUlAqooaZ2l9atiy8j+LFo\naGjQokU4W7cmAxro6V2gU6cyJTpm7uyNmpoqa9f+w/nzZzh4cB8SiYRbt26yZs0GypQpy9q1vrx+\n/VbkRVFRSdZHzuuc9zlWCu3bd+B//xtWosdQ3KxdewIvrxZkZ5cFIDIyiMOHKxVrthjA09ON8PBH\nvH79mvbtO1Ctmlmx9l8QZ8/e5syZpxgbq9O1q73gLycgUAIIwZyAgMA3QXJyMocPH+CPP/ILduQQ\nFRUp8/r6Fsh5oDQwMERXVxexWIyhoRHZ2dJAK7ck+dq1K3nw4D7Pn0cRHx+PRCIGpN5nr169YsEC\nby5fvkhMzP1c3mcxyMmJ0NHRQVNTk3XrAgqdy4dwdKzC2bMHefq0LQoK0XTq9AJ1dfUP70jxnfdP\nWW946tQJGjVqXKzBXNmyKe+8Ty22vj+El9cfVKu2j+fPRdSvr83vvzf+YmMXxLJlXbGxOUhMjJhW\nrSrRoEHJWhfkZHjs7GpTsWJllJSUaNOmPRoamuzevQORCLS0tElNTeX48SO0aNG6SP2KRCJq1arL\npElj6datF7q6uiQmJpCamoa+vn5JHtJnc+fOa1kgB/DggSVRUZEyE/fiYsaMOcXa34fYseMCEybo\nER/vgIJCNDdv7mb27N++6BwEBH4GhGBOQEDgmyApKZHt24PeG8x9q+SWJNfU1CQ5OZnQ0P/Q1tYh\nMzMTX9/lmJqao6GhxZgxExg4sA9374ZSv35DtLW1CQ9/RGRkJLa2Ndm8OQA7uzpMmjQNJ6c+dOrU\nmR49ejNkiBPHjx+hefNWRRIqeJfatc3YtOkJhw5txshIk99++70kTsV7ad26MZ6eSwgM3ChT9Vy0\nyAMLi+q0b98BHx9vzp49jby8PHXr1qdp0+acPXua69ev4ee3hjlzPDE0/Pz1ZTNn1iUhwY9Hj7Sp\nWDGJ2bO/nPeagoICo0e3/WLjfQh5eXkGD27zxcZLSkoiIOAsCgpymJur4Ovrg5ycCAUFRcaNm8yp\nU8dxdOyOnl6pPDL3uSlIJGTHjq0yIZQxY4YhFktQUFBg7NiJ30QwFxS0iZ07t2JmZo6LS14LhmrV\n5BGJ4pBI9ACoUuUe+voNAdi8OYDff++czwj+e2DbtkTi46XBeFaWPvv3qzNrlkTIzgkIFDNCMCcg\nIPBNsGKFNxERz+jfvxd2drV58OABSUmJZGdnMWjQEOztm+ZpHxHxDBeXiUyYMA1NTU2ZOIiioiJ1\n6tRjwICCPZzeR1HsA/KKAuTfLicnR48ef7J48XySk5OJjo7EyKgihoZGREVFsnfvLlRUVElKSmTl\nyr9RV9fA0NAIb+9FzJ27gNat2xEQ4P/G2Ls6mZmZPH36hOnT57BgwTz8/NbmEyooKtWqVaRatYof\ntU8OYrEYDw83bt26QZkyZZk7dyEHD+5j9+7tZGZmYWRkhIvLbDIzs+jXrydbtuwGIC0tjT//7EpQ\n0C4kEgnLly/lyZPHDBs2iIkTp8rOZ2JiAqdPnyAgYCsgLT1VV9fA3r4JjRo1pmnTFp8074KoVMmA\nbds6I5EID5ZfksTERBwcDnLtWj8gi8aN1xEY6IeS0tuSSTMzc5kwSG5yr7OqWbNWHmXEd9dgtWxZ\ntGzel2THji14efnIrAly4+zcksjI3Zw9q4aGRjpjx1aRrWUNCtpE27a/fJfBnKJi9nvfCwgIFA9C\nMCcgIPBNMGTISMLCHrFuXQDZ2dlkZKSjpqZOfHw8gwf3zxPMPXkSzsyZU5k6dRYmJlUZNWqITBzk\n5MnjuLpO/6RgrijkLhOzs6tNVFQkIpFIZi9w7dpVjIwqsHLlOqKiIpk0aQy9e/fDzW0GqqqqVK1q\nikgkx6JFy9i/fw93795h9Ojx3L9/V+Z9VqdOPXx8lvLw4QMePnyAsXFVGjVqXKBQQVH53FLJ8PAw\nZs50Z+LEqUyfPpmTJ4/RrFkLfvvtDwBWrfJhz56ddOnSnWrVTAkOvoKdXW3OnTtNvXoNkZeX5/Xr\n1zg49ODIkUP07TuAhQs9ZOWT6uoaKCkpM3fubBo2bCwTvYCS894SArkvi7//2TeBnBygxOnTf7J7\n93G6dGn2Uf2sX7+aQ4f2o6OjK1N8ffDgHklJWmRlKZOdfQ8vL28g7w80ly5dkK3DMzQ0YsoU6Xey\na9eOtGrVlu3bg8jMzKRcOX0GDhyCoaERy5YtJi0tDW1tHaZOnUGpUqULVZZ1c5uJuroGd+/+x8uX\nLxk6dCTNmrVk/nx3IiMjGDt2BG3atOf06ZO8fp2BsrIykyfPoGLFSkyf/is+Pt5cunSe1avlePGi\nExKJhNjYGEaOHIyOju5HCR59CwweXIWQkD08ftwCLa3bODkpCd85AYESQAjmBAQEvglyP7BLJBJW\nrFjGjRvXkZMTERsbw6tXcQC8evWKyZPH4e6+gEqVKpOamsqtW2/FQaKiosjISKd//17UqVMPiQQu\nXjyHSCTC0XEALVu2lmWI3v08N3fu3Gb+fHfmzPGkfPnCpdo/R5K8IO+z8PDHZGTI4+3ti4qKCsHB\n99iy5REHD+5hxIgGlCnzddT5RCKRLBNoZmZOVFQkDx8+YNUqH1JSkklNTaNevQYAtGjRmmPHDmNn\nV5sjRw7RpUs3UlNTEYvFrF3rS1xcHDExz8nMzJKdW3l5eVat8uPKlUucOHGUbds2yx5ei/IA+LHB\n6v79e6hTpz6lS5f+lNMh8AnIyYmA3IF5NvLy7/eACw29w4EDexk9ehxr1qwkOTmJ69eD8fPbRGZm\nJk5OvdHXN+DQoaNERMwjObktVas24sqV29SuXZ1jxw7TqlVb4uPj8fdfi5fXcpSVVdi4cT3//vsP\n/foNRCQSER//ihYt2mBqasa9e6HUr9+AceNGMm/eIrS1dTh69BC+vsuZPHn6e5Vl4+Je4uOzlvDw\nMCZNGkOzZi0ZP34Kly5dwNt7JQoKCvTo0Rt5eXkuX76Ir+/fzJnjya5d23n+PJr16wORk5MjMTER\nLS0t/v03AG/vlWhplYxIT0lSp445e/aU5syZI1hYVMDSstnXnpKAwA+JEMwJCAh8cxw6tJ+EhHjW\nrt2IvLw8Dg6/kZEhVbXT0NCgXDkDbty4RqVKlZFIxGhovBUHiY6OYsKE0axbF8CJE0fZZKTsEgAA\nIABJREFUuXMbfn6biI9/xcCBjtja1uTmzRs8eHAv3+c53Lx5gyVLFjBv3iLKli33xY570aJDeHsb\nkZJiQs2ae5k6tRKjRmUSEeEASLhwYT07dvzyyXYCRS2VVFZWITIyguHDZ5CUlIyNjV2efuTk5MnO\nzsDdfTbz5i3ExKQq+/fv4dq1qwA0atQEX9/lJCYmcu9eKLVq1SE1NQUQsXTpCoYNG4Svrx/p6ek4\nOfXG2tqWtLQ00tPTaNCgEVZWNnTvLl3Tp6amRkpKyruH8tns27ebKlVMhGDuC9K3b2P27VvHpUuO\nQCatWgXSoUP39+5jbm6BubnUa1EkEhEVFUnjxs1QVFREUVGRRo0aExf3iqwsBaSPNPIkJrbB13cf\ntrZmnD9/lmHDRhMcfEUmLARSNVgrK2vZOL/88huuri68fp1BeHgYz59H8+jRQ0aPHgpIvzulSpUh\nLS2tUGVZkUhE48bSCoLKlasQFxeX73iSkpJwdZ1BRMTTPCqcV69eolOnrjKDcy0trY8/wd8g5cqV\npkuX5l97GgICPzRCMCcgIPBNoKamRmqqVFUwOTkZXV095OXlCQ6+QnR0lKydoqIi7u7zGTNmOKqq\nqrRu3Y7y5cvLxEHEYrFMzjwk5DqtW7dDJBKhq6uHra0dd+78x82bNwr8XF1dnfDwR8yf787ixX9T\nqtSXe9BPSIhn1SpNUlLqAXDtWl9cXecRETH5TQsR16//xrlz12jVqt4njfH06ZMil0p6eS2gV69e\nNGzYgvXrVxfYX1paKnp6pcjKyuLgwX2ywFdNTQ1zc0u8vObLDJ/V1TWQkxNx+/ZNmjdvRZ8+3dHR\n0cHMTCqPnpqawqRJY99cOwkjRowBoGXLNnh4uLFly7+4us57rwBKdnY2s2e7cO9eKJUrG+PiMouw\nsLB8pXIhIdcJDb3D7NnTUFZWZvToCWze/A9ubvM5ffoEM2dO5eDBk2RnZ9OnTzc2b95ZaGndq1ev\nWLhwLs+fRwMwcuRYrKxsWLNmJc+fRxMVFcnz59F069aTrl3ze3P9KERFRTJ27AjM/8/eWYdFlbZx\n+B6GlBIUMQETkEZsbF111bWwXQEDYy1s7Mbe1V0DXUEUY0WxVtfuTsDCVhqR7piZ749ZRhAwcY3v\n3Nfl5cw5b533zDDvc57n/T1mtQvM/+3bwaxZsxKJRIKZWW22bRvL/v1/c+3aEeLiXjBo0N/Ur9+A\nESPGcPLkcTZt2oCSkhgtLS3++GN9oX2sr1694sGDvRw9eph+/QYAoKKijNzjJwMkKCkl8fDhafr2\nPY+urq5C4t/BoT6zZy8ocvwmJiZ4e29l9+6/uHDhLKdPn6Rq1eqsW1dQgTUtLfWtyrIqKq/FkN4M\nD5bJZPz55zocHOri6bmMqKhIRo8eVmx5AQEBgfdBMOYEBAS+CnR1S2NlZcOAAb0wM6tNaOgLnJ17\nY2pqjrHxa1l6kUiEuro6S5b8hrv7CEqV0iwgDpKRkfGvF0hetrgF0pvH80L5ypY1ICcnm4cPQ2jY\n0PEzXW1h5OMunX9EiMXqQCZ5OdHU1aMwNCxdVPX3okKFSu8dKnnnTjAbNngRH59OkybN2bixcKLf\nwYOH4ubmQunSpbGwsFQY4yAXoZg500MhTpGUlEiZMmX5++/9xMW9QllZmQYNGuHiMlhRZ8MG30J9\nWFnZ4Oe3872uLzT0BR4eM7G0tMbTcy67d+/k3LnTeHquoHTpgqFyAQH+jBzpjqmpGbm5uTx69BCA\noKBAqlWrwf37d8nNzcXCwgqg2NC6lSuX0bNnX6ytbYmOjmbChFH4+fkDcuP599+9SEtLpW/f7nTt\n2gOxWPxe1/ItEhYWytSpsxTzv327H/v372HVqnVUrlyF+fNncfjwQX766UcOHVpXQOwGwNf3T1as\nWE3ZsmUVx/Ijk8lIS0tFV7c0S5euxM3NGRUVFVq1+gE1NSnKyuHo6m6ibNlUSpcuTc2apjx+/JCo\nqEhq17ZkxYrFRESEU6lSZTIyMnj1KpYqVeSCQPHxcVSoUIkGDRpx8uQx7t+/S2JiInfu3MbS0orc\n3FzCwkKpWrVagYdHH6osm5aWphBBOXTogOK4g0N99u0LwN7eAbFYrAizzPNMf4thlgICAv8NgjEn\nICDw1fA+eZDy9qBpaWmxYcNmxfE8cZCkpEQGDfoZAGtrW/bt20P79h1JSkoiKOgWI0eORSKRsG9f\nQKHjz549RUtLGw+PGYwd+wvq6hoFVPM+J4aG5Wne/DT//GMDqGFgcJ7Jkx3w9vbl5MmGqKkl4+IS\nhpVVx4/uI38KhXeFSuanfPnyqKu/TmDcp09/xesuXQqmkli8eD69evWjefNWnD17FYBXr2IZNWoo\n/fu70L17z7eOUSKRsHz5VqKjE3F2bo+NTU3Onz/L8+dP6d/fhY0bvShVSrPAGPIoV84QS0t56Fzb\ntj/i6+vN06dPcHcvGCqXR55Br6ysTKVKlXnx4jkhIffo3bsfgYG3kEol2NjYvjW07vr1q7x48Uxx\nPD09nYyMDEQiEY0aOaKsrIyubmn09PRJSIgvUs3we+HN+d+06U8qVqxE5cpVAPke0YCAnXTv3rNI\nsRsrKxsWLJhFy5ZtaNascGieSCSideu2iEQiRo8eSm5uLoaGhmhqaqKursK0aZmcP3+WlJQ4UlIy\nOXv2NOXLlyc8PIy6deszbdpsZs+eSnZ2DgBubiMUxtzz58+YNWsa2dnZxMW9Ytq0OSgpKbFy5TJS\nU1ORSHLp1asvVatWe6uybEG12/x7PUWIRCL69h3AggWz8PXd+O/DInmZTp26EBYWirNzH5SVlfnp\np65069aDn37qyvjxozAwKPfNCaAICAj8NwjGnICAwDfNzp0X2bUrBbFYypAhFWnZ0kbh4WvQoBE1\natTAxaUPIpGIESPGoKenT7NmLbh7N7jQ8efPnyESgZ6ePkuW/MqECaOZOnUW5uYWn/06RCIRGzZ0\nZ+3a/SQkQPv2xtSvb06zZtaEhoaioVEeQ0ObEu+3uFBJKysbDh48SMOGLTh69PB7tzd58vRCx3R0\ndLG1Hcy5c2Kys8/Tp0/RHk+ZTMYvv+zi+HE91NTiOX48mXXr7uHo2BRHx6bA28VQ8p+TyWRoamoW\nGSpXVHkbGzsuXTqPWKxMnTr1OHx4FlKpjF9+GYNUKnlLaJ2M9et9C4TX5aGsnN94ViI39/uWZn9z\n/rW0tElOTipwDIoXu5kwwYN79+5w6dIFBg36mY0btxTZT58+PzNwoBtz5kzn3r27VK9eg3LlyuHs\nPIBHj+7g5jaYunUbFKpnb+9Q4AEQyI3vKVPmU7myIb6+2wvV+eOP9YWOVahQsUhlWQ+PmQXmIE/5\nFsDffx8AlpZWRYohicViRo1yZ9Qod0D+4EEmk9G9ey+6d3/7vkIBAYH/bwRjTkBA4Jvl/Pk7TJtW\nnqQkeRLm+/dPsG9fZCEP34gRYwrVHTFiTKHj+fNXGRqWZ8uW9wvvKylUVVUZM6ZdgWNKSkqYmJiU\nSPtFGULFhUqOGTOBhQtnsW6dF46OzYqsm5GRwcyZU4iNjUUqleDsPJg9e/wZNWocpqZmtGnThB49\n+rBjxz4yM9N49uwku3encOGCB/Hxj4iNjUFNTZ3SpfWQSHJp2NCRmzcvYmgYjkwmJjv7Bl5e1iQm\nPuHBg/uK9A/FERMTrQiLO3bsMBYWlhw4sLfIUDl5+NrrUD4bGzvmzZvJjz92onTp0iQlJZGYmEC1\natUBig2tq1u3Af7+O+jbV+4NfvToITVr1vroe/Qt8+b8m5mZs29fgCK08ciRQ9jZ1SlW7EaeW9GS\n2rUtuXz5Ai9fvizQvkwm4/z5M4SGvuDZsye8ePGcfv0GYGJSTVGmXr2GBATsws7OAWVlZUJDX1Cu\nnCHq6oXztD19Gs6gQbe4e9cRff3HTJ36kAEDmhQq9y4OHbrB0qXRJCerU69ePKtWdSnSuC+O/AnF\np0+fy+TJezh+XBdV1RyGDtXA1bXZuxt5C5+alkRAQODrRjDmBAQEvlkuXw4nKamH4n1kZFPOnz+A\nsXHFj2rv2LFb7N37ElXVHMaOrYOxcYWSGuoX580UCm8Llcwrv2PHDmJjUwCKTOR85cpFypYtx9Kl\nKwH53qe9e3cpzmdmZmJhYUliogGqquvR1d1JfPxw7t27jZ1dNcqUKYOpqTmuroM5fvwoXl6rSUmZ\nQ05OJnp63iQkuFCuXCYi0buFIUQiEUZGxuzZs5NFi+ZiYlINJ6fe1KvXsMhQuR9/7MSyZZ6oq6uz\nbp0PtWtbkJiYgI2NXNW0Ro2ainQYQLGhdWPHTmDFisU4O/dBIpFga2vPhAlT/h3TO4f9XfHm/Pfq\n1Q8LCytmzJiMRCLB3NyCLl2cSExMxMOjsNjNmjUrCQ8PQyaT4eBQjxo1anLr1g3FPIpEIqpXr0l4\neBjZ2TlMnOhBx45dFLkeQR6uGBUVyaBB/ZHJZOjp6bNw4dIix/vrr4HcvdsXgPh4I1av3kX//lKF\nouT7kJGRwaxZibx4IRe3CQvLxMRkH5Mn//jebeRPKO7jcxJf307IZPoAeHpeoGXLMIyNq7x3ewIC\nAv9fiGRfiXxS3oJB4PvDwEBbuL/fMV/y/v7992WGD69FVpYxALq6V9m7VwULixof3NbFi/cYNAji\n4uRKkZaWWzlwoBWampolOuavHX//S5w7l4yeXg5Ll/5Eerq02LJhYaGMGzeSli3b0KhRE2xsbBk1\naqhCWKRly0acPHmRJk38yM7+i/R0R2Ji5mNqaomzszNBQbcYOvQXLC2t2bzZmz//9EJLqxzx8dmI\nRNmoqNTBz288d+/eICTkHu7uk/D2Xo+GRqki98wJfBgl+d39Fr0/Q4YcZd++7or3hoaHuHGjPqqq\nqu/dRkREOA0aZJKV9Tq1Sb9+u/j117bvVX/p0oUcOnQAIyNj2rfvyM6dRwgLkyKVahATM5fs7LIM\nGTIPS0tTxWf+5597snTpKmQyKRMmjMba2q5AuhE1NTViYl4wadIURCIR9erV5/Lli9/UvRF4O8K6\n6vvFwED7g+u8/+MnAQEBga+Mjh0bMGbMVczMArCw8GfGjNiPMuQAjh8PVRhyAHfutOLWrfslNdRv\ngh07LjBhggk7djixdm1Pevb0f2v5KlWM8PbeSvXqNdiwYQ0+PhsKnBeL5cEfw4YZIhanIxa/xN7e\nF1XV1z89efvKlJREaGhocOjQAVxdu1O3ri2HDs3CyOjb8o7GxSUwbNgefvrpGO7ue8nIyPiodiZO\nHENaWiqpqans2fPa23nz5nUmTXIvkbFevXqVO3eCS6QteL/k7p+TR49CWb36Hw4cuPBe5du310ZH\nJ+/602jaNOqDDDmQh2PXrv16DlVVX+Dg8P55ICdOnErZsgb8/rsXUVGRWFmZkpg4l1ev3ClffjI1\napylcuWCojn55zk8PIzu3XuyZctOtLS0OXPmJAAeHh6MGzeZTZuKTqEgICDw/SCEWQoICHzTTJjQ\njgkTPr0dAwMlIB2QL8S0tZ9TuXK5T2/4G+L06TQyMvL2e4m5fNmYlJRktLWLTmD86tUrtLW1+eGH\n9mhqavH33/sKnM/KygSgV68W+PrOw9FRyuzZ7XByWs39+3cBkEolpKXJE5Nv2LCOhIQEVFVFhIbe\nJzU1DS0t7QJpJIoLJsmvcrlxoxc2NnY4ONT7xBn5cMaNO8k//zgDIi5fzkUk2s6KFV0+uJ280NWo\nqEj27PGna1d5KGx8fByBgYUVRz+GK1euIJMpKxQoP4U3w3j/ay5fvsfw4clERPRERSWSa9f2M3fu\nT2+t061bQ7S1b3H2rD+GhiKGD+/+1vJFoayszLp19Vm8eBupqeo0bSqmX7+WH9yOTCbj9u0gFixY\nio3NC/bvT+H580iWLDHkzp2nxdYrKt1Iaqr8IYCNjS0Abdt24PLlix88JgEBgW8DwTMnICAgAAwZ\n0pKuXbehp3eCChX2MW5cNCYmRl96WP8pOjpZyBMvy9HTS6BUqeLDTJ8+fYybmwuurn3ZtOlPnJ0H\nFTifl85AWVmZFi1aExh4g0mTxlKvXgOioiK5f/8e8+bN5Pnz51SpYoyOjg7jxv3CwYP7iY+Px919\nBCdOHEMkEim8EfLXhceS31sxaNDQL2LIATx9qkue3Dwo8/hx0fO3bdtmdu2SGz+rVi1nzBj5nsQb\nN64xZ850evT4iaSkRNat+52IiHBcXfuyZs1KQIRUKmX69Mn06+fE3LkzFG1ev36VgQP74ezcG0/P\nueTkyCX4nZw6KVQlQ0LuMWrUUKKjo/jrr7/YuXMbrq59CQoKLHKc/v476N+/B/PmzSjy/KFDB/j1\n1yWA3KDevt3vQ6arEHv37ubw4YMfXG/z5lAiItoAkJNTkYAAXbKyst5Zr00bO+bNa8fIkW0/Ogdg\n1aqVWLeuE35+bXBz+3BDLj8ymYxu3RqyadMP6OurY2lZDbFYjEz2OtxZvtdQTuF0I4UVU7+S3TQC\nAgKfCcEzJyAgIIDc4PDy6kVKSjIqKqpFqt9970yZ4sjDh94EBlpQpkw0c+YYvnWBW69eA+rVKygB\nn5ckHFAsQG/evE5ERDj16jXk2bMnlCtnqEgYff/+XVauXE5qaiqGhhVYtWodISH32LFjK0uW/Mqq\nVctRU1NnzBi5+/XUqeMsXSqXhff13cjhwwfR09OnXDlDzMzMAViwYDaNGzehefNWODl1on37jly4\ncA6JJJd58xZhZGRCQkICc+ZMIy7uFZaW1ly7dgVvb79PTs5cqVIKDx4oZoBKlQonvwawsbFnxw4/\nnJx6ExJyn9zcXHJzcwkODsTW1p47d4IRiUQMHz6aZ8+eKtIiHD9+hKysLKRS+dxevnyR7dv9CAy8\nwaNHD1m1ah1RURF4es5nz55d9OzZp8jwx/LlK9C7d29kMjG9exe//zC/OEdRFJ9X7ePo0uXDvWPy\nvgu+V1KSffGwzw/F2tqOo0f/wcVlMDdvXqd0aT1KldKkQoWKXLhwDoAHD0KIiop8aztaWlpoa2sT\nHByItbUtR4/+818MX0BA4AsheOYEBAQE8qGtrfNVG3Il4f0oDn19PQICnLhypSwXLjSmX7/Gn9ji\n68X048cPGTt2An5+/kRGRnD7dhA5OTlMnTqJJ0/qcOHCTEJCunL16pN/a8iYPHkPGzaks3JlFr/8\nshOpVKpYoIeE3OfkyWNs2rSdZctWEhJy73Wvb3jySpfWw9vbjy5dnBRz5+OzHgeHemzZspPmzVsR\nExP9idcqZ/HiBrRqtQVz87106LAZT8+iPTWmpmY8eHCf9PQ0VFVVsbS0IiTkPkFBtxSKmlC0V0Um\nk9G3789s3bqL0qX1ePDgPk+fyo3kypWrcPDgAbp06UZQ0M13jvdtTpulSxcSGRnB+PGj2LHDDw+P\n8Tg792HoUFeePHn81nYfPXqAm5sLzs59mDp1IikpKSQkxDNo0OsUDk2a1OXlyxgAevXqQlZWZoHP\n98iRbqxd+ztDhjjTp083hfcwMzOTGTOm0L9/T6ZOnYibmwutW0OVKv8AMtTUXtCzZ9oH73/7csg/\nrwMHuvHgQQjOzn1Yv34N06fPBqBZs5akpCTz8889CQjYSZUqxq9rvmGw5r339PRkxYoluLr2LbKc\ngIDA94PgmRMQEBD4hvjcizIlJSUMDQ1LvF1zcwuFd6dGjVpERUVSqpQmKSmqBAfLpfwfPmzIkiXb\nmT+/PK9eJXL4cEt0dJKRyUqxa1d3Gjc+9W9rMoKDb9G0aQvU1NQANRo3blps382ayQ2qWrXMFAIR\nt28H4em5HID69RsWuy/wQzE2rsD27e/eI6esrEyFCpU4dOgAVlY2VK9eg5s3rxEREYGJSdW31lVV\nVVPsczMxMSE09AWNGzfh4sXzpKSkcPfuHTp06MTDhyGAPCG1VCq32rKysott900mTpzK1auX+f13\nLzZu9MLU1BxPz+XcvHmd+fNn4uOzrZCxmffxnD9/FuPGTcbGxo6NG73w8VnP6NHjyc7OIj09jeDg\nW5iZ1SYw8BbW1jbo6emjpqZeIIxWJJKHlG7Y4MulSxfw8VnPb7+tISDAH11dXfz8dvL06RNcXfsy\nfrwJu3frcOzYLkxM9GnTpsN7X+eXJi+hOICn57JC59XU1Fix4o8i6xaXbsTCwqKA+MmIEaNLYqgC\nAgJfIYJnTkBAQOArx9d3I336dGPEiMGEhr4AYNSooYSEyNU2ExMT6dFDLvYgkUhYvXolQ4YMwNm5\nD/v2BXyxcedHReW1l0QsVkIikSASgURS8GcoIUG+zy4zM4fc3PKAGJACusTF5eTbL/SmUVu8iylv\nX1Fev4oaX3gvkY2NLdu3+2Fra4+NjR179+6mVq2CCcdLlSqlSOSeR357XiaTGz29evXj5csYdu/e\nQcuWrTl69DC2tvaAPKQyz3N55swJRV1NTU3S09PeOc48cY62beW50+ztHUhKSiq2bp4KZ56HsV27\nDgQG3gLA0tKG4OAggoIC+flnV4KCbhIcHFjAG5mfZs1aAHJPZnR0FCA3xFu1+gGAatWqU726XADE\nxKQiQ4a0o02bL7Nf8mtAJpNx9ux1AgJOv9eeQQEBgW8fwZgTEBAQ+Ip5Vzjhm/z99z60tLTYsGEz\nGzb4cuDA3nfusflSGBmZoKKSjIbGWQBEojgcHOSJug0N9TA3DyAnpxJqavcwMTmAlVWpf69FhK2t\nHWfPyhes6elpXLhw/oP6trKy4eTJYwBcvXqZlJTkEr2298HGxo74+DgsLa3+9UypFTJqdHVLY2Vl\nw4ABvVizZhUgIisrizt3bgMQFvaCKlWMqFChIqam5mzatJGzZ08hFosVyeBdXd1YuXIZgwcPQCxW\nVnxuWrRowdmzp3F17UtwcNECKPkpbPx+uJfY1taOoKBbxMRE06RJMx49evhWYy7vIcCb4h5f2hD/\nGpHJZIwe7U/PntXp3t2WHj32kppa9J5NAQGB7wchzFJAQEDgK+ZDwgkBrl27zJMnjzl9Wu6BSUtL\nIzw8jAoVKv4Hoy1IQXGMwueVlZVZufI3PDxmkJqag7q6MgsW+PLkySNUVVXw9bVh3bqr3LnzgFKl\ngrl82U6xX6hWLTNatWqDi0sf9PT0qV3b4n1GpBiTq6sbs2dP48iRQ1hYWKOvX+atyp2fgzp16nLq\n1CXF++3bX3tR/f33K17PmjVf8To6OgpjYxP27NnJokVzMTGphofHTAB69OjNrl1/sW6dd4F+5B7A\nwh5aExMTfH23v9dYixbnKJhPTSaTIZOBpqYW2to6BAUFYmNjy+HDB7Gzq/PvWOzw8lqNnV0dRCIR\nOjo6XLp0gWHDRuVr5+1jkRvix7G3d+DZs6c8ffr2/XtfA6mpqRw7dliRYuJzcPVqMP7+LZBK5Sq8\nly+7sn79LsaN+/Gz9SkgIPDlEYw5AQEBga+aor0f8n1Qck9FdnbBcKpx4yZRt26Doqr9pxw9egaQ\nh+XZ2zsojru7T1K8Nje3YO/egoaGnV0dxeJ/0aIuQNF70AYMGMiAAQMLHZ86dZbidX6jyMzMnFWr\n1gFyxb8VK35HLBZz504wDx7cQ1n56/9JLF++Alu37ipwLCbmJbdvP+XKlct06vT2/Xo5OTns2XMO\niUTK0KHvs8h/Lc7h6TkXZ+c+aGhoKMQ5iksbMW3abJYt8yQyMgI9PT3WrNmoGD+gCAG1sbHj1atX\naGlpve6xWIefiI0bvVBVVSUxMYH+/XtibGxM1arVCtT/GKRSKUpK8mClkSPdGDnSXaGOWhKkpCQX\nyBf4OUhPz0Qqzf9AQkx2tiB8IiDwvSOSfWSswuLFizl9+jQqKioYGRnh6emJtrY2AF5eXuzevRsl\nJSWmT5+Oo6PjO9uLjU35mGEIfAMYGGgL9/c7Rri/n5eHD0NYsGAO69dvQiLJZeDAn+ncuRuhoc8x\nNTWjSxcndu7chr//Dvz997N//x4uXbrAvHmLUFZWJjT0BeXKGX6UQuf3eG/T0tJYuvQUL1+mEB29\nEx0dDVRUlBk/3qNEF+//FYcO3WDKlBxUVX9HRSWXuXMn0aZNnSLL5uTk0L+/P6dO9QfEtGixHV/f\njp9VvdXbez0aGqUKiHN8anvq6ho4OfVCVVWViIhwxo79he3bdxdrjEdFRTJ+/CjMzGrz8GEIJibV\nmDFjDv369aBVqx+4du0K/foNQFtbB2/v9Tx58hgLC0s8PZejoaHB2rW/c+HCOcRiMfXqNeCXX8aQ\nkJDA8uWeChXU0aPHY2Vlw8aNXsTERBMVFUlMTDQ9e/bByak3s2Z5cP78WYyMjKlbt8FnESTJycmh\nT59dnD3rCqhQs+Yutm+3xsioQon3JfBl+R7/NgvIMTDQ/uA6H/0Y0tHRkYkTJ6KkpMSyZcvw8vJi\nwoQJPH78mEOHDnHw4EFiYmJwdXXlyJEjiideAgICAv/PtGnThGPHzr13+XPnzmBgYFAgnFAkkivX\nzZjhwf79e2jY0JE8D16nTl2Iiopk0KD+yGQy9PT0Wbhw6We6mm8LmUzGwIEHOHVqICBGS6sRy5dH\n0bXrl/difixr1sQQHd0LkCfMXrfuL9q0Kbrs7t1nOXXqZ0AeHnnqVH/8/PYyeHC7Eh3Tm/n/TE3N\niYgIZ8WKJSQmJqCurs7kydPQ1y+Li0sfdu06AEBGRgb9+jnh77+f6OioQuWNjEzIzs4mKOgZ/v49\nUFMTExv7En19fWbO9MDDYyba2tqMHOlGzZqmBAbeQCKRMGTIcMLCQhk/fgrKyspcuHCOXr26IpFI\n0NUtzdq1fzJ79jSuXr2Cg0M9qlathrFxVf76ayvduvXg3LnTiryIaWnyPWgrVy6jZ8++WFvbEh0d\nzYQJo/Dz8wcgLCyUqVNnMWXKOHx8NtC1a49C+QJLkvyeRD+/rmzYsAdlZXU6drShSpXyJdZPVFQk\nkye7s3nzXyXWpoCAwKfz0cZc48av8w/Z2Nhw5MgRAE6cOEGHDh1QUVGhcuXKGBntZbufAAAgAElE\nQVQZERwcjK2t7aePVkBAQOCb58PCnkQiEXXq1GPZslWFzuXf7zRkyHBAvtjs3Lkbbm4jhNxSbxAX\nF8e1axbIFTIhNdWSkycf0LXrlx3Xp5CZqVLgfVaWSjElITdXSt61y1FCIilZIZH8gj1yT3J/TE3N\nWbJkIRMnelC5chXu3r3D8uWLWblyLTVr1uLmzevY2ztw8eI56tdvhFgsZsmSBUycOLVA+XnzFrNz\n5yPCwxuRmLgUC4vWLF/+G/b2DgXSH4hEIrKyMvHx2UZQ0C0WLZpHuXKGXL9+FQeHerRr14Ht27dw\n9eplHB2bsmfPLjIzM9HQUCcsLJTQ0OckJiZQp05dNDW1UFVVw9NzLo0aNaFx4yYAXL9+lRcvnimu\nOz09nYyMDEQiEY0aOaKsrIxYLEZPT5+EhPjPKtiSP9RVXV2dUaPaC54bAYH/I0pkg8Du3bvp0EGe\n0+Xly5fY2NgozpUvX56YmJiS6EZAQEDgu2Lbts2cOnWc7OwcmjZtzqBBQ4GiPRvvw9q1J/njD1VS\nU8vQqNEpvL27oqGh8Tkv4ZtCS0sLXd2XvBb4k6Kt/W3Jtw8fPpC1a18LnLRrJyEkJJzs7Mqoqz+j\nfXvYuXMbnTt3Q02tYPikk1MT/P03c+mSKyCiQYOt9OtXjBvvIylKsCc7O4s7d4KYMWOyolxOTi4A\nLVu24eTJY9jbO3D8+FG6d+9Jeno6t28HFyq/adNFIiPtADFKShLS05WJjMzE3l6e/mDGjCmK8q1b\ntwXke/IyMtJRUhJz9eplLlw4S1ZWFomJiYB8L1tQUCB2dnXQ1S3N7NkLGDiwP5MnT8fU1AyADRt8\nuX79KqdPnyAgYCcrV64FZKxf74uKSmHjWVlZfkwikRAX94qRI92oVKkKMpkMH58NXLx4jqysLCwt\nrZk0aRoA/v472LcvALFYjIlJVebMWUhGRga//rqEZ8+eIpHkYmtbh9u3g0hLSyUyMgIDg3IkJydh\nZGRCZmYmP//ck7lzF1G+fAVcXEYRF5eARJLLkCHDcXRspgg3tbS05vbtIMzMatO+fUd8fNaTkJDI\nrFnzMDe3YONGLyIjw4mIiCAxMZF+/QYU2ospkUhYt+4PAgNvkJ2dQ7duPejcudunfXgEBAQ+irca\nc66urrx69arQcXd3d1q2lCdhXbt2LSoqKnTq1KnYdoSnwwICAgIFuXr1MuHhYWzYsBmpVMqUKeMJ\nCrqFmpp6Ic/G++zlio2N5bfftElIkP9tPnHCjpUrdzNlSuHkyYcOHeDBg/u4u0+id++utG37I66u\nQ0r8Gr821NXVGT9enWXLDhAfX4E6dQKZPLlkQww/N/kNOYAJE9phYnKB+/cvYW1dms6d29Cjx0+0\nbftjIWNOXV2dHTs6s3nzHqRSGePGdSMjo6Q9RoV/72UyGVpa2kWGGDZu3JT169eQnJzMw4ch1KlT\nl/T0NLS1C5dfterwR48qNvYl6uoaLF68gq1bfTExqcru3TupUkWu/GhsXJV9+wKIiAgHICsrk7Cw\nUMqWNSAzMwMTk6rcvRtMQkICAHXrNsDffwd9+/4MwKNHD6lZ83WOwJ07t/HixXMqVqzEb7+txcvr\nD+7du42jYzNOnTrO5s1/MW/eTC5cOEfjxk3YutWXXbsOoKysrAjl3LzZGweHekydOou7d+8wZsxw\n9u07zNatm9i+3Y9Bg4YSHBzIgQN72bVrB23b/kjVqtWQSCT88ccfZGTISExMZNgwVxwdmwEQHh7G\n/PlL8PCYyeDBAzhx4ihr13pz/vwZNm/2USQtf/r0CV5em8jISMfVtR+NGhXUPsifAiU7O5sRIwZT\nr16DL6KaKyDw/85bjTkfH5+3Vg4ICODMmTP4+voqjhkaGhIdHa14Hx0djaGh4TsH8jEb/gS+HYT7\n+30j3N/3RySSz9edOze5ceMqQ4bIF4MZGRkkJr4kLS2N9u3bUblyWQDatGmNpqbaO+c4NjaSpKRK\n+Y6okJ1dCgMD7QJKfQDa2upoaKhiYKBNxYoV6NChbbHtl9S9bdmyJQEBcs/DgQMH6Nu3LwBXrlzB\nx8eHdevWlUg/RREeHs7w4cM5cOAA7u7tcHNLIzExkQoV7L+5/dx2dnbcunWLK1eu8Mcff6Cnp8ej\nR4+wsLBg8OBlbN68mVevYnF3H4G+vj6+vr78/fffeHl5AdCsWTOmT5+gaO8TRSAL0aKFI1OmTMHd\nfRQ5OTlcuXKBXr16YWRUhRs3LtCuXTtkMhkPHjzAzMwM0MbGxpp1636jdetWlCunA+gUWX7ChLbs\n3z+OsLAGSKXKaGpKqV1bHwMDbXbsOE7jxg0xMNBGRUXMxYunadu2BdevX0dHRwcdHR3EYjHDhrnS\noEEDhgxxZefObZQpo4WjY0MCA6+yZMlipk+fyKNHj1i8eB4eHh5UqVKO8eMnkJqaSmRkJPPmzcPA\nQJt582Yzd+5cBg3qh0QioW7dujRqNBtNTTU0NdVJTVVDR0cHLS1NypTRpH//Pty+HcjkyWOJi4tj\n4MC+JCUlYWVVGwMDbczNzfD0nEXr1q1p3bo1pUqV4ubNq1y5cgF//23Ex8eTnZ3F8OGuREdHI5VK\n8fffRk5ODiKRiNDQZwwY0A83twHk5OQglUoRi8WIxWIiIsJZt+43rly5QpkyZfDwGEfXrl2Jjo4k\nOTmRlJRYHBxs8PX9EwMDbbS01Gnb9gcqVSoDlKFRo4aEhz/BzMwMZWUxBgbaBAff4MGDB5w/fxrI\nSxQfh4GBacl+oASKRfjdFcjjo8Msz549y8aNG9myZcu/4RRyWrZsyfjx43FxcSEmJoYXL15gbW39\nzvaE2O7vFyF2//tGuL8fhkwm/3uXnp5N377OXL58kZcvYxCJlEhKSiczM4sHDx7TqVNnpFIpKSlJ\nODn14cWLGBYunMPFi+eoUsWYgQPdiIgI5+7d29y5E0xychI1ayqTlNSC6OhfqVHDmsDAslhbz6Bc\nOQPq12/ElSuX0NTUJDk5mZSUFEJDI3j69Bnbt/szZowRI0e6YWFhxc2b10lNTWHRIk+MjU3JzMxk\nwYLZPHv2FCMjY169imXcuMkfpP4olcqIi0slLS2NLVv8aNNGHs2RmJhOVlbuZ/0MxcenkZsrKdCH\nqqoOcXFpn63P9+FjJPDzPj+Jiencu3cPPz9/ypQpy/Dhgzh58jzt23fF29uH335bi46OLvfvP2XJ\nkqV4e/uhpaXNuHEjCQg4QJMmzT/Ld9fAoArNmrWiQ4eO6OnpU6uWOWlpWUydOodlyxbx+++ryc3N\npXXrHyhTRv7wwdGxBTNnevD7716K8RRV3sVlME5O1Xnw4A729gdxcFjG4sVLC6Q/iI1NISdHglQq\nol279kREhDN3rie///4r9eo1RCqVcOdOMF26dKVmTVNycsS0bt2RI0fGMGzYMOrVa4Cqqjrjxk1W\nhFmuWeNNVFQkEyeO4fz5y6xb54WBQTk8PZfz6lUsK1Ys4cqVa9jY2ODt7YeRkQmrVi1HJpPh7b2N\nkJD7zJw5lZSUVCSSXCpVqoy39za8vdcTH59MbGwKCxYsJzDwJhcunGP16jX4+u4gN1fKnDmLqFLF\niN27/+LVq1cMHfoL7u6/cP36VdzdJ1O+fEW6dm3Py5cvmTRpMr//7kVwcCC+vn/SrVtPevXqR7Nm\n9RGJVFm4cDmTJ7uTkZGBikopGjduilgsZs0aLwYMGEhWVjaxsSmkpWUhk8kU9yIzM4eUlKwC36Os\nrBzGjJlQKAWK8Fvw3yD87n6//KdqlvPnzycnJ4eBA+U5fmxtbZk9ezY1atSgffv2dOjQAbFYzKxZ\ns4QwSwEBAYE3qF+/ARs2rGP+/CWUK1eO8PAwJk92x919ImvWrGTz5r8oW7YsLi79EIlg06Y/0dTU\nonLlKvj6biclJYVHjx5w/fpV1NTUOHz4NO7uI8nOVkdHZxdXr2bRtKkjY8dO5MWL5wwY0IudO/dz\n/PhhduzYStu27enUqSsuLn0K5AmTSqVs2ODLpUsXWL16NUuWrCIgwB9dXV38/Hby9OkTXF37vvXv\nuofHBF6+jCE7O4sePfrw009yhRGZTMa6db8TERGOq2tf6tatT8OGjmRkpDN9+mSePXuCqak5M2fO\nA+QiE2vWrEQikWBmVpsJEzxQUVHByakT3t5+6OjoEhJyj9WrV/L7714kJCQwZ8404uJeYWlpzbVr\nV/D29gPkecQWL17AnTtBioV4/geRxfGmV7MkyS9c8TGYm1tQtqwBADVq1CIqKgorK5sCZe7fv4u9\nvQO6uqUBaNOmHYGBt2jSpPlH9/suisv/t3x5YREfgObNW3H27NUCxypUqFhk+WHDRhZ47+Xlo0h/\nkD/XXNu2HejRow+TJ7tTvXrNf0NsJ7/ZHABqamq4uAxmx46tLFhQvPJrWFgos2cvZPLkacyc6cGZ\nMyc5ePAAEyd6IBaLGTNmuELYRSaDlJQUxo3bwPPnf1OjRlXs7R348891iMVi0tPTOXXqOC1btkEm\nkxETE429vQPW1racOHGUjIwM6tVrwK5dO3B3n0SdOvUYN24UPXv2pXZtC27fDqJsWQNmz54KyENo\nZTIZlStX4dKlC5ibmxMcHEjNmqZIJBKFcEsezZq15MGD+1SsWIkbN64VOCeTyTh//gw//+xKRkY6\nt27dYPjwUWRnZyvK1KvXkICAXdjZOXxyChQBAYFP46ONuaNHjxZ7btiwYQwbNuxjmxYQEBD4bslb\nvNet24Dnz58zaFA/0tLSUFJSQklJzJ07tzExqcbkye7o6eljaWkFwI0b1xg5ciz3798BQFtbm5iY\nGCpUqEiZMmWZN28mxsbGqKqq4O7eFkfHady4cQ1X176kpqaioqJKZmYGd+7cViwgq1evgb5+mQLj\na9asBQCmpmZEREQAcPt2ED179gGgWrXqVK9e863X6OExEx0dHbKyMhkyxJnmzVsqrv1NifabN6/z\n6NGDAh6m27eDqFXLjIUL57Bq1ToqV67C/Pmz2LNnFz179inWAPLxWY+DQz3693fhypVL/P33PsW5\nohbiP/zQvkjDs02bJnTu3J3r168ybtwk7t27w6FDcvn8jh270LNnn0Iy7du2bSEzM4OBA90KeTin\nTJmJjY0tWVmZLFw4hydPHmNkZEJWVtYnqRyqqKgqXovFSkgkuYXKiESiN/r4fKqKJUVReeGmT59D\n//49ijTiAR4/fsiwYQNJTExESang56NChYqMGTOBSZPcWbLkV27duvGv5wzi4lKwsBiMiUlasQ8V\nQkLus3z5IpSUxKxZs4pp02ZhampGcHAQN29eY8CA3mhqliItLQ1VVfkDgkuXnpCbq8fx46Foa0ej\npVWWrl2dCA19waFDBxg/fhS1a1sCcjGRefNmkpaWikwmo0eP3mhpaeHiMphVq5bj7NwbqVSKnp4e\n48b9QkZGJllZWQwePABlZWWMjEzQ19fnwYP73Lx5nR9+aMfBg3uJiopCU1MLZWVlxf7JvO+Oqqpc\npEVJSQmJRFLgnEgkonr1mowePYzExERcXQdTpkxZoqIiFWWEFCgCAl8PJaJmKSAgICDwfhw9ekbx\nunr1GlSpYsyvv65GTU2NUaOGUrOmKaGhLxQLyTyOHZPn65RKXy/Gc3NzABnLlq3k1q0bbNniw4MH\n9xk9ehwikRILFy6jShUjzp07zZkzpzA2Nvm3ZvEL+jwDQUlJTG7ua+PgQ4wOf//tnDsnv86XL18S\nFhb21nYKe5giUVfXoGLFSlSuXAWA9u07EhCwU2FUFsXt20F4ei4HoH79hmhr6yjOVahQiRo15Eao\nqakZUVGRQNGGZ2ZmJhYWlowcOZaQkPv888/fbNjgi1Qqw83NGTs7e7S0CobC5Peyvenh9PFZz2+/\nrWHPnl1oaJTCz8+fJ08eM3Bgv88SuVKqlNyw0NHRxczMgt9+W0ZSUiJaWtocP34UJ6feJd5nSZOX\nq83S0hpPz7kEBPgXO1cymYwnTx6zfv1rwY6yZcsW8CTlZ8cOP8aPn4KX10P++acTV67ooa+/i4oV\n77FzZ4DioUJwcCC1a1vy229LmTjRg/nzZ9GhQyfWr1+DiUk1Tp06jo6ODgcPnmDNmpVcvnxRYdy/\neKFDfPxQkpOd0NAIIienF2pq6nTr1pM7d4JZu3ZjgTGtWfNnoXGqqakxceLUQsejoiLp2bMzixat\nwNLSikWL5lGxYiUiIyMwNCyPrm5prKys6NixC05Ovbl16waGhuXQ0dHF13cHPXr8BMDUqbMICbnH\n5csXqVChIr6+OxR9VK9ek+nT5xToN38ZqVSKm9sIhg79pbhbKCAg8B/xbe38FhAQEPiOyFPtU1NT\n4/nzZ9y+HcyxY1e5deuGwthITk4CoG7d+pw6dYLExHiSk5OIj4/jxYtnREdH8fjxQ2xs7JBKpchk\ncjEVsViJXbvkCy9zc0uuXbtCcnISVlbWnDp1ApFIxNOnj4mPj3vnOK2sbDh58jgAz5495enTx8WW\nvXnzOjduXMPLy4dNm7ZRs2YtsrPfLv9f2MMkKbRwl8lkimNisVhh1GZlZRcqVxR5ngiQG6p53gh/\n/+24uPRl6NCBCsNTSUmJ5s1bARAcHPiv1L46GhoaNGvWkqCgW0UaFvn7zu/hjI6OAiAoKJAffmgP\nyA35d3k4iyJ/v8XZgT/91JXx40cxZsxwypYty7BhIxk9ehiurn0xM6uNo2PTD+73v6ZcOUMsLeX7\n7du2/ZHbtwOLLSsSiWjSpBmqqqro6pbG3t6Be/fuFFveysqGlSuXc+nSfcRiCSAmI8MEZeVKlC1r\ngEgkokaNWkRHRxEa+pxnz54wd+4MwsPD2LzZm9jYWLKzs8jNzcXIyIRTp47Ttm0HZDIZjx8/AkBZ\nWYJIJEMq1f733xMAjh7955Pm5dGjF+zZc5by5SuyZ89O+vfvQWpqKr169WPq1FnMmDEZZ+feiMVi\nunRxypuhN2eswOuiPsvFfbYyMjJwdd2Jnd05mjc/xOHDtz7pegQEBD4dwTMnICAg8IWoX78Re/fu\npl+/HiQkKJOcbIWPTzuqVoVJk9wRi8Xo6+uzYsUfODsPYsWKxYjFynTu3I5KlapQu7YFhoYVGD58\nEFKplFKlStG/vzNaWlqoqqqSm5ubL0RLn6FDXdHU1EJDQ4MjR/4hNvalwiNWFHmLvG7dejB//iz6\n9++JsbExVatWK7A/KT9vGqh37xZcVJcqVYr09PR3zo2RkTFRUZFERIRTqVJljhw5hK2tPQDly1cg\nJOQeM2ZMLpD/Sm50HqNfP2euXr1MSkryW/vIb3jmeUazs7NQVVUr4GXLT55Rmd+gBLmUff6y+T2c\neYZjSZDn2bW3d8De3kFx3N19kuJ19+696N69l+J969ZtFXnXvhXyz6V8zpXeasQXrl/8s+r+/V1o\n1MiRfv18qFKlD+Hhcq+YsvLrOnkPFQCqVq3OrFnzmTJlnMIztWmT3LM2c+Y8li1bRGRkBNHRkZw/\nf4YaNWpSt646p08/ISHhJWJxW2Syvbi6nqNu3QYf7Y3dv/8qHh6qxMa6UqaMBb17pzJjxmsPfp06\ndfH23goUFMjw938dbpybm4uXl7fCa21mZs6qVQWVZAcOdCt2DIsWneDgQWdAmehomDPHn9atc1FW\nFpaTAgJfCuHbJyAgIPCFUFFRYdmyVdy//5BWrTTIza0NwL179WnV6i9mzHidI05DQ4Np02a/d9tH\nj5794PHk7T8CKF26NCdOnCA2NgWRSMT06XNQV1cnIiKcsWN/wdCwfJFt5Bmo/fv3oEoVY8Wevzxv\ngDwEzIYBA3rRoEFjGjZsXKQXQFVVVeFpkEgkmJtbKDwNrq5uLFo0l8zMLMRiZcXi2NXVjdmzp3Hk\nyCEsLKzR1y9DqVKapKWlFWmUvcvwBLCxsWXBgjn07++MVCrj3LnTzJgxDz09fYWXVF1dg4sXz9Ow\nYeO3zq+trR3Hjh3G3t6Bp08f8+TJo7eW/1SysrLw8TlFVhb07l0XQ8My7670lRATE82dO7extLTi\n2LHDWFvbkJ6eRkjIPRo0aMSZMycUZd9HsCM/ERHhVKtWg19+ac+qVS9RVb2CkdFzqlbVKVTWyMiE\nxMQE4uLi/lWYzCUsLBQXl0GcOnWc2NiXLF++ijVrVnH58gVcXAYDsGLFPCIjo3jwIBh7+5/Q1R2g\naHPEiNEfNScbN8YRG9sTgLi4Rnh776R79/evf/jwLebMiSE21pDatU+wYUNLDA3LftAYXr1SJf/S\n8eXL8iQlJVGmzLfz2RIQ+N4QjDkBAQGBL0xurgSpNP+fYxFSacnupfL3v8SmTUlIJCK6d1dlyJAW\n76wjkUgYPXoXp07poK29mrJlZejpaTJhwpRin8TnGaiF+3/tHZg1a36Bc3Z2dRSv83uYHjy4z48/\ndsLJqTerVi1n/PhRrFy5ltzcHMzMavPq1StUVFRITk5m6FBX5s1bxIoVv5OcnMzMmVNITU1l+PCB\njB49Hl/fHWzc6EVkZDiRkZGUL1+Bn37qxpIlC2nZshGqqmqYmFQFCnqFatUy48cfOzJkiDMAnTp1\nVSSHdnEZTIcOrbGxsVPULRp5e126OLFwoVzIw9jYBDOz2m+p82nk5OTQv38AZ864ACoEBGxn586G\nH7x4/1IYGRmzZ89OFi2ai4lJNbp27YG5uSWLFs3lzz+1sLOr80GCHfJy8v/9/bdz8+Z1RCIlWreu\nRLdulcjN1WfPnieFxqGsrMy8eYtZuXIZqany1AK9evWlatVqTJ06C0/PuYhEFOlxe/z4FTduJJCV\n9Yh27ep+8pxIJOIC73NzxcWULIxMJsPTM4InT+R7Ti9fbsKCBVtZtarzB42hbl019u4NJyenMiDD\nwuIR+vo276wnICDw+RDJPkVKqwQR8mV8vwj5UL5vhPv76UilUgYP/ou//+4HlKJWLX/8/GwwMalY\nIu3fu/eEbt0yiI9vCICm5gO8vV/SooXtW+v5+Z1j3LgmgFzso3Tps5w+bUjFiiUzrndx9+4dduzw\nY968RYwYMZjc3FzWrPmTLVt80Ncvw7Jlnixe/CuNGjmyZs0qcnNzCQy8QWRkJGXKlGHSpOn8+WcQ\nt2/vwMFhKDVrRnDt2hXWrPkTVVVVZs+eRrduPbC2tiU6OpoJE0bh5+f/QWNs06Ypx459uBf0c3P0\n6CX697cH8ow3GRMn+jNxYntFma/1u/umUui3yNat55g1y4jkZEvU1Z8yfvwtxoz54ZPa9PE5w9y5\nNUhLM6NUqYdMmXKPYcNaFVn2zXsrkUiwsztHdHQnxbH27Xfj6/vhY/LyOsHFixJ0dTOZNq3RN/OA\n4Hvia/3uCnw6/2meOQEBAQGBkkFJSYkNG3qybdsxkpNz6NbNgQoVit/L9qFcu/aI+PjX8VhpaaYE\nBd2mxTuccxERueQZcgCJiTV4/vzRf2bMmZqa8eDBfdLT01BVVcXMzJyQkPsEBd1i7NiJqKio0KiR\n479lzbl+/Qre3lvp2LENqqqqTJgwjYQEPcRiMVu2dKZJk3F07NgUVVX5frbr16/y4sUzRX/p6elk\nZmYWyJW1bdtmVFVVFd7BJ08es3LlWm7cuKZIfbB+/RouXjyPmpoaixYtR09Pn4SEBJYv9yQmJhoA\nS8sfiI8vS2rqecqUUSEqKpKYmGh69uzzWdQl1dSUEYkyef24Voqy8lfx7Pa9+Jrz0z56FMbs2bd4\n9UqT2rWTWLy4o+Izlcfu3RkkJ8tTD2RmVmPfvkDGjPm0fl1dm2FsHMitW7extS1Hq1ZFG3JFIRaL\nsbd/yaFDuYAyKirhNG78cUvAoUNbMXToR1UVEBD4DAjGnICAgMBXgFgs5uef339x9iE0aGBK2bKX\nePVKvqdLS+s+dnZF73nLT5s2lfnzz0CSkuQePHPzc1hb/3dKiMrKylSoUIlDhw5gZWVD9eo1uHnz\nGhEREZiYVEUsfv0TpqQkyic0ImP9el86dDhDaGhXRZm4ODVFvq385VRUVCgOGxt7duzww8mpNyEh\n98nNzSU3N5fg4EBsbe05fvwIlpbWuLmNYM2aVezfvwdn50GsXLmMnj37Ym1ty/z5f7F16188f36M\ncuUeUr36GXbv/ou0tFT69u1O1649EIvfP2TufWja1IHOnf9i797OgBb16m1nyJAfS7SPz8WbMvlf\nG+PHX+fyZfkeuFu3stDW3s3cuZ0KlJGrZL5GWblkRHBatrSlZcuPq7t2bScWLfInNlaVevXUcHH5\nyIYEBAS+KgRjTkBAQOA7x9S0KgsWXMbHxx+JRISTkzrNmjV7Z722be1ZuvQ4Bw/uRlU1m7FjrYtV\nsfxc2NjYsn27H1OnzqJateqsWrUCc/O37zWrW7cB/v47KF9e7lVUVQ0hO9sMLa3sIsv17fszAI8e\nPaBmTdMCZT7GOwgFvX5PnqQgEskQidLJzdUlJcUMZWVldHVL/+vFi3+rqujHIBKJWLeuJ926XSY1\nNYsOHTqhoaFRon38PyKVSnnxIr9QihrPnqkVKjd4sCEhIaeJiWmMnt4NXFw+PHSqpNHQ0GDOnI5f\nehgCAgIljGDMCQgICPwf0LVrA7p2fXe5N+nSpT5dury73OfCxsaOLVt8sLS0Qk1NHTU1NWxs7IA3\nc669fj127ARWrFhMbu4jatdeR1ZWDapUaUXDhpULKGfmlXN27oNEIsHW1p4JE6YU6P9TvYMqKip0\n6XKIixd75WuTfHWUyM0tudQF+VFSUqJdu0afpe3/V5SUlDA2TiYqKu9IFlWrFs6j2LatPaam4Vy4\ncAB7+2qYm79d6VRAQEDgYxGMOQEBAQGBr5Y6depy6tQlxfvt2wMUr/NyrgE0b95KkehbV7c0c+Z4\nvrPt9y33Kd7Bvn1/ZtSoSoSFrScsrBM6Og9xdCwsgS/w7bB8uQOzZ28lNrYUlpYpTJ/eochyJiaV\nMTGp/B+PTkBA4P8NwZgTEBAQEPi/4+nTcDZtCkYkkuHm5kClSobFlv0U7/xS3VsAACAASURBVGCe\n169bt9o0b16LwMByQk6ub5yaNauwdWuVLz0MAQEBAUBITSDwHyBI6H7fCPf3++VrubcfKlX/4sVz\nZs2aipKSEvPmLaJSpYLekcjIl/ToEcijR90BGbVrbycgwBF9fb3PMPqvl6/l/gqUPMK9/b4R7u/3\ny8ekJlD6DOMQEBAQEBD4Ypw9e5oWLVrh7e1XyJAD2LPnxr+GHICIe/d6sn//1c8+rri4eHbtOsWt\nW/ffu87IkW6EhLx/+fdh4sQxpKWlkpKSwp49uxTHb968zqRJ7iXal4CAgIDA50UIsxQQEBAQ+OqR\nSCTMnTuDhw9DMDGpxowZc3j27Bl//PErGRkZ6OqWZtq0WTx8GMKuXdtRUhJz8+Z1Vq5cy44dfhw6\ndACAjh27ULp0OZSVQ6hceQwZGbaoqwehojKAbds2c+rUcbKzc2jatDmDBpVcMq17954xePATHj9u\nj4bGY8aMOcq4ce9O2CwSiT4o55pUKkVJ6e3PaZcuXQlAUlISe/b407Wr03u3/zYkEkmJp1h4kzZt\nmnDs2LnP2oeAgIDAt4RgzAkICAgIfPWEhr7Aw2MmlpbWeHrOZffunZw7dxpPzxWULl2aEyeOsn79\nGjw8ZtK5c3dKlSpF7979CQm5zz///M2GDb5IpTLc3JyZPn0ubdse5OHDUGJj3WjZ0pQaNcpy5kww\nGzZsRiqVMmXKeIKCbin2xn0seSGiOjoDePy4N3p6GxGJMti58yCqqvcICrpFamoKU6bMxMbGlqys\nTBYunMOTJ48xMjIhK+u1UuLVq5fx9l5PdnY2lSpVZurUWWhoaODk1IlWrX7g2rUr9OvnTKtWbRR1\njhw5xK5df5Gbm0Pt2paMGzeZXr26sHHjFlavXkFERDiurn2pW7c+DRs6kpGRzvTpk3n27AmmpubM\nnDkPgJCQ+4UM5zJlyjJypBu1apkSHBxEmzZt6dWr3yfN17v5epOJCwgICHwJBGNOQEBAQOCz4+TU\nCW9vP3R0dD+qfrlyhlhaWgPQtu2P+Pp68/TpE9zdRwByj1SZMvJcbTKZjLzd4MHBgTRt2kKRLLxZ\ns5bcvh3IwoUdGT58L1u21KBq1aqsXr2Sa9eu4OraF4CMjEzCw8Pe25g7f/4sz58/pX9/lyLPSyR5\nP7eif8eohESSy4YNvsyfPwsfn/X89tsa9uzZhYZGKf7H3n0GNHW1ARz/BwhhJYg4UARFRBxMte5t\naaWOalUcxYWr1FG34sCtddVVd0VxK65XrVqte9Sq4N4DZYsDgQgEEvJ+SEmhYB1FcZzfp+Tm3nvO\nvWHkyTnnedauDeHu3Tv4+emCo2fPnrF6dRDz5i1CJjNh7dpVbNq0jm7deiKRSLC0LERQ0Nocbd6/\nH86hQwdYsiQIQ0NDZs+ezv79e/WjfUOHDuXGjZusXLke0E2zvH37JmvXhmBtXQR//x5cunSBSpVc\nmDt3JtOn/4SlZc7AWSKRoFar+eWX1a90nwACAoYSH/+Q9HQV7dp1pGXL1nh51aNdu46cOnUCmUzG\njz/OxsqqMDEx0UyYMIa0tFTq1Hl3BesFQRA+FCKYEwRB+Mj988Nz8+ZfM23aRG7evI5EIqFZs5b4\n+HRCqVRy4MA+WrduS1jYObZv38SkSTNfuZ29e3fz2Wc1KVKkSK7XXmeqYF6yH6/VajE3N8fBwZEl\nS4L+dd9/tqvVavXBjEIhp2zZsvrXfH278fXX37xR/+rWrU/dui8ONtq3L8Hx4yfIyACJJJXChdNp\n0kQ3zfLo0UNYW+vu2cWLF2jXrgMAjo7lcHR0AuDq1cvcv3+P777zAyAjQ42rq5v+/NlH47KEhp7h\n5s0b9OypK4qenp6OldXfSV7yyn9WsWJlfQHzcuXKExcXi4WFBeHhdxk4MHfgrGv75dNFswsICESh\nUKBSpdGrV1caNmxMWloaLi5u9O79PYsWzWfnzu107dqDefNm8c037fjyy6/Yti3ktdoRBEH4FIhg\nThAE4SP3zw/Pzs4Vefz4kT47pFKpBCA5Oek/raHas2cXDg6OzJ79Y66RlyxeXvXo0aNPjjVsPj4d\nCQ5ewbZtIdSuXY/Dh3/HxsaGpUtXIZPJuHPnNnFxsXTs+A116zZg9+4d+Pp2Y9euHVy5chkXF1fU\najWRkRE4OJTN0Sd3dw+mTJmAr29XMjO1HD9+hLFjJ+UIZAIChhIefpdHj+JRqzNo06Y9GzasYceO\nrSgUlpQr54SxsTGDBg3nxIljrF4dhFqdgUJhybhxk7GyKsyePbu4efM6gwYNZ8qU8ZibW3Dz5jXi\n4+PJzMykYUM3Fi48w+TJSwENGRkZhIff4/jxo6hUKuLiYpk0aWye9zWrr9Wq1WD8+Cl57mNqaprn\ndm/v5vTp0zfHtr17d7/wPZRKjfWPDQ0N9EXQXxQ4A5iY5N32i4SEbOD4cV2NwPj4eCIjI5FKpdSu\nXRcAZ+eKnDv3JwBXrlxi6tRZAHz5pTeLFy94rbYEQRA+diKYEwRB+Mj988NzRkYGMTHRzJ07k1q1\n6lK9ek0AlixZoF9DZWRkhFxukef6qVWrfuHkyWOoVCpcXNwYPnw0hw//zo0b15k4cQxSqZRly4IB\nrX7kJUtmpjbXGjZPzyp88YU3QUHLaNPGB41GTWTkA44ePcQXX3izaNE8bGxKUKlSZfbs2Ulmppa2\nbTtQvXot5s2bhVKpRKNR0759J30wlzUgV758Bb76qjm9enUFoEWL1jg5lSc2NkY/apcV7G7YsIaF\nC+exbVsIMTHRLFu2CgcHR374wR8np/KArubcsmWrANi1awfr1q2mX7+BuUYAnz59wuLFQdy9e5vu\n3b8lKSmRyMhryOUymjf/mrCwc9jZlaZFi1Zs27aZQoWsGDt2Eps2rePAgX1UqVKNe/fucPfubSQS\nCZUru/LTT9OJjo7C1rYUqampPH78CDs7+xe+71WrVmfkyCH4+HTCysqKpKREUlJS9K+bm5vneP4i\n9vZlePYs4aWB86sICztHaOhZli5diUwmo3//PqSnqzA0/PvjiIGBRB9ECoIgCP9OBHOCIAgfsbw+\nPKvVGQQHb+TPP0+xY8dWDh06QEBAIP7+AwgPv8fKles5fz6UUaOGsmbN5hzrp9zcPPjmGx+6desJ\nwKRJgZw8eZxGjT5n27YQypVzIiLiAX36dOfx43iSk5OJjIxEpVIxffoUMjM1mJtb0KePHzKZjOrV\na3Hx4nmio6OwsJBTrpxuWmHJkrbExsYQFhZKXFwcZcs6kpDwjIkTf2TevFnIZDKcnMrz88/Lcl2z\nn1/vHM/bt/82V2KOEiVKEhy8EcgKdo8AEoyNjfH2bk5ExAOcnJwBaNSoCZGREQDExz8kMHAkT58+\nISMjg5IlbYGcUxYlEgn16jUAwNHRCSMjI3r16oqpqRlKpZLz50NJS0v7x2iaLhhs1aotU6dOwNe3\nHaVLl6FChUoAFCpUiNGjxzN+/CjS0zMA6N37+38N5sqUcaBXL38GD+5LZqYWqVTKoEHD9W1ZWVnh\n6upOly7tqVmzDrVq1SGv2bBGRkZMmjT9hYHz60hJeY5cLkcmk3H/fjhXr1751/1dXd05eHA/X3zh\nzf79+167PUEQhI+dCOYEQRA+Ytk/PD94cJ+rV6/w7FkCGo2aBg0aY2dnz6RJgUDOgESr1eLm5pZr\n/ZSbmwdhYWdZv34NKlUaSUlJlC3rSJ069QAwNpZx48Z1tm37lUGD+nLnzm1SU1NIT0/H1dWNo0cP\nUaxYccaPn8KiRfO5fv0qJUuWRCKR5Ehrb2BgQEZGBosXz8fKyooVK9Zw8OB+tmzZmK/358cfV7Jr\n137S0nrx+eepyOX7KF26DA8e3M92L/7ef86cGXTs2Jk6depx/nwoQUG5g0kAqVSqf2xoaMSmTTsA\nePLkMadOnWDbts1/jXhWACSEhPwPAJlMxoQJU/M8Z5Uq1Vi+PHeikZCQnS+8viZNvHKtp8tqC2Dc\nuMk5XvP0rKp/rAv8dF4UOC9YsPSFbeelRo3a7NixFV/fdtjZlcbFxRV48TrHH34YyoQJY1i3Lpi6\ndRv857WXgiAIHxsRzAmCIHzE8vrw/OjRI/r3/w6tNhOA777rn+exxsa510+pVCp++mkGK1asoWjR\nYvpU+VksLQuRlpaGRqP+a/80IiIekJ6um5JpZGREePg9VKo0HBwc2bVrBwMGDCEqKipH21otJCY+\nIyLiPhkZGXTs2BpjYxkpKamYmprky72JjIxm7VoJRkZliYlpx7p1YTg6TqdFi9ZcuBBGcnIypqam\nHD16SD9imJLyXB/g/tvas7zExcVRtGhRWrRoRXq6itu3b9K0aTOMjIxQq9UYGb36v+RLl25z8eI9\n6tVzoUwZ29fqx3+lUqmYM+cgjx4ZUq9eIVq1qvHKx0qlUmbNmp9r+/79R/WPGzZsQsOGTQDdCGr2\ntXq9evn/h54LgiB8fEQwJwiC8BF70YfnrIyJ2ZmZmb10DVVW4KZQWJKSksLhw7/TuLGX/vhy5ZyQ\nyWR06NAaCws59vZluHXrBhqNBnv70kilxvo1bEqlEjs7O/16tH+OukgkEhwcHBkwYDDTp0/BwEBC\n3br1uXHj2hvdi3+6dSuK+Pi22NpeonTpr8jIcMDS0p5ixYrRuXN3evXqikKhoHTpMpibWwC6KZxj\nx45ALldQtWo14uJi9X190ehS1uPz58+xYcMajIyMMDMzZ8yYCQC0bNmabt064uxcgbFjJ7203ytX\nHmXq1BIkJraiZMkjzJnzmEaN3PPlnryK77/fwa5dXQBjtm69SVraSTp0qJOvbSQlJbFlyx/I5ca0\nadPgpYXQBUEQPlUimBMEQfhEbN9+mjVrEtFqoVMnOe3a1c7xuqVlIf0aKplMho1N8VznkMvltGjR\nii5d2lO4sDWVKrnoX/vqqxbMnTsTqdQIQ0MjhgwZSdmyjvTo0Zm6devra8xlrWE7fPh3/vjjJAAW\nFhZ06OCrP1e9eg2oU6c+vr7tSE1NIzh4A2q1mkWL5lOxYqV8uR+ffVYBR8fT3L27HACF4jIDBybi\n4eGOs3NFWrZsjVqtZvToYdSv3xCAunUbULdug1zn8vZujrd3cwBGjRqX47WsUafs+2Tn798ff/+8\nR0fzsmpVKomJuumQMTGf88svm99ZMKdSqTh92hbQjdqmpDhz8OAVOuT+buCNPXnylPbtj3Dpki+g\nZN++TSxf3v6FAV3W9GAxBVMQhE+RCOYEQRDekL+/H4sXB/H48SPmzp3F5MnTC7pLL3Tp0m1GjbLk\nyRPdKNrVq6E4OFynWrWKOfbLvoaqaFE5jx4lAznXT/Xq5Z/ndLcGDRrToEFjQkPPMnToAFxcXJHJ\nTJDJZPri2/82evXPz+KGhoa0adONiRPHkZycgFarxd6+DPPnL37Du5CTQmHJ0qVlmD9/I+npUlq0\nsKBxY12AGxS0jHPn/iQ9PZ3q1WtRr17DfGkzy5495zh58jG2tgZ8993nrzXypFYb5niu0by7USup\nVIpcruTRo6wtWszN0/K1jRUr/uTSpS7oErVYsmvXl8yYMZNr18IAXTmL+vUbMmhQXypXduXmzevM\nmjWf4sVt8rUfgiAIHwKJNq+qoQUg6wOD8PHJ/oFQ+PiI9/fDsHTpXsaO9cmxbdy4zfTt6/3CY17l\nvX306AlLlpxGozHg228r4+T04uyKr0Or1TJgwBZCQpqQmSmnVq2trF/fAnNz83w5f0Fat+44Y8aU\n5fnzCkASnTptZe7cV6/tN2PGXhYsqIFKVZpChcKYNu0RbdrUfvmB//Cmv7ubN//B1Kkq4uNL4+ER\nxi+/1KNkyWKvfZ4XmT59L7NntyMr66ZMdpAaNaawbt0mfTmLwMBJ9OjRmSVLgnKMDgs64u/yx028\nvx+vokXlr32MmIQuCILwhry8dBkcY2Nj6NKl/Ttt+3Xb9PCwQ6G4pH9uYXENd/eS/6kPSqWSTp2O\nsGBBexYt8qFz59uEh0f/p3Nm2bBhL5s2NSQzszRQmD/+6M7y5cfy5dwF7bffUv8K5AAUHDtmRWZm\n5isfP3y4N0uW3CIgYAvBwelvFMj9Fz4+tThxoip//CFh586v8zWQA+jWrTqVK68HtEAKVapspmlT\nb2QyE0xNTWnQoDEXL56nePESIpATBOGTJ6ZZCoIgvLEPZ41OjRoujBlzlHXrbqHVSujQQUrduo3+\n0zn37j3DxYvtyboP9+61Yvv2EAYP/m/ZFR8/fsKPP0YATbJtNSI9/cO53//G1DQjx3Mzs/TXTvDR\nrFlNmjXLz169HgsLORYWr/8N8qsoXtyarVvrsWlTCBYWRhgbe6JUKnPtl19ZTQVBED5kYmROEATh\nA6XRaJg4cSy+vu0YM2YEKlUaN25cp1+/3vTo0ZnBg/vz5MljAK5fv8rhw4spVSqY1q2vc+zYEkA3\nwte3by/8/Hzx8/PlyhXd6F1Y2Dk6d+7MmDEj+PbbtkycODZX+0WLyjE0fJRtSypy+X//t3L06CXi\n4noDuwA1AIULr6RDh3eXsfFtGjy4MpUqbQLuU6zYAfr3L1TQXXrvFC5shb+/N507e+HpWZVjx46g\nUqWRmprKsWOH9WswBUEQPnViZE4QBOEDFRHxgICAQFxc3Jg2bSJbt27m+PEjTJv2E4UKFeLgwf0s\nW7aIgIBApk6dwMiRgVSu7MKSJT/rk48ULlyYOXMWYmxsTGRkBBMmjOGXX3SFqa9fv86aNZuxti6C\nv38PLl26gJubh779Bg2q4eu7nQ0bPFCrTfjiiyN07+6TV1dfi5OTLebm4Tx/3gH4FXhO376G2NuX\n+M/nfh84O5dhz55i3LhxF3v7chQpUqSgu/ReK1++gr6cBUCLFq2RyxUie6UgCAIimBMEQfhgFStW\nHBcXNwC+/PIrgoODuHfvLoMGfQ9AZmYm1tZFUSqVpKamUrmybn2Rl1dTTp06DkBGhpo5c6Zz585t\nDAwMiIqK1J/fzc1NXyC7XLnyxMXF5gjmJBIJM2d+Q58+d1GpkqhYsUO+1ANzcyvPoEEHWLUqnIwM\nKd7eGfTr1/o/n/d9YmZmRpUqrgXdjQ9GVjmL7IKDNxZQbwRBEN4fIpgTBEF4Qy9Ks18Q7Wu1WszN\nzXFwcGTJkqAc+yUn58x6lj2J8aZN67C2LsLYsZPQaDT61PwAxsbG+seGhgZoNJo8+1GunON/uo68\nDBjgRd++GjQaTY5+CJ+uGzfuM2PGFZRKYxo0kNC3r1dBd0kQBKHAiTVzgiAIb8jRURfElChRskBG\nCR4+jOPKlcsAHDiwj8qVXXj2LEG/Ta1WEx5+D7lcjpmZGdeuXQHg4MH9+kAwJeU5hQtbA7Bv36+v\nlVXxbTM0NBSBnABAeno6ffteZvfujhw50oZp0z5j3brjBd0tQRCEAieCOUEQhNdw4sRVOnTYQ6tW\n+/Hw+PblB7wlEokEe/vSbN++GV/fdiiVStq27cCkSdNZsmQB3bp1onv3Tly9qktoMnLkWKZPn0L3\n7p1IS0vDzExXr61163bs3fsr3bp1IiLiAaamZgV2Te+T9etXs2WLLkCfP382P/ygK5IeGnqWiRPH\ncvbsab77zg8/P1/Gjh1JampqQXb3vfcqXxIolUq2b98C6BLwDB8+SP9adHQU16//PS01Pd2OsLCU\n/O+oIAjCB0ZMsxQEQXhFCQlPGTToEQ8e6Oq7xce7U6KEBS1b1njnfbGxKcG6dVtybXdyKs/PPy/L\ntd3BwZHg4A0ArFmziooVKwFQqpSdfjuAv39/AKpUqcaXXzbSF6YdNGh4vl/D+8zdvQobN66lbdsO\n3LhxnQcP7nPw4H4ePLiPo2M5goODmDt3ESYmJqxdu4pNm9bRrVvPgu52gQkIGEp8/EPS01W0a9eR\nli1b4+VVj6+/bsO5c2cYPHg4sbExbNmyCbU6g0qVXBgyZGSONZbJyUls3x5C69a5C6gXK1YcW9vT\nPHiQFdA9p1Qpba79BEEQPjUimBMEQXhFFy/e4cGD6tm2GBAWlkDLlgXWpVd26tQJ1q5diUajwcam\nJKNHj8tzv4iIOMaN+5OHD82pUkVFYKDXJznV0dm5AjdvXicl5TnGxsZYWVkRExPNpUsXqFu3Pvfv\n38Pf3w/QJZFxdXUr4B4XrICAQBQKBSpVGr16daVhw8akpaVRubIL/foN5P79cNatC2bJkiAMDQ2Z\nNetH9u/fS9OmfxfLW7JkAdHRUXTv3gkjIyNMTEwZM2YE4eF3cXauyMSJrfnpp40olSeQy68QFmbG\njBmhDB8+GoB+/XpTubIrYWHnUCqTGTkyEHd3jxd1WRAE4aMggjlBeAdiY2MYMWIQq1dveqX9z58P\nRSqV6jMVCu+HihXLUKzYZeLji/+1RUv58h/GtMQmTbxo0uTlCSMGDTrF8eO6FPDnzqWj1W5hypQW\nb7t7BWLjxrXs2bMLgObNW1G/fkOGDOmPm5snV65cRKlMZufO7bi6unPhQhh3797h3r27pKSkUK1a\nDcaPn8LZs6fZvn0rI0aMKeCrKVghIRs4fvwoAPHx8URGRmJgYEDDhrrC76GhZ7h58wY9e3YGQKVS\nYW1tneMc/v4DCA+/x8qV6zl/PpSAgCGsXRuiL41ha2vAgQPNSEqqh0KhAGDSpEBOnjxOnTr1kEgk\nZGZmsnx5MH/8cZKVK5cxd+6id3gXBEEQ3j0RzAnCeygs7BxmZuYimHvPFC9ejKlTH7Bw4SZUKmO0\nWg0dO9Yr6G7lG61WS3i4ZbYtxty7Jyuw/rxNN25cZ+/e3SxfHkxmppbevbvi6VmFqKhIJkyYxogR\no+nc2Yc1a1YyceKPREQ84OzZP/Hw8OTu3Ts8ehRPdHQUv/66iy++aEpkZAR2dvYFfVkFIizsHKGh\nZ1m6dCUymYz+/fuQnq7C2FiWI+Oqt3dz+vTp+8LzZM+yqtVqqVixcp6lMcLCzrJ+/RpUqjSSkpIo\nW9aROnV0v4cNGjQCdCOrcXGxb+NyBUEQ3isimBOEd0Sj0TBx4lhu3bpBmTJlGTNmAr6+7QgKWotC\nYcmNG9dYuHAeo0ePZ+fObRgYGLJ//x4GDhwupgq9R1q2/Ew/rdLLa+JHVbhYl1QliaiorC1q7Ow+\nzsQely5doH79RshkJgA0aNCYixfPU6KELeXKOQHg4uLGr7/uxMXFld9+24NUaoS7uyfOzhV59Cie\nsWNHcu/eHcLD79K7d98PMpjbu3c3GzeuQyKR4OhYjsaNvQgOXoFanYFCYcm4cZOxsirMihVLefgw\njtjYGB4+jMPHpyNt23YAdBlR5XI5MpmM+/fDuXr1Sq52qlatzsiRQ/Dx6YSVlRVJSYmkpKRiY2Pz\nwr5JpblLY6hUKn76aQYrVqyhaNFiBAUtIz09PdcxBgaGLyylIQiC8DERwZwgvCMREQ8ICAjExcWN\nadMmsm1bSJ6BgI1NCb7+ug1mZmZ06OBbAD0VXtXHFMhlmTmzGoGB63j40AxPz1QmTPiioLv0Vrzo\nvTM2luof29uXoVu3nvqAb+DAYTRs2ITY2BiGDx9IixatefLksT5pzIfm9u3brF4dxNKlK1EoLElK\nSkIikbBs2SoAdu3awbp1q+nXbyAAkZERLFiwlOfPlXTq1IbWrdthaGhIjRq12bFjK76+7bCzK42L\niy5JSfZ7XKaMA716+TN4cF8yM7UYGRkxZMiIHMGcmZkZKSn/nqEyK3BTKCxJSUnh8OHfadxY1JsT\nBOHTJYI5QXhHihUrrp82+eWXXxESsuFf99eKRG3vvf37jxZ0F/Kdk5MdGzbYAVC0qFyfzfJj4+7u\nwZQpE/D17UpmppZjxw4zduxEdu7c/q/HXb16j/79r5GQYMW9e8sZMGDEO+px/jt9+jSNG3uhUOim\n1ioUCu7evUNg4EiePn1CRkYGJUvaArrArHbtuhgZGWFpWQgrq8IkJDylSJGiSKVSZs2an+v8//z9\neNm6TUvLQri6utOlS3tkMpm+/mF2crmcFi1a0aVLewoXtqZSJZd/ucK392XL666DfpEVK5bi7u5J\ntWrVX76zIAhCHkQwJwjvSPZvqbVaLRKJAYaGhmRm6qI2lSr9RYcKBUypVDJ//lFSUw35+msHqlVz\nfittHDiwL8+07EL+K1++Al991ZxevXTJXlq0aI1crsg1Ypf9uUQiYebMq1y50gm5XIGBwRpWrsyg\nfft32vV8I5FIcqxTA5gzZwYdO3amTp16nD8fSlDQ32UujIz+HrU0MDBArX61aYz79oUxb14cqanG\nNGyYyrhxzV84Mjpu3OQ8t2cvjdGrlz+9evnn2mfMmAlkBXCFChUiJOR/r9S/gtSjR5+C7oIgCB84\nUTRcEN6Rhw/juHLlMgAHDuzDzc0dG5sS3LhxDYCjRw/q99VNN3peIP0UcsrIyMDXdzdz57Zj6dJ2\n+Pklce7czXxvJ6vG1vvg34o3vw2xsTF06fLuI6L27b9l9epNrF69iXbtOmBjU4Lg4I361zt29KV7\n914AjBo1jgYNGpOcrJtyaWoaSmJiO/3zD1HNmjU5fPh3kpISAf5ax/Zcn3Rk797d+n3/GfS9qmfP\nEhg1SkloaHuuXWvNkiVerFp15D/3PTutVsvAgVuoUeMxNWvGM2zYtjfu7+vIzMxk+vQpdO7sw+DB\n/VCpVOzcuZ1evbrQrVsnxowZjkqVhlKppG3bvzPCpqam8s03zVCr1UyZMp4jR3R/+9u2bcGKFUvx\n8/Ola9cORETcByAhIYGBA7+nc2cfpk+fTNu2LfTvmSAIggjmBOEd0CWWKM327Zvx9W2HUqmkdet2\ndO/em3nzZtGzZxcMDY3031bXqVOfY8eO0L17Jy5dulDAvf+0Xb16i1OnGgOGAMTFNWbnzvB8byd7\nja1Fi3JPWXuX3qfA8m04dOh3fH3b8cMP/pw/H8qVK5de6bgDBy4QHn4de/vmmJkdx8pqGUWLrn3L\nvX17ypUrR5cufvTr15tu3Trx889z8fPrzdixI+jRozOFChXS/02ShAqJvAAAIABJREFUSCS8yRLR\nu3cjiYr6eypkZmZR7txR5dclALBt23E2bmxJSkotnj+vzdq1Tdm9+1S+tpGXyMgI2rTxYc2azVhY\nyDl69BANGzZm+fLVrFq1ntKlHdi9+39YWFjg5FSesLBzAJw6dZwaNWpjZGT01339+x4XKmRFUNBa\nWrVqy4YNup+tlSuXUa1addas2UzDhk14+DDurV+bIAgfDjHNUhDeARubEqxbtyXXdnd3DzZs2AZA\nQsJT7tyJJDk5CTs7e4KD/31NnfBuWFnJMTN7QkqK419bNJiZ5X+WvOw1tgpaVmDZqlUrQJKreHNg\n4CQAzp07w6JF89BoNFSoUImhQwOQSqW0bdsiV5bWBQuWkpCQwIQJo3ny5DEuLm6cPfsnQUG6D6xZ\noxxXrlykaNFiTJs2G5ns7ZRF2L37f4wYMQZXV3dWrFj6SmVAEhOfMXJkIlFRo4H9lC49gXLlPmft\n2pePWqrVaoyM3s9/t97ezfH2bp5jW926DXI812g0tGnjo19bB7zyWrHy5cvg6HiWu3dLAyCTReDu\nLv+Pvc4pPv45mZmFs/W3GHFxb3etZ3z8QwwMDPSZT52dKxAbG8Pdu3dYvnwxz58rSUlJpUaNWoBu\nWurGjeuoUqUav/++nzZtfPI8b4MGjQHdNOCjRw8BcPnyRaZNmw1AjRq1kMsVb/XaBEH4sLyf/10E\n4ROzZ08oo0alEBPjgqPjWebNs6V69QoF3S0BKF3anj599rJ0aSapqdbUrXuE/v3zv4j2u5gW9qqy\nAssdO3awf/+RXMWbL1++SPnyFZg6dQLz5y+hVCk7Jk8ex/btW/Dx6fjC9VBZIwy+vt34888/2L37\n7zVNkZERjB8/lREjRhMYGMDRo4f44gvv/3wtAQFDiY9/SHq6inbtOvL06ZO/PhxPxNHRiUuXzuvL\ngAwaNBw7u9LMnj1NP/oxYMAQXF3d+fnnBWRkKLGzW4eh4WOMjBJ5+vQwISE2XLx4npiYGExMTBg+\nfDSOjuVYsWIpMTFRxMTEYGNT4oVrwd53e/eGMWlSHI8eFcPF5R7Ll39OkSKFX37gX+RyBXPnlmTe\nvE2kpEhp0kSLj0/+Zkht0aIKwcH/4969VgCUK7edFi2q5msbefv751xXCkHF1KkT+fHH2Tg6lmPv\n3t2cPx8KwOjRE+jatQNJSUncunWDqlU/y/OMWdlUs0oxZHmf/j4IgvB+EcGcILwH5s+PIyZGV7Pp\n7l175s7dyPr1Iph7XwQEeNOlSzTPnj3D2bntezvKkl9eVrw5NjYGExNTSpa0pVQpXeZLb+/mbNu2\nGR+fji8877+NMGSv75Y1ypEfAgICUSgUqFRp9OrVlZ9/XkZo6Fn69RvEiRNHSUl5zmef1aBDB1+W\nLl3I3LmzsLcvjUqlQq3WEBg4ku3b95KRkYZcfpI7d86i1Rrj6OhJ1ap1iY2Nwdm5ItOmzSYs7ByT\nJwfqR1cfPHjAokW/YGxs/JJevp+0Wi3TpsVy547ub9PJkw2ZMmU9c+a0fK3z1KhRkfXrK76NLgJQ\nqlRxgoNTCQrajESSSY8ertjYFH1r7f1Nq68damhoSN269VEqk5g5cwrp6RnExcXqs1TOmTMDa2tr\n5s2bSXJyEkFByzh58jixsdGUL69LqKTRZDJq1DASE59RqpQdV69eJikpEVdXdw4dOsC333blzJnT\nJCcnvYNrEwThQyHWzAnCeyA11fhfnwsFz9bWlsqVK7y1QO5VamwVlLyKN/9z9E2XoVXy1z4vztL6\nohGG7PXd8rPgc0jIBrp160SfPn7Ex8cTGRmpf61Zs5bcuXMbrVY3zfPQoQNERUVy6tRxDAwMMDQ0\n4MmTJ0RHRyGVSilatBANG26nZs1tyGQaqlZ15PLli3z55VcAVKlSjcREXRIRiURC3br1P9hADnTJ\nf54+zT4lUkJiommB9effODuXYfp0b378sRlOTu+meHtGRgbffNOOtWtDMDY25tq1q8jlCh49eoSh\noSEVK1bi1q0bgG49nKurBwcO/Iapqal+bZy9fRlOnDgGgFKZhIdHFdas2UzVqtX1NfW6d+/NmTN/\n0qVLew4fPkjhwtaYmZm/k2sUBOH9J4I5QXgPNGyYioHBYwBksvt4eX18xaiFf5e9xlZBJ0B5lcDS\n3r40sbExREdHAfDbb3vw8KgC8MIsrVkjDMA7GWEICztHaOhZli5dyapV63FyKk96+t/JN2xsSiCT\nyXj0KJ4zZ07j5OSMRqOmf//BrFq1gTVrNuPl1ZTw8HsAWFiYsmnTV+zc6YWx8d9B/YsC1Kxi4x8q\nY2NjqlSJA3SBtVQaRa1aH/eo9KsqVqw4xYvb6Nda+vsPIDNTS2LiMxQKBWp1Bo8fP6JkyVL6Y1xc\nXDl27AzGxjL92rgBA4boX7e1LUXz5l8D0LZte/0aRQsLC376aQGrV2+iWbMWWFtbf/SzAwRBeHXi\nr4EgvAfGj29BmTJHuHtXhaengjZtPi/oLgkF4H1ZV5UVWLZo0QJDQ6M8izcbGxszatQ4xo4dgUaj\noWLFyrRqpauR1717b378cSK//GKBp2dV/Yhd9+69GT9+NL/9tofKld30IwzPnz//1/pubyol5Tly\nuRyZTMaDB/e5evVKrn1cXd25fPkiT548olmzlty7d4czZ07TooVu/VVychISiQQDA4Nc008B3Nw8\n2b9/L9269SQs7ByFCllhZmb+0axxWry4GVOnbuLJExnVqxvj59eooLtUoPz9/Vi8OAjIXTvU3Nwc\nBwdHliwJeul5XmVtXHq6mhYtDpCWpqFQodWUKKFAKpUyfPiY/LocQRA+AiKYE4T3gEQioXv3T/tD\n0qdoxYojnDiRjkKRyujRdSlWLHfQVFDGjZtM0aJyHj3KmRUwe/HmqlU/IyhoXa5js2dpzS5rhMHQ\n0JArVy5x8+Y1jIyMKFGiZK76bvmhRo3a7NixFV/fdtjZlcbFxTXXPr6+3fDz+5Y7d27xzTc+dO7c\nncWLF9ClSwcyMnSjKwEBgYSGnuXp06dkZGSQlpZGeroKAwMJfn69mTZtIl27dsTU1JQxY8YDb57K\n/31jbm7OlCn5n/DnQ5UVyMHftUNdXFw5cGAflSu7sGvXDv02tVpNZGQEDg5lX+nc2dfGHTy4n9TU\nFO7ebU1mZiGgHa1aHcTf3+stXZkgCB8qEcwJgiAUgNWrjzJ+vBsqVWlAy/37QezY0S5fRqTeVw8f\nxhEYOJLMTC1SqRHDh49h4cIDHDmixcwsnSFDKuDmVi7f2pNKpcyalXvK6oIFS/WPHRzK0qxZS+Ry\nBe7unri7exIefpfTp09hbCwlICAQK6vCDBgwGCMjIzp3bk/JkiWpV68BJiamKBQKpk2blasNP7/e\n+XYdwvvDy6seBw4cJyEhAWNjY4YNG0BaWhouLm4MGjSc6tVrMW/eLJRKJRqNmvbtO70kmJPkOXJd\nokQpNBorMjOz1sZZEhWV/yVRBEH48Em078lckH9++yt8PPL6dl/4eIj3983067efzZvb6J/L5Sc5\nc8YWa+v3Z3Qu672NjY1hxIhBr1xb7FVt3HiCoUMrk56uS1hRocImfvutEaam7y7JRmZmJj16+DJ5\n8gxsbUvleO3WrQjmz79MWpoRDRtqqVu3Avb29hgY5L3cPCkpifHjD/PokSmurmqGDm36wn3fhdTU\nVAIDR/Lo0SMyMzV07doTS0tLfW1ADw93+vUbilQqffnJBAC8vOpz4MAxNmxYS0ZGOl26+KHVaklN\nTcXMzOyNzxsdHUto6C2qVStPyZIlOHv2TwYNmsytW0cAMDG5w/z592nVqsYrnU/8Xf64iff341W0\n6OvX4RQjc4IgCAXA2jodUJP1Z7hIkVgUireXvv1VZBXQTkl5jru7J97eTXK8HhZ2jo0b1zFjxpx8\nae/8+ef6QA7g5k0PIiOjKF/e6bXP9SaFucPD7zFixCAaNGicK5BTKpX07HmFGzc6AP9j5045RkYa\nGjXaSFBQmzwLmn///W/s398NMOC33xLQavcxYsRXr30t+eXPP09RpEgxZs6cB+iuqUuX9vragLNm\nTdbXBhReT6VKlZk2bSJqtZp69Rri5FT+jc/1v/+dYfRoCQkJpbG398fWVoKVlZyAgAFs3bqBtDRj\nvLyMadWqYf5dgCAIHw2RzVIQBKEAjBzZBG/vYIoV+xVn5w0EBhYp8BGSrOlePXr00dfHypKZmcmG\nDWs5fz6UwYP7oVKpuH37Jr17d6Nr146MGjWM5ORkEhKe0qNHZwBu375FvXqfER//EAAfn69RqVQk\nJCQwZsxwrl9fjL19a0xMwoBMHB27olD8nXK9Q4fWJCQk6Pfv1asLvXp14fLli4Au+Jw0aSz+/j2Y\nMmX8a1+vg0NZNm/+H337/pDrtbCw69y40QAIB2yBxqjVHhw40J2FCw/l2l+r1XLtWmH+/rdqxaVL\nBft+Ojo6ce7cnyxevICLFy8QGxuTozZgq1atuHgxrED7+KFyd/dk4cLlFC1ajKlTx7Nv369vfK6l\nS58QH9+YjAxX7t49iETSm+XLV9OsmRdBQc1Zv/4LundvmH+dFwThoyJG5gRBEAqAqakpwcE+pKen\nI5VKC2ytXHDwCvbt+xUrq8IUK1YcZ+eKTJ06gdq169KuXStOnz7FnDkziI6OwsnJGU/PqpiYmHD0\n6CHWrVvN4MHDcXf3ZMWKpaxcuYwBA4aQnq4iJeU5ly6dp0KFSly4cB43N3cKF7ZGJpMxbdpEfHw6\nMXGiG4MGrebcuR8wN+9L5cpVCAsL5auvSnL16hVKlCiJlZUV48ePxsenE25uHsTFxTF0aH/Wrg0B\n3l5hbgeHElha3vmrrlqJbK8Yk5yc+72SSCQUK/acqKisLVqKFHmer316XXZ29gQFreOPP06wfPki\nqlb9rED78zGJi4ujaNGitGjRivT0dG7fvknTps3e6Fzp6TmDfpVKfDQTBOHVib8YgiAIBaggi0rf\nuHGdQ4cOsGrVBjQaNX5+viQmPiM5OZk6deqhUqmYMWMKY8dOZPr0KX8VCwdn5wpER0ehVCbj7u4J\nQNOmzRg7diQALi7uXLp0kYsXL9C5c3f+/PMUoNXve+7cGR48CNf3o3hxCevXN+HOHTtWrvyFr75q\nwcGDv9GkiVee+6ekpJCamvpWC3Pb2ZVixIi7LFkSRWzsCTIyBgASihc/SrNmDnkeM2GCM2PHruPh\nQ3MqVkxg3Lgmee73rjx+/Bi5XM4XX3hjbm7Btm0hxMXFEh0dha1tKf73v//h6Vm1QPv4ocn60uX8\n+XNs2LAGIyMjzMzMGTNmwhuf09tbzc2bEahU9pia3qF5c8P86q4gCJ8AEcwJgiB8oi5dOk/9+o3+\nWv8lo06d+ty7dxfQTRu8d+8eJUvaYmNTAmNjKV984c3OndsxMDBEqXzx4nsPD08uXjzPw4dx1KvX\ngLVrVyGRSKhdu95fe2hZtiw417TS3bv/x/3793j27BnHjx+jW7deufbv1683I0cGYmpqyubN62nf\nPn/KGOSlZ88G+PllEh//mMWLN5KWJqVVK3uqVXPOc/8aNZzZv9+ZzMzMAk18kuXevTssXDgPAwMJ\nRkZShg4NQKlM1tcG9PT00NcGFF7N/v1HAfD2bo63d/N8OeeQIU1xcDjF9et/4ulpzVdfNc6X8wqC\n8GkQwZwgCMInSzfKkDXVMjU1FSurwhgaGhIbG8Pq1SuIiIhk5sypfxU2/jv5sbm5BQqFgosXL+Du\n7sG+fb/qR3nc3T1ZunShvmC4QqHgjz9O8t13/QH47LOahIRspFOnrLV1N3FycmbkyLEsWjSPBQtm\n4+DggEKhyLW/RCIhIuIBzs4V9P3PT1lJYLJq3RkYGGBjU4wJE/L+4P748SPmzp3F5MnT9dveh0AO\noHr1mlSvXjPX9qzagCIj3uvJzMwkMHAX586ZUahQGqNGVcLNzTFfzv3NN7Xz5TyCIHx63o//OIIg\nCMI75+HhyYED+/j9999YtOgXZDIZ8fFxAGzZspmGDRuiVqu5fv0asbEx7N+/j9u3b7Jhwxq2b99C\ntWo1WLRoHp9/Xo/9+/dy7tyfdOnSnoSEpwBUquTC1KkTuHfvDs+eJXDhQigA/fsPYvfuHTRuXJtG\njWozZ85MAPr1642jY3n279+HSqWiZ88udO7sQ9GiRbl58xpdu3bk+vWrHD2aPQGJlhUrlrJ58wb9\nlqVLFxISspE38TprF9VqNUWKFM0RyL2vjh27Qo8eO2jXbgJ//HEdgIcPHzJmzIgC7tn7Yf361WzZ\novuZmT9/Nj/84A9AaOhZJk4cy6xZP9KyZWt++20dDx5Ec+hQJ4YMucKiRfPx9fWha9eOLFw4ryAv\nQRCET5QYmRMEQfhElS9fATs7e65evcLo0cOpXNmVhw8fkpKi5PlzJbdv32batFnMmTOT58+VxMXF\nkpGRzu7dvwPw/LkSc3ML+vfvg52dPcOHj+bixfNMmzaRbdt+ZenShVSrVp1Ro8aRnJxM795dqVat\nBkePHsbR0Ym1a0MwMDAgKSkJ0AVSZco4cPz4WZKSklAoFGg0GgYO/J6BA4fh6FiO/v374OZWk6NH\nz2JhYUGbNj6kpKQwatQwfHw6kpmZyaFDB1i+fPUr34eskUmFwhKNRkOTJl/QrVsnzMzMWLToF549\ne0avXl0ICdnJnj27OHr0EGlpaWRmZjJ69HiGDfuBNWs2s2fPLk6cOIZKpSI6Oor69Rvy/fcDANi9\newfr1q3GwkJOuXJOGBsbM2jQ8Px/U9GVIDhwYB+tW7clLOwcv/yynJMne/HoUSNsbTfTt+8ztmyJ\nokaNih9EIPouuLtXYePGtbRt24EbN66jVqtRq9VcvHgeD48qNGzYhHv3qnDmTCtKleqGsfFN7t+3\n5ujRlWzatAPQ/T4IgiC8ayKYEwRB+IR99llNKlSoRI8efQBYsGAOFhYWbN68nqtXrxIVFY2xsRQj\nIyMqV3YlMfEZc+fOpFatujmm8H3++ZeAborl8+fPUSqVnDlzmpMnj7FhwxoAMjIyePgwjtDQM7Rq\n1VY/HTFrOmV2hw7tZ+fOHWg0Gp48ecz9++GUKePAjRvx7NhRCpWqIpUqPUetVmNjUwJLS0tu377J\nkydPKF++Qp7nzEv2JDDR0ZH4+XWmSZMv/no171G627dvERy8EblcTmxsTI7RvDt3brFq1XokEgM6\nd/ahXbsOSCQSgoODCApah6mpKT/84J+jLtnLintXqFCJoUMDkEqltG3bAi+vppw+fRIDA0OGDx/N\nkiULiImJpmPHzrRq1Ybk5CRWrlzOnj07SUxMJDk5jdjYRtjYDEIqjUCrXcSMGUWYP38CPXv2YvXq\nTezZs4vjx4+QlpZGVFQkHTp8i0qVzu+/70MqNWbmzHkoFAqio6P46acZPHuWgImJCSNGjMbevgyH\nDv3OqlXLMTAwxMLCgp9/XvZK9/994excgZs3r5OS8hxjY2MqVKjIjRvXuXTpAgMHDuPQof08eLCa\n0qVXYmj4BGPju9jZPcHU1JRp0yZSu3Y96tSp9/KGBEEQ8pkI5gRBED5hHh6eTJkyAV/fbmg0ak6e\nPM7XX3+DTGaCoWEJYmM7YGCwlwYNKvPDD0Po06cvf/55ih07tnLo0AECAgLzPG9WfDNlykzs7Oxz\nva7VanNtyxITE83Gjev45Zc1WFhYMHXqBNLTVWzbdownT4oBxYESpKZaEBJygj59vqZ581b8+usu\nEhKe0KxZy1e+/uxJYIKDV6DVZrJp01pSUlKwsyvNmDEjuHPnFgkJCfpjypd3JiBgCKmpqZiYmPy1\nnhDWrFmFiYkJAwb44+X1JUWKFGXYsIGkpKSQkZFBeroKuVxOo0ZNiIyM0J/vZcW9J08epy/uLZFI\nKF7chpUr17NgwU9MnTqeJUtWolKp6NKlPa1atWHKlPEkJj7D2toahcKShIRn2Nn5YGiYgFYrJT7+\nJ9q3j6Bjx46YmJgCEBsbw5kzp9m9+3fOnTvD6NHDKFKkKIUKFcLZuQL79v2Kj09HZsyYwrBhoyhV\nyo6rV68we/Z05s1bTHDwL/z000KKFCnyQY5QGRkZUaKELXv27MLV1R1Hx3KEhZ0lOjoKmUzGxo3r\nWL9+DdOmHeaPP/ZSseIRpkzpQOXKqzl37gxHjhxk27bNzJu3uKAvRRCET4xYMycIgvAJK1++Ak2a\neNGtW0eGDv2BSpUqI5FAmTJNiI6+zpMnvxAdLePkSTvi4mLRaNQ0aNCYXr2+4/btm4AuMDt06AAA\nFy9ewMJCjrm5BdWr19SvQwK4desGANWq1eB//9umD4Kypllmef78OSYmppibm/P06RNOnz711/YM\ncv7bkpCaqgagQYNG/PnnKW7cuE6NGrVe4w78Parm7z8ACwsL2rf3xc6uNBER9xk4cCjz5i1Go1Fz\n6dIFNBoN165dZcqUGaxYsYZGjT7n6dMnujNJdOf75ZfVtGnTngcPwunZsw/9+w+kVCk7li1b9Nf9\nytmDlxX39vZunqO4d926DQAoW7YclSu7YmpqSqFChZBKpSiVSuzs7PWjhcnJSaSlpeDhURy1uiMG\nBml07LiNRo2q5lofaGEhx9TUlN27d2BpWYhly4JZtGgFTk7OxMXFkJqayuXLlxg7dgTdu3di1qyp\nPHmiu3ZXV3emTBnHrl079O/rh8bd3YMNG9bi4VEFd3dPduzYSvnyzvqfR4VCwfDh9bC0vE+/fp44\nO5dCqUymVq069O8/mDt3bhX0JQiC8AkSI3OCIAgfqX9mZnyRLl386NLFL8e2gwf3ExdXg8KFl2Fs\nHEFi4k3u36/IsmWL0GozAfTZKSUSCcbGxvj5fYtGo9GP1nXr1pP582fTtWsHMjMzKVnSlunT59Ci\nRSsiIyPo2rUjRkZGtGzZmm++aadv28mpPOXLO9OpUxuKFbPBzc0dgDZtarFixWwMDIYDUqTSR1hY\nPGbRonl8//0PVK36GfHxD5k7dyaDBg3nt9/2sGXLJtTqDCpVcmHIkJEYGBjg5VWPdu06curUCbTa\nTNRqDb6+3UhJeU5KSgoAhQsXJi0tlSJFirJ583qkUilxcbE8ffqYpKREBg78HgCVSoVardb33c5O\nF4BFRNwnJSWFn3+eg1RqTGRkBAYGhqjVao4ePUS5ck7Zjvn34t5arTZH4GVsrCvpYGBgkKO8g4GB\nARqNGq0WChWyYuXK9YSFnWPNmpXMmTOVqKhIevUypUmT0nn+HBgY6NpwdXXnzJnT7Nu3my+//Aoj\nIyM0Gg1abSZyuZyVK9fnOnbo0ACuXbvCH3+cpEePzqxYsQaFwjLPdt5X7u6erFmzEhcXV2QyE2Qy\nGe7unpQr55Tnz2NKynNGjhxCeno6oKV//8EFewGCIHySRDAnCILwkXqdzIxZTp++xoYNEdy5cxOl\ncghK5VcAeHqupkaNWtSsmXcK9S+/bMaAAUNybJPJZAwbNirXvoaGhvTvP4j+/Qfl2L5gwVL941Gj\nxuU67v79cD77zAkbm6aAIenpZ7C1tSU4eAXffdefq1cvY25uweeff8n9++EcOnSAJUuCMDQ0ZNas\nH9m/fy9NmzYjLS0NFxc3evf+nkWL5nPr1g26deuIubkFMpkMiQQaN/ZizpyZ+Pl9S61adQHJXyNO\nEhQKS31AExsbw8iRWR/idfXcQDf6ZmZmxsiRgXh4VGHnzu2sX7+G77/vSenSZTAzM9df18uKe//2\n2x48PKrkuh95TVWVSCR4enpy4MBeUlNT9fslJCQgl8vRaNRoNGr9+5Ale0Dq69uNLVs2oVKp8Pfv\nwddffwOAmZk5JUuW5PDh32nU6HO0Wi13796hXDknoqOjqFTJhUqVXDh9+iTx8fEfXDBXtepnHD78\nh/75hg3b9I//+fOYnJxEYmKi/udLEAShoIhgTsg3/v5+LF4cBMDChfM4ffoktWrVZdy40QXcM0H4\ndGRlZrSyKkyxYsVxdq7I7ds3mTlzGiqVClvbUgQEBCKXy3Mls2jbtiuDBklJSrLA2vo0Dg6NMTZW\nULJkV8aOdX+j4DA/hYae4d69uyQk6AKp9PR0Hj1K59EjCY0bN6F+/Tpcv34ZV1d3tm7dxM2bN+jZ\nU1fLTqVSYW1tDYBUKqV27boAODtXJDk5iblzF5GY+IwePTrToYMvYWHn8PCowowZcwD0RdK//bYr\ne/fu5sqVy7i4uFK0aDHGj58KgLW1NR076tqzty+NpWUhjIykaLVaGjRojKurO3Z29owePYz69Rvq\nr+tlxb0rVqycrbj33++BRCL5x3uie1yzZh2MjWV89113UlNTSE5OJjU1hZIlbbG2LsKyZYsID7+H\njY0NMTExANy8eV1/fHR0FFKpMe3adSA8/B5Pnz7RtxMYOJlZs34kODgItVrN559/QblyTixaNI+o\nqEi0Wi3VqlXPMfL4sQkKOsqcOYY8e2bDZ59tYdUq71dOuCMIgpDfRDAn5JusQA5g167t7N17uMA/\n/AnCpyR7ZkaNRo2fny/OzhWZPHk8gwcPx93dkxUrlrJy5TIGDBiSK5nFmDETiYnZS+nSLYiKCkKj\nseLHH0Pw82vxr+1mH1F727y9m9OnT18Adu48w4ABpTAyuoKx8W2OHn1M69b18tw3O0PDv//1GRhI\n9Gu8LC0L4erqTpcu7ZHJZBQubK3fLyMjg9DQs3h7N+fbb7syfPgPFCtmg0ajpn37Tjg4lAX+Hg2V\nSqVMmjSdsWMDiYpSkpmZhExmSIkShalRozb16jXUn/tlxb2zCwn5X47r8/ZunudrNWvW5u7d21ha\nFsLBwZGSJW31bVWoUAlv7+Y8eHCTkSMD6NmzC56eVfWjcyEhGzA1NaF//+8oW9aRvn0HYmSku2cl\nSpRk9uz5ufo1ZcrMXNs+RkqlkjlzJDx86A3AiRPuzJy5iUmT8i4qLwiC8LaJYE7IN15e9Thw4Dgj\nRgwiNTUVP79v8fXtTocO3xR01wThk5A9MyPIqFOnPmlpqSjHQyKVAAAgAElEQVSVybi7ewLQtGkz\nxo4dmSOZRRa1+jkSyVNSU6tgYzOStLSq2NuXLaCrya1q1eqMHDkEH59OWFlZcfx4FOnpFUlL88Le\nfjHJyVaUK/dNnvsmJSWSkpKKjY3Nv7YxbtzkPLd37tydESN000JtbUvh4uKuH7XL8s+g1sbGhhs3\nviMmJisYTqV589388EPTN7j61/Oi68he265atWo5phJmGThw2Cu3o9VqOX48lMTEVLy8PsPExOT1\nO/sBUSqTSUwslm2LAUql9IX7C4IgvG0imBPyke4b6enT5+DlVT/PRfKCILxNrz4SnlcyC61Wy5Ah\nW9m9uz4SyR3q1LnI0qVbqF7d9b1Y/1SmjAO9evkzeHBfMjO1PH2agpGRM2lpNUlPL4ep6WVq166V\n575GRkYMGTICGxubHDMGXnX2wJIlC4iOjqJ7904YGRlhYmLKmDEjCA+/i7NzRQIDJwG60dGff57D\n06fPSExU8/BhIFJpBCVKDCQiYhtxcRIiIyMYN24UQUFr8/8m/Qdbt/7B8eNJWFllMHx4E0xNTf91\nf61Wy8CBW9m0qQmZmYWoXj2EDRu8kcvl76jH716xYsWpWfMYR45UAQxRKC7g5VWkoLslCMInTARz\ngiAIH4kX1YyTyxVcvHgBd3cP9u37FU/Pqi9MZvHTT23p0+c6pUp9TZkyfWjVqvV7lcyiSRMvmjTx\nAkCj0TB48HaOH3+IuXljBgxok2NqZPZ9s9u//6j+ccOGTWjYsMlL2/X3H0B4+D1WrlzP+fOhBAQM\nYe3aEKyti+Dv34NLly5QqZILc+fOpFu3AfTtqyQhIYMiRX7m4cNNZGZaIJcfoGZNBXv27HqtWnjv\nwqZNpxg+vAypqc6Amtu3V7J2bYd/PSYs7CqbN9clM1NXR/DMme4sWRLCsGFfvYMeFwwDAwOCgpox\ne/ZmkpKkeHkVpWnTqgXdLUEQPmEimBMEQfhIZK8ZZ2VVWF8zbvTo8cyaNY20tDRsbUvpM/P9n737\nDIji6ho4/l+WooA0ARHsiqCiYDeW2KKxPyZ2LIAtajRqSGLvsWM3KhZQsPfXxB5iN5ZY0BixYqHY\nkN7Z3fcDYZWIHUTw/L64M3tn7p0dBA537jkvS2bh5+dDSMh9lEodXFyqf7TJLJRKJQsWdEStVqOj\n8/qyqXfuhPPjj6e5d68QpUvHMHduPWxtrV97HGTOHKnRaKhQoRKWllYAlCtXngcPwjE2NiY4+BYT\nJ45DoTCjcGEVaWmmgC/W1kWoVWsTX301h27dZrJihd87XXNOOXw4/t9ADkCXs2fLEBcXh7Gx8UuP\nSUxMQqVKz8ppZuaHqelGzp414tgxQ4oXL0mpUqXfe1zh4WGMGDEcP79N732u7GJsbMyECbJGTgjx\ncZBgTggh8pGsasYBeHv7vrDvdcksrKwK8fhxbPYPMpu9SSAHMGbMGY4cSc82GRwMY8b44+vb/p36\n1NPT175WKnW0SVRKly5LyZIdmDevMxkFzgsUOM/8+ZWZNGkUJ08ew9GxwkeX/dDYOAnQkPGorqlp\n5Gsfs6xTx4WGDbdw5Ig7pqYb0NPrzKxZn7Fu3Qrq1WuQLcGcEEKIV5NgTmSbd1mHIoT4OERGRjFs\nWAA3b5pRtGgc06dXw8qqYm4PK1s9eGD0yu1XMTQ01BYUf5kSJUoRFRVJ796W/PmnD6dOfYmR0WV6\n9ozC0bEttWt/hpfXDG1R9Y/JiBH1uH7dhwsXqmBpGYanp8lL66dt3LiWPXt+BeCrr1pjZNSH27fv\nYme3kaNHYzhx4hgXL15gzZpVTJ06G41Gk6kExogRYyhRohRTp07EyMiYa9f+ISIigkGDvsvykVeV\nSsXkyeO4fj2IUqXKMG7cJIKDg1m8eB6JiYmYmpoxZswEChe2JCTkPrNnTyc6OgodHR1+/nkm5uYW\njBzpSWxsDCpVGv36DaR+/YaEh4fh6TkEJ6cqXL4cqM3y6eu7nMjIKCZMmEKFCpVITExk3rxZBAff\n/jdLbH/q12+Yo/dDCCHelARzIlukpaXh7e3L06cRWFgUzrQmRQjx8Rs79hB797oBCm7cgJEj/Tl6\nNH8Fc+XLR3P5sgpQAmmUL//ms46vKluQQVdXlylTZrJggRfm5jE0aLCOL79sTf/+3wDwxRctOHr0\ncJZlCHKbpaUFO3Z05OHDB5ialsDQ0DDLdkFBV9m79zdWrFiDWq2hf383xo+fwujRP+LtvQoTE1NC\nQu5Tr14DGjZsAsDQoQMzlcCYM2cmCxYsBeDp0wiWLvXhzp1gRo78Pstg7t69u4waNR4npypMnz6Z\nbds2c+zYYaZPn4uZmRkBAQdYvnwJo0aNZ9KksfTq5UGDBo1ITU1FrVahq6vH9OmzMTQ0IioqigED\nPLTBWGhoCD//PItRo8bTt28vAgIOsHSpD8ePH8HPz5fp073w8/OhRo1ajB49gdjYWPr3d6NGjdr5\nPnOnECJvkGBOvLeYmBh69drLmTN1MDW9wdChlxgwoHFuD0sI8RbCw415PhtmWFj+y0jo5dWCggXX\nc/++IaVLJzBpUsu3Ov5N0v3b25dn8eLlmd6PjY3hzJmrBAWdpnXrdh/tkws6OjoULWr7yjaXLl38\nt/xFeiDTsGETLl688EK7jDWGCQkJ/P135hIYqanp9ewUCgUNGqQHVaVKlebp06dZ9mltXQQnpyoA\nfPllK9as8eH27VsMHz4IALVaTeHCViQkJBAR8URbw09PTw/QIy0tjWXLFhMYeBEdHQVPnjwmMjK9\nr6JF7ShTpiwApUuXoUaNWv++LsuDB+kF1c+cOcWJE0fZsMH/3/Gn8ujRA0qUKPXKz0oIIT4ECebE\ne/PyOsrJk70BHSIinFi0aB+urtEfTfY7IcTr2dsncPx4CqAPaLC3j3rnc/3441AmTpyKkZGxtv7k\nx5DIwsjIiLlz322N3Lu6du0uffv+Q2zsAQwM7tCzZ78P2n92yyoQzSo2zWin0agxNi700lI16QEX\n/7bVZNnm+T41Gg1GRkaULl2WZct8MrVLSIjP8vgDB/YSHR2Fj89alEolnTq1Izk5BQB9/Wf96+jo\naMejo/NsHSSkryMtXrxElucXQojc9GarxoV4hYQEfZ7/UoqNtSIuLi73BiSEeGtTprSkd+8t1Ku3\nnY4d/Zk/v8k7n2v27AUYGWVkQfw4Z6E+lIULL3PtWmfCwlYSHPw7q1frolarc3tY78zZ2YWjRw+T\nnJxEYmIiR48e0hakz2BoaEh8fHpgZWRkrC2BAenB2M2bN96qz4cPH/D335cBOHhwH5UqOREVFand\nl5aWRnDwbQwNjbCysubYscMApKSkkJycRHx8PObmFiiVSs6f/4sHD8Lfqv9ateqwdetG7fb160Fv\ndbwQQuQkCebEe/vySyvMzM7+u5VGnTrnsbEpmqtjEkK8HX19fWbMaMeOHc1YsuQrLCzMX9p2/Xo/\n7S+3CxfOYejQgQCcO3eWSZPG0qlTO2Jioj/IuD92KSn6mbaTkwuQlpaWS6N5f+XLO9KqVRv69XPj\nm2/cadv2K+ztHTK1adq0OevX+9O7dw/CwkIZP/5nfvttF+7urvTs2YXjx5+tqX5d4iyFQkGJEiXZ\nsWMzPXp0Ii4ujo4duzJlykyWLVuEu7srHh6uXLlyCYBx4yazdesm3Ny6MXBgH54+fUrz5i0ICrqK\nm1tX9u3bTcmSpV/aZ1bjcXfvS1paGm5uXenZszOrVnm/xycohBDZS6F52XMNH1heSH8tXi4g4CIH\nDjzE2DgVT88mmRbP55X05uLdyP3Nv152b69c+ZuNG9cyZcoMBg1K/0V3yZKV+Pv7YmFRmLVrV7Nq\nlT8mJqY0a/Y5Bw8e/Sges8wNv/56Bk9PM6KiqgPRuLpuZ/78jrk9LCD//9/9VL/mIP/f20+d3N/8\ny8rq7dery5o5kS2aNnWh6YtJyIQQ+ZCDgyPXrl0lISEefX19HB0rEBR0lcDACwwb9iNr167O7SF+\nNNq2rYWp6WWOHNlC0aK69O79dW4P6aPwf/93mv37oylYMJkff6yDjY1Vbg/pBcnJyXh6/sqlS+YU\nLpzAuHGOVKtmT3h4GN9/PwQ9Pd1PMlAUQnxcJJgTQgjxVnR1dSla1I49e36lcmVnypYtx/nzZwkN\nDZVC0Vn4/PPKfP555dwexkdj//7zeHpaExPzBaDhypXV7NrVDn19/dce+7bep0adpWVzNm/uh6Xl\nPBITjzN0aBQTJw6jYkUnkpKSePw4mlGjPLl16yaNG39B6dJl2LZtEykpKUyb5oWdXTEiIyOZM2c6\nDx8+AOC77zypXNk5269TCPHpkjVzQggh3pqzswsbNqzFxaUazs5V2blzG+XLl8/tYYk84NChx8TE\nVPl3S8GFC3W5fftOjvR1795dvv66E2vXbsHIyIht2zazYMFsfv55FqtW+dO6dVuWL18CwKRJY+nY\nsTOrV6/H29uXx48LY2x8CAODa9y9u4unT7/jl18WEBkZiUajIikpiXPnzhIZ+ZQtWzZw4cJfqFRq\n7t27S/fuHRk8+Btmz55K48bNMDExIzk5hWHDvuXevfRrnTp1IvPnezFwYG86d/4fhw8H5MhnIITI\n3ySYE0II8dacnavy9GkETk6VMTe3wMDA4IWshvD6BBfi02NpqQaStdsWFvewtn6xCHt2+G+NutOn\nT2lr1Hl4uOLn58Pjx4+zrFFXoYIOBQueIja2DaCgTJkEqlatzq1bN3jy5AkAc+cupkmTZiiVuvz5\n50mUSh0mTpxGuXLlUSjg1KmTzJgxhYcPw1EqdTA0NGT27Gna8WUUTZ81az7Lli3Okc9ACJG/yWOW\nQggh3lr16jU5dOhP7faGDdu1r7ds2UViYiIpKSkcOJCeubBoUVvWrNn4wnnEp2Hw4P4MGfI9Dg6O\n/PnnL7Ro8ZDTpytibBzDkCH6WFjkTDD3PjXqPD2bc/Hibp4+TcbWNpHx4+vg738RhUKBqakpiYlJ\nODlVISUlhT/++J3IyEiioiKZOHE0aWlpFChQELVajUaTpq1fZ2lpSWRklHZsb1I0XQghXkVm5oQQ\nQmQbjUaDp+dWatQ4T82ax5k790BuD0l8ABqN5qVFvyFzUKWjo8PixV9x7lwFTp1qiLv75zk2rvep\nUZeWlso333SgYsUwVq5sg6lpQQIDL1CunD2g0BZL12g06OjoYGhYkIoVnZgzZxGffVafgweP0qBB\nI/T0dPH1XY+v73pGj57A2rWbteN7k6LpQgjxKjIzJ4QQItusXXuYtWv/h0ZjAcCCBZdo0iQIFxfH\nXB7Zp6lRozrY2tphZmaOtXURHBwq8PnnjZg7dxZxcdHo6urj7FyVo0cPkZKSQqlSpXn8+DHx8XEM\nGvQdjRqlpylev96PQ4d+JyUllc8/b0SfPt/8m9VxMJUqVebatavMnr2QtWtXExT0D8nJSTRq1JQ+\nfb7JclwajYZNm9ZTqJAJnTt3A8Db+xcsLArTqVPXbLn252vUzZgxmVKlytCxY1dq1fqMBQu8iIuL\nQ6VKo0sXV0qXLsO4cZOZPXsaK1d6o6ury88/z6Rhw8ZcuXIJd/duKBQKBg0aiqmpGdHR6bNrf/99\nmYMH96HRqNHR0eHhwwfcuRMMpBdH79SpG+fPn6VDhzYULGiIi0tV2rfv+G9AKIQQ70+COSGEENkm\nPDxZG8gBJCaW49at3yWYywVXr15BpVKxZs1GUlNT6d27Bw4OFZg1axo//jiKqlUrcvjwnwwdOoCN\nG3fg7f0LFy6cY/DgYZQqVYaRI7+nUaOmnDlzipCQ+6xY4YdarWbkSE8CAy9gbV2E0NAQxo2bTMWK\nTgD07z8IExMTVCoVw4YN4tatm5QtW+6FsSkUClq3bsfo0T/SuXM31Go1f/xxkBUr/LLt+m1sirJu\n3dYX9tvbl2fx4uUv7C9WrDgLFix9Yf+gQUMZNGiodvvBg3Ds7IoRFRWJp+dgNBoN1avXomdPd+bM\nmcGSJQtRq1Vcvx5E374DWLnSHy+vGUREPOHixQtYWlppgzlZUyqEeF8SzAkhhMg2zZqVxc/vOI8e\n1QfA3n4vjRrVyOVRfZouXw5EqdRFT08PPT09ChcuzObN63jy5AmDBvWlSBFrwsLCSEpKwtNzCEql\nLtHRUfzyy0KMjY2IiEhP8nHmzCnOnj2Nh4crAImJSYSE3MfaughFihTVBnIAf/xxgF27dqJSqYiI\neMKdO8FZBnOQHmyZmppy48Y1IiIiKF/eERMTk5z/YN6TjU1RNm3a+cL+tLQ0Vq70R6FQsHfveRYu\nfICXlz6NGp3Dy2vBC8Ha6NETMm1nrC8VQoi3IcGcEEKIbFO1qj2LF19i8+Zt6OqmMXBgBQoXtnj9\nge8oLi6Ogwf38dVXHTl//i82blzHrFnzcqy/vEUBpK/DOnPmFLGxsfzvfx3YsWMrDg6OfPvtQEqW\ndKBTp3YsWuTN4sXzMTIyomPHLjRs2IRmzZ6tZevRw53//S9zwfPw8DAKFiyg3Q4LC2XjxnWsXOmP\nsbEx06ZNIiUlmVdp06Y9u3f/SmRkBK1bt8u+S/+A0tLS+O67HZw4YYmRUSJ9+ypZuNCQsLAuAAQF\nPaZkySN4eDQCID4+nsmTAwgPL0ClSmn8+GMLdHQkhYEQ4t3Idw8hhMiHwsPD6NWrS5bvDR7cn6Cg\nqznWd6NGVViypDkLF7aiQoWcLSIeGxvDjh1bcrSPvKpKFWdUKhUpKSmcOHGMu3eD2blzK/HxcQQF\nBXH37l00Gg2pqamZjvtvIo7ateuwe3d6hlKAx48fERkZ+UJ/8fHxFChQECMjI54+jeDUqZOvHWPD\nho05ffokQUFXqV37s/e42tyzeHEAW7d2Izy8HTdvdmHmzEeEhT2brVSrrbh1K0m7PWTIXnx9u7Jv\nXwfmzGnB9Ol7c2PYQoh8QmbmhBDiE6NQKPLN+pxlyxYRGhqCh4crurq6FChQkLFjRxAcfAsHhwqM\nHz8FgKCgqyxePI/ExERMTc0YM2YChQtbMnhwfypVqsz5838RFxfLyJHjcXZ2yeWryh6OjhVRKnVx\nc+tKUlISZcuW4+uvO1G9ei28vGbg5+fH8uUrSUp6Fmg8/7WR8W/NmnW4c+cOAwZ4AGBoaMi4cVNe\n+Dqyty9P+fIOuLp2wNrahipVnF87Rl1dXapXr0mhQiZ59mvywQOAgtrtyMjaFCv2JyEhJQAwMLiL\ns3Mh7ftXrpgDyn+3TAkMfJbRUggh3pYEc0II8RHau/c3Nm5ch0KhoFw5e/r2HcC0aZOIjo7GzMyc\n0aPHU6SIDVOnTqRevQbarIPNmjXg4MFjmc6VnJzEtGmTuHXrJiVKlCI5OTnfpEEfOPA7goNv4+u7\nngsXzjFqlCdr126hcGFLBg7sw6VLF6lY0Yn582czc+ZcTE3NCAg4wPLlSxg1ajwKhQK1Ws2KFWv4\n888T+PouZ/78Jbl9WdlGV1eXDRu2c+LEUSZMGEPJkmUoWtSWkSPHYmNjjkqlR6dO6Y83jh49gfnz\nZxMfn15z7fk1XJ06dc0yy+R/awf+dx1YhkWLvLWvt2zZpX2tVqu5cuUyP/88690vMpfVrWvOxo3X\nSEhwAKBKlSAmTizFkiWbSEzUo0kT6NSpmba9lVU8wcEZWxoKF0748IMWQuQbEswJIcRH5vbtW/j5\n+eDt7YuJiSkxMTH8/PMEWrVqS4sWrdm9exfz53sxfbpXFrMZL85u7NixlYIFDVm7dgu3bt2kd+/u\nH80syKpV3hgaGtGtW49M+8PDwxgxYjh+fpteefzzQalGo6FChUpYWloBUK5ceR48CMfY2Jjg4FsM\nGzYISA8gChe20h7XsGFjABwcHHnwIDxbrutjkZqagoeHKykpKVSvXgMvr2kAFCxoyPz5cylQwIzn\nv2aaNm3OzJlT2bp1E1OmzMDOrliOjGv16iNs336P6Gg/Pvusdo718yG0a1eLuLjjHDz4N4aGyXh6\nVqNMmWLUr18ly/YTJzoyZsxawsNNcHB4ysSJDT/wiIUQ+YkEc0II8ZE5f/4sTZo0w8TEFAATExP+\n+ecy06d7AfDll61YunThG58vMPCidlalbNlylC378dS4yu6gUk9PX/taqdRBpVIBULp0WZYt83nl\nMTo6Sm37DyWrmdTsdOTI6Ze+Z2VViEePYli6dJX2PlSu7JypqHVOOHDgPJMmlSM+vg0wiLi4vQwf\n/pgiRaxee+zHytW1Pq6ub9a2Ro3y7N9fHpVKhVKpfP0BQgjxCpIARQghPjIKhSLLxyCz2qdUKlGr\n0/er1WrS0lJfaJOd1q/3Y+vW9EfrFi6cw9ChAwE4d+4skyeP4+DBfbi5daVXry4sXbpIe1yzZg20\nrw8d+p1p0ya9cO6goKu4uXXD3d31jZOaGBoakpDw6sfUSpQoRVRUJH//fRlIzz4YHHz7jc6f83Jv\nhlSlUjFgwCZq1w6lVq2/mTVr3wfp9+zZR8THP6s7eP9+Xc6evf5B+v6YSCAnhMgOMjMnhBAfmWrV\najJ69A907dr938cso3FyqkJAwAG+/LIVBw7sxdm5KpBe8+ratas0afIFx48fJS0t7YXzubhU5eDB\nfVSrVoPbt29y69aNF9qEh4fh6TkEJ6cqXL4ciKNjRbp27cT8+QuIjIxiwoT0RCL79u3h0aOHBAQc\nICUlFaVSybff9qNUqTIUL16CZcsWY2FRmJ9+GsPixfM4duwwDRo04vmg5b+zcRmb06dP4vvvR+Ls\n7MKSJQve6LMyNTWjcmVnevXqgoGBARYWhV9oo6ury5QpM1mwwIu4uDhUqjS6dHGldOkyWZwxe4Or\n9ev90NfXp2PHrixcOIdbt26yYMFSzp07y2+//R8Ay5cv4eTJ4xgYGDBjxhzMzS0IDw9j+vTJL6yR\nzE6LF+9jxw5XwAiAX365SOvWN6hUKWdnbh0cCqGvH0pKih0AlpYXqVKlVI72KYQQ+ZXMzAkhxEem\ndOky9OrVm8GD++Pu7srixfMZNuwn9uz5FTe3bhw4sJehQ38AoF27r7h48Tzu7q5cuXKZggUNtefJ\nCJrat+9IQkICPXp0YtUqbxwdKwLQsWNbYmKite1DQ0Po2rUH69dv4969u+zZs4elS30YPHgofn6+\nlCxZmhUr1mBiYoKrqxuPHj3AyakyVatWY9eu7RgbF8LBwRGNRoO9fXmaNWuBt/cSDh8OeO01x8XF\nERcXp80k+eWXrd/485ow4Wf8/DaxYoUfM2c+qzE3fPhPtGzZBkjPtLh48XJWr16Pv/9m2rRpD6Qn\n5nBwSJ8lMjMzY8uW/3vjft+Es3M1AgMvAukzj4mJiaSlpXHp0kVcXKqRlJSIk1MVVq9ej7NzVXbt\n2gHAvHmzadWqLWvWbKB58xbMn+/10j727v2NJ0+evPXYHj9WkRHIASQmluT+/cdvfZ7nhYeH0b17\nR2bOnErPnp35/vvBJCcnc+PGNfr3d8fNrRvnz+/km28O4Ojoh4NDYyZNSiE5OZ4GDWry6NFDADp3\n/h/Jya+uUSeEEEJm5oQQ4qPUsmUbbSCSYcGCpS+0Mze3wNvbV7s9cOAQAIoWtdVmGjQwMGDSpGkv\nHPvfxzmLFrWjTJmyQHpAWbdu3X9fl+XBgzDi4mKZN282kZFPmTNnOmq1mipVXLh9+xYajQZra2vu\n37/PV191/PeMGhSKF0shvMkv6R8i2+bOnae4eDGKChWM6dKlfo704eDgyLVrV0lIiEdfXx9HxwoE\nBV0lMPACw4b9iJ6eHnXr1v+3bQX++it9jdvbrJHcs+dXSpcui6Wl5VuN7X//c2DFiqM8epReHNzJ\naS/16zd+l8vMJCTkPpMmTWfEiDGMHz+KI0f+YN06P77//iecnauyapU38fF3OXrUk549N9C6dWX2\n7v0NR8eKXLx4gSpVnLGwKIyBgcFL++jYsS0+PmsxMTHN8XWHQgjxMZNgTggh8qm4uHh++mk/N2+a\nYmMTganpIWJjo1GrVbi59QVg69ZNnDhxjKSkRCA9gIqJiebChb+4dOkC5uar8fDoh0ql4qefhmNr\na0u3bj3ZtWsHcXFxFC1qx8KFc1EoFERHR3P3bjBXrlxm69aNREZGYmtrh0ajwcLCgrt371C8eAmO\nHj2EkZExkB60aTRgbGyMsXEhLl26SJUqLhw4kLOFlH/55XdmzHAhObk0enphBAfvZuTIN58NfFO6\nuroULWrHnj2/UrmyM2XLluP8+bOEhoZSqlRplMpnP4Z1dBSoVCrCw8OIiYlh1qxp/PPPZQoXtkSj\ngRs3rjF79nSSk5OxsyvGqFHj+euv0wQFXWXy5LEUKFCApUt9XhkEPa9mTQe8vSPZsmUL+voqhgyp\nibGx8Xtfc9GidpQrl/6opoODI6GhIcTFxWofDW7RojXjxo0EwMnJmUuXAgkMvEjPnh6cPn0S0FCl\nyqtr/WV+VPfjyMwqhBC5QR6zFEKIfGrMmANs3dqDixfbc/x4Ma5fT2X16vX4+W2iTp3PADAzM8fH\nZy3Nm7ckOjoKSC8XYGJixsiRI/nmm29ZvHgeGo2G1NQUjIyMcHauytOnESgUCkxNzTAwMECpVLJq\nlTd2dsU4evQQSqWSZs1aEBoagkKhYMCAwfz00zAGDuyjLR0AGbN26a9Hj57A3Lmz8PBw1b6XU/bt\nU5OcXBqA1FRbDh58swDoXTg7u7Bhw1pcXKrh7FyVnTu3Ub58+Vceo1arsbOzw99/M/Hx8RQtasvP\nP0/k22+HsmbNBsqWLYev73IaN/4CR8cKTJgwFR+fdW8cyGWoV68S8+e3YNas1hQvnj1r8vT19QgP\nD6NXry7o6CiJi4slPj4eH5/lbNmyEU/PIdy5E8zEiWNwcamKn58PV65cpkGDhty4cZ1582ZTsmT6\nvRk16gf69OlJz56dtY+gvsyUKeM5duywdnvSpLEcP37k5QcIIUQ+IDNzQgiRT927ZwykZ8xLTnYg\nLu4uS5cuom7dBly79g8ajYaGDZsAUKZMWW3ylMuXA/EeK58AACAASURBVLGzK4ZCoaBq1RrExsZi\nYmJC5crOHDt2hFu3btKzpwfr1q0BYMOG7TRr9jnGxsaUKFGKnj09aNWqLQAREelrsBo1aqotbP68\n3r37a187ODiyevV67fagQd9l/4fyLwODzIliChRIybG+nJ2r4u/vi5NTZQwMCmBgYKCdpXo+YH3+\ntY2NLefOnSUg4CDJyUnUr/85hw4FZDm7BR/msdR3ZWRkTIECBjx48IBdu3bQunU7kpKS6N27H7Gx\nscydO5NixYqjUCgwMTEhMTGBChXS13WOGjUeExMTkpOT6NfPjUaNmmJiYpJlP23btmfTpvU0aNCI\nuLg4/v77MuPGTf6QlyqEEB+cBHNCCJFPlSwZz4kTKkBJamopihXrTdmyZqxYsYSbN29gZGSEvr4e\nANbWRbSJUSA9kHJ2duTx41iUSiXe3r5s2bKR7t174eraC4CAgAPa9hqNBrVaTdGiRd86sEhMTGTj\nxmPo6kKXLo3Q19d//UHvaciQ4gQH/8b9+zWxsQlk0CDrHOurevWaHDr0p3Z7w4bt2tcHDjybOcoI\neENDQyhQwEC7RnLDhrU8efLolX18LEXgIatspQqaNv2SP/44SHx8PLt376J37/7o6CixsSkKgK1t\netFwZ+eqnD//F4aG6YlZtmzZwLFj6Z/Ro0cPCQm5R8WKTln26+JSjTlzZhAVFcXhw7/TuHETdHTk\nASQhRP4m3+WEEOIjFx4ehqtrB6ZNm0S3bl8zadJYzpw5xYABvena9WuuXr3CqlXebNiwVntMz56d\nGTq0Ch06+FKhQjsqVaqHQrEVpVKXkiVLER8fR0TEE0aN+uGF/qpUqapds3b+/F+YmZljaGhE0aK2\nXLsWBMC1a0GEhYUyePBeatWaRVJSIq1adcLZuRoBAQdRq9U8efKE8+fPvfLaEhIS6Nx5FyNGtMPT\nsw3du28jJSXnZskyNGxYmd9/r8yWLVf4/fdytG5dI8f7fBP791+gc+fD3LyZTMeOm3n6NBJIn90y\nMTHRZsbct283VatWB9Jr7cXHx+XamJ+XkXgno/5ht2498PDoR6FChWjbtj0HDhxh/Pgp3L17h379\neqFSqXB17aWdievZ0wNr6yJA+tfeuXNn8fb2ZfXq9djbO7z2a6NFi9bs37+bPXt+o3Xr/+X49Qoh\nRG6TYE4IIfKA/5YNCAg4wLJlz8oGZDUbUrBgQbp0saRVq4rMnDkRAwN9/PxWcf36NQoXLkzhwlba\njInwLONk7979uXYtiHbt2rF8+RLGjp0IQMOGTYiNjaFnz85s374ZPT0LTp7swJ07U1CpjNi504iG\nDRtTvHhxevToxNSpE6hcucorr8vf/yinT7sDeoABR470YNu2o9n62b2MubkFDRvWxNra6vWNPwCN\nRsPPP4cSHNwWlcqYo0d7M3VqepZGhULB6NETWbJkAW5u3bh16yYeHv0AaNWqLV5e0+ndu/tHk87f\nwqIwUVFPiYmJJiUlhZMnj6PRaHj48AHVqtVg4MAhxMXFERMTQ0hINIcOHUOlUnHtWhDh4WEAJCTE\nU6hQIQwMDLh79w5Xrvz92n5btWrL5s0bUCgUlCxZKoevUgghcp88ZimEEHnAf8sG1KhR69/X6WUD\n7O2zSqihoGxZe375ZQEmJiZ8//0IbR23Tp3asWqVPyYmpgA4OlZg4cJlAJiYmDB9uhdWVoV4/DhW\nezYDAwPmzl2s3T5z5iBpaemFn2/dOo+Ozg4iIiLo0cOD4cN/eourk8yEACkpKTx9akpaWjHu3v0V\ngKioAnTr1k7b5vkyFBkaNmyiXfv4sdDV1cXdvS/9+rlhZWVNqVKlUalUTJ48jvj4ODQaDV991ZE+\nffZz4sRgbG2H88UXrWjWrC7Fi5cEoHbtuuzcuY0ePTpRvHhJnJwqZ9nX83/IMDe3oFSpMnz+eaMP\ncZlCCJHrJJgTQog8IGNtG4COjg56enra1yqVCqVSiUaj1rbJeBytePES+Pis488/j7NixRJq1KiF\nu3vfbBlTxYoJnDiRCBQEVKSmXqR2bXPUaj3atTvCvHkdXruWq0ePBuzatZqzZ90ANZ9/7k+HDh2y\nZXx5jYGBAS4uYRw8mL7OUU8vlNq1X/wxvX79cQICEjAySmLEiNrY2RV56742b15Pnz5u2u0ffxzK\nxIlTMTIy1tZtCw8PY8SI4fj5bXqn6+nYsSsdO3Z96fve3vs4frw9oEdoqB+hoVEMHXqc0aMnaNt4\neWVdX2/Lll3a18+vO0xKSiIk5B7Nmn35TmMWQoi8RoI5IYTIB4oWteXEifRH8p5/VO3JkycUKlSI\n5s1bYmRkzO7d6b8Ep6+zitfOzL2LiRNboau7k2vX9FGp/uHEiX6kpaUnstiwoQJ16x6hc+dGrzyH\nkZERW7a0Yf36Hejq6tCt29cfJAHKx8rbuzVTp24iIsKA2rX16d07cxHvHTtOMWpUGRITHQANN26s\nYdeudtrg/k1t2bIRV9fOZPwaMHv2AgDi4uK0WU3f1NSpE6lXr0GW2UpfJTVVQ+ZfQwxISnq7vjNc\nuHCD5cv3c+PGDnr27K5NoCKEEPmdBHNCCJEHZLUm7vnXDRs2Yd++3fTs2ZmKFZ20j6rdvn2TX35Z\ngI6OAl1dXX74YTQA7dp9hafnEKysrLVZE9+Wnp4ekya1AcDHR8ORI7ba9zQaCx4+THyj8xgaGtK3\nb4t3GkN+Y2xszPTpbV/6/okTMf8GcgAKAgOrERoaQqlSpV96TGJiIuPHj+Tx48eo1SoaN/6CJ08e\n06tXLwoVMmXBgqV07NgWH5+1xMfHv3Uwl14r8O0fj+3e/TN27vTj0qVegIrPPltL+/bt3/o8ly/f\nonfvJ4SGjgJGsnGjL126JFGgQIG3PpcQQuQ1EswJIcRHLiNDYIbnH0N7/r3n17NlsLGxoVatOi/s\n79ChCx06dMm2MbZuXZ1Vq3Zw40b6I5IlS/5GmzavTn4i3p6VVRqQDKQXB7e2vkfhwlVfeczp0yex\ntLTWzr7Fx8exZ8+v+Pv7k5qaXocwIxhbtmwRGo0GDw9XKlSoRETEE3r16oJCoaBXrz40bdoMjUbD\nvHmz+OuvM1hbF8k0K+jru4KTJ4+RnJyMk1MVfvppDKGhIYwbNxIfn/Rsq/fv32PChNH4+Kxl8+bG\n+PtvQVcXPDzavVMAtmvXDUJDO/27peDcuTacOnWJRo1qvfW5hBAir5FslkII8QlITk5m7NhduLoe\nYNSoXSQlJWXr+YsUsWT1akfc3TfRq9dmfHzsKF3aLlv7EDB8+Be0beuPtfUeypTZzJgxBhQqlHUR\n7Qxly9rz11+nWbp0EYGBFzEyMn5p24EDv0OhUODr+6wUwJo1G5k/fwlLliwgIuIJR48e4v79e6xb\nt5WxYydz+fIl7fEdOnRhxQo//Pw2kZyczIkTx7CzK4axsTE3blwHYM+eX2ndOj2pi4WFOUOHtuTb\nb1tiaGj4Tp+JsTHAs5IFBQo8wMrK7J3OJYQQeY3MzAkhxCdg9Og9+Pt3BfSBVOLi1rNo0dfZ2oe9\nfQlmzSqRrecUmenr67NqVReSk5PR19d/o8cb/5sEp3r1mi9t+3zB96CgfzA2NkahUGBuboGLSzWu\nXv2HwMALNGvWAoVCgaWlJdWrP6vRd/78Wdav9yc5OYmYmBjKlClLvXoNaNOmPXv2/MqQIcP544+D\nrFjh934fxHMGDGjMmTO+/PFHAwwMound+w6VKrXJtvMLIcTHTII5IYT4BFy5Ykx6IAegxz//vHo2\nR3zcDAwM3rjtf5Pg/Pbb/2FoaERcXBwGBq9KgPPyQPH5oC9DcnIyc+fOYtUqf6ysrPHxWa6te9ew\nYWN8fZdTvXoNHB0rYGKSfV9/BgYG+Pt35dat2xgZmWNr65Rt5xZCiI+dPGYphBCfgCJFEjJtW1sn\nvKSlyG9u375J//7ueHi4snr1Stzd+9KuXXv69u3L0KEDM7V9/lHHChUqEBcXj1qtJjIyksDAC1Sq\n5ISzczUCAg6iVqt58uQJ58+fA56VwzAxMSUhIYFDh37XzhwaGBhQu/ZneHnNoFWrdmQ3HR0d7O3L\nYWsrj/YKIT4tMjMnhBCfgEmTahIb60dwsAklS8YyeXL13B6S+EBq1arzQhIcBwdHBgzoqy0Kv2XL\nLu1s2xdffEmvXl2oU6cuX33VAXf3bigUCgYNGoq5uQUNGzbm/Pmz9OjRiSJFbKhcOT3RTaFChWjb\ntj29enXBwqIwFStmniH74osWHD16OMuEPEIIId6NQpPVsxK5IOMHish/rKwKyf3Nx+T+5i0ajeaN\n08jLvc3fnr+/06fvYft2fZRKNd276zBkyBfZ2ldsbAxr165GV1ePfv0Gvv4A8V7k/27+Jvc3/7Ky\nKvTWx8jMnBBCfELepR6YyN927z7FkiWfkZycnrxmzpyr1Kx5mTp1KmfL+VevPsrSpb5oNDHY2LSj\nU6dozMzevVi9EEKIZ2TNnBBCCPEJu3kzShvIASQkOPDPP6HZcu6EhATmz1cRHLyVO3cOcOrUIGbN\nOpYt5xZCCCHBnBBCCPFJa9SoLFZWJ7XbdnZ/0KRJ9szKxcfHEx1t9dweHeLi9F7aXgghxNuRYE4I\nIYT4hDk72zNvXiotW26hdevNLFxoRKlS2ZMV0tLSklq1/gZUAJiYXOKLL8yz5dxCCCFkzZwQQog8\nKjw8jBEjhuPntym3h5LnNW9ejebNs/+8CoUCH5+2eHltJiZGj6ZNC9OqVa3s70gIIT5REswJIYQQ\nIscYGRkxYUKb3B6GEELkS/KYpRBCiDxLrVYzc+ZUevbszPffDyY5OZnQ0BA8Pb+jT5+efPttP+7d\nu5PpmIEDewPw4EE4Bw/uy4VRCyGEENlDgjkhhBDZIi4ujh07tn7QPu/fv0eHDp3x99+MsXEhjhz5\ng1mzpjF8+I+sWuXPoEFDmTNnZqZjli71ASAsLJSDB/fn6PiaNWuQ5f6dO7exb9/ulx53/vxf/PTT\n8JwalhBCiHxCgjkhhBDZIjY2hh07tnzQPosWtaNcOXsAHBwcCQ8P4++/Axk3bgQeHq54eU0jIiIi\n0zEZAdayZYu5dOkCHh6ubN68IYdGmHVdv/btO9CiResc6vPVOnZsS0xMdK70LYQQInvJmjkhhBDZ\nYtmyRYSGhuDh4UrNmrXRaOD06ZMoFAp69epD06bNsr1Pff1nae51dJTExDzF2LgQvr7rX3FUeoA1\ncOAQNmxYy6xZ8965//Xr/dDX16djx64sXDiHW7dusmDBUs6dO8tvv/0fAMuXL+HkyeMYGBgwY8Yc\nzM0tWLXKG0NDI7p160FIyH1mz55OdHQUOjo6TJkyA4VCQWJiAmPHjiA4+BYODhUYP37KO48z09VL\n4XghhMg3ZGZOCCFEthg48Dvs7Irh67ueihWduHnzOmvWbGT+/CUsWbKAiIgnOT4GIyMjbG3tOHTo\ndwA0Gg03b97Isq1Go3nv/pydqxEYeBGAoKCrJCYmkpaWxqVLF3FxqUZSUiJOTlVYvXo9zs5V2bVr\nB5AeUGXEVJMmjaVjx86sXr0eb29fLC0t0Wg03LhxjWHDfmDt2i2EhYVy6dLFtx7fqFE/0KdPT3r2\n7KztO0NCQgI//jgUd3dXevXqQkDAQQD++usMvXt3x82tK9OnTyY1NfU9PiEhhBA5SYI5IYQQ2eL5\n4OjSpYs0a9YChUKBubkFLi7VuHr1n2zv87+zTAqFgvHjp/Dbb7twd3elZ88uHD9+JNv7zeDg4Mi1\na1dJSIhHX18fJ6fKBAVdJTDwAs7OVdHT06Nu3fr/tq3AgwfhmY5PSEggIuIJDRo0AkBPTw8DgwKo\n1WoqVKiEpaUVCoWCcuXKv3Dsmxg1ajyrVvmzcqUfW7du1D5eqdFoOHbsGJaW1qxevR4/v03UqfMZ\nycnJTJs2icmTZ7BmzUZUKtUHXwcphBDizcljlkIIIbKdQqF4YeYrux/vK1rUljVrNmq3u3XroX09\nZ87C1x5vaGhEQkL8G/cXHh7GDz98R5UqVfn770CsrKyZPn0OFhaF6dfPjbi4OB4/fgzA/fv3+eGH\n71Aq03/MJiYmMnfuDOrWbUBoaAj79+8lJSWZw4f/IC0tDYCpUyeir6/PjRvXsbGxQU9PX9u3UqmD\nSqV647Fm2LJlA8eOpQezjx494v79+0D6vXBwcGD69BksXbqIunUb4Ozswo0b17G1taNYseIAtGzZ\nhu3bN9O5c7e37lsIIUTOk5k5IYQQ2cLQ0JCEhAQAqlRxISDgIGq1msjISAIDL1CxYqUc7T8tLY2d\nO4+ybdthUlJSXtouI6gsV84epVKJu/ubJ0AJCbn/QvbMiIgI4uLiGD9+CkOGDGPHjm04Ojpib19e\nG4CdPHkMe3sHFAoFs2ZNpU6dz+jc2ZUhQ74nOTmJY8cOA+kB18KFS2nfvuP7fRikZ8Q8d+4s3t6+\nrF69Hnv78qSkJGvfL1WqFD4+6yhbthwrVixh9eqVLwTc2fEoqhBCiJzz3jNzPj4+zJo1i1OnTmFm\nZgaAt7c327ZtQ0dHh7Fjx1K/fv33HqgQQoiPm6mpGZUrO9OrVxfq1KlLuXLlcHfvhkKhYNCgoZib\nW+RY32lpabi5bebgwa6Akg0bNrBu3VcYGBi80PbAgfSZKl1dXRYsWPpW/WSVPfPJk0ekpqayaNFc\n7Yyks3NVzM0t+PPPEwD8/vsBKld2JjQ0hMuXLxEcfBsdHR0OHNiDubkFW7du4vr1IIyNC/H06dNM\na+reVUJCPIUKFcLAwIA7d4K5cuXvTO8/evQIfX19mjdviZGRMbt378LVtRfh4WGEhoZgZ1eM/fv3\nULVq9fcbiBBCiBzzXsFceHg4J06cwNbWVrvv5s2b7Nmzh927d/Pw4UM8PDzYv38/OjoyCSiEEPnd\nhAk/A+nFvNPS0hg0aOgH6Xf79qMcPNgdMAbg6FE3/P130bfvl9o2cXFxzJp1mOhoPRo3NqN9+9pv\n3U9W2TNNTEz5v/97sfh4QkICVlbWxMTEcP16ENOmzSYhIZ5z585m2X7atEnUrVsfW1s7LCwKM27c\ns+yVw4f/9NZjrV27Ljt3bqNHj04UL14SJ6fK/76THiVev36dadNmoKOjQFdXlx9+GI2+vj6jR09g\n3LgRqFQqKlSolC2zhEIIIXLGewVz06dP58cff2TQoEHafQEBAbRu3Ro9PT2KFStGiRIluHTpEi4u\nLu89WCGEEB+/detOsGhRLHFxRtSrF8Yvv3RAVzdnl2inpKgAvef26JKaqtZuaTQaevfezeHDHoCS\nXbv+QaM5xVdf1Xmvfp/Pntm48Rfa7Jn29uUxNDTE0bEiCxbMpl69BigUCoyMjLG1tc3U/tatm9rZ\nPgAvr/2sWVOA1FQDvvwyhHnzvn6nP4jq6enh5fXi2sEtW9JLJpQtW581a549XhoTE83hw2ewty+G\nj8+6d/g0hBBCfGjvPF32+++/Y2Njg6OjY6b9jx49wsbGRrttY2PDw4cP332EQggh8oynTyOYPl2H\n27c78ehRK3bs6M6iRb/neL8dOtSnVi1/QAWocXFZQ/fu9bTvN2vWgL/+qggoAYiPr8gff7x94ew3\nyZ554sRR7ftNmzbj4MH9NG3aXLtv/PifX5pt886dMBYtcuDhwzY8fdqMDRu+Yu3anMvGmeHSpZu0\nbHmazp0r07TpQ9auPZ7jfQohhHh/r/xTqYeHB0+evFgXaNiwYSxfvhwfHx/tvlctkn6TDGZWVoVe\n20bkXXJ/8ze5v/nX297b8PD7PHpU+rk9BYmNNfgAXyOF+OOPbixbtgeVSsM333TA1NRE+66Ojg4W\nFhHExWXsUVOkyMuvLzY2ll9//RVXV1dOnz6Nr68vy5YtY8+e3do23303kLFjx2JkpIufn2+W5+nU\nqT2dOrXPtM/KyiHL9vPmebFxYwCJiWWe22tGbGzO/R/LOK+3921u3OgAwNOn1qxYsY3hw+X/dV4m\n35fzN7m/IsMrgzlf36x/OF2/fp2QkBDatWsHwMOHD+nQoQObN2+mSJEiPHjwQNv2wYMHFClS5LUD\nefw49m3GLfIQK6tCcn/zMbm/+de73FsLC2ucnfcRGJj+2KCR0T/UqPHhvkZ69WoEQEpK5p8rGg0M\nH66Hl9dmlMoNGBtHEBRkxI4dBahfv+ELZQdMTEyJjo6iWbO2BAb+w+nTp2nTpi01atTm9OmT+Plt\nYs+eX1GrFZiYWPP4cSw//TSMbt16UrVqdby8ZhAU9A/JyUk0atSUPn2+AeDPP4+zePF8ChQoiJNT\nFS5c+JsaNbrx+ecl2bNnMzdv3qB8+SmEho4jPr4pRYoco169Yjny+T1/f2NiMv9BNi5OyaNHMdle\nTkJ8GPJ9OX+T+5t/vUuQ/k6LGMqXL8/Jkye1202aNGH79u2YmZnRpEkTPD09cXd35+HDh9y9e5cq\nVaq8SzdCCCHyGAMDA1aurMWcORtISNDnyy+NadWqbm4PC4Du3evRrl0sERGOlChRkpiYGAYM8KB+\n/YZAetmBSZOmM2LEGL7+ujVPn0bg4eHKvXt3KVmyNLa2duzevQu1+tlavCNHDtGqVTvs7ctz48Z1\npk2bhKGhIU2bNueHH0aiUqkYNmwQt27dpFix4syePZ0lS1ZiY1OUr792IzjYlH37OlGq1FB69SqF\nj88ELlz4hx9+GE758g/p1q0ULi72L7ukbNOmjTEnT/5NbKwTCsVTmjaNlkBOCCHygGxZkf78N/xy\n5crRsmVLWrdujVKpZMKECfIDQQghPiElSxZl4cI2uT2MLBUsWJDt2zcTGHgRHR0FT548JjLyKZC5\n7EDz5i3ZvXsXixYtx9W1A2FhIcyaNY+oqCi++caDy5cDM533+vVrpKSkMGHCz7i4VGPTpnX07t0D\nlUpFRMQT7ty5jVqtwtbWDhuboiQnJ3P7dh3gNgBq9X127LjAuXN/AGBurs+oUZUpUaLUB/lcunSp\nR+HCFzh5cgvFiunj4fHVB+lXCCHE+8mWYC4gICDT9oABAxgwYEB2nFoIIYTINgcO7CU6Ogofn7Uo\nlUo6dWpHcnJ6gfHMZQcUQMajhxoqVKiEpaUVUVFRGBjoEx4ejlKp1La3sytGUlIiW7ZsICwslB07\ntrJypT/GxsZMmzbp3yLmz/6wqVAo0NFR89wkH6VLd2Plyh45ePWv9sUXVfnii1zrXgghxDuQ4m9C\nCCE+GfHx8ZibW6BUKjl//i8ePAh/ZXtjY2MMDAqQlJQMQEDAAUCBSpWGjY0tiYkJaDQaEhLiUSp1\nsbd3YN++3cTERGNkZMTTpxGcOpW+LKFEiZKEhYXy4EE4+vr6lCt3Dh2dBECNnp4N1tb/aPu9fj0o\npz4CIYQQ+UjOFv4RQgghPgIZj/s3b96CESO+x82tKw4OFShZsvQLbQD09PRJTU0FwNW1J0uXLsbD\nwxUXl+ro6aXP4Dk7u6Cvb8DYsSMoXboM9vblcXGpxuefN+Lbb/vj6toBa2sbqlRxBtLXE3p6jsTT\ncwgFChSkVq2KWFndp0aN7TRqNJitW/1xc+uKWq3G1taOmTPnfaiPRwghRB6l0LyqpsAHJFl58i/J\nupS/yf3Nvz71eztp0lhu3bqBnp4elpZWzJw5D3//1QQE7KdLl+60bNmGIUO+YfDg4SiVSqZNm4RG\nk/7c5IABQ6hd+7MXzpmYmEjBggUBmDNnJsWLl+DzzxsTFHSPqlXLY2pq9sGu71O/v/mZ3Nv8Te5v\n/vUu2SwlmBM5Tr7p5G9yf/MvubfpAgIOsnatLyqVChsbW8aMmZAp6Lp3L4Rr10KoUcMBc3PzV55r\n8+b17N37G6mpaTg4OFCuXHOmTCnAkyeVKFPmTxYvLkaNGg45fUmA3N/8TO5t/ib3N/+SYE58lOSb\nTv4m9zf/ys/3tmPHtvj4rMXExPS9zrNu3XEmTzYiMtKJMmWOvnUw1rjxPq5c6aTdbtlyE2vWtHqv\nMb2p/Hx/P3Vyb/M3ub/517sEc5IARQghxCdHoVCQHX/L9PaOJTLyc8CC27fb88svN9/q+KQkvUzb\nycmylF0IIcSbk58aQggh8rXExETGjx/J48ePUatVuLn1BWDr1k2cOHEMlSqNKVNmUKJEKRITE5k3\nbxbBwbdRqdLo3bu/tqh4VpKTMwdjKSl6L2mZtaZN4wgOfoJabYmh4TVatDB4+wsUQgjxyZJgTggh\nRL52+vRJLC2tmT17AQDx8XEsW7YIMzNzfHzWsmPHVjZsWMuIEWPx8/OhRo1ajB49gdjYWPr3d6NG\njdoUKFAgy3M3axbPypWPUautKFToCm3bGr7V2KZMaYe9/RHu3EmiZk1LWrV6eeAohBBC/JcEc0II\nIfK1smXt+eWXBSxduoi6dRvg7OwCQMOGTQAoX96RI0f+AODMmVOcOHGUDRv8AUhNTeXRoweUKFEq\ny3NPmdIOR8ejBAcnUq+eDU2a1H+rsSkUCtzcGr3bhQkhhPjkSTAnhBAiXytevAQ+Puv488/jrFix\nhOrVawKgr5/+SKRSqYNKpdK2nzp1NsWLl3ijcysUCnr0kNk0IYQQuUMSoAghhMjXnjx5gr6+Ps2b\nt8TVtRfXr197adtateqwdetG7fb160EfYohCCCHEO5FgTgghRL52+/ZN+vd3x8PDFV/fFbi59QEU\nz7VQoFCkb7u79yUtLQ03t6707NmZVau8c2XMQgghxJuQOnMix0k9lPxN7m/+Jfc2f5P7m3/Jvc3f\n5P7mX1JnTgghhHgHarWaESO2U69eAM2a7WH37nO5PSQhhBDitSQBihBCiE+et3cAvr7/A8wAGDv2\nN+rXj8LU1Cx3ByaEEEK8gszMCSGE+OTdu6cmI5ADCA2tQEhIeO4NSAghhHgDEswJIYT45FWrVggD\ngzvabUfH85QuXTLXxiOEEEK8CXnMUgghxCevU6e6REQEEBBwDkPDFDw9HTA0NMztYQkhhBCvJMGc\nEEIIAQwY0JQBA3J7FEIIIcSbk8cshRBCCCGE/MFDnAAADGJJREFUECIPkmBOCCGEEEIIIfIgCeaE\nEEIIIYQQIg+SYE4IIYQQQggh8iAJ5oQQQgghhBAiD5JgTgghhBBCCCHyIAnmhBBCCCGEECIPkmBO\nCCGEEEIIIfIgCeaEEEIIIYQQIg+SYE4IIYQQQggh8iAJ5oQQQgghhBAiD5JgTgghhBBCCCHyIAnm\nhBBCCCGEECIPkmBOCCGEEEIIIfIgCeaEEEIIIYQQIg+SYE4IIYQQQggh8iAJ5oQQQgghhBAiD5Jg\nTgghhBBCCCHyIAnmhBBCCCGEECIPkmBOCCGEEEIIIfIgCeaEEEIIIYQQIg+SYE4IIYQQQggh8iAJ\n5oQQQgghhBAiD5JgTgghhBBCCCHyIAnmhBBCCCGEECIPkmBOCCGEEEIIIfIgCeaEEEIIIYQQIg+S\nYE4IIYQQQggh8iAJ5oQQQgghhBAiD5JgTgghhBBCCCHyIAnmhBBCCCGEECIPkmBOCCGEEEIIIfIg\nCeaEEEIIIYQQIg+SYE4IIYQQQggh8iAJ5oQQQgghhBAiD5JgTgghhBBCCCHyIAnmhBBCCCGEECIP\nkmBOCCGEEEIIIfIgCeaEEEIIIYQQIg+SYE4IIYQQQggh8iAJ5oQQQgghhBAiD5JgTgghhBBCCCHy\nIAnmhBBCCCGEECIPkmBOCCGEEEIIIfIgCeaEEEIIIYQQIg+SYE6I/2/v7kKzrB8/jn98uPkF1cl0\nbJJYoJRFrA6DDkpbc2s6FM0jBTWwDkKWppAPGPYgaxAdFQpp5YFgaCFoBLpSpFYY0QSDEmQo6UzN\npzrYXNf/IBr/KP3lw4953bxeZ7vu2/GVD0Pe933NGwAASkjMAQAAlJCYAwAAKCExBwAAUEJiDgAA\noITEHAAAQAmJOQAAgBIScwAAACUk5gAAAEpIzAEAAJSQmAMAACghMQcAAFBCYg4AAKCExBwAAEAJ\niTkAAIASEnMAAAAlJOYAAABKSMwBAACUkJgDAAAoITEHAABQQmIOAACghMQcAABACYk5AACAEhJz\nAAAAJSTmAAAASkjMAQAAlJCYAwAAKCExBwAAUEJiDgAAoITEHAAAQAmJOQAAgBIScwAAACUk5gAA\nAEpIzAEAAJSQmAMAACghMQcAAFBCYg4AAKCExBwAAEAJiTkAAIASEnMAAAAlJOYAAABKSMwBAACU\nkJgDAAAoITEHAABQQmIOAACghMQcAABACYk5AACAEhJzAAAAJSTmAAAASkjMAQAAlJCYAwAAKCEx\nBwAAUEJiDgAAoITEHAAAQAmJOQAAgBIScwAAACUk5gAAAEpIzAEAAJSQmAMAACghMQcAAFBCYg4A\nAKCExBwAAEAJiTkAAIASEnMAAAAlJOYAAABKSMwBAACU0A3F3JYtW9LS0pLp06ens7Nz6PqGDRvS\n1NSU5ubmHDhw4IYPCQAAwF+Nvt4/2N3dna6uruzcuTOVSiVnz55Nkhw5ciS7d+/Orl270tfXl4UL\nF+bTTz/NyJHeBAQAALhZrruwtm7dmsWLF6dSqSRJampqkiR79+5Na2trKpVKxo8fnwkTJqSnp+fm\nnBYAAIAkNxBzvb29OXjwYObOnZv58+fn0KFDSZJTp06lvr5+6Hn19fXp6+u78ZMCAAAw5Kq3WS5c\nuDCnT5/+2/X29vYMDg7m/Pnz2bZtW3p6etLe3p69e/f+4/cZMWLEzTktAAAASf5LzG3evPmKj23d\nujVNTU1JkoaGhowcOTJnz55NXV1dTp48OfS8kydPpq6u7r8epLb2zn97ZkrIvtXNvtXLttXNvtXL\nttXNvvzpum+zbGxsTHd3d5Lk6NGjGRgYSE1NTaZOnZpdu3alv78/x44dS29vbxoaGm7agQEAALiB\n/81y9uzZWblyZWbMmJFKpZKOjo4kyaRJk9LS0pLW1taMGjUqa9eudZslAADATTaiKIpiuA8BAADA\ntfHhbwAAACUk5gAAAEpIzAEAAJTQsMZcT09P5syZk5kzZ2b27Nnp6ekZemzDhg1pampKc3NzDhw4\nMIyn5Hpt2bIlLS0tmT59ejo7O4eu27Z6bNq0KZMnT865c+eGrtm3/Do6OtLS0pK2trY8//zzuXjx\n4tBj9i2//fv3p7m5OU1NTdm4ceNwH4cbdOLEicyfPz+tra2ZPn16PvjggyTJuXPnsnDhwkybNi2L\nFi3KhQsXhvmkXK/BwcHMnDkzzz33XBLbVpMLFy5kyZIlaWlpyVNPPZXvvvvu2vcthtG8efOK/fv3\nF0VRFJ9//nkxb968oiiK4scffyza2tqK/v7+4tixY0VjY2MxODg4nEflGn355ZfFggULiv7+/qIo\niuLMmTNFUdi2mvz000/FokWLiilTphS//PJLURT2rRYHDhwY2q2zs7Po7OwsisK+1eDy5ctFY2Nj\ncezYsaK/v79oa2srjhw5MtzH4gacOnWqOHz4cFEURXHp0qWiqampOHLkSNHR0VFs3LixKIqi2LBh\nw9DPMeWzadOmYunSpcWzzz5bFEVh2yqyYsWK4sMPPyyKoigGBgaKCxcuXPO+w/rOXG1t7dArvhcv\nXhz6cPG9e/emtbU1lUol48ePz4QJE/7yrh23vq1bt2bx4sWpVCpJkpqamiS2rSbr16/P8uXL/3LN\nvtXh0UcfzciRf/zz8NBDD+XkyZNJ7FsNenp6MmHChIwfPz6VSiWtra3Zu3fvcB+LG1BbW5v7778/\nSXL77bdn4sSJ6evrS1dXV2bNmpUkmTVrVvbs2TOcx+Q6nTx5Mvv27cvTTz89dM221eHixYs5ePBg\n5syZkyQZPXp07rzzzmved1hjbtmyZeno6Mjjjz+eN954I8uWLUuSnDp1KvX19UPPq6+vT19f33Ad\nk+vQ29ubgwcPZu7cuZk/f34OHTqUxLbVYs+ePamvr8/kyZP/ct2+1Wf79u157LHHkti3GvT19WXc\nuHFDX9fV1dmwihw/fjzff/99GhoacubMmYwdOzZJMnbs2Jw5c2aYT8f1eP3117NixYqhF9iS2LZK\nHD9+PDU1NXnppZcya9asrF69Or/99ts173vdHxr+by1cuDCnT5/+2/X29vZs2bIlq1evzpNPPplP\nPvkkK1euzObNm//x+/jg8VvP1bYdHBzM+fPns23btvT09KS9vf2Kr/7a9tZ0tX03btyYTZs2DV0r\nrvJxlfa9NV1p3xdeeCFTp05NkrzzzjupVCqZMWPGFb+PfcvFXtXr119/zZIlS7Jq1arccccdf3ls\nxIgRti+hzz77LGPGjMkDDzyQr7766h+fY9vyunz5cg4fPpw1a9akoaEhr7322t9+j/nf7Ps/j7kr\nxVmSLF++PO+9916SpLm5OatXr07yxyuFf97Wk/zxFvOft2By67jatlu3bk1TU1OSpKGhISNHjszZ\ns2dtWyJX2veHH37I8ePH09bWluSPV/pnz56dbdu22bdErvbzmyQ7duzIvn378v777w9ds2/51dXV\n5cSJE0Nf27A6DAwMZMmSJWlra0tjY2OSZMyYMfn5559TW1ubU6dODf26A+Xx7bffpqurK/v27Ut/\nf38uXbqU5cuX27ZK1NfXp66uLg0NDUmSadOmZePGjRk7duw17Tust1nefffd+frrr5Mk3d3dueee\ne5IkU6dOza5du9Lf359jx46lt7d36C9KOTQ2Nqa7uztJcvTo0QwMDKSmpsa2VeDee+/NF198ka6u\nrnR1daWuri47duzI2LFj7Vsl9u/fn3fffTdvv/12/vOf/wxdt2/5Pfjgg+nt7c3x48fT39+f3bt3\n54knnhjuY3EDiqLIqlWrMnHixCxYsGDo+tSpU/PRRx8lST7++OOhyKM8li5dmn379qWrqytvvvlm\nHnnkkXR2dtq2StTW1mbcuHE5evRokuTLL7/MpEmTMmXKlGva93/+ztzVrFu3LuvWrUt/f39uu+22\nvPLKK0mSSZMmpaWlJa2trRk1alTWrl3rLeSSmT17dlauXJkZM2akUqmko6MjiW2r0f/fz77V4dVX\nX83AwEAWLVqUJHn44Yfz8ssv27cKjB49OmvWrMkzzzyT33//PXPmzMnEiROH+1jcgG+++SY7d+7M\nfffdl5kzZyb5IwIWL16c9vb2bN++PXfddVfeeuutYT4pN4ttq8eaNWvy4osvZmBgIBMmTMj69esz\nODh4TfuOKK72yy4AAADckob1NksAAACuj5gDAAAoITEHAABQQmIOAACghMQcAABACYk5AACAEhJz\nAAAAJSTmAAAASuj/AKSSWUR2kw4CAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2ee65e10>"
]
}
}
],
"execution_count": 0
},
{
"cell_type": "markdown",
"metadata": {
"id": "QB5EFrBnpNnc",
"colab_type": "text"
},
"source": [
"---\n",
"\n",
"Problem\n",
"-------\n",
"\n",
"An alternative to skip-gram is another Word2Vec model called [CBOW](http://arxiv.org/abs/1301.3781) (Continuous Bag of Words). In the CBOW model, instead of predicting a context word from a word vector, you predict a word from the sum of all the word vectors in its context. Implement and evaluate a CBOW model trained on the text8 dataset.\n",
"\n",
"---"
]
}
]
}
| apache-2.0 |
swirlingsand/deep-learning-foundations | gans/gan_mnist/Intro_to_GANs_Exercises.ipynb | 1 | 385686 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Generative Adversarial Network\n",
"\n",
"In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!\n",
"\n",
"GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:\n",
"\n",
"* [Pix2Pix](https://affinelayer.com/pixsrv/) \n",
"* [CycleGAN](https://github.com/junyanz/CycleGAN)\n",
"* [A whole list](https://github.com/wiseodd/generative-models)\n",
"\n",
"The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.\n",
"\n",
"\n",
"\n",
"The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can foold the discriminator.\n",
"\n",
"The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.1.0\n"
]
}
],
"source": [
"%matplotlib inline\n",
"\n",
"import pickle as pkl\n",
"import numpy as np\n",
"import tensorflow as tf\n",
"import matplotlib.pyplot as plt\n",
"print(tf.__version__)"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Successfully downloaded train-images-idx3-ubyte.gz 9912422 bytes.\n",
"Extracting MNIST_data\\train-images-idx3-ubyte.gz\n",
"Successfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.\n",
"Extracting MNIST_data\\train-labels-idx1-ubyte.gz\n",
"Successfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.\n",
"Extracting MNIST_data\\t10k-images-idx3-ubyte.gz\n",
"Successfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.\n",
"Extracting MNIST_data\\t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"from tensorflow.examples.tutorials.mnist import input_data\n",
"mnist = input_data.read_data_sets('MNIST_data')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model Inputs\n",
"\n",
"First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks.\n",
"\n",
">**Exercise:** Finish the `model_inputs` function below. Create the placeholders for `inputs_real` and `inputs_z` using the input sizes `real_dim` and `z_dim` respectively."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def model_inputs(real_dim, z_dim):\n",
" inputs_real = tf.placeholder(tf.float32, shape = (None, real_dim), name=\"inputs_real\")\n",
" inputs_z = tf.placeholder(tf.float32, shape = (None, z_dim), name =\"inputs_z\")\n",
" \n",
" return inputs_real, inputs_z"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator network\n",
"\n",
"\n",
"\n",
"Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
"#### Variable Scope\n",
"Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.\n",
"\n",
"We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.\n",
"\n",
"To use `tf.variable_scope`, you use a `with` statement:\n",
"```python\n",
"with tf.variable_scope('scope_name', reuse=False):\n",
" # code here\n",
"```\n",
"\n",
"Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.\n",
"\n",
"#### Leaky ReLU\n",
"TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can use take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:\n",
"$$\n",
"f(x) = max(\\alpha * x, x)\n",
"$$\n",
"\n",
"#### Tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1.\n",
"\n",
">**Exercise:** Implement the generator network in the function below. You'll need to return the tanh output. Make sure to wrap your code in a variable scope, with 'generator' as the scope name, and pass the `reuse` keyword argument from the function to `tf.variable_scope`."
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):\n",
" ''' Build the generator network.\n",
" \n",
" Arguments\n",
" ---------\n",
" z : Input tensor for the generator\n",
" out_dim : Shape of the generator output\n",
" n_units : Number of units in hidden layer\n",
" reuse : Reuse the variables with tf.variable_scope\n",
" alpha : leak parameter for leaky ReLU\n",
" \n",
" Returns\n",
" -------\n",
" out, logits: \n",
" '''\n",
" with tf.variable_scope('Generator', reuse=reuse):\n",
" # Hidden layer\n",
" h1 = tf.layers.dense(z, n_units, activation = None)\n",
" # Leaky ReLU\n",
" h1 = tf.maximum( (alpha * h1), h1)\n",
" \n",
" # Logits and tanh output\n",
" logits = tf.layers.dense(h1, out_dim, activation = None)\n",
" out = tf.tanh(logits)\n",
" \n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator\n",
"\n",
"The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer.\n",
"\n",
">**Exercise:** Implement the discriminator network in the function below. Same as above, you'll need to return both the logits and the sigmoid output. Make sure to wrap your code in a variable scope, with 'discriminator' as the scope name, and pass the `reuse` keyword argument from the function arguments to `tf.variable_scope`."
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def discriminator(x, n_units=128, reuse=False, alpha=0.01):\n",
" ''' Build the discriminator network.\n",
" \n",
" Arguments\n",
" ---------\n",
" x : Input tensor for the discriminator\n",
" n_units: Number of units in hidden layer\n",
" reuse : Reuse the variables with tf.variable_scope\n",
" alpha : leak parameter for leaky ReLU\n",
" \n",
" Returns\n",
" -------\n",
" out, logits: \n",
" '''\n",
" with tf.variable_scope('Discriminator', reuse=reuse):\n",
" # Hidden layer\n",
" h1 = tf.layers.dense(x, n_units, activation = None)\n",
" # Leaky ReLU\n",
" h1 = tf.maximum ( (alpha * h1), h1)\n",
" \n",
" logits = tf.layers.dense(h1, 1, activation = None)\n",
" out = tf.sigmoid(logits)\n",
" \n",
" return out, logits"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 96,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Size of input image to discriminator\n",
"input_size = 784 # 28x28 MNIST images flattened\n",
"# Size of latent vector to generator\n",
"z_size = 784\n",
"# Sizes of hidden layers in generator and discriminator\n",
"g_hidden_size = 256\n",
"d_hidden_size = 256\n",
"# Leak factor for leaky ReLU\n",
"alpha = 0.01\n",
"# Label smoothing \n",
"smooth = 0.1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build network\n",
"\n",
"Now we're building the network from the functions defined above.\n",
"\n",
"First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.\n",
"\n",
"Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.\n",
"\n",
"Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`.\n",
"\n",
">**Exercise:** Build the network from the functions you defined earlier."
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"tf.reset_default_graph()\n",
"# Create our input placeholders\n",
"input_real, input_z = model_inputs(input_size, z_size)\n",
"\n",
"# Generator network here\n",
"g_model = generator(input_z, input_size)\n",
"# g_model is the generator output\n",
"\n",
"# Disriminator network here\n",
"d_model_real, d_logits_real = discriminator(input_real)\n",
"d_model_fake, d_logits_fake = discriminator(g_model, reuse=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropys, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like \n",
"\n",
"```python\n",
"tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\n",
"```\n",
"\n",
"For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`\n",
"\n",
"The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
"Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images.\n",
"\n",
">**Exercise:** Calculate the losses for the discriminator and the generator. There are two discriminator losses, one for real images and one for fake images. For the real image loss, use the real logits and (smoothed) labels of ones. For the fake image loss, use the fake logits with labels of all zeros. The total discriminator loss is the sum of those two losses. Finally, the generator loss again uses the fake logits from the discriminator, but this time the labels are all ones because the generator wants to fool the discriminator."
]
},
{
"cell_type": "code",
"execution_count": 98,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Calculate losses\n",
"\n",
"# One's like for real labels for Discriminator \n",
"real_labels = tf.ones_like(d_logits_real) * (1 - smooth)\n",
"\n",
"d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(\n",
" logits = d_logits_real, labels=real_labels))\n",
"\n",
"# Zeros's like for real labels for Discriminator \n",
"fake_labels = tf.zeros_like(d_logits_real)\n",
"\n",
"d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(\n",
" logits = d_logits_fake, labels= fake_labels))\n",
"\n",
"\n",
"d_loss = d_loss_real + d_loss_fake\n",
"\n",
"\n",
"# One's like for fake labels for generator\n",
"generated_labels = tf.ones_like(d_logits_fake)\n",
"\n",
"g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits = d_logits_fake, \n",
" labels = generated_labels))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So we need to get the variables for each part build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.\n",
"\n",
"For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables to start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance). \n",
"\n",
"We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.\n",
"\n",
"Then, in the optimizer we pass the variable lists to `var_list` in the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`.\n",
"\n",
">**Exercise: ** Below, implement the optimizers for the generator and discriminator. First you'll need to get a list of trainable variables, then split that list into two lists, one for the generator variables and another for the discriminator variables. Finally, using `AdamOptimizer`, create an optimizer for each network that update the network variables separately."
]
},
{
"cell_type": "code",
"execution_count": 99,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"# Optimizers\n",
"learning_rate = 0.002\n",
"\n",
"# Get the trainable_variables, split into G and D parts\n",
"t_vars = tf.trainable_variables()\n",
"g_vars = [var for var in t_vars if var.name.startswith('Generator')]\n",
"d_vars = [var for var in t_vars if var.name.startswith('Discriminator')]\n",
"\n",
"d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list = d_vars)\n",
"g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list = g_vars)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training"
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/80... Discriminator Loss: 0.4425... Generator Loss: 2.8760 Difference Loss: -2.4335...\n",
"Epoch 2/80... Discriminator Loss: 0.8649... Generator Loss: 4.6707 Difference Loss: -3.8059...\n",
"Epoch 3/80... Discriminator Loss: 0.5695... Generator Loss: 3.7862 Difference Loss: -3.2167...\n",
"Epoch 4/80... Discriminator Loss: 1.1659... Generator Loss: 2.9606 Difference Loss: -1.7947...\n",
"Epoch 5/80... Discriminator Loss: 1.8704... Generator Loss: 1.8585 Difference Loss: 0.0119...\n",
"Epoch 6/80... Discriminator Loss: 1.8201... Generator Loss: 1.9842 Difference Loss: -0.1641...\n",
"Epoch 7/80... Discriminator Loss: 1.6348... Generator Loss: 0.9816 Difference Loss: 0.6532...\n",
"Epoch 8/80... Discriminator Loss: 2.0758... Generator Loss: 1.6577 Difference Loss: 0.4181...\n",
"Epoch 9/80... Discriminator Loss: 1.7692... Generator Loss: 2.2681 Difference Loss: -0.4989...\n",
"Epoch 10/80... Discriminator Loss: 1.4375... Generator Loss: 1.6568 Difference Loss: -0.2193...\n",
"Epoch 11/80... Discriminator Loss: 1.3330... Generator Loss: 3.2855 Difference Loss: -1.9526...\n",
"Epoch 12/80... Discriminator Loss: 1.0370... Generator Loss: 1.7489 Difference Loss: -0.7119...\n",
"Epoch 13/80... Discriminator Loss: 2.4128... Generator Loss: 1.7430 Difference Loss: 0.6697...\n",
"Epoch 14/80... Discriminator Loss: 0.9600... Generator Loss: 1.8819 Difference Loss: -0.9220...\n",
"Epoch 15/80... Discriminator Loss: 1.4469... Generator Loss: 1.1186 Difference Loss: 0.3282...\n",
"Epoch 16/80... Discriminator Loss: 1.4471... Generator Loss: 1.6183 Difference Loss: -0.1713...\n",
"Epoch 17/80... Discriminator Loss: 1.0488... Generator Loss: 1.7481 Difference Loss: -0.6993...\n",
"Epoch 18/80... Discriminator Loss: 1.5066... Generator Loss: 2.4485 Difference Loss: -0.9419...\n",
"Epoch 19/80... Discriminator Loss: 1.1833... Generator Loss: 1.8220 Difference Loss: -0.6387...\n",
"Epoch 20/80... Discriminator Loss: 1.3408... Generator Loss: 1.2924 Difference Loss: 0.0484...\n",
"Epoch 21/80... Discriminator Loss: 1.3709... Generator Loss: 1.0623 Difference Loss: 0.3086...\n",
"Epoch 22/80... Discriminator Loss: 1.3033... Generator Loss: 1.3027 Difference Loss: 0.0007...\n",
"Epoch 23/80... Discriminator Loss: 1.2793... Generator Loss: 1.3861 Difference Loss: -0.1068...\n",
"Epoch 24/80... Discriminator Loss: 1.0635... Generator Loss: 2.6765 Difference Loss: -1.6130...\n",
"Epoch 25/80... Discriminator Loss: 0.9273... Generator Loss: 2.5718 Difference Loss: -1.6445...\n",
"Epoch 26/80... Discriminator Loss: 1.2080... Generator Loss: 1.5664 Difference Loss: -0.3584...\n",
"Epoch 27/80... Discriminator Loss: 0.9275... Generator Loss: 2.1867 Difference Loss: -1.2592...\n",
"Epoch 28/80... Discriminator Loss: 1.1091... Generator Loss: 1.6780 Difference Loss: -0.5689...\n",
"Epoch 29/80... Discriminator Loss: 1.1394... Generator Loss: 1.5004 Difference Loss: -0.3610...\n",
"Epoch 30/80... Discriminator Loss: 1.1007... Generator Loss: 1.6363 Difference Loss: -0.5356...\n",
"Epoch 31/80... Discriminator Loss: 0.9284... Generator Loss: 1.6571 Difference Loss: -0.7287...\n",
"Epoch 32/80... Discriminator Loss: 1.0327... Generator Loss: 1.5925 Difference Loss: -0.5598...\n",
"Epoch 33/80... Discriminator Loss: 1.0271... Generator Loss: 1.5354 Difference Loss: -0.5083...\n",
"Epoch 34/80... Discriminator Loss: 0.9506... Generator Loss: 1.6436 Difference Loss: -0.6931...\n",
"Epoch 35/80... Discriminator Loss: 0.9758... Generator Loss: 1.8441 Difference Loss: -0.8683...\n",
"Epoch 36/80... Discriminator Loss: 1.3653... Generator Loss: 1.3617 Difference Loss: 0.0036...\n",
"Epoch 37/80... Discriminator Loss: 1.1974... Generator Loss: 1.1603 Difference Loss: 0.0371...\n",
"Epoch 38/80... Discriminator Loss: 1.1631... Generator Loss: 1.2691 Difference Loss: -0.1060...\n",
"Epoch 39/80... Discriminator Loss: 1.2434... Generator Loss: 1.4074 Difference Loss: -0.1640...\n",
"Epoch 40/80... Discriminator Loss: 0.9168... Generator Loss: 1.8218 Difference Loss: -0.9050...\n",
"Epoch 41/80... Discriminator Loss: 1.1142... Generator Loss: 1.3254 Difference Loss: -0.2113...\n",
"Epoch 42/80... Discriminator Loss: 1.1721... Generator Loss: 1.4403 Difference Loss: -0.2682...\n",
"Epoch 43/80... Discriminator Loss: 1.2639... Generator Loss: 1.4644 Difference Loss: -0.2005...\n",
"Epoch 44/80... Discriminator Loss: 1.3026... Generator Loss: 1.3177 Difference Loss: -0.0151...\n",
"Epoch 45/80... Discriminator Loss: 1.2626... Generator Loss: 1.4706 Difference Loss: -0.2081...\n",
"Epoch 46/80... Discriminator Loss: 1.0161... Generator Loss: 1.6525 Difference Loss: -0.6364...\n",
"Epoch 47/80... Discriminator Loss: 1.1347... Generator Loss: 1.4505 Difference Loss: -0.3158...\n",
"Epoch 48/80... Discriminator Loss: 1.3174... Generator Loss: 1.3299 Difference Loss: -0.0126...\n",
"Epoch 49/80... Discriminator Loss: 1.0591... Generator Loss: 1.4575 Difference Loss: -0.3984...\n",
"Epoch 50/80... Discriminator Loss: 1.1734... Generator Loss: 1.9260 Difference Loss: -0.7527...\n",
"Epoch 51/80... Discriminator Loss: 1.0059... Generator Loss: 1.7600 Difference Loss: -0.7541...\n",
"Epoch 52/80... Discriminator Loss: 1.2851... Generator Loss: 1.1668 Difference Loss: 0.1183...\n",
"Epoch 53/80... Discriminator Loss: 1.1780... Generator Loss: 1.2625 Difference Loss: -0.0846...\n",
"Epoch 54/80... Discriminator Loss: 1.0170... Generator Loss: 1.5435 Difference Loss: -0.5265...\n",
"Epoch 55/80... Discriminator Loss: 1.1132... Generator Loss: 1.3062 Difference Loss: -0.1929...\n",
"Epoch 56/80... Discriminator Loss: 1.1084... Generator Loss: 1.3557 Difference Loss: -0.2473...\n",
"Epoch 57/80... Discriminator Loss: 1.2846... Generator Loss: 1.2462 Difference Loss: 0.0384...\n",
"Epoch 58/80... Discriminator Loss: 1.0062... Generator Loss: 1.4142 Difference Loss: -0.4080...\n",
"Epoch 59/80... Discriminator Loss: 1.2745... Generator Loss: 1.1870 Difference Loss: 0.0875...\n",
"Epoch 60/80... Discriminator Loss: 1.2649... Generator Loss: 1.2455 Difference Loss: 0.0195...\n",
"Epoch 61/80... Discriminator Loss: 1.2507... Generator Loss: 1.3175 Difference Loss: -0.0667...\n",
"Epoch 62/80... Discriminator Loss: 1.1241... Generator Loss: 1.2867 Difference Loss: -0.1626...\n",
"Epoch 63/80... Discriminator Loss: 1.1645... Generator Loss: 1.2192 Difference Loss: -0.0547...\n",
"Epoch 64/80... Discriminator Loss: 1.2231... Generator Loss: 1.0268 Difference Loss: 0.1963...\n",
"Epoch 65/80... Discriminator Loss: 1.0558... Generator Loss: 1.5315 Difference Loss: -0.4757...\n",
"Epoch 66/80... Discriminator Loss: 1.0592... Generator Loss: 1.4043 Difference Loss: -0.3450...\n",
"Epoch 67/80... Discriminator Loss: 1.1810... Generator Loss: 1.4129 Difference Loss: -0.2319...\n",
"Epoch 68/80... Discriminator Loss: 1.1422... Generator Loss: 1.4156 Difference Loss: -0.2734...\n",
"Epoch 69/80... Discriminator Loss: 1.0945... Generator Loss: 1.3094 Difference Loss: -0.2148...\n",
"Epoch 70/80... Discriminator Loss: 1.1504... Generator Loss: 1.3257 Difference Loss: -0.1753...\n",
"Epoch 71/80... Discriminator Loss: 1.1245... Generator Loss: 1.1868 Difference Loss: -0.0622...\n",
"Epoch 72/80... Discriminator Loss: 1.0467... Generator Loss: 1.2523 Difference Loss: -0.2056...\n",
"Epoch 73/80... Discriminator Loss: 1.1899... Generator Loss: 1.1791 Difference Loss: 0.0108...\n",
"Epoch 74/80... Discriminator Loss: 1.0329... Generator Loss: 1.4332 Difference Loss: -0.4003...\n",
"Epoch 75/80... Discriminator Loss: 1.2118... Generator Loss: 1.2174 Difference Loss: -0.0056...\n",
"Epoch 76/80... Discriminator Loss: 1.1392... Generator Loss: 1.2048 Difference Loss: -0.0656...\n",
"Epoch 77/80... Discriminator Loss: 1.1396... Generator Loss: 1.5353 Difference Loss: -0.3957...\n",
"Epoch 78/80... Discriminator Loss: 1.0808... Generator Loss: 1.6528 Difference Loss: -0.5719...\n",
"Epoch 79/80... Discriminator Loss: 1.1598... Generator Loss: 1.4892 Difference Loss: -0.3294...\n",
"Epoch 80/80... Discriminator Loss: 1.1646... Generator Loss: 1.3657 Difference Loss: -0.2011...\n"
]
}
],
"source": [
"batch_size = 100\n",
"epochs = 80\n",
"samples = []\n",
"losses = []\n",
"saver = tf.train.Saver(var_list = g_vars)\n",
"with tf.Session() as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
" for e in range(epochs):\n",
" for ii in range(mnist.train.num_examples//batch_size):\n",
" batch = mnist.train.next_batch(batch_size)\n",
" \n",
" # Get images, reshape and rescale to pass to D\n",
" batch_images = batch[0].reshape((batch_size, 784))\n",
" batch_images = batch_images*2 - 1\n",
" \n",
" # Sample random noise for G\n",
" batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" \n",
" # Run optimizers\n",
" _ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})\n",
" _ = sess.run(g_train_opt, feed_dict={input_z: batch_z})\n",
" \n",
" # At the end of each epoch, get the losses and print them out\n",
" train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})\n",
" train_loss_g = g_loss.eval({input_z: batch_z})\n",
" \n",
" print(\"Epoch {}/{}...\".format(e+1, epochs),\n",
" \"Discriminator Loss: {:.4f}...\".format(train_loss_d),\n",
" \"Generator Loss: {:.4f}\".format(train_loss_g),\n",
" \"Difference Loss: {:.4f}...\".format(train_loss_d-train_loss_g),\n",
" ) \n",
" # Save losses to view after training\n",
" losses.append((train_loss_d, train_loss_g))\n",
" \n",
" # Sample from generator as we're training for viewing afterwards\n",
" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\n",
" gen_samples = sess.run(\n",
" generator(input_z, input_size, reuse=True),\n",
" feed_dict={input_z: sample_z})\n",
" samples.append(gen_samples)\n",
" saver.save(sess, './checkpoints/generator.ckpt')\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Results with 128 hidden units\n",
"\n",
"Epoch 72/100... Discriminator Loss: 1.2292... Generator Loss: 1.0937 Difference Loss: 0.1355...\n",
"Epoch 73/100... Discriminator Loss: 1.1977... Generator Loss: 1.0838 Difference Loss: 0.1139...\n",
"Epoch 74/100... Discriminator Loss: 1.0160... Generator Loss: 1.4791 Difference Loss: -0.4632...\n",
"Epoch 75/100... Discriminator Loss: 1.1122... Generator Loss: 1.0486 Difference Loss: 0.0637...\n",
"Epoch 76/100... Discriminator Loss: 1.0662... Generator Loss: 1.5303 Difference Loss: -0.4641...\n",
"Epoch 77/100... Discriminator Loss: 1.1943... Generator Loss: 1.1728 Difference Loss: 0.0215...\n",
"Epoch 78/100... Discriminator Loss: 1.1579... Generator Loss: 1.3853 Difference Loss: -0.2274...\n",
"Epoch 79/100... Discriminator Loss: 1.1481... Generator Loss: 1.1773 Difference Loss: -0.0292...\n",
"Epoch 80/100... Discriminator Loss: 1.1529... Generator Loss: 1.6801 Difference Loss: -0.5272..."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll check out the training losses for the generator and discriminator."
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x2bab019bba8>"
]
},
"execution_count": 72,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAEICAYAAAB/Dx7IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnWd4HNXZhu8j7ar3Llmy5N5t2ZZtjGkxGBM6CYQEhwAJ\nLQkkQAKkA6mQj1BCCIFAIHQTwBBqaDbg3nuXLFmy1XvfNt+PM7NNu2rW2rvyua9L1+zOTjlb9Mw7\nz3nPe4SmaSgUCoUidAg70Q1QKBQKxcBQwq1QKBQhhhJuhUKhCDGUcCsUCkWIoYRboVAoQgwl3AqF\nQhFiKOFWnHCEEOFCiDYhxMih3FahGK4IlcetGChCiDa3pzFAN2DXn9+kadpLx79Vx44Q4vdArqZp\n157otigUvWE60Q1QhB6apsUZj4UQpcD1mqZ94m97IYRJ0zTb8WibQnEyoKwSxZAjhPi9EGKpEOIV\nIUQr8G0hxHwhxFohRJMQolII8VchhFnf3iSE0IQQBfrzF/XXPxBCtAoh1gghRg10W/31rwoh9gsh\nmoUQjwkhVgkhrh3Ee5oihPhcb/8OIcQFbq9dKITYo5+/Qghxu74+Qwjxvr5PgxDiC7d9coUQy4QQ\ntUKIQ0KIH7q9dooQYrMQokUIUS2E+L+BtlcxvFHCrQgUlwEvA4nAUsAG/BhIAxYA5wE39bL/VcCv\ngRTgMPC7gW4rhMgAXgPu1M97CJg70DcihIgA3gXeA9KB24GlQoix+ibPAt/TNC0emA58rq+/EyjR\n98kCfqUfL0w/3gZgBLAIuFMIcba+32PA/2malgCMBV4faJsVwxsl3IpAsVLTtHc0TXNomtapadoG\nTdPWaZpm0zStBHgKOLOX/V/XNG2jpmlW4CWgcBDbXghs1TTtbf21h4G6QbyXBUAEUkytui30AfBN\n/XUrMFkIEa9pWoOmaZvd1ucAIzVNs2iaZkTc84EETdP+qK8/CDzjdbxxQohUTdNaNU1bN4g2K4Yx\nSrgVgaLc/YkQYqIQ4j0hRJUQogX4LTIK9keV2+MOIM7fhr1sm+PeDk32xFf0o+3e5ACHNc+e/DJk\ntAzy7uJi4LAQYoUQYp6+/n59u0+FEMVCiDv19fnASN1CaRJCNAF3IaNygOuAycA+IcR6IcT5g2iz\nYhijhFsRKLzTlZ4EdgJjdQvgN4AIcBsqgVzjiRBC4BLbgXAUyNP3NxgJHAHQ7yQuBjKQFsir+voW\nTdNu1zStALgUuFsIcSbyYnJA07Qkt794TdMu0vfbp2naN/Xj/QV4QwgRNYh2K4YpSrgVx4t4oBlo\nF0JMond/e6h4F5glhLhICGFCeuzpfewTLoSIcvuLBFYjPfqfCCHMQoiFwPlInztaCHGVECJBt2Na\nAQeAft4xuuA3I1MmHcAawCKE+Il+jnAhxDQhxGx9v6uFEGmapjn0/TTjmAoFKOFWHD9+AlyDFLYn\nkR2WAUXTtGrgSuAhoB4YA2xB5p3749tAp9vfPk3TuoGLgEuQHvlfgas0TTug73MNUKZbQN/TjwEw\nAfgMaANWAY9qmvalnhp5PrKjtFQ/5pNAgr7f+cAePSPnQeBKTdMsg/8kFMMNNQBHcdIghAhH2h6X\na5r25Yluj0IxWFTErRjWCCHOE0Ik6ZbHr5EZG+tPcLMUimNCCbdiuHMaMpe6FlgMXKZbHwpFyKKs\nEoVCoQgxVMStUCgUIUZAikylpaVpBQUFgTi0QqFQDEs2bdpUp2laX+mqQICEu6CggI0bNwbi0AqF\nQjEsEUKU9XdbZZUoFApFiKGEW6FQKEIMJdwKhUIRYqgZcBSKYYrVaqWiooKurq4T3RSFG1FRUeTm\n5mI2mwd9DCXcCsUwpaKigvj4eAoKCvAsbKg4UWiaRn19PRUVFYwaNarvHfygrBKFYpjS1dVFamqq\nEu0gQghBamrqMd8FKeFWKIYxSrSDj6H4ToJXuEs+h7qDJ7oVCoVCEXQEr3C/9QNY+fCJboVCoTgG\nwsPDKSwsZMqUKcyYMYO//OUvOBxyToiNGzfyox/96JjP8Y9//IPnn39+QPuceuqpgz7fc889x9Gj\nRwe9/1AQvJ2Tllb5p1AoQpbo6Gi2bt0KQE1NDVdddRUtLS3cd999FBUVUVRUdEzHt9ls3HzzzQPe\nb/Xq1YM+53PPPcfUqVPJycnp9z52u53w8PBBn9Ob4I24rZ3yT6FQDAsyMjJ46qmn+Nvf/oamaaxY\nsYILL7wQgM8//5zCwkIKCwuZOXMmra0yaHvggQeYNm0aM2bM4Gc/+xkAZ511FrfddhtFRUU8+uij\n3HvvvTz44IPO126//XaKioqYNGkSGzZs4Gtf+xrjxo3jV7/6lbMtcXFyPukVK1Zw1llncfnllzNx\n4kSWLFmCUTH1t7/9LXPmzGHq1KnceOONaJrG66+/zsaNG1myZAmFhYV0dnby6aefMnPmTKZNm8Z3\nv/tdurtl1eCCggLuvvtuZs2axX/+858h/SyDM+J22MFuAUvHiW6JQjEsuO+dXew+2jKkx5yck8A9\nF00Z0D6jR4/GbrdTU1Pjsf7BBx/k8ccfZ8GCBbS1tREVFcUHH3zA22+/zbp164iJiaGhocG5vcVi\ncdZDuvfeez2OFRERwcaNG3n00Ue55JJL2LRpEykpKYwZM4bbb7+d1NRUj+23bNnCrl27yMnJYcGC\nBaxatYrTTjuNW265hd/85jcAXH311bz77rtcfvnl/O1vf+PBBx+kqKiIrq4urr32Wj799FPGjx/P\nd77zHZ544gluu+02AFJTU9m8efOAPqP+EJwRtxFpW5VwKxQnAwsWLOCOO+7gr3/9K01NTZhMJj75\n5BOuu+46YmJiAEhJSXFuf+WVV/o91sUXXwzAtGnTmDJlCtnZ2URGRjJ69GjKy8t7bD937lxyc3MJ\nCwujsLCQ0tJSAJYvX868efOYNm0an332Gbt27eqx7759+xg1ahTjx48H4JprruGLL77oVzuPheCM\nuJ3CrawShWIoGGhkHChKSkoIDw8nIyODPXv2ONf/7Gc/44ILLuD9999nwYIF/O9//+v1OLGxsX5f\ni4yMBCAsLMz52Hhus9n8bg+yM9Vms9HV1cUPfvADNm7cSF5eHvfee++gcq97a+exEKQRtx5pW9tP\nbDsUCsWQUVtby80338wtt9zSI5e5uLiYadOmcffddzNnzhz27t3LokWLePbZZ+nokHrgbpUEGkOk\n09LSaGtr4/XXX3e+Fh8f7/TgJ0yYQGlpKQcPytTlF154gTPPPDPg7QvOiNumX9lUxK1QhDSdnZ0U\nFhZitVoxmUxcffXV3HHHHT22e+SRR1i+fDlhYWFMmTKFr371q0RGRrJ161aKioqIiIjg/PPP549/\n/ONxaXdSUhI33HADU6dOJSsrizlz5jhfu/baa7n55puJjo5mzZo1PPvss1xxxRXYbDbmzJkzqCyX\ngRKQOSeLioq0Y5pI4egWeOosiIiDXxwZsnYpFCcTe/bsYdKkSSe6GQof+PpuhBCbNE3rV35kkFol\neqRtaQc1mbFCoVB4EKTCbWSTaGDrPqFNUSgUimAjSIXbrfdWpQQqFAqFB0Eq3G6dkkq4FQqFwoMg\nFW43sVaZJQqFQuFBcAq3TVklCoVC4Y/gFG53sVb1ShSKkKa6upqrrrqK0aNHM3v2bObPn8+yZctO\nSFtWrFhxTJUBg4UgFW7lcSsUwwFN07j00ks544wzKCkpYdOmTbz66qtUVFQE7Jy+hrUbDEa4ezve\niSJIhbvD92OFQhFSfPbZZ0RERHiMJszPz+fWW2/Fbrdz5513MmfOHKZPn86TTz4J9F5qddOmTZx5\n5pnMnj2bxYsXU1lZCfQs9frOO+8wb948Zs6cyTnnnEN1dTWlpaX84x//4OGHH6awsJAvv/yS0tJS\nFi5cyPTp0zn77LM5fPgw4BodOW/ePO66667j/Kn1TXAOefdIB1SdkwrFMfPBz6Bqx9AeM2safPX+\nXjfZtWsXs2bN8vnaM888Q2JiIhs2bKC7u5sFCxZw7rnnAr5Lrc6bN49bb72Vt99+m/T0dJYuXcov\nf/lL/vWvfwGepV4bGxtZu3YtQgiefvpp/vznP/OXv/yFm2++mbi4OH76058CcNFFF3HNNddwzTXX\n8K9//Ysf/ehHvPXWWwBUVFSwevXqIZ0AYagIUuHuBBEGmiNwEXdnI3z2ezj392CODsw5FAqFBz/8\n4Q9ZuXIlERER5Ofns337dmcBp+bmZg4cOEBERISz1CrgLLWalJTEzp07WbRoESBnlcnOznYe272E\nakVFBVdeeSWVlZVYLBZGjRrlsz1r1qzhzTffBGTNbffo+oorrghK0YagFe4OiE6BjrrAdU4eXgsb\nnobpV0Le3MCcQ6EIFvqIjAPFlClTeOONN5zPH3/8cerq6igqKmLkyJE89thjLF682GOfFStW+Cy1\nqmkaU6ZMYc2aNT7P5V5C9dZbb+WOO+7g4osvZsWKFT0mW+gPgSrJOhQEp8dt64IYfZaKQEXcdot+\nLjWkXqEIFAsXLqSrq4snnnjCuc4o07p48WKeeOIJrFYrAPv376e93X8p5wkTJlBbW+sUbqvV6nNy\nA5DR+4gRIwD497//7VzvXpIV5KTBr776KgAvvfQSp59++mDe5nEnOIXb2gFRidIuCZTHbZc/FiXc\nCkXgEELw1ltv8fnnnzNq1Cjmzp3LNddcwwMPPMD111/P5MmTmTVrFlOnTuWmm27qNYMjIiKC119/\nnbvvvpsZM2ZQWFjoN0Pk3nvv5YorrmD27NmkpaU511900UUsW7bM2Tn52GOP8eyzzzJ9+nReeOEF\nHn300SH/DAJBcJZ1feZcMEXBkc0w62o4709D1ziDrS/DW9+Hb74MEy8Y+uMrFCcYVdY1eBmmZV07\nwBwjOw2VVaJQKBQeBKlwd0nRNkcH3ioxBFyhUChChCAV7k4p2hGxcjKFQKA8bsVJQCCsUMWxMRTf\nSZAKd8dxiLgtnkuFYpgRFRVFfX29Eu8gQtM06uvriYqKOqbjBGketx5xm2NUVolCMUhyc3OpqKig\ntrb2RDdF4UZUVJRzcNFgCT7h1jSwdYJJF+62qsCcx9k52dX7dgpFiGI2m/2OGFSENsFnlRhCqqwS\nhUKh8EnwCbch1OYYZZUoFAqFD/ot3EKIcCHEFiHEu4FskEu4oyEiJnBZJQ6VDqhQKEKTgUTcPwb2\nBKohTtyF+3hYJSriVigUIUa/hFsIkQtcADwd2ObgGilpZJXYOsHhGPrzOAfgKOFWKBShRX8j7keA\nuwC/CiqEuFEIsVEIsfGY0o88Iu4Y+dgWgKjbGXErq0ShUIQWfQq3EOJCoEbTtE29badp2lOaphVp\nmlaUnp4++BbZvDonITB2iUoHVCgUIUp/Iu4FwMVCiFLgVWChEOLFgLXIEGlTlGtmmkAUmlK1ShQK\nRYjSp3BrmvZzTdNyNU0rAL4JfKZp2rcD1iKnxx0js0ogMLPgqM5JhUIRogRhHrf7ABzDKlERt0Kh\nUBgMaMi7pmkrgBUBaYmBR1aJYZUEwuNWA3AUCkVoEoQRt3tWiT5ZZ0AibmPIuxJuhUIRWgSvcJui\nA9w5qdIBFQpFaBJ8wm3rhPAICDcdJ6tEpQMqFIrQIviE26qXdAU5Aw4Epl6Jqg6oUChClCAU7g5X\npB3IiNuhOicVCkVoEoTC3eUm3CodUKFQKLwJQuF2i7jDzRBmDnDnpIq4FQpFaBGEwt3pEm4I3GQK\nRsTtsAam+qBCoVAEiCAV7hjXc3N0YDsnvR8rFApFkBN8wm3zirgjAhVxW9zKxqqUQIVCEToEn3Bb\nO2VlQINAWCUOO2gOiIiTz1XErVAoQoggFO6OnlaJdYitEsPfjtSFW3VQKhSKECIIhbsr8J2TRoSt\nIm6FQhGCBKFw+8oqGeJ0QGfEHS+XKuJWKBQhRHAJt6Z55nGDnlUy1MLtHXEr4VYoFKFDcAm33Qqa\nPfBZJYZwOz1uZZUoFIrQIbiE232iYINAWiVGxK3SARUKRQgRXMLtPlGwgTl66IXb4eVxq85JhUIR\nQgSZcLtNFGxgjpXCarcN3Xm8PW7VOalQKEKIIBNut4mCDYzHtiH0ub3zuFXnpEKhCCGCTLjd5ps0\niNCj76HMLOkRcSurRKFQhA5BJtxuM7wbBKImtzOrxPC4VcStUChChyATbl9ZJQGYBadHVomKuBUK\nRegQXMJt82GVmPV5J4c04vauVaLSARUKRegQXMLtLx0QAmOVqJGTCoUiBAky4faVDmh43AGwSswx\ngFBWiUKhCCmCTLh9pAM6s0qGsLSrEXGbIsAUqSJuhUIRUgSZcPvKKglE56Qu3OEREB6pIm6FQhFS\nBJlwd4IIk4JqEJB0QN0qCY+QUbeKuBUKRQgRfMJtjgEhXOu8hbvuINTuP7bzGLVKws0q4lYoFCFH\ncAm390TB4GmVdLXAcxfAmzcc23kMqyTMLCNulQ6oUChCCNOJboAH1k4weQl3WLiMii3tsPwP0FYF\nHfUySjZF+D5OX7hbJeGqc1KhUIQWwRVxe89+YxARA+XrYP1TkDJaWh21ewZ/HrsFEPKiYFJWiUKh\nCC2CTLh9WCUgfe7ydRCTBl97Wq6r2jH489gtMtoWQqUDKhSKkCNEhFtfd96fIGemHAZfuX3w57Fb\nXZkr4REq4lYoFCFF8HncUQk91yePgpQxMPXrMkrOmgpVxyLcFplRAjLi7mwc/LEUCoXiOBN8wh2f\n1XP9VUvl0kgTzJoO214BhwPCBnHT4BFxK49boVCEFn2qnhAiSgixXgixTQixSwhxX8Ba4ysdEGQn\nYli463n2dLC0QeOhwZ3HbnWLuFU6oEKhCC36E652Aws1TZsBFALnCSFOCUhrrJ2elQH9kTVdLiu3\nDe487laJSgdUKBQhRp/CrUna9Kdm/U8LSGusHZ6VAf2RMQnCTIP3uY2sElDpgAqFIuTol0EshAgX\nQmwFaoCPNU1b52ObG4UQG4UQG2trawfZGrNrcoPeMEVC+qTBZ5Z4WCUq4lYoFKFFvzonNU2zA4VC\niCRgmRBiqqZpO722eQp4CqCoqGhwEfldxf3fNns6HPgINM2ztkl/cI+4VTqgQqEIMQaUkqFpWhOw\nHDgvMM0ZAFnTob0WWqsGvq/D6mmVqIhboVCEEP3JKknXI22EENHAImBvoBvWJ9l6B+VgfG53qyQ8\nEhw2cNiHrm0KhUIRQPoTcWcDy4UQ24ENSI/73cA2qx9kTpXLwfjcdov008FVqMqmom6FQhEa9Olx\na5q2HZh5HNoyMKISZMGpqkGkBHp43JH6um6gHxktCoVCcYIJrlolAyVzKlTvHvh+3gNwQHVQKhSK\nkCG0hTu5AJrL5dD3geCRx60P+FEdlAqFIkQIbeFOGilFuL1mYPvZbT2tEhVxKxSKECG0hTsxTy6b\nyge2n0d1QF3AVcStUChChNAW7iRduJsPD2w/X52TKqtEoVCECKEt3IOOuH11TirhVigUoUFoC3dU\nAkQlyg7KgeBdHRCUVaJQKEKG0BZugMSRA4u4Na1ndUBQnZMKhSJkCH3hTsobWMTtsANaT+E+WSLu\nT38La/5+oluhUCiOgdAX7sQ8GXFr/SxI6LDKpbdVcrJ43Jufh91vnehWKBSKYyC45pwcDEl5YGmF\nriaITu57e7tuiTgj7gjP9cOZziZZUbE/swwpFIqgZXhE3NB/n9tuRNwnYTpg/UG5bK0c+GhThUIR\nNIS+cDtzufsr3HpkHabfbJhOIuGuOyCXDpuMvBUKRUgS+sKdOFIu+x1xe1kl4SfRyMm6/a7HLUdO\nXDsUCsUxEfrCHZsGpugBRNxeVsnJlA5YfwCE/pW3HD2xbVEoFIMm9IVbCEjMhaZ+Dnu3e2WVhJmk\nmJ0UEfdByJklHyvhVihCltAXbhhYLre3VSKE7KAc7h63ww4NxTDyFPnelVWiUIQsw0O4jVzu/uBt\nlYBMCRzu6YBNZfI9pk+A+CyZWaJQKEKS4SHcSXnQUQeWjr63dUbcZte6kyHirtNTAVPHQcIIZZUo\nFCHM8BBuI7OkuaLvbX0Jt+kkEO56PRUwbTwk5CirRKEIYYaHcA+kLrcvqyQ8Yvh3TtbtlyNLY1N1\n4T7a/zIBCoUiqBgewj2Q0ZPetUrg5Ii46w5KmwSkVWLrgs7GE9smhUIxKIaHcMdngwjvX2aJd1YJ\nSOEe7p2T9QcgTRfu+Gy5VD63QhGSDA/hDjfJKLI/EbdPq2SYR9xdzdBW7RLuhBFyqYRboQhJhodw\nQ/9zuX12Tg7zdED3jBKQHjeoDkqFIkQZPsLd31xuZ5Gpkygd0JlRogt3XKYcLaoiboUiJBlGwj1C\nL1dq7307nwNwhrlw1x2QfQDJo+TzcJMU71Yl3ApFKDJ8hDs+GzR73+VKfQ7AOQ7pgB0N0FAS2HP4\no/4AJBe4Jo0AV0qgQqEIOYaXcEPfYuQ34g6wx/3hz+Gpr4ClPbDn8UXdQZdNYqCEW6EIWYaPcCfo\nwt1XDQ7v6oCgpwMeQ8T98T2w6d+9b1O2Wk6vtu3VwZ9nMGiarFOSXOC5Xg17VyhCluEj3PFGpkRf\nEbdF+r1h4a51x9o5uX0p7H3P/+utVa5RneuePL4jFruawNLmGqRkEJ8N3S3Q3Xr82qJQKIaE4SPc\ncRlSkPuMuC2eNgn0mg748rrD1LR2+T+epkFHfe+jEMvXy2XR96BuH5Qs772NQ4lRvyUx13O9M5db\nVQlUKEKN4SPcYeEyU6IvIbJbPW0S8Btx17Z284tlO3h5XS81UCztUvR7E+6KDfJicc69EJsuo+7j\nhVO4vSJulcutUIQsw0e4QfrcfaW42S09hdsUKTNS7DaP1Y0dMgo/WNPm/3gd9XLZl3BnTYeoBCj6\nLuz/H9QX997OocJvxN1Pa0mhUAQdw0u447Oln9wbDmtPq8TPhMGN7QMUbl/etc0CR7dA3lz5vOi7\ncrq09f/svZ1DRXO5fH+x6Z7rB1OvpLMRdr89dG1TKBSDYngJd0LO4KwS54TBXsKtR9wlde3YHX46\nFDsa5FKz++7oq94pK/HlzpHP47NgyqWw9eW+BwsNBc1H5OcS5vVVm6MgJnVgg3DWPw2vfafvi6NC\noQgow0u447Ohu7n3XGmfnZORrtfcaOyQqYMWm4OKRj+z6xgRN0BnQ8/XKzbIpRFxA4xdJNtZu9d/\nO4eK5oqe/rbBQHO5K7fKZX8nZlYoFAGhT+EWQuQJIZYLIXYLIXYJIX58PBo2KJy+bS9Rty/hDu89\n4oZe7BJ3sfblc5evlxcUI4sDILdILg1RDyTNFT39bYOkfGg41P9jVW3Xj9nP+T0VCkVA6E/EbQN+\nomnaZOAU4IdCiMmBbdYgMXzb3m7/e7NKvCPudgvhYQLoRbg9Im4fwl2xQdokQrjWpYyG6BQoD7Bw\n223ys/An3BmToP5g/3LYOxtdkXZ/J2ZWKBQBoU/h1jStUtO0zfrjVmAPMKL3vU4Qzg63PiLuMO90\nQD0C7xFxW8mIjyQtLnJwwt1WI0ctutskIEU8d07gI+7WStAcvQu3ZofafX0fq2qH63F/5vZUKBQB\nY0AetxCiAJgJrPPx2o1CiI1CiI21tX0UegoUCf2NuP143F7C3dRhITkmgrEZsRys7UW4oxLlY2/h\nNgbeGB2T7uTOkYNxOpv8t/VY8ZcKaJAxRS5rdvd9rErdJonPDi6r5MAn8M5tJ7oVCsVxpd/CLYSI\nA94AbtM0rcX7dU3TntI0rUjTtKL09PSeBzgeRMZDRHwfEbevATh+0gE7rCTHmhmbEUdxTRuar3S/\njgZIHSsfewt3xQYZ3WcX9twvTxfzI5t6eUPHiL/BNwapY+R7r97V97GqtkvRzi4Mroh71zLY9Gzg\ni4QpFEFEv4RbCGFGivZLmqa9GdgmHSN9DcLpLavE2yppt5AUE8HY9DhaumzUtvnwgjvqpaCZY3tG\nz9U7IWOiTL3zJmcWIKBiY9/vabAYkXGCH2cr3AxpE6BmT9/HqtwuBxEl5gaXx91UJpfulpVCMczp\nT1aJAJ4B9mia9lDgm3SMxGf3I+L2Eu7IBLn0Sudr7LCQHGNmbEY84KeDsqMBYlIgOtmV023QWgUJ\nfmyKqATpMQfS526ukO2KjPO/Tebkvq0SayfU7Yfs6XKKuO5mOY9lMNCoC3dfddgVimFEfyLuBcDV\nwEIhxFb97/wAt2vwJOT0XmjK15D31LFyKq8aV161w6HR3GnVPW4pfMXewm0UmIpJlQLpbZW0VskB\nN/7ILZLC7a9aYHud/337Q8sR/xcOg4zJcrvehuxX75admEbEDcFhl9it0KK3o73mxLZFoTiO9Cer\nZKWmaULTtOmaphXqf+8fj8YNCmPYu79Rib6sEnMUpIzxiDxbuqw4NEiOiSAzIZK4SFPPiLu7VQ6h\nj0mFGC/htlmgo64P4Z4jy67WH+z52oGP4cHxx1bTpLccboMMPbOzN7ukaptcZk+HxJGuY59omitk\n1gwc+0VOoQghhtfISZARt2b3/4/sq3MSelgGDXqdkuRYM0IIxmTE9cwsMXxVXxG3EQHGZfpvq5Ft\n4ssuOfCRfB9Ht3iu1zTY92H/OuOay/sW7kxduHvroKzcLjNnkvJdxwuG0ZOGvw3KKlGcVAw/4e5r\nEI7Dj3BnTJajCPXh8sZw96QYGZ2PTY/rGXEbnnZ0ilO4n/6yhOdWHYLWas/2+CJtgvTXfQl36Uq5\n9Pafj26GV66EVY/6Py5AV4v0ofsS7oQREJnYu89dpXdMCiEvRGHmoYu4HQ54/tLBFd1yv3go4Vac\nRAw/4U7wHIRzoLqVP76/B4dRJMqXVQK6ZaA5B6M06cPdkw3hzoijuqWbli6rax+jM9Mt4n59YzlL\nN1a4fPb4XiLusDAYMauncLfXu4TU28IwIvB1/wCLn/op4Kqz3ZdwCyGj7mo/wm23yWg8a5qrzYkj\nhi6Xe/+HcmKJ/R8OfN/GMjl5RlwWtCnhVpw8DD/hNqYw0yPup74o4akvSthbpVfu85VVAm5erxQw\nI+JOcRNu8OqgdFolesTtsNLV3kJ5QweaUUGvt4gbIHeuFEb3jJTDq+UyMa9nJFy5XYpVRx1sfcn/\ncfvK4Xb61rkbAAAgAElEQVQnY7K8QPjqJK0/IKsbZk13rUvMG7qIe/Vf5bJmEAW3msrkhSk+S0Xc\nipOK4SfcsekyQ6SlEpvdwSd7pGWx+bDuP/vKKgFIGQWmaGeEa9TiToqV2xrCfdCncOsRN6B1NtDW\nbaOr8Yhsh3cdbG8mXSQ72Ha5pceXrpRtmfFNaCz1rHZYtQPyT5WCv/qvPSZ/cGJExH1F3CDTErub\nfc+GY4yYzA6AcJdvgMNrIGmkzA7p6jGuq3cay+S+cRlKuBUnFcNPuMNN0odtrWR9aYMzct58WJ/o\nwJ9VEhYO6ROcnXSNHRZMYYL4SBMAecnRxEeaeHd7pWsEZUe9jH6jEp3CHedo0186ArEZnpMS+yJr\nmhx67j77e+kqWd8ke4Z8btQSsdtkBJ49A067XXq8u5b5Pm5zhWxbb1ktBpn60HdfdknFBjDHQNp4\n17qkPGkF2a09tx8Iq/8qP7uFv5bP6w4MbP+mMkjOlxfH/gp3ez0svfrks1Ys7b2XO1aEFMNPuEEf\nhHOUj3ZVM9NUxi+yN7ClrBEcenTqK+IGl2WAtEqSYmRGCYApPIzbFo3n8/21fLhTt0GMHG4hZAcl\nkCikcNuaK3v3tw2EgBlXSoGsL5aWSfVOKDitZ6qeu20x/jxInwgrH/ZtcTRXyI7Hvi4cICNugBqv\nzBJNg4MfQ8Hpnp9ZYq68S/BXy7s/olhfDHvekRMoj5gt19X2YwSngbUT2qohqQBi06Rw+8uHd6f4\nU9jzXyj9ov/nGg785zp444YT3QrFEDE8hTshB63xENO23scbpl9wY+PDaA3FNLTqEYd3dUCDzMnQ\nVgUdDTS2W5wdkwbXzM9ncnYC972zm7Zum2vUJDgj7iSkcIe1V8tOs/4w7RvSVtm+VFoHaJC/AJIL\nwBTl8rkN2yJrmuwkXHCbFNsDH/U8ZvOR/tkkRtsTRvSMuOuLpVUzbpHnesM399VBWbYGHhwHBz/t\n/ZxrHpcXg3k3yfcZHjmwiSWMjBIj4rZboLsfVotR5TAY0hmPFw4HlK0a2IXxWKnYCNau43e+k4zh\nKdzx2YjGUi61f8SR7HMBmCGK2VGmR4K+rBJwizx368PdPbczhYfxh8umUt3axcMf79eFO1W+aAi3\nkBeHqK7a/tkUIDNhRp0p7ZLSlVKsR8x22TdGxF21Xb5m2BbTLpcjI32lBjaXy+yP/pIxWc5w4x61\nHvxYLsee47mtU7h9+NyrHwM02Puu/3PZLLDtFXnBis+S7zNtfP/KyxoYQ92T8qUlBf0bhGMId2NZ\n79sNJ+oPgqVNZlr1567kWGmthmcWweZ/B/5cJynDU7inXMrelHO42PYn4q76N5o5lpnhJew4bAi3\nP6vE5fU26VaJNzNHJnPV3JE8u+oQXS01bhF3EiAj7qw4E7G2xv4LN8CMb0nPdsuLcmCOUZgqfZKn\ncGdMlj6+8T7m/1BGU+6TMpRvkMcyvOv+MOE8WY/EvejVgY9lOYCUUZ7bGhcE72JT9cWw733prR/4\nxL9I1OwGaweMXehalz5hgBG3LrzJ+dIqAVn/vDc0zS3iPomE20ghtXX2XtpgqGgollZa9c7An+sk\nZXgKd8Fp/NB6K4kFM0mOj0bkFHJK5CF2V+gRmb+IOz4LopL8RtwGdy2eSEyECWtrnSviNkdjDYsi\nSbRxWraDMLSBCfekC2WFwe4WaZMYZEySqY2djXqFvmme+836jmzzaj3qdjjgg7ukTTNnAJ7m9Ctl\nSdwN+kAYS4eM/scu6rmtOVraE95Wybon5Qz2Z9wJzYflhcAXhpDkzHStS58o7YtuP3XPvWkslXcf\ncZmuzJ2+OijbqmUaJQQ24l7xADx34fGZDLo/uI++7a2Oz1DRWCqXtX6+f8UxMyyF+2BNK8W17Sye\nogvniNmMtZdQerQPq0QIyJyCZgh3rO/tEmPMjEyOJtrW7BJuoDM8npSwdgqTpLdni8nof6MjYmHy\nxfJxwWmu9UYH5YGPZV0T97Q8kJX/5lwPe96FuoOw/VU5unLRfb1XBfQmMh4KvyWzVNrrpGjbu2Hc\nOb63T8zzFO7OJnm3MPXrMPPbrjb7onKrzCZJdovk0yfIpT+xX/5H2cFm0KSnAgoh0wGhb+Gu0iPA\nEbNl2x2O3rcfLHvfgdIvYevLgTn+QKncKtNLoffKmUOFIdz+vkvFMTMshfuTPfKW+dwpelbHiNmY\nNCsT7Hq6mT+rBGSEW7Mbq91Bsg+rxGBUgh0Tdmc2CUBbWDzp4R0URMrBPrWk+NvdNwt+DDOu8pzq\nzPDdty+Vy6wZPfebd7O8GK34E3xyr7Rapn1jYOcGmeFht8Dm56W/bYqG/NN8b5uY6+lxb34erO0w\n/wcyXTB9ossj9+boFjkhg/s8nOkT5dKfz73vfZnrflSfab6xTPrb4Lp49uVxV+s2yYTz5ftsq+p9\n+8Fg7XJZW5/9vv93EENFe71np6DDDpXbYIxuS/nK1R9qjAmoOxtObPGv9jrY/ELw3PkMIcNSuPdU\ntjAiKZrsRD3K0NPN5oTpouAv4gbImIzobiWHer9WCUBBtP7P4RZxt4h4UsPbyTHJWtWHrfEDa3jG\nJLjsCdfEDiAFMiIeij8DhKsolDtx6TBzCex8XdoB5z0gs04GSsZEmfq38VmZqTLqdN+TQICMuJvK\npW/c1Qzrn5L7GrnnY8+BstU9hcvWLbNXcrxmBUoZLbN9fPncDoe8mwA51B+krZKsC3e4WXYO91Xa\ntWqHrG5otDEQdknNLpl2euqt8sJgjAw9XvzrXHj/J67ndQdkf8KE8wBx/KwSI3Ortw7nQHaU7nkH\nHp8H/70F9v8vcOc5QQxL4T5Q3ca4TDebIDEXLS6Teab+RNxSGCeElfvsnDTIjewEwBaV7FzX6Igl\niTbStQYcmqCkI3bwb8JACH1SXwekjZOWii/m3yI7BWdcBbmzB3++uTdIf7qx1Le/bZCUJzu7Hp0B\n94+U1sP8W1yvj1sko9rSLz33q94lC325+9sgO1zTxvkW7pYj8lwxabDzDSniXU3SKjHozyCcqp2Q\nNdUVqQ8mJbByW++jRo07gjk3wJSvwaq/+s93H2rsVtlBvPNNWXIYXP527lz5GQ0m4u5qgW1L+y+0\njaVQoPfT1PUi3M9+FT6+Z+Dt6Q1rF7x5Iyz9tszWEuGBnR7wBDHshNvu0CiubWNchptwC4EYMZsx\n6J5sb8Kte62jRSUpfjxugJwIWeCpEVdUXe+IJV5rI9ZaTz0JlDUN0TyIhl3i3THpTuoYuOkLuPAY\nJymacL6rvoo/fxtg1BnS7siZCQt/Bde8q0d1OiPny85Wb5+7Uhc2b+EG/5klhld69q/lxeAT/Z/d\nEGCQKYG93ZZbO+UApsypLsEfaGZJUzk8sxjev8v/NpVbZfSfNBLOuVdecD/93cDOM1haqwBNRti7\n35brjm6R30PaOClkg/G4ty+FZTf2b25SS7u88yk4TY649TcatrVKjlk4NMQDoXa/Ldt7+k/ghuUy\ns+pIAKcHPEEMO+GuaOyg2+ZgXIaXTTHCFYU2WwR+iU7GYk4gX1Q7S7o6qdnjrMiXHi4jmmqb6wJR\nY40m1tFKWGsVTeEplDf0Ur1vIBgdlFnTe98ua6rM+DgWws3wlV/IaDFltP/tMqfATZ/DN/4ts0hG\nne75uikSRp8pfW73SO3oFpkF4y66BukTpX3hXfXQ+OefcD6MO9eVI57sLtxpvacD1uyWIpo1Tdo/\ncVkDt0o+/JmM/Eu/9F8j5uhWl3+fnA+zrpYWlr/tfdFwSHY2f/kQfPCznlPigbScvCNgZ2QvYOsr\n8mHlVtmhHRYuB1n1Fv077L49eWMyDyOVsjeMzzRltH4H5SfiPqTfidXuG1rLpG6/jLLP+rn8LY+Y\nDUe2BK4j2p3OJhkgHAeGnXAfqJY/vLGZXhkVbsJd29HLlygELdG55Itqz85JWzc89RV4T/qHyciB\nNlVWKZQWm4MaWwwmzQKNh2iPSOfwUAn3iFly6d5pGUhmfQeuePbYjzP2HGlHuEddR7fIaFv4uHim\nTwC0ntkIdftlFkpsuuyINfCIuPuwSoyMkqyp+r4jBxZxH/hYXjBy58iUTePOwR1bt7y4u/v3I4rk\nXUJDSf/OU74B/loIS5fAp/fBuid6DmbqboO/THB1WBsYNeinXAZlK6XgVm533d3E9zGR9urH4LHZ\nPUXOaHu/hFvvmEwukIOq/GWWHPpcLq3tgysRfOATePmbPtpaLL9b4656xGxZQK3hGGaS8uaT++DD\nn/dcv+JP8FjRcRHv4SfcevW+sRlewu12a97oY7J2d+ojRpAvqkmMdhPuhhIZbW1fCvXFJNKCVQvn\nSIfcprHDQhP6OeuLscVkDJ1w582FWzbJqoChxLhz5VD+jc/I50bGhXfHpEG6bgl5R2l1+6UICCGz\nI4wJKKJd/QvEZUjf29/MQFU7ICJO1jYBGQ33V7itXfD+nZA6Dr7xvFxXsqLndoZ/n+32/txG4/YL\nY5q4b78Jd5fJjmmj1IFzm+0yr997diQjmj79DkDAp7+Vv1mjPQk5cj9/wnJ4rexQbfHy8A0xrtre\ncx9vjFTA5FHye2ou9x3Fl37pmh3Ku6TvzjdkllJv7FoG+z/oKfr1xdI2NDACtqHyuS0dsoN87d89\nS0S0VsOm52D0Wcd+19sPgla473l7J6+uH3jn0YGaVjITIkmI8vKxo5OwJo8FoKEP4a4KzyE3rFam\n+xkYkYNmhy8eJNraRCPxVLXKgzW0W2jS4pzbhCVk0dxppbnzGCvoGaSNHZrjHE+S8mT0vuFpGXVX\n6xkXvvxt0DNLTD197roDrmH+QsDFj8FX/+wZtRujJ41Su95U75T+tpFtk5Qv67n0ZWFYO+Hz+6V4\nnf9nKX6ZU317s0YUnu2Wspk2HhD9HxVaXyLTMMcslKNxs6b2FMxKXdy9O1dbjsp9M6dK62r3W3K9\n8Xkn5Li284VRy8Q9SnbYXWJctb1vW6Ox1HVRTde/M+85VRvL5Haz9bx878/m8/+DLx7s/TzGqEz3\ni7ymSZspxU240ydIj3+ohLv4U9mHgIAv/s+1fs3f5J3VabcPzXn6IGiF++1tR/nLx/ux2gfmTR2s\naevpb+sIPduiodPzx9fWbeOu17dR2SwjkXKRhQmH5z+G8WOefR1sfxVxZBOtYQlUt8i0wIZ2C824\nMj4ik+Ww8KHwuTVNY11JvaucbCjxlV9KMfn4N1DpY8SkO6YIKXTuNkRXs4wC08a51o2cJwcLueMc\nPenD53Y4XBklBsn58iLsHV2CFPPP/w+ePgf+lCcrME75misXetQZUL6uZxGlo1ulf59c4FoXESNL\nBvQScXda7Ly5uUJ+vw0l8gJmXJSypsu2u+ciG5krvoQ7IUevOHmVfv44WbYAXMLtKyXQ0u42cMbN\n2mo5IgUpa7r8LvqyNRpL5WcrhIy4oaddYmQaTb5Ediq7C3dXs3zedLjH52u1O2QgZLe5cuXd922v\nBUurZ99MWLj8vQ2VcO/+r7wonXqrjPpr9so+iA3PyN/IcQqwglK4HQ6N5k4rta3dfKpPhOCLl9cd\n5rfv7PbY72BNW0+bRMc0ch4A1V0mj/VbDjfy2sYKHvpI/sAOOfSReMYtIsjhu4l5eqdHJFTvpMOU\nRE2LK+Ju1FwXjPh0WZlvKIR73aEGrnxqLSsPhuBM5nEZcMZP5ACa9U/LAUu9zcoz6gxZYdD4pzXy\nt93rgfuit2HvTWXyH9o9K8fwx707KO02mUGx/PeAkAOKvvkKXPakWxvPlOV1y9d57lu5VUbb3v69\nW7lgXyzbcoQ7XtvGrqMt0otNdROe7OnSB3b3yN0jbveLuSHcICfoMMfK9hh3GfG9RNzukau70BqD\naSZfIpfuPnfzEXj2fJfggy7cBfJxymjZUehtfR36UqZ2ZkySYwfcxffIZkCTf+7/f8Bv39nNooc+\nx153QI7qBc90Q6MT1d0qAdlHVLVD9kEcC7ZuOcXehAtkZU5zjIy61z4hv6PTf9L3MYaIoBTu1m6b\n8/f48nr/V/h3th3ludWHqGuTX8jR5k46LHbPHG53Zl7NnZG/psSS7LG6WhffN7cc4VBdO/utugg0\nuP1w6vbLqC8+E+Z8DwBLRJJHxN2kuSLulCwpDEPhcxu+/bbypmM+1glh3vdlh1HtHv8dkwZjzpa+\nrDF9myEi/RZur4tbez18cLd87B7pO1MC3aJWuxXevF56rOfcC9d/DIt+CxPPl3cDBvmnSkEyOtjA\n/8AikNky9cV+hWPXUTlgq7imWQqf+62+kUlkiLWlXYpVVJLsJHUvGuUu3JFx8PWn5fswcM7H6kO4\njQtLbLpnxG1cMCZdBAhP4d7xH1ngzBja73DIC6FRysAUIe823C8EmiZtplGny99B+iTPzBL3Imdu\n7ahu6WLphnJqWrs5vGe9q63uFwWjA9I7G2rEbHnXcKxFrw59IT/zyRdDbCrM1X8ra/8uPx9fg+MC\nRFAKd7M+a01+agxfHqj1G7UeaerEocEnu2VUbgicP6sEUwTFifOdQm9giK8pTPDXTw9Q0hFHt4hy\n/Wg1zdNnPfVHYIrGGpNJlbtw47pgxKWOIDnGPCTCfbheZrDsOjrAqb2CBXMUnHOffOyvY9KgYIEc\n2WrU867bL31vd/vBF74i7uLl8MSpcjLi8x7w9J4Tc2XHqdFB6XDAG9fL299Fv+vdq4xKkGLg7nPX\n7O7ZMWmQMUnaMn5ymndXyu+1tqJYCox7xJg+UY5CNHzu6l0yrXHC+fK5ceFxOKQFYgg3yAuOeyZS\nZLz0n31G3HvkneTYc7wi7hK5PnWctFzchdvIdtn9X7lsrZSRsPt3lTbB83j1xTKzZdQZ+vubIEvO\nGhbMkY2yVDF4eOP/WnkIm55B0lC8WX4mE873FP36Yvlb8U41dXZQbu75vnujdKVnoazdb8vO4tFn\nyeen/kh2RFra4PSfDuzYx0hwCrfeoXf96aMRwCs+OikdDs3pSX+4S9acOFhtCLf/4kqpcZHUt3lm\nHtS2dhMfZeLaUwt4a+sRqlu7aYrKdQl3y1F5K2QId3wm3LicXeNvprXLRofFRkO7hajoWPkjB4jL\nJC8lZkiEu6xeHiOQwl3b2k1pXQCntppyGVz4iCyI1RsRsXLwTvFn8nndfhnB9TZoCqQohUe6crl3\nvw0vXCpF9obP4JSbPbcPN0uBMKySXW/Kzryz74EFP+r7/Yw+UwqBMU+m4Tv7ujAZefg+OijtDo29\nlXJMQGeVLhLuEbcpQgq/kVlinMcoSGYId0edvHDEuwm3L/ylBNbskZ2J6RNl2YQueRdAQ4kU4rAw\naTUZF5CWSjlrU1K+FP26A24ZJQWu46aPl4JqdAIbMw+NOlMuM9wyiTRNHnP0WTLPXhfu5g4rL64t\n46IZOUzOTiCsZpcU/KxpMgI2PPuGYtmecE8rlMRc6aUPxOfuaIAXvib7OY5sku3f+x6MX+wqSRGb\nJgOS+bf0HZAMMUEp3E2dUlgnZsWzcGIGr22s6NFJWdPajdWukRxjZvXBelq6rBysaSMtLsJvVT+A\ntLhInxF3ZkIUN505hhhzODaHRltMnssqMXw099v1jEkkpcjqgzUt3TR0WEiJjZQdFzFpEG5mbEYc\nu4624HAcW6eiIdyHGzpo6RqiLBUvfrFsB9/51/qAHBuQt8VF13lGhP4YezbU7Oapd76k/vDuvm0S\n4/hx+uhJayf875eQOQ1u/Nz/iNPkfCl8dqssCJUxRRb66g+jzpRRdNkqOQR+3/s9Kx4apI6VkaCP\nDsrS+nY6rXbCBIQZgYL3rX72dFdGR+U2+fsaeYp8zbhjMKLovj7fhBw/VsleaVsYn7XRt9BY6qrH\nnjVNfl6dTbDvPbnuwoflcs9/fQt32gR5QTH86kNfyIuL8R6N4mI1e+Q2HfWQWyRtSV24X1xXRrvF\nzs1njuH0cWlkdx3Emj7ZVVHSuCA2lPT0t0H+NnKLfAu3psmRrd6jQre9Iu8ezNHw/GWw9nFZNMu4\nYBrMuxEW/6HncQNMUAq3EXEnRZu5at5I6tq6nXaIwZEmKWbfPiUfi93B8r01HKhp9dsxaZAeF0FD\nhwWb24VACnckKbERXLugAICuhHz5Q3K43eJ6CUhmgizAVNXSRUObRQ6Rj0521uFeMCaNhnYLe6oG\nHylrmkZZQztj0qV/vjsAUbfN7mBNcT2HGzqoaQ3cdFPNndb+ZcaMORuAoxveJqHjsGdGSW8Yc0+u\nfULeei/+g8zq8EeSnsu9+Xn5XZ9zj3OOzg92VDotNJ/kzpH1wJfdBA9PkUW5pl3h2783RUjx9tFB\naXyf88ekEtdehmaO7VnHPWuGFLSWo7IDNKdQ/s4iE10R94CE2yurpKtZZtdkuAv3fj29rsQlsobf\nXr1TjuxMHSszbUYUSbuksVTaT+6dz8bx1v8TXl0i9xt9putzikmB2AwO7t7Ilys+1D/bIinAdQfo\nstr518pDnDUhnUnZCZyVF0aWaKTMNNqzoqSmyVRKf6N9R8yS76nTq5+oehd8+SC882OX5aJpstBa\n7hzZzxGdKLOiTNE9Z4M6QQSlcDfpHnditJkzx2eQnRjF21s9o4SKRmmTXDg9h/T4SD7cWcWBXlIB\nDdLiI+XvscNll1S3dJMZL0X4htNHc+7kTNJHTpJ+Y8tR+YVHJrrqPutkJUbq+3e56nfnFjmjodPG\nydzilQcGnw1S09pNl9XBBdNkx1Ig7JKdR1vkHJrA9vLmIT8+yD6A+X/6lEc/7cdM7plTsERncDkf\nY8ZGZ6KPKMoXsenyu/ryIRj/VSkQvZE0Ut5mr7hf2jPj5DR3+6pa+f5Lm/nRK1v8X2jMUTD7Wike\n59wHt2yEC/7i/1zpE30Ld2UL5nDB4ilZ5GmVWBMLeoq/UYO9Yr08huHVJ410E269eFR/hLut2jN/\n3ejgy5gk70LCzPJzbKuWOctO4dbvXA59KVP6Jl4o2zrpInlBOfSFtJ/cO3LTxkkxX/+k7Hic8z3Z\n4etGW+JY2sp3cnDzCqzh0TLyTx0HnQ288Olm6tstfP9M+RuYHSV1YG17tvy+o5Nl+9uqpZ2Z4ue3\n4vS5veqWGJZcxQaZMQLyLqr+gEz9TRoJ174n76Smft1/kbfjTFAKtxFxJ0SbCQ8TFOYlsb+61WMb\nQ7jzUqI5d3Imn+ypprXL5j+jRCctToqt4XNrmkZNaxcZevScFBPBU98pIiNfv5o3lMgfcfr4Hv9Q\nxj41Ld3Ut1tIjY2AS/7m/AfOTIhifGZcr2l8y/fV8M2n1vgdqGPYJEUFKaTFRTozEIaSNcVy0EqY\ngG0Vgclc+Xh3FR0WO39fXkxxbR81qoVgb+wcpoaVAlCC59yZH+yo5E8f+Eivi82QEbS1w0Mc7A6N\nbeVNPUXYqHXSXiO9bf37fXmdtB/WHWrgzc29VNP76gPwvY/gtNt4qzyG1zb2kuOcMVlGpBa9H6G+\nGJb/kT1HGhmXEc+EzHgKRBXN0T5SJTOnAkLOSarZXR2gSSPRmg7zxIpiysv0jjmjk9Yf8dmg2Xno\nrZWU6Z3eTgsnY5L0/o1MEMMqNOyf+Ez5Ga9/Ug6kmnihXG/YB+VrIaXA83xRCXDVa3Ddh3DHHjrP\n/iOOGFcbHQ6NLxpTGRd2hIWxpWy0jOLZteU0x8rjfPD5ShZOzGDuKFnbPqJOtvW/VSl6VspEKdzO\nVEA/EXfePHmHtP9/NHVYuPyJ1dzx2lYatn+IljpeCv6nv5OdvJuek4HalMucnzO3boaLfMzteoII\nWuGOMocRZZa3rWPS4yhr6MBic9kbR5o6SY4xExNh4rypWVjt8p+yL6skVfe/DZ+7scOK1a6RmRDp\nuaERZTQekj3LPnzW+EgT0eZwqlq6aGy3+KwmuGBsGusPNdBl9V3M/a0tR1hb0sCv3/KdqlSq/3Pl\np8YwJSchIFbJmpJ6xmXEMSErgW0VgYm4P9xZRVZCFJHmMO55e1eflsm77a7Uqu2dnmL03OpSnvy8\nhBLvC4AxerLou65Re8Cf/7eXSx5fxYMfeeUTG9kH48+D/PkAdFhsvLn5CBfPyGHmyCT++P4emjo8\nO7O92VDawB2vbeU3b+90ZkT1IGMSoEmRcThg2c3w+QOYjm5kck4Co1OjyBO1HA33ETFHxknr4MBH\n8rlbxO1oKOWBD/ewYftO2iPSnFaPP6qQ9eM/37iNrzy4glte3kxj6XaZk5yop0imjZf2oNNzd/Pt\ns6bJFMS4LFcUmzJa9ieA7+yfcYsgfz57a9o49f5PufKpNTS0y8902ZYjrGpJJ5Yu8rv30Zw6nfve\n2c1Vy2Swc+sM+Od3ihBG0FS9i/aINNbXhlPT0qVPMr3HLRXQT8QdESttjj3v8NyqEjaWNfLF7nJi\nq9bzQv047u/+GtTs4rlHfoFt51tsSz2PD/Y102nR/2/Dwnp2ep5AglO4O6wedULGZMRid2gcbnBl\nPRxp7GREsqwJcMroVBKi5Ifal3CnxUuBNoTb8DENv9pJwgiZlnZ0a8+RezpCCLISozhY04bNofkU\n7tPHpdFtc7CpzPckrRsONRAXaeK/247y9tae0d3h+g5MYYIRSdFMyUngQE2b34vAYLDaHWwsbWD+\nmFRm5Cb6jkyPkZYuKysP1nHRjGzuXDyBlQfreHe7//KiR5s6ea1xLBqCOhLZ6pbhZ7U7nHcFb2z2\nGvWYM1OK8Vk/c65aU1zPU1+UkJ0YxePLi3lmpVtufk6hnKR58R+dq97ZdpTWbhtXz8/nD5dOo6nT\nygMf+q8p3dxh5bZXt5ISG0mX1cGbW/zU6nZmT+yV08tVyI7gud1rmJydQJqtGrOwU2LP9L1/1nSZ\nBmiUjAVIzifc1kFuZCcTYlrZ2xHPI5/s9/v9aZrGo+vlxe6xCzK58YwxrNhXy/4d63GkT3QN1Ekb\np99p7pP56m51z0tMMqD50jSP8ia3PoBJF+ltKvB57tK6dq5+Zj3hYWFsq2jmsr+vYlt5E3/6YC+O\ntIy4DU4AABwGSURBVInO7c5edCEXTMsmNmMMWpiJr6S1EB7mdqdbtQOHPqn3yoN1MuLubJSDocLM\nvQ/umnQxtFaycdUnLJqcyZpvRRMprNhHfYWSjHMpM4/mOy3/wKRZ+emh2Xz/pc3c8vIAUwiPE0Ep\n3E2dFpKiXSI4Jl2K8cEaN+Fu6mREkhRuc3gY503NIiM+kvQ4r8jZC8MqqWuVV3yXcHvtFxYuf4RG\nlOMnsyEjPpI9eh6uL+GeNyoVU5jgSx8+d0VjB0ebu7hj0Xhm5yfzq7d2UtHomT5YWt/OiORoTOFh\nTMlJxO7QethGx8L2iiY6LHZOHZPKjLwkmjutTnvGm42lDfxi2Y4BZ7Z8tqcGq13jvKlZLJmXz7QR\nifzu3d20+jnO5/traSKezqw5HIkc59G5u6eyhS6rg7hIE29uPoLdPWNnyqVw23Zn5N3caeUnr22l\nIDWWj24/g/OmZPG7d3ezzBBXczRc9g+PTISX1h1mfGYcRfnJTM5J4LpTC3hl/WE2lvYsrappGr9Y\ntoPqli6evqaIGXlJvLzusG/hTB4l0xUPr5UdXblzaMg6jXPDNjI5Ox6hR7fbO1N77gu0JEnhr4yZ\n4LR0miJlJ+Z3Jgomx7VjSsrlkU8O8I0n1/DK+sM9ov83Nx/ho3L5Lz/S3MzPvjqRx5fMYpRWzlGz\nW+5z2niZCVK8XNab0VMxbXYHz5fJwWvP1E9l4V9WcM/bO/lwZxUlWYvRwsy0JU+mtK6d7RVNlOt3\nyZXNnSx5eh02u4NXb5zHKzecQluXjUseX0V9ezdLLjzXeWrzyDk8vmQWr/3gdETyKOk1G9itULuX\nuLwZJMeYdeHWM0v2fSitr96i4vGLsQsTp9tWc8tXxmIuXQ7hEVz3rSU8dc1c8q+4X07ynXcKb9/3\nPW5dOJZP99b0CLp2VDSzwcfv4XgSlMLd3OkZcY/WhdvwRjVNkxF3kitj4J6LpvDWDxe4bqn8kBBl\nIiI8jLp2GXEbQ9Yz4n1M0ZU8ytXpY9Rd8CIzIYoavdCUrzTE2EgTs0Yms/Jgz6HYxpd/yuhUHv5G\nIZoGd7y2zSN98HBDB/mpskNkSk4CMLQdlKsP1iOEvMDMyE0CfPvcO480c+2zG3h53WGuf26j6xay\nH3y4s4rMhEhm5iUTHib4/aVTqW3r5rpnN/gcXLViXw05iVFEX/0qH0/6PfuqWp1ZQMY/0W3njKOy\nuYtVvfQf/PqtnVS3dvPIlYXER5l55JuFzB+dyk//s527X9/OXq9sn+0VTWyvaGbJvHzn7+i2ReMZ\nkRTN9/69ka1eI1dfXFvGezsquePc8RTmJbFk7kgO1LSxodTH3VW4Sdo3m/8tUxbPf5AdCWdQEFbN\nFHOl81Z/XXNyz32BVe3SQnm3LtP5mb1XJn9vlxRYES1HmT5pIvdcNJn6dgs/f3MHRX/4mOv/vYE3\nN1dQWtfO79/bzaiRI9HCI5y/69NywsgQTaxudet4N4KUqu0eWRpvbj7C803T2XDmv7n/J7fy9Vm5\nvLC2jJtf3MTC544wo+Nxpr5o56wHV3Dx31Zx+p+XM+HXH/CVB1fQ0mnl+e/OY2xGPLPzk3nrhwuY\nkZvI9aeNYuq4UdI7T8zzzKhJG+dKSwRp39gtiOxpnDo2jRX7alnVYhQXq+thkzgcGkeaOp0X0i5T\nPGuZxqWRm5mRmygvTCPnuzKPxp0LZ9wFi+4jJsLE988aQ1pcBA997LrjOlzfwVX/XMsV/1jDXa9v\nG7oicgMkeEwbN5o6rOSluEQ5LtJEVkKUU7gbO6x0Wu1OqwSkQMZG9v12hBCkxkX0iLgzvCNucP1o\nw8yeRfvdyEp0CX6qn/zx08al8fAn+2nw8sHXH2okPtLEhKx4wsMEd391Ir9+aydbypuYnS//gUvr\n2rmkUArqyJQY4iNNQ9pBuaaknolZCSTHRhAfZSLKHMa28mYuKXR1CB6qa+faZ9eTGG3mjkXj+d17\nu/n+S5t46uoiIky9X/s7LDZW7K/hG0V5hOm3vDPyknjkykJ+tWwn5z3yBfdcPIUrZucihMBic7Dq\nYD0XzchBxKYyKi+P7rUNlNa3MzYjnk1ljeQkRvHtU/J57LODvL6pgjPGSw98xb4a/r6imMZ2C40d\nVurauvnJovHMyJOfX5Q5nKe+M5v7P9jLG5srWLqxnFNGp3DOpEzmjkrhhTVlRJvDuWyW673HRZp4\n5YZTWPLMWpb8cy3PXDuHkSkx3PfOLv63q5rTxqZx8xlSMC6ckc3v3tvNS+vKnJ1pHqRPkiMPi74L\nOYV8ZK/jTCC+9ENoq8USHsPu1ijaum3Eef2WX6zIYKIYyQrHbFa8uZ1nr53L0zttLAEyOw6CtR2R\nOILrTh3FtacWsPNIC29vPcL7Oyqdk2ebwgR/+NoMxKtZzpTA8DqZA/1hdRIL27rlHalRlArQkuUg\nuG6bnUc+2c+03GSKzpIB0v1fn84vLphEaV07h+raqWjsJMocTnKMmfgoM40dFo40dlLX1s0VRXlM\ny010HjcvJYa3b3GbiHr6N+QgKndSx8oRtA67vAM2cq0zp3JdQhbrSupZ8lo5u6KiiaWT8rBs4jss\nRJrCeWNzBc+uOkRxbTvzRqXw6wsns/lwI7sts7nf/DQc/ETOD2qM6AV5J7Pwl86nUrzH8rt3d7O6\nuI6i/BRueWUzQsB1Cwp4fk0ZK/bV8sDXp/OViZ4ZZ4EmKIW7xSviBuldF9dKq+SInlFiWCUDxX0Q\nTnVrF0kxZiJNPjp1DOFOGe135F5GvEvw/U0ufNq4NB76eD+ri+u4cLqr82lDaQOzC5KdHt5F07O5\n97+7WL63htn5yTR1WGjpspGfKi9iYWGCSTkJPiNui83BJ3uqnZ0+QsA5kzJ7evdudNvsbCprZMk8\neVEyhYcxNSfRI+Kubuni6mfW4dDg+e/NZUx6HNER4fz8zR3cvnQrf/r6tJ4ldN34Yn8tXVYH503x\nzE2+pHAEs/OT+clr27jr9e18sKOS314ylYrGTtq6bZw1QYrxpGx5l7G7spWxGfFsLmtkVn4yUeZw\nLinMYemGcpo7rWw+3MhNz28iKzGKKTkJJMVEMCY9lmtPLfA4b3yUmT9cNo07F0/g1Q3lLN1Qzu/f\nc2WoXFmU1+P9jEyN4T83ncqSp9dyzb/WEx4mcGgad503getPG+28IMVEmPj6rFxeXneYey7y0Vk9\n5ivS2174KwDW1pgojpzEmL3vQUwqnfEF0C44VNvuIXJHmjpZVWHl/cXLOD/GzC+X7eT7L27iUJsJ\na0Ii5sNr9TcnU0aFEEzLTWRabiK/vGAS2yqa+XBnFWMz4piQFS/7byq3ypxqvab3bnsu/916lO+e\nNgotKpHm8BSS7A28VmJiYWs3724/ytHmLv58+QyPu9qEKDPTc5OYrt+tDRpfg1hSx8pBMM3l0rY8\n9Lnsd0obR1G4mdU/O5vP9lZT9d98xlj28uROwYvbPibKHEaX1cG0EYncunAsL607zEV/W0mMOZy5\nOWej1f0LYdSvMSo++mHJvJH884sSHvpoPzPykthe0cw/vj2b86Zm8bWZudz5+ja+++8N3HPhZK5d\n4GPwVYAISuFu6rSS5CXcY9JjeXPzETRNc/rAucmDFe4Ip71R45bD3QOjNz3dt78Nnp2aqXG+hXv6\niETio0ysPOAS7oZ2Cwdr2rhspiu6S4qJYHZ+Mp/ureGniydQqnvNhlUC0i55dX05dodGeJigw2Lj\nlfXlPP1lCZXNngNG1pY08Ni3/JRQBbYcbqLb5mD+GJevOiMviZfWlWG1OzCFCZky1W5h6Y3znX0N\n35o7krYuG394fw9fHKjlulMLuG7BKJ9W0Qc7q0iOMfuMQHOTY3jlhlN4dnUpD320j3Me+pzxmfGY\nwwULxspb4LEZcZjDBXsqWyjKT+Zocxc36Hcjl8/O5fk1Zdz73128t6OScZlxvHT9vJ5TzvkgKSaC\nm88cw81njqG6pYv1hxrYebSZq0/xf2f12k3z+f5Lm0mOMfOrCyZ73BUaXDVvJM+tLuX1TeXceIbr\n1t1md/AeZ1IyaTZXWqJJMtkoqWuncvxCxpQ9DlFJhI04DaqkJegu3B/skNHxBdOyyU+N4b3tlXy6\nt4aRKTGYEvJduckJnmmTIEW8MC+Jwjw3YR15iixVu3SJfB6VSFpKAW9uqeC7p41i6YZy8i1ZzA9v\nYHltHPc/LItpzR+dyoKxvj34gGAkBNQflHNUbnlRlkzQg6gIUxjnTc2Gg7Nh616+dd5ZjLBP5GhT\nJxcX5lCUn4wQgutPH83jyw/yyrrD3LB4LuLLU+UMQbHpeqqlf6LM4dyycCy/emsnG8sauWZ+PudN\nlUHItNxElv1gAT9+dQv3vrObyuau/2/vzoPjqq4EDv9Ot9RaWrssyVosa/Ei77JkEba4wATwgtmc\neMyESSrlCdQQahIqk4CTSk0gA0yKYYpkSJwFEqgESFLESRzPEDLgFB6bJRgDwTu25X2RLVuykYQs\nWXf+eK9brVarW1tLr7vPV+WyepF8jyWdvn3uvedx/+Ia/wt5NEVM3CLyM+AmoMkYEz7KUXCxu4f2\ni5f6zbirCzO40NnN6QudHGuxZtzDT9wp/sY+py50hi6TQO+MO8yRa1+pJCXJRVpy6K1YSW4XV1bn\n88quJto6u/GmJPnr28EJ7bqaQh59aTfHWzr8+2x9M26AWSXZdHQd5Nvrd3CwuY13D7fwUWc3l1Xm\n8cjtc/x18Mdf3ssf3j8W8m23zxv7m3FJ3zHMLcvm6c097D11gQ+OtrJlXzMP3za7TyIB+OLCKq6o\nzufJjfv4/sZ9/HjTAaYVZTK1MIPKCV6rbUBnN6/sPMVNc0tIcocuqbhcwuqrK1k6ZyIP/XEnL20/\nyZXV+f4xe5JcVBdksPP4ebYdtmrHvjLSnNJsphVl8Lt3jzGjOItfrh5c0g5WlJXK8nklLJ8X/vBK\nfkYKv7n7irDPmVaUSUNFLo+9vIdNe8+wqKYQEXh6c6P/7MHa1w6wcNoE66BezTI49AP4uIW0idNw\n7aTfNscNfzvBrJIsKiZYL+DfXTGX29daC2yyv7y3f8hg2gmA1THwqq9YdfXm/ZBZzIrjZTz4x538\necdJHtqwk+9nVULbTtb8/VLufaWD7cdb+dri6RHXkEaVr2RzaoeVtLPLrNOtwewdO7Pm1DErYAeM\nT3ZaMt9YOoNvLLV39jTfbCXuqmt7d9KEsXLBJJ7e3Ig3xc0a39ewpXncrL2znm+v38GPN1mTp8c+\nMzf0O/hRNJgZ9zPAk0CEawmNDv9x9/TgGbdvZ8lHHD3Xgdfj7pfcB2tCptVoyhhD0/mPmVo4IfQT\ncyug4YvWiakB+Gbr+V5P2B/quxZWsWLtGzz5l33cv7iGtxvP4klyMTcoIV43w0rcG3c3cc4ue5QH\nzOzqynMQgef/epjpRZncXFvCirpS6if3fQFY2VDGr7ce4eXtJ1lRXxZyTG8eaGZmSVaf/0ffzOzl\nHaf4+eZGLq/K446G/r8MALNLs/nRP9Sz99QFfv32EfaeusDr+5tZ96618OX1uMlJ97CyIcwWLVtx\ndhpr76xn68Gz/co7M0uy2PzhGd45dI7UZJe/fCIi3Pepafxm6xEeX1kbtkfNWPreqvk8+/pBXt3d\nxEMbrAMj9ZNz+dfls6iZmMmPXtvvP6xTOaMOtk6F5g9JmjCF8rx09gc0+zp6rp33jrTw9cW9i+OT\n8tJ5c811VomtOeAdgl0qGZS0HGsftr0X++aCTh7+713c89w20j1u6hYuhy3vM3nKLNZN83Ci5WPK\n88O0D4gGb4F1EOa1x6x+6neu618HB+sEa15Vn22LYc1Ybl3WzddjPAJPkov1916FJ8kVMiG7XcJD\nt8yiOCeVN/Y3Izhgxm2M2SQiFVEfiS3w1GSg6oCdJcdarD3cw331z/d66O4xnGvvoulCZ/+tgD4u\nNywLfwkl32w9UtKon5zHiroynvq/A3ymvoy3D56ltiyn3w9CdUEG5XnpbNzdRG66h4lZqf6DSGDt\nsNl8/yLy0j2keQZ+Va8rz2VSXhq/f+9YyMR9sbuH9460+OvbPuV56eSkJ/NfGz8kJcnFd1fMjfjW\nb1pRJt+6qffAzMddl/C4XcN6y7igon9JZWZxFuu2HePVXU3MK8shOWD2vmROMUvmDCFhjYGSnDTW\nLJ3BmqUzONTcxked3cwq6X2Bfvi2Odxz7RQaT7dZ6zQ1y2DLE5BfTVWBm/1NvTPulz6wOl8uC4rR\nv7fZt2juLeh71HyI8jNSuGZ6Ia/sOsV3bp1NXm0pfMK6ylAyjH3SBmuhJr8ajm+D2s9azcdCScm0\n/g8HK6sE7j8YueNkgMww6zjWUIV7rpnC3Qur++47jxLHbQdstTsDBr/lLcpKwetxs/90m70VcPgX\n5CywFxT3nLzApR4TdgEvktRkNznpySH3cAd7YEkNqUnWwt724+dpqOy/9UtEWFRTyJZ9Z9hz6nyf\nMolPaU5a2KTt+zq31payZd8Z64RZkB3HW+ns7qGhIrff580ty8EY+Jcbpveprw9WarJ7VOt8vhn2\n4bPt/jJJrJic7+2TtH1Kc9L8vWxoWG3NGotrqS7w0nimzb8ldMMHJ5hdmjXw98E3yxzKbHsADyyp\n4d9vn9NnR9G4K6m1Yrvh30b36w4haQ/py45B0oZRTNwicpeIbBWRradPh7h81CD5ZtzBZRARobow\no8+Me7h8h3B82+pC7uEegoaKvL6LPwMoyEzhvuun8VbjWS71GBpCzC7BKpd0dvew/VjoxD1Yt9SW\n0mNg/fv923hutfca11f0T4SrGiaxoq6ML4zhKnk4vsQNxFziHpSccqsPRnIqVQUZdHb38E/PvcOn\n177O+0daWBruHYUvcYdYmByqKYUZrLpskOWGsXLjo3DPm1YXQeU3aonbGPMTY8wCY8yCgoIIjW7C\nCOwMGKy6IIMPjrXS2tHV5/DNUPkSt2+BcsBSySD99HML+OoNoQ/oBPvcFZOpmZiJSwZOQpdV5uG1\nZ9TDmfH6TCnMYE5pdr/OimBtRZycnx7yRWvpnGIeXzlvzGYPkeR5Pf7v0fzyOEzcARoqcsnzeth1\n4gJJbmHlgjL+bkGYNQJ/4h7kwmSsSU616vGqD8dtBwzsxR2susDL7961Hh/ZjNsqa/gaNo2kVDJU\nSW4XP/xsHTuOnx+wbpaS5OaTUwv4046TI5pxA9w6v5TvbNjZ5yLKxhi2HjrHtdPH9tDASNROyuFQ\nc/ugSlKxbEphJtu+df3gPyElEy7/knWZMpUwIs64ReQF4A1guogcFZHV0RyQb8YdvDgJvQuUMPyt\ngGDVz13Se43KgsyRzbiHqqogI+LWs+tnWs2GIjXNimT5vGJcQm9/DuDAmTbOtl3sV992skdvn8sz\nX7gs8hMT0eJHoOLqyM9TcWMwu0ruGIuB+LR2dJGZmhTybXp1QBIrG8HipNsl5Hmt05MTMjx9dik4\nxW3zS6ks8FIzMSvyk8MozExlUU0Rz791mHuvnUqax807dn071A4Op4r3mbZSQ+G4jBXcYCrQ5Px0\nXAIet8tfpx4uX7lkpAuT0eJyCXWjVM+9a2EV59q7ePEda+/w2wfPkpue7L8cmlIqtjgycQcfvvFJ\nSXJTnpdOSU7qiLeb+cojI12YjAUNFbnUTsrhqc2NXOqx6tv1k/PG9hScUmrUOC5xt7RfDHsictnc\nYm4Ialg0HL5OfmO5MDleRIS7F1ZxqLmd5986ROOZtpiqbyul+nLkrpLi7IHr11+7sWbAx4bCV2op\nTIDEDXDDrIlU5KfzyP9YbTxjqb6tlOrLcTPu1o6ukDtKRtuEBCqVgLUg+4+frKKj6xIpSS5ml45s\n0VMpNX4clbiNMWFr3KPJN+MesKVrHPp0fRn5Xg+1k/r3SFFKxQ5HlUraL16i65IZdte/oaiZaPV9\nnlo0sn3SsSQ12c0vVn8iYp8TpZSzOSpxhzs1Odpml2az48HFES+9FW9mlmiJRKlY56isFa5PSTQk\nWtJWSsUHR2WugToDKqWU6uWwxG314s4eg8VJpZSKVQ5L3DrjVkqpSByVuH017uFc8FUppRKFoxJ3\na0cXbpf4LyKglFKqP0cl7paOLnLSkrX5kVJKheGoxB2upatSSimLsxJ3e5fuKFFKqQiclbh1xq2U\nUhE5KnG3dFwck+PuSikVyxyVuFvbdcatlFKROCZxG2NYVFPIvEk54z0UpZRyNMd0BxQRnlg1f7yH\noZRSjueYGbdSSqnB0cStlFIxRhO3UkrFGE3cSikVYzRxK6VUjNHErZRSMUYTt1JKxRhN3EopFWPE\nGDP6X1TkNHBomJ8+ATgzisOJBYkYMyRm3IkYMyRm3EONebIxpmAwT4xK4h4JEdlqjFkw3uMYS4kY\nMyRm3IkYMyRm3NGMWUslSikVYzRxK6VUjHFi4v7JeA9gHCRizJCYcSdizJCYcUctZsfVuJVSSoXn\nxBm3UkqpMDRxK6VUjHFM4haRxSKyR0T2icgD4z2eaBGRSSLyFxHZKSI7ROTL9v15IvK/IvKh/Xfu\neI91tImIW0TeFZEN9u1EiDlHRF4Ukd0isktEroj3uEXkPvtne7uIvCAiqfEYs4j8TESaRGR7wH0D\nxikia+z8tkdEbhzJv+2IxC0ibuAHwBJgJnCHiMwc31FFTTfwVWPMTOBy4Et2rA8ArxpjpgKv2rfj\nzZeBXQG3EyHm7wF/MsbUAPOw4o/buEWkFPhnYIExZjbgBlYRnzE/AywOui9knPbv+Cpglv05P7Tz\n3rA4InEDlwH7jDEHjDEXgV8Bt4zzmKLCGHPCGLPN/vgC1i9yKVa8z9pPexa4dXxGGB0iUgYsA54K\nuDveY84GFgJPAxhjLhpjWojzuLEuiZgmIklAOnCcOIzZGLMJOBt090Bx3gL8yhjTaYxpBPZh5b1h\ncUriLgWOBNw+at8X10SkApgPvAUUGWNO2A+dBIrGaVjR8gTwdaAn4L54j7kSOA383C4RPSUiXuI4\nbmPMMeA/gMPACaDVGPNn4jjmIAPFOao5zimJO+GISAbwW+ArxpjzgY8Za49m3OzTFJGbgCZjzDsD\nPSfeYrYlAXXAWmPMfKCNoBJBvMVt13RvwXrRKgG8InJn4HPiLeaBRDNOpyTuY8CkgNtl9n1xSUSS\nsZL2c8aYdfbdp0Sk2H68GGgar/FFwVXAzSJyEKsMtkhEfkl8xwzWrOqoMeYt+/aLWIk8nuP+FNBo\njDltjOkC1gFXEt8xBxoozlHNcU5J3G8DU0WkUkQ8WEX89eM8pqgQEcGqee4yxvxnwEPrgc/bH38e\n+MNYjy1ajDFrjDFlxpgKrO/tRmPMncRxzADGmJPAERGZbt91HbCT+I77MHC5iKTbP+vXYa3jxHPM\ngQaKcz2wSkRSRKQSmAr8ddj/ijHGEX+ApcBeYD/wzfEeTxTjvBrr7dPfgPfsP0uBfKxV6A+BV4C8\n8R5rlOK/Bthgfxz3MQO1wFb7+/17IDfe4wYeBHYD24FfACnxGDPwAlYdvwvr3dXqcHEC37Tz2x5g\nyUj+bT3yrpRSMcYppRKllFKDpIlbKaVijCZupZSKMZq4lVIqxmjiVkqpGKOJWymlYowmbqWUijH/\nD9FEYuKz+r53AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2baac7f9710>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# With 128 hidden\n",
"fig, ax = plt.subplots()\n",
"losses = np.array(losses)\n",
"plt.plot(losses.T[0], label='Discriminator')\n",
"plt.plot(losses.T[1], label='Generator')\n",
"plt.title(\"Training Losses\")\n",
"plt.legend()"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x2bab09f7748>"
]
},
"execution_count": 101,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAEICAYAAAB/Dx7IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYVFf6xz9n6B1pgqICNhQLKrao0ViiiSXZJKb3anrZ\n1N1sNslm97fZmGzqpppiemJ6L/auaOzYRUERUKTXgfv748ydxgwMfQbP53l8hpm55cwI3/ve73nf\n9whN01AoFAqF52Do6AEoFAqFomko4VYoFAoPQwm3QqFQeBhKuBUKhcLDUMKtUCgUHoYSboVCofAw\nlHArOhwhhJcQolQI0bM1t1UoOitC5XErmooQotTqaSBQBdSant+iadqH7T+qliOEeAqI1zTt2o4e\ni0LREN4dPQCF56FpWrD+sxAiE7hR07TfnW0vhPDWNM3YHmNTKE4HlFWiaHWEEE8JIT4VQnwshCgB\nrhRCjBVCrBNCFAohcoQQLwohfEzbewshNCFEgun5B6b3fxJClAgh1gohEpu6ren9c4QQe4UQRUKI\nl4QQq4UQ1zbjM6UIIZabxr9dCDHT6r1ZQogM0/mzhRD3ml6PEUL8aNqnQAixwmqfeCHEV0KIfCHE\nISHE7VbvjRFCbBZCFAshcoUQzzR1vIrOjRJuRVvxJ+AjIAz4FDACdwNRwDhgBnBLA/tfDvwNiACO\nAP9o6rZCiBjgM+AB03kPAaOa+kGEEL7A98APQDRwL/CpEKKPaZN3gBs0TQsBhgDLTa8/ABw07RML\nPGo6nsF0vI1Ad2Aa8IAQYoppv5eAZzRNCwX6AIuaOmZF50YJt6KtWKVp2neaptVpmlahadpGTdPW\na5pm1DTtIPAGMLGB/RdpmpauaVoN8CGQ2oxtZwFbNE37xvTef4ETzfgs4wBfpJjWmGyhn4BLTe/X\nAAOFECGaphVomrbZ6vVuQE9N06o1TdMj7rFAqKZp/zK9vh9YYHe8vkKISE3TSjRNW9+MMSs6MUq4\nFW1FlvUTIUSyEOIHIcRxIUQx8CQyCnbGcaufy4FgZxs2sG0363FociY+24Wx29MNOKLZzuQfRkbL\nIO8u5gBHhBDLhBCjTa//27TdYiHEASHEA6bXewE9TRZKoRCiEHgQGZUDXAcMBPYIITYIIc5txpgV\nnRgl3Iq2wj5d6XVgB9DHZAE8Bog2HkMOEK8/EUIILGLbFI4BPUz76/QEjgKY7iTmADFIC+QT0+vF\nmqbdq2laAnA+8JAQYiLyYrJP07Rwq38hmqbNNu23R9O0S03Hexb4Qgjh34xxKzopSrgV7UUIUASU\nCSEG0LC/3Vp8DwwXQswWQngjPfboRvbxEkL4W/3zA9YgPfo/CyF8hBCTgXORPneAEOJyIUSoyY4p\nAeoATOftbRL8ImTKZB2wFqgWQvzZdA4vIcRgIcQI035XCSGiNE2rM+2n6cdUKEAJt6L9+DNwDVLY\nXkdOWLYpmqblApcAzwEngd7AH8i8c2dcCVRY/dujaVoVMBs4D+mRvwhcrmnaPtM+1wCHTRbQDaZj\nAPQHlgClwGrgBU3TVppSI89FTpRmmo75OhBq2u9cIMOUkTMfuETTtOrmfxOKzoYqwFGcNgghvJC2\nx0Wapq3s6PEoFM1FRdyKTo0QYoYQItxkefwNmbGxoYOHpVC0CCXcis7OeGQudT4wHfiTyfpQKDwW\nZZUoFAqFh6EiboVCofAw2qTJVFRUlJaQkNAWh1YoFIpOyaZNm05omtZYuirQRsKdkJBAenp6Wxxa\noVAoOiVCiMOubqusEoVCofAwlHArFAqFh6GEW6FQKDwMtQKOQtFJqampITs7m8rKyo4eisIKf39/\n4uPj8fHxafYxlHArFJ2U7OxsQkJCSEhIwLaxoaKj0DSNkydPkp2dTWJiYuM7OEFZJQpFJ6WyspLI\nyEgl2m6EEILIyMgW3wUp4VYoOjFKtN2P1vg/cW/h3vYZVBZ19CgUCoXCrXBf4S4+Bl/eJMVboVB4\nJF5eXqSmppKSksLQoUN59tlnqauTa0Kkp6dz1113tfgcr732GgsXLmzSPmeccUazz/fuu+9y7Nix\nZu/fGrjv5GRlsXwsOd7wdgqFwm0JCAhgy5YtAOTl5XH55ZdTXFzME088QVpaGmlpaS06vtFoZN68\neU3eb82aNc0+57vvvsugQYPo1q2by/vU1tbi5eXV7HPa474Rd3WZfCzN7dhxKBSKViEmJoY33niD\nl19+GU3TWLZsGbNmzQJg+fLlpKamkpqayrBhwygpKQHg6aefZvDgwQwdOpSHH34YgEmTJnHPPfeQ\nlpbGCy+8wOOPP878+fPN7917772kpaUxYMAANm7cyAUXXEDfvn159NFHzWMJDpbrSS9btoxJkyZx\n0UUXkZyczBVXXIHeMfXJJ59k5MiRDBo0iJtvvhlN01i0aBHp6elcccUVpKamUlFRweLFixk2bBiD\nBw/m+uuvp6pKdg1OSEjgoYceYvjw4Xz++eet+l26b8Rdowt3XseOQ6HoBDzx3U52HStu1WMO7BbK\n32enNGmfpKQkamtrycuz/bueP38+r7zyCuPGjaO0tBR/f39++uknvvnmG9avX09gYCAFBQXm7aur\nq839kB5//HGbY/n6+pKens4LL7zAeeedx6ZNm4iIiKB3797ce++9REZG2mz/xx9/sHPnTrp168a4\nceNYvXo148eP54477uCxxx4D4KqrruL777/noosu4uWXX2b+/PmkpaVRWVnJtddey+LFi+nXrx9X\nX301r776Kvfccw8AkZGRbN68uUnfkSuoiFuhUHQ448aN47777uPFF1+ksLAQb29vfv/9d6677joC\nAwMBiIiIMG9/ySWXOD3WnDlzABg8eDApKSnExcXh5+dHUlISWVlZ9bYfNWoU8fHxGAwGUlNTyczM\nBGDp0qWMHj2awYMHs2TJEnbu3Flv3z179pCYmEi/fv0AuOaaa1ixYoVL42wJ7htxV6uIW6FoLZoa\nGbcVBw8exMvLi5iYGDIyMsyvP/zww8ycOZMff/yRcePG8csvvzR4nKCgIKfv+fn5AWAwGMw/68+N\nRqPT7UFOphqNRiorK7nttttIT0+nR48ePP74483KvW5onC3BjSPuUvlYlg+mWWiFQuG55OfnM2/e\nPO644456ucwHDhxg8ODBPPTQQ4wcOZLdu3czbdo03nnnHcrLywFsrJK2RhfpqKgoSktLWbRokfm9\nkJAQswffv39/MjMz2b9/PwDvv/8+EydObPPxuXHELf+zqKuBykIIjGh4e4VC4XZUVFSQmppKTU0N\n3t7eXHXVVdx33331tnv++edZunQpBoOBlJQUzjnnHPz8/NiyZQtpaWn4+vpy7rnn8q9//atdxh0e\nHs5NN93EoEGDiI2NZeTIkeb3rr32WubNm0dAQABr167lnXfeYe7cuRiNRkaOHNmsLJem0iZrTqal\npWktXkhh+TOw9Cn5823rIGZAywemUJxGZGRkMGCA+rtxRxz93wghNmma5lJ+pPtbJaAmKBUKhcIK\nNxbuMsvPaoJSoVAozLivcNeUg1+Y/FlF3AqFQmHGfYW7uhRC48DLT0XcCoVCYYUbC3cZ+AZBcFcl\n3AqFQmGFG6cD6sItlFWiUCgUVrhxxF0KvsEq4lYoPJzc3Fwuv/xykpKSGDFiBGPHjuWrr77qkLEs\nW7asRZ0B3QU3Fu5y8AmE4GgVcSsUHoqmaZx//vmceeaZHDx4kE2bNvHJJ5+QnZ3dZud0VNau0xzh\nbuh4HYUbC7eVx11+EmprOnpECoWiiSxZsgRfX1+basJevXpx5513UltbywMPPMDIkSMZMmQIr7/+\nOtBwq9VNmzYxceJERowYwfTp08nJyQHqt3r97rvvGD16NMOGDWPq1Knk5uaSmZnJa6+9xn//+19S\nU1NZuXIlmZmZTJ48mSFDhjBlyhSOHDkCWKojR48ezYMPPtjO31rjuLnHHQzBMYAGZSdklolCoWg6\nPz0Mx7e37jFjB8M5/25wk507dzJ8+HCH7y1YsICwsDA2btxIVVUV48aN4+yzzwYct1odPXo0d955\nJ9988w3R0dF8+umn/PWvf+Xtt98GbFu9njp1inXr1iGE4K233uI///kPzz77LPPmzSM4OJj7778f\ngNmzZ3PNNddwzTXX8Pbbb3PXXXfx9ddfA5Cdnc2aNWtadQGE1sI9hVvTTB63KeIGKMtTwq1QeDi3\n3347q1atwtfXl169erFt2zZzA6eioiL27duHr6+vudUqYG61Gh4ezo4dO5g2bRogV5WJi7NognUL\n1ezsbC655BJycnKorq4mMTHR4XjWrl3Ll19+Ccie29bR9dy5c91StMFdhdtYCWjgG2gRbjVBqVA0\nn0Yi47YiJSWFL774wvz8lVde4cSJE6SlpdGzZ09eeuklpk+fbrPPsmXLHLZa1TSNlJQU1q5d6/Bc\n1i1U77zzTu677z7mzJnDsmXL6i224Apt1ZK1NXBPj1svdzdbJagJSoXCA5k8eTKVlZW8+uqr5tf0\nNq3Tp0/n1VdfpaZGzl/t3buXsrIyh8cB2UI1Pz/fLNw1NTUOFzcAGb13794dgPfee8/8unVLVpCL\nBn/yyScAfPjhh0yYMKE5H7PdcVPhNjWY8g2CICXcCoWnIoTg66+/Zvny5SQmJjJq1CiuueYann76\naW688UYGDhzI8OHDGTRoELfcckuDGRy+vr4sWrSIhx56iKFDh5Kamuo0Q+Txxx9n7ty5jBgxgqio\nKPPrs2fP5quvvjJPTr700ku88847DBkyhPfff58XXnih1b+DtsA927rm7oRXz4CLF8LA8+D/ekDq\n5XDO0603SIWik6PaurovnbOtq76Igo/JYwpSudwKhUKh46bCbWWVgKl6Mr/jxqNQKBRuhJsKtz45\nqQt3jIq4FYpm0BZWqKJltMb/iYcIt+pXolA0FX9/f06ePKnE243QNI2TJ0/i7+/fouO4nMcthPAC\n0oGjmqbNatFZG6PGQcRdVQQ1FeAT0KanVig6C/Hx8WRnZ5Ofr2xGd8Lf399cXNRcmlKAczeQAYS2\n6Iyu4CjiBhl1d+nV5qdXKDoDPj4+TisGFZ6NS1aJECIemAm81bbDMaELt0+gfFTVkwqFQmHGVY/7\neeBBoK4Nx2KhulSKtsHUJ0BVTyoUCoWZRoVbCDELyNM0bVMj290shEgXQqS32FOrLrNE22AR7jIV\ncSsUCoUrEfc4YI4QIhP4BJgshPjAfiNN097QNC1N07S06Ojolo2qutzib4MswAFllSgUCgUuCLem\naY9omhavaVoCcCmwRNO0K9t0VPqyZTpePhAYqawShUKhwJ3zuH3tWiqqXG6FQqEAmtiPW9O0ZcCy\nNhmJNdVlshe3Nap6UqFQKAB3jbhrym2tEjBF3Eq4FQqFwj2FW1+2zJrgGNloSpXvKhSK0xw3FW4n\nHrexAqpKHO+jUCgUpwnuK9w+9h63qp5UKBQKcEfhrqtz7HGbc7mPt/+YFAqFwo1wP+GuMa1+Y2+V\nhMTJxxIl3AqF4vTG/YTbvjOgTohulajMEoVCcXrjhsJtt2yZjn84ePtDSU77j0mhUCjcCPcTbmdW\niRBygrJERdwKheL0xv2E25lVAtLnVhG3QqE4zXFD4datkuD674Wo6kmFQqFwQ+G2W/3GmpA4lVWi\nUChOe9xXuB1ZJcFdoarYso1CoVCchrixcDuySlQut0KhULixcDuanDTlcivhVigUpzFuKtwCfALq\nv6dH3KrsXaFQnMa4p3D7Bsm8bXtCYuWjirgVCsVpjPsJd42Dlq46/uHg5aeEW6FQnNa4n3A76sWt\nI4SMupVwKxSK0xj3FG4fJ8INUriVx61QKE5j3FC4HSxbZo2KuBUKxWmOGwp3ecPCHRyrGk0pFIrT\nGjcU7gY8bpARd1WRFHiFQqE4DfFM4QblcysUitMWNxRuFzxuUD63QqE4bXE/4a5pxONW/UoUCsVp\njnsJd60RjJWOG0zpBKt+JQqF4vTGvYS7poFe3DoBXUzVk+24Ek7ebvjhfqira79zKhQKhRPcS7gb\n6gyoI0T7r4Sz92fY+CaU5bXfORUKhcIJbircDVgl0P5rT+rLqVWVtN85FQqFwgluKtwNRNzQ/qu9\nVynhVigU7oObCncDHje0/9qT1SbBVsKtUCjcADcV7saskq7tWz2pIm6FQuFGuJlwmwSyMaukvVfC\nUR63QqFwI9xLuGtMEXSjwq1XT7aTz61H3LqAKxQKRQfiXsKtWyUN9eMG2SEQ2i+zxBxxF7fP+RQK\nhaIB3Ey4XbVK9EZT7RRxK6tEoVC4EW4m3GUgvMDbr+Ht2rt6Uk1OKhQKN6JR4RZC+AshNgghtgoh\ndgohnmiz0VSXy4wSRyu82w5KZpa0V0qgOeJWHrdCoeh4vF3YpgqYrGlaqRDCB1glhPhJ07R1rT6a\n6tLGc7h1gttpCTO98RWoiFuhULgFjUbcmkQPNX1M/7Q2GU1jiyhY015rT1ZbibWanFQoFG6ASx63\nEMJLCLEFyAN+0zRtvYNtbhZCpAsh0vPz85s3mqYKd3vkcVvbIyodUKFQuAEuCbemabWapqUC8cAo\nIcQgB9u8oWlamqZpadHR0c0bTXVZ41WTOiGxUFkENRXNO5fLYzKJtfBSVolCoXALmpRVomlaIbAU\nmNEmo6kpa7gXtzX6ggqlbdxqVY+4Q2KVcCsUCrfAlaySaCFEuOnnAGAasLtNRtMUqyQgQj5WFLTJ\nUMzoHrcSboVC4Sa4EnHHAUuFENuAjUiP+/s2GU1TrJJAk3CXt7FwmyPuOFmSX1fbtudTKBSKRmg0\nHVDTtG3AsHYYS+MrvFsT0E7CrXvcod3kY1UJBIS37TkVCoWiAdyrcjKgCwRFubZtYDtZJdYeNyi7\nRKFQdDiuFOC0H3dvdX1bf1PU2+YRt+5xW0XcCoVC0YG4V8TdFLy8pXi3R8QtvCDIlOKocrkVCkUH\n47nCDdIuaQ+P2y8Y/ELkc1U9qVAoOhjPFu6AiPaJuH1DrIRbWSUKhaJj8WzhbpeIu8Qu4lZWiUKh\n6Fg8W7gD2kG4q0plbrmKuBUKhZvg2cId2A5Wie5x64VBSrgVCkUH49nCHRAhhdVY3Xbn0Ks5vbxl\nHxVPnpysq4W8jI4ehUKhaCGeLdztUYRTVWqxSfxCPDsdcM9P8L8xsPn9jh6JQqFoAZ1DuNvS564u\nsdgkvsGebZXoa3T+8Gc4urljx6JQKJqNZwt3e3QIrDJ53CAjbk8W7spC+RgUBZ9dDWUnO3Y8CoWi\nWXi2cJsj7jYSIGMV1NVYIm6PF+4i8A6ASz6Qfcy/uF51O1QoPBDPFu627hCo52ybPe5Qz87jriwC\n/zDoPhxmzoeDy2DJPzp6VAqFool4tnC39eSk3mDKHHEHe3ZWSUWhpSXt8Kth8MWw+sW2zcpRKBSt\njmcLt0+AvPVv64hb7xHeGawS/zDL855jQKttO6tJoVC0CZ4t3ACBkVBxqm2Oraf+WU9OenI6oL1w\n673Py090zHgUCkWz6ATC3aUdIm6rPO7aajlp6YlUFlr6mAMEmoS7TAm3QuFJeL5wt2WHQN3j1iNu\nXw/vV+I04lZWiULhSXi+cAdGtJ3wmCNuK6sE2naC8lQmrP0faFrrHlfT6gu3irgVCo/E84W7LTsE\nVtunA7ZDa9c/PoBfHpF51q1JVQlodbYLHQd0AWFQHrdC4WF4vnAHRkjvtq6u9Y/tNOK2tUqe+20v\n//xhV+ucsyhbPhYebp3j6VQWyUfriNtgkBc+FXErFB6F5wt3QISMJPVy7takugS8fMHbVz73c9za\ndfX+E6za30p2jS7cpzJb53g6joQbpM+tIm6FwqPwfOE2F+G0QUqgvoiCjl+o6XVb4S6uqKGksqZ1\nzll4RD6eau2I23Rhs84qAelzq54lCoVH0QmEO1I+toXPXW3VYAosVkm1rXCXVBopqTS2/Hx1tVB8\nTP7cbhF3pIq4FQoPw7ujB9BiAtqw0ZS+ULCOk1VwSiprqDTWoWkaQojmn680Tza1gtYX7gpTxB3g\nKOJWwq1QeBKdIOLuIh/bIpdbXyhYxzcIEDbCbayto6y6lto6jYqaFnba0/3tgIj2mZwE6XFXnFJd\nAhUKD8Lzhbu1OgSWF9TPndaXLdMRol6HwNIqi0VS2lK7pChLPiaMkyLems2fdOHWfXqdwChAa/tF\nlxUKRavh+cLtHwbCq2URd3EOPNsf9v5s+3qVnccN9RpNWXvbxS0WblPEnTAB0CxC3hpUFoJfGBi8\nbF8P0ucIlF2iUHgKni/cQshCkpZEjPkZsgdJzlbb16vtPG6o19q1qMKSTWIdfTeLomwZEccOls9b\n0+e2r5rUUdWTCoXH4fnCDTIlsCURd8Eh20edJkbcLU4JLMqGsHjokiCft4dwqw6BCoXH0UmEO7Jl\nEfcpk2BbC6Wm2S4UrGPX2tVarFvF4w6Lh+BY8PJrXeG2XkTBmoYi7pMHWj+fXKFQtJjOIdwt7Vei\nC+Qpq4i7pkJWZDYScRfbRNytJNwGA4T3bN3MEqdWSQPplF/cAN/d3XpjUCgUrULnEO7ALi20SjLl\nY2kuVJfLn6vt+pTo+NpbJZaIu6QlHndVqUzLC+shn3dJaB+rxMtHVlPaR9yaBif2Q14r9WBRKBSt\nRucQbj3ibk4rVE2TAhkULZ/rYqmLs5/95GQbedzFR+Vjmwl3Yf1ydx1H/UrKC6RVVJrbdisMKRSK\nZtE5hDswAmqroKa86fuWn5QClTRJPtfF0lnErQu36SJRXFFDoK8Xgb5eLfO49dS/sHj52KWXjJJb\nQzRrjfLzOIq4wXH1pPVFI39vy8egUChajc4h3M0owikoq6amts4iUElnyUfd59aLbOp53MGAJotz\nkBF3iL83If7eLfO49Rxus3AnmMbTCj63nr7oTLiDoup73NZ+f/7ulo9BoVC0Gp1DuM0dAl0T7mpj\nHZOfXcaryw5YUgC7D5c51PUibgdWCZjtkpKqGkL8fQj2825ZHndRtlzUICROPm/NlEA9aneUVQIy\nK8dZxO3lBydUxK1QuBONCrcQoocQYqkQYpcQYqcQwv3SDMwdAl1rNHUgv5TC8hp+z8i1CFSXBGlP\n6EJeZbfepI5eMm4S9uIKI6H+3oT4+1DcEo+7KBtCuoGXqe9XeC/52BqZJc76lOjoEbf1YhSnMiG4\nK0T3UxG3QuFmuBJxG4E/a5o2EBgD3C6EGNi2w2oiTbRKdh2T1sH2o0VU5e+XUa5PAHRJdM3jBrP9\nUFIpI+4Q/1aIuHWbBMA/VH6u1oi4zb24G/C4tVrbxShOZcqLWXSy8rgVCjejUeHWNC1H07TNpp9L\ngAyge1sPrEk0cTGFXTlSdDUNSo/vl4INUqgKD8tOec48brvWrq3mcRcegfAetq916dVKwq1H3A1k\nlYDtHcupw/L7iOoPRUfadp1NhULRJJrkcQshEoBhwHoH790shEgXQqTn5+e3zuhcJcDU2tU64v71\nUfjxQYeb7zpWTEq3UEL8vPEuOmzxkyMSZc+S4mMuRNxSuIsrawgNMHnczRVufQEF64gbTCmB7WCV\n6FaT7nMbq6E42xRx95OvndzX8nEoFIpWwWXhFkIEA18A92iaVmz/vqZpb2ialqZpWlp0dHRrjrFx\nvHyk96xPTu77Hda8BPt+qbeppmnsyilmSHwYExKDCavJl4INthOCVSXgE1i/m57dSu/F5ojbp/l5\n3PoCCo6Eu/BIy3tlVzRildj3KynKklWjulUCkL+nZWNQKBSthkvCLYTwQYr2h5qmfdm2Q2omeofA\nymJLmbaDtRSPFVVSVFHDwLhQpnevAuCEj57JYRLwU4dMnQGD6+1vve5kZU0t1cY6Qk1ZJfqCCk3G\nnApoZ5WE95KCri9n1lwqi8DgbVoIwgH2/UqsJ2wjkuS+SrjbhpLcjh6BwgNxJatEAAuADE3Tnmv7\nITWTwAjp0f7+uKxC7HeOLKwxVtlslmGamBzYLZRR4dJCSC82RaJh8bK396lMx50BwWql92Kzpx1q\n8rihma1d7YtvdPQ7gJZmlujl7s6WVbOPuK2F28sHInor4W4LTh6QfeC3fNzRI1F4GK5E3OOAq4DJ\nQogtpn/ntvG4mk5gJBxNh/QFMOY26Dddvm6Xn7wrpxghoH9sKLG1xwFYcjxQvunlIycICxqIuL39\nwMsXqkvN1oieVQKmsveaCtvUusawL77Raa1c7spC5zYJyM/kG2K5QzmVKfO3g2Pl8+h+cEIJd6tz\ndBOgwfJ/Q20LWwIrTitcySpZpWma0DRtiKZpqaZ/P7bH4JpCiQiByiLqwhNh8qNO+0zvOlZMQmQQ\nwX7eiFOZVBkC+CXTyuLQe4TYL1tmjansXY+4dY8boKy0GP43Fn77m+uDL8qWq9PYi2tYvCzKabFw\nFznPKNGxXu39VKbMaDGYfj2ik6HgYL27F0ULyd0pH09lwrbPOnQoCs+ic1ROAltP+QJwZ9l1/Ly3\nGM0+U8LErpxiBsSZJhhPZVIZ3JOiSiPbj5oyL7okSo+7qsSxVQJm4dYLbvSsEoCQjS/K/fU/Slew\nz+HW8fKRr7c0s8RZZ0BrrPuV6DncOlH95WTlyQMtG0dTyNna+dfBzNsFMQMhdgiseEb2lFEoXKDT\nCPdXfnP4s/dfORA0jHkfbOIvv+TIN6xyk4srazhSUM7AONMEY8Eh/Lv2BmDVPlMKY5cEmQ9efMx5\nxO3rKOL2ppc4TuyON0wna8KEot6H2xGt0SWwohGrBCwdAvVuidbCHd1fPrZXBWXJcXhzCqx8tpWO\nlwuFrbh+Z2uRuwu6psCkh+XFfvvnHT0ihYfQaYR7R2koJT0n8/2d4/nbrIEsz5bWR12pJad8d47M\nvR7YLVR60IWH8YtKYmBcKKv2m6JNPTWwLK/RiNve437M+33qDD4w8PzWFe6Cg64fyxGVRc77lOgE\nRkmPu+KUrAq1ibj7AqL9epZsXiizaY5vb53jfXM7fHpl6xyrtagolLnyMQOh/7lyndEV/1FRt8Il\nOo1wHyusoFt4AN5eBm4Yn8ijF43FqBk4dNhiM2SYKiYHxoVB6XEwVkJEIhP6RrHp8CnKq422gmXf\nYEpHt0p7eBuIAAAgAElEQVQqLFklkceWMsXrD7b2uRW6DZMZLZX10t3rY15AwYlwR/aVkXBLbANX\nrBLd49a7Alp/Dz4B0vNuj4i71gib3pU/t8b5NA2yN0pbwp1EMS9DPnZNkdk+Ex+SF+gdizp2XAqP\noFMId3FlDSVVRrqHB5hfOzsljiIRyqEjFuHedayYiCBfuob62aS8jesTRU2txvpDBbaC5TTiDjZH\n3EJAkMFI2LK/sa+uO5u6Xgyhpo4AJTkuDN5uAQV7ovTKxf2NH8sRNRWyV7krHndtNRzfIZ9bfw8g\nfe726Fmy7xf5nfQcKxdxcJCL3yROZcqsmtpq21a1HU2eaQ4kxtT2p/9M6DpIet0tLbhSdHo6hXAf\nK6wAoJuVcHt7GRBBUdSV5rM1S1YO6hOTQghLF8AuiYxMiMDHS7Du4EkpcHrTKqdZJbL96xWbL+Mz\nv6cwLJyNoTCTJ41XU1wtILSb3M4Vu0S3H5xF3FF9Tds1s+S8sT4lOnoWztF0+ah3J9SJ7i/L3ts6\nat24QHZJHH+vfJ6f0bLj5Wyx/OxOXQ5zd8lMIv3/3WCAM+6SF2jrMSsUDuhkwu1v83poZCzRhlIW\nrDpETW0de3JLLBOTpw7JVLuwHgT4epHaI5x1B012hO5zO4u4R1wLqZeR5xOHj0BmoIy6ha2+w6Tv\nHWqqxGxMuI3VsOSfEBoPcUMdbxPeS+aNN9dfbqxPiY5ePZm9SS7jZv/Zo/vLqLU1FzC2p+AgHFgs\nv9/YwfK1vBYK97EtsvITIM+NhDtvF8QMsC2KihsiHwvc6M5A4ZZ0CuE+WlgJYGOVAHiHRNPTv5wf\ntuewav8Jqo11cmIS5C10WDx4yzTC0YmR7DhaJCsfdZvAmcfdLRXOe4UXo5/g4bCn4fb1cO5/ZL+S\nKqOMGKFx4V79gowoZz4LvoGOt/HylmXnzY24zX1KXMjjBjkee5sE2qdnSfo7snJ1+NWy1a5/WMuF\nO2ertCPCerpPxK1plowSa/TvvaWT0YpOT6cQ7mOFFfh4CaKC/WzfCIyiC3KC8O/fSE9xYJwp8iw4\nZOlNAoxJiqS2TiM9s8DyurOI20RJZQ2hpsIbwNLa1cdfVnKWNCDcJ/bJLIKUP0H/GQ1/wKi+LY+4\nXckqAUtzKUdjgJZbF86oqYQ/PoDkmfKORQiIHtAy4dY0aTt0S4WYZPcR7uKjUFUEXe3a2vsEyIu+\nirgVjdBphDsuLACDwa4XR1AUhqoizk2J4khBOb7eBpKiTY2W7HKVh/cKN/ncVhOUzjxuE8UVRnOp\nO0jhNrd2DenmPOKuq5ONsHwCYMbTjX/AqH7S2mlOWXRjiyjo6B43OBZu/zAppDu/Ni+U7JC6OhlN\nrn8dFj/pejbMrq9ld8eRN1heixkgLYWGztcQhUdkxk5cqrR6TrSBR198DLI2Nm2f3F3yMSal/nsR\nSSridleMVbB/cdPaWbQRnUa47f1twNxn+uYRUrT6dw3Bx8sgy9nLT8gUN31TX2+GxIez/tBJSJwA\n8aOkcDRASZXsxa0jrRKTuIZ2s2SM2PPH+3B4NUz7B4R0bfwDRvWDOmPzIjFXJyd9AsHb9B06Em6A\nsbfB8W1wcFn99ypOwRc3wfw+8OpY+OlBWPkcvDFR2hUNYaySbXgj+0LiRMvrMQPlhafkeMP7O0Of\n5OuWKi86tVWtszCFNV/fCu/Nalq6pjmjxMHvV0SCEm535edH4IMLYGvHNwXrJMJdaZNRYsYURQ4O\nr+H81G7MGmKaNNSr6OwyJ8YkRbAtu4iywHi48TfbKNQB+uo3OjaLKYTGQbGDdMCKQtnHpNc4GHaV\nax/QnFnSDLvEHHGHNrydEBa7xJlwD7lENp5a/Xz99377O+z4AvqeDef9D+7ZDjculqltC86GLR85\nP/evj0LuDpj2hO1knS5szbVn9InJmBQrj74V7ZIc00XMWNnw57Mnd5eckHZkX0UkyeIvteKQe7H3\nF9nAzuBjKpTq2KZgHi/cxto6jhdX1puYBCxCVH6C5y8dxi0TZXk7hUfko13u9OhEk899uPEl0DRN\nqyfcNsuXhXaXUb19Y6Zjm2UUfOYDliZOjRHZAuGuKATvANkBsDH0CUpnwu3tB2NulWJ17A/L69np\nstpxzK3wp9dg2BUQ3hPiR8DNyyF+pIxMv78Xqsttj7njC9jwBoy9Q/rb1ujC3VyfO2eLPIaPv2Ul\nn9b06Ne+LO202CGQ/rbrlk7ervr+tk5Eknx0p5zz053SfFl9G5MCF74l79q2ftKhQ/J44c4rqaK2\nTmsw4rZvNEWRSbjt1ngc0asL3gbB+oONF32UmxZNsJ6cDPb3llklYMnlti/C0bMy7DMKGsI/VGZZ\nNKcIx5Vyd53AKJl6GBLnfJu062Qe++oX5PO6WvjhPgiJlT037AmOhqu+hnF3S3F7/UxTO1Ok5/zt\nXdBjNEx9vP6+QVEyNTFvl2vjt0bTZMQdlyqf+4XIC3VrZcUUZcuLzvCr5UWn4AAcWt74frU1cgwx\nToRbnxhXE5TugabBd3fJv6ML34SB58nK6BXPdGjU7fHC7aj4xkygg0VwQVolBh9Lv2kTQX7eDIkP\nk4U4jWBpMGUR7lB/H6qNdVQZay3iZz9BmZchC3yCmri8W2SfZlolLpS763QdKH8p7Zdrs8Y/TIr3\nrm+kF5v+tvSwp//TsqybPV7eMO1JKeA15fDWNFj6L/jsahnFX/SO7IToiJhmZpYUZcnJzm6pltei\nk1svl3v9a/KPevQ8+cccECG/i8Y4uV/2YXF24dZrCFzxuYuPNd//V7jG5oWw50cZWOjtCSY9IusZ\nmmKPtTIeL9xHTcLd3eHkZAQgHETcpqZODqyK0UmRbMsukn1LGqDY3GDK1uMGk6jrZe/2wp2/RwqI\ns9VonBHVTwp3UzMsGltEwZqpT8K1PzS+3ZjbpHf8++Ow+B+QNAlSLmh8v95nwa1rYNCFsPxpKcgX\nvAlh3Z3vEz1AfmdNnck/ZpqYjBtmdaz+8jtsaUl5ZRGkvwsp58sJbh9/aQ/t/qFxIc21K3W3xz9M\nTqq7YpV8fCl8fFmTht4h5O+Fr241L7DtMZSdkBOSiRNh9K2W1/ueDd2Gw4r5soiuA/B44T5mKr6J\nC3MQcRu8TEua2Ql34ZF6NonOmKRIjHUamxrxuUusenHrmJcvqzQ6LnvXNDk5prdJdUBWQTkL12ai\n2Qt0VD8pGGX5DvdziiuLKOgYDM4jX2tCYmHopTLqrimHc+e7fiEKCJe3nJd+DBe9DX2mNLx9zAC5\nGlFRE9uy5myRxTzWXnJMK2WWbF4om4iNvcPy2ojrZObP5vcb3jdvl7zo6T1oHOFKSmBRtrzTObYZ\nTjSzj017kfEtbP0Ifn+io0fSNA4ug5oymPJ32yBPj7qLjsjP1QF0AuGuICzAhyA/b8cbWC8QoFOY\nJSvpHDCiVxe8DKJRu6TYqhe3jk3E7R8qJ66shbs0T0bAeoaDAz5Yf5jHvtnJoRNltm80N7OkKVZJ\nUzjjbrm82YT7LGNrCsnnwiAXonQ9Mm2qXXJMn5i0uqC3RmZJbQ2sexUSJkD34ZbXI3vLO49N7zYc\n0efukpPNpopdh3RJbNzj3ver5Wd37yiozytsfBMOr+nYsTSFzFVyPsdRO4q+06B7moy6ayrafWid\nQrgd+ts6QVG2HrexSrZ0dRJxB/t5M7h7GOsPNpyXW1xhirhtskpktOo0l1sXjBjnwq33DF9rf+HQ\nI7SmCrcriyg0h6g+8OfdMvJoS/TvqikTlHrFZFyq7ev6nY6zi0BVCez6VqYnOiue2r5I/p+ecWf9\n99JukD22rUXVnrydzjNKdCKSZETd0FJxe3+VmTu9xssxNbdIqT3I3y27PYb3hG/vlFWynkDmKjlu\nLwdBoRDS9y7KgiVPtffIPF+4jxZWOPa3dQIjbSNufWHecMcRN0i7ZGt2YYM+t2WF9/pWiTklMCQO\nrSSHOz/+gzkvr+L1RdI/vuHHUg7mO87T3X1cluivPWAn3KHdZZFMU3qW1NXJRRFczSppKoERTffq\nm4p/mPzsTYmSi7LlxbqbnXD7hcj8afvMkj8+hPdmw9OJ8NlVshjoZwcZMsYqWPYv2QCrz7T67/c/\nR054r3nJsZBmb5I2nbOGYjoRiYDmfMm6mkqZwdJ3Ogy+UHZtPL6t4WN2FHW1MtjoNhxmvyAnZ5e7\nUC3cVhirXIuQS47L7zVhvPNtEidA2vWw9hU4sq71xugCHi/crkXc1sJt8kqd9b8Gzuwr+3O/tty5\nz1hstfqNjo3HDRDandrCo3y39RjGWo1+XkcpMwSzOBt+3ZVb75gFZdXkFleZrRobn9tgaHpmSXWp\n7D3SFhF3e6KXvruKXqlpH3GDqWeJVcS9fRF8c5v8Qx17m5ycPfNB6d8fXmu7b/o7UninPuE4B9/L\nByY+KKti0xfYvmeshm/vkK0QRlzX8Pgby+XOXCXnFvpNl6stGbzl52gKdXVt2zBMp/CILFCK7g+9\nJ0PqlTKVVP8/qiqVwUjWBji0Avb9BhnfydzptmDR9fIi3RiZq+RjQ8INMlsqrAd8fVv9GoU2xKOF\nu6SyhuJKY8PCHRgly5F131EvvnFilQCM7R3JRSPieXHxPhZn1BdYeW4j3gaBv4/lK7R43BarxFCW\ni4E6/nF+CmdFnCKoewo9IgLZll1Y75h6tH3OoFhOlFazL88uKo/q27SI29U+Je5OzACZmeBqn5HD\na+TEZOyg+u9FJ8vvsK5WRrTf3yfbG9y6Vv4RJoyH8fdIgf31r5ZslspiWTGXOFEKkDPSrpfv//o3\n28WVVz8vLz6znmu8ilUXbmcTlPt+kUVVCePlXU/vybDzq6Zl3qx/FV4Z1Xg7gpaiBxr6/ML0p2Qw\n9e4s+L8e8H/d4eU0WDBNCuqHF8ll5t6aItsotCYVp2Dvz3JFpMY+9+HV0t+OHdLwdn4hcN7LMo9/\n6T9bb6yN4NHCnVMkvbJGI240yy9BYZbswx3qPAVNCMFT5w9iUPdQ7vl0S/2JQkydAQN85KIMJoL1\niLvKUvZu0GqJoog+MSGmjJJkhsSHszWrqN4xdX/7+vEyl7eeXRLVT154rG71jhZWUFnjZDIsx3T7\n7GpWibsSM9CUDeJCilzBIdj4lkzV83HwexGdLCPAgoPw5c3yjuTCN219TN8gmPKYLBTa8YV8bc1L\n0n6Z+njD9pAQMOdlWSfw9W3yApG3G5b/R6ZB9j+n8c8QGClbCjuaoNQ0WX6dNMny+QZdKO8kszc0\nfmyQvz+rTG0LtrRx3w3d4tIrVwO6wAVvyNTQoZfKjI0/vQ5XLIJrvocbfodLPpRzDF/e3LoNnfb8\nLDN/ENIea4jMVdBzjGN/256kiXJ+ox0tE48W7gZzuHVMjabMPndRloymGkl78/fx4tUrRuBlEMx7\nfxNlVbbRnn1nQAA/by98vQ22Ze/AoOBSwmoL5R9+dDJD48M4WljByVLbyafdx4uJCvZleM8udA8P\ncCDcfQGNU9kZvL3qELNfWsW4fy9hxvMr2J9nlyObuQq+vEkKVdJEPJnS0D4AbN+8uvGNf/mLtA6m\n/cPx+3rk980dkLVORsCOSvyHXCK96N8fl+mDa1+WuerWmSTOCOsO5z4jj7/6BTkh5xfsWidIkOIf\nkeg44j6xVxZ/9Dvb8lryTNkgzNouqSqBda85Xt1+03uyH0pkH5mR0parGuXvgeCuUrB1kibBxQvl\ndzThPingfadJz7jHSBgwC2b8n5zkXfls640l41s5x5FyPmz/zPnkb0mu/J4bs0msmfakvIv/+rZ2\nyTLxaOFusGpSJ8jSrwSQv8gN2CTW9IgI5KXLhrEvr4SHv7RdcbyksqaecIPMMrEvex8SVmYVefRn\nSLyMgLdl20bdu4+XMMC0Qs/Y3pGsO3SSujorn9uUWfLYgq948vtdaGjcO7UfpVW1nP/KGoutc3gt\nfHixLDK65juPt0rSK+M4qYVQtOET2+/Dnr2/yiq3iQ84L+rRM0uy1sHgi2HIxY63Mxjg7H/KLJG3\nZ8jVfyY/6vqgh1wMA2bD4idkJDzjaVn+7yrOhHvvL/Kxr5Vw+4VIv3vX11KEd3wBL4+Enx+SBTrW\nWRw1ldK26TVOevVl+XBgievjaiqN1C04ZeSN8v9n6T9lK1UdTWvewtlVJfI4A2bL5m4Vp+TviiMO\nu+hvW+MXDOe9AqNvkWmybYzHC7eXQRAT0lDEbdevpPBIgxOT9kzoG80dk/vy3dZjNlFtSaXRJqNE\nJ9jP0miqNliWvScHlloJdzKDuochBGy18rlr6zT2HC8hOVaWjY9NiqSwvIaM45aV4vfWdKVOE5wd\nU8yv957J93dO4O6pffn2jnEkRAVy48J0vvzmC7QPL5LdCa/5DoJjXP6s7sqWYxV8XjuJMTXrWb7J\niTdZUylbyUb2gTG3Oz+Yf6jMKArvBTPnN3zixAmQPEv2mxlxrczVdhUhYNbzlPpGkRd3lvMLhDMi\nkuTvqn00vO9Xuaiw/Rqlgy6SIvzaeDkBFxwj7zpyt9tmyGz5QH6eiQ9K8Q/oAtsaaZhUa4RlT8MP\n98ve466mHmqanJtooG7BKULA7Ofl/MYXN8o7n/f/BM/0hv8kwoY3m3a8fb9Ku23gHBnxh3aXC3c4\nInOVtKpiG8n+sSfxTCncrjaPawEeLtyVxIb642W/gII11hF3rVHm4LoYcevMHSH/SJbvtWSnFDuJ\nuEP8fSg1TU5mVQZQpXmT4FMobxn9QiG0G8F+3vSJDraJuDNPllFlrCM51hJxg63PPX/pEY4RxfSY\nIvp1tfQF6RYewOe3nMEFA0OYuvkOsmpC+HfX+SzOFlRUe/6K4VuzClkVNhNvUcfRxa/XryoFWPuS\n9MDP+U/DxS0Al34E137f6J3I1qxC/lJ+OZ/VTeGxojkccJLC6YyMYl9GFz/NdRX3ND1tsksi1NWQ\nm21VFVlRKCderaNtHV2ES47JpfBuWgrj7pLNvTa9A9sXcbygWHrb8aPkJKu3r7R/dv8gJ18dUVUK\nn1wm0yA3L4QFU2U0v/K5xiPf4mOywrQ5ETfIuYaL35fzBGtekhem/udC9xGy1UJTMk92fQtBMbKh\nmcELUi+XEXiRg575mauhl5P8bTfBo4Vb5nA3YJOAlcd9UkYaWm2TIm6QlklSVBAr9lp+UWRL1/oR\nt3Vr1715ZeRpXYgRBZZbRtMf8JD4cLZlF5pFKCNH/uEkx0lB7hYeQEJkoFm4t2QV8uuuXCqjBuGb\nvbZedV6ArxfzB2cTKsr5KO4RFu6o4ob30kl76jd2HK0/EeopaJrGlqxCuiUO5Hj0OKZU/MySnXbF\nMYVZsOJZeRvcWAk9yDzsBvL41+w/weVvruO8V1bz/RFvViQ/ymcZ5Ux9bjl3fvwHe3Nd67nx1spD\nlBHAzuNlHDnZxFQxU2bJA298I5fTA2lpaLXSFrHHx1+20L1ri7QZ9EZhk/8GPcZQ+81dfP3cbXKO\nZ+JDlgvJ0EvBWMnBlZ9w43vp/OWr7byydD9fbs5m667d1L59Duz/HWb9Fx7YD3NeksHQ4ifg9Ylw\nfHv9sehY3WU2m6g+cO92eOQozFslMzjOf02Woi9+3LVj1FTINMMBsyzfS+rlgFZ/UYTSPDixp2k2\nSQfg0cLtdOUba7x8ZGRVlm/J4W7gj9YZZ/aLZv2hk+YMjoasEj2rZF9eKTlEEFaTX8/rG9ojjBOl\n1RwzZcbszinByyDoE2NZLm1s70g2HCrAWFvHs7/uISLIl+4TrpKVn5kr651b7PgSwnry8E1X88dj\n03j/hlEIIXhndWaTP6+7kFVQwanyGob2CCfqrNuIEwWs++UjS9Rda5STsMIA0/8FQEV1LTlFzZsg\n+njDES5/az3780r5y7nJrHlkCi9fPpxVD03mljN7syQjl/NeXk1+SQNVjUBucSXfbj3K1AHSqvpl\nZxO7+JmEuwfHuf2jzZwoLIJ1/5NdCONHOt6nSy9TYzUrvHzgorcpr/Ninvd3ZAUk217c4kdCRBJV\nmz5i5b58ft5xnGd+2cNrn39P5KczqTy+h/u9Huba7YP4/WCFbGN7/c+mRTKMcpGMXd84Ho+eJx7V\nzIhbxz9MXph0ovvJRmd/fCCLmqw5tEKmeFrfDexfLIV+wBzLaxFJsm3BHx/YWj+u5m93MB4r3LV1\nGseLnKx8Y0+gqQinsPnCPbFfNJU1dWw4VEBtnUZpVf2sEjAtX2aKuPccL6HIOxqv/F3ywmEVeZgn\nKLOkz737eDG9o4Pw87a0VB2TFElJlZEFqw6xct8JbpvUm4CUc6X/tu0z2xOXnYSDS2HQn0AI/Ly9\nmNA3mtlD4/hxe44lt9zD2GKaBxgaH453/xmU+3dlQuE3LNfvfpb8A46slVV54T3JL6ni/FdWc84L\nK6mpbVoq2W+7cvnrV9uZ1D+aFQ+exc1n9jbn5kcF+/HwOcl8Nm8sFTW1/NyIEL+7JpPaOo3HZqUw\nMC600e3tyRNdqNJ8OCumjMLyava+frXMP575bMNtdx2wrSSIOypvpUQL4OnqudjM7wpBTcpc+lds\n4cYhfmx+dCp7zzvGz4F/JzoAfkxbQG3f6ezLLeWOjzdz+KQpNTY+DW5eKlM1P7salv6fOXXPWFvH\npsOn0PJ3m1oYN7ySVLOY+KCsUv3xz/K8mibtlIXnyeKnBWdbKk8zvpU2kr0Yp14h7TXr/inN9bfb\nGY8V7vySKozOFlCwJ8jUaMq88k18w9s7YHRSBL5eBlbszTdXRjoWbm+zSO7NLaE2ONaSQ24l3APi\nQvDxEmw1+dwZOSVmf1tH97mf/nk3cWH+XDmml8zdHXie9Oys044yvpUR0KALbY4xN60HFTW1/LDN\nwTJqdqw7eJIvNmU3ul17sjWrED9vA/1jQ8DLG99R13Om13Y+/WU52p6fZIbEiOtgyFzyiiu59I21\n7MktobC8xmGRkzM2HS7gjo82M7h7GP+7Yjj+Po7FcWBcKL2jg/hhm5NeJkBZlZEP1x1mxqBYekYG\nMmNQLJsOnyKv2PUeHcv2nOSwFsOosEK+Sl7GGRXLWNHzdtcac9nx2vIDbPYdwVfTVvF92QB2HrP1\nszeETMMgNC7VfoCPL8X3l/sxJIzD7/Y1zJ09m/9eksqiW8fibTDw8BfbLXc7IbGy0nTo5bD835C+\ngKyCci55Yx0XvrqGE4e2Na+FsSv4hcDZT8mVmDa8Dl/cIHvMJM+UOeFlebKoJztd5m/3n1k/BXjg\nHKoMgdS+dx7aK2Nk4c/u713P3+5APFa4LTncrkbcJ2UbxqBox4UZjR3C15uRiV1YsS/fXO5u3dJV\nJ8RfWiU1tXUczC/DO9zqImEl3H7eXiTHhrItu5DiyhqOFlaY/W2dmBB/+sQEU6fBXVP6WsRkyMVy\n0mfPT5aNd34pMyrsKr2G9Qind3QQn7sgyP/3027+8tV2t5rQ3JpVyKDuYXKRZ8A77RrqhBcz8t+m\n9JMbKQxLpmraP8kpquCSN9ZxvKiS164cATgoYHLC/rwSbngvnbgwf96+diSBvs7/aIUQzBzSjQ2H\nCsgrcSzEn6VnUVxp5MYJ0u6YMUgu2OGozYEzluzOI9c7jpCjKxm4/3U2dJnJ1XvPYMlu148BcOhE\nGT/tOM5VY3oxM7UHQsBiu2N8e8SPP7T+9Mh4Cw4slamLVyyyWcg6LiyAR85NZu3Bk3y60So33Mcf\nzv8fxI+kdPmLnPvCcvYeL6FnlwD8Tu2jtqH2tSayT5WzJavQ8aRzQwy+CHqeIbNmdnwpi6Yufl/m\nhF//Kxh8qFtwNlQVoQ2oX+a+I9/IJRUP82bNdHZWRKDlZsgga+AcBydzLzxWuF3K4dYJMjWaKsxq\nlk2iM7FfNHtzS9lnSgsMdRBxB/t5U6fJycbq2jqCo03n8w2uF+kPiQ9je3YRGaYIaEBs/VLoWUPi\nSOkWykUjrPZNGC+LiHS7pOQ4HFopo2276EYIwcVpPdh0+BT77UvorThRWsW27EKqjHWsOXDC6Xbt\nSU1tHTuOFTE03qryMzQOkTyT87zWILQ6zsu7mTOeWcMF/1vDiZIqFt4wihmDYkmODWFdIx0eAdYf\nPMmVb23A22Bg4fWjiQxuPAd35uA46jT4ZUd9+8NYW8fbqw8xolcXhveURSd9Y4JJjAqq53PvOFrE\nmf9ZWu/7rjLWsnJfPiKiN6KmHJImMeSWtxkYF8YDn2+rVwzWEG+sOICPl4HrxiUSGezHsB7hLNmd\nZ36/rk5j8e5c1na/BpLOkvbHmHkOU9ouG9mTMUkR/POHDI4XWS5aWacqeLd2BsFlR7gsYg8/3j2B\np6Z1JZRStlc1sAwe8u7ksjfXcf4rq7notbUszsh1XcCFkAVUPcfKC82EP1t+/2OSKb7iJ/Zr8ZzQ\nQvm9qn5HxjdWHGS/bzLF4//GrBO3c2XgKxTff1T6+C5QXFnDok3ZvLXyIM/9tpcnvtvJv35sxTVN\nG8BjhTv7lC7cjUxOgiXiLjzc5IwSa87sJwsovjfZDo6zSuRrm00LMUR3My1FFdWvnqgOjQ+npMrI\nTyYBsI+4Ae6Z2o/v7xxvjjgB6XEOvhD2/ya97V3fAJrTVWj+NLw7XgbB55ucL0awbE8+mgYGgc0f\ntjMKy6v5ftsxsgrarrHO3twSKmvqSO1pW7IvxtwGviEEzn2Vp66fw/BeXTAIwQc3jmZELzk5N7Z3\nJOmHC+Qycg6oNtbx7592c+mb6/D3MfD+DaPoGRno0rj6dQ2mT0yw+ffAml925pJVUMFNpmgb5MVz\nekosaw+cpKhc3q2VVRm58+M/OFJQzn9+3mMjVhsPnaKsupaAIXOkLXbxQvz9/XnqT4M4WVbNu2sy\nXRpnbnElX2w6ysVp8USHyAvSlAFd2ZZdZLZt/sgq5ERpNd1HnQ9Xf93gWqgGg+DfFwyhpq6OR7/e\nTuaJMh74fCtnzV/GM0f6U+obxSMRK+kREciEcHkxev+AH8YG5hr+9WMG2acquHVSb44XVXLDe+nM\neJjkU/MAABY/SURBVH4lP27PcSjgP27P4ez/LufG9zby2cYsTgYmycnSvlPrbfv8hlLmVD3Jlb4v\n8MziQ9RamftZBeX8sD2Hy0f35MEZycyfO5T1Bwu4+PV1vL82k4VrM3lvTSYfrj9MYXn9VW7yS6q4\n+LW13P/5Vp76IYMXF+/j8/Rsm8yztsS9jZwGOHyyjMggX4fiWY+gKJlGVXCo/kriTaB/1xC6hvrx\n2055q+kwq8QUhacfPoUQ0L2XqWjDQUrUkB4yj/irP44SFuBDbKjji5Bw5BEOuUROxuz6SlbKxaQ4\n7fMdE+LPWf1j+HLzUR44uz/eXvWv10t359E11I8h8eEs3Z2Hpmn1zlttrGP53ny+3JzN4ow8qmvr\n8DII5gztxryJvaUP3Yro/VxS4+16rfQaCw8dwuDlwwRkkZQ9Y5IieWd1JluzihiVaJtpsT+vhLs+\n3sKunGIuG9WDR2cOdL4QhwOEEMwcHMeLS/aRV1JpLgCrrKnl+d/3khAZyLSBXW32mTEolteWH2Dx\n7lwuGB7P49/uJPNkGRcOj+eLzdms3HfCHBgs3p2Ln7eBgWPOBt9Z5mMM79mFyckxvLHiIFeN7VXv\n96+ovIb80kpC/H0I8fdmwapDGOvquHmCpXBocnIMz/yyh2V78rl4ZA9+25WLt0Ewqb9rhVoJUUH8\neVp//vljBot35+HrZeDKMb2YN7E3wVtukZWOJ/YhTM2lVhVG8d22Y/xpWP15pRV78/lw/RFumpDI\nQzOSuW9aP77beoz/LTvAbR9uZlRiBH+fPZCUbmEUllfz2Dc7+XbrMfp1DSYjp4TfM/IwCBidGMn/\nXTCYhKgg87H355WycG0mc0f2ZlyfSO746A++3XrUPI4Fqw5hEHDduAQALhoRT9dQP277cDN/+2an\nzThfXrKf5y5ONc855RRVcMVb68kprGTBNWmkJUQQ7OfdcD1JK+PBwl1OLxcjJHP1JJrTlW9cQQjB\nmX2jzX6xs8lJkBF3z4hA/Lt0l1V6DvqF9IkOJsDHi6KKGkYnRjgWaGd0HSRn9Nf+T3Ymm/y3Bjef\nmxbP7xm5LN+bz5QBtqJSU1vHir35zBwSR2qPcH7blWtTfq9vM+flVew+XkJkkC9XjunFtIFdWZyR\ny0cbjvDVH0eZOqArz84dSligCxdTF9iSdYougT70iHBghzXSa2ZMYiRCyAlXa+E21tZx9YINVBrr\neOOqEZydEtvAUZwzc0gcLyzex887jnP12AQAnvllD/vySnnv+lH1/oiHdA8jNtSfn3ccx8fLwOeb\nsrnjrD7cOaUPaw6c4IXF+5jQV/6eLtmdxxm9IwnwrT9Bet+0fsx6aRVvrzrEPVMt/vG+3BIufHWN\neWUmndlDu9ncSSTHhtAtzJ/Fu3O5eGQPfs/IZXRSBGEO5muccf34RPbkltAl0IebzkyyVC6PuFau\nfr7hDdDq0PxC6RLWk5eW7GfO0O4230lRRQ0PfbGN3tFB/PlsmS7o42XgguHxnJfanU82HmH+L3uY\n9dIqzhvajTUHTlJQVs190/px66TeeBsEO48V8+uuXN5fm8nc19fywQ2jzcHDP3/YRYCvF/ef3Y8u\ngb4MjDvAc7/tZebgbpRWGflk4xHOS+1us+ThhL7RbPzrVEoqjQgBAlkY98Dn27j8rXXccmZvLk6L\n55p3NnCqrIaFN4xiZIJd+mU74bFWyeGTZfSKDGp8Q5Aet04LPG6w2CXgRLhNkduxokr6xshMCO7Z\nJgsd7PD2MjCouxRHa5F0CSFg8Fwp2tBotsHk5Biign35LL2+XbIxs4CSKiNnJcdwVrKMvOztkh+3\n57D7eAlPnpfCur9M4bHZAxnbO5JHZw1kzcOTuXdqPxbvzuX1FQfqHb+5bM0qYmiP8KZd0EyEBfow\nMC603gTlb7tyOVZUydMXDmm2aAP06xpC35hgc7bO6v0nWLDqEFeP7cXEfvXvAAwGwfSUrizfm89f\nvtrOsJ7h3D21L37eXtw6qTebDp9i7YGTHDxRxuGT5Uy2u7jqDOoexvSUrixYech8C59fUsV1727E\nz8eLZ+cO5anzB/HQjGTumtKXh8+xvQsTQnBWcgwr951gz/ES9ueVMtXJuZzhZRDMnzuUv84caNtu\nIjhG2nVbPoLsdER0f+6a2o+D+WX8sN3WVvrH97vILa7k2YtT62XweBkEV4zuxbL7z+K6MxL5flsO\nEUG+fH37OO6a0hcfLwNCCAZ1D+O+af34fN5YDAIueWMtW7MKWbonj6V78rl7Sl8ig/0wGAQPzOhP\nVkEFn6Zn8f7aw1TW1HHzmUnY4+/jRXSIH1HBfkQG+zGiVwTf3zWeS9J68NryA0x9bjnFFUY+vHF0\nh4k2eKhwVxlrySmupGdEUyNumlzubs/4PlFmq7ohjxugf2xwvfft0fO5k5tjMwyeKx+7DbP0cHaC\nj5eBPw3rzuKMvHrFKUtNt7zj+0TRNdSflG6hLLUSbk3TeGPFQXpHB3Hl6F62fjsQHujL3VP7cu6g\nON5fe5iiipbnjJdWGdmbV2I7MdlExiRFsunIKZu2twvXHqZ7eACTk1vew+XcwXFsyCxgf14J93++\nlaSoIB45Z4DT7acPiqXKWIemwYuXDjN/jxen9SAmxI8XFu9jSYb83hsa373T+lFabeTNlQeprKnl\npoXpnCitYsE1aVw4Ip4rx/Ti1km9uW9aP4dZV1MGxFBeXctTP8jFKextnRYx+ma5gEfOFojuz4yU\nWPrGBDP/lz08+d0uHvlyG7d9uIlFm7K5dVJvUns4//8NC/ThsdkDWfvIFL67czyDujtuUdAnJoRF\n884gxN+bK95az6Nf7SApKsh8JwQwqV80IxO68NLifby3NpMpyTE2bSMaItDXm39fOITXrhzOGb2j\n+OTmMQxtYNztQaPCLYR4WwiRJ4TY0R4DcoWsggo0DRKiXBRu6wKAFkxOAnQJ8mVIfDj+PgZ8vet/\nfcFWUbgrvxhpvWTmweD4ZnTwC+8h20lO+btLm189NgEvg+CfP9jOfC/ZncfopAizzzslOYbNR05x\nqkxGdGsPnGTnsWJumpCEoQEf77azelNSZeT9tZn13ssvqeLjDUf4ZstRlu/NZ0tWYYNFQTuOFqFp\nNPiH3RhjkyKpNtaxxVTktC+3hLUHT3LFmJ6t4kfOHBKHpsFlb64nr6SK/16S6tDe0BmVECHtpIuH\n0sMq6PD38WLexN6sP1TAW6sOkhwb0mCaa3JsKDMHx/HO6kxu/3AzW7MLef6SYeYgoDHO6B2Fv4+B\nlftOMCAulPguLv4duUL3EbIXCkBUfxntTu9PbnEln6Vn8XtGHjuOFnPu4FjumuLaItPRIX71ggV7\nekQE8vktZxAb5s/Rwgr+OnOAzd+nEIIHpieTV1JFQVk1t0xsQsMwEzMGxfHBjaObfnfcBrjicb8L\nvAwsbNuhuI5evdUzwkWrRI+4/cMaX33EBa47I8Fpypy1fdI3pnHhnjEolu/uGE9Kt2a2Xh13t8ub\n9ogI5LZJffjv73u5bNQJxvWJ4sjJcg7kl3HF6F7m7c5KjuHFJftZsS+f81K788bKg0QF+3H+MOeL\nTwCkdAvjrP7RvL06k+vHJ5rzocuqjFzx1jr25tqmI0YF+7Lw+tEM7Fb//2SrSWxbEtmMTIzAIOSF\nZ0xSJO+vO4yvl4FL0lp28dbp1zWEfl2D2Ztbyr1T+zU6Vm8vA29dk+bwvctG9eR/yw6QW1zFBcMb\nLxC7Z2o/ftyew+Ldefz13AHmXHFX8PfxYlzvKBbvzmPagDboHjlmHizaYF6B6OyUWPY85cICEi0k\nNsyfRfPGsjW7iDP71q/WHJUYwYyUWIoqahiZ0MXBETyHRiNuTdNWAM1ogNt2HDY17ElwdXLSx9+U\nR90yf1vn/GHd+c9Fjktig0xiZRCQFN34hUUI0bxou5ncMjGJXpGB/O2bHVQZa80FHda35kPjw4kM\n8mXJ7jz2HC9h2Z58rj2jl9NqQmvumNzn/9u799gq6zuO4+9vr/QCpaWX9cL9KrciNEoRRVAnGMWE\nzAS2MjWbzs1lOrcoxsTNxGSJc8bFbC4oc+zWZRPcDGYXUSI6DVhQsKUCKgXagsWCrVBHof3uj+cp\nPZRezoGePr/Tfl9J03OeXs6np+d8z3O+z+/5/Th+qpXy7V4vXVV5cMNuPmo4ydrV89j8wDVs+G4p\nvymb6xXRte90TqIUYlft54zJSiUrrY+Z/nqRkZLIjIIM3vmkkZOnz7JxZx03z84Pa6x2uO5ZNJFb\nigu4d3Hke3ChUpLiuWeR1+4Kp+c8KTedH984lQdumMK3rx4f8e11tEcupc/foxkr4M5/euPCB9jI\n1CQWTcnp8bjIs2Vz+fNdV17UcROX9NuoEhG5G7gbYMyY/imQPTl0vIX05ITIntTped4kPFEWHyek\nJyeQOyI5rEI30IYlxvPT5TO484V3ef7NA2w7cJwJOWnnDaWKixMWTc3h9Q8biBchJTH+vD3y3swb\nm8WV47N4busnlM0fw/q3a3hl9xHWLJt2QZGYVTSS1c9vo2zdNp4tm8fiqbkcafqSzdUNvP1xY7fD\n/CI1f0IW698+SPm2Q5w8fZbVpf37GFgxtyisPeRw3HnVeOaGnLjTl+9dO+mib+u2ktHMLMzosW98\nSURg7IL+/739INYLdod+K9yquhZYC1BSUhLhuauRqWk8xZis1Mj+CSvWnr98UhRlpCRe3MHGAbJ4\nai43zsjjmdf3094O3+ymmC2Z5o373vheHbeXjiUzghfJ7y+ZxOp123nkpUo27qzlpllf4TvdHMEv\nHJnCX+8p5Y4XtnPX+gqm5A1njz+97bhRqdyxYNxF/40dSieO4rk3D/DUq/uYVZhxST3zaIuPk7CL\ndn/cVlSKthkQMTmO+1BjS7dnGfaqqPveYjQ8vXIOOf34djwaHr1lBtf/4g1a29q6HcFw9eQcEuKE\ndtVzixeHa+GkbGYXZfDijlom56bzxNeKe3yRzU5Ppvyu+Ty0YTcNzad5aOk0bpiey8Sc9H7ZOyoZ\n5/W5vzzTxurSsYNmj8sMbTFXuNvalcMnWqLTm+snQY7vDFfhyBTWLJvG79+poaSbvBkpidxSXEBK\nUnz44+V9IsKaZdN4fFM1z3z98nNTo/Zk+LBEfv2NeRHdRrhGDEtkVmEGB4+3sLy4ICq3YcxAk74m\ndBGRcuBaIBv4FPiJqq7r7WdKSkq0oqKivzKe5/DxFq5+Ygs/WzGLVVdEt5duBofKuiZaWtsuOPXd\nGJeIyA5VDas10Ocet6quuvRIkVNV1r11gFvnFJ6bIAe8A5NA+Ke7myHPerlmsHH2zMnqI1/w+CvV\nrO8yE1rHUMBI374bY8xg4Wzhrqz3Zobbuv/8aRIPNp4iKT6ux5n0jDFmsHO2cFf5K5N/UNdE48nO\nhVkPNrYwOitlQKdQNMYYlzhbuCvrm8lMTUQV3vqo8/TymkhmBTTGmEHIycLd1q7sqW9meXEBmamJ\nvLHXa5eoKoeOt4Q/K6AxxgxCTo7jPvDZSb4808bsopGcaDnD1v2f0d6uNJ5qpaW1Lfw5SowxZhBy\nsnBX1nmnPc8szECBl3fVU320+dzq49YqMcYMZY4W7iaSE+KYmJNGpr8M1hv7jpHnr7YR7qKuxhgz\nGDnZ466sb+Ky/BEkxMeRO2IYl+WPYOu+Yxw83kKcQFFmz5PMG2PMYOdc4W5vV6rqms+txQiwaEoO\nFTUn2FPfTH5GCskJ7k2XaowxA8W5wn34RAtfnD7LzJAVYa6Zks3ZdmXL3obwlyszxphByrnCHXpg\nskPJ2CxSk+Jpa9fwlyszxphByr3CXd9EQpwwOa9zhfSkhDgWTBwF2ORSxhjjXOGuqm9mSt7wC/rY\ni6Z4y1jZGG5jzFDn1HBAVaWqronrull5+ubZBeyubaJ0woWrNxtjzFDiVOE+2vw/Gk+1djt/cmZa\nEj+/rfuV1Y0xZihxqlXScWByRoFNfG+MMT1xrHA3ESdwWaQLARtjzBDiVOGuqm9iYk46qUlOdXCM\nMcYpThXuyrpmWx/QGGP64MyubevZdhZOzmbhJBs1YowxvXGmcCclxPGkjRoxxpg+OdUqMcYY0zcr\n3MYYE2OscBtjTIyxwm2MMTHGCrcxxsQYK9zGGBNjrHAbY0yMscJtjDExRlS1/3+pyDHg4EX+eDbw\nWT/G6S+u5gJ3s7maC9zN5moucDebq7kgsmxjVTUnnG+MSuG+FCJSoaolQefoytVc4G42V3OBu9lc\nzQXuZnM1F0Qvm7VKjDEmxljhNsaYGONi4V4bdIAeuJoL3M3mai5wN5urucDdbK7mgihlc67HbYwx\npncu7nEbY4zphRVuY4yJMc4UbhFZKiJ7ReQjEVkTcJbfikiDiFSGbMsSkVdFZL//OTOAXKNFZIuI\n7BGRKhG5z6Fsw0Rku4js8rM95ko2P0e8iLwnIpscy1UjIh+IyPsiUuFKNhEZKSIvisiHIlItIqWO\n5Jrq31cdH80icr8j2X7oP/YrRaTcf05EJZcThVtE4oFfAcuA6cAqEZkeYKTfAUu7bFsDvKaqk4HX\n/OsD7SzwI1WdDswH7vXvJxeynQaWqGoxMAdYKiLzHckGcB9QHXLdlVwAi1V1Tsh4Xxey/RL4l6pO\nA4rx7rvAc6nqXv++mgPMA1qAl4LOJiKFwA+AElWdCcQDK6OWS1UD/wBKgX+HXH8YeDjgTOOAypDr\ne4F8/3I+sNeB++0fwA2uZQNSgZ3AlS5kA4r8J80SYJNL/0+gBsjusi3QbEAGcAB/8IIrubrJ+VXg\nvy5kAwqBw0AW3pKQm/x8UcnlxB43nX90h1p/m0vyVPWIf/kokBdkGBEZB1wObMORbH474n2gAXhV\nVV3J9jTwINAess2FXAAKbBaRHSJyt78t6GzjgWPAC3576XkRSXMgV1crgXL/cqDZVLUOeBI4BBwB\nmlT1P9HK5UrhjinqvXwGNo5SRNKBDcD9qtoc+rUgs6lqm3pvYYuAK0RkZtDZRORmoEFVd/T0PQH/\nPxf699kyvNbXNaFfDChbAjAXeFZVLwdO0eUtvgPPgSRgOfC3rl8L6HGWCdyK96JXAKSJSFm0crlS\nuOuA0SHXi/xtLvlURPIB/M8NQYQQkUS8ov0nVd3oUrYOqvo5sAXvOEHQ2a4ClotIDfAXYImI/NGB\nXMC5PTVUtQGvV3uFA9lqgVr/HRPAi3iFPOhcoZYBO1X1U/960NmuBw6o6jFVPQNsBBZEK5crhftd\nYLKIjPdfSVcCLwecqauXgdv9y7fj9ZcHlIgIsA6oVtWnHMuWIyIj/cspeL33D4POpqoPq2qRqo7D\ne1y9rqplQecCEJE0ERnecRmvJ1oZdDZVPQocFpGp/qbrgD1B5+piFZ1tEgg+2yFgvoik+s/T6/AO\n6EYnV5AHF7o0928C9gEfA48EnKUcr091Bm/v41vAKLwDXPuBzUBWALkW4r3V2g2873/c5Ei22cB7\nfrZK4FF/e+DZQjJeS+fBycBzAROAXf5HVcfj3pFsc4AK///5dyDThVx+tjSgEcgI2RZ4NuAxvJ2V\nSuAPQHK0ctkp78YYE2NcaZUYY4wJkxVuY4yJMVa4jTEmxljhNsaYGGOF2xhjYowVbmOMiTFWuI0x\nJsb8H5ffU2fN5tKpAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2bab53e90b8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# With 256 hidden\n",
"fig, ax = plt.subplots()\n",
"losses = np.array(losses)\n",
"plt.plot(losses.T[0], label='Discriminator')\n",
"plt.plot(losses.T[1], label='Generator')\n",
"plt.title(\"Training Losses\")\n",
"plt.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator samples from training\n",
"\n",
"Here we can view samples of images from the generator. First we'll look at images taken while training."
]
},
{
"cell_type": "code",
"execution_count": 102,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def view_samples(epoch, samples):\n",
" fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)\n",
" for ax, img in zip(axes.flatten(), samples[epoch]):\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)\n",
" im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" \n",
" return fig, axes"
]
},
{
"cell_type": "code",
"execution_count": 103,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load samples from generator taken while training\n",
"with open('train_samples.pkl', 'rb') as f:\n",
" samples = pkl.load(f)"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x2bab4a00c18>"
]
},
"execution_count": 104,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAD8CAYAAAC4nHJkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAADWxJREFUeJzt3X+oHfWZx/HPx5gIJvWSbM01WDENBLVcNSVXWVCWLt1U\nVxqSIISqLFk2bPpHt2xhkfUHamAVZNl20X8KCQlN167pikpCXbbUuK67IsFENP5skr2kNCEm/ig2\nxWi88dk/7mS56j0zJ+fMOXPufd4vuNx75jkz8zDkk5k5M2e+jggByOecphsA0AzCDyRF+IGkCD+Q\nFOEHkiL8QFKEH0iK8ANJEX4gqXP7uTLb3E4I9FhEuJ33dbXnt32j7V/bPmj7jm6WBaC/3Om9/bZn\nSdovaYWkw5JelHRLRLxRMg97fqDH+rHnv1bSwYgYi4hTkrZLWtXF8gD0UTfhv1jSbye9PlxM+wzb\nG2zvsb2ni3UBqFnPP/CLiE2SNkkc9gODpJs9/xFJl0x6/ZViGoBpoJvwvyhpqe2v2p4j6TuSdtbT\nFoBe6/iwPyLGbf+NpF9KmiVpa0S8XltnAHqq40t9Ha2Mc36g5/pykw+A6YvwA0kRfiApwg8kRfiB\npAg/kBThB5Ii/EBShB9IivADSRF+ICnCDyRF+IGkCD+QFOEHkiL8QFKEH0iK8ANJEX4gKcIPJEX4\ngaT6OkQ3cDaWLFlSWn/mmWdK60NDQy1ry5cvL513bGystD4TsOcHkiL8QFKEH0iK8ANJEX4gKcIP\nJEX4gaS6us5v+5CkE5JOSxqPiNE6mgIk6aOPPiqtL1iwoLQ+b968lrWHHnqodN6VK1eW1meCOm7y\n+dOIeLeG5QDoIw77gaS6DX9Ietr2Xtsb6mgIQH90e9h/fUQcsb1Q0q9svxURz01+Q/GfAv8xAAOm\nqz1/RBwpfh+X9KSka6d4z6aIGOXDQGCwdBx+23Ntf+nM35K+Jem1uhoD0FvdHPYPS3rS9pnl/GtE\n/EctXQHouY7DHxFjkq6usRfgM4aHh0vr5513XsfLvuyyyzqed6bgUh+QFOEHkiL8QFKEH0iK8ANJ\nEX4gKR7d3Qfz588vrc+ZM6e0fsUVV5TWn3322bNtaVq4/fbbS+uzZ8/ueNnbtm3reN6Zgj0/kBTh\nB5Ii/EBShB9IivADSRF+ICnCDyTFdf4+qLrOv3fv3tJ62SOoJenmm29uWdu5c2fpvMiLPT+QFOEH\nkiL8QFKEH0iK8ANJEX4gKcIPJMV1/hpUfR//zjvvLK0PDQ11tf6lS5d2NX9TqrbbDTfc0NXyT58+\n3bJWNfx3Buz5gaQIP5AU4QeSIvxAUoQfSIrwA0kRfiApR0T5G+ytkr4t6XhEjBTTFkj6uaTFkg5J\nWhsRv6tcmV2+sgF27rmtb4nYvHlz6bzr1q2ru53PKPu+/4cfftjTdXdj48aNpfV77723q+W/8MIL\nLWvXXXddV8seZBHhdt7Xzp7/J5Ju/Ny0OyTtioilknYVrwFMI5Xhj4jnJL3/ucmrJJ0Z8mSbpNU1\n9wWgxzo95x+OiKPF329LGq6pHwB90vW9/RERZefytjdI2tDtegDUq9M9/zHbiySp+H281RsjYlNE\njEbEaIfrAtADnYZ/p6QzH2Gvk7SjnnYA9Etl+G0/KukFSZfZPmx7vaQHJa2wfUDSnxWvAUwjlef8\nEXFLi9I3a+5loK1e3fqCRq+v4+/bt6+0furUqZ6uv1dWrFjR0+VffvnlLWtVzxKYrtv0bHCHH5AU\n4QeSIvxAUoQfSIrwA0kRfiApHt1dmD17dml9/fr1PVv3Bx98UFqvupQ4Pj5eZzu1WrhwYcva8uXL\nu1p21dfR33vvvY7nzYA9P5AU4QeSIvxAUoQfSIrwA0kRfiApwg8kVfno7lpXNsCP7r7yyitL66+8\n8krHy64aDnpkZKS0PjY21vG6m7Z79+6WtWuuuaarZZ88ebK0Pnfu3K6WP13V+ehuADMQ4QeSIvxA\nUoQfSIrwA0kRfiApwg8kxff5++DAgQOl9el8Hb/qWvqll17as3VXPX67bBju559/vu52ph32/EBS\nhB9IivADSRF+ICnCDyRF+IGkCD+QVOV1fttbJX1b0vGIGCmmbZT015LeKd52V0T8e6+anO5OnDhR\nWq96lkAvXXXVVaX1qjEDZs2aVVove25/tz755JPS+vDwcM/WPRO0s+f/iaQbp5j+zxGxrPgh+MA0\nUxn+iHhO0vt96AVAH3Vzzv992/tsb7U9v7aOAPRFp+H/saQlkpZJOirph63eaHuD7T2293S4LgA9\n0FH4I+JYRJyOiE8lbZZ0bcl7N0XEaESMdtokgPp1FH7biya9XCPptXraAdAv7Vzqe1TSNyR92fZh\nSfdJ+obtZZJC0iFJ3+1hjwB6gOf2F84///zS+sGDB1vWLrroorrbQRvuueee0voDDzzQp04GC8/t\nB1CK8ANJEX4gKcIPJEX4gaQIP5AUl/radOutt7asPfLII33sJI+PP/64tH711VeX1vfv319nO9MG\nl/oAlCL8QFKEH0iK8ANJEX4gKcIPJEX4gaQYortNjz32WMvayMhI6bxlQ0VL0pIlSzrqqQ4XXnhh\nab1qGOwqJ0+ebFl76623Sue9++67S+tZr+PXhT0/kBThB5Ii/EBShB9IivADSRF+ICnCDyTF9/ln\nuNtuu620vmXLltJ61XX+qn8/9913X8va/fffXzovOsP3+QGUIvxAUoQfSIrwA0kRfiApwg8kRfiB\npCqv89u+RNJPJQ1LCkmbIuIh2wsk/VzSYkmHJK2NiN9VLIvr/H22Y8eO0vrKlStL63b5JeN33nmn\ntL5w4cLSOupX53X+cUl/FxFfk/THkr5n+2uS7pC0KyKWStpVvAYwTVSGPyKORsRLxd8nJL0p6WJJ\nqyRtK962TdLqXjUJoH5ndc5ve7Gkr0vaLWk4Io4Wpbc1cVoAYJpo+xl+tudJelzSDyLi95PPBSMi\nWp3P294gaUO3jQKoV1t7ftuzNRH8n0XEE8XkY7YXFfVFko5PNW9EbIqI0YgYraNhAPWoDL8ndvFb\nJL0ZET+aVNopaV3x9zpJ5R8rAxgo7Rz2XyfpLyS9avvlYtpdkh6U9G+210v6jaS1vWkRVYaGhlrW\nzjmnu1s5qi4FP/zww10tH82pDH9E/I+kVtcNv1lvOwD6hTv8gKQIP5AU4QeSIvxAUoQfSIrwA0nx\n6O4ZYO3a1rdYbN++vatlP/XUU6X1NWvWlNbHx8e7Wj/OHo/uBlCK8ANJEX4gKcIPJEX4gaQIP5AU\n4QeSavsxXhhco6O9e0jSBRdcUFrnOv70xZ4fSIrwA0kRfiApwg8kRfiBpAg/kBThB5Li+/zADMP3\n+QGUIvxAUoQfSIrwA0kRfiApwg8kRfiBpCrDb/sS2/9p+w3br9v+22L6RttHbL9c/NzU+3YB1KXy\nJh/biyQtioiXbH9J0l5JqyWtlfSHiPintlfGTT5Az7V7k0/lk3wi4qiko8XfJ2y/Keni7toD0LSz\nOue3vVjS1yXtLiZ93/Y+21ttz28xzwbbe2zv6apTALVq+95+2/Mk/ZekByLiCdvDkt6VFJL+QROn\nBn9VsQwO+4Eea/ewv63w254t6ReSfhkRP5qivljSLyJipGI5hB/osdq+2GPbkrZIenNy8IsPAs9Y\nI+m1s20SQHPa+bT/ekn/LelVSZ8Wk++SdIukZZo47D8k6bvFh4Nly2LPD/RYrYf9dSH8QO/xfX4A\npQg/kBThB5Ii/EBShB9IivADSRF+ICnCDyRF+IGkCD+QFOEHkiL8QFKEH0iK8ANJVT7As2bvSvrN\npNdfLqYNokHtbVD7kuitU3X2dmm7b+zr9/m/sHJ7T0SMNtZAiUHtbVD7kuitU031xmE/kBThB5Jq\nOvybGl5/mUHtbVD7kuitU4301ug5P4DmNL3nB9CQRsJv+0bbv7Z90PYdTfTQiu1Dtl8tRh5udIix\nYhi047ZfmzRtge1f2T5Q/J5ymLSGehuIkZtLRpZudNsN2ojXfT/stz1L0n5JKyQdlvSipFsi4o2+\nNtKC7UOSRiOi8WvCtv9E0h8k/fTMaEi2/1HS+xHxYPEf5/yI+PsB6W2jznLk5h711mpk6b9Ug9uu\nzhGv69DEnv9aSQcjYiwiTknaLmlVA30MvIh4TtL7n5u8StK24u9tmvjH03ctehsIEXE0Il4q/j4h\n6czI0o1uu5K+GtFE+C+W9NtJrw9rsIb8DklP295re0PTzUxheNLISG9LGm6ymSlUjtzcT58bWXpg\ntl0nI17XjQ/8vuj6iFgm6c8lfa84vB1IMXHONkiXa34saYkmhnE7KumHTTZTjCz9uKQfRMTvJ9ea\n3HZT9NXIdmsi/EckXTLp9VeKaQMhIo4Uv49LelITpymD5NiZQVKL38cb7uf/RcSxiDgdEZ9K2qwG\nt10xsvTjkn4WEU8UkxvfdlP11dR2ayL8L0paavurtudI+o6knQ308QW25xYfxMj2XEnf0uCNPrxT\n0rri73WSdjTYy2cMysjNrUaWVsPbbuBGvI6Ivv9IukkTn/j/r6S7m+ihRV9LJL1S/LzedG+SHtXE\nYeAnmvhsZL2kP5K0S9IBSU9LWjBAvf2LJkZz3qeJoC1qqLfrNXFIv0/Sy8XPTU1vu5K+Gtlu3OEH\nJMUHfkBShB9IivADSRF+ICnCDyRF+IGkCD+QFOEHkvo/pI9BCZ8nc+oAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2bab45b1550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(mnist.train.images[3].reshape(28,28), cmap='Greys_r')\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 5, 7, 3, 0, 9. Since this is just a sample, it isn't representative of the full range of images this generator can make."
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvWeUFNX6vr3HrJhBSSKDEsUISDD/VVRQwZxzOsZl1qUe\nD8ecMB4Vc0ZU1KOiHBUDKiIoKAYwC4ogSQTFHOb98Hvr4Rqtx6ma7t7TM9zXWizvVVZXV9eu6j37\n7idUVFVVBSGEEKLULFbXJyCEEGLRQBOOEEKIKGjCEUIIEQVNOEIIIaKgCUcIIUQUNOEIIYSIgiYc\nIYQQUdCEI4QQIgqacIQQQsShqqoq87/GjRtXhRAa3L+Kigr7F/N9u3btWhVCmJ1nDBalcamrf8UY\nl8aNGyfH0b/i/dOzUmb/8j4ruVY4lZWVeXavNyyxxBL2Lybjxo0LIYTPCz1OMceloqLC/i2qFGNc\nKisrk+MIUOCzVlbPisj/rMhSE0IIEYW4f9KXKb/++mtdn0IUuGrxiraqmGv9YqmlljL9yy+/1OGZ\nZOO3336r61MQdYhWOEIIIaKgCUcIIUQUZKktQsguq794dmh9sNGESNAKRwghRBQ04QghhIhCg7LU\nXnrppRBCCJtssoltyxLvv9hiC+fd77//3vRyyy2X6/2zRIEJURt0P4mGgFY4QgghoqAJRwghRBQa\nlKW26aabhhBCWHzxxXO97qeffjJ9yy231Lg/j//777+bbsi2Rxa7kPvQykyS/bzXLbnkkqYPPvhg\n02+88Ybpjz76yPSPP/6Y9bSFEGWEVjhCCCGioAlHCCFEFBqUpZZEmK244oq5XkdL55hjjjF93HHH\nmWYkG220hoZnF+ZljTXWMD1//vwQQgg//PCDbevVq5fpiy66yHTPnj1Nf/PNN6ZfeeUV0zfddJPp\nESNGpL4/7bs//vgj17nHIM1yrC/QOt12221Nv/DCC6az3DsDBgwwfd5555nmPcixKwfLmvb7Msss\nk7oPrw8jXVmzkbYwv1tqgtd17ty5ptu1a2c6ed7KEa1whBBCREETjhBCiCjUG0uNy+zjjz/e9BVX\nXPGXfa688krb1qFDB9PbbbedaZZ15xKY7/P55wv7CnHZW44WTRayRJp5VkiWyDSywQYbmE6sE15z\nXsOOHTumHo/WaJcuXUy/8847pjletKbKZYy8+4afM2bCMO3jnXfeOYQQwtJLL23bRo4caXrmzJmm\nvTYIr776qumff/7ZNO0evvaRRx4xffjhh6eeYzlb1p6NRjiGtJH5uWrb4JD3+2qrrWZ66tSppvP+\npBATrXCEEEJEQROOEEKIKJS1pbbKKquY5hLdI1luenYKI4NoC3jLW0ZacZm81157mX7ooYdqPK9y\noVh2jXe9uJ2219VXXx1CCGGjjTaybb179zb99ddfm6ZNwEie9957z3TTpk1Nf/fdd6aXXXZZ0wsW\nLDCdJWItT6RQHvh+fI9Sd5lldNS1115rmjZWTbYOLcrOnTubpnXG6EF+Vo4jr//EiRNNDx8+3HTf\nvn1Tz6E+1ifkted96F1vWm3Jtd16661tG5+lhx9+2DQjBBs1amS6ffv2pmfPnm163rx5pnktY/5c\noBWOEEKIKGjCEUIIEYWys9RatGhhesqUKTXuzyVrYqmwxQChRTBhwgTTtHoIEw+5BK1PNppH3mU0\n9+e1YNQMI6C+/fZb088991wIIYTXX3/dtrE22nrrrWea0W2MtjnrrLNMf/jhh6nnSGuC58JkPY8Y\nUW0ltyswRrR9DzvssNT9k3H0rB5a0EOGDDG98cYbm2ai7qWXXmp6v/32M53UOAwhhLFjx5q+6qqr\nUt837RzLHV7DF198MXU74XdRZWWl6T59+oQQql8nsvvuu5vm9xO/84466ijTL7/8suknnngi9bxi\nRnRqhSOEECIKmnCEEEJEoewstenTp5v2LBKy8sorp+6fBpeRG264Yeo+PAaTRhsaea0KXjsm8tHG\nYfQSSWo7MUrmmWeeMU1rgImHjPahRUcY7cXPxO3Fqg9X7jAp0UuyTbsW/P98Hdlqq61Sj8fn9aCD\nDjJ9yimnmC7n2l7FgvceoygZJbbCCiuYXmmllUzzmt91111/OTZ/ZpgxY0bq6zj2PMbkyZNrPF/C\n42SxovOiFY4QQogoaMIRQggRhbKz1GjReMt7RmTUNsLCix454ogjTNeXCJliwutCG9Nrz0BNu4aJ\ntckynTbmbrvtZnrSpEmmaTs8//zzplnXzhsXbue5N2QbzUsm7dSpU+p2RkclyZkcK9b+Yn0uJthm\nYc6cObn2b0gw6oztTpLadSFUjxxkl9v+/fuHEKp/xz311FOm27Zta9qzs1u1amWaCdNZIlNLYaMR\nrXCEEEJEQROOEEKIKJSFpcalnlfTikvG5ZdfvlbHZiIboRXz9NNPm2ZUVUNoT0Cy2FK0YnjtaLvR\nomE9J9pYiTXK2k+bbLKJaV5nRtgwAornlaVVgtdyoiGMHaHtzLH4+OOPTTPhlsm0TJpOO15Du1Z1\nAaMxjz32WNNMnh09erTppFUErf3111/fNMeEx6Zd5z0fbEPBOoUx0QpHCCFEFDThCCGEiEJZWGpc\nJlL36tXL9J133mm6prLqnv1y5JFHpu5PK4KJVd4xPdi58oMPPqhx/7qE9pdXe47XmZYarwUTb5mg\nRtsziZhK6kSFUL2E+vjx4017kYlZrj/3YeRVqVoPlAO0PXlNL7roItNsCdCtW7e/Pd6iGJlZSk49\n9VTTTCRfd911U/dnwmwCx2Tw4MGmb7rpJtP8DvPGsNQRaFlouE+iEEKIskITjhBCiCiUhaXGRCm2\nJPjiiy9M09LxuiUm25m8RsvHs1batWuX63w9vLL55Yhno3lwOc5r2rVrV9McowsvvNB0YrXRZuMY\ndu/e3fTmm2+eug+TEPPaPg052opjQZuG0WiPP/64aXbRZafVhPrYYbOcYT1Arx5kTXBMdtppJ9Ns\n2ZFl3MphPLXCEUIIEYWyWOFwVcNKq8zbYAw5Vypp+RaseJqFadOm5drfoxz+giiUpIldCP6PjMyJ\n4g/+Xbp0Mc0cmsaNG4cQqq+A+EP2mmuuaXqzzTYzPXfuXNOsKJ2lzMqi8pc6m9edf/75pvn5uf2a\na675yzGOP/5401wNffnll6Z5DblS9VbKDfma5+GEE04wfcghhxR8vORZCqH6M3b55ZebPvPMMwt+\nn1KhFY4QQogoaMIRQggRhbKw1MjMmTNN84fnli1bmmbMOX+Iq6lHO+GSn8dbVPBK9XjXguVhuA/t\ny1GjRpmmHdOvX78QQvUfPIcPH276uuuuSz02f/imHeeVQsqSi9DQeP/9903zB2oGzjC3bO+99zb9\nyiuvhBBC6Nmzp21LqhWHUL26d5MmTUzTUj3ttNNM33jjjaYXletfEywf1KZNG9NnnHGGaVaUri0n\nn3yyaVlqQgghFnk04QghhIhC2VlqtE647Bw4cKDpRx55xPQee+xhmrZbTYwZM6a2p9gg8HJTPFuK\n1Z/5WvarZ97MJ598Yvqee+4JIVQfN+ZY8Xh8H0am8b5g+ZtCynVksV6LCT9DITYuzztpohZC9Ygx\n2mvvvvuuaUaY7bPPPiGE6vkcHCNGRBHamMzlacj5TsWANjObqg0bNsz09ddfH0KoPk6rr7566vG+\n/fZb07Sf+RzyWSkHm1MrHCGEEFHQhCOEECIKZWGpsTzHrFmzTDMCjct19gP3kkDTYKIUEwzFQvJW\nZfYaOTGBNNmHY5vFfuH7cH9W5eYxGeGYhdgWQyE2mhdVOGnSJNNMvG3evLlplh96+eWXTSeJta1a\ntbJtQ4cONb3RRhuZph1I/fDDD+f4FIs2HENaoWyQlzRby1LBfcCAAama48P34bNSV2iFI4QQIgqa\ncIQQQkShIEutWPWq5syZY9qr6MztjMjIA+sa0d7wrLjYUUx1BT8nEzkZAeaNL23Ptm3bmr7vvvtM\nJ/W77r333sJPNoTw6KOPmmZy8N13312U45cjngXpNZ3j9scee8x0WsXi2bNnm37ggQdM04JhA0Tv\n/bOwqNS4S4OVutk8jdeB0YVpcF9aZx7vvfeeaS/aLSZa4QghhIiCJhwhhBBRKMhSK9aSOE+kWSEw\nomZRscuywGuRN6mSiZosv05rICl5X8j9wtcy4Y0JpGmtKkJo2LXyeF2o2fKD8FokkYSspcaotwcf\nfND0DTfcYLpRo0am33rrLdNslZDlfBc1WFeN7VZolybNCrO0TNlzzz1r3Kd9+/Z5TrHkaIUjhBAi\nCppwhBBCRKHOEj8ZPRHL3ir1+9Bq8BK3ygXamLQ5WIae9gvtNV5H1q/bcsstTTPxk1ZCHvg+V155\npenKykrTY8eONb2ot5zIS2K3MLpvt912M80x965n586dS3R2DQ9G1/Je5bOYWJorrbRSjcfLYpcx\ncrEc0ApHCCFEFDThCCGEiEJJLDXWbmLnQXYn5HKQyz6vsyPhcrTYNtkbb7xR69fuu+++pm+77bZi\nnE6t8OpuEW8765F5Nlq3bt1MP/3006YZmcbosTzwGIyY23rrrU2ztDvvr3KHHTQnTJiQuo83dqVI\nmDzyyCNDCCE0bdrUtnFsaXvTIiWMUhR/D9sQeN9bF1988V/+P5N189rT5fZ8aIUjhBAiCppwhBBC\nRKEklhqTwWgLcGlIu+SII44wffvtt5vOYh3QgmjWrFkIoXobAg8uWT///HPT3bt3r/G13nHq0kYj\nhXRe9CLtGGFz8MEHp+5P2PEzqc/G5T1rtvEYJ554oml2nLzkkktMszZYIcSu6+XZaCRLzTTe8yus\nsIJpXl8eh88aoxAT+4zHW3vttU2zc+Sqq65qeurUqaZHjRrlfZRaw6Td+m7Z8dq+8MILpvmzA7n0\n0kur/bc28PqV27XUCkcIIUQUNOEIIYSIQkksNc8W4BKdMHotr7XB98pipaW9z5prrpnrPb3jlCN5\nl9SMUmPE2Pz5802fdtppplnPiRYcrcnEJhs/frxtGzhwoGnaOIyM23vvvU2PHDnStHcf5aUux44W\nVdJ5Myu857/77rvU7Yz25PXi+CYWHC3lU045JfU9GUnKqLZijQUpB+unWHBMnn/+edO8znxGa8u8\nefNS37Pc0ApHCCFEFDThCCGEiEKd1VIjr776al2fQoOlEHuCUU+M6Prxxx9Nt2vXznTr1q1Nf/31\n16YTe+3ss8+2bbSRWL+L1h33aWi10fLaaB6MQPv5559Ns7tj0h4ihBAGDx5sOulAyUTaLJTCRlsU\neOaZZ0zznmfUZfKcsdsqIwuLYb/VJVrhCCGEiIImHCGEEFEoC0tN1C8Y3UV7jYmNtOCSREFaCoxo\nY/fDLF1Gi0XsxM9S4F2vr776yjQjBvk5r7vuuhBCeUc1NVSeeOIJ017NyIbIovNJhRBC1CmacIQQ\nQkRBlprIhGc5eZZO2v5eafWYNhqprzZaFvjZmAR66KGHmr711lujntPf0RDsTVEzWuEIIYSIgiYc\nIYQQUZClJkQDh0mzxbDRSlHyXjbaooFWOEIIIaKgCUcIIUQUKvIsZSsqKmaHED6vcUeRh9ZVVVWr\nFXIAjUtJKGhcNCYlQc9KeZJ5XHJNOEIIIURtkaUmhBAiCppwhBBCREETjhBCiChowhFCCBEFTThC\nCCGioAlHCCFEFDThCCGEiIImHCGEEFHQhCOEECIKmnCEEEJEQROOEEKIKGjCEUIIEQVNOEIIIaKg\nCUcIIUQcqqqqMv9r3LhxVQhB/4r0r2vXrlUhhNl5xkDjUj/GpXHjxslx9K94//SslNm/vM9KrhVO\nZWVlWHzxxe1fISy22GL2b1Fl3LhxIRShGVRlZWXB5yIWUoxxqaysTI4jioeelTIj77Oy6H7bCyGE\niMoSeV/w+++/59q/oqLCNLuL/vHHH3nfWgghRD1GKxwhhBBR0IQjhBAiCrkttbzQRisEBinktfVE\n6fAsUyGE+DNa4QghhIiCJhwhhBBRKLmlViyKYaMtu+yypn/88UfThdhCi4qltMoqq5j+9ttvTe+3\n336mX331VdPz5s0z3aVLlxBC9TEcNWqUaUYseuO8xBILb9Xffvst17kT5n0pUrJwOF6F5uaJho9W\nOEIIIaKgCUcIIUQUytpSW2qppUy3bNnS9FlnnWW6U6dOpnv06BFCCGHJJZe0bbS57r//ftONGzc2\nffrpp5t+//33Ta+wwgqmaRHRRmvINGvWzPR3331neumllzbNa7pgwQLTH3zwgemOHTuGEEJYZpll\nUt/nyCOPNH3bbbel7pPXRuO988svv5iWjVZcttpqq1z7J/dCCCHMmjXL9Ny5c4t1SnXO0KFDTe+5\n554FH2/TTTc1PXHiRNPz5883XV/sfK1whBBCREETjhBCiChEtdQ8m4McdNBBphlJ9sMPP5jecccd\nTTdt2tR0WuVpWjE77LCD6cmTJ5umBUe7iEtWUl+Wr4UyY8YM04xA4hJ//PjxpjfbbDPTb775punp\n06eHEKqPFW3JW2+91TTttcQi/fP+1J5F5t1fonBatWpl+umnnza93HLLpe7P54XPaH2PahsxYoTp\nRo0amd5kk01M8zM+++yzpl944QXT/ImA35Fpx+D1Y4TgWmutZXratGmp51sOCfNa4QghhIiCJhwh\nhBBRKJqlliWhzrM5mNT3+OOPm6bV1aFDB9OMbmEkWbKs5fswWmrYsGGmV111VdOdO3c2zaTGxAoK\nIYRff/3VND8fl7u07xqa7cbP/Morr5imBfn222+bpsXw2WefhRBCaNKkiW3jmJPBgwenbuf1bGjX\ntq7hPXzYYYeZ5nhOnTrVdDKeIfjjSLzkaFo8WY5TV/D8l19+edP9+/c3PWXKFNP8HuD3BqM0t956\n61qdi9fiZciQIaavueYa04yYI3VVm1IrHCGEEFHQhCOEECIKRVvHFpJQx9cywXC11VYzPWnSJNNH\nH3206XXWWcf07NmzQwghjBkzxrYxum3NNdc0/a9//cv0cccdZ/rzzxe25+a5MPGTS+a8tdRoE9Yn\nvM/2008/mfYiyQ444IAQQggjR460bRwLjv/uu+9u+vrrr0/dRxSHPn36hBBCePTRR20bbR+OOaMR\nixVdVl+sUZ7nGWecYfqxxx4zzfv9tddeM82Izjzvxff8/vvvTfOni3fffdf0nDlzTA8cOND02LFj\nTTPqlFZfTLTCEUIIEQVNOEIIIaJQZ6EhTHDi8o7JY0y85JL1ww8/NP3NN9+YTiww2jzt27c3zUi3\nnj17mqbNxfphiUUXQgg///yzaSYkMmIri71WV0vZP5O3TH9e65A2QJLAe+KJJ9o22jikdevWNR5b\n1J6rr77a9EknnZT5dWussYZpPherr756ja/l/cIExS+++CLz+9clfFZoxdNe22mnnUwzATqLpcbn\nb9CgQSGEEO69917btuKKK5q+/fbbU89r2223Nc02LFdeeaXphx9+2PQWW2xhmj8plBqtcIQQQkRB\nE44QQogolNxS8zo1etYSl5de0hS7T2644YamkygMRqZtueWWpplsResmS6IWP8cbb7xh2rOayr0T\naN6oryyfwWvbkFy77t2713i8Qw45xLQi04rDPffcY/rAAw/82305LrSRacXdfPPNpp955hnTHF+S\nVuPwz9D6OfXUU2vcPya0/2nXX3755aZp19Oi5z1Mze8Tfl8l1+HLL79MPTbfn999XvRr0m03hBB2\n2WUX008++WTq/qVGKxwhhBBR0IQjhBAiCiW31LxOjVy6MzKNy07W6WLNNEZkcGmalE1njSO+T7du\n3UzT/mE0HDsPvvfee6bZIZTnxbpti2K9L15HzzpJxpctC4YPH266d+/epkePHl3sU1wk+eqrr0wz\n8jIN1tLivU3rms8IbedevXqZ5vgfeuihprPYy+VmoxHaWIR1Fz/99FPTLVq0MM0WK9yfdv2xxx5r\nOvn+YXItLTfWhmzbtq1pz85nVCDhOMe0/7XCEUIIEQVNOEIIIaJQFjXBvegNRslwWbtgwQLTbDOQ\n2AiswcaaXVzys/Q6l/OvvvqqaS4vuazlMnlRh9eI7QfYQiIZ39NOOy31/w8YMMB0uSTGljNeNCAt\nG5bR90jGxWsNwPpchBFRG2ywgem33nrL9J133mm6IdnLM2fONM1Isk6dOpnm+NCurKysNM3EzvPP\nP990cg1pifK7hxGHEyZMMM36knwOvWu/1VZbmfa6iJYCrXCEEEJEQROOEEKIKJSFpcZlnJfsR+uM\nltnmm29u+uOPPw4hVO82SfuNS90nnnjCNMuJe5FmtPcYYcLjM5Lt66+/Tv0cDQ1eU9bYIkniGu0y\nWpq0D7zlfbkn0paaESNGmN5///1NM8Izi43G9g///e9/a3Uu999/v+nddtvNNC29li1bmqYlVB9Z\neeWVTZ955pmm//3vf5umzcj7drvttjPN8dl1111NX3HFFaaT+5+tUajZ4oNJtxdeeKFpJumutNJK\npnfeeWfTbK3AaER+b5XiOdMKRwghRBQ04QghhIhCWVhqtAVoXbH2z2WXXWY6sc5CqJ4QmiQQsjw3\nLTomdeZdOnKZzHMki4qNRpo2bWqaLQmY8LvuuuuGEEI499xzbRttSXYuZN0qjgstC9qr7NDakOHn\np6XG6+XB5OTHH3/cdB7LhBGGTKymBcpn8Z///Kfps88+O/P7lCO0Cq+99lrTDz74oGkmutJqY/I4\nW6kw2TnpiBvCwnYPTPCkncxjeBFlbDdw8cUXm+Yzx+eG9SYfeeSR1GMWC61whBBCRKEsVjicwdmk\ni5Vt2QCKOu04PB7/0mazKMa+s6Hb888/n/paL7CBfzXwr736/kPpn+E15V+4d999t2ler5dfftl0\n586dQwjVr8lZZ51lmg2mmOfAIAwGh7BPO0uAkFLnE5QKr9JwmzZtTB900EGm+YOvF/DSp0+f1O01\nceSRR5o+5phjUs+Rx2NAwrBhwzK/T33i2WefNc3rw+8QPgfMieHKnEEVXPnz/k/gNc57X3OFw1Uq\nV51c7WiFI4QQokGgCUcIIUQUolpqXkkO/sj/zjvvmGYMOX+44w+lrHqaLDe5pPXK5vBcaNGxVAer\nG3t2BUvueJ+vIUC7kI2n+IM08xUY85/A63PLLbeYbt++vWkv94aBIl4plobQsI25SrSAme9CO4TX\nkQ25+GP1+++/n/peyXhdd911tq2mBm1/hmWemBfSEMYigZ+FFuZzzz1netKkSaaZb8NAor59+5pm\nwAHv+cSuLFaJp7vuuss0n2F+R3I7fyLwqmQXglY4QgghoqAJRwghRBSiWmq0oriMo102fvx406zi\nzGqojIBh1eEkJ4RRNIx04tL4gQceMH3JJZeY5rL3H//4h2kvx4ZRUl6zOZKlv3s5QnuLZTT+85//\nmKY1QNszeS3Hf8yYMaZ5TXg9WSpnxowZpvfbbz/T11xzjWlafaz6XZ+gpcF7m5FESdRfCNVzn2jx\neCWCGDU1derUEEK2XB7C52jixImmS2HBlAO899n8kfb/pptuappRlCzhNGTIENNetFmxrcgddtjB\nND8Hf4ro0aOH6VJXa6+f335CCCHqHZpwhBBCRKHkllqWKr9eP25GI7G0zSeffGKaVkuyP60tlttg\nf282T9piiy1MM+rKi0wjXBrTxvCWxvU1eofnTQvmoosuMn3GGWeYZsXuxCbiMW688UbTe+21l2km\nknrX6rbbbjPNZENGEHEsWDqJ1b3LESY+X3rppaZ57+64446mr7/++tTj8L5kE0KWtslrpSXw+erZ\ns2etjlFfYQIurzETPx9++GHT8+fPN92sWTPT06ZNK9UpVoP3vhdFy1JJL774omk2eCsWWuEIIYSI\ngiYcIYQQUaizWmq0P7jUu+qqq0yzQdTrr79umlFtjLZIktAYpcYlLSutsqIql53Ujz76qGn2AKe9\n1rFjR9Negl1DgJ+ZUThsSHXUUUeZZmJb2jFYG42Jcqw+PWfOnNRjM1GY78PItIceesg0a1iVO//6\n179St3/22WemaeV4lhqfAV47JjbngVGFm222men6ahHngfctowVp+ScV0UMI4ZBDDjHN7zbazNy/\n2HX/vPcnfM+9997bNJu3lQKtcIQQQkRBE44QQogolNxS43KUS1AuxZngyfLfrAdFa4zJgVwyJglx\n6623nm176aWXTDNCiXbZgAEDUs+dNoYXpebZaIxmmTx5cuo+5Y4XdccEv1NOOcU0S5unLeU5bhtt\ntJFpWqe0yLp06WKaVidhohqvOdsfsGHeoEGDTLPkfrmQJfEuS+uLc845J1WnkaVlAeut1dfWD8WA\nz8FOO+1kmt8V3bp1q/E4tKWz7J/GJptsYpr3xJ133lnja1ljLWYNSK1whBBCREETjhBCiChETfzk\nUpyWCpemSX2nEEI477zzUjWjPTp16mQ6qWfEhLZx48aZZoRJu3btTH/11VemGd0zePBg07SX+Jm4\nxOY+9dVGo+25yy67mOa4MBrsu+++M812EmnLdNb9YgIia4Cx4yFrtnXt2jX1fHnN2WaCvedZT6oc\nbTTCpM6hQ4eabt68uWkmM+fp4PlnEouZidS0ND/66CPTtKDF//HFF1+YZosNXk9Ca5fff0xkTrpy\nsqbeG2+8YZotK/Im7tJ2Y7dSr2tuKdAKRwghRBQ04QghhIhCRZ4lebdu3arYPiALXqQT2wYwqozL\n+Jtuusk0l4NM/GQttXfffTeEUN3aYfQIk0SZsEmb5Y477jDNWlaloKqqKlRUVIyvqqqqXZjK/09t\nxsWDVhiX2hyvkSNHmqYFOX36dNMsoZ9c91133dW2MZGQXSN5j6y44oqmL7jgAtOsScXEU451IRRj\nXLp161Y1bty4giKACrHLPFjzK7FMaZfy+tO6ZhJuHVJWzwrhs8JIw7roAswxTL4TQ6jeEbZY5H1W\ntMIRQggRBU04QggholDyKDWv1tK8efNMv/XWW6a5jGe0R4sWLVK3s/ZWYhHQlmOHPkZGffrpp6bX\nX39901m6FrJrYhargdEkbH9QLngtJFiGntFj66yzjmmOF8e6devWphPLbMqUKbnOi/fICSecUOP+\nWdpD1CdbB4CuAAAgAElEQVQ23nhj07QgiRc9SbzafzVBq1P8PYzAZR0/tt4opb3GMWZ04z777FOy\n96wNWuEIIYSIgiYcIYQQUSiapUbbiJrJflz20fJghAdbCDBKjNYYy9lvv/32ppPoEFoxTHBipJvX\nqTMLeSN2ytFGI3mjobi/10GzLlo1NAQbjTBpmQm5hDYNo/qYTE1rVJQe2lhnn322af4UkMde4/fH\n8OHDTR944IGmy72TbYJWOEIIIaKgCUcIIUQUimapcdmXxUKiLTN37lzTXGoyYuyxxx4zTQuOiZrJ\nMT1rxbOOGpoVIxo2fEb69etn+sknnzQ9ZMgQ07q/6w5+t7FOHtumsPVGmSTYlgytcIQQQkRBE44Q\nQogolDzxMy+e7ZWly2FdkCXZTohiwnuLycyi/GDE7P/+97/Ufcr1u60UaIUjhBAiCppwhBBCRKEg\nS82rwbUosah+blEe6BkU9QmtcIQQQkRBE44QQogoFGSplcMSXpaCWJTRPS/qE1rhCCGEiIImHCGE\nEFGoyLMkr6iomB1C+Lx0p7NI0rqqqmq1Qg6gcSkJBY2LxqQk6FkpTzKPS64JRwghhKgtstSEEEJE\nQROOEEKIKGjCEUIIEQVNOEIIIaKgCUcIIUQUNOEIIYSIgiYcIYQQUdCEI4QQIgqacIQQQkRBE44Q\nQogoaMIRQggRBU04QgghoqAJRwghRBQ04QghhIhCrhbTTZo0qfr666+L8saLLbZwrvvjjz+Kcsw8\nrLHGGqa//PLL1H2aNm1qeubMman7rLrqqqbnzp2b6xy6du0axo8fP6fQHh/FHBdRnHFp0qRJVWVl\nZfjuu+9s20cffWQ6S2v0xRdf3PS6665r+u23367taVUjeQb5/C2xxMKvhN9+++0v+/55f8LX8vP9\n+uuvppdaainTv/zyS95T1rNSZuR9VnJNOJWVlSHLYHkPE2/aRo0ameZD6R2HuqYbng+K9wCdeuqp\npk8++eTU4+2///6mr7rqqtR9+vbta/q+++5L3cdj3LhxoaKiouBmUFnHZVGCX9a///57rtcWY1wq\nKyvDuHHjwsiRI23b//t//8/0kksuaZpfyHxeVlppJdPPPvus6ebNm5v2ngtvO5/BZZZZJoQQwo8/\n/mjbVl55ZdNz5swxveyyy5rm/jw2X8v9+Qddy5YtTU+ePDn1vAivR1VVVVGeFf5hmKUfGL9DvHuJ\nx8nyx4RH8tpy6FOW5XPkfVZkqQkhhIhCrhVOVrzZkH8Neasa7zj8q2769Omp+2+zzTYhhBCeeeYZ\n28ZVDVdV3qqGs7q3qiFc1Xh/CZXDXyt1yejRo0MIIWyyySap/7+Qvwg98q5qSkVyT4ZQfdXF+3L9\n9dc3vfHGG5u+4447TLdq1co077Oll17a9IIFC0x3797d9NixY1PPrUePHiGEEF566SXbxpUy7WKu\nwjheXJl4q+wVV1zR9JQpU0zTsj788MNNX3zxxaa9lWAhZLnHdtppJ9PDhw83XYp7ldT1d4U3tnye\nuE9etMIRQggRBU04QgghopDbUivWkjJvtMqMGTNqPAf+sJrG999/X+P71PZHvhCq2yT1lWKNL4+z\nxRZb/O2+dW0jlBIvwIX2GqPOGMnG6zJkyBDTe+yxh2k+O6usskrq8b0ftMeMGfOX/08L64cffjD9\n888/px4jy9gxyIDMmjXL9CWXXGKaVk5dPVNPPvlkjfvQ5v/qq69Ml+v93LhxY9Oe/clzzxIgkRet\ncIQQQkRBE44QQogo5LbUvOVU3mV23oiTLMmhyft657LOOuuYfv/990170UNZyHs9+F7lSLHsAB6n\npmtKK4i5J7RRzzvvPNNnnnlmMU6xLKF1xWtIG43baU1/8803phO77M/wvkzei8fjc8ZcGj6vSf7O\nn/npp59M047h+Hv5PLTyvHuwWFFqXs6Pl8fknQ9tNMLovvnz56cevy5st7y5eozq9XKv8qIVjhBC\niChowhFCCBGFoiV+cpnqLdEJ92EyWGVlZcHn4i1XJ02aZJrJc17pDy6r8yYSelYez0H8H0wCZvIi\nrZgsNhrHjuPrRUEefPDBpu++++5sJ1sAzZo1M0270Ht2iBdp5t273E4bN237csstZ9tobXFcaKPx\n/Xlt11prLdMff/xx6rlzTHlePA5LALE0ULHwrg3Ja3nxOJ61SFq0aGGa0YDJ9x+/J3iMvN9DWaKB\nvfJfWaJ686IVjhBCiChowhFCCBGFgiw1Lq25FGekTRYKsdFoV/3zn/8MIYSw2moLK2U//fTTpu+6\n6y7TXGrOnj3bNJesxWqb0KlTJ9MffPBBUY6ZFSbUnXXWWVHfOyu85rQmvGrhrB/mRc9ksQ9i2Gg8\nb1ZfXn311U2zejGvRd5oqhVWWME07RDaYWzLkezDaCRet+WXX940671NnDgx9bw+/3xh0WC+J6PL\nvMrYfC8+m0xW5PUrFp5Flbd9BO1Efifxerdv3940bbejjjrKdDLm/A596KGHTNNi5Hebl5jrPQfe\ndzctNe7D2pNZakx6aIUjhBAiCppwhBBCRKEiTzRGt27dqphcxiV0luiJmqJlQvCTBLnsf+qpp0x/\n8sknppNlLe2KNddc0zQttf/+97+m3333XdOMkuKyNwt5k1+rqqpCRUXF+Kqqqm653uhPdOvWrWr8\n+PGp/6+uOquyFcG3334bQqjetZL//9FHHzXNsZg3b55p2miM6ikFxRiXbt26VY0bNy506dLFtrFm\n2i677GL6scceq/beaZp4tiNhMzQm0zZp0sR0Yv3wnue1pV3JJmpeFOq0adNM08rx7kHabkwI/ZsE\nxZI+Kx7ec83tU6dONe1ZZxw3JoeyBmSbNm1CCNUtMt77PB6bSI4YMcK09xMBz5fJ1kxOzWsx5n1W\ntMIRQggRBU04QgghopA7So3LUUZfMZHNw7MLvMgcRkawIyDtgl69eplO7Dgem1FJtHT2339/07QL\ndt5559TteWq5/R077rhjjfvUBkYoMWEvpo3GxEZaBkkdNHahZLLhPvvsY5rWCq22Qw89tLgnGwna\nK++9955pfrYslg3hM0KbhtYLx53WWGLZhLCwiyijv/j+r7/+umla07Rs+Fov2onwM3nRa/xM3O5F\n7ZUa7/uE21u3bp36Wu+ngz59+phOayvBOm1Mon3llVdM9+7d2zRt0xtvvNG0l8jOyEgPr+4dowjz\nohWOEEKIKGjCEUIIEYXclhqXf6xvdcUVV5jea6+9TDNpictRb1n2/PPPm+YSndYELThaeckxGeHx\n4IMPmj7llFNMc6lJC4qRNp4dVUjkFyPsigk/Q0w4pq+99prpxK4JYWFkDfe9+OKLTTOp0Lu/YlqD\nxYT3/yGHHGL6nnvuMc37nDYGo8c8u5b3Iu0nWpocCyYo9uzZM4QQwrhx42zb2LFjTa+44oqpx/Oe\nP699gFeWn+fO7wNa9THbeWSJMqVV6NXA4znT6r788stNs90Er3NynDfffNO2vfTSS6Y5fuutt55p\nPkPsDsuIP8+i9fA6tWbp0OyhFY4QQogoaMIRQggRhdyWGhMwL7vsstR9nnjiCdNefSsuQdu1a2ea\nkWRMDOPSndYEE66SZeVnn31m284//3zTXsIcbYxSJ0rWVaRNqejXr59pRurQ4kssI0aj0SbguDCZ\njeNSX+F433nnnTXuzzqATMjzum963TSbN29ueqONNjLNSLYkEXXChAm2jeNGe5NRhbS/eDwvIorQ\nVuW4MzqUNjhrrBXLNvaecS9CkFGxTHzncRglRkt/t912M81x4/Hfeust00knYtZJY7Jn586dTb/x\nxhup2z0rLIstS7L8pJCXhvXtJ4QQomzRhCOEECIKuS01lj33lqZerStGbHB5yWXzsccea/rFF180\nPWvWrNTX8piJdbPffvvZttGjR5veYYcdUs+LFpyXsMbPWojtVkjSVLlAu4ZRWLQJOKaJJcAIREZg\n0bKgtXLBBRcU6YzrDq8jp5dASIuY+9OO5mv5LNBSY1QZbTpaQonmPbn22mubpn2+2Wabmb733ntN\nezaX11qC78XoPNaTy1uTMC9ZnlmeA68Zz79ly5am2bWYVuG+++5rms8Ez+H+++83/cUXX4QQQth1\n111tG79zadGxlqXXqsCLpMvSldmjkDHRCkcIIUQUNOEIIYSIQm5LjUlZSURFCNWXl0yeJLRRuOzk\nEnDYsGGmuZT1lnFc0ifdNLlEZRsCb6nOLnq0K7zud972LEvNQpKmygVeIy9ihdfl6KOPDiFUHyse\ng20jGLEYM6KvVBFxHTt2NP3RRx+Z5r2SJWGSeBGWrHdGO4xRS9xn1KhRIYTqls2GG25omt02+Uzz\nufRqo5EstdH4HcDoVEbB8fuj1HgtATgmkydPNu1ZiBtssIHpBx54wDTrNPJZSK4523fwJwp+f7Ro\n0cL0oEGDTGdpMVCIbSlLTQghRNmjCUcIIUQUcltq/fv3N01LjUtuLte4VOYSnfYKuzzmjZhIS9xK\nOhmGUH3ZSbi0f/nll1PPPUvtIS4vGW3FbpU8Tn2tCUauueYa0941Yi2o++677y/7Mrpwu+22M80o\nIEYVPvzwwwWccc14yXKFcsQRR5hmUqvXibFHjx6mWdeM8B6i9cNETd73tMAYKZi0FmB9Lo4L7bfp\n06ebph3E58iLfKKlxvHl88LrTwsrb9fdYsH3ZTSdZ4lzH14Tdnbt1m1hU0wmx7P2ZGKlcSxZa42t\nBxiBy5YRHp4Vxui5UtuWWuEIIYSIgiYcIYQQUchtqXn10wgtAi7tGQ3DfYpVvyyp9+R16uSSMqkj\nFUL1BCpGoGUpq07tJY2WInktNhyvb7/9tsb9//e//5lOoo5orzLRj1FJvFa0DOorp59+umlGlHlW\nEa3ILJ1AeU2Z4Ondo6uvvrrp5H5ld0l2kaRNlESAhlA9qorPiGf1ebYrbTrPYmQNN35/FAKPzxpo\ntMF5vbNElnJ/XmO2DeAzQdufNmYSpclznDlzpukOHTqYZhsC4t03XgRuzOg/rXCEEEJEIfcKh/DH\nQP6FwlmVDYC8v/S9uHGPmvIzmjVrZpozudevnX9t8q8A7y8b/iXH6tbs7x7zr4YY8IdFBn947L77\n7qZvvfXWEEL1BlSbb7556uv41xn/CuRf4fVpxchzzZIf4a3w+cMx/9Ln/cr7b4sttjDNH+T513JS\nxqZNmza2jVXZOeb8sZ+fgz/8c7XlBROcddZZplml+oUXXjDNvJNSBHPwe4urGg+vPAzHhJW96QCw\n9NOBBx6Y+r59+/Y1nYw/V5dcAfXq1cv0VlttZfrjjz9OPUcvICBLHk4pKudrhSOEECIKmnCEEEJE\noSBLzbMIvB8svdIX3g+i3jG9JeCWW24ZQqieP0BLbeLEiaabNGlimnkKXtkazz585513Uvfnj51e\n9ez6BD8D82O8CrTM7UhyP1iJOEuO0xlnnGF63LhxpmlfZLHXvPyoGGQp/eLlJ9E6o11FeL+2atXK\nNK8/A2T4I3kSrLHxxhvbNgbQPPfcc6ZZxoVWs3deDJDgObIEC3PxaP3wXitF3poX3OPBc+BY8T4k\ntAFZtXvo0KGmvaCZ5B6hzc/7l9fp3//+t+nBgweb5vcTAxhoqWV5bkrSgLLoRxRCCCFS0IQjhBAi\nCrktNa98BaNlGNHC7VzqeU2kvOgJWg1etMWkSZNCCNXzcM4999zUfS+66CLTXKZ6sfheIy2+lkts\nb1ldV6U6CoWf/9prrzV90kknmeb40oJMLM4sNhrHllW889poJLaN5sG8CTbm4rX1cpy85m20rubO\nnWuaOUy01PhsJhbcmDFjbBstN1o5vP60rD/88MPU86ItxnuBNhqtLY5R165d/3KOIVS3oYoFv1d4\nbrxOtBD5WbJYc7wO2267rWlGBvL7L4niY3QbK/SzDBfzrgYOHGia0Z19+vSp8RzzVo7O8hx7aIUj\nhBAiCppwhBBCRKGgKDUvAZN2UtOmTU17y2wehwlPtJ8YDcOyGYzwSF47YsQI20bLgcvzrbfe2vTd\nd99t2lteehEbXIbzXHjutDr4uesrF154oWlGMg0YMMA0bYhLLrkkhBDC8OHDbZuXVNa+fXvTTFKs\nT8mehOe9zz77mPY+P/f3IiO90jJM2pw6dapp2mSMyEwsaCYT8l7luTCqk5WJeV60hrzILm6nbcXt\n48ePN82K9MWC58Pnl3hJ37TRvPEh3IeJrkzU5DOUWGlMmGc1fUYu8vuGib6eXUeaN29umvcTE6xL\nUapLKxwhhBBR0IQjhBAiCgVZah6MbuHym0sxLtcYKeIlSXJ/LgFp4/Tr1y+EUL15EaN+mIy50UYb\nmb7nnnu8j2J4kRm0AmijeZZJ3rpx5QLHjtd01KhRpmfNmmWajceSmlNekihtDVoJDaFZXRbrzLNx\nec/Tak5LFAyhesQYIyNpozERMLHPeDxGPvE9CeueebXOstiBtMk9m6YUSdMck0KexyyvZfQdxyFJ\nUs8CrwGvGcetbdu2pj/66CPTrHvI2m+0XHmv0ObMax9mQSscIYQQUdCEI4QQIgpFs9RoCzCSwrNR\naAVwqUm8ZTYTz7hkTOwAr4kXl4UtW7Y07SV8eVE3WaI0GB1XrMZR5QI/P5f1tNfSEmh5Hbi895p7\nZWl8Ve54peJ5b9GK5XPkJUczOZbX30sgZYQZo5CSMeA27kuLjgmHXqsILzman8mLfGJdsPPOOy/1\nOMWyo0th1dKiZ2SdV2vOi9xLPi/vFd4HSV3CEELo37+/6QcffND0sGHDTPM+4D3E70La2F5ierGu\nvVY4QgghoqAJRwghRBQKstS86Bou3RjpkqU9gXd8anY2ZERcAi0yJp5effXVpqdNm5Z6bK9HO/Ei\nNnicq666yvQxxxxT4zHrK7RDr7vuOtNMzt11111DCNWjEQltoVJ0eKxLaNFmKbvPe8urMeh116X9\nROuKUUi0NZN9eAxGGn766aemac3kvYezPN+XXXZZ6j6leF6yRAjmxatXx+N7NRg5nsn3JRM5maS+\nzTbbmL7ppptM8zp5UYS091q3bm36s88+S/9QJUArHCGEEFHQhCOEECIKuS01LhFpV7GOEyPADjnk\nENMXX3yx6bw2Gi0ar6NoEs3BsvZHHXWU6TXWWMM0I3AaNWpkmtYBI6lo0zGSh/W+eL7/+Mc/wqIA\nl/KMKqN9dvTRR4cQ/OTZnXfe2XR9rZnmQRuje/fupl9//XXT3j1PvH2868UoSXbxZNfVZOx4/9Ne\noS3ntSLhmGfpykv4TNP6yftZCyFvOX7uz58LqPm9wWvC70i2e2DSZmJ/nnzyybaN9hfHlRG6N998\nc+qxvcRjz0bz7r9iXXutcIQQQkRBE44QQogoFNTxk20ANthgA9OMAJs8eXLqa7PA2me777676f/8\n5z+m09oZsLMil/y0Frh0ZLITo4S8FgpcMjOqJ4sd0tAsIw8mkyVdDJ999tnUfXm/NGTatWtnOmkN\nEEJ1u9Yr6+9Fo3m2M60XRk0xSi2xPVlXizY5nxfabl5CrhdRxvYItHu8KLw333zTNBMqiwXfi3UX\n2ZqBeFFttBx5fVj6f6eddjLNhFBew+uvv9508t3iJfTyvqG1T1vu1VdfNe11XPZay3hj2KxZM9OM\nEs6LVjhCCCGioAlHCCFEFApK/FxvvfVMe8mQrJOVdLMLofpy1KsfxQgfLlkvv/xy0+eee67pJLFu\n4sSJto3RL4z2YNdKRgxx2cuIHkZ1DB061DTtAq9zqVdPKQZZEm9LDZf4aTRkm5HW1gMPPGCadlWL\nFi1S9+dzRKuDVgqjKmkJ8fnifdmhQwfTU6ZMCSFUf/4++eQT07R9aPt5lrL3HUAbzau9xueoFDaa\nBxOXaT2yC/C+++5rmufPsfIiw+69917TTz/9tGl2NaUFl1xzRvQOHjzYNL/PGPVGa5DX9eyzzzZ9\n/vnnhzSyRAzzvQpBKxwhhBBR0IQjhBAiCkVrT8AlNJfWWeCSjpYal3TDhw83zSg1Ll+TqBvWGOrb\nt2/qvuxIyQQqRux458g6SN4+Xhn22NSVjUZowSTw+jRkS43103j/tWrVyrT3+fkcebUEmWDLaEva\nuOziOWbMGNOJhUQ7i6+jNUMrjrYb8Ww8L8LOa6fg7VMseD68xrQQaaN5eFY57TImvjNJnFFobLeS\nWHw8F14D2n6kT58+pu+77z7TbPuQl1I8l1rhCCGEiIImHCGEEFHIbal5S+W8NYm4jGd3yAkTJpg+\n44wzTHfp0sX0I488YnrzzTc3ffjhh//lPZnoxgRDLocZgeEleRFGhDDKxVv+560x1dBIri8tn112\n2SXa+5900kmmr7nmmmjvG0L1KMGOHTuafvfdd017FlKWthmsQ8dukLTRGLXZq1evv5xD+/btbRtb\nEvC8WHswSwsJniNbiLBbKTuHMuGU3w18LSP7CsFr9ZCXLM87o92oPZsx2e4ly3pJt7TRvFp0WZKK\ns+B9L2ZBKxwhhBBR0IQjhBAiCgXVUjvuuONMDxo0yDQToriE5lKMrQJoe3Xu3Nk0l7uPP/64aUZ1\nbL/99qaT2mtvvPGGbeNylVYAo1NuuOEG00ceeaRpb6lJGy0tSi6E6svghtzRMgvJtWbnyZjRc7Ft\nNMKoSy8akxFRtEa4f2VlpWlawN7+jIhiZBNrHiZ1udhOhFF1rGXI8fKsdM9qoWXufQd4bU+8iLhC\n4DNbiKXmkTeyLs324ndiFssrSxfiYtV0LOS1WuEIIYSIgiYcIYQQUchtqbEEOstq0yKgjUa8MttZ\nlqBcMjI5k0mFSdQNbSseO607aAghnHjiiTW+vweXl7TRCCNLConwqE+kRQItinYirwPveUY6st6W\nF1XkRY95zw5tFUYHvvjii6YTq4vvzxYSvXv3Ns2oKS9SKou95iVHc3shLU2yUIiNVkhHTM/S4ndq\nYmnSwuR3lZdQ7n0mLzLNI8u9pSg1IYQQZY8mHCGEEFGoyLNkraiomB1CKE72lUhoXVVVtVrNu/lo\nXEpCQeOiMSkJelbKk8zjkmvCEUIIIWqLLDUhhBBR0IQjhBAiCppwhBBCREETjhBCiChowhFCCBEF\nTThCCCGioAlHCCFEFDThCCGEiIImHCGEEFHQhCOEECIKmnCEEEJEQROOEEKIKGjCEUIIEQVNOEII\nIaKgCUcIIUQUlqh5l4U0adKk6uuvvy7VuSxydO3aNYwfP35OoU2lso5Llt7oyyyzjOmffvqpkNMq\nGaussorpb775JnWfLl26mH7zzTdzHb8Y49KkSZOqysrKMHnyZNs2d+7c2h4uNG7c2HQpn8Gll17a\n9M8//1zr43j3WpZ78G+I9qyIbOR9VnJNOJWVlSW92cuZiooK08VqWjdu3LhQUVFRcPfBysrKal9m\n3vmtuuqqpmfNmmWan62ystL0Bx98UOiphRBCWHzxxUMIIfz+++817rvYYgsX3X/88UfqPr179zY9\ndOhQ0/zcY8eONb3kkktmP9lQnHGprKwM48aNC/vvv79tu//++01n+Zykf//+pu+44w7T3n2ZXPMQ\n/OuenAPff4011jD96aef1vg+accLwb/XmjRpYnrGjBmpx/kbSvqs5H3GS/GdUJfvUxvyPiu5JpxF\nmXIb6D+T5fwaNWpU42unTZtmmn9V//LLL6YXLFhgmqsN7y/45Etm5syZNZ5jls/x0EMP1biPN8n0\n6NHDNCcl/uVdTIYMGWLam2Q4OVDzmnOS4blyRfLDDz+Y5kr1+++/Tz03vlfCZ599lrov35Pn7mnv\nDxpvkvGuTSm+bL3jeNu9c8h7Pln+CEj74yzveZUz+g1HCCFEFDThCCGEiEKDstRq+q2gPi5Biwl/\nwPagRfbFF1/UuL9no/Faz5kzJ8PZ/R+lHhfaaKQWP2DnhlYRLaQsv20ddthhpmmveeftWYQcl19/\n/bXG963Nvn8my5iW8/PondsGG2xg+u233zbtfc9k+V5K26dYll5eSvF9qRWOEEKIKGjCEUIIEYV6\naalxqde8eXPT06dP/9t9Yy7bs0SklCO00QrJmchiJdQ1Me4N77heKLS3/c4770zd7kV3zZ8/v8bz\nST5/IaHBK6ywgunvvvuuxnNkVN2PP/6Y+l7cnzqG7ZkH2mgkS9g4x6qm65wlSs3bniXkPu/7FoJW\nOEIIIaKgCUcIIUQUys5S4xKdCYaECYk1JRMWsizs2LGjaS/rPm9ESgyaNm1qOkuypQctjHKK8MuS\npZ+lFMzjjz9uul+/fkU6Ox/PosxijeS15rKQ9r48R9rCnTt3Nv355wsTy1n+qFmzZqaZ+MmqA7T6\nvOvB+/err76q4VOUB949udRSS5lmIi855JBDTN94440hhBBuuukm23bOOefUeAzv/bOUgcpCsZ5/\nrXCEEEJEQROOEEKIKJSdpeZFrhBaJFz2p1kEeSM2uDTlcp7RcNxe1/ZSGrTRxowZY7pnz561Pmbe\nz1lKC47HO+mkk0y//vrrpr/88kvTtBJ4Dxx55JGm0+qKFQMvqY8FSJ977rnU1xYt2Q73NOvptW3b\nNoRQ/Zk74YQTTK+22sICwDvssEPqsWnx0Aa64YYbTPN+9JJfyezZs00vu+yypnmepaCQe9b7buFn\n3HrrrU1vuummpv/1r3/9Zf9jjjnGtg0aNMj0xx9/bNr77ltuueVMz5s3L9sHqAElfgohhKhXaMIR\nQggRhbKz1LzkLi4fGfnxySefmE4abb322mu2bfDgwaanTp1q2isP36pVK9O0ZRgxlyVKKm+/k0Lx\nIp169epVlHPia2m17LnnnqZpNR5++OGmDzjggBBCdWsr7xKdfWW22mor04x62myzzUzvs88+pr3P\nWkgEX1a8hmYvvPCC6bx11bLACLB27dqZ3nDDDU0nEaFnn322bVtppZVM89rSmmHUGS2vXXfd1fQV\nV1xhmp+vprphIVT/DoiZ7Jn3nvSSXtkag5Yjx3z06NGmt9lmG9Obb755CKH6d1KWRoi8xmxTUW6W\nv+aDQoAAAA7PSURBVFY4QgghoqAJRwghRBTKzlLzoNV18MEHm+Zy88MPPwwhhDBw4EDb5tlI3L76\n6qubXmuttUwny9sQQhg2bJhpLp+948ew0QjtCVqOtCQ6dOhgupD20WxDfO2116a+180332w6sWa8\nml20D3gM2jtsTbzRRhul7n/hhRea3n777U0/9dRTf/t5QijdePH8SmGzelYq7wHuwwTOxHZcfvnl\nbRs7vtIioxXHREUmR7NbaJcuXUyPGjXKdF6LbMCAAabPO++8XK/1KNY4eDYan0Xv+Nwnbf8szwrt\n2k6dOpn+6KOPTPOngGLZa6eddlqtX6sVjhBCiChowhFCCBGFgiy1mPW1WF+JUTe0UR5++OEQgl9v\niPB8aT8wwu3VV181fe+99+Y847h4SXQcIyaN5YXWyUsvvZT6vowYPPnkk02nRSN5ded4vozqeuCB\nB0zffvvtpr///vvU1xYShVfMe5mfjRFdvOe+/fbb1Nfm7ZTpPY9M2mS9s6T7Ka2wW2+9NfXcZ8yY\nYXr8+PGp5/7YY4+ZnjBhQup55aVYNhopxEbbfffdTbMWH5MtvfGk7cb9GUmbRGDSOuvRo4fpoUOH\nmmY0GiNqS50gy58sGI2YBa1whBBCREETjhBCiCgUZKnFTCqivcJ6T4WU3E5gnbS33nrLNC2QcirP\nn4ZX6r1YLROYQEo7iMdnDaw87+VdT0YgeoltxepuWCr42Xje1CRLOXsPXotlllnGNO8Nnk9y37/y\nyiu2jRall0BIO+jXX381zSjIJ554wnSWyDTaTTymV8OwrnjkkUdSt3sdVjkmjCqjzbnuuuuaTq4V\nrwcjNL3vIT573J7lu8o7ZpZurnnRCkcIIUQUNOEIIYSIQlknftIWYDKTZ0fUBLtAMpKD0TVcRhKv\nPhKpS9uNtkX79u1NM5GPdkleWHqeFg1tLEYv5cGzAwltFkbw1GVn1Sx4EVpeVFxeG82D9zejClkT\nLencScuG1jWfBSZez5kzx/Qtt9xims8rxyuL1eklyJaDjUY4nlnsXG+ft99+2/Taa6/9t+/Zp08f\n00yo5n3jJbXnjXQktNHU8VMIIUS9QhOOEEKIKJS1pUZ7obYdGVdZZRXTXJruvffepldeeWXTXDoy\n2TRvMmlseN60HwtJuiPe9WdH0SuvvLJWx2YtOybNedapV7eqELwoo0KhFTV9+nTTtD2KZaPx/uPx\nGfnGaMNnn302hFA9Eqxv376mt9tuO9O8PozknDx5smnW7SJZ7Bgvsoo2ODv91hWFRIBxHBI7M4QQ\nnnnmGdNJBC7r2zHZ03tPL8qvWHgJxnnRCkcIIUQUNOEIIYSIQm5LjWWw33///aKezJ/hMo5LRq8r\nYbL8ZsIg7aVJkyaZZrl1RuZsvPHGqccud1q3bm16ypQppgux+Wh1ebZI7969U/epCe675ZZbmmY3\n0cTyCaH6ODIairXB+Lk92rRpY5p2EO+pYlqj7E56zz33pO5D+6tly5am2aE2CzxvWqC0Z5J6gyEs\nbL/Bdh+MTOMzx8g0Phe0QAtpz+FZQuVgoxWSjEvLlxGCHPN33nnHdGJLs2Pummuumfo6L6k7r73m\ntWvwnnlFqQkhhCh7NOEIIYSIQm5LrdQ2mgeXsv369TNNC+KSSy4JIfjJWYwYYsLaqquuanrixImm\ny7E2lwftpLxJWo0aNTLN5NBZs2aZ5vWn1cVrRKuL1zSxXZjcxwjArbfe2nRaXakQQvj0009NMyEt\n7xjRRiOMVCwmno1GOEZ5bTTC2n9Mpl1nnXVMMzpq9OjRIYQQ9t13X9vmtbng9aHF4yUf5r0HPevH\nuzdjUqwoQg9ansn3K7vq7rnnnqZvu+0203w+C0nM9J6hUkTdaoUjhBAiCiXJwylWGYQsK5WDDjrI\nNP+qS2CJDzY6Yi7ByJEji3K+dYl3rbJ8Hua78Mfm9957zzRXGE8//bRp/pXFv475Y+/6668fQgih\nsrLStvFHUeZE8a+9tm3bmh4xYoRpNnpjgEghuQgxAkS8v9aL9YzwB3/mr3BVN27cONPrrbdeCKF6\nBWQGBbFEEoM5CPPc5s6da9r7TDxf3mveD+B1taopNVxVsIr0brvtFkKofm1YBofffTNnzkw9diG5\naV4AQbHQCkcIIUQUNOEIIYSIQkkstWLZUjxOEhAQQgiHHnqoaf5QmtZLfI899jDNasb84TlLg6hy\np5A4eVpR/DG/e/fupmnFXHrppaZ5/WlvMZjjzTffDCFUt1/YxIt5DrRcaAux4nHPnj1N0worxBaL\nYaVmsYfy2qG0kZk3tcsuu5imvUmr5oMPPgghVM+DYq4IX8cGX3x2unXrZpq2p2fNUGd57kpdgT1L\nNe9SVCTnOPCaJLYzn4kDDjjAtGePFuvalDpQSiscIYQQUdCEI4QQIgplXS2ay1pGTHHZ/+STT5pO\nlvQPPvigbWM0FO0HRlo1NJg3wKV5lv0Z+cLtnTt3Nt2xY0fTF154oekk6imE6nkEiZVGC4XWAKPR\nOEa0O2jd0N5Ji0wsJ7y8Fs8CzRvdRRuN14LRg8ybYomaJPJsyJAhto0Rgyz/lOTshFC9FNQXX3xh\n2osSzGv3eGNaCuv71FNPNc1q53lttLzWH62r0047zXTXrl1DCP59Uw73O233vGiFI4QQIgqacIQQ\nQkQh6vosb9VVLjvvv/9+04yGYVOrtKXsXXfdZZoJgx06dDDN6KpSRKTEJouNRhgxttZaa5lmmR/a\nGbQ3WXaDJVRozSX2DseTUWys4u01euPxOEalaDZVTLL0uidZbCkmCjIys3///qZpWTI6kPf6tGnT\nQgjVo/tol7ISN5NWaaPRXuMznSXayUtW5r1W28aLWRk4cGBRjuPZaF60Hvdncvo333wTQvCrl99w\nww2Fn2yBeAmnWdAKRwghRBQ04QghhIhCVEstr/2R9PcOIYQLLrjAtJeoyIS0BNaAoi3AatFXXHGF\n6QkTJuQ6x4YAa6mxGniW5DeOKRtJ1RSps9lmm5mmLXr33XebfuKJJ0zTJqQFUe5kaWLl2UmeBc0E\nUkYtsSYax45RnbTUEmj1eHYlz+vjjz82zerWeaPRskTn1UeLO08jwhCqVxRnUnsCx56W91dffVWL\ns6tbtMIRQggRBU04QggholBySy1vQhT3p9XlRV7RJkssNZZpf/31102zzPdDDz1kmlYQo2Lq43K+\nUIr1mWsa9+uvv970iiuuaDqp7xVCdeuIyaHvvvtuUc4xBvzstLlYg46WJvfJEtVJqytv9FDSCqJ1\n69a2rU2bNqbZUI+Jv8cff3zq+xerzQKPQ8uwFImfpS7H78HPy6Z4SSRtixYtbButTZ5v3u9W3nN5\nbeli1bTTCkcIIUQUNOEIIYSIQskttbzLL9oCjEbzOOyww0wnSZ7Dhw+3bVySJ930QqjenbAUlNoK\nqI8wAZGtB3iPnH766aYHDBhgmsmmvC9oAca0RLLC+4Cf02tVwOvCmnFNmjQxzbYBWZ4vry5X0j1y\n2LBhtm3VVVc1zYRQ1hnjuRfrmnufoxTPDu2hUtwzWaIReV/wHM4999wQQvUakUz0pbX52muvmc5y\nnbhPXiuxWO0PtMIRQggRBU04QggholD3ta5D9aUmI3a8BCraKKyxlpRev/XWW20bdZb6bcUito3G\nBNiRI0ea7tSpU7Rz8OyDhN69e5vmMp7L+1deecX0qFGjTLNmV4zunMWC9wFbCdDS5f3MCEt+5qRr\naggh7L///qZ5vQhrovXq1cs0EweT2ne06zgud9xxh2k+Z3UVzVWKTsKltr698+eYM0pz/fXXDyEs\njCAMofr3Vo8ePUyzTiSP510nL/E+ZmSuVjhCCCGioAlHCCFEFMrCUuMScNCgQabZuTMp2x1C9eiZ\nNEpdwptRUtS0A2PD6L6YNloe2E2StgztpSRKJ4TqFkDe+lRZiJ30x89A64z3NtsKMCGTtgujymi9\nEC9BkLXUkhprTKSljXnRRReZLsX18ewm1mpr165d0d+XlNr6pl3lWV2sAfnSSy+FEKpbW0zY3HHH\nHU2vvPLKpmfMmGE6730dM8FdKxwhhBBR0IQjhBAiCmVhqXFpzcgLLv/Z2bCuodVTLh0nixXNU6zj\npL2WdimTcBklVYrryc/Ur18/02x/UCpob9D2vOSSS0xvsskmpnfYYQfTrLHF7pu04Hidad/QKvr0\n009Njx492vTtt98eQqhet+vRRx81HTMajfZQqW20UuA9N3ktu6SW4DXXXGPbTjvtNNO0n5kYTLxx\nq6u6cdXOoU7eVQghxCKHJhwhhBBRKAtLjUvQvCXWY8EaU6Wuw1YbSpEUlwVG6Xl2WJKEOGLECNvG\nJT3bUBTrvLzXPv7447U+Tm3wrItzzjnHtPfZaNMwaZT11s4+++zUfdjRllFfjKRMs3tiJtXyvdiV\ntD6St6add18k25n0y2TP8ePH1/YUy6LWoFY4QgghoqAJRwghRBTKwlKrD2Sx0cohCiSEELbYYgvT\nL7/8cuo+xeqwmCWqLIm84fuwm2SpI/2YHLlgwQLThXRAzIrXqZb1sbJEBk6fPt00x+Wqq64yzXu0\nLjrXep/D61y63377mWatthjjUhfk+U644IILTJdDe5NifbdphSOEECIKmnCEEEJEoSSWmreELidK\nYTnUpY3Gz0MbjQl1rNnkfeZCugLWBI/ndaEsBbTRSAy7JkvZ+EaNGplmN03u37x5c9Osm+VZvXxf\n3hvLLbfcX97L61CZF689hWcfPvDAA6nH4T1YivYEWajr77BysNFIsb7btMIRQggRBU04QggholAS\nS61cbTRSn7pGZsGzyLIk1Hn2Yiktwmeeecb0dtttZ7oc6sAVE15bPheMBvQsP36eqVOnpm7PAq9F\nTZ1TeWxqni+jCvNe5yz2XRYbstTUh++wUncrLQVa4QghhIiCJhwhhBBRqMizZK2oqJgdQvi8xh1F\nHlpXVVWtVsgBNC4loaBx0ZiUBD0r5Unmcck14QghhBC1RZaaEEKIKGjCEUIIEQVNOEIIIaKgCUcI\nIUQUNOEIIYSIgiYcIYQQUdCEI4QQIgqacIQQQkRBE44QQogo/H85TFMYGfu2twAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2baacfeecc0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# with 128\n",
"_ = view_samples(-1, samples)"
]
},
{
"cell_type": "code",
"execution_count": 105,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXm8VWP7/+9TlFl1RKl0NImoKFOIlKh4PKEeepQp8zyE\n72OI+IZQNKBQyBDVk1kImVUnmdJAlKFUSubZ+f3x+67L+7Duzlrtve+zzzmf9+u1X69Pq7XXWnvd\na+11rs++rusuKCkpcUIIIUSuqVbeByCEEKJqoAeOEEKIIOiBI4QQIgh64AghhAiCHjhCCCGCoAeO\nEEKIIOiBI4QQIgh64AghhAiCHjhCCCHCUFJSkvhVWFhYUq1aNXs55/TK4NWuXbsS59zKNGPgG5fy\n/iyV6ZWNcSksLIy2o1f2XrpX8uyV9l5JFeEUFRW5DTfc0F5pqVatmr1ySaj9rI2CggJ7+SguLnbO\nuSWZ7quoqCjTTQiQjXEpKiqKtiOyh+6VPCPtvSJLTQghRBDWS/uG77//PtX6Z5xxhumRI0em3d06\n8ccff+R0+4xafM1PK2pT1CSfTQgh1gVFOEIIIYKgB44QQoggpLbU0louoWy0TGByQRI7jp+b7+Xy\nimpHlcdxN2jQwPTnn38efP9CiDAowhFCCBEEPXCEEEIEIbWlVl5WUS6zpzLZXq4z4iorHM8+ffqY\n3mGHHUzffPPNpt96660wByZEObLeev//K/m3336zZbxXRo0aZfqEE04wfdddd5k+9dRTTefb95Mi\nHCGEEEHQA0cIIUQQUltqpHr16qZ///33jA/mr6TNHisLHi9tNIasvs/RoUMH06+99lrGx1KViLLQ\nnn76aVtG68zX/ufXX381ff/995uePn167HuTWKO5vmZD4GvZxHvk+uuvN3355Zeb/sc//mF60qRJ\nf9set1FRz08+wXO7Zs0a0z/99JPpunXrZryfk046yfTpp59uWpaaEEKIKokeOEIIIYKQkaXmC7lD\n9uOKs2N8dtnAgQNNX3jhhaYZ9q5cudL0OeecY/qpp54yvfHGG5vmOWCYTGrVqmWaYXVVYdWqVc45\n50aPHm3Lbrrppth1aVfyXL3xxhux66e9viqDTeSzSUaMGGGatiOtycmTJ5vu2LGjc865b7/91pYx\nY/CXX34xffXVV5v++eefY7ct/s7FF19smrbX3Xffbbpp06am999/f+ecc8OHD7dlSTrzv/jii6Zr\n1Khhmtlu+YAiHCGEEEHQA0cIIUQQCtJYEu3bty+ZPXt21g8ibeZQYWGhaU6o9PrrrzvnnHvzzTdt\n2e677x67DVoB3D/f26pVK9Prr7++6X79+pkeM2aM6U033dR0ly5dTE+bNi32GEpKSlxBQcHskpKS\n9rErJCRX45IJW2yxhekZM2Y455xr1KiRLYsK3JwrbYvRrqHme7/77rvsHuxfyMa4tG/fvqS4uHit\nE/BlgyZNmpieOHGiaWYBEl7fbdq0Weu2N9hgA9Mff/yx6T333NP0l19+mfxgM6fC3Sscf9+1UNZ3\n8Pbbb296zpw5pgcMGGCadmrI4vy094oiHCGEEEHQA0cIIUQQMspSSwIzwHr37m16woQJppPYaM88\n84xphvRxGRy77babaYaXtNFoJzDUZTYaj50W0B133GGarfWJz0arzNCaZLFhw4YNnXOlzyHPOa0z\nWje1a9c2ffzxx5seO3as6Vzba+WJz2pmluR7771numbNmqZ53R933HGmI3vTuT+zAK+88kpbdvLJ\nJ5vmGDVr1sw0rePAllqFIxtTlvA6WLRokeklS5ZkvO3QKMIRQggRBD1whBBCBCHnlhqL1Gij+aCN\nxSwxaloKcZkf3Cf1Cy+8YHrBggWmGY7SCho3blzsMTLE/f77703TMvIdQ2WD48XswcMPP9x0dL44\nVrQ3afkMGjTI9FZbbWWavcHuu+8+0yxOpK5sMEuycePGpnkt8jpj63qer7hrsUWLFqaTZNWdcsop\npq+44grTP/74Y5nvFenp3LmzaX6Hzpw5szwOJyMU4QghhAiCHjhCCCGCkHfTE2y00UamaW9tvfXW\nZb537ty5zjnn2rZtG3tcSTI52EuNGThczqJOn01U2fD1x2OWIMduk002MR3ZOLRz2LOL5+22224z\nfcMNN5jmtXbttdeavuaaa0wzw62iZO2sDZ8ty15Zb7/9tulevXqZZgaTj2hM27dPV0vJHoOXXHJJ\nqveKtdOyZUvnnHObbbaZLfvmm29MX3TRRaZ57VcUFOEIIYQIgh44QgghgpCT6QkygVlfnJ3Qx9ln\nn236iSeecM5l1pKbmWx77LGH6eXLl5tmNk5lsG6SkGSG1GOOOcY0s80iS4CzdnKcaZfRSqB1xgxA\nsnTp0thjrKice+65pm+++WbTzMxs3ry5aZ5nnoskREWEPOdJoL3HImvNhJscZnc+9thjpg866CDn\nnHM9evSwZd27dzdNO5WZixXFzleEI4QQIgh64AghhAhCzgs/08JQk0VORx99tGnOUHj++eebjgrc\nuA1f0aUvw47WDbOeqjo8p4TFlk8//bRp2juffvqpc85vefH8c5ZPjvPmm29umhlYLDb9/PPP/R+g\ngjBs2LDY5Sx8jqxj59Lbu506dTLNqT3SwGLPd955x3SSmX55f6XNIK3o8B7aa6+9TNMyi+CMuMxG\nY3ZnRZy9VhGOEEKIIOiBI4QQIgh5Z6kxTGTGDrPEzjzzTNNR63vn/rTdhg8fHrtthrS77rqr6Y8+\n+sh0VW+3znNEzcw/n2VJ2+uNN95Yp/3XqlXLNAtJaddEmTzOVczit6TwM7Nvlm/aDGYq8b20j2+8\n8cbYdcrivPPOM/3BBx+YZr877mfhwoWx28kkg7SiU7duXdPTp0+PXSeyFlmMS9uaBfC8Pzgr6OTJ\nkzM+1lyhCEcIIUQQ9MARQggRhLyz1Mjq1atNs4fQddddZ3rFihWmo5lAx4wZY8s4m+SLL75oevfd\ndzfNflBsg18Vefjhh0337Nkzdh3aOLQJ9tlnH9Oc8TQum4a2UNeuXU0/8sgjpmnRcP0hQ4asdduV\nBWZu7b333qZfeeWV2HV87+W4MNstWofWGi1SWtojR46MXadp06ammWEo/g77Dv7www+m2Xcwyjpk\nlhpt5vHjx5tu1KiRaRYGH3vssabvvvtu0/mQCagIRwghRBBSRzj8kZbdfFetWhW7fpLc/CTwvaw9\n+Omnn0wfcMABzjnnpk6dasseeugh061bt45934gRI9b5uJLAeofFixfndF+Z8s9//tO0r1aJLTUa\nNGhg+vbbbzcd99ccW6jUq1fPNKMqtu4gjE7ZCqSqMGvWLNOM9pJEeO+//77pDz/80HQUnTBi4eRq\njFK5Dq8LJgEkSbjJRYf5igIjQF+X7Xfffdc5VzoZ6oILLjDNqJOtt2rWrGn6pZdeMs3O9qxlLC8U\n4QghhAiCHjhCCCGCkNpS+5//+Z9U6+fihyraYbRmDjzwQOecc3fddZct69Chg2naAjwubi9b0DrI\ndxuNSQC0vb7++uvY9VnvwdYm9evXN81kjch269atmy275ZZbTPNc+WD33Hz48TMEm266qWm2+UkL\nr+/999/fdPRj9S677GLLnnzySdPs6E1o6XHsaIdy/H2dxqsaTBSgjR93PfMcv/rqq6bZBqdJkyam\nmUDABBMmE+QDinCEEEIEQQ8cIYQQQchJHU6uJwZimMisucMPP9w5VzpDipkwtH+YBZKku3RaKlIG\nDs8nW5XQImEGElttsM0M7UvWDpx66qnOOf8kaj7YrbtOnTqmfVZPZSMTG43QGqX+6quvnHOlx5O2\njw/aaOxcfeedd5pme5WoW7hzpSdVZAbVaaedVuZ+Kzo8bzzncfB7iK23WGO4xRZbmB44cKBpfp/x\nO69FixYpjzj7KMIRQggRBD1whBBCBCEnlloubLQddtjBdDTRmnOlC56ibJxevXrZMmaD7LjjjqbZ\n8TbX0JoqK5TOJbQaOUbMLmMIzqI+WpfUzGpjMZtvwrY0sIUNrT5aNJyAja2QqkomW1qYJRZ1G05r\ndTLrbZtttjE9ePBg0xy7L774wnS/fv1MVwUbjdcnf2pg93tmbE6cONE559zs2bNtGceM9yS75vtg\n66FsFeFngiIcIYQQQdADRwghRBByYqkxdPN1ovWt7wv1ok7QzpW21+69917TF154oXPOuW233daW\n0dqhtcV1BgwYYJqdqLNFedpohD3oaKMw7Odyahb8cl51Zr6sa1Efx5w2S9RXyrnSmTotW7Y0vWTJ\nknXaZ1WFY7TTTjs555xbsGCBLUvSp43WECcB4zhG96Jzzl1++eWmn3vuuXU57AoFs9EeeOAB01Gv\nR+ec++STT0y3adPGdFyPNZ5XnntmgvrgGOaDzawIRwghRBD0wBFCCBGEjCw1Wi7MnuD82myNThja\n165d2zQzjcjYsWNNM0xlxkxk2UVWgXOli9EYrnLSoyOPPNJ0Liw1Up69pLhvhtpTpkwxTduT9gqz\nAbfbbruMj4XXC3s/zZgxwzStCWr26eIx5oNlkCs4bQSnZ0hSYMxx33XXXU1Hk+fRal25cmXs+5jh\n6JtojdYcs0Bpe1fmMYrglB2+Yktmd37++eemTz75ZOdc6cw18t1335lOkgk6f/78MtcJiSIcIYQQ\nQdADRwghRBAK0oS47du3L2FBUqkNIfzefPPNTTP8Zrt1WirM2GAWBltuM5T0HXMU9vsKAGkLEBZH\nMRvKR9oCKt/6JSUlrqCgYHZJSUn7MjeyFtY2LknwTdvA7LoNNtgg4+3PnTvXlrVt2zZ2/z58Uxgk\nsZTSzjKZjXFp3759SXFxcUYWKo+bPc44KyfnrE9yHmnxvPLKK84550aNGmXLON0HrXH2yeN1wX1y\n2+wDx953GRYflvu9khYWZw4fPjzx+3zWtg+eS87EzGzBXJD2XlGEI4QQIgh64AghhAhC1go/GdIx\nhGZhGMNs2gVnnXWWafY+YzYSt0PYtj6ybFjg6ctiYuv7zz77LHbbPpIUx5F8ycxhwSSzV5hFdNJJ\nJ5lmRhOLMFetWmWan582wO2332466rG1bNmydT72TKZ7qEhTRRAeN7O+okwm50r3lfMVVXJGT451\nlKV2xRVX2LK/Wr4RtMbZIn/kyJGmaWXTdvNNV+LLcq1McDqGNCSx0ThlCAumo35s+YgiHCGEEEHQ\nA0cIIUQQcj49gW+qAtoFnHGSoSHDSk4twEya+++/33Sc7UZbgMfSvHlz02ln+ayoFo2vCIwt48nL\nL79smtlFtEIGDRpkmjYabcpszaJalWnSpIlpWsa0yGhZc33eA75svwgWbw4bNsz0Qw89ZNpX+OnL\nyPN9B1RWG42wf1o0w6pzyfqgRXD8aEuzwLSioAhHCCFEEPTAEUIIEYScWGppKS4uNs0ZJ1u1amW6\nf//+sToOhqC0GdgGPNc2D2fRzCQ7K1/wZdpddtllgY+kcuMrjKRdvGjRItPMEhs4cGDsdsrKeOK9\n0L79n/V7LDZNkmmZL9mY+Qp7RlZVFOEIIYQIgh44QgghgpDaUmN4ni1bihYBt8liQ2avsT3+0KFD\nTfft29c551zv3r1tWXlllFUGG02EJ4ktxd5/ZPTo0aaZAebriRcVJU6aNCl2/7LIRLZRhCOEECII\neuAIIYQIQmpLLRfZXcwk88HisY4dO5qmxffwww9n98CyRHnO8imqDswq88EZclnMKUQIFOEIIYQI\ngh44QgghgpAXhZ+ZUFYmja8F+oQJE0wfeeSR2T8woGwfIYRQhCOEECIQeuAIIYQIQmpLzdfrKVv4\n+j75suPKOgZfC/Rc22hCCCFKowhHCCFEEPTAEUIIEYSCNLZYQUHBSufcktwdTpWkcUlJSd1MNqBx\nyQkZjYvGJCfoXslPEo9LqgeOEEIIsa7IUhNCCBEEPXCEEEIEQQ8cIYQQQdADRwghRBD0wBFCCBEE\nPXCEEEIEQQ8cIYQQQdADRwghRBD0wBFCCBEEPXCEEEIEQQ8cIYQQQdADRwghRBD0wBFCCBEEPXCE\nEEKEoaSkJPGrsLCwxDmnV5Ze7dq1K3HOrUwzBhqXijEuhYWF0Xb0yt6rXO6V9dZbz15p31u9enV7\nFRQU2IvrFBUV2aus7W200Ub28q3j24/vVbt2bXtxebVq1ezle2/ae2U9l4KioiK3atUq+3f16tVN\n//7772k2JZxzxcXFrqCgIOPJoP46LiIzsjEuRUVF0XZSvY/r52KuqrLuWe6f+o8//sjK/tdb78+v\nnN9++y12X2v53Fm5V1avXm3/rlbtT5OH54PnqU6dOqZ5n/Gc8Jj5WTbffHPT3333nelff/3V9KBB\ng0z369fvb9ug3nHHHU3PmjUrdv8bbLCB6R9//DF2O1y/S5cupidOnBi7nR9++MHFkfZekaUmhBAi\nCKkinL+iqKZy4PurM1tEf0Vm66/kysyGG24Yq/lXeSaRD+/ZTTbZxDlX+i9vbjuT/TBy4Lj7rq/y\nmnmYx8Zjrlmzpulvv/3W9DfffGO6cePGpjk+3OZXX31lmvcZOfbYY00ff/zxzjnnxo4dG7vuzJkz\nY4+X0csvv/wSu5wRy08//WR60qRJsetzHcLoLy2KcIQQQgRBDxwhhBBByMhSq8jk+sfZikQubDQi\nK23t+GyPJIkgmVzHtNLiiCy3JOv+lSRj7rPdQsLzR8trs802M920aVPTG2+8cZnb9CVm8D6jZffz\nzz+bHjdu3Fq3TZuVCQHrr79+7H74+bg+4WdiMgN1thJIFOEIIYQIgh44QgghglDpLTWGgltvvbXp\npUuXmk5ST1QVLbi0n5lhPe2JKNvFV/OQD6Stl8kUn53EbCcfacelrOubY8XjYpaSL8Mp7TH6MqtC\nQjuLn6V79+6mH374YdNffPFF7HZ4Xml10X70nYeyMsB4TSSxxWh/kSTXR5J7MVvff4pwhBBCBEEP\nHCGEEEGoVJZa1Pbh/ffft2UNGzY0vWLFCtPM5GCYylYUDDV9rSuqir1Wu3Zt0yx+q1u3rmnaBPfd\nd5/poqIi55xzBx10kC3bcsstTb/55pumy+t8htgv7STf/nJ9bfG8n3baaX/bz6OPPmr666+/Nr1k\nSbquMr5j91lFJNftdZgVRjvxiSeeiF3fZ0lS+7L4fN8bhNdFZF36stt85yNtxp/P3vMVpzJrb82a\nNWVu34ciHCGEEEHQA0cIIUQQcm6p+UK0XBQbvvfee8650gVr1IcffrjpgQMHmr7hhhtMJ8nYqGw2\nmq+XGrP6Pv/8c9MsFGM2D3tLMWumXr16zjnnRo4cacueffZZ08waKi4ujj2WXBQGhrZG01odmaxD\ni6VJkyamzzrrLNPNmzd3zjnXoUMHW3b66aebXrx4senrrrvO9PPPP2+afcbS3tO+z5HrbEbul8fs\n+67yjVva64efa9NNNzXNwtIo07OwsNCWzZs3z/T3338fqzfaaCPTtLy4T1qJNWrUMM1z4DvfnTt3\nNj1lypTYdZKgCEcIIUQQ9MARQggRhJxbarnu08WsmzvuuMM551zLli1tWf369U2zbTf1PffcY/qT\nTz7JyXHmM74xoo1GGI5vscUWpjkWtBgiS2K33XazZbQULrjgAtPM9nnsscdMjxgxwjSLdjMhtDWa\nawuP9slrr71mmvZMXH+2yy67zDSLHGl1brvttqbPOecc0/fee69pFq2yLT9JkqUWsiiYx8D9Jhkr\nLk8ysRyLQ5s1a2a6bdu2pg888EDnXGnbku+jhfnRRx/FHhcnS2MGGrPtaHlzua9IlzaaCj+FEELk\nPXrgCCGECEKFLPysVauW6Xbt2pmOQlP2fWJGFTPWyC677GK6KlpqxFfkxnPas2dP06+++qppFofR\nVogssGnTptmyQw45xDRtT4brZ5xxhmlaADfeeKNpFifmO7m28Gjf3HbbbaavuOIK09tvv73pKKuz\nTp06toz3SNeuXU23bt3aNO+/Sy+91DSzoHbaaSfTPpuOtltIe9Nnf/G7ghlgPnx2nG8d9hpkRmeU\nxemcc3PmzHHOOTd37lxbRmubPwXssMMOpmmVfvnll6ZpqfksQI4/Pwe3yc/B4vi0KMIRQggRBD1w\nhBBCBCEnllousnFouzDrZuLEiaajMPiiiy6yZf379zf9wAMPmL7mmmv+9j7n8mMWwhAwS4yZLz5r\ngJbWp59+anqPPfYwvWjRItNHHHGE6chSY7ZNt27dTDMzjeuwmO3CCy80zQysl19+2XQSG6SyQZuG\n9O7d27Qvy6lBgwbOudLWCTOc5s+fb5oZhr5CQY4j++ZNmDDBdJLpF0gu7kdfVmba68f3Peezq849\n91zT22yzTex7P/74Y+dc6XHimLCnITMHaZVyfd9xcZ2VK1eapl3G9bkdvjctinCEEEIEQQ8cIYQQ\nQciapeYLL7Nlr7ElPu2gq666yvSQIUP+tp9x48aZ9rWHZxYPe3xVJNKeZ9+Mg7RoaKMxAy3KpHGu\ndO8tFoHGFY1yGggeLy2dRo0axa7DYznyyCNNT506NfZzVAZoKTIDjNBe5rjvvPPOsevQqonsLWaU\nzZgxwzT75HXp0sU0LVUW+zLrjEW77O3l+27wXXe5yF7jeeU1ySw12oM+W4+a2Z2cEmW77bYzTZuR\n2YC8V6JiTt9+aI/yuFq1amX6s88+M81zz2uI55jb5Ponnnii6TFjxsTuNy2KcIQQQgRBDxwhhBBB\nSG2pMRRk2OkLfZn1wDDOlw3ls3qYGUELhj22ygq/fX2cfO28fVkxLILk5+DnC00S68FnUbVo0cL0\nwoULTW+11Vamec5pGdBeo+0W1yeL1wL/n7OG0lrhZ2LG1NixY/+27b9uMx+nkEhyfOxTRwuE6/M8\ncvn48eNN0zbyFc1G1gttNBZmclzOPvts0+zhxayz7t27m07S7843TQBhplQu7i9+3iSzdnJ8WIRJ\nS43fYZzWgZm23Nczzzxj+sknn3TOlZ4agvvx9Unj+WNRKTNHOW68z5idx88R9aZ0rvT1lEl/TEU4\nQgghgqAHjhBCiCCkttR8YacP9rpiaMrQzdemnPC9tLF8hW9lwaIpFj6xwI1WA+2lo48+2jQtijZt\n2ph+++231+m4conPxqGNRpYvXx67nFlPtBc5LQQzZaLMs2iGSedKh+v9+vUzzUw3XhfM8GGWGq+j\n6dOnxx5vEpJcg5mSJHuT9gnXYQYVzzktp+OOO870iy++GLudp556ynRkgdK6Y6YZ7aOo75pzpa0c\nWtCc5oO2Hz8T7ZvBgwebvvjii10cuSi+pi3F64dFmrQKfePDz07NHmecTfjyyy83zR6Er7/+uumo\nlyPtQ44fx4TFnsyGo2a2IK8b3/e4bwoDnjP1UhNCCJH36IEjhBAiCEGnJ2CmQyb9eBgOMsSMg+Eo\n24CzIJQWWZMmTUzvv//+pj/44APTt99+u2mG27SR8p1MMrp23XVX0yeccIJpZsS88sorpiNbhAW7\nTZs2Nc3z+eijj5pm1hsLFlmQ9s9//tN0JgXHobPakuyP1kiPHj1MswiPBX9LliwxzRkjObskMxIj\ne+jggw+2Zffff79pWq2+WSxpb/MzscdelHnlXGkLnBmmJEnb/0zwbT9Jnze+l99n3A4LY9u3b2+a\nGWvMjGX2WGRX+qZN2HrrrU3vueeepjlr6KRJk0zzJw1f4TvxZQLyc9NWTIsiHCGEEEHQA0cIIUQQ\nglpqtNE4ayDDyyQwc6VPnz6m77rrLudc6dDR14afYeHw4cNNM7uHGWhchwVchMWR+U5aC4n2QdSz\n7q/wnLLHVqQZljPTjRmDzPSbOXOm6RdeeME0e39ddtllpv/zn/+YZoZdEnuN2V75wocffmh66NCh\nplmQyV5g1A899JBpX5ZYlBlGO4hFvb7sRWYy8V6jDfT000+b5oy6zN70FYfm2t70zWqbxJKl5vmm\nVUhrnf3o9ttvv9jt83sp2g6PkdvmfUOrjb0mfQX2nAnUd465nGPLfmuy1IQQQuQ9Ofmzjn+Z8gfJ\n//3f/zV90kknrfP2GeGwniP6q4B/AbMTK2tp+BfwYYcdZpo58fyrnpN+Ed/86CT0pG6+v874Vwr/\nOvPBzzZs2DDTbAcS1Q0459wbb7xhmn9NRdx2222mGSXynLRu3do0O0ez5oDnk7Un/HF83333Ne37\nqy1bSSxrY8cddzTNWpYk+H6oJ3QHOC5M4CA8v7fccotzrnTUwx+8eU64fyZz8C9rwgnGGNVwOzxe\n1vZwXLg8W/cOkwPotPA6SVKTw+iB1xUjD0Yvs2fPNs0EJv7gH9VBsZaHP/zzvPL+ZLTIhCjWVfki\nNR/8TBw3tjdLiyIcIYQQQdADRwghRBByYqntvvvuphm6nXnmmaZpl9A6SNJltiw6deoUeyy0eVjv\nQSuI4TzrB+67777YfSUJ80PYaMQXLrMGY968eaZ9PwLSRuQPvwy1L730UtOcDI11GJF9ytobjjlt\noeeee840E0J8kz4x1GfyAS2LL774wjQtFFoiuRqjuInoksLPxrYktFs4drx2eR/xs9ECjaw0nn/W\nuDHhhjYaf8Sm7earmWG7qGXLlplm3dChhx5q+pFHHondTrYoKioy7btX+Ll86/Ca9HWdZtsgWmAc\nN9ZbRfcoz/GCBQtM8xpnixl+h3HbPhvNZ9H61uHnyyQ5ShGOEEKIIOiBI4QQIgg5sdQYlrFVDCfO\nYrh+zDHHmM7EUovC0cMPP9yWRZk4f13et29f06eddpppZqQwNGZdCTPckoTboS01H0k6WNO6YYYV\n6wLIzTffbLpXr16ma9eubfqdd95xzpW2FJjpQuuSLVlo0c2aNSv2GAnrU2ij8diTtC/JJswSSotv\n0jVeW9OmTTPN+gveR7RG7777btORvUb7iHYMbVFaqk888YRpn2XE4+W4cBxpsbKrca5JMnGkL4sz\nSZdvfrfx3ud1yHonZo9G1wuzBTmWzJ7jeMeN61+PMYmN5qurytZ9owhHCCFEEPTAEUIIEYScWGps\nN8JiS7Z24KRbnNObGRu+0Nc3MdWcOXOcc6XtFIaCRxxxhOn333/f9FtvvWWamTYdOnSIPUZ2bPWF\n5OVpo2VrFCIyAAAgAElEQVRi5zG8972Xn5nW2bXXXmua2WBXX321c865Z5991pZFNptzpTNyeL0w\nq5C2j89SmzBhgmm2AGFWTSZdsjPFt29+ftokHEdmibFomuvwvPD8s9hzxYoVpiMbiB3XuT12S+dY\ncJI82kS00WjH0R5ikfXEiRNN83wkKabOBN7jvH5ZYEnrip/dZ0vRIqa9xnNFW573Fr+LonZGPK98\nH4tEH3/8cdNz5841zaxDX6ajzzL0ZbX5rtG0KMIRQggRBD1whBBCBCEnlhp7pvlsGYbu7PLL8J8W\nGCdAY5jISZyijJn+/fvbMmbx8H2cvIg2A+0K9phisV2+k9ZG41iwNxZ70jHspwVD25OTgQ0YMMB0\nNCEU7RFaPrSLFi9ebJpZb1yHMLznsfuK0/LFRiNJLApaw8xC4rU+ePBg0zNmzDDN88Kix+i6p13C\n88zxZEYZ79fOnTubpvXEnoS8FngsDz74oIsjF5OuEV+nZt43/Cy+ictoe3EMaV3RUuNynk/eW9F3\nDjP7DjzwQNMNGjQwzWvC1wGbsC8dzwE/N5fnYiI8RThCCCGCoAeOEEKIIGTNUvOFaD7uueee2Pcy\nfGVWG+exZ4YFJ6mKWnfTRiMMh2nv0EZg2Otrn54JviyXEPiyf3zj1bt3b9MszmSmDLN8yMsvv/y3\nffH806488sgjTdPiiCbU+ytcXlxcbJqZhKQ8i3AzsfB4rDxfo0ePNs1JAjn9A62cV1991TSnDomy\nqXyW3kUXXWSaGYDnnHOOafbnYxEwr/MxY8aYnjx5cuw6aVvnZ4skVpHPcuJy3ge+TMO9997bNCeo\nY1ZtBPviMeOPmX18H3vUJTmvvmLPJJmpmaAIRwghRBD0wBFCCBGErFlqvjm4fQVGvtCNIS5nmWQo\nyaIsZuysXLky8fEyW4YZU+wNxWPPVpZG6CwpkqSIjuE4M52YDcjCtilTpph+4YUXTDPbLPrM7DE1\naNAg06eeeqppZsDxWNhPatSoUaZpqdEyJOVZhMv7gtZF2uI5Xots688ZT5mxdvzxx5tmNhMtteg+\nZaYh7wvfrKy08Vgsyc/Evom8RnjtMGOO1wuLwsePH286W/cO72Vm3DG71ofPlmJWJD8jrTaeexY+\n876MbPydd97Zlr300kumOXUD7xV+5/I7LIlVybH1zYLLY+BUEmlRhCOEECIIeuAIIYQIQtYsNYaF\n2ep/xJCO2WgM6Y899ljTPXv2dM75Z79j6Mjwki3ky7PXVrZgPzSfpemDn3n69Ollrs9pHjp27Gia\noXnU2p4t6GmL+vZPiybKQHTOP1VCLvpuZQrtG2aOcYqLJPC65Odk9uSdd95pOuor6FxpW6dly5am\no8wm9iPkGO67776mP/74Y9MsPuRy9srzZaORzz77LHY5M1h9RZeZwO3Q5uK+eMy8n2g/En5X8dpn\ndiFtNF4XtIKjHoAcYxbIcv++nwJ833NJ8J0DXguZoAhHCCFEEPTAEUIIEYSc9FLLBczIOPnkk03T\nXtl9992dc6UL3dKGlJmE7fkyy2daG40kmRWQ6zRq1Mg0i3OvueYa05EdxhbuPD88XmZXPfTQQ7HH\nkiRjMEmL+9D2aVobjfiOj+eC0wP4eoRxyoF3333XOVd6xlv2MuS2ad0xM5T2EYuDuY6vsJvjwvGi\nzlbBNeExPPfcc6Z99yztsiTwembmLK05fp+x8DzKBvvoo49s2Ztvvmma1wHHmGOVybVMy6558+am\naaMmsdp9KMIRQggRBD1whBBCBKHCWGoMrRnG54uNlQ/7T0MmfazYOp0Fe6effrppFo1GY8TiOGag\ntWnTxnSa4t1MCZ2F6Gshn8Ta861Dm5LWDDPPmM207bbbmo7uKS5jASGLQJmNyL5d1ElmkSS+Vvi8\n13Nxf3M7tLl87fvTXie+z8WZgjt16mSaRdCRLZrknDEDN5Nr2fdZabVecMEFpnmNpEURjhBCiCDo\ngSOEECIIqS21fCuMrEg2Vj6RZOwYOtMCY080WmDMmqF9EF0znO4hk0y6JOR7EShJMha+ddjLjNBu\n4Wy5zz//vOktt9zSOefcrbfeast43qL/d650gacv0yzJvZhk1tO0U51kgu86zOR7zmdR0zqmXTlv\n3jzTUX+5q666ypbxHPPe4xg3bNjQ9IIFC1Iduy8D9bzzzvvbcTlX+lpIiyIcIYQQQdADRwghRBBS\nW2q5sNEYXjLTZl2hFXTttdeaPv/882PXz5ZNmG92Y6bQ5mCG1aJFi8p8b5ytkGsbzUe+jEu2Mq74\neWjTcRoCn9XGz79mzRrnXOn7hdvjNny93PiZkhTbEt/5CDlGvK55DDw2n4VI2BuQ48CMWlpnzAwc\nOnSo6alTpzrn/uwL6VzpTECeG85OPH/+/NjjSpsBSWvu008/Nc1s1ExQhCOEECIIeuAIIYQIQl4U\nfmZio9EOiEJG2gI+G43kou15ZSNbM55GhLS5ynNcfBlXST6/z3Lq2rWraU4JwHWSWFTRMSSZfTTJ\nbJFpbcLyyjBlIWxkKzrnLwLlOLCglsfPYmhmY3KmWlrK7I9GKzLa5v3332/LfAXDvmNMUsjN701+\nDtpoSQqV06IIRwghRBD0wBFCCBGErFlq5ZUJlMQOqGpwLI466ijTDNOT0KJFC9MLFy5c5+OJwv3y\nykQqT3yfk/aNr/29z3KKWtj/dZ20Vke0frbGIpPvgLQZbplAG41wZlRfZhhtLNpMtKI4nvxcvu8q\nft7GjRs755xbsmSJ/wPEwCLdFStWmPYVbPoKbQln2eXxZGKFKsIRQggRBD1whBBCBKEgTehbUFCw\n0jmXLtYTZdG4pKSkbtmr+dG45ISMxkVjkhN0r+Qniccl1QNHCCGEWFdkqQkhhAiCHjhCCCGCoAeO\nEEKIIOiBI4QQIgh64AghhAiCHjhCCCGCoAeOEEKIIOiBI4QQIgh64AghhAiCHjhCCCGCoAeOEEKI\nIOiBI4QQIgh64AghhAiCHjhCCCHCUFJSkvhVWFhY4pzTK0uvdu3alTjnVqYZg4oyLk2aNLFXeR8L\nXwUFBfbK5bgUFhZG28mrV/Xq1e1VHvuvVq2avdbh/ZXyXqnIr7T3yp8TbiegqKjIrVq1Ks1bxFoo\nLi52BQUFGU8G9ddxyWRu+ST45kDnvq677jrTvXr1yvoxlAXnkuec8UnmmM/GuBQVFUXbsWVJxiWT\nsUvy3k022cT0119/nfH20rLBBhuY/uGHH9K+Pev3isiMtPeKLDUhhBBBSBXhiIpBkr9Gq1X782+N\nOXPmmG7Tpk2Z7+Vfvn/88UfsOmVFNdy/bxtJ8G2HUQ3xRTUhSBLV8PNsvvnmplevXp1q+77ohFFN\n9erVnXPO/f7776mONwm+KJhRTbauAVFxUIQjhBAiCHrgCCGECIIstUqCz8Ig66+/vmlaS23btk21\nL9ofaX5YTmLFpSXJdiLryDm/fVSe0Frij+pJbDQfSeywXJ6LJPahbLTck2/XviIcIYQQQdADRwgh\nRBBSW2q5rvEQ64bPqqCN9ssvv6TaZpIsojTXQC7qSnzrb7TRRqa///77VPvNJr5zuOmmm5r+9ttv\nTSc51spyD1aWz5EpcVmKvG9/+ukn0zVq1DCd5H7OBxuNKMIRQggRBD1whBBCBCG1pVaVQ998JhuW\nV9JthsJ37L7MG1oTtKZ89lUIfOcwk+NIay9y/Y033tj0jz/++Lf/pwXI5b59+jIfkxSh+jIrK7rV\nxuPfcMMNTffo0cP08OHDTW+55ZZ/2wavX27jnnvuMX3iiSeaLu97NSmKcIQQQgRBDxwhhBBBUOFn\nQmhFpM16uvDCC00PGTIka8eUBF9PsWyRpHM0OzRH0ApLYpvQRqOuWbOm6cgicq601cPlPrtjHToX\n5wW+PmxcXrduXdO1a9c2vWzZMuecc+3atbNltHfat29v+u233zb90UcfmV6y5M9GwezCzMwqX8ZV\nEss019dvtqhVq5bpL774wjSvPa5TFrSBaVUeddRRpm+44QbT8+bNM82xb9mypekFCxaYLi8LThGO\nEEKIIOiBI4QQIgiVylKLLIVchIuZFA+GttGSkEkmEC0P9mHr3bu36f322890s2bNnHPOTZ482ZbR\ndvjvf/9reunSpaZpp5x22mmmzz33XNPvv/++aVpKXbt2Ne2zy7g8SS+6TMnWBGyctoCWDe2yrbfe\n2vTPP/9sunHjxqZHjBjhnHNuiy22iN02rVC+b+bMmabr169v+rnnnjNNG433js/2I/lWrEh4zLQi\nP/30U9O8P7788kvTY8aMMU1rjN9XjRo1cs6VPk+8Tnl/fPjhh2Uer89qKy8U4QghhAiCHjhCCCGC\nENRSY9ZLcXGxaYaG48ePN/3CCy+YZtEUs77i8FkRy5cvN00rwEdFKkBL22Mpk8/DfV1//fWmGzZs\naJrZSNOnT3fOlc62oeXWt29f0998841pZpHRYqBFw0I4WkebbLJJ7Po+QoxvkmJI33Fss802pnmO\nCgsLTdOaqVevnuntt9/eNK/7aJsNGjSwZb7CT44XbdT77rvPNC3QZ5991jT72nFMOf0C35vkPIWE\nx/zKK6+Y3nXXXU1PmTLF9AMPPBC7PrP4hg4dappTUkTngTbaVVddZXrGjBmmmTnLmVx95ykfvsMU\n4QghhAiCHjhCCCGCkBNLbYcddjDNLCLaaAsXLjTdtGlT01dccUWsToMvG4M2A8PL008/3fQtt9wS\nu06+k3bqgbTQFuE52n333U3TFnnooYdMz5o1yznn3GabbWbL3nrrLdN9+vQxvdNOO5letGiR6aef\nfto0s7EmTpxoes2aNUk+isHrhJlFIUhybdHeYhYUx6JFixamed/179/fND8bbZgoI41ZYbR9fMfL\nAkJmA65cudJ0p06dTD/11FOm2UMuzkpyLj9sNMJMwN122800x+HYY481TZt59uzZpnnNl9X7kJbw\nqFGjTPMcFxUVmf7ss89M06rMtx5rinCEEEIEQQ8cIYQQQciJpUYbjTBbiOFotoiyoBiSx/Xx+isj\nR440zcyT4447LotHl1tybUOw8I9Fa7Rr5s6da3rq1Kmmo0JBnk9mV7EglL255s+fb5oWHcc0k4Jc\nnqdcFRtmMmupL1uL9ikLC/fZZx/T7MXFrEKO0f333++c89tctLqZHUXOOecc08xku/TSS03T1uF9\nT6uKVl/oKSTKgtYmrxNee7wPOG0AlyextyIr7dBDD7VltPy32mor08zu5FjRUss3FOEIIYQIgh44\nQgghghC08JM9m84//3zTV155pWmGrz5oNTDzKSqWYui6YsUK02zTTmhXVCQbLdcwfPdZThyLSZMm\nmf78889NR1Yn+zrRQmFBaNTfy7nSrfLZe422jC/TKa2tyO3kC+xHxvPP67hz586mt9tuO9OcQoAW\n5IQJE0xHGVQsJOW906VLF9O07nie2VeNvcWYTUVbiTYU7zsWOvI7gLq8pirgOfHNcMp7hQXIBxxw\ngGlmknE7TZo0MR19n3Xr1s2WcfxYuMvtJSn8zAcU4QghhAiCHjhCCCGCENRSY1bK1VdfHat9M0Ey\n5GbhX1nZRcyGqszkIoxmUeett94auw57ptHGYWFvZIu8/PLLtox915hVQ5uiQ4cOppn5SCuGGVjf\nffdd7DrUvkwhXpvZhOPis4t5TFyf2Wi0YHjuTjnlFNPM6mPG2o033miaUwhE++X+eT+xUJt2FosS\nO3bsaJr2Ne1QFpPyHLDH23vvvefiCF2QWxac9oFWJK0zFuDS9rrmmmtM04Lj+Y+uZ55vjj2tZZ4b\n/lzB9/Ia4r1VXijCEUIIEQQ9cIQQQgQh72b8ZDETW58zq6ksG42WGzNG2Gac5LoPWUWCFiSzB9mH\njrYI7YA5c+aY5nmPrDlaLsx6ok3A4sEBAwaYZqbOI488Ypr2Qc2aNU3T6suXrJ20fa1omXAmzm23\n3dY0s77YV439y9iHjfZMVGDpK45m5hOtpDp16pi+/PLLTXOakX333dc07VBfTzYf+WADERYmE06r\n8vrrr5t+++23TfP7h+ecVnA0Pr5MPdqZLLplMfbixYtNR8W9zjl30003xR57SBThCCGECIIeOEII\nIYKQd5YaC9Noqfkyk2ipRKHn8ccfb8tos/hgNlZVhNbNgQceaJqZW0kKcv/1r3+Z5hQGkQXjs7aa\nN29u+uijj/7b+5wrbWXQ6mG7+HPPPdc02+ZXVGjB0Vp69913YzWzo2i98N5hZlW03FdQSVuUtiev\nC2aptWzZ0jRnYqWNx30lscvybaoCHzzfLGrnTwQsUuc9Rx1lEXIZ74OlS5ea5hQUtOtYGExbPB/O\npSIcIYQQQci7CIdP3pNPPtk0uw//4x//MD1mzBjT0Y+mvXr1smW+v8wvuOAC05wYqaLCuhf+eEz4\nVxMTL6g50dngwYPL3K/vx82ePXuajv4qY6IAfzRlogDfx2uBdRr8AZuRT48ePco83tAwgYUTxCX5\nC5PrMNphogDPxb333mu6VatWptk5mskfUaTo664e92O2c6VbsfBYmjVrZpqfm+Puq/nxJaLkM7yf\neN7Y2ZwJSYwMjzjiCNNMCPnvf//rnCsdsTCi53llkgbX53UzfPhw00888cRaP08IFOEIIYQIgh44\nQgghgpDXlhrtMrLzzjubZngf/VjWqFGjMvdDS42tPyoq/MHWR5JJxmj7cG52TlJHaLUcdthhpqdN\nm2Y66nDLTre+FidMCOGPypyUi1YCfyBN2004xI+omXTx5fHRuuIP1KyzoN3CVidsM7PHHnuYZo1I\nBFux0NqiLUf7platWrHHvmzZMtMcR76Xlh27dXO/rKfKN3g/0V5jggWv1VGjRpmeNWuWabbtiq4R\n3+dmm6CTTjrJNJM0aO/xu/DOO+80fckll5hevnz53/afKxThCCGECIIeOEIIIYKQd5ZaEtjahEQ1\nBmzhMGTIkNh1ma1TGUib2UO7hhOaMRynNUBLh+vTFqHtxTnZn3/+eeecc08++aQtY6siTvRFa4J1\nIGyLw89KOyAtIWoRMsm48nWa/uqrr0zTAuX55/q0KWmjRduhLcnx5/t4vzCrihloPK7u3bub5sR8\nPEbfBGz5hi+7k/D6HDt2rGlmrPFccWzTXIc891OmTDF90UUXmR42bJhpXn/HHHOMaVqkbIvD1lb8\nTNlCEY4QQogg6IEjhBAiCBXSUvMRhY9prRKGkcwCqczwHLH9D5e/+OKLpjnHOtvP0C5p0KCB6e22\n2870jBkznHPOffzxx7aMls9OO+1kmhlN62o75BO0jYjPLvNZcL4iSXYm3nHHHU1/8MEHpt955x3T\ntL2iQsSVK1faMlqn3A+tOGZecaK3xo0bm2Y23Jtvvhl7LD6SWFgh4TH4MhuZrUnrmF2zaa+RuGuE\n2+N+ioqKTPNcssDz1VdfNc1J9Miuu+5qmlmPuf7+U4QjhBAiCHrgCCGECEKlstQiWLDog9k97KBb\nUcmkFxUzh2hpMdSnLTJv3jzTLOSbPn26aWayRTATiUWgDRs2NE0rgX2ocmGphe6e69tH2vFigSvP\nIy0tdpH+6KOPTHOso/PLa4fHyGJMdlRv27ataY5Xhw4dTM+dOzd2/7xe2FuM5HMvNd8Y9uvXzzQn\nDmRxpu8epYUY2Vscp6222so0bTTfsSxatMj/Af4PWmdt2rQxzfucGajZQhGOEEKIIOiBI4QQIgiV\n0lJjqOnLEtpzzz1N59u86aHxheZczuwlasKiQWasRVMncCyY+cOJqUiux6U8bbRM4HlevXq16Zkz\nZ5qmHcnzGHdO2bfLN1XBGWecYZr94aIJw5xzbvbs2aYXL15smkW+zIhLct3lG7S/WDxJ+6lp06am\nfVMCMFuQ00pcccUVzrnS90fa4uYXXnihzHXYj3KbbbYxzazHXKAIRwghRBD0wBFCCBGESmmp+Ww0\nwtC+MkAbon379qZ9hV8kbVt/H75spygjh3YE+z35ZmWl1ZMLm4VFq//617+yvn3n/BZVWruQ544Z\ngJzxk9M8MJOQUw7EFVJy/FkEzewoZhLyWDglAo/luuuuM00LNknBK7fJDNJ8KALlMbN/2amnnmqa\nn5FFlb5pF8q6FnyFp4T9CJlFyH6EhGPVt29f09n6LvChCEcIIUQQ9MARQggRhEplqTFrpCwqW880\nhvEMl3MNiwOPOOII0++9957pyIJhkWCPHj3K3HauLRQeb67guPj6odFq4fmkBUerg7bKK6+8YprW\n1UsvvWSaM9ouWbJkrcd7wAEHmN5///1NM9Ns/vz5pqdOnWqa04ZwrGnB8XNwOc8BM7iS2OMhof3F\nWTN5vh977DHT/Fwcc86Uyntl7733ds6VtkFplRJ+340fPz52He6Tthv7unE5M+ySFJCmRRGOEEKI\nIOiBI4QQIgiVylI75ZRT1vr/+VxQlk0effRR07nuF8YsmMmTJ5um9RDNHMnMJfbUIjzG1q1bZ+04\n46BlFboI1Lc/Zi/5MpxYKMsCT87cScuS1ghttygLjdYZs8JatGhh+o477jA9dOhQ07R1OEOszwKk\nxRN3jThXerqMXPTzyhYcExZb0paKCjmdc65Pnz6m2Udu3LhxpqNpJWitUtMup23pOy4W4NJ+Pfjg\ng037CuVzMU2EIhwhhBBB0ANHCCFEECqVpXbVVVet9f/zOTzPFJ91lmuriNunHcRwv169es4557p3\n727LfNlHtOiYrZQtfBlTIfBZF74x4vXKYl5OFcDW/82aNTNNq+s///mP6TgbkdNGjBkzxvTYsWNN\nP//886Y5tlFWlXPOPfXUU7GfiVOB+Madth4z3yoKvPaZCXjiiSfGatqfW2yxhenIUjvyyCNtWf/+\n/WP3w2uZ55iZhryGfIWnvjHJRZaoIhwhhBBB0ANHCCFEECqVpcbsljjSFIZWNJJYZ7nIWGN2ETOm\naFdF+6Kl8PDDD5tmb7Bly5aZPu+880zfdNNNpjOZEZI2AfdLWykfYev/pUuXmp44caLpKVOmmN5h\nhx1MMzOMlmV0Hs866yxbxuxB2jScgZJ2z4QJE0zzmuIUBkmuO9potOwq+tQhPtuW1zl1xF133WX6\nnnvuid0Gx5XXdT5n4yrCEUIIEQQ9cIQQQgShwltqacLHfOvLFIJMbLQk76WNRmh7ffLJJ84551q1\namXL9tprL9PsJdW1a1fT06ZNi91eEnxTJVCXp42WNmONy1lgyUwlFhYy86ldu3am2QftzTffdM45\nd/zxx9uyUaNGxe6TvdRGjx5d5vHyM/k+n69XXD5MQ5BP+K79TKzl8kIRjhBCiCDogSOEECIIeWep\npbWA6tevbzrK3vFZZ926dTPNIrXKTJJzyKwgX1YN26mz3xYtHV9GURT6P/7447bs3HPPNU1LLRMb\nLW6f5U2SKQZ89ppvnbhr3rnSBYeRjelc6Qy3OFjs6bMfmaWWxJpOct35zke+jJ3IPopwhBBCBEEP\nHCGEEEHIO0stbSYVM3ZmzpzpnHNujz32yOoxVUZ8BZs+WARIktgftWvXds45t3r1als2bNiw2HWZ\noeSzbny2Uz5aMT6LMol17Ps8LBRMktVWFuyrlRZmAxIee5JjofVYXsWeuZ7KQyjCEUIIEQg9cIQQ\nQgShIGXh5Ern3JIyVxRpaFxSUlK37NX8aFxyQkbjojHJCbpX8pPE45LqgSOEEEKsK7LUhBBCBEEP\nHCGEEEHQA0cIIUQQ9MARQggRBD1whBBCBEEPHCGEEEHQA0cIIUQQ9MARQggRBD1whBBCBEEPHCGE\nEEHQA0cIIUQQ9MARQggRBD1whBBCBEEPHCGEEEHQA0cIIUQYSkpKEr8KCwtLnHOpXuutt5690r63\noKDAXr51GjVqZK+ytlejRg17pT0W36uwsNBeaY+9Xbt2Jc65lWnGIFvjopf/lY1xKSwsjLajV/Ze\nulfy7JX2XlnPpaCoqMitXr3a/l2t2p8B0u+//266oKDA9BZbbGF6xYoVpv/444/Y9UnNmjVN//rr\nr6Y5adxFF11k+owzzljr9rbeemvTixcvjt1/2gnpDj74YNN33323aR77Tz/9FPve4uJiV1BQkPHs\ng0VFRW7VqlWZbkb8H9kYl6Kiomg72ToskYWZOnWvZJe090qqB85f8T1kqPll+80335hu3ry56S++\n+MI0v/B//vln09WrVzfNB130kHHOue23394559y8efNij8X3kCHrr7++aT7k6tWrF3u8fMhwmzx2\nwmMXojyJrteqPOsv70f+ESxyg779hBBCBEEPHCGEEEFIbakx/KaFRMurRo0aphmybrLJJmVu3xfi\n0r7z2VK00spal9vbYIMNTNMC5HtpoxFacNym7zeqqmxfiPxC16JstNAowhFCCBEEPXCEEEIEIbWl\nRrvsl19+Md2pUyfTzz77rOkffvjBtC8zjJbWjz/+GLsOw39aVyRu+751CT8HYbhNe43HQkvNF57z\nuBTCC1E14U8KXbt2Nf3www+bruzfD4pwhBBCBEEPHCGEEEFIbanRfqIVNn369Nj1kxRW+Wy0JDA7\nLiKJjUZ8nRG4HR7jb7/9ZpqWIe3GJEWxQuSKWrVqmf76669N0w6+4IILnHPO3XjjjbZsvfX+/Erw\n3Ue8p3kvVESuvfZa0xdffHGq9w4YMMD0zTffbPryyy83femll5pmhwOOT1FRkemoeJ0/S4wbN870\nO++8Y/r66683ze9BFqznG4pwhBBCBEEPHCGEEEHIqJca+4UxFCe+TK8k2RgME2kF0PaKKw5lNsiX\nX35pmuE/7QJmmrHwk/thHzh+DlpkvlD2tNNOMz1q1KjYdcTaoQUxd+5c0w0aNCiPw8l71qxZY7pO\nnTqmac90797dOefckCFDbFnPnj1NP/bYY7Hbrug2Gklio/kKt1999VXTvPf5HcLvmVNOOcU0rXja\n9dtss41zzrmGDRvasqOOOsp0nz59TNO643flc889Z7pHjx7xH6qcUIQjhBAiCHrgCCGECEJGlhpJ\nEr+0EuIAAA/0SURBVGb7bDRfvzOGiZxfhiEuM8NatGjhnIvvqeZcaduP76Oltvnmm8cu33DDDU0z\nBPbZhDzGimqj+T5zWta1Df5WW21letmyZX/bnnN+y7aqwM/ctGlT01EGmnPOnXDCCaaZZRpng48f\nP9407wVS1XoD+j7ja6+9ZprnftCgQaZptTGr7fTTTzd96623mo7GivOO8acLZgZvtNFGscfFInzf\ndCvlRdW7Q4UQQpQLeuAIIYQIQmpLzddTjPYXbQ6fjeZr689wnZbOZpttZppWS9w01L7eaLQQ2rVr\nZ7qwsNA0Q2MWWS1Z8ucsqrQaeOwssCM8TwyJ8x3frKUcIxat1a9fP/a9W265pXPOuTlz5tgyZp0t\nX77cNM8VbQVfwaxvdtmKdJ4zgZ9/4MCBpvfff3/TvvMSnWue81mzZpnmPc3rnPdRPtg0ucZXDNu3\nb1/TzGj9/vvvTfMcdu7c2fSnn34au6877rjDOee39rn/uKJ355z77rvvTB922GGmH3zwwdj1Q6II\nRwghRBD0wBFCCBGE1JaazyJjllqSfmEMxRmydujQwTQzk2jdcH3aBdGsnLRzeFy06PbZZx/Tbdq0\nMc2CrMWLF5veeeedTc+cOdN02iwdn92Xj/iy7hjuf/zxx7G6rEwm3wyqmfDhhx9mfZv5CM/tSSed\nZPrggw82zeJnWpa8NyKbmtfz+eefb5r2Da3rJH0CK9OMt74M3Pvvv980CzVpBdPSWrp0aeJ98nvo\niSeeMM2pDNi/bf78+aZvuukm05MnT068zxAowhFCCBEEPXCEEEIEIbWl5stGI5mEzbvvvrvpzz//\n3HSzZs1ML1q0yPRTTz1lOsrO4HH5erA1btzY9AEHHGD6rbfeMk1b4r333ovdpg9fhk9FpUmTJqaf\neeYZ008++aTpM88803Q2rJPi4uJU6++4444Z7zOf8FlRtIbPPvvs2PdOnDjRNM/L4MGDTTdq1Mg5\n59xHH31ky2j5Rn29nCttY9Oio93Evnbs8/X++++bHjZsWOzxVkT42VeuXGmaRbe77rqr6TTfA/vu\nu69pFnJOmDDB9FlnnWV6xIgRpq+88krTDzzwQOJ9hkARjhBCiCDogSOEECIIGfVS82WlpGXjjTc2\nvWDBAtMXXnih6TfeeMM0Q3pmc0QhLo+F1hZtod122800PwctNWbJMRsuCb4CrYqYpeNc6Yw9WjRp\nz0tZdOvWzTSLc31UtsLDevXqmWYmH4udu3btavq2224zPXToUNN169Y1ffTRR5tmn8HI9qI189VX\nX5lmr7CRI0eaZl89Xs/HHXecabbIZ5Ejexhy7PL5vohm4XSutJ1P+5GF6ZzywFc8TeKyejmDctQj\n0rnSNufjjz9umn3VRo8eXeY+ywtFOEIIIYKgB44QQoggpLbUfD2VGBYmycZgTzbqPfbYwzSzPbp0\n6WKafc3ioIXFzBlaarQFWDTFz8ECrrSfKW4mUuf8M6PmO8wenDFjhulsWCE8b8x6SwItmsqAryD2\nsssuM80MMBa7spffIYccYprXOs9XZB+3bt3alo0ZM8Y0bR32B/Px6KOPmmYW6EMPPWSaljmtwXye\nRdQ33QnhuPEaTvJTA++h6F7g9wTPJa1Sfs8x05aFvPmGIhwhhBBB0ANHCCFEEDLyd9L2TyMsXmNv\nLmaBbLrppqYnTZpkmpk0DD2jEJMt2LfbbjvTzCphqNuyZUvT1113nem0hYc+e8nXRjwf4bEyw4bj\nm+3PwwLfJKS91ioqtBp9Rci8d/r372/aN0Mrr9GoP9rChQttGft2JYFjsWrVKtO8d1588UXTBx10\nkOl8ttGScO2115pmZloSm5ljy++w6CeF2bNn2zJamzfeeKNp/hTAKQy4/3zL/lOEI4QQIgh64Agh\nhAhC1nqpMXTz9YBiGMmCQW7n+eefN7333nub9k0zwIy1yHbgMVKzr1HUR8q50hYdC+/SWje+8DWf\nQ1znnKtTp45pZuadccYZplnYlgRfxl4ELQCecx+0OqsKvFYOPfTQ2OW8L+66664yt8liy6i9/n33\n3ZeVY1yzZk3s8v322880M9lOPvlk05988sk6H0N5QRvNB+8DTlXAz0v7c+rUqc650t9bzCzkPnm+\nn332WdPMOmQhez6gCEcIIUQQUkc4nOSJf60QRiBsPcO/etjOhjn+nBhtl112Mc32EvzR9N///rfp\n6K9z/kXADtEdO3Y0vWLFCtOcPIn59L65zJO09OFfNkmWlyeManwRKT8zkzJ8rW14vqJtMvGDf+35\n4LlN8tdkZYOTnvFaZMulTCb0y3a0zWvBd+3wL/s0E5JVVJj4xAnbnn76adPdu3c3HZ0r33cMx4zt\nbAYOHGj66quvNs1kk6ibfnmSf99+QgghKiV64AghhAhCakuNXWDThuQMs2kX8AcyWifsFkxLgSFm\nnEU1Z84c05xciskBtWvXNs1aBrbT4eRuvkQIX30Kj5EWY5IWIaGhLeOrjWAtAG3PJETnqFevXmWu\ny/qNJN2iKzOtWrUyzWuLFnDbtm1Nl3dCCu8j3hdsudOzZ0/TTBqorNDG4jmhjUZ7P7LgmFRDaFWz\nrRG7rNNey1atE2usCgsL13k7inCEEEIEQQ8cIYQQQUhtqTFn3GczMTPNV8vyzTffmGb4yOyNNm3a\nmPZNaEZLLbKrpk2bZstYm3Duueea3mmnnUyzhQutO058xC63tKB4XKxVoX3H85Ev8LzRuvnggw9i\n1z/22GNNs/1QtmGtVFWHXYI5T33nzp1Nsy3NusL7KUlXdB8cO182Fe/7smq1Khu00ThZXrNmzUxH\n339nnnmmLfvss89Ms36QrYyuv/762H1my2bNxEYjinCEEEIEQQ8cIYQQQciotQ01bSZfqxTC7AkW\nJ9ECe/31100z1G/evLnpLbfc0vQrr7zinCttZ7G4bMiQIaZZeEjLi+Ers4FY7Egbg+0lmI3DUDZb\nlkU2oYXhs9EIs/1ok3Kue9pubDkUFQQy6++SSy4xXVRUlOygqxjPPPOM6REjRphmq5hMiMZx5513\ntmXsQEyrmS1xmHXJwmoW9tIu43tvv/1208xU9XW3rijQiudEj/xZgBO50Ro75phjTEc2Gb/D2OJr\n7ty5pvk9xO8Y308dvmJ7H/xM3E4m32GKcIQQQgRBDxwhhBBBSG2pJZl0jeEgM9AYWhNaUVyHfc1o\n2dFqozUUWTdJQkraOLTO2O9o6623Nh11cXUuvk/Y2sgXGy0XsKM0dVmw+3M+ZvGVF7x2mRnEospL\nL73UNO2YtETXLvt9sVciO7fT8uKEebTMmY22cuVK07Sdx40bF7vNig6/F5nFec4555im/czvxQsv\nvNB0lIG45557xm77hBNOMN2vXz/TzMzl9ymvJ5+N5vu+zMUEeYpwhBBCBEEPHCGEEEFIbakx5PIV\nayWx0XzbZGYMQzpmYdCCYTZMtA4tLP4/exZRP/bYY6Y59cG7775r2ld4mq3sjRD4PkN5wEyet99+\nuxyPJL/g9cQsrrFjx5pmFihtrLTWZJRtdvrpp9uyl156yfQhhxxi+oYbbog9LhanElrg7InHbSbJ\njqyIcAzPPvts00cccYRpTnrHc3788cc755wbMGCALfv4449Ns0iUGYKLFy82TYuM07rQlmUWqS+T\nOBcowhFCCBEEPXCEEEIEISNLjZlGF110kem0sxD6bDqG7tTffvtt7PplZYwx1GQRYocOHUwzzPdZ\nZNwntW8mzJYtW8ZuPzRbbbVVue3budLZUJXVTskmzHY677zzTPus0cGDB5v+8ssvTQ8fPtw075Eo\nI43/z+JNTuHhs2B5LMxMo5XDe4RZoJUVnqvZs2ebrlu3rukTTzzRNAumo/fSIuPMx8zc5U8O/H6k\nXcbC+Ndee800v6tmzpxpmtlxvutMhZ9CCCHyHj1whBBCBCG1pUZYgOYLuZixxuU+K6xGjRqmmVXB\n/k3MfPNNFRDB0JEWAacnYEHoXnvtZZqzmxLfjKPMsCPsT1We0GbJNbQvo0wmLuvbt6/pQYMGpdpe\nec9sGYok1gX7XXXp0sU0M5g4tUFcIXTcrLl/hfYN7aDx48eXeby8pysiSWb75TnkLJ++mTtJXAYu\n7Wf+P63ojh07mr7zzjtN03Y76KCDTPfp08c0x2qbbbYx/e9//9v0PffcE7t+JijCEUIIEQQ9cIQQ\nQgQhtaXGMJLWlq+vWtp+PMzuYiju2xcthQjaaPXr1zd9wAEHmGZWB3sMcUZCHgvh/qlptbEgj+3f\nX3311dhtVjY4c2vPnj2dc6XPcxIbjfhstHyc+iEkvI579+5t+u677za9atUq0yzUjGxqnltaQ7y2\nmYH24osvxq7jI23War7hu/Z8Rd+c4oQFzr738jsyGqtly5bZMvZM4/X+6aefmu7atWvs+pzK5cEH\nH4zdPy21XI+VIhwhhBBB0ANHCCFEEDLKUmMGBu0khpe+YkjiC8t94R1tNM4WGtluO+ywgy1ji/dH\nH33UNK0zXyYJl/MY+Tl8WXjMEpoxY0bssVc2hg4dappWZpIsqDTUq1fPNDNyqiJsRc+C6H333de0\n7/6KxuX666+3Zez9xWlGmL3J3l5VAV6/tKLatm1rmrN5duvWzfScOXNMcxzYE43ToES9HGmzpf1Z\ngtllZJ999jH98ssvm+b3bK6zQRXhCCGECIIeOEIIIYKQUS8139QDDEE5q58vtKfNRGuuU6dOpmvV\nqmV6+fLlphn2R0VT7F/ETDcWeO62226mGYLSiuD6n3zySeyx+4o9uT5tPWYMVVRYlEbrjAWBxcXF\nptd1KgRfeD969GjThx566DptuyLjOy+8d3zr0OKOrl32aTv//PNj95nEXmFhNe/LfCaJheSbhoV2\nGVm4cKFpfof49rV06dJkB7sW+P3IfXJ2VtpoPnJdVK0IRwghRBD0wBFCCBGEjAo/ffgKyXyhKYvX\n2IfoySefjF2fmWnMzIk7RmaUrVmzxjT7tDFLhO9NYgXxs/qss8pgoxGec2pabdmG41UVbTSSxPbw\nrePLFE2zbR8VxUYjIfvyreu+eO0zK5Hfrfxuo05CyOJpRThCCCGCoAeOEEKIIKS21DbbbDPTDO+S\nFHgyY4zFTMxk81lwtLribDTiayFOWKjl2yePkdtkCMrltM6qeo+vbMBzy2tNiIpIkp8X4vBd+0my\nEpMQ8vtJEY4QQogg6IEjhBAiCKktNV94x3b8tNR8haK+WT59fX2ShIxR9hoz3XyhK7fRunVr0++8\n847ppk2bmmYxV5IQlP2+WNhVVWarFKIqkcQuS2OjpaWifK8owhFCCBEEPXCEEEIEoSBNKFZQULDS\nObckd4dTJWlcUlJSN5MNaFxyQkbjojHJCbpX8pPE45LqgSOEEEKsK7LUhBBCBEEPHCGEEEHQA0cI\nIUQQ9MARQggRBD1whBBCBEEPHCGEEEHQA0cIIUQQ9MARQggRBD1whBBCBOH/AW16HX5wbqaLAAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2bab29f4e10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# with 256\n",
"_ = view_samples(-1, samples)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!"
]
},
{
"cell_type": "code",
"execution_count": 106,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAKhCAYAAABkTRjXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs/Xe8ZUWVPv4/93ZO0DRNBkFJiigiCIqOYxhBRQR1BhEV\nGFHBGRTEMGJkdIyMyhgwIIoKZjFjAkwoBlAUVATEQLRp+EDTuel7fn/ge+9z6nKnz27wym++tf65\nr3PuPntXrVpV+3nWWrVqpNfrpUqVKlWqVPlby+jfuwFVqlSpUuX/G1JfOFWqVKlSZVKkvnCqVKlS\npcqkSH3hVKlSpUqVSZH6wqlSpUqVKpMi9YVTpUqVKlUmReoLp0qVKlWqTIrUF06VKlWqVJkUqS+c\nKlWqVKkyKTK108VTp/ZmzJiRadOmDXw/f/78JMnNN9+cJJk9e3aS5Pbbb0+SLFu2bOD7NWvWJElG\nR0cH/k6dekdzRkZGkiRjY2MD12+wwQZJkuXLlw9cv3Tp0iTJwoULkyTXXnttkmTevHlJkpUrVyZJ\nNt5444Hr3WfDDTdMktx4442Le73eJsPoYtq0ab0ZM2Y0bZw1a9bA31tuuSVJMnfu3CTJihUrBv7O\nmDEjSbJ27dqBvk6fPn3gb6kL1+vbrbfemqTV7W233TbwXGPiepUlfDY2dDJ//vwsWbIkK1asGBlG\nD0kyOjraGx0dbZ65atWqJMkWW2yRJLnuuusGnskuPJPOyj7qO3tjJ/6vL/quL3RLF1tuuWWS1i78\njo7Zr9/73fz587Ns2bKsWrVqaF2wC8/Qljlz5iRp7cKz6YqNT5kyZaCNE80NQmfEc0o78xxz6Oqr\nr06SbLLJHeZuLHw2N5YsWZLkjrlzyy23ZPny5Z10MXPmzGb8tN18u+mmmwbavHr16oG2zpw5M0lr\nL3RUzhE6ch37KO2RuI92XHPNNQPXuw979ft+u1ifOTJ16tTG1ktdmKf6ZPyNi3H0vTYS/6cztkz0\nhV2Ua+eCBQuSJDfeeONA+9hjqUv2sdFGG+W2227LypUrh9LFSJfSNptuumnv4IMPbhploB760IcO\nNF5nFy9enKRdeO51r3sN3I/R+/573/vewP0Y6mWXXZakVYbn7LnnnklaA/rTn/6UpFXm9ttvnyS5\n4YYbkiRPe9rTkiRnn312klaZ2nHeeedd1Ov19hxGFxtuuGHvYQ97WLbaaquBNm6++eZJkk033XTg\n2SauZz7iEY8Y+P8vf/nLJMlOO+2UJPn+97+fJNljjz2SJA94wAO0MUmr2/vc5z5Jkl122SVJcsUV\nVyRJ/vjHPyZJtttuuyTtok53973vfZMkF154YZLWwJYsWZJLL700S5cuHXoyzZs3r7f77rs3fb/k\nkkuSJK985SuTJB//+MeTtAvLb37zmyStrjbbbLOBvv/oRz9y3yTJRRddlCTZeeedk7S69bL91a9+\nlaSdDE960pOStLr+9re/naSdlI997GOTJH/4wx+SJCeeeGKS5NRTT02S/OAHP2h+/8c//rHTwrLh\nhhv29tlnn3GL1KMe9agkyZ///OeBtpWL6V577ZWktSd9tJB85zvfSZI87nGPS5I88IEPTJL87Gc/\nS5L89Kc/TXLHQtCvC+348Y9/nKQdC9d53utf//qB5/y///f/kiRXXXVVLrnkkk52sdVWW/WOOuqo\nxlYvv/zyJK3tASIWXXPE4mbdAAjYFbsAILbZZpuB+3iRabvFESD12QvOIrzjjjsmaQEqu7z++usH\nvh8bG8s3vvGN3HTTTZ3nyG677ZYk+drXvpakHR9903frAjvae++9B9rEpq2d5sCDHvSgJO0aePHF\nFzdtTtqX8z/90z8N/M5YGAP38fJ+2MMeliT5+c9/niT59a9/neSOsbnsssuGBiLVpValSpUqVSZF\nOrnU1qxZk+uvv75BZ5AmNwHXhrertyh0BUnssMMOSZJLL700Sfu2f8ITnpAk+f3vf5+kRRYQDFbw\n4Q9/OEn71v/c5z6XZDya/8tf/tK0O2nRX/k9RoU9DCOrV6/Otdde2yAGSJFuIBNsb5999knSIlbf\n/8M//EOSFpX95Cc/SZIcddRRA22C8qG+3XffPUny0Y9+NEmrI+ht1113TdIyF8gaC3QfLHXbbbdN\nkuy///4N4xtWRkZGMmPGjAZlQ5qYDZcWxAmdl24njOeqq64auL/rsTf/1+fHP/7xSZIzzzwzSWsX\n73//+5O0uoKMMRuI++STT07S2gfd7LPPPk0fhpWVK1fm8ssvbxAh/WOWpRsH2/LZuEGWxguiPeKI\nIwbuhw2y/X/+539Oknzxi19M0iJWOuM6KVmG8cfurrzyyiQtCzj44IObNg4rS5cuzQUXXNCwOGxs\n0aJFSVp0bl148IMfnKRdR9ihNps7bJzu6MC4Gr/73e9+Sdo58oIXvCBJO8fYGzcjXWgv+9Re7q69\n9tqr8cYMK6tXr87VV1/dMBfjVXqB9I13Zuuttx7QBfuxdlkr99tvvyTtHMGIrbWe96UvfSlJO+fc\nj45LZs7z4nnsyBzbfffd8973vndoPVSGU6VKlSpVJkU6MZzp06dnm222afz+fO588vyLfO1QAL+l\nt6X///a3v03SIliIk/9QkB8Ccr9DDjlk4Hu+WW91/lCICgODGvmEvfXLoOIwsnDhwhx55JGNjxTb\nw9YgC8iDz1PfMRY6u+CCC5Ikz3/+85O0vtVHP/rRSVqkixlBc8cdd1ySFqFgb3z0UJs+loyKrstg\ndBcZHR3NnDlzGsZBz+IFvn/KU56SpGUS+saeHvnIRw60bd99903Som4xO2gQA2ZXRx55ZJJWd9Ah\nxn3OOeckSR7zmMckSR7+8Icnae2QPUO+55xzTsMQhpXNN988L33pSxvULcbn2caJ7/7rX/96kjYG\n99///d9JksMPPzxJ8u53vztJcsABBwz07bnPfW6S5Jvf/GaS1rcupvfkJz85Sasz7BKiFbMxx+gU\n+qc7aP+2224bl6CwLpk5c2Z23nnnRofuhW2zufvf//4DfcNcjK85hB3wSLAL8c0yAYad0TXmxANi\n3TBneSGgeSzAHKWjJUuWdNbF7Nmzs8ceezTJAZ7N9tkJhvu73/0uSbte8KSwk09+8pNJ2tjg+eef\nP/B76xEG9Y1vfCNJGyPUN2PDbj7zmc8kSf7lX/4lSTsnzOUnPvGJSVrme9FFF41LUPjfpDKcKlWq\nVKkyKdIpS22bbbbpHX/88U12CL+it7AsMm9PvtHvfve7SVqEAGnwrUM8/MriIZCnt6m3tvv/8Ic/\n1K4k7duc//MrX/lKkjbVE7rDLjAgv3/Tm940dJbawoULewceeGDj54XWtA3KKtNZoTJoHsLEiGQH\niX9pu6w1iBWzomP/h/74u2W9iHPxm2NAkK/77Ljjjvn4xz+eG264YWjKs8022/SOPfbYBjVjWdAW\nNmZcIEjIErqDlKBzjLbM0IGEy7RnTNb3+uh5mMt73vOeJC3K9D17ZodbbLFFvv71r3fKRjJH2KY2\nQ9V87uaMZ/ISYJzYuvH+2Mc+lqTNtDQXMON//Md/TNLqGgJnJ8adverzpz71qSRt7BHbMIbsY6ed\ndsqXvvSl3HjjjZ2z1Ng+D4Znk3K9MEfMV3OIbdMV+zJ/fU/XBLMSf+DhMEfY3xe+8IWBz9ptXRMT\nWrBgQU477bRcd911Q+tiyy237D3/+c9v2iB+LS5tTTLvjR9mjHGycez8q1/9apI2jmkuuD/7ww7Z\nlblqjvgdOeOMM5KMzxgUz2KnN998c37+85/ntttuq1lqVapUqVLlniOdYjjLly/PRRdd1CCP/u+T\n1vcumwNihZrKjVz8lN6i/JPQobc/dPbWt741Setf9LaVUVNmakCH4h/iGPa22I+DaXWRsbGx3Hbb\nbU2f+GLdGxIpN2rJxBPn0AeMiK7KPQXiDnyqMm9e+9rXJmn3LEEyfLKer10QFjSp/Xz3N998cyef\nbHKHH/i8885rkCp74HfmJ+ZnxnD9lT3m77e+9a0kLRLlpz7rrLOStDriu3/DG96QpI3tiVvx4YsF\nYVQYlKwrume34i9z587tHMO59dZbc/bZZzdt5PuWgeVZMvroyB4QaFrfoH0sr8yo9LmMzbz85S8f\nuD9vgRgStsEu2C+5973vnaRlzn/+858762JsbCwrVqxo0Dr70AZtxWDEN/wfc2Hb4qDmDpRtvOjc\nHJGlWMYdjLtMQu0QS6Yr65K/1qUddtihiR8PKytXrsyvf/3rZpzol81hVWzWXLCOsA86NF95gx7y\nkIckacfL79n6CSeckKSNc9pTZP6XjPfpT396ktab4Dpzm9dqzpw5nWLgleFUqVKlSpVJkU4MZ8aM\nGdlhhx3yiU98Ikny1Kc+deD/fKdlhgWGAoFC0JAGf7SsFG9bb+FPf/rTSZJnP/vZSVrEAwFBC2IE\nUAHk8x//8R9JWiSMCfHtYwMyhoaRqVOnZpNNNmlYEgbCj6zv3v50I2Zz8MEHD1xftgWzgdahfXn0\nxx577MDvoD3xMLqAsCHYU045JUnyohe9KEmLgDCwe93rXg3CG1ZmzJiR7bffvvGBizNoizgFdMQf\nfOCBBw5cD+GW/mzMCEtwHTSG8UJ7UKR4hlid34mH0MXxxx+fpM1mgng33XTTJrtnWJk5c2YT70ha\n3zp0DcnSidgddK7PGAwUbvzFgMwZdiVLzZwsMzgxIcwJWjeXZcfZq2JMxAr22muvfOADH+ikiylT\npmSDDTZoGCumKT5EjJM4AtYlM886gf1ZH7B5aN64i2vJyBSnwJxcR4dYYGkP+nvooYcOXDd79uyG\nmXTRxfz585sYrYxNa574swoh5ohMzpe85CVJks9//vNJ2nHXR3Yh5iszWIzHHGEXMgHt17J/y1r9\n6le/Okly0kknDXyWHWk9WbFiRcN2hpHKcKpUqVKlyqRIJ4azatWqXHnllQ0ygP74PjEPsRNIApoT\nN+BPlFlD/B664md+4QtfmKTN4PL8sr4YpANNQg2Qi303/JLiGzJ0usjy5cvzy1/+skGe5557bpIW\nOWAoskswEXtGVBKAWLAujEbbIGSZgfbp2H8BvUFc9iBhUiWqUysLI5LNAj3uuuuuDZIbVlatWpUr\nrriiYUn6xC6gLshWFhh2Rxf/+q//mqT1RxsXdgP9+93znve8JMk73/nOJC3LhBL1uUSPdMsOxRjY\nhVhFmU01jKxduza33nprg9a//OUvJ2kZrRgaZuNZWBU7kFUodoOl6csznvGMJG0WGQYjnsleSqSL\nYbFbMQFeAJlZYgHuv+OOO44rGLkuUZkEGlctodwLgtXLqBKrgco/+9nPJmnnvXFhp5gyJiROqg88\nJWXdOYJheb49LuaOdccc3mqrrcYVMF6XrFq1KldddVWTGcf7IvMN+9cGNi/m57O204FxNP+xQnPt\n6KOPTtKyNSyTF0o/MC06M0fe/OY3J2nHyFpr3TjwwAM7sb3KcKpUqVKlyqRIJ4ajfhhmIcffW1Y9\nJv5kyEamjQwMVYTLelAls+G7h8og0Gc+85lJ2rgDRuOtbx/G/vvvn6RlDfyckBWfPlTRRcbGxrJk\nyZIGNUFJdIHZ6Ds2Rwf8zM95znOStOgM0oXuxEH4q/UFwpCRg93J/KITqAw7EN8Sb9FODGfLLbfs\n7J/G9mT7YSDaAnVB7cbXdWIxmAq7YEdQv1gAHYhPlOwRw8b+oHYxP3EKMTtxNmwDS9h+++077yhf\ns2ZNFi1a1PjWyzpg9I0BQ+0YyLOe9awkyete97qB32mH+/7iF79I0mbe8fGLd2J/4lqyjNgZ1nnQ\nQQclae1FbIdO/N100007o/qlS5fmJz/5STNHrBey0mShioNqo7kklihjynyXhcqbgBFh9xgPO8Em\nrUdiyPpmTKB64y8TTByLvS5YsKCxuS66OP/885uYqbXIesGTwTsgM04bPvjBDyZpmS0GYzzF7qwr\nvtd3doSx6hNd+148HEu0/mDm1kpz5ZprrmlsZxipDKdKlSpVqkyKdKo0sPXWW/de9KIXNQgVIvG2\n5h+EovmPofNS+APf9ra3JWnRFX8lBAspew6kZQ+LeIVc9dNOOy1Ju79GO739td/9ZYS87W1vG7rS\nwGabbdY75JBDGpYE8UBb2BV0rU4TZKrN+ioz66UvfWmS5C1vectAH8SfoDM61gfMCcuT6SMjC6Lh\n26cDWSv9eyC+9rWvddpdbxe1vkFnmKvcf2hJPANjpTuoDHtTEQBzgWD5k2XUsBs6cr2d6HTxoQ99\nKEkb22FHUB5kC/nuuuuunXWx+eab9w4//PBm3O0Z8QxsjUCUfPM+Q5KyiI455pgkLYPhZaBr9mBO\n0BGGjclgF2JLGDI2AckaK+h/s802y5lnnpm//OUvnaouHHfccU3fsC1tFJ/CqGVWllUO6AIL/J//\n+Z8k7fqB/WGL5YGQPBriFuImPCeYd7mb33pTVnjfaKONctZZZ3WqurDFFlv0jjjiiKZyAF2Ib/No\nsEnzulyf2ZG/r3rVq5K0VTncjy48pz8Wl7TMWLwUCzVH2KHYkmxX3iM62n333XPuuefm5ptvrpUG\nqlSpUqXKPUc6MZyNN964t99++zUIEML0VvbWKyuRQlH8zzJtvH35s6FwWSlQXHmWCMQDPZYI1/Mh\nItksMjEwL4jH/9///vd3qqV2wAEHNG9+SMF+Cii7PMa4PGkRexNf0FdxD2dN2NdT7mWRyeUvxgIl\n6pt2akdZgRnqXL58ec4555yhEUuSzJ07t/eABzygQYJy+jEWDAbqKhEvZsxeIE1szP4YdiEeBoXz\nU7OHkhGXrNDzxTHYhT0GzluaPXt2vvrVr2bx4sVD62LBggW9xz72sU0sjl1gvE4VZYPapC2YsO+h\ndIyJLjAUdoMps326Zn8QcH82YtLGsXx2ppCMQXHUFStW5Oyzz+7E9jbZZJPeU5/61MYuZO71ny6b\ntPFH44DVQ93WKLYrlqIChT1PbNnzxM/Ko8h5IcpsRHYBxWun+8qy22ijjfKZz3wmixYtGloXG220\nUe+xj31s4+1RVYVYi8ozxsrKI/5qk77bo4ih0A2dWxfKc7o8h73yBrAvGX6ea67Kyh0ZGcmXvvSl\noedIZThVqlSpUmVSpPM+nD/96U8NAoGa7Jp1OuJhhx2WpEUQ0Li3qErJ4hbiGdAX339ZK8lbVh4/\nBA2J2BcElTmr3p4Vb3VI2f4PGT5ddXHVVVc1mTb8/3SjLbJKMAzxKsgVc5GNwncq3qQvdCHTB2uA\nlKE+fbTnRGaXbDjxEYgampcdpUZbF3GaIZQlo8aeIbEYrA3K0nZ2Is4g9x9KgwqhKszI/ggIle5l\nzdAFu8J4sUb7s9z/xS9+cZKWoX3sYx9r0O6wsmbNmixevLhhNmJl2iZzSt/51ulfnIpdmWP6SHfs\nwu+Mo2wlzIevnhcC69P3d7zjHUna2ljiG/ZtqEN26qmnNux7WFF7ESPFEFS5MBf0wbhhPMavPCGY\nhwMDtj6IW2Eq4iDGgs78nqdFu17zmtckae2El0A1BqzvuOOOa8ZtWFm2bFl++tOfNvcwz6w9skZl\n3mmr+JQ4tLhXGZvF9tmbtVIGoD5bX7S/ZNDWcOuWmBO7tI5Z808//fSGUQ4jleFUqVKlSpVJkU4x\nnC233LJ35JFHNv5+CAFa86aDPGQnYTJ2gkMsZf68tkCk3vZ8t7Ka5OHL0BHrwSogY5kc0Js8fH/5\nSyHnCy+8cOgYzvz583uPeMQjGuTAF8oXThd8s1gdNC9biS9XlpC2ln5nLFBfMSK+WQiIzxeywQYh\nIMgIAvYccbYvfOELueGGG7J69eqh/dObbbZZ79BDD23YlLYab/5gSBN6kk1IN+IcYnIYsRgftsGP\njB26XqaePnsehMruZNPZ5yM7SoYP9nfxxRdn0aJFnXSxcOHC3pOf/OQGnUOObBJjKWN1ZfwKK5A1\nBnWX+2OwSjrHYDBeqF+f7KJnJ+Yau6M7ujDHfv7zn+c3v/lNli1bNrQutt56694LX/jCZr5iMOIK\nMuaMrz0q5oLaebLJMA7ri/ETt7LXjM5dzyuAOalPZ88LVqc9vAvEHNSOb33rW7nwwguzZMmSTmcD\nHX300eMycXkqrBfGCVPF3sSzzH/xLmsxLw5vkuv0DYsX87Fnks4wWllsdKy9GDq76Pc+/e53v8vy\n5ctrDKdKlSpVqtxzpBPDWbhwYW///fdvmIQdvfzLkIm3p7ertyGxoxw6g0Rcj/lgIvyY7ssf7f8Q\nCRTJn61mFwZlpzIkA3lp3+tf//qhGc6GG27Y22effRoECplAb6XvFbrWJkgW4sR4VGGV0YfBQMT6\nwEcrEwcKwwpkO6mdJoNP1glUKbML0po/f34+/elPd9pvsckmm/QOOuigJkMGSobiSmTLXlTlpcP3\nve99SVoGY3z4izFl48dfzY+N8dCRDCwVd9/4xjcmaRkVhIyd0gl2sttuu3XOzNp44417j3/845v9\nMxAj5guRYphldV+M9+STT07S7svS1rJmGt2xMz568QsxI3Zhzqmdxn4wGUK37rds2bLO+3CsF5gn\nm5Y5B6Wb93SAbbNV8Q3jaJxkfLJ9TIe9sT/PM5dkkNKlk4ExYqyCB8f9eEz22GOPfOxjH+t0Ku4G\nG2zQ23PPPZu4o303xkfbMQk2KJ5ofqrKoe3apFKBtstis56U+/CMO6+ROWHtxJQwL/Fyf9nxE57w\nhHzuc58bOmOvMpwqVapUqTIp0ilLbcqUKdloo40a9ASd2fHL5yrmgqn4C+39+7//e5IWyfALQoX8\nlzIiyhP7+J1VNuWf9H/n7si4cOInVlGejwE9dpGRkZFMnTq1uRd2BVFgY3zzkIKMGKiOrxUiwUSc\nVigOIs5QVl7WN2jRPh0ISB0qWTH+L9NL+93vkksu6ZyZNTo6mrlz547bIyCOJENOG2XIqGlGB9Ac\nJCseYSe4zC0xGPtm2KMYEruxB0l8Q7zEdbKeIGsoE3P+0Y9+1Dkza2RkJNOnT29sXV9kDZZ7xaBz\nKLvck6btEKcMQGwB2xfvhMq1W1/FK82dI444Ikny9re/feB6Y1d6GzbeeONxu97XJdOnT8+2227b\noOKyqoY4FR3YG+b/5pCYC5vmsZDJZe5hBXSP0dBJuf8Ls4XuxTfEx7A+DEk7r7766k71w5I7bOqB\nD3xgw0jpElMwfuzEs51TpI9YmLqTWLy5VsZgzBHeJ+uI39m/pz/GvaypZyzEBPvrXXaZI5XhVKlS\npUqVSZFODKfX62XNmjXjMiogC29taNmuVW9tGRH8yTJjMB2ZVDIyIBAxIwhY5hdUIENDBhbfr9+X\nZ5dDvt7MGFYXGR0dzZw5c5o4Q+kT5bP3DEiX713cCFqXsSX+AFXpsz7qO8QDsdrDYo/J6aefnqRl\nCdAlFkoXxg6qv+666zpXwr355pvziU98okFLUDc9l7XKsDbsCtrGSCFXdoE12rdhXPXxuOOOS9La\nj30dspCcjgpNYhHswu/E16DBLbbYYtzplOuSsbGxrFy5shl38SZtNu6YA/bOK8CmsW5xJ3MJapfR\nxbugvpizo/RVzIYu7KuAiKF7SNa+jHLH+wUXXNBpv0Vyxzy87LLLGhsUp6QbzEOcCIPxvUw6aF2M\nT4UT8Q+/kwFortCtLDWsQD06zMt6wVsg/lmeVEtH68Nwbr755px55pnNs8wVGXVYPx3LiGOTdIF5\nWC/cR1+c0GktfNOb3pSkPbVUdqt1RXYanbAb7N9azItkbMztjTbaqNN5YpXhVKlSpUqVSZFOWWqz\nZs3q3fve924yaWQbQcTedN7OvseExAb4ISGXMkMDGpPJ4TM0LrPKaXaQs70HfMN8stA8NuAtrp2e\n//nPf37oLLUpU6b0Zs+e3TANvnY+WsgWMoFkoDFt5asv0be4Al8rXfCdQhjQOfTGv+0+xoiOMCSZ\nQxCXDLLkDl93lz0G06ZN6y1YsKBBqvzEnsX37Xt24URQqKk8kRXrsp9LZpUKBhCtvukDv7W4CHRG\n12I80J0YECTbX5eu656kGTNm9LbeeusmLsXG2J44l2eWGZiQsyw2unA/14lfyk7CiMxnfcFgMCrP\no1tZU/os4xOal/02f/78nH/++bnllls61djbbbfdmnGli3LvmO+tB1A9u4CysXSxQF4E6Fy80hwp\nM6rEjqF864J4mL7L9MLAjR0Wsv3223euIj579uzeDjvs0MwFngYeEvfmBaJ/6wXWb+1k8zIz2csZ\nZ5yRpI3FsTPjb+0sKx5YW92Hzuz/0m4ixrRo0aJcdtlldR9OlSpVqlS5Z0mnGM60adOy9dZbj9td\nz5cKzcsC8RaW+SDO4fdYAMbEtwuJqHnm9EL+dD5a+z6cTieTB3oXB5Gdxm+pXe4P4XSRDTfcMPvt\nt1/DjjyLLviBibiGGA2EgPm4Dz+3/6tLB5VjVHRlDMQdoHwxAfEz19OFWAK/9bvf/e4kyb/92781\naGhYmTJlSubPn9/c2z311bjzvUOeJXK0f0ccA2OCfN/61rcmafcKYDqQsO9f8YpXJGkrF2iHWAJk\n7Tnl3gd+8Cc+8YlNltewMnfu3Oyzzz7NeOorxmlc9E1MxRxg47KBZOZhOFijzD99ZjdiMJg2Xz47\nYp/sgV3ahc/nLzMQwz7ooIOa/SvDysyZM7Pzzjs3Nmmc6QLLklllPTCP6cr/Za9B78ZVnErdONmI\nmBJ2YL3AjIyB9QC7ZIfWMzqj6+23374Z32FldHQ0G2ywQbP2ma/YnvHmBRDfNhcxHwy3XNuwNTE8\n8VB2YU12nbnErspsNeuKs6uMCRtw/7333ruxtaH0MPSVVapUqVKlyl2QzpUGDjjggMa/CJGIA3g7\nl7WRvDUhTL/3FoVkvOW91aEBCOOZz3xmkjZ+Ue7md19IBxrgy+fPhMAhGOjuhBNOGDqG42RHGVTQ\nOl8nRFmev+7ZdAYdQBD67C+2Ji6F3YnZuI+x0Eefxb+MgdgRhNZ/0mdyB9L58pe/3PkMmMc97nEN\nSoLS6QTKguogUmgLyoOAxR/4m6F/dgExlwiX3UHvrtN3vn59l/0oroIpYU633XZbTjvttFx33XWd\n6ocdc8xSbjIoAAAgAElEQVQxjZ7dU9/EVDBb8Q3sT5uMq0y9cne+LDJ/PY/d0QHWxr7YH4RqjmBO\ndCFbCtOeN29ePvnJT3auNPCkJz2pmRP6RBfQtXFj08ZL/KqsH2f8MB3sv6ycrkIF+xKTMTeMjZiN\nMbB+mBNlZfe5c+fmpJNOyp///OfOVReMuww4sRKeC23FuktmLKuVTq2hYnky8vTRGilz0/did9ie\nWLD4FnE/sWAMR6X92267LR/60IeGniOV4VSpUqVKlUmRTjGc5I4sGLvny0wsn+2zsHNYdhB0dsIJ\nJyRpEbD9FBCySgPe3vzY/Jqy3sQnoAEoTeYFhiXzAkKW7SLX3Fu+i6xevTp/+MMfGh89BEAX/MJQ\nk13OPkM4r3zlK5O0LA4bg8b4o6F9PlWxBf5tY4Jl0r0sE8iajmXyQE76sdVWW63XjvLtttuuqRQB\nfYmtYYEy7eyeVosP6uZX9lksxh6UY445JknGnaapGjWmy87sw5CtqH1ieexUHMXY2O+BLXQRVReg\neAyBDWIcmEnp/8ba9N1nsRjMt6w+7n7iFeYib0BZkcJcKLPmsJCSjey9996d9lskd6DrFStWNGwL\nUzCfxXD0BeqWvSi+dPjhhw+0xampYnvWC/NZTFYmn3ZD+1ijzD73k7mFyZRV7DGpBQsWNCx8WFmz\nZk0WLVrUrHnGwZzAKNkgm7WGaYtMTeMu9qqP5pT1ho1bLzxXfEsGp/VApp4xwcCtV7JxVWDffffd\nO+1JqgynSpUqVapMinSK4WywwQa9vffeu3n72e2q6q+3rrctXytGIp++rHHkr7ctBAqdiYP4nbes\nN2u5k1h1WeiQTxea54f0tofyfvKTnwwdw5k7d27vAQ94QIMUZLw5rRJq5qfmQ+eLd3IfxIth6COE\nyS/Nn8ynW15HJ9Ck5+g7fzhkJp6GjUDaW2+9ded9ODNmzOhtueWW405+lW1Y6hmbwyxlzNGB/VpQ\nuj5Bvtpslz07wKTZoUrcKi4bGzYPVdIh/3V/Re7FixdnzZo1Q+ti3rx5vd13371ByWwRO4NwMWJM\nlh3oA9uHOI2vcZX5aY5h+3TH7sTNsAXtUnWY7swxc1d7IN9NN900l156aZYuXTq0LubMmdPbdddd\nm3HTF6gba6cLsb9yD5Px0Sbjb9e9+CiGa46I+WBv7ALjFhfFrMRytcP1dNBfjaHLGTDJHXsY73Of\n+zS6KCtgG0e2qc8YRhkDNl7WYp/LcSZsHdMWKzQ3eU54m1zPPnmbMKf++y5fvjxr166tMZwqVapU\nqXLPkU4xnBkzZmTbbbdtsjggUEhSPALakgHjOogEo4H6IEu1raBy7EEtLvnx0DhfPgTD9w6JlNlu\nEBM0oH1y2csMjf9Npk6dmoULFzZ+YwzkrLPOStJmyEC0UJO4A1YGsagnBlVBOvZDyMSyS19ePT80\nxiILBpORBSOmRFeyYsoKurNmzWrQ9bAyZ86cPPShD20yaPjmxVbsAKcDuoGu2A953etel6TNFhIL\nkrHHZ6+dZUYfdCaehdlA83SuneyM7sQG5s2b17ly9rRp07LFFls0CFV8UV/EI6BxyBG61kb7X177\n2tcmaeeOvvLp22uk72zZnhX3F78wt+jeXwhbDBIz8rvNN9+8mW/DyqxZs7LLLrs0+sRUtYENludh\nYTzl6aVq5rEzdoC9y2Yk2AFGTafiJOJd5oj1wnolCw7D0a4ddtihYePDyuzZs7Pbbrs1todJWsvK\nCuniTBgMRuK5L3nJS5KMz2K1hrETfcOQxaHYurVYTKbMJLZeWB/YKbu43/3u12ndrAynSpUqVapM\ninRiODJw+LihIfEEWUb2P2AU4hvQlywS6AtCKX24UByk6rliMcSOYWif31HsyP2gRPWJsJP1OQ9n\n6tSp2WSTTRqGAImIQ5144okDz4bSMRsZO+IYEA8ko88yrTAWjAnCgFwgVehNhg4dYEZ8u3QhC8b1\n11xzTaPnYWVsbCxLly5t0JtYDTTkDBfPNn4YEGTLbrAKbWY/0Lz4WFm5AmsoM3R8hlyhtyc96UlJ\n2uw12XBiBYsXL+6si2nTpmXLLbdssg2xaPEKsRM2q8q3PmK4WCCmiyVgQBBnWemaHegrKTM1zUU6\nxsS0G6OGcH/2s591riKuAgX9awMGqpYdz4Z9eMaD/Yh7QPfWC3YiQ4/9lexRhpWxxFQwHs+ha3ZI\nF9YLz7/yyisbG+oiIyMjDVvze0xDFiIPiFid6u/axG70EXuzhpkT2Kj7WBPpwJjwPjh/y3XWJyzP\nXJUFhyldccUVnXRRGU6VKlWqVJkUWa8TPyEVKFvGlbet/TLejuXbGOrm+5OBAa3x0UJ1dtFCIPzT\nGIr4xL777pukRS4QDj8lH684C9SgH11kZGQk06ZNa5iJuBAUr4/aCnnKItFX2SFnnnnmwO+hMugB\n2xPHwirts3Ed3zvd20UNObuPrLl3vOMdSVp0ee2113ZGsrNnz86DHvSgJnZHIE/sDKriW8futJ1P\nHvvSB4iWv9pzIE/jJxYkHqHvGLXMIOifb94YnHzyyQO/nzlzZoNAh5Xbb789N910UzM+GK/aeu7N\nxsXoMFO/M/5sGLKlS793f4zH3MQSMGIVKl70ohclae1NfJQd26Pm/2zh5ptv7sz2RkdHM3PmzIZR\niCdg79g5G7ZOiM2Zt9pmvmNEdGSdMKesJ7LVzD1xNVXG2TwdWF/MURmi7Eg/Vq1a1XnNsFfNXkF9\ntE4YJxm0+qyN5Z7EU045JUkb6zG//dUnXgG6sj4Y54985CNJ2rnETswRrNEa7BwlsnLlyk66qAyn\nSpUqVapMinRiOKtWrcrll1/eZJt4+5Z7CSAMSEHevKwgcQqIlV+wf7d70mZw8C+6jxhAee4K1ABZ\nizHZtSueAlnZBe66rtVwx8bGGmRans8OFUEYkAi/sDZA3dA/f7K+65PPUDndin/wi+uDdvDBY3P2\nIEA4/o81POhBD2rQ1LBy00035YwzzmiQDrQtlgPF7bDDDknamAs/MJRuDwBd8N1DrpAt9CajRjwC\nGxHnwAb8n38c0/YcyBfC1t4FCxY01w4rU6ZMydy5cxvEyJaNBybsPBTMRR+13ThjPNggXdEh27aX\nyfiam+wCOxHDYWe8E2W2JaGTPfbYo7NdrFq1KldeeWWjX0xTXAHq5pnQprJeHMarr9YLjKlkKli7\ndQKbL08K9X/f0xUWUGZoGZudd965c8bebbfdlvPOO6+xUeOO8ZqPvDCuM++tnd/+9reTtCwNK7P2\nWg9Kb4D7WfN4Fawv5oq9kmI41mR2ICZJR495zGMaVjSMVIZTpUqVKlUmRToxnF6vl9tvv73x70FF\n3oblyX5lTri3cVkhGfMQe3E/SKfMy4f2oEVvf6wCgpG5g3FBVK9+9auTJK95zWuStGiziyxfvjwX\nX3xxU8tMnEEMBlKEIMSNIASIBoK1wxyqU+UZ8oDe6FitNM+T/QadYzrGSDuhfWxEJWdZKDvvvHPD\nPIYVe5KMG380FAh9G6d3vetdSdqTOSFgPneIVWaf/ReQMWZi3GTo+J2aW8bEfSF0fS4rH4hbqHSx\n4447jsv2WpcsWbIk5557bsNwIEGMls3zCrB5DBjyhbZlt8nI4lPHmNgH5tPPVPv/j13SgV3/qnOo\n2YdNyFITC5o+fXrneBaBvsVatV2f2bx4gj0p7EnfoXdz5Z3vfGeS1n7oxnrhMyZj3XE/c5N92BfE\nfrAAjIpn5t73vnfn83DEfI2POWKN8mwsSlzLs8VerX3mMUaipprx1kfXGQMMx//dV4YwnfDYsFNz\nRFWZF7zgBUnuYM5dqtVUhlOlSpUqVSZFOtVS23DDDXsPf/jDG58rRgEReGvzvXur+j+fq9PrvO2h\nb29RSNbv/IUCzj333CTt2xiC4Wv19saQsAkIG/rHQuyFOOqoo4aupTZ//vzeox71qCYuoE3lmTDQ\nnPiD3c0QrH02kAQkjB1A2K6H+iAfCFSfZdZAYNA/FIlt0mm5637PPffM6aefnuuvv35oODtt2rTe\nggULmn0s4kvQPQQJdWPApc/cniAMS4wOsjbekLLv6VZ2JOF/xjbYA7aI+bqOfcrMOuyww/K+970v\n11577dC6UG9QXLBkfWIpmE5Zf9C42CMElZsT/efTJK09mTtHHnlkknavkt9hNhC1/SDmDMGQyxpu\nj370o/Pud78711xzTae6cg9+8IMbu6ADKFxfzaGy0gO7gbaNn3gk+9GH8nRbrE2lZN+b99Y+bN/v\n6QDDYQ/m8i677JL3vve9nXQxffr03iabbNKwOrasT8ZfX3h99LGM/bFVa591QqyFN8hctCbb14MF\nsn33NReNjb1smJCxY7/3v//98+lPf3roc5Iqw6lSpUqVKpMinRjOZptt1jvkkEOaty3kYpc63+t/\n/ud/JmmZjLc6JsMXCm1BIIccckiSjKs3xA9pzwIU73s+XCiurEKrfdojniKnXcbH5Zdf3unEz8MO\nO6zZDyGWAsXJ/hEnwjigarEcsRhtO+OMM5K0e0OgLsinZAVQGKYkO0UsAMKma7EauuYHF7c499xz\ns2jRoqxevbrTiZ/77rtvg7qgJdkr0L4TN9lNWWsPWn/GM56RpN2J7rOYDF0Yv7e85S1JWkZkz4D4\nlQwwv8MmjV2521+cbMWKFbnqqquyYsWKoXWxySab9A466KAGuULtbJJ3QN1Btmz/DF1omz6qxSbr\nUTYaJIyhsh9zkdA1RCsWAAHb6S6m4z6Y1ic+8YmsXLly6KrASbLVVlv1jj766IZRisHwjFgPTjrp\npIG+ia2VJ71i59gbmzXnrGUYij7IjrMeYJnWC3NEPISdYc5ie+z2wgsvzOWXX96pWvRmm23WO/TQ\nQxubxNKsTSpLiG9aPzAWTNPayC7sHRMPtS5YG+nyM5/5TJI2lqcyCjsV38ZsxEPZofZYrzCclStX\n5g9/+MPQc6QynCpVqlSpMinSieGMjIzcmORPf7vm/N1l216vt8kwF/4f18XQekiqLvql6qKVqotW\nqi7ukE4vnCpVqlSpUmV9pbrUqlSpUqXKpEh94VSpUqVKlUmR+sKpUqVKlSqTIvWFU6VKlSpVJkXq\nC6dKlSpVqkyK1BdOlSpVqlSZFKkvnCpVqlSpMilSXzhVqlSpUmVSpL5wqlSpUqXKpEin06VGRkZ6\nd3YIk2oFim367K/jARxXoHiewoHKf5dl6BU89FkZcQXtymNSXT9RO8p2ur5PFg9bomF0dLQ3Ojo6\nro1EWz2r/F5byt9NpMs7aeud3n+i5ygKWerCdWTq1KlZu3ZtxsbGhi5MODo62psyZcq4e5Z99L1x\nLv/qo7b67D4THQA2UbWM8rl0NVH7yvuMjIxkbGwsvV5vaF2MjIz8ny7d0UUX5ojxNM8nGk/jYjys\nDw4lm8iO+to28H057hOtD+X6Qcr79K9PY2NjnebIyMhIb3R0dNz8dm86sjZOJBOtYfpQzqWJ1lLX\nlXO21M1Ec9b306ZNy+233z60Lrq+cJrFPmmVo3Gq8Ppeo5xj4wRQVYVVdfWZ0t1H5VKfvbBUQlaF\n1jkVKil7wTFw7WG4/u/+fYM3dK2j0dHRzJ07t3mmar10UT6LOJNDm7SdeImq8kqHzk0pJxXdlIum\ncysYmmqzdOIvnfafLdT17PopU6ZkwYIFTdv13Wd9VNXbs5zVUp7Z4ix556FM9HL22XPKycJW6cIZ\nMvpMtyp504n7TJ06tfltF+lv5529xPq/X9dLdCIwNdH9ywWs/F0JMMr2lPftByzrWgxLGR0dzfz5\n85szW1Qm7l+s+j8bR+OmIrGK6eaSMSlPY2Vf7MlnvyvXB89jF/5P6Mx12jtz5sxmPg4ro6OjmTNn\nTnMvOrEeqITtHK2JXpJsVB/MGX1wnfOx6MJzrFNs3onD2uW8JWPi//rOHn2/6aabNuv3MNLphTM6\nOprZs2c3A64cPIOw0BDKcQjY4sWLk7SLafk29iJx6JTOlYupFw1hKJQy0eJPieUia1AosYtY8N2D\nITrwzEvNZGUo5SRkKAa8NJB73eteA/d33xI1lou4vpeH2mm3v/q+fPnycYvSumRsbCxLly5t7uEF\nYxIpH2+8tdmCoa8mgcmiTxMx4RKRlkha35Vqp3OH27m/6/XbWK1Zs6azLty3RIQTsSl9MD7a4rry\nJVqK6/TdwjFRu8sXnfuXL5NywVufmoujo6OZPn16Y+P6aA5YD/TZs9iBoxTMifJlW34uj33WZn3T\n5/IgtnLOlZ4Tf7UzmVi/E4kXTmmbPtORcWTz5TiUc4ZNmzPmYLnGEvd1vfu7T7k+ePm7j99rz9Kl\nSzvposZwqlSpUqXKpEgnhjM2NpZly5Y1rrDS9QJRlG9dh/tAChiJ30PEjg6GgLxVIVQHMb3qVa9K\nkrzhDW8YeC5WAVFDD1hC6SP2PerdRUZGRjJjxowGIUAWUFzJ5jxTnyGVEtlCLiWFRbUJFxkde452\nONALEnFsr7FZHzY3kfR6vdx+++1Nm7AwVLtE+yWdvzMEmbQ6Mj50MpFrhw5cz84wWsy8tIPSNcOe\nIN0uMjIyMuB+Kn3mpQ/c/yeKUxi/kpGUzKl8HqFr99fXkm2WLrfyuevDcG6//fbccsst41yZ5mcZ\nVzQXHIimTaXnxLwt50rpStV26wJ7u+GGGwbu62A+x3TTWem21v6VK1d21sfIyEhGRkbGsalyXMtn\nle68iRiy8TcHS/e1Y91LO7N+EGux59IFnXNz68fq1asrw6lSpUqVKvc86XoAW08WU794K5dv1dJf\n7Jjb3//+90naty5E3O8XTFrE6m36y1/+Mkl7VGyZ2eF5jpS95JJLkrRvbW/zL33pS0na456hhxUr\nVgx9xPSUKVN6s2bNGhcE9LaHJMRexKX0GQMq+0CX/v+EJzwhSfLDH/5wQBeQDGSERUIimBTUWPql\noT1osD9mcNNNN2XNmjWdspFmzJjRPMN485FDrCV6J6X/GKoq7Yh9HXbYYUnuOPY4SZ7+9KcnST71\nqU8N3LcMoDvWF1uUnABNei5mNmXKFHGcTtlI0Oyd9blEtGU2UMlQJsrccx/2QNiPOaVvJZOeSCbK\nVvLsLllq5ohxY5vajIHqUxnPMh76Uo4X0afdd989STvvHY/91a9+daBvZRyiZB2eY06W8ZHp06d3\nPm57dHS0N3PmzGaOlH0s1zCftY1d6Ls1rUwOYuPsw32sdd/61reStOsDXZTeBM+zzvCQYIPGZMqU\nKVmxYsXQuqgMp0qVKlWqTIp0Zjj9+y0gCsyj9Pd665a+dW/PvfbaK0n7tn3yk5+cJDn11FOTtCzh\nrLPOSpK86EUvStK+jd/3vvclSbbbbrskbVaUt/9//ud/JmnR/7ve9a6B9t1Jps7QDMd+CwgBsiwR\nR38qZdKiPH5lfTz++OOTJG9+85uTJI9//OOTtJk67n/44YcnSU488cQkLdLYaaedkrQIR2bgn//8\n5yTjU0W1509/+tNAO7fccstcd911WbVq1XrvMcBAMYkytbfMPitTxE844YQkyRvf+MYkyUknnZQk\nOe6445K06bLs7zvf+U6Sdhz/4z/+I0nyxS9+MUny05/+dOD+b33rW5Mkb3rTmwbayX748rvuMaCL\n/sygifb49F0/cF2ZkaevULY+uN7/jfvvfve7JG2cwljsuOOOSZJzzz13oD1lluNE+73EpdZHF9rK\n5ulbX6B2uhDzMZcwZcz2lFNOSZJ88IMfTJIceeSRSZJ/+qd/StKi8vPOO2/g/h/96EeTJO985zuT\nJD/60Y+StCzioIMOStKuNxgNBk6nc+bMyfLlyzsznH7vkDXMelBu4cDGSib08Ic/fODzN7/5zSTJ\ny1/+8oE+Wg/MCazPemPt/NCHPpSkXS/KrNYyHZtO6HTWrFlZtmxZZThVqlSpUuWeJevFcLx9d9hh\nhyRtTKbMaIBsxCOOOOKIJK2vHcr+r//6ryQtU3rZy16WpEVt3/ve9wa+//KXvzzwfIjmV7/6VZLk\nve99b5Lk4x//eJLWJ2v/jrczfyQEddlll3ViOKOjo01fy30vZeaTvurT/e9//yQt4oSu6MzeJjrb\nbbfdBvpI11DixRdfnCT59re/PdAnYyPPv/RHl5ts7bPqgt5KhqOvJVry2f/Ljby+d/1973vfJMl3\nv/vdJMnBBx+cJHnd616XJPn0pz+dpI2P0SEmBMl6DqbEzuiCzo3Jfe5znyR36PK2227L7bff3lkX\n5R6OsrqBPpZZRlhWuYn22c9+dpLk85//fJLkbW97W5LW9j/wgQ8M3B/zMc6QMHsp98Jgyhjw3VF1\nQQwHOsa2MAVtKffTGBdxB6xN/FPb2e6DHvSgJMlznvOcJO2477LLLkmSf/zHfxy43/Oe97yBdphT\nl156aZJW9yXLtF788Y9/zC233NI5zjl16tSGTfH6aINxF++0x9GaZd0wj9mq9Ud8XFuf+cxnJkmu\nuOKKJC1b5PHg2TDvrR/sBdssN7j6f39Msct6URlOlSpVqlSZFOm0DycZRD7lvhlvPegbUuC7PeOM\nMwbuAU1hJN663u78kZDM1772tSQt44E45PVDSv7avwO5YAn8ldCE3PIuYh/ORJl1ZR05qI3/2v+h\ne0h25513TjJ+r9JnPvOZJC1zwXyUC4Kkn/rUpyZpmRO/NpbAHw3V0QFEM3369PXaozM2Ntbcw7hO\nVGrGdcZPG8p9MtpBN3Qo1ve4xz0uSRvr+fGPf5ykRW1id3z/0GCZaUOn7OIXv/jFQDu6Sq/XGxcj\nKeNV5V4icQvPpEMMpsxaosv3v//9SVrdvP3tb0/Sxi++//3vJ2n3rL3mNa9J0uq6LCdTtm+imnvD\nyNjYWFasWDEuk7KshWi98CyZmZgoJvSzn/0sSfKv//qvSZLPfvazSdpM0H//939P0q5D5ogYHxbA\n3j72sY8laVmm5/Kg0L12Ywd/rTXYWR9Jy2zdqyzLZc2yTmD5fmcPJLbPVs0pbO/MM89M0trLgQce\nmKSdA/rMk8J+9t9//yRt7NicmChbcsWKFXUfTpUqVapUuefJejEcjMPbztuxLMbJ5wp9y4vHUCDR\nc845J0n71uRDh/Ke//znJ2kRh6wUvnvokJ9b9tE///M/J2mRlEoFrof+HvzgB3dVQ3q9XtasWTOu\nGF5ZK6ksHPmQhzwkSbLPPvskaX2ydFNev8ceeyRp2Rk2py8+H3LIIUlaZAvFlTEBbK+sdFAWNFwf\nKYt0lvsq7I8y3vROF+IJGO4LXvCCJC3a44vHrJ/1rGclaRnqySefnKTNyIFoIV/teOITn5gkecYz\nnpGkRdyYOLnxxhvXC8n2Z6mVdd/K/RF0pg3mFrsyfpCo+BT7gHRdT4cYrDnx9a9/PUnLtMQ1ofeJ\nKn331/Jan2oD/bvr/d56gW1bN8raaRisvmKi7MK4iunJuOIxse6IX33uc59L0tqdOSfLVQzwoosu\nStLG/sqY0aJFizpXJ1GNwz3FWsxT9mHtZBcPfOADk7Rrpiw1bfJ/ngxxTdVY6FRsV0wH63e/o446\nKkk7l2TD/va3v03SenAIT86MGTM6FfutDKdKlSpVqkyKdD6eYNq0aQ0K5juVRQKZektCT1CS+l52\nrfJjPuxhD0vSvrVVAoB8+HKhPcjGsQd88VDi/e53vyRtRo92QRHQ4CMf+cgu3R8Qu8lLpgDF0Y23\nv4wZvlpZIQ996EOTtHtKxKkOOOCAJC2ygOaPPfbYJC0TEgOClPh8IVtjAzFBVsagzPtfvXr1etWJ\nmjZt2rg9PtpI32UlAuxO7A4ShVA//OEPJ2n3xTz3uc9N0o7nN77xjSTJv/zLvww8T+WB888/P0m7\nL0cM4IUvfGGSiSsOkPVB9BP9Tp/ZOF2VO7whR9fZS2bPCQbLlv3OXOE1wGQgY3EvzIe9sr8LL7xw\n4Hdl5ez+LMRhZXR0NDNmzBi3O543AGPgubAeYO/mp1iN+JRYsDayC2gdk5HVKmZ39NFHJxk/91QP\n147yOARiXVuzZs16zZGZM2c2a6FxMg6y0NwXMzF36M546JP7+P1+++030PcXv/jFSVrPCu+RPsvc\nY2d098lPfjJJu/6Y09ohu+6ve7OG1kNlOFWqVKlSZVJkvWI43sLQMzQvS4iI4ch8kDUiY+bf/u3f\nkrS7XjEdPl47gfnu+afFbiBfwsfLd2u3rbc4RFzW7lqf83AcwFbuDOd/huKgbugI84AwsDNsDBNy\nPdRlTxGES1dYAzRPoESMB7KyixojKvfh6E8X4Z+eqLqzPsqo0XZZQViXzDr1nqByPnesDPLEUGQb\nie289KUvTdJm/PjdYx7zmCQtsuXDxyrLWMOUKVM6HzqW3HkMxz3pgs1BjMaZlIcM2jtirtEVnz8b\nL89P2XfffZO02Wx8/ZDsb37zm4Hf6e+6zuEZRnq9XsbGxpp7mQslSoaixfge8YhHJBkfh5SRCa2L\nX/AalLUSVaywTslWM/fEPdmfuUFn4h5l9eiZM2eu18F8vV5v3D497AC78yx/jY85gPVpmznCTqyR\nvEnvfve7k7RrKHtxP3FPcauS1cma9X+xZOvFvHnzmnEaRirDqVKlSpUqkyKdKg1Mnz69t3DhwnEn\nOJYZN3ziUJpaVuIZ0JZsIv5C10FzdsnLBS+ZDpSnJptMHBkXfL72pkCR3shlBd21a9cOXWnAzmF9\n78/a+Ou9Bp4hE0b2B93pC+QDdfPJf+QjH0nSojcZVlgcxqO2mvgH9CfDr9SR50OHENfq1as7VwWe\nOnVqb8MNN5zwfCT+5jKWA91BZ694xSuStJl56kOJ7YjFYE76pjYaJqOGmv0aYgjQ3atf/eokrd+a\nLsoMPWy+iy5U4yjjhWWV4LKGFjYmUw5Chc6h/3LflzgpnemjuCdWYBc+hiW2w87KU3bLqsV9+hha\nF9OmTestXLiwsQtzQ9v11V99sX5gxDKqVBaR5Yj121WPGWEsPC76JJ6hJqO5Z0zMvdNOO037k7Rj\nR6RyCPUAACAASURBVPdjY2PrNUf6j9sWt/RsMRIM1v+tZezBuJpTpNxb5r50i/Vh9zI02R0PiTgX\ne6JrOnT//goaXXRRGU6VKlWqVJkU6RTDWbNmTRYtWjSu8jA0xNcqdiPzhf/PWxyzUVMNwlUhGXKx\nj0LWGX8mRMrvueuuuyZp/dja9bSnPS1J+zaW6YUFQCzleTldRN/5dGVQyV8XV4K+IQmZMBgLnyof\nKfTNR6sOlTx78SZ+aDrE3lzv+T/4wQ+StDEdSMX1/WfXrO/eEyyJz944QIgyaL7whS8kaRnwoYce\nmqStD+V6MRkZfPzW9mXQFQYEjfud7DV7V6DH1772tUlaeyxPnuw/ZXFd58fcmfR7DcraU+XplWwQ\n+ucbl01kLxmvgnORxEWNuz1lWB1fvzkGrdvzxGuAEZW7/ct45sjIyHqf+mn+ladXkrLenLgijwbm\nYbf8U57ylCQt+mdP7AKbx/55UDBd91WhAsrnTShPxbU+YGqzZs3qXI1j7dq1ufXWW5v5Vu6zcj8x\nXLYstst+7LsyJ/bc8w6HDGZyzDHHJGljL//93/+dpK1XaQ01/80Fe57MCXaGLZrL5blOy5cvr1lq\nVapUqVLlniedYjhTpkzpzZ49e9zZ9Hyh/adGJq1/WOzE2xsigeqxAjEcvlpZI5At3zy/trc4FAcd\nnn322UlaX6zsI9dBQJgWNLFmzZpOJ37OmTNnnK8bGvLW91mfsD+sjW8egoDGZBPRzQMe8ADPTZKc\nfvrpA99DPJCM52MB6tJBOOU+Duhv3rx5ufXWWztVSB4dHe31o1ZoDOsrKyezB/upZA/KOmMXfPqy\n2tSD43/GiOheBWUxAMxHLND+CyixrP0GbdLF3nvvnQsuuCC33npr5xhOOa/Kz+Xudb52zKaMsUGe\n+g6N22XPLswRyBRztZeFr99+HExbn8uzovqz1tYnblGeSJq0MRxtZjsYqJirfVrugRWodQbVsx+s\nD0PB4spMMLEh+7HUH2OPMkQxGvaEoW233Xb57W9/m2XLlg2ti+nTp/c233zzpu+Yrr90IRaM1ZVn\nCfk/b5DYnEroxPjKuONhMacwd2uxOJhYHt3xjFgvygrw06dPz8033zx05ezKcKpUqVKlyqRI5/Nw\n+s95gboIn6oYCUTAR0ogDW9p+yigOf5qGRLYgber0wvdV7yirGsGDcp+wir0AXqA5lasWNGJ4fSf\n1w6heLasEnsNoDe+ddfpE+QipoOx0CnfvHiV30FMkCg2SKBBWWv82sZdNgyZN29ebrjhhqxevbrz\nGTDlnhM6MV6XX375QN8xHbuqIUr7J17/+tcPfM/fzPcOrWHCMgH5+ks7wx7EscQCxPbKqtbJHTbc\n9ZTL/vNdyvlVnoMj7mCPENFGMRa+/7333jtJm4GF4UL7WAF2qXYW1g/5ug4C5rP3HHO3P2ut63k4\no6OjvX5dlpl7Ynj2jLmWFwDjxcLEAMV4sXVVGN7ylrcM9OGCCy5I0npC6E5cxPU8L9YT7eQRKb0X\nIyMjnU65pItp06aNq0hizpSZeqomiGNj89Y6npD3vOc9SVrvjnORxHZlpdGVdYPnwz4cDEgWHLYn\no9jcLfdS9Xq9ynCqVKlSpco9TzrXUhsZGRmXhQSZyLSA5vkDxUzs9IW2jz/++CTtGR3YAMRiRzCk\nI+sMgvWWlrnlueoIQch2VUNOEIv7QnFddTF16tQGrfMT841CHNASnzp2BbVBa/ac8O1DGpCKvopD\niDe4v2yl8jRLsSCISHYKpIJZQbzQZ1fp9XqNHkudlGeusBOojT295CUvSdL69GWZYXHQm2oNWIG2\nYzh0KeYD5YmXvetd70rSon4oU6zA89anfph+91cbSMazvvJ7qBwDgSAxILqxF6msN8cXj61hrpiQ\n+xgL95c1yasAgZeZY2V/ukh5yqnxZ+vmpTkj25QN81Bg+VA5NiCOJaPT+KtUAtU7Uwqbw7zLdcT1\n5V4p7Z42bdp61xt077KyOu+O781n4y5Gg+WLK4lnq77AG2RdYE/+8qBgb2I1xt9eplNOOSVJO6c8\nh/TXr+yii8pwqlSpUqXKpEjnWmrJ+PiD0+Vkl0DT3qr2pGAg3r4Q5Ve+8pUkrb8Z4pH9Bl1BaTIz\n+BWxBW95z4EmoTqZOGUufLk3Yhjh04Z+tBGDKfc9iB/wJ5e5/49+9KMH2iIGBPlAFPYQYGcQknNu\n7BCWlQTh6iufv8weMQK+4euuu2696oeNjo42GVfaKiMK0+WDh6K0FcMVy9EXMRZZZRCy2mfsUEwH\nIsZ4IFw+euelqC+F3RlDv8fE1mcPTnKHbbCHkj2zRbbPptmqfTcypVwv45LOZB1C9TKt6N7eN30S\nz9Ku8mRRumBvdwezSe7wJojVQdGyyIyP6t4Yh/lfVsZ2zpXzcMSf2DgPCvQvw9OcU5mCx4M9ym60\nG1+frRe8Aex7+fLl61U5e9asWY1ejQs7oH8xWnZj3KxtGJA55bN1Q8yHLukam3Rf9oMpq75QZi2a\nw3Tg+/46hXUfTpUqVapUucdJpyy1adOm9RYsWNBkDXlbQoKQBSTjrWpfRXn6pGwRqA4qg3jVyFI9\nGDq3X8dbn29VbEi9MGdEQDYytryloYK+2l5DZ6lNmzatt/HGGzcIBSKFjj2DTjAYCIJOnDKIGckK\nkZ1mHwVEoa3QHPRWnhXkvipq23NUnmYobkbmz5+fxYsXd8pSU0ut9HVDPvzA7EIfxOJUBsBYZNqV\nFY7VziOQsb46J4XPnx1gd/Y2yF4qT200Bv3Vh7tmZsnYI+X8gp77s3yS8b53O8jFq9785jcnaSut\nq4XGTrRZnIIusUn7LCBgdgpBlz56Y9gfe+q6D8d6QR/G32f79MoTYsXczC3/x1DtQaMjbB37413A\niPRdzM74ywzjmRE3Kf+PNVr3li5d2lkX9u2VXgDrA2+OcbPWYf3qwIlzYWdiMdgc3TojiM7FucSA\nZAZag8U3rRN0xZPSf15WMliHcvny5UNn7FWGU6VKlSpVJkU6xXDGxsaybNmycbGRMtNGDTW+Vihb\nFoh4AXTGVyvryNudH9JbXrzBOSqy1iAfGR3iH7JdZL15K4tRuP4Tn/hEkjbrZRjp9XpZs2bNuDN5\nCHYHncu4sxcIG4Ak7KMQf4LyICFoHRIRE/J8p1liQuIc4hl0yKcLsZSMbPr06Z399mvXrs0tt9wy\nDs2LN8kWcx4ShqqNEKU+y7SzT8J4YnPiU3QF4dq/o89Yp/PdoUi/wxIg4rIiwvTp08dVkB5GRkdH\nG7ROl+VfSNazMYq+qhdJ2nGX5SguKltNNWjsXkyILTtzim7VXCtZxUQxm/7qIV1r7LGLMiaIzWG2\nxgfaxsLFZvSN3ZjPYnNQt3UEK5S5J2vN3CirzatbiG3IUixPKtWPDTbYoJmXw0p5+inpn3dJa8My\n6VTJYB+y1bTJuvKOd7wjSctUVUS3F9FaZ7+NGA5diWvRiZgNlimuJqvNXJ8zZ844T8H/qoehr6xS\npUqVKlXugnTehzNjxozm7Q5NQV/exnyiTl6UCSETo9zlLobjrBi/s9uej96+Gn7GctesncvQobc5\nFF+iVdlK65OV1ev1snLlyuaeEACWV54Jr62qJ6jqyudOl7JCxLH0zW551V/tmna939uHQVf80IQP\nWLvLasaLFy/urA97kvyOnxr6huJlFYoj8InzL/u9bCF1nNiN8RUPgwrVxNIHz3/Uox41oAPoTNaU\nuBcUjxlp7+23375e+3D6s9TKrDBtFF/UFqj+gAMOSNLaiTkBlcsA1VZMGuvDYKF9LKA8A4q3wNzA\nuGRPlfuF1qxZs96nf0LjnoHZEEwE87Q/S4zO72WxivHRib1sshqNc1llQzxDlmt//cCktU+oHvtj\np+xi2bJlndne2NhYVqxY0dice/pr3DAV2a28Qf4vbqVPstXUUPTZXiW6sv6I3WCZ7IE9mTPYpdgg\n5lRmN65evbpmqVWpUqVKlXuedGI4znTwVizrNfG1Q9EyarwNnXsCPZUndPo//yUfPgTirS9DQ/aJ\nrBXZbBCOc1CgNu2TKVZmYHSR0dHRzJ07t/ktnzl0pLoCpCoeJdvE/httFk/QVjoWz9JHcSsxmfI8\ndvcR7zA2Yj0QLT+1z8Zk6tSpneMWvV4va9eubZAohomxQGfiTNgXxEl3Ym6yi2TelFV8ZSPZryPT\nDsqDEiFWaA6rxBLpGkvAPmS1dfXTk/6zY8rYCD1D5xCubEQ7/2XU6QN0LbMLc/nqV7+apI3RYAcy\nOGVosiNMB8MqK2NMdCrr+p6H49TUpGXTdMErwBPBo4G9Q+sqTpQne9IRRmzcMVw6E/dUlcG4sgu6\nwJTYE7twHzGeq6++urMuxHzZcFmd2zM8EyvfaaedBvomJldm8LEHe9bsjRQzxqBV1MaIeZ9UZC9P\nDC2rhFhv2MWNN95YKw1UqVKlSpV7nnTahzM6OtqbMWNG4w+EoqCwch+GcyeOPfbYJG2eu2wTmVbQ\nlVPn7DEpT+KU5YTB2KnsrQvtua6sleYtbV8INCh77vbbbx96Hw5d8PNCx+INkCJ0Ly5lxzhfPcRp\nX47fiW/JIlGtQfxDvAyjUV3W2GAJ4h58uVhH6Zc2ZmvWrBG76FwVGNqC0thDeeIju+Av5qfWF0hX\nBo44FjvD8qA4WU7YImat4rL9XFAe3WlfWcGZ8E933Yfz178D32M2kCnvADRvfKF2/2ezMv5k5KmJ\nRYyfLDYZWezJHiXIGrssT64sq5+X5+J03XvSbxfG2XxnJ/4vS03cim36HjovT/oVX7Cv653vfGeS\ntgq9uSRTy/pTziGMih3QVVlFZOnSpZ3nCF1Yb3kgxLOwLPPXmimTk80bL/YhziVzD5NlN9ijuUB3\nbJ6ng11hYDwi+izmZ33rZ2h/1Ufdh1OlSpUqVe450imG0+v1snr16uYtCk3xK3sLQkdQNwYCScgS\n8RYVW+F/xISgcj73ww47LEmLODwXIvGWl33mfu4vViDLDYL2Fu+SnTU6OprZs2c3qF0bIAbIUhaS\nvQBqXvHNQjbQnqwQiARrw/7ky8tS4evFaDCl8pRCKLLMSiPQ/syZMxv0NKzI2MNI+79Pxp9VrwZW\nWSdM3MseASje/1UeYAd88+JifPI+Y7jQpAw+vnpxMGitrCd2V/bhTLSXiW7pBjqHODFe6F6byirP\nfPNiPzL92Lr7lswWwyprcBl/dlHGNdcnhjM2NpbVq1c3fSjtyrPZxfOe97yBvosvqJWnL1jhqaee\nmqSN9crsFOcQszMHZc9C8a5jd3QgNlhWudbeefPmdY7vieHIKhVH9gxeHPNTZXReJOuKc23MAd4g\nNfXMERXRVahwH8+xH8s6ZS3mkdFOjIiUsb4lS5bULLUqVapUqXLPk84nfk6ZMqWJvWAMEIp7Qd9Q\nO9/qkUcemaRFUfzVslW8de08l6Xk7e10O4zJ95APJOUtDMWV/khIq0Qua9euHTqGo34Y5CGTrqw1\nRCdQVBnzkVcPJdhT4j7YHuShr9CaSttYpay08mx79yn3JJXn+CxZsqRznajyJFh9xrLK7EAoDstz\nxg97Ue9JXAOLk3V44oknJml9+jK+oHy78MWK7F0ps+bEMbCRsjrAxhtv3Ok0Q7roZzj0W1YxgOL9\nNU5ia+aUfRv68D//8z9Jxu/XwZSxd7rG4uhWpiB7KSsN2CtjjFx3V2I47KE8C0YsFeo2Lz0Li9A3\nzBfjUZlEzMfeE4wGQ+ZRkYll/M0Re1CwPzorz28yVrNmzcqSJUuGjlsk7Ymf9KwN1g+68Nc4lVXF\nZXLKpOPNoWOsXrajtc/cUfnEHGI/PCnWLSywjPGV3opVq1bVWmpVqlSpUuWeJ50YDsQCHUNNEAq0\n5O0nbvDKV74ySXvmAsQr+0QGhvx62UcQMn+lOIa/0J+4BXQnMwsK0F6ZO5ATP6S39vXXX9+J4UAf\nSYvCy6qvng2hiDMQGXWQBISh7TK2MJBvfvObSVoW53s+e23yXGgN8tFOcQvMBPpcuXLlep1dP3Xq\n1HHnyLhnedolJgrNsQNxCeMDBZaVK8QQZaNBtHSL2bAjaJ9AvlAdnYjd9J833xXJ8gKU5+GUGXtl\n5pM5Y05B4+KUECcGS1fQv53h7EUVYXPSfTDdMvZISrvt18X62MXMmTOb7DSMEoPxbDZPF9YBcQzj\nzYb12b48+7p4RJwkzC5kQ6rpB9Vrj7/2yslqE8cwN43dypUrc+utt3ayi2nTpvWsZ0m75mB1ZRVx\n89P+KvUiZa2yfeOMGdON66y5mJH4l8xNmXn9p9zqY9KuJ9pbXrd27VprRmU4VapUqVLlniOd9+FM\nmzaticnwgUIsJcL1ViyrsELpmBFEIouIL17Wmcwsvn4sQoYOpAQFQnPuD7WVVU0xJCygSwwH24PC\nIUKo3rP9H6qH4sTBoG8ZOuJYMmzEbCAf6Mt9VJvmX6Zjz+trb5IWJbpeu/vrh61YsWJonyxdzJo1\nq0Fppc+bHUCypDw5FpOR7YjlPfKRj0zS7quAztgNdlBWDtAOzynPQSp3a9NFf/zlrzvlOzGcO8tQ\n62cKd6aDiapJG0eMxvjaX+H/WID6c/4PpWPEZeWD8nPJePrHsOvek9ILUO4tcu/yZFVzxnhibdoG\nxYuLymK1J0XVDVmqZS1HfTYmZTxTm0vG2y9dUH1yxxyZPXt24+mgA+NSVo32f30W4zOP6Y43RzzU\nXjPrx8te9rIkydvf/vYkrUeFLngT6ABzwQ7poPSIWI+WLl2alStX1hhOlSpVqlS5Z0knhjN16tTe\nvHnzGjTk7SgrSO53uXehfIa3tre4ty3GoaKpGlqQKkbluaV/HLL1/9JvTkpU14f2OlUamDZt2rgd\n2SUy8RcicR3Whx2qlFuiL3Ene4ZUGuCPLrNdtEefocTSR4xFiGOJY6xcuTKLFy/unJk1ZcqUpu+Q\nLAZaxvjKzCe/0zbjjbnYb6P6r1p6YjUycUrGQpdlnSo+e+J32tlvL+t74mfJaCDDkkGU5xL5Xbmn\nyTiX+yC02fVYfsmkyr0S+mgMfJ5oT8X6xHBkchoPfWMX5mmpE/MWy+OxMI76zEtgb4p6YrwGGDKW\nxy7795z1twcrJKWOzZFbbrkla9as6cxwZs2aNU6/4tlssswWLJmPucDbY4+ZNde81mZ73lSawJTY\nPF3RkXXE/ejAnDSW4l033HBDli1bVhlOlSpVqlS5Z0nnGE5/bSRvT9Wd7Slx4qfr7JfhW+XHJK6D\naCGa8i3Mn8jXL8uo9AFjTHZtl35PJ/zJ67ebdunSpUMzHKi+3NFfZlhBVSWr689YSdq4lIyecle2\n++pLeTZ6WcG7jAUQSKb/fPb+6xYuXJhrr702q1atWu9aamXsRs0rWYS+LytU6BMdaSP0jaG4Dmsw\nfsa9rBNX+qf7M2z6P7tvPwLumo1U1lIr97uU7K5k38R1dOWz+crHXrK1/rPm+9tRzhHPLZlY+blf\nV13jWWW9wZJ1qWXIo0GsD8bROlDGKY2/7LTyrKdyLkLpYng+s7dSVz6zi/4zjf56kmln5ouJ0nPp\nhSm9BNYJn8t4tDnh/3RHF+VptmUsxtiUcauSBWpvyYRXrVrVKbZXGU6VKlWqVJkU6VxpYHR0tIk3\n8J2XNci8FaFpO3m9VVUWkHElR9wphf2+0qRFJO7n7S5bxd4Cb2tveW/9EumWFXD7zuXotA9n3rx5\n42pQlSclQgyQgT6UPlr34TP1fz75/tMGk/EVA4yJPpdxLsi3jFPQmT0xXX2ySWsXJWou/dVQlL5q\nO53xL7OrMpOvzKTyV80+VYBJGRso0VmJFjFx56vYc9bFV19WGpgoljJR1lq5T6e0r4nO2Zko62yi\nyhLlWJH/LZtufTKzZs6c2cwz6L6MpWAQ7MD/fWab9oyY3xPNBcwFOyjjIKXdldlqGJE5pA6ZvU6b\nbrpp5zgnL4C2alOZqWf+lwx5oioZZeantdJzyvO1/J8npWSRZTZjf0WBv/Zj4PuRkZFOuqgMp0qV\nKlWqTIp0ZTg3JvnT3645f3fZttfrbTLMhf/HdTG0HpKqi36pumil6qKVqos7pNMLp0qVKlWqVFlf\nqS61KlWqVKkyKVJfOFWqVKlSZVKkvnCqVKlSpcqkSH3hVKlSpUqVSZH6wqlSpUqVKpMi9YVTpUqV\nKlUmReoLp0qVKlWqTIrUF06VKlWqVJkUqS+cKlWqVKkyKTK1y8VKr/8flsUdStv8n9ZF10PH/pZt\n+XtL1UUrVRetVF20MqwuOr1wJlvKMzq6/n895G6vdVRW3V1XWyfq07r6Wla+nejkxnU918mO6yMT\n9XWi78szX8ozNyY6q6W8Dyl1UP7tqtuRkZG707bu9JlkfZ+jKrCK16WoMk3Hw47t3TW37kyH5b3L\n8V7fZ050qmp5imp5Iuz/1vb+3/eP2f+/lwRb1wmvf7PnTurTqlSpUqXK/2flHsVwylMGJ0KokEx5\nMt/6oo67kymV95ronus6jwRad115fo7nOD+jPCF0ovZM9P+7KqOjoxOe0TJRG8qTICe6rjwTZKLr\nnC3izI91IWd2tK773h0yrF1MNB4lG/BXXwldladmdpVyzk2ZMmXcuVdd7tMvpS4mQtnrsgvjXY5j\nebqqc7OcDDvRKasTSTkms2bNmpBR3lOk1AkpT6CdbKkMp0qVKlWqTIpMKsOZyMdeovjyrHFvaafW\nQUQTvaW7ItS7wozWFVcgE/lMS7Slz9ib+5W6gdoWL148cJ+Jzh6fKGYwbPvXJf39KhlJec+ybRMx\nGtftvPPOSZLf/va3A7+jqwc+8IFJkssvvzzJ+JNdJ9LJuhD73RHD6eorL2MuJVrfeuutk7Ro3UmN\nELeTGP2utK+ucRLXrQ+7SQZ1OCy6Nm4LFixI0tp8uS7stNNOSZJLLrkkSXuKpTnhM3soT00tY4jl\n88u543cTeRP+HoLlleNU6pid8JD8vaQynCpVqlSpMikyKQynRNelb9Zb+jGPeUyS5Ac/+EGS5MEP\nfnCS9kz7RzziEUmSb33rW0mSpz/96UmS97znPUnaeAbk4m0+mZkY6zrLvjyzXuYMFIbJHHDAAUmS\nyy67LEmyaNGiJMkJJ5yQpD2r/Gc/+1mSFu2de+65SZKlS5cmadGg36+L8dwdUsZEymesi+WJP0Bp\ndLThhhsmac9d32STOzLYf/GLXyRJjjnmmCTJBz7wgYF2sIcNNtggSXLTTTcNtG/YbLZhpR/VT6Rv\nsi5GXLb94x//eJLk8Y9/fJJk9913T9Lq5CUveUmS5O1vf3uS5Pjjj0+SPPe5zx24j+eyo7uaITaR\n9Pd7ojlAypheGa/E3jAffXzmM5858P0+++yTJNltt92StOvHgQcemCQ56KCDkiQLFy5M0s6R66+/\n/k7bQfoZ0d8rS20i28Rg9OUvf/lLkuRPf7oj8fY1r3lNkmSbbbZJ0q4P5or7Wn/WN/a3LqkMp0qV\nKlWqTIp0OmK66+alEiFANpgIhHrjjTcmSe51r3slSR7ykIckadHYd77znSTJQx/60CTJjjvumCT5\n5S9/maRF+dtuu+3A9WUG1xDZMRf1er09h+xb787uWYo+Qx6YjM9Q2BOf+MQkyVe+8pUkLWpz3a9/\n/euBvxDLH/7whyRtfOuLX/xikuThD394kuTFL35xklbXmA5EpD2ynaDz9dnUNtH+GaKNnml8xB8g\nSChMHIt9YLaf+9znkiQ33HBDkhaVETEfCPiRj3xkkla35fX6XtqFzLu7oot1sWtxBaING220UZJ2\nDlxzzTVJWt3svffeSZKDDz44Sct8scBPfvKTSZK3ve1tSZKf//znSZL73ve+SZIzzjgjSTJ//vwk\nyc0335yk9TZgh2X710cX7mk87+S6JOP30bAXc8D8/973vpckeexjH5skud/97pckefSjH50kOeqo\no5Ik//Vf/5WkZTJXXXVVkuQLX/hCkuQNb3hDktZzwqNCV5tuummSlgWWsZu/5cbPieJdxpcnY889\n71iuPvWpTyVp2f5pp52WpJ1r4p8f+tCHkrRzwrqD9WORpf0aizIrkgyri8pwqlSpUqXKpMjfJIYz\nURzDWxuS2W+//ZIk3/72t5O0MRnxi6uvvjpJ+7bda6+9kiQXX3xxkpYRnXfeeUmS3/3ud0laNM8H\nXGYp/T1y0Euk6DPU9bjHPS5J2xe623XXXZO0COZd73pXkuSkk05K0iIOuvzNb36TpGUyMnV22GGH\nJC1bgGBLxHJXfNMT7fCfCK2Jzeyyyy4DbXOd+IOsI8z2iiuuSJJ8+MMfTtIi5+c973lJWkQKEdPh\nT37ykySt7sU9ulZ1GEaG3cXOJvWhzDoSbzjzzDOTJIcddliSltl897vfTZJstdVWSZJnP/vZSZLj\njjsuSZvNeN111yVpdUPnvi/bfXfGs9a1X66M5ZaZeWIzb3nLW5Ik++67b5LWPjbeeOMkrc1j9RhL\n6R244IILkiSHHnpokmT//fdP0jIbwj7uLCb5t47hTLRGLVmyJEnLTP09//zzk7Rt1PZf/epXSZL7\n3Oc+Sdrxtea6fvvttx/4/PznPz9J8v73vz/JxMymq1SGU6VKlSpVJkXuVoYzEaPhgxU3gGyvvPLK\nJK0/UTwDQ4H2IReIBDqDAuTnf//73x+4L2TE93p3M5v/bZ8GXfB9Qm/6huVB9SeeeGKSNnsEM7nw\nwguTtKzv61//epLk9NNPT9LGMT7ykY8kaZHLc57znCTJP/zDPyRp0VtZpWGiHcldZWRkZJ1ZaWIn\n/MQ+0xF/NN859E5nP/zhD5O0sbqzzjorScsC3vzmNydp7UbcA4rHJvj0MacydvC3rB82UWwHUvV/\nfWbTGCyGwj5++tOfJmmR77Oe9awkLbqHfNnPG9/4xiStl8AcufXWW5NMji70sXyWdQLaFuPz+b3v\nfW+SNi6FvbkPL4DfWSfKuJfvZYCK6eyxxx5J2jlWZtOtK+Pw7hTrhYxN89X6IBZHt8ZdpuZHBa/h\nYwAAIABJREFUP/rRJO26IpbjetmMYnfmhL4/4xnPGGjPRHUPu0plOFWqVKlSZVLkLjGcid70ZbaS\nLBLoDJKBuqC5973vfQO/f9WrXpWkZUSy0vixP/jBDyZJrr322iQt6pO5Ve6q/VvEcNa1Wxkygeox\nCYgCMvnxj3+cpNUBNH/OOeckaXUB1ctS8/nkk09O0vq5ZTd94xvfSNKiwBJd3l2+2b9mtiWZuKKE\nbDR/oa4nPOEJSdrcf7EafmRZR9A6FPf5z38+SeuDx2jYlSykMgsOq8SsMK2SCa8vku31euNqnpXV\nmrVF/EGbZSHJKnra056WpGXxr3/965O0cQgZe6eeemqSdo7xGmBAhx9+eJI2+/Giiy5K0vr69Zmd\n3l21wsbGxibc4V9WQ6B/6Nt4i0OIX2JlYjgy+l7+8pcnaRnQj370oyTJk570pCQto5HVKu5Ft9aX\nssrD3VWNIxk+JuY6zFPmpViv8ZZddsQRRyRp49ji3aecckqSNub7ile8IkmrG/EujMr+rjIOf1eZ\nDakMp0qVKlWqTIrcLTGcMqMFuoa2MBBvSYjWrmn+aVlHxx57bJIWvWFE/M7Qvcwdu2ohY+isrDxw\nd1WX7u/3nexTGHgG/zH0JosIypKlhsWpGMAfrU++t2cAm3N/uvY7OhY3I9rxt6x2O5Gv+973vneS\nFlHa2S1GRwdiN9ifDBt/9QkyftnLXpakZXnsCHOx/wbSpgP7OLBAY9dfz2x9baRkd6WdyBr8/e9/\nn6TdO2ZcxRvsr4HaxXTsOcGE/F4MDwKGbLE5Oi/jE+YIRF2ykLtSV66M0Rh/zxaDO/vss5O0ngu6\nwf4OOeSQJK1dQO8y9oyj3332s59N0noJ7E0R9xTL0VfxEeuGdpaVMO6KLtb1uzIT134pfcZotMm4\ninNheezLX14B64nMTVlo4uP28fF83F2xPFIZTpUqVapUmRS5SwxnIt9mySSgaf5p2UHeznzqL3jB\nC5IkRx99dJIW3UHrfLDe5tttt12SZLPNNkvSMqbyZL8Srd1dMZw7y8svfZ76CjFAWfzUkIxsFHXk\nZFbJvJJdpIKA76E/8YunPOUpSdo9KZdeemmSdu8K1C+WdHefKXRn39GFCsfGz/fYnswqdmL8xRmw\nQ/5qzPhrX/taktYvrc9QnUw/MSOxPWyhrPF1V1Hd1KlTx1XtLfVrjxk2Zfyg7P8fe2ceb91Y/v/3\ncx7CU8bKkETmyJxQimSep5CUeZ4yRMnwlRKRKbNkzFRkzlwoGdKAZCiUIQkZXvqR4fz+4P3c51xn\nr7Pnffaj6/N6Pa/97LP3Xute17rXWp/PNd0yU7djfOGoo44CStahKs3aFBWucVF7rZnRpXrQC2Hc\nzJiP6rJq1cxmMTAwMPG3UTFod8+bx6ptFlpoIaBcG2Yvel3bG80xO39Ud84Xv+f2VUqHH344MLKP\nmMrH+Fe8RroJ9ymMuRnH9B7n+fX+oqr3Ovf8eh/RK6CCtf+kx6rNVIVV/RDbRSqcRCKRSPQEXanD\nUblEv7AdayPzjdWzZqPIdK0xsZfWkUceOWy/sZ7DuIbxEX32VetbtIrRfu+xuy/jDzJZ2Z6+eFm6\nNtDfvdtuuwFlrRfz72WqMh9tbPbbZZddBhR/thk51ihFVt9uR+1atnCbsngzoOxga62QWUb6qxdc\ncEGgKCHPozY1Zuf37Zllpo1rxsjWZIH6v2V/Kp54DO3Oi1o1TVEBx9UqVRpmn9nzynimx6CqV/E6\nr8xu9HtmH3nMiy66KFBsaA8t6y7sT1a1Vkw76yRVdR7xvVms3gdUb173egdUOrJ7Y3Yei+rfrDQz\ntvzceaEy1hPi97WFitvzWG/l2E6iKjvMNZ9UZXaSiH0ojf1pM7sreCzOfaFNzX7ze/X637WKVDiJ\nRCKR6Ak62i06Pp1lrioVfbKyuL333hsofknjDva8sgrW3HF/53oXMlwzK5Zffnmg5O3rC9bn2wBb\na7lbdI3PgcKOZpllFqBkodjzbN999wVKtbOMRR+rmTsqHOs2rMqX8cqEZSzux1jAzjvvDIy0Qa3e\nWa12i65nC/ehPzl2YfD8mZGnQlG9qfpkwsceeyxQmKzZSKpFFbVZbBdddBFQsh9VF9ZtVc2LdroC\nV6066t/NiHIsKlhVnTEble7RRx8NlLiUCsb6CWtXlllmGaBcG9deey1Q5pVxD2MGxtdkxlWKtxO2\nEJ53baKydQxR/XtsdiQxA+/KK68EStzJjCsVjNeANUx+/7zzzgOKojEOYlZtrKWL6Ga3aPetsnFV\n04MOOgiAgw8+eNj3zNj1WrAeT4+JcSz/rkr0WtRLYE2b95VGkd2iE4lEItFX6OqKn8ZOZBr68Hfd\ndVeg+BuNK9gjyziHefYyXZ/Shx56KFAyvczskeHqfx66xsvQ1076YOv1UotrfZgtJIOwNkWGYgaN\ntQLGXrShWSj6nWVpF154IVA6D8jiVY+ySdVelT+9E6tcRvh3FY1MVNVnZlWsz3HND897rIewWt66\nLBWxx25Wk/2kZMhmqRn/ctXDoccydNztoN7aQPrMVW/GGfTRq/bM3NRmqjwVstmOqkRZvPFQX1XC\nziuVlOM0Hhp7b8X/t4L4e+eBc9N4gx4Rv+/80GZ2AVfVeZ+xm8JOO+0EFLZuzMaapS233BIoSsjM\nTuNf2sBrJXZK6OaKn3GeOIe1gdeCGZwqFP9uJq/K2fot76V6OrzWVH/ON5V0t5AKJ5FIJBI9QUd6\nqVWtfyIjUdnYxdentisyyiDMxzerRGbq9r7whS8ApbJY/7ZsL/qEY/1NN7NLYufbuFKetST2RLIe\nxywjmYc+fH3r+lplLPpoZaZm9MgKZXvWbcji3Z82iqtcDlUPrdhp6G9i5ltc80W/sjZbYYUVgMLW\nZPHGo1zFUJihpXrT5y67P/vss4HCXFU2vrcHm7UHEUPVabvZe9EW2kn7y9adN14jsnWZq0zULCMr\nxfW9G4cyHmHVvfVa9uoTqgPjWsbJZPXduFZi5pvH7LxQ9XveL7/8cqDEfq2rMj5pfFPbqFxUi9po\n//33H/Z746FeU35PL4HjFN2qSamFaHfVmfU4ni977Lk6shmd2spYjdeInbZVvmbyqny85+o92m+/\n/Tp3UEOQCieRSCQSPUFHs9RiBo6+UJ+6xmpktPqrzbiyyt5+QDIV4xYyYtdrN+/ezspm7jz22GNA\n6S+mv1KMkk/fVJbaaGt9RFsYg9EXb52FmVQySyu+PWZ97jIb62w8RqvljX+ZwadPX/VnRp/1HpFl\niiG2aTlLLSpfVZX79BhkZTJU/+750gb69mW0MlPnh4pGFuhaIMaCrEmSSasmjd04T2r1l2slY2+0\neJaKV5h1aOaV59O6GWN+roYrC7e3lmxfRWxcy/kmW/fVa8XuHM6LGK+oUjrN2mJgYKCyk7rnMXZQ\nN8POujs7jXg/sVu8KtAMLr0IHqPzzu3Yfdz5oG1VvGaOOv9iP7EafRM7lqVWFTf02K0R8t7o+TEG\nbPxaBaOy9R5rpp9KWE+J59/PvSaNETW6TlZmqSUSiUSir9DRLLWYkaNykX3LYIR9fMweMXvI71tz\n4Ep81qpYmezTWt+vGVvuRzYfu9SKdrORRquuFzLLuJqpqs/Yiz5TGYc9kOz+a9zLY7UK22w163c8\nRhWQtpWtybCr+lp1shNurGOI8SPrLDxvZidab6VicWxmbBl/0AYyULMZnRf6uVVAMmTjHjHrrd7x\nNIrRfhdt4YqszmnjCao7j9V4hjbV567S0Zfv94wFqvJ+8IMfAKVS3biq88B5aXakaLcTRa3fxd5q\nxqVU/c51j9X3rkLpXFcJOUa9B9pU1ee1ZuxPW1jjoo31kKgK7NIhulV9DyPvnXYOsB+c3cCNP6l0\nncvWLlpPpfpTQbs2lL33nBfOM1VfXB+p00iFk0gkEomeoKMxHJWEfuC4yqS+euMKZhVZE+BTfMMN\nNwRKB1wZkL5an75mGZmxFXtm6Y/0d2IUttZ0p4EqyMrMvIqxHFWY39NWZmjJQGSBZpkYbzDrSGZs\ntoldFtye7/WX+3vPe5WPthP+6dg3zPMW1/ARZiXqj5btG8Nx3Rz7fnlsZrGpJv1cdqdtrLs488wz\ngTJfZazOU2tQzFLrpK/e7htxDpqtaC2Rat85bH2EPnoz/ezWIYzhaFuz1ZxHqkdjAK4ke+CBBwL1\nMzpbsUVUklGx+rnZhsYxzbjUFl5LsvWtt94aKNeMbF+1podD1eb9xXlpHMNryU4nZs9WxTlFJ+eF\nHdD14njswmvIVxWqx2otomNWCcVOBN5bnW/2JWxXyWYMJ5FIJBJ9hY4onJidJGuXOboGuYxzueWW\nG/Z7fff6o62vifUYKh4r0H0q67uP7Mz9y/Zk853qpTZallpVPzmVhp2Sje2YgeVaLvpa3b6KyOwz\ns5bcjuzd+IWrXMb1d1QJjk9m1G42Uq21gUT0feufXnvttYeNSYXi58Zc7AOm791jk/1rO8dg3Mvt\nGA+TKcvyzGaL52woy2u1r1yNvw87RuOSqjMzr4y5GZ+Stft7rwFtYbxB3711G6o/r0UZrvNQteD8\n1AsQM/W6MS9iJ3V7qOmpsFZNGHcyPmWHEmMvxoI9FlfF1ZtgRp5z3c7aXlOOQ0WtSvS+VNWDsZu9\n1PRQCPtJmqXmWFU62lCvkedd23kfMKvRa1LbaHv7E7oSqPOxXrw7FU4ikUgk+godjeHIXIy5yOaF\nDFN2J8uSqeq/VtGYeeNT2BoFma+V4/YBktUZI5KZxNdRntZNKxwRtyVDUYnIQPWZyiRlLH6ur96e\naGbiuIaMK3zaJ8pVUmU2rpNjjYlxLeMS0S8duzEMOZ62mWzsmC2MG6gwzDoyq0y2pSK1atpqeLOQ\n9NHbbSGuBWKWpPPFeaYtnSdVKm/I8XS83kK1b0am50lbOFazCu2yEdcMsore2jRjf7J8lbKqzvnn\nsXtNxmukG/MiImaXmSWmR8Lzay2KY5Wlez+wW4M2Ubm4XVWiGZ2uFWRXBr0GHnusv/EcDO3N2Cnl\nG2EXaFWY6t/7iWuBmXGnClOZmJ3mPTSuFWZvNe8zepWcP61m7qbCSSQSiURfoaMxHFmR7Mp+Xmaj\nxC6sdvmV5euntIZE/7ZMyNiOjFeGI/ORtcmQWlirvu0sNZmINrFuxsw5fez6m2XnrsXh5+uuuy5Q\n4hAek3nz1ixYYxJXs5TVaRvjJ7GTdlwXR3QyhuM+9anLtmXjsi+zyez/ZPaQ/mRZmZXkrmEv27Mr\ng+pPdWm9hfNPW5oJFHt8DUWnmGzs7+caPVaQx9Vx9c0bnzKzTxVgjZrZSM4L45sqYfdrHNVry/3E\n8VV1nhjyvuUOFLHzhPPBsXosekBUOKp/swuNe7rWj5l31qa4XWO7dmBXRfq5alJbeE2YvRjjWe2q\nvUa+F1cXtZOAysRjce7qRfJ+4bE4x1VArg1mXFz1r3q0z1yNcQ8bTxVS4SQSiUSir9CRTgOx47BV\nr77XD2l1tJ/LVPWpugrhPPPMA5QV/Vw/RwaiKph55pmBUhEc1yCP8YqqSvhOrAHjttyXdRIqj8hI\nZCpWQcu6VlxxRaBkE6narDmIawDph1ZNWr2vDfRnGx+zHiOytXbz8GFk7Ca+V2UZuzHjykwrj93a\nAlWfasDYj6rAYzXGp5o0g8u1YszYkbnG2oNerFWvXVVZqjnPo8dgHMtaIrMOvVbM7LNmRK+A8U6V\njCrCGjfVQuy2IaqukXbnxWjXiHPeKncVhfPEfl6ye3uimUW2/vrrAyX+IEs3C9ZjteZEpavK85rw\nnLhfxxGvkW52GoieEfdhjNZ7p94Bs8eM9TlfrCFSNapkYqcRbRnv1X5eaz2kTiAVTiKRSCR6gq50\ni5bdy97iinnm2etv1DdrZobdpFUHZi3JfGWHxitUUD7Foz9a/3gDnU9bjuHEbByPebHFFgOKf9ox\nyyBUMtbRWFdj3YQ2kK3LZPTZawsZrkzY35kJqK0dlwyqSuV1wlcfbeJYZN1mixmfsMI8Zg8Zs/N7\nKiIzcvRLu19VpDVNqsvYETmu0xPrLbqRjeRc9BisrjdrTdZtnYVs3PNt1qKqz2PXRs6D448/HiiZ\nW3ZCFrErdJwXVehGTZJK1W7xzhNVmSzdjgFW4xsD9piNFXttGcfwe8ZD7DDg/cL7ivcRr1H7inXy\nGqkH41fWRXk+ohdJRawCdt0kx64XwR6N2tL4qJl93i9EzE7MGE4ikUgkJkl0VOGIuHa9ikfI5swi\nspLcmgR7Zxmjkb3pv45+Rlmaiir6ips4xo4pnNghQIVhdprxC1mXcSlZv8dqbEab6Zs1C83+dKoB\nbeH+qupv6qGTTDbW4zgWffhWjJuRdcwxxwBF8cry9MXLRFXCZmb5feeV6y8JbaVaiOOLSridtYGq\noA30vctQjb0Yh5Kduy6O8Qgzq2TpMlrnj94Drx3jVdpQBWX2o9lLjcZoOpmxJzwvejJc00mbeF0b\n03V+WGviWi5u1y7RzpeVVloJKLFeFZTZbWYEqoSjJ6RW7LdbdTiOzWP2mKy/0iNirMZjMMZr/Z4Z\neZ5/bWnvxQceeGDisQw9xuyllkgkEol3BbqicCLbNwsk+gX1L6to9GvLfPVnuiKf2WsyV331Ps1r\n+FgbGe5QtNxLrSp+IUPRBh6b/mHVmt1iXRtGv7Y+ehmumXwx+0wm4/fiOajqB1WFTqxyWVVlri38\nPMb4HKvHLvO0k4D1OzJWmaxsX8VTqzca1F4DaOj+h46/00w22iRmB6myzIiyElz1pjKR3dsx3cws\nV8E1fmV8whhOnAeNZqG1aouh8yJmBVYpTMccs8iss1LdG9tRFW655ZZA6cpgJ23jnHZduOCCC0Y9\n9ipbxFqzbvZSi2uHeY8TdhwwlqfNtt9+e6DEQY35GvvzmrG2qVNZaKlwEolEItFX6KrCqWK8VSst\nqliMO8h8rZ+I1dFVDLaNp3bH1sOJqGJ3sjM7GmsDlYrv9cHKcPXdqhq1UcwMrMo6iucosr1uVlHH\nMcjujT9V2Ur/tepQm8T6DX3w2sBjir75ehk43fTVxzGIeOy+9zWyf22gcjYOEn8fUZWxWU/9tWOL\n0fqqDd23c1qVF8fieTUeaq2amX1eS76KGPt1f43aYmhHim7PiyoYyzULNWaVaRtrz4yPmrVWda9s\ntt6q1XmRCieRSCQSPUFXFE4D26n5virTq+p9vb9HNPAUb0rhjB8/fkTWVyOseShiH69Y9RxZmL57\nWV20XT2b+V4m5HY7wWSrVFPcdz1WFdeKGbIfoNjIOopa9TOj7TeiSlG9w2I7Gs+qF+eqim+Iqjqq\nql5o8e/15mfsjBzRrC0GBgZGnN+qeGeVLap63TnWqGCjlyBuv8oW0SbGUYyfdFLtdQr17mlm4NlT\nsVv7SYWTSCQSib7CmCicPkbTMZxmFU09e9eLrTRa+VvlL6/H8tuJ4dQ71npsvtH3o4yj5u/aHU8/\nMNl6aNcH3+j3upm9GNHo7+L3qlRa1e/r2aKXcc5JFalwEolEItFXaLZb9LPA37oxkD7B7E1891ng\nbw30GGpqAPH7rWbgNbvfsJ9m7ABt2qLRuFM9NPu7BsfTki2a/E3baLZCvEWbNm2LwcHBEbZoNYu0\n0d+NEn9qa7uduEaa/M2kgoZt0ZRLLZFIJBKJVpEutUQikUj0BPnASSQSiURPkA+cRCKRSPQE+cBJ\nJBKJRE+QD5xEIpFI9AT5wEkkEolET5APnEQikUj0BPnASSQSiURPkA+cRCKRSPQETbW26bcGdM02\nLGwAzw4ODn6wkS9W2cJFo6oWPhPve9/7gLJgWrOICy91GtmYsODdYItGm3XWw7vBFp1C2qKgUVs0\n20uNod1f402v2Und6APDtct/+9vfDvt7sw8aV0d0tcQaaKrX0VBbuOKmq0/WQ6MPmtlmmw0oqxdq\nazvixjU/HI8rQP7nP/+pud2ZZ54ZgKeffrqhcfQDukAwgM4/vAcGBir7ujXb/TuuWzR0H0N/52qX\n995777Dtxv3XQ1wltdO27iY69VDt1vYmZXTKFulSSyQSiURP0NH1cBpdG6bRfUaWHtlhFfubaaaZ\nAPjnP/8JlBUAVR9VqyPSwno4VWPtFKaddloAXnzxxWF/X2ihhYCRjDauCLnNNtsAcPrppwMwzTTT\nDNveKCuFtr12fb8xw1bH1awtxo8fP3EfVatdDtn2sPdRubiGvefLOasqc3teA66GGpV2PPbpp58e\nqFb73ZgXvUan70cR/WgLXfrOh15dg7keTiKRSCT6Ck0rnFor+Ikq/7RPXT+vinP4+Te+8Q2gxC1+\n/OMfA4W1L7744gA8+uijALz00ktACcS/8MILw7bbhI++ZYVT43NgJMOYeuqpAXj55ZeB+muO+/uH\nH34YgAUWWACAiy++GIA11lgDKIxm7733BsqaIKeeeiowkhH7WpXc0Av21uiKm2L55ZcH4P777wfK\nWvMe2wc/+MFhv3/yySeBohKee+65VobZ1iqXjcadPAZfPS8qVrc3zzzzAOUacs77vd///vcAzDLL\nLMP277XU7CqqQ46LwcHBMWH1VZ4MYTzykEMOAWC77bYDyrF9/etfB2CVVVYByjWjjb0vtLCmUN8p\nHOe6xxTvhd1CKpxEIpFI9BVaiuE0ytqqWJSszL+baSU7++xnPwvAJZdcAsCqq64KFFZnHEKoEmS8\nVWvai1HG3bTC+fKXvwzAOeecM+zzb33rWwAcdNBBw8YUffSO/V//+hdQYjYyk7nnnhuAW2+9FYBf\n/vKXQMncW3jhhYHCjGWB0ac/44wzDtuP3998880BuO666wD4+9//7viaZm+tsGYoNnFePPjggwBs\nuummAFx55ZUArLnmmgBccMEFQGGyzp+ddtoJgHXXXRcoytrXKhUZx9OJuEXVtur9XXjeomo7/vjj\nATjwwAOBcsy77bbbsM9PPvlkAB544AFgZIamDFgl3GiG3liy+mg7x27GpoplpZVWAuBvf3s76fRX\nv/oVALPOOitQMkT1lDz00EMtjWcsvADOi0UXXRSAe+65ByhZssbmvC+dccYZQLm+P/e5zwHl/qDH\nxPtKq0iFk0gkEom+Qkt1OFEhxBjJRz7yEQD+8Y9/ACPZnP7lRx55ZNj377rrLgDmnHNOAI466iig\nxHRkwjLdE088cdh29W/L5t2/T+8llliiqWMdDR/4wAdYf/31J8ZIImSgZ599NgBf+cpXgKKuZCQy\nFmM72sqxP/bYY0BhOltuueWw95Gh+vsrrrhi2OfaXMgGf/jDHzZ+0KOgVmwvZgduvfXWw/YpG/v3\nv/8NwHrrrQfACSecABTmqjKRpQkVsLbwPBu7Ofzww4GSoXfTTTcBsOKKKwIjlW4nM3qq1HWsYRMb\nb7wxUNTbb37zm2F//+Y3vwmUua0Ctk5LL4CfG69SIctozaKU7ZvlGLMso5oYLXbbLqabbrphxzSK\n0gTKfcDYjapcW9x9991AmfPOE6+F888/Hyg2Mj4633zzAWNbe1SV7eoxq9Y32GADAP7yl78AxStw\n4403Dvt8l112AYqy3X333YFy3u+77z6g+TrCVpEKJ5FIJBI9QVMxnMkmm2xw6qmnrpv5YFxCdvXn\nP/8ZKCxc5vvHP/4RKE9h4ff9/PrrrwdKZtf6668PwA9+8AOgMGLjKK+99hoAa6+9NvC2GoES4xGx\nhoEmYjhzzDHH4AEHHDCxzqUKqjXVXNy39teXagaWjOPoo48GYIsttgCKIqpigR6jPvuf/OQnAHzp\nS18a9r16LK6dzKwqLLXUUgDccccdQFFxV199NVBUmcrEz43ZyeY8ryogz5/xKTP4jF84f1R1qsZG\nO2W0Ygu3Fe0sU/X1wx/+MFCyizy/yyyzDFCyDs8666xhvzMuYQxHhXzhhRcCheGqGjfZZBOgKCe3\n7zV25513AsVGVfUcvYxb1KufiRl83h/OPfdcoMQEPVazWpdbbjmgKN8dd9xx2PbnnXdeoFyLVeim\nLTzGRRZZBChzWdXmeTZG84tf/AIo5zfGRf3cjhTON21hLEhbxnhnvXOSMZxEIpFI9BWaiuG8+eab\nE1lELfgU/NCHPgQU/6B+SX2kX/3qV4HCRH399Kc/DRRfvD7XfffdFyh+R5mvfkn34/Z9OssWZYf6\nuevl9TeC559/fmJ9EFT3MpNVVX1PqOoef/zxYWOWncnaPMbIgE855RSgZODI2vXJqnj0W2sDmY5d\nGeaff/6JCqAZDA4OVh6b+5JNm4n3sY99DCi2ko3rgxeysx122AEonSRk+dZh2X3BeIfbVyH97ne/\nG7bdmJnVao1KxDv1KsP+ppr61Kc+BRR76y3YaqutANh5552BwmidP7JwGaxZaCobVaGZfWZeWXOy\n2WabASV+ps3iuVZpGxMYpStH26hqdFsvs8/z71w3U9N549h9731CmxoX83vf+c53gGILY0pVGD9+\nfNea5joPVC7Gp7yGjHd6LzOmaxarr8YrV1hhBaBktRkX91i9V3ren3jiCQBWX311oHhIOhW/S4WT\nSCQSiZ6gpTqcRhmgDMZaggUXXBAofkPjE7Kwn/70p0DJZpJp7LrrrsN+Z+WwSkeloaJZZ511ALjt\nttuA4os1DiIbrJGR0XQdjplxf/3rX4Hq2IjZQ88888yo2zV2I7P0WG655RagMNPYbdrMK8dj/EwG\nLEN2fN///veBkk0XlWsn/dMxYyuqrTnmmAMotllsscWAUjNgJqCKVJbn/DCWJ2P12FXGsjgzf1Qb\nKuhO+aff2dawa6TGtoASf/J8em2YZSQrN77leZSNW2Ny7LHHAmVu23PNjE9tqXKSQcv2vXZUWn7f\n+Ta0a0i3Og0411W6VZ3UYydrfzf//PMD5Rozi9U5H+8/xhDFRz/60WHbjdm13ezGUVXTqC2cR8al\nfb/00ksDxdMRMzs9314jxjGNr3v+99prL6B4nbxGoo3rKbqM4SQSiUSir9DRXmoyEDvBMf0JAAAg\nAElEQVQFqDDMSptrrrmAkR1vVTZWjK+22mpA8XPL1sxO0xevL9fKcvPyzWL62te+Nuz3jnuURdI6\n1kutVcgsTjvtNKAwELOZVAPGs+yRZVwk9o/Sl289kKjqZjzddNPx8ssv88Ybb/SsojwyV+eFsUBZ\nu4rU8ydbk8XJ+mV3xxxzDDByvqmUGsmGapXVx23LFD1W40sqHM+vCkZGa5cF/+7593wby7Gy3A4U\nJ510EgAHHHAAUFS+88ZryJiSNq6qfZlrrrl44oknePXVV9ueF+3GyLSNGZnXXHMNAJdddhkAN998\nM1DinX/4wx+Acv7NyDL2e9hhhwFF+cRzpRKO6EXGnrVFKlDV37LLLgsUpeNaYV7vehFU/9bfqGCc\nT3ZCcR6a6em9sdFOGalwEolEItFXaGs9nFrVyDDS7ycr07+4xx57AHDwwQcDpQOAfmp//6Mf/Qgo\nfmqrsPU/xtqVmKUm+/ep7jjtGnvttdcO299bb73VtMLp9MqZ3/ve94CibIwNqfa0hdXRMlaPTT+2\nVflmqcgKo3/cLg/GT1QR3WRvMkdRpThiRbndGmSyQnVghp+xPBns7LPPDpRaqCq/ufMzMtpW6nBU\nYR6LsTkZq1mJMksVrfFMa0Euv/xyoNTJ2CFg//33B4rvXZvI4s3sk6kav7AuTIX185//HCjzwlie\ntogV792I7dVj0bEPoPVY2tIsRDP47Exippbzzev929/+9rDPtVGstq+6n4luXiPW35hNpvfH86+a\nd647RuOeXu/ea7WVfeb0CjnvzGKzn6WIWbcx+3XI91LhJBKJRKJ/0JEVP6vWm1GxyCDsoCxLt15C\nFmemhXny+uatktdPbSxn2223BUqHXH26xoCsOZAZxfHV6B80ZjGc22+/HSg++NhryzhYrNJX9cnW\nZPlxjft6Hb5VOLLJVli9qDen6o3FY9XXLrtzPhiTMxvJGhPZ+3nnnQeUnmpDquQbPZ74u6aZbDxG\n3wtjMKpzj9m4lOpelWac07il59/aJK8R1dyee+4JlCzEL37xi0DpXydT1kYqYhWO88/xj0Wngfje\nbDNjNqoA1aLsXtZv1qK2Nt5h/ZZ/t3rf7zfaS60XnQa0uyrNe5iZvMb4rEEz7qm3R2+Q90i9BN4T\nVVBmu1kTGeOd9ZAKJ5FIJBJ9haYUzoQJEwbnn3/+EX6+iM985jNAYag+lfUr6nM3TrHRRhsB5Sks\nA9F/LPvT362C+fznPw/AF77whWHb95hUQMcdd9ywcYyyrnzDCmeaaaYZXGqppbjhhhsa+XpdqExU\nGMYA9FcLffx2yv7ud78LlKwjj1Hb+d6KZWM29dAMexs/fvzghAkTKusnmoXM1fiE3RCcTypcY3Rm\nWpmdKHv705/+BBTG6qvz06ps0aleapNNNtkIZqhyib54z7M+clWbld5menqsqjcZrbZR3RvvMk7p\n+TZ+YXxTxaQP32vLa8ZrqUZH7aZsMTAw0Hb3ZW3nsRqfiufRY7L+Kp5PlYzzI56juGZQPYyFLZwn\nKmZ7qtkzLdYk2alC5WJtkp97b42r4TbbjSUVTiKRSCT6Ck3HcGqxtyrF4FNYn6r1OTIN/czGdlQ6\nMhmf1sZa7IC7zz77AIX5mJ2ij3f77bcHCmMxPtFA/n/DCmfKKaccnH322SeyehloRKOdb2WU9n/S\n36xPPa6Sar69/cmsDLf2ROZSr0K4ah2MZtlbI/2lqmJ9Q7YDlOp3M7OOPPLIYZ+rEsyksveefmtV\ngvNUlhcVcKPoRB2O742x2CHdLgoqGZmlisXYnp/bO8+eWM59+xBaT6NysaOEnSi0vSrBGJFxVOdB\nN6vrI6rq4rx/GNdUHegB8fweccQRQFHxxr/s0qESMjvNa9YsWTP+mkUvYzjCa0ib7bfffkDJYvVa\n8b5gZqbdOcx+tDO7Csn7jPMldtCuh1Q4iUQikegrtJWl5tMyrgkuu/ZpLIszP16maZWrnZFlqrI7\nc8Vdt0LmYqaN1fPGNXxK668UqgMze2ocFwCDg4NNZakNDAxM9KWb8aLSaBRRhcWsFPPtZbSHHnoo\nUHztZmhpIxmvKsE6HFEvQ0y0sx5Oq5XkzhePyWM188YaJRWLWYtWYcvmXOHReWEcQwUd99epPlFQ\n5kVU+e5DZuqcVGH4Peu5fvaznwGl95ndgWWka621FlDimHaWUP1ZPe/v7fJx1VVXAaUTgYxWm5nZ\nGdfDeccObbH6qrln5p2xlZhV6O+MP5n9Gler1IPieTf+aR8xa02Ml6qI9JQ0i15m7PnqnLX/m+fP\nmJ33OHviOff1fHhP9XMz/Dzf2qbR+4RIhZNIJBKJvkJH6nBiDMensLEbn5L6FY1PmPdulbR+ZVmW\nPnp7IfmU1ueqOpD9yfKXX355oDBfFZF+zDjuISy06Tqcemy+XraH2WUxXiWbkwn7e+sujAEYt5DZ\nesxmQcVaqHp45JFHWHvttbn33ns71jMrvq9iTbJwq6GNX9gl3KxGj9EuDK7oanxEdaDicd65vUZj\nOVNNNRWvvvoqb731VtsxHOeBtUT62lX5fm7dlHPezteeX1WdCkbfvZlV1tXogzem47FrC23mfDLe\nYQzHWKLKbEg9Ts967DnHtZWxOddoMWtRReOxet/w/qNN9D647pLXfavrYnXCFlUrAlfBMTuvrKOx\n64rbMV5ljMeaR+t29BqYneh5VyHVq8NptVYtFU4ikUgkeoKmVvwUNZ5uNb9n1tiGG24IlBoBWZr9\nnaySVtlYZ2HOuezcHldmpVhfY6dU4xaqBHu4GQeJfknH3c7qffWYQPy7vtLFF18cKGxe/7VQ2Vhn\no29fVSdD8XNZ3lJLLQWUY3T/8dirVJ+MqxXUmxfxfez6rE9dtiazteOxbMyMLPuBaZNDDjkEKJ0q\njKtZj6OPP9rCccQeaqqKVhDjWZ4H6x2sAPd8ycZVOq686LGY2encd0VI57zeAV/1xXsNmuHpfFM5\nGfNzXNpKtFs30g60kb3SvNa0rdln3idUj17/XtfGiJZcckmgxD9k9SqgsUBUNh6LdXTOHz0g2sR4\n1Pnnnw+U7EVjdm5X1W/sznuiCtrO6sa9jb/HuR/jna12+k6Fk0gkEomeoKX1cKrgU1AfalylTvZm\n/yg7FthhQHZlZoU9k8xy23zzzYESs9H/LPO1Mt0sJyvWrZGRDejrrYGWe6mp3vSpy7Jk72beyTDN\nKnHMsm5tpY1kYWaxWU1vJbqZOmbsWXWv7R2HGGUtoGHohH+6qj4rZt4YT7BruDUC+pO1nZlV2sLY\nn2pPlejaHyoeFa7bl0WqGowFdHLFz8gUY5aRykPfur3MjMnJys3M9NWOAQsvvDBQ5ofV9TJcM7Q8\nRq+JuM6JmaMqqZ122gkoyqaXHZK9Pzg245CeV+NbsnQVjV03vO9suummQGH3ZvLZpcEYkLbymh0y\n7mHjqEI3bBE7qVfV4bgejrE749t6k7w3urqxc97YsNfMlltuCZRsN+dTs0omYziJRCKR6Cs0HcMZ\n+sSTCciaY88qawNkIj6VZd9WDBvLUdG4Rod+aLNL9DNbgW62kk9nOyarKqxdsW9QVSVzO35qbSBL\nMiYiC3PMZmDpmzUDJ7J+mYVxDI/dTrhm6FmTYtW0lej+3Y7cMhptog2Mb6j23P+UU045outAo6ha\nzyayZL9nTz3Pv/U1KlYzpeydZ52Wx+Z7bW4M0Cp7tyfM0NGWMW4WlVc786LKhmYNOi/0nZuJ55y2\nXsIsNhW08QxjgLJ2Y3wyWZWwHQZcP8n55/ftOizbj9dIu6tzjoZ4/Rl/MovMue5502OhR8T5ofI1\nbuGYVYV2QlYB2UHba7YqtjsWqOrv5nkzm1BbqaBVys59laqxn5VXXhkotjn33HOB4iXwnvzJT34S\nKPeTeI+vWv20UaTCSSQSiURP0NEVP2UKsme7OJsd5KsZEjIPIYvTd282iTUERx99NADnnHMOUBiq\nTEUmZK+1GEsS+tdl/0PQ9no4dl/Qh+57YzKy/eirjbCDQYwvaGN9+cYn9MW63bj+SlxPI2aS1Yi3\ntO2fls3HOIZZhcadVGUqXpmsY9tiiy2Awtatt1Ixu4a9dTr6p2VrxgJUHWZBOl/0i5vxJYsU7dgi\n1nqpUGSyri2vGjeWo80cq6+ydo9VheS1YDaS6sA+ZNtssw1Q6r6sMNeW1sRpc8dp945O1uHo8VDN\nCTMzVe1moZld5nxS9cm6vb61iatcep0bD1Pl+7m1Kq2iGzEc56r3JhWrWahmpWobv2+2oeseeezO\nLzM6VcRmLepJ8dqLWXJR5bfbezEVTiKRSCR6gpYUTsx0kpmYCeO6FD5lY7W8tQQyULNGdt11V6DU\nGMjK9Rtad2M/KX25Mhz91jJiWaIMNlaY16i/aVrhRP+vNnGfMkQZozC7xHqY2DU6KiA/l/nIDl2r\n3N5Iqr3YN856D+NfnkPrPxyn6AR78/wbbzBryJiLbN1u4XHdImM0/l6fvfPJVzO+zMhyFVT7yKn+\nVIXGcOxHJyuspdjfeuutlvrKxfhV9IU7Zs+jCsbYimO0XsZso4suuggoVffGBvUqaEsVj754syON\nj+kFcBzaxmstxhS1Syc6ZwtXpVVtec1oA1endIVX57RsXiXsPPPaMVPTTFBZvFmunUInFU68p/re\njhIqFa9flY3en0svvRQo17GKRlvafUXvkpm72l4b61nx786XenHNVDiJRCKR6Ct0NIYj05A1m3Xm\na3xamo0iM9U/aG2KHQis09DPbVaKfmq379Nd/6OKyqdy7GtWo1twwwpnYGBgcIopphjhy7RS3w7a\nMZYig5TBDNkeUGzpmGVtKiIzcWRt0R8uY43HajwrdiCIeM973sPrr7/eUv8wESvCzZQxI85VUu3e\nrJKxilrmKqzDkcXbkcBYjT3VVHkyYTO9PBfG06xd0gZV1dWiEzGcGIOz1sz5om1ixwhricw+Mi5q\nnOnkk08GShxLNef6NjfeeCMA88wzD1BUg+dEZRPvA1UZW51k9VH1xRitttpkk02AMg9Url7v3jfs\noK3NjHeo9ozdqKTbRTdt4fVqNpm98bxnqnyc89rM7Edju859la7H7vxwHlqP5f3Ja7jRVXxT4SQS\niUSir9BSLzURM5xkiD6F9TPLun2aysb1S1uvIzN1JT5/b6cBf2fsR1aoQpIB68O1LsMslVhRXKV8\nGj32WrUWKhAZigxBn6rZa1XKUiXjOu0yUet6ZHn6WmU0sX4i9lCTuZipU1VJ3G6e/dBtOy/0B7u+\njedN5unnVs/LrvQze95k67J7WZ6KyXVPZPMemzEgs+M873He9gLuWwZqPEtVrpqXgVo1rw/e73mN\naUv7y5kJqjfBzD7Vg5mgxn5iDLLVzsmtwPNjJwD7gZl9aDcNz58xHzPtVDTawEyr2IdMpROVTVXX\njUbXSeoktIUxXa8Nu6PELizGr806i/e27bbbDijH5u/1HnlvtU9hzEYUVbZotT4rFU4ikUgkeoKW\neqnFjAUr+e08qg/Vp6JsLPqF7fejb9WOATJdc83NqLE6XxanotEPHRWHdRXGguqtE97MejgLLLDA\n4HnnnTeRQao07Gklq5IxGmcw60hVZdWz/eGsONdW2sbq+ioGWo+J+PcYX4mYMGECr776Km+++WZT\n/unJJpusUjW5/pE1RTJQYyxm3tkHSni+rbY2i1GGa9zCmgKz3lSX7if26LJ2xf3XY2udyMzyvQzW\n2JwMVNuZfaTSVK37O68tFY/zwUpzFbFdHKy/McNPlaDaMzvOzM/YLcTxjx8/njfffLMjcQvnoOpK\nGxi7sxNyXBdLZWt3BMeu7aw5suda7GNYD36/Rn1eTXQjhhPj4d7T7MZhNpl9KL3vGAv0/uL9RgXk\n+dWLpKo33h6zaptVeRnDSSQSiURfoaNZahFmEck0YzxDhuPnxnp8Spuh4X5UND6FI9uP42iUscig\n/vvf/zaVpTbllFOOqKKPnW71L8tYZRQyXI/ZNTlij7Nu+5Njdtxrr73G0ksvzd1339019tboWFTO\nsjhZvbGcWBWtkml0ddN6aJXVjxs3bsSxxmMb8n2gVNEbe1HVWb+ll8BYjGtKqVTMVjNj02vNzgX6\n+J2vMuchc7/muBzv5JNPzhtvvNFW9mID3x+2T2HcwuzEelmFMSbb6X5wvbCFiNd/7MbgtWBMxlpI\n7y/WbcWVhDt1jYhUOIlEIpHoK7SlcERVllesQZFNGY8w5qO/2cydGCOK7DD2XKtCveyzGt2i2+6l\nVrUGTESza5m3i6oeSGJoXVCv2NtYoVnG247CqZoPzs04x6squmNPNmM6nk/rsYwpGuvRW2BWmlmS\n/q6eKoxegm6uh9MtdKvjdTdjOGONep6VGh22U+EkEolEon/QEYVTBVm17Mn4hb7XKtYtq4pVrvGp\nWuUXl+1Z49BEnU1TCqeWrz7CTDtrBPy+Csc1W7rFbMzoc//a3LhHVcbQpMhk68H6HNeGaXQ9pG7Y\nIiofz4sdJMzEizG/2KPN97EbuH+307KV5lVKqiq2FPf3bpwXreLdaItWahIhFU4ikUgk+g3vdIBt\n6B8wOPTfwMDA4MDAwGD8e71/76iDjv+u1fHcf//9g/fff/8g8NtWbdHov1bH2K6tqmw3YcKEwQkT\nJkx8v8466wxOO+20g+3Mi3fLvz333HNwpplmatoWtezsefc8VJ2PRj+P25188skHJ5988q7Nv3nn\nnXdwiimmyHnxjg2Brtqi1Xtkr7bnv2mnnXZw/PjxDdsiFU4ikUgkeoJmYzj/Av7WveGMOWYfHBz8\nYCNffJfbomE7QNpiKNIWBWmLgrTF22jqgZNIJBKJRKtIl1oikUgkeoJ84CQSiUSiJ8gHTiKRSCR6\ngnzgJBKJRKInyAdOIpFIJHqCfOAkEolEoifIB04ikUgkeoJ84CQSiUSiJ8gHTiKRSCR6gsma+fKk\n0mK7DTzbRGubd7Ut3o2t11tF2qKgH2zR6LIS3UY/2KJfkMsTtIZ3a6+jnmDcuHEj1nkZ7e/tbrfT\niPvpxj4HBgZGrITbzve6hbHe/2iYcsopJ64fNBpqnc9Wzqm26NU8bAb9OKbR0JTCSSRGQ1Vfvnb7\n9fWq31/cTzf2Kyuvt6RwZO9TTTUVUBYv7DTieFyYz/dj0XOxykYuHlgP7Z5PbVC1SF0/oB/HNBr6\nk8IkEolE4l2HVDiJjqGeb70eq+/U/seSlTcKx1bPJn4elY3se8KECUBZjr1qu37fpaLrjcelxscS\njZ6/97znPUBRgR6jSiguv+38fN/73gfAyy+/XHO7fl+bdHv+/i8gFU4ikUgkeoL/CYUTGcpYZ7e8\nW1HPro0yw0aZZAyWxvhIs/sZCwYb9xXHEBWKxzj11FMDhYVPP/30ACy44IIArLXWWgCcdNJJACyz\nzDIAXHHFFUBRA88888yo4xkLNJuF9sYbbwBF5ZlQEH8fYzFVyqYK3bBNowq3H84LtD+eVDiJRCKR\n6An6UuHoc91///0BePrppwHYeOONgcLazjjjDADe+973AtVP30nBp58o593z9OEPfxiA559/Hihs\nfv311wfgIx/5CAAPPvggANdccw1Q4g/14hDdykobN25cw+qsagwqkFdffRWANddcE4AXX3wRgFln\nnRWAD37w7bIxbbfwwgsDcNNNNwFw6qmnAnDLLbcA8OlPfxqA22+/Hagf2+kE4rFOPvnkQPX5icok\nqjvfe+zGaqaddloAnnjiiWH79f6g7eqNo0pldgP1th0/V/356nnzverOeRPPa7vnOxVOIpFIJCYJ\njGvmSdVutWyjvtkPfOADAPzqV78CYL755gPKU9mntPDvkbmIu+66C4All1yy3hDvHhwc/ES9L0FW\nDg9Fs7aIMRaVisxUpjrvvPMC8M9//hOA7bffHigZW1tuuSVQ2P3FF18MwKWXXgoUH/1f//pXAP77\n3/8C8NprrwEwxRRTAPDKK6+MOt5eVJR7bahsnMteK9rIsTrHtYXXiGrvK1/5CgA333wzAM8++ywA\n66yzDgAnnHDCsP1qkwYYd8+q6yObNhvt/e9/PwDzzz8/UI5NRbzLLrsAcM899wBw9913A/D73/9+\n2O+uv/56oCgc41zeL4wNVcX4emkLz7fXhmrtvvvuA+D8888H4Je//CVQ5stcc80FlGPSJn/84x8B\nuPXWWwHYYostgOJN2G677QA47bTTgJHKO2ZNZqeBRCKRSPQVeqpwRtnusFefnj7Vq7KOoo9VRjLL\nLLMA8MILLwCFJcqE/V4NpMJ5B91kb7FeZrrppgPKedE3/53vfAeA2WabDYAPfehDAMwwwwxAYVu/\n+93vAPjTn/4EFFbm9lQ4+rf/9a9/Oe5h4xilRqXrtohz1PeOWRbuNaH6q8oy8/va7vHHHwdKJpe2\niYw5xgRiZlc3bBFjKTFOobLRs/Hd734XgJlnnhmARx99FIDVVlsNgAceeACAX/ziFwBcd911AHzi\nE29f2r/+9a8BWGWVVQC45JJLgMLuHY+KeMjxAGOjcLTBsssuC8AGG2wAwAorrADA3HPPDYysHdp2\n220BOPbYY4GS3fjb3/4WgMUXXxwocXJjgCpp55/va8XX3nzzzVQ4iUQikegv9EWWWqw1kMn+/e9/\nBwqTrZchYfaStQjGgISs7s477wTgk5/8ZGcOYAywxhprAHDVVVeN8UgaR8w2inELlcvyyy8PwGWX\nXQYUBaQ/2gycfffdFyjn9cILLwQKG3vkkUeGfS6Ddh5FpVsve6qTaLQGyGOdccYZgWK7z3zmMwBc\ne+21AMwzzzxAUSx33HEHMFLle4zGQdx+VDRR7Q0MDHStfi3uS5XnWGeaaSagzAtjfR//+MeBws73\n2GMPABZddFEALr/8cqDcD8z0E9pG26rynI/Og1o1Ud3M6oOiaMywM67teTOeaZzyvPPOG/b9v/3t\n7T7E2k5l6zwznu17bXrEEUcAxYb14t7N2iEVTiKRSCR6gr5QOEIGpS91p512AuDkk08GytP89NNP\nBwpD/f73vw/AWWedBRQf7UsvvQSUzAwZSj8rm1hBLgOx1kC/s9koVZhjjjkAeOyxxzo/yBbh+ZWl\nqXhWXXVVAK688kqgMFOZ50YbbQQUW6y88srDvidLlxXaX0wffKxZcB5EVt8NZVMVN6zqehFVlu8d\n64EHHgiU+WBmltvRFnoJZp99dqDUKBkf0xay+mmmmQYoTDjGL1pVN43UJGkj9+n5M35gbOYf//gH\nAF/96lcB2GSTTYASz5DVe73bK81rSpstvfTSQIljGANy/tTrQNBtdQPFFs4b7a9nw89Vtt4znSee\nT+fRnHPOCZTsRc+J3gDvid5LrdPq9NpDqXASiUQi0RP0RZbaKPsDSvaRtQa77747UKqoP/vZzwIl\n99ysE320TaBnWWqNKhAZh2rPuJaMw/x5ffb21JLRWIMQ8+frZex1IgPH8+e+rfVQ4cg4jUfIqhyj\nx+KxyjytHTBL6d///jcwkglbZyPcruOqysiK6GVNkraRsS6wwAJAmS/a0PjV/fffDxQlZJzL+hu9\nA6oAM7ZUEWaveQ0ZE4pqUDRri4GBgcqK/Wh3a4Ts92ZMz9iLGVQf/ehHAfjmN78JlBhO7CTg+f/e\n974HFEX80EMPDdu/8QsVlX93ezWOi8HBwY5eI9E2nk+vT+OYnv/FFlsMgN/85jc1f+92zdj12BdZ\nZBFgZFakNWzOA2M/3keMh1Yhs9QSiUQi0VfoqxhOxHLLLQeUvlD6+I3h6Mc0ZqNPdptttgHgqKOO\nAqqZay/6SFVBZSO7l7XLTGSgKhoZT8xW0e8s9OmaiSdiZfAotUgtoZav3vfGFcRzzz0HFEbpscf1\nS8y4sm5GtqYtZKAy3Fi/FTPA9GtHH32cH+32i2qml1rcl8ckO5eNy/JVNtrOa8JMrP322w+Agw8+\nGCg1SNakRJt5Dd14441AmRedWrZ4NN9//Cx2srZjwFNPPQWUa0ZW71jj3Pba0abGdIxTLLTQQkCp\n3zL2Y7wjZu5FhdbJ3mpV24o1SXb/NnbrPU/E+aQNvaYuuugioGT2GatTRdp5IKq8el04mkUqnEQi\nkUj0BH2pcPTRmmWiH1pfq35M/Zoy1vXWWw+AI488EihxjaWWWqrmfsZC2UTI7iNkKFYIW3WvL16W\npg9ephqVjZApW6HeaYzG+mJGlixK+8eMKBWOLE8l+uUvfxkoLP0vf/kLAD/84Q+Bwnj9fmTp/s5a\nBdlbVdZaq6hliyrVFDsg+7rXXnsBZc5vvvnmQIlnmnllp4EbbrgBgOOOOw6Agw46CCjqwFdt63iM\ni6qEtEEcby/WkHIf1n5cffXVQOlxZjzBa8ZjN1PPOIO/d54Z/1QJeS0Z39QmUYmP5TpJwvOx1VZb\nASUu7byInSCM0RjH9BpSxXnNqQK9Jpx3Kh63Zx/Djh1PR7eWSCQSiUQFmlI448aNY4opphjBBDoN\nn85mrfzkJz8BYNdddwXKOjgxC01FI6qUzVhARqFP1QwsmaqxGpmFHXBlV2al6Hf2d/Xg77ulbMRo\n1df+XcapDYRjlGVZOyIrk4WrcIzl2Afqxz/+MQAbbrghAH/4wx8AePLJJ4FiU/cbff6drjWohciW\n4zH7uQzT2Nxtt90GwM9//nMAVlppJaBk9O22224AHHrooUCJ1chsvUasv5EZr7vuukDJXhLGjqKN\n2kGjCkGlYRzS/mBeC74ax7TWyGN2nuyzzz5AydjzvBoT1INibFhbGd+wA7PohxWCrR0y1lY1JhXJ\nmWeeCZT7hnFNa470DpnRe8455wDw7W9/G2hczU055ZQTPU6NIBVOIpFIJHqCphTO4OBgV9WNTMgO\nt/ps/bs+1yomrR+6HxBZc2T11o74KiIDNrPKrBS7xVahl6sVDkUj8bB6c8dtaBPjVfrc7Y33xS9+\nESjZbsazZOe+ymgffvhhYKS/W/TSN+/5id0PVDp2xzB+aW2ZXYHNTjRepU1URLjayQ4AACAASURB\nVDJgM7qs3zG+obKxT11cIbIb13c9+3rsHpNru+ywww4AbL311kBh72Z2ev697g844ACgeDZi12fZ\nvJl9eh085tiZIqq9oTHBTs+Z2LVbD4bZic4HX4VqzazDzTbbDCiZvNYgGbdUwegN0pvksTdamyaa\nnS+pcBKJRCLRE/RVlpoMQr+yPlkzrBqNW/QDWvX7RmViBp6sraozQWSqMt6YAdYPqFprRUbquiXG\nM/TR2w1cFmZ9zo477gjA/vvvDxQGbObWWGQXiSrF6THIomX3znkzr44++migxKNUutaiaANVnL83\nW814hJl8xgqNBdl5IK7D0w1UxXJi5tTaa68NlJid8QbVn8do3Z028RpQ+agaXO3SYzfmYBcHFZJZ\nj7GGRXRzHqlstJFxJZWocUuzUh2jsVmvKbMTVTTG8FTCrnpqreK3vvUtYOR579Y8SIWTSCQSiZ6g\nLxSOfsk999wTKGuOCxnN17/+dQBuueWWHo5ubCH7U9nUWzelaq2XfkI99iRj1T9t9pkKSJbn52Zo\nmdUmqzfeoTKWIUd0s84iblNm6vnx/BqvjJXfdsvw/M8666xAiSvI5u0rp0rwmFV7Zu7JnI31qLBU\nwr2wRVUcy2MzvmDWmPMlrlL6+c9/Hig2NY4R1w6yP5zvPWZtYncG2b7b14ZutxfQRvYy0waxdszz\naJaiHhC/57ywo4AxQG1hx4oYg6l3/tudH6lwEolEItET9IXC8alt76QI4xj6dsey8rfXkOG4DsrG\nG2886vdjrKAfbRV7VAkZrGv+6Hs/8cQTAdh0002BogJkcbJz41bWcRjDMT4hVNSx00AvoDIx+9B6\nLOe4DFUFYveMe++9Fyh1NNaYmGWkCjSrzd+rfIyD2k/Mv9uVWmUkIxbdqFGKc9QYjbGUL33pS8PG\nbD2OysUxa0PHpu1ULsZ4VCiqSGMz2tCVYrWBNu0lnLuqPdW6c9y/G9+0BsnaJOeF508vkPEq18FR\nRcbsyKru4BHtXiupcBKJRCLRE/RU4ehr1W/o09IMDBlLfIrKPPx9ZGHvZujPjqqg3no2op+UTWRT\nqq/YHdoYjEpEn7s2MMZjry0zcFQD9huTOZup4/6dP43asBOIHQVk42ZWqXRUZ65zY+2IbN8uDGY1\nmaUkE7bvmJXpVpo7jx544AGgxLNih+6IbmatuW3Ph+c3do7wfuH1b52eMT2VkV04zOwzFmy8w5ok\nPSmur6Oi8txoY1VDrdVaO31dxRog54exHMdsvMlrwixF57zn3X5z1jLFa++II44A4Kc//emw/Xa7\nq0IqnEQikUj0BB1ROPHpuMQSSwClM4BPV/3XPr31J2655ZZAqTC371Nck0Gm0ii78PdmM/VTJ4J6\ncKxWDFfFO/oR9Tojx+/JuvTNOz9k4frk7bJgbz2VjvGIU045BSg+f79vPEM1YbxEVt+o/7oduA9Z\ntjUh3/jGN4Dii1e5ONetx7GPoGpOH78+fSvS3b7qTnzuc58DSid1rymvkbj+Sic7qceu3VVzOY7Z\nrNSVV14ZKHU5rm+jKrRuz/uNNUnOC5WOmVlux9VynW/GO8yCrJoPnZwn2kbFoqJRlZuJZwad50db\nqWS0oVlofs/Yb1Q4rppc1ZGkKpOwXaTCSSQSiURP0BGFI3P1aSjT0O/sU1vmIPPU3+ja5PZM8mks\n4zCDo1lW77gmJWUjrKqX3U9KXRaq2JJ/V2lUKVar6o1nuMaHXYJd3dI6G7PRZH3WrOjXdjvWtsT+\ndp1a3XIo4jH73mNzrK7g6IqOiy666LDPPfaPfexjQKmncHv64M3AslpeG9sR2RVAjRVUXUsxvtYJ\nNt/oNlS0xmpUoGboeT8xQ+vss88GSg2KtjWupYo0jnXYYYcBZR0dY0OxKt/YkJ/HLh6dRFwV12Nw\nbttlw2O3E7bz44QTTqi5HTtLxHupcSl761XBjEBjRJ2aD6lwEolEItETdDRLTeZodpF57rIqWZr1\nFH5fX6rMVOapX9O+P2YxmZHTKPqxFqUerB2Qoay22moAXHXVVWM2pnbhscSVPGMcwWxFY36yLWMx\n1pLYB0z1Jxvz+/rwVRGyvKjIe9FhwPeq9Zg5ddZZZwGlBsmuv9bV+Hsz+Fyj3mtHNu81cuqppw77\nnopGFRFXYa0XZ+kGqlYV9b1jNQZr7MYYjefvmGOOAUpca6ONNgKKErIeR6Wk18AOJm7HbtSOQ6Xj\nuRIDAwNtZ3Op4pzjXgsqG2vQVFfeU7WZHa+jIvVVhWNsz/15LN5j9T6p+uJ6XMa/zJrMTgOJRCKR\nmCTQ0Sw1X30qR1bn5/aHkiWYiaXv1ZjLBRdcABT/ZbPKRkxKykboVzZza1JWNto/Zso4L6zDkqHK\n+ly7xZiNcQprSR588EGgzDcVtVXW7iey+Mjuewl97Kqym2++edjf9dGvscYaQDkm63Fc+8djV8FY\nq7biiisCJZvN+WMGqNdgVJtV56ibqFoF1fNvNqH1Vr63E4BdOLxfbLLJJgBcf/31QOkzZqaf3aFl\n96pFtxfr/KruG52YN1UrqrrvvfbaCygdAjyvxiXt+uy14+88f8Z4fL/ddtsB5VoyhhOP0d+ZLamy\n6VQcKxVOIpFIJHqCjmap+Rr7M8XsD2MzQsYqwzBTx3z5ZrPMJsWYTRyza49rM9FLBtopxA7WHoPz\nRWXjset7l4VFP7UxHivOzX40W0mWdumllwIj4yZjaTv3bR2M8QjH9tRTTwElhnfeeecBJf6gb12f\n/jXXXAMU5uqKjmZ4xRVlPQdV8ate2qZKcTrnZe32zpNt+95jUAWcdtppQOkgYLas8+i2224DSmcB\nrzGPWQU1FnAMqi+PQWXh59bdOFZt5pzXe2S3BueJcS69BPG8x2y2qm70Ec12XUiFk0gkEomeoCu9\n1Hzq7rTTTkDJGpKRGqsxM8dX/dLWVbSqVCYFZVO1EqRZJTJe/dHdqBXpFao6WAvni3U2KmQ7Tpil\ndPzxxwOw+uqrAyP9yioaaxmErLHevOiFMo4ZeWZiqfodq10UjPXoU1eheMwyU70AMl+3F+MNvewf\nJ+rFjepV9Gsjs12N5apcjdlZx6ctVImqvyuuuAKA7bffftT996qvWC04lmOPPRYoymbvvfcGYKut\ntgJKDCd2Y/Eauf3224GSvbjzzjsDRcFEuJ+q2FK98TaKVDiJRCKR6AnGNfOEGjduXEvUz0wKs0Gs\nFbDy1zXp+wB3Dw4OfqKRL7ZqiypYNa2v3jqMiy++GCi9lHqFwcHBhiWVtmhWIUS2bQzPLsH67Jdb\nbjmgsPef/exnQGFl+vpjfU+j8YiqrgBDGHDTtmgXVYo29rYy3hEz8RpVMM2u8NgLW8RjN2YXlarH\nrk1UQNEWKiHZe9V5Nt7hfKpnm07aompf8fzqBbDmzGOznktla2av3VxUgbHWqVFU1SSJRm2RCieR\nSCQSPUFHFU69p+AkgJ4rHJmNdTdW/FpxrC39Xq9sOxasPmavxWrsmM1UpWTajcV0ktV3q4JfVh9R\nb8XXdm3TjXkRx9SpTMyqY23VBt1Ue/XiRs3GlVqNQ8VrrlGkwkkkEolEX6EnMZx+RQ2mM2YxHFHF\n7lplHq1iLBROje3WfK3yQ3cry6ybtmhXgaiMzVLqNvphXjSLyPa9xkRUhY3aflK0RUS7GXnW4aTC\nSSQSiURfoSt1OJMK+rFep8pv3Stl009ogXHW/Hs/d56o6irdKHqlbHqBbp2nyN7bXfPnPe95z6Qc\npx6GdmuNsg4nkUgkEn2JZhXOs8DfujGQPsHsTXz33WyLZuwAfW6LNhnzu8oWbaKrtui1Am11f+/U\n++S8KGjYFk0lDSQSiUQi0SrSpZZIJBKJniAfOIlEIpHoCfKBk0gkEomeIB84iUQikegJ8oGTSCQS\niZ4gHziJRCKR6AnygZNIJBKJniAfOIlEIpHoCfKBk0gkEomeoKnWNv3aYrtduGzrs88+++zg4OAH\nG/lNq7b44Aff3rxLxHYKcVmDZpfLjejF8rn9gmi7flhiuttodZGzTtrC5ZFdGnpSw7txXrSKRm3R\n027RVRPMNRm80Ntd6a9ZPPvss/63Y72OZpllFgD+8Y9/DPv7zDPPDJQHTqduxtFmPmhEve27Wusb\nb7zR0lhcFwNav5FMmDABKGvXTz311AC8/PLLw77nfJl++ukBeP7554H6x1hlazvmxs+nnHJKXnvt\ntaaOYVJB1TXWS3IQ58dkk719O3rjjTfaGlO/E5yxQL+sxpwutUQikUj0BE2v+DkwMFB3DYWhbBma\nZxpVTKfd1enEbLPNBsDjjz8eP2p6xc+///3vAHzkIx8Bytij66xd1tZrNOsuGBgYqLu2i+dvyO+A\nkSt46u7xVSZc9fd24TmT9dc4jnSdvINWbDH77G83E/7b32o7EDp1LXgNPvHEE8O2G+8XVaurjqXb\nuVPo1D2yWeSKn4lEIpHoKzSlcGaZZZbBrbbaikMPPbSh78en7Vg9fZtA0wonYrrppgPghRdeqPod\nUNail5UZc3nyySeB9lclbBYxiNwJ9jbllFMC8Oqrr1b9zn0Ne18FYzwzzDADAE8//fSwMUelom09\nF867F198ESjzMe5/aEynmfXa3/lNKpx3MG7cuMGhsb1G4XnxNXoHPP9ud9VVVx32/eOPPx6A22+/\nHYCNNtoIGOl9eOihh5oal5hpppl47rnneP311/9n5kW9uGwqnEQikUj0FZqO4XRxLJWIGRZRKU01\n1VQA/L//9//a3VVTCmdgYIDbbrsNgKWXXrqpHUUlJHu/7777AFhxxRUB2HLLLQE46KCDgOqMqhrj\nG/Xz+L0a8ZSW2VvVvqsyZSKj9TXGaj7xibdPjVmFW2yxBQC/+tWvAPjzn/8MwBe+8AUANttsMwBO\nPPFEAE4//XQApplmGqCwNrcXlfcMM8zAiy++yBtvvNH3THallVYC4Prrr+/I9qquqV6qPeeRiuS5\n554DioKddtppgTJPfvCDHwDlWlp00UUBWHzxxQEmZhx67T311FM199tolmUnbTEJeH+GodXSgVQ4\niUQikegJOqpwYhxARqtPdfvtt4/bA4qP/9Of/jQAN91007Dv33nnnQBcdNFFACyzzDLDtq9vVt98\nG2g5hlPF6qv+/tGPfhQo/mmz3X76058ChZ3J6q3rMQMnMs8pppgCKDUs9aCC0tY1MnkaZm8DAwOD\nk08++UTlEo9Z9lYvLhXVlgW5js241+c///lhf9cmCyywAABbb701UGykOnT/N954Y83xDWFrwNvz\n+c033+zrGE60pdeANUqdZszdUL4Rng/rsIxvev48zyeccAJQFIzfF9Zn7bXXXkC5tmaddVag9RiO\n6Od50StMNdVUvPrqq7z11lupcBKJRCLRPxiTGI5M55577gFgwQUXBArbV7HImK1l2WCDDQBYZJFF\nANhnn30AmHfeeQH48Ic/DBS10ALazlKr8T2gqD/Zm/5oIXuXkf7lL38B4KqrrgKK+ttll10A+P3v\nfw8U1uf23V/M7BHRN28m2RJLLAG8fU5eeeUV3nzzzaazkdyW227UL+3v4vn39+9///uBMk/WWGON\niWOFYrullloKKFlL+vSPOeYYALbaaiugxDn+9Kc/1RxfVDr9zGS10SuvvAKMzAz0fEdo0zgP66Eb\nCie2YYqI9VsbbrghAOeddx5Q5v6QMQLw73//G4Cdd94ZKB0rzF5TAcXfNYpOzItoEz0PN9xwQ83P\n+xUZw0kkEolEX6GnvdRkrsYnZKw+xY3JvPTSSwDcf//9AMw///wAXHjhhUBhOD/84Q+Hbf+ZZ54B\niv/aDLBusIMZZpiBVVdddWJcSXY+xxxzAPDYY48BMN988wHw4IMPAoWtRUXjGGV51113HQAHHngg\nUDJszjnnHAAeeOABAK699lqgKCJZnTUoqsIzzjgDGFkfJBN+9NFHgZF9y5pBjYymYe89z7Jws4Bi\nnY7zRMWqTYxj3X333UA5Fl/9njbdaaedAFhllVUA+O1vfwuUOIfbM1spnotGumqMNazbMoYnvvzl\nL4/6u2aVTSdQNR+isomxYM/B7rvvDsDRRx897Pdx+/7O+KSeEm3k/cQM07FUD7G7RlQ2zcJ74yWX\nXAJU1zIJsxt/+ctfAs33Wmu2zioVTiKRSCR6gq7GcGLWkU/xX//610CJG/gUVqFsvvnmADzyyCMA\n7LDDDsM+96l8wAEHAHDvvfcCJXtFtt8oixviJ+1YDMdYi5k0Mogf//jHAJx88snD9i2sFTE+pZ9Z\nxnrccccBpQbhr3/9K1BUgfEK2d3nPvc5oCgjFVCEcZHrrruON954o+Gsk3eOoaYtrIeQNVWxJ5Wt\nr3PNNRcAyy67LFAUiTEa62bOPPNMoBy7Nrd313LLLQcUdmd2m/PC7drBW1XqORkYGOjbLDXPv8fi\nteX1/Jvf/AYosb9OoRe2qIpbGJv1fHneVUDGdLzm/vjHPwIlXuW8UNnqNbj66quHbadRdMIWZtY5\nFsfmsTvX9R7499iv0s+j0jVrVY+Haj7GSb0WrFFqFhnDSSQSiURfoaUYTr0eWRFmyug7XWyxxYDy\ndDULbe655wbK09qn99577w0UxiyDMd5g3MSntttpVOF0wocbs8Qco1XSM800EwAzzjjjqGOQpct4\n3K6ddo39CONdfu+www4DSo2B/uyTTjoJKJlaP/rRj4Ztx8w/s+JaQcxKizVBsdNAzKAypnPssccC\nJY6lX/rnP/85UHzvnm9t6tpDKmDZo3VcKmfrcoyvRZXovOvn+I2xu5ih5fxbb731ej6mWhg3btyI\nrNN6qOoybiae9wdjefbU22677YByX9IW9lK74447ANhtt92AopDtzeb9opcxHY9JGJdea621gHIs\nUcE6R73GorIRXmPG+uyiEOHvW12Yr1GkwkkkEolET9CSwml0FcRPfvKTQKmX+Pa3vw2Up7I9rYxv\nmK1StSJjzGaRwVxxxRVAqU2xQn3NNdcc9r1uPLVlT2aryeI9BjOlzj33XKBUPcfYzVFHHQVUq0ar\npGPVfsy0Ue3p45fp2uH7tNNOq7n9RjuANwPZlGOV4cqiYt2NNjDOZJcF58s///lPoMwns9hUwCrb\neeaZByiszXkhw3W/Zg5GFila6XTcbWirhRZaCBhZhyWMd441BgcH215l0utZtm586tZbbwVKlmK8\ndqzvWXnllYHSucT5oXfA+8dYnGvP23777QeUsW677bYAXHzxxUA5zx7rNddcAxRvU4T3TD0W3gur\n4DXhflR9sVZpzjnnBEp8vVmkwkkkEolET9BWllqjXVU/9rGPAcWnbndf1YCZEY32Qot+atWFGRi/\n+MUvgBIP0U/agE++qSy1oQzY/kz6St3XwgsvDIzsDCD79verr746UJiLMMNGv7VZbjKXn/3sZ8O2\n7/dlTg8//DBQYjRmq5iRJXyvQmplxU+P2Xkhs62qvxCObckllwTg4IMPBgrrOuSQQ4DCWK3PMuvM\nTJ499tgDKDEdGa+KyRiif48rfGqzWI/Tj1lqVddt7A/Xhf02ZYvJJpus5dVuY7zS2jM7qltj5rFa\nb2VMzhivSjaqQL0Dyy+/PFA/xhRjfJ2YF3oizj//fKBcr1/96leBErc2Q1NvUJW3RpsaB/Vauuuu\nu4DiBYjf11tQ1UE7Ina7zyy1RCKRSPQV2uo0EJVNVeWv65SYBy9DsL6m2S7Ps802GwA/+clPgMJw\nzGE3C6WdqvlGMDg4OPGYYxZIZFNmqZlJpQ2M6Zh1FCE7l83L6rStxxx7pMnGZP9+LyobYfdqOyQ3\ni7feemviMRprUdHGrMM4T/z7+uuvD5TYnvPiU5/6FFD8xr6us846QGFnqrvYtdqapqqeXfVWae1H\nxPiX0Pb9gloV7o16VfRMGLPzvNpxwPNtlqtZjF4j1qTFa1EYIzSTtB67r6rWbwfO8ZtvvhmAyy67\nDChrOnmP8/pVfcdVlIXdWL72ta8BJRajByaubuv9yEy/RtHqtZIKJ5FIJBI9QUd7qdVjLioOn9rm\nwTcKn8rWmlQpqpjbXoVGY1CjjUe1pS/WPm4yF9mXdTT2NLMe5jvf+Q5QOtjqa5W5yCRkPnY4Vk3I\n9h9//HGgZODo+5W1qcBki9ZCaTMZUzuZfJFdu62obNyn7NwuB9pMn7sZdXZ/9pi++MUvAmWVVZWL\nttL3f9ZZZwFlvRznXxxHFVvrxyw1EZWN2HjjjXs8ku7Ba8DsRTMpY7W9154ZW8ZDnfOy/Ag7lFx+\n+eVAUTxjgcMPPxwo2YfGpYVrOPl3PRXWqOnJcK7HeRuVjdhmm22AxmvOPv7xjwMljjbnnHNO3Gcj\nSIWTSCQSiZ6gowpHZqnCiGvUy3it8Pb71llUsWufymYnGW+ITNUMDF/NaolQhVT1FWsUg4ODExVM\nXINHv7GszGO135sszC7NKg9/J2uTyZqRpy/3lltuAUpsx/iYzEOf8Ne//nWg2Gy11VYDRq6+KVph\n9VNNNRVzzz33RMbo+Y6dBqK/2Yw4K7wd44c+9CEAtthiC6CoRKuvrTA3A8cYTewsYd85awmcl1Wd\neGPvv37uNFCFbsctewmzF7///e8DJdZm1wz7C7oelnV/XjPOrwjnt9ekXUGqUGsF227NDa+hXXfd\nFShrOhkPVe3bcT/WwxjLtVZSBePf9eboHTC7tVF4fxHN1uOkwkkkEolET9BRhRNjJ7J0feRW5etr\n1WdqV1eZqh0JVCA+lf1dVY3B2WefDZS8+gif8m435tW3gri6pa8ykH333RcoMZbY7fnII48c9juP\nUYYjuzLTzwwda408JqumzdCJ6s3K88jyY93GGWecMbHXWDM2GMp8ZH+xv1xcSfMzn/kMUOaHx2S3\naMfksZmtpm3tHCCTdTv6t2Ww2l7E3lmiX+M1Q1HVzdc57LX0boAK1qxF1zMy3uE1pFo3E8s4g9eG\nn8v6Y8/FetlpMf7RDXWz7rrrAnDppZcO26fKRk+JMeOqzF7vR8aCVG/Gio17GQvuNVLhJBKJRKIn\naKrTwBRTTDE488wzj4hXiKgYZOsyi9hLy4wsK8xFVY65263Kq48ZYmLo+iYwaiZWx9bDkWUZd7Lj\ngAzUPHtX5ouZXNrSDBqVi5l9scraOIW1TfZei+fX9VFck6gKzVRRDwwMDE422WQj6l8iM4y1Q9pI\nv7Wrm/p9FYv1Fsar9DubnWb8yp5bm2222bBj1JZxXlR1QBg67sHBwb7qNGDFuVmNwiwla0q6hXZs\nEbuJR/i5WYj7778/UDpE6OmQrdtRQiVr5qX9vkRcN8f7jsrXbuIxllN1b5x66ql55ZVXePPNN9ue\nF1U2iXFmv+f5VZ1737Cbi3U13ntdG8xjWWaZZYBS96cqbBfZaSCRSCQSfYWurPgp4zQ/WwZh1klc\ne1wGEpVIRFQ4ft+sJbNURIwlRGVTo6dTy73UGkVcaS/WAMVYkF1eZfv+XoYSVdtnP/tZoPSJqjHu\nYe8dvz7flVdemXPPPZenn366ZfYma9I3HuNTwjGrdBZffHGgrIMjXMfGugozseydpl9bxWMsyJhh\n7JFV75ypqIasj9I3CkebqhLF9773PaDEDLuFbtrC61eFYz+xCM9nrEWKmZdV9xGz3JwHKqmY4Rd7\n6kV00haN9peLUNWbkWudn1loejTsQm2MyF6OxnTaRSqcRCKRSPQVOpqlJmIlsFX1Zh/Z40h/5Kmn\nngrAjjvuCIz0teqbjbGhr3zlK0DJXqnyDdfrrNoqhv5ehhLXGo9jquonJmKvJOtpZHtVmXpuT59t\nM2OHEkd5/fXXm+5t53jMoFKJOCYVipX/UfG4P/s5GY+wa4IxGztdW1ugYo6q0LiYLK6qa3UV4hog\n/QBtOfPMM9f8/PTTT+/lcDoKFaXxTmO+VdXx0SMifK9Hw67gzgMVzCabbALAsssuC5SsVjuwx+7h\ntbpddzqjsdXtmXVq5qWrntpFxRiwtY96PrzX9hqpcBKJRCLRE3QlhiOq6lxUAdak6F80u8S6C5mP\nWShf+tKXANh0002B0lvL+gyZURUziXAcQ3z8TcVwRuusXM8n69gdc734khk51rvEbCR/7/o4ZsGZ\nxx/90/XG14x/euqppx5cbLHFJrKn6PvWznZ1Nh5lZo01Rq7h4Zof119/PVBWTbU7g35r55d1Gvqx\nrVVyRUj3b7ys0ZieFeX9EMMxU0tb1dhvN3Y7Ap20RczQMv7k9WiNWrvH5vaNyflqDNB6rptuugko\nWbNxftToT9a0LVqN1VTBe6TeATuX2HvRrtHeb+wMYA1S7JzeKjKGk0gkEom+QlcUTmQusmzXFD/n\nnHMAWHvttYHyFLZLsN+LFcCyA5nrEkssARRGIhP2tR6bOPfcc4FSt0EbdTjGG/Qbx+r2UbYDFJau\nkvHYZSKqPmMtcTVE92vVvZ0F4rGb3WS+vizPLg2tZmYN9Wt7/u115WqGKk7raVRrdji2i/iKK64I\nlLiVTNMea8aK3J492+yoa3dha55a7STRT3U4znXjlSKqyHa6fTeCbtjCOKWq3VhvVQZVleLRFnoN\nIuwrqBfAeWrM0GsoxlGr0A/zYuedd3b7QFH9egvi9V+l7ttFKpxEIpFI9BW6GsOJ8Ol6ww03ACX7\nzPVtTj75ZKB6fRKzlByz/koVkWtFmLnRQs+jhhXO+PHjBydMmDDRB1qviroKMpK4hrnb1Z9tFb4+\n28jy/J7s355KIp7nGvGr+P2mOg1MPvnkI2qK3EfsdOvaQCqRCy64ACjHJqzjcmVPlazqzmyy8847\nDyhZcGY7xY4VrfbA6gcm69ir2L3H2O1+cJ2wRayTcc6rbFThdtWwJ5qZeKpz11+yJu2AAw4ASlak\nWa52IbfzslmxK6ywAlDiHcaQva/E2F9EP8wLa8/MuNP7E/taxtV4O41UOIlEIpHoK4yJwrHbq1kp\nKp2HH34YGNnzSqZh/vyVV14JlLiJvnv7D+mzt2LZGEID6FgvtSpEH6qK370NGQAAIABJREFUxHiW\nsZqrr74aKDUExm7s4iBUQrFOo2r10yplY+xoSOynZfYWWXhksmYb2tdJ9bbnnnsChY35fRnmSiut\nBBQl4zzRX+3KocbmPFZ98xHaXkVdFfPrByZbdZ26vlJV9loXxtFxW1xzzTUAbL311kCp47JDsllk\ndqBwPlT1wvPVbEY7MZ9yyinDfhdX/I0qsd69sR/mhdeO14Tegwi7f3h/6fS6SalwEolEItFX6KnC\nEfpk9dXGVeOq1mqxMl0fq9Wy++23H1B6MbWxXkXDCmfChAmD888//4gV82LVe60qZahmZ/F97Aat\nz1aYcWPXBRVNvWyUqriGtUWdZG/HH388AEcffTRQlOhyyy0HwIknnggUlaXykJmussoqQFE8+vCN\n3VnfYwZX7CwQbdFopk4/1OGsv/76QIlPxk7pvaq/Ef3A6qtQLy7ZafSDLbyXxnW5YszPTDxX/LW/\nZaeQCieRSCQSfYWeKJx2V9asWl9FmMdvp+Q20HQMx07FjdbdqNJi5ktVRpXHarzDzC37hW2xxRZA\nqbKvsrH7NZ7RyU4DVZ2z6ymJOAbnidlCxmxUMGaj7b333gDstddew7ZnTEfbxe7Bwu7AhxxySM1x\n6dufbrrpeP7553n99dd7zmS1hbUpqrqxRj+w+n5BJ23RbH2MdVnW6bn+lb83488MUb0LZvQZz4or\nA3utxNWa6yEVTiKRSCT6Cj1ROJ3uHxQR2UEb+2s7S61ZplI11k984u1hPPbYY0CpztdPbdzK6mm7\nwtbbbqPoRJ+oevGqGGPxvQrFYzXzLnaPVtH4+yplU88Goynofuk00C9IWxR0whYqiaoO7Xo8nJN2\nUVDZmJUWV9M1tmsXaftNGvNx7SlrkOohZnSK1VZbjV//+te8+OKLqXASiUQi0T/oSS+1bqNVVeHr\nkHG2rHD0uTuGaFer42NdjJC9W4sku3dsZnaZrRZ7aFWtvzPK+IHCeOxHJtpROHEfVWOqWn1UdXfP\nPfcAI+skrE0yHhUrwtudfzHzJ1l9QTds0W0PSKcQ51U350VVZqWd0O3SIYxH2m0hZstW3Zc6hYzh\nJBKJRKKv0JLC6RQjadTn3ypayMtvO4ZjRW9c9bLRY4pdf/1dZN2iU7aKnbM72TOr3hhdf92KclGV\nlVg1X6qUa/x7rCSPWZTWc1mrkAqnoNkee5NNNtlEu/a7gqmHDTbYAICLL74Y6M95YZ1ep9a5qYLr\nM5kdmwonkUgkEn2FZhXOv4DazXreHZh9cHDwg/W/9q63RcN2gLTFUKQtCtIWBWmLt9HUAyeRSCQS\niVaRLrVEIpFI9AT5wEkkEolET5APnEQikUj0BPnASSQSiURPkA+cRCKRSPQE+cBJJBKJRE+QD5xE\nIpFI9AT5wEkkEolET5APnEQikUj0BJM18+VeNyZ04a2nn366qd+10QT02SZa27yrWzT0Y2PCsULa\nouB/yRb1lj0ZC1tUNfEdazRqi6YeOBGuPf/II4/U/Ny1GERcn6TeuiUvvfRSze/Vmwh2/7VLdL0H\n0JDP3629jhKJRJNodH2tTqBRktxvD5pmkS61RCKRSPQETa+HM27cuKZdVXFd7qhourXWy5RTTgmU\nlSEbWBm07fVwmkUVs2l2FdNO43/JdVIPaYuCtEVB2qIg18NJJBKJRF+h6RjO4OBgw/7GuOKmSua1\n114DitLxe9NNNx0ATz31FADvec973h7kOzEZf9co63eNe+Hvpp12WgBefPHFhrbTCVTZzGOvGmun\nEONgnVxdddy4cUw++eQjjmG079fad1x5s1n4e7frfHruueda2t5YotcKt9Or7baCddZZB4DLLrts\n2N/bnRfim9/8JgDHHnss0P1VMfsZEyZMAOA///kP0Dkb10MqnEQikUj0BE3HcAYGBiayZFmzr80+\nHaeeemoAXnnlFaA8dX1/5plnArDFFlsAzbOveuOrwep6HsNpFY5dZiITXmCBBQC47777hn2/2XTK\nSck/HWN1008/PVDO6wsvvNDW9iclW3Qbk5ItvJ/oYfEa8T6w9NJLA7DuuusCcMghhwDvrmsk3jPN\nKF5qqaUAeOyxxwCYYoopAFhkkUWAYqOHHnqo0f1kDCeRSCQS/YOmFQ7Ur6+p8Ttg5NPWv8tEDjvs\nMABOOukkAB599FGgMA792qutthoAt99+OwDPPvtso+Mf9r7GsU8yCkfMNNNMAPzud78D4JxzzgHg\n//7v/4DC+jfbbDMArr76aqDEsbRxxKTA3lR3733vewFYaaWVAHjiiScAuOuuuwCYffbZgZH1YvXq\nwEQ3bOHYHYMsvN+XfJ8U5kXEDjvsAJT7injmmWcAmHHGGYGigIyrOq+qYj39bAuv99NOOw2AG264\nAYB55pkHKHHy3XffHYDDDz8cgMUWWwwoXgK9B6eccgoA22+/fc39pcJJJBKJRF+hqSy18ePHT4y7\nAMw777xAYZJV7Cz+3XiC7M4YjVkqSy65JAC77LILAI8//jgARxxxBADzzTcfUJTP9ddfP+zzqmwp\nx6FSsnXOk08+WfuA+xgew7bbbguUY9l1110BuPXWWwG49tprAbjjjjuAongWXnhhoFrhtIJGFUO7\n27/ooosAWG+99YDibz7++OMBmGGGGQC45557gOpj1IbdGu9o6HQ2kLYxs9Pz/L8MbaKq9/r32thn\nn30AuOmmm4ASrzCO8Yc//KF3g20TnnczeYXz4M477wRgrbXWAmC//fYDirdo9dVXH/a72267DYCN\nN94YgB133LEj40yFk0gkEomeoCmF8+abb/LSSy9NZAo+NcWee+4JwHHHHQcUZuFTVPg0vuSSSwC4\n8cYbAdhjjz0AuOaaa4CSrSb0N/o0XnPNNYGimBxXvZoCmc+krGxk81tvvTVQjsl42OWXXw4UJq3C\n2W677QBYddVVgf/f3nlH21GV//tJQiR+RZQmJRRp0pWq0otIFRVpUkRpNgSRJkVREEGQjhQhiEhV\nBERApIhUEQSRUARpCipKEbH9FmqS3x/wZN+z7507Z06ZM4nvs1bWXefknDkze/bMvJ/9thTN1q4f\nbDT6pRQ8n/qnttpqq5b/d81d606VZ45BEfpN6qBoTrarCj3v3//+9wGYa665gBRpJTfffDMAt956\nKwDHHXcckPwRXnvPPvts9YNoONZ2/POf/wykMden5xied955QPJreP9YccUVgTSmTzzxBAB///vf\nW35naKRuFTqp0lLGF7/4RQCOOOKIEf/f6LPjjz9++j4AHHvssUBSdQ899BCQVkrWWmstoPfXdCic\nIAiCoBY6qhatRTlx4kQgrZGfdNJJACy33HIAbLTRRkCy4nxfK2vxxRcHYKGFFgKSD6fIMtU3o+/o\n4YcfBuB3v3u1yHO7WdlatrPNNhvQXcZxv/0WYty8lupHP/pRIJ0L0YLSOrv33nuBpGg23HBDIJ0r\nLaAmoxKdf/75W973fHvMp512GpDWp/3bBIos26J5YxTb5z//eSBFB6lsPG8q2KeffhqAq666CkgW\nrdGKrhZsvfXWQFK0WrztVoloInn1DF+7UvLpT38agKuvvhpIPhw/P888r3Yk0ec3adIkAN7//vcD\ncMUVVwDpHHZ6rfcjAtHzW8RHPvIRIPm73Qejz7zXOlZeU9tuuy2Q/KW9qkQQCicIgiCohcoKZ+rU\nqdOtIdc2tRT863qg1rdPTddSjZQwmuiss84CUmx4ni8jWnf2yVlllVWAFInRRr+blvd7UUtJa6fX\ntYgcO/1f+rccc/fd33V9eoEFFgDSOrZqUjWqpatauP/++1u+P23atIFEbY3Eqqu+mhL1l7/8BUhW\nvepumWWWAeDMM88E0tgcddRRte7nSORzrqwquH4Ez6ufV9l4XvVT7b///kCyyrXaF1xwQQBOOOEE\nYHiklupepdxtFYZBUqYY3vOe9wDJX2X0mfNb5SNeI+L9qB/KpKy2Ypl/UYWS50TmXHLJJSP+jrjq\n5Bjpw1HZSNF9bZ111pmeA9gOoXCCIAiCWqiscIZGaJRFNuVPxd133x1INYu01vTlaN0VdQa11bQZ\nwj6177jjDmC4dbDwwgsDaX07V05F/XnaYdy4cbz5zW+eXom4V8pGC8OxMupMv5V+LtWi56Do91Wj\n99xzDwBzzz03kFSDCqgfa/hF/i3H3fPlecytOvfZqMSNN94YgOuvvx5Ia/K5ws6jG4voZ4Xc3KIs\nUjqqf+e+iuetb30rkLLgvVbcV31wObPPPnvL6/z3/J26lE0/IrOcs6P9JgyPXq2KlUz6QdE+lSkb\nIzStnlCE0aujtMcGUs7jCiusAFS/FxoN2S6hcIIgCIJa6KiWWlW00g8//HAAtt9+eyAplksvvRRI\nlUvz9cM8ssL1bKNItPavvfZaIK31v/TSSy3fl7xvyhArYGC11FxTt+qC1RWMMnOsOu2PomVk7pNj\nVJSRXkedqHZ7sOQKJlemVS1Y68/p5ypbN+/HWLTr0zGvxugyz7/zI8caWPmxqfKtK9cpg6wfZp6N\nEZg5eS20ftWlmzhxIs899xz//ve/ax8Lr9ei6FL/3/lThn5x8/Gsseg9W8oieqOWWhAEQdAoOsrD\nKSO3GI0msjKA/oM11lij5XNSZPW5XZ++5u+4Zu9T3fXpvE9Kvt26uimOhpbuhz70ISDl25x77rlA\n9S6nRdtX2TgG+mzq7iw5lHYtUD+Xf15VmPs3ysg/V2fFASk6ds+DEZxmkqv+yzBSL/dPrbvuukB9\neWP9oKw3y2OPPQb0v+J2LyqU2I22zJemYrVSiMomX53J8/GKyCuSmJ9jxK9KOO951qvuqKFwgiAI\nglqorHBGizpxPdDIrbyW0frrrw+kiCutbNdmn3/+eSBFoZgFm1f11bI1T0MfkP+vVeffPDott3DN\nvre2UhXyY66KlobdTbW2L7zwQiD5vexKqFq85ZZbgHTMRUpFCyVXCeuttx6QoqCM128yuQ/HY61q\nrefnqklWv7kiWuuPPvpope8buefYOFb6Bp1PZTRpTPTZej8YWrF+KPZ6adc3OEhyZVOkePRne2w5\nZcomP4/+XX755QF44IEHgDTfhubj9YNQOEEQBEEtdBWllvtqcgs0R0VifkVeA8n1SZ/2ri+6Hm3M\nt2u5Zsdab8rtuf5tZFe+f6Nk99YWpea+PP7440BSeZLnZ+inMvro5ZdfBpI6K4rYKrP2ipRRP6OR\n2l2/HrJ99wlIvjqz6u3k2S8/VB2RWap2z6OWrZGYZdeplqxZ3yolx8RuqM4f6xAWUTRvBhGl5hh4\nDPbJcqxcEXGfXcGwuvzSSy8NpMoCZWPZrl+zzkjOXGl6DEYdFkUtitecPr4ddtgBgKOPPhpI0WlG\no/m77eaqRZRaEARB0Cgq+3DGjRs3/clfFF1WlFWtYvGpbOSN1plP0zzKTD+HSsRabN/97neBVKnA\n39FnVLV6dBVe//rXs8QSS0xfA+0U68LlaLV77EaPWDMrz0Vot9uqONZ1RKflClZ11i4eg2v3Kl0t\n3m222QaAyy67DCg/n2U5MHVG7GlZmjmuP9KoMiPwnAdFlu6XvvQlIHVyFS3TK6+8EkiWbpmPpkn+\nD3s7rb766kDy/dq/puh8WTHb82oNvjzHJMftnX322UDqqttP8oof5l+ts846I37eOWzFibxHVE7R\n3M7rxzkf3J7zpleEwgmCIAhqoS+VBorqcxkZZb9sf1srT2tfC9V6Ulp/e++9N5CUzn333Qcka1Br\nLldYbq/oWIdknlfy4XTa+W/ovrl279r6oYceCiT/xOmnnw6k/ByVjnWe8nXrIqpGHfVjfVory2rO\nBx10kL/V1u9omaoqjXb02BZddFGgPF+jKHIvx4jMfo6F9f60plUqKtmifAivAVVjkd9UPEYrKLv9\nfN60oXz67rfoldJ0pSO34svGyur1dsctop/zwl5i11xzjd9v+Zxj4/mvOlbm95gTOWQ/R/x83h8n\nJ3w4QRAEQaPoS6WBXNnoLzA6TWvLCCt9OVY+9vOuuRpdkltf1pfSNyRGMdnJz46gRWv3qouqtKMW\nRon2AVIejGpt7bXXBlIejmNh35pHHnmk7d8eaV/Lok7e+MY3tl1tuSr62r7whS9U+p495g844AAg\n+bdUOI6JlStUOLmfqmrHxjr8GDvvvDOQrgVVmn4uj00rXeVbpM5yC1VFrC/ozjvvBIrPfx15N17H\nO+64I5Cs7VNOOQXonQ/NsTOPx7Eoo0zZ9JPvfOc7QJrbRYpDP3enY5UrG+eRv++8lCJlU5VQOEEQ\nBEEtVFI4Y8aMYcKECcMURRlaU1pZZuebM2Cts9z3Y/y80Wrm3ejzMabc7eXRT/qEBpk1XZb/ourz\nmIxOyfuo55398uoLRfH6ea5Uma/HMe0H9i2yp4++vCKWXXZZIEXiaKF67FqwjpGWsgrXY3VsV155\nZQBuuummbg+la7RMjzjiiJb3n3rqKSDN6fx8ek14DNbI0zK97rrrgOF9cRzLfvT+qYrHdP755wNp\n34w+tMttVaXtvPD+5LxwBePAAw/sZre7qmAwduxYJkyYML1aQo77rurzXleEVVl6hceUK5teEwon\nCIIgqIVKCmfatGkt/VOqPvG1bKwAkHd+ND9n/vnnB1JkhHzjG98AkqXsOqbb1bJ1vdv6QP2iSjdD\n1ZtVEbRUzYvQ8tFiVdHk9cKsqaYFZAdPq8nmXVgHUQm5iP333x8YHqGVr607LzwWK1T4VyWTc+KJ\nJ7Z8389Zh6oJyianaP4UqfHcL5Gz3377Ackfos9nkMqmqJeK50X/pUpE/4IRnEX77jWy3XbbATBp\n0iRgeD8cx6Bb31A3Pr2pU6cWqhsYHpmX513lKxxHHnlkpd/3+0YK+zu+71j3OxctFE4QBEFQC5Wj\n1KZNm9bxUzD/vJaIFoxr++Yi5ArKp/0vfvGLlv/XgtIqsD5Zv6li8eiX2nzzzYHhNYv0U1188cXA\n8LGySrRVnf2elqzx+lUxe1/rqx+WzZ577gkkxepvqlhytLaM4FOl6e8q8zM5NlrKqr+c3LdnvteZ\nZ5456vabjDlpp512GpBUXbs1sfpBUS8VrwlzSfTleB487/71fuH37IZrjloe0eXnmtD3qow8steV\nD++FBx98MJAqnZuvd9FFFwFJmViNwTwrV3vshuwYO/dVxEWdf3tNKJwgCIKgFipXGhg7duywfiQV\nvt/yOo8u0oJ1bd/PT548GUhZ0kaf+X2f7kXWW9ExamkPsZh7Xi3aYzAnyBpoWnVWed1ll12AFGln\n3o2WyAUXXADAJptsAiSfkMdQdX15pZVWAtL6eU4/sqiPPfZYIFmm8803H5BUWtEx6JvLrbB2j7nb\n/iiDqJDcKebZ6CNcaqmlgKQyRvMjtEM/xuLuu+8GUob/N7/5Tb/f8jfHSC39mGKE30svvdTurnZE\nJ2NR5M8qwqjVNddcE0j3uiHbBYb3u1HRigpKv/eXv/xlAM4444x2D2FUotJAEARB0Ch6Ukut0/Vh\nrXer/uqHyLvO6d/I1znNXLeSQJ5R3kH+Tc8VTq6iFlpoISDl2Sy33HJA8lfk/om8krbVgFWDvcZq\n4P2wZPOcoE72DYqVdVENv26ZkRSOnRyNdnR+9SpasZ9jYU8oa+wtscQSQOoULPotrrrqKiApJCtQ\n9JtnnnmGzTbbjMmTJw9sXhRV5pc8Cs3z7zWUKyBp1z+f3/ND4QRBEASNoqtaavn6YR4rXqQs/J5W\nvX6L/Puuc2655ZZAqufj5zbYYIOW9/PeMmXKpt2qwd2gYvG39tlnHyAplbLf9hi02vulbKSfET1a\nWZ1Wfij7vH6xMoUzI/S87xTP37777gsMVzZGAParXl43WAVcn4yVSTwGFZArGoPCVYpB4NzVr+n9\nRd+c3Y5ViV/96lcrbb/d67/TaMdQOEEQBEEtVPLhjB8/ftqcc87Jc8891/J+u+t+1rRS0ZgtrWVq\nFrXrgyocI7y0XLWAjELp1CofwdLtuQ8n9ytYRcFqC8bbuw+OzaCt76pr9d30Bmo6M4IPR+ViHTF7\nSf3qV78ChtdW65ROxqJMUZ5wwglAUmUzCp2MxSDrOvaT8OEEQRAEjaJylFqV+mG5oilCFeBT3/44\nRqm4llvU+6Nsf4ryf0ag5wqnaWvm5jyV5SjMCFZ9XcxIY2GUmpWRrf47pKstALvvvjuQ6o+1u0ox\nI41Fv5kZx6JqnpCEwgmCIAgaRU/ycLrFasFWGNDPYSZxnkXbLtZWq5Bd3XOFM6PSZOut7nXwOsbC\nqKOqvaZy9BUa8bXaaqsBaRWh25pZTZ4XdRNjkQiFEwRBEDSKjhSOPRWswqtVVpbpnWeat7tunK8/\nj7BfQE8iuyornKKeLt0y6GiWqtbbUN9e3o3UqMNOs90H7QdrkiVrLkpdWfU5TRoL1ZqVSOqmSWMx\naELhBEEQBI2iqsJ5Hhhsmm9/WWTatGnztPPBmXws2h4HiLEYSoxFIsYiEWPxKpUeOEEQBEHQKbGk\nFgRBENRCPHCCIAiCWogHThAEQVAL8cAJgiAIaiEeOEEQBEEtxAMnCIIgqIV44ARBEAS1EA+cIAiC\noBbigRMEQRDUwixVPjyzFqAbUhzyhQqlbfoyFmUFUEfYD6B3Lalf97rX8d///pcpU6bUXphw4sSJ\nAPzhD3+o9L1ux6Ds+00q0tjr812VJo3FoOlmLAZ1Hjv93aLvzTrrrPznP/9p+34RCgdYYYUVWGGF\nFaCGWkfjxo1j3LhxjB07dnpF6KEssMACLLDAAoXfHzNmTEsH0/HjxzN+/PjC7VVl4sSJ06s7V6Vs\nH/J9z9lzzz3Zc8892/69WWaZhVlmmYVZZ52VWWedtfTzRb/vGM4ItHusUjbmddCEfWgazl3pdIyK\nvlf0fv677VL0vQUXXLDStdOIBmydkj91LYffxY235w3YcsXiybE53N/+9jcgHYPH5N+8PUGRpeFk\n+O9//1u23yN+P6eq9TZ27Njp2+y0FXi/WHLJJQF47LHHKn1v3LhxTJkyZaay6staCJe1gpiZxqKM\nsmuqmxYeMwtjx45l6tSp0Z4gCIIgaBadrZ30idwS1tpSFSy33HIA3HHHHS2fk14sKXVLvg9507G8\n2dxIa6KQlE3uy/Hzc8wxBwAvvfQSkMZIa8z9sBma+9EvC2u0RnH+Zt6Ar9cUNfQrUzZFCqysMeBo\n5Mq2U5XX6zErUjYyqCZ3/cQGbVXba5etFlRl7NixhXNqkUUWAeB3v6u2qj/oRo1Vf3fwd+ggCILg\nf4KOfDjt+gtmQPruwxnyfSCpuNVWWw2An//85wD8/ve/B2CeeV4Nmttoo41a3peHHnoIeNV5BzD/\n/PMD8Ne//hWA5557ruV1EVpK06ZN81/ltfrjjz8egP3226/dr7bF0H0b+rcuOhmLfkfODYoZ2YfT\nazXQi7Ho9DwXHcug5k34cIIgCIJGMUNHqfWBjhVObnGUqUA/rwJ6/PHHAVhzzTWBpFgeeeSRlu39\n+c9/HvH3XAN+9tlnW953zdjzXOTnyOmlJZvva9E+5GGcr3/964E0ho7Nm970JgB+8IMftLuLo9Lr\naKRO9mHeeecF0vkdFEWW8/zzz88LL7zAv//9756PRbfKw/nkHH/jG98IwMc+9jEArrzySgCeeuop\nIPlyXnnlFQDWWmstAB5++OFK+zEjq70iPvKRjwBw6aWXAsmH+Pe//x0oVlChcIIgCIJG0UiF41PU\np2u7Wfc9oJLCmWWWWaZb6UaXaT2ZZ/Ovf/0LGG7FveUtbwHgzW9+c8v/63OZffbZgZR17+/kCir3\nb/g5x7BIyQwiu77oN/P3tVB33HFHII3p1VdfDSSFc9999wHwxz/+EYDNNtsMgCeffLLdXW+hyNKu\nw5JtV3kOiqr5FtD/+8Vee+0FwLHHHgswLCHW1/vuuy8AW265JQBzzjknAIsvvjiQVhfe9ra3ud9A\neYTgIMciXw3w2nHFRF/uKqusAsDll1/e8nnnuisjv/rVr4B033L7SyyxRMv2i6LoQuEEQRAEjaKR\neTg+Zf/f//t/bX2+24iMTrfzWhY6MDzGX2WTVwzQkt18880BuOKKK4CUY/SnP/0JSGumSy+9NJCU\n0P777w8ka+yaa64B4LTTTgPgt7/9LVCekzSI6KcyP9K73vUuIB37pEmTgORbMaLP+XHccccBsOqq\nq7ZsvyqjVXXo1zj5m6ozLVKpmn+jv2uPPfYA4IknngDghhtuANJYd6qg+pHnkUdwzjXXXAC8+OKL\no37PagmnnHLKiP/vOdOfqY9G6/y2224DYPLkyUA6tlw19CNfrNt7Vq7Cv/SlLwGw2267AbDQQgu1\n/L8888wzQLqWvMaWWWYZgGFla/ydtddeG4Dzzz+/o/0dtv892UoQBEEQlNAohbPGGmsAcOONNwJw\n++23A/CBD3wASFbBJz/5SQA++9nPArD33nsDcNVVV7V8rl06tTba+V5RvTeVjX4JlYyRND/5yU8A\nuPjiiwHYfvvtW75vhM0vf/lLIFlv/k5RxFVRXlC/qwAMRetpvvnmA5JFq//KY8lr46ka9fGcffbZ\nQJovWrRVGcWP1dH2qvzmD3/4QyApXjP9b7755hG/d8wxxwBJyah8zznnHCD5I7R8nV/+3uGHHw4k\ni7VTf1cvyOdgmbJR4RbllOUKOq9P+Jvf/AaAc889F0iKqt3z7DWrL6gTup1TXhObbLIJAIcddhgw\nfEUjV0KO2aGHHgrAl7/8ZSBdc16L3gdy33ROx/lDlT4dBEEQBB3SiCi1H//4xwBsvPHGLe/nquC6\n664DYNNNN3V/gOQ/0QLqYr25ch5O1Se9n9e6evrpp4GkaIxOU8VtuOGGQMrP0DK95JJLANhll12A\n3q2x9zIaqSy/Yu655wZSxWwpikrM19i1VFU6v/71rwH4y1/+0tZ+t0s/opFUmg8++CCQ8q5E5WJ+\nzsorrwykaKMiH51KZ+eddwYYVjreWmqqxKoMMjLLYy7yQ6n+Dj6Coi3ZAAAgAElEQVT4YCBdk0aE\nas1bW08/aBcrHLWNhcfuSsc3vvENIEVsiisf999/PwDbbrstkGouuvLxmc98BkjXjLlKXquOifNJ\n33Feay+qRQdBEASNpBYfTpEKMIt+qaWWGvF7WjKumVolOl/r1Ypz7bbO+kLtbtN9NMLmjDPOAFLt\ntB122AFIForb1VpXAXks5hJo4WjBVKXIx9QJecXqsm15Hv3tdiPrtFjNu3HsjEa6++67K+23Y3Dr\nrbcCKTKnnyy77LIALLzwwkBaK1f56K+69957gRTBl+OYWHPvkEMOAYYrG3H+zYh87WtfG/F9x8AV\nkPyafP7554E0Jm9961tH/Fy7aNUPAn1zroQ4Tx544AEA1l9/fWB41Kz3Ruf6AQcc0LId3/faVfm8\n5z3vAdK8zBVOVIsOgiAIGslAfThl0UFGHamAfN/se601M8432GADIOXvdFDNum0fztixY6fNMsss\npVFdWg725Nhpp52AtBavhZArlDzT10xgLZWTTz4ZSDkFRiOV0a+On6P9f5kvp90IOY994sSJQIrk\nMsfACKybbrqpnd1um36s1Tv+RmIutthiANPbi7/73e8Gkqr32PVv6dMzfyuvdZVXnBDPgYqoqr9r\nkD6csjmrSizyAXq/0JdjPpfk1UHa2J/axsI8q2222QaAk046CUirBPk9Mh8rFcp2220HwHnnned+\nAWkeHHXUUQCccMIJwHC/WdRSC4IgCGYIBpKHc8stt4z4vk9N17eNJvEpqwrQEtGSed/73gck/0eR\nsullH59p06bx3//+t+1Kt1rvxvK//PLLQLLuc8vBtdWf/exnQLLetDSMyPv4xz8OpIoD+XZGsERG\n3L9+dg5sd2zaxZwB/R/mLunv6BUTJkyYPqeqUpTvVPT/KpVHH30USPPD8+UYqd6trqCykU996lPA\ncGUjWrK9juTrJ2XKxrytspqLRujp59C3Y5a+OVFNRJ+M1RVOP/10INWR8xpzXuX3FaPWVNLi/cR6\nc0bB5rUZpVs/eCicIAiCoBZqVTj6Me655x4A1llnnZb/11ozI1i0QPJKpj5tf/SjHwFpHdPIrfzp\n3OsOpXbHHA2VivuiBVIWyWXUSZ4N7XbsDeP7jk0eRaKlk2dp5/XM3M+yzqCDxLHKs+e/+tWvAsPz\nebolj/SpQpm1rWLxPKrOtthiCyDlyXh+jKwybyvHfJ2iSC6xskC7HSO9ZrsZi36x4oorAsl6L8Jj\nMmftrLPOApLCsULJIGjXp5pX53C1xu+vt956QDr/Vi7J83RyrKXmalKv9zsnFE4QBEFQC7UqHK3t\n3XffveX93JoyAsNsWiN38nVpVYIW70MPPQQkn47Zs4PAfXUt3sxxqwOrMFQ8/l100UWBlIUvWjhu\nd8kllwSSJa2Fqz/DnJQXXngBgBVWWAFInfxyy0Rls/TSS0+vON0pvc570prLrXHVwS9+8YtRfy9X\nc3XWjSvCMTIXTct13XXXBdKx5GvxRWO71VZbAcUVBLxWzOexOrXRbnmGufRC2XQ6H6xAkqO/oUzZ\n2BF26623BlJFdWszGqllNKznQNqtXt0J9qEp6i+Tk1f79ppw5UK/lL69MvThVVU20nEOU0ffCoIg\nCIKK1JqHo4LJe8VoaRolYo6AVv873/lOYHh3y8suuwxI65RaaXvuuSeQeoJUoFIttTFjxpRGheX7\nnGfLa5lY8Xr11Vd3+yP+rtbWHHPMASTL9dRTTwXgpz/9KZDWqd3e73//eyDVaNOyttLB0L4+r/mm\nas+3yI85jyq0Ori5Akap5RULcsr8EGURenWMharyve99b8tr1Vm+7+Zj6PsxXye30sXoNi3iGaF+\nWFGfGpWNPpycD37wg0AaMytIqOKdT6rHoqoMZTSh+6n77uqOKyRGV3q+xTExEtgVkarkqwaRhxME\nQRA0ir76cHLrXstCJWN16DzSynVmc098Kmupap1fcMEFAKy00kpA6vHQqcVSlaFWYlnVhLxemJ35\nLrzwQiBZDEXfVxWq+rRYHROrCVt3TuXiGq1jpAVtHL/RT3k/nUGQ+y2cL6o0s5+1eFWH+qWKKPND\nDKouFiTlaXXnI444AkiRmVqu++23H5DGxj5J+Zq+OJb6Qaw6XqTABzkGOXndr5zcv5mjAjKizzFS\n/fm+11IdjBkzhgkTJpR2Ma6KY+WqkNu/6667gFQLzff1/VbtHWXtRn0/jum4ceMqdZENhRMEQRDU\nQl8VTr4G61+te5+MRm65bm2lUtdoteK1zrR4tc7yaLQ6o4/aqEnW8lrfimvwRcpGHEOrS9sDxjh7\nM49VhVq6Q30ykDKItZg9F455kTU5CDx/nt999tkHSPvomBRFMXWKEV5d1OIbRpmCsCeLGeAqHSOk\nnPvHH388kKKbJFc24r67hl/UuTHfL2t29doSr8I3v/nNUf9f312O88MumObdiH7Tbv1YnTBt2rSe\njmleF855Yi7jpEmTgFSz8dvf/jbQ+Xk12janirqBUDhBEARBTQykWrQ5AEZS5HWdiuLirVCw2mqr\n9WI3RqLvHT+NDrHTY5mysOPecccdByQrTYtDX435OG5Paz2vUGBUivkeRx55JNCaGzWoKLUirKFn\nLpOvXcsv8z8UWe2qg7J6UXWOhftkr5+8L47Z8UXK2GOxYvZGG23U8v/dVg7o51jkqs4q4M5pfbxF\nVnrZtaga0N+Rf68qnYxFvo/t3j+c+6p/I+5yhavC8R6q70Vl7Nh1qu6K5k9EqQVBEASNYqD9cHLK\nepbnUW99oLLCqYoWgnW/iiLqtNqNq7fnvf4MI2187Zq9lo9KyO3kCmiNNdYAUp8dGTt2LFOmTGmE\nwnFf87pk9oqpWh3a+aPVb4UCz4H5PLkPsOpYjBkzpudz1H13H1VtuW/GCFD7nmiJ9qr6Qx3zwuix\nvFJ3p9d/3s3S7ajyzdOpsr1erQIUVb1QwX74wx8G0vX/la98peV7ubq3ysr3vvc9IKnCvGZfu37u\nXvfPCoUTBEEQ1MJA+uEUUVSp2HXrflFnLoIWp506rZidZ9Vb1ddKtubXuAar5XPiiScCKRfFaDYr\nEWihGJevpaSF4xqvlnPVqJN+YlUErT3PT5myKfLZ+P3rrruuZbtF0WidKpV+Rj/ZL8eoRDHqMe8k\nW7RPva531w55dnrRPqhonaNeG+aQ5NXky/D7XucqmjvvvLPaAbxGp2M20nzKlYb5cd4LP/e5zwFp\n7PIVEVWg/ZSsoWhenQpn8cUXB6qvCvR63oTCCYIgCGqhEQonj6wqol/W2CCyrDfddFMg5QRYCUCL\nxP4WViLQ52POkXXizMPRN6Ri0vdjXanDDz8cgIkTJwJJ0fQi/2bcuHHMNttshbH67eK+FPlUjjnm\nmFG/p7Ixeq2od4xRSkYtjdKnvYOj6A/Oi6JqwO2q9Fxl1EnV7pH6cjz/rgpYGb0MI/W8lvw9IzKd\nJ1Wz7jtlpOPN5545ROZlWRm7SLHefvvtQKoKb/UV7xvbbrstkFZKis67+1HmR4+On0EQBMEMQSMU\njv0qcvLKyjMTrlP71yrPxsvfd999QPJfqUzsbprnYdjXRGVz9NFHAykbf5VVVgHSmm8vqzFMmTKl\na3UDw+tCWQXh7rvvBpLFmluFqkTX6q1PJvnnVTbSDyWjIjGPplu09ovyb4xKKltjb5KPrgz9kFr3\n5ulI0bHuv//+QKq15/+bv+e8GkQ/pNy/mO+7SsXcRPfZaFL3+eGHHwZSZQrJt6cqHFLVedT9K+sA\n2y2hcIIgCIJaaEQeTlHfixrybnIq98Pp977pm9F61/rPOwW6H37OLqmu5S611FJAWv8uW+sfZB6O\nisV+R1qq1tyz/pjHuPnmmwMpQq/onOgbyutONaEfThlW+b7++utb3jfqyFpZRiuqeHtFL3NP2iW/\n/vVPHHzwwUCqmmFEVx6ZKaqJXXfdFYBLLrmkm92aTi/Hwjmf58u5z9ZOO/DAAwH42c9+BsCxxx4L\npPuBVTgci3/+859AUtrmbf3jH//Ij6Wt48h7CLndyMMJgiAIGkUjFE6+D8aMm4tSI41TOGJEjWvA\nWvv5mnxu3eW5Jkbs3HzzzUBxpnM31lu3FYf1V1lHzqoIRuYZqWWnV3ObtLbynKZuaYLC0SLNOzia\nj6Ofq98MYixyBWoO2plnngmk+aafy2vyoosuAmD77bcHyiuzV6XqWIzWOyY/RiN2neue57322gtI\nKx1Gr1599dVAqj9pdXEr86vqvFb8nXZ9jWXXVCicIAiCoFEMVOG4Fm/2dN4VcwBUrqVWpBD6hRbu\nkLVT9wcYnpWfr4OXxeEP6VDac0u2LOLFfV1iiSWAlDWtGnNd+vHHHwdgk002AVKOQW6l5TknnVaU\n6GQsrO5bVD2jCC1Uv+e1kVcLtqLAQQcdBAyvuN4vBqFwvMZUzJ6/LbbYAkiVI6y6YXa+80W/Rq/p\n5Vjk14YKRx+Mr5dZZhkgHbPV540Sda5bS0/fjgrY7Umv7l+hcIIgCIJG0VOFU2ZB2gdHq8z1SKOL\njLDRoh0APfPh5L6Uqr6eorHMLRI/5/q1a7RaykYr5d0yy+il9XbUUUcBcMghhxR9399s9ydrpQlW\nvWOkD846czvuuGNb2+tVhYFOxqLXPrWm0Mt5UeRL6XdliF7VkQyFEwRBEDSKrhRO7idoF603Kxjb\nl8K8iAHSdT+cQVnr+Xq1fd+L6om5n8blG//vOe3Geut1lv2Q3wHKx7ZXVtvYsWOZOnVqV2PxoQ99\nCEg+l6pYGcJKER6T3W8d6zJcXei2blgTIvbqxhyoG264oeX9bsaiaC6XRXh2en/Jr4lTTz0VSKtM\n3RIKJwiCIGgUtUapaa3lXQobRCWFowUMKXosjwLpFXX27IHq1tvQsWh33dk8m912263T3SzaH6B3\nKrOOiL1O1+rtZzQzR6m1i5FcqgN9R953er3qMIhIzm4/3y9C4QRBEASNoqrCeR74XekHZ1wWmTZt\n2jztfHAmH4u2xwFiLIYSY5GIsUjEWLxKpQdOEARBEHRKLKkFQRAEtRAPnCAIgqAW4oETBEEQ1EI8\ncIIgCIJaiAdOEARBUAvxwAmCIAhqIR44QRAEQS3EAycIgiCohXjgBEEQBLUwS5UPzyzlxkfhhQql\nbVrG4i1veQsAzz33HDC82Ga7xTeLijjmRfoWXHBBAH7/+9+3s7vTG7TZhqCMJhdprJsYi0SMRSLG\nItHuWFR64HTL0ksvDcAjjzwy4v83oPJppVpHY8eOnb6vzz///Kif9XMe44QJE4DUoTPviugDyv4Y\nfs7ttFsd2O34oCl68Pn+tGnTBl55NggGQQPuPzM9saQWBEEQ1EKtCqdI2ciMZFmMGTOGcePG8Z//\n/AcY3pdEa0lUMC5t2bNDZeESmq/nmefVlb2//vWvALz5zW8G4MUXXwSKFYvKyf/PlZV9e/LuqkP7\nsvS697x9SvrV0dVumPfee29fth/8bzAj3X9mVELhBEEQBLVQuePnmDFjZlhLYPz48QDTVckIVOr4\nOW7cuGG+EMdGJaECOeqoowA45JBDgGTtq3hUFQYN+Lpq5z//ul8qK1/79//+7/+ApLTe/va3AzB5\n8mT9OAN3iJatqde15t6EsShi/vnnB+DZZ5+t5fcGORb6gI8//ngANt9881E//6tf/QqAFVdcsZe7\nMZ1BjkUejDRoouNnEARB0CgqK5y+7MRrluqdd94JwLvf/e6W96tasF1YvpUUztAotbJ9WX311YHk\nq7nrrruA5KtRafzjH/+otO9FyiYfAy0hfUFFUW4TJkzglVdeYerUqbVbb/k+H3bYYQCceuqpQFKm\n+qd8/b+scOqmjrFoN4XA+aKKf+WVV4AU0WmqgtdU/j2ZY445gPYjP6VJ8yKPehXHxmP22nFs99ln\nHyBdY+2OfU4onCAIgqBRNErhLLbYYgA88cQTI/5/2b76dF555ZUB+OUvfwlUelpXUjgAc889NwD/\n/Oc/gaRUdtllFwDOO+88IPlIXFeeb775gORX+tOf/gQkH47HotWW+4bMz/H/VU6rrbYaAI8//jhD\n98/fzaPiJPdv1WG9FZ3XN73pTUCKOrvuuusAOPDAA4GkCh988EEA9t13XwD+9a9/AfC9730PKE5y\n1RpcYIEFAHjyySdH3c8mWbKd4ljn53/TTTcF4Nprr21rO3WOhXPRuanfcaWVVgLg7rvvBtJ53mKL\nLQC47LLLAPjd715Nq9O/teaaawJpHh1++OEt359rrrkq7V8dY6FCkdNPPx2Aj3/84219/+ijjwbg\n85//vPvR8v9ee963nAfbb789kK7FF154YdTfCYUTBEEQNIqBKpz8abvMMssAsPzyywPw8MMPA+kp\n+/LLLwPw1FNPAcmizXNNpN8+nKGvtUT861pqvk+zzjorkHwpG264IQAnnHACkKyys88+G0jHvtFG\nGwFw6KGHAvDYY48ByQpU6fh75r74vhaMUXG+r/rz/de97nX861//YsqUKQOz6suiCVWBlhFyLPP1\nZyMCjznmmFF/z2P3e3ke0oyscGabbTYgWe8q4JtvvhmAl156CRiueIvox1jkStfXyy23HJDuA54f\nVb73AeeL80BUAWeeeSYwPKLLa8m/brddmjgvNthgAyApFed2GY6tuZJGBHqtlREKJwiCIGgUHSmc\nXuU/uB2t+4997GNAskR8uqpk9Fv88Y9/BGDZZZcF2rfO2qBylFqOlsLnPvc5AH784x8D8OijjwLw\nnve8B4Bdd90VgA9/+MMt3xOPKVcgrje7Nqv1pqXqPi266KJAqoAgd9xxBzC8SOg666wDwG233dZ1\nHk6/82NUbx6LijhXk3vssQcAkyZNGnV7Wsgqmzzib5CWrPvi+VphhRWApO5U1CrY3B/hfNNfoU/P\neaJVn0c3FTGIsXAeeUzWLRxaHWMon/3sZ4HkyzPnLY9WE1cd2i1sO2S/GqNwXAn585//DKRjKqNs\ndcgIPleXRtlOKJwgCIKgOQzUh+PT02gjrS8tTWPEn376aQAuv/xyAG699VYA3v/+9wOjVg6oStsK\nZ+zYsdPGjx/P7LPPDiTrKfelqDA23nhjAD7zmc8AaS1d6yw/D77OKwSoZLbaaisA/va3v7X8rtEk\nef0y/18ca31GYiWJJllvKlut8gsvvBBIkXinnXYakJSMilj/mH6MIiW86qqvnvL1118fgK9//est\n/9/PsShSgx6r0Y77778/kJRrrnytuXfSSScBKSrR86vPxvnmvHWVoKzOodQxL/KISiM4PZ/uqz7f\nP/zhD0AaG8fU1h0eq2OVW/Pyvve9D4Brrrmmrf1swjXi+XTFxGshz79x7nvdq1hUgd5Pisam6H0J\nhRMEQRA0ilqrReeYD+HarGuo3//+94GUw+JTWIzYUiX87Gc/6//OZkybNo0pU6ZMVy4XXXQRkCwB\nc0XWWmstIFmeqrqh24Gk6rRIVSpG4txzzz1AWpPXMn3mmWcAeOihh4Bk9enn0vLVEtJfkTduU0X8\n+9//7qVPrCvMu7jvvvuApO6speU8cQwdG5WvFnFeoTvHsfVvnXiM5nGJ1v1vfvMbAN72tre1vJ8r\nYJW0PpmbbroJgLXXXhtIije3fN/61rcC7SucOrD2mfvo+fZ8LrXUUkA6dpsR5iy55JIA7LzzzgCc\nfPLJo/6ueXszEl7XRtrl59f7wMSJE0f8/rbbbgsUq/9eV3gPhRMEQRDUQtUW00yYMKHQUqyyHYAj\njjgCSJanT+dTTjkFSCpB6z+PvPjJT34CJOu8bqZMmTLdnyB5B9BFFlkESMdkfTDHQP/TO97xDiCt\nreqbMbfAqsDWhzLqzWx5VZ+KRv+Gv/PRj34UgHPPPbflfXF7Cy+8cPsD0GM8/1qsP/rRj4BkhZst\nfeWVVwLFUXDOi/vvvx8oVzg5dXZ+zJWNc3mvvfYCUg6R8yGvJ2fFZJVunhGubzG3fD223/72tz06\nks4544wzANhzzz1b3i+zuvO8mxyvJf0aziMrEiyxxBJAGuO6Km73EquzGGWo6tMP9YEPfGDU7xdF\nqYmRns7Lbu/9oXCCIAiCWqikcKZNm9b1Ew7SGuwOO+wAJOVy5JFHAskfYU001+7zeHtjzuvuCTIS\nWpB5/owRNloQWh6uL6+xxhpAslytlaQ1rz/CKLO9994bSBnFjtm8884LwFVXXQUkhaXPxsifvJq0\nf1Vib3jDG3pyjqvg2DkfXGtXmdhLyGMrUx5afWZLa9k+8MADQHltvTqUjT4VrXoVsMdsnpVVxY2k\n09fyzne+E0jn18g8fTj6R1XguQXr67L8ijowb8Zx91iKuP7661s+3y777bcfAAcccAAAv/71rwG4\n+uqrWz5nVKz3qbqvh9FwX7bbbjsAvv3tbwNpPunj81opUusqFpVzjp/Xh9yrMQiFEwRBENTCQKLU\ntOKN0FEVnHjiiUCy9u1PoZWfY3ZtE9Ze9TNprb/3ve8FUvSaFoUVbs0dULm4rmxU2zbbbAMki0Ul\n4+8YpaaycS0+t1i05o3AcXvuj2v8WkLjx49vO+s8J69e0C4qVPOs7B108MEHA8kvVYZr+kYlLb74\n4kCaR253EFGNOfohVHU77bRTy9/11lsPSFFmF198MZD8HZ5XVwdUvPol7G9StDbv95tw7eiPyq1w\n57r3AxVK1S6X9tdSLTo/rb6gv9NrQZX56U9/GkhRcoNkt912A9L51o+Z4xgahZqPqfcLjzmvRi2O\nkTmSvSIUThAEQVALA6k0YGSOCsd90Lo37+K2224Dki8nt9asOGCGeNUudSNQuVp03nUwrwxQNL55\nPoXKx2PNo5e0bFzfVoX413ygF198EUhWfd7x0+3Yj8eaXPnv1ZlFrf/C6s6qvnYrSHgOnAf2Q9Ga\n069hlrWVtnM8h3VWizY6UB+aVryRds4jo8+0uq1959h985vfBFKeV1nkphasvp78mIvoZ7VorW59\ncDnrrrsukO4L7d67vM/oh3BeDc09g1SpwBUYo9uKKg/UcY2471aPVxEX4Zh4/Zu/5bH94he/ANL5\nd877Pd/3vuL3y5RwVBoIgiAIGkWtPhzXme1zYcSN1rd+DLtjugavlZfXHbMTpE/pqtVee4F5MFoA\n7mteyywnV2Pf+c53gGSJuI5sFJJ/tTyM3NMyNtJGpaPfI4+a08oz+mSk6KU6orQgWW/6o4b6kaBc\n4ThGdnL86le/CqSoNI/5pz/9KZCqkVtbzTV751+7Vn4vyP0QHvMHP/hBAL71rW+1fM78qa233hpI\n59Hse8mVdZEPRz9WkaqrE/e1SNmIKxplmKumetffMXnyZCBl39tnR+z86hhuttlmbf1eP9hxxx2B\ntBKhT7cMz6Nq0WhV55E+XiM29W95b/XYzevyvtar3LRQOEEQBEEt1OrD8SmrdaVl+4Mf/ABI1rvr\n1VaLdp3Zp+wTTzwBJJ+P65VuX6XTgU+nUrXoWWeddbq/4V3veheQ8l2qRnq570ZYWWXBPB7X7M3P\n0JKxnphWvVnT9snJcxq0ZLTyiyLA6lifVgW6rqyVb6SVY1IW9ea8yLOhc/+VPhwt33bpxVgUWYi5\nIjE/y6hD1Zl/DzroICAdk2Mmzn3Pc567ZnUPfT5a++3Sj3nhfcD8uyLylY52rW5VnFa7qqEI5481\nHotyUPoxFkUdg/O/+TFbB9DoV1eL3PcrrrgCSGNoHy59um7P3KMiP2cR4cMJgiAIGkWtCkfLRH+D\n2dLi011r3s/llU6NZvra177mfrX8fxfrjB13/NRyaNf/kOOxm5OSd+5zDLQ8/B27XWqxmn/hurUW\njp/TEsorIww5LqZOnVqLwvG8WeFadaZ11ilFfovcr2HNNi3fIvoxFuZVqeatiO758PyrAlXSRt6Z\ns7TSSisB6dqycoBKx2oL+vysKuzvV6WXY9Gugs0/3+n17bVVpOpcDdC3eOeddwKpGkhOP+aFysMK\nEbmvzxWJvAtq3v3U+5E5jFYPX2ihhYDhatJzoLJ2laFdQuEEQRAEjaLWKDWfvlrf9i/R4jQ7X0sk\n757pU9zcg5yqlk+nakSmTp06LOKp6rZya1xfkErGjGEtYRWP3Qn18WjB2PPerHvHWosmj0rSP+Z+\n19kLx7wZx84aV2WRU3nuUz7mzoOiCrf+v8pGi7ashlcvMULTShQqlXvvvbflc3mUo/usPyq3gD1m\nLd/8fHaqbPqBdQHLyDt5dqpwrNlWhOrf6g5FyqYfeGzOwaJqCmb+u485+fk2h8j3zXHMcf7pH+8X\noXCCIAiCWqhV4WiZ2NVS683qrFpv/jXySvIeMvl2q9KpshmKGfqd1hHLc4vMDXCd2e2pbPy8EXxW\nVv7hD38IpDGywrI11Ix6MddASzhXkXWiX+oTn/gEkCL07EGvP6KoaoMVBMzHMfpM61AF5P/neVrW\nLbvgggt6cjxV8DetDJArmyI8tvzaEMeqKV1bR+OEE05o63Na8+eff35Hv6Pfa8sttxz1c64uuMJS\nJ/oTv/vd7474/879Sy+9tK3tuXozadIkIF1bRVjxot+5jKFwgiAIglqoNUpNi9PeHlrbeV5EnlWf\nr2d2G60yCpVrqXWqbET/gcdkNJkWhyrQ9edPfepTQPJ3OVZacebfmG/h9s3Sth6VSiqvrWSlgTqi\n1LQkVbyumZuL4pq6VRHcR8+7a/t2S1XlqRr0Tznf8gq77WbZ1xmxVzanrSNmDpp4DKq5flWL6MVY\nOFeNxDNHxCoLOXnkVbtYgUL/pmOTYx6f1eeLKijn9HJeGD1mjqKKJ8eai9tuuy2Qrp0c7xv6mIvI\nc5s6JaLUgiAIgkZRqw9HK8y+FEVWWFEdKKOZmoRWtwqlXSvMbGd9KW5H1WcUkvXkDjvsMCBFXGkR\nqVBcozUKSaveGlxmqGsh+z0tIP0lddVRg1Tn6ZOf/CSQul9aGTevT6cfS7+T1RisvmD+lgrHKCiP\nOcf5uMoqqwDt+1G6oWie5ArH184T/ZpFlqg+nTrPX6eobNhHXcIAABaWSURBVMR6cB6zFZFVJB7z\npptuCqQais4H/Q6eT+uOFflDRP+G88So2UHgsZb1+jF3UdXv+T7nnHMA2GijjYByZZNXi66LUDhB\nEARBLQykH04RPm2tJm1dMjHnpI9RJJV9ODm5Bevr3EqzL7vWuFVcF154YQA22WQTAD7/+c8DKa/G\n/Bw7AJoZrHWotXj77bcDyRpU6Rx33HFAsnC0rLSkjRisw29h9JG/rXLRd+P5HvI7LX/vv/9+AG65\n5RYgqb8vfOELQBpzlbG5KfYMapeqY9GLitvOG/1Qeb+iIfvW8vl+04954b57XlUsHvOPfvQjIFWR\n95opq4lWxFZbbQUk35GVmatGK/ZyLDx2Vy6KfDPd0iufTU74cIIgCIJGUe8CXgmuwZpVn6sEu881\nidzqzmuq6YvZY489ANh1112BZMEYjTbnnHMCKfPcDGHXo12z1R9hlJm/ZydIrTYjb2688UYg1VgT\n989oGH1HdeBYeSzW+1KpWBfuK1/5CjC8p49r9/qh8rpTRdV9qyqbTumFHyXvX5TjtZJXi54Ryf1Z\n5ldphat8/ZzVN4rIfTp5lQ2r03ueBpGHlaPf0utYP7c+m07z5Bw7lfKgCYUTBEEQ1EKjfDiSV5HV\nWjd+v9fdCYdECFXy4Yy2Vp/nCpkrctZZZwHJT5XnTWjd33DDDUCKuzf6xAq2KiXXud3uN77xDSBF\n3rgfxuWb21RUZaGfeThaa/poPGb/qgK18jzvm2++ect2nAcem34sLeJez49+jIXn3X0ti27M59kg\nKkO8th+19UnK68gZ0Zn7s6wvZm2+vNutY2Vu2he/+MVOdmsY/RgLc9D0O379618HYPvtt3c7LX9z\nVDTbbbcdAFdddRXQUW+wSoQPJwiCIGgUjVQ4uaVqhJaVVHtRA62ArqPUcuyvroWhX8K+F1pzWm0q\nm8suuwxIFQKMYlPpODZ+Xktor732ApKfw4geVYJrxfnvDo1emTJlSl8t2bLqzK43a63JoHJM6rDq\nRT+D0UrmrFx77bVAqjDQ6yijdqlzLIrQx+P86XZe6CdTQbVLE8bC+8SBBx4I9L/acxGhcIIgCIJG\n0UiF4/qka/T22TYyq+x7dXX8HM2H026dLqOMVBhFx2B+zsorrwwky2bI/rS8zjPWfW1EmL4c18n1\nl/jZJlhvPTifPaHOWmrf+ta3ANh9990BuOOOO4BUOcIIraJq0f2mCfOiKcRYJELhBEEQBI1ioAqn\nqCNjTredOUXfgNb9CFRSOOPGjZuuPIyUyqPTimpmuS9lx55/L8ex0S+i30MfjhE7eWfSfEzzCgmD\ntN66rcDdawYxFo6B8yTvBDmosQmrPhFjkQiFEwRBEDSKRvpwBkjHUWq5slFBmPWcK5v8/dznou9H\nX5DbM7rMSB2VlRTla+SVECTvNTIkNyast9eIsUj8L45FkT/2f3EsigiFEwRBEDSKqrXUXgD6U8a0\nGSxS4bMtY5Erh7w3uMqhXZ+NaFX5t+r382z+nAJfQJVxgJl7XsRYJP4nx6Ig0vR/ciwKaHssKi2p\nBUEQBEGnxJJaEARBUAvxwAmCIAhqIR44QRAEQS3EAycIgiCohXjgBEEQBLUQD5wgCIKgFuKBEwRB\nENRCPHCCIAiCWogHThAEQVALlUrbNK0Anc3IfvnLX7a8b4FLm4tV4IVp06bN084HmzYWRdie2zYF\n7RKFCRMxFol+jIWFZW3HblvtphPzItHuWFStpfbql9rsZpn3WMmxl4y9Pl544YVK+/Hiiy+O+L4P\nmryvSl6peYT9mulqHVV90ARB3Vhea0Z50ASdE0tqQRAEQS10pHBUNvvttx8Axx9//IifK1I2Yn92\nlUhV7HL5ute9ruW1Vr1935944glgeKfPvBfNjMxcc80FFKu+IJhZ2HjjjQG47rrrRvz/N73pTQC8\n/PLLLe+XXe/eR/JK7/+L9OveGAonCIIgqIW+dvzs11Py9a9/PZB8RPaIyRWVCifvijkKHXf8HBRX\nXnklAOuvvz6QlM5//vOfrrYbDtFEE8fCVYGnn34agNVXX73ldb9o4lh4n5G6ViyaOBaDIjp+BkEQ\nBI2iIx9OGb1eC3V7r7zySsv7kydPBuCKK64A4Mtf/nLL/xcpm3nnnRdIUTFl0XRNQstWP5rW3Hrr\nrdfyfjBzoRW/6KKLAknB7rjjjgAcffTRANx0001AigD9wx/+ACT/5UUXXQQ0e57k0aVlnzvggAOA\n5Ls5+OCDgbQS8uCDDwKw1FJLAcOPfUa6/qvyhje8AYADDzwQgO9///st/7/YYosBaaWk34TCCYIg\nCGqhKx9Ov3w0Jm761NV69/e0RIyO8+ndLvl+D3ndeB9OPtaOxayzzgr0znKN9elEnWORW/da30Ze\nPv/88wCssMIKQFIws88+e8vnJVfC5qJ1as33cizcF1cuOr2POGauaGyxxRYA3HfffS3bzcemXRZZ\nZBEAfve71jS9OudFfs8yItccRjFHcvnllweS+nvXu94FpMjg973vfQD885//bNlup4QPJwiCIGgU\nXflwcn/CfPPNB8Cf/vSnUb+XR5XIo48+CqSn9nLLLTfi530qu/5YVWnlFs+MsHZ78cUXj/j+Nddc\nAzR7Tb6pfPCDHwTgBz/4wYD3JJH7LRZccEEA7rrrLgD++Mc/ArD33nsDqaqGJYxycsX03HPPAbDN\nNtsA8NOf/rRn+14V/Qt5flzZ541KzUvirLPOOgA89thjLd/z+h4/fjxQPYIzVza9oNN7luTKRrX4\nsY99DIBDDjkEgIUWWqjl+0bunnzyyQB88YtfBJI/u8xv1i2hcIIgCIJa6MiH49O0zDLJo9W0tiZO\nnAiknAE/Z1TJzTffDMCKK6444nZ33nlnIK3Zur0555wTgNNPP33E77WhaBrnwzGvpqjOnGPaa5XW\nJB9O1TwLP29uij7B66+/vtJ2hnxuYGPhmvyee+4JJNX/zne+E4Cll14aSFZ7fs05L2abbTYgWbAq\npcUXX7zl/TIGMRaeTxWK++pr/ZdGqZ1zzjkArLHGGkDyEc0999xA766VQc4LFe3+++8PJF+NY1K0\niqQ6dMVE399TTz0FwHvf+14gzS9XTjbccEMAbrvtNmD4vT98OEEQBEGj6GulAVFZ5FFhuaWhwsnX\nJ3P0Efn5nXbaCUgx5kbunHXWWQCce+65QHq6n3/++UBawx9CYxSO+2aO0Sj70Zffb4LC0c9w9tln\nAzDHHHMAxcpEtacq/OQnPwnA17/+dSBZZc7HJlv1WrAek604rChx6qmnArDaaqsB8POf/xxIx6Y/\nVR/Q9773PSApII/9Jz/5CQCbbbZZW/vVi7FoN89mhO2N+Nr7iCsvyyyzDACHHXYYkKJYc99Otwxi\nXriKs9VWWwFwyimnAEnlld0PvHdaZ85ryXuuq0q+1udn1Jv30JxQOEEQBEGj6Ejh+NQzOqTrnXjt\nqWxERVFUyD/+8Q8g+TP8vOvXWjj5Mbm/WnujRHQNXOF4DEYfuYafo1XXaaXtMga5Vu+xq2BdNzYf\nq+h7n/70p4FkvblO7XxoQu5Jhe0AKd9C/8RKK60EJD+nqq1ILbgdmxQ+8sgjAGy33XZA8u04Rm6v\n6L7QBOU7ZPvA8KhTlYzq7ROf+ETL53pFnWPhsemzsbKEY1CkbMzbMqJX5eK82mOPPYB0L3f7zgOV\njX7zr3zlKyP+TiicIAiCoFF0lIfTrbIxkkKlseWWWwJw6aWXjvh51w1dx77jjjuAZLG6Lp1bsNZU\nMmot/90mYgZwkbIR1drMQN7HyPPk+dx6661H/b6W63e/+10gKaN+5xT0ktxaz9fWV1llFQCefPJJ\nIF0TZVa7itlotmeeeQZIUWxGeOr3nJF6Q+X7mvuvzjjjjBE/1y1jxoypbZw8ps985jNAsbJxf7y3\nGZnn5/OKAs4f75Hmorli4uf+8pe/AHDkkUf25nh6spUgCIIgKKEv1aLL0Ofi0/nDH/5wy2tZd911\ngaRofOpaQ82KuOYU6PvRCnR7RnScd955LdtvYsfPSy65ZNT/v//++wF49tln69idvqJPzgzynMsu\nuwwozkHK8XP9itzrJXlOWFEWvGNz5513Akn55nXIVPmuvTsGjz/+eMv2l1hiiZbXN954I5AUVFmE\naJN5xzveAaSxNQ/Hmmq9os77xUsvvQSk85JH5nkNqWzMbTRSz3tjHiG8yy67AOn833333UCK+HW1\nyfnYq2MOhRMEQRDUQl8VTllfHJ+aPsWNTrImkta8mDF+6KGHAmm90e0vu+yyQIpKM29DhVT0+01Q\nOmb2lkWdGXXShH1uF49Jy1NrrEjZyA477NDR7/k7RthYo6/dml11kPsb82vEYzeHzIg7Kw54Lej3\n8lr7+Mc/DiTfzDzzzAOkMdHy1b+lP3bbbbcFiqt0NBnn19VXXw2k+bXxxhsD6ZhmhGtFVKAf/ehH\ngZRT6Lzx/OmTM3rsnnvuAWC//fYDUnUNFbGRve9///uBlHez1lprAck37EqL+9GraycUThAEQVAL\nlfJw3vCGN0xbfvnlp6/3tUtRDTPr9ljx2P83asnXVjQ9/PDDX93pbI3+29/+NpDWJcXIHHMPimhC\nPxwtTzPGtWDdN9fqtXg23XRTIFWH7bTLapFS6mWOQZ5Z7rpwWSTe5ZdfDiQfXBm54vXYHJtOoxPr\nyLfIz4Nz39fXXXcdkOayf2+44QYgRR0ZoWf0kfOkKKrRsf3CF74ApEjQIgaZk1R0r/L+8u53vxtI\nnX9ViUU+QOefY101T6uOsbDihLlo1tJzjufVVTzv4v3BatD6xVXC+vhcXbLCiQpZv7hRbkVEHk4Q\nBEHQKGqppZZbKFqiVirVAjESQx+OERRabf7NMQvWGmldMPBKA1r/WuOOiRnh8847L5CiUcw5sH6Y\nHf3q6uAH5WPhvhtRk3ezLMP6YVpd+ui0ULVo9YPl6CvqNAKrH5Zsru58bVb8iSeeCKSxsm/Nbrvt\nBiRfnvPEv47poosuCiQ/VlHPHy1br0V9Ol6TudXfyVh062/Ul2vduFzFO3Za89YfNIck/133Z599\n9gHSWFelDoXzta99DUhKwxp6rnhYG83+NyoeV0y8H6jyL7zwQiBVf3ZsPN/eX8qq1OeEwgmCIAga\nReUotU6ybPPP5xUCVDzWi3I92tdFkVtu99e//vWov+92rLHVZIy0M3fg2muvBVK2vWu1rqlqtTc5\nf0Jlk/ujihRrTlFXynZ9QSqsJo1R7k8yGmiDDTYA0tzWmr/llluA4n434mvzL/JqC0a13XTTTUCK\nThPVYy/pVNmo1rTSJ02aBKRIPSOnVL4PPvggkI6x6HetrGwlgnb3o87OwN7z9FvnlSG8l02ePBlI\nKx4e80MPPQSkfXferLrqqi2f86/zIFc8vSYUThAEQVALlRXOSFaDFma7UUBuw8gJ+dvf/gYkC8SY\nctdu8zV/LWXzLIoskRlB2YhdTPU7GGmjOtB6szf5jITnXcWpStO6L0Nr/dhjjwXgoIMOaut7RuYU\n1eobJEYjet7NHfNYN9lkE2B4/cAy/H4eoamvRsWcX8+d9qrpB3boVK2pdFXMnldXAYy8MtIzx/uD\n19aLL77Y1n7UqWzy31TxGqXoHPZ+4L3Sjp1G+KpovF9IHv2a11brN6FwgiAIglroqNJAXvdJi8Ns\n1nbR4jBXwM6M/jUnoKg21lJLLQWkSBsjM3KfTpOstjKMIvGYtEhEC7VJ/oiqOG+0wsTXzqcrr7wS\nSOfVKETV3dvf/nYgZUnna/J5V8sm4TXkHNbPJFqc5l+0i6sN1trTAtaSNefNHLX8WmnSNeI8MHIv\nVxrm53nM+bVSRG71N5G8CovHrq/Ga8XVG+eP6k3/qN/zXpr7w/3+Aw880IejGE4onCAIgqAWKiuc\nsWPHDrNQF1hgASApES1P4+fz9UJjvc0NMH/CKtD2IM/X9v2+lo9PeymKVsutNteGjcQYRBRKEeZN\nFFlrVSsJzEh4bCplz4eReSrf/Dx5PnNUgeZjNAGvBa8h6wI61/3/L33pS21tT4v2nHPOAVK0Ub4q\nsO+++wJw0kkndbzvdVOm4vUFev2WRZ316voeN25c35WgFQbuuusuIB2j6sw8Gf/qz7bagvPq1ltv\nBYrrErp6UNeKSSicIAiCoBYqK5ypU6dOz9DVWjKCYu211wZSlIhWlT04rNdkVIn92cXPF2Hc/Zpr\nrll1t1vIo1OaoGzENXstj5yjjjqqzt0ZCHmPGH02+XnS6jOnJMcs7CaRVyj/wAc+0PLa/7fKcxH2\ngnriiSeAtDafKxsjt8xhmRnwvFsf7swzzwTqqwZdh59Lf6WrOFZ/9hpQteerM7/5zW+ANPd33XVX\nIK0aOEaLL7440J+8q9EIhRMEQRDUQuVaaqNVGtDqMqfASCt9PXk16KoYoeX6d9UeDf7uKOuVA6ul\nZv6F6qsoMk+/15Zbbgkky6XXvV4GURV4hO0CKRfFaDMtTHMP7PGRo9XfrYLtx1hYG8trJsc5ai6a\ntdPMy3CNv2ie6A9zXvVqjb5J80IfrBXU7YdTRK+jVfsxFkaXeR/QX+2KhzXyjC7zXqgf3dUk/Vne\nH/JeVN5Le5V/E7XUgiAIgkbRk0oDWhy33347kKyrPfbYA0j9avK8i7Lf8OmtMunWMil6mvdLJVTB\neHstkKLs+y222AJIa7XmU8yMOA/0+eUYtXbKKacAaeysnNsk31yO1TPyDHHxtVFHjoXXUJGysbaW\nlQRm5HytHI/ZSDyv2x//+Mcjfj6vO1d2/6haMaUf+NtGlTm39eHoP7cqi/Mkz410bDxmrwWrTQ+q\n+2konCAIgqAWOqo0kGOWq31JLrjgAiBlr/q0LbLKclQabrdXlmrRU71Jve6tD2ZOUo5jqLLpdmy6\n7VUySLR0XefWXzFIC7UMrWijjNzXoh5BeX5OjvXoXJNvsqrrFsfGaFfHxqoKeWRf1RWRJswbFYpz\nWd+dfZBUbR5rPl/0U3lPU+3r33ryySeBUDhBEATBTE5PFI7rxMaOayn4VDUL1vXHvA9K3gm0V0/f\nJlUQaJfNNttsxPe1WNrtIdMuM6KyEWtsPfzwwwPek/bx2sh7QNnL5Yc//CEAH/nIR4B0TS222GIA\n7LTTTkCy3mfk81cVI/SWW245IKk+c5G83v3br3yZXlYaKFphOPfcc4HUvyavFp37w73HXn755UDy\ne66++uoAnHzyyZV+v1+EwgmCIAhqoXIeTpufA4ZnVfva6tA+hfv9lN1qq60AuOyyy1retw6V6+AM\nMA+naTQh36JfWBGj3UrMM/NYVGWQY2HukVFpN954IwDHHHMMkHy++nT6TR1j8Za3vAVIPr8ll1yy\n5bUrHkbiWW3+He94BwDzzTdfy//3i8jDCYIgCBpFTyoNjKAU8u8Bwy1L168b1J8iFM5rhFWfiLFI\ndDIWTY+E7NTXO4h5kY+l91D7HJ111llAqhLtsRmd1i9C4QRBEASNoi8+nByzpa0i3WCLJxTOa4RV\nn4ixSPRyLBp8H2iLmBeJUDhBEARBo+ipwslrF1VlUHkzQ6rIhsJ5jbDeEjEWiRiLRIxFIhROEARB\n0CiqVhp4Afhd0X92G+s9qIoAQ7KGF6nwtVHHYganyjhAjMVQYiwSMRaJGAsqLqkFQRAEQafEkloQ\nBEFQC/HACYIgCGohHjhBEARBLcQDJwiCIKiFeOAEQRAEtRAPnCAIgqAW4oETBEEQ1EI8cIIgCIJa\niAdOEARBUAv/H7NipH+sPjvgAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2baac78f668>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# with 256\n",
"rows, cols = 10, 6\n",
"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\n",
"\n",
"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\n",
" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\n",
" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)"
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAKhCAYAAABkTRjXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3WeAXFXdBvAnySYBCRBaCEgRxAYigiKoiBFEiAoWUBQU\ne++9ooK9FxDsigo2FEVQQVF4RbAgWJAgoIJUTQQCEUJCmPdD/M3dObuTndnsDvF9z/Nls5uZe+/5\n33PufZ5/O1NarVYqKioqKiomG1Pv7AuoqKioqPj/gfrCqaioqKgYCOoLp6KioqJiIKgvnIqKioqK\ngaC+cCoqKioqBoL6wqmoqKioGAjqC6eioqKiYiCoL5yKioqKioGgvnAqKioqKgaCob4+PDTUmjFj\nRqZNm5Yk2WijjZIkN910U8fnli5dmiS5y13ukiRZvnx5kmTFihVJknXWWSdJ8u9//ztJstZaa3V8\n/5ZbbkmSzJgxo+PvuiL4/A033JAkmT59epLktttu6ziv7/t56623JklmzpyZJLnxxhuNy/UsarVa\nm4xtiWT69OmttdZaq31Nm266aZJkyZIlHWM1lnXXXTdJcvvtt3fYxLWy4axZszo+Z0xrr712kuSO\nO+7ouA5jW7x4ccfYbr755iTJeuutlySZMmVKx/FdJ1v6/tprr50lS5Zk6dKlU3qxQ5JMmzat5R4k\nySabbNJxjmXLlnWMyTWCazNG99W1siWbORfbl90yyvljPhrr1KlTO87Hxq7LvVh77bVzyy23ZNmy\nZT3bwhpxTXPnzu2whZ9sYS34vDG61nLOsoXPsx0YmzVqHrAF25h3vm9+soV55vcZM2bk1ltv7csW\nU6dObQ0NDbWPtcUWWyRJFi5c2DEGtnDN5Rxff/31kyTXX399ksY25ff97jjGZr6wffm8sP79NO88\nn8o1NTQ0lOXLl2fFihV9rRHXlTTPC2Nyf5zT78bmmtnin//8Z4ct2Mz8MRY2MC/AvHJca8T3/N38\nZDvPk3/9619JVtrmtttuy/Lly3uyRV8vnFmzZmXevHltIz384Q9PkpxyyilJmkn8tKc9LUny1a9+\nNUlzoxjcA+W+971vkuTAAw9MkvzgBz9IklxyySUdxznttNM6ju9497jHPZIkj3rUo5Ik1157bZLk\nl7/8ZZLkmmuuSZLc//73T5L87ne/6zjf6aefnqS5GRdffPEVvdpigw02yEEHHZQLLrggSbLvvvsm\nSfv3q6++Okny/Oc/v2NsJoifv/nNb5Ik++23X5Jk1113TZL8+Mc/TpL84x//SJI88YlPTJJ8//vf\nT5Jst912SRpbbbzxxkmSffbZJ0ly4YUXJmleJFdcsXJod73rXZMkf/rTn5IkL3zhC5Mkxx13XJKV\nE+j3v/99r2ZIsnJS7r777rnqqquSJE9/+tOTJF/84heTNPf9oIMOSpL88Ic/TNL95bvNNtskSV70\nohclST70oQ8laRanv59wwglJkjlz5iRJrrzyyiTN4mOLRYsWJUl7XI7DZmz0mMc8Jklj4/XWWy9/\n//vf+7LF+uuvn/322y8///nPkyTPfvazkyTf+973kjQPuYMPPjhJ8rOf/SxJ8yIwlssuuyxJs0bM\n4e985zsdYzr00EOTNGvQvPjrX/+apLEtW5gH5g0ywPYeZE960pOSJMcff3ySlfO9X1vMnDkz2267\nbXsOP/nJT06SfOUrX+mwxUtf+tKOv3sYloRg2223TZI84QlPSJJ87WtfS9I8/A477LAkzf3beuut\nO8bKtnvvvXeSxobnnHNOkuZlbr56gZkXJ598cpKVz0Hf7RVrrbVWtt9++/a1WiOf/exnOz7HFuzu\n5WeOegF4Ibz+9a9Pknz4wx9O0pBo886z0OcvuuiiJCvv53BbXHfddUmS888/P0nzjC0J6gEHHJCk\nmW9DQ0Pt7/aC6lKrqKioqBgIpvTTvHPTTTdtHXzwwW0Ggs2TbRgF5kqe7bbbbkka5vHnP/85ScPG\nMM7ybe64D3rQg5I0rA0wWa4917XLLrskSX79618naVgBV8/mm2+epJH22Ogll1zy21ar9cBebDF3\n7tzWoYce2r5G58IY73WveyVpFIpzbrnllh3nLN0Jxrj77rt32MbYHvKQhyRJW034f8zpfve7X5KG\n2TzjGc9Ikvz0pz9N0tiYiuAuwHwXLFiQBQsW5N///nfP7oINN9ywte+++7bZlfvrXNxKVNW8efOS\nNIz1u9/9bpLmPnFpkfmzZ89O0ihRY6YqzzrrrCQNa3MdbO162PQPf/hDkmTHHXdM0swfLJ/a+OEP\nf5irr746t912W8+2mD17duvhD394ex44l2vhVsI073a3u3X8PPvss5OMdB+6vzvssEOShvVjlw97\n2MOSNGx9ww03TJL87W9/6xjrH//4xyTJU5/61CTJiSee2HFdW221VZJGgWO6l156aS655JLccsst\nPdti3XXXbe2yyy7t++Va3SfrkQIxH7bffvskjcp3P7hzrIVhrvAkzTyhXHkZ2JCCcb89+5zXGnYc\na8S8cL7TTz89N910U26//faebbHeeuu1zL+kmRfOYQzu8z3vec8OW5x77rlJGhVvvvDieH6wjbXk\n2WuNWJNswhZsbOzlM9n53DvP6B//+MdZtGhRzy61qnAqKioqKgaCvmI4S5cuzaWXXtp+63kr3uc+\n90nSMMl3vetdSZJ3vOMdSZLnPOc5SZpA2eGHH56kYel8sS94wQuSJJ/+9KeTJK961auSNH5G7O1x\nj3tckoYNYIvYGbZ+73vfO0njl8QKvaX9XWzhPe95T8+2WLZsWa688sq2XxhjoGQw1Xe/+91JGp/n\nnnvumaRhvB//+MeTNOzJ2P3d9z/5yU8maRjPT37ykySNTxWb+9WvfpWkuSd/+ctfkjTq03XxyWJd\nmNKee+7ZZlG94o477siSJUvabAk7xkjdj7e+9a1JmngRX7x5Yb5gZ3z62Lj7c+SRRyZpFDImzDaY\n9G9/+9skDfsXF8H6zjzzzI7z+755ttdee7VjL/3Y4uabb27PA8Ff8Qhz7k1velOHLaj4nXfeueP/\nzYsvfOELSZI3vvGNSZJnPvOZSZoYgO+fdNJJSZo1Yq2K6bGZNfPgBz84SaOAsX6fM3+222679n3s\nFcuXL8911103IllAHNHzQmzEfRbfcN9e9rKXJWnWO/Xu2s2bt7/97Uka2xx11FFJmjVHSRmH+Bjb\nsL37T92JqzrvTjvtlPPOO68vWyQrFRblal5QDhTPxz72sSTJ2972to6x8Ap4RvKceA7sscceSZpn\nq7inOU3ZiuVdeumlSRqvg+cFheT+W0Nsb54Z/4477ti2Sy+oCqeioqKiYiDoK4az1lprtbbYYou2\nn4/f0NsWY8BsZZFhiXe/+92TNCmYCxYsSNL47DEJx3/kIx+ZJPnABz6QpMkuoyqwecxFPMJxZXx8\n6UtfStK8vbFPDIq/8qijjuo5hrPhhhu29tlnn3a2SpneSF1hmGyBkfALUwMUCjYoNsQXLxuJepS1\nxqcv2wkj8T0xocc+9rFJGibLZ4zdY51Tp07N5z//+VxzzTV9+ad33XXXNmtiX/EDTJStZDfKYhSX\nMhd9TzbjQx/60CSNQhWXOuaYY5IkL3/5yzvG+j//8z9JmhiQe0PhmA++JxZIBbLFJZdckvPPPz83\n33xzX3GLBz7wgSOymKwV6k16q/tnjYj9mR/muGvyfT+pxhe/+MVJGkYsPmLM7jsb8i5g0tSj/3/A\nAx6QpPHxX3/99TnjjDNyww039GyL6dOntzbccMN2nNK6xpbNUfPFzzPOOCNJE9/wPLn88suTNM8b\n7F28g2KWuWWeUPOeE7IVzTfzjFLiXXAPzQsq45xzzuk7njVz5szWZptt1l53noGll4hNPAe+9a1v\nJWkUh/9nC/dRjI6SftaznpWk8Qa85CUvSdI8ZzwjZSVSfZ47r3zlKztswYbm5wMfuPIx+ctf/jIX\nXnhhlixZUmM4FRUVFRVrDvpSOBtssEFrr732ajMF9RBYmLcuRsBHy2+J7fOhYxreztSBfH3+TDUq\nWIDMGuzQW1sWiuw5v2NY/NGYivoeDOmUU07pWeHMmTOnddBBB7WzzTBLbMm5ACsrM/j4jf0/5kD1\nqQE49dRTkzSsT10G28vMYWv+Z8rHebH5smBV3GbDDTfMySefnEWLFvXM3tZaa63WVltt1T72U57y\nlCRp122YB4A5uib2dy1YOdtQgRjsZz7zmSQNi5MRVqpHNjRvxNHKYkos0fncuyVLlvTNZGfNmtXa\ncccd24xx//33T9Jk9Ti2c1NfQAnttNNOHZ8Xq2PLsnbNPMGMqUeZfdYWhvrlL385ycgMMLVqFLTf\nZ8yYkfPOO68vtTdz5szW5ptv3r4PxuCYsgldmxiPa3bfxR1+9KMfddhG9qNat9e97nVJRioUtsD+\nxVs9j6wRn6c+Pc/MO+dfd9118/e//72v4ui11lqrtfXWW7eVKW8OxSOG4xopD7YTd+aV+cUvfpGk\nmbO+R9WJf3/9619P0qypb3zjG0katUnR8MCokXMv2Ni8E0+nmGfOnJnLLrus5zVSFU5FRUVFxUDQ\nV5baLbfckvPPP7/NSGRzyHTwtlVFjWlQIny33qp8pphF+Vblo8cWZVJ5m8tKU9H+vOc9r+M82H7J\njLBL58Eu+sHNN9+cs846q81cZR9hqFTXW97yliRNNhHGi3Fg4/6O3elAgBHJTnKt2BeGTCWK8ai6\n9nesHsunKviEKazzzz+/zXp7RavVyrJly9rzQtYRW2BnlCuWha3JoHF/ZCWxgbgCBSR7TaxHxpUY\nIUUsbiX7iVrAGs1f81PMh/K69dZbR7RZGQvLli3rqMh3DsqDssUU1aa5Vt+VxcgWlLM57Xif+MQn\nkjQ+eeqeUpYF9YY3vCFJU6NmXoi7mVfulXvJS/CPf/yjbZdesWLFiixevLgdr8CejUHN2HOf+9wk\nzdx9xCMekaTxgJiP4hnuI1XOo0LteR55TmDzlAoVwIPCS8F7YD56vlgb5vPixYvbdunHFv+p3UnS\nZIt6flAYr371q5M0sRfZhu4rVebZ6P5Ri2qKZI7xRpXK2ZqwBtlCzI4KFBc1bzyD3cP/tPjp2Q5V\n4VRUVFRUDAR9KZx11lknu+66a5ulYc3YGnb+qU99Kknje8U4fO/Rj350koapYtt77bVXx/e9fTFY\nvdVkw1E2vo+pYg+YyWabbZakUT6Yscri1772tUma3PVebSEWNXzsWDYGKfai35uKXxk2rpmNMIv5\n8+cnGVkTIGajyl42kVomx1Vf4x7JgvL/bMFWmNL8+fPb6qxX6BMlkwVLwjxl7ImZsZtsJNfqc9Sg\nOBUGbL5QxI6n9oAa8bu4Bubq/6kBKgFjxh6pz/3226/vnlmzZ8/OAQccMKLDAKVBUfKBU7ZYNpuJ\nqfDVm8NUonlFPbi/shl5EdR1WUt+Ug/uNbVP/eszaPw77bRTO9bVK2bMmNEez/BrohzYBpuXjWhs\n1rW18L73va9jDGKF6m+wd3VYatjMN9lrnleOTwF5XlBG4itspVfjvHnz+q7DmT59ejbbbLP2/aIK\neIWod9dIpevCQbEao6xC88GzUe0RpSP28pGPfCRJ80x+xStekaRR1p5bvEllRwIeHB6X4THKMg65\nKlSFU1FRUVExEPSlcO64447cdttt7SwTfj2sHTPw9nvNa16TpGFRmC9GgemoBHZc/mb+TscTE8L2\nHI8ywsYwGp11+S+xCm9vzBlj6kfh3H777Vm4cGF7bDKhqKYyliPrB5vG9oxFnAID5rPXtRewLaqP\nDxhTkoVExaltwEzYgNpUr6FWZv/992/XsfSKFStW5Prrr2/HQNyXiy++uOMn37gMGvfLtfHpGxvF\no7aI39k8ExNQVyN2xFePJWJ52CHVR925XmDz3Xbbra0wesXixYtz+umnt2Nz2B8byIByTbp1Y88Y\nMFXmWikkKlKGaKmsxb38tBaoSOPB7mVLlV2C1bqpkXrUox41IvNyLJgXlEJZVe8axR/URVEovATm\nhfmDleswYd2y+Xvf+94kTW0SNa+WRaxXhwE2Mu/dC1ly1ox5NX/+/BF9HXuFGB1Fw7NgXRs79ebv\nFAul415Yt2wjU88z9ogjjkjSKCLH4xkRL7PGZBK6R7wBniPupczAu9/97u3v9oKqcCoqKioqBoK+\ns9QuuOCCds0HBYIh8pFjbZ/73OeSNL3UsH+sHMvGjL1VveWxfzEbrJAioqzEL5wH68P6v/3tbydp\nMiywB35PsaB+MHXq1NzlLndpX3u5+ROFItYiG0n9hO6vGAPGQulgfxgQhoP18Tc7PkXDZ//4xz++\n47pU9+vdhaHJgvH5L33pS21G2Ctuu+22XH755W3/P8WCIRojf7M6GnEt88H9KeMmstooYGzeNZsH\nspjEgMTmsDGs3vhk7LGl+cC/ffjhh7cZf68YGhrKxhtv3Fa2FGtZIe5cbCEbDWsvO2m7RtlK1AKm\n6vPuq+xIcTLZbHpumaeUlDXk3rk3hxxySPv61Ib0iuXLl2fhwoVtVUfJeE64BuofOzennc+Y3Dc/\n3W898dTX+b5Y8LHHHpukifXwbBx99NFJmrgmFeo5ZD5aI1TCM5/5zL7XyNKlS3PhhRe2n2ngvuok\nYU7rruJ+gexBytlPY+HhEJNTHyiGoyejDGE9+3xfpjAl5llv7ZV1Pq94xStGbMC5KlSFU1FRUVEx\nEPTVaUDPLDEQb1PZK9gUZSGuwSfKJy/rBHuTg64TKV9qGfvh3/Z5b3sZXpivbBbZRliF6+Kf5vdU\np7NkyZKeOw3Mnj279bCHPaztNxaPKvs1UWfOjeHyqctSc63UmUwa8SsMA7PFEqkKPlaKCHPFXGTV\nYPkUD3YiNvCd73xn3FXUrgErwgLdH0xSzEytAHYnxuK+Unt87OVOruYhVu785pEsNpk5/NVsxtbY\nvHmMeZ999tm58cYb+9r3ZNasWa2ddtqpzepl+bCz+WGsFIq5aAxlBwoKRsyFt4DqL7csttbMfb54\nY6W0KWPfFw81H6jTs88+u699T5JkxowZrblz57btWc5dvn/335qQsefzPBI8H9Si/zcvjMWYzQvH\nZ1MZguIV4lQ8NuKr4iWuH/v/85//nNtuuy133HFHX2tkiy22aHfFcB+dU2zNfdDB3rNJtp/+ktQY\nJVPuf0SZq2HybORVMjbPHdcjg3j4lvFJs6asacc599xzc8stt/S83XZVOBUVFRUVA0FfMZxkZUwA\ni6Y8sCeMUX493yzf6Tvf+c4kDTvzNuVXxIxlj+hYIGtJlgklJUNDJo9sJX8X68E2+fYxHm9t58Ma\nesHQ0FDmzJnTZgjYlrgF5UONYbI+L9NGnQ3lofcRxkEF6huGCasIx5jKXl1YIiajxkGFML82FYr9\nbbLJJm0F0SumT5+ezTffvO33pSCwc0pERpz7SAXKStTTSg2KuhvXiL2rNcH+jE1WIgaNhenSIE5i\nfFSArCYKzPH6zdZLVqqzzTffvK0oKVxMU4adOSmbSMzP3vTiUli6ue1+ujbxJrY0j3gVKCu200Fd\nXMI9Mp/ElCh283DmzJnt9d0rpkyZkqGhoXZMDhun8s0TP7Fw80D1u/tM/fFgiNFReWpYxHTMG7Ec\na1Hc1d4y5hNVQH2qD2ILCuzaa6/tq/YkWamSNtpoo3Y8it2pJveZjcxN8WVzWzxa/Zb7L25edjgp\nu3qwHe+UeSfGwyauy/z1DDcfKO7zzjuvrQh7QVU4FRUVFRUDQV8xnE022aT1+Mc/vu13pBSwbswU\ni8a2vAG9HaHsWYSBnHDCCUkaP6K3LFYhG0XvJOfxdrfroTiG+Afm6zoxNkz4Zz/7Wc8xnLlz57YO\nO+ywdpyBqsNgHJv6wkyxPbUF4lJ8+/zP2JmeSdRfqZTEetSUUA+Yi9oUPl71Fo4HGPc111yTc889\nN4sXL+6Ztmy00Uatfffdt12vwL7UlnOxFTZn7GIrYmu+55opD/Eo6hFrw8bEaqgDnxNDUsFeKpiy\nR5jzLly4MJdddlluvfXWvm0BFA3fOmZoTmLN2LW4gjlpjZgvGDDGae6Lc4mLiHtQE3zv1ruO6+YL\nG2H/Yjfm44033piLL764r87Z6623Xmu33XZrZ6fp7ECNmQfORcH4nNiKeeU4vifepLOE54NsVSpP\nvLLcl0vsh5ehrMdxXjGc4Vi4cGGWLVvWsy3EfK1/3hXZq7wA4FnoGcYWlBFbiO2YRxSyeKS15fjU\nGy+RNWc+UpdqLD1XPMOpUbjjjjty+eWX97xGqsKpqKioqBgI+orh3HTTTTnjjDParEi/pbKjsben\ntyqWL+bDf6gmxFvf5/zUqUBcQ6UvBYXt8497K2MB2L3d7hzX/hjiLuPB4sWLc8opp7T7fdmLBRun\nwsSHsCUZWBQRtqVHmrFQd3z8agfUS5RZLlQiFYclYjjf/OY3kzS+XowF63e+/2Tf9GWLf//73/n1\nr3/dZmXmhWtXW4BhUqziC1SAGI9aFExYbIgKVN/Fn43psq37TGWKJYpzqb/h/5YJiPW7N9dff31f\n/ulkZXbXL37xi/bcFy+yZsT4jFVWEpZPHWL75o84KeZKHeo4wCvw9Kc/PUmjJtmCYmJ7a8RaENtx\nfWIGFFE/nhDQXZ4nhN1du/Vcsmr1N2X24Zvf/OYkjfo3f3gVzHHzQg2R+VzuVCymR9WZt+rFPGes\nEfds+fLlfcdwbr311vzhD39oKxKxMircs07Mlo2cx/30fc9EsVcKlVLRR45C4QnxDKaojclzgWdE\n1px7VHbs9uxcsWJFjeFUVFRUVKx56Ltb9G677dZ+86tildeOjWHL/MuYCGbKhy6rBHuifDAiCkhV\ntreqfdz97u2uBxZWSXFhPpgMFuk6+W6xi16gQzJWjU3J4MNMMFdjw6YpGr51dRGYhDgCxmmHRnUU\nlBWmRCXI6CsVlrx+HQ4wIQwLA583b96IHTrHwowZM7LNNtuMiENQJHzi5o3/l60oow7zpIgwU6pR\nHIzKo/rEiPwu+9G8xA7Fhtwr88bf2dp83WWXXfrukDx9+vRsueWWbV+3mjN7t1DzbKOvFzbvfvHR\ny1aSRSYGRA1gujI61XXpoYUBU+BUnnts3yQdDMSMzEuMeIcddujY56cXzJw5M9tuu21b3ZvjYmxs\n4j5bvxSFWKzuGuJW1r14hOeJGJ+ebOa0MVLCFJXrEuvB8qlF88G8VJs0b968dtywVwwNDWXu3Lnt\nscpSpUDEkXgsZIv5f7YwBnsHmWdiQsbGhuaXNfLsZz87SVPPox8hWxgjpSxOTrF7XrjO/fbbr22/\nXlAVTkVFRUXFQNBXlppq2XIfbawNKyprP/gD+ZMpGKxNvQWfOh8tVYBpiMXwd2LUWBnm5LzUguw1\nvl457PL4ZYCceuqpPWeprbvuuq2dd9657YPHIDBI14aN+en/sW6xFiyKGnjlK1+ZpIm1YLoUE9Um\nRuNzbOCeUHFsidGwjUwvqnH33XfPOeec01eW2owZM1qbbLJJ+xz8wuZHWTmOmapVEV/w/3z22Ls6\nGf9v/sisU3NAcWORFCsGxv/tumQpiRlQDZ///OeTrMwM+93vfpclS5b0bIu11167dbe73a09Jtdq\nnlASlANmSpmW80GMD8N929velqTJPsOUMVA1J85LHVpj1iC1KUuJ8qa8KGlZT1tuuWWuuOKKvjpQ\nDA0NtdZdd932OYzNuSkm8UdZhuJK2Lu5b0zmheeBeWcdW4vWuflBRcoMMy/Z0DxhA5mF9lUa3q3+\nqquuym233daXLdZbb732s9HYzBPzgudCrE0cmgJhK2uBiheDk81Y7r9EaevRZg2IW1FYPscWnpnD\n98tKmp6NW221VS688MKe10hVOBUVFRUVA0FfCmfjjTdu7b///m02Vu61ojYEC1PZr/KfX1JMBuvi\nD8XasTBvbayN8pGxg8moe+CL54OVw05J6ZjLV4wlYhFLly7tWeFsuummrYMPPrg9ZoxBhpNj68Z6\n/PHHJ2kYp8wp7Iv/mQ8f+1YHYW8XWSLOI9uIchIf4R/HjJ2XjYyZr1as4thjj+27T9Ts2bNb8+bN\na9f4sLt5wRbiCnYldN/EVPj4jd08M2aQraRDAX+0e0G92T/HmFWgy8ShMsU3KCS2O/HEE7N06dKe\n+0QlTR2Oa6e2ZPBhiq5dPAqzdZ8pXN4Bx6O+xOjUmIjxqdMBNpFtRHnzzVOJYoq6lOvSQSEfd9xx\nabVaabVafdXh7L777u1YHYVCvVHhYrtiL1h0uZOnteG+8VCIJ+hkoi6HemcDcVXdw8V6dTSwpnhU\nZLs5P5xzzjl922KDDTZozZs3r60keCY8+/w0Zs8NnxOzoYhlcJpfujdTjzpvU6ieC7xBbC9uZc57\ndopNsy3Pie7V7sFJJ52UO+64o2dbVIVTUVFRUTEQjKuXGgaLQWBf3nrYdtm7yFvZWxrzwLb1BZMv\nL0ODQnIcmRq6AWMq/JkYL4aCvWFOMoD4kPl+fb8X2A9Hvjz/MxaGIch4kgmHSejbJpNGJ1zXKpMO\ng/F3mX+YDP+27DOMmEpQgUzpqETnt3Y9fj7xiU9s967qBytWrGj76t0fWWBYN7Ysxkb5iFvpF1eq\nPIyT31v2IpbP1s7L1y5jh01kcJmHfPVUApbpvNtvv317bvdjh5tuuqkdUxELobJKr4C5SrVjnpSO\nbELMWBxENhFbOJ7/9zsbYLZUKB//F77whSTNmjBfxArFdu5///v31WswWTlHr7766va5ZB9a967N\nHPdcsB8NFSbD0vd4A1yzmCGPiXng+WONUETGQfEaMyXtuJ5vvEDuxdZbb913v0G7JZedRKxjsRLP\nQHNSXJyHhAqnlHl/KFXPDbEZHoxyDelfydZ+lrV01qjYk2cwG971rndtP7t6QVU4FRUVFRUDQV8x\nnI022qg1f/78Ngsr+0RhVd7SKnYxGD5UikLGBF+7mAwWzo+M3WOLWBfVgB14y2OwstO8pX3OdVJQ\nst7e9a539RzDmTNnTuvAAw9sx5uoO/ED5zBmjLXcGVS3BH5kcQ0qkuryOcyKbxdjZSv/7zxYPEYk\n28X3XIeUEdwOAAAgAElEQVTfX/ayl+XYY4/N1Vdf3Zd/eu+9924rW3AtWD0W7347N+UjzlTu0GgM\nmJR5YiyyiCgZWZTOZ57KisMqzRM/zR8ZOgceeGC+973vZdGiRX376s15bNm1YpjmCxZtzZQdAWRU\nUUIUM1u7ZrEZ8UndGnSFpjatHbZ0j8TwrG1xLsp3/vz5+fnPf54bb7yxZ1usu+66rV122aV9LHa3\nLt1HasqcNnfZSuaVmjM/rd+y9x7bsoUOF7LaKFi2lKXIJtYCRcXGbDR//vycddZZfdligw02aO21\n115tFe3c7pu14HmhXoYXhjLy0xqRsecZp5uDmCB4PlCV4uhUpOdWWZvkWczrMLznYrJy7f34xz/O\n9ddfX2M4FRUVFRVrDvqO4UydOrXNBFSxyu746Ec/mqTxxWMWMnL4tWVO8B/zncpSwniwcvEGWS5q\nSfgd1TTwU/NXiq+UNS/e3ny9mFI/mDJlSqZPn97On7fXt3oYvn9VznymuvhistiaWhN+aJlbGKlM\nH7ZQUyL+obJY1ppKcr5iLBMLpDrK7gBnnHFGX3uUJyvZ2frrr9/2cavpMU+wKDbQAcJP88I84KNn\nG/uS8GNjnhSu+4rFY2NUQKnIzQ81DRi1uAjbnnnmmW379IqpU6dm1qxZbTWlA4Bzm7PsLePu1a9+\ndZKRewFRvhit/UzsX8KXbk8XtnDd1iCmbF6IHZa998wPqpK6uPLKK9sqrFfccccdWbp0aVsZqLMT\nc3n/+9+fpMkqMz+MGZuWVeb++7w6K/PNc0NMRl2VPWWcX9Yqz4w4iZig54XaKb+LBZ133nltRdAr\nPC/cBz3wxLdk9srYk736wQ9+MEkzJ8sMX9lrYjnWP9VHNXpGu6/UHhvz1FCfMvPKsYvhON4FF1zQ\nly2qwqmoqKioGAj6iuGoKMcE+B29BSkK7EqMBsPFOLydZVzxN8r15uPHTDFfb3cMBTujMmRqUQVq\nDygi4Nvnu1XNfeaZZ/Ycw9F1QRdW+er80li7uNE73vGOJI0SwSixdTEaDFcVNB+8+4ShUnuUCuaB\nWfMVU4niZhivzC6slerbaKON8oMf/CD/+te/evZPT58+vTV79uy24uB75w8Wj+JnNi+wObEb1ypD\nhwrkl8YKzTN1PeIbeqhRaMYqnsam1ACF5Xp1l/b9FStWZMGCBfn3v//dsy1mzpzZ2nzzzdvZPti8\nHlQUBKWjYhsLx2QpFxmaMv3UDPEGGJsO7e4rBWUsxk7F8Qaoq1APRAmziXl93XXX9b03kE4D5jpb\nuCbq2xrQYYCKE7NVtyVWZ857rlDE4k3Yu16N1pZ7wBPj+cHWbGp+AptZI7Nmzcr111+f5cuX97VG\nNt5447b6Yle20C/OfbHDK+XDa6TeivKkwjw7eQMoFvU4noXutzWk7obtqBUxH54XcVbPC8/OmTNn\n5uqrr+6560JVOBUVFRUVA0FfCmf99ddvPfjBD26zdnUN2DUGW+5XIx7hbakqFpvzdlbLQrFgxtgi\nHy5F4jx+YmdqTkr/I2WEBar3wWDe85739KxwZs2a1dppp53aLAlDcS3GAFg7xYJRYtuUjThIuee4\nOBVGgw1i9+Il1FvJiMUz+O7L/eQd9+qrr85xxx2Xa6+9tq/+Ydtss037WDKsKFSqDHtyn7Eu6k+c\noqwlUANgrpZ7z/PNm1eUN2aMSZsXWCW2iQ3yZ5uXM2bMyDHHHNNXxt5d7nKX1r3uda/2Oah4jNba\nod6MzS6VfPZlJ2xZQZQzZeOaxYhk9vm+OAXffdmDi1fAPTF/ZUux0T/+8Y+cdNJJWbhwYV899ubM\nmdMeO4Uj1mJ9+n/3k1KlNCgS8QVKmKIWN8W6rTGZXjJEqXw1TY6n7sz8kgnGtpS6NX7jjTfm5JNP\n7it7ce21125tt9127bFSKGK94kigD5ys1Re/+MVJmu4t1gDvjY4BngPmg2efehy1iO6345lPpVfA\n9z0fZF16lt5666192aIqnIqKioqKgaAvhYPJUhiyTzAM9Q98slgbX7v+UHarVCsgHoGNYWfYoLe4\nt7I8eYyZb5XC4uPFgLAJvl0xKJ+n0E477bS+FM5973vfdqYTNo9hYBJiKnyrduLjn6YG+G6pQsxH\nlhOGy2bqN3wPY6YmKCzKCpvkB5chhP277iVLluS0007rOa8+aZgsZYBNi1eU80LWomwkfuXSv4yl\nUbaUkOPblZIapDbNS2pPnY3rwVSxdzEDsUSK99Zbb815552Xm2++ua8Yzl3vete2khCroarNCyzd\nnHQ/MFtK1LwSyxGfxNoxTnEM2UOYNBbvd/Ew84yt/a7rB0Y7fPfNM844IzfccEPfcQvrW6yEZ8GY\nzHX1cBSr3oviUZRJWUf3oQ99KEmTpSi243PGYI1QE9am9c/2nhsyxSgjz5lFixblqquu6qtz9lpr\nrdXaeuut23NQthqvgDVibntWugaqz/wxNopU1qJda9Uuiu3xEpV717A9pet61DDpCmJ3VM8rz6MV\nK1b0FdurCqeioqKiYiDoS+HMnDmztdlmm7V7HvEvyyLzFhY3UOeCSfJrUwUYrLerWA8W5i2Lffsc\n9qXKlj+R71/FOcZNkamaxfZcBya8YMGCvmM42DW/7ze+8Y0kjbJQPyPDTmxFtgdGKksEsH0sDBuk\nytSaYEz80NSd+4rp+F32CWUkbx/rP/fcc3P55Zf3lY0kexGr56t3v7AidjYWNmIL36OYsTFxDr3z\n+OgpGR2OfY5icT3qbvTO0vONfxwLlMUkW+3yyy/Pddddl2XLlvVli7lz57ZZMbXkGmXkUV3qtFyr\n+BOmScG4JvOi7MbBC6D+gnK1RmSKWSOyJY2ZihBDZFvM+z+V9X1lZk2bNq21zjrrtD0MxmZOs5H1\nap26FnOdmqNQ2JL6V7/Do8JTwhvgPLpJs7WxU6HWYqnUKaLhneBvvPHG3H777X1l7M2ePbs9RnNQ\nLM36cy1Ulr+zneeN+cCTIYtNPY6ea2xo7TmumBD1aV54rjgPZUQ98ir5/JVXXpnrrruuZqlVVFRU\nVKxZ6Evh6Jml9kTWD6XARyuzyp4vWLa3prcuhSQbDaOQuYUJebuC8/FP8z/zd/pdXr3zY5ViQWJE\nFE8/MRx7wGBPGATfu1iKn2IuGKgxiztgMJgPW2Lh2D4fPrYnP54tMQ81CLLY1ECxqbGrRPb3ddZZ\nZ1w7fs6ZM6cde2NnYF/sSbcELJtiphJl4GBXYjV8+mzquFgh22Fhjqsam/9b5o15hTGbn3z+uif0\nu+Pntttu21YGjiUDy1w0d3kFqEHXZj7ITnRfKVmsX2zOvKKMqEQKmHpkC/ddFp15xZaUGFuvv/76\nueiii/qqSaJ8KQ81H1Q4dU0FmuuUrLFj85QHD4cYjjiYa6XSHNe9YHPzT8yI0qbErD2xYvPI8Zct\nW9b3jp9iOK5VNpgxWo+8QOLM1DelYx6Y+xSTnntiP9azMbu/1pQ1ooO3uJk1Yl5Qi/rPlTvUbrDB\nBjn//PN7jnNWhVNRUVFRMRD01Uvt9ttvz8KFC3PMMcckafLUZUzwxYpXqDXxVpUBg3WJ4VAsOpnK\nOvEW5rcWHyk75vq+ty82wJdPkelbpcJdHzJvd8yqH/CdUxjUnW4K2B3WJIbj3BgqBYLh8t27JqqQ\nb9bOj8aOgVBSbMAmGJXj6z+lnkfW1GGHHTaihmgsTJ8+PXPnzm3vzYK1id3xsWOW/NblTrHiSuW8\noOLUY6jjYAsZP5SRn+IWbM5nr4cflSn7zbwQv9hhhx363g9nypQpmTFjRpt9U23iVCr+xSmsGdli\nVKAxWCt68Jlnatd4BeyOW3ZvwPYxWepCHAMzpg5LW1AJu+22W5uF94pWq5Vly5a166GoL88NthBX\noHjLrt3mg/VOSctGU7tkLZnzlCuoLVLLRCmxtfgHG8nMUh8mM2ufffZpZw/2iilTpmTatGntPpJA\nVYuDyyJVg2buWpOUKoUjbml+GQNbiZ96fhiztea+++lz4vDWEO+CTgfW7N57791WoL2gKpyKioqK\nioGgL4Wz7rrrZs8992z71DEWygMzwfLlcHur8ivKoMHKMQ7ZaJiKrJBtt902SePjlXuOsVILmAn/\nNwaNjWDIro+fFIPq1xZ77LFHO/MJ48DeMRNMg0+0zJhji3JfEr50NmZLbALz5dPFUDAPDFYVPVWI\nCfHl+z4VOTQ01Pb/94rZs2fngAMOaKsuCkTdBMWDYbpP1BZ2x2bmgbGUHSwoE79TQsZirFghtq8W\nxjwte2u5PsdRYd4P1ltvvey1115t5Wsui73IqDQ2ykbXDrYw52VIybiiCigd8Qm98ygqY3Fc8xLj\n5T0QQ7QG2ULsia3HY4sNN9wwhx56aJsVm7vWvftQKg+xGvEHmVTUHPZPfTmudWxNgfkk7ilzVPZi\n2YHEWtatnLfB/LzlllvadusVG220UQ477LB27Zlrcb+NUSzO/Xdt4o3mptiKNWaM5gHb8pwAb4Hz\nUeKUlmcm23sG81aZF54vm2++edtuvaAqnIqKioqKgaAvhbNkyZKcc8457ewzvnOMtmSe3s4YM+aC\n9WNfmIb6Csf1tqYO+LsxGgwHY8ZMKBjxE/tmUBE6HVAP/ezJDTfccENOPPHEdhYYJot5UAwYg+pq\n9TbYtTFiHhgtWxijWIJ4lONhnjLD+Hhdj0wgmX+UFVWAnWBvN910U99s9qabbsoZZ5zRVqDUmcyY\nsped+4k5lllLmK7rkD3kvoslqOfBmI2ZwnFc5zEv1b7o0OyeYH1+rrPOOn35p4fbwrzAFDFRisSa\nkSHl/lIobEcdgmp41+W+m9PWgLnt/803tmEr/cYoKAzWmhQTXLBgQd/z4uabb85Pf/rT9hhlclLx\n1ggF6z4bM1bveWAtGYNrY2PrmDfAXDd2x3F/HYfCEhsS13Q83gQ///nPf7bt3CsWL16c0047rb1+\nZbxRNOYL+1Oi1qe5Xu5OawxigmKAjuMZS2GbX9aCGI3nkLWnN5uu1Z5rPCnmwoIFC9pelF5QFU5F\nRUVFxUDQVx3OlClTFia5YvIu507H1q1Wa5NePvh/3BY92yGpthiOaosG1RYNqi1Woq8XTkVFRUVF\nxXhRXWoVFRUVFQNBfeFUVFRUVAwE9YVTUVFRUTEQ1BdORUVFRcVAUF84FRUVFRUDQX3hVFRUVFQM\nBPWFU1FRUVExENQXTkVFRUXFQFBfOBUVFRUVA0FfzTunTJnS0ZZAA8F+W3VPNDQHnYCuCYv6aG0z\nIS0aVvfaJ3DsHWi1Wj3vUTBRtlhT8f/ZFuX8+v9sixLVFg16tUVfL5xk5QQ0+XRvLfel6PYQ7PZ7\n+ffyReZ45d99z94SZTfb8kXoc75XHifj6HU01t4x5djKz7sm12IM5Zgdx9993vd1f+31esrjdrve\niv4xfI2s6jPJ2PYu72d5/8wDe0CVny+7Go91vHJNlvPrvwH9kjBjHKsD9GSRu/9P6PuFkzST24sG\nPCy7vTDKhyX4uxb93R6e5fHceOcd6+Herb36ZCi18pjdXgy9tjkvHwDdXlDl+cv/L+9Bv5utVawa\nU6ZMydDQULutvG0Ihv9/MpJAdHuIdbuP3QhIt//vRtag2/n7bcM/Gei2PrvZrrTZWOh3DVaMHzWG\nU1FRUVExEIxL4ZSyG9OgfDCLko13Y9U2i7L9cXkcn8caSxca1VAyIJ933LHYYr8Y7jop3YklkyxZ\nVDeXFlB75YZaxup357OhFtv5nt+7uSdHY9p3dkzuvxmtVivLly9v279fl2vJ5rutGd8rvQLlcUov\nQKl0x1JKw3/eWfOi2xop5zoYq03k/O5zY7kR/y+ifKb2iol2I1aFU1FRUVExEKyWwsEQSiVTxidK\nBVSyNckHWBpm8tjHPjZJ8tOf/jTJyi1rk7S3NLUtrq2Cv/71r3dcX3m9kxkgLxMRum1NbOwl48RU\nwf/bHhfWXnvtJI1t/fS5UumUzLWbf/v/g6oZZNC3W3B/rC2ru8UpyuOW88i2ybbpHm+sbk3JPB0N\n5f3rZitj8Dzx+VLtl/fk/5Ly6TXWa2yeuUuXLp3U66oKp6KioqJiIOh3i+nW1KlTRzABKLPUSh9r\nGefYaKONkjTKxdv4D3/4Q5LkQQ96UJJks802S5JcccXKrOW73e1uSZLrr78+SfLPf/4zSfLWt741\nSfKud72r4/wlE3Kdo/g1f9tqtR7Ygym65tWXaq6M5fh/MRg/ZfxtssnKMiBKZuHChUmSHXfcMUmT\n9UTl3XjjjUmSDTfcMMlIhuv/y7hXmU47XI22Wq01osagm9/5AQ94QJLk97//fZLm2l/84hcnSY45\n5hjXlWT1GWq/tlhVWnS3MZXs3Oew9PXXX9+1JGnuv3ni+z4/a9asJMkNN9yQJNlggw2SNGulZP3l\n9YwWR53oeTHW/enmCdl0002TJH/96187vv+sZz0rSXL88ccnaWwxe/bsJM0aM1+22mqrJMnf//73\nVV5HNwxyjYyVkVcqWTbyPPC9d77znUmSI444ouP7pRrsF73aoiqcioqKioqBYFwKR/ZXGUcY9rmO\n3zEJ7Iqf0Fv4oIMOSpIce+yxSRp/9KmnnpokOeSQQ5IkZ5xxRsf/Y/WXXXZZkmTu3LlJGob7hje8\nIcnILDXKaBQfbd8KZyzfOKboHBRNaUOxly233DJJo2guvPDCJMnee++dJPnTn/7UMVYsD0Mx1muv\nvTZJsttuuyVJfvGLX3Scr1v20jBFdqcrnFtuuSXJyDiWefKZz3wmSXLBBRckacZMEZfoltE1FsZj\nC/cdutW/QKlsSoXz1Kc+NUnyzW9+M0ny0Ic+NEmyxx57JEkWLVqUpFkzvAAU8w9/+MOO82+88cZJ\nkquvvnqV1zWcWU+28mUDqs1zgu2oPOv63e9+d5JG9T/60Y9O0nhIPF94CSgcxzW/2PCcc85JMnbt\nGgxijYwVU+uWJXvllVcmSR7ykIckaZ6Zl19+eZLGZosXL+443vOe97wkyWc/+9m+rrMqnIqKioqK\nNQp9KZwZM2a0NtlkkzaTLOMSJRPA4tddd90kDXP4xCc+kST5yEc+kqRRKk960pOSJD/60Y+SJFdd\ndVWS5PGPf3ySRsl4O7/mNa9J0rD6t7/97UmSV7ziFR3He9rTnpYk+da3vpWkYTaj9InqW+FgFsZa\nZoV0i93wK4uxYKzYHcb6zGc+M0nDyvipKR0+2p/85CdJkvXWWy9JowZ9joISy2Gz0djcihUr1giF\nU8K1f+c730mSHHjggR1/F9co1UW/tQclxmOLUvmWMRrXRHWZJ7vsskuS5Le//W2SRtm4/xTJ61//\n+iTJe97zniTNmvL7c5/73CRNnOtLX/pSkiamYx7edNNNSZo1MWzMHdetDmci5kW3eIT7WMYVwN8p\nl9133z1JMmfOnCTJDjvskCT52te+lqRZU9i6Nfqwhz0sSfOccZ4yq7ZbXOs/dhjoGilrCsXozB9x\n8Je97GVJmvlzySWXJGmUjr/zOlFCfpbzsldvQFU4FRUVFRVrFPqqw1m+fHmuu+66EeynhJzuMj7h\n5xe+8IUkje9dfMLb+AMf+ECSkSyNGvjKV76SpGG6J5xwQpLkz3/+c5KGtcGXv/zlJA1D6tZxYDxg\nC2ODktHyP2Mq/M187ljXueeemyR5+ctfniSZP39+x/cOP/zwJE3sho3ue9/7dnyOjR/xiEckaXz4\n3WqjYHXVwHhQsqluPfWoxwMOOKDjd3EK7I+iNl9gkDUm3XqllT/vec97JmkyMCkZ8wPzlIH5s5/9\nLEny4Ac/OEnD3j/5yU8mSQ4++OAkTRzjsMMO67iOD37wg0mSD33oQ0mSZzzjGUkaxkwldovtTQTG\nihe5j2W3DXOczc4+++wkTWzm/e9/f8ffN9988yRNXFQs8Ne//nWSJuuNN8Fziw1KDHJtlFmCZWbt\nAx+40hHjmffEJz6x4/8//elPdxzPWF/96lcnSQ499NAkTRyMN0nmsDj3RKMqnIqKioqKgaDvTgOt\nVmtE/U3J2soaFFloWLY4hLcuvzKl8uEPfzhJ43emaJ785CcnaWI0stH4cvluZWKULB7DoYC6bWvQ\nD7qpI2N3TiyNv/kb3/hGkoaZiMH4u2v7y1/+kqRRLuJnRx11VJLkBS94QZJkzz33TNIw4K233jpJ\ncumll3Z83/llDFJm3TpuDwJj+Yldk8y8sivDv/71rySNgimVDZQsfTIVD8WAfXfrMCF2YoyUie9j\nshjn9ttvn6SJ5XzsYx9L0txXa+Re97pXkiZWiPG+9rWvTZK89KUvTTKyNX/ZlXwiukWP1cfLuYDS\ncJ/LtYCNl2N785vfnCS53/3ulyR5znOe03FeXgFz39rjDXAvxuqsPZkoVZ36Kc/IfffdN0nyq1/9\nKkmj5j03KFhZrr/5zW+SNJ4U3qJ73/veSZLf/e53SZpnsZ/WVFnXc911163W+KrCqaioqKgYCPqu\nwxkaGurarRmL9pbeddddkyT/8z//k6TpAODvep9RKttuu22S5IUvfGGS5q190kknJUmuueaaJI0v\nVz0Gdnf++ecnaWpOZG6Icxx55JFJGvYwyh4iE9ZpQBZQqXTYSJ84vnTxKPEmKk4GH7+zfPrTTjst\nSZM3z9cvO43/mnJSz7PzzjsnaRhSaYupU6dOWDbSKJ9L0p0xGutY/uOy79NYLKxb/6hesTq2KNV+\n2afLPMHKX/WqVyVJ7nOf+yRp1o44w93vfvckDbuncN7xjnckaebPS17yko7vHX300UmaDM8//vGP\nHf/vOijesh/i0NBQbr/99gmdF2XtSPn37bbbLkmjRIzB84eSvf/975+k8WyY8zKz9tlnnySNepTZ\nuc022yRp4mdiN2P1bIPJWCPd9tGSrej+UzJU/9/+9rckTfYZRWT+sIX7Tjkbs/OW+zd169w/Sl/K\nmqVWUVFRUbHmoO8YzooVK0a8fcu3srfmz3/+8ySNPxEb87bWE4u/WWYOv6IMG/5s7P0xj3lMkkbR\nqL/BDjEXsR2ZXmNtWd0vhveVg7JC3O8yb2RU8aViZ7LU/L/jimPxrT784Q9P0mSnPP3pT0/S+HYd\nRwdtTFj2CaUDZaUyhTMZGEtZYGUlyqw1yuYe97hHksbfrMZAPIvqY3uY7Gy14b3UMENzGIMs56D7\nqdpdX7j9998/SRNf4AWgZC6++OIkzf2V6ckGz372s5M0/cJkP6pZobSphW6sfjIytLpl8lFVWPtH\nP/rRju95TpRd48tO6TL5fvnLXyZp4h2eR54zlDGbOF63+UHtTQbKZyuIT5svMu/cZ7FCa8j94hkR\ns1HnpQNJWbvE86FDP08LrG48qyqcioqKioqBoO8YzpQpU9qMxFvYMbBwfkXMku/U2xSLo0AwVwxV\nnj0fLn+2DBu55BiNzC2fdxysEGsoMz5KprtixYq+YzhlHQs4tnNiuK5ZryuZeX7KPnKNmAsGjJ05\nPsbq+GJCmDTGK/7leOWeIMPV32RXUY+190a3/+/mPy7/XnYBXl2sji3KOEV57WJyOkyYL3zsfPbm\n8ote9KIkycc//vGO46gwp4jUc1HSOk6o15G9ZN5QOGWMaTL6h3WLqWHTZb2djEz1eebF2972tiTJ\n+973vo5r1zuNMjrzzDOTNJ1J5s2bl2SkIio7qY+l6iZjjZj76vbKfpG6ruj/5pmoi4quKtY5L4BY\nHRtRvrq9dMvI67XjQI3hVFRUVFSsUehb4UybNm3MnfbEE/gBAYvjb5b//qlPfSpJk5223377JUl+\n8IMfJGnevuIZmI3zqcL+3ve+l6TpJybfvuz1Bo47zB/bl8KZNm3aiD2ASiaLPelgjClQY+JNFA/f\nKkZ78sknJ2niU1gZFWfPIH5o8TG1RmoWjLGsNSg7DwyrqbrTe6k95SlPSZJ8+9vfTjIyLlb2fSpr\nSWCs/x8LE7kfzrDPJWkYrfuhpkRHZPcb+8feqTi/8yKY82rZHNdaonDYsNyLClbRKWHSshdlVorJ\nub9lrFinCfEGNrDGKCRdGNhSTE+PRVmwZabmWDuKDmKNlJnA5nC5w+t73/veJMkb3/jGJM39FLdW\nlyfeJVvWs1j2mi7kzitrkadlrFqqqnAqKioqKtYo9J2lNhp7K2Mh2BS2LhPmcY97XJKmy6/sEezM\n2/gJT3hCkiZnnC9XbOdNb3pTkuYtLZtFpgXFIyOD0iqr6l23t37ZMXcsrMrHW1aWi6moGVIrYkyU\njgpw/uaddtopSWMjLA3bd1xV2BiK85Q1TzJ1uvWL6oWdTzbcF9dcxslkaqm3kLHDRs9//vOTNBk6\nbFXG8CYLo9mPkikz5mQdysAUd8BoKVljMl/ML/dXnIIXQFcPHZHFgsqYUKl4y0yxyUA3L4BYLHZd\n9lgsd7NVd+Pzeqmpqvf8YBP1Xep6PD/UxlFKY+09MwhYx36au9SbuLY6PDEfzwNjEgv87ne/m6Sp\n9zK/rCFjNr9k8HXrnD1eVIVTUVFRUTEQ9KVwpkyZkqGhoa6db7EkbB3jlDn1qEc9KkkTv9Dvyx4e\nIIuEUsHu+GR1LBDLkcFFycjY0WEAq/dWLzOzurH9sTBaPKtUTxgKFie2UsYnxJ3e8pa3JGmUjIwc\nPlv7oBib2A2UHZOxNteFCcliKfvi2Q/nzkQ3m/I3Y6jmmR5a6rFkYIlnUHuUTdnnbKIxWp1G2RVh\niy22SNLUfKi/+upXv5qkyT4Ur5BtpFfa6aefnqTpHCEe8cpXvjJJU9vGm6DmTbYaRcy2mC3VAMYx\n3vqs4XFOKJVCaSvZrpQN21GJMi55Jighn+MhkQ3rfsvwkrElA8y4rNGyBqZUpZMJqqvsQk+Jek6o\ncSxjNbxG6vN4SswfWYvq89hYnQ5VCLwHE5XxWRVORUVFRcVA0HeW2nCm021PFcwTk8C2MQrdo9WU\nHH/88Uma6niZOnvttVeSkTng3s6YrT0dVBbzX/L5YgVlpla510e/vdSmTJkyInujjGdRFM5VMk0M\n5KgQtmAAACAASURBVKKLLkrSME1KRr84XYLFxbB4/mvxCnvVU4f81q6LLSifUt0Ns8WkZ6mVvvxu\nPbVKhmxeYXHGroYJE+4GvbWoi7Ewniy1bnsulTVrfqfCKGA7vcq8UldD5WO29kdyPmzf2hGzYRu9\ntcrrEyOwx32pOlYnM2us+ilwTea0nxQK2+iQjnVTPHY9lcFnDOJZ1J/jeR5h/WU2a7cO38YyiCw1\n11h2QHe/KFxdV9iorL+joD1rzSPP0gULFiTp7J2XNM8D96KbN6hmqVVUVFRUrFHoS+FMnTq1NX36\n9LZPs/T/Q7k/O0Xh7WinT3EJ/cT4Gfnoy74/mKyaBBkZ/Nz+7u3P/+jtX761S6V2xx139N1poMzu\ncSz+5XKnPlkiGItaJJW/xoqZGJOsFN/D2tiIT9918NHrhIvBlDUGo/nlB7Vfe7eK81Il8kvbpVBW\nor1+sHigHsyPsmPzILpFl2Mr626odgzWNVFf4hAyMmVqHnLIIUma+63K3pitNfOIsrH2fO6hD31o\nkkYRsVG37LSJ7EDBFuU1g04lYnBsxGZ6qYnJimdSe2LA5o1MP3ExWbSeQ2UNXdkxeTRlNtFrpFsH\ndB4JyoXNxB95PjzreI/Y5rjjjkvS7ILqWel+ewbrzec4stR67TtYFU5FRUVFxRqFvmM4yciYjbef\nanksXOxGfv2JJ56YpGHzMm58T8cBHY2xO9loWLq3vCp7x5Gpo95HFS4FVe75MArD7juGU8axsDBq\nCoMo92zhO8VAKSK+UllsYjoy8bBBx8eMdBTA6tjQvjm6SGNQZTfjEoPcD6dbFXO3XSfL45hn1KPs\npDJGN16Mxxal8i3HbGxqih75yEcmaeppfF4Mxx5QmKceWLLdxLV0ZNeZwl5Tjqf+i0q0psp9cEbZ\n78TPcc+LsWJ2bOLvp5xySpJG1Zm71q/OBGzA8yJWY2yq6M0z/cf0pRurN1+3Z+RkrhHPAWNST6WL\nS6nKxKU8R3zPmHXYZ0sq0XzRnXy8GZxV4VRUVFRUrFFYrW7R5Xcf8YhHJGmYiLemeIQeSbJJ+BP5\nbPlY+ZUpFRkWZ511VpImA8fbnIIRq8Fg+DGxgZLdj8Jkxq1wyh0dwTXyrfK9y6jD3jFZvtpyF1OK\nyPnUNLGtimKKid/aTqLDrjtJwxLLXmqDyFIrK/7H2gm09CNTNLIQ2bhfjNUfCsaTpTbK3x0rSaNM\n1Y5RoLLTeAOwd7E6GVW6QlsT1p5uwXqmqeuRLUkpiQGWcZRunZJXR+GU96/MAnMfZFjKoHRt1Jfn\nBFXIc6J2SB9BGaC8CZ4DVAIWX859cS69HtXCDVLhgCxTNYfiVJ///OeTjMzgU9MoZsuLRMkaC9v6\nu7GpceMdKLtATNQaqQqnoqKiomIg6LuX2n+yM5KMzP6RRYY928NB9Sz/oziHfdj5mfWFkrmF5fFH\n//Wvf02SPOtZz0rSVNfKanMdfLv8mN7qmDAm003p9IqpU6eO2NGzZG+uieJQI4RFqa/we5klgtnq\nnmBsmK34lxomLFCPJCzOcTGdbtc5iF5qZS8zDLT0O2NVZX8vmXvup4w82Wrl98tYUK+sbXVQZn2V\nqsff9bii4sXqzAtdNnQ4VmOiW4daJApFnY06Lt4AdRfWEFAf1uSqamb6nRdTpkzJ9OnTR9h5FDWd\npIkvUfP+n1JR34eFY+UytcwLnUvUvB1xxBFJmrqrMjOvjF/xGgyid1q3uJbsQ0qYZ8Sz1H5I4lWe\nF5SLZyPvD9vpyM8L9MEPfjBJo5zLrtQTvUaqwqmoqKioGAj6juEM7xOFrZdV9iC3WzU9ViZPHuvi\nd8Q8+CftY3HSSScladiartBiPKru1SqUefRllhPWgNmsTgwHHANDAIoDA6VI+NRf8pKXJGkUCsYh\nloOViX+97nWvS9LUHJT9o3QbxnTcI/tklLudjtYhYbLrcMQrMNVe62PYVgaN+1iyQ35tY4ZeawpK\nTER1fakozXFxCmzbnMfKKRtdxCldikR9Fp+/fVEwYfU49o6xv5I1Uu67Uu4RNTwbasWKFZOamUWh\nHH300Uka1W+dlh1HKB9rys6gVLxejlSjeKj4KFbPFn52mx+D6DTA3rqwiFPJQiyVM5XPRmJ+6m54\nSHyfF8C88XygtMfqe9cNNYZTUVFRUbFGYVxZalhRt53xyp5IsoowFPtTnHDCCUmat6vaE/5GTFjv\nJIpJnyB+am9tKkDWCkZcZuCUSmzYOPpSOMPVHvbj2H66hrIOh3/5yCOPTNKoNUqHzfS2ksHDv2x3\nUzY2Nr3TZKeV+7Z32/9kuC0G1WkAyirrUhVguu5vqVSw+bLP03gVTYl+bTFaZ+VumVkYqj2jQNYR\n1q3i3G64O+ywQ5JGJarfwVAxXZl8MkNBvKzsE8aW5TwZFk+bsHlR3h9sWxajDgNiwa5ZDYlYjQ4U\n4ls6Hls7jmct6GBQXoe11G0ewmTs+NktdkahUmueocbiOSFzjzLyfBAb9Ew1H3hAHG+8XTigKpyK\nioqKijUK4+oW3a0yt9wDRiUvJYOhqnpVFa+G5Pvf/36SpgOqWI0OAuIZMi28zcV2xD1KddDNnz4K\ne1vtGE7JYLE29Q8YC5Ume003Bf5odRbiUhiv+gr7V1B9Mntk+uj2QGFhbWXmVxl7wngGqXBKdFMm\nxoh9j7VPCVVI+ZSxvV6xOnU47GselLERnSh8zn0Wd3jnO9+ZpKma//CHP5ykqdexY6i6LvVeFLRs\nRbFEHShcYxkXGWU8Hdc3kb3Uuv0dKy974YE4lDo+a4H6F6/QpYNC6tavzHnGehaWSnoi14j50S1T\nE0rvkpivuJRno2xEStf6Nla/e86w6Xh3eq0Kp6KioqJijcK4Yjjd6nDKHG7/r18PtkbJeDvzsfq8\njBxvZ6zf/9sLhJLRL0x2Ssniu9UBjBK/GHengW57t2Ak/MOAbRnLHnvskaRhsnzylJH6G/n4/NBY\nP5+s45bqrtzbY1V7kwwqhlMqmd133z1Jo3yhZH+lioSSnU1Uvc1EdBoYdqyO39lAtpqYDq+AWjVj\nNx8OPvjgJE1GF+XCBjL17BnD5+//XUdZo7Sq/nWDmhdl5whdFHgwzjvvvCRN1hkPiSw3PRQpH2qx\njK/6ybaDyF7s4/NJmniVzhCyDWX6umbeHjVpPk/5lmutW43aeFEVTkVFRUXFGoVxKZxhvyfp3iPJ\n371Fy/26ZZm9//3vT9IwGYyEYtEbyX45Mnb4q3UmoHiwudLH7zpKP+l4d/wcPtYyP77MAnNubB1U\nSxuzz1M0fKxUor3q2YQPvsywGaXGKMnIWM1oGHSWWgn3caLqaFYX41E4Y3Wx6DY/zB9zXOaVteDv\nfPHiCSrHeRHMH102SmUzbGwd1wOjZdkNal5Qe+JZ1Jq4Z5l95v/9nU1kucnMKu9Ftz2AumWllRiE\nLcrni/XrdzE8iobHQ72d54puDN2eT6vbVaEqnIqKioqKNQrjUjjd2Hw3pYOl2bOljHfw2Ypj8OFT\nIqryxS3K/k/dqrlL9tYtlgMTkaVWVm6X1+D/gQ0xEwql3O/C39meoin3rSjjHeX9Le9RqfL8+85U\nOCUmmo31i4nIUuumzrrtGFvWxVCsZS2ZNTDafVzV8cu10O1zpc0HUXsCxlTaxJjVtFE4ZQdkny89\nG+PtnVhiIjP2VvdaxnoGl3+f6DVUFU5FRUVFxRqFvhTO1KlTW0NDQ11rObDrUnmU/mmszee8nfmn\n1ZBAN79zNxZWsvdu8YpRmHNfCmfatGkjKnS7dTEY5fuj/p0N1JqUDLaM1ZRjHK8aGMXGa4zCubMx\nnk4DYymJbnGobh0gSrbvfot3lTUrZcxmlHjlqOeFbtc3nnnRrQ5u2DF7Ol45hpK9l5hsZbwmrJHJ\nUiz9oiqcioqKioo1Cn3HcKZNmzai/9Kw/08yki11q4Mo6yhcC9YmPtFtT5FutSS9+i1L1nj77bf3\nnaXWjRl2iydByXS7sb+xYkJlJmCpdPrN6BpkNtJ/C8ajcMr7OdZ96HVul/e/m9rvpv5LjDVPJrI+\nq9852atC6ZXlT7QaqGukQVU4FRUVFRVrFPpVOAuTXDF5l3OnY+tWq7VJLx/8P26Lnu2QVFsMR7VF\ng2qLBtUWK9HXC6eioqKiomK8qC61ioqKioqBoL5wKioqKioGgvrCqaioqKgYCOoLp6KioqJiIKgv\nnIqKioqKgaC+cCoqKioqBoL6wqmoqKioGAjqC6eioqKiYiCoL5yKioqKioFgaOyPNPhvaUC3Gk36\nFvXR2ua/whbdtmseC7UxYYNqiwbVFg3+L9pivM/OSWneuc4662S33Xbr60JWhWnTpo3oGD0R+E9X\n20yZMqXrvjNd0HOvow022CAHHXRQ/xfXBRtuuGF7D/ZVod8x3Xzzzat82YzDRqNiaGgoU6dOHdE9\nezxwnLGuzf+Xnxvr72Mdr2LiMJHru9t9Hc81jXZdk3n/d9555/aeRROBu9zlLu2dkicSnp2ThepS\nq6ioqKgYCPreD2cSr6XNjst9M/ycPn16kpF7w0zgG7nv/XAmG90Uw+qOfSzp3K+7wD46vRy7G7rt\ny14e1zwod7Xs9Xz9Xt9/k+tksneAvDNtUc6PtdZaK0mz++0o508yfluMtX/Pmjgv7IvlJ9tsu+22\nSZI99tgjSfKVr3wlyeD3BqoKp6KioqJiIJgUhTPeHfg233zzJMk//vGPJMl6662XJLn11luTrIyb\nJMmcOXOSJDfddFOS5Nprr02S3HbbbUmSt73tbUmSI444YpXn58cdtiPppCucbrYpdwgt/74KlrXK\n862//vpJmj3vqYKxsDrsbaKY5bBr6fi7RIjFixcnaZiu+99N8ay99todn4PStqPslrnGMdlRzptk\n8ve2H4Qt+h3LjBkzOj7vp7neTan43tZbb50kufTSS/u6zsmwBWXS6zqFpz3taUmSb3zjG0mS97//\n/UmSmTNnJkkuvPDCJMm73vWuju996UtfSpK87nWvS9LsGDxW7E28+frrr09SFU5FRUVFxRqGvtKi\ne0XJTMq35Z577pkk+cMf/pAk2X333ZM0b98//elPSZJ//vOfSZJnPetZHf+P4V588cVJkl/84hdJ\nkm9+85tJkic84QlJknve855JkksuuWTU6xymbAYOcQhMYdGiRUkatg4Yx+zZs5Mks2bNSpJstdVW\nSZK///3vSRpbYYfUIfb2q1/9ahJGMTp63Xu+VJjf/e53kySPf/zjOz5P2VLAf/7znzv+v1RxFEzJ\nEvmzMV7nLVXlmrApYcl0SwVsDOaRz7PBjjvumCT5/e9/3/F5LH8Udb/GoLT/Rz/60STJq1/96iTJ\nNttskyRZsmRJkozI/qJcNtlkZYXDYx/72I7jYP1s8re//W1iB7AaKOes++Q+UzKehda5MX32s59N\nMjKW87vf/a7j844rg7VUg2y6zjrrjHqdlE2/qAqnoqKiomIgmNQYTskk73rXuyZJ/vWvfyVJFixY\nkKRRIt/5zneSNL7UffbZJ0nztt1hhx2SNGz+e9/7XpLkYQ97WJLkoQ99aJKGIVELmBCsYsyTFsPB\nNIBiYQss3ede+9rXJkluvPHGJMnJJ5+cJHn4wx+epFF31MBJJ52UJNl1112TJF/4wheSNIpo4cKF\nSRrFNFam30T6p7tlm5kf2FkZW1FncLe73a3jd7Y49NBDkySHH354kuRxj3tckpGsDcM9/fTTkzTM\nV+wPY8Z0J9MWq/hex++lTfbee+8kyU9/+tMkyb3vfe8kzdooFcuyZcuSNPPL7+JY4qL9YpDxrPvf\n//5JkssvvzxJo1zcX4r3r3/9a5Jkiy22SNKse/f94x//eJJG3XneOM51112XJHnIQx6SJPn1r3+d\npFkr3TCZtigVrvvr/olf+tz555+fJLnmmmuSNNlo1r/5ZX5Q+56Nm222WZLG47LddtslaWwxFmoM\np6KioqJijcKkxnCweP4+TGKjjTZK0jAO7F4mBcXie+ecc06ShuFgtHLJsbePfOQjSZI3vOENSZIX\nvehFSZoYj593BowVq8c8+aXFLzCYU089NUny4he/OElyxRUrmyC89KUvTdJk8vGxyjbZa6+9kiRf\n//rXkzQMGGP2E8PpVsOwOijjBeYDJYGxUiyyDl/zmtckSV74whcmSZ761KcmadQZZfOyl70sSZOR\ng93tvPPOSZqx+7s41z3ucY+O85uH3ZTNIFGqcsx2yy23TNKofmtFHJMXAOM1pi9+8YtJkrvf/e5J\nGtt8//vfT9IwXsy536yoiUS3GJr4033uc58kyQMe8IAkyQknnJAkOeCAA5I0KvDZz352kobli2Md\ne+yxSRqlwwY///nPkzTz8qKLLkoyUtmMVY8zGRBrGZYFlqRRpqXXQDzcs9B8eNSjHpUk+fGPf5yk\n8YRYW2wnxkNVHnfccUmSV73qVUmSH/3oRxMyrqpwKioqKioGgoF0GsDasTNKh99QBoa/A7Z2r3vd\nK0navcvEfmRk8N1irmJFstWOOuqoJD0x2AmP4ZTsjaL52Mc+1nFNZWaN2M3cuXOTNAyjzH8Xyzny\nyCM7jvOkJz0pSVOT9NznPjdJw/LKDK0yW2k8/ulusRrApo3xlltuSdL4kR/5yEd2/F1WEWBhxvb8\n5z8/SZOxI9ZDEYtnmRdqDWQtYoFs7box3KGhodx+++0D8dVjz5QLhitW475Suj7PR//pT386SaMC\njRlrx4DLWA+GS2WWa7DEIGI4lMspp5ySpLHRAx+4cmli8bJdf/aznyVJPvnJTyZp4p+U63nnndfx\nd96Epz/96UmSz33uc0ma55N5YF50qwtak7oujHK+JM39ZtMf/vCHSRqlNH/+/I6/O675Ixt2LNQY\nTkVFRUXFGoUJVThljytvWXEGb2NxBazN58UXdtpppyTJfvvtl6RhsPzbWPrLX/7yJMmmm26aJLny\nyiuTNMpInMN1ON8q4hZ9K5yxOgdgZ6VfuKxNYjufk43mmufNm5ckOeOMM5I0NqL6xHA23njjJE02\n029+85skjW2pB0zGdZbXNxEKxxjd9zLzxjWIrfHB8x+7j9g3JnvMMcckSV7wghckaXzy5gvbmBcU\n8lVXXZUked7znpekiQGWPftKDKKiXLyTwnEfZWRi4WzCRu6/+yqrCDMV78RoKZqyLyGUGZ0lJsMW\nFAhFKkPKen7MYx6TJHnwgx+cpBn7t7/97SQNG9dZRNzqggsuSNLMqxtuuCFJ8tWvfjVJ83wQMxbn\nYLN3vOMdSbr3bBtEJmfp8aDuusH80TtNHAw+/OEPJ2nipSVK5cSjYk2deeaZHdcJVeFUVFRUVKxR\nGEgvNQwBiy4ZMPbtc/zXGIgOAuosZObw0WIBYjv27MHyxTHe+ta3dlzfKJk5ExbDGcvH2q2SHPPk\nn2YT2SNU3Xvf+94kTRU+5vO1r30tScMSsT6+2pKl+b3s2TYR7K3bPMCyZeCpv3rf+96XpMnQk41U\nZq2deOKJSRpb+F12oiw12UqYsrjXwQcfnCR5ylOekqSx3SBqkkCcEes2DzBUypbSoWCMiY1e8YpX\nJGligtTCT37ykyRNZp5aFTEaGaFlV+GJ7pA8derUrr3qoFwLlIyY3P77798xxtNOOy1JsyY+//nP\nJ2nuu5gtdchDItvtE5/4RJKmg4n4529/+9skjTfBvemGNbHHXukpMX90MnF/zXHx76uvvjpJEzM2\nz6wNz2hZsmwMVeFUVFRUVKxRGJfC6caCumUlrSITKknjh8bafvnLXyZpGCvf/Ze//OUkDTPBEr3N\nvaXVd6i25dd2vd72o2Bg++F0620l7uDnm970piSN7161/Jvf/OYkTXaJeMTZZ5+dpImbycTCkLFJ\n96K8hxjpRLC3Mk7lnPzBKv3LDgEUjSwl98u8cP/1VMOAjz/++CRNfY6agw996ENJmoyuP/7xj0ma\nbuPmy2j9of6zA+KkMVmM1P0SQ3niE5+YpIlPWEOulVKRtSZORTXK4Lzf/e6XpIl3lEpaPVip9rt1\nLZ7IeVE+D8xxcxXblk3m/pY986h8sRvf/8xnPpOk6brh7zL21GmJnz3jGc9I0ijtid4zavgY2b0b\nyhhbrzVAMjTLWLCaRDVJUManPJesRbWNaqAe/ehHj3reqnAqKioqKtYoTGgMp1uWEr80RlIqHz2x\nMJKXvOQlSZoMCSzvsssuS5L85S9/SdKwL75WDAdzlt3yrW99K0lPnXFXW+H023kYoxC34r+WsYOh\n6hPHhjKzfvCDH3QcTxYJhcR25fWNdV0TuR+OOiz3HUM1VrE6sTiKVt2MnlmUCvAvU8jmi2w0WUpq\nEPj+1S4NYm+gbigVBJauNo3SMS+MqWTIOgg4jlgNxipeoWLcGpD1VNZjTea8WMXnkjQ2YBvKl0r3\nu+wx91ucSo2bjsqeA9aC+WbNqPOS7Wheugc8Jt0wEfGs1YVnpRoktqAOKWdrgbegfBaWzy22YDuK\npxuqwqmoqKioWKMwqZ0GyqwkDLc853Oe85wkTZYZ5srXyi9pFztKR+Uwv7UsFPvp8NmWHVZXgYHF\ncKDMGsFQZNhgWfqHYTJiOXy9r3/965M02SXj3a8CJoLJlhkzfOUysNSGPOIRj0jSME7xKTE4NQXG\nRqG8+93vTtJU2es8YP6o0secqUTxLvOi7DRQYjLrLQCrv+9975ukyQpSR6GDwGGHHZZkZLYhm6kl\nKfsZ6qyOYZddo3vdF2cyFI45r4uz54VYn4w7fQJlkRmjdU75iPX5/L777pukiQk7rlggW1ABsmJL\njNIjcNJie91qf0pQ/+quZCmyjbkuPkUJmw/U/zvf+c4kTUcTz14xH6qxG6rCqaioqKhYozAhCqdb\n1omMGiwKU6U0vH1lWoGYj95aqui9dfmv1ZrYx0I2ipiOeh3sELNeRbXupPVSG2sXTH7k7bffPknj\nq5eJJctEvEM84oMf/GCSxqZl1Xyv95cKYLuJiOGUv5c/+eDdH7n9Rx99dMcYZMhQQnrkyTrD2vxu\njyCZWpSPuAimij36flnlPawuZ9LiFmXPK7E7aq7cM8r8wIBlamKmYnh20dUJmWKmfO2vI75Z1mF1\nw0TWZ5UKmMrz/zwVlK/Ynp5qstZ4QHxO3JJychw/dd6mpMRJu3Vo9lybDIVT7sU07PMd11Ce27PU\nWKk5c/9BD3pQkiarrPR4qM+x1tQoOh5b8wrIcjzwwANHHV9VOBUVFRUVaxQmNIaDdZW541tvvXWS\n5u1pjw8ZE7r/equqAC8ritUc2OOBz5USkqWCvWHOJZO6M3b8HPa9jmtgM2y/zLzSUQD7429WQ6Bq\n3p4vZbX8ePd4mYheaiXKmhOsSixGVpFsIvcLo1WfI66lkwS2hq1jrL7vJ9XoOvWlc7xudWKToXDY\nglozV6l2P/XCUzMk+0jcQicJ3TTs8UIxYfGvfOUrkzReArbGnMuOF4OIZ4H4gXoqyoQNsGsKhlJV\neyTr7O1vf3uSpg6LLcTDdOHQeUJsyN95QGRoDdIWvDrWd9kZoNv94eEQw5XpyVOhWwNVRyGbf561\n5o8+hfoNuhe+3w1V4VRUVFRUrFGY0B0/+cQxUjUB8tplmYlDqLNQUY61eXtjGmI83t6YKL+0bq/q\nc3STxg4pKhXmznNnwNgoFkxUNlHZD0pcomQ8OixTRmV+PWbbLfuo17qLXlHGbUb7GzUntoeRUqbG\nxgbUXtm3SWxO9pFYjf1yZGxhzPaEsQum+y8WyEbl7pdTpkyZ8F1Ay64b6qmMxVoR93StMjDt2eKn\nrDaZe5gyBWwfJJmd1pDrcE+ohjtj11NxBOtc3MrzQ4xWjEVMl6fD52RiYfXWvQwr2WllDz9ZaWW1\nvS7TerUN37uq7K6+ulDnImPXM4wS8Syz7vU08wwFMSEKp1Qmflf7qBefjF/jsmbYyPzkdRovqsKp\nqKioqBgIJjSGw//IFyqT4pBDDknSMFfw9pR9JE9eLyOxGftXAIbMN2uvEPGMt7zlLUkan2+36tpR\nMGExnDILqcz+MQb/L6uEr/6Nb3xjkka9qfi1F4gOyT6P0WKsZa+mfpnrRPqnqTnXhrVRFFi8WgL/\nr49TqQJ22GGHJE3sRiYfln7WWWclaRQ125f9yti+W8dsmIy4hcw7cUhrhpIRb8LqqTfxSddcsnq1\nJeaNuCf1IBtRzA+jvTM6DTin2K6YjEw9cQR7uIjtsZUaEhma4hNiQtYGBayLvNomVfq+L9OPSlSf\nVcamh8WCJ8wWzkGFyS6j1t03Hg2KVbdnNlOfZ96UzwE2p+J4fXgDPFc8j8yHsbpy1BhORUVFRcUa\nhQlVOBin2AtGwedqvwl583qfYe3YHR/9pz71qSRN9axYD98tPyRG7LwUzY477pikqZbFXMUGRqkf\nmvAsNUwCMAe2wLqpQ0xHPYVYDH80JqKvmN/FeuTzlxXK3bpTd6vXmYgstTKG4xrPPffcJA1b93dj\n4WO3340sNj8pZtlF+oRhyvZNcTyKRx2G+y/WqMO2uEmJyVA47kfZURuTFKNRf6M7tPsq1gMUEVUo\nLiI+Zt4Zo3vk/vfaA3Ayq+utU/vTiPVa5+IHOiDziFA0bMY29sGhsH/1q18laeIjlHNZ2+Lz5W6Z\nk7lPkrmrN55MOs8F59ZVQyyGKnNfzRcdJ8Aao+6NnZeJ10BGsaw32YxlH8QSVeFUVFRUVKxRmFCF\no3eVnkb6fsnykGmBjalixcbk3csOsUe9egs+VR1w1TDIvNF7i0+/rBT2di7HzG/6+9//ftJ2/Cx7\npvGx6o0lS8W1ykLB4vl0ddR2XFkrlBKmVJ5/rL2LXNc973nPXHHFFVm6dOmEsTc+d/edinONlCvm\nqmpaFqI4RFlHwYZ+qrvweapA7Md5xTmg7DTguqZMmZIVK1ZMah1OWV1PwWCqMi/ZDsT0+PDnzJmT\npPEy2DsKQ1brht2XdR29dqaYDFtg1e6reNRjH/vYJI3SoWDENbBw8QvzwM6wni/2w/L8kNFHZKmN\nWQAAIABJREFUSVG44iTlflnl2pk7d24WLVqU5cuXT5gt7N0kLiX+RJlQGDwY4p1+d42ewb5XPvPE\nS60F91+cS1zLM5EXgLepxAUXXJBDDjkkF110UVU4FRUVFRVrDsalcEpfPZaGtcnp5juX567WxN4e\nGIlsM35IcQsxIG9zmRkq1PVikzXivLJdZL/JcqEaJqLTwNSpU1vTp09vXzuFwgYYh15XCxcuTNL4\naH3PmPbcc88kTc80WWf2AFGLInMP28fOKBtMqOyqUN4jTHqifPXDFVN5zDJjj7/YPMDCxRn4jWVa\nsZHPY2+qoO17JJPrmc98ZpJm/mDMjquzAHWAWXfrzjCZMZwypqbmpNyVtKwpueSSS5I0DJQNqXvz\nQY0K22O4bOk6KOuxMjknwxZlHz9zVId0a8GYxWgoFWqQApJ1JsYjy1XHAs8Ha0CfMbE9/ci++93v\nrvK6J9IWnlW6X8jUla3aLT5aenE8hyjeslOB+Kd5Z37pQ0khW1tUoDhaN9QYTkVFRUXFGoVxdRoo\nGSCl4u3Kly6GU+7tgInqPOpty+8sQ0t/H/U0+opRQFic3HTxDPU+stn4Jbt1MR5PdXWr1cqyZctG\ndJ4u89+xLQwDm/J38Qo9kfz/hRdemKSxnQw+iobtZN5guGUfOz+dv9ddLvvFaDYs41ZlVwS2cu3Y\nu/ss+wzDtc8JRVOe29jNO1mQKtcp6NJXXyqbie7CkIzc4bOM7YH76XPUuawivnQ1KdSeMZYKRiYg\nL0OpfM3f0TpFTDScQ/8u65XCVFOkFoRXgEoz5+fPn5+kqWWjYEtb2iuGLcWv2M6eMGCtnXrqqau8\n/omcF9SZde3Z+aY3vWnUz3uGljEYql2vPB0oZNrpRykDWEcDmZ+6k4ujyl4TyykV+XhRFU5FRUVF\nxUAwIVlq3rKyRTAYb+3DDz88SZOFht3zM/LRi9Wo2/H2F7PxOX5G2WqyUmS7qL+hlPiG5aCD7sPD\nMjBWO0uNL16MptwfXW2JzCy+Uj2R2EoHXH5qY5NNgvliHrLY+GL5wd2bklmPMp4kE9shudzhVQaN\n7DNsG1N1PykZcStjEq9wPIrIvGNLPdowWopXTJHSkv3UjblORrfobrEbc9p9ov7MXapMbZHu0jqs\nY+3iDzoYUDylYu5WczQWJsIWpQ3Yv9w/S3ajDC5rRGaWWhTfF/fSxcH6ppDZUAeDMtbTLfbo7zIF\neS8mcl5QIOrzyvhU2efP+va7tUTJ6iKuowQYi9iQ2ibHo/p4myhuqhNGyb6tMZyKioqKijUHE1qH\n423Hx8pHi5Vhbep0MBI+WsoIA/UWlZklg4PfGlvji6cqSiUDpR99FEx4HU657w3I1BKn4Mfmo8W6\nsHcM5zWveU2SJpsNgy17JJXszJh79cVOJJMts9T0qgJ+5v9l78wDbRvr//+65x5cV6YQihSljBlK\nURkbNMkYiWggSlKayZSkJEMkQsaQFCoNZhqMpZSUoRQZK0q4vtc9vz94nefszznr7L32dDa/z/uf\nc/e+a6/1rGc9a633+zPKrq644gqg2Ju9/s6R0WWyeD/L6ox2k73JcPVXOC5t/zLmfmTXV6kp16b5\nNbJo+9+4xvUveC8Io5rMxzL6yOOpoGKOSV2fXi8rDYz5HTDeJ+Oat+q3fgifI/p4tAKo+mT9Pjf0\nV8Rzr4q+rZqjbs6Fam6Memr4rCIxMtdqHSpge0BZLSHuN/rq4r1Zla8nzH066KCDJvz/VDiJRCKR\nGCh0ReFE1uxbVWagH0PmIRORtUc/gyzNt7f7laFU9aKvYnE10DWFE2tkqe6cGytayxj83vwafTlW\naTB6RB+QbD7OhSovRs/V7QBal70NDQ019Q85J+uvvz5QMsGdA23k2vD1wTkHrhsj+WR9ZmdbNbyq\nc2fst2RemLb8flaLnuB3DWMzcs/rqF9S/5f+MCM2XfsqG3161idTxYl+doKtsX08VsNn75Htt98e\nKDUZzT3yehqd5px53e0NtPnmmwPlnpmoD9JEx4/oxlzoozHHSD+WY7bqihVJvHe6jQnqStZCKpxE\nIpFIDBS66sOZ5HfAeNuof42wkNXFnuLNmPMEEVbtDBO6oHCqMoJVgTJRmaoZ5LJso0VkODEqRUYr\nquzLVjgwOq4uepldL1OVVemnku2pbMw9Ovvss4FSdcHIGaMahV0K43rRJ2ieWOx/UxWdNuZzzxWO\niLZ16wQ6dm300W9pzkpcH861+6uq9tsq+qFwzLq3hqJwbvzr9fc5oi/P6Njol2hmKdG36Fw3Qz/X\nRRU6zY+JkXftIhVOIpFIJAYKPVE4VcxRlh6z4ePvqt7azRRPF9D1fjhVtlFZmeeqrT52F4xzGXup\n142s6ZV9etq0aZX7rKrwIJwDmafqzioMRpvJ5s2/Mb8mnqss34gvq0Y3q0dVhalQOBNVrh4L74FY\nvWHMOBr20y1MBav3uREtIfr6/BzrGlb5I1TOVmdoF53MhWvTXLAx27nvjsbWq/1VIRVOIpFIJAYK\nffHh1EUVS+/D279jhdOqTbVZd8xmfqnYsVN0a256oXCqznWCYwPjFbE2dv1dsZJBrIzbrfpPg2Cr\nd86ckyrF22sMwlzol4rRsPpkXBexcrqYqnukzr7bfdb1S9EIo1NT4SQSiURioDCQCmcKUVvhdItF\nR3QaF98p2mFvzfIoqhD9FvH39jkxx6SZD6bbLG8QWP2gIOei4OkwF+nDSSQSicT/l6jbD+cB4I5e\nDGRAsEyNbR8A7uhVxNxUKZunUGce4Km5aJdFNZtDfTYRk9Q+a2scFWhrLro5gAFCzkXB02Iu+uTL\naXkuapnUEolEIpFoF2lSSyQSiURfkC+cRCKRSPQF+cJJJBKJRF+QL5xEIpFI9AX5wkkkEolEX5Av\nnEQikUj0BfnCSSQSiURfkC+cRCKRSPQF+cJJJBKJRF9Qq7TNM70YH/DAyMjIYq1s+Eyfi6dDYcJ+\nIeeiIOeiIOeioNW5qFtLrRY6raRc9/ddqNz8TK379LRA3Y6c7VbC7VWF707Q6rn0euy9rC7cbN+D\neF0GBa1Wj4+V1wetdFma1BKJRCLRF3RF4VQxk06ZSt3fJzOaWsR1UJctV/XDEXF/sr7YGbYZmnVX\nnQosvfTSAPztb3+b8P8dY6/XeC/noJly7df92+r1rtpueHi49pqri9jNNiqbOLb55psPgP/9738A\nrLLKKgDceOONQOkU26xDbK/7cKXCSSQSiURf0BWF04yZDAKDTPQecR20er1dH7Kwxx9/fMLt3N/w\n8JPLVhYmK5tnnnkAePTRRxs+2+u+03H2ElXKRkzVGHtx7071fLeruEUv1Y1WAte2az2u2bjd4osv\nDsBPfvITAFZYYQUA/vSnPwFwyCGHAHD88ccD5bpGK0Gv+3ClwkkkEolEX9DTKDXRLqNZd911G37/\n8MMPA/Cb3/wGgIUWWgiABx98cMLfR3tkZGvPetazGvb7TMSMGTOA8Sy/n5ClVTHDqoiaaJcWXs95\n550XgFmzZjXs3/3Ec372s58NwL/+9S+gd8p72rRpPWPxjjky3Cq/lPBeEP4uzv1k++/1OUXE48UI\nrLXXXhsoinaTTTYBYOONNwbg29/+NgDnn38+AMsuuywAl19+OVBUQ9VzII5r7Bz1ai6iH9T5V/3H\ne2juuecGYJtttgGKj+aLX/wiAK961asA+PCHPwyUZ6dz96tf/QqA1VdfvdunMiFS4SQSiUSiL6jV\nYroqeek///kPAAsssEBXBvWhD30IgO233x6AjTbaCChv/W9+85sAHHjggUCxUx599NEAfPCDH3S8\nDX+jHXQChnv9yMjIy1sZY7cSuWSe+++/PwB77703ADNnzgTglltuAcocv/3tbwfg9ttvB8Yz1W6x\n9m4mtVUxReG5+v2SSy4JwL333gsUZnrbbbcBRbk4d17X+eefH4CHHnqo4bjNrrv7ken6+zHj7XuC\nn8w1MlrnasEFF3RsAJx55plAiUq67rrrALjzzjsB2HHHHQG44IILAPjhD38IFEb973//e9LxDA0N\nMWfOnL7MRVS2nvOqq64KwKc//Wmg+L08N+dMxaOy/uc//9nw96Mf/ShQIrl8bri9z7FmSrgbc+G5\nPfLII63up+Gvqv1973sfAC94wQsA2GmnnRrGfOKJJwJw6aWXAnDPPfcAcNlllzXsr93nRqtzkQon\nkUgkEn1BVxROC78Dxr893/rWtwKFbS2xxBJAYWEyGlnYGWecARTfjUror3/9K1Bs+jKcNtC2wqny\nN1TBscpwZKLLL788AH/+858BOOqoowBYaaWVAPjRj34EwM9//nMA/vCHPwAlIqvV4zdDL5lslc3e\n66y92s/6aIzEUbH41xwWlYrsTdYoU43+ikUXXRSABx54oGFcvWCyk2zfcEzP2fXkPSBz9e8b3/hG\nAO666y4A1lprLaBE+DknrjNt9aq48847Dyjr6OKLLwYKu6/yi/ZD4Thmr/d9990HwC9/+UugKJL3\nvOc9QDn3GHGlFeC5z30uUOZWy4n+TZXRaaedBpT1p5KO1gO/66fydewvetGLgGLxuOiiiwBYccUV\ngfG+n/vvvx8o5+z6cP1ceOGFAFx77bUN/++5NotaW3bZZbnzzjuZNWtWKpxEIpFIDA66onB8+8oY\nZSSytMgUok1dZaMvpsoX5O+MKdff4ds4ZtFql1544YUn3N8EFRI69uFUseT4vTZ4/QWO5ayzzgLg\ns5/9LFCUy09/+lOgsLGrrroKgA033BCAX/ziF0BhLoPgw4nnrI/FaKDos5FdOScyTe3UsvZddtkF\nKPZn92c0kj4/Wb1sPdq/X/Oa1wBw5ZVXAoVZR3t6L+ZCyLJlks7Fq1/9aqCweu8N14Pn7L3m7xdb\n7Mnas6797373u0DxW/j9rrvuCsChhx4KFH+G577OOusAZW5EN+aiKnLS770OW2yxBQCnnHIKAMss\ns0zDWE866SSgzMk111wDlHtE1v+Xv/wFKOvKa7DZZpsB8PznP79hPK4X59bnQz+Vr3jta18LFAXy\nzne+E4Cvf/3rDdv5/PDcvb5eT+8t83RcL/rB9Yu1ah3yOO43fTiJRCKRGCj0xYcT4dtRZSNz9S1r\nHL1RIzIP/RfGnO+www5AeWv/4x//AMbbw0ULtZr6HqW2yCKLALD++usDhdEaRy/7MidJlibrF//9\n73+Bog47rbzbTfYmYxWyKP0JKhmZrKzbaMM111wTgG984xtAmQvzLDbffHMAXvaylwHwta99DSiR\nObK8qGBiVJJsLeZjdHMuYj6F10l/hf4k/ZpLLbVUw+/1X6y22mpA8fW5jmTC73//+4HiA1Jdes76\nDM3HcE5UYl6jfrD6qmhS50YF41/XgexfH67+TCM+fa7ox1ABHXfccUBZZ57rBMq2YRwTVKjo+lzo\n0/UZ6bNPy8XHPvaxhv/33tB/5RpWKbs//Zqeg8+V73//+0BRRPqM9Yu1ilQ4iUQikRgodLXSQLOM\ncuFb+O9//ztQ3qZvectbgPE+GVnhVlttBRTG8cpXvhKAU089FWi9+myr4+wEjtG/8VgxR0Cm8d73\nvhcoOSebbropUFiYvh8zhs0Q1l9m7oqMeSoh69JWbrSYEVGqOv0T2223HVDyrPTB+Nn9fOpTnwIK\nK9N/pQ9x5513bji+iicyWH0CMuSYjd8LxLwpr6dRR/qfPCd9L56D23vvmH/z4he/GIDllluuYf/e\nO9/61reAwnj1AR5xxBFAyWWpqsrRC8RjVOWSufb18fz+978HSsTWb3/7WwBOPvlkoPixZPEqHdWg\n95rPFyM7vWe8h0Q/qlh7nVyj5p798Y9/BIrvzfyql7/8SUOMCkh15zm6nqLfyufRD37wA6D4ub7z\nne8A8MIXvrDLZ9aIVDiJRCKR6Au6qnBaVQy+RWUmsi4ho5BxylRkATJbmaz2zFZzYXrdywLG54pE\nO3Acg98bV3/uuecCJVJGNq46VNn4OxmNtt666AWjlS2bP+W+vV4/+9nPgFLZ1rHvtddeQPHZmUWt\nKtRXJ/vTFq/qUw2okGIugetKFdlqzkEdNOv54lqWufrZXJBzzjkHGK9s9dF476hsbr311objqFxU\nPKpJbf6XXHIJUHLZPL7XJqrBXtQPq9pf/N6xGbl50003AaUKx69//Wug+Hi8F/zdG97wBqCsB6NW\n9XupArQ2NKuM0S6s1jARYoSt/kvPyag073ufoT5H3vWudwElIq9qzM973vMAOPbYY4His3FOnFNr\nsOlT7BZS4SQSiUSiL2grSq3V7nFVkEUZ468t1goCMgwjLXyrG2mj/THGx7c7njHoe5SaUAFZfcEI\nLBmOfgYZa2TQd999N1CUUKcqrp0InCpW7/X2ehlhZ5Sh9uPDDz8cKDkgRp+53mSg4stf/jJQclY8\n7p577gkUtaCdu91Oj3XnohU1ECsfWyNPJeN1dg5UYx/5yEeAMided2tn/fjHPwZKrpqVCfSfmcNi\npJ/MVp9RM39FN9dFjf0AJWLPSD2rLBhpd8cddwBlbqNCNrpNK4Jz53MjKvCYdS/aXReT/X/se+M5\nGK2or0U/pflVe+yxB1BUWpVKd/9G9Or/NlLUe8TPddV+RqklEolEYqDQlg+nU5umLMvoEe3LKh7z\nIqz/Y5a9kRi+/c09iXkeT0fIbGQg+hlkJqrAGEXk79ZYYw2gP/6pKjTrkOhYtQvrZ/Cz3Qhlnn7W\nnuxf8y+skSVD1YdnfTDnrmp8k9ROm/xEm2BkZKQpq49RZEad6ZNR2ep3MCPctX7AAQcAsN9++wHl\nHrLunDlJ5rTJiM1Ncn05V73CtGnTxvXWqQuj01Q2+mh9PgjrEBrFqF9D5azfy7muQuw4GyO8uuHT\niZGy/tWf/ZnPfAYoPhbzaHw2qmi83lVw7lwPv/vd7wDYYIMNJhyPftF3v/vdQIlmFJ1at1LhJBKJ\nRKIvaEvhdMqiVSb6aIwusjaWPhsrD3zyk58E4MgjjwSKLdbopqcztBdra1fFRXYuYvUEbbjveMc7\ngBKhNUhQ2ahAYm01o4ys/iuLkp1dccUVADznOc9p+J37MdrtpS99KVD8E7J5UdeH08q2VWimpvzs\nuchcPWfvDaOKzJKXcbo+ZK7OofeM/gsrVxh9pL9Mn2Av2PtYTJs2rePoP/0L5t+o5t2v/ilV2777\n7guUyD0tJ1pWzPuqy9Jdx8PDwx0/A6t+7/det8997nNAUahGp51wwgnA+AoRwrmwHt3WW28NFB+x\n23s8O4Kq/m644QagRPLpP+3UT54KJ5FIJBJ9QUe11Hzr+RZsBlmU8fTGx1vl1wxgI2aMZvKteswx\nxwCw3nrrASU6xcxibf8dYMqi1GRxMteqrPdYfUHWZSSOFXQ7RS8r4ap0HPtuu+0GlKg1M761vatw\ntW/7O+3XzokRVy95yUuAEtklpqKuXGSerlXXtmNU6apUvf777LMPUJinOUiudfdn90sjPVdeeWWg\nRHLJZI1i05avaoi1uCJ62fGzWd0//9/73jw8x3z99dcDZZ04p56rPkIjP819ir1j6qKTudAPGatx\ne/3MJdJvZf1Iq3RYgeJtb3sbUCpOCHMXXWf6r8zj8pmtwra2ns9mn8X6DKvycYzIzCi1RCKRSAwU\npqRatG9dI2+sEvylL30JKDHiskMjdz7xiU8AhdmawS7DaTeCwnHsvffeU6ZwtMVqw6/qijlR90Eo\nETvmnnSKXiocGat+K3MMZFP6XlR73/ve94Dip5ClWTn39a9/PVAU0O677w6UCJ8x4wTqK526czFR\nRnn04bhWPUdVn+rMPBx9Lc6VOUZWQNY64PGsHHD22WcDpVq0meX6L/R7GO2kWogVMoR+i352uRQ+\nL4xK1K+l30u/hArXnlJbbrklML4ChbkmWmhiVYVmmG+++Xj00Ud54oknujYXsdOram2TTTYBimKN\n6l7F4xxp9Tn99NOBEo2mcor9l1S01inU1+d4/J0KqQqpcBKJRCIxUJgShROhopGJyL78bL6Odk3f\nxrI/c1dkuh1gyhSOjDf2IYnMU6Yco9Xe9KY3AWUuOkUvu1zG/7dCcuxiaU+Xr371q8D4/Kttt90W\nKAzVCrpGMRmhE9mcCrjVSKNesHrZd6wSfsEFFwCleoKfrS+n+ou1rlRGRjfJlK08YSVua7Rdfvnl\nQFE8rfoxetkPJ64TFW/MNdE/4ffW4PN5Ya8g2bnnaiVlc5hUEc0Ubz/74XisSy+91N8BpfpGHEus\nRu9zxHvJOXQ/3js+Z/SXGtFnhJ8VDqxbZ3dcqzlEpMJJJBKJxEBhShSOb2Xt17Ir//qWtn+38fOy\nfTv2aX/uQnSa6LvCkXlYvdc8C6NFtLmam2RmeGSFMqCYGdwu+hGNFP1Qrgevv9n2srWoAmVv+jWM\n5HIuzEkxKqlqrbuuXH/OuZGD3ZiLeO4x/8pj6ZewbtiNN94IlGg0oYIxysz97rLLLg3/L1R1MlQj\nuLQayJAnU6N1opGe+k1X75GVVloJKOtEZetzwO/N1/L54f8bkaVarFJ1VYqr0xp7rWxnLT3HFvvZ\nuFZdL94j0ffm9v7ee0ZVqI/QXmRalVynsWdZM6TCSSQSicRAoav9cFqFb+EY8+/bVTZmBI7sS6aq\n/fsLX/gCUOzg+naeTpCJmAGuv+LBBx8ESkVk7c/OmcxG1qVNv1sKpxtotZ6Y111lIQuTlUWodMwl\nMCtfO7S9Q2TE+jUcj8pIlhijGv2+m4j2f9e00UfWTNMns+GGGwLFL+Hal4k6d0bmOSdG8Nkl1fXi\nfg477DBgPJNuhk4qEEQFGRH9klFpGn2mn8soNNWZ6s8cJX2+RlZZidsq83Y31Z/lvSZa7dPTTRhl\nFhWn/W08R+9758Yxec+4zq6++mqg1CPUz6Xf07wb14PPF/N59N14bcwX0pfTLHeqCqlwEolEItEX\ndMWH061ukdq1fbvL+tyv+Tj6M+yKZ2XVLjCQKfPhOHZt+kbgCVmezNUILLHVVlsBpeZSp+iGfTr2\n+Ii+m6rOjvox9t57b6DUk5Kty67Mp9BvIYyw0f/hulK5eJy4vyq21k1bfVQWzoHfu7ZVKioelYwM\n1wgsc0nMv5ARW3nCyD2r/3pcIwFVe0YvNUMnc1Hlw5Otez08V1W7CkVFErtaqgr0e7l+rCfnOnId\nqGjN4p+KChTN4FitKGAtNOtHqso8V608zoG/00qg4nGu4z2wxBJLAOXZq9/UdebxJqmwnj6cRCKR\nSAwO+hKlVpVlLdMw30J7o29ho1B8ext9ZESX/S66iLYVTqcqT+YiW7MGlvt1zow6kemacxIzgbvQ\n06Xr7K3Klh+j1WTCsn6jjlwv5hzpo5EJq3iMajRSS/9HVDoRsUdJJ5FZzVScc2BOyZprrtlwDvYl\n0Y9pXo5Z9qo3la8Vsr0ntMGbl6VvLyqZWDW42bppp+rCmKguoLBm7+/Yz8jeT6p182iMsDN7/uCD\nDwbKXFpXzLkzp+Tee+8FSl26Cy+8EGiIQmw4vv12xpxHw3aiHxF7rkn/6rfWAqKSMSLPnEafE86Z\ntduM0PMee93rXgcUa5JwHcbnTZVfNRVOIpFIJAYKHUWptcrqYwy5b2uZjcrGOHl7f7h/o8/MitZn\no/256q3bT7SrKGKnvar9GpkTo1O0xRvBY5+MQUSziKiYUyQzPe+88wDYf//9geKfcPvY88X6Ya6j\nmLsg4vqN4+tEJVb9Vn9BjDL0s719nAOjFmWwqjR9O/p8jMwyL8d+Jtr0VUaLLrooUHxEsvmq2n2d\nYiL/SKz8YJSh11W1tdNOOwGlarjbmUNiLyC7ngpVpNdbC4m+H+fKHBOfH1U11WL9wl5Gq0U4V9G3\n4vXzfndM+q28d/T1ahUyv8/KE/YW0yqgP9TK2l4/56jTOUiFk0gkEom+oC8+nBiF4jHtt77zzjsD\nJRol1rjSBq+9WpbXA0xZLTWh4on+BjuB2tVSaIs14mbTTTcFSmXddtFN+7S2c2tYRcToJW3pKl57\n1cvqjMjTfm2OwEEHHQQUNqb9OfoIJxg/MGn+RderApvhrSrzum+++eZAUWlvectbgFJdw3PWN/Pm\nN78ZKHlcRjOpDjyeyilmrldVH+/lXHiuMQ/LmnrmjOjXMgLP6+o60c/g88J7xueF6s0eQ9ddd13D\n7/0bK0tMcB4N4xVTUXWhCrGyhM9a1b35W7fffjtQ+iEZwef3nqs5blV9cCLSh5NIJBKJgUJbCqcq\nb6FZPkOs8qrd2gq4ZlcLxyYz/cAHPtDScTrAlCscYRSKcxYZqLZdv4+ssV30smaWtvUYERXH7rnJ\n2t/znvcAxWbvejAnyd4w9ntXDRjtJPO1Am9ddCNKLVb3dkwyU23pRg3JUPVTxvwJ/VPmrDhnWgk8\nnj4+/ROOx+NXdfic4Ly6vi70SxlR5zpQ0ahMrITtuXpu/vX6X3bZZQBcccUVQKk8Yf3BKl9djfNp\n2M8gKZxWIz2tOOGcaT3wmdzu8yMVTiKRSCQGCn2tFi1L0w+hndlulUcccQRQOnvaw9xq0PZt7yG6\npnBkVdYeiqjKSTEKxWgjo5CMOjEvwyoL0f6s3Vsm0y66wd5aZdGyeLezh4vXWz9F7EFvJJYVKKwP\nJZuX3Vf5K1pd+3XnQjUQvp/wmEZcWQfMqDJzi9Zff32g5J6Yk2K+lp08zbdwjlwPE7DyZuOfdLtu\nzEWzY6lkVMLmljg3Rli59u386r1j9Gu7z4sa0bcDo3AmOB5QnjPeYypkfTrWcIsV1ZvVv4tIhZNI\nJBKJgcJA1FLTju1+Ym6ArM23sW/nHmDKfTies5FYMln9XOYQaHuN+Tt1bfNV6CV7k8GqRGJX01hf\nzOx4oxSdI6tCm12vj8d8i1hZucb5jI5r9uzZHc1Fq71V4vf6N50ro89OO+00oLD/2L00zm0VtPHH\nShbNKmV3w59V93kRfX9x7LLwWG2613kzg6xwRFU9w2WXXRYYX5euys/aDKlwEolEIjH0A02CAAAg\nAElEQVRQ6IkPR3Z+9tln1xrMAPR06brC0V918803tzWgWN+rX+gFe2uXccYqv5GFxWjFqjlrFt3Y\ni971nnNU681QNZaqiL5eYyo7fk42ponQ6vrqVAG1Mxd1fSOi3d/1C6lwEolEIjFQ6GuU2tMAU+7D\n6ReaKadOmKwx/0aJicjaW+0EGSNnoq+nWzD73xwX0Q0mGyukDwrq+lcGSeFMcDygf7XOBnku+o1U\nOIlEIpEYKNRVOPcDd/RuOFOOZUZGRhZrZcNn+Fy0PA+QczEWORcFORcFORdPotYLJ5FIJBKJdpEm\ntUQikUj0BfnCSSQSiURfkC+cRCKRSPQF+cJJJBKJRF+QL5xEIpFI9AX5wkkkEolEX5AvnEQikUj0\nBfnCSSQSiURfkC+cRCKRSPQFw3U2fqYXoAMeqFHaZtL2ud1GFiacOjyT5qKqgKqfbdf95z//ueH/\n3WbOnDm156KqmOvTHXXWxdDQ0MjQ0BDPetazAHjooYcm3G6q2pE0w2QtP+bMmdPyXNR64fx/gJZr\nHU2bNo3h4eHRasCt9jlpF1Yb7rST5/+P6PfLejLEHi5VY6qq4uwLI/5+kurOQHlxzJgxAyhdde2q\n+vDDDwNw3HHHAbD++usDMP/884/uy86rdTBt2jTe+c53AnDEEUe0/JuxY38mYGhoiIUWWmi059cF\nF1wAjD/HRRZZBIB7770XaP4C6tZcNavcbrflSBpmzpzZtLvsWHTUnqBZQ6tBWTg1xlG7PcEyyywD\nwB13TP6uGrQGSk/nMvT9Rt25mDZtGosvvjgA//znP4HSlmDRRRdt+H7eeedt+H8fLPH6NGvRYGvp\nRx99tGE8bh/bM7/whS8EyosmPkiq2hX0c100a5fe7OXdbI378m3WVrsK3ZyLOFaV5i233DLp9sJz\niW22m51b3Wd0bGFeV+GkDyeRSCQSfUFbCqfVt2Kr5oNeN6f62c9+BsAb3vCGZpv2rAHboKi9VpEK\np6CduVh66aUB+Pvf/z7hdjJEGWPVvRKtCH52+4UWWgiAf//73w3fR2VUte6ateMeq3TqMNmnftPR\nuqjbHE4873nPA+Cuu+6adLtXv/rVAPziF7+oNa65556b//u//2vLnzXmMzBekUzwuwn/xu01fWr2\nbLb+ms1tlbq84YYbAFhttdUAWH311bn55pt55JFHUuEkEolEYnDQ1xbT2o3/8pe/TLrdAQccAMB5\n550HlLe29swddtgBgJNOOqmT4UyEriucKlY2VdEoVXbrPffcE4BDDz0USIUzFnXmYvr06SMzZ84c\n9Y2IKgXj9ZCxuh5cH6p+t5s1axYACyywQMP3BgG4H3/vOPTl+H28/nF80Vc077zz8uijj/LEE090\nvC6q7gn9Ww888EDD97b+vu666xrGVBfxuMsuuyxQnkdxPM1aote9R4aHh8dd33j/q1RWWmklAK66\n6iqg+Pock9fb7VXMjs1z/e53vwvANttsA5T15Hb+XkVj9Fwz5RUVUPpwEolEIjFQ6IvCqYpmu+ii\niwD49re/DRRF85vf/AaAJZdcEhjPtmRnH/rQhwBGI4K+/OUvtzO8seiZD6ddaCvVdtov9ELhfOpT\nnwLgyCOPBMZHVEVsuOGGAFxyySUAvPKVrwRKjkj0Wyy22JMpVDHiqlP/WS+ikaLvRUR/ptvHe0Df\nz8tf/uRyNUpy6623BsYz4KOPPhqAz3/+8wDsscceQGHa7jdGyY2NShoZGenJurjzzjsBWGqppYCy\n5v/0pz8BDSwagCuvvBKAjTbaqOH/DTn+5S9/OeFxDAGXxUfF4tybN9TMB9TOXMS16PVTvY3ZvmG7\nOPa6cB2suOKKQJkjn83Pf/7zAdhxxx0BeMlLXgLAPffcA8DHP/7xCfc7Y8YMZs2a1bI/KxVOIpFI\nJPqCvvpwZFPXX389UN62F198MQBvfOMbJ/29vhyjS2S0vq3bjacfgylTOBtssAEA1157LVAYarus\nvNPIv376cGRZ/pVly/oWXnhhAF7wghcAJYfF6y+cs2OOOQYo6+ULX/gCUJhsVNznnnsuAJtuuumE\n42snDydeN23e0SbezEbuGN1u7733Bor/crPNNgPgYx/7GACHHHIIAB/84AcB2G233YBiBTCCS9u+\nc6b/5HOf+xwA7373uxuOO9dcczF79uyOIrOq4PV98MEHG76Pc6gq/M9//tPwO9fDmONOuB/9IFXK\nOkbmNfNj1F0X5qxMdMxW/VL6s6655ppJt4uK+PDDDwdg9913b9hOdeizWegb9DninDk3MSoufTiJ\nRCKRGCj0ReGssMIKQHnr6mt5zWteA5S3ZYwJF3GMJ554IlCY7M477wzABz7wgXaGNxYdK5y7774b\nKP6nKjgXz33uc4HCWJZYYgmgKJN99tkHKGxfBdTMlrvccssBcNttt026XRV6oXBilrLQV/PrX/8a\nKOVVVLz+TrYm64rrRIWr4nV/u+yyC1BYvvWs7r//fmA8y4zrre5cTJ8+fZQVv/SlLwXg5ptvnvR3\n0ZfiGPzevAr3a+kZ7wWZZoxq+8pXvgLAj3/8Y6BEeKp0/va3vwHwxS9+seH36623HgA/+clPRsfY\n7Si1KgXh+vB6OWavmz5AFYvnLlt3//6/68XIvpibov/C7/19MzXSyT1SVXlEZavK91hGmf3whz8E\nGBcFGfer+v/d734HFAXbLP/mpz/9KVDuPVWkc+x49tprL6BYD1LhJBKJRGKg0JbCaWYLFW9961uB\n8vaUeWpv3mKLLYDCxv71r38BcOCBBwJFAc0zzzxAsVu/+c1vBmDttddu+NwuxsTE11Y4sq4qxjHB\n74DxxfBiUUYhO5MJxdpYjl0fkCzNXIaY09Aq+unDufTSSwF43/veBxQ159zGnIVPfvKTAOy7775A\nUciyc9eLGeRGAqmU4pp//etfD8CFF14Yz6utyKzJqojHPKjoN7A231//+teG/5edq1TWXHNNoKwH\nt5P9qw7WXXddAL73ve8BhaGqrIX3lr4bo9l+//vfj27TrSg1x2zlD8/J771HXPteT/1NXveDDz64\n4f99Xpx++ulAYfdaVPT1+BzyeD7P9A2JmAsVUWcu5p577pElllhi9P5sNw+vVZ+PtdiM9KuyGvn9\nWWedBZRnst87tzHfq90ae6lwEolEItEX9MWHU5V7oP3YOHwjKGJMujAbXuarXdy3c7sY87bueZSa\nzFOmI4uL0B6tfXnVVVcFCuM0Tl6m49wafSROOeUUAHbaaSfH3fC7KtTt9THPPPOMsvaqvJfIzvRz\n6ff64x//CBQlcvLJJwPFjqwS0c5stOMrXvEKoDBZ14+5C2bn+7ku6szFggsuOLL22muPjrHVHKDo\nw9Fn4/X33tD34nrQ9/elL32p4Xjm5TjHMl19AN5Dzqns3kgx15P+FK9tJwqnmW9Wv9Rll13W8L1j\n0YrgdqoD1ZkWF9m9x/voRz8KwGmnnQaU54/5NrYCaFahOaKTuTjjjDMARls3TLC9x2j1EECZqxtv\nvBEo60V1d9NNNwHwohe9CCjrw9wmVaLrw+uusnnZy14GlDladtllufPOO5k1a1YqnEQikUgMDrqq\ncCKDjW9pa6kJmYX/X+UTkpleccUVQLEnasdu1X/SAjpWODH6xIZKsS9KjHuv2o9zY/WFlVdeGSjR\na1Zb8Hhmazv3skDt1lZz+OpXvwpU16/qhw/HMZpbYjSZ7EsVt/HGGwMlgsdseutNqYhcF/o/ZOey\nMxls3Vpc7ag9fXT/+Mc/Gv4/3hOx+rPnKFM96qijgBLJJ1xHNvIyUlPo1zIb36glI0ZVwq6D173u\ndUBhtGP7nTjebvmzVG1aOERVZez4PIk+mx/96EdAWcP6u4ys+vnPfw7AtttuC4yvphB90q0+E+vM\nxfDw8Mj888/PdtttB5Tr2m1cfvnlQKm64HPG6hw+S12f3hs2x7P6y69+9SugXINbb70VKPXnxvZn\neuKJJ9KHk0gkEonBQl8rDYzZz4TfV3Xs0865zjrrNPy1tlasO9VBz5m2FU6zzH4ViL15ZO0RsjnZ\nujZWM8etaRQZcow60a5t/H6sjTXmPBp+L3qpcKqOad0m2Zd+LH01+nS0xYuYu2BOiVFQKmBt9296\n05uA4gswSq4K7WSUy8JjJ8+qCsTxuqs8//CHPwDFb6WqO//88wH47Gc/27Bff29VBm3uqkcju1yP\nzrGq0MrJk/TV6fq6iBFbse11VOueq36sww47DCis3u3NaXOOtTLEe6aqfbuKWHY/9h5rN2JPpRr9\nVJ22qPeZaGSm+1O1WUHC/Dzn6B3veEfDdvp8XL9+btbROBVOIpFIJAYKPVU4desERch8Yiax9aGM\nTpOtVdU8qoGOfTirr746UHwusiwjsZpBRisbl32p5jxHGUnskyFk/ebnmDEuQ26W+d5LhRP9XEan\n6e+S3btunAtt86q0eL1lbUZ06c/ys1FJdSvudtL3JI4t3m9eX8/ViLy3vOUtDZ/NPfrwhz8MlPqD\nRuDFOnGnnnoqUKLdhLlum2++OVDyc7bcckug+G6mQvmqbPVfybJdw1//+teBsubnm28+oFSUMAL0\n+OOPB8qcWKXceyauv6qsfxEVUSdqr1mkXruIfi6Vqj45z/39738/UCpJWJ1Fheu94u+8JkbVRj9X\n3ejFVDiJRCKR6AsmD5XqEJ3aJWVxMh3/qnzGdN4Dip9DJjQVUNkI/RKRgVT5sVQgVZBtGScf/Vf+\nlflG5WO0ylTC62bEi4w11nsygkbGa92mmPUs/J12bHMLXvva1wJwzjnnACUiS3SqxCNmz55d6QOZ\naNuxY4is3Cx8o9CMNjQKTQbq8Yxe1K+hNUClY1Sa68ztvAaO0/XTDQZepZZijxcj6Lx+Vl1wzbo+\n/N71oPJVCesnUeFa98s5Vkmr9syu108Wq1Z3a11Mnz599BkW6wmKVisQ6F+ytqJzbB1CfTZeZ/Ow\nzEmy2ou/s+afqlElbfflqJTaRSqcRCKRSPQFPVU4rUIbqvZsGYjM1LewDEa2JtOVuXzjG99o2L5b\n9tF2EGtmGZWiPToi2uD1W6lkYr5GrCYsIzJjXNbn74zQ0RdgFemzzz673VNsGbH/uTDyJeZFCM/B\n7cwdiSwr/k6/h/40s+sPOuigCcfXTYUzzzzzsMwyy1QqSdeF5xyZrHkzVnleZZVVgMLqY+09bevv\nec97gKLeVAmut8985jNAqS5tT6nf/va3QFlPjs91NbYfSrvzU3UfRl+aa9KoVBWsY1DVqRKMxDMf\nx2hGc45k9UZ6qlzM17EGY1Wlkma+nbp44oknKpVNq/C6WyfO6yWMXvQ4bufcqiqjknVO9fVqLbLf\n0gknnACMt6SYn9Xy+FveMpFIJBKJDtCXPBwZimzOY2ov9G1pFVirTGun1E9h1rbZ9jIXWZxv4Q7Q\n9VpqMhCjz2Ttt99+O1Ds0iogs6FlmLEigWzLXi7+v6w+9hrRp+T3sv6q3jSil9FIjk0GGWuwxXpv\nRmyN7c0yGVSFVhPXb+E12HXXXYGimCNijbd25iJWiqiC18FzNhPdLHyjyfRnqoC+//3vA/CRj3wE\nKLZ2FY5zt/zyywOlArv3UFwn+jNi5Ymx6rHd3JOq6gpRMbmG/X99MPqlzDVR4WoJiVaAWPdLhazK\n11/hPWT1DddZq4q3k3URI+Q8lurMc9aXYsfOrbbaCihzpUJVUVvtW1xyySVAqZiuSoyIfZicA/vi\nWIHAa7n//vsDTz6z58yZk1FqiUQikRgs9NSH49vbXJTYaU9mK0MxC9oeHlb/3WOPPQD42te+9uSg\nn2L1MhajkerGuFfVEesmPEdt8e9973uBMlaVjrZUGa0RXHY1NWrJOHrr0Mlsq/rprLbaakDpmqja\nVD3KkPoJ2ZS19Yy8suqzkX1mRTezoceOjeZlyMqsyaYdu0rZiFZzpqowNDRUmSMUGaTwe1WYytT1\nojL13DyHo48+GihRSbJ3K6ub46SyiX7PWIcwzo0Rgo899tjoWu4UVZ00jZzacccdATj33HMB2GST\nTYBy31dVJHG/9jWyRt+ZZ54JlHOzbpjX+W1vexsA73rXu4DST6dK6eyyyy6jEY91EdeF+15jjTWA\nsuaNLvTZ6LNKZeN19Pq6Tvze+9xqGvrLYh8toX/V4+vvink37l8FtsEGG4xGyrWCVDiJRCKR6Av6\n2g9Hti1704fjW1+Gayy5NlrfzuYiWNvorrvuAkoUlL6dqn46LaDn/XAm2A9QGIc2epVHM7aturOO\nlLZ/bbrHHnssUOZsbAfHydCPatHap2XnKmKV7iGHHNLObsdF5sVe9trD/dsM7czFiiuuCJT+IxGy\naZmyinb77bcHSmSdGePmlnhPqAK+/e1vA8UHY60+oxGdQ30DRj+qVszTMN8n+ludyyWWWIL77ruP\nxx9/vON14Zq3FpprXR+d6t37WoUTO7bKyt2fzwmrJnhvqO712Xjdzftxf6qEb37zmy2dXyf3iMol\nVg7RqmOUmM/ICK+PCsk6g0Yn+lm/lD4/nzPRGqTfS5+NyjbmtllbzXU9xveTPpxEIpFIDA664sOJ\nGd0ySZWK3QiNCTerOdaBMpokZp7LUGXCRuL4tpatyQZFVT5Ou/3EewnZvdnOrSpP2aA9P6yRZK6S\nPqFBOldhHxOrN1tB25pY7UJbfYxe0tej3yJGDHUzHyfWqnMtagO334hM1jpvP/jBD4BiS7/hhhuA\n0vvJKhoqHVWAfjDXj/eCEZxGJ1lnTAarqvDcq6qda03oBPF+NCfE76P/0r9G7nmf2w9JxWMOif4M\n/WBCFWjvICsUeE+oCo0AE1pMtAo4h6rEOpg2bRpju+LGmnV+Ni8uVnWP1eD9bGdPq4H7zBQq1qqq\n8sKcJn03zo3PEe+p6OObqG7gZEiFk0gkEom+oCsKR2UjY/StKGPQnq3C8S2vMtKWb8avWdXC/ZqL\n4GcjOY488khgfN927dyiKuN9KiDjMD7eSI9myiZG/tkfR4Zk1Jt9UuxZr528WV+LfkJWb/a7Csc8\nmHZhdJLrQgWjsjGTXbYvulUzayzri0xSda2S0PfidbMagj169F/Iru2Gavdbo8/0W1x99dUN+zU6\n0sirmO/hZ/0b+gy06XdjTmLNNKEa9znxne98B4BbbrkFgDvvvBMoa9h14X4cm3/t7WLUaYzAUx3q\nr/Jesm+SakBYY02F046yESMjIzz22GPjIupi5QnzaKoi8WKUo89e9xf713hOnqtwe6stqFy8V1RO\nrp+oAmPUW6tIhZNIJBKJvqAnUWq+VY2UMs5dxqGPx7e0uQPWQvKt6Vv5qquuAop9Uzu32336058G\nikpwO5mR9YXEJEqnb1FqRuzJeM2KNiteG/sExwVKnoX+MXMYDj30UKBkoKt8VBGtopMInFZ9Ia4H\nt/evlQC+9a1vtXR8o5BksNq/VQ36bszjMku61b44defCPu9Q/FHWQPO66q+wEoCq31wh14Nq3chL\n87CsG6i/Ux+P3U6tkKyKNBrOa+K6UzWoKiJiTcBuZtf72XwsVZVs2xwS82pE9MHq61G5uF/9Y86d\n94K/79TSUXcu7BQKRYXpb9Ji4XpoFUa3WUOxmf/zmmuuAUp/rSqotOyrpN/MnKbY4Tij1BKJRCIx\nUOhqpQHrNVkTTdunuSTah42wsZeHETAyjvj2NLrEPBwVzymnnAKUiB6VlG9ho6CEbFBWEI/TT8jm\nrKHmnMjajKzRdqp6i/1QZEwqIysP+Lsq5tpLtGr3t1aW/gNZmlFJUeHITM0xiVUWYj0oFZRRTG7X\n64i9secvY5V161tRychsZd/OgbASsizdte05uYbdr+rdyE7vQe8R87Fcf36Ovib33417I2bXx8+y\nbbuPqrqsFBHh9TMK0RyRsVURoChZfUWi6pyaVYfuZvVorTrmirXrK/OZ5t8I7wWfec2UjfDZKqxv\nGatR10UqnEQikUj0BR35cCKzVMFon7YWkvk41gWTrWlPlKn6VpVJaJN1v7I4WZ2+IH015hzIAiOz\nsQ7RJLW0+ubDkWnIgM0MlmnKSOLcxs6hViYwQs+opU7RiQ+n1X5EXg9ZtopXBhkrGrcKf68Px1pq\nqsi6tfM6qZAco4TMObr88suBkv9gRJQ+E+8d+9zog1GpyPLNZXPurDShLV+1YA5b7EBq3oY+phgF\nFbfvxG8R10WsXeb/q1TMkjd6NSrTM844Ayhq32oMbuf6itFsVdD3p0KK2zu+lVdemVtvvZVHHnmk\n7XvE+1m1peKMNc7qwueI/kyfsXXhuVbdM66Pueeem1mzZjFnzpz04SQSiURicNDVKDXfejIOo4Ce\n+9znAkX5mP8Q8y18m5qHI1Mx98AYcGPE9RWphIzsiexM+6Ysc5J4+rYVTt0uo7FSsrZ8GY/MOCoa\nIWs3o9y5kMl2il7UUjOaSOVhzkCMTmoX2pVdb9bEMj+jXdSZi2c961kjq6222qht3ooDKheVh4xR\npms+hTXxVL767mTvH/rQh4Cy1s2aN5rIqCf9GvrHhPeAyqgq8zx+P23atFp9T576zYTrIvaAid1r\nPaZKtaq6tP2OrBNmDT6jEZv5n7wmcS5aRZ25mDlz5sjyyy8/6lPz3LT2mO+iZcPcpUmODRQ/lzXQ\n+tXl2FpqK620Uq0+SalwEolEItEX9LVadNWxZHlGxshUYydIcw+OOuoooCidKpjFX6N6dM99ONra\nZVX6payJptJR4cj+YxSKVYCNSjIPx7kyh8GM9broR7XoCCtUmCUdWXeEc2MUpD1+6qrNZqgzF0ND\nQyMzZswYFwkpo409XWIelhGZMlcrChiZJ9u3koQ+HRWQ/XGskWa0mqq+St1Hf2y0EvjvbuZnxc8q\nH6PP9OFYXd5aac6pUY5WMjHa1fpz3cbYOWlnLsb6syb4f6BU7/YcrJFonpXPSHPL7B3VLTS7d1xn\ndhL1nFLhJBKJRGKg0NUoNVG3GnOrmelxv92s7vsUuqZwmo1Nm6315GSiVmu1s6O+Gus96Y8w50nm\n3O06cVOhcPoFc5y23XbblrZvp9KA95XXX1Yeo7701RhxKXPVn2U+lWxf2765SvrwrFNo/TG7Wlo3\nLnbrjFF0/lVdqLjHqsxOFU6E1TZk8yqceO9U5b3Eflo+F6qeO1oJxlRNaOU0xrH+uqz+qd+MQImE\n837V31jVN6nfaPeZmgonkUgkEgOFjhROt23lA4C+d/yUdWl/1odjhrm2UtFJT46JsOmmmwIl70N0\nk8kO2jqpO55O5kLWLrON103V7nW10oCKV8UaM7tj1WH37/ey+Faz4o2eU9motMzrmTlzJo899hhP\nPPHElClfz80s/b/+9a9A8YeKZuy8KseoLrpxj/TAStMRVP1aASLMqbSq+R133JE+nEQikUgMHvoS\npfY0Qt8VjrlHa621FlA6Nsp4Vl99daBE6vQLz2QfTj8Ujr4264NVKY2Y72IUkqw91vszd8QouBbG\nM+FxYo6aiigqGxm44+/muqiqZdjtjrxGhhoRWgXzwrQ2xErZEe3MRVW1k6rcpKr8qLrYaaedgJKb\nFhGvxbrrrguUKMlm90wqnEQikUgMFLqqcAbNVt+MoUyAlhXO8PDwyAILLDCu++AzBc9khVMXdedi\neHh4lFWb6T82Y/+pfQLjK0moKGS8MerQChX6L6ICEdE3EPN/3N6otNibyOOP3b6dyKy6Pe8HAfEa\nxS6onUSpWcHeqEPhvLfaq6eqcnX83uvr2OOz2ejGVVddteF7q0Pbj0lYJca+TAsuuCAPP/wws2fP\nToWTSCQSicFBXYVzP3BH74Yz5VhmZGRksVY2fIbPRcvzADkXY5FzUZBzUZBz8SRqvXASiUQikWgX\naVJLJBKJRF+QL5xEIpFI9AX5wkkkEolEX5AvnEQikUj0BfnCSSQSiURfkC+cRCKRSPQF+cJJJBKJ\nRF+QL5xEIpFI9AX5wkkkEolEXzBcZ+Np06aNWLhuMlQVlus3qpobTVLy+4EapW2e1iUaLBLo3MQ5\nGoTinYNSDLYbc2FLYRurPfDAAwCssMIKQLkev//97z0mML4Ns2hWwr/u3MV7tmr/g7AuBgWDPBet\nNnaru06q9tvqXNR64UDjwzp2HRTNKtfGz/bksBdDqzeRXQ5jN0QRj+dNP0n16GdqrSMWWmghAB58\n8EGge71GeoFB64JYB0NDQ8yYMWPcmvTFcd111wFlLd99991AuS5eJysUW83Xar++sOL1s2+SL6Y1\n1lgDeLIjI5ReMK9+9asb9us9F6sTu3+vxUc+8hFOP/30lubgmYJuE55IdMfuu+pYkQhU9RCa7BiT\nIR7PdWe/Jfsz+Tnek0NDQ7Xu0zSpJRKJRKIvqFW8c/r06SMzZswY7UbYrsksvs1jP/UXvOAFQOn5\n0azrXbuMOPYomTNnTt87fvYbVUwqfv9M7NfeLurMxfTp00fmm28+/vvf/zZ8H3sz2Q9lv/32A+AV\nr3gFUObstNNOA2D77bdv+L0K6B//+EfDZztIXn311QC88pWvbDi+JjL/ylxVTuLlL39y+V911VUA\nrLPOOgD88pe/BAbTjFRlwq9af93qKFp3LoaGhkbvM8dat6Nnsw6ucTsR+yZp7RHOUbtzkh0/E4lE\nIjFQqOXDmTNnDo888giLLLIIAP/85z+B1oMEqhiHbFD7pArK/uru/1vf+hZQ+sWvvPLKAFxyySWT\n7j/Ct7usoJ/+jFb7q9e1Hy+44IIAox1Iq9DMRtxKUEiriNehqotgv9HLYIQ5c+bw3//+d9xa9Lrf\nc889ANx5551AUTYxiGPbbbcFirK55pprgLLmX/e61wFl7dvZ8cc//jEwvmPnTTfdBMBaa60FFJ9R\nhMrG8aps5p9//nFqqFV0a75VhXbNdG5cu9Hf4H2uf8pxuF287+uqjbqYM2cOiy66KFCCRqqOEa+f\n6yIqG+Fc+Aydf/75gbLe/N7fb7DBBgD89Kc/nXTMza7dzJkz63RUToWTSCQSiW3kBBYAACAASURB\nVP6gbsfPkenTp3ct3LkqoiLau/XxyN5lLI4j9hyPkC3EPvHxOEDXfDhG3sm2OkWvQ8232GILAM45\n5xygM1t93bHKzh9++OFWD1k1job92Hf9/PPPB8r6eOlLXwrAzTff3NJ+25mLqjUZo4wcswpHVb/+\n+usD5Xr89re/BUpkptFqN954IwB33XUXUCI2v/vd7wLFF/S85z0PKHMTo9I8vtfMa6jSmTVrVq3e\n9U+dW8O6UPWJVn17zqXbO/ZtttkGYJy/TL/WrbfeCsCpp54KlDk59NBDgTJXnvt//vOfhuM0Uzx1\n1sXQ0NDIXHPNNW7e24Vj81zPPfdcoEQrHnzwwQC8973vBcqz0zWvb7DK9+McVN3LKijnPn04iUQi\nkRgo1FI4Q0NDIzNmzBinMKrsfBMoCKCwPG2obud+fUv/4Q9/AMZH1MhI9PXEyA+ZlG/nqph1MYZh\n9zxKzbHKVGN8e5xLz0G/WWSo3fY/6cPpRjRSr1VZXEeyLRlxzCVxPHVRZy5WWGGFkZNOOolNNtkE\ngPvuuw8o/scPfvCDQLknHJNjjczVse+1114A7LrrrkCJ6Fx66aUb9qdvRp+e6+w973kPABtvvDEA\nn/zkJxu2jyrB33vPOb5eRKnFNR99L86Bf70XvG/f/OY3A4XlO6f+/9577w3A2972NqA8V1SF5hfp\nk9a/onqMWHDBBdtWexP5TMeeu4g+wKrotC9+8YsA7LzzzkDx2XzsYx8D4MwzzwSKIrn22msB2H//\n/QH4yU9+MuHxI6oi++add14ee+wx5syZkwonkUgkEoODWlFqIyMjPP744+MYa9XbUQUiY1Fp+Ne3\npuzsJS95CVBsqbJB7de//vWvG/ZbFZUWY86rlJbbdeI7aMbiZZQyiR133BEoNvoddtgBgNe+9rUA\n/PznPwfg7LPPBkpkl+fg3MhsDjnkkEmPXxfdjMzpdWkj149qQmXjOXh9ncOIXkSr3Xzzzay99tr8\n6le/AuBVr3oVUBRGPKYKYokllgDKGnWN63dQ9R911FFA8UM95znPAUr+jffQFVdcATxZIQBKfo0w\n0vOII44AxvscHZfXcKGFFhqngrqFyNp9PkRlqqJVsay33noAnHjiiQCcfPLJQFkPsn2vhXNmlQXn\nwDkyl6nZeTaLBK3CRP7vqrUXfSh+dg5e+MIXAkWtmZelv3uXXXYB4G9/+xtQ1tOyyy4LFOXdKqpy\nmer6qFPhJBKJRKIvqB2lNvazDMS3XYz+ksVrE/3Nb34DjM8ZWW655YBSb0q295rXvAYojOb2228H\nChuT0ZrTos3WzzImtzcqZZJ6RF334TiGnXbaCShz8Ytf/AIoTFS2ZVSJjNhzjGpOprT77rsD8M1v\nfrPh+07Rz4xyz23hhRcGii29Cl6/l73sZQBcfPHFQIncck3LbF1H7SqZunMxbdq0cUpG1m0OUoyY\ndPvor1h77bWBovK9/trkrcUW14f71/fzvve9r2F/KpiqfByhj+iuu+5izpw5fV0XMTdp+eWXB4q1\n4N3vfjdQotC8/7UWGKX2ta99DYA3velNwPiaij6PPvvZzwLwjW98A2i+XupGqc0zzzyjx2yWM1jl\ns/Gv0YxaQlZccUWgRCW6rs444wygrD9V3FlnnQUUFej2rUYORstORqklEolEYqDQkcIRsWpzVel7\n7c3aGS3Fbvb0t7/9bQAuuOACoNgbd9ttt4b9V9Vyk6no53AcRrGcd955Db+bIPKibYUTVZMMxnh3\nM8K1H8fMYNWeakyVtuSSS3q8hnOXpRmZ43GqKmerIm+77bZWTq8nTDayOmvmmXXfQR2nhs+yNf0W\nMdqoru+mk7mIa0wWfdhhhwGFZXudY4TWYos92S1DW/wee+wBwJFHHgnApz71KaBEnQn3I/O1ZptK\n2nXarKZeRC/WRTznOBbvEbP0vX9dPz/72c+A8hzabrvtgMLi3c8+++wDlLlyexW1z4lbbrkFKGpg\ngvPqWiRnXXgPqeocuxF3f/rTn4CiiFWyqj/Xoz4ffTBVz8T4udP2BKlwEolEItEX1O6HMxa+7bbc\ncksAvv/97wMly/WAAw4Ait9ChqKyMb/G3IJY50cbvG/ZWFcoZrvGaDPZo+OK9tBuRlHJGKPKOuWU\nU4DCuvQzxEi6733ve0BhVR/60Icaxqyy0QZ/5ZVXAkUJVSkbGY42X1VmVZRKN2upiTXXXBMo/ior\nEKs82q0mrVKOcE7f+MY3NhxH9Lqh29gMdZmha/Wggw4Cxte2WmqppYDip3S9/OUvfwHKveK95JpX\nMWlTjwpF/5W12awc4H6iqnQ/jkMV0UnF72YZ+1XKxu28t1yzRpsZqWkUoizfKvPxeF/+8peBkuNk\ndQ3V5fXXXw+Ue7MXUYytZu5XQcuIfu2TTjoJKM8b/VvRV+T/W3GiykrU7HOnld9T4SQSiUSiL6it\ncMbGkvu2k8VrE5WdC+2HvsX9bASN7Eslc8wxxwCFvemfkInI2rRTfuELXwBgmWWWAUplXBmKqsK3\nvFnf1trqZra+DMWsZpWHtvfYhdToss9//vNAiRoyf+e5z31uw1jNFDbT3DmPkEmZY/CGN7wBKMz2\nwgsvBCbsg1P3lCvhOlHRmDvgOTr2unlQnpsRNhH6N77yla/UHHHnGB4e5tnPfjYvfvGLgVJt2bWn\n6t93332BMv9//vOfgXJ9Vcr6t37wgx8AJR9Hf6e+PxWQc+rvzaI3msl77v77728Yd6xzpiLWR/Tl\nL3+5kyi/hs8t+Ikm3N523N5LPhf0c8VzipD1Oxc+j/74xz8C4yMHWz2fOqj6bas5TkZyagl5+9vf\nDoyvCCE8Ry0bPgd87rQ6PqH16dJLL21pvBGpcBKJRCLRF3QlSq3K5un3RqH49o0MVdZvvwvZnm9t\n3+qydXNPjj76aKBkX/vWV9Fo043ji/k3YyoR1IpSm8jfYZ+Syy+/HCjMU1bvsZ0Dj210mn9VIrEW\n1mabbQaUigQyXplOjEZSFR5//PEArLvuukDJgO9HNFKzat6tIvq9Ipxb2VyzHJNmmGuuuZg9e3bL\ndaKgdHZ0TesvUNF85jOfAQrbVknYodNz1O9l/oz3ijkixx57LDC+F4zrxQoC+mJkpKr/qA6r+il5\nzyy88MI89NBDHVWLbhfeIyeccAJQ8mzMZdMvpk/Ge6AK5vN4j1VV0G6Gdu6Run6hGBWm/8pnnWN3\nu3iPmdPoOes/9/j6gOMzO1o8qr4XGaWWSCQSiYFCR1FqIkYuxPwa7YiyOnNC3C5Wf5apymxkIr7d\njcywcoGszIiav//97w3jkmFHO2nMOK6LiVjKRRddBJSIPH04nqt5EWZwO0aZSWQo/l52Zx6PTPY7\n3/kOUM5R1veBD3wAKMz1wx/+MFAicXrZ9TLCczJqrFmXwSpUZV8LoxqbKZtWq1g3qzJehbFz6lg+\n+tGPNmyjkjW/xr9mxW+11VZAuX7eC/opHFvsXrnRRhsBxVavojHvx46g/tVaYPSa0D9iLstDDz3U\ns9p4zdai/jCtBqpB7x1Vv37JZsfR/+m91euafxOhSvVX+VS9/q4TrTgqYasqRD+Uf10HwmdhVFBV\nvYCsPv3Vr3614fu6z49UOIlEIpHoCzpSONqnI6NcddVVgfL2VEGodKyAawTW61//eqCwdxGrSmvP\nNqrN+mTCXucyoBtuuAEojMZ8IXNY/L4dDA0NMXPmzMoIK1WZjME50K+0yiqrACVTODKMCBmRc2uk\nn4pFdfi5z30OKH6v2Mf91a9+9YT733DDDYFSEaEX6FTZ6B+L7Mv1pN+qGSKjrVJOnURlyUhVHjJM\nVXqssmt+hHk3sf+RPjfvKfN4nJOPf/zjQKkabR8UfXtrrLEGUK6vmeYqG9eX4zIKzuNst912o5U6\neoXoJxA+JzbffPOGz1YisQZjZN9xv1bS9r7X/6n1oSqXrReo8mdWrTmfhZ6Dzxe7nvr/Pl/02eq7\n8fra8VN/uFGTsTJ3tPpURXzaD6dVpMJJJBKJRF/QkcLRDihr9u0Zq/3KmoysUHnY38b6P7Hng5Cd\nGb3m23ullVYCSt8c2aFMR+YjM5IJR4bcDubMmdNS/oiq7kUvehFQcgZknvp8msE5ldEYrSRD3XTT\nTYFSPyzWs7Oyrr+XrXpt6vbH6CdkfUZ0xSzqrbfeumG7dvcfP7dbdWFoaGh0jCpN/ZmxmrNQcZhD\nZFSb19G17hy4n7XWWgsoitl7xChG1405UOZE6Q8RsfOs8PNxxx03mvfWbXg/eiz9W6pDLSmeu75b\nc5PMo1H5aMnwHlG5GJmn79b9qEYjnPsxFZHbPkeYuB+OqKpR5hj0T3s9ve8vu+wyoORrWT1cJW31\naK0L/vXc9Y9ppfL3rWLppZfmjjvuaHn7VDiJRCKR6AtqKZx55pmHZZZZZpRF+bZWoRjTLWLFZCHb\nM7JCdq4tVfanXVLfTuwcaoy5rF5WJ6t0P9FXI1Op6tPdTWirveaaa4Dir5Ittuov0C8lizMvx2gj\nz9kaS9pc3a8+BNVlVJHx8yBBhvv1r38dKNc1Zsd3G+0y2mnTpo3W7YpVnGO+S+xm6Zq2QoFVNT79\n6U8DJbrR6hreE0YvWWldxWT+zYEHHgiUdacq0Dek78ccF/2c9rTyXukmYr8qVaG9W/TJOjeO2f5H\n3lP6M4zQ03ogrKiuteG6664Dyj1TpTq6/VyYrA5Z1f/5bPS6uV581jonWltcV+YmWuHCZ7AVsa1o\noQIy6tUqDM0iNF3HvgtaRSqcRCKRSPQFbVUaaNatLlYWsIKpTMYsaCsLaE/WzqwvRn+H9aCMxJLx\nWF9szz33bBiP/TGMZouI52zE18MPP1yr0sDw8HBTFiSLk6WrQMwZuOqqq4DC7mQwMlSZpXZmM9W1\nuVuzzZ5Bbq9a9HeqwKhGq7L3p6LXR4S1s+zbLhxrv1RZnbmYPn36yMyZM0e7kZoXVQWZpfXB9INq\na1edx6g3ow5dy37venrXu94FjI+KtOulfk7XpSrB/aoyzMOxekIn6yKq+egjsaq7c+Hc7bDDDkDp\nU+N9rt9CeB9b/8114/aqRZ8Xdtf1eWH+Xqv5V+3Mhfd3rHxvbqJK9Z3vfCcA559/PlAUinUmY26h\n+/Oe0G/t9l5n/ejm5+yyyy5AUdSug1hRP9aljBUpstJAIpFIJAYKtRXORJE7KhdZt6xZBmPuiJ/t\nX6HCMdLikEMOAYqy0ccz5vhAeXvLwtxeNnD44YcD5e08plbahOdlNNsNN9zQdsfPCf4fGK+mZGXm\nEMTaakbWGE0m4zRPQ0Uj09h///2Bwng8rrZbe4bIbGW8O++8MzA+H8C4+rr1w1rdthXEKtKxBp7X\ns9PeHK2il2pPn41Rgl5Xo5CsnuAcWMEiri9rpsnq9XfZC0hm6zrTR6MSssJ7rPQurrvuOrbffntu\nuummrs2FqlvfinX+9LnIol2z3s/OmVFnzsVxxx0HlAisGNWm8jnjjDOAYjHR31HXZ1N3XUwW9eh1\niZG63teOLeZvRaXk3JiHpaqLlgyVqxUEzO+xZ1Xs4iyi37tu99NUOIlEIpHoC2qFniy00EJstNFG\no90pfbsaiWPVVhmoykOGIVs38sV6X9oNVUoylle84hVAecsaGWEEljZdcwtUPEbyxM5/oyf91Fta\ntmjkVl1MFFcvM6myA8sk9E8Y5aHfy2gh7dbOhfHxsjIrA2i3jrWXVHNmrHuNjOwxOkmbv4gMqp/w\nXB27cys765eyiZFadTF9+vTRtS8LN1dM5SH8f9eka9w5UOUZnRiVjbXVzJp3zvRvep31mxrFZqV1\n91/Vw17VoBrpJoy88n79xCc+AZTqCfoZjJxSmThnsnDXhb4YVb35elpUnFvr2pmr4j1kLor3Yt3q\n0ZNh7rnnZskllxzNWfE5oW9G/5Vqzwg6o9ROPPFEoKx9x+iYvUf0g+ur9Rnqs1efj7X1PEcjgbX2\nVOVcRRU4NDRUqxZdKpxEIpFI9AW1FM6DDz7IOeecM+57/QhCdh+rM9unRLuydmerCBudZsSGtdO0\n4ZpB7P59e1sZV7amIoqMWfhGNgKoWdRdFSZ6szeLcNFn4rGtouC+nCOZRKyd5VzbtVTbv74hWZxV\nqT0nGbYKJyobMWPGjFEV1W/IrswZ0a6tWqi6Pl5n7d11O4hGqGzG9rWpgyeeeGJcvxl9c0JW73XT\nR2c1jIMPPhgoTDfmoN12221AiQD1e2uq+b31Bo1G0sZv9XHXowrKdec9Zxfdk08+ebT6QadQRS21\n1FJAyYvxuvn/Rl7Kwl3bsnWViX4Kq3mYe6QlRsUas/WtI6YfI/qiI1qtMj4RHn/8ce64447RyFl9\nLFa+33XXXYGiKLXaGG269tprAyUHybF4zt4DqrZYWdsx+zuvu3PrdVYZRV/TPvvsA5R1o7Kq2+Mq\nFU4ikUgk+oLaUWrTp08fFxkhZCayctmS28uu9NnoX9CfYZSK7Mo6P761rRt16KGHAoUZ6cvxdxOM\nu+Gztt8J3s5di1JrBpmrrF5moW9GP9cPf/hDoLCv+Flbq3ZpVaW2eq+JrFD7uJFAVehHHk70F8Q8\nK9eNFbD1EY45LlCupyy/m7b3p8bR8lwMDQ2NzJgxY1RVV3VMlL3r05GBGiWmgjWa0arg7scoRFW+\nvhrnyjwOLRIqYXvSx/HI6q0CIrN2jrXVd2NduE+ViGzZqFVzUWJEpWzdiiJGcqri9MmaY2Yej88V\nFbBz7b3gPVRXzXaj4+eOO+4IlCreXhfnwPvWDq/64qyNaL7XqaeeCpSIYNeH1iIVts9S/dY+Q2Mf\nnPhesJ+WeT1juzfXWRepcBKJRCLRF7RVacBICKPAqvZh9IjMVYbh9tFvoe/F6tPGhMtcZY3as2Vl\n7i/aWKtiySdB3xSOUOHo19JOrVLRn2FUSfQ7RbUZa17FLG6jXpqhHwpH9mVelfXHIlQDskDrRxnR\n4zroVlXfiDpzsfrqq49cdtllo/4C2bsq3rEL1Zz5MOZHGK1o3xLZvbZ21b7M14rZ+oZk+a6fk08+\nGSh+D8cTK2G4P9m/VojZs2dz9913M2vWrI7XhezcbrUbb7wxUHwuPi/0b9gF1XOXnRvh5Rzrv9J/\nYQSfPhrXhT4dVeOY8TZs12wdtXOPuGa9v6v8jzFiVz+m6l01qELy/jYKzv357DOCz3skRoLG7aPa\na9YzKhVOIpFIJAYKbSmciMi29U+oXIzE8e081v4H5S3bLAopRtLEt3GziImq6tBj3tZtK5xm+TeT\n7AcYXzE3zkX0a8RzqcqjqDpeL9ibaDXqT7+VfoqqisTao808twbWkksuCZR1pm+vhfECrSuhTjLK\no/8wHtOKAioSlYxKQ/+FikQbukrJc7eSgAzaqhuLL744UFSBSmi//fYDSk+ZKkbrPTo8PMysWbO6\nUoEisnbHaO6ZfbKM1NKiodL1d9aHU+3p2zHvz/3q9zQC0HP3Xq3ySTdDN+vKVVVPiDXS9OmYlyP8\nf3MbfTaqXGKNNGvpWbfOey/OyVgf3tjv41ylwkkkEonEQKGjWmpV7E2WFSNqZPEqnVZt7rE7Yqxg\nKtP1rRtzIIR2apnyBMftmQ/HuZCtyerNRdKubGSNeRn6wWS0MZrEz5HpOsdGKRmVZjRLM/SzWrQ9\nOfTlyOJilQUjr6wv5rnHvIhmCsb/lxU2i2prZy70wcjSretltJh+p6hwVfGuC5WOa1Zb/GabbQbA\nN7/5TQD22msvoORl6B/xuhvJqYKOSnj33XcHSsdRxzWWKXdaLTrCte38e4/E6x99dH4f505En220\nCngPxkjCur6/bsyFfmbnQOXh9RCuH/OzVMQqVKs9e094bj6LfYb6fBDOiffUmmuu2eopje43o9QS\niUQiMXCopXCGhoZGhoeHR+18MaIq9mtvlXlW2fzdPrKx6C8xYuOiiy5qOG70p8T9OH7VxE033dT1\nfjjNEG2j8XvZ/Xrrrdfw2WgW58KcBCN7IkuMttxm6GcejtFn5kv0CnV9N6LOXCywwAIjr3rVq0b7\nHRk1Zq+VuqjqIaOSken6vX2UYq+gGBnq+vJelWEbxWYk6tioutmzZ3e1QrKI93+716kZmlWNr4tu\n5OFEGKEb+yg5R1YqsOKAUa5WlojWJ69nrPoSo+VEu9UUUuEkEolEYqDQVqWBqrdf1VtzzO+B6rd7\njAWP28XIi5gPVBVl4vYt1P3pmg/HmkPWg6uC9mRtueYUaMvXP2VvoNhpr1tsMKrGbiqcXjHWKlhH\nzu6ZnVaXbmcuXHMx6kdfihn9se6bOSfa8KvmrKqicbNoyXgtosKOvkH/f2hoqC2F0+q2T0fUnYs6\ntfmsKGAUmZn+VgyI6yoqk2Z5M+3ek1XWqFQ4iUQikRgodKRwtA/K0qKNtFNmu/zyywOF3cdokmY5\nDiK+/bV3Rzb3xBNP9CxKrdXIqchYjE4xl0lm04ypNpvzZuN5OjPZbiuqunMxffr0cf6IuFbjWnR7\n/5pDYmWJeK+1i1bnRl+hOXWLL744Dz/8MLNnz+7aurAaQ1XfqkFH3XUxPDw87jpXwf5G5hRZ8cGI\nX58PVf6odivgx3UaO5H6OSroVDiJRCKRGCjUUjjTp08fmW+++UZ9NJFV2489+hmqst+1U5uHYcRN\nXbYeUVWvKCqaCdhez2upVTFMOypavVVU5SA183c1O15E9HMNosJpl7V1irrVoueaa67RnC/zHmSE\nKhfrfLnmzTS3X5FVf0X02cTrFbtful/hPeg6i/2QnFvvHZl0XDe9iMx6uqKduXCejTK0r1GrUWFe\nX//q0zFKtWqujciNz+ZuIRVOIpFIJAYKdX049wN39G44U45lRkZGFmtlw2f4XLQ8D5BzMRY5FwU5\nFwU5F0+i1gsnkUgkEol2kSa1RCKRSPQF+cJJJBKJRF+QL5xEIpFI9AX5wkkkEolEX5AvnEQikUj0\nBfnCSSQSiURfkC+cRCKRSPQF+cJJJBKJRF+QL5xEIpFI9AXDdTYetDL0VYgF7JZZZhkA7rijaWWJ\nB2qUtnlazEW76Ebxzqdb0caq8Q5iIdOpQidz8XRbD2LeeecF4NFHH234PtdFwdOqeOdyyy3Hcsst\n1/L206ZNY9q0aaywwgqssMIK4/5/ZGSkYVHfdddd3HXXXZX7GYNnaq2jnmPatGkMDQ2NVsOF8ddh\ngvme9Hux5JJLjnY+bQXPf/7zR/sI1YHjnWuuuZhrrrk44IADRjuvJjpHXA/t4vjjj+f4448f/bz8\n8suP9s7qBR599NFxL5t2MNkaj3AN9grzzjvv6Iu0nxiIF04ikUgknvmo3fGzyf8Dnfdm6bTvSezw\nKZZddlkAbr/99qqf9rwfThXiOcd+J62iW2aLTswFsTtl1fWsuk7dQtz/c57zHAAeeOCBCcdThTSd\nFPRyLjbccEMALrnkkpa2tyvp0ksvDZTrHDsCx6643eqn1E4n2Kq17thUajfffPOk+4v9kSK6dW+1\nOmdPK5NaIpFIJJ756KrCqQvfnrJ4bZb77rsvAMcccwwAP/3pTwFYY401gML+q/p5d8Dy+65wmjGI\n1VZbDWC0g+TPf/5zYDyb6zYGgdX/7Gc/A2DjjTd2TEBhb17n2F+9U9gN81WvepXHnfK5GBR0Mhd1\nFcaPfvQjgFE/mvf/oAQdDEJgTbetBFUBEs2QCieRSCQSA4W++nDE3/72N6D0TV9xxRUB2GeffQD4\n/Oc/37C9jEiG9O53vxuAU045peF4J5xwAgA77bRT03OpwJT5cISMZbHFnozOvueee4DSs/6RRx7x\n+MBgKJzp06ePzJw5k9VXXx2AK6+8csLtdtttNwC+/vWve4yG/99vv/2Asg7Es5/9bAD+9a9/Nfxu\no402AuDyyy9v+H699dYDYJNNNgHgYx/7WMP+4ty5f9fZgw8+2LD9VCqcTv0OVZFR7a6bXszF0yVc\nOo6zHwon/n+358r1NTz8ZIZMlU+oGVLhJBKJRGKgUFvhjGVM0aYe7YiRlYuLL74YgE033RSAf//7\n3w2/l8351vU4MS7d7c4//3yg2B/f9ra3AbDAAgsAxR4ZxzEBplzhjNl/w+d4nfx/I8L++9//dvX4\nddnb0NAQM2bMAMo8G0mzxBJLAEXZjvkdABdccAEA//jHP4ASdfTa174WKLb8tdZaC4CllloKKOds\nYq/rYIMNNgBgzz33BOCQQw7xnFo9pdHxPZU7MuU+HPOQjMzy3lp44YUbvp9//vmBoozvv/9+AI46\n6iigqLeTTjoJgFVXXRWA6667rqVxdHMu9t57bwAOPPDAhu9dR1U+2gh9PK4f19VHPvIRAI488kig\ne9Fpos5cDA0NjQwPD4/eEzH6tEq5RIXrM7BTv6XH85k5a9ashuP5/80UT917JBVOIpFIJPqCgYhS\ns8qAymeHHXYACvtaf/31gaJcVFS+5X3r6wuS6a6yyipAYUoqptmzZ1cNacoVTqtRJ+aUyHzMLekW\nusFkvb5nnXUWAO94xzvcN1Cux0orrQQU38/2228PwC233ALArbfeCsDJJ58MwJZbbgnAr371K6Aw\n3Msuuwwo60Tl/NKXvrTVU2nA/PPPz//+9z+eeOKJvimcmF8h219wwQUB2GyzzYCiDjz3Zr4a15Nz\n/tBDDwFFIcXtq9CNdWEU6he/+EWgnKvr5eUvf/IWvOaaaybcb7xHogpwLozsdB10G90s8xM/a7nw\nHP1//1ph5aabbmr43meicxGjWV1ffu9nlbHKy79xXC9+8YuBcm+KVDiJRCKRGCh0ReF0K5Kmaiwy\nGvMxvve97wGFrYk///nPQGFI1k+bZ555gGIHj1FIYzAwlQaq4Dmbk3DDDTcAhdl0K3qlLnvTltsK\nVLSnn346UHwyZlk7B9qVI1S0Kp6//vWvALzxjW8E4MMf/jAA//znP4ES8feHP/wBKNFucd3JiGV3\nCy+8MP/617/4v//7v777cFzzzomRm6p+q2a4XYSq/oMf/CAABxxwAFCYXGrE+wAAIABJREFU8yKL\nLALAG97wBqDkuvVC4Zg3t+666wLw4x//GCjqzeuskrXigD4/x1TlExZaOL761a8CsNdeewHw29/+\nFpjUstEWOlE4UaVF34z//8pXvhIo12nbbbcFil9Sa45r3eeIf91v9Ku6nx/+8IcAbL755kCJ9DVy\n89577/VcJz2/VDiJRCKRGCh0pHB+97vfAYV1dZr1OrbS8FiY33HRRRcBhenE2HGz8GU6xx57LACH\nHXYYUHwFiy66KFDe7mPQd4VTN67ec/d3Mhht8lOlcCarEyWqVJznohJVkRh1FO3YrjNZvr6ht771\nrQAcccQRAOy+++5AiXaTaTtXkQ26P5Wy6EfuSfwsE3XMqnOZqjZ3c9n0e8mQVY2nnnoqUO0PacGv\n2YBu+vbG5LM0/L/Kx3NxXURl49r//e9/D8CLXvSihv27zvz9ICmcqGj8rH9Sv6fPsje96U1AWQcv\nfOELAdhqq60ajuN1d/0873nPA4q1R5+dVgCVsP5Pj+tcxfXpvRfnMhVOIpFIJAYKXfHhdCv7Nb5F\n/XzFFVcAxZ4ZI3LMx5AZ2QtF27Bv48MPPxyA973vfcB4RTVnzpwpj1KLY4oRXVFFyIDNNeoWi+tl\n7kmVEva6XnvttQC8/vWvB0qUkSxQ5rrNNtsAxc/h/qy0a/6O38e8DiN9/vjHP0463l7MRWThzomf\nY45bZOsy43gvmFfh9nWrjTdD3bkYHh4etybNj9HvoBI1z8q8LXOJJthvw2ctFW9+85sbvtdXGyPx\nuoV2ctXi9Y6Rdl73LbbYAoCXvexlQPE/6ms588wzAbj66quBcv+r0lV9iy++OFByEg8++GCgVOnw\nuH//+9+B4tvReqVS8hmrgoo5dalwEolEIjFQaEvhdLuej5Ez5pb4dvbtGu2JsgQVjT6c66+/Hihv\nfT9/4AMfAOB1r3sdMJ5Zj7ElT7nCmeA4wPi5Nh7ezod33nknANttt92E29dF3SzqGTNmjCrKWPuu\nWeSdKs28KdmcikQ2by6K+73vvvuAkkmuUrntttsAuPTSSxuO06x6QxV66cOpGoss30oBVWqw6ve9\nqk/Wi7lQgdg/qW4WvT46LSHC50avOmd2Iw9Hn6zX13N/wQteABSlYb1Aq3AY8RfvERWufmqVyWc+\n85mG761H6XF33XVXAM444wxgvL+syu9at65cKpxEIpFI9AW1FM6CCy44ss466/CTn/wE6Dz/RgVj\nlNGJJ54IVDMS3+L6M8x21ZZvLoG2/xtvvLFhfBP4bOIhBk7hOGarLcji7FpqFIrnsvbaawOlNla7\nTLeXPpzPfvazABx00EH+HqiuE7XOOusAhfXpm9FXY87Ab37zG6BUGlABRbzrXe8Ciq8oRqVtvfXW\nwJMq44wzzuDee+/t+lx43cwJkqk6BzvuuCNQrru29arotjHHB8q6GaTIrEm2A4qfwSjCVqFCViGJ\n6C/pNtqZi1ZVtgrGGnl77LEHUO4dzzn6uaJVSMXj3BqtqDXJ6LXvf//7QKnU7tzpG8qOn4lEIpF4\nWqGrtdTMl5FpNsvL0ady4YUXtnT8GLMuo5E1mBWrUrJWUw0FNmUKJ1bGdszaeGUqZmlbHyzWXDIj\nWf9VXbYopqJCsqzNyCrXj+doHx1r7ZmD4tzos3EOZHmdKvFezsVHP/pRoOQOmWehzd41bXUNo5PM\nu9FfZXdUo9iMVrJ7abfQzlx4/aICEfYr+trXvgbU9+FYucJKBULLh7kl3UYv1sUnP/lJoPT60j/t\nWndNR8tGrLgf602uvPLKQFH17teuytZiPProox0v0LwKfVaLTiQSicRAoisKR8XRrIeCsdv6bGRx\n2h2r4Bh925plHe3ZRvTIqGTMwmgY4/MnOPe+KRwjrmR99nQx2izmWUS2LyORveu/0n8RlVJddt9J\nLTXHrJ1Ylh5R5bOJ2e+eo/XjrHlmHSkh6z/nnHMafue49AH95S9/afXU/H3PFE5cw9YBNLN8tdVW\nA0qdONVcVPveG7vssgtQbPtmkHcL3ZgL67iZh9MpYuVk4XOiSllV+TddX5PUXPR3Hc+F97X5LVo0\nnBvnKuaKWWnAMXouKiHvd/2b+iX1Bfn88ff6CL1nnEt9OFVWqlQ4iUQikRhIDDffpDlkCFW2V9++\n2lqNHpKla7f2rWx11/e+971AsVNb8dZM5chQZNRGcEVo51QlWLOrLuPtBmJkjeosRhVFhWI0kzZ7\nM4aNLml2DXrVN35kZGScz65K2Yh4ro4xKl7Xh9fPiBujEDfZZBNgfCWBeK5VmetTiThGq38bgee5\n6+90zmSeqkEZsTZ49+PavuOOOyY8fq/XxUSIlY077cRpJJfnYIRmlbIRZu2rlJ1LWX/0KfYC3ite\nn1jrzG6osd6g68BnmXMZlYv7NxpNxbveeusBcNxxxwGlbqFRrlW190S76yYVTiKRSCT6gq5GqcWu\ndFZv9e1q1ebXvOY1QKl5JhOONbEiZCCyPSO2RKykG8+thXPtmw9H27tMRVtrlV3b7bXdWmPJvBwV\nUmSLMqa6XQ/r2KenT58+MnPmzEpGKesyYi5GLcVIOysWWAnXagqyLnNTfvnLXwLFPu06MptaBS2T\nteaW6qDVuZmKiL1mHTwjtPXbS0bG6l9VgNeimfqswlTMRRVU1EbuWX9Mlm7FEaEKsL6YkV4qatdT\nq+jmXETFoC8n+sN9DvisdG1bR+6SSy4BShSrEYCuce8VfX4qpvPOOw8oUWu77bYbUNZJlb9VpA8n\nkUgkEgOFriocYf6L9Xt868osjYu3H7s5CP5/M+i/sKKAkCmrdNqwS/c9D6dZbxCZj+ruyiuvBEqF\n3V//+v+1d+bxuo3lH772OcdUMoQopJQhKcmcIUOJKDOVIplCRVJSitIkkSRTFFJkKJIoSpJUSgPJ\nlKG5jKGfDJ39+4PrPPu99157vePa79F9fT4+29n7fdfwrGetdX+fe7oWaD8ard1180FYslqknqP9\niW666SagWFGHHnooUPwPBx54IFAieRwTI27OOOMMoMwfrTYVlTX3VFBVUZRVDJNV3y5xtUF/hNFu\nV111FVCUT7sMw1ioSMyzsfOrqwVe/zjHjeBzXlg3rC5fsOrv3VSLrrvPnaurrbYaUFS9+9YPbrTi\n7rvvDpTIOvOuzj//fKD4LVVMbj9WEPD5EiNMrcLh51TQPtMlFU6SJEkyVPQlSk3MszHqw3VDraqr\nr74agK222goolmbVenXEqsBR2Wgt2PHTigd19CtKphuq9u3vtUisG6bfK9Yd89xds425CJFBnmtU\nY673WuHWYzaK0CgzLUjP0Rpr++yzDzDe2jKfxkgsc4/Mzo7WvdackXxuv9scpdmBaEnr77Qit37O\nqi67g6TXyDi/pz9TXNmoup7HHnssUBSQx1HXqbbbDsaRiY4rRpfp17ROZMRqCp7DRz7yEaDUXtOX\nZ86aq0FG5Oof1YfjM1h1aN1CVxccaxVVVDadkgonSZIkaYS+KBwtWvvYGA2khXr22WcDJacgRjrU\nWTpaInvvvfeE39MyrooyqYqw0OJoMhchVvO1KrDx8K69GnFThZUFttxyS6BEudUpnEFSlY+lovE6\nqN7Mm7H3i9aT0WOx35E9gFRE5mWZr1VVDdwx17d48MEHA6VSs5UJjKZ0O4ssskjfsuHl3HPPBWCX\nXXYB6mtV9Qtr66299tpA6fAYqfNn9INu7zOvi/PLlRMxP6uK5ZZbDqg/t0E+D+K2Y1Vmz8E8Gn0z\nVhDwc94T+rOskbbZZpsBZfXAMVP96b9y/96Tbkefkf4u69t5T7r/satSnYxTKpwkSZKkEfoSpeZb\n1Ph3fSkS+3bHaKWIf3fN/UMf+pD7b/mcdabsihe3F/M/JNbqGkNjUWrmAKhoPFZzl+ryMFR1VuZu\nN8KvXXrp9RF/ev2tnWd1BH9qZbm+rLVm9WdzjrQGzSS33pjnrgL+4he/CJTILK+/ETZed3MP9GdE\nZdZpnaixY1FF7NVkFrtKJ9bO857pNLIu4j2kKtS/6ljoJ6tjGKLU5LLLLgPKPBqz3wn/3e6zzs9b\ncdtKJ5F+jEXMx1PV+zxwFSDWSPMZpm9ljz32AIrPxkoVMXIvzivvHatJ223X/bSrdDNKLUmSJBkq\nelI40ZLQj2CGdxXWUjN6yag1o4xi9emI6sAs6ir0GRmLPkyVBjw3q0Tre9FiqeKcc84BSsbwAGuj\n9Wy9HXXUUUDJdlbBqEw8F1Wdf/e6bbDBBgCceOKJQLHW3K75W0bgWB/K+WEWttnTKh+jKZ2vW2yx\nBVAy0430ufHGG5k5c+ZArHp9d+YQOR+skqBvzrV0o4dUOu32jFG5mG+jZWtlCqt9uN1B5GdVddzt\nFe8V1ZrPjdjhs1OFE2uoVX2/m7GICsN/q2RULvpUvCfct7/32WnEpnPY63zqqacCpVKAikkl7XZU\nMN5bziv9qj47J1kV8vhS4SRJkiTDQ8dRamP7nvjTt7TWVFU2qvg53+p1eTjux6i3OmUjMYtai6jf\n/o5u8JzuuOMOoFjVWhQx4saOj/YSmh1Q2YiVJbwuVnm2QkTMCTAqzd9rrRnlppIxK9ucBOejvhkr\n7p5yyilAUdRmZWsNGl3ZbZ2xdvDYzPT3XL0HvP6uyZtrYvVgIz7tm+TafKxjp+qL/lT9Hb3mU3RC\nVDbmjOh/7DZSz3nh982ziXTqu4nVoWOfp25WFeaaay6WWGKJWf6gqmhAlYTKxs9Fn8oKK6wAlIhL\nlY73ghUJ9F9673luqkJVvvPF3LZYWb2qMkJWi06SJEmGkp58OL59Xfv27WrMdrc5DB6TuQNut1/E\nt/OYfzdeSy2y+eabA6VaQ11E36DoxW8Ro9NiVYU4/lpXWu0qEmunaZVZqeLjH/84UPJ79N24/hyz\n6N2P29PK1D9iLa5YA1AG4cOp8mc4RlbE/uY3vwmUenNWClCV6dvRf6GK8/uu9VtdONZS65RhilJz\nTLzehxxyCFB8dZ0S52ldTlInYzFjxozRZzzjGbPyYVRnq6yyClCedSoco8ZU235P/5I11FT5+imt\nRBDrCuqzcVUpVs7Wp+f2HNt2lU36cJIkSZKhoieF41q6VVcPO+wwoLxFjUaztpnrzPonzLdQCTVt\nxU9AzwpHC8Gs9U6JUSpaNk3TifU2bdq00TnmmGNcrki0ELXaVBhW+7V6uL49x87oNRWO2fHmzxiZ\nY9VpcwjsEbTuuusCxcqvyq4Xs/Cj9T8VVr3X/4gjjgCKmjPPItahU91pnRspqhr8/ve/D5R7Uh9B\np/7MYVI4qj8j+lQJq6468S0c502v9JKrpsLw3thxxx2B0tvHHCAjMf1ptJl5OT4frLKiTzBWf1YF\nRj+V80b/dvQF1kWndZqrlgonSZIkaYSeFE5dteW99toLKOuLTWEFAiMu6nrOjGHKfTjDQi+WrHk0\nWuUxt8joNCOw9PkZZSZGr9VFMVmRQotX63/M8QHV172q2+KYvkqNWfWxGrgWsMekonE1wWg268LF\nShVarFY4uPTSS3s5vI7GYs455xxdeOGFO+65U0eVL1CrXWs+4nxyDPVv6L9wO2b7u1JTRTf9cDy2\nWP3Ee2C33XYD4LjjjgPKs2vNNdcESj8sI/IOOOCAlu3FOR7zfhwzlU3VPRGVTd09lAonSZIkGSr6\nUmmgH3HqvVC139jbvg1S4TxJN1Z9tIratRR7paoaeKcK2wrdVo+WYfJb1DHoHk+DGItua535s6rT\n5yArXsNg50VUuvq9jVI0h8zVBPvXjDk2oES16RPUv1WndDutGp4KJ0mSJBkqulI40SJpt/ZQrxhR\nY9+dmJ/Th/2mwnmSflpvVZEuXi8jb+wB0mvtq25xv9F3NDspnEEzjGNhVrz1vyY5HqDzrPkq1dhL\nlFq7PcDi3Lazr6sG/oy18uKxxior3T4rMw8nSZIkmS3oi8KZ5PMtnzOrtddaVVX7b3fdMVrcrm8+\n+uijPSucurj12YVeLFnzacz5sCaafdq7rsPUZrRhVd6NWfZ2S61ibI+SfvfDmd0ZhrHoVqlEer1X\nOx2LkZGRWVU1vDfqiPk0E/VsCscEtH+v9Gs1KhVOkiRJMlR0qnDuAu4c3OFMOUuNjo4u0s4Hn+Jj\n0fY4QI7FWHIsCjkWhRyLJ+johZMkSZIk3ZJLakmSJEkj5AsnSZIkaYR84SRJkiSNkC+cJEmSpBHy\nhZMkSZI0Qr5wkiRJkkbIF06SJEnSCPnCSZIkSRohXzhJkiRJI8zo5MNP9cKEwN0dlLYZirGwYKmN\nmP785z/3tL2RkZEsWBnox1jEttXd0q8CuN0yO8+Lfjenm53Hot80WrxzZGRkXNXSdj7f6fcGtZ0x\ndFTraPr06ZX/VeGxxs/Fc6g6J38/bdo0pk2bxrzzzsu8887L/vvvz/777z/r91XMmDFjVgXaiZhj\njjn6NZYJZY6suOKKrLjiim1/r+r677TTTuy00079PMS2mGxO9Zs+3s8tzDPPPLP6wkxE3b2T9E5P\nLabb+DzQfenrfjdya2N7HbcniBNU66mq/bYTXkvX3/vy8fvxewsuuCAA9913X8vnJFpvdS0c/Hws\ndy5pvRV6GYuoSGzu9tBDD026nUG3io4885nPBODee++d9HP/S/Oi7hr8L41FHdmeIEmSJBkq+qJw\nbFhV1Ryo00ZtVda6tNt4qQsrsW2FM23atNEZM2bMat7kvlUwjzzyyKT7rhsb/+7Yut0HHngAYFwj\nJ8/19a9/PQDnn39+R/uLpPVW6KbRluPdlEIZFM94xjOA4Wq3HdV+t2qw1xWUYRiLYSEVTpIkSTJU\n9KXFdK+Wwuqrrw7Az3/+cwDmnntuoLR+jS2je20tOwkd+XCmT59ea1V1ekwqGs9ZH4Dq8T//+Q9Q\n7wOoo8qXk1Fq4+lmLMa2qX5yG4M4tMboZl7MMcccowsttNAsJfLoo48CsPDCCwNw9913d3UsVYrG\n58Amm2wCwCWXXAKUuR5bSb/oRS8C4J577pnweNq4t4fuHpl//vkB+Ne//tXE7maRCidJkiQZKrpS\nOHPOOSdQrOJurTfDc7U89FOsuuoTIiNaib/5zW+AYv0//elPB+Cuu+5qOY46v4hM8LmOo9Q8ZvMs\ntCyWXnppAG655ZZJj0kcU63AiFadPz2XddddF4ArrrgCGB/lVkUc+8gwWm9Txew0FtG/0W96GYs4\nx+si4+pWLhZaaCEAlltuOQCuvvrqls+vtNJKAHz2s58F4Ktf/SpQxugb3/gGUHLXXvjCFwJwww03\ntHUcTc6LV73qVQBcdtllEx7bX/7yFwCe85znAEXp6HvzufDHP/4RgOc+97m9HM44UuEkSZIkQ0VP\nUWp1VnK7aLUvvvjiQHlLv/a1rwXg+OOPB+Dhhx8GYLXVVgPgpz/9KQD//ve/gXqrvo1olo6j1FR5\n7a6dxuiz6AdbYIEFADjwwAMBuPXWW4GimLbddlsA7rzziRzV173udUAZg3YjdZZddlkAbr755nHH\nN1U+HNfao8+uire+9a0A7L777gAsueSSwNRZbzB+LKoiOLfffnsAzj777La2672x8847A8UK/+Qn\nPwnA85//fAC+/vWvA2VsevUdOS9HRkaYOXNmX+ZFv/Pr6nKbnFfeo/6U22+/HSjPB+/B17zmNQCc\neeaZE253kPeIfuwPfOADQLmePhsnSy6fjH322QeA4447rqvvV5EKJ0mSJBkqOlY4llWBYol2Ggcf\ns+f9vpaHfpE77rgDKMrGY9V306lV30a+TtdRalURe1X/1ufjGO66664A7LnnnkBRNFrIjsH9998P\nwDHHHAPABRdcAMBf//rXls9NctwtxxP9ZP5tKv0WKhRzjjxnj/VjH/sYAPvttx9QfAPivPJ7vdLE\nWMR7SIv2pJNOcrstP1XS0bp3XnmP9HpvRD/LMPmzfvWrXwGwwgorAPCpT30KgEMOOWTS7zk2zhvn\nvv6OdhnkWHhszuW///3vQLmevZbg8TnhfOmVVDhJkiTJUNGXSgOdrsm6Rqr1pMWxxBJLAHDttdcC\nxapy+8bvu76pVe/6eLTm4jpnG76mjhTO2Ki3dnOStFw8Vv0O119//YTbkUsvvRSAG2+8ESg5BvPN\nNx8AF198MdB+3ocqMo7dyMgI//3vfwdqvXn9PcdXvOIVAPzud78DYMMNNwSKj04L9txzzwXKOdat\nY2sF9uor6MdYRH/nTTfdBMDyyy/fcoxx9aCNY3O/QLmOFvj89re/DcAJJ5wAFEv53e9+d3snNH5/\nfZsX3fqAo79zu+22A8r8Uf15T0VUDS95yUsAuOaaa4AyJp/4xCcm3f8CCyzAgw8+yOOPPz6weyRe\nzzplU7eiEvnZz34GwLHHHgvAWWedBZR55/ef9axnAaWiSRWpcJIkSZKhoqN+OFW0WytNa974+c02\n2wwob29zStzeV77yFaAonTXWWKPlc1deeSVQLN3TTjsNgD/96U9AUROuV/Yz+3vatGnMPffc43wm\nddvUgjDa5Itf/CJQ/A1aaVq+hx9+OAA//vGPgRI5Y/+b3//+98B4S8QxrbKUHYPog2oiI95z3Xzz\nzQG48MILgWKpvuENbwDg1FNPBco5fuhDHwLaX7+2coVRjf2OjuqEaMW/8pWvnPBYYgRVxOvpvFMl\nqPo9R32Aft57yDH03vDv7Sqqbqga926jWx2jt7zlLUCJ2PN5YF5NjFZcaqmlANhqq62A4gv0nvL5\nEOvHRfrlG5yMD37wg0BRX6oxr7N43fRnOzZf+9rXAHjjG9844fat7uJY+JxxzNxunbLplFQ4SZIk\nSSMMpB+OFo2WqJWNl1lmGaDEglvZ+Lbbbmv5vBnDL3/5y4HyVteSUSnpw1lsscWAsvb6ne98Bxhf\nkaCN+mMd5eHMMcccs6wi+9u06zvRitp4442Bkkuij0b/lqrNuk/6bhwb12I9DvuuWB+qznJVLaqs\n7r///r7lW0S0sl1DF8dMX43+jejX0KI95ZRTgM5zEWLPoXbp51jECMto/et3ePGLX9zyPRXRj370\nI6Aom2222QYoa/BiBN/pp58OlPmx//77AyW/473vfS9QqpsfffTRk57fMEWpxXmhIvb6xvmhqvPe\n+u1vfwuU582b3vQmoFybOpoYi/g88VjXXHNNoPi1VV2eu1VZfG7EfDD/LSoon5FGCHdwnOnDSZIk\nSYaHvvhwtLa0plUk66yzDlDelptuuilQsuVdw1WxWA9MxWMEllnx1113HVDWN7XKVDSqhrnmmgso\nqqNO2XSztj86Osqjjz5aW08u5k/4ea19c030a2mt+XnrO+nn8NysbKvFrIXjmNRFzWkd6htqwq8R\nlY1Y7aCq7pyWqvkV/rsqQkslrVKK89P54HzpN1ZrmIhoPcc+Sl5Pfx9rYon3zuWXX97ye3075mm5\nHe/Jww47DChjZR6XY9WEn6tf+zCq9cQTT2z5vWo9Yg03x9J59Itf/AIYf21i7bdBjs1ee+0FlKoq\n4nW+6KKLgOJzede73gWMr0O37777AvDSl74UKNe5KrLT55EVTQbdvykVTpIkSdIIfY1S86c9W4wW\nU6FYP8q3qFFErkubKaw1Ftf0tep9S2vtH3TQQQCsssoqQLEK69Zi+2Gx1H03jo3nrkWrgrEWVvR/\nqdK+9KUvASWKxLFwrd/cJT9fZ6nEbqpacXPPPffArBz34fXzpxF7VfvVCnM+eF1jtJrZ+Spk1YKq\nTxzzQdHJfPIY/akKNAPce6mK8847Dyi+OyPyqnpGbbnllkBRxFrOTdIvhWAUq/PG1QL9mnVYh9Dn\nVCRWbh+k6ovKRvS1xGfV5z73uQk/H32D73znOwHYbbfdgKJ8xPlVN8/6RSqcJEmSpBH6qnBitV8t\nSf0TrqV/5CMfAUoehlEj/jQb2rj6aFlES1i/h5E6WsxGsdUddy90q5K02lVvUbW5PSPw7Olx8skn\nt/z9W9/6FlDdHbWOWJ9uEFZc7OUT15GjT6YKLU4zyVUD+i20eOPno6+n20q7/STOG/0KZs+3+/2X\nvexlQJkHVdb68573PKAoYytXTAWd1l6MmFuy3nrrAeP9VIceeuik3/ceMb9rUL2D+km796UVJsyz\n8bo7v+K9YCWKpkiFkyRJkjRCXxROjHv3p4pFX429P6zr5NvVdUUjLmLvkGgNRjVw1FFHAaWbXZMW\nS9VaebsVB6r8TCoW1Zo5A56zEV2ild+t1eiYV9Ve6gWPyWOPKuzggw9uazuO6fvf/36g+MGq1rOr\n+MlPfgIU628qiP7Odi1YrfhFF10UKGP75je/ueVzUc3p4zPyaipVXrdz1GM2d0zfXOwtdeSRRwKl\nYoW4wtK036IJVPuOzdprrw2UagpWmHCMjOzTx9MUqXCSJEmSRuhJ4USfjT+1JOwZrrVu/woti7vu\nugso9Xpcc3eNVwtWy1g1YASPPcu1dLT+6nrCSK9ryWPptFtlXLv33LXWHEN/brLJJkDpf6JvR3+X\neTrd1sSy0sEpp5wysGgcFa/n6rm1qzS02q0/1+5xep1ds/c4jPhTGTdBVMAxWrAK57a97VWkVvGI\n21UB2evevxsR2s1xT0UNOijXz5WQHXfcESgrGY6BY+n1tHaa0Y1m5VtnbJD145oi9iQT//3hD38Y\nKPPCe8+8n6ZJhZMkSZI0Qle11Or8FFqucc1ey1JLxPo9Rtb84Q9/aPm+683mFhhJdcQRRwDFwtlj\njz2AUodKldDFGm1H/XA8Tui+8q3naH25Aw880O0DZW3WMXQ/WnFmy7/tbW8D4LLLLuvqOERLtp91\norS2jCKMlqcVJTxnrXlzinpliy22AOD8888HxlfEqLt2TdYPi6rbOb/33nsDJRLPigFa+0Z8WkPL\nmnvmponzpVufXz/GItb1qsKx8Dli7UXz7qxg4rlrvav6raAe/VZWYF5rrbU8p3ZPqYWprCvns9So\nw059r/321WYttSRJkmSo6MqHo0VQZaloMfozZlP/7W9/A0rfCt9TfbNqAAAgAElEQVTSKpnFF18c\nKB34XHc2m9rPq5Bc11bhNBF9MjIyMqs7Jozv/d4u+qmsEm3Gsedu9nQcc/vlOMZmkHs8scZWFfrD\ntP7aqKjdMVrR5mVpkXrOsRZav5SNGOkn/eoEOhnd+ge9Do6JfktVvfeGlY2dD+ZpmfOmVW914dg/\nx78P8l4ZGRlhxowZ454PRqnuuuuuk37f54V1w375y18C5TmhT2f99dcHilJ2jNyvyscVEXOWhhl9\ntfF+tIqK/u9ulUq33VZ7JRVOkiRJ0gg9RanVrcGKVprWv9a5b2/f2ioerXqjkX74wx8CRdno8znn\nnHNavt+txdpNtNLo6CiPPfbYLAujU2Uj+hGscKvPRsvVCtpG+Bl9ZG0kP2clbnOe3G6dBaua8DyW\nX355br/99q7OpY6VV14ZKHXhjDI04k7l2y/lYW214447ruX30VfUbv+TTtCCjPW4qoi9o/RDRKUU\nu9c6Z4301Oo3ctPvGYVolYbYObKuy+Wqq646qx9Vu3iPROqUjefsue68885AmR9evy9/+ctAUQPi\nmFsJ3XvK58n3vve9WcfXDv2MZq3Dc/PZGNW4Ks1xValGYkWBiNWh9af6nPBZao09/WbtRv7WkQon\nSZIkaYS+VBqIVFUG8PdaYSoL13T10fg5rT39Er6FzbpXEWkNmM9hteB26SYPY/r06cw333w9VzVQ\nGVn12Sg1rTTXo43M0eeiX0JlEy3eaFnHOP2q/jg33njjwHwbWv1GUNnXyK6TdT182sV5pZKKaPEO\n0ofTrrIRrWfr/8UePrFrrT+/8IUvACW7PqL/I6rWqHyjsnHemcdjz5gmcCy8Pvb2ufjii4GST6W/\nysrXdjG1b5J9lqyy4Of82enxNIH7UqH6U2VqlQw7ftZtp6qihMpGVLzub7vttgPg2c9+NlDmT6/3\nTCqcJEmSpBH6qnCqsu1jJQJ9MN/97neB8f4Pre1f//rXwPh1a+PvrZysX0MroFO6saj/+9//8uCD\nD/ZsjRslcs899wDFp+JYmhXtWq3RKZ6rlqfKRss4Hk/syxMZq4D6nYHtGLldK9pqgW600UZAiTY0\nH6tbnB9x/drqwp1auFNBjB5SkdjNVJ/e4YcfPuH3VfneQ1XzNP7ef6tsmiAeg3PRaMaPf/zjQKmZ\nF/0aWuUqIdWf/W5UQtbs6zQSs4kuqPqtxdwjf/o8eMc73gHAueee2/L7SK+18vSPO9b9GoNUOEmS\nJEkj9FXhxLo+ce3TdWIzfV1L9/OuI+rjiREbRu7ox1hxxRUB+OY3vwnUV4muekt3+9aeOXNm7Xer\nxiIei9Ehrv1bG+26664DihrQT3XqqacCJVrNvjquV0ficTrWRrtoUc8111x9X7N230YnbrjhhkCJ\njNI/0Wu0mPOvKjLnqquuAkp31UFF4409hnbnVsxpsy+OinedddYByqqA5xotWf2g3kPtdqQVLWp9\nOL2qzcmoqzhgJWNXQMyziXjM3juufOjnsPqGVRnMaWrXzxbHaKmllpoVMdcvPLeq6+U9csEFF7S1\nPVXfe97zHgA+/elPA+XZWUdUkf1Sd6lwkiRJkkYYSC21urh1s+u1cH0b+xY3k1hL2Kx5/ROf//zn\nW7Zn7we7H6p4qo6vat16dHS0o1pqVhsYe64xGqxOLfh9s/A9N30zZuObX6Nlu8MOOwDFOjQL27V7\nfUKqhnaPY/r06Tz++OON1InSL7XxxhsDxRKt8gGuuuoTl8Zzdf60q2y7pYmx0PI8+uijgZKroqq3\ni6V+CscuVpu22oY5Tz2vuYd7uR9j0a7683MnnXQSUPKqPCb9Hvo19XfaZ8uul3YE1leouu82d076\nOS98trWb26iqcx44VvrHY+dY/67vZ+utt275e1XUqvUO63KwspZakiRJMlR0pXB63umTb1vXcM23\n0cozs3i55ZYDSr7GtttuC5R1SS2bT3ziEwCceeaZQPtVaCdYn+xI4UCxTGLuQLvjGrPetVz8t383\nSsnInbe//e1AsWRVNFp1WsbidlWTsQ+82f5GeE1FJVx9cuZZ9apM+lURt59j4TE511Wgzkl9aX7O\naETVf8xpixGgRvpdeeWV7R7ypMepH+WEE07gscceY+bMmQObF3XKx7nqWHlPxKr03v/66qwarTJu\nV0WIKyc+b4zgG+Q9suSSSwJFkVg3sl0fzAT7b/l3HGNXnYwIVjlZxaFODabCSZIkSYaKKVE4orVm\nhJZv02WXXRYo9cW0yjfYYAOg5CJYH8o+3mZpV1FlQY1Zp+5Y4dRZDlU5BlEJ+Tn/riXjv40aMqPc\nCD9VwZ133gkUa8xs+xhlFNfkY0b7yMiI0XeNKRytK5Vu7IvULnEsh1Hh1KHCidFncb7ETHKz7PUB\n9bsK9LRp0xqfF70Sc9J6zS+L9/IgxiLuQ6XRaeWKTvEZ3G0uYyqcJEmSZKjoOA9HS6cfxPVno07M\nmnc90Y6N+insehj9HHVrwFW/7/Z8ZsyYMS4j3FwTo8ui1V3Vwz5aruYeWWPNqq2qPTt8WkFbhWPk\nlr+PVNUr8+cCCywwLut50Hidve769hxbrS7X4p0vRmzpZ4gRgsNEXCOP2PF1l112AUq0ogpG9a/P\nzlpY1hfTL9HvMaiqHtILTWTuw/hqDb1WfR708U60j0EpGyP+fvCDHwDd1ZPshuG9Q5MkSZKnFB37\ncNpRON1aEn7PbHrfuv7eGlzG27tOHSN2qvwkbRxX2z6c+eeff3Sttdaalfkd8ZiMoIlr6lqOHps+\nGVWccfTW/XItV0s2XrdoidZ19IvRdWOZ3dbqB003Y1Hn26vCeaDK7HdduzraWCV4ys2LunOuupee\nimPRLenDSZIkSYaKgUaptbtWGxWJEVrWkRr02mk3lQZmzJgxusACC8yKT6+r01ZV3aDTDOM66izr\nGI0SrbfZMRpp0HQ6FiMjI5XX3T4jVuOtYpNNNgFK76BBc9pppwElB26S+dzxvOhXx0z9YLH+Xx32\njNLfVUXdqoAsuOCCPPDAAzz++ON5jzxJKpwkSZJkqOhK4bRrsfTLshl0VEu3tdSgRA+ZMd5ufbkq\nJdLt2r/EuP2qKKOoKsfmATVVS212oRcfThORTU2S86KQY1FIhZMkSZIMFZ3m4dwN3NmuYulXvs6g\nrcQx219qss8F7gbubLd7YByLTnOF2iXG7VdFOVUdz5O/72Qc4Mmx6PA7swtdjcVTTdk8Sc6LQo5F\noe2x6GhJLUmSJEm6JZfUkiRJkkbIF06SJEnSCPnCSZIkSRohXzhJkiRJI+QLJ0mSJGmEfOEkSZIk\njZAvnCRJkqQR8oWTJEmSNEK+cJIkSZJG6Ki0zVO9AB1w9+jo6CLtfPCpPhZZmLCQY1H4XxgL27Q/\n+OCDk37uf2Es2qXR4p0jIyPjqhzPpnRU6+gpcs7/81x88cW1vVKSzlliiSU48sgjp/owOubBBx+s\nfdn8r7Hwwguz8MIL97ydXFJLkiRJGmGgHT9nQzruh/NUJZcLCjkWhWEcCzt17rjjjgD84Ac/AOBP\nf/pTW9+v6ttV19NoGMdiqsh+OEmSJMlQ0Wk/nKRhqqys2bmjpL3pH3744YFs/0UvehEAv//97yf8\n++w8drMj/bre//nPfwCYe+65gaJM/u///g8o3W7vueceAJ75zGcCsNdeewFwwgkntGxvjjnmAOCx\nxx6bcH85P/pPKpwkSZKkEQbqw3Ft9fHHH5/w38OCltC999475T6caH1/7WtfA2DTTTcFYNFFFwXg\nxhtvBOD5z38+UMZUq8/17LPOOguAF7zgBQDcfvvtQH031k7Wp+eZZ57RpZdemhtuuKHdr3SFY/Oc\n5zwHgL/85S8D3Z8M41p9ld9h0DQ5Fka4vfOd7wSKIpF//vOfADzrWc8C4JFHHgGKAlpggQUAuO++\n+4DS/fbf//43APPOOy8A06dPB2DBBRds+Xwdwzgvqhj0szd9OEmSJMlQ0UiUmhaE1tjWW2/d8veV\nV14ZgLvvvhuAY489FihWvt+rs+riuWjpuPbbBlOucCbYDwBPf/rTAXjooYeA8evXfs6/77333gBc\ndtllQFnXbpdhtN60UD13ifOrDj/v9uqYyrHwXF/4whcC8MMf/hAo1vtmm23W8nvvAedDVMy9+iUG\nMRbxvl588cWB8QrWc/7jH/8IwM9+9jMA1l9/fQAWW2wxYPxc99554IEHWvYnjonzQp+OqqCKYbxH\nll12WQBuuummlt+rbKJK7BepcJIkSZKhoq8Kpyr653e/+x0Ar3jFK4BSMsJ4+ZVWWgmAD3zgA0Cx\nysW38/333w8US0WLKO5PS0W/xc0331x3ajJ0CmeS/QNwxRVXALD88ssDZV1apfP6178eKNZgu9d7\nmKw3LU3X6KOF+otf/AIofi6Vcrvow3NexqilqRiLD37wg0BRqvqtIl5P/RmXXHIJAJ/97GcBuOWW\nW1o+ryIWx1a1Vzc/+jkWvUYLLrnkkgCzfIcqoDrl6nX2Xom0q5in8h5x9cZno+fsz1gFxfmhCux3\nBF4qnCRJkmSo6GsejuuD8W37pje9CYB//etfQCmO96tf/QqApZZaCoDnPve5QFEm/luFEv0VVRaS\n8fh//etf+3RmU4/RaRtssAEAF110EVByTd7//vcD8K1vfQuA+eabD4CrrroKgL///e8ALLPMMsB4\nS3eY2W677YDxykZUyBtttBEA3/jGN4Dq/IrIvffeC0xtbTyVhveK11NrO/pmxH87P97whjcAsPHG\nGwPFx3P99ddP+P0mI0b1pRglFu/bo446CoD999+/re1ZScDoshVWWAGA6667btLvnXnmmQDsvvvu\nLb9XQTcd+dcN0S/tdfV54FjIV7/6VWDqc4tS4SRJkiSNMJAotWjJRLRUXW82N0RF8pvf/AaAnXfe\nGShKR4tVy0Q/hd+P2+/CUhlaH45r+YceeigAr3vd64CSVa+Fc/TRRwNF4TgGKhot5qc97WmT7m8Y\nfDgea50Vbq6SuUf9ZpBj4TkamaVf83nPex5Qrl9U9a4WzDXXXC2/1/952GGHAWUVwb9HX02nfpRh\nmBdVrLfeekDxd5mDNuZ4gOLj03fnuf/jH/8A4NnPfnZb+xumsTj++OMBePvb3z7h33/5y18CsOqq\nbT3eOiZ9OEmSJMlQ0ZPC6TZ7df755wfgt7/9LQCPPvooABtuuCFQMn3f+MY3ArDNNtsAsMYaawDw\nk5/8BIA99tgDGB+v30X+jQydwtEfpUJxrK1P5TUwKsk1/IUWWmjC7cWxPPDAAyf83DBYb9tvvz1Q\n1p9jXoTX17EYFIMcC61u64x5jqr0v/3tb0DxLzjX3/GOdwBF+X7nO99p+Vnlv9LPuuKKKwIlesnc\nlbp7ZhjmRRUnn3wyAAcffDBQ/JbimN555xNtr5ZYYgmgrMR4bxntVscwjYUKWb9W9NXp4/N695tU\nOEmSJMlQ0VOUWqfKxvVqrW9jwo2LP+CAAwD45Cc/CcA111wDlMgsLdl11lkHgNe+9rUAnHLKKUBZ\n7+5C2Qwtqj3Hzp9aqq7hW51B/1bMLD/kkEOAkqVtJNcwc/bZZwPFyjfnSOvtc5/73NQcWB+IykYl\n6++dy5deeilQ7g19MCrZfffdFygKqG7FwnvvjDPOAMq9Zq6cPp/ZCe8J7/sqK94xtvaa6A+9/PLL\nB3WIA2ettdYCqiMtB6VsOiUVTpIkSdIIfcnDcW3U9Wd9MpFFFlkEKL4ZrTV9Ov7UElEBbbnlli37\nMcJqzTXXBOC0006bdL+zI+bTVPknll56aaBUjVYJ2fPDNX5zGqy1ZQTg7IA+On040XpbbrnlGj+m\nXolRYV43741Yz+v8889v+Zx5VM75dnON3K+VJ5wHp556KlAUk0pndrqXVIP77bdfy78jjqHPF/nC\nF74AjM9dmR0w6uxd73rXFB9Je6TCSZIkSRqhkWrRYu2iX//61wDceuutQLE89CtY9+vrX/86UCIw\nzC3x51133QWUaJN2rb1JGJootarroip0DIxeM3dAS1ZlZMSNcfgd7L/xCJyYP+Vau1b9lVde6f6A\n4tupqjPWLwYxFt4L5p7FvCgjqS6++GKg5NXoq/G6+rm6+9i8ntVXXx0o/k+j01TMRgZO0gVzaCKz\n2l1ZkThG+jW6fX4Mw1h4n3suVfXhBl1FI6PUkiRJkqGir7XU6njlK18JlExfqz9bGTdG7FgPSkt3\nzz33BOC9730vUNa9d9hhB6BE3syOaIG87GUva+vzjpFWmda+1p4qYXaoCyXxWLXa/KlfymoKWv9j\nOrY2cpy94HW2okCsFKBitcqzHV3Ns9JvdeGFFwLwla98BYA77rgDGD+G+mZWW201oPhu3va2twGl\njqG+mz6sEtTSa5Vo8Vxf/epXAyUHKSpl8/Z+9KMfASXqdXa6N6rQj13V52aqa6dFUuEkSZIkjdCI\nD0eLRoWjH8K+NlpX5ghYJ8q4eq32XXbZBSiRWFoyfn7hhRcGeqqAO2U+HM/x6quvBmCVVVaZ8HP2\nftGyiVaalk6vluowrE+L19n1an13VpRQ6Xba1bRdBjEWVkRXyVgX0Gx5fXJa5fZ+0f+pmjOHTV+O\nqwSx2ob3iPPD+16lpY/v3e9+96TH3clYTJ8+fXSeeeaprKnYKz5XjOwzx8xq9EZmqu58vvSr6+Uw\n3CPeG/r2qrqUpg8nSZIk+Z+iER+O1tSPf/xjoKzBG4VmNWgrH3/3u99t+b6Kxeqvdg51fbqJdedB\no+qznpw1kYxGcwytjFy1/txkf5Om8NxVfzE3aXY8Zyucew9svfXWAOy1115A8dnoqzvmmGOAolRe\n+tKXAqUaR1SB+r3iCoZjpXJSUZnrZLRcP/olzZw5syN1U+fbUcnErpb2v4lVnvVrWZFCv5cRfvqQ\nnwo4NlX0y2/WK6lwkiRJkkZoNA9H7JejFeW/XYfUgolW/LbbbguUvhWuf8d16h7e4o37cKLl4b+t\n5mtnT603FY9r9fqtYoRWrxE4TaxPd2p1OS9i508jvQaVHT+IsYhVM1T/Rt5Z6fi4444D+qfiVdDf\n//73ATj33HMBeOtb3wpU97CSQYyF/iYrkHjOdvI0t8To1ojPkah8VTjmIDnPfE64/W4ZBh+OrLvu\nukBRrhF9dXbF7Tfpw0mSJEmGikbzcCRaUVU9ziNGIdkTJPZ4cDvD4NOJ680Ro0k8Z610/611Zn25\n7bbbruVzKhzX5E866SRgfJ/2YaZdZaMCjspGrPZ73nnn9efAGkAF6vxQ3Z944olAUTj6N//whz/0\nZb8qG4kVB1Qbg0S1bu6YKxRf/vKXgaK6jD6MfW1Uxp///OeB6nqDViiJ37NfzlOJWCU+RqUtv/zy\njR/TRKTCSZIkSRphShROpM7S9W2tgtHi0ULSwj3nnHMGdYgdY/WEz3zmM0CxVM2KNidpt912A0o/\ni0suuQSAgw46CCj5GVZdsJ6YaB3OjpVu26XOr6C6m50Ujuh3UuH8+c9/BkquSL+UjdFsEVcLVNRN\n4H1rDpF5M3afPeKII4AyFvpw/Lz5NVtsscWk+3GVweeLqwFV9cZmZ3bddVcA3vKWt7T8XgVtvbip\nJhVOkiRJ0ghTEqXWKeYixF4dZttvs802QOnt0QN9i1KzZpX5EhGrLLhObZ8Sc03MMTI72q6mWocx\nT8J1bH07vTJMETii0omVlbXiqrKse2WQY6EV/s53vhMokVPm3ay//voA3HTTTQBcf/31nWyeffbZ\nBygdYSMqZK1+fUtVz4VOxmKVVVYZ/elPfzqu/0ysddav3BCVkfl8ViYxus0cJ/P8zIWK+//whz8M\nwMc+9rGW44w5SsN0j1hh3wolUd1V+T/7RUapJUmSJENFoz6cbrNdjTqz/pRru1bK3Wqrrfp1iH3j\nJS95CVDWzq3nJFqW/qwaG304WrxVGeD9UjbDiNaZYxUVzqCst1NOOYWPfvSjA9m27LvvvkCphG1k\nlT1+VG0333xzy7/rqiuohF784hdP+jmj0/qtNgCuvfbaceoG2n8O2MXSuR/x+95bdT2fXvOa1wDF\nT1q1/6pr3o/qC/3GuW/kX6w4YH25QTEyMtLRnEmFkyRJkjRCIz4c37ox+73dfWsRxR4vRqvFePse\n6JsPRwtUK82+6Z3iGL3vfe8D4Mgjj2z5/aAYpvVp+91YYaLKV6O11++xaWIszLfSR2e+lQpXJXT6\n6acD4+8lfXhGclXV1vJ75japGtuln2NRd528npdffjlQKo2oyjq9zmuvvTZQ/Forr7wyUHw+nTIM\n94idWquiGVVl+gZdLZqqeyQVTpIkSdIIA1U4Wij+NJpogmiPqv0BpeOnikb10K++FmMYWC21eI5G\nqVkbrerz5mdYM21QvUUm2P+UW2/i/DE6MVrvjlVVXbleGcRYVEUVarGqZPTBHHXUUQAcfvjhQDlX\n87f0Z7pdx0SLdscddwRKrlK3Fm4/xyJWbfaYmoqsqiJG0VUxDPeIx2pUrDUYI47pfffdBxR/eL8q\nZqfCSZIkSYaKgUaprbrqE2LBqs5a9YstthhQrHV/rzWvArJvTuzXbgXlYenxMBmqMI81dmJ0Xdkx\nMN9iUJWPZydUMjvssANQrn9UOFrx/VY2g6QqqvC2224DSlVn549+K/0ON9xwAwDLLLMMUHLVHCPv\nJSM4Y4+pYUDr2ntj0F0p64i+4tkBj3X11VcHioLRByiem3l/U3WOqXCSJEmSRmi00oCWqQrGSgFa\nsPbDsB6QvUHMIN57772BYhkZvdRHGu+HM6wMw/q09aHsiqnvToVsp0drcQ2KqRyLaPXH+9U1/JVW\nWgmAW2+9FSgWbJXPr66aeRXDMC+GhWEeC+eN/XHslzMo0oeTJEmSDBVDXUvNXAEjdYzg0eIdgO8m\nFc6TDLP1FtHPMag+SLPTWAyaHItCjkUhFU6SJEkyVAxFP5wqXH+2HpkZxjI7RKlNFf9LYzMMHV6T\n4cNeVAcccAAAp512GgA777zzlB3T/zqpcJIkSZJGGGofThUDtN7Th/MkuT5dyLEo5FgUciwK6cNJ\nkiRJhopOfTh3A3cO4kA6YYB+iaU6+OxQjMWA6GQcIMdiLDkWhRyLQo4FHS6pJUmSJEm35JJakiRJ\n0gj5wkmSJEkaIV84SZIkSSPkCydJkiRphHzhJEmSJI2QL5wkSZKkEfKFkyRJkjRCvnCSJEmSRsgX\nTpIkSdIIHZW2GXQBuiEoqX/36OjoIu18MIvxFUZGRkZHRkY6vm517ZMjtlO2fXLdduu2N8888wDw\n8MMPT/r9LNJYyLEo5FgU2h2LRvvh2Hv+wQcfbPl90y+a2M99zIPsqVrraOBMmzZt1nhKvK5VD/gF\nFlgAgMcffxwo8yN+3xeN10vmnntuAB599NGWv7u9pz3taUDpr+S//+///q9lP295y1sAOP300wGY\nMWPGrG0kw0u7hsj/AlXP0n49Y3vdTi6pJUmSJI0w1P1wBt2rfoK3dfbDeZJOlgumTZs2Otdcc/Gf\n//wHKEo2KpkZM54Q1H4uKk2Zc845W34f/171vSrry/1GRStaxn7P7YyMjDBz5sxcOhlDjkVhdh6L\neK/UqcS6v2c/nCRJkmSoaNSH0yl1yqZdp/O6664LwJVXXtnW55POGB0d5ZFHHpllBT300EOzfj+W\n1772tQB8+9vfBoriiL6dKmUjVb+vup7RD6PPR9/R3/72t0m/P5Wkf6I5nkpjHVW8Kv+MM84A4Oij\njwbgJz/5CVA9971XXJXodYxS4SRJkiSN0IgPZ+yaOJS3o2vxE62dw3jLtArfum6vB5/P0Phw9IM8\n8MADLb+/5JJLANh0000Hufu+hEVvuOGGAPzwhz8EynV/3vOeB8Add9xRt12Ppd3jmPB78fsxqs3j\n8nvOI+ffVKzVq/o8xt133x2Ab37zmwAcfPDBLX+/6KKLADjnnHNavj/ffPMBZQxUh0bkff3rX2/Z\nTh2DGIteI5+03p/73OcCcNNNNwFwzz33APDyl78cgPnnnx+A3//+9y3f32abbQA477zzOtpvP8ai\nSjF0OyZ+z+3qB7/vvvuA8jzZYostAPjpT3/al/2mDydJkiQZKrpSOFoUUYFUvR192/rzxS9+MVDW\nzrUo3/WudwHwzGc+E4ATTjgBKBaLa/xx+34/Wq5jLNSWz/vWn+DvA1c4cYzuv//+lnMwQkvivyMx\np2nJJZcE4F//+lc3hzeLTq23adOm8axnPQuAf/7zn8D4dWTHPUavTbA9j6Hl93Eexc+bX6Ol6+fW\nWmstAC699FIA7r33XqCsSztfoiKaY445eOyxx5g5c2ZjCsdj9lw8NsdukUWeyEu+8MILgfG5Rv7d\ne+HQQw8F4Mc//jEAV199NQDPfvazgc79V8MUmfXpT38aKOpv3nnnBcq9FH28qgjHdM899wTga1/7\nWsvf2/VP9HMsOk2CjvhMVrn47FxooYUm3K4///GPfwCw+eabA/Db3/4WGB+5mVFqSZIkyWxFVwqn\nyifjWzC+RRdccEGgWOPbbbcdUKyxT33qU0Cxyn71q18BxSo7/vjjgaJ0qixfLRvf6gceeCAAn//8\n5wG4884nCgnMNddcwPhM89HR0YEpnOhf0sp/+tOfDoy3ZLvFa+F2uo0m6cZ68zpUxfhX+eSidTfm\nGFq+r19r6aWXBsp69CabbALAiiuuCBRrX6XlT+fXSSedBJQ1fv0arvGrDpvIw3GueiwSVZx88pOf\nBIp17vxxLju/VM4/+9nPAPj73/8OwBFHHNHyd1Veu0ylwnFMrBjh9XSeOAbi2IjX2c+7etCt72gY\n1J5jsM466wBw4oknAkXlR5zbnrvPoV/+8pdAUXtnn302UMamarVIUuEkSZIkQ0VXeThV0T/RmtYi\n0ZraddddgWLNuwYb/RTLLbccANdeey1QIizcnpZKtKRVUh7HRz/60Zb9m3fxyCOPTHg+g8Rj3mij\njYBijVX5JeqOqUoVTFUugWrA/x9LnbKJ11EF6u+XWGIJAAb9VBsAABL5SURBVPbdd9+Wv8fafAsv\nvDAAyy+/fMvfvd5axn7+uOOOazk+50lU7oMkKhtx36q1jTfeGIBXvvKVAPzud78DYPHFFwfKqsA3\nvvENoKzpf/e73wXg+9//PgBveMMbALjmmmuA4gs699xzgaLE9XMNAy95yUuA4vv1eeG5uWLyoQ99\nCIBddtkFKKpORey5ib6fk08+GRi/UjPM+TiOwUEHHQSUe0M/Vnz2vuc97wFgr732AmCZZZZp+bv3\n2Fe/+lWgs8jQTp6fqXCSJEmSRmgkD8e37cc//nGgvI1df9T619K84oorADjggAMAuPXWW4GyPh2r\nD7/iFa8A4JhjjgHggx/8IAC33HILUOLu3f4kseYDj1LT8lxllVUA+NGPfgSMV3kvfelLAbjuuuvi\nfoESZXTjjTcCxZqPfo9u6SYPJyrQST4PlLHwp0rEczHixvXpl73sZUCpZPDHP/4RKLkErltrmS62\n2GJAWZ9eaqmlADjllFOAMq+cR6rOWE26ybX6Kv/XZz/7WaAoGcfAnzvvvDNQ7p0VVlgBKBbrVVdd\n1bIf70W394IXvACAI488ctLjm4qx0M/kvPrWt74FlAg7fbOquNtuuw0oVrxqznkWt19FrMEXlW83\nYxGvb7t5L/Ge8fqal6c/3GM1T+8HP/jBhNvxp6sBPivrfDVVx5s+nCRJkmSo6Esttbq3tGvrRo34\nFtWiVbnstttuQFlPjr6iuB8tmKOOOgoo65Hf+973gBYLta3jbALPXassHotWufHxET+vdef69J//\n/Geg+L+aXoceHR0d58OpqiDh57TGYuUJ83m0unfYYQegWKpGL2qd65vR8nWtX+vtda97HVCUUMz/\nch56fEbuzDnnnAOrVF5FnA+OgXPcY3fNfb/99gPKaoFRbI7pq1/9aqBEJxmJp6rbZ599APjCF77Q\n71PpGc/Re+biiy8GioozokqfsNetKk+wU/x+P++luryWqt/7vZVXXhmAs846C4BFF1205e+33347\nUO6Rqv3rB3WVoMqfKv16dqbCSZIkSRqhLwqn6m3oT3MNVl31CfeI1pg1tr785S8DxUKt2q7o73j3\nu98NFCv/5z//OVAs3mFSNhEjaGLdriplE/FcjCbS76FltPbaawPjK2QPirHr4Z5TzNyumidadc4L\nq0pruZpboDXm9qwTZnZ0tN623nrrlu2bj6MFXJUfNDZnquk547HF6glGYPl364O5du/1VzV6j7iq\n4L8dwz322AMolSliRvowsNpqqwFFjb3+9a8Hyvyw0vFvfvOblu85BhtssAFQlI9j1GnuUT9XCerq\nSVbtKz4z/bfbMydNf3asjRefyfqA3Z9K9xOf+ARQVotkMp9ORqklSZIkQ8dA+uFES/Ovf/0rUPwL\nWuV/+MMfALjggguA8VFovo1VMP7+sssuA0rUkWvwX/ziFyc9HhkmxaMFq78hUlW9QaKKePOb3wzA\nV77ylZafO+20Uz8Pu4WRkZFZ1xqqLcgY9ROtOf+ttfaXv/wFgPe///1AiULUYnX92urTRiPqt7D6\nr1akuStxjd/tqIDqouwGiWOgH+ozn/kMAOuttx4wXgFVRXJ5T2jpmsu2+uqrA8X3o8/QezHmNk0F\nVhHXhxMjtLwHYs5JfO4YwWn+n36PuirlgyTev14vzy3eE6o7/eDx+ou+vVin0LFR0X7sYx8DSs6i\n94AKOEYQ1z0jO32GpsJJkiRJGqGnWmrtKgfXh7U8zTFxDf7uu+8Gylq90WVaKn4vZoZr4ey9995A\nyTmIFrZv7zZ6fgxNPxwtG7OmPfc6tHC0UBzLWFeqjl5yDGI+TuwaOOZ7QLHarP9m9JEZ5ubROAbm\n2ziP9FfZ28X1Zy1ZVd9HPvIRoIyJSjv2wTHS67DDDuOhhx7i8ccf7zn3JN4bjolKxDFQcRx77LFA\n8VfUVaIwH8f9GOlpt1sj/VZaaSUAvvSlLwFFBW6//fYtx1VV0XuQeTidVnhwDIxuNbfo+uuvB0pn\nWWsp2p9J3+9mm23WyeFNtP+ux6Ld6tCugHiORis6V73HvvOd7wClkoB5fvpkll12WWC8QoqrSdG3\nVMXYuon//e9/Mw8nSZIkGS4GUmkgxpLb30aFoWVqXL2KRR+O31eZxExwrTAtVKsEG53mduospgkU\n2ZQrHI9Jv5cWjvkTVTgmZhYbvWQeR6eVB/ppvUWfScxF0JrSOlPBWD9Mn51qwAgb55X+hl//+tdA\nGQOvuxGB+ob0U6isox9srBX4+OOPD7QfTvTF6GvTIrXaRvR/OYYqkV/84hdAsea9BxwTfTT+3nsq\nXgNVZtVqwCAVzoc//GGgKNF2id1MVTjOJ58P+sOcL0boiSsmqsU29juwsfA6vOY1rwHK2DgvvD76\nLe+66y6gVCAwz0/177PTz+kzjn4xO8G6WjTJ+bR8LxVOkiRJMlR0HKXWTtx1XAf0ba0VfsMNNwDF\n4tWXU9Wpz/1p7esLuPzyy1u2H6u91kUbDWOejhFT+r08JmsdvfCFLwTKuRnJoxW/5ZZbAsV616IZ\nJCMjI8w999yzFEjs/VOnMFUs+mzMn/Dczb8wskarXcXivDJSR8vVXjCxx1DMgZK4Lj6I+RDVv/tU\nddkbymNQuXjOVkD3usbqDt4jqn0tWNf+3/ve97Z8Ps59LWT31wRen0MOOaSj71k9wRWTP/3pT0Cp\nvafvz6x7x9rVgve9731AqVrfrrLpJ85du9JaW9Hrb4V71ZeRlM7hz33uc0CpumH9wRe96EVAWSWy\nfqD+cBWO88eIUFcH6p6J3d4bqXCSJEmSRuhY4Uz0ZquKeNBK19rWkrG2lRap1l1V9da4feuGmWMS\nfQMx+sm/G8vu8Ux2TlOFEVr6pxxDlYxorVk7KXa59NybyCAfHR3lscceq+wJH6vtjv0elPVlo8us\nPPH85z8fKIpWhaN/y3M1mnGrrbYC4LTTTmvZj2og+gjjccUou7H14fpFVS0tLVNVmfeEOUhWDZ8k\negwYX2VDC9e8nniOa665JlDmS5PKRmK9ulhrz5+emz6+2OFTrEBQVzn9Ax/4AFC6oE7Fc8BzdbVG\n9KVYKeSiiy4C4G1vextQKp3bE8h7xLnvvWDumc8TV0BiLpwKyHtlUGORCidJkiRphIHUUhMjKYyY\n8m3qGqoWipaqa/lVSkcfgZaJmcSu2ZtNbQROjLSJykaGwYfjWq7HbMVk/x0tklh/zPXn008/HSjR\nTb1WzG2Hsb1w/DdM2DMDGJ8ZrvI0ksocAq0t+5zo64s+GNf+XdN3Xjl2sRp09N3E44x+kH4S96Xa\nN2/GXKI4dzutfhBXGcxBceydLyon/R7W6moSr6e1EK25GPtoWWsxKiLPdZNNNgHg6quvBkqXywki\nqgDYc889W/4tTVRa9xnonI2oXPS1WC/OyE1XeeIcdXuuEsRnaeybpTJS5XV6ziuttBI333xz259P\nhZMkSZI0Qk95OHXd61QaRl6pQIwqiWvqWrqvetWrANhmm22AYu1r8RpbrmXk92NdqHg8MWpugppf\njefhREvHMTMj3GO2yq+fj51AI56zGetG5LRbKbebHIOqyrfxOsTOi/pq9MlZIUBLVevOeWCOgfkU\n+jms1XfwwQcDZS3fc/a6q/ri8RkRNLYCwcyZM/uab+G5q0yf85znAHDmmWcCsNFGGwFFlVX5bCbZ\nf8t+zD1505veBJR7TKxH6Pyq6yXTRMdP/RleH58fPjfqrHCvs2MX56VVN4zIu+mmm4Ci+qoqY0S6\nGYuqXJ+qlYv9998fKKo7+nh9Bo7ZT8u/3Z5+zqiIYmX3bsk8nCRJkmSo6CkPp2qNXrTStDjMrzBy\nwp4e9mI4+eSTgZJVq7Vltq05Clq4cb8qG1ljjTWA0iPCWlyd9sPoJ6o2rXcjrkSrzO6UEXMNzEHR\nrxHR0tGydX9a0v1k0UUXZaedduLoo48Gxld6iJFR0ZrS2nPd2nM7//zzgRJpZdVw83VcO3aeuK7t\nuTqWzg+tdlVkjJJTgUfF3k+ck1V9ivTBmXvULjEPx663RqH5d8fae09lI034/OrQl+Nzwesd503V\nCobRjtFXFysy+xyJamNQz4cZM2ZU5vqMrU0GRc2r7sy3iTmLrnjE6t6u9lhJ/cgjj5xwv037rVPh\nJEmSJI0wkFpqVfhW9q1tVV4t0muvvRYo9YF8S9vH2yxYLZiotKIFpJXgeqfW2ySVWvvuw4lWvdFG\njoHWVLR86iLnNt10U6BUia3i1FNPBeAd73gH0H7kVafr0+1UoFBZqHyjD0UlbM5RzNPSv6HfQwvV\nMXYe2TW1qr+Slm5UYlUVKvrptzCPwryHiNFkMS9jgv0AZSyM5HI1wLnv56zErmrods2+CR+OEVZv\nfetbW37v9bLvlTXX/L3zJ3bNjQrIf+uze/vb3w6U58oJJ5zQ1nF2MxbtRsDFuep11hfraoDdbn2e\neE8Y8avCNa/Hf0d/aq9KJ304SZIkyVDRF4WjZRHj46vwrbrtttsCJQvaulHXXHMNUKxxcxW05rUO\nYlZ1XH9uN9pkDAOLUtNK33zzzYHir7KyrWv70dqP+RixTpmfN1pFy9bPdTEGQGfW2/Tp00fnmWee\nWb6QqrV1I2X8qaqrmjdag4svvjhQlI+RVvpwVCTmc7meXeVrrLMy9YM8/PDDjI6O9sWqNx9GP1Gd\n2vb6x2oIqkR9L1rp0XoXa3PZ+6XX3KImFI5dSa26UIfzzusWueKKKwBYf/31gVJPzF5T5uuoqNul\nyX44UbGo4lz90bdjJK+Rvp5zjNBVIenj7bXDayqcJEmSZKjoS6WBdpWNaLXZD0erTetPxWOkjm/n\nCy+8sGU7WrruX1+NUU1xLd74+0FkkNehRWuuieekNWdklkrl8MMPB0rmubklBx54YMt2PUctoEgT\nEXkzZ87k3//+97ioIFVdrGxtbpBW2kEHHQSUCDy347ywhprdK60r5fU2Gk1Lt9s+7Cofx2zatGkd\nZ/hXYe6Y1S7ch+coWr6T5MG0fK4KlXGsvD07YNWDOmK9uIjKxlUFx+yYY44BSkXlqcBjt7aZEZlV\nn1OBeJ9bXcN7xWou+qHM6zNydNddd23Zrsq42wrZdflaVaTCSZIkSRqh0Sg1ibW09DP4llaJHH/8\n8UCxYF1vdB3SSC07QqoOtHj8XrvrpQzQh9OphanlYJ8KK+SK+RpGHfVbtfUSpRb9FeYCnHTSSUBR\ndVpj1sKL9b3iz7POOgsoVp3r2+bfRJ+N6qTOZ1OVnT2mL07f/BbmEhmB6Rw3i75btGitD6Yy7jdN\n+HB23nlnoERYtnFM7g8oY+EYqyb9u8+bTqs4TLDfxjrBqoTXW289AN74xjcCpbqG52q0mgrX6FTH\nyJwm512sNl9VgbuO9OEkSZIkQ0VffDiRmDUb18G1NH2rahGbNbvffvsBxTJ2e0aTWDXWCBxVgBhX\n71s8+jGmojp0p9nrrpFa66oql2AYGBkZYcaMGbN8affccw9Qrpu5AXabtNqBdaWcH65T+z23YySf\nCihasjGfJ/6sylCPOLaDzLa/7bbbgKLK9EPp39Lnol/L39u10rX4WEPrqcQZZ5wBlFpnu+++O1Ai\nsIzIMtrRMTXqzI7CE+RTAb0rmyZwjsZKIkahXnDBBUA5d2vmma/jKpGrCkZ02i9HZeN+qiJMpdNI\n5CpS4SRJkiSN0Ndq0RN8fsK/u4aqhav/wbX8fffdFyh+CysMaPEa6SVuXzWgRW0XRa2BNmi8WrRZ\n9+YAeA5G5HVaU6tfdLM+HasxxygiI2O8/uZdWSPPtXt9NvrmzjvvPKCMVVSLsYpD3XyM1prH47/d\nzhprrMF1113HQw89NHC/xexCEz6c2YVBjEX0N/rvvffeGyiVKszj8xlphQl9NLfccgtQ8nD0p77g\nBS8ASjUXid2Qq46jyg+aPpwkSZJkqOhK4VQplzrFE9+SddsxMsMIHqvIVr1lY2+Hqj49k9C4whlW\nelE4sbaV/9b6slOrClc/hcrW7peu0dsPx+tnhe3tt98eKNFrzpe63IIYreS8UUHFdeq06gs5FoVO\nx2LGjBnj/IOq/1hRpEphVFXo1+frT+8dq3RERRO/X0W7td9S4SRJkiRDxUDycHqN6W6XAfQeT4Xz\nJN1YsioYo8pUEvrmtO5iFJvKIn4+VoMec2zAeAUVoyKrPicqm1iZN/qK0qov5FgU+jkWzsV+VbYY\nFFWrRalwkiRJkqFiSioNTDWT+HRS4TxJJ9bbtGnTRueee+7Kyg6igtCKq1KmrmvHaDexJ8inP/3p\neMwTbs/jMd/LGlpXXXXVhMfhcXoMadUXciwKTVQa6Fe+Xbv+7Xb3G1eXUuEkSZIkQ0WnCucu4M7B\nHc6Us9To6Ogi7XzwKT4WbY8D5FiMJceikGNRyLF4go5eOEmSJEnSLbmkliRJkjRCvnCSJEmSRsgX\nTpIkSdII+cJJkiRJGiFfOEmSJEkj5AsnSZIkaYR84SRJkiSNkC+cJEmSpBHyhZMkSZI0wv8DkOUU\nqLKi7L4AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2baba3fe5f8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# with 128\n",
"rows, cols = 10, 6\n",
"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\n",
"\n",
"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\n",
" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\n",
" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise. Looks like 1, 9, and 8 show up first. Then, it learns 5 and 3."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sampling from the generator\n",
"\n",
"We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"INFO:tensorflow:Restoring parameters from checkpoints\\generator.ckpt\n"
]
},
{
"data": {
"text/plain": [
"(<matplotlib.figure.Figure at 0x2baa8d03438>,\n",
" array([[<matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2A9E5C0>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2B5AA58>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2ABB080>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2DAB828>],\n",
" [<matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2A25BA8>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2CB86D8>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2D07860>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB2D449E8>],\n",
" [<matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB32D3B70>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB3311F98>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB3367128>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB33A5898>],\n",
" [<matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB33F29E8>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB3437198>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB3483400>,\n",
" <matplotlib.axes._subplots.AxesSubplot object at 0x000002BAB34896D8>]], dtype=object))"
]
},
"execution_count": 77,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXeUFcW2xmtMoIKAAwgiMoBgAEQEzFwRI4pZRNDrM6Ne\nxZwFFJHnNV8jKmJGhauCWcwZFYwgAooEQbKAYNZ5f7zV299oF9M955yanuH7rXWWn02fTtXdNfWd\nvXcVlZaWOiGEEKLQrFHZByCEEGL1QB2OEEKIIKjDEUIIEQR1OEIIIYKgDkcIIUQQ1OEIIYQIgjoc\nIYQQQVCHI4QQIgjqcIQQQoShtLQ08ae4uLjUOadPnj4dO3Ysdc4tTNMGapeq0S7FxcXRdvTJ3ycv\nz0pRUZF9cjmemjVr2icD16ZSPmmflVQjnJKSkjSrB6GoqMg+VWnbzjk3fvx455ybmet2stguhWSN\nNdawTyHIR7uUlJRE2xH5Iy/Pytprr22ftPCdUFJSYp+skrV3mCw1IYQQQVirEBvlX55//PFH7Do1\na9Y0/dNPP5lmT5yksCjXWWut/z+d3377LfnB/oUk+/cd++pI/fr1TS9atCiv2+ZfoL/++qtp3z2V\nhPbt25v+5JNPKrwdUXX55Zdfyl3HNyLgu2369Omp9pvk3RJtP8k9nuQ9m0txZt+zkstoSSMcIYQQ\nQVCHI4QQIggFsdSSDAc33HBD03PnzjXtGwImsW5ysdLK2z+pDjZaWuvSx+LFi/NxOLHQRiNJrAQf\nstFEEnzPxO+//266bt26ppM8B7SIfbZemvs5F2s5yfPve1ZyeV9ohCOEECII6nCEEEIEoSCWWhJo\noyUh3xFQIcmXfZVP0h6HL2ehuLjY9Lx580zHnXMuVhjhdngeSc6Jx8Xt0CoRIglp7eQk0XFpiKJy\nnSv7c0KS901lvYc0whFCCBEEdThCCCGCUGmWmo8s2k+5suaaa5rORyRdKGrXrm169uzZpjfYYAPT\nviSw5cuXm47a8euvv7ZlAwcONP3kk0+mOq5criHvqVxsPSF8hHqH+Z6DuGT4Va2f5HiTbCcJGuEI\nIYQIgjocIYQQQSiIpZbLkLIybDSfLcRjWWeddUwz2oR2mS/SiUNQrh8CVrKdMWNG7DqtW7c2PXXq\nVNNbb7216Tp16qTa7/z5801PmTLFOefKVE/mED0JbCN+t3nz5qZp43H/WYvUCY0vqi9iv/32M/3Y\nY4/Ffo/Xdty4caZ32WUX0xtttJHpqpgcvdNOO5nmOaa1XpNYWr53TlSncZNNNrFlfD6XLl1qetas\nWaa///772O398MMPscfCc+Lx+t7djRs3Nk17PS0a4QghhAiCOhwhhBBBSG2p+YZcSaylqsA222xj\nevLkyaZ9db3Snmvoa+Oz0dhetNE47B4+fLhpDsF5D3z++eem27VrF7uvqObUrbfeasv69etnulWr\nVqbvuece0y1atDA9YMAA0zfccINpn/WxuthlPm6//XbTJ5xwgmlf4mvcv/Ma1qtXz3T37t1j17/m\nmmtM33zzzaZ5f2UBn8313nvvmU5ro/muW5JIMn43elYYCbreeuuZ3myzzWK3x0T6BQsWmKb9z/0k\n+RmB6+RioxGNcIQQQgRBHY4QQoggpLbUOOTy1aLKJUqN3+3SpUvsOm+88Ubs8uh41l9/fVvGKBpG\n2nzxxRemOcRmFAjJV5LgV199lZft/JWNN97YNGua+Y47SUQdI1w4y6nPXiS07CJr7KOPPrJlnTt3\nNv3+++/HLm/Tpo3pzz77zPSFF15omhE8W2yxhel81W2rSjzxxBOmDzrooHLXj7sufF5//vln07wv\natWqFbv+KaecYprP0aBBg0wnuXcKDc8lX7P35vKeW3fddU1H9tl2220X++/333+/6V133dU0bTSu\nzzamveZ7Jnzvbi5nNGJaNMIRQggRBHU4QgghgpC3xE8mRjKipWfPnqZvueUW002aNDHNCIuRI0ea\nZjQMLZp7773X9F577WW6WbNmzjl/otsrr7ximrW8PvzwQ9O+EuL5qo/UsmXLvGznr/Aa0tpgtBJ5\n8cUXTe+5556meZ4dOnRIdQy0tw488EDTkU3AKQ723ntv07Q0d999d9MLFy40feqpp5pmtNu1115r\nenW00WidJbHRaCdF98ndd99ty3z3JJND//vf/5r2WVJMRMxy/cCQCap8tvgs8B3ZqVMn51zZa/bq\nq6+aZvQaI1DnzJljmlZoviI3+V1a9mnRCEcIIUQQ1OEIIYQIQk6JnxyuUR966KGmd9xxxz93Buvk\niiuuMM1kS9oCvnpbJ5988iqPkRFYHF5+++23phn1xP1wqEvNKJCsQxuNUwzQ5qCNRngtkkQU8X64\n6aabTH/yySemo8Q/2qW0YHfbbTfTO++8s+njjjvO9JAhQ0zPnDnTdI0aNUz76klVZ2iHJaF9+/am\nmbRbHs8++6xpn0XGROn77rsv1XGtDvBngfr165tu0KCB6aieG62+Dz74IHYbjPoMaSHnUg9SIxwh\nhBBBUIcjhBAiCDklfvqWs8Q5bRQO4Tksp73F7dAaY8RScXGxaUZnnXPOOc65ssN/WjcrVqyI3Q9L\nga9cudI0h7rcf9brdNHmos2UJMktrY125plnml60aJHp1157zfQLL7zgnCt73ahpC/mmMKBFwwTH\nrLdFIejdu7fpDTfcsNz1eU+nsdEIIwB99xcTbxmxyKkiVjd89csOPvhg00zgjJKd+d7aaqutTDO6\ns7IiMXOpB6kRjhBCiCCowxFCCBGEvCV+csjNiC5aHg0bNjR94oknmmZZcw4ft99+e9NMeGJyJi27\nH3/88W/HRYuIVhzL3TORiSXKv/nmm9jzyAVGvhUK37HmK8mN1sDTTz9tmlZX3LQIvEfYtqzNdddd\nd5nedNNNTbP9CZcvWbKkvEP3EleqP6vwGUkC6wmmYcsttzTN5GhGBvL54rNDnTWS1AsrhFXrexcy\n2TmyKHkv9+/f3/TEiRNNF/p4fShKTQghROZRhyOEECIIqS01zj7H8vW+6KY77rjDNBM2hw0bZpo2\nCmGCH2e6Y2QabaJoiMmhJqM9jj76aNO0azgNAuu9+aYqyIUslGd3Lre6Y1x/2rRppn2zCEYw2ZT1\n0MjgwYNNjxkzxjRr77FWHyPjCIf9jAhiHTCS9dprvLZMlE4CbefNN9/cdGTD0OZt3ry56QkTJpjm\nc8RjufHGG00zkjDL9dN8VpTPlsrFuuL6tH8PP/xw07z+UUQfozw5pUkWZrVVlJoQQojMow5HCCFE\nEFJbarTRkgw1+/btW4HD+vs2v/7669jltIYiu48JnhyCsq7a7NmzTZeUlJju06ePadYkq24Jhj4L\nidfTN3MgbUyfJUFLq1evXmX+65xzjRo1Ms0ad02bNjXdrVs306eddppp2mhJZjT12WhVlXvuucf0\nvvvua9pX53DWrFmmGXkZRZtddNFFtoyJvLyGvvs/SrZ2rmz0KCOrsgavTRJrOV/PPhOZ+bMAn4W6\ndes65/6sqeZc2eeN9Qr5Dqsq7yeNcIQQQgQhp2rRSXpV32RoufTI/NGYo5ZomzxG/njJH7j51/YF\nF1xgmn9hJznX9ddf3zRLiFQl+BcWcy/4FyuDHZiTwb+CWYl47NixpqO/7KK/3pwre20ZiMJcqi+/\n/DJWZ/0H/nzBa3TIIYeY/vjjj02zjSZNmmSak+exdAqJRpZsW5aZatWqlWlfnhKX77PPPqazPMKp\nrPwV5t48+OCDpjnyiYJjWrRoYcsYvMHAJ+Y6cULFLKMRjhBCiCCowxFCCBGEvFWLLvR3//nPf5qm\njfDOO++Yjn4Q5X5oqdGKaNu2rWnGwbPStS84gZYOj6WqwlJEzD2iBcDyM08++aTpxx9/3PR2221n\nmhNMlZefQ0uH1YxZ9ZvlP0aMGLHK7VVHGMDBnJirr77a9MUXX2ya9+j5559vmm0X5bmx4jStnKuu\nusq0zyJj2zK3LctU1g/s0USEzjl3wAEHmH7mmWdMR5bygQceaMtoiTLAidb2Sy+9ZDrLAQQa4Qgh\nhAiCOhwhhBBByFu1aB8c2nP4TRsriS318MMPm46LTHPuT9vLN6RkdBstolGjRpn2TWjli93n+r6J\npnyTMBWKtGVrfDk2y5YtM838K+Ze0A7gubFNo5wcX5XZE044wTSj27g9VvReXeB9zDwkRoNxYkC2\nEaux0yaOK0tCS3XgwIGmWU7q0ksvNe2LAuV9UVXo2rWraZaTKQSMaH3kkUdM8x0SlbFh6SdOnMhI\nWFZc58Rs7777rmk+w1lAIxwhhBBBUIcjhBAiCAW31BhRwwQn2mJJErE4dPdZRnHf5bY5ERW3wSgp\nX/ImkxZ5LEnma89XwmtSfDYm981hPJMtqX3DcW6HCYY9evQwTXuiZcuWzrmyJWZYObdTp06mH3ro\nodjzWB2h7cwyS4xGu/nmm03feeedsdtJU92XbTt9+vTY5bynGJnIKNCqQqFtNMJ3ISfR42Rr0TPH\nez9JhXlOYsmkdllqQgghVkvU4QghhAhCwS01DsVpEbRr1870Rx99ZDouusm5spEatH24ThR5xmgd\n2gm9e/eOPS7aOD5q165tes6cOeWunxV8Fh6H8WmJ5l13rqy92Lp1a9PNmjUzHUXesIo3LbXqXJU7\nLT67mJFkvF95vfiM8PouXrzYdJpEZe6fk4A1btzY9CWXXGL6iCOOMJ3lCdhC4otQ/fTTT02neRb5\nUwQtOtYjZGX9rKERjhBCiCCowxFCCBGEnCw12lm+SBgu32OPPUxzIijfMJ/bZ6n0KVOmmObQPdKM\nKGNtsKeeeso05273TRJHe4MJdmkTK6sbjJqhpcM25Vz3kdXju26M2OHkaoxqXL58uWlOEvbcc8+Z\npk2RJDIwi/ad7356/vnnTfuOe4sttjDNSLazzz7bdFQ/LQms30aLlLbOzjvvbPqwww4z/eijj5Z7\nvFUR3pNpbUO+lxg9xvdf9IzwWenYsaNp/pxAi27AgAF/20YWye6RCSGEqFaowxFCCBGEnCy1JHYS\nh+Ws6eSDw0QODX1JaLR3ovWZvMlhLOeCZ6QP98my4PwuZ+ijTZjEVqxMCjG7ISNiunfvbvr666+P\nXScOti3vi7j2/OvyGjVqmB48eLDpaAZL5/6cOdE557p06WL6zTffXOVxVTa++8nXdoxMY3TS/vvv\nb3q//fYzHSXhOvdntCWvM+sNPvHEE6YZEUXN6M0dd9zRNGuFVSfS2mhst++++840LTW2eVRvjdf4\nyCOPNM32fuONN0yzHmSSRNHKQiMcIYQQQVCHI4QQIggFSfykjZN2eOezyzjTHRMvORyNIkhouTCi\nhgmhHLKeddZZplke/5NPPin3eGl7FMK+Sopv3/k6Dl5n2iic5uHggw82/fTTT5tme5SHz1Jl0jDh\n1Aa0Pbmdt956K/H+K5tcbNlDDz3UNKOpeC1oK0f2IhOiGzRoYDpJkijvLz5HVQVaVJyagzBKbMKE\nCaZ9zxzfLbTlmeDJnyM22WQT09Gz1a1bN1u20047mWby9JAhQ0wnsV+zgEY4QgghgqAORwghRBBy\nstSSJNSlqd20KmbMmGGaw0cOR+vXr++cK5ukSfuNESZMMHz88cdNs2ZUWipzKJskiomWgS8J01f7\niZYa23TkyJGmGRlGSy2y2niMd911l+m5c+eaHjZsmOn+/fubZptzRsMRI0aYZo0vtq/P1q0OCby0\njHlNGSVI62X33Xc3HSVis515nX1Tf/ie7zp16phmRFaW4fXzQRstyT3D5UzU5HVjrbtjjz32b8s5\nwy0jdA855BDTs2bNit12IWBSL6cZSYtGOEIIIYKgDkcIIUQQ8halxgRPDiM5s2Takvi0cbp27Wqa\nyXs77LCDadbVivAlanHYyygqX5QUrYYkdlRoe43RYoxk8VmaPjvAN7Mjt+NrRyYeMjJst912c86V\nnZKCSZq+/Z966qmx6/jwbdNHFqN5ktTqSnKfjRkzxjQToe+4447Y7UTwvuBzNnToUNNMMmT0YJYT\nDonv+WXSKy1BXieuz/cTl7Pd+Cxy+1yflnK032OOOcaWnXzyyaZD2mgkFxuNaIQjhBAiCOpwhBBC\nBCFvlhptNMKhaZLhd9u2bU0zMu2LL74wzUiNcePGmY5mokwbcfTyyy+b7tevn2lGp7z++uummzZt\nGrudyrRoOHQnuURfpf0urQROT3DTTTflfCxJSJLER7JoqSWp1ZXkuDktxyuvvGL6qKOOMl1cXOyc\nc27jjTe2ZVdeeaVpWnFx9ptzVcdGI7770BdZ57veSZJ0ad+dccYZpidNmmT6gQceMB1d5+iZWdX+\nSdZrOkZohCOEECII6nCEEEIEoSC11AiHg7QLfEP0V1991TRtGQ7db7/9dtOcwTCyBk477TRbNnHi\nRNOcNZEJg4weYS01lhD32Wg8j169epmuruXZK0KopEqfjdaiRQvTTKKrzrCeF8+5ouefRfsxH+Qy\ng6cPXyLtoEGDYpfng7Tb80U6crqPSy+9tNz106IRjhBCiCCowxFCCBGEgltqPhi9QcuDszOyrhlt\nGd9seaNHj3bOOXf88cfbMpYWZ90kzjLJ5FFG5iSBw8uqZKOlrbGWlizVKfPZSJWZqFtoFixYUNmH\nkFnY7j4brVGjRqZZ14z47vG0UW1xyeb5ssh8+NZh/cJCPB8a4QghhAiCOhwhhBBBCGqpcVjGIeO0\nadNSbYd1w1gSnzWJIlh7iBEpvtpj1c1a8Q37fRFd+bK/KttGS0J1a2uRjCTt7rPRSL7ucR5P3DZb\nt25teurUqeVuI1/HUgg0whFCCBEEdThCCCGCUJRmCFVUVLTQOTez3BVFGpqVlpY2yGUDapeCkFO7\nqE0Kgp6VbJK4XVJ1OEIIIURFkaUmhBAiCOpwhBBCBEEdjhBCiCCowxFCCBEEdThCCCGCoA5HCCFE\nENThCCGECII6HCGEEEFQhyOEECII6nCEEEIEQR2OEEKIIKjDEUIIEQR1OEIIIYKgDkcIIUQYSktL\nE3+Ki4tLnXP65OnTsWPHUufcwjRt4GuXNdZYwz65HFO+thPqU1RUZJ8stUtxcXG0HX3y98nLs5KB\n86g2n7TPSqoRTklJSZrVRTmMHz/euTxMBlVSUuLWX399+6SlqKjIPrlsJw1rrLGGfXzHkoS1117b\nPrlsh+SjXUpKSqLtiPyRl2dF5I+0z4osNSGEEEFYq7IPQOSH77//vtx11lxzTdOc6fWPP/6I3Q5H\nH1zHt83ff/89dp1GjRo555ybN29e7PY4CuFx+ZaTX375JdV2qH3nJHInSduJ1Q+NcIQQQgRBHY4Q\nQoggyFJbjaDl9dcf6yOSWGQMKKAt9eOPP8Zun1ZaxHrrrWf6559/jt2n7wd/n0XDY//tt99i15e9\nEwZdZxGHRjhCCCGCoA5HCCFEEGSpVXN80UK+CC2fjcbtrFy5stz9lhcBxuiyunXrmv7pp59MN2zY\n0PQXX3xhukaNGuXuc5111ondly/yriL5OlmgR48epp977jnTN998s+lLLrnE9HfffWc6siB9be6j\nZcuWph977DHT22yzTartiNUPjXCEEEIEQR2OEEKIIMhS+wtrrfXnJWGkU6G/m0/q1KljetmyZRXe\nDqO+8pEkye01aNDA9EYbbWR69uzZptddd13TQ4YMMT1q1CjTvXr1Mk1bjCVMvvzyS9M8j5o1a5qm\nlVeVeOGFF0zz3Pr162d64403Nk1LLbLSNtxwQ1v28ccfm27WrJlp2rHTp0833blzZ9NNmjQxPXfu\n3NjvsgTRr7/+Gn9SotqiEY4QQoggqMMRQggRhEqz1GrXrm2aQ2taG5VRjykXK2zKlCmmGckTmuXL\nl5tOmzxJ0kYv+YhslFatWtmy/fff3/Rmm21met999zX99ddfm95ggw1Mf/jhh6bPOOMM08OGDTM9\nderU2GPh9aDFV5Xgs/O///u/sZq26ueff77K7b322mummzZtapoWHe8XbpsRi9S++8tnoyVJOBZl\nYd3DSZMmme7SpYtpPjeLFy8Oc2CrQCMcIYQQQVCHI4QQIgiVZqklKaef1kaLkv2Y6EeSlNvPBdpo\nrDeWJFEyV2iz8NpWllXB/V5wwQXOOeeOPvpoW1ZcXGx68uTJpocPH256zz33NP3DDz+YZhLo/fff\nb3rLLbc0PXHiRNOMRmPUXoh2KQTz5883zXZn+86ZM8c0LTCuE0XyMWLQB5+Xb7/91jSvOSMMk0yF\nQZjMy7YWZalXr57pWrVqmd5+++1N8x5ne/O9OHr0aNPHH3983o/Th0Y4QgghgqAORwghRBCqZOIn\nI42i2SSdc+6tt9762zIOIxmxweEo1+Hwn4mcXO6LtKE11KZNm3LOIr/47KHKivjZZJNNTO+4447O\nubLXnPbmO++8Y5pTGQwcOND0okWLTLPGGqc5WLp0qWlGG3K5z9JhBF0W4fXiteX5MIF2wYIFpvfa\nay/T99xzj+nIavRFMvI+p0XGa/7yyy+bHjFihOlLL73U9JIlS0yz7YhsND+0hGkh+2DCtA9GiRb6\npwaiEY4QQoggqMMRQggRhCpjqXHYx8iccePGmY6icTgE5fCf0IKi1dO4cWPTtHFWrFhR7nExYic0\nvlL7vki/QtQRY52sq666ynS3bt2cc2VtLtovjLr66quvTH/yySemmczKpE6eN+3DJHW6aBNNmzat\n3PXzSdroQZ4n66GRnj17mmbS7H333Wea7R7N0Lpw4UJb9sYbb5g+6KCDTPMZ4f1FK/KAAw4wffHF\nF5seNGhQ7HeZZMoIN80WWvZZ6tu3r2m2PZ9brp8koXns2LGmC22jEY1whBBCBEEdjhBCiCBk2lLj\n8P/nn382zVkOGQET2WEcItLyIr179zbNoSmH9r4EUhJyOJqUJJYEh+C5WGq0SNq3b2+6a9eupqOk\nPpasp+XDiCpGlEWWz181LQPfPcJrwHugY8eOpsePHx97HiFIGz3osys/++wz0+edd55pWmC+qKXo\nnC+66CJb9o9//MP0hRdeaPraa68td3u0lDnLqO/+4v3ANlrdaqnF3XtctsUWW5hm3UEmbF5zzTWm\nOR0F4TNxwgknVOxgc0QjHCGEEEFQhyOEECIImbbUaGnRUmDtJ1okr776qnPOuR122KHcbdOKoS2W\nxEarDiSpZZcEzhZ57rnnxi6PIsYYpcZIMyYycpbJCRMmmPZZXrTXktgynNGShLbU0rLrrruaPvXU\nU00zaomJzazlR3hdtt12W+dc2Qg9ziAa1SZ0zrnrrruu3GPk+nxejzvuONO0dSpzVtwswWsSRdXy\n3vclrLPuIK+9b9t8tmhzsq5hoacw0AhHCCFEENThCCGECEKmLTWWQadFQwuGiZ1RIhnth8cee8z0\nQw89ZDpJTaKqRMh6SBy+s35Xp06dTNOiiqLBaLl9+umnptmGtMiY4Mt98lxpGdAOpWXgs3F82wmN\nL1GX15aWFmv8ceoBX5Iz4TlH0U+cqZbXnMm2LVq0MM2pDwjtOk43wH3Syo6mR3Cu7JQTqzNRpGXr\n1q1tWZL7nct9s9r67vGQM4FqhCOEECII6nCEEEIEIXOWGoeDvlLmtNrivvvuu+/aMpY9Z4JbdavX\nlNZSS7I+24Ka9lavXr1Mf/jhh6ZHjRplesyYMc4556ZPn27LaAfQfqFdVLduXdNt27Y1zcgs2gGs\nfeezGEhWknZ99yLr9zVv3tw0La1NN920wvvt06ePc66sncVE6t133930m2++aZqJhVHbOld21knS\noUMH02zf9957ryKHXa2JovtoT/JZ5b3M54bwvs7ae04jHCGEEEFQhyOEECIImbPUjj32WNM+WyRN\nkh7rPjHxifZOdSBJEh2vW1rbjW1BG22nnXYyzejBF1980XQ0iyftGiYmMjKKtaIYpUV7jcfOBEMm\nMNK6yXqCoS9KjZF2tKsYjfbBBx+Uu31uk9cuega+/PJLWxYlgzpXtt4dpzBo2bKlaSaK+s6Dddh2\n220302y7qp5wnWRKkCREtjCvTRJYR5DPU9bQCEcIIUQQMjfCefDBB00//PDDpis65zn/8uCPoxz5\nrC7VafmXl28E4PuBkn9Vb7XVVqbbtGljmn8Fz5o162/bYS4Vt3fggQeaZhkPTugVjZKcc+6kk04y\nzQACTrrGEdGyZctcHFn5QdV3HEcddZTpRo0amf7Pf/6Tavsc1TD44JtvvnHOlW1z30R0vBeYw9au\nXTvTl112mWmeE/NteCzPP/+86e7du6/yHKoSzI1iCSmfq8ARYJJcqgiOgFktOsvvM41whBBCBEEd\njhBCiCBkzlLz/XjIH5lXrlwZu06cNUErgD/Eff7556Y333zz1MdZVfD9mOmboIzrczlj/jkZ2vz5\n803PmDEjdv0dd9zROVc22IB5NWxz2gGsYss8EK7vsyk4kVtV5Z577jH9/vvvm+7fv79pXwAN23fw\n4MGmeV2iZ8oXhEEb+6yzzjK93Xbbxe6TliZztXyWGgOEqjq0KmlLDho0yPTNN99smtfhnHPOSbwf\n5mbx+fAFhmQNjXCEEEIEQR2OEEKIIGTOUvPB4T2tnrhJt2gz0H5jZBrzPUJWWg4BbRHaHLwurNrL\nGH5eI0avsersK6+8YppWwsyZM00fcsghptu3b++cc65Jkya2rH79+qZpB7BUDc9jwYIFphkFRAuO\nx5ukHXlOWZyAjZYJc5iSRNfR1qGVQ0smbjt8znhNWLaIzwvxHdd5551numfPnqYZ1VjVYV4fSwKx\nDBCj+A499NDE2/bZzFUxd0kjHCGEEEFQhyOEECIIVcZSIxzqxyU5cWhP64j4IrOqA7TRiK9UECdG\nYxIarxGtLto1I0aMMM3kPZbXiJJAmbzoi57jfpgoyiQ3fpd2YBIbzXfvZOUe4DWnjUaSHGurVq1M\n01Yur4q2zxZjOyeB96BvAry+ffuavvfee1NtP8u89tprpnmNmcgeTRbpnHMHHXTQ37bBe3n48OGm\nfc92VUEjHCGEEEFQhyOEECIIVdJSK886SWuXsX4Xa3NVN3xzy3O+etpr77zzjuk33njDNCfAY101\nRp5169Zb4tvEAAAgAElEQVTNdBRNw6gwWgO0tlj3bOTIkbHHwu8yCTUJPssoK3XVSC4ViPldRoNt\nvfXWpqOoQto7rBzNCe181nSS/VPzHqhONpoPthujK1k1Ow4+E2effXbs9qoiGuEIIYQIgjocIYQQ\nQaiSllp5vPrqq6nWZwRUvXr1TFcHe82XpEcrimXwqadOnVruNrmdvffe2zStk6h+F6cYYMQaJ/oa\nNWqU6UcffdQ0bVRGpqWF5d8rOuVFIfHZxUzITWsj1qpVyzTb9OWXX3bOOde1a1dbxmkr2EaEtift\naF5PXud//etfpm+88cbYbeZrArMsw7qDrDUYB9shi/dpRdEIRwghRBDU4QghhAhC5iy1hg0bmmbi\nW5p56XfYYYdU++zcubNpRmNVJXyWBC0arsOy6YxS4wyOtFRolx155JGmObUDbR/WPnv66aedc87N\nnTvXlrE215QpU0zTrqF1Rhsvl4itqmpP0PalpcZrngRaNWzTNDzwwAOmhw0bZpp27CWXXGKaNb84\nbcHqRpL7Nlpn+fLltqw61HeM0AhHCCFEENThCCGECELmLDUmqTG6pkGDBqY5xGQdogMPPNA5l37Y\nXlVtNFJejay/Luc5d+jQwXS/fv1MDxkyxDRnXJ0wYYLpiRMnxm6zS5cupqOkTdpZjJbicl9tNOq0\nllp1i3piBBinG2AbVRReq++//970wQcfbJrTU5x//vmmGYXImUWZqMvkR99+qxN85ngdfIm0zz//\nvHPOubfeequwB1ZJaIQjhBAiCOpwhBBCBCFzlhqH1q1btzbN8uiMzOGMelE0DG05DuFptaUt833S\nSSeZvvPOO2OPJW1CXqHgTJmM7uO1feqpp0xz1s4jjjgi9ruTJk0yzVkHuQ6jCqOkQuf+rAvFa87E\nUNpoIa0VTn/gmwog67Rs2dL022+/bbpx48ameY/GRTPSruRzNnr0aNM+i+eUU06JPRbWwZs9e3Y5\nZ1F9YR00TtlBWDdt6NChzjnnnnzyycIeWCWhEY4QQoggqMMRQggRhMxZaoTRUIx6YvQME+Iii6BT\np0627KOPPjLNml3NmjUrd/+0i5gwR7IyAx+tEiba0f6qW7eu6enTp5v+6quvYrdJ24uzRtJ+8pWe\nZ6JmdI18ETshSTKjZmXC9uLspz5Yn2uzzTYryDGtCtqxpHfv3qavvvrqUIeTOXzvDcLn4tlnny3k\n4VQ6GuEIIYQIgjocIYQQQci0pUZYm6s8xo8fH7t80003Nd2nTx/TUWSIc2XLrXM47KtVlqbGWyHx\nRXfRlvFZNL5zY/RMkvLxjHbid+O+V1nl6LNelyqJjZZVmHi6OttohLOa9u/f3zQj97bcckvTSWYo\nrspohCOEECII6nCEEEIEocpYavmGsxz66juRrNd64lCcOl8WEmcoZKJmIfYVt+0k199nR/DYGdXo\nmw1VVAxGMor/h1GErA3pI+vvmVzREyeEECII6nCEEEIEYbW11FgbrTqQZEoCDumZPMthvM9mohVF\nfBZA3PFw23FRbH9dJ61F5zsW37GTrEeviaoD6ztylluhEY4QQohAqMMRQggRhNXWUqvO0B6itUUb\nLe1308LS/1EyI200n+0Q0trKYkRQLpaiyAay0fxohCOEECII6nCEEEIEoSiNrVBUVLTQOTezcIez\nWtKstLS0QS4bULsUhJzaRW1SEPSsZJPE7ZKqwxFCCCEqiiw1IYQQQVCHI4QQIgjqcIQQQgRBHY4Q\nQoggqMMRQggRBHU4QgghgqAORwghRBDU4QghhAiCOhwhhBBBUIcjhBAiCOpwhBBCBEEdjhBCiCCo\nwxFCCBEEdThCCCHCUFpamvhTXFxc6pzTJ0+fjh07ljrnFqZpA7VL1WiX4uLiaDt5+ay99tr2qezr\nU4kfPSsZ+6R9VlKNcEpKStKsLsph/PjxzuVhMii1S37JR7uUlJS48ePHuzXXXNM+aVljjTXsU79+\nfftklVzONSF5eVZ4XYuKimI/PniOSdZPS5rtFWL/aUn7rMhSE0IIEYS18rUh9rKcRdS3vLqz3nrr\nmf7hhx8q8UhEZfL7779X+LtrrPHn34Pz58+PXadu3bqmly9fbvqPP/4od/vRs+l7Xtda68/XA7fn\nO6dcznX27NmmmzZtWuHtJCHJtUny3bTvs44dO5qeMGFC7Do1a9Z0zjn3448/ptp2vt6zDRs2NL3u\nuuuanjkzP7Nya4QjhBAiCOpwhBBCBCFvlppvGJcvG61OnTqmly1blpdtRhTC9pONJnLlt99+K3ed\npUuXVnj7cfc6l/36668V3jZJ8nwV2kbLhbXXXtt0kjbx4bPRSBorrRA/USxYsCB2eb7ekRrhCCGE\nCII6HCGEEEHIm6WWL9q1a2d64sSJppNElvzrX/9yzjl333332TIOUTmkbd68uen111/fNK0w7pPR\nQCRJDPzqFJ0nqg5RFFLaiKi0VPX732ctMoqPVhvzkBi5R2suX3ZlIfG923LJ+9EIRwghRBDU4Qgh\nhAhCTpZarVq1TK9YsSLng3HOuc8++yx2+ffff2/aN5S97bbbnHPOTZkyxZa1aNHCtK/kBq2zu+66\ny/TgwYPLPd6qbhdUFdLaEUyazCXRrzpTaCstghbME088YfrQQw81Tevp3HPPNX3ttdcW9Nhop69c\nuTLVd3nMrVq1Mj1ixAjTAwYMML3PPvuY3n///U1HPwU459zDDz/snHPuzTfftGXHHnus6cWLF5su\n9LuH28/X86QRjhBCiCCowxFCCBGEnCy1tDYaa/P4hvPFxcWmlyxZYprDu3nz5pneYIMN/rYOh/BM\nZKpXr55pRqOts846po844gjTBxxwgGkOmUV4WIfqoYceMs2IxEGDBpnOuo0W1cxyzrmff/7ZdFWw\naPl8sfbW5MmTTdMCZURoz549TdOSql27tmnWISx0LUbaaL598Vy4Dq1d1oJr3Lix6cjmd86VqfTN\nbV5++eWmo/fPkCFDbNkVV1xhmvYb4fFyP4sWLTKdiy3G9fkeT4tGOEIIIYKgDkcIIUQQgiZ++mw0\n2guMwuAQkJFphxxyiOmhQ4eajuoxbbHFFraMZd195dN32WUX07RrOMz/6KOPTL/44oumzz///Nht\nitzhfcE23XjjjU1feumlpjt16mSadmgW+emnn2KX09795ZdfQh1OLLz/+ezyWdxwww1NN2rUyDSt\ncdra//M//2P6wQcfNN2tWzfTtEYLgc8681l2PK85c+bEbufOO+80TYuUlv8NN9xgmpYZ27lJkyZ/\n23+HDh1Mn3baaaYZ8UeLbtasWbHnkS+bOZfoRo1whBBCBEEdjhBCiCBkopaaz16gpcbh7tdff216\nxowZpqNhOYfwNWrUMM0h5eGHH276pJNOit0/h6lt2rQxTUtHllrF8LUtr+1NN91kmjaqDybTMQqR\nUU+VSevWrU1PnTo1dp1cbDTacbzXmRwdZyexLWijcd2ddtrJNKcSuPXWW2OPhdOJkOHDh5u+7LLL\nTLds2TJ2v0cddZTpBx54IHabaeE7gdfbZzkxAs3H+++/b/qUU04xzfswSZRddJ0322wzW8Z2pXXX\nvn1706wTyfeW72eEyoqG1AhHCCFEENThCCGECEImLDXC4T2Hgxxmf/vtt6ZptUTrc2jMoSOH0hdc\ncIFpDk35XdoeHBozwY0w4YvHuLoTtR0Tb99++23TkyZNMr3VVluZTjsLJK95XLRPZcOorO222y7V\nd30l74mvxhyfKW4niiRjMuGZZ55pms8Ct0HLmhacbzbMhQsXmqbt+d5778Wuz2c2XzYaoYXvS5Lk\ne2XgwIGmjznmGNOMWLv99ttNMzLNV5+N15NTn1x11VXOubLJlf/+979Nv/zyy7Hb4PvJZ6ESLg+Z\nJK0RjhBCiCCowxFCCBGE1JZaoWsb+YZ33JcvAicODp8Z7XH11VebZjlxDlNZw2jkyJGmfdMc+Gy0\nQl+zLMJkudGjRzvnytbUatCggWlGb3EaCpaOT0L37t1N+65zs2bNTM+cOTPV9isC76ckNhpr9jEa\n0zejpO88uV9GjJ1++umme/fu7Zwre01oO/tqhY0bN840owp5jEwOZTvSRuMx8hnxWYaFgDYar9Pj\njz9u+sknnzTtO062w9KlS1MdA/cbbZ+zHT/66KOm2T7HHXec6fvvv9/0nnvuaZr3OK1Qn53pe7f5\nft5Ii0Y4QgghgqAORwghRBAKEqXmi/yoDDhsZwIgh6A+OJRm1BMTRVnLy8fqYqNxqB3NXOicc507\nd3bO+cujM/nOl3jog9f2888/N00LwGfdhMBnEfuuxbRp08rdJhP7aGPxuWNCMpMnuU4U2cTtEdpo\nTJSmXcYpRHr16mX6iy++iF3O9qUlxCTfymLZsmWmGTlGi8yXsJz2GffdF88++6xzrqzNzGPhO4nb\naNeuXexyti0j/miL8r1IG5U6Xz8LaIQjhBAiCOpwhBBCBCG1pZZkOMVhdmXDGTxZh4i2APn0009N\nsww3o0OYCCb+hFMIdOnSxXR0z/juHV7bJJYX61YxkZAWAKNtGJ1YmfjsGOK7L2mdMfKypKTENGdF\nZRIybTRe3379+jnnnNt8881tGafqiKLYnCs7bQjb6+677zb92muvmY6sob/C0v200XzXg5aQL7E1\nLb4pIHhtfJFmhUiSZHTr2LFjnXPOHXbYYbaM15X3EGcT5TQsXOfUU081ffzxx5vmeSSZcZbLfZFs\nSdAIRwghRBDU4QghhAhCQaLUOFyrjKTHjTbayPQ555xj2pdIyGF1z549TSeJHvLVRMqSrZhvWrRo\nYZoRLpxxkzOkRhZQrVq1bBlrptFG8llqvHc4myeT2XxU5syZAwYMMJ1kJkteN0Ye+fjuu+9MX3/9\n9aY32WQT075n8J577nHOlU089M2+y6g/Xk+uw9k/fdc8rSWVLxuN+I7N935iDUBe73xBSyuyPzlj\nqs+KZZI0ZxClncp7LklSfRJLO5fEXI1whBBCBEEdjhBCiCAUfHqCkEmP0XCQUTScqdM3aygjnb78\n8sty90PrjMli1dlGo+114oknmmakDEuns/ZclCjLduFsj75S6Sy5ftppp5lmRE7WoaWRxF6mjeZL\nDiVMyOT61ITXNIpq+/DDD23ZihUrYr/H/fv0Bx98YJrnWl69w6yzfPly0/n6iYDboQUWzVrsm4mU\nlusTTzxhmtf4m2++SXWMaW1ORakJIYTIPAUf4fBHZf51lRb+xdahQwfT/Ms7ygMZOnSoLfPN773X\nXnuZ/uqrr1IdC3+sq85la/hXGAMxXnnlFdP8a4ptwdFMlEfAedf5Yz8rR/Me4Q+hzzzzTOrjzwJp\n/yL2lVTx/ZjL3Cfm2/h+CJ47d67p6Fpznxzh8C/fJHlN/Cu7qo9qfO3GezyXgAa+l04++WTT22+/\nvXPOHyhwxx13mB4/fnzstgv9TlLQgBBCiMyjDkcIIUQQCm6psTwM7TVONPWPf/zDNO0wVrxlZVnO\ndc/hY9xQn//OqrXTp0+PPV4OpWkj0CJo2bKlaQYZVHb+Ub7x/bDJ68xrSruG9tkZZ5zxt+3RRuP3\nOGHUddddZ7oQ+RghSNv2vpIqvsAKVsj++OOPTTPP6fXXXzfN5yjNRGEsoTNv3jzTnGiPE4WxRE7W\n8D2btLGYU8Rco1zuQ75PWH1+xx13NB09Z7TuWPqGgQI+ayvL7x6NcIQQQgRBHY4QQoggBM3D4Zzu\nZ511lulbbrnF9CGHHGL6scceM/3uu++apqV26623mo6sHtp4PXr0MD1p0iTTvhwHlr9hSYuFCxea\nXrlypWlOlMRJp3xD2dATgOUCrwvzjXhNec4jRowwTQsuuta+/I0zzzzTNPMMqqqN5oOWStpIH1+u\nxPPPP2/67LPPNs32YnVt3t/RPUrLiPcnIzlpl40ePdo0z+Ott94q5yySQeudz3K+7CHfdniNmVPn\ns93S5q8wcvOUU04xHUWmcR22wzvvvGOa7x4fhbbRlIcjhBAi86jDEUIIEYSCWGqsCswh8VNPPWWa\nFhUna+Jc25wwjcN4lqWJi97hUJcROuuuu67pZs2amebc7YxGa9++vWkOa2k1RBV3k5K1qJGkMBrv\noYceMs2yH7QgfaVVIvbbbz/TtHw22GCDnI4zyySx0ZJMwMZrS4uFbUFbistZRTpKeGYSIu2Se++9\n13Tt2rVNs5LxoYceatpXhTmtlZhLgnguMPqS15sVtFnZOQlsTz77vA6MLoyiZ4888khbdvrpp6fa\nZy4kiXBT4qcQQojMow5HCCFEEHKy1HzDL2oOQZnUx0m8CCM2Lr74YtOM8OA2aZPF/buvZhEtIkZG\n0Q5kkhUTGR955JHYY6/OsK2ZBMg502njxEErxpd0yOiq1RFaObRjeF+y3hnvdUaSHXbYYaY5Yd3B\nBx9seuedd3bOOffSSy/ZMiZbs8Yg25bPd5LJ7XKxYAqB773lOxe2QzSZoHNl6wuygjnXP/DAA01/\n+umnpmmZsbJ6dM2ZUM1JIfkzA0li1fNd6IsALbTlrxGOEEKIIKjDEUIIEYScLDVfCfSuXbua5jAu\nSaIUh6Njx441zaEsh6bcb2TZcdjJCBMmlU6cODH2PDis3meffUwz2o22x7bbbht7jEnqNVUlmKgW\nTajmnHNbb7114m0wWkr8Ce8VatZJ23zzzWO/S2uE932dOnVMM4F62LBhpqN7kbXsOnfubProo482\nvffee5t++umnTTORNElSog/aSrSTCmHx+LbJdwWfZdZV4zq00Wjt83pynd69e5tmZBqty2jqFb4r\n+/TpY/q+++4zHZfE61zZyOATTjjBNKey4ISGhPcf673NmjUrdv20VM23nxBCiCqHOhwhhBBBKEoz\nZO3UqVMpo7WSwAgVn3VAfDZdEiLb54EHHojdxhFHHGGatb6Y4MYIrH/+85+maSOxlhuTRtOWBS8t\nLXVFRUUTSktLO5W78iqoSLskgXboiy++aHrXXXdNtZ2o3tqWW26ZnwMrMPlol06dOpWOHz8+9T1M\nG5eWMqOaeH+nhbbKk08+6Zxz7qijjrJltJppzTBKlDDZl2X0fdB64vZ9dtZfKOiz4nt+eY48Zp+F\nTmvz8MMPj/0ubTraZ1HUIe0yvkMZ6ctEVe5/6tSpptmexxxzjGnOmsxZexkl/Pbbb5v21ZBL+6xo\nhCOEECII6nCEEEIEoSC11Dj8Yg0mJvuxvlISK8pnTXB4PGrUKOdc2VpM/B7L5zPSjENWRun07dvX\n9IwZM0xvttlmqY69KkFr4/777zfdrl27VNthyfs2bdrkfmDVAF9NMc5+269fP9OceoOJ0rfddptp\nRoaNGTPGNKOQ2Ka0co499ljnnHOTJ0+2Zb46Zoze5Gytvllu+Q7gudJW4nlPmzYtdr8hYYQso//4\n3uKzT3uL58jrSVv68ssvN027lHUFo58F2GaM7qTVxnqUjGKkFcbIONqpDRs2NM198bsk7VQMPjTC\nEUIIEQR1OEIIIYJQ8FpqrJ+1yy67mH7zzTdjt8M6ZUw84zr/+c9/TF944YWmo6gR7p82BofJHAJz\nfdoS1113nWnaQrTjqhuMyGnbtq1pWjFJIgnr169fgKOr2vhqitFO2nfffU2z9P/w4cNN06ZmjTM+\na7z+3O+UKVNMf/fdd865ZHYJ1/HVDeOxJEkCZT1DwueUllQh8CU60kKvW7euabYVnwnaXozopBXJ\ndxGfs6FDh5pm0mgEE4AZLRi1n3Nlfwo499xzTbds2dI06+7xWEK+zzTCEUIIEQR1OEIIIYKQt1pq\nvuVMjGSCESMjkiZJRjCSpzzSDhdpP5x99tmpvlsdoMXgS9T02WiLFi0qyDFVZXwJcyeeeKLpu+66\nyzSjAQcMGGCa1hKv//fff2+aNci4Lx4DEy/zEVXJ5yvts+azZgtto/napGPHjqZpY3FqCLJkyRLT\njPpilBoTL33Q3opL6vVdG9qZTPZ8+OGHTdOe5HnHWXer2i/J5b7RCEcIIUQQ1OEIIYQIQkESP31U\nh8TI6giHzj169DB91llnmb7hhhtiv8tEPkb5iP/HFwFGG4189tlnplnvat68eaYZjda+ffvY7dCy\nZqQS651FEVS0wvKV4JeWkO8G3zlyGgdq4rPjmOjsi0b0fbc8K9I3fYpvhlLf/rlPX007337zhUY4\nQgghgqAORwghRBCCWmrVnapaV43H+uijj5petmyZaUZD3X333WEOrJqR9v6gBcIoKLLHHnuYZmIf\npzN44YUXTDPZMipvT2vGZ/uQJOskWb9Ro0amaRmSJNZPIfC1FWuZ8Znw2VjEV3euou+KXLbBa8n2\n4ZQHvmkiuE5aNMIRQggRBHU4QgghgiBLLY9UJRvNB200Jpaxxp2oGDklzMH24My1gwcPNk37qX//\n/qYPOeQQ00OGDDEd1dxiMqEvYfSvszymwWe7+Ww0JkIW2kZjUietRVpkPP4VK1bkZb+8hrRLFyxY\nUKFt5ALPz2ej0b7zRcclQSMcIYQQQVCHI4QQIgiy1ISXXOpklccOO+xgety4cXnddnWEtgdnriU+\nO+Shhx6K1ZF1RfuI2ldLizXeOItlvkgS8ZUvaJGljb7LF6xBGNmbrIFG0s6O7KtXl9aOy5d9pxGO\nEEKIIKjDEUIIEYSiNEOloqKihc65mYU7nNWSZqWlpQ1y2YDapSDk1C5qk4KgZyWbJG6XVB2OEEII\nUVFkqQkhhAiCOhwhhBBBUIcjhBAiCOpwhBBCBEEdjhBCiCCowxFCCBEEdThCCCGCoA5HCCFEENTh\nCCGECII6HCGEEEFQhyOEECII6nCEEEIEQR2OEEKIIKjDEUIIEQR1OEIIIcJQWlqa+FNcXFzqnNMn\nT5+OHTuWOucWpmkDX7t06NDBPpV9XlX9k492KS4ujrajT/4+eXlWMnAe1eaT9llZy6WgpKTELV68\nOM1XxCoYP368Kyoqynn2wZKSEvf666/b/9eqVct0UVGR6XxNtpd2m2us8f8D6T/++KPc7RHftpPs\nf8011zT9+++/l3uMJB/tUlJSEm0nl82IsuTlWVmyZIn9vyagzO0dkfZZSdXhiOzCTobwBmrYsKHp\nBQsWlLvNtdb68/b47bffTEcdiHPJXua+jibuGJOQZP3y9lldYFvk+5wL8cdKFsjyuTz00EPOOeeO\nPPLIYPsMeT30G44QQoggqMMRQggRBFlqqxFJbLSdd97Z9Ntvvx27TtrfRCqDLNsm+cRno9WrV8/0\nd999F7t8n332cc45N2bMGFt29dVXmx40aJDpJPeOqBi0LitqpdWpU8f0smXLcj6mQqERjhBCiCCo\nwxFCCBGEKm+pMfw1shdWFzulEPhsNJFNGJ24YsUK07TRCJc//PDDf/v30047LY9Hl5zqFBGXNnIw\n7nzZrrSw58+fb7q4uNh0SUmJ6Y8//jj2WLJwXTXCEUIIEQR1OEIIIYJQJS01DiV//PFH01EVhJo1\na6baXo0aNUz/8ssvOR5d9aFJkyam58yZU4lHUhh8ia1ZhzYJbbR8bztk8mwW7J58kct1u/76651z\nzh1xxBG2jPfpwIEDTX/22WemeR9wfT63LVu2NM33ZpI2b926tempU6eWcxZ+NMIRQggRBHU4Qggh\nglBpltozzzxjer/99jPNaJXNN9/cdN++fU2feeaZiffDobqvkGLdunVNK8HtT3766ady17nkkktM\njxo1yvSJJ55oevLkyc4559566y1b9s0335j+4YcfYred1t5JG+lEG61Pnz7lrp8VeC3WXntt04xm\n4jpNmzY1vXDhQtNRsiBr7A0fPtw0k4B9VnMuRVKzRmXZiT169DB9+OGHO+ecu++++2xZ586dY9el\n5c13KJNAW7VqZZo2Gu+bX3/9tdxjXH/99ctdJwka4QghhAiCOhwhhBBBqDRLjUNAwoSnV155xTQj\nz84//3zT11xzzSr307ZtW9Pjx483zeHzRRddZPqcc84xXZVK3CeppcToFdoftKJ4Xb7//vvY9bkO\nGTx48CqPkTYXbbQLL7zQ9K233mo67fVPYqn5bJMRI0aYjkrEZxVaZLNnzy53fSYLHnPMMaajZ4d2\n2ejRo2O3se6665peZ511TC9fvty07/pXlaTOQj/vtB9nzZplunHjxqZXrlzpnHPuww8/tGU33HCD\naR4jk3jXW28903xWfXa1z0bztdVHH30Uu35aNMIRQggRBHU4QgghgpC5xM9TTjnF9GWXXWb63nvv\nNZ0mOXPixImmO3XqZPrZZ5+N1YzMefPNNxPvp7Jh1IkvcsiX3OizOX7++WfTPhstDRyuM+rlyiuv\nNM0oKZ8dwO1Qb7LJJqbnzp1rmueddprrLEIbzWeHst1pn5x77rmmI5vswQcftGWMAOU91a5dO9NM\nAnzuuedML1q0KPZ4c7HUqlMUHOudsWbhAQccYDouwZoW6hdffGGa14YRpUmizkja6Dzf7MKJ9lXh\nbwohhBApUIcjhBAiCJmw1DjkZpQMh+j5qHE2Y8YM06effrpp1gZiolTa5KjKhNcqiT3EiDVGyUT1\n6JwrmwS70UYbpdp+GhgBNXbsWNO77LJL7Pq0ZTbeeGPTXbp0Mc0k05kzZ8Zuh1F4tWvXTnHEuZOv\nOm68Fr7IMFoyzZs3/9sx0MampcL2p+3CROlp06aZTmKp+axZn5VT1W00nnv79u1N9+zZ0zTbLUqI\nf/31123ZkiVLTPM55D3EqLe0pI3Oy6V+n0Y4QgghgqAORwghRBAyYalxSJlL6es4aIsxAo1DXVou\ntO4KYaMxsiSfJIkE4jq0kObNm2e6UaNGsd9l7btu3bqZ5rCe9hZtoosvvtg5V3Y2SdporPEUrbsq\n2KZHHXWUadpotEZ9lhqvQegotUJMh0BrhMmZ48aNM832ivsey+I/+uijpu+44w7TDRo0MP3JJ5+U\ne1y8H3n/Z92mzgdMyHzggQfKXT+6tr6ajnxW2W5ZTqglGuEIIYQIgjocIYQQQciEpZZvaBtsuumm\npt5JQogAAAvDSURBVD/99FPTrAFFOGT1kUsiW6GibpIcB9dhHSbCpEJGidFGGzlypGnWIPOdW2ST\n3XbbbbaMdkr37t1Ns418kVysvXbBBReY5oyGaaMaC2VJhJxVlBFgX375pWmfTRp3zmPGjDHNsvif\nf/65adaa49QGPuuS1k9Vqk+YD2j/0l7z0a9fv1X+O61SWtFVBY1whBBCBEEdjhBCiCBUSUvNZ2lF\nlsKNN95oyxh188QTT5hm1A2nLUhrTWUF1jdKm5jlm9pg+vTppr/66ivTaWsvRVYbLRdug9E7tB2Y\nYMikXdZhY1uwDptv+ovQFNpGI7169TJNq8sXgRe1C60ZRg/SrpwwYYJpWnRJpkdIUu+turLvvvuW\nuw5nv/VNLRLBKD/WtOPzkY8k+UKhEY4QQoggqMMRQggRhExbakmS8TbccEPT0aygTAakvdS7d2/T\njz32mGkmALK+VlUil/pGHMYnKQefj0gjboORPJyS4MgjjzTti/BhtFsSG4023dKlS5MdbAbgs8A2\noqXIe/rOO+80XaNGjdhtRttZuHChLTv11FNjv8fpCZj4yQjDm2++OXY/tOm22WYb0++8807s+oUm\n7YypuUCbl9Bqbdasmek4u57tzXcbr+v9999vmhYpo9qycL9rhCOEECII6nCEEEIEodIsNV+kmW82\nR1owXM6Imd122805VzZ5jeW8mbDGoebQoUNNH3/88aY542UWI9MILSffTJnEl5AYKnKoXr16pnmd\neVwdOnQw7Wv/K664ItV+s2ArVATef2yv4uJi07SGGcnnI9rOtttua8tozbItaLuxZh0jomip+Y73\n3XffNe2rp1doCm2jEU79MGzYMNObbbaZ6fLeLdF7zbmy7ydGlzLBvW/fvrHbPuOMM0zffffdiff/\nV3KpO6gRjhBCiCBU2ggnLn/mr/h+nOZ3WXIjqjTNv8BYKoXf419vnTp1Ms0f5d544w3T/Mtv7ty5\nscdVmSQZ1ZBc8kN47Tgi8v2lFOWEHH300baMZXNee+0100899ZTplStXxm6b1//f//53mkN355xz\njunrrrsu1XezAp8XlijafPPNTfvcgauvvtp0lIvG68z25MRfbdq0id027wVf+3MUxGOviqVZfDlr\npE+fPqaHDBlims8cA5iYNxhdf45YLrroItMM3uD2OKGkryI9cw+vvfba2GN57rnnYr9LcnF7NMIR\nQggRBHU4QgghgpCJPBzfvOxpiYaYSSaFIrQZ+OM7f2COm7gqS+RSwdqHz+rkcuZq+Gy9Jk2aOOec\nO/PMM21Z/fr1TXft2tU0rTYGhDCwYNdddzXNc2UgiK+8R8hSM7nCa8R70RfY0bZtW9OcdO355583\nPXr0aNOR1ZYkr+qll14yzWv47bffmr788stNDxw40HTIitmFhpMIsiTW008/bTrJu2LQoEGmGfgS\n2WG+H+Z5/ZL8LEG4ziWXXGKaNiFLIvkmgcsFjXCEEEIEQR2OEEKIIGTCJyqEHVQetBF8kScc9vbv\n3z/IcVWUQl/Dww47zDStK+Y2+aIAX331Vedc2evM60+7jHq77bYzzeE9o6poMdAy8OV4sOQL8UX2\n5JO0bfTTTz+Z9llR3Caj/Vg2hhPTTZky5W/boC3KfXK5r7ROZJc6Vzaa6rLLLiv32LNA2jbhOfLe\nT3v/sJxTGubMmWP6mGOOMU3b1FfKyPd80g7ks1UINMIRQggRBHU4QgghgpAJS81XtqSQ9hojpli2\ng4mitNFYlTiLFGKueG6TlYgZyUebjO3FaJ4NNthglfuhFXbooYeapu3AquDLly837UtwpDXEdXzJ\nhiFK+iS5n1nGZP/99zd99tlnl7tN2o5nnXWW6VmzZpnmfRxdF9or1Ew+ZBv5IqhYUurZZ581fdJJ\nJ5n2lZWpDFu9Ivtq3LixadqJtLd43+ZSBiaC92y/fv1M00LlBIlbbbVV7Hb4fHz44Yemc6k0nxaN\ncIQQQgRBHY4QQoggVJqlxqE757pv3ry5aSbv5WPIzW1wwqLFixfnvO2qRpLr6ZuMjQmevrpaG2+8\nseloKM/t+SLKfLYYLRrWfmKl42uuucY0bSRaQ7R0stjWUUTfXzXhteM50O6hZcykUdZee/31151z\nzm2xxRZ/W7aq/RAuP++880x/9tlnplmTzUfW2sJ373OCxi+++MI0LS1aaowQTPLMRZYn98/7gNGH\n++yzj2nfJG6042i18Z3rS1QtRHShRjhCCCGCoA5HCCFEECrNUuNwjUPNL7/80jTttYpGESWpSbRo\n0SLTnNCqOuAbxlNzsi5fqXriW04LZvDgwaajofw//vGP2OPyWTesq/bRRx+ZpgXASa0YMXfsscea\npr1WHfDV0LrhhhtMczI2RgmOHDnSdGRZ0r7xJTAyYZTTIDBqite5c+fOpnlP8bhoT9WtW9d0FibJ\nS/u+4flyCoG333673O8y2TmqQffAAw/YMtYU5LVntCiT1GmjsQYebTQSMjFXIxwhhBBBUIcjhBAi\nCJlI/GR0DfHNde+jZs2azrmykU60ExihM2LECNO0YpJEklSlcuu+c+Bc67fffnte9sWoQiYhRrYL\n61CxNhttIc64yiggXnPuh8t9SaCENoQv2i7rsE15nowGY5TYlltuaZrXK4oO5D3MdmNCNMvWM1Hw\nkUceid022y4JWbDRcoEWXJJ3AtuQ9dEeffRR51zZ68H7ndYZ93nllVeaZgLuzTffXO6xhEQjHCGE\nEEFQhyOEECIIlWap0drwwYiZr7/+2jSTqdq0aWO6e/fuzjnnNtpoI1t26aWXxm67Z8+epjlrIWuA\n3XLLLaY5BM66jZZk1r6hQ4ea9tlJtLqaNm1qmvXmWAr9/PPPN80IpEhz6gfWgWLkzdy5c037SqWz\nfefPn286SfIgbTQmPKa1gEIT2cXOlU2I5TnTjuQUElyfz1S9evWcc2WtuCSz7zKpd9KkSab5vDBK\nkfC+qE7wGnMm0B49epjmNABMQB4wYIDp6N3iqz/48ssvm+azx+jaHXbYIdWxh0QjHCGEEEFQhyOE\nECIIlWap0dqYOnWq6datW8euX1JSYtpXYy3SXNa3b1/Td911l+n33nvPNIevrIPEqJusT09AfDYa\nLTImpzEhjJGBrE12+OGHm65Vq5ZpXuurrrrKNK/XFVdc4Zwra6nRlqEFyG0T7oc2Wtoae1yf913W\no9R80y3wnH02GmFkExOe00ALmhGmvpkm0+KrY1YVGTt2rGlauFdffbVpPouRpcznZ+LEiaafeuop\n07T2s1aLzodGOEIIIYKgDkcIIUQQMpH4ySgllvlu0aKFaV/9qDgrZNSoUaZpBSVJ2KxK1hnxnRuX\nM/GVNa169epl+oQTTjC9xx57mE4yZKelc/rpp5seN26cc66shfXxxx+bvvzyy0136NDBNO0In7WS\n5Lh8Fk3WbQje50zw9B23z0bLN4Xef1W30QjPZdq0aaYPPvhg03HvsKzfmxVFIxwhhBBBUIcjhBAi\nCEEtNV90DZczqTPf0GqqTpEwzvktQi6njUai+k3OlY2YYcQYk8lonXDGTX73v//9r+nIGuJ0E0x8\nY103Wm1J2iVJlBq3k4+ZY0PhqwcnqhdZvw/ziUY4QgghgqAORwghRBCCWmqMuqnsaKHqYKMRX+Ji\n2mvL2nNDhgwxzVkEmSjLZM7JkyfHbjOyhjibKyN2ciHt+a1O9kV1oBAWqK8unSg8GuEIIYQIgjoc\nIYQQQQhqqVU3GytL+OwGJs9ySoK99tqr3G36ytovX768IodYEDurKs2+KtJTiHtGNlrloRGOEEKI\nIKjDEUIIEYRM1FIT+YXRgDNmzDCdxEYjvsTDLEV65WKj1a1b1/TSpUvzcThCiFWgEY4QQoggqMMR\nQggRhKI09khRUdFC59zMclcUaWhWWlraIJcNqF0KQk7tojYpCHpWsknidknV4QghhBAVRZaaEEKI\nIKjDEUIIEQR1OEIIIYKgDkcIIUQQ1OEIIYQIgjocIYQQQVCHI4QQIgjqcIQQQgRBHY4QQogg/B9Y\nCse8A/FQ1AAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2baa8d03438>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"saver = tf.train.Saver(var_list=g_vars)\n",
"with tf.Session() as sess:\n",
" saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))\n",
" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\n",
" gen_samples = sess.run(\n",
" generator(input_z, input_size, reuse=True),\n",
" feed_dict={input_z: sample_z})\n",
"view_samples(0, [gen_samples])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
gmarceaucaron/ecole-apprentissage-profond | notebooks/classification/lasagne_nn.ipynb | 1 | 24455 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This notebook explains how to define a classification task for vision with Lasagne and theano.\n",
"\n",
"To execute a cell: Ctrl-Enter.\n",
"\n",
"The code was executed with the default configuration of Theano: `floatX=float64`, `device=cpu` and the configuration for GPU `floatX=float32,device=cuda`.\n",
"\n",
"Tested with:\n",
"- Python 3.6.2, \n",
"- Theano 0.10.0beta1.dev,\n",
"- Lasagne 0.2.dev1,\n",
"- cuDNN version 6021,\n",
"- GeForce GTX TITAN Black"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import os\n",
"os.environ['THEANO_FLAGS'] = 'floatX=float32,device=cuda,mode=FAST_RUN'\n",
"import numpy as np\n",
"import theano\n",
"import theano.tensor as T\n",
"import lasagne\n",
"seed = 1\n",
"lasagne.random.set_rng(np.random.RandomState(seed))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Hyperparameters"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following are hyperparameters that will have an impact on the learning algorithm."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Architecture\n",
"N_HIDDEN = [800,800]\n",
"NON_LINEARITY = lasagne.nonlinearities.rectify\n",
"\n",
"# Dropout parameters\n",
"#DROP_INPUT = 0.2\n",
"#DROP_HIDDEN = 0.5\n",
"DROP_INPUT = None\n",
"DROP_HIDDEN = None\n",
"\n",
"# Number of epochs to train the net\n",
"NUM_EPOCHS = 50\n",
"\n",
"# Optimization learning rate\n",
"LEARNING_RATE = 0.01\n",
"\n",
"# Batch Size\n",
"BATCH_SIZE = 128\n",
"\n",
"# Optimizer\n",
"eta = theano.shared(lasagne.utils.floatX(LEARNING_RATE))\n",
"my_optimizer = lambda loss, params: lasagne.updates.nesterov_momentum(\n",
" loss, params, learning_rate=eta, momentum=0.9)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"An optimizer can be seen as a function that takes a gradient, obtained by backpropagation, and returns an update to be applied to the current parameters. Other optimizers can be found in: [optimizer reference](http://lasagne.readthedocs.io/en/latest/modules/updates.html?highlight=update). In order to be able to change the learning rate dynamically, we must use a shared variable that will be accessible afterwards."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Dataset\n",
"In this example, we are using the celebrated [MNIST dataset](http://yann.lecun.com/exdb/mnist/). The following are functions that download the MNIST dataset, resize it into a convenient numpy array for images of size `(n_example, n_channel, img_width, img_height)` and split the dataset into a train set (50k images) and a validation set (10k images). The pixels are normalized by 255."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import os\n",
"def load_mnist():\n",
" \"\"\"\n",
" A dataloader for MNIST\n",
"\n",
" \"\"\"\n",
" \n",
" from urllib.request import urlretrieve\n",
" \n",
" def download(filename, source='http://yann.lecun.com/exdb/mnist/'):\n",
" print(\"Downloading %s\" % filename)\n",
" urlretrieve(source + filename, filename)\n",
"\n",
" # We then define functions for loading MNIST images and labels.\n",
" # For convenience, they also download the requested files if needed.\n",
" import gzip\n",
"\n",
" def load_mnist_images(filename):\n",
" if not os.path.exists(filename):\n",
" download(filename)\n",
" # Read the inputs in Yann LeCun's binary format.\n",
" with gzip.open(filename, 'rb') as f:\n",
" data = np.frombuffer(f.read(), np.uint8, offset=16)\n",
" # The inputs are vectors now, we reshape them to monochrome 2D images,\n",
" # following the shape convention: (examples, channels, rows, columns)\n",
" data = data.reshape(-1, 1, 28, 28)\n",
" # The inputs come as bytes, we convert them to float32 in range [0,1].\n",
" return data / np.float32(255)\n",
"\n",
" def load_mnist_labels(filename):\n",
" if not os.path.exists(filename):\n",
" download(filename)\n",
" # Read the labels in Yann LeCun's binary format.\n",
" with gzip.open(filename, 'rb') as f:\n",
" data = np.frombuffer(f.read(), np.uint8, offset=8)\n",
" # The labels are vectors of integers now, that's exactly what we want.\n",
" return data\n",
"\n",
" # We can now download and read the training and test set images and labels.\n",
" X_train = load_mnist_images('train-images-idx3-ubyte.gz')\n",
" y_train = load_mnist_labels('train-labels-idx1-ubyte.gz')\n",
" X_test = load_mnist_images('t10k-images-idx3-ubyte.gz')\n",
" y_test = load_mnist_labels('t10k-labels-idx1-ubyte.gz')\n",
"\n",
" # We reserve the last 10000 training examples for validation.\n",
" X_train, X_val = X_train[:-10000], X_train[-10000:]\n",
" y_train, y_val = y_train[:-10000], y_train[-10000:]\n",
"\n",
" # We just return all the arrays in order, as expected in main().\n",
" # (It doesn't matter how we do this as long as we can read them again.)\n",
" return X_train, y_train, X_val, y_val, X_test, y_test"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load the dataset\n",
"print(\"Loading data...\")\n",
"X_train, y_train, X_val, y_val, X_test, y_test = load_mnist()\n",
"n_train = X_train.shape[0]\n",
"input_shape = X_train[0].shape\n",
"print(input_shape)\n",
"input_shape = (None, input_shape[0], input_shape[1], input_shape[2])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"n_img_row = 3\n",
"n_img_col = 3\n",
"plt.rcParams['figure.figsize'] = (12,12) # Make the figures a bit bigger\n",
"for i in range(n_img_row*n_img_col):\n",
" plt.subplot(n_img_row,n_img_col,i+1)\n",
" plt.axis('off')\n",
" idx = np.random.randint(n_train)\n",
" plt.imshow(X_train[idx][0], cmap='gray')\n",
" plt.title(\"Label {}\".format(y_train[idx]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following auxiliary function creates a minibatch in a 3D tensor (batch_size, img_width, img_height)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def iterate_minibatches(inputs, targets, batchsize, shuffle=False):\n",
" \"\"\"\n",
" Return a minibatch of images with the associated targets\n",
"\n",
" Keyword arguments:\n",
" :type inputs: numpy.ndarray\n",
" :param inputs: the dataset of images\n",
" :type targets: numpy.ndarray\n",
" :param targets: the targets associated to the dataset\n",
" :type batchsize: int\n",
" :param batchsize: the number of datapoints in the minibatch\n",
" :type shuffle: bool\n",
" :param shuffle: a flag if we want to shuffle the dataset\n",
" \"\"\"\n",
" \n",
" assert len(inputs) == len(targets)\n",
" if shuffle:\n",
" indices = np.arange(len(inputs))\n",
" np.random.shuffle(indices)\n",
" for start_idx in range(0, len(inputs) - batchsize + 1, batchsize):\n",
" if shuffle:\n",
" excerpt = indices[start_idx:start_idx + batchsize]\n",
" else:\n",
" excerpt = slice(start_idx, start_idx + batchsize)\n",
" yield inputs[excerpt], targets[excerpt]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Model definition"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The next two functions are general functions for creating multi-layer perceptron (mlp) and convolutional neural networks (cnn)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def create_mlp(\n",
" input_shape,\n",
" input_var=None,\n",
" nonlinearity = lasagne.nonlinearities.rectify,\n",
" n_hidden=[800], \n",
" drop_input=.2,\n",
" drop_hidden=.5):\n",
" \"\"\"\n",
" A generic function for creating a multi-layer perceptron.\n",
" If n_hidden is given as a list, then depth is ignored.\n",
" \n",
" :type input_shape: tuple\n",
" :param input_shape: a tuple containing the shape of the input\n",
" :type input_var: theano.tensor.var.TensorVariable\n",
" :param input_var: a theano symbolic variable, created automatically if None\n",
" :type nonlinearity: lasagne.nonlinearities\n",
" :param nonlinearity: a nonlinearity function that follows all dense layers\n",
" :type n_hidden: list\n",
" :param n_hidden: number of hidden units per layer\n",
" :type drop_input: float\n",
" :param drop_input: the probability of dropout for the input\n",
" :type drop_hidden: float\n",
" :param drop_hidden: the probability of dropout for the hidden units\n",
" \"\"\"\n",
"\n",
" # if input_shape is None, then the mlp is used on top of an existing model\n",
" if input_shape:\n",
" \n",
" # if input_var is None, lasagne create \n",
" # automatically the associated theano variable\n",
" network = lasagne.layers.InputLayer(\n",
" shape=input_shape,\n",
" input_var=input_var)\n",
" \n",
" if drop_input:\n",
" network = lasagne.layers.dropout(\n",
" incoming=network,\n",
" p=drop_input)\n",
" else:\n",
" network = input_var\n",
" \n",
" for i in range(len(n_hidden)):\n",
" network = lasagne.layers.DenseLayer(\n",
" incoming=network, \n",
" num_units=n_hidden[i],\n",
" nonlinearity=nonlinearity\n",
" )\n",
" if drop_hidden:\n",
" network = lasagne.layers.dropout(\n",
" incoming=network, \n",
" p=drop_hidden\n",
" )\n",
"\n",
" network = lasagne.layers.DenseLayer(\n",
" incoming=network, \n",
" num_units=10, \n",
" nonlinearity=lasagne.nonlinearities.softmax\n",
" )\n",
" return network"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"# Create a network\n",
"input_var = T.tensor4('inputs')\n",
"target_var = T.ivector('targets')\n",
"\n",
"network = create_mlp(\n",
" input_shape,\n",
" input_var=input_var,\n",
" nonlinearity=NON_LINEARITY,\n",
" n_hidden=N_HIDDEN, \n",
" drop_input=DROP_INPUT, \n",
" drop_hidden=DROP_HIDDEN)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Optimization"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the following, we want to maximize the probability to output the right digit given the image. To do this, we retrieve the output of our model, which is a softmax (probability distribution) over the 10 digits, and we compare it to the actual target. Finally, since we are using minibatches of size `BATCH_SIZE`, we compute the mean over the examples of the minibatch."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Create a loss expression for training\n",
"prediction = lasagne.layers.get_output(network)\n",
"loss = lasagne.objectives.categorical_crossentropy(prediction, target_var).mean()\n",
"params = lasagne.layers.get_all_params(network, trainable=True)\n",
"updates = my_optimizer(loss, params)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Compile a function performing a training step on a mini-batch (by giving\n",
"# the updates dictionary) and returning the corresponding training loss:\n",
"train_fn = theano.function([input_var, target_var], loss, updates=updates)\n",
"\n",
"# Create a loss expression for validation/testing. The crucial difference\n",
"# here is that we do a deterministic forward pass through the network,\n",
"# disabling dropout layers.\n",
"valid_prediction = lasagne.layers.get_output(network, deterministic=True)\n",
"valid_loss = lasagne.objectives.categorical_crossentropy(valid_prediction, target_var).mean()\n",
"\n",
"# We also create an expression for the classification accuracy:\n",
"valid_acc = lasagne.objectives.categorical_accuracy(valid_prediction, target_var).mean()\n",
"\n",
"# Compile a second function computing the validation loss and accuracy:\n",
"valid_fn = theano.function([input_var, target_var], [valid_loss, valid_acc])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Training loop"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following training loop is minimal and often insufficient for real-world purposes.\n",
"The idea here is to show the minimal requirements for training a neural network.\n",
"Also, we plot to show the evolution of the train and validation losses.|"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"#%matplotlib notebook\n",
"plt.rcParams['figure.figsize'] = (4,4) # Make the figures a bit bigger\n",
"\n",
"import time\n",
"def train(\n",
" train_fn,\n",
" X_train,\n",
" y_train,\n",
" valid_fn,\n",
" X_valid,\n",
" y_valid,\n",
" num_epochs=50,\n",
" batchsize=100):\n",
" \n",
" ###################\n",
" # code for plotting\n",
" ###################\n",
" fig,ax = plt.subplots(1,1)\n",
" ax.set_xlabel('Epoch')\n",
" ax.set_ylabel('NLL')\n",
" ax.set_xlim(0,50)\n",
" ax.set_ylim(0,0.5)\n",
" \n",
" train_log = []\n",
" valid_log = []\n",
" ###################\n",
" \n",
" n_train_batches = X_train.shape[0] // batchsize # Warning last examples are not used\n",
" n_valid_batches = X_valid.shape[0] // batchsize\n",
" \n",
" for epoch in range(num_epochs):\n",
" \n",
" train_loss = 0\n",
" for inputs, targets in iterate_minibatches(X_train, y_train, batchsize, shuffle=True):\n",
" train_loss += train_fn(inputs, targets)\n",
"\n",
" valid_loss = 0\n",
" for inputs, targets in iterate_minibatches(X_valid, y_valid, batchsize, shuffle=False):\n",
" loss,_ = valid_fn(inputs, targets)\n",
" valid_loss += loss\n",
" \n",
" ###################\n",
" # code for plotting\n",
" ###################\n",
" train_log.append(train_loss/n_train_batches)\n",
" valid_log.append(valid_loss/n_valid_batches)\n",
" #print(train_loss/n_train_batches, valid_loss/n_valid_batches)\n",
" if ax.lines:\n",
" ax.lines[0].set_xdata(range(0,epoch+1))\n",
" ax.lines[0].set_ydata(train_log)\n",
" ax.lines[1].set_xdata(range(0,epoch+1))\n",
" ax.lines[1].set_ydata(valid_log)\n",
" else:\n",
" ax.plot(epoch, train_log[epoch], 'b', label='train')\n",
" ax.plot(epoch, valid_log[epoch], 'r', label='valid')\n",
" ax.legend()\n",
" ax.grid()\n",
" fig.canvas.draw()\n",
" time.sleep(0.1)\n",
" ###################\n",
"\n",
"train(train_fn, X_train, y_train, valid_fn, X_val, y_val)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following training loop contains features that are interesting to consider:\n",
"- early-stopping\n",
"- logging and filenames\n",
"- checkpointing\n",
"- adaptive step-size (optional)\n",
"\n",
"The first three are the most important ones.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import time\n",
"import pickle\n",
"def train(\n",
" train_fn,\n",
" X_train,\n",
" y_train,\n",
" valid_fn,\n",
" X_valid,\n",
" y_valid,\n",
" num_epochs=100,\n",
" batchsize=64):\n",
" \n",
" print(\"Starting training...\")\n",
" train_loss_array = []\n",
" valid_loss_array = []\n",
" \n",
" # early-stopping parameters\n",
" n_iter = 0\n",
" n_train_batches = X_train.shape[0] // batchsize # Warning last examples are not used\n",
" n_valid_batches = X_valid.shape[0] // batchsize\n",
" patience = 10 * n_train_batches # look as this many examples regardless\n",
" patience_increase = 2. # wait this much longer when a new best is\n",
" # found\n",
" improvement_threshold = 0.995 # a relative improvement of this much is\n",
" # considered significant\n",
" validation_frequency = min(n_train_batches, patience // 2)\n",
" # go through this many\n",
" # minibatche before checking the network\n",
" # on the validation set; in this case we\n",
" # check every epoch\n",
"\n",
" best_valid_loss = np.inf\n",
" best_iter = 0\n",
" test_score = 0.\n",
"\n",
" epoch = 0\n",
" done_looping = False\n",
" \n",
" if not isinstance(N_HIDDEN, list):\n",
" n_hidden = [N_HIDDEN] * DEPTH\n",
" else:\n",
" n_hidden = N_HIDDEN\n",
" \n",
" exp_log_filename = 'mlp_lr-{}_arch-{}_bs-{}_seed-{}.log'.format(\n",
" LEARNING_RATE, \n",
" '-'.join(str(i) for i in n_hidden),\n",
" batchsize,\n",
" seed\n",
" )\n",
" with open(exp_log_filename, 'w') as f:\n",
" log_line = '{} \\t\\t{} \\t\\t{} \\t\\t{} \\n'.format('epoch', 'train_loss', 'valid_loss', 'valid_acc')\n",
" f.write(log_line)\n",
" \n",
" while epoch < num_epochs and not done_looping:\n",
" \n",
" train_loss = 0\n",
" start_time = time.time()\n",
" for inputs, targets in iterate_minibatches(X_train, y_train, batchsize, shuffle=True):\n",
" train_loss += train_fn(inputs, targets)\n",
"\n",
" # And a full pass over the validation data:\n",
" valid_loss = 0\n",
" valid_acc = 0\n",
" for inputs, targets in iterate_minibatches(X_valid, y_valid, batchsize, shuffle=False):\n",
" loss, acc = valid_fn(inputs, targets)\n",
" valid_loss += loss\n",
" valid_acc += acc\n",
"\n",
" # Then we print the results for this epoch:\n",
" avg_train_loss = train_loss / n_train_batches\n",
" avg_valid_loss = valid_loss / n_valid_batches\n",
" avg_valid_acc = valid_acc / n_valid_batches * 100\n",
" print(\"Epoch {} of {} took {:.3f}s\".format(\n",
" epoch + 1, num_epochs, time.time() - start_time))\n",
" print(\" training loss:\\t\\t{:.6f}\".format(avg_train_loss))\n",
" print(\" validation loss:\\t\\t{:.6f}\".format(avg_valid_loss))\n",
" print(\" validation accuracy:\\t\\t{:.2f} %\".format(avg_valid_acc))\n",
" train_loss_array.append(avg_train_loss)\n",
" valid_loss_array.append(avg_valid_loss)\n",
" \n",
" with open(exp_log_filename, 'a') as f:\n",
" log_line = '{} \\t\\t{:.6f} \\t\\t{:.6f} \\t\\t{:.2f} \\n'.format(epoch, avg_train_loss, avg_valid_loss, avg_valid_acc)\n",
" f.write(log_line)\n",
" \n",
" # if we got the best validation score until now\n",
" n_iter += n_train_batches\n",
" if valid_loss < best_valid_loss:\n",
"\n",
" #improve patience if loss improvement is good enough\n",
" if valid_loss < best_valid_loss * improvement_threshold:\n",
" patience = max(patience, n_iter * patience_increase)\n",
"\n",
" best_valid_loss = valid_loss\n",
" best_iter = n_iter\n",
"\n",
" # save the best model\n",
" with open('best_model.pkl', 'wb') as f:\n",
" all_params_values = lasagne.layers.get_all_param_values(network)\n",
" pickle.dump(all_params_values, f)\n",
" eta.set_value(lasagne.utils.floatX(eta.get_value() * 1.2))\n",
" \n",
" if patience <= n_iter:\n",
" done_looping = True\n",
" break\n",
" \n",
" else:\n",
" all_params_values = pickle.load(open('best_model.pkl','rb'))\n",
" lasagne.layers.set_all_param_values(network, all_params_values)\n",
" eta.set_value(lasagne.utils.floatX(eta.get_value() * 0.5))\n",
" \n",
" epoch += 1\n",
"\n",
"train_log, valid_log = train(train_fn, X_train, y_train, valid_fn, X_val, y_val)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"!ls"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"!tail mlp_lr-0.01_arch-800-800_bs-64_seed-1.log"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# load the saved model\n",
"all_params_values = pickle.load(open('best_model.pkl','rb'))\n",
"lasagne.layers.set_all_param_values(network, all_params_values)\n",
"\n",
"# After training, we compute the test error.\n",
"test_loss, test_acc = valid_fn(X_test, y_test)\n",
"print(\"Final results:\")\n",
"print(\" test loss:\\t\\t\\t {:.6f}\".format(np.asscalar(test_loss)))\n",
"print(\" test accuracy:\\t\\t {:.2f} %\".format(np.asscalar(test_acc*100)))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
jeanpat/DeepFISH | notebooks/LoadingDataset.ipynb | 1 | 148039 | {
"cells": [
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import h5py\n",
"import numpy as np\n",
"import skimage as sk\n",
"#print sk.__version__\n",
"from skimage import io\n",
"from matplotlib import pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from skimage import filters\n",
"from skimage import feature\n",
"from skimage import io\n",
"from scipy import ndimage as nd\n",
"from scipy import misc"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cy3.tif\n",
"DAPI.tif\n",
"LowRes_13434_overlapping_pairs.h5\n",
"overlapping_chromosomes_examples.h5\n",
"\n"
]
}
],
"source": [
"from subprocess import check_output\n",
"print(check_output([\"ls\", \"../dataset\"]).decode(\"utf8\"))"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"h5f = h5py.File('../dataset/overlapping_chromosomes_examples.h5','r')\n",
"#h5f = h5py.File('../dataset/overlapping_subset_pairs.h5','r')\n",
"pairs = h5f['dataset_1'][:]\n",
"h5f.close()"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(2853, 190, 189, 2)\n"
]
}
],
"source": [
"print(pairs.shape)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"95"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pairs.shape\n",
"pairs[0,:,:,0].dtype\n",
"pairs[0,:,:,0].max()"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(1427, 190, 189, 2)"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"subset = pairs[::2,:,:,:]\n",
"subset.shape"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"h5f = h5py.File('../dataset/overlapping_subset_pairs.h5', 'w')\n",
"h5f.create_dataset('dataset_1', data= subset)\n",
"h5f.close()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Loading a subset of the overlapping examples"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7f7cf035fb90>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXIAAAC5CAYAAAA1fLTKAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXd4XNW1t9/pTaM26pIt2bjbmGKa6dhAqIkDBEhyE0iB\nBFJIuwmQ5AbSSMglySUJJJAE8nDz0QmhhEDoXGrANsXgbrnJVi8jTZ853x/rjEcY25Kl0YxGWu/z\nzDPnHJ3Ze81o6zdLa6+9NiiKoiiKoiiKoiiKoiiKoiiKoiiKoiiKoiiKoiiKouSdM4C3gdXAVXm2\nRVGyiY5tZVLgA5qBKsAGPA8ckk+DFCVL6NhWxi3WLLd3BLAcaAOSwH2IF6MohY6ObWXckm0hr0MG\nepp2oCbLfShKPtCxrYxb7Fluz0C8lcE4339abUBrlrtVlDTVQKtlDBoextguM6B7DLpWFNjX2M62\nkO8EKgedVwE73n9LK3ACcGKWu84mz6L2jYZnyZ99145Vw8MY293AD8aq/yzwLON73MD4t/FZxuPY\nznZo5TXgcGTA24Fzgaey3Iei5AMd28q4JdseeT/wZeAZwAHcAbyQ5T4UJR/o2FbGLdkWcoBHzcc+\naBqDbrNJU74NGIKmfBswBE35NmCsGMbYHs805duAYdCUbwOGoCnfBuyRbIdWhklTfrodNk35NmAI\nmvJtwBA05dsAZY805duAYdCUbwOGoCnfBuyRPAm5oiiKki1UyBVFUQocFXJFUZQCR4VcURSlwFEh\nVxRFKXBUyBVFUQocFXJFUZQCR4VcURSlwFEhVxRFKXBUyBVFUQocFXJFUZQCR4VcURSlwFEhVxRF\nKXBUyBVFUQocFXJFUZQCR4VcURSlwFEhVxRFKXBUyBVFUQocFXJFUZQCR4VcURSlwFEhVxRFKXBU\nyBVFUQocFXJFUZQCR4VcURSlwFEhVxRFKXDs+TZAKRTmAzbzeBMQzKMtipI9bv7Zo7uOf3f74byz\nuiqP1owMFXJlCJqAOUAAKAcGgFlAK/BC/sxSlFHytUte4XMfX8GC2W27rp1+0jqCAy4OXHJZHi3b\nf1TIlb3gBT4EVIPFC5ZicAKxABhRMIqR4fM8kMynoYqyXzQ29NL86q/3+jOAd56+icPPuIRwxJFL\n00aMxsiV3SgCGoCLgKlgD0BJsTjmtcB0oNIF7npgLnAk4M6XsYoybBbMaePMpev2KuKDmT+7nXtv\nuZe6msIIIapHrgyiBDgWmAGeMvAALqDU/JEV8coTQJsN1gaQ2HkSWA7E82K1ogzFwfN38udfPsQh\nC3YM+zVnLl3Hzdc9ykVXLKOnb3w7K6MR8meBRiBint8B/AH4KzAN2Ah8AugeRR9KznADS8E+B4qc\nUAX4AAci3gvAcXoUZ1WEgZdK4F9Auw26KxAxf4cJJOTPomN7wlBT2c9dN9/P7AM69vu1Hz51DcX+\n6LgX8tGEVgzgXOT/67nAT4FfAPcDs4G/AdeM0j4lZ5wKlplQ6oSFQB0wFTgMOBwsV8Z4/qTFvD5l\nEUd8/jk42pBwi8cFVALn5M/07KNjewLRsuKGEYl4muGEYvLNaGPklt3OlwB3mcd3AWeMsn0lJ5QA\nFeAyPXEnIuTVQD2wCE5pfIyjblvBAX/czOGpN7A5U+A3X2pzIS8813zR+PZehomO7QnAYQe1YNn9\nN7mfWCywY+UNHHP4Vmqq+rNjWJYZTWjFAO4DosA/gP9EctTSswN9SL6aMu5ZDJYycNsknFKK/OYq\ngQogAGv65nL3x8+lK1TKv7aeQnKjTUaADwhZIe6HxFyITwVWI9GJcJ7ez6jRsT1BuP/We7LSTk1l\nP//34J958J9zuPTbZ9Pe6c1Ku9liNEJ+OjLQPcBfgCv4YB6ac88vfXbQcZP5UPLDbOAAcBSJU12F\nSFYl4m37gRhsfmwGX/H/jninnb7lZbAN+X8ufU8UiNuhtwS6FkGyGLg7B/Y3m4+somN7AvCtL75E\nZWAgq20uO201ZSVhTjzv4qy2u2eaGe7YHo2QR83nMPAwkofWi/hoA8ifeNeeX3riKLpVskcTkqUS\ngHqLZB2WI9GRciRCEgI6gT4r7W3V0IaMGi8QQ4S/GBkNIWT6L2qHvhk5fA9Ng86fy0ajOrYLnM9e\nuIKffOdpnM7sr3E4YfHmrLe5Z5oY7tgeaYzcRWbEOoCPAi8BTwMXmNcvBJ4cYfvKmFMLLAVHHcyw\nynipRGLiPkTIA8hvN4nkbxhImnk6LTE9IToTPJeHCPy0Hff5YTgEcDuAT+b4PWUFHdsFzrLTVvOn\nGx4aExFP0/3ez8es7ZEwUo/cAlyL/BlHEK/l/wFPICla30EKchTkX/LEJoDEQk4EWy1U2sQTr0Vi\n4w7E27YjX/MOpMSKFfmtpyeOytjltdsWx1l2zF2cE32Qf8w+g3ucn2RgnR9a9hJ9GN/o2C5QTjtp\nPVPrevnD9Y/k25ScM1IhjwAn7OF6B7KuWxmXVAOHAo1gK4dau2RLBxARr0IEO4VM6yWRxT92RN6s\niMi7ke+CAFAG3ml9HOF4jXO2PkJRQ5DnFixhY7UfWhzIUtCNuX2bo0PHdgFy1ilr+f11j1Jf25eT\n/ryeOF+/9GV+dcvinPQ3FLqyc9JQDpwMNIDLBQ1W8cIbkLCKG5m+Sy8CSiAxcDvikfsQYR98n0ea\nHegt5ZHE2QSmdPG2fQEd/RVmlNkCbM/he1QmI4cf1MJffv0g5aW5y5KKRO3c+bcDc9bfUKiQTwpc\nwBlgnQLVLhHuckTIyxBxLiMTQjHM4wgi6OnzBt4fcjHDLKntNp5qPZOXFywmvKYI42EnbAFoITNv\nqCjZp74myGv/uDXn/aZSFna2F+W8372hQj7hKQOOl3h4tUtCKenslDIkROIlk0wXR4R6gMxUuA0J\nu7gHnVvN537zsR1CT5TDeqTsSiiECLmijA0nHd3M0/f+JS99//2fs/PS795QIZ/QVADHANOh2CMC\nnp7Y9CEZKE4kPm5HQidRxAuPIqEVD5miWW7ECzcQjzyMJOUFEc1uRqYB21OQagPeyMWbVCYhZ5+y\nlt//PH+Tmhd/fVne+t4TKuQTmqlAE3iLocEiqYU1iAdejnjVdjKjwEpGwHuQSc8EkiduRcTfal5L\npyR2I3tMbAPWATuASC/wzNi/PWXScvThW6mrzk+J2QsvOy8v/e4LFfIJSwNwNNjLZPFmOjulCBFk\nJxI6tyPi7UQWnicQEe9FvPF0GKXbPE/H0O1I+CUMbAa2AhsNiHYjmXq5WjShTCYsFvjo6e9x5Zf+\nL+d9J5NWLrvqTO5+aH7O+x4KFfIJiQM4ERzlUnS1BolxVyNCnp7YhIwHHiPjYfchAu1AYuYGIvpB\n87VRJBmvH9iJJKa8C0Q7kdVnq8f6DSqTlBJ/JGv1U/aHSNTOtb88gVv/emjO+x4OKuQTkjlgqYRS\nq4TJSxABLjIfbkSYk4hX3YMsr0/nj/cicXEbmRGSjp/vRES/F4mHr0EmOMMh4HEkvqIoY8OVX869\nJw5w5U9P5n/+eGRe+h4OKuQTihnAbLDMhRKvTGpWIbHxdIaKD5mwTHviYcSzDprX+hEvPEZmpWcE\nc79O82cDiKBvQnR7ZxRSO1ERV8aKKz7/Kmefsoalx27KS//jWcRBhXwCMRU4HqiDarvUQalCPHI/\nIt52RIijZNK7g4go9yOCHUfE2zB/nt70Z8C8pxcJvawHNiCTnNEOZK8FRck+F37kHW74ryew2VJ5\n6X/WsV/JS7/7gwr5hKAOOAWsNVBjz2yUnPbC44gnHkMEPEJGmPuQkEo6QyW92MeFZLd4EVGPmfe2\nIBUQtwCbkxDfDjxGplS3omSPs05Zy5033Z+Xvts7fXzqq8tYt2n8l55XIS94moAlYK2EgEOyU6qR\nSobpKoVWRLx7EcHeSaaOSnoZvgMR/nSaYRHixadf349McLYjCSkbEhDfgRQBHP6GtooyXD574Qr+\ndMNDeem7o8vL5VedwePP5qoc8+hQIS9oZgBHgaUOiuyScVhBprCVx7wtLcS9SEy8j0wKoY/Mis30\nebo4lsM8jpNZ/NOF5I3HIkjO4ZaxfYvKpOSKz7/KT698Km/9t7T6ue/ReXnrf39RIS9YGpFVm1NE\nxGuQhTsuJF/cQiZUEkXEuxsR9BiZHPISJJYeI5Olkl6mnxbwdI55mEzuOEHevxuOomSHi89fyc+u\nehK3O5E3G5ae/+m89T0SVMgLkjpgKVhNT7yOTJphuo5PCPGuU2QyUaKIlw0SRikx73EhsXTDfF16\n958kkpoYQbzwHuTLIJ6+EBvTd6lMPs48eR23/ervebVh45YyOrrG156cQ6FCXlCk1fpUsJdAhV3i\n4X4yO9p7EQFOkclOGRwLT+eQl5n3+smIf8q8J2E+uhER70e2e2s1r8X7gUfH+L0qk4mlx26iobaP\n23/9YL5N4ZBTv5BvE/YbFfKCoQ5YDEwFjx+qrDAFCYuk64W7yKzYTHvgYfO5CAm9pLdqS4dhnGRC\nKmHEKw8jmSndZFZ6pmPj4Tiwkg/uRawoI+P0Jev5w88fYUpdb75N4Td/PoJIpPBksfAsnpSUAUuA\nKeB3wUwy6YU1iBCnw4lOJDxiR8Q4ggh3Ol6e3hAi7ZmnJzpj5utayVQz7EQEvBOJjUcTYLwCvIq4\n74oyOhYt3MHtv36Qqizvdj8Sbv3roVz9s6XE4rahbx5nqJCPe5zAMvBOgQpzk+TpSHphBeJhpycq\n0ys1HYgAp9MKU0jYJV3wyo945INL1vabr9mJLPLZijlBakDKQPIO1wL5yyRQJhYV5SFef+yWfJtB\nZ7eHV95o4NJvn51vU0aMCvm45zzwN8BcKxyAPNI1xdObQVgQAQ+az52I151C4uCDQygg4t1nnqfr\nrbQi6eBbkTzxnTGzwa2Iyuum8Up2aX/7F3nru7W9iFeW1wOw7LMX5s2ObKFCPq45EOzTYKENlgJz\ngClJ3FNC2D0JHNY4RtxKOOEm2umBoE0c5xASUu8hswlEjEwGS4pMedoYstCng0z9lM5eJC7zIrJb\nhKJkl8sv+nfe+g5H7Fx+9Rk88I+5ebMh26iQ54wKJHaRnpnsGeL+2cBSaHLAEcBJSfzzuykv7qTc\n2YnPMoCHMCE89KTK6K4sIxguob+lHMNiFa+8FPHQ05UNE2SqGxrmeQQJpXQj2h3qBeNhpIHuLH8G\nyoTkW6fC756BCj8snQO3v7TP2y/79Otcd3V+QnSf+upHWbsxwGsr6vPS/1ihQp5VbMAsMksjk2SC\n1Ollk+nSgiDxjXfJVKhKUwOcBKUlMrF5NFQsaGdBxQoCdFJMLyX04SJKCA/9Vj8d7gAt7jrWWObQ\n76yAdRbR4V4kBm4nUzMlinynBBHx3gHEUsgLnkAqYimKicUCxW548Tt7v+fiozPH3zpVnhdeK2PO\nyIzvs05ey03X5T51NZWy8KWrz+B/71+Y875zgQr5qEknZ09DllSWIkFpHyLUHvOeQYVLLABhMIJI\n1cJNiHgmzPuqwFMMsy1wIDinhZlSsYGpbKaWHfgIUUY3CfPXF8KLnyAWDMKlXtYnncTqiyFpkeb6\nkTh4elVmFxJK2Q70xiEVAV4DXhjzT0spIMp9MK0CfrIMGsr2//Vv/QBe3ghX/w3ag9htKebPbs++\nnUNw7yPzOP8LH8t5v7lEhXxU2BAhriGzRr4ULG6w2sAoh5QDLFaw2sGZApctkz0SiUM4hnwBJBBB\nt4HtWKj3wiHAQvBODVLLThrZQik92ElgJYWXAQwsWEkRwU053dSwk1C5l20DThIDHvkucZjN95PZ\nY3Mr0B8HViCxlbdy+cEp450iF1x9Bpw2ym3NFk+H/zoLfvAQRYlOfnZ17ibN//74bFatreK7P1uS\nsz7zhQr5qLAjq3IagDqwuGTJvBtzY2NHJqriAorMtJE44qj3OSDogP4mCIaQ5O0jwR2QJmcBByWo\nCWyngg78BPExQAgvA/hwEsNPEDcRyugmjp0ENpIWG8FAMZ2hGuiySbNhJCyfLkEbCgFvA88jrrqi\nDKLYM3oRT3PSbLixiHt++PvstDcMHn1qJpdfdSYtrf6c9ZlPVMhHxWxkVU49lHolV7scEe1iJN+7\nHRHOUmS+M2QenwOuQ3uJ3l8C99rhjTqIXAoWB5TZYAGwAKrnbaXO2oKPAcJ4cBLDgkEILzaSOEz5\nLqcLLyEMrLRSQ7V3JwNlJUTiRRIXb0dEvAUYCCMi/gS6QlPZIw9entXmPsefOOX4jVltc2+sWlPF\neZecTyQ6eeRt8rzTMcEHlIPfK5GVBvNSFdg+nMC1IELkLTepx+wSSjkS6IKpR27k9/WfYdG/nufv\n513EN0tuJFhdIdGNHuT7YQY4Duin0bqZJpoJ0ImTGF5CDOBjOhtJmWGValoxsGBgYTv1lNHNDmqw\nhpISC9+AfJlsSkFvEAnhPJaPD0wpFLzOoe8ZAls8RsWm1Rz3h5/QsO4N2tZA1ews2LYPVq2pYsGS\ny8a2k3GICvmIKUHi4aXigVchi3RKgKngO7ybedXvsMYzl+73asQTnwekUhxQs4GGn23moT/C+Vc/\nwNPfPom7y/8D436bhF2qgbkpKmvaqKGVKtqopA0XUaykqKMFJzHsJCiiHxtJktjwEKaEXpLY6A4H\niGzywntIYsyaFPSld0t+Iy+fmFIgnJ2dzI6jb/sFS2783q7zPy+DK9/LStMfYMU7tbyyvJ5vXPOh\nselgnKNCPmLqAA84HJn6JV7EKw9AaGMxG33TcZZEsS2OkdzsBBtYauNssTWy6rJDObl0Ox1nlmDx\nJXEfGCLc55dwtRvcswaodbdQQQduIlgwsJHCQWyXiNtIEsaDgYU4Droop4MKOo0A3a0BUssd4uW/\nC/RvRrzwjnx9YEqh8NWlo27itOuu4Mi/3pgFY4ZmzYYKPvuND7NyVU1O+huPqJCPiGp27YdmcWUq\nC3qRBBQbJNa6aI9MwTl/AOeMCOEBJ3SD4XPS7SrljoM/yduzF7DRM431zKB4ShexQzwkHWCzp6iq\nbaHc2oWdBAZgI4mHEDGcxHEQwksKK2HcpLDSRzEdVLKK+axOziX0UokszHwDCHYD9yL/FijKPrjq\ndKga+QThwofvYMlvvo+/dXsWjdo7hgEnnnsRO9uLhr55AqNCPiIcgA+sASiziq6nC1ild+jpBaPN\nStTul2udYCVJ1dItFFv7WMssVnoOIkAXSaw4UjGq527GYw3jJkIFHVTSThH9Zp8W4jhxEKeTAFGc\ndFNGL6UE8RPCy8bkdNaFZtH1Wp0UKFxrQH8X8Jt8fEhKIVLqBZt1v17i7e7AHg3z9ZOn7vO+aD88\n+HVY9qvRGPh+rA0/yF5jBcxwhPxQ4DbgIPM8APwVWQGzEfgEmbXc3wU+hUR6/xP4ZzaNHT+kZzSL\npAphDfKp1CKph0mkwuAA0AyWshSOxRGqm7ZRZ23BTZgkdkJ4KaMbOwn6nbJkP4yHOA5sJInioo9i\nAJzESGAngZ1eSuggQBvVtFHFjnAdPX3l9GytIP6OSzzxVwzYFILEhpx/OgWEju1RUrnhXc658j+o\neW/FkPe6irIr4k++MD17jRU4Qwn5DcBFSNJaml8A9wO3ApcC1wBXAMcDpwFzER/1OWA+mUrZEwQf\nMqNZCzU2CZVPQQQ9gKQfOpAohhOsniT+BZ00TN1Cg3UbU9lCGd0YWAjiZwAfSax4CRHHjpVSBvBh\nJ0EMJz2mxx3GsytWvo0GtjCFraGpBNvKCW4sxnjXLrHw9ORm93aIv4qkrCh7QMf27ixqhAV1w769\nfOsGPvxfnxuWiGeTd1ZX8fs7DptQRa9Gy1BC/k3gRuCRQdeWIIMb4G7gdfN8KXAPkmi3E1iFJNy9\nmEV7xwE+RLX9IuKNiHg3Ip65A6ll4pPnwJLtlPm6mGNZzcGspIo2KugghpMgfrYyhSB+ttFACA8h\nvCSxEcRPED8Wsw5LG1XYSNJLCTGcbOmbRs+bFRiv2+BNYB3iQ3YlIbYGyREfqjDXpEbH9u7MrILG\nwPDuNQw++YXTKN+S27o8wX4nH/nMhWzcMoKSAROY4YRWLLudB5BySyAlmcrN41rEH0zTjkjbBMML\n1EK5TcIntcjCnxJkbZAlgSViI7CwhZKSbkrp4QA2cCBvsYBVzGE1LiKE8NJNOVZS7KSGHkrZTCOb\njUZcRPDgJWTxYjHYlV6YMGwMDBTRv7ESViMy8zKw3oDWBKIx9yG/FmUY6NhOY7WAc2g5sMVjXHzx\niTS8+fJ+dzHS1MNEwkokaueosz7PqrWVI2tkgjOSyc7dlwI6h/mzQTw76LjJfBQCHqAJLMVQbJUy\nKwEkLh4A7CkclgT18zZSXbKdIgaopJ0ZrOcANjKNTVTGO/DEowzYB3A6Y0Rw7/LCDaCnLYDVnpAH\nkIg6sNqTJMIOEts8sNkqIv4m8IYBWyOQWoMU3XonPx9LXmkmizXTJ+/YnlEF3953Dravq53Tf/Ll\nEYn4SPnnszN45sUmrr/pmJz1OX5oZrhjeyRC3osEDgYQP7TLvL4TiTmkqUQKpO6BE0fQ7XjABpSD\n0yXCXYakHfoBbwKrPcmssveY7X+XYnrx00+ATqazkSY2McXYQmlPBGsUXO5+nGUxum3lOIiTwE4I\nH4mQCwwXFkcSI2qFuB2SKdhplZ3WliO54RsM6H0HUuuY3AWvmni/WD43msYm8djeN/ZohNN/+hXm\nP35PTvq79+F5vPVeNT/+n+Nz0t/4pInhju39yzMSngYuMI8vJLMH2FPAx8w2a5GMgNdG0P44ZhpQ\nCj5nRsTT9VWcSeZXv8VC/wpmso65rOYgVjKPd5nPKqanNlHcFcMal5asZonmBHbCeHYdY1ggbsMI\nOSBql5yJdVaJyq5E/sF/OwFd2yGZVnUlS0zesf2jj+zzx5+65BTm//PuHBkDDz4+Z5KL+P4xlEd+\nLbAMiQL/G/gGknr1V+A7SNGOT5r3Pof8IbyL/Bt6ORNuBUoZ4AOvRQTchlQ3dMQ5puYFGh2baWAb\nDWyjnm0UMUAjmykxevFH+7HHUrLxThlghS5LOa1UE8dBBDctbfUi5AYwYJEStG1IfattSPTkVSAZ\nQcrPbsrDZzBh0LE9mPl7z1b5wnmHULN65aia/+ITw7/393ccxp0PLhhVf5ONoYT8B+Zjd/YWTPuR\n+ZigeMDpk1C5Ux728jjzat9kjmM15XSykLeYwlaK6cNBDH+sH/9ABG9fSkrJugEbdPn9bLM20EU5\n26kngguXN0J/JA5hp9QO70A2Qm4hEy5LRYD/zsu7n2Do2B4Cb08HZ13zhVGLOEh5/uFgqdcFPiNB\nV3buF8Vgs0tIpQJsTQlmzVvFISWv00QzB/IWjWyhLNmNMyX1UCo39YtnHUE8eDfggj6KSWElhpMU\nViJ4CIc9EHFI3kS3+ViPCPlaoC0Mxr73Q1SUbODq7+O0677G3CcfyFmfv73tiJz1NdFQIR82swAv\nOOyyHP9kaDxqPQdXvcHBZix8trGGir5e3KEYxA2pA76TzLSYE3mtH/ypPuxUYzfXlNjSSRFxi6R/\ndyLhlO1IwcK2OCQ7gFdy95aVycHPz33f6dnXXErJji0c8OLjOTXjuz+f+Dv5jBUq5MOmCqx+iY2f\nACUntnFg8UoOZiVH8iqNbKZmSw/WLiOz0XEnsq1aFKm3EkUiqwlwGxFcRAnjMQtjWUglHHJ/LyL+\n68znLUlIdSFzbvHcv3VlYnPCrF2HZ/3wixzywJ+wpFI5NeETXzqHYP/oa6BPVlTIh40THB44Gmyn\nRVjoW8lc3uUg3qQhsY2q7X1YtxuyaNvcY5l+ZKVnLyLs6S3gLGCkrATxk8K6a7KTpEXuDyOTnNuQ\nFfapIDLf1pzzd61MDmyxKMfdeh2L7vlDTvsNRxx87+cnceeDB+a034mGCvmwqYUD7HAcVNa1UWVr\nYwYbmBrfSs2mLuzbUiLcLiSvwYOIspdB2S1IhUQHhGxeDNhVT6XXKCHZ6hSPvYfMFnH9CfPg3Zy/\nY2VysPDhOyjr2c4JN1+b875ff7OWX96yOOf9TjRUyIfFdAhMg4PtUJOiyNtHLTuoo4Wq/g4cHSnJ\nMEkhXnd64XdayOOIp25mrJCApGEnipt+fLRSTevWOhJbHZKlsgaZ3GwHUt1oXFwZK752ySuU3fAk\nqcjY7d160Hngr/3gdcOAn/322DHrdzKhQr5P/MAhwCxolEqH1qokXucARfTjN4J4EmERagci1k4k\njm5HYuJh87nHvB6ARLGFuNNqeuNldBul9G8pwdhqzVQw3AJEeoH/RWunKNnmsIUt/PV3D1BfE+TG\nu5JEI2PX15RF4Cn54PU5x3+ZtRuHWaRL2Scq5PvkGGAKlFbDIgssBHtNHLdDJipTFitRtxuPZ2BX\nyIQUIuxRJB6+HQm1RBCPPAJRm5OgrWhXGdvucIDwFo+USnkXeNeAriBwJyriSraxWODfj92669xb\nDtHgPl4wBhz30c+oiGcRFfI9Uoq4z01gD0CNXTzqSrA7E3isYalIaFhxJ8KSV55ANNeLCHoHkge+\nEQm1WJAJzyKwTDOI4mQrU2ijiq5QBXTbRPRbgb4IkrIysRYPKvnnhKM2Eyh//7i64iW4pj53Nqxa\nU0Vnlzd3HU4CVMg/QBmwCJgDtmKodUA9ItAWcPkiOMzNjw2LlYjHjdsbylStMZBJzzCiwzbz3IJM\ngBrikfdQSicB2o1KIq1uCaV0ADsMSOwAXkJWEilKdjhz6Tr+cP3D1Nfkzv2uPRCmHJY5f3dtJZ/5\nxod5b31FzmyYDKiQv48yJJwyE/BDpRVmI5tGeMFSk8TlGcBFjJhZxbTdVY6rKIEnGRPPPIjUzgNZ\nEORCwioAHkhWWOksL6WFeropY3uynthGn0xu7gD6Y8BD6KYQSjY59ogt3PqLh6mtzm0MpXIGVM+T\n4+CAk49+7gINqYwBKuS74h7HArPBUgtFVtk2oBHZBageqXC4GVIzrCSxMYCPDgL4LUG85QMEHAnc\npOQTTSDeuBcRdbNIFrUQr7Ozw1bDdurZyhS2bZwGK22SqbIDJBajIq6MHrsthdVqEG3+8ZD3XvYk\n3Hzy2NoaShczAAAPMklEQVQTjjhUxMeISS7kTsT7ngY0gbtCdmSsRAS8yvzRVDm22IGkhV5KaKeS\nFuoooZdSeqjq6xNvPISs6HSQmeA0QypUQHtdMeuZwQoO4b3wfHjNLhslb0xAfB2yo5iijI7qygFu\nuf5hPnzqmmHd7/RCYDp0bhwbe/69sp4jzvz82DSujKge+QTBARwMLALrHCipENGegXjiU5Ga7j5E\n722QCtsINpfRasju9S3UEcQPGFiSyDYE6XzyOPLppjeeaIT+WW5W2efzJgexou8wWl6dJrs+vhOB\n6BvAwzn9BJSJSUlxhN/++B/DFnGAskY4aox09rGnZ3L2xR8fm8YVYFJ75EcBB0JROZTaZbuAeiRh\npQgJrdSQibxEgThE+9x0R8vocFfQRYAkNlzxGNZoKpN2GDMf6Yn5KkhOg7UV01nDLJYnDmHr6iZS\nD1vh1QS0pDffDOf0E1AmJg/ddhfHH7U532bgq4DYwdP42nfOorXdl29zJjSTVMhPAuZJKKXeIh54\nMSLkRcgEZTUZbzyGaKwNUs0OwmVF9MwrxbBYiOLGsFggaog3HkOyVGyIkHuBqbCzqpI+i5/1zGR9\nxxwiy32yefKbz0DqZcSNV5TR8d5zv2POjI4RvXbRJ6H5ZViVpX8Mv3f7dizn3EQ0NkllJodMok/Y\nigS+m4ADwFEpXngtUlq2AomN+xARdiLRl3ShKymMAlaIxtwkU1YMmwUrSRwpsyKhDRF8KyLgxUAV\n9AfctDirWMU81qdm0tVeIZsnv9ZqbhShIq6MHI87wfe//hxXffn/RtWO1S6P0dJT18Sf/t/LxGIe\nUBHPCZMoRu4B5gBTwFYlE5kNiJCnPecSxCP3kwmLJMgstQ8hueRFETzWMAnsJHBgi1mwdiJiH0UW\nBiXNRwqSKSsDFNFOFb3xEqJrffAMEOnng5uzK8r+MXNa56hFPFu0zTyQe391H/0VNfk2ZVIxib4u\n5yE5hHXgd0j8uxKJiQfI7MFpRzQ/hQhzmF2CjCH3OLxxWeeMuSGEzcCwgSVkvj5ORp87wVMRxe2L\nELW5WN0+V/bg7AH5Hh3mHliKsheu/96/8m0CAPf99110TZ3BjnmL8m3KpGOSCPmhwBSgAYqKoNoi\n4l2OCLgXEW+zMqG5aY+kE2JeLzKf/WC1JfETxEaSAXz0uouoqOrF1puSkuEuZII0KG2lGuAN2yJe\n4wgGUt5MbXILYGhYRRk5o4mJZ4sHf/IXNh21hL7qhrzaMZmZBEJuR2IlFeDygduSqVCYLjNbyvu9\n8PTKzLh5zYcIeQqsZXEoNojgJo4DgD5LMYmyndiKUiLibrPLSog6nKwoX0gbVaSwYmBuHuEELH4w\ntOaEMjKqKwZoqM1eGYe37oc1+7G7W099E69fcBlvfuTTWbNBGRmTQMgbEffbLAZubn6Mgbx7J7Jw\nx45MZtrJiHd656l0iVorpLodxNrc9DaWELa46aWETgIMuNy4auKZSIkDuqf72VA5hXZKsZGUyIzV\nIO7EnEBNIUF1Rdl//vTLv1Pki2WtvYXnwrpn4O2/DX3vW2f/B3+77o6s9a2Mjkkg5OnQRVLE24KI\ndIX5nCQTC7eat9sRTz0t9inzdUkgCrGgh85IgJ2eWrZTRzWtrC3updbWhq9ygE5LgAF7EX1+Dyls\ntFFFK9Vsp4HIhiJZ+WkAligYk2i+WSl4Vi9dxoZjPsTr538x36Yog5gEQr4NmA5UQzwldVROAE4x\nwJaC92xS48SBhEPSBfAd5nM6bp5EQi0DkPQ6CTorWdMwC5cvSswsSVvv207I52EntfgYoJQeeihl\nHTNZycFsXjcL1lilXG0PkDLIBOQVZf/40tVncsIzN1HkzZ5Xvi82H3YCD19zC6Gyypz0pwyfSSDk\ncaTItx8MJ5SVwSlw3LFPEEz5eddxMLFWr4RbvMgnYjWfLUjYZcA8HwB2AishdayNztYGXpnvY1tJ\nA35LkOJkkBZbHbW2FooI4iFCH8XsNGrosxQzZeY6WvpmEH3dhZFIN748D5+JMhHYvK2E7h53VoX8\n3N/Cltegd/v7r/fWNXL77c/uX2On/iprdin7ZhIIOcjWOw7AB1s8sM1NKOwjGC6FLovofAkSQvGT\n2Sw5imhtD5k64+3I/Y8DTRbC75WzrrRcXtMF1vkJts+agt8dpMjTS9jiIRj1c5b7Eb609WZWN8zl\n+s99hzXLF0B3TNpVlBEy9fCv8/wDt3Pckdlbkj/tGFg5qHbb5kXHc/tfnsta+0r2mSRCDlLwuwy2\nOeDHU3ijazH0mbvyGOyKf++a2Owns7inG1kM1G4edwItwMwYVDvlvgHgQEjZ7YTK/YQ8PvoCXlIx\nB14jzCHeFRzxyJvML1nHSyccw5oDFsCbNo2sKKPmy989nTef/H3W2lv2K6mT8uJNsHrJR3jkmluH\nfpGSVyaRkIeB9YANVtnhhw2S0HIINHxxEzMr1rC8+zB6l1dIzZQuRLSDiIDvRMLtISAagng3LG8D\nbwvEjwVnCfghcEk7p01/iLjVzmrrHNb0zyXYVcaL/mM57qMv0Wsp5u3uBdJeMjexTWVis2FzOb+8\nZTHfuPTlrLU576IiPr/iO3R9/3MMlGtMfLwziYQ8heynZub+tRkQmELV+du46+DzOOJfb3HLKZ/m\nh5Ef0XZPnSzsiSDe91YknBKPIj8YAP4FRtjMObdBbAmkHDTOXMtVwV9Q5uvges+3WB2ZS/wFFw+u\nv5C/z74A1oNxswVW9ILxZB4+B2WiMRBy8M1rT6W2KsjHl70z6vaajvwaW7aXYBgJeHo7XFC7/41o\nfDynTCIhT7MemdkMQBRc/XGMFheOFxMc2/gKjRWbaeuvk72Po4hX3pWEeBAJz7yNKPtgXgF8sGEa\n7c808MQZS6hy7WRV74HEni+W7TdbwIhZYG0KWtNtqUeuZI9PfOlcXK4k55z+3n6/diDs4Ae/OIkb\n/rD4/T/40SPgcUBTABYOc+VmcydEtYZQLrHkoU8DfpCHbndnEbiPh1P8HHXpS5y7+D56AkXc+ean\n2HjdbHgCiBsQikCqGwmKLzef94LVDoeehP/sUuyNlXQvr4InU9BuiOce74d4L7AS2IAE4JXsci3k\nZ1zDOBnbN1/3KF/89Ov79ZqvX/Mhfn3rUXu/wWWHy0+Cwxv3LuhdA/C3lfDY27B65371rwyHvY/t\n4Qz4Q4HbgIPM84uBXyFRXpBpwcPN4+8Cn0Jy/v4T+Oce2hsXg13STOaAYz7UFWE9oRbv4SHCW7wk\n/+aA9SFkF/t0qsrrSJxlGDgrwBOA0OEQN5eEkgReRYLsbWPwfhRhv4R8Qo5tjzvOj779DN/8wvBi\n5hdcdh73PDR/eI1Pr4CpAfjtbjv+fOte6BiA15v3z1hlPxi5kN8AXIS4oQvNaxcBi4Cv7nbv8cBP\nzOdq4DlgPh/MyxgXg12wINGl+bLdm3uOXAp1gNGBiO4qJLYeH0H7jt3OR9KGsn8MW8gn9Nh2OpMU\neWO88OBtzJvZvsd7fn3rUfzo18fT3evB2N802BLP+8/7wppKO+bsfWwPFSP/JnAj8Miga+nNz3Zn\nKbJzsIF4NKuAI5FdKccpBiKuKyG1EkKVyN9nEHgjC+2rcI9jJvTYjsVsdMU8zD/xcgBOWNzMTT/9\nBwDzT7p89B306raE44nhTHbuPrAN4BPAh4BNwBXAamSLhsGzLO1I1e8Coh14Nt9GKLlj0ozt515u\nyo6AK+OSkWSt3An8xTz+GHA3mRjj7lPVTvbIs4OOm8yHooyEZvORFXRsK+OIZoY7tkci5INz5u4H\n/mge70T23ElTiZSj2gMnjqBbRdkTTbxfLEe1lFzHtjKOaGK4Y3skNVSPR6p6A5yDJFEDPIV4MVbk\nX9FDgddG0L6i5Asd20pBMpRHfi2wDDgAGbjfAo5G/v2MIIvWLzHvfQ54GngX+Tf0ciTtQ1HGIzq2\nlQnDJF4QpExMdEGQMlHZ+9jW7WkURVEKHBVyRVGUAkeFXFEUpcBRIVcURSlwVMgVRVEKHBVyRVGU\nAkeFXFEUpcBRIVcURSlwVMgVRVEKHBVyRVGUAkeFXFEUpcBRIVcURSlwVMgVRVEKHBVyRVGUAkeF\nXFEUpcBRIVcURSlwVMgVRVEKHBVyRVGUAkeFXFEUpcBRIVcURSlwVMgVRVEKHBVyRVGUAkeFXFEU\npcDJk5A356fbYdOcbwOGoDnfBgxBc74NUPZIc74NGAbN+TZgCJrzbcAeUSHfI835NmAImvNtwBA0\n59sAZY8059uAYdCcbwOGoDnfBuwRDa0oiqIUOCrkiqIoBY4lD30+C5yQh36VycFzwIl56nslcFCe\n+lYmPvkc24qiKIqiKIqiKIqiKIqiKIqiAGcAbwOrgavybEuaZ4FNwHvm42ogAPwTWAM8BpTlwa5D\ngTcHne/Lpu8in+nbwGl5su9ioJvM5/jvPNuXa3RsD4/xPq5Bx/Y+8SHZ9FWADXgeOCSfBpk8g/zi\nBvNn4BLz+FLgf3JqEdwAdABvDcOm44EXkAykGuQPwp4H+y4CbtzDvfmwL9fo2B4e431c783GyTy2\nP8BJwAODzr+KfJvlm2eARbtdawb85nExsC6XBpk0It/yaZrJ2FRCxqZrga8Muu8B4JixNo4P2ncx\n8Js93Jcv+3KJju3hM97HNRTg2M7lgqA6oG3QeTvyLZZvDOA+5N+jXyIeVQAImj/vA8rzYNfuOf6D\nbeolY1Mt8lmmydXnurt9BvAJYC3wODDHvJ4v+3KJju3hM97HNRTg2M6lkBtAcrdrzhz2vzdOB6Yh\n/wo3AFcwPu3cl03jwd47kT/KWcAfgbsH/Ww82DeW6NgeOeN9XEMBjO1cCvlOoHLQeRWwI4f9742o\n+RwGHgamI56Bz7xeAnTlwa7d2ZtNu3+uleTnc40NOr4faDKPx4t9Y4mO7ZEz3sc1FMDYzqWQvwYc\njrxZO3Au8FQO+98TLjJLXh3AR4GXgKeBC8zrFwJP5tyyD7I3m54CPob8LmuRya3Xcm6dTPy4zeNz\ngFfM4/Fi31iiY3vkjPdxDZN7bO+RM4F3kNnd7+XZFpBfznNkUrSuN69XILGwNUhqVCDHdl2LpD8N\nIKlOxw1h0/eROOgqJA0uV/aFkIF7PHAlmc/xX2S8lnzYlw90bA/NeB/Xg23Usa0oiqIoiqIoiqIo\niqIoiqIoiqIoiqIoiqIoiqIoiqIoiqKMW/4/qhJiw35mFYsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7cf04285d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"h5f = h5py.File('../dataset/overlapping_subset_pairs.h5','r')\n",
"subset = h5f['dataset_1'][:]\n",
"h5f.close()\n",
"grey = subset[10,:,:,0]\n",
"mask = subset[10,:,:,1]\n",
"%matplotlib inline\n",
"plt.subplot(121)\n",
"plt.imshow(grey)\n",
"plt.subplot(122)\n",
"plt.imshow(mask)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Try to convert greyscale into uint8"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def toUint8(array4):\n",
" a = array4/16\n",
" a.astype(np.int8)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(24, 190, 189, 2) int64\n"
]
}
],
"source": [
"sub25 = np.copy(subset[0:24,:,:,:])\n",
"print sub25.shape, sub25.dtype"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"greys = pairs[:,:,:,0]\n",
"masks = pairs[:,:,:,1]\n",
"g_ex1 = greys[200,:,:]\n",
"m_ex1 = masks[200,:,:]\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7fb599bfbd90>"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAC5CAYAAAA4YsSNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXmcpFV197+39qre93Wme5gZZmeRHdkHRzYzCDESk4Ag\nRkTyEmPeVzC+QU0U1Bg1RnABFfLGIKggi2ELi1F2GJZhmH16lp6Z7p7el9rrvn+cp6ZmSM90T3d1\nVXf1+X4+z6eqnnqee089fftXp85z7rnGWouiKIoy83Hl2wBFURQlO6igK4qiFAgq6IqiKAWCCrqi\nKEqBoIKuKIpSIKigK4qiFAhTJujGmAuMMeuNMRuNMZ+fqn4UJZfouFamM2Yq8tCNMS5gI7AS2A28\nAlxhrV2f9c4UJUfouFamO1PloZ8MbLLWbrfWxoF7gdVT1Jei5Aod18q0ZqoEvQnYecDrXc4+RZnJ\n6LhWpjWeKWrXjLLvoNiOMUZrDihTirV2tHE4GcYc16BjW5l6DjW2p0rQdwFzD3jdjMQc38PZwDlT\nZEI2eBa1bzI8S/7s+/JUNDrOcQ1wy1T0nyWeZXqPG5j+Nj7LdBzbUxVyeQVYYIxpMcb4gCuAh6ao\nL0XJFTqulWnNlHjo1tqkMeYG4AnkS+Mua+27U9GXouQKHdfKdGeqQi5Yax8DFh3+qNap6j5LtObb\ngDFozbcBY9CabwOyzvjG9XSnNd8GjIPWfBswBq35NmBU8jxTtDW/3Y9Ja74NGIPWfBswBq35NkAZ\nldZ8GzAOWvNtwBi05tuAUdGp/4qiKAWCCrqiKEqBoIKuKIpSIKigK4qiFAgq6IqiKAWCCrqiKEqB\noIKuKIpSIKigK4qiFAgq6IqiKAWCCrqiKEqBoIKuKIpSIKigK4qiFAgq6IqiKAWCCrqiKEqBoIKu\nKIpSIKigK4qiFAgq6IqiKAWCCrqiKEqBoIKuKIpSIKigK4qiFAgq6IqiKAWCCrqiKEqBoIKuKIpS\nIKigK4qiFAgq6IqiKAWCJ98GKDONZYDbeb4VGMqjLYqSPe649ZH9z7//s5NYu6Euj9ZMDBV0ZZy0\nAouAaqACGAEWAp3Af+fPLEWZJH997Yt84k9fZ/nirv37LjxvM4NDPlasvD6Plh05KujKGISADwK1\n8tyUgQ+IA6koUIoMo+eAVN6sVJQjZW5TH9tf/u6o77U09wOw9unbOemiTxKOeHNp2oTRGLpyCIqA\nJuBKYC64q6G8TBz1RuAooMYP/iZgCXAK4M+XsYoybpYv6uSilRsPKeYHsmxRF/f/8H4a6wZyYNnk\nUUFXRqEMOBv4YwjUQ2UF1HihHqhDHpuBo4G5HqASWA4ch/7oU6Yzxy7dy93ffYBH7/mPcZ9z8fmb\nuP3WRykrjUyhZdlhUv99xpg2oB/5rR231p5sjKkAfgG0AG3An1hr+ydpp5Iz/MB54F4CJV6oQZx1\nn7MtA++FUXx1EYb/UAZPAfvc0FsNLAXeBhJ5sz5b6NguPOpqhrj3jl+yeEH3EZ+7+oMbKS2O0j8Q\nmALLssdkPfQUcI619nhr7cnOvpuAp6y1i4CngZsn2YeSU1aBWQgVXlhhJOrSApzobDfF+N15p/Jq\n8wmc/Mnn4DQLLQaCfkT9L8+n8dlEx3aBsWfNtyYk5mm2v/ydLFozNUxW0M0obawG7nae3w1cOsk+\nlJxRClSDzw81Rpz1RiTM0gicAKtafsspP32Do+7czkmpV3H5k3JaGeA+UNTrgOntzYyBju0C4oRj\ndmPM5NowBvas+SdOP3EH9TWD2TEsy0xW0C3wuDHmFWPMtc6+OmttB4C1di/yH67MCE4DKiHogmJE\npCsRMa8GqmDDwBJ+8aeXcefVV/LkjlWktrrFly0CitwQLAXPEuBjwLnMYFHXsV1A/PrOX2Slnfra\nYf7wm59y+62/pbpyOCttZpPJ3sE63Vq71xhTAzxhjNmA/COMk2cPeN7qbEp+WAQsAG8R1BqRqmrk\nsRQoAeKw/bGF/FXx90n0eOl/rRx2GZlnVIZ8CUSBhAf6y6DnBEiWImHnqabN2bKGju0C4XOfep6a\nypGstvnhC9dTUR7m3D/+eFbbHZ02xju2JyXojpeCtbbLGPMgcDLQYYyps9Z2GGPqkZknh+CcyXSv\nZI0W4AygEppdEjevQlLPK5HQSxjoAfpd7Ouql7+qGwgiIp4W/hgy56gXiLphYEGOPkMrB4vmc5Nq\nTcd2YXDNFWv46k1P4/cls972Oadtz3qbo9PKeMf2hEMuxpiQMabYeV4ErEJSHB4CPu4cdhXwm4n2\noeSCBmAleBthgVvGTS0SZilGBL0a+epPIOJtnfeCSESlEZgLLITgp4ep+longT8ZgeMN+L1I+GXm\noGO7MLj0g+u561sPTYmYp+ldd9uUtT0RJuOh1wEPGGOs086/W2ufMMa8CtxnjLkG2AF8JAt2Klmn\nComjnA3uRqhxS255PVCOpCiGEC/cAF7kr+xyXuM8ViCiHwD3qTEuPeMXXBZ9kEePvoj7fX/G8KYS\n2O3L7UebPDq2ZzAfPGczc5v6+dE3Hhn74AJjwoJurd2GzCR57/4e4PzJGKVMNXXA8UALuKugwSNR\nlypEoGsQIU8htbdSQJLMaHEhYh9AwiyVsgWPGuQkz8tctuMRipsH+d3yc9lau8gR9KOQYl7THx3b\nM5dLzt/IHbc9QnNDbrJQQsE4n/3kC3z7x6flpL+x0Gl9s44KYCUwR9IT57gyMz9bkTCKF8la8SI1\nW6JkvPMiROADiBdf5JxTCSP95TyauISquT287V5G12CNnAtAe64+oDJLOfHYdu7+zgNUVuRuRmck\n6uHnD67IWX9joYI+q/ADF4OZA/V+EfAKJAZegQhzOTIqDCLcPiBCZvKnBxF/NyLwPudYC6l2N//V\ncQnPLz+dyIYi7MN+2GmB3Ryg7IqSdRrrB3jlt3fmvN9UytDRVZzzfg+FCvqsoQI4E1wNIuZzEWGu\ncLYSMlP8DeKZGyRjJX3r3IXcME2nlqdF3Y2EZoaA3RB+vBI2A2uAkRFgz9R/PGXWcs7p23jm/nvy\n0veDjy/OS7+HQgV9VlANnA7Mh9KgpCU2IwkuISRjxY/kknuReHkEyWaJIKmIae+9FBF0xyvHh4h+\nmP2CzjZn60pBqgt4LSefUpl9XHL+Bn749fzd/Lz6s9NrsrAK+qxgDtAqszibnfosDYhIVyFetsfZ\nLCLWMSRKki5PlUTE3IV8AbiQMEw6lbEHycrehXjnuy2E+4FncvMRlVnJ+0/aSWN9flbN+uh1069u\nkQp6wdMEvB88FbDISDZLNRJeKSZTRdGDCLMfGESEuh/oQ4Tf7WwHvk455w0jnnwbsBPYkoJYL/AE\nkKvJF8rswnLZheu56YY/5LznRNLw6Zsu5r6Hl+e877FQQS9oPMC54KmEo4x45XVIHLwEiZ2nlweN\nIHHzXiR80ocIeoRMtkv6JukQEn5JAPuc13uQRJZ1QKwbmc22Yeo/ojIrKSuN8qs778t5v+GIh6/8\n89nc+fMTct73eFBBL2iWgKmGCpeEVsoQES8mEzcPIMI8jIj5CCLcg4igp0U/LfwpxJPvIBOSaUO0\newsQHkY8801T//GUWcvNN/w+P/1+bSXfvevUvPQ9HlTQC5L5SLGtJVBWJJ55ejp/+sZmERIHT3vm\nI4inPYgI9ZCzP4Z8EaTTF8PO++lz9iCCvhnYG4VUByrmylRx4yde5EOrNrLyjG156X86izmooBcg\nc4CzgEao90CjUzmxBgmzGMTbjiMCnU4PH0K87iEymS1eDr5JahBPPu29DyBCvhXJN492Ab/OwWdU\nZiMf/aO1/NMtT+BxH0HRyyyy8Iwb8tLvkaCCXlA0AKvAVQ91Xpjn7CpHQiwJxCtPZ7BEEIEeRsQ5\nnc0SR0Q/fcM0hHj01jl3APHMO5CboNuTEG8H/hP5RlCU7HLJ+Ru4945f5aXvzn0hrrzxw2zeVpWX\n/o8EFfSCoQVYCa5qqPRmqibWIFkpPjIhlnQqYgcZAU+LuBeJm6en+ae9er+zbwi5EdqJlKfaEof4\nHuBJdAKRMhVcc8Xr3PWth/PSd1d3kM984WIefzZXZaAnhwp6QTAfWW2oAYq8EnWpJlNAKz0RKB0y\n6Ufi3wOI1+1BPPiA8zpdy8U4bRw4ezR9Xi+wF4hFETd9Zw4+pzLbuPETL/K1m/8rb/3v6Sjhl48u\nzVv/R4oK+oxnLrI4RTOUeCXEUoJ41NWIECfJhFrSYjyEhF0CiICXId582lN3IyGaA+PtXiR+Hka+\nGMI4DU5uMQlFGY2rPvIGt37hvwgGEmMfPEWc9ydX5a3viaCCPqNxFqdwNYpnnl5pqAzxsEE86hDi\neacnDKWrJ4LE18ud4wPIl4F1zgsiYp5wXkeQME2vsyXCSOwlNqWfUpl9XLxyIz/7Tn7XD9m6vZzu\n3lBebThSVNBnJNVI7uEqcJdBtVdK4JYgoZO0QCcQ7zx9EzThPPcg4u1H4uXpei7pMEuSzGSi9GSj\nCOLVdyOi3gPEh4FHp/7jKrOG887YSnP9AHd/N/+LQR236rp8m3DEqKDPOBqBU4EWCJZArUsKbdUi\nf810xUQ34mmnPfIwIubpG53pJeTKEGFPn+Nxjk05j53IrNFeJPbeiwh6OIaUU8zfz2GlsLjg3E38\n8OuPMLdpIN+m8C93nUwkMvPkceZZPKupAM4F5kKxDxaaTC3zeiROnl4+MV0F0Y141el4eTqeXoR4\n5unZon4yNz7DiGgPItUTe5w2enBi7wngJeBl5FtDUSbHCSt2c/d3HqS2eiTfpvCjf38fX7htJfGE\ne+yDpxkq6DMGH7AagnNk/c9WZFW3auRmZhEixi4y2SheRIjTJXEt4pGn1wQtQSI36QUsosjNznRY\nJZ28MmhFzG0KyVncADw9tR9XmTVUVYzw6mM/zrcZdPcGeeG1Zj71fz6Ub1MmjAr6jOFyKJkDi92S\npTgfSU9sQLQeMgtSDCFe9j7EC08h4ZX0snEuMuGYATKe/QiSirgXEfI2oCNdB2CH85i/FDKlMNm3\n9pt563tvVxEvvd4MwKXXXJE3O7KFCvqMYAV4joIVblmieDEwJ0mgeRhPKInXxEglXEQSQaL7gjDk\nhi5EoBuQGHg6vzxGZvFni4Rk0qGWLuRLYC8i5t39SBD9D84ORcku11/1St76Dkc8XH/zxTzwn0vy\nZkO2UUHPOVVI/CJ9B7NvjOMXAedBqxdOBs5NUrK0h4rSbqp83RSZYQImQpggfclyemsqGRgpY3h3\nBRZ3JuslQqaSYoJMPRbI5Jm3k1moYqQP7MPOjt5sXgClUPncKvj+M1BTDCuXwM+eP+zh1135Crfe\n/FSOjDuYv/hfl7JxSzUvv9GUl/6nChX0KcENHI3EMoKIiqYD2WkhT5cyBIl7rBulnXrgHCgrgwXA\n6ZaqZV0sr1lDFd2U0U8pAwSIMEKQIXcJ+9zV7A40st61mGF/FWxyiR73kck/t0736ZWGBpGY+V4L\nsRRywhNIPVxFcTBASQCev+nQx1x9eub5366SxxVfBuxB988vXrmRO2797VRYeUisle36L1zM//vV\nsTntO1eooGcNNyLe88jM7gkg4t3vvOd1jnXm4huAMNhBZMbnNkREE/I+NRAog0UuWAG+eRHm1myh\nhe00sIcihimnlyQeLBAmRAmDGCzh8iCbkz5ijaWQdO6CphdyTs/y7EZCLO3AQAxSESRzJT+1ppVp\nSmURzKuGf1wNcyqP/Py3b4Hnt8DfPQBdQ7jdKZYv6sy+nWNw/yNL+eh1H8l5v7lEBT0ruBFBbiAz\nw6cCjB9cbkhVgvUALnB7wGfB587cnIzEIRJFUlYSSLzaDa4zoSkExwPHWEJzB6hnDy1sp5w+3CRx\nkcLPCBaDmxQRAlTSQz17Ga4oon3YR2IkKN8pXg5ezKIT2GFhOA68gdwJfTuH102Z9hT74QsXwgWT\nXG7t9Pnwfy+BWx6iONnDbX+Xu5vrv3l8Ee9sqOHvvr4yZ33mCxX0rOBBBL3J2fxQ4slUKPT4Mutv\npp329I3IADDohQEvDLXAUHrViFMgWCWThhYBxyWpq2qnmm5KGCTEMGFCDFCGlzglDBIgQjm9xPGS\nwEPSuBmqLKF7uAHK3NJsenm5TmS5z5ERYC3wO0TpFeUASgKTF/M05y2G7z3NfV/+YXbaGwePPLWQ\nT998MXs6SnLWZz5RQc8KRyOze5qgLATlRl6ma6PMRwR0J5kiWMPOKR8G3/v6iP26HO7zwmsNEP1L\nwAPlblgBLIPapTtpcu2mmCFGCOEljsEyQohihvARw02SCnoIESaFiw5TR11oL0OVZUTjJRKy34fE\ny3cDI2HEI3+SzIwkRTmAB6/PanPXcBerzt6a1TYPxdoNNXzkLz9CJOod++ACQQU9KxQBFVASgnoj\n+eEhoA5cH4oTWB4l8laA1GMe8dRPAXpg7ilb+EHT1Zzw5H/z4OVX8rmy7zFUXwNvISGRRcAC8Mwf\notXVRittVNKNjyghRhgmxDy2YTG4SFHPXiwGi4t2mqiglz2mAddwSuLlW5B08m0p6BtElhp6LC9X\nTJkhFPkn3YQrHqN663rO+tE/MmfT63RugNpFWbDtMKzdUMOK87L7ZTQTUEGfNKVAOZhy8BupqdLg\n7J4LxSf1sqTuHTaEltC3vl4886WATTG/fgvNt23nN3fCR29+gKc/fy73Vf459lce8abrgSUpaho6\nqaeDGjqppQs/UVykaGQ3PuJ4iVPEMG4SJPEQJEw5fSTw0DtSSXRbCN4F3gHWp2BwK7AReDU/l0yZ\nGVxyTFaaef9Pvsl53/vi/tc/uRRuejcrTf8PXn+7npfWNPM3X1o1NR1Mc1TQJ00TEASPN1MfJYTE\nvqtgZGsZ24rm4SuL4jotSqrNDx4wtTG2u1p459Pv4/zy3ey7pAxXURL/ijCRgWIYMhCEwNFDNPjb\nqWYfAaKO/53CR3S/mLtIEiYIQBwv3VSxj2q6bRW9HVWk1njF619nYXg74pXvy9P1UmYMN07+JuIF\nt/4vTvn372XBmLFZv7mKa/5mNW+uq89Jf9MRFfRJUcf+8oWuQKaSYQjJXPRAYpOfzuhcfMuG8c2P\nEhnyQw/YIh99/nLuOe7Peevo5WwNHcUW5lPa3E3suAApL7g9KWoa9lDp7sXjVDV0kSTICHFHzkcI\nYTGECZDEzQCldFPNWpazPrGYkRfKZKLna8BQL3AfzsoUinJobroAaid+I/GYh/6Nc7/3RUo727No\n1KGxFs7544/T0VWck/6mKyrok8KZJGQqodwl+l5NZjm3SmTOUIeLmLtE9vWAsUlqV+6gzN3PRo7m\njdCxVNFDChc+G6Nu6XZCrjABIlTRTQ2dFDHszMswJPDiJUYPlUTx00sFfZQzRDEjNsTW1Hw2jhxN\n70uNUhRxo4WhHiA3npJSAFQUgdt1RKeEervwRCJ89gNzD3tcZBAe/Cxc+u3JGHgwruZbstfYDGZM\nQTfG3AVcAnRYa49x9lUAv0BWJm4D/sRa2++89y/AhUi0+OPW2jemxvTpQDFQC+4SiZ3XI555AyLe\nKcRjH0auUkUS36lR6lp30eDeTYAwSTyMEKKSHtwkGPKVyMQggsTx4iFBlAADlALgJ0YCDwk89Dve\neAd1dFHD7pFG+gcq6d1ZTWJtQDzzl1KwNQyJzXm4PtMbHdvZo3rLOi77/J/RsH7sSxIoya6YP/Xf\n87LX2AxnPB76TxHX7p4D9t0EPGWt/YYx5vPAzcBNxpgLgfnW2oXGmFOAHyCrMRQgISQHsQHq3SLi\ncxBhr0K8cw/7y9iaQJKSFftonrODOe5dzGUH5fRiMQxSyjBFpDCECJPAg4sUQxTjJkkMH32UMUgJ\nEQIEiACwi2Z2Moedw3MZ6KxgcGspvOt1bn4iMfOe3ZB4EZ3GPyo6tkfjhLmwrHHch1fs2Mzq//uJ\ncYl5Nnl7fQ0/uOdEfl1AxbUmy5iCbq39vTGm5T27VwNnO8/vBp5B/hFW4/xzWGtfMsaUGWPqrLUd\nWbR5mlCEJJSXyH3RFkTEWxBP3YvUSnEBUUv1ee1UFPWw2LWB41lDLZ1U0U0ML4OUsotmBiilHT9h\nAgwTIoWLQYoZpBgXFouhk1o8JOijnDhedvTPo+/NGuxrLnjTwCYkG7EnAbGNwONkqnApB6Jj+xAs\nqIPWqvEday1/dt2FVO3I7S/AwSEfq6/+U7btqMhpv9OdicbQa9MD2Vq71xhT6+xvQqbPpGl39hXe\noCcENEClU9GwEZlAVAaUW3AlIeKi6pjdlJf1Uk4f89nCCt5mGWtZbNcTIMoIIXpMJW6S7KWePsrZ\nTgs7bAs+ogQJEyaIAdwkSeAmkfIwMlzM0LYa8cRfAV4AtljoSCD1b3+JCvmEmN1j2xgpSzEG7liU\nq64+hzlvvnjEXUw0ZTGecBGNujnlkmtZt7F27BNmIdm+KWpG2XeYNcqePeB5q7PNBAJIEa4SKHXJ\nrP8qZ3elBW8KD3Gal+6grqydIkaopZP5bOEotjKPbdTGuwnEI4x4gnh9MaLGzwghkrixGHo7qnB5\nkrg9CYyxJKI+XJ4kibCX5M4A7HBLbvlbwKsWdoUhtRHYjEzln220McU122fH2F5YC5+/4LCHhHo6\nueirN0xIzCfKY8/M55nn5/GN29+fsz6nD22Md2xPVNA70j83jTH1yMR2gF1IJDlNMzLJ/BCcM8Hu\n840bqASfX8IsFchEomIglMS4kyyqeJdFpesoZYBiBqmih/lsYR7bmJvaSXl/BBOFQGAIX3mUXk8F\nHhIk8DBMEckRP0kg7k1CxA1xN6Qs7DGw0cj6zG8Bm1PQvxZSm5jdhbVaOVg0n5toQ7N8bB8eTzTM\nhV/7K5Y9fn9O+rvv4aW8ta6Or/7LWTnpb3rSynjH9njzkgwHeygPAR93nn8c+M0B+68EMMacCvQV\nZIyRo4ByWai5AgmzlAJVFnxJlte9yTGla1jAZhaznmN5k2W8wzLeYV5qKyU9UVxxacllwRpDEg8R\nAhgsSdxgXSLiwz6IuqHXwEYXrDNSGHEd8HYcetshtYbZLeaTQsf2gXzljw779l9c+wGWP3ZfjoyB\nBx9bPMvF/MgYT9rizxF3o8oYswO4BbgNuN8Ycw1SHeQjANba3xpjLjLGbEZSu66eKsPzSwUQgpBL\nxNyFU00xwfvrf8dc3w7mSP4JTbRTxDAtbKcs1UdpdAhPzMI+MBVgDfRSSQd1xPESJsDuziZ5I2Xk\nKg4ifuJbSOR2M1K2PBlF1H1bXq7CTEfH9igsP/QKPp+6/HjqN0wuk+VTj4//2B/ccwL3/iZLlR5n\nCePJcvnYId46/xDH3zApi2YEQfAWyZoVftk8VTGWNLzFYt96KulhBW8zh52UMoDXxiiND1E6HCXU\nb2W5t6CUSO8uKWaXu4keKtlFM1EC+EJRiMQg7Bfp6EJCaLudx20WkhHgn/L0+QsDHdvjI9i7jw99\n6S8nLeYgywOMB9OkE4Umgs4UnRAl4PHIpKFqcLckOHrJO7yv/BVaaWMFb9Nit1Oe7MNvY3hsnJpt\nw5J0EiGzuJEfBigliZsYvv1T+CPhIER8srpQeknPLUg9840WOsLA4ddrVJRs4Bsa4ILbbmTJfz2Q\nsz6/95OTctZXoaGCfsQcDRSB1ytp6Cth7mmbOLb2dY7jDZbwLovsBmoG+vEPRzHppUP3INmEIDnq\nNUAxlKYG8RLH7dQj95CU3ImYkYUoupHbce3ABqAzAal9QO4yDJRZwtcvO+jlJV/6S8p2b2fB80/k\n1IzZsLLQVKGCfsTUgimR2PlZUHpOJyvK3uR41nAKLzGXHTRs78P0WIwXEeduJFs5Cvicx2EwCQjY\nCD5ihAniJkEKQyrhkZh5P/JFsNl53J4A2w08DU6xLkXJGmdnipRf/OXrOP7Xd+FKpXJqwsc+cxlD\nw76c9llIqKAfMV7wBuA0cF0Q5pjiNSxhHcfwFs3xdmrb+3G1W1kAKL0E3RBypfsQgQ84+w2krGGQ\nEiyGOD4iBLFJV6ZsQHqloy0W7BCyVFxb7j+2Mitwx6Kc8eOvceL9uVsmDmAk7OGL3ziP/3hwRU77\nLTRU0I+YRpjvgbOgpqmLWncnC9nM3NgO6rf14G1PiYD7ECc6hIRYgkjsPOW8VyyPYVcIgKhTr6Xf\nlpLq8ImY9yNly3cAQ0lkEdB1Of68ymzhmIfuoaJvN+fc8ZWc9/3aW418+0en5bzfQkMF/YiYB5Wt\ncJwX6pOUBPtpZA+N7KZ2uBtvd0oyUlJkvHPYX2WXhLMFnH0JSFjJPx+mmA7q6NzZSGKnV0R8A7Kw\nUBeQ6kFq4SpK9rnx2hep+NaT2OjUhViOuRxKG/7nfmvh1n89Y8r6nU2ooI+LEuA44Gho8UAjmJok\nQd8IxQxRYocIxUcgTsYz9yOTjdJFusJIhks/En+vhEQpxH0uYvikprmtYHBHGXanSxzxdYhTHukH\n/h9SXF1RsscJx+zm59//FY31g3zv3hTR6NT1NedECJb/z/2LzryBTdvGWQxMOSwq6OPidGAulNXB\niQaOAW99nIBXbmimMESCAYLBEfHEvYiXniBTcbEdiatHEA89ClG3n0FPCYOUMEwRPSNVRHaEpPzt\nOpzytwPAf6BirmQbg+XV//zx/tehKogO5daGMy69WsU8i6igH5YyZ5sHnipo8EhOeA14/AlC7hE8\nJEjiJhiPiEceR7Q3HTvvc7YtZCaZW0T4Wy0xvOyimU5bS+9INfS4Rfz3WugPI/Vwh3P9wZUC56xT\n26iuGDlo343Pw5cOPVE066zdUEN3bzB3Hc4CVNAPSQVwArAI3KVQ75USuUWAsfhDEbzE8ZAgZVxE\nQn78wTCm+oAmBpFQyzByQ3QYEfQwYCHm8dFHuSzqbKsJdwQko6ULSVNM7kUmEA3m7FMrhc/FKzfy\nw288QlN97sZVwwoJuaRZt7Gaaz67mvWba3Jmw2xABX1UKpAwy0KgBKrdsAhZvKIITH0Kf2gYHzGi\n+DFYunxV+Es6CKbi4tQPkhHwOBJTjzjNByFZbdhXWc5uZNp/e7KZ2LYiuRG6FxiOIvWg+nL70ZWC\n5v0n7eDjTdK1AAAQcElEQVRH33yYxrrcxlaqF0D9Unk+OOTj0muu0FDLFKCCfhAGOANYDNRDiVsW\nfm5FvPMmoArsDkgtdJHCxTBFdFFNsWuQUOUwVd5+AjYlVzaOiHrQeaxAPPV6iDV52eOup50mdjKH\nXVtbYY1bslr2WGTZIRVzZfK43SlcLkus7R/HPPbTT8IdH5hae8IRj4r5FKGCDkiw+2hEuedBoFqE\nvBoR8RrZTQtQCy6PhYSLPsrZRzV7aKScfiroo7Z/QPLQR5A6LF4yN0KDSPy8BroaStnMAtZwPO+G\nl8HLXnjRwtY4xDcBuak3rRQ2ddVD/PAbD7P6gxvHdby3CKqOgu6tU2PPy280csrFn5yaxpVx10Mv\nYDxISuIJYBZDabWI9wJEwOcgr4uQlEQXpEY8DLRV0JmqpYM6dtPIICXSXNKKkO9Dslrics7+BTDm\nwuDCAO94l/Emx7Jm4ER2v9gqofJ3whB9HXg4h59fKVTKSiJ876u/HbeYA1S2wKnXTo09v316AR+6\n6k+npnEFUA8dWbh9BRRVQYVHFnhuRuLgJYinXsf+qfpEgQREB/z0xCrpDlTRTRUJ3PjjMVyxlIh4\nBHmMIRkvALWQnAcbq+exkaNZEz+OHe+2Yh9xw4txaH8NUfYIijJZfvOz/+DsU3fk2wyKqiF2XCuf\n/fwldO4rzrc5Bc0sF/RzgSUQqIFmIx55KRIvL0FuZNaT8c7jSIaKB+x2L5GKYvqWlmNdhigBLGCi\niHfuFODaXyq3CGwL7KmtZsCUsomFbO5eQnRNEbwKvPks2BeQBHZFmRzvPvevLF7QPaFz3/cxaHsB\n3snSD8Uv/rQdc/ntRGOzXG5ywCy8wgYJjLcCR4G3FhoQ4a5C4uW1iIi7kRi4j0wtFot43S5DJOYn\naWVRZzdJvDYh77sRJ9vlnFcm7Q5V+dnjr2UdS9icXEBPZxW8YeDlvWAjqJgrkyHgj/P3n/0dN//V\n7yfVjts7/oUoDkdfYwt3/fsLxOJBUDHPCbMwhh5EchDngLtWxLsZEfUiJDySjncXO68tmVmfI85m\nwF8SIWjCJHETx4M7ZjDdiC5HkSSVFBJLt5BKuhmimE7qGEiUEd1UBM8AkSHnIEWZOAuP6pm0mGeL\njoXLue/bv2SoZpTiLcqUMQu/NpcClUAjlPjEM68ByhEPvQzxsD1IZopFRLmfg8QZF3hDCayR9YXd\npLAumyl7m05bTB/fDcGqCMHiKFG3n3e7lsDbRtrFzaz8blWyyje++GS+TQDgl9+8l565C9iz7IR8\nmzLrmGWCfjySttIMRcVQZ0TbKxBBT3voaTFOX530hDoP4rW7gBJwu5OUmEFcpBghxECwmOqaPjx9\nVopqBZAIzyCQhFST4TXX+3iZkxlJhTK10QENtyiTYd2z32fJwn15teHBr/6MraesZLC+Oa92zGZm\nkaB72L8IqK8YAkZi4+Vk6pWXO49pr3rEeYw7j15E9C2Yihi2NEXEBkgYuYz9ppRkhQdPcXz/4tGU\ngK2GmNfLmqpj6DB1pDBYXJn4vCkGG0JRJkJt9RDNjdkr3vbmr2D9OFeds0B/YwuvXHE9b66+Kms2\nKBNjFgl6CxJTCYBxi2fsRxxjL5mp+W4y3nmS/QtRYA7Y5wLb5yPeGWSgpZQwQfooo5tKhgMB/A1x\nacdI273zSthaO4cuKvA4S8e5TEr6dYH8W0xh3VKloPnJtx6ipCiWtfaOvRw2Pw1vPzj2sW9f8uc8\ncNu/Za1vZXLMIkFPZR4tIrZFSPw8RMYrDyMim0KuTuiA5+kmEnJsbCBId6SKPcF6dtNEHZ1sLO2n\nwd1FUc0Q3VQx5ClhoDRIChed1LKXOtppJrqlRCYgWch8kyjKzODd8y5ly/s/yGsfvS7fpigHMIsE\nfRcy5bMOYkmp03I2cL4FdwredUtRLC8SmSkl45WD6G0CEfUYMAzJkJcBXw0b5iwiUBQlho+dzKGp\nqJ1wUZA91FPECOX00kc5m1nIGo5j+6ajYaNLTOrFEfV4Tq+GUjhc/4WLeOe02ykuys0YajvxLB75\n0o8YqdRKidONWSTocWTF5VLABxUVcL7hzDOfYDBZwjrfccQ6QxJ6CSLCnhZ0F+JEDzuvh5Hytm8a\n7BkeejqbeHFpETvLmylhiNLUILvdDTS49lBiBggQZcCWspd6BimheeFmdvfPJ/aKXxaEJgKsyf0l\nUQqCHe3l9PQFsyrol38fdrwM/bsP3t/XMJe7f/bckTW26jtZs0s5PLNI0AHWsj+Osj0Iu4KMhIsY\nHCmDHgMdiN6nyMTR0x55hIw3PYTMBt0LPA60uAivq2RzRaWIfy+YpQnaF82hJDBIcWCAsAkwFCvh\nYv8jfGbXHaxvXsI3rr2JjWuWQ2/M8dIVZWK0nPxZnvvVTzkri1P9550Bb9yXeb39hDP52d2/y1r7\nSvaZZYIOUp+2Etq98NW5vNZ7Kgx4JPwBIuARMjdABxFB70cEfQRZgKIH6AZ2A0dHoc6fme6/Aqzb\nQ7iqlHCwiMGqIpJRDyHCHB9aw8mPvMmysk08f9b72Th/Obzh1nlFyqS54YsX8dZTP8hae5d+W+qw\n/OF2WH/uah7+8o+y1rYyNcxCQY8gy7q54B0PfHmOJMAcD02f3srCqo283nsiA2uqRbj7kRmfg2RW\nEmoHRixEwpDohdc7IdgOiTPBVwolhqpPdvLBox4mYdysdy9mw9ASBnsqeL7kDM788PP0m1LW9i4X\nLz+VvQwFZfaypa2Cf/7hqfzNp17MWptLriri2jU30fP3n2CksjZr7SpTwywU9BSyzptTC7cLqJpD\nzUd38Ytj/5iTn3yLH33gSr4c/Qe67muCNuQ7YB/ixXcA8Qgyc2gIeFLqsIwAeCB2HiS9zF2wiZsH\nv0lFURff9P4t68NLSfzOz4ObruDBRVfIGqN3AK/3g50eM/yUmc1I2MfnvrKK+tohPvbhtZNur+Xk\nG9nRXgYk4Old8NEJTOP/wLcnbYcyfmahoKfZAgRk1k8U/ENxUrsDeJ5PckbrS7RUb6drsEmc+SjQ\nY6EnCYkhJGzzFpk4TZoXgRBsPYp9zzTxxEXnUhfo4J3+FcR+VwovIN59DNiYhM4hZM059dCVbGH4\nsxsuJ+BPcNlF64/47OERL3//T+fwzz88/eA3/uFRCPqgtQqOGedM0LZ9EEscsQ3KxDHW5udunDHG\nwi156ftgTgD/mbCqlFM/+QcuP+1X9FYXc++bf8HWry2CJ4F4CkaikOpBguavI7GXQ+DywPvOofiS\nCjytNfS9VgNPpaDLiicfG4ZEP5LZshWnoIuSVb6Mtdbko+fpMrZvv/URPn3la0d0zl/f8kG+e+ep\nhz7A74Hrz4ETW+HYQwh7zzA8sAZ+uxY27D2i/pXxcOixPaagG2PuAi4BOqy1xzj7bgE+ieQBAnzB\nWvuY897NwDVI1vaN1tpRJxFPl0EvaSlLwLMUmopxndVA6OQw4R0hkr/2wpYRRHDTqS2vIndDx4G3\nGkKVMHwyJBJOXwngJWQGU+dhT1cmw9iCXuhjOxiI8w//+xk+d90L4zr+o9ddzn0PLx9f4/OqYW4l\nfP9jB+//3P3QPQSvbj9Ca5XxMzlBPwNRs3veM+gHrbX//J5jlwA/B05CitI+BSy0o3QyXQa9YJCZ\nQ8vBtQgCS8BYGNkHdh/iVr8D7AAm8hPS+57XOolo6hmXoBf82PZ5ExQVxfn9Az9h6dGjF+/69o9P\n4R++cza9felqckdAafDg1wPhiRmqHAGHHttjxtCttb83xrSM8tZoDa4G7rXWJoA2Y8wm4GTEJZ3G\npAuevwGpN2CkBimzOwQc2U/W0VEBn47MhrEdi3uI9XlYdu5nADj71DZuv/VRgP37JoUK+LRiMkW4\nP2OMecMYc6cxpszZ14SkkKRpd/bNMLqA58iOmCszkIId28+92Mqycz+THTFXph0TzXK5HfiKtdYa\nY/4R+BZwLaN7NoeJ6Tx7wPNWZ1OUidDmbJNGx7YyzWhjvGN7QoJure064OWPgfRysruQFSTSNCNp\nIYfgnIl0ryij0MrBonmE9UYcdGwr049Wxju2xxtyMRzgoRhj6g947zKkSArAQ8AVxhifMWYesAB4\neZx9KEo+0LGtFAxjeujGmJ8j7kaVMWYHcvv+XGPMcci0yzbgUwDW2nXGmPuAdcidwOtHywJQlOmA\njm2l0NCJRUqBohOLlELl0GNbl5pXFEUpEFTQFUVRCgQVdEVRlAJBBV1RFKVAUEFXFEUpEFTQFUVR\nCgQVdEVRlAJBBV1RFKVAUEFXFEUpEFTQFUVRCgQVdEVRlAJBBV1RFKVAUEFXFEUpEFTQFUVRCgQV\ndEVRlAJBBV1RFKVAUEFXFEUpEFTQFUVRCgQVdEVRlAJBBV1RFKVAUEFXFEUpEFTQFUVRCgQVdEVR\nlAIhz4Lelt/ux6Qt3waMQVu+DRiDtnwboIxKW74NGAdt+TZgDNrybcCoqKAflrZ8GzAGbfk2YAza\n8m2AMipt+TZgHLTl24AxaMu3AaOiIRdFUZQCQQVdURSlQDDW2vx0bEx+OlZmDdZak49+dWwrU82h\nxnbeBF1RFEXJLhpyURRFKRBU0BVFUQoEFXRFUZQCIS+Cboy5wBiz3hiz0Rjz+XzY8F6MMW3GmDeN\nMWuMMS87+yqMMU8YYzYYYx43xpTl2Ka7jDEdxpi3Dth3SJuMMf9ijNlkjHnDGHNcnuy7xRizyxjz\nurNdcMB7Nzv2vWuMWTXV9uUDHdvjsmdaj+vD2Dj9x7a1Nqcb8iWyGWgBvMAbwOJc2zGKXVuBivfs\n+zrwf5znnwduy7FNZwDHAW+NZRNwIfCo8/wU4MU82XcL8DejHLsEWAN4gFZnDJh8/92zfD10bE98\n3EybcX0YG6f92M6Hh34ysMlau91aGwfuBVbnwY73Yvifv1hWA3c7z+8GLs2lQdba3wO9Y9i0+oD9\n9zjnvQSUGWPq8mAfyLV8L6uBe621CWttG7AJGQuFhI7tcTDdx/VhbIRpPrbzIehNwM4DXu9y9uUb\nCzxujHnFGHOts6/OWtsBYK3dC9TkzboMte+xqdbZ/97r2k7+rutnnJ/Hdx7w03k62TdV6NieODNh\nXMM0H9v5EPTRvuGmQzL86dbaE4GLkD/amUwPu8bLdLmutwPzrbXHAXuBbzn7p4t9U8l0/YwzeWxP\np2s67cd2PgR9FzD3gNfNwO482HEQjleAtbYLeBD5ydSR/nlnjKkHOvNn4X4OZdMuYM4Bx+Xlulpr\nu6wTWAR+TOan57Swb4rRsT1xpvW4hpkxtvMh6K8AC4wxLcYYH3AF8FAe7NiPMSZkjCl2nhcBq4C3\nHbs+7hx2FfCbfJjHwR7AgTZ9nIxNDwFXAhhjTgX60j9hc2mf88+Y5jJg7QH2XWGM8Rlj5gELgJdz\nYF8u0bF9BKYxvcc1zMSxnY87scAFwAbk5sFN+bDhPfbMQzIS1iCD/SZnfyXwlGPrk0B5ju36OfJN\nHwV2AFcDFYeyCfhX5A77m8D78mTfPcBbzvV8EInVpo+/2bHvXWBVvv/uU3RNdGxPbNxMm3F9GBun\n/djWWi6KoigFgs4UVRRFKRBU0BVFUQoEFXRFUZQCQQVdURSlQFBBVxRFKRBU0BVFUQoEFXRFUZQC\n4f8DplAW62P7To8AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb5fba12190>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"plt.subplot(121)\n",
"plt.imshow(grey)\n",
"plt.subplot(122)\n",
"plt.imshow(mask)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "ImportError",
"evalue": "No module named mahotas",
"output_type": "error",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[1;31mImportError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-17-2ca8953dc5d4>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[1;32m----> 1\u001b[1;33m \u001b[1;32mimport\u001b[0m \u001b[0mmahotas\u001b[0m \u001b[1;32mas\u001b[0m \u001b[0mmh\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[1;31mImportError\u001b[0m: No module named mahotas"
]
}
],
"source": [
"np.apply_along_axis(\n",
" func1d=lambda x: subset[:,:,:,0]/16,\n",
" axis=1,\n",
" arr=dat[:2,0])"
]
},
{
"cell_type": "code",
"execution_count": 96,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"gabs = filters.gabor(g_ex1, 0.2)\n",
"images = []\n",
"factors = [2.0, 1.5, 1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]\n",
"for i,k in enumerate(factors):\n",
" images.append(misc.imresize(g_ex1, k))"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjwAAAIkCAYAAAAaivFsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmQJPdd5/33L++su/ru6WtmNKc0ksaSJfk+sPFtL7Yx\nYGMw+xDLPssR8ATHmsWwrA0mYFlDLAF+Fh4wNw9mfRswNrYlW7asw5JG18xozp6Zvru67so7f88f\nWf2MwiFZFp4+puf3iujoqursqV9K2Zmf+v6OFFJKFEVRFEVRdjJtqxugKIqiKIqy0VTgURRFURRl\nx1OBR1EURVGUHU8FHkVRFEVRdjwVeBRFURRF2fFU4FEURVEUZcdTgUdRFEVRlB3vmgo8QghLCPH/\nCCHOCyGaQohvCiFe9222/7+EEAtCiHr/98zNbK+yPQkhfkoIcb8QwhdC/Nm32e49QohYCNESQrT7\n31+2mW1Vtq/v9Djqb6vORcrTEkJUhRCfEEJ0hBDnhBDvfIbtykKIPxdCLAkhFoUQ/3Wz27rVrqnA\nAxjABeClUsoy8GvAR4UQ09+6oRDitcAvAa8EdgPXAf9t85qqbGNzwAeAP/0Otv26lLIkpSz2v39l\ng9umXD2+o+NInYuUZ/FHgA8MA+8GPiyEOPw02/0+4ALTwB3Ajwgh3rNprdwGrqnAI6XsSSnfL6W8\n2H/+j8A54Nan2fxHgT+VUp6QUjbJTkz/fvNaq2xXUspPSik/DaxtdVuUq9dzOI7UuUh5WkKIHPA2\n4H1SSk9K+TXg08CPPM3mbwJ+W0oZSClnyYL2/7F5rd1611Tg+VZCiFFgP/D40/z4BuDYU54fA0aE\nENXNaJuyYzxPCLEshDghhHifEOKa/ptT/k3UuUh5JgeAWEp55imvHSM7Zp6O9i2Pj2xUw7aja/bk\nK4QwgL8G/lxK+eTTbFIAmk953gQEUNyE5ik7w13AESnlCPB24J3AL25tk5SrkDoXKc/kW48N+s+f\n7tj4HPBeIURBCLGPrEqY2+D2bSvXZOARQgiysBMAP/MMm3WA0lOelwAJtDe2dcpOIaU83y8dI6V8\nHHg/8P1b2yrlKqTORcoz+dZjg/7zpzs2foZsrM8p4BPA3wKXNrR128w1GXjI+i6HgLdJKZNn2OZx\n4OanPD8KLEkp6xvdOGVHE1vdAOWqo85FyjN5EjCEENc95bWbeZphGlLKhpTy3VLKcSnljYAO3LdJ\n7dwWrrnAI4T4v4FDwFuklOG32fQvgR8XQhzu95X/CvCRzWijsr0JIXQhhEN2wjCEELYQQn+a7V4n\nhBjpPz4EvA/45Oa2VtmuvtPjCHUuUp6BlLIHfBx4vxAiJ4R4MfAW4K++dVshxF4hxIAQQhNCvB74\nD2QD4K8Z11Tg6U8//wn6n5CesjbKO4UQU/3HkwBSyn8Bfgf4MtlMrnPAr29R05Xt5X1AD/jPwA/3\nH/9K/xhqrx9DwKuAR4QQbeCzwP8GfmsrGqxsS9/RcaTORcqz+CmysTjLwN8A/6eU8rgQ4iVCiNZT\ntrsVeBRoAb8JvEtKeWLTW7uFhJRyq9ugKIqiKIqyoa6pCo+iKIqiKNcmFXgURVEURdnxVOBRFEVR\nFGXHU4FHURRFUZQdz/h2PxRCqBHN1wgp5YatD6OOo2uDOoaUK0EdR8p365mOoW8beAB4TB0fO96R\njV8Lz1z91tXPlZ0kGipv+HuU/YUNfw9lazWd8Y1/k99Q17Qd7X3PfD1TXVqKoiiKoux4KvAoiqIo\nirLjqcCjKIqiKMqOpwKPoiiKoig7ngo8iqIoiqLseCrwKIqiKIqy46nAoyiKoijKjqcCj6IoiqIo\nO54KPIqiKIqi7Hgq8CiKoiiKsuOpwKMoiqIoyo6nAo+iKIqiKDueCjyKoiiKoux4KvAoiqIoirLj\nqcCjKIqiKMqOpwKPoiiKoig7ngo8iqIoiqLseCrwKIqiKIqy46nAoyiKoijKjqcCj6IoiqIoO54K\nPIqiKIqi7HjGVjdAURRFUZQdJAUkINhWZRUVeLaDBPgGUAN2AbeSHSiK8h2SEuKLBVjTIC/RZzw0\nK97qZilXodZ9wxCCXonJH6lvdXOUq00XmAMagAXsBXJsi7SxDZpwDWsD3wQ332b07XOEukm52KB9\n/wCXTu+B5211A5XtLok10uM53OubVPZdQuQkAPWTo0TLOcwbe1vcQuVqELdM0kcMRo1l9t90mk7e\nJdf0aR+rMmeOY14fbHUTle1Mkl3P5oEqcBQYAELgGNACKkCeLf0wv42KTdeYFRicX2DmJ44T3GLR\nDissPjHN2cZ1XJoYZ+IHT8HCVjdS2c7Sng53O9z+sq9QLLaIdJM4NLC0kKSacvPL7ye6r4hMt7ql\nynY3c+9FXvryO1k7OIBXcVhoTbIyMMTKzWVuK95PPGdudROV7SoGzgMd4DbgIGCShZ0WcAi4CZjt\nb7uFVODZbAnwAHAmgtsks189jG0FtPUc6aAgnncwWwlzJ/ZQcVbgzi1ur7ItRZ8vMLhY59DbHuK+\n4y9D80Eg8epF2ssD2FbAqcXDDH/vBeIHClvdXGW7eshg4J8b8L0RX1h5Ne5Ak47Mo5di0paJHkpO\nTuzn+uUThI84W91aZbvxgDNAj6xHYo6s0gNwkSzg9IAmcAtwP9k1cIuowLOZUuBPYPd7noCqie/Y\nOAfbeKdLhHeW4L8aJP/gEBkOLBs0qkMc+eH7trrVyjYT3V3kljd8g94BmwvdGSoHFln65gSNJ0fx\nP1qi9XcDyMSgt1zADx2u/94HSRdU77VymUyg97sVbnvB15ndv4+OXWTf8BlatUFmHz/E2u/uYvHO\nSZycR2N+mOOH93N06mGSnr7VTVe2ixA4DdwMvAQIyLqzGsDXgE8DnwPqZIHHBF4HPLEVjc2owLOZ\nzqcc+O+PMLcwzc1v+DrdC4NEvoa+GMJd8NEPvpXXv+cT0NKzg0dENNwq/P1WN1zZLqJLJQZftMBs\nbgrH9pBSo7VapnrHEtyv85Kf+zy3/uzdBI8UoBrTXhpiiRFE00Am6s9dyZin4JZfuIdH4pu47cBX\nWW0M0egOYp2LcB/s8Vuv+AVedvTLLMxOwmAIBvQ0B+2z6hhSyD68nwNeRTY2xyar5LT7j8/A/s89\nwq0fuCcLOx2y4FMmG8eztiWtVoFn0zTA+FLMk/cfwXY8jp15EVa5S9J1oSLh1ZB/8Sf5xODboCdh\nEegaXPrMPqbedxJ+HXh8i/dB2VJJrMGTKcJMiROdKDWxHR+dlG47DyPwsXt/iD+u/RR6NYSmRT7X\nojY3zuQLThP/YZ7kgo1M1RTAa1nq69jnAx7vHqEgOjzcOkop7RHnwBcOlZkmr//VD/Eh8xewawmx\nb2HrIaecfbzgXV8l+cMcyUVVMbymeWSzigVZoOmSpQmdrMLzKjhx9838cvzbuAOd7OcCOAXcQNYN\ndposCMnNa7YKPJvl12Dqg2dA0+g8UQUpCS0d5jQqUQPOwC8de4CRr9fhgoAxCdUIJiQXL+4h/xsN\nnv+ar8CHt3pHlK2SzjvsffsTrK6N0l6r0G4XCZou6ZLN1MBFKKS8fOYufuC+j5HcYyNakkDToaZx\nqTbF0Hsvcuu+bxD/jRrTcy3r/kWFoTfOEycmNW8IN+9hFAI6xwapTtRZGynxgT//a35s7i/wOg4i\nEchII/Us7ktvZ9fPnOH7Op8k/Lwa03NNksCjwFuAC1yu3kDWM3Ed0IK3r3yM3/rSr+Dfm8vG7cRk\nYUgAbwVek2SDnaPNa7oKPJvhC3D9vz7AuccOZgsBDAtogRUljLzkPNZbOtCCx3/4Vlq/V8kOmmnA\nt6ACWipwRro88PhLeelb/nWLd0bZCvGSg1FP6YRFMFMGR5ex7RCz6GPPdFgJhsFKOPEXN3LmH/ej\nH4koHawRN4sM3ThHXLcp0OGh2h287qc/ifTUn/61KL3P4JXv+BcupDOYhYCc3UVIST2ocOjWhymN\n1IhPWHzsCz/Mo1+7CWc4oFKq0QoKDBcXSFYtul6Rj06+g1cO3LnVu6NsthQ4Cxwgq/K4ZON2BFlw\nGSZbc2cJPvk7b+Obf3Qb0tFgpr/97WRdYReAEwJeGWXVnk2q8qiz3kb7HdDfEPHEfbfgzLSgGuLK\nHhQFg5OLNJpDLJyahjeC8w9r5P+hhnZTAqcFudE1+LiGDDRqfzABpuD8vj3ZIoXKNSNZtMnrHgOv\nmKMdFCgN1GnVB5BSYIiEaqlGu1tGm0rgXT7We3tMPP8srYUBzHKb1XumsYZ6nP/y9SRNjYeDo6Sz\n7lbvlrLJvM8Uuf7gYzwycgRLD9FIIQFvrcxE7hLLjHLRn0Z7uUfp+5cZ/7FZcpMNau0hiqUWzYeG\nMKyI+X/dg6nFrE2W6XxpYKt3S9ksXbIuqQqwp//cIavw5IECUCQLMAeBNwI/CryCbHxPQjbruAic\nAC5q0DCzEOVtzi6owLNR5sA522P/nxzDGuhAXeBfLKIbEi/KwWLCyulJwsAGS0Mb6+HfOUD3awOk\nbR3jhW16XxrE2BPyuzf8DG/98b+Fu2FVH86mtSs7XuKb5GUPYzHFHuviRy5OzscgJWy62HkfBNQ7\nVcrDa+SHmzgFn0RI5uqTDB2cI+3piOGInxv8fX7+De/HsX3W6sPIY1u9d8pmiedMco9E7H/xCc7m\n9xLGNgCu49GNC+RGGnRlAYsQx/Uouy382GItGSCMXXZV52k8Okphus1v6f+Fd77pI3iPlThf3EPy\nuFqf55pQA5aBEbIw0yQbgGyQBRaLy2miShaAyv3X18gqP2uADq/55U9x64fuhhJZaDoJ+JuzGyrw\nbIRFmDx4Gv+QwalTN2HlfcQNASzr7N/7OKwIsATxrA1dgbOrSbqYg2kJw4L881cxZAKPQe5wl586\n/b/4mYn/CUfBe7TEez784WyNA2XHSiON9AsOqQPa8wI8zaJktmicGIeehmalNBerrF4YJ1goIYQk\njk2CVp4kdDEKIW2vSFJzGdRqfF/wKX5r9v1Mli4QphY/+RMfIn4kt9W7qWywtKlxsPYk7fESs6VJ\nhJ1SMDvULo5wODpOt5fD8xwazSFWGsO4pkcvdklDg1jqFIsNcFLMTkTFrPOO5if4D/5HMKcilloT\nfOjHfpLgkqoW7lgSWCELOzeQrZ68yOWVlbv9x8tk43jqXF50MOz/zOx/lQAf7jDv4y2jn8puobQI\n/AhZaNqEBVKFlM/ceSaEkDy2iUOod4InodipI14f01stEHsuxaROOyhhDkRoF1LCSRNdxIieJKqa\nFIt12msDUNMw3AB9V0zwcJHqbUvUvzzKq/7dZ3A7Pp8983aGzCVWf20cPngF23xEIKXcsKk7Qghp\nrjY36p/fcdJEw7hXZ+INZ/CxWTs9ij3RxW+UKFXWiFoWQcFARhqkGoYZ43cddC0h9Qz0QoywYvzZ\nEuPXn2P+rv3s2/84Pzj9t/zOpfciDIj+JI/xU50r1uZoqLzhx1DZV0uPPxfxeZPdJy/Qeq2LEIJe\nmEPoKREmg1qN1eVxchNNfN8BATmzh5+4hG0H2/KJTYGmS7zVEgO7lpi76zpefPsXqYoGX1t5BXax\ny+KHZij/ytIVa3PTGd/w44jfUNe071ibLMzcQdYtFZB1Xa13Z0VkXVVa/7HoPw/7j22ywcoBWVi6\nC0pvbTB4ZIVzn92f/d4xYHf/51fi//z7nvl6pio8V9Ia6LmA4BUG7YUBYt8AI8af1mFYEnsa8lCK\nDDXs4R5JaEJP0D47hFPoQJCS39skqDkUDtQxSgGY8MWfezOf/cg7YFUjnUnhTVu9o8pGSWKN5GN5\nnFc1aMUlWn4Zc8on0XTIh6x1q/iWQxyaGFZEEugIK8YoBAgB1kgX2+0Sdl1K0zWW66NoBz1OHz/A\n73ztV4lrOfKFDuKF6n4TO5kMBKPtFWpvLiMtjdAyiHQDyw1Bl6zIYczJHo1WlWFnBT906ZHDj21y\nAy16jRKjzjJBaGMNdBkLF9FnIu752Cv57De/n0ZcZiJ/MbsQKjuPJAspXwJe1H8ccznQ5MhCT8rl\ngAOXE4XJ5WnqJtm4HQuYhtYnK5z7tf3ZOJ7dZF1gDptyjy21mMKVUgN9OcA8GOE/WUSbijEqHjQN\nRFuHizqUBZYZEDZy+E4OiinUbCgnaKWE3HSP5sOjFI+uUMi1WTg2w8grLhDsydMxXTRfx7o3yUa6\nKztOmgjSnsXN//Eejl16PpXRFXJuFwR43RxB18UpdhFA2iwgcj0KY01aayWEJnEdD93K1m3Pmz0K\n+Sa9tsPuiTPMFSZIU42c3cYgJN0fo9bM3ZnipsXwmVXSG6G7UsYo+eRkDysNCbsWaWhRKDUpRB08\n4dJulXENn17XxbYCHBHA0CrzjSmKxRZWHHCutZ+9Y0/ivSKPNCUdJ0/7wQHKr75y1R1lG/HJhk38\nLFkwGSILLpAFnDow2H+8/mWTVYR0shBj9J9rZGN4FoGXkY1BXR/j8zBZaMpvwj6hKjxXzj/DxJvP\n4bcd2OczNDJH1MhhjXUJZ3MwFVOZXsIu9MhPtEhCE70OLAFNQe/MALmJBu5Um/bSIAuzM1glD81K\naM5XkLrFTc+7j8V7p1VM3aHkqsXgyirHHn0BpeE1mvPDRIFF/eQ4acvCcEKKxQ7C0yiO1UgWHOrn\nRxCrBumiQ5A4FLQOtghI7ZSVxi5k22bFH0IDNC1lzF5i5XMzGIXwWdujXJ3SLxrsv/0ES70xnIE2\npbRJVxSoiibtqEhsQBoJUl3LQm8xJYpNgotlgsAmSQ0G3Drl0hpSCHpJkVA3CHSTzqhDWDV4i/Fp\nZudmtnpXlY1ynmxplIfJZmW1ya47AVlAMcmqQOtBxyCbrbXW/76+jdP/apAFoVmy6lCh/++uAFOb\ns0ugxvBcGY/C5EtOs7g2gTHqI6VBvGxDGxLPhHHQ0wiz5BG1HZKugWmFRJdcOBRj+jFRYqHlE0qD\na8SP2nT22ewZP8u5J/Zj1KE4WaN+93h2A7YrTY3h2XJxqDPWXUFUoSmLWIWAMLQJIwNNgp3z6LQL\niMggN9DAWyhjDXp4i0Xc8SZeu0Ap18Tv5SmaLSJHR8vH6GFCp14hiC1uG7ifB++8HW4PEcaV/btW\nY3i2B+/JEkcr93OyepABc402BYQu8QMHgcSxfISekqY6MhHEsUEkTeK6Q3VyhSTQSTsWJbeBJx1E\nmmK6EZYZsLQySWpJbjl1jIcWnof+misfmtUYnm1giSzAHCar5FSA1f5rEZcrPSFZ5WaFLMwskFWC\nBFngKfUfW/3nBbI1fAyy6s6dZF1aQ1e4/WoMzwaKgC/CpWAGGWr4p8sQSNJAwz7SztJsE5IlA//J\nMs5oB6viEbVdCjevwZMGUWBBopGm0FitEt0AWs/g3OlDuGNdDt/6MPXf26Cwo2wL8ngOb9qibhax\nKj6dxQFEmpAv9BisriBDg7SdI19uEawWGJmZo7dSYergGXrLg8gVm3aUJxEGtfoowolJejq6G6Mb\nKddNn+S+n3gJvDC44mFH2R6Suo7xDwlzI7vQtISVxhianZKEOqVci1yuh0wErUaZdqeIY/gIQ9Jd\nHmRodJGVJ6aysWLVmJqo4Fs2+WKXEIt2XCI30OSO4F7uO33HhoQdZYtJYJ6sC6tEVpUxyMLO+oTO\nHFl3lU62ds4iWYWnRhaM/P6/M0JWFRL955Ks+lMmqxLdw8aEnWehAs934/fhlpmvMfwHFzAdj2TO\nRB+PCHoF5ECKlAKx28Pe3cwOivGU7sIAcduFDgR1m5nXnoA4xR5rgadDbBL4NiN7LjK65wLimMmj\n778d/uNW76yyEZJLNnvELM7hDlFgkYYGjZUKxclV7EKAa3TpJnksEVCZXCARGhRiGp0q+ZE1ltbG\nqe6eh3xKwe3iFlo4400EYOYigsghcVLadw1h/EEboW6jtSP1/qrM0c4xhn/5EmFqE7dcCoMNDGI0\nXeJIHyElhpdgE+E6HoGwSWMNp9yiGZXZf/2jBB0HR/joWoppRjTSCnqSoCUpVjvivn95Kc5br9zs\nPmUbuUjW/fQqskHGEVn1ZowsKThklRpBNoB5kOy6tv75SQKT/d/z+j8zybq91odhdMlWZx5l08MO\nqMDzb/fPcOSP7+PB+16E1CGS2cpLZiGA4xputYvXyCEfyGGUIsZeMAvnNdAEqa/BGkRxjtk/PIQx\nHiNy2RB4d7wOFxwW/2kPHb8IBwP4d1u9s8pGiC84lFotlswhpJ0QRwYiloyNLtJYGiCODFpemdCz\nsqnnvkt3oUTUydGbrxI1XJJEI1mxsIdbSB2kAblCh6hn0Vgcxu+6WF3JkjW6KbMglC1wl86bf+Dj\n3D/wfEwnAiHxNBNH86mtDmHbPo24TL0xQL7QoZJfozNXpV0v06sX8bsujuEzf2wPpWKTQNrEbYe8\n5+F3HBpJGdsMqBxrI16zSSvEKZsnIVv8zwQO9V/T+q9Pk1Vm1oNNDLTIws9FsurPpf7rkC1IKLg8\nQ6tGNp29RlYZioDH2JKwAyrwPHcSeD/k3lPjsXNHMQ75tJYGMf0EpiX+3SXEjTHe8SoYkHvZKt1j\nwyx+bg8gcfLN7MA6CIwEcHtE3Lahq4Ob4t07kPWb7pd03zNE79JgVl5UdpS44VI5sEJwWKdztspk\n9SKanoCTsjg7g2GHeJ6LacUE9xWRliT2LIxygOlHGCMdwiCHW+zhJQUcJyDs5Om18/idHL2VKokU\nhKsFWmsVzIM9lXd2oN7flTlw03Huzr+Yot4hwEbokkKlzXxtktHqIkFoY4YpeavLWjDEhdpu3JEO\nhhmj6wn5aptU0zD3tUkjHV1LsAtdWhTRjIQBvQ4fsTi3ZwatopYz2HHOkFVmricLN4Nk4250sjV4\nArLuKcgqNCHZWJwKl1dZjsmqOIKsIiT6261XeFKy9XaeJBsbtEXJQwWe50ICn5eM/+VZguUSnDfQ\nvYTwokWkm7gjDcqvXkB2BewKGBlaxuvloCRhROLc3MJfKCNyKYbw4YSFWUwpTy/iSxsiHX0iQEti\nrIE2/BJZaVHZUZJFm/zjPYp2m6DrULiuzrI3gmlHlN0WlZFlCqUOsWdDIkkndJafnCGNTYSQRI7G\nQHENc6BF6FtoWogE3HwL2bMw3IhUl1w3epL0XgNzvLvVu6xsAHG34NY3fIPz1d0EsYNV9qm1hrBN\nH0sLGR5YpEseP3JAS2l7JbqBiyMidCfCDy2qg6s4bo+0Y1LNN9CtGJFKOt0SphUS9vKUF9qsvLKK\nPpps9S4rV1JCdiPPHFnYmSer3CyTVWIGyQYlV7g8+yrqb+c+5WsXWcXG4XL3VUo2nscnGwtU6r/X\njWzpLGMVeJ6L34TCj66w8MQe0ljDvaFJEDnYhzqIeR2/W6S5OIwz2Ya2zfLJaeSck607MBZSHVyF\nagJuQtxzoCygmDAQNLPxO2YEwxG7Xnue8OfLKuzsQEnTpuh1yb1+jdXOEEYxJGjnSVKdJNZphwVi\nqRN4NhJonR9CaBLSFMsNGK4uY+RDYmlgWSG6SDAK2UVKCh2n3EWPYqpOnfN/cxjte1QXxE7U+6sy\nN9/2IMfzh4gwyZldWrUBpvMXaAdFEk1HCg1dxPiezWpvCPSUuOtSGVmhKupYdohmpbRbJRITVr0h\nRrUlOl4eMx9gyZCp4jnO/+M+9PFoq3dZuZJisgAyBBwh65YqknU/rVdqWmRBZ/3GnqtcDjRuf/v1\nwcwOWUFAJwtFxlN+fgNZl9neDd6n74AKPN+JBvApcH63SWdtEDyBmffxZ0uISoxYE+gTIfZgBzyD\nZMEGPYEO6M0IjkaICyYLS5PY1S6yZpCfbKEVE2LP4Ly/Gy0EPZQU3A5jDy7Da7Z6p5UrKY01oscL\nsKwjD4d0vBKalaIhsYo98m6HbrOIocX4vkMSGshUUN63giYTtCGfyLOJNQPH9Wm3i8SRieWEBL5F\nIdch1SDVJIYbo+cj0n0auq0uVDtJVLMQX9C45Xse4DHrCJ7nkqdLr14kN9CiHpcJAgcXj067DIHA\n0FNcy8MyI3KDTdr1Kj2RY7iwQrNZZVd5gbzokYY6C2IcxwqwjYAk0Rl9ZIX4lRpCXSl2Do/sQ3iZ\nbPBwyOWqi0FW0VkmG7ezPhsr5HIFJ9//mUYWaNZ7OQv9xy5Z+Flfi2eVLGAV2PJxhOowfjbnYWbP\nCSbeexp/qQSXJPZIh7BnIQERCoyxiHjVRPOBNbCmu+DG5G6okezWsWe6yGKCmDMIzpRwDjQJOzqm\n6SF9gWyZaG5EEluU8i0efuC27MZqyo4gY0H6JZfbXvJVZm45ie+7eOfKdBoF0qaF57usrQ4xMLxK\n7NtEPQfNTrByAe2lQezJNkNDq1THF1ldHoYULDck7rkkqY5b7LFwYoY0FUSBiVfLs2ttAW1GVXd2\nkmRF5+jKw0y+9hwnx67D8/LMFC5Q86rIfILnu7i2j2WHCCRBamBbAWgpxWKbUqHJYK6Gng+JUpOF\n2jhusUs9rmDkQlJD4Hdy6EZCGFsM2atc6u7G3tfb6l1XrpRVsjDzMrIByTWyMNIm635KuTwdPeXy\nzUFtsm6pif739ZuHrt9aYv1eWhbZVPX1f2uErJIkyQLTFlOB59v5Goy055l/bA9z/7QPa7oFZYPU\nESBMqAnSuk3ndP8uw5dKkCQEpwpUojZ+owCBQVAvIEINhmOcw3XEso41HhDUitiVAFoQhyZ7J0/A\nJ3XiW62t3nPlChL3Wux+80nuP/EyFlpTOHGEPdHBjWJy5Ta2EWMZCVHdxW/lYMFCNk2irkOptErQ\nytNsVug2K5h6gmP5yESQL7XwmzmSWEcf8gjbOSatRUYeqfHow0fR8mrMxU4RPWJz8MRpTu/ew+n2\nfjRS8nqXnuVS0H3CWgHX8lhsjUEPmmuDGD50ggIFo0scGnS9PPVeFYsA04yYGJpD9ASj1hKNbpVK\nrkGUmKSxxhHjMXJ/EbG6p7zVu65cKR7Z+JtbyELP+kDjlCyM6GRBZf3u5qtk43bC/rb5/s8jLk85\nL/a/l/uv61xee+co2YrNHbJwtQ2owPNMlqH8yiWW94wSuSbW/g7h35Qxcj5x24AzKdpYCmnK0Mg8\n3koRTcS85A5pAAAgAElEQVRQ17GGPVoPVtGsiL2HH4MHDOSARFoC6RtEuo7XymNe1yQ4XWD6wFny\nI03m//sUF0evyw4e5aqXxhrR7xXZ/ZqTNOwyhZkVKpVVZE8jbtiEOPi6RSIgSjU6l8rZCWhQEgob\nM+/RXhuiUGzgRBFRomEVPNrdIkmqg50Qd23CnoPtBOwfPU5g6ZwZOITxcvWpfKdIWxqHOMkTzz9A\nbFq4BY/eQhXX7ZJInZZXYnT8Es1mhYOlE7RaA9iVLt1ukYrboLtQRbMT9uVOE8Q2ia3j+S5dmSMy\nNeZ7u8ibXRZnZ7iueIpDyUmW/miK4+/cjz6uQvOOEAKfBF5KNgvYJRujk5KFE6//eL1iE/e/PC4H\nmgWygczrFZ5+jwYRWbVn/fcGgcMSLgB3kY3d2SY37lOB55m8D5LQBpGSm2oQruTh1ZK47aCtATfG\npF0DSimr7SFoQ3rKYvyNZ/FP5ii+pka8muPs6cMY0yF2pQMCgotF0q5Jumwy0qphftaj++US3T8f\nwv+BPAxs9Y4rV4p8wuT2n/8qp1YOkCQ6oW9Raw5iTvRI0UnNGA2JTDVGBxbBhDTUGd5zkdJQDSEg\nNiW5fA/PMhgZXEIgEbrEtCI6ayVMN8KZS9B8yRN338rSwjTmdPvZG6dcNfz/UaF+cwEhJPlejyg0\nGZhZpBlWaC4Mka+0WGyOkS90qDGEaUasnp5icuostdoIhak1gp7DxXiKUr6FLQPyVhdiQTYeXlDx\nmkx9fJbe/WXu/9IdLL1bnYh2jBi4H/jR/uP1Wz3kycbrdMkCicbl+2X1yALRFNk4nYRsHR1JFp7y\nXL5WuVy+aej6Ss1/BzwEvJhtde9HFXiezp/BC776RTqdCpWDq/TaVYhSiAX6dIdkWkLNgFOg1yR8\nwcI44sEeWLhrL+luQfPrQxBpuCNNkqZJsFZE8zUopJT3reJOtZHnNKK3udQOj8LryA4cZUdIFmwK\nYZtHO7dQGVjDMkNi36RcadJaqlKaWkVGJl47T97oMXd8H5UDS5g5n9rKIN1uHk2AjAyWVsawjIhO\nUKCzXMUkoWi1qZZqTI6eo+MV8DQX8/oO5oCagr5TSAnJ31q86wN/xnxrmkPlE9TkMJV8g2a9gq7H\nDO1aIAgs4rU8wtOZv3MvYyNz6IMdar1BCsUW7V6RSJpopMhUIDWBF7pE0mTYXmawV8f8umTtp0us\nPK+K/WoPvaAqOzvGGbKZUh2yK/76ncrXu7CGyUJQq7/9LNkA40GyYBT3t21weXyOIOsWc/rbVslW\nZV6/1cQhka3ts43CDmy3m4emZCs1rpGlyAowvnlvD8ATsO+1j3D66zfChCA/s8pofpGzF/ah13Sm\nDp2hR45Ws4w0BNQFgcxjaAHWeBf/mxXSioE12CJMLOjYkIJwE+SjBrvfeBz7ZMTJszdl9xLZDsN1\ndtjNQ+OuA76W/QGbQAmM0uZ28RwITrGkjbHa2EV59xK25mPJiEgapKFGbBvEsUUU65hmRKdRRKQC\n3YpJA4s0lUxOnufSxX04pTZhbCJ9izTRGKnOc3PpYb74969H3BGilbf+4rTTbh6apgK/6yA9E6SG\nlg/IlbrIdPM+I3YfrHB07/082L2dkeE5sGDIXmUlHSZsW4wWluiSp5fkqJgN1nqDFN0mq7Vxxgcu\nstIZJui5VMpr9GQOXUsQhkSkkm43z03uI5jHE451jiKOJOjbYMzXjrp56PpaNAGXVyJ2yc75m3Xe\nXw8oB4FTZONqqmTXWNlvx/q9sODy7KoWWZCx+tuOkwUaQRaYgv7XEFmI+hxZxWc7dF9dFTcPbcos\nQQpwzQ4UZLZ09f1AGj/LL18hAfA5mH10H+xN4aQkb3aZXdrNgakT7LvlMXzTppPmMeqSYLVI4piw\npCE0Se+bQ1g3tiGQhJ4NvoUY9OAiyC8b7Hn745z/wcOcPHYTHGB7hJ0dREqI2ha0dKQbUzm6hIhB\n9CC5z4VA59vk+ysmuljgRHyEuiiDSPGXS2hpiicdGpfGyBe6tOeGKLt1JouXGBSrIKA03CBetLlp\n9AG0RDB38TqMUhcCHUOPIda4YfeDOF+M+MJH3oT+Gm9bhJ2dREpIOga9+SqmkVDONXGLTaRn0PjG\nOJFnkKYbP7c29TXyX+gxW5qmuGuN1c4oA9oazU6ZQq/L/sIpgp6DE/mMmMu00hKu0ePS7HXYbpfl\ni1MU7TZWMSDAxrU9ykaDwLPxuw4vML/BEx98Hg/az8e4I9wWYWdHicnWtgnIrrL7yca+BGQVl/XA\nsZHC/vtMkIUel8uLBz51sHFINpuqxOWZWUb/9fVVLWT/NYfLs7OeR3Z9vqe/f/vZ+rDzLLa+4CTJ\nbhP/Vp9cvocMBF6vADJC7BLIpon5ZEhU1KEkNnYxvs/A+IfPsPDNGfK71uieH8Z0Qg5Xj3Ni5RDx\n2QJi0keEBqmbwgrEngVDEZEwMW5oI2s6VuIRnnEZf805Fk7uwdAj4j+zOLf7BvjgBrb/GpYGOknT\nIl/pkFa7hJ087ZUy+UM1DD2m6Y4QLeRgzM/uN7RR7Yg1+LqG+Q4fwwnwmibkQ4QuKdOkYQ/RbFUo\nDtdotqsEwiOxdKwkoTE7QH5Pi4ceeBHV588RtnMkGjhDHt1Wnv17H+Hs8QMEh23MUXUDx43QPTdA\nNb9CfnyeSNdJpYZrBpRKLZbEOFEjB4M9klTDdDbujuHhV1xe+qtf4qHerbiuR+DYRJgM5NYQXXii\neT3D9godUSTtCdphEZeQkak5Wq0y+bEmXq9AzvVotssUhjp0ZIFdYo7gL0s8+qJb0N/bw9j6K8DO\nE5MttHeIbPxLQBYiymTdRz2y0BCSVUVMrvz6NJKsatMhCzzrM7TWZ2AZZBUbnyyQrY/jWb91REpW\nCTpLdiuIOpfX0oklohoh/8bKnh+4wm3fQFtb4UmAL0jcd9fA1+g1CuwqzWd9g79tIb9pZjfZ9C04\nGML5DYzEx8C83WPh2HUwr9M9V8G+rsXcPfs5dfEIthPAWYH8kossROSrbfQ4gsGY4mgDYh03jdCG\nYkLp4t5RZ+HJPZhmyKHDx+D9ZH2ayhUXdyyStRzF3WuQS8gXulTHlom/XqD96VHqX5jIPqnEUMx3\niE4WNqQdMtRIvllg+j8dJ/Adglqe0kSNJNFJhEYtHmRw1yL1x0eJUwthJaS2QCZgDfaoTK9hxTED\nt1yi0ygRSR3bDQhWc4zkljn5qVuIRzT0UbWY4JWWRoLu6TKjhy/gjHUJNYPhcA39pGD5j3Yz90/7\niZsORhgxwSIsaSA25nwUPWazf/BJ/vXi6xCLOlqaUiy1WWhM4yUu87lxYs/m0pm9xJpOGhsUnTZu\nuUOl2cRMYwbtGqYZ4OsWQ9Vl2l6RvNdj11eXaby1QHKzRKiwc2VJsqncZ8nWUbPIgkwJ+Cjwx8Bf\nkoUMi+yeU8tk18ErKSELOyvA88lmS62SBROPLNSskp0T7wSWuFz5qZANVK7223iYLLClZGN6AByB\n/JKVbXfdFW77Btu6wHMR+DLoP9RD+jos2hi5kDOfPgJftPjw//pRPv+el8AKGBMRzNpwW5iN/L6S\nfOCP4YZ33U9a0eBR4KYYrRAT4GLsaxN8zUXqkH/rCoPvuIT8pxymiKncvgQrFt5ikb2HnsCrucRr\nDoYVEEYWtCXJnxg8tnSbCjsbQEqIForoyzC+7yzthSF6K2W8ToHVe6dgVPLpH3o1H3zTz5KeNBm7\n7Rzt2hDloyskK/aVbcfxPNavSKovnsOXLpXxVaKmhZPrMTa0wPKFSfQoZfnPdjP9olO0ZwcxzBhp\naASJTZpoDNkryJ5BfW2QgaEabrFH+5Eh3iI+xaV79mO+pPXsjVGeM7+dIzhRYvrAGbzIZaE+jmWG\nnJs7wOr94/zuO3+a//2CN6HNCYpJm9lwksHqKt0TV34mU/tvh3jb0MdYvGkYmiZhxUTTUlzNI19p\ncurSEaprTapyjanRWerfGKNotxhzFuh5OVq5IlOD51n2RiAvyRtdYkMn34rI/UXMQ7fejDamuq+u\nuITsmqYBLySrkoRkgecTgCv5wMd/kR/+8z/NxscMkIWdAbLqyZUSk3WZfRl4Ldl7RWTdWQ7ZmJtZ\nsu62FbJp6u1+O4v9r/U7mxe5PG19tL9vLeBfyMYEVa9guzfJ5g9aToBl0AoR0tEgEEhbQAj6UEjy\nVzbGWoi/YPPV8/Ajnz3FpXv2YdzYJfZNdCTJmgHVK9BZ2AH7QpfRl8+zsDJB1DIhNsFN0HYFVOwm\nvU6BaMGivLfOWlSmYHSwSz5R1yVNNErlNVoXB0kdQVSziaSLle+R3GMy/vpZLj20b/uHnatw0HIa\n6iQrOQaMFYxdPrXOIEQCMx8hhMT7WoWRV11g4Y0zpK+Dg287znx1DKlrWLZH+8IQ2qCPbn73J//o\nWJ7Bo/M4ts/cygx0TCjGODmPiluji8tAbo3lpQkqo6vEDYswp1MwOgSpw4Q5x/LyBDW9RLnSZOXs\nNJoTUi7U2L14gYe+eDvmu7Z3F9bVOGg5TQXBSo6i7OEMt+iKPKnU0LQUR/NZvnOa3EKXs/fs49Li\nKj/+J9/g0caN5KZaEOhEPRvsBCsffPdtWdUZ+UaNyvetcKJ2hDjQMSshuh5h6DGFpINlB3SSIoln\n4eY7hG2XkeoCDcrk6ZGTPebZRdI00HMxte4gea1H5YkW5XyLU6W9235dnatu0PJT16OpklVtamRB\noUxWTfl74IjkrluHcV9hcvsnF7LXC/3f75EFku+m8JySVW/OAreRLfT3jX7bxsiqNcX+++TIQtEg\nl+9oPkhWyRkgq/7Uybq4zjzlZx2yatAN30U7N8O2GrRsJLAnInddE2lpyOEI3CRLofWUwV+8SHzG\nwvnVHr9w31e49L590AQRAms6qQVE+uX7d/xbPQjiownW9/S4ML+XaCUHgZnd/yqNcQs9QmFCKSbJ\n26zVB6Bl0D0/QO3YJHFs4OS6LM5N4eESBnZ2AhQwPjNLkphcWrkKws5VSErQAoE7s4Z9uMVyYxdp\napCkDimCwdwyw6+6yPKvT/PCT9/Jm/7Lxzl74hD+UonIs2kvDVKaqZEu5J79zb6NuOsQfabE+O3n\n6VJg7sI+nHIXYcRUx5YwiXAsjyQxWLg0hShG5JIeLVnCtkJCzUIzEi5FE/g5nfGBedZWhyCBA1OP\nUf/0OI8Ub9r2YedqJCX4XYfKxCrOdIu1eIAwsgh8myg0IZIcfdU36Jwqs/dnn+D9/+9f89DXbiNe\ndTHNiF7gkB9rkHS++0ph554qlb/v4L3O4JH6TUgnQa+EdJoFhEgZsxaJdYMgtWlHRfLFFqmuEbo6\ni4wBggiDWTmDTYBZDFlcHQcB3+N/iaXWKGf2zWz7sHNVCsmCxhhZF88Klwf+nicLC+8CPgvva/8D\nP/nwJ+DzZEFHcLlrq8O/vWurS1axOQnsIavyHCMLNgNPea+ILFzNkl35e/22WmQThhIuTzk3yRYa\nzPe/HiGbQX0Vjdd5Optb4YlTaGhYY13SrgZFSXyPC7fGmLWQ6K48Ez95DsMKmP3Ph7LbziegvzZE\n2+8hT9qIyYT4bge5X4Pcc/wgEAAfg11vPo+4JcKfLVDrDIOmkbdaeLpLXnSJHQMjDWn7VcyeT2lv\nnbWvjCAPaxRyLTq1EqViE3O4R1K3iMuC3rkqIkwoXGrTvHcY3n3l/rNtuKuswmNZIUFgkS90iWMD\nTU9pXxzBHGxhy5jOEwPc8LIHWO2NsnT3NBzw4ayDc8va///H7xY96l/fhXn9c1+kL6oVYS2GUzoT\n7z7DwvI4jh0gBcSRwcBgjWazQrncoNMtIoSk5LboRAU0LSVNNNJEw3JC9Cgh73RY7Q7TbRXI5XyC\nyCB+soh2XRfd+G6T/ea42io8UoJYM8gPNGjGZfK5Ls35AfKFNlHbxTtZ4Obb7sMi4r6PvQQ5DGls\nkLutxczEaeY6k1QKdZafGMfYHTzn/09pqBF+2WX3xHnKu9e4yG7aXhF7tIN1SSJ3xRg1gRiMkCnE\nmARhjkq+RrJm0ata2HpIJyhQEk1G7GVW/FGKbpPZtb2YTsDIQzVmL+3G/r6rZ9Xtq6rCk5CFgx6X\nqyAGWVWkSlYN6QE/QHbe+W/97yNkXUnTZEGjAnyKbLzNcxlXlZAt8ueTBZ1bySo8PtkH7fXFAA2y\nUNMlCzLDZGFm/bYSPbJQUyULcHa/7bX+798D3NHf5mqwbSo892pogyHh8TxxxSDpOlAVvOaGf0Q7\nEkEN5j6/h9X6KPqvdjHe1YOjkFg6yUWX2LCIZh2sF/Xg7vUbdnyHfOBjcP1vPkDzSJ65c3vwqhbW\nkAdJyu7Dp8gNtCnOrBG0HNqNIXQRE1UM4p6NHDcZnp4niB10R9Iy89QujuPlLDpnhxBuTNJ2cOzw\n6go7VxlNS+g+MEg+16XTKBL6Nt2VEkJLeOXglxlz5mEFnnjkKLEpyL1wFaFpsDtGpBq2FeLPl+jV\nijg3NIhqz+2vODpbZGrfk+y//Qm4KaXeqSJDk8hzkU2HkcoynpdD01OCZp4k1gl6DpYIMYiRscA0\nIpDQrhfp+kWa3QoAphkhOzqvc76AcJOrJuxcbTQtofXVUWzLZ3l1FyW7RRA6BJ0Cr6v8MzdPPUAS\n6zxUex4X8pNM/vvTVL9nEW5OMQY9zrdmEC2dNW+A4esX8R6q8FzORTIC/X/qvP7Nn2H+0CiPGjcS\n56E8VqO+NsANU48QxA67x04TCJt6MkCom0grxdV7LBuDWGaELUJct0fXLPCkdxDDiZjt7iZX7RA+\nXCJn+VdV2LmqyP7XWbIqikd2NV0FcpLqf1pBe2GchZJ7yULFe4DXk41/Wd92hSxcHOw//k6lwOP9\n33sh2To5T/bbkSNbc6dENm4n5fL08oQs+KxPS++vU0bQ/12PrHsuJRu3s6v//bsrhm8bm1fhaYMo\nBGi9FGs0wAty6LkIlk1efctnmWcCN/U5tnozwdcrMBNTLdWpa2Xogp6XSCMlPemCBmKfj0VI0C49\n+3v7YF3sYj8/oN0cYGB0nl6Qx5EB7eMV9P0BYWgxXF6mvjiMPdGhN1fGaoXEVQORj5mcmmXx1DT+\nQh77hhZBvQi9NJupsawzYs0hWhpLzsTV1411FVV44kYOq9omiQ1sxwchiVZcpKHz2unPcJEpyrR4\nzL+BtX+dwnpBCy2SSCdFQxInOqYdIQKNqGYTShdRDNGtEPEs8T/6dJ6Jl1zAm7JoLVdxnACsFM93\nsFopznCXYq5BvTuA43oYWkQsLWqXRilPr+DoAbWVMYSUpEKiOTF6JEgiQVAv8bzd9zD3sd0sizHM\nN1xd3VhXU4Un8C1MM0ILBNXyKu2gRBhb/H/svXmcpHld5/l+7iPuiLyvqqyq7qruOrqbvruBboQW\nEAVExWHRddxVUbwHZ3RGdx1m3XFndJ1Zld0RlxkXRsFRRNRGoEGQpoG+u6qrq+uurKzKMyLjjuc+\n9o9fBIkOhwfdVZX9vF+vfEXmE88R8dRT8Xzi873CtsUPzr+XFWboUaRFhWcevwdjd5tCoYOmRgSx\naP6omhGeZyJ7Eprh4QQ5FDNClr/+52XqSMx8dgP1dS7Lvb2UjRZeTiOKVOKeiaJE2PIAw3Koh+NM\nWhvU4zGUnoRRHSD7KVPaOuf8PQShRV7vkqgyg04RyQoJL+U4dPkoFBROj+1FmXuReph9k7hmHJ5R\n2EpHuCAj0XARmEiYf/cZ1p/eRegacEyCv0Dk1qQIsTFKaraGy/oIsVFAuEZfL0U1QSRC/w/D7dcR\nLhEIV2dUbTWOSDLW2W4o2EIImCoiDDZguwR9a7htH1FS/7nha1lEuD4vfPupbw5XhcPjwNwNS+i1\nEL+XQ3YkzJJDvKLziVNv4tn33cljS3dhFlys+5tILnRbRaziAEmDRElJLhhYh1tgQWm8iX+8SG7h\nG8jiJ4D/BcyDHr2VKvp4h+aTM3j9PO2jNZIJSVwMzxo0zs8glyKSQCetJPh5i7irEa1aLL3/Rgp7\nmrDfw+9a8JQMdopspSze/zybD82zse8aFDvXGl3YUzmPmXcJQp0w1JErEeEpg7/47Pdw9Im7Oda7\nhWlzHfPeFkE3h2xHSFKKbvvISoLbtzGKDrk9bdiQMeQQvs5nbOhphJ8s8srb/op6tUKvWaVQbNP3\nTHTDI1/pMrH7Mq1Tk6xvzuHGFpbqMtgo46MjlwJcJ8fmo/PcPvkFzGqPGBm/UcLzLPyVPDcf/AJP\n/+bdNF+XR339tSV2rjl8hZvSY6gFn4GUQ9ITqvkt6Ev8fuf7+bPH3sZjrTuJAo09B59DswOcIEeq\ngGwkaGaA7xsUrS5KKWDc2yKua1ia+zUbW6YpRKdMpF/TSF6fcGrzCLurZ6i3p6hKTZJAJjZjKkaD\n9fo8TXeccatOu1/FICQtJzQaEyS6xIVj+1m0lsiVegyiPI1L09i5HtMrDV45/2lOdA9x7uZd15zY\nuaaQEFGDBUSysTx8XAAuyFx6137C/2TCo5IQC4cQgsZChJJstsu8NbabAvaGz3216yhBiJK/Ar4L\nkavTRjT8S4b7HSVONxDiq4tweUZl5w5C5JxHiKKJ4bFPDd+PihA7Hx1ud/3w8VoRO9+AF8/h8YEw\nAkvGqvVxfRN7rIskpwyeHgNNgrIPjoEchyS2DPkIaVOB8ZiJqTU2ju2CcoLUS0mLMazr4mLhazQk\n/F2Y+PmLtI5OEoYG5r1tvPUyxd0bdFslaFpQ9tBMn/CZApRi6KtIVoI25RI0c5i7Onhny1gHtvAe\nL5HmZdHPZaZD/10l0u+RYR//uAz7K8215PD0LYhkjMIAIzeg3y9g5xwmrA1WOvOEjkWcSMh6iGV6\nxKlMudCi1y+RAnEsIykppumBDGks0Tk6QfWmdTr94n/3DT0a6BhJzMT4JTaDSbzNIoXpLVQzQFVi\nAl8nilXCUGOysMHq+i7sck8MinVMAk+nOr1JFKv4jkWp3MIZ5AmaFuZkn+nNTdY703TbFaTrvWs2\njHUtOTxRqBBv6OTH+hRKLbzEwk4d7NhhafN6ZD0kUhSQIOnraGMDNCUkTSUkNaUodelSRJNDtDik\n3y7iL+WR5mPUogvyf38a3PcVOfw9T3Fe2UM/zTFTXaUbFqnoTQIMeoMCmhGiphGDThHNCuj7NoXU\nRVUCXN1AVWIkL0UxI1DBaefw3ByHJ59h8zdm8O4xcOdNtOl/fNXYleKacXhG1VVdxDgFFSEKXERv\nmmcRoSED4eTYCGFRQAgVFRFekhnewxAhrZMIAWPxN0VGjOinkwJ3IcJgIaISTEU4NhsINycYHmcN\nIWJG1WIDRGK1N9zfKNxVRzhU4fD4PkL0jNyma42rwuExgCUVnAT3dAGaCk6zwODCGIylEIA904Nm\njD49gLYCiYQ25mFXe2yc3Q1tCewQc7IHgYF9ZAs2JPKHv4rL82dw+DceZfPCLkJbg+sTvI9U4GJK\n9+gkEima6cOaTkF3YFqGSIWFWIidEznIJahWAFKCu1Yh3R8xeetFHrjjQXpvr5D+vCxmk1zLYuca\nQ7Y8Ui8mjhUcJ4capridAmudOcYr60iDhFylg6FERAODOFLoukU000czAlIkJMD3DLqNCp3Lk5T2\nNGkem6FQ+psJzPGWRnraIM7HbEYTxJFCfrZBmKr4vonqRaSyxFihQS434PLz+9CKDoNmAdcx0RUf\nXQnQ1QA1TUgjic3Tc+Ao5KMB3f88xanVQwymDNQbnWtW7FxrKEqMFxVBTWgGVbq9IuvONBfd3dSm\n10gDhUKljWJFlKpbBIFOLCnIcoImh6z2polCBT8yaAUVXE1n7PAK3iUTXQlI4r/5WZt+XOX1P/an\nnNRvJLZkKuUW641ZFC0mjlQ0P6ZkdIhaOnbgkFoJsaNhFxySXELLL6MTMk4DP7KROhL9rRJlr829\n2sMc+83b6L7TIrpDuqbFzjXHaPimi3BQ2sPHowinv4xwfGYRIsdnuww8QgiiGCGamghxcTNCgPxt\nTXZ5uOx+RL8fn+1EaX14XB1xLxpDCJdRUnVn+NxIdCnDZWvDYxvAnw+3uREReitybYqdb8CLm7T8\nchfmQ9iU4IICZzWkmovUScm9rI7TzTP5ikt4yyXMG1sw0AkGeQbPljCKPYzbWyiBhGSmsJTidPJw\ni0f/+Pj2BZICvw68NeTZc7fCVIgyG0FPQnqdw8wDF+AsXDd9mjDSoBjS3KxBkMJkBBdUglYOro8x\nTI9pew2plDKz/zw8abIvPstDZ78D3oe4KDJeVNJEprS7Sa7cIWpYBKGNJoWYtkMvKDF5/WXyVp9I\nBjkfIMkp7moFp5snlSRM20eSEmzdpTTWAiOkFxRQcwGdJyZIYvFfIo0gf9aldNc6ueIAO+8QbVmo\neoLfzmOZLpuXFjDSAM836VycRJ5y0ZOQVE+II4UUhcpMg16nRK9TxrA9pFzIorRE89gk6nf30K7r\nf8PcoYxvMhIUZhvIaUK/XSAKNJE7o7sMkhzWZBeVmJLcpkeOfL6POxiWo3s2pXwHXQ/JK31y+gDd\nCGl6VSr7G2ydmxENJYefR4PfqbD4ijN8zrsPq9hHNwLCUGO+tkQh6bHSmEWLQtJEwsi5bKSTRJGK\nantEgUqSysznL6OqIWGiIA2P614ocENwisdad5L/iSay/iIOec7YLt3OI5wTB3E3HTkz6whBEg1/\nRstjtiuxLLbHShSGz+nD59sI9yVGlLcnwMsQzQpHobAEcQ9qIETXqPy8iRBbCULk2MPj7EKEzEbi\nJ4fopPwwcB9wEy/MmIuriBf3o/aMAccN8Q9zMEXWEnL2gHRjmKF1zGTjM7thl493ogLrKVghFCXM\nvEu0laM80cBdLSEd9pieWYVlA5IUaT0SF97HUw797mNwSUNqx5SSFjSgsLdBumqy+pE93PSdj3L6\n1BHGZ1cg1FDUAKoBtFWkQoyddLEnOkRdlTNfvAnklLVPL/K6+z7CIz/1wIt6yjL+JrIS09us4XSL\nYLEAZckAACAASURBVEpUZlYJUOm3i7iOiR/qbFxYIOrmiAKNqK6T6imaFRD0DZy+haoldDcq+L4O\nKeS0PuZMD2UsxtB9wrpO6f/xqL1incFGle56jSSUWFg8S2erhG57hF2L1AB3YNHqVylO1pE9GUmS\nkJKUanWLyNWQopTBuQqq7BNdtDm8cZyLR3eh3DVAUrKb1JVCViP8roWmRRSqXVEIocX06hVy2oCt\nxiQbg0kMy2dreQbLdpBIkeSERJKJYxkliSGQkaSUXG6A285TLjdxG0VIQXso4f4f+wTnuI7YV7Bi\nhzSQMBKPfphjsz/BYuk8K+k0Mgm+apD3HGqFLRJkNCXESAN6tk2/U+JyZxem4RGumrx67ON87tn7\n0Be9K30qX9qMwj4h20JhNEFcQSQJj5KRQ4QjNEpQNhCCRmNb6MQIQWMM111ChKtuQjgyMiIUNcV2\nPs4ojKUg3KFROfn08LnyV+x7fbj9qGvyZxHl7KVv4jm5inlxBY8mQylGmo6hJ5FMJESocChg0Mkj\nXxfCDT5qCwgSmIrBjJFbMIhNiKDv5dCKPmndoN0ri4vMkEgfV+HdYL+lzfLyHoz5PmnXoHNqgrgq\nE6UashaDCUf/+i5oyNQfm4dQJlFUWDFgzCftKjhWEZoqkiLBZED6tMT3P/C7fHztO+FnXtQzlvG3\nSFMZxQhBiUiVhF6viKTFWOU+5XILXQvJjbUxql1kJSa1FXJjbSQlIU0VClafMFSpzmyi6SG6GeKl\nBgPPRglDAsdEb8d4P6SxWp9jYtclkBP662X6Up7aRJ0kUvAlFbng4nk2UdcGJUU2E7y+jWJGdDdr\n6EWX+uk5Zg4ugSJx0+KTHPvQ7QwOm8h61gTuSpIkMtggySn9Xp4wUAlSHXusi4vFdPUShWIXLQoo\nzW2SpApOaJOmMgWpTxIrSEqKbnmoaoQbWEi1gAEWylKM++sldh9c4qR8gPF2E2+Qp9EdJ5FlMCVC\nWSeVYCWaQ5JSLq8s0muUKdhdNtZnSGWJfj+PMyhQidsUtS5WuU+rWeH+sU/zSPhyzNcOrvRpfGkj\nsz0Xy0AIEBCOThEhcsYRAmaUPKwg7lmjaq0Q4bSMBM9omOcysBELYbQArCASkj22c3M0hODxEc7N\naYQDNOqv00AIodGyFYRQ2hjucw0hpmrsaFfnK3lRBY+50EHqykhTAbgp+YUO3noR03IxpQBNDqBv\nkIzFMJ9AoMKaQlJKiVYKJGaClkRgR7Al4fZt8Y9eTygkbfZ/6ChOs0J3s4TlOTAZYL+ygbyekkYy\nWhSgHAxhd4q50MFQHXAS0g0D82ATOjrVwyuYk23iYoqt9+CczuLrT/H+V//oi3mqMr4GSSxjlPpE\nHRMrP0DTIyZqG/TbBXq9In0vD0pCzhogywloEYONCv16kVypS6pK6KZPLCmEvkaqxtiVPpKUEuZ0\nok/mmLhjhSQHSjWk06+SBBqTM6v4rkmcqFQnN5BjSGMZ1ASt3CdOVVIlQq8OKBa72FMdTMshzUPL\nq6CoEWc+fyPqv+gL4Z1x5UjB1Dy8lkWt30LTQyaKdVIkcvIAKUrppCWIJCJVI4ll/IFF0tYxFY/V\n9gw5fYAmhSBBFKuoWogsJYz36hSP97jjxz7P6fE9eBsFBlWTwliLicoGUkfBThxkP0Enoqh30dSI\nsbBBrtyl0Z9gZvoSuuKzR71IsbBFNykSWjJeO89d5cf4/T/8p5mzczWQIsTCBtu5ORbbfW9Gk8dH\nZeIgcmdGYyVchODIsS2CFLab/13wRTPCC8P1o+HyGtuJyhXEXdwePpdj212qDpcX2K4MC4avZQnh\n6ny1Yp8dzIsqeLxuiVRWwFWR9Zh+u4Bqu3iOjVfPUZ3fAD0iuZxD8WNxYbQ1ipMdkCTSlk6tXCdY\nKqDMDZPzXAltj0fuh9uc+vObwI6hJuGUc1RnGzgnyyQTMmouwG/miLUEOhLepTzBnAx5GbvWxjte\nJh+26Wl5gpN5/M+VGRwtYB5us/yb18G/fTHPVMbXQtUjPNck0YTT41ysUm9MoWgxZs4lDDX0dooX\nmASBhmm7EEpIvkZB6+F7Bm7HJvI1wn6OfKmP07VJ/oPN5K5lrG9vs/LsXnKFHkkqodo+at6lNahR\nsDs4A5vNlTncTp54PUfiGNi2Q29pjP3VU0iOzNbFOZxGmcFGkZnpJYLn8hzInWQrHMvCWFcBkgx+\nbEApJpiUiQYmfmSQJiArKW5oUYo7RJLKoJejaHSRpBRPUTFinyhS6fpF7MSh45WY0tZJIgXpnExN\nbqD8U5cvnHsVmhwQlkEpRkzra7TcKkkuQVJSmpenSXXYbE/QaRdJFmIkUnJKn0Z7jGRLxytoeFg0\n1mYJLucYK6+z/oE5cj/8zZw2mfEPRmZbzIz66XQQ4iXH9uDNNiKvJo8IZyUIcdRne0ZVDxEKSxBJ\nz3cAr7BFufgC22MiYDuM5SLcmwgRyhrl63jD7XuIkFqKcJjS4bYm8DiiqeBLxNkZ8eKnS45BckIj\nCSVUL8VUA0glpqdW2Lo8gVpykcwIyUqgmICZ4HUtZCsgZ3e5fHIflb1r5JI++l/HzGxdBCNl/fxu\neBJypTaKH6O6AaFjYmkuxbEWg1MVirc0kI7r6LsGUI1RcuIbmlyOUWYC/HEdIhmtHKDeMUA6EmN8\nLiS+T8sqsa4iJAk0y8c7VSS32ABSCvkeTj/HWNDGGHNIYhnT9pAk0Md7SHFCvTWJKblYvo8b2JQr\nm/hLOfiSxh0/8QXqjQlUzcf2e5RODyimfQJXR5UTkr7KVn1ajISwHBQ1hDClMLVFa2Ocqf0X2Qgn\nkfMhxdlNtMKAWFXYWJlh8tAyT3z8XrS7sv46VwuSBIbtUT+1C1Nx8BITU/bphzmKSRdPM7F0F9P0\nCAIN2+4TRSq9tMB4oU4uHbAmTVPUOrQGVeKHDW5sn2BzvkbPKyFvxFT8LmY/Rg1DXN8k9RQM06fj\nF1lYPE3o6uTzfSqFNrKUEMUaZnlAodzDmHKQpRiFBLvcpjq5wdSHt1h/oIakZqL5qkFiO0k5YLvc\n20GIGQ0hiMaGzy0ixIeHaADoIIRLCVEl9TzwZoRAyrHtGOWG64165YwqvKrD45QRzo8z3O8ywr2Z\nYHtI6KhB4p8gSttH5fAvIV58waMBB2OUuYiobdI/W0av9Vn7zAKBbxCdzSMHKdGWjmyFEMjEOQmS\nlEFoE4cyradm6P7OGNNvXmb1wAJhO4dhOujv6OP0ihTnt0gSnd7ZKu64hhpFpH2VXqtMOi8TfNKG\nVCNaLSBFMe7zBQzFx4484lWTRIfoWI4bF47SWRrfVtYZVw9yijwTETo6cSLTXp9AVSPWm9Nsbszg\nrlUIfZ0wVIkilTQESY/pbI2jTXtEPZ3WhQkoJRz4luOcGt9DMrAoFHu4ExYbszXinITnmAQti9xE\nF30lIE0lgvU8xtgAZdqlt15D1kMa9Wm80MS/nKNotTEtjzDUSWSNcRqomdi56pAkkMcHpPmUKFLp\nR3lM1WPVm6E1KNNojJHTB7iJTSpJJB0bTQ9xsHGCAo5n0/cK+B8o8PIHPsO5e3bTdivoscf8d5xj\nJZpn1/hZYl3h/JlDaAWP2WiV1to4bpwjpzj4oU4oqTiJjW76rA2mKdHGWg9Zru9Cl3y6gyIL0jJP\nj9+aDQC92hhVa8F2OKmDEBf+8PmI7ZlWPkIQpYjGgKNmgl9C3GduQwibcLhOnu3qLX/4owy36SAc\nnFEu0WD4XG/4dzI81mC4r2mEUDrM1+/kvIO5IgWxspwQHzPQqwOoRgQnCrBHQq156Nd3iQ2Z/O42\nUi6GqRCWFdEJd0uHjykoukv+J1tc3NwrGjyVPXxNw4h9VC+k6xaIchLatAtrJh2/jFINKCotkHww\nJNADUANSDeS5GKdegmKEaoWkgczBBx7nuf96K3zblThDGX8Xwp5B0DMwcy5mpYuiJqSVGK08oLiw\nSb7Uo5TvoBohaiVmUK9gjvXoN4uU4zaRqlEsdjjv7MMgpDa/wubqNBNzKwz+cAxdDTD0CGu6jePY\nJPtidC3E2tUiClRqU5vkZ5rolo+Sc3E9i+JUi7Vzi3S2yoyVN5DXUo6duA3pJWYdXyvk8g7euRKW\n7iLLCW5qoWoRluUxX7uE55nUrC1kNcGaauK1cxiqT6Kl8KhGfsWl8vZ1vhjcg7ueI5/rI6mAkzLW\nr1OPx4k8lbHrLxH4BpfVGey8i+xAaqXgqpTNFnKakCYSZs5n1ZnFK+rMVy/h9W1eW/o4px48SOG+\nrSt9ujK+GqNS7hXEHTVAuDgBQngUhsvLbOfTtBD5N2sIUaIiQkwthCgpDB/3I6YFjJykEkLQlIb7\nHh8eZ2L4fB6Ry1NHCK11hOuzB3ia7Q7LL1GuiOBJZA0KCfGaDi0dygrMeEzV1lCShPG9K8hSQnzS\nhk0Ne3pAYgBn4WU/9wjJjMT+64/zisXPCCXsykinZHppAVPxiZ8rEC3ZLO45BUTET5vEoU5neRwi\nXVxYzxoo0z7GxIAwUeEidM5PEKzZjOc2ee7ltxPfoV2hM5TxdyIfosgpoWeQShD4GoblocVivpXb\nt3G6JdJYxsp3UeQIr2eTHDUpLDSxxvqUjRaLtbO0tsbonh9HtX36nQKL//Nz1E/NIfUl3FYRlRh3\ntQQp6EZI7Os0WzWipgmIBGZDimi2xtBtjzRUsc4GRLaMen02wPFqJZVAm+0DKaQQeAa6HjAu1xlg\nU9Va+KmB61jEsUre7jDwcnhni7zqvk/SmStwS+FpbtGfIjQV+lsl/GaezcEUUjnm4qVFOpvj3MBJ\niBU2L84RpCr1uEYUqWDErF5cJG/20fQQVQ5xO3laSYlLq/uomE0+8ZNvxn2TfqVPVcbXo4wQGjLC\n6fERosVCCBofkdwcDddVEA0EXYTzcgghWm5CCJkWIh+ngei8/DzbuTgRIu9HZntYaIdtJ2mUT9RE\n3B+j4fZLw+O8hL98XbnbeUkiXlNRpgNYTbBzDlutCSQjgUii2y/BVApSyuB8CR7UqdxU55I8R+rI\nPHX6bp7YvB32SGhaQnpzhOQpaAUPOqB7LueXDlC02mBK6IrLwm2nGF+8zOS9F7Be0SJ+1MZ/qgip\nhP7KDvaeFuQTorMa/AIvWdvvWkHVI+JNk9JqD38tRxopyEqCpMcoSkIYqah5j8QzcFZLxA0TzQmZ\n33uWRn0Kt2MReCatsIzsR0ztWUZKZXK2w/mL+0UzymJE0jawcg6zC8tEiUL78iST1VXmapdJzBS/\nUSQcWMhaRKKBXhlwc+Uptp6bQJnMOt9ezUhSijewCc/nUF0xdiKnDWiEY0LkShaxpGAZLvR02t0x\n/M8WOGQc5Zy/j8jXeCy9gxZVbMVlvLqOPO5jqh6pJpHULUrVOmed67FTh0KxQ9luMplfJ5/2Wagu\nM7N7iX6rTL+dR0kS8tUOBb2PUepSeryP9a+/OWNZMl5ARsnCCiKReNRbJ2Q7vFUYrrOKyLHpA7cg\n3JjRhPJRiGzUF6c8fH4UJht1Rt6NcIhSxLyr3YjQ12g/xnAfRUTS8zpwkJdk3s5XcuUEjy2BJRM7\nKsxJSEqCpMX49QLN9UnwFYyxHtW7VkiOKvCtMW29Rv38NJRT1H6E27dRFvuEkQR1nYkjyzQvTkAX\nAssk2lLptmuQhyQvsyVVqTfH2XhyF+5jZaZecwn5ZQOsag87P8A5WuPmO75E/akZoaozrnrUvT0a\nvRl27TuL1yoSDgwsw0HTQkjBdUxKEw2Ku+qwlKDNeARzGv1eBdmI6CRFNpfmkMcCWn6FOFJwTxap\nztdBTnE7ecr716ifn6HhjqFpEcWpOi2/wiCxST2N3FST2fkl/EYB0wmRUnjqj+7Gf72UJZhe5UgS\n2NUBXadMUWmhajFuaqGlIXKa4AUGnmOiqQFz5SWs5z2mXrfM6twUZ3rXYdkDzMRj6fz1lIsten4B\nI/ZZtM8zuFQmRxcvtunJNl1yqLaPrgdEmkqgarS8Cl2nSKVcp1beIpf0GdMadJtlvu/y73MiugEt\nE81XPxJCnDyH6F48yrcxES7NONs9d0AIlcnhshbbScvnERGIkSt0FhHWGjlEk4gQVh/h5EwMl3fY\n7vkzKkdPh6/pL4fHNV+Yt34tcWUDNjLsXXye3EKDQTcPcoo13UavDDAnuvh/UgQP9vzMcbikIBdC\nlEoAjkbtyCr7dz9P8mkbGgYTBy6x8eRuKCpCxWoRyCrs9iCMiVydwSfHsSt9MdpiN2y0x0lWbNx6\nnv5Glb03nuSZX74Hvv2KnpWMvweSBFLRJ4o0irObWMUBQaiTt3oUKx10JaT5x9NoUcTMW87jd3K0\nowrGZAdFSemsjHHd7pNoSoQfGEShjDet0Xx8Br3ow0md0DHRxh0UK0TTA2QlQZUjHCeHVnSwDBfH\ntUmNmKSacJ11Gvl1WRjrWsKe72D3XWxzgCpHmLqHSkTOHFC0uzQen8OOHCZvXmF9eQHJTCjaPXxX\nzGvbO/08W/Up4kglkhSW2I2f1yEPwbJN3LDI5QcEPYtUknBaJXQ1RDFiJC0FCZzIoueVkRLYXz7B\nez/xU+ivyPrtXDOMxEwXIT4MthOPR5VZzyAqtW5B3Kd6CIESIQTJwvD3UQfmBDiBcIeWEeJI/4pt\nu2yHsEaVWC2EKzSOKGuPEWGzl3Aoa8SVFTzzcO7dB0mbMqTgPFKlf2wM92QF74Ml7vzez9ELily6\ntEjhUJPYhfQLJmMLqyhpzOmnjsD9PhO3XGRzZR48SShkBTQpAC+ENR32hHAuQb5TDGiUjRh7ponc\n1qEQQl9Hz7nUnx+HN17RM5LxD0CZ8Vn+ywNIaUq3VSJMDPpegU69CgMF7T4H39BodSvIVkAYqBBJ\nWLk+C3vPspZMYik+xUIXPecT9HQwQFFj5CMOXtMmCRRSCTzHwtJcUMC2XGQlwVA9BkEOPecxJdV5\n/A/vQ8maC15TKPmIs89ez+zZVZJYptGeohWU2doaY/DJCjfe8hSb9hhtpcyuPWdIYplo3aRW3KJm\nbrFpj2MWe0yXVtHNgE63hBtbOEWD2vwmka3idHLkax1avXGMYg9ZTggcnWLUpz/II0USHgZyEBP9\nmUnpJzau9GnJ+PsgIcJLv4cQLVuIpOTm8HGAqMLy2G4gaCJcnjmE2OkgxEwV4fr4iDydcbbDVu5w\n/122e/tEiOTk/HAfFYTwOY4YSJqJHeBKCx6AHwTnQzUmapuYt3UglLH7PbhN4pn0CEWjS21yg97l\nMtQ10peFNH5jjkSWUWsh6UBm8+F5UEKUA324SYQywraNeagPpxSsnAu7EpI1k96JCRJNfPhoNQfU\nlGpuA+dfVujqtcz2uwaRJNBe3sXQPQhVBvUKvUfHuX7qJFGqkkYaNWuL6dIq/sWSGH0Tq3QfmqTu\njZMgUa9P06pXiUKV8q4GWNBbL2HkXeJUQzqjEKzl8V2DzdVZBmsVGpdmCXyD1Y1ZVCXm7vhLXPjM\nfrTXdK/0Kcn4B2DeP2B5eR92NMDID+h1ikw83yTdL9NUa4wbdaaMddY3p/FjE2t3m9Uv7aKbFDHi\ngH6YZ6mxl3avzFR1HXusAy2Ntprn4OTTeJfLlNIuhuESJDo9X5S2pwr4ik6iyMxoK7R/dYqlV81d\n6dOR8Q9BAb4VEZ6qINyXswghMouoxppEODIOQsAUgU8hhIqMEEcXEMJmLyLEtYoYCzEqO4dtZyhA\nCKMBYqp6ZbjOo4g5WRlfRkrTr51jIElSyvEXIQdhAGylsBAiv19i8RdP0zdsGpdmoZ0iKylaJcC/\nYFC6dYt+u4yUC8g3HdrOGJX9GzQuTmLmXHLWgObKGOmmjjrhogcRTqOAcbiH38qjdAPikg4XQZ6M\nUC/FFItNGqWZl67YOSSRpukL9h1AkqRUa7zwiZfhszlq4+v0kxK55x16d+WYnLlMGsl4nk2vX0I3\nA9RBRKXQYLM1g1+UyacDur0yRtklVaCg98npfS5f2kMUSViTfdIVk8JkC1eyiGIV3XaRSHFXStRm\nNiis9jn9iYNob3tp9tsJx0ov+DVU8tZeqN1/mbipUD3XYXDExPyriOJ9baz8gHo6RturkTfa5DSH\ndmOcqcoleutVBhM6qpfgSxqKGRPEOpbkUDbaNDs1ekEVyQio0mFja5KJXWt4sYEhBUSxSs8pUAm7\n5M4MCHSD9g0FpJfo9POOOf2CX0f8ygt8bhNEBdZobtb4cNme4bIm200AOwiHRkOIndHMq9Jw25E4\nOs12abs73DYYHq+CcHvqCIfpOURF1mFemve0X/ra97Mr7/CAiH1+TIItFfvHB5x75gY2PrZImg8w\nF/sYUw5GyUGuJDQvThD2FeKuyVY4TVxNaPzJPFIkUSi3accFqtMN1Jt6RL6B08vBZfAfzzG57yLx\ntISh95DmI25ceIYgMmlMvoTFzg5C2u+x9cQsTCbEb4xQSy6rJxaxNJdYkcCOsKtdlGmfllomtmSs\nnEdSkJD0FG+1QCHfw7b7OIrN9O4lZnZfIu0YRHmJVlhm4Fmohk/YN+hcHGd8boX1B+c5Z+x9yYqd\nnYRSjVlZWxCjJt4YsxFOcfyY+Jpcy9XRlAhFiknKMSveLJ4mQpxG3sOyHJoXpijoPSb1DUJ0iqUu\n+8eOI8sJbalAbEg06tOUtA69II+fmChawuGVZ1mfmKB9KP+SFTs7hlG/nPOIe5s9fDyHEDqjv7cQ\n+TijOVkJwvVRh4/V4foycDsiQXk0cX1zuI48/N0drvMQQlDdTnZP+ypcHYLHgz3/53FIZFw/x8zC\nMpW718k1QgYna8R2SuvJKcxZh2KxRaXWRlITtJ4LzxoUv32D8nwdQw8wiIgNifQxA86kYMjiwqvI\nbD0zCQ2dtJpSa9U5/oHbRUZ9xo4gfd7mhrc9iX+8gKyklAsdqvvXOfvsIdzYYqK8SbMxhqW6mHkP\ne6JLmoLXzJPEOvsOPUenU0JNY+JEptOsstGaxAtsVDkkbSjYhQGSmqIZETccOMrqiT1I93nIuehK\nv/2MbwJRU+Pg/c8QtnXSusx4bo3ZW87S26iy6YyjJDHnN/dRkHvktAFWtYMXm/hNi2Zzkhv2HiUf\nOMhpihYFlGlzcv0w0XkTOU1JnzBRLZf26jihZzBhbnDo2Ake7r0CZVeMlLXC2BlsAW9AVFDJCJdn\nEpG0PECIFodtp6eCED49RBjs8HC7yRTUVLg+pxHOzQbi71FYzB7u+0HECIuswvhrcuVDWh7wMPCG\nCIwITphwHhZ/4DmavQncbg7qEkFkQTlEySfErg5bEvpCn3BgkNrApsrhOx6jHo6z/vE98FFgHyK7\n/Z4Ya6bL9bVTGLrHY3ffD/8CYf9l7IiQVjQwmZq9xNrSbuxqB/dcgTSSueHWo1zy5nC7OYrjbQat\nAkmkoeoBiQzxZQP7ug5FtcdWp4ZlO0zkNhgLmzzy4GtEqLWUiGtFSpg9dIHxwRato+Nc7O9DvmmQ\nJSizM0JaaQr2n8Zwe4o7JeNerhA8Z/LAG/6Mi9IuOlqRoJGj065RGt/ELHh4iUHrzBQTey+R+DLl\nYpv1jXnunPw8vbTAkydeTvywgnRDShpI2Lc3KSddxiob3Bo/yX/5V+8k93NN1FL4gr63a4UdEdJq\nIpKSR/k5RxGuz5sQYad1hKMziXB1RkNGm4hE5gXEfVEHFlKx7rskIW7KiDL1CUQy8jTC1XkYuA8h\nfl7qCcpfJ6R15QXPX0DxR9bpPjcOMwlSIyUtp/A5g+J1W7CYkjyrEtwiE7VMkjUde7yL0ymweOAU\nfl6FSCFQFTQ1ZOvsBMH/V+Dbf+zD/IT+2/zc1r/neOd2brznCVbetUjn7hrcSHZRfCU7QPCEny9i\n3tdE8SXiVCbVU5K+RnpW5ZX3fIrj/hE2l2fQZ3pY3RAPC1WKqUxvIIUSShCjVX3kJGErrtH46ALm\n3g4/vu89pIWE9zzz05T2N8gbA87/7kGUV3rIE9lNasROEDyDx8rceM8zXIrnKUR9HMlGShOC52yq\nxQbhvILftlGnfIKtHK5skPMHGFMOBb9HpKqU5TaqHNGjwPrKHI0vzfA9d3+At/Y/zH8s/SSPR3fy\n8rnP0P+FCsfecATjjqx9wVdyzQueAFEZ9R2I/JyRmOkihM+bEAnIoyTjMYSgUYe/mwi3RwPKIaxq\n8B9AnQt44N/8JeXZBn/8H7+PsGaAk8CfduD6iqjyujriNVeeqzmHx/jBNkFqQF6GtkyqKEwurlH5\n3jW6YY3uL42Rv7FLcCZH8oxO7e4VlN0+tCUGFZNQ1lh/dJbeczWKepdgtQAn4abq07z2w5/lrsNf\nhCThxMJtdL67JrpNZmJnR5G0Vfa94RhxrBCoMqmREHg6hekmY/es8pk/ej2bfzLH1N6LBCeK9LtF\ntAmH3HyLpl9FykfMVZZZ702jyiGym0Ae/DWLd2q/zT/hgxRubLH5nt2c/yeHUN/Sy8TODiP2FfYd\nOcWmPI6tOfTUPG5soioxpVu3aKlVVn5nL/lih43zu2g2q0yVVyhNNtlcm8XVLWa1FVbDGZb6uxmn\nTicqwpNwSD7BGz/xIK+vfJxJZ5XPvOkNnHr3vkzs7ETawL1sj37wEM5NANwJPIYQRDmECFpH3I+U\n4c8otPU8cFYTTQtTkI2IN89/mB8334O9rwsfAt7bgDtKwhG64nfyawP1Sr8AKZUIlvKosz3i52zS\n52U25Bn4tApvjuAXYfP8DPJ4RFJU2PrULBzxse5uoakhC+oyrWCa3N4Oy8v72H3TKZby+/mtT/0s\nl39ylj9+69tBlan8UoNWeexKv92MF4h+kkdKwMh79JerpGlKc3MO2Qyw3tiCnkSrNQZ7fOxil6ht\n4tViyoU2Rbr00zy+Z7AkLWLmPPI31+l/epxvkx+kfnqS5qdmuO27H+GJuXuQsg+XHUmAjhRDhELs\naYQXc9QLNvKaRPnWDfLvaLD27G4KR+qoQcryxb3UFtYZn16lKjeJUQiaOQpjTU6yn/npi5w/yps3\nnAAAIABJREFUcAP/qfejFN7Z4n2//SM0pBl2/bPztMhf6beb8UIwGusQIFyaLYSwSRCOzi6EsLmI\nEDf2cHkBkaScQwggA5GnUwMOQvCczS8//it09ALu/16B/xF4aGK72WHG34krH9L6r1D8pXV67SLp\n4zaFV2+iqQHNx6bhmAK3RdBRYU4M9+MiWK9o4nZyvGz+CbpJkbPPHwYlhXMyuCksSyJ2+kfAPwd2\nB/CEDkde2LdyzXKNh7TSBKJniuTv2UTyZXzHpDJWZ9LY4Oz6AZzzJYwbOkTLNvb+FoO1KmrepTLe\nQCfEShx6SgE/MOmsjxE/bjL9pnPUT04TrdmQpGiTPupqhDubQ5vrfeMX9RJjR4S0Hi5z/auPsxlP\n0D4zwYHrj1FTGizFu7l45gBj+y7TXy5jT/RRpBAnsKmVtoiRmZLXaScVvMSkHxboPjZOQeogeeDP\nqni/VUD62ZD5iQssn7+O0qHNF/S9XKtc8yEtD1Ek8y2IXjwSaK90yU33aH9qQnRLriLCXROIBGV3\nuGw0bLSNSF7eAr4IvAzRm2eZbQepgKjO2kcWsfjbXM0hLd4I3Q9NkbYtWIN3FX6Nd1v/Kz9033tg\nN+SPtMCG3OwW5lwbmuD2bYhhl3SRs188AkjwqAyzAbPffpa3vuv3oJfCv4mY3r8Ev6YLJZ2xI5Fk\nkGZDvMtlnEGO6LLJj5jv5c3SR3jV9EPIp2KsvAOVBN81uH335wnXbeJYwUtMZqVVNo/votMoET9p\nUrt9lV3RMrulC9gHtuBAQG1qHT+0UKez0vOdinl7n+bnJ5HDhLSv8Orkr/gB3s8DykOMp2vk5T5m\n0WUsajDNBqmnk0YSrm8zxQbr/Sk2WxP0n6oiV3x2XXeOH3jgveQv9uGfRSzMnyf+qIUxl11DOxYD\nIV4u8OXy8kP3HuO1L3uQiTdfFs7OHkS+DmzP2JIQbs3+4bangE8jiiVei8gJmkIkJs8hxM8Mmdj5\ne3LlBU8RuBGU6gD2w79+7Nd4OriF//fzPwUnoP8747ACg+UK3gcrHPj+p1G2NHjO5COPvA2mfSh4\nyGsR33nLf2PpD27gIrso3NyCsZQwJ4sk5X1X+o1mvJCoky7ROY3FsbMkLYX/7XO/yl9238CDT72F\nRFJpf3QaNY2IPpvnyUfuZfq6JTrLk3RbRf760msYX1gh7mlMvuY8/23mu/jw77yN6o11nCdr1Ow6\n49IW0g0+kpL1SNmpKGZEb4/NZLeOpMf8X8/8PJ/wX8eHLr+d+qlZlv7wRry+Tictc/yLN3F48ikG\ncY5BL88j/XuRBjLFXBer5/Bzh/8dDz/+as7G1yHNwvjMCrX1Fpt7xzHLWe7OjkVCODejcNQWnP7I\nfv78yTez+X/MCffntxCC5TQip6eCcIaWgD/my/k98rdFvPu3/zkPvfpe4fwYCGenM9x3Fs76e3Pl\nQ1ojHoLCD23Se3RClN79NPDWiD0/dZLzP30IfiDC7js4a0Vmbz/PVrFC1LY5sPsox//iNuRnY5IN\njd/47R/lYV7BRz/1vSQfUOFnEbHUjK/NNR7SGhF7OsrFFP2gw+BMDUox/IGC/UNtimqL9QcXKX3v\nOp0LNdTVhMUHTqISctmZI1i1SWywa31uGzzFHbVH+cTZN3C6eB39C1XkGQ/FzhKVvxY7IaQFIjwa\nPppj793P89z5l2GYLv4HbfTbXe489AgPf+w15L93CxOP/skqu8bPkp/tcjmYo5Y2Oe1ej9WIqDzT\n5hff/MucMG/gQ2e+j/Yf1FB/xEGpZi0Mvh7XfEgLROrFAJG4PIVIUi4Cn4Dqz68TmDr991fhjuG6\nS8D9iGqtNsKGWAfJTLjlVY/S3l3j/Meuh88hqrsOIgRP5u58da7qsvQRKfBQwtQPX2T9wUU4Df/2\nx9/Fv3zvb3DvTzzEFz7wLbBPRj/cI3rSJHlWFTk5psSt5Ud48vfuFcPSrluBeBZWA3inLnoZZHx9\ndojgAYgdFdlXKM1tsnV2DiPo8/ShI5TaDgd5lvaZCaSJiLzdpe8WSV0F1fCR1sHa3aXbr6H0feJ3\n9OGnJuBIirY7y9n5RuwUwfNlnlSZOLzCmdOHwZF4z40/zDvf9z6+5x0f4M8efQvBjMbs9UtsNacI\nn9SI9yuMN+vcO/g8H2+8geC8wR7pIc4eeAC9EWC9PZuv9ndhRwieEU2EgBlHzLiags/8q3uYps7L\nP/YwjfdNwQFECGwdUZE1gRA8PqLBYAM4839D/p0il+fOF+elX9Nc1Tk8IyTgAZn1X1lk71ueBQf+\nS/9/wv9ule/Pvx8OyHABdMUn3QV8Z8L0fRfgeXjSuBfeAfwC8F2z8FbgZzKx81JEsSOSfMTWX86z\n6+DzhC2dX5ffRaLKfPfEB4EUKU3Jj7WQkpSxGy9hawPCgo6bM9EmB8h7I7RPmWhv7GZi5yVKenPE\n8oeu45U3fxKlEfHh3JuJ75f5jsJHCedNVCcgr/WRjJDcq9oc3H2U9kqFTx+5D+2BPrl3bLHxwy+j\n8KotrLe/OGI/4ypjlIjcQ7g5W/Bbp3+Gh/xvoXBvG8ZS0ZywhqjeuhPxxX8Z4RCVgXngbe+E7yMT\nO98Erh6HZ0QC0udi0rtS+M8qVGDPz5ygXa/SvDwFFSgtbCDFMu0PjsFrM1/vH80OcnhGxK6OupqS\n2DLRLxmoP+Cz/3XHWO7toXeuijzvMjW1QnNjEv+yjbovy6v4x7DjHJ4h6qdTlFtiGh+ZJJnRuO21\nn+fiYJFev0BajpgsbmD0Atafm0e+NfjGO8z4uuwohwdEOfoKwqkpAX+1gfEtRcJv00iOKbApiY7L\nu4EziGqsXVwFDWOuYb6Ow3P1nVYZ0lcqcArMmwZ4Czk2nWn6GyUmjyyTr3VY+tUDxIc0+NYr/WIz\nrlYUKyCa0kiOa+x5zwk2uvNcSufpOUX23/EMmhxw/P13wJ0p2r6saibjqxO9WqL53DQzBy6xWlrA\nlQwcw2BevcRC8TzP/PntrOypkr+1eaVfasbViIxwaTRE2Or2SXwHMU29ixA6Y8DHEPk+i1xNcZcd\nx9Xn8HwlfaABcj8kiTSwUshJwgK0rtzL2nHsQIfnKwl7NqzIVPZt0nIqsKlDJUWtDJDkrOrqm8FO\ndXhGxI5K1NAZW2qwMTtFwe3ilGzUcR/FzBKRv1nsOIdnRIrIy+kjxE4ZMUYiGD6OpqpnYucfzzXl\n8HwlefGTfLnMKgtfZfz90QoOHIA+NlrRh6J/pV9SxjWGYkcoCxG9BRubLjFgkIVBM/6OSAhhYyK+\nsAcIEaQhOi9nvChc3YInIyMjIyNjJzEaHZHxopMZaBkZGRkZGRk7nkzwZGRkZGRkZOx4MsGTkZGR\nkZGRsePJBE9GRkZGRkbGjicTPBkZGRkZGRk7nkzwZGRkZGRkZOx4MsGTkZGRkZGRsePJBE9GRkZG\nRkbGjicTPBkZGRkZGRk7nkzwZGRkZGRkZOx4MsGTkZGRkZGRsePJBE9GRkZGRkbGjicTPBkZGRkZ\nGRk7nkzwZGRkZGRkZOx4MsGTkZGRkZGRsePJBE9GRkZGRkbGjicTPBkZGRkZGRk7nkzwZGRkZGRk\nZOx4MsGTkZGRkZGRsePJBE9GRkZGRkbGjicTPBkZGRkZGRk7nkzwZGRkZGRkZOx4MsGTkZHx/7P3\n5lGWn2d95+e9W1Xd2peu6upNrW7tki15F8YYB2Jjg/FhScJilsyZBJMhLDOTOYfATIAwDAyQM5PM\nACYnxJwMBBOOA4TNS8DY2OBFkq3VklpL71XVtW93v/c3f3zfR+9tRRJqqbuW28/nnDpVdeveW7/u\n31Pv+7zP8n0cx3F6Hnd4HMdxHMfpeUKWZS/+wxBe/IdOT5FlWbhW7+12dH3gNuRcDdyOnFfLi9nQ\nSzo8juM4juM4vYCntBzHcRzH6Xnc4XEcx3Ecp+dxh8dxHMdxnJ7HHR7HcRzHcXoed3gcx3Ecx+l5\n3OFxHMdxHKfncYfHcRzHcZyexx0ex3Ecx3F6Hnd4HMdxHMfpedzhcRzHcRyn53GHx3Ecx3Gcnscd\nHsdxHMdxeh53eBzHcRzH6Xnc4XEcx3Ecp+dxh8dxHMdxnJ7HHR7HcRzHcXoed3gcx3Ecx+l53OFx\nHMdxHKfncYfHcRzHcZyexx0ex3Ecx3F6Hnd4HMdxHMfpedzhcRzHcRyn53GHx3Ecx3GcnscdHsdx\nHMdxeh53eBzHcRzH6Xnc4XEcx3Ecp+dxh8dxHMdxnJ7HHR7HcRzHcXoed3gcx3Ecx+l53OFxHMdx\nHKfncYfHcRzHcZyexx0ex3Ecx3F6Hnd4HMdxHMfpedzhcRzHcRyn53GHx3Ecx3GcnscdHsdxHMdx\neh53eBzHcRzH6Xnc4XEcx3Ecp+dxh8dxHMdxnJ7HHR7HcRzHcXoed3gcx3Ecx+l53OFxHMdxHKfn\ncYfHcRzHcZyexx0ex3Ecx3F6Hnd4HMdxHMfpedzhcRzHcRyn53GHx3Ecx3GcnscdHsdxHMdxeh53\neBzHcRzH6Xnc4XEcx3Ecp+dxh8dxHMdxnJ7HHR7HcRzHcXoed3gcx3Ecx+l53OFxHMdxHKfncYfH\ncRzHcZyexx0ex3Ecx3F6Hnd4HMdxHMfpedzhcRzHcRyn53GHx3Ecx3Gcnue6c3hCCOMhhN8PIWyF\nEJ4NIXzXizyvFEL4YAhhPoSwFEL4wxDC7E5fr7M3uQI7+tMQwmYIYSN+1EMID+709Tp7j5drQ/G5\nrw8hfCra0lwI4Yd38lqdvcsVrEU/FUJoxHXI1qTjO3u1u8t15/AAvwrUgAPA9wC/FkK4/QWe92PA\nW4C7gEPAOvD/7NRFOnuel2VHWZZ9Y5Zlw1mWjWRZNgL8NfCfdvZSnT3Ky7KhEMIk8GfArwHjwE3A\nx3fwOp29zcvd0wA+HNciW5NO79RF7gVClmW7fQ07RgihDKwCd2RZ9nR87D8A57Ms+4nnPfdXgY0s\ny348fv+NwL/KsuzFDMm5TrgSO3re644DTwEnsyw7swOX6uxRrnAt+jngSJZl37/zV+rsZa7Qjn4K\nrT3ft/NXuje43iI8twAtM4zIg8CdL/Dc3wDeFkKYjUb1fuBPd+Aanb3PldhRN98HfNqdHYcrs6F7\ngdUQwmdDCAsxvX50R67S2etc6Vr0zbFE4+EQwg9e+8vbW1xvDs8QSk11sw4Mv8BznwTOAheANeA2\n4Gev6dU5+4UrsaNuvhf40DW5Ime/cSU2dAQ5yz8MHAVOA79zLS/O2TdciR39LnA7Sn39APAvQgjf\ncW0vb29xvTk8W8DI8x4bATZf4LkfBPpQznwQ+H3go9f06pz9wpXYEQAhhLcBM8BHruF1OfuHK7Gh\nKvD7WZY9kGVZA/gZ4K0hhL/NwXZ6n5dtR1mWPZ5l2Xwm/gb418Df24Fr3DNcbw7Pk0AhhHCy67G7\ngUdf4LmvBX4zy7L1LMuaqGD5zSGEiR24TmdvcyV2ZHwf8J+zLKtc0ytz9gtXYkMPAc8vtsyAcI2u\nzdk/vJK1yLjubOi6cnjiZvOfgX8ZQiiHEL4aeB/w/73A078IfF8IYSSEUAR+CLiQZdnKzl2xsxe5\nQjsihNAP/H08neVErtCGPgR8awjhtXEt+t+Az2RZtrFzV+zsRa7EjkII7wshjMWv3wz8CPAHO3m9\nu8115fBEfggoA5eA3wZ+MMuyr4QQ3hZC6F5A/hlQB04BC8C7gW/d6Yt19iwv144AvgVYy7LsUzt9\nkc6e5mXZUJZlnwR+AjVNzAMngO/ehet19iYvdy36TuCp+NhvAj+fZdlv7fjV7iLXVVu64ziO4zjX\nJ9djhMdxHMdxnOsMd3gcx3Ecx+l53OFxHMdxHKfncYfHcRzHcZyep/BSPwwheEXzdUKWZddMj8Ht\n6PrAbci5GrgdOa+WF7Ohl3R4AHiv20fP88c7oD11j9tRT/PlHbChe92Gep7P7YAdvdHtqKe578Vt\nyFNajuM4juP0PO7wOI7jOI7T87jD4ziO4zhOz+MOj+M4juM4PY87PI7jOI7j9Dzu8DiO4ziO0/O4\nw+M4juM4Ts/jDo/jOI7jOD2POzyO4ziO4/Q87vA4juM4jtPzuMPjOI7jOE7P4w6P4ziO4zg9jzs8\njuM4juP0PO7wOI7jOI7T87jD4ziO4zhOz+MOj+M4juM4PY87PI7jOI7j9Dzu8DiO4ziO0/O4w+M4\njuM4Ts/jDo/jOI7jOD1PYbcvwHEcx9kjZF0fAT8SO1dOp+sj1/WxB3CHZ6/QJi0y+V2+Fmd/0oof\nOfSXvUcWGWef0Eb200CbVR4o4bbk/O2Yk9xE9tNA9hSQDfUDfbt2dc/hDs9ukqEFZil+bADjwDQw\nhhacsGtX5+x1uheZNWCd5CwPABNokXEbcl4Ks6EtoBa/DvHxHFqTBvCDmPPCZMi5qQPb8XMHeRdN\noIocoCG0Hu2i8+wOz27RBFbRIlMEvgEYBJaBB5HhHGRPeMXOHiQDWpmc5KWgU9TtwFFgETgLnAFm\n0UITcMfHuZznHOYMngYqQc7NSWQ3K8CjwDPAYfQztyPn+XSACnAROTejwA3AcXQIOwfMA5eAm9jV\nPc0dnp0mIxpBG07mtZAMIafnNDqVvx54FngSuBmFAx3HyIDtDNZakBXgVrTIlJGjXADuRjZ0CjgU\nf+443WTAHHBxC24pw8G81ppB0on8bcgZeiK+ZmJXrtTZq1TROrTRhKF+OB6d5iEU9SkDx5CT8ww6\niM0AI7tzue7w7CRttMA0gNmgE/lptEltIS+4gk7rs8AwcD/wWvxOOaIDrHdgNcBwHW4typ4qwFYG\n7W3I8rA6AJMoZTqH0hHDu3jdzt6igQ5UBeCuQTgRZEMBWEDRnX60eU0CbwTuQxvXIB7lud7J0L61\n1oF2BtN5ZSQCsq25GmzPQZiAkTIMFvXzRbTXFZAztMP4NrpTZKhOZxX4JuBiTptXG52gTgG1v4Sx\ne+DWMRnF7ciAHgdu2ZWrdvYSHbTIXMzgzhwcGpL9bKJT1sI2NFYhG4GZAT1+M4oePr0OJ0b1tXN9\nUwcuxM9vByo5ndQXgfNt2HwQ2uehcBMM3qGozjRwBK1Td+F2dD3TQSUZK0CWwXQObszLGb4AXKyR\n7yxTvusc1XaB9mqJbKsox7kJbLe1D4Z8qjHcIQfaa+93imYGmxl8HdqkjgDn0R1YXYEbm9z90TGO\n/+yKTlgtFP7rQyevufiYc/3SABY6cnaOo02ngjaujU1yJ8/zju98kK/6h4+RH20odToHTAGjTZjf\n1ELT2a1/gLPrWO1gFXgnao44horeAVpf4fZ//AQ//ucf5Qd+/o/0s8X4/BPI1h7PYCXz9eh6xBpt\nNpEdHc3D6/NKm1vjxNYq5WPneM1Hmhz8SJW+tzZUwtFATk9owEpT+1yDVEu2A7jDs1OcR3UUbRTp\nqaPFpw1QhB8PPDD/en76TT8JpTY0OjKeNkppbRELC3fl6p3dpoMWlD60aCyiaI+1EZcy+u6Fb3r/\nX/DW7/s0uZtXodFIJ/dbp2AkyPYW8c3qeqSD1p0Kitq00Kazgbqw2kBrkLefeIzvOfhx7mqdhVId\nGut67Rbwtcj+5pEtNXbh3+HsHhnxgEWK9KwhO2rGnzPFLc+0+c0f/QC/Mf+P+Ibif4Dmeb0mDxzs\ng9GS9rcLaB3bIYfHU1o7wSpwKsA/QDd4AFWsl9EiMzsMH4HvPP5hnvrDo3CxBuWyCruW0Qn9XWij\n+mQGd8euHOf6YQtY24JbBpQOzZMWmGGgMELz/iK/u/Z+tloNWl+sQmlUm1pAjs9tQzqJPYLsZxQ/\n8lxP1IGVFtQbcLisDQfktAS03kwc5HOf+CY2H76F049Pw1MrkI3Jfqqo4PSmoE3uLNpBxvCd5HrB\nipQrdTgyAIWcbMH2ozGgXeTC1gl++f7/hc2fKfCVR05CuyTHpggUc1qHDgJPof0RdqTGMGTZi7tW\nIYSM9+6Q69WrrKEN5j1oUaihhaePeDJHm9afA9tPKNx37E44mJNDlEeOzixKYyxm8NmgqM/V4o8D\nWZZdsyxqCCHjHrejV8wmsNCE6Q4cLKl9eABtUiY02AGercLm09CpQ9+NMDwGpZwWkmc3YGZEG1ap\nCl/egMMzV68W48s7YEP3ug29Ijpoo1rOoN6BmRaM9CUF3BJyngdQa/HCNjQv6cFsGnJjcoayDKpb\nMDoINwa4P+j1s6iQ+WrwuR2woze6HV0RlnKqAGsZVFswWIcby9DKaR0aRvub6cottKBVgdWoPlgq\nQaGs5+WQvZRJEZ5R4ABXR+vpvhe3IffLrxVt5OycQa2doBOV3exttFBso5t+I1C+Va+bQbUX62ix\nCsCnUJvxjUFe9BZq/XN6lw46/Sw21UUzUYJc0F+ttQ0PkNqLyyXI3wB9AUYHYCknG7oE3FWG+zNY\nasOtJZga03tP79K/zdkZ2mijWu7o66M5ONCX6rg66PA1jJyeIlAI0AowUIbymA5pm8BMRvHvV2n+\nRRkWgjap1UzOVDl451Yv0i0quABUOzAa4JYhrT2WjjIb2oqvq7VgbQXCAIyMQHEg2glMFJfIKoHV\n1UmlR7cz2VgrXHNxSw9oXwvqSGxpC7gDnY5WkEdbQEZSQotNhlo/Z0jV6tX42Dko37LN237vLzn5\nwccJ9Vjd3oq/ww8qvUsbRfaWgZkCjOUV2cmQrWygv94+ZFPjwGgexoYhG4J6XnUaVeAkfM9/+RBf\n/eBfwE15eCwPS0Wot3fn3+bsDHboWkZrxgRwIGjtyCPnpoYcIrOjMjBehonjMHhErelDQBX6T9T5\nwE/+Fm/4n++jL1dLu0cDrwnrVawL9BSypeEczOT1eBvtY3m019XRYX4KmOqDoSMwPQXD/SlK9B74\nwAf/X/773/x1lXicR/thGznc1xh3eK42NZSXHEYtweYFjyCDCKSC5Yvxcy5+thNWDkVxRqEw1OAt\nt/4Vt3/7Q4TDHS1OR+PvcoenN2kBl+rS1LkNnahWg2xjHS085kSfRjYHsoeV+PosPmdA3985/TA/\nesP/DbfG+q+jAcZyXnTaq7SRXtNapvt9KAcjuTQ+wuZlVeP3qyRHKJAOYwHZ0BiUqPNt4Q+567se\noO/GmuywEaATYvOF01O0kF1cQjZwO3AkQClGmS1KmCF7WkMHsRZQDNBXgEJezRJTyJmuwszAAgdu\nuQRvziCfpcjgDtiQp7SuJk2kSHozUlCuohNSQMZwMD52AHU5TKJFpkXqnAjoxm8Dr4eNT47yb3/p\nh2kfLdBpFXTHvhLf30PIvUUGdDKdyBsluL1PjvMqOjm1kWT7RWRXdWQPVeQkt5GjPIg2uSW0SN1X\n5Z//d/8afrgOD6GF51QGg5naSp3eooM2nkuZ1pwb4kJRQ06zpSBqxNoc5AjZ/KyAbMTWrgJwCLa/\nOMg/feCXWAozbFeGZJuV+Bo3o97BojFr8SOgdecQqTOrn3RYssyEzWGrxddbTU5ffN0E8BX4yw9/\nPa3DeaXhS0A+pIHH1xh3eK4WLSSdPY2Ki20RyKFFZpzUyldBC40tFk20MNVJBYQV4E7g0RybPzcm\ng7oZiX418KGQvUb3IrPZhtsKSiU0UK2ETSGej98vkwqOm6To4Xh8rIpOVQVgdgB+uwq/NaBF53AG\n7QDBA7w9hUV8K6gucDQvvS9rOS/FzxbZGUARQaMdHx9GG5qlqWJhc7ud57F33wL5YdUC2STsPtzh\n6SVMRXkF2cQ00mOyMgyLINv+E7pet4XWoxJaf0w2I0MHsXPwB0/8PdmXFTAHZD870HnsDs/VYpG4\nmaAQYLf8+hoylBF0g5dJE4mtVa8fecQLaKObQdGiN6HC5yJypD4dv5699v8kZ4fZzLTI3FKQvSwi\nW2ii720CcY4YNn7e62fiz1eQ41NA0aEbUdFgC0WAmsBmB475LtVzNIBLHaURZoJSoA20HpmjY7UW\n5u9m8Wc1FNkZIWmEjaC1aQN4aw4eGYu1QMAXkA12v5ezv7FhsmfQ+jEdtKeB7MHSV1soQ5Eh29hE\na9UWcmQOIwfGaletq7SImm+Ij83F97WasmuMm+nVYBOdqGbQzbMTuXm3+fh4QItHARnKMlqA7HuL\n3OSQ03QELU4jaLTEcvz+EH7neg0TgTvQ0ckoQwuCYWnOPHJaYj6cTeQY1Ugn8hFSQeoIaaG5DRjJ\nYCGDobxrOfUSFiFcBNYqcKKjtWQIbUAmFtdGtjCE7MikDVbQwaxKErecQOvMNnKITLvpFiSPUc/0\nfbedOvubJqkO5yDag2ytqSJbsJrBXPyZdQufJznU1q1lDvQAsqEc2ifHifP/kPNskelrjEd4Xi1N\nNITvPcgQ7PTdh26m5SbLyBDqaMExr3gKLSQb8fEyMoxJtCCdQwZ1Gvgc8Dp8gek12sBiA4aLcHte\np3KbNmx58g5ylq3zpoFsa5004boaHx9ANjdE0nEaBs5kMN+AUsHb0XsNS0PMAe8ZlG1YissKlO2w\nZeNI5klpVKshHCYNDrWu0hG0Vp1FdvYpZFOHSU6Ts/9poKnnqw0YHoCpkGq8QPtagWRD2/E15gRZ\n0bt91NA+aLVgVhDfBtabsN6CwX5FI/t35p/oDs8rJUM39BQShcsX9b2dqjto8SjHx+bRDbeUxAo6\ncZ8niTCZZoYp4D6BFqFzqNj0LeyYYTg7RA3NJVpswZ2lNDrETtQmTjlAmlVjm9ciaWMqIXtrkza7\ngJzuPHrfp1ow2dFkY48Q9g4tYKUDZ7ehnYeVfingtpHTa2rblma3QcYlUl2PdZGWkD1ZfY4pejfR\nIex+ZK+HSGlTd3j2N5Zd2ATWM2i2FXXpj9pKOZITUyQ5LqaQXCVJG1h5hmmF9ZFSpvZ5ralZWu1M\nB68Bdmw9cofnlWCnog3knLy9mNqBD5Dqc1powxlBN9bmaVkaax3V4liVewMZzGZ8bT8ykAuo28ad\nnd5iC4kKHi7ARJ9sYhMtEoMke7DcuX1tM7VqyMmx/LgJhFknhZ3M+oEvoc1vesCdnV55uWaeAAAg\nAElEQVSihlKh6wFuKcNAgKE4M22C5LRYt5XZhr3WhoaW44d1jEJagzaRjeUzjaaYKcTItIsN7nsy\n5HisZbKhTkkCp2No/amTHGCLMNs4GxtobdGdKS6TwiAXf2avqaFo0GpVTRPTw6mudYdwh+eVsJnp\nZt8VtKhUSCMiqsg4ppBDU4ufbZFZJLUT50mnr4H4PBsnAcqhfg45SRPX/F/l7CTbKDJ4AuW06zHq\n0iB1y/SjxzZIg2RtgamQikxtI2vFz42uxwaBp9rQzsFM0Z2dXqJOGhfx1jzk8rrfdRR9sbXF0utW\nV7GNHCJT0W2h9QpSZ2mdtEFZZ9ejwGBehzp3dnqDJlHNvQbHi3CsKHtpkTTiTMbABG+3kS1tonWo\ngtYcm4VlDnYV7Yv1+HgLeByoD8mhGmbHbcgdnitlFengfCNaBNZR9MYWBhMZjKNontPZWUMnbLvB\nffHnwyQHJ3S9zzDw8fg7TuB3qpeoApcqcLwAk0W4FJQuCF0fLZLjs40WnlWSzIGNHDF5gu50hS1C\n/cDjbVgM0mLxCGHvUEVjQuptOFm4PBJTQs5KdxeoFbibKm632JsVrxfR2tVdAE98jyeJUaTgkhi9\nQg2JU6424YYCTOVkC1Zzs432rwqpDMPWFnOeLfJjUgb9pIhzHdmdZTqW4nuO5+Tw7EKTqG+jV8Iy\n+sP/hjjzYwOdpC6iE5JtQGYQ/fE15fh4CTk9fSSHB9JiZfORGqgtcB14A34q7yUqwEJFyrcHizAf\npHGxjJwW+4vsXmDstGX1FVYndoiUJy/G59nYkjyxgytIVdnnrvUOFRQpbgc4kofBXHJ21lEEpk1K\ne66TTuV5kgRGBUUXIbWXW3OF1W5YimsdKbx3H9qc/Yd189WB9TbUOjAZ4EBBg4ZN7b9Ius8NtD5d\nQnZmTvIYlx+88sgGrRTDurLawFYmmx0DxsKuNd64w/NyaKNirovAu0JSTs6jhWACbU5WlByQN2t1\nOeX4nEmUb+9Hp/XuIq8t0gA2S2Hcjjs7vcQ2MNeGG0owkde4iAJKj06SOh7MGbYWURs9Mo7saI3L\n2zzXkPPTR5qxNgCca8FU/nJNKGf/0kH2sdzRfT+eU7rbuvmapDowS5ebw1MlFbQPI1saINmaiclZ\nWjSP1q2tTANCJ3Mp7eXsTyyF2UBTzLfbcmBvLaWoXvfoIxv1YBPQ10gHqhlkD5byMufYDlv2+4a7\n3q+IsiFldm1f8+30b6OGdEvmM7g704JyHt1U826bJEOwavdA0rLo9njHkbc8gd7LNAtMK6UAtJvQ\n15ZhOPufDlownq7CVENdUpWQIn1FZDcLJBE36/grkIQmzeYmSbYziaI9IBu0NuINYCsfCw7d29n3\ntNEhaS6TrViBqLWYQ7KXDdIpvoJspog2n0lSV0w/qU7DFN5bJGfHJDIqmSJCporr7E+sC3geWNqG\nwRYcKV7e2dkgRfRsoOdGfKyI9i3T0bFC+ALJ2bHZbAWemwcpJ52U3dhFr8MjPC9FBbWG3wHcHIsr\nLLS7yuVOj02PXUeb1iRaUEbje5kh5NGNt4XJpqdb++ck8KWgsJ8vLvsbm4211IJGC94yIHuZQ3ax\nShodYZoV1nZeJYl29cf36haohJTeaqPoo21QNwBnWjCUg/6c29F+p43azteDNp3JAINB65ONHOkj\nDSq2WUbmCJn4ZB6tTZDsySQOLG1a63reNkq5Dua9/mu/Y4NAl5EtnCyrm68YyzNMw6tE0okz+2oi\nGzI9OavhKpLqv8wZbpK6jE15uYJ+zySpoHmXcIfnxWgCj6HRDuNBE9BNrM1CxqaZs4pu7jlSW/kQ\nMo4NtFhYMZh1Z9VIxV1L6MT2dcBvA9sFdWj5RrV/eW4QaAbbAU4OyF4COvkUkO3YnBl7jeXILT06\nSEo1ZF2P2aZmBYUWSr4Z+GIGT+XhRPC/8P2M1VusAktxEOhklwNr6XDbrMyWtkmb1SCpNixHqqmw\nGVjdBzUbLNoPVDMJDa7F0QI+hWR/0j2jbwXZxBEkPmrrSreMikV7ujv0TBB3hNRFnCEbKpDazk37\ny2qAWhmczmSfo7k9MYLEl8MXoo3mfRxDodzH0c21SEyZVHNTJ9ZLkAzoCDrF96HFYju+r7WtW249\nQ47RXUBfCz5cULjxTnyB6QU2gKUO3BoHgc4j27E6HWvzbJMG7Zk6d5l04p4gbUwWEbTuP5vRNgwM\nt+FLGTybV5THTvPO/qUCnGsqDXo0p02rge55lSQKZ919Ju62ShrOaHpNJohqtRqrpJoOi1SXgVYH\nnu6oe3A6n9qNnf2HHYpW6ypynyrJcV4h1QBaF6jJD9iB3Ircbdq5RXQsjRXi45b6apGcplamw9t8\npuiOHfJ2mT1wCXuMDG1MNeS4VNFJ3Gon1kmbkglzVbpePxt/djB+b6kKKxjr3riqwFxHxndqA8Yn\n5Oz4jKP9TzWDszWYihPKbXSInYC2kB2YAxRI0Z0RZGsWEbKTk7UMd5CTba3Gq7E9eakBjQ4cGfFN\n6mqQPe/7nYy4ZmjTON8BtmB6CGq5VJRuqQar22qR1inbqKxVuNP1nhYhNMmDEZLa+2pHXX1LbT33\nSMHt6NXwfPvpZidsyUQFF4HKKhzKw60HUr2NZR6WSTZikhfd6dApZFM2sNj0c1qkYvh2pucsAJsh\niRbO5GBi97qyns/edHisOnw3ohwbyOG5GW04x5BRrKIbOEQqQjVv+CJycGxullWl28I0Ft+7gm78\nDPBZ5AjNow3xpgkZk5eRvzrshGtS5pDE1HZqw2ohR3ZqEyYGdB03Ihuymgs7oW/Ery/GaxwjpbGs\nlqcdHzNHqYRs5rEMih1p7QxWYWg0FTc7rxwLz9uJF/7bSMq1/v1Wl1XdgEMjMJxXJ55tPmbbE2gN\nsYaH0+h5HdLq3kCOcpOURjVxyhKyofsCVGswWIQDxTQ2wnnlWDTNnFNLU1vK51rTQiK5m1swOAJD\nJe05R5HTYoOtJ1FGwmzEDloTpLrAYZQWq5Nmrm2QUlxrwNNtOeXFoJ8fij/fiX/ry2TvmLSF3tZI\nf/DW629CSNeaBlIT/Wakt2MterPx5yayZIuLbUDHSO3p2+gmTyEjsuJkS1HMIuHC08BJ4NbcXroL\n+xsr1DSHs1sLokzqTrnWtrTQlm2cmNbpaoAkt26nJBsY2123A7KFAZKku6W8LIVlEu0LGZzuQH8H\nZksw5mHBq4KtPRvo/9zSPX2kydDXuvCyg9rB54B3jcHTQdc0TdpcurusJuL1rADH0Rp0ENmV2VMD\n2c9y/B35TK97MMBTyzA6pkLWPXIS39dYacMmadSLNRvkSKNjbMjvtbClDtpPlwKU+6C/AFledjSD\n1h/ryOue27eB9HYCSRTXZC7a8fEKKVMxh2arLSM19/Ggf1t/SNo8e6gWdfe3WltgbBbVIFpUcuiE\ncxadgHfC8Vnr6JSTK6dU1Vj8nEceq21OR0ijI5ZI062HSSKC3SHmGnJwPtyEgRy8IS+DcK4OGUk+\n3/7QbB7Mcnx8kMtnT10Lqqhu5zXFZNtbqBasyOUigSOk1II5ZjZxuIls0KJTFm0YBR5Zg+0xfT1Z\n3FMnqH2PheUt+jGG/u8vofVoiNSWe61oI0eZKjAgG56LH0PIRvrR49V4jXPxtdvxYz1+b0XIw8jm\nrKW904E/24D2GJyYhFEvcL8q2OFkkxTVsXq9TaCRQSGDWtDf/2CQnV3tyH4d2GxCpQ43lCGXu7wM\nYwzZjonfWqeopdnt2s0hypHWzYyk7bRISqGOx+7iXW49fyl218QtZL+M/jOPkgqBWxkciH+Ei6QZ\nMaNc/c3KoktPVuH9g0lTJ4vXdjD+7qdIHvoyKd1wCOXBx0gquJA2qZPAX6DC5tmi/p171CD2JeYw\nW72VSQKsN5VPzgpp/pS14l4L5eEWMF+DUEytvtbOa6ekBdKA0O4ojwnAmYiXDeqzsPgMcKoK5/qg\nldeGO+pTz68aGXJqVpBzcBQt/MtoeG/3qIZVdA+PcPX//5vASgM25+GuI3JQTAOniO77OnK+LArY\nIUWkRklTz23ERINUO9YEPpfBdgfGR+K06pxr7LwaLL3YRv/fG8iODsSPUkfTwbcKcdxCBrV8it6O\nkA6/r+YedF/HRge2alBcg5F+qShDivxYpNC0v/qQbdtga3NszOmxYaB9yGlby+BsgFaAkbDrgoIv\nl91zeFroD3cDzYqC1Bb5ReDiPPSPwqGCco82t8qK8a4W5q2eB44MqiNrlKRkuxF/Zx2luerIgbGw\npHVvTSCHx+aHWEFYEbg/Pj5D0uVxrg428XkTuAndtwypwz5zCaoBcqMw1geNgu7lHNrQrqa2SAVY\nbEAnD7fntHlOkWohlpA9LAJn2jAbNBLgACkqBfq7KJPy6Jb+OtuGi3kYDpoy7FGdq4PV2V1EjsEJ\nUgvuJeDcnJwDDl8up99Am9o4V69mqobsY60AM9PQzKWuUIvonEfr1bMd1Wcci5HiA8jObMaR1epA\nilato0PbNpp4PhZSg4Q7O68OO3Rtof/vm0hjONaq8MxT0D4K2TCEQuqeW42vn+Dq2FELOTHrNdn2\nyCwsxK5N65Q6h+77Y8ApdEC8IV7DRPzZSPxsBcym19QALrXh2Rr0DcDBfNLo2Qc2tDsOTwMtJn0o\n5zyOblIReLAGF1u88zN/xddv/w3/x7//STYuTKUaiDXS6fhqcAEtdncgAz1PUrK1CeWPkaa7jqFF\n42vi9Zoi7lG0kFh73iAy4MfqUCnAbXnfpK4226QamdeSnM028NRpSt85z4+978/4ysCdfPSn3ktz\nMQ/NIHtb4uoV+C6hSECuIIHKhZDqvEbj71glFQVO5dIctlG0kMyTRAYXSKf1IeCZDJ4NMFVU6mGP\nn6L2DW3kKC+he3ULSYRtG5h7BO6Bb7nhQe4aPMWvHP4nrP6fM6nDZZF08Hm192ST1B06koNivzZQ\nKxy1ep3NeG0DAbKQ1p4p0gl9ljQFPY/syJy6GnA46DFPYb16zPm1hoQh9HdtqeulM7C9AN9wM1/3\n1/87+W8+xJmD7+bJX74jHc4qpLFCr9RpMBXlS/HzQEl22i6kVvIhkh2dj9d+kGQjh+LzrGXdJqLX\n479lG5jvyO5H+zQEdIDL527tcXbW5K2odBUt7haqPUvqZNq4BBzin438FM/+9hpvee27+MSZ92hR\nstPyOmlY5yu5Bvv8DNqoPgA8glSVp0mqpE2ko7OGDOp4/NlXkebWnEDGcYZ0ipqN70cG6yW4yTep\nq44Jad2M7pVJog8D23Won+ENN36GsQc/xnvu/TSPl1/LqZXb9NxZ9MdsheavlCYxDdKGNwblyc+i\nReIgqWjanJ75eH3WxWDRyiOkOoxL8dqG0QJzX6b3OBDc2bmaNEkqsFZfZRFdi/w1F2F2hNboJcb4\nBHfe8zY+szUFI1F5eBDda6vNutL1yE7Pa1GaopiT02Wn9O6U5nD8PWvxsemQOmCmkB3b5rUU/202\nD+l0Tetco1/P2aVJ1T2H7WcbpCJfE3PciF9vlKA6DLkxvvk1f8PTb38zT5bi5On+ISjkk3NhRcwv\n92/cagSrQKWj9WIjzjwrF1LbeB8pyjdAOniNoKyDjUGaIg3/vEQaOptlMNdSxLGC1rmJXOrQ2kfs\nrMNjJ5Qych5WSPL6dfQf/lXH4JNf4h/+3h/wjm/8FJ/4xb8rEcA3oZswjTYGk1O/EqzDZT3T720F\neCfwBVJUxpQmQTfzLElzwOow5uPnUWQUh0g1JNMonPh4PxwLCm36JnV1MenyE+jUYvbQQBvCLSV4\n/Wu475dO8tAP/SC5v8lReXwFcnWY7tcmMROfa3LqV4KlV+eBRgNuy2kx2EaLSD5+Ni0L026y+iET\nD7S6tGWS2ukcUfwNeKAFgxnMFnSi3yenqD1PB60DdfT3aqM7bKL4GnJC77wJ5qrc96W7mG8NsPJ0\nP+QbMDOQUtZnSbODrmQ1rZLsIkNryTjJbsZJqQXT2bFaL1PWtvbmOkmPp4AOXxbd2VhXPUd+UE6R\n2afz6jGHYhvZi2ljmaBjaENzGnKz8ERG+Z4bWF6+iTOLk1CswuBgGuFhQpEvtw6mAzQzvXYt/t4s\n0+sPk+zZZuuZQ24dYzYrbZhU72UF1kOoi3gJTVMPLTjV0c/G8lL73qeipjvn8Nik3z7kTXZrktyA\n6mPOtuDbc/Btr2PuQwv8zr/6Lmh24DZSmHaIpF9y4Ap+f5s4NA0Yz+B1Qe9zFt28UZLa7Qyp4yfE\n32PTz60IEFLNUQ6F+YaAhXV4og339Hu9zrXAUoZDpNlBsyjtWEJ1NKEC75ygOTBG8xc/hzyK18Od\nRdneBloUnonv83IdHltEzlehVoNj43KuljPYiqmyNpIpqKBUw1r8mCR1cJjo5AYp2mTaTgNIPPDR\nCkxmcGgIcu7sXFWsu8lSjlV0v7bRQexZYHEFbp+Edov5tUnmL7wZnmjBUF6OwyaKlDxJ6oR6uavp\nOmrlrQJ9QakBc7rspD8TP1t3lT0+TmqVN6Xu7mGz1lEzCCxUYK0FgwNS2O3HD19Xkwr6Px8j1W+2\n0f/zAHB6G8bzcHwQ1uADf/I/wH9agtJTMH6vDsqBZH9Wy/dy7MgyJXNEhzko6jeC7KNMqtkxWQyz\ne5NWsCzGJimyU0HL5UJ835U6XKoDI3AopGj1PmXnHB6b3HsSLSzmuOSh/C9XqXxmHH4lJ0G+W4E3\nzai+xoT7zpP+8E8AX+Ly6vaXooOKkSeAdwCV+FdfQxtODd1sMxYbDNokybM/NzmYy0N+g/H548gx\n+nIfHCu5s3MtMC2LDXQyt9PxHHAsg58EPp2HXy/BXzfhZAm+6qtVpGfjPBqolqEP3SPrEPzb9CI6\nUUn0TIBDA5qNZe/VDHr9FrJd64JYil+XkVNlLefdwoiPxp+ZXeWBjQyGSzBd2teLy56kQ9Josoiu\nKRaXYeT9K2w/O0z7s20pD/ePwFQnbmY5Oa6m9RS7xp/7+qWiPCZmuAHMN5UWGwmpOHQb2ZNFjsZJ\n0UAbR1MiCVDarCwbV2NT0a3DLwdsdaBvCKb6ZIPO1cMO65DkJeLffeGeBtM/ep6Vj01S+0x/itqO\n360XFooaAGu2aPWilv0wgcLnY2KkW8BqE2otONEvW8lC0o3KSJPNx0kNEGZHQyT5FIuWB7ROmvCg\ndfaFojq8DoboKO3vw9fOODy2uI+TdCMqPOdtVvJj8LoMfjSnDeBDKOpzkqQTMEhKCywDd8fPY7x0\nMXAHOBXrIL4hwN+gja4vfiyihWSKpENg3vomSVl1Gl0bxLlFyNGxhW4buA+Y6k9jJZyri8kYHCXN\n/bG6hrGM/JEa7TvL8MNlOcR/jiI5VivWj2zoJCkCcy6+3mp5XuiP2TQ0zrXgUFEF7hukiKOJCbZI\nG4+dqNqkyM04spnzJK2gbgXvdhQTbOc1w8h1mq4+3alpExG19NAY9M9UqJXLtHMH4MuoFi/kUv3e\nOMnhrpNsyApPX8hxtlqLVWChDiMdCY6WcknAzezHNrs+YpqCFL2x2iKrWVslbWRrpO7VxTVoDEFu\nKEk0OFcXS0GXSSKCsVC808yxvTZCe7wfbsrreY8GKI5oPRoiKfabTfWjGlJTUn/+zmzO0SawUVfm\nYySvVFo5pMOg1edY+twUtS1j0Ua2Mt71HJM0MDutZ7DagnorOvlFdfTtk06sl2JnHB7zTMdJgkZl\ntGg8C/yvQTf7DuR4vIkkoDXW9XpThLSOhHPxazvZPJ8N4HwLCh14awk+hYoCbVJ5Lr73CFo81lH6\nrEXaiBZ4LhLFUWRwT8T3z6MaizbwQAOO97m0/7WkTZpLZoJ8BfRH/3iO9o+U5VwcRxuISezbZOhA\n0pwwkb9BUhG8TSnvpo6EBBsBpoKcpTWSJIGduMxGLad+HNlKNb7HHLLHIWT38/Hnzw3nq8LjfVDe\ngpnRpOXkXF0s0mK2M0CqX9iAS792JKUarQNrmxQBtnUsI9Vg9SFl5DpKUeWf9/tamQrbl/MQGlI0\nzudTLYV1wGyQ0lPn47X1kdJtVntkjo0VXtt09Gr8x62tQq4fDhdShNq5uthYIRsHZNHZOnQ2C6z/\n4VTqGO1Ha8w0OnxNkByYboV1Ozj3c3n60Yrb1+NHrgNDAcZLqdvO0vLrXe+7Ft9vtOtrK7+w6++Q\nZD0aQLsNzSasBii1lSqbyO2rTqyXYmccnhz6j10g5aAtxHoP2qQGkSbA06Q2ue48o0VkzCvtI20c\nM6QBi8ZifK93FHSzFtA8ow5JS8Nmy9hpKo8K/kyUyTY1S0tcII2OqKKQ4mn0gjd42PiaUyCNHjFN\nFNOtOYHSjNsoumP2Mkiy8m77sA3PCtJXSc61Pa8KXOxIOOy1BagWZKuTXN7xYAufiWSWkL1tkZRt\nLfVgadEmkHWUKruQg/YaHJiFyVGXL7iWmIiaKaEbk8g5WETO6VnSPTVHxzYnG/NhjscISn9tBhWX\nm8OToZP4WgsWm3C8DMXh2DARX2f3ukNaP1ZIaf8mad6a1V7YfCbQaJFCByp5XXepA4ePpxO5c20w\nbTYTNLUOrT5kW59Fe5NFgaZIzqdF8qyjy2qyRtC93ySOZ4i/q4ls5mKmteXEgN7LggCDpEYHm9e4\nRNL4MTFEs7Eq2ufKaP1ZA9odWAlQaUJuG/rGYabvchvtAXbuT8JUP2uk/8BtdOMHSIWe9nMLEdup\n27QyLN94CZ3CLsTndleNLyBn5+uRga3E37FOUrDtj+8/gIxhjbSYmFLpdLyWRXTi6j6JLSHxuONB\n8uB+irr2mNKn2UYBLQZ2+jiINi4rArbwroV7+0hRlhAfs1STObL2XlVgrg6Debgzr8XDnmOFxxmp\n8NXmypiQpYWVS6TC2Eskx7qwCpcGlC7py8GhWf1ujw5eW8zRraGUuDnPl9C9nSBFbqw2xxwMS102\n4+ODyBYz4EBeG5zJHgSkSLvchpUteM1EcpAtldYdtTZn25ydJqng3TZN00ixkTbNNrTqsFSHwpim\nUh8q7NzsweuZIlo/tuP31lLeRvfR1iJLM9l9NEyo0PTarDnGUk8rKEJt0hfLmdave0lz0Ww9Mx0o\nWwNXSI5UjdSaPh6vKSAtuQVko/MtyJahPQz9Zel9DYYUteohdsbhCaSQnW0+5nxYWsCGmq2Tirds\nHkyJ5MHaH/MwaXLrOZSKytBNvAD8HVL9jXVQHEGLUjW+7wQyqHWSwW6QTntWg9FBi5gNNz0PvAXo\nc2n/Hcck0E00DlJNg431GCaFky3sb6dlSxPYID9zSCrIiZ0hpjLrMNxW4XMzpJoPW5xsAxyN72Md\nfea05EjaKda6apHLTeB8E8plhaXL+Aa1k9j9ryB7WSOJ81nkx+YJmYNhqXhLZVlq1JznQdLmsgEM\nZFGQsgA3TWjt6ZBs1uxxKf6uA6S0hb3vClp3rKajW0YhAyqbsL4GB4/rcOY1XzuLzchqoPtqqVHT\n0rE0utmONe7kSRFiO/ybmOU4SUNpEx20bPj0cdI61J2SsoixiR2ukfbKPCla1IdslHh9OaDdgtYG\njA5qyOhALjnXPThuZOciPN2hZOt+6i7cvBGdkG0ROk8q/m2TCvlswymQCv0mSamONeQFV0miXGaY\nF0kKtzbw7BwptG0pLtPCWCYNU6u2tRit5uFteLh4t7B8uRXidQv41dDCYZ0HtiBY1M4WBUiOsznb\nkySnp1aFgxn098NykBPUHRmwbqtuYTjbqAaR7Y0gW7Mi+xHiZPSG8uPD0/qdPZIb3zfYIciKhQ3r\nlLlEUlG21JVFY6x7M5AijBaVthSXpUdXmrDdgsMDeu3TyHkxB9gUwi3ifI5U8zVGmlpu6rjn4u88\nQjrUtUbhyKjWOGdnscNSi+R0dNdkWQ2OpcgtMmwz2QZICtomdNtANtQEthuwtA7rY9BXVPRuhOSE\n2JpRIRXiW23aarwGK4we6np/mycI0KzpY6wAE4NQzqeapB5l57btjDShdSR+NqOZjF/bRHRrRbfK\ncXNYxkgLzTJJb2IDOHsRGofUvWWOlSmhWs2Pna5MYOxcvJZN0kwc85CtSNEcsI06nMng1kF3dnYT\ns5nu1KhtSqZ+a4Jb+fi8HLI3E9sKyJa6U08doLkMyxtwbALKQ7CVSzlvc3yt2Nmc8IvxGmwYqW2G\nVVIrus2g2QJO51QIOEVP5cb3Dba5mBSBOTVW5zBNih6bM2ORH3vtDKnmYpg0yLMNLG3B4jIMFeCG\nQ6qlWY3va519s2jt2SJFB01nZ5LL1y+zvRGSFtjaNlQymB5KKQpnZ8l1fZi+lu1Ntg4VSSUZg6S6\nUXOChkgOUg3tQwVUV7Ndg855KMUUk+2dE6SDFmitM324DWRHY8gubK0zx6tbh6eawXoVOk04PH3d\naDTt3D/RojKryFmx07C1gW+SWv2si8t0UyzPaSFAU0O2U5cVAc6gG2fRHXuNGeLB+L7mCVtKzWaa\n9JOEvOyEZQWDp8pww6CHjXcbK2RfQffcTtY5koNjf+T2/A1kW3aaKqL7ayclGwS5OQiFSSgPQiOf\nxA0LaJOyor9RUp1Zf/z95mBZi7PN1bHhlBnQF9NkB/Lu7OwmZkMmsmbFpgdIYwG6T+aD6B6a82qT\ny612wlJca8D2AIRZGJxWV187vm8Z2ZDJaBwgbYKQCk9tIxwnCQla27mtn0sDMDSQ5Bac3cGis93y\nJGW0ZlRI+jfWsm5pdxs3Y4dq299GidHoFnRikc7hnB63Oi+TMBghDbm2yJHVo1mXl82ctPEnFpEq\notqy9jBMTKW18DpgZx0e+2MOxPA+KTVhi9A2aSOzlINtIsukEOLh+Npn0ELy7kNpc5lAoV9TjrTN\nxcY/WLHiLGmomqk/m5ruUvw4ifQ4csjIrhPD2LOYQ2zzgKyWx+orTKvpOSeDJL9vzzFhLRMfbLRh\nswlH+uHwCGwUUsRxiMtDwVZ4b9FHW1wGSHUaNlvnEkkIrC+DiwUYL169wbfOK6sK4nYAACAASURB\nVMMOX7YhtEmFwpYGtfov26AgOdOQilNbpHEO5zOpJt9QglZR99+c6w5J5NLspxI/mxM9gNYuK3K3\nerXnpyvyOek0eaR5d7FosznENrzV6qys1srqaexgbdPHrTDd2sXX0Z5TzMMNQzBzDNqlJCJomRCr\nC6qQosgWgT4QPybjdZkTZHOxAvAVoJFTQ8ZQ7vIUWY+zs+cDKzbeIHm7ln80LR0L6VpouY3y1Ta2\nfhkZz2ngAeAu5PxsowXGRJ2sen4DGYZpa7SR4R0gGdxU/Hoy/l7r+DoCfLKjFlWfibV3sJPVBVIh\nnhUkj5Dy49356yKpW69AHPoJPNyCjQa8rhBVtzMJbw1xeTTPFiZzuEx7x5yXUZKA4Dhqk7cOsnIF\nHlpSQeBg7rpZXPY0NvDT1iJLC9hBa4gkS2Ezh8zBtuddQLWGD6OanJtRLWL3INEZUlH8Clq/TJvJ\nNi071Fmhq0UAZkl6YRPA8ho0KmmCurO7dDvOpnJsH+YwQ4ogdq8pdv9XUXrzaaRJVwJmcnEUyJBE\nSPtJUZ5NtPZsIHuyAmfrGLUDntUc2tgk4jV1OurqG0BK39dZpHnnzwiW46yT8pLdRceWNmiQwnBj\nyCDs8U+hm3w32lysHfQu0tyiFulEtYlu9pMkdcv1eC2TaOGyAmf7vXYya1bgTVag4ewJrPPO7pNF\nXSw6N0RKNVhXzXp8/HFSfdgTwME8vCEP61ZrEWAtkx2MofbNVSQ6eZY4FJBUNG+n7wXSwnKMZFNl\nYKUfSiXJybuzszewtFQWv7fUkUWfLb00SDpR25BOSIXwc2gNuQPd323kHJlwpKUgrEanhjYqW+u6\n9cWszitH6uKqIAdnDljvk7quOV/O7mJpdJNLaZLsBNI6YQd3S7mbWKTZ3CYp/TWLbM6iQmYj5pBb\nesrU3+3AZZpRpvNj6XaLMhWAVge2WlBswWjh5Q8q7SF23uExwSXTNCmh05HdIBs/YbO2yqSU13J8\nj1Hk7FhXjbWQH0Qbm538rTLdurcOksThrDDRCgPN27bTVz/wX4Fb3NnZk5ha8lPA69GJx1KhbdLp\n3KT5B9F9H0Mnqg6ae3VT0GZiCrYZcHvQc6zbweQS+pHd2hwv67KxdIM570/G3z2VwXpdQwSPTbqz\ns5ewWi4rcrdNxcY5WG2fOSJWD9giRY0tKnxHfM9ltAn1dT3X9FcszWr6PxOkiI4Vv1onj3UYrpE0\ngs4AwwNJWdfZG5hdWDODNStYpHCUODaGVGtjYpLzWUyjxiaGt5BmNHZQFsLSYJfi77Pa1XW0Ph0j\njbKxrcrKRTZINa82LmK+CUfKUmq+Dp3m3fHvrIrdbp7lxodJRV6LpNOSCQ+eRTO2bkQpphtJwoCQ\ncpoW9htChrGFFhgLXw+QnCoTIZyPz3s2/vzzyPlyif+9yygpRRpIehWmDloh1dGMIpGtxzPZ27tR\nfdatKP1kBfBVUhH8Y6Tiw3mSiml355dpOoHs9SKyo0VgsQWPzsPhyesudLwvsCLTStf3tmF1NzPY\nPc6jMRHzbY2KOJ7JhmxemzVZWN1GE6W8rHXYNsRxUqFz9wBk02/aInVnFYGzGRQyvc6bJvYW5sza\nEFirzbFaQovAdNendpCQ4EoDBttag96MMhRHSHWt1pwzh/YlS5tZzeIMSfjUFOW7BRBrpBqwc80Y\nHOhPaf7rkN05K/SR6iksJTFJqsPYJHXe2Kj6p4FvJEVrHkPebRPdeIv02ByaN8XPw1x+2u+gXPtK\n/ICkqlwC3phpc5uK+it+Kt+7DCIHo4Y2ru7UQIm0GNmJZyFWmN6E7v0ScoQtzWqRmgFUDG/phlW0\noNkIE3OSTc9lO17LEFqoZlHb8DMFGDnuwxv3Ktap2R/l9Q+gmWnQJVXQ9dwGWos2Mrg5xOeThshO\nkiLY5oCvkU7eVj9obe3d6X1zusokPZ5yBqdresOZ4AKVexGr6TMJFIvwdUglGZaOso7QjSZUalCM\nQn+m57RImmbere/T/b629tgAa+sMNSfbDnfmNNWQs7SS1/Mm8j0xBPSVsjsRnjw6rTxNMhgL49qm\nY4WEDWQIr0M3bD6+Rwf4Ilo8+tCGlEfprHE02dxyq+YpT8Tn2rC06fiYqZkOAfVt+Hxd7+Gn8r2N\nRQofJ7WFt7j8VGUO0PkM+nM6jR9BDnMJ2csCqU24iJyoPmR3p0lF0mZHpp0BstchtMjYWIIMeKSa\nnHFnbxJISttzyMmwugm4fHp5FTnJGwHGCxo38mTQhnKBmHJCNmCn+TUUmTnTSZ05NiOwn8sVba2o\ndRitS2OZikvnGzCZXbcpiD1Pt8NjkgYWCbY1wtJZVnezjYZOT+Y1VsZSXBdJMhum/L0UX1Npw2IN\n6p1UG2hpLJPPKHV9tp83M5ivycZG85ePYLoO2b2SJdO3WECS2dbya47OBnJu2sDXktJPFsIrkUbc\nmxd9idQuvIUWIhuyVonfE59j6qlFtNjl4vv9fhVu7U+nMmdvY0rac11f20A/23SWkEN8cw7KQZE/\nawWGJDdgNriBhLmGMjk9ptDcnZZok/L0liKtIYfqFNCpwGHfpPY8OeRMDAZYCmkDsYOSbUbWXXU0\nflwgaTs1uXy4qI2ksLR8vZOmn3fXcthzM5LyvNnaaAYPV2BsWBuV1+3sXWwN6EMOxmoGw5ket+id\nlVlUgGIRbhxRw4Q5RRa9sahyd0RxE2i0YHNb72/T001U12oX88hZrsX3amWw1oawDZOtJK57nUZ3\nYDf/jAIqIn4ifn0c3bQqaSDoXaSq9puRQ2POzSxaRLZIp6M2qdPiFmQsF+Nzt9FmZBXuVsC6SmoL\n/WPg5AGv29lP2LDGOeTAHCAp2lrk5jAwHlLbuBWmttCAvjWScJiltlZRJMhSWjVkr6YYbuFjK0Y1\nYbhzbbiYg+NTHiHcD1jx8mEUcS6SVGqryIZKqM7LilBtTTItqCOkkRImmmppjRDgSEEO00W0zq2R\nIn/dKs71+LMsg2cD9E+kRgtn73OAJER4kZQu30QRwBtQvY5F9kwQtYTspXstsv3xDLKtgRKMj8FS\nLik0Z6QhpiZvEEgF9QttuNCEyVEYyvvhi93+U7KbPA98DfAISk9MozoL0x/onoreD3yBJBi4gTa7\nIlqArCW4igrBPoZOT7PImMaQMRZQEfRkvI7PxPc4wnXtAe9LRlFx+jl0iqk0YbENM/3ayCCdnJbQ\nAnIAbXBW92W6On1ELZXYYnwDMZVBWjDshGWTtAeI9URt1f6Y9oqzPzCRyUF0/4bQpnUhfn0jScPL\nTtI5tE49Gd+jjGzEBh8fR3ZxMb7vIeCzaBOzGp+t+Hu2SWmINRQhzLXgtmI64Dl7H7uHm+gw3gba\nmfatQ0F7k9XdWLOOCQdeJHWBmtMzgEo5zgObQUKBTVLksVsU1bq/tpCNLlUV3RkagLEclFwSA3bb\n4Qlo49kC/iNaDHKk05QpLds0Y9PGuZ1Ugb5GEpYbRw7LGDpRzaFIT7e65ToyOnvdYqbIUR9w3I1i\n33IQWGjCE5uQG1U6ahTdc+tgaHD5fJlh5GxnyC5swRpDp7PTyMasGHWDVJjcXeC8Acw1YS0n0bBJ\nN6J9yY3I4Xkki4JtQY7KGGkeUYmUdgoojbqO1qMlYgqLFFk0za8qWtcsfWWSGxYFIHYPXgxqU761\n6MXu+40cMBCUIVgALm1BLq8hxDb2yIQBLR1qKSaL7pkT3EG2dYA01NYcY5ui/twQ0Pj8BnAxg6wF\ntY5+93j+upmT9XLYG8HSWeSgLKNJ5JYvv4kkwJR1fbbCKwv9NUhzZZrI6TmIokV5ZHwVtFmZwupU\n/D1f6sAN+eRkOfsPS0uU8nBpQOJss/kkRmihX9PHsK6adZLNmIiYzbjpR6d0O7XXYjvykUJScX7u\ndFaFQh6mc6oFcTvafwS0LpSByho0yzDTpxVyDjk+VtBsHXq2elq9mJ3YD6M1LY/qfbaBB4lDjuP7\nHYyvs4LlS234ShsG+3Sg83To/qSEHJ5LwGYVhorST7L5WnZIsoJ5K4q3A5m1rg8jOxpDe9VABg9n\nUGiqA3QjnvIt2mgjduaQsOBYSWNsrvMi5eezNxyec8hJqaHamluRM3IB3ciDpBEQtjHZRGwTkLOB\nfG10Mj+D6oOsZsNqfEbQonYaLT6v8cr1fY+JC27kYHYg6ePcTtpkBkkna2sLnkJ2tIU2MdtoJtHi\n8wBwsaVBog0gZKmDx1pBz6D8+mSAojs7+xbT29lE89TWczpFn0Brxxw6OB0m6fS0SYNjTV/nBGlY\naAl4CPhCliKJnXU4NAS5uPQWgAt1idAd65PtXcdtw/sei7QA9E9d3oHcQGtRDjnQJp/RT7SD+LrD\nKNp4DNnDeWAugwcbyJNqQ3kYWlPpELcQX98JcLjf1bhfhN13eBaRx3sifr0GfAR4B6ld9Bxp6vB5\nFOK7iByhE2jjsjDyPPCFBpzahJEJbXi3BqW2jqL8+B+i/PvN+CDHXsCK1Q+hTWcRpRfuQ/d8AtlV\nPf58izRMdBXZ0UGSvkUZ1YmdeRS2p4EhCP1wsgD3xPd6uAKbbRgehrF8al139h+mrbSE7GUwr7XH\n9L5mSemFNbQhldEadADZEGiNMRsciq/9YgUunoP2zcAGHBqEv5PXa55C+1euKPsbCXthRXZeKR10\ngNoEbkMHIKsPvB85L6PI3h5HdmIdnsTHj6M97TiK7lSAR9qSWTlSghumdcgajVmJzwP1GmQ5KJfi\naIpw3XdjvRi7m9kzJdJ3o5t9EBWJvg6NdZhDTkkVXek5dBOX4uO2UQ0gj7gGfKYDTxYY/Y3AP3rq\nVyj/zLaiR5Mt+IUWfOKiur9uwp2dXqGJNo4bkJ0cJqknfy6TsNxR5OScIbUMZ/E1h1HkbxZtYGeA\nB56FmeO85+lP8x0bH4Z7AxwLsLIB//XLsNWB2SEtYu7s7G8yUmfLODoMTSLnpYzs4TSprfxU/FhF\ndjcO3IlO5DbYcx744hoMPsOhf9fiD376W+j7SBtuzsPnA3zhUbiwpHTWdA5Gcu7s7HeaJB0wm1pu\nEioNtO4sxM8VZFfzXd8fQXvTjchhDihC+MRF7pr6I37+n/wEP//en+aeY1+BrVV45iFYuQTtNpRz\nsj1Tmff16AXZ3T+xTTQTa56Uw7RWvXuQt/xp5O1WkQN0gDQUzSaqLwJfRpvcVgP6Ml5/9+f4yad+\ngQfe/noe+LdfBR+9BOPD8OZDO/kvdHaCZeQkm7DbBqrPmcw0DPRLLajl4I4gsbgVNH9rm1ToDuq4\nGUR2tn0Wjo3zs8P/gjsaT/O7X/t++IVP6I1Hv1uLktMbmBL3UVJ3XYPUhdePDlMPIRuzcSYmVDmE\nbGgGpSzW4/vNNaG0zcDoOF/77k+ThQG4eBaefRj6T8LkoE7xprvi7G9apGaI7mn2HdIoms0sShcE\n2ZClyIfQ4euW+P0SsrkHgLl5xt76CHd//wNkC4GPff4N8EATzs5DcRzGR2CkkGqCnBdldx0eE/5r\nx49FZASg0/gRtDk9gup0xknS2VbtbsP1aihMOFqCUOXTH3wHP/DmD/L4h1tQ3YbxUbil2wqdnsEW\nlBxyYhbiRx45PQcLcKYOF4oaGVJA6YjbkdM8FF9n8u7FDgzeDQ8E3vj5L0IrwC88A+HrpIw6vQv/\nRufaY6uhHbw2kTOUJ7YCZ1DpqPPFBE1H4ocpLJt2zxrQ7Ie1aRY/NMH/dO8v0/rrs3B2HFrHoHwE\nxmIxq9MbdHduFtHetQ40M3L5Np1SXnaxhqKD1sUXSCrto2g/ezLWfV3qQDvw+fyb+e7899A5mKMS\nnoTaRSjMwsQhpbe8o+9lsbsOzzByZr4J5Sg3gfei+p0/J9Xa9CMDuQ1tSDaLqx+luRZQVOgvWzC+\nDneM0/5w4BO/MwFjd8ON/XDBjaJnmUR29Caem49W/P46+WNt6h/rI3s0DyN92sQm0analJHr6FQ+\nj2zrVAuWKnBgEIY78L7TkM1D+S2Q709F807vENBmcwmdzKMNjXzTCsO3r1N5aIjVvzigDa0c6yOO\no8hiDm1uJph6BjjdgEsVyNowdZCNT8KHnrgNTvfDxCQszSTxOad3sK7NReS4nAduh75vr3LwbWeZ\n/4Vj1D89oL2qSUp/dg/SfgqlT+8HHsqgdg4mD9F8fIyNtz8IWYPO6mugeFiF76M57+i7AnY3kGoz\nsB6On+tw6F3P8tVf93EG378CMx1odOT0HEAGZRmpfuQh15Cj9AXIjQTG3wel9zU1bG/4rXD7oPQI\nhvGanV6lD93bMyhKMwhj713i4AfOUHhrA1qbUG4qYrhBmqlmxctbaMDek00IWxy5d54TP/YsxbcB\nhTYMvB1e0wfFdpI2cHoHc3ga6AAV5xfl3tIi/71NwusyFYZubkAul6LRJng5j9KhXwYe2oKz2xw/\n+jR/9wMf4/D3Lqi771QLDhyDQkFrnWlDOb2DtZfX0XqyCOSgf7bKTTefor9Sg/Uz0HxCzs0lUlRo\nHUV+ngIe7MATHXKdjH/wz/+U9/1ff85N75unc2qWzjOvhbXDEIahPAD9Ybd38X3F7v/JHUQ3OUpj\nX/yVG1nfHmX73wzBAwuaaXR4RlNen0a1GuYh349OWZeAIhz8j3P8m3f8Y37+Uz/F/X9yr1QuOzVY\nHkgt7U7vYcNo55FzvNBh9cPjrD4wSusP1mDtDKxOwegxqBfhoSDnJ0OneZt43qjD1xT55l/8M0bu\nXOHf/cA/ZTncAcObsBZ1DcZdor3nME0dU2EfAlZg7ePjrC1PwKc2YO4UtJpQnYHRw7K1u0mdflvE\nFEYLJgJ3fddZvuNHPsK///I4F377KDx1F+QyWMvgYEhaLE7vkCONiVhBNT0XoP3RImvnxmk9ugm1\nKhQ6UNuA5UEo5+X8lPVcNpGztAHhcMZXf+uDnL7rGE9kJ5CHPQKhKPuxQbRuRy+b3Xd4TJxrHTkl\nX4TtBybgmUWG37lN9rVttn79AJyPbXiPkiakr5PGBORg/XfG+JWV/5En//g2pSnWgFIniYY5vYkN\n7xsnTirOaP1xAbY3oDzPLd92nvmJDhu/N60W4CppDIUVDuaAgSGY6/Dwx18Lf1Vh+7FV6JRgsQGd\nIThU2gt/Mc61YhCtLSbr/1+K8LtbMHaRw/c8yInyHI9mr2Hls6MwNaRUutVzmaR/fgwGaqwsFXny\njw6wfmYFWhch68DKKMzmtFG5HfUmfchxNp24x2HrS2Xu57UwM8eBsRZ9+TwL/Qs0n52Gi4NQL2jv\n2wK2O7DagXwThrZZPdPmVDbOs6fHgTqERRjsh/F+rV/u7FwRIcuyF/9hCBnvffGfXzUytPGsIufk\nFFBv8h2/+hF+4q6f472n/oRz7zsadXeCFpbzKE1lgxu3alBb+f/Ze/Mgy7L8vutzzt3emnvWktVd\nNdOLZiSNNTOyRghJjAfJcgj+MCE7wBizRGAIHIGBCJBFCEQAHhsFhPwH/GGbP9jCCLAgjLVgECgU\noTBGDkmg0Yyk6Z6lt+rqrqqs3N7+7nb449xf3puvs7qrqquyMl/+PhE37suXb7mZ77xzvue3wsY9\n363WfRa+L/DuC4sOjA/jVwzOuWf2HzLGOD53BuMox7sjCiAo4WgIXwj48l/6q6x99wFf/pn/gPv/\ncwidK75WRYYXSJ0Ckn1Ih3A/g60jn+03W4fuDqyu+WBntRA+nK+cwRj6gTMYQyneelNQta95B/5Y\nyZ/7C3+fn/6ev8KXx/8Of/sHfxxmV3wl5nH1J5dAMIF5AekhfiAegXkTopch+aJPW5d4DeV0/uEZ\njKPve4bjSCq7z/DWwgFQDoHX4a++yk/91n/Gd5Zf5T/6a1/mvR8fk915BYKrfu4qATeBcuTjBoOv\n0e68SW4LsuwmzP4RWP8kbCTQtbWlWde2k/zOw8fQ+fjqSRfiLt699U8BNuQb77zEt3Ze4I//2C/D\njztIp17ArOLT9z6B36lP8Ip3eweiz8Mf/V74E4G3/KjJ7/IQ4oOSnYOJgZUVeNDlN77yIxyYdcy/\nZGElrpuCbuLjwMbAvRDSBDY7UPSgtw3XX4KdNdhWsXNpiPEbK2nQGNyE+zc5eLvP2Lb4kvlN+PQO\nhHtw0/lxdK167uSuFzitia/91OpB7ydg54s+y7SHjqNlR7KuEvz80pceNK/AL3f5+hc+x2v/4Wd5\nafVdInsL7Jpfzz6BtxaGmS8iyDUovsh0+BNkg38a7I/CzZteZIvYkfdSHpnzYeFpInUsOiV8fQ9e\nSuCnVnzW1ut4k/Ma/gP/XepeI/rBPznLYuER5s4HDE4MZEfw4u+w+n03GL38CsUvhF7gSGHCI+Bd\n5yendqM1hEEnlcdhWSw8wgy/mRoAbgz5HD7fh387gl8H/jf8InUD79r6Oj4O4wp+sVOejItu4WmS\nAYMS9lxVt+k2L/7oV7jyjw8Zr3yON/7aq6SHLT9uInw8ajqF0EEUctxl1FhoVcHuuoH/aD7EwnP+\nPMk38RPIwMJqx/cQ+b8cjIy37rTwoijDW3DWnuO1KueT2PixsQvsJ/DGpzh6pwXfb/wue4IPaH8N\nX/5dgkh1960ILXxs4fvA7gx4E75m4Sc/DzdM3eX8N/AxP9fw92kGnyJE+Ara1vlqyPMDbv+y5fb/\nfRM+9UfqRrQ5XmDP8LWZVmjEnGpq8dPk/AkeqK04G10veBpp6xzgF60VdCelnI50Ir4GrCWwdwOO\nMvj9SvTP8ZPLJn5i0VLsymkkVG1p1mF3FXbnsP8Aim1vJfwWPubwBbRasnI6EbBqoB3C3c/D4EU4\nyHwPrB5+Hgrwbq3r+I3X+VyVl4Lz+6+V2iob5mSfGxW8yqMgqcbdynpzLfLjyFJV6TYazK58ODKG\nehba1mdYzRM/FzXFsgaPKh+GbMCuA5urvtTKGD921jnZNUBF8zPl/AoeqCeQ7nO9CuUiI7E4gVGL\noPL4SAyXBULrW4s0W5moyFE+imYgcxR5YdOp7hPBbNB4wTPgfAseRVGU88KxeH7eF6JcWMTCrJuv\n54Ia0BRFURRFWXpU8CiKoiiKsvSo4FEURVEUZelRwaMoiqIoytKjgkdRFEVRlKVHBY+iKIqiKEuP\nCh5FURRFUZYeFTyKoiiKoiw9KngURVEURVl6VPAoiqIoirL0qOBRFEVRFGXpUcGjKIqiKMrSo4JH\nURRFUZSlRwWPoiiKoihLjwoeRVEURVGWHhU8iqIoiqIsPSp4FEVRFEVZelTwKIqiKIqy9KjgURRF\nURRl6VHBoyiKoijK0qOCR1EURVGUpUcFj6IoiqIoS48KHkVRFEVRlh7jnHv4L415+C+VpcI5Z57V\na+s4uhzoGFKeBjqOlI/Lw8bQhwoeRVEURVGUZUBdWoqiKIqiLD0qeBRFURRFWXpU8CiKoiiKsvSo\n4FEURVEUZelRwaMoiqIoytKjgkdRFEVRlKVHBY+iKIqiKEuPCh5FURRFUZYeFTyKoiiKoiw9KngU\nRVEURVl6VPAoiqIoirL0qOBRFEVRFGXpUcGjKIqiKMrSo4JHURRFUZSlRwWPoiiKoihLjwoeRVEU\nRVGWHhU8iqIoiqIsPSp4FEVRFEVZelTwKIqiKIqy9KjgURRFURRl6VHBoyiKoijK0qOCR1EURVGU\npUcFj6IoiqIoS48KHkVRFEVRlh4VPIqiKIqiLD0qeBRFURRFWXpU8CiKoiiKsvSo4FEURVEUZelR\nwaMoiqIoytKjgkdRFEVRlKVHBY+iKIqiKEuPCh5FURRFUZYeFTyKoiiKoiw9KngURVEURVl6VPAo\niqIoirL0qOBRFEVRFGXpUcGjKIqiKMrSo4JHURRFUZSlRwWPoiiKoihLjwoeRVEURVGWHhU8iqIo\niqIsPSp4FEVRFEVZelTwKIqiKIqy9KjgURRFURRl6VHBoyiKoijK0qOCR1EURVGUpUcFj6IoiqIo\nS48KHkVRFEVRlh4VPIqiKIqiLD0qeBRFURRFWXpU8CiKoiiKsvSo4FEURVEUZelRwaMoiqIoytKj\ngkdRFEVRlKVHBY+iKIqiKEuPCh5FURRFUZYeFTyKoiiKckExxqwbY/5XY8zIGPOmMebPPuRxXzLG\n/Lox5tAY88ZZX+d5QAWPoiiKolxc/jowA7aBfx74G8aY7zzlcWPgvwJ+8gyv7VyhgkdRnoDH2FX9\nW8aYbxtjjowx7xpj/poxRr93yuOMoZ80xnzNGDOoxtKlXbCUkxhjOsCfAn7GOTd1zv0D4JeAf2Hx\nsc6533bO/Tzw5hlf5rnh0k28jzrJNB4fGWNeM8a8c1bXqFwIHnVX9UvA551zq8BngM8B/+aZXaVy\nnnnUMQR+AVsD/gngLxpj/pmzuUTlnPMdQO6c+3bjvt8Dvvs5Xc+55tIJHh5vkgH4KeDuWVyYcjF4\nzF3Vm865QfVjAJTAK2d2scq55DHH0M85577inCudc98AfhH4obO9YuWc0gOOFu47AvrP4VrOPZdK\n8DzOJFM9/pPAPwf87NldpXIBeKxdlTHmzxpjjoBd4HuA//LZX6Jyzvk4O/N/DPiDZ3JVykVjBKws\n3LcCDJ/DtZx7LpXg4fEnmf8C+Gm8RUhRhMfaVTnn/sfKpfUq8DeBe8/28pQLwBPtzI0x/zFggP/m\nGV2XcrH4BhAaY15u3PdZVBCfymUTPI88yRhjfgIInHO/dBYXplwonmhXVQntPwT+xjO6LuXi8Nhj\nyBjzF/Fu+H/SOZc9w2tTLgjOuQnwd4C/bIzpGGN+CPiTwN9afKzxJEAMWGNMYoyJzvaKny+XTfA8\n0iRTub7+U+DfkLue/aUpF4iPs6uKgJeeyVUpF4nHGkPGmH8ZH0/4I86598/g+pSLw78OdID7wM8D\nf8E593VjzA8bYwaNx30RmAK/ArwITIBfPeuLfZ4Y59zzvoYzoxIy+8B3i1vLGPPfAXecc/9e43Gf\nBX4L2MOLnRhYxQ+oH3DOacbWJccY8z8ADvhXgc/jJ5EfdM59feFxfx74dgGQ9gAAIABJREFUJefc\nrjHmu4BfAP5359xfOutrVs4XjzGG/hzwc8CXnHOvn/mFKsqScKksPI9h/vsaXgF/Dr/r+lfwmVqf\nBW6f3RUr55hH3VX9EPA1Y8wQv6D9CvDvn/nVKueRRx1DXwY2gN82xgyrejx//Tlcr6JcaC6VhQd8\nHR7gvwZ+DHgA/LvOub9tjPlh4O855xZdXhhj/hjwt5xzN8/2ahVFURRFeRpcOsGjKIqiKMrl41K5\ntBRFURRFuZyEz/sCFEVRFOUsMMaoS+MS4Jw7NbNaBY+iKOceXaguDw9brJ4aX9GhtNR87uHD50MF\nj04yl4dnOcnoOLocPPOF6q/oMFp6fkZLninPjo+28Py4TjJLz/9xBpPMP6vjaKn5n3ShUhTlfKNB\ny4qiKIqiLD0qeBRFURRFWXpU8CiKoiiKsvSo4FEURVEUZelRwaMoiqIoytKjdXgURVEURXkyniQB\n9zkldargURRFURTl6XCaADonVStU8CiKoiiK8vFwD7ltGj8/Z+GjgkdRFEVRlCfHPeTc5BxYeVTw\nKIqiKIry8WiKHTlE5JwTK48KHkVRFEVRPj5u4WiiFh5FURRFUS48i2LnHLq1VPAoiqIoivJwHhaj\nI8KmbJybty1e5NjGIT/DSQFkTrnvKaOCR1EURVGUD6cpZBbPRXUs3g6qwzZuy8+mcW7efoao4FEU\nRbnsPGrxuHMQh6E8B8SSI0KmbNzOq9unncPGESzcFuEjBzxz0aOCR1EURfE8TPio0FFE6IigEVEj\nR9Y4y+1o4Qgbt5sWIDiTMaaCR1EURfnwGiqgoucy07TwiNBpCpz0Ief4lENeK+Rkqrrl0S2NT4gK\nHkVRFMVzTrNrlOdMMyC5oLbiiLiZn3IWwZNQW4Uk7qc5zpoxPGLteUao4FGUi85pO/MzyHhQLhiL\npf+bAab5wtGMrWi6IQLqBUrH1uVCLDxNF1YKzPACZ964LecWJ+N+FosPNjO4nrF1B1TwPH8W0/ua\nKXuK8qjIAiacQcaDckFpuieaO3JZqFJOBpu2qsNRix4dX8vHaXV0RKTk+HHRtOJUh8lKgqLAUmKD\nAhuXBKbERgVFGFCGltIElM5SZJaSAFdYb/lpiiEh5KSgXrz9MVDBcx4oG4dMJoryMJoieXGXLjQz\nIWRXrijNxSzHL15TYAKMq2NKHW+RAB3qmiqn1U9Rlodm9lUzvVysOc2jui8oCyJSojAjDlJ/m4zI\npWTEZMTVPTFZEZMWUMxtbSlatP40x5rhg7V7PgYqeJ4HzQknw086MrAMfoHq4Ccc3UkppyETkuy4\nxIQsJNQ78wT9pl9WFt1YzWBTETqT6va8ur8ppFPqOUgsQjK2Ek7fhSsXE/ncF92bTffVKcHJNiiI\nw5RWMKUdTWmFU9rhlFYwY5q1mWXt4zMZFFlAsSioxMJjOLnxl5iep2QE0GnwLJHJR3bjM/xEk1W/\nC6gVr4iiBBU9iqc5fpr+c3FDZI3HNndNMnaaO3TlciHzyZyTIkfOErcTUQsZGTcytobV7/rACvV4\nUgvictAUuosWncUg5cbPQVwQByntcEqvNaTbGtFrj+gmI0aTPuNJj2CSQw5FHpBOY//cpuCReUqa\njIqFWjCcnMueEBU8Z02Gn2COqnMBbAObwBpwCOwC+8Co+p3u0BWoJ6QJfvEZU4vlVfxYkYVtSr2Q\nzYE20MWPJeVy0YzHmOPHzhF+HIlghnp8dDhZQK4ZuxFV9wXU85LGHS4PzZTzZlxX9vAjMCVRK6Ud\nTui1Rqz2D1ntH9LvDYgP54SmEjvTgDSPsdPSv+ZiEHNzQ9aMaW12Wv+Y6DJ6VshAGuAXqjn+v9/H\nL1YxfgIy1X2yWB3id1Md1NJzWWn6tjP8ODnAL1wlfuxcqQ6ZRHbxY21KbTmUTBt1P1weFmunTPAb\nqUNqV3oBNipIWnOS1TnxakqeBxRZ6M9HlmJiyY8sDguBhchAUgWeihW6KXp0fF08mi6tpgW56e7M\nPni2UUFMbeFZ6R2yvrbH+toBAQXkhnwaktqYadEhmBV+DC6mpp9mLZT7m0HNHwMVPGeFTDb38QNo\nFbgKXMd/6HvAN4Fr1WHwVp771fNj6sVKuVzIRDTCixzZaW/hLTct/Dd5n9r3HQIbeHE9rA6LH4fy\nHGX5KfGLlriujvBCeIIfK32gA53+hJub73Br42121t/j0KxyiD+ObncYfLPNYL/NbNiCMAaXQBr7\neWyFum2AiumLzWJsoLg9RfA0xU51BO2C2KW0wim99pC1/iGb63tsbu1C7rxlZxAzNW2iPPMWHhE8\ncLLPVsgH+2s1LUEfExU8zxrZYQ3xomYD77raqH43AO7iBc2X8INphP/wZUc+xA+uTfxi9YyLMynn\nDJmExnjLjcEvNOt4N1YbuAc8oN5xx/jxAt4aNKEeiwEqeC4LBX7RGuCtOmP8/DLGC5U+cBU6VyZ8\ncvNNvrD123zP5ld5N9o5Pt7rbPD+/hoz1pgN++B6kFmYxH5eCvDusGZmjXI+OS31XI6M2qLTDGgf\nA7nDUmIosbHDxKX/2TjaqxNaq1OS3oyonRImGUGUY21JHKW0WxN63SHZSkw5s9ispB1PyZOQPAkp\nkpDchuRlSD4PcAQnXVoihiSp52E8wrhTwfOskQlHdue3gE/gF6z7+IXqEPqbR9y49g570212y2u1\nu6JXPW9GXYq7i+6kLhMz6kWqwC9U1/FjKAM7LWi9OqH7A0M+tfdNPrX3TV7b/zS/d/dzjIa9eoc0\n8o8/9olLto2yvIiF5wgviGVBm1ELnh1o35zyye03+YHtf8iPbP06r3Ve5bXOd9DtvIrNd5h98yp7\nZDB0kFoYJ15ESUbpBrWF5ykElyrPkGbV5GYaugieU0SPKR02KgiigiDKT5zbK5Xg6c+J2hlBnGOD\nEoMjDHNarRm97giXWmxeEpPRbY+Z2RZzm1TnFrOyhZu1yMtqRy9iRwpfynUvurweAxU8z5ocP9FM\n8AtMG/9fl8DBOfAKfFfxNX7yF/8yf/dzf4af/+Sfh29Uv38Rv2vaB97HD8YX+GAUu7K8TPGfvwT6\n9fBjoA28ATYv6H1pwLUfucOP/e6v8qd/9+/yC/t/hjduv8Qo7fnHGeo6K7IoraGCZxmRInFiLd6v\njgO85a+Pt/7dcPBCidlxzLYj3u7e5LfsF5hNW7x7tMO76Q630xvcu73CtNsl+kJM7yZkM8hnUGR4\nsZPhrdcd/FiTeEPlfNKM62rGdzVjdhYsPMaUBLYgSjLCJCNqZ4SdlKiT0emNafWmxL05UScljItK\n8EAUZrSTKa5nCMqCmDmdaMyk22VU9BjnPUZFn3FRUuaWrKishs2YnhA/bk8TO48prlXwPEuaGREB\nfhcU4AeVuBZWgRYcDdf46tH38v6bOzBzfnIqTN2PZBU/ICUgdQ0/sailZzlx1NkxR/gFK8Jb9/rU\nbqsOuNyQpRGTB13uPHiBP3jwGd7b3yE7ivyk0aFONZagxBG1ANfihMuF1NgZU48dETzbeMG8Ddx0\nmBdKzI2S2WbMW/YmpbHcnt7k4N4qh/fXOLy3yhRL2nPEX3D0Usf0HszuQfEAP2Yy/Kaujx+3Em+o\nnE8We2I1s7KmC4dYeAKHTQpCmxHHc+LenHjFB7m3O2Na7SlJu7LwJN7CA44wzGi1ptiiIDEp3XBM\n2how7bU5nK5xNJtjpyVuZkjTmOm8PF3siBWqWfjyCSyJKnieJotFvsZ4v/kIH2B6tXG/pV68HsBr\nk+/my6s/C98Gfrfxu0PqTC7wO6nb1HEYauVZTiT9fIBfrA7xY2gdPx5k0tqAsgwY3VkhO0z4tW/9\nCb76rc9z7/2rDGYrfozIWFurniMp7e3q0FpPy4UIHhE7e9SCZxM/fl4Ac9NhXiwxOzmz1Zi3prd4\nb3qDaFyQvxeSvx6Qvx4SvzCl8/kh7c8NibrANyD/Bsy/hR+fEgid4YVO7+z/ZOUxWMzGWqzpdZqF\nJ3YEvZLQ5MRJStKd0Vqb0tqa0WmNacVT4nhGFKeEDZdWFOQESUli5pTRhLJlKXuW+TQhGcwJhgUO\nS5bFTMoOdlbWNekivNiR8giLjW2fYL5SwfO0cfhBcoifYDK8W2oLPxHIByk1LJoZOLuVzW7d+PtW\ngO+snp8AX6WujSD9TFroQrVMiC99Ti12xMrXw1sJ+9SfeR9cYcn2W2TfbjF6d5U37rziRQ3Q3pzQ\n+/SA+EoKbchHEcM/6DN5u1dna1m0Ps9FZjH1XKzKstky+Lmk5eAG8IKDF8FddZgVIDbkRUQ2aTE6\nCHD7obciHwAD2JpO2cwPuWFvEyQFd1Ze5M52zHha7cJEQEf4OUkWJ0Hnp/NDs4+aZFo1q7U/LIbH\nOWzhLTxR7AVPe21Ke2tMO5mQBFNiOycKMoIgxwQ+jzwMM6wpsZHDJiW2KLGFI5tF2NBRYknThMm4\nQ1yuYOeFvzZZI8UC1SxQeBqPOMZU8DwtZBDN8AvVAP9BJfg0c4mXED/kB8pmO8gd9Iw/BmC2C8If\nzvjk1bdYnQ14/dufYuBW67RBWQjVX748SK2mo8ZZhM41/A69S52+GVPHaryPD4Tfq14rgY1PP+DV\nP/ka66/sYYOSwdurvP7gu3jnD3t1e4C4ek3l4iIFTWfUm60D/DzRxddo6gG3HNx08KKDNYdLDOQB\nzMHtBri71idS7HG8oVqxAz45fovvufd7RGnGV/OMyUqfezd2vNC5T71oZpzeFVs5Wx4mDJrVlD8g\ndlwteOZg5u7YrW6jkpCcMMyIW3OS7pzW6pT2xoRWPCVhTkxKSEaAbySKgyAoiIKMiIyQnMj520Ua\nMitaTOYdhqMVEjsnLHNs5j7YxmKx+8DHGFMqeJ4WEnOxS51RtY0XOiv4xSWibgMgAy/A77TXDEwD\nPzm1gTlEt1K6f/qQf3Hw3/JHX/sKP93/Wb7S/nxdTyXFx2coFx+ZhEQwH+K/7BLndR1vJVyjDuBr\nTmoSLzanzsBqQ3Jrxvr37XHlj9wlNBmttSm3f/UTJ3dzOQ+fIJWLQUrtAj2kFj2GKl6nOq45uO7g\nWgkxOGdwuYWhgV0Ddwy8ixdPleBZNUM+OX6b77v3uyTZjEnY53b/lp+rdqktOyknFycVO8+P0zqe\nNzfli7E6lVi284KAEhuX2H5xfI67Ka0rU5L1OWE/w7YLiKA0loKAgoDcSyK8pPFH4QLmZYItHaYs\nsc5hS0c2j7g/u8p+tsmgWGVCh9TGFGG1e4842QDZ8FTiVVXwPC3EjDzFi5CreNdDl7pgYEFdSEkK\nOYXVOTF1G4nKalNkAfNf6/Db7e/n3tEOD9Ktk5OJWnaWhwy/WA2p4yG2qON2JEg9oW4C2VxkLLUV\ncZPjiWK/v8kfZJ/h9vQG7WTKnBaHrNXjRyxFysXixIJW7cyH1BW45/jPuANmy2FulZhPO9x6fZBb\nGBsYWTiwftyNgInD2hLTK7ErJa3elC4TekcjkjKl1ZkTdgo/dpoWa7NwfSp4nh/N1PPF7ueLNXaq\nAHeTOgIKL1vinDDOCHtexkTdlHhrTrw+J+pnBO0CF0JharHTFD0ifFxpKQt/uLw6F5b5LGF/vslB\ntsGgXGFClyyIKSNbz0sieJ5ifScVPB8XGVRS5yLB78g/Qf1hSYCYWHQkzgf8h5hSuxXkw12FYhQz\n+e9jfvHVP+UXvSG1f7xZ2VS5uDSbOkrcxRw/BraBT1PH2khmgvS2EUthQV2McKN6bjXhHXbXOJz2\niA9m9LtD7NQxKlZP1rjQgOWLhxSKk3FwiHdD3cd/nn3gmhc74SsZ4UsZwQsZeSskTwJyApha2Kss\nO0fVa60BbYiTOUlrRpJMyZ3lzfwWf7/4IubA8fv3PsNuuu3HqVSOX8dbssXdquPp+dIMTG72RRPX\np7QYGdeHyRxBXBImGXGcEifz43PYzQjXcsLVjKCfY9slRO5UC4+InYiMzMVkRUyWRWRZfZ7NWwzm\nqxxlq8cWnrmNKUNbN7FdFD3mQ45HRAXPx0UWqjl+UZJGoBEnrTmSHiw+Sah7aonbq0c9icXUgclv\nA29SV8uVehcav3PxkeaeYtmZ40WLZPVJkUmxBkbULihJI82p66tIXI5MEIWBrwUUrydMUrB3IH87\n9o/rVK8fowvURUOC26fA1MCRqwXPGj7e6xaYWyXhzYz41pT4hTnzMgHXoihD3NTAvoE7+MWvB6yC\n6Tmi/pxuf0i/d0Q+sLx1/xb3dq+RHcbcv3+FB/e3/PuJaF7zzz22aOu89HxpBrLLmiJWYSlZIG1n\nRtVROGzf19qJkzmt/pRWf0arPyXs5phuiemW2F6JaZfepcXpgkdEz7RsMcvbzLIOs7TNdN7251mb\nyazHOOswKXpM6JLahDKqqiw3XVrNDZm6tJ4T4lYYU1t2NvELVb96TDNzojkJyCInTdkkLqNDrcrl\ng57hM3VEVGX4iUUKGOpCdbGRHmsieBx+HL2CHxc96qw8ETxZ9VyJ90nxQltEc596sjgy8NWAYjdg\nuhv7RWpg6ho8IniU889i2QtZvEbOzw8H1AUA+8BLYL6zJLyekVyb0bo6xo2hGEeYscFNrH/8nep1\nPoGfW25CvJHS3Riytr7P5L0ub+U32b+/zfSgB2/h+/7dxhfAfAGf/bVavbfOS8+fxeBksQQ2+2NJ\nm5Gq154pIUgKQjKSeE6rN6WzOaGzOSbo5bjE4BJwsfG3o4e7tDIiQnLmZZtx0WOU9RmnPcbzHqNZ\nn8m0y3yekGYJ8zJhTkJmK5eW48NdWh8jlkcFz5PiqHvU7AEv44MCO9S1A+SQx2fUGVYiYCS2R0yO\nHeogQEe94I3xwYQRsENtOlYuJrLjOsQLZon9WsFn1GxSp4pLRl9BLY4kFVjaTZT4sdHGL3YyUYxN\n3YfrgfHvF1LvxqU8gi5Q5x/ZDOXU2VjiBk2psrDA3CoIbhUENwqCKxm2n+FiyIqI4jCgvGvhroH3\n8McRtUWgyvzLgogpHQZln/m4TbqbUL5j4Z3q8VTv1zxk7lPrzvPntM7nko11muA5AkNl4cEXF2z3\np3Q2x/R2hthuQREEx0du/flhLq1jC49rMSp6DPJVjuZrHM3WOJqsMZ72KWaWIgsoi4DCBRSB9S4t\nw6MFLWsdnjNCdlb38IOlRV3ALaGO05FeRRIZv09dFEysOPKYiNr8KC4MeZ/7zr9XC1gxfkHTzukX\nG7HsHOI/W4MXsi/gBc8aH2ygJy4MCW4eUbs5S/y3uYVffGRHJNabtPEcyfbqoq0lLhLNLtYjarG8\nTy10r4B9qXJj3ZgTXMkwrRIXieAJce9a3DeNd38dVK+TcCx4XAx5EDGlDUVBNo6ZP0go3w684JFM\nwEXBI1bnZRc8H5XRuPj7xZ8X5+0nbYi5aPFr3m4KnWZGZjNQWTwMx4kPDmscNiwJWjlhNydaSYnX\n59heQU6IqYrH+anJUGJxzhy7tnJCUuLjtPRJ0WGc9ximfQbzFY4maxyMNxhP+nXaeVFdt5TZkHnr\ntBiej/qffAQqeB4HCVCWKqZD/OASN1ZTkYof0lIPKilEKLt7cStIxWQRO2LxkQXxQXW+gQ8O1FT0\ni4lMRM1aO3PqWJor+LHUpR5DsvNeLGi5jx+Hhlq4SNbMlFoESaXdQfVzwnGsBm2Wf3FaJkpOpp/v\n49PCd6mF8gte8ES3UuIbU8IrGYXEWRSht/DctvCH+HEkc9MqdfB7bMiCEGiTFYZyHJLtJhRvVxYe\n2dgtCh5pX3LZNmKLYmMxFbyZWbt4NFslnHb+KE57H0lsGHMyG0vO4iKXTZL0PosM5Zqh7FuKduCD\n28OQ1EQEWC9uMN4ShK/LYykJKDA4CheQElM6W1l32gzzPuN5l+m0TTpKyIchbmD8tTQbmEoijmzu\nJFs54oNBy0/yf6pQwfM4FNTN+Eb4HbmkDcvORnpkyY5JouElVVSycMT90Kke3+xtItk4h3g/eYEP\nZF1HC8RddGTBOqCO/bqGH0fb+M9ZesdIVW7ZBQ3xxQX38GLJVs/bwC84IX5sibBO8S6LO9V9UtNH\nAky1Lcn5ZrHJ47iK1ZGilJLduQ7mWom5VWJfcgQv5rDiKAnIB1BMAn+MAvJ3Isp9i8sMhKa2SG+W\nBNsFdq3EtgrMvKQcWLK0RflGQPF+iBtYL9Z7eNdrs1yCLEyXidMsLIup4M1DFm3bOBaFUJOPWsyb\nG6LF9xJrjqw9ch5zMmVd1q0WPj5n1VD2LGUnII9DsjAiMzGODNe4oKByZIkAwkHpLCkxmYuYuQTj\nHOOszzjtMJu2mE9i8mFIeWTr9krN+ByZ76TKslh5Fnv9qYXnGSMBghKg7PALxjXqZnzNOByJv5G6\nFjL45tXryQfaqZ4rboUx9UAcUFt2eqZ2QegndvFoWnaa9ZosfuHYwe/OJehTrIIyoUnMzj61cIY6\nM0vicWJqN6gUoHufuj2FxAjJblw5/0i8jmSD7jl/TICWgVUDV8G+XBK8khG8mmHXSlzLko4TOIJy\n11LuWtwDS3EYUg4CX/erYZ2xW47wZka05Tte5wchxZ2Q/E5E+Y2A8r3AZ3WF1XMki3CFy90d3S2c\nm/Vuck4KVrFUNM+npVw/6v9ysdZO8/0kTkfmG7EojziZ8h01zh1wYuHpBBRJSFZZeLwu85ad5tng\njl1bhQsonT1xTPIu03mnsvA0BM+I2oITV0fQuB03ft8snfGwGB5tLfEUkQDlffwC8gI+SFnK/DcH\nrwicEriLX3Qk4FR2R/LhrlJXYRYfq8T7fKt6LnhhdeXZ/onKM0R2XGO8dUY6S1/DV1B+AW+lkb5W\nM+pUUcnekh29BLbLYrVBvehIKYMZPi7obfwkN6leW3bkGrdzcRDBI5bl+84fKV4orwI7BvtyQfgd\nKdGn5rjAko8jinFCsRfAWwb3lsG9Ay62XuzIeNj2h9kuCbczWltTks6U2aTD7O2A4isR5TsBvG9g\nZurmoFv4sSsLk7qxPE3xIXE0clusFXJuvkZT6DxOW47F92sGtUtQ8oC61cgQv2Z1qDPq5PaK8Rae\nSvB4l1ZEZn0gYEh+LHbElRWSk7uQzEUUWDIXk7qIrIzIyph51mI+bzGftpmPE7JBiDs0/rrEw9EM\nUhZ3acTDU9NP+988YqFLFTwPQ9TzFP/hHOAH0i38l11cDWNqc5w8b4T3q484aQKWpo8yuLuN57aq\nx0yoBVObOt34sk0oy4BMRin1DmtY/ZzgRawEKEvcjjx+iBdGe9T+94Q6XkeCk1epA0Zl4ZEYoffx\nAiimDmrVsfRofFhg6rP8/zV37aXzn/3AwaGrmoE6PyeB/1xX8ZaWDYfpO0zicBmU44B8N6J4P/Ib\nr/vAvsNsOsxqid1ysA3uqsFdMZiNEtsrMK0S40oYOrhrcd8OcLuBf08f1uPfU1yjT1D8bWlwpxyL\nqeDNo6COs5OVV/5vtnF+1CrVp72nBAKLV0EsPBL3N6DOxpMg8w7+s1wDt+JdWj6Gx1t4QhNhFiw7\nAcVxAwmAzEWULiB1sa+9U7aZli3yPCZLY/JpTDZuWHikiK6IHYnhkSSeRXF4moXnCVDBs4hMdAV1\nQbhD/ODpUKeESz8rSTsXH2PTpSCpwgl+odniZACbqHzx7/apA8qo3m8brZNyUcmpd1j7VO5J/Bi6\nSl1/SdxXlrrFhKQcH+HHSb96/Bb1RBVTi5944b5mpuAGtWXnsi5OT8riLvxZI4HJMg/sl7BXwn5R\nCR0La9a7szaMz9psQzkLyO/GkBrKmaU4CHH7pl7gNoEeBNs54XZKtJVRrhqKfkjeDyCBvAyZT1oU\no4DsqOUDTCemLnYqVsWqGvOlFjtNPkzwpI0j4oONVRcDcRcF1EdlaZ0msJrFBWX+kUrcEvsn2cMi\nYtfAbYDrWS94OpY8CcnDiNTkldOqPGHlCcmJSSmxddCy88HKo7LHuOz5tPN5SDkNKccBxTCkPKwE\nj4idNrXgkc2ZxPZoa4kzQKoj7+IHjfQ12sSbgaWmTtl4vAy8KXWJdvFPSjaWpNvJwJY6CePq/h5+\nV35QPVerll5M5LMVy47EYg3w4+I6XoRIvRxxQ7nGcyTQcIYXy1KfZwc/lgSZDKSWzuIkmuDH7Cp1\nBWbl0ViMz4Bnv7hLBW1ZrPZK2M3hfg7GQC+EVQvrBjaNHxdtKOcB+T0o7/tYm3IQ1EHGfY5dn8GV\njGR7RnJlStmyzIMYFyQ+BDULKCctsmmL4iikGAVe8ICfi2QcXgbx/GEWvsUA4ebRtOhITI2sE02B\n0vzfyWIvrYfEW2AWnrt4bZmr5g7X6HJe3R46zNRhMjDOYQKHicF0HbZTEnRKbKfEtutz0C4Iksz3\n0IoywiDD2Cr43YUEZUHgSqyTJqD+nBYxaZmQFgnzonV8zIoWbmxx0wCXWso8wJUWZ8zJMJCQD8YU\nNUWOVlp+xoypd9dSNl1ib8rG4yQ42VD3JSmoxUqfWq2KqQ7qbCx5LWkXcJ863ViqpWqfo4uHZGJJ\nf7UBfhys40XLCv6LLj2xDHVtlQl1XQxxc0pWlQQnh5wsGw+1lfA+PjNrUD1fXGBaEO50TlvYFnfs\n8r9dDC49jSf5rjavoXAn6+wclLBXwF4OHQNrBrNp4aqFLYdbNdAxuEFAMQgojhuAVkcM9JwXPJ9w\nBFcKoitzWlcm5CagnDnyuaWYWvJ5iBuFuKPQb7pEcIsrdRs/hsWqeFnG02mByYsxM82g4aYAgtr6\nL+NHxlXWeF5z4V+0AjVjhJpjc4bP3JuU1dkdn+20JJiXWOPFTWC90Anzgng9I15P/bGaEbVT4jAl\noKA03nlVYigNlBgKDEUZkBUR5IYyD8iLiDRPmBcZs7zFJO8wzTvM8xZZnlDkES4PcIfWi57MesGe\nmLqOnCRQdKhr0Z0WxA1PbQ08f4LntAnorBZ8BzhXL1QpsGX8jlwG4Yz6vyZBpBH+OfvUfvUE/8H2\nq+eKq0G6pMuiRuP+N/ELlsT99FCxcxHJqMfQA/yYuQm8iB8bfep2FcuJAAAgAElEQVTgdKgqIuNj\nLcTkHOPrLu1QBxtLVWSxHi0GKzr8+HkLP55koWrjx6jyQZoLSLPvUEZdo0bioMRau5hB8nG/o82d\n/xQYFF7k7BaQu6pHWki4VRDfnJHcHGGvwrzTIu0kpO1W7QqdVtdsqASvg76rrDMlRcuQmgiTtSiH\nAem9hOJ+RLkX+IVpZLx18b3qtaRekwTGS0DpZUlBP01sLI6TtHEWmmOiabURZMMCtYVWRJIUlRWR\nJGtP81ziLTuTKt5qUMKwPqwrCExBaAqiTkHY8bdjm9PuTen0JnS6Uzq9Ke32lE44JTA5MxJmJmFu\nYn8bfy5c4MVOGpCnEUEaE6QlQVowzxJmWYtZ3mKetcmymDwLKTMLExE85qTgkZjCPrXgkWSe0xqF\nPiXOp+BZ9HGeFWJKPsj9RHMzrM3GzYE+5WQH9Hn1OxE5UitH/g6JRM8a98/wPtUD/Kcg8R4JXmBJ\nEKvyaJzmR5f77cLxrMaU+NGHpY+9mAArFq5ZL3ZuUGcfzBuPl4Uur65NXKAy8YlvW0y9zdYCD/Ai\nSf7mIXVRSxHN2jri4TQXELHMLZbeH3EyhqVLnenSdD88Kc0WAFMHgxz2MribwUpQHRHhiwXdl6b0\nXh4SXi0ZssKIVVLX8mLH4MdFysmq230HK64SPJbURpQZuL2A/I2I4vUIdyeEsYWRqYvCFdRB8WJd\nlPiwy2DdWYynkfuaAcLzhUO+r81D3DcnAtI5acl5WHzP4nOaFqQp3qIzKOGw8MeRv22SnKCTE7Vz\n4nZG0s6JOzlJO6UfD1lJhqwkI/rJkJV4SD8cEpqCgekxoM+QHgN6lPSZmZjChd6yk4aYGf6YOswM\nsjQiTRPSNGaexmRpQpFGuNSLJJdbyAzO+F5cBA03qWSINYX0othZKsHTXKSadQSgHigSqf2sBJC8\n/wQftyNm3G28C0J25BL9LmW5RcTMq+uTiVBqnDR3h1AvbmN82rC4O5pfDqmVchlKtD9tmqZicRk6\nTvqGn6WIlrYhAwcH1e78hRBetN5Sc61xbeLHF0uPlCQQ96e4UOFkQS6oBdIe3ppzh9oaIc1DZVcu\nViHldJoCeU5dxbiZynuAX/DXq0OEaczTie9x1IJn5ioLTwp3Z9BqQS+AWyHhq9D51JS1Tx8QXUlx\nE8N80vLXLO1JxE0qyRLHgqf0gicwlCYmS0PYt7g3Qsr/L4BvBXVvthn13LdNbZWUhenj/K0XlUVL\noAge+e7KmtCsJQP1vC79FZuvUTTuWxQ7zcKEzdo+RePnmTspePYKH9y+X2BXU0KbEXVSkk5GazOl\ntZHSXp2zZg/ZMAds2EPW7QHr5pANe0hoch6YDR6YTSI2qmoaiZ+mygBXWEgtbmpxE+MtNxNLPgvJ\n5/7I5hH5PKSYhV7wWHDWgBytRvyOdBmQo+nSkv/DUrq0ZNJvxi9AVe4a/0Vr7nifNs1g0btVYOA6\nfrLYxi9WErwcULuvxNc+o04LFrMc1d8jIi6ktuzcBV6jrqnS52Rq8fn4VC4GstuRDvRNV49MRuIb\nl126iICnZUGTyUoKUx4YyCy0nHeJvkht4RHTt9TXkXTRpntKrAjNPlhSlDKrnvM+tWie4b8X0v1c\n/OLaGPSDLLoGJGB8sYu0ZNU0C36G1WOH1JNyzkkXV5MP+7/LNTgqkeOq8VDAfg6jDLKUoA3BlZLg\n5YLuSyO6OyP660Pi7pzCxpRBAIEh247IBhHpLPLxEkm1uPSAyMDUwK7BzQLczGFmFt6yuDct7Flf\nY0ey+mLqMhornGwye9k2YYtWnmZwsgieSeMQSw3U84tsWETouIXXOE3sBI3XaRoCmrclhmdYwmGV\nybebw26OcSlBNyUyc5LOnNbGnM6NlO6VKWvFAZv5A64UD9jOH7Bd+CMkp82YgJzSwMzEDEwPwBcV\nzEOK1IsZybgqRiHlJKCYWcqZnC3FLMDNqmzCFrjqfFwDqukabn5/TjNsLI2FR1SyTDASrW6p+wyV\n1F88qUrcLDP9tK5jn9o1sGp8RpZEza9Rl+1vuhikhH/cuL9ZLAnqgFSpdinZOpJ+t+gb1yDlx0N2\nxzP8/1WaaRbUgefy2azj08ElLuFpCR55vxFezI4M2MCP2+1K8HwSX8NJJisZC+9VryGBsSJ4pFw/\n1d92QF2A7i6+p9E+tQVLApubuyUVO6fTDDptFngU60iG/7/Kd7PNSfeW9NATkS0CdbG2yochY6bE\nL1p7Du5XAcpHOUz8hYS9kuR6SvJqQP/WkN7mgG4yIrFzysh3OIrtnNHVHiPXo+j0yNMITNV12hrv\nQhhU7qoHDvbAPXCwZ7zYmZg6S1TilCRIvs/lDXo/Teyc5tJqpoCLBUzWCLktzaFlbIjHQMIh4KTY\nkUKFzfdbPKaLFh4vdribYZOUYGtGZGcknRntzRmdF2b0X5ywNj1ga7bLteldrs/ucm16j53ZXcKy\nIDIZpTGkRAzpkVQLc+EC8jzyNXVmMdkkJhvG5Eext/ZMDEzBTYGpOT4fZ/aJRacZ9rFYa6dZc+cZ\ncbaCZzH4S0zIQ/xgkkleLC5H1Co4bzxfmmd+nMlcXqvAD5wHVOWuTb14yHvIl11UuSww4vPvUC9Y\nkooui41Mqnv4gNJm9WTZPYr5Unl0RDjILktMyhkf7M3SFNYHnPTJnxZQ+Cg0J0J576Nq8imNF81r\npt4hi6iVDJoCv5D0qUsdtKvrb1YajarXFqEsLhap8ySNR2XMiiXiKRXqWjqasXgpdVFRsdjK/0tq\nZ12vjvfwfe0Oqa2IErchorPZYuGj/u/NXf4EH/N1p4T7BWS5P0gJe9C6Bt1XHf2dEb1kSDce0zIz\nbFQSBynteEzIJkUHJtsJZm5xGZBVBQOPTHU4X3377eo8x4shKXy62jhanGxsvKxz1GlJMnJ/M26m\n6UqS9ahpyalciEGSE8b+iKKMMMoJw5wwyMmDkNyGZCYiJ/SHCymK8GQPxaYYkrCJRbEjQeoTIDPg\nDIQW2hb6AUHPkbRzOsmcfjRmJRixypi1csC2e8Cm22eNQ1bcgD4jOkywriTOU8JZji1LTI631owj\n8jQmH0bkg+oYhhTDkHwUwMyeXKMNJ6smLx5NT8hiu41nPGedvYXHUVcolqrCsovq4Cefe9SuCFHJ\nI2qlu2hFedLrcNQFmQalf92NoK5XIsr0EHgDP+kdULu5LH5yaPoZTeP1Q/xAeAMv3hzeciQurKb7\nS3k8muXTB9TuRhELsgBtUu/MC+q+UlBnsjzpZyCT05AqAL2EvKjK9lcB7y1qV+YAv2jeps5SMNRC\nRQJOZScpu22xBEnlZRFH0jRU3F8izFXonKQpcBdFsrgiptQLjAVjCqJ8TOzGRHZM3mqTrnTItrqU\no6BuDCyioQX0K2tKM0i1eQ3NoNO5q489KS5YetdWbCCx0A8JN1Na2ym97ZTOxpiY9Li0fzcY0wkm\nlM6S9GcESYZZKRkP+6SHLdKDNsU4qjdb9wy8C9yuzs32NlLYUopUNuuiLOtYepjYkd8tpp83LTti\nlRFLTpUcESY5nfaETntCuzWlE0/ohBPawZSJ7TCxHaamzcR0mNBhSpvChbVYEKuhiAHHB4WO3J5U\nrsrCQhj4jDwHRBBuGZKVnG57xkowYrM4ZGN2yObokM35PuvpISvpkE4+JS5TrCvBGVxqcIX1dZ3G\nIbn1rSXyLPLtSkYhxbjK6BsbGJv6fyNCR4wEJXWgfzMTqxmr86wTSRY4O8Ejk45MNmNqs53ErkyB\nIYSjCTfy3yJ5MWX0j77K0e9vMf5D70skNv65kvn0uJO7LFISfzOs3jfC+xfli97Cf/ktVVwGXrSM\nqbujr1C3gJBqmrJoNTNpROzIbl4yZ5Zxx/SsaWbUyIIlAb9SG8SBKQra9gHd1gOyfp95tEa+m5Df\nDnAHVYxDbOrd2UeNo6Z1shnkOqeql1Jdj3GVq9LVmS1Rdb0H+IXnDsctQ8xKiVkpYG5wRxY3tPUC\nLO4V2QQc4serxCKJ4GkWIlQ+SHO33uxNNaLOuBTLcrWoBHnK6t3brE/fYG33DQadFzhc+QSH1z7B\nfNiDOyXujvOfTSuATgD9oJ7Qm5N4c86RmKFR4Y9hUVntjP9dGMBq4q2D6xHhzhGtlSm9cEyLGQ7D\nhA4llj5DVhjQY8SKHbAaHbFuDtjf32L//jb7b2wxuVMJnj0H+84vkgYvxsWlLkfTlbqsFp2P4rTv\nebNlQ7OgINSCpzpHcUYnmbDaOmItOWQ1PmItPGQlGHAYrHFkV/1hVsFARsS8KWoWKRvv2RQ7x2nx\n1rcgiYJq42Ogbwi2DMlqQbc1Yy0YsVkecGX2gO3hHmv5gNXsiJW8EjxFSuBKChfgMkM5txRlQFGE\n5FVPrCyNKWYhxTSknAWUM+ubyUrBVBnvYqQQ91yncTQrwi9WUH6StfwJOFvB48O+60wA6cvSwk/y\nbwFTaBVH/ED6n7P+nQe8+Z/8a7z2c19g/JWef7zEP0jtgsfdnYuF6YB6l5MAm9b/blK9tjTIk0aM\nGXUGjDTz3Kn+JrH8NOMs5tRxFgne0nCVy5PS+awQU6+IgpK6oKPEwIzAjjNu8v/wqvl77H3xs9z7\n0R/k8OvXGPxSn+xeC8aBFz2SzSK78g+jGS8kbqYDarEbGOgGvrt9y9bFBter50hvqy5+PFyHYCMj\n7s5gBPM32hTzuF6M96lbUkgRzB3q3mzNOB/lwxGxI0JZCvuJxWVR8GQpK7Pb7Oz+Di+Ev8ndT38W\nc71g8l2bZIOEMivhduk//07krTuzagA1d7rN+A+ZG4Z4a+BBDvuZj62ZBjAPKsFjYCeEF0rCnSmt\n1ZJ+MPaNGgmZ0KHAssE+m+yxw3usBkesmUM27D7vZRPMfcv49T6Tb/W8K+uoCoxu4QNJt6hjI5uB\nySLYLpuVcNEa17TwLNZlKhqPXaiMHIUZ3XjMWnzIdrzrj3CXzWCPXbvNrt0mMhlYSE3M2FQ1TJrB\nyM2jKXQWzxhf28ZaCF0lVP3P4aqhVVl4VkNv4bk63eXa8D7dckyvGNMrx3TKCUmZYinIXYBLDWVq\nKechRRqRz2Py1AueMg38kQWUqcWlprasR6cczdY3zRY4zeDkRynm+RQ5O8EjbiypEbFDbfGRgMGq\nGnGx0mbvj3+J4XekfPPXPsv+m1v+C7lBHTwshdUkVuPDaNYoke7R0qBzC1+mvRmUto5frKRWigT0\nSbrvFvXOXRbcCX5B28dnWhwW/sLWgrqWxbNOi15WmpORxOLMqeN1pJq1pIVPwe4XbNhv8rL5P2mt\nl8y//2Xmts/4N1pkd2PvdxZLoQiH08aRvHfTqiP9aXbx1j8RTa3Kh75O7bYUd8EYv8CKpW8D2AZ7\nrSTanOMOIHsQUxjn/4YD510P75h6zGxSl0nQdPMPpzlmFnfqklkzBgJ3nEBgMr/SmcIRpTP6w3ts\nTl7nxvS3yK/HHHVeJHx1CkcF5s0CTIEb4evXjEP/elBn2BhOxn1I9e1DvMVFKiinsnAF0LWwFWBe\nNJhXIdoJSVYL2uEUgyMjZEaCc2Ao6TJm2+0SlRlJOaddTsnHMYd3N4i/NYc/lCq8+Gywa3hBvkkd\nY7bCyVYRl3lD1rTwNKuZS4CyWDRks70QdBuGOZ1wwlp4yHa4y43oDjfCO1wL7tK1Y2KbgoXMRIzp\nEpKftAA2e2/JHPcwwRMC7WpzFePnnlYJbUfQMSTdgl57zmowZLM44Opsl+vmLi3mtJjRcnMS5sSk\nBFQurcz6rKtxQDEOySeRb/qZxpSF9e6u3OJKg8tNXX9OiqWKd0TCVBYzsZoZss21cGlcWk1X1pi6\n1swaVZE2TlprEsivt7nz+S/irOWdX3yV/K2oDqaTgksycTUDND/svSf43dghdYCYBHtuUtdAifAL\nVkxdsVR2P7K4yuQwox6AI3wGxC6+s/GwhCu29onrTvzjcVxdFP+/FpeiBMJJcF9VWbjYjrjd+UHK\nTshg+jIHf+cVxu9tkEdtuOILYh0XkRThc9pnJEJYGslKOrnEBImPuukaWKcWJ0n1OBHKsqD0/csX\n84DZqA2HUOyHcM/Bmxm8WcA4gjL0O36JtdD+ao/HaTt1w3G2iFktMesldqMgCjLiWUoym9MeHcLd\nHvt3P8M33w+4H30XB5OXSN/r+/YLqcV1Qv/9jkIvoHep48Mi6vElVm2x1B0CWFgNq/gtA3EAcYBZ\ngfBWRngrI7qVE+9MMWuONIgJyQko6DAhcAVHxRrfKl7hQb7N+KjH+LDL5LDL/de22Huzz+xBAbOR\nv7710Auqrcq6I+1ymlmvl3Uz5k45L8bwNAWP/I+aNXYq61gUZnTshNXgiO1glx37HreCt7lp3yEK\nTlp2Dsx6LXjkPcRyLcdpokdut6uNemz8GOo632dtFcLY0IpyutGMlWDMRnnIldkDrud3CW1BaHN/\nmJzQFlhbQomP4ZlYymFAfhiSH0VkRz47y4EXRRhcdT5GYm2bBS971PGU4cLt5ubyDEXP2QieZtCX\nFLCa4gfJi8Dn8B/sLwMx5GHI23/zFm7PUOxVFpJr1ePFspPjB8dHpaln+AnmXepFUrpUQ50CuEVt\niRFLT05d10QG4oB6YAbUKedH1d93UPjzTuTdZNIgUvl4HBfbwosNyUqSL5Whjp3ahNJG3N74IW5v\n/hC8Dvwv1WPWgCvGi1PZ6cuX8TRk9yWp4VLZeIIfS6v4sdM8pFmn1PyROC+pzCsB1UAxDylGVRbN\nnoW7JbyRwTdS73JLQj+GbuDHuqaaPzqLC5fsnOE4zsBcKwlu5QQ3M1qdKb1iSK8Y0h6OKF/vs/f6\nZ9gtXmIUX2M4uU56p4+bR7jUQcdVcX6NTJUqaPQ4c3NAPT8cNX7esLBZzRErxlt2uhazVhJdT2ld\nn9LamRL3Z7DiSEM/YQUURGTg4ChfZS/dJp9HpHcT0ncS0ndixm/EDN6MmT/IYT6ClRb027AS+fG/\nbuoGoGdRkPMi0ozhWbTwNN3fErNSfb/DIKdjJqyZQ7bNLjfMHT5p3uRl820vdmzMyPY4NGt0zITQ\nNASPuOpHnIwxO03wZPg5JjZVbypTe0GuQGAMiSvoMmPNDb1LK99lh7snm3U2rS0OH8MzsRRHAcV+\nSP4gIt+LfakDiblZDDgWI4ah7n7ew4+xgA8+72mXlXkMzkbwSF2LmDqNVrKtEmox873ALriBZfJ+\n3wfYrZi6aR3U/YckgFhaMIiAEcTn2kzhlU7Vq/h/vLisZMETpd4sRgYnUzOl8JikJE6p01oPAIw3\nGW8Z6JoPXpfy+MgYkuwFCbBMOA7gtWs50dYcGxdk7yTk7yY+WPNd/CQisWKrVJVyjf8cpX5Ou7pf\nrIWySEoj2WF12+Lr6VRdqmlTj5/uwrU5amuQ1DSR3f6D6m8qDTjr48R+38C3rbfs9CyshXWFXwmM\n1IXp0WiWDVgUPGLhaYG5XhK8khF+d0qyMWbFHLBh92kNZzzobbNfvMTuwTZFFFGOQ8r3AsitH4si\neMamrlIc4seBjDNxfe5Vt8VCuGphzcLLAVytBMgamPWCaCujvTWhtzUgtjOwJamNK7GT0mZK7kL2\n8m3eT3e4O9nB3bW4b1rc7we423PKu2PKB2PIR373vx7DdVO75mUjpuPpJKdl1jVdojlgHaZ0GJy/\nHTpM7DAthw1yn1NhQqamxdD0ODBr7Jot9os1BmWfiWszIyG3AS4AY3OcKyErYVqAKaEoYV5ABsYY\nbGIwbYsxBmMNxliClZJgs/DHVnVeKwj6BdvmPj03IHQZGSFD1+O+28a6HFfij9TXzZGfR/M+7wyu\ncvdok73xKsN5h7mLKQJbWZH44BFRjyfp29dsE7GYiXXGLqxFzlbwyAIhux9ZWFL8zviLwG/i4xZ6\nkRdCN6jdSRIwGuMnjTFecJxW5VQypN6tnncFb036BHXWjAghKeE9pzZFS/aNBGW1qYsIStYWlW98\nz/jHzo13l8guXyeSp4OMIbGqSfaT9JxaA3urIPmeCeFaCv/AkO8l/rP/Jn5RkoKDK9RujQC/EI3w\nX1gRvwF13MURPqtqSJ1Cfgv4DmqTtuzKutRffKn/M6jOkqUgAuoBfiEcABNbN/3cMxBHfvxvmXoz\nIJkPyqPR/F/JwiU7dZn1AsAYysBSBJbMRkzLDsMsZ562GbLGJF4h7fZ9V/L1ErPloCxxgfG7ankt\nETwHrm4EWZg6mWFCLdB3IH51TvzKnOTVOeWWIevFZL0I1wXXMmRZxPSgQx5EpGGLKMyYZnOS6Zxk\nOqOYGA4HLYaDgunRAN5I/PFOAIcBuAhWEh/MuhXBeuA3j7IgPWn9qcvComBuBhEHDuN8aQBjS2xY\nYqISm5QEQXFcuG9iWgxMj32zRpsx+8U6R85XvZnZmCwIcKHDBAVkGcxyiDIcGRQ5ZBkmc9iWJUgC\nbCvAJpagFWCTgGglJ15Nidd85/NkLSVaTUl6KZtmj54bEpCRupCB63OPbdIypJzhjxTKKcc/j6dd\n7kyvcneyyf50hWHaYeZiytDWliwxDDSPZo85GV8SanJaJtZz5NkLHolZEJOdBHw1TfP/L/Db+EVD\nuoVLHxgp5iVVjyW/X760Es8hokjiaaRysiyOzeqOUlSw1biuw+p5R9SuEVvdlqJvM/witYsPOpzl\nlSUo9NacbfziKs1DlaePLFyG+ssFuJElfzvG3bMU74d1jE2M/+y3qIMzpZdVhhc8zUaRYuWTLB6p\nqivBzVKD6Qb1DkfcFQ6/uA2pBbhYCaV+zi5+jL9XwHtV3ZWZ85k6owCCwGf8SId0qQh9DiaLC4n8\nz5pxPLKQ/f/tvcmPZUeW5vczu/Mb3T3cI8jgzCRz7GplqRsSulBaNCBAWjWgBiSoN91LbfUHaKmN\nFtpLSwnQrgVB0EIFLYRGCRK6KqsrK5NZOVSSTJLBmHx+z99wJzPTwu7xe8MZzExmkREeHvYBhvs8\n/Pl7Hn7tmX12zne+o8AaBU2Ea2LKbYGqNE2VEy0sm82EyhW4QsGORd2xqDdtNx8iXKF9Zd6WvsXH\nOb3ZqOgNN93vcKcbtyF/q2T29jmztxaYuWaVTVinYyqdYWtNtShoj1Ki3FyOeN0Sn7TEJw3upOXi\n2FCerOF4CcczOJr6q9M+FToe+XVpL/UaHkn/3mRvna8TwwjPIMqjAGUdWlm0NujYEKUGnbU+wqOg\nJmajCpZqyim7JKrm1O2yUDNWekQZZzRJjE3xhGfbwLrCxRVKlThbQV1BY9FFTJTHRLOYeBYTT/3j\nfNpQTLcUky3FdMtourl8PGbNhPVlhGfhphgUSzPFWDAlmArMCszSj8264Kh5haP2FifNnGU7prQd\n4ZFq5mHFlXw9LD2/GuEZCuGfc3QHnlWdh1QtiIBPoibgFwc5ZYuHjeLJ/KIsUMPqB/mDS/+SzqaH\nkn7xifGRHdHsSPny0FBLrL2l1FiiPTF901DpQH2Bt/U/7Uo8jevzlqLlkNN9wNeH4YdmmL+WKoAa\nzMOI8sEIVTnsSeQ3HsVlNRS36cmzaC223etLhEYikI7e7E+q8MRD6Q4+6rJH/8GXD/ph9zPiljx0\nFpW0hkR2PrfwWQNrA9aCiiDOvJfLfvc7h15Yfz8M/25DLUZHdtDgWo1tI2ztsNuIZpWzXs9QZ/gq\nFRf7Cq4d1xGe1v9wDi5VPiV5TJ/uvixgGLyvGLDN8C1Gvg/Z3S3z1864ffcRbRETqz2MgrbW2OOY\ndpFjT2LUxPkxdagzh/rMou853Odb2odHtA8P4eEJ1PtQWagSmBW+4ehB5o1Up5FPkU744uYT8OX4\nsgiPcmhn0Rgi3RJFLVHSEmctOm6xKGqVsCFnyZRM7aKwnLDHQs9YR2O2SUaTRrgMVNzCuoZlCfEG\npzYos8XVW1Rr0DohylOSWUKyn5LsJ8T7CeNpxaRY+TG6YCqPixWRaom6KFSDj/CsGaFaS1t22bna\nZzzbU0V7BNuLjIU64JxbLNScCzWmJMXG6gmd0hNGwbJmDsnQMMKjnjKeI55NhEeIygX+BKzo20NI\nqmuCn1Dn9OW7IhST50l0p6J3qhWNxJS+xP0RfmP6Fr12Q/7QoqEY0bvbiqBaIjvDxnnymnKK+wTY\ndpR/P/J5eOk3I1GmgK8fUskn+iohKTK/nMZWuq9usPSmlsMTrVTiCVEZd49r/P2VD+1F914S1ZGu\n0UJ0ZCMbLohD40nZVCWPvca76j4CHjlPjk66FSDXMFL+vURUL9q0a7BIvJBQVx7LRg99W4AKWCnc\nSsMmxmiHbRSNUSgUTitcovqoX7e4q8SiW0esDBiFfaCwqeqiRQNnuFTDKIVJCrdj9BsW9Y5Ff9sS\n77ToHQupD8i4bh45ozAmojUJpk18mlxS/8fOt5/4yPr2EIcpHMZwKOk11WnJFMxiH9m5FT/pgRLw\n1fAUDY/SoGxPeOK4IU4b4rxBR6bT8CRsKFgwJVINFs2J3mURz1glI8omo8liXNNFeBY1Lt+i4jWo\nFc6uoF6DMWiVEuUZ8Swj2c9IX0vJ7maMJlum6YKdtDM4TBfMu8ctSVdw3hWeu+7apjQX3bmxxj8+\ngfoh1MuUdbLDJt1hm87ZJCOqNMUkup//48GQNJZEdNIr12ui2xni2UV4RKAsVU2GPucnomA5TUsV\nlqSThD0OvVJEZ3GB30jud1+7Lh0gqSWx3R+WF4qQWdFXX4n4Sk5jGT0ZAr8ZXhoQKph1osOJenk7\nCT9LyByCXlvzgL4iahhOlQ0C+jTGMDUlUTmpahAh6RF9FYFUU+3jdV936OemxadM5XQjonUxrRQy\nJfN6KH5+5OAz21myJ35juoMvPR/pJ3Pg12CBuBEQsiyaA6mGKfH2AWcKzjUqsmht0ROLShx2FWPP\nImwc+RLc2hMjPWpJ84bkoEFjqH8TURcxNRFPeBeMUnhtD+7uot4cE3+7IX63JnmlxuFYlxNsqWlV\nwkqN2aoJrU0xTYTLgQPrdUBGwYWCYwuHNTys4VEJqwTMHv/vC2oAACAASURBVOQ5TKd+zArYSX1k\nZ6a+uG4G/H64quEZkp7IoZxPaUXaEMUtcVKTZHWX0lI0xGwoiLocak3CWbTLop16wmMyGhNh247w\njBrIKlyyAdXlmeolyrYonRPlOfEsJ93Pye7mZO8YxuM1s2jBjj7jVnTCXnTKnj7lVnTCBVMWzFmg\naRixZMKCHZbNhDpVPpZQQ72C+hTqR9CcJzSjMe14QjOa0IxHtEmKjfSTER4RvktgQObXcDzNFPga\nrGfPTsOT4jcYadgX04ud5CQrolGJ5Ag52cX/ocXYSMp7JbXxyPqhOpfSN+n8MejLLgcuqqzoUyPi\nvzOn31BlUzsb/B/E9TYDDrRPa8jvE/DNQiIlcn+EQAg5EW2WRPIk2iKeKGJ6KXNQUk1SuXdm4aLx\nQybNbkecD1TvrC33WjQ/F92/SQlpS186LmRHBNfSQFack7Xypci7qvdFkc0p4OuFpMgzeksJaRq6\nrzq9n4KxQ08s0aRBTyzmzHn9ThyB07hGwUaj05YkrxntrImzms1eih0l1KT0/UMeew3NaxZ+UKC+\nUxC/1pC9viV/ZYNbRKzOJ1ycz2lNTBMlNFFCG8e4BE94psZ3OV9qWCpvVPi4ggdbeFR7YbLbg3zf\nk5zbKdxOYBZ58jzSfdQ5HMZ+Pyie7sczGMqCciJcNkTKEHXeNipynWg5ZqsyNGNcJ2JeRjNW8ZjS\n5tQ2wVjfFkLrFjducEWFTSuIt6DXOFYo1aITQ1QY4qklvmVJ7ziy16AYbxizYsaCOefsccI+xxxw\nRORaapdw4SbddcqRu8Wxu+XJjoGqgmqjqJdQnUF7GkGbg8ohzqHIQCe+QksOdxLZGbp0D20NhuMa\nzrlns13LxpTgT1ciQBYGKD2QxJhQfitJG8CTVtWKXpS6BDadq+D4FszG/YYzHbxPTp9WkxRVQ89Y\nRQTd0E9u6MvT6+41XqXXBF3DG3pjIad0CZOK7kr0YGJ2Jd5IUjUzTDVJhGdGn9Y6AjIL0YKeXe/A\nNIbXlb/fInaWqGKLj9aI7kvmmLRKEYI9rAySBqOVglj7OSRER5yTw3z6ZiCERyI8oieUHlbnCha+\nJFxPLPGoQactTBS2iDBplxNtFG4N5Ip4ZEgnFUlU0kwtOnc+rWQ2wDmoQ5hN4bVd+E6N+iNLtNuS\n7NWks5LtxYTNZsT2cIKp456EjxzMLeQGNTe4Et8N+ww4snDUwlHt21IUOeQTGE36SsTX6NOhoRLr\nD8Nwwx5GfLu9yWlwVmGbCFPGqJVFpc43D00NbVxjohgbRdhY+9LzyKGU9VEhZYhVS6oaUlXTRgqb\nWcxIY2cJZm+EvbCorQaMJ7F7KWqWoIsUlWi08qzMoTBEGCIaPOkuySmbnLIpKOuCqskp65yqzqm2\nOc0jaM4U7RaMAZuAGwM2gnnq/ZrmsSfOc+2DCOIcP+yJJen6p5GdaxDNeRqeTYQHnvTKkciKEJrf\nFg6TqoqrQjsxoGvwC82e7iu7duh9UuQ9JM0hJ7yG/tQnQix40mxKqi1O6UuS9+i9VwKeHYQMSDRQ\n7mWnIb00vBLdzrD1gtgZGHpTOElzpoC2EJcQL/zphhnMHdxVfhMRvVe3/lx2Phfn3KGZ5bDz+Za+\n3cUSv7kavEPqHk9uToHsfHOQCKEUK0jkTez8OxdktXREM0NsW+KoweUx7TT1HFgqOpdgiaiaHF1a\noiqjLBPaLIGDGNwuRBZ0hno1Q93eQR9E6Fnjq3dWGa5S1I9z2qMEd6K7CLiDwsHMoicGPWrRmcFW\nDnuksB9ruBfBIvOCn5GFndx7NYlb/Iz+IBaEyb8/JKozjO48jfRIIY1WWKexjcaUMawcRP62NHlD\nmyaYNMamkRe2Zwoi0LguItQSq4ZEN6R4wmNSix5r2lkKuxY2Clsn4AxqX6N2ItRUo4oI3REehcOh\nsGhaYt+IlMwTnrag3OaUm5xyU1Ctc6pNQb3KaQ4Vzbnn5tZ6M3c3xvfkmqcw71Lt88hLN8REVWQD\nwyag15zgXMWz27alrA36Bn5yQpcS8GF/EvHDkZ5XImIW8nLcjQjYH8Gk8EaFY3zZ8Lh7nry++OyI\nlkf0GcMQnbyPePxISu0efuO7RSA7zwuy+AhJlfs6NIms6ReogSnhEy7NkgqzeMJyjG8kmsy9h5Ie\ng47hFeWFylLZIhEi6Ye06F5jhF8QbtGLjeneT9oJPKL3YpEWKbv0UZ0XZLF4YTFMiQ4js0KEO32V\nunBEpSGxDXHUYPKUZmJ709MuomzqiHqbY9cRumlptxFtquEgAr3rq+3iHXhNo1/JifY10azBbRX1\nKqMpM8zjuCM8ykd1dhwUFjW36FFLPGqIshZTQ3ukcR/FuPsRLFKw2v/Mbgx3op6Ui15xePIO+P0w\nJD3y9dOiPLGXiTqnfYRn67rKXt+Hqh21mKLCFDHWapzyHjYq8dQkUpYIn/5KnCc8JlK0maUZaZil\nuD2FbRKU7U7st0HtdZV6BejEXRIe4JLw1KRUZGwp2LY5221BuSwoFznV5ShoF2AWXEZ4nMhLMt21\nO+kIz6yTiMxVH9kRHaNIRa6Wm1/zOffstm4JK8uQVIM0Y5SUgbgxC4uUDU2cSkUDtMVvMBmemUJf\nni6lxdJkUvQckuaIBu83jBgo+jJiyfNXPGmu9BxtsV9aDD9QQniG6SKpzBJLALm/IzyRFWH6MCoo\nKY0TYBNBNofRvCfdd/CEWJrICjm/oPdlEhHfDB+xkV5XEiE0dELl7me29GaaMr9DZOebx5DwPC3C\n0/lvqaVDlz7Ck0Q1TZ6hJ9avMzLHSrCriGodUS8zX1kljY8PFCQ5JDuQOtSrLdGdhni/Rs9q2jKj\nXaW0RxnuEDhSfv5Z58MDhYW5Qee+xDnJaprKl6mbjx0carAZuNTPu90u5foGXzR5C/jqeFqER+bO\nMMLj1GVKixKcU120JyItG9pJgjExlggXKR/lUe4ywhNjSGhJaMh0jYk0KnMw1rh5gq0TrBUiZVEH\nLey2qKlBFS0qadHK/PYIT9NFeJY51WlOeVxQHedUZzmmMxs0pTd0vkxpobuoTjS46j5bctVw8GoV\n6TWqxvoyPFvCI+JlSUWItgL6PluyCcgfTTaKqvs3SUkd4DclcU1e029AQqYu6DdESWM5eqYqaTM5\n/cvXUrJ63n1P2gUUX8tfIuDvA0lJCaGQ1JE0oW3wc+gWT4o1t/jU5JpeLxHhN4wD+iiRfIDj7rny\n+kKYNvQkOKcXTEu0QETK0iTylN6I8BW6/jeEKqxnieFpXbQ8QoYjekPRHYW7q7G1xuoIlymYOtQt\ng3vYeW896JyUX4lwuUZNIbnbEBct8UFDW8a0VUJbJb5k/RDML8EeWkwZY6sIVylU5lD7BjW2qB2D\numN8dCc2qJXDnWjabYb5JMY91r3vV6H8mKu+mCO58v8M8+r3w5DgDP9NoK+Mjvg4q3yEpwVXerKj\nS4uKY5qmonUJRvnqPptpMKAcHTXpNDy0JKohdTUm1pBFuFGEnSYYE6FUhEo6Zr5boXYr1LRGFxU6\ntWjdXhIeQ/QE4dlSULY55bagusgpTwuqw5zqYU51nOOs59jW+ZYSViI8sepSWNpfLx+rvhjj6rhK\nsK/53Hv2hEdCYZKuEp8dEYTmeGKxpN+8TvCbRoTfNL5PXyX1G3qyMu7e42P6hU0ckqVjtbSIkDJ5\n6MPadD//Of5UfoLfoO4SyM51gRCeDT0x3dD3xWrpjQFlzgnZEfftjN71VkTo8n1Jayb4OSEVYVKZ\nJaRIyjSF8Aj5EuIjGmixQLjVjTlBoPw8IHNhKHAXvdUW38NvDnapMXWE0hEmU7ipA2vgsYVz47vY\nZxpGMbyaoPYUyayieHVD3myojgq2h2PsUYStNPZ+1FkYOOwowo40jECNDNFOi05a9MwQ7bXouUFp\nh1nG2Icx9cMY+2GEfaS9WBrn5/6+6lOosp7Btd9sXij8lpQWLVinUY2CxqFUhPE9xGnajJbEi5ZT\n7d24rWdWCteltHyX8oQa4yJMpHFZhhsnGJsQ6QydZDDyei013aCmW38dWVTSoFTP1LpascuUVkLD\nVjQ8y4LqJKd6lFN+XlA/zn1xXwqkyl/l6wJPbubddab6BslDbdjVaOILNO+eLeGBvjS0ot+sht46\nw9OvbB4XBhbOe0vkqnctlTJjaVlh8ZvSffzN26XX60iX9oInO7eqwc9VeJIlHbGl0mtC2KCuC67O\nkQZPKIZ25kOXbvBz7JjeK0cEnne7McfPAfFmkajOMX21HvSVXULKx/SCZiHsZfc+9/GkWdIdssFK\nleELtEi88BhuXqIlHOMJg4jKN+DmCrtUnvCoGJsrnHWo2IBucecNfNzCKPJEOYpQe4o0rxhlK6b5\nOauP5pgkotrkuGPfcdquu4n4msK9ruA1hdqx6P2WeL8mHjdEmSHOWthCtdC0n0Y0P89xvwH32MHa\n9b5iB8rbJIiANMylPxxf9re7OmdE8J5232y9SSQGnBjXGjAmptUJbZLSZCnNKKWuUuo2w3bK5hhD\n5io0jsS1ZLamsjmlaskTS5lD5RRZ5OdNPnJkI0eaQhQpFBprfFSndimxM0TOohzgvKB6tZmyXk/Y\nrEZsLwqqZU6zSGnP015nKOuWpP+HjWXFVFC88oa9/F6gFNZVPHv5rVQ7SKpKfHVEmyG5QdlAFsDC\neOOAmYIi6rU4Cn9jJFUlTRkf4W+aTNIZ3QKFn8AjegGq3EgRNYsJXYv385HO6gHXA0JihNxIg84M\nH9URMqTpvZeWwEP8vYXLfka8Rd9yQowHJZojjt8RPcEWwbEYbomjqJBt8eM5BT6lNzIc+lYEDdjz\nwbBaVATtM/p7tgaOFfYwpn2U4G4pjEu88FRazRTK9zmbOPTcoGcNydyRj7eMRmsm4wvMSUKZjtDG\ndi0mHO64yx9k+jLyGGWWZFqT3toSZQbVCevtKsIeR9h7EfbXkW9jUznIXT+HZA5e7UkY8PXiaWTH\n8EXLiUHhhLWaNo6pkoxtOiLKWlRusYVGW4eylsQZUtug7RrlHM4o6iqjrjPqOqeqM2qTU5PREqGc\nA2NRxkFjsXVEGRVYIoxJaExKbTJKU7AxYwqzZXGyw2I5Z7WdUjYFNSkmiZ5s4D2+Mq42AH2aAP4F\nn2vPnvCIeFBcly/wGgpNXwYuUZZV9/xXI+9dMtNP6m6kLYVEisTcbUMvVH6Nvn+S5CFFoFwMXivD\nE7APu+/doidiL/hNvlEQEaFE9zbdWNL3RRMhqpBXS19dl+DvrVS0XPqfdP8m5oAnBs5t562i/WYl\n5Fm8c4YRQrFZWNKbC26799odvF/A84F8hiWtLq1p6u7fS7BnGvN5DL/KMC7G5BE2j72+IlHwmoY/\njtETS/KeI75dkk0aimxNEW8o2LJtauJt6zU3CwuLFpZdmWjd7Z5pTJS0pHHNKNqCgWab0mwymscp\nzcMU+yD2UUKr/Ly5TWcRpfq5HMjzN4enRXfE4kQ0okObk+4Qbp2mSRKqNCPOClRuoVCYIia3Jbkp\nSY2/ykhMS2NSmjal7q6NSWlcSq1TKpdQW98WomoTqjqlUjmNTWmalLrJqJqKrKnImpq0rlidTrlY\nzlhvJmzbgoauCahEp2W9m1y5flkDUHhyrr2g8+7ZEh4JE4oOQ4TFJV8UGdfdb7eHj+pk9NoK6Kss\noBcjNvTGhlLNJcSn5smO6urKz1zQ6y5eoa8AC8Zd1wsyh3L6VJR0KJdqLInQSbPOiL6SJceTkIS+\n8gr8vZ51Xz/G6zXWFWQR6BSmuteJyYIgeh8hPjU9YRJd2RxP6KVxbcDzw7BwQqK8q+5agjtTmM9j\n7EijaofbVdhdjdtVkGh4LYaZQ08b4jdKsjsVo8mGItpQ6A05JWlbE20Mauk8YV62sKy8N0+TgtKQ\nQpQYsrim0BvfO2uT0pyllI9H2EcR9oGG+8r7Qc07XcWu6nU7Qw+UgG8GQ6F7Qv95lzSoHK7kwLXw\nhKdNE+osQ+cWV2jMOKYep8zbBWnbkLSGcbth3i6YtwtG7ZaWmNb52q3W9Y+35Fy4KUs75cJMcc2U\nkpytK8BAUjVUZUNSNSRlTVI1pFXD5nzEZjlmsx2zbUbULsXEVyI8QnqGKaynlZ5fnWcv8Jx7Po4y\nMf60Iqfzc/o0hJSCfwsfnRmaFa55UlU/TI1pel2FiJ1F37PA39ChzqfFb0jSl+k33XW3G5J+CLhe\nkA+bWAWU+Dkg2pkcfx9H+Hsf4QmOVPRJdFGq+6SPmhAfcekWrx/t+opCOeHJEB2atCw5wncVkJYT\nsphMeaEXiRceVytvRIsF/SGoBS7APqZvUvuaglZBqlGpJXrFoV93JNOWfLcm39uSF2tytqRUpDRk\nVBR6wyRao3WCsS1t22IN0MTQ+PmkaofeGuK1gVLjjjTt44TmXgoPlSfq5/hGoDleqCw+T0NTzYBv\nDsMIj5Ad6P2+hhGeJXAG1kW0WUyVZ7hC0Y5j6lVKOc5Jm5ZpsyauW8bNhr3mnNvNIfN2gYkirI4w\nOsZEEUb7sVYTjtw+qT2AVlGqHOc0pRth6oho2xJvDPGm7R9vW6pV1pkNZpRNTk2KTaKnR3gkZS+G\nrJKqlwjPUNLxgq9jz+djI6cs8S+5wBMd8DdE/EwkdSAbkxAUsYav6Hwsutd7o3u9Y54MOQ77dzn6\nEmNpTirNHxP8xigN0V7wm3ujMRTbjfEk9nM86RCi8RbwNv3pRfLuw0aykgo7xs+DOfAPgeMIDjNv\nZml8aemlPkeii92p7jJ19oi+ia1UZAnZCXPp+kBIj6NPaeZA28B6A4drcA0UY7g1gmhMkW8ZFSvG\noxXpuEaNWnRsiGnwNTqamoTR3prXvvU5d9whq70RJx/POE1mrC4mvlnsiYaPoD1O2M7HMAez0ZSH\nKebQweMGHnclMK9E3gtql77oQnQVAd8shh48lj6zoOkrNYeE5wI47SI8RYIrFGYUU09Sqqkh3jRM\n6zWmiklqw7jaslef8Ur1mH1zjEs0NtG4VGMT5R9rzZIZqatxVlOZjAVznI0oTUFdZeiVQa8sem39\ndWWJ1pa2jGmqziKh8SXrJh4QnmHncyE9UnEq6dJh2vSGrF/Ph/DIH1A2g9/giQvAO/gUwIi+Jb0I\nUKWEdEWv0zmjP7V/C39DHwAPnU9NiAncAlCq3/Rk83pAd5LCLyy3Cc32XgTIyUM+wBsHxw5K5zvY\n72hfgSXahxme5Ei+XdKdq8FoHOq2Rb9nsfc1Lkvg0MGZg9r4Bo5FNzFaPLk6ws9dMcZc4ef1Ln3q\nLMyl6wPZxORxNhimhfUF1CdQb2H/lu99Fo3I8y2701P2Z4ckRU2TxrRdF3UpSq5Jme6smX5rxXRn\nxdl8h0/itynLMav7GbSRJ9IOmiKFAtoiwa6hPVSe8Cyazhilq8Qa9luTVFaYT88Gsg8M0zqiQdX0\nWp5hhAdNM0poRzFq4lAXDrVy6LXlVnWGLSPi0jCuNuyV57xaPeZu+8A3i80VLvcaLacVJHCmdnEo\nSpOzdDNS2+BaTalHbLYFagUsHWrpjTO58I9dq7BW4azGGeWL4mPV69e+LMLzZaXnNwTPNzAqKSbo\nP8Sihm/wZGbBk13JRVezwDPtEX5ReAu/wTn85nNm4O9M18Fa+z43YkooaZDPu9e8jY8MDYWoAdcb\nco8uU1AWohqUgTiFrMuFyoI0FCGKWF0MBWv8h/4A0rsV2asbmp9lVGcF9tjCduuJTFpAlPbprEd4\nwrzshkQIpfdM2JyuJ+TUKlFCITybBjYXUB3C6gLeUFCOIII8L9mdnPLq7n3fIV2N2DCm6sy8HIqG\nlNHuIXd3PueNd+5xPDugLEc8PnodFrlfe06ABbRRQqsTttHI224cNnBYQ9X49ehA+7nU9bK9rAoM\neHaQNUO6pg/tU65am8h65BTOKdww9W0A42hNjHMahSNWhlTX5NGWkVv7jJkBW3vTbduCqyCKIrRe\no3SJ0w1WW4xWtDqm3aZ9lHl5ZcCTpEV86cRkULSIotmRVJb6LeMG4PkQHplAklqQlg0O/0cXTc6m\ne77clGG4TTQ7c+BNC+9ZX8l1qD2ZGQHfs/DYm0MR0bekkOaP4qIsi0pYUF4siPA8xROeuIao8QLT\nNO3Tl+LXI6Hcy5YO7rJnmrrjUG84sne3jN9dsq3HNB+muM8aVLvCrcFlEeikT6k+xKewtqpvG3EH\nP5dE8Bdw/SDrj6E3kRzjmwq5MbhbkI9Az+E4g59BtZuxmO2QzivS3Yp2N6Ldi4hGht3ynL3tGXvl\nGaN8zThf43JFnle8NfuUfL/h7f1POdoccLjZ5+h8H1QDugFdd/qxrlGjjmE/gluqT2WJK/wN2XRe\naAyFzLL2XE0RCZGQNUDuXdxNPa2wCdhMYVtFaxSt9W0e2tbR1tCuoLWdV2oMqwi2kS/0a2Nw4hAu\n6fSLK0N+t/TKY/EEGxZfDKuxbhC5eRqeH+GRxo8VfqPI6SumHvKkuGrR/VwxGHn3c+8B7xjUmw3u\nVync1/AL4E8U/LMI/iyCv9WePH2Kj+pIOu0ufZ+QkBd/sSDRQRESZxpez7rWv13C/bB7rlQkDE0D\nZbxhiSYN+wfH7B2cchFPWD2Y0oxi4j+pmb13zu7JQ9wnEccfpCzvjXypcWagjiGLe/sCEZWGyM71\nxtBGQNJaYyBJIJ12hLmGeAKHBawU5ajgfLxHO07I7m6J3muIk4ZpvuRgdcx7px/x/tnHbHcy1nsj\n1klBEje8PfmE9259wmp/wgeH3+dnix9wdLIDbECt/UhjyMZwawzjBHa6HkZSKTo0fQt4PhgSgWFq\nS/RfkiKSdUbu2+CA7mJ8b62k679lFcYpTKtoSp9FrRp/rbeOuvSJikUCqxi2iV9yTNItcdIbUCw4\nhun5nF4rOzTbHA2GEJ5hi4jh//EGkp/nR3ikNLyg71q+wZMdidBs8BoJKQtM8KceITvvWPS7LW7k\ncMcx/FTDT4Ea/vTs/+VPP/5z/ve9/4xf3LkD/98v4fh1aN/2GqGhzX84ib94kBO6EJ5cw27mDdqO\nlT8aHeHFyLIYCeGZ4yMxbzh4wxK/W3Iwe8h7kw/59f3vcvTgVdzMkv6TLXv5Ge/wAPOjmOrRPssf\n7fnTeVTDPIeduI8Qhoag1x8S3bH4Q9cwwjNJYDKD8QgSB+cRHEVwDmVS0KQpy3RO/v6GSXzB+M6S\n+d6C/dUJ3z3+Nf/h/R9xr77LJ8mbLGZTsqTmzcnnvLX/Oe5UoRc1R9UOHxy/z2V5qjrz82isPeHZ\nTztdheod3oOm8Nnjy8qwh6lxkV8MnYqvGveJ3kciPAqcUlilsAqsVphWUy8cZe3Ytort2lGew3YB\npzUsU1ilsE2hSqGVaE1Fb8K7GjyWauaUPhUn7VQkYphf+R2/rBHoDcPzIzyWXnQqE0WMBMUuXYTF\nsmGJG7PG57nfdag7LZxq3C9T+BHwMwcJ/ODTn/NfNP8rf/3uP+YXqoB7fwubBMZv972Wgqngiws5\npcsHOlbdpqV6n57LNhHOtybJuu+jYA+SuGE6OWO6c45L4IF9leWvZ7R/HsN3Lc0/SaimGZtshBuX\ntNGnYJcQ70KyC5PIzyNpLPu0ZnoB1xNucJXHSdcs8SCBsUNPDXps0XmLXbe065b6pMWOaqIzS1xF\n1CqliRLaJMJkGpcqVOSIlAENVZKxzOe0hWIdaRq3geoxxBUkNSQRjBKYxj6ys6P76GP21N884Hlh\naF75tAjPhD5yIoefQUrLdWkwF/nHNlbYyKe06hq2F7BuHeu1Yn0K60PH2dbLv1YZbDOoMzAZXuQs\n+kQpxNgMRkTvNSU6xzF9Xywha1dJGU+53iA8vyqtocr9jN4g8Id4/50PgJ/jT+kl/sZITlvKSq3G\nfpbhfgn82+759/33/uz4P+XnH3+PX/7oPdiOYPsfw95OX3YeUlgvNiTCI2aUUtE3wX+49+jbQzxw\n8KhzTd5Vl+L1JKk5KA65NT7kuN3no/Jdth/MsP+bxv1TsO+nrPfGnCc7wCE1H3vjuOyHMHnVu97u\n0+fqwyn8+uNqyH6YXpc2N7dB3XbEd1uSqiKpaprfbGg+WtN8tMGtLG0VU5mYtR5xPLnFZ/tvsJOc\nsZ6NKacZebSlVAWfqrf4WL/PQo/5ld7jEQ74DeQFTAqY7PnIzt4EZknf/TysT9cDTyMBw5SWRHiu\naniuprQUECtcqrCDYTKFMYrmAqoINi2s1o7lGVw8gtMVLApY5bApoMqhLTrCM+gD98R1S+8jJgfC\nYT+/q/0Gr7p230CiI3h+yRz5A7f0TR0zuPXmETt/esqj5V3WnyRgF9COwUz6ySXl6Q8V7lEEH4D6\nwHL37XtkPyw5jO/w+S92+PTHE7A5qBTiqRcF7hLSDjcF8sGUyrsT0LZl9O6a/PUtm0djNo8mUF7A\nZ+d+LrQ74DLQYFVEVReszuZcPJizvL/LvLrglR8cstodc3a0Q7lRnG0NfOCoHk8gyWE6gt2oDw+/\ngF2DX2oM9QlDwiOn8wNQ7zjiuCGLt+TxhuovzuH8DPPLM+w6pi13qM0Om2jM0fgWnyavk85L4rRB\np4YsKlkx5VP1Fp+pd7ivb3GuFpyrBfAxZHdhXsD+ric7e12UZ1gaHHA9cJUIDN2XhxGe4Rwaipbl\nfka+K7krwBUK2w3TKupjL0retHCxdixO4fwhnC1gMYLVyJ/b61FHeIYVx9sr15LegHcY4RHCowa/\nk+KlWr+en/GgMEzwUZyupPedvV/zR9/+Cf/37n/COp6A/RXwFtjJk8xaPFA+Bn4F+p7lj//rv+LW\nf37I/8N/xKP/XrH50Rr0tyAd92kzSYkFvNiQsDL4D/YGOIR41XLrPzhi/58e8vCT19h+MsKdnsDf\nfgh2D3QGUQYxNC7lcPkKZ/duUf1FhvmrhDt/9CHf+69+zr3NW2yPfsDm3xpOf75EfeyoH70L2Ssw\nn/lIoWxOL8FCceMwXOglxe46O11lUWlDsrthtHfBhjPu7AAADg5JREFUZPeC9vSQ+uPHNPPHmKTA\nNWDPZ6yPRpwwJ+cAx5ZJs2Zqt0zaLcvVjHvr1/jZ+rt8urkN9cfgthBdQNHCPIH9mSc8U/r1KeB6\n4Kp2Z0gUhi7MwwqozEHmUBmQO1TeXTOHTRVVlLJWE87sDkfNAYXeUDURy9KxrCyLyrGsLcvaX8+b\nHZbNbVbNHtt6RhUXmDjBNWqQiu2uQ3HyLr3xqQipJeJ0w0vPfxueX4RHFORj+nDcY7j3r99h8xcT\nTj+8BXEC//Jd+PHMV159Qs9iH+FPZuKuG4HJIqo6Y/PxnPqBWDFbyDoTr+Czc3Mg5FcsClpgAco4\n1GOHOrYoHBzA6P0149NHNMewKhvarsmsuR+z2U4hcvCXLeqvWpJ/UDL6RxdkPy/RPwbz1xrzNxqO\nCigOYH73yW7VL8lCcaMwPPBIX60ZgIHHJfxNhT7cMHp/we63F+zvnDPev8/oB58zqj9nVc657woe\nfHCH5SdzTruJuCWimO2Rz1PyWcr5+R4PP9pj/ZGBTy/gMIH6wFdiTe7AdA6zuCc6IY11/fA0UjAk\nO8Py9BRIPblRmUPlFpU7VOHQhcVEilLnLO2Uk+YWqfWWBItqwmplWW8sq9Kyqh2r1rJylgumLN1d\n1u6ArduhdhNam/qmsiLtGLZKEU3aPn1hjqT5w3r1nJ2WxfdGOpWfwuN/c5vHZh/ejZj/wyVv/oNT\nHl8kHD6ewanr+ht1d6y0cNRC3eKSmtNPHeVfJqx+DO2HMcQF5FHvtSPph4AXH3IfZcPqeqY1Jwkn\n/9c+6w8LNt+d4r6nOPj3Wr71w5KzH9V8/H9aFvfwi8Kj7nVaC/dK3KMN56ucT92bHJ0d0Pw6gc9y\nWO9D6mAv9wuJtB4Jc+nFxDC6k9E3Mi4NPNrCgwv0x0tG5pTd3TNefe+Mu/uf8er3fsOrs485un+b\nf/fgDosPKg5PYk47snNKRPzqHvHdA5K7+2yXIxYfxmw+bOHBha8prm/D+A5MxjCdeMIjJpWB8Fw/\nXCU60BOeYSf1Ts+jMlCZQ2cWlVl0blC5RY8s1mlKl7F0M5KmgQZqlzLZ7rJZWbYby6aybBvLxli2\nzrJhxJo7rN1ttm6X2k4wNsMZ/UXSNfx6h7569MsIz0tIfp5vQbZEefbwG9B9oClhvoH/csq/P/1r\n/pv/47/lf3r3X/E//4t/Cf8aL3CWjtgXLWxPwSywesHP/4dzosmW7epD2L4Bs+/AK3lPdsKCcnMw\nTG8WeMKTgV1oLn4y5uKDHEwM7yhe+d6GP/72EfeaEY//vPGE53PgsfMtKTYtlCU0Fywfaj7/zQ6r\nj0Y0H2k4yoA9T3L2cn9qkoqsgBcPV/UYQpgNULbweAsPFmhOKHZP2H3vhFfdCd/Z/4zvzT7ke+/9\nHZ/+dMXiwfv88oOa7V9HbN1g13lvD95/G779Hqw1/PrUj8cbGO/5MdrrS4Tn9M7fAdcLku4UsiOV\nxVcJj5CeywiP9SQnN+iiH7ZVlE3ORTuFVlG3Kat2Sr7eUK0M1dZSlZaqNlTGUjlDSU7p9ijdLUq3\nS2XHtDbD2W4CS3Tn6pjiD/rSCV00RU8rPX+JSM/zXbZlIhX4m7MGiHxX4Q+3nE4y/t3qj3kwvutN\nAvfwJ7Gkm4VWeav/bAQpXCzeh2UD8T4UM7g19WRnxEvJZl8KRPSb1i7ervS8hHILzRi2Ma+dP+BP\nDv+SnzUbfnLwjz1pNkBloao92Wk34LZs/mKBrc6o72WYz24DGdyZw1zBPPNzNfnyXyfgBcBwHRCr\nC4MXDc8K2MwxteLiJOPxTyfoaI96Z8zZ/IB7s3c4rPb5u+b7nJt9L4BnimfCDax34DCFuAUTebe4\nYgK3C5iOYZr6p+93NgrBQfl6Y3hvrpKeIdnphkolwmPQuSHKW3RhiIoWUypKm0Ezo2oyVtWE07Ii\nuahp1pZmY2hLQ9MYGmNpnaFxCTVTGjejtlMaN8HYFGe1/93kwCfERoi0mPYORdRPS2m9ZHPv+Z9T\n5aZJI1GXw4MY/pdDfvLKu/zkh/8dpBGUnRHXLn6hKPHdh213YtoB7Hf8RJTGo0EAePMhi88IPwec\ng7qCau1TCMuc/aNjvh//gtVmRrG78WmpU2DtoKl9VJEadEP50w3lTxd4dt3CnTHcnsG+Du0ibiJE\n6KmAJvK1v6XCrDOWZ1PUT2+xeVBy8s4dPvvWO+y8u2BVjvm0eYMze4DfSaQzrYb1zBOeqoHYeefv\nYur9n+YZ7CQ+qiONG0PU+XrjKiH4XRGezKG6KI/OO9JTtERFg7WKssmobYpuJ+gt6LVDLS12ZTAb\ng60MtjGY1mCdwaIxLse4AuNyrM27lJb6IuEZprGkLH44gobnGi3fMX4ReAXfJuDxDiwq+OkJnEz8\n6egBPsJj8JNunydvrIQfZTIGvDy4NNrS0I68idyRhX9zwo+nr/M/Tv85n2/e4/HJvk9/iRZsnnmz\nuSSBpNuF1B3Qu6ALmGiYqeCzc1MhhCfBR2TKEdQ5xlkuTi2b+5ajrSX+R4bYtMQ7LaaMKOuMygpT\nktNaDusYqgROGk9ydtJuxLCrYa+zxogI69R1xzClNfy3p2l4nhAt20GUpyXKGx/hqRNqlWBcQlsn\nmDKhXSXYZQSrFrYGqhYaA9aAa7v3jvs3dOJcOIjwjOhS7vg98YAvlMM/cX2JcX0Ij8YvPDt4wtOO\nYKHgYguf2j5aE+PDitIXJPTBCoCe8CQa1AiSDA5P4G+P+bF7nZ+pf46d79Ic3OpO83gTwWnm0wzF\n2Lel0LdBO4i0b0b7EnlUvJQYepHk2kddWr+gtGfQbqEq8RHBz/FkZYN3gU+BW8ZbHWjnG3+qwYuO\nI9iNYTfpIzviyh3m04sHIUBXnZZbehPUXOFijUNjmwi1dZil/2FzEWMvIuxFhFtp3Er5uVQCbbfI\nxNqvQxPXidydn5eXQ3UDP5/EjFda50jvrGH5fFi/LnF9CI9AIj1vA2UG5QFU2pMcSVUJow6n7gCB\nfKAj1YlANdgCoh3a0ncgJh75rnsxnUVBp6MYqf6ENtwAg4XBywNF77QMT6YqJJDzmL4H1zl+nr2u\nfPPPJINUg+p2FwVkEYxjGOl+Qwr6rxcLwyiPXIcFEyk92VFApnCRwjqNaiJPaBQ4o7CrCLOKsSuN\nXWncWuE2ykecTfdmiYbC+fXJKmgdFJEnO4XuyY6kscQiYzi/rhKdsIZd4voRnsvTFv7m59qfxg1P\ndnYN4bmAp0FE8KnyYvbdHJbOV/UpDTryc0gqF4ToXE0vhEXi5YHc6wS/cYij+9BJt8UTngf00egR\nvlVJEXcbUtJtMB3hiboNLFZPlg0HvJgYRniEDHdelUKCXAwuVpcRHraAAVdq7CbCrv3VbTRurXtf\nuVb5eRMrb6VilT+QObq5pfqRq76VhYiUh4RH9sar/kEB1/TjN/Q9CCeigK8COX1pBSruyYxovMQK\n4Wm9bgKBfvkw3Ahko5D5IRtbiq/sO8OntlK8TmIC7Cl/Ah9FT1aDhk3m5kCIjjweprSGutEYUAqn\nNc6BbXxkx5Uaqy1uq7FbPbgq2CpPeEw3YSTCo/GHNkVHdK6QHqnCGl4L+ij10whPmI/XlPAEBHwd\nkA1MyjQFsmDJ4hUWgoAhZF6IE7wQH6kEjOg9TiQiNPQ4CfPp5uGqcFkIz5DspOAMYBXWaFSjUFbh\njEZZhysVrvIEyJXq8mtpCIDSvrJPO092rPOvXSifdr+88mQlcjp4LBGe4TwM8/ESgfAE3EwMP/AS\n4QkI+F2QOSNpK6niErJTD753NR0ayM7NwTCqcxVXD0wxXnJhgVrhKsAoXOOg0qjaeVJT4wlOLc/r\nHrf4dJa8llae9Cj8/CrwRGc0uEo0J74yhums4f8lAAiEJyAgIMDjanpLyE7Ay4nfRhSGlVBuMJTq\nyA6eADW+Xyxb/5gGT3Lkcds975K0qN7vSzRkw9TV8PGw9PxqoUUgOU9FIDwBAQEBAQF/CK4Si6Gg\nOcWTGfl3ITjtlceGL0Zqhk1JpSpLUlZXiU5Ipf7eCIQnICAgICDgD8HTCI/oe+zgOZqe3Fy9Wnod\nUHTlsUR5JIU6JDyB7HxlBMITEBAQEBDwVSAE46oTs5AVN/jeUOcjww4eD80MZejBa0m0SHp2DZ8T\nKrG+EgLhCQgICAgI+ENw1ZBQyI18T8iJRHyeNuBJZ+ThGPbrGno5BWPBPwiB8AQEBAQEBHxVPI1o\nCOG56tcjkRwxKrw6hsLjq9eh0e7w8dWy80B8ficC4QkICAgICPhDcTWlNYz0XCU4POUqr/G01NTv\n+veAr4RAeAICAgICAn5f/C6iIY7tDk+AvszP52mvG6I23yiCmX5AQEBAQMDXha9KWkK05pkhRHgC\nAgICAgK+CQxFzb/Pc4fXgK8dgfAEBAQEBAR8nbjacPSr/FzAN4aQ0goICAgICPi68VVTVYHsfOMI\nEZ6AgICAgIBvCoHIXBuECE9AQEBAQEDAjUeI8AQEBAQEBHwdCNGca40Q4QkICAgICAi48QiEJyAg\nICAgIODGIxCegICAgICAgBuPQHgCAgICAgICbjwC4QkICAgICAi48QiEJyAgICAgIODG43eXpf9Z\nqLMLCAgICAgIeLGhnPt9e9cHBPxhUEqFSfYSwDn3jZ2Owhx6efCNz6O/CVPpRuOH6kvnUDAeDPjG\n8U0uYAEvB8IcCggI+PsiRHgCAgICAl4KhEjhy4EvOyAFwhMQEBAQEBBw4xGqtAICAgICAgJuPALh\nCQgICAgICLjxCIQnICAgICAg4MYjEJ6AgICAgICAG49AeAICAgICAgJuPP5/L6/3m+g2YyUAAAAA\nSUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7feed0105690>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"filters.gaussian(im, sigma=3)\n",
"from generator_tools import ResizeImages\n",
"plt.figure(figsize=(10,10))\n",
"for i,im in enumerate(images):\n",
" plt.subplot(3,4,1+i, xticks=[],yticks=[])\n",
" #plt.imshow(im, interpolation = 'nearest')\n",
" plt.title(str(factors[i]))\n",
" plt.imshow(filters.edges.laplace(im, ksize=3))\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "IPython (Python 3)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
MinnowBoard/fishbowl-notebooks | Slideshow.ipynb | 2 | 5792 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Slideshow Project\n",
"\n",
"This complicated project uses all the major components of the other projects to create a system that will display images and show information about the images all on the electronics connected to the Minnowboard.\n",
"\n",
"### Review the wiki page at http://wiki.minnowboard.org/Projects/Maker_Slideshow for hardware requirements and setup.\n",
"\n",
"Start by importing all the necessary packages."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import time\n",
"import sys\n",
"import os\n",
"from PIL import Image\n",
"from pyDrivers.ada_lcd import *\n",
"import pyDrivers.ILI9341 as TFT\n",
"import Adafruit_GPIO as GPIO\n",
"import Adafruit_GPIO.SPI as SPI"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we'll start by invoking the GPIO class, which will identify our board and initialize the pins. We will use two pins for input for scrolling through the slideshow. We default to the spidev device at <code>/dev/spidev0.0</code> for the minnow\n",
"\n",
"Additionally, the Data/Command and Reset pins are defined for the TFT LCD display."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"myGPIO = GPIO.get_platform_gpio()\n",
"\n",
"myGPIO.setup(12,GPIO.IN)\n",
"myGPIO.setup(16,GPIO.IN)\n",
"\n",
"lcd = ADA_LCD()\n",
"lcd.clear()\n",
"\n",
"SPI_PORT = 0\n",
"SPI_DEVICE = 0\n",
"SPEED = 16000000\n",
"DC = 10\n",
"RST = 14 \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following functions collect all the images in the specified directory and place them into a list. It will filter out all the non-image files in the directory. It will fail if no images are found."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"imageList = []\n",
"rawList = os.listdir(\"/notebooks\")\n",
"for i in range(0,len(rawList)):\n",
" if (rawList[i].lower().endswith(('.png', '.jpg', '.jpeg', '.gif'))==True):\n",
" imageList.append(\"/notebooks\" + \"/\" + rawList[i])\n",
" \n",
"if len(imageList)==0:\n",
" print \"No images found!\"\n",
" exit(1)\n",
" \n",
"count = 0\n",
"\n",
"print imageList"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we'll initialize the TFT LCD display and clear it."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"disp = TFT.ILI9341(DC, rst=RST, spi=SPI.SpiDev(SPI_PORT,SPI_DEVICE,SPEED))\n",
"disp.begin()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This long infinite loop will work like so:\n",
"\n",
"<b>Clear the char LCD, write name of new image</b>\n",
"\n",
"<b>Wait for a button press</b>\n",
"\n",
"<b>Try to open an image</b>\n",
"\n",
"<b>Display the image on the TFT LCD</b>\n",
"\n",
"--If we fail to open the file, print an error message to the LCD display--\n",
"\n",
"----If we failed, open up the next file in the list. If we're at the end, restart at the beginning ----"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"while True:\n",
" \n",
" lcd.clear()\n",
" time.sleep(0.25)\n",
" message = \" Image \" + str(count+1) + \" of \" + str(len(imageList)) + \"\\n\" + imageList[count][len(sys.argv[1]):]\n",
" lcd.message(message)\n",
" lcd.scroll()\n",
" try:\n",
" image = Image.open(imageList[count])\n",
" except(IOError):\n",
" lcd.clear()\n",
" time.sleep(0.25)\n",
" message = \" ERR: \" + str(count+1) + \" of \" + str(len(imageList)) + \"\\n\" + imageList[count][len(sys.argv[1]):]\n",
" lcd.scroll()\n",
" lcd.message(message)\n",
" if(count == len(imageList)-1):\n",
" image = Image.open(imageList[0])\n",
" else:\n",
" image = Image.open(imageList[count+1])\n",
"\n",
" image = image.rotate(90).resize((240, 320))\n",
" disp.display(image)\n",
" \n",
" try:\n",
" while True:\n",
" if (myGPIO.input(12) != 1 and count != 0):\n",
" count = count - 1\n",
" break\n",
" if (myGPIO.input(16) != 1 and count != len(imageList)-1):\n",
" count = count + 1 \n",
" break \n",
" except (KeyboardInterrupt):\n",
" lcd.clear()\n",
" lcd.message(\"Terminated\")\n",
" print\n",
" exit(0)\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
wjladams/youth-isahp | javascript/InitClassIdea.ipynb | 2 | 4216 | {
"cells": [
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"class PwModel:\n",
" def __init__(self):\n",
" self.alts = []\n",
" self.pw_votes = {}\n",
" self.nAlts = 0\n",
" pass\n",
" \n",
" def addAlt(self, altName):\n",
" if altName in self.alts:\n",
" raise NameError(\"Alt already existed\")\n",
" self.alts.append(altName)\n",
" self.nAlts+=1\n",
" \n",
" def addUser(self, userName):\n",
" if userName in self.pw_votes:\n",
" raise NameError(\"User name alrady existed\")\n",
" self.pw_votes[userName] = np.identity(self.nAlts)"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['Kitchen', 'Math']\n"
]
}
],
"source": [
"model = PwModel()\n",
"model.addAlt(\"Kitchen\")\n",
"model.addAlt(\"Math\")\n",
"print(model.alts)"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.addUser(\"Bill\")\n",
"model.addUser(\"Jeff\")"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "NameError",
"evalue": "User name alrady existed",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-43-de252f210060>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mmodel\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0maddUser\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m\"Jeff\"\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m<ipython-input-40-5d10fcea6941>\u001b[0m in \u001b[0;36maddUser\u001b[0;34m(self, userName)\u001b[0m\n\u001b[1;32m 16\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0maddUser\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0muserName\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 17\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0muserName\u001b[0m \u001b[0;32min\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpw_votes\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 18\u001b[0;31m \u001b[0;32mraise\u001b[0m \u001b[0mNameError\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m\"User name alrady existed\"\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 19\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpw_votes\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0muserName\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0midentity\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mnAlts\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mNameError\u001b[0m: User name alrady existed"
]
}
],
"source": [
"model.addUser(\"Jeff\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"hide_input": false,
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
UWSEDS/LectureNotes | Spring2019/06a_Objects/Building Software With Objects.ipynb | 1 | 883476 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Why Objects?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Provide modularity and reuse through hierarchical structures\n",
"\n",
"**Object oriented programming is a different way of thinking.**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Programming With Objects"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtAAAAIcCAYAAADffZlTAAAAAXNSR0IArs4c6QAAAAlwSFlzAAALEwAACxMBAJqcGAAAQABJREFUeAHsnQd8FMf1x5+6BBISovfeezPVNGMwxr3ibnDBiePYf7e4xHF33GIncRK3uMQJ7gbcKMbYdFNM71VUCZAQEhISqvf//ea0x97pJJ2kU+XNh2Pb7Mzsd/d0v3n75k2AA0k0KQEloASUgBJQAkpACSgBJeATgUCfcmkmJaAElIASUAJKQAkoASWgBAwBFdD6ICgBJaAElIASUAJKQAkogVIQUAFdCliaVQkoASWgBJSAElACSkAJqIDWZ0AJKAEloASUgBJQAkpACZSCgAroUsDSrEpACSgBJaAElIASUAJKQAW0PgNKQAkoASWgBJSAElACSqAUBFRAlwKWZlUCSkAJKAEloASUgBJQAiqg9RlQAkpACSgBJaAElIASUAKlIKACuhSwNKsSUAJKQAkoASWgBJSAElABrc+AElACSkAJKAEloASUgBIoBQEV0KWApVmVgBJQAkpACSgBJaAElEBwdUbwwd9nyPpVuyQ4OEiuuHmcDB/b1zQ35XiqfPzObNm2KU7adWopk2+/QJq3aixZWdny3399Kxt/3SE9+nWWK28aKw2bxLou8cv/zJNVS7eIIy9fptx7uXTr1VYCAoMkNydPPnxjpmxcs9Pk/+0jk6Vh4xjJyc6VJT+slc8+mCv1G0bJqPEDZeKV55ryTiSflK8+nC/rV2+XYWP6ysXXjpSo6ChZuXiDfPf5Ysk4dVqyTueIw+Ew+bms36CePPbSHVI3KkLy0Ia1K7bKR//8RkLDQiQzI0uCQ4KkU7fWMv6SodKlV3tXu+0r+/fEy/t/myl7dxySjt1aSZfu7WT4+f2kZdsmEhAQIPn5Dtm6cY989MbXuLZA6XtOZ7nujkmmiL07D8nfnp2OdmVJUFCQhIQES2BQgGRnsZ2CNpyWG+68SM676Bz5ZeFG+ebTn801dOvVTm753cVoZ5gpf/G8X2XG9B8lOiZS7n3yZmnYKNrexHKsO2THpn0y/e3v5fCBo/LEq3dJ284tvJa3ftUO+c8/Zplr7NG/o9w47UIJQ/s2rtkhX3/8sxw/liotWjeSKb+/HPe0vvP6wezff/0K9yZT7vnjjdKhc0u3suN2Hpb53yyXOx+82m2/fePI4ST531vfy/qV26RVu6bSpUdbGXZeX+nQpZUE4Tll+mHmUlkwZ7Xk5ebJxdeMklEXDMTeAMP3Czwzy39aLy3bNZYpv7tcWrRpbM5JOnpcZqHdG1bvlB59OsjleHabNG9kjh3ef0w++PssORAXL7fff6UMGNrd3D8ezMRz9s8/fyKHDx6TZq0ayoNPT8E9de8XJyedlC//M18Wz1stSUdOSFT9unLJ5NEy6epREtvQee9W43vx2XuzJT0905QdFh5inqes09nm2cjJyZXLrz8Pz/8I0yb+dzojU77+ZJG8j+8p21E3qo75fkzFdysSzzivmSk7OwftnyHrVuyQQSN6ydW3jpN6MVHmGP+bN2uZzJmxTOrUCZUX3rrPtV9XlIASUAJKQAlUVwLuv7TVrJWXTD4PYni7pKWmu8QzmxjTIFoGndtL9m4/JN16tzPimfvDwkKl/5BuRly+9Ni7ELObuNuVLoUA2A5x2alHO+nYtbURzzxI4TrmwiGyYtEmiakfacQz94eEBkvnXq2MOKCw6z2wM3ebVD+2nkTHRkouRFI/1EnxzDR4ZB/JgAjZvfWAEU+Tb7tArr/9Qplw+TCIru2SAaHMFASR07pdEzl1MkP27Tkst959qRE1e3celCkXP2EEk8lo+28V2nfXVU+bNj7y4m1y8kSavPrE+5KelunKFRgYIB27tIb4aiBL56+RC69wCn5mSDp6Qg7FJchl142Vm357sUTjWpMhNC+8ciTE3KUSFBAo+/fGQ2BmydDRfaRV26Yy96ulYNzeMGIZLL8bBN7mNbtkyMjefhTPIp+/P1dmf7nEiPj2XVrKydRTrNJr6tC1hTRuFiurFm+U9h1bGPHMjL0HdIGwbQYhvAz3uI3p+FgFsMxj8cnSvGUjadu+ibXbLCkUF85dJR/96xs5tP+I2zFrYxM6WPfe9KKkJqfKH164TaJi6spfn/lI9u46jGfJKRaZd9ylwyUOYv1kchrEdX/scR6LqBMuQ0f1lk1rd0poaIhLPPOchk0aSK/+nSVu+0Hp0J33zymeeYwiOzK6jqxZtkX++Js3JOFQEnebFFE33IjWFT+vl3GThrmJZwc6UysWbZAbxz8EHkvljvuvkv/Of0luufsSeefVL2Qdnkcr7di8F+cG4ZkdjWfxEjxbp8z36NLJY2Ty1AukQaN6pt1W/hQwePy3/5CP3vzWiN7v174pL7x5r2xdv0d+c/UzsgvPv5V4rf0GdcOzd1Re+eMHsuC7VeicZluHZcJlwyUBHQCro+M6oCtKQAkoASWgBKopgWptgabAa9i4vjRsesaKbHGMgqBo0jJWGnkci4mNgvhoKHu2H5CZ/1sgvSB6W0NQMdHi2qBxLARJQzehwWOR0RGwqNaFOD9jGeP+Js0aQFyfI9Pf+taIrxZtmhirMq29rKP/OV2lJfbZUzTEdSOIu2GwmEdF1zWHaBnu3K2tiCPflTUoOAACr56EQ1idM7KX2d9/SHf5+7P/g5icI6Mn9oeFvbUr/7efLzQW9+thbaXAeuGt++Wn2SshFFsYa6GVkVZlXmcdiKtoWL2tRCvpH1+9E4K/u9m1e8sBycnKlSEQy7FoR+uOzSX5+EmXGLzxNxfL918tktkzlsjAEV0kLDwIzXfIT3NWGEv5JFhX/ZVS0Rn44B/fyHuznpbmrRvL469MK7boqHqRMmJcf5k7c5kc3HfULW8HCOVGuH52TGhVj4yKNMfzYWZPOnZC7n/yxkL3n28AVi7aKHl4G/HLzxtgJW3qViY3Fs1dLXVxr264a5J07dXBdCSGjuoLK38ndCzO9EXZyaiP54jPZnDwmf0sIyIyXGJxT9hR80y04DZGxycyktZb99SwcbQ0bdVIjsbTAv6t/P6J62CxdT5bFJ7RsdHSAm8h8IDh4xTs7Aw9/X9vSjN0GF776A8SU2D1vQgi+XjiyQIrsbOeAUN7yMSrRkqDAov09+jIBKCTN+y8flIX7ek/rLtsXrvLZKZlffWSzeC1QZ771++NRZwH2JH87aPXyp/u/qd8BYv3Iy/d7iwc/zfCdTVoEiNHjyTJR299I4NH9UTH98z3pjGOtcBbJE1KQAkoASWgBGoCAfdf95rQ4hLamJubL2ERYXLHA9dIPF59/+/N7+RkSloJZxV9OCQUVu2h3czr+SU/rjEZKZ7TUOaBPUdgLWzjEslFl2JZbtsWEvye5/CV+hC4hJxMOSXHEk64HU46lmJcKAICnG4hYREhsD4Og3U4xC1fURsNIML6Dela1GFpDMHXFS4JEeDHVA/i/8obx8vPc1bK3p1OkZoAF4aP/vG1PP7ab4ospywHvvhgPlwQGklsKdxBaFHuCveSX+ASYU/LFqyXdLhprIbFNhVWYCut+2WrEa/t0JHAHbF2mw7RwbgjsmNzHIQerNpwZ/CWEsGf7ghBBWI5OCQQnasB5o2It/z+3Mc3Hd1h+Z8A6/as6T+jrQdNu4uqIx1vNr748AfJOJkpd8LybIlnKz+t0OfgLY7lYtStT1uXeLby2JcU0YNH9jS7UlPS5Z2/fGlE9eiJ59izSXe8rbgQbk5L8PbjyKFE1zHWExYeKtfAmp2EtwCzpi80bkuuDLqiBJSAElACSqAGETijImpQo4trKrSt5MKnd8T5/eVc+CzPgz+qp4WyuPO9HaM7REe8Vt8I/1T6gjJtgO9zMFw8GjWNKXQKxQJFtgitzRS7+fB5zsPSN9y0CufDUk1Lpj01bloffqTb8Hr8EIQ0y2MKdLM+O/cV9T/L860NVgnX3XGhxMCi/iXEWE5OlnFx6HNOF2ltrJ1WrpKW5JBvfNTp++1k4uwEOBmJ8c8dCHEfGGztL6lMgZU32rjwHDmcKEdgmWVKgQX9+NEUvHVoKonw901PO+0q6JeFG2BJ7ylBcNlx3h/nodOZGcb6PPDcnnAV6if7dhxEBynddZ61wrchO+GasHHtnhL58xmgn7nz+pzXz3IC8DzY67bK9mV5OjNLpt53uelkvPfal3I684wbhOf5J8BhwbcrpEf/TnjD4Bw74JmH7TjTFl+ei0BXZ4PuU6MmDPIs0nTmusKtKgOW/wPolLgSHr2TYDrh0hEy7uKh8HP/VuJ2HcJhstGkBJSAElACSqBmEfDlV7NmXVFBa/NycmTaw1fB4hgt7702A4PKUsp8HQ0axcg5w3tK/IFjeHXt9Ktev3KHGUTWrGXDQuVSOGVBQBzanwjxfgy+pjvkjec+LpTP245Nv+7EQMivpWvPdmaAmj3PTXCp4OCzh257DYMPv4OAOiMO7fn8uR5RJ0weffFO+e6zhfLVRz/JSvjaPvD0FFThu9Dl4MW3XvlC7r/5Jblq+H0y+4ul8IF1dgC2bdwnf39uuuzZcUC2bNgrr/9puuzast+nS6CLCgViGqys8fudFvIlP/4q9WLrynW3T5IAdEK2rt+NQaLOTs+ieWtkOKz7dOWxp9OZOXDbWIdBdaPlAgyS2783QZYvdLdqM/8l142SPnDXePEP/5bXnvyvJCcV/UzxGTielAq3h72uD/2Dd2w+YAaQ2uv3dZ3tjMa1PQbXiBUY5Pnpu7MxUDGn0OkU7/SlPxp/vGAAY6EsZd6Rk5Mta37ZBrejMOEbAG+JbijsdHl2XOn+k4OBvg8+PwUdzwby50f+LaknCndUvJWp+5SAElACSkAJVCcCtVdA5zrg1xsjt/7+MkSUWIfIB+sMd9pgS5s4mLAtIjZkQ4jtRaQGpn103+jSWhph8JdniqgbJnswsOyBW16R3171jNx744ty6IDNGmc7gRETtmMA1++R57ZL/mTyMnLIHzBIsF79M/7LPKUj3EWefeMe+Ag3kpcgPv7+7McYYJmBIxVrxRs5vr906d1WXn38fURDOR/ih1EtfCN5LOG4vP3KV4iK0lH++dkT0g8RJN55/UtYJxN4SdK0RUNp26GZsYSOgTsABzd2RCQSX1Mj+M7WjQqHb3OqOWXn5v3Gn3vUxIFSB24H2zfsMwPWdm87AIu+GD/vM1ZXZy2JR1MlKTFVRsD6TBeaZuC7cK7TXcfejjbtW8hj6Ez0HdxF3sUgPArp+IN0UyjcmQhBFIst63bLS4/+W1585F3zeeHhd9CR+My4gdgHHdrrKG6dLzXycvKN73ffwV3lMwy6TE93Dkq1n5eLzmNiQoqEwxWHVnPPtG93vPzj+eny8qPvy7IF60wUFs88RW1TBKfBXz04ONgM2vWWj4MGo+DPTfcZ+v7bU25+vvGpZjSPreCzfuVOHHbAsm3PpetKQAkoASWgBKo3AXdTXBnb+ptLnpZNcG8ob1qaML28RRQ6/9Lrx8oy+Mi+8fwnMhwRETxDfBU6oYgdzTBgsSHEGoXYjs37jJ91u07NveY+BbeBLrAgv/r+gwjXFSmn0jLkp+9WeM1LQdIUgx5vuusi2bBquwnfNuy83vDtbe81f/e+HeXD756TN1/+XD5553tZ/MMa+TcG3jX1Ygn3WkCZdjpk/KXDYIFPlEkYgOZrykSYs49hJe01oJOcO26AOY0h3WZ/uci4WnAHQ/sxOgX91ofC1YDhCEuTOPCMftvbN+6FT29P2bc7wYQ8pD83Q6Ytg2X59gculR+/+0V6IrRhWLh7n5Eh/JaC4QAMkmM0FgrosRDys79cLPsxCLFNB/cweu3QkXrj48cQRvF7+TfcKBju72/THzXRX+ztzsKgxHMxyPHpN+62uUkI3kocld+gU8X7Xp70GAZZ3jzhYQjhj2XqvVe4FUVxztCI+RCrublO67s9Q+v2zeDnvdmEabx66niT1368+PUAjAfgnw2KXu/XwHrp6mTCJHq4IVllT0OowLW/bJHnH3wbvtR/dYXls45byxHNbrBWdakElIASUAJKoNwEeiO877++frLc5biriTIW5w/xXMaqfTpt8u0TTTSG2V8tQUi6LDdB41MByBTbqL6069wa4bYSER5vI6JzxBrrqffzHcZ/OQSCjFEYGE3k8pvGec1KEcLX3YPgm3vBFcOkTfvmsvRHDIKD6C4qRdarKw89N0WmPXSNHN53BAOyfjQxh4vK74/9dElgpImiRJO3OtjZ2Lh6ByJ2cNCeM1HQMRKFFTOZe/chtnVE3Qh8Qgty+b5gtJPusG7vQfg3hmyLbVzPDIZkCcMRn5lxjxMOpsiWtbvNoLfQUOcASasGxvpeircT2fA7n/XfBfL9Z4sQ7i8FMY6zZTVEprdEyy5F6yMv3iG5OP/L//wgKbbBitY5FJIVldojPvbNCH04C5Fm1mJwZHj4mesKDg4RimSGiuPz6pnoW0/XphaIghGFZ6k0ieEX6bZEf2wOJvSWGPnkZNopRN2I9nbYte/uR66TUwj5+P7fZkhgKHz5fXyr4SpAV5SAElACSkAJlJLAxlXlN/iySr9YoK22V4QF2Sq7PEvGhqbY/OCNGfC5PGWEYGnL46vw4WP7yNuw/M6dsVSuumW8iRpR2nKKy9+ybXO5btokee6Bt+XzD+bJVEwCUlziNf2KSBMrETVi6n1XuonS4s6rrGNHEW3hBCbx4CQ0Vtq2Mc4Zn9kWXo9WWVr3Q8PK8jgGmFCFnITk43fmyNgLB5sweKyvH0KztcBgwnf/+iUGFCYjbnUvt4glDkee7Nm2H9FU4o3P+eYNu018br6lCIcbzroV23GfJ1hNL7S85Loxsm7VVlmPfOknT6EjdOY6C2WugB2MNPMjYiq//tRHsKy7R2Khm0+fwd1lwfcr5dZ7LvNb7Yz4wsGWAQiVyImHOImQZ6IPeUZ6hrRFfO7iUu9BXWTClcPNxDe0Vg8Z3rtQ9ur6N6VQQ3WHElACSkAJVHsC/nyr6RcLdEUTS/di6eIgtFMYPBYe4ZvVcvJtEzEzXVOcc8q4rPrmwet+Ze3x+p7CirPRcea/0qd881q9uPN6wpo6cFgPmT9rOcS+06/XW37LEhwDl4N6iIldHY13aQillouoG3a3mQ0Qm73h0mGfNCM5MQVuLA2Mj7K3ay1pXwvEjQ6FtX/t8i1mAhm6hTAxrncbWGIXzVklHbq2MmHU7GXlwRq++Me1mJSntzz8wlTEyJ4mj2KmyN89fo1079te4jD4kdEsvCUX/9gYxBCPLNNbDW/llmYfwxlyYCnFO8Pr2RPji0/CBDl7tx00kWjsx8q7zpjhI84bIPO//qVQUSeSU+RXdOiaNm2E+OiFY2l7nnDnfVfjzUO4nDyZ7sWT3DO3bisBJaAElIASqB4EqrWADgx0GAvXOkybvAIhyKzEWdBmTV9gYir3RBQGXxL9W6c9dLUZYGaJH1/Os+fhjHC9B3Q2k4g0aVl4cJY9r+c64/h+/PZsibfFxvXMw21OIX7xtaNMWLaNv+5yy/Ljt7/Inx/+N+JDJxnBlgSr6hqIRs4kyOnOq1tilAyG5MsoGOg2+4tFCFMXKOdfOtQMJLPaeyz+hInn7Gs8a+s8a8kZCVtiZsFWEMst2zaydptlr0EdjY/vueMHwdf6jJsDD+bmBiCG9Aa54LIRbuc0xCQsYzEz5X74U1tRV5hhNVx3XnrkPUw3vtfw53Tty35aC19nDD4sRfxqt8rKtREgF10zAp/RchptMZETC8qjRXf0pIFy7oQB8uZLn8l2THtvT2x7oP0E+8ES1un2cfv/XWlmsfzHC+7RZdYs3WYGJk68egT8/4t3D+H3sCmmH7/vTzeJw7hqe/epLqE5elgJKAEloASUQKUTKMs780prZGBQsEy593LZsSVO7r7mObkYr8zbYrY8+rqeTMmQx165vVBbNiAM3LZNe0yc5gHDuhnfWisTY/wOG9NPcmB55Kx0luSkryqnpj5y6LhsQ6ixolJ0/SgItMbGstmsuffBbikIy8VpvA8iysSrT3xoxBv9RhMxjfZKDDibcMVIV/EZ6dkmUgP9V5mfU1Azte/cHAPeOsln783DeivMnOi0dv8MS+o3cFVIST6JKcbbyuzPF0tfzLQ4csJAN7cU+qb+unQTfFRPGT9e+ld7puOYkW8Lw6pBDB6GCwWtikWnAPDcicgOx00s7LGTzik6q+1IK0xVHoUZHufNXA5XjjQzQcktv7vMDLC0snEacs5+2KN/Rwkxg9OsI74vGVWjMaOh9AkoNJNkX0wh3QDuN+3gM2z3u+Y9nzdrKYTlXsSFdn8fkYfJeHIxI+Hx46kyc/pPZoY9zir4C2Yq/ASDIvftPmxmjlw4Z7WJNjHp6lFmIKSzxQ4zZXUcIl0wukcCOkzWwEjGwN6FKCH0+d4F/3B7Ynv2Ii7ydoTw4zTYAxE2kdFfrLQNIf42w2Ui/kASpjBv6LJ4BwQEwRf6ElmA2SE9fa4bwm//4eenmoGGd175lJyL2OjdMDiV0UGWwvJ+6z2Xex1AyPvBNvC5iMO19sAELp6RS9p1biZ3PnCl/Pv1GXI0IVkGY1IW+pn/BJeRiVeMkGumTLSabpZ8HvciVOF6hMDrjU4vrc5WmedfMlQ+/McsV4x1txN1QwkoASWgBJRANSQQACtQuc0+lk9JRfkrMvbsT9+tlpVLNprIAZxB7YLLR0BgYGpptN76IWZEBVqr01JPQYwFIWZvVwgqd2FIt4IsTEBBi6E1UQmFzS+I+5uFgVGMMNCX5xXhz0ohzEo9pxC37i1jHh/ce8TE+uVEFxbeQKj1aLzqHwg/3FBYB1nnAfiKMnpEOGYUbNKikZlpziqH4d/WQmx079PeWFZ5jaz7GGL7rkO0jiSIlqHwPx0wvBusz2f8X1kffYopuMIQiaFuVIQRY1a51pIxghlGjC4WreAnzGm+7YLNysclJ8CgrzUNliEocyim/nZOEmLP5X2dApKv+ukHfe75/cA1xi0jOy5/Rji4v338qLG+ux0sxcbBuKPGCt8YMwmyw2IlPh9b1u1CaLw2bu4+ORDIywpmlqwbWQduHGc6GRzYxklzOFCOzwinyO7YtbUR+py0Zeu6PXII04f3Rudl6JjeEM8RVnVmSYGahHvFWTFbtGnkiqjC53M97l1KcjqijoSY+90I03AzceZAPgvsgNXFIMvufTtg8KnTp5ozIPJeZWB2xZatm2AK8fbw5T4jrh2YVIfxpdui42UfTGgKxn90VWHYxdX4/jCWeT2UO3hUH+mMyYE4O6Bn2rV1vxHPnPyH1vheA92nKmd+Pmd0ITmMWOczMZDxMMpt2qKBjL1oiPTyeCvEONzrVm6HS1Ka6egNGN4dnVC7vzieWUR4oQ9HS7zl0aQElIASUAJKoCII+FOv1ggBXREQtczqQeCr//4o+2B5nfbgNRJZD77cmpSAElACSkAJKAElUAEE/Cmgz5jqKqChWqQSKInAhlU7MLXzEEx6El5SVj2uBJSAElACSkAJKIFqQeDMe+Bq0RxtxNlAgG4Kc2cukVwMMGyGQWSckIYxpjUpASWgBJSAElACSqAmEFABXRPuUi1rYwwmlpk81X2QWS27RL0cJaAElIASUAJKoBYTULNfLb65emlKQAkoASWgBJSAElAC/iegAtr/TLVEJaAElIASUAJKQAkogVpMQAV0Lb65emlKQAkoASWgBJSAElAC/iegAtr/TLVEJaAElIASUAJKQAkogVpMQAV0Lb65emlKQAkoASWgBJSAElAC/iegAtr/TLVEJaAElIASUAJKQAkogVpMQAV0Lb65emlKQAkoASWgBJSAElAC/iegAtr/TLVEJaAElIASUAJKQAkogVpMQAV0Lb65emlKQAkoASWgBJSAElAC/iegAtr/TLVEJaAElIASUAJKQAkogVpMQAV0Lb65emlKQAkoASWgBJSAElAC/iegAtr/TLVEJaAElIASUAJKQAkogVpMQAV0Lb65emlKQAkoASWgBJSAElAC/icQ7P8itUQloAQqm8DOnTtlwYIFcurUKYmOjpZJkyZJ8+bNK7sZWp8SKJKAPqNFotEDSkAJ1EACKqBr4E3TJp89BCiIs7OzpX79+sVe9JQpU2T58uWuPDfffLP85z//cW3rihIoL4H8/Hw5ceKEZGRkmM5ZUFBQqYr09zO6d+9eefDBB2X79u1Sp04dueqqq+SRRx4pVZs0sxJQAkqgrARUQJeVnJ6nBCqAwNq1a2Xu3Lmyfv162bBhg+zevVsoXMLCwmTAgAFy4YUXyh133CGNGzd2qz0vL6/YbbeDuqEEfCSwatUq+fjjj2XevHmya9cusZ4zPo8dOnSQLl26SOfOnWXq1KlmWVyx1rlWHs9ta7+vy6eeekpmzpzpys7vy1133SUxMTGufbqiBJSAEqgoAiqgK4qslqsESkEgJydHnn76aXnxxRddIsV+elZWlrEw08r8/PPPyxtvvCG33XabPYuuKwG/EeBbjyeeeEJeffVV04HzLJjP49atW82Hx/72t7+Z/A899JCEhIR4Zq+Q7YSEBLdyc3Nz5ddff5Vx48a57a8OGw6HQ5KSksx3m2+T2AHRpASUQM0moIMIa/b909bXAgLbtm2TIUOGGGHsi1UuMzPTWNro3qFJCfibwMaNG2XgwIHy8ssvexXP3uo7ffq0PP744+Y8+jpXRho5cqRbNQEBAdK2bVu3fdVhg9/pVq1ambdGzZo1k6ioKJk/f351aJq2QQkogXIQUAt0OeDpqUqgvAROnjwpY8aMkaNHj3otiq4a/OzZs0conK1Ea9uxY8ekXbt21i5dKoFyEzhy5IgMHz5c0tPTC5VFn+devXoJReC6deuEeT0Txfdvf/tb+fHHHz0P+X379ttvl8OHDxvXksjISLnyyiulY8eOfq+nvAXyu8p2Wolvmw4dOmRt6lIJKIEaSkAt0DX0xmmzawcBumN4E89/+MMfjDDgsU2bNpnoGnw9fcMNNwgtbUyhoaG1A4JeRbUhQLcNT/FMlwP6GqekpBjhPHv2bKH7BEXgrbfeWqjtjAbz/fffF9rv7x0U8m+99ZaJPvP1118LB85qUgJKQAlUFgG1QFcWaa1HCXgQYBQB+o7aU3BwsLz99ttmUJZ9P0UzBxH+73//k2nTpskHH3xQ7jB1ycnJcvDgQeGyQYMG5jVzSdE+7G3iOn074+PjJS4uTmihbN26tbRo0cIzW6Htsp5nFcTz9+3bZ4Rc165dJTY21jrk07K89ftUSTkyVUX72FF7//333VrdtGlT+eGHH4zl2e0ANnif+Rw2adJEXnrpJbfDDz/8sFxwwQXmmXA7UMQGB8rSlen48ePSs2fPUt/PIor1uru8z45VKNvMN0OJiYmGRZs2baxDfl1WxbPg1wvQwpRAbSWAL2e50/Cm1zv40aQElIDvBBB2y4G/K24fWNF8L8CWc/DgwW7lwFJtO3pmdceOHY4HHnjAAdHplt9qR7169Rz33XefA6/nz5zkZW3//v0OvEJ3IHxYoXLgh+p49tlnHXhVXejMsp5nFfTJJ584RowY4WA7rTZzCWuk4+KLL3YgpJmV1euyvPV7FooOkAPi3YFBYQ7E33ZcdNFFnlnctjFQ1IHOismPaBEODBp1O+7v9rkVXsLGxIkT3ZiS66efflrCWQ4HfHwdLVu2LHTunDlz3M719oxisKIDAxXN/bPuJzqLju7duzseffRRB9wf3Mqwb/z0008OiFZHeHi4eR4QocZ+uNB6eZ8dq8D33nvP0b9/f1Ov1WYu0Xl0PPPMMw6E+TNZP//8cwe/C2yjPR/X+QxwPz9ww3L8/PPPVvGuZVU+C65G6IoSqGUE/KlXaUEqd/Jng8rdGC1ACdQQAhhMVOiHFT6kZWq9N3HiWdA///lPByzcher0/HHndt26dR1FtWXJkiVGAHo7z77v22+/dWtCWc9jIampqY4bb7yxxLZT0P/rX/9yq9faKE/9VhmeS3YU7NfMdbjaeGYz2+xQUDTb8yNusStvRbTPVXgJKxSqiJ7h1raGDRs6EG2jhDOdhzGA0O1cXuPf//53t3M9n1EK9lGjRhU6z87niiuuKLIN7LzY87L93pI/nh2WC5cVB6zqbnXa67fWR48ebZpxzz33lJjXOueFF15wa3pVPgtuDdENJVDLCPhTr6oPNP6CaVIClU2AA7DS0tLcqmUkDg7SqqhEdxEOaPIlMcIH403zNbU9MRTX1VdfLQxjZiW6l3DWQ083Ck66YaWynmedT3cAuq/YE0OBecbD5iQfHMTGuMX2VN767WXZ12Fxtm+adfrjekuLFy82fsT2Y4zrzVRR7bPXVdz6gQMHhIPb7In32Vc/ewhd+6lmnS5KxSVYqGXRokXFZZEZM2bIvffeW2yekg6W99lh+fwe8F4zRntJaenSpSYLo234mux5q/pZ8LXNmk8JnO0EVECf7U+AXn+VEIArRaF6KzqCAP2rmTjVN8UxhR79Xime8DrcRF+wN2rlypVusxvyGP1h7dEX8OpeeC2MMkD/VQ4ue/3116V9+/ZC/1krlfU8no9X4fLLL79YRQle2cuHH34ojGDCQZb0v2bkCHviIEy7+C9P/fZyPdf79u1bKPJDUQL6m2++cTudg+CsdldU+9wqLGaDE/Z4Jk6U4mvyNm18SQLaKpsdoeuvv15+97vfSadOnazdruVHH31UqOPhOljCij+eHVYBtw0zuZG9OrhnmNjXfBb/+Mc/uiLiWDGe2algB2nChAn208w6O8qwwJsPXI+Mv7iVqaqfBasdulQCSqAEAv6wzvvTJO6P9mgZSqC6E3jnnXcKvd597LHHytxsz9fj3nyg//vf/zr+8pe/GHcIbxUhLF4hv04MKnPL+n//939u7aYftC+prOfRhYA+ovgz5vrwGjwThHshtxJYoV3Zylq/q4BiVuira28f1yEeC53heR0QjK48Fdk+VyXFrNC9x/MaYPEv5gz3Q3QBoe+yvQwMBnTL5PmMMi+ZYEIWVz6WM378eLdymM/THYQnlOTC4a9nBx01R6NGjdza1K1bNwc6b652c4UuOs8995zjuuuuc9uPGNlu5/J6PL9X9hOq+lmwt0XXlUBtI+BPvaoWaPw106QEKpuAt8kmfIleUZ52wodY7r//fsEAPK/FQCQUsqYyyoA9Md6uPX333Xfi7Vrsebhe1vNWr15tLMxWeYGBgSYKibVtLWnthj+ttWmWjOpgpbLWb51f3JKuDp7J0wq9efNmt+tgfvt5Fdk+z7Z52/ZmLYYPtLesXvcxAgvfbNgT30gUlxj5hdZWiFFXNpbDKDSeqSwTj/jr2Vm7dq2JtGFvEzq7hdyH+IaHk8lw6vPypKp+FsrTdj1XCZxNBFRAn013W6+12hCw3CnsDWKc3apK9I3mRC12X0y2BQOw3JrUr18/t226c3DfXXfdZWIEux20bZT1vF27dtlKEeNrTZcTimPPT0REhFteu1tCWet3K7CIDZbt6e7gKaA93Tco+BFNxFViRbbPVUkxK7AyFTrqee8LZbDtoLuMp08/IkzYchRepW+yN7clukb07t3b7QT7RCRuB4rZ8Nez41kOO3H2zk8xTSjToap+FsrUaD1JCZyFBFRAn4U3XS+56gl4Ew4UhpWREOpNaEHjVMhWDGVEMBBEsHDzNfbWlksvvVTwKt7tEAfu0WqI0F4yaNAgmTVrlttxbpT1PE/xwsk7EOLM68dTtDLGtZXKWr91fklLT0GFKAomvrZ1nqeA5qx5FGJWquj2WfUUtfS0HjMfZ7r0NTEWsuc09J6dCl/LYj7P74c/BHRZnx3PZ5Bvaiw/59Jck695q/pZ8LWdmk8JnO0EzvwFP9tJ6PUrgUok4CkQWDXivlZoCzjo7rzzzjOvzP/85z8LRR4HANqjZZTUAIo+zkpnDX7zzM/ZEi+//HK56aabBDF+XYfLep431wJXoSWscICjlcpav3V+SUtPAU0xSfcWJlrpV61a5VaEZ/6Kbp9b5V426E7hmUojoL0JXG/PuGcdRW17TuhTGmu4Vaa/nh37mwyWTQFdkamqn4WKvDYtWwnUJgI6E2Ftupt6LTWGgDdxQZ9Nho9DDGa/XwetxIwIsGzZMreyWRdfmdPflf6na9asKeS24XYCNhg9guHHMDGFvPLKK4J40Z5ZTMg5vsLHoCrXsbKc52kZpf/2mDFjXGUWtcLwdhiM5Xa4LPW7FVDMBq3vjDxiF220iHN6aQppu4sEZ+4799xzC5VWke0rVJnHjj59+njsEROZBRODFNrvbQfDzXmm8ligPQVzWcYH+OvZ8bQ2l+Tb7cmhLNtV+SyUpb16jhI4Kwn4Y4SlP0c1+qM9WoYSqO4E4DPqgM9uodH5nJWtLMkzwoFnFA7OwoY/cG4f1gXB7lYdLMtueTgZRElpxYoVjsmTJ7udx7o4Q5y32Qit8nw5D1NEu5UL8WmdXu6lL/WXphKEznNrKyejgV+5mZ3Qzh5xqn0q1t/tK67S9PR0BzpQbu1nm+G+UNxp5hgjZyCMndu5jMhhj67BjCU9o/aK4AfsVt7YsWPth816SVE4/PXseE4SQ06cQdHXVNooHN7KrcxnwVv9uk8J1BYC/tSr6sKBXwlNSqCyCXDykalTpxaqFqJW6KtZXKJ7ACehwB+04rK5HVu+fLnbNmPTYkpv4/fsdqAMG/SJpjWaE7XYE4SDcRGx77Ov+3KepxWTcZ/58Ufypf7S1OPplsG3CfR9XrBggVsxnvncDto2StM+vmHgoMp9+/a5xb+2FVfsKt9EXHvttYXyYKbFEp8zvmWIj493O5dxne3RNdwOFmwwtrc9priVh5Ff1q1bZ22aZUkDEt0yF2z469nxLIffP09/e3v99vjj3M/vumcq7TNcmmfBsy7dVgJKoGIIqICuGK5aqhIokcDTTz8tmNrZLR8FBd0BvIXtsn64eZzuGL6Ej7MK9/Sv9vajzoFg9oF31rn2JX/4KQy9JQ5+8kzW6++ynodYwp5Fiq9uBfYTy1q/vYyS1gcMGOCaTMPKixjRJrqJtV2U+0Z52vfjjz+aSWs4uBJxlc3zw4gqpU3PP/98oZkHOYkJ4hq7+bNb5bID9+CDD8pTTz1l7TJL3nOWVVKiuwt98vncWYnPuLeZB2GBtrL4vPTXs+PNvYWdhuTkZLe2sO10aaK7iV1EczZHT3cST594e0HleRbs5ei6ElACFUzAH2Z5f5rE/dEeLUMJ1BQCdKPAV9zrp1WrVo5LLrnEMW3aNAcsxg74Rbrlw4A912XCQuV2zNOFw3OyDwxUcsAf2nU+fJ8d8OF1K4Ptsk/2wcycJAJTdjsg/h2wdrrOhwXUQdcE+7Uwn5XKeh7PR/xqt3JZByycjg0bNhgXCebhZBeI1+t47bXXHAgP5+BEF/ZUnvrt5ZS0/vDDDxdqq53Jb37zG69FlKd9l112WaE6EQnFaz0l7USc8EJlsf0YZGgmOHnkkUccEMwOhKBzoPPnNS8ZeEuez6jFBQMGHZyQ5+WXX3ZgOvtCZbZu3dqrK1BJLhxsgz+eHZaDDmuhdmHWRAc6c47p06eb7wMi2rjyYGAuT3MlhOVzHeN18/uHwbYORK9x3HbbbQ7MBOrKW55nwVWIrigBJeCVgD/1Kl/PlTv5s0HlbowWoARqEAHOlkb/TktMlGYJC7TrSj3FiaeAxoQVXuugaKZAKapeTwGNaYfd8lL8dOnSxUF/X88y7OeW9TxeICI8eC2f9VGIwOJZqG5MRuFiw5Xy1O9WUAkbGAhaqC12LnahZC+qPO0bOnRooTrfffdde/E+r2OAnKNz586FyrNfQ3HrcAMxnRlvFXo+o96eGW9l//Wvf/VWXIkzEfIkfzw7LIedNT5r3trnbR87dPZ09913F3vuCy+84MpenmfBVYiuKAEl4JWAP/WqunDgr58mJVBVBPh6l6/gMVVxqfyRr7nmGoEFzOdmn3/++XLnnXcWys/X6Fb8aQgEwQ99oTz2HYzYYU8MgcdQeJ5uHYwxDWuwK2tZz2MBGKBmfKy59Ex8VY5OiOdu8QzLVp76CxVezI6BAweKZ11WdkYGIRdvyfMcX7myLG8zBtJVpCwJbw0EYlFgaRZvk/0UVSbDznEGvk8//bTQZDzezqEL0ezZswvNUOmZl88jOmKeu33e9sezw8o4sct7773nU4ScXr16FWLAGQoZZ72ohAG3rkPleRZcheiKElACFU/Aq0Qv5U5/KvpSVq3ZlUCtIcCIB4xmQQugt4gItNjROjV37txC1wxB7WbhwkQphfLQ2g0fTeOCgb8sbvlpRaZ1lNEYaL21jsOX1a2cpKQkB2YddCCcnCuPlZdLup3w1TpdOuyprOfZy6BV77777iuybtZPtxFa3+3uLSzDH/Xb21Lc+ptvvlnIKg4x6mBUiKJSedqHMHluEV0g4ArxL6re4vZjIJ9j0qRJ5p5C8Hq934iJ7LjlllscGPhaXFHmGHzkXWXAT9jsQ+fLMWrUKNd+61nCTI3mOSquUFqmrfxcYjKgIrOX59mxF8rvKMIoOtDxdaub9aMj46CLC0Lw2U9xrdNNyjO6CM/jWxxauK1UnmfBKkOXSkAJeCfgT70awCrwJS5XGtHsBnP+0oTp5SpHT1YCSsBJgBEsGFWBkzhwem1aFDkoijMGFpUgEoTRGJifURWKSszD2QhZNsSynHPOOW5WTE6AwmnFORjMc/CTVSan/qalEn7QZgpnWvo4gI2f4iyXZT3PqtdacpIPzhBHCzrro+UUHY9Cg/is/NbSX/Vb5RW15IAyMiRLto+DRYu7d1Y5ZW0f4ybHxcUZKyejRjCmtz8Tnxk+L3zbQIs/JxPhYLkePXp4jTJRVN0Qh2aAHa3mfONhJd5LxhMnNz6PnlZYK599CbcHoWXXSmyTL5O/lPXZserhkveJLBCqz9xfPve0UtuvyZ7fWufPLQfq8nr5fPB7w0HB1mBbKx+XZX0W7GXouhJQAu4E/KlXVUC7s9UtJaAElIASqAEEMPDQuFVYTe3bt2+h8HfWMV0qASWgBEjAnwJaZyLUZ0oJKAEloARqBAG+8aAlnCEc6XNtT2WZrdB+vq4rASWgBEpDQAV0aWhpXiWgBJSAEqgyAi+++KIg9JvX+n2doMbrybpTCSgBJVBKAmec0Ep5omZXAkpACSgBJVCZBDDI1Wt19H9HzGevx3SnElACSqAiCKiArgiqWqYSUAJKQAn4nYC3UIaY1EWWLFni94GTfm+8FqgElECtIqAuHLXqdurFKAEloARqLwFOoT1u3DhB2DxhXG3GXG7Tpk3tvWC9MiWgBKotARXQ1fbWaMOUgBJQAkrAToATD40fP96+S9eVgBJQAlVCQF04qgS7VqoElIASUAJKQAkoASVQUwmogK6pd07brQSUgBJQAkpACSgBJVAlBFRAVwl2rVQJKAEloASUgBJQAkqgphJQAV1T75y2WwkoASWgBJSAElACSqBKCKiArhLsWqkSUAJKQAkoASWgBJRATSWgArqm3jlttxJQAkpACSgBJaAElECVEFABXSXYtVIloASUgBJQAkpACSiBmkpABXRNvXPabiWgBJSAElACSkAJKIEqIaATqVQJdq3UVwLbHw/wNavmUwJKQAkogQog0PV5RwWUqkUqgZpNQC3QNfv+aeuVgBJQAkpACSgBJaAEKpmACuhKBq7VKQEloASUgBJQAkpACdRsAiqga/b909YrASVwlhAIhsNdcNBZcrF6mUpACSiBak5ABXQ1v0HaPCWgBJRAEP5SfztXZN4qkRAduaIPhBJQAkqgygmogK7yW6ANUAJKQAkUT4BDaYOaiLy7SCQxBZZo/ctdPDA9qgSUgBKoYAL6Z7iCAWvxSkAJKIHyEshDEIQxXUWa1ReZs1kkv7wF6vlKQAkoASVQLgIqoMuFT09WAkpACVQ8AQcEdN0IkeuGi/y0XITbmpSAElACSqDqCKiArjr2WrMSUAJKwGcCuXkifTqINIoVWbkevtAhPp+qGZWAElACSsDPBFRA+xmoFqcElIASqAgC+bA6R4aKjB4gMnOjSF6WSIDOM1QRqLVMJaAElECJBFRAl4hIMygBJaAEqgcBWqHHdBdJzRRZux9WaA1rVz1ujLZCCSiBs46ACuiz7pbrBSsBJVBTCdD1uU6YyDXnivy4TSQHglqTElACSkAJVD4BFdCVz1xrVAJKQAmUmUA+RPMg+EIfSBLZcwzh7dSNo8ws9UQloASUQFkJqIAuKzk9TwkoASVQBQQY0i62jsiEPiKfrRQJVDeOKrgLWqUSUAJnOwEV0Gf7E6DXrwSUQI0jkJ0rMg6+0Ht3iuxIEAlVEV3j7qE2WAkogZpNQAV0zb5/2noloATOQgL0ha4LX+iLh4rM+FUkFzOrqCfHWfgg6CUrASVQZQRUQFcZeq1YCSgBJVB2AgH46927vcjqTbBEwx9aQ9qVnaWeqQSUgBIoLQEV0KUlpvmVgBKoEQRokQ2GawOFJdcdsNI6MACPHw7Es38YHs5fH3u51rpVL+fgZlsYfo6foHL8BWZ72zQV6dtO5IclzmutETdGG6kElIASqAUEgmvBNeglKAEloATcCFA0c7rrrfEI97ZDhD7DiVjmZYukYX8qhKyV6A5xANu2XdahUi/hVSFNIYotXWxcLdCW2IIdUXXhetFeZCg+9TApStN6Is3ri5xG+0o7PTfz0/d54jki/1mMMnKcgry05ZT6IvUEJaAElIASEBXQ+hAoASVQqwjQwsvQbl9huus/znH6B1fmBWJMX9HpFA4h9NzbK5xZejcQuQzRNC7tD0EdAYEPFV8aAcw40P3biny7FtN778UkK12dQrroBugRJaAElIAS8AeBAruIP4rSMpSAElACVUsgEMKZbhEzq0g8268+AGZwbx97no3HRZ75SeTOt0VmrUHbYVUu7eyCgbjeS/qKfPOLSHqW+kLb+eq6ElACSqCiCKgFuqLIarlKQAlUKgFanvn5AtbYp+Y6Lc9BQUEyceJEadKkiWRnZ0tycrJPbaLwjYmJkdDQUFiE6YjhTNx/+vRpmTt3rqsslt29e3epV6+eNGgAkzJSnTp1JCQkxHmS7X+en5GRIcePH5dly5ZJfDx8TJDWpOEzW2QDrMjXjRTpAt9m+jjbqraV4r5Kq3XvFogJjWYu2YXwdt1gyT7TZPfMuqUElIASUAJ+IaAC2i8YtRAloASqkgB0qXHbmAXL85MQzzkQlRTPd911lwwYMMCs5+fnS04OHIV9TBTAgTTv2hLLPHLkiMyeDbWLREHMOpo3b27qsEQz6yoq8RweHzRokMycOVNWrFjhEun/2y6ycK/Ic5Mw2yCEMK3ReRDSxSWK7LpRIr1a4dzlmGClh9MVpLhz9JgSUAJKQAmUj4D7r0P5ytKzlYASUAKVTsASz/O2ijxRIJ7ZiJtvvlkGDhwIAZonWVlZRjxTvPr6odjmefYP9x0+fFhSUlLMdfbo0UMaN27sEuhWXuYr6kNLeG5ursTGxsqUKVNk6tSpEh0d7eJ2CAMdp84UeelbuGSgmmAfzBxZ6BcM6SWSgI7EUViz6cqiSQkoASWgBCqOgAroimOrJSsBJVDBBGggpt/wrHUi93/tjGbBKidPniwjRowwItbugsF1Xz/emk7hGxcX5zrUu3dvCQ8PNxZl104fV2iFpphnOx955BEZPny460zarz/aJPL7DxEhJBGCGNdZnCimG0fnxhhQCCv0bEysEuKD6HZVpitKQAkoASVQagIqoEuNTE9QAkqgOhAwghLi+dP5Io9+j1B1Ba4OgwcPllGjRrncIvzVVopdWo/pcsFE9w66bni6eZSmPop5Wqppxb7llluMRbpu3bquIpbCmnztO7jGpagP11eciKYrx4TeInPgA56YWnxeVwW6ogSUgBJQAmUioAK6TNj0JCWgBKqSAH2D8yEYX4PV+YnVGHBX0JimTZvKNddcYwbwFeeHXNa2nzp1So4dQxw6JA4YbNiwYZmsz571082EaeTIkfLQQw9J//6Ia1eQknDo6YUif/nGGc+aIfq8JfJoGCnSpB4EtLpxeEOk+5SAElACfiOgAtpvKLUgJaAEKoNAMP5qHTkJUTkL8ZQ3n6mRETNoxaVvcUWIZ1qat23b5iqbApoff9ZFa3SrVq1k2rRpcv3115soILxCunS8BR/vW9/D5DAINB1eOMCH6VA0hiv1uL4i36/yLYLHGXq6pgSUgBJQAqUhoAK6NLQ0rxJQAlVKgDPvbUbkt1s/hFsDBKU9MVxd586dzQA9+35/rVNA79iB6QwLUrNmzTDAL9jvriK0RrOucePGGd/obt0QjqMgrUkSufcLke9gdaefs+dU4LRC18Vn004NZWcx06USUAJKoCII6FCTiqCqZSoBJeBXAvT9DcfU1z9jgNxjmF0w3vLZKKiFvshjx451DRDkbivahr0hnv7KzOOZPPPwOPNR2J44ccKVvWXLlkboUkSXJ3lrg1UeOwT333+/iRn91VdfSVpamuyHe8a9s0VWHBK5G+MOm2PwYCaicEBzSyImZpm+DMfAZz2OD2zjjCdtladLJaAElIAS8A+B8v3l908btBQloASUgFcCFIXB0LjHMQX2+4tEXl8KP2AvOc8//3yJjIw0ItcSpOnp6ZKZmWlycx8jaNgnUuEAvsTERFdpzEN3DOZhXnuyykxIODNR96FDh2TTpk2mTnve0qyzvqQkmJWLSaybn06dOsnatRghiESXjukbYY2HQfz2iSLndXfGwQ4KF4loBtEMC3QaLPWB7ZDR6V7N0zQpASWgBJSAnwiogPYTSC1GCSgB/xCgTdiEYcNKMuIgJ8Pf+TXERZ6H9aLSrFmzXJObWHmseMvWNgUz91mJ29bgPWtfaZY///yzLF68uDSnmLyWGOdGWdvAMtq1ayenwurI/d9ukzu25MnNF4m0ihUZCtG8Yp/IsD6YUMa9H2Dq1/+UgBJQAkqg/ARUQJefoZagBJRAOQnQRQOa0HxOQ/St3gDrKoJdLICf82aEZDtdQvmpqchUxsTBhxx4yOm3uc5EYc2IG/bkbbAgXSo48M/XRMHsLT9nMOQsh/Y66BoSFRVl9ttD29HS3qJFC2ndurUR4AldO8uMVb/K7LcOyLRhIqlsNqzORwCtbZ2CKcF9baDmUwJKQAkoAZ8IqID2CZNmUgJKwN8E6DocAheNXIi9E/DrPZqBwXHw390Er4r1+JzCYLjKSJZrB8Uw/Z8pVimmOTsgxSrXKbApaClymYcWYG5T8HJpCWNuWx9v1m3m48fuZ20vlwLebqG2yraWPJdt4McS4i2aN5OJ48+TzVt3yJ8W/ioBednGa2PdPpH6YBwBEV0nzDmokJ4pHGioSQkoASWgBMpHQAV0+fjp2UpACfhAAMZlmJfNPxM5ghpuz0FYSeGWsQ9uyt/CE2INBHRVJApeunZY7h0U0t4SRSvFNK3CFLlccpuh7DiFNwcY0ueaH4pylmMXw0a3QgBToHP2QiarHLbBsoRbYtlqgz1vWFiYyUeLNeu2hDjLHHLOAGnbuqXsP7BfEhGr+sn5CfLhnNMyfJDIOc1FYhD6rlM7kXqoOg+NQVPEAWdq+lNbifs0KQEloASUQMkEVECXzEhzKAElUAYCDLEWiLBz+CcZWXDDwCcDau2HNSIbIZ5XHIbVuQb56NKiTFFclMD2FVFGRtl6ChTblgWcApoCnuKdriaW+OdxCnAOoMxx5MkW8N6yUuQdNI6SvQcGGLbESnN0Zpq3F+neSqQd/KYDkI/eK3VwjBqaVmqK61x8NCkBJaAElEBhAiqgCzPRPUpACZSDACc64SDAYxj8d/QQQqtBrC3eJrIKk55shzCrji4EMRCPl18h8sk3EPpl07dFEiOP6zHAry9CzgXACsyZwL/43N3yW+TJtgN037Cig1AwUzgfOXLElqP4VfqRr0EQEfRfnGqShtMAAEAASURBVGmv841AC7SvFe5Rh04i5/ZCHGkcrQ8hHREt0rq+Mzwe+g6SBzGtBmoLni6VgBI42wmogD7bnwC9fiXgRwK0Oq/ZDyszoq2tR3S2uKPwb/Zj+RVVVDe4OLz2rMiidSJ7d/ivlqYNRD58X2RQQ5ElqxG/GkW/8oLIJeeLTJmGkHxVbOGlID6ENqCfI79sF/kfPkxoNnzARXo1EemIVwg9eooMaIeOEdZD8atBv3UV0waV/qcElMBZSkAF9Fl64/WylYC/CQRDXB3E4L/HZkCEugew8HdV5S6vRw+RRnBd2LceH7g8wwUZvssQhRCGTOEYeDcWvsOnEGBjNfLYvS76doGohLBcsgUWdkxcYqVBsN42QZkb40QOHIDlFgceu06kC4Tn4PNEdoMN05dviXz2g8iDD4m88JLTwjsEdcVGwEIPJbt7tzNfY/x1BlK4ZIhEooztELeV5aPMyzqOwCZ7C4KbBKLu5mjHBbjGS/vD7QMdAlrWVUQ775X+rwSUwNlHAH8SNSkBJaAEyk+AoeiOwty871T5y6rIEl7/szNGciIEczu4KtzwJNw2DjprzIZgHjZE5MVnIF73Q0BHQbyGwVr8mMiObSL/fBh+w6Nw7LTI4xC8j/wN1naI4VeeheAeAbcVWK9j+2HCl7+IfP6ZyGUQ0G9/cUY8s5afIEZvu1swgQqEOup//x3nbIIZe0QaDhR5F9vvvidyDc696AIcaw3xDH/xyddXnoD25E+3m0Ng82+8WfgYHYpvYT1vDTO1+kh7ktJtJaAEzhYCNJJoUgJKQAmUiwC0s2RhQOBPEJ1V7JVQ7HVcfSFm7Rsv8n9/gnCeIrIQovieG5xuCbSmZmaLjIG7QvwqkVF3QsBCtOahQ3AhzmtfV2TiZJE/wnI86mqRjz6FNXYiLMzwHR6L5f0Q1xdAWH4J4TwBYrp+KMQ0jm1GWZ7pm29Flv8CAQ9x3AZW67tR14UQ1cuWidxyizN3WFOI+dEQ4//C8XucVnLPcqpimwNBD9MyzZuuSQkoASVwlhJQC/RZeuP1spWAXwlATOXDQnk0zq+l+r0wukpsXQTx+quz6GcgpNvDkorgFUYP1qsj8vJHmM2vvch9d0Dcwg+4Q3dYfmF5PYJTMo+LPP0afKUXw4UDrir/RN6GOEdOijz7DAQwyv5mpshfd2F/I5QJLoxmUVTahXxTbxYZP1Tkissg7oeIpBfkD0Obvl8o8sEnRZ1ddftX7YNbSruqq19rVgJKQAlUNYHAqm6A1q8ElEDtIMAoDUcgMKtzqt8G0SVgGbYSJ2/5Be4bjoK/hKfSRX4D4fyfrxCVYxgiUsAsnYhr4sC5jFMi116OqcWTRa66Anm+EXngd7BWo4ybYEHedRgC+EKRT78TeQnW6CTkS0PZbdtbtZ1Z/ucPIk9OEWkMX+LPf4B4Rjktm6EDsg/Tb6MjwkTxzTqrY6JftiYloASUwNlMQAX02Xz39dqVgB8J0HB6zI/lVURRu3di8BtEtJVuuETkiSexhcbTzzc8BMIZ+96bLjL8VpHbX4UQhrtCNtxTBnWCH/Lv4ZsMt44+8FV+5c8QvhDUo0YjTN0tyHsH8pwLC/UzIpNuhgtHhMjs7+HvfBPKtf2lHddN5GLsS4AP9sPXwnidBrcRCO9pjyJqCfyL0QRXCrCd59pZDVZOxledP3Y1uHxtghJQAkpA1I6gD4ESUAJ+IUABfQQitDqnmV/DinyNyJ//iHjMi0Rehd/xSx/B6psFazMEbx6EMiYUlN59EBMZYnjCcMziB0v0GrhaODDg7wYIY2SR+QtFhnTFbIqHnQJ4ygQIZgjt/y0TGd0R0UgOwHINt46XPxCZcRGmKIeQngmLdTtYla+F2J69Bq4ZM0T+cDXOi0U9Y3GsEc69EYVDQWPmcONWEh5WPWmmH0W7eK9xPZqUgBJQAmcjgWpq3zgbb4VesxKo2QSCIKYoois7RSNgcdu2baVr167SpUsXadKkCWIYR7umuba3ZxsGDT75GCzIEL/3PYUBf3NF/jUdYvc0XCkgcFPhjvH0C7BSQxw+BTeMAGw/AKtzb4jifXCC/gOE98DBIs8/i2NwuXj6RZF1EMOPPAJ/6UEQ5s/BRQRuGQ/BmkyL9va98HG+GOfuhtvHpYirDOv2+/8VuXMqRHs2xPvnIvMgrh95CAMGx8F95H5Yobc7xfuq1fCzXmpvffVZDwiqPm3RligBJaAEqoJAAGa3oh2hXGlEsxvM+UsT8EukSQn4kcD2x9XE5UecFVYUY0AvhUi87VOncKywigoK5lTWPRDMuX379kY8t27d2ixTU1MRg/mA+Rw9elQOHjwoGzduFE7D7c8UgMfS21/OovaXtu6SyuGU3fzEwlTNGQmzsrJc03mXtq6y5L8mWuSZ34KBfj3Lgq/GndP1+XLLhBp3zdrg2knAn3o1uHYi0qtSAkqgsgmcgLW2MqbppnV5/PjxxuJsLfMxE0oGZjsJR2DlOnXqyOHDh2XBggWyZcsWobieM2eOXwWmN/FM3kXtL+29KKqcmJgY6d69u7Ro0UIiIyMxAYzT5s8pvuPi4mTv3r2lmt67tO2y8gdXxasGq3JdKgEloASqAQEV0NXgJmgTlEBtIMCJVCo60eJqieZbEDCZYjkJM5LQwhwAsy2tsckIk1G3bl2ZPHmyEc7LEFx5zJgxMn/+fJfgrOh2VkT5gwcPlk6dOhmrM11V+vbtKxTUTLzuXYiJt2LFCtm8ebMsXboU0TwKwnlUQGNiOzijhKhdsgLgapFKQAnUCAIqoGvEbdJGKgElQFE8YcIEady4sVx//fXGheHYsWNmGRjoHM5BEc2Unp5uLM7MfwKjAump1q1bN2ORrmkkeW0DBw40grlp06Zy6aWXGqs63VV4XbxmWt47dOggQ4cOlXnz5km9evVMh4FW+YpIQVEolahVQVcEXi1TCSiBGkBABXQNuEnaRCVQIwhUsJgaNmyYEYa9evWSqKgoY2mmH7C3RNFJC2xaWppccMEFsnv3bunZs6ds377d7/7Q3ur35z5anfv162eunVZ3XvORI0cKDZJMSEiQiIgIueKKK8wximu6rlSEJboSXjb4E6GWpQSUgBLwOwGNwuF3pFqgEjj7CNAAfHxPxV13aGioNGzY0IhBWpJPnz5tLK/F1UjLLMUjrbOtWrUy4pIW3Jok/jhYktZnposuusi4rLBTYFnc7dfPfZmZmcadg24uFN60SFdEGgEXDt5zTUpACSiBs5WA/gk8W++8XrcS8DOB/Fw/F2grjpbVYEx/x0FzXLdcNWxZvK7SCstzaLGmGKUPtdNr2Gv2areTVnO6rjRo0EA6duxo3FG8iWer4TzGzgWvdfTo0dKmTRsz4NA67q9luL679BdKLUcJKIEaSkAFdA29cdpsJXA2EbDCtvGarQGDvl6/FamC4jIIwrILpvKuKVbo+vXrm84Cre8MVccOQUmJeRiVg5E6OMiSLi++djhKKpvHw/EJLbkZvhSleZSAElACNZaACugae+u04Urg7CGQgvmu6Z5AKzRD1NEtwxcxSeEYFhZmQtwxf0B2jrSA+0FN0X8UwOwAcOlr4jXzWnkeLdEM+8elv1JLdEDqYIZEH7S8v6rUcpSAElAC1Y6AvoirdrdEG6QEaiYBB/6ahLJL7s28C8UaieOx0IHFCa8GOJcBHhhmmDMbNkF5TTqK7E3JkfiEROkJF4yVK1eaQXW0ShdnjaaIpO80o3AwxFs2rLI5RxLksvNEOmAWwdwskaM7UBHaxiZnYJmCiosT1yYf8iYWlwnH7akRTqL8Le6UhrjOMORjnph6YNVe5ACmyz50KkNa4jpPnjxpRDTdM0pKpqMAEc1rp4jOB4cQBuguuDe5pZhThqcE2sZpNsOFXNcf96QB3wSU1BI9rgSUgBKovQRUQNfee6tXpgQqjUAe/J/PwRTXb/eC4KLK9Ei5EKYt4HzcAdNc5xWnJHGe5+lh+Cu1bq/I40v2Sl63zibu85IlS0xIu8TERGNt9XRRoIiktZr+0j/88IMRkvHHTsiQDskyAOJ0SCeIVbTDMdqjoT5sltB8ryV4XpPXTAU7mZczO67fj2tegxB8nR1y6NAhE1GEluSSomqQBfPRUk+3j7SMTBkVnSPXnI+CUfgJlJvvo/iNhGCOaF7AChfetxU6AzBmUzyXhUNx163HlIASUAI1iYAK6Jp0t7StSqCaEqAo7gGrLrRbkYmClUK6pOQpzE5jPpBurSHeQvbJ5m27pW+vLrJ48WIjkDlBijWNNf1+KR5pmaaLBwX0rFmzZM2aNcb3ee/a9XLzOXCHgPtBZnZJrfDvcc9rKrF0nNAQQrXOob2Snt3XdAB4zZdddplrpkHPTgPLtNw26O/NCWRCYIU+ejRZpowQGdNVJAfCN7BLibW7MphOhu2e0XpdUgfIdbKuKAEloARqMQEV0LX45uqlKYHKJOCLOC5Leyg+g+FLcMUwWGTnLpYDMZHSpmVzM1U3p64ePny4mVzFik5BIb1jxw75+eefIR6PGh/oX1avl96RcTK4R+WL57JcMy28rVuKDG+XKit37JOB/brL6tWrpXnz5jJo0CA5fvy4sURTRFtCmuKZFndO8T1jxgxz7RkI45e4eY10xpuBHAhhCmjhR5MSUAJKQAmUi4AK6HLh05OVgBKoDAK0fPaDFfr5idnyxzmzJfnkKOndraMcOHBAdu7caaa05rTWFJEpKSkmFnIo3BgCYIldumqdxCSvkt9e4PStroz2+qOOLLjFXAu3mKVfLpMDjetLq+ZN5euvvzY+3dakMvSJzs7ONiKaIfq4/eWXX8r6deskBIMnN65cL1d1PC2t6fON8jQpASWgBJSAfwiogPYPRy1FCSiBCiaQXSCin52QLf9b8qPMizso3fr1lGYNY4yI5Ox8Lmss2hKXcFTift0kg6J3y5SJIm0w8C2nBolI9AWkSWOR64dky99WLJbwUeOkccMG8tNPP8k6COQePXpIs2ZQxki0usfHx8u2bduMr3QYXFhWrtkoHU+tljuvwoBM5EFxmpSAElACSsBPBFRA+wmkFqMElEDFE8iGAO7bBv7WTRyyMm67LNi9U1b82lSyI+tJdBTCVyClppyQiPSTMiD0qEwdAct1Rwx4g292TRLPFklajS/tiwgdwUny+txvpHX/4dKpc3tJT0+X5cuXG4u7lZe+33RjyUPEjbk/LJLuuZvk+Wvg/oK/8nmqni1MulQCSkAJ+IWACmi/YNRClIASqCwCdOcIRCzi0fBnHtg+X06djpeV++Mx2A5WVjhMN4XA7tNSpC7+ukVEimRxwCAdqWtgYrM5aG8CrrV30wx56ev58v2mptKp7wDMThglYaFwUwkIhJDOk8zT2ZIYnyhxm9bKlc1TZdrVIiFgUFG+6TUQpzZZCSgBJeA3Aiqg/YZSC1ICSqCyCDA6BKNzUCDWR+DoCzFIzp6sSBFGPNsP1MB1XivH/TVvBB/wG0W27TsiG5K+lzXfBYojqK65ogCMOgyOzJDLEaO57UUi3RGqj3/cVTzXwBuuTVYCSqBGEFABXSNukzZSCdR+AoEQivT7pbNuDqJuwCPBzP1R3JXjFBPPmZbn2p5oea8Dy/vQ7iKDwOjqnvmSm5dmrOsMHxiC8HychIUoEHzD3eeZXHEAHh6SX0yowdrOUK9PCSgBJeAvAiqg/UVSy1ECSqB4AhBwDgo5z0TFh08KxGEUJloJg6U1MxUW5kMi9SCieViTkwA7CrS8MxW4fDs3Cv7PKjjmtpMA60M8h4PxcYjwTHROIKSZrLjdFmNru9BsNs7s+r8SUAJKQAkUEFABrY+CEvAzAYoTzsYH11S3ZE1Kcba9VqfB8zQUWgYCRjRpbhPRENP5EMsRiI7RAMI5B3+NQpA54VdMZQ3xnIN1S9i5gdQNQ6A0VvdciOYsWKe73IwOCiZoSYkXScdU4SlHRE6hs9KKHRXAzsdM4dTgwbB259N3XJMSUAJKQAl4JaAC2isW3akEiidAUWhZ6YKwQbEcAAHC9WN4q54EUZKdBB9U7LOseuERIqGx8FHFhyKbkSGMCEIey2eXihH/alWiMAuBWG4P/9wmiGtcVApOFtk3D8x2ghmiT9DdQJMfCOA5C87CMxcHEb0c92I8BloOPFMunzdkwcMIy/8xkeNYHv0anRiIbIcf7gHLpjuO9X1hVTUlse2MYGJci2pKo7WdSkAJVAoBFdCVglkrqQ0EOBteIIQAhXIGLXX4UBRsOoiBXVshOoJD5ASiIuxJry8JjbpJelRHyWyMzPgBpuNpbHyGRGxdK12DD0mTvEyJyc2RpvXzpRGsr4NaQ+Sg7GD4sYaFOi3YnDWO4rMmJyPMeAGwZp5cD0+CnuhEOMe9uV1WEvid+AFcYRUNx/X7Q7i5VVDdN/iM+EGsFnmZuBEB+GuftBECGYybXol70cqZ23WPUH9EUwjsDRC8eKYDYKku7+PHZzod4n3mIoh31FuTErlk4r5cMEKkU1t839Gp06QElIASsAiogLZI6FIJFEGAIiAE4uIQ/EcTEyCU8Y574cZQ2RbWQXbHtJJT9dqKjIV/Qkuow+YwL4dg9gvjx4GTXOpEJJnmZpizDjvwPj0JaiIRnyP4HN4skWvTpFv6bmkXtE2GwaWhQxNYbCGqw1C3mX65iLZV690QH/TXzYsQaTgI/sxdIZ7RQfBMx3fAaj8LqNILxLNnhtq+TZUaCf2Mx6I0bhllwcLwfwF4jre9C7eN8/AZiVJszyjLDIJwFjzCGXjW2Zkpq7APwbObclLk9fl48wBXnSFj8XYBnUK/Jo+2+7NsumEl4pl8+TuRp68XaRbjHtXEs+rydjb82XYtSwkogYonoAK64hlrDTWYQD6sTj9tEll+JEx+TW0n21qeL/l9EAZhAMzGjfCLWqc+Ag7DpGre89JxFKoxH6oRizMJQtqYr7EMpXkZo7mawyG1RWdsQ63A7JyelSWr0xJk9ZFj8nnybqnz7c8ydvVcmdwvTwZ3dBZfE36gKSo4+QfFR1Bz9CkQXi6gvUhsCycNhCs+o8dgld6xEMbp1ehz0JrvB4unsxbv/7NtRqBihevVJuHG5qLDlHoQuhXs/K0xPa+T1v0GqPMYhG19iNzI4chhA9IQj3dwS7DCW4HkzWjbfrQJjeKELHQ78jUdThF59lORS64QuWcszvLSefK1LK/5KhoUK8U1h6ND+/wckT9dhOe4Dp5XfL2Z+CxZb4jMmAewoasKObHzQLcsctOkBJRA7SSAr7omJaAEPAlQ7ybCenb/glhZ0Ry/nOcOhMjAL2ReioQGHJPonKNSf+NxCcnM8DzVYztf8vMiJa1BtKTg9PTQNjDFQnB3hEqhL8P+fbBA73b+EodF4xca5trm/SXjD+Plu6T7Ze77L8k/0n6Q8/pDyFTnH2OKBQiL07hGBwRzix6wOvaGWMYlshOSuAf7d8KNYxem1L4cAgMG+52zYaFcKRLNv0LgXdGJfZuj6LvEYhmGNqHJ1SaFgVPMCFh950KwoY0V3TYK4UgwPzQP9wosokbiPmHf8TVoA0Ris3Z4PIegTf3gWgMRHbcFjz/uXziewRD0Ad36hx4UKR5Xxon8HaLzpd91lFFX3oD7i53+NK/zu3j0INRslkft/t+8/SKHZOR8L3+elywt8BXN3ovvIgBkow8cjPvGexUBhvmw7EtL51e4b2u8QYoC2xZwA0FHUZMSUAK1j4AK6Np3T/WK/ECAYmvG0iBZMeB2qMIsuRbuFcO6tsJ00U0QMaKhhIWFSUREHbzu5vvu4pODs8RlZEpW1mmEEUuSpSvmy5sO/Kq2GyRd5n8pd57TUOpExcieuN34sXVIMpT2Mswod6D/eMm94W555ckfZEAX6G5oa39qkOJb7cNRKAcTlo4KAmKhUS8Ii47Q/zCsG4smOiAHVkCAbYTYgKCKhOahlti9HiIM+1JWwQJaghjzoRW+ZUEbc3Cr6qN94fvAEWLfbnX1rZCKyQUskpwk0nMMBO0aMIXlVqA3KzpRRPPWHfoRQg/Pe13ct+NYTzsBf+VWuKV90AlCP6/BAOcnAZ2fJLjbJPO+4UScYgbPemsn3Y769gqVUeddj94KCoC/v2/XxBb5mFr09DFjObOho3HnHYNlYJevJSDroEQHBZvnvi6eeXZ2mPLQ+0g9kSwn8w5L/HGR1fHw+14qcg6E9MXohNANrFp9d53N1v+VgBIoB4HgcpyrpyqBWkkgDN+KhXDbeC21t9TZv09eu2KIjBg9ViLqRkIxBMBLIx+vbh2uT0kQAnCO9QmB4G4EAf7urE2SGxAtY5s45NLJN+LVb7CcPp0pDpiZHZAmh/fulXs++1Z2tBoisd37yc97NsuVvXMkG8KkOiQH9JADlsrMWAj7trC29XW6bLBtJ47iv90QW2shmLEeDKUVUSCUQ6GPHNifheuIhqClCKuM5EB9QRCD0Z3Qvm0Q8JVRqa91sGMB0VwXXkGx49Dp+NK4RFe4FZrNoyGXLh0JC8FnD3ZkghFEYR78n1PwSVsN8QwBGAB2zcCuCT7Z54Ahvh+n0BHKgvCnOKQ4tktfujREdIIib9wVNznNhzcMODsAD4lQkdpLwmapE5+q8pZhqxRFhddrI8MumoZrYc+rINmrAcgWAfxy5hoWV+QFyIH4tfLMK5/Iv5cclWmjgABMVERb8HSpBGo+ARXQNf8e6hX4kQB/5FLhj/sVxEF+SLY8Ob63nHfhxZjZLUeysv3zLvZUxinJpS80BhG2b9/CiOfMTCgXJjhRBgeFYkKRxoiJnC2Bqbtkyu23y5dvPi/D28ZLY1i9qiSONESE8ffkEuozBtbJCAwMjGgNccG/ItANJ/CaPx1+s/F45R9JgyNElQlfRuubuTinYAvgBjijqMpJrA9Cv8ckkfUrYImG100orPmVVn8JV8l2NIOIpchviI5I2i4I03VAVEkq34hotCH3AP5DO8ztKfhlyIewP0ar9GIYkntBD0MTN4Pht9l54AhhnXYQXkgL0XYI6bq8BhRB96d96Dh17ouT41+DGveFNMUnfCI44wvD3HhLRewulDWgCXZF4uPrCYVKKGIHHtoSU0EevJppXTda/vXiVHnmry/L24vz5M6RKqJLxKcZlEANIqACugbdLG1qxROgNS3+gMictFbSv1cTGX/hJAwE4o+7f5ID1us9e2CeDY9GgQhtF9vAWLQ9S89IT5PE2BipF5IrHTt2kEZtBsmhuK+laX/k9I+O96yyyG0HxDEHU+WjyXktEdJrDIQzoipQBGfAuLh/P/ajw5G9B3nQ+agP4ZdfSeKvyEYXHKAWy0T7G0Dw0c0kBNv+u5sl1e77cUvqUX61HCuyB9bfgERIQIjRSkve6kKDGP6uPqBlrkTQGLjeHIJVujuEfgSEdCw6UpFdsA+dp8PfQlijscfTRVbgWfjrpEPoJOJDRe4t4btmfN958VbdWM/GM0QO9sQsDGwTRAO1lbiTHybeVM96WIhnQczLekuTWC4/Vl2+npvMjlo9eXJCnjyEr/w7i0XuGInq0Sa1RPsKUfMpgepLAH8aNSkBJWARoO/z5sxgyT+ZI9dDPEdFRRnrM10w/JHy8nJl+a6DIr0H4F39IQkOCTbuHfayAzGDSDoE9NGMUImFGg3Bdt+Ro+Xooq8lGM2oLP1s+TeHNIX2hLWxMSyQ8DoxKfOI8xV+HKzNoRAKDLdHscIwadQa1SUx6kf9HgjXhg9TY3wS0c7SaiFzciX9F9oAQvR8kV2fwiaLhpYm8kVFNREeCRJK8Yqb64A43h+HADQb8CZiCPbF4L5DVDekWw/u/zL4SfeDm0fH1s78LnFsbxx+eQ7ga7AtGeMIEIkmLTXLTJxzKMshG7Zi3Z6XxaDeMLw16IkOXJ2CmxeOZy6Sbi/I3BrLZjBes6PHm5uPfccg5DnG1/7V5TNNf3MmXJKk4sNZMrnumfhI49IkBv+1xSfEMmoX1G8a6Xmidcwq7PRJwVdcXpgictf7Iu8tcYponuaZ1TpFl0pACdQMAiqga8Z90lZWAgG+ej4FT4q3VrWUZn06Sp9uHSQp/hAG+p92hasqTzOCYd7eumW7zDiKn+Y2XfGe+4CkJx6XjJOpRnTSD9pUBL+HI/v2QjE0l7zANDmeEC8tmsTI+78EysAOmHgFQqGiInJQuDCaBq10oXwTDot3K1gZGTCEAQ+S18PaiEFk0RDNOSch8KgyYG2ujmLAiCWIvlYXOtuI/6tlO9kuzxTTCY/IOPiRz4c4JVxPoeZ5QmVtox0BuOdsTuZOvIE4gBXcf8bwpqUa/UNZuU5k8h3OfF7N/Tj/QLzIw1+1kzajp0pkcLhkROQZoRsY7pD6A2CCLiLthADGP5M47XsW5iEPzMqUY2t3yHnNF8rUMTiEhzgTz+pTM8Nk38nuUieCTzW/Wg5EnKwHoV7QC8R2PgYC14mOMf7JJlPBf0TuQGjK04nH5FTaMclI/FVevzVb2qFzwx/NXBS5ENe/ayvakxcIHigLPZ1GTfPNwEJ6rTBiSd/meP4o+lHlv+4S+d17Ih8sFpmGdp4GK3LUpASUQM0kwL8FmpTAWU2Ar1QZjjklBT9yCxCya/T5iLIRIfe9952kRUbJgVQoxVK5cRT8LNL0xTm++TNJ52rOTZ2Cn/+rL8Y+LLv2lieWfSJ99/8br77rSD24gBo/Y/wYLz8MM9mAqyU1KUWu+uC/MLXBBFa/rfzt573ywAQIWFjj/P0amK4aJ9Cshh1QHV7PMwID3VIpWFLWQPT8AhF9BMewTYtkIJhVR+GM5plG58Aa2vUStDfW7KlZ/+Evc/0RCPuHZzIH3CvLH7o0kNgmTrku7HAV/JLweUhFB29gW6zwmJeUAWH5/JxQaT3iJunWvhW+Wu4ZS/O2h5bpQPh27G/cTjYv2yR5I47Doo3bjzoysmNl5AW3SoP6dY14ZlPMV9JmkjbbXtpo7eKzn48IG0tWtJbktE9lIb4Ho+CywrCDT/9wvgzs08O8QeL3lmWtwR+RbPQ0A7HBc//0+UJZ8sxh2bAd9xMi+rlrRKb+FZb3QyJdWgKd+6Vb1epSCSiBGkBABXQNuEnaRP8ToLWZ/s7Z+AHbnSgyb5HIYukq6y68H7+QI2DZypAt2fhF5CQpVqyqYpuBvJxBgSkDL4YR+k7S0qAm9mIdKigBlSRgZFX+KZEtcBhtgl9hzOGdfPXd8hPfKZ/gIEIcs2xSvVrAbAUl0hzqpC98Jxh8N/GwfPbDAum46gW5/TwUS+Hij4QffwcstQ2Hokmd8UPfGgZoXEoempO4TOQgLG11D0I04JIYoaTaiuYCFrgTZtxaoxHwfe7jD0AVXwbb7JloYW12LnyL8fjk4R6YvphnpqreZsMLGs/v1K8HEJEFj3aTKOz3Jg4humcvFtmbM1au69QG7lHZ5b8CPJBBcHZnR9ie2F8NgvmeH1qfzyTbOlZtW2eyFKyxyDBEzgkPjZVT6EefxvN/Ejtj8F3o3qWzDBk8COEpsWHlt4nzcPzdmH7ypBxJOCxrT4j840ORuU+LPHqnyLNPwEJ+E8IHwj1KRbRFT5dKoGYRKPjFr1mN1tYqgbIQ4I8hRTM/+49BGEK3LtgtMn0dhPRgmCqvg3jm+1ZONUafBWhWYxI+DUfK4lIgvkYMYbVxExRnHN67o9BEmmqb4ReyB1RQjEi7jiJD4RPBX3U6RVpWN4r0qMaw9LJ1/BQkhmRg7FyzC6oD8aGlQRuR0RPk62felcsGJko0TMGcALG8ia4O4fAhbXSBs6TjEMsOXEYyLofhzOriOC/RgU91T8TFjkXUKJGmY6p7a8+0zzxheC6thLst8T/hGV0P/hBuoXhsuK86J77FWb5NZBzYew2kgZuDfql8sraejJmIGT398fBWAhBjpQ4IM1/ZaPxNyISHSb066B+np5vxEbmcerOIVL9BA9mEvvOobiKPfxIqj33jkI9vz5HEGzHJDDoSj09AxxXfY3+/TSqiObpbCSgBPxKoAT+JfrxaLeqsI0CrGDVrFgxdNHb9uAM/8gnBsjq/v+w6jV/8XRC7v39UZMR4/OpDweQWWMR8USuM0UbXjn2/wnz9NYQxBHJbmN+GXQ/RDGfJQP4y4jjfM1P+mF9Jz4KxTeuY5277nbKsZxTUsY1lc4dJ8uOaD+WSwRBWYWhycefayylqHcImEEWnwjC+Fx8HRFBQJi1vTiTEUtNSPm7jcbw2j+3svP9W+8uLyirHn0uK/uNo2Cm0dzeezyYdIf7R70rahz5TMh4x8K+O7bYzoIdSEl64bINYvL8ljnhrMH5t5qCzmlNvrDRuGI3Hnt+Likk2Q7CfKnCY70M7fKVT8YKpLVybslPhroHwlnQ5cbdwO6tkvPjGjZvIxsNBcv6APDm3b0vJqDtA3prxhfzmcpG1B0X+u1TkkYvR6cPz6g2ZnxqvxSgBJVABBFRAVwBULbJqCVCQ0MjLH3XGoz1yXOT7bYHyQ72hciwa7hDTLhLZGof3qfNFXn8aVuK2ELdQkBS7vqYQ+DzE7YTvx/swEbYTuegemKVgaQ7DfopqE6wZpip/Jk6HvH8tVG2CPCpT5B8/rpcnWq6TCf2dg6Z43d4SOxCcprmoRNeA0xA+CV/COp8FUc6/ChDmNfEHnW0Oh/DPXYXbg0/O/7P3HnB2XdXZ9zO99z6jmdGo92ZZki1ZluReMcbGJRhMCwn1C0kg8CZASGgvyUsJkECooRhwbGNjhJEtuQjJktV7l0bSjKb33r//OneudDWaUZ/RjLTXb86cc0/Z5dnn3v3stdde60kI6WjwgYiGYjdeRt3a4G3wn2FTP/OykcGrUvxbygQJLcVkIwsCPYZ2PXyA+owEAs07ZJMuSUmQfiZU+gPXgm++eShEE6ZMwz94sDoH0aE5vJb0zcMNZbkMYumYlVUO9Sss4uuBBjoc9zOtTHdE2QvXjxiBTkpKIRpnuGKjWzQpq0bRk2foly8dUsG2zfqX97HY8tvSi6ulu2/kvbyAn59+snOnHAIOgSFGwLpKJw6BqwIBs4G0jq4ZEvjKJmkLpHBVyzQWBT4qvWMckTSmYFaBrcKKH6KG3i793T+iooT0dtGzX4iEwWj2rpB+sUp6G6qkWbPImARMU3w5bDr7K4tVrJIKPfNL6clP0ZOPV3Fdhf7qP7+jb+z6id7GmKDfOC88VnGCatL5G5EeyCWap+Sm+BaZfCQS50DIrPym3EzNwCwlE5vVSprrRxxDfkK4GDkMBweY6XqBVKIoW0i5j/CrgHNxVIa281ymBVZyGBzbK2++me3dt69ENQRw3mjMZzBzOEO45wiDg+3VM/XIbaMZYw4iWySvZryCdHWnMkNzebo4cx+56RiaZ96nI7SHeaoJra1mDUW7ogaIa2la6QR84DUE06g04oSEGm0qLdGd9z+qzz93SNeNr9N//IX0nv/DgI5Bx43j+fnoPAM5d8Ih4BAYpghcnl+XYVo5V6xrBwHjl3V0bFuOS9/fM0mb8udBNB+jN09jxU8CQHCDMav1kN613PQhSKgti/fbIp8XVKRh9gyv/EHatwHTj79hrp302+hN/WYW55XORdxkiwhffAbPHHehrswnz2bqBSP8y4/r/35vi26atkOTx9JRdwf2wMZuWpXL/4pXwGcrRIdjw+pqF3MjVgfZKYihvtsYN9VDTpogfNTdbODtVRiOYq9XLYQ/rohXa4ZvQWf9TtrNONgwEnuHOuDAto6gvtVHoPdzPH0ahbSXrO+YlFdxzxEGNWkTWWsb4tkOD2Z1jJ6HswA45DKtvLT3JRmtcySzGPatimIfFlHFAkLc78X1b8Jh9QszTXvUaJVVbdWUcdLvXj2uO25bppplH9Z//+nf9Nl7O/S5T0qf/Slp0sZz+LK2W+GdOAQcAsMeAUegh30TuQKeDwKmIfoqrrGeSXsP2uY7pZkzfSYZZn9s87nGTMoxMH35BemvP43KJxbyfCE9FRnYSq7Nf4Q8w2ie+HtYGezMyPMF0zHSMvuSfm2i+6mtkYBy1MiCocx5yPfcsWPS6l/gC2uRSu78G/3P77fqbY/+BVo36979EkzJmpUZv1ozbvu8dqXgz3rltUGgQyFxBZA5Iz57IdCJfPZH9bNzw1WsbLH8KnfsobwQ6M4x7Pdy0i7wygwXMcXuhkKI34up+AmfoQYcqNcc2aIXboVN85U7Qyj7tm0hmnT91MHVPvdm3EgZuonyGc6USn/2yWeU7xwnzNoEE2al8h41HeXrS/1TUrpJO5iZncDvHE1FW/XQWKZlP1Fapmo8cdjzExivFxdt0vf/2wa5wVqzOloJhHL5yCO4xGOs/+nvYT/O+HheQe9PwznKZJctL7cA8TyAcrc4BAYBAX4GnDgERjYC5j3umdfYgqepIKleC0pWaPn25ap720dgI6iNrEM3wrrqOemBd0GemRe/IM2zPU8mh2E1q9E+/8XnmJGFKDQxT5yc6lNpnq/9tJHhLrTHR4sxdM2HlNMje+yI3UBiHXTFIWI807Nm5HgRDPW1v9GcmFq1nDimPQ9+SNtaxmpe5xx8M5s27PSEymtvIIswTZj/SW1aiylDmw+S0++6ej6ZOUQFzT5hHPUsQZtbRfVp/pEi5kKwkLFeBhrzgvGM13hde3jVhsvMgZWjHnOMn78UqunLlmh8Xo4aiVxysOuA0uP5XvR5/zzceWZPbbjm8n25HIQ2sC09UwkGs0dikyCq+IEmrzbK19USg/fHEL7qRlgvTXpgqWYWZONwmwwK4ziYaKXF5XUkTMAVVgHW42KkGWP76vISdTdWEiAJM43Eev3dsgZlQZ7tFVz+4RNER2QwzIewu9lsZgHIls3Eouxh6dvPE8UxRbppDrMPXOvXm0lvVXhNvDF8GlZo/hmBwQqw1Jul2zkEHAIBCNh30IlDYMQiYDaYBPPTf++LUXR6iH7+yUe18KZZeu43P9aDr6NuveU+5u15zddznEJPMxZGckGaZ6Ax0ttURu/3S2nBE9KfX9F90biwohN9qRmmthS1UVwy/WjXOXCk1wxqUMTKH+nGkja9mp4n3fcO1I3nINHWczdSyZg00oedbPidFsDb28LTVLRvFx5AXtLo265TeEg32ih6+L5C9Usa7tDYmDiljmpQ935u6Oe2vo+N1M/WvAUTITgQnf17aRYIiq2/HClCaysNztdK2eOv49VLhyhBoIeL8G3QPiZDjqaN1y1Z6djet0NS0cYG1Somlov9EWhOp8e0acfOXZo/dybtQYP0Hel5Fez/4bORbtMAt2E8HNTScnKQUU0yYTFJmOuE4gSnG75q9PXCxEpiz2GkoYj2BqWwPtjqF8JXvYPi3zKtRiuP/If27uzCQ0etsvgaj8lgTJ3FxBD7ieMIeGTZ2maNioyyr3Bf6b32yK0s0+CZVVukt8C3tNxby9svnEaYI5n8Kq3AbGYK5j6866PJdzybI9F9AXafHQKDgwBdqxOHwMhFwDqSshrpUEye3nXTTI88Qy11+913auFT/641LbfRk/KaH0Cldys9lOfM2MwuLkBC6Z1e+i29Z5amlv1BP37frZo2c7Y3dfrn19/UO374DTW/8x/o7TCM7Le7683LVFe/flpB//sDhb7/o3q4fp+eXv8mpJwytsPyBhIzQ2lvoXceg9HpMWWuflGzbrmJjrJbB/cfoLd9XsfGJePOrptFXSH98hKjAZ70z08GynnEnTeuUg9cqVM5oMphRyA7VvURRKANdHMDvp+x0VwI9CS0k0do5jBjrsNAjPu+uDFYBWPHQVh99r/1DY3KS+xWohHovvbPVmbq85m3d+uzv/yufrVjuhLwjxxNGO3IiF71qd0DoY5NTVWoZ3ZhJ+yUvbCRSkpOQgPc/8trZXjl1df0/pnFCofkGlk9VguRbC7Xof17sODqVGVlFW7VKZj9YJyH2KxWcHCXysrKPReYkxL3auo0flmYPGIo7Xm7vHOedOf1VWpuIuZRDCftHTMybMW0zRTf/mMOPbHrAwkYTRvNNo4beM7SHVCohv0slEK0t6ME37UZT0Mv42+aZx9YANyWrxOHgENgUBHgZ8KJQ2DkImCdyGvH6cQJqTtnAT2azYfSi8XEZSgzEcZhTKSK3rQKVc2oSfSAbRdWWdM+YyahBghseII+c/N8zVt0S28+dKD33a1/P1anv37tDXxRoYkeSLttWvATRURueVatEN+Xf/BtpcWhvR5TL02+nh4Y8t2vRs6qQyWLuW9iHOr2SuXGhjONHKFQ7k/LyFDj4cOanJ+nUMxBTltDeGE1vSrutuZORvsXn43bMZT2dSdYnIVmcMTxCV67JF7ZDl5dQYoaIGipvLpnc0c4FA1ollC2aHBPY6gmpqb5tLuQ0qaWBk3O4z3lr1/hfCqmCT/4WLf2l25TNeTQLJNK+Ur4vzJGbUupo31F/TTXvhJFR6n/ORrwHbT3o3NIwO5je3g22tySp72lA55nCyPWtp2H2NctPsFnndUF9ibjGBhgDaIW0jYMvALaOJzP0WaGYce2Xarw/vrHutGMt88l43IpW570IOS+AUz/9hsMvAr5qcgfQBNN2W0MMZJMms6FgbvuELhSCIReqYxdvg6By4GAx48rM5m7LFCQRc84KaYZs96CXq96H94rpg/Qo5x8oP8D6y3XrMEw8RZN3fmC3v4ObKhZmHdKWvTYY7fq8y/8P5X33H3qdN8j055teE3ZnSVqR8tWWVmpigbS2bacVW6PUj7I/0AE2mMlEGjzaYYtdFR0tKeZs6nplORkFaMWGzfjFs87wED8pW9xrtbP5sGgM4fJAAhPy06a30wfjOCMMDFyad44Io7jsZBXd8xkxoAbUHKeB6kazKraZI6ZxVQ3JSkGtxGmIQ6isO3NLcpMPkfOvS/nhCzu42vlyfje/dl2fIXPKZa2EdjePGIhy/PG8tkIsD8vDs9b+Lp6ZNz/gKXBZp4yulFBh9p16z1tP1hyPl9mfzkpm9U5GyIdxBaax77v89xjSzfaeaci+enxzJqsXk4cAg6Bi0LAEeiLgs09NGwQoANpDULFSGiwIoucodvZWNTT0q2qDrS6nvnGLrxy3MFpU+9cgJiqxgysy4/SGy/U9MwkRUeTVx+JT4jQTCIsvFyFLUkKqitTYZ0mpNPRoqgdf9Cyu+5XbEKCNm7cqE2bNnkERG++zlz9Ap7o+1xvIjwOS+EflbXFjAHSg/ouJCaKNYKQayeKgOCkTvAheXQHRIHmGkyOM1iQW5l5exV6gKaHQLdDBtsg0Ciir2x9eBdNQ5yUCgu297IX3FbsjyMGeH2563QJvO98vpIXo9m1cp1P2qeXbMBPJRWYiTUwgOH9qoWErtoPWWUdgr/+/gdtDBzBVzWerRca/6Xz3ttzZiaTSLSf806DtmhGf2DjxezbU5Q2OpbflkCgfWmFhNQrurNOu1bxHeFnMYRnnDb6vJvG3egQOA2B03vj0y65Dw6BEYAAHUc0LrQUPVW/3HhA79myX9NmT9Wmdav1etQYGBQ0pKhUWoJ67Lx7o956W1TBV54mzDfzwbCFFrRsp7GG3tt6uoLQSXPNOGx/eZjj4XVbNa61RQmEauuml507d66qqqp05MgRaetLeKj7IHPGkG+/FtrIu5l9GOlvoMfGhlNJsMHOUjU3N3u2p7Z4qqysTN1R4ZSuv4x7C3iN7MxjQQ1WMRMmAVs5UJZQcRt3jFAxV3wHd0PGGPtl5UJceYU7mYjwxlJXqE7GmbEUUHBcjMefrRi20K6NWRALXHNVCpXeBzN9HdJsWt5jtMHaowzUMK/xf11P1pt7O7i3uRhc+NpflPAed/HVb0jy/dqcTxr2c1FLubYfj9Psmt+oLHI0Li1P/02wGbmQkBblxTylqW//sg6Sfj0/PTEMCk6/83xydPc4BBwCjkC7d2BEI2BkIjaTuW58rZbcfJ8+8OUf6sGF8/Wd1aju7vwQvRBqow5usjnxCxHPbzS9ZOtxafTDqAOTtOe1BrJpUXw8LO2ktjhYx4s7tK2SrxL3nBlKjJ6tBw8B63+tGVMneeTZpr1DUDFNmzZNhYWF6qlHvbVtE+W920eYPbOTauyeD2EUupMVQgwAZt8Jc4FIb9rBOsKjug7PBx34t67AFCQH7XVCHMT8dIXThdT26riX+meOh3RACArRrkWgufT7fh6JFTR75yTGZeY1JYwxXG0a73rdla+J8cJu860eICH4jjubB46AWwc+pL7egCfwq2rMzt7rK/luU4abxzAGH005INAnCqWPLpQKzBSln3LZ99AWrlp1Llbsd82/ENAgYNnEmWQ9MHHuf20d78m0f1JE3i2qtuYJxLH3XkuruuFf1VXUpYIJX1PHWtLlZ+WSCtubtts5BK41BByBvtZa/Cqrr/HiWWl0Cyyu07ylWn9XvNYXnWAp+mKfazlbQDgK1Z0Xc/gCKm+dz85X6SUXwFrS6WU6tX/KbP3n//uRPv2Fj3ER9aBJT7u++1/fV+OCt6Ee7Kc3NUev29/QpPpCxU9fQidoXRj9Lr1sImF+owhpZhplnXiDDePFNyHS5ZDmOp5LZg7XVgndNQU77NXS01/FC8c+laNuMvMPI9CtEOnU5DGKi03w1kt6iV+D/6y56iAt46dzgPeDzsNgzOcLbfbhBp2Z4O/djoUPBHoidSs+eOVLGA3YnQxM7U0OJIlnaGPPp6i9Wlpby9DAV3VPGa84X19L1ywQUjNxBcfiwwkMHmKskT32bhfPJ/HLd4/nj9kKxWa7kwsJ7UMfMdvii4og3lu3bshvUQk/B0aCST+GuppbvPBY3+f+SLuR5aZw8mUxspl/WKjxgaSb349jne/X9FFf8zxjNhWSjWMCA8HlzjsEBkTAfW0GhMZdGO4IWB+Kxyu8WXBQetRHYNMmYYc8jmN6EAugYIFK2tlfSO8ewjMnthA4hfnzJ74IE+vtjWbcq3945hfK+N4PtXjZUi/J3z61Wl8voXebN8HX458GGr1fa41CXnhe08dO8BZb9QSoiSMw2DUS7RFoiLGqYA659JJz3mGrtCDSx5kv3qhbq6I1MTdS//n8Pq/vNBJuNtR+ufHt9yiUTrF9iEmFP//hsDeyHM84JyIbTW0VTV+K/TBEYsRDwisUjzlKF5MU4ROx5IEkZVDXfoZqQ9IM5mM4C4zbNx3zfD+HWtSSixXqUgxhXrMX8whe9TqO83OkPCPKNJxpYCv5GuCJTkWFvgAji2exn+pzWuO5ibvYvC/2Oasu2znfq3PeEFAAemHzRLLmgLQRHLYegqBT76wCsiKvNgYWTDSpgIHEnQvxesl74LkKDMyD49n8DP18zzbKZhesoANLcFCktwjS8+o58G3uikPAIXAWBByBPgs47tLwRiCct/e1bdI3XyWcbsof1P0z5iKnoaabchPMOoY+BJqB/1jPjON8o5GZStvMPr71G0J+Pw4A1hH10hUj1g88ofe+9aqC33idbgrL4zx6s3vQUp9B0HnOjFiff0rjqrco7YZ7B4yIFh4ersy6Oh0LQRNtc6/bf6rpyQVaOG6SRt/7SeUXTFd7W4teXr9V+zesOq1Rlj3xSd2w8G6189i1KtZCrYyRInKxoqHZm3fAL7AHDYUjjHSx17G5BltoxlcTFjEhwWRELT5/bd3slRAj0KMZqEwLb1FxSanG5I86WQwje+cl1Mne12+8KG2BPN89nih8t0EQMwnOwsCnqZ1vHBwwNRqTnFRfilhoaddh6eVd0vfekD7/dvAo4BrtPmRi9eMrSvRthVKHyyIM8qqp8z+CRQSKgHv4+XofJDkxitR7f3bsJ6gN3F9nJuL7r0ormKD6+zt41yMC7gEvUyTE1O5WGYuZUwnsFDBW76eovYkb13biEHAIXBQCjkBfFGzuoeGAgHViZuocPesOPZ6ZqPqqQyp+dbv2Pf8LVqPnSDcuw75jBiHQktFQo921MNhmu2m9s0d46US8hTa9vYgxgE6OX3wKVc84mMI0n2rIX1l7xrx6LLlb3c2QdbvfnMB67JVr9tkiMNjiP/OnVrJfeu7HCs5JYcr3ZCgTf2oUoYep1g71JMQr8/qFCv7Ds5qPu7y5T/6tUgumYGsd540BzI9tFFOz7/38D/TW/35LmzesUwyePG569GHdtPRdpAPTuIbFaxaaIX4szQUOFbtpFghmb6uOaGSsDqG8ptFHeb0g0N2QzUYmHzDuuWL1M2J23fhufWvzNuXlZPLKhykc+wLz6Sy+bmcVvrPNjRDgn0H20Jh+7QnaC0L68+W4SIcYHoUot/EVtXrj7lyjIIVzZkv3M0a9boJ0AxroF5gc+hee//pHIdh8tU8SzbNmfBku8vU2d/CtqZBdI6+X+oLxM8G4WZ/9BTbW86SHaN8wBn27t0n/tQmNNMS6gi2SfBfxbt++RPoqk1PfXyn987PSlx9CUw0B90t8kjQmZJ2qi4qVPvVcBNr/lNs7BBwCF4sAX2EnDoGRi0AHnWxOVobiE6MVhznEKKoyFXXVij89rfxNB3VweaMaUpPUvge1ZNHDrMqiRzatdLT1PPS+yYk+0mtqnk7mTZf/GsJND377X0KCOdff4sMuGG0EDM3ENNu24scMDxthBodRFVYcIVzZCeaeN8MWqlXfHKXW1laIRqhHmn0Pkjz2yzX0oKZNXLzsQc258QH4OXkiRgo72vx38hlmOHbcWI39zLf1WO9pu9PIjN17LYtVvx3Nc/Y4MKtGQ3uUZqU5rhZYzAqp8hh1YmIkmRe8mde2k+Mr5Y3DTCvugci+dahQ+44c04xJ4z3bW2/h2tleRF7YDt7XL/8WM42x0rsY337xaem7L3Ge8WhfwaJDhyrQvB5GW/0MnignS5+8gyApPGeL6r76IgT83XwV+z44iJ/JVp2Woe9rekk5WdCjLz7HOH+O9NhiMADXf/+99OmfUj+08IFiGHzpZTBbiLb6QekXb0o/Bbf3PkBR+Lmylz2UcfSC0d16vWo7H6cHPu6OHQIOgUFAwBHoQQDVJTl0CPhJkmlzvQV6aHpb0P7e98Cd+vKXP63GhjbC7rbhgq5J1RXlKm+s097j1V5o3yNHq3WkuloNbd1qTktT24H9cOBgdd9PL712Kz2T6TMDxHpt0zJ7K4jsPMS5hzndILr6/QcVtm+/4AUalxahsooSbdi513u4pqZGLfjJjY+PP0mgzQuHBVMxEp1IMJSx48Zjz42Wmk51IDn7lOxAT139581SJ7KAejI2Knud6W8+d9M0V4uYJ5FgCHMPJCpqJlrQdEgjmssrtUDSBmxRaEr/mq/Jh59eqSoMmduJKnKo074b/m9kP+gzqPnftyCKDHqfuE36/74r/Wx1P/cNcGrbHuk9bL9bK/0nmuvtpLMCbfx9C3igD+EcIIlLPm3rhDMgrOFU9ZKEnnf5BuBiwPfEe0iJ9H62BlOWH3COQXtkZLi30Nh+HwLlF9xz8AgRHT+OBp53ffZ+tvHcYb8blM18Rzc3VZ7DfCMwRXfsEHAIXCwCjkBfLHLuuWGBQDCdWeHRIqXNnOB1PEai2yHMiUmpSk3NZWPO1RPr8axzp5exzQ5Z5t/D6rO29jDV1lSourpGew7U6OMf/6zyc/M9l3PcdVIam5qwfaRzIxKgqX2NSIRh0hEdHanYmBilXA8Jxnd0MCYczXssPx+BtkWCFRUV3oJB875h5Nl8QK9dCxNA8kbfrBRCiJ2NPHs3un9nIGAoN9OcE0zhxr7yAOSGfX8TB2c8PEJO2KtqwTkO78BCAgKdT13LD1/Zwtu63Hw04V+5q107dm5WGZ8P1vrsl2P8X7XAInKugkHAa+sxv3iXjwT/4c+0E/fQXKdJdna24uLivEFnaWmpN8gMvOE5SHgsg6WPvl36MRrcO9CGW5ht7zsdeOPlPqYODfUMXPjNscXLFy1UuhIs/ov6//sfCXsHAABAAElEQVQ74c6UfR9j8K//CjvmjEzduGC+srKymNzq1I4dO7RhwwaPTPvz29yVqy/+sVsPzyrWf7zCYCL31IRYFDdFUU57Z5w4BBwCg4uAI9CDi69LfRARsE78yRtY7/fcq3r5xB4lZ4zR6ILRasUJa7c3x0pP4u2tdzVtsn22Lpu9+aWynRFivgWZ0RnKzMnWuIlNaK4zNW/BAlbGn66BDkL77Gm5SeGU+Ii0nTdy7GmouVhSUnLqFo7+/Oc/ey7r0tB027VVq1axVpFeFFn0jvu9knkf3L8LQ4AmCsUmNXQM5Ibp/uhKCJk18dUm1Kn7KC7e0NgGFXqv7hWvoWljZ+Rhowz2nShKv/ALaQdlXGAa0dMVp16BzcNE1mi+gZDf//oZpJfbAsmzkebFixd75DEyMtIjzvYd2bJli/bu9Q1GrdL23IrXpL/EbngM+a9k0HTXVE7yezDY0kSBwzJOEdaLyo/fm3WbwS0L93SjILuYan3nWTyStGbonW+/iwF5tPfbEwZLv+666zzzr23btp3MKqKjSfvS79Thxl8rLKpb23jv5+VwmZ85JtdUEZ3tDSDdjNVJyNyBQ2BQEHAEelBgdYkOBQJmUTEqDVvI93VpV0mx1u0o1s4Nf9bBymC1Vtyo7/33z5nSDFFaWgb7eMXGBik6KkVJiZGKT2AO+mToQOvGbYNmk6iRYdP+9CXQ3g38M9IN9z4pRqyDMEgNxW+aab937Nmnffvp1QOkCe31888/z30+Eu4n4jnjx2jWwjs9bXbA7e7wPBGwNaDRMfA1tJ+NRZDoGrSTNO1Vp4HjhYuClDauABgb+9mYcBiIkWgjz+Yy8O2LpW8/j63++9GkJlC4QEJL+QswL5h6o/T7P/I9gzRWBzRSDDM49913n5IxZ7LvnX3/bKbGPi9ZssSrqZ9Ek51CyPfN3dJNpPfyFgj0RO+Wwf1HHQqP+8xXQkzVSx0uWEijvZkAp4XSBxfyNLi9SPm/90qI7rlnvgwHq7uJ/UbY78WcOXN0+PDhkwPuBszOJo/K0urjN2hGyxqteBUC/QEG7cWsWd4TpTl3zTnt98lLzP1zCDgELjsCjkBfdkhdgkOJgHXgplSezjTmdQUEJGzpUTkRNSoqV6v0+dX6NVPGhyBVVaHhCkkOVlxCgTLS45WaHgOJTmGlf6gyRo1SZma2MnFwm5EWTBSxTnWyUqqDxL30Aypk5s9VVZXqgChb52ZeNFqxb25uaWLRX7Oa6mo0PviE4ugYLbBHoFiH6CfOdj4Y93WP/9O3lUwM5N4+M/B2d3weCATzC9YAqWn9KcOhCDw7oJ4M4GXnkcLIucXqdaUWDp4LJRvMTskjUOYJ6UPfxpb3cTSsfCeJPyQiSOtgFd8HJlzCYL8vs7wgF631RgiwX2bMmKEkwtz7yaOdt++KkWmzCbbrBw4cODmoTSHN9QelT5DPt/+X9LEJz6b9L1Ts+xzoyeKsz1OXLvKZRz1PU52f9aE+F8lvOxrjGn4bJo/jGo36qzfRquN2LiMj/WT9/E/ZrJaR6pycnNO08C2s11j6kW9rzU/+VXtXvagaXJfsb8/X2Mf+TXljCpw5mB9At3cIDCICjkAPIrgu6aFDwDrwFjpniwCWj1a6IN2bNdbt2IuaG7hu5pR30LkfKd6j0sNMc+5Hm8QzzXRkB7FrjMT7RTi2HNHRBCQhIsnGlZXqxAFvflL3GX1lJJmlofo0YhBBB5hELxg3Gu3aKDpxNG/mQu1PzDj/A14CzJtdfxLMTe/75A91/YJ76DT7u8OdOx8EjFRGMVjpgZw10Y7DRTN7PmW/mu6B68piqjx5IwNWNKHf/TmxiFh+kI25hg1wg/gOxtr3kHumZvOdw9QgUAoKCk6z8w28ZiTSNNGpqakqK8NYGOGrrmpIufmCX3YDs1BPQc5J+4KE+9twnBOB+cP5ROKjGvrYPMwucjnouKCcTrv5BLMlN4NBMIO9rfxOrHiDxX/pUbgC9C0cPO1mPlj98/PzTyPQhceL9GjWZD30T79W3UcqVd90VFPSzPXltR2RtC927rNDYDARcAR6MNF1aQ85Ajalb1Hp/GLe5cwts8mNY9nG0XEt4QNi2icj10esMzcG0NsroljGTVaZ54c2N5n07FIfCTxlx/a4hR7mz5s+vRubzNxEaTPEbkNdtIqKxzIlbZbZ3Zp03WLl3/KI5t+w1HNP52XdJ/2R9NHT4oFZfzgF1sNw5e8MOQ3L3g/nSiswEe8RI2mBJ6+RY8P+bOJdDgS4783cYG7pLod4bUZaYyGH//J2TArQ1mZhtuEXG3Ca2Pv+Vcw4AsW0zGcTn5nUqcpamb3BEvsPLmFb1s/TXOtX/Mmwb+T7WY9Jxblw9NLh/iQGyN6L1l/alq4/7f4ytmf4gbh9GsSfgb2NApbv8cVOSm5p9BZNRkVFnTGQsLqbJ5/ThTUXjLwjIqOUmpGtNGV7uAb+9p1+v/vkEHAIXG4EHIG+3Ii69IYVAl4/19vZWYyUvmL93RgWofUr3N9yEZomfzZz0GzNvVv6QPpCrS7+qXpiorz+NTIqViH4kbbObqSTZwtm04gt6Lpj0s4iny1sf1iyrlO5KUzzZ2IaC4mwHx6/xtBm3hnneK60I7BnDiPNZPZ+HG1Q4h+gWDrXitiAw8PID0SfihsmlQ24Xexz3v/R1sl2Wni7EFSddpelgw1IjyVsh6iGg9pKlWo242cjft7d5//PiLQt8M0g6/5mYCz7eBzZBMrx48c1bRqeaPqZjjFyXVtb63mu8T/TwTsSDwEtKvWdsXfGE14kq4phwzpEz1uGVdvEqyIfcIrjw4Kd8fYoNv89dl9/Ys+2clMJWu9+F+dxQw/lsUAr/Q1IrB2LuX4UBToTVJ62vp0meXaNLzerXzW2zbm5uWcQaDNlOXbs2GnFCps4QUForL3vBeU6V/lPe9h9cAg4BC4LAo5AXxYYXSIjFQHreCw88WBIGyQikt4yJiZUUXEYesT5CLTl5XWy1ivbNtgyEMO6xHxt4Vg1U+Bf+j2k4qiUAhEZKCsjVeXk9xZ7I1BWfz/sNrABKrWyBWfwD8ymZEFsOMSiRkm2xfIZ8j2LQUlgGGUjEBeirSbJESGmEW1oCdLmxvnqwStDkLlc9IgvF3qlG9a7pzIDLAE+QEK4N6hXHdwWF69ui44JUN1MxVhAn0QCDQXzuZrp/ujuOt2kZzQ/t6tf4heQ7AUf9l0/4E8gjPdmUb70TU7QfJ5s3rzZ876RkpLiEUj/WgG/ZtrcuXVYFNFeWYwW92FmeTZsZN6Il27jUdLihWo4wnvEy2TVT2RgHI0G3M4banBbz/a4opgDf8YcpnLRBnBnE0O4kme6eA+Tc/nQ90XnBgsfP5pBQ7wN/gLSt3Sj+IyHS6XcCYGPuV8H2z7iBTW9Pu+4tn31b9RZ26B169Z5ri7N5jmw/gcPHvTcYFo6fll4wz2KjArzFnD6z7m9Q8AhMLQIOAI9tHi73K4xBKwj9TpTI0AcBze2Kxhm7dcCDjYcQWTaFQ8VPcW7LkuWRvCqCdz4tZfZH5aWQBqMhLRCLPzcwrRudh98WBZg0T77Nw6FqbnHY2xv2jijR23YhxqhbodtV0CE7FwD1xo4V82v1SgIUToZJVCl6xfhRg2SRMRz2WDF0rxaxN6VmHAWsoZFa13bbIV1tCi6p1VhxMGOxF95jxkcI4nBqGD9FbeHQkq1ZvxfaGXcaBoC5pjJOWJBR7cf07eW/4dC25pIq5VHeggalKjdqXdpa8xDmtH9G89/ME8MupgGNwvTqBnMSGxDo2ti7upWrlyppUuXegGHzIWbiQUg2rlzp3bt2uV9tn/2Li1hgDVnCu8bsx9W7dE2i8S+g3P+988zqeKciUFkdeM1Uchc/gWI6efPR4xE24LDMBvZ9aYb+Jxp8ZP4Hng+qQMv2O3c38mz6YuJlJkyQxuabvcGktMo7e6tK/TGr3/r2XcvX75cixYt8my+LQnzg224BGrmx8yeo5kL72Bg4G/4Ppm5jw4Bh8CQIOAI9JDA7DJxCNCJY6vQ8O1X1fbqThYtnW+3fWnI9RAvOO4bH1BPrtHbyye2eOtHrzMFvZNFXEuWKJgtFNLTxCKvNrScpkGr5bid+fIwtpA2zjU1qrO8VK1oQGNgI1YiuJ3nsSSOzxYAIoF0jSB5/ASIbO9t3gmIMoSpFBZUBPF665c8C2H55KPSJAiVmQ2MdKHqPuHAyNrtiatUisa0UgWaUvRzZTKk8AhiP0zXTDZa8a/2UjLATWJUcTIyT7CaO8cruqNStgDWr7CO6qnW9NI/am3OA/pdwyN6KP43nmmNn4D6i3K596aZzmJ9wEMzINCvnkrdgg09/fTTnhlDenq6p4kuLCz0TBtO3UXkwckswrue75KZYvRKopFaE96HgeQktv3c0Pt69XOln1Nnudlms/qd0eKZbt7tVsw42lo7hBMfj9QHE07y4b/6knav2q7K8r2epvm5557zFkzaokIj0J5/+d5iRHLuXR/+FIGi8NxzSiHfTyHdKYeAQ2CwEXAEerARduk7BPwIQPBCbhqt8LGYcgyRuwh8hcBKmTs2ddxlEgs889Ra6SebIHi3364vfelLXodvHb1/yt2yssiN5pasnan3TmxbLSxxMxrFFgi2nTt69KjqsfvsRPtYCVGoOlGs8qOF6uS5WAh3Yk+HonjONM7hEGwj20a8x8IPJzAYMa3efgjJP/5M+vKT0njMP4a7jbRZYfhDcPvXzRmx829mc28mCRZcwxTIZr58U/gq/anpMe0edZ+Sip/1NPoDcbjg0DZIdrFm7O/UKFwqpqC5joqtUljxYSLone5Rxjh4cki15la+qDdD7tUv2+7XI8kvKIr27c+Ol9svm+B1TfeiCS5sZCC24VSyfnvfvja//jvumiD97W2Ur8/rfNKMZyBg/AkMs721cVb2OH3i336l7/7Te1V6dJtXwsrKyjNKGhkXqb/7t+9p1rKHPAJ+xg3uhEPAITCkCDgCPaRwu8yuZQTMJ27U7Ik4rGYbQjGNWNBlYkRmv7rhEFHnXsZd4KTJ+tSnPqWEhARvqr1vlUJgiKEREYpkM08CJoHeFOawaMz4jpEm24wEGeEvKSkhtHqNaiDXxcXFKjlxQqVFRQotLVHEwT2aEtTuTcXvgmTGkexcSPUXf0VY5A9iYxoN8RxiEuXVzFc9q4A3NX+SHHOe4nlieyPIhdXcRps0wZH46JmvmBmLHW87joa9MUwdLTGq6o5QYmSHMmKrlRa3Sq3T364tCbdrXs0Kzx90YDX9ZQiDJD/x2rd85bCyeDnzj+P+IjRSDGVhL7O4aoXezLxPT5XfrcczlyuSwl6mV8ZfgtP2VvZYBkEfXYqrO+yKn90u7eo15zjtxt4PDAH1BIT7PQuxSsGMZ7gPlPqrw0DnzAf85AWz9Y8/f0bLf/A57X51lQqLMc3plZy0RGXNvUN3/+WHNHP6zZBn/xvlv8PtHQIOgSuBgCPQVwJ1l+c1i4CnCO6jPRspYJjZxk7MCT71AguiEhL1lX/5ouefNnBxV9+6GDE28e/7Xvd/NqLnM+sNUj6BbUbjjcC02Rb1MRjybZEcG9hWr1+v7f/wN9609phP/5NiWGC3/oufUwzT4s9ulD6yjGlyY6KDJKY9NnJs5TUaY14mjABhKePz580F80f+1hGfBrn6GLbbPNTIQ7WYuNSxNPJQbRbT+dGqxpC7jbp1jx5tAGHgnYtqnUQJBuTFJQ+iItsPwapLFBNUousqXtKY+Uu1t22RJrb82VuEZgTY8jeNrL1WhraVyzavrAx4zA6dnXfNrpvY3ki8iRHrlJYi3VD2e62DRC8/tkz3Zq9SSJjv+mD9N1MO03a/f7F0z0xpzWG21y2ktQ8Cq08qZZu/AJON0b6w10bqryby7MfW2jA9Y6w+8LmfquI9hSotr6SNfK2VnpKshOyximBFcgfvlhOHgENgeCDgCPTwaAdXCofAsEbASJjZGP8EglPYGKxvfuMLXojhNjNKvszit/kMXDhlYZ3T8NBww9y52l4wQR0H9yonLU33E/65ZM9udf3253oVLeYDs3GfhoZyIA8QF1NUbyEkv5RG8MvwbVzOIKINdoeTDM913+HSEFXXR6iCkPHlIYkqS05Qd1gqq80wyF3EFouK1TxhxKAet+gZDTDEYMhxEysmbaq+mf1xEv0TtgydJTBbrhtLNFJtK+7YNfWE6I19J1QTtUWRC+ZR//2sFyzXIQhmUSFtUhusEiyYOxSheDWpILhb2UkssMwle5LIpKxGqs3O3PaURFEU0QYD9jmB8zltRZpfvlxvsbBwbVW77sz/s9fmHjn3cTnuvLxiyZpWPgWI7scm+i7smwM13xTLc0Vn/tyvBhv3s6Fn5hztQWFKzh+v1ILxJ2+1V8A2I9lOHAIOgeGDgCPQw6ctXEkcAsMXAZjOz56TfneQoBV/+QHdeuutLOi7/OT5bACYpjsJc5HW3HyFQaALce9lXkamLbhBb/3m5xrFojILTPHk/LOlcv7XPFtliMtxOO4rW4is1xmkvVUZ2ps+QXW5o2CgsNObIMR4ylAS+3iYewhMMJYVbYd24zT4hHTsuLSjHLU4TtTK2FeQWOfFqBEpCLJr+3bCzaepM+dePbX+WTU1QL4DBT/PVbRVld1e0bsFXDelspFSC4VtC+/gawrlfiLYy8KiJ+uoysavU3tMlao2YiKTh0vBHN+iP+PzFpTIyCyHnpjbZv9x76mL2vkHPLY0wMoYKGaSYxr+q1Ko7yk7G18NgfQMG29vlGMjncshVyuWlwMbl4ZD4AIQcAT6AsBytzoErkUEIuGGy7dJX4ecLr3pJv3lBz+IQjX0NO8AQ4WLmWwkY95htLHiwH7V4dFj+pQp+t/kTM2tK9XGddjK4qHhUsU0s3Vk8pXfBuvlOcvUsOg67AlQ2WZkal5ECOYNodg6h6nLfkFhlsGQvBbsc7Z6vtMgyDkQ7PRMaRq2CeVlvugdeJlQYz3sFopUA9vvgVDXctyB8a+xUwtTbTYhJz1kn1kL086/9upK3XPPvXrbvXfpd3itaPZUk8aYydeieZyUXsZltjcmGRnqMFt0PDmUYIJTYnG1iWEHhYZN08gZbPiNVmY64TkP+hxwH69XZFWlJtcUaXRlqQpGdWjRZN+izhgMk0dlcczjVmrToF4ObfXlIOQUZ0RIcE2TgmtsRsLaYvClOxh/32kM8iIuFxsf/DK7HBwCwxWB3l/W4Vo8Vy6HgEPgSiFgXTo80VOc/ufLcKvMTH3i7/5OScnJnkcNs0/2d/v+xYH+BYFWZr/ds39/OephaWVmZakMltV17Kia8OqRnZOjjOvmKmjVi2pCKb4HHjodYufXal5MvgSK1P9Cxp+992Oaet8ypeAzrJC8Q9lM776D/NPxEjKB1X9doBCCHpY1cVrK5hFAFk72WCg8JDgpUc0Q11Ijr4ZYL2jBaIuP1ME622t4CAJcW82GPUM7Ww8Eu5WNRZSe+UcVJBsXgKrpVGdZo15cs08PPHCTQt72AHYkO3FBMp77UGeaHbXnQxmCFARRMmJmbu0s72QcL5uEUzkItEfaA/XHVnAj8nZuBsTfnuHPvEZvgfxvsTJA+P5fJQCjXR+996CuTzig1LBu5ZFdGmOGSWirzYTG6Lz3OM97ePC51xqFIyeGQBCrilt+/gdVLD+Arb+pogdZaNuwuB6lfPUR2p9ZEycOAYfAJSHgCPQlwecedghcnQgY7zICtB/O9vVfwpeaIIxhrXruRz/SS4kJRHlLw09xiGLRyhp5zmThXwImDOGQtwg0nFEQyBC01Oa31vzZRkdFeUCZBtU2P9EOtHM+HyTt2Wzy2oItQc2Bfaquq1MGZZh/y61a9dKLGg8PeW0rQTYwPeg0pnsRYnWvhMu+HD1JoxfNUTortzrJd2xvWkYoZ3EMJHqjlw1nszd6aprYFCij/bCaeYnNlnezN3I9hq2vpGMi3RULmTUxDTeZm631ZubsO8iTkYqvISwKnzn+tQzwtNEFYX0GTbhnU3HvvRpDmLvD1mDg7jWcl6DRWMRvVOytYOWzkWRL90KEhWxe+cyuxdTMPF/Y1OptOn4UQ+wTCt5zWGl7KzQRf9Pj46o1KqFbC/JxP0gxo+DwKSi7zYuLlcpcVF/KAOdCij5c7+0h8kr44ulKmzdpyIpI6ykknhmGHoz5nTgEHAKXhIAj0JcEn3vYIXB1IWAczAhcBwTnP1ewrg3TjaWQn2VoFTs6a9X96gtqgcRZZEAjQoVG6BAL0W3SA4EOSUhWd1q6IiDN7YSLDomLUxKBMeKxX05lIaDt0yCLkWhos9Amx3G9x8iiX4zgIX7NtX9v54xAJyUlqR1ybr6iD+3bp0ljx2rmrJl6MSpaWWhuN2NmXAu7JdLxRbm0MwJdWyvVRxUoMyKcyIi+8hgZNgmFIJO00O8qg81ISTkE2kyO7fgwxwYLXFEYfnDO93wvVCc1slxSONX23W2f/HdIN9hHEyuMiWmNbTPpPXUyod7zo7gUQoSOGm6A/+uY3Xu5xEiztbgfBCPS8WgxExgB5ED8qWk3L09ZAxumNG/UgIaFqqwuU8r6jcqpr9KsjFLlwe+zKf9ozEAmZve2D58NIYPZv79cxR7W6aB1Dpo52fNvPlTlNHzN1Ebd9oY4cQg4BC4FAUegLwU996xD4CpCIBROZKG41++QfvomZAzLgkfgSCkwQQuvHWXsEEnis5/D9Z46+bkNs4bO5jK1HinzCLal18GzxrvqOWbyX234R2uMSVAzWuTgxERc4iUoIzdPaZhipGZnK4bPuXn5hOiO9TTa0WhVzZe0EW4j0KMLCtQaGa3czlYVHzliRVIy6eTfvExdr76otmLW8JHRrHwUpX7C5911/v9s4VpCTh6DgGh1t2Oj2ke4fFKMj6RD/YxMmxiBtWyprtbYCT5P478RavvBje9lvpaGPRuYFh9Pl17yftrJszxg+Vr66Is1inyt5Fhaq4jtsoq/DF75/B/IAT6tWDScudjQGMlmJFa19GZVYZayvR6TlGPH2IqUsX6nxgRXaGxrg0ZFt2kxI40UBmqRjEoS2DxlOwr38/bpbeD6X8bLWtFBToyXJAC9Qc6sN/khz3BoquVycQgMNQKOQA814i4/h8AwRMAUnVUoDL+1ErMNTGpvxHx3tKlYESPAJv1xOd+V0/+bnjSsl8wkGrEJEJ+WsYNIe5W+s82laofw1m5fr2rIxCE2I9pt5BmbnaMotqTRBZDZHOWOGeOZa+SwiDCJ86OOVGvzli0eATHvHKOvv14VK19UJnnvxVx3Rm5Axhd6SP7dEa3qDjGK27+Yf2rPDxyV6grQoPsJsj11E5vZSG9mb0YTcERh9OKRayO5aZTe4KXKl41IWXpwT88u25rQtnzy3MTeymB5DZp4ifPPNNZWCJP4ON8+DSOXsTQKeJXpUZVhU/1mNQ2164C+uruchYoHNL3jgG6a0q38sZQZLXUMj9psiBV6wPePCvecYJjSwOZ6NB/W7r9DwCEw6Ai4n5tBh9hl4BAY/gjYYsHlW1iztgutM6QlDG5oWueLkcDHBiI9fg22pW8hurNgljkc23n/1lJfjKvkYrXsfEtNEKjNbPVorythV7EsqDNy3rxxvX78wx9qyvTpKiNyYSgPW6jvN1fjV3iqz+Y2sDyW3/kI6/vUc+yEgppb1WP+3fpUxOy+Xzc7j8JCBefna2FyEuUO8kxR+uZnCwz9Jhnt3GOT54xVxDgFsdqyBpANt82eRAdQ6YHpe+/N59j5y2JmJP4yVFo5ec6X/zkSuByXT6qR/aWxRKlZCjVOhVTjRcWCx+xprdGe4jr99kiVosvf0qS923THrFI9fLOUN4/3JCoDD4BMi/QZAoQEdyocHl7OKKV+K2Ma3hMnDgGHgENgsBFwBHqwEXbpOwSGOQKmfa6AC74Igb4VzXM4n408+6gd3HGQy2/pGz/ty3tMeZ3AP9v8Zek0E5HivZ7pQxcnbw1t1a5vfE2beNiChMyLIkgI5Le8Eb/NbAWJULULrIDdHk06DVt2q/htrZqWFK9Oc3jcK1aWSrvpO/+BO44dRPIL1r7H3q0J996NNwWu9iHb9pjfksSIbBqfbculVvbZCC0eAk+KLUg0TTXWM5iF+OPR+fC5wKqcTNMO/GVI6m3RJZwrJK9C9ldEPGINroatNbYFnJkUj3F0rpq7Z2hzfZM279iur/z7Dt3PKsTb7rpHeTMWes5Geqvg7ZJi6zUu/nvKuv8pr5INm3hfbBrEiUPAIeAQGEQEeidaBzEHl7RDwCEwrBHwCDTmqfGNQWqGoe1rQxPN9HstpLSRzUw4jLiZdtfjhxxfCpE7XzAsD+NYthkJts3Iq2nHjSzz0bMpvg6meR/c6xbsb/2R9sbwy/bUWq6jIjBLiwsRs8bAyYjemVWsip88q12YI4SagXivhECYdxcVSbt3e2fe88Rf6C6Mdo/87DceRv77BtpbuW3zLy40M46lbKYhnsjGBIBHai31V6nxa71bHXszB+lk62YzznmBVeMJX96Wvw0JRpPvTWyW7xi2KyZWIK+hKZUZQNtKt0QadckS4rN/TC8sWqqP//iX2njkqFoyZ6g+xbc1sC8MX6SXm3+p2uL7lTaH+pnNiqXnxCHgEHAIDCICTgM9iOC6pB0CIwEBU5i+ytR315gJKs/J0vRl16n2RLGO19Wwb1ZUaZF6So8puLlLo2PClM3COltt2Nzd4PGUU9TSV9uLIXUXilMgP+pramKf56BBfg4PIk+hgX74Rh9ZPN88vLQh0U/ewRPPvqivfKtdoR/8gCbGhXia6B4WP8bv26t6NKep+MSeM2cunkRi1fK7F1T+1gZ137hQwXjDOF+x/Ew7HAaaWb0PmZ20yQG2cu9IojqnyRTuMUVrMs9ZGkaIL1T8z2SRAlUm/yAZcTdDiSETyHIG3ls6u4MJQR6iycnRmk5wmDrMdDq7yxQXEqXZ8+frf0LCteqNFZo051a00FEnFf02kOhilHSw4V2akv6Cz+ibAaE3whiySriMHAIOgWsNAUegr7UWd/V1CPRBwMhXWUWUajpa9JUvf1QLF1zHGTvbTqS/VnwiV6q6ukbbdxdq/a9W6s6bRimqO0KtDdWqPd6h6s4uBRceQh0arLZ6SHfZUXwg+5IwUnY2GSyyba747keV+9TrKDFnoVGG83sWA2crTMA1zwqDNN73MHzsjyv0f77UoK5P/AVhrbPRwpvphU8KcKFnURnt/tnz5+kPa9YqZuYsNeFaLrgfU46ALM44NMj8hNavnZ7COUy5PSmF3BrRNlJt4tN/21GQZz89jTbz42lpXYgE5gtcaialCvaHLySRC70XfJIxvv9WZo6OvPm6psUdVU8MluRdSzRu0jT9+dAfdM9dzWpqrtemzXV6bMIc/cvuLWpubVd8DCOkALGZkdqGPHXncdI00PgvdwQ6ACB36BBwCFx2BByBvuyQugQdAiMHAbig6lGWHuoJ1fVz52r8uBwKb9pTo1RBBEeJYMvT2NFjNHbsOBXiGDomM1ZxybFKCU7Bu0M4cT24t30KT6AJJUJGOwRn99FodZaUKbGJhXgW9KRwv5rq29VM6OqgRvOajNa1q13t2EuYBtHESKmVx8S454WSQN+Tvv9GlqNJK5tE39glPTTvwgi0vwxmzvFONNFx297Up792UHse+6AyF8xVQ6/vZSuuLSg093pphMpOCw7XgePFSp4wRj0MLC5VAlMwe2jLz+/Fw65t7M3ANMaruWr8kQDieJPzBXHpvXxBOyPpxFHsTStI+/jMGr1zi4HlHzRg5nKyMQd6knv/FZ/eBW3typu4X4uWJqqxvUXLX3pda9bUaN7MCuWNtiAjnTp6fJ8O7k9QTlyS4mIZDfXzcgQFWf7c3s+1gYrgzjsEHAIOgYtFwBHoi0XOPecQOB8EYDxGe3pO6izP56HBuMenMzWCGsgvIrEB+P0atJkl3Xri72YrPdXolxFo/08DpKRXL1qF2zGrS1hoBJwGrwmH6/XM66uVkJyq9GiCmOCnOSg1XelZ2WrIS1FX3jilRdaqIKoK5fRstbUGQaK7FVxX6WmD21ua1VxTq9ITweouLcGhxVE1VJZ4SGEtoQhfkX3EmlKYlvFCtMg8olTSKIIBBs3nQ2DF7WIfOUneA85bfvbYHTNxq5ZWoR/98Mt6Ye3NjDqw00UqKivVQZTAMEwQTBOdXzBKq2oqldRd4F2/nP/8ZNoCufhlSe/BMdrFiG8t2zG2FD5PCbiv97bz3lkOlp95EJnO3ryHnGBfyOaR5F6CbB5DJgDSaNpmZkoqEQfDeD/CtI9Zix80t9jdPvGDy6cxbOMgz4sIcb40K1P/8Z3v6TMfjlIwpkHxUTGaOLFaf1xeTFo2tLL3L1gpKZ365VsrNfOW9xDZMoxBGqedOAQcAg6BK4iAv5e8gkVwWTsErl4EgnC8GxRXoa6aRnhHlG+R2Sn+MyQV90hnUJ1CwtrUBjc2LxtWBCOkOw4SbfBEgdLyI/TUr1/QseL9mjhhhqZPJzR3QhKOEWIVHR3DPlr7du9XR3Mt7sQKILIdysb33F1oY+vq0EK3NKno+AntPFCimTemKJ1wc8FoplduKFLM/h2qSUvDr3ScMjLaFBkTrBxId0ZCKoXI1xjMQb75kxVqvnmxEqLDiRLdpmOHD+ELulttDQ2KqWpUdGUpmlepIClBbY1158TN6lYFA7R6tiZAwxgodHNuQOFaq9nN8kwM4wOiLJ8US8MUq9PzpC+9X/pg5ev6zDM+N3BlZWVcszt4FJvobPxVRz7zmppmzVEsdiS+K97lQfnnJ9V55GRF7iK8ehsE9gSEdTWfZ7MlsSivE5viiy2L5WGkfTT7XNJ9Jz6349oIxx7UopS4VGXjii6IPPbjy7urY6c6GxJ0/7h5emLyJO1jgBEL4U3jPYog3Lh1OOZhpIc2bqVt16xZ40WiVEMTZ60GPaqpblVewXRtLzyuvDFVampr0rp14TpUWqdls24iD25z4hBwCDgErjACjkBf4QZw2V/FCKD97MI3bea0DVqa9yHtPvxxXJbdqK7wcI8qDEXNe1SvUcHYl476JzUda1fLcQgM5TKBU+m5qqV65NPvVkdbi2fnXItv4zVr9+tPKzaruRlLWOyajdikEI6wFP+8H79/OprWLi+4RUxUqGZPMVoLNQuy8CFZehwGur0hXieIhBICi100IVbdCaNUyjR9c0eNjpTUqx7+O2ZSnBbFhioUBWNRWYPaksbo29/9mGJjzIDVL91qaKxRSWmDTpQU69nnX1LZ/jolrX7JchxQjDyXQbK+AyczTvzXE3AH9/jZtdemIK2vxx0xtgpdaOThhmfY0LaRZhhu/magQl3GtnM76YORkehx48Z5BDqZRYVRYXXaTCGWQWa9MOAQbD/JHrDQl3jBSG4Q+fUcParKDRt03BoXKWQ7hmlO3sRJiu9sx9TkbMjZE/2LPWXBbRbGRGsaIBSV/RBznyDtPxCk6K53E/q8Rll5W3Xz4mTVHK/T17//WyXsmqOszBRNnjVLx48fVwnvVls7umzAtsGGmXjYAC0rO0vPvrJTi9rKVIcbmJLqBSzMnKHjRbFaufxNtUeOVWl5nZJnZqihpVXhEYRSxyVM77il/wK7sw4Bh4BDYJARcAR6kAF2yV+7CBj37CpmIdbv8ZRw+3O6YdQf1B0zXT1mAjFE0tXVoJCmHeqgHGU4KEiABJl2NZTZ8XVH8Lowex4L/ro9E4QsptNzWCRnBMekqanJ21paWtAyNyh+WpZeO9KmnTvLlULo7LjxMcokUp/5gAiCEIXzXBSmHLnB1RqTVI+Gu0exMOSgvDzPDKMHG9lgpv5NC96IxtLsMYLDQnS0tFQz5o1VjDlf9gwRjK75JC4Wm9dxKZowbgKkKU7/9973agnFM5d2tlDQpK+fZ6qm1yHARp5NDlYXqCryCUwtzBygfzETm/TUYmVMobFyyrWDXSz2EIGaaHvSSJuFB58xHgwh0EZTV65cqfHjx3sYWv1y0AAXfu0renXxzQwwWAaI5j0OXEwjb5rgwZAgzEeiN23UWwSVqa6w5X8+8bxprPiTqhct0px3PKLIxDiFDKCNbjdiyxZh7dLPEMXgTseoo7R4m26+KVi5+aM1YWK5nv/DajU1pur2WxO5o0dJuSmad30tOI1Cu5ygjZs3KwRyP2oUi0+jophhaPdwsNDsu3EFmDsqR2PGLdXh3RtV39ym7Nzx2rp1s2ces3FzqYqOruf9YyErdhulVQ366N9+g3fh9EWEvdV1O4eAQ8AhMGQIOAI9ZFC7jK5FBFibp/bdaCvZsse3K3XSJkKqDR0SrWhhy3dCho9hFwsDwlOYJ2bCegzb4PTrsiGFTMfDDE0r6GkGe4sXjqY8IsJH9rFM8N0DubJ7K1DX7jpYzv2QLj6HtLQTQjtIcQlRnGvC/KPBI9ChuCWLbmtFax2mRGxk4VFKTg5SjLFcNNuhPNPJwrHw8HiIewznzLjVCHTgZqSzR5mZkWrtbEXTak9iosHpdm5LA+NeLu2R6mqUmwfhyjYQsLKWEZRjS+s/Q9x4aADhNi/H+Lp9Wpb3kCbft1P7fsJCxDDf+cDHbG3gQrTaS7Okl0tYyLdxo1588UXNmDHDG3Ds2QngREXs2bpVW8PC1b1oibJnzVBIwWjloW21H90esLYaUkD7f2kCqGEHD2rL976n6rp+zFswlej54x+16UCloj/zEc1NiPNNPwTkan6lJ3a0KQ6Q9sYnqIHPYeZdxVdK353gWQABDu0uUWoiC/kYPiQmRCsj8pi2lkRBilHhy0g05hmMkk6UlCg3F9d0BQUMmtrQ8NergbLYO2b7Eq6b3biR65eWv6h9+w+oAvJfhj18Y2Mj70kyMx8ppJGpyZPHaev6tZowZq430OoxlbsTh4BDwCFwBRFwBPoKgu+yvkYQgKymU9U2CGsRRDqQkww2AnAeRfAtj4R0BupfzWFC9hhpz4lCTUqeAflBI9xHjHzaFihmHuGfek/Cg0IoqmxbQGd3dZJoE8Snk0V1R5taUTD3eCYaUUGd6mbRYdtxbLDN0LgHekbB2tCEprS2qAeSv2LVM2hyX9ecWbOVn5fFQrIEpaVleBpLI99hYRE6gPlGdHuXQuFuB9BiP4WWmZ3ugOTeDPe2gC9ArSKIcvrMmVo2caKe/u1vMSWhyLZxbSAxnExqgydqW+U/aFr6uxRs1ikWd9sj+3b1lJgG/69ukdb+gsEJ9X722Wc9Et13EDImrF2fT16hjS+v0FstqdqTOkbVc27QxBnTFB8fqyi0sCEMYLoG0AqfynHgo1BIb9EPvq+y/shz4GMHN6j5C1/Xui/8vebHAZi9BL3SiTr/xnUndOOaDapk0LNvSpJWLl6o4hjslnvvs4FSfGyMGuMKVFqzVgXYltdWY69+Ilvz5l2vFS/v1S3L4nTw0EF1dd+lm26araKiY9q3b59M21xTU6PDhw97Ji+HDh2i/vHeu2OLUxOwqzZzjjjSz8LkI9o09ozyDE8j36XFxylXvJ68/QGvjfv6/vbXw+0dAg4Bh8BQIeAI9FAh7fK5phEwqhLEt822oRYjt6fTYB93KkCD+tVnf6UEPGdkY77RAYk7l0bUSE1lZZX+vHo50fpyIUp4n4ChhuHPNyYmhi3aI0Lmp9c+G7k24hXEZgTb3L11Edmvp9cW13hrF+T9pglV2NHW6+DBUm3bdkjNv2n0tJT2fHx8HFuCColCl4HJR1F7t15BUe2ZJ/D8Bop9HQBHkpgpJk/w78Ybb9QYTAZ+B7FtxhtEK4FfQmDRFOOsEgbRPlE/XRPTohWR2ayeSm7vh0B3kt+cMeB3v/Q5TGOsLGaa0FfumQm5n0GI8YnSh7oqtWFPpXa9+ZZWPh+qPXkLFbXgesWMzlMWpjORRhiNSJ+rkAGZ9ITjcO6lP+ogxLSvGCk1rbi1WWtrK7huU+vxXWp/+tcqfs97lW/a/968QrGDWTsvTydSIpUGAR5XyywBmHXH+gAzDXUcRD82KkwxGdP05vrd+Ptu055dUZp43Z3Kz81RfNxH9Mtf/5liZDNbEK+33lpHex7UiRMnPBto0zrboMvKNWnSpJMkeSy+tE0LbYMq87FtOJZj1tOE6VB5KbZHzII0RoTrvo99VslpqQz2+tbUfXYIOAQcAkOPwBXozoe+ki5Hh4BD4HQE4Lt6iwWO+wrL9M1vfVPvfte7NHbMGEw8TFWLaQVT66Ec88kj1aZNNmJnJKe8vEqLFk3WXXe/TY0EU2lsbFUN/p1rcElXVGTbMZlWsRozBiOE8RCm8PAoJSb6vHqkpaV4U/NGpk3CWJSWEz0KG1mCaJC+bSa2N+JnNthmj50zKlcheOroxLND8PLlGJf7SGMZHK+ZpKKpk5l07IRAT4uL84h8CoSttvY4ixGrlJyQBnn3kh7wn9k8RzYRBKULtfY5pAUid88sFoliEfHjlXg0YQFiI/lnkEYS2+PLpAVTWZgIr7aamunJjUao50gPYn9SgzeP5a+9rq0VydqG3W/LjLnKnz0L+/J4hdNAhr1n6jEAoba2igHjva+87A0cAos7depUPf7448rOJvAL95km18jsj3/8Y5WuWKHDc29U+pzpCoesGkU2U42DaJ73TsqWpuTi4xvtfkenwnsNzFtpq3sTmRWAsIfmoDkOf7eOlZZjlhSjKiIGbtqw3tM0Hzt2zGsvM8GwfM0EwzTNgYTZP0CwMnWQRw9uNWorynlfalXR1Kjy5g7ioGAWhPeW93/uvzR+zjzFpGcpJT5txJNne7UtyJA1ae9rHthsQ3bc1TsqvJJlGLLKuowcAoOEgCPQgwSsS9YhMKwRoCNvNs9hSAVeJL7xjW8oA9K8eOIEAqfEK46Ff1EpqepmsWAQGsB4ptfN3CAWrbKZbeTk5GvG9Ok8be4qSMyjYZ2edrmLYCqd2M8aQWpn4VdlZTlayB5VVddry5bNevnlzXriiSe8qXke9Ii5n1TZ50AxzWQcZNhImBFqI3vKy9dizETS9+zRW9gft+MJwzvPJTPjKGKzBYtmBpCEHW1RWz1ErZHn0wKTHvC4xwujOODlkxes1m2Q6FljpK+PMhMW3yU7b+Q3EvNxKxcK95MCLASQwQ48AR/VSdJHCiDX7dXadGS9dq9drxUvhWl35gL13DhfOQX5SmBmIBY7atPS+wcc/sRCCVBTUlyk4320zzb4efTRRz3ybD6qTQw7W+ho57/1zW+qZ+Ur0qTxjF5g9b0E3Xw+hxhhpsB1tKm/Ht7zZg9PGoXkdRzt8FG8fZhnjS1btnh+sE2rbO1khNnMNbwBGOWwfG3zi29Bar0322CeO3q6qrW9huA7BeMABDCuT2F1Js+tW6OPPfFV3fzwB3iPKKLhBtYjWaz8Ldgc5UZv1PYm7MSDInwD1CGslL2PZv6S1r1WxDFSly05ONU8Q1gSl5VDYOQj4Aj0yG9DVwOHwAUjYH2mmR34xchZCdrI/bt26h7MY6N3rFUNpKUJlWwIC8fakjPUhjeJjpg4vYmpxYwZ7+p91Lpk/4a1A+YcISHhaJztnEkMpCoNm2Y7DsbN2Tg9+tgX7MN5iRHrvuTaytqGZvrJJ59UDQvT9rFYzzxyWJ1qe0mWkTbzeNEJ+2qoqlENXkSyzo8/n1e5Am8yQmw20bYFip9QB57zHxup9hPrIBwjL5gsLWI88kBthypOrNYra1brjacStXv8dHVPnqbEmTM0Fs09al2PdNkAoQevHqEMfqzefrQt/YmAncjAJ9Djh2FoZHratGmaNn2adrz5hg7eeZumTCFjY6h9xMi0Xyz91j+8qJ8dLVQ0mmUa2CPLRpqvu+46jzAHtpFhb23UzUDKPK2UMWNQXm4a5mrPVGP+/Ot1993TNIpBWH3VMb3jR6tRy9/CaswtGstCxwW50zTu3V/QjIWLaGd/KUb43t5PCGvtFgxcpq3UAr1P6yufVFvQbMxWGEkNgViLhvcc1ezkH2lC3HdUtI7fgCK+obCAU609BAVxWTgErhIEHIG+ShrSVcMhcKEIGDHqK1sgdtVwpEdYqJeLFYOF3wjqalZn+RF1lXt8yNOirVm/WeMmjfXIWzQE29zXxaGljo2OUHSUpez352zqVyNo1kWbp49Oj0R5ttEQNyNa/ZFkbj5DjJiZRnrHjh14Zsj1rkejETfvInBQryyHe9dCdpO2aTtrIG/h2FFHYe87mCThUtM2so2bZiUBWyqcFrfSel9LrbYXr9Zrb6zWztei9WbiLHUuuEHTJxQoLDVN0QQoOQaBxoIEjfEpMW2933vKqbOnjm64YSEY7lTVehjUNGxM+iHQ1oI2Hghm9qHixd8rgZmDcZDvEDTRpmG2trB2s72JtYsNahpYKNgCya7Cb3MFwXaKWxo1f1S63vPupQTnmaoJ43MVHRNLGuaGLlK7dmxWVsnzWloXoznv+6AyMqcpIpZg5Tgr71Wee+lfDf+ATj1HpCPP4RHn5l9p2ahf8b0xryVD55anh3eqm3aq2YoXnpWUg0a+1Hf3amgbVweHwMUg4Aj0xaDmnnEIXMUIHKVHtSAkj9GvT2fzezwwQkX8Ck3ANGHvD36j//v933g+mIMwMQhLz1F49ihFpscrGDd1iWidzfY5KSlZOZxPZJ+fn6IjR8p0rOiE1r75pkfEjOyZqYXdG9iRGy3zqBkEzX9shG0F9rtmGnLbbbd5BK4UgpzODVFmM4Ec61Wm7sG8w9zwVeGZInfcaCVhXhCYvu/u4fffr5m2OocziJk3AZd5EOqapmbtO7JWu7au1bO/idG+8XMUMWmyIg4VKpu619k45TzE7JIzMzM8TCMxvwjG5ribENpma+0Xy7ueO7ZxENqG/fTuYj0yrkCx1ka0Af88ExnztlJTVa0qTDFqqmtUhbb42NhsKS4e85DZ+NPG90x5iZakxuuDH3yEVPsWsl1NDTW6711/o/ufeFzNDNwsee+uM53C+Is3Yvfe+8eXqA3/4Qf24pM9ny291veeD1GtuirQgmOrT2BSpVpTWmM7cQg4BC4KAUegLwo295BDYOQjcLa+E2dz+imE6G541VxIdAQkzQiA8dRwHpxrCkTEzrX3tKuj+ojaq9g4QZRnGf8pZL+PzUJLd4bFqAWfwRWsqJtAUIyME7vUiUuSesw9ytjqWUgYNBGmiF1vFAFVoo1Ys+gwkn0oGu56FhFawJK33npLn/jEJzxybO7NzCxgMoWKh5jUUVazfzZ55ZVXdODAAY/wJWbnKT49Y0SFgPaqwb9ek2QvvPgCTDzmYhXxwKwmHaterefQTDd3hagdzeaeAFMHG2AEaod9iPj+23kbWISx9bBwr2v7TtXPuU5JeE0x42wzCzHzkFLy7mHw0tFUq+hgov+FJagRrFsh3DUNjTqMSUYR97WHZ6t7ag62y/eiNk/GuBvyjIZTdYzAGmsxy9itkGXzydwWZTapsrwW++daHS1s076jx/Xyq6+qYNH7PR/dJHdNCK+4EnlXu/cz2wORHkoxd46MobzpBUeehxJ5l9fViIAj0Fdjq7o6OQTOA4GEc9xjOsnfw4RDsBF4P67YiJmiqoNosBogxb1E1Z+EkeqIXkYe6KrPNIo+Ol2rnjqfti0Izap3vqdTcbayqpNFgObQeVOpl5z5mm6BTNVTgFr2q7m2vZdcGfkz21sTc4+Gew6vLOvga5Xo8iLNJGHnLs/e17xOmNx4/RKu9DJ+78zI+2de/1ox8TAxBe80IJhewGAmrAsiTTut9F2z/8XFxV6IcfOr3J+YbbSZzrSzX/1vX1fo4luUhS10NwsAY7IzlJKQqFILoIM9u2qKFXZor9aUVehEVoqagyDJY0ejGocUj2MRYirOsu1Fqasmes0RCDMeUuorNLktQtOy09Uxaar2HT+kX//qaYK81GpbSY9KK7oUERaLLfBkLXjfvyojdbxnvtJfWa/Wc932XWFMYVzWiUPAITAyEXAEemS2myu1Q+CSELAZ+9HwnxCmk/2L2QZKEDfFmnkbmma4bgtu29pafLbQpkkrgzMd3Mx5O0cCRgjMiUUvlz4jSS75yPMZV06dMLJoPp1xOexpu7f3Eke7I4eQiObpwUwRCgsL1YiP5+i771Xs3Q8qK3WGbk3r0SdvW4jm1vdQcHC48m54AMJ4Kv2RfmT4+O1RuhhcLJrDwsH1aPsxgTCxgYVpec08xrTRgWI2yxbt79QCwx79NO0VtZe9oleWB6sxKkkVsfEaj1lOeUeM6qbNU90DD6kuKRP/fCx2I7S6l3kLI5a9DFCOvKLcut3Kjk0mDPoyXb94qVIzZyoqPVPJhA0/UVaq/a/8j9Y1jFbu6OmaMzcF94LJ2MnjOI82QeHttc3V1D6BeLtjh4BD4OpFwBHoq7dtXc0cAgMi0AFxmTdOyucX4HAAQe37QAxE9iZIMwEDPaIdhvY4HC8dfjE+lY/S98Aa9Mzc24IisqLklN20/77A/UDk2n+PXfcT7TYoeVswNiQsZDTxh342DaoRaJuGnv7AezX/tgeJgAgZw2D7zsf/Wn/4xbe8+2+4+6+UjycLI2tXoxhOCcDz3sXSP+Aa28TMNMyE5cknnzy52M/OG3k2s5dVq1bZR08m0p5jsMBITzRba0DqqcJxRpVn676vTFq/e7PWVeP7uzFLTTR8OwOXJEw4pmaVKDOiW+mYj9z/bXAP+6p2Bn1aISiurfGMEJubxKS4TC148FPeiIrsvXaw2Qe8GzpxCDgEHAIjGgFHoEd087nCOwQuHgGzhbwF8nt4y8BpPDQDcwEIll9LbeTHM78IeAQlr6bebgQNYgRpaqjkfrsv4B47tOudEKcDK0+/0NybJgpkBYeOU2HQHWqvblJ0ySsKmzxHzSeKMMtAzY004/PZtKoWqGXb1q2KSE9R8phxPp+2DAqC8Wf32N9+SpGj44W3Pd19/4cUFhHiaTpPz/Xq+WTtsXQiWmgGMfvqfPVau3atp6m/8847PY8cRp5t0GHk2RZY+uXhBSiWIc82u+AJbWTTB/ZxYjaDk3zpoaYeNXWcUCdta76DI7g/DbMeHGWog1mC2DRmImpI3xLwp2PHSH/vi++K++8QcAg4BEY2Ao5Aj+z2c6V3CFw0AmZr/J5FaBkPYGPcO/0fmNjbp0gfvdXjU4GnzzyGwJkLNpNgCFUihNvEuFhfMUKVmtf3rI9oxb/blpk9iJutLysoEnbG/H54dLAiPvTOkwS6pKTEC95RifeNWjxszJ99jwryZpwMsmEmAeFR2XrnE1/0yJuZlNi5q1lscJMCof3HpdiqPw8ZBmPTQr/wwgvav3+/5syZoygWYtrx6tWrT0KRzq//4twzBzr+GzzXepiIRNKmUQySgmzmgUa1NjTLkGbIspmTxHjM2f+U756AT+7QIeAQcAhclQg4An1VNqurlEPg3AgY8cpEm/hdiOtP35Q27IIQ8dgYzt2zGI8P+Xi3MOcMdvI8xdM4noOwmieAMwQi5hlQszdNdZCxe1uNyC7Ecxvge8K0qP/zP//jaVPtzIIH7juDAZr5gF8CDv2nrso9EbG1cCZtiTeSjzzrI9FW0b1793pbf5V+8kbWAY7Gpr2jv6unzgXaXJ86O/BRjyVo7TlUwjvCqsShys3l4xBwCDgEPAQcgXYvgkPgGkbAbKEzk6W/vZPp+Ft9QJiv53BsWc1u+ELI86DASBnG5ufprYDEjUSbhCYmaMLsGzyNaMDla/bQeOut06Vf8Kv+jy9J+3vNOfoCkgHJ/tAS6cHrAkw3+t50CZ/3P/4NtdVUMfbpb6R0CQn3+2iPQln0OPF3n+WqMWknDgGHgENgaBBwBHpocHa5OASGLQJGkk3rG6jEs/DUw0JMk5md3W9RHv7wh5WWan38UgAAQABJREFUNY2Fg/1eviZPmqu72ROkH2fg/m+/iGIoHcfu3JZgjmax4a1LWDzKtfF5Ps2zzRhcbsn++7epm7DwQ0NoiYZIpEl7f4dW7X25UXPpOQQcAiMNAUegR1qLufI6BAYJgUHgUpdcUlM2T7nubsw4PsVCxlOsfvy4mbrzzvcPkZbzkqsxpAnY4CcDP9HvmMsiSuzYLZKk6ezDIJlEPvfIZus5zDYupcAJi1nROJTKYOpnixudOAQcAg6BoUTAEeihRNvl5RBwCFwQArZYbdKECfrrz39O//XP/4xJSbeWLlmiez/2XUVnjlWX0z73i6d/BiECG3ascTw+awMk//l+H7pMJ7stKM5Qy1AS9qGum8vPIeAQGJYIOAI9LJvFFcoh4BDwI9CNLe2ihz+jqYvfj9eHbiUQICSKaIQdg6hF9ec90vd+E43hOLsw0rF15XcIOASubQQcgb6229/V3iEw7BHwgqAEhSklO8crq5FCR56HfbO5AjoEHAIOgasaAUegr+rmdZVzCFwlCECaA0ygr5JKuWo4BBwCDgGHwEhFwBHokdpyrtwOgasdgfP9dbpc3tJspZ1tThwCDgGHgEPAIXAOBM63izpHMu6yQ8Ah4BC4jAjgq7jrVbw/19T63EYMlLQtWCu+DBa+lkQ2nosfnHX2/AYqhzvvEHAIOAQcAtcUAo5AX1PN7SrrEBgZCJhf3+pVu9W29ygRCmHTA0hnLIE0IlIvzQWweXAgCknQpkZl3nczHisqB8jNnXYIOAQcAg4Bh4APAUeg3ZvgEHAIDDsEenBfl/mJ+xXkrRYcyEdZjzpw0xYajtPjSxLS74RANzWRXph6Wi+DRvuSyuMedgg4BBwCDoHhjoAj0MO9hVz5HALXIgJw2K4UYowPxJ17MQmy+y4H3w3CW3J8rLOBvhbfNVdnh4BDwCFwEQg4An0RoLlHHAIOgSFA4FTgwSHIrDeLy7UgcehK7HJyCDgEHAIOgSuAgOsurgDoLkuHgEPAIeAQcAg4BBwCDoGRi4Aj0CO37VzJHQIOAYeAQ8Ah4BBwCDgErgACjkBfAdBdlg4Bh4BDwCHgEHAIOAQcAiMXAUegR27buZI7BBwCDgGHgEPAIeAQcAhcAQQcgf7/2TsT+P2G6o+Pfd9ljWRfsqSEbD9UiAhlK0pSpAgt9kQiCiF7dpJQ1uwkyhIRZcmeXbbs6/zPezj3P8997r3P3Z7v93m+v3Nev+/v3mf2+czcmTNnzpwZBdAtS0PAEDAEDAFDwBAwBAyB4UXAGOjhbTsruSFgCBgCo4+AzCLej/5U4r1cuIPZwx6mD0cfMCuBIWAIjAUEzIzdWGhFq4MhYAgYAiONAIzq2/LvKedmnPUuN9GLb8nPSd7jYeGn27DPXVQn8pc83uXvXedmmuEeN8Hr4iS3v7vR5+eLSm5+hoAhMAYQMAZ6DDSiVcEQMAQMgdFA4N23nHvqNueW2vwEt4ybzt33wubudTeXe+21SfovCRbGeZJJ3nWTT/qsm32ia93i8+/gHr/FudeecW6aSfvPv48G3panIWAIDA4CxkAPTltYSQwBQ8AQGCoEJhY+eeIHnHv0EufmWfoQN8cch7jXJ1jWvf7GZCKJ7q8I2ksOE0/0rpti4gfdlO885u69zLm3bhbmWcrU35yHqomssIaAIdAnBIyB7hOwlqwhYAgYAuMLAq/d4NzttwrjOrtz0818o/OzSs37zcWie/2Sc8886dwLj0m+8j4hbqa+Mb50O6unITCqCBgDParwW+aGgCFgCAw5Au8f3Jtc1DkmeNi5Nx+S+ohO8ojQ+3nPAONss9mIQG6ZGAKGwHsI2JBjPcEQMAQMAUOgOQLCzHoYWkgMYowk9VvYPZJ1sbwMAUNgOBCwza7haCcrpSFgCBgChoAhYAgYAobAgCBgDPSANIQVwxAY7xFAgpmIMEcPjUEow+jV3nI2BAwBQ8AQKIOAMdBlULIwhoAh0HcEOBA2+eTvugnkJNhobcl7yXiyycS+w4SixKvqCH2vuWVgCBgChoAhMGwImA70sLWYldcQGIsICOP67hPOzb3kce6BR9ZyT722knt7golHnIedWLj4hec91k0lTy/2hCcwEcNY7G1WJ0PAEDAEGiNgDHRjCC0BQ8AQaAOBd2537qWFXnCrzLuae/Dp7d1zfhVhoEeSg33WzTvFGW7qKa9yL4hdY/e0/I3wYbg2cLQ0DAFDwBAwBPqPgDHQ/cfYcjAEDIEeCCDpfeNl5x47y7lX53ZuwUUOc/MvfNjIMrDPO/fATc49fL9zUzwq0mdjnnu0mnkbAoaAITD+ImAM9Pjb9lZzQ2CgEIBhneAVYV7vdO7xu517Qm6UG1EStWeupp5C1ElEe8TIEDAEDAFDwBDIRcCmiVxozMMQMARGHAGRRE/0vtaGf3vEczep88hDbjkaAoaAITCUCIykguFQAmSFNgQMAUPAEDAEDAFDwBAwBGIEjIGO0bB3Q8AQMAQMAUPAEDAEDAFDoAcCxkD3AMi8DQFDwBAwBAwBQ8AQMAQMgRgBY6BjNOzdEDAEDAFDwBAwBAwBQ8AQ6IGAMdA9ADJvQ8AQMAQMAUPAEDAEDAFDIEbArHDEaNj7wCGw8H6jdanzwEFhBTIEDAFDwBAwBAyBAUHAJNAD0hBWDEPAEDAEDAFDwBAwBAyB4UDAGOjhaCcrpSFgCBgChoAhYAgYAobAgCBgDPSANIQVwxAwBAwBQ8AQMAQMAUNgOBAwBno42slKaQgYAoaAIWAIGAKGgCEwIAgYAz0gDWHFMAQMAUPAEDAEDAFDwBAYDgSMgR6OdrJSGgKGgCFgCBgChoAhYAgMCALGQA9IQ1gxDAFDwBAwBAwBQ8AQMASGAwFjoIejnayUhoAhYAgYAoaAIWAIGAIDgoAx0APSEFYMQ8AQMAQMAUPAEDAEDIHhQMAY6OFoJyulIWAIGAKGgCFgCBgChsCAIGAM9IA0hBXDEDAEDAFDwBAwBAwBQ2A4EDAGejjayUppCBgChoAhYAgYAoaAITAgCBgDPSANYcUwBAwBQ8AQMAQMAUPAEBgOBIyBHo52yizlySef7MaNG+c233zzTH9zNAQGEYHxpd++88477uCDD3af+9zn3KKLLuqWX355t99++w1ik1iZxnMEXn75Zbfuuuu61VZbzV1++eXjORpWfUOgHAITlwtmoWIEGGyuv/569+abb7oPf/jD7iMf+UjsPWLv1113nfvTn/7kJp98cnfqqaeOWL4jkdEFF1zgTjvtNLfAAgu4n/zkJyORpeUxQgiM5X6rEL777rtu1VVXdX/+85/VKTxvuOEGt+2227oZZ5yxw91+jD4C4/OY8+KLLzrqD62xxhru05/+dK0GOfLII93VV1/tPvOZz7itt966VhoWyRAYFgSMga7RUjvssIM74YQTQswJJ5zQ/fvf/3bzzjtvjZQsSh4Cu+++u7vjjjuC96abbuoWW2yxvKDmbggMHAK/+93vEub5s5/9rNtqq63ca6+95q688ko39dRTD1x5rUDO2ZjTrBfQv3fccccgWPrjH//ovva1r7mJJpqoWaIW2xAYYARMhaNi4zBIMDkqIWlCUmrULgKzzDJLSJAFyqyzztpu4iOc2jbbbOM+//nPu/POO2+Ecx7/shsUrE8//fQA/vTTT+/OPfdct8EGG7gvfelLYeE96aSTjn8NM4o1vuqqq9z666/vttxyy8Dc5RVlLI05eXXspzs7odNOO23IgjF7UJjnsu3fT2ws7bGJgDHQFdsVJuill15yMHazzz57iG0MdEUQSwRnkXLxxRe7e++9180888wlYgxukGOOOSYwz1dcccXgFnKMlGxQsP7Pf/4TEP3Yxz7mJptssjGC7nBWAzWaP/zhD+6kk04KY3deLcbSmJNXx366TzDBBO7vf/+7u/DCC91f//rXfmZVKe2y7V8pUQtsCAgCxkBX7AbKLK+00kphW5boqHDceOONFVOy4EUIzDDDDG6ttdZy8803X1Ew8zMEBhKBxx9/PJSLfmw0HAjYmNO8nT74wQ+6tdde26k0v3mKloIhMLgIDDUD7b13jzzyiHvjjTdGBOGnn37aXXrppSGvTTbZxG222WZJvspYJw4NX1ANeeyxx9yrr77aMKX3onPgEanYf//738rpgfOjjz7qnnrqqdJxOWj50EMPBb3P0pFqBmw7ryZY1axCbrQnnniicNs5N2Lk8eyzz7oXXnghcul8pX3JBxzr0ltvvRX6F5Yn2qTnn38+9CPapN/UBtZaRi3vxBOXP2ai3xlY1iXiPvjgg+5///tf3SRCPA6VMd4xDlUhxpeHH37YUZdeVBfvkewTveqAPzuSdfEG4+eee65MNpXDUK5nnnmmcrx0hH6WEZXIKvNKumx1+2k6nfRv/RablC2dpv0egwhIR2lMK8y2medvpEgmaS/mofx0003HKO1lkvIbb7yxl8Gir0U47LDDkvw0ryWXXDK4feADH/AyaTbKXyYr/6tf/covs8wyfsoppwzpyraYX2qppfxRRx3lqXdMX//610MY0T2LnZN3yihms/zHP/5xLyonISx4TTPNNF4k6P7aa69Nwma9XHPNNX7FFVf0U0wxRRJXJAt+++239zKJdUWRScT/8Ic/9CKF8JRb22aFFVbwF110UVf4IgfKPdNMM/mPfvSjmcHazIsMmmKVLuTvf/97P//883uRoCfY0V/5rX977bVXOlr4fc455/hPfepTof5gOMkkk/gllljCy+FVL5NiZhyZhP1cc83lZ5ttNn/PPfd4+tJBBx0U8NO2kIOu/sQTT+yILyoPfp555gllpI+IRRkvJ+k7wsQ/fvzjH3uxIBHaGXfy+sIXvhDKSFnlgJxfffXVvWyHx9E63nv1WzGjFb5nUd1JsKNsc889t99ll126MBhprDsqE/247LLLkjbX7w08tL3Fooy/8847oxg+1OUHP/iB/+QnPxmw0/aWQ7NeDmF5YTI7wsc/9tlnn9AWovcdnGlbxYz8f/7zn8fBe74/8MADfqONNvIf+tCHEtxFh9uLmczQznEC6f4mTJaXHaMk3pxzzullQRZHCe91+jYRq/YJ4ogVlIA9/RVc+ROrSUl7LLzwwh34Fo056fqS/hFHHOHFNGGYf/jGFlxwQb/nnnt2jdOEjUms0ISyib5wUi7KqP1En8wFVQmcRN/b863rd8+YDRZiqSk3ORGQJGU54IADQh2Y78AL3EhrkUUW8WJBxgvTmpvOhhtuGMYt+m4eyYLe02cZa0RPOqRPGcVyhxcBVV60xL1sP63a/mRQdc5LCmUvQ4NAm/wqkoLG1GaByhRm3333TT52HRh5wiiKBKZMErXCfOITnwj5rrnmmkn8n/3sZ0lZxAxQ4l71hQkIxiOuT/pdrFF0JFvEiNx9991hco3TkMNLXekfd9xxHWnqD9w1LgsUmBcYb3U78MADNWh4MlkutNBCiT8TL4y0MhIsCKpQUd3azqspVln10sWW4pX1TLen7Db4b37zmwmGxGFi0UmG32D8z3/+syvLeAKUQzOBqc3KE7df/vKX/vXXXw8TbV6YXXfdtSsPHLRdZAfGn3HGGR2LqzgtJtzDDz+8MI2shd+3vvWtjvqTTrrfwoiK5CpJe6SxTjJOvYiObUfZYzz0nbZRuuWWWzx1Ub+sJwyxnLvQKB1PbQvGIxbY6fhiRqwjfNEPsc2dMPDpdPjN9yv6rUkScX+75JJLOr59jS87aEn4Jn27Tp8g45hx1jKlnywAlRTPrH4Z11fMtHnZfezCW9MWFYawgNV04yfjpoajbzNGpvu3+n/729+Ooxa+I7xhIUaaGj/ryQJJdqO60orrx7dfNBctvfTSXiSzXWngAFNMvgheskjMroY6a9nAWlRnkjJT/t122y0ranCr0k+rtn/VOS+3kOYx0Ai0ya8OHQPN6heJnH6A6WfRKrtJq8JkaV58xEqyXZkMWkjB69IWW2yRpE86cvAhSEVvvvnmMDAiBUbKHVPRgA9zQ3mRNPOukiwkt7/5zW+SQYsJOj2gyjZsIgEX4/oeiYESk75YE/C//vWv1Sk8GbzJTw5MeTlEkviR39FHHx0kbIljiZeiurWdVxOs8qqCpBjGQsw5Je0qF2qE37jxJyo1HdG///3vJ2HFHFTSZjCLp5xySrKAYaGYpngClMOtIZ3lllvOi2qRp++y0FNGHKmoXJgQwiCFQ9IFIyGmGf1UU00V3Fk0kWaatF2QdDPZ8S0iFf7Xv/4VGHsYhJghoP+mSdPIYlSQ4iGpB4tbb73Vw3ix8yLnDLxYskjwEdvgSbIjjXWSceqFsmqbK46rrLJK0uZIB99+++0Qi+9Rw9AuSJP/9re/eb4XOYDlxaRasvjkmxJ1qFRu/7+YYeeBdqDNdtppJ49EHnz4zssQba9jKswMCwFRAwl5spNAf+PbjiWicX9DYor/4osvHvopffUb3/hGWKRp/k36dp0+Qb4w/HxnjFeUj7/f/va3SXsgbYypqF/G9dXvi51BdmvkoLNHsj7HHHMk+Zx//vlx0uGdsVNxXm+99TzjLITQB+m3lpF3+kB6XA6Bc/7beeedk/hycNWTP31MVBzDbpDulJIHi/Q0xfXTcYKdUHYOGafkEGaYS7SMzAtZVMRAP/nkk8kijV0vFiK6a4tUmYWgpp8ljKraT6u0f505L6v+5jb4CIzXDDTbX/qRZT2/+93v9qUF2ZojPyb99BYWq238YHLTfmUKA5OhkoMvf/nLmdILGJSf/vSnHckVDfhsOcKE5xHSQcWPreeYxPpF4nfXXXfFXrnvKp1vsoiIEy+qW9t5NcEqLnPeu+JcJFGCQYJRIixMUBbBDGtaTNgxxRMgYWDWdXLScKjXaHyeSJLSqjgw0RqGiTxN2i6EYUcCiVKaWGBqGmI6LO2dSLGzGGj6LO2RRSwkUA0gbVQeskjz7SfWWfmm3diBoSxI6rOIrXAta7zgjMPCiGoY1CjSFLcF40dZhjmdzjrrrBPyYeGTVjEhLAuYX/ziF/72229Poqb7G8xWnnpR077dtE/svffeCY7KtCYViV4Uz6x+ma4v6gbxLgjJgI+2l9j+jlJ+7/V73/te8EdokcYKlStVnYHZrUIIcXTsYMH2yiuvdEWHGed7p3wstGLJO4HT9WN3TM4WdaTD3CY3aoY0YLLJN01FDDRqG+TPAl4O2aajhsWl7mKCAZjEVKefEr9M+9eZ8+Ky2fvwIDBeM9AwdDpIZT1R72ib+JBVFwwpWJqQQmhZYECq0le/+tUQn0kwPbAVpVU04BfFw4+JUsuMHmxMrP7VL81cx+Hid6QexMljbOKwZd6L6tZ2Xr3KU4RVr7j4K5ZFTB36zYRj8s5jIGFkUOkgXJoxjSdApMuoaKSJRZiWBX3GeGdBwyJFVQlUOg/CaLvQV4v6BlvT5MWiMj0RaxpZjIqWI++JvjXpIgXMIq1fP7HOyjftVsRAo9oAE0NZ0XUvImVIUIVK9wvFkXTqCg5gbhUz1BLKUtzf2DHIYqY0raZ9W9PJe/bqE2UYKNJWPLP6ZVxfdGvTzLOWjYUEeMIIpom2xo/FbRaxk4M/bZ31/WbFwS1WcUHAlEdnn3120tbp/hLXj/EjvfjWNJkrtL/Eu0Dqr/01rcLBGRPt8yzk8ygW7MR9qm4/JZ8y7V9nzsurg7kPNgJtMtBDZ4VDtvOcTP7yDXeTTPzBhE63TzOXv/zlL+FkO6lgfSNNX/ziF50MDsG5jjUOYZpDXNkCddRvJCi+nEQGt44sZcvWyVZjcOM2Ka5e7kXCOIcgYCWHDAvtrfZKq5f/SOZFWYqw6lXWsv566yI3LuaZPpOJNVwdT5r3339/btJcoysSqS7/+LZMMBQdwa4wwvAm9VVTbF2BxIH0i6775fY9SBgNV5ROCFThP22LdJ+tkERyw2UbWFfJV8P+4x//cKLKEX5+5StfUefMp443soh39913X2YYvtX9998/06+Xo449hBNGtFfwTP/vfOc7Ts5IZPrh2GbfzsqkjT6RlW6eG1ddC5Od6S2CluCe1ee1zdVGeDoBkcwGJ75BHX/TYbJ+i2pIcBZVGicHtrOCBDdRu3Ciyx7esa+fR4wfefmLFDiJltcfkwDRiwi+kj4vzHXk0/kqB68Th3iMa6OfJglnvNSZ8zKSMafxDIHyNpYGBBiYCNFzdgximOdSEolYmETEaoM6tfZUppgBLh5ANAPZknMMOlz8IXp1weSbSODUu+dTB6IqcXomGgVg8KJcohMX/mT7sNA0mui3Otm+d6JrHOqCzeuVV17Zie6cY7GQNbj+6Ec/CpcVMDmIFCHczsjNX9wMJwelotI0f+1nXlWxal6b91LAljjEpMFgnkcaDvONVQmml79eZh9FNSMkLVKwqlkk4WOGSqRbTnQeE78yL+TN98S3Qb+FYYYBEb3oMtELwyiG/cS6qAD6vRMmXtRkxYlxEz1RJxLOrmAIDvIYuq7AKYe4LHXHH2X8UkknP9vCu599IilswxfmAogxNk0inQ3j8G233eZkV8vxW0lkdk7UssJP3JnnypK2Ya++xLgtetrhm6Iv1SHiIyziW+S7LkvaBwgvEmgnUuHMqKJ+krjHY5zWEc+6/TRJOOOlzpyXkYw5jWcIDB0DTftwuxcDEIwa0g0+KNHZcjB6bZNsZbmzzjorJCv6l04O0mRmoRJoJEVyKC0wn5kBU47Y3lVpmmzPp3yb/bzhhhuc6N2566+/vjAhBu80yaEfJ4eTQj1gisXkXfhj8DvkkEO6pFVics4hCUH6DF7YahVTg+7QQw91ohftxFJCazcK9iOvJlilsav6O56MRFcx4NgrDb6BOsRCE9JnVhrqp8+sML3cYum26E72Cp74i5qKEysA7vjjjw99KPFIvWT12VSQzJ8jiXVmAcRRDuglXkzcRSQHhxPvftikjRmptscfCt4G3v3uEwnALbwUMb6iNuHE0kNYwLKzIFZSwhXvopft5HxLuMWPIiDRL0sw6ipI6tWXSJP+BDPapC+xQ8acxRhflh6SOwGURJVMX3Ofoo/v2JFV6nc/JZ+qc56WzZ7jLwJDyUDTXLpi7HfTIQUT3cOQDdtIfGS9CIk10tsyxHadruirDEi90oaZRUovp/odDOdWW23lll122YAbgxNMjejkFSbDIM+2LpIRMZPl5MBYkDoghT722GPDBBAnwOAsB5mc6MYFfyYL6oQb5UF6KJYH4ii139vMqw2saldEItL+ojMbsBo3blzAqyg9GNt+MDtFeVb1i/syC88yBFMs5wHC7gXhRdc0XFYkh6sStRaxbZ0saMukmQ4zCFjT1kqMLUWSQ5grpViqr25Nn7rbQDq0GVi3SU3xHok+0WZ9i9JCuAIe7ACJKUoHQ81fTNttt50TqyGxU+E74ymSZS7Q0XmqKIL2pyZ9iTkFKvtdE1Yl87xz1XcvAQC7GvHORr/7KeWCqs5578Wy/8dXBIaWgR6pBlP1DbZIYUiLCN1GpEtIxeVEtpOTxEXBgx/br0h6iVdlS6xXwqg5MNAhLeCacfTjYlKpBW5FkkYGfCTI/IkZLid2RMOtdki2YcqzJC7kJWbTnJjiCiocMNDo3MGEE69NaiOvtrBqUi/qIWbMwk2RZSRJTfIaibixxKnsZM1CRr83pHDsWqRJFw5FfTYdJ/17tLGOGWa++SKVnVhftm1VKHBRnV3eKYuYZuO1VWqC90j1iVYrnJOYHPZzqCig1oYqhNj3DjfpyoHYcK5HDr66Iv3grGQZf1n0IFXuNX+wGNEwdfsSkmtVAauy2KIPKKGKU3WMG4l+quWrM+dpXHuOXwiUV7Qav3AJtWU7ndUyxKEosYVZ+IfkVUkZAf1d9NTBAcYbfc+mxECpahtImePBq0naHBpTyTrMeazXlpWu3LTlTjrpJKfSAybDflHdvPqFVVxPFkmQSn9iP33XNgJTrs4ddELihb54FrHlLqfagxcLuFidIyu8uom5Mn0NTEbyo8LLMGCtbU21zj333MLaiR3m4M/hrzheYaQKnjr2EEVugasQs3xQLXedvt1mn6DERd9g+RpVDwnTqXVBwixmUcOCmW8dYcuZZ55ZmXnWUii+CHBiXWH116fYdA6Hevkdq0eovz5Rj8wjmH6l+MCfuuU9tYz469yUFzbLvUk/1TGBdKu2f9U5L6vs5jZ2ETAGuqBtmbx0ta2n4QuCOzGOn5xyRg+aLbsypKff0beW63czoyA5KCu9hSkkLUgu0chMT8ztZbrjqHXOCqCnuPGL9TPz4rC9yIoeUulh+NHgvzbzaopVmWqotEUM++cG121b6ob0ftAJJhkVC7ai08SiSS5NCM5iGiztnftb+ywBsvot0lh2QYpoGLDmIKDY0w3VYIzJW4iwYNdFJ1v9dQ8KFuElNtXDDhhh5Crw3AU844WYLSxKKtevSd9us09QwKJvMLcCLXiw4NT5QEytOqwVIYRAR7wpofYEMZZx+JtnmpD64gchbEAankcIfzjLkk4H6blcXx6iMQ9w7qgsiVm/RG0D9T8dH8rGb9JPdUwgr7z2z5tTiJM35+HH4oedMrn4hp9G4xsC8pE0pjbt6jUuTIsJcIuf9IdwY1iWcfqsrDBATxz+uHmsDMnH62U7LIknk6UXSUIwJI8tTGGqw82Bsl3XkVyR3VIxZ5SkJwxNYotXVuAddkMpZ9p29vrrrx+ucuXaYRn0kzyxh8ytZ8TBjrCSnCr32L3loheuJFeSQdtzLaziwS1gZSmvbv3IqwlWZeojFkwCBrSfHKwMFx0IM+iFOeqIrrcDghc3ucluRIc/N3lxAyThuGUrJllgJTgfcMABsVfHuzBhIRz45hG3E1IG0cfuCqLtom0qi6hwNTgXI9C3sBMri6YQXyx+ZF6YoGlQlpj4XjRd2kTUmoK3MOv+arm1LL7pTaRKcdTkfSSwTjIreCmyA000bnbTunLlMDZ61S43dqLloG5iN5eLN7IuaMrDsaBYmV7cFKplEXUbL5LocNEHNsHl8LAX1bXgz22JSmX7m4av27fb6BOMY1q/5ZdfPtz4yO1/V155ZYe95SI8y9YX++Oal9Zdn6LfnPhpGJ58J3JOxWPfXphhn3V7p6aR9WSM1ktSSI/LuEQaHS4mYW4RFT6vl0/hn3VBUlw/UY8K5eTOgyuuuCLYhOaWTC6P0XKLilVWUQqv8ubSJY0vB//DrZ2UT0kWE14WFl6Y98zbEuv0U9Iu0/5V5zzSBXfajTox5pXlEYhrNHoItMmvsspsTG0WqHFhWkqAyVsHEpE+l041NsguNl5Lx2PS0klXBxllRPQ3zEFMRQM+BvVhMjQuaXP1LEwcblx4ssQSS4T3NAPNbYJxPDEN6EVnLsGDAZ9BWUkkaEl48pTttjCgc8GCpsMAFTPjGjfvmVe3fuTVBKu88sfusj2b4AAe2q5gEhNXbrMwUcx4MkBzOYFI7xP8cWfyjymeAEeCgebWuvj6efqV9i3Kh3985X1c1ry2pX+stdZaHfXnRjKdpOh3XO5C+nkM9EhgHdcl712/5aKxg+uXdYyhTvzBTOs7T9GX7vjW4vzycIzDlHkXKa/nauk433R7gnd8cU7Z/qb51+3bbfQJ0tAb9LSO+g1ye6BSEZ5l61vEQIvEORFAaDnyngceeKAWq9QTwYKoVHS0oRzCC9+h5kFfQzgTM62aeFw/LgYTKXWSlmKl6TB3iBUOjdrxZKwiXPoiFQ201157dcxLsjsZLp2hn3PpkuaB8CpNdfopaZRp/6pzHumy4NXy8uRKd6PBR6BNftUY6Jz21mt0GXQuueSSnFDdznzkKilDmlOFYNpXX3315FpW/ThZrSM1SN9+xUqdMEy6WUS55bKIjo8cRmy33XbzSGC4EYv4SEVjkgNg4QpilVZqOXgijbrpppvi4OFdtuXCQBiH5R3pmVzy4JFmVaGiurWdF+Wqi1WZOiFBRToPU6n40K/AJU1I7WkfbtrTsPpkImPyYoJDWhMTkn9dMMmWYuzV8a4MGvjmkUqzsq4jTjMZsqXbwfRRBhZcoueYl3yQMFGnrH4rliCCfzxpM8kiORQrLkF6SFwm+CwaCayz8k276RggFxGlvTp+sxACr7hvUD/GDjFzlil51gSKvhENU+UpJieTq9K1z4E9/SD9zZftb3H+dft20z5BGVh4I+HVevHkGyNtpSI8y9ZXzoiEPGTbX5MNT8Zb3dHklkJ2oHCDqZaDeaFfwzTrd8/4QJmrkJhEDbuLcrFMRz1hTJFAiw50bnKUgUUT+bL7KfrqYS6K8eJ75Tpu2jGPejHQxKMvMY6xII7T513ULbwcTvfcmppHVfqpptGr/evMeaRNPSg38yyMutHgI9AmAz0B1ZUO0IhWnP09szvXPXF6o3QGLTKWKtA7rGp6TQbGYKkCMzyYqatK6MVhMo8Tz9i4zrudkKajjBzSk8EoMxvCcCsWl0Zgdig+zEE+6OHJwJgZF/1DdFw5eIG+Mwc5RKqcGVYdZfvZYbMTHVnCU35hqtS79LNM3drKSwvVBCtNo+gpkp9wyAdzYZyC1xvU8uJgalAG/nDwBzNQxKE/5pEsUpxMbrntSTzKgO1YkermWl+hX3CAlgOA6bbDdi02mikHtwxC9BN0C4nHRUaxzmAIkPqvTNtSF/osGJBm/A3iJgxn4bfVb6xTVer6CSZ8W0U4x5HAjkN2fGvckJj3TcZxyuAYhy/7Thn47hm7RJ0n6MxmxS3T37Li4Va1bxOnaZ8gDXRv6VeMmeih6/kM/HrhWaa+mgZjf/ytikDGceukMKhBbzbvEB/nB7iACsoyFRo8SvxHGzJ2MG4wf6S/46wkuJOA8uuhb8KICmHAC0s6ZQ4N0l+Yu0QQ5ET9IyubxE0YzmB9SgRHIU/mJ+aLslS2n8bpFbU/4erMeZgPLPO9xuWw99FDoE1+1Rjo0WtHy9kQGDoEshjooauEFdgQGGEEZCciHNLEZF3WNd9aHG4pZMEIcRC9ykE9TWM0nwgFRFof7LeffvrYEqiNJq6Wd3sItMlAmxWO9trFUjIEDAFDwBAwBLoQQBIMYaYUJjmLkMiqpQxRp3BykDYr2MC6ccMgzDOEnWsjQ2CsI2AXqYz1Frb6GQKGgCFgCIwqAmLRwonubrgxUA6DBwmt6M8GFQvUWVBjkEO34cIpCioHgR1qE4NOqLXsvffeQWXvrLPOSoo7bJLzpOD2YghUQMAY6ApgWVBDwBAwBAwBQ6AqAsstt5zjRlY5qBhUOMTco+MvTUhud9llF8dNnMNA6EgfdNBBHUXlRkU5iNzhZj8MgbGIgDHQY7FVrU6GQJ8QWHPNNR2HILl+3sgQMATKI7DhhhuGy7YuvvjicJAQdQ5UHlDvmGeeecIhPbGMlHsgvHxOIxeSa+l32mknJ1YswqFxsR3v1llnnZErgOVkCIwiAnaIcBTBt6wNAUPAEDAEDAFDwBAwBEYGATtEODI4Wy6GgCFgCBgChoAhYAgYAoZAFwJmhaMLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MxBAwBQ8AQMAQMAUPAEDAEuhAwBroLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MxBAwBQ8AQMAQMAUPAEDAEuhAwBroLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MxBAwBQ8AQMAQMAUPAEDAEuhAwBroLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MxBAwBQ8AQMAQMAUPAEDAEuhAwBroLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MxBAwBQ8AQMAQMAUPAEDAEuhAwBroLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MxBAwBQ8AQMAQMAUPAEDAEuhAwBroLEnMwBAwBQ8AQMAQMAUPAEDAE8hEwBjofG/MZRQS89+7xxx93L7/88iiWYvzI+t1333Vvvvnm+FFZq+VQIPDGG284xoDxkV599VV3yimnuKuvvnp8rH5f6/zss8+6E0880d188819zccSHz8QMAZ6/GjngarlO++841544YXMMjF5bLfddm6aaaZxc845p5t22mndNttsk4R9/vnnHQyfUXUE8rBbcMEF3WSTTeYuuOCC6olajBFDYOeddw7t9P3vf3/E8hyNjE477TQ3+eSTu2WWWWY0ss/Nc6TwP+aYY9xXvvIVd9xxx+WWZRA88saTQShbXhmeeeYZ97Wvfc1tuOGGNo/kgWTupREwBro0VKMX8Pzzz3ef//zn3aKLLupmnnlmt8QSS7hvf/vb7vbbbx+9QtXMGUnn7LPP7maccUZ3wgkndKXyve99zx155JHu9ddfdx//+MdDnVVacPDBB4d4880333grneoCrKRDEXYq5X/llVdKpmbBRgMBJn++n6effno0sh+xPLU/6nPEMu6R0Ujgj3DhsMMOCyXZZJNNepRo9LyLxpPRK1XvnBdeeOEwf/7nP/9xl19+ee8IFsIQKEDAGOgCcEbbi8F07bXXduutt54777zz3F133eXYgrrjjjvcr371K7f00ku766+/frSLWSl/pBZMRGzPPvjggx1x//e//yVM9dFHHx222e688073pz/9KYT797//HZ6odsBgDzv9+c9/dmeeeaZ77rnncqtSJkxu5MhjELFrq25RNe11wBGgr9PnaXujbgQY5x966CE33XTTuTXXXLM7wAi4lGmjQRxPykKz8cYbh6BZApyyaVg4QwAEJjYYBheBffbZx1188cVukkkmcT/72c/cF7/4xTCw3nvvve6MM85wMJkwk8NEs846a9Dve/TRR90WW2zRUfQHHnjAofsIbbrpponf1FNPHd7ZQp1jjjncRz7yETfFFFMk/sP6Qv2ZLBnIt9xyy8xqlAmTGTHlOIjYtVW3VFXt5wAjgJrQV7/6VTf33HO7hx9+eIBLOjpFO/3000PG66+/vpt00klHpRBl2mgQx5OyYMFA77777kEoxWKB3VAjQ6AOAsZA10FthOIgqYF22GEHt+OOOya5fuxjH3P8/fCHP3RTTjll4j4sL5tvvnlmUXUxAHM81VRTdYWZf/753Z577tnlbg69ETDsemNkIQyB0USA8x9//OMfQxEGWX2DAg7zeIIKIOqBf/vb3xwLlu985zuj2eyW9xAjYCocA9p4DKa6TbbUUktllnKWWWZxKp2NA6AKEZ9gR7eVwQIJbxVCxeLvf/97IhUuExe1E1RNbr31VvfSSy9lRnnrrbcyrWuoWsbEE+ev60jz7bffzkw3dqxadvQtb7nllqA20kT38sknn3Q33XRTqH/eQUktZ9xG6pZ+lgmDXiz9Rem///1v2CJ/5JFH1Ck8y2JH4Pvuu8/deOON7rXXXutII/3jxRdfLGwP4uelUaZucX70Y/ThH3vssdg59530kXKi5kR96hL99V//+ldIh35FH8+jdFsQDrUl+pb277y4sTvtyTcLvk0oqzz0UXDM6p9ghorYP/7xj8J6pstUtm2qtrnmw8FhypXu0+qf92Ss+Oc//xnigkVZqot/k3Hk0ksvDd/KTDPN5FZfffXColYZZ+KEyozPZduozHhSFX/mrviQuPbHsu1eFn9V48DaiZEhUBsB6aCNaYXZNvP8GbWLwPTTT48dJ7/11luXTljUAUIcOYznZRLwstXmRZob3EhLVCj8T3/609z0ZAAK+WnexBGG1suJeC/MdG68J554wsu2oxdrDkleonriRe3Ey4GNjnjzzDNPCPOHP/whuB9++OFJHPKL/8hbDk2FcCeddFLwkwVFR3r6o07ZRR3Gr7XWWl15igqJF4ZHky58itqJ//nPf+7lgEpHOtTjox/9qBd9zyS+MGNeFj1d4bTOH/jAB3yZMEmC8vKhD33ITzDBBF7UYjxYigWDJP2//OUvIWgRdvQJ8v/Nb34Tygq+Wh7acOWVV/aiahJnGd7lIFEIh38W0e4TTjhh+KNsUNW6EUcO+3hR2wnpaLnkMK3fddddQ3qEiUkmYC8HsbwwIkk9iEe/E5WoOGjhuywC/Re+8IWO74d0wHeXXXbx9Lc0xW3B9/KJT3wiKTd9Wc4zeGFc09GS3/fcc49fbrnl/EQTTRTKDn4rrLCCl8W0l52b4CaqL0n4Xi9xeWRB5JdccskEE1ER8Ntvv70XJickA84LLLBA4i+7W36PPfbw4JlHZdtm//33T9LVNoyfcqYjyeKoo44KYRdaaKFQNtlu9zPMMEMSn/56zjnnJOGzXuj3yy67bMe3AP5ybsRfd911WVGCW1382xhHGLPBJO97qjLOpCtYZnyu0kZF4wl518FfzMuF+n/jG98I7S47rB3fcFG7V8X/sssuC3nxLRf17zSO9nv4EWiTX0VS2ZjaLFDjwoyhBD73uc+Fjxzm6IgjjihVM518ZAvQyzZViC/6hv5Tn/qUF5Nw4TeDtJjC6kpPpHVeTJqFMGJCzospJS/WPrwyVDDHF110UVc8kQwlAx3M+rhx4/yqq67q5SBMSIuJLKaYYcP9d7/7XWBuRKIewlNfmB3+YEpFKhGia92YWNNUp+yi/+bBBjxEJcb/4Ac/8LKd5xdffPHgJgcY09lk/maRQhpM0Ex+YiYpMF7KwIGbSP9DXAZrJnHqRnjiwQxqfYlfJkxcEMVTdOZDejBd6nbFFVeEoEXYadh11103lAmmeZVVVglMK+Xj74Mf/KC///7742zDQgw/FldZRHiNX6X+cVr77bdfWBzQJ1ZbbTW/0047hUWZLgrpayJVi6OExQz5iiqQF33bwGizkIMhhCEuQyLF9zCYpEMf2WCDDfxWW23ll19++aROWQtbxfLAAw8M+REfpnWRRRZJ4uXhBYOrC1f6Boy0WKwJ8XAXKzzhvQoDreU54IADAh7gCFPP961tw2JAzlMkOKf9f/zjH2dCVqVtYLjo4/R18mWBoH2eZ8wQa1+ljCKJDeHFrKVfaaWVkjGMeoiubma5WNjpt8WClAUy/Vn7DHn/8pe/7IpbF/+2xhH6Mthstlm2MKrKOBNXruz4XKeNssbiuvhruzMOrbHGGqXbvQ7+sqMU0gdvXdzHmNn72EWgTX7VGOgB7iey7dwhrUQSdeWVVxaWWAchnaSQjKqECekfUmL8YLLSUkWkrvjBqMRSMhgUGEv8YLBJJyad5GC0kXQoyRZfkNTBnMakkzoSz5jOPffckAeTZRZp3bIG7TplF3N5IT8WGmkmDMkaEvwydNBBBwXmW7ZVO4LDhCmDvu2223b48QPGAUzZNcijMmEUT9pUdBP93XffHZITVYdEil6EncanLGChzC6JXHPNNcmuApKhmNjJIE4eQ5jFQMfxe9VNtt4DowXD8/vf/z6O6pkAdYEi27AdfroQE4sGHe5i/SVIxjocc36I2oX/zGc+ExaMaQkVzDH1Bm/R2+9IIcZyscUW89RBCak48fiT7Xp1Tp7KQIGL7trQLy+88MKEcSQukuiyFJeHhRtjCiTqDB5GhfRYMPFkt0T9+cbFdGZwh+kVNZyOLOu2jUou+S7ySPsqZYJRlgPUybfIN6YLCRYzadJyEZcxS8c+womaiRfLFqFOLK7SjFNd/NsaR3TxxEI+i+qOM1XH5yptlB6Lm+Bft93r4I9Qhj7C37XXXpsFt7mNUQSMgR6jDZtVrdtuu83LoYfkY+eDRzKlksV0nHgQYkssTTC1TB6kw/asEtvNTFZMpjEDpf5sV+s2KhO6Egy9DkSi56nOHc80w62TelsMdN2yI4Wn7KIP11HeNn/stddeIQ8m5zT1YiAJXyaM4snCQxmgdF7aL9ITHuE0PgsglfbH8XfbbbdQByR4sX+/GWhl4L7+9a/HxUnekYDSfjD9SjBJ2h9FF1+dW33CfKqEkwVGTIolKieqeqT+MOK6wwOmMYlOclLuq666KvYK7zfccEMina7DQIvteM+CLiYkk4pVL//0t12nbci7CnPGeBSrdmjZ5eBXKDf+qDXEhIoMdWKMzCIWxcqosrum1AT/NsYRFijaFiy0qlLeOFNnfK7SRunxpC7+1FfHqKrtXhd/3SGlvkbjDwJtMtB2iFBGrTokkiEnK9faf5gvK0Oy/RsOwWC4frbZZgtRZDJ1opIRTg8Lc5qZDLfLYS4qTRw6JC7EISUl6iKfkCO/D3/4w+qcPIV5Cpea4CB6gom7piFqD8EudeIRvQizEf1q/7Vu2TGHB2G2CXOB/aC55porJFv24FuTMsgk6jhhXpdE8hVugEzHF/WF4MRBMQ6IjhSp/W8uEcoiUTUIznF/xCqN9l/qw0GntkkWmU4Y5ZBsXrsKg+xEfaAja2EMnCxSgptanNEAojMaXjHTKIstdU6eogblRKUr+V31RdQ0HIfTYhIJeWIqTfTJM/31203Xs07bxHmXeRd9bPetb32rK6hIyoMb4xWH6ZT4zUE8SHZ81LnjiYWfjTbaKLhxkFKpCf5tjCMcNFUSdSl9Lf3MG2dGcnxugn9c0TLtLjudSZS6+CvOIjBK0rIXQ6AKAv3lbKqUZMjCckpb9Opqlxo7lD/5yU9KxeeaZczYMZkcf/zx7kc/+lG4UEX0ooNd6Kx0mKzziAEKiidFtfgh25pOtnYzo4p0M7jH9lvVbd55582MMxKOdcuOqShu/cJCAhfWiN52mHixwaqMQ5Xyw2DK4ZRgKYABPmY4RfpYJalaYXVCqBVZIuX1GRZjSvQPZVzVrR9PLgxSpkK2rh3XG6dJLVTAJBNWdkhCEFGxCEwSCyOR4DvRVXbf/OY3E8Y6nU6v39z4SR+hTbkEiMWzSOJDtLx2zcNSmeq0BQy1MsBNaXlxtZy9/DVc/MyKg5tIY3NvNsRfzk2Ei37oy0pN2kbTKPPMKjPxFEPeaXdRB+E1jGdq6UR0zoNb1n9gDMWMUxP82xhH4v6ggpKssuNWZZwZyfGZ+aQu/nFdy7Q7eMkB2RCtLv7gLConZo88Bt/eKyFgDHQluP4/sOhl9jQ19P+hu9/qSAphpLfbbju34YYbBuadC1XkcJDj+msmwrKkYZUJIJ5OIDAIsu2XmxQTKtIwpQfFrBcUT2rqN1LPumXnogIkaUgLjzvuOHf11VeHPwZm2U50cvioVBVgopB2HnvssX2ReJYqRB8DiWqIo7/DOCrT2sfsQtLapvzALGDepIrEWbaRw0JSyyQHBcM1vVz2APPLJURyFsDJoVh3yCGHBKZQwxY9kVAiyYR5bovAMYt0MauLgKww/XDLw1XzUn994t6kbTTdJs88DOOFPSY+80gl8VyiwbcruuyJMKEO/m2MI2INIiku5cqiOuPMSI7PTfDPqm/aLa/d6+KvC3TiGxkCdRAwBroOahKHiVv0kGvGbhaNlTOMM1vrMDWiJ5257ZuXCxIkKJZYqtRDTj87sbSRF7XLXW9xwvbwaFHdslNeVFPkRL5D/UF04RyqMkwE66yzTmCmxSpGz2qJLmVguJl8f/GLXzgwpEwMzKeddlrmNnTPRAcoAAst+hkU9xktovrp7zae2qakxSJHDipWShY7unwXxGWXQQ4hhhsf5XBe2OaPGcKshFELoR2ZZD/72c+67373u4FRVwZLDrI5pPFtEVc3Q7Eksq20206nadu0XR5NTw476mvYoVMJZeL4/ovopoc31B5gnqGm+DcdR1SoQVnoo1lUZ5wZyfG5Cf5Z9a3iVgd/xTnGvkqeFtYQMB3oIe0DSN2U0D2rQmxbQbr1ybuqYMRSBNx7keqbxtuhveK07V+37HE5kEohseTCDHQskfbI6e44SOY7W5a//vWvgx9PMbPm0C0lPSS3sWQpMwFxJK9eVCZMrzTq+oOJUsyUKDOZt3gq2y+z6gaThr4qVLVPall5omYlJtLcySefHJzFukqHDn8cNn4/44wzAvNMXzj//PPdpz/96fC90Kb8KeMVx2nyLibbQnR2lfKoLJ558dtyb6Ntstq8aflQ19GFkViiyU1O/VSVjYBt4V93HIGB1z6VtTCrO840GZ+rtlET/HMbq6JHWfzl8KnTcUvHsYpZWXBDwBkDPaCdACmxWL7ILZ1czhH8mDC41jtN6AWLebS0c9iqRFUBErN4ib8ezIG55hbBsiSn90NQbi7Li5c1IZRNv0y4umXPSpuJTGwGB6/4oEpWWNyYjPWGsyy9S90mzIqvt0iqnmLdMFnx6rghPc/aPua6W0hsEnfoEfMb4kCcSvWCg/zHDWQcXFPKYv6K6k+/1gN3p556qiZT+/nlL3/ZoQIFlWlXVD8g9L/TW8dMvnm3K4ZINf4TSyIhFlIxPfgVJ4MaiVw8FJyysIzD9vu9Sdtom9MGnCNpk2hfHY/EAlFm0nyPZ555ZvBjZ0GpbfyrjiMwzyoUUcmolo1n3XFG8agyPtdtoyb4x3Vt470X/qhM6XeUNW63UQZLY+wjYAz0gLax3CgXmBWYGl0pa1E5HIXOLSRmgzJ1OpEeiPkvd+ihhyYHO2DIYQ7Zcme7bcstt9Qkndi8dXJRQfgtF4FkXn3MiXe5cKFDYkp6KuUgvVg/EmaMbccsBj/JuIWXumXH8gDXPMcENhwEhJSBi/3T70i/VeqljKaG4ZrYmIlUd32q1IsFjVqLSFtVKRNG02v6hHETG+AdElpUH9AHh1BjwAKFkpgKC0wpzDL9UVU5nnrqqXCI7+yzz9agmc9eddt3331DPPo7Osw64Wli9HHUqOI2xEINh2rTi08whvGFsDTTi/SMAupMsd43C1vUQzgr0CahLoIED+I7ilU5LrnkkvB9pusUAo/Sf3XahqJqm9NXxBxmUnr6UBu09957h2ToF3x7cZ+h7bDowiE8sI4tfDTBv41xhEKrICBL4FB3nKkzPjdpo7r4h0ar+V8d/GOMFfea2Vu08RkBGWAaU5t29RoXZowkIOoA6GWEP5FOeNk6DzeIqZ1Z/LAPLRKVjhqrLU051JfYEOYGQm7x4tpS4mHDVra0O+Lxg6uLZQsshMFWNBe3cKsel5RwGQrlIH5sC5h4XHIh+r7Bjyd2ebnNTO1NcxNbTFqHtuxAk3adsnPpCPWhfMK0eC4KkW3d4Ca6g10378V1iN9FuhnikBZ1l4Oeye2NXDKCO22VJrGoksSTbUQv6gaefGMqEyYPzzgd7Rdpu62E0fhi9jApD3aBFQvKL5NMV7sTV5iQJI7olPoVV1wxXH4iiwqPbVrtT+lbDIlbpm70P/LnT5iIcBEQdqHFakpyqx23EyqJznkIK1K0cG02tn6xTauXhcgiQIMWPrGRrN+LSLPC5SVyeDfYEOZGQy5JoUwiHe9IR7FM920NxNXZxMOOcppkwZHYlxZpXrjNE9vchJdFariFkfc6dqDzytOrvNp+IrVNFzeMDZSHvzJtQwLYhBfmNcQhHt8HcbkkRKmorxJGFuZJfOzkp0nM1CX+fE/CHIcbJHU8YmxM2+8mjbr4tzWOiLAklJvvKIvqjjNVx+embVQX/7rtXgd/HXvo30bjFwJt8qus0BtTmwVqXJgxlACTHrdtKeOqkxXMlqz0MxmaeBDi1i4mapgZ4vKEgeKWvTzi8gcYZhgQzY8nZYCJ5tanLOIiAib7uKxysMNz3bFIJDuisBggTQb2mMQWc3BngssiLoYhXpoh17BVy86FMDCKcT155wY6LmcpS1xOw02DLEw0LW5v4wpkkXoFTGC40sSFHDCg2j7EhVGNqUyYPDzjdIqw41Y4UVMIjAkLN/DXetCGMGwitYuTS9656Q0GVpkT4jGhwYxAIs0K9ZNt6SSOvpSpG2HPOuuskGaME/kw+VE2UYHRJD1tQZ+j3FoHDbv//vt33aKZRMx44bZAvhdNB4w++clPhtsFqTPuXEMfU6+2EEl9iCemt+JoybtIvDvyZPFLWNmF8owH5Jl3sUySSPTSqzy0PWmmv0VNgvbDX9RH1KnjWaVtNKLsGHQw0eDKLaRKRfuKu0wAAEAASURBVH2VMCzg+dboD3mX5cAgwajHfYZxk0WQqI9oVl3POvi3NY5QF7DmT3aDuspWd5whoSrjM+GbtlEd/Ou2ex38WYCDc5XFKLgYDT8CbfKrEwCHdKRGtOLsXwrxr3viPV3JRolZ5C4E2ELmIBU6g6hLiNSoK4w6oGKB6S306fSwDDqqxMf+aZUDE2xzEQ99MrY8VTdO88p6sj3KoTP04cgvy0QQOsPokJJumrD4QFz+soitbU5cx6oEWeGqlB3VlIceeijkyVZpVrmy8ki7UXf0mYWZDLqz6o87dqXz6sTWPPE4cIjOrSxCNGryLApThGeSgLzkYccBJbbUwRVCjeTOO+8MZcbaRFoHOARK/Ud8LlnhRHtsqYO02Z4v6jtFdYuzof9jHYPy8Q0Icxh7d7wThrB8O2xJY3GhTD06EpEfDI/oS/INgYXWA/UR1G7SfaVXW5Ae7YA5yKLyoG6ALiwXFMXhiKtmBdNlzfrdqzy9/FF7oQ3T9UznVaVtiAsO1A/dedRl0uNSXl/VfBk/6HPaHuqeftJG9APM2sWHptPh0r/r4N/GOMIBZMZPVKIwv5hFdccZ0iozPmueTduIdKri36Tdy+JPHowf9H1ZOAa1Hq2zPcc+Am3yq8ZAj7H+ksVAj7EqWnUMAUPAEBiTCMiulUOPGEHJaFo2GpPgvl8pzJVyzoBFLEw3Ag+j8QeBNhnoblHX+IOj1dQQMAQMAUPAEBgYBLbZZpuwU8UFKFnWWAamoENcEFE7CqXnhlJjnoe4IQeg6MZAD0AjWBEMAUPAEDAEDAFUC7bYYosAhOjXGyAtI4AZQyy0oAKIVSEjQ6AJAnYTYRP0BjCuHKwKtySqjd4BLKIVyRAwBAwBQyAHAcyyYbo078xETjRzLoEAZxkwWThu3LiOsxololoQQ6ALAdOB7oLEHAwBQ8AQMAQMAUPAEDAExhoCpgM91lrU6mMIGAKGgCFgCBgChoAhMDQImA700DSVFdQQMAQMAUPAEDAEDAFDYBAQMAZ6EFrBymAIGAKGgCFgCBgChoAhMDQIGAM9NE1lBTUEDAFDwBAwBAwBQ8AQGAQEjIEehFawMhgChoAhYAgYAoaAIWAIDA0CxkAPTVNZQQ0BQ8AQMAQMAUPAEDAEBgEBY6AHoRWsDIaAIWAIGAKGgCFgCBgCQ4OAMdBD01RWUEPAEDAEDAFDwBAwBAyBQUDAGOhBaAUrgyFgCBgChoAhYAgYAobA0CBgDPTQNJUV1BAwBAwBQ8AQMAQMAUNgEBAwBnoQWsHKYAgYAoaAIWAIGAKGgCEwNAgYAz00TWUFNQQMAUPAEDAEDAFDwBAYBASMgR6EVrAyGAKGgCFgCBgChoAhYAgMDQLGQA9NU1lBDQFDwBAwBAwBQ8AQMAQGAQFjoAehFawMhoAhYAgYAoaAIWAIGAJDg4Ax0EPTVFZQQ8AQMAQMAUPAEDAEDIFBQMAY6EFoBSuDIWAIGAKGgCFgCBgChsDQIGAM9NA0Vf8L+vLLL7t1113Xrbbaau7yyy/vf4ZDloPh006DnXzyyW7cuHFu8803bydBS8UQaIjAaaed5tZff333/e9/v2FKgx/dxrHBbyMr4XAgYAx0jXZiALr00kvdBRdc4O68884aKQxmlBdffDHU6eqrr3a33npr7UIeeeSR7otf/KI77rjjaqcxiBHbwmcQ6zaSZbruuuvcn/70J3f22WePZLaWVw4CjGMbb7yx22OPPXJCjH3niy66yP3hD39wxx9//JivrI1jY76JrYIjhMDEI5TPmMpmhx12cCeccEKo04QTTuj+/e9/u3nnnXdM1bFuZV577TW34447ujfffNP98Y9/dF/72tfcRBNNVDc5i2cIGAJ9RmD33Xd3d9xxR8hl0003dYsttlifc7TkDQFDwBAYfgRMAl2xDWEQf/e73yWx3n33Xcf2n9F7CEw++eRu2mmnDT9mnXXWgWGer7rqqrBFu+WWWwbm3trLEDAE3kNglllmCS8IA/hmjaohMEhjyzbbbOM+//nPu/POO69aJSy0IWAIVEbAGOiKkDEwvfTSS47JZvbZZw+xjYH+fxAnmGAC9/e//91deOGF7q9//ev/e4zy25///OewRXvSSSeF9hvl4lj2hsDAIIBA4OKLL3b33nuvm3nmmQemXMNSkEEaW4455pjAPF9xxRXDAp+V0xAYWgSMga7YdMosr7TSSm6rrbYKsVHhuPHGGyumNHaDf/CDH3Rrr722U8nW2K2p1cwQGH4EZphhBrfWWmu5+eabb/grYzUwBAwBQ2CEEBhqBtp77x555BH3xhtvjAhcTz/9dDg8SGabbLKJ22yzzZJ8lbFOHCq8INH+3//+VyFG+aCk/cwzz5SPkBOSuj/33HM5vs2cUYt56qmnaifCoRjKhzrNaFHdNnz++efdQw89VEuthMOsxAW/0ST03f/zn/+4//73v6NZjMK86/YxxphHH320Uf+MC9YEqzpl6UcfaWMsqPu9KJZPPPFErW+G+GDCmDEIpG361ltvDUJxwu5ck7moSbsMBABWCEOgAgJDyUDDKB1yyCEOycmHPvQhN/XUUweGtt8T+G9/+1v39ttvu4knnth94QtfcIsssohbcsklA9z4FQ2CMEpzzz13UPtgqxT61a9+5T75yU+6GWec0U0//fRuoYUWcnvttVdjRpDtuw022CBIlKabbrogCUa3EfN0VRh9cD788MPDAUnis7276KKLum9961uFDD/YEFYl9KGyqf9gxrfddlu3+OKLu2mmmcbNNttsQf9yjTXWcJdddlkqdPfPBx98MFgOmGeeeQJ2lG+mmWZyW2yxRdiK1hjUef7553eHHXaYOrllllkmuOFOGz755JOJX9UXtkyXXXbZ0BfLtiHtwwLsAx/4QGj7D3/4w26KKaYIfXnXXXcNE3xeOWA8dtllFzfXXHMFXXPionO+4oorhm34vHhp949+9KMBL8pRRHfffXcoF+35+9//PgnKt/bTn/40YEnZ6dvUh7KsvPLKjm3tOrTzzjuHcmHmLo8ef/zxkB87HOecc05esLDgq9vHsBLCLtNUU00VsNb+yQHiF154ITfPLI+mWFUtS9U+QjvSvksvvXRW8YPb9ddfH8YPxhP91vje+IbiPyzwKLU95p177rnu05/+dCjrHHPMEcZ9xt/vfve7hd8M5Xn99dcdfYvxhjow5i611FLu4IMPdjCxdaju2AID/8Mf/tCtsMIK4XvhW6affeQjHwljZtXxCOshCyywQGgHrcepp57a0S4/+tGP1CvzWWcc04SatIumYU9DYCgRkMGjMa0w22aev5GifffdlxGv6+/jH/+4Fya2b8X4xCc+EfJcc801kzx+9rOfJeUQc1CJe/pFpFhJODET50V6nfxO10XUH7wwr+kkev4W6Zb/wQ9+4EUPOTdt8tpoo428MAFd6cVlFEbOr7766rnpyGTrRWrclQYOMhGEeMLUZfoLQ+BFzSNJWw4eelkMJb8p/2677ZYZF0exI+xl0ZSET+M35ZRTetHDDvFloswNp/Huueee3LxijxifPffcs1YbyuKjozzUddJJJ+1wk8nQi8Q0zjq8y8TrZZGVhBWGPeAo+vjBjXqXJbH3HeKQv0ixc6PRDorTP/7xjxBOmGqfxjVdB+KIGcPMdL/+9a+HNGn3NMkBqOAnDGvaK/lN/lqmQw89NHGPX5r0Mcqt6cti2cviwMsiL3E78MAD46wK35tiVbUsdfpIUXtQOeqreNBf+Haz2psw3/72txM84u+lyZj36quv+m9+85tJGchHFk9erPskbnwX//znP5O84xdhSP1yyy2XhNW66HO99dbzosIS/PmmylL6G9D04md6bLnllls833ccJv0uixkvZ23KFsOLcKAwPdIX6ypJenG71B3HSKxpuyQFshdDYAQRaJNfZfXdmNosUK/CyNabn2SSSXIHDFl590qiln88acPAKT388MMJwyq2VNW56xkPWnL4MJRfJCBeJDZeJNJeJGlepCpJvc4///yuNHo5iIQlif+xj33Mk4ZsqXlRc/FyUMiLtCbxZ0JKU1xGnZxEWuvFRqqXLXovkg4vUrkkDZiwLCpioJnMlPkV6bFnYoXxhx544AHP4kQnlKwFCROStj9MtxwK9CKNDkwgdWQRRXyR7oc0YaTFnJ7/0pe+lKQruwXBDfdrrrkmhCvzX4wPjBX5VG3DBRdc0IsEzMuFDV5sbYdJ6J133vGiR+9l1yAp409+8pOuIrE4Is/JJpvMyyHNxF+2XP3RRx/tZTcjcev1AgaKcxFDKNLFEG6JJZZIkjzjjDOCG32Bd/oYRDl+85vfJIshGIGshVoRw9YGA92kj4m02LMQARv697PPPpvUG+aHfvTrX/86cev10gSrOmWp00eK2oM66/cGo0mZIAQV++23X9KHeJdDwx3tHX8vTcY8vhXtq2IiM+lvLDJPOeWUZHHDt59Fulgkjc997nPh27/rrrv8AQcc4MX8aJI2/nybZanq2MJ3IpLmkB/j6z777OP/9re/he8G7MScoNfFMN940cI2LqPsOPhLLrkk1Etx0noyxvHH+K0Ut0vdcYy0mraLlseehsBIItAmvzp0DLRcwtAx4OmAoU/ZzutLW7BSJw+kZjDxMSFpxU+2srv8NFw8aBH2M5/5TJeU8fbbb0/q9tnPflajlnrCyDPokvYqq6ziX3nlla54MDNIjgnDwJmWjqTLiNRC9Ms70qHuosYR0mASIN80FTHQYmYpxIWJlq34dFQvKjKJlBWGPy2JX2eddUJ8JGByiU1XfJjRX/ziFx4sY9p7771DPOquTEDsX+Y9jU+dNhTVBi/qK5nZwRDMOeecoZxZzLDugBQt1DITznBEeiTqFiEv+kQWwTyBF38xk035qUceidpPEk/UcbqCFTFsbTDQTfqYWKNIyg6T1ZSaYFWnLHX6SFF7fO973wt4sBiCUYuJb1NU6II/32qa2vheYCJ1XNtpp53SWYTfopaWtBmCiJj+9a9/JQIOUf/o2qEUfW7P4lD7eRUGWvMpO7aIOlGST7wA1nR4siDQsshNnbFXqXeNG+8EpCMOQruky2S/DYGRQqBNBnrodKDRuyuiXv5FcfP8pGET3WFhbIPeWhxWDxNyUKlIJ1PjrLrqqsHUEDaTY5KBPOiU4nb//ffHXj3fRZUkOUwp0iAnUrSuOOj+yZZ8cEeX+6ijjuoKow7o93HlsjCq6hSe6LiiBwoJs+rQtStLwrgmN31tt912iRnAOL4w5U4G/+AkTHA4nKb+wqwH83j8Rs8668IHzAvKROvAsp9Utw3RVUZ3P4voD8svv3zwEql6VxDwhjiw15TQW95www1DMtw6iSWZNKHXD4EpF2woUX7qkUdgo5RVD/Xrx7NpH1OMKVsbODfBqk5ZNE4bZQeD2267jUfol5w1iUnUOZJ+wUUsRYe5634vnHUhXb6NvJsS6Ztq8QfzmTExxjF+Q8LohvMrsT96+9hx5vxJPwm9fb2Z9VOf+lSwUpSVH9fbowsNnX766Q498n7SaLVLP+tkaRsCI4XA0DHQsgUeDn5lAQTzhfm0tukvf/mLU0Yg69AV11aLRDdkW+aQHgfl0syzlplDYRADbhUSaWEIjikqDqfkkWxnJsy1HmbMCivSVSdbt1leTqTAift9992XvPd6EYleOIRJuCIGjENJSvFCQiTm6hwY6OTHKLyUaUNOpFclDmhBWZZTOHAK0R+33377xvasRR0hpMd/yiwnDvKiFwbJjobDNGFZ0joQPqseZdOpE65pHxM1gKTfc4sm1473k4qwqlOWtvsIC20ojyFXppoFWd54Qfwy30vWmKc3JLJYzlt4ssDTcTMeL8iX/gBx6FCxCQ7RfwhdOFQLsSjoB8n5gWTs+8pXvlKYhc4xHOKuMr4WJprjWaZdssaxpu2SUxxzNgSGCoH3uL4hKjKDJVJPPnzRT0xKzsC3//77JwNh4tHCizLFTBYx86hJc4IdhpPLCESnNpi9qsJwaDo8SQviJH0V0oG215XiTHJMJoQXneMqWSRhic+CgclVtgMT914vsZSTU+hIhLJI1E8SZ8wUKmkd+V0XX02rn09twyJzUFgFoL9QJyYoGE3wRBqcR5yk58Q9zAzWUeiX3KzI7WOcwq9KSJ9oSxiXM888s0PCd9NNNyWLxi9/+cu5ScOg0OepA3/0W0y1jRY17WNY22AHR3SJQ9/GEgdWReTMgGOhXMQk9qpzVazqlKXtPoI0lPZFEi0qU4l0lLoi2dUdN8IxNtch/V6yxjxtTxhjFhR5pOHi8YKw+lsZ7Lz4/XaPx65eY7ScDUmKwxiN1aDRIG2XrHFM8a7bLqNRH8vTEGgbgaFjoAFADsiFwRwmgpUwzBTbeEx2bRPMwFlnnRWSFf3UYHouKw+VQCM1kINDYQLOCtfLrc4kxMSjiwkm3V7EtiUDehPby0iDYPqqbDFis1hJdBP1NfeJ+ghmp5Rihl+3bNVvkJ5FbcgWO6bqjj/++ELsdNs5rheSMnYakD7TJ8EeM1xiiSKY9MNUn056cby8d8rJdyM6404sGIQ/VYvRPs9OCeoyabrhhhuc6Mc6zJsVUVY9isI39Wvax8hfDkcF03Uw0SxWrr322vDHog+Vgiw8isrdBKuqZWm7j2AiDtUD1CiQjG699dbBRCaqMpi/49ZR6Dvf+U4RBIV+ed9LvEDHdKDushUlxtwQk0rO+6HaF+fT6113MAnXa4xmfFZqMkZrGnWf/WyXumWyeIbAICEwlAw0AKp0pt9gIiXEZjGECgETWi9CMsjkO1KEDVEkY9ih1rIW5c3kB2G7ty6pVIJFRVmKmTt0FdOTXTodJP66RYwf9qKVYB6xAT5MBDP51a9+NdGnRwKM/jz10O3pgw46KFmwZdWNyVUsXTix0uGOPfbYwNyABW4wGEiw6Q9lCekyDDSEFFpMRAbJojLQcpq/S+effNgBog/AmGDvG1vYfJMserikAj3PJlSX8W7ax7TMMIswykhY0aPFFjO7LUihwR1Gsgy1gVXVsrTZRxAIIByAgWaRBUPNX0ycZ4jVgWK/Ju/ki211+ve4ceNCHy9Kj13I9MKab4GzKfTJ0STqocQYXSSF1vGZ8E3GaM2v7Wcb7dJ2mSw9Q2A0EBhaBnqkwFL1DSRxMA1FhJ4bkgak4hyAw8j/SBCSApgwpMq9VCpgTDRMnW1/6oNURA8MVWFi46uCUWHoJYlJYxdvw1IHLkIYJoKZ0v6ExC6+3EXroQxAL11MsOTgqJi+CiocMNDotMPsIRkuS2DI5TjsCKAHDQONxFQld1nqG6gJwDzD9HOFfdyu5Ku7Ibz3qgdhYtLDrzBNdSguS50+FucJoyAWT8Lf5Zdf7sR+erhEBXxZNORJ6OI02sKqTlna6CNcmoRKFWpCqPuIfeKgFiFm6cJZFA78Fp1niLGo804dxNRbuOWy6nhBfizwYUgfe+yxOtm3FidmmBm7itRR9Nsj87pjdGsFz0moabvkJGvOhsBQIVBPaW2oqli/sGwb6qlurG+gf1r0h1RQSRkl/d3vpzIOMPGxvl06X7HpnFz9HKtHpMOh75hHTKJK8YE/dct7ahnx77X1n5VGzEBfeumlWUFy3ThgqhRLeNRtJJ7x7XwwJG0QVlFOOumkRDoPk16VlElGrxEJth4oRLosF0x0JMcCTNsOKXPcph0Ba/6ASYNQncprp6I6xuXRctYsSkc0bsDTXSUWD6oD2hEo9aNfWFUtS90+wiJZ+ywSZjHlGZhZrvJGQMCORT+ZZ+DU9gRv8q1Kqk/MmJg+YKhpsdDSw4bqVuVZZmzRepAuN/cVkR7eZTEZxyuKo35alrxvR8M1fWq56rZL0/wtviEwCAgYA13QCgxkKmnVk9EFwZ1cNJBYuEAPmu3PkSJUAyAmbQ5B8UwTEwV+EJMq0qU8YgGArm06HaRRRxxxRIjGAB+bN8tLS90xFaVqG2yDV72yVmzcBt1U0jvxxBPDoTVNO36ecMIJXdeBx9Ir1duM44zEe3y4Ti7m6coSyROSzjzSvpj2R30HCSWkEux0mKLfqJGopJh+qxM4Etf0oTn6g9Yjqw7kA/51Kd6yRqqeJq4T176OX7p/Nu1jeRiTl0rHeY/1VPmdRU2xqlOWvDh1+ggqYTqGsTOB9RcWD2qZI6vObbupagj1YselKsXjE2dm0kS6jO0sCKB0f0qHz/pdZmzhICA7PRDfVx7DjoBGF4ioyuRZa8oqB25aln6PcU3bJa/85m4IDBUCMmA0pjYNUzcuTIsJ6K173B6VdTFJVlYyYMO5hj9hhpIgsm2XuHMDVh5hAF/j54XJcpeJLrkkhfgiVfRcvSyTXbgMRbbavV6ygL8w0l3JxGUUhiqUg9vxrrjiinBbILdmcXmIlk/UELrSwKHoIhWuWNb4cvgz3KAlk1iSDuWVidoL8x6u70083n/hxj2NzxXLIokOFzxwMYgc9vKiZhP8ueUrJrH1msQTW8vhBjBuU7vyyiu9LCzioLnvMT512pD+oGUXU4Ne1H1CXnKw0F8tNzKK9DXxF0lSRznECoLnmmE5uOW5/EGJsnPtuqYr0mP1qvTUvs5lQJqWSHAz06DsGkak38llOyL18umryoXx6kqj6OIOrocXpiGkL/rv4QZN6shtnWIHOFwAJIuF5HY8OdTXlX6TPrb++uuHK+zpL3xTSlzaM9dcc4VyLbLIIurc89kEq6plqdtHitpD9JuTttY258nlJrJD4WVB7GVB42+++eYuLJp+L5qg2KRPyvCNb3wjuYlQ/bl5ktshCcftgDHJYs+LqcAkPjd8itWZEIQxUXT3g5/2+zoXqZQdW4Q5TsrBNeBnn312ctOlqJh4+jJ9G3xFlz/3Uq64ful3sRgT4ot6kZcDxmHekoW5F6Y8CToI7ZIUxl4MgRFGoE1+lRV3Y2qzQI0L01ICMDfKRIqEonSqXD+tE43Y+0zitTVoJQlmvDCB6tXLWgaYEG7t09/USSQbCdMTJxOXkSvGRUqdxBMJVvJOWtyUJ1Y44ujJexEDTaC99trLwyBqmZg0RHIYrtXViQw/mLo0MSFypbDG5clkwZ+6kXb6BjyYIb1BUcNpnUT6lM4m83eMTx0GmjKISkRSTsrBDW4wIrzDlIhZuvCeZqBFYpXEw0/UWcKCiQlf6wPDFTN9mZXIcTzmmGOSdEhPdDZzQnrPbaBx+8HYc6W5tgF9Q293q8pAk2m8IKAs2k68w1iw2BBJWyivWCDJLGfdPsYtj4on9RL7wF70UJOxgDaC8SpLTbCqWpa6faSIgRaJc7JwUFzynvFtleDT9HtRjGWnw7NoifPlm2GckR2XpG3wZ0GcJsYChCBxfNlNSH7LhUJeF+a0eVWqMrbsvPPOHeWlTDDTcdn49qr0sbi8olbTkZZ+O4wNSoPSLloeexoCI4lAm/yqMdA5LadXqsJwXnLJJTmhup1h8FSSiIRUCamhMh1yeEydu56iZxkGQAb4OvTyyy8HKWAsdWFwhjFFAi060LnJIv2DCaLOojPoRb8tSOPiwZ3BnquSi6S2vRhoCiB2hgMTDkMSp887zJEc0vJcw5tHME567bXGhxHnCnTSziIYDCRmGp6nHIbycmAtK3iXWxttSF5I13ViowyUG6m46B8HyThuLF7SJGovyTXncR1gKsUGukcKX5e4clrUEhJsihYI5ME3ISbvkvCUB2ZGbroM1yWL9Y7ghxQsTdSf8PSlPEIaFzMWSKXZXWBhC4lua0gDxj+P6vQxro5mwaxS8Bhn8s/rW3llwL0uVnXKUqeP5LUHOzS6M8ECF0kmbjDVjBXsSME08w2BE+MG35hSG9+LpsV4Q9/SvOJ24Vti0cainx2sLIIhFTWKRMJLfJhyyg8DzBXguJF+HaoytsDkszCLBRvkzXwh1l1qSZ61zOxmsUsVp027MD4oDVK7aJnsaQiMFAJtMtATUGj5eBvRirO/d6PZdU+c3iidQYuMNQF00KqYBaMO6A5yABETbMK4JtUSBsfJROCEMUjc0i80B/kSl7ybEAdJZGAPtoG5wVEY+J7JCQMe9ABjk3Fcoc0BHPRTyxwaXHjhhYPJv9VXX92J+kdhnjJ5BcslwhiFg3Ccmq9ySQp1xLwWOJMvut29CN1r6kMd0UsUBrZXlMS/rTYkHcqAeS1uQYv7GG6Yg4v7TlIAecGiADaxsSnNwUrwKtO2cRpZ76SH9QvyLoMjfZVLWKgH7aYHi0gbPVn0ZbP6uvZx8JcFVFZREjf6BRe0LL300h3fA7qr6ONnpZ9Efv+lTh9Dz5t+Rf9C3xmcRdqfTrr077pYkUGdslTpI3ntIUIEJ7toQT8eHeG8Q8ccYuVCHyht4q+t7yUk/v5/fB+Ma5inw2whlirKjpXEQT+Y9hRmOU429H2+ubJpdUR+/0eVsYVvhEN49DHsr5fpy1l5ZrnxfXBwku8ZfOIbLwk/aO2SVQdzMwT6gUCb/Kox0P1oofE8TQZrkXIEG8ennz62FlXjedNa9ccjBLjKnMO6MJpZ12wrFNxSqFdhcwg1PrinYexpCBgChsAgINAmA21WOAahRcdQGbAnDPMMqUmyMVQ9q4ohMN4ggHQXYgcAJjmLkO6rZR9R/3JyaDIrmLkZAoaAITDmECi/dz3mqm4VagsBtgP33nvvoFKgN9iRtkmi2kLY0jEERh4BscATrolHJU2sO4QdJdE1DmoTqFGgXnPyySeHC3wonejND+TNeSOPnOVoCBgC4wMCpsIxPrRyn+uIPqLaONWsuKEsy+6q+tvTEDAEBh8BrjKXQ4aFKhzsNO2yyy6O2zWNDAFDwBAYZATaVOEwCfQgt/SQlI1ranfaaScnVgPC4Zxx48a5ddZZZ0hKb8U0BAyBPATExFu4IOriiy8Ol42gzoGKFuod3PLHoWKxuNLzMGhe+uZuCBgChsCwImAS6GFtOSu3IWAIGAKGgCFgCBgChkBpBNqUQNshwtKwW0BDwBAwBAwBQ8AQMAQMAUPAOWOgrRcYAoaAIWAIGAKGgCFgCBgCFRAwBroCWBbUEDAEDAFDwBAwBAwBQ8AQMAba+oAhYAgYAoaAIWAIGAKGgCFQAQFjoCuAZUENAUPAEDAEDAFDwBAwBAwBY6CtDxgChoAhYAgYAoaAIWAIGAIVEDAGugJYFtQQMAQMAUPAEDAEDAFDwBAwBtr6gCFgCBgChoAhYAgYAoaAIVABAWOgK4BlQQ0BQ8AQMAQMAUPAEDAEDAFjoK0PGAKGgCFgCBgChoAhYAgYAhUQMAa6AlgW1BAYDQTeeecdd/DBB7vPfe5zbtFFF3XLL7+822+//UajKKOa58knn+zGjRvnNt9881Eth2Wej8Bpp53m1l9/fff9738/P5D5DD0Cw/wtvvzyy27dddd1q622mrv88suHvi2sAqOHgDHQo4e95VwRgQsuuMBtvPHGbo899qgYc3iDv/vuu27VVVd1O++8s7vwwgvdXXfd5W644YaAwXPPPdezYmMJs+uuu8796U9/cmeffXbPeluA0UHgoosucn/4wx/c8ccfPzoFGKBc//e//7mddtrJffnLX3Z//etfB6hkzYsyzN/iiy++6BgXr776anfrrbc2B8NSGG8RmHi8rblVfOgQ2H333d0dd9wRyr3pppu6xRZbbOjqULXAv/vd79yf//znEO2zn/2s22qrrdxrr73mrrzySjf11FP3TG58xKwnKBbAEBgBBK644gp3yCGHhJzeeOMNx7dsZAgYAmMHAWOgx05bDm1NttlmG/fkk0+6Lbfc0q233nq59ZhlllmC34QTTuhmnXXW3HBjyeP0008P1Zl++undueee6yabbLLw+0tf+lKpavbCrCz2pTKzQIaAIZAgoN8eDnPMMUfibi/9QeCqq65yhx9+uGOsPOaYY9ykk07an4wsVUPgfQSMgbauMOoIMNhBc801VyEDjQQH9YUFF1zQzTzzzKNe7pEowH/+85+Qzcc+9rGEea6Sby/MymJfJU8LawgYAs6tsMIK7u9//7t79tln3Sc/+UmDpM8IsFOH+hD085//3M0000x9ztGSH98RMAZ6fO8BQ1T/GWaYwa211lpDVOLmRX388cdDItS9Do2PmNXByeIYAm0jMMEEE7illlqq7WQtPUPAEBgQBOwQYc2GeOuttxzSQSwk1CHiP/jgg46DJr3opZdecs8880yvYD39kYTwV4fQu33qqafqRA1xqtS3diYZEZ944gn35ptvZvjkO3nv3aOPPtqovlmpa7pgUZa07BNPPDhrXa1Hk/6Qrj+HJR977DH36quvpr1q/QY3vs///ve/lePXqR8n+x966KGgn145wxoRnn/++ZCf9o8aSYQojC1lxqCs9KkzB7L6RXX6RFu4MG7QD0aDmrRJk/K2Nc9ULUOdMbpqHmXDN8V+kOpSts4WrgECMkg0phVm28zzNxbpxz/+sZ9xxhn9D3/4w1C9e+65x3/hC1/wk0wyCaOrl4NcfvXVV/eyVZ5b/X322SekIfqmIcyJJ57oRQUhxBd9Xi/bTV1xxbyOF3NQft555/UiyQhhRafOi0UGf+qpp3aFVwdhkP0HP/hBP+ecc3phSLww+P6www7z8803X0iDMosKhN966629TDYaLfNJWpT5Ix/5iJ9ooomSMnzmM5/xl156aWYcHMvU9/e//72ff/75O8o13XTThd+Ulb+99tqrIw8x3eZlW85/9KMf7XBP/zjnnHP8pz71qRCW+tJWSyyxhN9hhx28DJDp4Mnva665xq+44op+iimmSLAC8+23374nVkkiqRfy+8EPfuBlCzf0FS2PHID0X/va17wMuKkY3l922WUJNvQP7WeKywILLODvvPPOrnhZDlmY1cGetNvGRxgk/6tf/covs8wyfsoppwz1pK+L1M4fddRRoe/Gdfr6178ewkw++eSxc/Iui0xPfT/+8Y97xQ3spplmGr/SSiv5a6+9Ngmb9VK1fsJ4hnGB702/UVnoeNm692KNIiuLRm6MCWKFJhk7qBv1nHvuuf0uu+yS27fFWosX9Sg/22yzecYv6IgjjvBiDtFTXsrOmLDnnnt2YZ4usCykvViWCGMCefO35JJL+l/84hee9txkk01CG4keajpqqd9V+wSJ1sUlPU7df//9Xs4WBJzAdtppp/Vi6szffvvtpcqeDgTuH/7wh/0HPvABL2cZOrybtMkZZ5wRxjbRq/Z/+ctfOtJN/9huu+3C3ENbZ1HdeabXtyhWg7ycUwl/fFdpqjtGp9PhN3MiYyPzNO3GH7jreLnwwgt3jLMiHEnCHXDAASHJo48+2n/iE58I81yV74HIbdYlFMb+6ysCbfKrrLIbU5sFalyYlhPQgYKJgYErZq70Y+XJRycHGDJz1zTWXHPNwBjE8XiHmVUSiVJguHRCTofV3xtttJF/4YUXNFryjAcHMZ3kxW5uMlhoXH3CVGYxcCQm5sICI65hYVpEHSBJi/LttttuSb7xS5n6wtRr2nlPsbQRJ+s13TwGSqSX/pvf/GZHujDAyvyTz0ILLeT/+c9/dqTLj+OOOy6JB1MBUwLjpWU78MADu+L0crjllls8zK6mkfVkIXXeeed1JHXSSScVxiEdOTDTESfvRxZmdbBvG5+nn346LDyzMFG3Ku1/9913d0ygpCGHiLpwpB5ZVLV+In0NfUnLCsMII62MOwuCNulb3/pWR134/tL1o6/B4KYpHhPEdJffbLPNOtLSOvBce+21AyOcToPfctDXL7fccrlx5QCwFxWr4F+Hga7TJ5rgot8G4zLfE4vzGAt9n2qqqbxYvcmCpNAtxl0ZNY0Q+1VtEzG9lpRTDl5rkl1PFniMldRjgw026PBvOs8odlljMYs5xY4FiFggSfJuMkYniaReYsZZ800/deFI1Bh7Fo11v4d+1CVVNfvZBwTa5FeNge7RQDpQIL1h0kKayQDxr3/9KzBiMFbxRHbzzTd3pahpIAUiPgwaUhwkgT/5yU/8b37zmyQOK3f9+OXgmD///PMDk/vII48EKTfSHvWHWUxTPDggoSAsElvSkS3t8GTFrmmss8466STCRIlknTDzzDOPZ4BnwIUeeOABz4Sj8cWeZlf8MvVFMnvJJZf4P/7xj0laclFI+I0bf5Q3Jk03a9AmnFzekKS14447JosDmIpTTjklYYiRUMYk2/yJBFQM7Hsk70owwUilfv3rX6tTqScLEyZecIKBR9r1t7/9zTOpsbAR83IJsyWWNbxs/yfpMjArNprGKquskmCD1Ojtt99Owhe9ZGFWFft+4LPFFlskbYVUVQ4AeSTIfD9I7FmoIrmLKasu6s/iFqyRNPOuC0Pw5vvSxR8LlvTCs079KCP50XZin1uLEdoXaRY7Dm0SEmJ2aOjjMFD0EXaX/v3vfwfmSL9HxpM0xWPC7LPPHsqNlP/II4/09957b5Cg6VhBOowVWcS3ofnotyp2yT3MITtl6seTslalOn2iCS7an+gTjMm05bbbbhv6It89u29ap6WXXrpqdToYtSIGuk6bLLLIIqFsLFRiBjUupFxqk5RfLPjEXr7pPKPYpcdiMduX5Anz/Morr3TkW3eM7kgk9UMOaoaxkXFa2+u3v/1tMl6mJeDx90C7E6fO99CPuqSqZj/7gIAx0H0ANS9JHSj4yJBIIplNk9zKlHy4WRKBOA2Y8JhhjtN6+OGHwyBOXjBM6cGHsEz+DOaE4eOPV9b4x4MDYZBUv/7663glBAO1+OKLhzSQmIkuduLHi04cMNFyiK3Djx8wb0hySR+Gnm3XmMrWV+OQDn/f/va31SnzqemmB20Cw4AyAZIOi5MsiicUtt2ULr744hCPuDAEbRATsdYrZrDitGHqNYzcrhd7Je9MkIRhB6QOFWFGepp/EfZt4wOTzHdA3nLJRFf/oVwsUH/605/ymlBRXdgShwnPI3aHtK6oyMRUp35s95IezP9IEHWjjlnEAhGVLcqTxbinxwRUsNKSatQUFB+xN96VDe2hbfbpT3/aix5/Rxikx+xoaRpVGei6faIJLtqfKDNjR5baDWp0Wqebbrqpo869fsS4FzHQpF+1TVBV0nLlLXhY5BCGxWPMZLcxzyh28ViMmor2kSzmuckY3Qtr/Pfee+8EExbFeRS3Sx3sSbffdckru7k3R8AY6OYYlk5BBwoGhvTEGyfC9i0fI5KzeLAijKaB/3e/+904Wsd7vB0pNz11+MU/5Ca2ZKBIpxcPDkiaVXIcx+c93rLed999E2+kgLoqV73vxDN6iRkSBuSYytZX44ALf0VMHGE13XjQ1jTQbyYN/PIYDSR2qHQQLl7oIEXXMhS1sebV64nuuWKILnYRoV9O3ixksso9CAx02/h89atfDXXmm0ovAIuwKmr/onj4oTOubSym+zqC16kfu0Okl8WwdiQ+Qj84l0F5kGamKT0mpJlnDY8uOmmwOE7Td77znQS/66+/Pu0dfsO06MK6KgNdt09kFiRyLMJF+xP9kB2vLIKp1n6TJ/jIiodbjHsRA804XbVNEHoos4oKQpoQtOjO6De+8Y0O7zbmGcVOx2J2zPRcUBbzTAGajNEdFcj5UYeBroP9SNQlp4rm3AICbTLQZoVDRscyJBIKJ5KX3KDcEgfJQOjU9Fg6sAwwbv/99087J79l2zC8y+GHYEM08Ui9yFaqEx3L4CpbsCnf//+5xhprOPLMItF1TJzvu+++5J2rokXCHH7LgbrEPf0iBwATJzl8k7zHL73qG4dt+q43FHI7IabbskiYVCeHS4JXXGZR6UhwkoN9jmtqm9A//vGPBMOvfOUrhUmJZDn4ixTfxe1QGGmEPdvGR5jmUAPZBQk2vUeiOvHFO2mLNnXqJ4xzKLYc4nJyyNTJrs5IVCM3D61fum7pCIwJwvSkncNv/Tayxi/GBYgLQbTuwSH6D7u7oi4WXIS5i3x6v/arT5TBhbFd1NIyC6mY4JmFS2akio512kRU65I5QiTQXdZfsIcswpNQkvSlS23PMyKZdxtuuKHDupAwz+GabJ2fYiiajNFxOm2+l8Fe1MG6shzEunQV0hz6jsDg2Mbqe1X7m4EcOksyEMmDY4BLk+jC5k5ehFUGSvQJ01E7fsOYMpERXnSSO/zK/hBJVWAaGfQor5LoVOqrEwm0k1V98jt+EfWS5KfoZyfv8Uuv+sZhm75ruWGMYYjySMPFZRb9didbok70WgMWokfrVl55ZSc65u6LX/xiwlznpZl213bEvVdbxv2EthQpYDq5Uf/dL3xk16YvdYPZE71Hx8THH8ytMhNZGdap349+9KNwaQOm8rj9TNSDwk2aov7k5DBfVjatuIk6lhOVk/DtUzcYZha8ohfdOH3RBQ5pZC0G9HuJGcrGGUYJ6DdTt0/0CxfFhKJm4RJVoS+vmn9W3qL+FBb7mBMUSbkTaXtSBtEBDu8f+tCHHONZTIp1r7GpzDxD3xNVEcd8wEJEpPSJcCfOk3cde+uM0em0RuK3Yi/nKLqyG7a6dFXAHFpBwBjoVmB0Tk4CJynVsY3KAKk2mpnQe5EcsAqTaBNbvEhqRXexw5ar6HYlWYveY/Ke9yLbhA5J4mgSg7guAmTr0qmEpahM3OwXkxwICTchwkTDFInJs/DHIkIOxnRMTnG8rHfZXk2ce7Ul7ajUpC01jX4928KHyV6lpKJO02pxuaXye9/7nhMVg8J0ZRewy79q/ZC20s+QPp911lkO+8MHH3ywO/TQQ53oRTuxdNLqbZnYm991113d8ccfH/LqqsD7Dll1ywubdmeHJo/4JiDq3TY16RP9xqUIk7ZxyEqvKH8W9/Q/FocwzMpAiyqYu+KKK0Jyot7h4t2AtucZUVVzLBrlkLQT1UUnqj6hLOm6tDFGp9Ps9+887IexLv3GanxNP3/EHF8RqVlvJlAlOdCjr6WfYm0hkXQyAPYi0TcMQWLJd684sT8TLcwmFJdXV924y+G3RIqn0rz0E6ZfDjUSfNSIQVx0hUP+YravZ5nFHJfjius0oU6BFPjMM890cogzeMOYM1GJzng6eO5vLQsBerWltiNh67YlcUeC2sBHzgg42guKv5mm5YeZZTsW5hkmj4WQHBQNv+WAWsJQFOVTtX4sfpC4oUZFfixIUcXBjWuc412aonx7+fGtio6wO+iggwJmorcZ+qPo6zvqxp8cFu6VTCN/xieojnCgV8Z1+8Qg4NKrbv30R2ijN7MigWYhAol1p6BOwTtS6pj6Mc+wGyNnPUI2LCZZPKaprTE6ne5o/B5LdRkN/MZSnsZAt9SaseS2DiPEapftNkilqXlFY+LQMHW3i2GEdVs7Li/610psiyJBLfoTSx0afFSfWm4Y0qLy4odeZCyViQvO4IgEERUAGBRlhpFswhyVoXhrVNspL55K9vCv25Z5affDvSk+qPWIOcdQtF7YVCk/kzhbrTCxN954o/vZz37mxPZt0NdFpSe+Ujmv7cmvTv3oe+THGCC2q0OxYarlMpgqVcgNy+IAFREICZ/YLHZyiCucyaBu/Kk0v6huuRmU8NBFNrdFtk11+8Qg4NI2FlXTU/1mzt6IPfkQHSYWQh990UUXDe/6Xz/mGdIUCxxBrZB8GCvFVKdmmTzbGqOTBEfxZSzVZRRhHPqsjYEu2YToCutBmnQUthHlJH9wZgKP1TnSYYt+60fJITTVU8sKj7SBARMqUp8gnTzikIlSfCBQy4Bfr61wjd/0yQQKxdLYqmlqudFNQy2lDeLQKJJFCOZM9d56pa1lIZzYXy0MrpJwDt3E8QojtejZBPu6+KgeLQdxWMg1JRaU2leRhLWFY9X6yc117qSTTnJi7jJUCQavDRJTbUkybJePBqmuPuNSfAA3LgsL7rwxMg6X9V6nTwwCLll1GUk39I/pdxBqHIyhLLCgtPQ5OMp/+n20Nc+QLgs48mcBylzJjoiqaqXzbXOM1rR56ljGe5O5hPi9SDHsV1165W/+g4GAMdAl2wEmma1TucWuKwaTJmoBEJKhusQ2LQRDwKE2nmliksIPYuAUk0TpIMlvuVAiSKwSh/df0IOTq3zDLxg39OSUxAyVU/3gY489NqmX+vfjiVQYEoP4tZNXSQx6eEgDqxBx8ig+TR7rK+eFx52DgCr5gUHOYypYxCiTJeYICw+YFuXXxK8M9m3jo7qa7IDINfaZxUc6jSSrDPGd6G6K3EiYGeWEE07IdMexTv3y4nDwCiYCUqlw+PH+f2Iz3ol9a3fbbbfFzoXvWjcCZdWPXQy5XKcwjaaeKlknHQ5Npgk8UIERe9LBK2vsSseJf9fpE4OAS1yH0XjHoopid+mllzq58CkcKoWZjNssLlvb84ymjdUmtTLF98u8Eu/aNRmjNY+ip45lhGkylxTloX79rovmY88BR0AGusbUpl29xoVpOQG1dynNCDcbbkf75S9/GS4YkVWux6asTJrBT04hZ148ommozcy8Ispgk1ySQl5cMiFSgnBxiUxQXramvV7ggD/G9NMkA1coi5aXp5gYClfRimTAcxkAdjrVXw6hpJMIl8WoP/atsfFJ/kpyiMKL+S5P3KzbEMvWV9MTixehPLIV6OUgVrhARpgCL8ylBgnPXunG9cL2qUg3O+JzFTE3ChKO26uUuCxh9dVXD9f50gZK2A7m9kiw4OavKiTMcYIxV81iu1tvOMRONDd2CaMVwojeuRfd0szk+20Hugz2beNDXxJ1pQQfbJmLZDNcqIJNcWGqw+UP9IeYitpfdI6T9GRBm/RXvtHY7i1tGds9J/2q9RPm19MuXPTCBSJKsrj1ctAvKYdI5NQrPLmMRL8rcC9L3Dyp8ainHFINUWVR76+WW0LjWwSFcepKNh4T0vaI48DYYdd8YnfehVn1ovqU+HPjoV6yxLi07LLLBj/s4JNGVTvQdfpEU1yK+pPWn/6jmOwtF3VUoSLci/ziPIraRMNxzbiWUfGX3RP17nq2Mc8UYceV7lqePfbYoyP/umN0RyI5P7iOXfNdfvnlw82vzHngw7ep1Bb2/ayLltWe7SPQJr+KlLMxtVmgxoVpOQEdKDBKH181y+TOn36w+HMjYRZpGr0YaOIyOYtKRZIu6XMjoBrF57foOYYLWWKmVvONBwfRAfVyoCpJSxl9LbNIDDwTRBbttdde4QpqDQuzxyUJot8bLotRd65OTlOV+hJXDu0lZSRdLSeMTUy90hXpXGB0tWw8qT+XlYg0MLl4AHcGVSVuk9M4MEZcfS76yEl4FkYwCVWJ63JpK02bJ8x0/Bs8i9LuNwNdBvt+4CPSssCExlhou6tbmsksan8uHoJ51LjgxvW8+o1y4YnelJdmoKvWT3YUknzIU9QPwsIXplHzp+/GizH6Dle5q78cdi3dnUhHDoslcUmDG0D126Z/cjEQ7v1ioCkslwzp1fJaD9mhScrFQp1rzPED/6pUtU80xaWoP2nZh4GBZiGlN1Fqu7CILKKm80wRdnI4OLnanfGPy2iU6o7RGr/oSX+Qnb+kP4KFjinctKkUz5F1F5Sk1c+6aFnt2T4CbfKrxkD3aJ/0QCGqDx1MEBMWDJfoYOamhKSWjxnmqQzJaeogNYslPsRHuoAEOh6Q0umlBwexKhGuidWBlScSTyQbWQx4nB7SahgPJug4Pu+yXea32mqrcOVyHIf3qvVlAkCal14kyHZgR9Jl0kXSsNtuu4Ub2dJlZjClPkceeWSQ6mvicvgrXJXNAicdRyw7BKm9hq36hFGnf8R1Iw85uOm33nrrXMmz5qPSRbngRZ0qPXthVgb7fuGDJBXJf7p/sevB7kr6drZedWGnRC7S6WhDFk70ByRRerUxuxwx1amfqDclt+7FfYZvi3776quvxlmEdzGzl5RN1FO6/IscYEqovzIE5MmiFkmb2IBOmHNR6+pKBim5Li7EQkKXvzqIvn8oH0xxHrHY48ZC3T2hHOzOHHjggWHBIJZPQhpZNyLmpRm7V+0TTXDp1Z8oFztDijl1rEJFuBf5xXmUaRPCsyjUfiiqZl7ObMTJZL43mWd6YcfuoZwFCGVCgBFTnTE6jl/0zuJWbwlVPOiL9BOlNrHvZ120vPZsF4E2GegJKJp0tEa04uxfCvGve+L0RukMYmRhcoLtVXTN9OAeunfoWGEPkpPOsZ5sVh2AGHNvHC4SZiErSK6bSECCDi3m5RZccMGOgxJZkTglr5cRyOo6XIZCONkaD4d/OAwUW4nISiPtJit7JxNb+KMOnMjXPNJh+V23vsLQh8OTMtgFixR6i5jmUTVdTG6hf0y7gR9WLmjHPKJd0XEHc/SdOdgkUsW84JXc6SscOCFtbksse9CUMnGAEdNsdSwslMWsF/ZUtl/4gA030WEHm35FP8+iMnUhDDfGcdCNfvp/7b0HYFXl/f//ziaDGSBswgpL9l6KA8GBiBT3Hq3fautobWtt/2rt0tbav3W2WlcVrQspiqIiyBLZe+8ddoDs3PP7vJ+b5+Tk5t4MuCEh+Tx6uec855mvc5O8z+d+ns9jF/uwPfZDlqHYn8r8+PPG0IfyIGI+Lxy/iNVgw8eDDz5oYorz9wVjrIsbS9BypWWKMDdz42ebv3tseDnWYZ48qIFh4QIT68kf+5BzZ3nLl5F1Svs5YVn+TPF3IH9GuCmTN/Hnl2Moqw1vncDj8n4mbL1T4WLnW9bvZc6V7fNnsKKpNO6lXbP92DGW554wjB3HyoXs8oBjmyjXe0X/zthxlcaOiwkZKpW/Q/m5DJYq+js6WBvB8rgmib8DOD6uRwnkEW72HENlzSXY/DTv1AmEU6+qgC7jPgQT0GVUqdLLoQR0lQ5KO1cCtZwAIxLw4ZV/uLnhygMPPFDLiej0lYASUAJnnkA4BbRG4Tjz9097VAJKoJYR4G6WFM/cYOW+++6rZbPX6SoBJaAEah4BFdA1757qjJSAEqhGBPg19vPPP2/cGhhOTxY2VqPR6VCUgBJQAkrgVAhUzFHqVHrQOkpACSiBWkyA27lzB0FZMBnSv7sW49GpKwEloATOSgIqoMu4bWPGjAEXxdjth8soXuWXuYBEQlqBC0r4dbEmJaAEqpYAF+1K3OSqHYT2rgSUgBJQAmEloIsIw4pTG1MCSkAJKAEloASUgBKojgR0EWF1vCs6JiWgBJSAElACSkAJKIFaQUBXs9SK26yTVAJKQAkoASWgBJSAEggXARXQ4SKp7SgBJaAElIASUAJKQAnUCgIqoGvFbdZJKgEloASUgBJQAkpACYSLgArocJHUdpSAElACSkAJKAEloARqBQEV0LXiNusklYASUAJKQAkoASWgBMJFQAV0uEhqO0pACSgBJaAElIASUAK1goAK6Fpxm3WSSkAJKAEloASUgBJQAuEioAI6XCS1HSWgBJSAElACSkAJKIFaQUAFdK24zUWTfOONNzBy5EjcdNNNRZnV9Ojo0aNmnD/4wQ+wYMGCajrK4MNatWoVbr/9dgwZMgTdu3fHhAkTsHLlyuCFa2gut5O/4oorcMEFF+DLL7+sobPUaSkBJaAElEBtJBBdGyddm+c8Z84czJo1C3Xq1MFbb71VrVHs378f//nPf8wYR4wYgUGDBlXr8drBTZ06FRT9OTk5Ngtr1qxBy5Yt8eyzz7p5wQ4yMjLw2GOPIT09Hffcc48R4MHKnQ15x44dw//+9z8z1NGjR2PUqFFnw7B1jEpACSgBJaAEyiSgArpMRFpACZSfgOM4+OUvf2nEc1JSEp544gl07NgRy5YtQ2pqapkNffXVV3jmmWdMOQrw999/v8w6WkAJKAEloASUgBI4swRUQJ9Z3pXW24wZM/CPf/wDDRo0wMsvv4zY2NhK60sbDk1g6dKlxtrMEr/97W9x//33m8KXX3556EqeK02bNnXPWrRo4R7bA73PloS+KwEloASUgBKoOgIqoKuOfVh7nj17NibpWbmaAAA/dUlEQVRPnmza/Otf/4rk5OSwtq+NlY/Azp073YJDhw51j8t7MGzYMFCEHzp0CMHq630uL0ktpwSUgBJQAkqg8giogK48ttpyLSSwZ88ed9YNGzZ0j8t7EBERgd69e5e3uJZTAkpACSgBJaAEqoCARuE4Reg+nw+7du1Cfn5+yBaysrJMmZAFyriwd+9e5ObmllEqfJfZH314TyWxHnnk5eWdSnVT53T6Z8SHbdu2gczDmY4fP44DBw6Uu0nv/YqOrj7Pp5XBh4sEudiRPwvhSEeOHDH30MuwvO1WdH7288qFqpqUgBJQAkpACVSUgAroMohxERjdIf7v//7PlFy3bh0mTpyIxo0bo3Xr1khISMD111+P3bt3uy1t374dV199NerVq2fKsP64ceOKlXELBxx89NFHJloB26cPLBei9erVy/jSUiQEJoYI4yI1b3SHAQMGmDzmd+3aFfv27Qus5p7v2LHDjL9Zs2amP/pQX3jhhVixYoVbJtQBx8MFc3Q7sHNNTEzEOeecgzvuuKPUfm2bjAgyZswYw5jz5bzHjx+PjRs32iIh3yluf/WrXxnG7L9du3ZmHMOHD8dnn30Wsl5ZF7iQ76qrrkKHDh1Qv3590C85JSXFhGOzUUEC2xg7dqxh/vvf/969dPHFF7v34e6773bzSzugiGzfvr3p85133nGLnsp9rgw+W7duxTXXXGMWRPKzQi78fN98883YsGGDO97yHpD1tddeiyZNmqBRo0bmHsbHx6Nt27Z4+OGHEewzb9s+lfnx88aILvyc8ueXn3vO4b777gPDJmpSAkpACSgBJVAuAmKJOe00rNn1Dl81Md155500yToi8pzp06c7IqjMOfO8LxE9joifUstIGDNny5YtQTFlZmY6P/rRj4q1KcLNiYqKcvM6d+7srF69ulh9ER3ude94vMfr169369j5SBg7R2LzOiJYg9YXgeF8/fXXbr3Ag8WLFzudOnUKWtf2zbY/+eSTwKru+b/+9S8nJiYmaBvk/OSTT7rX/v73v7v1eCDCyiEP25eIOadVq1ZOZGSkyZMHm2Lly3Milk/nF7/4hSNuFG67tn3vuzwcOSK2ijUpETZKrXPuuecWKx/qRKz4bjt//vOf3WIVvc+VwUdiiDvyQOeOz8uEx2Qu/tvumEPNxRb48Y9/XKwtcpfFr8Xy+BmTbxVsFff9VObHz5sds3w74LRp08apW7eum/fUU0+57euBElACSkAJ1DwC4dSr/Mr+tFM4B3TagwlzA1ZwUgzyjy5Fws9+9jMjFL755hunf//+7h9giXXrxMXFGRHHenPnznW+++47R6yTbhmxZAcd4UMPPeSWeeCBBxxxZzDlKB7efPNN9w89+/MmCpZp06Y5N9xwg1v/vffeM3nMnzlzpre4Y+dDsUKxyfFyTLI4zaEoFkup207fvn2L1bUnHBsFNsUIBf7vfvc7Z9GiRY7EMHbmz5/vPPLII66QZfviWmGruu9Llixx+xHrsSMWdEes+86UKVMcsei716zgkdBubl0eUOjyGtuXuMvuNY7hpZdecmQBnptX3gPeV9tfv379zFg4V7HSOxJOzpFvAtzrfNjxJrHYG+behyAKNt4DvsSi7i0e8jiU6KzofQ43Hz6E2Ycd8e12Xn/9dUes0ebeko39OXj++efduYWaiy2QlpZmHkj52efngQ+RBQUFhpV8A+CyFqu+reK+V3R+Bw8eND+7vL+yuYsjizTdtvi558/Pq6++6ubpgRJQAkpACdQ8AuHUqyqgy/h8WMHJP7zy1bIjYcSK1eAfYopqK7woSikuvEn8gh1aqFmGwpOWTm+iwKQQ5PUHH3zQe8k9FtcBt48PP/zQzbcHsvmGe51iIVTyzod9fvrppyWKiguF29b3339f4joFt52vV7x6C1L02zKy66H3kjkWNwBznQI8mKX7xRdfLGYJDhTQAwcONPXZTjiSuN249+C8885zTp48WaJZWp35UMF58WHKa9m3hWkpt/PmA0FFU1mis7z3Odx8JAyfmRctxLLLYolpUfg+/fTTzvLly91rZc2FD22HDx92y3sP+ODIb2zIMtjDUEXnJy497n1Zu3attys9VgJKQAkogVpCIJwCWn2g5S90eRKjIzBM3Pnnn1+sOP02vTF+xQKHW265pVgZLiajnyeTCDNwsZw3ceMMbprB3QF/85vfeC+5x9ddd53xi2UGd7o73WTnc+mll5ZoSkS2m7d582b3mAeMMiGWVZN30UUX4bLLLit23Z5wq3D6QjO9/fbboG+vTVx49sEHH5hT+vbyFZjoM8y41qGSCDZzyRs2LlTZ8uSLu4i7c+Af/vAH49seWI/+0L/+9a9NNhePisgPLFJtzsPJhz799jPHHRa5NXlgkgdHyMMfevbsGXgp5Dl91UNFKuHPArdBZ6LfdWCq6PxsebYTrs9M4Jj0XAkoASWgBGoPARXQ5bzXYq0FF4UFS1z0ZZNXTNs8vouPrHvqDXXGzJUrV5prFCahBAUFChfJMQWKWpNZwX84Hy7eC5ZsP7wWKPa5uNBGHgl8UAhsyz40MErDpk2b3MtcIGgFDQVZqESBbhMFvzfZGMnz5s3DT3/6U3BB2ekk+RrfVOfCQS6KDJXk639XXJ/KorlQ7YY7P5x8xNLuDq+0++UWCtMBF/cxBYuCUtH5iYsJxAXFtHf77beDW9prUgJKQAkoASVwqgRUQJ8qOU89WibLSrJYyS2SnZ3tHvPARpygMOYf+lAv+erZ1GPkjMpMjIRhk/gU20Pz7hXC3geHYoUKT7wPDbJ40i3iHX9ZbbiVAg4effRRE0WB2bRUM2qD+DC7LAOKl3lq51XWeCjC7A6B3jmV2cEZLhBOPpYNpyALNcM+E/48MPqMLOKD+P/jxhtvNN/YyKLdkH1VdH6MtsFvFpjEtcRE4hBXHTDSyemEXgw5QL2gBJSAElACNZqACugw3F6vddR77G3am+89pjWXf9CZGEaLltBQLytmZYGbt+mwH9PaHSp5v06nKCktMTSZTd54u96v0E91x0TWIydauTleuoj87W9/Q5cuXUxYPvEDt12X+U7rNXf+YyprTixj5+WdE/OrUwonH++Dgner8dOdL7+FkMWA5oFkwoQJJiSi+JAblx9ZCOs+DIlrXomuTmV+slgRkyZNch+8vv32W8jiQRM20LoUlehIM5SAElACSkAJBCEQWikFKaxZ4SdA/2jG02UaOXKkcZmg20SoF2M6S9SD8A+knC3asbK4LAArtZZXxErIMLcsY/DaxM04TjVRyFIQ0ZWCQozuL3QXYR7dMOhvXp7E8div98uaE9uz8/LOqTz9nOky4eLj/fbE68t+OvOhKL711lvxl7/8xTz8cG0BfetpdV64cKF5MZZ6aelU5scHLj4QvPvuu6AFmokPsIztbn37S+tTrykBJaAElIASIAEV0NXgc0C/WyYKM1pAS3vRL9RrwT7Tw/e6OFjLeagxeC3NEs/XLSbRFdxj7wY0bmYFD8iPiwAlmgm42JKJorq8i/xowaYLCFNZc6Lws2W8czKVq+k/p8vH6xNv5366U+W3B3ZTmp/85CeQ6Dbg4tVRo0a5LkzW2l3W572i8+NDKzeDkRCPRrDbh8Kf//znYdtV8XT5aH0loASUgBKo3gRUQFeD+2MFNH2hGaHiVJKEg3OrWQupmxHGAztWNkm/1dKStZRLmD+zq58t6/WN/vzzz212iXeJDVwir7QM7kYoIQRhLaYUaeVNdl5cJOn1+Q2sL2H/3O3Ce/ToEXi50s9P5z6fKh+vgP7iiy/CMkcJYee2U95dGt0KIQ5OZX4U7Pz2gokuUnY9QoguNFsJKAEloASUgCGgAroafBDoh8nEUHa0pJ5K8vruyqYbp9JEuepwm/Bu3bqZshTIdmFjYGWG/LMC9v777zch+myZ3r17G19lnsvGKWCYtMBE6yC3A7cp0A+WrIIlumLQwshkLZjBygXm0Z2Aif1wsVlgf7zGxW52IRrFmuykx+wzmsp7n8PJR2Iuu37Dr732WonILBbAv//9b2PRteelvUssdPeyxMt2j+0Bv72QnTLtaYn3is4vVHk2zAc8m6x/uz2XuNaQTX4gGwTZLH1XAkpACSgBJaAuHNXhMyA7FbqxkLkQTnazA32dvYkL1ihQLrzwQixbtsx7yRxbCypP+Aef4pULFPnVeGnioURDZWTQAvrHP/7RlKKgZCxf2djF9YdmiD4uBKNPKRMjevzyl780x95/ZDMWc0qrH0P/MawYxytbNEO2sDYhAzlu2bjDW80cU9RQSP7pT38qFuKM5WUXRDfmdGnh6AIb5Vf6skmKyaYV++abbzbhBbnQjWJPNpQxPrOys6Qpwzl5o5UEtldZ5+W5z+Hmw5CH5MpEv/LBgwcbocx7JRuegNZkhkTkA8+CBQvKNXXvQlh+5ul+w0Qfdj48sQ8bPi/wYeZU5kfXHoZFlN1Diz0crV69GrIBjOm7a9euYFx3m9gvf97uu+8+c+9lp0R7Sd+VgBJQAkqgthOQPxKnncK5s8tpDybMDdid+2Rjh5Ati+BjmADzEh/RoOVk0ZJbRgRCiTLctU7+gLtl2J5EGnBkMxJHLKnFduULtnOfCA9HLMPF6os11pyL4HD7K898xAXEbecx2eEwWOK21+Kb6pbjeEV8FDsXf2lHBFWw6g53muOWypYb37nTo21T/FLNFtgdO3Y0ZbjDn03cSc7W406G4mJgdgiUcIJuPndTJJOKJHkwcWx/tv2kpCSHu+/Zc45PLOqOiPWgTVf2ToTluc+VwYe7Z44bN87lQB7iO+5u2c5z3gtZBOhy4c+C5cafEW/iPC655BL3Ostxq3R+5nksot257bbbzDHb9aZTmZ/d+ZJt87PVp08fR3zY3c8b+wv8rHKXUTt+votfvXcYeqwElIASUAJnGYFw6lVaY047hXNApz2YMDcgm3SYP6IUh6GSWHxNGXEdcMSHOWgxcVVw/xgH/qG2FcSi68hOd07z5s3dsvYPOMUwtzR+4YUXHLHU2irF3iksxLJXrC7bksgJbrnyzEciYzhWfEtsXrdu4AGFPIWIV2ByvBKdwrnrrrsctlNa4jwoRsWa7I6ZglV2N3S3yRY/Y3Pt5ZdfLtbUP//5T6dz585uPctJrMKOWKYdsRYWK1/eE7GqOuKa4chizWJtU9xz++hgW5972+a4OBaKS7Gqei+V65ifHwpGtsHPVbBUnvtcWXz4gGC32LbM+bmXHS2dwG3fy5oLP5f8PNrPGttjW7IDoSP+786iRYsMB3GXKYGhovPjvZAIHA4fhO247fvo0aNLjN12yJ85lpNNjir8QGbb0HcloASUgBKoHgTCqVcjOCX5A3FaaXhzvw/vnL1vn1Y71bEy8TBGMBem8avsUInhz7j9sNefMrAsQ7Yx4oNd5BZ43XvOsiKUzFfkdBVgxAe2X55E9w9uysJ+6K9sfYJZt7zz4Vfz/Mqa8XbLSnS94OIrLl7kborer8HLqmuvM7QY69ONwjteuk8wTnOocTCKB+vS1YKL3bjRhwhQ2+xpvXM8vAfkn5aWVu52GeqNrifecH0VGQi50z2mLI6l3WfbX2XxIRu6P8iDhfFnp094sFSeubAMP6/8zMsDWTFuzCNL9hMsVXR+/Dxx3Bw//Z35mSlrIyT+bJd1L4KNTfOUgBJQAkqgehEIp15VAV297q2ORgkoASWgBJSAElACSqASCIRTQGsUjkq4QdqkElACSkAJKAEloASUQM0l4I/3VXPndxozcwo3VZBnDHHjiIzIk7coRERJVAZxF4iIjEVMBF0FIk6jD62qBJSAElACSkAJKAElcLYRUAFd6h3zu4fnZhXgrZenY/WKnRh5SW9cPrEnxPdFtLOK51Lx6UUloASUgBJQAkpACdRAAurCUepNjZBFfxGYMnkGDuxJx08fGYdPJi3B7q2ZiIrML7WmXlQCSkAJKAEloASUgBKomQRUQJdyXyXmr7kqoeBw+BBwcG8WEpKiEZ9Iw70a70tBp5eUgBJQAkpACSgBJVBjCaiALsetbdysPjJOZuCzyfPxg9v6oXGzJBT4VECXA50WUQJKQAkoASWgBJRAjSNQi1RgYbhrJ0IWA+bLKw+RUYyr7LcyO45PXJp9sp0gnykiJVfK+RwpV4CP352Bh343Hp26ppoPQIFsN2yt0yZD/1ECSkAJKAEloASUgBKoNQRqkYC295SL/3wikWOxcdUezJqxFJ26tMCIi3qLZPaLZ0QUSGE5i4rEjM+/R+tWzYx49onIjoyIFP9nlqMg10WElqq+KwEloASUgBJQAkqgthCoRS4cFLvyisg3luZjh3Pwtz+9j0YNG2PKB3OxZP6aQj0sIerESg0UICMjA9/NXYfx155nzv2Wa58c0zItbzySgzBs5uhvTP9VAkpACSgBJaAElIASqPYEapGApuLli1OORnZWDuITcnDVDQPQsVMKdmw7aK4Z8eywTAw+mzIToy4ZiKT6CXLuiOWZBnu6gNDBg+8qngWIJiWgBJSAElACSkAJ1CoCtciFw5qMo8wGKSmtGmLYiD74yY3PoVW7Brjhzr5y4wtw5PBx5Gf7cPRIDvJz49B/SBr8rht+VAzMcfJ4NgpkM5V6DRJr1YdFJ6sElIASUAJKQAkoASVw1sVis1Zkvy250OfCWIONcdneUXpglEjFM2WfQYy4YDA2rDmAhx6/AXm5OXjpr1Nw8OhREdAHsWZpJn752C1mr5Q88dqILPAhOjoSMz9dhDdenia1I3D+Jf1x010XSKxoEdcRMja6fujmKiXIa4YSUAJKQAkoASWgBGoSgbPMAi0C1YhUv3T225TpkywvClfjeiGnvFBcLxdlSD4XBzIdPHgIzVrXB/Xv3x+fhJQmjfCrR28FN+j+Xnyf33zlI7TtdBuSJYydI77Ts79cjy8+WY1Hn7oLsQmx+O9b0/HN9IW46NJhUoNjYKualIASUAJKQAkoASWgBGoygbPMB1p8jilUJRoGXxF8uXdHdgY00TPcjBAHRX7Le/ceQaPG9ZCZmYm9OzNx7S0XISomD/lR+Rg0sisSE+pj+/o9po/IiGh8PnUpRk/ojtQuzdCiTQNcde0FWLJgt4zFL+X9yt0eh+hes5WAElACSkAJKAEloATOagJnlYBmTOYCX7aIaAkzJ+HkIJrZl0v+UciXLF5niLrSkyPGar/IPXTgEJo3ayw+zrJAMLpoYaAxUEusZy4STG7a0K+LZfFh9x4dsWzh9sLmI7F86Vok1RV7tbptlI5cryoBJaAElIASUAJKoAYROKtcOLjJSWREHTgFEfhiymzM+WopsvN9uHj8YIwaM1huiyhqpiKztP+82L9FzwwHxIWjX79uYmmOR/eeLfHBO99i/E3nIVos0FP/+z3y83PRskNTI9a3bduHk5n7sGnlXjzz/72H+KQ4rFm7Db/63bWi4kWQs1n1gS5GWk+UgBJQAkpACSgBJVATCZxVApoqNTKyANM+WYyZX6zBj+6fYCzPzz89GXHRSThvVBezuI8mY2poo6ONe4UPPhHak16bh00bNuPKq0eg14A0ZJ88iQaNEsSA7MP1t47Bj295HnPmL0dsdAwS4xLwwCNXI0Ys019N+x4bN6TjqokjcNvd9bFq6Q6JwuHDzXdfjoR6UcaDg/ZrtUTXxB8RnZMSUAJKQAkoASWgBIoTOLsEND0vxF1i+dI1RvC279pAMuJx/Y2jsXjRShHQnUXGcjvuPMnnNt0ipenVER2ND9/5Ejs2HcXgoT3x4l+/wO+eaoa8zHgJRccYz9GY/NHnmHjTEAwa3k0MyjlonNIEh/Zl4KW/T0bb9s3xo3suNosNHScavQd1NG3bf9SDw5LQdyWgBJSAElACSkAJ1HwCRf4MZ81caYX2IT19n4yYcZgjkb43HVtksd/h9JMioKMkh/ZgunOIeo70+zsfPnIcaeekYNj5vSSqhk/cMTIRW6cOYuJjsHHNbmxefwAXj+2LRk1jjXj+9msJV/fqB7hk7DCMvmSouI4QUKy0a3w1CkW6v21e0aQElIASUAJKQAkoASVQOwicXRZocbWgR8b4H1yIp//0JnbsSRdhG4fVizag75Du+NsfJqFj57a49MrBaNqikdxBWWEoCwYd2VVw4o2j8I8nP8b77y7A3fcPRU5ejrhvxMMnxuq335yMm26eIBE4YnHsQAYmvTVVdh8Ebrp9PD75YA7WrFqLxDqNMGbsAAy7qJe0y+2+Y6Tt2vEh0VkqASWgBJSAElACSkAJFBGIkEgTp21GHd78BtPinL1vF7VcCUeMvuEUyFJCCdy8b9dBzJ69XFww6mLI0O7yHo+sk/n4avp8zPt6NdK6tMGl44cgpWWyZyS5mD6FdRIlFnQ+jhzMEA0cjaOyecrVt4zB4nlrxb96EUaN7SWuHOfghaenoCAnCtffNQz7dx3BU0+8id8/fY/sXNikcMGgp2k9VAJKQAkoASWgBJSAEqi2BMKpV88qAc3FgUbui+SP8PtUFN6kvEKXijgRxFHIysrFzOmLMHvGCqR1ThU3jIFIaU2LdD72bDmCv//5YzSoXw8JSTHIyj6Ce392PT7+4HMcO5qPW384FnXFMp2RnoVf3Pc3PP3cg0g0Gjweb/1zOurWrYMrrzuXQ1ELdLX9EdGBKQEloASUgBJQAkqgOIFwCuizy4VD5LFZsFfMdYJxn+n1nACfhJNjeGga1S8ZNxQXjR6EmV8uwLNPvoa0rh0xYGgvvPHiF1j47XYpL2LbyUf7rsl48emP0LNfO4y+tCuWLFmJVUv2IX3PCRw+dAK79+5HWnKq2Whw986dGC4+1HQNYUg9Wq81KQEloASUgBJQAkpACdQuAjVKAXIPlXffnIb5s9ehUXID/PRnE8QdYyhGXToE82asxB8efht7tmUhLqYh4mKjUJCfjy3rMoz7x+oVu7F82Xa0btcQI87vhvadW2HR/DT87c+T0K9/dxzcfRiZOTkYMKSnROmgSo/SqHW162dFZ6sElIASUAJKQAkoAUOgBgjoCNebYt/eg/hGYjb/5dmH8N9JU/H4r15Cr0HdRezmIypKzNZimY6LkygeEubOyc8WAPkSmi4Sx45l455rh4pobiGbGhYFJhk5ui+69WyHJQs3okffVPQb0MVE7TC+G8Ws4PppUgJKQAkoASWgBJSAEqgtBM56Ae3ZMgX16iYiKSEOC75dgV1b96P/oG7oM7i7RIYukGgbPsyauk42VMlDTFSMuF8w3B239fYhL7cAn06eL5blbDRMboQmzRuiafP6SElJRnJyfYy5grsc+tNXn8qmKit2oO+Arhh0kYhzTUpACSgBJaAElIASUAK1isBZL6D99me5Z7KNdmL9BPzfQ9dh+mfzcf7lI3DeRT3EWBzl3tDLrhqOp347HY3qZ0skDwlDJwsBjxw5iTvuH4Vr7hiG40eOYePaPThxPFP8nzOwevVG8X2OowEb9RrGoyArFrO/Xo4JN/bHx+/NRWr3Zkhpnmx8riN0NxWXsx4oASWgBJSAElACSqAmEzjrBbQbCkNcKnw+Hzp2ayOvtuaeOY4s9mPYDvFZzs/xYd++XbjxR/2w5LvlEpbuJOLqRODRX0/A3kM78eW0edi8Jh0bV21ATExdXHXTuRh12xBp1MHJEydw8mQOZkxfjK49W6F3/85497X5OHDwkBHQNfkDonNTAkpACSgBJaAElIASKE6gyOG3eP7ZdcaQcuKoQZ/mAtkZha4YPI+IiJWNVmTvQBHXr//rI7Tt2Bz3/mYs/vjcjzHo/I54+E/Xo27DWNx1z0TMnr4BSXXr4vf/eAA/fmgCXn/lPSxduMbsZJiYlCguHY0w4dpzkZWThd8+9BL6ynbeXbp0YMealIASUAJKQAkoASWgBGoRgRpggbZ3y6hoE1ou0heB7+eukS2+j6Nbr7ZYtXyN+D3H4rIJI8RrI0NcPaIRHe+g9+AOePWlaeg7sD1yTzi4bFwfxCcVoE2npjhvxHCslB0O+wzoJnVEjIs+j4mLxgMPX43c7HzEJtA1xL+SUN037D3QdyWgBJSAElACSkAJ1HwCNcMCXXifIiOikS+7dz/95Lv4+J1ZSE8/iqcemYRl323HLXddYRYTwpHtu2X5YIFYq2Pio5HavhlWLN4tVuo8rFy2TVqqA0dcQdav2o/EhAZyLpu3RDLuMw+5fXcBYusINtkRUZMSUAJKQAkoASWgBJRA7SNQgyzQImrFXWP18k04npGJP75wt2yqEomx44fhySeeR07eCYn/XEfusKwIlAWHEQV1JDJHtmyukopJ//4Gd/7kcrz63P8wR7YB352ejqTEGFw87gdSXqzMTqy0ZQWzvEfwuEY9e9S+T77OWAkoASWgBJSAEjAEhrW78ZRJRMgOdqniIvv6Z39EdHRR4AY2OO2j2fjjz18R19oCt30aO+/9zbW45vYxbp49uP+mJ7FYPAi85e21UO9zt/4n1KVKza85AlpEMbXu/n3paNq4vhHPFMv16yeKVToCBbnRiEyMFZjR4s7BuNAFiIyKQ3KTeCTI9tx58t8v/nADli5YizoJ/dFrQAdx52B5SmWvWK45yMzk9B8loASUgBJQAhUkcP3116OgoADvvfdeyJrlKROysl6oEQToCmvEWbHZOFi7fHOxnLPxxKsMz8bxy5hpES4cuuOT+MxdsGnDNsz5krGgD+HlZyehY1pLJDVIkJL5yM3Jx9tvfI5Fc7fgsw8XGHeNwcN6Yeqn36F+4ySMvGwABp+fhviEGLnmb944QJ+ldHTYSkAJKAEloATCSeCxxx7DpEmTJDrVyZDNlqdMyMp6oUYQyMvNw7Lv14n2opgqSuIYi9XLNiMrM6co8yw8qgECuoi6I4qX0TLuunsivpq6GM89+SEaNamPO+6daLbt5uYpX/xvPnZs2oXn33wA0z6Zg3Wrt6BLj7bIPHkce3btL2xMbrf4QfvFuXXdKOpHj5SAEjh7CTC0ZUZGRpVOICcnB1lZWWYMx48fL/x9U6VD0s6VQJkEdu3ahcsvvxyPP/64eExay1XxauUpU7yGntVUAls37sau7ekSTjhAQMv5/t2HsH3TnrN66jXKH8E85fjy0bVPWzzW5zbj7gxZ9+fjzaOLh1igmzRpgqyTPuzesVdENcWxuHZInLvB/bvgH49PRZ9B7dFvaGd06NZCbnqeXBd/Hokj7Vq5z+rbrYNXAmc3gbVr14J/oCNlfUPDhg1xzjnnIDbW72pV3pmdkLju7777Ln74wx+WWmXmzJnYvn27+Zp64MCBpq9gFb788ktcdNFFrqDYuHGjxJKPQWpqarDiJm/lypXGenfeeefhk08+MfWbNWsWsny4LqxZswbZ2dno27dvhZvct28fVqxYgdzcXKSlpZkXG8nPz8eiRYtw8OBBNG/e3LRtxRW/4l+4cCEaNWrklj9w4ACWLVvm9t+2bVv3mpupB9WOAB/6uneXnX3FuPT666/j0UcfLTHG8pQpUUkzqgUB+jF7U6Do9V6zx7YO3wvyi3yc7fWlC8T6XBD8QQsSLW3F4g3o0rOdLW7e2Q7bs5vkBRuH7bdYxSo4KU6sCgZw+l0W3hx5ixAxHBFJB3YRzBESjiPGV/jVgSwaNIsACzBoRDcMH30O3nrrI1x2zQh07ZGKA3uPYtqUBbIBS4oJT/fSs59g/sy1chPZFl1EZOEh3zUpASVQpQQoThMSEtCxY0fs3r0bFK+VkXbs2IFt27bhpptuMha3b7/9NmQ3S5cu9W/YVFhiz549smnTvpDlK+MC++NX6mUlivTWrVuXVSzo9dWrV6N9+/aG/dSpU7F3715T7osvvjAPA3zI4APHd999Z/KPHTtmxsR75uVBAZ2ZmWnaYnuNGzcO2p9mVi8C/Obm9ttvx4YNG3DLLbcEHVx5ygStqJlVTqB1uxTYV6vUprJOrHR5GFcnFm0kipmt07pdM9eIYCezeO5qOQyunejGQfeOwNS8VRO3TbYfGydWUE+KiopCy7ZN3TLsv6pSjbJAM+qGP1FU+61SPCr6pilOhDRw5dUjceXEkVTcknyY9dVidO7SHnc8cLmc56NH7/b48xNvo9/gByRknbTD3QyLGmElTUpACVQRgeTkZNBqSSsvxZtNhw8fxpIlS4xFtEePHmjZsqW5RMFGkUvLWb9+/VCnDqPx+NORI0ewfPlyjBw50maZ97i4OONiQUGwefNmt61ihcp5QsGxadMmJCYmgiIzPj4+ZM1gc6BVj5ZfWtopzi+55BIsXrzYPEDQ4su5LliwAJzLV199hT59+oCMgvVL6zstyPwmjpZhcuT8o6OjMXToUHDeodKFF17oXiLnQ4cOGcsy+dx7773mW4EhQ4bgs88+A9/5h278+PGmfVqpvalBgwbo0KGDN0uPqzkB/tw888wzpY6yPGVKbUAvVhmBN6f9ye2bv/ceuPlJrFi4MWg0DDFJon7Dunjhvd8gsW6Cv57oKa/oPnbkBNbIQsFgFmRWoMcAFxKePJGFxKSi34m/+NPtsv7ML7ozjp7ArZc/giMHMqS8I+GGI9G1V3s8+/bD5veNO+AqOrCKs4q6P5PdGiltOjQ3VHZG8Tn8pZ4vN7jA8wfShyYpDSSMXQP/IkLj/B78CepMjl77UgJKwE+A1sz169dj3rx5risC3RI+/PBD2R20i3nRLYK+xVzk9P777xvXgq5duxr3D8uRYvKjjz4K6mqRkpKCpk2b4pVXXjFtXHbZZWB5itlgiQKXQpSvdAmDaRNFLMX74MGDjTidPHmyvVTiPdQcKHjnzJljrLidO3c2gp7W8QsuuMAIZQrrdu3aGWHO+SclJRnxHKxfjo2WeyYy/Prrr8E26Y9dmpXdO1iOhw8lFO+0MrM/utQw0a2G3JmYz4eGYGnr1q3m4YeuH2xPkxJQAlVLICZWIpQVvmj17TOoi8hkY2UsMTCK2YP7j4grbLpbJyamuD123cotOHr4hBG+JRqQDIr0g/uPYusG/+8jW4Zh8Ow46ENtxTOvy77S4mLbDbR+2zJ8r6pUiwR0EWK/MZmiOFJuYgwGDO6Bz6bMlqetddi36wRe+9dU9OyTirgEWrHFryeCW4OriC4iqEdKoOoIULRRwNHPdt26dcZHecuWLahbt67x76W1s169eti5cycoNCmEaaWltZXWWaa8vDx88MEHRoSmpqaaPO8/dFegmwHFKUUhLbQUmHRRCJYo1FmeL7ZtE9uhJZyWZfoBU7zSLzhYCjUHluU4Ro0aZdweaMGm9Zc+x3SBoHilRZnW41atWpn38vZLy3ubNm3Qq1cv016wcQXmzZo1C3wYoZWbrK14ZjlanUPNz7bDMV988cXGn3b//v34+OOP7SV9VwJKoJoQ6DWwi3/9WKjxyNqw5QvXh7qKhXNWGcEbsgAvSBsrFpXWxkr5PU9XWn9ibOi+g7vZ0yp/r5UC2myC4kSZpyufLwupaU1x/69/gI/f/xJPPj4JjZKTcO2tQ8UCLavkfeJ/IxupaFICSqB6EKDFdPjw4ZgwYYIRrPRXpmWYwo3WT7642IlikpZVugsEJgpiCm7rx+u9TssIXSHGjRuHiRMnGgsyXSa4eJFW12CJLgv2ZV1HWI7j4stawykcvYLT21aoObAM3VVsvRYtWuDSSy81bhzvvPNOUMFa3n7tYr/yCF+Ogxwo3q07B7+yt9FEeJ3H9FEvLbEO58D7w3Z4/8hckxJQAtWHQKdubVG/UaLRScFHJT7MskgwWPIV+LD0u7VidiwefaNk2dBt0I1jibRh1rTJv7SGN2xSD2nd25Zspopyqs72XUUTdruVbyYiuCNhZJz88gbSerbFo0/+RFaS+hAVw+eKPJNvysuuOZqUgBKoXgQoEinYaJGlhZbuE7SkUmhaQcYFaqtWrTL+z8yn5ZoCjsKRbhlvvvmmEXOBVmjWp1WZgvnqq6/Gv//9b2OJDuWSEIoMLcMcn7V80w/bitbAOrSUB5sDXUe8iS4PFJ98cVxHjx41ll+6gNhUkX5tHftOrrRuex8EeI0cGcWDPCi4mWidJytakun2wgWDtDCXljhO3gMm+nTTMh+KSWnt6DUloAQqj0CDRnVFrKZi0Zw18jNe8lszusKuW7UVJ2Tn56R6xR+a9+xMB90vjLtsKUMsq40t63eJFdz/cM3IG117tke9BkmltHhmL9VuZSgiOpJh6mySc794ZkaM/FK3F/RdCSiB6kCAltgZM2Zg7ty5RhQzHJsN/0YXjddee012H61vLNNcwEZhTDH56quvGtHHsHfduvm/AqSIGzt2LOiXzKgC1nJKMUdLMV0LKBDpljFgwAAjqClY77jjjmKCz1qGvXysIKTvM9un6wfLUYAzjq69zjo85ouCNdgcvGVZnm4rFNrWvYRjpDC34cXo6lGRfr1j4DHdTOhzffPNN/PUTbTKs8833njD5HGso0ePNq4lnCN9npmuvPJK805RPW3aNMONIpt+z9dddx1mz55t+uC9pFinNV2TElAC1Y9Ab3HjWDSHVuCSiX7Q9E/evH6n7NzcuViB5Qs3IC+nLOszHWP9bWxatwPsy5sY4i432xsBLQL9h53jLVLlxxHyi+20vzsb3vwGM5E5e9+u8gnpAJSAEqi9BOjGQVFmxbAlQasthShFGxPFphW+3mNb3pax1lJblm0HRqoIrG9/pXqFL+vxnAKUyVsmsH6wOQSWoZ8187xjYZvsx1p32U9F+rV9UCjzoYQPG+VN7JuMveMprS7Lsj/vWEsrr9eqH4FUeTjlZ4QhDUOl8pQJVVfzq54AfZzvveYPIX2hI+Xb+bt+dhVuvueKYoN9/P4X8NWU7wsDNRS7VOKEbdz54Hjccu+4YteeePAlTJ/8ndtGlCwufGXy48YqXqxgBU/CqVdrqQ90BYlrcSWgBM4KAnQtCBTPHDiFqxXPPLeCOPCY5zaxDNvylg0mEL3XWZdC2Suemcd6VjwHlgmsH2wOgWU4l8CxsM9AQVqRftmHFeUVEc92PoHjYX6oRBaBYw1VVvOVgBKoGgIdOrdGo6b1SveDDojlnHUyGysXbwzq9hF8FiXjQXOLb1qgrQ813TdatmmK1I7+0KTB2znzubXbhePM89YelYASUALVlgBF9IgRI6rt+HRg1YcAI9yUlcpTpqw29HrVEaBvc+dz2mF++oqggpg+zBvXbAdjPtdv6Hfh2rRuJ/bvOWzcM+zIuQCQ7hrBEtvYsHqbhLw7DvpdM23dsEsioh10fagZvq5n/7QSm6oEa+9M5p0xCzTDHXEBD7+6y8jIMIt/uACI5/yalH6GPGeIKuZxpTfzGbeUC1qYx1XwDAdFKwm/mqSPHb/uZFm2ybBVXJTCxT/Ms+2wDOvYF79utGGnmMc22TfrcJwcA+uwPssyj7FnbR32bcfEuizHubGcPWd9jo91WJd+hXbsLMt89s12LBv2pUkJKAEloASUgBJQAtWBQJ9BXWUYwReEGR/mgxnYtHaHO9TF82T3QQnQYFNkZAS6yuZ0oRLbOHbkpBHitswi04ZXnjoS/7m7vVxt3r0jrNRBUXR+8803rqilmOTGBxSQ3EGLK80pgnnOFxexUEBz8Q3rMgwU47DSP4/CdObMmUa0UqjymIKUwpflKUwZoJ/9cSMDfiXKrzcpUFmeYnnt2rVGuNLiwtXlFN/sk4KdIpxlGe+UibtucdGOFfEcKxcxcUxcEMNzLmzi+LiNLet/+umn5jrnxnlQ/FMosx2KaS6u4Ty4uImLa9hX4Ne+lXpDtHEloASUgBJQAkpACZRCoCcXCMrGc6ES4zQvlz00mKibFs9fwyNzTuFdt34ibvjh5RJL3xOwofCqfaOF2RtTuvgW4LJ2JD4aPfp2ssWrzfsZEdDWskq/Pb4Yg5UrthkLlEKXvnPMp5jlSnSK4I4dOxr/Q4pPimOGgqJQ5YpzrqqnDx03C2DbFJ7MZx2GUmJ8V66053WunmcZtrNs2TKzexkFK/vjZgu8xnrcjpbt8hrDQzE+LK3iFMOpsliC5xTiHCPFNsU+58E8ivKePXsaCzbLU6CzDYZz4thYn5sOMEzVFtnwgbuFMTYthXS7du1MHkW/JiWgBJSAElACSkAJVBcC7Tu1RNPmpYWaLPJhPpR+FOsltJ1P3DKYIkX/tO3QEoPP64mmLZJFD4WSnI4roA8dOIb14tJB1w4maqj2aa2Q0rKxOa9O/4SaTVjHSAAUm7QsU6BSCNMayw0RuEjH7t5FCy8XltDiTCHNleYU2hS2FMAMAUVxzPrcCcu6PlB88sX6rENRzLKtW7c2/bJ/Wrxp8WX7tBx7N0Sg6KbluUOHDqYNinWW5xgouim2uaiG/lycB8M3MVQWhTNfTOyT4aPoBsIxU5BTdNMqzmscK8fI1e20RrM/imgK8LS0NDOmsELXxpSAElACSkAJKAElcBoE4hPrmPjLtBIHSxS6m9fuROaJbKxZvhlZJ3KlmLVAR6L3oM6okxBX2EaRa4e3LbZBN5ATxzOxbsUWnMzIkhb8bbBf7j5IV5Dqls7IIkIKSIpQblxAIUzLM8Uu80aOHGlEaHZ2lliiY43IHDRokLEwU5xSMHOjAIrc8847z1iNmU/RzboU17QyU9hSoHLjBPZHocx2eEwBTcFM6zEFOzcDoADmNb6Yz3iwtEgPHSo7EEoexTcD/NMazrGxXVqVaXmmwO7Xr5/po3///kYws05SUiLuuusuc84dtiiSU1KamfYaN25iRDTrsU3upEYOHBuFOnc9Yxs816QElIASUAJKQAkogepAoM/grpj1+ZKgQzE+zEdPgrGcl5qdCYs0DKNo9Bvi913uK2188+mikG0cP5YpftA7Cnc3pFj3W6BNG0P9sfuDVq7CzDMioK0opGD0J4n/GSc7URnOjlhhGebJv4LT5ytAXHycPMCI34tcoHuFTd7wVHTZ8D/lOMYiTPFJtw5af3nMsm3atLFVjUimiKYVvEePHsZtxL0oBxTLTFFRfiQ851aStDbbxHZtOYpePiDZMVFU8ymqUaMGpn+Ws2VZrnHjZNNehDxF0fJuE63ebJcCXZMSUAJKQAkoASWgBKoTAUbAiIgSIcN9TYIkWolnT1+MlYs8oedE4DVqzN0M/RqqR79OiBR55csL0oBksY25Xy/BioA2GjRKQufuqcErVXHuGRHQnKMV0f6nisInFLkfsp+2AQfH//UArfSiW/3aOigcU8lzxd9WUfvevoqKUaRaAUyLs03eeswzBmB2wTFIMT5d8TRSRhRYNnCQfv+egK163eHKPE23zGAqZMAjtTobIvqPElACSkAJKAElUL0ItGnfHC1aNcGu7enGUBg4Om71Pe2j2ciUGNBFvsvceruDu/V263bSRusm2Ll1v1vG2w7b+PyjOSXa6CLbd9cvDG/nLV8djouU5JkaDYVyYYgTSknxuvBrSepJ8xIBimw5LnpMofAtnvymfdOOJ1xK8TIlz8otVI22ZR+F/XjEbvFWfeaDYMU5rzkyP77cVKwtOw+T6RbRAyWgBJSAElACSkAJVEcCcXVi0a13B1FCHm3jGSjNjEcPHUdONv2fbYpAv2FFoedi42LQvU/HCrXB+NH9hlRP9w3OMjgNO//KejdCmWKTPr+ROLgvA1Pem4k3/zUV+3fLojuf+HQ4RSFPWM6/UBAoyI8Qn2mvuC3fICme+fJan4PVzMnKxf8+miGRP0TEG+FsRW9gaY5JSsj42W7myRxxgBfHdzMnzs1bnicMo0fcMvli17zl9FgJKAEloASUgBJQAtWLAH2YS0v+7+qLStDlo/fALkUZcuRvI7QACmwDkT7441AXa6banITVhcPuMW5nN2fv2/aw6F1cNqyCpJhlAO0nn/gXBg/sC588vEx6ayru/8WNReVdteng+ef+jbGXX4q27VLkulioZQ/1ks8AfrHqaSDgsPTruTk+vPfWLAwZ1heJSQkidxllI1gdvyBftHA5WrdqjZUr1+HQwaO4YtwFEppvKUacO8TTr18487lhwXcs31K+Dind5zmQpacxPVQCSkAJKAEloASUQKUQoMW5dYdmxoL8o4evQWwdiUQmcZi5RCyUD7N3IDQs0l0jtaNd9+a/Sgt0VEyE0Xre8sGO2UZzcRtpl9YSPjGazv1yKWZ9thArF27A3p0HTF6wemcyLywCuseANDOpEgM3cfwixRFCwrj5shEdESsWYFqWaUGmqCzA0QMZSIhOwoRbLjT5JzJOyNUCcY32W3ZpsY2MzDZ+0WOvvAzJjSR2M69LaSueC3z5cu6TcrGS5xe7juTR4z0iwi5WZHnZkbAgU8rJdpH+BowPiWPEeIyxJrNUUlx9KSPPQvl0J4lCnpOP2BiJ8uFkSVzDeBTk+eSD5BfQC+euh9O/DkaeP0jyZYfC9GOYO2M9hg0dJHXFnSPyhPQlcymQccQAi2ZtQJ3z4uWDIXEV5XpegUQjiYqVUXPchf7gHIQmJaAElIASUAJKQAmcYQJ5efnIkm/VuUX3kUMZEoM5GS1TU9CqXTNs28iN5qx7a/CBUdsE23q7ZdsUtBFf6C0bdperjXP6pYFiPvNEFk5KiDu+srNyTls89xyYFnzgFcwNi4B+ccqjwbsV4WmVamREDHKzffjwnVlIl62sO3ZsjcvGD0SLtskSI7A+Xnpqsojo4WiSIpbZQoPv8sWrsXD2FjRMrodLrx6A3Tt3o65E6EiSiBf/+3AmNq0/jm49m2L0uH5I33sU305fjwwJp5Kb5+AHNw1C4yb1cGjvccyauRD7ZG/2MVcOkM1NWmPhjI2Y+/1aNJW+Jl43CNFxIuYL+6QQjxLxHSObu3w7fSnWrdyOfcePom3L1rj+1uHYuWM73nxlClq1bI+rrhuMlUt24MgBMZ3LByor5yScgkh8N3MjPu48Hds3Z2DcxEFgIPLX/vkZLr1iINYs2S/505DcfAJWLNuJdWu3iKU7HldeNQIpLfyRQAgzqPU+OGXNVQJKQAkoASWgBJRApRGIESPiOWJB3r5xn8il0gU0BVX/IFtvczdCRuPYumFv+doo9KFOEI00ZuII86q0CZ5CwzQDV16iuwYtveIjHCXuFm+/8imdmMXN4VzZrWYHPp0yR4RqLB74zUR06J6CZ/7wX3z49jwznq8//w7z56zGuRf3RIOm8cjMyMWSeVuRnZGHWdO+F0vvAYyd0A9Lvl8u4VNW4+SRPMyYNg/DL+yB/Lzj+OT9b5B53IcXn/tAnnhaYNCwnji8X3bJWb4V06ZMx5ixfSTsXQ7e/c80GZ6Yhs1A2TUHLJZysTzv3XNIVn8m4ee/ulEE+m55akrHojnr0UxC0o25bCAaSMi6vhLe5dKxI+RpKgKHDpxE9x4dMfyCXhg77iJs25yOnExuIx6Nndukrbr10VvK33LHVVgydyc2r9mDW++8Et06dcT7b8yVz1yR3zdHokkJKAEloASUgBJQAtWBgN8fmdbG0lKEhCIWsR1i6+0+simK32JZWhvyhX2ciO0QbZRe88xdrVwBXShK2Ul+TgFWL9mC+Lh4bNy4BY1T6stuf+lyJRt1EiMxSgTpI7+/A998+Q12S5iT72auwzXXXIa0bs1w4eiBSG7SQFxAxOUhVwT0jFUSf7kF1m/cLTv7tRNxK/4wsmqv75CuSDunJUaOGiQu0jEirlehU5cW6D+ks6zkTEX/Yb0wbepcsXg3xPZtuxATXQd7d6eLZTxHdHPhh4IL/RwxzMtpTEwBOnVvLBbiWKS2aysLC0/g8onDEZtYgI8/+Mb4PMeKZ0ZcHYllHc0VhQVy032Iic1GbEK0xE3MQSRjJ0pjEXI9KlYeJGJyEZ8UYXYp3LfrBN7+5xdYunAT8sW1xO5qeOZuv/akBJSAElACSkAJKIGyCTASB4VtkcGxZB1u382tt+m/HCx169VefKpLb4P+z+3km3v6UVfnFBYXjtATpHSmRZe+xLLddl4uOnVrhW59W2HfzqOg7/KXU5bIlUiMvmKw7PAXKbv7CVhZt5cgQps7EDZs1lJcMkR8ympM46ssgrROvRj5GqCNBNdOEZeKg2bDlQzZnjs/yh/lO1r2YYmM8JntvDOObS8cQzRyZYvwhKRGSGmeiIvGDBR/mly0bttARC5jN7Mufah94pd8Ut7lS4qCKBTk+p8x8mRQ1NYHDx3DjXdeg0mvz8L3czeInbqOlGToOpmhuG84vkgRwjJn+b9JSrJs0S1uHXKSeTxP/pVrErqD/kPxiXFo2S4Sd/3kCmxevws7t++Rcfj7ks41KQEloASUgBJQAkqg2hCgoGVM6M1rd4X0Yea6sd6DusrSL2q/kqlZy8ZI7dASG1bvCNkGPQBo7a7umqiSBTTh+X1lomKjccWNF+LFFz6UCBe9sHrlWtxw86Xofk4n/PbXLxp3h4MHDqFjWnu0SG2KyyYMxysvTDaBuLl74E23jUVCokhc8cMZN/5cTHrzEynbFmvXbcRtd08Qa28UYuP8ApriNSrWQc8BnTB/3hL8/3+eJFbiOHTomIKrrjkXf/3zP5HzrwxsE7eK5q2TJNRKmohcylzRvbI4sGVnLlSMQGJyHGKSYuQmO6jfMAr1ZFvxdSt24Jk/viEfgPYYN2EYZs2aJz7UYoUWq3XdRrIYUJ6+kpsnSB3g8vHD8dlns/H9wpXo2qsNoutEo0FKHBilb/w15+Ofz32E55+ejPXr1uG6Wy4SER/8A1fyI6g5SkAJKAEloASUgBI4cwSixId50IgeOHFMAirQiBwk0ZjYf3hR/OfAIhTFA8/tYSKwhWqDIYJLayOwzao6jxBxWOi7UAlDYMuFYevE9VncHCKxa+tBWfy3Da3aNkHHLm1FaObLzcjBetkDvUGjRMlrI8ZfMUGLmDy47xi2bN6DVq1T0KxlQ5w8cVy2AE9EjIRUSd97GOtWb0Gb1OZIFVN/ZlY28nJyUbdePXEXyZeA3jlIqi/W4QIHq5ZvM+K4k7RdR1wrMk9mYeXSLYgWF46e/SSwt1i3I6MKJPIGxXIE8vPlWPr3ydh4g42sNUOKEgtzBPbtO4Tk5PqIiY8y8akZjo9WZaIkTdNeRJS0ESN95SJLxpYsCxp9YnH3STkiieLTmRNjFjfGxkWjUVPZytzwUit0JXwStUkloASUgBJQAkpACYSNQOULaA6VWlGUJTdDiRJLsU2OT9wi6MAhYpOh3qg+/eFRaA+moKWBXK6JsKT4NF8JSDlH9vqONF8PUNqKa4h7LmdSluKXlRwJWEhNGhkpJmLm8CJD2xmNyoWDbJcWcoa7Y1g6yeMY5NwIYdMON0ChPZrXeVkEsNT312OejIcNsYwpz/bMqfwrIto8YnHuEnpP3EpMG7wuQlz+letSm+4f4voRadgwX5MSUAJKQAkoASWgBJRAdSVQuQKaszbqUt6NLuSmJDygWJY3m6xm9OaxAPNFXHqTKeJm+SuIxPUWkWMpYOuZNgIve8v7Ba87LlvUW8TmmXe5YPu3fXivB/bnlvUWKjwWQU3xDnDRolH1RW0HKa5ZSkAJKAEloASUgBJQAlVPoPIFdNXPUUegBJSAElACSkAJKAEloATCRqDQ7Bm29rQhJaAElIASUAJKQAkoASVQowmogK7Rt1cnpwSUgBJQAkpACSgBJRBuAiqgw01U21MCSkAJKAEloASUgBKo0QRUQNfo26uTUwJKQAkoASWgBJSAEgg3ARXQ4Saq7SkBJaAElIASUAJKQAnUaAL/D5nWLcJ0fPllAAAAAElFTkSuQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='Classes_vs_Objects.png') "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Initial concepts\n",
"\n",
"- An **object** is a container of data (**attributes**) and code (**methods**)\n",
"- A **class** is a template for creating objects\n",
"\n",
"Reuse is provided by:\n",
"\n",
"- reusing the same class to create many objects\n",
"- \"inheriting\" data and code from other classes"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"# Definiting a Car class\n",
"class Car(object):\n",
" pass"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [],
"source": [
"car = Car()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Attributes"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtAAAAIcCAYAAADffZlTAAAAAXNSR0IArs4c6QAAAAlwSFlzAAALEwAACxMBAJqcGAAAQABJREFUeAHsXQd4XNXRHVmSJdmSi2S59957xx1jYwy26SX0XgOhl/ATEjqEEEggEFpoCWC6cQEb3Hs37r13W27q0v7n3PVbv31aSbvalbSSZr5v9dqt591dnTt37kyECyIqioAioAgoAoqAIqAIKAKKgCLgFwKV/EqliRQBRUARUAQUAUVAEVAEFAFFwCCgBFoHgiKgCCgCioAioAgoAoqAIhAAAkqgAwBLkyoCioAioAgoAoqAIqAIKAJKoHUMKAKKgCKgCCgCioAioAgoAgEgoAQ6ALA0qSKgCCgCioAioAgoAoqAIqAEWseAIqAIKAKKgCKgCCgCioAiEAACSqADAEuTKgKKgCKgCCgCioAioAgoAkqgdQwoAoqAIqAIKAKKgCKgCCgCASCgBDoAsDSpIqAIKAKKgCKgCCgCioAioARax4AioAgoAoqAIqAIKAKKgCIQAAJKoAMAS5MqAoqAIqAIKAKKgCKgCCgCUeEMwQevfy3LF26UqKhIueja4XLWsK6muSmHj8ln70yUtau2SrNWDeWKm8+V+o1qS0ZGpnz85g+ycvF66dCttVx8zTCpVSfR08Xx/5kiC2evFldOrtxw74XSrlNTiagUKdlZOfLhG9/IyiUbTPo7H71CatWuIVmZ2TLrp6Xy+QeTpWatBBk8oqeMunigKe/okePy1Yc/y/JF66T/0K5yweWDJKF6giyYuUImfDFTUk+lS0Z6lrhcLpOex5pJ1eTxF2+RqglxkoM2LJ2/Rj765/dSOSZa0lIzJCo6Ulq1aywjxvSTNp2ae9ptP9m+eY+8//dvZMv6XdKyXSNp076ZnHVON2nYtI5ERERIbq5L1qzcLB+98R36Vkm69m4tV94y2hSxZcMu+ftfPkW7MiQyMlKio6OkUmSEZGawnYI2pMvvbj1fzj6/t8ybvlK+/9+vpg/tOjWT6+6+AO2MMeXPnLJYvv50qlSvES/3PnWt1Equbm9iEOcuWb9qm3z69o+ye8d+efKV26Vp6wY+y1u+cL385x/fmj526N5Srr7tPIlB+1YuWS/fffarHD5wTBo0TpYbfn8h3mlNd/+B2buvfYV3kyb3/PFqadG6oVfZWzfslp+/nyu3Pnip1337xb7dh+STf/0oyxeslUbN6kqbDk2l/9ldpUWbRhKJcUr56ZvZMm3SIsnJzpELLhssg8/tibsRBt8vMWbm/rJcGjarLTfcfaE0aFLb5Dm0/7B8i3avWLRBOnRpIRdi7Napn2ye7d5+QD54/VvZsXWP3Hz/xdKjX3vz/vgwDePsn8//V3bvPCD1GtWSB5++Ae/Ue1585NBxGf+fn2XmlEVyaN9RSahZVcZcMURGXzpYEmu5390ifC8+f2+inDyZZsqOiY024ykjPdOMjaysbLnwqrMx/geYNvFPemqafPffGfI+vqdsR9WEKub7cSO+W/EY4+wzJTMzC+3/WpbNXy+9BnSSS68fLtVqJJhn/DPl2zky6es5UqVKZXnuX/d57uuJIqAIKAKKgCIQrgh4/6cNs1aOueJskOF1cuLYSQ95ZhNrJFWXXgM7yZZ1u6Rd52aGPPN+TExl6d63nSGXLz7+b5DZVbztkbEgAOtALlt1aCYt2zY25JkPSVyHntdX5s9YJTVqxhvyzPvRlaOkdadGhhyQ2HXu2Zq3jdRMrCbVE+MlGySpG+okeab0GdRFUkFCNq3ZYcjTFTedK1fdfJ6MvLA/SNc6SQVRpkSC5DRuVkdOHU+VbZt3y/V3jTWkZsuGnXLDBU8awmQS2v4sRPtuv+Rp08ZHX7hJjh89Ia88+b6cPJHmSVWpUoS0bNMY5CtJZv+8RM67yE34meDQ/qOya+teGXflMLnmzgukOvp6BETzvIsHgcyNlciISrJ9yx4QzAzpN6SLNGpaVyZ/NRsYNzcYsQyW3w4E77clG6XvoM4hJM8iX7w/WSaOn2VIfPM2DeX4sVOs0qe0aNtAatdLlIUzV0rzlg0MeWbCzj3agNjWAxGeg3fcxEx8rAJY5oE9R6R+w2Rp2ryOddscSRSnT14oH735vezavs/rmXWxChOse695QY4dOSaPPHeTJNSoKq/9+SPZsnE3xpKbLDLt8LFnyVaQ9eNHToBcd8cd97O4KrHSb3BnWbV0g1SuHO0hz8xTq06SdOreWrau2ykt2vP9uckzn5Fkx1evIkvmrJY/3vGG7N11iLeNxFWNNaR1/q/LZfjo/l7k2YXJ1PwZK+TqEQ8Bj9lyy/2XyMc/vyjX3TVG3nnlS1mG8WjJ+t+2IG8kxuwQjMUxGFunzPdo7BVD5Yobz5Wk5Gqm3Vb6FGDwxJ3/kI/e+sGQ3h+XviXPvXWvrFm+We649M+yEePfEva1W692GHv75eU/fiDTJizE5DTTeiwjx50lezEBsCY6ngd6oggoAoqAIqAIhCkCYa2BJsGrVbum1Kp7Rots4ZgAQlGnYaIkO57VSEwA+aglm9ftkG8+mSadQHobg1BRqHFNqp0IQlLLi2jwWXz1OGhUq4Kcn9GM8X6dekkg173l03/9YMhXgyZ1jFaZ2l7W0b13W2mIe3apDnKdDHLXHxrzhOpVzSNqhlu3ayriyvUkjYyKAMGrJrEgVr0HdTL3u/dtL6//5ROQyUkyZFR3aNgbe9L/8MV0o3G/CtpWEqzn/nW//DJxAYhiA6MttBJSq8x+VgG5qg6ttyXUkv7xlVtB+NubW5tW75CsjGzpC7KciHY0bllfjhw+7iGDV99xgfz41QyZ+PUs6TmgjcTERqL5Lvll0nyjKR8N7Wqo5BgmAx/843t579unpX7j2vLEy7cVWHRCtXgZMLy7TP5mjuzctt8rbQsQ5WT0nxMTatXjE+LN81yo2Q8dOCr3P3V1nvfPFYAFM1ZKDlYj5v26AlrSul5l8mLG5EVSFe/qd7ePlradWpiJRL/BXaHlb4WJxZm5KCcZNTGOODajos7cZxlx8bGSiHfCiZpTqMGtjYlPfDy1t95Sq3Z1qdsoWfbvoQb8B/n9k1dCY+seWySe1ROrSwOsQmCA4eMm7JwMPf2Ht6QeJgyvfvSI1Dit9T0fJPnwweOntcTuenr06yCjLhkkSac10j9iIhOBSV7/s7tJVbSne//28tvSjSYxNeuLZv0GvFbIM2/+3mjE+YATyTsfu1z+765/ylfQeD/64s3uwvE3Gf1KqlND9u87JB/963vpM7gjJr5nvje18awBVpFUFAFFQBFQBBSBsoCA93/3stDiQtqYnZ0rMXExcssDl8keLH1/8tYEOZ5yopBc+T+Orgytdr92Znl+1tQlJiHJ8wmUuWPzPmgLm3hIcv6lWJrbpnkIvzMPl9T7wiTkeMopObD3qNfjQwdSjAlFRITbLCQmLhrax/7QDkd7pcvvIgkkrFvftvk9ltogfG1hkhAH/CjVQP4vvnqE/DppgWzZ4Cape2HC8NE/vpMnXr0j33KK8uDLD36GCUKyJAZgDkKNcluYl8yDSYRd5kxbLidhprEIGttj0AJbsmzeGkNem2EigTdi3TYTop1b98n637aC6EGrDXMGX3IQ+NMcIfI0WY6KroTJVQ+zIuIrfSjvcaWjPTT/I6Hd/vbTX9HWnabd+dVxEisbX374k6QeT5NboXm2yLOVnlro3ljFsUyM2nVp6iHPVhr7kSS6z6CO5taxlJPyzl/HG1I9ZFRvezJpj9WK82DmNAurH/t2HfQ8Yz0xsZXlMmizD2EV4NtPpxuzJU8CPVEEFAFFQBFQBMoQAmdYRBlqdEFNBbeVbNj0DjinuwyEzfIU2KM6NZQF5ff1jOYQLbGsvhL2qbQFpayA7XMUTDyS69bIk4VkgSRbhNpmkt1c2Dzn4Ogf3NQK50JTTU2mXWrXrQk70rVYHt8FIs3yKJW8tM/ue/n9ZXn+tcEq4cpbzpMa0KiPBxnLysowJg5dereRxkbbaaUq7Egcco2NOm2/3Zi4JwFujMTY5/YEua8UZd0vrEyBlre6MeHZt/ug7INmlpICDfrh/SlYdagrB2Hve/JEuqegedNXQJPeUSJhsuN+P+5H6WmpRvvcc2BHmAp1k23rd2KCdNKTzzrhasgGmCasXLq5UPw5Bmhn7u6fu/8sJwLjwV63VbY/x/S0DLnxvgvNJOO9V8dLetoZMwhn/qPAYdoP86VD91ZYYXDvHXCmYTvOtMWfcVHJM9mg+dTgkb2cRZrJXFuYVaVC878DkxKPYOgdB6Yjxw6Q4Rf0g537D7J14y48JjYqioAioAgoAopA2ULAn/+aZatHp1ubk5Ultz18CTSO1eW9V7/GprKUIvcjKbmG9D6ro+zZcQBL12676uUL1ptNZPUa1spTLolTBgjEru0HQd4PwNZ0vbzxzGd50vm6sWrxBmyE/E7admxmNqjZ01wDkwpuPnvoplex+XACCNQZcmhPF8rzuCox8tgLt8qEz6fLVx/9Igtga/vA0zegCv+JLjcv/uvlL+X+a1+US866TyZ+ORs2sO4JwNqV2+T1Zz6Vzet3yOoVW+Rv//epbFy93a8u0ESFBPEEtKx7trs15LOmLpZqiVXlyptHSwQmIWuWb8ImUfekZ8aUJXIWtPs05bFLeloWzDaWYVPdEDkXm+S2b9krc6d7a7WZfsyVg6ULzDVeeORdefWpj+XIofzHFMfA4UPHYPawxfOhffD633aYDaT2+v09Zzuro2+PwzRiPjZ5/u/fE7FRMStPdpJ32tLv33P49AbGPEmKfCMrK1OWzFsLs6MY4QqAL6EZCiddzokrzX+ysNH3wWdvwMQzSZ5/9F05djTvRMVXmXpPEVAEFAFFQBEIJwTKL4HOdsGut4Zc//tx8CixDJ4PlhncqYMNVLiZsCk8NmSCiG2BpwbKNppvtGksydj85ZS4qjGyGRvLHrjuZbnzkj/LvVe/ILt22LRxtgz0mLAOG7h+jzQ3jfk/k5aeQx7BJsFqNc/YLzNLS5iL/OWNe2AjnCwvgny8/pfPsMEyFU+KV4s3aER3adO5qbzyxPvwhnIOyA+9WviH5IG9h+Xtl7+CV5SW8s/Pn5Ru8CDxzt/GQzu5l12Sug1qSdMW9YwmdCjMAbi5sSU8kfgrybCdrZoQC9vmYybLht+2G3vuwaN6ShWYHaxbsc1sWNu0dgc0+mLsvM9oXd21HNx/TA4dPCYDoH2mCU094Dt9sttcx96OJs0byOOYTHTt00b+jU14JNJ7dtJMIe9kIhpeLFYv2yQvPvauvPDov83nuYffwUTic2MGYt90aK+joHMuauRk5Rrb76592srn2HR58qR7U6o9XzYmjwf3pkgsTHGoNXfKtk175B/PfiovPfa+zJm2zHhhcabJ75ok+ATs1aOiosymXV/puGkwAfbcNJ+h7b9dsnNzjU01vXmsAT7LF2zAYxc02/ZUeq4IKAKKgCKgCIQ3At6quCK29Y4xT8sqmDeEWqbv+CjoIsdeNUzmwEb2jWf/K2fBI4LTxZe/FdTDhsVaIGskYut/22bsrJu1qu8z+ymYDbSBBvmV9x+Eu654OXUiVX6ZMN9nWhKSutj0eM3t58uKheuM+7b+Z3eGbW9zn+nbd20pH054Rt566Qv57zs/ysyflsi72HhX14cm3GcBRbrpkhFj+0MDf1BGYwOav5IGN2efQUvaqUcrGTi8h8lGl24Tx88wpha8Qdd+9E5Bu/V+MDWgO8JAhBvPaLe9buUW2PR2lG2b9hqXh7Tnpsu0OdAs3/zAWJk6YZ50hGvDmFjvOSNd+M0Ghj2wSY7eWEigh4HITxw/U7ZjE2KTFt5u9JphIvXGZ4/DjeKP8i7MKOju7++fPma8v9jbnYFNiQOxyfHpN+6ymUkIViX2yx2YVPG9ByOPY5PltSMfBhH+TG689yKvokjO6RoxF2Q1O9utfbcnaNy8Huy8fzNuGi+9cYRJa39e8HkE9gPwZ4Ok13cfWC9NnYybRIcZklX2bXAVuHTeann2wbdhS/2axy3fgHq/s5LoURFQBBQBRUARCDkCneHe983vngq6XG82UcTiioM8F7EpPrNdcfMo441h4lez4JIuw4vQ+Mzg42Zick1p1rox3G0dhHu8lfDOkWi0pz6S4pbL2C9Hg5DRCwO9iVx4zXCfSUlCuNzdC7a5517UX5o0ry+zp2ITHEh3fhJfrao89MwNcttDl8nubfuwIWuq8TmcX/pQ3KdJAj1N5EeafNXBycbKRevhsYOb9txCQkdPFJbPZN7dBt/WcVXj8Kl8OpX/B3o7aQ/t9ma4f6PLtsTa1cxmSJZwFvwz0+/x3p0psnrpJrPprXJl9wZJqwb6+p6N1YlM2J1/+/E0+fHzGXD3lwIfx5myCCTTl1CzS9L66Au3SDbyj//PT5Ji26xo5SGRLC5pDv/Y18L14bfwNLMUmyNjY8/0KyoqWkiS6SqO49UptK2naVMDeMFIwFgKROh+kWZLtMfmZkJfQs8nx0+cgteN6r4ee+7d9eiVcgouH9//+9dSqTJs+f1c1fAUoCeKgCKgCCgCikCACKxcGBqFb0g00FbbZ+/91DoNyZEBTkIh9A1NsvnBG1/D5vKUIYKBlsul8LOGdZG3ofmd/PVsueS6EcZrRKDlFJS+YdP6cuVto+WZB96WLz6YIjciCEhBwj4thqeJBfAaceN9F3uR0oLyldSz/fC2cBRBPBiExpK1K7e6/TPb3OtRK0vtfuWYogzHCOOqkEFIPntnkgw7r49xg8f6usE1WwNsJvz3a+OxofAI/FZ38vJY4nLlyOa12+FNZY+xOf9txSbjn5urFLEww1k2fx3e80ir6XmOY64cKssWrpHlSHfy+ClMhM70M0/iYrhBTzNT4VP5b3/6CJp1b08sNPPp0qe9TPtxgVx/z7iQ1U6PL9xsGQFXiQw8xCBCTqENeerJVGkK/9wFSedebWTkxWeZwDfUVvc9q7OE+jekoPr1mSKgCCgCikDFQiCUq5wh0UAXN/wnfWi6uAntFDaPxcb5p7W84qZRiExXF3lOGZNV/yx4vXvWHMv3JFaMRsfIf4FLrllWLyhfR2hTe/bvID9/Oxdk323X6yu9pQmuAZODavCJHY7KuxNwpZYNrxt2s5kVIJudYdJhD5px5GAKzFiSjI2yr74Wdq8B/EZXhrZ/6dzVJoAMzUIo9OvdBJrYGZMWSou2jYwbNXtZOdCGz5y6FEF5OsvDz90IH9m3yWOIFHn3E5dJ+67NZSs2P9KbhS/x4J9YAz7E44u0quGr3EDu0Z0hN5aSvNO9nl3oX3w0AuRsWbvTeKKxPwv2nD7DB5zdQ37+bl6eoo4eSZHFmNDVrZsM/+h5fWk7M9x636VYeYiV48dP+rAkd6bWa0VAEVAEFAFFIDwQCGsCXamSy2i4liFs8ny4ILOEUdC+/XSa8ancEV4Y/BHat9720KVmg5lFfvzJZ0/DiHCde7Q2QUTqNMy7Ocue1nlOP76fvT1R9th84zrT8JohxC+4fLBxy7Zy8UavJFN/mCfPP/wu/EMfMoTtELSqS0AaGUmQ4c7DTeglgy75Uk9vdJv45Qy4qask54ztZzaSWe09sOeo8efsrz9rK591ZETChogs2AhkuWHTZOu2OXbq1dLY+A4c0Qu21mfMHPgwOzsCPqRXyLnjBnjlqYUgLMMQmXI77KktrytMsAimOy8++h7CjW8x+DNc+5xflsLWGZsPA/Bf7VVZUBcRcv5lA/AZIuloi/GceLo8anSHjO4pA0f2kLde/FzWIey9Xdj2SvYM9oeFnNPs4+Y/XGyiWP7jOW/vMktmrzUbE0ddOgD2/wWbh/B7WBfhx+/7v2vEZUy1fdtUF9IcfawIKAKKgCKgCJQ4AkVZMy+xRlaKjJIb7r1Q1q/eKndd9oxcgCXzpoiWR1vX4ymp8vjLN+dpywq4gVu7arPx09yjfztjW2sloo/f/kO7SRY0j4xKZ1FO2qoyNPW+XYdlLVyN5SfVayaAoNU2ms169X1vdkuBWy6G8d4JLxOvPPmhIW+0Gz2IMNoLsOFs5EWDPMWnnsw0nhpov8r0DEFNad66Pja8tZLP35uC80aInOjWdv8KTer3MFVIOXIcIcabysQvZkpXRFocNLKnl1kKbVMXz14FG9VTxo6X9tVOOYyIfKvpVg1kcDdMKKhVzF8igOcGeHY4bHxhDxvdO/+ktieNEKo8AREep3wzF6YcJ0yAkuvuHmc2WFrJGIac0Q87dG8p0WZzmvXE/yO9atSmN5QuEXkiSXZFCOkkmN80g82w3e6a73zKt7NBLLfAL7T3ekQOgvHQfOjw4WPyzae/mAh7jCo4D5EK/4tNkds27TaRI6dPWmS8TYy+dLDZCOluscuErN4KTxf07rEXEyZrYyR9YG+ElxDafG+Efbhd2J4t8Iu8Di78GAa7J9wm0vuLJWvh4u83mEzs2XEIIcxreTTeERGRsIUeI9MQHdJpc10LdvsPP3uj2Wh468V/koHwjd4Om1PpHWQ2NO/X33Ohzw2EfB9sA8fFVvS1AwK4OD2XNGtdT2594GJ5929fy/69R6QPgrLQzvwXmIyMumiAXHbDKKvp5sjxuAWuCpfDBV5nTHqpdbbKPGdMP/nwH996fKx7ZdQLRUARUAQUAUUgDBGIgBYoaLWPZVNSXPaL9D37y4RFsmDWSuM5gBHUzr1wAAgGQkuj9dY/YnpUoLb6xLFTIGOR8NnbFoTKmxjSrCADASioMbQClZDYzIPf3wxsjKKHga7Ml489K4kwK3WGELfeLX0e79yyz/j6ZaALC95KYOvVsdTfE3a4laEdZJ07YCtK7xGxiChYp0GyiTRnlUP3b0tBNtp3aW40q+wj6z4A377L4K3jEEhLP9if9jirHbTPZ+xfWR9tikm4YuCJoWpCnCFjVrnWkT6C6UaMJhaNYCfMMN92wmal45EBMGhrTYVlNMrsh9Df7iAh9lS+z0kgudRPO+iB53QDrjW8EnLi8jzcwf39s8eM9t3rYQAXO7fuN1r42ogkyAmLJRwfq5dthGu8Jl7mPlkgyHNOR5asGl8FZhxnJhnc2MagOdwoxzHCENkt2zY2RJ9BW9Ys2yy7ED68MyYv/YZ2BnmOs6ozRxLUQ3hXjIrZoEmyx6MKx+dyvLuUIyfhdSTavO9khOGmMHIgxwInYFWxybJ91xbYfOq2qWYERL6rVERXbNi4DkKIN4ct9xly7UJQHfqXboqJl30zoSkYf2iqQreLi/D9oS/zaii3z+Au0hrBgRgd0Ckb12w35JnBf6iN79TTO1Q503Oc0YRkN3ydf4ONjLtRbt0GSTLs/L7SybEqRD/cyxasg0nSCTPR63FWe0xC7fbiGLPw8EIbjoZY5VFRBBQBRUARUASKA4FQ8tUyQaCLA0QtMzwQ+OrjqbINmtfbHrxM4qvBlltFEVAEFAFFQBFQBBSBYkAglAT6jKquGBqqRSoChSGwYuF6hHbui6AnsYUl1eeKgCKgCCgCioAioAiEBQJn1oHDojnaiIqAAM0UJn8zS7KxwbAeNpExIA19TKsoAoqAIqAIKAKKgCJQFhBQAl0W3lI5a2MNBJa54kbvTWblrIvaHUVAEVAEFAFFQBEoxwio2q8cv1ztmiKgCCgCioAioAgoAopA6BFQDXToMdUS/UBgw4YNMm3aNDl16hS8k1SX0aNHS/369f3IqUkUgZJBQMdoyeCstYQWAR23ocVTS1ME8kNACXR+yOj9IiFAQpyZmSk1axYcaOaGG26QuXPneuq49tpr5T//+Y/nWk8UgWARoF/so0ePSmpqqpmc+et60ao31GN0y5Yt8uCDD8q6deukSpUqcskll8ijjz5qVadHRaBQBL766iv529/+JocOHTJj+s9//rMMGOAdCCrU47bQRmkCRaCCIqAEuoK++FB1e+nSpTJ58mRZvny5rFixQjZt2mQCesTExEiPHj3kvPPOk1tuuUVq1/b270sfw3ZxXtuf6bki4C8CCxculM8++0ymTJkiGzduhL919zjjeGzRooW0adNGWrduLTfeeKM5FlSulddK47y27vt7/NOf/iTffPONJzm/L7fffrvUqOHtG92TQE+CQuDEiRPmPXPCkpWVZTYqx8XFyeDBg+XVV18NquzSyMzxd91115lVO9a/fv16ef755+XHH3/0ao5znDqvvRLrhSKgCBQZASXQRYauYmfkP6Snn35aXnjhBQ9JsSOSkZFhNMzUMj/77LPyxhtvyE033WRPoueKQMgQ4KrHk08+Ka+88kqeiIyshONxzZo15sPrv//97yb9Qw89JNHRZwIR8Vlxyd69e72KzkaAm8WLF8vw4cO97ofDBQPlUMtJ8sXVJE5Aypp89NFHMn78+DzN5qT/iiuukN69C4+oGigOgabP07gCbhw/ftxDnq1k8+bNs07LzLE4MSozIGhDywUCuomwXLzGku3E2rVrpW/fvoYY+6PdSEtLM5o2mneoKAKhRmDlypXSs2dPeemll3ySZ1/1paenyxNPPGHy0Wa0JGTQoEFe1TC6aNOmTb3uhcMFv9ONGjUyq0b16tVDuPoE+fnnn8OhaQG14b///W++6blKUZgEikOg6Qur3/mcE5mOHc9ETOXz5s2bO5OF9XVxYxTWndfGlTsEVANd7l5p8XaIWpChQ4fK/v37fVZEUw1+Nm/eLCTOllDbduDAAWnWrJl1S4+KQNAI7Nu3T8466yw5efJknrJo89ypUychCVy2bJkwrVNIvu+8806ZOnWq81HIr2+++WbZvXu3MS2Jj4+Xiy++WFq2bBnyeoItkN9VttMSrjbt2rXLuiwTxx07dnjtsXA2+osvvjBmHAX5nw8Uh0DTO9vkz/Vrr70mb731lhw5ckQaNmwoXEEpS1ISGJUlPLStZRsBJdBl+/2VeOtpjuGLPD/yyCNCgmARAi7TcamUG16o7eF15cqVS7y9WmH5RoBmG07yTE3d+++/b0wjSFQtISn84x//KB9++KF1yxzpDYZ2pPQEU5xCIv+vf/2rOKvQsk8j8L///c/85liA0NPPsWPHrEuhOc306dNl2LBhnntl4eTss88WflQUAUWg9BFQAl3676DMtIBeBGg7apeoqCh5++23zWYd+30uT3MT4SeffCK33XabfPDBB0G7qaPWZefOnUb7kpSUZJaZC/P2YW8TSfyePXtk69atQu1k48aNpUGDBvYk+Z4Hk5eFMv+2bdvMP+62bdtKYmJivnX5ehBs/b7KDOW90mjfqlWrDFG296Nu3bry008/Gc2z/T7P+a45DuvUqSMvvvii1+OHH35Yzj33XDMuvB7kc0EPHzRlOnz4sFlWD/R95lOsz9vBjh2rULaZK0MHDx40WDRp0sR6FNJjaYwFZwec5hvcq3HfffcZW3grLSf24UigiR9XRuhBpkOHDpKcnGw1OehjSY7boBubTwHBfh/CYXzm0zW9XdYQwGAKWs6qe5WLH5XyjQDcbrkwvr0+cD9XpE736dPHq5zf/e53PsvBTnPXAw884ALp9EpvtaNatWou/GN0YXneZ37e3L59uwvacRdch+UpAzaorr/85S8uLFP7zB9MXhaIf+QuuJlysZ1Wm3mENtJ1wQUXuOAhwGe91s1g67fKsY6YALlA9lzYFOaCVs51/vnnW498HrFR1IXJikkPbxEuEBGvdKFun1fhhVyMGjXKC1PiCs1jIblcLthhurD8nSfvpEmTvPL6GqPYrOjCRkXz/qz3icmiq3379q7HHnvMhSVqrzLsF7/88osLpNUVGxtrxgM81Ngf5zkPduxYBb733nuu7t27m3qtNvOICaQLbtBccPNnksKswcXvA9toT8dzjgHe5wdmWK5ff/3VKt5zLOpYwITW9cwzz7hgjuDCxr8CMfRUVsAJJjZe7SfeMD0z3zd7vzD5dmFzaZ6SAsUh0PRWhXfddZcL9uUueAZxYU+Juc3fuy5dunjaDwWFi/csIUZ8F+wTJoIubM62HnmOoRy3V111lfmd4O8FJqeuTz/91FOP/QSE34wL9qVq1aouKE9cMOHzJCkqRp4CcBLs96Go49PeBj0v+wiEkq9SMxa0hLJBQTdGCyg2BPhjb/8HxHP+cBZFfP3IO8v55z//6eI/EGedvq75o+2rLbNmzTLkz1ce+70ffvjBWb0rmLxYLnZdffXVhbadpP7NN9/MUzdvBFO/zwJxk5MFe795Dk8QPpNzUkHSbE8Pv8WetMXRPk/hhZyQqMJ7hlfbatWq5ZMQ+SoKGwi98rKPr7/+uldS5xglYYcLtDz57PhcdNFF+baBkxd7Wrbfl4Ri7LBc2C27oFX3qtNev3U+ZMgQ04x77rmn0LRWnueee86r6UUdC5yQOCczzkmaV0V+XDz11FNe/Rg3bpzJRXJutd86fvfdd3lKDBSHQNNbFdrHFydhWB0w5Nhqm3WES0Yri8ueh899KR6caYIZt5xQWe3gESs1nrbYT4ijPR3PsefFk6SoGLGAUHwfijo+PR3Qk3KDQCj5qnrhwDddpXAEuAGLflXtQk8c3KRVXEJzEW468Ufo4YP+prlEaQndcF166aVey7Y0LWHEQ+eSO5dL7RJMXpZDcwCar9iFrsCc/rAZ5IOb2Oi32C7B1m8vy34OjbP90pzjn1+ee7wxc+ZMSUlJ8XpGv96U4mqfV2UFXHCTGDe32YXv2l87exBde1ZzThOlggQaapkxY0ZBSeTrr7+We++9t8A0hT0MduywfH4P+K7po70wmT17tklCbxv+ij1tMGOBJlnODYocd8GI03yD44IyZsyYPOPDmZbp7H3jdUHCtIGmz688EH1jEpTf86LeL6lxW1D7gsEo2O9DMOOzoD7pM0VACbSOAb8QoNN+p1gbBp33Q3VN+2oKNwCRHJPo0e6V5AnL4cb7gr2uBQsWeO28py2s3fMCd62zH9xMRttVbiTiJke6gqLtrF2CyYvlSrH7Z8Vyq9m4Rg8m3IBJG2x6jrALN2HayX8w9dvLdZ537drVs9HTepYfgf7++++tJObITXBWu4urfV4VFnDBgD1OYaAUf8VX2PjCCLRVNidCWNqWu+++W1q1amXd9hzpf9g58fA8LOQkFGOHVcBswwQ3slcHbaLxfc1NlNxMaXnEYX8onFRwgjRy5Eh7NnPOiTI0meYD0yMzQbQSBTMWnJMglunrnlVXYUduXLa7JeR3j+2l8HfE2TeOcad7zUBxCDS9rz5AvWd+26xnMPnyEHOsrFi3gzoW57gtrGFFxSgU34dgxmdh/dLnFRyBUOjlQ6kSD0V7tIzQI/DOO+/kWaJ7/PHHi1yRc5nR11Lkxx9/7PrrX/9qlvB8VcQlQtoC4ivs+cD7gifpH/7wB899pqEdtL9S1Ly0qaSNqL1N7INTQN7zmJbYl2qLWr+zHl/XtNW1t4/nII95kjr7AcLoSVOc7fNUUsAJzXucfYDGv4Ac3o9oAsJlc3sZ8LHrlcg5RpmWmCAgiycdyxkxYoRXOUznNAdhhsJMOEI1dmjvi41nXm1q166dC5M3T7t5QhMd2h5feeWVXvfhI9srL/tj/155JcZFMGMB5DXP/gDa+RZVECrdq+1jx471KsqXGUd+dr2B4hBoel/ji2OSNva00+cHEV692u/M4+t305kmmHEbKhMOqxOBYBSq70Mw49Nqtx7LDwKh5Kuqgcavi0rhCNi1OlZqfz1YWOkDPcKGWO6//36hNsaXcHe6UwtOLwOW2F2Y8d6ECRO8tFNWOl/HouZdtGiR0TBbZdLPLL2QOIUab9jTet2mVwdLilq/lb+go7WkbU/j1EL/9ttvXv1gWnu+4myfvV35nfvSFgeiqaMXFmok7cJViYKEnl+ozQIZ9SRjOfRC45SiBB4J1dihFpaeNuyCyW4e8yGu8DCYjD9BRexlOc+DGQvYAyDUAlOjT00xbOyNdtxZhz/X+BcvdF9nF/uY5X1/zTjsZZTkOb3DYNO0CTvO3w5sKAy6+uIet0E3MJ8CQvV9CGZ85tM0va0IGASUQOtA8AsBy5zCnrioy9T2Mop6TttoBmpx2tbZfb1269bNq3iac/De7bffbgJreD10XBQ178aNG71KoqkATU5Ijp0f7Fj3Sms3Syhq/V4F5nPBsp3mDk4C7TTfIOGHNxFPicXZPk8lBZyQLDnF/u6dz5zXNJdx2vTDw4Qzmdc1bTGdEzYmoGlE586dvdLaA5F4PSjgIlRjx1kOiZiTSBbQjIAfBTsWOJGEFtgQ6eeffz7fCXNhDaMtt92emuYbJMx24aQJKwb2W2b/AV1klrZwTwk06CFvRnGP25A3+HSBznEcjr+lxdV3LbdsIKAEumy8p1JvpS/iQGJYEgJXb0INGkMhWz6U4cFAqL2y2xo724LlW8FyptdtbtqjxhBuvaRXr17y7bffej23Loqa1/mjz3/ocHHm8+MkrdxQZUlR67fyF3Z0EirsUjf+ta18TgLNqHn2qG3F3T6rHfkdndpjpmOkS3+FGlqGFbaLc1Jhf1bYufP7EQoCXdSx4xyDXKmx7JwL60dRnpf2WLDa7NwQSHtn5wSbaZ1jnzbX48ePt4optSPHHzc5l6SEYtwWV3ud47io34dwGZ/FhZOWW3oIKIEuPezLVM3OH1o2Hn41i7UP3HTHqFtcMqdmiiSPmwCdHjPyawQJ3zfffOPZ+OZMB/dtcuGFF8o111wjcKfl9bioeX2ZFngVXMAFNzlaUtT6rfyFHZ0kgmSSJi4UauoXLlzoVYQzfXG3z6tyHxdclnZKIATaF8H1NcaddeR37QzoE4g23CozVGPHvpLBskMZiMNqq/1Y2mOBbeGK1JdffmlvltAMafjw4Xk+DIXtFCf5dj4vr9ehGLfFhU2ovg/hMD6LCyMtt3QR0EiEpYt/mandF7mgjRp3sMMHc8j7QU0xPQLMmTPHq2zWxSVz2rvS/nTJkiVeIXq9EuOCniPoeoz/IF9++WUT4cuZhu7muHyPDVVej4qS16kZpf320KFDvcr1dUH3dtjs4vWoKPV7FVDABTXw9D5i/ydFjTgC4xgibTeRYOS+gQMH5imtONuXpzLHDV+2ofTMgsAgjpS+L+luzinBaKCdhLko+wNCNXac2ubCbLudOBTlujTHAts7depU41rR3nbuh7DvibA/c57TdR6jlPryzuJMW56uAx23dk9BxY1DqL4PbGdpj8/ixkrLLyUEQrG3MpS7GkPRHi0j9Ajgh9NEzMIw9drlzh3jRRHnTnHnbnIQXq96WC/r4q59u8Ctmlc6OuwvSObPn++64oorvPKwbHrzoFeCgsSfvNgE5FU2o4WFSvypP5C64DrPq60MRsPoYYxOaH/P8FPtV7Ghbl9BlZ48edKFCZRXO9lmLPsWlM08o+cMECWvvPR+YPeuwYSFjVF7RbAD9ioPIaLtj815YV44QjV2nEFiiBMDlvgrgXhKyK/MkhwLbAMjotrHbFHOX331Va/uBIpDoOkDGV9Ww/zJ408aq7zCxm3r1q29cL3xxhutrF5HTL690hF/eyAVK3EgGIXq+2DVbT+W9Pi0163npYtAKPmqmnDgm65SOAK0zcOPZ56EILVeG3fyJMANmgfQmT++Nr4e+7w3d+5cr/u0Z+TudNo9ByP452K00QzSYhf8sBvzEPs957k/eZ1aTPp95icU4k/9gdTjNMvgagJtn6dNm+ZVjDOd10PbRSDt4woDN1Vu27bNy/+1rbgCT7kScfnll+dJg0iLhY4zrjRQ22gXeoGwe9ewP7POaW9v9ytu3aeWc9myZdalORa2IdEr8emLUI0dZzn8/jnt7e31O7WKvuxwAx3DgYwFtoVtwKTI3iy/z/ndde5laNSokfFgwZUKXx/npk9W5vRGEigOgab3u4NBJgxm3HL1yS6+NPocX9wE6o8EgpFzHIfzb6k/fdc05Q8BJdDl750WW4+efvppQWhnr/JJKGgO4Mttl/WPm89pjuHLFZ5XYbYLp321rx9ebgSzb7yzZTen/MElKfQl3FjiFPvSd1Hzwpews1i/zQrsGYtav72Mws579OjhCaZhpYWPaOPdxLrOz3wjmPZxuZ1ePbi5ksE8OD7oUSVQefbZZ/NElmMQE/g1zmPTzrI5gaOXgz/96U9eVfG9s6zChOYutMm3u4jjGPcVeRAa6MKKy/M8VGPHl3kLJw1OTxNsO82aaG5iJ9GM5uhcPnfaxNsbH8xYYDkID202OXLDH82znJMRe12+zn/88Ufhfgm7cMIAH8r5flasWCEMKmQX7omw248HikOg6e11F+d5MOOWpg92oakLA1ZZwg2Y/L4x4IlTfClMAsEoVN+HYMens196rQh4EAiFMj2UKvFQtEfLKD4EaEaBwePzA62PC26jXPB77ILG2IUfX690+AflaRg0VF7PnCYczmAf2Ajigj20Jz9sn12w4fUqg+2yB/tggAiE7HaB+Lug6fTkhfbTRbMEez+Yzi7B5IX/aq+yWQ80nC780zYmEqyHwS7gr9fFZWO4h3Mx0IVdgqnfXk5h5yAvedpqx+WOO+7wWUQw7UPI4jx1QoPos57CbsJPeJ6y2H5sMjQBTuBX2AXC7IIrLxcmfz7TEgNf4hyjFi7YeGWC8rz00ksuuB7LU2bjxo19mgMVZsLBNoRi7LAcTFjztAtRE12wEXcxcAi/E/Bo40mDjbnM5hFoaD3P2G9+/7Dh1gUPNq6bbrrJBXtzT9pgxgImI3kC2hCDQAQeYrzaymA3/ggmTV752E/iY5dAcGC+QNI7x5fzN9DeDuvcnzzONMGMWwbasfJbR/hVdsEVqIvmcjRRs+47jyCuVrO9joFgFIrvQzDj06vhelEuEAglX6VWJmgJZYOCbowWUKwIMDoU7TudP5b+XEMD7Wmb80fe+c8DASt81kHSTIKSX312Ao3ADF7pSHzatGnjoq2vM789HxsZTF54ePBZB+skEYHGM0/9/Kdkl2Dqt5dT2Dk2guZpix0bO1GylxVM+/r165enzn//+9/24v0+xwY5l9NO097+ws5hBmImM74qdI5RX+PGV/mvvfaar+IKjUTITKEYOyyHkzWONV/t83WPEzq73HXXXQXmfe655zzJgxkLq1evzlMPNt16yi7sBJvg8kQjZTRCf4T28k4snBPZQHBgnYGkd44v52+grz74k8eZJphxywkO/NXnwcmJG+IEuLAR2itdfgQ6EIxC8X0IZnz6egd6r2wjEEq+qiYc+CVQ8R8BLsFxCR6higOyR77ssssEGjC/KzrnnHPk1ltvzZOey5GW/2kQBMGPcZ401g0uB9uF7u/oBs9p1kH/0tAE25OapWT7jUDycic/vX742tHPpXJMQuxFm3OnW7Zg2p6n8AJu9OzZM09freT0DEJsfEkw7fMVMdBpa+mrTl/3sHIgXI5nBDtfwX585eE9uu+izSsj1/nyFezMRxOiiRMnijOqmTMdxyMmY87bfl+HYuywMmj55L333vPLQ06nTp3yYMAIhQXtN2CQEkuCGQtOkzCWyXfqr/Cd0AbaLvRZ7o/Qs5AzCAzt8rGZ1JM9EByYKdD0noqK6STYccvv6lNPPVVg6+gmkSZ8DARjF19md3weCEah+D4EMz7t/dFzRSAPAqGYS4SS0YeiPVpGySBADQ49WlAD6MsjAjUfnP1Pnjw5T4NAqL20FQiUkicNtd2w0TRmGBi4XumpSaZ2lN4YqL21nnNZ1pJDhw6ZpUa4kvM8t9LxSJMTLqvTpMMpweS1yqJW77777nPlVz/bQNMRap7s5i3MH4r6rXYUdoRf3DxacWqUuAs+PwmmffA37aXVAoHz+Q7yqzu/+7CddY0ePdq8V/zz9vnO8c/edd1117kQlCG/Yjz3YSfvKQN2wuY+JmCuwYMHe+5b4wk23WYseTL7OKFm2krPI4IB+UjlvhXM2LEXyu8oNbqY+HrVzfpBjlw0caEW15fQTMrppYH5uJJDDbclwYwFlkHTEAsXkHbXlClTrKILPWIi78nLMmDX78IktdB8VoI333zTKz9/x7j6ZRd/cbDy+Jven99Aq0zr6E+eUI9b1k2vSHzv1nvikZ6LaCoEhYZpHs29rOdMi0ifVrPzHP3FyMoYzPch2PFptUGP5QOBUPLVCEKCQR+UDKj3O5N/9l7/duIGVZlmDksEqAWi9oabcKjRo0aRm0AYMTA/wY+i0BsD04Ns55fMpGE0QpZNDWDv3r2NH2grA4OgMKw4N4M5Nz8xDYMsUEsJO2gTvplaDW5e46cwrWUwea328cggHyAzxu8y66SWDROPPJv47Hl4Hqr6neU6r7mhjBgSS7aPmsGC3p2Vv6jto//ZrVu3Gi0nd9uDuFhFhuTIccXxwhUHavypJeNmuQ4dOgQU7Q3/fM0GO2riuOJhCd/lypUrjYcZjkenlstKZz/C7MFo36x7bJM/wV+KOnasenjkeyIW1K7y/XLsU0tt75M9vXXOfw/cqMv+cnzwu8NNn/YNt1baoo4F5ue7Ymh1tsuXVtqqw9fR+h1hm7iyEKhwAyvLYF/z+y0KBAfW7296q+351eurL/7kCeW4tdrAPnEFkJsz+X2gxtk5DqzfEK6oFfad9hcjq37rWNTvQzDj06pbj2UfgVDyVSXQZX88aA8UAUWgDCBw8803G7MKq6n0AhGoxwkrrx4VAUVAEVAEAkcglARaIxEGjr/mUAQUAUXALwS46kHtKl04Ov0MFyVaoV+VaiJFQBFQBBSBYkdACXSxQ6wVKAKKQEVF4IUXXhC4fvPZfX8D1PjMrDcVAUVAEVAEShWBM0Z9pdoMrVwRUAQUgfKHQH7R9Wj/Dh+35a/D2iNFQBFQBCoIAkqgK8iL1m4qAopAySPATXdOQVAXmTVrVqGbrJz59FoRUAQUAUUgfBBQE47weRfaEkVAEShnCDCE9vDhwwVu84R+telzuUmTJuWsl9odRUARUAQqHgJKoCveO9ceKwKKQAkhwMBDI0aMKKHatBpFQBFQBBSBkkJATThKCmmtRxFQBBQBRUARUAQUAUWgXCCgBLpcvEbthCKgCCgCioAioAgoAopASSGgBLqkkNZ6FAFFQBFQBBQBRUARUATKBQJKoMvFa9ROKAKKgCKgCCgCioAioAiUFAJKoEsKaa1HEVAEFAFFQBFQBBQBRaBcIKAEuly8Ru2EIqAIKAKKgCKgCCgCikBJIaAEuqSQ1noUAUVAEVAEFAFFQBFQBMoFAkqgy8Vr1E4oAoqAIqAIKAKKgCKgCJQUAkqgSwpprUcRUAQUAUVAEVAEFAFFoFwgoAS6XLxG7YQioAgoAoqAIqAIKAKKQEkhoAS6pJDWehQBRUARUAQUAUVAEVAEygUCSqDLxWvUTigCioAioAgoAoqAIqAIlBQCSqBLCmmtRxFQBBQBRUARUAQUAUWgXCCgBLpcvEbthCKgCCgCioAioAgoAopASSGgBLqkkNZ6FAFFQBFQBBQBRUARUATKBQJKoMvFa9ROKAKKgCKgCCgCioAioAiUFAJKoEsKaa1HEVAEFAFFQBFQBBQBRaBcIKAEuly8Ru2EIqAIKAKKgCKgCCgCikBJIaAEuqSQ1noUAUVAEVAEFAFFQBFQBMoFAkqgy8Vr1E4oAoqAIqAIKAKKgCKgCJQUAlElVZHWowgUBYF1T0QUJZvmUQQUAUWgwiDQ9llXhemrdlQRCBcEVAMdLm9C26EIKAKKgCKgCCgCioAiUCYQUAJdJl6TNlIRUATKEwK6rlKe3qb2RRFQBCoiAkqgK+Jb1z4rAopA6SGA1fasTBH98S29V6A1KwKKgCIQLAL6Gx4sgppfEVAEFAE/EYiA6jkrW+SFj0TmbxGJivQzoyZTBBQBRUARCCsElECH1evQxigCikB5RsAF7XNcrEi3HiLjfxHJBJlWUQQUAUVAESh7CCiBLnvvTFusCCgCZRgBV67IwLYiRzNEZq0RqRxdhjujTVcEFAFFoIIioAS6gr547bYioAiUDgI50ELXShA5F1roFZtFSKhVFAFFQBFQBMoWAkqgy9b70tYqAopAOUAgO0dkVDeRzXtFth+ALbT+EpeDt6pdUAQUgYqEgP5sV6S3rX1VBBSBsEAgF1roGlVFRvYR+eJXkQj9JQ6L96KNUAQUAUXAXwT0Z9tfpDSdIqAIKAIhRIBa6IHtRPZkiexNUS10CKHVohQBRUARKHYElEAXO8RagSKgCCgCeRGgFjqxikjvFiJTf4MWWqOr5AVJ7ygCioAiEKYIKIEO0xejzVIEFIHyj0AONhCe00lk7iaRfccRXEVJdPl/6dpDRUARKBcIKIEuF69RO6EIKAJlEQFqoetWF+mcJDJhkQZWKYvvUNusCCgCFRMBJdAV871rrxUBRSBMEMiADfSFfUUWboQt9FG1hQ6T16LNUAQUAUWgQASiCnyqDxUBRUARCFMELHMHy3a4JK0foDj2CKMLUpNcVGHeZGigayKgykwEVrm0X1FL0nyKgCKgCCgCJYWAEuiSQlrrUQQUgZAhEItfrmPp7lDYmafcwUigyBU4tjBCMs0o2bwXjLAcBgqMxMfiyDy3ggdGVxaJgTs6bgYkEWZo7qKQaU4GLhsm8s5XImN6QguN/pGYqygCioAioAiEJwJKoMPzvWirFAFFwAcCJJokqN+uEPkOn+Mg0ccQiITR/U7gAy5thLZpeCShCPJnEWh3ySLgy5JAZg2Jx8PEhiLtkmHLHAu/zgiOUhtRBkl+swOonJsJOzWCJhqf1XtEujdFfms2YGrSP4qAIqAIKALhhIAS6HB6G9oWRUARyBcBy2Tjv9hs9+ef800W8gfUYts12STmh0GQjWTi7xaYXuBD+XC+yHUDQaTh37lOTeSjGtwPIeGOARkf1V3k+2UiXRq73dqpFtoP8DSJIqAIKAKlgIAS6FIAXatUBBSBwBCgnTOVvp8sFHl2mjtvpUqVYOrg/gnLyfFPXcs8EZbRtKMJWVlZ0BxbzBhmG5GR5sNkiYmJUr16dcnNharYJixv165dkpaWZp5tzwC5nyryGYj0o0NFBnd1a6OpYS5MstCFnk1Evpkosma3WyOtWujCUNPnioAioAiUDgJKoEsHd61VEVAE/ETA0jx/DPL8DDTPpLj169eX66+/Xho0aCAkvkePHs2XGNurSUhIkJiYGPstQ5I3bNggr7/+upCIs8xx48ZJcnKy1KhRw5B0km6SZV/CPCTREyZMkN9+Q0QUyKaTIrf+IHLVDpF7B4skQRtNbxsFCbl7HJo2aojIV7NFOlxeUGp9pggoAoqAIlCaCCiBLk30tW5FQBEoEAGLPH96WvNsked7771XateuLdnZ2VK5cmWJj48vsBzroV3DbN2Ljo6WPXv2GPLMe/369ZO+fftKRkaGl0baSu88UgveunVrufPOO2XWrFny1VdfSWZmprG//gR22mu2idyEDYIj27s3ORa0yZCa6hb1RD6dI5IK85A4mHWwzyqKgCKgCCgC4YWAb5VKeLVRW6MIKAIVEAGSZ2O2sQCaZ5hF0HqCZhQ33XSTIc+WyQVJMU0r/PkwrfNDsrt161aDMLXM7du3dxNglOlMm981iTyJ+IgRI+Sxxx6TDh06eN7Y0mPQQn8D8xNoz2k9ElnAry43HjarA/MNhPeevlqkMgi0iiKgCCgCikD4IVDAT3n4NVZbpAgoAhUDAZLMXNgEvw3iSZtnam1pk0yzjebNmxuzjVAgQcJM84+1a9ea4pKSkgw5d9o6+1MXyTVJfZMmTeSuu+6Sa665xmjHmZd7Cf8ELfoDn4lshpcNuuHLT2jOPQabCScsETkKUxBLC59fer2vCCgCioAiUPIIKIEuecy1RkVAESgAgSg4Ws6EvfAz40X+isAilsnDJZdcIl26dAkZeWYTaNt87NgxOXHihGlRp06dDOklGS6qWNroYcOGyUMPPSTt2sElx2n5YYvI3R+KzICpNL1u+CLHUEJLHbjCqwwivR/aa19prPL0qEDO3DoAAEAASURBVAgoAoqAIlA6CCiBLh3ctVZFQBHwgUAUfpH2gTQ++TXsgDedSdCtWzcZMmSIMdM4czc0Z+vWrfMU1KxZM7Np0HOjiCeWNrpFixZGG33RRRd5PHpsBkO+FZr1v8GkIxMkmX22C7l7tTiRc3qLTFuhNtB2bPRcEVAEFIFwQcDx0x0uzdJ2KAKKQEVDIAaa5+U7RK58F67cNp7pPe2eqX3mZsGimFacKSnvGYnu6tUwNobQnIMmHPm5ucubu/A71EbHxsbK6NGjjTa6adOmJlMmSPIbc0Ue+ULk4HF35EHaR1tC/Xc1fJZDA++PCzwrnx4VAUVAEVAESgaBAizxSqYBWosioAhUbARoohCDX6IpCJDyxGSRQ7RhOC0ks3QpZ7mr47X1sdLw6CS9zmt7WuuchJn+m1NSUsytuLg447aOeS3/0lZaf48F1cuNhY888ohMmjRJJk+ebDYqToRJx7p/izx4Nrx0wGd0DrCgycpJhFT8Yp7ILPiV3nJYpHVtjUzo7zvQdIqAIqAIlAQCSqBLAmWtQxFQBPIgQNMFxkHZfwQeKuBp41/4cLOdXapUqWI25dFO2dI+p6ene2yWmdbpB9oixRaZ5fH48eNy8iR25NnEes5NhBR641i6dKls377dU5cteaGnLI9knPXnJyTtFPqY3r17tznfguS/nyByxWaRG4aItIQXDnocqdYIhBq20tkwaRHcU1EEFAFFQBEIHwSUQIfPu9CWKALlGgHwS7MhjpYK5JG7Dons2QdPG9Pgso0k0YekpqbKM888k+eJc5Of8zpPBj9ukIiPH4+diyUsTZs2laawvZ68YassfWebPDBWZEhH+KNuJrIApLpdc5Bo58yihNuo1SkCioAioAh4I6AE2hsPvVIEFIEQI0CXdJXxS5MKc4QjUAIv2wHb3pUiP+0X2ZkKbWsB9ZEYF4UcUxtM22lGEqxataox8aAbPGqvqQXmOW2qeU7NtlUHz6mt5jXL4IdiaY7tTeUzBlshybeE+VkuNeeWxpzPmJ/toK9oHvmM99i+evXqmTytW7WS9Zu2yB0TZsq5SzKlWlWRNART2QfMmtQSSQd+lkcSqz49KgKKgCKgCJQOAkqgSwd3rVURKLcIkDCTd7rAjCNwvgM2vIvWisyDtnkOHF4c4g65YhYSYJpT0PSDQrJrEVvaOjOcN69JaHnND0k1N/xZ4b5JpEmOSZIZrjs/0wwrL0kx87NMSrVq1Uwd5sL2xyLlvMVztpV5ma9T+7bStHFDWbJshaxbs1oicrLk3Vku6QMC3R1a6Vog1UhucGV+nvOjxJpoqCgCioAiUHIIKIEuOay1JkWg3CJg2TNHgMztgUnxfniWmLFMZCmChqyHi+X96aXTdUuzzCO1z/z4EkvDTBJNIssjiTOJLT/Mb5XlzB+BWQInDBQSYqsslsMP81tSs2ZNc0ryzvDj1FSTaFMTTaHXDuZv3aKZNKxXR/bu2yefrFwnn+SkS6P5MOeIEWnfXGQQyHQs6oyvLFIlXiQRxJq1sCqae+A1qCgCioAioAgUIwJKoIsRXC1aESivCDDYCZTLknXaNncDzDGWwCxjew40zRvgWQIE+gxtLD0UqA0nmbRxWJ+NsUguj7SFLkxoktKls8gJeMtYt54E+0wOaqspvsqxAracSe0+s0i31Q7nc15vx0SEn8mHRF5FVENwZ2kMZXfd+iI94KWjNgh1vbrQVLfDM5yT1IOLC98VNdR0h2dvp6869J4ioAgoAoqAfwgogfYPJ02lCCgCpxEgKdtxUGQrvL/NWSyyClrm32Cfm+7mjWGF07t/QuhseLl45vnQNKsSyOjvbxO592KRYzjPqSJyAJOH224BJjBRKaoURJzzKxPm0bIJXH/TdpHZ+FDQJKkzGaQav+wtE0XqNxfp20ikOq4bg2hXBevOxKQnx0b4TUb9owgoAoqAIhAQAkqgA4JLEysCFRsBmmos2Cry0Jcie8ngwkwqx0LjijalnrbUSADBrYo2WwKLCYkGyzwGTa5dEkAsOTE4djqf9SwR0UyOQ8ucfXpycPMIkYd/L/LUg4gSOA2aXWh+33hK5KNPRM49H5MI5Gc5iQjFfRzEHZ7xjLAJ1MhDKSyV0MCcYvKqwWbuQZ38LOXexl34QJLw6doCH9hSn9cTxLq6ua1/FAFFQBFQBIqIAP/XqCgCioAi4BcC0fjFmLM8PMnz728VGToUhBksdc4vIk+/c3qD3Wnm+sD9ImMQrAR8WLbBBfPjL4ukYIPjfb8TGQXymwCWOwXBS57+OwhmXZE/PyzSCoTzSBxc7b0L04nJIrffjAAnk0T+PeE0XND83gMC/dgTCAYDEt6pEyYXD4rUBEE/BZL60WciX38j8rvhIt26wIYZ9f+0BGG8X/ML7pAlQjdl2mb3591FmACMEhnXQySjmIh8yBquBSkCioAiEKYIUDGioggoAopAoQhEgpjug23zPNjghpuMGSly/Y0ib70l8jI+F10LMt3fbaOdDQLdBCrYq/qK/OVvIn/4P9gJN0fgkitEOoIo3367yB9fELnrWeQZJnLOEJE77gQJro/AJiDDM2eL3H0TzCDwa9mgG3xWQ/Nsl207YcKBMo4Bm9/jeHCdyC0g1L8i35M4Uuog3833oaxVIhMnuu+V1t9jwGMhiL9acZTWG9B6FQFFoDwgEFUeOqF9UAQUgeJHgC7pToAk7j9a/HUFWsMIkOXZIKY/zXTn/NMfRI7ucLt74ya67SD9N0ED3bg5PFg0g7a5pkhcLEwuYmDSgc/osTB5mAciDC32zn0ig3shLcj1+RdhwgBt8+cfwwQD6SPxi5lz0nfrML+Qxx8R6VBdpFdPaJsbQhte1Z02GthNmiXy/Eu+85b03TUHYLuNd5mE9qk9dEmjr/UpAopAeUBACXR5eIvaB0WgBBCgVwdGwz6cWQKVBVhFTZDiFGh+LfkGZgo0OKbNNu2NG4EMv/05boFUr18B22SoX/mMG/DuvwMa57+IXDIGdsswvbgXJPopEF2cykUXQzON6wXToUEGOT4B049GLfAA15Y0T4QdNJ5d9yTKgtnH2QNFFqP+6tD0WjFWiN3hI1aO0j+yPfyoKAKKgCKgCBQNAfwLUVEEFAFFoHAEyLfS8Cer8KQlnmLzFmiV25yp9s1XEQ57kNuEg+7bRo2A+cl+kd5XiFzzPMwsUtCXdJHh3aEpHowNgOeJdIbW+CTSjLnSbdO8fBnKGC5y9dXwZHEu7KGbikz4AUT6WriJs/1y3nsjvF7AtrlFbdgVDwWRxibDG/H5YTK03KjbEm4uDBc5eRSTiFQl0eHyPrQdioAiUPYQUA102Xtn2mJFoFQQIIGm8jkcbWc//0Lk4/dEnn0cmt9IkZHQEj++ACYUF2JzXw5c2W2CSUZjkVtvgHu3BiDLILw7sbNuBTTF116PoCQw4zi8F76U64jM/Y/IABDrN+8XeQlmGD3x2b1FZOMOmGCgjvEgyfTAMWcWyqkl0gbE+2bYOq/Zg82VB2E3DYJ9dheQ8zHwxtEIGws7uokqYqeEjaRiFpQN14PGLUjYtEoboggoAopA2UFACXTZeVfaUkWg1BGw3LkVd0MYWITR+po2bSoNGzY0obb3ISrf4cOHhSG2jxw54hXhb/UamFrcDg3wpdAio3FXYcNeCjTM//gviDHI4tKlIn9/BW7c4CVj5XyYZoyD1hkEdwHu334XNNTQMDfpIPJ/f4Ot8iSRn/HZhrI69gV5hlb6lXsweUB5e/C5ZLTIhVeBOCP9HJh0PIU8iza6EbnlIWigL0IYbxDxh/4IIt8HGw8biHz1tUgyyHa4SAQbYv6ES4u0HYqAIqAIlC0EIhCeNmiF0oB6vzO9nr3307LVe21t2COw7gn9Lx8uL4lv4hVoXt+FZrc4pVmzZtKxY0fp0aOHtGvXTmrXri0xMTFy7Ngx2bZtm6xYsUL27NkjK1euNNfF2ZbiLjshIUGSk5Ox2bCqCeF96tQp2bt3r/BYnFIfL/OT62HPDe16SU2KirM/Fb3sts8G/W+8okOo/a8gCISSr6oGuoIMGu2mIhAKBIqbbHXr1k169eolF1xwgfTs2RMb3SIkLS3NaJupjea9/v37y/fff2+I55w5c2TdunWh6FqJllGjRg3p2rWr1K1b12jY4+PjPfWTQK9du1aWLVsm+YX+9iQu4kkcCDQ3USrtKiKAmk0RUAQqPAJKoCv8EFAAFIHwQICEkgSZ5Llfv35y6NAhycnJ8TSORJqmHYmJifDhfIV8+OGH0qdPH6OxpXa6rEgD2HQMHz5catasKX379jXa9jp16pi+ZWVlGfMUatenwdCany1bYIAdYqkKc5LoBBSaG+KCtThFQBFQBCoIAmG0L7yCIK7dVATKMAIR2KBXHNKyZUujeeaRpPLAgQNG60wNtPUheabQBjo6OlrGjh0r1NySRJcVocaZ5JlmKdddd50MGjTImKfQvptmKZw00PZ7KEIq3nHHHTJu3DghJqEWeibJVfVzqGHV8hQBRaACIaAa6Ar0srWrikBREaD9cy5I13F4mgi1kBjT1pnSvXt3+Jo+KdyaQeLsS3ifNsL169eXFi1aGNvo6tWrm6Ov9OFyj+0eMGCAsXcePXq0UOt89Cj8yUEiI8/MTDIyMiQ9Pd08v/zyy+XgwYPGjGX3buxYDJE0SUSkxSpKokMEpxajCCgCFRAB1UBXwJeuXVYEioQANJanDhYpZ4GZSKCrVKlizDWSkpI8mueCMpGMZmdnGxLNDYb1oNkNIy9xPpvetm1bYf/oVaRDhw6GPLMf/NiF18SEZimNGjUymym5odJOsu3pi3JeD+YbVWPVBroo2GkeRUARUASIgBJoHQeKgCLgNwIM5x1qiYqKEn4srbOTUOZXH+2FmZbEMi42VloWQ9vyq7so92m+QWkMh9S05y5MiAdtwGnCQZOP5s2bF5bF7+cJasLhN1aaUBFQBBQBXwiE+b8cX03We4qAIlBaCBSH2Wx6RqYhlCTR+/fvNzbB/njXjIuLk8zMTONJIjI3xwRKKS1c/Kk3ISHeaNdpbkIzDX8mCtSy096bdtHURodK6sPpR/AOTEPVGi1HEVAEFIGyh4DaQJe9d6YtVgRKDQFqoCN9TLtJrKNgiVAzOn+zABoqNEBey2AhCSe1kkVSEe96376DRsu6ZMkS6dSpU4HkkuSaJg4kz8uXL5eMrGyRQ/tkXD+Rhghgkn4cQVR2uuthuw5D28oIivkJrY8PI+EJP2cHyWg33cDllxymxZKIQrlJj2YS1bEHcNch9DMt07Sb9tvVqlUzts3sR0HC55xY5MIAnefGUhpZXNQgF5TR9ow18L2xvXxH3aqLnNXDHebclkxPFQFFQBFQBAJAQAl0AGBpUkWgoiJgyCJI2JVjEYkPnuXAw7yEGwxrVhVpCyuFgrw7kMxZwjKiwAh3Hxb5w6SNktmhnWzfvl0WL15sPHEw6qBl1mHlsa5JQGfOnGn8JO87eER6NT0iw7APcSg+1KyyPXYx7bffcJzzeWFprCz2Plj37Ec7NjxnCO9lW0WeXnVEWjRvKhs2bJDBgwcbQmzP5+uc5JmbB2nKceRwityG/vUF+T2Vgg2dB/K+B2cZbGsCXdbVEMnBPCMJ76gd3hF5e0HvyVmOXisCioAioAh4I6AE2hsPvVIEFIF8EOBet37N8ydtJK7ZIK6RdgbpKMtJUkniGtYWGZi0T+atXCe9enREKO1JJlfv3r3NRkGaO1gaWG4YJKmcO3eu/Prrr2hMhOxCZMLb+uXivkAb7a7QaatdQJNMhsKeO7rhN9lmvhz0sS400VX3bJa07C6ya9cuE02Rfq/pts6XFpr9pdkGtez0Cc1+ph49IJecJ9IMhJjzA2cfnW20rs1k4jTw1jtS8myho0dFQBFQBIqGgBLoouGmuRSBComAP5EIT3M1v/AxacEGx8CV8+JJ82TT5mrSskVj+fHHH2XTpk3GAwWj9pFkklSSfJI8b0NI78jIKFmycrX0rLlVurQ+Q579qtiRKJA2O7IWeslYMA0biPRvdEQWbt4hndq1kClTphiTFbriS0lJMX2zF8TQ3rR9Hj9+vNGy795/UOqe2iXJ0CBnoDwSYRVFQBFQBBSB0kNACXTpYa81KwKKABCg1ppa1edGZ8mTP06U+SlnSfdObWDqsFFWr14tCQkJRutMbWxqaqohljlQoc6au1CaZi2VO6GVpZY3nIWa8Sv7i/zyxUzZl1xT6tZKlA8RSXHgwIHG9zW16vQqQhMVap5pJ/2///1Ptm7dKumYtWxfuFCeHpYrcDYi/kxiwhkLbZsioAgoAuUBASXQ5eEtah8UgTKOQBa1tAju8eLYXJm4YJZ8PmGd1G/bSerUrQ9ThbTTJhMuSTmRJvt2b5LjW9fJta33y9nd3QFBSMLDWWgyUQOb9+4dli7Pzpgs6T2HSbOG9eSnn36S+fPnGw8bJM4k0NRIU9POc5Ln6ZMmy+N9dku3NtgMCTtmFUVAEVAEFIHSR0AJdOm/A22BIqAIAAFqVmsjwMf1Z4uMOn5Qfv7tF1m2KlKWpiVIXFyspJ46IS3i02VEVI6MvBgePKrBlAHGy+FOnq2Xy/DZA1uKPCnH5KM5P8j8/X2kTatmRqO+es0aQ5iZNgp+ralh37Fnr2ycPlOePCdFzuksknbavtsqT4+KgCKgCCgCpYeAEujSw15rVgQUAQcCFhlOBjm+dqDIVTAg3nUULicg9BzRqKbZT2fIdjbNNsLcdMM0/PQfNpWa9gGtRLrUy5Z3ZsyRhT8tk1M1G0mNarUMkXahQ8ePpUh0+iFJOrVbXjof4c1h363k2Y6knisCioAiUPoIKIEu/XegLVAEKg4CpwkvPXoUxH1p8kBzBXrHaAzTDktIQMu6sF+IXC73jsSGwOxUWbJxvezbtl4QC8ZIHFzO9YBpCjcMYh8h0th6bIEWqNsQWxF6qggoAoqAIhA8Akqgg8dQS1AEFAEgUAnkzul/mf7W6DGCnihc8IccGYd0+Bw4JoKYJ4UGAyFftLTS5QlkmnNQKuMXeEBHYAITDXJiix8jAKHx0+zcMBgB4k1/zlknkBcaebqy44fa+XIwtzCY6B9FQBFQBMoCAkqgy8Jb0jaGPQLUqJIA8WgXkkfzsd8sh+fs43FoS+OxUc4igTxx4boqzS5AnnOhSY4Cec7dKRKzyI1LOYQioC4RK0OS/WC/HFtpMG2p2gSa6RgESIFlC61bsvHBvkOhot4+/CohSI3nXQTUKk2sCCgCioAiUBgCSqALQ0ifKwI+EKgEpsLAHTxC+Scn0hGq+SQ0g6m4OM1aSHii4kWqYWNcFZBLKh1pmkAtrVOz6KOKsnULfaoBs4PGQ23EGH11we0atazEKH2PyN7ZOC5HeGvc4wZAFf8R4CQlaje0+BmwBccmyujG8ECCGOW5GHvpuIe5iUQgTfo+RDYHIT81ExMVhBB3EfwghKHbGTHSi50HUV5xZ6V2nxp8FUVAEVAEihMB/BtTUQQUgfwQIMeDUwT38jrISQ48IfDeASyhr1olchDXx/F87dFo2RPXSU4kNJasqvgPjkSVj0VI/Kkt0iJnjTSPz5EEkJokLMEnIpRyl/ruZfcIkkuSE5RdVk0ViIcLfXNtxmcQSBsmDE45tFRkz0/A8jg+mEygu+VXrM4RmBALJ22ZR0Q2vg/yPEqkHgLQCLT7JM+WxCCyY+ZaaKUPisRibFnNsZ4HcuTkZ+MBkZUrMKTxjsNd2MRG+H717aou/8L9XWn7FIGyjoAS6LL+BrX9xYIAtcfRIB/UGO+C5vQUtHxLd4gs31VPNiXWlt0JTeVwnYYiLTqAxdQDU4FFbyyYDD8kTvzwvzlUg8vTkTkNasE9+0X2HZBKB1ZIq+0p0jJtqzSN3SH98A+/EUgPQ1pTe2bZxxZLx0JZKLBxQdN3EseaTWC+0d6NmbOKvfNhajAZPI9aQZDnci3AgoTW2IPT7VwxkGiq8yMxTg7+iA8mLR3G4RoTM7vkQiMdiU2I6TDtgHtp9xKAPYEf5yTPqzHmP5iHKIqt8X7B0qkFD2cBLPLFYnxvsfJxVjt3dEqnWZWn/af7EuZd8jRXTxQBRSC8EFACHV7vQ1sTDgiA9CAQnMxYI7LgVKLMO9FLdnToJ9IHauMLwHbjYYhaA6HzrB1yxsiZ/4bxyTztrDcCTJFkMR7q2ESkzQHJbgxGjbXw3KhYWZ+RKeuP7wap3i3/3LNWmk2eKOcnLZbLerqkblL4mniQD7rAUmiCEgXSltAFUICo1Gnr1qjn2pfOU0XWTEWGZXjGyQQ17cUgbBMnOiSrPC9VQTsiMDwOA6Oah9GSYmoQzV9iUFcaVkH2oa4GF6EuG4muAw1sVEMMu5XQREN7nA1TDgo12CSZhQlJ5/xNIh/+guA2D4t0a4Yc7AtxDkZYBsdCsOXk1wZMLgYPFLnvDWjlQfg74itL8xYKo1VaE4BItIMbL4lHLL6nxNN4eCmudrmboH8VAUWgHCGgBLocvUztSvAIUOu2YQ9cjC1uJxuanyPSviX+82LN3BUpjWP3SvzBbZKwEWo9ssh8BRHkXIlyMilCtmHXV04V7KRrCRVeYiMwK7Cq1Qvd/8ljcD8JasIWA2TrUxfLG2t+k5mfPiL/uGCn1MHGu7AKT01igS6ngyDnoNmxnUWad4J2s7EbhANbcNwocmwdtOkX4D6Iy9rvkH455hDY8BasHW6+UOMBNfYHQR5rYe6CGCvFxs0KaoPXM7Sh1gDYxU/Ahj88KC5ORtIXB+3y8dVuzX/tcagMpPHgIqwKYBw3aIP3MAzu8GCbvuM3kSMg02nQKMfjmXkfJLM+hPbO32HSMwfv89N/XCbJHcHGMwFyKISs9fB+94aBfFXDwVXUsX2kPH3Pcnn29QXSBPPWnM2YQOAlcNxG44Ww29FpIMwncQ8LR20xYW2O+13wFeUkr8ysAAUHk+ZWBBSBIBHAT6mKIqAIEAH+Pz8JzfOHC5NlQ9dx0ir1iFyVdELaN2kKpXM1qVo1AcvhlaUyouIVxoqysjMlKyNLTp04Lnt3bJX/mzledp1/r1SfOkH+3Lmy1K3fUDZv3SWpmTly4FCW/Dxjp2wdcZ2saDtSvpz3rtwLEkp3ZaUtEeBNVKpHgajFNEOkwC4gHzgmgHRQ23wcBHkziFnuBjwHcSQ72QwCF4VjOu4nAKoQUS/fUIAYZYKgJ0MDHokVA5qUFJfW13cDvO9yUyk9YjStDS4L3nkSWJiVCO9kIbsiOaeHk0PAmudJfUGUf0W90DhnNQL+HYBNN5EmIPQNe4ns3yayezbuY/GDZh7ks2aHJw4eQUEZeJdnD2ojye3HIiHYJW1GChTWzo8fUhsvCzgVp5zVYJC8Xnu2pB5YJtWioo3mmb63Yyq725iRVUlOpW6RY2knZG1KpMxYmi4TJ6fKlb0xn8W7w9dSRRFQBBSBAhFQAl0gPPqwIiFA7fMEEJHPM1pJv2M75IV7rpP6jZvin30E/gEjRpztUxguEae1a5UqNZSWbdtKl2XbZNeu3dL91CYZMfZJiQYR79oXbA+2B5XAus5evEAu/2Wi1K1VVXZn9ZLN+xdJs2RozgrjLYU1pAjPyW2MP2fU7SJRbgpi1gLkuT0eYLn7FJTou2EXmwnCmr4NpATpuNESSnojLmhEaVIRD2JX3M0nYa7WD68IGvuTS9A8EsJSFGqFI9LRDhxrDANhhRa3ynHcO41NcTWtErA+AtxToNx1QbtKe+UcnKfsxSRnBbyetEMbQOjrQytdD5+MHVAEL8AztE+giWX76E8ar81IDMqLa4tlhuhMt6q2QMLLXAn4oFJPCaYY33+MyZPvRyG7GxEnLbuNQHOGexdpddD0B6MTx274c9XvjsqkKd/Jmx9MljvxvWyO7155CNrj3Xm9UgQUgVAioAQ6lGhqWWUWAbrq2n9U5ON1lSWuVro8dsMlUr9JM8nKgvq1CEKyTckFE83OSJeNx0+AtaRJvcQqEhsbK2ncWHhaIsBeXJExWF/fL2e3aS1t242Tid8skjvPs1KU0BFNplY5E8eqMMGoDsKc0AO0qAbIGJqQsQ0YLQOBXg/iDKziQKadxIstNXMHEBOLq/BecQjbmosl+OYgqkumQpGKV1UZGu/irregvrDueIwlauMrVxdpBv6272tgwgcFktCCSvXvGd+FC5MbapRNdSTtvHcEZh2/4h1igrG7AUzxB8E+uxFMPC7FxAjvcdc8mJtsxqoB0lUGp6Tp0LpdIndE/ySyfpofsyBkEnQWpNXdUR/tZYP4KVBa4Sn/JRWasMBSvB/6AzrqgzucUUPaSq2qa+TZv26ROwfD6gokWjXR3mjqlSKgCJxBQAn0GSz0rAIjwKXsXSAfK/bXkrsvHCTtOnQsMnm2wxiFXUqbN2yTbdytBGZZr25dROXLsSfB7Qg5SNvo5JrwmRwhXTt3li8+SUa6g3mX171yhugC/MG4oQP/qQGlYw54TAMs/VdCk0m+Ns4GkdiK6+2oD9pNaiqrlDJRNRwLBL4ulIyCuUcN8KRUnKIrYSFWO2p0ATndj0nHHOAH3IqbROcxxyAaqDca7ysaczbXJpGtIMspmCDVhLlCEiZJLTFR27cUdtLfYuKEd74U75rBb7rXOWa00z4BZV+sYczORqTILpR/4IAZ5nmy1MdEpzbelyWnF2gMwTcvzQCGmRn5ri/OS45uiQWude08Mj8nD0xnz8f7bLclfG4va51IL/T7z5eLPPlfkVsHwz4a7VZNtAWYHhUBRcCOAH4uVRQBRYAE8sc9yVIZvuQuHnO+REdHYYc+/wsXXSLABCKh2v5l6kzJxEZBstRolBkD843c0+YgLJ3XBw6AQFdqhDSp0qZVK8lu01UOHf1Z6kILVmxmHCAPNIHIrYJNgW1gI9sTbWnm7u/R3eBHG+B+bhmIKexpaTpKxyJGQYiDnXe4c5TcX/IgmJdL9UHYrNfOXW8C7/FBmAl9fDfqK/LbFhBYYGowLK02gjwSIuiKJWsXyO4ebPoEcXbhnedCC10DLzUT4+GHxSJjQSLNu8Z1HsF/jVlI8/WOfpLUMFl270zDOI+QI6kZsns3BosPScAYiztNXqsAk+p1sRoTkSEtqu2ToR1yOHc0sv2UyE9oU65FznGX36FDB6pIVia+IujA4agYyagc58WFmTkXM7sa6acQpOeENK+RKQO7wztMIh/wKVZNMGaOYDJjxi7+8N3QSY4lCTBboXTuJHI36n/pS5GHhmAVAWZMYbWh17RS/ygCikBpI6AEurTfgNZfqgiQI3PD24pN8DhwoK40bN9Kfp0+XX6cOg2b+3yTgXwbzP/M1q4s/KePwH/orOwsmZAG9jAQBqhHT8nM2Zul7jdfSWKNRImPx32aeqD+mfPBYEbeLTNmfCYRO/4qy7YekldAJP5yNcgrvqWnLULyrTqQB4Y0k0Bgb1gCyEI8CF4CuDv3iR2GDfhueGzIWIv7JDHAJ8amOQyknuJKyyhzmTBFqAsCbclpjmRdhtWxEshhaxDSzZ8CThC44txU6E/HiRUD+JBJ0hZatuEa75kfWBlJGu73w3iwiCfOzgjyrdgi8urCPjLsouslDsbSdVohAwTDGAQX+wXM1Zk/vM979jGcmpYGV4jZ8sOqdbJ/7r/knvPRKiTcvgvfw1VDpUevfliBcbN3ruJUaRdnVmpYUFLlaLiog0rdIZywstxjaRny9spVsj/ySxnSDGMb/aqMsf7o9w2QoglysUWUbJwdMGdsW5UTh+QPF5yQJpi0Dm8Nwn2ByD+/Enn5SuRAFnv7TSb9owgoAhUaAf6MqigCFQoB/jOkH1j+H92+D17ltoOoHhwqWfc/IFtPpMmf4RVDGtSB6wJ8PQr7r8nCaNNAdRYNqeF1Q9IPYncWjuZzFM+g2iLrS0qUuZfeJnP3YvfdGlQciWfcdRaFfBfcBXVZS9ky8GrZEgdVW7P+sm7WVGk29wu5e0hWyJaR6b6sMshnWkPYDg8EOabmD909CAxSQJ6zF6A7IM7V0eRcpA07QduiYJPd9TIcQYrKisTWwpAaC1OJ8WgxhoaHw5VmBzh08bFUuTzfDzuYZGj16ybiPsaFl+A5uKk8M7GKdB4yTqrGRoHknklEkozX45dUgfPlqKg4adawrmStw3fHxtYb1EuGGVM7eKFxE2hr8669YGuPgf0ez6tXq4o5bCWJxHcqd8+XsgRWIc3qoU9oWE7yRTKgX9czpllocFaWu45KkVGyeNUmWbvtFTmKScRrMGd59w+YLIBffzxF5LqRyI/+F/Zz4GyPXisCikD5RUAJdPl9t9ozGwLkCdTk0jsEg6Tsxud/M0WmbI2S/Rc+if+Ql7hVrdWQAOSyQD/PZAokzTDzkBPHsA6O/7Kb5kPFuA22EAmwKwDDi4F2mQyvCRhqHI4k2PQdHQ/1VqthIm3YIn5OC3fE0Y4EGxeN1EX6lgPks79skIsOLZJ6IGAMXhKMuMB14kCOmoB8RsRAiwuicHwVFOMgzYe24xnKrwRts4nAGExFxZSX8OUC3gYXA9raxVRJCIrlGHP6vU7djDG31v3Gw3Fewm5XxpCbjtWHEQPQTo5xp+D5T8sxRpLGSJOGdTwaYmcyf64tUsz9AIbE2zKZjbcgz9lF3MDL/NFQOR/C17JpR7cZdyLGfoRkwm92FBZVMJBOSyw7DYmEG5lGdarBtWSkdOmYI9N3VJLnJuXKHy8UuXOJyFdYDbqou/8ThNPF60ERUATKMQJKoMvxy63oXaO9pPVB4D9ZBBKzHlYZXxxsK2tWbpDcNrBdeOpu7BTqDXaK/7AksRRf5MH9BH9RKLRVkgk14uLpiBayGvegru3aB/9h+4N9giDzOT+WVppqK6NNI7NiQagnPzJsBWhhNAf4rz3Q8SKZvmKRXHM2soF5BWUPjbrpniwVnH//Gmid58IFXDrKJa9H2a4wM9UgUnahXWwmiDNDVDsFbyUshOT4MBqTdBLaWow3mOtKjYYYJr9ibrUJo4cYhyGDJolNw3dk02GR2zGEbRzTgytMnGX83CTpci5csxT8JfHkKa0TEnRaUzXG13D9QXxDm8A85dhxYzbiS3tN0l2zWrxsOtVAqlXeIWchusove9rJOctnyrP3iVz9Aua9wKV7M7ctdWn1S+tVBBSB8EEAPy8qikD5QoCKYZpoHAZRPJAC385rKsniiNaysP4gkbOHiXw/UWTUufiveANYDTTF3J3kj9BIFP9oZe43MMHA2nCPgTC9uB4aZzAk41MNDM+zxgu2au75U7CPNGQ0WWC32dvk2QP9Zer/s/cd8HFdZfZnVEe9d6tbsiy517jHJb2YFEgHkiwQ+EN2l74sC2R3ycKyywLLbnYDhCSUENJsNokTx7Hj2Ikd915k2eq9d43KzP98b/SUUbMtW5I18vf99DQzr9xy7pt555773e++WY7Pp+RjWQ4f4CQyQ5mh5JE0MOchTchbK0ldYwHJEr1HwkmmZVjaCHU25BUTa6cny+9fBJx7mlEi2KGYyv5KF1V0Uc1r2DSy2pyVRR6u/uNRG94dCGF5mjc5OyrtccA1XwLSqYQWnyPUbJ+JaFKuohKWjPdEbDxfB4JIfA8VsNNlnY3VURGXpT6fr/5Ot2e5KS/PJAVZNZNTDdBSzNEVfs09UIdOxqUbqg2EVAcE+KG8PhxB3kWYk96MhKgV+OfNZfj1I3n4D7bht/+HMbTZeWP1L68je3lV06sVAUVggiCgBHqCNIQW4/IQMJVmiRB35AxVpzpgQ2kKPsqg8+LqOZSOSHYllNyfKCVlks2s/wQJLk928eE8bwnEZcNBRv7nP5Md8cl85yOMy0U5VDIUojvaJjHktm4kOY+B7cffwPtNNfjg6X/DM9aXsfwaKrHGkPTHmQp57mA/wE4FUaIdDHQhMM7kOVJUGZ73pzLKkrudiZeLxFiOCqWiyLocfZYQhbHefC+QTQSTRVR6eKsQYvjz1cZRD48MthnZvQ9vHXF7nygmZFKKI2479bx/FqezjIKj9ARcjfve4mDLHHYaHeYoievx0XjPglSVE7OA4MEEfoTpy+Tgk5UWtNgcKOJogAwAeTOcTBf9oLx8vViH/j0E+ezv74dO7xDYeG4Gh2ZKWhswa9V9+MGbP8SvH7Xj/lX0jWbf+e8/wzKyk3RZo0EjrI+erggoAhMPgQnyyJl4wGiJ3AcBY/iZhPIUH77PnUrF2+GLYV/zKUqslP+iOO4qjKWH7OAPzznDTtx+Oz/zKTlIZhumzqI815KRv/ZLMog1wKKVvJQsTtw+xsKkQqXFlPyocj/+debFskZGo+dL38Pf/W8RXv/r/chI4fLEooa7mqUTLWfp1/wui0bSIKSoP00gWWLSwpgG7ndNZiK/l+LXh9CFfBoVXsLjS5g6SlhXqRZ/zSZCvYwy9BLTFhLoqnyGslvI2zHZWWZR0ieCSTll8aBquVeInXQ6Z7NvKSMS/Qg0QW+hx1JJfRpmzY8eRD5Hsy5cYZtKcCDb0UDxkpMWfhxAnP2pGMscXq5dROW5hkSa3yUS6KFMongERUTjWAWQw/vr+dfP4qGHV+GNukfwxy2/wYPXOVDJy3/yDvC1tUzflz8jA76CQ6Wr+xQBRWByIjD0L8nkrKvWapIiwGAAeGEX8ETd3VSbbyHBpURrzBjk066TxJm+xNjxKslzMHD7ej71hPhe5ANalOduSoiv/BJYfgcJNJmQyLgyU+yijQxE1G9RvAeS3qHSECZ4YgewjMq5P8eey/lE3/osZ89lomzt43ju7aNYf/d9VMCETjpNSuPlXYYF6f8Ja/SbKPgTSRGJ0UT0t+0t8iW9iFdMOt1YpE+TxwmQPgJB76/YSFrkkjIf4UVSHivL2XOK2wLecWnckTvCRMbodFGeq0mKH3vJB8EZS6i62lF37gD+77rWwV8N1qG8jFgHLCC5tbLjxvt4jKyK7RkQGjK4czjC/EQdTo9yIIEEur2I98sKdmDoziE3joTFExO/5x4GeO7haxf9f2rr61BZXYN23mMzA9lpqD2I3z37Gx6z4x/2eCM5uhN/y5+Pf6gGfvwXkmj+1IQxfemUnu/ek2Mi2ivZNmDXf4rApEGg99EzaeqjFbnKEJCh2gN5wM8LpiJ9tgfuCjyFtzZsx5G1X+ATM4xo8OlWXUxFNx/41NdGRp7lWv7hld/T35mTBKMSSWwPc4ZYAjf6EFyU+wcT8CLhOHKA18Q7HUxFvR7WeL6sSV1IefXBr1NObgb++/uYWvYRglKycPCmR3DSNxOL7bP7uQJIMXu6ZmEbJ0jekL4SnunF6DnIpEiUJotJHZtZn6gs1pU8z5+krlt2TmCTuaQVvD9jqO6mZHNBle28Hdinu9JuHBI58U/vchJp1nIsnDOD7j89yOs+hcggAjuEqiqh3Vqs4bCyY2qzOU8Y6AYx0mYQAhsSEoIKX3ZsZQ1yfpfrSz3glxA00qT6zpdVPWWT0RkPfs1kHq/Vr3eEoqEVp/NKEMSVXNraOtDACDp2ez26uKKMl6UAaZ61+NsFHViS5ux/v/ZYJeNiv238Bnh+kulQcbaQXH/vHq5W+CLwJDupGVO58Aq/1l5kyUORaHGX8iXWMfT2iufPkSzIItF0RtT/7qudvlEEFIGJhIAS6InUGlqWkSPAB9LGwz5osPXg//72ISxfPgd379yI5c+8ic5bHnCSgb88z8mDNzvZ5EjUM1Gqdr3KJyBnDTU14MFTGzE/Owwvv7cZHyTnAAuu4xORT9RhjexOvmHv/gZ31zTjuN0PJ6+/kTOb+NQdjkQbLLGBM9FC+NS3MnTIm1jqXYMQLiyxbdv7fIq/hoTbroM3n8wMANYvZ/ED7+BCETV1qxER8zya+h/ud647fhD1Wfog4dwq80mmOTAgS0/zFpiwJlQzlISp4bhz4RcLyw6WfUDTjWv5RX0uqwf222ORPS2DgzSdnEfr4OqbTQjibTcIUAIcQ/JXvWk7jibEIz4m0iivrKrpWg8fhoJz3WHhPXq+1TxFCa6ta0BQF6Vw3qvy1axAIKZaA0g0GceZfhg9Itte5H3sVHmZCC9oqKvBMiG2HHzqpvLcyb1/taYGH5b8CCWldswioY2O4deM/eCwWRzcYZ84kATZ6DxIErRQqtBw5fJyo/GYD7+W//gQBxNWM3JlFePIF3NQSjIYopyCdZucw85sGPsJFMWxlqMRqcy/NwQ1L1RTBBQBd0RAHu9qioBbIiCEkaISdjT7YenalVg4bwrr0Yq5i5Zh1VM/wTsy044PUkTxSTmF8h9VqYs2GZdtaKS8LU++SLy6Jgrrb3uQER888egnm/A33/9vPHM6jhMSSaSHI+Ui/+blcTmzn2NLchLWLV+K039+AfYvfI8kRZ628kQeYOKbwHBbSIwyCL/Pe+8gKycb/sGhOHX8BPL3bEHZsnnO6BlDXU4GYJEweUMcG5CT230U1a4tibDQp9VCgd7K5nSHaoo/blUuIzisIFGbyWgXfO9Hsnalyi6+8adKSSyDM+DLD6IkixqbEt6DAGI7aAEVksbkRJLGG0/i2Q//EXu8EhDACXcORwR9ij2cfvVyN0XIPSskmsZbv72NfUCfcPpXk8UOqi1VYjLe3CPv46kH+T3l+Z30jEoI7kRT/hbU2rw5SbQNjY31hqJspHmBf5GRHmhurkNrWyuiPBux7l5WhUm38D4RHp6VzC1JPjAh88lnNoLs47n9TI6Zx10PMAn57clK4ZYK3LJwmPN6rxFi30yCfZJE+hAHsH7/PnAPr5nKn6sh3Trkp0FNEVAEJjwC5s/IhC+oFlARGIiACF5F5MfnkuZi+cxZnCQkTx47vLiIQkhQ70O76AylJD6pZGETCdtwsSYP/f0fknhn4rOBLVh/+92M8sCnPNMPCgvDE199GO985WUUp2cNqTwZ2QhJfvVZ45qGwgK8ys0hawpfeycwnUxqqEmIQrqbqUDbKAU2tSKO7h9+MhOKFsGoH4UlJVgycx6VPdLkgQ9846xJ/I+/VlPZX+mycfXpE+zXsImG4jcTDQHpE/mSPDVXk7elkVSKqim3otxO42zyDengffNBPvGbwpEVmrg8dJCsxkWRRQ4HKPtki2dzm9WNhpZCo+gt9C6SIDSmNZMo8s8w6X/K9IP2ViYpaUrGrta7L4r92sxYHmD6XJwQ37lJXCteNci3TD8YeJlrEgPfc+6hEX5d9vvzWpkYaWNdZQEho15SVrOAl/vdkfKzzBdjUodgdpgWJ3HLAFL4c/TWW5wIm+ok+APTEEzFVcSHnRmzuAPP0c+KgCJw5RFQAn3l20BLcIkIyAO2rZYXR2Sj01bJN+bT3ItDqnxsiWTZU9wbMHgET0x5+ssyZvkFQPYsrF9cT/JMAg5KaoZ1YUpKHJYnd+IFUYs56WkQ8xDn15JziK09gRmrr6Xv5VkUF7MsnWQU+3Y7leve1Aa9WFhWkVmpoBu+lcJAuAUFBMCaloyQRJmRNuiqSb3Dg0yiicPtXskkZVSfQ9gUV9qP+GIBl9uplYMZbQV0hVjEOiTwtqQKLX2lcTeWxUbsinN9EJYl97STQNva2xEjgbTPZ72EMVT6czyV646c35jXBU2yNL+2fO9DEh0tvN7pJXLBy/udMETxfUhcvYm9xAs3WP8Q54yIpffL8BI+8KstLiBRN/BnYz05uFn33qREA2hl56onj/7gJ+hBwnvEZa7wJWSolygCisBYIaAEeqyQ1XTHBQGLPICSI/Fubh5quWpKTFIoqsurcMpBUivL9OaW0FeZks9wbhZDlVLijH34ATCD6jLHWP0DRDIc8KQjg4gK437GikU4md3AWUEiOx7di/ksWzpJeOrUDLz99tsoKiqiz8nLjCN9H2VJPkn7MWE+PY3hbl7LkHQyC6rb3mUohKIStjQ3U3XuZlZXny4lSmIqfVXF7bbgOKEhmZso4eCGuoVc9wlnk5BqDUfJC0mgA6bSrYAE6UqZMZEtNBh+jO0m7hseZPLtnFRn3HoXUyjz9hv4lbiYay90joA1FMm90HWux0k6C0qBXx1w3iO7Koj9VnZeSMwHfnWkExbGPq2XWSfXdC7ivfRtQxOZD/u7F1NuuX/fO8n+86r5qI+6y/g+u2Zj50zKAP9STJn9LILmtaH8Ff6MccRlXEm+a4H0vSKgCAyLgBLoYaHRAxMdAXkY+on4W96K6iW34Ns//h2+8pl78eyf38DptNUcqyYJbSHzMsJWXeRTWWTtFo611+/jaoXfpA/0CTQ3ibrNJ5+LOezeOFdJaStnKPLMp3JdFWJ2vo64pVTHOZbtw/HY+fPno4QqtL2u0LmS4SIqyQaxF5mJjFBCSxxgvtu3AZ+4wyDnVUWF6MhJhR/ZTWVlJVdWC0aAn/ifuhRmsr9lXXuoJCLTKeBbi6ncETK3Mt4+siKeg7dWzAxO4nuXKjoJ6JVQ0eXW6WSHzEOk8T7rQSyV8YshgX2XuL6RpMzN3C8ZXSIxNZO4pFfmGcFpD48sdhLoJpLpm2czYgbrN3AahBS5oY73E79+l2ICoUzWNS83+tHDfTflPJLh8spEpKc+g/2ts4acg2znCEFkzcNYknwzvLOr4eBPgkS2VFMEFIGJhYB+LSdWe2hpRoCAEOiQMCpAx/eiIe2LeLa9Cb9/+i10p84jsaVcKcFr42U8eAQmZPvwds74msOnL8nx1CT8fttW3Hj9CiM+rVOJ9mZUuoPY3jOV5FwY/IAnpkh5RzYhi1lb6b8sizf00LExiou6RERGorqaLOrkO4x/lUMnbrKqBpbzdDlJ+xmq6VS9r13LWV4c49/2B7RXFCHvXD7C6HddUl6O7PT5CAyMHEQERlBDtzvV6CjRTzYyjuvZ5HOOJeELouI3APUJXS8pqz9ZVgmH5ZNWcdAilWTqNHdegV9gcnlY2zvoIdTNyYwEstcuqVMmHRlJkMSwjv2/ppZeHs39gRygCeVmzCsUtVq2cTJxfQgiiZalyaNYhlR+F1Pl81CEnvfWiIxE2OgsSL3Zpp0kvJKsNKVXAP/17h90g3J/G/vcbxWnIHHaLEMNN6Zt8BJXE0ir7Qtwtuk7mD3zb5FLJV1NEVAEJh4CV+Dne+KBoCVyTwRkKDqNvpJTbfXY18IneM5N6M5cR2bFx5kouuJkakz8u8j6icxTR1ZTRJZzx9eYBhVsSlkbghfih//yv/i7bz0MX79A5B4/i8d//DKar3+cD1I+TV2Zh8xsrKpC2JZ3kL4wwyDOZu4yVB4bG+sk0FXHGKHjEGdAnnP2AtKTmV8USf8xrOO+M2++isJqSmO0HTt2wJPpStzcmauvhT9Xjulkda8mcxAeC8lQG2ELZLOy6d3O5LbsPMvbciXrkM3Q5LzNAnnLjWtdmJk3cQwLbUUrSXRokDC+SzCWW75iBXSP2Mg2OcevjZX9zQCSaMPYRp7h7DC0cFESZnH9TH5P01l3XjduRFoIu/wUsM5GtAu+v+y8pb26GM+7Bth5kv3eU0w/mHWlN5aDdfcmmV4wDVgzl8Sdnft+kT1YHi+OpDia8tDeUYnggJhh2144ut0jGZZovpEPaoqAIjDhEJCfMzVFwO0QEN4qw66vUZ05l1/Ap9lLHOLnOG3CVKpOnBwl8ZkjKDvVkITKA+hCLEUSlGt+8wrAOMvw5VNflv/u4oWL1uFf9lnx0l/9CtGc6n+omURu1aPO9Pv5Vvc+6d7+FRZF+cAvMKQfgRY/Zol9K0Q6sLAYTRIzLC2HpP04Es/lYd6UMMy89T7MnjUXmxJm4Jkn/8ZoFyHOsiXmLMIN6z/ljDnrdi12aQUWRNu5ZdPtwcFOQwVF+hD2US7UnJeW29heJfNKbWUccKimOppK8kzCKaRrPKNxCG4BflywM8eO50sqkNAb01lqLl+BizLW41AJ8MxmEkKW/+Y1wKeX8ztB8ihJSH8ylqqv+PvWkUDvOAr89j26sLwPfOMWKvAJPIlftXExIdEs11BK74jzZ30IGX62hd5hrOiNs4BbH2RdOeAk/WZxDynnPbrhPeDxPwGfYUfpxizmIqD3bjKpMcWrgv3mk5g3J2ZIF46Py8UE5To1RUARmJAI8KdQTRFwPwTkgVjZwIlChxOxauVCtJ3YivKjb+OUJQSdPimUgfhEn5ZGlkK20MKnuMSolbhvhpOiPJj4ZOpTjpmYqM9vv8TArmQ1GYuc5NmExcGn/eIVyJu5EHkdfEKGBDqZgkGeea24fcgTVKIYnN7B0HXPwe8Tt5lX93uVSVsWruaWsXAxil77HRZnXYP5y69Bwv2LERHOJYz5wJciLrnj82hjXjte/ZUxU3/hnetxy91/zZB2CYMmQvXLYLJ9YFN5cejdksi+0HFGfiCbvhJ+w6MCK28VO29F+1mS2CXsGLBevnmsG9Xa8TRZ5jojmkT+w0NoykxFWEgQffR9xW3feV+frzC8zTdsdarOn7+R5JFfhS37gT+8xVufqmwX0xa1N5XqawK/cuv4VVqxkC79q+iRdBr4/nPADz5DT6V4ZiLkdiyNeHd3MHwg+6n+VmbE79UlG7/i+UVcwvtl4G72r9fRS6ybbbmTdf8f7i8q5X3KxGfHAauWMTb0AuDf32AHgpjcz5+ivrxZ57mZDvz6ow+wcMG1FyDQl1xavVARUATGAQH5zqspAm6JgPDVkCkxSE5KQiddI9LoZzyfwWnffvsZJDTsQt7GHjTS3cHeRiU58xo6ZJIch/FJ6kF5zMpx1+AAZ72FIG95lco1GcTNn+eTkYxmIKkReUlWv5AnsYzFy8NYwkAw/Jfhr1ydT3m0nAF2N/CAHQ1chCU+XqS2j03Ic21tLYeAu7nwy134m2V30iXEz4hdK7FfJb6xacFBfrjzC9/E7Y/QlYTmyQUvpNMgIvnVZBKzOJruDuxzoDaXGLEpxQXBHU1uGYl1XExFNowEOn4aCRbJ9HibhE5LI9F7IKcRLxw4jHVrVsDKEIk1JJvnNbaBkOV3TwL/8lfAi+8BPyJJrKgYfNXB3l3/SWIdE8tVAFcCX74DePhTvOYvwL99jp2IwZeN+h5+U9HFASkJinPJxt+CllbgH9i/fvw2DkjxfjzLOn/hGWKxe3CqFv6UfHEd8KUbgF9voetKJK/J4Xm8l8WlZHE6O/4f7TUmF1vol9TXjx+clO5RBBSBCYwAfxLVFAH3RUBCupkuDjIGbXN44ub1N+LJJ7+JVvpFd9NZuKOt2fA7LqipRSmXLiwqrkJZXTMqW9vRwoVNbLVVqCysR9t1qznevIfkmAzD1YTdisJsmoVPQU9G5uCiJgEnTyOVT8XUcB8Oy+bieBnlKFoFWUV2Np+0vSZuG/X19SgrK2NSHsjIzIaV6rgQYkaqG2QmR/foXdlNijSgVIOumXQ7yDi9OYDgO5X9FBIYEFpZHMOtjZ0guXXsVey/CRF7h4MjvJ34N64m/cG7SOIPvX4Y77zeAYtfEM62kSlKwO2hjOUuqgeeex948lGupvc28K3fX1y5K0k2f/hn4CWSzVceo0qbBvxlF3DfKmbEDtFYmqjtEfx++V5OJvzqP0sifDvba1GW8178/NPA1n3sBDDEpTc7t01NTcbvkGQjhPi/2a4FvF+/8wDwNOuayk5EFPvv0vGWOcahfk1cMbEDQf5KoC+nafRaReBKIuDuj6MriZ3mfYUR4HMLDQXFqJhej3C6VXiSpNrpVhESGs6IF0ncqA4bxqe/IRkLOeATzNj4wo8tLZ1oa6lFYWkrHn3km0iIT+JROcdpstywrd0Gq6jPvWPtFnp6Wq2+3KwImpMKb19fHvJEFeM04xyfmrSzZ89iwYIFCAkJMT63U6nevn274ROdkXMjIhPmXHVqsgHECP5JJ8JG9S48gdEdqD63cThc3MY/bp0RJDZBTjXcT3hb5h2jG8Ua+gOTkDUd5q2Yl6E5AABAAElEQVRFUjWeJm5Cour/3fV2nMg9iTqSzG0k9o1tHNWRsgwEmft++y7w6I0khiXAL//gHKSRb5Rp3t7emDFjBvz9/Y2Rlry8PCMCjXk8l1+NR37Fle2/CrzwOgd75jAvkaFdEzFPHo1Xfu07iLU305ev76A6XUwexOhAHrCnnK4an+EFHlTPNxGrA1asu24F0lJTjXkN0mGWOO+trdLTc9p7XdMRu6se2cEV+M0HwLepXksvmEnAV+p80U7nzvT0vyKgCEwsBJRAT6z20NJcJALiZykR6v5xeTWe2/8iTnQlIJrLaveQGYRHxtCPuJMuD8IC5MkpTyt5bxLpXi3Xw4FArrEbGJyIqLguRHIJtIys6VSQ5PyPTSb/ifuFq8lnc5MHocR6Ligo6Dulq6sL27Ztw6JFiwwSsX//fkN9lhOW3n0L3RAsSqD70Br+TSQJpjiXVpBw+rPD1L8Vhr9uIh/hAAS66caRT0UXBdyu0K+wfIdCqPCvnE9SR2ALXwH2nqV/7wyWiYS6z/i1kb5hK1+zkoCv/9J5hIMnhsn3IzMzs6/DKKMtErpx1qxZeP/9943RGDlRvn0n8ukrTTeQ7Gl0B2Fed5FEjxmBZtJt/KrbqPwaaxbx84iNbfXG+5xXPJP3H8n+8TPAL14Erl2zElnTMo0OsYyAxcfHY/ny5XjnnXf6lGgLZ4seCb8B80L/gOIydvbZOQn1J5Yk9cfKY7FYJjurKQKKgNsicIV+ut0WLy34BEJAeO5SPoAXzujEqYJ8nGCQ4L0lXHywIAmfb66j37A3gsOi6IMZgykJ/lSDk5GREYSY6Cj4+tD3mE7FFj7sPcgeHCTewpH7SLFLPU3y3CPj3r3WIwSa1wgJaWhqxtGDB4yFTszj8lpaWorXXnvNdRdiMtKwcPX6fvv0w9AIiEDXSFU0nKTFVkyeyc9CwtzdxB/Xs5beC9WsDwma1PNKmSjRNpJliZhx20pOfKOrRRSJ4uzU/iXyowL91evov13AzkwhfbelzLxWLC4uDqtWrTKU2D53Ku6XuOfr1q3Dyy+/jI6ODuN0P163+zTw2L3AH+kWYRBopj1i6837vNcRW1n4M4x5erGjgI7znj34IK+vYSenhuW7kQRaiP6TVJ+9IlORlZHeT12XDkN6ejpyc3ORn59vpNXKGYSzk1KxJW8FvI7uwAeJ7Kxw8uEP3+REwlvugj9XSmU/W00RUATcFAEl0G7acFpsJwIyIUom183O4LokUznbfy6fk7Yiqj1F2HWID/xyEmo+APOooDU1eKOHrhY2ul70MKZYRnoK4hISkJqajtSUQJRW1pJwVxjxcUXJNk0Utk4bfalraozhVz5XYRFJzqcVwdZmRHi24oEEO14gIcptMK8a/OrjHY6HvvsUomITjYAgg8/QPf0QINCOU3Q1Jx+RIW+7AD9ZjPfsZU1sG2Uc5HuUHAHcy9Bs//YcfX2XUm2OJObcL7d0MTum8rDIL+WkwBj6AdOdxrSZM2fSD5jfLZkr4GLyOTg4GNOmTcPhw/RToYVwO3oSmB7NKDpUYp/7kESb5H0kFsDz/UL7+Puwl4q7jIQ+vC6Tp5hy+bBnD3GA1+8qpJtNOMMOEpszxODlHcCy5ens9AwelRLlfcqUKcZIlNnpbimrwZqv/BZ7Xnse/3X6Izxb7YuEm+7DomvvVPI8BOS6SxFwJwTkN1FNEXBrBITqdvY+ICWinCxOIetDpNBfU8i1eHKUNtLfubGLoeG4OTrQxf37C2oYBWEfavK49gmf/ct5jaMkF9OsDmTH013RhQ9YGLTDn8SBlxmbDL5ayQYiuD+c14nNSmWYrv/jEHUdR8BJ+Ezz5EX+iSn4/N//L5Ysud5tH5ziemCopR/3LcwqOkHhfpm0NZomkwYlSIrbhq4bTTDGOC1pu+VTeR9zwtt2qv5v0m1mGu95GXiJIWmVez91CjujgfRhPvpxYSIYb90kjB/vdb4TUimraJrWyTc2fq9k5OZbHIg5W8z0h7qfzAsGvvIePMZOcSsJPJM+r0kesoR3VhxP4z10KZZMLObI9az8b7bwd4YVsAzjcyLqu9TVlVw3cOJwfGw67vjKE4yT3QFfX2+6y3hSvb6U0ug1ioAiMJEQ4ONJTRGYPAiYrsryTJaV0kyLDiIJINkVAihEQLal6SRmAx7edMygawfVtiEezuap8mq85wNaHv7tvcOwM0m6//g5KqZUvD4qfgAVnYt4Zg8foDEIy16FuCkJRkxn7nQrE6yEyFY006WCqqF0Sgaa4BDoy9i/7FQQlqHNAI2H+Orytu/DsERqiPyGzmBi7x3iluorsHlf9u0Y4RvBfFj8RpCWdET96e5w2xxnevJdEDPbS74XRYf42dzBY21cQSVUQkQOYUKs5bhpQqC9SaCF/GZO4ZbEHQPb1yVt87p+50hlXTq3fecM9UbSlvRG+KSzMY9qkvQIllM6wCfPApt7Ow0SSUdU9YEmq4WWMDKPEGnT7MFBRrvY6T7iw+UKJeLOx0fNs/RVEVAE3BGBEf6suGMVtcyKgFPxulgcRLmSbaQm13j5cPj7BmBKw1qc9nrYWLpYfLVlKNwdYzgLWZYl05//iKrkfgp5H3OhfvAYnId1j+Vwt5Arcmn481rhLyLQSzr+VPM82YnJoaIXRRXTk7hQ2ISVJMXL6pzQJhdIfqLQuZI0nua2Jhh0sf1b7b7wMMIhOtmfQxbv4UEhaGeqkzlKEsH35o3nQXw4EbaXbrWHRsHBuOM99PvolDhoXBTIizdcj6yNbW/FfMcmTI1ykt7LBUqIeKeziINGFHrYVjMSSIJZZlmkU+z48eOGH7Sr8ir7RX220fVJonGYFkExegk7mi9v5h42vnTIjBCNdLWQmst9EpfkJNh8a+zjrYAyKtUSA9zwGednItCPU/NjP2Mx0cjyVTMRqwwX9Za17yTuby8bWpj25THpKHSS4Pd4x8BmX0m+bkFrIGV5HDTqM3v2bERGRva5rUhdJdJOcTEL6mKp8xc7R224b7Lczy7V07eKwFWNgBLoq7r5tfKjjYA8JLv5oO+klNcpBJFEpDf63dj7vApJ6CU+o1EvITCS5HMkz3vfoy8pmbCsHePKRYSoiBnn8oCjluSHnztY91Zu/EMjy2TjMVnJrYOvH3CT/XKe4d4ifDCZC0ykkIDzFymEZHpqOt1wSMilU+LuxEPU5W76DL3ecBsqfOPg5eiiS4oHvLnoj2fvWD7Xp+Q+QdFpFjBmeEQ2Sn2EFdvhiOQxsta4xrOYn5+HnpZ6+He0oc3bF6VRs/AWbsajXW9CJvuNhhJtlmPgq6QtkwwX0D96V7XzqIRsjOVCRhLCToikmDFvgP4OBw4cQF0dfZp6bSVdQr50N1VrKrI2MuOj7JCJi05ThZPMCgLFfG+a3M71zNP1HpBzwvlPXs9n0olLJh6hMoGQabiapOfLjsAMkvlBJvkx8WiWsyn6c9jb+k9GyL+0M7vwD3cu5/e7G2+99Rauu+46REdHG5fLJMLdu3cb8ebN9CKSEjB/wU39ym4e01dFQBFwfwSUQLt/G2oNJigCQpwdVU1o/4+3nNLaGJbTQabpmTMFfp9dOiq5CN/gIo743S4uX/wusCZ7OmrmzqX/djdKqbLJAjZdVBd7GhrYSehBYEcrPDo74E1SJ4p7MNVFiZohal4cSYw/sZD3vnzli9G5EFItWzvP57xPlBVSzSRjKuXmRVeQNVmc1LaWJJqfpTzuakI6A/wc+ITvBjxb8yn4tHQjq+EN+HeL7CpdCUHE/G+8pdJsx6+mLcWuadNZeZ5j5TlcgnFOfis+t+tp2Ni5oCstLMQmsfwMdsfdjc229bjNa6PRMZFUx8KEePqxg/PIShLoV5w5iMvCzp07jQgUEolC/IBbWlpw6tSpfpFpAngf3LuKSjIJs/BsriGCZewoiVlmOOs/sJ0FGSc6xml9/+S8gef2Hex9I9dJeQW+oUyul8mTg4wH7LzYcKvhBAoW1RhBmpa1GPd/80f43T9/E42NjdiwYYMRvk6U6MrKSiPqjpmW1O+zf/MEIuLotsUOtZoioAhMPgSUQE++NtUaTRQE5EFM1bA9mUzBeAyPXcEclPF8Ir1AnjYqJuT5SDEXzNhK5XnddfjBPz5hhCWz90qBojBKaDJRF4VAiZ9rJ2NyNZJQN3JVNjlWwhhitTxe39aKFpLumnNnYWf0Em8ymnASDCHZkdwCuYVwE7cAKb4Qn1aSrPf3MFwayc+X1vUq0aNSs9FNREiWqOiuLM/4yH/CjQ01mK/SCQjx7Mby7s3Y6ncnqm2pyGk6ZqwaP7BEMunVTjwCrE0IbChFdkM9Quzt8OHn1FP7YSMR7ZZMxPgaiHbMqvk/7PK8E7aOm3BX2CbDj5/ZjolJXRamkyAu4Ap9+5xZiK+zkEjZhjIr6/Ovt9NHnsq1OdFU2lpcWwwzX3s/TsSXHvqv3HDXl1F5ogabX/1XI4xdEe9x2VxN3FAee+KHWHrbg4bbiesxfa8IKAKTBwEl0JOnLbUmEwwB4ZqeoUGI+uIn+hGsMSkm8xJC4hhSUhtZjl4kO8V0xfjq81SMk9Lwnb//DqIZ01cWh3E1b/rzxjGmmZBp180cxu+gQi1D2xI/W8i1XN/MldpEwW4lyS7na3V5OQ6RgHhXlCOkLB+Z9HlpZ0UKKM5mkCge3Au8Rr/ZO0jWRqFqrsUf9r3BTU2C2nuWEYGE72VUgX+GyWszXRGq6cfb1UJVnWUW32Fyf2Mrqefks0oumNNhRX2nN4KCuhHrX4OgyIMoSFiBkLYGxPeU9PO6kWzFfUBI9IO7for7uz3hTX9nT95MFlnthE3AXf2sh+fHdDdgec0m7Ipbj5dq1uHu6C3GCIBB4PudffkfJE1Rj/96NfOlf/Gf9nMRlo8X4BuUwTyOJvzVdeyIUUwX8u2uJvMYfDjD8jMkx6lLErHz+f/CyaOnDHckqZPV2wNJs5bhxse+xLjYd/DeFycSNUVAEZisCCiBnqwtq/WaMAjIpLgLjjePRmmZjxCwyzGZPFVPMvT91+mzbPHBc1SeJbbtQPJs5uEaccDc5/rqRZItm9VHVHgqzhzeT0tM7CPcMk4u6nUDCfUO+pDm/sM30MyJctnf+wHK6Vub8Iff4pX3GDElkz6pQU4l2khoFP9JnWXI3cSugwzYLt4VJExCFmU7VERXEw7F15cyLjIvaOUFTaxTpS0Ihc1RaPcLQAsbuSE2jr0OEqdI+i5H0dchjQk3sjdC9RmHzkp4FqT5H0TWbB/4pq+FV9lbiPWsNEizKLMSBUNuF1GPPZu7OVmuGwxZbvjPMyV4EEY5LpuYdNLERUFcDiJs5VhWuRG7Ym7H5hIbbojbMWZ+9+Kb7seyfOFa4JbZwKZjwOGP6H7D8vPPwDKVHZ919ChansjFTPheFmxxd5N7wouxMq+/48tYseITyM87h1Zx6KZFhgcjKjkHfiFBhpuKu9dVy68IKALnR0AJ9Pnx0aOKwOUjYLKdy09pzFOQ4ecNdJ14rxD49re/xrjVS4xlyi83YzNOsPnqmp43CUkClexVzCs3aSq68s9gZk4ObrnhBvx46xZEMQTDhoPAF68dHQJtul1IXYWUFlZxtTlubWynFhKk3fkWVNf7o56rdVQGx6A0OAKdfpRRLQwdMp+SayA3iaYh8d4koHgbJWhPssNysmvx2ygmePtOMzHOsnMw9l872bgwXZFfefhcixcKPtyLGyIi4Z24FLWHNqCIvaxyqthnCj1Q4SBBp2NGEJqRQifnKbFUNyPJx3ltELMTd2j54ZZV/QJYFB9GNhFGHcrPsSTRi6v/gt3htyKyvg2r4vcbqrgUy7wNR0uVlirJRMA4QvPwMkKxgFV0FsUg0KLaW9mXELI9Gcgzq2aY1FsigniHTUH2NVP6hiQkmojR6ZIehJoioAhMegSUQE/6JtYKKgIXh4C4bmzeCfwLtwceeBD333/fqJDni8ldXDzCGEu4IykF3iTQuSdOYN6sWQhZdA2C3yjGrgOMTTwLiGe4YdOH9mLSHXiO8F4b+e5JuupuPumNYosVZ9vSUZCZifYgMlVZZm+BN0ky1eMAsj8rSbM/pe+yc/QrKWCQb5LkE9zaGT5CluerbyRrGqm02mmo2tu3vIOQ9Z/AidC1eHvbVhaVTNMwobpdqCXlpXaN/cwOsrmYEH+W0CDUMjlPSLH4k3uRUId7VaA+cz/aUIxTbMvgePosJ/Nc8n2J5x3I6khby8iIcHohuJdjZnt4UpFmsh8b0xdFfdIYce7z3+FbVk88aj7umRhDBLLjMk0SZp9LTRFQBCY2Avw5VVMEFIGrHQEhVoUUTP9+B1eiy5mBr3zly/Dz8zN8mIdSjccCL3/mF5WcDHJbVJw5Q9cEOxasXYsdG19CFElFXjmXVY64dAItbhqtFIR/8KI3Nq64Gx7rZ8IeHonw8DDME+ZHadqDTs4MKMcPXFKHL6fpH1HHlSs9okmuIxmybL4D/pwY2dBBFl5FwMTxuZJyZFeDrCFPKbuOJIvHqnmsjOSakykpUXMbbOK68u6mN3Hr+vVYOHc29h6kzN5Hol2digOYJhsompTZjwyZodPsZL1tfG3zEfbM44y2XeDHSkSTxfrzMwMu7+KiHkaYk4omlrEWGadPIpGq+DVZjUjkKUHEIy3ZucCQwaGpYIsZtec/89W598L/Ba9Ja5SXLUfLYWlgG/fiNBZ15WwCdPt3oSczhckLI1dTBBSBiYqAEuiJ2jJaLkVgnBDw5a9AI4nlLzZK1AtPfOvRR2An26xjRA2ZHOjjzeWH+TnA3994Fb9nIdWuW88ozA6TdCPj41FCItZcWECl2Y4Z2dnYHBmL+PoK7DjDRTgySStIYC6Fq0lYvY/OARtv+3+Yf+taBDJOcQPz8KR8W0oGWcRUk0hgKdAa1CWcnyl6G5TWYfh79OqrcbGwEZeW9KkG6ZaTPUm86zibr7BdCDNlVyHOHSTWMqtQAh3bSKK5gp3h+lFRQfcO+muUtKO6pRNvt3Uh+LrrGY8uiSSdvhqBVL1FCReyLBWlL7pRaQllIWvVW0mkha2yPYz0jJP4WfYJE5ZXcYyW8olJmBDKzWfYnmdYvq1NLIuQ68ISpO7OR2xPMaY2c8np0E7MTGEnhS4ZvlSrpRiyuqS4ZUjzjtckTinyhDK2r0dzG+qefxMt55o4mXPsGLR8p/xjfRD8949wuGXs8plQ+GphFAE3RYC/xmqKgCJwNSIg7gzyiP7gHFcafJsiKsXTNR52HPqPn2D/f/8SXvTRdZCwdQUHk4R5IYyLZfiSvEnc26CQECPer6jGgTwuC2lYOXnOeOQbSq4zMoenyL60gaTb2Dngn5wTxwmLosOWHz+G2tpaxFFlDVy2AgFvvIQTJ0msyTNDSeqEI47EpFw2ctqNlQlIvzkbwRIhhKyQXNEw0XBJX6l+Wwy3CeGhp521QSrfEwlyUwtdFISkknRzX2i/+BlUdLkvWWLxiYeyDz8xcVEUa7iH0DKsSIb8H2QSGpD6NeIWLkQsX+u5Sf5F3PqZWWnzVaKiyDacmb4Z5ilBZMTB3GJYxoxk46p8Viefbii7ZLGTkmoq6K3wP3USaW1FSOsoxPTQLsSzMAzGgmwCJFmLGC7NyrdOzs7j8n7SGutnt/oh7BufRJg071gbwezyZztJ+/X22cY6S01fEVAERo6AEuiRY6ZXKAJujYBwAF+O/FeS2b11Anh1Bxe04OcMcr4eMiRHUzm65SFeec4gRrLYiRAn2ScureV8LeDWTiYly0o3czU8S1Aw/INJqqmi+tMlIiwuHt4BAUhMTUUQCXaAEG1+9icBD+CrkG0hzEIexVVDFGxR38JJzruo5ga1NKKosBBJCQnI5rLJxa+/RMJKsn8auH0OCY3IoiM0UVDbHZGIDgww1G25nNXoM3kfxz10GTb2U383+As9R1zINBV5fo7hGYKjXNOvKAKUWO+rfGI8DkTLvoswSUtIvaTNWCUG3vl8X8Xtsq1v9mBvGc0Ew9hBCie6WST4DDDdZluOY3RHOcaZf3/JZ+5nz8G3pBLpZ8uQ0dyAVK9KLM1mh4HkLogiOPtOhhAu+IpSPSB1Mxf3fqWPkyOSoUTGywzf8UmJ5HghqPkoAmOOgBLoMYdYM1AEJg4CQsyECG/cB7yxha6yFLnuo/wqqwQa4fZ4XM7x4T/ZxKiFGUZheYDJU55bD31+6R7QQ+m0Jf+osYy3LIAiy3mfZl70GoUlJJwsMgZdYeHwDY9AdFycscVTcY5kjOlE+j6Lq0hySgoc9OGN6GhG/rlzWLl8ORYsWID9AaHIZNzk/XnAJ+YxwX6sdUCxhvvIsniGh8CDBB5UoAeaVE+W0xbaImQ+uJcKTuVn2WR/MdGhtwvyDJS4MAjfm4Tbt/d8Vrv3Hd/QRlpU83wPpkKxHVnccrjVMc98vtKjeXTNINbMVdivmDeZsQ8xEosm2NcsoMuKB07Q7eREM3MvqcLPaqvgQ5eU5D3HMT8wHzmWbkwjSKJSe8lkRXqZSHKGQC7ADWMWquPGfeUcqBjmrAmwW+pgNsx4FOc8mI1H9pqHIqAIXBgBJdAXxkjPUAQmDQIy52zjR8CLm4FbyZFCyZWEP5nk2azoUM9vU1w1zxn4KgRUVhSUNOP4Xj7LJryju7MOXcXc6JcgBFPIdSG59wkSswYq2faQMETNnI1oLhceTNeR2Kpm7Nu1CyuvvRZBDCLcERGDaE7UO1RClwPKsUl0FR6xTy4LY7FVw6OLk/sslE7FT7jXpJw2+iXUi+8yGV04SbwPFzARIu1qKb3UOJ41k2so4mMvN/GSkH3kjZzO53T5kCslh/4pcMcIzLxWuiphTEnU6W7mU8tXivFjY5JpX73NWnCfldq7P7X0eLYub5rOnm6coUp9poSYlRzlOux5yMgrxeo5x7AwqwtzFtKlJZ1JyT1GIPqSZFJCmo1RBI6ANB/he86Z5K2gpggoAoqA2yCgBNptmkoLqghcHgISl7eS3PENMr7byfKE7ApxNkna5aXuvNoQM4dISMimqNyyiQWzLLEk86ROnIPXie62StR/uBnl2zcjgeUK4bHorW/gJ6dPoSsoCEFlBfDl/iBytQIq3SniFzECkzqKzzfOVqK8qhWJsYGMMOJCoEmea+vrkferX5HRUWMmkV9y8y3w9rPCYSqzvNwUIU21WRToJG6NJLWE1jhOKsk6WQzyTE8HQ8GXrJkS/zvxNtMxdlzkP/Ma8cPmFEND/W5lPqV8z37F2JsUX/xyTd9qyVF8gWTJyMyVwOrVONPcijOVVXj6+CnM2bkb18eWYN3t9yMqaRorLng7MbAz1nV4YA0Sl/4IgTM7UP4Cj4i0LkCpKQKKgCLgBggogXaDRtIiKgKjgYAQ6GKqt10koBL5rI6MzJ/75Eegl9c6h9P5WYiwUB1z/2jk76ROH6dkqt4mMQxnQSK5Cc2S/Kf5OJBWlQc749rJaoFyfRK52psHuLpdurNsA9P8OPXB7+iqzVXx6rDl3T3wenA9YhhNwd7L+LtJoPPy6B+yby+CuMLgtSkpOPm7lxD50KfojsBMh+kZSP6iDgeydPQkNiyBqImDCL1kcI4bOb9hSdwvdRO8k3g+q2SY7BMbSV3kXFG9hcin8VXSPsxXCrnja1IQowEFBW4BrN3URJLqJBzqWItDeUX4yT++jUdvn4/r7/50/zmPBCm06iGS7GsQNrMaNR9Ix0NNEVAEFAH3QEB+y9UUAUXgKkCgm/xmx1mSvSmpOBYVitj0RJw+d4aCazv8uX53YGs1rGRzsiBHOGPbWag0dvW6OQwk0gM/jwZ8wlFNMinpyWcRJCUKm5j4bguBzj0H/HY7V79b6dwvHO5iTFwI7lnBjsPLz+IXz9MR4t47Ee3ZY0xmNBx2jTjMnFC5Zg3u+/Sn8eH2HTj63jbYb76JhRGCOLxJGQweyVfxXfbj62puUvSWXkItBNe0AuOI85Oo1HJ+EK+T88+fk/Ma879Zd1GlF3GnfJbJj4fME8b6VXwzJLQeFeUISvzzfDwwnTdafUM9PL1tyJk7DaV0jH7pf57HwutWIywk0XDnMIvV4EjjiMLnEZzyQ2AP9wqIAoKaIqAIKAITHAEl0BO8gbR4isBoIdBJybKiJBQt0aF4+tVfICVRHAF6UMcg0BVcR7q2pgBnzlXj3Re3Ycn0cIRbA9BaXYnaii40M36wR2kRLFzCrqk8H7JyoPAck8ANV8ax4EJrqZ5v+JAxoekVkM0ZfBfrCy2E3IOM/MufYifiL7/Hk/9WD9tjdyGZESi6ZbabsegJ/XY5odHGSYaz589F3saNcDCcXgv9sD2ELI7ATCIsrhviG93L94m4czKguHyIYkw34F6zGCr2TH4ywuXx9UL4mlfKq5mfTH68lp8ZsZiTHcdg0iHTNIyN+6O4GLQdPoisoCIG8PBFesbtaGltZ7STjYzh7cCRwzuxIPpzyJsWj/LKakSG9SfQcn9UNc5GkNyKEt6E81HVFAFFQBFwBwSUQLtDK2kZFYHLREDWfmgkRyzmhL0VC+cjOTGCKYoTANXmkCBuMj0tGSuWc/no3HoERDciKi2KvrbxmNrjzSWZu2GX1fdo3VwUpKbOgYIiDwRW5sHP246minI0V9ejrZnRklvoJyLncRJeF2VfUZHFTCVZlOCREEPn1c7/cp2EWp5GJXrnKWA657ONxAwSzes/ezsV34/ewPf+7SwsDz0Ca1a6c51rJuZJJVUmD3rwNSspFZuPnET0umvRI4GkL8EG1lUUanJ/Q2wVH2YhkRwYMOI/ixswPRkYD9pi+FYH8FyTGHP3RZnkJ0KuuJUw4h9JugX7L+ZKo2F6Syuz/GQbztiZ+GZYKK7zsaIx5QSWr/BFRWM9Nm/dCs8eD9x+mw/Co+MYL7wU771/FJa6NsRGR/VznzaTdjq2mJ/0VRFQBBQB90BACbR7tJOW0p0QIO+wS+iBK2JCz+h+MSBvWW1wG1nUkYo2fOv6BWSw3GGcJP+ENIm62kVluRP1XI7aL5EevV09OJnXjI0ffISQ8ChMYQxnWd5bFlSxxCSjIzwA3h5ZyAwog6Rv7/ZEGxfY82ioZZzlHnQw7FlzXTMVbKqgZ88i78xJekp0w8osA+jsKjnL6oBCiOXV9Inm7gtaBPMrPc48V1zwVGPRD1ft2CTRd1zDuW+Fp/DLn34X2+ZeB5wsNhKr52RCWYFR4lQnJMah4cw5BFGR9uW+gVE5Lpz70GeYpFgIsphTdXYu5EIIDb9p8WgQIk1qb7iF8GVE1kuFGRXEYbiTSBg8UaRbhShLj8qTK0zy82y6p6TyNSc4FL7sYEk4wSNN9fi9rKoo5wqR5p9YErep3GYwlvYDSYnY8NKr+MydXvBmByyRoQoDAorRWBlieHXIfRUc7IczudsREJyAyIg4Kv2SipoioAgoAu6PAB9DaoqAIjBqCJCpOTg5yi/2BOy1vdzDZDKjlsnQCRnZOJrhZy1Bncl9eKpwpY9OeuCjzvmYRqb2P0//Drv2fIRpmWlIox90KMlPaFgEwrmgRmFxIUrPnUbI6lUkkF1ITPDDLYwD3N7ug9a6akawqMex2lZkB0+Ft3cPSmracfLVA6jnQhORJFCRYW3wD/JAZsIUxE2NMlbWi21y4Mnf12LO7X8ND0cPmiorUNHaRt/rRnjUNMORdxxWyuMzY+PQWVc6dOV690pdaimvlpOIdVN97pEg1cPhy3PFdbmJsm4oFWtx3zBNSLTYnDTgl4924nDhG/gchXNxqajjqnxCoIUsB4WHI/bU+yifV4vUGK5HKIRyFM01NSHV0ayMeDPYqX5P5eqP+SyHKNKLma8/Ox+yeuJITfKQtCUM3gx+WB0UgAUkyvUNlVyYMBjpSZnwYvqnjrwHb69ctFUHIittKb6QORV59Q1IYRQUf1nGnWUxFlqku0sTMZIwg6LSd9Y5gbXb27naox9C4+fh8LE3MGtaBQ6ctOH992uw5NHH2E76uBlp2+n5ioAiMHER0F+0ids2WjJ3Q4CEzdJJ8kPpMPtT/86ABD3IK7ofLYEyYD/25mffhxkJv4J/51YUH/s4ZJyN7Glbz/W447H7GI+5g2ueNKKxsRH79ldgx84C1NcLYRQS1IFWEts752ZQfCaV7PKAr78PZk0PowBJ5uWRagiRth4LdtdzgiE7CxkRjJm8NhV17TY0U73uaLejvroHhYE9iArv5pocFnx4rASrbrsZX/nyvcxDCCCB4mZ3tKChkSHMKqrwl03voPCtw4jfUzosHxbyzOTxR0q0Z1mcm+mFkvgQkzqPSazh9jYSY0bu6KBizWAbhqBqXtJJbDzpe7sgA5hH3+odjGBXVFTEDkM7OwjesHIJ5zjK3Qe4MuKU6Aju48lM1H4JRNbM83yvPSSpFpJSe24uSrZtQ3nvgi8nWJb2G27AfPpnWwmE3TWU3PkSdDkmXusBLPuy4HDU5G7E4vkl9Ht3oDDvJrZFAJLST2PJNeGoKqrDz369EZHhs5CemsSOVA9Onzxh+IV7EEBR5q0ciQgIDGTnqwNvf1SHJlsRShqtSEy6E3FxaTh9wo6NG4+h3haJ7jDeV92dqGtoRmhwEK93KZS+VQQUAUXATRFQAu2mDafFnpgIWPiNauLCEC1UPENm/AxrU37GoMfjU1ZyPLQVc4GSbYw5XMc8yYkpDGMXZ6nFz1xI0tVNAsloCRHhiIqK7FNZOzsZh5k+zjZbJwl0C/K52lz1hy10s/CAdYqNUTm66btK0kQyF0xCGcih/hm+xQgMIdmjculBX9hkIX7M0un6AHQKc6XM60U3gTPFBXiYYeOcPteihYrxOoIVHhrMLYLl8sXf/ctvkSCJCFeXV5qrW4e4G+RR3RfyLHaqLgEnbf9heBk49wz8z2W3KUFHR+xF6q2/QnFYM1op57Ko/UxEZVnE4/rFJNBbmO6pUzh8+DCuueYaA6+gAMrcT/wAH65ejbTZc+BISsGUmChYhAnKxdxGS5kW8uy7fx/2/vznaGgj8+818nr2grbiwJp1SH3g04gN4tTEIWZPCgHvJnieLJaHtI2Ur9eEt8b6+qC9uowjBIWYOTOdezrx2obdKC3NxHVrRM7vQTRXqZk9oxBxCQvRwpuqmpMoo2NikMBl1WXJdXFxkUmW+fn5SE5JQvrUtdj30W40t7TDs7YYmzZtperfgpOnctmhaiE23Xjmn76Kv3tqE9taCXRvc+iLIqAIuDkCSqDdvAG1+BMQAX6ruvfSR1dUT7oZeAgvGQdrFQJdSfcREkRDUGaeQgybqrnPN4gE10FO6yR7oiKaJqTah7GPfX19ERISTIKZYCxp3UVS3UTVsJ6vQqB9SYS82rgCXUMXh+qbSLob4c1JZOGcVOjN41ExcYbCGx3DEHEsg+QV7NWJnmaSqeNViImsoo8sCXigL8+TkAvsZfQq0sF0+xC3cQ/ya2aBw5yvKGfMYnw3k+9KGLsDXVS8Sf7rqqu5vHQUzvZ80uCwZl2Gej1aey+yrXOxYM1D2HuU/RmyUYeZqMsF63KA3+1mmLwWB5555hmcpd92GKNvvPHGG2xI+sRs2oQiblmZsTgTm4mK+Uswc3oGfIODEejDiMx08HXF1SXpi3vLcHCWM2dwZAB57ruYGHdt2YzcknrUfOPLmBns30+J7iRxXlHThOyycuyNicXZUB90cE1tk0L3sD2ifa0I7G5j58dM1RNRXs0o4o1SWlbB9k8kQS5GdU0ASsr2saMVhiC6cIhbi3QsnB0tGztarZCO14EDB1BcXEx3HI5YSA+HZZTzZcvMSDVe86hex+dMR2J8Mq8389VXRUARUATcGwEl0O7dflr6CYqA8MMAMpe2chbQZDBjXFYhrbKOhWt2FJ0xnX7Pfzr2AZbFrSexHV4tFRXVVFJFaSwvLzcmDQYHBNGVwYfpMgMhnjxP3siLhaRNVGi57hzdQtqomracZuRjnieh7iK7O6hezsZ//fy3ePppP4aIS8XU9GAEc6nBiPBoEtRQugIE49iJYgQ0Uq1kvLd3ycW2iqcH7fMkZVncJ0q0uG90xMfji599GD/58Y941Bnhw7W+xkUD/rF/gPyOW5DYsQBh0/ehexdPGPDLJ4sSRpFUfmcd8FcbWHaSw3feeWdASsAidoh+fksFY1FX4NAH72PbKwE4MXMtIrJz4D01HQkRdHcx8OGlJJMmnoMSGriDgHkzzmDlS39GpYvyPPA04/Opvaj7r6dx/GtfRjbDCpp5OJiGf0Mn0t8/i5yKbahOicWv77sFVf7eVKTZRrxYuk3xiWk4eiII02e1ob7ChuMV2Vi1ciWOn6CbRV0lSkqCMGv2vQgNDcTRo0cNNV7uh8LCQhLlZqNjIZ2tiIgIo9MVQ3U6KcnXiF4inTG5RaTD1dzUiMqyUhyvrMTnvvKfPG6B3I9qioAioAhMBgQGPEYmQ5W0DorAxEBAVE5TCR6vEg0kk0JkKQDjDy/9Hzi9D2vXrIYPyY+jl9wJ0ZH3riYkqLa2Hnv2vIlFi5aioOA4iVMHCZA3yRojLnBJP/EPlvNkcpmQKR8fbyrL/oZrSGLiFBJooVFCcS3oojL70KJFBikVgm2zdZGcd5CIlfF9Ad0EWukLXYewa1bgZGE+DjSV8EpnmY7Qp3waCTS5Fwo5cTAyYQpSU1ORk5ODkyV1qKqpRExUzHn9aqUoPTYrujpi4RFuFEqKNsi6SO5WzgaeIeH+3iYuGU4V3NWm+wMPLwcigjipj+ddwxhx9za0oqz+L9j25l+w1yMKuSHZqFq8BDlTU2ENDzOUaTt9w02S65qe63tx3eghWc09dMh1N6NZeOHOO+/ErFmzDLwrSUY3MjZ1wYEPUPPOdLTdejP8ia+0uy/9ondmRmFv8g0IJqbT6e7S6eNJQu9M0pskejpdOAKoDidM+RRepY+yv08EFizM4QqBNgQG5eDtLe1oqO9GTc1/GsqylNvK6CvS1qGhoWzjQCxdutQYsTDbuIsdJRsdzUWVrq6sRWlzA+rLKzF94UpEzFuOzy+/GelpmW5JnukE0689xvfDlcx7fGuquSkC7oiAEmh3bDUtsyJwkQiQl6HkHIkUydWLf3oBuadPIYu+rBHcfAMCEMOQdIF0QSBDMqIsCFGSTUjRwoUL6fr7NeYkTNLDGKavrWtFY0MTlcpaEvNmtFCRbGqqY0QHO6qrW1FZWU4/WQfWrl1rpCHFFBogBFFC4AnhFjPJlxA02YzPvfnmv/wyPvzgA0PNlsVGxFgNnCGBtvEcIZUxdFE4ln+GpLyc18YY55zvn5BIDyGS/fsKgy4ht8dSunI8E0tf61JZRZD+5NzEnWR2IqN5kIDLpEzTyCe5iAhV/mSONtiqce7cdhzcvx3bXgzBwYx58Myagci5cxFD319Plt1Q66nm9nJaMxm6f3Qj/7VXOTGzfwEfeeQRLFmypM81JC4uzvBF/vlPf4rSP7+M3CWLMZ8qfnfvdTb6uXRQlW4MC6FbBoV2trsENiRIdOPxxiyeKx0aTy8r2jvDcfDoKZz54wYuftJi+DaLK0+wuKSwYtOmTTOIsnlPSGHFhaOL4Q0bGmrY3pW8BzgRlCtZ1gaEoy6D8nzWdODDbfjr//c4Vt73LWfHhtmzym5n0kZhlqpBbTUeFZEoMRZHLf+NR26ahyKgCFwKAkqgLwU1vUYRcBME5Pnb4FLWg1yu+jC3h8gKo60eKOPkvUa/YK5OGIcYkjP/qGj4c5JhIVcnnJIgPspCI4TUiW+rlRudkpOj+TmDm1Bj2WwGwbORWYpC+oXHfsx9/c1UYM3X/kfFK4T5CAnkljF1KpYvW4Z/fvJJeDF6g5iUoJGnyGqAEk5NVNFuTlorr6oGA0WMKkEjP0QiiXJqlJO/CAKyyX5RqV1NiI5sYhThMZPkO4eFvWtuI85Vb8Oundvw/nshOBwxD16clBibmoiw6BjGW2Y0C1GOpd6sjweV+QpG/3C1eLqrZGdnGxP3TN9qcaWIiorC+jvuwFNPPQXL21vR/cAnndjxYoMsS3kkXdNEgueEw7rTp/Hctq0oZISPBrrbSIdGRhJEWRY3jJSUFIMwm5fJq4xO1NU3svPUxFGJBqNzFR8XRNcbCXUXgyc28+568H6gjI72nQ3IqGvBTZ99HCtuf8SI+exaDNd0J/J7Ay7edjX5jHc96wWktn0CZ7sWs50kGs3YmrSaFzusKdZ3Mdv333H2A2kDZi09SDVFQBGYUAgogZ5QzaGFUQRGHwEhn64mn//AOXEP8Mk824/qMpdeRn4les4dQhsPylZPAuH16N1obG0gaeih6ivKrze8GEzZw/QJMBIVRimqNRVOP09ERoaQ3PoaKrGQPiGI5uZahqHeC5krKSkxJp5FR0cb6nhYaZFB0ZtJXktYrjQSTyGRMqlNbKhIFEOlPdJ94hMt20hMyKIsly7mQ6E9J4WqdTrwSca7LinZhp07tmHznyORm5qDhpy5yJw7C6FBgXSBsaKM5DmckS0qjaud/2I5OiAdBYNku+wXXNPZyYgm8a3ctxPNt17PeM5cd5D7XU3InnRvHGybpjdfR+DpXJTFRCOWHSW5XtIVdVlMRgAkNF8nw/d1caujC08dV8WpruekxMxgzJkzG7NnraIPexrjh0+hD3sU3TWK8U/P34fZuY1U7ZOQlrwekamz4MdyufNkQSGx0hlyMJpOWUwTZs+5CYn2ZVzGPkuOCFxjap6dBYj234TagyTxuznq4WyiMc1TE1cEFIGRI6AEeuSY6RWKgNsjILT3efrIriUxvcklSoisEBhEtSuMvwzvPfMq7n3xTZ5pQWhaOqIyshBCUhebGojgqECEcxJgIN1AgkgCg4NCOCkwmO4drailen2WhFBcLfxJAEXp9CU5NomgEBR+6PssRE+Wzz5+/LjhdyvuH+Ir3cQVUOJZFjneSm4oSnoNFe5ahlU7TRXVz98XyYwrLBMMJ5oJmZaoIULCRbSfOZ2xwSnaf9ZWgyNF2/HRh9vx4WYrPopbjrhl16CiugrZZJ1VrIhZHcHEdHVxrZ90IMK5wEtcSgoq6TPtWVUFC90uXAm0YNZG5Or5xtHsgO3AMSxesRje9FeX68VEyW9va0Ur1eXWpmaS5Vac9ehBDdsNIUmcMTmDjuCF+N037seCRdlyhXEd9X6+ctXKzlbccuOD+Mw3fkBy6Wsck0mCsniN2xtxIxSo3gRU0C09esYHCIuhHDwO1lFAd6Uy4ljIZpCbQRpTTRFQBCYcAkqgJ1yTaIEUgdFFYLjnrzybt5Ds1DVxUZIAEj3yI+N5zX8yYnyjP9mfo80ggrYzR9B2+ogRCeMoj9t4qEte+XS3+IfAMyIalthQ1DB6hc/hY+g8thcd1kDUWv3R4R+IzpBQcOYaSbUnAvwDEMjwcFaSbz9OaLPxmt27dxvh4r70pS8ZbgSy0EtLQwOSWS5flquGZEZoW2FBAf70pz8ZriIx9N0IZVQPCTk9kU1cPExl2osC5sJM+lmTjz7Q0IHKmi3YvHkLdtcGsa4OnGGIPQ4OGGZ2OIaqmxwTVw4xn4MH0D4lCX4B/kZsaocRg9uOIuZbRfUZNRXI5ARP8b9uoXLfRn/n8rp6FJK0N3kEoX4KXXIS53IGZQzX6namaTRubSVCdh7l5ELpYfmiiy4azUK0q7uQxxGLrdvfhV9IBjxJym0cxJhsJpOAfblZGEmnuZjhIInneJiEnjQ2+RIO9+Udj4JoHoqAInBeBJRAnxcePagIuD8C5KDntQMkw6WcLfevC5xqaSvdWatJGjpdCIMPH+TW3l8Leaabz3WJLWx3NMBR04AeXifmTcXVg1Kkgz7KdpmFR2MWAGMwy3WSbAOJO7kiTnG1w7fJxCVmtExgk7jLYsWlpaRsdNugS4Rs+dHx8KEq3VnXgH379hnnLFm8iip0vFtFd5C6G+4hdJEJZcOEcwLitGTgK1yCvYTy8+7nnPWVCpaVlRlKvMRUHkimRZnukNjUtN0vvgjL6XzELb2GbroR8I+PRlBIGKoYcQM+bLSzp9BSVoS32CaFQRGwM9Y3fTKMDg1XQmFj8RxG0EB+ARPbB8/6Kszs8uVk0zhUcVGVze+8j2NH9+N4cSvyKrrR2uLJZdrTELnsYayNYQQPjmRMZnMIoSWU5j0/meuqdVMEFIGLR0AJ9MVjpWcqAm6HgCxWl5JKHrWHhPg8Q+uh9PmcvZoEmmKjjVyKrs/G5DjhViXHueVyHxfGEwIowpiYSSjkVTYRO00zJ9aZu8xrzONRzE9IeROjRJjnyqQ5k0DncsJbD/1zQx7/NhxTF+OhmbPh/8t/wpYXfmMkQa9rpC+/x0zOLV/F9aTXm0LmESKRQSzWUZl+9rCzOuXl5QwnV2NExXCtoJBnWWpc/MXFpE2+G7gHcxr24M0tFjRaw1EbGIY5dJvJRwwa49NQdvvd9AegupxItdnCGaQ97JWUFgLHNiO5+giSGfM5Iu06zF+yGuFxMxFEX+lgusccO7AdeRx5qHUsRuSCWKwNj0IQF8OR8jp4b4nb9QDXa6NM+k8RUAQUgcmOgBLoyd7CWr+rGgEh0LNTOKHNHzhIV43h7J5lYExgkmyKmkKag8m1TMtZCaTPA8rPcg+ZcDl9QhvqnQo1edQgE0J3IRPySBEWrR6xzJBT58iixWdaNlnEJJer3oVS5Zz3ya8ijAt2CEO/6Z4v4r1XnkM3ewJp825E9uI1RoSCC+XlDscpwBtM+P6lwJ+p1MtETlGdN3Hlw8cee8zwETcjcchkS1lqXBY2EWOoZ8xJA+Zzm5VK33J7LUl1reGxfK7yJE5VvIcdxz0YZo+qdJsvXXU6MTWqETOju+DHfBZ/kytVxn8L+zu/DU9ya2HkQorb2ZHKmL4KmTmrjHykjBIRojcwirFP/ykCioAicLUioAT6am15rfdVg4AowzdyxP7g+0NXOTsSWEPlU1RFMYMoCaFzMYkqkUY3WSGyCSRqjMDWpxz3ncZjMoHsHPMx/ZIlGVlB0DsUiLmG5LvlMZR6ZMOn4AgCwzs5+Yz+Hn/8XyMJWeVO4gyL60IByeHcWz9BH+mAvnBoKTnz8MSLb+HAseNYOP8WBAX79eXTVwY3fiOuHansK3yanZX/cXqpGEtly8Ipa9as6VOiC+gH/tJLL5Hk8gLafGKbk0icpUci1tuOcjQtgS4iPLZmpp2TLWvRRVLsSd8Yzu00Okwy6c/KzlITHX6N5AaMUhj7nNkYSes/RUARUAQUAScCSqD1TlAEJjkC4iJxH8mrzOx/Oa9/ZRdwRP+JO0iK6XosavVwJqRaSLMY1+CA8N5BJmyZ5G3OnQOOMF0756fFPgzsO/MwfEMWGeqoD9MJ+d3vydidBLqK0SQ2bNhgKKsSUWLx/LXwI9MTVVysq8uCzOy1yMpZa0TeMEm68+jk+C8QPraSvuGljIJCP3SxN954g6tC7kFaWppBmmV5bdP/WY4/tpyk2GPo9pM2lc2bv/QcYGCIObnC2UkSwi1uGN7cXJc2Z2jw8TFW1j7J/afHB0jNRRFQBK4EAkqgrwTqmqciMI4ICIG2kj19/y5GfzhCIl3sJFPT04ElWSRV9EceScxjIdOG4+1QdeAxujX3NxI0UaaFLDm4EoldlFIhTyTbVrojiGBqJMmEt23bZlzrw0Vbsq9dPshdQHyGhe9NVhPsGJwE/3of8O0/AlsrnDWtrq5m9IveWZoulb93FrCAoweDMHc5R94aowoD9g310cGbpXHnGRLrgY041NmXt8+DKyP6z+FNqKYIKAKKgBsioATaDRtNi6wIjBQB4UOiQt7OSBuei5yEVfaZ20jTG43zhdSFcMlpk0C7pjnv1jsRHZPldCtwPXAVvBfFOIwk+qf3A7/5EHiB7hw1Lq4VdHlGMkcAvrYWWEby7E31eVRiYbMhpINT+uQr6GmTuHTSMmNjjLsC39gopD/7+NhkoKkqAoqAIjDGCCiBHmOANXlFYKIgIITVWI56oki4LIc1LgUeXITFztX6TAvibMZ7HvgiPDx9rkoCLTgIifaj3/nj13HyJFXm05xYWEUSLZQ2nX7NizhyIGEFZXRhVMizZMq0RBWe9tK3nB9k31gane6ZpZoioAgoAm6JgBJot2w2LbQi4P4IcL4gUpKn4XqqzW++8FujQlbGLX7oq/+LpIyl9Hl2/zpeTg1kAp84UmTQT33a9SS3vYKwjBoIdiNxuxlJOSwiaY+HkT1Lp05NEVAEFAF3REAJtDu2mpZZEZgECAh38vS04J6//T6iknLQ1t6BeXPnYOqSW9AlzFHNQMAgyuOJh5JavfMUAUVAEbggAkqgLwiRnqAIKAJjhYBE0rAGJ2P9F75mhNGTsGpmtI+xylPTVQQUAUVAEVAELhcBJdCXi6BerwgoApeFgCzOYYaqu6yE9GJFQBFQBBQBRWCcEFACPU5AazaKgCLggoC42Uo4ifOZ+PyORiAIqtpqioAioAgoAorAaCKgBHo00dS0FAFF4MIIkDg7iqtgP3ScC3gMzaK5MB48mnheLR1yL5VEiy+vtwMe62JhiU7ih0tN6MJV0jMUAUVAEVAEri4ElEBfXe2ttVUErjgCHuTMHcXVqPnDe/DwGnrZO4eFS08H+TJ2dShDnV36rDZ7VSXC025BQJzkc+npXHHQtACKgCKgCCgCEwoBJdATqjm0MIrA5EfAzvB0fnMykPKLx+EwY7MNqrYD3X6e8PLiiiKXyntFcG5pgd3PDw7bVR4TbxC+ukMRUAQUAUXgchBQAn056Om1ioAiMHIESIgdvj4kyBHnvdbC84xFQi7V80KId3iYk4C3yMp6aoqAIqAIKAKKwOggoAR6dHDUVBQBRWAkCAi5vdgVEeXcSzXJ41IJ+KXmqdcpAoqAIqAITHoExmnJqUmPo1ZQEVAEFAFFQBFQBBQBReAqQUAJ9FXS0FpNRUARUAQUAUVAEVAEFIHRQUAJ9OjgqKkoAoqAIqAIKAKKgCKgCFwlCCiBvkoaWqupCCgCioAioAgoAoqAIjA6CCiBHh0cNRVFQBFQBNwTAT4FHI4r9yi4knm7Z4NpqRUBRWAiIKBROCZCK2gZFAFFQBG4Ugi0ANaYeoChsu0sgwQtsYxx5BJHb2QVyc9qbYJHB9/IBzVFQBFQBNwEASXQbtJQWkxFQBFQBMYCgapDwMyHn0J22UwUtN5FHh2G7i4q0hKIeyyM67R7eDrg7dmCKK99mJH+BPI2kb8Lkfe59HVzxqKomqYioAgoAsMhoAR6OGR0vyKgCCgCkxwBC5dV9y8GKrYCs+Z/CRnB/4qWnoXo6PCmCj02BNpBAu3tbUeATx6CHfuQ9y5BPgj4eit5nuS3m1ZPEZhUCCiBnlTNqZVRBBQBRWBkCIi3RttO4ASVaMeUAgRFFwBcJNI+Ri4VForbNqrNLZXAWZJ372pwyXYWYozdRkaGip6tCCgCisD5EVACfX589KgioAgoApMbgV7i6tnMap4gmT4+TtVlvn6SN5VnNUVAEVAE3A0BJdDu1mJaXkVAEVAExgKB3kAcKgSPBbiapiKgCEw2BK5c7KLJhqTWRxFQBBQBRUARUAQUAUXgqkBACfRV0cxaSUXgCiMgsiY3mUB2RYz5GnlfoeyvSJ01U0VAEVAEFIExQ0AJ9JhBqwkrAoqAgYAQ51bAsx0IC69F9xhNThsO7R4Gk/Dx7UJgYD3s3cOdpfsVAUVAEVAEFIGLR0AJ9MVjpWcqAorApSBAAm0hefaoArJSvolEn62wO9ohQdLGeuthHkE4g1nx30eIx044OEkODN2mpggoAoqAIqAIXA4COonwctDTaxUBReDCCJBAe5DJVrzOWL/2k5gfvxYe8TmUhf0ufO1lnuGQJe8a8xg2rRHntjE0WwkT1F+9y0RVL1cEFAFFQBHQR4neizn7xQAAQABJREFUA4qAIjD2CHCsq5sqdOuLQH0oEJvKWGkBY5+tLA/dStJcwy1IstNfvHEAXbNQBBQBRWDyI6CPk8nfxlpDRWBiIEAl2ioxfxlvuOYAX8V/Y6xN3EdI3kP4SzfOrtdjXTNNXxFQBBQBReAKIqAE+gqCr1krAlcbAgZnJqH18Bnfmit5Hl+8NTdFQBFQBCY7AjqJcLK3sNZPEVAEFAFFQBFQBBQBRWBUEVACPapwamKKgCKgCCgCioAioAgoApMdASXQk72FtX6KgCKgCCgCioAioAgoAqOKgBLoUYVTE1MEFAFFQBFQBBQBRUARmOwI6CTCyd7Cbl6/rB+OR6gGNwdJi68IKAKKgCKgCCgC44qAKtDjCrdmpggoAoqAIqAIKAKKgCLg7ggogXb3FtTyKwKKgCKgCCgCioAioAiMKwJKoMcVbs1MEVAEFAFFQBFQBBQBRcDdEVAC7e4tqOVXBBQBRUARUAQUAUVAERhXBJRAjyvcmpkioAgoAoqAIqAIKAKKgLsjoATa3VtQy68IKAKKgCKgCCgCioAiMK4IKIEeV7g1M0VAEVAEFAFFQBFQBBQBd0dACbS7t6CWXxFQBBQBRUARUAQUAUVgXBFQAj2ucGtmioAioAgoAoqAIqAIKALujoASaHdvQS2/IqAIKAKKgCKgCCgCisC4IqAEelzh1swUAUVAEVAEFAFFQBFQBNwdASXQ7t6CWn5FQBFQBBQBRUARUAQUgXFFQAn0uMKtmSkCioAioAgoAoqAIqAIuDsCSqDdvQW1/IqAIqAIKAKKgCKgCCgC44qAEuhxhVszUwQUAUVAEVAEFAFFQBFwdwSUQLt7C2r5FQFFQBFQBBQBRUARUATGFQEl0OMKt2amCCgCioAioAgoAoqAIuDuCCiBdvcW1PIrAoqAIqAIKAKKgCKgCIwrAkqgxxVuzUwRUAQUAUVAEVAEFAFFwN0RUALt7i2o5VcEFAFFQBFQBBQBRUARGFcElECPK9yamSKgCCgCioAioAgoAoqAuyOgBNrdW1DLrwgoAoqAIqAIKAKKgCIwrggogR5XuDUzRUARUAQUAUVAEVAEFAF3R0AJtLu3oJZfEVAEFAFFQBFQBBQBRWBcEVACPa5wa2aKgCKgCCgCioAioAgoAu6OgBJod29BLb8ioAgoAoqAIqAIKAKKwLgioAR6XOHWzBQBRUARUAQUAUVAEVAE3B0BJdDu3oJafkVAEVAEFAFFQBFQBBSBcUVACfS4wq2ZKQKKgCKgCCgCioAioAi4OwJKoN29BbX8ioAioAgoAoqAIqAIKALjioDXuOY2wTPr7u5Gbm4uDh8+jPr6ekyfPt3YYmNjhy352bNn0draahyPiYmBbJPRamtrDVxOnDiB6OhoZGdnIyMjA76+vpOxulqnMUDA4XCgoKDAuI9KSkqQmZmJGTNmID4+/ry5yT0n302xxMREhIWFnfd882BjYyMKCwuNj56ensjJyTEPucWru5ffLUC+Cgqp37vRbWSbzYbTp0/3JZqVlQUfH5++z/rmKkKAX67LtmWx9ztkc1cjAXZ88YtfdJAMOtj0g7Ybb7zRQaI8ZPWWLFnSd/53v/vdIc9x553btm1zkOj01dEVn9DQUMdTTz3l6OnpcecqatnHGIGqqirHPffc4wgODh7yPoqKinI8/fTTw5ZCjpv33bPPPjvseQMPvPDCC33XSd5X2o4dO+b42c9+dtHFmGjlv+iC64kTAgH93jmbYaTfuws13qlTp/p+V+R3aThucKF09PiVQWA0+epV78KxZ88ezJkzBySCkJ7lUPbWW28Z6hUfaEMdnpT7Ojs78fWvfx1r1qwxVPmhKtnQ0AB2PLBixf9n7yrgrSi6+KHj0SDdISKhqGCAKBZSgrSKioEtqCCKXVifoqKgKIiUikiHiFJSoggiJY10d9f7zn/em2Xu3tzb975z+D127+7s7Mx/9sycOXPOmWstLbyndHIt4yIwdepUqlmzJo0YMYIOHTrkEYjdu3fTQw89RLfccgtt3rzZY5pEvojVrC5duqh+ZtasWYlcFSl7giAgfEdqFVn4LkE+2AQtZoY24di3bx81btyYcNRUu3ZtuvLKKxXzTZo0iY4cOaJunThxgh544AGqVatWwi0F67o5Ob7zzjv04YcfWo/kz5+frr/+eqpYsSL9+uuvtHTpUuvevHnz6LHHHqPBgwdb1+REENiwYQO1bt3a4iEgUrZsWbrqqquoXLlytHLlSpo7d67iNdz75ZdfqFWrVrRgwQLKnDn0uX1KSor6XpF3njx5cIgJdevWjQYNGuT43fFSfscFlwdiioDwXRr8wfJdTBtPXp5YCIRDiR5OlXg4yhNoHo8//ri1FJMtW7bUfv36uTx6/Pjx1KeeespKwy2bes8997ikSUYTDrYbTc2VK5dVbxZ4Ujdt2uRS7+XLl6cWKlTISpMpU6bUtWvXuqSRHxkXgXPnzqVed911Lt8HD2ipvMrjAgqWmZs0aWKlA4/BLMikYE04zDxied6pUyerfjxBiGVR5N1JjoDw3fkGjhTfiQnHeYwT8Syc8mqG1UBD+/XFF19Ys53OnTsrcwTrAp/kzJmT3n77bRo3bhxhVl+kSBE6ffo08UdDLDCaSb2eY0l66NChBGdDFhaIBVOCU+JNN91EzZs395jP4cOHlTYXjgp4HuXAM9AAN2vWjLJmdW+2YJ7xVujnn3+eePKgbsM5YuTIkVS6dGmX5HAi7NWrl8IM2sJLLrmE1qxZQ5UqVXJJ57T+aJNjx46pPO6//35iQZ2GDRum6ozVAizze6q/y0vlR8wR+Pnnn8k0V7jzzjvpgw8+cCsXC8c0duxY5awLHgG98MIL1KFDB2Ibe7f0uACn3W+//Zbmz5+vePGyyy4jtrFWzq3mA+AfrCKB4OzKE2bztjpn+30aPXo0LVy4kHgCSJUrV1amFi1btlS86vZA+oXff/+dfvvtN2L7SsUr0KiDp9lfwnoEToADBw5U37C+CB7p3bu3yhvmT74okPLj+W3btik8UBaYycCpCStlt912G+XOndvrK+AwDXwWL16sNP7g4YYNG6r6e30oyBuB4GVmjXaZMGECzZw5U9UPK4BwHoU5ULt27dRKhpkejt/Tpk1Tl+D8zZM3ZZaHdmUlh8KifPny5iNJeS58RxQq3+kPA2aM6GfwDcGJvm7dutS2bVt92+cx0HHv+++/V983MoNTNcZ3O5nfNiv66Mknn3RJEk0+hpwxatQo1e+hv4RMVLVqVeLJCqEvt1PS83E4ZhDhlOjDUZ5A8vjss88srRC0p3YNq5kHtK34w+zeTr400NBos/e/9R7+uFzOWahw08jxgOai2bU/c8UVV6QyY7sUI5hnXDKw/WCmsMrJZiu2u+d/wnmQbe1SucM6f9E4C6b+prYRz7OwbJWFo3+k8gTGeIOcxisCbNJjtRvacP369T6LypMkKz2+eRaGrPTmN8HCdSpH7nBJi/Q8wUxlExDrGZz4c8LjiCCp9erVc8sL+fEEMfWff/5xyQ8/WEBNZXttj8/gOfQHbPOsnoNzEa55+sPqjT/yV348D9y89TEcJSd19uzZHl+D/o8n5m5l48lw6ssvv5zKUU88Puf0ohO8dN5sE5/KEwC3smkcWZBO5cmZTq6Offv2tdLfcccdqTwRsH7juT59+rikT9YfwnepyqlPfyv2YyB8h2+DhdJUNud0+YaQV+HChdW3ZOZrdyJ0Mu698cYb1jvQz9nHdpSFJ/NWGvsKVrT4GOVA/8omeFZZTAywYs1makhmUbzycTjlVWhwQqZwFijkwgSYQdeuXa0PAYJZsORNgGa74FQI5vojQ4QPDPzo/PU1HMFAmrZv357KtsbWfQ7vpZa3wcgY2PRzPXv21I+kBvOM9bCHEwz++j04ojMIhoKpP95jCkumGQnK8sQTTwRTFHkmBgjUqVPH+o5Yq+u3BKyxsdLbvzvzm9DfJiZ59s6cta2pHB7PepcvAZQ1mqlsz+/yTg5B6cKzbIOcumPHDis/nGAA02XAEd+o/TuF8AaKtADNjpluwrPZT6B8+G1ORlAuRDwx6wDzNQgG5jWY24SDnOCl34eoR2ZZOHRhKiYDZn+KtoGJnSZTgLa3ByYYO3fu1EmT+ih8FzrfYfKICbT5DXrqb/R9U4B2Ou5t3brVRUk0fvx4l+8TQij4U7+LAxpY96PJx7xK5SKDoDz2PgN8ZvY18crH4ZRXM6wAbdpd8hKw9VE6PfEmQLP3r9XhcySLVDZLUFljhslLQRZDNGrUyHrl8OHDreu8HGxdxwkYBx9tqVKlUtn0w9L6BvOMS8a2HxyVxCoD3mdnaFtyrz+DqT8yswtLvGSWykv8qRjQ//rrL6/vkxvxhQAvl1vfkf1b9lRSrGaYAwUmuJrs38RHH32kbym+gOCsBxjYPWryJUCz+ZH1DAZHNtNS4RjZtCu1QYMG1j2zHFht0e/BESHpMNgiDOZ7773nco9ND9TqErTYbEph3bvxxhuVZhsrWv7IV/kxUJurM+hH2ORDabDYtEQJnLqsmCigjCCOnOPCY/DpwKQDE4qvvvrKKieEUDYN8VdEn/ed4oXMsBKYN29eVQ4IzKbAgH5A1wlHNuGx3m8K0LiHNsU1aMWSMbyoVXHbifBd6HxnF0zZ9MxC+aeffko1+xt8a6bvTzDjnqlhZqdr6104+eSTT6xvHm2LfhIUTT7G+8yVOjb1skL3oR9jkymrjGxmiuRxzcciQKsmCu0/cxkYAm6w5E2ARn5YvuQoA6mYZZr05ptvWh8cNAaa2F7Sus5RA1Jff/31VLZ/skxHwDR2CuYZex7m7x9//NEqAzoHDMbBktP64z2msAQNo6llCrYc8lz0ETAdTLGkHghhJQjfHP4wcdJkfhOeePXpp5+2nsMKjiZfAijb9FvPIAa8SRMnTrTuwcxBC59se2tdt5cD5l0Y/B588EG1xAtHI03BOjP5Kj/MvzRWbH+tBGD9Phx58xkX7XT//v3V7QEDBljPQTuNFSyTYCKm84UpRygULF7AEkKJve+BkG8KLzBd02QXoPE7I5LwXeh8Z2pO9WqS+S3ZAwuYAjTSOR33tHIMfIeVao4KZr0Oyj3Nj5AbNEWTj9GX6DLgaOdLTGyh1HvxxRdTsSqmTV3jlY/DKUC7e6MxQhmBWJOrDOFRVx5EIlJl1qTQNddco5wE4IiH8Fxsk0h//vmn9T4z9jQcX+Agh13XED7v1VdfVX+sTaGbb75ZORjAyYA3hbCeD+YZ62EPJ8DFpFCwcVp/8704h5MlHCiFEg8BFuqs8JBwqPFH4APEg9aE5z0R+MBOrH0l1kqry3AggsMPLy/ak1m/4aTKk1rrN/hr8uTJ1m/wH5x14DAM5zW9ayKc+jSB70xibSnx5NO8FNHzGTNmWPmzFtltR1A40rHWSDk6IiEckUBwONLEGi1atGiR/qmOcGSC0xQITkKhULB4AUs4IyPkIZwP4SyKvhPhM7WDMcpl9p32csLRMCOS8F3orc7+GlYmcFq3E/obXn2yX7Z+Ox330KdVqFBBBSrANw3HQjgYwylY8yebRxCc6jXFio9RDvQrJrVo0YLwZ6eMwMcZVoCG5yg8lkHwYvdFiJ4BwhbWTog1WcTLh9bg5elZ1gJZlzFo8MxSxZuG96qmPXv2EGuj1B8Ge14utpgpmGd0vp6OwMUkf9hgm2V4/Zv10M87rb9+Th+9CVH6vhzjFwF8E4juAEIEG3+ELbdZu2Ils3+H+gai0djJvhU48vIlQEMwNN/Fmh17li6/IWxDsDQFSqd9gUuGIf5A38C22VYuGHw9EWK2s7ZI3QKfghAFRBMEhaZNm+qfbkdzkuF2M4ALweIF5QFr+dTmOzoOv6fXeepzkI611Co6gKdnkv2a8F3oLczOxVYmJUqUsM71ib2/0df10em4h+8YUcAQfQg0ZMgQJUDzrqvqN/4Dn5rvjRUfQ/7wxndWYdNPMgIfZ2gBWjc4tFaY6SEclid6//33lYYLMy92ilFhZDAT80XYVAQbr2hBGOGXMJtlGyE1s2RHQPW4/WO89957VRqEc0N4L14KdnkNhGleJlYzVoScAgXzjEumxg+EiuIlc0sbOH36dDWYGUmsU2xAg10cedlQzUAfeeQRwkY0oGDrb2XOJxgIhRITAVMAhiCGkHZ2ra1ZM0wQTTKfN69j90s7mVpJ3EMn74sQmtEkNsPyudEKNCkgbCaEEHog7C4YK0Lfg41hEFIKpI/28qBf06QxMeuOSQBC13kjdt7zdiug68HgxcvfKpSe1ryhnug30deh72TTGatvsvedulAZud8w+Ub4Tn8Rzo4YA9npVD2E79FOug+wX8fvYMc9aJex4oxVL6y6QIiHJloTdmo1Kdp8rN/tqf/V98xjRuHjDCtAo1PGR4hYjyDEe/a0BAuBFXGc2Z5HmV9giQXaEX+E/LTwjPizHG7GesTcxc+TIA7NK2IsYzdAaICxXItYtYhHjTyhPcNvLUAj42CesQpkO4GZCDvfqKuYTaO8mADYCXUCw6OzYccLQuxcTaHUX+eB2L1CiYkAzG84woziG9SgR48eatdBmCjZCdpUc9dLLN2zLa49mfqttdrmTXM5Ezxtj1lupsU5TBcgFGstNEwgMPnzR9BC6xUZ0zxBP8c+C+p+9erVqX79+h4n5OhHwkGog+5HTJMwnTf6CRMrzb/QSmtCW7D9ZcAaJf1coMdg8EJcai08syOjiqGN70GTOSnw1HciXUbuN4TvQuc7rOpqARr7RdhJr+bYr+N3sOMeRwBSSigtgzz33HOWmRkmsmZ8ebwn2nyMd4Ig/0C4R/+jCStZ2PWR/crULs2QHzIMH/MgEjKF0yg75MI4yIA3DMGasfWHnQn5A7FyQGgt0yMfaXl5xbqPE09OhAg9Y+YLz12TTCcFhKjTBG9xtplW4WHguW8nFvqtfB9++GF1O5hn7PnafyN0lxlOD2GkTI93pId3Ow9gVnkQqkw7DwRbf+RrOozhHUKJi4AZkxb8AE9u7HJp0pw5c9zC0fHk0Ezi8k3AicyMz4y44Kbjm+mU68sJz3wGPG4SHGF4gFKOMegjWMOrbnfv3t363hGlggcS6zHW9qWy8G7df/fdd617cCzU/QGi/wRKvsrP2iorT/AhonKYhMgB+p08WUhlrZa6zRNi6zru8wqT9RgiiqA/u/LKK1NZI5ZqOulZiRycBIOXuTssymES+iBdJxwROUWT6UTIygR9OUMehe/Smj1YvkO4VP2dwSmTTdCs7whO7TxBtu4jHZsqqfuhjHvIAHGW9XvNI3jdTtHkY1YiusSMx/dlksmzvPmVcvw3r8UbH4dTXoUWJmQKZ4FCLoyDDNhGJ9X0xsdHi+gX1157rRrs7fFEIQCYAjZe5UmAxkBkPoutsNH54w8Dk8kciG+qyR4K65lnnlEbBrADTSqbkbgM0LxDknosmGf0+3wdzfA5urw8M0+F8M82ly514KVUl8Es2PqjPKYAzTZgvooo9+IcAcQUR2xl/f3gCGGONZOpmAwiJKN5D+e826RbrcxvAmnYHEFt9oFwU6zpdckDA4smXwKoPdoMNkfhlR4VIxnx13W5TC98DJBmHHdEDYGAzdp1l0kAPOkhUGsyo4RgAoDNYO6++2592+vRV/kxyQWOupx4JybV6CfMsFi4bw54mOSyNtp6DpFuoBRgBz1VJp0fjvbNSrwW1MuNYPBiDZ5VNpQBIQuxCQ9C7EEwNsuHEJ6aTAGatWP6coY8Ct+lNXuwfIewjub4DR5B2EvsiWBGxdDfohagQxn3UGLwJhRROl8cMbZ62uQtmnyMsiEij1ku1jKnQknAttku4TT1Xg3xzMfhlFcztACNDwNaJLuW2fxQ9DliHbJ3Px5xIU8CNBKYzKvz0EdodPU5Bj6t4cLsFvFc9T1vR/Z4tbS9wTzjUgEfPzAoYcD3Vg593dNmK8HUH0UxhSURoH00ToLcgvCDkG/6W/F2hGDNW9SmYlJrJ/ObsE9AzfzsMVR9CaAYgBCz1Xzefo7dDc1wdCgXhDZT02x/Br+xO6BJY8aM8fgeNkcwk7md+yo/EkOINsNxeioLJgAIq2USNkUw+yBPzyFUVzjIKV5YoTBXv8yyQZgwJzeYiGgSAVojkXYUvktNDZbvgGDv3r098iy+R/Qz5jeqBWg8F+y4h2dBdoUYBFRvFE0+xj4W5iY9Jl/qc6ym6/47nvlYBGhvX1SQ19leUGlusDRjmiXgw2AvXMVM+IA8kTcBGjFLwUzmZgeY1WJgQl6mNoVtrK2s8RzbPnvUzkGQYFtRt9jIwTxjvdDPCQQIMLF91yEMZjAz8ba5SbD1N4UlEaD9NE6C3Iawyk6xqZdffrmLZgf8hSVSdg5LxcYj3sj8JjBY4bswtdfYlQ4x08HHJmGVRnfuHPrRvGWdIy9ocvE967ToAxCHmj3drXTmCWKzY1XJ3ldgAPFk9oDNk+677z4rf7wHWvQNxtKwmb8+D6T8WF5FHGvsnIZJiK4D8MH21cDeE3FkIaWpNgUBPIt+CcJoOMkpXjDrMTdnQLnQNyOm/tdff23VEStimkSA1kicPwrfBcd3GkEI4JhEa55CH/Lss8+qfgb8q6+bOxEGO+7pd4IvzQk6Yiz7omjyMczlXnvtNZdVOGAAuQar5eiLTIpXPg6nAJ0JFWYQQqL6Je5Sz8/ZPjykfOLhYWYAFSWDl2NULFIevEMqFrxR4eQExxbEZvXkROXpBdz5qfjUOoYujPbhaMCDpKfk6lowz3jNzMMNxMNlAYYQ2gehs+Cw5Y+Crb+/fOV+YiKAb5QFRxVbmc2XXEIzOa0RQjnxCoxyXGFh1u1xFo6JBVd1HREntGOQW0K+AM96OOWBT+Ggw4Klp2Qu19BXwKEIfQWe0ZEuXBIZPxCfGlF1WEj16+iIx5yUH+kRFQf5w3nPX1mQXpNuDzhfwmHPE5Y6bShHJ3jhO0E4QkSSQGg2J/UJpYzJ+qzwXeB8Z/8GwB+IPlGrVq2AeSMW4160+Bj4QBbgVQ4lC6A/8yYLxCMfh1NeFQHazi3yWxAQBBIaAQjVCG2H2KqsRVJ1gYDLmqKEqFeilz8hQJZChh0B+W7DDqlkGAEEwilAu8eUikCBJUtBQBAQBKKFAGKqmjFU8V5oZROF4qn82ERqwoQJjqFje0mlsXP8oDyQsAjE03ebsCBGqODCx5EBVgToyOAquQoCgkCMENBbUevXw2xK7/Klr8XzMZ7Kj2VabNzklLBbKpa8hTIOAvH03WYc1AOrqfBxYDg5TSUCtFPEJL0gIAjELQLYGClnzpzKVhFHjquudgTl0JRxW2azYPFWfnacctmwySyrr3Nz8xNf6eReciAQb99tcqAavloIH4cPSzMnsYE20ZBzQUAQSAoE4BsNB5ZIOcRFGqREL3+k8ZH84xMB+W7js12kVOcRCKcNdObz2cqZICAICALJgQCi1SSq8IwWSPTyJ8dXJLVwioB8t04Rk/SJjIAI0IncelJ2QUAQEAQEAUFAEBAEBIGoIyACdNQhlxcKAoKAICAICAKCgCAgCCQyAiJAJ3LrSdkFAUFAEBAEBAFBQBAQBKKOgAjQUYdcXigICAKCgCAgCAgCgoAgkMgIiACdyK0nZRcEBAFBQBAQBAQBQUAQiDoCIkBHHXJ5oSAgCAgCgoAgIAgIAoJAIiMgAnQit56UXRAQBAQBQUAQEAQEAUEg6ghEfCfCpRv20bL/DkS9YvJC5wjUKFcAAWhp2cb9zh+WJ0JCoGiBnHRhqfxU5oKUkPIJ9mHh02CRi/5zwqfRx1y/MdZ8unn3UVq99SDtOnBCF0mOcYzADZeUYPlnv7RXDNoI/WTNCoUi+uaIC9AQnkf8tjGilZDMw4RAg/JqAwdprzDh6SCb6szsRQvkipkALXzqoLFinVT4NGYtEGs+PXD0FE1fsoOWi1IqZt+AkxfXKF+QZnB7iRLRCWphSsv9ZKQFaDHhCFNbSTaCgCAgCAgCgoAgIAgIAhkDARGgM0Y7Sy0FAUFAEBAEBAFBQBAQBMKEgAjQYQJSshEEBAFBQBAQBAQBQUAQyBgIiACdMdpZaikICAKCgCAgCAgCgoAgECYERIAOE5CSjSAgCAgCgoAgIAgIAoJAxkBABOiM0c5SS0FAEBAEBAFBQBAQBASBMCEgAnSYgJRsBAFBQBAQBAQBQUAQEAQyBgIRjwOdrDCm5MhKVcvko3PniFZuPkAnT/OJUMwQqFQiLxXMk10FrN/Emw0ICQJAQPg0vr4D4dP4ao94Ko3wavy0hrRFYG0RtwJ0uaIplCt7Vjqbmko79h2jw8fPBFajMKe6rHIhuvP6inT2XCp988taFpYPqje0vKYstb22vDr/8qdVNPnPrWF+c3JkV75YHsqZLQthA4Ad+497rVSObJmpLHbh450QN+44QqfPBj4hyZI5E33YuY7K+9Cx03TPB7O9vkduhBcB4dPw4hmr3IRPY4V8dN6bN1dWKlEoN2Xm/vX4qTP0367YKRlkTA2tzaPBqyLfBNZGcSlAN6xVnLq2vNiqwd5DJ6nzJ3OJZVg3QoeQK3sW1Sl4uo8HcvL9VBbEg9ES33hpSapcMp96b/3qxSwB2ixIJspk/gz7eSB1DPtLw5Bh8YK56OOH66qczjH+D348l/YdPuUx58ebX0QNahRX997/cRnNW7HLYzp/F/lzEIoSAsKnrkALn7ri4euX8KkvdMJ/74MH61Ax7o81fT7xX/p50Tb90+Xo7zv2d98lMw8/4mFMDUUm8FClqF2KyZgaYfkmauBF4EVxKUBfzwK0SYXz5SBsifnPhv3mZZ5NEw1/7lqlqYZ285FP57vcx4/bWVN8702V1fWPx6ygmUt3uKXxdWHdtkN0TbULlPC+akua9tlX+nDfC6SO4X5nuPJDm+APTI9O98qqF9BPC9019Vm5kldUKaJee5ZtYpZu2BeuIkg+EURA+PQ8uMKn57GQs/hCoFqZ/C7CM0oH3vUkQPv7jv3dD6TmsR5TQ5UJAqljpNLImBopZIPLN+4E6AIp2Xn/8oKqNqfPnKNsWdP8HBvUKOYmQPN6vxKekTh3jiweEcjNtsqacnlJo+97Oo6et4l+WbyNTQpS6cSps56SRPia/zpGuAAhZT+XNcmt65VTeVx1kWcBGu2t22nJ+v0xM9cJqaIZ7GHhU3uDC5/aEZHf8YHAtTx2atJj6kUsVBdhxdQeXt11JX/fsb/7rrl5+hXrMVWPNShbMDKBpzpF85qMqdFE2/e7zkuXvtNF7W696kWVthIvHPHbBup4QyX17qtYC/zF5FV0hgVZ0AX5c7JN1/klqSyZM1ONcgXUvW1sM72fTQWqlc2v0qmL/F/JwrlVmjNs6/Fvui0zOhLYh63acoiOHD9N9S4upvL9c80e2sC2uHlyZqULS+dnZ8FUWrnpIJ047VmIhh1unQuLUBm249229xit2HSA9h9xNVeA0FGlVF5Vh+X/HaBTPEHQlC93NrqwFDslsqnDiv/S3uOvjqY5BDQDFdmRrgLbHKfkzEab9xyltVsP0UG2CY4lzV2+0xKga5QvwGXLSkdPuNqzQzOtCZ2DJkyKqpcrSKW43TCR2nvoBK3nNtm484hO4vPoFG8zs3jF0yxjLM+FT4VP9fcnfKqRiL8jVv7qXVxUFWwrjwmreUxoeEkJdjXJRBCsx7CCSJO/8QZjrK8xV49H0RxTL+YxPk+ubLR933HabHMev4jH7Xwp2Wgnr4LC5hvWfYHIBBqP/PxsFTbfhG/OgaOnadPuI7R222F9O2bHUMZU+KxUZVwKsMP9MR6Hd/OY+ve6fQGbt8qY6trscSdAQ9MMOsmC6sQFWwhaS9gg52Gh8PLKhWnBqj3qfudbq1BdQ/CCYPbWvZepe9OXbKcJCzbT250uV7/1f82vLEP4Az30yTzae/gkvXtfWpoRszZQheJ5rDxhqA9b3BZX+3cWLH1BbvrkkbpUugg7waUTnOA+GLWMFvybVl5cbtegPDWpU1ql6D16Of22bGd6aqKW/J5W6ZraT8evpGl/byd/dewzbqV6vihPJp6+/WLuHNImEDpTOIt8/fMa1qBv15eifoTAu50nNHBgQQdch0017GY0daummW+cYcx+/3e3KuO9N1WipnVLU/as7isL81fuov/9uFxNNnxVyCneOq94xlOXMdZH4VMi4VNi8zjh01jzoq/3X1KxIOVnxQ0IygktQOM3eNgUoP2NN1Am+RpzMR5BkRStMTUvC856jIfS6rG+v6NairKzwuXd+9PG9t0HT7AP1Twqz+O7Tq/T2WWCXZwW1KROKep0c2W38WfJ+n30ybgVXn15dL6RPAYzpkKegYxQrmget6LBwf+TsStoMQvS/kjGVFeE4ioOdNECOdXsCEVcvHaf0vaazmTmUpQ3TTCehanFSR/mFmkOha6a5MbMMGbngHzs5M1ZsPEVpV2EZzyXLUtm6tGmBpU0tOT2/Lz91n5w/uqI5xG9Ah0FhGfUayFrzsHkIEQxebx5Nbq0YiH1O1b/mVrlKy9KE5Z1WaqUzEuF8uZQP2G+Ae00JkO3X1NOdV74vZptz2F/jkgooKurFaXbrkqbCKkLIf6n8UY2iYBniNUN+XHh0zQI9XcjfJpF8a3wacisFfYMzDET/TC0jXoFsELxvDxu5bbe6e879nffyij9JJpjqi+nVH0vUJkAQvVDjauq8WfXgeM0858dKooUqnUJj6U92tS0VzXqv52OqTddWsISnrfyZGPpxv28optmvgOtcpcW1VS0rHBVRPeNyC+Zx9S40kBfy1EuNM1ZkaadxYdyT7oTIEwkEBINjNxvwioaMWsj9X38KvUIzC+6D1iozvexZhnmEYj60Lp+OYKAC/qetcxgBtiBwbQBs2VN+XJnV9eHTFvHsYSPezXV0Ontx/G/b6IffttIF/AkoGe7mlS0QC6lcW10eSkaxOHvgiF/dUSeEDS1APrVlNVWOL2LWaB+u1OaRv6O6yvQ3+lCdTDlCPUZtGGb+uVVNpfxKgK0A9p85UpeYdA0N73NsbQ0h00/5q3czRr83ZbgjPZ/sUMtlRyTgrHzzy8/6jxCPSYCnqHWMdTnhU9dERQ+FT51/SLi4xeUOFjBBcF8Q4eu+2PVbmXGgesQsL+buQGnfsdUmIP4GnNVJsZ/8TambmMzD38yAbTs7XmlGASHvWe+/IOOnTxLWbNkohfa1yKMXzBRqV2pUEAaW5VRBP5zOqYi/C7MQyf+sUXtlYAiQf55h1fgYTpaME8Ogpb63wgESkjmMTWuNNB6tnzqzFlauHqv+ux2HjjBdkeH1HkOFp71cj+EaNg9acLHoT1UtXAGB4kjRvzog+mxiGG64YmwJAvTD5iJQBsaKP3KToZfT11LR1jwg930tzPSOiQ8XyvdITLQvMx0gdTxWrYZB2FS8PNf58MSwQb7QLoNdkXWNJyfKphviM45MMESGwhteCl3Ppq0/TNMXrS5C/TMH4xarkLZaa0z0mvNOs6LFcyJQ9gpEfAMe6UdZih86gqY8Okua5ILZIRPXb+PWP26rEohyznb1Fia59oUC2X09x37u++pnvE2pvqTCTA2waYaNJ3NKCE8g+B79Ue6+Sh+Y0OgWJLTMRVtDhllF8tTmjC2LmNNtCasLEaCknlMjRsNNJzvMAMCLVqTZr6hGxNmHDoWc4OaxVxsh3WaUI/QYJs2yU7yw8dsEnYm1FQ4X2Q+SuQPBXpRHduTz3ul24Drd2dn8w4QHPAK5s0eU7stMLDeeAZaEXRGcEhBu4OWYGnxpKtzYWE27bjm4guUNh8OHVh90JSVtSvhpkTCM9x1DzQ/4dNAkTqfLpG+K+HT8+2W6Gc6rj7qYQrN2owDpnLwTanMZnSRcI5LxDG1JOOhqeElxZXGWf82I31hhTnW5JRX0Q9hglCtTAFlF5+PJwpl2KlQk4ypGonAj3EjQOtZCoqOJRI45WlC0HNNWLpH1Ixw70wIrWe4SM9akR/sfyJFWCLDMh0IR+DmiY6xYGpq4j2lifQ1k9kR81nHhdbvncMCtklwToIDJ9JFixIJz2hhYn+P8KkdEf+/E+m7Ej71356JkAJj5hVVCltFfaZVdescJzBJ0AQtdCQE6EQcUwtxaD9NmFyUOL9Yqi+rI8w8Y01OeBW+WK/fXdslKpm9/JEYahOp77PjEcjv+BGg06NvoNAIsYI/T4RZ0jXsROYpCLyn9LG4Voi1vZr2pHv14jfMTDTBlCFUOnTsFC+dnlO21kdOnKZn+v/pMUtsb63NWjwmiMJFhJ6D8wJC0iFk38Xl8vPGKmkOhTA/gV2epqs5ZCHspkBb2Hbve7bR28qRPLCM9umjV+pkfo9O8U4kPP1WPkIJtPkGshc+DQzkRPquhE8Da9N4T4W+1RxjPEVf0HXADruDeHn//Oik78TP0dOYCqd5TWZd9bVgjvsN887vZq6nGUt2uGUD0wdvZqBuiSN4wQmvPs9+WQhTCBrHvkOIdnWYV92b1S1Dt15RKuBSypjqClVcCNBYQsJsDwQ7ZoQpsxNMOGryboQgDOIQoMFA+ENMSyxHmc5p+nnEb9akne3073Adr7m4qNpsRQupEPA17dh/3uboEMeS1FTWWDopyJMF05lOp8HRVx1RNdg0ATuE+cvMazTAL14J8SvbNaigincrO1dWTdeYL16317I1w03dzjhHx/7X2jR7eCxBOSGneCcank6wCEda4VPhU3N1Tfg0HFwVmTzMie6Mf7Zb/jDm2xBtAgopjIvVeQ+FZbw3ga/xBs/6u2/mH8p5IGMqfI60AgkmfghrB6EQ1NiHUOhLJjDHT4yrOqxdKHWJ5LOBjKlQWJVND1+3Zushl6AGmNxrMuYj+pLbUcZUV0jiQoA2HRmm/rWVsFORnTB4f/BgHXUZzA77WMwCsVkJOgDEGL6Hl/0RyxAaTb3ttzlTRKeCWRuEbcwszdmU/X1OfqM8b91TW3m4YncnRP7QhM5Lk8mcjS4vqcp+mh0mm3FHVsywqTKXUiD++6rjnOXnbYuf4TiPn09axd7WR9SkAhvHXMY2T9BAz+DoI7EmLDlpARpaD02og0l6IoJr2KVwEQvQsOd+pElVM5nf82DwTiQ8/QIQ5gTCp8Kn5iclfGqiET/nMHFElAgQQtb1Hf8vYfMwO8GfAeZ0IPgWKQGaz32NN/7GI5VZGP4LdEzVCiSM/z3a1qBpvOcB7HyxVbkme/hZXzIB5AcdShXywhoOYIDIXbgGXLEJyeVsGjP413Ux2plY1yrtGMiYCj7VikbsWQGFHdoYG8/dmh6hDLmZcofrW87/kjH1PBY4iwsB2hSmELrME8FGCzsKFWOnOWic63P0iXG/b6YlG/ZRw1ol1CNYjsDfrKU7LAEaXqZYckHIluL87LMcmxmEOIimR6q6GOR/2CgEuxU+w38mQVg341hj2QSRQBDYHhuE3HNjJSs5HA9h3O+JfNXxxzkbVWeB5RmU4aOH61r11XnN4I1l4kGARhglmGSYG84g4sofq/fooqojHAxbcJxntDM2mGnInSG2X4UzJKJ1aLtvl4c8/AgG70TC00OVI3pJ+JRI+PT8JyZ8eh6LeDrDCigEShD2BfAkPOPeXFZcaAEasfX7T16txg5f4w2e83cfaUKlQMfUKQu30n23VFGvw4qIXhWBwIuda7Xm1SyPL5kAkb2+ZdONzrdeqGQGHPGnNd06H2xAg/0mYk2BjKkoJ+SdWhUKqb0hBjxVT8khUDxiPHVCMqa6ohU5DzfX93j9BcFP2ztjswxzhmN/yNzBDsIiaCjHbV7JIdtMMrf0ROzHr35arXY21GmgkcUMDLMy7NYHgqOdJzpuXNdpkQ47JYJw7YVvFqkA9eoC/wfN9l9r9tKLgxfxub5Kyg75teF/q4mAvgpGHz5jPb0/cpliUlw/bmNMX3U8efqcilU5ddFWixl0fGvUb8OOw247/+l3x+L4q21XRMyg7R0RQvBBkw4vbhAmHMAUNmnj02M/m894a0fMvJ3inWh4RqsNhU+FT02ew3cnfBot7nP2nioc1xeEPhPKJG+ECZAe3xD/GP4pIF/jjb/73vpilXH6f/qd+BnqmIqws+NZkabDneL92G3x2QF/Ko26/R347UsmwP1JHCu51/dLrNCruKYnJBivsUvwnoOeQ+EibbQpkDH1ozHYaTDNFBLyAYTn9dsPU89Bf7FvUZoQbW40462NZEx1bd1M/MEZIp7rzUB/1S9xl0o6Z/twt0cg9Iz4baPbdfMCbJfhFWza15n3zXOEMsPk+jjHZzQLjmUJmE/sO3zKo4E/3oGwaYjqsJm1oHBIA+F3zuyZlRBnCrvmOxFJAyiZS5a4n4s9nXFNM28xjqOIgOQwobALwWZ+OIdAkoeXhP5jLbV+LzDAxw0hzhP5qyNshItwvkU4dN4JFuwxGQkEU/0uBJCH1hcbzkSS0BbQJp/lNkBsUW8ETXPJwmlthpm2NrkB7sBI/8bz/toxGLxDxdNbvTxdx5Jlh+sqWBoUT2kieU341DO6wXw3wqdpfavwqedvKpSr0CSif17O9sreCK4iuXKkjU16nPOWFv0m2gmaSPv45u879nbfX1+MsoR7TMWYApMUbNsNBZmmtG/wrDXG6us4epMJzDQIXQdbaIxX2FcBq+BpX7eZyvv5m2zaOYLbC+YxkaRAx1S0GcxFoeHHZnIgyB1ZWaiyj8Xe2kjXI5i+MZpjKuSZO66vqItrHX3Jq1aiAE/iwoQDjJuuCPZbbHsj6wegUcafN8I79E5MZhoIYf6ETG8CrV1IxqYv+AuEwOi7D7qmRGfnq8PzV0cI4jBLCZdpimvpwvcrrb09TxLMt6BT99RmdtzxjL92DAbvRMHTxCyS58KnaegKn7p+ZcKnrnjE+hcEPH9jmi4j+k17/H19z9944+2+v74Y+Yd7TEXftI41qnbyNFboNN5kAn0fR+DoKV8zTTycBzqmemqztP7MXZHlrY10fWVMZcWdBkOOgoAgIAgIAoKAICAICAKCgCDgHwERoP1jJCkEAUFAEBAEBAFBQBAQBAQBCwERoC0o5EQQEAQEAUFAEBAEBAFBQBDwj4AI0P4xkhSCgCAgCAgCgoAgIAgIAoKAhYAI0BYUciIICAKCgCAgCAgCgoAgIAj4R0AEaP8YSQpBQBAQBAQBQUAQEAQEAUHAQiDiYeywXSRxPD6h+EdAtRXHBUX8RKHoIoCYmgV5w5hYkfBprJB3/l7hU+eYheuJWPMp+gjszKq+gXBVSvKJGAJFuV9veElxQpx/oegiEA0eibgAXZO3j8SfUOIgoLdDTZwSJ0dJ9c6LsaiN8GksUA/tncKnoeEX7NOx5FPs2ntT7ZLBFl2eiwECxQrmisFb5ZXRQEBMOKKBsrxDEAgAgZy8I5iQICAIxDcCseTTWL47vltFSicIRB+BiGugDx89SUePn99aM/pVlDcGikBKrmwqqbRXoIiFLx22ik3JlZ23VY3NnFb4NHxtGemchE8jjbD3/GPNp2d4x72Dh0/QaT4KxT8CBfPlpCPHTkl7xaCp0E/mTckR0TdHXICGMLZz79GIVkIyDw8CxQqnqIykvcKDp5NcwOw5skecHb0WSfjUKzRxd0P4NHZNEms+PXP2HO0/dEKUUrH7BBy9OU/u7NJejhALX2L0k5EWoGOj7gofRpKTICAICAKCgCAgCAgCgoAgEFUERICOKtzyMkFAEBAEBAFBQBAQBASBREdABOhEb0EpvyAgCAgCgoAgIAgIAoJAVBEQATqqcMvLBAFBQBAQBAQBQUAQEAQSHQERoBO9BaX8goAgIAgIAoKAICAICAJRRUAE6KjCLS8TBAQBQUAQEAQEAUFAEEh0BESADqIFT506SbOm/0xrVq0M4ml5RBAQBKKBgPBpNFD2/A7B3jMuctUzAmtXr1Rj6smTJzwnkKsJhUBqaiotWvg7rVu7KqHK7bSwsQs867SkcZQegnPXx+6lq+tdR58PHBFHJZOiCAKCgEZA+FQjEfrxwP59tHfvbiujnDlzUdFiJShbtrTNl6wb6SeCvR0R+e0LgU8+7EWzZ/1Kg7+bSJfUvsJXUrkXIAIQYjdtXE9nzp5RT2TOnJly5Mip+DZr1siKfjt3bKP7O7akSlUuolETZgZY4sRLFlkUEw8PKbEgIAgIAoKADYHWza+jvXvOC9C4nSlTJqpQsQp1fvRpatzsdtsT8lMQEARiicCPI4ZSr9d6uBUhb9581PCmxvRU95eoUOEL3O7LhcAREAE6cKwkpSAgCAgCGRIBaKBBTzzVkwVnoqNHj9LaNf/SbzOmUs/uj9K5c+eo6W2tMyQ2UmlBIB4R0Dx76WV16aprGtDZs2dp/749NGnCKBo/ZgQtmD+bRk2cRXny5I3H4idEmUSATohmkkIKAoKAIBB7BB54uIvSPOuSfDdsIL331os04IuPRYDWoMhREIgjBGpffiU98kR3q0T3dX6SOt/bhrZt3UTfD/uaHnykq3VPTpwhkCEEaCw9rl61gk6eOEHVqtekYsVLekQJji/r166mrVs2Uemy5Xl5sjJlz57DY1p/F3ft3MHvXE5ZsmSlymwHdEHRYm6PQGuzhp0nSpQsTfny5acN69fQqpXLqPKF1dQzbg/IBUEgiREQPk28xm3UpIUSoP/buI7OnDlD/mwr0S8eOLCPqnAfBxMQk6Ax28G2k5UqXUjZsmc3b6nzo0eO0Kp/l9GRw4fowouqU/ESpdzSyIXoIBBtXg10bN69aycdOnSAKlWuSnhm/pyZCpC6V19LuXLljg44cf6WUqXL0o23NKGhg76gf1cu9Vhap7y2fdsWll2Ws9xUTmHvMdMkvJjUAvShgwfo3bdeoMkTRrs0XaMmLem1Xr0thkLH37/vBzToq8/UIKATw+D+qWdfpg533e/W2es09iME9Z7dHnXzPsUs8K33PiV8vJpWLv+H7mp7K3V64HEqfEFR+vDdV9UtLKnMWbhGJ5OjIJDUCAifJm7zHj92TBU+hfssf8IzEvZ4+iH6e9EfNHLcDKpStZpLxT/64E0aN+o7+rDPQB7gm1r3Tp86RR/zveFDvrKu4aTWpZfTe737KwWEyw35ETEEos2rTsfmN17uppwRJ0z9nbo+eg+tX7daYdG95xvU8d6HIoZLomWcN29+VWT7pMIpr2HS273rg7Twj3kWBBdWvZiAd0agpBagn3ykIy1ZvJDqXFmPmrdsR5mzZKHZM3+lnyePpSbs9HLdDY1UGz/LH8CMaVPUzKlN+7u5Qy5DK1f8Q8O+6a+0K+g0Hn68m9/vYemSv9jz9HYWwk8rofuKutfQ4cMHaepP42n+3Fl0Z5tGNOHn+ZQvfwGXvObNmaE05HWvqk8QtKEBFxIEMgoCwqeJ2dJYQYPpBqhFqw5hqwSiB5jUjftn2FpDqG7b4V7KnTuFpv8ymQZ/3U95+o+bMjfolULzPXLuH4Fo82qwY3P3Lg/Qrp3blXLq2LGjVLp0Of+VyyApjrH/wsRxP6ja1ru2oUutnfAa+PTh+9ryqtByFTmlecv2tGP7Frav/oGeeOgul3yT9UfSCtAQkiE8IyQOQs1p7Uiz29pQ63Ydlfc4GvWP32cr4Rne5EO+n0QpefKotr7+xkbU4PqbqWO7xvTNwL7Upv09VLiIb4/V3u+/QadPn6JX3vyQWrU9/wG1aHUHPfPEfTSTY0cP/LIPPf3sKy7fE7TW8GJ/+3/9AtZ0u2QgPwSBBEVA+DSxGu61l55RBT554jgrGZbSfxvWKeG56zMvRqQicHSC8HxN/YZKM61fAu3zxg1rVZ86lrXW7e7opG/JMUIIRJtXQxmb//tvA30zfBxddHHNCKGRONmuZgF39MjhdJZX2rdt3UyTxv9Iu3btoGYt2hJW4zU55bXZM39RwnPlCy+i/oNGEkJbgu7o+CDbWLdO0/7bJsP6XclyTNqNVKBRBt1594OW8KwbDZpebZM86ofh6vLd9z1iCc86XfWal9KVbDuFZcrf5/2mL3s8bly/lhb/tUDZ5dm1MYi/2OnBJ9Rz0JzYCbZ8L7/+gQjPdmDkd9IjIHyaWE08fvT3hL8pk8Yq4Rml/23GLzT6x7R+NNy1mThupMqyQ8f73bKud+0N6tqSRX+63ZML4Ucg2rwaytjc5emeIjynfwJzZ08nmLb0ev05GjTgM9rHkTje+eBzZVJq+iE45bVffp6o3oDJqxaecQGKxg8/HZj+9uQ+JK0GehPPQEEI5O2L4PwCgrDsiapVv0QJz1u3/OfptnVN51ONZ7xZ2FTETnBeBMHYHuFkzDRwVsydkmJ/RH6nIzDi20G8S9VUFzxy5sqlNFI/fPeN13swvXnp+S5q5m0+jNWBmxo1My/JeYwQED6NEfBBvnbRim1qoo8+bDdrsaAQ6PPRO/TOGz05HFa+sEfi2Jzej08Y+4Paqc4s9v59e9VPMXkzUYnceax4NZixuXrN2pEDIsFybtK8lVpBh0nLmB+/VeHrBn75iVph1yvuqJJTXoMsA6pWvZY6mv9ZttU2R2EzTTKcJ60AvX3bVtU+BQoU8tlOO3dsT0tX0HO6fPnTjO0PHtjvOx/+OEEFvOQDh0T8YatS2GQhmLlQYAjs4LbEVq8mwWkJ5OveyZMn1XNYujLpgJ+2NNPKeWQRED6NLL6Ryh0KAKyc3XlPZ/WK999+mYawTXK4Y0HvTO9XYebmaddDLB/Xa3BjpKop+RoIRJ1XwzQ2G1XIkKfFipeiy664StUdJhuP3N9OCdFfft7bxZzUKa/t3r1T5Zkv3SExI4KbtAJ0ocJFVNBwLFcU4QgX3qgILzcguDi0GcV4a1o77d29S10yo2fY0+B34SJp79BaEXuaI0cOK+E5L4erE+HZjo7v3115xyT8eSJf94oWK04/TV/o6TG5FicICJ/GSUOEUAyECANtYDM2fwRzNhB8RQIh8DA0XW+/39frKmEg+Uia0BGINq+Ga2wOvebJkwNMNro9/zq1a3EDjfx+sNpFVG+k4pTX8qcHQzjIK70ZldJ6sySsvRZ4ly9d7LN2ZcqWV/cXL/zdY7pFbNcMqshxJX2RzucfjsRx+vRpt6SL0vNHjFMhQUAQSENA+DTxv4R9e3erShQoUNBvZQoWKqzS7NmTppjQD8CjfxfHgLZT6TLl1SXEyxeKLQKx4tVQx+bYohZ/b0eYOWik06JxpPkYoJROea14idKqcpB57KRX9u3Xk+130grQN6fbuA75+guCLawmhF4a8vXnVtzCpuyJCho2+EsOe7NDJ1PHieytumLZEsIHB8dDX4SNAapycP99e/fQ0G++cEl66NBB+vzT/6lrcFYUEgQEgTQEhE8T+0tAHNg+vd9RlWh4U2O/lSlbrqJKM5m3E9YE4RkOTgj1CTLD2MF+EzR4YD+Xflxd5P+wWQZi1wpFHoFo82q4xubII5N4b9BRwkZ+P8QqvFNe098DNNlYYdeE2NsIP6goyaNwJK0JR5PmrVWc0LWr/6UOrW6hG25uTFg+nDNrmgqv8sEnA1T73nhzE44TXZ/+XDCHOvKmJhgEipUoqQTnX9nLNFfu3PTcS73Us/oD8XTE0sgzz71Gj3e+g/p82Iv++mO+iul88OB+5WgDR5cGDW9x2SDAUz5yTRDISAgInyZWa2MjFE0H9u+n5csWK00WnLUf69JD3/J6RAjRwRwWFFE8jnF0oypswzzj1ym0edNGqx82H0akDfSbCGXXruWNhO+lLK8aHuVYtiuWL1GOha++1ZtuvrW5+ZicRwCBaPNquMbmCECR8FnCif7dN1+gdWv+pcW8sVHty+qSU16DrIQdH9etXUX3tG+qdjc8fOgQjeUoPeDr4xzqMtkpaQVoOLkMGj6eer3Wg6ZNnaw2RUFjwo6rS7cXWaBuYrVtvwHfKfYDJJ8AAEAASURBVA0xZlKI+ADCFt7YgOWl196nchUqWWlxkjVbNvU7a7bsLtcR8m7oiMn05qvPsjZlJiF8DKgo21bDVhc7DprkLR8zjZwLAsmMgPBpYrRuRTY9gxnFL1MmWAWGL0f5CpVVRBuECzVDWXnr20qXKUef9h9Gr/TsqoRiCMYQvr8eNob+XbFMKTKy2frV3p9+Td8M6KtW9r7mOPqaUlLyKAdCbD4lFHkEIsqrWdNEEb1fg66N47HZSz46v4x01E632bO7yinAALx6W6v29O2QAUrBBwEa5ITX0FYDh46hns8+Rn/+Poe++vxj5d/V4vb2bGf9GrVsXN+SlVTmSfhfJl4uSw21XvVLpG0aMmf7cLesduw5Qjv3HnW7Hs0L2A4UYeayZs1GZctV8BlvefeunWr3wHLlK7mEmrOXF/ZD2XPkcIsxrdNhaRFhf4qwc6G3yBxI6y8fnV80jsUKp6jXxLq9olHXeHtHSq5sVLxIHsqT272zi0ZZhU+FT8P9nfnr27CpA4RlHZMf7z965IhbPH6zXHAK37l9G+/mml/tGKudEs00kTyPNZ8eOXaKwKtHj7v72USy3va8wz2mIr9THDXJVzjXQMbmQPKx1yWSvyuVKRjT9oJpBSaaZrxns764j509PfGRE147wdpmOPtCbtJ5QQbKxP+yeRDgzTJE6hzyDMZUO/mSV+1p/f3OEAK0PxDkfhoCIkDH7kuI9cAcDwJ07NBPrDcLn8auvWLNp/EiQMeuBRLrzbEWoBMLrfCWNhoCdNI6EYa3KSQ3QUAQEAQEAUFAEBAEBAFBIA0BEaDlSxAEBAFBQBAQBAQBQUAQEAQcICACtAOwJKkgIAgIAoKAICAICAKCgCAgArR8A4KAICAICAKCgCAgCAgCgoADBESAdgCWJBUEBAFBQBAQBAQBQUAQEAREgJZvQBAQBAQBQUAQEAQEAUFAEHCAgAjQDsCSpIKAICAICAKCgCAgCAgCgkDEdyJE3Ewdt1Tgjm8E0FYgaa/ot1O2rJkpa5bYzWeFT6Pf5sG+Ufg0WORCfy7WfIo+omC+nDHbcCl0BDNWDvhepL1i0+a6n4zk2yMuQGfPlsXrLjiRrJjk7RwBMHumTCTt5Ry6kJ/InDlTTAVo4dOQmzBqGQifRg1qtxfFmk8hQOfKmY1ynAt5A2G3usmF8COQhdsrN7fXWWmv8IPrJ0f0k5GmiAvQp8+co2MnYrvtaKRBTJb8wegQoKW9ot+iYPZYaqCFT6Pf5sG+Ufg0WORCfy7WfHouNZVOnjpD4Feh+EcAiokT0l4xaSj0kzmyR/bVkRfRI1t+yV0QEAQEAUFAEBAEBAFBQBCIKgIiQEcVbnmZICAICAKCgCAgCAgCgkCiIyACdKK3oJRfEBAEBAFBQBAQBAQBQSCqCIgAHVW45WWCgCAgCAgCgoAgIAgIAomOgAjQid6CUn5BQBAQBAQBQUAQEAQEgagiIAJ0VOGWlwkCgoAgIAgIAoKAICAIJDoCIkAnegtK+QUBQUAQEAQEAUFAEBAEooqACNBRhVteJggIAoKAIAAEtm3dSnNmz6Jjx44JIIKAICAIJBwCEd9IJeEQkQILAoKAIJABEdi5YwetXLmc9uzZTSVLlqLLLq9DOXPmjBgS77/3Fn03fCgNHDSMmt3WMmLvkYwFgWRB4MyZM7Ri+TLasGEdZcmchWpecimVK1c+WaqXcPUQATrEJjt79ixlyZIlxFzkcUFAEIgkAsKn3tE9evQovfTCs/T9t8Po3LnzO9zly5efXnr1Dbq30wPeH5Y7gkAYERA+9Q7m9Gm/0AvPd6cN69e5JLrq6no0YNBQuuCCoi7X4+VHMrepmHCE8JXd2b4VlSpWgNatXRNCLvKoICAIRBIB4VPf6D77TBf6dtgQqlq1Gr33wcf01ddDqHuPnpQ/f36+Ptj3w3JXEAgTAov+Wkgli+anxx95MEw5Jk82K1Yso/vuuYM2b/qPHnzoUfpy4GD68OPP1MrNHwvm05K/F8dlZZO97xUNdAif3fHjxyk1NZVOnDwRQi7yqCAgCEQSAeFT7+ju37+PRv04gvLmzUdjJ06hAgUKpiVuQfTUMz1o+bKl3h+WO4JAGBE4ceK4yu3YsaNhzDU5sho25Bs6ceIEdXv2eerx/EtWpTre3YnWrF5FRS64wLoWTyfJ3vfGtQC9a9dOZe+DD6dWrUupZKlSbt/G0SNHaPHiv5TdXrFixanKhVWpSBH3jwn2fQcO7KeqF1WjkydP0swZ01Re1za4nnLnzu2Wr68Lhw8dot27d9Hx42nOL1s2b6ZcOXNRpkyZqFz5CnTw4AHCtUqVq3jM+8jhw7Rx4waqULESpaSkEJY4/l25gsqWLUd58+VT5ft9/lx1vOzyKzzWR5cPAjyWdP79dyWVKFGSql1cPaJ2i/q9chQENALCpyfZXjgx+XQV9xug0qXLnBee0xs2W7ZsdGnty9J/uR6c9jvow5cuXULoO6+oU5dgHuKLgunXkR/6ZWgyUR/09VmzxvUQ5wuCiNyLV17977+NtG3bVlVnmBStX7dWnecvUIAKFy7C49sKHtdyUXkeXz0R0mfOnJnKV6iobmO8P3z4EFWucqH6jTESk0GMzxdXr+HT7BLj87Jl/9Ah/lar16hJpUqV9vTKqF7TfFq9ek2390LmMSkUeQL5QD5avepf2sRtAjyBYY4cOcxXqHNfMtXZM2d8ykhoK01wJkb7HuN2R9tUrFRZ34r7Y1z2LhB0X3iuu9KMmAi2vL0NfdSnnxJKkebFns/S2NE/EgzrNaHT7/JUN5dZGu4989Tj9OsvP9OChf/Q3Xe1Ux8Irr/x1rv08KNP4DRgervX6/T1gP5W+ns4P01jJ0xhz/Lf6IP331a2g+9/+Im+ZR2f6/E0/fjD99T3iwHUpm0HWvrPEmp0UwNV5ouqXUw9unVVEwL9QNv2d9DHfT53Gwz+WvgnPfrQfYTOR1P27Nnp9TffofsffFhfkqMgEBEEhE8Tn09LsaAJWrVqpdJk2QdjTx+O035n5A/fUbennlADM/LD4PnCS6+p1Tt7/sH266vWbVbjAfpVTVBgDB3+g1Jk6GsZ9RjPvLpv316qe1kNq2lmzZxOV9e9VP2uV78BfTtiNN1yw7V0+vRpWrTkXypRsqSVFicbN6xX6SHsYXwHYbyf9utU+nftJurOJkoTxo1R1/FfoUKFaci3P1CdOlda13By6tQpevP1l+nLL/q6XL/iirrUn00mMCmLFZUqnSbET5o4npo25+UhHxSsPAE5CnLLp5/0dpGp4Ej8ymtvKZkCSkJNvmQqKAh9yUhXX1NfKQ4h6wwfNtilL4BMBNkoESguBei7OrShhX8uIDBP+w53UeYsmenXqT/T2DE/Uqs27ajRrU3op0kTFVPg/g033qyWMKDFffftN+nD/72rPMhvurmRWxvc3+ku2r5tGz3+5FOEmS5mpE6pbbs71Kx0yDcDlfD60COPE7TfGBgwg4IxPz7EcWNH01vv/I8g1GqCJuanyRPVjO6WRo31ZXUcz+nff/ctuq7hDdSu/Z1Kiz3gy89p5IjvlMbm7Xc/sNJDy9K8yU1q6RVCeu3alyv7KAj3PZ/rRllY8yLOPxZcchIBBIRPE59Py5QpS3WvvJpgR9mqZRN6738fU5Omzb1+LU77HQz4TzzaWfWBT3R5mipVqkI/T5lEb73xiketVrD9+u23NVZh8aAMueiii9WgjDHk0Yfvp6nTZnutT0a5Ec+8CrOhN3u9pyZwQwZ/rWzx23W4UzUNFEoQ4Jo0vY3GjB5JY8aMpMce7+rSbGNYiQa6rcXtLtexStKy2a1Ks/1cz5cJ3/rkSeP5bwK1vb0ZzV2w2EW7/ADLBlN//kkJqBg7U1LyqPT9PvuEWjS9heb98bfHb9blpRH60bpNexrx3XClVMySNQu9+novnyvTKIYTeQLpH7yvo5JN4AtxT6f7qTTjtfSfv+mLzz9Tzov79+9XvhFIa5InmapO3at8ykh4vv8Xn9Gwod8ovLt0ZZmFgzHMnj2T5vw2y8w+rs8z8UeWGmoJ65e4S2UxZ/twt6yOHDtFx06cdrvu7QKE5Icf7MTLfFfSuIk/u2hdETO0SpWqVKx4cYLt3qmTp9S5mddgFmoxq7nn3vvpf737WLfu6tBaaaBhrjF+0i9Us9Yl1r1gT9Bpz5s7m6b/Np/sSytNGjUkaGoGDxtBtzZuar1i0oRxhA+uOTP7gK+Hqut/L16kNND40fXp7ko7ox9YvOgvuvXm65TWfcnyNdbS523M0At+n0eTpkxXS6I6/bKl/9CN11+jcMFs3ckSZu6c2dgMhejo8cDbS79XjqEhkC1rZkrJlZ2yZ4tNRBfh04zLp5s3b6I72t2uBBh8xZdcWpue7vYcNW7SzO2jdtrv3HxDffpnyd/02edfERQPmqAYwAoiCP0g+kNQsP36BUWL0uixk+nCqhepfGB7efkl1Wjv3j00c84Cqlaturoe6n+x5tNTp89y/3yKTp85Hy3FX50SZUzFWIoxFRO4QUO+c6nWjOm/Uoe2LalGzVo0beY8l3vX179ShV/8be6fymwHN/V4j3CMY8b/ZJl2QNy5+8629MvUKfyN96DnX3hF5fXbrBnUtlVzanjDTfT9yLEu+d/bsT1N+WkSTy4/ok73d3a55+9Hgbw5HbeXtzz7fPwh9XrzVXUbckzHe+6jJ7s8Q0WLFXN5JBh5YvZvM6kNTyqwAjVl6kzKkzevlSfygwySi98JDX/Romnv0xj7kql8yUjtWt9GWG34a8nKiGj3Ic/kyX1eeakr5Ete1WkCPZ43RAn0iQinmzJ5knpD54cfdRP+6l97nSUwFyxYyDo3i1SzZppgvGXLZvOydY6lw3AIz1aGXk7a39FR3Rk1coRLijE8QQCZg4lOADtKlM+k2pddrsqLzQbmz5urbm1iT1wIzxjoYE9oEmy2MJjAPmkLD4xCgkAkEBA+fc0F1kTmU2jmfv5llhIocqekKI/+Tnd3oBbNGqnVOl1Rp/0O0kN4xgAPDZpJiCTQomVr85I6D7Zf7/NZf0t4Rka5cuUijBegzZsydj+YDLx63fU3UPESJQgKItjnaoJtMGKXY0yHzbudEKlC20XjHkwQ7mblGggmnZpgZgR6oPMj+pJ1bMgr3KA//1hgXYvFCUxToVSEchHyAExN6l5eg6A09ESByhN4Fk6KoEcee9JFeMY1+EE0uK6hslHGRMNOwcpU4HXQ+HGj7VkmzO+4M+FYv36tAg9LN4HQoUMHWQs8h3bs2E779u6lnTt3qMdgL+WJLmWBNBrU8vbW9PILPXhJaLJynIFzIExGfuWZLz4cmJ3YCWk8EcxCYNe0fdtWdVvHgTyAJZWnn3R7JFvWbOoabKPNzsMtYYJcGDTwS172nexSWsyGv/5mOH3z9Vde78Hu78nHHnKx50Im8FyWjRtc4HT8Q/jUHbJE5tOUPHmUNg4DKAZmLFvDkfn2Fo1p+qz5agXMab+jJ/A1atRS5m12xHKnpDlvQ6ixk9N+3VPfqSMT7N+3z559hvqdDLwK80jYxn7W5yNlxtDzxTRN7Lixo1Rb4p4n8vRdgE9BMOXUtGH9enU64vvh9DNrm03CKgYI42msCTGfJ02ZRnPn/Ka00Vjlxoo78LmbNdImeao77tv7KVxbt24NDsoUVJ3Y/qvFG7ZAW/zfxo22OyxgBylTwdxq0sRx9PorL9K0X6aqyQvMcxNpX424E6C3btmiGqhQwcJuDWVewFLMay+/QN8M+kqFd4GXaL78+ensmbMqWRgsU8zXOT7Pn78Am240YzvoUcrmqv0dsK+azJE7jhO003B2DJS0xzoEcJBmfNgkLfzzD7ds8G7M1mHukgyE1QRoGUxC2C2Qr3snT5yklSuW05mzZ8xHaR+b/wiFhoDwqTt+ycCnsEdFmCyYVMB+FELzDyxUYOnaab+jlRnojwKlcPbrTszXAi1fIqZLFl6FvxME6NE//qAme5h4jR0zSgmPrVqfd+T310b50hVVR48esZJq5RR2+cuezX3ZHyZAN950i5U+1ifwD4P5JmK4Dx0yiN7t9YabAO2tjPZ+Cuk0b8PB0hPp8JZQSoWLoCH/ic1F3njtJYJmGya6UPh92re/8ssI13simU/cCdAIQYetZHfv2eVm22MC0fuD99i4/VO1TPfu+72V7Q7uL1++lG5ocLVaqjHTx+IcQjME6B9Hfs9C810qYgjK4cl8w1f59u5JmwFr72MIx6C6V15Fw79Pm4H7ej7R77386puEP0/k6x5wgn2VUPgRED51xzSZ+BQCQ+u27WngV1+oZXPU1mm/U7BA2hIt7JoDpUTo1wOtS7ykSxZehX07TKXgF/TnH7/zqkiK2sTs+oY3+pQV7O1wnk9LWbeKcwhYKGP6fTHQa+hGK3GcnGAC0fOlV5UADZkJZpvwD/NH5+t/PpoJ7JqRB7TtWs4w80H4QxBC7YaTYHozcvQE5X/x8Uf/U9HJ7mzfmuYtWOyoTcNZJid5xZ0NdNlyaQ3096JFPuvx0+QJ6v77vHNWIKGXfGYW5E299Ah7JE+kGRszKwQ7x1acmGHZ7Zb1s3t273YzN4BGBkupoHLlKqijNsuA/Ze59a66Kf8JAlFAQPjUdVUjGflUm4JpJyWn/Y4OvYVd0hCb1k467q95PR76dbM8yXCeKLyqx9OjPjZS6ZDuW/Qj+xbBORLUpp1n8w3c27l9Ow4uNG/eHPW7XLny1vXyFdLGVqxYJhLplWwcCxRM3wQpvQKByhNIruuvZQ07Bvq6dtK13/f2W7epNxlJPwcZru/nA9TKF+J3z5s3W9+K62PcCdDNb0vzxv68Xx+18YlGD4Jiv76fqKgXuHb6VJqN8waOAakJnfQ3A7/SPyN+1Bu2eNutC7Y8sM1C2R9/9EEVZ7INa3W8EfJ55KH7XIRohHnBQIMPDEseoPLlK9DlV9QheM9j+cYTYcMCIUEgUggInyYHn6KfHT50sEufg28G2jisnIFgdwly2u+gz0JILGigEetVkzLTeOUFmjVjurqE35rioV/XZUmWY6Lwqh5PVyxb5hX6lq3aqJCIiOuMPSAQAQIh7rxRlycfUQ73+j5s67/o96n6iVVhTdrJte9nH7vIHfo+NhdBnOhYELTCTz7+kDKnsr8fkTlAl11exy3EXqDyBJ5vkx4hB/4PO2yTDjhYYhIM22lsPOeEdJt6kpHg12UnOP+CCuR3nQzY08XL77gz4cCyIRxYYPN6c8P6ijkyZc6kgqLD+3bgoGEKu1tubax2r3mBYx5j1piHnWBGjxqpTDhg+2Z2ypECu05dDrXHJhqw4Vm7ZjXvXHRQbcpihrQDk6I+eq96b84OKCPsjCaOH0vX8MfapNltyi5pwvgxyhzlObZL1LM5pH3jrfeoZfNGyoEA9kMICg+74M2b/yOE/Dlx/ATNmutuH41nhQSBUBEQPk0OPl27erWKxfpOr9fV4IjlWywFI14utEZ3dbxXeeDr78Vpv9P1me702MMPUM8ez9DvHEUIGizEgUZ0Dnj2273646Ff13VNlmOi8Cr2ZEAEqd27dlHTW2/k7+N6JbSa5nsYIxs1bqr2gMAGLBhPsZuvN8qRPQe1btlUOe1jQoc9GNatXaN2GLytRSvrMTj1Y18GxIGGCSgwq1ChEh05cpiWLFnMjoWT6aNP+lrhFq0Ho3CCcL0/fP+t+sNkFrsNQ+MMrTD4CJFzPvwobVJgFseJPNGU5Q1ErcFqeaObG3AIy+YqjvPffy9SMgnegX0o4KzohLzJSJUrX0g3NaxH19S7VoX5LVykiNpBFHteYGUAzyUCxZ0ADa3t+MlTWTB8Snlows4ZhM1JXnrlDSVY4vezz71IsOX57tuhKig/hEsE7/51+hy6rdktbk561lJHeoQK5BEqIQ4jPjjEiPyqfz81M37sCdcg7wjqj7AzCOoPrXGFipW8vvaS2rWp80OP8c5JT9LnffuodIhj+Q7beJuxpHEDZiC/zJhDz3V/mjeVmaA+cp0x3glveiFBIFIICJ8mB5++8PJrlC17dqXNGz3qB+tzgb0zdh9DH2eS034Hmj1olXu99aq1syxCbY4eN5l3kNugBGi8X1M4+3Wrz88euMO2LkcyHROFV7HhWO+P+6qNdzBe4s+TwglRlPTOgr7MN9CG/foPVBuR4dtGJCe8Aw6yH3/Szy3aA2JPw0kRGmqt2UUeiIl844230JVXXYOfUSdMatPK1ltp07U5BYRZxMxGRBJMDuzkRJ7As4h/jY3cBg8aSIh8BUJwBjgs/o83a8POniZZ/OVDpvImIyFf7Hnx9YAvLasC5I1whRDUERUoESjuNlIxQcPWkpgtoqEgeJoaWJ3u6JEjtIm1rqVLlSEdtgW7/aHT0A2MtMjrJF+PRMNgiRJh9MqWKecx/6e6PErfDR9KcHa874GHdNGtow58jh0If/hxvLIXXL36X0IkkkCcAhCyD97yZ8+dVbNG7WVrvSDAE9lIJUCgIpAs1hs0ON1IxYRA+DTx+RRmZjAJO3TwIJUsVYoKFy5iNrHHc6f9DuJCQ1to5n3k8GG3uLN4WTj6daxCIn89LnishMOLsebTYDZSMauYCLyKMm76byPvQJyFYDZkJ3yndWpXV7sPL1m2xk0QRnq9ycdEDvmG1dndu3epP2g+zZ2B7Xnr33Co27Z1K+UvUEDtYOhU86rzCedGKsgTq9xbtmwmaNbLsqbWlHH0O0OVJ5APVqEOHjyghGbIUp7IiUzlTUaC2S1kF5jIlClb1tooztP7nF6LxkYqcaeBNkGCKYan4OhmGgjE9l2msPWnnZBX1gjNahDXWQcFt78XtsjjONQO3t/i9tb22x5/44O118ljwvSLYCKnxv2+8pN7goATBIRPA0MrnvkUAoLpVBVIjZzWx5MHv7njmfnOcPTrULiEU3g2y5eo54nAqyhjxUqVvUI8nP2CMDlq3bq9R+HZ04NYwcZfoATbXW2/G+gz0UgH5djFF+d39Cqn8gQyh+LOn/IO7RSoTOVNRkLZKle50FF94ilxXAvQ0QJqPnvlIj5zIJSXl3NgKhIojeKlI9gSwgTDW4zFQPOSdIJARkZA+DQjt77UPVEQgBPaihXeHQHt9UAos0CFW2gsYbYJatv+/Nbw9jzltyAQDQQyvAANwbll81sDxhpeohu37A44/XfDh6i07drfGfAzklAQEARcERA+dcVDfgkC8YrAl/37Ut9PPw64eLC1f/zJpwJKDwd5COhYoa1Rs1ZAz0giQSBSCMS1DXSkKm3PF5ot7FoXCKXkzaNsqgJJizQ6VAtm2d4ItoR/LfyDNyoo6dHmy9tz4b4uNtDhRjTw/GJtWxmKDXTgtQwtpfBpGn7Cp6F9R6E8HWs+DdUGOpS6B/osdrXDHgWBUo1atQI2l4BdLnYLhMmiaUtvf9d/bEO9besW5cDvyU7Ynj5Sv8NtAx1IOeNFngikrJFMEw0baBGgI9mCCZa3DMyxa7BYD8yJIEDHrnXi683Cp7Frj1jzaSII0LFrnfh7cywE6PhDITYlioYA7SyoX2xwkLcKAoKAICAICAKCgCAgCAgCcYOACNBx0xRSEEFAEBAEBAFBQBAQBASBREBABOhEaCUpoyAgCAgCgoAgIAgIAoJA3CAQ8SgcsBmDLYpQ/COAtuLQqdJeMWiqzLxdfWaAHyMSPo0R8EG8Vvg0CNDC9Eis+RR9RI7sWSlb1tQw1UiyiSQC+F5ySntFEmKveaOfjDRFXIBOc3o4Hel6SP5hQCAlV9pE5+hxaa8wwOkoCzB75lyZeMOdyDO9p4IJn3pCJT6vCZ/Grl1izadnzp6j4ydO0+kz52IHgrw5YATwvRyT9goYr3AmRD+JyWYkKbK5c8khjO3cezSSdZC8w4RAscIpKidprzAB6iCbaDC7r+IIn/pCJ77uCZ/Grj1izacQoPcfOqHG1dihIG8OFIE8ubNLewUKVpjToZ/Mm5IjzLm6ZhcbdZdrGeSXICAICAKCgCAgCAgCgoAgkDAIiACdME0lBRUEBAFBQBAQBAQBQUAQiAcERICOh1aQMggCgoAgIAgIAoKAICAIJAwCIkAnTFNJQQUBQUAQEAQEAUFAEBAE4gEBEaDjoRWkDIKAICAICAKCgCAgCAgCCYOACNAJ01RSUEFAEBAEBAFBQBAQBASBeEBABOh4aAUpgyAgCAgCgoAgIAgIAoJAwiAgAnQCNFVqaiotWvg7rVu7KgFKK0UUBDIWAjt3bKM/fp9Dx48fy1gVl9oKAgmEgIyjCdRYCVLUiG+kkiA4xHUxMUDf37ElVapyEY2aMDOuyyqFEwQyGgL9Pv0fjRv1HX3wyQC6qVGzDFX9kydP0D9//0XFS5SiMmXL+607+rJlS/+mIkWK0kUX16AcOXL6fMZpep+Zyc0MjUBGH0cD4dW9e3bTgQP7PH4nBQoUosJFLvB47/SpU7RyxVLavXsnXVy9FpUoWdpjumS7KAJ0srWo1EcQEAQEgSggAK37m690p82bNlKDhrdQn8+HeH3rimVLqHvXzrRt6yYrTZYsWahjp4fp6Wdfsa7pE6fp9XNyFAQEAXcEAuHV06dPU+MbrqBTp066Z8BXal5yGQ0dMdnl3rlz5+jtN55nBcL3dPr0KeteqdJl6bMvh1OFilWsa8l4IgJ0Mraq1EkQEAQEgQghcOjQQfro/ddpzI/fEoRgEJbHvdGypYvpkfva0QnWVrftcC/Vvao+7dmziwZ99RkNHtiPzp49S92ff9163Gl660E5EQQEARcEnPDqmTOnlfBcrHhJuvb6m1zywY/qNS5xu/Zij8fpp4ljeDWpJjW9rQ2VZM3z9F9/oknjf6T772pJQ0ZMCmhlyi3jBLkgAnSCNJQUUxAQBASBeEDg7vZNaAtrnTve+xBdeFF1eqVnV8qUKZPXovX9+F06cuQwPf/y29ThrvutdFdfcx21adGQRgwfRA899gzly5df3XOa3spQTgQBQcAFAae8iocrs6noS6+975KPpx9LFi9UwnPpMuXoq8GjKG/efCrZjbc0pcyZM9OEsT/QqBFD6alnX/b0eFJcS1onQtg7zZ09nX79eSL9t3G9W2Pt3rWTNq5fa13f9N8GlfZftuOBRsQXHT1yRDn1/TZjKu3YvtVXUnXPafrt27bQzGk/09o1//rU7Ph9sSQQBOIQAdjLLWc72KlTxrPz3Ww35zvw36p/lyuhC8XHkuLv834j8Nu+fXt81giaUPA7tCDQZMLuzxc5TY/8MHCgbzl8+JCvrJP2Xp0r69GIsdOoe883KE/6oOmtsrt27lBtV+SCoi7CM9KXr1iZ6l97g1r6nT51ksrCaXpv75Xr4UFAxtHw4BirXJzwqtMyThj3g3qk04NPWMKzzuMunlyDpkwem9QyTNJpoDH49nqth1peNJcVmzZvTb3+11e3L73xcjea89s0mvX7Snrz1WfplykTrHswlv+E7fkuqX2FdQ0nGPg//uBNGj7kK5frtS69nN7r3d/NcN5p+gP797Gd4IO08I95Vv4XVr1YDVTWBTkRBBIYgcV/LaAXezzpYgsLzUX/QSPp4vQlQkxi72p7Kz3WpYdynH3r1R603xCcm7VoS6/1+oiyZnXtvpYu+Yue7/Yobd1y3s42W7bs1O3519yEN0DoNP1EXpZ846Vulo0gtCxPPN0T9gsJ3CLOix6IdkrnOo8nGuiHMZB7oksuq0Mzp/9Mf/OkpGWbO8lpek95yrXQEZBxNHQM4yEHJ7zqtLyzZ/6qHvHE21V5ZSpnrtxKwbhr53aCWUgykusIlAQ1HD74Sxo9cjhhGeH+zk8qGz0Y0OPPTujY77+7Je3csZ0H6+eoZCm23/llstJePXxfWxr70xzlXa6f68bCLbRgyBu2fLlzp6j0g7/up6JkjJsyl7Jnz6GTk5P0KAveCc0bBPfmLdvzx7eFxo/5gZ546C4rTzkRBBIVAYR569blATpx4ji988HnvPx/MQvSm2ksR7DYyZ2sFqB1/X7+aTyt6/M+XV3vOmrWoh1hZebboV/RxHEjlebz+Zd66aS09J9F1OnO2yglT156kZcfa9S8VOX96Ufv0LtvvsD9QFbm2XuCTj+N+4WXejxBEMjvY41LufIVleDX58NeLjxvvUBOFAK7d+9SxzJlK3hEpEyZ8ur6gf171dFpeo+ZysWQEZBxNGQIEzaDY8eOqv4UioFixUvRBUWLuZloQV7Zy34MIE/Rd2DSBUfCdbyKvp8VgyJAJ8jnMG/ODFVSOKXoUCowcL/n/kc91uDwoUP07Y8/Wx8BDOG7PHoPzZ75C436YSg93vV59dyC+bOV8HxN/Yb0YZ+BVl7QPm/csFYNphAE2t3RKaj0eB+E58oXXqS0cTlz5lL53NHxQep8b2tav251htN0WSDLSVIgsGrlctq3dw+1aNWBGje7XdWpUuWqdO11N3msHzrfBx7uQk8+/YJ1/6p6Dahj28ZK6H6863PW0mHv915Xplef9R9O4ElQNQ6nVIrt8zrcfhN92e9Dup01nFpr7TT9gC8+Vnm+2qs3NeM+AgSN6XdDB9B7vV5SvzGoCLkisHfvbnUhD09sPBEmPKADB/aro9P06iH5L+wIyDgadkjjPkPtx4BVwrvbNbHKC01ym/Z3U+dHnqL8BQqq64cOHqAzZ85Qrty5lb2zldg4yZMnj/p1MJ23jVtJc5p0NtD52fwCZJpk+GqtV978wBKekQ4fUZt2HdUjs2dNsx6F1gvUoeN5Jxh9sx7b8YGWLPpTX1JaMvwINP0vbKsNggCuhWf8RtzFDz89L7DjmpAgkIgIFEjvfGGitC9dsPJVjxq1LnMRnpG2Rs3ayuP7BGuzF/05Xz0Okw10+tBga+FZ54ulRPAQfB6gwQYFk37l8n8IdrxNmrXSWavjHXc/SLc0buFyTX6cR+AwR+wAZcue/fxF4yxHjrQVu+Os9QI5TW9kJadhREDG0TCCmSBZQe54tuebbPL2Or3y5ofU7bnXqDXLQvAPHvZNf3r4/nbKjBXV0f4f5oq7vZrZs6fFeIdGO1kp6Uw4OnZ6iKb9Mol6c5glCMB33P0AXccxSnW4JXtD5smT5jlqXq/CdscgmHZo2sxOhiB4ls5imz2T9u9LW340bS+dpteDO7RmdsrFM0BFPjzd7c8k0+8R3w5izKe6VClnrlxqJeCH777xeg+z5Jee70JneaZsUqu2d2W4DS/M+sfqHE5jDW+8lWZMm0Itm1zLk8V7uYO+21opspcrb17PWkv4BcBOGmYfIMQhBkHTgbjEdsqaNZu6BP7EcqPT9Jo3q15Uw6O2BVoYkNbgqB/yn0JAe+bDkdoTIfYsSGu2nKb3lKdcCx0BGUdDxzARc7jr3s5uxX748e7UodVNqs/9kVfl7+j4AOkVpaMcXccb6bjQWnHiLV0iX086Aboma62GcbDvj/73BsHs4s8Fc9Sg+ca7faj2ZXUDaivtWa61InhID9arV61gO8i0AdnMDKYX9RrcaF1ymh47+IDy5U0L5WRlJCe0Y9tWWrt6pQsSeunX172TJ0+q5+wCtF4udslQfkQFgfc//oq+GdCXhg3uTwO++ETFAoY/wTPPvRqwLXGedMH62NE0zQYiBYAwYVry90K3euTNl4/t+IpzUP/K6p7T9HvSeRP5CDlDQAvGhw+naaLtT6PNQIUKF1FHp+nVQ/Jf2BGQcTTskCZshkWLFVfmbwP791GO1xCg8+UvoBQGMOOAb4ul5DNqqVeTChVK423jVtKcJp0AjZaBzTO8+jesX6MGaQT1fpId8cb+NFctw/prPa1RLlq8hJUUHxE0UW+/35eqs4OSP3KaPj9/kKCD6QOKv/wz0v2u3V8i/HkiX/fQBj9NdxeoPOUj16KDACafnR99iu594FGaMmksfcYxgr8f/rUyWwo0XqjmT+2YUrRYGp9eyhPkT/sP81sRp+nz5U+z+xPe9AutW4KChQqra1s2/+d2Dxd0iNHi7KwEcppePST/RQQBGUcjAmtCZlqkSFFV7hPHj6sjIhDl534R235vZd6ufGE1l3pBsAbPI12RC4q53EumH0lnA202DraR7PX+Z3Tzrc1VTNm//jwfHk6n271rhz61jn+l21aWLl3Oula6THl1vsamCbUS2E6cpi9eorTK4R8OxWUn05TEfk9+CwKJiABs5267vT31G/CdKj5CmdkJDofoiE2Co96ihQvUpdJlyqqj9gJft3YVYWtZf+Q0fYmSacIdtpf2FCN+V7oG3N97M+L9q65uoKq9gON429sSNxBPG3Rjo6bq6DS9ekj+iygCMo5GFN6EyBwr7yBsnKQJDt2gubNn6EvWcdHC+SoG/9X1rufISGnOhNbNJDpJOgEatpF20k55efOlaXnN+6+80FU5IOlrMI4fOugL9fO229vpy9SkeZrzELae1cuO1k0+wWYPiPusyWn6mxs1U4+O/H6wtYEELiD6xrMcPk+RePmn4SD/JyQC0Eho5xNdAb30ly+/u+kSotL07P6oi+CFEJUwwcCgDidDEHbCqnnJZSps3agfPGugsROeJqfp8S5EC4GNNbav1gRhHr4W8+fOUpckCodG5vwRdu/QZAL/IYM+P3+Dz7BZFJw/y1eoTDAZADlNrx6S/8KOgIyjYYc07jP85++/PG489TcHR5jAQRTgR3b9DY2sejRuers6h4/S3j27reuQhbCyCGresq11PRlPksqEAw3XodXNdEXda+h6dlYqWLCwimeICBqISXhp7TpubZg9Ww7q3KkN1bu2IVWseCFNn/YT/bdhHcF7/+Zbb7PSI9JGA3ZGRBzodi1vZIG6NZVlh6SjbIe5YvkS5Vj46lu9lbYbDzlN3/CmxmqQhhbtnvZNOdZ0E/ZIP0RjR39PVdi++jjHzhUSBBIZAQi3o0cOU2HgqlarQfDO/uHbb1SVED7STrCzw06i0Pwi9jpWYn79eYKyvcMmK6bTHrzHEdMdmygtmP8bx1Kvw44ueZRQPW/2TDrBOwiOmjDTeoXT9A883JVeePYxjindkzXg86lipaoqdOW/K/6hK6++VvlbWJkn+cmX/T7iSCZpJhnawXLVymX06gtPqZqXq1BJxeDXMHTtxiZYHBoUMbOXLVnE4QUvoU3/rSeY1qWk5FGb4ui0ODpNbz4r56EjIONo6BjGSw5OePXtN55XZqrYHbRMuQpqA6TVrMTA6iCUA126vagmw7pu13A6hPVFyMO7WWZpeGMjyp2SQtOmTlaKv0ZNWrKzfnOdPCmPmRiY1FBrVr9E2kYfc7YPd8tqx54jtHNvmrOP280IXPj0o7dpxPBBLlrcq65pQM+/9LbSbuhXPvlwR47S8Sv1++o7mjh+pNrTHVBgo4Tr+UN47a2P3JYesAQJB6ih33yhtFE6LwwCcCDs8cKbLjbWTtNjJ8KePEj/yZu+4Fl4pENQx05qLRvXp7z58tOIMb/q14b9WKxwisozmu0V9kokaIYpubJR8SJ5KE9uz+G+Il2taPAplgGxkx+22NYEpzFseHTvA4/pS2qbb+xEiA1UECburVeepV3pplawe+758juKR60H0k/gaNrr9efpH3YkNE0tKlW5iO7u9DC1bH2HyyNO04/jySz6lz3pm4Ngkv38y2+rqB6v9OxKH/cd7LFcLi8Nw49Y82nrZtcRJvreCOEEEVvfpD8XzKX/vf0yreXY3jCzyZEjpwo7iHj9nnxKnKY33xXJ81jz6ZFjpwi8evR4WvSSSNVVxtHwIFupTMGotJe30jrh1SmTxhAcBU0zVSgpEBnsiad6srB8vdtrsOoOwXvGr1OUPTQSlCxVRkW5eqr7yx6jFrllEqEL6CcxptrJl7xqT+vvd9IJ0KgwBk+EkTvJGmk0pg6NZIKhBejB301UO/8hLu3ePXt4ObGS15il5vP7eGvhndu3sTdqfg7DVcbvh+IkPXZqg2anXPlKVr7QCmTif97iqZplC/Y81gNzsOVOhudiPTBHQ4DW7bSfd50D72BCWLxEKbcQk8uX/q228oYA/fnAEYqfN7ApE2LTYlcsf4TQaJs3baBz3A8U4/w98b+Zh9P0CIcHTQtWuDQhTFu0bP0SmU/hsY/dJ8uWq+gxmpHGUx+dptfPReoYaz6NlgAN/GQcDf0rirUAHUwNDnHsdvTPWbJmIewUGqjMgVWpHDlyuSgRg3l/uJ6JhgCdVCYcGnjY6sCWzgkVKnwBh1K6IOBHEJrFSXgWJ+lhsw27S5N8BSw308m5IBDvCEDwNIVPf+UFP9u9vH09g0gfFStd6CuJyz2n6WEOZqdoCc/29ybab9i8w548UHKaPtB8JZ1/BGQc9Y9RMqbIx4oN/DmlUkbQBafPJmr6pHMiTNSGkHILAoKAICAICAKCgCAgCCQGAiJAJ0Y7SSkFAUFAEBAEBAFBQBAQBOIEgaQ04QgE2+df7kWdHnxcObIEkl7SCAKCQHQQQKzRr4eNJb3hSXTeKm8RBAQBpwjIOOoUMUmfTAhkWAEa9joZ0WYnmT5eqUtyIgCb5MuuuCo5Kye1EgSSCAEZR5OoMaUqjhEQEw7HkMkDgoAgIAgIAoKAICAICAIZGQERoDNy60vdBQFBQBAQBAQBQUAQEAQcIyACtGPI5AFBQBAQBAQBQUAQEAQEgYyMQMRtoBF4Xgf+z8hAJ0Ld0VYgaa/ot1a2rJkpa5bYzWeFT6Pf5sG+Ufg0WORCfy7WfIo+omC+nDHbsTR0BDNWDvhepL1i0+a6n4zk2yMuQOdNyUH4E0ocBKS9EqetwlVS4dNwIRm9fIRPo4d1vLwpZ46shD+hxEEgR3Zpr8RpLWcljZ3Ky1k5JbUgIAgIAoKAICAICAKCgCAQFwiIAB0XzSCFEAQEAUFAEBAEBAFBQBBIFAREgE6UlpJyCgKCgCAgCAgCgoAgIAjEBQIiQMdFM0ghBAFBQBAQBAQBQUAQEAQSBQERoBOlpaScgoAgIAgIAoKAICAICAJxgYAI0HHRDFIIQUAQEAQEAUFAEBAEBIFEQUAE6ERpKSmnICAICAKCgCAgCAgCgkBcICABCr02QyqdO3eO7/IcIzWVMmc6zYcslCnLWTp19ixlypydsmXKwvczec1BbggCgoAgIAgIAoKAICAIJB8CIkD7bNNUdffU8bM0tP9UWv7PZrq+8aXUrG0tysRCNWUS4dknfHJTEBAEBAFBQBAQBASBJERATDh8Nmomypw5E40fO512b9tFXV5sQeO+W0RbNxyjLJnP+HxSbgoCgoAgIAgIAoKAICAIJCcCIkD7aNdM6RrmEiVK0L69RHu2H6fcebJSrhQo7kV57wM6uSUICAKCgCAgCAgCgkDSIiACdABNW6R4fjp09BBNHjuf2tx3ORUpnofOnhMBOgDoJIkgIAgIAoLA/9v7EsCqqqvr9V7mARISIEwhCUOYJMgYRkEFQWakiKKIE9a29v/FVv+qrUMnh6/W/nX8Wq1KS7FVESmTqAgyz3MS5hlCCBAyT++9b6/zcl9ekpeoH0NCsk/7cu89wz7nrhviuvuts7cioAgoAvUOgQbEAt16ZrhsshmwVD4lsPsFywN165hdLqdImp2Q7YJSZ5da6ed0ST8HPv1wOR7/9SR07BJvfgEcsrnQ8k6bCv2hCCgCioAioAgoAoqAItBgEGhABNp6ptz85xSKHIj9u09h5fJt6Ni5FYYMv14os5s8w+aQznLlZ8fypRsR26aFIc9OIdl2m130z+xHQq6bCC1U9agIKAKKgCKgCCgCikBDQaABSThIduVjKzWe5ovni/DHFz5CVJOmWPDxGmxdl1LGhyVEnXipAQeys7Oxfk0aJt0x1Fy7PdcMbUfPtBx4Jif8aFEEFAFFQBFQBBQBRUARaBgINCACTZLLD2/ZH4UFRQgJLcJtd/VFh44xOHYk07QZ8uxinwAsXrACI27th/CIULl2ieeZDntKQCjw4FHJswCiRRFQBBQBRUARUAQUgQaFQAOScFguYz+TICWmTRMMGtITP737dbRJiMRdD/aSB+/AhfM5KC10IutCEUqLg9BnQCLc0g03VAzMkZdTCIckU2kcGdagfln0ZhUBRUARUAQUAUVAEVAErrlYbJYX2e1LLtNcGG+wcS5bT5QKjCqlYqXkGcSQm/pjX8pZPP78XSgpLsLbf1iAzKwsIdCZSNmWj//33AyTK6VEVBt2hxP+/nasWLQZH/z3Ehltw4239sH0mTdJrGgh1zZZG6UfmlylCvJaoQgoAoqAIqAIKAKKQH1C4BrzQAtBNSTVTZ3dPmVqkuVD4mqkF3LJhop8ubxC6rk5kCUz8xxaxEaA/PdPz89FTLMo/OLZe8EE3RtF+zz7nXmI63gfoiWMnUu006u+2IvPP9uDZ1+eicDQQPz778vw9bJNGD56kIzgGmhViyKgCCgCioAioAgoAopAfUbgGtNAi+aYRFWiYfBj48fzdCQzoIme4amo5qRct3z69AVENW2M/Px8nD6ejztmDIdfQAlK/UqRPKwLwkIjcHTvKTOH3eaPpQu3YeTkbojv3AKt2kbitjtuwtYNJ2UtbirvZu7WeTXTa7UioAgoAoqAIqAIKAKKwDWNwDVFoBmT2eEsFBItYeYknByEMzuLib8fSqWK7QxRV3NxibPaTXLPnT2Hli2aisZZNgj6l28MNA5qifXMTYLRzZu4ebFsPuzWvQO2bzpaZt6OHdtSEd5I/NUq26gZcm1VBBQBRUARUAQUAUWgHiFwTUk4mOTEbguGy2HD5wtWYfWX21BY6sQtk/pjxKj+8liEUbOUu6Xd1xV+lr8znBUJR+/eXcXTHIJuSa3x8T+/waTpQ+EvHuiF/96I0tJitG7f3JD1I0fSkZefjgO7TuPVZ/6FkPAgpKQewS9+fYeweCHkNKsa6ApI64UioAgoAoqAIqAIKAL1EYFrikCTpdrtDiz5bAtWfJ6CHz462Xie33hlPoL8wzF0RGezuY8uY3Jow6ONvMIJpxDtue+txYF9BzHx9iHo0TcRhXl5iIwKFQeyE9PuHYUfz3gDq9ftQKB/AMKCQjHr6dsRIJ7pL5dsxP59GbhtyhDc93AEdm87JlE4nLjn4bEIbexnFBz0X6snuj7+E9F7UgQUAUVAEVAEFAFFoCIC1xaBpvJC5BI7tqUYwtuuS6RUhGDa3SOxZfMuIdCdhMYyHXeJ1DNNt1Bpqjr8/fHJP7/AsQNZ6D8wCW/94XP8+uUWKMkPkVB0jPHsj/nzlmLK9AFIHtxVHMpFaBrTDOfSs/H2n+Yjrl1L/PAnt5jNhi6XP65P7mBsWz9UwWEhoUdFQBFQBBQBRUARUATqPwLleoZr5l7phXYiIyNdVsw4zHZknM7AIdnsdz4jTwi0n9TQH0w5h7Bnu1vvfP5CDhKvi8GgG3tIVA2nyDHyERgcjICQAOxPOYmDe8/ilnG9ENU80JDnb76ScHXvfoxbxw3CyFsHinSEAAWKXaPVKCPpbtts0aIIKAKKgCKgCCgCioAi0DAQuLY80CK1oCJj0g9uxisvzMaxUxlCbIOwZ/M+9BrQDX/83Vx06BSH0RP7o3mrKHmCssNQNgy6JKvglLtH4LWXPsVHH27Aw48ORFFJkcg3QuAUZ/Wc2fMx/Z7JEoEjEBfPZmPu3xdK9kFg+v2T8NnHq5GyOxVhwVEYNa4vBg3vIXaZ7jtAbDeMXxK9S0VAEVAEFAFFQBFQBBSBcgRsEmnikt2og1veZSyuPj2n3PIVOGP0DZdDthJK4Ob0E5lYtWqHSDAaYcDAbnIMQUFeKb5ctg5rv9qDxM5tMXrSAMS0jvZaSTGWLeCYMIkFXYoLmdnCgf2RJclTbp8xClvWpoq+ejNGjOshUo7r8OYrC+Ao8sO0mYNw5sQFvPyb2fjtKz+RzIXNyjYMepnWU0VAEVAEFAFFQBFQBBSBOovA5eSr1xSB5uZAQ/eF8tvcmoqyh1RSJqkIEkLsh4KCYqxYthmrlu9EYqd4kWH0Q0wsPdKlOHXoAv704qeIjGiM0PAAFBRewCM/m4ZPP16Ki1mluPehcWgknunsjAI88X//iFdefwxhhoOH4O9/WYZGjYIx8c4buBT1QNfZfyK6MEVAEVAEFAFFQBFQBCoicDkJ9LUl4RB6bDbsVZBOMO4zVc+hcEo4OYaHplP91gkDMXxkMlZ8sQF/fuk9JHbpgL4De+CDtz7Hpm+OSn8h265StOsSjbdemYek3gkYOboLtm7dhd1b05FxKhfnz+Xi5OkzSIyON4kGTx4/jsGioaY0hCH16L3WoggoAoqAIqAIKAKKgCLQsBCoVwyQOVQ+nL0E61alISo6Ev/nZ5NFjjEQI0YPwNrlu/C7J+fg1JECBAU0QVCgHxylpTiUlm3kH3t2nsSO7UcRm9AEQ27sinad2mDzukT88cW56N2nGzJPnkd+URH6DkiSKB1k6X4ata5h/VvRu1UEFAFFQBFQBBQBRcAgUA8ItM2jpkg/nYmvJWbzf/35cfx77kI8/4u30SO5m5DdUvj5idtaPNNBQRLFQ8LcuUoLBYBSCU1nx8WLhfjJHQOFNLeSpIblgUmGjeyFrkkJ2LppP7r3ikfvvp1N1A6j3ajgBdffJkVAEVAEFAFFQBFQBBSBhoLANU+gvVKmoHGjMISHBmHDNztx4vAZ9Enuip79u0lkaIdE23Bi5cI0SahSggC/AJFfMNwd03o7UVLswKL568SzXIgm0VFo1rIJmreMQExMNKKjIzBqPLMcusuXiySpys5j6NW3C5KHCznXoggoAoqAIqAIKAKKgCLQoBC45gm02/8sz0zSaIdFhOJHj9+JZYvX4caxQzB0eHdxFvt5HuiY2wbj5V8tQ1REoUTykDB0shHwwoU8PPDoCEx9YBByLlzE/tRTyM3JF/1zNvbs2S/a5yA6sNG4SQgcBYFY9dUOTL67Dz791xrEd2uBmJbRRnNt02wqHpz1RBFQBBQBRUARUAQUgfqMwDVPoD2hMERS4XQ60aFrW/nEmWfmcslmP4btEM1yaZET6ekncPcPe2Pr+h0Sli4PQcE2PPvUZJw+dxxfLFmLgykZ2L97HwICGuG26TdgxH0DxKgLebm5yMsrwvJlW9AlqQ2u79MJH763DmczzxkCXZ9/QfTeFAFFQBFQBBQBRUARUAQqIlAu+K1Yf21dMaScCDWoaXZIZhRKMXhtswVKohXJHSjk+v2/zkNch5Z45Jfj8PvXf4zkGzvgyRemoVGTQMz8yRSsWrYP4Y0a4bevzcKPH5+M99/5F7ZtSjGZDMPCw0TSEYXJd9yAgqIC/Orxt9FL0nl37tyeE2tRBBQBRUARUAQUAUVAEWhACNQDD7T1tAyLNqHl7E4bNq5JkRTfOejaIw67d6SI7jkQYyYPEdVGtkg9/OEf4sL1/dvj3beXoFe/dijOdWHMhJ4ICXegbcfmGDpkMHZJhsOefbvKGCHjws8Dgvwx68nbUVxYisBQSkPcOwlVvmE9Az0qAoqAIqAIKAKKgCJQ/xGoHx7osudkt/mjVLJ3v/LSh/j0nyuRkZGFl5+ei+3rj2LGzPFmMyFckr5btg86xFsdEOKP+HYtsHPLSfFSl2DX9iNiKRgukYLs3X0GYaGRci3JW+yM+8xTpu92IDBYYJOMiFoUAUVAEVAEFAFFQBFQBBoeAvXIAy2kVuQae3YcQE52Pn7/5sOSVMWOcZMG4aXfvIGiklyJ/xwsT1h2BMqGQ5sjWCJzFEpylXjM/dvXePCnY/Hu6//BakkDfjIjA+FhAbhlwg+kv3iZXYFiyyLMcrTxvF69ezS833y9Y0VAEVAEFAFFQBEwCAxKuPt/jYRNMtjFi0T2/cW/h79/eeAGGlwybxV+//N3RFrr8Nins/ORX96BqfeP8tRZJ49OfwlbREHg3d9qq+645vA/qmu6ovX1h0DNM99tAAAg2ElEQVQLKSbXPZOegeZNIwx5JlmOiAgTr7QNjmJ/2MMCBUx/kXMwLrQDdr8gRDcLQaik5y6R/z3xu7uwbUMqgkP7oEff9iLnYH9SZW+yXH8gMzenPxQBRUARUAQUAUVAEbgCCFAKa8hZBdsupO44WKHmWrzwZobX4vplzfQIly3d5ZT4zJ1xYN8RrP6CsaDP4b//PBcdElsjPDJUepaiuKgUcz5Yis1rDmHxJxuMXKP/oB5YuGg9IpqGY9iYvuh/YyJCQgOkzW3eCKCvUXR02YqAIqAIKAKKgCKgCFxtBEqKS7B9Y5pwL5Kp8iLCWOzZfhAF+UXlldfgWT0g0OWou4TxMlrGzIen4MuFW/D6S58gqlkEHnhkiknbzeQpn/9nHY4dOIE3Zs/Cks9WI23PIXTuHof8vBycOnGmzJg8btFBu8m5Jd0on0fPFAFF4NpFgKEts7Oza/UGioqKUFBQYNaQk5NT9vemVpekkysCioAicFkROLz/JE4czZBwwpUItFyfOXkORw+cuqzzXW1j9UqPYN5ynKXo0jMOz/W8z8idIfv+nHx4lHiIB7pZs2YoyHPi5LHTQqpJjkXaIXHu+vfpjNeeX4ieye3Qe2AntO/aSh56ibSLnkfiSHu83Ff7Cel8ioAi4EEgNTUVJ06ckH+zdjRp0gTXXXcdAgPdUitPp285yZW47h9++CEeeuihGnuuWLECR48ehcPhQL9+/cxcvgZ88cUXGD58uGzBcH8Vtn//foklH4D4+Hhf3U3drl27JLZ8HoYOHYrPPvvMjG/RokW1/S9XQ0pKCgoLC9GrV6/vbTI9PR07d+5EcXExEhMTzYdGSktLsXnzZmRmZqJly5bGtoUFsdu0aROioqI8/c+ePYvt27d75o+Li/O0eSr1RBFQBK4qAtQxe5fKpNe7zTq3xvDoKC3XOFvt2zaI99nh/rto1XmOEi1t55Z96JyU4KniCe3QnpUkz9c6rHkrDKyFi4qI1cICLn3KsocjB5uQYZudAnYhzDYJxxHgLPvqQDYNmk2ADiQP6YrBI6/D3/8+D2OmDkGX7vE4ezoLSxZskAQsMSY83dt//gzrVqTKQ6QtSkRk4yGPWhQBRaBWESA5DQ0NRYcOHXDy5EmQvF6JcuzYMRw5cgTTp0/H2LFj8c0331Q7zbZt29wJm8p6nDp1SpI2pVfb/0o0cL65c+d+q2mS9NjY2G/t56vDnj170K5dO4P9woULcfr0adPt888/Ny8DfMngC8f69etN/cWLF82a+My88SCBzs/PN7Zor2nTpr6m0zpFQBG4igjEJsTA+rSJby77xGqmh0HBgWgrUcysMbEJLTxOBGvZW9bskVPf3IkyDso7KpeWbZp5bNJ+YJB4Qb2Kn58fWsc19/Th/LVV6pUHmlE33IWk2u2V4lmZY0jOgoRIAxNvH4aJU4aRcUtxYuWXW9Cpczs8MGusXJei+/Xt8OJv5qB3/1kSsk7sMJthuREO0qIIKAK1hEB0dDTotaSXl+TNKufPn8fWrVuNR7R79+5o3bq1aSJhI8mlLKt3794IDmY0Hne5cOECduzYgWHDhllV5hgUFGQkFpR7HDx40GOrQqfveLFv3z4cOHAAYWFhxpMdEhJS7Uhf90C5Bz2/9LSTnN96663YsmWLeYGgx5f3umHDBvBevvzyS/Ts2RPEyNe89L7Tg8xv4ugZJo68f39/fwwcOBC87+rKzTff7GkizufOnTOeZeLzyCOPmG8FBgwYgMWLF4NH/odu0qRJxj691N4lMjIS7du3967Sc0VAEahFBGYvecEzO//uzbrnJezctN9nNAxxSSKiSSO8+a9fIqxRqHuc8Clv0n3xQi5SZKOgLw8yB1AxwI2EebkFCAsv/5v4xAv3y/4zN+nOzsrFvWOfxoWz2dLfJeGG7ejSox3+POdJ8/fGs+BaOrEYZy1NfzWnNVTaTGgeqGRGcbr4R71UHrDD6z+QTjSLiZQwdpHuTYRG/O77Depqrl7nUgQUATcC9Gbu3bsXa9eu9UgRKEv45JNPJDtoZ/OhLILaYsokPvroIyMt6NKli5F/WDiSTM6bN8+n1CImJgbNmzfHO++8Y2yMGTMG7E8y66uQ4JKI8pMhYTCtQhJL8t6/f39DTufPn281VTlWdw8kvKtXrzZe3E6dOhlCT+/4TTfdZIgyiXVCQgJIzHn/4eHhhjz7mpdro+eehRh+9dVXoE3qsWvysnsvluvhSwnJO73MnI+SGhbKaog7C+v50uCrHD582Lz8UPpBe1quLgLTpk3D1KlTfU66ceNG8+LDb3n4kjNx4kTzwuazs1bWGwQCAiVCWdmHXt+eyZ2FJhsvY5V7JJnNPHNBpLAZnjEBARX9sWm7DiHrfK4hvlUMSAVJeuaZLBze5/57ZPVhGDxrHdRQW+SZ7ZJXWiS2XUHvt9WHx9oqDYhAl0PsdiaTFNvlIQagb//uWLxglbxtpSH9RC7e++tCJPWMR1Aovdii67ExNbiS6HIE9UwRqD0ESNpI4KizTUtLMxrlQ4cOoVGjRkbfS29n48aNcfz4cZBokgjTS0tvK72zLCUlJfj4448NCY2Pjzd13j8oV6DMgOSUpJAeWhJMShR8FRJ19ueHtq1CO/SE07NMHTDJK3XBvkp198C+XMeIESOM7IFEmd5fao4pgSB5pUeZ3uM2bdqY43edl573tm3bokePHsaer3VVrlu5ciX4MkIvN7G2yDP70etc3f1ZdrjmW265Bd26dcOZM2fw6aefWk16vAoIPPfcc0Zaw9/ZyoUvVPz2gC+n48ePN59169aZb06WL19eubte12MEevTr7N4/Vt09yt6wHZv2VteKTat3G8JbbQc2iI2dm2uysUv+zlNK6y6MDd2rf1frstaPtUfda/XW5b1B+DBF6k5nAeITm+PRp36Auf9YgKwLdkntHYcfTBsoHugC6SNfLZBx+34Rq9W70MkVgYaIAD2m9LSyvPfee6BemZ5hEjfL+0lyRjJJDzDlApULCTEJN3W8CQkJFZrpGaEU4r777jPkkBsOWbh5cciQIRX6WhckHRaR9Paocl38WOsicbT6WWOtY3X3wHbKVaxxrVq1wujRo41sg0THlyfxu85rbfb7LsSX66B0hOR9ypQpvDRyGCuaCK95To16TYUSGt4DC/XPr732mvFGWWupaay2/e8R4O/vww8/jEWLFpmXT1+WHn30UfNNBmU5/AaB5emnnzb/ln7+858biZSvcVpX/xDo2DUOEVFhuFitF1k0zLJJcNpDY6rcvNPhxLb1qWRYVdoqVlRvgzKOrWLD7GmTn/SGN2nWGInd4iqaqMWrBkqgzdOQhILySOxB8scbSEyKw7Mv/VR2gDrhF0DHfImpN89GsuZoUQQUgbqFAEkiCRs9svTQUj5BTyqJJkkwCwna7t27jf6Z9fRck8CRrFGWMXv2bEPmKnuhOZ4eOsoUbr/9dvztb38znujqJAnVIUPPMNdneb6pw66OKNJT7useKB3xLiTofDngh+vKysoynl9KQKzyfea1xlhH4krvtqUht+qJI6N4EA8SbhZ654kVPcmUvXDDID3MNRWu09KhU9NNz3x1mNRkR9u+OwJ8pnyp5O/f+++/j2effbbKYEuiRHmHRZ7Zif+GRo0aZYg3x1svclUMaEW9QiAyqpGQ1XhsXp0i/8arfmtGKWza7sPIlczP4Y0rvjSfOp4Byi+MXLYGVL7NxqG9J8QL7v5bzsgbXZLaoXGk+8WuBrNXralhM0PxKtsZps4qcu0mz6wIkD/qVoMeFQFFoC4gQE8sv0pes2aNIQMMx2aFf6NEgx7piIgII6XgBjYSY5LJd99915A+hr3r2tX9FSBJ3Lhx40Bd8owZMzyeU5I5eoopLSBBpCyjb9++hlCTsD7wwAMVCJ8vQmERQmqfaZ/SD/YjAWdUD6udmPKcHxJWX/fg3Zf9KVsh0bbkJVwjiY1Fjij1+D7zeq+B55SZUHN9zz338NJT6JXnnB988IGp41pHjhxppCW8R4t0UTPLQlK9ZMkSgxtJNnXPd955J1atWmXm4LMksaM3XcuVRYD433///XjiiSfMS6EvAs3nx29sKhdKkhhZhVIfX7/rlfvrdf1B4HqRcWxeTS9w1UIdNPXJB/cel8zNnSp02LFpH0qKvs37TCGA28aBtGPgXN6FIe6KC70joNnQZ9B13l1q/dwm/7Dc9P4SljK45V1m9OrTcy7Big5VBBQBReDSEKCMg6SssoyAXlsSUZI2Fm9Pmve59+yst7ylFnGg7cqRKiqPt/6kehNfjuM1CSiLd5/K433dQ+U+JDWs814LbXIey7vLeb7PvNYcJMp8KeHLxnctnJsYe6+nprHsy/m811pTf227vAjEy4slny/DEX5b4Uspyffzzz+PZ5555tu6a3s9QoAa50em/q5aLbRdvp2f+bPbcM9Pxle46+cffRNfLthYFqihQlOVC9p48LFJmPHIhAptv3nsbSybv95jw082F74z/3njFa/Q8XteXE6+Sq2CFkVAEVAE6gUClBZUJs+8MRJXizzz2iLElc95bRX2oS3vvr4Ionc7x5Ioe5Nn1nGcRZ4r96k83tc9VO7De6m8Fs5ZmZB+n3k5h0XKvw95tu6n8npYX10hFpXXWl1fra89BLip8Ec/+pEJ//jkk0/W3kJ05lpBoH2nWEQ1b2z0x74XUDWWc0FeIXZt2e9T9vGdbUiKb3qgLQ015Rut2zZHfAd3aFLfdq5+rRLoq4+5zqgIKAKKQJ1EgCS6uo2SdXLBuqgrhgA3z1Jew6yTlOJ4v4BesUnVcJ1CgNrmTtcliEPAN1Wkhnl/ylEw5rNVDqQdx5lT5408w6oTl4J1WuVIG/v2HJGQd+7wl+xweN8JiYiW6dFQM3xdUp/EKklVqhi7yhW+UbkCi2C4I27g4Vd32dnZZvMPNwDxml+TUmfIa4aoYh13erOecUu5oYV13EXMcFD0kvCrSWrs+HUn+9Imw1ZxUwo3/7DOssM+HGN9+HWjFXaKdbTJuTmG6+QaOIbj2Zd1jD1rjeHc1po4lv14b+xnXXM818cxHEtdobV29mU956YdCxvOpUURUAQUAUVAEahNBF599VVwM+GgQYOMZp37CLQ0TAR6JneRG/dNgI2GOTMbB1KPecDZslayD0qABqvY7TZ0keR01RXauHghzxBxq89mY8Obnrok/nM3q7nOHL1XeEUXRdL59ddfe0gtySQTH5BAMoMWdwCTBPOaH25iIYHm5huOZRgoxmGlPo/EdMWKFYa0kqjynISUxJf9SUwZoJ/zcVMEvxLl15skqOxPspyammqIKz0u3F1O8s05SdhJwtmX8U5ZmHWLm3YsEs+1chMT18QNMbzmxiauj5stOJ6hgtjOe+N9kPyTKNMOyTTf6Hkf3NzEzTWcq/LXvlf0gahxRUARUAQUAUWgEgLUOj/22GMmjf3SpUvNptxKXfSyASGQxA2CkniuusI4zTskhwYLedOWdSk8M9ck3o0iwnDXQ2Mllr5XwIayVutAD7N3TOmKKcBl70iIP7r36mh1rzPHq0KgLc8qvwLihzFYueOXsUBJdKmdYz3JLHeikwQzCxL1hySfJMcMBUWiyh3nfBumho7JAmibxJP1HMNQSozvyp32bOfuefahne3bt5sA8SSsnI/JFtjGcYx7SbtsY3goxoelV5xkOD4+3lyTiHONJNsk+7wP1pGUJyUlGQ82+5Og0wbDOXFtHM+kAwxTdUgSPjCGLWPTkkgnJCSYOpJ+LYqAIqAIKAKKQG0h8NZbb+G5557DrFmzTLQVb91+ba1J561dBNp1bI3mLWsKNVmugz6XkYW9EtrOKbIMFrvwn7j2rdF/aBKat4oWPlQd5XR5CPS5sxexVyQdlHawkEO1S2yDmNZNzXVd+lHd3VzWNRIAkk16lklQSYTpjWVCBJJkK3sXPbzcWEKPM4k0d5qTaJPYkgAzBBTJMcczE5YlfSD55IfjOYakmH1jY2PNvJyfHm96fGmfnmHGd7UKSTc9z0xbShsk6+zPNZB0k2xzU80RyWrG+2D4JobKInHmh4VzMnwUZSBcMwk5STi94mzjWrlG7m6nN5rzkUSTgFNjxjVpUQQUAUVAEVAEagMB/jfpqaeeMv9NplOLCVQqf/jfYS0NC4GQsGATf5leYl+FRPdg6nHk5xYiZcdBFOQWSzfLA23H9cmdEBwaVGajXNrhbYs2KAPJzclH2s5DyMsu8GioOS+zD1IKUtfKVYkDTQJJEsrEBfwHSM8ziSrrhg0bZkhoYWGBeKIDDclMTk42HmaSUxJmJgogyR06dKjxGrOepJtjSa7pZSaxJUFl0HfOR6JMOzwngSZhpveYhJ3JAEiA2cYP6xkPlh7pgQMlA6HUkXwzwD+94Vwb7dKrTM8zCXbv3r3NHH369DGEmWPCw8Mwc+ZMc33zzTcbkhwT08LYa9q0mSHRHEebgwcPNjhwbSTqEyZMMP14rUURUAQUAUVAEbiaCFBWyP/Wsrz44os+p2YcaY2e4hOael3Zs38XrFy61ec9Gg1zVh4Yy3mbZCakbMMqjKLRe4Bbu9xLbHy9aLPVVOFIGzkX80UHfcxkN2SGDisDobEx0B27v8KgOnBx1eJAk2CWk0NxzUsOdDfOJLEOaXOj4XTKm4tdtDIiQqf7v+bCtxx+3JnHLPsV56pogV5w/gGgl5iFfVnKx5pLsx6mkrR5vfVUscuhXkvkWxSX7O7npfcp61fZnnsmq7+XIatBj4qAIqAIKAKKgCKgCNQiAoy08cCEZyRTc9WMhFwWYznf8eBIIdCpSNt1RDiQcCH5X5Sk3v7HspdM9sCDQrDvH/8MSkuYHKVqoY2pD96CnZv3IWX7IY+NyOhGmCM2IiQz4uUolzMO9FXxQPOmLYLqfqsoI4uGWApJ5dsGCbUU8lVy6OrpZCXWWtaz3L73XMak+UFSyw+9yvQ4W8V7HOsMZ+cUXAOXZf5Hii6/DpUJfaVFuvU9lVL1epZLMs4ZWMFSPriKXXcH/akIKAKKgCKgCCgCikCtItC2XUu0atMMJ45mGGJbeTF0gi6Ztwr5EgOa5JmFfKhLUntP6u3YBLER2wzHD5/x9PG2QxtL562uYqOzpO++XOTZe77LcV7OJC+Hte9ig0S5LMQJqaSoLtxcknzSfPjmIjorW4nHGolvxeJ+QMaOV7iUin2qXn1nomq4Lecom8eL7Fa06jS/CBY5Z5tL7o8fT6lgy7oPU+npoieKgCKgCCgCioAioAjURQSCggPR9fr2woS8uI3XQulozDqXg6JC6p+tYkPvQeWh5wKDAtCtZ4fvZYNe7N4D6qZ8g3fpGw3r/q/U0RBlkk3KOuzITM/Ggn+twOy/LsSZk7LpzkkJR7kEgv3cGwUhXyHYRDPtTW6/2yJJnvnx9j77GllUUIz/zFsukT+4WYILtUhv5d5ck/SQ9dNufl6RCOBF+G7uiffm3Z8XDKNHuMVmhTbvfnquCCgCioAioAgoAopA3UKAGuaaCkm0d7H5uXB9v87eVbIZkDYq9vPuUNkG7E6441B796o755dVA135tlafnlO5Sq4JngWg3QTQ/u0v30T/fr2Qk1uArJwLePSJu93c1UgmSFTdY954/QOMGzsacQkxQlrpoaYCpfI7APvW5OGtuT0nqxA/uu8F/OntWWgaEym2HLJaI+CQ84qFJHnL5h2IbROLXbvScC4zC+Mn3CSh+bZhyA0DvJZRNqccNmxg/9bydUjNIVksnU7FGfVKEVAEFAFFQBFQBBQBReBSEPDNT7+fxcuige7eNxG7Nu2rOrPRwthFCCFh3JyF8LcFigeYnmV6kEl8Hcg6m41Q/3BMnnGzqc/NzpVW2VQo3lq35IJe40Kjix43cQyioyR2M9ult0WeHc5SuXZKv0Cpc5NVl9QBUm8L9iKykpHQkS/9RIxucWxxI7sgZNwWIH3dZDw8KEL6yLtQKeUkfihxlSIwQKJ8uApEox0CR4kTfv5uj/amNXvh6hOMYTcmS71kKMy4iDXL92LQwGQZK3IOu6S4pJfaIesIADav3IfgoSFo2UbiKkp7iUOikfgFyhq47jI9uJxpUQQUAUVAEVAEFAFFQBG4vAgk9Uu8LAYvC4F+a8GzvhcjxNNiqnYhqMWFTnzyz5XIkFTWHTrEYsykfmgVFy0xAiPw9svzhUQPRrMY8cy6OTB2bNmDTasOoUl0Y4y+vS9OHj+JRiFBCJcwcv/5ZAUO7M1B16TmGDmhNzJOZ+GbZXuRLeFUiktc+MH0ZDSVHaDnTudg5YpNSJfc7KMm9pXkJrHYtHw/1mxMRXOZa8qdyfAPEuJcNieJuJ+Q7wCJg/nNsm2yo/Qo0nOyENc6FtPuHYzjx45i9jsL0KZ1O9x2Z3/s2noMF86K7kdeFgqK8uBy2LF+xX582mkZjh7MxoQpyWAg8vf+shijx/dDytYzUr8E0S0nY+f240hLPYSw8BBMvG0IYlpFeXC8HG9HHmN6oggoAoqAIqAIKAKKwCUg8OIv3sGif68WZ6LvSBqWabtkJ/zVHx/CLRMHWVWe4389/TcsmPvNd7Lx1B9m4tbbBnvG1rWTyvqHy7s+m7BSenpFiuEnIUrmvLOIImaROdwg2WqOYdGC1UJUAzHrl1PQvlsMXv3dv/HJnLVmDV8tXY91q/fghluSENk8BPnZxdi69jAKs0uwcslG8fSexbjJvbF14w6sWrYHeRdKsHzJWgy+ubuEScnBZx99jfwcJ956/WO0TWiF5EFJOH9GsuTsOIwlC5Zh1LieEmu6CB/+Y4ksT1zDZqGcmgsWT7l4nk+fOie7P8Px81/cLQT9JA7ty8Dm1XvRomk0Ro3ph8ioSPTqk4jR44aIvtmGc2fz0K17Bwy+qQfGTRiOIwczUJTPNOL+OH5EbDWKwPXSf8YDt2HrmuM4mHIK9z44EV07dsBHH6wREl6u++ZKtCgCioAioAgoAoqAIlAXEHDrkeltrKnYECSpt6+rJvV2T0mK4vZY1mRDvrAP8quT6bu9V31lCXQZKeUkpUUO7Nl6CCFBIdi//5DoiyMk21+GtBQiOMyOEUJIn/7tA/j6i69xUsKcrF+RhqlTxyCxawvcPLIfoptFigREJA/FQqCX75aEKK2wd/9JyeyXIOT2rLzNuNBrQBckXtcaw0YkAyUBQq53o2PnVugzoJPs5IxHn0E9sGThGvF4N8HRIycQ4B+M0yczxDNeJLy57JeCG/1c4piXy4AABzp2ayoe4kDEJ8TJxsJcjJ0yGIFhDnz68ddG8xwoyoygYJdIOrij0CEP3YmAwEIEhvrD5lckIa1pV6QZ0u4XKC8SAZLpMNxmshSmn8jFnL98jm2bDqBUpCVWVkPvB6TnioAioAgoAoqAIqAI1DYCjMRBYlvucKy6IubvYOrtlhL2zlfp2qMdAoNrtkE5bYJ8c8+wd3W5XBYJR/U3SOpMjy61xJJuu6QYHbu2QddebZB+PAvULn+xYCvVyxg5vr9k+LNLkhMBVmJ1hwrRZlakJi1aiyRDyKfsxjRaZSGkwY0D0L13W3QSr/XxY5kIlHTY2ZIKu9TP/bWCf5Coo21Ok847++LRsjX4o1hShIeGRyGmZRiGj+qHvJxixMZFCsll7GaOpYbaKbrkPDnK5kWHHxzF7neMElkUuXXmuYu4+8GpmPv+Smxcs0/81MHSk6Hr5A5FvuFy2oUIyz3L/5vFREuKbpF1yEV+Ton8lDZqrkXuERIWhNYJdsz86Xgc3HsCx4+eknW455LJtSgCioAioAgoAoqAIlBnECChZUzog6knDI/xtTDuG7s+uUuFJHTe/Vq0bor49q2xb8+xam1QAUBvd13nRFeYQBM2bhiEeF/9Mf7um/HWm59ggHiC9+xKxV33jEa36zriV0+9ZeQOmWfPoUNiO7SKb44xkwfjnTfnm0DczB44/b5xCA0Tiiub+SZMugFzZ38mfeOQmrYf9z08Wby9fggMKtPlCHn1C3QhqW9HrFu7Ff//xbniJQ5C+w4xuG3qDfjDi39B0V+zcURkFS1jwyXUSqKQXNJc4b2yObB1J25UtCEsOggB4QHykF2IaOKHxpJWPG3nMbz6+w/kF6AdJkwehJUr14qGWrzQ4rVuFCWbAeXtK7plqIwBxk4ajMWLV2Hjpl3o0qMt/IP9ERkTBEbpmzT1Rvzl9Xl445X52JuWhjtnDBcSzxVoUQQUAUVAEVAEFAFFoG4h4Ofvh+Qh3ZF7UQIq0Inso9CZ2Gdwefznyl1Iivvd0N1EYKvOBkME12Sjss3aur4sYeyqXTzVC0YaIXEzhNv6+dtx4nCmbP47gjZxzdChc5wQzVJ5GEXYKznQI6PCpK6tOH/FBS1kMjP9Ig4dPIU2sTFo0boJ8nJzEBwUhoDgAJFtnEfankNoG98S8eLqzy8oRElRMRo1bixykVIJ6F2E8AjxDjtc2L3jiCHHHcV2sEgr8vMKsGvbIfiLhCOptwT2Fu+23c8hkTdIlm0olXSV/BqCQnk+YENrzZL8xMNsQ3r6OURHRyAgxM/Ep2ZsaXqVSbRJnI09EdFz42R+XjEKZG3RsqHRKR53p/QjJH5MuegKMJsbA4P8EdVcUosbvNQLXe3vkzYoAoqAIqAIKAKKgCJQBxC48gSaN0muKMySyVD8xFNsFZeTMZaFvArZZKg3sk93Gkj6g0lo6SCXNiGWJJ82kk7p55K40HaeG2or0hDPtfSTviS/HORylnCo9BUXMWtMPGna4RU3DtIuPeQMd8ewdFLHNci1IcLGDhOg0B/NdjYLAZbx7nGsk/XQEPuY/rRnLuWnkGjzisV7l9B7IisxNtguRFx+SruMpvxDpB92gw3rtSgCioAioAgoAoqAIqAI1FUEriyB5l0bdilHwwvFjWtOSJbZWFYszuhdxw6GY1qN7r6mi6fKPUAormWp3KCQUlOMjcrN3v3dhNezLqurdxerzhylwZrfmsO7vfJ8nr7encrOhVCTvJuEMCZLoZxa/cu66EERUAQUAUVAEVAEFAFFoG4hcOUJdN26X12NIqAIKAKKgCKgCCgCioAicEkIGDHDJVnQwYqAIqAIKAKKgCKgCCgCikADQkAJdAN62HqrioAioAgoAoqAIqAIKAKXjoAS6EvHUC0oAoqAIqAIKAKKgCKgCDQgBJRAN6CHrbeqCCgCioAioAgoAoqAInDpCCiBvnQM1YIioAgoAoqAIqAIKAKKQANC4H8AlcMTV7RPE+wAAAAASUVORK5CYII=\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='ClassAttributes.png') "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Attributes are data associated with an object (instance) or class. Object attributes (and methods) are specified by using \"self\". Instance attributes and methods are accessed using the dot \".\" operator."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"class Car(object):\n",
" \n",
" # The following method is called when the class\n",
" # is created or \"constructed\". The variables \"self.x\" refers\n",
" # to the variable \"x\" in a created object.\n",
" def __init__(self, color, car_type, speed):\n",
" self.color = color\n",
" self.car_type = car_type\n",
" self.speed = speed"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [],
"source": [
"car1 = Car(\"blue\", \"sedan\", \"very slow\")\n",
"car2 = Car(\"red\", \"sedan\", \"not so slow\")"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"very slow not so slow\n"
]
}
],
"source": [
"print(car1.speed, car2.speed)"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"class Car(object):\n",
" \n",
" # The following method is called when the class\n",
" # is created or \"constructed\". The variables \"self.x\" refers\n",
" # to the variable \"x\" in a created object.\n",
" def __init__(self, color, car_type, speed, sunroof=True):\n",
" self.color = color\n",
" self.car_type = car_type\n",
" if isinstance(speed, int):\n",
" self.speed = speed\n",
" else:\n",
" raise ValueError(\"Bad speed value.\")\n",
" self.sunroof = sunroof"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {},
"outputs": [],
"source": [
"car = Car(\"blue\", \"sedan\", 100)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"# Creating an object for a class with arguments in the __init__ method\n",
"car = Car(\"Blue\", \"HatchBack\", 100)\n",
"car.color"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"# Creating an object for a class with arguments in the __init__ method\n",
"joe_car = Car(\"Blue\", \"Sedan\", 100)\n",
"dave_car = Car(\"Red\", \"Sports\", 150)\n",
"print (\"Type of joe_car is %s. Type of dave_car is %s\"% (type(joe_car), type(dave_car)))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Type of joe_car has (color, type, speed)=('Blue', 'Sedan', 100).\n"
]
}
],
"source": [
"# Accessed instance attributes\n",
"joe_car = Car(\"Blue\", \"Sedan\", 100)\n",
"print (\"Type of joe_car has (color, type, speed)=%s.\" % str((joe_car.color, joe_car.car_type, joe_car.speed)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**EXERCISE**: Change the constructor for Car to include the attribute \"doors\"."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Instance Methods"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtAAAAIcCAYAAADffZlTAAAAAXNSR0IArs4c6QAAAAlwSFlzAAALEwAACxMBAJqcGAAAQABJREFUeAHsXQW8HLXzn7q7u7u7G1baUgqUlsIPKxR3KA5/3EtxK1IoFCi0UKO0UKhTd3d3d+/955v3si+7t+d37929N/P53O1uNskm3yS7k8nMJJOHiYQEAUFAEBAEBAFBQBAQBAQBQSAoBDIHFUsiCQKCgCAgCAgCgoAgIAgIAoKAQkAYaOkIgoAgIAgIAoKAICAICAKCQAgICAMdAlgSVRAQBAQBQUAQEAQEAUFAEBAGWvqAICAICAKCgCAgCAgCgoAgEAICwkCHAJZEFQQEAUFAEBAEBAFBQBAQBISBlj4gCAgCgoAgIAgIAoKAICAIhICAMNAhgCVRBQFBQBAQBAQBQUAQEAQEAWGgpQ8IAoKAICAICAKCgCAgCAgCISAgDHQIYElUQUAQEAQEAUFAEBAEBAFBQBho6QOCgCAgCAgCgoAgIAgIAoJACAgIAx0CWBJVEBAEBAFBQBAQBAQBQUAQyBrPEAz+8DdaNGctZc2aha65+RJqc1FDVdxD+w/Tj4PG0cqlG6lStbLUp9/lVLpccTp9+gx9/+kYWjJvNdVpVJ163nQRFS1R2Kri8O8m0Jzpy8lz/gL1fehqqlWvImXKnIXOnT1P3370Oy2Zv0bFv/epPlS0eEE6e+YcTftrAQ0bPJ4KFc1HHS5rSl16tlP5HTxwhEZ8+zctmruKWndqSN2va0/5CuSj2VMX09hfptKJ46fo9Kmz5PF4VHwcCxXJT8+8dQflyZeLznMZFsxaQUM+GU3Zc2SjkydOU9ZsWaharfJ02ZWtqEa9yla5zZPN63fQNx/8ThtWb6OqtcpRjdqVqM2ljahsxRKUKVMmunDBQyuWrKchH43iumWmhs2r0/V3dFNZbFizjT54ZSiX6zRlyZKFsmXLSpmzZKIzp1FO4jKcov/deQVdfEVzmjl5CY3+eZKqQ616leiW+7tzOXOo/KdOmEe/DZ1IBQrmpYdeuJmKFitgFjGCcw+tXrqJhn7xB23fspueH3A3VaxexjW/RXNW03cfj1R1rNO4Kt14V1fKweVbMn81jfpxEu3fc5jKlC9GfR+8mtu0UFL9GbOv3h/BbXOSHnjuRqpSvawt741rttPfo/+jO/v3soWbF7u276MfPv+DFs1eSeUqlaQadSpS64sbUpUa5SgL91PQX79Pp3/+nEvnz52n7r07UIfLm3JoJoXvr9xn/vt3EZWtVJz63n81lalQXKXZt3s/jeRyL567huo0qEJXc98tUbqYurd98x4a/OFI2rJxB/V7tCc1aVVbtR9unuR+9skbP9H2rXuoVLmi1P+lvtym9nnxgX1HaPh3f9PUCXNp366DlK9QHrqyT0fq1qsDFS6a1HZzeVwM+3ocHTt2UuWdI2c21Z9Onzqj+sbZs+fo6hsu5v7fVpUJf6dOnKRRP02hb3icohx58uVW4+M2Hlt5uY+jzqAzZ85y+X+jhbNWU7O29ajXrZdQ/oL51D38TRg5g/78bQblzp2dXv/8YStcTgQBQUAQEAQEgXhFwP6ljbNSXtnnYmaGV9HRw8cs5hlFLFikADVrV482rNpGtepXUswzwnPkyE6NW9ZSzOVbz3zJzOxSBFvUgxmAVcxcVqtTiarWLK+YZ9wE49qpa0uaNWUpFSyUVzHPCM+WPStVr1dOMQdg7Oo3rY5gRYUK56cChfPSOWaSGvEzwTyDWrRvQCeYCVm3Yotinvrcfjnd0K8rdb66NTNdq+gEM8qgLMzklK9Ugo4fOUGb1m+nW+/roZiaDWu2Ut/uzyuGSUU0/uZw+e6+9iVVxqfevJ2OHDxKA57/ho4dPWnFypw5E1WtUZ6ZryI0/e/51PWaJIYfEfbtPkjbNu6kq66/iG66tzsV4LoeYEaza8/2zMz1oCyZMtPmDTuYwTxNrTo2oHIVS9L4EdMZ48oKI+SB/Gsxg7ds/lpq2b5+FJlnol++GU/jhk9TTHzlGmXpyOHjeKQrValZhoqXKkxzpi6hylXLKOYZEes3qcGMbSlmhGdwG1dQEx+dAfLcs+MAlS5bjCpWLqGD1RGM4uTxc2jIp6Np2+Zdtnv6YilPsB666U06fOAwPfn67ZSvYB56/+UhtGHtdu5LScwi4l7Sow1tZGb9yIGjzFw35pCke7ly56RWHerT0gVrKHv2bBbzjDRFSxSheo2r08ZVW6lKbbRfEvOMe2Cy8xbITfNnLKfn7vmIdm7bh2BFufLkVEzrrEmL6JJurW3Ms4cnU7OmLKYbL3uc8ZhOdzx6LX3/91t0y31X0qABv9JC7o+aVi/bwGmzcJ/tyH3xSu5bx9U46tGnE/W57XIqUiy/KreOf4gxePbej2nIZ2MU0/vHgs/o9c8eohWL1tM9vV6mtdz/NaGujZrV4r63m955bjD9M3YOT07P6NvU+ao2tJMnAHqiY92QE0FAEBAEBAFBIE4RiGsJNBi8osULUdGSKVJkjWM+ZihKlC1MxRz3ChbOx8xHUVq/agv9/sM/VI+Z3vLMUIEgcS1SvDAzJEVtjAbu5S2QiyWqeZg5T5GMIbxEqSLMXDenoZ+PUcxXmQollFQZ0l48o3HzmlSWw0wqwMx1MWbuWrPEPF+BPOoWJMPVa1Uk8lywombJmokZvPyUkxmr5u3rqfDGLWvTh6/8wMzkn9SxS2OWsJe34o/5ZbKSuN/A0lYwWK9//ij9O242M4pllLRQR4RUGfXMzcxVAZZ6a4KU9LkBdzLDX1sFrVu+hc6ePkctmVkuzOUoX7U0Hdh/xGIGb7ynO/0xYgqN+20aNW1bg3LkzMLF99C/f85SkvJuLF2NFh3mycDgj0fT1yNfotLli9Oz79zlN+t8+fNS20sa0/jfZ9DWTbttcaswo1yM64+JCaTqefPlVfcvsJh9356D9OgLN3q1P1YAZk9ZQud5NWLmpMUsJS1pyxMXU8bPpTzcVv+7uxvVrFdFTSRadWjIUv5qPLFImYtiklGI+xH6ZtasKeHII1fenFSY2wQTNSdBglucJz5580J6a6eixQtQyXLFaPcOSMDH0IPPX88S26S+BcazQOECVIZXIbiD8S+JYcdk6KVHPqNSPGEYOORJKpgs9b2CmeT9e48kS4mTntOkVR3qcm17KpIskf6DJzKZeJLX+uJGlIfL07h1bVq2YK2KDMn63GnLGK/F9OqnDyqJOG5gInnv09fR/933CY1gifdTb/VLypz/i3G9ipQoSLt37aMhn4+mFh3q8sQ3ZdwU53tleBVJSBAQBAQBQUAQSAQE7F/3RChxgDKeO3eBcuTKQXc81pt28NL3D5+NpSOHjgZI5ft2tuws1W5VSy3PT5s4X0UE83yU89yyfhdLCytYTLLvXLTktqIXw+9MgyX1lqwScuTQcdqz86Dt9r49h5QKRaZMSWohOXJlY+lja5YOZ7PF83VRhJmwRi1r+rpNxZnhq8kqCbkYP1B+Zv573ngZTfpzNm1Yk8Sk7mQVhiEfj6JnB97jM59wbvw6+G9WQShGhUNQB4FEuSarl8xklQiTZvyziI6xmsZcltgeZimwpoUzVyjmtRJPJLhFdLCaEG3duItWL9vIjB5LtVmdwY32Mv5QR8iSzCxnzZaZJ1dN1IqIW/xohmGlozZL/juzdHvk0Elc1q2q3L6ecYxXNn799i86ceQk3cmSZ8086/iQQjfnVRytYlSrQUWLedZxzCOY6Bbt66qgw4eO0aB3hyumumOX5mY0qs2rFV1ZzWkar37s2rbXuofn5MiZnXqzNHsfrwKMHDpZqS1ZEeREEBAEBAFBQBBIIARSuIgEKrS/ojJvS+dYp7ftpY2pHessT2B9VKeE0l96t3tQh6jKy+pLWD8VuqCgxaz7nJVVPIqVLOiVBMwCmGwiSJvB7F5gnefzfAwObkiFL7CkGpJMk4qXLMR6pCt5eXwbM9LID5TZJn1OCvP1j/yCK4PO4fo7ulJBlqgPZ2bs7NnTSsWhQfMaVF5JO3WsQEfgcEHpqEP3OwmTpElAEkak9HObMnOfOasOD5QnsZS3gFLh2bV9L+1iySzoEEvQ9+8+xKsOJWkv6/seO3rKymjm5MUsSa9LWVhlJ6l9km6dOnlCSZ+btqvLqkKNaNPqrTxBOmal0ydYDVnDqglLFqwPiD/6APTMk+qXVH/kk4n7g/lsnXcwx1MnT9NtD1+tJhlfDxxOp06mqEE40x9kHP4ZM4vqNK7GKwxJtgPOOChHSlmC6ReZrckG1Kc6dG7mzFJN5mqyWtUJlvxv4UmJRdz1jjCmnXu0pUu6t2I99zG0ce02vg1shAQBQUAQEAQEgcRCIJivZmLVKLm058+epbueuJYljgXo64G/sVHZobDrUaRYQWrepi7t2LKHl66T9KoXzV6tjMhKlS3qlS8Yp9PMQGzbvJeZ9z2sa7qaPnr1R694bgFL561hQ8hRVLNuJWWgZsa5iVUqYHz2+O0D2fhwLDNQKcyhGS+a57ly56Cn37yTxg6bTCOG/EuzWdf2sZf68iOCZ3RhvPj5O7/Soze/Rde2eZjG/TqddWCTJgArl2yiD18dSutXb6HlizfQe/83lNYu3xxUFaCiAgbxKEtZd2xOkpBPmziP8hfOQ9f360aZeBKyYtE6NhJNmvRMmTCf2rB0H6o8Jp06eZbVNhayUV1HupyN5DZv2En/TbZLtRH/yus7UANW13jzya9o4Avf04F9vvsU+sD+fYdZ7WGD9YN+8OplW5QBqfn8YM9RzgJct2dYNWIWG3n+/OU4NlQ865UczDt06Xfv2J9swOgVJeyAs2fP0PyZK1ntKAdhBcCNoIaCSZdz4gr1n7Ns6Nv/tb488SxCbzz1FR0+6D1RcctTwgQBQUAQEAQEgXhCIP0y0Oc8rNdbkG598Cr2KLGQPR8sVLhDBhsqwZiwIntsOMOM2Ab21ADaBPWNGuWpGBt/OSlXnhy0ng3LHrvlHbr32pfpoRvfpG1bDGmckQAeE1axAdeDHOf2K/9PxYXnkCfZSDB/oRT9ZSSpyuoir3z0AOsIF6O3mPn48JUf2cDyBN+JrRSv/WWNqUb9ijTg2W/YG8qlzPzAq0VwSO7ZuZ++eGcEe0WpSp8Me54asQeJQe8NZ+nkTlSJSpYpShWrlFKS0E6sDgDjxqrsiSRYKsa6s3ny5WTd5sMqyZplm5U+d4cuTSk3qx2sWrxJGaytW7mFJfqk9LxTpK5JT9m7+zDt23uY2rL0GSo0pRjfyeOT1HXMclSoXIae4clEwxY16Es2wgMjvWMr1BS8JxPZ2IvF8oXr6K2nv6I3n/pS/V5/YhBPJIYpNRDT6NB8hr9zLGqcP3tB6X43bFGThrHR5bFjSUapZrpzPHncu/MQ5WRVHEjNnbRp3Q76+LWh9PbT39CMfxYqLyzOOL6uwQQfZX31rFmzKqNdt3gwGszH+txQn4Huv0nnLlxQOtXw5rGC8Vk0ew3f9rBk24wl54KAICAICAKCQHwjYBfFhVnWe658iZayekO0afKWIRFn2eOGi2gG68h+9NpP1IY9IjhdfAX7gFJssFiUmTUwYquXbVJ61pWqlXZNfpzVBmqwBHnAN/3ZXVdeOn70BP07dpZrXDAkJdno8aa7r6DFc1Yp922tL67Pur2VXePXbliVvh37Kn329i/006A/aOpf8+krNrwr6SIJd80grEAPXdajNUvg91I3NkALlk6ym7MfWUpar0k1andJE5UMLt3GDZ+iVC0QANd+8E4BvfVWrGoAd4ShEAzPoLe9askG1umtS5vW7VQuD6HPDZdpM1iy3O+xHjRx7Eyqy64Nc+S0zxnhwm86Y9iEjeTgjQUM9EXMyI8bPpU2sxFihSp2N3qVeCL10Y/PsBvFP+grVqOAu78Phj6tvL+Y5T7NRont2MjxpY/uM9QkiFcldtM9PKlCu0dCz7CR5c2dn2BG+Ee67aFrbFmBOYdrxAvMrJ47lyR9NyOUr1yK9byXKTeNvW67TMU17/s/z8T2AHhtgOl1rwOeC1Un5SbRoYak876LXQUumLmcXuv/BetSv2+55Wtb6n86ihwFAUFAEBAEBIGoI1Cf3ft+OuqFiPO1cxNhZhcL5jnMorgm69Ovi/LGMG7ENHZJd9rG0LgmcAksXKwQVapent1t7WX3eEvYO0dhJT11icpBHqW/nI0ZMnhhgDeRq2+6xDUqmBAsdzdj3dzLr2lNFSqXpukT2QiOmW5flDd/Hnr81b501+O9afumXWyQNVH5HPYVPxrhUEmApwlfTJPbMzDZWDJ3NXvsgNFeEoGhgycK7TMZoZvYt3WuPLn4lz05VvAHeDupzdLt9ez+DS7bChfPr4whkUMb9s8Mv8c7tx6i5QvWKaO37NmTDCT1E+DrezqvTpxhvfOR3/9Dfwybwu7+DrGP4zM0l5lMN4JkF0zrU2/eQec4/fDv/qJDhrGiTgNGMlZUmf1j38yuD0eyp5kFbByZM2dKvbJmzUZgkuEqDv3VSdCth2pTGfaCkY/7UigE94tQW4I+NowJ3QieT44cPc5eNwq43bbC7nvqejrOLh+/+eA3ypyddfmDXNWwMpATQUAQEAQEAUEgRASWzImOwDcqEmhd9uk7h+rTqByxwUk0CL6hwWwO/ug31rk8rhjBUPPFUnibixrQFyz5Hf/bdLr2lsuU14hQ8/EXv2zF0nT9Xd3o1ce+oF8GT6DbeBMQf4Q6zWNPE7PZa8RtD/e0MaX+0qXWvd3sbeEgb+KBTWg0rVyyMck/s+FeD1JZSPez5winO2ZSrgqxCcmPg/6ki7q2UG7w8LxG7JqtDBsTfvn+cDYoPMB+q+vZPJZ4POdp/crN7E1lh9I5X7Z4nfLPjVWKnKyGs3DWKm7nzrroXscrr+9EC+esoEUc79iR4zwRSqmnV+QYBMDTzET2qfzei0NYsm73xAI1nwYtatM/f8ymWx+4KmpPh8cXGFtmYleJ2HgImwg5CTrkJ46doIrsn9sf1W9Wgzr3bKM2voG0umWb+hTtd4i/58s9QUAQEAQEgYyFQDRXOaMigY41/MdcJF0wQjvOxmM5cwUntexzexfema4kpzmuVFaD0+C116wyL9+DscJudNj5L3S6oJbV/aWry9LUpq3r0N8j/2NmP0mv1y2+lgQXZJWD/OwTOx6Fd0fZldo59rphqs0sZmazPqt0mJtmHNh7iNVYiigdZbe6Bgorw36js7O0f8F/y9UGMlALAcGvdwWWxE75cw5VqVlOuVEz8zrP0vCpExfwpjz16YnXb2Mf2XfR07xT5P3P9qbaDSvTRjZ+hDcLN7LwL1yQfYjnDWtVwy3fUMLgzhCGpWDe4V7PJPgX78Yb5GxYuVV5ojHvRXoOn+FtL25Cf4+a6ZXVwQOHaB5P6EqWLMb+0b19aTsT3PlwL155yElHjhxz0SR3xpZrQUAQEAQEAUEgPhCIawY6c2aPknAt5G2TZ7ELMk3YBW3k0H+UT+W67IUhGIJ+612P91IGZpr5CSadGQc7wtVvUl1tIlKirLdxlhnXeQ4/vj9+MY52GL5xnXFwjS3Eu1/XQbllWzJvrS3KxDEz6Y0nvmL/0PsUw7aPparzmWnEToLY7jzeCF4y4JLvRLKh27hfp7Cbusx0aY9WypBMl3fPjoPKn3Ow/qx1On3EjoRleWfBcswsl61YTAerY71mVZWOb7vLmrGudYqaA26eO5eJfUgvpsuvamtLU5Q3YbmId6bczPrU2usKIsxl1Z23nvqatxvfoPDHdu0z/l3Aus5sfBiC/2rbwyK6yERX9G7Lv450isuiPCcm5weJbsduTald5yb02VvDaBVve28Syp7ZTGDeDHAOtY9+j/RUu1h+/Lrdu8z86SuVYWKXXm1Z/9+/egjGYUnefvzh/7uJPEpV212nOkBx5LYgIAgIAoKAIJDqCISzZp5qhcycJSv1fehqWr18I93X+1XqzkvmFXm3POi6Hjl0gp55p59XWRazG7iVS9crP81NWtdSurU6Enz8tu7UiM6y5BG70mmWE7qq2Jp617b9tJJdjfmiAoXyMYNWXEk2S5V2N3Y7xG65sI33VvYyMeD5bxXzBr3RvbyN9mw2OOt8TXsr+xPHzihPDdBfRXxsQQ2qXL00G7xVo2FfT+DzcrxzYpK0exJLUkezqsKhA0d4i/GKNO6XqdSQd1ps37mpTS0Fuqnzpi9lHdXjSo8X+tVO2s878i2HWzVmBrezCgWkir4pE+O5hj077Fe+sC/q1tx3VONOOd6qPB/v8Djh9/9YleOo2qDklvuvUgaWOhq2Icfuh3UaV6VsyjhN3wn+CK8axeENpUEmr50kG/IW0kVY/aYS6wybetdo8wkjpzNjuYH9QtvXI87zZjxQH9q//zD9PvRftcMedhWcyTsV/sRGkZvWbVc7R07+c67yNtGtVwdlCJlUYo/asnoje7qAd4+dPGHShpHwgb2WvYRA53st64ebhPJsYL/Iq9iFH7bBbspuE+H9RdNKdvG3jFUmdmzZx1uYF7Uk3pkyZWFd6CvpH94d0qlzXZT19p947TZlaHhnzxepHftGr8XGqfAOMp0l77c+cLWrASHaA2VAv9jIda3DG7g4PZdUql6K7nysJ3313m+0e+cBasGbskDP/F9WGelyTVvq3beLLro6oj9uYFeFi9gFXn2e9ELqrPO89MpW9O3HIy0f67aEciEICAKCgCAgCMQhAplYChSx2EfrlMRKfxG+Z/8dO5dmT1uiPAdgB7XLr27LDAZvLc2l1x9ieFSAtPro4ePMjGVhn701maGyM4ZQKzjNG1BAYqg3KgFjM5P9/p5mwyh4GGiIdD70WcEI46HOLcR128Ln8dYNu5SvX2x0oeHNzNx6AV7qb8p6uNlZOohnbmFdUXiPyMk7CpYoU0ztNKfzgfu3Bcxs1G5QWUlWUUc8ew/79l3I3jr2MdPSivVPm7SpxdLnFP1XPA86xWC4crAnhjz5cilmTOerj/ARDDdiULEox3rC2ObbZNh0PByxAQZ0rSGwzMZ5tuKtv5M2CTFjuZ+DgcRSP/Sg213aiHEtaIuIicsb7A7ugx+fVtJ3280QLrZu3K2k8MV5J0FMWDShfyxfuJZd41WwqfucZQZ5RvLOknny5mY1jpRJBgzbsGkODOXQR7BFdtWa5RWjj01bVixcT9t4+/D6PHlp1ak+M8+59OPUEQzqPm4r7IpZpkIxy6MK+ucibrtDB46x15Fsqr2L8TbcIOwciL6ACVgeNrKs3bAKG58m6VRjB0S01QneXbFs+RK8hXhl1uVOYa49vKkO/EtX5ImXaUyoMuY/qKrA7eJcHj/wZZ6f823RoQFV582BsDugk9au2KyYZ2z+A2l8vab2rcoRH/0MKiTb2df572zIuJ3zLVmmCF10RUuq51gVgh/uhbNXsUrSUTXRa9KmNk9CTX1x7rPs4QU6HGV5lUdIEBAEBAFBQBCIBQLR5FcTgoGOBYiSZ3wgMOL7ibSJJa939e9NefOzLreQICAICAKCgCAgCAgCMUAgmgx0iqguBgWVLAWBQAgsnrOat3ZuyZue5AwUVe4LAoKAICAICAKCgCAQFwikrAPHRXGkEBkBAagpjP99Gp1jA8NSbESGDWngY1pIEBAEBAFBQBAQBASBREBAGOhEaKV0VsaCvLFMn9vsRmbprIpSHUFAEBAEBAFBQBBIxwiI2C8dN65UTRAQBAQBQUAQEAQEAUEg+giIBDr6mEqOgoAgIAgIAhEisGbNGvrnn3/o+PHj7MGoAHXr1o1Kly4dYa6pm1y5y5wwgbZt26Y8F9WtW5eaNw/ODWjqllSeJggIAqEiIAx0qIhJfEFAEBAEBIGYI9C3b1/677//rOfcfPPN9N1331nXiXAyfvx4xfibZT1w4AAVKhTaRlxmejkXBASB+EBAGOj4aAcphSBAkyZNohdffJH27dvHPq2zUu3atWnw4MHs21k8lGTk7nHmzBkaMGAA/fvvv+w//ryCIkeOHFS+fHnq169fyBLNQYMGERi7gwfZp30y5c+fnx5++GHq1KmTDkrzo66rLojzWofH8/Ec+2B3kluYM45cCwKCQPwjIAx0/LeRlDCDIDBx4kSaOnWqVdslS3jr8LfeUoySFRhHJ9hMBcw+GBtI1MDUCUUfgXHjxtGzzz7rmjEkstOmTQuaif7ggw8Uo+yW2eLFi2nTpk1ut6IWJn0malBKRoKAIJDGCIgRYRo3gDxeEEhEBMA0lytXjooXL06lSpXiLc3z0d9//52IVYn7Ms+dO9dnGSGdfvPNN33eN29A8okJmS+Cnm4sSfpMLNGVvAUBQSC1ERAGOrURl+cJAukAATBj27dvt2py9uxZZShlBchJzBBw+kwfO3Ys7d+/P+DzIMneuXOnFc+Zj3UjRifSZ2IErGQrCAgCaYKAMNBpArs8VBAQBASB8BCoVKmSTa0Hk5eff/45YGbffvutLU486TvbCiYXgoAgIAgkAALCQCdAI0kRBYFQEDhy5AjNnDkzKKmkmS/0UyFVnj59ukpvSpjNeNE6hzcC6N3CeBL63qZRW7jPCLfu5vPgemzt2rXKA8TmzZvNWwHPgeHGjRtVWtQvFgTJce/evW1Zf//997Zr58XevXsJkmpNefPmpR49eujLkI+pUc9AhQK+8NIRjPTdV17Hjh2jOXPm0NKlS+nUqVO+ogUVvmHDBlqwYAFhQhMupfYYDLeckk4QEAQYAR6wEVObkjd48BMSBASB8BF45plnPBiS5o8ZOK8M77vvPg/rHHty5crladmypXX/ww8/9DRr1syTJUsWK48KFSp43nnnHSuO2wmewd4cPLlz57bS6TJUrFjR88orr3iYKVBJf/nlFw/CkK+Oo49FihRR4bjHUlIPM8Zej1u9erXnscce89SsWdMrPfJhbxAe9gbh2bVrl1daBES77uZDvv76a0/jxo097PXEVjb2duF5+eWXPSdOnDCj285/+uknT9u2bVX5NR44sn64p3v37p5Vq1bZ4ody4ewX1apV88ybN89WRjyL/Sb7zPb999+3xWeXcJ6vvvrKFoZ+E4jCqWe4faZFixa28v3vf/9TxUM7of9kypTJuo8+F6if67rxBFG1CfqxmQdPTDyVK1f29OnTx7NlyxYd3e+RJ0senoh4ihYtapUF47Jr164ejKtRo0ZZ4bpf7NmzxyvPUMagV2IJEAQEgaARiCa/Kgx00LBLREEgtgg4GSV8cN0YaJOxAAPAUjRPr169vD7U+oON4/XXX+9hyapXBdiDg4e9Z/hNi/RjxoxRaR944IGAcfVzX3/9ddvzPvnkEw+75wsqfZ48eTwslbalx0U0664zZ+M5z+WXXx6wXB07dtRJrOPhw4c9N954Y8C0mJx8+umnVrpQTpz9Agw0CEeNNY7PP/+8z2wbNGhgizthwoSQGOhI6hlunzHbGvXjjVQ8LHm31cOsP87BZLv1cwDDEmbPE0884QGj7EznvMYE9bPPPvOZF/Jj6beHjWh95sWeaTx33HGH130nAx3qGMSzhQQBQSA8BKLJQIsKB785hQSBREWAXyHEUmj69ddf/VaBJYcEIzKT4IKOGW86ffq0FcwMudrtrXDhwlYYTrR6BbxtBEvOuHChFqwPXOw+x8wHQZ3CF0VSd50n8r/iiiuUX2Qd5usI1RYnMeNNP/zwgy0Y7vzgncQkll7TvffeS8y4msERnbOk1JZ+6NChEIjYwnCxaNEipSqjb5QsWZIuvvhifRnUMZJ6OvuBvwf6i/vHH38QS7P9JSdgAB/XboSdDN9++22/fUqnO3r0KN1zzz3kSzVmx44ddNFFFxEzwzqJ1xFj5ssvv/QKN9sonDHolaEECAKCQJogIAx0msAuDxUEoofAsmXLrMxYBYHAWBUrVswK0yfYjMOkv/76i1hVwgoqW7YssYqF0oOGXik8Nrz33nvEy9oEpgt0zTXXEC9PU+fOna10+qRevXrUpUsX9WO1BQLTZRI2hwFhW2Ywx7y8rXRPeblcbRLSpk0bMzrNnj3bthOd7WbyRbh113mxOoBiMPU1jry0TyzNJRjdPffccwSjPZDTzzWYOeiaa8KGN0gDPezdu3crXWhnnZ588smgGDidp7/jddddZ7sNHdwZM2bYwnCBzXhMQjpW1zCD/J5HWs9I+oyvgvnr5++++65Xst9//11tC27eQH9/4403FMMNRtdNJxzt76YbjcmgM5xVmOiWW26hW2+9VfVx81m+zsMZg77yknBBQBBIZQR4NhwxRVMkHnFhJANBIEERcC7V86sgoAoH4uDHEmO1pKyrDrUEZhBsy8fQzTTpkUcesd2HHnSwhOVw/Wx9/Oabb/wmZ2meh5kbD9QB3AhL2079Y2eezmX9cOuO5zOj6+GJhq0etWrV8jDzayse9L9fffVVpQajb7DUXul567rjiLo5iSchXioyUJ8IhZz9QqtwIA+etNjKf+edd9qyRjlN/VyUk/1KqzjB6EBHs56h9plw2xrqMiahDlWqVLHhhGuMESc9+OCDtnjAiyeetmjov9DVN9seqhw8gbHinTx50sMrG7Y4Or7ZvyIZg9bD5EQQEASCRiCa/KpIoPmtJiQIJDICULfALoatWrWyqlGmTBm1BG0F8Al/1C1VDITDE4NJ8NLAhmhmUFTPWVeYHn30UcK20W4EqXnVqlVtt9avX2+7dl6EW3fkA48J8E5hEjOrXuoXkJxjJ8Aff/zRiorNTeBtQxM8Y9x111360jpCct+hQwfrGicrV660XUdy4VTjgCoPM4xWlmhTqAloql69OjVt2lRfBjzGSz1R0GDbGuoyzORadcNOjc5+hJUAjBEn8USJeKJpC3aq7uAaqwwmvfTSS9ZKBcKxGjFixAi1WmPGc56n9hh0Pl+uBQFBIHwEhIEOHztJKQjEBQJQm2jUqJFXWerUqeMVZm6k4UwDdQ6E3X333bRw4UKvtLEMgG40GHynDqzJCLk9P9y6Iy+4qjMJTDB0woMhZ9rSpUsTVFHAHDt/ToZs3bp1wTwiqDhONQ7o3UJXWBNUSkxiIzvzMuB5vNQTBQ23rZ11QF7OiQfCQOh/l112WdJF8j9UY0xiw17zkmA34NZvsmfP7jqpQnxN8TQGdZnkKAgIAsEhkKSUGFxciSUICAIJhICbHrQpnYTOJy+TK11jXS1I77744gv1g6QSkterrrpK347KkV260ZAhQ5S/aRhh4aeNFKPyAM4kUN3xHCdjhTROPWdf5XGmxTbYtWvX9hXdFr5161bbdSQXrIpA7LqQzO2+YfgGvWPoYf/555+27CNloNOqnrZKOC7c2hqTMU3OVRVIsp0TNR0XR2xRb5K50oBwTJRMYhUZgv5zOJRWYzCcskoaQUAQsCMgEmg7HnIlCKQbBCBRdZIp/cJ9GFc5Dd10GvY1TFdffTXddNNNdObMGR0c9hHL3vD+wHrGyngLS+swWow284wCBqo74jglwW6MGOK5kVMq6RbHVxiM16JJTmkqvK1gkxF4BzG9nsBbCxjuUCie6umr3IHa2lkHp4cUZ75gsE2CRw7TYNA5AQqXecYzUnsMmvWSc0FAEIgMAZFAR4afpBYEEhoB3uiDpkyZQnBzxxtRqB0BnRUCI8YbVRD0Q8MlSLbhvcPpJYL9PSuvF5DiwTPE/Pnzbfqr4T4vmHROaXMoO9rBk4hJ0OsOZmtsMG9sOGYmjfgcuxL279/fcmGHyc6wYcO8vG+EKn1GweKpnuEC5axDoAmbcwdJtBl0mjWxkaI+VcdDhw7ZrkO9SK0xGGq5JL4gIAj4R0AYaP/4yF1BIN0jAMYVBn74wXUc71pHP//8s63ecA324osvknZFZ7sZxMXo0aO9mGe41YOvXZMh4d38bPFMiXkQjwkpCtzzmQRVEmzDnC1bNjPY9dyZFnrOI0eOdI0b60BItIEbJPqaePdI5YZQX6PdnPrS+p6/YzzV0185/d1z1gFGlZhkQEfZjaCmYhJ7PTEvvYwPkR/8lmMyGC6lxhgMt2ySThAQBNwR8F7jdY8noYKAIJABEIBONKTR8HNrEpawoW6hyY2xhc6tL+Jd22y34Eeat/S2Mc+2CKlw4VRnOH/+vPJN7evR5qYuzrSou7/6+8ozWuFONQ7TWBTPuPTSS131wgM9P5r1DLXPBCpbsPedDDTa2TS0NPOBmhE82pgUiIGGmoyvDXICbXBkPkefBzsGdXw5CgKCQNogIAx02uAuTxUE0hwBMHyQnLmR26YSpsoDpHfOpfE5c+a4ZaXC3DwXOCPDpZxTv9QZJ5rXvL21V3ZQU3Eu4YPhgnoL3J5pJrpu3bpeaV9++WWvsNQKuPbaa/1ujoLVhXAomvUMtc+EU163NDCGdTLvb731lmvf5+3n6dixY7ZsgK1JbjYDcGNnjiX0k4ceeshrl0rkww5rrewiGYNWJnIiCAgCaYKAMNBpArs8VBBIewSgi1u+fHkC42cyuPBggC2PTYJhldNHM/SiTcLOgvD+MGjQIOJNWWjSpEnWbadLPezAZkql4ZMZRm5ODwcms2FlFqUT7GYHvWyTFi9erMoBFQj4fQY2YCKfeOIJtWuj9v9bo0YNpfJipv30008JesZLliyxjM5ggAaXgNjRsV27dkF76jDzDeYcerrYWtqNoFrgNiFyi+sMi3Y9Q+kzzrKEew2jVaf+N1SVYND63XffqW3OoWKESQYYa5MuueQSwhbgJiG/jh07mkGqzcFYY2fDjz/+WPWhDz/80BbH7SLSMeiWp4QJAoJAKiEQ9PYtfiJGc2cXP4+RW4JAukbAueMcvwKC2omQmQNXXHibaYi6bD9m5qy4vN227V6hQoU8zDB5mOGyhSOP+++/30qnT+677z6veObzWJqno3qYYXaNy8vrHmbiXe+5Pde5O124ddcFY4bZw54QfD7frA/OmYHWST3bt293xQrxkCdL7L3y5Y0zrPTBnjj7hbkToZkHb0vu9TyUxRdGwexEiPyjWc9Q+kw025oniF67XDrb1nnNeske9A83Gj58uCvWzjxwjXFlhrPU2coy0jFoZSQngoAgEBQC0eRXRQLNbzYhQSAjIlCxYkVbteGdAHrO5lI0IrRv354GDhxoi4sL+Ig2DQCdEUzPBdDB5W2mnVEILsa01BkuvZjB8ooTy4D69esTM55BGYDxttk2/8HYPAX64jg6CUv4ps9tfT8Sl2c6D19HSP/dDOOc0ldf6X2FR7OeofQZX+UJJxwrLTDyDNaFIFZbYJSJ/uFGPXv2DOiVBpL/X375xWtjFlOdJNIx6FY2CRMEBIHUQUAY6NTBWZ4iCAREAMZOppcLbAPttu21cxncea0fBNdw5lbB2DyCpWH6Nr3wwgtq10G3ZyASNpSAMeH48eNdPVPA/RaYDOduakiL52CJ3KSPPvpI6RI7/ewiDlQFYLyFJXSzzHiGSc66Oq913EB11/FwvPXWW2nRokXKDZ0bA4q8nnrqKbXxi5kO5yxBJGwM8/DDD7u2lY6POoORxfbOoRKYLHhp0OQ07NPhBQsWVDvfYSKiqWHDhsqAUF+bR7SvWV9f+SJNtOoZSp9xtq3zWtcl2LaG4ery5csVRuY40PngCEwefPBBpdbRqlUr85bXOSYD2HTIaaQIWwGoeMyaNUvtUGhOsDDWzJ0pIx2DXoWSAEFAEEg1BDJB5h3p09qWStoedvrOoZFmJekFgQyNANxrwa8sGGk3RlODA11c+FYGU+zPfRYM4LRRHPIzGTGdF7wIQPd306ZNBJ1dfPArVaqkfiZDr+M7j3iFwPgPu/Oh7EgP/WLT6NBMg3KD6cRGJmCWmzdvTmCCNGkMkN5pqIg40ay7fqY+AgtI4VesWKHaADhACmkypTqu2xGu8IADJOu6DatXr66wdIsfbBik2cAWzJevCY/OCzrs2AIdzLG/PoT4cNuHlQe47vPFVOp8zWOk9Qy2z8SyrVEHbLuOvgsmGHr6bv3NrLev8127dhGrTCm84UXDXH1BGmCMfo32cHOTGOkY9FUuCRcEBAE7AtHkV4WBtmMrV4KAICAICAKCgCAgCAgC6RCBaDLQKWt96RAoqZIgIAgIAoKAICAICAKCgCAQbQSEgY42opKfICAICAKCgCAgCAgCgkC6RkAY6HTdvFI5QUAQEAQEAUFAEBAEBIFoIyAMdLQRlfwEAUFAEBAEBAFBQBAQBNI1AsJAp+vmlcoJAoKAICAICAKCgCAgCEQbAWGgo42o5CcICAKCgCAgCAgCgoAgkK4REAY6XTevVE4QEAQEAUFAEBAEBAFBINoICAMdbUQlP0FAEBAEBAFBQBAQBASBdI2AMNDpunmlcoKAICAICAKCgCAgCAgC0UZAGOhoIyr5CQKCgCAgCAgCgoAgIAikawSEgU7XzSuVEwQEAUFAEBAEBAFBQBCINgLCQEcbUclPEBAEBAFBQBAQBAQBQSBdIyAMdLpuXqmcICAICAKCgCAgCAgCgkC0ERAGOtqISn6CgCAgCAgCgoAgIAgIAukaAWGg03XzSuUEAUFAEBAEBAFBQBAQBKKNgDDQ0UZU8hMEBAFBQBAQBAQBQUAQSNcICAOdrptXKicICAKCgCAgCAgCgoAgEG0EhIGONqKSnyAgCAgCgoAgIAgIAoJAukZAGOh03bxSOUFAEBAEBAFBQBAQBASBaCMgDHS0EZX8BAFBQBAQBAQBQUAQEATSNQLCQKfr5pXKCQKCgCAgCAgCgoAgIAhEGwFhoKONqOQnCAgCgoAgIAgIAoKAIJCuERAGOl03r1ROEBAEBAFBQBAQBAQBQSDaCAgDHW1EJT9BQBAQBAQBQUAQEAQEgXSNQNZ0XbsQK3fu3Dlas2YNLV68mA4ePEi1atVSv5IlS/rMaf369XT8+HF1v0SJEoRfeqT9+/crXFasWEHFixen2rVrU7Vq1ShHjhzpsbpSpwgQ8Hg8tGnTJtVftm3bRtWrV6e6detS6dKl/eaKvoUxCCpXrhwVKlTIb3x98/Dhw7R582Z1mSVLFqpTp46+lRDHRC9/QoCcgQsp4zG6jX/69GlavXq1lWnNmjUpe/bs1rWcZCAEeHBFTG1K3uDBL1GJGWDPPffc42Fm0MNN7/W7/PLLPcwou1avVatWVvznnnvONU4iB06aNMnDDJBVRxOfggULej777DPP+fPnE7mKUvYoIbBnzx7Pdddd58mfP79rfylWrJhn0KBBPp+G+7p/ffvttz7jOW/89NNPVjo8O61p2bJlnvfffz/oYsRb+YMuuESMawRkPCY1T6jjMVCjrlq1ynrf4H3lizcIlI/cTxsEosmvZngVjjlz5lDDhg2JGUHCzNKNxo8fr6Ra/KFzu50uw86cOUP9+/eniy66SEnl3Sp56NAh4okHtWvXzpLCu8WTsPSPwF9//UX16tWjYcOG0ZEjR1wrvHfvXrrzzjvpsssuo61bt7rGSeRArFo9+OCD6n0yZcqURK6KlD3BEZDxSGoVWcZjgnfkOC9+hlbhOHDgAHXp0oVw1NSoUSNq0aKFGnx//PEHHTt2TN06deoU3X777VS/fv2EWyLWdQvl+MYbb9C7775rJSlQoAB17NiRKleuTBMnTqSlS5da9/777z+699576bvvvrPC5CTjILBx40bq2bOnNVZQ8/Lly1PLli2pQoUKtHLlSpoxY4YaU7j3999/0zXXXEOzZ8+mzJkjn8PnyZNH9UvknTdvXhzShB577DEaPHhwyM+Ol/KHXHBJEJcIyHhMapZwx2NcNqoUKj4RiIYQPZoi8WiUJ9g87rvvPmspJlu2bJ5PP/3UlvTkyZOehx9+2IrDLei5+eabbXHSowoH65N6cuXKZdWbGSHPli1bbPVevny5p3DhwlacTJkyedatW2eLIxfpH4ELFy54OnToYOsH/OHy8GqOrfJYTu7atasVD2MJ6j8mhavCYeaRlue33nqrVT+eIKRlUeTZGRQBGY8pDR+r8SgqHCkYJ+JZNPnVDCuBhlTs888/t2Y1d9xxh1JHsAL4JGfOnPT666/TqFGjCLP6okWL0tmzZ4k7DTHDaEb1eY6l6u+//55gbMhMBDFjSjBKvOSSS6h79+6u+Rw9elRJc2GogPQoB9JAAnzFFVdQ1qzezRZOGl+Ffuqpp4gnD+o2jCN+/fVXKlu2rC06jAhfe+01hRmkiA0aNKC1a9dSlSpVbPFCrT/a5MSJEyqP2267jZhRpx9++EHVGasFWP53q7/toXKRaghMmDCBTHWFG264gQYMGOD1fGaOaeTIkcooF2MB9Mwzz1CfPn2Idem94iMAxrk//vgjzZw5U425xo0bE+tYKyNWMwHGCVaLQDBq5YmxeVuds54+/fbbbzRv3jziiR5VrVpVqVpcddVVakx6JUgOmDVrFk2dOpVYj1KNCUjUMXbZLsJKAiPAr7/+WvVVHYixMHDgQJU31Jz8UTDlR/odO3YoPFAWqMnAeAkrYldeeSXlzp3b5yNgGA18Fi5cqCT+GKudOnVS9feZKMwbweBlZo12GTNmDE2ePFnVDyt9MB6FOlDv3r3VSoYZHwbe//zzjwqCkTdP3pT6HdqVhRkKi4oVK5pJMtS5jEeiSMej7jBQY8T7B30LRvTNmzenXr166dt+j8F+937++WfV75EZjK3xfXeS2edZ0EcPPPCALUpqjm/wGSNGjFDvQ7xHwRPVqFGDeLJCeMc7Kd2P72jMIKLJ0UejPMHk8fHHH1vSIkhPnRJWMw9IW/HD7N5J/iTQkGizVwDrOdy5bOfMbHhJ6vhDZ5PsOtM0bdrUwwPbVoxw0tgycFzwoLDKyWorjrsplzAeZF07D7+wUgKNs3Dqb0ohkZ6ZZass7P3DwxMY4wlymtYIsOqO1T5oqw0bNvgtEk+GrPjo28wMWfHNtmfm2sOeO2xxEZ8nkh5WAbHS4CSQER57BPG0adPGKy/kxxNBz5IlS2z54YIZVA/ra7umQTqMe9Z5VulgRIQwtx9WaQJRoPIjPXDz9S5hbzieadOmuT4G7zmegHuVjSe9nueff97DXk9c04UaGApeOm/WiffwBMCrbBpHZqQ9PDnT0dXxk08+seJff/31Hp4IWNdI9+GHH9riZ7QLGY8eZdSn+5DzGMx4RJ9hptTD6py2voW8ihQpovqYma/TiDCU797LL79sPQPvP+e3HWXhSb4Vx7mylVrjG+XAe5dV86yymBhgxZrV1xDNongd39HkVyHZiZiiWaCICxNkBg899JDVEcCYhUu+GGjWC/aAMdedDB4+wBDgo6DDcMQA0rRz504P6xpb99ntl1r2xkDGB0+ne/rpp3USTzhprMQuJ2AK9HNwxMsgHAqn/niOyUSZaiQoy/333x9OUSRNDBFo1qyZ1V9YqhvwSSyZseI7+5fZ9roPYjLnfGmztNXD7vGsZ/ljQFmi6WG9fdsz2dWkbWyyDrJn165dVn44wYdKlwFH9EVnfwTzBoo1A82GmV7Ms/k+QPlwbU5GUC54PDHrADU1MABmGNRtokGh4KWfB+9GZlnYdaEHkwHzvYm2gSqdJpOBdrYHJhi7d+/WUTPkUcZj5OMRk0pMrM2+6fYe0vdNBjrU79727dttQqLRo0fb+i2YUIxb/Sx2aGDdT83xzatXNh4E5XG+SzD+zHdQvI7vaPKrGZaBNvUxeWnY6pShnvhioNn61/oQsCcLD6slqKwxw+SlIGtAdO7c2Xrk0KFDrXBeJrbCcYKBg05bpkwZD6t+WFLfcNLYMnZcsFcSqwx4nnNAO6L7vAyn/sjMyUTxkpmHl/49+NDPnz/f5/PkRtogwMvlVn9x9lm3EmHVwvwgYCKrydn27733nr6l+j8YZ/0hgX6jJn8MNKsZWWnwEWR1LOV2kVW4PO3bt7fumeXAqop+Do5wSYePKtxdvvXWW7Z7rHqgVpEgxWZVCuvexRdfrCTbWLkKRP7Kjw+yuQqD9wWrfChJFauWKIZTlxUTBZQRxB5ybGMJthuYdGBC8eWXX1rlBBPKqiGBiuj3fqh4ITOs+OXLl0+VAwyzyRhgvOs64cgqPNbzTQYa99CmCIP0Kz26EbUqHuSJjMfIx6OTMWWVNAv9P//802O+h9AHTdufcL57poSZjbGtZ+Hkgw8+sMYC2hbvT1Bqjm88z1zBYxUwy3Uf3m+sSmWVkdVMET2ux7cw0KqJIvszl4fB4IZLvhho5IdlTfY+4MEs06RXXnnF6nCQGGhiPUornL0JeF566SUP6z9ZqiMYNE4KJ40zD/N6+PDhVhnwcsBHOlwKtf54jslEQfJoSp/CLYekix0CpiEpltSDIaz4oG/hhwmSJrPt3cbkI488YqXDSo0mfwwo6+5baeDr3aSxY8da96DmoJlP1r21wp3lgBoXPnL9+vVTS7kwKNIUrtGSv/JDzUtjxfrXigHWz8ORN5+xSae/+OILdfurr76y0kE6jZUqk6AKpvOFKkckFC5ewBLMh/MdAybfZFKgoqbJyUDjWigFARmPkY9HU3KqV5lSEPZ4ORYwGWjEC/W7p4VjGI9YqWavYNbjINzT4xR8g6bUHN94x+gy4Ogcr5jwQqj37LPPerBaplVd43V8R5OB9rZGY4QyArEkVynCo678cYlJlVnCQq1bt1ZGAjDEg9su1lWkuXPnWs8zfU/DIAYGctiNDe7zXnjhBfVjKQtdeumlysAARga8WYSVPpw0VmKXE+BiUiTYhFp/87k4h5ElDCiF4hcBZuosN5AwnAlE6O/wB60J6d0I/d1JLH0llkqrYBgKwbCHlxGd0axrGKPy5NW6xjgaN26cdY1xBqMcGAbDeE3vmgijPk0YXyaxtJR4kmkGxfR80qRJVv4sRfba+ROGdCwdUoaOiAiDIxAMizSx5IoWLFigL9URBkswjgLBGCgSChcvYAmjY7g8hPEhjEXxjoSbTG1IjHKZ70hnOWFoKJSCgIzHFCzCPWM7DispjNadhPcQr0o5g63rUL97eNdVqlRJOSpAX4dhIQyPYSysxy2rRxCM6jWl1fhGOfC+MalHjx6En5MywvjOsAw0LEdhsQyCdbs/gvcMELawDoVYwkW8rGh91NzSsnTICsbHhGeWyt80rFc17du3j1hKpX5gAngZ2RpM4aTR+bodgYtJgbDB9svwBmDWQ6cPtf46nT76Yq70fTmmPQJoe3h3AMFTTSDCltssRbGiOfubvgGvM05ybgWOvPwx0GAMzWexBMeZpe0azDYYS5OhDHXM2zKM8ALvANbNtnLBR9aN4JudpULqFsYjCF5ANIEh6Natm770OpqTDK+bQQSEixeEBOwmVG2+o/3tuz3O7d2CeCylVl4A3NJk1DAZj5G3PBsdW5mUKlXKOtcnzveQDtfHUL976N/wAgavRKAhQ4YoBpp3Y1XX+MP4NZ+bVuMb/Iev8WgVNvkkI4zvDM1A6waHNAszPbjJcqO3335bSb4w82JjGeVGBjMxf4RNRbDximaE4ZYJs1nWEVIzSzYEVMmdnfGWW25RceDODW6/eInY9hgw07x8rGascEUFCieNLVPjAi6keCndkhL++++/6iNnRLFOsQENdnHkZUM1A7377rsJG9GAwq2/lTmf4AMpFN8ImAwwGDG4tHNKbc0aYCJokpneDMcul04ypZK4h5e5P4ILRpNY3crvRiuQmICwaRBc6IGwu2BaEd4x2BgGrqNA+ugsD95fmjQmZt0xCYDrOl/Exnu+bgUVHg5evMytXOlpCRvqifcj3ml4R7LqjPUOcr4jdaHk/aCRSDma40nGYwouoZzhG8jGqCoJ+qmT9LvBGY7rcL97kC5jxRmrYViNARMPSbQm7OBqUmqPb/1st/eyvmceM8r4zrAMNF7W6ITw9QiCv2e3pVkwrPDjzPo8Sv0CSyyQmgQi5KeZZ/ilZXczVhJzFz83RhySV/hYxm6AkABjGRc+bOGPGnlCqoZrzUAj43DSWAVynEBNhI1yVChm0ygvJgBOQp0w4PGyYcMLggIRuuUAAEAASURBVE9dTZHUX+cBn75C8Y0A1GzYk4waHyjpE088oXYdhCqSkyBNNXe3xNI96+I6o6lrLdU2b5rLlhi7Tt/kZlycQ3UBTLGWQkMFApO8QAQptF55MdUTdDq2TVD369SpQ23btnWdeON9EQ1CHfT7wlT90nnjfWBipccppNKa0BasZxm05EinC/YYDl7wS62ZZzZkVD600R80mZMCt3ck4sn7QaOVcpTxGPl4xKquZqCxX4ST9CqPMxzX4X732DOQEkJpHuTJJ5+01M8wwTX9zuM5qT2+8UwQ+B8w93gvacIKF3Z9ZLsytUsz+IcMM7754xIxRVMpO+LChJABbxiCtWTrh50JuYNYOcDllmmpj7i8vGLdx4mbESFcz5j5wnLXJNNIAS7qNMGKnHWmlXsYWPQ7iZl+K9+77rpL3Q4njTNf5zVcepnu9OBeyrSER3xYvfOHzSoPXJhp44Fw6498TUMyPEMo/hEwfc+i38NiG7tZmjR9+nQvd3Q8CTSj2NoeRmSmf2b4/zYN30zjW39GeGYajGWTYPDCHyJlAIN3AUt41e3+/ftb/RpeKviDYSVjqZ6HmXfr/ptvvmndg2GhHvfw8hMs+Ss/S6WsPDHe4JXDJHgI0M/kyYKHpVfqNk98rXDc55UkKxk8iuC91aJFCw9LvjymkZ4VKYSTcPAyd4FFOUzCu0bXCUd4TtFkGhGy0EAHy9FAQMZjEhjhjke4S9X9D0aZrJpmoQujdp44W/cRj1WY1P1IvnvIAH6W9XPNI94BTkrN8c1CRJsvefQvk8yxzJtiKcN/Myzexnc0+VVIZyKmaBYo4sKEkAHr6HhMK310Wni/aNeunWICnH5GwRiYDDYe5cZA4wNlpsVW2Pgo4IcPljk44PdUk9NF1qOPPqo2EmDDGg+rkdg+3LxDkkoWThr9PH9H032OLi/PzD1g/lkX01YHXmK1feTCrT/KYzLQrAPmr4hyL04QgO9w+FbW/QRHMHMsmfRg0gfXi+Y9nPOukl6lN9secVgdQW32AbdSLOm15YEPiCZ/DKjTqww2R+EVHeUjGX7WdblMa3t8CE1/7fAaAgabpeu2SQAs5sFQazK9hGACgM1gbrrpJn3b59Ff+TGZBY66nHgmJs94H5jur3Df/LBhMsvSaCsdPNpg8s8GeqpMOj8cnZuV+Cyojxvh4MWSOqtsKANcFmITHrjYA2Nslg+uOjWZDDRLwXSwHA0EZDwmgRHueIS7R/P7jbEDd5jYE8H0iqH7qGagI/nuocQYsxBE6XxxxLfVbZO31BzfKBs89ZjlYimzB8ID1s22udnUezXE8/iOJr+aoRlodAxIl5xSZrOj6HP4OmSrfySxkRsDjQjm4NV56CMkuvocH0Qt+cLsFn5e9T1fR7Z4taS94aSxVcDPBT5WYAR8lUOHu222Ek79URSTiRIG2k/jxNktMD9w+ab7hK8jGGveitaDyauTzLZ3TjTN/Jy+Uv0xoPjQwDermd55jt0NTXd0KBeYNlPS7EyDa+wOaNLvv//u+hxWRzCjeZ37Kz8ig4k23W66lQUTALjPMgmbH5jvGrd0rI5mJgn7PFS8sEJhrnKZZQPTYE5uMBHRJAy0RsL/UcajxxPueASyAwcOdB3L6Kd4/5h9VzPQSBfudw9pQU6BGBhUX5Sa4xv7WJib9JjjVZ9jNV2/1+N5fAsD7atHhRnOeoRKooOlGVMtAR2DrXDVYEIHciNfDDR8mWIwmZsgYFaLDxbyMqUsrGNtZY10rPvsKrUDg8E6pF6+kcNJYz0wwAkYCwxi565D+MhBzcTX5ibh1t9kooSBDtA4cXYbzCobv3qaNGlik+BgHGEplI3DPNh4xBeZbY+PEtrflF5jVzr4Rsd4NQmrMfolzi4ezVvWOfKCJBf9VsfFWIcfarZot+KZJ/DBjtUj5zsBHwo3tQdsktS3b18rfzwHUvSNxhKwmb8+D6b8WEaFH2vskIZJiK4D8MH21cDejdiDkJJUmx98pMX7B8xoNClUvKDWY27CgHLhHQzf+d98841VR6x8aRIGWiMR+CjjMbzxqJEFA47JtR5reLc8/vjj6v2Dca3DzZ0Iw/3u6WdivJoTd/hY9kepOb6hRvfiiy/aVueAAfgarJbjHWVSvI7vaDLQmVBhBiEialvqfyr99J1DI8onHhLzAFBeMng5Rvko5Y96RMWCNSqMn2DwAp+tbsZVbg/gl5/yT61960JpH4YG/PF0i67CwknjMzOXG/CTy4wNwbUPXGrBkCsQhVv/QPnK/fhGAH2RGUflW5nVlGwumEItOVw28UqLMlBhZtYrOTPHxIyrCofHCW0A5BWRA2BBD6M8jEcY4jBj6RbNFoZ3AgyH8E5AGu3pwhbJuIB/anjPYSY1oKEjkoVSfsSH9xvkD+O9QGVBfE26PWB8CYM9Nyx13EiOoeCFfgJ3hPAYARdsodQnkjJmtLQyHoMfj86+gXED7xP169cPesykxXcvtcY38AEvwKscihfAe84XLxCP4zua/Kow0M7RIteCgCCQEAiAqYZrO/hQZWmRKjMYXJYISfkTAgEpZHpCINHHY3pqC6mLbwSiyUB7+5ry/Vy5IwgIAoJA3CAA36mmr1QUDFLZRKF4Kj82ixozZkzI0LFepJLMhZxQEqQ7BOKpP6c7cCOskIzvCAH0kVwYaB/ASLAgIAjENwJ6K2pdSqhH6d28dFg8H+Op/FiOxQZNoRJ2RcXStpAgEE/9WVrDjoCMbzse0boSBjpaSEo+goAgkGoIYAOknDlzKp1EHNl/utr5k11QploZInlQvJWfDaRsGzMFWzdz85Ng00i89IdAvPXn9IdwZDWS8R0Zfr5Siw60L2QkXBAQBOIeAdhAw1AlVgZxsQYg0csfa3wk/8RCQPpzYrVXRixtNHWgM2dEAKXOgoAgkD4QgFeaRGWe0QKJXv700YukFtFCQPpztJCUfBIBAWGgE6GVpIyCgCAgCAgCgoAgIAgIAnGDgDDQcdMUUhBBQBAQBAQBQUAQEAQEgURAQBjoRGglKaMgIAgIAoKAICAICAKCQNwgIAx03DSFFEQQEAQEAUFAEBAEBAFBIBEQEAY6EVpJyigICAKCgCAgCAgCgoAgEDcICAMdN00hBREEBAFBQBAQBAQBQUAQSAQEhIFOhFaSMgoCgoAgIAgIAoKAICAIxA0CMd+JcMOuo7Rp97G4qbAUxDcCFUvkpUx8e6O0l2+QYnSnYJ7sVLpwLipZOHeMnuA/Wxmn/vGJp7syTtOuNdJ6nO46cIJ2HDhJh46fSTsQ5MlBI9CoSmHauOuYtFfQiEUvIt6TlUvmi16GLjnFnIGevWovDZu6yeXREhRvCFzXvqLa2OHnKRvjrWjpvjx1KhSkPh0qpRkDLeM0cbqYjNO0a6u0Hqd7j5ymETM20/LNh9IOBHly0Ai8cnMj+o3ba5m0V9CYRSsi3pOxZqBFhSNarSX5CAKCgCAgCAgCgoAgIAhkCASEgc4QzSyVFAQEAUFAEBAEBAFBQBCIFgLCQEcLSclHEBAEBAFBQBAQBAQBQSBDICAMdIZoZqmkICAICAKCgCAgCAgCgkC0EBAGOlpISj6CgCAgCAgCgoAgIAgIAhkCAWGgM0QzSyUFAUFAEBAEBAFBQBAQBKKFgDDQ0UJS8hEEBAFBQBAQBAQBQUAQyBAIxNwPdHpFMU+OrFSjXH66cIFo5dZDdPosnwilGQJVSuWjQnmz055Dp2jL3uNpVg55cHwhIOM0vtpDxml8tUc8lUbGavy0hrRFcG0Rtwx0heJ5KFf2rHTe4yHsvnT05LngahTlWI2rFqYbOlam8xc89O3f65hZPqyecFXr8tSrXUV1PujP1TRu7vYoPzl9ZIfdgHJmy6J2Ytp18KTPSuXIlpnKF8tDvJMLbeKdm86eD35CkiVzJnr3jmYq7yMnztLNA6b5fI7ciC4CMk6ji2da5SbjNK2QT53n5suVlUrxLqeZ+f168sw52rwn7YQM8k2NrM1TY6wKfxNcG8UlA92pfkl66KraVg328+5Ld3wwg5iH9SK8EHJlz6JeCm73kSAn3/cwIx6OlPjihqWpaun86rlt65SwGGizIJnUBthmSHTPg6ljdJ8YndxKFspF79/VXGV2gfHv9/4MOnDUfQva+7rXpPZ1S6q4bw9fRv+t2BNWIbg7CKUSAjJO7UDLOLXj4e9Kxqk/dKJ/b0C/ZlSC38eaPhu7iiYs2KEvbcdA/TjQfVtmLhfx8E2NhCdwqVKqBaXJNzXG/E2qgReDB8UlA92RGWiTiuTPQXUrFqIlGw+awTybJhr6ZDslqYZ08+6PZtru4+JqlhTfcklVFf7+7yto8tJdXnH8BazfcYRa1yqmmPfV25Kkz/7iR/teMHWM9jOjlR/aBD8Merx0W9QoRn/O85bUZ+VKNq1WVD32POvELN14IFpFkHxiiICM0xRwZZymYCFn8YVArXIFbMwzSoex68ZAB+rHge4HU/O0/qZGyhMEU8dYxZFvaqyQDS/fuGOgC+bJTvUqFVK1OXvuAmXLmmTn2L5uCS8Gmtf7FfOMyLlzZHFFIDfrKmvK5SOOvu92/O2/LfT3wh2sUuChU2fOu0WJcVjgOsa4ABFlP4MlyT3bVFB5tKzpzkCjvXU7Ld5wMM3UdSKqaAZLLOPU2eAyTp2IyHV8INCOv52a9De1JjPVRVkwtY9Xd+0UqB8Hum/Pze0qrb+p+luDsoXDE7jVKTXD5Juammj7f1YKd+k/XqrdbVOnuJJW4oHDpm6kGy+qop7dkqXAn49bTeeYkQUVK5CTdbpSlqSyZM5MdSsUVPd2sM70QVYVqFW+gIqnAvmvdJHcKs451vVYlazLjBcJ9MNWbztCx06epTa1S6h8567dRxtZFzdvzqxUvWwBNhb00Moth+nUWXcmGnq4zaoXpXKsx7tj/wlaseUQHTxmV1cA01GtTD5Vh+WbD9EZniBoyp87G1Uvw0aJrOqwYnPScwLV0VSHgGSgMhvSVWKd4zw5s9HWfcdp3fYjdJh1gtOSZizfbTHQdSsW5LJlpeOn7PrskExrwstBEyZFdSoUojLcbphI7T9yijZwm2zafUxH8XsMFW8zs3jF0yxjWp7LOJVxqvufjFONRPwdsfLXpnZxVbDt/E1Yw9+ETg1KsalJJgJj/TsLiDQF+t7gG+vvm6u/R6n5Ta3N3/i8ubLRzgMnaavDeLwmf7fz58lGu3kVFDrf0O4LhifQeBTgtNVYfRO2OYeOn2Xj9GO0bsdRfTvNjpF8U2GzUoNxKcgG9yf4O7yXv6mL1h8IWr1Vvqn2Zo87BhqSZtBpZlTHzt5GkFpCBzkvM4VNqhah2av3qft3XF6NmhuMFxizV29prO79u3gnjZm9lV6/tYm61n/dW5Qj/EB3fvAf7T96mt7smxRn2JSNVKlkXitPKOpDF7dHq8DGgmWL5aYP7m5OZYuyEVwywQhuwIhlNHtVUnkR3Lt9RerarKyKMfC35TR12e7k2ERX8XOuSZbUfjR6Jf2zaCcFquOHo1aq9MV5MvHI1bX55ZA0gdCZwljkmwlrWYK+Uwel+hEM706e0MCABS/gZqyq4VSjaV4jSX3jHGM2a9VeVcZbLqlC3ZqXpexZvVcWZq7cQ+8MX64mG/4qFCreOq94xlOXMa2PMk6JZJwSq8fJOE3rsejv+Q0qF6ICLLgBQTihGWhcYwybDHSg7w2ESf6+ufgeQZCUWt/UfMw46288hFb3fjIL1VKUnQUub96W9G3fe/gU21D9RxX5+67j63hOnmAPxwV1bVaGbr20qtf3Z/GGA/TBqBU+bXl0vrE8hvNNBT8DHqFC8bxeRTt0/Ax9MHIFLWRGOhDJN9WOUFz5gS5eMKeaHaGIC9cdUNJe05jMXIryJQlGWqhanPajbpFkUGiXJHfhAWO+HJCPk3wZC3ZpWtbGPCNdtiyZ6Ylr61JpQ0ruzM/XtbaDC1RHpIf3CrwowDyjXvNYco5BDoIXk/u616KGlQur67T6M6XKLWomMcu6LNVK56PC+XKoS6hvQDqNydDVrSuolxeu17DuOfTP4QkF1KpWcbqyZdJESAVE+KfxRjaJgGeE1Y04uYzTJAh1v5FxmkWNWxmnEQ+tqGdgfjPxHoa0Ua8AViqZj79bua1nBurHge5bGSWfpOY31Z9Rqr4XLE8ApvrOLjXU92fPoZM0ecku5UUK1WrA39Inrq3nrGqqX4f6Tb2kYSmLed7Ok42lmw7yim6S+g6kyg/2qKW8ZUWrIvrdiPzS8zc1riTQ7djLhabpK5Kks+goNycbAUJFAi7RMJA/HbOahk3ZRJ/c11IlgfpF/6/mqfMDLFmGegS8PvRsW4HA4IJ+ZikzBgP0wKDagNmypvy5s6vwIf+sZ1/CJ32qauj4zuPoWVvol6mbqBhPAp7uXY+KF8ylJK6dm5Shwez+LhwKVEfkCUZTM6Bfjl9judOrzQz167cmSeSv71iJFiUz1eGUI9I0aMNr21ZU2TTmVQRIB7T6SgteYdA0I7nNsbQ0nVU//lu5lyX4ey3GGe3/bJ/6KjomBSNnpiw/6jwiPSYCnpHWMdL0Mk7tCMo4lXFq7xHxcQUhDlZwQVDf0K7r5qzeq9Q4EA4G+6fJG3Ea8JsKdRB/31yVifEXb9/UHazmEYgngJT9Ol4pBsFg79FBc+jE6fOUNUsmeua6+oTvF1RUGlUpHJTEVmUUg79Qv6lwvwv10LFztqm9ElAk8D9v8Ao8VEcL5c1BkFKvioGjhPT8TY0rCbSeLZ85d57mrdmvut1u3hhjHXvCAOVg5lkv94OJht6TJnQObaGqmTMYSBwz/Ecf5qUKxIHqhhthSRaqH1ATgTQ0WJrIRobf/LWOjjHjB73pHyclvZCQvn6yQWSweZnxgqljO9YZB2FSMGF+ilsi6GAfStbBrsyShpSpgvmE1DkHJlhiA6ENG/LLR5PWf4bKi1Z3gZx5wIjlypWdljojvpas47xEoZw4RJ0SAc+oVzrEDGWc2gGTcbrHmuQCGRmn9v6RVleNqxW2jLNNiaV5rlWxUMZA/TjQfbd6xts3NRBPgG8TdKpB/7IaJZhnEGyv5iSrj+IaGwKlJYX6TUWbg0fBRmOa8G1dxpJoTVhZjAWl529q3EigYXyHGRBowdok9Q3dmFDj0L6Y29crYdMd1nEiPUKCbeokh5IfOrNJ2JlQU5H8semUyB8C9OLatyefv5asA66fnZ3VO0AwwCuUL3ua6m1hAOuNZyAVwcsIBilod9BiLC2ethsXFmHVjta1iylpPgw6sPqgKStLV6JNiYRntOsebH4yToNFKiVeIvUrGacp7ZboZ9qvPuphMs1ajQOqcrBNqcpqdLEwjkvEb2ppxkNTpwYllcRZX5uevrDCnNYU6ljFewgThFrlCiq9+Pw8USjHRoWa5JuqkQj+GDcMtJ6loOhYIoFRniY4PdeEpXt4zYj2zoSQekaL9KwV+UH/J1aEJTIs04FwBG5udIIZU1MS7xYn1mHmYIfPZ+0XWj93OjPYJsE4CQaciJdalEh4phYmzufIOHUiEvg6kfqVjNPA7ZkIMfDNbFqtiFXUR6+pY53jBCoJmiCFjgUDnYjf1MLs2k8TJhelUhZLdbA6Qs0zrSmUsQpbrJduamTzSuYsfyw+tYn07nPiEcx1/DDQyd43UGi4WMHPjTBLas1GZG5O4N3ip0VYYZb2atqXbNWLa6iZaIIqQ6R05MQZXjq9oHStj506S49+Mdc1S2xvrdVaXCOkQiBcz8F4AS7p4LKvdoUCvLFKkkEh1E+gl6epFbsshN4UaBvr7v3MOnrb2ZMHltE+uqeFjhbwGCreiYRnwMrHKIJW30D2Mk6DAzmR+pWM0+DaNN5j4d1qfmPcvC/oOmCH3cG8vJ/yddJ34ufo9k2F0bwms646LJzjQUO986fJG2jS4l1e2UD1wZcaqFfkGAaEMlafYrssuCkEjWLbIXi7Osqr7lc0L0eXNy0TdCnlm2qHKi4YaCwhYbYHgo4y3JQ5CSoc9Xg3QhA+4mCgMYDwg09LLEeZxmk6Pfw3a9LGdvo6WsfWtYurzVY0kwoGX9Ougyk6R0fYl6Sm8sbSSSGeLJjGdDoOjv7qiKpBpwnYwc1fZl6jAX7xSvBf2bt9JVW8y9m4skayxHzh+v2Wrhlu6nbGOV7s89cl6cNjCSoUChXvRMMzFCyiEVfGqYxTc3VNxmk0RlVs8jAnupOW7LTsYcynwdsEBFL4LtbhPRSW8d4E/r43SBvovpl/JOfBfFNhc6QFSFDxg1s7MIWgLn6YQn88gfn9xHdVu7WLpC6xTBvMNxUCq/LJ7uvWbj9ic2qAyb0mYz6ig7yO8k21QxIXDLRpyPDX/O2EnYqchI/3gH7NVDAGO/RjMQvEZiV4AcDH8M287A9fhpBo6m2/zZkiXiqYtYHZxszSnE05nxfKNcrz6s2NlIUrdneC5w9NeHlpMgdn5yalVdnPssHkFfwiK2HoVJlLKWD//dVx+vIU3eJH2c/jZ3+sZmvrY2pSgY1jGrPOEyTQk9j7SFoTlpw0Aw2phybUwSQ9EUEYdilcwAw09Lnv7lrDjBbwPBy8EwnPgABEOYKMUxmnZpeScWqiET/nUHGElwgQXNZ9MnoVYfMwJ8GeAep0INgWKQaaz/19bwJ9j1RmUfgL9puqBUj4/j/Rqy79w3seQM8XW5Vrcrqf9ccTgH/QrlTBL6xlBwbw3IUw4IpNSJqwasx3E9en0c7EulZJx2C+qRinWtCIPSsgsEMbY+O5y5M9lCE3k++wPyXlSr6pKVjgLC4YaJOZgusyN4KOFnYUKsFGc5A4t2XvE6NmbaXFGw9Qp/qlVBIsR+A3Zekui4GGlSmWXOCypSSnfZx9M4PgB9G0SFWBYf5hoxDsVvgo/0wCs276scayCTyBwLE9Ngi5+eIqVnQYHkK534381XH49E3qZYHlGZThvbuaW/XVeU3ijWXigYGGGyWoZJgbzsDjypw1+3RR1REGhj3YzzPaGRvMdOKXIbZfhTEkvHVovW9bIpeLcPBOJDxdqhzTIBmnRDJOU7qYjNMULOLpDCugYChB2BfAjXnGvRksuNAMNHzrfzFujfp2+PveIF2g+4gTKQX7TR0/bzv1vayaehxWRPSqCBhe7FyrJa9mefzxBPDs9SOrbtxxeXXFM+CIn5Z063ywAQ32m0hrCuabinKC36lfqbDaG+Krh9soPgSCR3xPQyH5ptrRip2Fm/05Pq/A+Gl9Z2yWYc5wnInMHezALIK+Z7/NK9llm0nmlp7w/fjln2vUzoY6DiSymIFhVobd+kAwtHOjk0a4jot42CkRhLBnvl2gHNSrAP6DZHv+2v307HcL+FyHktJDfnHoIjUR0KEY6EMnbaC3f12mBinCTzoGpr86nj57Qfmq/GvBdmswaP/WqN/GXUe9dv7Tz06L40THroiYQTtfRHDBB0k6rLhBmHAAU+ikjU72/Wym8dWOmHmHinei4ZlabSjjVMapOebQ72ScptboC+051divLwjvTAiTfBEmQPr7Bv/HsE8B+fveBLrv612sMk7+08/EZaTfVLidHc2CNO3uFM/HbouPfzVXSdSdz8C1P54A9/9gX8mv/bzYcr2KMD0hwfcauwTvO+zuChdxU5uC+aa+9zt2GkxShQR/AOZ5w86j9PTg+WxblMREmxvN+Goj+abaWzcTdziDxbPfDPaqban/qajTdw71SgKmZ9jUTV7hZgB0l2EVbOrXmffNc7gyw+T6JPtnNAuOZQmoTxw4esZVwR/PgNs0eHXYylJQGKSBcJ0ze2bFxJnMrvlMeNIASuaSJe7nYktnhOnBW4L9KMIhOVQonEywmR/OwZDk5SWhzSyl1s8FBujcYOLcKFAdoSNclPMtyq7zTjFjj8lIMJjqZ8GBPKS+2HAmloS2gDT5PLcBfIv6IkiaSxdJajPMtLXKDXAHRvoa6QO1Yzh4R4qnr3q5hWPJsk+HSpYExS1OLMNknLqjG06/kXGa9G6VcerepyIJhSQR7+flrK/si2AqkitH0rdJf+d8xcV7E+0ESaTz+xaoH/u6H+hdjLJE+5uKbwpUUrBtNwRkmpL64HnrG6vDcfTFE5hx4LoOutD4XmFfBayCJ/VuM5bv81dYtXMYtxfUY2JJwX5T0WZQF4WEH5vJgcB3ZGWmyvkt9tVGuh7hvBtT85sKfub6jpV1ca2jP37VihTkSVyocGDgJguCAxbb2cg6ASTK+PkiPEPvxGTGARMWiMn0xdA6mWRs+oJfMISBvvewPSZedv5eeIHqCEYcainRUk2xly56V0nt7T5JMJ+Cl7pbmzlxR5pA7RgO3omCp4lZLM9lnCahK+PU3stknNrxSOsrMHiBvmm6jHhvOv3v63uBvje+7gd6FyP/aH9T8W5azxJVJ7l9K3QcXzyBvo8jcHTL14wTD+fBflPd2izpfeYtyPLVRrq+8k1lwZ0GQ46CgCAgCAgCgoAgIAgIAoKAIBAYAWGgA2MkMQQBQUAQEAQEAUFAEBAEBAELAWGgLSjkRBAQBAQBQUAQEAQEAUFAEAiMgDDQgTGSGIKAICAICAKCgCAgCAgCgoCFgDDQFhRyIggIAoKAICAICAKCgCAgCARGQBjowBhJDEFAEBAEBAFBQBAQBAQBQcBCIOZu7CqVyKt2krOeKCdxiwDaCvt5Yuc/odRFAJsYYKvYtCIZp2mFfOjPlXEaOmbRSpHW41Rt0125MBVnf/9C8Y9AQd4EDNuqw2eyUOoioN6TMX5kzDdSiXH5JXtBIN0ggJ0X8+bKlm7qIxURBNIjAmk5TtPy2emxLaVOGQ+BaG6kIiocGa//SI3jFIGcvCOYkCAgCMQ3Amk5TtPy2fHdKlI6QSD1EYj5mvGJU2fp1OlzqV8zeWLICOTMkdQdpL1Chi7iBFl52/IczEDjmBYk4zQtUA/vmTJOw8MtGqnSepye591ZT/BK1Tk+CsU/AvlYhePkqXPSXmnQVHhP5s4Z2xXdmDPQR46dpt37j6cBfPLIUBEoUSSPSiLtFSpykcfPw6obJYvmZSY68rzCyUHGaTiopU0aGadpgzuemtbj9CxvWb3nwHE6zky0UPwjUKVcIWmvNGomvCdjzUCnjbgrjQCVxwoCgoAgIAgIAoKAICAICAKRIiAMdKQISnpBQBAQBAQBQUAQEAQEgQyFgDDQGaq5pbKCgCAgCAgCgoAgIAgIApEiIAx0pAhKekFAEBAEBAFBQBAQBASBDIWAMNAZqrmlsoKAICAICAKCgCAgCAgCkSIgDHSkCEp6QUAQEAQEAUFAEBAEBIEMhYAw0GE095kzp2nKvxNo7eqVYaSWJIKAIJAaCMg4TQ2U3Z8h2LvjIqHuCKxbs1J9U0+fPuUeQUITCgGPx0ML5s2i9etWJ1S5Qy1szP1Ah1qgRIgPxvmhe2+hVm060GdfD0uEIksZBYEMh4CM0+g1+aGDB2j//r1Whjlz5qLiJUpRtmzuGxUI9hZUchIEAh+8+xpNmzKRvvtpLDVo1DSIFBIlEAJgYrds2sCbuCRtZJc5M2/WlSOnGrdZs8aW9du9awfdduNVVKVaTRoxZnKgoibs/diimLCwSMEFAUFAEBAENAI9u3eg/ftSGGiEZ8qUiSpVrkZ33PMIdbniah1VjoKAIBAHCAwf9j299uITXiXJly8/dbqkCz3c/zkqXKSY130JCB4BYaCDx0piCgKCgCCQIRGABBp0/8NPM+NMdPz4cVq3dhVNnfQXPd3/Hrpw4QJ1u7JnhsRGKi0IxCMCesw2bNycWrZuT+fPn6eDB/bRH2NG0Ojfh9HsmdNoxNgplDdvvngsfkKUSRjohGgmKaQgIAgIAmmPwO13Pagkz7okP/3wNb316rP01efvCwOtQZGjIBBHCDRq0oLuvr+/VaK+dzxAd9xyLe3YvoV+/uEb6nf3Q9Y9OQkNgQzBQGPpcc3qFXT61CmqVacelShZ2hUlGL5sWLeGtm/bQmXLV+TlyaqUPXsO17iBAvfs3sXPXE5ZsmSlqqwHVKx4Ca8kkNqsZeOJUqXLUv78BWjjhrW0euUyqlq9lkrjlUACBIF0jICM08Rr3M5deygGevOm9XTu3DkKpFuJ9+KhQweoGr/joAJiEiRmu1h3skqV6pQte3bzljo/fuwYrV61jI4dPULVa9ahkqXKeMWRgNRBILXHarDf5r17dtORI4eoStUahDQzp09WgDRv1Y5y5cqdOuDE+VPKlC1PF1/Wlb4f/DmtWrnUtbShjrWdO7Yx77Kc+aYKCnvXTNNhYLpmoI8cPkRvvvoMjRvzm63pOne9il58baA1oPDi/+KTATT4y4/VR0BHhsL9w48/T33+d5vXy17HcR7BqD/92D1e1qeYBb761keEzqtp5fIl9L9el9Ott99HRYoVp3fffEHdwpLK9HlrdTQ5CgLpGgEZp4nbvCdPnFCFz8PvrEDMMyI+8cidtGjBHPp11CSqVqOWreLvDXiFRo34id798Gv+wHez7p09c4be53tDh3xpheGkfsMm9NbAL5QAwnZDLmKGQGqP1VC/zS8//5gyRhzz1yx66J6bacP6NQqL/k+/TDfecmfMcEm0jPPlK6CK7JxUhDrWMOnt/1A/mjfnPwuC6jVqE/DOCJSuGegH7r6RFi+cR81atKHuV/WmzFmy0LTJE2nCuJHUlY1eOlzUWbXx49wBJv0zXs2crr3uJn4hl6OVK5bQD99+oaQreGncdd9jAfvD0sXz2fL0ambCzyqmu2nz1nT06GH668/RNHPGFLrh2s40ZsJMyl+goC2v/6ZPUhLy5i3bEhhtSMCFBIGMgoCM08RsaaygQXUD1OOaPlGrBLwHmPQYv5+haw2mulefWyh37jz079/j6LtvPlWW/qPGzwh7pdB8jpwHRiC1x2q43+b+D95Oe3bvVMKpEyeOU9myFQJXLoPEOMH2C2NH/aJq26ZdJ1utQxlrGKd39e3Fq0LLleeU7lddR7t2bmP96l/o/jv/Z8s3vV6kWwYaTDKYZ7jEgas5LR254sprqWfvG5X1OBp1zqxpinmGNfmQn/+gPHnzqrbueHFnat/xUrqxdxf69utP6NrrbqYiRf1brA58+2U6e/YM/d8r79I1vVI6UI9rrqdH7+9Lk9l39NeDPqRHHv8/W3+C1BpW7K+/82nQkm5bBnIhCCQoAjJOE6vhXnzuUVXg06dOspBhKW3euF4xzw89+mxMKgJDJzDPrdt2UpJp/RBInzdtXKfeqSNZat37+lv1LTnGCIHUHquRfJs3b95I3w4dRTVr14sRGomT7RpmcH/7dSid55X2Hdu30h+jh9OePbvoih69CKvxmkIda9Mm/62Y56rVa9IXg38luLYEXX9jP9ax7pkk/XdMhvWz0ssx3W6kAoky6Iab+lnMs240SHq1TvKIX4aq4Jv63m0xzzpenXoNqQXrTmGZctZ/U3Ww63HThnW0cP5spZfnlMbA/+Kt/e5X6SA5cRJ0+Z5/aYAwz05g5DrdIyDjNLGaePRvPxN+4/8YqZhnlH7qpL/pt+FJ79Fo12bsqF9Vln1uvM0r6zbtLlJhixfM9bonAdFHILXHaiTf5gcfeVqY5+QuMGPavwTVltdeepIGf/UxHWBPHG8M+EyplJp2CKGOtb8njFVPwORVM88IgKDx3Y++Tn56+j6kWwn0Fp6BguDI2x/B+AUEZtmNatVpoJjn7ds2u922wnQ+tXjGm4VVRZwE40UQlO3hTsaMA2PF3HnyOJPIdTICw34czLtU/WXDI2euXEoi9ctP3/q8B9Wb5556UM28zcRYHbik8xVmkJynEQIyTtMI+DAfu2DFDjXRxztsL0uxIBD48L036I2Xn2Z3WPmj7olja/J7fMzIX9ROdWaxDx7Yry5F5c1EJXbnaTVWw/k216nXKHZAJFjOXbtfo1bQodLy+/Aflfu6rwd9oFbY9Yo7qhTqWAMvA6pVp746mn+WbrXDUNiMkx7O0y0DvXPHdtU+BQsW9ttOu3ftTIpXyD1e/gJJyvaHDx30nw93TlBBH/nAIBE/bFUKnSw4MxcKDoFd3JbY6tUkGC2B/N07ffq0SoelK5MOBWhLM66cxxYBGaexxTdWuUMAgJWzG26+Qz3i7defpyGskxxtX9C7k9+rUHNz2/UQy8dt2l8cq2pKvgYCqT5Wo/RtNqqQIU9LlCxDjZu2VHWHysbdt/VWTPSgzwba1ElDHWt79+5WeeZPNkjMiOCmWwa6cJGiymk4liuKsocLX1SUlxvgXBzSjBK8Na2T9u/do4JM7xnOOLguUjTpGVoq4oxz7NhRxTznY3d1wjw70fF//RDvmISfG/m7V7xESfrz33luySQsThCQcRonDRFBMeAiDLSR1dgCEdTZQLAVCYYwhiHpev3tT3yuEgaTj8SJHIHUHqvR+jZHXvP0kwNUNh576iXq3eMi+vXn79QuonojlVDHWoFkZwiHeaU3o1LS2ywd1l4zvMuXLvRbu3LlK6r7C+fNco23gPWaQZXZr6Q/0vksYU8cZ8+e9Yq6IDl/+DgVEgQEgSQEZJwmfk84sH+vqkTBgoUCVqZQ4SIqzr59SYIJnQAW/XvYB7STyparqILgL18obRFIq7Ea6bc5bVGLv6fDzRwk0kneOJJsDFDKUMdayVJlVeXA8zhJr+w7w9PbdbploC9N1nEd8s3nBF1YTXC9NOSbzyy/hd3YEhX0w3eD2O3NLh1NHceyteqKZYsJHQ6Gh/4IGwPUYOf+B/bvo++//dwW9ciRw/TZR++oMBgrCgkCgkASAjJOE7snwA/shwPfUJXodEmXgJUpX6GyijOOtxPWBOYZBk5w9Qky3dhBfxP03def2t7jKpD/sFkGfNcKxR6B1B6r0fo2xx6ZxHuC9hL2689DrMKHOtZ0f4AkGyvsmuB7G+4HFaVzLxzpVoWja/eeyk/oujWrqM81l9FFl3YhLB9On/KPcq8y4IOvVPtefGlX9hPdlubOnk438qYm+AiUKFVaMc4T2co0V+7c9ORzr6m0uoO4HbE08uiTL9J9d1xPH777Gs2fM1P5dD58+KAytIGhS/tOl9k2CHDLR8IEgYyEgIzTxGptbISi6dDBg7R82UIlyYKx9r0PPqFv+TzCheh37BYUXjxOsHejaqzDPGnieNq6ZZP1HjYTw9MG3ptwZdf7qosJ/aU8rxoeZ1+2K5YvVoaFL7w6kC69vLuZTM5jgEBqj9VofZtjAEXCZwkj+jdfeYbWr131/+xdB5gURRMtLhEOOHLOOUcBRUBQUXKOAooBEBEwIAICIoj6qwgooEiSLCCSc84gOeecczw48t+v93puNt7u3YbZvSq+Y2Z6erp7Xm/P1FRXvaadYmGj0mXKk6tjDboSVnw8fuwwvd28tlzd8O6dOzRbsPRgXD8QVJeBLgGrQCPIZdzkuTSwX3dasXShXBQFnQk/ri6ffyUU6lpa344YPVVaiPElBcYHCJbwxgIsvfv9SDlz59XyYickNFQeh4SGmaWD8m7itIU04OsvhDVlNYE+BpJB+FbDVxcrDurFXjn6PLzPCAQyAjxO/aN38wjXM7hRLFs8T2swYjly5c4nGW1AF6qnsrL3bMuWPSf9NnIS9e3ZVSrFUIyhfI+dNIsOHdgnDRmhFs/VX34bS3+NHi5n9sYKHn0l4eHJZQAhFp9i8TwCHh2rISZVRK3XoO7G5XeznXJUeQlpq4Juw8LM9RRggLFar1FzmjJhtDTwQYGGuDLW0FdjJs6inl98RFs3r6dRvw+R8V31GzYXftb9qEHNSpquJAsPwP8Siemy5/G9r0qZTYuGrL842aqoS9fu0eXrkVbp3kzAcqCgmQsJCaUcOXM75Fu+euWyXD0wZ668ZlRzlu2F/1BY4sRWHNMqH6YWQfuTTgQX2mPmQN7YylHleWObMW24rMbX/eWNezVaHeFJQylTuuSUPJn1w84bbeVxyuPU3b+z2J5tWNQByrLi5Ef9kffuWfHx69uFoPDLFy+I1Vwj5IqxKihRn8eT+74ep/fuPyKM1cgH1nE2nrxvy7Ld/U5FeY8Ea5IjOldn3s3OlGN5L548zps9tU/7C64V+NDU8z3r7xfnsbKnrXHkyliLEtZmBPtCb1JlQQdKJP6F2lDg9W3w1D70GbxTLcWRvmqZN7bjBKFAxwYCnzchwAq0734Jvn4xG0GB9h36/lUzj1Pf9Zevx6lRFGjf9YB/1exrBdq/0HJva72hQAdsEKF7u4JLYwQYAUaAEWAEGAFGgBFgBEwIsALNvwRGgBFgBBgBRoARYAQYAUbABQRYgXYBLM7KCDACjAAjwAgwAowAI8AIsALNvwFGgBFgBBgBRoARYAQYAUbABQRYgXYBLM7KCDACjAAjwAgwAowAI8AIsALNvwFGgBFgBBgBRoARYAQYAUbABQRYgXYBLM7KCDACjAAjwAgwAowAI8AIeHwlwiSJQyh1yiSMtB8ggL6CcH95v7MShwVTcFAi71ccXSOPU59B73LFPE5dhsxtF/h6nOIZkSI8jMJCg912T1yQ5xAICQ7i/vIcvA5LVs9Jh5niedLjCjSI5/HQYTE+AhjsEO4v7/dVUKJEYuVL300I8Tj1fp/HtUYep3FFLv7X+XqchgrFOVWKJPQs/gsIxx8MLiFWBEJDg7i/YkXJMxnUc9IzpZtK9bgC/fDRU7of5dtlRz0JYCCVnSxJqFjyUyyn6+NlYgMJU2fvJTQkiMKTimW8ffStyePU2Z7yfT4ep77rA1+P02fPnsv36eMnz3wHAtfsNAL42IH+w/3lNGRuy4jnZGiIZ1+ovjN5uQ0mLogRYAQYAUaAEWAEGAFGgBHwHgKsQHsPa66JEWAEGAFGgBFgBBgBRiAAEGAFOgA6kW+BEWAEGAFGgBFgBBgBRsB7CLAC7T2suSZGgBFgBBgBRoARYAQYgQBAgBXoAOhEvgVGgBFgBBgBRoARYAQYAe8hwAq097DmmhgBRoARYAQYAUaAEWAEAgABVqADoBP5FhgBRoARYAQYAUaAEWAEvIcAK9Dew5prYgQYAUaAEYhG4ML587R+3Rq6f/8+Y8IIMAKMgN8h4PGFVPwOEW4wI8AIMAIJEIHLly7RwYP76dq1q5QlS1YqU7YcJUmSxGNI/Pi/b2nq5Ik0ZtwkqlOvgcfq4YIZgUBB4MmTJ3Rg/z46efI4BQcFU/GSpShnzlyBcnt+dx+sQMezy54+fSqWYPbsajfxbCJfzggkeAR4nNr/CURGRlLvXl/Q31Mm0bNnMSvcpUwZQb2/7k/vtH3f/sV8hhFwIwI8Tu2DuXLFMurVoxudPHHcLNOLL71Mo8dNpPTpM5ilG+UgkPuUXTji8St7q3kjypoxFR0/djQepfCljAAj4EkEeJw6RveLz7rQlEkTqGDBwvS/n4fQqLETqFv3nhQRESHSxzu+mM8yAm5CYMf2bZQlQwR1+vADN5UYOMUcOLCP3n27JZ09c5o+aN+R/hwzngYNGSZnbv7bsol279ppyJsN9GcvW6Dj8bN78OABPX/+nKIeRsWjFL6UEWAEPIkAj1P76N68eYNm/jONUqRISbPnL6ZUqVKbMtcn+uSz7rR/3177F/MZRsCNCERFPZCl3b8f6cZSA6OoSRP+oqioKPr8ix7UvUdv7aZat2lLR48cpnTp02tpRtoJ9GevoRXoK1cuS38f/HBKlChFWbJmtfptRN67Rzt3bpd+exkzZqL8BQpSunTWPyb49926dZMKFipMDx8+pNWrVsiyKlepSsmSJbMq11HC3Tt36OrVK/TggSn45dzZs5Q0SVJKlCgR5cyVm27fvkVIy5svv82y7929S6dOnaTcefJSeHg4YYrj0MEDlCNHTkqRMqVs3+ZNG+S2TNkXbN6Pah8UeEzpHDp0kDJnzkKFixT1qN+iqpe3jIBCgMfpQ+Ev7J/j9LB4bkCyZcseozxHd2xoaCiVKl0m+sh84+pzB8/wvXt3E56dL5QrT3APcSRxea6jPDyXYcnE/eBZHxJi6FecIwg8cs6oY/X06VN04cJ5ec9wKTpx/Jjcj0iVitKmTSfebwfEey0p5RLvV1uC/EFBQZQrdx55Gu/7u3fvUL78BeQx3pH4GMT7uUjRYg7dLvF+3rdvD90Rv9WixYpT1qzZbFXp1TQ1TosWLW5VL3QevcRHn0A50I+OHD5EZ0SfAE9gmDhxYn0Vct+RTvX0yROHOhL6SgmCidG/90W/o2/y5M2nThl+a8inCxTdXl92k5YRPYINGjahwb+OkEop8nzV8wua/e8/BMd6JXjod/nkc7OvNJz77JNOtHzZEtqybQ+1adVM/kCQ3v/bH6hDx4+x67R8N/AbGjt6pJb/bVGektnzFovI8rX084/fSd/BHwcNVae07ZfdP6V/pv9Nw/8YTU2atqC9e3bTm69XkW0uVLgIdf+8q/wgUBc0bd6Shvz6u9XLYPu2rdSx/buEh4+SsLAw+mbA9/TeBx1UEm8ZAY8gwOPU/8dpVqFoQg4fPigtWZYvY1s/HFefOzOmT6XPP/lYvphRHl6evXr3k7N3luXH9bl++PhZ+T7Ac1UJDBgTJ0+XhgyVllC3Rh6rN25cp/Jlimlds2b1SnqpfCl5/HKlKjRl2r/0xquV6fHjx7Rj9yHKnCWLlhc7p06ekPmh7OH9DsH7fsXypXTo2BnqJlyU5s2ZJdPxX5o0aWnClOlUrlwFLQ07jx49ogHf9KE//xhulv7CC+VppHCZwEeZryRrNpMSv2D+XKpdV0wPOZC46hPQo6C3/Db0FzOdCoHEfft9K3UKGAmVONKpYCB0pCO9VLGSNBxC15k8abzZswA6EXQjfxBDKtCtWjShbVu3EAZP8xatKCg4iJYvXUKzZ/1DjZo0ozdr1KJFC+bLQYHzr75WXU5hwIr7w3cDaNBPP8gI8terv2nVB++1bUUXL1ygTp0/IXzp4ovUVWnarKX8Kp3w1xipvLb/sBPB+o0XA76g4MyPH+Kc2f/St9//RFBqlcASs2jhfPlF98abNVWy3M4V+X/84Vt6pdqr1Kz5W9KKPfrP32nGtKnSYvPdDz9r+WFlqVvrdTn1CiW9dOmy0j8Kyn3PLz+nYGF54eAfDS7e8QACPE79f5xmz56Dyld4ieBH2ahBLfrfT0OoVu26dn8trj538ML/uGM7+Qz8uMunlDdvflqyeAF927+vTatWXJ/rDevVJFiyYAwpVKiIfCnjHdKxw3u0dMU6u/eTUE4YeazCbWjAwP/JD7gJ48dKX/xmLd6SXQODEhS4WrXr0ax/Z9CsWTPoo05dzbptljCiQerVb2iWjlmSBnVqSMv2lz37EH7rCxfMFX/zqGnDOrRhy04z6/L7QjdYumSRVFDx7gwPTy7zjxg2lOrXfoM2/rfL5m/WrFIPHTRu0pymTZ0sjYrBIcH09TcDHc5Moxmu6BPI/8G7raVugliIt9u+R9kEXnv37KI/fh8mgxdv3rwpYyOQVy+2dKpy5V90qCPh+pF/DKNJE/+SeHfpKnQWQcawbt1qWr92jb54Q+8nEj+y5/FtYaXMrWQR6y9Otirq3v1HdD/qsVW6vQQoyR0+aCum+SrQnPlLzKyu4AzNn78gZcyUieC79+jhI7mvL2u8UGrxVfP2O+/RT7/8qp1q1aKxtEDDXWPugmVUvERJ7Vxcd/DQ3rhhHa1cu4ksp1ZqvVmNYKkZP2ka1ahZW6tiwbw5hB9cXTHYR4+dKNN37dwhLdA46PppN2mdURfs3LGdalR/RVrdd+8/qk191hMDesvmjbRg8Uo5Jary79u7h16rWlHigq91V6YwkyUJFW4oRJEPnO8vVS9v44dAaEgQhScNo7BQ3zC68DhNuOP07Nkz1LJZQ6nA4FdcslRp+vTzL6lmrTpWP2pXnzvVX61Ee3bvomG/jyIYHpTAMIAZRAieg3geQuL6XE+fIQP9O3shFShYSJYD38uyJQvT9evXaPX6LVS4cFGZHt//fD1OHz1+Kp7Pj+jxkxi2lNjuyV/eqXiX4p2KD7hxE6aa3daqlcupRdMGVKx4CVqxeqPZuaqVKkj6xbUbtkq3HZxU73vQMc6au0hz7YC60+atprRs6WLxG+9OPXr1lWWtXbOKmjaqS9VefZ3+njHbrPx3WjenxYsWiI/LwdT2vXZm52I7SJUiicv9Za/MX4cMooEDvpanoce0fvtd6tzlM8qQMaPZJXHRJ9atXU1NxEcFZqAWL11NyVOk0MpEedBBkoo6YeHPkMFUn8LYkU7lSEdq1rgeYbZh++6DHrHuQ59JnizGeKluyJG+qvI4u41xRHH2Cg/nW7xwgayhXYeOVspfpcqvaApz6tRptH19k4oXNynG586d1Sdr+5g6dIfyrBVoZ6d5y9byzMwZ08xyzBIfCBD9y0RlgB8l2qeX0mXKyvZisYFNGzfIU2dEJC6UZ7zo4E+oF/hs4WUC/6Rz4sXIwgh4AgEep/3MYPXncQrL3JJla6RCkSw8XEb0t23TgurXeVPO1qkbdfW5g/xQnvGChwVNL2ASqN+gsT5J7sf1uf7rsJGa8oyCkiZNSnhfQM6eSdjPwUAYq69UfZUyZc5MMBDBP1cJfIPBXY53OnzeLQVMFcovGufggtBGGNcgcOlUAjcjyPvtPlRJ2raamOGGbP1vi5bmix24psKoCOMi9AG4mpQvW4xgNLQlzuoTuBZBipAPP+pspjwjDXEQVV6pJn2U8aFhKXHVqTDWIXPn/GtZpN8cG86F48SJYxI8TN04I3fu3BZW4PV06dJFunH9Ol2+fEleBn8pW1JKKKTekAYNG1OfXt3FlNBCGTiD4EC4jCwXX7744cDtxFKQx5bALQR+TRcvnJenFQ/kLUypfNrZ6pLQkFCZBt9o/cPDKqOfJIwb86eY9l1o1lp8DY/9azL9NXaU3XPw++v8UXszfy4UgshlXrjBDE6XD3icWkPmz+M0PHlyaY3DCxQvZkxbI5C5Yf2atHLNJjkD5upzR33AFytWQrq3WSKWLNwUvA2lxlJcfa7benYqZoKbN25YFp+gjgNhrMI9Er6xw34dLN0Yen5lssTOmT1T9iXO2RJbvwuMUwhcOZWcPHFC7k77ezItEdZmvWAWA4L3qa8FnM8LFq+gDevXSms0Zrkx4w582giLtF5s3TvOWz6nkHb8+FFspCuo3LH4r4RYsAXW4tOnTlmcEQp2HHUquFstmD+Hvun7Fa1YtlR+vMA915/W1TCcAn3+3DnZQWlSp7XqKH0CpmL69elFf40bJeldECWaMiKCnj55KrO5wTNFX53L+xERqYTrRh3hBz1T+lw1bwn/qoWCueMBwTqNYEdnRUWsQwGHqIEPn6RtW/+zKgZ142sd7i6BIJhNgJVBL6Ddgjg69zDqIR08sJ+ePH2iv5RuCPcflvghwOPUGr9AGKfwRwVNFlwq4D8KpXm6UCowde3qc0cZM/A8clbc+Vx3xX3N2fb5Y75AGauId4IC/e8/0+XHHj68Zs+aKZXHRo1jAvlj66OU0YaqyMh7WlZlnMIqf2Gh1tP+cAF67fU3tPy+3kF8GNw3weE+ccI4+mFgfysF2l4bLZ9TyKfGNgIsbYmit4RRyl0CC/ki4S7Sv19vgmUbLrow+P02fKSMy3BXPZ4sx3AKNCjosJTs1WtXrHx79ED88vP/hHP7b3Ka7ocff5G+Ozi/f/9eerXKS3KqRp/fF/tQmqFA/zPjb6E0t5KMIWiHLfcNR+27fs30Bayij6EcQ8pXeJEm/236And0vb+f6/P1AMKfLXF0DjjBv4rF/QjwOLXGNJDGKRSGxk2b05hRf8hpc9ytq8+d1KlMU7Twa3ZW/OG57uy9GCVfoIxV+LfDVQpxQVv/2yxmRcLlImZVq73mUFew7IeYcZpVO5VJUMDCGDPijzF2qRu1zAa1K6iqAABAAElEQVTZwQdEz95fSwUaOhPcNhEfFpvE3H8Mmwn8mlEGrO1Kz9CXA/pDCKh23SlwvZnx7zwZfzFk8E+Sneyt5o1p45adLvWpO9vkSlmG84HOkdPUQbt27HB4H4sWzpPnfxQrZzlDveSwsDieVFOP8EeyJWpg48sKZOdYihNfWJZ+y+raa1evWrkbwCKDqVRIzpy55Va5ZcD/S7/0rjzJ/zECXkCAx6n5rEYgjlPlCqaClFx97ijqLaySBm5aS1G8v/p0IzzX9e0JhH1/GavqfRrpYCGVFtGxRf+I2CIER0KaNLPtvoFzly9exMZMNm5cL49z5sylpefKbXq3YsbSn0TNZGObKnX0IkjRN+CsPoHs6v6VrmGJgUpXQbqW5+0dqz61pyOp66DDDf99tJz5An/3xo3r1ClDbw2nQNetZ4rG/n3Er3LhE4UeFMURw4dK1gukPX5k8nE+KTggleAh/deYUerQ41u1YIu91brgywPfLLS9U8cPJM9kE2HVsSco58P275op0aB5wYsGPzBMeUBy5cpNZV8oR4iex/SNLcGCBSyMgKcQ4HEaGOMUz9nJE8ebPXPwm4E1DjNnEPhdQlx97uCZBUosWKDB9apEumn07UVrVq2USThWYoTnumpLoGz9Zayq9+mBffvsQt+gURNJiQheZ6wBAQYIUNzZky6dP5QB9+o8fOv/GPGbPMSssBIV5Dp82BAzvUOdx+Ii4In2hcAq3LlTe+lOZVk/mDkgZcqWs6LYc1afwPVNohlyEP9wyeKjAwGW+AiG7zQWnnNFVJ/a0pEQ12UpCP6FpIow/xiwzGeUY8O5cGDaEAEs8HmtXq2SHByJghJJUnRE344ZN0li90aNmnL1ml6C8xhfjclFEMy/M2dIFw74vukfyp4Cu1x5QbUnXDTgw3Ps6BGxctFtyUOqp7TDIMX9qLXq7QU7oI3wM5o/dzZVFD/WWnXqSb+keXNnSXeUL4VfovqaQ97+3/6PGtR9UwYQwH8IpPDwCz579jSB8ifqQRSt2WDtH41rWRiB+CLA4zQwxumxI0ckF+v3A7+RL0dM32IqGHy5sBq1av2OjMBXvxdXnztdP+tGH3V4n3p2/4w2CxYhWLDAAw12DkT2W0b1G+G5ru41ULb+MlaxJgMYpK5euUK1a7wmfh9VpdKqd9/DO/LNmrXlGhBYgAXvU6zma08ShyWmxg1qy6B9fNBhDYbjx47KFQbr1W+kXYagfqzLAB5ouIACs9y589K9e3dp9+6dIrBwIQ0eOlyjW9Qu9MIO6Hqn/z1F/uFjFqsNw+IMqzDGEZhzBg02fRTom+OKPlFb6BtgrcFs+ZvVqwgKy7qSx3nXrh1SJ0EdWIcCwYquiD0dKV++AvR6tZep4suVJc1v2nTp5AqiWPMCMwO4zh/EcAo0rLZzFy4ViuEnMkITfs4QLE7Su29/qVji+IsvvyL48kydMlGS8kO5BHn38pXrqV6dN6yC9LSpjmiGCpQRXwEPI35w4IgcNXKE/DL+6GNzkneQ+oN2BqT+sBrnzpPXbrUlS5emdu0/Eisndabfh/8q84HH8nvh463nksYJuIEsW7Wevuz2qVhUZp78kauCUSei6VkYAU8hwOM0MMZprz79KDQsTFrz/p05Xfu5wN8Zq4/hGacXV587sOzBqjzw26+1lWVBtfnvnIViBbmTUoFG/Urc+VzXnvlhzgdsq3YE0tZfxioWHPtlyHC58A7el/izZXACi5JaWdCR+wb6cMTIMXIhMvy2weSEOhAgO2ToCCu2B3BPI0gRFmpl2UUZ4ER+7bU3qMKLFXHodcFHraltv0hrunKngDILzmwwkuDjwFJc0SdwLfivsZDb+HFjCMxXEJAzIGDxJ7FYG1b21Is2vhzoVPZ0JJSLNS/Gjv5T8ypA2aArhKIOViB/EMMtpKIHDUtL4msRHQXFU2+BVfki792jM8Lqmi1rdlK0LVjtDw8N1cHIi7IeinRPdAymKEGjlyN7Tpvlf9KlI02dPJEQ7Pju++1V07WtIj7HCoTT/5kr/QWPHDlEYCJxJigAlH2Iln/67Kn8alRRtloFTu7wQipOAuWBbL5eoMHVhVT0EPA49f9xCjczuITduX2bsmTNSmnTptN3sc19V5874IWGtVBf9r27d614Z1GZO57rmIVE+eq9YPMmXEz09TiNy0Iq+lv0h7GKNp45fUqsQBxMcBuyFPxOy5UuKlcf3r3vqJUijPxqkY/5gvINs7NXr16Rf7B86lcGtixbHSOgDitbRqRKJVcwdNXyqspx50IqKBOz3OfOnSVY1nMIS61ex1F1xlefQDmYhbp9+5ZUmqFL2RJXdCp7OhLcbqG7wEUme44c2kJxtupzNc0bC6kYzgKtBwmuGLbI0fV5oBBbrjKFpT8tBWWFeOirBrzOihTcsl74Is8RVDuov37DxpanbR7jB2t5TzYzRidiELnq3O+oPD7HCLiCAI9T59Ay8jiFgqAPqnLmjly9H1sR/PoVz/R1uuO5DoOLO5Vnffv8dd8fxiramCdvPrsQTxZxQfg4aty4uU3l2daFmMHGn7MC313lv+vsNd7IB+NYkSIRLlXlqj6BwmG4i814h35yVqeypyOhbfnyF3DpfoyU2dAKtLeA2iSicsHP7IykENM5cBVxVmaKqSP4EsIFwx7HorNlcT5GICEjwOM0Ifc+37u/IIAgtAMH7AcCWt4HqMycVW5hsYTbJqRp85il4S3L5GNGwBsIJHgFGopzg7o1nMYaUaKnzl11Ov/UyRNk3mbN33L6Gs7ICDAC5gjwODXHg48YAaMi8OfI4TT8tyFONw++9p06f+JUfgTIQ0HHDG2x4iWcuoYzMQKeQsDQPtCeumnLcmHZwqp1zkh4iuTSp8qZvMijqFrwlW1P4Eu4fdt/YqGCLDZ9vuxd5+509oF2N6LOl+dr38r4+EA7f5fxy8nj1IQfj9P4/Y7ic7Wvx2l8faDjc+/OXotV7bBGgbNSrEQJp90l4JeL1QLhsqj3pbes67Twob5w/pwM4LflJ2yZ31PH7vaBdqadRtEnnGmrJ/N4wweaFWhP9qCflc0vZt91mK9fzP6gQPuud4xVM49T3/WHr8epPyjQvusd49XsCwXaeCj4pkXeUKBdI/XzDQ5cKyPACDACjAAjwAgwAowAI2AYBFiBNkxXcEMYAUaAEWAEGAFGgBFgBPwBAVag/aGXuI2MACPACDACjAAjwAgwAoZBwOMsHCHBQZQkzOPVGAZQf24I+kpQp3J/+aATg8Vy9cDeV8Lj1FfIu14vj1PXMXPXFb4ep3hGhIUEU7CLSyq76/65HNcQCBIdFhbK/eUaau7Jjeekp8Xjmu0zQXj+5OkzT98Hl+8GBBAgI7qL+8sNWLpeRBA9eybA95HwOPUR8HGolsdpHEBz2yU+HqfiGfFU/PE71W0d6tGCnpPor6fcXx4F2U7hIUKf8bR4XIG+c+8hXb4e6en74PLdgEDGtOGyFO4vN4DpYhHhSUMpU7rkYolWFy90U3Yep24C0gvF8Dj1Ash2qvD1OH385BlduRFJkQ8e22khJxsJgbzZU3N/+ahD8JwEE4cnxfMquidbz2UzAowAI8AIMAKMACPACDACXkaAFWgvA87VMQKMACPACDACjAAjwAj4NwKsQPt3/3HrGQFGgBFgBBgBRoARYAS8jAAr0F4GnKtjBBgBRoARYAQYAUaAEfBvBFiB9u/+49YzAowAI8AIMAKMACPACHgZAVagvQw4V8cIMAKMACPACDACjAAj4N8IsALt3/3HrWcEGAFGgBFgBBgBRoAR8DICrEB7GfC4VPdcrG6yY9tmOn7scFwu52sYAUbAgwhcvnSB/tu8nh48uO/BWrhoRoARiA8C/B6ND3p8rS0EPL6Qiq1KOc01BPCCfq91A8qbvxDNnLfatYs5NyPACHgUgRG//URzZk6ln4eOptffrOPRuoxW+MOHUbRn13bKlDkrZc+RK9bm4Vm2b+8uSpcuAxUqUowSJ07i8BpX8zssjE8maAQS+nvUmbF6/dpVunXrhs3fSapUaShtuvQ2zz1+9IgOHthLV69epiJFS1DmLNls5gu0RFagA61H+X4YAUaAEfACArC6D+jbjc6eOUVVqr1Bv/4+wW6tB/btpm5d29GF82e0PMHBwdS6bQf69Iu+WpracTW/uo63jAAjYI2AM2P18ePHVPPVF+jRo4fWBYiU4iXL0MRpC83OPXv2jL7r30MYEP6mx48faeeyZstBw/6cTLnz5NfSAnGHFehA7FW+J0aAEWAEPITAnTu3afCP39Csf6YQlGAIpsftyb69O+nDd5tRlLBWN23xDpV/sRJdu3aFxo0aRuPHjKCnT59Stx7faJe7ml+7kHcYAUbADAFXxuqTJ4+l8pwxUxaqXPV1s3JwULRYSau0r7p3okXzZ4nZpOJUu14TyiIszyuXL6IFc/+h91o1oAnTFjg1M2VVsJ8ksALtJx3FzWQEGAFGwAgItGlei84Jq3Prd9pTgUJFqW/PrpQoUSK7TRs+5Ae6d+8u9ejzHbVo9Z6W76WKr1CT+tVo2uRx1P6jzyhlygh5ztX8WoG8wwgwAmYIuDpWcXE+4Srau9+PZuXYOti9c5tUnrNlz0mjxs+kFClSymyvvVGbgoKCaN7s6TRz2kT65Is+ti4PiLSADSKEv9OGdStp+ZL5dPrUCavOunrlMp06cUxLP3P6pMx7SPjxwCLiSCLv3ZNBfWtXLaVLF887yirPuZr/4oVztHrFEjp29JBDy06sFXMGRsCACMBfbr/wg126eK4IvltnFXyH8Xf40H6pdKH5mFLcvHEtYbzduHHN4R3BEorxDisILJnw+3MkruZHeXhx4Nly9+4dR0UH7LlyFV6mabNXULee/Sl59EvT3s1euXxJ9l269BnMlGfkz5UnH1Wq/Kqc+l25dIEswtX89urldPcgwO9R9+Doq1JcGauutnHenOnykrYffKwpz6qMVuLjGrJ44eyA1mECzgKNl+/Aft3l9KJ+WrF23cY08Kfhqn+pf5/Paf3aFbRm80Ea8PUXtGzxPO0cnOWHCn++kqVf0NKwgxf/kJ8H0OQJo8zSS5QqS//7ZaSV47yr+W/dvCH8BD+gbf9t1MovULCIfFFpCbzDCPgxAju3b6Gvunc284WF5WLkuBlUJHqKEB+xrZrWoI+6dJeBs99+3Z1u6hTnOvWbUr+BgykkxPzxtXf3durxeUc6fy7GzzY0NIw+79HPSnkDhK7mny+mJfv3/lzzEYSV5eNPe8J/wY97xPWmO2OdUqVuFB8aeA7jRW5LSpYpR6tXLqFd4qOkQZO3yNX8tsrktPgjwO/R+GNohBJcGauutnfd6uXyEltju6CYmUqSNJk0MF65fJHgFhKIYv4GCoA7nDz+T/p3xmTCNMJ77TpLHz040OPPUvBgf69NA7p86aJ4WX9JWbIK/51lC6X1qsO7TWn2ovUyulxd97lQbmEFQ9nw5UuWLFzmHz92hGTJmLN4A4WFJVbZyZX8aAvqhOUNinvdBs3Fj+8czZ01nT5u30ork3cYAX9FADRvn3d5n6KiHtD3P/8upv+LCEX6LM0WDBaXxUNWKdDq/pYsmkvHf/2RXnr5FapTvxlhZmbKxFE0f84Mafns0Xugykp79+ygtm/Vo/DkKegrMf1YrHgpWfZvg7+nHwb0Es+BEDFm345z/hXiudC7+8cEhfxdYXHJmSuPVPx+HTTQbMxrFfCORODq1Stymz1HbpuIZM+eS6bfunldbl3Nb7NQTow3AvwejTeEflvA/fuR8nkKw0DGTFkpfYaMVi5a0FeuizgGiC32Hbh0IZDwuJhFvykMg6xA+8nPYeP6VbKlCEpRVCpwcH/7vY427+DunTs05Z8l2o8AjvBdOr5N61Yvo5nTJ1Knrj3kdVs2rZPKc8VK1WjQr2O0smB9PnXymHyZQhFo1rJtnPKjPijP+QoUkta4JEmSynJatv6A2r3TmE4cP5LgLF0ayLwTEAgcPrifbly/RvUbtaCadRrKe8qbryBVfuV1m/eHh+/7HbpQ5097aedffLkKtW5aUyrdnbp+qU0d/vK/b6Tr1bCRkwljElJY0CllFf55LRq+Tn+OGEQNhYVTWa1dzT/6jyGyzK8H/kJ1xDMCAovp1Imj6X8De8tjvFRYzBG4fv2qTEguPmxsCT54ILdu3ZRbV/PLi/g/tyPA71G3Q2r4AlUcA2YJ2zSrpbUXluQmzdtQuw8/oYhUqWX6ndu36MmTJ5Q0WTLp76xl1u0kT55cHt2OHtu6UwGzG3A+0BHC/QKid8lw1Ft9B/ysKc/Ihx9Rk2at5SXr1qzQLoXVC9KidUwQjDr5svDjg+zesVUlSSsZDpzNv0z4akOggCvlGcfgXRz0W4zCjjQWRsAfEUgV/fCFi9KNaMXK0X0UK1HGTHlG3mLFS8uI7yhhzd6xdZO8HC4beOjDgq2UZ1UuphIxhhDzAAs2JC75D+7fQ/DjrVWnkSpablu2+YDeqFnfLI0PYhC4Kxg7IKFhYTGJur3EiU0zdg+E1Qvian5dUbzrRgT4PepGMP2kKOgdX/QcIFzevqG+AwbR51/2o8ZCF0J88KS/RlKH95pJN1bcjor/0M+4W95mWJiJ4x0W7UCVgHPhaN22Pa1YtoB+ETRLUIBbtnmfXhEcpYpuybIjkyc3RY7q0/MLv2MIXDuUnBVBhhBElq4RPnt6uXnDNP2o9710Nb96ucNqZilJxRegFAeR7pbXBNLxtCnjBOZLzW4pSdKkciZg+tS/7J7DV3LvHl3oqfhS1kujpq0S3IIX+vv31T6Cxqq9VoNWrVhMDWpVFh+L74gHdBttpsiyXSlS2LZaIi4AftJw+4CAhxgCSwd4iS0lJCRUJmF8YrrR1fxqbBYsVMymtQVWGIiy4MgD/k8ioCLzEUhtS8A9C1GWLVfz2yqT0+KPAL9H44+hP5bQ6p12Vs3u0KkbtWj0unzm/iNm5Vu2fp/UjFKkYNexJ4oXWhlO7OXz5/SAU6CLC6vVJEH2Pfin/gS3i61b1suXZv8ffqXSZco71VcqslxZRXCRelkfOXxA+EGaXsj6wuB68XKV17QkV/NjBR9IyhQmKietIN6hSxfO07EjB82QUFO/js49fPhQXmepQKvpYrMC+cArCPw4ZBT9NXo4TRo/kkb/MVRyASOe4LMvv3balzh5tGJ9P9Jk2QBTAAQfTLt3bbO6jxQpUwo/vkyC1D+fPOdq/mvRYxPlsLiGgFKM7941WaItr0afQdKkTSe3ruaXF/F/bkeA36Nuh9RvC8yQMZN0fxsz8lcZeA0FOmVEKmkwgBsHYls0I5/uLtVsUpo0prGtOxUwuwGnQKNn4POMqP6TJ47KlzRIvTuLQLzZizbIadjYek9ZlDNkyqxlxY8IlqjvfhxORUWAUmziav4I8YOE3I5+ocRWfkI637Vbb8KfLXF0Dn2waKW1QmWrHE7zDgL4+GzX8RN65/2OtHjBbBomOIL/njxWui05yxeqxqcKTMmQ0TROS4kP5N9GTor1RlzNnzLC5PfHYzNWaK0ypE6TVqadO3va6hwSFMVoJhGsBHE1v7yI//MIAvwe9QisfllounQZZLujHjyQWzAQRYjnIpb9Pi/Gdr4Chc3uC4o1xjzypUuf0excIB0EnA+0vnOwjOTAH4dR9Rp1Jafs9q0x9HAq39Url9Sutt0e7VuZLVtOLS1b9lxy/6iFJVTLYLHjav5MmbPJEvYIKi5L0buSWJ7jY0bAHxGA71y9hs1pxOipsvmgMrMUBBziQawXBOrt2LZFJmXLnkNuVRT48WOHCUvLxiau5s+cxaTcYXlpWxzxV6It4LHVmxDPv/hSFXnbWwSPt2Vf4gT4tCGvvVlbbl3NLy/i/zyKAL9HPQqvXxSOmXcIFk5SgoBuyIZ1q1SStt2xbZPk4H/p5aqCGckUTKidDKCdgFOg4RtpKSooL0VKk5VXf75vr64yAEmlwTl+4rg/5GG9hs1UMtWqawoewtKzatpROyl2sNgDeJ+VuJq/+pt15KUz/h6vLSCBBLBvfCHo86RwlL8JB/7fLxGARUIFn6gbUFN/KSOsXZfAStOzW0czxQsUlXDBwEsdQYYQrIRVvGQZSVs3c7ptCzRWwlPian7UBbYQ+Fhj+WolUOYRa7FpwxqZxCwcCpmYLfzeYckE/hPG/R5zQuxhsSgEf+bKnY/gMgBxNb+8iP9zOwL8HnU7pIYvcM+u7TYXntolyBHmCRIFxJFVffVN7T5q1m4o9xGjdP3aVS0duhBmFiF1GzTV0gNxJ6BcONBxLRpVpxfKV6SqIlgpdeq0ks8QDBrgJCxVupxVH4aFJqZ2bZvQy5WrUZ48BWjlikV0+uRxQvR+9Rr1tPxg2qgighHBA92swWtCoW5MOURAUqTwwzywf7cMLPz621+ktRsXuZq/2us15UsaVrS3m9cWXNO1RET6HZr979+UX/hXPxDcuSyMgD8jAOX23xmTJA1cwcLFCNHZ06f8JW8J9JGWAj87rCQKyy+41zETs3zJPOl7h0VW9EF7iB4HpzsWUdqyaa3gUi8nAl2SS6V647rVFCVWEJw5b7VWhav53+/QlXp98ZHglO4pLOCbKE/egpK68tCBPVThpcoy3kIrPMB3/hwxWDCZmFwyVIDl4YP76Oten8g7z5k7r+TgVzB0/Vy4YAlqUHBm79u9Q9ALlqQzp08QXOvCw5PLRXFUXmxdza+/lvfjjwC/R+OPoVFKcGWsfte/h3RTxeqg2XPmlgsgHRFGDMwOwjjQ5fOv5MewureKIh9ofUF52EboLNVee5OShYfTiqULpeHvzVoNRLB+XZU9ILeJBDDP43tnlTKbFvpYf3GyVVGXrt2jy9dNwT5WJz2Q8Nvg72ja5HFmVtwXK1ahHr2/k9YNVWXnDq0FS8dyGjFqKs2fO0Ou6Q4osFBCVfFD6PftYKupB0xBIgBq4l9/SGuUKgsvAQQQdu81wMzH2tX8WImwp3hJbxWLvuBaRKRDUcdKag1qVqIUKSNo2qzlqlq3bzOmDZdlerO/3H4TflpgeNJQypQuOSVPZpvuy9O35Y1ximlArOSHJbaVIGgMCx698/5HKkku842VCLGACmjivu37BV2JdrWC33PPPt/LMapdEL2DQNOB3/SgPSKQUO9qkTd/IWrTtgM1aNzS7BJX888RH7N4vlyLXhwEH9k9+nwnWT369uxKQ4aPt9kus0rdcODrcdq4ziuED317AjpBcOvrZeuWDfTTd33omOD2hptN4sRJJO0g+PptxZS4ml9flyf3fT1O791/RBirkQ9M7CWeuld+j7oH2bzZU3ulv+y11pWxunjBLEKgoN5NFUYKMIN9/ElPoSxXtaoGs+5QvFctXyz9oZEhS9bskuXqk259bLIWWRXioQQ8J/FOtRRH+qpl3tiOA06Bxg3j5QkauYfCIo3OVNRIejCUAj1+6ny58h94aa9fuyamE/Pa5SzVX39DLC18+eIFEY0aIWi4ssf6Q3ElP1Zqg2UnZ668WrmwCiQS/+zxqerbFtd9X7+Y49ruQLjO1y9mbyjQqp9uilXnMHbwQZgpc1Yrisn9e3fJpbyhQP8+ZpoczyeFKxO4abEqVmwCarSzZ07SM/EcyCjKtzX+9WW4mh90eLC0YIZLCWjavOXr58/jFBH7WH0yR848NtmMFJ5q62p+dZ2ntr4ep95SoIEfv0fj/yvytQIdlzu4I7jb8XwODgkmrBTqrM6BWanEiZOaGRHjUr+7rvGGAh1QLhwKePjqwJfOFUmTNr2gUkrv9CWgZnGFnsWV/PDZht+lXhwRluvz8T4jYHQEoHjqlc/Y2ovxbBnl7egaMH3kyVvAURazc67mhzuYpXhLebas19+O4fMOf3JnxdX8zpbL+WJHgN+jsWMUiDlSCsMG/lyVrDrSBVev9df8ARdE6K8dwe1mBBgBRoARYAQYAUaAEfAPBFiB9o9+4lYyAowAI8AIMAKMACPACBgEgYB04XAG2x59BlLbDzrJQBZn8nMeRoAR8A4C4BodO2k2qQVPvFMr18IIMAKuIsDvUVcR4/yBhECCVaDhr5MQfXYC6cfL9xKYCMAnucwLLwbmzfFdMQIBhAC/RwOoM/lWXEaAXThchowvYAQYAUaAEWAEGAFGgBFIyAiwAp2Qe5/vnRFgBBgBRoARYAQYAUbAZQRYgXYZMr6AEWAEGAFGgBFgBBgBRiAhI+BxH+gkiUModcokCRljv7l39BWE+8v7XZY4LJiCgxJ5v+LoGnmc+gx6lyvmceoyZG67wNfjFM+IFOFhFBYa7LZ74oI8h0BIcBD3l+fgdViyek46zBTPkx5XoIODgny2PHE8sUlwl6OvIL5aTjrBAa67YbwYHz95Rkl1ad7c5XHqTbTjVxeP0/jhF5+rfT1O8YxIEhZCoWKVOBbjI/Ds+XPuLx91k3pOerJ6jyvQ+FpmYQQYAWMjwOPU2P3DrWMEgEDK5IkZCH9DIEmov7WY2+skAuwD7SRQnI0RYAQYAUaAEWAEGAFGgBEAAqxA8++AEWAEGAFGgBFgBBgBRoARcAEBVqBdAIuzMgKMACPACDACjAAjwAgwAqxA82+AEWAEGAFGgBFgBBgBRoARcAEBVqBdAIuzMgKMACPACDACjAAjwAgwAqxA82+AEWAEGAFGgBFgBBgBRoARcAEBVqBdAIuzMgKMACPACDACjAAjwAgwAqxA82+AEWAEGAFGgBFgBBgBRoARcAEBVqBdAIuzMgKMACPACDACjAAjwAgwAqxA82+AEWAEGAFGgBFgBBgBRoARcAEBjy/l7UJbZNYrt6IoJDgRPX76zNVLOT8j4BcIJAsLoRTJeHlXv+gsbiQjwAgwAowAI2ADAcMp0NfvRNH8/87R0fN3bDSXkxgB/0egToVsVO/FHP5/I3wHjAAjwAgwAoxAAkXAcAr0k2fP6VbkI7pyOyqBdgnfdqAjEBn1JNBvke+PEWAEGAFGgBEIaATYBzqgu5dvjhFgBBgBRoARYAQYAUbA3QiwAu1uRLk8RoARYAQYAUaAEWAEGIGARoAV6IDuXr45RoARYAQYAUaAEWAEGAF3I2A4H2h33yCXxwgwAt5D4O79x3T/Eft4ew9xrsmbCIQGB9GTp88pQ6ok3qxWq4tZqjQoeIcRcIiAN9iuWIF22AV8khFgBFxBYNWeizR/yzlXLuG8jIDfIJA/a0qqUz6bzxRoZqnym58KN9THCHiD7YoVaB93MlfPCAQSAmAYYQadQOpRvhc9AumF5RlMUb4SZqnyFfJcr78h4A22K/aB9rdfBbeXEWAEGAFGgBFgBBgBRsCnCLAF2qfwG6/yvJlTUOrkYQRfuzNXI73ewKRhwYQ2PBVWnqMX7kh/Q683gitkBBgBRoARYAQYAUbAAQKsQDsAx92nwpOESOUU5d598JhuRz6OtYqI8FBKkdS07DMCtG6LP09JcFAiGtSunCz+jqjn7Z/Xeaoqu+U2qZSTGlfKJc//Oucgrdx90W5ePsEIMAKMACPACDACjIAvEGAF2kuoZ0mTlIZ2rECI4layYtdF+m3uQXVotYUy2frVvFr602fP6LM/t9LpK3G3DAclSkSw8j4QTAmOXPlENp9IIl3FQp9nYQQYAUaAEWAEGAFGwHAIxGhzhmtaYDUoj3BL0CvPuLvXSmWmXBmT27xRKLlNoi2xKkNwUBBlTpNMHbq8hUI6+cvK4q8Kjfj4JZev5wsYAUaAEWAEGAFGgBFgBIhYgfbBr+Dq7Sit1molMmn7+p1KRTNQEqFEQ67ceqA/FY99WJ9Nkw7JEpvKjkdhfCkjwAgwAowAI8AIMAIJEgF24fBBt+84dp0qF8tIyRKHyO345ces3CleFdZpyO3IR7T75E2qXjqp3ZbCsgwLd25hzQ5PEkpnr0XSsfN3zPyl00ckEdbrmDJgzS6WM5Us88KN+3Tj7iOb5eO64rlSyXJPXrpL+07fspkPiVDKc2dKQTnSh1NYSBCdu36fcI29slMmC6XC2SMoS9pkdOryPdor7pOFEWAEGAFGgBFgBBgBoyPACrQPeujxk2e0+dBVerVkZkqTIjGVzJOGdh6/obUE/tKFs5uU2/X7rxCC++xJBqHgftqwCBXOYcqv8sHHeeySo7RspykIr12N/FS+YHp1WijEIfTtO2XkMQL1ELCnF9RYt0J2evv1vGauJ/8dvkY/z9xHj8Q96KWK+CBoX6sAJRcKvF4eP31GM9aeopkbTktmDXWudN409EWTYvIjQqUdE6wbYP9gYQQYAdcR8DWDDlqMj+dUgsXn8s0HdJnHsuudyFf4PQK+HofMZOW9nxAr0N7D2qymdfsuSwUaiVWFG4degVbWZ5xbs/eSlg/HekkcGkQ/vFdWKuHPnz+n7cKyDT9rKORw1ehUtzBdvf2Qdp24QVGPn+ovNduPemR9Lrlg/nj/zfxm+XBQvmA6eqNMFpr/3zntXK1yWal9zYLa8a17jyg4OJFkD0F73qqWh4LER8Dfa07KPJlSJ6XeLUtafRjky5KS8KdEF0+oknjLCPgMAczg4GMWSzlfuxMVK8ViiMiLhTdwzTMRsXvpZpSYafLMIhxGYNDBWP9VBEpD4KbWbuhGn/UVVxyYCDCTVez9ykxWsWPkrhysQLsLSRfL2X3iJt25/4hSJgujCsIynCQ0WCq5sPxCoYZcFK4VR4QrBizVtqRhxZxSeca5UYuP0MKt52W2IsIa/V1bk3W5ZdXcUoEeMe8wTVtzioZ3elHmuSdo9LqN3ib3b9x9KLeW/90S7iMjFx6mo6INsERXKWZqF6zNSoHGA61l1TzyUigHv8zcT+sPXJHH1Utnlko8Dhq8lIMWbTsnqfvqv5RdU55hdf7pn30E9o1Wr+ahykUzymv5P0bASAh0rldYBv2qNoGGsu/EncJF6Z5KMtuCfvLnD8oRXKCUbBDjAr/1+AjiIvCx/PCx+QyQvkxffXjq69Xv69vG+4xAXBFgJivnkGMmK+dwckcuDiJ0B4pxKAPK5saDV+WVeCm+WNjkXlFKuDakS2l66a7de9lhyZVFoCEELiFLtl/Q8h44c4tgBYbkET7JUMphgb54IyYYEfVfEtOs+LN0x8B1KLPPhJ20SbTx2p2HNGH5cSRLSRvdPhyUy59O46neduS6pjzjHNxHjpy7jV0ZEFkwW4Tcf0FcowQKOqZ60Y7B/+4n+IezMAJGQ6BQtpiZEbQN3OzNK+e228xa5bKZKc/ImFX4+sdHGlbMQX/3eIWm9axKVYubPmbjUx5fywj4EwLMZOVPvZUw2soKtA/7eb1w41Ci2Dj01ma4b9gTMStMGYQrhBSxP1D4M//wblntL0y4d0BCRTBf6hRhct+V/6Bwn9WtRHhdKNFq+jl50piJiyxpYwITD0Ury/p6DgvrtZKMqZIS2g2/b8hDUcfRC3fVaRlIiWBCJULHZ2EEDIeAYtF5oUBaoUjHjAXVUPET12aN3MeggyDdmLqSMouOgpu3CRABNQZx6+rdaQkDM1lZIsLH7kYg5ons7pK5vFgR2C8YLeA+AYWyeO7UlF0E4FQoZLLOwrXhgs5ibFkYXD8UrzS2hQSbhS25//AJ3XvwxNYpl9Kgy8KPM0j4NutFb42OFNPalvJA1K8E7h4pBPOGCopE21gYAX9DYP3+ywT3qRAx7ioJl6NF20yuU+o+SuRJrVmf14qPZEs+d5VPbeHukV/4/iMA75ZYnfTM1Xt0TPdhiRFXOEeEViauA3MNWHSeiDF56KxplkeVp7aeZNBBHfmypKACWVOK2arntPfUTfksU3XzlhHwJALMZGVCl5msPPkri71sVqBjx8hjOaCUwi8SbBdYIfCLxkUF/ZuJn9mR9RkNgv80ViYEHd29qMf02citNtuJJbltuWjYzByHRL3/dES4taUbEflK4KYBZR4+nPDTQqAilOmnQglgYQT8BQEw40CBhiBewVKBVrNI+F0jryMFGgG4bavn08a9wmC3CPwdOueApIDMlSm5iGkoq07JLZ4Z+IO0F8F613VxDFC4Pcmgg+DlTxsWpRcLxbD6PBFsO9MF2w4LI+ANBJjJioiZrLzxS3NcB7twOMbH42fBxqEkRwbTqoR48a7bZwrEU+cst9A5FeUbqOPAcnFFRL5b/unZN6C44g8CazC4muMrUIqVlMmXVu3KLT4KyuaL8Xc+J/ipcW83o/2zYTkvJRhDlKBN5QrE5FfpvGUEjIQAfvPKtx9+/WCVUQIudKVYQgm+ec92gC7yQ8kFew0+muHqsXrPJWGBNsUugEmne5PistiHNlhyVH2mgEJzFh3FoKNmqFRexaCjjrGFAv9Zo6Ia/SRiJxAgCcH1YNBpWjmXPFb/oc3qHlUarPHIqySRjLxQR7xlBNyPgP7dqQLvVS2WTFYq3XKrmKxAA4uxtO3oNcK4hSgmK/WO0r9LLctxxGTliXGomKz0bl1oE1isKhYxxUbhmIN5gYLnhC3QnsPWqZLBsnFZvDzhH6xkz8kb2otUpdnawrqlXm6fCS7o3xccptNX7knrLqZ4y4iARFigV4kXMwSqM5RXuIzAcg1mDdDn4Wt+TxwXMQEvdGTUE6mQw42kXY0CtHTHeTm93bRSLkqb0uTvjCleNS29UVjd60RbzzrWKUiTVpwg8EW3eCW3dGORjRX/8eBXSPDWaAisE24cBaKDYuGDOTWaohEuHYkFow7EURBwcvGx2LxKLpkPCvlnf/5H9x8+FeMmEfVqXoLwMYrxBCsTxugHQzZQ40o5qeYL2eQ1oISEwo2xe1uMceUWJU+K/zzFoJNWPDteKW5iyoHC8Yd45sBNpbRob6c6heRzQLWBt4yAJxFgJiuTOyUzWXnyV+a47PibIB2Xz2edQACKsF7WxMK+ofL+s/6U5FvFMV7mgzuUpxlfVaOZvavRbx0r0Ltv5KcSwrdaL7uFcq6kTvns1EfwMb8WveqhSndlC2vV1NUntEtql89GQz+sQIPaldOYRUCZN0Ys6qJkwdZzQlkw+T+DceQTofxjURX4gB+/GBNUqPLzlhEwGgIYsyqo9pVo2km0UY0lBMhisSR7ArYdWIohK3ddlMoz9sExjY9SJViUAQImHH0sA1YoheKtd91Q13iSQQeWcVibITuO3aAlOy7QA2Ehx0fxgCm7VRN4ywh4HAFmsjJBzExWHv+p2a2ALdB2oXHviQfCugSLDXx/Iy2C52BJqiMUT1iu8GK0fPFGCh9nCK7HCoNKwAULy1Wb1/JSNcEVjakiZYlCXjBarLZg8pi44jhlEtZu/cqFim1DlY+pK6XgqrqwhYUsZbIgq3PghMbLHAuvZE4TQ9X16MlT2iWsZ38Iqjr9ct6g0+s9fgd1a1xMBkOhbAQbLt5+nuZsOktjPq0oLeRRj+xz3eIaFkbAVwhgJueACAIuliu1dOGAtfiusAQrqsYth69K6sjEYbZtFFl046RayUzS4qzuBW4gSjLoZqZUWmxbeww6cKlylUFHWdnVDFkGsTCMkn2nb6pduT1xKebjVziLmZ3jA0bAEwiAyapG2ayyaMwE4V2qYhCQ6CiWyBaTlb6NlkxW+neYPp+9fU+NQ2eYrJQ7pVADWDyIACvQHgRXXzRWCWz23Rqp4Fr6UkGBbfnDWsGVHETwpYJ/s14mrjxBM9aZlsKGq4Ne7oqgvBHzD8up1HRi0QZYdKOEkg2FFgqvpeAh0POvHZRaBPelE+4VOFZWLNTb6n/rtHZYXtt2EM6JBV9s+GRuO3pd+I9dF1RbwZLvFm4daIPlvagyT4gFKD4avlm2A4GGp4Wyr/I2/34NhQgXE0uc1LW8ZQSMgADcOKBAQ+CDid+8kthmkdJEuzYhPz46M8eEAqgi5NYdNHh4nLiDQQcNSqULFL6vu1/ZWP6PEfAyAsxkFfPM8TL0XJ1AgBVoL/4MoPyKmV2bgukoWwqvyhybMgnlE0GFKrBQXWdvCwuaCubT53HUDtThqI0oB+f13M76sm3t22oHprGfPLUDlK1COI0R8AECGw9cFUGABeRsSSURuKPYbsCQs1O4NziSmzrWDLhArdptzfmOgFv1ceuorLiec5VBB/WoAEPsR+gYdnDMwgh4GwF8HDKTFTNZeft3p+qzPb+ozvKWEWAEGAFGwCYCUCYRyASBP7NaIEjvH23zQpGI2RklsEBbsufg2FJ5hhVZiapLHcdlq2+DmvJV5dhi0ME5/QIW+hVFcc7eghY4x8IIeAoBPRsHM1kxk5Wnfme2ymUF2hYqnMYIMAKMgBMIYFEVS3Hkd6nygllDuXxULpaREHwLGkcIVjd8IX9a6lCrgHSZUtfoFWpc87Kwer9RJou2oJLK5+xWMeggv2LQyZkhnBC42F0E9dpi0IFvNzifIVhE5SPBvAGmEHBZf1i7oEzHf0xjp0HBOx5GQDFZ6atxhclKXQcmq9wZk8vVchFLhKD2+i9mN/swxCesmrlVTFZlxVi1DNZXZTqzjcs4RNCuEjBZVS2eST4PsBox2q2EmawUEp7ZsguHZ3DlUhkBRiABIICA3461n1FoNKc6rLqHz8UsX28PAtBLThGuG6B9xMsaW/ypxZHUdbM2ntFiDvYJKki4dSA/eGDBXAMBRaSzrluqXGwVg84Hol4IlHj86cWSQee2WClx+c6LVOMFU+AWFHj8QcA8Agt1tnQxL3B9WbzPCHgKAcz6NH45p1Z8bDEIKiOYrBC/gFU7FZOVGmMqz6rdFzUqWKSByapaiczyNJis8IeP5rhSwcZlHILJClzX4IFWTFaqvWCyUuw9Ko23nkGALdCewZVLZQQYgQBCIDI6IBdK4lPho68EPv96K/RSwSSjlydimWtcA7Fktlkg2GsG/r2bLly/r10CqxYE1ukVgt7u2u2YhVguCPaaUYuOaOUhHxRxWMQUgw7SLOsxpdluAxh0vp26my7eiGkD8oNB5z9hbe7yxxbJ5oM0JaDNQtvVfSH9pGDg6DF2u6S2w3FsMRvIw8IIuIKAYrLCNbaYrNTvMS5MVli7QAXo65ms8Lu2xWR18Mwts6ZbMlnhpCfHoWKy0j87wGQ1a+NpSSeJD3EIM1lJGDz2XyLx4I15G8SxmkqZW8kr11+cHMcSYi6DNQWLBCC6loURCEQEsIBGy6p5AvHWJCf4tLWnAvLekgoGGlBHKv5n/U0mERSUoG7DeUuBPzFWPANfsj0Bew18oWHJxmqAl4Ul296DGSuIZk6TVEw1J6KzYnVPBN1CcGyPyQfUV4pBR+dKbdYcZxl01EVQNODycV1wVGMxFyUoBy9uWzipPP66LZozlVzwqXg0+4q37yOhvx8VVautDzRHv3/0E8YorMtKUbbsO4wRZ5is1HW2mKxwzlE7PDEO0Q5LJissyJTQmazsvWfdqa+yC4caDbxlBBgBRsABAo4UYFsvdFUUFElH1yIfLNnOLiIEto/TVyJV8drW2ww6UEZAR2kpsTH1WObnY0bAWQSYycoaKWayssbEWymGU6CzC/+5zxsVtfuV6C1guB5GwFMIhAu/NRZGgBFgBBgBRoAR8F8EDPcmx0pZaqlY/4WVW84IMAKMACPACDACjAAjEKgIcBBhoPYs3xcjwAgwAowAI8AIMAKMgEcQMJwF+qGIJD138z7dj4oJSvHInXOhjICPEEiXOhllSMNUXz6Cn6tlBBgBRoARYATijYDhFGjEk4Oo/7EIlGFhBAIRAf2KcoF4f3xPjAAjwAgwAoxAoCPALhyB3sN8f4wAI8AIMAKMACPACDACbkXAcBZot94dF8YIMAJeRaBuhexyhSyvVsqVMQJeQgA8xOD59ZUwS5WvkOd6/Q0Bb7BdsQLtb78Kbi8jYGAEkicNJfyxMAKBigBcDH0lzFLlK+S5XkbAGgF24bDGhFMYAUaAEWAEGAFGgBFgBBgBuwiwBdouNHyCEWAEXEXgyo1IuiZYdFgYgUBEIFmSUEovWHRCkoX55PaYpconsHOlfoiAN9iuWIH2wx8GN5kRMCoCYBhhBh2j9g63K74IwH0DTFG+Emap8hXyXK+/IeANtit24fC3X4XB2zt00EAaN3qY1spnz57RwH5f0ux/pmhpvMMIMAKMACPACDACjIA/I8AKtD/3nsHavnXLBho36je6dOG81rKgoCDau2cH/fzD1xQV9UBL5x1GgBFgBBgBRoARYAT8FQFWoP2150S7nz596tXWx1bfpPEjZXtq1G5g1q4atRrQvXt3acXShWbpfMAIMAKMACPACDACjIA/IsAKtD/2mmgzrLpli2alr77o5JU7+Lh9K3qhWDY6ffK4zfquX7tKa1cto4yZslCpMuXN8rxRs548nj2T3TjMgOEDRoARYAQYAUaAEfBLBFiB9stuI3oYFSVb/uCBdxgP4H7x/PlzevjooU3EVi5bKM9DWU5ksdBAlqzZqUSpsgQXj/PnTtu8nhMZAUaAEWAEGAFGgBHwFwSYhcOgPfX40SM6cvgAnT9/hlKlSk3FS5alpEmTydZCCb186aLcv38/kk6fOiH3U0ZEUOrUac3u6OSJo3TyxDGp1GbLlpPy5i9I8EvWCwL9jh45SJmzZKOUKSNE/qN0+OA+ylegMGXKnJVgXY56YPJfvnj+LCVOnMRUXvacWlkrVyySRb5Ro66+aG2/+pt1ac+u7bRw3ixq1/ETLZ13GAFGgBFgBBgBRoAR8DcEWIE2YI/t3L6FvuremS4I5VlJihQpaeS4GQRrbu3XK6hk2rxxLdWvUVEel6vwMo0aP1Pur1i6gIYO+pbOnD6p5cVOwUJFaeBPwylf/kJa+sH9e6hV0xrU9v1OlDZ9BhokAv4gyZOnoDr1m9Lfk8dqebt+9I62P2biLCpb7iVped63e4dMz5O3oHZev5M3nyn9+LFD+mTeZwQYAYMggA/cf2dMpnfe70i58+QnfFh/378nFS1Wkho0ecsgreRmMAKBjQCYrGAMe/eDj+WN8jg0bn+zAm2wvoFLxudd3peMFd///DsVKFREKNJnafbMqXT58kUqVKQ4fdFzgLASH6F/pk0kKKZ1GjSVd6FXin/6vi9B6Ube/AUL0yPhejFLUMlBse7X61OaNMNkMdbf/sb1q6TVu/yLlah02QrC3eIM1a7fhDJmzkL//D1BHrd6ux2ly5CRghIFiXKLyMvPnT1Nd+/eofDw5BSePLm+SG0/Q6bM0XljPgq0k7zDCDACPkcAH9z4eO/8aU/ZFsWgs2j+v1SjTkNKkiSpz9vIDWAEAhkBxWTV/K13tdvkcahBYbgdVqAN1iWHD+6nG9evUf1GLaimeGlBoCRXfuV1raWt3mlH2/7bKBXonLnyaF+qWgaxM3zUFMqTt4CZP/KLFV8R1uvytG/vTrp29QqlE9ZmvcBlBHV+99MIs+uKlyhDG9aulAp0/cYtqUC04qyuPX3KFFiIAEJ7os6dF8o2CyPACJhYdIKDg70CBRh0HNWFWajtWzcRPp7TpkuvtQkMOkN+HiAZdGrXa6yl8w4jEAgIxDYu3H2PsdXniMmKx6G7eyP+5Zk7w8a/PC4hngjA3xkCBfnG9atxLg1Kt2UwX0hIiOa6cfHiOauy4e/c55ufra6zymiRcPvWLZmSMdrKbHFaHsIanjRZMrp58zrdj4y0lYXTGIEEg0BsrDbuBMIZxh7MTkFq1DZ9tKv6mUFHIcHbQEPAmXHhznuObcwzk5U70fZOWaxAewdnp2vJlScfVXuthrT2NqhVmYYN+Z4uXrBWdp0t8MC+3bRg7kwaP2YEjRw+SLqD4Nonjx9bFZFb1J0sPNwqPbaEu3dvyyzp0md0mDV9hkzy/IULZx3m45OMQKAjEBurjTvvPzbGHrDrrFy+kPCB/Vr1WmZVM4OOGRx8EEAIxDYu3H2rsY15ZrJyN+KeL49dODyPscs1/DhkFP01ejhhOmf0H0PF6n7DqGmLd+izL7+msLDETpWHKdnePbrQ8aOmoL0IYdnGC/LObZOyi5emu0S16e4dU9n2yr1754485Wgq2d61nM4I+BMCly9doGNi7D24f1/GCsDVCoIFhZxhtUHe+DLoICbCGcaevSIAGC5dFStVIzwnLIUZdCwR4WN/QICZrPyhl/y7jaxAG7D/QkNDJdUbouEXL5gtrNA/SCYMBPF88kWfWFt85/Yt+vD95hQpXtZffzuIatVtLKnncOFnH78rrE2LXHbTcFQp3DMgl4TSYE/wMLt545o8nSJFhL1snM4I+DUC8HEc2K+7DNjVf6TWFmMQ7DfDBn8fK6uNuxh05i/b4hRjz57d2yXmefIVsIk9M+jYhIUTDYwAM1kZuHMCqGmsQBu4M2HZrdewORURNFJN6lal1SuXaAq08m+2tZAKHh63b90U/owNqGGTVm65Q60+YVGzFBWMqLipLc/j+MoVE281rOC2rFy2ruE0RsDfEJg8/k9JBffaG7XpvXadZeDef5vXE/4gzrDauItBJ2VEKqcYew4KNy+ICvSVB7r/mEFHBwbvGh4BZrIyfBcFTANZgTZYV4ISDgqmsuqieWoBFXBDKkmTNp3cPXxov0rSto+j/ZvPnj6lpWEHbh07d2w1S3P2IHUaU31HRH0lS79gdpmis4OFGXR5yqVDn0kp1+CXhYWdhREIRARABQnp1uMbuTAR9kE9+fZ7HbFLYLSJjdXGnQw6zjD2qIWY7AUBK8WaGXRkF/J/BkeAmawM3kEB1DxWoA3WmTOnTxIWrElUp14TKli4GGGlwelT/pKtrC3SlGBVQdBNwZ/ynZZ1BP1UZRkY2LVbbyrzQgW5CMr+fbuo1xcfSd/GQ2JlQfBGJ05s8qHWTy+rMh1tSwmleemiOTT45/508uRRunf3LrVu20FS2mHBlew5ctHZM6dEwON5Uv6e+vLAZQ0pXLSEPpn3GYGAQiAiVRp5P8sWz9OUZldvULlM6K9TDDrwrQaDjpr1UXniyqCD62/fvimLyZjRNg2lJYNOXAKNVTt5ywh4GgFLJqs0aWNoGV2p25vjMC5MVjwOXelNz+RlBdozuMa5VPAwbxXTvZMnjNLKgEX60y/6kp5cPTQsjL4eMIi++rIz7d65Tf7BzxKCB8Yvw8ZS/z7dxNLZ/8o/TOd26PSZXOzku296mFmBQ6ItwiGhYVqdljuNmrWW09BwI5kyYbS4PsxMQQDHNBTo9WtW2FSg169dIYtEPhZGIFARaN22Pa1YtoB++fEbWifGQss279Mr1d5wyMFsDwsw6Jw8cUwE+F2WCyupj1B3MuigbhXca6mU69sFBp0zp04QGHT0Czbp8/A+I2AEBBST1aoViwlMVs1avkONm7XRZoRcbaM3xqErTFY8Dl3tQc/lZwXac9jGqWQsUoJVAsGXfPniBUqRMoJgXbLFXFFFvJhXbdwvKe9wPlv2nFqdsEjPW7qZYLECXU8OwQIAP2ZYnuvUa2pGV4flvTduP05h0dZprRDdDgIYh4wYL32rr165JJYUz2FWRvUadWjG3+Np2eK5hGljvYC+Z82qpQRFvUq16vpTvM8IBBQCcM+YNG0hDf6pP23ZtI62blkvZ2f6//ArlS5T3ql79SaDDhoUJj7GIVhN1J4oJdvWc8jeNZzOCPgKAWay8hXyCate5oE2aH+nTp1W+k5mzZbDpvKsmo2pXbhM6JVndQ4KM5TvnLnzaqwbSLM19YM0lBWbwBqer0BhqzLKlqtI6cUS37t2bpVLjuvLwSqGoPOqIlZThLsHCyMQyAjA53nkuBk0a+E6gtsVZmY6t28lqeJiu2/FoHP65DHJoLNl9ylas/kgrVi/V6xG+pq8XAX0xlaWs+fxkQ65fPG8zUuYQccmLJxoYAQUk9Wytbuo//dDhbtjBsl+M2Loj0612tvjUMU8MZOVU91jmEysQBumK/y7IbBMtXq7vbyJ5Yvnm93MkkVz5XGb6EAqeRtt2gAAQABJREFUs5N8wAgEKAIImB344zCqXqOu5H/evnWjdqdKCcaHpV4Ug87rb9aRDDqJEyfRn47TvlbXA/O6VGFq6e7Ll01MOSpdbZlBRyHBW39DQDFZjRg9VTYdLohKHI0Lj45DizGP9ij3KRVsr9qo3/I41KNhjH1WoI3RDwHRiiYt3pYMImtWxTykwIu7fu1yKl22gtNT2AEBBt9EgkTg0IG9VvcN9ydIipSptHN6VhstUex4gkHHEWMP6i4gXLggl4TLmC1RL3Vm0LGFDqcZDQEwWVm6IxmNycoSM0smK8vzOOZxaAsV36bFPmfv2/Zx7X6EANwzVm7YZ9ZiWKbXbDoo/Z/NTvABIxBgCIDCsUWj6vRC+YpU9bUaBDesvXt20Pw5MwiuWKVKl9Pu2B6rjScYdBwx9qBBhYuYmHEuigBBW6KCF5lBxxY6nGY0BJjJymg9ErjtYQt04PatT+4MCrNloBEYQ9R0mU8axZUyAl5AANPF73foQrBC//x9X/qqeyf6e9IYqvBSZRr+5xSzuAGw2lR99U26HxkpWW0WzZ9FQUFBGoMOYhrAoNNbsOzMnTVNMuh06vqlvAs9j7ozDDqKsQe+zmDsGfX7YLqic9dA+zA+N61fQ5gxshRm0LFEhI+NjACYrLJnzyWZrPr27Eo/DOhF169ftctkZWtcKCYrd45De2NeYakYqsBkZUt4HNpCxbdpiQQrw/P4NqFSZtNqd+svTo5vUXTv/iO6dO0eRT54HO+yuABGwIgIZEwbTpnSJTdi0+LdJozdy9cj412OPxcAJfTs6ZP0UFiks2TNbrYokuV9YcVQW6w2eCzbYtCBz7RlEDCUcDDoxBYE/OTJE5uMPWjTu63qE/w+/xg7nV6sWEVrJhh0qlUsKl1LVm86kOCDgMOThsqxmzyZiblEA8pLO/x+dB5oZ5isUJqjceGJcWhvzP+3eR21b9tUzlT9NXWe2Y3yODSDw6kDe+9Zd+qr7MLhVFdwJkaAEWAEnEMAMzDgonVGwGqDP0uBRRgMOnpBmqXyjPO20vTXqX3F2KOO9dtadRpJBRqLJekVaMWg8+rrNRO88qzHi/eNjwBcqPAXmzgaF54Yh/bGvCWTVcaMmbWm8zjUoDDUDrtwGKo7uDGMACPACHgfgToNmlIqsYriymWLpEVOtYAZdBQSvGUEPIsAPryZycqzGLu7dMNZoJMmCaHcWWOi1d19w1weI+BrBIQhkYURMBQCYClo9U57Gj70B9q7e7tkzWEGHUN1ETcmASAAJqtxo4eJhceWaAuS8Tg0bscbToF++vQ53Y96TE+ePjMuatwyRiAeCCRNHELhSX3jQxmPZvOlAY5Au46f0DvvdxQrEyaWdwqLGDPoBHin8+0ZCgFmsjJUd8TaGMMp0GgxHPefPYt3bGOsN88ZGAFfIBD/sF1ftJrrTAgIKOVZ3SsYPFgYAUbAewhYslihZh6H3sPflZrYB9oVtDgvI8AIMAKMACPACDACjECCR4AV6AT/E2AAGAFGgBFgBBgBRoARYARcQYAVaFfQ4ryMACPACDACjAAjwAgwAgkeAUP6QCf4XmEAGAE/RSBDmmSUPnUyP209N5sRcAIBH7LoMEuVE/3DWRgBgYA32K5YgeafGiPACLgNgQcPnxD+WBiBQEQgJDiIkiUJJbHxiTBLlU9g50r9EAFvsF2xAu2HPwxuMiNgVATAMMIMOkbtHW5XfBF4HuR7dihmqYpvL/L1CQEBb7Bd+eg7OiF0H98jI8AIMAKMACPACDACjEAgIsAKdCD2qo/u6dv+fWnYr4O12pcvW0Kff/IxXblyWUvjHUaAEWAEGAFGgBFgBPwdAVag/b0HDdL+DevX0m9Df6Fz585qLcISpJMm/kVTJ0/U0niHEWAEGAFGgBFgBBgBf0eAFWh/70HRfiiqvpaRvw+TTWjYqInWlGqvvk4pU0bQlMkTtDTeYQQYAUaAEWAEGAFGwN8RYAXaz3vwreaNKGvGVHT82FGf3QlcNJYuWURZsmSl8hVe0toRJpYBrlWnLp06eYI2bVyvpfMOI8AIMAKMACPACDAC/owAK9D+3Hui7Q8ePCBEZUc9jPLZnSxcME+2oX6DxoJ70ZwktWHDprJdbIX2WfdwxYwAI8AIMAKMACPgZgSYxs7NgLq7uAvnz9OhQwfofmQkFSlajPLkzSeruHvnDl29ekUo0Pfl8bmzZylpkqRSgc2ZKzcFBZl/G126eJH2799LwcHBVLhwUcqYKZPNpl6+dInu3r1D+fIXkOdPnjhO+/ftJZSJ+nG9pSwSCjSkbv2GlqeoUpVXKCIiFc2fO5sGDR5GsEqzMAKMACPACDACjAAj4M8ImGtZ/nwnAdZ2+DWDwaJMyULUsllDev/d1vRS+VLU6cMP5J1+N/Abebxzx3Z5/HarZvL4xXIlacvmjRoaUJqrVCxHJYvlJ7h7NG9Sn0oUzUf1ar9BZ86c1vKpnc8+6USVXipLt27dpA/ea0MoD3W/Xu1lKlYoD23dukVllVtYv3ds3yb3CxYsZHYOByEhIUIZz0/379+nszbqs7qAExgBRsDrCFgy6Dx79oy6d/uEpkya4PW2cIWMQEJFwHIcMpOVsX8JbIE2aP+M/GOYZLCoXbc+den6ubT8rlu3mtavXSNb3LRZS8qaNRtN+GsMnT59itp/2IkyZswkLc+wFEO2b9tKDeq+SY8fP6b3PuhAL79cmW7fvk1z5sykNatW0huvVqbN23ZTqlSpZX71H5TiBnVq0IUL5+nLnn0oe/YctHDBXPE3j5o2rEMbtuyUdSP/6VMn6c6d25Q8RQr5p8rQbzML32iirbKdefPl15/ifUaAEfAxAopB593322stwQzWju1b6d9/plPDxk0padKk2jneYQQYAfcjYGscKiarHDlzUddPu7m/Ui4xXgiwBTpe8Hnu4tUrV8jC+3/7A5UqXYaKlyhJH3XqSlOm/SvTy5R9gT7u8illzZZdHrd4q7U8/ujjrtJlAonffP0VPXr0iH4e/Bt9/79BVKdeA2rV5h36e/psqlGzNt28eYOGDv5ZXm/53+3bt2jpirX0WbcvqWnzljR2/BSq/kYN6XM9cfxYLfvx48fkPgII7Yk6B2WbhRFgBGIQMCqDDlrYsFFT6c61YP6cmAbzHiMQgAgYdRwyk5Wxf2ysQBu0f1KnTiNbNneOSWF2tZnHjh6RrhywUrd8q43Z5bAuQfmGwKpsSwYNGUa5cufRTiE4sM0778ljTCspgRIOyZwli0qy2qpzsJSzMAKMgAkBIzPooIX1GjSSDWU3DlN/8f+BiYCRxyEzWRn7N8cKtEH7p0PHjyk0NJS+6fsVNW5QWyq6rnwlK8twiZKlbAb+FS9RSt75ubNnbPJIp0iZ0goZ5Rpy8cIF7dwd4RICgfuIPcmUKbM8dVbUxcIIMAImBIzOoAPXrRdeKE+YWuaPX/7VBioCRh+HzGRl3F8eK9AG7Ru4aCxaupqqvFKN1q9bQ+++3ZIqVihN/23Z5FSLLwr/ZUiaNGlt5k+SJAnh78mTJxQZec9mHsvElNFKtT5/WOLEMptSpC2vwbE6FxxkzeBhKz+nMQKBgAAYdFauWCYZaE5EuzrhvsCgg2M9gw6OwXiD4D1LefjwIe3ds5sWzJsjGXFwbEvAoIOZJyUoD+w3uNbex7cjBh2UU6d+A1kcfKFZGAF/RMBd4xBMViuWL6XVq1YQxpo9cfc41DNZwSWTxTgIcBChcfrCqiXwe57x7zw6euQwDRn8E/0z/W/BpNGYNoogvgwZM1rl1yekz2A6f/36NX2yto+XeFRUlPSXxmqBzsj1a6ayTEGBpisioq89f/6c3SIQjAiJiHCuHrsF8QlGwA8QgLLa/fOuNHnSeMmPrprcpGkLGv7HaAKDztjRI1UygUFHyex5i+mlipXkIT5uf/7xO/pt6C/yQ1flwYdv337fysBgPe86GHTwgj907Ax1+6wLzZszS10iP6QnTJlO5cpV0NJiY9BBxkKFisj8hw8d1K7jHUbAHxBw1zgEk1XHdu/R4cPmY6DCixVp2O+jKEeOnGZwuHscKiYrkAKAyYoD8c3g9ukBK9A+hd+5yvMXKEjDfx9NsDzhpbhx4zpq0NC0ZLZ6gYImTi+5cueWhxh0YOGAO4heNkdT3RWwQT2HfJfF17albIxeTTCniAhWohR5vVuHOqe2SoFWeVU6bxmBQETAHQw6wOUDQR+5aOF8KliwML3d9j3KJlwq9u7ZRX/8Pox69egmgoBvUrfuPc0gdD+Djim24fRpDgA2A5oPDI+AO8YhM1kZvpt92kBWoH0Kv/3KMe0KC7ReFJVUqogY2rl06dLLLFjsRG9dKlKkGBUtVlxO+f4x4jfq3PUzrSgwbPz4w7fyuONHnbV0/U6Xzh9S+gwZCF/ZEFDVoRxI85at5Bb/oR7ItWtXpYKfONqlQyZG/6eU6yJFi+uTeZ8RCEgE9Aw62aJZchSLDm4Y7ln4g7UYvsVg0ClqMTbWrV0tlWd8PC9cslKjiAR7TvU3alKN6q/Q8GFDpGKdIXq2SYGpGHRUEHCTZi2ozVtNadnSxQQGnR69+sqsKk5CseSo6/Vbde70qVP6ZN5nBAyPgDvGoWKyQlB96zZttXtu2aqNdKtcvGiBZLL6+puB2jm145lxyB+yCl8jbNkH2gi9YNEGWJqxcEnDejVppLA2/TPjb2lxmjFtKsH6W658zDSs2u/frzf17tWdunzcQa44CMt0v/7fyYVMQM6OxViG/PIT9evTi6pXq0R7du+iN96sSeCZtiWJwxLL4EVMLw/4po94YVeVriRQyuvVN0Xn4zoEG6oX9flzZ20VpS2ggoBGFkYg0BGIL4MO8Jk04S8J04fiAxcc63oBrSViI7A66do1q/Sn5L47GXTg3pUsPJzgChZ5z7lYCasGcQIj4AME4jsOmcnKB53mZ1WyAm3ADoMVF6TpsEL37d1Drj44ZtQf8qUJHujw5Mm1Vrd++13J6YyX26iRI2jWzBka6wZesghELFmqtAx8+F74Xv4+4ld69PgR9fl6AE2YbD8waMTIMVJRXrpkEQ37dbBUgrFU99z5S7XyVSNeqfqq3NXT26lzx48dlVa23HnyygVZVDpvGYFARSC+DDrA5fjxoxKe0qXL2oRJfYzasgy7k0EHlWssOufO2GwLJzICRkQgvuNQzdAwk5URe9cYbWIF2hj9YNWKXr370eHjZ2nD5h20cs0mOnryPE2fOVcsi13ALC/cOsZPmiYDh1av30KHjp7RAn+QEYN/6Yp1dOrcVVqz4T86ePQ07dp7RPJAK/9pswKjD2D1ghK99+BxWrVuMx0/fYlGj51oZQ1D9rpigRbIXF3QkkwQ/82ZbeKxrmPH0q3y8ZYRCBQE4sugAxyU25M9Fh21euitWzedgi2uDDoonFl0nIKYMxkMgfiOQ2ayMliHGrA5rEAbsFNUk4KDg6XCDLeJ2JgyMF1VuHBRM+u0KgdbWLURUW/vhazPq99Pnz6D9HMGobs9qSiWCM+YKRNt/W+z9uJXeedGK9BYDpiFEUgoCCgGnfWbthN8kE+dPCEZdK5cvuwUBMqv2R6LzpUrpnIsGQDsFR5XBh3QZiG+ARIRkcpe8ZzOCBgSgfiMQ2ayMmSXGqpRrEAbqjv8szFQ9Dt8+LFs/Ly5MdRZoN87eHC/dD2xDJLyzzvlVjMCriGgGHTg/nT37h3JoKNKUDNAlgw6OK9YdDZv2qCym21Vui0WHXcy6Fy8aFo0CVRaqdOYVkc1awgfMAJ+gEBcxqEag4rJyvI2mcnKEpGEd8wKdMLrc4/c8dtimW9YweEzrQT7UBLUsuEqnbeMQCAjgNgFS4mNQccyf5NmLWXSn38MJyzgoJcZ06fS7l07CSuDVq5SVX9K7oNBZ0s0TSUSnGXQsSpIJKhp7AIFCllRYdrKz2mMgFEQiO84VExWV69e0Rio1L05y2TlvnFo+pBlJivVA8bYMo2dMfrBMK347n+DpMJbqlQZl9qEwKX9h80pdj76uCu16/AROXL/cKkSzswIGBwBxaADtyZQzqVNl452bN9G9hh05syeSWDQQcQ/FF0EPmG2pnadelSp8ityFdI3q1ehmrXqUtas2WjXrh1ydUEwY3z3w88UFGRtA1EMOq++Vp1geQOXNIJ57THowL0EDDp58uazQvfsmTMyrXhJc0pNq4ycwAgYCAF3jUMwWYHBCkxWGzesk7SutwT/+sIFc2VwvDNMVu4Zh6cluip42EBQJ+imsAKdoLvf+uZBk6dfKMU6h/0UuHLoBdZnVp71iPB+oCOgGHTGjv5TvnDV/YKpBgqvJYPO+nVrCFyyYNDBWMFHp5K/Z8yWfO3jx42hcWP+lMko/+VKVeinQUPtrkiG4F8o7P/OnE5LFi+U5cKFZMjQETYZdKBAg0GnvQ0FGlzVEMW0Iw/4P0bA4Ai4axwqJqtun3WWTFYrVyyTd545SxbJZNWp8yd2kXDXOGQmK7sQ+/xEIrFy1fP4tqJSZtPCGusvTo5vUYJi7SlFPnhEj588i3dZXAAjYEQEkiUJpeTJ7AdlGrHNzrbp3v1HdD/qsbPZAzYflhE+eeK4XFwoe44cDoOAb968QZcuXaQc2XOaKdh6cC5fukSYNsYyvpYfqipfqxaNpSI8f/EKuagSpp7xly9fAbsfsliwpUnDOoJb/kWav2i5KkpuHzx4QEUK5qLHIpDw4JHTkvPdLEMCPAgNCaLwpGEUFmpuLPAWFPx+dA1pd45DWLVPnjxOCPB1FIzv7nH4y8//o/99P0Auhta7b3/XAEjAue29Z92pr7IFOgH/wPjWGQFGwDMIKAYdZ0pH7AD+HAlYbvDnioBBB3+OxJJBB5Y1JSuF9RmLtdSqXZeVZwUKb/0KAXeOQ8Vk5SoA8R2HzGTlKuLey2/tQOe9urkmRoARYAQYAR8iAAXDFoMOmqQ43Dt26uLDFnLVjEDgI2BvHDKTlbH73nAWaOE2K6e34+9YYmzguXUJF4GgIPEjZ2EEDIIAGHR+G/qLZNBp/2En2SpMfS9fvkQGTZWv8JJBWsrNYAQCFwFb45CZrIzd34bzgY4UPpRXb95nP0pj/264dfFAIF3qZJQhTXg8SjDupewD7bu+OX36FF04f45eKFfBZco5KMwQWMKUYBGV0NBQSUWp0hL6ln2gE/ovIPb7d+c4RIja48eP7cYwxN6ahJsjQfpAI6LxydNnHESYcH/3AX/nz57FO2434DHiG3QdAXcy6KB2ZtBxvQ/4CkbAneOQmayM/XtiH2hj9w+3jhFgBBgBRoARYAQYAUbAYAiwAm2wDuHmMAKMACPACDACjAAjwAgYGwFWoP/f3nkARlWlX/xk0gsEEiCE3nvvVUFFUEBAxAaKjdVd3VX/rq6u7rrqWte29rpWxF1FFAuKSG9SpffeQ0+vk//33cmbTIaZIWgmmUzO1TCv3Hfffb83k5z3zXfPDez7w96RAAmQAAmQAAmQAAkEGIGAc+EIMD7sDgmQwDkQiIoMq7BJJs6hm6xKAr+KgLpEVWShS1VF0ue5KxOB8nC7ooCuTO8I9pUEApzAidNZOCYuOiwkEIwEdGR/bXHRCQ8rdispz+vMzS2gS1V5Aue5Ki2B8nC7ooCutG8PdpwEAo+AOozk5dsDr2PsEQmUAQF1iKpIDx26VJXBTWQTVYJAebhdMQe6SryVeJEkQAIkQAIkQAIkQAJlRYACuqxI+rmdfz/3ON5755VSnUXN11etWIod27eUqj4rlSSwYN4sPPq3e3D82NGSO7hGAiRAAiRAAiRAAkKAAroSvA2W/7wI7739Mg4fPFCq3h45fBA3TRiN++6+tUT9RQtm4z9vvYSTJ4+X2B6oKxXVX7vMyvbFZ5Px5dRPAhUN+0UCJEACJEACJFCBBKq0gLamr61A/qU69ccfvGnqDRs+ulT1vVV6/B/346Xnn8D8OT96q1Lu233dg4rqb78Bg1GtWnUR0FPKnQdPSAIkQAIkQAIkEPgEqqyAvuN349GjQwPs2bUjoO+SphGo4E2qWw9duvX6TX294urrMPjCYejavfdvaqesDl63dhW6t6+PB++93WOTFdXf8IgIXDDkUuzbuxsrly/x2DduJAESIAESIAESqLoEqqwLR3Z2FjRXOCc3J6Dv/uwfvzP9vPiSyxDyG01Ib5r0x4C61pzsbNOfrCzPtmcV2d+hl47GV198aqLQ3Xv2DShu7AwJkAAJkAAJkEDFEqhyEej09DTs2b0T2VlZhvyhA/vM+t49u2C3O+y38vPzsWXzBpw47nkQ2fatm3D4UMl8ZD1Wj0lNPW3a3bVzG77/dhq2b9ts1t33a+qCRmA1z9fbefTA2T/NMMdfPGykefX0z6GD+zH3px/MufShwFvRaPbWLRud16n13Pvl3m/XtrRtZTd71gysX7caOTkOAexax3U5Ly/PnO+nmd/il1XLoetWObB/D44cPmRWMzMzTLvatmt+tqf+Wsfra648/GzeuA7avrLXdU/laMqREgMqlfe82T+YY/Reeyq9+gxAterx+PGHb5CXm+upCreRAAmQAAmQAAlUUQJVLgL9ygtP4tPJ/3He7jv/MNG5/O5H06DRRv3a/tYbx5mv8Z9/ubiuVlThfMVlg9GiVRt8Pn2u89hNG9Zi/LhhuOHm25FYuw6ee+phsy8urhoWrtgG1/39Bg7GX/7vNpw8ccx5/G13/Bn641pUsK5fs8psata8tesus3zq5An8+c5bsGLZYue+Vq3b4c8PPOpcd134x4N3Qx0mPvz0W3Tq0t3scu2Xp35bx69bsxL33/N7HNi/19qE8PAI3HP/P3D1+Juc26wFFfSP/v0eeTgovsbadZLw98eeQ8dO3TD8ouI0kqWL52PUsH7m0J69++PtD6aaZU/91R0qet989VkZWPmKWTaV5Z/IyCjcde/fTH9co/XqqKHXPf/nzXj68Yfw7fTPrUPQuGlzvPTah+bVuVEWwsLC0ET2rRP+B+UhS+uxkMCvIaAOOtXj43HjLXeU6nAdBKwPkx07d0N0dEypjmElBwENCDz56ANo36EzRl9xLbGQgJPAuXwO9W/v6pU/I75GTTRvcebfXmejXPBIQP/ezpFA2+133o/EWrU91gmGjVVOQA8fdQWSkuvh808/NGJw/PWTUEuEnS3EhpYiPktbvAV6Fy+cY6KuGsHUXGNXwalt6xvro/ffMPnMw/50H1KOHDL2dG+88izayS/98wYNcXZh/749SEtLRWxsHGLj4pzbdUE/4CryNfLauWsPjBx9lYj7/Zg+7X/Q/G5fRY91L776rZHyG669TPpQDQ/+4xl06NjFiMqX5WHkqcf+itDQMIy7+npnk4sXzsVdt080glYfClq2aos9e3biv5Pfw6v/fhqffP4D7n3gMezauRWf//cj8wtqxOhx5vgWLds427EW3Pt7rzw0zPnpe3PcFVddh+R6DbFp41p8/P6bePqfDyL19Cncevs91uHO11uuvxyHRZxMmPg76HmmicvGmtUr8MC9fzB9clYsWtC8cxXQ+yVaTgHtTofrpSFgOehcde2Npalu6rz28r/wlQxgffbf7+CioSPMttOnTmLqZx+bz9LA8y8qdVsVVVG/WduyaT3GjBuPmjUTy60bNpvNfLM345svMGzEGERFRZfbuXmiwCVwrp9Dy8mqufydmPr1XOeFVdT72tmBc1yoqP5aTlb1GzTCzbfeeY69rjzVq5yA1uin/iyaP9uI21Fjr4FGbcuqaIrEJfKL+4l/veYxZ1m9ma+9/hbc99d/Ok+pUeoX/vWoybl1FdB7djsGOKqQcy8L5v5oxLNGwt987zPnH4prJtyCSRPHYueOraqy3Q/zuu6r388//Qg05eSVNyc7I9dt23dC/YaNcfWYi/DWa89hjER7NGqr9azo+7MvvQPXP/ZXXXMj9BeZ/pEbP3GSiZyrgG7cpFmpo3PLli4w4rlps5Ymkm49WAy6cKh5+Jhw5SV4/91XccVV15/x5HtcUjfe/2Q6mjVvZTjoH9hLBvfAxvVroGk5LUTou5akpGSzqg8yLIFFQN9noaEVM53yuZAoKwed+fJ5f0ki2cn1GmDG7BXn0gW/1fV1D9RB5+CBvfIZrINRl1/ttz54aniYjF948dnHJLXrOwy/bKynKtxWRgR8vQfK6BRl0kxZfQ4r8n3tDYSve1BR/XV1sgpmAW3zdlO4/dcRqJtcH3975FmP4llb1K9lXcWzbjtvsCPqrKkCruX0qVNmNamuQ8i57tPcXC1XXnODUzzrun5d8tzL7+riORVv/dYIun6VpdFxK+3Darh1m/bmfJpjrHnYWvaLc4U+JDRp2qKEeNZ9KnZV6P6WMvV/k83h19142xlR+fYSGe/ddyCyMjOhaSHu5dEn/+0Uz7pPo1M95ZsCLe7sdZv14OL+LYLuY6k4Amdzb6m4npU8c1k66HTu2hODLhiKK6+9oeRJKmjtbPegohx0FIcOuNZCH3eDwW//0MnKb2hL3XCgfg6ripNVlYtAl/qd+SsrNm3WAjGxsV6P1mize0lIqGU26de0riUtzTEgsVbtJNfNZtkSrBoJdi/OvMlzcO3w1m+1ctOifXvs7yVztHV7WFi4vphofsNGTUyqhq5rZNwfxYrKq1j2VNq272zEsw5SdC9xcdXdNyEh0cH+lBt7rVi7Tl1T35O4PqMhbig3Amdzbym3jpzlRGXpoNOocVO8+NoHZzlj+e0+2z2oSAedevUbmod9/bZLfw/Ub9C4/MBUoTPRyarib3Ygfw6rgpMVI9AV/xlAqKQ+eCoREZFmc1qRs4drnaNHj5jV6tXiXTeX+bLmgmnRvOI1v6w446da9eroICkxKsC1WO4kNWTwhT+K5dxRo2aCx+Z1sJYW94cRj5VlY5iPNADrAcZmC/xUAW/XF2zbS+PeknLksBmH4J47ryx04O1myc11dVYpjRPNr3FyKY2DjjrZaB6+5irqeAdvRfuoaVYa1XYtrv1SFxp1l9Efd2tIZVEZHXTc741+Xa1RN+Xly71oyFCHa9F3X09zxcXlMiBAJys6WdHJyvFB8qzcyuBDVpmbsBwcXG3XKuJ6dDY8LTrwzb3Ex9cwm06LsPVnqVOUB6yTuLz85sdnPZUVTXd13zjrQedQoZakqKh7yckTx2HlKLsefvxoilnVwQu/tVgPD9XlIYGl4gmo+C2Ne8t9d/9ObBOX4bOv5sjA4JJ57S9IbqwO0HvupXdx4cXDzUWVxonmXJ1cVLD6ctDRE38jbjCPPnSP035RxwbccfcDHscuWH3sO2AQXn/nU+fNsPr19cyluPP31zvGPshedeLRwbJaKrODjnXd6m5UWvcivWbLOWHHdoeNqG5jKRsCdLKikxWdrByfpSoroC2RrPmy7iUhwTFq/Pgxhxhz3X/40Jli1nV/WS7XEjs8LVbU1bXtuskNsPaXlVgr9nLuucme6rseey7LmpahRfOaNRqkf+R9FUu4bhJ/5rPVd94DLxOpeDqP9mebDPhbvWIp2rTtcEaVVZKvraVZGVgPWRx1IBRLxROoLg+N5+Le4qvHnqLTvpxorLZK6+Tiy0FH2/pJJkh66L47jBWk2tvpQNq5EjnWgYLWN0/WOUu8ehkY/Oc/3WwcfVRoqq96g6K0BY3WBoODzrm4FymvOkXjRvbv21sCH1d+OwE6WTlcsNxJ+vr9ESyfw9L+/rPYBLuTVZUV0DWL8o63FtnAWTdcX+vKSPew8HDj3awTi6jjg5ZtWzbh7ttvMMvn4nDhOODc/7Vs9TTiql/Puv5hHSL2VjNnfIXPPv0Ao8VJxMqtVvcNtXkzxcsf23PpSQNx2tCBj2rnNvV/H5ewq7Pa0a/0rPO3koGFKnI1d9q9vk6brv21fKqt/GO14ittGT5qnJnI5eMP3pII4gjUSXLkKevxGtFTRw11VVEbwd9aLAGt18RS8QR+i3tLaXrvy4nGOr60Ti5Wrr41ENU63np9540XzeLDjz+PEZddYZbVt3jKR+8Yr3Ld4Enkm4oe/tkjE0G9P/krtGnXscTeYHHQORf3IgVgcT9AB50S74eyWKGTlWeKvn5/BMvnsLS//yxC1rfEwepk5TucaFEIwtcu4p2s5YVnH8UzTzyEvz9wp8kx1G0qBoePHGv+gOkT17+f/aeZ+EQt0po2b4mocprcQPthRYAPHTygXXOWwRddYr6mVFF6/VXDxV/5KePJfO0Vw4zPtc6iV1ZFo376QPH4P+4zE7d8JH7L0z6fbM45Xs438RpHvqGeT63FzNfQsqz175HI2Ovia3v/Pbdh7GWDsMTFHUOjZOoaoukeE68ZYTyilbWvcuGQS9Gz9wAzaHGCTFyjkyb85+2XTb80ohcdE4O/PPT4WSPlvs5h7VMbLi1t3USJtZ+vwUXAmxON61WW1snFl4OOurpoaoJ+w3TpiMtdm8c1190iLhKjSmwrzcqfJPXDXTwHk4POubgXKS9Nf9PfBTqzaWZGRmkQsk6AEDjb5/Bc3gu+Pod0sqKT1W99y1fZCPTlV07AsqULzdemn3z4jvkq9fqbfu/keb+IsCyZ7nvWD1+biU70l7Ee83/3PYyhg7oaQemsLAsqMLWEyex8noqv/aGSFqHRNauO6/F9+p1vorkL5/1kvua19qnnss6cqJOALJfrePv1F80fjVFjrjKzA46+ZMAZ7ekxWqxXs3yWfmsdTRH5dOpMPP7I/WZ2oVlFFnq6T43mr7vhVl10lqEiAKJkVsAnZZIVnWZbfzRdo0+/86RvjzjrqdXNwzIz4YN/+aMZSKWDqfTBxSpWP61Xa/tr70wxolyj2f/95D2zWaPzOovhQzLRi/ukJ9bx1qvVjr7qbIqur2ZF/tEHExUg6n6go/pZgp+ANyca1ysvrZOLNQDVl4NO6zYdPD7o6e8aLVaKk+v5vS2379j1jF3B5aBTevciC4S66OyVGR0PHtxnJk6ytvM1sAmc7XNofdvpehXW2Bv3weOl+RzSycqVpASM6GRVEoiPtSoroNUDWG2h9AN3NOWwiKRGJeznomNi8cwLbyI7+0UjpBo3ae4UnjqRgc5c6FrUE3nxyh2IiHQ4Z7ju02Vf+/Vci1ftQKgHt4chw0aYtIcfv59uJh9xbVedKHRAkdoJqa2d9tHKUf5yxkKEyH+u5V8ys1luTk6J6/TVL9djdZKR9+QrYh1YuW/vLuhMQ0nieW0NdHStq8vni2et/pyQ9BN1RVARWt1DVPy8wRdjzuINhrFGrzVlxCqe+qv7wkX0/+n//mp+1IVAf0nqtXubWMNbO9rWn+55EDffdqczBUW3aflhxnTzqmkiLCTgi4AnJxcr3cqTg86xIgcddbDxZ7EGwVoOOu7n0vOryKysDjre3Ius60xLdbiaePu9YNXja+Un4O294OtzWFFOVu60K/vn0NPvP+sarQeYYHWyqrIC2rrBOte9/ngrKrStEd1WnUiJrnoqvvyftb6v/d6mnO3es5/8kUvCL6uX44hM+23lFLmeX4+18rSt7dYvDmtdXzUC6ykK66tfrsfrsopXayY/932e1jUyYEUHPO3XbdonHUTlXrz117WestEfX8VXOxrl8xTRmPn9V6ZJnVWSpXIRsB4i8/JyK6zj1oOlJwed6vGO3zd00Cl5e8rSQUdtCnXsiJZqfrb6LHkVXFMC1rcndLKSAa10spLgmX+DBRX1qSsZRq2oXvC8Xglo9GT89Q47qlnff+O1HneUHQEdOLp962Yzq2FZTvNedj2s2i1Zf5zdvY4tKjWLXHSOubno6KC8FA+WkNZxZfnqy0EnuV59cyod8Kq+xu6lrPpojZ+wHHTcz+O+7u6g477fdf1s98C1rrVs9UcddDyVsnTQSUk5ZE6hD8++AiSe+sFtpSPgfA9UYicrvVJ1snIv1gBy9+2/Zt1631fFz6HFMVidrCigf80nopyPueLq680fgXlzfijnM1fN082bPdNEUG6c9MeqCSDAr/ps7i2NGju+zfju66nOK1Hx/Pgjf8GSRfPMtnNxuHA2cg4L7g46rofqt0X6rZamj037/BPnLu3T8888UmZ9tBx0dCZNdcTxVNRBxyqWg46mg7nX1zEBzz75d6uqcwbPc3XQ0QbUQUfTulyLvxx0lLV+a8ZS9gRcnazcW3d3srL2V7STldUPfVUnKy06lsb1c+AvJ6uq/DkMVierKp/CYT5BAf6PphjMXrQ+wHsZPN2bePMfJOo/CTrIkSXwCFjuLTorn7q39OozEPmSm3/nnx8ynR0rg30/ePdVfP/tl+KJnImWMq38nFnfm8G46uCy/OeFfr8oy0FHB/Kpg457itLNt96Jv8oA4KceewCrViyRtKjWZkDz5o1rzTcfPy9ZUCZ9VAedm64bbRxxfl4yH5279pSUpTjoH/PFC+YiW2ZCnPr1XHMu/bZLHXT+cvetpv7SxfPM4Du15JslA4F1nIFVznYPrHqur5aDjvJXBx11EkpKrmesJ3Vgctk66Owzp/Y0QMy1T1z+9QTUyUqtVNXJateubUhPS8MEGVCu39rp+18HhH/1xadQJ6vLRl8lgzn3Y+5P36N9xy7I2pD16098Dkf6+hxaTlYaGVYnqwsvvhSaN/+l9Fl/Z2TJ2KKyKlX3c7jXIAxWJysK6LL6hPi5HQ6E8TNgl+b1q0mKZxcgAbZ4NvcWjbzqrJlqTTl/zkzzo24x//l4GjZvXG8EtOW+opdmud94c9AxdTw42FhYrLasV2u7Nwcd3X/pyMtlQG4uXn7hCXz39RfmEB3Q+/YHU43QVwHt2p63PmqKghbr1ay4/FPpHXR8uAT5ci9aOP8nQ0HvAYt/CNDJysHV22fTlXql/xz6+D1j/Z6yXq3rrgpOViHytWGhdcG/9nVA8nhz6MJDk39tE87j0jNzcfhYOjKy8pzbuEACwUQgKTEWdWvFBdMlOa9FP7tHjpeP725+fr5H9xZnZ2RBI636i911oGlGejpiJQrrWtQrWB10vAlRPZe7g411vP4KzchIP2Mw6rKlC/C7G8ahi0R935/ytVX9jFe1S9SBvDVrOmZA1Qql7aOvfrmfqLQOOtZxZ3PQ0Xre7kFp+lUaBx09h697ow5E6l7k+sCr2wb3a28cg+Yu2XjGfdE2f22JjQ43n924mIr5dioQ/z56c7KyGOv90Pe4q5NVjnzzoU5WrvdN6/u612fb7+m9oMeU5nOox7o7WenkZepk5dpHb+/rs/Vb+2GVyvg59Hbdek3efv+99doLeO2lp6GpkHeK21V5F29/Z8tSrzICXd53lecjARIoEwIqdt1TI9wb9uTh7S6e9ZizOdHoubyJa/3GQr8qdi+lcdDRY6zBe67Hl7aPvvrl2p4uV0YHHe23r3vjyb1o0fzZyJLUnQskRcTTfdE2WcqOAJ2sfL9H3UlXxs+hr98z3n7/VQUnKw4idH93c50ESIAEyoAAHXTKAOKvaMLycL/OZWKsX9EMDwkSAvwclv+NrCpOVgEXgY6MCEXjevHytUD533SekQTKg4DNVnKCm/I4J89RMQTUQee9d16BOuiMnzipYjpRhc6qtoAL589C1+690bVbryp05bxUXwT4OfRFp+z3VRUnq4AT0OFhoWV/N9kiCZAACVQAAU0hoINO+YHXaOO8JZucA0PL78w8UyAT4OewfO9OVXGyCjgBXb63mWcjARIgAf8SoIOOf/m6t+466Mt9H9erLgF+Dsvv3lcVJyvmQJffe4pnIgESIAESIAESIAESCAICFNBBcBN5CSRAAiRAAiRAAiRAAuVHgAK6/FjzTCRAAiRAAiRAAiRAAkFAgDnQQXATeQkkECgEatWMQUJ8dKB0h/0ggTIlIJbfFVroUlWh+HnySkSgPNyuKKAr0RuCXSWBQCcQFipfatFIJ9BvE/tXSQnQpaqS3jh2OygJMIUjKG8rL4oESIAESIAESIAESMBfBCig/UWW7ZIACZAACZAACZAACQQlAQrooLytvCgSIAESIAESIAESIAF/EaCA9hdZtksCJEACJEACJEACJBCUBCigg/K28qJIgARIgARIgARIgAT8RYAC2l9k2S4JkAAJkAAJkAAJkEBQEqCADsrbyosiARIgARIgARIgARLwFwEKaH+RZbskQAIkQAIkQAIkQAJBSYACOihvKy+KBEiABEiABEiABEjAXwQooP1Flu2SAAmQAAmQAAmQAAkEJQEK6KC8rbwoEiABEiABEiABEiABfxGggPYXWbZLAiRAAiRAAiRAAiQQlAQooIPytvKiSIAESIAESIAESIAE/EWAAtpfZNkuCZAACZAACZAACZBAUBKggA7K28qLIgESIAESIAESIAES8BcBCmh/kWW7JEACJEACJEACJEACQUmAAjoobysvigRIgARIgARIgARIwF8EKKD9RZbtkgAJkAAJkAAJkAAJBCUBCuigvK28KBIgARIgARIgARIgAX8RoID2F1m2SwIkQAIkQAIkQAIkEJQEKKCD8rbyokiABEiABEiABEiABPxFgALaX2TZLgmQAAmQAAmQAAmQQFASoIAOytvKiyIBEiABEiABEiABEvAXAQpof5FluyRAAiRAAiRAAiRAAkFJgAI6KG8rL4oESIAESIAESIAESMBfBCig/UWW7ZIACZAACZAACZAACQQlAQrooLytvCgSIAESIAESIAESIAF/EaCA9hdZtksCJEACJEACJEACJBCUBCigg/K28qJIgARIgARIgARIgAT8RYAC2l9k2S4JkAAJkAAJkAAJkEBQEqCADsrbyosiARIgARIgARIgARLwFwEKaH+RZbskQAIkQAIkQAIkQAJBSYACOihvKy+KBEiABEiABEiABEjAXwQooP1Flu2SAAmQAAmQAAmQAAkEJQEK6KC8rbwoEiABEiABEiABEiABfxGggPYXWbZLAiRAAiRAAiRAAiQQlAQooIPytvKiSIAESIAESIAESIAE/EWAAtpfZNkuCZAACZAACZAACZBAUBKggA7K28qLIgESIAESIAESIAES8BcBCmh/kWW7JEACJEACJEACJEACQUmAAjoobysvigRIgARIgARIgARIwF8EKKD9RZbtkgAJkAAJkAAJkAAJBCUBCuigvK28KBIgARIgARIgARIgAX8RoID2F1m2SwIkQAIkQAIkQAIkEJQEKKCD8rbyokiABEiABEiABEiABPxFgALaX2TZLgmQAAmQAAmQAAmQQFASoIAOytvKiyIBEiABEiABEiABEvAXAQpof5FluyRAAiRAAiRAAiRAAkFJICwor6pMLqoQdrtdWpJnjMJC2ELy5CUUIaEFyC0oQIgtAuEhobI/pEzOxkZIgARIgARIgARIgAQqBwEKaJ/3qdDszc0qwEdvzsSGtfsw6JIuGDGuE0JEVCOE4tknPu4kARIgARIgARIggSAkwBQOnzc1BDZbCKZ/ORtHD6bgTw+OwldTVuHArkyE2vJ9HsmdJEACJEACJEACJEACwUmAAtrHfQ0pijAnJyfjxHHg2KEsxMSFITpWA/cM3vtAx10kQAIkQAIkQAIkELQEKKBLcWtr1Y1HakYqvvtyCa64sTtq1Y1DgZ0CuhToWIUESIAESIAESIAEgo5AFVKBjnxmFIbIYMB8+cmDLTRKbqgjj7mw0C4pzXbIcEHZZpOtUs9eKPUKMO3T2bj30TFo2baJeQMUyOBCKzptNvAfEiABEiABEiABEiCBKkOgCglo657q4D+7SOQIbFt/EPNmr0bLNvUw8KIuIpkd4hkhBVJZ1kJtmP39MjRsUNeIZ7uIbFuITfKftZ4Kcg4itKjylQRIgARIgARIgASqCoEqlMKhYld+QvJNpPn0iRw8/+RnSKhZC9M/X4RVSzYW6WGxqJMoNVCA1NRULF20GWOuPt+sOyLXam2nkWl50SVZ0B8WEiABEiABEiABEiCBqkGgCgloFbn6o5cchuysHETH5ODy8T3RomUS9u4+ZvYZ8VyodcLx3fS5GHJJL8TFx8h6oUSeNWCvKSCa4KGvFM8ChIUESIAESIAESIAEqhSBKpTCYYWMQ80EKUkNaqL/wK7444RX0KBpDYy/pZvc+AKcPJGG/Gw7Tp3MQX5uJHr0bQVH6oYDlRpzZKRlo0AmU6leI7ZKvVl4sSRAAiRAAiRAAiRAApXOi82KIjtiyUU5FyYabILL1h3VDIwzSsmNMs8gBl7QB1s3HsW9j4xHXm4O3nh2Oo6dOiUC+hg2rs7EX/4x0cyVkidZG7YCO8LCbJj77Qp88OYMOToEgy/pgesmXSBe0SKuQ6RvmvrByVXOIM8NJEACJEACJEACJBBMBCpZBFoEqhGpDunsiClrTrL8qHA1qReyqjtK6uXiDbJdBwdqOXbsOOo2jIfq3xcfmYKk2gm4/+EboBN0L5Pc5w/f+QKNW96IRLGxK5Tc6QU/bsEPX23Aw89MQkRMBP730UzMmbkcF13aX47QPmirLCRAAiRAAiRAAiRAAsFMoJLlQEvOsQpVccPQnxD9cd4dmRnQuGc4N3hZKM5bPnToJBJqVUdmZiYO7cvE1RMvQmh4HvJD89F7UFvExsRjz5aD5hy2kDB8/81qDB3bHk3a1EW9RjVw+dUXYNXPB6QvDinvUO7WspfTczMJkAAJkAAJkAAJkEClJlCpBLR6MhfYs0VEi82c2MlBNLM9V/mHIl826X61qPNdCiVY7RC5x48eR3LdWpLjLAMEw4oHBpoAtXg96yDBxDo1HbpYBh+279gCvyzfU9S8DWtWb0JcNYlXM23DN3LuJQESIAESIAESIIEgIlCpUjh0khNbSBQKC0Lww/QFWDhrNbLz7bh4TB8MGdZHbosoai3FYWnHeol/i58ZjkoKR/fu7STSHI32nerj80/mY8x15yNMItDf/G8Z8vNzUb95HSPWd+8+jIzMw9i+7hBe+Pt/ER0XiY2bduP+R68WFS+CXJtlDnQJ0lwhARIgARIgARIggWAkUKkEtKpUm60AM75aibk/bMStd401kedXn/sSkWFxOH9IGzO4T0PGqqGNjjbpFXbYRWhPeW8xtm/dgdFXDkTnnq2QnZGBGgkxEkC249obhuEPE1/FwiVrEBEWjtjIGNz94JUIl8j0rBnLsG1rCi4fNxA33haP9av3iguHHdffNgIx1UNNBofGrxmJDsaPCK+JBEiABEiABEiABEoSqFwCWjMvJF1izeqNRvA2a1tDNkTj2glDsXLFOhHQrUXG6nTcebJdp+kWKa1ZHWFhmPrJj9i7/RT69OuE15/9AY8+Uxd5mdFiRacez2H48ovvMe66vug9oJ0ElHNQK6k2jh9OxRsvfonGzZJx6+0Xm8GGhYVh6NK7hWnb+ocZHBYJvpIACZAACZAACZBA8BMozmeoNNeqUWg7UlIOS4/Vh9mGlEMp2CmD/U6kZIiADpUtGg/WdA5RzzZHvvOJk2lo1SEJ/Qd3FlcNu6RjZCIiKgrh0eHYtvEAdmw5iotHdkNCnQgjnuf/JHZ1736OS0b2x9BL+knqiAKKkHZNrkaRSHe0rXtYSIAESIAESIAESIAEqgaByhWBllQLzcgYc8WFeO7JD7H3YIoI20hsWLEV3fq2x/OPT0GL1o1x6eg+qFMvQe6gjDCUAYOFMqvguAlD8PLT0/DZpz/jtrv6IScvR9I3omGXYPXkD7/EddePFQeOCJw+moopH30jsw8C1900Bl99vhAb129CbFQCho3sif4XdZZ2dbrvcGm7arxJeJUkQAIkQAIkQAIkQALFBELEaeI3h1EHJI83LS48NLm4ZT8sqftGYYEMJRTj5sP7j2HBgjWSglENffu1l9doZGXkY9bMJVj80wa0atMIl47pi6T6iS49ycXM6XpMrHhB5+PksVTRwGE4JZOnXDlxGFYu3iT51SswZGRnSeXogNeem46CnFBcO6k/juw/iWce+xD/fO52mbmwdtGAQZemuUgCJEACJEACJEACJBCwBMpSr1YqAa2DA43cF8kf4sipKLpJeUUpFZEiiEORlZWLuTNXYMHstWjVuomkYfRCUkONSOfj4M6TePGpaagRXx0xceHIyj6JO+65FtM+/x6nT+Xjht+NRDWJTKemZOG+O5/Hc6/8H2KNBo/GR2/NRLVqURh9zXnaFUagA/Yjwo6RAAmQAAmQAAmQQEkCZSmgK1cKh8hjM2CvROqE+j5r1nMM7GInp/bQGlS/ZFQ/XDS0N+b++DNeevo9tGrbAj37dcYHr/+A5fP3SH0R24X5aNY2Ea8/9wU6dW+KoZe2xapV67B+1WGkHEzHiePpOHDoCFolNjETDR7Ytw8DJIdaU0PUUk+j1ywkQAIkQAIkQAIkQAJVi0BQKUCdQ+XTD2dgyYLNSEisgT/dM1bSMfphyKV9sXj2Ojz+wGQc3J2FyPCaiIwIRUF+PnZuTjXpHxvWHsCaX/agYdOaGDi4HZq1boAVS1rh+aemoHuP9jh24AQyc3LQs28ncelQlR5K17qq9Vnh1ZIACZAACZAACZCAIRAEAjrEmU1x+NAxzBHP5n+9dC/+N+UbPHL/G+jcu72I3XyEhkrYWiLTkZHi4iE2d4X52QIgX6zpbDh9Ohu3X91PRHM9mdSw2Jhk0NBuaNepKVYt34aO3Zqge882xrXD5G6UiILz3UQCJEACJEACJEACJFBVCFR6Ae0yZQqqV4tFXEwkfp6/Fvt3HUGP3u3QtU97cYYuELcNO+Z9s1kmVMlDeGi4pF+o3Z1O621HXm4Bvv1yiUSWs1EzMQG1k2uiTnI8kpISkZgYj2GX6SyHjjLrW5lUZe1edOvZFr0vEnHOQgIkQAIkQAIkQAIkUKUIVHoB7Yg/yz2TabRj42Pw+3uvwczvlmDwiIE4/6KOEiwOdd7Q4ZcPwDN/m4mE+Gxx8hAbOhkIePJkBm6+awiuurk/0k6exrZNB5Gelin5z6nYsGGb5D5HagAb1WtGoyArAgt+WoOxE3pg2n8XoUn7ukhKTjQ51yGcTcXJmQskQAIkQAIkQAIkEMwEKr2AdlphSEqF3W5Hi3aN5KexuWeFhTLYT207JGc5P8eOw4f3Y8Kt3bFq6RqxpctAZFQIHv7rWBw6vg8/zliMHRtTsG39VoSHV8Pl152HITf2lUYLkZGejoyMHMyeuRJtOzVAlx6t8el7S3D02HEjoIP5DcJrIwESIAESIAESIAESKEmgOOG35PbKtaaWcpKooTnNBTIziqZi6HpISIRMtCJzB4q4fv/tL9C4RTLueGgknnjlD+g9uAUeePJaVKsZgUm3j8OCmVsRV60a/vny3fjDvWPx/jv/xerlG81MhrFxsZLSkYCxV5+HrJws/O3eN9BNpvNu06a5npiFBEiABEiABEiABEigChEIggi0dbeMijbWcjZ7CJYt2ihTfKehXefGWL9mo+Q9R2D42IGStZEqqR5hCIsuRJc+zfHuGzPQrVcz5KYXYvioroiOK0CjlnVw/sABWCczHHbt2U6OETEu+jw8Mgx3P3AlcrPzERGjqSGOkYRM37DuAV9JgARIgARIgARIIPgJBEcEuug+2ULCkC+zdz/39KeY9sk8pKScwjMPTsEvS/dg4qTLzGBCFMr03TJ8sECi1eHRYWjSrC7WrjwgUeo8rPtlt7QUhUJJBdmy/ghiY2rIukzeYlPfZ13U6bsLEBEl2GRGRBYSIAESIAESIAESIIGqRyCIItAiaiVdY8Oa7UhLzcQTr90mk6rYMHJMfzz92KvIyUsX/+coucMyIlAGHIYURIkzR7ZMrtIEU/4zB7f8cQTefeVrLJRpwA+kpCAuNhwXj7pC6kuUuTBC2rIEs7yG6HJQPXtUvXc+r5gESIAESIAESMAQ6N90wq8mESIz2DWRFNn3v3sCYWHFxg3a4IwvFuCJP78jqbUFzvY12HnHQ1fjqpuGOdBeQQ8AABnSSURBVLdZC3dd9zRWSgaBa31rn7fXRbs+9rbLr9uDR0CLKFate+RwCurUijfiWcVyfHysRKVDUJAbBltshMAMk3QO9YUugC00Eom1oxEj03PnyX/3PT4eq3/ehKiYHujcs7mkc2h9lcquYjl4kJmL4z8kQAIkQAIkQAIk4AcCmgprxFmJtguxac2OElsq44qrMqyM/Zc+a0S4qOuFdvFnboPtW3dj4Y/qBX0cb740BS1a1UdcjRipmY/cnHxM/uB7rFi0E99N/dmka/Tp3xnffLsU8bXiMGh4T/QZ3ArRMeGyz9G8SYCupHTYbRIgARIgARIgARIobwJ5uXn4Zdlm0V4qpoqLJMZiwy87kJWZU7yxEi4FgYAupl4oilfdMibdNg6zvlmJV56eioTa8bj5jnFm2m6dPOWHr5dg7/b9ePXDuzHjq4XYvGEn2nRsjMyMNBzcf6SoMbndkgftEOdW6kbxebhEAiRAAiRAAiRAAiTgncCubQewf0+K2Am7CWhZP3LgOPZsP+j94EqwJ6jyEcxTjj0fbbs2xj+63mjSnSHj/ux68zTFQyLQtWvXRlaGHQf2HhJRreJYUjvE565PjzZ4+ZFv0LV3M3Tv1xrN29WTm54n+yWfR3yknVHuSnBT2UUSIAESIAESIAESKC0BzWN2Le6i13WftWwdo68F+cU5ztb+1T9L9LnAShGwtha9ilva2pVb0aZT0xI7tB1tz5okz1M/rPOWOLACVoJAQBfdHHkJKQyT3GddF8EcIoMFw8M0wUOKDBo0gwAL0HtgOxw+koKPPvoCw6+6AG07NsHRQ6cwY/rPaN+htbGne+Olr3D51YPQd1BrOVZTRKQtFdJU0cKAhQRIgARIgARIIJgINGya5LwcnYDu4N4UFBSUjBw7K8hCZFQE6tavVTQTsw0NGtcW4Vukx4oqrly0QZY8f4uvaRya3nHljUNdm0Vyg9o4cTTVDCLU9g7tPyqptxrMdJTQ0FAkN6xtAp/Wtop6DQIBXYxOXTccRW+iYwCgLhXf00gR0sDoKwdh9LhBRXrYjnmzVqJ1m2a4+e4RUjsfHbs0w1OPTUb3PneLZZ20o7MZFjcidVhIgARIgARIgARIIDgIfDjjSeeFqIC++/qnsXb5No9uGBKSRHzNanjtvw8htlqM4zgRW6GhlgYDTp9Mx0YZKOgpgqwHaMaADiTMSM9CbFy089z3PXmTjD9ziO7UU+m4YcSDOCmCWgW3TQRc287N8NLkB0RAF5/LeXA5L1R8D8rtgo2UNmczN1RmRrEXamQ5X25wAerXr1/UEztqJ9UQG7sajkGEJvnd8xNUuXWdJyIBEiABEiABEiABPxEIjxCHsqKfiMhwSWdto9/dezybitljR05KKmyK85hw+cbftWxetxOnTqQb4eu63VpWkX7syCns2nrA2mRe1QbP6ofmUFviWXfKvNKSYtvORL+tOvpaUaUKCehixI5gsopim4jncPTs0xHfTV8gT1ubcXh/Ot57+xt06toEkTEaxZa8nhCdGpwiupggl0iABEiABEiABIKVQOdebRzjx7xdoIwNW7N8i7e9WL5wvRG8XivoDmlj7QpfbayTL/+LfaXVG7pbn3Y+myzPnVVSQJtJUApDzdOV3Z6FJq3q4K6/XoFpn/2Ipx+ZgoTEOFx9Qz+JQGdJOrWMQpSJVFhIgARIgARIgARIoCoQaNmuMeITYo1O8ny9ksMsgwQ9FbvkTq9euknCjt5zqB3HeW9D0zhWSRtmTJv8q9HwmrWro1X7xp5OWSHbKi72XSGX63JS+WYiRGcktEWaFOdWnRrj4af/KCNJ7QgN1+eKPLPdHCGz5rCQAAmQAAmQAAmQQFUgUCOhmojVJlixcKNJc3W/Zk2F3bx+F9Jl5ue46kV50EWVDu5LgaZfeMt/tto6Wxs7t+yXKLjj23913mjbqRmq14izDq/w1yoagS7iLiLaJl8POL8ikHWHeNb94bJdos+eU4Aq/MaxAyRAAiRAAiRAAiTgLwJdJI3DmwjSPGjNT96xZd8Zp1+zfCvycs4WfdbEWEcb2zfvPaMNtbjLzdZxalb6bAh69O9wRr2K3FC1BXRFkue5SYAESIAESIAESCBACXSRgYRWCoXnLkoe9LIzc5hXLFrvubrHrV7aWKgWeMURzJDQQnTppdbCgVMooAPnXrAnJEACJEACJEACJBAQBJq3boiEOtVN/rHnDjm8nF33ZWVkY93KbR7TPlzrFS97aEOm+NYItJVDrekb9RvVQZMWllta8dEVuUQBXZH0eW4SIAESIAESIAESCEACmtvcukNTSWf1LBU1h3nbxj3G89nq/vbN+3Dk4AmTnmFt82aHp/u1ja0bdovlXZpVXazt9osj2jFnDrXa13Xq0QpqrxdIxTMVP/QwPz8fR4/KjDK5uUhNTUVWVpb50fXs7GxkZmaa9dOnT5s6x48fN9tTUlJw7Ngxs23//v04ceIE7HY7cnJycOTIEZkppwBaV9vct28fDh48iIyMDLNN29Z9WkePsX7Uf1Dr6Dl1m7ap/dG62k/tgx6jx2td3Xb48GHnMXpuq096rNbTa9N61roer/3T8+ixBw4ccPZd6+p2Pbe2Y7HRc7GQAAmQAAmQAAmQQCAQ6Nq7rXSjOJXCtU8mh/lYKrZv2uvcvHKxpF6IQYNVbDI7dFuZnM5b0TZOn8wwQtyqs8K04SpPC8X/ub21O2BeXXvo106p6JwzZ45THKvQnDp1qhGQJ0+eRHp6uhHBKij1Z+HChUZA79mzx4jltLQ0zJ8/H7NmzTLCdO7cuUa0qlDVZRWkKny1vgrTFStWmPNt3bpVZsfRgYIys7oIVK2vYnnTpk1GuOpsNuvXrzfiW8+pgl1FuNadN2+eYbJq1SqsWbPGKeK1r4sWLYL2acGCBabvs2fPNv1bunSpOf7bb781+/Xa9AFBxb8KZW1HxfSMGTPMdbz77rvYtWuXOZf7NJh+vSFsnARIgARIgARIgAR8EOjUU/KOZeI5b0VNGNbIHBpaVDetXLJRl8y6Cu9q8bEY/7sR0AlSvBWNMLt6SpecAjwEEdFh6NitpbfDK2x7uQhoK7IaHh4O/QkLC0NcXBzq1atnhG5kZKTZrmJWZwRUEdyiRQvExMQY8aniODo62gjVmjVronbt2oiIiMCGDRvMDVPhqdv1mKSkJFSrVg3t2rUz+3v27GnqqIj95ZdfsHjxYiNYtR/Vq1c3+/S4HTt2mHZVzDZo0ACHDh0yEWoV002aNDHrKsS1jxrp1oi3XoduU1HeqVMnE8HW+irQtY1mzZoZ4a7HJyYmok6dOti5cyfatGmDGjVqGCHdtGlTs01FPwsJkAAJkAAJkAAJBAqBZi3ro05ygtEynvtUnMN8POUUtoi1nV3SMrTYRJs1bl4ffc7vhDr1Er2mgqjgtgT08aOnsUVSOjS1Q4vqu2atGiCpfi2zHkj/lIuAVgAqNjWyrAJVI7gajW3durURyZpKkZeXZyK8UVFRJuKsQlq3qdBWwawCODY21ohjPb5t27bO1AcVn/qjqRR6jAp2rduwYUNzXj2/Rrw1pULb18hxcnKy8z6o6NbIc/PmzU0bKta1vvZBRbeK7Q4dOmD37t2mvcaNxWA8Pt4IZxXPWvScQ4YMMSJa+6yCXEW4RsV1n16v9rFu3bomGq3nUxGtArxVq1amT84OcYEESIAESIAESIAEKphAdGyU8V/WKLGnokJ3x6Z9yEzPxsY1O5CVnivVrAi0DV16t0ZUTGRRG8WpHa5taRuaBpKelonNa3ciIzVLWnC0oefV2Qc1FSTQSrnMEKICUkXo8OHDjRDWyLOKXd02aNAgI0Szs7MQGRlhRGbv3r1NhFnFqUaTT506ZSLL559/voka63YV3XqsimuNMqtAV4Faq1YtI1hVKGs7em4V0CqYNXqsUe2NGzcaAaz79Ee3jxw50rTdr5/MQCjbVHwnJCSYaLj2TdvVqLJGnlVgd+/e3YjxHj16GJGvx8TFxWLSpElm/cILLzSiPCmprmmvVq3aRkTrcRphHzBggInAa99UqI8aNcrZ10B7k7A/JEACJEACJEACVZNA1z5tMe/7VR4v3uQwn8qAejmvNjMTFgtdddHo3teRu9xN2pjz7QqvbaSdzpQ86L1FsxuqWHdEoE0b/QJn+m7XCygXAa0iUYsKZ0exIyoyStNjpBRKFBYinh2zy9jtBYiMjpTNkvciOzS9wioqfq2iKRuOp5xCaERYBaymdWj0V5e1bqNGjazqRiSriNYoeMeOHeV8cg6XomJZS2ioA4mu61SS2rZVtF2rnopefUCy+qSiWp+iEhJqmPNrPauu1qtVK9G0FyJPURp5t4pGvbVdFegsJEACJEACJEACJBBIBNQBQ32YofOaeCgaJV4wcyXWrXCxnhOBl1BLZzN0aKiO3VvCJvLKnuehAdmkbSz6aRXWurVRIyEOrWVGxEAs5SKg9cItEe14qih6QpH7IfNpG3AodHw9oFF60a0Obe2RmDnIZY+jreL2Xc9VXE1FqiWANeJsFdfjdJvR+noK7YNU06crXbVJj9zrunfSYfViL1nP2V25TnNa3aCliIEuFT1gmM38hwRIgARIgARIgAQChECjZsmo16A29u9JMYFC924VFhZgxhcLkCke0MW5yzr1dnPn1NsNm0obDWtj364jzjqu7Wgb33+x8Iw22sj03fEyrXgglmIlWV69U6FcZHGiUlKyLhxaUvWk+REBimxZLn5MUeFbsjhC+6YdF7uUknXOXCu1UDXaVs9RdB4XsVuyVbt5I1jiXPcVyvXpj7OUaMu6DrPRWYULJEACJEACJEACJBCIBCKjItCuS3NRQi7axqWjGmY8dTwNOdma/2yVEHTvX2w9px7O7bu2OKc21D+6e9/ATN/Qq/RMw7p+f70aoaxiU/OTbTh2OBXT/zsXH779DY4ckEF3dsnpKCy2PNF6joGCQEF+iORMu4rb0nVSxbP+uEafPR2Zk5WLr7+YLbZ4IuKNcLZEr3tt7ZPUkP5ru5kZOZIAL4nv5pr02lzr64ra6CluufgS+1zrcZkESIAESIAESIAEAouA5jD7Ko7v6otrOKbe1qnAi4ujDe8CyL0N2Oxw+FAXtxFISyEi+LxfTSl7OiB5vMeaCw9N9rBdT2ed0mYMtP/50Gvo06sb0tKzcCrtJO66b4JDu5rUBhWqjmNefeUDjBxxKRo3TRLRqhFqzUBxfwbQur4ivL73p53Kxu9vfBIvvnE3aiXVkLYKpLcmgUOWSxYlt3LFGjRs0BDr1m3G8WOncNmoC8SabzUGntfXpRtF55SXn3/W+vXl6xDfOc/emJbsAddIgARIgARIgARIgATOhYBnfXouLTgU6Lkd4aF2x56tsG751jP3GB8/myRCiI2bPRthIRESAdbIskaQVfgW4NTRVMSExWHsxAvN9vTUdNlbIKnRjsiuqlCbLdvkRY8cPRyJCeLdrPultiWeC+z5sm6XehGyzSFWC2WbZryHhFiDFbW+zEhYkCn1JJ/G0tgSRi6EiPGQcBNN1lpxkfFSR56F8jWdJBR5hfmICBeXj8Is8TWMRkGeHaFhjoj28kVbUNgjCoMG95btMkNhymksmr0F/fv1lmMlncOWLm3LtRRIP2QWyhXztiLq/GgkNxBfRdmfVyBuJKER0gftd1E+uHaChQRIgARIgARIgARIoEwJdOrVqkzaK5NBhK9Pf9hzZ0R4WkrVJgI1N9uOqZ/MQ4pMZd2iRUMMH9ML9RonikdgPN545ksR0QNQO0kisw4NjDUrN2D5gp2omVgdl17ZEwf2HUA1ceiIE8eLr6fOxfYtaWjXqQ6GjuqOlEOnMH/mFqSKnUpuXiGuuK43atWujuOH0jBv7nIclrnZh43uKZObNMTy2duwaNkm1JFzjbumN8IiRcwXnVOFeKiI73Bx6Zg/czU2r9uDw2mn0Lh+Q1x7wwDs27sHH74zHQ3qN8Pl1/TBulV7cfKo5P3Iw0JWTgYKC2xYOncbprWeiT07UjFqXG+oEfl7b32HSy/rhY2rjsj2GUhMHou1v+zD5k07ERsXjdGXD0RSPYcTiMIsi6cjzzeFW0mABEiABEiABEjg3Ag8df87+PZ/CyWY6MWOo6g5m8xO+Lfnf4eLR/c/4wT/evA/mD5lfqna+Ouzk3DJ5QPOaCNQNrjnP5Rtv8RhQ8Ks8iNx3JAwTH7nW01iljSH82S2mr34dvpCEaoRuPuhcWjePgkvPP4/TJ282PThp++XYsnCDTjv4k6oUScamam5WLV4F7JT8zBvxjKJ9B7FyLHdsWrZGrFP2YCMk3mYPWMxBlzYEfl5afjqsznITLPj9Vc+R6Om9dC7fyecOCKz5KzZhRnTZ2LYyK5ie5eDTz+eId2T0LDpqJ5aOyyRcok8Hzp4XEZ/xuHP908QgX4AO7emYMXCLagrlnTDhvdCDbGs6yb2LpeOHCj5zSE4fjQD7Tu2wIALOmPkqIuwe0cKcjJ1GvEw7NstbVWLRxepP/Hmy7Fq0T7s2HgQN9wyGu1atsBnHywSEV6c9609YSEBEiABEiABEiCBQCDgyEfWaKOvEiJWxGHo4GXq7a4yKYojYumrDfnCPjI0IKfvdu21fwV0kSjVk+TnFGDDqp2IjozGtm07Jb84Xmb7S5E92YiKtWGICNIH/3kz5vw4BwfE5mTp3M246qrhaNWuLi4c2guJtWtICoikPOSKgJ69XvyX62HLtgMys19TEbdH5WmmEN36tkWrDvUxaEhvIC9cxPV6tGxTDz36tpaRnE3Qo39nzPhmkUS8a2LP7v0ID4vCoQMpEhnPEd1c9KbQgX6FEpiX1fDwArRsX0sixBFo0rSxDCxMx4hxAxARW4Bpn88xOc8RkpkRGSVe1mE6orBAbrod4RHZiIgJE9/EHNjUO1FTM2R/aIQ8SITnIjouxMxSeHh/Oia/9QNWL9+OfEktsWY1dL1BXCYBEiABEiABEiCBiiagThwqbIsDjmf2SKfv1qm3k8X2zlNp17kZIqJ8t6HmDE3lm3u1vQvkUiYpHN4vUKWzRnQ1l1im287LRct2DdCuWwMc3ncKmrv84/RVmr2MoZf1kRn+bDK7n4CV2bFjRGjrDIQ169aXlAwRnzIa0+QqiyCNqh6Ojt0bibl2kqRUHDMTrqTK9Nz5oY6vFcJkjhRbiN1M5516ek9RH8KQm5ODmLgEJCXH4qJhvZCRlouGjWuIyFXvZj1Wc6jtkpecIa8yeLEgFAW5jmeMPOmUautjx09jwi1XYcr787Bs0VaJU0dJTbWukyuU9I1Cu02EsFyz/F87KVGm6Ja0DlnJTMuTf2Wf5lxLukd0bCTqN7Vh0h8vw44t+7Fvz0Hph+NccnIWEiABEiABEiABEggYAipo1RN6x6b9Rsd46piOG+vSu60M/VLtd2apW78WmjSvj60b9nptQzMANNod6JrIzwJa4emAQZnhLyIMl024EK+/NhV9JRK8Yd0mjL/+UrTv0BJ/++vrJt3h2NHjaNGqGeo1qYPhYwfgnde+NEbcOnvgdTeOREysSFwZzDdqzHmY8uFXUrcxNm3ehhtvGyvR3lBERBbl5ch9C40oRKeeLbFk8Sr8+6kpEiWORPMWSbj8qvPw7FNvIeftVOyWtIrkhnHoIgnlOohPb3eIDA6s31oHKoYgNjES4XHhcpMLEV8zFNVlWvHNa/fihSc+kDdAM4wa2x/z5i2WHGqJQkvUulqCDAaUp6/E5Bg5BhgxZgC++24Bli1fh7adGyEsKgw1kiKhLn1jrhqMt175Aq8+9yW2bN6MayZeJCLe8xvOAOQ/JEACJEACJEACJFBBBELDQtF7YEeknxZDBQ0ieygaTOwxoNj/2b2KiuJe53U0Dmze2lCLYF9tuLdZUetlYmPntfOavWBSI8Q3Q7RtaJgN+3cdk8F/u9GgcW20aNNYhGa+3IwcbJE50GskxMq2RhL8lRC0iMljh09j546DaNAwCXXr10RGeppMAR6L8KhwSds4gc0bdqJRk2Q0kVB/ZlY28nJyUa16dUkXyRdD7xzExUt0uKAQ69fsNuK4pbQdJakVmRlZWLd6J8IkhaNTdzH2lui2LbRAnDdULIcgP1+W5fyaKK832Mha06VQiTCH4PDh40hMjEd4dKjxp1ZvaY0qq9BW4WzakyR6HTiZmZGLLOlbogxotEvE3S71FEmoPp0VhpvBjRGRYUioI1OZG16MQnt9P3EHCZAACZAACZAACQQAAf8LaL1I1YqiLHUylFCJFFul0K4eyyJeRWyq1ZuqT8c0kBoPVkGrAXLZJ8JSxaf5SkDqFYovtM18PaDSVlJDnOuyJnVV/OpBhTLpumpSm01CxLrF+ElrO7qmAwe1XY2Qq92d2tLJNu2DrBshbNrRCVA0Hq37dbcIYDnecZxuk/5oQ1rH1Nf2zKr8KyLaPGLptYv1nqSVmDZ0vwhx+Vf2y9Ga/iGpHzbDRrezkAAJkAAJkAAJkAAJBCoB/wpovWqjLuXV6EIJ45oFFcu6s6hYmtF1m1YwGtPa6ahrqjg3OQ4QiWu1VNygiFJTTBvuu13rOwSvs19WVdcq1jbzKjus81vncN3vfj5nXddKRcsiqFW8GztuM0uhLFr1i6rwhQRIgARIgARIgARIILAI+F9AB9b1sjckQAIkQAIkQAIkQAIk8JsImGSG39QCDyYBEiABEiABEiABEiCBKkSAAroK3WxeKgmQAAmQAAmQAAmQwG8nQAH92xmyBRIgARIgARIgARIggSpEgAK6Ct1sXioJkAAJkAAJkAAJkMBvJ0AB/dsZsgUSIAESIAESIAESIIEqROD/ASrAimG6cSKuAAAAAElFTkSuQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='InstanceMethods.png') "
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAAFyCAYAAACNyaN2AAAMFGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdUk8kWnr+kEBJaIAJSQm+CFOkCofciHWyEJEAoERKCih1ZVHAtqFhAVHRFRMW1ALJWLFhYBOz1gYrKyrpYsKHyJgV0fe28e8788+XOvXe+O7kzZwYAZVt2bm42qgJAjiBfGB3ow0xMSmaSegEOMEAHJoDA5ohyvaOiwgCU0f7v8u4mQCT9NWtJrH8d/6+iyuWJOAAgURCnckWcHIiPAIBrcnKF+QAQ2qHeaHZ+rgQPQqwuhAQBIOISnC7DmhKcKsMTpDax0b4QswAgU9lsYToAShLezAJOOoyjJOFoK+DyBRBXQezJyWBzIb4P8YScnFkQK5MhNk/9Lk7632KmjsVks9PHsCwXqZD9+KLcbPbc/3M5/rfkZItH5zCEjZohDIqW5AzXbU/WrFAJpkJ8XJAaEQmxGsQX+VypvQTfzRAHxcntBzgiX7hmgAEACrhsv1CIdSBmiLPivOXYni2U+kJ7NIKfHxwrx6nCWdHy+GiBIDsiTB5neQYveBRX80T+MaM2afyAYIhhpaFHCjNiE2Q80XMF/PgIiJUg7hRlxYTKfR8WZvhGjNoIxdESzsYQv00TBkTLbDDNHNFoXpgNhy2dC9YCxsrPiA2S+WKJPFFi2CgHLs/PX8YB4/IEcXJuGKwun2i5b0ludpTcHqvmZQdGy9YZOygqiBn17c6HBSZbB+xRJjskSj7Xu9z8qFgZNxwFYcAX+AEmEMOWCmaBTMDvGGgagL9kIwGADYQgHfCAtVwz6pEgHRHAbwwoBH9CxAOiMT8f6SgPFED9lzGt7GsN0qSjBVKPLPAU4hxcG/fE3fEw+GXBZo+74K6jfkzl0VmJ/kQ/YhAxgGgxxoMDWWfDJgT8f6MLhT0PZifhIhjN4Vs8wlNCF+ER4Qahh3AHxIMn0ihyq5n8IuEPzJkgHPTAaAHy7FK/zw43hawdcR/cA/KH3HEGrg2s8UkwE2/cC+bmCLXfMxSPcfu2lj/OJ2H9fT5yvZKlkqOcRerYP+M7ZvVjFN/v1ogL+9AfLbHl2GGsDTuDXcKOY02AiZ3CmrF27IQEj1XCE2kljM4WLeWWBePwR21s6237bT//MDdbPr9kvUT5vDn5ks3gOyt3rpCfnpHP9IanMY8ZLODYTGDa29o5AyA522VHxxuG9MxGGJe/6fJOA+BaCpXp33RsIwCOPQWA/u6bzug1LPc1AJzo5IiFBTKd5DgGBEABynBXaAE9YATMYT72wAm4AxbwByEgEsSCJDADrngGyIGcZ4P5YAkoAWVgDdgAtoBtYCfYA/aDQ6AJHAdnwAVwBXSCG+AerIs+8AIMgndgGEEQEkJD6IgWoo+YIFaIPeKCeCL+SBgSjSQhKUg6IkDEyHxkKVKGlCNbkB1IHfIrcgw5g1xCupA7SC/Sj7xGPqEYSkXVUV3UFJ2IuqDeaCgai05H09E8tBAtRlehm9AadB/aiJ5Br6A30B70BTqEAUwRY2AGmDXmgvlikVgyloYJsYVYKVaB1WAHsBb4P1/DerAB7CNOxOk4E7eGtRmEx+EcPA9fiK/Et+B78Eb8HH4N78UH8a8EGkGHYEVwIwQTEgnphNmEEkIFYTfhKOE83Dd9hHdEIpFBNCM6w32ZRMwkziOuJG4lNhBPE7uIj4lDJBJJi2RF8iBFktikfFIJaTNpH+kUqZvUR/pAViTrk+3JAeRksoBcRK4g7yWfJHeTn5GHFVQUTBTcFCIVuApzFVYr7FJoUbiq0KcwTFGlmFE8KLGUTMoSyibKAcp5yn3KG0VFRUNFV8UpinzFxYqbFA8qXlTsVfxIVaNaUn2p06hi6ipqLfU09Q71DY1GM6WxaMm0fNoqWh3tLO0h7YMSXclGKViJq7RIqVKpUalb6aWygrKJsrfyDOVC5Qrlw8pXlQdUFFRMVXxV2CoLVSpVjqncUhlSpavaqUaq5qiuVN2rekn1uRpJzVTNX42rVqy2U+2s2mM6Rjei+9I59KX0XfTz9D51orqZerB6pnqZ+n71DvVBDTWNSRrxGnM0KjVOaPQwMIYpI5iRzVjNOMS4yfg0Tnec9zjeuBXjDozrHvdec7wmS5OnWarZoHlD85MWU8tfK0trrVaT1gNtXNtSe4r2bO1q7fPaA+PVx7uP54wvHX9o/F0dVMdSJ1pnns5OnXadIV093UDdXN3Numd1B/QYeiy9TL31eif1+vXp+p76fP31+qf0/2BqML2Z2cxNzHPMQQMdgyADscEOgw6DYUMzwzjDIsMGwwdGFCMXozSj9UatRoPG+sbhxvON643vmiiYuJhkmGw0aTN5b2pmmmC6zLTJ9LmZplmwWaFZvdl9c5q5l3meeY35dQuihYtFlsVWi05L1NLRMsOy0vKqFWrlZMW32mrVNYEwwXWCYELNhFvWVGtv6wLreuteG4ZNmE2RTZPNy4nGE5Mnrp3YNvGrraNttu0u23t2anYhdkV2LXav7S3tOfaV9tcdaA4BDoscmh1eTbKaxJtUPem2I90x3HGZY6vjFydnJ6HTAad+Z2PnFOcq51su6i5RLitdLroSXH1cF7ked/3o5uSW73bI7S93a/cs973uzyebTeZN3jX5sYehB9tjh0ePJ9MzxXO7Z4+XgRfbq8brEcuIxWXtZj3ztvDO9N7n/dLH1kfoc9Tnva+b7wLf036YX6BfqV+Hv5p/nP8W/4cBhgHpAfUBg4GOgfMCTwcRgkKD1gbdCtYN5gTXBQ+GOIcsCDkXSg2NCd0S+ijMMkwY1hKOhoeErwu/H2ESIYhoigSRwZHrIh9EmUXlRf02hTglakrllKfRdtHzo9ti6DEzY/bGvIv1iV0dey/OPE4c1xqvHD8tvi7+fYJfQnlCT+LExAWJV5K0k/hJzcmk5Pjk3clDU/2nbpjaN81xWsm0m9PNps+ZfmmG9ozsGSdmKs9kzzycQkhJSNmb8pkdya5hD6UGp1alDnJ8ORs5L7gs7npuP8+DV857luaRVp72PN0jfV16f4ZXRkXGAN+Xv4X/KjMoc1vm+6zIrNqskeyE7IYcck5KzjGBmiBLcG6W3qw5s7pyrXJLcnvy3PI25A0KQ4W7RYhouqg5Xx1ec9rF5uKfxL0FngWVBR9mx88+PEd1jmBO+1zLuSvmPisMKPxlHj6PM691vsH8JfN7F3gv2LEQWZi6sHWR0aLiRX2LAxfvWUJZkrXk9yLbovKit0sTlrYU6xYvLn78U+BP9SVKJcKSW8vcl21bji/nL+9Y4bBi84qvpdzSy2W2ZRVln1dyVl7+2e7nTT+PrEpb1bHaaXX1GuIawZqba73W7ilXLS8sf7wufF3jeub60vVvN8zccKliUsW2jZSN4o09m8I2NW823rxm8+ctGVtuVPpUNlTpVK2oer+Vu7W7mlV9YJvutrJtn7bzt9/eEbijsca0pmIncWfBzqe74ne1/eLyS91u7d1lu7/UCmp79kTvOVfnXFe3V2fv6nq0Xlzfv2/avs79fvubD1gf2NHAaCg7CA6KD/7xa8qvNw+FHmo97HL4wBGTI1VH6UdLG5HGuY2DTRlNPc1JzV3HQo61tri3HP3N5rfa4wbHK09onFh9knKy+OTIqcJTQ6dzTw+cST/zuHVm672ziWevn5tyruN86PmLFwIunG3zbjt10ePi8Utul45ddrncdMXpSmO7Y/vR3x1/P9rh1NF41flqc6drZ0vX5K6T3V7dZ675XbtwPfj6lRsRN7puxt28fWvarZ7b3NvP72TfeXW34O7wvcX3CfdLH6g8qHio87DmHxb/aOhx6jnR69fb/ijm0b3HnMcvnoiefO4rfkp7WvFM/1ndc/vnx/sD+jv/mPpH34vcF8MDJX+q/ln10vzlkb9Yf7UPJg72vRK+Gnm98o3Wm9q3k962DkUNPXyX8274fekHrQ97Prp8bPuU8OnZ8OzPpM+bvlh8afka+vX+SM7ISC5byJZeBTDY0LQ0AF7XAkBLgneHTgAoSrK3l1QQ2XtRisB/wrL3mVScAKhlARC3GIAweEephs0EYirsJVfvWBZAHRzGmlxEaQ72slhU+IIhfBgZeaMLAKkFgC/CkZHhrSMjX3ZBsncAOJ0ne/NJhAjv99ttJKiz7yX4Uf4JEL9tBtKO/vwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGdaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIj4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjMyNDwvZXhpZjpQaXhlbFhEaW1lbnNpb24+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj4zNzA8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICA8L3JkZjpEZXNjcmlwdGlvbj4KICAgPC9yZGY6UkRGPgo8L3g6eG1wbWV0YT4K5ekzvwAAABxpRE9UAAAAAgAAAAAAAAC5AAAAKAAAALkAAAC5AAAotLGEljsAACiASURBVHgB7H0HuBXF+f6gFFETwAYiXVBAgoBgQBEBDUUBQYolwKOClBDBiESa+lii1Aj4JKETEUFBiiCIAQEVpAsICtKrBVSE0ARk/t+7/8z8dvfs7tm995y9u+d+8zz37u7MN9/MvLP7nqnf5JHkhIc7deqUuPTSSz0k0hvE6TP+/P7x95delvk/7XmYEP8PDKc7JmQmZCbk3EPITIhOLGjyY0JkQmRCZELUlMCEwITAhJB7CEF/+P+7yW3fP7cQ7W+A7Tm3vRC24gsuP/8g5qYfRE9CzJMnj/374GdGgBFgBHIEgSTzvynJExNiSmBkJYwAI5BuBCJDiGFkJN1gsn5GgBGIJwKqpxoGD/lqIYaRkXhWFeeaEWAE0o0AE2K6EWb9jAAjEBsEmBBjU1WcUUaAEUg3AkyI6UaY9TMCjEBsEGBCjE1VcUYZAUYg3QgwIaYbYdbPCDACsUGACTE2VcUZZQQYgXQjwISYboRZPyPACMQGASbE2FQVZ5QRYATSjQATYroRZv2MACMQGwSYEGNTVZxRRoARSDcCTIjpRpj1MwKMQGwQYEKMTVVxRhkBRiDdCChC/O9//xs4qcsvvzxQHDbuEAguFmYEGIGwEQiVEE+ePOl66t5ll11mlJ2t3YT9CnB6jAAjoBBQhHjkyBHl5fsa1No3txB9Q8uCjAAjkBMIKELkLnNOoM9pMgKMQKQQYEKMVHVkfmaOHz8uli9fLpYtWyY2bdokfvzxR+Pv7Nmzonjx4qJEiRKiZMmSokyZMqJdu3bGc+ajwiWMCgJMiFGpiQzPx4EDB8SQIUPE+PHjxZkzZ3yV9uKLLxYtWrQQPXr0EA0bNhTqZfUVmYUYgSwgoN4x7jJnATyO4g+Bf/3rX+LJJ58UaAVm1bVt21ZMmTJF5M+fP6sqOB4jkBQBJsSkELFAVhHAigG07kCIqXCNGjUSs2bNEmpFQip0sg5GwIwAE6IZDb5PKQKDBg0S/fr189RZpEgRUaVKFVG6dGlx6NAhsXv3brFv3z7XOPXr1xdLly51DecARiA7CDAhZgc9juuKwIoVK8Sdd94pfv311wQZvHRPP/206Nmzp+OkyWeffSaGDx9utAYTIpPHnDlzxH333ecUxH6MQLYQYELMFnwc2Q2BBg0aGDPJ9vCiRYuKyZMnC3R/k7nXX39d9OrVS9gX61erVk18/vnnnpMsP//8s9i2bZs4ePCgwITO6dOnRbly5UT58uWNv8KFCydLXpw4cUIcPnzYIpcvXz5jFlx5bt68WaxZs0Z88803Rku3VatWKoivMUQgTELEi+3qCDvsYnEN54D4ILB27VqjLlWdmq8rV64MVJCXXnopQRftCJCrV6921EMEJTt16iQvueSShHgqHxdddJEh8+233zrqUJ4zZsxI0HHFFVcYwRcuXJC9e/e2hBcsWFBF5WtMEVDvCM0yy6B/QYvsyXYqI0GVsnz0EHjiiScsRKHqtmnTpoEzi+2exYoVkzVq1JB9+/aVS5Yskb/88oujnqFDhzqmq9K3X2kzvnzrrbccdcFz4cKFCfpApiDDF154ISGMCdEVytgEqHckKBlCPqjjrXuEdm5wRF5iw4YNCUWllqOoWbNmgn8yDyzXSbbcZuzYsaJr167JVCWEY8Z648aNRjfaHvjxxx8LTOLY3Z49e4zuMZG1JYgIUZw6dcrixw/xQiDMLjMTYrzejSzlln4pBWaO7ZMp2H2yf//+LOlMFgkb8bHL5fz58xZRpDly5EhRp04dQa1KMX/+fEHd3ISF4bfffrv49NNPE8YkMbmDMLvDhNCwYcPs3oIJMQGS2HmESYjcZQ7apo6hPG3HS+hK0lch69atm7bSjBo1yjFNdHntbvDgwY6ytNTHLmqMUyLv9r9ChQoZfjQxJOfOnStpQkVu3bpVLlq0KEEHe8QLAVXX3GUmJNhlHwG3bmb79u3Fm2++mf0EHDRgJvqTTz4xZoXRQsXsMI31iaNHjwps/zM7zDiXKlXK7GXcL1iwQNAYp8V/3bp1olatWhY/9YB91jT+KPLmzau8+JoBCITZQuQucwa8MMmKMHv2bHH//fcniA0YMEC8/PLLCf7p8qB2SUIXGGmhK1+gQIGELj32Wffp08eSHTdCBAliHBGGKNhlFgJMiJlVnzlemnfffVdg37Hdvfjii+LZZ5+1e+fIM9YgHjt2zJI2xhbt44JuhNiyZUsB4meXeQgwIWZeneZoiWhZjLjrrrsS8vDYY4+JCRMmJPin2uO7774ztvbt3bvXaMVhIgfWdTDhcu7cOeMKs2P2SZ8ghEhLbsRzzz2X6qyzvgggwIQYgUrIpCxgCUv16tUTigSSXLx4cYJ/qjywUwTd3jFjxiTMIvtJ46mnnjK2C5pl3VqI48aNE507dzaL8n2GIMCEmCEVGZVi/PDDD+Lqq69OyM71118vdu7cmeCfCg8Yg8Dax59++inL6oIQ4rx580SzZs2ynBZHjC4CTIjRrZvY5qxixYri66+/tuQfExHovl577bUWfz8P2I8M5zSJgUXbd9xxh7Gf2K4L/pjggSUdrI1EHjDrjH3UmIk2uyCESMt5ROPGjc3R+T5DEAiTEHkdYryWZGU5t48//njC2j36XiS29GXFkWUbiS1zWPc3bdo0SYYatBoyGuuYFu1akTROqOXUDRGopF0vCXGwL9nu3PZkO61vtMfl53gigPcUf2GsQ2RCjOc7EjjXH374YQLh4CWj5S6S1gEG0ke7RRJ00SyxpB0ohh7aNZIQjrSoe+6YzqpVqxzlqYWYIM+EmABJxnswIWZ8FedMAclElyPx3HPPPZKWvPjKFBmLlbT9zlEPHVRl6Lj77rsTwmENx83R0poEeXwETIhuiOUufybE3FXfoZV25syZjsSDF44mWCRaX14OhEdjf446HnzwQR2VjNA6ysAMmN2BYK+55hpH+S5dutjFjTyqD8R85S5zAlQZ46HqOYwuM+9UIbRzkyOSEVii4uRgvQZb5W6++WZRtWpVUaFCBfH999+LXbt2ienTp7seEwADCpiwgeEGuO7du4vRo0cnJGHfGQNDr7BcQ3uOE2Th4bQsyG3ZDU+qOEKYEZ48qZIxv23RKwgmP8jSjGOLjL6ewP6wX4jxSbP75z//6aqH1kPK/v37y3r16kmaXdZyHTt21PcqHzQDbchu2bJF0qy2kQSPIZqRzh336n0Io4XIkyq5452ylBKk+PDDDycQkHrx/F5hJHb9+vUW3Xgg+4OSjgXwrb9JkyaSdqxIkKtb2s8//7yRDhOiAUOu+qfeCSbEXFXt4Rd24sSJsmzZsq4kpF5E+xUtu9atW0uM/7m5ZcuWSVirtse1P4MM6awVQw2dBugqz4TohnTm+6t3hgkx8+s6x0uIlhkdMCXbtGkjr7rqKldCwktJi7CNLqzfZTogTNo94qgTLcgRI0ZY1iWi5UpmwyxdaaSLliONexpYcQsxx1+Z0DMQJiHypAqhze7/I0BvutixY4dxqh22+9EvssCJfNhVAnuFmDzJioMVm+3btxvbBMmQq6GvcuXKjqbAoB+GH4hMjZ0rRNKiTJkyhi3FrKTNceKPQJiTKnlwYJAbZDjbAg4fCjtGgBFgBHICAUWIOJYiqKP1r4GicAsxEFwszAgwAmEjoAgRPZagjoZbAkVhQgwEFwszAoxA2AgwIYaNOKfHCDACkUWACTGyVcMZYwQYgbARYEIMG3FOjxFgBCKLABNiZKuGM8YIMAJhI8CEGDbinB4jwAhEFgEmxMhWDWeMEWAEwkaACTFsxDk9RoARiCwCTIiRrRrOGCPACISNABNi2IhzeowAIxBZBJgQI1s1nDFGgBEIGwEmxLAR5/QYAUYgsggwIUa2ajhjjAAjEDYCkSPEsAHg9BgBRoARsCMQGWs39ozxMyPACDACYSMQGUJkA7FhVz2nxwgwAgqByHWZmRBV1fCVEWAEwkaACTFsxDk9RoARiCwCTIiRrRrOGCPACISNABNi2IhzeowAIxBZBJgQI1s1nDFGgBEIGwEmxLAR5/QYAUYgsggwIUa2ajhjjAAjEDYCTIhhI87pMQKMQGQRYEKMbNVwxhgBRiBsBJgQw0ac02MEGIHIIsCEGNmq4YwxAoxA2AgwIYaNOKfHCDACkUWACTGyVeM/Y++//75o2bKljrBy5UpRq1Yt/cw3jAAj4A8BJkR/OEVaat68eaJFixY6j2vWrGFC1GjwDSPgH4FQCfHkyZPSLWuXXXaZEcTWbtwQcvdnQnTHhkMYgSAIKEI8cuRIkGiG7KWXXhooTh4iO1dCVBnxEAmUWG4SZkLMTbXNZU0nAoqH2EBsOlFOs24mxDQDzOpzDQIZTYg///yzOHv2rFGZV111lbjooosysmKZEDOyWrlQOYBARhPiHXfcIZYvX27AeujQIVG8ePEcgDj9STIhph9jTiF3IMCEmIV6PnDggPjiiy/Eli1bxOWXXy7Kly8vKlasKEqXLp0FbUJgAPfLL78UX331lThx4oS48cYbRaVKlUS5cuVE3rx5k+rMKiFmN12aJBPff/+9kT+8SGXLltV5XbFihdi4caM4duyYqFu3rqhXr54O4xtGIKoIhEmIApMqbo4AwoSLW3CW/OlDNHRCL7UQs6RDRTp37pzs27evLFKkiNap8qyuzZo1k0QCKorn9fz58/Kll16S1JV31Zc/f37ZqFEjuWfPHk9dc+fOteigZTeu8qlMd8aMGTpdepHkhQsX5KlTp2Tjxo21P7B54IEHXPPDAYxAlBBQ3zJNqsigf0HL4cl2KiNBlXrJp4oQ9+7dK+vUqWP5yFV+7VcQw4gRI7yyJbdv3y5r167tSx/0/+Y3v5Hjxo1z1emXEFOd7nvvvWcpA7VuZdeuXS1+yD8TomvVcUDEEFDfc1AyhHxQF0tCRMvS3CoE4bVp00YOHTpULly4UE6dOlX27t1bFixYUBMBTd7ImTNnOuKD1h6tudSyqADaZSLHjBkj0bLbuXOnnDVrlhw4cKCk7rhFbtiwYY46/RBiOtL94IMPLPlbvXq1BD4oE1q3+BHBX69evRzzzZ6MQNQQYEJMUiM9evTQH/0ll1wi3377bccYIJyiRYtqWZCZ06/GI488omVAnIMHD3bUB090v0uUKKHl0b120umHENOR7pIlS3Te8CJ16NDBeH7mmWeMrrNrwTiAEYgoAkyIHhWzb98+o6WjQBo0aJCHtJSzZ8+2EMTkyZMt8tu2bZMXX3yxlunWrZsl3OnBTjqvvvpqglgyQkxXujSDr8sCjPLlyyfxA8KOEYgrAupb5y6zQw12795df/AgsmQTM7TmURYuXNjoPpcsWTKhq6haUAr0DRs2OKRq9cJERZkyZXQ+rrzySvnrr79ahJIRYrrS/eyzz3S+UCa0eA8ePGjJGz8wAnFCQH2bYRBiSrfunTlzxmLQgAqS4NauXSuwOBsOyz4KFCiQIKM8aBxQ0OyoejSu1apVE5s2bTLuGzZsKD766CNLuNMDzUYLaik5BYnKlSuLrVu3GmE1atQQ69evd5Szew4YMEC88sor2ptIR1x33XX6Odmym3SlC6s6t912m84H8KNxVf3MN4xA3BCgMXAjy0SIgbOOJXiBnNcvBSkyWhteMuYwzGiqOKm4TpgwwazeuC9UqJBOo3PnzgnhQT1o87fW1759e9/RJ02apOOhrGiZmV2yFmK60rW3EIm4zdnie0YgdggoLgmjhZjSWeZ0EyK1LC0k1K9fv2xV7uHDhy36MDPt182fP98S1z6x40WI6UzXToijRo3yWySWYwQiiUBsCRFja1gf6PVXs2ZNTSSrVq3ylMUvgtlhhleBg+trr71mDg58jyU1Zn1YtuPXUdffEnfIkCGWqF6EmM507YQ4ffp0S774gRGIGwLqG41dC9EP0NlZmL1o0SILCY0dO9ZPkq4yCxYsyLI+LKhWFYUrlrWYnRchpjNdOyEiLXaMQJwRUN8ZE6KtFmlvsYWEaFLDJhHs0d7idFo+46bRTjz2rqkXIaYzXXu+mBDdapD944IAE6JLTdnHKHv27Oki6c/bPiYZZPeGfX0jCNDsvAgxnekyIZprge8zAQEmRI9aNBteSMV+XPMWwCD6Ro8ebWmtkqUdS669CBGC6UqXCdFSDfyQAQgwIXpU4i233KKJCAut7QuinaJOmzZNYs8xlvFgdtjsqlevrvWRqSzDOow53O2+S5cuOh4q7Pjx4xbRZISYrnSZEC3VwA8ZgAATokclYvJCAYQrjDl4Ocx8FytWTMdp3ry5RRzmw8z6Fi9ebAl3ekDXHdZuVDxaLJ4glowQ05UuE2JCVbBHzBFQ3xlPqjhUJBlQtVicadKkiWcr0T7WN378eIvWH374wUJusHKTzNm7y04TF8kIMV3pMiEmqz0OjxsCGU2Ib7zxhnz55ZeNP3s3029F9e/fX7fOABZMf9G2wYToZCFamne2YPwRRGR3zz33nEUfdsDAaKuTmzhxomEwQVXSnXfe6SQmkxEiIqUjXSZEx+pgzxgjoL61MFqIKd3LTBkPxR09elTQWKIg8146vVKlSgmc1wJ/mMinxc+CbAPqcOxlpnWMgghM+6kbyN96662C1hYqL+NQebKMbVxxEBb2T5NtQfH+++9rGZz5unTpUiOu9vzfTbK9zBBLR7r2vczUehVNmza1Z4+fGYHYIBDbvcxh/ghh6Urbtm0tLTuqYcdn2EFEy9TLYVzw0UcfdYzvpJcMKMgdO3a4qvTTQkTkVKfLLUTXKuGAmCKgvr8wWogp3cucE3jDqjVmnmEoVgGnrrAQDXNh3333ne+sYU8yLEqbJ02UPrLMI6tWrWpY5k42u+2XEFXGUpUuE6JClK+ZgoD6/sIgxFh2mQmgBEcEJajFZpy6R8cBiBtuuEGQzUJBNhMTZP140Msk9u/fLzZv3ixoPFHcdNNNxol7WdXnJ03I5FS6fvPHcoxA2AiE2WXOGEIMu5I4PUaAEQgHASbEcHDmVBgBRiAGCDAhxqCSOIuMACMQDgJMiOHgzKkwAoxADBAIlRBPnjyJ2VlHh8kJOAz0s2MEGAFGICcQUIRIu9QCJ4+1wkEcT6oEQYtlGQFGIHQEFCHSspvAaQc9ZIoJMTDEHIERYATCRIAJMUy0OS1GgBGINAJMiJGuHs4cI8AIhIkAE2KYaHNajAAjEGkEmBAjXT2cOUaAEQgTASbEMNHmtBgBRiDSCDAhRrp6OHOMACMQJgJMiGGizWkxAoxApBFgQox09XDmGAFGIEwEmBDDRJvTYgQYgUgjwIQY6erhzDECjECYCDAhhol2Lkurfv364uDBg4LOjxEDBgzIZaXn4sYRASbEONZaDPJMR7CKq6++2shpr169xIgRI2KQa85ibkcgowmRTssTZ8+eNeqYzkkWOOKTXTgI4AjV5s2bG4kxIYaDOaeSfQQymhBxdvLy5csNlA4dOiSKFy+efcRYgy8EBg4cKP72t78ZskyIviBjoQggwISYhUo4cOCA+OKLL4xT92ADrXz58qJixYqidOnSgbWha/nll18KEDb+cKJf2bJljb8KFSqIIkWKJNVJhnfF999/b8ihQhFfuRUrVoiNGzcaB9XXrVtX1KtXTwWl/Aobcsqw5iOPPCI+/fRTIw2MIYIglbviiitE4cKFBXA8d+6c4Z0vXz5RsmRJJeLrCrx++eUXQzZv3ryiVKlSxv3x48cFcIWz43HhwgVBx6eKXbt2CToyVlx77bWievXqolKlSgI6suLQE9myZYvxBwxwamKVKlV0frKik+PkDAJ4X+DCsIcY+rnMRAD6/GT6eLJ1dCx9uLJv376SCErrJNws982aNZNEPr7SWbVqlfzjH/8ocZ6zXY96JpKQf/7zn+Xhw4c9dc6YMUProAqV9NHLU6dOycaNG2t/6HzggQc89WQ3cNy4cZb0VDns10GDBhlJPfTQQ1qejlyVQeqIXlhZsGBBHf/+++/X2R8/frz2R9rAAm7ChAmSSNMSpvKGs7a7dOkiiWC1nmQ30Eck7qgPen/729/KTp06SeSVXTwQUO8D6izoX9ASxpYQ9+7daxwor8DyuoKQaALBE5t///vfEnJeesxhOMj+448/dtX53nvvWXSdOHFCdu3a1eIHfVEjxKVLl1ry+Oqrr7qW0R7w1ltvWeLOnz9fi7zzzjuWsG+++Ub269fP4mfG13xfp04dCXkvR61P2apVK1/6oJta+nLdunVeKjksIgiodyEoGWblRy+WhIhWi7lVCCJr06aNHDp0qFy4cKGcOnWq7N27t6W1QpM3cubMmY5VPHfuXInWkAIeZEdjbBL+a9eulWg54mO/7777tAxkqRvs2tL44IMPLLKrV6/WhIsWKD5y/CGddDrq+svXX3/d+DO3fGn5jfZHuJkcbrjhBp133Pt1NGGj41133XXy/PnzOiqwV/jiOnr0aOMZ9YKW5KRJk+RHH30kQZyoO+o2W+Rr1qypddlvjh07JkuUKGGRb9SokcSPHHoHO3bskPiBeuqppyR1wbUcWvs0hGBXx88RQ0C9N0yILhXTo0cP/VKjW/X22287Su7Zs0cWLVpUy9LYoiOB1a5dW8vQwVpyw4YNjvrgiZamqiBc//rXvzrKLlmyxCLXoUMH4/mZZ57R3UXHiGn0RPlV3p988knXlPDDouRwpUkwV1kVcPToUctQA1p/ZjdnzhyLTuAMgv7www/NYvoePQAzMXvlg8ZCtW78OA4bNswYotDKTDfr16+XNJGn5Rs0aGAK5dsoIqDeRSZEh9rZt2+f5cNTY18OoobX7Nmz9csPYCdPnmwR3b17tyUc3Vovh1bPjTfeqOOglefkQCKqInFFawREnpPOLyFifNTcmnzssceSZhtjd+byolVmdmhtm8NxP2TIELNIwv2mTZsscdq1a5cg8+2330o6WU3L4YcnmZsyZYqWRz68hj6S6eLw9COg3hsmRAesu3fvrl9mP4P+tOZR0uyp0X3GYLu9i4qWDVpz6Ga/9tprnq1DlR0QhKqkQoUKKW/LlWZNtQxk0TWkHSIWmbAf/BIi8oWxTVVGxMMYqJf7wx/+oOVp1jxB1E6IqBM/Yzy/+93vtF50d1FfZvfEE0/ocPQW/GCMCa6bb75Zx7v77rvNKvk+Ygio9zB2hHj69GmJD8PrDx+CKiA+HC9ZjAfanflFbtiwoT3Y8RmkmEr34osv6jKgLLRUJEG9nRAxu5zTLgghYjxP1ROuGONzc7S8yDIG+8YbbySI2gkREyB+3EsvvWTJh33FwC233KLDb7vtNj8qDZm//OUvOh6IFCTJLpoIqPcwdoSIVoTKfCqu6IbZHVpkSnfnzp3twaE8jxw5UucBeUE33u7shEj7hu0ioT8HIUQQBK3l1OV0avWpAvzjH//QcljWQmswVZC+2gkx2VCHimifucZkldmZJ9ewRMevs3ebQersoomA+t7DIMQ8gIASdHQ0QG34e4hY4mExMn10Fr/sPBAhCuqeahU0m2gsHlYeNHAvXnnlFfWYkiuNWwmacRU0ISNoYN+4UkUYi5Vp/FDgD4t+8accEWLCgt+VK1cKarEoETFq1ChB3Tv9nBM3NHsu6EfLSJomVQQNEXhmg8b4BE0CaRkaFzQWvGuP/91gYbla8P3444+LsWPH2kXEvHnzRIsWLbT/9OnTRdu2bfWz281//vMfQa1rHWx+J1AH5kXyNEEiaExXy3rd0DIeQbPQWmTNmjWiVq1a+plvooOA4iF8h0FdYD7y+k2gxI1ffi8ZcxhaFZgd9PrD8gmlF8tZvGTxi2B26C6puLhizC9VDgPr9kXT5rS87lEGu7O3EIkA7CKhPwdpISJzaDVhMkiVvX///gl5pp0tejkR5FCnTs7eQnQaDnGKh1lhlT6uL7/8shb7/PPPLWFmuaD37777rtbLN9FCQNVlGC3EWK1DXLRokeUDoJZISmoOi48V6OqKCRsM6GOMk1oysmPHjsYOh27duknaj22R90OICxYsSEles6MkKCEiLZRdYYK1frSN0ZKF4cOH63DaHmcJMz/YCZG2L5qDXe+3b9+u9SMf5mVOixcvtoSpfGblmsofV9fCcECWEFD1yYRogw+LjBU4uFJ32SYR/BEtQ/OibNy/8MILnjOgWRlDjCsh2n+E7C076mbqOsH6PzdnJ0S/eFBXVutHnYOAlXMiS9rPLrPyl2wrpkqTr+EjoL55JkQb9vZJm549e9okgj+SEQH9waF76GdNGiYEVCXh6mdSxS8BBC+B/xhZaSFiGKRcuXK6vO3bt9cJkjEG7Q/svCYm7IToNWutE6Ab4GbGGsujlDtz5oylu/7000+rIL5mEAKq/pkQHSqVbCjqDyS7+4BhNMA8RuY1k2rOin1PciZ3mVFu85ACtjUqwwwYz1Mva7JlNHZC9LtHGgvpVRq4Llu2zFwVll0nTgu3LcL8EEsEVP2HQohYIuH2pzKSShSza+3GvO4MC63tY1pOeZ02bZqxnQvLeMwGB7BFT5URV6wvTOawU8VuTSXTCRG7Qcx7gNUEROXKlTV+ZHzWEzo7IfrZUQKFzz77rE4DdYRustndfvvtOpzMvZmD+D5DEFDfKJmxk0H/3LjNzT9WkyqoX+wFVgDhah/Tsr8D6PIVK1ZMx4EBAuWwsd+sy2lBsZJV1zFjxljiID62/9mdfZY5al1m+44de/7tzzDAoLDCRIv5xwR7g/FD4eXshIjtdjDKkMyZt0nS8QfSvsjevnDb/IPnpfvrr7+WIHF8GOyijYB670JpIXpBoTLiJRM0LLstRPxCmMfCmjRp4tlKtO9lhl0+5TDmpcqIa58+fVSQ4xWWWDDpAgMC5niY7bS7KBKieVE7Zs2DOPzwqDKDzMxbKGGTMpmzEyJ0wcqOl4MFHpUmrk7LfvCRXHPNNVoOLcZkvQb8SN51111GHOxS8TJ04ZU/DgsHAfUOZCQhohWGsSf8kRXlLCGKD0OBhCtMf2GA3e6wtMNMAhh/hN08s0OrQ+nCLgunCRLIYx0huo0Yc7TPMjvZWowiIWJZjCorTJfZW1tmXOz3IJkyZcro+NibrXTZu7H2uHi2EyLGImFAwm5sQ8XduXOnYV5NpYEfov3796tgy9VeHzD99eOPP1pk1ANahGYjuNCPmXR20UVAvQMZSYipgP2nn36yfCwADFaXYe3673//u3z++edl06ZN9QeLcBCZfUAeeaEdJBY5bAXDWCLs582aNcsYe7z11lu1DJ1JYhgYMLcSr7zySomZZ9qdoj/EKBJi69atdTmACX4gMEEEC+AwkpDMmSdR1EuKNZl+nJ0QzesXW7ZsaeCHVihMuWGfsdlsG9Ki4w9ck8HkWI0aNSxlwzgv1oxiiAPb/SZOnGi0BM1b/aAX7wy7aCOg3jUmRI96om1blkXDCjSnK7rYbuODGPuCUQCneHY/7EdGdwvOvGDZLKdIN4qEaM+TOd9YhJ7MwWq1eXIF8SdNmpQsmhFuJ0TsQAHBmn9YzPkx3//pT39KOkYJUsSibXPL1azD6R4GY5N1r30VjoXSioCqOyZEHzCjBYCZZ4wFKeDUFV0yjHU5WaMxq8bZLGjhme3qKR34YGFVxz6LCp333nuv5YNGHtBKhLOTTxQmVZAvtJTQXVXlwxUkgjE1P85sNRx6kpkFUzrthAhL5HCYBDHPFKt8IU+YNUYLPojDOlIYfTUvz1I6ccWZL1hLqX64guhm2ZxBQNVfGISYUuMOlPEcc/RLL2B8ACetkTVmQdaWBY15CRp78p0nGG6gGWNBM5CCxpoEmcE3jBngFDg3Bzka2xL0AepD4N1ko+JP461i27Ztxml8OJUQONGPh6/smY+RpZabIEs3vuLZjTvYjSngtD8aNxS0xMfAnbrAggjXl243Idp9YpyeCEMO1AU3jrxFWemHzy0K+0cQAWqUGLkiQgycO+odBoqTMYQYqNQsnCUEqNUrqDVnxMVL+tVXXxlHvfpRlowQ/ehgmdyJABNi7qz3yJeaZm8Fzcga+cQ9nYfiO89MiL6hYkEbAkyINkD4MecRQNeYZqN1RtBa9Gt7EJGYEDV0fBMQASbEgICxeHoRgFFWmpwyjOQipQcffFDQdshAiTIhBoKLhU0IMCGawMgNt2QmX9ApfWkpatWqVQ0yC6L8zTffFJiIoMXNgmZtBSZAlMMkDJ5pd4jy8nVlQvQFEws5IMCE6ABKJnvRWSBi3LhxaSkizPbTIvNAummhtGMczLrTImdBaxYD6YMwE2JgyDjC/xBgQsxlrwLZdbSc75HK4t9zzz2Cdn8EUmknxAIFChjdZJyxErRlqBJmQlRI8DUoAkyIQRFj+ZQiQPu9BZ1vbKxTxCFOWNNJ+7yzlQYZ0hC0GFvrICMflgPDdADfMAI2BJgQbYDwIyPACOReBJgQc2/dc8kZAUbAhgATog0QfmQEGIHciwATYu6tey45I8AI2BBgQrQBwo+MACOQexFgQsy9dc8lZwQYARsCTIg2QPgxugjARNfp06eNDJLBVYG1iuwYgVQiwISYSjRZV1oRgG1BRYi9e/cWw4YNS2t6rDz3IcCEmPvqPLYlZkKMbdXFJuNMiLGpKs4oEyK/A+lGgAkx3Qiz/pQhwISYMihZkQsCGU2IdFqeoPOAjaLjHBI6TMgFBvaOAwJMiHGopXjnMaMJ0XxI0aFDh4yDf+JdXbk790yIubv+wyg9E2IAlI8dOyb27NljWGeBhRY6N1nglDz8Va5cOamVluPHjwtYd4ED8GXLltWpQxdM5e/atUvQsaOGzurVq4tKlSoJOp9YywW5QQsZJwPiD6eI3XTTTaJKlSqiVKlSQdQkyKZD7969e8W6deuME/pg9QZ5pCNZjVMNVQaYEBUSfE0XAmESovA6aZUKaJzf6yUTNIzMPukzgamFGDS6lt+8ebN89NFHJdnq0/pUftUVZ/A+/PDDcsWKFTqe/Wb8+PGW+KdOnTJEyGy+JAKwhCm9OH+ZjLpKHI7u10FfyZIlHfVBL5nXkp06dZI4ezaIS4feyZMnu55rTMc6SrLfKOkoUyObwFjhQstugmSdZRkBXwio9yuMc5ljSYj4YBVIfq50NrMks/iO4L/zzjsWXWQ6X/br18/i55YGHbIkIe/lqPUpW7Vq5Usf0qlQoYKkVpmXSiMsXXqfffZZX3mtVauWcUg9CFLhQwuzk+abBRiBoAio9ysMQsxDB63jhXZ0OPAdjgrgGJ4Vz+yOIa5atUrUr19fUOvMSB4HkHfs2FHUrl3bsOaMvKJ7u3TpUuMgJHQl4dDsXrhwocDxmWY3a9Ys0bp1a+01evRo0a1bN2OyB5ajmzdvbnQV0a3GWSJTp041DlNXEWrWrGkxfKr8cUV3HF1idOWVQ/rUahXVqlUzup442xjnlowaNUqcP3/eEMuXL59YsmSJgBFVJ5cuvYMHDxZ9+/bVSRYqVEj06dPHwPb6668XW7duFRs2bBAjR44UOAQeOMEat8IYO1WGDx+u4/MNI5AKBFSX+ciRI4HVYUgnkPNia1Jk/Pp7yQQNy26X+aGHHtItEhrvk99++61rFoiIJI3Pafl77703QXbOnDk6HOWlHwGZP39+SWcOJ8jCg8bVJFmQtsShA6IcZQcOHKjlqFIl7eKQNC7pKLt+/XpZvHhxLd+gQQNHOXimQ++5c+cknZmi06cVABJ5cnLAgM5VMWRplYCOwy1EJ7TYL7sIKB4Ko4UYuy4zupQKoOeeey4p1p988okhjw/897//vdHNM0eaO3eu1qf00n5cs0jC/aZNmyxx2rVrlyADoqZfJy3XoUOHBBm7x5QpU7Q88kItR7uI8QOQDr0zZsywpE2HXiWkbfbYvXu3BMkrzHBlQjQjxPepQkC9Y2EQ4v8DAAD//+jM/toAADq6SURBVO1dCfRW0xY/Zp4hIaUyZCkeKiWFlKIokSzSqmR5tELiRSlDeihTpcgyJimlZBaNKlQkwzMUkhISopc8ItN9+3eec5xzvjt/33d93/+/91r//733nH2m3z13f2fYZ2/hhZAQwsNfIemYY46ReSLfzz//PFHWv/32m7ftttvq9Ndee22s9N9//30g3zPPPKPzQ5123XVX77///W8gv4qoX7++Trf11lt7GzZsUFHyevHFF+v47bff3luzZo0V7/fw+++/ew0bNtTp2rRpk8NWrHyPP/54Xe4222zjrV+/PqdsN+DEE0/UaYDdZZdd5rLwMyOQNwLoW/jDd5n0L2nhWyABFeZLW2yxhQwPYbHS/fTTT6Jjx45WmPvw2muviW+//VYGt2zZUmy33XYui37u16+foI9OP+MGaRYsWCDDDjroILF48WJRpUoViyfJw7Rp06w6n3baaeKJJ56IzGLo0KHimmuu0XxvvfWWIGGmn5s0aSLeeOMN+Xz00UeLRYsW6biwGxIqYtSoUZKFBKnYtGmTUO8BgcXKd8899xRff/21LPeEE04Qs2bNkvdh/yZPniy6deumWVD3W2+9VT/zDSNQCARU/ydhmDi7nXbaKVmaMAlKOUnJHMZjxmEkptIU4jp27Fgze3k/ZMgQq4x9993Xmzp1qvfjjz/m8MYJcEeIN998c5xk3qRJk6x6zJgxw0pXtWpVHd+rVy8rLuxh4sSJOh0w/Oqrryz2YuT7888/e9TpdLnnn3++VWbQw6uvvqrToK48QgxCisPzQUDJkqSjQ/AnpYKOEH/44QeRWCJTa4OIBKI499xzrWiayol27dqJ119/3QpHuccee6ygqZ/ACOeQQw6x4oMe3BEiCVfRuXPnIHYdPnv2bGv0atYVI2ASXJq3devW4qijjtLPYTdr164VDz74oGZZsmSJOOKII+RzsfL97LPPxD777KPLvOqqq8QNN9ygn4NuPv30U0E/SDqaR4gaCr4pIAJlO0LEGtjq1atD/2jKp0cVNN0N5Q2S8AgnoafzIexz7mvXru1hpPPyyy+H/ki4I8SZM2eG8qtImg5bZdIUWkV5b775phXnV7+4YY899ljR88V7MOszcuRIXWbYDS2RWOl4hBiGFselRUD1zSxGiKE7JqoiaRvily6fTRU3PwivU045xcOmhaqr3xXCk0ZBbnL57ApEWuvz5XMDP/zwQ6vMAQMGaJbnn3/eivOrU9wwWk8ser7PPvusVd8xY8boMsNusMm15ZZb6rQsEMPQ4ri0CKhvJQuBWNApM1U8klq0aCEWLlwo+WiXWdSsWTMyTRQDNh7mzp0rSEAKEkaChFVOEto9FvPnzxeHHXaYFedOmadPny7at29v8fg9YHOoadOmOgqbCZgyglasWCHq1aun40hYirPOOks/J7mpUaOGqFatmkxSrHxfeeUVgY0fRcOHDxf9+/dXj4FXbMJgM0YRT5kVEnwtJAJlO2WO8wtQyBFiUHmYtg8bNszbb7/99OiFXpBHwtDDBoJJ7ghx3LhxZnTgPQlOK++HH35Y82IqaW5SkHDRcfncFCvfjz/+2GrLwIEDY1Vz6dKlVjoeIcaCjZkSIoBvF39ZjBDLesochStt8nikRmN9tPPmzbOSuQLxpptusuKDHiZMmGDl+8ILL1isNPLV8WeeeaYVl89DMfJ11wJ79uwZq4o0KtdtRIdlgRgLNmZKiAALxISAhbFDwdgcrd12220WuysQe/ToYcUHPZAOoiUMsKZoUvPmzXU86UuaUXndFyvf3XbbTdcXZcShwYMH6zQsEOMgxjxpEGCBGIAa9Bxp/dEbPXq03MkNYMsJpjU4/eGSOokV7wrEv/3tb97GjRstHr+HAw88UOeJ/N2puKsv+dxzz/llkxO2fPlyD5scGN36UbHyJZUl3R78gJBKjV/xOgwbKqSqo9OwQNTQ8E2BEWCBGABop06d9AeIY2NxiPT6dBoAO2fOHCuZKxDBc8cdd1g87gPpQFp5kt6eyyLXO2jDQfNh1AUhEkZQW1JH6LBz3rdv3xx2rKMUI1+sgaqOh+uNN96YU7YZ8Oijj1r8SMNTZhMhvi8UAqpfVsg1xPHjx3vQ2cPfd999lwgzV52lT58+3i+//BKYB9bGTH1FnDkm5WaL3xWIO++8szwvjTVCP/roo4+8OnXqaGGw1VZbBY6mbr/9ds2Hl4q6BJ0Rxoiwa9euFr8rvFV9ipHv5s2bverVq+vygRVO4/gRhCfOlO+www4eKcTrNH4C3C89hzECSRDIUiBmrnZDjcuL2rZtK1VrVCZQ+8DJkoMPPlirgNBxN/H++++LKVOmCJxsUUT6dYI2DNSjvLpqN1CfwRlqEI1IxZFHHilVdXBKhI6qCRIGAvkrOueccwTtTKtH60rTaHlChRS1dfjee+8tOnToIBo1aiRPh3zxxRfinXfeEfRDIchAhObr3r27oGN8+tm8KVa+OJ0yaNAgXRTpGMpTP82aNZMnUt599115PhtnyalDixEjRoh77rlH0I+ETEOGJwQtZ+j0fMMIFAKBCq12k+SXwY8XZ5ZPPvlkPSohwCPvoTyMDQA/ckeIOIGC0au5ERNURu/evb1ff/3VL1sdhpEXlLZNBeag/FQ4pp5R0+ti5Ys11jht79Kli2x7gwYNNP4XXnihbjffMAKFQkB9FxVyylwIkDBNJos0HlnW8TC1U4C51x133NHDtBrT3CByBSIpXEtWbIKYO7oqbwg27BpjYycJvfjiix6dafb22GMP3/pi+knK256rvhNVRjHyffzxxz0IOj9s69ata62xok0KGxrVRlWX4xmBxAio/pWFQCy7KTOBYxGBJHDi5csvv5R/tKYnMC3FH0554DmM3CmzaUwB6WD4AFNCTG1r1aolGjduLGidMSzLyLh169aJZcuWCRhyoHU7eVqHlMgF7XBHpg1jKHS+NAoVmCbTzrcgtRw5xY9rNCOsnhzHCCRBIMspc9kLxCTA+vFGCUS/NBzGCDAC2SHAAjE7rAULxAzB5qIYgRQIsEBMAVraJCwQ0yLH6RiBbBBggZgNzrIUFogZgs1FMQIpEGCBmAK0tElYIKZFjtMxAtkgwAIxG5xlKSwQMwSbi2IEUiDAAjEFaGmTsEBMixynYwSyQYAFYjY4y1JwDA/WrxWRAVsB69pMjAAjUBoIsEAsjffAtWAEGIESQIAFYgm8BK4CI8AIlAYCLBBL4z1wLRgBRqAEEGCBWAIvgavACDACpYFApgIRhkmDmk3WYmQUmacIYuFwRoARYASKioASiHB7m5SSGkyp9MYdkgLM/IwAI5AtAkogwrJVUiKL7omSsEBMBBczMwKMQNYIlJxAzBoALo8RYAQYAReBkhkhuhXjZ0aAEWAEskagZAQib6pk/eq5PEaAEVAIlNyUmQWiejV8ZQQYgawRYIGYNeJcHiPACJQsAiwQS/bVcMUYAUYgawRYIGaNOJfHCDACJYsAC8SSfTVcMUaAEcgaARaIWSPO5TECjEDJIsACsWRfDVeMEWAEskaABWLWiHN5jAAjULIIsEAs2VfDFWMEGIGsEWCBmDXiXB4jwAiULAIsEEv21XDFGAFGIGsEWCBmjTiXxwgwAiWLAAvEkn01FbdiOK9++umni2eeeUY28qSTThJPP/20eOCBB8T5558vw6pXry5dttasWbPiAsEtKzkEWCCW3Cup+BW6+eabxZVXXikbuvfee4t///vfYvfdd5fP3bt3Fw8//LC8b968uZg/f77YZpttKj4o3MKSQIAFYkm8hspTiblz54oTTzxR/Pbbb2LrrbcWL774ojj66KM1AN9//71o0qSJWL58uQy75JJLxO23367j+YYRKCYCLBCLiW5A3q1atRJr1qwR//jHP8TVV18dwFW6wWnr/9lnn4nDDz9cKAc+I0aMEP369ctp6LvvviuaNWsmfvzxRxmHEWPXrl1z+DiAESg0AlkKREFrR4FEDYO7vcD4ihJBwkC2E2395z//WXbNyqf+HTp00G0/6qijvN9//z2w/bfccovm3XnnnT2Uy8QIFBsBJYfIYraX9C9p3UKlnapI0kzD+Dds2OB99dVX8o+maGGsmcVNmzZNf+jlKBDT1v/ll1/W7ca7njlzZijmNHX29thjD52mf//+ofwcyQgUAgElh5IKQ/AnpcwF4jHHHKM/qM8//zxpfYvCT1NkXadyFIhp63/88cfrdtN0OBa2tPmi05DPW++LL76IlY6ZGIG0CGQpEDN3Q9qiRQuxcOFCaqMQJBBFviocGzduFB9//LFc/8MaIE35xF577SX/Dj74YLHLLrvIstx/9Ouh183OOeccsWDBAsmCNcRBgwZp9t12203suuuu+tnv5ptvvhHLli2T7UGbsDlRp04d+Ve3bl1RtWpVv2RW2A8//CBo5CzDsGaC9IoWLVok3nrrLYG20g+KaNmypci3/i+88IJo3bq1KkI899xzAqo2UYQNlv3220+sX79esvIGSxRiHJ8vAhV6DbFQI0Ra5PdIeHnbbbedHrEQ8Nb9Djvs4HXr1s0jgZLz4zRmzBiL102rnjEiCqLFixd7pJLibbvttoF5kXqK16dPH2/dunVB2cjwRx99VOdBHUCu5W3atMmj3V8djjp16dJF8udb/zZt2uh8DzvssNC6uZHXX3+9Tgv8eS3RRYifC4mA+hZ5yhyA6oQJE/QHqcAKu2611VbeQw89ZOWWr0B58MEHPQiusHLNOGxCkDqLVQfzgZSgrbywXkcK0VYY8iuEQKSRpkfqNTrva6+91qxK5D1+jMy2TZw4MTINMzACaRFQfS0LgVh2U2YalQmomGzevJlwEgKnJ84++2xx5JFHij333BNrouLLL7+UysOTJ08W3377reTDsJs2DcQJJ5wgn9977z0xb948eQ81k59//lneI2+c2FBEO69SLUU940qbGOK0006TU2M8k7AT5557rqA1OTlVx5R55cqVYurUqfK0B3hAmAa/8847Yqeddvp/gPEfdWvfvr0OefXVV2Wb0B4ageo6NG3aVNx2220in/o/9dRTsv6qMEzJTb1DFR52xbIEcAb16NFD0I9UGDvHMQKpEeApc8hPCem+6dEJCZjQRX1aU/QOPfRQzQ8VEz8iAaV5+vbt68dihZHw1fw77rijR6c6rHjzgYSX5qUe4Q0YMMCM1vcknC0+EjLyeeDAgR6mzmGUtP4XXHCBLovWWL1ffvklLHvfuLPOOkvnUaNGjVB1Hd8MOJARiIkAvhv8ZTFCLLtdZtqk0B/i4MGDIyF96aWXJD/URbCTiqmoS0kEyqpVq3T5eEmY1obRr7/+6h144IE6DXT9/Ig2mjQP8sXa40UXXeTHmhOWpP5IjB8S1ck6duyYk1+cgPHjx+s8kBdt+sRJxjyMQGIEVF9lgehAB71FcwMj7tqXnxA0s04iUKBHidEcndTwRo0aFTo6VGXQdFoLjypVqqhg6+rqBG655ZYeRrhxKEn9aZqr64KONnz48DhF5PC4Pwx33XVXDg8HMAKFQCBLgbgFqXvgA/Elmg7KcGqUb7wb+NNPPwkacbjB1vNrr72m1/WgPkK7lFa8+YC1PZyxNQlplIrMQQcdJLCmSELGZEl8jzVAqJOAaMosSNAlziMswZAhQwSNZjUL1t6w9mnSK6+8Yq3jod1YV4xDSeqPNcyGDRvqbCdNmiRoJ14/x73Bu6ZdfM3+r3/9S9APlH7mG0agUAioNUTSZkicJenKJksTJsEpJzmaCOMx4zASU2kKcR07dqyZvbwn4WKVse+++3q0eeHRGdsc3rgBSUZYcfM0+cgQglXnTz75xIyW9+4IEcrWcSlJ/Z9//nmrLrNmzYpbTA6fWW7v3r1z4jmAESgEAkqWlN2UOQuBSErQHllesT5qAIaPE5smI0eO9JYuXZroPZgfdpxNFTNzrJ3df//9HgQYdBJpt9arX7++R6NX74ADDvBIidkjxW6rvnEE4ujRo81iQu+T1J923q26vPnmm6F5h0Wibaqzdu7cOYyV4xiB1AioPlZ2AhGGAVavXh36ZwozKDaH8QMAP0I4qc/oj1EBZl5r164tNzww8oqiJAJF5QWdQldp2iw/7B5tdskdIWLUG5eS1B+C1qwbWbuJW0wO3xFHHKHzInWlnHgOYAQKgYDqr2UnEOM0vlAnVVAWjBGccsop3vbbb68/TAWeeYXwDPvwkwgUlHvTTTfllAflb4wM27Zt62G0RLqR3nnnnedBxYWOK1r8cQTi9OnTUVQsSlJ/bESZ2ESp9IRVoF27djqvBg0ahLFyHCOQGgHVX1kgxoQQG0Nk+t7DOla9evX0R6qAxBXT1iB9wSQCBSNDCD+VN+6vu+46qSMVVN00a4jFEohk71DXHW2IOlIY1CaEmz9uWCpgYgSKgYD61lggpkQXI7Bhw4bJ9TsFJq44s0snUnJyTSIQGzVqpAUKdAXDjuOpgkwLMahHnDXEYglEV3+QjFKoaia+mvqVp556auL0nIARiIOA+oZZIMZBK4QHI0c6YqcFGICFDqFLcQUiHReUCtPqBZEKkJuV77N7JvmvnDJD0Kr640pWb3zrHCeQLAHpvHr27BknCfMwAokRUP2VBWJi6HITkJkqywgDjtK5FFcgYsqtXg6usPoSRTipQk6brHR/pUAkPVCrLrCyk4bQLtO4BTmoSpMNp2EEIhFQ3xwLRAcqqPXgiBt2SpOoi1SrVk0LgRtuuMHJ1ZMqOwr0MAOxpBCu8wE/pp9RdO+991ppkA6nPFxyd5nTTpnD6o8yIYxVW3FNe8LEPfECdScmRqAYCKj+ygLRQbdTp076Y4bKSxxau3atTgNg58yZk5MMx+kU6NgdDiK4PlB8uF5++eVBrDL8kUcekRsw5kgK6aAc7VI+AjFu/VEmRnamXiR2wtOQO/WePXt2mmw4DSMQiYD65iqkQMSoaujQofLvu+++iwTDZHBPWcDwapilFjpeZukrwgYgmQMzs5T3hxxyiBZ0MHzgt/GiEpmjTViK8dsgAS/0CFEeNl7cXWa/aXs+AjFJ/VG3M844Q7cXJ33S0KWXXqrzgCHefE4KpSmf01QeBLIUiJnbQ6TG5UWk5ydIMOo8YAOR9P4E3AXgHgRT/O+//76YMmWKNnWPcDIKK2jxH7cWkYAQjz/+uA4jyzjSJiIJM4FzlDRF13F33HGHgNl8RXAPQMJBng+GHUSaDks7iEuWLJEsNEUXpA4k4IqAurAMgwN4Gl2KY489VpCakIxzzzLTCMyyj6jK87smqT/SA4devXrprFasWCHoVI1+jnNDeocCrklBpI8oZsyYEScZ8zACiRFQZ5lphJg4Le0PJEsT9jtDOclRQBhP1nEYiZx88sl6dKLqGHaF5ZgwU2Hu6MzMC8rWJmHKCZ07kyfoHsf5lFtPKGv78aldXrcOSdYQ3bRmOW790RaMak2eu+++22xi5D0cS5npYfWHiREoFgKqr1XIKXMhQMM0+YknnvBgy880ha+AU1cYb8W0+qOPPoos9oEHHvBg5l+lxRWCFJ7pXEL50C2E1zmTH/dYLzzuuOO8Z5991kqGTQictTbXE3HChkaGks8VakkEIjJIUn/w//3vf9d1T2oTEe4TzHbTaBxZMjECRUFA9bUsBGLZTZkJHIswjIanO5jUwh+dHBGk5iL/yJKzfLYShDzApNUHH3wgvfHR2pog4wXSfH9QEhotyiny8uXLBbzm1apVS049YV4/iMD36aefCkzLaT0yiC1VeJL633fffYL0I2U5JPilSwJStI4sl3q8IAV36QoBzHDJQBZzItMxAyOQFoEsp8xlLxDTglzZ09EoV0AAwoUriFwCCHLEFQmL648Fvl/g54WJESgWAiwQi4Us52shQFNfAT/UIIysMTqO2lxp3LixIAV1mYYMawg6Qy7v+R8jUCwEWCAWC1nO10IAu+LYnf/www9l+DnnnCPGjRtn8ZgPEH50ZlkGoZNCMJrWt01evmcECoUAC8RCIcn5RCIAFSa4K6DdcDlKnDt3rlQHchOSzqh0hUobVDKKNqsEVJCYGIFiI8ACsdgIc/4WAtCVHDRokAzDhhBZAdc6nYrxzDPPFHTuWT7CBzZZ+QndcFLp+MoI5IsAC8R8EeT0iRDAzjGmwtOmTZPp2rRpI3eOsfsMuvPOOwVGhCAov9M5crmjLgP4HyNQZARYIBYZYM4+F4GNGzfKKfHKlStlJDzowZPeG2+8Ib0B0nFGOaWms+CidevWuRlwCCNQJARYIBYJWM42HAHoR+LIIwijQ4wU4bYU+p0gHD8kPyrynv8xAlkhwAIxK6S5HEaAESh5BFgglvwr4goyAoxAVgiwQMwKaS6HEWAESh4BFogl/4q4gowAI5AVAiwQs0Kay2EEGIGSR4AFYsm/Iq4gI8AIZIUAC8SskK7E5UAZ+/TTT9fGGU466STx9NNPC7KrqM2CVa9eXZCXPlGzZs1KjBQ3/a9GgAXiX/0GKkH5ZOBWkOtQ2VLYj4ShBrg2AHXv3l08/PDD8r558+Zi/vz5Au4UmBiBvwKBTAUinLkHNZIsTssojCaYKg4CMOAAgw6wdkMWx+W5ZHKLoBtI7l5FkyZNBAzfguBDhhxl6Xi+YQSyREAJxK+//jpxsWTVPlEaNhD7B1ytWrUSa9askfYByRdKIhDLifmzzz6TR/RU5xoxYoTo169fThPgQKpZs2aCfNjIOIwYu3btmsPHAYxAsRFQAjELJ1MsEOltfvPNN9qcPzl6F+QmtNjv+C/Lnxx0ieeee06Wf9RRR4lFixZJz4J+FRo2bJgYOHCgjCJ/M9JdAlwfMDECWSJQoQUi+UUWMBQAwselLKpkCbBbFjmEErD+DKrIAtF1dTpz5kw5dXbxUM/w/wK/MvjBAPXv318MHz5cRfOVEcgEgSwFInwFBxK1FouHgfFpIo455hiZJ/Il51Bpsih4GrgLVW0lgVjw/EslQ3gQVO2k6XCsasG7oEoDL4NwQcrECGSJgOp/FdLrXosWLcTChQupjUJ6y8tXpQNmq+AoCet/+IPlZxg5xR/M4++yyy6yLPcf1iPUOhpM5y9YsECywMeIMpaKAFh42XXXXd3kOc/Ia9myZdJ7HTYl4MCJXH2K/fffX25c5CRwAmCRWo3E8ItYp04dzYE2kZtSAdNcsDyDtjVq1Ejmj02ROET+ny2zXZg2Q9UmitAWjBLXr18vWXmDJQoxji80AjxCjPHzQ4v+Hgkvb7vtttMjGHoR1v0OO+zgdevWzaN1spwcx4wZY/G6adUzRkhBBKf1Q4YM8WjqH5jXtttu65GrTo+EdlA2Mvz++++38ti0aZMMHzt2rLfPPvtYcapu8Ovcq1cvb/PmzaF5I5JMeek8yI1oJL/JcP311+u0wJuEvxnN94xAURFQ/T2LEWLofFhVpJCtLcSUecKECfoDVXUMu5JHOY9cbFrNyFcgkmMmj0zpx64HbUp4KDOIHnnkESuvtWvXeqQnaIUFtZE2RzzwBxGNoj0aSeq8yPhrEKtvOH58zLInTpzoy8eBjEAxEFB9LwuBmPkuc75T5sWLFwuoyNCoiHASAqcpzj77bAE/HzBvTy9ETiuhTDx58mSBTRwQht3YRIBjddB7770n5s2bJ++hdqI2epA3TnAowk7s4Ycfrh7ldfXq1eLQQw+VzulVRKdOnUT79u3lVBbTbBhWhal97Fhj2qkoSM3liSeesMq95557xAUXXCA3nZA3Nn1opCin1UuWLJGK07Sep7KVeoM4VeJHri9l7Cybeod+adwwTNOVodgePXoI+lFyWfiZESgKAjxlDvmZIV04PVqhdbbQRX5aU/RIcGn+Dh06+Oa80047aZ6+ffv68piBtOao+WmX3LvlllvMaOueHDZ5tWvX1vyYXuOXziUSWpqHepVHSvEeptuzZs1yWeUzCWWvXr16Vhpam/XlJcGq+WhN1SMn9b58YYHkyF7nUaNGDY/WNcPYOY4RKBgC+B7wl8UIseymzHXr1tUf5uDBgyNBf+mllyQ/BBF2Vmm0lpMmiUAkZ+4epuDqJUHYRBGNRDU/0t100005ScjnscUDPtIDzOEzA95++20rDXnGM6P1PX44VH07duyow5PcjB8/XueBvCDomRiBLBBQfZcFooM2HTWToyYFUNy1MD8haGadRCDSdNESDHQG2MzK9x6jKdqp1enozLCHtpjkCkTa2fYdSZppcF+/fn2dL9YJN2zYYLHQNFfHAzfSI7Ti4z6sWrXKyueuu+6Km5T5GIG8EFDfexYCsaBriD/99JOgEQjVP5iwzqXW9Vq2bClo1zKQGWt7OHNrEtIoFZmDDjpIYE2xSpUqJkvie5zCUOt8NGUWo0aNCswDqjzKEVPjxo2lV7pAZiMCxwFvvPFGHQIVoVq1aulnuAA1sTvttNME1hWjaOjQoeKaa67RbPCp3LBhQ/2MtUzzedKkSYJ23nV83Bu8W9q11+zwyEc/SPqZbxiBYiFQtmuIGIkRKAX7g8qJS1BzMcvYd999valTp3p05tZljf2cZIQI5WRVPtbV4tK4ceN0OqQnvUIrqTtCDFP3MROSgLPynTFjhhntPf/881Z80JqklSjgwcSpd+/eAVwczAgUFgH1vWUxQizoGmIWApGUlz2yxGJ95AAMHys2TUaOHOktXbo00RsxP/SwTZV169ZZ5dIINnY5pAhtpZ0yZYqV1hWIEPJxCAJOdRhc3R8R2mm34mnnO062vjzmtL9z586+PBzICBQaAdW/y04gYq0Mu59hf6Ywo+luKC8A8COEQ9lZAeV3xc7u+eefnzMS88svrkAkdRerzCTrcbRUYKV1N0xcgUgqQn5VzQkjR/JWvjSFtnhGjx5txZO1Gys+yQP5ZNZ5kXpSkqTMywikRkB932UnEOO0uBCK2aocCA3Sz/NwYkOB5neF8AwTBHEF4vTp061y7rvvPlWVyCsUuc26kRUZK40rEP1O11gJ/nhw8x0wYIDFho0ns1x1AsZiivnQrl07nVeDBg1ipmI2RiA/BFT/ZYEYE0cYuYVAwbqWq5unwMSubdCOcFyBCFUTlR+ufuozQVXGmqGZFiM3k1yBCOEbh9xR66233molI0Vwq1xM+9OS+WNGit1ps+F0jEAiBNR3wwIxEWx/MmPKjimpueYFUHGGl06k/Mn4x11cgUi745ZwSWIZ58knn7TSQgCa5ApEbMLEIXfUSoZcrWSu/iAZoLDikzyQwQrdhlNPPTVJUuZlBFIjwAIxNXR2QowcSX1Ff8QAFkrSLsUViEhXtWpVnV+XLl3crAKf6SieTod6kDqMxesKxLijT/dcN1m1sfJ1BaYbbzFHPNCRRN2Gnj17RnBzNCNQGARYIBYGR5kLma3ySI9Jf8h0tjgn9yQCkcxu6bxwAiTuETZYpVEvFlcy92XVwxWIUACPQ6SDaOWLNUWT3M2cRx991IyOfQ/LPiaOMDzBxAhkgYD6bnjK7KANtR6c18X6WxL1kWrVqmmhccMNNzi5elJlR4EeNQ2+4oordF5IAz2/KEK9Ye1GleFnfssViNB3hJWaKDKnsWinuySA5QNVLq5pT5i4J16g3sTECGSBgOq/LBAdtMnqi/646QSLE+v/CLNYClBc58yZk8NIJ100D1nOyYk3A6AHaQo31CmK3Omy34aJKxBR1zvuuCM069dff13XG/xXXXVVDj9GdthQUhicd955OTxxAtyp9+zZs+MkYx5GIG8EVN+tkAIRi/zQlcOfO22MQs49ddGnT59Qyy103MzSV8RZX2yMuHTIIYdogYFpsDvKcvlhVEK9JFyxngbB40fk+N0jn8aa/9hjj/Vjk7vkZp4QurB2gzVCP/roo48802gDDE58+umnfqzeGWecocvHyZ40dOmll+o8YHg3n5NBacrnNJUXAfVdZCEQC3qWmSpedGrbtq0gwajLgQ1EOjUh3QXgHvTVV1/J88Z0GkSbvkc4GWgVJLxwaxEJDPH444/rMDi/gk1EOGfHOUqaous43MBtQdOmTQWt1+lwUlqWthZxheMsskQjXn31VQEHVorgIxZ2GpHWJfcsM6nPaPegsIcIe4801ZbnwJEv3IKinYrgBoF2ptWjdUW7aQ1Th61YsUIccMAB+jnODekdCrgmBZE+oqAjgnGSMQ8jkDcCZXuWOYvfMIxMyJWmHq0Q2pH3sFkYZirM1RE084Q1GT/CuiBcGJi8YffQ2yNB5JeVDHOnzDiBglG0uZERlD/0L4NGqMj8k08+sep59913B9bDLwKOpcyyyfiFHxuHMQJFQUD1vSxGiAU9y1wUNHwyhYFTsgTjwbafaRpfAaeuMLKKaTWml1GEqa25Nog8IEjhqS6McCYZJvzdtEgP/yM40YEjfq65LzdPVyBidxiEM9DNmze3BJKqG1n7kRtMbl5+z+TwSueR1Cbigw8+qNOibLL241cEhzECRUEAfQ5/WQjEspsyEzAWEUjSex/M2+OP1tLE3nvvLf/IsrN8thKEPMDEFRmAld74aK1NkGK3oHW8kBR/RlFPELSGJ6eVNFoTtC4pPe6hPnHInTLDTQCm34ro6KEgwS7gNgBmw2B6jISwio680jFDQWe7JR+m9HChAM+AUYR2YaoOM2IguGAggxJRyTieESgYAllOmcteIBYM9b84oyiBmG/1aFQtBSB5/5NZkekyQY63IrN1/bFg/dJvDTQyI2ZgBFIiwAIxJXDlnKzYAhHY0NRXwO80CCNXjIajNlcwEqUz4DINHF3R1F7e8z9GICsEWCBmhXQJlZOFQKR1TLkbr3bHw3amAQ2EH51ZliihU0Iwmta3Swg+rkoFRoAFYgV+uUFNy0IgomyoLMEtAx05lKPEuXPnCtKNzKkW6YhK96tYtwTR5pQgRfEcPg5gBIqNQKYCEQYQghpEu7QyCgvrTMVFICuBiFbQ8UUxaNAg2SD4W4YfFqXDqVpJHvwEnXuWj9CBfPHFF2NvMKk8+MoIFAIBJRC//vrrxNlB9zcJ8aZKErSKyJulQMQPHKbCKBPUpk0buXOM3WfQnXfeKUeEuIegpHPjlkMshDMxAlkhoAQiNEqSEhluSZSEBWIiuIrHnKVARCtw2ubwww8XK1eulI2CBz140iOFcEFK5IKOL8opNZ39Fq1bty5ewzlnRiACARaIEQBVxGgcw4OLVkVknVqQUQb1WJQr9CaVS1WMDjFShL4h9DlBZP/Q0oUsSiU4U0YgAgEWiBEAcTQjwAhUHgRYIFaed80tZQQYgQgEWCBGAMTRjAAjUHkQYIFYed41t5QRYAQiEGCBGAEQRzMCjEDlQYAFYuV519xSRoARiEAgS4FYlvYQSbGYKSYC8AoIV6xwMYA/MtAQ21NgWBHwVKjyvPzyy3NYYa9SxeNK56BzeDjgTwQqCl7333+/fu81a9b0Pv/88z8bmfKO5CWOymViD5EFYsqXVC7J4N9ZdSiyE+nBSVYhCH5VVL79+vXLyZJcMuh48LFAzIHICqhIeHXr1k2/exg3jvJRZAHh86D6WRYGYlkg+ryAihIEp1wYnaFDwbL4okWLCtY0FogFg1JmVJEEIgSX6R73kksuyQusLAVi2R7da9WqlVizZo2073f11VcTZkwmArCwjaN56kD8iBEjtNMqky/tPQ7Nk38bmZxGiAL5m0R+XMQLL7ygg2BLESdfKhvF7acVDS84JGvWrJnuI3CK1rVr11Svn9cQI35P6CPXQ/Iox/IRWVXY6A4dOmiM4PMFa4mFpKgRYiHLKte8Kns/veWWW3QfhM8h4JGGSIrKfCrklHnDhg0enduVf1GOl4LAI0MIGmgWiLkouV4EZ86cmcuUZwgLxGgAK3s/hWdKcumrv9X+/ftHg+bDUaEFIhkt0ACl3YGiKbLOgwVibg+Cp0DViWjakstQgBAWiNEgcj/1vJtvvln3RVpm8eDSNimpvpzFCDHzNcQWLVqIhQsXUhuF9JZHW/PyPuofgaHXw2D6fsGCBTIJfIQoY6cIwDqVaSXGTIf4ffbZR9AGA24DiV6YUM6YwOTmiTAyrKsdxWONo06dOgiWRJsX0ugqTGzBak3Lli1VVGg6MMHaDEz1r127Vmy//fbS50ndunUFuRzVeYTdYN3ONNdFbkzFSSedFJYkJ2716tXi9ddflz5XqlatKjE77rjjhDIYjARRa4gmPuCvXbu2ZWDWjE+CH/Lyo2+//VYsXbpU/uGdw+vhoYceKuvuxx83DGuxeCfIG7b14IMG7wJeGf3I7G9J+qmJB/J18fIrC2FYI162bJn0okgjMulIjFzOSo+PUf0c6c1y3feA+Hz7I+oE75Xr169HdoI2WMTtt98u7+P+Q71AwDYpJbWHmPkuc9oR4pgxY/QvDYESeI9fJJPuvfdei3fVqlVmtO89dRIrDVRXXCJr0pqHXphco9u0aZNH5vl1OOrZpUsXK+nTTz9txSuVBPqR8Bo1amTFme0kM/+x/CGTCS+dB7kPtcqOepgwYYI1xTHLh94hdgvJVavMJmqEGLVrmhY/tw1jx471oE5k1tW832WXXbzzzjtP6rC5aYOe4ff7iiuu8OjHIDDfk08+2SNL4zlZpO2nUXiZBZGbW2/IkCGB7wrtJ/e5HrmM9eiH3Uyac1/s/ogCr7/+eo0jfJUnXUtU75MEYmJdxJwGRwSwQPQBKI5AdDsS1kvI77F+8eolugKRfJhYPP/5z3882oGTHVilCbqik5MBV58a/z+IRqRSvUalJ6OvgbxuxDXXXGPVS+XhXslXtIe2QkCquMsuu8zNzov6wNPipwqCPiUUzlUdoq40yvZo1KuSB15pdOxhEyoqP8Tjh/C2226z8iq2QCQHYR65dIhVP9QRmxmoUxAVsz+qMmnH2arvxIkTVVSsq3oXLBANuGha4JGTI/kHwaBAIrUGHY54t9MXa4Q4Y8YMXQfUhfwVyw8E96gfPir8uWuc5JvESgddQTXaIrP+Hk0nPJr2evPnz/fuuecer0GDBhY/RqBB9OSTT1q8cfUOzXUe1L9KlSre0KFDPdQNI4zp06d75IfFI3cCMv8LLrjAo2UJXVYagZgWP7Qdgp+mlLp81BmjIXKzKkdtK1as8CBwUS/oXyIef9tss41HSy1B8MlTFeaoEALvjDPO8IYPH+5hYwo/XFBCV+8LeZJhXSn8VaZp+2nUDwjyx7ugZQvdHpTfqVMnD318yZIlHjkE83DihZaQrB8s8JFalKqidS1mfzQLqlGjhq53jx49zKjIe9QffywQA6AyRyd9+/YN4Pp/cLEE4rx58/QLxsvCS8Z14MCBHqbOQYQPUr1gXPFhY7F5/PjxvkmwI+9+/EGjRAgqlTemipj6RRF4atWqpdNhVzAof4ye6tevL3khCFRZaQRiWvzQHnzwqmwILXzsQWpFaAuOkCl+Wl8NhOSiiy7SfLR+602ZMsWXF4KpevXqmhf9ER+rS0n6aRyBSGuSukzgD7WWIMJ03uw3eK9+dSxmfzTrdtZZZ+m6QzgGvS8zjbpX744FokLEuSbpaMUSiFjzUy8KV4w+8EFFEUZtZjrcB/16q7zIP7KVBmt9fkQbO5qvY8eOfiw5YeZaHuoSNr1CYqzBQgiZbUgjENPih11K/ICo8uOMNjBFU/y4YlTkEilGW8sW7lq0y++Oxv3eSZJ+GiUQP/jgA33qCG3Aj18UuT86fmvhxeyPZv3wg2++A7/1V5PfvFfpWCCaqBj3STpasQSiq+uHX2w6OWPU0v/WTYdfcTrx4c/8Ryj5SLaEEKazLpEfFKvDYZoXh0wVHQh12g2MTOZuHKURiC4OcfG7+OKLdTsxiouDOUYjDRs21Omw8eTShRdeqONx3DFKJQybYVg2wPQZmzru0gjyT9JPowSimoEo4RDnbDjaTTu8ul2777675+r+uu+hUP3RxRc/pKruuN51110uS+CzSld2AhEfdtu2bUP/zLUnUkcJ5Q1SKE7S0bISiGFre+abdjsgPsQ4hMVx1TF69eqVk+Ttt9/W8eCbNGlSDo9fQLVq1XQ6rMPFIaylqbrgWgiBGBc/Oo6oyybvgHGqK3kuvfRSnQ6C1J2ymQKTVIxi5as0BIKYk/TTKIFIqjS6/o0bNw4qMif8qquu0unwrtwfkGL1R7cikA1mnyEPjy5L4LNKV3YCEbuPqvKFuEKlwo+SdLSsBCKUcOOQ2wHjjuTMdTBYE3EJGyAm5rNmzXJZcp7xQZvTX+ySxyFsIJllFUIgxsXP3PTw+2EIqr87bcbarEnYSFJt6tmzpxmV+j5JP40SiOYyAdbj4tK4ceN0u9A+9D+TitUfzTLUvYlH7969VXDkVb0XFohlJBBHjx4d+WLB4HbAxx57LFY6U9fOTyBOnjzZ6vjkXD4yX3JDaqXBaCIOYb1NdVJcCyEQ4+CHY59mudggQZ3j/JkbEsgDu7KKSKnbyvfKK69UUXldTQEQtfkXJhDXrVtn1c/P3FpQRUkx30rrbhQVqz/61cecvnfu3NmPxTdMvfOyE4iYhmAnMuyvSZMm+gUtXrw4lBcA+FGSjpbVCHHq1Kl+Vc0JczsgVFriUJRAhEBRHQdXOmERmS3wN9OMHDkyMg0YoJxtpiuEQIyDH4S8WW4+9+YPERb4zbxGjRoVC4copiT9NEwgQnib9Ys7q0D9yNe3lXbYsGFWtYvVH61C/niADqtqB9Tl4pJKU3YCMU4D055UMfNO0tGyEohxBVuxOiCUsFXHwTVM9Udh+eyzz1pponaYVToszOerdpMGB3dZwGxv0ntT6M2ZM8fC4b777lNNzeuapJ+GCUT0LbN9SeoHRW4zLdTCTErzHpA+6gfaLEPdt2vXTtcF+rVxSdWfBWIAYkk6WmURiFDdUR0HV0yzosj9GOKOPNwpXCFGiHF+UNyPe8CAAR6dtU31Z+IDZWoTuxtvvDEKuljxSfppmEB0R7B+6jNBFXLfsbs04cbHeQ8oK41ANAdDSTbE1LthgRjwlpN0tDQCEbpu6iXg6tcB03aktOmiOqCr54WPPIqgYGy20x09BKUnQwdWuqwEIqbq5iZQWnNSbrvczcB8LTyr/JP00zCB6K5x+qn4qDLdq6svCZ1Wk4rVH80y1L1pRRunsuKS6qMsEAMQS9LRXIGIUUYUucqqfiOGtB0pbboogehOq3D8L4rctcC4u6vu+desBCLaY+62n3nmmVFNjB1v2u1zz5/HzsRhTNJPwwQisjV315PUD8c/lUDBFSNqk4rVH80y1D1ZjdJ1idvXkFbVPxOBCEMGQX+qIqpBhbiaw+Yo5deg8pJ0tEceeUQDiva4Z539ysCpA9V2XMtBILqL5ziBEofMTgqHQHFo8ODBFj5ZCkTUUb0bMsMVp7qxeEz9Rvz4uArMfplgZx9LFVAPw26uS0n6aZRANC0h4USSq0fplq2eoZqk8MIVSv4mZSUQYaHHHN0n2clX9YeVnKR/QbItKLxsrN2YL9HsaFHTh1deecXqEDj8HkXYAVMvAddyEIjY2TfrHPckAMyKqXTosFDFCSMICrIpqdMgbZYCEWavVH1x9RNEfvVfvny5h00kfAh+hOUCM9+gQwEqLQSSabAA7l1dStJPowQizJGZ9cMGUxRhKcBU6PczB5eVQHRPUsXVaEAbVbszGSGGgaoqEsaTNK4QI0RTifbss88OrQJGoaoduMI2XhjhQzD5cV8OAhG/wOYpoKh2KgzcUyd+bVW8uLpnn4FPlgIRH4WyuoOyMWKMGs1BeKkjijil4qcTiJGHKcCwIxqWr7s2B3/ELiXpp1ECEebOTOEGKzdR5E6X/TZMshKI7pLO7Nmzo6qv49X3WCEFIhb/cRYXf+7wXSMQcUPWkLXQwvQh7AgVOrW57gRwTR00syiMHiFU9tprL8+cSvqdHU7bkdKmi1pDRDtgqkp1HrLobDYt8H7z5s2W5RaYywo69qfsNuL8rik8/ARM1AeeFgc0BCbSVDtxxZHDoDPYGBGStzeLH2o2fuQecwOeyiCuyY81ZlPYYf3Rz991kn4ahRfKd5cqsA6HH0I/euCBB6TBEYUTZgJ+lPY9xOmPZnnm0Un0n6jz+2Za1YYKKRDNhqa9P/30060Ojg6JY2d9+vTxcPjfJfeXEsegMIK6++67PRzpwrExfFQKeIwSYVBUPV933XVuljknTvx+fXMSUUAxOyD001SdcYVdwDgEgW+mg44hRkg4b4oPC50Z587VGhDWzciUvk7jh3nUB54WB7QHQhznec064wOFBRhsosHWIuoNQW1uRoC/e/fugZDAWK9pMQj8WB5AGkzxgEf79u2tcmEQI2gDK0k/jcILlcZuc7169azyoeyM/vvUU0952EHGkgKseZvYoL/juKUfpX0PSQWiMhuHeqFvJSHVFhaIAai5L1EBhiuAdwk2/8wTMia/eQ9BoNY2TMOssCbtkluHUhCI7pE6CPy4BAOwSuCZmLj32OHEqMTEx89ARdQHnhY/1R4IReghmgribl3dZ0ztw6bByBtCB8fK3LR+zxglB9mxRF5uG8083H4ahRfyA2FdkPwIxaofyoO+X9gPo1vHuP04iUB01dhMpfj/tyr8v8KNBWIIThgBmGsqAA0fB9aK/AhCETbuXIvDCmysRZkGEcy1Tr8pYdqOlDZd3A5oWkWJaxNR4YWPEoLOtDKt8MGIGRbJFeEcsYrzG3VFfeBpcVDlqytsG6IuptqMqheumJ7BGELQKE7l414x0sTOM9YczfxwD4vo+BHARkEUxe2nUXi55eBMMiyyu98A6ge/JXiPULSP+gFI+x7i9kfUG5bMTQzff/99tzmhzyptFgJxC9SECvQlGjHI8BAW33RZBdL6jvQMRwvi0gsaHR63PLv51YM6iKCdVEG/mtJjGe0USk9qtObmx152YTRtFrR8IOtNPxDSGxspxCZqB42+BPnBELQzKz0OwlMhvNiVOtHpE+mBDh4LyaK1oLVjgT5BU8bUVUd/QV+B1z14HaQpq8yTbCbGzjNNP42bOb5N9Ge8Lxq5y/e0//77iyT1i1tWGj7Uj3a3pfc+pKelKUEDj0RZKTlEAjFROjDTKD5RmrIWiIlaWkmYaSQsXVHSKRTZYhodiYceeqiStJ6bWWoI0NqmIGdgulq0limaNm2qn+PcsECMgxLzBCJAUxQBf9UgjBTI/LwcBQcm4AhGoEgI0OaX9DOO7ElXU9DGT+KSWCAmhowTmAhgmnfwwQcLOqYog8kWoBg3bpzJwveMQNERgPCjM8uyHAg1cnsgyDJ54nJZICaGjBO4CNBJBkFm+QUpJctRIp0/FqSL5rLxMyNQFARIx1jQppQg16gyf1KJE7Qpl6osFoipYONELgKkSiPIZacMJmVzQWakBJ3ycNn4mREoOAJkeEPQqSaZ75FHHilIGyBywzOoEiwQg5Dh8EQIYIcPU5Zp06bJdORtTu7wYfeZiREoFgJ33nmnwIgQhB9gsnQuyPd36uJYIKaGjhO6CGzcuFFOXVauXCmjyLK2oBMXLhs/MwIFQeCNN94QpAwu6DitXKqhY5KC9ETzypsFYl7wcWIXAeipkTKsDMboECNF1clcXn5mBPJBgNzhClJYl1mQPQBBRwvzyU6mVX2V9RDzhpIzYAQYgXJHgAViub9Brj8jwAgUDAEWiAWDkjNiBBiBckeABWK5v0GuPyPACBQMARaIBYOSM2IEGIFyR6DkBGK5A8r1ZwQYgfJHoGR2mcsfSm4BI8AIlDsCf7lABICbNm1KZU+OLPsWBH/YkiMjnQXJC5lAJw9WN1atWiXiAFzo8pM2hMsv7PsvR/yrVasmYOPwpZdeEuTLJWkT8uIv9/5XUHuIQLIiCURy0i2VksnBjewkLBCjv5Vy/yCiWxjOUQrth0AEwYgxObjKVCiWQvvzGRCxQAzo3+RMSpBvW4GjbCBo0ZMPkgDuP4PLvUP82ZJ0d9z+v36EqgQi3iCsl0+ePFmQi4B0LzRhqnJ//ywQfV44OW0X5IhcxsAeG44Xkc8UQd7ZfLjtoHLvEHZrkj9x+0tHIKq+i2kzOYPKRCiW+/tngeh88+QMSGB0CCJvX9K/Aw6bs0B0gAp4LPcPIqBZsYNLof1qhLhhwwbRqlUr+YOelVAshfZnOWX+H3HP8O/M42HxAAAAAElFTkSuQmCC\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 10,
"metadata": {
"image/png": {
"height": 200,
"width": 200
}
},
"output_type": "execute_result"
}
],
"source": [
"#Class diagram\n",
"from IPython.display import Image\n",
"Image(filename='SingleClassDiagram.png', width=200, height=200) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A class diagram provides a more compact representation of a class. There are three sections.\n",
"- Class name\n",
"- Attributes\n",
"- Methods"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Instance methods**\n",
"- functions associated with the objects constructed for a class\n",
"- provide a way to transform data in objects\n",
"- use instance attributes (references to variables beginning with \"self.\")"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"class Car(object):\n",
" \n",
" def __init__(self, color, car_type, speed):\n",
" \"\"\"\n",
" :param str color:\n",
" :param str car_type:\n",
" :param int speed:\n",
" \"\"\"\n",
" self.color = color\n",
" self.car_type = car_type\n",
" self.speed = speed\n",
" \n",
" def start(self):\n",
" print (\"%s %s started!\" % (self.color, self.car_type))\n",
" \n",
" def stop(self):\n",
" pass\n",
" \n",
" def turn(self, direction):\n",
" \"\"\"\n",
" :parm str direction: left or right\n",
" \"\"\"\n",
" pass"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Blue Sedan started!\n"
]
}
],
"source": [
"car = Car(\"Blue\", \"Sedan\", 100)\n",
"car.start()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**EXERCISE**: Implement the stop and turn methods. Run the methods."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Inheritance"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Inheritance is a common way that classes reuse data and code from other classes. A **child class** or **derived class** gets attributes and methods from its **parent class**.\n",
"\n",
"Programmatically:\n",
"- Specify inheritance in the class statement\n",
"- Constructor for derived class (class that inherits) have access to the constructor of its parent.\n",
"\n",
"Inheritance is represented in diagrams as an arror from the child class to its parent class."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtIAAAK8CAYAAADClFiAAAAMFGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdUk8kWnr+kEBJaIAJSQm+CFOkCofciHWyEJEAoERKCih1ZVHAtqFhAVHRFRMW1ALJWLFhYBOz1gYrKyrpYsKHyJgV0fe28e8788+XOvXe+O7kzZwYAZVt2bm42qgJAjiBfGB3ow0xMSmaSegEOMEAHJoDA5ohyvaOiwgCU0f7v8u4mQCT9NWtJrH8d/6+iyuWJOAAgURCnckWcHIiPAIBrcnKF+QAQ2qHeaHZ+rgQPQqwuhAQBIOISnC7DmhKcKsMTpDax0b4QswAgU9lsYToAShLezAJOOoyjJOFoK+DyBRBXQezJyWBzIb4P8YScnFkQK5MhNk/9Lk7632KmjsVks9PHsCwXqZD9+KLcbPbc/3M5/rfkZItH5zCEjZohDIqW5AzXbU/WrFAJpkJ8XJAaEQmxGsQX+VypvQTfzRAHxcntBzgiX7hmgAEACrhsv1CIdSBmiLPivOXYni2U+kJ7NIKfHxwrx6nCWdHy+GiBIDsiTB5neQYveBRX80T+MaM2afyAYIhhpaFHCjNiE2Q80XMF/PgIiJUg7hRlxYTKfR8WZvhGjNoIxdESzsYQv00TBkTLbDDNHNFoXpgNhy2dC9YCxsrPiA2S+WKJPFFi2CgHLs/PX8YB4/IEcXJuGKwun2i5b0ludpTcHqvmZQdGy9YZOygqiBn17c6HBSZbB+xRJjskSj7Xu9z8qFgZNxwFYcAX+AEmEMOWCmaBTMDvGGgagL9kIwGADYQgHfCAtVwz6pEgHRHAbwwoBH9CxAOiMT8f6SgPFED9lzGt7GsN0qSjBVKPLPAU4hxcG/fE3fEw+GXBZo+74K6jfkzl0VmJ/kQ/YhAxgGgxxoMDWWfDJgT8f6MLhT0PZifhIhjN4Vs8wlNCF+ER4Qahh3AHxIMn0ihyq5n8IuEPzJkgHPTAaAHy7FK/zw43hawdcR/cA/KH3HEGrg2s8UkwE2/cC+bmCLXfMxSPcfu2lj/OJ2H9fT5yvZKlkqOcRerYP+M7ZvVjFN/v1ogL+9AfLbHl2GGsDTuDXcKOY02AiZ3CmrF27IQEj1XCE2kljM4WLeWWBePwR21s6237bT//MDdbPr9kvUT5vDn5ks3gOyt3rpCfnpHP9IanMY8ZLODYTGDa29o5AyA522VHxxuG9MxGGJe/6fJOA+BaCpXp33RsIwCOPQWA/u6bzug1LPc1AJzo5IiFBTKd5DgGBEABynBXaAE9YATMYT72wAm4AxbwByEgEsSCJDADrngGyIGcZ4P5YAkoAWVgDdgAtoBtYCfYA/aDQ6AJHAdnwAVwBXSCG+AerIs+8AIMgndgGEEQEkJD6IgWoo+YIFaIPeKCeCL+SBgSjSQhKUg6IkDEyHxkKVKGlCNbkB1IHfIrcgw5g1xCupA7SC/Sj7xGPqEYSkXVUV3UFJ2IuqDeaCgai05H09E8tBAtRlehm9AadB/aiJ5Br6A30B70BTqEAUwRY2AGmDXmgvlikVgyloYJsYVYKVaB1WAHsBb4P1/DerAB7CNOxOk4E7eGtRmEx+EcPA9fiK/Et+B78Eb8HH4N78UH8a8EGkGHYEVwIwQTEgnphNmEEkIFYTfhKOE83Dd9hHdEIpFBNCM6w32ZRMwkziOuJG4lNhBPE7uIj4lDJBJJi2RF8iBFktikfFIJaTNpH+kUqZvUR/pAViTrk+3JAeRksoBcRK4g7yWfJHeTn5GHFVQUTBTcFCIVuApzFVYr7FJoUbiq0KcwTFGlmFE8KLGUTMoSyibKAcp5yn3KG0VFRUNFV8UpinzFxYqbFA8qXlTsVfxIVaNaUn2p06hi6ipqLfU09Q71DY1GM6WxaMm0fNoqWh3tLO0h7YMSXclGKViJq7RIqVKpUalb6aWygrKJsrfyDOVC5Qrlw8pXlQdUFFRMVXxV2CoLVSpVjqncUhlSpavaqUaq5qiuVN2rekn1uRpJzVTNX42rVqy2U+2s2mM6Rjei+9I59KX0XfTz9D51orqZerB6pnqZ+n71DvVBDTWNSRrxGnM0KjVOaPQwMIYpI5iRzVjNOMS4yfg0Tnec9zjeuBXjDozrHvdec7wmS5OnWarZoHlD85MWU8tfK0trrVaT1gNtXNtSe4r2bO1q7fPaA+PVx7uP54wvHX9o/F0dVMdSJ1pnns5OnXadIV093UDdXN3Numd1B/QYeiy9TL31eif1+vXp+p76fP31+qf0/2BqML2Z2cxNzHPMQQMdgyADscEOgw6DYUMzwzjDIsMGwwdGFCMXozSj9UatRoPG+sbhxvON643vmiiYuJhkmGw0aTN5b2pmmmC6zLTJ9LmZplmwWaFZvdl9c5q5l3meeY35dQuihYtFlsVWi05L1NLRMsOy0vKqFWrlZMW32mrVNYEwwXWCYELNhFvWVGtv6wLreuteG4ZNmE2RTZPNy4nGE5Mnrp3YNvGrraNttu0u23t2anYhdkV2LXav7S3tOfaV9tcdaA4BDoscmh1eTbKaxJtUPem2I90x3HGZY6vjFydnJ6HTAad+Z2PnFOcq51su6i5RLitdLroSXH1cF7ked/3o5uSW73bI7S93a/cs973uzyebTeZN3jX5sYehB9tjh0ePJ9MzxXO7Z4+XgRfbq8brEcuIxWXtZj3ztvDO9N7n/dLH1kfoc9Tnva+b7wLf036YX6BfqV+Hv5p/nP8W/4cBhgHpAfUBg4GOgfMCTwcRgkKD1gbdCtYN5gTXBQ+GOIcsCDkXSg2NCd0S+ijMMkwY1hKOhoeErwu/H2ESIYhoigSRwZHrIh9EmUXlRf02hTglakrllKfRdtHzo9ti6DEzY/bGvIv1iV0dey/OPE4c1xqvHD8tvi7+fYJfQnlCT+LExAWJV5K0k/hJzcmk5Pjk3clDU/2nbpjaN81xWsm0m9PNps+ZfmmG9ozsGSdmKs9kzzycQkhJSNmb8pkdya5hD6UGp1alDnJ8ORs5L7gs7npuP8+DV857luaRVp72PN0jfV16f4ZXRkXGAN+Xv4X/KjMoc1vm+6zIrNqskeyE7IYcck5KzjGBmiBLcG6W3qw5s7pyrXJLcnvy3PI25A0KQ4W7RYhouqg5Xx1ec9rF5uKfxL0FngWVBR9mx88+PEd1jmBO+1zLuSvmPisMKPxlHj6PM691vsH8JfN7F3gv2LEQWZi6sHWR0aLiRX2LAxfvWUJZkrXk9yLbovKit0sTlrYU6xYvLn78U+BP9SVKJcKSW8vcl21bji/nL+9Y4bBi84qvpdzSy2W2ZRVln1dyVl7+2e7nTT+PrEpb1bHaaXX1GuIawZqba73W7ilXLS8sf7wufF3jeub60vVvN8zccKliUsW2jZSN4o09m8I2NW823rxm8+ctGVtuVPpUNlTpVK2oer+Vu7W7mlV9YJvutrJtn7bzt9/eEbijsca0pmIncWfBzqe74ne1/eLyS91u7d1lu7/UCmp79kTvOVfnXFe3V2fv6nq0Xlzfv2/avs79fvubD1gf2NHAaCg7CA6KD/7xa8qvNw+FHmo97HL4wBGTI1VH6UdLG5HGuY2DTRlNPc1JzV3HQo61tri3HP3N5rfa4wbHK09onFh9knKy+OTIqcJTQ6dzTw+cST/zuHVm672ziWevn5tyruN86PmLFwIunG3zbjt10ePi8Utul45ddrncdMXpSmO7Y/vR3x1/P9rh1NF41flqc6drZ0vX5K6T3V7dZ675XbtwPfj6lRsRN7puxt28fWvarZ7b3NvP72TfeXW34O7wvcX3CfdLH6g8qHio87DmHxb/aOhx6jnR69fb/ijm0b3HnMcvnoiefO4rfkp7WvFM/1ndc/vnx/sD+jv/mPpH34vcF8MDJX+q/ln10vzlkb9Yf7UPJg72vRK+Gnm98o3Wm9q3k962DkUNPXyX8274fekHrQ97Prp8bPuU8OnZ8OzPpM+bvlh8afka+vX+SM7ISC5byJZeBTDY0LQ0AF7XAkBLgneHTgAoSrK3l1QQ2XtRisB/wrL3mVScAKhlARC3GIAweEephs0EYirsJVfvWBZAHRzGmlxEaQ72slhU+IIhfBgZeaMLAKkFgC/CkZHhrSMjX3ZBsncAOJ0ne/NJhAjv99ttJKiz7yX4Uf4JEL9tBtKO/vwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGdaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIj4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjcyMjwvZXhpZjpQaXhlbFhEaW1lbnNpb24+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj43MDA8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICA8L3JkZjpEZXNjcmlwdGlvbj4KICAgPC9yZGY6UkRGPgo8L3g6eG1wbWV0YT4Kd981fgAAABxpRE9UAAAAAgAAAAAAAAFeAAAAKAAAAV4AAAFeAACIlMJ5EyAAAEAASURBVHgB7H0HuBVF0nYJCAImEERFkmtOgIgiYsAAYkDMa2JNa8SIAUTRNYu4gH6GFSMmlDUhmAMqiICKJDGjIAbARfhlUQHn72qp2Zk5aeZMn+l7b7/9PNBnZjq+XdX1Tt+a7jU8Fchg+O9//0sNGjQwWGKyolA/8If8Qf+SzRrmUmP+wfyD+Qfzj7kZJVlJmH/szD9rgEgnE9RSqSHIdgRZxgX4A38QGRAZmQ+yjjH/YP7B/OPe/LPGsmXLjK5IZz1xoT4gYBqB2rVr06pVq0wXi/KAABAAAkAACACBGoYAVqQNDyhWJLAigRUJ91YkZBqB/kP/of/Qf5kPso4x/9iZf0CkDUs6BNmOIMswAn/gDyIDIiPzQdYx5h/MP5h/3Jt/QKQNz7SYSDGRYiJ1byKVaQT6D/2H/kP/ZT7IOsb8Y2f+AZE2LOkQZDuCLMMI/IE/iAyIjMwHWceYfzD/YP5xb/4BkTY802IixUSKidS9iVSmEeg/9B/6D/2X+SDrGPOPnfkHRNqwpEOQ7QiyDCPwB/4gMiAyMh9kHWP+wfyD+ce9+QdE2vBMi4kUEykmUvcmUplGoP/Qf+g/9F/mg6xjzD925h8QacOSDkG2I8gyjMAf+IPIgMjIfJB1jPkH8w/mH/fmHxBpwzMtJlJMpJhI3ZtIZRqB/kP/of/Qf5kPso4x/9iZf0CkDUs6BNmOIMswAn/gDyIDIiPzQdYx5h/MP5h/3Jt/QKQNz7SYSDGRYiJ1byKVaQT6D/2H/kP/ZT7IOsb8Y2f+AZE2LOkQZDuCLMMI/IE/iAyIjMwHWceYfzD/YP5xb/4BkTY802IixUSKidS9iVSmEeg/9B/6D/2X+SDrGPOPnfkHRNqwpEOQ7QiyDCPwB/4gMiAyMh9kHWP+wfyD+ce9+QdE2vBMi4nU3Yl0jTXWMCxNKA4IAAEgUB4CnueVlzFFLtg/d+0fi42r4w8inWLSyJfVVUESLFzuP4i0SAFiIAAEbCMAIp39CLhs/xhtV/sPIm1Y11wVJIHR5f4LkbZhwAR/xEAACLiNgM15yOX5n6UO/XdzRR5E2vCcC0VyU5FYjGwaMMNijOKAABCopgjYnIdg/9y1f6wuro4/iLThydJVQRIYXe6/TQMm+CMGAkDAbQRszkMuz/8sdei/my8SINKG51wokpuKxGJk04AZFmMUBwSAQDVFwOY8BPvnrv1jdXF1/EGkDU+WrgqSwOhy/20aMMEfMRAAAm4jYHMecnn+Z6lD/918kQCRNjznQpHcVCQWI5sGzLAYozggAASqKQI25yHYP3ftH6uLq+MPIm14snRVkARGl/tv04AJ/oiBABBwGwGb85DL8z9LHfrv5osEiLThOReK5KYisRjZNGCGxRjFAQEgUE0RsDkPwf65a/9YXVwdfxBpw5Olq4IkMLrcf5sGTPBHDASAgNsI2JyHXJ7/WerQfzdfJECkDc+5UCQ3FYnFyKYBMyzGKA4IAIFqioDNeQj2z137x+ri6viDSBueLF0VJIHR5f7bNGCCP2IgAATcRsDmPOTy/M9Sh/67+SIBIm14zoUiualILEY2DZhhMUZxQAAIVFMEbM5DsH/u2j9WF1fHH0Ta8GTpqiAJjC7336YBE/wRAwEg4DYCNuchl+d/ljr0380XCRBpw3MuFMlNRWIxsmnADIsxigMCQKCaIiDz0P/7f/8vcQ/WXnvtxHmCGWD/3LV/LAeujj+IdHAWMPDbVUES6Fzuvxgwz/MEDsRAAAgAgUwRkHkIRDpT2HVlLts/BsDV/q+xbNkyWP3s9Q01VmEEateuTatWrUrcwoYNG+o8INKJoUMGIAAEDCEgRHrhwoWJS2zQoEHiPMgABFxHACvShiXA1TcygdHl/osBA5EWaUAMBIBA1gjIPIQV6ayRd3dFVpB21f6DSIsEGIpdFSSBz+X+iwEDkRZpQAwEgEDWCMg8BCKdNfIg0q7afxBpw7rmqiAJjC73XwwYiLRIQ82Mly5dSuPHj6dx48bRtGnT6KefftL/fv/9d9pkk01o0003pRYtWlDr1q3p6KOP1tc1Ewn0qioiIPMQiHT2o+Oy/WO0Xe0/iLRhXXNVkARGl/svBgxEWqShZsXz5s2jQYMG0b333ku//vprrM6xv33Pnj3pnHPOoX322cff2SVWZiQCAmUgIPMQiHQZ4KXM4rL9Y+hc7T+IdErFiWZ3VZAEB5f7LwYMRFqkoebEd911F11wwQXEq87lhqOOOooeeeQRqlu3brlFIB8QKImAzEMg0iWhMp7AZfvHYLrafxBpw6rkqiAJjC73XwwYiLRIQ/WPeSx5NZmJtInQrVs3evrpp0l2eDFRJsoAAkEEZB4CkQ6iks1vl+0fI+xq/0GkDeuXq4IkMLrcfzFgINIiDdU/vummm6h///5FO9KoUSPafvvtqVWrVjR//nz66quv6JtvvimYZ++996Y333yz4HM8AAJpEJB5CEQ6DYrl5XXZ/jFirvYfRLo8fSmYy1VBEkBc7r8YMBBpkYbqHU+YMIH22muvvHuK81hffPHFdN555+X9mPDdd9+lW2+9Va8+50Ph2WefpUMPPTTfI9wDAqkQkHkIRDoVjGVldtn+MWCu9h9Euix1KZzJVUESRFzuvxgwEGmRhuodd+3aVe/MEe1Fs2bNaMSIEcRuGqXC7bffTueffz5FZaJdu3b04YcfFv348Oeff6ZPPvmEvv32W+IPHZcvX06bbbYZbb755vrf+uuvX6p6+uWXX2jBggWhdGuuuabeVURuzpgxgyZPnkzfffedXlk/7LDD5BHiaoiAzEMg0tkPnsv2j9F2tf8g0oZ1zVVBEhhd7r8YsChpEmwQVx8E3n//ferYsWPeBk+cOJE6deqU91m+m9dddx1deeWVoUd8ghy7d+yyyy6h+3wxc+ZMGjp0KD366KMFdwepVasWnXzyycRlb7TRRjllyI1///vfxB85BkPjxo31dn0sp5dccoleOZfn9evX18ZQrhFXPwRkHgKRzn7sXLZ/jLar/QeRNqxrrgqSwOhy/8WAgUiLNFTfmF02eDU5Gnr06EEvvPBC9HbRa9aJv/zlL3qPaV7F5n+777573t07Bg8erMlt0QIDD9dee23617/+Rccdd1zg7v9+vvzyy3TAAQf874b6xSR85cqVdO2119JVV10VegYiHYKjWl7IPAQinf3wuWz/GG1X+w8ibVjXXBUkgdHl/osBA5EWaai+8U477URTp07N6cCUKVNo5513zrlf6gZvm1dq27t77rmHzjjjjFJF5TznHUA++ugj7e4RffjWW28Rf9wYDXPmzNFuHMuWLQs9ApEOwVEtL2QeApHOfvhctn+Mtqv9B5E2rGuuCpLA6HL/xYCBSIs0VM+YCQjvxLFq1apQB/i0wrlz54bumbpYuHChXrHmleJg4DqHDRtGu+22G/322280duxY6tu3b47LB69wv/POOzk+1/zRIz+LBv5Qkle/owFEOopI9buWeQhEOvuxc9n+Mdqu9h9E2rCuuSpIAqPL/RcDBiIt0lA94+nTp1Pbtm1zGt+lSxdNVnMeGLjBbiTsThINL730EnXv3j10m09XvOyyy0L3+IK33GvZsmXoPn9EuOuuu4bu8cV6661HS5Ys0W4mffr00avsfM0fNu6333456XGj+iAg8xCIdPZj5rL9Y7Rd7T+ItGFdc1WQBEaX+y8GDERapKF6xoXcIU444QR6+OGHK9Ip3tnj7bff1rtsMAHi3TbYl3nx4sXEx4wHA+/gESXM/Jx9t9mHOxiKfTR59NFH6w8a69SpE8yC39UcAZmHQKSzH0iX7R+j7Wr/QaQN65qrgiQwutx/MWAg0iIN1TN+5pln6PDDD89p/IABA/QuGTkPKnSD5UhkKlgFu5zUq1cvx/WEV6p5F45gKESkmTyzn/Smm24aTI7fNQABkRkQ6ewH02X7x2i72n8QacO65qogCYwu918MGIi0SEP1jPNtGcc9ueaaa3K2sbPVQ95Dml0xgoF9p6N+z4WIdK9evYhfGBBqHgIyD4FIZz+2Lts/RtvV/oNIG9Y1VwVJYHS5/2LAQKRFGqpn/MYbb9C+++6b0/hTTjmF7rvvvpz7pm/88MMPeo/pr7/+Wq8a8weOv/76q96ybsWKFTqeNm1azop0EiL9j3/8gwYOHGi66SivCiAg8xCIdPaD4bL9Y7Rd7T+ItGFdc1WQBEaX+y8GDERapKF6xryVXPv27XMaz+T6tddey7lv6gafLMjuGbwvNBPnpOGiiy4KHa7C+QutSA8fPpxOO+20pFUgfTVAQOYhEOnsB8tl+8dou9p/EGnDuuaqIAmMLvdfDBiItEhD9YwXLVpETZs2zWk8H6ryxRdf5Nw3cYN33OC9q//zn/+UXVwSIv3888/TwQcfXHZdyFh1EZB5CEQ6+zFy2f4x2q72H0TasK65KkgCo8v9FwMGIi3SUH3jrbfemj799NNQB/gDPXaz2HjjjUP341zwtnIc8n3cx4e17LHHHsRb1UUD3+cPH1u1aqX3tuY28C4efDoi7+wRDEmIdL5t9YJl4Xf1RUDmIRDp7MfQZfvHaLvafxBpw7rmqiAJjC73XwwYiLRIQ/WNTz/9dGL3h2g499xz6bbbboveLnnNH/fxKjDv0XzyyScTX6+11lo636OPPkq8tV408CmHd955p94GL/iM/aT5aHAm4MGQxEcaRDqIXM36LfMQiHT24+qy/WO0Xe0/iLRhXXNVkARGl/svBgxEWqSh+savvPJKzkEo3Bvedo7dO/KtLBfq7cSJE6lz586hx7zrBn/wx4ew8JZ10d02ODHXw+4k0TBp0iTq1KlT9DZhRToHEidvyDwEIp398Lts/xhtV/sPIm1Y11wVJIHR5f6LAQORFmmo3jF/cMgfHkbDgQceSI8//jitu+660Uc517xX81577UV8iEo0jB8/Xh/fvf/+++d8xNigQQNatmxZNIu+vvXWW4mP+I4GEOkoIm5eyzwEIp39+Lts/xhtV/sPIm1Y11wVJIHR5f6LAQORFmmo3vHTTz9NRxxxRN5O8ErxyJEj9dHaeROomxMmTKDjjz9eH90dTfPXv/5Vk3G+v/feexOfphgNM2bMoO233z50m4k5r0YvWLAgdJ8v2B2Fd/wIhkK7dsC1I4hSzfot8xCIdPbj6rL9Y7Rd7T+ItGFdc1WQBEaX+y8GDERapKH6x4V8pblndevW1Udyt23blnbccUfaYost6Mcff6Qvv/ySnnzySb0XdD4E6tevrz9kbNGihX581lln0d13352TNHqSIpNnJt2zZ8/OScs38m3PByKdF6oafVPmIRDp7IfZZfvHaLvafxBpw7rmqiAJjC73XwwYiLRIQ/WPeT/nffbZh9jP2UTgjwSfeuopveuGlHfXXXfR2WefLZehmN1LevToQewGwivcfDw4h969e9OIESNCaXlHj0svvZSOO+44Yh/s5s2bF9xHGivSIehq1IXMQyDS2Q+ry/aP0Xa1/yDShnXNVUESGF3uvxgwEGmRhpoRM5k+9dRT6bHHHkvVoY022ojGjh2r94sOFrR8+XK9oh13j+oDDjhA7wDSqFGjnC3wpNyrrrqKrr76ahBpAcShWOYhEOnsB91l+8dou9p/EGnDuuaqIAmMLvdfDBiItEhDzYofeOABuvbaa/Wx3Ul6xvs+83Z3t9xyC7Vp0yZvVvaR5pVnJtXFApNo9s1eb7316PLLL6cbb7wxb3IQ6bywOHFT5iEQ6eyH22X7x2i72n8QacO65qogCYwu918MGIi0SEPNi1euXKk/Ehw9ejSNGzeO+BTEQoG3yGMXDPaBjrNdHn9IyNvhjRkzJqfIzTffnPr06UO8j3WtWrX0c14p79evH/3f//2f7/LBD9h9ZMiQIfoIcPhI50BZ42/IPAQinf1Qu2z/GG1X+w8ibVjXXBUkgdHl/osBA5EWaajZMY/z559/rnfQYELNxKVZs2b6FMKWLVsSf1RYTliyZAl99tlneh9pXnnmUw233XZbEvmKlsmE+quvvtJuHk2aNKHWrVv7ZDuaFtc1HwGRExDp7MfaZfvHaLva/zXUXqVe9uKGGoFA1UWA/xQvH3UlaWXDhg11chDpJKghLRAAAiYRECK9cOHCxMXy/uUIQAAIJEMAK9LJ8CqZ2tU3MgHG5f6LAQORFmlADASAQNYIyDyEFemskXd3RVaQdtX+g0iLBBiKXRUkgc/l/osBA5EWaUAMBIBA1gjIPAQinTXyINKu2n8QacO65qogCYwu918MGIi0SANiIAAEskZA5iEQ6ayRB5F21f6DSBvWNVcFSWB0uf9iwECkRRoQAwEgkDUCMg+BSGeNPIi0q/YfRNqwrrkqSAKjy/0XAwYiLdKAGAgAgawRkHkIRDpr5EGkXbX/INKGdc1VQRIYXe6/GDAQaZEGxEAACGSNgMxDINJZIw8i7ar9B5E2rGuuCpLA6HL/xYCBSIs0IAYCQCBrBGQeApHOGnkQaVftP4i0YV1zVZAERpf7LwYMRFqkATEQAAJZIyDzEIh01siDSLtq/0GkDeuaq4IkMLrcfzFgINIiDYiBABDIGgGZh0Cks0YeRNpV+w8ibVjXXBUkgdHl/osBA5EWaUAMBIBA1gjIPAQinTXyINKu2n8QacO65qogCYwu918MGIi0SANiIAAEskZA5iEQ6ayRB5F21f6DSBvWNVcFSWB0uf9iwECkRRoQAwEgkDUCMg+BSGeNPIi0q/YfRNqwrrkqSAKjy/0XAwYiLdKAGAgAgawRkHkIRDpr5EGkXbX/INKGdc1VQRIYXe6/GDAQaZEGxEAACGSNgMxDINJZIw8i7ar9B5E2rGuuCpLA6HL/xYAJFoiBABAAArYQAJHOHnmX7R+j7Wr/QaQN65qrgiQwutx/EGmRAsRAAAjYRgBEOvsRcNn+Mdqu9h9E2rCuuSpIAqPL/RciDdcOkQbEQAAIZI2AzEMg0lkj7y6RFKRdtf8g0iIBhmJXBUngc7n/YsBApEUaEAMBIJA1AjIPgUhnjTyItKv2H0TasK65KkgCo8v9FwMGIi3SgBgIAIGsEZB5CEQ6a+RBpF21/yDShnXNVUESGF3uvxgwEGmRBsRAAAhkjYDMQyDSWSMPIu2q/QeRNqxrrgqSwOhy/8WAgUiLNCAGAkAgawRkHgKRzhp5EGlX7T+ItGFdc1WQBEaX+y8GDERapAExEAACWSMg8xCIdNbIg0i7av9BpA3rmquCJDC63H8xYCDSIg2IgQAQyBoBmYdApLNGHkTaVfsPIm1Y11wVJIHR5f6LAQORFmlADASAQNYIyDwEIp018iDSrtp/EGnDuuaqIAmMLvdfDBiItEgDYiAABLJGQOYhEOmskQeRdtX+g0gb1jVXBUlgdLn/YsBApEUaEAMBIJA1AjIPgUhnjTyItKv2H0TasK65KkgCo8v9FwMGIi3SgBgIAIGsEZB5CEQ6a+RBpF21/yDShnXNVUESGF3uvxgwEGmRBsRAAAhkjYDMQyDSWSMPIu2q/QeRNqxrrgqSwOhy/8WAgUiLNCAGAkAgawRkHgKRzhp5EGlX7T+ItGFdc1WQBEaX+y8GDERapCF+PGbMGOrVq5efYeLEidSxY0f/Gj+AABCIh4DMQyDS8fAymcpl+8c4utp/EGmTWuSwIAmMrioS918MGIi0SEP8+Pnnn6eePXv6GSZPngwi7aOBH0AgPgIyD4FIx8fMVEqX7R9j6Gr/11i2bJlnSohQDhCoCQjUrl2bVq1albgrDRs21HlApBNDRyDSyTFDDiCQDwEh0gsXLsz3uOi9Bg0aFH2Oh0AACOQigBXpXExS3XH1jUxAc7n/YsBApEUa4scg0vGxQkogUAwBmYewIl0Mpco8c9n+MaKu9h9E2rA+uSpIAqPL/RcDBiIt0hA/BpGOjxVSAoFiCMg8BCJdDKXKPHPZ/jGirvYfRNqwPrkqSAKjy/0XA2aSSP/888/0+++/a3ibNGlCtWrVEqhrVAwiXaOGE52xiIDMQyDS2Q+Cy/aP0Xa1/yDShnXNVUESGF3uvxgwk0R6jz32oPHjx2t458+fT5tssolAXaNiEOkaNZzojEUEZB4Ckc5+EFy2f4y2q/0HkTasa64KksDocv/FgFUHIj1v3jyaPn06zZw5k9Zee23afPPNaeutt6ZWrVrJUCaK+cOmWbNm0ccff0y//PILbbXVVrTNNtvQZpttRnXq1ClZVrlEOm296mNr+vHHH3X7ePzatGnjt3XChAn00Ucf0ZIlS6hLly605557+s/wAwhUVQRkHgKRzn6EXLZ/jLaz/VdG32jgXUBsBtQP/G3Jn5pHeAcco9UrAqfL5HLVinSqslesWOH169fPa9SokV+mtFnigw8+2FPkMVY9K1eu9K699lpPuZwULK9u3bpet27dvDlz5hQtc/To0aEy1PZ3BdObrHfUqFF+vYqAeH/88YenjIHXvXt3/z5jc8wxxxRsDx4AgaqEgOiyItJe0n9p+wH7C/ubVobS5Lclf2atvkLAVkcEfNQPRRZZyDoWA2ayXlNE+uuvv/Z22223EDmU9kZjJpRDhw4t2o3PPvvM69SpU6zyuPx11lnHGz58eMEy4xJp0/U+99xzoT6o1XTvjDPOCN3j9oNIFxw6PKhiCIg+JyXRnD5tgP2F/U0rQ2ny25I/uHaoWcdkcPZPG6tBdLn/8idVNREYEykTPtLfffcdbb/99rR48WLdLm7nEUccQbvuuivtsMMO9J///Ic++OADuvPOO2n58uU6DX/UqFZr6fDDD8/piyLlujw1afnP+FTCHj16UPv27alx48babeTDDz8kRci1q4ckHDx4MPXt21cu/TiOa0cl6n3ppZd0u6UhkyZNIvWCwAsMpFbTqUOHDvrRLrvsovsi6RADgaqKgMxDihgnbiK7eaUJLs//jBv6/1+yuRe5NfzTsP98eW29EUhbUD/eiEUWso7VPKpXMk3Wa2JF+pxzzvFXWNdaay1v5MiReZvI7hfNmjXz0yqjqv80HE180kkn+WkU4fZuvvnmaBL/mt1ENt10Uz89u4HkW/mKsyJdiXrfeOMNv208fieeeKK+vuyyy7SLh98R/AAC1QQBmYewIp39gIF/uMk/4NphWNegSG4qEouRGDCTIpWWSH/zzTce+ylL22666aaizXvmmWf8tJxnxIgRofSffPKJp05+9NOceeaZoef5LqJk9cYbb8xJVopIV6petSOK3xfu75prrunxiwcCEKiuCIiug0hnP4Kw/27af7h2qFnHZLD2p4XVnUD99v60JH9SVdO3MZFK69px9tln01133aXbw0efz507t+gWeuqDRNpwww3pt99+I963ml072D1DQu/evenhhx+WS5o6dSq1a9fOv873g/Hg3TvYNYPDBhtsQAsWLAjtiV3KtaNS9U6cOJE6d+6s28X/sUsLY9S8eXP/Hn4AgeqEgMxDcO3IftRgf+3ZXx5tW/iDSBvWNVsDKd1A/fYUWQxYXCL966+/Us+ePWXo8sZTpkwhPpSFA2+/Vq9evbzp+Cb7HqvdJkLPmeROmzZN39tnn33o9ddfDz3Pd8FkWq3M5ntE2267Lc2ePVs/22mnnbRvdd6EkZsDBgygG264wb/77bffhshqKSJdqXqjRJrxY79pBCBQXRGQeQhEOvsRhP21Z395tK3hb/qPH/jThpt/2hA5cnn8lR5rNwHBolTMO0RIHhPxfffdl1Pleuut59dx2mmn5TxPekN9SOKXd8IJJ8TO/sADD/j5uK/vvvtuKG8p145K1cvtCGKvCH+oXbgAAtUNAZFnuHZkP3Iu2z9G29X+w0fasK65KkgCo8v9FwMmWJSKK02k1Up2iCT279+/VJOKPlfuGKHy1Ap40fTBh2PHjg3ljX7wWIxIV7LeKJG+7bbbgs3GbyBQ7RCQeQhEOvuhc9n+Mdqu9h+uHWrWMRms/WlhdSdQv70/LcmfVNV8EkukOB374xYLRx55JL3//vs6yXvvvUcbbbRRweTsexzcvopdOoL+y0OGDKELLrigYP5SD9jNhLeBk3DLLbfQxRdfLJdFY+5Dx44d/TSDBg2iSy65xL8u5tpRyXqjrh1PPvkkHXXUUX678AMIVDcEZB6Ca0f2Iwf7a8/+8mhbw5/fIkwGV99IBEP0313XFqXHetVVZMFEnGbXjldffTW0CnzPPfekatILL7xQdnl8kIrgwzFvLxcMxVakK1lvdEWa60IAAtUZAdEzrEhnP4qw/27af7h2GNY1KJKbisRiJAbMpEilIdKzZs3y28RtUx/7pWoa7wktfeQ43zZ2hSqIEtaoC0UxIl3JeqPtApEuNIK4X10QEB0Fkc5+xGD/3bT/INKGdQ2K5KYisRiJATMpUmmIdNQH+7zzzkvVtKjP9fnnnx+7vOj+1Eycg6EYka5kvSDSwVHA75qAgMxDINLZjybsv5v2H0TasK5BkdxUJBYjMWAmRSoNkeZ28EmC0q5jjjkmddMaNWpUVnl33323n4/bM3369FBbihFpTlipekGkQ8OAixqAgOg7iHT2gwn776b9x8eGatYxGaw5u6/uBOq397GDfOSjpm9jIpX2QJadd97Z3+u5RYsW+lAUPnSkWFA7atD8+fNJkVf9ceOBBx7oJ+e9o/kQFg5t2rShL7/8kqTffqI8P8444wxSPtr+k6VLl9I666zjXxf72JATVare6MeGyrWDevTo4bcLP4BAdUNA9FER6cRND36snDizygD7Y8/+8HgBf0v4m35nwxuZm29kIkcuj7+ax/Sqq2BhIk67Is0f9Um7OFaHjRRt1h9//OGpnUH8PIccckgofb9+/fxnXN5rr70Wep7vgl1MFGn286mdRHKSlVqRrlS9WJHOGQrcqOYIiL5jRTr7gXTZ/jHarvYfrh2Gdc1VQRIYXe6/GDDBwkSclkgvXLjQU6tMPok94IADvFWrVhVsWtSX+d577w2lXbRoUYgU9+rVK/Q830XUrSPfB32liHSl6gWRzjdiuFedEZB5CEQ6+1F02f4x2q72H0TasK65KkgCo8v9FwMmWJiIH3roIe+6667T/5Q7RFlFXn755T6R5jaqvak9dTx5TlkTJkzwgichsn81E9hoGDhwYKg8PjFx5cqV0WT6+v777/fUceN++r322itvulJEmjNVol4Q6bzDgZvVGAGZh0Cksx9El+0fo+1q/+EjrWYdkwE+SpZ8lFYPok38xTdRzScmRSp1WYsXL6YOHTrQnDlz/LJatmxJ7H/N95csWUKTJ0+mF1980X+uyC+pfahJEV//nvzg9Hwwi9obWm7pw1a6deumY/bB5sNgJk2aRGPGjPHTqGO+6c033wwd6iIPS/lIc7pK1AsfaRkBxDUFAZmH4COd/YjatD/cW9Rvh3+ASBvWNQiyHUGWYbSJvxiwqkakGRsmoX//+99p1KhRAlXBmD84uuOOO6h3794F06iVBzr33HPpgQceKJgm+KBz586kVtdp8803D972f8ch0pzYdL0g0v4Q4EcNQUDmIRDp7AfUpv3h3qJ+O/wDRNqwrkGQ7QiyDKNN/MWAVUUiLfjwzhn8Tx3WQsq9Q27ruG7dunTqqafSVVddRc2aNQs9K3TxxBNP0LBhw2jmzJkUNdz16tWjrbbaik488US66KKLqNhuIXGJtLTDVL0g0oIo4pqCgMxDUX2M0z/s2hEHpcJpbNofbhXqt8M/QKQL60RZTyDIdgRZBssm/mLAqjKRFpzUB4f0+eefawLcsGFD2nLLLal169ZUu3ZtSZIo5j7PnTuXZsyYQcpfmrbbbjvabLPNyi4vbuW26o3bPqQDAlkjIPMQiHTWyIPI2rS/PNq26geRNqxrtgZSuoH67RF5MWDVgUiLvCAGAkCgZiEg8xCIdPbjCvtrz/7yaNvCH0TasK7ZGkjpBuq3p8hiwECkRRoRAwEgkDUCMg+BSGeNvD0iJz2F/bdj/0GkRQINxRBkO4Isw2cTfzFgINIyGoiBABDIGgGZh0Cks0YeRNqm/eXRtlU/iLRhXbM1kNIN1G+PyIsBA5EWaUQMBIBA1gjIPAQinTXy9oic9BT23479X4M30JZBQAwEgADpD+T4Y7ykgT/a4wAinRQ5pAcCQMAUAkKk1ammiYvkvd4RgAAQSIYAVqST4VUyNd4I7bwRysDYxF8MGIi0jAZiIAAEskZA5iGsSGeNPFakbdpfHm1b9YNIG9Y1WwMp3UD99oi8GDAQaZFGxEAACGSNgMxDINJZI2+PyElPYf/t2H8QaZFAQzEE2Y4gy/DZxF8MGIi0jAZiIAAEskZA5iEQ6ayRB5G2aX95tG3VDyJtWNdsDaR0A/XbI/JiwECkRRoRAwEgkDUCMg+BSGeNvD0iJz2F/bdj/0GkRQINxRBkO4Isw2cTfzFgINIyGoiBABDIGgGZh0Cks0YeRNqm/eXRtlU/iLRhXbM1kNIN1G+PyIsBA5EWaUQMBIBA1gjIPAQinTXy9oic9BT23479B5EWCTQUQ5DtCLIMn038xYCBSMtoIAYCQCBrBGQeApHOGnkQaZv2l0fbVv0g0oZ1zdZASjdQvz0iLwYMRFqkETEQAAJZIyDzEIh01sjbI3LSU9h/O/YfRFok0FAMQbYjyDJ8NvEXAwYiLaOBGAgAgawRkHkIRDpr5EGkbdpfHm1b9YNIG9Y1WwMp3UD99oi8GDAQaZFGxEAACGSNgMxDINJZI2+PyElPYf/t2H8QaZFAQzEE2Y4gy/DZxF8MGIi0jAZiIAAEskZA5iEQ6ayRB5G2aX95tG3VDyJtWNdsDaR0A/XbI/JiwECkRRoRAwEgkDUCMg+BSGeNvD0iJz2F/bdj/0GkRQINxRBkO4Isw2cTfzFgINIyGtU/3nvvvenbb7+lk08+mQYMGFD9O4Qe1HgEZB4Ckc5+qG3aH+4t6rfDP0CkDesaBNmOIMsw2sRfDBiItIxG9Y4XLVpETZs21Z04//zzaejQodW7Q2i9EwjIPAQinf1w27Q/3FvUb4d/gEgb1jUIsh1BlmG0ib8YMJNE+ueff6bff/9dd69JkyZUq1Yt6SriCiMwZswYOuSQQ3QtINIVBhvFG0NA5iEQaWOQxi7Ipv3hRqJ+O/wDRDq2isRLCEG2I8gyOjbxFwNmkkjvscceNH78eN29+fPn0yabbCJdRVxhBK644gq6/vrrdS0g0hUGG8UbQ0DmIRBpY5DGLsim/eFGon47/ANEOraKxEsIQbYjyDI6NvEXA1YdiPS8efNo+vTpNHPmTFp77bVp8803p6233ppatWolUMaO2QVi1qxZxESf/61atYratGmj/22xxRbUqFGjkmUtW7aMfvzxR52OceT8EiZMmEAfffQRLVmyhLp06UJ77rmnPDIeM/lYuHChLvekk06id955R/9mH2km1hIaN25M66+/PjGOK1as0LfXXHNNatGihSSJFTNev/32m05bp04datmypf69dOlSYlw5RPH4448/6N1336Uvv/ySfvjhB9p4442pffv2tM022xCXUU7gv3ywLPA/xmC77baj7bff3m9POWUijx0EWF44gEhnj79N+8O9Rf2W+Icy+kaDMohGy0taGOoH/kllxlR6NY95/M9kUMRRl8nlKtKVqmhF+Lx+/fp5itj6ZUqbJT744IM9RVpj1fPee+95xx9/vFe3bt2C5Sly6fXp08dbsGBB0TJHjRrll6GIgKfIoqeMgte9e3f/PrfxmGOOKVpO2ofDhw8P1Se4ROObbrpJV3Xsscf66WvXrp1ojBTR8erXr+/nP/zww/3m33vvvf59rpux4HDfffd5imyHnknb1lprLe/000/3FDH3yyn1g8tT5D9veVzuuuuu65166qketxWheiAg8sBjlvRf2h7C/sL+ppWhNPltyZ9Zq68QsNURAR/1Q5FFFrKOxYCZrNcUkf7666+93XbbrSBhkrZzzERWfVhXtBsPPvigThfMV+z3Ouus47311lsFy3zuuedCbfvll1+8M844I3SPy69qRPrNN98MtfHGG28s2Mfog0cffTSUd+zYsX6SJ554IvTsu+++8/r37x+6VwhvHmdOXyyo1W7vsMMOi1Ue16P+suC9//77xYrEsyqCgMhFUhJt4mUJ9hf216Ya2JI/uHaoWcdkwJ9WLP1pZfUg2sRf/qSqJhJjImXCR1qRKv1n+sWLF+t2cTuPOOII2nXXXWmHHXag//znP/TBBx/QnXfeScuXL9dp+KNGtUpMapU0py/PP/88KRKmXTj4oSLJdMopp9C+++6r3QzYtYPdDp588klSBNnPz+4a7E7CriTR8NJLL1GPHj3825MmTaJOnTrxiz6pFW/q0KGDfrbLLrtUdPeMjz/+mN544w1dV9++ff0PPXkbPMZMgiKrfpu22mor+uyzz/SjLbfckj799FNJVjTu2bMnMZYcmjdvTt988w2pVW19/fTTT4fqu/vuu+nMM8/UH5v26tVLfwTJbiDs/jF58mR67LHH6Pvvv9d5+b+dd96ZpkyZ4l8Hf7DbCLtu8LZ+Erp160bHHXcctWvXjho2bEiMg3rxodtuu41Wrlypk7HrCmPD7jUIVRcBmYcUMU7cyHy6maQQm/MvtxP1u2t/rY6/6bcHW28E0g/UjzdikYWsY6XIeoXPZL0mVqTPOeccf+WR//w/cuTIvE2cM2eO16xZMz+tMqp5/6SvCK6fRpEub+rUqXnL45u8si24cHzppZfmTasIWijdiSeeqK8vu+wy360hb8YK3uT+S9svuOCCgjXdcsstfjpOrz4OLZhWHqiXmpBLDK82B8Ozzz4bKpNxZheal19+OZjM/81/cVAkPpSnUDuUr7efjv/6MHjwYO1K4xcW+KFesDz1gaufvmvXroGn+FkVERCZxYp09qMD/uEm/4Brh2FdgyK5qUgsRmLATIpUWiKtVjlDhE18ewu18ZlnnvH7wf0ZMWJEKOlXX30Ves7uF8WCWs301Iqtn4fdDvIFJn2CH8fsW80vADZDXCLN/t9BP3G1Ol+y2eybHOzv559/HsozevTo0HNOO2jQoFCa6MW0adNCeY4++uhoEk+tWnsNGjTw0/ELS6nwyCOP+Om5HcVcdEqVheeVR0DkCkS68lhHa4D9d9P+g0hHNSHlNRTJTUVisREDllKEQtnTEumzzjrLb1ecj+HUntWe2o1CfwTHH6Gpbd9C7eGVVF49Vq4E3pAhQ4quRktGJpaCzXrrrSe3Q7HahcJPw2mVa4mnXA9CabK+iEukuV3suy195Hzs410s7L///n56tQtJTtIokeYxiePDqlx1/HLVDh4ej1cwnHvuuf5z/utEHIz5w8+2bdv6+fbbb79gkfhdxRAQOQSRzn5gYP/dtP/wkVazjskAHy13fbTEN1FN37FE6tdffyX2ky0W2M+VtybjwNu+1atXr2By9ulVu1yEnrPPq1qp1Pf22Wcfev3110PP813wdm7sD2sqXHvttTRw4EC/ON6yTbmQ+Nf8Y+LEidS5c2f/HveD/aZtBvb9VoRYN0G5dpB6cSjYHPYdZh9xCQ888ADx9nn5glrB1vuBsy85h4ceeoh69+4dSsq+00HZYJ909psuFa677jq68sor/WS8baAiwf41+06zPzwHxpu3FowTLrroIr//ioBrX1SR9zj5kSY7BGRcFJFOXKl6CUycJ5gB9s9d+8dy4Oz4m35nwxuZm29kIkcuj7+aR/SqnWBRKuZVS8ljImZ3gWjgFWAp+7TTTos+zuR62LBhfhu4LexuEg3RFekBAwZEk2R+nWRFmldt1V7cfj/zrTJLB+644w4/HW8vl09noivSpVxypOzoTiAvvviiPNJxcOtD3iovboi6d6g9v+NmRbqMERB9x4p0xsCr6vLpcpatQP12+BdWpNWsYzI4+0a2GkSX+y8rQWrijCVSatLLu4NFrMx5EikirXfPkEd8gAkfGiJBfdBGN9xwg1waiXm1W22LRupDRVIfvOmYV8J4VZt3e+B/vKIuq+pcKe9OIQePSCOiK9K8W4RyQ5DHVuIkK9LcQOXDTOrjSL+tyu9ZH3Tj31j9g/+yIAe9/P3vf6d77rknmkTv5hFckeYdUI466qicdNEbr7zySuivEkGZ4DEIHo6jPhwk3n0kTuCdX9SWh35S3imkY8eO/jV+VB0EZB7CinT2Y+Ky/WO0ne2/6bclvBHZeSOScQT+9vBX84heaZSxKBXzKibvtlDsn/pTvL96yQegFEvLK1DBwAerSJs4Zp9mU4E/OIselhKsq9hv7kM0RFekFXGMJsn8OsmKNDeOV2n5I0np++WXX57TZnUSYmj/bR7TfCG6Iq3cXPIly7nHu2xI/RwrVw8/zYcffhh6FkyX9Pe///1vv1z8qFoIyFhiRTr7cYH9tWd/ebRt4Y+PDQ3rmq2BlG6gfnuKLAZMxsJEnOZjw1dffTVEnNTKp4kmeXzoiPRVYv6QkT9044/o1Mqpp3x+9Yl4au9jT+2FHUofh0i/8MILRtqappCkRJrr4r4LJptuuqmn/KBDTbj11lv952ov59Cz4EWUSCtf5uDjgr/VftZ++dyO4HaDr732WuiZtLOc2ORLWcHO4EFZCMh4gkiXBV+qTLC/9uwvD5wt/EGkU6lNbmZbAyktQf32FFkMmIyFiTgNkZ41a1aIOCm3jtRN4pVoJs3SV/79j3/8o+iOEuX4SFdXIh19eYmuJCt3CB873r+5UIgS6bh4KJcLv3weIybuEvKRbHVAjlfOv1JHvkudiLNHQHQTRDp77GF/7dlfHm1b+INIG9Y1WwMp3UD99hRZDJiMhYk4DZGOfsx43nnnpW5S+/btfaLGbgxx9hTmD+UEG47jfGwYlzim7lCRAspZkWZ3nc0228zv7wknnODXoE579O8zdsU+2IsSabULiF9OsR+MWxBr3qZQgtolJuRWcvHFF8sjxDUIARl/EOnsBxX215795dG2hT+ItGFdszWQ0g3Ub0+RxYDJWJiI0xBprr9JkyY+seK9jtOE3377LeQDXGxnimA9fGiLYMNxTXbt4H4HXV/UB4v+yYzsryw4qO3sghDl/I4SaS4zTuADdKQOjseNGxfKFjylMN+BLaHEuKiWCMj4g0hnP3ywv/bsL4+2LfzX4IqV4iEAASCwGgHlrkCyx28SUNQxzjq50uck2YqmVf7FpE7902nmz5+v9x8umiHyMLhvsDpghRSJJXXYSSRV+FIdIU5cF+/wsNFGG9GBBx6oE/CexGpF2k98zTXXhPYs9h8EfjCObdq0IfWRnX+X29CqVSv/mn9Ed+1QK6vUo0ePUJqsL5Lu2iHt432yGWvesYSD+jCPjjjiCFI+0fTxxx/re2PGjKGDDjpI/873X3QfaXUCISmSnC9p6B7v1837dktQ7hy0xRZbyCWpFzN/7+itt96aZs+e7T/Dj5qBgOzasXDhwsQdUqdeJs6DDEDAeQRMv7PZeiOQfqB+N98Iq8L4q8lErwZKW0zEaVek1XZsuk3StqjPbrSN7JqgyLOf55BDDvGTqC3b/PtcnjpIxH9W6Me//vWvUB7Ox8eMR0N0146q5toRPeEx2v7o9eGHH+73mz9AnDp1qn/Nq8J8dHqxEF2R5mO91XaGxbLoZ8Hj2Js2berxSZXBoEi23w4ei7FjxwYfF/z96aefeor8W1vxKdgwPMhBQHQdK9I50FT8BviHm/wDrh2GVQuK5KYisRiJATMpUmmJtFqV8oK+vgcccEDOThLB9j7zzDN+P7g/9957r/+YfXqljxxfcskl/rN8P5544gn9YaJaIQvl490joqEqEungYTa8C0mSwC8sghWT4OBR7f369StZVJRIc1m333570XxqP2+/Tk6fb/s9Jlcbbrihn2733XcvKg9cIb9cqVMbdR4+Vlyd8li0HXhoFwGROxDp7McB9t9N+w8ibVjXoEhuKhKLkRgwkyLFq77sW8v/li5dWlbRTKikbRwfeeSRHn94Fg28xVqQPLJ/9aJFi0LJeJVTyuJT+fJ9OMgZeB/oOnXqaJ/q6K4dQ4cODZXJF1WRSPP2dNJX5Z6Ss7qb04nADd72rnXr1n5+5U7j/+bdM0qFKJFmX+u6det67AOdL3zxxRcet1Hay7upzJ07N19SLzoe3bp183766ae8aXk+O/bYY/1yuXzemQSh6iIgMgAinf0Ywf67af9xsqGadUwGZ0/2WQ2iy/0X30Q1fZsUqdRlLV68mDp06KBPHZTC+GRB9r/m+3wCIp9Up46TlsekdpUgRZhor7328u/xD7UqSmr3D/8e+1FfeOGF1LZtW+1Xrtw2iE/h4/I4XH/99XT22WdT48aN+aVd39tggw1IrWbrsrfcckv9rCr6SKsXDnrqqad0m/k/9WKhfZ0ZGx5rPn2xWOC+X3HFFaEkjPnbb78dupfvIuojrbaxo759++qkvXr1ok6dOlG7du30iZGTJk0itTsHqb8Y+EWddNJJpHb68K+DP5S7hz7RUB3Q4t9mn2722WYfeJaN77//ntS2eKRe5IjlR8Lxxx9P6rhwuURcBRGQeUgR6cStU3+9SpwnmMHl+Z9xQP//Szb97K3hb/qdDW9kbr6RiRy5PP5qHmWmKFBUqVgdDx06LETami9mV5BC/s/s29u5c2fdz3x5g/cGDBig3QIYiOBBJcE0sqtEVVyRjrYp2G4+fKZUUMdq61X5YL6429hFV6T5xEL+q0TUTSZYtvxWLy4lfbB5BxY+rCW4Ui75C8UXXXRRSTeQUpjgeeURkPHDinTlsY7W4LL9Yyxc7b9xq+8qkKJQ6L+7LxJiwEQWqmLMH/+pVWiPfV2lvRKz6wD78qpdJ4o2fcWKFR7vDc2+v5JXYiZ6++yzj/4wLVgIl6lWPENEkNugVqJ1sihprQofG3LD7r//fo/dKqR/HDP5ZJ/hOOHQQw/183I5vLd3nBAl0lOmTNHZ+ONA9msOtkfapHbh8NQqeZzi/TS8D3jXrl1D2yQGy65fv77He2HLC4+fET+qLAIyfiDS2Q8R7L+b9h+uHWrWMRms/WlhdSdQv70/LcmfVNX0bVKkKlIWb0v3+eef08yZM4m37WMXC+XTS7z1X9zA27uxK4fa0YGUAaHmzZvT5ptvThtvvHHBIjid8t3VbhLK37pguqr0QPmT0yeffEK8nRhv28c4qZeOWE0Mbl/ILi533HFHrHxR1w52lVGnIvp5eTtB5RetXTAY95122ol4u740QZ1WSOo0TFIr6dSsWTO91SL31eafatP0x9W8Mg/BtSN7CYD9tWd/ebRt4Q8ibVjXbA2kdAP121NkMWDVgUiLvCCuHAJqlZ3U6rGugGWD95DmvZvjhFJEOk4ZSOMmAjIPgUhnP/6wv/bsL4+2LfxBpA3rmq2BlG6gfnuKLAYMRFqk0e1Y7YahP9hkFPj3yy+/HBsQEOnYUCFhBAGZh0CkI8BkcAn7a8/+8vDawh9E2rBy2RpI6Qbqt6fIYsBApEUa3Y3ZhaNPnz4+ALw6vdtuu/nXpX6ASJdCCM8LISDzEIh0IYQqdx/215795VG1hT+ItGGdsjWQ0g3Ub0+RxYCBSIs0uhnfd999pD7aJPVRpgbgr3/9Kz3++OOJwACRTgQXEgcQkHkIRDoASkY/YX/t2V8eYlv4g0gbVjBbAyndQP32FFkMGIi0SGNl4kcffZTGjx9fkcJ33HFHTYKTFP7www/rD/TUoSakdsHw99DmMvjjRP5QUJ0mmKRIApFOBBcSBxCQeQhEOgBKRj9hf+3ZXx5iW/iDSBtWMFsDKd1A/fYUWQwYiLRIY2Xi008/nYYPH16Rwnv27EnPPfdcorL5gJR8eXg3DT7kRu05nag8TgwinRgyZFiNgMxDINLZiwTsrz37y6NtC38QacO6ZmsgpRuo354iiwEDkRZprEzMJys++OCDFSn8wAMPpJEjRyYqO0qk69WrR+zOMWjQoMQr0VIxiLQggTgpAjIPgUgnRS59ethfe/aXR88W/iDS6XUnVIKtgZRGoH57iiwGDERapNGNeNGiRfTtt9/qfab5yHTek3vddddN1Xk+7lsdwuKX0aVLF1p//fX9a/wAAoUQkHkIRLoQQpW7D/trz/7yqNrCH0TasE7ZGkjpBuq3p8hiwECkRRoRAwEgkDUCMg+BSGeNvD0iJz2F/bdj/0GkRQINxRBkO4Isw2cTfzFgINIyGoiBABDIGgGZh0Cks0YeRNqm/eXRtlU/iLRhXbM1kNIN1G+PyIsBA5EWaUQMBIBA1gjIPAQinTXy9oic9BT23479B5EWCTQUQ5DtCLIMn038xYCBSMtoIAYCQCBrBGQeApHOGnkQaZv2l0fbVv0g0oZ1zdZASjdQvz0iLwYMRFqkETEQAAJZIyDzEIh01sjbI3LSU9h/O/YfRFok0FAMQbYjyDJ8NvEXAwYiLaOBGAgAgawRkHkIRDpr5EGkbdpfHm1b9YNIG9Y1WwMp3UD99oi8GDAQaZFGxFEE1llnHVq+fLm+fdFFF+m9pqNpcA0E0iAg8xCIdBoUy8sL+2vP/vKI2cIfRLo8fSmYy9ZASoNQvz1FFgMGIi3SiDiKQIMGDXwi3bdvXxo8eHA0Ca6BQCoEZB4CkU4FY1mZYX/t2V8eMFv4g0iXpS6FM9kaSGkR6renyGLAQKRFGhFHEQCRjiKCa9MIyDwEIm0a2dLlwf7as788OrbwB5EurRuJUtgaSGkk6renyGLAQKRFGhFHEQCRjiKCa9MIyDwEIm0a2dLlwf7as788OrbwB5EurRuJUtgaSGkk6renyGLAQKRFGhFHEQCRjiKCa9MIyDwEIm0a2dLlwf7as788OrbwB5EurRuJUtgaSGkk6renyGLATBLpn3/+mX7//Xc9vE2aNKFatWrJUCOuhgiASFfDQatmTZZ5CEQ6+4GD/bVnf3m0beEPIm1Y12wNpHQD9dtTZDFgJon0HnvsQePHj9fDO3/+fNpkk01kqBFXQwRApKvhoFWzJss8BCKd/cDB/tqzvzzatvAHkTasa7YGUrqB+u0pshiwqkyklyxZQnPmzKFvv/1W//vjjz9o44031v+23XZbWnfddUWU8sZLly6lRYsW6Wfc3zZt2vjpuKx3332XvvzyS/rhhx90me3bt6dtttmG6tSp46dL8oNX5GfOnKn/MTHYbrvtaPvtt6eWLVsmKSYnbSXK/frrr+n999+nTz75hBo1aqTbuM8++1DDhg39+kGkfSjwo0IIyDwEIl0hgIsUC/trz/7ysFjDXxl9o2HZsmVGy0taGOoH/kllxlR6pcce/zMZunTposvkctWKdNlFz5gxwzv55JO9evXq+eVJeyWuX7++d9xxx3kTJkwoWM+9994byq8mLp32vvvu8xS5DT2Tctdaay3v9NNP93777beC5UYfcHktWrTIWx6Xqwi/d+qpp3qKLESzFr2uRLkjRozwlNtN3rauvfba3nnnnef9+uuvul2MseCitr8r2lY8BALlICDyxbqR9F859QXzwP7C/gblIevftuTPrNVXqNnqiAwY6ociiyxkHYsBM1mvCSLNRE/aFieuXbu29/DDD+ftxhNPPBEq67vvvvP69+8fuleojt12283j9MWCWu32DjvssFjlcT1bbLGFp1aBixWpn1Wq3CuvvDJWWzt27Oj98ssvHhNrwUcdyFKy3UgABJIiIPKVlEQnfSnN1y7YX9jffHKR1T1b8rcGV6wUDwEIAIHVCCgiSatWrUqMh/wJX00aifMWypDWR/q9996jvffem9RqsK6iWbNm1Lt3b+rUqRNtuOGG/CKt3TDefPNNevzxx4ldHjjwn4dfeukl6tatm76W/55++mk64ogj5JLuvvtuOvPMM/VHkL169aJDDjlEuzSw+8fkyZPpscceo++//95Pv/POO9OUKVP86+APdhth1w12O5FP8KV6AABAAElEQVTA9atVcmrXrp12kfj444/prbfeottuu41Wrlypk6255pr0xhtvkHrpkGyhuFLl3nzzzdSvXz+/rvXWW48uueQSje1f/vIXmj17Nk2dOpWGDRtGCxYs0DiNHDnSx5hPNrz11lv9/PgBBEwgIK4dCxcuTFwcux4hAAEgkBAB028Ktt4IpB+oH2/EIgtZx0r19GqjyXrTrkgfe+yx/gqo8mf2FKkt2DxFYD3lf+ynP+igg3LSPvvss/5z7q96efDq1q3rvfzyyzlp+YbyG/a23HLLUB718WTetFdccYWfTpEBT5365ym/67xpP/jgA099eOmn79q1a950fLMS5a5YscJr3ry5Xz+7dnCb8gXGYIcddtBp1a4rfh6sSOdDC/fSIiDzEFak0yKZPD/4h5v8A64dyXWlaA4okpuKxEIhBqyogCR8mJZIs+uDtGvgwIEla3/77bd1eiaGu+66q3ZHCGYaPXq0X56UO2jQoGCSnN/Tpk0L5Tn66KNz0jDBV6thfroTTzwxJ030xiOPPOKn57aolepoEv3iUIlyR40aFap7+PDhOXUHb3z11VcevxwIZhyDSAcRwm9TCIiMgUibQjR+ObD/btp/EOn4OhIrJRTJTUVi4RADFktQYiZKQ6SVe4peLZZ2XX311bFqZV/eQiFKpNdff/1YH/zJiiy3Re3g4S1evDhUxbnnnuvjxx8n8up4qcCr1W3btvXz7bfffjlZKlXuvvvu69erXEu8n376Kafu6I3u3bv7eRgHEOkoQrg2gYDoO4i0CTSTlQH776b9x/Z3atYxGaxtv7K6E6jf3vY74puopt5YIqV2cqCePXsWTcv+xOK3vOeee5LadaNgerULBCmyFnrOed555x19b+uttyb2mWZf3nLD888/H2qz+jCQ2G+6VLjuuutIfZjnJ/voo49IkWD/mn2nlWuEvu7cuTOpnUP8Z8V+sJ/xkCFDdBJFwPX2RzIOfLNS5bJ/ufigsh+3cm0p1kz9jH3Q2d9bArcdPtKCBmJTCIj8KyKduEj1MWziPMEMsD/27A+PA/C3hH+y963SqfFG5uYbmUiGy+Ov5jG94ihYlIp55VfymIh5a7douPbaa0N1tGrVynvyySe95cuXR5PGuo6uSN90002x8j366KOhdrz44ouhfGrfZf85b5UXN0TdO3788cdQ1kqUq06aDLlpnHHGGaE6C11MmjTJ7yOPN1akCyGF+2kQkLkEK9JpUCwvr8v2jxFztf9YkVazjsmAN0JLb4SrB9Em/rISpOaTWCKlJh1KuwIUrEgRaTrllFOCt0i5HNABBxygDwoJPuB699prL1IuCnpnDt4tI06IrkgrUk5HHXVUyayvvPJKaLU82FZececDTCSoDwdJbZUnl0VjtZ0ePfjgg34a3ilEbTWnrytV7rx580IHwlx++eV0/fXX+20o9GPu3LmkXmT8x1iR9qHAD4MIyDyEFWmDoMYsyqb94Saifjv8A0Q6poLETQZBtiPIMj428RcDFpdIczomV8XCkUce6ZNgdsvYaKONCibfYIMN8hJztfKtt6xjMlsobLrppqR26aC//e1vRUlslEjzFnlRd5J8dXz44YfUoUMH/xG7egwYMEBf8xZxO+20k/8szY9///vf/vZ8lSpXrSzrLe6knf/85z/pwgsvlMuCMW9ByO4nEkCkBQnEJhGQeQhE2iSq8cqyaX+4hajfEv9QxtxocHVpX0BE/911bVHzmP7TvciCiTjNx4bR+hXp9dQ+zx5/zCdtzRcrn19PrbpGs+vrqGtHsVMQgwV89tlnoTovvfRS//Frr70WepavTXHvKX/pipc7ZsyYUHtL7dghDeKPP7H9naCBuFIIiK7AtaNSCBcuF/bfTfuPFWk165gMeCO09Ea4ehBt4i8rQWqaNSZSaQ9kydcQxuj111/XB64oEkuK5OYkU7txEB/SwgehBEN0RfqFF16gHj16BJPk/c0fTe6yyy7+M/7IjldkOXz++eek9pr2nymSTSeccIJ/neQHr9g3bdpUZ6lUuRMnTiT+IFLCLbfcQhdffLFcFoz540T+SFECVqQFCcQmEZB5CCvSJlGNV5ZN+8MtRP2W+Efhd6vynuCNzM03MpEWl8dfzWN6pVKwMBGbXJEu1B4+MIT3gm7dunVopVWRaI8/rAuG6Ir0Aw88EHxc8Lci3KGy1YmHflq1e0no4z1FSv1naX5Uqtw5c+aE+nLZZZfFaubMmTND+RSRjpUPiYBAEgRkHsKKdBLUzKR12f4xgq72H/tIm9EfvxRXBUkAcLn/YsAECxNxFkRa2sljp7azC5E9dfS2PNZxlEjfeOONoeeFLkaMGBEqd9y4caGkwVMK8x3YEkqc4KIS5TJBl7Hm+LTTTovVIvVXgFA+EOlYsCFRQgRENkGkEwJnILnL9o/hc7X/INIGlCdYhKuCJBi43H8xYIKFiThLIs3t5YNF1J+GfcI3dOjQUDeiRDrOCYRcgNpD2i+TcWKf6WDYfffd/edqv+vgo1S/K1Vu48aN/fZyHXECnywpMsIxiHQc1JAmKQIiYyDSSZFLn95l+8foudp/EOn0uhMqwVVBEhBc7r8YMMHCRJyGSPM+1ePHj/duu+02T+2aEbs5ysfYJ3xqW7dQviiR5uO3lyxZEkqT72Krrbbyy+Tyoy4j0f2ux44dm6+YnHuffvqpxx//FZK7SpWrtg70+8MvHmr3lZy2BW/wh4YtW7b084BIB9HBb5MIyDwEIm0S1XhlFZqH4uVOnwr123GtBZFOL7uhEiDIdgRZBsEm/mLApC0m4jREulevXj5x4+Op4wS1L7Ofh/vz6quvhrJFiTSnuf3220Npohfvv/9+qEy173I0iT5mXH2I56fjVV4mn8UCHxEuR3XzTiQXXHBBTnImE5Uol328Zbw5vuGGG3LqDt4YNWpUKD3nwYp0ECH8NoWAyCWItClE45dj0/5wK1G/Hf4BIh1fR2KlhCDbEWQZHJv4iwGTtpiIH3roIU/tuaz/LV26NFGR0W3l+vTp461YsaJgGez7y1vfST/q1KnjqUNNQumjRHqdddbx6tat67EPdL7wxRdfeG3atPHLrF27dsHV22HDhvnpuA3cFnY1yRd4nI899thQ+ijpl3yVKFftCe01a9bMr5+x4tMb8wUm3YxR/fr1PXUQjp8nH/HPlx/3gEASBER/QaSToGYmrU37wz1A/Xb4B7a/U7OOyYDtZyxtP7N6EG3iL9tOqfnMpEilKmv//fcn3uJOAm+/xicRbrvttv5WbOpYbZo9ezaNHDlSn4QoadX+yKQ+pJNLHUe3v+Nt7Pr27aufqRVwfVAJb5nHpwrywSWKRBKXL+Gkk04itdOHXIZi5e6hD4Phw1sktGjRQh8U0759e32a4Pfff0/Tp08n9YJBixcvlmR0/PHHkzou3L8O/qhUuXya4RVXXOFXpfaI1qdE7rrrrvoEwxkzZtAHH3xA77zzDi9Y0ODBg+nuu+8m9XKh85x77rmk3G78/PgBBEwgIPOQItKJi0t70qrN+Zc7i/rdtb9Wx5/fYkwGvBHZeSOSMQT+9vBXiqxXG2UsqkK8fPly7+CDD/ZXQaWNxWI+NIQ/jMsXoivSiijq1fLgB4qFyj777LO9lStX5ivWv8crvXxYS/DgkkLlyX12kSjlBlKpctmHPE7fjznmGN33HXfc0R+Ls846y+83fgABUwiIXmBF2hSi8cuB/bVnf3mUbOEP1474OhIrpa2BlMahfnuKLAZMxqKqxOzO8fTTT3s9e/b02AVB2hmNGzZs6LH7B7tjFApRIq0OWtFJ+ePA4A4ZUjYTYt6Fgz94TBLeeustr2vXrl6TJk3ytpfdJNShLV50G71SdVSi3KeeespjgpwP2y222CLkQ859EmzUKnqp5uI5EEiMgMgXiHRi6FJngP21Z3958GzhD9cONeuYDPjTkrt/WpI/qSp9NilSRsviP/fOnz+ffvjhB/1P+SwTu0/wPz4VkK+Lhahrx+TJk6ljx45+FnW0uHZdYBeM5s2b00477UTKj9p/Xs6PBQsW0KxZs0h9CEnKL5nU3tCkDo8htWNIOcX5eUyXq1a9id051E4ipLbH064o2223nV8ffgCBLBCQeQiuHVmgHa4D9t9N+w8iHdaD1FdQJDcViQVHDFhVJtJpBbwUkU5bPvIDASCQDgGZh0Ck0+FYTm7YfzftP4h0OdpSJA8UyU1FYpEQAwYiXURB8AgIAIGKIiDzEIh0RWHOWzjsv5v2H0Q6rzqUfxOK5KYiscSIAQORLl9/kBMIAIF0CMg8BCKdDsdycsP+u2n/QaTL0ZYieaBIbioSi4QYMBDpIgqCR0AACFQUAZmHQKQrCnPewmH/3bT/INJ51aH8m1AkNxWJJUYMGIh0+fqDnEAACKRDQOYhEOl0OJaTG/bfTfsPIl2OthTJA0VyU5FYJMSAgUgXURA8AgJAoKIIyDwEIl1RmPMWDvvvpv0Hkc6rDuXfhCK5qUgsMWLAQKTL1x/kBAJAIB0CMg+BSKfDsZzcsP9u2n8Q6XK0pUgeKJKbisQiIQasJhNpPu5bHcLia0CXLl1o/fXX96/xAwgAAbsIyDwEIp39OMD+u2n/QaQN6xoUyU1FYjESA1aTibRhdUFxQAAIGEZA5iEQacPAxigO9t9N+w8iHUM5kiSBIrmpSCwjYsBApJNoDNICASBgEgGZh0CkTaIaryzYfzftP4h0PP2InQqK5KYisYCIAQORjq0uSAgEgIBhBGQeApE2DGyM4mD/3bT/INIxlCNJEiiSm4rEMiIGDEQ6icYgLRAAAiYRkHkIRNokqvHKgv130/6vsWzZMi+eiCAVEHADgdq1a9OqVasSd7Zhw4Y6D4h0YuiQAQgAAUMICJFeuHBh4hIbNGiQOA8yAAHXEcCKtGEJwBupm2+kLEZiwECkDSsVigMCQCA2AjIPYUU6NmTGEsL+u2n/QaSNqdCfBUGR3FQkHn0xYCDShpUKxQEBIBAbAZmHQKRjQ2YsIey/m/YfRNqYCv1ZEBTJTUXi0RcDZlikUBwQAAJAIDECINKJIUudAfbfTfsPIp1adcIFQJHcVCSWAhDpsC7gCggAAXsIgEhnjz3sv5v2H0TasK5BkdxUJBYjIdJw7TCsVCgOCACB2AjIPAQiHRsyYwlh/920/yDSxlToz4KgSG4qEo++GDAQacNKheKAABCIjYDMQyDSsSEzlhD23037DyJtTIX+LAiK5KYi8eiLAQORNqxUKA4IAIHYCMg8BCIdGzJjCWH/3bT/INLGVOjPgqBIbioSj74YMBBpw0qF4oAAEIiNgMxDINKxITOWEPbfTfsPIm1Mhf4sCIrkpiLx6IsBA5E2rFQoDggAgdgIyDwEIh0bMmMJYf/dtP8g0sZU6M+CoEhuKhKPvhgwEGnDSoXigAAQiI2AzEMg0rEhM5YQ9t9N+w8ibUyF/iwIiuSmIvHoiwEDkTasVCgOCACB2AjIPAQiHRsyYwlh/920/yDSxlToz4KgSG4qEo++GDAQacNKheKAABCIjYDMQyDSsSEzlhD23037DyJtTIX+LAiK5KYi8eiLAQORNqxUKA4IAIHYCMg8BCIdGzJjCWH/3bT/INLGVOjPgqBIbioSj74YMBBpw0qF4oAAEIiNgMxDINKxITOWEPbfTfsPIm1Mhf4sCIrkpiLx6IsBA5E2rFQoDggAgdgIyDwEIh0bMmMJYf/dtP8g0sZU6M+CoEhuKhKPvhgwEGnDSoXigAAQiI2AzEMg0rEhM5YQ9t9N+w8ibUyF/iwIiuSmIvHoiwEDkTasVCgOCACB2AjIPAQiHRsyYwlh/920/yDSxlToz4KgSG4qEo++GDAQacNKVQWL4zE+4ogjaPTo0bp1Bx54ID333HN0//330xlnnKHvNWvWjKZMmUKbbLJJFewBmlRTEZB5CEQ6+xGG/XfT/oNIG9Y1KJKbisRiJAYMRNqwUlXB4m666Sbq37+/blmLFi1o6tSptMEGG+jr448/nh577DH9e/fdd6c333yT1lxzzSrYCzSpJiIg8xCIdPajC/vvpv0HkTasa1AkNxWJxUgMGIi0YaWqYsW9/vrr1L17d1q1ahXVqVOH3nrrLercubPfyl9++YV23nln+vTTT/W98847j4YNG+Y/xw8gUEkEZB4Cka4kyvnLhv130/6DSOfXh7LvQpHcVCQWGDFgLhDpvffem7799ls6+eSTacCAAWXri62M5bZ/3rx51KFDB1q4cKFu+uDBg6lv37453ZgxYwbtuuuutHz5cv2MV6iPPfbYnHS4AQRMIyDzEIi0aWRLlwf776b9B5EurRuJUkCR3FQkFhIxYDWdSC9atIiaNm2q9eL888+noUOHJtIR24nTtP/ggw+msWPH6i7stttuNGHCBH/co/0aNGgQXXbZZfr2OuusQ1999RU1adIkmgzXQMAoAjIPgUgbhTVWYbD/btp/EOlY6hE/ERTJTUViCREDZpJI//zzz/T7779rAWQSVqtWrfjCWKGUY8aMoUMOOUSXXh2JdLntnzhxYsiF46WXXtIuHoVgXrZsGbVu3ZqYuHO4+OKL6ZZbbimUHPeBgBEEZB4CkTYCZ6JCYP/dtP8g0onUpHRiKJKbisSSIQbMJJHeY489aPz48Vrw5s+fXyV2gLjiiivo+uuv122qjkS63Pbvt99+xP7RHNht47333tO/i/138803U79+/XSSBg0a0JdffkkbbbRRsSx4BgRSISDzEIh0KhjLygz776b9B5EuS10KZ4IiualILBFiwKoykV6yZAnNmTNH+zezj/Mff/xBG2+8sf637bbb0rrrrptXuNkoi1/wSSedRO+8845Oxz7STEwlNG7cmNZff325zBvzCu2sWbOIXwz4H3+016ZNG/1viy22oEaNGuXNF7zJq70//vijvsW4c34J7G7x0UcfEfe1S5cutOeee1La9o8bN466du0qVWj3Dt7yrlTgDw95Vfqnn37SSfHhYSnE8DwtAjIPgUinRTJ5fth/R+2/MvpGgzJwRstLWhjqB/5JZcZUejXtevzPZFBEUJfJ5SrSWXbR6uM3T5Fer169en550l6J69ev7x133HGeIqI59QwfPrxgPsnPsdoWLiev3FAruJ7aGs6rW7duwbLUNnFenz59vAULFki2vPGoUaP8MhRx8NQLgaeMmKd20/Dvc3uOOeYYnT9t+9VqtF9uu3bt8rap0M1rrrnGz8v4qxeSQklxHwikRkD0URFpL+m/tJXD/sL+ppWhNPltyZ9Zq68QsNURAR/1Q5FFFrKOxYCZrNcEkR4xYoRP5KSNxeLatWt7Dz/8cKgbaYnogw8+6DHhLVZv8Jn6OM9T28qF2hC8UIefhMpSK7+eOggldI/LM0Gk1cq2p7a588u++uqrg00p+ZtfYoJ9e+SRR0rmQQIgUC4CImtJSTSnTxtgf2F/08pQmvy25A+uHWrWMRnwpx1H/7SjhEj+pKomAmMildZHmv14eau33377TbeJT9vr3bs3derUiTbccEN+kaYffvhBHxry+OOPE3/cyIH7wh/TdevWTV9//PHH9MYbb+jfvN2bfADJZfMJfxJ4JwveHi4Ynn/+eTrssMO0Cwff5x0sTjnlFNp33321Swm7drDv8JNPPqlPB5S87K4xffp0WnvtteWWH3PbevTo4V9PmjRJ94n7o1a8/TbssssueleRNO1/9tlndfulMnYdCe4bLfeLxew+wzhzOPHEE0m93BRLjmdAoGwEZB5SxDhxGfl0LUkhsH/u2j+WE2fHPw37z5fX1huBtAX1441YZCHrWM0jeuXRZL1pV6TV3sX+aqgipt73339fsHnKZ9rbfvvt/fQHHXRQ3rTK2PppLrjggrxpgjcVaffTN2zY0FOnAAYfh36rrfT8tIznpZdeGnouF4rUh9Ipcqqv1XZz2sVD0uWLk7b/zDPP9OtSPuTeihUr8hVb9N4JJ5zgl6E+NtSuKEUz4CEQKBMBmYewIl0mgCmygX+4yT/g2pFCafJlhSK5qUgsC2LA8slFuffSEmn18Z7froEDB5Zsxttvv63Tq632PLUzhccuE9GQhIiqvZP9+hkfdr8oFlauXOlttdVWfh61wp03udrJxE/D5bJv9TnnnJM3bfRmkvZzXn4BkbHt2bNntLhY1w899JBfBpelPoaMlQ+JgEBSBERWQaSTIpc+Pey/m/Yfrh1q1jEZnP3TxmoQXe6//ElVTcfGRCqNawfvyKE+IPTdMJRvL1111VUl26aMAamV44Lp2DWDd6PgoFakaciQIQXTsquIWoHWbg28ywa7gqiP9Qqm5wennnoq3X///TrNeuut57ubBDNF93Tm/bXnzp1LzZs3DybL+ztJ+7nNwe3qeB9o3g86aeCdUjbbbDM/25133klnnXWWf40fQMAUAjIPwbXDFKLxy3HZ/jFKrvZ/DX6Dii8mSAkEaj4C6mM73583SW+FfMYl0r/++iupFc6iVUyZMsUnkryNm9r1oWB69l1Wu1aEnnMe2apu66231nsfMzlNE5IQ0XLqufbaa0mtnvtZ2beYfbuDIUqkud/sNx0nJGk/+2i3bdvWL/bRRx8ltbOJfx33B481v9RI4BcafrFBAAKmERAiLdtVJimf9zpHAAJAICEC6f+YES4Bf9pw808bIgUuj79SPf3ne8GiVMxuE5LHRHzfffflVKlIaaiOVq1aeeqjPm/58uU5aePeSOoaEbdcSTds2LBQm7/55ht55MfvvvtuKM2AAQP8Z6V+JGn/a6+9Fqrn5ZdfLlV8wefBes8+++yC6fAACKRBQOYSuHakQbG8vC7bP0bM1f7DtUPNOiaDq3/aEAxd7r+sBKn5ROAoGqtJJ++OFEUzFXmoiLTeDSOYhA8COeCAA+j9998P3tb17rXXXnrnDN6ZY7vttgs9L3aRZEU3Ws60adN0W9jV4euvv9aHw/CfoNUHfKT8o/U/dgeR3UM4vyLS1LJly1BR0RXp2267jc4999xQmkIXSdo/cuRIUh9s+kV9+OGH1L59e/86yQ/ehYT7zOGoo47Su5ToC/wHBAwiIPMQXDsMghqzKJftH0Pkav9BpGMqSNxkrgqS4ONy/8WAxSXSnI79eouFI4880ifBvJVd0F83mm+DDTbIS8zZn5m3qHvllVeiWfzrTTfdlNQuHfS3v/2NeAu7YiEJEZVy1EeMdMMNN5Ba0ZVbsWMmn2olPZQ+SqR56zwmp3FCkvbffvvtxKcRSpg3bx4xVuUE3oqPXXU4sK/4m2++WU4xyAMEiiIg8xCIdFGYKvLQZfvHgLrafxBpw+rkqiAJjC73XwxYXCItmBWL03xsGC2XSewdd9xBr776KrHPbqHAK9S8ul2IMCYholyHOu2Q+vfvH6qO/dD5SHJ+MeAjxdl/WO28of/x8eHi182Z4hDpF154IbSvdKiyyEWS9v/jH/8I+TKzfAd9nSNFF73kfa/Fj3vHHXckXp1HAAKmEZB5CETaNLKly3PZ/jE6zvZfGX2jwVUfGQER/XfXR1zNI9qfVmTBRJx2+7t8bWAZHT16tMd+ultuuaVus7RdYkVuC+73HPT1LbWPNJ9OyCclSrn8W5FTfXRxvrbxvXJ8pBWRLlRczv0k7R88eLDfdu5DqaPLcyoL3AiOpTrQJfAEP4GAOQRE1xSRxhHh5mCNVRLsv5v2H/tIx1KP+ImgSG4qEkuIGLD40lI6ZZB8zZ8/v3SGMlKoFV9v0KBBXuvWrf0+cF/UNnWeOsEwp8QkRFT5E/tl8l7PxY79lorUCrafh9sR52PDShHp6P7ParVcmpk4Du6PfeihhybOjwxAIA4CMg+BSMdBy2wa2H837T+ItFk9cvarVYHR5YlEDJhgYSLOgkhLO3ns1FHeIRLLJwhGQ1wirY4l1welCC5qK75oUXmv+dAWycMxE/1oiO7aUSkizeUG2zJu3LhoU2JfN27c2C/rtNNOi50PCYFAEgREXkGkk6BmJq3L9o8RdLX/INJm9McvxVVBEgBc7r8YMMHCRJwlkeb2ql0+POVj6RM+PrI7GuISaT4KXDDh+JprrokWlXPNJxu2aNEilM8mkVYfB4baMmrUqJw2x7nB/QriqnzG42RDGiCQGAHRORDpxNClzuCy/WPwXO0/iHRq1QkX4KogCQou918MmGBhIk5DpHmfaj5KW20N56lt22I3p2nTpj55vP7663PyBYn0+eefn/NcbqgPBv1yGBt2kygV/vWvf4XycD4+ZjwaTK1IF2s/18kkXsaVY3UiYbQpsa7VoTKhcv75z3/GyodEQCApAiKvINJJkUuf3mX7x+i52n8Q6fS6EyrBVUESEFzuvxgwwcJEnIZI9+rVyydv6uS/WM357rvv/DzcH7XDR04+dTKin6Z37945z+WGOl7bT8dlXXLJJfIob/zEE0/oDxODK7ecjw9FiYY0RDpu+7lOXknmDy9lbNXx5dGmxLqOuoiorQhj5UMiIJAUAZFVEOmkyKVP77L9Y/Rc7T+IdHrdCZXgqiAJCC73XwyYYGEi5lXc6667Tv9bunRpoiKjp/L16dPHUwefFCxDbYnnqa3vfNJYp04dTx2MkpNeHd7ip1GHjOT9IFEyBVe311133bwfDnJaPm2R6+MPEqO7duRzL0lDpJO0n9um9vL2+8snQ5YTLrzwQr8MtX1eqpMly6kfedxBQOYhEOnsx9xl+8dou9p/7COtZh2Twdl9FFeD6HL/Zf9WNZ+YFKlUZe2///6kCLVfxoYbbqgPLuE9nPk3B7VyTLNnzyY+xY9PQpQwfPhwUh/FyaUf8yExTz31lH/dpEkTfeAL7wPNGPApgxKiB5o0atSIFKmktm3b0qpVq0i5begT/iZPnqyzKFcSUtvykfowj1/y9T0+aEatZhOfxKi269PPogeyqBXf2PtIJ2k/N4BxOP3003Vb+L/PP/+cNt98c/86zg/eN3rGjBk6KZ80+eKLL8bJhjRAIDECMg8pIp04r3LbSpwnmMHl+Z9xQP//Sw0aNAiKRKa/reHPbxEmg6tvJIIh+u/m9jc8/mrG0P9EFqpCvHz5cu/ggw/22yZtLBbXqlXLGzhwYMHmR1eDg2XtsMMOoXzsGsF7JgfTFPo9YMAA748//tD51SmFefPIrhnRNiTZtSOaN9ieaPu5Mbz9XjDNXXfdFepjqYvvv/8+lH/IkCGlsuA5ECgbAZFVrEiXDWHZGWH/3bT/cO0oW2XyZ4QiualILA1iwPJLhr277M7x9NNPez179tTuE9LOaNywYUOP3T+++OKLko29//77PXVCoN9nLosJ+L777puTl+vnvaHVSkUoPedhf+h99tnHGzNmTCgff5ynjiwP7XSx1lpreWolWqeLkuEkRJoLSNJ+Tr/NNtv4bWcck4QHH3zQz8t9Vqv/SbIjLRBIhIDoNYh0ItiMJIb9d9P+w7VDzTomg7U/LazuBOq396cl+ZOqmpFNipTRsvjPvepgF1JEVf/jo7rVdnP6Hx/XzddxAx8z/sknn9DChQtJ+Q6TOtCF6tatWzC7Wp3WrhyffvopKYNDzZs31y4SG2+8ccE8nG7u3LnE7iPK37pgunIeJGn/PffcQ2p/a12NemGgjz/+mNQBKyWrZVlQB9vQ9OnTdVo+fp2PakcAApVCQOYhuHZUCuHC5cL+2rO/PCq28AeRLqwTZT2xNZDSWNRvT5HFgFVlIi1ygjgZAmpVXRPnOXPm6IwnnHACPfzwwyULefbZZ0kdcuOnmzRpEu2yyy7+NX4AAdMIyDwEIm0a2dLlwf7as788OrbwB5EurRuJUtgaSGkk6renyGLAQKRFGmtWrFw06OSTT9ad4pV7Xo0v9dHhTjvtROpgGp3nkEMOodGjR9csUNCbKoeAzEMg0tkPDeyvPfvLo20LfxBpw7pmayClG6jfniKLAQORFmmsWTHvMsK7nXz22We6YyeddBI98MADBTvJpPnQQw/Vz1k2mFDzbiUIQKCSCMg8BCJdSZTzlw37a8/+8ojYwh9EOr8+lH3X1kBKg1G/PUUWAwYiLdJY82LeSlAdbkNqdxHtT/7666/rbfmiPVV7flOHDh1IfbipH6mPOIm3AkQAApVGQOYhEOlKI51bPuyvPfvLo2ELfxDpXF1IdcfWQEqjUb89RRYDBiIt0lgzY97r+oorrtCd4w8lP/roI39Pbunx0UcfTaNGjdKXnTp1orfeeqvoh5iSDzEQSIuAzEMg0mmRTJ4f9tee/eXRsoU/iHRyXSmaw9ZASqNQvz1FFgMGIi3SWDNjHl922Xj++ed1B/fbbz+9Ewfv5sHhjjvuIF6B5sCH3nz44Yd6hxJ9A/8BgQojIPMQiHSFgc5TPOyvPfvLw2ELfxDpPMqQ5patgZQ2o357iiwGDERapLHmxkuWLNGuG19++aXu5NVXX01XXXUVffDBB6QOoKHff/9du368+uqr1LVr15oLBHpW5RCQeQhEOvuhgf21Z395tG3hDyJtWNdsDaR0A/XbU2QxYCDSIo01O+b9rflodQ68Gs0r07xfNO/RzYGPOe/YsaP+jf+AQFYIyDwEIp0V4v+rB/bXnv3lUbCFP4j0/3TAyC9bAymNR/32FFkMGIi0SCNiIAAEskZA5iEQ6ayRt0fkpKew/3bsP4i0SKChGIJsR5Bl+GziLwYMRFpGAzEQAAJZIyDzEIh01siDSNu0vzzatuoHkTasa7YGUrqB+u0ReTFgINIijYiBABDIGgGZh0Cks0beHpGTnsL+27H/INIigYZiCLIdQZbhs4m/GDAQaRkNxEAACGSNgMxDINJZIw8ibdP+8mjbqh9E2rCu2RpI6Qbqt0fkxYCBSIs0IgYCQCBrBGQeApHOGnl7RE56Cvtvx/6DSIsEGoohyHYEWYbPJv5iwECkZTQQAwEgkDUCMg+BSGeNPIi0TfvLo22rfhBpw7pmayClG6jfHpEXAwYiLdJYc2Ie0yOOOIJGjx6tO3XggQfSc889R/fffz+dccYZ+l6zZs1oypQptMkmm9ScjqMn1Q4BmYdApLMfOthfe/aXR9sW/iDShnXN1kBKN1C/PUUWAwYiLdJYc+KbbrqJ+vfvrzvUokULmjp1Km2wwQb6+vjjj6fHHntM/959993pzTffpDXXXLPmdB49qVYIyDwEIp39sMH+2rO/PNq28F9j2bJlXvbihhqBQNVFoHbt2rRq1arEDWzYsKHOAyKdGLoqneH111+n7t27a5moU6cOvfXWW/r0Qmn0L7/8QjvvvDN9+umn+tZ5551Hw4YNk8eIgUCmCAiRXrhwYeJ6GzRokDgPMgAB1xHAirRhCbD1RiTdQP323ojFgLlApPfee2/69ttv6eSTT6YBAwaI+NW4eN68efoocCElgwcPpr59++b0c8aMGbTrrrvS8uXL9TNeoT722GNz0uEGEKg0AjIPYUW60kjnlg/7a8/+8mjYwh9EOlcXUt2xNZDSaNRvT5HFgNV0Ir1o0SJq2rSpFrnzzz+fhg4dKuJX4+KDDz6Yxo4dq/u122670YQJE0jGOdrZQYMG0WWXXaZvr7POOvTVV19RkyZNoslwDQQqioDIJ4h0RWHOWzjsrz37ywNiC38Q6bzqUP5NWwMpLUb99hRZDJhJIv3zzz/T77//roeXSVmtWrVkqK3FY8aMoUMOOUTXX5OJ9MSJE0MuHC+99JJ28SgEvHKTo9atWxO/aHC4+OKL6ZZbbimUHPeBQEUQkHkIRLoi8BYtFPbXnv3lgbGFP4h0UbVI/tDWQEpLUb89RRYDZpJI77HHHjR+/Hg9vPPnz68SO0JcccUVdP311+s21WQivd9++xH7R3Ngt4333ntP/y72380330z9+vXTSdjf9Msvv6SNNtqoWBY8AwJGEZB5CETaKKyxCoP9tWd/eYBs4Q8iHUs94ieyNZDSQtRvT5HFgFVlIr1kyRKaM2eO9m9mH+c//viDNt54Y/1v2223pXXXXVdEKRSzURY/4ZNOOoneeecd/Zx9pJlYS2jcuDGtv/76clkw5rJmzZpFH3/8MfHHeltttRVts802tNlmmxF/0FcqLF261F/5ZdzbtGnjZ+E+vfvuu5rE/vDDD7pv7du31+XHKZsLGjduHHXt2tUvk907eMu7UoH7wqvSP/30k06KDw9LIYbnphGQeQhE2jSypcuD/bVnf3l0rOGvjL7RwLuA2AyoH/jbkj+lx7wDjtHqu3TposvkctWKdNllq4/hPEV6vXr16vnlSXslrl+/vnfcccd5yg84p57hw4cXzCf5OVbbxOXklRsrV670rr32Wk+5qBQsq27dul63bt08RfYlW9743nvvDZWhJlCd7r777vNatmwZeibtW2uttbzTTz/d++233/KWGbypVqP9Mtq1axd8VPL3Nddc4+dlvNVLQ8k8SAAETCEg8q6ItJf0X9o2wP7C/qaVoTT5bcmfWauvELDVEQEf9UORRRayjsWAmazXBJEeMWKET+ykjcVitf2f9/DDD4e6kZZIf/bZZ16nTp1it0N9rOdxnYXCE088ESrru+++89Q+z6F7hfqoPhr0OH2hoFbtPbVy7Zd19dVXF0qa9z6/tATrfuSRR/Kmw00gUAkERPaSkmhOnzbA/sL+ppWhNPltyR9cO9SsYzJY+9PC6k6gfnt/WpI/qaqJwJhIpfWRZr9e3qpOrcLqNvHpe7179yZFamnDDTfkF2li9wc+ROTxxx8n/riRA/eFP65Tq8P6ml0w3njjDf2bt3+TDyC5bD7xTwLvbNGhQwe51PHXX39N22+/PalJzr/fq1cv6tGjB7HLBbuDTJ8+nT788EO9Awi7R0gotN3c008/Har37rvvpjPPPFN/jMll88eQamVau39MnjxZH5jy/fffS7F632c+hTBfePbZZ+mwww7zH/FOHZ07d/av4/xgdxnGlcOJJ55I6mUmTjakAQKpEZB5SBHjxGWtvfbaifMEM8D+2LM/PA7A3xL+adh/vry23gikLagfb8QiC1nHah7TK5Em6027Iq32MvZXR5UfsafIZMHmKZ9pTxFeP/1BBx2UN60ytn6aCy64IG+a4E3lU+2nV7uOeOqDvODj0O+PPvrI23TTTf307AaSb6VMkV0/DeOuDsPx2C3k5ZdfDpUnF4rMe1tuuWUoj/qIUx6HYkXI/XTKZ9xbsWJF6HmcixNOOMEvQ31s6Cm/7TjZkAYIpEZA5iGsSKeGMnEB4B9u8g+4diRWleIZoEhuKhJLhRiw4hKS7GlaIr3FFlv47Ro4cGDJyt9++22dngms2qnCU6vDOXmSEOlPPvnEY1cRwYZJaqmgVr799JzvxhtvzMkyevToUBpOp/ZxzkkXvDFt2rRQnqOPPjr42P/NLxzS3p49e/r3k/x46KGH/DK4LH5BQAACWSAgsgsinQXa4Tpg/920/yDSYT1IfQVFclORWHDEgKUWokABaYi0OuZcr9JKu+L6+uYjz4EmeUmItHJr8HHhdkydOjVYVN7fvHqrdr7w822wwQYe9yUYokRa7RSSd+U6mId/77DDDn657Ae9ePHiUBLljuE/5/aqfaBDz+NeqMNYQuXceeedcbMiHRBIhYDoO4h0KhjLygz776b9h4+0mnVMBvgoWfJRWj2INvEX30Q1A8cSqV9//ZXUimfRtOzHK37Le+65J6ldIAqmZ9/l7t27h55zHtmqbuutt9Z7Ia+33nqhNEkv+NQ+8WNWrh00ZMiQgkXwlnqzZ8/Wz3faaSf64IMPCqYNPuBjx2+44Qb/Fm/V17x5c//6+eefD2HHPs3sN10qXHfddXTllVf6ydRKMbVt29a/Zl/t4PWjjz5KaicT/3ncHzy2ahcUP/lVV11F6kXGv8YPIFApBGQeUkQ6cRXwkU4MWSiDTfvDDUH9lvhHWa9dRTLhjczNNzIRCZfHX81jehVSsCgV88qv5DER89Zv0cDbzQXLbtWqlffkk096y5cvjyaNfZ1kRVodSuLXz37DccMDDzzg5+P2q32hQ1mjK9LFtt0LZlTEOFTuiy++GHzsvfbaa6HnhXyuQ5kKXARxOvvsswukwm0gYBYB0XesSJvFNU5pLts/xsfV/sO1I452JEjjqiAJRC73XwyYYFEqzoJIq+OqvZ133jlEDrmdTPL4Y8J//vOf3syZM0s1NfQ8SBCLfWy4YMGCUL1qxTxUTrELdQBKKO/IkSNDyaNEml8O4gQmxjJOHEdfPtTOJaHnaieROMXmTRN0TznqqKPypsFNIGAaAZFvEGnTyJYuz2X7x+i42n+4dqhZx2TAn1Ys/Wll9SDaxF/+pKrmk1gixenmzp1bNO2RRx5J77//vk7DW9kVO25a+RKTIrk55bEbBm9R98orr+Q8kxtqpwxSxJr+9re/EW9hVyzEde1gt5RddtnFL0r5G9PFF1/sXxf7wX3u2LGjn0R9SEiXXHKJfx117eCt+qJuLX7iwA/eYi+4PR+7erAbiYTbb7+d+DRCCfPmzSPGppzAfZct9nibQN5iEAEIVBoBmYfg2lFppHPLt2l/uDWo3xL/4LcIk8HVNxLBEP1317VFzWN6NVNkwUSc5mPDaP2KbHpqf2WPT/iTtuaL+WRBRSCj2f3ruCvSL7zwQqiee+65xy+j1A8+wCXYtssuuyyUJboine80xlCG1RfRci+99NJQMv4gM1ivMkyh50kuDjjgAL+sHXfcMUlWpAUCZSMg8osV6bIhLDsj7L+b9h+uHWWrTP6MUCQ3FYmlQQxYfsko765JIi0tYBllIsp+u9G9laUPvAtGoR024hJp3vJNyuM43zZ20qZozD7Rwby33XZbKEmUSDNpjxPU4Syhcm+99dZQNnUATOg5u6eUG4Jjpw50KbcY5AMCiRAQvQGRTgSbkcSw/27afxBpI+rzv0KgSG4qEkuAGLD/SUP6X0EyNn/+/PQF5imBDyvhPZiDPr3cl3bt2nnqBMOcHHGJtNptxMeEyzv//PNzyip045lnngnlZeIcDFEizR8nxgnRVfLHHnsslC26//OsWbNCz5NcbLXVVn4fDj300CRZkRYIlI2AzEMg0mVDWHZG2H837T+IdNkqkz8jFMlNRWJpEAOWXzLKu5sFkZaWseyqbeT8fnB/+HCUaIhLpDlfo0aN/PKOOeaYaFEFr9WR334+bofali6UNkqk4652q6O6Q+WOGzcuVG6UaEefhxKXuFBHn/t1nXbaaSVS4zEQMIOAzEMg0mbwTFIK7L+b9h9EOomWxEgLRXJTkVg0xIDFEJPYSbIk0tyon376yVMfK/l9GTp0aE5bkxDp9u3b+2XxiYFxj8o+/fTT/XyM69KlS0PtiBJpPvglTlB7SIfKZZ/pYFAfB4aejxo1Kvg49u+VK1eGcOzfv3/svEgIBNIgIPMQiHQaFMvLC/vvpv0HkS5PXwrmgiK5qUgsEGLACgpHGQ/SEGneXm/8+PEe+xcn2catadOmfl+uv/76nFYHiXQpd41+/fr5ZTE+vE9zqcDtVjuD+PnYxSQaokSa96tesmRJNFnOddDdgvsZdV1hNxcZR47LPZEwekIibzOIAASyQEDkF0Q6C7TDdcD+u2n/QaTDepD6CorkpiKx4IgBSy1EgQLSEOlevXr5bVJbwwVKLfzzu+++8/Nwf1599dWcxOpkRD9N7969c54Hb/A+1kFSzG0qFaJuHfk+JIwSaW6r2rquaNFqSz2/3Zz+8ssvz0nPK8n8oaWM5amnnpqTJs6NqIuI2nowTjakAQKpERDZBZFODWXiAmD/3bT/INKJVaV4BiiSm4rEUiEGrLiEJHvKH7+pvY71v6h7Q6mSoqf09enTx1uxYkXBbOpYa4+3vpN+1KlTx+MPBqNhu+2289Owu0Z0VTeafuDAgX56Lpv9hZmw5gv333+/t+aaa/rp99prr3zJ9K4j0k6OmazXrVvXYx/ofOGLL77wuK2Sp3bt2p7awztfUk/t3e2n45MgywkXXnihX4Y6KjzVSZLl1I887iIgMg4inb0MwP67af9xIIuadUwGbIhuaUP01YNoE385CEFN3yZFKlVZ+++/PylC7Zex4YYbkjplj7bddlvi3xx+/PFHmj17NqnTA0n5SPtphw8fTor0+tfygw+Jeeqpp+SSmjRpog98UQSYGAPlSuI/4x/K5UIfzKL8kf37fNiKIu360JVatWrRtGnTaNKkSTRmzBg/jXLX0IeYBA91kYf/n70rgb1r+P7zs5XUUq2lVC1NRRuqtBWltVSLRLoQSlBJG6KW2CWUShtLUKKW2CKidlGKRtFQNPalC6VKUbUVtYf/V1DzP59Jz3Tuffe9e+97816Xcyb5fucus53PPTPnc+edO5PekIWWsTO0c6K7TbPepn///oZcQgy9CLhyaXUOJyfnHz16tKGVPvg0EUNu8tH21xYvXmy6d+/uz4sc0LrRZsGCBS4prSdtaCvyItk0jSLQMAI8DhGRLl0WuW2VzhNmWJ3jL9qh9cu1v6v1+cd+Z9M3MplvZKxHkp8/dWQ3C8lYrAlxW1ubHTp0qJ8d5TbWionYWswiVwvpNZ7Dsnr16pWZDX7PY8aMKdwOrLtMBDazLFxMu3bMmTPHzdqHH0qG7QqPsX52tRlxlL106dJEO2+//XZcLhyWLVuWyD958uTCeTWhItAoAqzrOiPdKJLl80u2f0BLqvzq2lG+r9TMIVWRGBTJ8rMBYyzWlBjuHNOmTbPDhw+3cNfgdqbj9u3bW7h/wA0iL8AFI/R9Rlkg4IMHD66ZlWa9LW1BXpEX+du1a2exAyBtJW5XrFhRs5w0kcZqGwgzZsywAwYMqJARbevRo4f78LJmwStv9uzZ05cB3MqEKVOm+LyQi2b7y2TXtIpAQwhwv1Yi3RCMdWWWbP8AmFT51bWDRp2YQX9akvvTEv+kSuNJTJWKWhZ+7qWNXQytKuH+yFfYdO3a1f117tzZ4LxoIJ9qs2jRIrN8+XJDvsSGNnQx5KdcKDswIh9l5/5As8OG/K5Nt27dCtefdu2gHQudmwhXTlucG3ohMDQ7bLp06WL69OljiPjz7dyYtjM3Y8eOdengerJw4UJDK37k5oNccCmhda9dWrivzJw5MzefJlAEYiHA45C6dsRCtHg5av9l2n8l0sX7SKGU2pFkdiQoBxuwNZlIF1LitSBRHpFuVASaxXfEecmSJa6oUaNGmfvvvz+32CeffNLQpjY+Hfy+s3y8fQI9UAQiI8DjkBLpyMAWKE7tv0z7r0S6QOcok0Q7ksyOBB1hA6ZEukyPqS9ts4k0WkUuGob8ul0DMVOP2fe8jw4x8z1v3jyXZ9iwYYZcUNyx/lMEWoUAj0NKpFuF+Kp61P7LtP9KpFf1gShH2pFkdiQoDxswJdJRulLNQlpBpMlP261uwquN1FrpA40FaR4xYoRrN3QBhLp379415dCbikBsBHgcUiIdG9n88tT+y7T/SqTz+0apFNqRZHYkKAkbMCXSpbpMXYlbQaTRMCwdSJvZGNra3Plvz5o1y9Da1hVtpjW+Td++fZ1fNm7SR5uGNoipSKcXFIFmI8DjkBLpZiNdWb7af5n2/3/4yrJSHfSKIiAXAfyMj9nIsoFWvXBZlEiXRa58+lYRabSMtkk348ePd43cbrvtzPz58/0a3NzyY4891kydOtWdYg3r2bNnF/7wksvQWBGIgQATaXwEXDZg7XYNioAiUA4BnZEuh1duan0jlflGCsVgA6ZEOrebNJyglUQazxMuG6gTYciQIW4lDqzmgXDrrbe6GWgcY5ObuXPnupVCcK5BEWg1AjwO6Yx0q5HXDWGk8h8l0pH7mlRFYhgly88GTIk0a0Pz4lYSaUiB3RnhuvHZZ585oSZOnGgmTJhgaCMYQ5vHGNom3bl+PP/882bQoEHNE1xLVgRyEOBxSIl0DlBNuC3Z/gFOqfIrkY7cmaQqEsMoWX42YEqkWRuaF2Nbc9qExVcwcOBA06FDB3/ejAOse42t1BEwG42ZaawXjTW5ETp27JhYy9pd1H+KQIsR4HFIiXSLgafqJNs/oC1VfiXSkfuaVEViGCXLzwZMiTRrg8aKgCLQagR4HFIi3Wrk5RJJRlqq/VcizRoQKZaqSAyfZPnZgCmRZm3QWBFQBFqNAI9DSqRbjbwSaan2X4l05L4mVZEYRsnyswFTIs3aoLEioAi0GgEeh5RItxp5JdJS7b8S6ch9TaoiMYyS5WcDpkSatUFjRUARaDUCPA4pkW418kqkpdp/JdKR+5pURWIYJcvPBkyJNGuDxoqAItBqBHgcUiLdauSVSEu1/0qkI/c1qYrEMEqWnw2YEmnWBo0VAUWg1QjwOKREutXIK5GWav+VSEfua1IViWGULD8bMCXSrA1rX4xnd/TRR5vp06e7xh9xxBHmqaee8pvt1CvRZpttZtra2lz2888/30yaNClR1BNPPGFGjhzpr7377rtmr7328ud6kERgXcHr7rvvNmPHjnXCbbvttm5Jx+233z4pbMkzHoeUSJcELkJyyfYP8EmVX4l0hM4TFiFVkRgDyfKzAVMizdqw9sXXXHONGTdunGt4165dzbx580ynTp0aFgRbLzORvuCCC8z111+fKHPatGmOwPNF1KtEmtGojNclvE488UTz0EMPOSEHDBhgXnrpJbPhhhtWCl3wCo9DSqQLAhYxmWT7Bxilyq9EOmInkqxIDKPUjgT52YApkWZtWLviWbNmmcMPP9ysWLHCbLDBBmb27Nlu18IYUiiRjoHiqjLWJSL9xx9/mH79+pmPP/7YCXj22Webm266aZWwJY94HFIiXRK4CMkl2z/AJ1V+JdIROk9YhFRFYgwky88GbE0k0gcffLD5+uuvzZgxY8yll17Kj0vjlQh89dVXbgvw5cuXuyuYMcbMcayQR6SXLl1qXn75ZV/dsGHD3E6J/oKQg6J6uq7htWDBArPvvvv6Xy0wQ3388cfX9dR5HFIiXRd8DWWSbP8AnFT5lUg31G0qM0tVJEZCsvxswNY0Iv3jjz+arbfe2j2ic845x9x44438uDReicDQoUPNjBkz3Nl+++1nXnvtNf8LQwyQ8oh0jDrW9jKk6yn85i+66CL3GOFT//nnn5utttqq9GPlcUiJdGnoGs4g2f4BPKnyK5FuuOskC5CqSIyCZPnZgMUk0r/++qv5+++/Hbwwquuttx5DXTh++umnDWY4EZRIV8L2xhtvJFw4nnvuOefiUZmy/itKpPOxk66nf/75p9l5550NXigQLrzwQnPdddflA5dKweOQEukUMC04lWz/AK9Y+cnoRw00GEQtr2xhWr/iX1ZnYqWnccTiL2YYOHCgKxPlfvPNN3UVTa4cvgwi0nWVsS5nGjx4sMeHfl5viqibbLKJr4NcRppSx9peqOqptfSxq9cTevmyy5YtK/1YeRwiIm3L/pWuLJVB7a/a35RKtPR0demfzkjTqBMziH0jWwmiZPl5JohGjmgqdcABB5hXX33VlUdE2hRdGguzUezvO3r0aPPKK6+4MuAjPX78eN++jh07mg4dOvjzMB8u7rjjju7DO58g4wDyLlmyxN9Jl4kbNMCZ77//3qUBTrvssotPDzeK+fPnm99++83Qi4M58MAD/b1a+ZDo/fffdytrfPvtt2bjjTc23bt3N7vuuqvp0aOHL6PWAfySBw0a5JPAvQNL3pUJX3zxhcFydYsWLTJbbrmlw+yQQw4x7du398XkzUiHciLTDjvsYDbaaCOfP7xfBj9fQOoAv3R88MEH7g/PfPfddzd77LGHa3sqaalT+JrjmaDsTTfd1D0PPIuddtops5xQ38roaYgHCk7jlVkZXUSf+PDDD83ChQsNPvLbbbfdTM+ePU23bt1y9RxlhvWmnwPuN6qPaBNmpX/66ScUZ+r58BDtQgC2ZQOeWSNB8vgP3FT+/zMY61ZXWG34x35doIEmdpGlu8hE1QAACEhJREFUytP6Ff9SChMxMQ0ebjYpYpG23hnpu+66y7WF21QtxgxYGO68885EPvLTDG9nHqPPheVfffXVFemmTp3q05Cht//995+lQc/SKhn+Oso47rjjEnlpDefEfXJzcffp5cLuvffeiXthGw466CD70UcfJcrKOhkyZIgvg5aby0pS9dp9991nyd3G5w/rJ0JiiQTZv/76y+XPm5F+/PHHE+XQ8neJeuvFL1EIndC6xZaW9UvUFbZ78803tyeffLKbyUznrXb+zz//2IsvvtjSS0TVcskH3dLLUkUR9eppHl5hRf/++6+94oorqj4ryE8vLfawww6z9EIYZq04brY+osLLL7/c49iuXTtL5L+iHbUu8PMkIq0z0rWAasI95R8y+Ufc36FJMVWRZCoSj0mSnz8bMMYiRryuEOk0AaGZN0sbUXjCwNiliTQtSZdI8/PPP1ta0cARH85TLQY5mjNnTtXHQDPglpa58+VPnDixatr0jcsuu8znq1Y/ru+zzz4WsoJYczrakCVdnM0jhvXixxWR36096qijfBu4LdVimtW3NMvO2avGNBtv6ePMQuXiBYo+dE2U1Wwi/cknn9j+/fsXah+woI/8LNpULTRTH7lOWsEj0d4HHniAbxWK+ZkqkS4EV9REku0fgJQqvxLpqN1IriIxjFI7EuRnA8ZYxIjrJdL087W95ZZb3B8IJbeNlhfz13E/TZaaNSP97LPP+jagLW+99ZYFscIx2gcyhr+0Dzet5ZzI98ILL1ie3R0xYoSl9XYtuWdY2sTC3nHHHXbPPfdMpMeMd7VAu+Ml0pKLSbWkieuhHyvav8UWW9grr7zSom2Y0XzmmWfsVVddZbfZZhtX/mmnnWbJfcbXVQ+Rrhc/NBwvDOT64OtHmzH7OmXKFDdLvHjxYguijnaFLxa0KYgll6CE7OEJfPbDWWg8z2OOOcbSB3KWPth0LzzwB+fnhXrpY1n30sDl1KuneS8eKB/PgtxrEnIfeeSRFjr+9ttv208//dTSetSWXJ0SLzpoJy1/yE1MxM3Ux7Cizp07+3afdNJJ4a3cY7Qff0qkc6GKnkCy/QOYUuVXIh25K0lVJIZRsvxswBiLGHG9RDqsO5wNPffcc8NbFcfNItIvvviiJwbACeQAMS335Vw8Khqy8gKIHOOKGIQQH2Hde++9mVnID7uCNFablQbB5bLh0gAXhbyANF26dPH54NpRrXzM1vbq1culBYHkuuoh0vXiB3lAFLlukF2QRLjWZAXIQn74Pj35j2clc9fOPPNMn4780+0jjzySmRaElra/9mmhjyB56VBGT4sQafK59nUC/2uvvTZdpT+H20n4soHnmtXGZuqjbwwdjBo1yrcdpLra8wrz8DE/ayXSjEjrYsn2DyhLlV+JdOQ+JlWRGEbJ8rMBYyxixOsKkYZPM+ODGLOdIGJ5AbPEYT4cV5st5LKmT5+eyANf5qxAHzz6dMOHD89KUnEt9FVGW2q5ASAzfMx55p3lqIdI14sfVn3AiwfXXWR2E64EnB4xZmHTgTZESbjXpH3t0+nTs/9ZzyQmkaYPP+3666/v5cBLU15Iv6xk+fo3Ux/D9uFFMXwGWf7lYfrwmPMpkQ5Rac2xZPsHhKXKr0Q6cv+SqkgMo2T52YAxFjHidYVIv/766wligBlC2mkxF6J0PswatrW11cz3+++/J8gr3C7S4bvvvku0B+4IRUK4VB5eBmh1hdxs6Q8q6yHSaRyK4nfWWWd5OTFrXARzzH727t3b58MHmelw+umn+/sgrHlLM+IjUbi3wM0DHzumXXhQfkwizb94cJ9Mf7yZlgfnkJtWzPByderUydJ28Ymk6ecQSx8TldAJXsC47Yhvu+22dJKq55xPiXRViJp2Q7L9A6hS5VciHblLSVUkhlGy/GzAGIu8GITw0EMPrfkX+tbSsnA108IvNSuUISjNcu1IE5BavsuhDOl8IHBFAj4a4+dx6qmnVmR57733/H2ke/DBByvSZF2gHSJ9PvgZFwn4OJLbgjgGkS6KX9++fX3d+++/f5HmujTnnXeezwcCnnYtCIk2LfVXqFxecaVa4jJ6mufaQUva+fb36dOnWpUV1y+55BKfD88q/eLRLH1MNwRjQ6gzEyZMSCepes75lEhXhahpNyTbP4AqVX4l0pG7lFRFYhgly88GjLHIi7GaA+eJEWNps6xQhqC0ikhj840iIU1cis4ch36+J5xwQkVV+DAwxHzmzJkVadIXQARDNw2sOlIk4MPKsK4YRLoofuHHgFkvFNXan3bvgO95GPCBJct0yimnhLfqPi6jp3lEOnRngb9x0XDPPfd4uSAf9C8MzdLHsA4+DvE444wz+HJuzM9FiXQuVNETSLZ/AFOq/EqkI3clqYrEMEqWnw0YY5EXSybSN998cx487n6auDz22GOF8oVrJWcR6YcffjhBmObOnZtb7pdffpnIg9nLIgH+xKwbiGMQ6SL4/fLLL4l68eEg2lzkL/xQD23GKhccaDOXRLnjxo3jWw3FIXHM+yi2FpH+4YcfEu0rs5MkbciTyJv+gLJZ+pgFXOhmMnLkyKwkmddY15RIZ8LT1IuS7R+AlSq/EunI3UqqIjGMkuVnA8ZY5MX4uRwrO9T669evnzfsb775Zs20MJxZoQxBadWM9KOPPprV1IpraeKCpeWKhDwiDSLKzwsx7ciXWyzwD/PccMMNuXmQAJuyhPliEOki+OHlIKy3kePwBQYfvoVlTZ48uRAOeYnK6GktIg3SH7av6K8YaN8777yTyDtp0qREs5ulj4lKVp5gDXKWA8tWFg2cR4l0UcTipZNs/4CiVPn/HwAA//+iPygpAABAAElEQVTsXQfYHUXZnYgiTbqAoIQgoAGFgA2kJYI0gRBAakRiwQpJlF4TFVRUSESKqBQBOySKgqBIIgiiIAldBSkCIsUAkp9m3H/OyrvMnTtb7+zOvXfPPM/3zd7dqed9552zs1NU5NktXLjQc4rlkmP+xL+cxvgLrZSK8OfTbbHFFnGaSPehhx6qlPQyyyyTpDFlypTMNL75zW8mYZHn3/72t8zweIg2J3WH/8UvfrErznXXXdcR5rLLLusK47pRNd4b3vCGJL/99tuvK+lp06Ylz1Hm//u//+sKY9/4+c9/3hHnW9/6lh3E+XvRokXRK17xiiTuZz7zma5wF198cfIc5bn55ps7wlTB4de//nVHmqaMyl6feuqpSXl+9atfdaR79tlnJ896uSijp1l4QbfM+pUp31/+8peOuEcccURHlarIAQnk6WNHJi/92GGHHZKybLjhhq4gzntS93//+99R2T9ngiVusv9l/1tCXbwHDaV/fnt9DUuoiohEmD8bsuhC0750YD7zJZGuRsDziMtXv/rVhKRAbo8++miu2GwS9ZWvfCU3DgIgbdEN+E0RaZsUHn744dEtt9xS6c/E5/bbb++oz0knnVQIh7xAvoj0vHnzOsrnerFLK4st469//esdQe3nRV8I8/SxI5OXfpht/93vfrcriPOe6FpZEo3wvTr2v+x/e9WhXuKH0j8S6V6k5ogbSpBSFOYfzpBJByay8OGbnWm/jkj/4x//yCUuVQlI1Xh5xOX888/vKDPIYZ679957O+LYo5Vp8W+77baOeE0R6eeeey4aMWJEkvehhx6aVsRS95955pkkTej8IYccUip+WmBfRPrJJ5/sKN/kyZPTsuy6P2vWrI64P/vZzzrC1KWPHZm89ONNb3pTUpbx48e7gjjviR0ikXbCU+tN9r/h+l8INhT+JNKem1UoQUo1mH+4hiwdmMjChx+aSGNUM8/97ne/Szp8YOAaoaxKQKrGyyPS9uf/OXPm5FUzAjEVGcP/yEc+khsHAa666qqOeE0RaeS9+uqrJ3nvtddeuOXFrbzyykm6e++9t5c0fRFpFGaFFVaoVL6zzjoriQcZYwTfdHXpo5mHXK+44opJWYrqGuKKjpJIC5LN+ex/w/W/kHIo/EcgY93w6IgAEXgJgcUWW0zpea2l8Vh66aXjOLo9l46bFmHLLbdU1157bfxYj0grTYzSgqbef81rXqP0KGL8XM+RVnq+a2rYH/3oR0oTo+T5jTfeqN72trclv10XF1xwgTrggAOSR5pIq6OOOir5jYvrr79e6c/TyT1NZNWOO+6Y/E67qBpvzTXXVH//+9/jZPUcaXXRRRd1ZIF6veMd70ju/fjHP1Z77rln8jvtYqWVVlL/+te/4sebb755Ipu08Lh/wgknqM997nNJEE2k1de+9rXkNy4uueQStcceeyT39BxpNWbMmOR3VRz0i5jSLzpxOm9+85vVnXfemaTZy8Xb3/52ddNNN8VJ6JcWdd999yk9DzwzyR/84AcKOqxJrlpttdXUTjvt1BG+jJ7m4bXJJpsoYAg3atQodc899yg9Ot+Rn+vHxz72MaXnVCePnn76aYVyiasqhzx9lPTFh/151atehYGu+BbaE9pVESf1fOyxx4oE7wiz1FJLdfzmDyJABAogABbv04V6I5A6MP92vhH2g/x1c4tHg6QsPnzfI9J5n7k1UYjrIHXRhCW3GmPHju2IMwgj0pr4dZT5jDPOyK0nAmy99dZJPEybeOCBBzLjYaGhJlFJHODa5Ij05z//+Y68f/GLX2SWVx7++c9/jrC4Ms2eYlqL6Aj8X/7ylxLV6f/3v/+NNHlO4uyyyy5d4cwR6Tw9zVpsiISPPPLIJC+UDwsv8xymrGjSnMTTLzJdUZoakX7kkUeScqD8p5xySldZ0m6IXDginYZQfffT2kt9OXamzPzD8B9O7ejUw55/UZHDKLIILiT+0oFJWXz4Poj0csstl3TKeuQ4s1iYhy31gP/hD384MzwIlBke14NApP/zn/9Eyy+/fFL2vHoKCN/73veSOGl1lbDw9Uh3R3jEaZJIg0ytssoqSRn0KHoEcp/lQHq32WabOM4SSywRuXZ60aOdkUl8scNEVrr23ONvf/vbXUUoo6d5RPrxxx/vIMW77bZbV372DXtah2shYVNE2p56dOWVV9rFTf0t7ZFEOhWi2h6E7H9QKeYfhn+QSHtuUlTkMIosYgyJv3RgUhYfPhbFfeELX4j/9GfmSklusMEGCZHSn7mjF154ITUdkCFzXi3q9JOf/MQZHqPVIKOve93rInM+J8pru6oEpGq8vDnSKJ+eypHgMnLkSLvIzt/PP/98tOqqqybxXvnKV0Z62ogzLEj34osvHi255JIdpNNFTPOIYVUcULCZM2cm5YU8t9tuu+iJJ55wlhntZ9999+0Ij+3uXO7oo4/uCAc8MY/cdphDb5JkzK8G0bVdGT3NwwtpH3/88R3lwzxjvEC53DnnnBPpqRRJeHx5cLmqciiij2Z+U6dOTcoC/Xn22WfNx5nXYodIpDNhquVhyP4HFWL+YfgHibTn5kRFDqPIIsaQ+EsHJmXpF1/PvU06ZZQRREbPBY0+/elPRwcffHBXMe2ROT1vMh6ZPvPMM6MLL7wwOuaYY2IyJvXFqPS6666b5DF9+vSuNKsSkKrxihAX7C8sdYD/17/+tavcrht4UTDjYY9ojMjqudARCBlI0FZbbZXsmIGt9tZZZ50kjgvzPGJYFQeUH+RfzxlO8kfZgc/HP/7xCPuGX3755XG5QfDNRXoIt//++7sgiO/pueIRXsxMLDCNBXEwFQF46HnwHc9BVtMWdpbR0zy8UEDs3rHeeut15K/nxcf6O3v27Ag7cmDqy84779wRBvp+ww03OOtdVQ5F9NHM8K1vfWtSJuhWGSfyIJEug5qfsCH7H9SA+YfhHyTSftpPkgoVOYwiiwBC4i8dmJSlX3y785dywkeHbbsXX3wx0ovJko7cDG9eg0DK3E0cGCHPjjvuODvJyC6D67N5VyR9o2q8IsTl/vvvT8qMsuNFoag78cQTE6Is9Xb52NECo6AmPp/4xCe6sskjhlVxkIxAprGPtHkwjKu85j1MQcmaroG0QVbf//73d+BopmFeYyoIvrCkObuOZlxbT/Pwkjww73nSpEmFyof8sF9z1guVXcaielxEH6XM9naS5mE4EibLF9xIpLNQqudZyP4HNWL+YfgHibTn9kRFDqPIIsaQ+EsHJmXpJx8jpeZCKpQVpApzYV0OZPpLX/pSpHcicZIQzLW94oorkqjmXG7X1IWqBKRqvKLEZfTo0Un9dt1116Q+RS5A5kCQMb1DZC8+RuhPO+20JJlx48YlYVyjvHnEsCoOSQFeupg7d26Espjb10mZ4WMawcSJE1NHje305DdGtvXuLhHmVJvp4RrTW/DygAV0ea6onubhZeejdwyJNttss642gPK9+tWvjuWIA3byXhyqyqGoPqLc5513XgeGeqcVuzqZvwV/EulMmGp5GLL/QYWYfxj+MQLg64bnzemjdlXILXSYP/EPpX+y7ZTnJuWtber5q+quu+5S2BZLzwlWa621ltIkJzN9TSyU3plC6VG6OB62LdPTFOL4mREH5CG2OsOWZ3D6xULdcccdSh+EUar0erRX3XrrrUrvdKH0XHGFrc70fN9SaYQIrE8rVPogGvXwww8rPe873loROtFL+4G+QFf0ITQK20HqqRWxnmFLyaKuip4WTRttE/oMeekvBbGc1l57bVWmfEXzqhIO5cO2h3r/6ji6ns+u9AtrqaTEDmkiXSoeAuuvBqXjmBHY/7L/7cV+mLpU5TqU/pFIV5FWRpxQgpQiMf9whkw6sH4l0qIj9F9GQI+8x8RZn1oY39SjsQr7YtMRgRAI6LnbasKECUnWeq62euc735n8LnIhdohEughafsOw/w3X/0KSofAnkfbbjoIJUqoRSpGYv0oOfCCRFm0YDF9/Sld6Hm1cWIxMYtQeo+50RKBpBMyDZPRe20oviCxdBBLpcIfKsP8lkS7dYF0RqEjtVCTRhTbLXzowEmnRhsHwMR1h/fXXV/o49LjABx54oDr33HMHo/As5dAgANI8fvz4uD6wJTiZcaONNipdP7FDHJEuDV3PEdrc/wG8ttafI9I9N53OBNqqSIJCm+svHRiJtGjD4Pj65Du1/fbbK30YSTxf9qqrrlJ6L+HBqQBLOtAI4ChyvVhT3X333XE99NaUSi9WrVQnsUMk0pXg6ylSm/s/ANfW+pNI99RsuiO3VZEEiTbXXzowEmnRhsHy9ZZ26thjj40LrQ+ZUfPmzVP6VMDBqgRLO5AI7LXXXkqfghmXfdNNN1V6d5XchcBpFRU7RCKdhlB999vc/wHVttafRNpzm2qrIgmMba6/dGAk0qINg+VDbvi0fumll8YF33bbbeMdE7CbBx0RqAuB008/XWEEGg4vbn/605/UGmusUTk7sUMk0pUhrByxzf0fQGtr/UmkKzcZd8S2KpKg0eb6SwdGIi3aMHj+U089FX9iv+eee+LCT5s2TekT+gavIizxQCBw0003KX0IjHrhhRfiKUX6OHal9/nuqexih0ike4KxUuQ2938ArK31J5Gu1FzSI7VVkQSRNtdfOjASadGGwfSxz7A+BCMuPEajMTItsh3MGrHU/YrA/PnzlT6oJi4e9iDXR5j3XFTRVRLpnqEsnUCb+z+A1db6k0iXbirZEdqqSIJKm+svHRiJtGgDfSJABJpGQOwQiXTTyLeXSArSbe3/SaRFAzz5bVUkga/N9ZcOjERatIE+ESACTSMgdohEumnkSaTb2v+TSHtua21VJIGxzfWXDoxEWrSBPhEgAk0jIHaIRLpp5Emk29r/k0h7bmttVSSBsc31lw6MRFq0gT4RIAJNIyB2iES6aeRJpNva/5NIe25rbVUkgbHN9ZcOjERatIE+ESACTSMgdohEumnkSaTb2v+TSHtua21VJIGxzfWXDkywoE8EiAARCIUAiXTzyLe5/wPaba0/ibTnttZWRRIY21x/EmnRAvpEgAiERoBEunkJtLn/A9ptrT+JtOe21lZFEhhZ//9TSy21lMBR2H/mmWcKh80K+Nxzz6klllgiK0ipZ9hTeZdddlF/+9vfVJGO2Xf+pQqrAzN/v/IfRPxf+9rXqrXXXlv99re/Vcstt1zZKvQUftD1b5lllump/rT/1ex/T6AbkYl/GPxJpA0l9HFJRQ6jyCK7QcW/H4n0LbfcEh9G8uyzz8bwkkiLlqX7g06k0mtW7Ek/1B9EGm7kyJHqd7/7XaNkuh/q38uLNIl0MT1PCzWo/U9afcreb2v9SaTLakpO+LYqksDC+ld7keg3In3hhReqI488UuHIbDicunb//feLmFP9QScSqRUr+ID1Dz8iLkQaIltzzTXV97//fbXhhhsWlGBvwQZd/iTSvcmf/V+1/q831F+OHQp/EumXZeDlKpQgpfDMfzAbcj8R6TPOOEMdccQRsUpttNFGCscYb7HFFuryyy8XNUv1B51IpFas4APWv3+ItOgupndcdtlljZDpQZc/iXTBhp4SjP3vYPa/KeIsfJtEujBUxQKyIbWzIYl2VJV/vxDpT3ziEwqj0XCnnnqqGjNmjBo3bhyJtAg4xx90IpVTvdzH/VB/GZFesGCBGjt2bPwi2BSZ7of6c2pH+TUquYpdMEBV+18w+dxgzD8M/yCRzlXNcgGoyGEUWaQ0qPiHJtKYwrHvvvuqa665Jp5TOmPGDHXggQeq2bNnqwkTJpBIi4Ll+INOpHKql/u4H+ovRBr7uT/55JOxHv/0pz+N9brukel+qD+JNIl0bkOtKcCg9r+9wkEi3SuCVvy2KpLAwPpXe5EISaSxMwdINBYXYuRuzpw58Ug0ZDpt2jQ1ffp0ddRRR6mjjz5axJzqDzqRSK1YwQesf/ipHW984xvV008/rcyDkfBSeP7559dOpgdd/pzaUbChpwRj/1et/0uBs/TtUPiTSJcWVXaEUIKUUjH/wWzIoYg0yPNOO+0ULyrEnFKMQK+11lqiTiTSCRLFLgadSBWrZXqofqg/vqBce+216uqrr46ndkhpTTKNBYhbbrmlPPLm90P9OSLNEWlvCl0yobbyDxLpkoqSF7ytiiS4sP7ViHwIIm3uzLH11lvHJHr55ZcXUcY+R6Q74Mj9MehEKreCOQH6of5pRBpFFzKN6zPPPFNNnDgRl95cP9SfRJpE2ptCl0yorf3/iIULF0YlsWJwIjDUCCy22GJq0aJFjdYRBqhJd/bZZ6tjjjkmzvKDH/ygOu+885zZY7HW3Llz48/iGLmmIwL9jsD48ePVdddd1zUiLeU2yfRpp52m9tlnH3nUer/KYVKtB40AtB4Bjkh7VoG2vpEJjKx//49I2ztzTJkyRcTX5QuRxiKtIp/CB31ErguAkjdY//BzpLNGpEWcJpn2OTI96PLnHGnRkGo++79q/V81tLtjhcKfRLpbFj3dCSVIKTTzH8yG3MTUjrSdOUR3XD6JtAuV9HuDTqTSa1bsST/UvwiRRm3wFWbSpElxxXyR6X6oP6d2cGpHsdbqP1Rb+QeJtGddaqsiCYysfzUiXzeRztqZQ2Tn8keNGqXuu+8+dfvtt8enxLnCmPcGnUiYdalyzfoPxoi0yNY3mR50+XNEWjSjms/+r1r/Vw3t7lih8CeR7pZFT3dCCVIKzfzb2ZCz5D9v3rz4UBXsqevamUPiuvwRI0bEt82txFzh5B71j/oXcp4t9A9z+TGv3961Q3TU9k0yjcW1J5xwgh2k8G/qP/U/tP4z/+a/SJBIFzaRxQLSkNKQ9pMhA0mYOnVqfDBF2s4cWZpNIp2FTvcztv/w7b8skYYUTTKN+dPnnntut3AL3KH8w8u/n+xvAZXxGoT6F0b/SKS9qrFSVOQwiixiJP4v4z9z5kwlCwmzduYQ7GwfI9grrLBCfIgFros44v8y/kXw8h2G+JcfkRYZ+CDTxJ/6TyLf/IiwtOFQ7Y9EWiTgyQ8lSCk+86chhyHHIioQA7hTTz01IdTxjYL/cMLhuHHjFEaycV3EUf+of6GJRJURadFttBm8fGJhbpWRaeo/9T+0/jP/5ok8ibRYUE8+DSkNaUhD9vDDD6tPfepT8eEqOO57xowZMSGoot4k0uVRY/sP3/57IdKQONYUYLeaKmSa8g8v/5D2l/Jvp/xJpMv3lZkx2JDa2ZBEKULKH9MvMHqMY79BokGEx4wZI0Ur7ZNIl4aMU7v0Yr/QROboo49WmNaEec4YVa7iqpLpkO0f9WT+4fUvtP4z/+ZHpJVeje/V4aTEkI75E/826t/NN98c6eO9cUpppHfmiO69996eYdC7F8TpwS/q2P7Y/orqSh3hoH9V9NZVFrQp/UIatwH9QhotWLDAFazjHvWf+t+hEA3/oP6F0T8Sac+KTkUOo8gixjbiP2vWrIRE6xHpQh2+4JXlVyEkbcTfxJD1D9/+q+itKUPzuiyZpvzDy9+UX9PXlH875U8i7bmlsSG1syGJGjUtf/35Oh4xw0i03plDiuHFr0JImq6/XVHmz/ZXRW9tPTJ/lyHT1D/qn6k7TV9T/8LoH4m0Z02nIodRZBFjm/DX8z8TEq135hAIvPnjx4+P08eId1HXJvxdmLD+4du/byINOWOqFKZM4YU1a5oH5R9e/q522dQ9yr+d8udiQ20ZfTou9uBij7oXe2BRIba3mz17dryosJedObJ0HzsXlDkhDmlR/6n/det/ls5C/04++WQ1ffr0+IRCnFToy6HdoU3Mnz8/XsSLkxP1uoSO5Kn/1P/Q+s/8m19sSCLdYQZ7/0FDSkNapyFDZ469nbGrgI+dObI0nkQ6Cx33M7b/8O2/LiINidtkWn+tUWuttVaiDJR/ePnXaX8TQadcUP7tlD+JdEqDqHqbDamdDUn0pU75gzyDRKMz15+Z4wNXetneTsqc5o8aNUrdd999Sn/W7iALaeFxv876Z+Urz5g/21+dRBp6ZpJpjEhjZFraIfWP+kci3/yIcGj7TyItEvDk05DSkNZhSDGNA9M5hERjj2f7s7InFU6SGTFiRHyt5xcm9/IuqP/U/zr0P0/v5Dn0r24ijbzSyDT1n/ofWv+Zf/NEnkRaLLAnn4aUhtS3IcOxxSDRcHpnjngk2pO6ZiZDIp0Jj/Mh23/49t8EkYbwXWR6vfXWC34gjW/741T0lJvU//D6T/mTSKc0z+K32ZDZkIfJkIBAg0jD6d0IlM/FU3GiKf9AElZYYYV4Hjauizq2P7a/0O2vKSItbQKnJ55//vnxF6LLL79cbbrppvKocZ/tj+0vdPtrY/4ckfZs6mjIaMh8GBKQV9mZAyqKhX9Y2FT3dA5pDlWOB0dc6j/134f+ix6W9aF/Z599tpo6dWqjL54mmTbnTJctf6/h2f7Y/kK3vzbmTyLdq+Wy4tOQ0ZD5MiQgsxiBxhZ0cCDRU6ZMUZMnT66dUJNIWw274E+2//Dt/w9/+EO8KFef8qmgx005k0zjpRcvv0076l94/fNl/6voDuUfRv4k0lW0NSMOFTmMIotIhhH/EISaRFo0qpw/jPpXBoF+qH8IIo32gukdmIaF7fCw000I1w/4k0g2P0dXdI3yD8Q/fJ/4w5N92nmyj+gR5V+f/PUn40iPssWnq2nDGekR6kiPWEcLFiwQ+L35VU+Ho/zrk38R4RL/hRHaCdoH2krdThPnSI88J20S+eoFwXVnm5o+5c/2l6ocDTxoq/5xRFpe5Tz5fCMM9Eb4kvzagH8TI9SYUlLldLg24J9lKlj/8O2/7hFprF+YOXNmPPqMfdbhcDgSpl3tvffeavTo0fG9EP+of+H1jyPyLRyR9/2S0tY3EsGR9eeIgOhC3X6dI9Qcka4mPbb/8O2/rhFpPV0j0vOg4y9BmiTHo9AjR46Mzj333ERZKP/w8k+EEeCC8m+n/JVvXaMitVORRI8o/+bl7yLU+OTcixs/fnxMFPSiqVLJUP7Ny98UEPH3P7UD7Wu33XbrmL6BaSO4bzviT/23daLJ39S/MPrHqR2ev7/x0xo/rYX6tIcpH8cff7y65pprYq3GoidM0cAhLmUddhzAbiGaLJTafYD6T/0Ppf/Qceifr6kdWDyI9mNO39CEOr6HtuVy1H/qf2j9Z/7NTy0hkXZZwx7u0ZDSkIY2ZCASu+++u9KLEGNNrkKoSaSrGQG2//DtvxciLfOfZ8yYEZ9cCC3Q0zcUtrbDHOi8fdwp//DyD21/mX/zRFasdaj2RyItEvDkhxKkFJ/505A/+uijatSoUbFKrLHGGuqhhx6Kr8sQasTHSBy28UobfROdM33qH/UvNJGoQqTnzZuXLCAUfcbJnqecckpMouVenk/9p/6H1n/mH4DI+56/wzk6YeboiByJP/HH9lu6w0+24cJiKCyKwj38aWIc5c2hlrCiV0V96h/1r6iu1BEO+oe5y9DfItvfzZ49u2v7uj322COOj+0ly24tSf2n/teh10XTpP6F0T8uNiyqoQXDUZHDKLKIp+3433HHHQlhxi4DpitDqEmkTeSKX7dd//qh/nlEGuQYL5J4oRQ919vXRfrE0EjaDEg4nmH3mjKuH+pfpry+w7L+7P9861SZ9ELp3whkrA0GHREgAi8hsNhii6lFixYNJB4HHXSQuuiii9T++++vzj77bGcdLrzwQnXiiSeqBx54IH6OqRtYVCWLEjFPFJ+14bR9iH3+IwKDggD0F1OaoNeYmiQOU5Vk/2eEgVtzzTXVpz71KTVx4sSO+c+//e1v1Y477hjPj9Yvp5IEfSJABIhAFwKcI90FSW83OEeOc+RCzVEDUZC50SAQIBJZTo/KxQT6/vvvj4MhPAg1FleNGzdO6VE5hZ1AyjjqP/U/lP5DT0X/RowYEautHs2KdViO7xZdhm5j8SB24UhzaA9oG/pLTuF50pJ/Wpp132f+bH/90P7q1vO09EPpP4l0mkQq3g8lSCku82+vIcXOAiAMGFkGSS7qbEKNnQkwYkciXRTBl8Ox/fVH+xMijd1nzJdBtA0Q6DFjxrwstJQrtItJkybFYW+++eaUUJ23Kf/+kH+nVJr7Rfm3U/4k0p7bGBtSOxuSqFEo+ZcdjZbymr5NqEmkTXSKXYeSv5SO+f/P/giRBi5yfDdeNDHKXMbhpfKpp54qvJ868af954hwgF0zXmrUodofiXQZq1ogbChBStGYfzsNuYxGY2405kD34kCoQSCyPnunpU/9a6f+iT70i/xBpDFFCVOV0DaqOsSfPn164a88/VL/qvXtNR7rz/bfxhcJEuleLYcVn4aEhqRpQyKj0Rh5u/7669Xo0aMtrWzuJ/Wf+t+0/pvaLfqH6RyY1tGrk7aFdIqsO5D8e823anzmz/bXD+2vqv72Gi+U/pNI9yo5K34oQUoxmH/7DOmECROU3g9X6a261OGHH65oSNv3aZHt/38I1GH/5GuP3h5P4cTDLFdH/ln52c+Yf/vsv6kDlH8Y+ZNIm1ro4ZqKHEaRRXRtwx8jb9hhA6PRGD1bfPHFSaSXIpGW9tC0P4ztD6cebrzxxvF0J4xKY9pTmhvG+qfV1XWf9Wf/18aBHBJplzXo4R4NCQ1Jk4YEJBpkGqPRmM9J/aP+Nal/tqkcVv3DNJG5c+eqU089Nd71w663/B7W+kv98nzWn/anjfaHRDrPMpR8TkNCQ9KUIbFHozFSRv2j/jWlfy7TOKz6h6lTmEKFXT/MQ15sDIa1/nY9036z/rQ/bbQ/JNJpFqHifRoSGpKmDIk9Gg2Vpf5R/5rSP5eJHGb9A4nGAS2zZs1K3dFmmOvvkrd9j/Wn/Wmj/SGRti1Bj79pSGhImjAkrtFoqC71j/rXhP6lmclh1j8sNJw6dWq8G8jVV1/thGCY6++ssHWT9af9aaP9IZG2DEGvP2lIaEiaMCSu0WjoLvWP+teE/qXZyWHWP5z2iVFpHNCCkw5dpyMOc/3TZG7eZ/1pf9pof0ikTSvg4ZqGhIakbkOSNhoN9aX+Uf/q1r8sMzns+ofjxWfOnJl6QMuw1z9L9rQ/tL9t1X8S6TzLUPJ5WxVJYGL96ydyaaPR7MjYkbH91dv+8g5oIf714i/9TJpP/Il/iIEEEum0FlnxPhsyG3KdDTlrNBoqS/2j/tWpf3lmsQ36Jwe0yJaTJiZtqL9ZX/ua9af9aaP9IZG2LUGPv2lIaEjqNCRZo9FQXeof9a9O/cszj23QP3mZxXaTCxYs6ICkDfXvqLD1g/Wn/Wmj/SGRtgxBrz9pSGhI6jIk0oHLKYauE9aof9S/uvSviG1si/5hoeH8+fPVueeeqzBCLa4t9Zf62j7rT/vTRvtDIm1bgh5/05DQkNRlSPJGo6G61D/qX136V8Q0tkX/zjvvPDVp0qR4Fw/zgJa21D9NF1h/2p822h8S6TSLUPE+DQkNSR2GpMhoNFSW+kf9q0P/iprDNukftsLDAS3YUxpHiMO1qf5xha1/rD/tTxvtD4m0ZQh6/UlDQkNShyEpMhoN3aX+Uf/q0L+idrFN+jdt2jQ1ffp0NX78eIUjxNn+aH/apP8um9DW+pNIu7Shh3ttVSSBjPX3T+SKjkZDBsTfP/6i20V84t8e/M0DWjC9AyPUlH975O+yB5R/O+VPIu1qDT3cY0NqZ0MSlalD/kVHo1GGOvKXuhXxmT/1v00j4rIV3gc/+EGFedPUf+p/m/Tf7hPaqv8k0rYm9Pi7rYoksLH+fjuSMqPRkAHx94u/6HVRn/i3C385oAU76GBUevHFF1ckUksVbS7ew7H9tav92QoUSv4k0rYkevwdSpBSbOY/XIakzGg0dIDyHy75S7su6lP+zcsfCw3nzp2rcEDL4YcfTiK9FIl00fbqOxzbf/PtHzIkkfasyVTkMIosYhwm/LGAacKECWrkyJEKI19F3DDVv0h97TCsP9tf0yPC8tUIc6Rvv/12EmkSadssNfab9i+M/SOR9qziVOQwiixiHCb8R40aFRNo+9AHqavLH6b6u+qXd4/1Z/trmkhDJ0GisRXeN7/5TXXQQQflqWltz6n/1P8Q+i8K3Vb9I5EWDfDkt1WRBD7W348hlwMfyoxGQwbE3w/+os9lfeLfTvylvW611VbxNI+yeuMrPPWvnfon+kP5h5E/ibRooCefihxGkUV8w4J/ldFoYDAs9Rd5lvVZf7a/UCNyWHD41FNPdRzQUlZ/ew1P/af+h9J/6G5b9Y9EulfLZcVvqyIJDKx/74ZcRrfKjkZDBsS/d/xFl6v4xL+9+MsBLbIVXhX96TUO9a+9+gfdofzDyJ9EulfLZcWnIodRZBHDMOBfdTQaGAxD/UWWVXzWn+0v1IicbIUHvZUDWqrocC9xqP/U/1D6D71tq/6RSPditRxx26pIAgXr35sh72U0GjIg/r3hL3pc1Sf+7cZ/4sSJ6qKLLlKTJ09WM2bMqKpGleNR/9qtf5R/GPmPWLhwYVS51TIiERhCBBZbbDG1aNGiIDVbf/31k9X/6JTpiAARGBwEbrnlFrXZZpspzJfGVnjw6YgAERhuBDgi7Vm+fCMM80YoYhxk/HsdjQYGg1x/kWEvPuvP9hf60/ZOO+0U79xRZtvKXnTejEv9p/6H1v825k8ibVohD9c0ZDRkVQ1JL3OjRXWpf9S/qvonOtSLT/37P3XllVfGBylhb2nMlW7SEX+2f7b/5k/WJJH2bOVoyGjIqhgyH6PRUGXqH/Wviv75MoPUv//pnxzQMmvWLLXbbrv5gjc3HeLP9s/2TyKdayjyAtCQ0JAMoiHxMRqNtkH9p/4Pov7n2fWiz/tF/7HQcOrUqWrs2LHxvtJFy99ruH6pf6/1qBqf9af9C2H/OCJdtcWmxGNDZkMu25B9jUZDJal/1L+y+pdiyirdpv79T/+efPLJ+NhwHNBy8803qzFjxlTCs2wk4s/2z/bPEemydqMrPA0JDcmgGRJfo9FoDNR/6v+g6X+XEe/hRj/p/5QpU9TMmTNVkwe09FP9exBj5aisP+1fCPvHEenKTdYdkQ2ZDblMQ/Y5Gg2NpP5R/8ron9uKVb9L/XtZ/8wDWhYsWNDIVnjE/2X8q2tx9ZjEv534k0hXbzPOmGxI7WxIogxl5e9zNBplKJu/lNuXz/yp/yTyL39aPvDAA9X555+vTjjhBIUjxOt2bH9sf2x/L7e/utubpE8iLUh48mnIaMiKGjLfo9FQYeof9a+o/nkyeR3JUP869W/OnDlq3Lhx8Wg0RqXrdsS/E/+68bbTJ/7txJ9E2m4JPf5mQ2pnQxK1KSN/36PRKEOZ/KXMPn3mT/0nke8cEcNCw/nz56smDmhh+2P7Y/vrbH8++7e0tEik05CpeJ+GjIasiCGT0eiNNtpIzZs3r6K2dUej/lH/iuhft+b4uUP969Y/aetNHNBC/Lvx96PZxVIh/u3En0S6WPsoHIoNqZ0NSRSkiPyxNRZGo+FfffXV8V6zEr9Xv0j+veaRFZ/5U/9J5LtHxOSAFt/t3W6LbH9sf2x/3e3Pbie+f5NIe0aUhoyGLM+QYdHR9OnT1dZbb60wh9Kno/5R//L0z6e+2WlR/9z6J21+/Pjxavbs2TZs3n4Tfzf+3gDOSYj4txN/EumchlH2MRtSOxuS6Eme/OscjUYZ8vKXctblM3/qP4l894iYeUDLvffeGx/WUkcbZPtj+2P7625/dbQ1M00SaRMND9c0ZDRkWYZMRqbqGI2G+lL/qH9Z+ufBxGUmQf1L1z/ZCq/OA1qIfzr+mYrr6SHxbyf+JNKeGpAkw4bUzoZURP51j0ajDNQ/6h+JdPMjUkXavxzQsvzyyyuMSsP37dj+2f7Z/ptv/yTSni0ZDRkNWZohq3s0GqpM/aP+pemfZ1PnTI76l61/Y8eOVXPnzq3tgBbin42/U2k93iT+7cSfRNpjI0JSbEjtbEiiRmnyb2I0mvrH9pemf6KfdfvMP9v+yQEtdW2FR/yz8af+14tAW/WPRNqzXrVVkQRG1t9tyJsYjYYMiL8bf9HPun3iT/zzvgjIVnh1HNBC/aP+5elfnTawrfpHIu1Zq9qqSAIj699tyJsajYYMiH83/qKbTfjEn/jnERk5oAXTPLCvtE9H/aP+5emfT32z02qr/pFI25rQ4++2KpLAxvp3G/KmRqMhA+Lfjb/oZhM+8Sf+RYgMFho+9dRTPJDJc6Nk+2P7K9L+PKudIpH2jCgbMhuy2ZCbHI2GKlP/qH+m/nk2b7nJUf+K6Z+8XPveCo/4F8M/V5ErBiD+7cSfRLpig0mLxobUzoYk+mDLXzrMuvaNlnzFt/OX+035zJ/6TyKfv/2WbIWHdunzgBa2P7Y/tr/89ue7PySR9owoDRkNmRiypkejocrUP+qf6J9n01YoOepfcf2TA1omT56sZsyYUQjfvEDEvzj+eVhWeU7824k/iXSV1pIRhw2pnQ1JVMKUf9Oj0SiDmb+UqUmf+VP/SeSLjYjNmzdPbbzxxvHBLL4OaGH7Y/tj+yvW/nz2iyTSPtHUadGQ0ZDBkIUYjYYqU/+of+xIm+9IpRsp2/7kgBZfW+GVzV/K7ctn/rQ/bbQ/JNK+LMhL6dCQ0JDAkIQYjYYKUv+of23syMSMD5r+z549W02YMEH5OqBl0OovcvPls/60fyHsH4m0rxb8UjpsyGzIL7zwgho1alQ8Ko19YjHq1JSj/lH/QnQkot/Uv/L6Jwe0zJo1S+22224CZSWf+JfHvxLQKZGIfzvxJ5FOaRBVb7MhtbMhib5A/ieffLKaPn26amqnDskbPvWP+kciPThTO9BmsdBw6tSp8Qt3rwe0sP2z/bP9N9/+SaRhyTw6GrJ2G7KHH35YbbDBBvFo9M0336zGjBnjUbvyk6L+tVv/KP/Bkz/WU2BUGge09GozKP/Bk3++VS8egvIPI38S6eI6WigkFTmMIotwQuM/ceJEddFFFynfBy1I/fL80PVn/u3Wf8q/mvynTJmiZs6c2bPdIP7V8M+zq0WfE/924j9i4cKFUVElYTgi0AYEFltsMbVo0aLSVb3//vvV+uuvH8e744471MiRI0unwQhEgAi0DwHTdjz00EPxlnjtQ4E1JgKDiQBHpD3LjW+k7XwjhRrJAQuhRqNRBupfe/WP8h9s/Rf7ccIJJ8S7/kCeZR3bP9s/50hzjnRZu9EVnoaEhiSEIanryN8uBc+5Qf2n/ofQf1FL6l91/ZszZ44aN25cPBq9YMECgbSUT/yr418K6JTAxL+d+HNEOqVBVL3NhtTOhiSjSfvvv7+68MILq6pPz/Gof+3UP1Ecyn+w5Y/FyfPnz1dVD2ih/Adb/tKOq/qUfxj5k0hX1diUeFTkMIos4giBvzkajbnRo0ePluI07oeov1lJ5t8+/af8X0agV/0/77zz1KRJk+JdPHBseFnXa/5l87PDM3+2/zZ+ESORti1Bj79pSNpnSGQ0GnOjzzjjDNVGQyLNhvrfPv0X2cOn/HuXP7bCw+LDKoc5Ef/e8Tf1uew18W8n/iTSZVtKTng2pHY1JHM0GiNIq6yyCom0PiI9lGP7a1f7s/VsGOQ/bdq0+ECn8ePHKxwhXsYNQ/3L1NcOy/qz/YcYyCKRtltij7/ZkNvVkM3RaHyWpfzbJX/bXFD+lH+vHbl5QAtezjFCXdRR/6h/vepfUV1zhWur/pFIu7Shh3ttVSSBrE31t0ej0eG1qf4ic9Nn/dmRsyPv/YuM/YJutrGsa7Y/tj+2v97bX1Ybcz0jkXah0sM9GrL2GDJXZ0f5t0f+LjNB+VP+PoiMvKQvv/zyCqPS8Is46h/1z4f+FdE1V5i26h+JtEsberjXVkUSyNpSf+noUG/z82tb6i/ytn3Wnx05O3I/I2Jjx45Vc+fOVWUOaGH7Y/tj+/PT/uy+Les3iXQWOhWe0ZC1w5C5RqOhLpR/O+SfZhoof8rfF5GRA1owZQwv60Uc9Y/650v/iuibHaat+kcibWtCj7/bqkgCWxvqnzYaDQzaUH+Rtctn/dmRsyP3NyIGEo2t8Ioe0ML2x/bH9uev/bn6ONc9EmkXKj3coyEbfkOWNhoNtaH8h1/+WeaB8qf8fRIZOaAF0zywr3Seo/5R/3zqX56+2c/bqn8k0rYm9Pi7rYoksA17/bNGo4HBsNdf5Jzms/7syNmR+x0Rw0LDp556qtABLWx/bH9sf37bX1pfZ94nkTbR8HBNQzbchixrNBrqQ/kPt/zzTATlT/n7JjJyQAtOTsUIdZaj/lH/fOtflr7Zz9qqfyTStib0+LutiiSwDXP980ajgcEw119knOWz/uzI2ZH7HRErYnekTbL9sf2x/fltf9K2snwS6Sx0KjyjIRteQzZhwoT4yN6s7ago/+GVfxFzQPlT/nUQGfkSNnnyZDVjxoxUVaT+Uf/q0L9UhbMetFX/SKQtRej1Z1sVSXAb1vrLVlTLLbecwghR2gEJw1p/kW+ez/qzI2dH7n9EbN68eWrjjTeO7U7WAS1sf2x/bH/+219ev0cinYdQyec0ZMNpyMaNG6dAprNGo6EqlP9wyr+oGaD8Kf+6iIwc0JK1FR71j/pXl/4VsYFt1T8S6SLaUSJMWxVJIBrG+hcdjQYGw1h/kW0Rn/VnR86OvJ4RsdmzZytML8s6oIXtj+2P7a+e9pfV/5FIZ6FT4RkN2fAZsqKj0VAXyn/45F/GDFD+lH+dREYOaJk1a5babbfdulST+kf9q1P/uhTOutFW/SORthSh159tVSTBbdjqX2Y0GhgMW/1FrkV91p8dOTvy+kbEsNBw6tSpKu2AFrY/tj+2v/raX1o/SCKdhkzF+zRkw2XIyoxGQ2Uo/+GSf1kzQPlT/nUSmSeffDKe2oEDWm6++WY1ZsyYDhWl/lH/6tS/DmVz/Gir/pFIO5Shl1ttVSTBbJjqX3Y0GhgMU/1FpmV81p8dOTvyekfEpkyZombOnKlcB7Sw/bH9sf3V2/5c/SGJtAuVHu7RkA2PISs7Gg21ofyHR/5VzADlT/nXTWTMA1oWLFjQsRUn9Y/6V7f+ZdnFtuofiXSWVlR41lZFEqiGpf5VRqOBwbDUX+RZ1mf92ZGzI69/REwOaLG342T7Y/tj+6u//dn9Iom0jUiPv2nIhsOQVRmNhupQ/sMh/6pmgPKn/JsgMvKij4OhMCotjvpH/WtC/0TfbL+t+kcibWtCj7/bqkgC2zDUXzqpvFMMpc6mPwz1N+tT9pr1Z0fOjryZETEsNJw/f74yD2hh+2P7Y/trpv2ZfSOJtImGh2sassE3ZFVHo6E+lP/gy78XM0D5U/5NEZnzzjtPTZo0Kd7FA8eG0/7Q/tL+hLE/JNK99JqOuFTkMIosougV/15Go9mRsSPrVf9Ej6v6zH+w7U9ZucsBLVdffXW8tzTl3y752/pC+YeRP4m0rYk9/qYih1FkEVuv+PcyGo0y9Jq/1KOqz/wHW/+qyl3iUf7tkv+0adPU9OnT1fjx4xWOEKf82yV/affiU/5h5D9i4cKFkQiBPhFoMwK//e1v1Y477qgwN/qOO+7o2Faqzbiw7kSACPQnAjigZf3111c4oAU2a+TIkf1ZUJaKCAwxAhyR9ixcvhGGeSMUMfaCf6+j0ShDL/lLHXrxmf/g6l8vcpe4lH/75C9b4eGAljPOOEM1NUdbdM70qX/t0z/KXykSaVMLPFzTkAymIel1brSoDuU/mPIX+fXqU/6Uf9NEVg5owVZ4t99+u1p99dV7VePK8an/1P+m9d9U1lD6RyJtSsHDdShBStGZfzVD5mM0GjIg/tXwF/3t1Sf+xL+NHfnYsWPV3Llz1dFHH61OPPHEXptR5fhsf2x/bWx/JNKVTYY7Ig3J4BkSLNKZMGFCPL8Qozu9OMp/8OTfi7ztuJQ/5R+CSMgXNcyR7tWG2Tpd5jf1n/ofQv9FR0PpH4m0SMCTH0qQUnzmX96QjRo1Ku58zIMNBM+yPvEvj39ZjLPCE3/i38aOHG1CtsLzYcey2ljWM7Y/tr82tj8S6SyrUOEZDclgGRI51MDXSA7lP1jyr9DEM6NQ/pR/KCIhtgzTPLCvdAhH/af+h9J/6Hso/SOR9mxtQglSqsH8yxkyn6PRIRsy5f8/BKj/5fRf9MaXT/zD4o8Fh9gKTw5o8SXXoulQ/mHlT/zD4E8iXdRCFAxHRQ6jyCKeMvjLCI6v0WiUoUz+UmafPvMfHP3zKXdJi/Jvt/yPOeYYddJJJylshQf71rSj/rVb/9oqfxJpz5amrYokMA5S/X2PRgODQaq/yMynz/qzI23jp11pQ6H1/84774wPaEF57r333njetJStCT90/Zk/7U8I+0Mi7dm6sCEPRkOuYzQaqkT5D4b8PTf7JDnKn/IP0ZGLAkL/PvnJT6rzzz9fTZ48Wc2YMUMeNeJT/6n/ofU/RP4k0p7NCw3JYBiSOkajoUqU/2DI33OzT5Kj/Cn/EB25KCD07y9/+YvaeOONFeZLY1QaflOO+k/9D63/IfInkfZsYWhI+t+Q1DUaDVWi/Ptf/p6bfEdylD/lH6IjFyUU/ZMDWpreCk/yl/I07TN/tr8Q7Y9E2nNLZ0Pu/4Z84IEHxp8+6+hkKP/+l7/nJt+RHOVP+YfoyEUJRf/kkKmmFx1K/lKepn3mz/YXov2RSHtu6WzIg9GQcRIYRm18O8p/MOTvW+6SHuVP+YfoyF36V5eNk7xcPvWf+t8v+u/Sz7rueSXSI0aMqKucTJcIEIEhRSCKIm81a3NHTvvrTY2YEBEgAkOKgM/+RiAikRYk6BMBIhAEAZ+GjUQ6iAiZKREgAkRgIBDw2d9IhWsh0nUUVApMnwgQgeFAQEZQfdoLEmmlfOI5HJrGWhABItB2BOrobwRTEmlBgj4RIAKNIlCHYSORJpFuVImZGREgAgOBQB39jVScRFqQoE8EiECjCNRh2EikSaQbVWJmRgSIwEAgUEd/IxUnkRYk6BMBItAoAnUYNhJpEulGlZiZEQEiMBAI1NHfSMVJpAUJ+kSACDSKQB2GjUSaRLpRJWZmRIAIDAQCdfQ3UnESaUGCPhEgAo0iUIdhI5EmkW5UiZkZESACA4FAHf2NVJxEWpCgTwSIQKMI1GHYSKRJpBtVYmZGBIjAQCBQR38jFSeRFiToEwEi0CgCdRg2EmkS6UaVmJkRASIwEAjU0d9IxUmkBQn6RIAINIpAHYaNRJpEulElZmZEgAgMBAJ19DdScRJpQYI+ESACjSJQh2EjkSaRblSJmRkRIAIDgUAd/Y1UnERakKBPBIhAowjUYdhIpEmkG1ViZkYEiMBAIFBHfyMVJ5EWJOgTASLQKAJ1GDYSaRLpRpWYmREBIjAQCNTR30jFSaQFCfpEgAg0ikAdho1EmkS6USVmZkSACAwEAnX0N1JxEmlBgj4RIAKNIiCG7d///nfpfJdZZhlnHBJpEmmnYvAmESACrUagjv5GACWRFiToEwEi0CgCdRg2EmkS6UaVmJkRASIwEAjU0d9IxUcsXLgwkh+9+ksvvXScRBR5S7LXIjE+ESACfYqAGLbHHnusdAmXWmqp0nGGPQLt77BLmPUjAkSgKgJ19jccka4qFcYjAkSgJwTEsHFqR08wJpEFTw5kJJDwgggQASIQIyD20Wd/I9CSSAsS9BtHYIMNNlB//vOfO/Ldf//91fnnn99xjz+GE4E6DBundnBqx3C2FtaKCBCBXhCoo7+R8pBICxJ95r/44otq1qxZav78+erhhx9WDz30UPz3r3/9S6200kpq1VVXVaussopabbXV1Lbbbqu233579cpXvrLPapFdnDe/+c1dRHrixInqggsuyI7Ip0OBQB2GjUSaRLpo42iDjS2KRRvDPf300+raa69Vc+bMifvZJ554QuHvhRdeUKuvvrp6/etfr97whjeotdZaS+21117x7zbiNCx1rqO/EWxIpAWJPvEfffRR9c1vflOdeeaZ6h//+EfhUoFQYzT3iCOOUK997WsLxwsZkEQ6JPrh867DsJFIk0jnaXabbGweFnU+f/zxx9V//vOfOAusaVh22WXrzK5w2n//+9/VySefrL797W+r5557rlC8xRZbTO26667qU5/6lHrPe96jxHYVisxAfYGAyIxTO/pCHPUV4uabb1ZbbbWVeuaZZypn8pa3vEX95je/GQgyTSJdWcxDEbEOw0YiTSKd1TjaZmOzsKjzGb6cYnAHo/5wH/vYx9RZZ51VZ5aF0sYA1ZQpU+JR50IRHIHe//73qwsvvFAtvvjijqe81a8I1NHfSF05Ii1IBPbxlrzpppvG0zh6Lcpb3/pWNXfuXLXCCiv0mlSt8Umka4W37xOvw7CRSJNIpyl+G21sGhZ13//Wt76lDjrooCSb0EQaC3Axmgwi7cNtt9126pJLLlGyU46PNJlGvQjU0d9IiUmkBYnA/jvf+U71xz/+sasUeKv/wAc+oDbffPN4XjQ+kWHKx1/+8hf1ne98J57b1RVJ3/jyl7+sDj/8cNejvrlHIt03oghSkDoMG4k0iXSaMrfRxqZhUfd9TH+4+uqrk2xCE+kvfelL6qijjkrK47rAwBO+6I4cOTJej/S3v/1N3X///a6g8b2xY8d21DE1IB/0BQJ19DdJxfSbmjenE8UG0t7Sa0tCeh/dGDfBT/y3v/3t0VNPPZUJwwknnOCMO3r06Mx4/fDwTW96U1fZ9WLDfigay9AAAqLnes5aVPYvrXjYFz+kC5m/4Bmy/v2ad1ttbAh56MXx0Ste8YoO266JdIiixHnqBYWRnuPcUR5pK5pcRYcddlikv1Y4y/e73/0u2n333Z1xkcbs2bOd8Xiz/xAQmZftaxA+z3FEWqMb2l122WXqfe97X1cxrrrqqnhhQ9cD68ZOO+2kLr/8cuuuUjfccIPCKEyew4ILbEN3++23q/vuu0+98Y1vVBtvvLFaZ511lDaIedGdz/ULgLrpppviv1e96lXx6meMUpjTTXoZkX7yySfVXXfdpR588EGFT7bPPvusWnvtteMyo9zLL7+8s1zmTcxFx8Ij00lZzXvA5Lrrrouxwbw4jFpg+swaa6xhBuN1SQTqGCHgiDRHpF1q2JSNddkU6PmoUaM6inX99dcrzNeG/cL0AEzre8c73tHTgjzsOHHHHXeoO++8M959Yt1111WwsfBf/epXd+Sf9sNVftsm3nrrreoPf/hDPA0RtnDChAlqwYIF8R/Sveiii9Txxx/fkcV+++2nPv/5zyf3sPBw5ZVXTn67LrBT1T333JPYeLRt2Fz8wdbrwSJXtK5748aNi3fmsB9g56vvfve7CtM08txpp52mJk+ejFHCjqBjxoxRf/rTnzIXHzbVV7nk0lHYlv+oo79JIM1j2mWe60TjN7cycRg2ij73uc8533j1Z6VC8Ojte6IDDjggmjZtWqS3jos06Yv++c9/5sbV5DvSezmnvq1rAx/tuOOOqW/rrgx0Y4422mijSCttV52WWGKJ6EMf+lAyyo5Rc9EZ8fXOI65kk3tI/8Mf/nCEtCSO7WM0BGH0FJgknuvixz/+cVcamugnQTFKsccee6TiozuHSBvJJDwvyiEgcvM5QhByRBi1D5m/4FlOCu0I3ZSNddkUyEUT1Bjon//855Emt112B2FgtzD6KWGLSEaT59im6p2anGlKunpwITrnnHNyk3SVf8UVV4zj/fe//40++9nPduSz5JJLxs+OO+64jvuii2l+1gj1r371q2iHHXZw9iFmeptsskmkd96INMFOrZeeLplaLv0ykxrP9UC/CHSlpadaRnrAyhU8qruvKiIXZ8FaelN0x2d/I1B6nYchBZXE6RdD4Ktf/WpXAwWWeg50sQRKhsJ0ERBNkVeeDyMN45bn0Em85jWvyU0XBBokV49mdIXNItJf+cpXusJnlX2ZZZaJ9OhIarGvuOKKxo50rQAAQABJREFUrvTwArBo0aJIj9BHa665ZtdzOz89ny7661//mpoHH6QjIFj6NGwhiSxqGjJ/wTMd8fY+acrGumwK5HL33XdHM2bM6JryIDIzfUzpyxsEgCR/9KMfRfosgVwbZaatR2cjvb4mVRF++ctfdqUHgg8SPX369K5nPom03iov2mWXXbryMMvvutZfXSO9S4izTgcffLAzPQwQlXVo23rNUgQCf+SRR0Z6d6zo+eefdybju6+qKhdn4Vp6U3THZ38jUJJICxIB/Z/97GfOxq6nWER6eoTXkulN6CP9mdGZHxRNf8ZzPoMxxdt/msPoNsKIsub548ePjzbccMOu8GlEWu+t3RU2Lw88x6h6GtHVO5s409TTPSLXaHlafnvuuWcaLLyfgYDg6dOwhSSyqGrI/AXPDMhb+6gpG/vb3/7WaVMwGpw2T1fkZvrrr79+/EKfJjB82TPDl7nG1zyQQJfD101XWvfee29sS+1nPon0xz/+cWfedp6u3/gK6lpPpKcoOtPESHUVl0aczbTq6KuqysUsV9uvRW989jeCKYm0IBHQ13PBIj331tngQWz1tj0RDDTe2Ht1eJMWhRIfBv7EE0+MMJUEIw8YPfn0pz/dFU7PaUv97LjZZpt1hUf6eBnAZ1WM1OgtkSK9B2cSzkXaXUQaxFaf2pjEk3LrU6civQVRPHqj5zFHp59+unPKh97xJK6XjR2mwEhapq/nwiX39Vy8CFM4MJIDUm6Gk2uMYlc1zHaZ2vRb8PNp2EISWcguZP6CZ5t0qGhdm7KxaTZFzwmObYc+LS8ezbz00ksjvRVb5ghs2kI2xBVZmz7s6Qc/+MHYDuLFAVMR9LxrZ1gMFOgT/Lrgw+I6M025PvTQQ533hUjjayT6DPxhepzEEx9TCOU5/O9///sdeWNBoIQVH/3S1KlTI71WKNLzvuMBEYTDAnt8bZRw4p966qkdaWLQyPXygn6jLldXX1VVLnXVcxDTFT3x2d8IDiTSgkRg3yRvInDbh/F473vfGxNTvbVQ5twwV3X0dj6RXnTSZYDSRppdpPtrX/taV9IuI4iyYy4gVnDbDqTdrpv8dhHpr3/9687w+NxlO73tnzOsa765XjDjDAtiDANsT63RC18ivXDHGQcGn64cAiJzn4YtJJFF7UPmL3iWk0J7QjdhY9NsCmSDaWB44bedPo3WaVO23nprO2hs811fFPXi6ujXv/51V3iQ5bRpfJh+YDvM9xU9Mv3lllsuvq8X5kUg6bDrILeuKX8YTTfj4hqjzVlOnzTYFUcvWEyNgn7IzgO7QJlu/vz5XWEQZ4sttjCDeb2uq6/yIRevFR3AxERffPY3AgOJtCAR2MeiEXyeEmEX8TECgZFgvKFjYUOe23fffbvSBzFMG+nGpzJ7dOF1r3tdpHfI6Mhqt91260oX5U/7fIjIegcPZxwXkT7kkEMivTo6woIZvdI6HhnGXGxXuR944AFnunrVfkeZ8SNrIQoMosulTQcBBnTlEBAd92nYQhJZ1D5k/oJnOSm0J3QTNjbLpmDAIc25yCfkCTJourRFfVkLCfGVEV/WRD/Ehw3FCKrpssq/1157RfqkQjO489pVlzwijelxUi7x02wwMkU5PvnJT0b6rIR47jkWSeJrgNknpE2HqHOL1RB9VVG5OIXVopuiVz77G4GPRFqQ6AMfn6Iwd1gEXtbHoousKQYgwXaaMEZZbuedd+6KgxEJ04Hc2unqLYoy5/jpI1a74iANF5E285JrdA4uB0Pq+pyHEQ/bpXUaWFCitwS0gye/Xftf4yWIrhwCojM+DVtIIovah8xf8CwnhXaFrtvGptkUe7TURl0fGOK0h+edd15HUBdJxe4NWTtXIIG0xW+2LU8rP6bWpe213FFA/cNVxjwijd2RRH/FxzQYm+jbeWX9xrQ/Scv0jznmmKxo3p/V2VeVkYv3ig1YgqIDPvsbgYBEWpDoIx9v1iDUrjnEogxpPhb8YU61PWqMLZVccex5ZTYMrukd5kgBCKdrq7tJkybZSXX8hjK7ylOUSHckZv2Qz5Bm+ti2yXZpnQY+AWc5l9E3t83ListnLyMg8vFp2EISWdQsZP6C58sI8yoNgTpsLPJKsynHHntsWlHi+/PmzXPawy984QtJPAwSuNbSYF50nsMuRKIfpm9P1Usrf5kvblWINMitWS65xvZye++9d4QFfJhKUsa5tvJDuliz0y+u176qjFz6pc6hyiE65bO/kbqQSAsSfehjj2JscfSJT3yi1C4SUJgpU6Z01ChtvhhWcGPuddqfa041Fp6Iw8JEUVDT18exSpBU32VE8og0toX63ve+F5100knRRz/60Wj77bePMJcQCwoxIo+tiVwj0mWItPmi4Co8FsuYdcU18KMrh4Bg6NOwhSSyqH3I/AXPclJod2ifNhZIphFRLLTOco888kiXTYE8zZFc7D4kMjb9PJKOfDESb8aRazN9hEsrP7a+K+qqEGnsCuKy21JO8bEVqz4AJsILAOJkOSxSlHimjx1PmnBN9FVl5NJEnfs5D9EBn/2N1JdEWpAYAP/xxx+PsDr66KOPjt71rnc5R4JFWTAyjZ0+xKV95pLwZXzMyRKHRY+uuKeccooESfVdUyTSiDRW3WOkOOsgFlc55N5nPvOZrnKkdRppq+UlAdfoCYm0oFPcF9n4NGwhiSxqHjJ/wbO4BBjSRqAXG4u00mwKdtrIchhtdm0fiql14mD7Rcamj92KijiM7prxcL3NNtt0RE0rf96LgJlIFSKN+JhmAjtqlzHtN/ACPlj/4po+oU+OdKZl19ksu4/rJvuqMnLxUbdBTkP0yGd/I3iQSAsSA+hj5XTaimwojbm/cdW9LUX5TF8fZ5uglfb5zN7xIolgXLztbW/rMnQuIo2V7pgHaJah7HUZIu3aDcQodoQRIDt/EmkToWLXgqFPwxaSyKLWIfMXPIuhz1BFEChjY5FeGhHF9mV5zrW95pZbbplEO/vss7vsDmSOL3RF3Oqrr94VH9vSmS6t/HkvAmYaVYk00sCi+bXWWqurnKLbab49so60HnvsMWc62JK1Ltd0X1VGLnXVeVDSFd3x2d9I3UfgQmfgxem5snE6HpP0Uq5hT0SPVCh9IlRXNfWIr7rrrrvi+5ocKn2aU1cYTbaVPhil637WDT0fWOnpDXEQPeqt9NSKruD6JDGlp1N03Tdv6JMDlV7AYt5SmkgrvRAxuae3b1K6M1F6W6nknlzgvj5SV+ltpRTKpBdeKP15UOktmpSeEy7BYl8TaaU/B3bcu/HGG5XeZ7XjHn4AKz1lpOu+3NAr55Weuyg/Y18TaaUbaMc9/shGQOxFFdyAt8vpRVdKj7y5HjVyL2T+giftr39RF7GxyDXNpmjCo/ToaWrB9EEfSn9t63quv/6pH/7wh/F9vdVcbNvsQDNnzlR6twj7dsdv6ATShz01HcqEsolLK3+eTZT48DU5V3fccYd5S2miq/S+2R330n7o9T0KeP/gBz9QqHNR+6C/WCp9emRHsnoLVqXnh3fcQz+hd3dSevF9x/0iPx588ME4mF4I2RW8H/uqrkK2+IbYx6L6ZEKV1t8kYXQD8+Z0ovEboLcEW5pQkdOTbGiwPZzgLz7mnMmiQxwLK/dNXxthO6lSv7G3spmeXGNbojznWjhjj0in7e7xsY99zLkrCPZNdaVbZo40R6TzJOfnueiKNmxR2b+0EoQcEUaZQuYveKZhw/svI1CHjUXqaSO6GE3Ocmnbdpp2Ky0MFoTnubTRWXO9C9JIK3+eTTTz72VE2kwH14sWLYqwEBPTV9A3YDco0XPb10Sp66hwrKOxw+E3jg6v4rAJAKaUYD9tHCoj/SvS6se+qkodhzWO6EHZvgbh8xynduQhVPNzHAGOA1FwoAcWzuHUJUxjwC4bZRwWF4qiiA8iLR07Og7XHLwihDerHNi1Q/IzfZwGmOXwCcwML9c2kU47UQuLHF3u97//vTNdTu1woRX2nsjcp2ETfQ9Vs5D5C56h6t6v+TZlY1H/NCKat/g67VArPcKawIp5wK55zuaalSSwdZF2UIw9xzat/KGItFWN+Octt9wSnzYr+m76mEduOpyoaz6XayyiL7qdn6TnOrUSB+HIYFQ/9lVSdvrxzItYF3z2N4IribQgEcjHBu7SuE1fGmfRYo0dO7YrHT1loyO6ngLRFQbxenVYSW2WHdfYDi5r1AfbOtlx8Nsm0ttuu21XOHQmaU5PKekKj3RJpNMQC3df5O/TsIUkskAyZP6CZziJ9mfOTdrYNCKKA1FcC+IEMdgnkZ/pX3zxxRIk9l1fHmEPsftIlnPtNIR8rrnmmo5oaeXvlUhjZNi3c525gIX4tnNhhrrvtNNOEQ4dK+JwKjAGuUzZyLUctNOPfVWRurUljMjLZ38j2JFICxKBfOzviU9SImTxMT3hJz/5SaFSXXDBBc7R5o985CMd8fE5S9I3fXw6czmcHoU9k9/3vvdF2BcanxCxGwdGBEyHEREzPblOKz8ItuukLcSziTS2tpP0TN91kiOM3SqrrOIMf9BBB5lFjq+rdhpcbNgFZaUbIk+fhi0kkQUIIfMXPCsJY4gjNWlj02wKZIPRUZfDdDTXYVlLLrlk14Ek3/jGN5z2Les8AJBsnGIo+iE+Fhoib9Ollb9XIq3X8JjZdFzfdttt8emE2OYVO2qAsGbVRyLjRF+pi/gYSLEdXkbkue1j4SHqnOVAlF2DUEhrn332SaL2Y1+VFI4XiQ747G8EVhJpQSKg/973vjcRstnQMTVj1113jbB1HebHidEDwcUWO1ixi83qEc6MJ9cXXXRRR60wT27ZZZftCvv2t789wp6XtnMZKmw/d//993cEdX3yQhlWXnnlriNuQaKxZZGU0fbtKSFYjW2HwW/7dKp//vOfmXttu7Y8qtppkEh3iL/yD5GrT8MWksgCiJD5C56VBTLEEZuysWk2BbLBlzt7EAI2HTZeZGf6rp0oMGcYe+Wb4XCNgRfsoGQ7vTgu2njjjbvCY/DGHo1G3LTylyHS7373u7vyw65G2AHF5bBNq10fvFhgYCTNYeqjq17XX3+9M0raXGnBDqPbxx9/fDx4hTMXrrzyykgvjozGjRvXVTYpK1500C+L68e+SspGn1M7hl4HMLqaNpIqjRY+jB9GFlwj2GY4XB944IFO3L74xS86DQOOY8V8aSygwMlPeLt2EfS0uX569wtnuphDNnHixAiHnGAet15FHYfDqY0g2na59S4cHeU+44wzusJIHBhSfMrbaqutOsp6wAEHdMXBUaoIi9EPdC5wVTsNEukOEVX+IXIkka4MYUdEwbPjJn/ECDRlY9Nsitg6HEKFwQLYQ6yLwaiwyM30sZ4FB7C4HNaBuPoAxNlhhx1i+40DS/bdd9+YvJvpynXaoSRp5S9DpF32F/liEAZ9AeznYYcd1lE1HKYlZRN/pZVWijAl5bvf/W70i1/8Iia3eiePmPCuu+66XeFXW2211OmEWBS42WabdcWRvMr6eDGwvzD0Y1/VAXLLf4iMffY3AilHpAWJwL7epi4CmRVh9+LjLVpGr+1qwaC49m8ukh9GddJG3LApPshqkXQQBqPdIMB2eL1FX0eR9XZi0TrrrNMVzo4nv9GRYMQehk7u2T7yhqvaaZBIx/D1/E/k4tOwpelnz4UtmEDI/AXPgkVtXbAmbGyaTcGuHa7dhERmtu8ajTYFhjUmroEOOx3Xbwx64OAZl0srfxkifdZZZ6XaXikPdvYwHV4OMOgiz8v6+NKKA1iyHPo+vMSUTdsOD8KOBay268e+yi5jm3+LHH32N4InibQg0Qc+PmVhPnJVA4lRD4y65i08AcnGZ6wyxBdzl9PIuUB3+eWXZxJYUWTMK8MUD8ybk3vi4yXAdnPmzInwGU3CpPkg0VJ3jJynhSORthEO81vk49OwhSSyQDFk/oJnGGkORq5129g0IorjqvG1D6OyIqc0X+xTHqI33HBD6oi2K20sSsQcYpyimObSyl+GSGMg4y1veUtmPW0ijfJg2otrrrirLuY9zKm+Wp+wW9Sdc8450ahRozLLZ6Yv1+iXsWYoa8pJv/VVRTFpQziRo8/+RnAjkRYk+sjHtjyYXoGRWNcnPFEI+Bh5xQgDttAz97QsUh0YTZBP14lXSBvTL/B5UFYlF0lTb+gf4TQuF/GFccUJi+Jcc8rMUxMlHHwYr7S51cAJ20Rh/qA4YIEjxe2XEuAlWz5V7TQ4Ii0o9+aLHvs0bCGJLNAImb/g2ZtU2hG7LhubZlMw5xYOI5mwY/ZWpLC1+FIIsl3GYUBi+vTpEaZGuL7CYbAE0+kwEos9//NcWvnLEGnkgTU8IJ2ik+Kj3li4lzb1ELto4FRcTC3M6vvwDH0FpnqAuJd1iIMpIzj9V6bdSBltH1+KMUBVdLu8fuqryuIyzOFFrj77G8GLJxtqdPvZ6dED9cgjjyi9GFDpxRrxKU/605LSG9PHf/qTlpfi65Fcdfvttyu9v7PS87WVfstXOHlQj2JUSh/l1os24lOl9CKb+PTB9dZbr1JaZiRtaJU+XEbpfaSVnm8Yp6tHN5Q2rGaw5Frvc620YYtPOtQGU+njZ5U25slzXoRDQGSmDVvpQmjS4IwT8mRBFChk/oKnNu5ObHjTjYBPG1v0ZEDYdJw6C5uudzBSeos258mG7hK770LumuzFdhx6OHr0aKXnEitN0t0RGrj76KOPxvWE3dY7ZMR/eg/nQjk//fTTcb+HNPRicqXJr8KJgvhD/6enyhRKJy8QcNPz0RXy0VNe4j521VVXjfsW9IF6UCgvCedz9lVOWILdFPvos7+RyozACIr86NVfeuml4yRoyHtFkvGJwPAjIIZN7yZTurJVX/BKZzRAEWh/wwurKJEOX1KWgAi0C4E6+xuOSLdLl1hbItA3CIhh8zlCEHJEGMCGzF/w5EBGOBUnkQ6HPXMmAlkIiH302d9IfiTSggR9IkAEGkWgDsMWksgCvJD5C54k0o2qcUdmJNIdcPAHEegbBMQ+kkj3jUhYECJABHpFoA7DFpLIAo+Q+QueJNK9amb1+CTS1bFjTCJQJwJiH0mk60SZaRMBItAoAnUYtpBEFuCFzF/wJJFuVI07MiOR7oCDP4hA3yAg9pFEum9EwoIQASLQKwJ1GLaQRBZ4hMxf8CSR7lUzq8cnka6OHWMSgToREPtIIl0nykybCBCBRhGow7CFJLIAL2T+gieJdKNq3JEZiXQHHPxBBPoGAbGPJNJ9IxIWhAgQgV4RqMOwhSSywCNk/oIniXSvmlk9PvYOvuaaa7oSeNe73qWwnz4dESACYRAQ+0giHQZ/5koEiEANCNRh2EISWUAUMn/Bk0S6BmVlkkSACAw0AmIfSaQHWowsPBEgAiYCdRi2kEQWdQuZv+BJIm1qGa+JABEgAio5/ZhEmtpABIjA0CAgxM+nYQtJZCGYkPkLniTSQ9NEWBEiQAQ8ISD20Wd/I0XjgSyCBH0iQAQaRaAOwxaSyAK8kPkLniTSjaoxMyMCRGAAEBD7SCI9AMJiEYkAESiGQB2GLSSRRa1D5i94kkgX0z+GIgJEoD0IiH0kkW6PzFlTIjD0CNRh2EISWQgsZP6CJ4n00DcdVpAIEIGSCIh9JJEuCRyDEwEi0L8I1GHYQhJZIB0yf8GTRLp/dZ4lIwJEIAwCYh8HhkiHgYm5EgEiMIgI+DRsIYkssA+Zv3QUg6gDLDMRIAJEoAkEfPY3Ut5aFhtK4vSJABEgAnkI+DRsIYks6hkyfxLpPE3jcyJABNqOgM/+RrCshUjz06LAS58IEIE0BIT4+TRsIYks6hkyf8GT9jdN43ifCBCBtiIg9tFnfyNYkkgLEvSJABFoFIE6DFtIIgvwQuYveJJIN6rGzIwIEIEBQEDsI4n0AAiLRSQCRKAYAnUYtpBEFrUOmb/gSSJdTP8YiggQgfYgIPaRRLo9MmdNicDQI1CHYQtJZCGwkPkLniTSQ990WEEiQARKIiD2kUS6JHAMTgSIQP8iUIdhC0lkgXTI/AVPEun+1XmWjAgQgTAIiH0kkQ6DP3MlAkSgBgTqMGwhiSwgCpm/4EkiXYOyMkkiQAQGGgGxjyTSAy1GFp4IEAETgToMW0gii7qFzF/wJJE2tYzXRIAIEAGlxD6SSFMbiAARGBoE6jBsIYksBBMyf8GTRHpomggrQgSIgCcExD6SSHsClMkQASIQHoE6DFtIIgtEQ+YveJJIh9dtloAIEIH+QkDsI4l0f8mFpSECRKAHBOowbCGJLKAImb/gSSLdg1IyKhEgAkOJgNhHEumhFC8rRQTaiUAdhi0kkYUUQ+YveJJIt7M9sdZEgAikIyD2kUQ6HSM+IQJEYMAQqMOwhSSygD9k/oInifSANQQWlwgQgdoREPtIIl071MyACBCBphCow7CFJLLALWT+gieJdFMazHyIABEYFATEPpJID4rEWE4iQARyEajDsIUksqhwyPwFTxLpXNVjACJABFqGgNhHEumWCZ7VJQLDjEAdhi0kkYWsQuYveJJID3OrYd2IABGogoDYx1qI9MKFC6MqhXLFWXrppePbNOQudHiPCBABEwExbI899ph5u9D1UkstVShcmwLR/rZJ2qwrESACZRCos78ZoUmvNyItBfWYZBmcGJYIEIEBQkDshc8RgpAjwoA+ZP6CJ+3vADUCFpUIEIFGEBD76LO/kYKTSAsS9IkAEWgUgToMW0giC/BC5i94kkg3qsbMjAgQgQFAQOzjwBDpAcCURSQCRKBPEPBp2EISWcAZMn/pKPpErCwGESACRKDvEPDZ30jlahmRlsTpEwEiQATyEPBp2EISWdQzZP4k0nmaxudEgAi0HQGf/Y1gWQuR5qdFgZc+ESACaQgI8fNp2EISWdQzZP6CJ+1vmsbxPhEgAm1FQOyjz/5GsCSRFiToEwEi0CgCdRi2kEQW4IXMX/AkkW5UjZkZESACA4CA2EcS6QEQFotIBIhAMQTqMGwhiSxqHTJ/wZNEupj+MRQRIALtQUDsI4l0e2TOmhKBoUegDsMWkshCYCHzFzxJpIe+6bCCRIAIlERA7COJdEngGJwIEIH+RaAOwxaSyALpkPkLniTS/avzLBkRIAJhEBD7SCIdBn/mSgSIQA0I1GHYQhJZQBQyf8GTRLoGZWWSRIAIDDQCYh9JpAdajCw8ESACJgJ1GLaQRBZ1C5m/4EkibWoZr4kAESACSol9JJGmNhABIjA0CNRh2EISWQgmZP6CJ4n00DQRVoQIEAFPCIh9JJH2BCiTIQJEIDwCdRi2kEQWiIbMX/AkkQ6v2ywBESAC/YWA2EcS6f6SC0tDBIhADwjUYdhCEllAETJ/wZNEugelZFQiQASGEgGxjyTSQyleVooItBOBOgxbSCILKYbMX/AkkW5ne2KtiQARSEdA7COJdDpGfEIEiMCAIVCHYQtJZAF/yPwFTxLpAWsILC4RIAK1IyD2kUS6dqiZAREgAk0hUIdhC0lkgVvI/AVPEummNJj5EAEiMCgIiH2sg0grbXS9OQ1ohL82uEsvvTRabLHFkr8//OEPbaj2wNVxmWWWSWR02GGHFS7/f//732jChAlJ3F122SXCvW9/+9vJvdVXXz166KGHCqfJgJ0IiL3Qhi0q+9eZ0su/Fi5c+PKPAFch8xc8A1S78Sxpf7MhrwufutLNrg2fNoXAddddl/Rv4DeXX355rVk32c+KfSzb1yB8nvPKeqWgeZkOw/Of/exn8UuD1JlEuj+luuSSSyZy+uxnP1u4kF/84heTeG94wxuixx9/PIm73377Jc8233zz6IUXXkie8aI4AtJ2fBq2kEQWNQ+Zv+BZXAKDG5L2N1t2deFTV7rZteHTphAAkRY7Av+yyy6rNesm+1mpl8/+RsAhkRYkSvo0KCUBCxS8CpH+9a9/Hb+Vo+G98pWvjH73u991lB4N8U1velNicA455JCO5/xRDIE6DFtIIotah8xf8CyG/mCHov3Nll9d+NSVbnZt+LQpBJok0k33s2IfSaSb0qYC+dCgFACpD4KUJdIPPPBA9NrXvjYhyV/96ledtbjlllsiM+3vfe97znC8mY5AHYYtJJFFTUPmL3imIz48T2h/s2VZFz51pZtdm/qfbr311tEb3/jG6Atf+EL9mQXIoWj9miLSIfpZsY8k0gEUMC3LYTUoafUd1Psm2S0yteN973tfQqI322yzeF50Wt2//OUvJ2Ff85rXRI899lhaUN53IFCHYQtJZFHFkPkLng6oh+4W7W+2SOvCp650s2tT71PYbWk7kydPrjezAKmXqV9TRDpEPysybiWRXrBgQfTPf/4z/lu0aFEANXRnOYwGxV3Twb5bhkjbRuSXv/xlZuWfeeaZaOWVV06M8KGHHpoZng87EajDsIUksqhdyPwFz06Ue/tF+9sbfqFi19U/1ZVuKJyQLxZQStsZRiJdpn52H1jHHGk7j6b6WZFxK4n0FltskSh5P+2QMIwGJaQxqyvvMkR6m222SXTtXe96V6EifelLX0riLLXUUtE//vGPQvEYKEpw82nYQhJZyDRk/tJR+NQt2l+faDaXVl39U13pNodMd07HHHNMYouGkUiXqZ9Ncusg0qH6WbGPPvsb0aYRuNAZeHGyT5/HJNWWW26prr322rh8mkgrveVYqbI+/fTTSu+4EMdB+UaNGpXE11uvKK046p577lGPPPKIet3rXqc23nhjNXr0aKUXmSXhXBf6LU/tuuuuySO9a4d6xzvekfx2XaAct99+u0I98KdH2OPyoEzrrruuWmGFFVzR4nt///vf1Ysvvhhfv+pVr1J6J4nUsK4HyO/555+PH6Fua665pitY7fdQDz2/WN12221Kb02n1llnHfXmN79ZjRw5snTe9913n7rxxhvVXXfdFWOHOr3nPe9RSy+9dJKWJrfq2WefjX/rqR1Kz3lOnpkXc+bMUePGjUtu/eIXv1A77bRT8jvtQo9Kq7XWWks98cQTcRC98FDNnDkzLTjvGwiIvdCGzbhb7BK643Ih93FGeULmL3jS/ro0Q8X9QFvsb1b/hH4Pfepf/vKXuN9Dn4p+b4MNNlCLL764G7yX7maliyBoy3oqQZIGbHJeXwp9vffee5M4K664olp++eWT31kXTz75ZNyXoD9B3qjDW97yltz+zSzngQceqK655po4m0mTJqljjz02ybJoWVBn6NYdd9yh0Cfoxegxj1h77bVz659k5riomm7V+l1//fXq3e9+d1ISTaTVjjvumPxG3z1//nz14IMPqiWWWCLuv8Fd0IcXcSH7WbGPwKasS+tvknS0EntzOtH4zc5bgjqhXkdEsO+vlAu+7uji4n3nO9+JdCPveCbhtIJEBx10UKSJZ2pVyryZ//73v4/233//SBspZ37IV5Pj6NOf/nT06KOPOvPcd999k7jY31ETY2c4102tOB0L43bffXdXsNru6ReA6Mgjj4z0i0JSB8Fa/J133jmaN29eoTJ897vf7ZhSIWnAx77R2EXjueeei9MqOiK97bbbJmUbM2ZMoXJIoM997nNJ3Fe/+tWcKy3A5PgiN+hn2b+0pEOOCKNMIfMXPNOwqXKf9vd/qA2a/bX7pz/+8Y9xRc4+++xojTXWSOyV6Ax89E8HHHBApAceUlXFTtfe9vWb3/xmR9p/+9vfUtOSB2gzZjmwJVqeQ/+NbUnNeOb1sssuG334wx+O7YorrW9961upcc108MUxzf3nP/+JPv/5z6f2RUgHmG633XaRflFIS6brvo90q9bPHpHGzhpw+sUr0gOFqZjpQajozjvv7KqLfSNkPytyLdvXIHye6/vt73o15D/84Q87hP/www9HRx11VMc9Adj2sdgM4V0uz6BInPPOOy/Sb0KF8kP+WLQ2d+5ciZ74V199dUcaRYyNRL7ooos64urRVnlUu69HjSPgaGPr+g2cZsyYkVmm4447rlBaaPSYwwxiLXl95jOfcab91FNPxdvcSbhp06Y5w6XdvPXWW5M8kMaFF16YFpT3DQQEb5+GLSSRRdVC5i94GhD3fEn7+z8IB83+2v0TdhmaOnVqh50SfbF9TGtLm6Jmp9s0kcZ+/jgoyy5z2m89Whrpr5Zd7aAq0ZSE9Gh+tOmmmxYuB/p15JnnfKVbtX42kdYj9dEPfvCDzEFAwR4vDX/6059Sqxi6n5Vy+uxvpLJDT6QvvvjiDmU/66yz4t+veMUrIozMnnvuudFVV10VgXBjVwc9vaMj/Nvf/nbBqsPPMygIjDAYPRYBojFhDhbuY4QAI9UguePHj0/CIKye6uF8k15vvfWScLgu6nAqn5QBoxF4423CYdTcHIUGUd5zzz2jr3zlKxEWGGDLOGBujhpDLpCZy5nzkVGf5ZZbLt6uCG/NeOPHfK4TTzwxWmWVVeL6fvzjH4/0J8Kk7mlEetasWUkYpGvvG+0qi31vtdVWS9L4wAc+YD/mbwcCopM+DVtIIosqhsxf8HRAXflWr0Sa9jeKQthfu3865ZRTEvuEr3+wpVdeeWV0ySWXxF8L7dFdPdXDqTN2uk0SaRCx17/+9Uk9oO8Y7cVgFb5m/vWvf41++tOfRrDz2P9f2gO+9oIQmk5Pw4hOO+20+M/8Ujx27NjkPp67SDj6Gj19MEkf+ey2224RRuOBx9133x3jqqeIdAzkIFzadqoom890q9bPJtLgJ/hCj7JDb/S0xQgvleBLRxxxRKSndHTgsP3225swd1yH7mdFH3z2N1LBoSfSs2fP7hA0GgAazhVXXCEYdPgYQTUJK8DHZw3b5RkUhDffWJHvzTffbCeT/MZIrAga/uGHH548kwsQUDOMq1wSVnysujcNBUbjm3Kf+tSnkvKiMeLN1uVgQFZdddUkLEaRoeymw/QQ85Mkdsu46aabzCDJNWT41re+NU4PxFwwSyPSINwSBp8EkVdZN3HixCQNkGocfUqXjYBg7tOwhSSyqG3I/AXPbNTLPe2VSNP+hrG/dv+E/geDOqeffrpTAfSc10ivDUpsGHTJJp+IaKfbJJEGMRUdx6AMSGmanUXfoOd+J+Ex9SDNmV8tp0yZkhYsua/nVCfpon/BNqhpDgTfJP/ot+y+TeLWlW6Z+tlEGgOLWER/zjnnSDE7fOyoptc3JXhAPmn9cuh+VnTHZ38jYAw9kbYbPsA8+eSTpf5OX0+m71CMvfbaqyucna5tUDA3TAQH/2Mf+1hXGuYNjBKbp+VhOoTtMH/aJMUf+tCH7CBdvzGXzCwH3tqbcPfff39HWbPmmqE89tsq5kGb7sc//nFHPfI+kwF/e0pNGpHGFwDBSC8gNbMtfH3++ecnaSCtovO9C2cwhAEFc5+GLSSRhYhC5i94+lSVXom0bSdRRtpfnxJyp+XCHV/rshxGMUWH4O+zzz5dwe107X6vrjnSmGoCQiflK/LVD1PsJDx815RJVLAM0dQL2zu+MoMc5rnf/OY3HeVwTcusK92y9bOJNHDDAF6Ww6CkifMFF1zgDB66n5Uy+uxvpKKtI9L41J/2RiigwJcRTYCPz0QY2TVdnkFBeDQgTF849dRTM0ejJV0QYxE2pi243N57752EgQHAPOAs9973vjcJv9VWW2UF9frsE5/4RJJvkcWRL7zwQjwNA9M88JnR3obI3DIHn+r0Lhm55cVnJsETvotI691aOsLkGY20TO0XpzPOOCMtKO+/hIDIxqdhC0lkUa2Q+QuePhXMN5Gm/fUpnfS07P4JfRhsXZ7baKONEnuIQRu9K0ZHFDvdpoj0wQcfnJQLXzcxgp7nMFpt1gcL3VyuDJEGgZd2Bj/rK7PkhXLonZ2SeCuttFJkn4lRV7ooQ5n62UQa5ZaF+1If24fNMwetXC9s/dDPitx89jeChQIIvv6koJJ4no/VwSB6WX/mHFcQwaywro297YaPhQpFHFbjSn3g2yOMdrq2QSmShx3G3P0BeboMH+Zzm+XCHO80h88u5hxtjJo25UwDprekK5QtyHSaM4/txry4Ig4vMSZWLiJtf33AnLAqDrps5nXCCSdUSaZVcQQvnLxV9s+XzRqmdATPokpE+9uJ1DDZX7t/wjqcIs7u92yiaKdr93t1jUi/7W1vS+yr3p6tSFXiMOYCSxBw11SQMkTTnP6yySabFC7H0UcfnZQf7dR+EagrXRSwTP1sIo3pmUUcpkSK/cGOZ7brh35Wyle2r0H4vH4i6Ig0RlOlcj58TGOwnd3w86YYSHx7p4vLL79cHsW+na5tUDoCF/yBifwmDpgeYTsYAr33chIua5QZ8+EkPSg6lKEphxF1yfsjH/lIT9mCYJtvvHnTZCSzG264ISkDyuIi0lioKOWEnzZ3XtLM8k2D9clPfjIrKJ9pBAR3nyMETeq4S4gh8xc8XeVy3aP97URlmOyv3T9Nnz69s7Ipv+x+zz6Qw07X7vfqItLmonUXUUupTryDkrQL+Bhcsp1pt/PmSJvTS7AupqjDgJdZDhBW09WVLvIoUz+bSOftoiV1MOej77fffnI78fuhnxX8ffY3UsHWEekf/ehHUvdM3573Y5P0PINiJ44RbexpjVOGsKc03qoxfQSrXkGM8QnFHH2H0F1EGulicYMoBfy0ec/6MJsk3Ec/+lG7SLX9xudAs3y9LnB84IEHOtLD230RB/zMcriI9Pe///2OMFnb9+TlaX6+e//7358XvPXPRTY+DVtIIguBhsxf8CyqWCGINO1vUen0Fs7un7BbVRHXa79XB5HGNEnRbfhYOIg+oMifuYAPcW3iD0yKEk2sUTLLgR2nijpsOWvGNRfe15WulK1o/RDeJtJYLFzEmbu+uIh0P/Szgr/P/kawCUqkMbqKHRay/rD9nACA7eKywgIg29kGxTX9w46D31h5KvnC/8IXvtARzE7X1UARAQsc7Lm6ZrpZ16iry+GtGvOEJa6LWOoTBDtGcYFdUw4vDVI2+Jgj3otD2c30sJVTEYe5XWY8F5H++te/3hEGuFV15ob12EaJLhsBkY1PwxaSyKK2IfMXPLNRf/kp7e//DhAT3Gx/UO0vJGz3T1jMXcT12u/VQaQxuGHLpurvn/zkJ10wFCWa6OPNfMusp8F2t2Zcc8FtXelKRYvWD+FtIm1/kZA0bT+PSPdDPyv4++xvBIegRFoKkeX7XuxSdI9gbIwuwMO3t6OzDZWLSGN1rpkGrjFnGSPRmOuNUUucJIUTmLD61xxBRtg0Qw68EFfSxvY69uKFr33ta8lzfWxqFsTen/3qV79K8kYZcZpWL+7nP/95R3p5O3ZIXsAkb/s7HL4iOMKXky8ljTL+DjvskKS14YYblonayrCCu0/DFpLIQogh8xc8fSoT7a8bzX62vyix3T+5trJz1QxfN0WP4Jft9+og0va0ALN8Za9dgzpFiSZIpZlfmX7N5hPYg1lcXelK+kXrh/B1Eel+6GdFdj77G8G4dUS66BuW/ZYIYmo621DZRBoj0eZCP1xjnhqEmOaKzNGTuDZZtUfazdHRrE3gJT2fvr2N0kknndRT8nbjLjoSYH8yc41IAxtpYPARp6ozSUeZBTFV8xv0eIK7T8MWkshCHiHzFzx96oWp0zhgqayz7STtb1kEq4Wvirs9clq236uDSNskFOQeJzVW+XPZ96JE0/7S6trGLk1adh+GEVpxdaUr6RetH8Lb5SzaXvNGpPuhnxX76LO/EYxbR6SzdrkQUODbb4nYAcJ0tqGyiTROhhLBYRpG2h6WZpr2yX1pc6QRB59l11577SQPc+HDPffck9xH3q4FFma+vq/tuZeHHHJIT1ncqw9sESzhm2/zWQnfdtttHfFcRNre/xkvAVWduQ940VXyVfMahngiU5+GLSSRhUxC5i94+tQN30Sa9tendNLTsvunorhjUb3oEfyy/V4VIo09os08bYKKKXrmYvNDDz00veIVnhQlmvbaH3uL1qys7XMSIB9xdaUr6RetH8LXRaT7oZ8VHfPZ3wjGrSPSdiMVIGwfB4II8PDnzJnTEcQ2VCaRfv755zvmMGftrGEmit0ozDyzpnYgnjl1BMePy7QEzOeWdIpu92eWw8c1TnCSMmDv616cPde56C4g9laBLiJtvzDZci5T7hVXXDGpc9Eylkl/2MKKfvg0bCGJLOQTMn/B06ee+CbStL8+pZOelt0/FcUdh2mIHsG37aGdrtnvoTQ2kcZocp7DdEszT9cXTHNXCNcBaXl5ZD0vQzTN3UPK9GtY7GnWEaPppqsrXeRRpn51Eel+6GcFf5/9jciwdUS6yIlIAOe4447rUHzbIGQZFOy9KUKDj/1J8xxONjQ/jyBeHpHGmzw22pe8ZCHF+uuvn9zD/OIQztz3E/Wy53C7yoSVvfgEhB1SsMrZdCZJ3Xzzzc1HqdfHH398ggMwchFp+1MmTlCs4iA/c9Sk151KqpRh0OKI3vo0bCGJLPAPmb/g6VMPfBNp2l+f0klPy+6fzC+W6bGiyDyGG/pUpt9Duj/84Q87bO6NN96YlV38zB60chFp2HzRb+x05dOVIZrml2ac1Icvw0UctuyT8sN/+umnO6LVlS4yKVO/uoh0P/Szgr/P/kaE2Doijf0an3rqKal/qm9+psdhIPZhIbahMt/MsbBDhAa/yEEo9ps84uG0vDy3++67J3lhAYxJ4vEWD4IXwmH6hYmBPYfbLhMM0mqrrZbE2WWXXTqCbL311skzEFZsiZflQNzXXHPNJA7K4iLSeFkxy1n1REL75KaiO4tk1WHYnwnuPg1bSCILeYXMX/D0qTe+iTTtr0/ppKdl9084MdY+pdAVe7311kvsYdl+D+ldf/31SXzo4yWXXOLKpuMedjgS3YXvItL2QTH2QEtHgsaPP//5zxEGk7LapUk086ZrHHnkkR1lxULIPIepjvhiLHUcM2ZMV5S60kVGZepXF5Huh35W8PfZ34ggW0ekAeZpp50m9Xf6eIsW0OG7tpezDZVJpDEn2Yx/2GGHOfORm3iLx2JEc0QT8Ys0UhBUyQudlHk0NxpnKIfTgMwGjB0tskal7Tlk2HPbdPYphS5ja4bHyLLgIr6LSONFw9y/GzuoVHH2p6srr7yySjKtiiNy8WnYsjrMJsANmb/g6bOevok0ykj761NC7rR++tOfdtk/LGbPcr32e0gbC1JFD+Hn2VOz/5J4LtsOG7HKKqskaWOEOqs/QVkwOLPNNtvEcXCqYdphK+bhYdhFK8s9/vjjHaR4t912ywoeP7OndaCvsF1d6SKfMvWri0j3Qz8r+uWzvxE59j2Rxmgu5vziz/4cIpXI8m3CizfDxRdfPMLnJJe7++67I3yyEdBBcF2jn3a6JpFGuuaR1jhVMG3hIA4owPQMLAq0d+0ocqoQjIl5EIi53Zv9Wc5V3zrv4QVEcIS/5557RpjvbDvMkTMbO+ZXw7CYDvPOV1111SQ9YJZ2nDdIN2SMURiTzKcZUpRLyjly5Egz28LX5lG0yBfHL9NlIyCY+zRsIYksahsyf8EzG/VyT2l/s/HqV/trD0xgkAU28bzzznNWCP2e2Y9U7feAhzmfGTopUw7tjDFajUGM173udZE5dc8+s0Hi2f3jdtttFz3xxBPyuMNHO9x3330Tu45yYKcrl8P2sNJ20PfbX5/tOPaUQayHSfvye84553Ssl8KX1TRXV7pl6lcXkUadQ/ezImOf/Y3Isu+JtBS0qm8TXnN/ZbxNYqcMvBXjpCGQIZOsAXicjORydro2kbY3IMdiAsyVxkgBDAjmAr/zne9MGvCJJ54Y4QQnc1R6pZVWisuHz2VpBgNlMxcXirJgT+rQ7l//+lfHSwnKhukWONkRUx9OOOGEaMcdd0wwwHO8UNgLXKQedj3x0oCRbqQDgwX5YWGnYAiMzePUDz74YEmqw8d+oIIb/LSTIjsiWT+wN7ikgTLR5SMgePk0bCGJLGocMn/BMx/55kLYdpL2txnsQV5FH+DDxoldNPs9rEvBAIM5rQ7hq/Z7qJ09AgsSj5HpM888Mz6yG6f7ggRL+dD/rrvuusnvtOPMMZiyySabJOEQH+tvcAYDpkZixxH0A6iPuXgP4dDnpLk99tijI00M5GDh/6c//enI1Wdgiow5BQbpY7tZ1AsnAULnMRVl55137kgXONxwww1pxYin3tSRbpn61UmkQ/ezom8++xsRZuuINE5uAiEToyLguvxPfvKTqW+adgdhE2m8oWIvYVe69j00QFm0YG70b4ZLI5cQ5MMPP9yx6BDxzj33XJFxUB9GJ61OZv1wjdHjvPnkeOEoIjusqIYMcDCK5INpLy5nHyUOg1/G2ds3uTb9L5NeW8KKXHwatpBEFnILmb/g2U/6Y9tJ2t9mpIOBIdEH+LBRX/7ylwvZzl76PdTuxRdfjMwTic1ymNcYCJG1JKadxkL/NAcyjX2kzS+vZpqua0zpy5oGYpNHMw0MkLgc5j1PmjSpA2Mznn0NLlBkgKaOdMvUzw7rmobiwsPcKMF1RDjihO5nRSY++xvBonVEGqtH4bBYwVwJLCCjgWJVsLlhuoBl+nYHYRNphIVBwYg33kQlffFBBt/znvfECyHMdLFo7X3ve1+HwcP8LoxKZznsWyxpY/oKGmQ/OYwYYCcP1EXKKT4+OYLkou5F3MUXXxwTZHPHEkkLIxvmHMxx48Yl+WWNSowePToJt+uuuxYpRhIGn0slf/h33nln8owX6QgIZj4NW0gii5qGzF/wTEe8+Se2naT9bUYG9ugfCCgcRm0322yzDnsFvfHZ7yEf6fuWXnrprryQH/reK664AkFjZ87FT5uCJ2Hh41wG2HZzm1XRf/iYXoedSrIGoMz0MJJtLggUTDDHOsvhhQV42nER/9WvfnXcT+EAsSwi70rfd7pF61cnkUY9Q/azoh8++xuR3Qhc6Ay8OE0O43Q8JtlzuS699FKliVGSjia8Sn+GSX7//e9/V3p+mNJv7GqNNdZQ+tOR0o0iee7jQo+MKr0Dh9IriJXuaON89JQDpeeGpSaPcHputtKGQun51qnh5IGeyqGuvfba+KceUVCnn366POorXxsUpd/MlT4sRWkjq/SnLKXn5ik9J690OXXnoG699dYYVz3HTulpI0rPByudDiLojkfpz3lxXN2pqDvuuEPpnVty04Ku61XYSu8LGofVnyyV7iBy4zGAUmIvtGErDYf+euGMo/dSV/rF1fmsiZsh8xc8aX87JU3724kHfqFvgR3WC+Nr6/eQD+y95KUXoCs9hUSh79NrUfDYi9OnFSp9kJbSX2aVnpqp9BztuE8pawf0+h111113KZQT5UO/pAd5CpURbQ71RH8EfUM/pA9Mq9SvmRn6TLeX+pll6uU6ZD8r9tFnfyNYtJ5ICxCD7Ou3SKXf8OMqQFlAAvWo+iBXqfGy6xGUmDjrUxTjvPVohtKHE+SWQ8+JU/rQmyScngOn9Nz35Dcv0hGow7CFJLKoacj8Bc9BItLp2jE4T2h/B0dWLGlYBEL2s2IfSaQr6EDeiHSFJPsuCkZB9YrkuFwcEa0uHj1FQ+l5b3ECGCHH6ARGT7IcvmDovbvjIHrva6U/ZWcF5zMDgToMW0gii6qFzF/wJJE2lKyBS9rfBkBmFkODQKh+VuwjiXQFVRp2Io0pHHp1cYIMRkf0nK3kNy+KI4DPkPpUSKW3DYwj6ZXrSi/aTE0ApFnPTY+fo5GCUG+00Uap4fmgE4E6DFtIIovahcxf8CSR7tSzOn/R/taJLtMeRgRC9bNiH+sg0q1bbOhaFKg7noF0OLQE28Xpxhb/7bPPPgNZj34qNPYalRXh2Es1bbEKTsc0t9bDVkl05RAQvdWGLSr7l5ZTyMV+KFPI/AXPNGxC3LcXG9L+hpAC8yQC/YVAiH5W7GPZvgbh8xznSGt0B8Vhzi4WVOg9pZVetaywcFIcFkfgtz79SW6l+vogk2RhYmqgig/0NkZK78BRMXZ/RNNb7Kljjz02LgwWhM6bN68L17322kvp0xPjMJtuumksj6ILU/qjluFLUccIQcgRYSAaMn/BUxv98MJ9qQTD9EWQ9rdv1IoFGQIEmu5nxT5qYlwavbTF7UlCeUy7zHOdaDwyWiZO3WGHaUTE3OJOsIavdxuJ9K4RhaH86Ec/moxim+n4uC67dVzhQjcYEHt66/nOCUbbbrttx/ZF3/jGN5JnOLb2wQcfbLB0w5OV6JvPEYKQI8KQTMj8Bc9+0hDa325p0P52Y8I77UOg6X5W7KPP/kakxhFpje6gOH0ildInIybF1ftUKj2dQ5188sldI6ZJIMfFIYccojDhvw630047Kb0HZh1JN5qmnrqh9L7X6p577onznTZtmtInKCp9oITSm+srfYxsvLURFnnq/UwbLduwZFbHCEHIEWHIJWT+gqc27n2jIsM0Ik372zdqxYIMCQJN9rNiH+sYkR56Io19MvUhAIna6Y3f1fLLL5/8HqSLxx9/XOnRz3ifS30EarwH87LLLjtIVRiosmJfUH24Slxm7C2tR6bj/aL1wTHxPexdbe5JPlCV64PC1mHYQhJZQBoyf8Gzn4g07W8fNDQWgQj0MQJN9bNiH0mk+1gZWDQiQATKIVCHYQtJZFH7kPkLnv1EpMtpBEMTASJABOpBQOwjiXQ9+DJVIkAEAiBQh2ELSWQBYcj8BU8S6QDKzCyJABHoawTEPpJI97WYWDgiQATKIFCHYQtJZFH3kPkLniTSZbSQYYkAEWgDAmIfSaTbIG3WkQi0BIE6DFtIIguxhcxf8CSRbkkDYjWJABEojIDYRxLpwpAxIBEgAv2OQB2GLSSRBd4h8xc8SaT7XfNZPiJABJpGQOzjwBDppgFifkSACAwuAj4NW0giCwmEzF86isHVBJacCBABIlAvAj77GylpLdvfSeL0iQARIAJ5CPg0bCGJLOoZMn8S6TxN43MiQATajoDP/kaw9EqkkWjVjuSZZ56RMvXkP/fcc2qJJZboKY1eIjN/4k/9q7/9pR3ZWtX+9NLmzbiDmj/trynF6te0/7T/tP/12/+0FlpX+0vrb6QcI3CkrfwI6aMDoiMC/YAADl/Rx5f2Q1FYhhQEllpqqZQnvF0FAdrfKqgxDhEgAm1AIK+/4Yi0Zy2o642oaDGZP0dE2jAikjZCMKgjwkXbd164qvXniHQessWe0/7S/rbB/qa1hmHV/7T+RnAgkRYkPPnDqkhF4WH92ZE00ZGkGbaqRLKofueFG9T8SaTzJFvsOe0f7V8T9i9NG6l/9ehfWn8jciCRFiQ8+VTkehS5qHiIfzvwTzNsg0pki+p3Xriq9SeRzkO22HPan3bYnzRtoPyHU/5p/Y3oAYm0IOHJZ0MazoZUVD0o/2bkn2bYqhLJovLNCzeo+ZNI50m22HO2//9v7w5W4whiIAznnPd/1pxzKoINTTdjjZSZ/U5imbHVrZL+EizYPfO/UkP91f+ObwRWfpM+tEinEkXRIBvkOwb5tD0/pf9WYHvqInuq7+69q/e3SO8qe/b8U+ZvVQ33539v9L+V32QOLNKpRFEEEiB5I0hOx6Or/1dgu7pInt5v995T81ukd8qePe/q/9Vp5Oc//Kf+z++t/CZzaJFOJYoikAEZkNWD7Pt4rsD21EX2+/2ufr56f4v01Yp//Tn8x3/8v5//X6fu36e75m/lN8lskU4liuJdQp4eT34g/wSQr8B2dZE8na/de0/Nb5HeKXv2HH/x9xP4u5qGt/b/ym9SB4t0KlEU39pIp+Vxf0bSYSQrsD11kT2dr917V+9vkd5V9uw5/uFfB/9W3aj/7um/ld9EB4t0KlEUNfI9jXwqj/p/Rv1XYLu6SJ721+69p+a3SO+UPXuOP5/Bn1U30P+d+q/8Jn1gkU4liqJBeucgnbYH/Xv0X4HtqYvsaX/t3rt6f4v0rrJnz81/z/yv1FB/9b/jG4GV36QP/5tFOpOCNYkAAAHESURBVAf6abxqJD/Nm5+X/8+v3f+lT63uiOqv/vrv9x2jdfQ7zZ/5M3/m7wgWN7w0xR+LdLGYU0LmGvIzMkbGyMKD7og/+IM/+NPNneSb4o9FOgoUxSkhc3z5GRkjY2ThQXfEH/zBH/zp5k7yTfHHIh0FiuKUkDm+/IyMkTGy8KA74g/+4A/+dHMn+ab4Y5GOAkVxSsgcX35GxsgYWXjQHfEHf/AHf7q5k3xT/LFIR4GiOCVkji8/I2NkjCw86I74gz/4gz/d3Em+Kf5YpKNAUZwSMseXn5ExMkYWHnRH/MEf/MGfbu4k3xR/LNJRoChOCZnjy8/IGBkjCw+6I/7gD/7gTzd3km+KPxbpKFAUp4TM8eVnZIyMkYUH3RF/8Ad/8KebO8k3xR+LdBQoilNC5vjyMzJGxsjCg+6IP/iDP/jTzZ3km+KPRToKFMUpIXN8+RkZI2Nk4UF3xB/8wR/86eZO8k3xxyIdBYrilJA5vvyMjJExsvCgO+IP/uAP/nRzJ/mm+GORjgJFcUrIHF9+RsbIGFl40B3xB3/wB3+6uZN8U/yxSEeBojglZI4vPyNjZIwsPOiO+IM/+IM/3dxJvin+/AUh9f14LqjsuQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 13,
"metadata": {
"image/png": {
"height": 400,
"width": 400
}
},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='SimpleClassHierarchy.png', width=400, height=400) "
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"scrolled": false
},
"outputs": [],
"source": [
"# Code for inheritance\n",
"class Sedan(Car):\n",
" # Sedan inherits from car\n",
" \n",
" def __init__(self, color, speed):\n",
" \"\"\"\n",
" :param str color:\n",
" :param int speed:\n",
" \"\"\"\n",
" super().__init__(color, \"Sedan\", speed)\n",
" \n",
" def play_cd(self):\n",
" print (\"Playing cd in %s sedan\" % self.color)"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"scrolled": false
},
"outputs": [
{
"ename": "AttributeError",
"evalue": "'Sedan' object has no attribute 'color'",
"output_type": "error",
"traceback": [
"\u001b[0;31m--------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mAttributeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-55-14d445517fdf>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0msedan\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mSedan\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m\"Yellow\"\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;36m1e6\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0msedan\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcolor\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;31mAttributeError\u001b[0m: 'Sedan' object has no attribute 'color'"
]
}
],
"source": [
"sedan = Sedan(\"Yellow\", 1e6)\n",
"sedan.color"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"'Sedan'"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sedan.car_type"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"text/plain": [
"'Sedan'"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sedan.car_type"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true,
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Type of joe_car has (color, type, speed)=('Blue', 'Sedan', 100).\n"
]
}
],
"source": [
"joe_car = Sedan(\"Blue\", 100)\n",
"print (\"Type of joe_car has (color, type, speed)=%s.\" % str((joe_car.color, joe_car.car_type, joe_car.speed)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise:** Implement SportsCar and create dave_car from SportsCar. Print attributes of dave_car."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsQAAAJICAYAAABmJ/IgAAAMFGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdUk8kWnr+kEBJaIAJSQm+CFOkCofciHWyEJEAoERKCih1ZVHAtqFhAVHRFRMW1ALJWLFhYBOz1gYrKyrpYsKHyJgV0fe28e8788+XOvXe+O7kzZwYAZVt2bm42qgJAjiBfGB3ow0xMSmaSegEOMEAHJoDA5ohyvaOiwgCU0f7v8u4mQCT9NWtJrH8d/6+iyuWJOAAgURCnckWcHIiPAIBrcnKF+QAQ2qHeaHZ+rgQPQqwuhAQBIOISnC7DmhKcKsMTpDax0b4QswAgU9lsYToAShLezAJOOoyjJOFoK+DyBRBXQezJyWBzIb4P8YScnFkQK5MhNk/9Lk7632KmjsVks9PHsCwXqZD9+KLcbPbc/3M5/rfkZItH5zCEjZohDIqW5AzXbU/WrFAJpkJ8XJAaEQmxGsQX+VypvQTfzRAHxcntBzgiX7hmgAEACrhsv1CIdSBmiLPivOXYni2U+kJ7NIKfHxwrx6nCWdHy+GiBIDsiTB5neQYveBRX80T+MaM2afyAYIhhpaFHCjNiE2Q80XMF/PgIiJUg7hRlxYTKfR8WZvhGjNoIxdESzsYQv00TBkTLbDDNHNFoXpgNhy2dC9YCxsrPiA2S+WKJPFFi2CgHLs/PX8YB4/IEcXJuGKwun2i5b0ludpTcHqvmZQdGy9YZOygqiBn17c6HBSZbB+xRJjskSj7Xu9z8qFgZNxwFYcAX+AEmEMOWCmaBTMDvGGgagL9kIwGADYQgHfCAtVwz6pEgHRHAbwwoBH9CxAOiMT8f6SgPFED9lzGt7GsN0qSjBVKPLPAU4hxcG/fE3fEw+GXBZo+74K6jfkzl0VmJ/kQ/YhAxgGgxxoMDWWfDJgT8f6MLhT0PZifhIhjN4Vs8wlNCF+ER4Qahh3AHxIMn0ihyq5n8IuEPzJkgHPTAaAHy7FK/zw43hawdcR/cA/KH3HEGrg2s8UkwE2/cC+bmCLXfMxSPcfu2lj/OJ2H9fT5yvZKlkqOcRerYP+M7ZvVjFN/v1ogL+9AfLbHl2GGsDTuDXcKOY02AiZ3CmrF27IQEj1XCE2kljM4WLeWWBePwR21s6237bT//MDdbPr9kvUT5vDn5ks3gOyt3rpCfnpHP9IanMY8ZLODYTGDa29o5AyA522VHxxuG9MxGGJe/6fJOA+BaCpXp33RsIwCOPQWA/u6bzug1LPc1AJzo5IiFBTKd5DgGBEABynBXaAE9YATMYT72wAm4AxbwByEgEsSCJDADrngGyIGcZ4P5YAkoAWVgDdgAtoBtYCfYA/aDQ6AJHAdnwAVwBXSCG+AerIs+8AIMgndgGEEQEkJD6IgWoo+YIFaIPeKCeCL+SBgSjSQhKUg6IkDEyHxkKVKGlCNbkB1IHfIrcgw5g1xCupA7SC/Sj7xGPqEYSkXVUV3UFJ2IuqDeaCgai05H09E8tBAtRlehm9AadB/aiJ5Br6A30B70BTqEAUwRY2AGmDXmgvlikVgyloYJsYVYKVaB1WAHsBb4P1/DerAB7CNOxOk4E7eGtRmEx+EcPA9fiK/Et+B78Eb8HH4N78UH8a8EGkGHYEVwIwQTEgnphNmEEkIFYTfhKOE83Dd9hHdEIpFBNCM6w32ZRMwkziOuJG4lNhBPE7uIj4lDJBJJi2RF8iBFktikfFIJaTNpH+kUqZvUR/pAViTrk+3JAeRksoBcRK4g7yWfJHeTn5GHFVQUTBTcFCIVuApzFVYr7FJoUbiq0KcwTFGlmFE8KLGUTMoSyibKAcp5yn3KG0VFRUNFV8UpinzFxYqbFA8qXlTsVfxIVaNaUn2p06hi6ipqLfU09Q71DY1GM6WxaMm0fNoqWh3tLO0h7YMSXclGKViJq7RIqVKpUalb6aWygrKJsrfyDOVC5Qrlw8pXlQdUFFRMVXxV2CoLVSpVjqncUhlSpavaqUaq5qiuVN2rekn1uRpJzVTNX42rVqy2U+2s2mM6Rjei+9I59KX0XfTz9D51orqZerB6pnqZ+n71DvVBDTWNSRrxGnM0KjVOaPQwMIYpI5iRzVjNOMS4yfg0Tnec9zjeuBXjDozrHvdec7wmS5OnWarZoHlD85MWU8tfK0trrVaT1gNtXNtSe4r2bO1q7fPaA+PVx7uP54wvHX9o/F0dVMdSJ1pnns5OnXadIV093UDdXN3Numd1B/QYeiy9TL31eif1+vXp+p76fP31+qf0/2BqML2Z2cxNzHPMQQMdgyADscEOgw6DYUMzwzjDIsMGwwdGFCMXozSj9UatRoPG+sbhxvON643vmiiYuJhkmGw0aTN5b2pmmmC6zLTJ9LmZplmwWaFZvdl9c5q5l3meeY35dQuihYtFlsVWi05L1NLRMsOy0vKqFWrlZMW32mrVNYEwwXWCYELNhFvWVGtv6wLreuteG4ZNmE2RTZPNy4nGE5Mnrp3YNvGrraNttu0u23t2anYhdkV2LXav7S3tOfaV9tcdaA4BDoscmh1eTbKaxJtUPem2I90x3HGZY6vjFydnJ6HTAad+Z2PnFOcq51su6i5RLitdLroSXH1cF7ked/3o5uSW73bI7S93a/cs973uzyebTeZN3jX5sYehB9tjh0ePJ9MzxXO7Z4+XgRfbq8brEcuIxWXtZj3ztvDO9N7n/dLH1kfoc9Tnva+b7wLf036YX6BfqV+Hv5p/nP8W/4cBhgHpAfUBg4GOgfMCTwcRgkKD1gbdCtYN5gTXBQ+GOIcsCDkXSg2NCd0S+ijMMkwY1hKOhoeErwu/H2ESIYhoigSRwZHrIh9EmUXlRf02hTglakrllKfRdtHzo9ti6DEzY/bGvIv1iV0dey/OPE4c1xqvHD8tvi7+fYJfQnlCT+LExAWJV5K0k/hJzcmk5Pjk3clDU/2nbpjaN81xWsm0m9PNps+ZfmmG9ozsGSdmKs9kzzycQkhJSNmb8pkdya5hD6UGp1alDnJ8ORs5L7gs7npuP8+DV857luaRVp72PN0jfV16f4ZXRkXGAN+Xv4X/KjMoc1vm+6zIrNqskeyE7IYcck5KzjGBmiBLcG6W3qw5s7pyrXJLcnvy3PI25A0KQ4W7RYhouqg5Xx1ec9rF5uKfxL0FngWVBR9mx88+PEd1jmBO+1zLuSvmPisMKPxlHj6PM691vsH8JfN7F3gv2LEQWZi6sHWR0aLiRX2LAxfvWUJZkrXk9yLbovKit0sTlrYU6xYvLn78U+BP9SVKJcKSW8vcl21bji/nL+9Y4bBi84qvpdzSy2W2ZRVln1dyVl7+2e7nTT+PrEpb1bHaaXX1GuIawZqba73W7ilXLS8sf7wufF3jeub60vVvN8zccKliUsW2jZSN4o09m8I2NW823rxm8+ctGVtuVPpUNlTpVK2oer+Vu7W7mlV9YJvutrJtn7bzt9/eEbijsca0pmIncWfBzqe74ne1/eLyS91u7d1lu7/UCmp79kTvOVfnXFe3V2fv6nq0Xlzfv2/avs79fvubD1gf2NHAaCg7CA6KD/7xa8qvNw+FHmo97HL4wBGTI1VH6UdLG5HGuY2DTRlNPc1JzV3HQo61tri3HP3N5rfa4wbHK09onFh9knKy+OTIqcJTQ6dzTw+cST/zuHVm672ziWevn5tyruN86PmLFwIunG3zbjt10ePi8Utul45ddrncdMXpSmO7Y/vR3x1/P9rh1NF41flqc6drZ0vX5K6T3V7dZ675XbtwPfj6lRsRN7puxt28fWvarZ7b3NvP72TfeXW34O7wvcX3CfdLH6g8qHio87DmHxb/aOhx6jnR69fb/ijm0b3HnMcvnoiefO4rfkp7WvFM/1ndc/vnx/sD+jv/mPpH34vcF8MDJX+q/ln10vzlkb9Yf7UPJg72vRK+Gnm98o3Wm9q3k962DkUNPXyX8274fekHrQ97Prp8bPuU8OnZ8OzPpM+bvlh8afka+vX+SM7ISC5byJZeBTDY0LQ0AF7XAkBLgneHTgAoSrK3l1QQ2XtRisB/wrL3mVScAKhlARC3GIAweEephs0EYirsJVfvWBZAHRzGmlxEaQ72slhU+IIhfBgZeaMLAKkFgC/CkZHhrSMjX3ZBsncAOJ0ne/NJhAjv99ttJKiz7yX4Uf4JEL9tBtKO/vwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGdaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIj4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjcwODwvZXhpZjpQaXhlbFhEaW1lbnNpb24+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj41ODQ8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICA8L3JkZjpEZXNjcmlwdGlvbj4KICAgPC9yZGY6UkRGPgo8L3g6eG1wbWV0YT4KULE+1wAAABxpRE9UAAAAAgAAAAAAAAEkAAAAKAAAASQAAAEkAABfQ5TAp4AAAEAASURBVHgB7F0H2NZEth4FQUQEFBcVaa69ASKKCCKoCBbE3l1Rr9gbFhTrWtdyBb0qa1kVG/YG9oaCCBaKWFFBBAugCFcuKGDunOAJk3zpmS/z5887zwPfZDItp82b85/MrGLJJDSm//u//xNrrLGGxh6TdYXxQX/IH/QvmdXQVxv2B/YH9gf2R59FSdYT7E82+7MKAHEygYuqDYHMJpBR9I26D/qD/gAkACRRdqJa92F/YH9gf4prfwCINVtGGEQYRBjE4hrErOYA+g/9h/5D/7PakbTtYX+y2R8A4rSSF9AOAplNIAPIGrsY9Af9AUgASGIbDM0VYX9gf2B/imt/AIhhELVSAAsCFgQsCMVdELIaA+g/9B/6D/3PakfSts9qfwCI01I+oF1WhgR0G7sY42NBwoKEBSm2wdBcEfYH9gf2B/ZHs1mJ3V1W+wNAHJvU8SpmZUi8UYJrYXwsSFiQsCAFW4jq3oH9gf2B/YH9qa6VCe49q/0BIA6mbao7WRmSalClEcbHgoQFCQuSYhJyzcL+wP7A/sD+5Gp0lMGy2h8AYoWYOrJZGZJ1DhgfCxIWJCxIWe1I2vawP7A/sD+wP2ntR9Z2We0PAHFWDnjaZ2WIp7vElxgfCxIWJCxIiQ2HpgawP7A/sD+wP5rMSeJustofAOLEJA9vkJUh4b1H38X4WJCwIGFBirYU1akB+wP7A/sD+1Md6xLda1b7A0AcTeNENbIyJNFgPpUxPhYkLEhYkHxMQy5FsD+wP7A/sD+5GBufQbLaHwBiH6JmKcrKkCxjU1uMjwUJCxIWpKx2JG172B/YH9gf2J+09iNru6z2B4A4Kwc87bMyxNNd4kuMjwUJCxIWpMSGQ1MD2B/YH9gf2B9N5iRxN1ntDwBxYpKHN8jKkPDeo+9ifCxIWJCwIEVbiurUgP2B/YH9gf2pjnWJ7jWr/QEgjqZxohpZGZJoMJ/KGB8LEhYkLEg+piGXItgf2B/YH9ifXIyNzyBZ7c8qixYtsnz6RREoYIwCderUEcuXLzc2PgYGBUABUAAUAAVAgXJRAB5izfzO+oaSdToYHx4aeGjgoclqR9K2h/2B/YH9gf1Jaz+ytstqfwCIs3LA0z4rQzzdJb7E+FiQsCBhQUpsODQ1gP2B/YH9gf3RZE4Sd5PV/gAQJyZ5eIOsDAnvPfouxseChAUJC1K0pahODdgf2B/YH9if6liX6F6z2h8A4mgaJ6qRlSGJBvOpjPGxIGFBwoLkYxpyKYL9gf2B/YH9ycXY+AyS1f4AEPsQNUtRVoZkGZvaYnwsSFiQsCBltSNp28P+wP7A/sD+pLUfWdtltT8AxFk54GmflSGe7hJfYnwsSFiQsCAlNhyaGsD+wP7A/sD+aDInibvJan8AiBOTPLxBVoaE9x59F+NjQcKChAUp2lJUpwbsD+wP7A/sT3WsS3SvWe0PAHE0jRPVyMqQRIP5VMb4WJCwIGFB8jENuRTB/sD+wP7A/uRibHwGyWp/AIh9iJqlKCtDsoxNbTE+FiQsSFiQstqRtO1hf2B/YH9gf9Laj6ztstofAOKsHPC0z8oQT3eJLzE+FiQsSFiQEhsOTQ1gf2B/YH9gfzSZk8TdZLU/AMSJSR7eICtDwnuPvovxsSBhQcKCFG0pqlMD9gf2B/YH9qc61iW616z2B4A4msaJamRlSKLBfCpjfCxIWJCwIPmYhlyKYH9gf2B/YH9yMTY+g2S1PwDEPkTNUpSVIVnGprYYHwsSFiQsSFntSNr2sD+wP7A/sD9p7UfWdlntDwBxVg542mdliKe7xJcYHwsSFiQsSIkNh6YGsD+wP7A/sD+azEnibrLaHwDixCQPb5CVIeG9R98t8/irrLJKNIFQAxQoGQUsy8rtictsf4jIeH68EOCFoLgvBADEmpcKGERzBhGAWLMwo7taQQEA4vzYCPtvzv4Tl0F/0D/LCwkAsWZbCYU0p5AMiPMEAJrFB92BAtooYEIfYP/M2T8SHNAf9M8CCLMan6LLHwBxVgnwtC+6QHgeJ/Glyec3AQASEwgNQIGcKGBCH0zqP5EV4wMQAhAWN2Qhq2nMqv8AxFk54GmflSGe7hJflnl8EwAgMYPQABTIiQIm9KHM9ofYiucHIAcgLy4gByDWvDjBIJoziCYAgGbxQXeggDYKmNAH2D9z9o8EB/QH/QHI0wNyAGJty8+KjmCQzBkkEwBAs/igO1BAGwVM6APsnzn7R4ID+oP+AMQAxM4iAoNQXoNgAgA4gocMKFDDKGBCH2B/y2t/SfzBf/C/yIAcHmLNixgMgjmDYAIAaBYfdAcKaKOACX2A/TNn/0hwQH/Qv8iANKvxyyr/AMRZOeBpn5Uhnu4SX5Z5fBMAIDGD0AAUyIkCJvShzPaH2IrnByAFIE0fspDVNGbVPwDirBzwtM/KEE93iS/LPL4JAJCYQWgACuREARP6UGb7Q2zF8wMQAxADEDsmHgYBBsGUQTABABzBRwYUqGEUMKEPsP+w/6bsP6kf5A/yl0X+4CHWvIhBIc0ppAkAoFl80B0ooI0CJvQB9s+c/SPBAf1B/yyAMKvxKbr8ARBnlQBP+6ILhOdxEl+afH4TACAxgdAAFMiJAib0waT+E1kxPgAhAGFxQxaymsas+g9AnJUDnvZZGeLpLvFlmcc3AQASMwgNQIGcKGBCH8psf4iteH4AcgDy4gJyAGLNixMMojmDaAIAaBYfdAcKaKMA68P//u//Ju5zzTXXTNyGGsD+mbN/oD/kD/qXTf8AiFOZ/eBGEMhsAhlM2eg7DAAsy4qujBqgQC2nAOsDAHF+jIb9N2f/icugP+ifxUO/yqJFi4Ae8rOXGCkGBerUqSOWL18eo6a7SsOGDe0CAGI3XXBVTgowIJ47d25iAmRZVBIPhgagACgACtQACsBDrJkJeEM194bKAACAWLNQo7tCUoD1AR7i/NgH+2/O/hOXQX/QP8vLPACxZlsJhTSnkAwAAIg1CzW6KyQFWB8AiPNjH+y/OftPXAb9QX8AYsXeQSHKqxAMAACIFYUIyC5cuFCMGTNGvPXWW2Ly5Mni559/tv/98ccfYoMNNhAbbrihaNmypWjTpo045JBD7OuArlBcQynA+gBAnB+DsP6Ud/0hKQP/i81/eIg120oohDmFYAAAQBws1N999524/vrrxd133y2WLFkSXFG5QzHdffv2Faeeeqro2bOnYDorVZCtgRRgPgEQ58cc2H9z9p+4DPqD/vAQK/YOClFehWAAAECsKISSveOOO8RZZ50lyAucNh188MHiwQcfFPXq1UvbBdrlRAHWBwDinAguh8H6U971h6QM/C82/+Eh1mwroRDmFIIBAACxW6iJHuTdJUCsI/Xq1Us89dRTgnf10NEn+tBPAdYHAGL9tA3qEfbfnP0nnoD+oD88xIp1gkKUVyEYAAAQKwohs9ddd5248MIL3YWeq6ZNm4qtt95atG7dWsyePVt888034ttvv/XUWnm56667ijfffHNlAXI1jgKsDwDE+bEG60951x+SMvC/2PyHh1izrYRCmFMIBgAAxCuFeuzYsaJ79+6++zoTvc4991xxxhln+H409+6774qbbrrJ9gav7HFl7plnnhH77bffygLkahQFWB8AiPNjC+y/OftPXAb9QX94iBV7B4Uor0IwAAAgXqkQPXr0sHeSWFmyIte8eXMxfPhwQeEPUenWW28VZ555pvDStX379uKjjz4K/cju119/FZ9//rmYNWuWoA/6Fi9eLDbaaCOx8cYb2/+aNGkSNbz47bffxJw5c1z1VlttNXsXDC78+OOPxYQJE8T3339ve7r3339/vlXaX9YHAOL8RADrT3nXH5Iy8L/Y/IeHWLOthEKYUwgGAF7gppnFhenugw8+EJ06dfKd77hx40Tnzp197/kVXnXVVeKSSy5x3aI3cQqb2GGHHVzldDF16lQxZMgQ8dBDDwXuZrHqqquK/v37C+p7vfXWq+iDC5544glBH/Opae2117a3iSNen3feebYnm+83aNDAXpj4uqy/rA8AxPlJAOy/OftPXAb9QX94iBV7B4Uor0IwAAAgXqEQFApB3l1v6tOnj3jhhRe8xaHXpFd///vf7T2KyatM/3beeWff3SZuvPFGG6SGdqjcXHPNNcW///1vccQRRyilK7Mvv/yy6N2798oCmSMwvWzZMnHllVeKyy67zHUPgHgFOVgfAIhd4lHVC6w/5V1/SLDA/2LzHx5izeYRCmFOIRgAABCvEOrttttOTJw4sULC33//fbH99ttXlEcV0HZtUdut3XnnnWLAgAFRXVXcpx0rJk2aZIdReG+OHj1a0Ed83jR9+nQ7PGLRokWuWwDEK8jB+gBA7BKPql7A/puz/8RY0B/0h4dYMXFQiPIqBAMAAGIhCATRzhHLly9XtEPYcbczZ850lem6mDt3ru1BJs+tmujEu6FDh4qddtpJ/P7772LUqFFi4MCBFaEU5HF+5513KmKS6eM+uudN9EEgeaO9CYB4BUVYHwCIvRJSvWusP+Vdf0iqwP9i8x8eYs22EQphTiEYAAAQCzFlyhTRrl27Cunu2rWrDTorbmgooPAMCtPwppdeeknsueeermI6Le+CCy5wldEFbfXWqlUrVzl9LLfjjju6yuiicePGYsGCBXb4xmmnnWZ7vemaPuDbfffdK+qXrYD1AYA4P87D/puz/8Rl0B/0h4dYsXdQiPIqBAMAAGIhgsIMjjrqKPHAAw8oGqMvSztRvP322/auEATCaHcIivWdP3++oOOf1UQ7TniBL92n2GaKcVZT2MeBhxxyiP3hXt26ddUmyEsKsD4AEOcnDlh/yrv+kJSB/8XmPzzEmm0lFMKcQjAAACAW4umnnxYHHHBAhXQPHjzY3tWh4kaVCogXzBd1CArlqF+/fkVIB3mOadcINQUBYgLBFEe84YYbqtWR/4sCTHcA4vxEAvbfnP0nLoP+oD88xIq9g0KUVyEYAAAQC+G3VRmpyT//+c+K7dMU9ck1S3sQU4iDmii22BsXHASI+/XrZwN/tT3yKynA+gBAvJIm1c5h/Snv+kOyBf4Xm//wEGu2kFAIcwrBAACAWIg33nhD7LbbbhXSfdxxx4l77rmnolx3wY8//mjvUTxjxgzbi0sf8i1ZssTeKm3p0qX27+TJkys8xEkA8RVXXCEuvfRS3VOvNf2xPgAQ58dS2H9z9p+4DPqD/vAQK/YOClFehWAAAEAs7C3MOnTooGjGiiyB5Ndee62iXFcBnRRHYQ+0rzAB4KTpnHPOcR2yQe2DPMR33XWXOOGEE5IOUZr6rA8AxPmxHOtPedcfkjLwv9j8h4dYs62EQphTCAYAAMRCzJs3T6y77roV0k2Ha3z11VcV5ToKaIcI2vv4l19+Sd1dEkD8/PPPi3322Sf1WLW9IesDAHF+nIb9N2f/icugP+gPD7Fi76AQ5VUIBgAAxCsUYvPNNxdffPGFoh1C0IdoFL6w/vrru8rjXNB2ZpT8PmKjQzu6desmaIs0b6Jy+sCvdevW9t7INAfadYJOu6OdKNSUBBD7beem9lX2POsDAHF+koD1p7zrD0kZ+F9s/sNDrNlWQiHMKQQDAADiFUJ94oknCgor8KbTTz9d3HLLLd7iyGv6iI28srTHb//+/QVdr7766na7hx56SNCWbt5Ep9bdfvvt9vZr6j2KI6YjmwlIqylJDDEAsUq5yjzrAwBxJW2qVQL7b87+E09Bf9AfHmLFukEhyqsQDAAAiFcoxCuvvFJxIAbdoe3OKGzCz9OrqJIrO27cONGlSxdXGe0SQR+20WEctFWad3cIqkzjUJiGN40fP1507tzZWyzgIa4gSeoC1gcA4tQkTNwQ60951x8SFvC/2PyHhzixyQtvAIUwpxAMAACIV8oofVg3adKklQV/5fbaay/xyCOPiLXWWqvinreA9vrt3r27oMM0vGnMmDH2scp77LFHxcd69Ka+aNEibxP7+qabbhJ09LI3ARB7KZL+mvUBgDg9DZO2hP03Z/+JV6A/6A8PsWK1oBDlVQgGAADEKxXiqaeeEgceeODKAiVHntsRI0bYRx4rxa7s2LFjxZFHHmkfqey6IS8OO+wwG1RT+a677mqfjuet8/HHH4utt97aVUwAm7zDc+bMcZXTBYV50A4VagraZQIhEyqVKvOsDwDElbSpVgnWn/KuPyRT4H+x+Q8PsWbLCIUwpxAMAACI3UIdFEtMterVq2cfldyuXTux7bbbik022UT89NNP4uuvvxaPPfaYvZewu7cVVw0aNLA/2GvZsqVdcPLJJ4thw4ZVVPWejEcgmMDzZ599VlGXCvy2hQMg9iVVZCHrAwBxJKm0VYD9N2f/iYmgP+gPD7FizqAQ5VUIBgAAxIpCyCztB9yzZ09BccA6En0M9+STT9q7RHB/d9xxhzjllFP40vVLYRt9+vQRFF5BHmc6tpnSMcccI4YPH+6qSztQnH/++eKII44QFKPcokWLwH2I4SF2ka7igvUBgLiCNFUrwPpT3vWHhAr8Lzb/4SHWbBqhEOYUggEAAHGlUBMoPv7448XDDz9ceTNByXrrrSdGjRpl7zesNlu8eLHtYY67x3Hv3r3tHSuaNm1asfUa93vZZZeJyy+/HICYCZLwl/UBgDgh4TJUh/03Z/+JbaA/6A8PsWLAoBDlVQgGAADEikJ4svfee6+48sor7eOUPbdCL2nfYNpm7YYbbhBt27b1rTt69GjbE0zgOCwRGKbY5caNG4uLLrpIXHvttb7VAYh9yRK7kPUBgDg2yTJXxPpT3vWHhAf8Lzb/4SHObALdHUAhzCkEAwAAYrdMeq+WLVtmfwz33HPPibfeess+1c5bh69pazYKbaAY4TjbtNEHc7QN28iRI7kL53fjjTcWp512mqB9kFdddVW7nDzXgwYNEv/zP//jhFLQDQrLuPnmm+2jmRFD7JAwUYb1AYA4EdkyVYb9N2f/iXGgP+gPD7FiwqAQ5VUIBgAAxIpCRGSJVtOmTbN3fKDjngk8NW/e3D5VrlWrVoI+nkuTFixYIL788kt7H2LyBNMpdVtuuaVgHnn7JGD8zTff2OETzZo1E23atHFAs7curuNRgGkNQByPXjpqYf0p7/pD8gP+F5v/q8h9Qi0dhgB9gAK6KEB/nucPr5L02bBhQ7s6AHESqqFubaUAA+K5c+cmfsQsXpbEg6EBKAAKgAI1gAIImdDMBLwhmntDZAAAQKxZqNFdISnA+gAPcX7sg/03Z/+Jy6A/6J/lZR6AWLOthEKaU0gGAADEmoUa3RWSAqwPAMT5sQ/235z9Jy6D/qA/ALFi76AQ5VUIBgAAxIpCIFtaCrA+ABDnJwJYf8q7/pCUgf/F5j88xJptJRTCnEIwAAAg1izU6K6QFGB9ACDOj32w/+bsP3EZ9Af94SFW7B0UorwKwQAAgFhRCGRLSwHWBwDi/EQA60951x+SMvC/2PyHh1izrYRCmFMIBgAAxJqFGt0VkgKsDwDE+bEP9t+c/Scug/6gPzzEir2DQpRXIRgAABArCoFsaSnA+gBAnJ8IYP0p7/pDUgb+F5v/8BBrtpVQCHMKwQAAgFizUKO7QlKA9QGAOD/2wf6bs//EZdAf9IeHWLF3UIjyKgQDAABiRSGQLS0FWB8AiPMTAaw/5V1/SMrA/2LzHx5izbYSCmFOIRgAABBrFmp0V0gKsD4AEOfHPth/c/afuAz6g/7wECv2DgpRXoVgAABArCgEsqWlAOsDAHF+IoD1p7zrD0kZ+F9s/sNDrNlWQiHMKQQDAABizUKN7gpJAdYHAOL82Af7b87+E5dBf9AfHmLF3kEhyqsQDAAAiBWFQLa0FGB9ACDOTwSw/pR3/SEpA/+LzX94iDXbSiiEOYVgAABArFmo0V0hKcD6AECcH/tg/83Zf+Iy6A/6w0Os2DsoRHkVggGAIg7IggKlpwAAcX4igPWnvOsPSRn4X2z+w0Os2VZCIcwpBACxZmFGd7WCAgDE+bER9t+c/Scug/6gPzzEir2DQpRXIRgQI2RCUQhkS0sB1gcA4vxEAOtPedcfkjLwv9j8h4dYs62EQphTCAYAAMSahRrdFZICrA8AxPmxD/bfnP0nLoP+oD88xIq9g0KUVyEYAAAQKwqBbGkpwPoAQJyfCGD9Ke/6Q1IG/heb//AQa7aVUAhzCsEAAIBYs1Cju0JSgPUBgDg/9sH+m7P/xGXQH/SHh1ixd1CI8ioEAwAAYkUhkC0tBVgfAIjzEwGsP+Vdf0jKwP9i8x8eYs22EgphTiEYAAAQaxZqdFdICrA+ABDnxz7Yf3P2n7gM+oP+8BAr9g4KUV6FYAAAQKwoBLKlpQDrAwBxfiKA9ae86w9JGfhfbP7DQ6zZVkIhzCkEAwAAYs1Cje4KSQHWBwDi/NgH+2/O/hOXQX/QHx5ixd5BIcqrEAwAAIgVhUC2tBRgfQAgzk8EsP6Ud/0hKQP/i81/eIg120oohDmFYAAAQKxZqNFdISnA+gBAnB/7YP/N2X/iMugP+sNDrNg7KER5FYIBAACxohDIlpYCrA8AxPmJANaf8q4/JGXgf7H5Dw+xZlsJhTCnEAwAAIg1CzW6KyQFWB8AiPNjH+y/OftPXAb9QX94iBV7B4Uor0IwAAAgVhQC2dJSgPUBgDg/EcD6U971h6QM/C82/+Eh1mwroRDmFIIBAABxcqEeOXKk6Nevn9Nw3LhxolOnTs41MsWjAOsDAHF+vIP9N2f/icugP+gPD7Fi76AQ5VUIBgAAxIpCxMw+//zzom/fvk7tCRMmABA71ChmhvUBgDg//mH9Ke/6Q1IG/heb/6ssWrTIys9cYCRQIJoCderUEcuXL4+u6KnRsGFDuwSA2EOYGJcAxDGIVLAqDIjnzp2beOZZvCyJB0MDUAAUAAVqAAUQMqGZCXhDNPeGyAAAgDi5UAMQJ6dZTW/B+gAPcX6cgv03Z/+Jy6A/6J/lZR6AWLOthEKaU0gGAADEyYUagDg5zWp6C9YHAOL8OAX7b87+E5dBf9AfgFixd1CI8ioEAwCdgPjXX38Vf/zxhy1hzZo1E6uuuqoibbUnC0Bce3jJT8L6AEDMFKn+L9af8q4/JF3gf7H5Dw+xZhsJhTCnEAwAdALibt26iTFjxthSMnv2bLHBBhtolpia0R0Acc3gg85ZsD4AEOukanhfsP/m7D9xBvQH/eEhVmwUFKK8CsEAoAiA+LvvvhNTpkwRU6dOFWuuuabYeOONxeabby5at26tSHP8LH049cknn4hPP/1U/Pbbb2KzzTYTW2yxhdhoo41E3bp1IztKC4izjis/6hU//fSTPT/iX9u2bZ25jh07VkyaNEksWLBAdO3aVeyyyy7OPWSiKcD6AEAcTStdNbD+lHf9IRkC/wvOfwketCbatcJkwvjlpb+0R7Rjilbxk0DM7pP6lR7iTH0vXbrUGjRokNW0aVOnT54z/+6zzz6WBIGxxlm2bJl15ZVXWjKUI7C/evXqWb169bKmT58e2udzzz3n6kNuuxZYX+e4jz/+uDOuBHDWn3/+aclFxdpzzz2dcqLNoYceGjgf3PCnAMuUBMRW0n/+PUaXwv6W1/6SdID/4H+0lahejazypxc9QCFgEAy+EDEA0KluugDxjBkzrJ122skF8ni+3l8ChkOGDAl9jC+//NLq3LlzrP6o/0aNGll33XVXYJ9xAbHucZ999lnXM0jvtjVgwABXGc0fgDiQdYE3WK6SgmGqnzZlXZDSjsvtMD4AGcuCiV/IX7HlDzHEctXQmfAnE3N/MuE/EUtDqI2lOmKIv//+e7H11luL+fPn2/OieR544IFixx13FNtss4345ZdfxIcffihuv/12sXjxYrsOfbwnvafigAMOqHgWCa7t/qTxde7RKXN9+vQRHTp0EGuvvbYdjvHRRx8JCaztEAqueOONN4qBAwfypfMbJ2SiGuO+9NJL9rx5IuPHjxcS6NOLupDebdGxY0f71g477GA/C9fDbzQFWB8kwI2u7KlBYTxpEuyfOftH/AL9Qf8sMbRpdF5tU3j50/0WhTekYr8hZZUHk/yXiml7FrM+g9peh4f41FNPdTyeq6++ujVixAh1CCdPYQ3Nmzd36kpQYv+p26nwV+bYY4916kjgbP3rX//yVnGuKfxiww03dOpTeIWfBzCOh7ga477xxhvO3Ih/Rx99tH19wQUX2KETzoMgk5gCrA/wECcmXeoGJu0fTRrjY/1NLbwaGhZd/hAyoUEI1C6KLhDqs6TJm3x+BgBp5h3UJisg/vbbby2K4+W5XXfddUFD2eVPP/20U5faDB8+3FX/888/t+RJfk6dk046yXXf78ILOq+99tqKalGAuFrjyh08nGeh511ttdUseoFAyk4BljkA4uy0jNuDSftHc8T4AMRxZbUa9YoufwDEmqWi6AKRlRwmn58BQNZnUNtnBcQnn3yyA/gIyEZ9mCf3PLaaNGliNWjQwGrZsqV15plnqtNxPKj8rBMnTnTd97ugD9XatGnjzGOdddax5NHYrqpRgJg9t7rHfffdd515Ud/k8Z41a5ZrbrhIRwHmFQBxOvqlaWXS/tF8MT4AcRq51dWm6PKHGGK5auhMhY+hyUgMk8/PMZNSuWM9xZIlS0Tfvn1D677//vuCDuegRNt+1a9fP7A+xebK3RFc99u3by8mT55sl/Xs2VO8/vrrrvt+F3I3CiE9pX63xJZbbik+++wz+952221nxx77VvQUDh48WFxzzTVOqQSdokWLFs51VAxxtcYdN26c6NKlizMPoh/FFSNlpwDrgwTEiTtDDHFiktkNTNo/mgDGRwwxYojXSKe81ErXmwH3U/Q3BH6OtL94fnNv6CTOSUSadjTgNjp+77nnngqxady4sTPGCSecUHE/aYE0dk5/Rx11VOzm9957r9OOnpU8s2qK8hBXa1yvh1gCd3VayGegAMs0PMQZiJiwKey/OftPrAL9Qf+EKuuqDkDsIkf2CyikOYVkABCXi9UGxNKz7AKhF154Ydyp+dabM2eOqz/pkfat51c4atQoV1vvh31hgLia43oB8S233OI3fZSloADrAwBxCuKlbAL7b87+E8tAf9A/perazRAyIVcNnQl/sjL3Jyv+E7GU7FgspXozZ84MrXvQQQeJDz74wK7z3nvvifXWWy+wvozNtU+d4woUKkEhE5xuvvlmcdZZZ/Fl4l8K36DtxzjdcMMN4txzz+XL0F96hk6dOjl1rr/+enHeeec512EhE9Uc1xsy8dhjj4mDDz7YmRcy6SnA+oCQifQ0TNoS9t+c/Sdegf6gf6aQkSxo2q8t3tDwhuYnF3mUSXtoe0F1jpXlo7pXX33V5ZW98847M03thRdeSN0fHajB9KFf2tZMTWEe4mqO6/UQ01hIeijA/IaHWA894/SC9Q/rXxw5qVYdyF82+UPIhGbJhEBmE8gs7GAAkKUPb9ssgPiTTz5xgVD5UZu3+0TXtKcwPyP9+m2fFtShF3h6QxPCAHE1x/XOC4A4iIPJy1lWAIiT0y5tC9h/c/afeAb6g/5pdZfaARBnoZ5PWyikOYVkAODDltRFWQCxN0b5jDPOSD0PauiNSfZuyRbWuXd/YwLAagoDxNUcF4BY5YLePOsDALFeuob1Bvtvzv4TX0B/0D9MP6PuARBHUSjhfSikOYVkAJCQZaHVswBi6phOhuN5HXrooaFjxbnZtGnTVP0NGzbMaUfzmTJlimu4MEBMFas1LgCxiw1aL1juAIi1kjW0M9h/c/afGAP6g/6hChpxEx/VyVVDZ0JQv7mgfv6ISMq8NpZ269ZNyNPU7P7koRpigw02SNT39ttv7+wVLA/aEDNmzBDy8InQPuQOEILGkiDU/ohvr732curT3sPyMA77um3btuLrr78W/NxOJZ/MgAEDhIxhdu4sXLhQNGrUyLkO+6iOKlVrXO9HdTJkQvTp08eZFzLpKcByIQFx4k6wD3FiktkNYP/N2X9iAOgP+uOjOgX14w2xvG+I0h7aXlBFHDJns3qI6eM1nhf9ykMnQudEp8rJnSycNvvuu6+r/qBBg5x71N9rr73muu93QaEbEvw67eTOFxXVojzE1RoXHuIKVmgrYLmDh1gbSSM7wvpT3vWHhAP8Lzb/ETIRaeKSVYBCmFMIBgDJOBZeOysgnjt3riW9bQ4Y7d27d8WxyeoMvLG+d999t3rbmjdvngvc9uvXz3Xf78IbLuH34VoUIK7WuADEfhzTU8b6AECsh55xeoH9N2f/iT+gP+gfR0+D6gAQB1EmZTkU0pxCMgBIyTrfZvfff7911VVX2f9kmIFvnajCiy66yAHENEe5t7Elj42uaDZ27FhLPdmO4o8JiHrTpZde6uqPTsBbtmyZt5p9/Z///MeSx0A79bt37+5bLwoQU6NqjAtA7MsOLYWsDwDEWsgZqxPYf3P2nxgE+oP+sRQ1oBJiiOWqoTMhhslcDBPHTEpZ18nSzH3Nnz9fdOzYUUyfPt3pq1WrVoLik6l8wYIFYsKECeLFF1907ksQK+Q+xkICWKeMM1SfDuiQewtzkX3oRq9evexfilGmQ0HGjx8vRo4c6dSh2Ko333zTdbgH34yKIaZ61RgXMcTMAf2/rA+IIdZP26AeYf/N2X/iCegP+iOGWEH7eEMs7xuitIe2J1QRhxqTpa3L5Als9vx4nkG/FGJBnumwRHHB/fv3j9UfjdOlSxdr2rRpgV3G8RBTY93jwkMcyJLMN1i+4CHOTMrYHWD9Ke/6Q0IC/heb//AQy1VDZ8Ibqrk3VPaISbukk6Va+6KdHuifPLRDyLAJV9/16tUTxx9/vLjssstE8+bNXfeCLh599FExdOhQMXXqVOH1BNavX19sttlm4uijjxbnnHNO6O4WcTzE6hx0jQsPsUpVvXnWB69cxBkFu0zEoVJlHdh/c/afuAH6g/5ZPMQAxJU2LVMJFNKcQjIAqMmAmIVr+fLlQnpsbSDbsGFDsemmm4o2bdqIOnXqcJVEv/TMM2fOFB9//LGQ8cRiq622EhtttFHq/uIObmrcuPMrcz3WBwDi/KQA9t+c/Scug/6gPwCxYu+gEOVVCAYARQDEisgiCwpUhQKsDwDEVSGvb6dYf8q7/pBAgP/F5j88xL5mLX0hFMKcQjAAACBOL79oWXsowPoAQJwfT2H/zdl/4jLoD/rDQ6zYOyhEeRWCAQAAsaIQyJaWAqwPAMT5iQDWn/KuPyRl4H+x+Q8PsWZbCYUwpxAMAACINQs1uiskBVgfAIjzYx/svzn7T1wG/UH/TB5i2iYkP3OBkUCBaArQh2X00VnSRB+nUQIgTko51K+NFGBALE9LTPx4WRaVxIOhASgACoACNYAC8BBrZgLeUM29oTIAACDWLNTorpAUYH2Ahzg/9sH+m7P/xGXQH/TP8jIPQKzZVkIhzSkkAwAAYs1Cje4KSQHWBwDi/NgH+2/O/hOXQX/QH4BYsXdQiPIqBAMAAGJFIZAtLQVYHwCI8xMBrD/lXX9IysD/YvMfHmLNthIKYU4hGAAAEGsWanRXSAqwPgAQ58c+2H9z9p+4DPqD/vAQK/YOClFehWAAAECsKASypaUA6wMAcX4igPWnvOsPSRn4X2z+w0Os2VZCIcwpBAMAAGLNQo3uCkkB1gcA4vzYB/tvzv4Tl0F/0B8eYsXeQSHKqxAMAACIFYVAtrQUYH0AIM5PBLD+lHf9ISkD/4vNf3iINdtKKIQ5hWAAAECsWajRXSEpwPoAQJwf+2D/zdl/4jLoD/rDQ6zYOyhEeRWCAQAAsaIQyJaWAqwPAMT5iQDWn/KuPyRl4H+x+Q8PsWZbCYUwpxAMAACINQs1uiskBVgfAIjzYx/svzn7T1wG/UF/eIgVeweFKK9CMAAAIFYUAtnSUoD1AYA4PxHA+lPe9YekDPwvNv/hIdZsK6EQ5hSCAQAAsWahRneFpADrAwBxfuyD/Tdn/4nLoD/oDw+xYu+gEOVVCAYAAMSKQhQ8u+uuu4pZs2aJ/v37i8GDBxf8afKdPusDAHF+dMf6U971h6QM/C82/+Eh1mwroRDmFIIBAACxZqE21N28efPEuuuua49+5plniiFDhhiaSTGHZX0AIM6Pf7D/5uw/cRn0B/3hIVbsHRSivArBAEAnIP7111/FH3/8YUtYs2bNxKqrrqpIG7LVpMDIkSPFvvvuaw8BQJyc0qwPAMTJaZe2Bdaf8q4/JDPgf7H5Dw9xWssX0A4KYU4hGADoBMTdunUTY8aMsbk9e/ZsscEGGwRwHsW6KXDxxReLq6++2u4WgDg5dVkfAIiT0y5tC9h/c/afeAb6g/7wECvWCwpRXoVgAFAEQPzdd9+JKVOmiKlTp4o111xTbLzxxmLzzTcXrVu3VqQ5XpZCCz755BNBgJ3+LV++XLRt29b+t8kmm4imTZtGdrRo0SLx008/2fWIjtSe09ixY8WkSZPEggULRNeuXcUuu+zCt7T/EnibO3eu3e+xxx4r3nnnHTtPMcQEkDmtvfbaokmTJoLouHTpUrt4tdVWEy1btuQqsX6JXr///rtdt27duqJVq1Z2fuHChYLoSslLjz///FO8++674uuvvxY//vijWH/99UWHDh3EFltsIaiPNIn+EkGyQP+IBltttZXYeuutnfmk6ZPmTQmAOA310rXB+lPe9YckBvwvOP8leNCa5MKqtb+knWH88tJf2iOL/ulMEgDafVK/Ejxl6loCN2vQoEGWBKhOnzxn/t1nn30sCT5jjfPee+9ZRx55pFWvXr3A/iRItE477TRrzpw5oX0+/vjjTh8SSFkS9FnSuFt77rmnU05zPPTQQ0P7yXrzrrvuco3HdPH+XnfddfZQhx9+uFO/Tp06iXgkgaLVoEEDp/0BBxzgTP/uu+92ymlsogWle+65x5Kg2XWP57b66qtbJ554oiUBttNPVIb6kyDetz/qd6211rKOP/54i+aaNPG8qG3Sf0nH4vqwv+W1vyQD4D/4z7bAxG9W+dOLHqAQMAgGX4gYAOhURF2AeMaMGdZOO+0UCHx47vRLgFR+QBb6GPfdd59dT20Xlm/UqJE1evTowD6fffZZ19x+++03a8CAAa4y6r+mAeI333zTNcdrr7028Bm9Nx566CFX21GjRjlVHn30Ude977//3rrwwgtdZUH0Jj5T/bAkvc/W/vvvH6s/Gkd6+q0PPvggrMuKezy/pGA4DfjmwbMuSNxP2l+MD0CWVnZ0tIP8FVv+EEMsVw2dCX8yMfcnE/4TsTRs2liqI4ZYgiP7z9/z58+350XzPPDAA8WOO+4ottlmG/HLL7+IDz/8UNx+++1i8eLFdh36eE96bYX0WlY8y/PPPy8kmLJDI+imBLviuOOOE7vttpv953sKmaA/5z/22GNCAl2nPYVBUJgGhWh400svvST69OnjFI8fP1507tyZXpiF9ECLjh072vd22GGHqu728Omnn4o33njDHmvgwIHOB420/RrRjJMEnc6cNttsM/Hll1/atzbddFPxxRdfcLXQ3759+wqiJaUWLVqIb7/9Vkgvs3391FNPucYbNmyYOOmkk+yPKvv162d/7EfhFRRWMWHCBPHwww+LH374wW5L/22//fbi/fffd67VDIVjUEgEbSfHqVevXuKII44Q7du3Fw0bNhREB/kCI2655RaxbNkyuxqFhBBtKGwlTmJ9kAA3TnVXHT8ZcVUIuID9M2f/iCWgP+ifJYY2QK1jFxde/nS8Fal94A2p2G9IKi/T5E3yX2qt7XFLM++gNjo8xKeeeqrjCaQ/q48YMcJ3uOnTp1vNmzd36kpQ4vuncglUnToSPFkTJ0707Y8KydPMdKHf888/37euBFquekcffbR9fcEFFzjhAr4Nq1hIz89zP+usswJHuuGGG5x6VF9+BBlYl2/IlxNXqAl5f9X0zDPPuPokOlNoyssvv6xWc/L0FwAJxl1tguYhY6GdevTXgBtvvNEOUXE6UzLyRcmSH3I69Xv06KHcDc8y7eAhDqeTzrsm7R89B8bH+qtTnpP2VXT5Q8hEUo5H1C+6QEQ8XuRtk8/PACBykgkqZAXE0uvoAl4c+xo0haefftoBP/Q8w4cPd1X95ptvXPcprCEsSe+iJT2oThv6c75fIvDG9KNfij0mIG8yxQXEFB+txlFLb3nktCl2V33eadOmudo899xzrvtU9/rrr3fV8V5MnjzZ1eaQQw7xVrGkF9mSHhynHr14RKUHH3zQqU/zCAt9Ufvi5wMgVqlS3bxJ+0dPhvEBiKsr4eG9F13+AIjD+Zv4btEFIvEDexqYfH4GAJ4pZbrMCohPPvlkB8zE+ehL7nlsyd0T7I+96GMrud2Ya/7k2SRvrvwTvXXzzTeHeoe5IQFEpk3jxo252PUrd01w6lBdGbJhyT/pu+rkfREXENO8KLaZn5HaUQx0WNpjjz2c+nLXjIqqXkBMPIkTWytDYJx+5Y4TFvFLTaeffrpzn/5aEIfG9IFju3btnHa777672mVgnukBQBxIIu03TNo/ehiMD0CsXagTdFh0+UMMsVw1dKbCx9BkJIbJ5+eYSam/sZ5iyZIlguJIwxLFgdKWWJRou7H69esHVqeYV7krg+s+xYRKz6Fd1rNnT/H666+77vtd0DZiFC+qK1155ZXi0ksvdbqjrcJkaIZzTZlx48aJLl26OGX0HBRXbDJRbLQEtvYUZMiEkC8AgdOh2FqKoeZ07733Ctq2zS9Jj7K9nzTFWlO6//77xTHHHOOqSrHFqmxQzDbFFUelq666SlxyySVONdquToJZ55piiylenBLRm7a0i5POOecc5/klkLZjRVneg9rzfQmIg6oElsuXisB7YTdM6j/NC+MjhhYxtGuEqWhV7xVe/xKA/1hVi/6GEOshQyrh+c29oUtNt71oIexx3SIvIrfR8Ut/hvcm8shy3yeccIL3di7XQ4cOdeZAc6EwDm/yeogHDx7srZL7dRIPMXlR5V7OznP6eX35AW677TanHm1r5qezXg9xVKgL9+3dueLFF1/kW/avuuUebdEWN3nDJuSe0ZFNWe7gIY4klbYKfrKkrfMYHWF8c+sPsQf0Lzb94SGWq4bOVPg3pIzEMPn87BGTdinWU0jj5bvjQqzGPpUkILZ3e+BbdJAFHR7BSX64Ja655hq+1PJL3me5HZeQH+QJ+WGX/UseQfIy0+4E9I883OzlpkFpNwU+gIIn4fUQ0+4G8s/7fNvIbxIPMU1QxvgK+RGgM1cZF2wfeOIU/JUhTz8f+PFf//Vf4s477/RWsXefUD3EtGPHwQcfXFHPW/DKK6+4/kqgygTxQD0kRX4gJ2i3jDiJdiqRW+05VWlni06dOjnXfhnWB3iI/ahTnTKT9o+eCOPDQw4PeQYPeYyXzkRV8IZU7DekRMz2qWyS/3I9sD1/PtPyLSKvIu0OEPZP/onb8SbSQRhhdckTpyY6YIPnRL8U86sr0YdV3kMz1LHC8vQM3uT1EEsA6K2S+3USDzFNjrym9DEgP/tFF11UMWd5sp1r/2biqV/yeohl+IhftYoy2hWCx6dfGULh1Pnoo49c99R6SfNPPPGE029QhvuEhziIQvrLTdo/ehqMj/VXv1TH77Ho8oeP6uLzOlbNogtErIcMqWTy+RkAhEwv8a0sH9W9+uqrLgAkPZGJx/drQIdP8LPyL32wRx900cdi0pNpyZhY+4QzuXeuJfdSdtWPA4hfeOEFv6FzLUsKiGly9OxMkw033NCSccKuOd90003OfbkXsOueeuEFxDLWV70dmJf7ITv90zzUbe5ee+011z2eZ5rfOC9X3C8AcSC7tN8waf/oYTA+ALF2oU7QYdHlD4A4AbPjVC26QMR5xrA6Jp+fAUDY/JLeywKIP/nkExcAkuESSYevqE+eYQK//KyUv+KKK0J3QEgTQ1xUQOx9CfF6dmWYgUM72v83KHkBcVx6yFAGp3/iEQFwTn5gWR6UYqX5F3UUN43JMgJAzByo/q9J+0dPh/EBiKsv5cEjFF3+AIiDeZvqTtEFItVDK41MPj8DAGU6mbNZALH3o70zzjgj83w6dOjgAB0KD4izJy19EMa0od84H9XFBYCZHyikgzQeYgqD2WijjZznPeqoo5wR5Ol9TjnRLuzDNC8glrtWOP2EZYhuKq1pezxOclcTV7jGueeey7eq8svzACCuCnl9OzVp/2hCGB+A2FcwcyosuvwBEGsWlKILRFZymHx+BgBZn0FtnwUQUz/NmjVzABLtlZsl/f77764Y2bCdFNRx6PAOpg391uaQCXpuNaREfpjnnLRH8bxMB7mNmkqiirwXEFOfcRIdpMJj0O9bb73laqaeOud3cIercsYLngcAcUZCJmhu0v7RNDE+AHECcdVetejytwo9gDScSKBAjaGADAMQvEdskknJ43Xt6lLLkzQLrSvjb4U8xc2uM3v2bHv/2tAGnpvqvrPyoA0hwaiQh154arkv5dHOgsaiHQnWW289sddee9kVaE9b6SF2Kv/zn/907Xnr3FAyRMe2bdsK+TGZU0pzaN26tXNNGe8uE9LTKfr06eOqk/dF0l0meH60zzLRmnbYoCQ/QBMHHnigkDHD4tNPP7XLRo4cKfbee2877/efdx9ieaKckGDXr6qrjPZ7pn2fOckwCbHJJpvwpZAvWM7ew5tvvrn47LPPnHu6M7zLxNy5cxN3bfJL9cSTRQNQABQABXRQQPcrQtHfELLSA89v7g1d6oPtncvKQ7V9Vg+x3AbMnhPPzRvTqo5FefqTvwTBTpt9993XqSK3CnPKqT95oIRzLyjz73//29WG2tHxz97k3WWipoVMeE/s887fe33AAQc4z00f2k2cONG5Ji8tHWkdlrweYjpuWW6jF9bEvqcek73uuutadPKgmiRYduZBvBg1apR6OzD/xRdfWBLEJ/IAsszBQxxIVu03YP/N2X9iJugP+mdRaoRMZKGeT1sopDmFZADgw5bURVkBsfTOWWosbO/evSt2PlAn9/TTT7sA09133+3cpphXfkb6Pe+885x7fplHH33U/gBPegpd7Wi3A2+qiYBYPdSEds1IkujFg2lFYFY9QnvQoEGRXXkBMfV16623hraT+0E7Y1J9v23fCJz+7W9/c+rtvPPOofJAA9JLkjyFz25Dxz3LU/tC58E3+fkBiJki1f+F/Tdn/4m7oD/on0XLAYizUM+nLRTSnEIyAPBhS+oi8sJS7Cn9W7hwYap+CBjx3Oj3oIMOsugDK2+irb1UEEjxx/PmzXNVI68j90WnrPl9IEcNaB/hunXr2jHH3l0mhgwZ4uqTLmoiIKZt0fhZZdhHhbe14iGUAtpurU2bNk57Gabi5Gm3h6jkBcQUi1yvXj2LYoT90ldffWXRHHm+tPvHzJkz/apaXn706tXL+vnnn33rkj05/PDDnX6pf9pJI07iuQAQx6GWnjqw/+bsP3EQ9Af9s2gyTqqTq4bOhJOCzJ0UxDGTUiF0sjRzX/PnzxcdO3a0T5HjzuikOIpPpnI60Y5OHpPH/PJtIXdBEBL4iO7duztllJFeSiF3q3DKKM747LPPFu3atbPjrmU4hKBT1ag/SldffbU45ZRTxNprr00vv3bZOuusI6R32e570003te/VxBhi+eIgnnzySXvO9J98QbBjgYk2xGs6TS8s0bNffPHFripE87fffttV5nfhjSGW26eJgQMH2lX79esnOnfuLNq3b2+fADh+/Hghd5MQ0oPvdHXssccKuTOFc61mZBiFfUKdPKjDKaaYZ4ppphhxko0ffvhByO3YhHwhEyQ/nI488kghj3Hmy9Bf1gcJiEPr+d2Uf9XwK44sg/0zZ/+IOaA/6G8y/r/w8pcFTfu1xRsa3tD85CKPMrkeEOLLY6jEY8hje12HRvBc/X4pxCIoPphiX7t06WI/p19btWzw4MH2n9tpsuqBFWod3gWhJnqIvXNS502HkEQledyx7SVX28XdPs3rIaYT6OivBN7wE7VvzssXkMgYZdoxhA7tUD3X3D7o95xzzokMr1Bpwv3AQ6xSpbp5rH9Y/6orYeG9Q/6yyZ929ACGZGNIuLhH3y0z/RkARFPJXA36yE16hS2KBeX58i/9SZ5iXeUuCaETXLp0qUV7C1NsLLflXwJsPXv2tD/AUjuhPqUH0gXoaA7SM2xX84LPmvBRHU3sP//5j0XhCvx89EsgkmJq46T99tvPaUv90N7QcZIXEL///vt2M/oIjuJ+1fnwnOSuEZb0Wsfp3qlD+0j36NHDtT2f2neDBg0s2kuZX1ychjEy3A8AcQxiaapSZvtLJMTzY/3XpEqpuskqfwiZkKuGzlT4PxlkJIbJ5+c/EUtNyvgU1W9O26FNmzZNTJ06VdB2cRS6IGNeBW05FzfRtmIUIiF3IBDSEIgWLVqIjTfeWKy//vqBXVA9Gdtqhx/IeOTAejXphoy3Fp9//rmg7cNouziik3x5iDVFdds8Ch257bbbYrXzhkxQCIo85c5pS9vYybhhO7SB6L7ddtsJ2iYuS5Knzwl5uqGQnm3RvHlze4s/eta0fwJlfUDIRBauJGtr0v7RTDE+QibS2otkku5fu+jyB0Dsz9fUpUUXiNQP/ldDk8/PAKAIgDgrndE+mgLS6y2kN9euSLJBexDT3r9xUhQgjtOH6TqsDwDE+XHCpP2jp8T4AMQAxGukVngA4tSk828Ig2TOIDEAACD2l82ylcrdG+wPE+m5Kf/yyy/HJgEAMT6qiy0sSkXYf3P2n9gA+oP+WV4IAIgVY6YjC4U0p5AAxDokuHb0QaERp512mvMw5C3eaaednOuoDAAxAHGUjPjdh/03Z/+JH6A/6A9ArFgmKER5FQKAWFGEEmfvueceIT9OFPLjQ5sKhx12mHjkkUcSUQSAGIA4kcD8VRnrT3nXHxIB8L/Y/IeHOI3VC2kDhTCnEADEIYKp8dZDDz0kxowZo7HHlV1tu+22NphdWRKde+CBB+wP0eThFkLu2uDswUwt6SM8+iBOng4X3ZFSA4AYgFgRh9hZ2H9z9p+YBPqD/vAQK+YKClFehQAgVhShitkTTzxR3HXXXVUZoW/fvuLZZ59N1DcdlOHXhnZ/oMNO5J7FifqjygDEAMSJhUY2wPpT3vWH5AX8Lzb/4SFOY/VC2kAhzCkEAHGIYGq8RSfl3XfffRp7XNnVXnvtJUaMGLGyIEbOC4jr168vKEzi+uuvT+wZ5uEAiAGIWRaS/ML+m7P/xCfQH/SHh1ixWFCI8ioEALGiCCXKzps3T8yaNcvep5iOsqY9nddaa61MFKBjmOVhHE4fXbt2FU2aNHGui5BhfcC2a/lxC+tPedcfkjLwv9j8h4dYs62EQphTCAYA2HZNs1Cju0JSgPUBgDg/9sH+m7P/xGXQH/SHh1ixd1CI8ioEAwAAYkUhkC0tBVgfAIjzEwGsP+Vdf0jKwP9i8x8eYs22EgphTiEYAAAQaxZqdFdICrA+ABDnxz7Yf3P2n7gM+oP+8BAr9g4KUV6FYAAAQKwoBLKlpQDrAwBxfiKA9ae86w9JGfhfbP7DQ6zZVkIhzCkEAwAAYs1Cje4KSQHWBwDi/NgH+2/O/hOXQX/QHx5ixd5BIcqrEAwAAIgVhUC2tBRgfQAgzk8EsP6Ud/0hKQP/i81/eIg120oohDmFYAAAQKxZqGtRd40aNRKLFy+2n+icc86x9yquRY/nehTWBwBiF1mqegH7b87+E2NBf9AfHmLFxEEhyqsQDAAAiBWFQNZFATKWDIgHDhwobrzxRtf92nTB+gBAnB9Xsf6Ud/0hKQP/i81/eIg120oohDmFYAAAQKxZqGtRdwDE8Zi55po4qS4epdy1YP/N2X/iBOgP+sNDrNgkKER5FQKAWFEEZH0pAEDsS5aKQgDiCpLEKsD6U971hwQE/C82/+EhjmUJCGXlAAAfA0lEQVTm4leCQphTCADi+HJa1poAxPE4D0Acj07eWrD/5uw/8QL0B/3hIVasEhSivApRDUD866+/ij/++MOWsGbNmolVV11VkTZki0YBAOJ4HAMgjkcnby2sP+Vdf0gWwP9i8x8eYq9Fy3gNhTCnENUAxN26dRNjxoyxpWL27Nligw02yCghaG6SAgDE8agPQByPTt5asP/m7D/xAvQH/eEhVqwSFKK8ClEEQLxgwQIxffp0MWvWLPvfn3/+KdZff33735ZbbinWWmstRZorswsXLhTz5s2zb9Dztm3b1qlEfb377rvi66+/Fj/++KPdZ4cOHcQWW2wh6tat69RLkiEP+dSpU+1/tFvBVlttJbbeemvRqlWrJN1U1K1GvzNmzBAffPCB+Pzzz0XTpk3tOfbs2VM0bNjQGR+A2CFFaAaAOJQ8gTex/pR3/SGhAP8Lzn/5Rb7WtGjRIq39Je0M45eX/tIeWfRPZ+ratavdJ/UrPcSpu/7444+t/v37W/Xr13f64/nyb4MGDawjjjjCGjt2bOA4d999t6u9NMB23XvuuceSINV1j/tdffXVrRNPPNH6/fffA/v13qD+WrZs6dsf9SuBu3X88cdbEiR7m4ZeV6Pf4cOHWzKcxXeuEthZZ5xxhrVkyRJ7XkRjpovcdi10rkW/yc9JPEr6L+2zw/6W1/6SzID/4H9a26GjXVb504seoBAwCAZfiBgA6FAs7kMHICbAxnOL81unTh3rgQce4Cm4fh999FFXX99//7114YUXusqCxthpp50sqh+WpPfZ2n///WP1R+NssskmlvTKhnVp36tWv5dcckmsuXbq1Mn67bffLALITB95MEfkvItcgZ8zKRhO+pKj0ijrgqT2lSaP8QHI0siNrjaQv2LL3yrEQGk4kUCBGkMBCQjF8uXLE8+H/zQujVvitkENssYQv/fee2LXXXcV0jtrD9G8eXNxzDHHiM6dO4u//e1v9EJqhze8+eab4pFHHhEUSkCJwiFeeukl0atXL/ua/3vqqafEgQceyJdi2LBh4qSTTrI/9uvXr5/Yd9997VABCquYMGGCePjhh8UPP/zg1N9+++3F+++/71yrGQrHoJAICufgRONLr7Vo3769HXrw6aefitGjR4tbbrlFLFu2zK622mqriTfeeEPIlwdu5vqtVr//+te/xKBBg5yxGjduLM477zybtn//+9/FZ599JiZOnCiGDh0q5syZY9NpxIgRDo3ppLqbbrrJaV/bMhxCNHfu3MSPliUOL/FgaAAKgAKgQE2ggK43I+4Hb0jFfkNiPqb9Ncl/qU+29y/t3P3aZfUQH3744Y5HUsb7WhKc+g1jl0kgasn4XKf+3nvvXVH3mWeece7T88qXAKtevXrWyy+/XFGXCmRcrbXpppu62siPBH3rXnzxxU49CaYseYqbJeOSfet++OGHlvzA0Knfo0cP33pUWI1+ly5darVo0cIZn0ImaE5+iWiwzTbb2HXlLiFOG3iIg0Mp/OgYp8yk/tP8MD7WnzhyWq06kL9iyx9CJjRrBhTCnELUREBMIQU8r0svvTRS2t5++227PgG8HXfc0f4zv9roueeec/rjfq+//nq1SkV+8uTJrjaHHHJIRR0C6tIr6NQ7+uijK+p4Cx588EGnPs1Feo69VewXgGr0+/jjj7vGvuuuuyrGVgu++eYbi0A+04x+AYgBiFUZ0ZGH/Tdn/4l/oD/on0WPAYizUM+nLRTSnEIy2PFhS+qiLB5iGfZhe295XpdffnmseVCsa1DyAuImTZrE+rCNPaQ0F7njhDV//nzXEKeffroDFukjPPJWRyXyHrdr185pt/vuu1c0qVa/u+22mzOuDNmwfv7554qxvQV77rmn0waAOBgMI4bYKznxr2H/zdl/4hLoD/rH19bKmtiHWK6MOhO2XTG37QrHTEoxj8VSufOA6Nu3b2hdirfluN5ddtlFyF0iAuvLXQuEBF2u+9TmnXfescs233xzQTHFFOuaNj3//POuOcsP4ATFFUelq666SsgP0JxqkyZNEhLMOtcUWyxDDuzrLl26CLnThXMvLENxuDfffLNdRQJpe9sh5gMVVqtfir/m2FiKc5YhI2HTtO9RjDbFQ3MqSwyxBLj8yLF/se1abFK5KsL+m7P/xAjQH/TP9P1DJUbOVoI3NLyhZZOg9K2lPbQ9gHF7IE8st9HxS1uKedOVV17pGqN169bWY489Zi1evNhbNda110N83XXXxWr30EMPuebx4osvutrJfXud+7RFW9zkDZv46aefXE2r0a88OdAV/jBgwADXmEEX48ePd56R+I2QiWAvcRANo8ph/2H/o2Skmvchf5C/LPIFD7FcGXUmvKGae0Nlz6RUiFgslcZTpPWE+Q0gAbE47rjjXLfkn/JF79697QMj1Bs0bvfu3YX807+9kwTt7hAneT3EElyLgw8+OLLpK6+84vJeq3MlDzgdZMFJfiAn5BZtfBn6K7dxE/fdd59Th3a2kFuc2dfV6ve7775zHQxy0UUXiauvvtqZQ1Bm5syZQr6QOLfhIXZIUZFJqxewf+bsHzER9Af9M3lIKyxBsoKiyx8AcTJ+R9YuukBEPmBEBZPPnxQQE3AmkBSWDjroIAfMUrjDeuutF1h9nXXW8QXY0hNtb5VGoDQobbjhhkLuKiH+8Y9/hIJRLyCmrdm8YRp+Y3z00UeiY8eOzi0KoRg8eLB9TVuTbbfdds69LJknnnjC2RauWv1KT6+9tRrP87//+7/F2WefzZeBv7T1HYV1cAIgZkpU/gIQV9IkTolJ+0fzw/gAxADEa8RRVf86WdzLfm3xJwv8ycJPLvIokxJu/0lc51hZPqrzzkOCV0vuE2zRR2s8V79fGRNrSS+ot7l97Q2ZCDvVTu3gyy+/dI15/vnnO7dfe+011z2/OcUtk/HEVe935MiRrvlG7TDBE6KPHLHtWnCYhHqAB9Ms6S/sP+x/UpnRWR/yB/nLIk/wEMuVXmfCG7q5N/SkHuI4fM96MIffGCQjr7/+un3whgSjQoLVimpy9whBh3XQgRhq8nqIX3jhBdGnTx+1im+ePg7cYYcdnHt0IAV5SClNmzZNyL2KnXsSLIujjjrKuU6SIQ/6uuuuazepVr/jxo0T9OEfpxtuuEGce+65fBn4Sx/h0cd4nOAhZkpU/sJDXEmTOCWw/+bsP/EH9Af9M3nIs6Bpv7Z4Q8Mbmp9c5FEm7aHtOdQ5lk4PcdC86OAI2ku4TZs2Ls+nBMMWfUCmJq+H+N5771VvB+YlcHb1LU+wc+rK3TZcH6lJcOncy5KpVr/Tp093PcsFF1wQa5pTp051tZOAOFa7olZifVA9v3HzaZ8Z9h/2P63s6GgH+YP8ZZEj7EOchXo+baGQ5hSSAYAPW1IX5QGIeXIkO3IbNRdok0ci82371wuIr732Wtf9oIvhw4e7+n3rrbdcVdVT5/wO7nBVTnBRjX4JaDOv6feEE06INSPplXe1AyAODp+IRVCfSrB/5uwfsQP0B/191DK3oqLLHwCxZlEpukBkJYfJ52eQlPUZ1PZ5AmIalw6YkKEfDnAbMmSIOh3LC4jjnChHHcg9iJ0+iU4UU6ymnXfe2bkv90tWb2XKV6vftdde25kvjREn0UmBLCP0C0AMQBxHbpLUMWn/aJ4YH4A4ibzqrlt0+QMg1iwRRReIrOQw+fwMdrI+g9o+CyCmfY7HjBlj3XLLLZbc5UHtNjQvY3Ad4Ca3E3PV9QJiGS9lLViwwFXH72KzzTZz+qT+vaEY3v2SR40a5ddNRdkXX3xh0UduQXyvVr9yyzrneegFQu4WUjE3tYA+qGvVqpXTBoA4GAxTWEXaFCQHaftL2g7jAxAmlRmd9SF/xZY/AGKd2iD7gkKYU4iaBoj79evnADA6NjhOkvv6Om3oeV599VVXMy8gpjq33nqrq4734oMPPnD1Kfft9Vaxj3+WH5w59cjrSiAyLNHRzXyEMu2ccdZZZ1VUJ3BVjX4pBpr5Tb/XXHNNxdhqweOPP+6qT23gIQ4GxSrtkuRh/8zZP+IT6A/6J9FX3XWLLn8AxJolougCkZUcJp+fAVLWZ1Db33///Zbcs9f+t3DhQvVWZN67ndlpp51mLV26NLAdxcbSlmv8HHXr1rXk4Rau+l5A3KhRI6tevXoWxQj7pa+++spq27at02edOnUCvalDhw516tEcaC4UwuGXiM+HH364q74XvHO7avQr9xS2mjdv7oxPtKLT+PwSgWeiUYMGDSy5e4LTxg/A+7UvahnLUdwP6dR6aZ/ZpP7TnDE+AGFa2dXRDvJXbPnDtmty1dCZsO2LuW1fqrHtWlbZ2GOPPQRtrcaJtv2ik+W23HJLZwswedyx+Oyzz8SIESMEnWzHSe6vK+QHY3xp/3q3XaPt0wYOHGjfkx5p+8AK2qqNTomjAywkGBTUP6djjz1WyJ0p+NL1K8Mo7ENB6BAPTi1btrQPDOnQoYN9OtwPP/wgpkyZIuSLgpg/fz5XE0ceeaSQxzg712qmWv3S6XQXX3yxM5TcY9g+9W/HHXe0T6T7+OOPxYcffijeeecdevEXN954oxg2bJiQLwl2m9NPP13IcBanfW3LsD5IoJv40bDtWmKS2Q1g/83Zf2IA6A/6Y9s15dUOb2jFfkNTWJk4K+2h7f1L3LCKDRYvXmzts88+jleS5xj2S4dH0AdgfsnrIZaAz/Zeqx/iBfV9yimnWMuWLfPr1ikjzysd2qEeYBHUH5dT6EFUeEW1+qUY6zjPfuihh9rPvu222zq8OPnkk53nro0Z5o/q+Y2bT0sP2N/y2l+SGfAf/E9rO3S0yyp/CJnQwQWlj6wMUbpKlS3z+AwAUhGuio0oTOKpp56y+vbta9Gf9nme3t+GDRtaFFZBYQ5ByQuI5YEbdlX6CE7d0YH7JmBLu0bQh31J0ujRo60ePXpYzZo1850vhR/Iwzss7/ZtUWNUo98nn3zSIqDrR9tNNtnEFWNNz8S0kV7tqOkW+j4/Z1wQrNZL++Bltj9EMzw/AGFa3dHRDvKXTf4QMiFXDZ0Jf7Ix9ycb/hOxNCw6Waq1Lwk6xOzZs8WPP/5o/5MxvYLCEugfnfJG12HJGzIxYcIE0alTJ6eJPPLZDgmg0IYWLVqI7bbbTsg4Y+d+msycOXPEJ598IuQHf0LG7Qq5t7CQh4iITH+akhPR3a/0QgsKk5A7Xwi5LZsd4rHVVluleeRa0Yb1gWQuaULIRFKKragP+2/O/hMHQH/QP8u6BECczu4FtoJCmlNIBgA1GRAHCk7MG1GAOGY3qFYCCrA+ABDnx2zYf3P2n7gM+oP+AMSKvYNClFchGAAAECsKgWxpKcD6AECcnwhg/Snv+kNSBv4Xm//wEGu2lVAIcwrBAACAWLNQo7tCUoD1AYA4P/bB/puz/8Rl0B/0h4dYsXdQiPIqBAMAAGJFIZAtLQVYHwCI8xMBrD/lXX9IysD/YvMfHmLNthIKYU4hGAAAEGsWanRXSAqwPgAQ58c+2H9z9p+4DPqD/vAQK/YOClFehWAAAECsKASypaUA6wMAcX4igPWnvOsPSRn4X2z+w0Os2VZCIcwpBAMAAGLNQo3uCkkB1gcA4vzYB/tvzv4Tl0F/0B8eYsXeQSHKqxAMAGozIKZjmOVhHI7Ed+3aVTRp0sS5RgYUYAqwPgAQM0Wq/4v1p7zrD0kX+F9s/sNDrNlGQiHMKQQDgNoMiDWLK7qrxRRgfQAgzo/JsP/m7D9xGfQH/eEhVuwdFKK8CsEAAIBYUQhkS0sB1gcA4vxEAOtPedcfkjLwv9j8h4dYs62EQphTCAYAAMSahRrdFZICrA8AxPmxD/bfnP0nLoP+oD88xIq9g0KUVyEYAAAQKwqBbGkpwPoAQJyfCGD9Ke/6Q1IG/heb/6ssWrTIys9cYCRQIJoCderUEcuXL4+u6KnRsGFDuwSA2EMYXJaSAgyI586dm/j5s3hZEg+GBqAAKAAK1AAKIGRCMxPwhmjuDZEBAACxZqFGd4WkAOsDPMT5sQ/235z9Jy6D/qB/lpd5AGLNthIKaU4hGQAAEGsWanRXSAqwPgAQ58c+2H9z9p+4DPqD/gDEir2DQpRXIRgAKOKALChQegoAEOcnAlh/yrv+kJSB/8XmPzzEmm0lFMKcQgAQaxZmdFcrKABAnB8bYf/N2X/iMugP+sNDrNg7KER5FYIBMUImFIVAtrQUYH0AIM5PBLD+lHf9ISkD/4vNf3iINdtKKIQ5hWAAAECsWajRXSEpwPoAQJwf+2D/zdl/4jLoD/rDQ6zYOyhEeRWCAQAAsaIQyJaWAqwPAMT5iQDWn/KuPyRl4H+x+Q8PsWZbCYUwpxAMAACINQs1uiskBVgfAIjzYx/svzn7T1wG/UF/eIgVeweFKK9CMAAAIFYUAtnSUoD1AYA4PxHA+lPe9YekDPwvNv/hIdZsK6EQ5hSCAQAAsWahRneFpADrAwBxfuyD/Tdn/4nLoD/oDw+xYu+gEOVVCAYAAMSKQiBbWgqwPgAQ5ycCWH/Ku/6QlIH/xeY/PMSabSUUwpxCMAAAINYs1OiukBRgfQAgzo99sP/m7D9xGfQH/eEhVuwdFKK8CsEAAIBYUQhkS0sB1gcA4vxEAOtPedcfkjLwv9j8h4dYs62EQphTCAYAAMSahRrdFZICrA8AxPmxD/bfnP0nLoP+oD88xIq9g0KUVyEYAAAQKwqBbGkpwPoAQJyfCGD9Ke/6Q1IG/heb//AQa7aVUAhzCsEAAIBYs1Cju0JSgPUBgDg/9sH+m7P/xGXQH/SHh1ixd1CI8ioEAwAAYkUhkC0tBVgfAIjzEwGsP+Vdf0jKwP9i8x8eYs22EgphTiEYAAAQaxZqdFdICrA+ABDnxz7Yf3P2n7gM+oP+8BAr9g4KUV6FYAAAQKwoBLKlpQDrAwBxfiKA9ae86w9JGfhfbP7DQ6zZVkIhzCkEAwAAYs1Cje4KSQHWBwDi/NgH+2/O/hOXQX/QHx5ixd5BIcqrEAwAFHFAFhQoPQUAiPMTAaw/5V1/SMrA/2LzHx5izbYSCmFOIQCINQszuqsVFAAgzo+NsP/m7D9xGfQH/eEhVuwdFAIKkUYhfvvtN0WK0meXLFkiVl999fQdeFouWLBA9OjRQ0ybNk3EATa6x/dMJ/IS4+vl/8yZM8VWW20l1l13XXH77beL3r17h/JAF/3XXHPN0HGCbsL+wv6msb9B8pS0HPIH+csif/AQJ9W4iPpQyGIqZE0ExASGd9llF/HNN9/YUgdAHKF88rYuQBg9kn+NaozfrFkz8fvvv9sDnnLKKeKiiy4SjRs39p2ArvEBiH3JG1kI+19M+x/J2JgVwP9i8x+AOKagx60GhSimQtREQHzEEUeI559/3hE9AGKHFIEZXYAwcICIG9UYf6+99hLvvPOOMzKB4WHDhol99tnHKeOMrvEBiJmiyX5h/4tp/5NxObg2+F9s/gMQB8t2qjtQiGIqRE0DxCeffLJ48MEHHU8geYtnzZrlXAcJpy5AFNR/VDnG1xsyQfS+5pprxLXXXiv2228/8euvv4rRo0fbbOjWrZsNjFu1auWwRRf9AYgdkibKwP4X0/4nYnJIZfC/2PwHIA4R7jS3oBDFVIiaBIhVMPzWW2+Js846ywZBL7zwgiAQFJZ0AaKwMcLuYXz9gJi8w+Qlbt++vZg4caIYMmSIuPzyywW9JJG3mEIoKJSCki76AxCHSXnwPdj/Ytr/YI4muwP+F5v/AMTJ5D2yNhSimApRUwAxeYUJEFN68803xa677mr/I68gAHGk+mkDhNEj+dfQBUi9vTdq1Mgu4j22yVN87LHHimeffdYu33bbbcUdd9whNt10Uy0fdQIQezkQ7xr2v5j2Px53o2uB/8XmPwBxtIwnqgGFKKZC1ARArILhe++91wY8JHwEigGI46lhtQBpvNH1eWi94/Xp00eMGTPGeUni+/QXBALG3377rV00YMAAcckll0SG1nD7oF8A4iDKhJfD/hfT/odzNf5d8L/Y/Acgji/rsWpCIYqpEKYB8ciRI8Xhhx9uy5gKhqkAgDiW6tmVaisgvuCCC+xt1y677DI7XEKlCHmLKYRi6NChdjHFFNNHd1HhNWof3jwAsZci8a5h/4tp/+NxN7oW+F9s/gMQR8t4ohpQiGIqhElAPGXKFDtGlGJCzzzzTDtGVBU6AGKVGuH52gqI+YWpe/fugrzCfmnSpEm2t3jy5Mn27X333dcOowjaos2vDy4DIGZKJPuF/S+m/U/G5eDa4H+x+b/KokWLrGD24g4okD8F6tSpI5YvX57rwGTITKSpU6eKfv362R9I/eMf/xD33XdfxTTI+3fFFVeI8847T5x//vkV91FQ+ylAB3R07NhRNGnSRMyfPz/0gb0f3ZHMnHjiiaFtvDezbG7v7QvXoAAoAAoUgQLwEGvmEt4Qi/mGaMJDTB5hOoWMfoPAMIknA+ILL7zQ3lEgTGRrq4c07JnVe7X5+bfcckvx3Xff2TtN0I4TYWnGjBn27iT80Z3fFm1h7eEhDqNO8D3Y/2La/2COJrsD/heb/wDEyeQ9sjYUopgKkTcgJhBMW2lRuES7du3sP4OT988vARD7UcW/rDYD4sMOO0yMGjVKeGPM/SmxovSZZ56xwyhI3ijRFm30YhWVAIijKOR/H/a/mPbfn5vJS8H/YvMfgDi5zIe2gEIUUyHyBMRJwDAJGwBxqMq5btZmQHzbbbeJQYMGhf41wUWMvy7SfHQHQOxHyegy2P9i2v9ozsarAf4Xm/8AxPHkPHYtKESxFSI2owMqxuH//vvvL8hz17p1a0EfQgV5hnkIBsR+OwxwHf6NMz7XrcYvxq+e/JOsdOjQQbRp00ZMnz49MfvoYzw65IU/uqPt2m6++eZI+UsyEPhfPf7H4QPoD/qbjP8vuvwBEMexMgnqFF0gEjyqb1U8f7hB7t+/v/3hHH35TwAlKhaUiEzgmUA0Hd1L+bAE+ofTP4x2Ou5Vm/6rrLKKPU36sC7qRSroefgFi+5THxSCQR926kjVfv6oOWL82i3/4H84BSD/2eQfgDhcvhLfhUBmE8jEBPc0qMn0TwOG6fEIOPfo0UOEbbnFZKjJz89zrOZvbX9+3oLv6aefzgRi6aM78hDTgS+UqF8CxuR9zpJqO/2jaIPnh/2Hh3aNKDWp2v3M+iePAtWaaBs3kwnjg/41Uf4k2KDtDe1/8kjmRFOk+tRWAuLIdpD/2i3/MmzGlgX61ZFILuVfK+w+pbfYkt7jTN1C/mq3/EUJB/gP/kfJSDXvZ5U/eIg1v6tkfkPJOB+MX/M8FLS3MHmHKZEXjjxzSRI8xPGpVdvln8Nn4vy1IC7V6KM7kkneoo3CeEhO44TzeMeo7fT3Pq/3Gs9f8+yvl0fVvAb/i81/AGLN2gGFKLZCZBUHL/8ZwFC/acAwtQMgJirES176x2ulr1a1xyfw2rRpU3vC0tOib+KyJ5IzAsbffvut3S99gEcfciaJVa7280c9MMaH/UXIQoFDFqIUPOJ+Vv0HII4gcNLbWRmSdDxvfYxfcxYE2hWAYn8JxPgdyezlXdB1kt0FwP+aw/8gfmYtJ88t7RQxceLEVF7csPFJVumkOzoZkRLFFNNOFHE/uoP81X75C5Mf8B/8L/ILCQBxmHanuAeDAINABkEFw2Gn0MUVMd5dIMorCPmr/fJHXtz777/fBqrkxa1GIvmlcXiLNgLE9BeOKG8x5K/2y1+YvIH/4D8AsaIhUAgoRJEVQhHlVFmS/zlz5tj7xZK3TQcYpokAEMdjRxnsD8ekx9mGLx7VgmuRt5i2aaPDZAgMU57+2hGUykD/oGencjw/1r+yr39Ffn54iMOsW4p7MIjlNojff/+92HvvvW0PMR3JTJ42HQmAOB4Vy6B/SUJo4lEtvBZt0UaeaP7ojrZoozAKv4/uykD/MGrh+ctt/8H/YvMfgDjMuqW4B4UotkKkYLnThDzC9PX/lClTBIFh+kgp6k/MTuOIDABxBIH+ul0W/SO5Iq8tnViXde/geJRdcUAMAWP+6M7vI9Gy0D+IZnj+8tp/kgnwv9j8ByAOsmwpy6EQxVaIlGy3m9EHdASCdYNh6pwBcdQJZZC/csifrgM6kso7vfTR8dHkNQYgrqQe9K8c+lfJ+RUl4H/B+a97k+SsGyNnnQ/Gx8bgWWUoTXv5AZJ9uAEdciC//k/TRWgbOpRDmlwr6lAPyH855J8P6JDxvKFyo/MmybUMk7DlkGRRhk1UdA/5K4f8VTD+rwLwH/wPko08yrPKHzzEQa96KcvxhljwN8QUfE97JHOSodgjKAGxoHxQgvyVQ/7oLxH0FwmK46Xt16qdhg4dan9QRx7i1q1bC9pfGzHElVSH/pVD/yo5v6IE/C82/wGIgyQ7ZTkUotgKkZTt9BX+2WefbTerxr6wPB8AYqZE+G+Z9I/DaKTnJZwoGe4SAKYXPgLAlGjXFJL5oNj4MtHfj6x4/nLZf68MgP/F5j8AsVeiM15DIYqtEEnYz9tfURu/eMokfUXVBSCOotCK+2XSP/LQ0j7BUX81iEe5yloEggkMEyiWoUCC5D3qgI4y0b+SYvioCvwvz/pXG+X//wEAAP//wUGuJAAAQABJREFU7X0H/B1F1fYg1vBJRBRQlKKCgiXEChZCFJEiBCwoWDAWUEGKigVLEgUVLAEVFQtFxa4YUVEshBc1YgVUwIIxgNhQBAy+orjfPJv3LHPnzuzO3Nm9d8szv9//v3dnpz7nzJmzs2fOqKzmsHbt2ppLjCuO9RP/OI6ZLPVpp52WKaXyP/xuOixYsCCv67zzziutivw/HP4/4ogjcp5YsmRJKU/EPrzuuuuyI488suBv8B7iQgL5bzj85+IH0p/0d/HFtOJS+U/V3dDUBqW2h/VzQKbyUFX+n/70p9ld7nKXRpQRX92i/CxfvtyXJI8n/w+H/+WlbNGiRaU8EfMQvL3DDjsUynAVv9llk/+Gw3827XFP+pP+Lr6YVlwq/62HhuqVrtrCTTfdpObMmVNbebEFsX7i3yT/XXTRRWrhwoXq73//uzrooIPU6aefHsuiE6VfunSpWrZsmdKrgQq/fYH8Pxz+/93vfqe23nprpV/OlF7B9bFEcDz4S3hr3rx5OW9r5Tg4PxKS/4bDfy7GIP1J/ybnXxfPmXGp/EeF2ESzht+pBEltAutvTiBBAZk/f/7UlWHwBBQVKsTVo2No/A9l+Prrr1erV69WW221VTVAjhTg68WLF6uVK1fmT/XXCHXiiSc6UlZHDQ1/GxH2vzn5a2Ptuif+xD9JIa97KTt1yTq1Payfn2xSeciVHzaU5qfkXXbZJdOrw8G2la4yY+JgJ6ongKzKXpT8Pyz+h7kE+GJSO/azzjqrMP+ZO3duVmWjXsWz5L9h8Z/ND6Q/6W/zxDTvU/mPNsQ1UyuVIKnNYf3NCSQoD9pMIoPiACVE/vbdd9/si1/8YirpSvNTIS6Fp3g4NP6HjS/4EHwZE/CCB74VHtarKpleKY4pwpl2aPjbILD/zclfG2vXPfEn/i6+CI2jyYSeEeoM/GTT/082sB/WCnD+t2LFioJ98PlaKxkKn5xjbS+LQjw/YKuMz9pa8cltOz3JaMM5sD0MMHOATTv4TW+I87HFSDzygJdgKqFf7tSGG26orrrqqpxvJzWVkAoo//ov/4TWrivpT/onmSy4mCoiLpX/qBBHgB2SNJUgIXWUpWH90xVIUCqgHENhvfjiiwvSwJ5TlONJbTuLwvQPUXy0C6z8t/nM/E36T5f+Jvb4PQv811tvvbwZ2FiHl7KyYG+cA+/iBQ+28Qj6K0jOt2VllD2bRf/N9rD+4fE/6X8rAuT/RP4PXUoOTcdPFvxkEcorTaSbJf/pjU3ZoYcemm255ZbFp2gtqnLbY73ylmRvDNtOlAWfsGVhlv1Hu1j/9Mc/eAK8UWb/a7tTs23RxfRCK9RJfEr6T5/+pjwg/sTf5Idp/+46/9GGuGaO6TpDpMLB/q8TyFBOYNfpsjfWq8nRSgcV4jDOHCL/iY9qW8kVxPAyBkUXSjNe1nyKsyjW2DA6aRgi/iZW7D8VUpMfpv2b/JfGf1SIa+ZYMmQaQ6aSo434YzOeeAOAUoI/KCjPe97zgjfjUSEO44w20j+s5ZOnAn+Bp+yvB/bGObygIc4X8Exe4GIP5JAyh4i/9B1X9p/y3+SHaf8m/6XxH22I9UxSZ6ANT6INTyIx2oo/bDX3228/tfHGG6t73eteTntjbJjzbcbDgSCw86zaPNXW/ieSNTj7EPsPG+CNNtpo5IAO2JyD3/AMG+dg4w6b9qogfApbZP0S5uVHXzlDxN/Egv2n/O/ypjKTlyf53XX+Xw9vFJN0nHmIQFMIrL/++uqWW25pqviZlHvwwQerM888Ux1//PHqsMMOU2vWrFFnn322Ovnkk9WVV15ZtAkb8I488kilV5SVvRlPNk/pMVuk5w8iAAS22267nI+gxMLziXiLeNzjHqdOOeUUpU0lgoF61atelfPlQx7yELVq1argfExIBIgAEegyAlwhrpl6XX9DSoWD/R9fIcEqHY7YxdV1ohhWf7GChz+cOiZB23IqbVaRK8dYsROFWH+GkyRjV+I/jv8YSA1GzAp/8MkZZ5yRrxKDzxC02UP+chXbXeTHlwi8tMWeWjer/ksfWf8w+Z/0X4cA+T+N/6kQy0iq6UqGTGPIVDK0EX8ouvD7qm08S12moe/4ZC1/pnKMz92IR6BCnMPg/NdG+jsbWnMkVoSPOuqovNR58+blL1c+85uQqsVEB2mx6oyXs5AwVPwFG/af8p8mE3NkOEz9mjr+qBDXTLJUgqQ2h/W3TyBDmcVnbH28br7iG0JjrNKJYmwe/oG8VIj9CA6V/0WB1W7/1LHHHlvpj9iP4K1Pli5dquC3GKY7OPQDXymqwlDxF1zY//bJX6HNNK6kf7fpT4W45lHCAdHtAZHKDjb9cXAHzCUQQg5OcNUvh39go5SsErvSIc6u35euqXjWPzv+B3888pGPVHWuUGFl+Pzzz8835OHQjqpA+s+O/qAN8Sf+dY7/qvFuP+86/1EhtimaeN91hkjsPgWydXSwfMrGJrkqZTYVe+Qn/3FCrHNCxMsYTC9gvhPyhYP8R/6rk/9iZSL5j/yXwn9UiGNHXEV6DkgOSHNAwlUaPmenHolbwXbFY/If+c/kv4IxEn6IDTxMJmA6ARMKXyD/kf/q5j8fr7niyX/kvxT+o0LsGlUJcRyQHJAyIMVcAn5gZed/AmsFZSX/kf+E/4IYJjCR2MHTD3Y5YBx/HH9NjL9yrrv1Kfkvjf+oEN/KS7X8IkOmMWQqEdqEP/wJn3TSSQoHbmCVbRqhTf2fRn/tOtj/Zsaf6YpNHxGtsOHOFYh/M/i7sHbFEX/iT4V8ci8XVIhdUiUhjgKJAkkEEjbTYZUYn5lTXGDFsCP5j/wn/BfDNyFpsWlv4cKFeVIfT5P/yH9N8V8Ij5L/yH8p/EeFOGSURaThgOSAxIAU5QEnhEEpnlYg/5H/UiaEKj6Vrx4+V2zkP/Jfk/xXxZ/kP/JfCv9RIa4aYZHPOSA5IDEg5eSw2JO+ItltLDn5j/yXMiGMMZQjAl87Lr744pzH4XnCDOQ/8l/T/Gfym/2b/Ef+S+E/KsT2iEq854DkgMSA3GijjbxHNSeyWGl28h/5L2VCKGWu/3sIrynwTwxXbLb3FPIf+a9p/ivjUfIf+S+F/6gQl42uCZ5xQHJAnnvuuWq//fZTOEIXysM0A/mP/JcyIYTyqvjXhiu21atXF6fYkf/If9PgPx+fkv/Ifyn8R4XYN7ImjOeA5IA88MAD86Oaly9frmBzOc1A/iP/pUwIMbwqp9jhet555+VZyX/kv2nxn4tXyX/kvxT+o0LsGlUJcRyQwx6Q11xzjdp8881zDpr0qOYE9uNJddZJgSlYTpJ3SOMfrtiwuQ6mE/LyN6T+u/iD/R+2/Cf9u01/KsQuqZYQxwHR7QGRQPo86wc/+EF1yCGHqGkd1Wy3l/w3bP6bNv1xHDnMgxDgim3bbbdVKSs0Nj/H3k+7/3b7WD/HH/l/cj/A9niKvU8df1SIYxGvSJ9KkIriKx+z/tkKZNgNX3LJJQq77+FpYtqB9J8t/YeIv7hig/eJ7373u1SI9abaWYUh8p+JNftP+ZfyQkKF2BxNNfzmgBzugIS/YRzGgaOa8RsbjqYdyH/D5T/w2izoD9MJ2BHDFduhhx6q3vve906b7Yv6ZtH/ovIZ4c/6b0WA9Kf8o0J863iYyYRgVM/6B2zDKTvvp3lUs8l7+M0JgRNCyoRg81PoPbypzJ8/P0+ODXZQkGcRyP/k/1nwv/A6+a/b/McVYuHkmq4cEN0eEClsIEc1275ZU8qMzUv+Gy7/gVdmSf+lS5eqZcuW5V9GTFdssTyckn6W/Z81/qx/tvxP/LuPPxXiFOnryEuBPEyFRFbItthiC7VmzRoHZ0wnivw3TP4T7po1/XfeeWd1wQUXqH333Tc/tEPaNa3rrPvP+jn+uELdXRt6KsQ1S2oKxGEKRNlYRBvKYdJfxMjQx/9ll12mdtppp9wV2yw2lg4df/af8ocK+eQKORVimclqulIgDVMgyVHNq1atUjvuuGNN3BRfDPlvmPwnnNIG+stJjdhUClds8FU8rdCG/lMhmVwhSeUT0p/yL2X8USFOHYFWfg7I4Q1I8cW65ZZbqksvvZRup+h2ypIK07tti/yBycSKFSsUXLFBKZ5WaEv/p9Vfux72f3jzj8kDpH8a/akQm9xUw28yZBpDppJgFvjD3/AZZ5yRn9Z18MEHUyGmQpzKxhPnnwX/m42V+uGKDcow7OmXLFmisOFuGkHqn0ZdrjpY//Dkv8kHpH+36U+F2OTmGn5zQHR7QMSyACZ+eJfAFTvrN9lkEyrEVIhj2ai29G2SPytXrlQLFy7M+zYtV2xt6n9tRI0oiP0f1vxjswbpn0Z/KsQ2RyXekyHTGDIR/qm7nTr99NPV4sWL1YIFCxQUANJ/WPS3+ZX0H6W/uGKDHTFMJ5o+rIb4j+Jv82fT98Sf+KfY8KbyZyr/USFOpYCVP5UgVnHRt6x/ugJJbCVlRz3xny7+9gAh/u3DH6YTOMUOpkUYJ00G0r999G+S3nbZpD/pn6KQUyG2R1TiPQfkcAakHNUMlrnuuuvy1S/Sfzj0d4kK0n+c/vDRjZPrrr/++tw3MV4imwrEfxz/prB2lUv8iX+KQuriqZi4VP6jQhyDdkDaVIIEVFGahPVPTyDJUc2LFi1S8DSBQPynh79rIBD/duIvY6VpV2ykfzvp7xqrTcSR/qR/ikJOhbjmUckBOZwBOX/+fIXVL/OoZtJ/OPR3iQ7S309/MS/CajE22TURiL8f/ybwtssk/sQ/RSG1+Sn2PpX/1lu7dm0WWynTE4EmEVh//fXVLbfc0mQVyWXDndT222+v5s6dq6655prk8lgAEeg7AvDEgjED04njjz9eHXbYYX3vMvtHBIhAhxDgCnHNxEp9Q0ltDuufzhu6HNV80EEHKXiakED8p4O/4G1fiX+78ZdDbEA3eJ3Ahrs6A+nfbvrXSWtXWaQ/6Z+yQk2F2DWqEuI4IIcxIOF7GJvq7Emd9B8G/X0igvSvpr+8TEIZhulEna7YiH81/j7erSOe+BP/FIU0lQdT+Y8KcSoFrPypBLGKi75l/c0LJDlwAEc1Qyk2A/FvHn8Tb/s38W8//jCdgB0xXLEdccQRChvu6gqkf/vpXxetXeWQ/qR/ikJOhdg1qhLiOCD7PyDlqGbXZE7695/+ZeKB9A+jPzajYlMqQp2n2BH/MPzLeDjlGfEn/ikKaQrvIW8q/1EhTqWAlT+VIFZx0besv3mBtNFGGxVHNeMELjMQ/+bxN/G2fxP/7uBvumLDsed1mE6Q/t2hvz1267gn/Un/FIWcCnEdo9AogwOy3wNSNgXNmzcvd7lmkD7/Sfr3m/42ve170j+O/jCdOP/88xVcssF9YWog/nH4p+Jt5yf+xD9FIbX5KfY+lf+oEMciXpE+lSAVxVc+Zv3NCiTxpbp8+XKFzUF2IP7N4m/jbd8T/27hDxt8bK6DKzbfmLJpXHZP+neL/mW0nOQZ6U/6pyjkVIgnGXUleTgg+zsgsRkI5hIIclSzzQqkf3/pb9PadU/6x9NfvrrUcYod8Y/H38XHk8YRf+KfopBOyneSL5X/qBALkjVdUwmS2gzW35xAgr/hxYsXK/OoZptexL85/G2sXffEv5v4y0ZVrBbDleGkgfTvJv0npbedj/Qn/VMUcirE9ohKvOeA7O+AlKOaTzvtNIUJ3BVI//7S30VvO470n4z++PoCZRgnQC5ZskQtXbrUhjbonvhPhn8QuAGJiD/xT1FIA1isNEkq/1EhLoU3/mEqQeJrHM3B+psRSLB1xGEcOKoZv3074ol/M/iPcrn/jvh3F3/x7w3qTuqKjfTvLv39ozr8CelP+qco5FSIw8daUEoOyH4OSHERZR/VbDMF6d9P+tt09t2T/mn0x8rwsmXLFNwZwnTC9+JJ/N0IkP/S+M+Nangs8e82/lSIw3k9KCUHRLcHhI/IclQzXEPB04QvkP79pL+P3nY86Z9Of5hO4BS7SVyxEf90/G2ejrkn/sQ/ZYU2htdcaVP5jwqxC9WEuFSCJFSdZ2X99QskOVXLdVSzTS/iXz/+NsZl98S/+/ibrtiqXkBtXiD9u09/m6Yx96Q/6Z+ikFMhjhltAWk5IPs3IOFv+KSTTlKuo5ptliD9+0d/m8Zl96R/PfQXE6VYV2zEvx78y3i87BnxJ/4pCmkZb4U8S+U/KsQhKEekSSVIRFXOpKy/foEkRzXDphGfc8sC8a8f/zK87WfEvz/4yyE4OM0Om+xCAunfH/qH0NtOQ/qT/ikKORVie0Ql3nNA9mtAyqEBIeYSYB3Sv1/0jxUHpH999IcrNmyuwyl2oa7YiH99+MfyPuUf5X/Xxx8V4klGfUmerjNESdeCHvWt/3JgQOixsn3rfxDRjUTsPxWSlBUag5Xyn6YrNn6hsdEZv+f44/irc/yNc1h5TNf5jwpxOX2jn3adIaI7bGXoU/+xQgXvEriuXr06X62yujt226f+j3UuIIL954Rc94QsNvwwV4LpRJkrNvIf+a9u/gsQe0US8l+3+Y8KccHK9fzggOj2gDC5QI5qXrBggcJKVUgg/ftD/xB622lI//rpjxdS2BHDFVvVxlbiXz/+No+X3RN/4t/lFxIqxGWje4JnFAj9EQiyqafsqGabRUj//tDfpm3IPenfDP3F9SFoUOaKjfg3g38I7yMN8Sf+VIiN0cIBwQHR5QEhrCxHNeP+uuuuK/1MK3lwJf+T//vA/yZPx/xukv9NV2wwYXKZTjRZfwgOrJ/jn+N/TshQaSRN6vjjCnHNZEklSGpzWH89Alkm30WLFil4mggNxL8e/EPxttMR/37jD9OJ888/33uKHenfb/rb492+J/1J/5QXEirE9ohKvOeA7MeAnD9/vsJn2rLPsy5WIf37QX8XbUPiSP9m6W+6YnN5fiH+zeJfNQaIP/FPUUir+KvqeSr/USGuQjjyeSpBIqsbS8760wWSmEvMnTs39zAxBnJJBPFPx78E3spHxL//+ItvcJhMwOuEeVgO6d9/+pcJAdKf9E9RyKkQl42uCZ5xQHZ/QIqbp4MOOkjB00RMIP27T/8YettpSf/p0F/8g0MZhn9iCcR/OvgL3vaV+BP/FIXU5qfY+1T+o0Ici3hF+lSCVBRf+Zj1pwsk+B7GKnHIQQA2QYh/Ov42pjH3xH8Y+MN0AsrwmjVrRk6xI/2HQX+fTCD9Sf8UhZwKsW9kTRjPAdntASknY4Ue1WyzCenfbfrb9Iy9J/2nR3/TFRtMJ7DhjvhPD3/X2CD+xD9FIXXxVExcKv9RIY5BOyBtKkECqihNwvrTBJJ8iq06AMBHBOKfhr8P19B44j8s/JcuXaqWLVuWnyKJLzq3v/3tVZcn5FA+96Uj/w+L/20+IP3T6E+F2OaoxHsyZBpDJsKfvEK00UYbRR3VbLeX9O82/W16xt6T/tOnP0wncIodDtI588wzqRDP6a4f2NjxZqfn+Jv++DNp0HX8qRCb1Kzhd9cZIhWCLvdfdq/Pmzcvd7k2CRZd7v8k/bXzsP+ckKa9Qgt7fyjF119/vTrllFPUwQcfbLPl1O7J/+T/afO/ydzkvzT+W2/t2rWZCSh/E4FZI7D++uurW265ZerNeMYznqG+/OUvq+OPP14ddthhU6+fFRIBIjAZAh//+MfVIYcckp9e973vfU9hDwADESACRCAGAa4Qx6AVkJZvaGlvaAEQlyaZFH/sWoe5BELMUc12Yyat3y5n0nvW303+m5Tedr4h0x8mEytWrMg312GT3SzCkPEH3uw/5U+XV8ipENcsNSkQuikQ4G948eLFKvaoZpt9SP9u0t+m46T3pP/s6G+eYrdkyRKFDXfTDqT/7OgPWhN/4p+ikFMhrllickB2c0DKUc2nnXaagqeJSQPp3036T0pvOx/pP1v6f+1rX1N77LFHTpZJ/Ijb9Iy9J/1nS3/iT/ypEBtSiwOCAyJ2QJhHNeM3joSdNJD/yH+x/Dcpr7nykf9uUsccc4w66aSTCldsKePZhXFZHPHn+Of4766XE64Ql0m3CZ5RIHZPIJ544onqqKOOUpMc1WyzCOnfPfrbNEy5J/3bQX9xxTapP/FJeYD0bwf9J6Vfaj7Sv9v0p0KcOgKs/BwQ3RsQclTzWWedlfsytUgadUv6d4/+UQSuSEz6t4P+5il2dYzrCrIXj0n/dtC/IMiUf5D+3aY/FeKaBwwHRLcGhEyckx7VbLMP6d8t+tv0S70n/dtDf/nyA5OJ1atXJ5lChfIF6d8e+ofSrM50pH+36U+FuM7RoMvigOjWgDjyyCNze8O6Pq2S/t2if83Dn+P/pnbRf5dddlHnn3/+1Fyxcfy3i/51j++q8kj/btOfCnEVh0c+54Do1oCQo5rr2pFO+neL/pHDuzI56d8u+puu2JYvX67wAtxkIP3bRf8mae0qm/TvNv2pELu4OiGOA6I7A0KOaq7LXAJsQ/p3h/4Jw9yblfRvH/1lnMN0Agd2YMNdU4H0bx/9m6K1q1zSv9v0p0Ls4uqEOA6I7gwI+Bs+44wzVJ0rR6R/d+ifMMy9WUn/dtJfTKOgDONrUFOB9G8n/Zuit10u6d9t+lMhtjk68Z4DohsDAp9S4V0CV2y42WqrrRIpvy476d8N+tdCbEchpH876Y9xDmV4zZo1qq79Ag7y8wtRy2zIXTRqMo7jv53jP5TmVIhDkQpMxwHRjQEhRzUvWLBArVy5MpC61clI/27Qv5qSk6Ug/dtLf/EoA8rCdAIb7uoOpH976V83rV3lkf7dpj8VYhdXJ8RxQHRjQOy7775qxYoVKvWoZptVSP9u0N+mW133pH+76b906VK1bNmyxk6xI/3bTf+6xrmvHNK/2/SnQuzj7AnjOSDaPyDkqGaQ+LrrrqvVPynp3376Tzi0g7KR/u2nv7hiw0sxDu2oM5D+7ad/nfS2yyL9u01/KsQ2Ryfec0C0f0CIw/5FixYp7ECvM5D+7ad/nfS2yyL9209/vBDDnvj666/nFyKbgRPvyf/t5/9EEpdm7zr9qRCXkjf+YdcZIr7Hozm60P/58+cr2BM2caRrF/o/SrF679h/Tohz5sypl6kiSgvlP9lDAFds8DrBTbURIJckDcW/pIikR6yf8idF/lAhThp+45k5INs9IMVcYu7cubmHiXEKpsWQ/u2mfxp1q3OT/t2hv+wjqNMVG+nfHfpXj+b4FKR/t+lPhTie50tzcEC0e0CIP9KDDjpIYZWo7kD6t5v+ddPbLo/07w79TVdsS5YsUdhwlxpI/+7QP5XWrvykf7fpT4XYxdUJcRwQ7R4Q8D2MVeK6jmq2WYX0bzf9bXrVfU/6d4v+cLm4cOHCnA3qkAmkf7foz/FfLwJd538qxPXyAx2zt9gxu0x+dR7VbLNP1wWC3Z/Ye/afCkGKDV8sv9npJ+E/+WoEO2IoxbArnjRMUv+kdbnysX6Ov66NPxcfTxqXyv9UiCdF3pMvlSCeYoOjWb9fIMpRzTypKpidohOS//z8Fw3mBBmI/2T4w4744osvVpAR8E0+aSD+k+E/Kd52PuJP/FNeCKgQ2yMq8Z4Dsr0DcqONNqr9qGabXUj/9tLfplUT96R/N+kPrzPwTwxXbCneZ0j/btK/LllA+neb/lSI6xoJ/1cOB0Q7BwT8De+3335q3rx5ucu1msleFEf6t5P+BYEa/kH6d5f+4p8cJhOrV6+eyHSC9O8u/esQDaR/t+lPhbiOUWCUwQHRzgEhLpaWL1+uYDPYVCD920n/puhtl0v6d5v+coodruedd55N3sp70r/b9K8kcEUC0r/b9KdCXMHgsY85INo3IOBeCeYSCHUf1WzzB+nfPvrbNGrynvTvNv0hK7C5DqYTk7w8k/7dpn+qbCD9u01/KsSpI8DKzwHRvgEhp1I1cVSzRX56GWmxlxGbVk3cc/y3b/zH0lnMq5Av1hUb6d99+sfyi5me9O82/akQm9xcw28OiPYNCDmqGbvHsYu8yUD6t4/+TdLbLpv07wf9xRVb7Cl2pH8/6G+P69B70r/b9KdCHMrpgek4INo1IMyjmvE7xcdoCAuQ/u2ifwjN6kxD+veD/jCdgB0xXLHFuGkk/ftB/0llAunfbfpTIZ6U8z35OCDaNSBk53hTRzXbbED6t4v+Nn2avif9+0N/uGLD1yUEbLCDglwVSP/+0L+K1q7npH+36U+F2MXVCXEcEO0aEHJUc4pv0Rh2IP3bRf8Y2tWRlvTvF/2XLl2qli1bln9ZCnHFRvr3i/6xMoH07zb911u7dm0WS3SmJwJNIrD++uurW265JbmKSy65RO20005qiy22UJdddllyeSyACBCB4SGw++67qwsuuEDtvffe6lOf+tTwAGCPicBAEOAKcc2E5htie94QZWNMjA1gKjuQ/u2hfyotJ8lP+veP/th7gM11cMVWtTGX9O8f/WPkAOnfbfpTIY7h9oC0HBDtGRByVHOs66QAMnuTkP7tob+XSA0+IP37SX9xxYZNuZAn8FXsCqR/P+nvorUrjvTvNv2pELu4OiGOA6IdA0ImsC233FJhhWdagfRvB/2nRW+7HtK/v/SX0y7LXLGR/v2lvz3WXfekf7fpT4XYxdUJcRwQ7RgQ8Dd8xhlnTHTaVAL5eTAHD+ZQc+bMSWGhpLyUP83JH7higzK8Zs0atWTJEoUNd3Yg/s3hb2Ptuif+xD9F/lIhdo2qhDgOyNkPyJtvvlnBuwQmMOwM933eTCCzNyvpP3v6pwhEL2EDH5D+/ab/ypUr1cKFC3NucLliI/37Tf8qMUD6d5v+VIirODzyOQfE7AfEZz7zGbV48WK1YMEChQlsmoH0nz39qRBzhbrJMS+u2PCiDXti87Afjn+Of8qf7sofKsQ1S04KxNkLxAMPPFCtWLGickd4zaTPiyP9Z09/TkjdnZBSx+S0xh9MJ3CKHUyz4HlCwrTql/rsK+un/KH8m1z+USG2JUriPQXSbAUS/A1vv/32ORWvu+66kdWbRNIGZSf9Z0t/4k/8p6EQ4BQ7nFwHV2zmoT/kP/LfNPjPNxmR/9L4jwqxj7MmjCdDpjHkhLAX2U444QT16le/Wi1atEjB08S0A+k/W/oTf+I/LYVEjoU3XbGR/8h/0+I/19xG/kvjPyrELq5KiCNDpjFkAvR51nnz5imcUGeu2qSWGZOf9J8t/Yk/8Z+mQiKu2LBajE125D/y3zT5z56byH9p/EeF2OaoxHsyZBpDpsAPf8PwLjF37tzcw0RKWZPmJf1nR3/QjPgT/2kqJPBkg811MJ1Yvny5Ovjgg+l2j24HJ50+kvNR/qXJPyrEySw4WgAZMo0hR9GMu5Ojmg866CB1+umnx2WuKTXpPzv6g4TEn/hPUyEGz8khQPi9atUqteOOO+LnTAL5n/w/bf43Gb3r/EeF2KRmDb+7zhCpEMyy//L5cppHNdt4zbL/aAvr54TICXHyXeb2eA69l5fxY445Rh133HGh2WpPx/HP8c/xP/n4p0Jcs0iiQJqtQPr+97/PFRp+sqx5VIcXx/E/2/E/K/xhOgGf57vtthtNJih/wgVGzSlnxf/Sja7XX6tCvN566wkuvBIBIkAEghDIsiwoXUiiLgtkys8QCjMNESACQ0agbL5Ilf9UiIfMWew7EWgBAmUCLrZ5qQIxtj47fUr9VIhtNHlPBIgAERhFoGy+SJG/qKURhbiswaNd4x0RIAJDRUAUwDrlRapATKVFSv1N4JHaH+YnAkSACLQBgRD5mCJ/0UcqxG2gNNtABAaIQIiAi4UlVSDG1menT6m/CTzs9vGeCBABItBFBELkY4r8BSZUiLvIGWwzEegBAiECLrabqQIxtj47fUr9TeBht4/3RIAIEIEuIhAiH1PkLzChQtxFzmCbiUAPEAgRcLHdTBWIsfXZ6VPqbwIPu328JwJEgAh0EYEQ+Zgif4EJFeIucgbbTAR6gECIgIvtZqpAjK3PTp9SfxN42O3jPREgAkSgiwiEyMcU+QtMqBB3kTPYZiLQAwRCBFxsN1MFYmx9dvqU+pvAw24f74kAESACXUQgRD6myF9gQoW4i5zBNhOBHiAQIuBiu5kqEGPrs9On1N8EHnb7eE8EiAAR6CICIfIxRf4CEyrEXeQMtpkI9ACBEAEX281UgRhbn50+pf4m8LDbx3siQASIQBcRCJGPKfIXmFAh7iJnsM1EoAcIhAi42G6mCsTY+uz0KfU3gYfdPt4TASJABLqIQIh8TJG/wIQKcRc5g20mAj1AIETAxXYzVSDG1menT6m/CTzs9vGeCBABItBFBELkY4r8BSZUiLvIGWwzEegBAiECLrabqQIxtj47fUr9TeBht4/3RIAIEIEuIhAiH1PkLzChQtxFzmCbiUAPEAgRcLHdTBWIsfXZ6VPqbwIPu328JwJEgAh0EYEQ+Zgif4EJFeIucgbbTAR6gECIgIvtZqpAjK3PTp9SfxN42O3jPREgAkSgiwiEyMcU+QtMqBB3kTPYZiLQAwREwN14443Rvfl//+//OfOkCkRnoRGRKfULHlmWRdTIpESACBCB/iMg8rFsvvjf//1fdcc73nEMDN98YSekQmwjwnsiQASmgkCIgPM1xCfgUhRSX10x8Sn1Cx5UiGMQZ1oiQASGgIDIx0YV4rVr19a2HLHBBhvkdKFAHwJ7so9EIA0BEXB/+ctfoguaM2dOdJ62Z6D8bDuF2D4iQARmhcA05guuEM+KuqyXCAwcARFwZW/8Poi4QuxDhvFEgAgQgf4hEDJf0GSif3QfTI8e+MAHql/+8pcj/X3Ws56lzjjjjJE43vQTgRAB5+s5FWIfMownAkSACPQPgZD5ggpx/+ie9+jf//63Ouuss9TFF1+srrnmGvX73/8+//vb3/6mNt54Y7XpppuqTTbZRG222WZq1113VU960pPUbW97206h8YAHPGBMIX72s5+tPvaxj3WqH2zsZAiECDhfyVSIfcgMJ34IMnI41Izv6Q033KC+853vqJUrV+bz5F//+leFv5tvvlnd8573VPe6173Uve99b7XVVlup/fffP7+Pr4U52oJAyHxBhbgt1KqpHX/+85/VKaecot7//verP/zhD8GlQjHG6uqrX/1qdfe73z043ywTUiGeJfqzrztEwPlaSYXYh0z/44ckI2dJzWuvvVb95z//yZsAm/0NN9xwls0p6r7qqqvUCSecoD784Q8rKEAhYf3111f77LOPOvTQQ9XjH/94JbInJC/TtAMBoVmZiR0V4nbQqpZW/PSnP1U777yz+sc//jFxeQ960IPUt7/97U4oxVSIJyZzLzKGCDhfR6kQ+5Dpd/zQZOSsqIkvkVhkwSo8wiGHHKI+8IEPzKo5Rb1YKDryyCPzVeAiMvLH05/+dPXxj39c3f72t4/MyeSzRCBkvqBCPEsK1Vg33np33HHH3DwitdgHP/jB6vzzz1cbbbRRalGN5qdC3Ci8rS88RMD5OkGF2IdMf+OHKCNnRc0PfehD6uCDDy6qn7VCDM9VWN2FQlxH2G233dQXvvAFJZ5d6iiTZTSLQMh8QYW4WRpMrfRHPvKR6oc//OFYfXhLf85znqMe85jH5HbD+HQFU4pf/epX6iMf+UhuOzWWSUccf/zx6lWvepXrUWviqBC3hhQzaUiIgPM1jAqxD5n+xg9RRs6KmjArOO+884rqZ60Qv+1tb1Ovfe1ri/a4fmABCF9It9xyy3y/zW9/+1u1Zs0aV9I8bpdddhnpozchH7QCgZD5IlUhVvrNq7agUYNP49rKG0pB2g9rjpvgJ9eHP/zh2fXXX18Kw5IlS5x5t9tuu9J8bXh4//vff6ztelNdG5rGNkwBAeFzbROWxf75mge/6rMMKfULHrNsf1vrHqqMnAU99Cbu7Da3uc2IbNYK8SyaktepN85l2gZ4pD0yVrSSlB199NGZ/nrgbN93v/vd7ClPeYozL8r44he/6MzHyPYhIDQvmysgJ1zPQ3tDP8Qa5VmHr371q2qvvfYaa8a3vvWtfAPA2AMrYs8991TnnHOOFavUhRdeqLCqUhXwVgX3Z7/4xS/U7373O3Xf+95XzZ8/X93vfvdTWjBWZXc+14q8+vGPf5z/3e52t8t3+2LVwTTjSFkh/vvf/64uv/xydfXVVyt8Sv3nP/+p7nOf++RtRrvvcpe7ONtlRsJWGxt0zCBtNeOAyfe+970cG9idYRUCZimbb765mYy/IxEIeeP3FckVYh8y/Yyflox0yQTw6dZbbz0C7KpVqxTsmSF/8Nkd5m6PeMQjkjaewUPCpZdeqi677LLcW8I222yjICNxvcMd7jBSv+/G1X5bpv3sZz9TP/jBD3LzPMiy/fbbT1133XX5H8o988wz1Rvf+MaRKg488ED15je/uYjDBru73e1uxb3rBzwjXXHFFYWMximOkJn4g6zWizaubGNxCxcuzD1J2A/gaemjH/2ogvlDVXjPe96jjjjiCKzWjSTdYYcd1E9+8pPSTXbTmmtcdBlp7MBvQuYLrhCHqv4tTvemN73J+QarP/cEtVq7ncme+9znZkuXLs20y7JMK2/Zn/70p8q8WonOtC9g79u3FvTZHnvs4X37dlWgB3U2b968TDPvWJ/0GePZ85///GLVG6vYeoyP/GlPGa5iiziU/4IXvCBDWXZeucfqBtJo05Iin+vHZz/72bEytMJeJMWqw1Of+lQvPnqSyLSwLNLzRxwCQi/XG31VnK+mlBVaX5kx8Sn1Cx4x9Q0l7bRkpEsmgC5a0cyh/vKXv5xpJXVMbiAN5A5WIyVtCG20EpzLRO0ZyFmmlKtf8rNTTz21skhX++9617vm+f773/9mr3jFK0bqudOd7pQ/e8Mb3jASL7zou5atGH/jG9/Idt99d+ccYJb30Ic+NNOeIjKtKHv7pc0Ive3SLyXefK4HWqEfK0ubIGZ64ciVPGt6rgmhi7NhA40U3imbG1JXiGu1b5AGD5ReE3f7He94x9hABZbaRnjiMssywgwDCqPQq+oKYQ0hVxUwWdz5zneuLBeKMJRVvToxlrZMIX77298+lr6s7XoVMdOrHd5mf/3rXx8rD4r8LbfckukV82yLLbYYe27Xp+3Vsl//+tfeOvjAj4BgWSbgfM98paYopL4yY+JT6hc8YuobStppyUiXTABdfvOb32QnnnjimCmB0My8wtSt6mUcdPvMZz6TaV/ylTLGLFuvlmZ6/4iX7F/72tfGyoOiDmV42bJlY8/qVIi1i7Zs7733HqvDbL/rt/6KmWmvFs4+vexlL3OWh4Wa2ICxqffkZFDEX/Oa12TaG1P2r3/9y1lM3XPNpHRxNm6gkcI7vjkB8VSIe8AcX/rSl5yDXpsuZNrsoNYeamfmmf7856wPDKc/rzmfQajibd4XsNqMNMK0VddFixZlD3nIQ8bS+xRi7Zt5LG1VHXiOVW6fwqo9cTjL1GYUmWv12lff0572NB8sjC9BQPAsE3C+Z75iUxRSX5kx8Sn1Cx4x9Q0l7bRk5P/8z/84ZQJWZ312rEI387r99tvnL9Y++uBLmZk+5je+jkGZcwV8LXSVtXr16lwW2s/qVIhf/OIXO+u263Td46uia7+MNt1zlomV40mCTwE2y2pirpmULma7hv5b+MY3J1Ah7gmHaFurTNumOgc+FFTtbiaDoMYbeGrAm7Ewllwh6I877rgMJhpYScBqyGGHHTaWTtuMeT8H7rTTTmPpUT6UenzuxMqLduWTaR+QRTqX8u1SiKGg6lP4inzSbn0KUaZd5+SrMdrONzv55JOdphTaQ0feLxs7mJZIWeZV25oV8drWLYNpBFZmoFyb6eQ3VpUnFdB2m4Z0L/iVCTjfMx9OKQqpr8yY+JT6BY+Y+oaSdloy0icTtM1sPvb16Wf56uLZZ5+daRdgpSuivg1byCu0Nq+QhwcddFAux/ACgE/82i7ZmRYv7PpEtjHyYxOZWab8fuUrX+mMF4UYX/cg8/EHszHJJ1eY1slzXD/5yU+O1I2Nb5JWrphXjjrqqEzvhcm0XXS+MIF02AiOr3eSTq7Lly8fKROLN66XEMj9pkJTc82kdGmqn10sV/jENydQIe4iVT1tNpUwIbx9hRB54hOfmCuY2iVOqe2VqxrthibTmzPGBJFv5delPL/zne8cK9olDNF22Nphx7IdoHzbfZN7l0L87ne/25ken6HsoN3NOdO67LH1xhJnWii4EMS2yYreIJLpDS7OPBD8DHEICM3LBJzvma+mFIXUV2ZMfEr9gkdMfUNKOw0Z6ZMJoA3Mo/DibQd9OqhTJixYsMBOmsts1xc6vQk4++Y3vzmWHkqvz7wNn/XtAHtY4SPzOnfu3Dxeb0DLoGxDLkNJdZnCYXXbzIvfWP0tC/rkuLE8emOeNwvmEbsOeB0yw8UXXzyWBnke+9jHmslq/d3UXFMHXWrtaAcLE37xzQlUiDtIVF+TsbkCn42E6CFXrChgZRZv3NgAUBUOOOCAsfKh4PlWnvEJy14tuMc97pFpjw4jVe27775j5aL9vs96yKw9TjjzuBTiww8/PNO7gTNsLNE7i/OVWtgqu9p95ZVXOsvVu9RH2oybsg0bEIyu4DOzAAYMcQgIj5cJON8zX00pCqmvzJj4lPoFj5j6hpR2GjKyTCbgxd8XXEok6Amlzgy+zWtlG+bw1Q5fqoQ/5AoZiBVNM5S1f//998/0yXNmcudvV1+qFGKYjUm75OqToagU7XjpS1+aaV/5uW02NgNidd6U6T4zgyZdc85irgmli5NYA4oUvvLNCVSIe8YM+EQE21ohfOwVmxPKPt1DmbXLhFAqC09+8pPH8mCFwQxQUu1ytWudUhs6fXTmWB6U4VKIzbrkNyYJV4BAdX1mwwqGHXyTBzZeaPctdvLi3uU/GS8zDHEICM+UCTjfM19NKQqpr8yY+JT6BY+Y+oaWtmkZ6ZMJ9uqljbs+OMIpz04//fSRpC5lE94GyjwtoADfJi9bFvvaD5Mzn6/ekQbqG1cbqxRieOMR/pUrzEtshd2uq+we5nBSlnl93eteV5at9mdNzjUxdKm9Yx0rUHjANydQIe4YQUObizdlKMYuG1thCt8VG9tgc2yv4sIVkCuPbbdlt9FlNmG++UNxdLlYW7x4sV3UyD2Y19WeUIV4pDDrRj4PmuXD3ZAdfJMHPs2WBZfwN921leXls1sREPqUCTjfs1tLGf2VopCOljTZXUr9gsdkNQ8rVxMyEgj6ZMLrX//6UoAvuugipzw79thji3x4WXftFYHdcFWA1xvhD/Nqm7D52h/zBWsShRhKqtku+Q23Zs94xjMybFSDiUZMcLmQQ7nYk9KWkDrXxNClLX2eVTuEp3xzAuLpZWJW1JlCvfBxC9c8L3nJS6K8HoBxjjzyyJEW+uyxsGMZtsm+P5fNMTZoSMAGPGFU86qP2ZQk3qtLmFQpxHBn9IlPfCJ7y1vekr3oRS/KnvSkJ2Ww1cPGOayQw6WOa4U4RiE2FX5X47GpxOwrfgM/hjgEBMMyAed75qspRSH1lRkTn1K/4BFT39DT1ikjgaVPocSG4LLwxz/+cUwmgJ7myiq83QiNzWuVso16sTJu5pHfZvlI52s/XK6FhkkUYnixcMldaadc4cJTHwSSQZFHnrKAzXiSz7zCQ8c0wjTmmhi6TKPPba5DeMA3J1AhbjP1Gmjbtddem2E38DHHHJM96lGPcq7MCtNgpRieKST4Pj9J+pgrbJ4kYHOfK++73vUuSeK9ukwPfAoxdplj5bbsQA5XOyTu5S9/+Vg7fJOHb3e4FOBaDaFCLOiEX4U2ZQLO98xXS4pC6iszJj6lfsEjpj6mHUUgRUaiJJ9MgGeIsoDVX5fbSZicSYDsFhqbV3jHCQlYbTXz4fcTnvCEkay+9lcp9GYhkyjEyA/zDchBu42+e+AFfLC/w2WWoE8CdJZl99lsex2/pznXxNCljr51uQzhI9+cQIW4y9Stoe3YKezbgQzmMf3jTupbUZjQvOpjSovW+z5r2R4aigzGj4c97GFjAs+lEGNnN+zszDbE/o5RiF3eK4xmZ1jRseunQmwiFPZbMCwTcL5nvhpSFFJfmTHxKfULHjH1MW05AjEyEiX5FEq4zaoKLreMj3vc44psH/zgB8fkBmiOL14h4Z73vOdYfrhDM4Ov/VUKvVnGpAoxysDm7q222mqsncLbvqu90o2y8PnblR6uPJsK055rYujSVJ+7Uq7wgm9OqEMhXg9g6IpqCdqWNC+nxiJraVffC9ErD0qfEDTWTb0Cqy6//PI8Xit5Sp/uM5ZGK81KH5AxFl8Woe1llTYbyJPoVWilTRbGkuuTpZQ2UxiLNyP0SXBKb/Qwo5RWiJXecFfEabdDSk8qSrtDKuLkB+L1UalKu0NSaJPeoKD0Z7v8bHttMy3J8qtWiJX+TDcS96Mf/UhpP58jcbgBVtoUYyxeIvROcaVtA+U2v2qFWOkBORLHm3IERF5MghvwdgW9OUnplTTXo6nEpdQveFB+1k+qEBmJWn0yQSsuSq9mehumD3xQ+uvV2HP9NU19+tOfzuO1i7NcNtmJTjrpJKW9G9jRI/fgCZQPeWgGtAltk+Brf5VMk/y4aiVbXXrppWaU0gqr0n6XR+J8N3r/igLen/rUpxT6HDq+9RdApU8DHClWu+5U2n56JA5yXnsTUnqT+Eh8yM3VV1+dJ9Mb/saSt3GuGWvkgCNEPpbxk97T5ByHvvliDE490GoLuvD8ja62AgdaUMhpOjY0cEsm+MsVNl2yuQ7HfUq8edXC2C4q6h6+ec3y5Dfc6VQF1wYTe4XY543ikEMOcXqxgN9OV7kxNsRcIa6iXD3PhVe0gMti/3wtSFmh9ZUZE59Sv+ARU99Q0zYhI4Glb4UVq7tlwefu0ZQ7vjTYuFwVfKul5n4OlOFrf5VMM+tPWSE2y8HvW265JcOGQ5iFQLbD+5DwuX3VCs/YEc7YJ2Knwz2OdJ4kYLM6TDXgjxmHi8j8iLLaONdM0se+5hE+KJsruKmu49TH0cw4GAMHO2CDGE7hgXkAvELEBGyiE4aRKxRimaAxgbhs3EIU17J2wMuE1GdecbpbWcCnKTO9/LYVYt8JS9jM5wrf//73neXSZMKF1mzjhOZlAs73zNdy4Xff86bjU+oXPJpuY9fKn5aMBC4+hbJqk7DvcCK94lnADTtZlx2wuSejSGz98B0YYtug+to/K4XY6kZ+e8kll+Snfwq/m1fYWZsBJ5yaz+U3NnuHupGT8lynEOJAFFkUauNcI23nNbdkyHnBNycgngpxxzkFjsBlkJtXGaSh3dtll13GytGmECPZtWnBWBrkSw3YOWy2Hb/hhqxsFQfuiOw8uLcV4l133XUsHSYVX9CmGmPpUS4VYh9is4sX+pcJON8zX6tTFFJfmTHxKfULHjH1DSHtNGWkT6HEwRiujV+CP+SL0M+8fv7zn5ck+dX1JQ/yDN4yyoLLsw3queCCC0ay+dqfqhBjpbbu4PK5jw3jdnBhhr7vueeeGQ6PCgk4pRWLTSZt5LccuNLGuSakb0NJI/TyzQlUiHvACfAviU9FQmy54rP/5z73uaAefuxjH3Ou/r7whS8cyY/PTFK+ecUnLVfAaULwubvXXntl8CuMT3vwHoE3fDNghcMsT3772g9F2XXyEvLZCjFcqkl55tV1Mh+E3iabbOJMf/DBB5tNzn9POnlwU90YlBNFCD3LBJzvma/CFIXUV2ZMfEr9gkdMfUNIO00Z6ZMJoA1WK10BZlquQ4/udKc7jR1M8d73vtcpn8r8wUNZxql0wh9yxYY61G0GX/tTFWK9R8WsZuT3z3/+8/y0ObgHhQcIKJ5l/ZHMOGFV+iJXLGjYAS8V8ty+YoMd+lwWoPC6FoNQ1jOf+cwiaxvnmqJx/FHwgG9OoELcEyZ54hOfWBDbHPAwedhnn30yuEyD/ZkIPyiqcA2DHapweo50Zj75feaZZ44ghM8JG2644Vjahz/84Rl8LtrBJbDg9mzNmjUjSV2fotCGu93tbmNHl0IZhqsdaaN9tU0tsPvYToN7+7SiP/3pT6W+ml2ueiadPKgQj5B/4huha5mA8z3zVZqikPrKjIlPqV/wiKlvKGmnJSN9MgG0wZcwezEAMhkyWmhnXl2eE2BTC1/pZjr8xgIIPPbYQW8Cy+bPnz+WHoso9uow8vraH6MQP/rRjx6rD1504LHDFeDe0+4PXhCwQOELMAl09WvVqlXOLD5bYsEOq81vfOMb80Uk+Nw/99xzM70JMFu4cOFY26SteGHBvCqhjXONtI1XmkwMhgew2ulb2ZTBiyuEIFYKXCvKZjr8ft7znufE761vfatTQOCYTdgTY6MBTgLC27JL0fbZ0mlvDc5yYaOFs+dx2AXsnPWu4TwdTuGDwmy3W3uNGGn3+973vrE0kgcCFZ/Ydt5555G2Pve5zx3LgyMykRarGZhkECadPKgQj5Bo4huho0/pLYv3VZqikPrKjIlPqV/wiKlvKGmnJSN9MkFkFQ4Twks75Bn2fWCVVuhmXrFfAwdxuAL2ObhkOPLsvvvuufzFwRUHHHBAroSb5cpv3+EUvvbHKMQu+Yl6sRgCWQ75d/TRR490DYciSdvkuvHGG2cw9fjoRz+afeUrX8mVVO15Ildct9lmm7H0m222mdfMDpvfdtppp7E8UlfsFQq+veLfxrlmBOSB3wiNy+YF2hD3hEm0e7QMSqkQPeWKt2JZTbbhgWBx+f8NqQ+rNL4JH87VoXSGlIM0WH2GImun167hRpqs3Vhl97vf/cbS2fnkHhMKVtAh8CTOvqJuhEknDyrEOXzJ/4QuZQLO98xXuY8/fenrjk+pX/Cou019KW8aMtInE+BlwuW9RmhmX12rwyYdsIfCteBgl+O6x+IDDiBxBV/7YxTiD3zgA17ZKe2BJwozQMnH4oc8j73iyyUO4igLmLvwMhJbtp0eijc2atqhjXON3cYh3wsdfXMC4qkQ94hD8IkJ9rqTCkqsYmAVtGqDBpRlfF6KUWBh2+tTsoUE55xzTqkiKgwNuy2YTsAuTeLkCmXeDitXrszweUvS+K5QhqXvWMn2paNCbCM8m3uhT5mA8z3ztThFIfWVGROfUr/gEVPf0NI2LSN9CiWOEcbXM6ySCp18V5EvVbS58MILvSvMrrKx+Q42tjgVzxd87Y9RiLGg8KAHPai0n7ZCjPbAnMRlS+3qixkHm+Pz9ImnoeHUU0/Ntt5669L2meXLb8yr2BNTZsrRtrkmFJMhpBM6+uYEKsQ95QK4k4HZAlZGXZ/WhDFwxUooVgzgus30qRgCDYQnlEjXCUgoG2YN+Gwnu3BDytSO4TOczuRSYCFkcWKeBJfNlnkKnqTDFULMZ3sMnODeCPZ5EoAFjnq2Xy6Al7gqmnTy4AqxoJx2FT4uE3C+Z76aUxRSX5kx8Sn1Cx4x9Q01bVMy0icTYJOKgJVFyCHbhSVkJb68QWmOCVgYWLZsWQaTA9dXLSxawMwMK6Pw+V4VfO2PUYhRB/aoQHkUnpQr+o0Naj6TPHh9wCmlMLkrm7vwDLIeJhRQwGMD8sAUA6exijmLtNG+4ssrFopC3bS1aa6JxaXP6YWuvjmhDoWYJ9VplNsc9GqA+uMf/6j0pjelNzXkp/7oTz5KOzjP//Snplqar1dW1S9+8Qul/QMrbc+s9Fu7wklyelViovLRbr25IT9lSG9GyU+T23bbbScqy8ykBa7Sh4wo7YdYaXu+vFy9WqG0gDWTFb9xco0WcAon12nBqfSxokoL9eI5f8wOAaGZFmTRjdDKgzNPyklxzgIjI1PqFzz0pBZZ67CT1ykjQ096g0zGKaCQydpjjtKuwZwnZMVQBnTXSlsuh8FH2223ndK2tkor2zHF1Jr2z3/+c95PyF3t0SH/0z6Ag+q44YYb8nkLZehNz0orsQonxOEP8yagym0AAC3LSURBVJc2QQkqpyoRcNP22gr1aFOSfI7cdNNN87kBc5henKkqwvmcc40TlplFinwsmy9ST6pbDysadfVQn+WeF0WBXheiLIcI9BcBEXDa7iu6k5O+qEVXNMUMlJ9TBNtTVahC7MnOaCJABBpCYBrzBVeIGyIeiyUCRKAcARFwZW/8vhK4QuxDhvEpCFAhTkGPeYlAcwiEzBfJK8R6Nbe2FWJpcI1FNocuSyYCRGCmCIi8oEK8jgyCB+Xn7NiSCvHssGfNRKAMAZGPZfMFFeIyBPmMCBCB1iIQIuB8jecKsQ8ZxqcgQIU4BT3mJQLNIRAyX1Ahbg5/lkwEiECDCIQIOF/1VIh9yDA+BQEqxCnoMS8RaA6BkPmCCnFz+LNkIkAEGkQgRMD5qqdC7EOG8SkIUCFOQY95iUBzCITMF1SIm8OfJRMBItAgAiECzlc9FWIfMoxPQYAKcQp6zEsEmkMgZL6gQtwc/iyZCBCBBhEIEXC+6qkQ+5BhfAoC8D17wQUXjBXxqEc9SsGfOgMRIAKzQSBkvqBCPBvasFYiQAQSEQgRcL4qqBD7kGE8ESACRKB/CITMF1SI+0d39ogIDAKBEAHnA4IKsQ8ZxhMBIkAE+odAyHxBhbh/dGePiMAgEAgRcD4gqBD7kGE8ESACRKB/CITMF1SI+0d39ogIDAKBEAHnA4IKsQ8ZxhMBIkAE+odAyHxBhbh/dGePiMAgEAgRcD4gqBD7kGE8ESACRKB/CITMF1SI+0d39ogIDAKBEAHnA4IKsQ8ZxhMBIkAE+odAyHxBhbh/dGePiMAgEAgRcD4gqBD7kGE8ESACRKB/CITMF61UiPtHCvaICBCBphC48cYbo4vus0IcDQYzEAEiQAQGgkDZfEGFeCBMwG4Sgb4iUCbgfH2mQuxDhvFEgAgQgf4iUDZftFIhzrKsv9Rgz4gAEagFgZBPYL6K+qwQU376qM54IkAEhopAyHxBhXio3MF+E4GOIxAi4HxdpELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfMFFeL+0Z09IgKDQCBEwPmAoELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfMFFeL+0Z09IgKDQCBEwPmAoELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfMFFeL+0Z09IgKDQCBEwPmAoELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfMFFeL+0Z09IgKDQCBEwPmAoELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfMFFeL+0Z09IgKDQCBEwPmAoELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfMFFeL+0Z09IgKDQCBEwPmAoELsQ4bxRIAIEIH+IRAyX1Ah7h/d2SMiMAgEQgScDwgqxD5kGE8EiAAR6B8CIfNFskK8du3arC7oNthgg7yoLKutyLqaxnKIABFoGQIi4P7yl79Et2zOnDnRedqegfKz7RRi+4gAEZgVAtOYL9bTymtt2qs0uMYiZ4U96yUCRKBhBERe3HjjjdE1cYU4GjJmIAJEgAh0FoGQ+SJ5hZgKcWf5gw0nAp1GIETA+TpIhdiHDOOJABEgAv1DIGS+aKVC3D9SsEdEgAg0hQBXiNchKwK/KZxZLhEgAkSg6wiUzRdUiLtOXbafCAwcgTIB54OmzyvEvj4znggQASIwdATK5otWKsS0IR46y7L/RKAaAVkRLRNwvlL6rBBTfvqozngiQASGikDIfEGFeKjcwX4TgY4jECLgfF2kQuxDhvFEgAgQgf4hEDJfUCHuH93ZIyIwCARCBJwPCCrEPmQYTwSIABHoHwIh8wUV4v7RnT0iAoNAIETA+YCgQuxDhvFEgAgQgf4hEDJfUCHuH93ZIyIwCARCBJwPCCrEPmQYTwSIABHoHwIh8wUV4v7RnT0iAoNAIETA+YCgQuxDhvFEgAgQgf4hEDJfUCHuH93ZIyIwCARCBJwPCCrEPmQYTwSIABHoHwIh8wUV4v7RnT0iAoNAIETA+YCgQuxDhvFEgAgQgf4hEDJfUCHuH93ZIyIwCARCBJwPCCrEPmQYTwSIABHoHwIh8wUV4v7RnT0iAoNAIETA+YCgQuxDhvFEgAgQgf4hEDJfUCHuH93ZIyIwCARCBJwPCCrEPmQYTwSIABHoHwIh8wUV4v7RnT0iAoNAIETA+YCgQuxDhvFEgAgQgf4hEDJfUCHuH93ZIyIwCARCBJwPCCrEPmQYTwSIABHoHwIh80WqQqyyGoMmQYa/IYSzzz47W3/99Yu/H/zgB0Poduf6qBWngkZHH310cPv/+9//Zvvtt1+Rd++9984Q9+EPf7iIu+c975n9/ve/Dy6TCUcREHlx4403ZrF/oyXderd27dpbb2bwK6V+wWMGzZ56lZSf5ZA3hU9T5Zb3hk+nhcD3vve9Yn6CfnLOOec0WvU050mRj2VzxV/+8hfnXBIKQq3aqzQ4tPIup/vSl76UK//SZyrE7aTmne50p4JOr3jFK4Ib+da3vrXId+973zu79tpri7wHHnhg8ewxj3lMdvPNNxfP+CMcARk7ZQLO98xXS4pC6iszJj6lfsEjpr6upqX8LKdcU/g0VW55b/h0WghAIRY5gutXv/rVRque5jwp/fLNCYinQtwouf2FU7D4sWnTk0kU4m9+85v5WzYG4G1ve9vsu9/97kiXMPDuf//7F4Ln8MMPH3nOmzAEQgScT/j5akhRSH1lxsSn1C94xNTX1bSUn+WUawqfpsot7w2fTguBaSrE054nRT765gQqxNPiMkc9FCwOUFoYFasQX3nlldnd7373Qtl9xzve4ezVJZdckpllf+ITn3CmY6QfgRAB5xN+vlJTFFJfmTHxKfULHjH1dTUt5Wc55ZrCp6lyy3vT/NMFCxZk973vfbNjjz22+cpmUENo/6alEM9inhT56JsTqBDPgDGlyr4KFulfX66m0hpiMrHXXnsVyvBOO+2U2w37sDj++OOLtHe+853zzzW+tIwfRyBEwPmE33hp62JSFFJfmTHxKfULHjH1dTUt5Wc55ZrCp6lyy3vT7FN8Jpexc8QRRzRb2QxKj+nftBTiWcyTQmPfnDAIhfi6667L/vSnP+V/t9xyywzY0V1lHwWLu6fdjo1RiG1h8rWvfa208//4xz+yu93tboUwfuUrX1mang9HEQgRcD7hN1rSrXcpCumtpUz+K6V+wWPy2sdzUn6OY9KFmKbml6bKnSWm2CgoY6ePCnFM/+w5rAkbYruOac2TQmPfnDAIhfixj31swext2tHfR8EyS6HWVN0xCvETnvCEgtce9ahHBTXpbW97W5Fnzpw52R/+8IegfEyUFbiVCTjfMx9+KQqpr8yY+JT6ReDH1FeVlvKzCqF2Pm9qfmmq3Fmi+LrXva6QJX1UiGP6ZyurTSjEs5onRT765oQ6FOL1wMi6olqC+ImrsUj1uMc9Tn3nO9/J26cVYqVdXUW19YYbblDaQ0CeB+3beuuti/zaZYjSDKSuuOIK9cc//lHd4x73UPPnz1fbbbed0pupinSuH/qtTe2zzz7FI+1lQj3iEY8o7l0/0I5f/OIXCv3An17xztuDNm2zzTZqo402cmXL46666ir173//O/99u9vdTmnPB960rgeo71//+lf+CH3bYostXMkaj0M/tP2t+vnPf67gS/Z+97ufesADHqC23HLL6Lp/97vfqR/96Efq8ssvz7FDnx7/+MerDTbYoChLK6nqn//8Z36vTSaUtgkunpk/Vq5cqRYuXFhEfeUrX1F77rlnce/7oVeJ1VZbbaX++te/5kn0Bjt10kkn+ZIz3kBA5IUWZEZs2E/6IQ7DifJzHU5dk59l8wvmLcyJv/rVr/J5C3Mi5q0HPvCB6va3v30pY5SVi4wYi/oTfVEGZGrVXIj5fvXq1UWeu971ruoud7lLcV/24+9//3s+F2A+QN3ow4Me9KDK+cls5/Oe9zx1wQUX5NUsXrxYvf71ry+qDG0L+oy5+dJLL1WQ6XrTdK4H3Oc+96nsf1GZ48ek5U7av1WrVqlHP/rRRUu0Qqz22GOP4h5z78UXX6yuvvpqdcc73jGff6F7YA4OCbOcJ0Pmi977IU5d4YDfWE3o4u+mm27CO0D2kY98JNODvYg302hGyQ4++OBMK5B5Wte/mDft73//+9mznvWsTAsrZ32oWyu52WGHHZb9+c9/dlWXHXDAAUVe+BfUCq4znStSD66RDWBPecpTXMkai9OKfPaa17wm0wp/0QcTb/x+8pOfnF100UVBbfjoRz86YqpglgW/w/D6oAdGXlboCvGuu+5atG2HHXYIaocketOb3lTkvcMd7kBbYgGm4ip0A3/G/vmKTlmh9ZUZE59Sv+ARU19VWsrPdQh1TX7a88sPf/jDvCMf/OAHs80337yQN8IzuGJ+ee5zn5vpBQAvW9jl2u5CTznllJGyf/vb33rLkgfgebMdcMVVFTD/wp2lmc/8veGGG2YveMELcrngKutDH/qQN69ZDr7g+cJ//vOf7M1vfrN3LkE5wHS33XbLtMLvK2Ysvo5yJ+2fvUIMTxAI+gUq0wt2Xsz0YlB22WWXjfXFjpjlPCl0LZsrYG/tem73w3ffej/EqQL905/+9AgTXHPNNdlrX/vakTgB2r5iUxXSu0KVYJE8p59+eqbfbILqQ/3YnHX++edL9uJ63nnnjZQRInQk85lnnjmSV69+yqPGr3oVNwOONraue+B04oknlrbpDW94Q1BZGPyw8YWCLHW9/OUvd5Z9/fXX5+7VJN3SpUud6XyRP/vZz4o6UMbHP/5xX1LGGwgI3i4BVhVnFDPyM0UhHSlowpuU+gWPCat2ZqP8XAdL1+SnPb/Aq81RRx01ImeEX+wrzL18plt2udNWiOHPHQce2W323evVy0x/BRzj7UkVRilIr65nO+64Y3A7MC+jzqpQV7mT9s9WiPXKefapT32qdDFOsIfy/5Of/MTbxVnPk9LOsrmBCrGXfOsefP7znx9h+g984AP5/W1uc5sMK6WnnXZa9q1vfSuD4gwvBNpsYiT9wx/+cGcNVYIFmZAGq7lCSAwq2DghHm/8WDmGsrpo0aIiDdJqEwrnm/G2225bpMPv0IBT1qQNWF3AG+w0AlaxzVVhKLxPe9rTsre//e0ZDPHhqgyYm6u4oAto5gqmvS76M3fu3NzNDt6C8QYPe6njjjsu22STTfL+vvjFL870p7ui7z6F+KyzzirSoFzb77CrLXbcZpttVpTxnOc8x37MewcCwpNlAs73zFFcHpWikPrKjIlPqV/wiKmvKm2qQkz5mWWzkJ/2/PKud72rkC/4mgZZeO6552Zf+MIX8q9v9mqrNqFwsoZd7jQVYihU97rXvYp+gN+x+opFI3wd/PWvf52tWLEig5yG/3cZD/h6CsXODNq8IXvPe96T/5lfXnfZZZciHs9dyjTmCm1WV5SPevbdd98Mq+PA4ze/+U2Oqza9GFlQQTqfG060rc5yJ+2frRBDv8AXb7QdfKPN+TK8HELfefWrX51pU4kRHJ70pCeZMI/8nvU8KfzgmxMQT4V4hGTjN1/84hdHCI6BgAH09a9/fTyxjsGKpql4ggj43GCHKsGC9OYbKOr96U9/ahdT3GNlVAiO66te9arimfyAImmmcbVL0soVu8xNgYHV8WmFQw89tGgvBiXeVF0BgmTTTTct0mJVF8xtBphdmJ8K4d3hxz/+sZmk+A0aPvjBD87Lg4ItmPkUYijOkgaf6lBXbHj2s59dlAHlGEdaMpQjIJiXCTjfM1/JKQqpr8yY+JT6BY+Y+qrSpirElJ+zkZ/2/IL5A4srJ598spPk2iY003tfChkEXrKVSGS0y52mQgwFU3gciyNQLn1yErJd20YX6fFJ3xfMr4BHHnmkL1kRr22Oi3IxP8B9pi9AUTeVeMw79twkeZsqN6Z/tkKMBT5s9j711FOlmSNXePDS+3cKPEAf37w663lSeMc3JyCeCvEIecdvbAEAUE844YTxhEaMNjofYZD999/feLrup12uLVhgeyUExPWQQw4ZK8OMwKqtefoZzAzsAPtiU7l9/vOfbycZu4etltkOvIVPI6xZs2akrWW2XGiP/fYJO2EzfPaznx3pR9XnK+Bvm6r4FGKsyAtGeqOkWW3w7zPOOKMoA2WF2kMHV9DDhIJ5mYDzPfPBkaKQ+sqMiU+pX/CIqa8qbapCbMs5tJHyswr19Ocu3PH1qyxgVVF4CNdnPvOZY8ntcu15qykbYphwQDGT9oV8RYPpmaTH1WVKiA7GKIx6A/bIV1soeVXh29/+9kg7XOaKTZUb2z9bIQZuWEgrC1gcNHH+2Mc+5kw+63lS2uibE6gQO8k2GmkLAHxCB3BVQVYYQQR8vsFKqxnscm3BgvQYSDALWL58eenqsJQLBVeIDnMAV3jGM55RpIEggJ1sWXjiE59YpN95553Lktb67CUveUlRb8gmwJtvvjk3b4D5BD7/2e5zTFcv+ISmvTpUtheffwRPXF0KsfYuMpKmSnj4KrVfgN73vvf5kjL+/xAQ2pQJON8zH4gpCqmvzJj4lPoFj5j6qtLWrRBTflYhXs9ze37BHARZVRXmzZtXyDMsnmgvDiNZ7HLteasphfhlL3tZ0S58LcSKdlXA6rHZH2zocoUYhRiKuIwzXMu+2kpdaIf2JFTk23jjjTP7TISmykUbYvpnK8Rot2wwl/7YV8gsc/HI9eLVhnlS6OabExCfvEIMMOr6kwbbgPvusRsWClvZn2kDCoWuLK3LQbQtAGDQHxKw+1T6g6u94meXawuWkDrsNKa3AtTpEoCwdzbbBRtoX8DnENOGGauY0wqmINOu0IKqhVLsC+ZxyrA7Cwl4GTGxcinE9tcA2FxNEsDLZl1LliyZpJhB5RG8IMRi/+qSWW0qR/AIZQLKz1Gk+iQ/7fkF+0xCgj1v2QqfXa49bzWlED/sYQ8r5KN2CxbSlTyNuZEQirTLxCJGYTTNSh760IcGt+OYY44p2o9xaiv0TZWLBsb0z1aIYbYYEmAqKPIHHrbs0IZ5UtoXO1cgfaicn6mXCaxuSifruMI8wA62AKj6dC/5bc8M55xzjjzKr3a5tmAZSRx4A4N3EweYHdgBAkH77i3Sla36wt5MygPDgymmFbDCLXW/8IUvTKoWirL5BltlfiKVXXjhhUUb0BaXQowNedJOXH225VJm2dUUXC996UvLkvKZRkBwL3vj9z3zAThNHne1IaV+wcNVriuO8nMUlT7JT3t+WbZs2WhnPXf2vGUfzGCXa89bTSnE5uZql8Ll6U7usUfGBa5Y5LGDKXerbIhNsw3s+wgNWHgy2wHF0wxNlYs6YvpnK8RVXpukD6a99oEHHijRxbUN86Tg75sTalkhLnpcww9pcGhRsxDon/nMZ4KaZ9vV2Mp2lWCxK8EKM3wi49QZ+CTGWzLMMrDLEwouPm2Yq+HA0qUQo1xsAhCscfXZBWun/EW6F73oRXaTGrvHZzqzfakb+a688sqR8vC2HhKAn9kOl0L8yU9+ciRNmduZqjrNz2pPf/rTq5IP/rnQpkzA+Z75wEtRSH1lxsSn1C94hNZH+dlP+Qn62/MLvCOFhNR5qwmFGOaDwtu4YoMcZHjIn7lRDXltBR6YhCqM2INjtgMejkIDXJWaec0N4k2VK20L7R/S2woxNsWGBNNLiUshbsM8Kfj75oTOK8RY7YRHgLI/uD0TIOCmrCwtALGDLVhcZhV2Htxjp6XUi+uxxx47kswu1zVQkQEbAWxbVrPcst/oqyvgLRl2tJLXpSDqk5lGVlWB3bQClH9pG66woU4JaLtZHlwQhQTYTpn5XArxu9/97pE0wG3SYDo+h/sfhnIEhDZlAs73zFdyikLqKzMmPqV+wSO0PsrPWw9cEuzMa1flJ+hvzy/YdBwSUuetJhRiLDKYdEn5/bnPfW4MhlCFEXO0WXfMfhG4STXzmhtLmypXOhraP6S3FWL7C4GUaV+rFOI2zJOCv29OQDzMI1zP7f767mdqMuFrlBlf96aQUB+zcLAtBMDVdoNmCyyXQozdqGYZ+A2bXqwMwxYaq4g4WQgn8mC3q7mii7Q+gQ58kFfKhlsY28j/ne98Z/FcH4dpQtr472984xtF3WgjTldKCV/+8pdHyqvyMCF1AZMqt2s4hENwxFVOMpQyYq677757UdZDHvKQmKyDTCu4uwRYVZwPsBSF1FdmTHxK/YJHTH1VaSk/3Qi1WX6ixfb84nKh5uoZvhYKH+EaO281oRDbn9vN9sX+di2uhCqMUA7N+mLmJVsfgA9fCU2VK+WH9g/pm1KI2zBPCu3K5gYqxMI1nqstWELfmOy3PiiYZrDLtRVirAybG9rwG3ZgIKYvhNjASV5b6bRXvs3VyjJn4lJenVfb/c9b3vKWpOLtQR76Zm9/ynKtEAMbGWi4Is+kwVQ+YjaOTFpf1/MJ7mUCzvfM1/cUhdRXZkx8Sv2CR0x9VWlNnow57l3KteUc5acg0+x1UtztlczYeasJhdhWJqGk4+S9Sf5c8jlUYbS/XLrcp/moas9BWDGV0FS5Un5o/5DebmfoeK1aIW7DPCny0TcnIJ4KsXCN52oLljKvDGYR9lsfPBaYwS7XVohxUpAQEOYNPh+KZpn2SWw+G2LkwefS+9znPkUd5gaBK664oohH3a6NCGa9df+2bRsPP/zwpCpW64M7BEtczbfzsoJ//vOfj+RzKcS2/2Ao85MG04906K7wSevqQz6haZmA8z3z9T9FIfWVGROfUr/gEVNfVdq6FWLKzyrE63luzy+huGPzt/ARrrHz1iQKMXwMm3XaiiZM18xN0a985SvrAen/SglVGO29LbZrz7JG2X7yQR8JTZUr5Yf2D+mbUojbME8Kj/nmBCrEwjElV1uw2IPVlxUHQwgBcF25cuVIUrtcUyH+17/+NWLjW+YJwiwU3hPMOstMJpDPNMnAsdDyuR/2zlJOqJs5sx11/MaJPtIG+E5OCbYtcKjXCttFnUshtl98bDrHtPuud71r0efQNsaU37e0wh9lAs73zIdFikLqKzMmPqV+wSOmvqq0dSvElJ9ViNfz3J5fQnHHoQrCR7ja8swu15y30HJbIcbqblWAGaJZp+uLoOnFwHXQVVUdZc9jFEbT20XMvIRNjWYfsbpthqbKRR0x/WtKIW7DPCn4++YEKsQmR3p+2wIg5IQcFPWGN7xhZADYgsEu1xQs8P0oxMMV/jGrAk6qMz9bIF+VQow3c/PMd9lwsP322xf1w/52FsH0O4l+2TbOrjZhJys+zcCjB3b1msFUNh/zmMeYj7y/3/jGNxY4AE+XQmx/YsSJeJME0M9cBUn1rDFJG7qWR8ZImYDzPfP1NUUh9ZUZE59Sv+ARU19V2roVYsrPKsTreW7PL+YXwLIazOORwU8x8xbK/fSnPz0iM3/0ox+VVZc/sxePXAoxZLbwNzwr1RliFEbzyy1OXsOX1pAAV3HSflxvuOGGkWxNlYtKYvrXlELchnlS8PfNCVSIR1jSfWMLFvgLvP76692JjVjz8zcOhbAPjbDLNRVibIAQ4uEaciCG/WaOfDj9rCo85SlPKerCRhFTGcdbORS1WQSYNZgY2DbOdpsgmDbbbLMiz9577z2SZMGCBcUzKJ5wxVYWoIBvscUWRR60xaUQ46XDbOekJ8zZJ/mEesIo60PfnwnuZQLO98yHTYpC6iszJj6lfsEjpr6qtHUrxJSfVYjX89yeX3CCp33qnKumbbfdtpBnsfMWylu1alWRH/z4hS98wVXNSBw86gjv4upSiO0DQ+wFj5ECjZtf/vKXGRZ1ysaVqTBWmUG85jWvGWkrNvxVBZgA4gus9HGHHXYYy9JUuagopn9NKcRtmCcFf9+cQIV4jC3HI2zBAlDf8573jCc0YvBWLODj6nJrZpdrKsSw2TXzH3300Ubp4z/xVo5Nd+YKI/KHDFYomlIXJivzyGQM0lkFGLebAxkeGMpWiW0bLfhsNoN96pxL6JrpsdIruMjVpRDjhcH0/wyPH5ME+5PSueeeO0kxg8ojdCkTcL5nPqDKJk5fnjrjU+oXPOpsT90KMdpI+VknhdxlrVixYkx+YdN1WUidt1A2Nl4KH+JaJQ/N+UfyuWQzxvEmm2xSlI0V47L5AG3BIskTnvCEPA9OqfMdumEeAgWvTWXh2muvHVFu991337Lk+TPbXAKy3g5NlYt6YvrXlELchnlS+Ms3JyC+95vqsLoKm1j82Z8pbKZ03duKK970cMY7PvO4wm9+85sMn1IEfCiqrtVIu1xTIUa55lHDOCXOt0EOB4XA7AGb32wvEyGnzEComAdCmG7G7M9lrv42GYcXCcER16c97WnOc9Vhg2YOetgfQ8CYAXbZm266aVEeMPMdswzlGTTGqoqplPsEKtol7dxyyy3NaoN/m0eMol4cq8tQjoBgXibgfM98JacopL4yY+JT6hc8YuqrSkv5WY5QW+WnvUCAxQ7ItNNPP93ZIcxb5jww6bwFPEx7X/CkmOLZFWP1GIsJ97jHPTLTpM322S/57Pltt912y/7617/K45ErxtEBBxxQyGW0A56VXAFuRWXsYO62v+baeWxTOuz38H1JPfXUU0f2A+FLpS80VW5M/5pSiNHnWc+TQmPfnDAIhdjHfKHxtuJq+ufF2yE8O+AtFyfPQKkxlS4QACfluIJdrq0Q246sYXQPW2K8+UOQwFb2kY98ZDGQjzvuuAwn+pirxBtvvHHePnzG8gkOtM3cRCdMA5/Gsw5/+9vfRl4u0DaYMeCkPpgULFmyJNtjjz0KDPAcLwb2RhDph91PKP9YeUY5EFygHzYwCobA2Dzm+mUve5kUNXKFP0rBDVffyX8jmawb+JaWMtAmhmoEBK8yAed75is9RSH1lRkTn1K/4BFTX9NpbTlH+dk04uvKhxIq/IArZJTINXPewr4LvOib5mZIP+m8hdrtFVEo41gpfv/7358fpYzTVqHMSvswf26zzTbFve+YaSxqPPShDy3SIT/2l8AHP0wG4SEDchz9MTepIR3mDF946lOfOlImFlSwQf2www7LXDIfpiemaQnKh5tS9Asnu4HnYeLx5Cc/eaRc4HDhhRf6mpGbtDRRbkz/mlSIZz1PCr/55gQqxF7WvPWBLdBxkg8UKxEuArLr+tKXvtT75miXayvEeOOEL1pXuXYcBqIY95sO4810PiURPb3mmmtGNtch32n67PU2BAgfX5/M/uE3VnOr7K3x4hBCO+wgBg1wQIbUA3MSV7CPeIbgjwm22yGX8/iY8oaSVuhSJuB8z3wYpSikvjJj4lPqFzxi6ms6rS3nKD+bRnxd+VigEX7AFTLm+OOPD5J9KfMWav/3v/+dmSfEmu0wf2NBQvZKmHIWG9J9AUox/BCbXzLNMl2/YepWZl5hK4FmGViocAXYBS9evHgEYzOf/RtzechCSRPlxvTPTusy73DhYW7odx3djDyznieFJr45gQqxi7JWnC3QsVsSAUb95s5XARsDFbtgTcfbVpH5rV2urRAjEQQLVqDxZinlyxVK3eMf//h8w4BZPjZn7bXXXiOCD/ZTWCUuC/B7K2XDLAQDs00BKwDwPIG+SDvlik+BUFbR95Dw+c9/Pld0TQ8bUhZWKkwbx4ULFxb1la0ybLfddkW6ffbZJ6QZRRp8xpT6cb3sssuKZ/zhR0AwKxNwvme+UlMUUl+ZMfEp9QseMfU1ndaWc5SfTSO+rnx7NQ6KJAJWUXfaaacReQO+qXPeQj0yd22wwQZjdaE+zJ1f//rXkTQPpq26zzRN0uIKv/yQzaZ7TuF/XGF2Bs8aZQtBZnlYWTY3vgkmsEEuC3jxAJ52XuS/wx3ukM8zOAiqTCF3lV93uaH9a1IhRj9nOU8Kf/jmhDoU4vXQSV1RLUEreXk5NRaZ3K6zzz5baQWnKEcrrkp/Hinur7rqKqXtr5R+A1ebb7650p90lB4cxfM6fuiVSqU9Rii9Y1bpCTOvR3/KV9r2yls80mnbZaUFhtL2yN508kCbSKjvfOc7+a1eIVAnn3yyPGrVVQsWpd+0lT40Q2lhq/QnJqVt35S2eYtup54k1M9+9rMcV23DprQ5htL2VtHlIIOegJT+zJbn1ZOLuvTSS5X2NFJZFnhd7zpW2i9lnlZ/SlR6oqjMxwRKibzQgiwaDv01wZlH++JW+gXU+WwakSn1Cx6Un6OUovwcxQN3mBsgR/UG7sbmLdQDeS116Q1LSptmKMxdeq8FHtcS9OlzSh+IpPSXTqVNFpW2Yc7nhNhxrP3Vq8svv1yhnWgf5hW92BLURow59BPzCfgN84g++GqiecmssM5yU/pntinl9yznSZGPZfMFMNKLbmNd9M0XdsLBK8Q2IF2812+FSr+x500H00CZ06vcXezKzNqsV0RyBVifipe3Qa9OKO3kvrI92uZM6cNPinTaxkxp2/Dinj/8CIQIOF9un4BLUUh9dcXEp9QveHRJIY7Bpq1pKT/bShm2q20IzHKeFPlIhTiBK6pWiBOKbk1WrErqHbh5e7hCOTlZtOmD0nZleQFYscZqA1ZDygK+KGjfz3kS7TtZ6U/MZcn5zEAgRMAZyUd+UiEegaOxG8rPxqBlwUSgkwjMap4MmS+4QlzBUn0X6DCN0LtpCxSw2qFtoop7/ghHAJ8H9Sl/SruryzPpndpKb070FgDlV9tu588xWKEYz5s3z5ueD0YRCBFwozluvaNCfCsWTf6i/GwSXZZNBLqHwKzmyZD5IlUhVvrzXG1Bkxb2yLWVV0dB9qYQ1+a3OuqZRRk4vAJuygT3Zz7zmbNoRq/qhK9L2QENX56+TR047dB06QYXPwxxCAjfYjNE7J+vppRNbb4yY+JT6hc8YuprOi3lZ9MIs3wi0D0EZjFPinwsmytSD+agDbFGuSsBNq3YeKB9Eiu9S1dhg6AEbCLAvT4NSKK8V32gRbEBz5towgfa/Y7SHiMmzN2ObNq1m3r961+fNwYbHy+66KIxXPfff3+lT8PL0+y44445PUI3cLSjl7NvRcgbv6+VXCH2IVNvfJ9WiCk/6+UNljZsBKY9T4bMF1whrni56tMKh+laTQ/FYmVYe8fItJeDCiRuffyiF72oyGuWU8fvWJdlt7aqPb/gE1rbAxcY7brrriNud9773vcWz3Ac6dVXX92exneoJcJvZW/8vme+bqas0PrKjIlPqV/wiKmv6bSUn+MIU36OY8KY4SEw7XlS5KNvTkA8V4g1SmWhTysc+oQipU+6K7qr/SQqbSahTjjhhLEVzCKR48fhhx+uYBjfRNhzzz2V9sHYRNFTLVObRCjtN1ldccUVeb1Lly5V+kQ8pQ8mUNpJu9LHg+YuebCZUfvTnGrb+lJZyBu/r69cIfYhU2885ec4npSf45gwZpgITHOeDJkvUleIe28yAT+N2pl8wa3agbjS568X9136ce211yq9Gpn7WdRHW+Y+fDfccMMudaFTbYVfSn3IRt5m+CbWK8W5v2F9gEgeB9/Hpk/rTnWuBY0NEXC+ZlIh9iFTbzzlZ714sjQi0DcEpjVPhswXVIj7xl3sDxEYCAIhAs4HBRViHzKMJwJEgAj0D4GQ+YIKcf/ozh4RgUEgECLgfEBQIfYhw3giQASIQP8QCJkvqBD3j+7sEREYBAIhAs4HBBViHzKMJwJEgAj0D4GQ+YIKcf/ozh4RgUEgECLgfEBQIfYhw3giQASIQP8QCJkvqBD3j+7sEREYBAIhAs4HBBViHzKMJwJEgAj0D4GQ+aKVCnH/SMEeEQEi0BQC2n9kdNF9VoijwWAGIkAEiMBAECibL6gQD4QJ2E0i0FcEygScr89UiH3IMJ4IEAEi0F8EyuaLVinEIMFNN92k5syZE02Nf/zjH9F5XBl8gLjSNhHH+v9X3fGOd2wC2qAyif8w8O+jQhzE4J5EIj/J/8Pgfw8bKNKf9Of8O65/+OYLexyth6NG7chZ3EORZiACQACHYOhjIQkGEfAiMMlLt7ewHjyg/OwBEdkFIkAEGkEgdL6o9aQ69IQrxHxD5Rvq+BtqI6PcUehQVoh8b/yTyh8HlBNFzap+rhCvI9dQ+N/HnOw/51/Ov+Pzr2++sMcRFWIbkcR7CiQKJAqkcYGUOKzGsvsE3KwUUmngrOqnQryOApS/lL+Uv83LX5F39rWt4883X9jtp0JsI5J431aGSOxWcHb2nxPSNCYkn4CblUIqA2RW9VMhXkcByh/Kn2nIHxnv9pX8107+880XNv2oENuIJN5zQLRzQCSSNTg76T8d+vsE3KwUUmGQWdVPhXgdBTj+pjP+hN/tK/En/m18IfHNFzb/UiG2EUm8p0CgQGijQEhk6+Ds0+J/n4CblUIqAM2qfirE6ygwLf4TettX1k/5T/nfPpMN33xhj18qxDYiifcUiBSIFIjNC0SfgJuVQipiY1b1UyFeRwHKX8pfyt/m5a/IO/va1vHnmy/s9lMhthFJvG8rQyR2Kzg7+88JaRoTkk/AzUohlQEyq/qpEK+jAOUP5c805I+Md/tK/msn//nmC5t+VIhtRBLvOSDaOSASyRqcnfSfDv19Am5WCqkwyKzqp0K8jgIcf9MZf8Lv9pX4E/82vpD45gubf6kQ24gk3lMgUCC0USAksnVw9mnxv0/AzUohFYBmVT8V4nUUmBb/Cb3tK+un/Kf8b5/Jhm++sMcvFWIbkcR7CkQKRArE5gWiT8DNSiEVsTGr+qkQr6MA5S/lL+Vv8/JX5J19bev4880XdvupENuIJN63lSESuxWcnf3nhDSNCckn4GalkMoAmVX9VIjXUYDyh/JnGvJHxrt9Jf+1k/9884VNv9YoxHbDJr2f1YQk7WX9N6nQc8MFszqvxJ/4k//m1Dmkosri+OP44/jj+IsSGjUmTpU/VIhrJAaKSiVIanNYPyckTkickFLlyKT5KX8ofyh/KH8mlR+p+VLlDxXiVApY+VMJYhUXfcv6OSFxQuKEFC04aspA+UP5Q/lD+VOTOIkuJlX+UCGOhrw8QypBykuvfsr6OSFxQuKEVC0pmklB+UP5Q/lD+dOMdKkuNVX+UCGuxjgqRSpBoipzJGb9nJA4IXFCcoiGqURR/lD+UP5Q/kxF2DgqSZU/VIgdoKZEpRIkpW7kZf2ckDghcUJKlSOT5qf8ofyh/KH8mVR+pOZLlT9UiFMpYOVPJYhVXPQt6+eExAmJE1K04KgpA+UP5Q/lD+VPTeIkuphU+UOFOBry8gypBCkvvfop6+eExAmJE1K1pGgmBeUP5Q/lD+VPM9KlutRU+UOFuBrjqBSpBImqzJGY9XNC4oTECckhGqYSRflD+UP5Q/kzFWHjqCRV/lAhdoCaEpVKkJS6kZf1c0LihMQJKVWOTJqf8ofyh/KH8mdS+ZGaL1X+UCFOpYCVP5UgVnHRt6yfExInJE5I0YKjpgyUP5Q/lD+UPzWJk+hiUuUPFeJoyMszpBKkvPTqp6yfExInJE5I1ZKimRSUP5Q/lD+UP81Il+pSU+XP/we3HLc6V/MCvQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 18,
"metadata": {
"image/png": {
"height": 400,
"width": 400
}
},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='ClassInheritance.png', width=400, height=400) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Subclasses can have their own methods."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**: Add the play_cd() to Sedan and play_bluetooth() method to SportsCar. Construct a test to run these methods."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What Else?\n",
"- Class attributes\n",
"- Class methods"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Object Oriented Design"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A design methodology must specify:\n",
"- Components: What they do and how to build them\n",
"- Interactions: How the components interact to implement use cases"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Object oriented designed\n",
"- Components are specified by class diagrams.\n",
"- Interactions are specified by interaction diagrams."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Class diagram for the ATM system"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1wAAAKYCAYAAABn6/nSAAAMFGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdUk8kWnr+kEBJaIAJSQm+CFOkCofciHWyEJEAoERKCih1ZVHAtqFhAVHRFRMW1ALJWLFhYBOz1gYrKyrpYsKHyJgV0fe28e8788+XOvXe+O7kzZwYAZVt2bm42qgJAjiBfGB3ow0xMSmaSegEOMEAHJoDA5ohyvaOiwgCU0f7v8u4mQCT9NWtJrH8d/6+iyuWJOAAgURCnckWcHIiPAIBrcnKF+QAQ2qHeaHZ+rgQPQqwuhAQBIOISnC7DmhKcKsMTpDax0b4QswAgU9lsYToAShLezAJOOoyjJOFoK+DyBRBXQezJyWBzIb4P8YScnFkQK5MhNk/9Lk7632KmjsVks9PHsCwXqZD9+KLcbPbc/3M5/rfkZItH5zCEjZohDIqW5AzXbU/WrFAJpkJ8XJAaEQmxGsQX+VypvQTfzRAHxcntBzgiX7hmgAEACrhsv1CIdSBmiLPivOXYni2U+kJ7NIKfHxwrx6nCWdHy+GiBIDsiTB5neQYveBRX80T+MaM2afyAYIhhpaFHCjNiE2Q80XMF/PgIiJUg7hRlxYTKfR8WZvhGjNoIxdESzsYQv00TBkTLbDDNHNFoXpgNhy2dC9YCxsrPiA2S+WKJPFFi2CgHLs/PX8YB4/IEcXJuGKwun2i5b0ludpTcHqvmZQdGy9YZOygqiBn17c6HBSZbB+xRJjskSj7Xu9z8qFgZNxwFYcAX+AEmEMOWCmaBTMDvGGgagL9kIwGADYQgHfCAtVwz6pEgHRHAbwwoBH9CxAOiMT8f6SgPFED9lzGt7GsN0qSjBVKPLPAU4hxcG/fE3fEw+GXBZo+74K6jfkzl0VmJ/kQ/YhAxgGgxxoMDWWfDJgT8f6MLhT0PZifhIhjN4Vs8wlNCF+ER4Qahh3AHxIMn0ihyq5n8IuEPzJkgHPTAaAHy7FK/zw43hawdcR/cA/KH3HEGrg2s8UkwE2/cC+bmCLXfMxSPcfu2lj/OJ2H9fT5yvZKlkqOcRerYP+M7ZvVjFN/v1ogL+9AfLbHl2GGsDTuDXcKOY02AiZ3CmrF27IQEj1XCE2kljM4WLeWWBePwR21s6237bT//MDdbPr9kvUT5vDn5ks3gOyt3rpCfnpHP9IanMY8ZLODYTGDa29o5AyA522VHxxuG9MxGGJe/6fJOA+BaCpXp33RsIwCOPQWA/u6bzug1LPc1AJzo5IiFBTKd5DgGBEABynBXaAE9YATMYT72wAm4AxbwByEgEsSCJDADrngGyIGcZ4P5YAkoAWVgDdgAtoBtYCfYA/aDQ6AJHAdnwAVwBXSCG+AerIs+8AIMgndgGEEQEkJD6IgWoo+YIFaIPeKCeCL+SBgSjSQhKUg6IkDEyHxkKVKGlCNbkB1IHfIrcgw5g1xCupA7SC/Sj7xGPqEYSkXVUV3UFJ2IuqDeaCgai05H09E8tBAtRlehm9AadB/aiJ5Br6A30B70BTqEAUwRY2AGmDXmgvlikVgyloYJsYVYKVaB1WAHsBb4P1/DerAB7CNOxOk4E7eGtRmEx+EcPA9fiK/Et+B78Eb8HH4N78UH8a8EGkGHYEVwIwQTEgnphNmEEkIFYTfhKOE83Dd9hHdEIpFBNCM6w32ZRMwkziOuJG4lNhBPE7uIj4lDJBJJi2RF8iBFktikfFIJaTNpH+kUqZvUR/pAViTrk+3JAeRksoBcRK4g7yWfJHeTn5GHFVQUTBTcFCIVuApzFVYr7FJoUbiq0KcwTFGlmFE8KLGUTMoSyibKAcp5yn3KG0VFRUNFV8UpinzFxYqbFA8qXlTsVfxIVaNaUn2p06hi6ipqLfU09Q71DY1GM6WxaMm0fNoqWh3tLO0h7YMSXclGKViJq7RIqVKpUalb6aWygrKJsrfyDOVC5Qrlw8pXlQdUFFRMVXxV2CoLVSpVjqncUhlSpavaqUaq5qiuVN2rekn1uRpJzVTNX42rVqy2U+2s2mM6Rjei+9I59KX0XfTz9D51orqZerB6pnqZ+n71DvVBDTWNSRrxGnM0KjVOaPQwMIYpI5iRzVjNOMS4yfg0Tnec9zjeuBXjDozrHvdec7wmS5OnWarZoHlD85MWU8tfK0trrVaT1gNtXNtSe4r2bO1q7fPaA+PVx7uP54wvHX9o/F0dVMdSJ1pnns5OnXadIV093UDdXN3Numd1B/QYeiy9TL31eif1+vXp+p76fP31+qf0/2BqML2Z2cxNzHPMQQMdgyADscEOgw6DYUMzwzjDIsMGwwdGFCMXozSj9UatRoPG+sbhxvON643vmiiYuJhkmGw0aTN5b2pmmmC6zLTJ9LmZplmwWaFZvdl9c5q5l3meeY35dQuihYtFlsVWi05L1NLRMsOy0vKqFWrlZMW32mrVNYEwwXWCYELNhFvWVGtv6wLreuteG4ZNmE2RTZPNy4nGE5Mnrp3YNvGrraNttu0u23t2anYhdkV2LXav7S3tOfaV9tcdaA4BDoscmh1eTbKaxJtUPem2I90x3HGZY6vjFydnJ6HTAad+Z2PnFOcq51su6i5RLitdLroSXH1cF7ked/3o5uSW73bI7S93a/cs973uzyebTeZN3jX5sYehB9tjh0ePJ9MzxXO7Z4+XgRfbq8brEcuIxWXtZj3ztvDO9N7n/dLH1kfoc9Tnva+b7wLf036YX6BfqV+Hv5p/nP8W/4cBhgHpAfUBg4GOgfMCTwcRgkKD1gbdCtYN5gTXBQ+GOIcsCDkXSg2NCd0S+ijMMkwY1hKOhoeErwu/H2ESIYhoigSRwZHrIh9EmUXlRf02hTglakrllKfRdtHzo9ti6DEzY/bGvIv1iV0dey/OPE4c1xqvHD8tvi7+fYJfQnlCT+LExAWJV5K0k/hJzcmk5Pjk3clDU/2nbpjaN81xWsm0m9PNps+ZfmmG9ozsGSdmKs9kzzycQkhJSNmb8pkdya5hD6UGp1alDnJ8ORs5L7gs7npuP8+DV857luaRVp72PN0jfV16f4ZXRkXGAN+Xv4X/KjMoc1vm+6zIrNqskeyE7IYcck5KzjGBmiBLcG6W3qw5s7pyrXJLcnvy3PI25A0KQ4W7RYhouqg5Xx1ec9rF5uKfxL0FngWVBR9mx88+PEd1jmBO+1zLuSvmPisMKPxlHj6PM691vsH8JfN7F3gv2LEQWZi6sHWR0aLiRX2LAxfvWUJZkrXk9yLbovKit0sTlrYU6xYvLn78U+BP9SVKJcKSW8vcl21bji/nL+9Y4bBi84qvpdzSy2W2ZRVln1dyVl7+2e7nTT+PrEpb1bHaaXX1GuIawZqba73W7ilXLS8sf7wufF3jeub60vVvN8zccKliUsW2jZSN4o09m8I2NW823rxm8+ctGVtuVPpUNlTpVK2oer+Vu7W7mlV9YJvutrJtn7bzt9/eEbijsca0pmIncWfBzqe74ne1/eLyS91u7d1lu7/UCmp79kTvOVfnXFe3V2fv6nq0Xlzfv2/avs79fvubD1gf2NHAaCg7CA6KD/7xa8qvNw+FHmo97HL4wBGTI1VH6UdLG5HGuY2DTRlNPc1JzV3HQo61tri3HP3N5rfa4wbHK09onFh9knKy+OTIqcJTQ6dzTw+cST/zuHVm672ziWevn5tyruN86PmLFwIunG3zbjt10ePi8Utul45ddrncdMXpSmO7Y/vR3x1/P9rh1NF41flqc6drZ0vX5K6T3V7dZ675XbtwPfj6lRsRN7puxt28fWvarZ7b3NvP72TfeXW34O7wvcX3CfdLH6g8qHio87DmHxb/aOhx6jnR69fb/ijm0b3HnMcvnoiefO4rfkp7WvFM/1ndc/vnx/sD+jv/mPpH34vcF8MDJX+q/ln10vzlkb9Yf7UPJg72vRK+Gnm98o3Wm9q3k962DkUNPXyX8274fekHrQ97Prp8bPuU8OnZ8OzPpM+bvlh8afka+vX+SM7ISC5byJZeBTDY0LQ0AF7XAkBLgneHTgAoSrK3l1QQ2XtRisB/wrL3mVScAKhlARC3GIAweEephs0EYirsJVfvWBZAHRzGmlxEaQ72slhU+IIhfBgZeaMLAKkFgC/CkZHhrSMjX3ZBsncAOJ0ne/NJhAjv99ttJKiz7yX4Uf4JEL9tBtKO/vwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGdaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIj4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjg2MDwvZXhpZjpQaXhlbFhEaW1lbnNpb24+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj42NjQ8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICA8L3JkZjpEZXNjcmlwdGlvbj4KICAgPC9yZGY6UkRGPgo8L3g6eG1wbWV0YT4KAEx8HgAAABxpRE9UAAAAAgAAAAAAAAFMAAAAKAAAAUwAAAFMAACTA15fefIAAEAASURBVHgB7H0J/GZT/f+ZJvsyyE4Y2kgxtkIZUxEhgyjEkD9SMWTLOhQVLZaIVMbYStLMyJKkMUjZskSRpMm+Zfk1Iab7P+8793PnPPc55z53Ofe5z33u+7xe3++9z7nnnuX9+ZzP+XzuOedzRgQ6KB3+85//qIUXXhi3tQSWT/zJf+x/tQgfXSjlD+UP5Q/lD+VPPQhQ/lL+tkH+jqDBNVfAsMOzw7ehw7uGU/I/+Z/8T4PDJR+qjqf8ofyh/KH8qVrOuPLvl/yhwRVRoF+A101wlm9HgPTngM8BnwO+XTpUH0v5Q/lD+UP5U72ksZdA+dMf+UODK+I/Mlx/GM7e3bmki/xH/qPCRYXLJR+rjqf8ofyh/KH8qVrOuPJvi/yhwRVxQFsI3naGZ/vtCJD/qXBR4aLCZZcO1cdS/lD+UP5Q/lQvaewl9Ev+0OCK8O8X4HZyc4aH+HPA5YDLAdclH6uOp/yh/KH8ofypWs648qf8aYf8ocEV9QAyfDsYngLPjgD5n/xPhZMKp106VB9L+UP5Q/lD+VO9pLGX0C/5Q4Mrwr9fgNvJzRku4s8BlwMuB1yXfKw6nvKH8ofyh/Knajnjyp/ypx3yhwZX1API8O1geAo8OwLkf/I/FU4qnHbpUH0s5Q/lD+UP5U/1ksZeQr/kDw2uCP9+AW4nN2e4iD8HXA64HHBd8rHqeMofyh/KH8qfquWMK3/Kn3bIHxpcUQ8gw7eD4Snw7AiQ/8n/VDipcNqlQ/WxlD+UP5Q/lD/VSxp7Cf2SPzS4Ivz7Bbid3JzhIv4ccDngcsB1yceq4yl/KH8ofyh/qpYzrvwpf9ohf2hwRT2ADN8OhqfAsyNA/if/U+GkwmmXDtXHUv5Q/lD+UP5UL2nsJfRL/tDgivDvF+B2cnOGi/hzwOWAywHXJR+rjqf8ofyh/KH8qVrOuPKn/GmH/KHBFfUAMnw7GJ4Cz44A+Z/8T4WTCqddOlQfS/lD+UP5Q/lTvaSxl9Av+UODK8K/X4Dbyc0ZLuLPAZcDLgdcl3ysOp7yh/KH8ofyp2o548qf8qcd8ocGV9QDyPDtYHgKPDsC5H/yPxVOKpx26VB9LOUP5Q/lD+VP9ZLGXkK/5A8Nrgj/fgFuJzdnuIg/B1wOuBxwXfKx6njKH8ofyh/Kn6rljCt/yp92yB8aXFEPIMO3g+Ep8OwIkP/J/1Q4qXDapUP1sZQ/lD+UP5Q/1Usaewn9kj80uCL8+wW4ndyc4SL+HHA54HLAdcnHquMpfyh/KH8of6qWM678KX/aIX9ocEU9gAzfDoanwLMjQP4n/1PhpMJplw7Vx1L+UP5Q/lD+VC9p7CX0S/7Q4Irw7xfgdnJzhov4c8DlgMsB1yUfq46n/KH8ofyh/Klazrjyp/xph/wZMXv27MDFBIwnAkSACDQFgZEjR6o5c+Y0pbqsJxEgAkSACBABItASBDjDFRGaXxja8YXB1a9Jf9KfX7j5hdslH6qOp/yh/KH8ofypWs648qf86Y/8ocEVcSAZrj8Mxw5vR4D8R/6jwkWFyy4dqo+l/KH8ofyh/Kle0thLaIv8ocEV0b8tBLezO/eQkf5UOKhwUOFwyceq4yl/KH8ofyh/qpYzrvwpf/ojf2hwRRxIhusPw7HD2xEg/5H/qHBR4bJLh+pjKX8ofyh/KH+qlzT2Etoif2hwRfRvC8Ht7M4ZLtKfCgcVDiocLvlYdTzlD+UP5Q/lT9VyxpU/5U9/5A8NrogDyXD9YTh2eDsC5D/yHxUuKlx26VB9LOUP5Q/lD+VP9ZLGXkJb5A8Nroj+bSG4nd05w0X6U+GgwkGFwyUfq46n/KH8ofyh/Klazrjyp/zpj/yhwRVxIBmuPwzHDm9HgPxH/qPCRYXLLh2qj6X8ofyh/KH8qV7S2Etoi/yhwRXRvy0Et7M7Z7hIfyocVDiocLjkY9XxlD+UP5Q/lD9VyxlX/pQ//ZE/NLgiDiTD9Yfh2OHtCJD/yH9UuKhw2aVD9bGUP5Q/lD+UP9VLGnsJbZE/NLgi+reF4HZ25wwX6U+FgwoHFQ6XfKw6nvKH8ofyh/Knajnjyp/ypz/yhwZXxIFkuP4wHDu8HQHyH/mPChcVLrt0qD6W8ofyh/KH8qd6SWMvoS3yhwZXRP+2ENzO7pzhIv2pcFDhoMLhko9Vx1P+UP5Q/lD+VC1nXPlT/vRH/tDgijiQDNcfhmOHtyNA/iP/UeGiwmWXDtXHUv5Q/lD+UP5UL2nsJbRF/tDgiujfFoLb2Z0zXKQ/FQ4qHO1UOEaMGOESi4wnAkSACBCBFiMQBIG31tPgiqCkwk2Fmwp3OxVuiAD2//b2fxpc3vQJZkQEiAARGCoEaHBVQE4qXO1VuMBOpD/pT4O7nQa3GFw+B9YKhihmSQSIABEgAn1CoIpxgTNcEfGocFPhpsLdToUbIoD9v739v4qBtU86AYshAkSACBCBChCoYlygwRURigpXexUusADpT/rT4G6nwV3FwFrB+M8siQARIAJEoE8IVDEu0OCKiEeFmwo3Fe52KtwQAez/7e3/VQysfdIJWAwRIAJEgAhUgEAV4wINrohQVLjaq3CBBUh/0p8GdzsN7ioG1grGf2ZJBIgAESACfUKginGBBldEPCrcVLipcLdT4YYIYP9vb/+vYmDtk07AYogAESACRKACBKoYF2hwRYSiwtVehQssQPqT/jS422lwVzGwVjD+M0siQASIABHoEwJVjAs0uCLiUeGmwk2Fu50KN0QA+397+38VA2ufdAIWQwSIABEgAhUgUMW4QIMrIhQVrvYqXGAB0p/0p8HdToO7ioG1gvGfWRIBIkAEiECfEKhiXKDBFRGPCjcVbirc7VS4IQLY/9vb/6sYWPukE7AYIkAEiAARqACBKsYFGlwRoahwtVfhAguQ/qQ/De52GtxVDKwVjP/MkggQASJABPqEQBXjAg2uiHhUuKlwU+Fup8INEcD+397+X8XA2iedgMUQASJABIhABQhUMS7Q4IoIRYWrvQoXWID0J/1pcLfT4K5iYK1g/GeWRIAIEAEi0CcEqhgXaHBFxKPCTYWbCnc7FW6IAPb/9vb/KgbWPukELIYIEAEiQAQqQEDGhf/7v//Lnfuiiy5qfYcGVwRLGYVLCGNFmJFEgAjkQiAIglzpfSQu0/9ZfnkE6sRf5HcdfFceOeZABIgAESACvhGQccGrwTV79uz+aze+kak5v0UWWaTmGrB4IjA8CGiZVKgxI0eOVHPmzCn0Ll9qLwIiv2lwtZcH2HIiQASIgImAGFzPPfecGZ3p3rVaijNcEXxlvrAKYThgZ+JFJiICVgTq7Edl+r+1MTkjWX59Sxrr5LucbMLkRIAIEAEi0AcEZFzwOsOljYRwhosDfvEBXwhDg6sPvYBFDC0CdfYjyr/i8s8HQ9aJf5185wM75kEEiAARIAJ+EZBxgQaXX1zD3MoM+EIYGlwVEIZZtgaBOvtRmf7vg0Asvz6Dr06+88E7bcvjgQceUJdeemnPZr/lLW9Riy22mFpyySXVUkstpdZcc83wT+jdM4OWJciKqwnLAgssoJZffnm14oorqhVWWEGtvPLKarnlljOT8J4INBIBkRM0uCogXxmFRwhDg6sCwjDL1iBQZz8q0/99EIjl0+DywUdtyOMXv/iF2mmnnQo1FcbXxhtvrCZMmBDmgX2fgxCef/559eabb4ZVwf6PxRdfvO/VKoOrWdnNNttMHXDAAWrHHXdU888/v/mI90SgMQiIPkKDqwKSlVF4hDA0uCogDLNsDQJ19qMy/d8HgVg+DS4ffNSGPHwZBqussoo6/vjj1T777FMrbP/617/CWaI33ngjrMf++++vzj333L7XyReuUnHMdF1zzTVqvfXWkyheiUBjEBB9hAZXBSQro/AIYWhwVUAYZtkaBOrsR2X6vw8CsXwaXD74qA15+DYMPvWpT6kf/vCHaokllqgFPpS93377xWUPi8GFBsHouvXWW9Xqq68et483RKAJCIg+QoOrAmqVUXiEMDS4KiAMs2wNAnX2ozL93weBWD4NLh981IY8XAbXQgstpBZccMEYAswY/fvf/45/p92sv/766qabblIud85p75Z99pGPfETNmDEjzmbQDC4YS9ibZQtQRp9++unwz6X/rLvuuuruu++2vc44IjCwCIg+QoOrAhKVUXiEMC6BU0F1mSURGDoE6uxHZfq/D0KwfBpcPvioDXm4DK7TTz9dTZw4sQMCnKHz4IMPqoceekhdf/316mc/+1nHc/PH+PHj1RVXXKHgbKNf4amnngqNmf/9739xkYNmcNlwjSsb3fztb39TJ510kpoyZUryUfgbdFh66aWtzxhJBAYRAdFHaHBVQJ0yCo8QhgZXBYRhlq1BoM5+VKb/+yAQy6fB5YOP2pBHHoMricdvfvOb0KEDDARbuPjii9Xuu+9ue9QR99JLL4WG3OOPP64ee+wx9eqrr4bL5t7xjnco/KUtT3zxxRcV/hAuueSScB+Zmfluu+2mvva1r8VRcKDRy1gpUx8pqAyuyAP6z5ZbbqmAcTJcddVVaptttklGd/320Y6uTHXEE088oR555BEl9IK8XWmllcI/zODBg2XR8Nprr4UGPbw8/uMf/1BrrLGGGjNmTMgH/TTei9af79kREH3Ep8GFThKG2bNny20t1yaXr8mFs8xqwY2FEoFhQaDOftRk+eOD/m1uf51854N2bctDz0KF463QTa56JiYTFNo4Cj784Q9b83jnO98Z6KWIznz+9Kc/BdrJRqCXLlrfR120kh2m0bNX1nyOO+4457vSFvOqZ7ys+SDSR30k87K4Ip/TTjvN2rbvfve7Uoz16rMdZgF6VjPYaqutAq08W+slOGvHHsGPfvSjQBti5uup99dee23w3ve+N9CeLq15L7LIIsHWW28daIM8NR8+HEwEhDe0wRXk/XO1KLYS2jzgApwy7RfCuEBmPBEgAr0RqLMflen/vVvWOwXLr++DX51815szmCKJgA/D4P777w/e+ta3WhXlqVOnJosMf3/rW9+yphf+SV4XXXTRQM9gdeXly+DyVR+poA9cJ0+ebMUIebuC73agHO1iP9huu+2sdUnSyfy90UYbBdprpKuqYfzLL78cGtTme2n3yyyzTADDj6FZCAhN8xpbSO8KNLgiZMooPEIYF8iMJwJEoDcCdfajMv2/d8t6p2D5NLh6cwlTAAEfhgHyOfTQQ60K+Re+8AU87gg/+MEPrGlFZrmumOV4+OGHO/LyYXD5rI9Uzgeun//857twwuySXsIpxXRcq2gHCrDVw0WjZPw666wTwKiyhVdeeSUYPXp0Vxslj/nmm8/6DLOemEFjaA4CQlMaXBXQrIzCI4SpoFrMkgi0BoE6+1GZ/u+DQCyfBpcPPmpDHj4MA+A0a9Ysq3L8rne9qwPGZ5991job9va3vz3Q+54CLB3Ue3eCs88+27rUcNNNNw20U4w4T72fKfjSl74U/umDmLvqgGVq8hzXn/zkJ/G7uPFdH8m8LK7Tpk2zLq/bddddpYiOa1XtuOWWW7owxbK/Qw45JLjhhhuCv/zlL6ERjHSTJk0KMBMpY49csTTSFr7yla90pUXeJ598cshPoDOMS9BN8pKr3ocXaK+ZtmwZN4AICN1ocFVAnDIKjxCmgmoxSyLQGgSkH/kUcFnBK9P/s5aRlo7l0+BK4w8+m4dAWcNAcoJyrF3JdynGmJEx93GdeeaZXWkgq371q19JVvH1lFNOsaaFcWcLa621Vld6zM6kharq48J1xx13DFCm7e8b3/hGcOCBBwbarX5XO4AR9sT985//tDanqnaceuqpXXXRB1xb64DI73znO13p3/3ud3el//vf/x4ssMACXWldM1c24wxlMTQDgSr0kRFous5Y0UtWcS9Z4s0kghJwMhABIpATAelH2uDK+aZS+itl7nfMFyj/iss/E8ei93XiL3xH+V2Uev19r6w3PbO273//+5V22GBGhffPPPOMWnbZZcN7uJrHGV040wuyCVd4n4OnQT270fEuPBaussoqHXH4cc011yjtQKErXs9mqT//+c8d8drgUuecc05HnPmjqvq4cDXLznoPXHbYYYfUA6WrasfOO++sfv7zn3dUVRt3ShuGHXHyQ+/3Co8TwBiy4oorxt4L9X6uDvrCe6SebZTXwqs2KJWeMetIJwn08kO12mqrxR4pEb/CCisobbh1nBcn6XkdLARkXPCqj8DgQuAX1uJfWDWbhF895iLJ/0SACBRBQPoRZ7iKoFfunTbLf+G7cgjy7X4h4JqJyeql0KznTjvt1DVjAX7QLr7NZF335hJB8yGcNWCJmfCUXDHrYgtFZrhs+fiojwtXaUPW6/ve975AH+Rsq2bPOB/tsNFUH9wcLsXsWYGUBNpY6qKrbb+fmcW2227b9c6VV15pJuH9gCIg/O5TH6HTjIjYZRQOIcyA8g2rRQQagYD0I58CLmvDy/T/rGWkpWP5xT94peGa5ZnwXZa0TFM/Ai7DoIjB9elPf7pLIQY/YJ9P0TBq1KiuPOGgwxZ8GVy2vCUua31cuEr/yHuFd74jjjgil6t1qbPtmrUdxxxzTBf+qPvCCy8cgN5w1JGXvth7ZWu/a6+X1N+2rBBLKRkGHwGht099hEsKNaoIZZa0yNSjZqG5mfE/EciAwJ133qk++MEPdqXE8hMcIJkMedMn3x/039KPtIDLXVUuKcwNWccLZeRfR0YFf9RZvvAd5XdB4vX5NdfSN21whUvD8lRngw02UHfddVfXK1gOtthii3XFP/3000rP3oQH3D766KNK709SOPgWy9L0vq/weu+996o5c+Z0vKsNLvXtb3+7Iw4/iiwpNDPxWR8Xrssvv7x629veZhYb36PPvPDCC+q5555TenYqjjdvcBDwZZddpvQ+LzO6495nO3D4MA6fTtKgo0D9QxuE6kMf+lD4p/ephcv/kmnk93333ae090L5GV/1eWxKHy8Q/07egCdef/31jujDDjtMaVf4HXH8MXgIyLjgVR8RO5NfWIt/YdWsEn79ECzLXOGO9Oqrrw4OP/zwQCvd4WZUvQ440GuLAz04BOPHjw83qWLzJQ/UK4N0/e/ecccd1q9mts3YqG3e9PW3MF8NpB/5/KKUtQaUf8XlX1aM09LVib/wXVr9+GxwEHDNxBSZ4VpiiSW6ZLA2tLoa+8QTTwR6z5HVC6HwT9r1y1/+cleeiCg6w1VFfcrgCicjf/jDH4I99tijC0/gog0g67aVKtoBXLFsz+Z90EUjuG3H8j/9sbPDoyTyQtDGqLVdrvzS4nfZZZe5mfL/QCMgNPSpj3BJYUTyMgO+EKYM98CTD1yJpp1gL+XIFWvF9cbU4De/+Y1VSJSpz6C+q7+khW544YrXdVbGoNY9Wa+8BlTe9MnyBv238LVPAZe1zWX6f9Yy0tKx/PoMPuG7NPrw2eAgUMYwMFvx/PPPW5XopIc6uHxfaqmlrGmFd3pdfRpcVdXHF64nnniiFaujjz7ahD90pV8VrihIO0MJ8LG6F22Sz21eIoueF5bMG7/1qpYOHPhjMBEQ2vnUR7ikUKOKUGZJi0w9araZm1nO//BIdPDBB6v//ve/Od+clxyeeS6++GI1//zzz4scsjt9ArzC8gZM0yPsv//+6txzz21sK7FEcMMNN+yqv57hUh//+Me74vOm78pgwCOkH2kBl7umXFKYG7KOF8rIv46MCv6os3zhu6Lyu2CT+VpBBFxL3/IuKfze976nDjrooK5afO5zn1M//vGPw3iMyR/+8IfV7bff3pUO8ViKtuqqqyp9nla4tAze+bAcHJ4MzaANLqVXpZhR4X3eJYVV1scXrlhaqGcOQ4+OZoPh9e+2224Lo6psh1nmq6++qvS5Z+qnP/2puv7667vqZKY17+FBEfwkAWOyzcvkpz71KQVPl3kCeEV/XM/zCtPWgICMC171EbEt+YW1+BdWzQvhVxTBMusVHnkOOOCA3F9gpLzkFUsQsblzWMN5553XgZU2uBrd1LwzVnnTNw0c4WefX5SyYkD5V1z+ZcU4LV2d+AvfpdWPzwYHAR8zMVgdAacOQnvzanrY0x8xrWkw9ug9Ql2gaEMi0B89u97x5TSjyvr4wFUAwWHPJqa4xxI/8UJYZTukDskr6HXPPfeEB1TvvvvuwUorrdRVR6mzVrYD/YE3zuKvf/2rNe0ZZ5wRp+HNcCEgvOBTH+GSwohHygz4Qpi87IZDA+Vd1xUn0esvacFnP/vZYNy4cYH+mpb6zuabb563Go1Jj/abONHgmmvou/Z8NYawUUWFtj4FXFYMyvT/rGWkpWP59Rl8wndp9OGzwUHAh2Fw7LHHdowlwgP6DK3YKECLtYMDa7q//e1vVkCwj0nyMq++lhRWWR8fuAoo2LNlth/3ODQYBilCle2QOmS5amcYgT5fq6uuqK+eGYuz0I4vAuzzSrYJXhgZhhMBobVPfYQGV8QrZRQeIUwetrvlllus53UgL3xdgdMMl1OM3/3udwFOf5dyk9dp06blqUoj0j755JNdAo8GFw0uEYZlmbhM/y9bNt5n+TS4fPBRG/IoYxhghuXrX/+6c+zFMzN87GMf6xpn4V7cFbQnwq70GJ/zGFz77ruvK/ugyvqUwdWssD7YN9RhknrJBz7wgThZle2IC8lxs/3223fRLbnnzPaxe5g/cOeAbyiTCv+KjpHn6gKEe7g0qghl9hDIWk8N8tzMMvzXszXqxhtv7Eq53HLLqQsvvNDqFjyZGGvQsdY4We66666r/vjHPyqpV/I98zdcuuKke5yWjnucnP6e97wnvOovUmZS5z3Wqz/77LMdz+ebbz719re/vSMO7lpvvfVWhSv2mq299tpKH5IYnuzekTD68eKLL8antF9yySXq+OOP70iGk9+/9rWvxXGLL764WnrppePfWeqlN9aG6/O1QRfWRzshid9Pu/GBW949WXnTu+oPN8YPPfSQ0od7hrSA294xY8aErnT1VzzXa3F8VbgKv2rBFpeV9YZ7uLIiZU9XRv7Zc8wXW2f5wndJOZqvBUzdLwSK7jXSjpbU3nvvra677jprVTfeeGN10003dbj51gq1mjlzZld6jBsYv8wAN/E45iM5FiLNfvvtp7TjBTN5eG/bw7Xddtsp7WWvKy0iqqxPUVzNisI9PPY62VztH3jggUqfQRUmr6odGNO0E7FwfNPLABX+sH8Oe+TTwgknnKC0s4+OJHDjD3f+ErDfDzpXMuhlilaX8Tgq4DOf+Ux4bMCyyy6roNvhqo3NUO9J5sPfg4WAjAte9RGxxPiFtfgXVs0m4dcRwbLX1bUXB/n8/ve/7/V6x3NtcHR9mcEXOL05tSOd+UMbC4HeGOxcw456YPocywLOP/9881Xr/eWXX95VByyFlICZOpz+Dq+KgpV5xZT+Sy+9JMnj63HHHWdNb75r3idnvGz1glckBHzpxLp68/2FFlooLtt24xs3Fx+4lgjmTZ9sw7XXXhvoAd5Jh0UWWSTQg6VzZlXy842r5Cu0yPMlSdJKHkWvlH/F5V9RzM336sRf+M6sD+8HFwHXTMwnP/nJQJ9v1PGnFelwNUgvb3X6Y12AmZlkgMc64Q/zisN1zfDMM88Ea665pjUt3vvoRz9qJo/vN9lkk653sNcJKzpsocr6uHBFmRiTXH8/+9nPAhwADJ0izcuyNnTjJlXVDm0wd+G5wgorWGkrlcG+d/3Bseu9pC4GD8ngE5MPcI/jeuA1ORkmTZrUlRb4zJo1K5mUvwcQAaGz6Bh5rq7mcElhhEyZAV8I4wI5Ga+/9HR1ROQBZTdvQL21575gvfXWC3Cq+W9/+9sA641dAcJRf2Wxli/tSF6xdwqbRl0BgjT5jv46EG4q1jMpAdbFJ58nf2O6/uGHH+4ooqzBhQEiWQ4MSRhbNte1aQZXFbjlNaDyphcwsUF8n3326cIiiY38xmZy7dFJXu+6+sTVzFzKzyPYJK2ZT5H7Mv2/SHnJd1h+fQaf8F2SJvw9mAi4DAOhY96rPtTXKe++//3vO+UmlHQsO9tss806PmLtueeeXe/ow3HDtPfff3/w+OOPx8Da0qL+UMyxbxt7zbC9QEKV9fGNq0kHjLdmqLId2htiF/6gMY7d0auHwnNOf/3rXwfac2GgV80EelVPV3roVDY9yrXvfuWVVw6wn+snP/lJ8NWvfjUYO3ZsB08IFkcddZQJA+8HGAGhmegYea6uZtHgipApo/AIYVwgJ+NtX1OQBxTqIsEmGGz54AuU1DXvFQMAjDlb0EsurPnqpRWpX/2SddAuVjuyL2tw6SWb1nrppR8BZnOS5bsMrqpwy2tA5U0PMF955ZVg9OjRXW2Vtuuln9ZnMEx/9KMfddBDfvjCVfKTq9Qpj2CTtJJH0WuZ/l+0TPM9lk+Dy+QH3rsR8GkY6GWEAc7AdAW91DVc6SGyqdd1q622CnAIMGapXGkx8yFBH2viTCfv43BkCVXWxyeuUndccRhyMlTZDjgusR1obdYp7R6zWHfffXeyyuFv7WY+WH/99XvSzJb/FltsUfteXWujGGlFQGgoOkaeqzVDHUmDK0KmjMIjhHGBbMZDAbYtrdP7ncxk3u9/+ctfWoUEFO4JEyaErlJxOjuWKOqzoaxpsWRCvAyZFdT7sqzp9f6yOH711VcPvQFhtsxm7ABDzIqZRie8BOGrFP6wRFFwliuWx8lzXPF1yQxwLiJpzavLQ5LN4KoSt7wGVN70wAKznmbbcQ/+O/nkk8OlDZjtg8ct4JdMp/fDWY8Z8IGrSSe5l/LzCDZJK3kUvZbp/0XLNN9j+TS4TH7gvRsBH4aB3jscwKW3bTxLlowPTBgbRD65rjC2ZGk8ZjJc6UyDC8aZ3gvmTIs8TIMLdauqPj5wNduMWR6M4RhjbKGqdqAseB/EUkKzPlnuoYfNmDHDVt04DjyDmTHMWmbJE2nghj4Lr8WF8KZ2BIS2omPkuboqT4MrQqaMwiOEcYFsxt97773WTvqhD33ITOb1Hl+TbLMc+AqkN5h2lQXB4FqChjXyyaAPhbS2CQYUlHt9iGTHK4888oh1Gh84HnLIIR1p5QcGHcFZrlgHnhawj03SmtdRo0aF8Ti3DEYm1strpyFdy0qqxi2vAZU3PfYkwBWv2Xbcu2aubMaZPqyzC+KyuHZlGEVIPfMINknryjNrfJn+n7WMtHQsnwZXGn/w2TwE8hoG+HCkHUkF2hlF6C0Q41XeAFm67bbbdslSyCzsddaH5Hacy4WZEHxwTH5cxczXD3/4w47in3jiiXCPs8g/uWKVAZba77XXXh3p8aOK+uTFVeoJwwP1hA6D/dhHHnlk6h5yszFVtEPyx1J66B4w/KCLSH2TVzzTzk7CJYYwgLMGjMcwsldccUVr3viYveuuuwbwSM3QPASET0THyHN1tZZeCjWqCFq5VtrZxNwfOf/rDhu+oUHu+SY8HsFDTzLo9drqoosuSkZ7+Q3vfqY3P8lUO8QIvTbJb/OKtuiBRGmBaEarxRZbTGmDSel9PnG8y3seEsArEbwTJQO8QWlBmIxW48ePV1OnTu2Kt3lz0gaXOuecc7rSSkRavXbZZRcFz4d6sJDkXde6cNN7pNTHP/7xrvq42uNKDy+OetavIx94oYRHSq0IdMTjh559VXpzeewZEnH6K2HIA3pJKX6GwVUPPMyC69xcuv9LP9KCrfthjxh6KewBUI/HZeRfj6wzPa6zfOG7LPI7U2OYaGgR0Ep86PlOrwpQ+sOd0oaG0h8DnR6B4REWYyg8u8KDLuSrNqSs+MC74YMPPqhQBjzH4q+Xp+Aq62OtZEWRVbcDYxu8VAJj7eBEacNK6X1X4Z8+ADn0mlymaXpmM/b6C0+E8NCs964X1inL1IXv+kFAxgWf+sgIfFn1U7325qKXyIWNzzJgw5jQZ2h1gaW9HqmTTjqpK95HhM1Y0d76lN68q/RSCWcRcIuqN+x2PYfLWriuleBSwPXG09DtuGvQgPt5uCc3wzrrrKPgZjUZbG0oanDByNL7uEJhmyzH/G0rsx+4uQwoF86u9PrLWzjImG36whe+oM4++2wzquMedNXLQDristI7K64dmRs/RMDBtXDegI8lMCLnzJmT91WmbzkCeeR3y6Fi84kAESACrUCgrD5iBUkbCWHgkpbiS1o0sOGUsmCZdrW51Mb78GxTRdBnQQT6zKuwflJPXLFvq1eAh0HzHblPLjNzLXXDkoq0AFfxkqdcTXfy5rtFlhS66qVn0cysrfd14qYNKGudXO2xpYerW8HUvMJ9b1qwLSvUs5Qdr7jqkQXXjowSP6SeeabuJW0iq9w/Kf+Ky7/cYFteqBN/4TtLtRhFBIgAESACLURAxgXRMfJcXXBxD1eETJkBXwjjAtmMv+GGG6yKMDzhVRHgal3qZ17hbrZXgIMP8x25T+6dcingSUU9WZ7NUQPWuNuCT4Mr6aLWVl6duNkMKNTRhbMtvWuvILxNAmPXn23PF5yMmMFVjyy4mvkk74W/8gg2SZvMK+/vMv0/b1m29Cy/PoNP+M5GF8YRASJABIhA+xCQcUF0jDxXF1o0uCJkyig8QhgXyGY83I1KevPqOhjRfLfIPbwEmeXIvV5Wlik7HKIs78g1WVeXAj5t2rTUMnB4pOQp134YXMlNy7ZK1ombzYBCHV0429L/4he/6MJWMM571fuyOiBy1SMLrh0ZJX5IvfIINkmbyCr3zzL9P3dhlhdYPg0uC1swiggQASJABGpAoAp9hAZXRMgyCo8QJgtP4LRySW9e9QbZLK/nTnPeeedZy7v00ksz5WXzwKP3NnW861LAbYaA+SJm2UwMcN8Pgwuu3nuFQcQtD84/+MEPurBNYp31Nzw4mcFVjyy4mvkk76U+YkTluSbzyvu7TP/PW5YtPcunwWXjC8YRASJABIhA/xGoQh+hl0KNKkIZL1myuU6zxNzMevy3OYuAwwF9AGPoFa7H612P4fwCAV53kuH6669X2v15MlrpM0jUQQcd1BVvRqA98E6n3cSb0Uq7x1VauY7j8jpzkBf1wcZdjkK0waW0oi1J4qvNgUVRpxnaELR6AYwL0zeDiFsenNHGrbfe2mxSeK8Pl1bvf//7u+LTIvS+OqWXf8ZJ8tQjfinDjfQjG/17vQ6+KRPK9P8y5cq7LL+4l1jBsOhV+C6r/C5aDt8jAkSACBCBZiAg44JXfUTsRn5hLf6FVbNPOJsgWPa67rvvvtbZB+0+vder1ufbb799gDM7cK4UDv/FGSAStBFnLQvOEXoF12xc1j09gzrD1atewGUQcXPNLNna89e//tVKdxz2WTbkqUeesqQf5ZnZkrR5yrGlpfwrLv9seOaNqxN/4bu8dWZ6IkAEiAARGE4EZFwQHSPP1YUIlxRGyJQZ8IUwLpCT8dddd51VGYbDgsceeyyZPPX3rbfe2pUXDjQWxRqnvNv2YSX35dgKcR1onNyrU1QBr2tJoc1ASbZ/EHHLg/Prr78eGuHCm3I94ogjkk3N/TtPPfJkLnXMI9gkbZ5ybGnL9H9bfnnjWH59Bp/wXV6aMT0RIAJEgAgMJwIyLoiOkefqQoQGV4RMGYVHCOMC2RaPk+/lPfP6iU98ItCHANpe6YrDKe36gD1rPubp5rayYITpw/q68jQjbF4EUdebb77ZTJbLmYP5YlmDCzOFaaGsYTBouOVtjz6Us4s39KHbaZBlepa3Hpky1YmkH+QRbJI2axmudGX6vyvPPPEsnwZXHn5hWiJABIgAEagOgSr0ERpcEb3KKDxCmDykv+KKK2IFU96XKxxoQKlNCzCobAo18vjMZz7T8epZZ51lLSvtTCYYY4sttljXe3CYofd0deRfVAEva3DpQ3o76pH8UbReks+g4Za3PViiKjxlXvXB0tLEjusbb7wR4Gy0bbbZJth7770DLDv97ne/G9x3330d6fLWo+PllB9SRzGi8lxt2b744ovB6aefHqy22moBDE0Y0PitD73uSl6m/3dlViCC5dPgKsA2fIUIEAEiQAQqQMC3PoIq0uCKCFVG4RHC5KW5ay8X8sNhxdibdfzxxwc///nPA5yr9Otf/zo455xzgnHjxlkVaby30EILhfuPzLrMmTMnWG+99breQRk4iDkZtBOOYMyYMV3p9SbCrtktvFtUAc9jcG2yySZd9YFHwyeffDJZ/fh30XpJBoOGW972YA/e4osv3oXbBhtsEDz11FPSzPg6adKkrrQ4t2vWrFlxGtzkrUfHyyk/pB/lMbQkrZntjBkzgr322qurLZI/rjik+YILLohfK9P/40xK3LB8Glwl2IevEgEiQASIgEcERF8QHSPP1VUNGlwRMmUUHiGMC2RXPJxbbLzxxqmKoeSd5QoDBPvDbOEPf/hDAIMpmQ+cbWy11VbBV7/61eA73/lOsOuuuwbLLLNMVzq85zqcuagCnsfg2nPPPa11gkHw2c9+NkBehx9+eEfTi9bLzGSQcCvSnm984xtW3LRHywD7ueBkBbQfO3ZsMHLkyK60Rx11lAlHeF+kHl2ZWCKEN/MINklrzmZJPrjio8XUqVPD0nDFb/M59jvCOPv9739vqVH/osrIHx+1bHP5wg8+cGQeRIAIEAEi0HwEZFwQHSPP1dV6GlwRMmUUDiGMC+S0eBhdu+22W4cSKPnluS6//PLBXXfdlVZUcNJJJ1mV6izlbLjhhsHzzz9vzb+oAp7H4Dr33HN7YrTWWmt11K9ovToy0T8GBbci7QF/rb/++j2xs/HAFltsEdj6RZF6JDG1/ZY65BFs11xzTWhwy7u4YqktZutsSwdRLoyzyZMnB+uss04HLlh6eMIJJzjfs9XZV5wNZ195Z8mnzeUL72TBiWmIABEgAkRg+BGQcSGPPiJpXejQ4IqQKaNwCGFcIGeJP//884PRo0d3KICSb9oVsxLYdwMHGlnCbbfdFmAfVlqe5jM41/j2t78dvPnmm87siyrgeQwu7C9ae+21U+tdlcGFhg8CbkVxxp47LE3VZ72l4mfSfffdd+/aqycMULQe8r7rKuWL0HJdseT1lFNOCVZZZZWO9pizWa4ykvEwyiZOnNi1HxJ7vrDkEMZZP0IZ+eOjfm0uX/jOB47MgwgQASJABJqPgIwLLj0kLd7VehpcETJlFA4hjAvkrPEwKi688MJAH04bLL300h3KpJQhVywJO/roo3O7kUdd4DL8xBNPDDbaaKMAyxAlT7lCMdeHM4czb4888kjP6hdVwPMYXKjEE088ERqXUk+5YlkkZjWwNMwMRetl5mHe141b2fbgfSwfXXHFFbtoDiznm2++cEmp6eHSbL/cl62H5JO8Cj1dguynP/1p7tmsZBlpv7HkcMKECcGoUaNifGTJ4bRp09JeLf2sjPwpXbjOoM3lC9/5wJF5EAEiQASIQPMRkHHBpY+kxbtaPwIPdMbqP//5j9KzGbitJTS5fDmROoLSC37I6+GHH1bPPvus0kv5lCauWm655ZQ2LJT+sq+0cwxv5eizv9QDDzwQ8sCaa66p3vnOdyqtfHvJv4pMgMmDDz6otPt8pT06hn/6DLMqinLmCfo0DTezMdoLZUjzf/zjH2rZZZdV+niBkK/qlAHSj8DrEvQB1OqSSy5RF198scK9BD2bpbSBrbTzC4nydgU22sBSeoZLzZw5M85XLzkMy9MzYgr3PkOT5Z8PHOpsv/Cdj3YwDyJABIgAERgeBEx9JGur9ESGNSkNrgiWMgO+DNg+DS4rtRhJBIYYAelHEHBXX311aGj98pe/jFuMjw0wsvDn2+CJC0ncwCCF4YU/7a0xfqpdzKuDDz5YwfDTs2BxfNGbMvKnaJnme20uX/jOxIP3RIAIEAEiQARocFXAA2UUDhmwaXBVQBhm2RoEpB9hBteczdLL/MKZpSpms/KAq88vU/ocr3D2C7OrEvTyW6WPUVDvfve7JUrBIMtjiL322mtKe9yM3zdvYGhWbWCWkX9mXYve11m+8B3ld1Hq8T0iQASIwHAhIOMCDa4K6FpmwBfCcMCugDDMsjUISD/C8kYs10SA0QJDS3sdrNzoyAP0DjvsEBpeed4ZhLTAE8ZgMvzvf/9Tei9kMrrnb+1cpGeaLAn0/lWlPaHmMlLT8s1jpArfUX6nIcpnRIAIEIH2ICDjAg2uCmhOg6sCUJklEciBgCngrrrqKnX22Wcr7cAjzgHKvSzjiyP7eDN9+vTQyML+LuzzkoC9lTBiMNMls1pYioi/rCHN4EFZ+uDzrFkxXQ4EYGQJ39HgygEckxIBIkAEhhgBGRdocFVAZBpcFYDKLIlADgRsAg5LC7/+9a8r7OV65ZVXwtywvA6GF5YaioGTo5hcSW+88UY1ZcqU0NAyjSx9hle4lwyzbz6W+5WRP7kapBOjTcmQtqQxmdb8jWWWJi7mszz3mOHSXkhzGalp+Wc1UmlwpaHIZ0SACBCBdiJg00eyIkGnGT2QKqPwCGH4hbQHyHxMBFIQkH5k+6KEPVPwVIhZr6qXG8KIECPLnKWq0mlHGfmTAmnmR20uX/iO8jszuzAhESACRGCoEZBxwaaP9Go4Da4eCJVROIQwHLB7gMzHRCAFAelHvQRcFcsN04wszGLBM6Jt71NKc3I9KiN/chXkSNzm8oXvKL8dzMFoIkAEiEDLEJBxoZc+YoOFBpcNFSOujMIhhOGAbQDKWyKQEwHpR1kFXNnlhnUbWSY8ZeSPmU/R+zaXL3xH+V2Ue/geESACRGC4EJBxIas+YraeBpeJhuW+jMIhhOGAbQGWUUQgIwLSj/IKOCw3vPzyy0OX7XJWFvZ2YVYqeUgxlghiuSDO1TKXC8IVPTwPVj2T5YKijPxx5Zknvs3lC99RfufhGKYlAkSACAwvAjIu5NVHgAgNrh58UUbhEMJwwO4BMh8TgRQEpB+VEXDwIIizsmbOnBmXhCWBWA6IZ5jVkjBq1KjQ5TyMrI022kgtvPDC8qjv1zLyx0dl21y+8B3ltw9OYh5EgAgQgeYjIONCGX0kicIIPcgEiGzzgFu2/UIYDthJ9uJvIpAdAelHPgQcZq9OOOGE0MgyDykWIwtGGP4kUP79p7UGp/Ad5bf0Bl6JABEgAu1GQMYFH/qIIEmDK0KijMIlhOGALWzFKxHIj4D0I58CDu7BsXwQM1tJI8usYZn+b+ZT9J7l12fwCd9RfhflXr5HBIgAERguBGRc8KmP0OCKeKSMwiOE4YA9XB2OrekvAtKPfAq4rC0o0/+zlpGWjuXT4ErjDz4jAkSACBCB/iFQhT5CgyuiXxmFRwhDg6t/nYElDR8C0o9ocPWftmXkn4/a1lm+8B3ltw9KMg8iQASIQPMRkHHBpz5CgyviizIDvhCGA3bzOxlbUB8C0o98CrisrSnT/7OWkZaO5XOGK40/+IwIEAEiQAT6h0AV+ggNroh+ZRQeIUz/WIElEYHhRYAGV/9pW0b++ahtneWL/OYHMx+UZB5EgAgQgeYjIOOCT31kxOzZs0Mvhc2Hp74WLLLIIvUVzpKJwJAh8Nxzz+VuEVy6jxw5Us2ZMyf3u3yh3QiI/KbB1W4+YOuJABEgAoKAGFxF9RHJx7xyhitCo8wXViEMB2yTtXhPBPIhIP3I5xelrDUo0/+zlpGWjuVzSWEaf/AZESACRIAI9A+BKvQRGlwR/cooPEIYGlz96wwsafgQkH5Eg6v/tC0j/3zUts7yhe8ov31QknkQASJABJqPgIwLPvURGlwRX5QZ8IUwHLCb38nYgvoQkH7kU8BlbU2Z/p+1jLR0LL/+Ga40+vAZESACRIAItA8Bn/oIDa6If8ooPKIo0uBqX2dki/0hIP3Ip4DLWrsy/T9rGWnpWD4NrjT+4DMiQASIABHoPwI+9REaXBH9yig8oijS4Op/Z2CJw4OA9COfAi4rOmX6f9Yy0tKx/PoNLsrvNA7lMyJABIhAexCoQh+hwRXxTxmFRwjDAbs9nZEt9Y+A9CMaXP6x7ZVjGfnXK+8sz+ssX/iO8jsLpZiGCBABIjD8CMi44FMfocEV8U2ZAV8IwwF7+DshW1gdAtKPfAq4rLUt0/+zlpGWjuVzhiuNP/iMCBABIkAE+odAFfoIDa6IfmUUHiEMDa7+dQaWNHwISD+iwdV/2paRfz5qW2f5wneU3z4oyTyIABEgAs1HQMYFn/oIDa6IL8oM+EIYDtjN72RsQX0ISD/yKeCytqZM/89aRlo6ls8ZrjT+4DMiQASIABHoHwJV6CM0uCL6lVF4hDA0uPrXGVjS8CEg/YgGV/9pW0b++ahtneUL31F++6Ak8yACRIAINB8BGRd86iM0uCK+KDPgC2E4YDe/k7EF9SEg/cingMvamjL9P2sZaelYPme40viDz4gAESACRKB/CFShj9DgiuhXRuERwtDg6l9nYEnDh4D0Ixpc/adtGfnno7Z1li98R/ntg5LMgwgQASLQfARkXPCpj9DgiviizIAvhOGA3fxOxhbUh4D0I58CLmtryvT/rGWkpWP5nOFK4w8+IwJEgAgQgf4hUIU+QoMrol8ZhUcIQ4Orf52BJQ0fAtKPaHD1n7Zl5J+P2tZZvvAd5bcPSjIPIkAEiEDzEZBxwac+QoMr4osyA74QhgN28zsZW1AfAtKPfAq4rK0p0/+zlpGWjuVzhiuNP/iMCBABIkAE+odAFfoIDa6IfmUUHiEMDa7+dQaWNHwISD+iwdV/2paRfz5qW2f5wneU3z4oyTyIABEgAs1HQMYFn/oIDa6IL8oM+EIYDtjN72RsQX0ISD/yKeCytqZM/89aRlo6ls8ZrjT+4DMiQASIABHoHwJV6CM0uCL6lVF4hDA0uPrXGVjS8CEg/YgGV/9pW0b++ahtneUL31F++6Bku/IAz+y0007qyiuvDBv+iU98Qk2fPl0JT7ULDba2aQhMnTpV7bzzznG177zzTrXuuuvGv5ty8+Mf/1jtv//+YXWXW245dccdd6gVV1yxVPWlD/vUR2hwRSQpM+ALYUpRly8TASIQIuBTwGWFtEz/z1pGWjqWzxmuNP7gs8FE4Jvf/KY66qijwsq9/e1vV3fffbd629veNpiVZa2IQAKBX/ziF+EHA4kG/zbR4EL9d999d3XppZeGTdl0003VjBkz1HzzzSdNy30Vvd6nPkKDKyJDGYVHCJObonyBCBCBLgR8CriuzB0RZfq/I8tc0SyfBlcuhmHi2hG44YYb1Mc//nE1Z84c9da3vlXNnDlTbbLJJrXXixUgAlkRGCaD69///rfaYIMN1EMPPRQ2/6CDDlJnnHFGVii60ole71MfocEVwVxG4RHCcElKF88ygghkRkD6kU8Bl7XwMv0/axlp6Vg+Da40/uCzwULgscceU+uvv7567rnnwop9+9vfVoceeuhgVZK1aTwCm2++uXr88cfV3nvvrY455hjv7Zk1a5a68cYb43y32247tdRSS8W/m3bzpz/9SX3gAx9Qr776alh1zHjtuuuuhZpRhT5CgysiRRmFRwhDg6sQX/MlIhAiIP2IBlf/GaKM/PNR2zrLF76j/PZByXbkse2226qrr746bOzGG2+sfve733HfVjtI37dWPv/882qZZZYJy5s4caI6/fTT+1Z2kws69dRT1ZFHHhk2YbHFFlN///vf1dJLL527STIu+NRHaHBFZCgz4AthOGDn5mm+QARiBKQf+RRwceY9bsr0/x5ZZ3rM8odrhuull15S//3vf0PaY7B/y1vekokPmGjwEfj973/fsXTwV7/6Vbi0cPBrzho2CYGrrrpKYcYJgQZXdsrNnj1brbbaagoGK8Jhhx2mvvWtb2XPIEpZhT5CgysCt4zCI4ShwZWbp/kCEYgRkH5EgyuGpG83ZeSfj0rWWb7wnU/5/eEPf1jdcsstITRPPPFEaY9ZPjBmHn4Q+NjHPqawfwsBy5f+8Ic/+MmYuRABA4Fjjz1WnXzyyWEMDS4DmAy3p5xyivrKV74Splx44YXVI488opZffvkMb85LIuOCT32EBleEb5kBXwjjc8CeR3beEYF2ICD9yKeAy4pcmf6ftYy0dCx/uGa4qjC4/vGPfyi4bX7wwQfVEkssoeAV76Mf/ahadNFFY9bCMjfsL0JYY4011BZbbBE/ww36luw7wu9VVlkldPiAe1fAuPboo4/Gj7HHA+VnCZjpu//++8M/lP3e975Xrb322mG5Wd7H1+pnnnkmTAr5MHr06Pg1LOO755571Msvv6w+9KEPqc022yxs+xtvvBGmgYcyYJQnwDh+/fXXw1fgCAP4mAH7XcaNGxdHAW+4gs8TSMf66ZiHXkXSgifRZ7D/Cn//+9//1AorrBD+rbXWWmrxxRe3Zmv2z7322kvdfPPNYTrs4YIBJiHZB/P2E8nHfA9xK6+8spp//vnlsTKfJ/sfEt13332hZ84nn3xSLbjgguod73iHeuc736ne8573xHlkvYGsQH9+4IEHQvkC+bXRRht1rA6ALECdECD3ll12WWv2cKCBWa4XXnghfF7EgQbai+BVH9HCNAy6EXJby7XJ5WuaBPhjIAJEoDgC0o+0gAvy/hUvde6bTZY/ZduO99vcfuE7HzhKHtoACMcE5K2VeIkudL3wwgsDvSwxzk/qi+siiywSHHjggcFrr70W5r3eeuvF6SZMmNBV3g9+8IP4Od7X+xu60iQjwBtmmd/4xjeSSbp+63NxAm3sdLxn5qEVzmCfffYJ+3nXy0bE5ZdfHuehFaBAK66B/jgRaO+AcTzy/fSnPx2+pTfIx/EjR47MhT1kzkILLRS/v+OOOxo1mXurZ7fi59p9dtfztAjSca6eNAh0TKNTmWfaaUOgjaNggQUWiPnE5Hvcg8d22223QH8w6Crqhz/8ofM9Mx99HEHHu3n7ibx8xRVXdJSn3cLLo/Cqz5TreK6XSYfxevY+GDNmTMczs35jx44N/vKXv3Tk5fqBMvSHFGte2ugKgIkE/VElTrfHHntItPX61a9+NU4LeugPTdZ0rkhpT15dBOldIbYS2jzgApwy7RfCuEBmPBEgAr0RkH7kU8D1LnVuijL9P2sZaelYfn0f/ITv0uiT95kvg+u4446LlQapp+2qvwSHY9jqq68ep//85z/fVe2qDS69byLYYYcd4jrY6mrG6a/hgZ6166qnRCQVPv3lOtAHnHblLwaXPnun41kW41DKuuSSSzre1bNX8ii86lmLQM96xWlOOOGEjudpP0jHTsW9Tjqm0anMMxjUJm/3uscHgYsuuqijyKIGV95+IoX2Mrj00tmONv3rX/8KtOe/QM+CdcTb2oo0d911lxTVdcXHExhFMMBt75tx6PNIr2fI47Rf+MIXuvI0I2D8mnlcfPHF5uOe9/KuT32EBlcEexmFRwjTk4JMQASIgBMB6Uc+BZyzsMSDMv0/kVWhnyyfBleScfAVW/oErqNGjQq+9rWvBddff33w6KOPBjAI8Ft7MgvTQQFZbrnl4ncw85UMVRpcMEj0kqS4fNR5yy23DC644IJALxUKHn744QCK4Ze//OUOw0Uv/Qv00qlkVcPf1157bUd+t912W6ygQaHTHgLDP73HJX7/Xe96V/wO7rMG7aAgfm+llVYK3nzzzY5Xp06dGj9H22wzFB0vRD9IxyAYJDraaFQ2TjtS6ZjVQj88/PDDAxg04O2bbrop+NnPfhYccMABgV6OG/MRjI3rrrsuLl4vpwu+973vhX+mUaPdw8fxeJ78SFEEXxTay+DSZ8vFdQXP/+Y3v4lngbfffvtAn3MV6GW2AT50nHvuucH73//+jvSYiXYFfAxBnvKHWSjILBhGMNT0GWHBzjvvHD8/66yzglVXXTX+rZcJurKO4/W+rTh9rxmx+KXoRurlUx+hwRWBW0bhEcIkCcbfRIAIZEdA+pFPAZe19DL9P2sZaelYPg0ukz/0PqQASr9tKzrSAABAAElEQVT0Cb1no0vJkvR6Q3ig90yEabU3xPidQw45RJLE1yoNLr3HJC4biqQ+myr8Kh0XbtxAoVpxxRXj9HpflPF03u1vf/vbOA2wgNKEq3b7HC4tnJdy3p32SNbxDpY/9Qovvvhix1f7o446qusVzBgKPbAkEjTqFUjHuQgNEh170azIc3MpK5bHPfXUU85s9J6uQO9jjHlpm222sabVe5TiNAcffLA1jUQWwRfv9jK4YCwKz+OKDyraCUUwZcoUKbrjqvdYdX10sc1yYWmi3tMW563dtwdogy3A8MLMMtJgCbXUpxcmyOuzn/1snB7GF2bJsgYpx6c+QoMrQr+MwiOEyUpIpiMCRKAbAelHPgVcdyn2mDL9355jvliWT4PL5BhzTwb6xXnnnWc+7rr/61//Gs/8SD/CTFIyVGVwQcGEIiZlZ/majC/Zkh5XfE1PBhhLZhrMhn3xi19MJuv4/eyzz3YYT5/73Oc6ntt+YM+ZWQ5m45LB3GfyyU9+MvnY+pt0nAvLINHRSqiSkVgaK/xz/PHH98wNM15Ij72Z2tNlgCWWyZDH4CqCL8rrZXBhFlfaJVd8SEkLV155Zcc7WGqZDMnlu5gdSwunnXZaR56oi02+JfOAYSj1xhUz7VmDvOdTH6HBFaFfRuERwmQlJNMRASLQjYD0I58CrrsUe0yZ/m/PMV8sy6fBZXKM9j4YKwr4uou9Ub3CRz7ykfgd9CWbQlKVwYWlQNJ/tbeyAF/xewV8bV5nnXXi9+CQIhluvfXW+Dnyxwxelryxp0vqA8XVptCaZWlvjnF6bMxPhqeffjp+jnwxi5YlkI5zURoUOmahWd40c+bM6TDws+7t68WTeQyuovj2MriS+WKG69VXX02F6JVXXun4+HPSSSd1pddeXOP+hKWE2BuWFrTn0I7lhOiDNvmWzANOgUQO4Pr9738/mcT5W97zqY+MwECvM2YogYCe5gzf1pQrkQtfJQLtRkAvQwoBMN1WZ0UEZ23oTchKD35ZX2E6IhAikFd+a4+ASs9wpKJ3xx13KLg5RoC7cq1UONMfeuihXQfnwt2x9AOc+6T3bTnflwd6A77ac8895afSCon6zne+E//GjZ4pU3oDehynFZIOV+vxA+MGRxYIRojWey/iM24k2QYbbKD00qHw5yabbKLgsj1LQB311+swKdxKoyyRA4hMHjKs94QoHDTcK+jlSaHLfEk3efJkBTfbtqBnxMJz0kR26K/iHTjiHbi/1sZh/Lr+Qq+0p7n4t+uGdJyLzKDQ0UWnsvHo4+LCHS7RcTab3nNZKlu9hE5poyzMQy+fi/uJLdOi+OrlemqnnXaKs9ReCpX2vhn/Tuar96ApbbTEz103cHuvDZXw8X777af0h56OpHrfaXwwMWSp3tvZ8dz2A2eRnXnmmfEjm3yLH0Y3kNXaK2QcPWnSJKUN4vh32o3IIZHDaWmTz6CPWIOYd/zCWvwLqwY2tKIFS16JABHIj4D0I59flLLWgvKvuPzLinFaujrxF75Lq5/5DF+m5R0fVyxnMwP2N2APlOQND11Zglby4nfwru0LcFUzXEsuuWRctlawslQ3TJNcVog9IGZIfmE/5phjzMfOe8ye6TOB4jrZZq3k5bPPPjtOh71ZNl6EswChB66mowPJJ3klHechMih0nFcjv3dwXmPyB5w7wElGr9mgtFqUmeHK2k/yznBlndk192fCBb4ZMFtlyjebnDLTy/0555zTgXHW90wce3k2lLJwFXr61Ee4pDBC2CZkTfDT7oUwaWn4jAgQgXQEpB/5FHDpJc57Wqb/z8ul+B3Lr8/gE77LSr2qDa5//vOf8WCPuh199NGZqqYP1O14z6aQVGFwweGEYIgrHGCgzln+9KxTx7u33357R1uTirr+wt3xPO3HKaec0pG3bV8W3jeXN+27777WLH/yk5905PXHP/7Rms6MJB3noTEodJxXI793WPKrZ3k7eAR9Aco+nGJ897vfDfQB4LkKNQ2FXg4iiuKb1+D6+c9/nqkN5hl8SYMrKaeyHt2QPPLBJt9sldMHIMd0gdfDrEFkmk99hAZXhH4ZhUcIk5WQTEcEiEA3AtKPfAq47lLsMWX6vz3HfLEsvzkGF2ZPoDSk/ZnKF2ae0tKC382QnKmCspYl4PBj6UO42hSSKgwuGB9muWXukwpdUpHErEHWgNkyONmQ+tgM18cee6zjazuwtwUYepIPrnivVyAd5yE0KHScVyP/d+jHOAbB5JPkPfZAYcYaePQKZQyurP0kr8F1zTXX9Kp2+DzN4NLLFDsw+tGPfpQpz+Q+Spt8s2W04YYbxuXBvX7WILTzqY/Q4IrQL6PwCGGyEpLpiAAR6EZA+pFPAdddij2mTP+355gvluU3x+DKQtkyBx9fddVVsYKAPoHDULMEbN433cLbFJIqDK7kcjvpx0Wu8EZmhqSinlXhkzzMc3yg7AIjM+g9bjHWOFTVFeAIwWyP3mvmShrHk44xFKGBYeJXFx3n1ai6O73HMMCZbnAeY7Y5eQ/jLM1wL2NwZcW3DoMr2S+yGof40GUePG6TbzaqbrXVVjEdcE5Y1iD08qmP0OCK0C+j8AhheFUxYxMLYlGUB3wKuKzCtUz/z1pGWjqWT4NL+CNpZGTdNwF36GafsykkVRhccElvlnvEEUcE2slEoT+0wQxJLLIqkpIHDok26wZl2Azm1+80d9d4ZuaTrKeZp9wn6046zhsT66Kj0KYfV8h0uEjHviHzMG6Tj3AIsnZUYa3OsBpcyRmuXkdeCDizZs3q6IM2+SZpzav58Us79DEfpd4LnXzqIzS4IsjLKDxCGF7nCVRiQSyK8oBPAZcqUY2HZfq/kU3hW5ZPg0uY59FHH+1QLHDIb5bwpz/9qeM9m0JSxODCGVtmX07uucBSRnMT/GGHHZalupnSJI2WvIo6voqvvvrqcf1xEKoEHBgt7cLSw6TDDkmHa/I8nwceeMB8bL0nHefBMih0nFej/t9hWfGpp54amHuKwH/aK2AAByvJMKwGV7JfJOVJEgf5jY8l0l9xtck3SWte3/3ud8fvbb/99uaj1Hspy6c+QoMrgrwuhUeIqV1PBnJfx3WYysf64VVWWSUXnsPU/iL8U7T9+HonggnT9VBosFfi2muvDaCUZK1L0fIl/1TJmeFhXf1fqsbyaXAJLyT3Yu2zzz7yKPWanM2xKSRJgwuzU71C8vDTr3/9612vmF7Jdtlll67nRSPKKuooFwqdyCjtajuQ5YA4H0jid9hhh9QqwtCTtLjeeOONqenxkHScB9Gg0HFejeq7g6wHv5n8pI8x6KrQsBpc8Nxotl0fi9HVdlsE9rKa79nkm+29pZZaKn7v//2//2dLYo2TskTHyHO1ZqgjaXBFyNSl8AgRyyqckk/R67CUb7oOhaKQFY9haX/W9ibTFW0/DiGFcSvCyXaFIYY17TDEfvrTnwY2uhQtX9rhEnBZ4+vq/1I/lk+DS3gBV1NJyLoMBjNhZv+zKSSXXXZZR5o777zTLNZ6f+GFF3a8YzO4Nt100ziNPofImk+RSB+KOmbozL0f4phjrbXWiuuMfSVpQZ+rFqcFxpdffnla8vgZ6TgXikGhY0yYmm9eeOGFjlnh008/vatGw2pwoaFYSimySp+t19V2WwQ+PMk7uNrkW/K9N998swPno446KpnE+VvKEh0jz9WVKQ2uCJm6FB4hYlmFU/Ipeh2W8rExWjoKZl+y4jEs7c/a3mS6Mu03v4CPHTs20AcUBrjiLBKhhe0KQw0umWGInXXWWeGsWLJeWX+7BFzW+Lr6v9SP5dPgEl7AFd60pM9guR72L6QFKBYrrLBC/A7etSkkyf0T+uDTtGzDZ2ZdkK/N4EqeQ3T11Vf3zBcJHnrooQDGjov/fSjqKGfHHXeMsYEjDeybEXwxOwf80gKWg0l6XPXhr2nJ42cmdqTjvGX2eZeGCqBl6Sj5+LzimIhbbrklgCfLLMcFSNn68N+Yp04++WSJjq+mwYUxNS0U7Sd1OM1AO3AunvQnfAyB/pEW8Byz0/IOrjb5lswj6dkwq8dX5CNlZdVBzHTJeshvGlwREi6BL0BVdRUilVF4JY8y12EoX2a39AnvYWfJs6xwGNpfJ/2/+c1vhpjjyxXWaJsB52dMnjw50Ke8h4bYOuusEwszEWrmFfSDIYY8s7bJLK/IfV39X+rK8mlwCS/gmjz3Ccvf0kJyj5FLIXniiSc6+l6v5YrJfRPI12ZwoZ8uu+yycd6Y8Up6BEzWH/urPvrRj4bvwKOb7ayhoopksiyzHQsvvHBwwAEHxHX9yle+kkze9RsGmflVvhdukgHpOBeJQaGj0MXndfz48TEvZZ2tefLJJ+N30KewHDgZRI/B8z333DP5uON3UXzrMrguueSSjvanOaxBQ9F+4GD+ZTG4kkuBf/3rX3fglvZDysqqg5jpXPnS4IqQqUvhESJR4S+/h03OfoByL7MrtuVrgrl5Jf7l8ccBjxBSWc+6wFfmqVOnhoYYNrNiVkyEHK4YcGA0Z9kL5hJwWePr6v9SP5Y/XAYXDCAYSfh75ZVXhMyZr6+//nqw3HLLxf0BX4Evuugi6/uQd3i+yCKLhH/Sh2wKCYwgc78V0soSu2TmmP2CkYGZM3NpnMv4O+OMM+L6Il+4vcbSKVsAv++6664d6W1KZ1FFMlkm2m06KzDd52fZx4b8PvWpT8X1xfiSJZCOc1EaJDpmoVueNMljEb70pS8Fb7zxhjML7O0zz+tC333ppZe60uOYAunLo0ePtjrWkJeK4luXwYV+YX6gGTlyZGDzVggdDeeWAYctttgiPEhaMLHJN8FDroccckiM4UILLRRg/1jWIOWYemLWe1cZI/BAZ6z0RlKlv/zgtpbQ1vL1dHSIt+6ESn/lqwV7FNr08i+++GKlv1oqPRAqvfxD6a+lSisASi8rVKecckpPXJve/p4N7JHAR/tffvllpfdFKK1gKj2bpfTZNT1KtT8G/YSG9957r9J7wJT+UqW0AWZ/Qcfq5RfOZ1ketFX+CDZtbr9e6hXCEA2FAkntVz2TpI455pi4HqinVtTUBz7wAaWNB6Vdryu9t0jpj0phGsg7vTRJaZfl4W+tkCh9zlT8vtxoxxnq85//vPwMx31t/Ch9WLPSy3bUX/7ylzBf/TU4TKNnh9SBBx6oHn744fD3iSeeqI4//vj4fbnRntbUxhtvrPSyKolS+iOY0h9i1JgxY5T+eKL0fqqw3togVS+++GKcbvfdd1eQ4cmgl0AqvYctjoYc2HrrrePfeW6AzbHHHtvxip5JVzfddFNHnOuHPg9N7bfffvFj4PGOd7wj/u26IR2VGiQ6uuhUJl4bA0obXnEW2phQeulqOB7iHkF7wQz7lt7HrPSHiDgt+Eo7c4h/y4028JU2iOSnWnrppdVOO+2ktEdNBVmglzDGz4riqz+qhHlKRvojqNJeE+VnYbqhr+szxsJ8dtttN6VntOI85UbPaqnDDz9cfobX973vfWr99ddXa6yxRqgD/PKXvwzl2eKLLx7KDegC0C8QtLMNhTzSAtJr761hEn0el9LOvNKSdzyTcUEbWR3xWX449RGxxPiFtZ4vrGIxc4al3AyLObsFnpY1+lmXFRL/cvgLH5tT+FhKWCZohSyQ5Yfwfihl2K5lysG7lH/1yD+hW5346wE0/AoqdRmkK5bv6YE//kordU1e0T8wi2Mue3N9AcbXd21c9cwTs0Cy5wGOb6TM4447zgkRvlzjHC5zBknec11RT9fyw6Jf7m0VxDIuzCaY9cDsYNaQPAcIS9izBtLx1g7cMU4UDWXpWLTctPcwc7Ltttt2tNHkM9s9+oj+cOHMNsn7Zh7aMOl4L5k2K751zXBJ5eE1FUcymG1L3uuPS+GZfnhHG15x2l7eDZPHWSQPVZc6uK5SD5u+0SvOmac8qHPAQx3aWr4Qjgp/cYVf9m4ll3ngNzpNlmWFxL84/sLDcoUnIOAOQQmjqUyA4Sxr2dP2dJUpA++2Vf4Ibm1uvwysgsWgXaEU4cND0lhAvXHGFJbyScD+JGmPy+BCWhhd6E9YhijpzSv2YF133XWSbWAeHmrbaxUnjG5mzpwZjBs3LtBf5a35Y3kPjMRe7tWLKpLJ+shvLF2WdmITPhwe5Alrrrlm/P4nP/nJPK8GpOO8PThZDQIXwGXp6Mq3TDz6FJbhgi9sfVX4Dn0Oyw7/9re/9Szu/PPP73IWAUMNex/NULSf1G1woQ16hjnYY489grXXXjvGDUsM4UUUe7tMHQJyQ3Ds5XHwggsuiNPiHT1zb0LW817KEb0mz9WVOZcUalQR6lpSwyWFc/Evs6QNy9gwfa2/Vqq99tprbob6f55lhWXKjwsscTNs5WMZEKby9YZipfdplUBGqWnTpil9bkmYhx6oFZYBJYNzCj+Z0PG7rv4v1WH59S1pl6UjepAUcgzkVc8ehX1Ke/ZTek9VuFxP7/MIlxdJhbEtQH9tD39mWXKjZ5bUP//5z3C5oP7opJZffvlwmRyWZvsKWOKo92EqPTOh9L40pfeQKf0xppYtDJAd2qNc2DQsNz/77LNzNVPvM1F6T0n4jlZ81Z///GelD1bNlQfpmAsua+KydLRm6jFSK+dKO6hR2kte+KcNiLC/Yokt+hh+Zw3QDR588EGF/ol+ib4z//zzZ329UenQVrRT7xtV2mjtqPu//vUv9ba3vS2Ocy3FRALIciyNxLJrBCzF1h+Qwvus/2RcAC3zBpc+QoMrQrIuhYcG11wCFDU4knu3zI5xzz33xHsHMOCnhaLlp+WZ59mwlQ8lDvs5sN46aQjnwUXSYj8Y9o5gH5f+mhfuB5FnuLoEnJkm7b6u/i91Yvk0uIQXylzzGlxlymrau5AbeuYurDaUKRhL+sywXM3QsxihgaU9sYbv6Vk6pZ2Z5MojS2LS0Y2SDzq6c+eTQUUA+8vWW2+9uHp6y4LSDrri3+aN+ZEW8bfddpvaaKONzCQ972lw9YSoeIK6FB4aXHNpVtTgcM1uCSfga5Bee6+0e16l11hLdNe1aPldGRWMGMbyxRjW+0oUhKO5GbcITJgtmz59utWJBg2uIojOe6cu+Sc1qLN8GVgHfYZLsEq7UlF3o4Ov3NoTYpigyBdvyVkvVVJ77713+BMzFZh9yOI8Q97PciUd3Sj5oqO7BD7pBwKYOdLLKsPZdb1EsmP2ylY+HAAddthh8SOsatLnrsa/zRsYZjDQELbbbjt15ZVXmo8z3cu4wBmuTHDlS1TXgE+Day6dihgcotBjmh1e7WxBlhXCC9a5555rSxLGFSnfmVmBB8NaPryhwUMRjC0RgAXgCV/RrnPDL1rwXIgvy3rvXpwVDa4YikI3dck/qWyd5cvASoNLqDF8Vywd1Ptm4oZhlgQz8EUClmHiQ592Jx++jmXsmMX3GWhw2dH0SUd7CYztBwJY1mtuDcAKFng2dgW9x1jp/aqxB9Z3vetd4YcOkd3mezCu9B6/MArPoXfoPbBmkkz3kjcNrkxw5UtU14BPg2sunYoYHL1mt5CzLCvEUrTHH3/cyRRFyndmVuDBsJYPV/FQbPA1auLEier0008vgM68V0BPLCNAvnrTv/riF78YPqTBNQ+jInd1yT+pa53ly8BKg0uoMVzXH//4x+GRIVgOiPCZz3wmXPFQppVwAa4PuVX68OZwP84NN9yg9DmCZbLseJcGVwcc4Y8q6NhdCmP6hYB2khHu7UR5cHWPmeNPf/rTXfvboLdNmDBB/fa3v42rhqMq0P+SAVsY4FYeM2cI+Mjyve99L5ks028ZF2hwZYIrX6I6B3zUlOXn28OBzollHWmzW8IBsqwQzhuwLM0WiH8+/G0YuuLE6MXzNBq43k/Gm+uzfeSH/En/6uifpJ/td534y8BKg8tGmebFYU8VHHTgrCPtLVHdfvvtcSMwXuC3nI0UPyhwY57rhU3+kHM+8kVVaHCpcG+cDzpihYU4SilA5tRXcM4Tzv9kyI8AjCbMROH8Pgn4MI6Zr8022yw8GxZ77+HsAqtbJMCBFs4Ps4VddtlFXX755eGjD37wg2H/L+pgRMYFnwYXvHmEoc1ugQEA29+sc3j0wBnoXhXopRwh/6b90zMrYVr9lcSZjPSvlv44AwP0wjlBpptXJ0F6PNDLD+L89JKBHql7Pyb9q6V/LwrUiT/4En/DEEy3yb3OqRmG9traYLoMF9riutJKK8Xn+djeyxunZ7cCvT8k5B3k/7GPfcx5nljevEnHIPBFx3333TemkckPPu7zHg2Qlw+GPf3VV18dLLjggpnoA3f4ekVLoI0vKyxnnXVWnI/+8BHomTFruqyRwh/a4Eo9A9T23FVGPMrUOeChciy/vQpPXvrjQF10BhhdWQIUcqSHsu8K5L/q+U8vuQnpoJcEusiQKx4GNOiq94eVNuJI/+rpn0bcOvGXgTWtfk15RkW9W1FfYIEFAsiKZ555xjsZofytscYaoRwCH+m9KF7KIB390fHAAw8Mz7LCuWu+//QSOC/0bnMmOKBYeyAOP4iILDav+hiJYOuttw7uuusuJ0x33nlnoGeywn6IM7z08kNn2qwPpA42g6pXnKsMuoXXqCLUuaSF5efDH3t4sFQkj7vxXssKSf/ql5RhWQDogP1XesYrPCct7HwF/yE/8AKcaJQ974v0r57+aWSuE39ZOqIHybQqNuIZzqnDviIEbDLHPte2heeffz7cr4vzfJZcckmFDfaLL754ZTDgCAx9qGqYP87m0jNdHWejFSmYdFSq33QsQie+4xcB6AbYs6WNMLXMMsuE3j/1QdE9C4EOgDPPEHBG4YYbbtjznV4JZFzQxlWvpF3PXXvKaXBFUNU54KMKLD+bwnfjjTeqcePGZdq7ZfYCOGs45JBDws2X2P+VDMQ/G/5J3PL+FvrhPXgPKusqHt4pkQcENbwcwdtRkUD694f+LtrUib8MrMNgcLnwZTwRIAJEgAhkR0DGBRpc2THLnLLOAR+VZPnZFL4is1vAF4r56NGjFc6E0nuIENURiH82/DtAK/hDXPXjdcx4wWACXXEt4unLNOKKOtEg/ftHfxvb1Im/DKw0uGyUYRwRIAJEoH0IyLhAg6sC2tc54KM5LL+3wieKNTzZYDlZ3gCFHlPPNqWc+PfGPy/eaenlEGNbGtMAw/kZ+N0ryAxm0UOWSf/+0j9Jzzrxl4GVBleSKvxNBIgAEWgnAjIu0OCqgP51DvhoDsvvrfCJkl506Zgo5XoDdXjmg8lGxL83/iZevu7hShl/ONfm/vvvDw1iW96YAZNZMBhhmBlLBhxAOmXKlNBA045VwtnMZBrXb9K/HvoLPerEXwZWGlxCDV6JABEgAu1GQMYFGlwV8EGdAz6aw/J7K3yiUBc1uGRZIQ2u7g40SPyHmUwYYXKdNWtWV4VlKaLMhmEpYhknGoPU/q7G9iGize2XgZUGVx8YjUUQASJABBqAgIwLNLgqIFabFQ7A2YT2y4G3UK6hjOcNclgyZkig0JuhCe036+v7fpDbD0NKjC+5wklGMsD4wpJCpEHAwdjnn39+eN/r3yC3v1fdfTxvc/tlYPWBI/MgAkSACBCB4UGABlcFtGyzwgE4m9B+KN5w84sAxxdQrvMELElzuZNvQvvztDVv2qa1H7OVYnzBeAZdbQHLUHF8QC9eaVr7bW0tE9fm9tPgKsM5fJcIEAEiMLwI0OCqgLZtVjgAZ1PaL0aTzfFFGltAOYc7eZfDjaa0P62NZZ4NQ/vFALv99tvVlVdeqfRhuiEk+uBEdckll4R7wFwYDUP7XW3LEs/2917SbMPx3//+ty06d9xrr72mFlxwwdzv+XqB5RN/8h/7ny95kjefYZM/znO4tFLS/NMe81KX6RuLwFlnnaWOPPJI53larobJ/q+jjz5aHXPMMa5kjG8wAvqEeTVnzpy4BTg89IgjjlCPPvpoGLfddtupU045JTzDLU7EGyJQAgEYqgxEgAgQASJABASBhRdeWG47rjz4OIKDX3iLfeHt4KYSP7Lij+VjY8aMCb3UiSLdq1hxloF0eMfm4S5r+b3KKvqc5VfHfzgMGR4qse8LSwvxe+LEiR2kIv7V4d8BtONHU/HnDJeDoDmjh+0Ld87mK7afM4ycYRyeGUbnDJf2zBTOcDV1wMsr2Fzp2f7mKFwwmOC57u677850RhMU7BNPPDF1Voz0bw79XX04LR5GNw5cnj59epgMDjZOO+20eJkh6T/c9E/jDTwrSn8aXL2QzfacBgcNDhocw2NwZOv181INW/+nwTWPtta7ogOuNbMCkSw/u8InywOhMEOJ7hUwq4HZDZzNhD1gtkD8s+Nvw69sXL/wxz4v8I+4mgf/4JiB+eefX7mWAZRtW5b3+9V+V11YfjH+p8Hl4qh88cOmcOVrveIMF/cwcg/nEO1hpcHVQwJS4SimcPSANfPjPPiLe/cs7uElrc0VvFm5POWb7/m6Z/n94z94u8QSQ8x6IsAgP/XUU9W+++7ri5y58yH9+0d/G3GK4k+Dy4Zm/jgaXJzh4gwXZ7jySw4/b/iWPzS4etCl6IDbI9vMj1l+doXLdA/f67BSWX4I1+CY2XAF4p8dfxeGZeLrwB/LDMET4lIes5/gE9sevzJty/JuHe0368Xyi/E/DS6Ti4rf+1Z48taE5dPgo8FHgy+v3HClp8HlQiaKp8JRTOHoAWvmx3nxxx6ce++9V6W5hxdX8KuuuqqCcp0W8paflleRZyy/Pv7DLCiWFsphyuJUo9fZXUXo7HqH9K+P/qBJUfxpcLk4Ol88DR4aPDR4aPDkkxr+UvuWPzS4etCm6IDbI9vMj1l+PoVLHGHA2xyWh9kCDr2FkwTs0UH6tED88+GfhmWRZ3Xj/+STT4bLCs8444yw+pjlwmyXa89fkTamvVN3+1l+Mf6nwZXG1dmf+VZ4spc8NyXLp8FHg48GX1654UpPg8uFTBRPhaOYwtED1syP8+Lfyz08ZrRGjx4dlv/iiy+G+3TSKpO3/LS8ijxj+YPBf5gVxWwXZk8RYLTDOUvVywxJ/8Ggf96+S4MrL2L29DR4aPDQ4KHBY5cO1cf6lj80uHrQjApP8xQe8T5oO1sLSjNmKyZMmKCwZKxXIP2bR/9eNM3zPEl/zJpiVjTt7K48+fdKmyy/V3rfz1l+Mf6nweWHE30rPHlrxfJp8NHgo8GXV2640tPgciETxVPhKKZw9IA18+Mi+MPhwZQpU8IZCBhYEuBUA7NbuGY9q6tI+VKejyvLHzz+wywp+Mp1dpcPuksepP/g0V9ok3alwZWGTvZnNHho8NDgocGTXWL4Telb/tDg6kEfKjzNU3jE5fv222+vpk2bFlNY4rO4jZeXSP/m0V9o5+OaRv/k2V0w9LHM0KdTjbTyfbSvVx4svxj/0+DqxVnZnvtWeLKVOi8Vy6fBR4OPBt88iVDujgZXD/yocBRTOHrAmvlxEfxlnxYUX+zTkoD9NjjYNs2DoaSVa5Hy5V0fV5Y/2PxnO7sLyw6xZNVHIP0Hm/4+aJyWB+lP+vPg9YXTukilz9j/2P/60f9G6HOMAnAyGY4M1w+Gc0nNovwn7uFnzJgRepTDTNcOO+ygsriCN+tStHwzjzL3LL8Z/Q9GfvLsLsx2gQ/LBNK/GfQvQ+O0d0l/0r+J428aT+d5Rv4n/7eB/2lwRVKBHb6ZHV6cY4h7eLjxxkG2UILNfV29hD/p30z696Jr1ud56Y9lq+AvX2d35S0/a7uypmP55P82KDyu/kD+J/+T/znD6JIPvuJpcEVIUuA2U+DK4caYYcASQjjLGDVqlMJMRJ49NqR/M+nvSxAWoT+WGcKToXl2Fwx9uJLPG4qUn7eMtPQsn/xPhZMKZ5qMqPIZ5Q/lTxvkDw2uSIqwwze3w4t7eDjJwOxWVlfw5gBC+jeX/iYdi96Xob+Ps7vKlF+0zeZ7LJ/83waFx+R58578T/4n//ODgykTqrinwRWhSoHbXIGLGQVx3Q1y2s7l6tV5SP/m0r8XbbM890H/5NldWHI4adKkLMVzD+1/yH9U+KjwZRIWFSTyIf/KVIvlU/61Qf7R4IqkBDt8czu8uIEHKTfddFN1yy235Jb9pH9z6Z+b2JYXfNEfywzhVEM+AGCpK5YZYm9hWvBVfloZac9YPvm/DQqPqw+Q/8n/5H9+8HDJB1/xNLgiJClwmytwxT08SCneCvN2ENK/ufTPS2tbet/0z3t2l+/ybW1Mi2P55H8qnFQ402RElc8ofyh/2iB/aHBFUoQdvtkdfsSIESElo1MOco8NpH+z6Z+b4IkXqqI/nGqceOKJYWnYa+g6u6uq8hPNdP5k+eT/Nig8rg5A/if/k//5wcElH3zF0+CKkKTAbbbApcFVTiSQ/6vj/yxndxH/6vDP0jOIP/Gnwk2FO4usqCIN5U875A8Nrqj3kOGby/DiGr7o/i2wAOnfXPr7GAD7QX8cyo39Xbazu/pRfhpOLJ/8T4ODBkeajKjyGeUP5U8b5A8NrkiKsMM3t8OLwQW38LgvEkj/5tK/CL2T7/SL/q6zu7bcckvVhgEnibv87hf+Ul7yyvLZ/9n/aHAm5UK/flP+tEP+0OCKehQZvrkMT4Or/LBA/u8v/99zzz3hbNe9994bEm+77bZTZ555plpttdXKE7NADqR/f+mfJBHxJ/40+GjwJeVCv35T/vRH/tDgijiaDNcfhnMJkDL4Y6nWDjvsoLbffnuF+yKhTPlFyku+w/Kby39JWub5Xebsrjzl9EpL/msn/wlfkP6kPw0+GnwiD/p9bYv8ocEVcVZbCO7qSE1uv3iCwyGzuC8Smtz+Iu1NvsP216dwYZnhHnvsoa666qqQLJjlmjx5cs+zu5I0LPOb9K+P/qAb8Sf+NHho8JSR4WXepfzpj/yhwRVxKRmuPwznEgpl8KfB5UI1e3wZ/LOX4k7J8v+jbr/99nCZ4axZs0Kg4GADhybDnXzVgfg3V/754A3Sn/SnwUeDz4csKZJHW+QPDa6IO9pCcFdnaHL7aXC5qJo9vsn0z95Kd8pBar/wM2oLYwu/J06c6K68hyeD1H4PzcmdBdtPg4MGBw2O3ILD0wuUP+2QPzS4og5Dhm8uw48fP15Nnz49XIaFWYEigfRvLv2L0Dv5zqDRP8vZXck2lPk9aO0v05Yi77L97P80uGhwFZEdPt6h/GmH/KHBFfUWMnxzGX7zzTdXM2fOVDNmzCi874X0by79h3nAS57ddfDBByvsVfS9zJD8T/6nwUGDw4csLZIH5Q/lTxvkDw0uGlwhAk0WeDS4igxxne80mf6dLSn2a5Db7zq7CzO7vsIgt99XG9PyYfup8LVB4XP1AfI/+Z/8X/0HlxGzZ88OXJ2Q8USgCQhstdVW6uabb1bXXnut2myzzZpQZdaxAgRGjhyp5syZU0HOg5Hlfffdp4444oiQ11Ej8Pq5556rVl111cGoIGtBBIgAESACRIAIWBHgDFcEC7/wNPcLz4gRI0IqBkHxbwekf3Ppb5VsOSObRP8qzu5qUvtzkjZTcraf/Z9f+Kv/wu/qjOx/7H9t6H80uCIJwA7f3A5Pg8s1jGWPJ/83i/+xzBD7uaZMmRISuezZXaR/s+ifvWdnS0n6k/5tUHhdvYH8T/7vB//T4Ip6IDtcczscDS7XMJI9nvzfTP6/8cYbvZzdRfo3k/7Ze3h6StKf9O+HwuniQvIf+a8N/EeDK5IA7PDN7PD40r/kkkuqUaNGKdwXDaR/M+lflN7J95pOf5zVhaWGL7/8cqGzu5re/iQ98/5m+9n/26DwufoF+Z/8T/6vfkktDa5IAlHgNFPg4Av/uHHj1NixYxXuiwbSv5n0L0rv5HvDQP8yZ3cNQ/uTNM3zm+1n/6fCWb3C6eqT7H/sf23ofzS4IgnADt/MDk+DyzWE5Ysn/zeT/21Uxtld2N81a9as8HGWs7tI/+Ghv40nesWR/qR/GxReVz8g/5P/+8H/NLiiHsgO18wOR4PLNYTkiyf/N5P/XVTOe3YX6T9c9HfxhSue9Cf9+6Fwkv/sCLD/taP/0eCK+J8M30yGv+CCC9Tee++tJkyYoHBfNJD+zaR/UXon3xtW+t9zzz3hbNfMmTPDJuOQ8MmTJyt4NTTDsLbfbGPaPdvP/k+Dg0sK02RElc8of9ohf2hwRb2IDN9MhoezgBNPPFFNmjRJ4b5oIP2bSf+i9E6+N+z0N8/uQtvRV9BnJAx7+6Wdrivbz/5Pg4sGl0s+VB1P+dMO+UODK+pJZPhmMjwURxpc5YcD8n8z+T8P5dPO7iL9h5/+abxC+pP+NDhpcKbJiCqftUX+0OCKuKgtBHd1mqa2nwaXi6L54ptK/3ytdKduU/ux73GvvfaKnWqMHz9enX322WrFFVd0A1Txkzbhb4OS7afBQ4OHBo9NNvQjjvKnP/KHBlfEzWS4/jCcS3gUxR97UrA/ZerUqQqKY9FQtPyi5SXfY/nN5L8kHYv+roP++FhR5uyuom21vVdH+816sHz2Pxo8NHhMmdDPe8qfdsgfGlxRryLDN5PhxeCaMWOGwn3RQPo3k/5F6Z18r630T57dte6664ZONXDtZ2gr/oIx20/5Q4OPBp/Ig35fKX/6I39ocEWcTYbrD8O5BElR/GlwuRDNF18U/3yluFOz/Hr732WXXaaOPPLIeJlhlrO73NTM/4T0r5f+xJ/40+CjwZdfcvt5oy3yhwZXxC9tIbirezS1/WPGjFFwfX333XerMl/lm9p+Fz3zxrP9VLj++9//hksM4YQGYYkllghnu8os1c3Kh+Q/8h8Vfir8WeWF73SUP5Q//ZA/NLiinssO18wON2LEiJCCQRCUksGkfzPpX4roxsuk/zz6Zz27y4Cv9C3xn4d/aTALZED8iX8/FE4Xa5L/yH9t4D8aXJEEYIdvZoenweUawvLFk/+byf/5qOxObaM/DhLH0sKXX345fDF5dpc7t/xPbOXnz6X4Gyyf/N8Ghc/VQ8j/5H/yf/UzzDS4IglEgdNMgUODyzWE5osn/zeT//NR2Z3aRf+0s7vcueV/4io/f07F3mD55H8qnNUrnK7eyf7H/teG/keDK5IA7PDN6/DwsDZ69Gi16qqrKtyXCaR/8+hfht7Jd0n/dPrj7C7Mdt17770hdNjXNXny5HCfVxLLIr+Jfzr+RTDN8w7xJ/5tUHhdfYL8T/7vB//T4Ip6IDtc8zoclMBx48apsWPHKtyXCaR/8+hfht7Jd0n/bPSv6uwu4p8N/yTf+vpN/Il/PxROF7+S/8h/beA/GlyRBGCHb16Hp8HlGr7yx5P/m8f/+ansfiMP/TGbjNmu6dOnhxn6OLsrT/nuVhR/wvLJ/21Q+Fw9hPxP/if/V7+klgZXJIEocJoncGhwuYbP/PHk/+bxf34qu98oQv9p06aFhtesWbPCjMuc3VWkfHdr8j9h+eR/KpzVK5yunsn+x/7Xhv5HgyuSAOzwzevwp59+ujrkkEPUxIkTw/ODXMI8Szzp3zz6Z6Fr1jSkfzH6w6kG+qF5dhd+T5gwISv0YTriXwz/XCCnJCb+xL8NCq+rC5D/yf/94H8aXFEPZIdrXofDfhIoepMmTVK4LxNI/+bRvwy9k++S/uXoX/bsLuJfDv8kP+f9TfyJfz8UThdfkv/If23gPxpckQRgh29eh6fB5Rq+8seT/5vH//mp7H7DF/1tZ3dhBnqJJZZwF66f+Co/tZCUhyyf/N8Ghc/VBcj/5H/yf/VLamlwRRKIAqd5Agd7Rs444wzOcLlG0Rzx5P/m8X8O8vZM6pP+Rc7u8ll+z8ZaErB88j8VzuoVTkvXC6PY/9j/2tD/aHBFEoAdvnkdfvPNN1czZ85UM2bMULgvE0j/5tG/DL2T75L+/ukPpzbJs7tOO+00tdpqqyXh5wzXf/zj3wVySgT5n/i3QeF1dQHyP/m/H/xPgyvqgexwzetwNLhcw0f+ePJ/8/g/P5Xdb1RJfyz9hSONl19+OVxaiN9YZmiGKss3y3Hds3zyfz8ULvKfHQH2P/a/NvQ/GlxR/2eHb16Hp8FlH7yKxJL/m8f/Rejseqdq+tvO7sJsl8xMV12+q90Sz/LJ/21Q+ITfk1fyP/mf/F/9kloaXJHkocBpnsAZPXq0giL36KOPWpcpJQeVtN+kf/Pon0bPvM9I//7QH8sM99prL5U8u2v++edXHPCrH/Bd/YL83x/+J/52BMh/5L82yH8aXFH/Z4dvXocfMWJESL0gCOxSPEcs6d88+ucgb8+kpH//6G87u+vUU09V++67b086VZWA9O8f/W00JP7Evw0Kt433EUf+bwf/j5g9e3Z5bdXFRYwnAhUisMgii4S5ax6usBRm3RQERo4cqebMmdOU6ra+npjl2n///dXNN98cYrHZZpupc889V6266qqtx4YAEAEiQASIwHAhwBmuiJ78wtC8Lwyc4fInjMj/zeN/f9Sv9wtr0bO7hqX9aAf7H/sfZ3i4pNanTMuTF+VPf+QPDa6IK8lw/WE4lxDIi/8999yjxowZo9ZZZx2F+7Ihb/lly0u+z/KbxX9J+pX93Xb6P/nkkwrLCnGuHgJcx0+ePDl2qlEW317vtx1/tp/yhwYfDb5ecrKq522RPzS4Ig5qC8FdHaZp7cfm+3HjxqmxY8cq3JcNTWt/2fYm32f7qXANgsKFvpz17K4kD5f5Tf4n/w8C/5fh4TLvkv/J/+T/6g1uGlyRlKLAaZbAocFVZnjtfpf83yz+76ZguZhBoz/O7cJ5XWlnd5Vrcefbg9b+ztpV/4vtZ/+nwl29wu3qyex/7eh/NLiiHkCGbxbD0+Byie5i8eT/ZvF/MSq73xpE+vc6u8vdmvxPBrH9+VtR/A22n/2fBhcNruISpNybbZE/NLgiPmkLwV3domntx9fvE088UU2aNCn8Eu5qV9b4prU/a7uypmP7qXANqsKFjyvm2V24x6HJSyyxRFb27pmO/E/+H1T+78m8HhKQ/8n/5P/qDW4aXJGwosBplsChweVhlDWyIP83i/8N0nm5HXT6287uwrLDCRMmtKL9XhqZksmg0z+l6l4esf2UfzQ4qjc4XJ21Lf2PBlfEAW0h+LAwPA0uFyWLxZP/qXA0QeHAMkPMcM2cOTNk9M033zyc7Vp33XWLMX70Fvmf/N8E/i/F5Ckvk//J/+T/6g1OGlwccEMEmiZwoXRNmTIlVLbg1axsaFr7y7Y3+T7bzwG3SQOu77O7yP/k/ybxf1J+l/1N/if/k/9pcJWVI5nfp8BplsDBl2185Z4xY4aXs3pI/2bRP3PHzpiQ9G8e/bHMEDPd5tld2Ns1fvz4jFSfl4z0bx7951Gv/B3pT/rT4Kje4HD11Lb0P85wRRzQFoIPC8PT4HJRslg8+Z8KR1MVDh9nd5H/yf9N5f9iEr/zLfI/+Z/8X73BSYMrkjsUOM0SODS4OgfMsr/I/83i/7L0Tr4/DPRPnt2FpcbwYpolDEP7s7TTlYbtZ/+nwl29ws3+Z0egLfKHBldE/7YQ3M7uSjWt/UsuuaTCkqIXX3zRi3voprXfRcei8Ww/Fa5hULggE7C/c/r06WFXgDMNLDPEB5q0QP4n/w8D/6fxeNoz8j/5n/xfvcFNgyuSQhQ4zRI4I0aMCCkXBEHaOJL5GenfLPpnJmzGhKT/cNE/79ldpP9w0T9jt4+Tkf6kPw2O6g2OuMMlbtrS/2hwRYRvC8ETfB7/bFr7aXDFpPNy0zT6e2m0kQnbP5wKlxwfAVLjoGTX2V2k/3DS3+jiqbekP+lPg4sGV6qQ8PCQBlcEIgVuswQuDS4Pvd/IgvzfLP43SOfldpjpn+XsrmFufxYGYfvZ/2lw0ODIIiuqSNMW+UODK+KethDc1Vma1H4sFxo3bpwaO3aswr2P0KT2+2hvMg+2nwrXsCtc06ZNC/d3vfzyyyH7Y/Zr4sSJ4cwX+Z/8P+z8n5T55m/yP/mf/F+9wU2DK5I6FDjNETg0uMyh0s89+b85/O+H4p25tIX+rrO7ttxyS0WFo3qFo5Pr5v1qC//Na3HnHdtP+Uv5M/zyhwZXJPco8Joj8GhwdQ7WPn6R/5vD/z7oncyjbfS/5557wtmue++9N4Riu+22U2eeeaZabbXVktD05Xfb8E+CyvZT/tDgGH6DI9nv5Xdb+j8NrojibSG4MHjy2qT2Y2nQDjvsoLbffnuFex+hSe330d5kHmw/FZ42Kjxlzu5K9qEyv9n/2P/a2P+kz5D/yf9t4H8aXFGPZ4dvTocXz2M41BT3PgLp3xz6+6B3Mg/Sv730xzLDPfbYQ1111VUhW2CWa/LkyT3P7kryUJnf5L/28h/4hvQn/dtgcLhkZFv4nwZXxAFtIfgwMDwNLhcVi8eT/zngt33Av/3228NlhrNmzQo7Eg5QxqHJcCdfdWD/Y/9re/9j+7mksGo568q/X/KXBldEgX4BXjfBh6F8GlwuKhaPJ/9T4aPCM1fhEfmC3gRjC7/hzbDKwP7H/sf+R4OjShmTljflT3/kDw2uiAvJcP1hOFenz4P/+PHj1fTp08NlP/gK7SPkKd9Heck8WH5z+C9JOx+/Sf/Bon+Ws7t80F3yIP0Hi/5Cl35dSX/Snwb38BvcNLgiiUqB1xyBt/nmm6uZM2eqGTNmeNtnQfo3h/5VKEGkP+lvU3iSZ3cdfPDBCntHfS8zJP+R/2z8V4Wss+VJ/iP/kf+qN/hocNHgChFoksClwWUbMsvFNYn+5Vpqf5vtp8LhUjhcZ3dhpt1XIP+R/1z854vH0vIh/5H/yH80uNJkhNdnFDjNETg0uLyyfpgZ+b85/O+f+vSSloX/k2d3QQ7Bm6GPs7uylF8F3SVPls/+T4W7eoVb+lvyyv7Xjv7HGa6I88nwzWH4ESNGhFQLgiAptwr/Jv2bQ//CRE55kfQn/bMqnFWc3UX+I/9l5b8UMVb4EfmP/Ef+q97gpsEViSgKnOYIHBpchcdV54vk/+bwv5OIJR6Q/vnoj2WG2M81ZcqUEPWpU6eqMksMiX8+/EuwuvVV4k/8aXBUb3BYO5+ObEv/o8EVcUBbCN52hmf77QiQ/6lwUOHIr3DceOONCo41MOtVJrD/sf+x/+Xvf2X6nPku+x/7Xz/630AYXDJjYXYA3hMBIkAE0hDgktI0dPI9a7PCwfEnH68wNREgAkpx/PHHBW0Zf0bMnj3b30aYgvgvssgiBd/ka0SACLQVAS27Opo+cuRINWfOnI44/iACvRDg+NMLIT4nAkQgiUBy/Ek+528ikERgoGa4fH4xSDaUv4kAERgOBGRGwqe8aMsXNhcHtLn9VfCTC2fGEwEi0GwEqpAXbZa/4Ia2tJ8GV7P7PmtPBFqHAAc8/yRvy4BnQ64KfrKVwzgiQASaj0AV8qLN8hcc0Zb20+Bqfv9nC4hAqxDggOef3G0Z8GzIVcFPtnIYRwSIQPMRqEJetFn+giPa0n4aXM3v/2wBEWgVAhzw/JO7LQOeDbkq+MlWDuOIABFoPgJVyIs2y19wRFvaT4Or+f2fLSACrUKAA55/crdlwLMhVwU/2cphHBEgAs1HoAp50Wb5C45oS/tpcDW//7MFRKBVCHDA80/utgx4NuSq4CdbOYwjAkSg+QhUIS/aLH/BEW1pPw2u5vd/toAItAoBDnj+yd2WAc+GXBX8ZCuHcUSACDQfgSrkRZvlLziiLe2nwdX8/s8WEIFWIcABzz+52zLg2ZCrgp9s5TCOCBCB5iNQhbxos/wFR7Sl/TS4mt//2QIi0CoEOOD5J3dbBjwbclXwk60cxhEBItB8BKqQF22Wv+CItrSfBlfz+z9bQARahQAHPP/kbsuAZ0OuCn6ylcM4IkAEmo9AFfKizfIXHNGW9tPgan7/ZwuIQKsQ4IDnn9xtGfBsyFXBT7ZyGEcEiEDzEahCXrRZ/oIj2tJ+GlzN7/9sARFoFQIc8PyTuy0Dng25KvjJVg7jiAARaD4CVciLNstfcERb2k+Dq/n9ny0gAq1CgAOef3K3ZcCzIVcFP9nKYRwRIALNR6AKedFm+QuOaEv7aXA1v/+zBUSgVQjIgPd///d/udu96KKLWt9pi8C3Nl5Htrn9wk9BELjgYTwRIAJEIERA5AXHH38M0ZbxhwaXP55hTkSACPQBAQ54/kFuy4BnQ074iQaXDR3GEQEiYCIg8oIGl4lKufu2jD80uMrxCd8mAkSgzwhwwPMPeFsGPBtywk80uGzoMI4IEAETAZEXNLhMVMrdt2X8ocFVjk/4NhEgAn1GgAOef8DbMuDZkBN+osFlQ4dxRIAImAiIvKDBZaJS7r4t4w8NrnJ8wreJABHoMwIc8PwD3pYBz4ac8BMNLhs6jCMCRMBEQOQFDS4TlXL3bRl/aHCV4xPn26+99po66aSTlG0QX3jhhdUxxxzjfNd8cO2116pbbrnFjPJ6f/LJJ4f5PfDAA+rSSy915r3llluqsWPHOp8nH7z88svq1FNPTUbHv9ddd1218847x7/lxlWPbbbZRm2yySaSjNcWI8ABzz/x2zLg2ZATfrLJalv6quM4dhQbO9LoMmfOHHX33XerGTNmqFtvvVU9/fTT6oUXXlAYpxZffHG19NJLq2WXXVZtvPHG6iMf+Yhaf/311ciRI9Oy5LOWIiDyggaXPwZozfijB5kwzJ49W277ftVkg3uovpdbZYGXXXZZ2CZpW/J6xx13ZCr+0EMPTc0nmW/e31KJK664IrWcrbbaSpJmul5yySWp+e2+++7WfFz1OP30063pGZkdgeeeey546qmnwj+taGR/ccBSCo/rAS/I++dqSp3yD3Vi+Rx/hDc5dhQbOwQ/86qN1+Dss88OVlllldTxSGSKXFdaaaXgzDPPDF599VUzu4G5HxZZnhfQQWi38EjesQfpXYHyvz75D5r0C//YyulXgTaGEwa2PWtq3Lbbbpsq4A866KBMTRsUg2v++ecPXnrppUx1RiI9e5XafhpcmaH0klB/zQ3mm2++mCb777+/l3zryETkBQc8f+jXKf/RijrLF37yh2a5nDh2FBs7kqjffvvtuQ0t4QW5rrzyyoGeEUtmXevvYZLleYAclHYLb3D8yUO99LR1yn/UrF/l0+BK54NCT5999tngrW99a6zcSgc1r3r5QvDGG2/0zH9QDC7U/eKLL+5ZXyTAV8XFFlsstf00uDJB6S3Reeed10EPGlyd0PZL4HaWOu8Xy6/vC6fI5XnUqO+OY0fxscOk2kUXXRQsuOCCHTJP6Jz3io+NkydPNrOv9X6YZHkeIAel3cI/NLjyUC89bVvGPxpc6XxQ6OkZZ5zRJejN2QXpsFdddVXP/I899thgySWXTP2z5Y0yRo0alfoe8pXgWsondcV1xx13lOSp16uvvrqr/WY+uKfBlQqh94fjxo3roAkNrk6I2yLwO1s971eb2y+yaR4a9d1x7Cg+dgjVrr/++kDvv+qQd0JjuS600EL/n71rD9mi+P77jSK6UBGZpkReKi3tQmWa0IVIzMAwrCyzssIoKMrKsii7GBYV3SHBii5/SFaWRJGF3U0Cu9gFDa3MzAxCyZ9EaTm/+Wyep5mdM/s8++w8u/s+ewbed3bPzs6cOWf2fJ6zO3NGDR8+XE2aNEmNGDFC6XXVqeX1uh3VCl4TD53Mu8mWZ5FTVfpNY0gcrizaSy9bF/wRhyt9HLR19bjjjnOM9/Tp0x3axIkT26o/edO5557r1A2jgPU6rSbO4dKLia16AUp6cWPTKqdOnWrdx33tEoerqRiDFVi/fr3aaaedLJ2Iw2WLty4G3+71f2d17j/9gPpPGuUdCXa0jx3Q2tq1a5UOgGHZOtIv8rPPPlutWLFC6SAalpJxDvqECRO89+6zzz7qu+++s+4r+qTbbHmr8qtSv2k8icPVqvaal6sL/kiUQv30hEzaaEeHH364VSWiL9bCMwAAErdJREFUH61atSqOgvTXX381rum3bHG0JERJypO04xbNnz/fqUI7XFGfPn0cOkdYsGBBpMHGujRmzJho0aJFFu2VV16Jxo8fb9HMk+3bt0d9+/aNfv311wZ59OjRkX7r2DjHgXa4Ij1F0aLhhOMDdB00I7rmmmtwaKUtW7ZEehqORdNf/KIDDzzQoq1ZsyaOToVcTxGJhg0bFh1xxBGRXhxtlUuecPUjStGAAQOsokuXLo2jYK1bty7aY489opEjR0b6DWocAcsqmDjZtGlThD8zaeco6t+/v0lyjtHO1q1bLbp2bKNevXrFNLNeHcAkmjlzplVWv9mNZs2a1aBRpK4GocIHEiUqvHJqEyWKER2NJ/2zgLlaHEmwIx92QFOXXnpppKf/OUrT0wujBx98MLryyiuda0nC448/Hump/I59RTlE1uWwFtdMm4tzpCrYcsGwf3UR6j/ZC+1wZa5yzz33ZO+ps/2FQGrTf/I9y/Qwtbzjt0rES0/Ob775ZucN2eWXXx53iVsM/dRTT+Xubqe+cOEL3JFHHmn158ILL0zld8mSJVZ56PaOO+5waKG+cL344otO3eZUyZ9++il+a+mbYoIpJWnBQLj60ScNYrEcMM1kyJAhDg8og69KmIZJZTnB6e0BnHux9qBZGjx4sHPf5MmTG7fddtttznV6zri8J33xIv7lDWND3bkPyrT/YL7M9mk85RZizgoEO/Jhx48//mgFBiK9ItdbnmTSzrPPPsvaT9j0lStXsnVV1ZYLhrHqaptI40rwp20ROjeWaf/BTFHty5RCR/XtE/TXHaW/rDiGGnPKkeBc0cNK+SmnnNJ+gzvu7JTDpfe+UjfddJPFM5wZ/WXFy3Ny6uSgQYPUnDlzrDrQ91AOl/4C59St30DFU0a+/fbblqJUHXTQQUp/gWT7xNUP/levXq0Qqh4ATLr05Zgm5JveWVWQZoVRESLJWQAvnEKKAhwfx2W2T+PJx1sRdMEOpfJih/6Kz9rio446SkG+WRKmGOpZEGx9eqYFW1VVbblgGKuutolkLwR/2hahc2OZ9h/MFNW+OFyO6tsnvPPOO46B1lO81N9//x1XmgxrigcXzgHezOVJnXK4sEj1vffec/oEA+5LBx98sFX+iiuuUA899JBFQ79DOVzvv/++UzfqR7Svww47jL1GBtPMMbefSx988AFbx9NPP910YbZZv55m6qwbQHtVBWlOFlWhkVwF8MJppCjA8XFcZvs0nny8FUEX7FAqL3aceOKJrK1uN9jFq6++ytanp6KzQ6KqtlwwjFVX20SyF4I/bYvQubFM+w9mimpfHC5H9e0TLrnkEsdA6znjVoX4akQPLOWzZ8+2ymQ96ZTDNWrUqPhrVjJ4hm/62ddff+30beHCheree+916KEcLuyRQnI0c7yFpPOBAwfG0ajgQOr1VQ06XUcOx5fbjNpXP8kE+7TMmDFDvfbaa+qJJ55Q48aNY+tHGwDwZOoUSONHxlVXXRX/4auk2VccDx06tHEd5ebNm5dkrbLn1BcBvHAqKgpwfByX2T6NJx9vRdAFO/JhB4I5IXw76ZJyBNDIk/bdd1+nTmAFNuBNpqracsGwpKbyndPYEvzJJ0fz7jLtP/goqn1xuEyt5ziGweei8eELkZmwPwg9sJTj60ee1CmHC2FzkbAOiXhFrgNxsF9r7r77bqsc1iJhIN9zzz0WHXWEcriwuaXJGx0DFLFuK7lGDlGmDjnkEPaeadOmOWrw1Y92MBVRB+Fw7klOwySeTj75ZKdsp0DabAjji3igHF8ee2qiPgjghdNgUYDj47jM9mk8+XjrNF2wQ6m82MG97INejz/++FzqAwbS+DBzfDVKpqracsGwpKbyndM4EPzJJ0fz7jLtP/goqn1xuEyt5zjGolx6ECnX0focx2Tz5s3shozLli1ru/VOO1xz5851+vbRRx85/CZDGo8dOzYu00mHC1+lSN7J/NFHH3V4BME3DVFHX3TKp9XPyYAq4Jwc8Ld8+XIqEudVBWmLyYqdkJ4F8MIppijA8XFcZvs0nny8dZou2KFUXuzwTZs777zzcqkPgaNofJi5jtbr1FtVWy4Y5qgqF4HGgeBPLjFaN5dp/8FIUe1HaKjsPxrAlgZ62AmcC+oH5ddeey3bi+QXI5T3LcRlK0gQO+1w6RDvTnCI6667zuIC0QCp35RjZ3ikMhwufIX7888/LR7NEy7KHxZXJ5MPrHB/WuKmUUIuzzzzjHVbVUHaYrJiJzS+MK3H/MMaSfOcOy7b1kn75eNNUgc0nsoa5oId+bEDDhDp0cxvueWWXGrlIkei/ieffNKpt6q2XDDMUVUuAo0vDl+a0ZK2R86rhwed1Il84cr16P17MyLQcWHH9d5MbO16Hw8HHHr37q22bdvGlm9G7LTDhfYxHY4MDXK9D5XFlt67xLoOeSBwBVIZDlczB5bb4NIMJ0+d84HVrbfeSkXY/IsvvrDkQbLD1BkzVRWkTR6rdkyylDeM4TQDkCkzldk+jacy+i/YoVQI7PCFPr/zzjtzqZXb0gTjBbM+kqmqtlwwLKmpfOdkLwR/8snRvLtM+w8+impfHC5T620e6w0VnR/XeuNab22Ys683wHPuef311733pF0owuHC9DwyNJR/9tlnDbZOO+0067oZ7r4Mh8s3nZAYRqAI6gfl0Eky+cCKA1zz3g0bNjj1o53k2qmqgrTZl6odk74E8MJppijA8XFcZvs0nny8dZIu2KFUCOxYvHgxa28vvvjiXOqbMmUKW+8bb7zh1FtVWy4Y5qgqF4HsheBPLjFaN5dp/8FIUe2Lw2Wpvb2To48+2jHKiIiHzRN9f8kNhfEQtzvfvAiHC1MGEYiCjA1yenu4adMmtfPOO1vXTIenDIeLiwhoapcDxywOF6ISpiVsBcDt0YXNr83E8RFi42OzDW49WdLxM8tX/ZjGoABeOE0VBTg+jstsn8aTj7dO0gU7wmCHb0YBQsXnSXhxSOPDzJNrcdFGVW25z+ESDGtvZNA4EPxpT37cXWXaf/BTVPvicHHaz0D76quvWINMD2WWfLfddlMIqpE1FeFwgacRI0ZYfT3hhBNiVpPTOeCYrVu3rtGNMhyuN998s9E+d4ApgUndZHG4lixZwlVr0bgQ9MkfAFUFaasjFTshvQnghVNMUYDj47jM9mk8+XjrFF2wQ6lQ2LFx40bnhSD02q9fv1zqQyRaGh9m/ttvvzn1VtWW+xwuwTBHhS0RaBwI/rQkrpYKlWn/wWBR7YvD1dJw8Be68cYbWYNMD2XWHBvqZk1FOVz33Xef1Vd81YLRueyyyyz6yJEjrS50o8PV7O0gAnZwuoeuzMSB9K677moWYY+x/1ey/smTJ7Nl5QvX/8XjFGPVl4oyuNI+L4Ey5U/PEc9Z56iCHWGxAxsSky4px8s/hIxvJ2HLD25tNpwwLlXVlvscLsEwTovNaTS2xOFqLqtWS5Rp/8FjUe2Lw9XqiGDK/fPPP/EbNHoAQ+SYipg1FeVwrV692gE0zGVP/viHY2ambnS4KAKj2U/zeO3atY6sMD6uv/56sxg7DQXltmzZYpUzT7Zu3cpOVxSH6z/HygeGphzN46IMrtmmeSztlxe0g+y2qY9OHwt2RCo0dnDrcqHbs846qy11Jl8k0jjxRT7kHK4q2HKfwyUY1tawaOC6D2PS6L4Wxf6XZ/+hk6LkLw6X7wlogf722283Hj4yxsix4z2+UjT722WXXZz7se4HP9azpKIcLvCE0OlmX8844wzrHNewubCZutHhQrjgtIQ9ukw50fHDDz9s3TZr1iy2HJxbX1qxYgV7jzhc4nD5xkwzelGA4+OjzPbp2fTx1gm6YEekQmPHxx9/zNpF6Beb/2ZJq1atctYl0ziB/eVSVW25z+ESDOO02JxG4yDNsfJd89Vepv0DT9J+MQ6fOFy+J6AF+kUXXeQY+CzrsL7//nvnfjzMcFCypCIdrrvuuovlmYwQFoEnUzc6XAMHDlTbt29PdrVxjn3KSCZm/vLLLzfK4OC5555jy82bN88qZ55gfzezTjq+4IILzGKNY25K4dSpUxvXe9oB9dcHaml0X18FcIoBnCrKn8aTj7dO0AU7IseG5cUO6Omkk05y6oV+Md3whx9+aEmVWJ+V3AaFxkhyurxZYVVtuc/hEgwztdf6MY2FNJzxXfO1IvhTD/wRh8v3BDShY8oXFxThnHPOaXKnfRkGnB5gyocOHWoXanJWpMOF+fDEJ5fDIUumbnS40PdFixYluxqfY8rfAQcc4MgJzjjtTUY3fvjhh0451G2G1aeyyOGkc+MO92RxuMaNG2dW26OOadz5QC2N7uuoAF49AI/TP40n7lonaIIdrrMFHeTFDujq3XffZYNnoH7ss9hs3RJmJiSnyNP4QPRYBDrxparacp/DhX4Jhvm06afTeEjDGd81X62CP/XAH3G4fE9AE/rzzz/P/lBesGBBkzvty5hiRg+wmX/66ad2wZSzIh0usDF48GCWZ/D/zTffOJx2q8PVq1cv9eWXX1r9hbN15plnsvLhQrGvX7+eLQtZXn311dZm2J988knDkQP4m+MFx+eff77FC52MGjXKKYuIjGi7Jybqtw/U0ui+/grg1QPwOP3TeOKudYIm2ME7XHmxg3Q1c+ZMx96RjhFEA/t+zZgxQ82fP199/vnn6qWXXlKIWostO5Lbm9B9yB977DFqgs2rasvTHC7BMFaVqUQaE2k447vmq1jwpx74Iw6X7wloQh89erRj1Pfaay+F6HRZ0i+//MIGQMC0sVZT0Q4XFg2T0THzIUOGsCx3o8O13377xTLYe++91aRJkxT2HZs2bZrC10lTJnSMtXlYF8Aln4OGe/E1C+H3+/bt26j3mGOOURMnTmycUxu+xeHc9CXcA6cN677wY2P69Okca5WkUX99oJZG93VIAK8egMfpn8YTd60TNMEO1+EKgR2kKwQkGT9+vGMfSc/t5L7ZA9Qm5VW05T6HSzCMtJYtp/GThjO+a76WBH/qgT/icPmegBT6zz//zDpJ7e5qf+qppzrg0Lt3b4XNc1tJRTtcy5Ytc/iFEfJFb+pGhwsRnhAchYxvs5z7ukW6xTQVbpNkrk6UW7p0qROKH2XHjh1LVVr5nDlzmvKJdV49JZFcfKCWRvf1UQCvHoDH6Z/GE3ctNE2wo3PYYeoKThciwpJu281h4x955BGz6tTjKtpyn8MlGJaqSu9FGktpOOO75qtU8Kce+CMOl+8JSKHff//9rCFvttmur8q5c+ey9SFsbiupaIcLPPXv39/h2TcNshsdrsWLFysEtuCm9pFBpvz2229vqsYHHnggdToL6gL4v/DCC3FdN9xwgyN/37qvbdu2qWHDhjnliT/k4nDVw+D7BmKdAZ+eA59sQtIFOzqHHZyeFi5cGAfMIB1nyY899liFadxZU9Vsuc/hEgzLqtl/y9MY8jlVaXRfi3W2v5BJXfovDpfvCUihcxssYi40fti2kzZu3Mh+LfGtyUm2UYbDlYzCN2DAgCRbjfNudLjeeuutuH9wMjH3P/mFCiH/Adhp0QYbAtpxAHDnxhbWHZx++ukKYY8pzZ4923Gg0iJo4c36hAkTnHvANzbynDJlClVd+VwAL7yK6gJ4nORoPHHXQtO451uwIwx2+HSFaLKIDoup33369HFsIOkf+f77768wnX/58uW+6lqiV8mW+xwuwbCWVOkUovGS5lj5rjmV7SDU2f5CBHXp///QWT2Aoj/++CPafffdcVh40j8o4zZ3sFJ4+9KgSMAnAT19Mho+fLhzWX/NjMaMGdOgb9iwIVq5cmWkF05HOtxupEMcR/rrV+N6loPNmzdHOhpktGbNmkhHO4wOPfTQqF+/flmq8JbVURJjPn///fdo0KBB8Z/eL85bvooXyF5oUMvMng4Wwt5Tpv0DQ9K+4A87MIUYXAJ6j8MI9lqHf49gQ7STFenIhPGfXpMbtL0q2HLBsKAqjQR/wsoTtdUF/8ThCj92pMYukkCrYNVFXa58VwTwwquoLoDHSY7Gk7zw46QjtJ4uAcGwsBokeyEv/MLJtS74Iw5XuDEjNXWhBASsqqdUAbzwOqkL4HGSo/EkDhcnHaH1dAkIhoXVINkLcbjCybUu+CMOV7gxIzV1oQQErKqnVAG88DqpC+BxkqPxJA4XJx2h9XQJCIaF1SDZC3G4wsm1LvgjDle4MSM1daEEBKyqp1QBvPA6qQvgcZKj8SQOFycdofV0CQiGhdUg2QtxuMLJtS74Iw5XuDEjNXWhBASsqqdUAbzwOqkL4HGSo/EkDhcnHaH1dAkIhoXVINkLcbjCybUu+CMOV7gxIzV1oQQErKqnVAG88DqpC+BxkqPxJA4XJx2h9XQJCIaF1SDZC3G4wsm1Lvjz/wAAAP//dK69UgAAQABJREFU7X0H/CRFtXWtq4gLuChJQZJZUREBMXwSFEEwIGIiKKz6VFAEDCigEp45ASr4jKAgPkQFFEk+BMQsiCQTIiCYQMVFVhFd56vT9G1qeurOdKrqmanTv99u9/9OdVf1ufeeW7erunrBwG7Gbn//+9/NokWLcBh9W7BgQVZn3pTo9bNCIqAhcPHFF5vNN9985Oezzz7bbL/99iNyCsIjIHzxt7/9rXZlK6+8svecPvkPDWL9jD9ew6SQCLREgDGsJYCl0xl/SoB08Gcq8W8BE64OrIWXmFsEli5dai666KKR+9tiiy3MGmusMSKnIDwCDHjdY5xKwPMhJ/bEB34+dCibdQQYw7rVoPAFH/h1h2sq8YcJV3c2wysRASIQAQEGvO5BTiXg+ZATe2LC5UOHMiJABFwEhC+YcLmotDtOJf4w4WpnJzybCBCByAgw4HUPeCoBz4ec2BMTLh86lBEBIuAiIHzBhMtFpd1xKvGHCVc7O+HZRIAIREaAAa97wFMJeD7kxJ6YcPnQoYwIEAEXAeELJlwuKu2OU4k/TLja2QnPJgJEIDICDHjdA55KwPMhJ/bEhMuHDmVEgAi4CAhfMOFyUWl3nEr8YcLVzk54NhEgApERYMDrHvBUAp4PObEnJlw+dCgjAkTARUD4ggmXi0q741TiDxOudnbCs4kAEYiMAANe94CnEvB8yIk9MeHyoUMZESACLgLCF0y4XFTaHacSf5hwtbMTnk0EiEBkBBjwugc8lYDnQ07siQmXDx3KiAARcBEQvmDC5aLS7jiV+DNVCVc7lfFsIkAEUkKAAa87bacS8HyISQfK9xtlRIAIEAEfAow/PlSayVKJPwuWLVs2aAZRd2ettNJK3V2MVyICRCAJBG6++eah+7zb3e5m/vOf/wzJyn8sWrSoLOLfiSPA+JO4AfD2iUADBMrxp8olGH+qoDS/ZaZqhItTOubX0HhnRKArBGREgk8Yu0LUmFSeMPoQE3ti/PGhQxkRIAIuAsIXjD8uKu2OU4k/TLja2QnPJgJEIDICDHjdA55KwPMhJ/bEhMuHDmVEgAi4CAhfMOFyUWl3nEr8YcLVzk54NhEgApERYMDrHvBUAp4PObEnJlw+dCgjAkTARUD4ggmXi0q741TiDxOudnbCs4kAEYiMAANe94CnEvB8yIk9MeHyoUMZESACLgLCF0y4XFTaHacSf5hwtbMTnk0EiEBkBBjwugc8lYDnQ07siQmXDx3KiAARcBEQvmDC5aLS7jiV+MOEq52d8GwiQAQiI8CA1z3gqQQ8H3JiT0y4fOhQRgSIgIuA8AUTLheVdsepxB8mXO3shGcTASIQGQEGvO4BTyXg+ZATe2LC5UOHMiJABFwEhC+YcLmotDtOJf4w4WpnJzybCBCByAgw4HUPeCoBz4ec2BMTLh86lBEBIuAiIHzBhMtFpd1xKvGHCVc7O+HZRIAIREaAAa97wFMJeD7kxJ6YcPnQoYwIEAEXAeELJlwuKu2OU4k/TLja2QnPJgJEIDICDHjdA55KwPMhJ/bEhMuHDmVEgAi4CAhfMOFyUWl3nEr8YcLVzk54NhEgApERYMDrHvBUAp4PObEnJlw+dCgjAkTARUD4ggmXi0q741TiDxOudnbCs4kAEYiMAANe94CnEvB8yIk9MeHyoUMZESACLgLCF0y4XFTaHacSf5hwtbMTnk0EiEBkBBjwugc8lYDnQ07siQmXDx3KiAARcBEQvmDC5aLS7jiV+MOEq52d8GwiQAQiI8CA1z3gqQQ8H3JiT0y4fOhQRgSIgIuA8AUTLheVdsepxB8mXO3shGcTASIQGQEGvO4BTyXg+ZATe2LC5UOHMiJABFwEhC+YcLmotDtOJf4w4WpnJzybCBCByAgw4HUPeCoBz4ec2BMTLh86lBEBIuAiIHzBhMtFpd1xKvGHCVc7O+HZRIAIREaAAa97wFMJeD7kxJ6YcPnQoYwIEAEXAeELJlwuKu2OU4k/TLja2QnPJgJEIDICDHjdA55KwPMhJ/bEhMuHDmVEgAi4CAhfMOFyUWl3nEr8maqEq53KeDYRIAIpIcCA1522Uwl4PsSkA+X7jTIiQASIgA8Bxh8fKs1kqcQfJlzN7INnEQEi0DMCDHjdKSCVgOdDjAmXDxXKiAARGIcA4884dOr9lkr8maqEi1M66hkpSxOBFBGQDjIDXnfaTyXg+RATe2L88aFDGREgAi4CwheMPy4q7Y5TiT9MuNrZCc8mAkQgMgIMeN0DnkrA8yEn9sSEy4cOZUSACLgICF8w4XJRaXecSvxhwtXOTng2ESACkRFgwOse8FQCng85sScmXD50KCMCRMBFQPiCCZeLSrvjVOIPE652dsKziQARiIwAA173gKcS8HzIiT0x4fKhQxkRIAIuAsIXTLhcVNodpxJ/mHC1sxOeTQSIQGQEGPC6BzyVgOdDTuyJCZcPHcqIABFwERC+YMLlotLuOJX4w4SrnZ3wbCJABCIjwIDXPeCpBDwfcmJPTLh86FBGBIiAi4DwBRMuF5V2x6nEHyZc7eyEZxMBIhAZAQa87gFPJeD5kBN7YsLlQ4cyIkAEXASEL5hwuai0O04l/jDhamcnPJsIEIHICDDgdQ94KgHPh5zYExMuHzqUEQEi4CIgfMGEy0Wl3XEq8YcJVzs74dlEgAhERoABr3vAUwl4PuTEnphw+dChjAgQARcB4QsmXC4q7Y5TiT9MuNrZCc8mAkQgMgIMeN0DnkrA8yEn9sSEy4cOZUSACLgICF8w4XJRaXecSvxhwtXOTng2ESACkRFgwOse8FQCng85sScmXD50KCMCRMBFQPiCCZeLSrvjVOLPgmXLlg3aQdX+7JVWWim7CANeeyx5BSIw7whIwLv55puHbvVud7ub+c9//jMkK/+xaNGisoh/J44A40/iBsDbJwI1ENDiT5VLMP5UQWl+y3CEa351yzsjAnOJgAQ8PmHsTr2pPGH0ISb2xAd+PnQoIwJEwEVA+ILxx0Wl3XEq8YcJVzs7SfbsVVZZxfzjH//I7v/1r3+9ed/73lcJC3RqdtllF/PVr341K7/jjjua008/3XzmM58xr3rVqzLZWmutZX70ox+Ztddeu9I1WSgtBBjwutd3KgHPh5zYExMuHzrjZaeeeqp5wQteUBS6+OKLzWMf+9ji72k/YDyadg1NX/uEL5hwdaebVOIPE67ubCapK2FoXBKuN7zhDeYDH/hApft/z3veYw466KCs7LrrrmsuvfRSs9pqq2V/77777uakk07Kjp/85Ceb888/39zjHveodF0WSgcBBrzudZ1KwPMhJ/bEhMuHznjZV77ylewBmpQCn89SwsV4JJrjvioCwhdMuKoiNrlcKvGHCddkW2AJDwJNEq7zzjvPbL/99mb58uXm7ne/u7nwwgvNk570pOLqt912m9lss83ML37xi0z2ute9zhx99NHF7zwgAkCAAa97O0gl4PmQE3tiwuVDZ7xslhMuxqPxuuWvfgSEL5hw+fFpIk0l/jDhamIdPMfUTbhuuOEGs+mmmxpZ6AAjYhgZK29XXHGF2WKLLYrRM4x47brrruVi/DthBBjwuld+KgHPh5zYExMuHzrjZddff7254IILikLPfvazzX3ve9/ibznYeuutzY033miWLFliDjnkEBH3tmc86g36ma9Y+IIJV3eqTCX+MOHqzmaSulLdhOtZz3qW+frXv55h9MQnPtF85zvfKUYqysDhfbA3v/nNmRjviv361782q6++erkY/04UAQa87hWfSsDzISf2xITLh0572Z/+9CezxhprZBfab7/9zFFHHdX+oi2vwHjUEsCETxe+YMLVnRGkEn/mNuH661//au64447MItBZx5LR3LpDoE7C9b3vfW9o6uDZZ5+dTS3UWmM/VWA22GADg0CN7Y1vfKN5//vfrxWnPDEEGPC6V3gqAc+HnNhTlwkX489dSJ9xxhkGI1/YpiHhYjy6Szc8qo+A8AUTrvrYaWekEn/mNuF6ylOeYr797W9n+v3tb3/LFe80S28or5Nwbbvttgbz5bFhuuD3v//9ibW+973vNW95y1uycqjrmmuuMfe73/0mnscC848AA173Ok4l4PmQE3vqMuFi/LkL6be+9a3mne98ZyaYhoSL8egu3fCoPgLCF0y46mOnnZFK/GHCpVgARln++Mc/Zr/CwTbccMOiJKbD/eQnPzFLly41/+///T+z5ZZbFr9pB3jieeWVV2b/4KgbbbSRedSjHmXWW2897ZSJcowAXXXVVQYJJf5hMQq0E/8e8pCHmPvc5z4Tr+ErcN111xks7/vzn/88uwba+NSnPtXIB0JxTtWEC/P7t9lmm6IaTCvEUvCTNiyggVGuP//5z1lRLqAxCbF0fmfA617XqQQ8H3JiT30nXKj/2muvLZqImRn3vve9i799B7feemsxEwC/r7nmmmbllVf2FS1kiEV/+ctfsr8x8wM82zTeuefhgg94wAPMCiusYBDj5H3dvfbay1x00UVZfXiHCwmYbHjfa9VVV5U/1X1X8ZPxSIWYP1REQPiCCVdFwCoUSyb+WJLPNkucchh9b/UxwL8uN5sIZdfEdW0yUvvSp5xySnG+dbDBf/7zn4E1ioFdZa+Q49ovetGLxl7705/+9MAufz50jtwv9jagDl7+8pcPrPOOvY77ox0hGtgl1Ac2sKnXtcupD1772tcObrrpJvfUscef+9znBjbIe69pg/jAJj2D22+/PbvGve51r6KcXfxCva59mliUs8sFq+V8PxxxxBHFufe85z0HNoD7ilGWGALiP/CZuv80qPrkP7SJ9TP+wA7WX3/9gvPA35O2vffeuygPv3jb29426ZSBTXqKcx73uMdl5ZvGuy9/+cvFtVC/XRY+u94nP/nJIbn4bHlvl2Uf296u4yfj0Vi4+WMFBMSG68aecX088n9//A+Vx8K/yHJiVeizZzFg329NZW0TLvsx3qGAYUdcBvbDvEMytFtLuOzo02DnnXceKS/3Wt7bEamBHVWaeLvHH3/8AAlg+Xztb7voxMAuvz7xugjU2jVc+eabbz4AFkjARG4/fOy9vh0BHNjl34tyhx12mLecJrQrFhbnoq4TTzxRK0p5QgiI3THgdaf0Pvkfd9Fn/WJP3aE5GDSNP6985SsLzrMzICY2CXFD2o896p20uUmdHW3KijeNd6ESrhDxk/FokmXw9yoIiL8x/lRBq1qZPvkfLYxVPxMuxR7OOuusoUD2gx/8oEh0MLJkV9rL/tk56SNXALHbqRVD52+33XYDJEt2KuLg6quvHiDAIVFxExKMStmpFyPXE8FXv/rVwcKFC4vrIplC/ZD/6Ec/GmDk6/Of//xgp512KsqAHOwUw7EjaHjKKCSC/eLFiwfveMc7Bv/3f/83sFNcBmeeeebAzsEf2OkqWblXv/rVAzsNpDhHS7hOPfXUogyua6diyq1U3tv3toprvOQlL6l8HgvOLwJiqwx43ek4VsDRWtxn/WJPWtuayJsmXPa7VgXf4cHauFH93/zmN0VZiQuITeOwtO/CFue4nNw03mkJl53qPvjIRz6S/XNnYtjl4Qs5fvc9ZAwVPxmPmlgyzykjIHzB+FNGpvnf4zir+VWrnxmrfiZcik6++c1vDgUmdPbhaHa58mxqoXJaJsZTQ3FKBE37zalsSqLvnEsuuWSw9tprF+Xt+06+YpnsCU94QlHOvk9VTN/wnWCX3i3Koi0HHnigr9jgX//612CdddYpymJKIdrk2+y7XYNHP/rRWVk79784R0u4kJgJDpg6ibrqbnvssUdxDSRfmNrJLW0ExKYY8Lqzg1gBR2txn/WLPWltayJvmnDZd5WGHsIhodG24447ruBGdzbFueeeq50ycKf62fenBv/+97+zsk3jnZZwuQ1wZ0Psv//+7k/e41Dxk/HICzeFNREQvmD8qQncmOJ98j+aFat+JlyKEdgVDotgBgfD6NNrXvMapfRd4t///vcDu6BEcW6VURlMlRMnxt43BdB+i2qoDKY3jtsQSB/2sIcV52BEzre5c/dRNwLyuA3tKE9p1BIujKzJfT3nOc8Zd1n1t89+9rPFNXAtjBBySxsBsSkGvO7sIFbA0VrcZ/1iT1rbmsibJlyoy65wWHDevvvuq1aP93il7W7CdNBBB6nn2I/IF+e40+GbxruuE65Q8ROAMB6pZsEfaiAgPsf4UwO0CUX75H80LVb9TLgUQ/jud79bBCY4GEZ0brzxRqX0XWIESHHIFVdcsdI5GLXZeOONi/PwYm95u+WWWwYIqieddNLgyCOPHDu6Jee+7GUvK66JaYK+7WlPe1pRBkmlXRXQV2xIVl44xJdw/eEPfyiuCzzsd7SGrlH1j3Kieeyxx1Y9leXmFAHxLwa87hQcK+BoLe6zfrEnrW1N5G0SLkzfljZhRoG23f/+98/K4T0uu0Jt8V4tZkJomztFGw+zZGsa77pOuELFT8Yj0TT3bREQ32T8aYvkXef3yf9oRaz6Z3JZeLtSnrEjJtbu9c2+02SwlCw2LNtuV7lTC9tV9kY+xFv+OKJNMgw+2Dtp22yzzYydkpcVe9KTnmSwhHyVzSYtxiZSWVGbqBksk2lHkqqcqpb57//+b/P2t7+9+N0GHbPWWmsVf+MAywjL8r32PTNzzjnnDP3u++MLX/iC2W233Yqf0PYPfvCDxd84uPzyy41NIguZfbds6JzihwkH0LVdEbEodeihhxq7+EbxNw/SQ0D8wga82jevLZmdzLK0CmIp37/Yk427CjrD4tDxB/EDcQQb2gZ+Xm211YYa8dOf/jT7tAiEdpVb86lPfco8/elPN/a9W2PfC86Wfbfv+Krn4Lp2NKmIB03jnX3nzOyyyy5FPXaVQmNXoy3+xgHagc98YLNTCos4lwlK/4WKn4xHJaD5Z2MEhC8YfxpDOHJiMvFHcsxYGZ7U5+4t+tmTOlc27hir5Mk5Xeyx9Gx5Kz/xO+SQQ8pFvH/bb18VbcOKU1W38rRC+w2wqqeq5Y4++uiiLcDp+uuvHyp7xx13DE0PnDRNUU7GAiIu7r4RLiy44ZaxiZycXnvvvgOwzz771D6fJ8wXAmJXfMLYnV775H/cRZ/1iz1VRTN0/MGMB1mgCG3DQhrlzeV2fM4Dm33AVnCu/d5h+ZRssQq510033XTo96bxrusRrlDxk/FoSN38owUC4kOMPy1ALJ3aJ/+jKbHqn8kRLgvOxI87WqeovNmEy9jpd0Ply0/8PvzhDxs73WGoTPkPjKi5HxvGB3/tu1PlYt6/f/e73xm7imHx2w9/+ENjl2Av/i4fXHbZZdnHie0qggYfKsYeT1zswhTGvr+V/UN7ZJQP59uEa+hDyzfccMPQ3wcffLCx01nKVY38bVfHMnZp4ULuG+H63//9X2PfFyjK/PjHPzabbLJJ8XedAzv3PrtHnPOCF7zAfPGLX6xzOsvOGQJ8wti9QpN5wuiBTuzJxl3Pr6OiGPHHvvtr7EO4rHLfR9/tSrTGrk6b/Q4exweH8XFhzObA9sY3vtHYadzZsfz3vOc9z9iV+rI/7WdAjP3OofxkmsQ7nNzlCFfI+Ml4VKiaBy0REL7gCFdLIJ3Tk4k/kmjGyvCkPndvcc+ezLmyccd4AmiTjLH/7NSE4mkflksfVx5PKspb+Ymf7eSXi4z8bZOKok65p6b7L33pSyPXhwALapTfoapaBzBwN+DinvuhD33I/Vk9xseP3fN8I1w2QR0qYzsF6vUm/YBvf0l9WFaYW9oIiC3wCWN3dtAn/+Mu+qxf7KkqmjHizwknnFBwHt7vdTcsiIRVX9HuBz3oQcVP4GW8Nwx5eQQL73i5o0eIb+7WJN7h/C5HuELGT8YjV9s8boOA8AXjTxsUh8/tk//Rklj1c9GMYb0Xf5UDEL5FNWkrT1sQx2yyx8IY5e3d7353EYTlmvj+Cl6stvP3B3b0Z/DSl750YOf0D7AErrvaFcqXE64zzjhj6HqTViiU9iB4T1oWHh85ljZib59gyOm19894xjOKaz3mMY+pfT5PmC8ExK4Y8LrTa6yAo7W4z/rFnrS2NZG3WTQD9WFKuX2SnvEe9u5iRnY0quDDV7ziFUPNw2dFcD/gZyy0JBs+9SH3ad8HK5aDl9+bxDuc22XCFTJ+Mh6Jprlvi4D4EeNPWyTvOr9P/kcrYtXPhOsunQ8dNQlAv/zlL4ugBqfEt6/sy7qN/t10001D7cHIlnzcEtfG8eGHHz72g8buPH+cU36Hq3yPVVcSRNuEdLD3jXDh22NumfL9DN3chD/czotdiGRCaf487wiIXTHgdafpWAFHa3Gf9Ys9aW1rInc567e//W2TSwwe97jHFRyKj/bKho/SS5vxoXt3cxOL008/vfgJ3C7nYGn48laOBVUeMOIaXSZcIeMn41FZ4/y7KQLiR4w/TREcPa9P/kdrYtXPhGtU95mkSQDClA55KgmntPPolavXF9v3n4qAieXbfd/qKl/1Pe95T3EO2lNOuOx7X0O/46POVbYrr7xy6DxfwlX+ftZVV11V5dLeMu73xOy7C94yFKaDAANe97qOFXC0lvdZv9iT1rYm8i4SLvtObcGz7geDZRQL7bbv/g417/zzz/ees8MOOxRyWWTDPbFJvMP5XSZcIeMn45GrbR63QUD4gglXGxSHz+2T/9GSWPUz4RrWe/FX0wC09tprF4HthS98YXG9Ngf//Oc/sw8vi6PbF6MrXQ6rDso52JenFJbfxSpPT9EqOe+884au60u48ITUrfuCCy7QLjdRft/73re4VtU2TrwoC8wsAmJXDHjdqTBWwNFa3Gf9Yk9a25rIu0i4vvWtbxW8Z5daz5qBqdn2EyeZ/OEPf/hI0/7xj38Uv8u7X1iNVlZ6xQNB3wq4TeNdlwkXbiZE/MR1GY+AArcuEBC+YPzpAs07r9En/6MFsepnwqXYTNMA9OQnP7kIkr6AqFQ3Vmy/bVJcE85uV5caWx4/4sXqddddd+i8csKFcm4yg7ZX2ey3vYau60u47HfQhsqccsopVS49Ugb34Y4aHnTQQSNlKEgLAQa87vUdK+BoLe+zfrEnrW1N5F0kXHbF2WJxDHkn69xzzy14de+99/Y2Td7dlXe/7Lcgi3OwAJFvaxrvuk64QsRP3C/jkU/rlDVBQPiCCVcT9Pzn9Mn/aFGs+plw+fU/aBqA3G+hwDF930PxVfmLX/xigEUsfIq3y/0WARPXxPSISdvHP/7xoXNw3q9//euR07baaquiHAK0XfJ9pIwrwIIZ6623XnEOrutLuJDc4Tf5d+yxx7qXqXxsP9ZcXAPXqrqSYuUKWHDmEBCbYsDrTnU+3unu6pOv1Gf9Yk+TW1m9RBcJF2rbeeedC/4766yzBpj2Le3VHmK99a1vLcqcdtppA/edLzws821N413dhGu//fbzVV/IQsRPXJzxqICYBy0REP9j/GkJpHN6n/yPZsSqnwmXo3T3sGkAghO6H63EEzskKeM2LDP8tKc9LQuSWNbXna+P8zAFRJwc+ze96U3jLjc4+eSTs0U13JEhnIdVoMrbSSedNHTtd73rXeUiQ38jyLttwbEv4cLI1KqrrlqUxcqJTbbyVBA84eWWNgJifwx43dlBrICjtbjP+sWetLY1kXeVcLkPzrAghnzuBNx+8803e5vmrvYHbt5xxx0LHsYKh76tabyrknAtXry4qB+r6I7bQsRP1Md4NA51/lYHAeELxp86qI0v2yf/o2Wx6p/bhAujQHiyh3+33nrreG17fm0agHCp8uqA22233dCyvm51UDRWjRInxv4b3/iGWyQ7XmONNYoy+AZLeQEMOQHfC7v73e+evfNVbsdRRx0lxYo93g9ba621imvj3PLKV1IYydkKK6wwuNe97lW8E4D2lhNEKf/85z+/uK79ULKIa+0POOCA4hqoF+8ocEsbAfEVBrzu7CBWwNFa3Gf9Yk9a25rI28YfqdNd2Ajv7spKteM+jwEssbAS7gvf45Jp41gOXnv41zTeVUm4Ntpoo4LD7UfsB3inbNxWjltdxE/Ux3g0DnX+VhUB4QvGn6qITS7XJ/+jdbHqn9uEa7KKx5doGoBwVSQx7pK+cFC8T4VvY+GJJaaGfOYzn8kSFfdjlCi3++67extW/nAjzsO7XFj69ytf+coAy94+/vGPLwLbO9/5zuw7LO4oFwIuVi7EU073uy7ulBO0Ae8L4NtXhx56aNZOJD0I9nIt1PXgBz+4qGvffff1tvkTn/hEUQbXvfrqq73lxgnxjTGci39oEzciIPbAgNedLcQKOFqL+6xf7ElrW99yvAssbZT9pKl5+HyGlJX9brvtpt5K03hXJeHaZZddhtqy+uqrD7Cg02tf+9qBL3aEiJ+4ccYjVf38oQYC4k+MPzVAm1C0T/5H02LVz4RLMYSmAUguh6CB73C5HwgWR9X2mP6hPYHElAhfEPVd65BDDhlgmiI2fAzZV6a8aiASNEmofOVF9qIXvSibnoEnrCLTXt7GKJyUwf5jH/uYwFNp//vf/37ofN/HoCtdiIXmCgGxKQa87tQaK+BoLe6zfrEnrW19y5FcSRtl735jy9c+LC4kZWV/wgkn+IpmsqbxrkrCVb62tAd7PFDzbV3HT9TBeORDmrK6CIj9Mv7URU4v3yf/o1Wx6mfCpdhAOUhU/RBk+XL4Xha+m4KneuKo7h7T5PbYY49BOQEqXwd/Y9UqjFAtWrRo5FpIlp761KdmC2+452LRiWc+85lDyRTeE/PN5UfwRCKFaYVuG3H8kIc8ZPCRj3ykuLT7LRhtVA6FH/GIRxTXes5znlOcX+Xg+OOPL85FG372s59VOY1l5hwBsU0GvO4UHSvgaC3us36xJ61tfcsxI0LaiD2mFf71r38d26yzzz576Bw8+Bv38fmm8a5KwoWGYkbHKqusMtImvLs8busyfqIexqNxaPO3KgiILzL+VEGrWpk++R8tjFX/AlRmDcjY73sY25HHYfTNJgtZnXlTotcfq0Ib8Iz9ALCxH6s09r0pY785YjbYYIPauNvRLmNXHDR2ZUNjDcWss846xk7xM/e///3VW0E5uwKhsYmfse+DqeXwg326aK644ors+nb+v7GrEho7D3/sOdqPdhqHsdNHsp9t0Dc//elPjf2QsVa8kMMW7LdnzOWXX57J7Dx+c8455xS/8yBdBIQvbMCrDYL9HpH3nD75Dw1i/Yw/XsOcI6H97qP5+c9/buxiH8a+05vFPvtOcOU77CJ+Mh5VhpsFFQQYfxRgWohTiX8LkNm1wKmTU1daaaXsOvOecHUC1oxdxI7KZQmWffk7a7kdzTN2asvEu7DLGRu7JHJR7gc/+IGx76gVf/MgXQQk4KHj5m5I6O1UWlc0ctzXQ6WRhlAwNQgw/kyNKoI3hPEoOMRzX4EWf6rcOONPFZTmtwxHuOZXt1NzZ3ZqoFmyZEnWHjsdJnvKiRG5cZtddMTYDz5nRZ797Gebr371q+OK87eEEJCAxxGu7pSeyhNGH2JiT3zg50Nn/mSMR/On05h3JHzB+NMd6qnEHyZc3dkMr6QgYBcCMY985CPNL3/5y6zEXnvtZY477jiltMmSq5122in7HeSGxGvjjTdWy/OHtBBgwOte36kEPB9yYk9MuHzozJ+M8Wj+dBrzjoQvmHB1h3oq8YcJV3c2wyuNQcB+jNNsv/322ZQvjHKdd955Zquttho5w34zzdhvx5hf/epX2W926WBjF+sYKUdBuggw4HWv+1QCng85sScmXD505lPGeDSfeo1xV8IXTLi6QzuV+MOEqzub4ZUmIGCXnjdvfetbs1JY4OMnP/mJWXPNNYfOeuELX2hOOeWUTPaEJzzB2FWqTJ0Xq4cuxj/mEgEGvO7VmkrA8yEn9sSEy4fO/MoYj+ZXtyHvTPiCCVd3KKcSf5hwdWczvNIEBNChwVTBr33ta1nJbbfdNlt5EIsdYDvmmGMMRrSwIRH78Y9/nK3AmAn4HxHIEWDA694UUgl4PuTEnphw+dCZXxnj0fzqNuSdCV8w4eoO5VTiDxOu7myGV6qAwNKlS7Mpg9dcc01W+rDDDjOHHnqoueSSS4z9sLO54447DKYcfuMb3zD2W18VrsgiqSHAgNe9xlMJeD7kxJ6YcPnQmW8Z49F86zfE3QlfMOHqDt1U4g8Tru5shleqiAC+B2Y/YpyVxugWRrrwvS37keZMhm9/bb755hWvxmKpIcCA173GUwl4PuTEnphw+dCZfxnj0fzruMs7FL5gwtUdqqnEHyZc3dkMr0QEiEAEBBjwugc5lYDnQ07siQmXDx3KiAARcBEQvmDC5aLS7jiV+MOEq52d8GwiQAQiI8CA1z3gqQQ8H3JiT0y4fOhQRgSIgIuA8AUTLheVdsepxB8mXO3shGcTASIQGQEGvO4BTyXg+ZATe2LC5UOHMiJABFwEhC+YcLmotDtOJf4w4WpnJzybCBCByAgw4HUPeCoBz4ec2BMTLh86lBEBIuAiIHzBhMtFpd1xKvGHCVc7O+HZRIAIREaAAa97wFMJeD7kxJ6YcPnQoYwIEAEXAeELJlwuKu2OU4k/U5VwtVMZzyYCRCAlBBjwutN2KgHPh5h0oHy/UUYEiAAR8CHA+ONDpZkslfjDhKuZffAsIkAEekaAAa87BaQS8HyIMeHyoUIZESAC4xBg/BmHTr3fUok/U5FwQTVNAb/tttvqaVYpffvtt5sVV1xR+TW8mPUTf9pfeP9beeWVvc7clH+8F2sgZP1/N4sWLWqAXDenNMV/XuLPxz72MfP+97/f3HzzzebMM880T3nKU7oBtuJVGP+6iX/4pthGG21k1l9/fXPSSSeZxzzmMZU0QPy7wX8S2Iw/foSa8q//avWlsepnwpXrhoQTh3A0VyD+xD9GwsmA5/fAWAHHX3vzB27a9erKm97/LCdcS5cuNccee6z56Ec/am699dYMsnvf+97mt7/9bV34Wpcn/3fH/6uttpq54447Mp0cfPDB5qCDDpqoH+LfHf7jwGb88aPTlH/9V6svjVU/E65cNyScOISjuQLxJ/5MuGZvhEfz57ryWAFPa1fT+mcx4cIoyDHHHGM+//nPGyRd7nbAAQeYI444whVFOSb/d8f/T3rSk8wVV1xR6A2jlf/zP/9j1ltvvUJWPiD+3eFfxtb9mwmXi8Zdx035964rtDuKVT8TrlxPJJw4hKO5BfEn/ky4mHBp/BBa3jTgzlLChUTr3e9+tznxxBMLOLfaaiuz//77myVLlpi//vWv5qqrrhrbMS9O7PiA/N8d/7/5zW/ORi532mkn85Of/MRcf/31ZvHixQajXfvss49Xc8S/O/y9AOdCJlx+dJryr/9q9aWx6mfCleuGhBOHcDRXIP7EnwkXEy6NH0LLmwbcWUi4LrrooizRwl62Pffc0xx22GFmgw02MMcff3yWcD360Y823/3ud6VI1D35vzv+R0K99957G+j4qKOOMnvttZc5/fTTM30++9nPNnhfDwmYuxH/7vB3cS0fM+EqI3Ln303513+1+tJY9TPhynVDwolDOJorEH/iz4SLCZfGD6HlTQPuNCdcmDKIf5JooZONzjdGtJBoyfbc5z4365CjI77HHnuIOOqe/N8d/0PfO+64o3nsYx9rLr300kyPp512WqZ7TCGFHWCK4bOe9axCx8S/O/wLUD0HTLg8oFhRU/71X62+NFb9TLhy3ZBw4hCO5grEn/gz4WLCpfFDaHnTgDuNCReSrHe9610GUwixoYONJAv/Vl111SEor7vuOrPhhhtmshtvvHFk5GOocMA/yP/d8v8qq6ySacv9mDd0jYT7wgsvzH7D9EJMM4R9EP9u8ddchQmXH5mm/Ou/Wn1prPqZcOW6IeHEIRzNFYg/8WfCxYRL44fQ8qYBd1oSLllxEIthyEIYWBoc0wbRydY2TDnDQhkvetGLzKc+9SmtWHA5+b9b/n/kIx9pbrjhhmyECyNd7gadwy5gJ1hIA6Ndm2++OT+LE+GzQEy4XEu867gp/951hXZHsepnwpXriYTfLeHXNX/iT/yZcDHhqssbXZVvGnD7Trh8Kw5iIQwkWeMSLcENo1sY+fjsZz9rnve854k4+p783y3/v/jFLzZf//rXzXHHHee1AyymAfu47LLLMl0feOCB5m1ve1t0vUuFqeifCZdofHjflH+Hr9L8r1j1M+HKdZSKw2smyfvvNuBpOGty4h8HfwY8vwXGCjj+2md3Dn9fCZe24iBGLrbeemsN5iE5Ot2bbLKJwbe3rrnmGo5wRBjhGFKA80fX/I8ppViR8tBDD81Gs5yqhg5hL4cffngmw0eS8R5f1Y8lD12o5R9d33/d5sSqn/HHr5lU4g8Trlz/sRzOb26Gc6hvj9PhJv5+BFKxfwY8v/5TCXj+u2+e8MVOuCatOKjdn0+Od7qOPvrobKlwdLpjjDD72gFZKvwT6/7POOMMs+uuuxqMdl5wwQVatZkcv2O0q8ry8WMv1OLHVPTP+OM3klTiDxOuXP+pOLzf3BnwqP80El4GPD8DpBLw/Hc//QlX1RUHtfvzye9zn/tk3976zne+Yx760Icy4ZqjES6MgG600UbZapTXXnutT/1DMnyDDQk4ppZiw8eSv/CFL0RbRCWV+Mv4M2R2xR+pxB8mXLnKU3H4wsJLB7z/NBKOktqLP1PRPwNeofKhg1QC3tBNO380vf/QI1x1Vhx0bmfiIZYJ33nnnY18eysV/9eAmcf7l5UKb7nllpHVKTUcJi0fr53XVj6P+PswYfzxodL8gZf/avWlTfm/bk0zn3DVvWGtfCzAWb8fAeL/d7NoERdN8FtHeCntj/Y3Lf6H0QZM9cNqcjjGVmXFwTpegilkGM048sgjs5EN2v/82T/e5cMS8Oeff37l9/pgQ7A52Id8LBnfacPiG+VPCtSxt0llaX/zZ3+TdO7+nor+mXDlWk9F4a6Ru8e8fxLetHQ4XbuMdUz7p/33bf833XRTlmgdf/zxRaK18cYbZwkROsBdbehQYzohNkw3w0eQaf/zZ//yjp4k1XXtx10+HjaCpKvqgix166L9zZ/91bGBVPTPhCu3ilQUrjkB75+E13eHk/VzhFPjp9DyPvkPy7JjSe4TTzyxuE0sdlBnxcHixAoHSOiWLFlidtppJ4MpZNj6vH/WHwZ/+cbannvuaaDzJhtsEyNcsnw8kjgkcF1vtD/2P1KI/0y4cuagw9PhU3B4LVDS/mn/tP+4CS9Wh8PqgO4qcugco1Nb/lit5rdN5FgKHkvCu99oov/Pn//DrrbZZptKKxVOsiN3+XjYJmynSxul/c2f/U2yKff3VPS/YNmyZQP3xnlMBIgAEZhFBBYuXGiWL18+i01nmxNCAAthYDTrW9/6VnbXixcvzkYR0KnF1K2QG0Ys8LFj1Pm73/0uZFW8ds8IYOroOuusk7ViMGjfzSt/LPmQQw4xBx98cM93yeqJwOwgwBGuXFepZNiaafL++YSJIxxxRzhcX6T/zb//YZEKJFVIerAh6cFoFv6FXJAgqyz/T0YqytPMaH/zaX9I4PF9rUsvvbSTESkkcbAhLOqCDe90YbSr7YMC2t982l9OOxN3qeifCVduCqkoXLN83j8JjwkXEy6NH0LL551/5L0pwRGdVLwbEyvRknoxuoWEr7xy3bzjL/ev7ef1/pEQYaXCU089NbM37f7ryjFdEfa7dOnSzIbxXlebhV3mFf+quPL+0+h/MeHKPYIGn4bBawRI/VP/TDiZcGr80IXcTbrQOUXSFXOTd3qwxLyMskn95L/55D8Z0Tz00EOzkSnRdxf7LpePp/3Np/1VtbNU9M+EK7eIVBSuOQDvn4THhIMJh8YPoeWp8A/eg8GoA0YGYnzfyNUbkjxMa9xvv/2yb3y5v6WCv3vP7vG83r984NpdkdK97y6O3Y8lY8RWRm/rXHte8a+KAe8/jf4XE67cI2jwaRi8RoDUP/XPhJMJp8YPXcrdpAsrvWF6X4yphfj2FkYl5Ntb7j2R/+aT/2BrWJUS71hB76E2jJgiocf0RWx4LxGjalXtmvY3n/ZX1d5S0T8TrtwiUlG45gC8fxIeEw4mHBo/hJanxj+xky6ZzogPKaPu8pYa/ind/4IFC7Lb7WKlwjJu5b/l21+QI8nDu2NVlo+n/bH/kUL/gwlXzhh0eDp8Cg5fDpDyN+2f9k/7j5twY7QJ0wvxUdkQ3zYS38Ye0xdPP/30bLoXRiLKG/1/fv0ftgUbKy+UUraBrv5GQg8bk48l4z0yjHaN22h/82t/4/Quv6WifyZcucZTUbgYeHnP+yfhscMdt8Pt+iD9L03/c5MuTL9Cp7jKiIBrO5OOMd0LqxNiu+WWW7zTvGh/82t/SH7w7h5WEsRUv1ibLNiB+iYt2kH7m1/7q2JvqeifCVduDakoXDN+3j8JjwkXEy6NH0LLU+YfJF1bbrmlueKKK7JkqOukS6Z5jVs4IWX8YdvzfP+S+PgWSwnp10jykODBvictSz/P+FfBmPefRv+LCVfuDTT4NAxeIz/qn/pnwsmEU+OH0HLwzz777JONRDRd6U1rIxZNwDSvcZ1e8t/88p98DmCrrbYyOA69YUR1yZIlRV2oF+8Q4p0ubaP9za/9aTp35anonwlXrvVUFO4auXvM+yfhMeFgwuFyQsxj8s+d/CPTv4A9ltfG3202JFpIuBYvXpyNNGjXIv7zy/8YYcIKlUjkMaU05Hb44YdnnxxAnbA5JFp4f3DSRvubX/ubpHv8nor+mXDl1pCKwjXj5/2T8JhwMeHS+CG0nPxzF/90mXRhStfRRx/t/faWq1Pifxf+Li6xjkPjj2QL337zfRKgi3tEYo9RLeyxYfoqki3UW2ULff+T2sD659v+p0X/TLhyTdDh6HBMOJhwTCLmUL+Tf8g/Lv+gs4oOLLYqq7xpdinf3rr00kvHLsZB+5tv+8NqmPhGVtcrFWIkCwk9bBTb+uuvnyVaqK/ORvubb/ubZAup6J8JV24JqShcM3zePwnP7fBpdhJKTvuj/dH+7nrgISNT4m8Y9cIUwzrbaaedZnbeeeesE4z3asZt9L/59j8kRJjuN2m1wHE2Uv4N74PhoYDYFhblQD1VR7Xc69H+5tv+XF37jpPRv/0YXrYtW7ZMDnvZs37i34vh5ZXS/mh/tL/+EKD/3eV/NrEa2E5J9m/fffctjm3SVUtBe+65Z3auXQ584nnE/y78J4IVoEBo/MWm7FS/1q2374EN7AOBwi7tx7QHdgS11XVD3/+kxrH++bb/adE/R7jydDuZDNv3eMHKeP98wsQRhrtGGBQ3CSam/9H/4H/uVEJZNAPvxWCKFt7BwQIEkE8aRZCFEmCwVd7bof3Nt/1hNGqbbbbJppViemnTDaOmGNWCfWHrasSM9jff9jfJ3lLRPxOu3BJSUbhm+Lx/Eh4TLiZcGj+ElpN//m6++MUvFu9tSbIluLtJFz6MjHdxxiVdkriN+/aWXBt74j///L9gwYJM5fZpv6v6SseYNnjAAQcYJFzYqiz1XunCeSHa3/zb3zh7SEX/TLjo8BkCqRi85vS8fxI+E04mnBo/hJZ///vfNzvssEM2cqCNGtRJuuTbW+XETbsP8t/88x8S9csuu6z2whmyKIaMar3sZS8zn/70pzVTaiSn/c2//Y0zjFT0z4Qrt4JUFK4ZPe+fhMeEgwmHxg+h5SnzDxIpTPdCh9a+d5VNK9TwRhlML0THGR1oJFTYuxtGIzbccMPsO0g4HjcSJueljD8wSOH+MR319NNPr/x9N9gOpg9iOiK2Rz3qUebKK6/MPmCMaYlV7Co7scJ/KeA/DgbefyL9L3mZjC8N8qVBsYU+9rQ/2l8fdid10v5of2ILMfdYbMB2XLMFCLDIRZUNixZgoQLbgcvOLS9YYEfIal0PddL+59/+xS6wn7TZ1QYzG4KN2Q8YD0499dTsFDuVMJPbFQknXaLW77S/+be/cQaRiv45wpU/duAThkSeMCiPmah/6p8jfBzhU+ghiBijVZj6h5GEZz3rWeZrX/ta5XrckS6MNOCdLhnpwugWrlnnm0vkv/nnP1k4A+9fyahV2eAw2opRLeyxlZd6hxw2i62OfWUnjPmP9jf/9jdG/UmMMOP+mXDlVkCHp8Ozw80O97igEPI38k9a/IOECdMI0YG1o1XmzDPPNGuvvXZtE8P3uT772c9m07tk9UJcFx+gRdJVdaP9zb/9wR6QjCNBt6OkQ6YBe8R3uo466qhMPu4DxvJNLyT4bVY8dBtA+5t/+3P1XT5ORf9MuHLNp6LwsqHL37x/Eh4TTiacwgex9ynxTznZwmjDCiusYJr6nyRd0Bk6wUjiMDIhnecqukwJfx8eqdw/ki18XgAJF46xwf7cDxhj0RZ8eFt+9+G1wQYbmOuvv57LwvvAaSBLxf40aFK5fyZcuQWkovDUDZ7370eA9s+Eu2mH329R9aQp2R9GoNDJxcgW9ujYtr1/N+kC8lW+veVqqG397rWaHLP+OPyDBVcuvPDCYgoqEi1Z6h32iM8JyNTUcXqE3cKOsWGUq8o5465H/cfRv6YD4h8HfyZcuQXS4OIYHB3ejwDtj/bHhGf+RxjRwUWn1i5EkCVb0lHtwv9xXXSEcU2MUNTZuqi/Tn3lsqw/Dv/BLrDMOxIvjIRitBW2ePDBB5sDDzywrJaxf7vXwvtcbTbqP47+NR0R/zj4M+HKLZAGF8fg6PB+BGh/tD8mXPOdcGnJFhiB/k//j+H/mGaKDxjLJh8wXnPNNWtPaUWyhuQeUwuPPPLI2km+tAF72j/tP4b9uzbnHseyPyZcOeqxAHeV7B6zfhJOCoTj2rx7TPun/c+z/ctoQHlkS3yA9k/7j2H/MhUQdojkC1NRsTW1P0xH3HnnnbNpsZhaiHe7mmxN629Sl+8c1k//i+F/TLhy76PD0eFiOJyP7CGj/dH+aH/zOcKFqX4Y3cJmv2dk8AHa8kb/p//H8n/YH2zSXRSjjf3JB5UxTbHp1MI29Zd9qcnfrJ/+F8P/mHDl3kmHo8PFcDgtGND+aH+0v/lLuNxkC8u2y4hCmQfo//T/WfV/TC3EyBZWP9QeKJTtvfw37Z/2P6v2X7blcX8z4crRocPT4VNweI0MaP+0f9p/twlf1WQLPkn/o//Nsv+JrWPUDCtkuqNnWsxx5bR/2v8s279ry+OOmXDl6NDh6fApOLxGBrR/2j/tv7uECyvAYdlsPP3Hd43wsdhxG/2P/jfr/idLzu+5554GCVidjfZP+591+69i7wuWLVs2qFKQZYgAESAC04zAwoULzfLly6e5iWxbAghcfvnlZocddsiSrd1339184hOfSOCueYupI4DVCp/4xCdmUwvPOusss+WWW6YOCe+fCAwhwBGuHA4+YeETlhSesAx5v/MH7Z/2T/tvP8LljmzVedJP/6P/zYP/YST38MMPz97pwqqFVacW0v5p//Ng/06XynvIhCuHhQ5Ph0/B4b0sYIW0f9o/7b9dwoXpg5tssom57rrrzE477WSwZHbVjf5H/5sX/8O3uS677DKz3377ZUvPV/EB2j/tf17sf5y9M+HK0aHD0+FTcHiNDGj/tH/af/OEC8kW3tnCCNfGG29s8L2jqk/34ZP0P/rfvPgffAAPHrBhlAsJ2KSN9k/7nxf7H2frTLhydOjwdPgUHF4jA9o/7Z/23yzhaptswSfpf/S/efI/mVqIZAtJ16SN9k/7nyf71+ydCVeODB2eDp+Cw2tEQPun/dP+myVcGNnCiFaTkS3xR/of/W+e/A8PIZBsYSENrtIpXq7v6f9p+D8TrtwHaPBpGLxGedQ/9T9PHR7NzjU57b+Z/S9ZsiRbAnvx4sVZ0lVl+pRPB8S/Gf4+LJvIiH/3+OMhBB5GYMO3ufBxZG0j/t3jr2HtkxP/OPgz4cqtjwYXx+B8zg4Z8Sf+THiajbBoPlVHTv+r739dJVvkP/L/vPrf/vvvb44++miDb3Sdf/75KiXN6/2rN1z6gfdfn39LELb6Mxb+TLhyNcUCXLMK1p+Gw1H/fgRo/7T/WUq4pSPZdmRLvIH2T/ufJfsXu520x9RCjGwtXbrUHHnkkQZ+49to/7T/ebT/sq0z4coRocPT4VNw+DIByN+0f9o/7b/aCOPxxx9vMLqF7dRTTzXPfe5zxY0a7+l/9L959T98HmHnnXfOVu3E1ELf6p20f9r/vNq/GxSYcOVo0OHp8Ck4vOv87jHtn/ZP+5+ccLnJ1nHHHWf22msv140aH9P/6H/z7H94KHH66adnDyfwkKK80f5p//Ns/2LvTLhyJOjwdPgUHF4cv7yn/dP+af/jE65QyRZ8kf5H/5tn/8PHwLGgDKYW+kaFaf+0/3m2f+lvMeHKkaDD0+FTcHhx/PKe9k/7p/3rCRc+5ooV1/BOSpVlrsv+Nelv+h/9b97976ijjjIHHHCAd2oh7Z/2P+/2jxjAhCuPhHR4OnwKDq91/Gj/tH/avz/hcpOtPffcM1sGXvOjpnL6H/0vBf/DaoUXXnih2W+//QwSMNlo/7T/FOyfCVfu8XR4OnwKDi8Brryn/dP+af+jCVeMZAu+SP+j/6Xgf5hauOGGG2bhB8vEIwHDRvun/adg/0y4Mnenw5PwSHgpEF7u7iM72j/tv2z/mD64ySabGHQSd9ppJ4PV1kJttD/aX9n+Qtma77ox7e+www4zhx9+eLZc/KWXXppNMYxZf9/3z/pHEUhF/0y4ct2novBRU79TwvtnwE8l4Pt8gPZP+3ftH8kW3tnCCNfGG29sLrjgAu9y1j5baiKj/dH+XPtrYkNtzoltf1hA47LLLiveh4xdfxkr1k//i+F/TLhyz6PD0eFiOFyZ6OVv2h/tj/Y3OqVP/CP03vW/2MkW7s2tP/S9+q7P+sk/MfkHDzIweowNo1wPfehDTcz6yz5A+6f9x7A/Jly559Hh6HAxHK5M9PI37Y/2R/ubjoQLI1sY0YoxskX/vxMB8l96/Lf//vubo48+Olsu/jvf+Q4TrkXTwX/CSTH3qfg/E67cqlJRuOZEvP/0Ap5rC9Q/9c+Eb5FZsmRJtgrh4sWLs6QLU59ibPQ/+l9q/oeRZPjX9ddfb9773veaAw88MIareeug/9H/YvgfE67c/ehwdLgYDudleyuk/dH+aH/9PuF9zWte00uyBU6g/9P/U/R/jCRjRHnVVVfNphZusMEGcIfoG/2P/hfD/5hw5a5Nh6PDxXA4LZLQ/mh/tL/+Eq7Xvva15phjjjGxR7aED+j/9P9U/f+5z32uOf3007Ml4rFUfB8b/Y/+F8P/mHDl3k2Ho8PFcDgtmND+aH+0v34SruOPPz6bSgjfPPXUUw06gLE3+j/9P1X/x9RCjGwtXbrUHHfccWavvfaK7X4cYf47/S+G/zHhyl2bAY8OF8PhtEhC+6P90f7iJ1xustVXZw+cQP+n/6fs/yeffLJ58YtfnE0tvPbaa4N+gsEXg+l/9L8Y/seEK/c+OhwdLobD+cgeMtof7Y/2FzfhcpOtj3/84+aVr3yl5p7B5fR/+n/q/r/jjjuaCy+8MBthxkhzzI3+R/+L4X9MuHKvpsPR4WI4nBZEaH+0P9pfvIQL3wHCy/qYznTooYdmK6QR/3j4l3mQ/Ef+u+mmm7JVCzG1MPbUXtof7S8G/zPhYsKVIUDCIeHEIJxyR0v+pv3R/mLZn5ts7bnnntnKhLQ/2l8s+xPOc/e0vzvt76ijjjIHHHBA9k4XPoiM1QtjbMSf/h/D/5lw5d5Mh6PDxXA4LXjQ/mh/tL/wIyy+ZAs+Sf+j/9H/wvtflfi39dZbZ1ML99tvP4MELMZG/6f/x/B/Jly5N9Ph6HAxHE4LHrQ/2h/tL2yHD9MHN9lkE3PdddeZnXbayZx22mmFO9L/6H/0v7D+Vzib51Qrb2kAADxpSURBVMD1PzwUgZ9iwzLxSMBCb279oevyXZ/1p8E/TLhy66fBp2HwPrKDjPqn/tnhmo4Ol+ajbeWHHXaYOfzww83GG29s8MFVd7oS/Z/+T/+fHv8XX8X7lTgOvdH/6f8x/J8JV+7JdDg6XAyH0wIH7Y/2R/sL3+HDqBaemLvJFnyS/kf/o/+F97868Q++GuubePR/+n8M/2fClTMAHY4OF8Ph6gQcrWwIecr2v2DBghCQ8ppEIENgMBhMRCJl/wM4vP/m8Zf8NdG9WGAKEXB5MRX/X7Bs2bLJ0WAKlcUmEQEiQARcBBYuXGiWL1/uiiodr7TSSpXKsRARaIKAjbFNTuM5RKASAuSvSjCx0JQhkCIvcoQrN8JUMmzN53j/zZ8wapjWkRP//vCXJ8TuE7c6umNZIuBDoI5d0f/783/obpbxr2NnPjuljAjERMBnr7Psf3WwY8KVo5WKwjXj4P0z4Kc6pdIXADQ/oZwIVEWgjl2Rf8m/Tfm3jp1VtV2WIwKhEPDZayr8x4Qrt6pUFK45Ee+fAb9pwNdsqo68T/vzBYA6bWdZIuBDoI5d9Wn/aDvrn13+r2NnPjuljAjERMBnr6nwDxOu3NJSUbjmWLz/2Q24mk7ryFPWvy8A1MGOZYmAD4E6dpWy/wE73n/z+FPHznx2ShkRiImAz15T8X8mXLmlpaJwzbF4/80DnoZpHTnx7w9/XwCoozuWJQI+BOrYFf2/P/+H7mYZ/zp25rNTyohATAR89jrL/lcHOyZcOVqpKFwzDt4/Az6nFHLBVo0fKK+PgK9joV2F/Ev+bcq/dexMsz/KiUAsBHz2mgr/MeHKrSwVhWtOxftnwG8a8DWbqiPv0/58AaBO21mWCPgQqGNXfdo/2s76Z5f/69iZz04pIwIxEfDZayr8w4Qrt7RUFK45Fu9/dgOuptM68pT17wsAdbBjWSLgQ6COXaXsf8CO9988/tSxM5+dUkYEYiLgs9dU/J8JV25pqShccyzef/OAp2FaR078+8PfFwDq6I5liYAPgTp2Rf/vz/+hu1nGv46d+eyUMiIQEwGfvc6y/9XBjglXjlYqCteMg/fPgM8phXyHS+MHyusj4OtYaFch/5J/m/JvHTvT7I9yIhALAZ+9psJ/TLhyK0tF4ZpT8f4Z8JsGfM2m6sj7tD9fAKjTdpYlAj4E6thVn/aPtrP+2eX/Onbms1PKiEBMBHz2mgr/MOHKLS0VhWuOxfuf3YCr6bSOPGX9+wJAHexYlgj4EKhjVyn7H7Dj/TePP3XszGenlBGBmAj47DUV/2fClVtaKgrXHIv33zzgaZjWkRP//vD3BYA6umNZIuBDoI5d0f/783/obpbxr2NnPjuljAjERMBnr7Psf3WwY8KVo5WKwjXj4P0z4HNKId/h0viB8voISMfib3/728STb7/9drPiiisW5VZeeeXiOMYB+X92+V/sbDAgf8XwFdbRDgGxV5cXy/yn1RCKF2PxHxOuXLOxANcMifXPbsDTdFpHTv33p38JAOyw1LFYlp2EgNiV27HQzil3OEJ1LLT6yT/98Q900gZ/sTPyl2bdlE8TAmKvLi+W+U9rbyhebON/Wlt9ciZcOSqxAPcpATLWP7sBT9NpHTn135/+JQCww1LHYll2EgJiV27HQjun3OEI1bHQ6if/9Mc/0Ekb/MXOyF+adVM+TQiIvbq8WOY/rb2heLGN/2lt9cmZcOWoxALcpwTIWP/sBjxNp3Xk1H9/+pcAwA5LHYtl2UkIiF25HQvtnHKHI1THQquf/NMf/0AnbfAXOyN/adZN+TQhIPbq8mKZ/7T2huLFNv6ntdUnZ8KVoxILcJ8SIGP9sxvwNJ3WkVP//elfAgA7LHUslmUnISB25XYstHPKHY5QHQutfvJPf/wDnbTBX+yM/KVZ93TIL774YvOEJzxhpDFnnnmm2W677Ubk8yoQe3V5scx/2r2H4sU2/qe11SdnwpWjEgtwnxIgY/2zG/A0ndaRU//96V8CQJsOy7/+9S9z6qmnmssuu8z87ne/M7/97W+zf3/5y1/MaqutZtZaay2z5pprmvvd735m2223Ndtvv725+93vXsdEWHbGEBC7cjsW2i2UOxyhOhZa/eSf/vgHOmmDv9gZ+Uuz7umQI+HafPPNRxpz9tlnZ/Fg5Ic5FYi9urxY5j/t1kPxYhv/09rqkzPhylGJBbhPCZCx/tkNeJpO68ip//70LwGgSYflpptuMh//+MfNxz72MfP73/++ssqReO2+++7mzW9+s1ljjTUqn8eCs4OA2JXbsdBaX+5whOpYaPWTf/rjH+ikDf5iZ+QvzbqnQ86E6049iL26vFjmP01joXixjf9pbfXJmXDlqMQC3KcEyFj/7AY8Tad15NR/f/qXAFC3w3LppZeaLbfc0tx22211VD1U9lGPepT55je/yaRrCJX5+EPsyu1YaHdW7nCE6lho9ZN/+uMf6KQN/mJn5C/NuqdDzoTrTj2Ivbq8WOY/TWOheLGN/2lt9cmZcOWoxALcpwTIWP/sBjxNp3Xk1H9/+pcAUKfDcsMNN2Tz8TF9sO326Ec/2lx44YXmPve5T9tL8fwpQkDsyu1YaM0rdzhCdSy0+sk//fEPdNIGf7Ez8pdm3dMhZ8J1px7EXl1eLPOfprFQvNjG/7S2+uRMuHJUYgHuUwJkrH92A56m0zpy6r8//UsAqNNhefzjH29+9KMfjagYUwVf8pKXmCc/+cnZe1v4mDSmGv7yl780n/70p7N3vEZOsoL3vve95sADD/T9RNmMIiB25XYstFspdzhCdSy0+sk//fEPdNIGf7Ez8pdm3dMhZ8J1px7EXl1eLPOfprFQvNjG/7S2+uRMuHJUYgHuUwJkrH92A56m0zpy6r8//UsAqNph+dOf/uSdArjZZpuZ8847z9z73vdWVX/YYYeZww8/fOT3RzziEeanP/3piJyC2UVA7MrtWGh3U+5whOpYaPWTf/rjH+ikDf5iZ+QvzbqnQ86E6049iL26vFjmP01joXixjf9pbfXJmXDlqMQC3KcEyFj/7AY8Tad15NR/f/qXAFC1w4JlfJ/5zGeOqBfJ1lOf+tQReVmw4447mrPOOqssNj/4wQ8MRs4mbcuXLze/+tWvzFVXXWV+/vOfZ1MRH/zgB5sHPehBZoMNNjB3u9vdxl4C75xhsQ93u8c97mHWXXfdQnTFFVeYH/7wh9mKi3jPbOeddy5+0w4QNH/xi19k7bruuuuy9myyySYGbZvUJu2akLe9bpX7RT1o83e/+91sv8IKKxjcN6Z7rrPOOvi59iZ25XYstIuUOxyhOhZa/eSf/vgHOmmDv9jZtPGXz+/Q1g033HDIDL/3ve8ZvA974403mpVWWimbqo3V/MY9uBq6QOmPtnxRulz251//+teMa9FGTCf/xz/+YR74wAdm3AZ+W3XVVX2nDcmaJFy4F9+0dfADVr0dt7XFwae/LuKE2KvLi2X+0+4rFC+28T+trV65ddJsW7ZsmRz2smf9xL8Xw8srpf2la3+WGAf4V3U74ogjsvJynuyvv/76Spe44IILBi996UsHdrRrcMIJJwxsJ3/wxz/+ceK5NmAPnvjEJw7uec97eutHOx75yEcOTj755MF//vMf9XqnnHLKyPn3ve99s/I47w1veMPQ7/e6173Ua+EHmzwONtpoo8HChQuHzhNcbCdqsMMOOwxsR2Xsdco/dnVd3/3a9+WK6tCuXXbZRW3/brvtNrAdrqJ81QO5f9uxGEz6d/PNNw+VqVpHV+XIf7PLf2JnVW0hFn/5/A5ttR35rKlnnHHG4OEPf7iXM+wDmsHznve8omyVe+uKL9y67IOnwctf/vLBiiuu6G0n7gdtRRk7ddw9deTYTkH3XsMuCz9SFoJ///vfGW+KfmVvk44BYoG2dYWDT39t4oS0V+7D5cQy/7m/ucdyja73sfiv6GXEqlADivXPLuFrOq0jp/6p/zr20mVZCQBVr/mBD3zAGzjtO1pVL1GrnP3GV5ac2e92eeuV9rv7jTfeeGC/BeatBwHeLYtjdBqQbNnpjiO/aQnX0qVLs45G+Vra33b5+8E3vvENb5tcYdfXPeecc0buyT5lHdiRwoEdkRust956I7+X72H99dcfXH311W4zJx7LNdwOg3Zc7nBMvHjHBci/s8u/YmdVTSIWf/n8Dm21o/ODo446KuMcabu2t9O0JyYyXfOF4Pj+979/Ii+47UYi9PnPf15OH9nXTbj23nvvkfrtCNPg3HPPHbk2BF3j0FWcKDdWMHO5sMx/7m/ucflaXf0di/+YcOUaiwW4ZiCsf3YDnqbTOnLqvz/9SwCoqq+vfvWrI4EQ17BT+gaXXHJJ1ctUKodk60lPepK3Pmm3tn/MYx6TBeFyRRhh851z7bXXDjAaVf7Nl3DdeuutAzs1aKSsnIuOgRy7eyR2n/rUp8pNKv4OcV27AqS3LXZa5cC+O+f9zW2zHD//+c8v2lnlQM5zOwzacbnDUeX6XZYh//THP9BjG/zFzqraQyz++ta3vuX1rc985jPqaLLci7vHqD0ejvi2EHyBeuy3Fb1td9vlOwZ/ag9m6iRcH/zgB0fqx0MiLaELgUMXccKnM8HN5cIy/7m/uce+63Uha+N/depnwpWjFQtwTTmsf3YDnqbTOnLqvz/9SwCoqi+MHNl3fEYCIq6DROM1r3nNAJ0NTAlpu33kIx/x1vPQhz50cOihhw6+9rWvDT75yU8Ott56a2+57bfffqQJ3/nOd7xl3/jGN3rlvoTrLW95y0hZTCl85zvfOcDUSoyW4Un2a1/72pFyq6++ujpVKMR1MWVTdOzu99tvv0Ju38cYYOrgNtts4006cR46POg0Vd2kLrfDoB2XOxxV6+iqHPmnP/6BDtvgL3ZW1RZi8Zfmd/bdrMzvHvCABwzg7+Aw++H4wbOf/ezCH+WeZH/aaad5by8EX+BBjG82gX3HdfCVr3wlG3Gz73sOjjnmGO9UQ7tCrXdKd9WEC3XgwZTcu+yRhGlbCBy6iBO+9sr9uFxY5j/3N/fYd70uZG38r079TLhytGIBrimH9c9uwNN0WkdO/fenfwkAdfTldtbl/PIeU0ye/vSnD/DOxPnnnz+wL+bWqWJwyy23DFZbbbWRwGsXchggQLkbEhy8h1RuA/7GewjuZhfn8JZbvHhxJt9uu+0GeApuX9Ye/OxnPxuZBvjrX//a+x6ZNnLl6wz4Og+hrmsX//DeLxIoJInlqaDXXHPN4CEPeYj3nAMOOMCFcuyx6MLtMGjH5Q7H2AsH+JH80x//QJ1t8Bc7q2MWMfhL8zu0F1N0kbSUtze/+c1ev9tqq63KRQeh+OLDH/6wtw2+d63s5zy8ZX3v81ZJuIAZHnCJTmWP92q1LRQObeOE1l65J5cLy/zn/uYea9dsK2/jf3XqZsKVoxULcE05rH92A56m0zpy6r8//UsAqKOvP//5zwO8JyXnVtlj9AuLXmBkqpwE+ep+/etf770+grJvw4vUvna86U1vGiquBX6c+8IXvnCAaYzjtl133XWkHiQo2oge3i3AIhVu2+5///sP7EpfQ9WEuu64+0Xnyrdp0xCf+9zn+op7ZXK/bodBOy53OLwXDCgk//THP1BrG/zFzuqYRwz+Gud33/72t9XmYgqh3JO7v+yyy4bOCcUXr3vd6waPfexjB3b1wcFaa62VjXivssoqXn77zW9+422rXcl2qK34Q8NDEjkkoKjPvWcc77777t4RM6kgFA5ae9GmKnFC2lfey/25XFjmP/c397h8ra7+buN/ddqwABVZALgRASJABGYaATtaYbBket0NSxFjs8RZ61QbCLKPHJ9++um1zpPCWALeTksx+H6Xb8My7/bp5dBPdiphtvT6kND5Y8mSJcY+XTVYPtd2ErK9TYaMnS5YlNKWJ7bTaIx9j8vYqT5FWd/B2muvnX3M2f1tn332ye7FlbnHdrqQsauSuSJjR9EM5LKFuq52v/hIte3kGLvqozRhaG9XUBvB2ibZ5ic/+clQOe0PO4KW/WQ7E1oRVY4PZnMjAlUQmFb+0vzuYQ97WLbEunZv+Ai8HRUf+fn44483e+65ZyEPxRdFBc4BYoP4syPO4g34oxx33ve+9xn7oMstajQ8bMKVLYVv39Ud+RajnW2Q8aZ9WDd0LfePUDho7a0aJ9w2useCY5K8KNlZrAxP6ivvWf/sPmEr67LJ39Q/9d/Ebro4xwaD7Kli02vhXYWddtope39LrlV1j7n6eOerPNpzxx13eF8s33fffZs2szhPe3JZZfQGSzr77u3II48sru878E0rdEeXQl0XbdHuF9Oqxm2+KZrucvLjzsVvgpP7hFY7Lj/hnXTtrn8n/84u/4qdNbWJEPyFtmh+99a3vnVsU+0DjcJ35N6wf8c73lGcF5IvikoqHshUbLetvimAGh6Yvv20pz1t5J433XTT7FMR45oREgetvVXixLg2C04uF5b5z/3NPR533Ta/xeI/TinMtRQLcM0oWP/sBjxNp3Xk1H9/+pcAUEdfvrL4VtMXv/jFAZbzrbP6Herff//9hy75y1/+ciQAo5zb6Rg6ocYfWiDFkvCTNkzrEbzcPb5Tg3fWtH++b4dhkQ7ZQl0X19fu1034pB3u3rfgB+6v6ib4uB0G7bjc4ahaR1flyD/98Q902AZ/sbO2ttAlf6Etmt9hkZ9x2x/+8Acvx7z61a8uTgvJF0Ul9gDf1jrppJMG73rXuwb/9V//NcAiRHifDAtj2BkKg8c97nHeB2N1Ei5tCqXvGm7bcBwSB01/VeJEuZ3u32KvLheW+c/9zT12r9PlcRv/q9MOJlw5WrEA15TD+mc34Gk6rSOn/vvTvwSAOvqqUvZPf/rTAB/3PPjggwdbbLFFtsqd1FXeY6QLKxvKhncAymXw9yc+8Qkp0nivBdJJHSFUiBW0fO1qIsN7ALKFui6ur92vtvKZtOmQQw4ZuVcmXIJOt3vyX3P+E9/rViODQRv+Qls0v8OqhOM2vAvqW6XvWc96VnFaSL5AJVjJESPg4z54LLj79nj/trxpePjOhwwrJV5++eXlywz9HRIHrb1V4sRQI0t/yP26iRQTrhJIof8k4TYn3C50Q/yJfxd21PQafdqfBICmba96Hlb9e/nLXz7SiZf63e88ad+BwdPWtpsWSCd1hFCv1i65hzr7JzzhCcWthLouKtDuV15WLxpROsDUp/L9MOEqgdTRn336P25hlusXG+1IFepl6vAXLqL5HZYbn7T5vgf4lKc8pTgtJF/Y9zoH973vfUd8X3Cusu8i4UI9+AYjVqDVtpA4aPqrEie09kIu+KWYcC3IATB2yWLT54u6rJ/40/76e1E+Zf+Tl3jvjAU2HATesHiEu1iEVOe+TG6DmnnOc54jPxV7+10uY6e6FX83OdBehsbL23bKzNhLoswOO+wwUsYmi8Z+aHlEPk5g34cq7iXUdVF/0/t929veZuwUzqFbsAmXsR2FIZn2h9hVlfK33367sU/Ti0uhnphbyv4PnGf5/sXOpom/gKnmd+A2O1qFIt7tn//855AvSCE7Im5OPvnk7M9QfGHfnTU2sTN2JViptthD/rznPc/YJe0NuAuLR2ChJixsYd+lKsrhwCZcxn76Ykim4YFCdkTP2PeAzamnnjp0Dv6wsxqMnc44IocgFA64ttZe1DkpTuB8bRN7dXmxzH/auaF4MZr/I+HCNstPeO68g3b/8/45wtPOgtqdTfvrz/4suWdP3Zpq0HYQap+KZYelXtnjm1CyeAa+fyVyd//2t7+9dl3lE7QnlzaQlouO/K29W3b00UePlK0jCHVdtKHp/XKEq44G25Ul/zXnP+GHphoIwV9oi+Z3k6ZFa0utu+80heKLE0880cu7r3rVqwZ2JcIRiLG40QorrDByjttWOUnDY8MNNxxcdNFFWTF8A1H0KXss1PPHP/5RLjO0D4UDKtHaWyVODDWy9IfcV4ojXHyHKzcGEn5zwi/5U6M/iT/xb2Q4HZwkAaDKpS655JIBPvCLD+DiBep11103m36C1aLqbFgkQ+qVPRIu8QN0gnzvMdhl38dWg49g4htSaOcvfvGL7F0EvAzvbm0CqdauAw880K2i9nGo66IhTe+XCVdtNTY+Qey+8QVanjjL9Qt/VIEgFn+hLZrfHXTQQWObim90yT25+6OOOqo4LxRfYCEft045/tWvflXU7R58//vf95avM6XwrLPOKi7585//3Lva7R577FGUcQ9C4YA6NP0x4XI1UO+YCVeO1ywTbj2V+0vz/pnw+C0jjrRP+5OgWuVO8VFMKe/u647wbL311iPXsVPyhpqAJ59uHTheffXVx36YGB/JLJ+D9xHcp7NtA6mdUjNSB+6n7Rbquk3vlwlXW41WP79P/0crZ7l+8fcqaMfkL83vHvjAB459LwnJityTu//yl788dIsh+GLbbbcdqdu+6jBUr/vHBz7wgZHyaHOdhKucwGhJ33nnnedWXRyHwAEX1/RXbm/RkIoHolOOcFUELESxWSa8LvDg/TPh6cKOml4jZfuTAFAFO4wa2TnoI0EW00q+9KUvVbnE4IQTTvCOXr3iFa8YOl/reOC7Lb4NI1lIyOR+ZI/vSblb20CKb4HJtd09vp/j2/71r38N0IZnPvOZA4zQ4ZtcH/rQh0ZW4Ap13ab3y4TLp80wspT5B4i2uX/xwSqaiclfmt+hveecc463uZiid//733+EX+51r3sNbrrppqFzQvAFlnwXPN39FVdcMVQ3/sBsgjXXXNNb/pWvfOVIeQ2PcgJz6623ejGwH70f2HedRq4bAgdUUrW9Iw2aIBBcmXBNACrkz20Ip4t2sX4mPF3YUdNr0P76sz8JAFV19/SnP90bZDEl0C50kS2djvcQ0HnAhoQDywxjdacXvehF3u+2oA2f//znh5pwyy23eBMoBPmrrrpqqCymlmCZdbkXd3/uuecOlW0bSLGE773vfe+RujbbbLPsuzVDldk/Dj300JGyWG75+uuvHyoa6rpN75cJ15B6gv5B/mvOf+LrVRUUi780v0N711hjjZEHLuBL8Kfcj7t3v8El9xmCL1CPW68c4xMR7oZ3qsZ9axEfMi5vGh7lhAvnfe5zn/O247DDDitfdhACB1RSp70jjRojEEyZcI0BKfRPJNzmhNuFbog/8e/Cjppeo0/7kwBQte142qk92ZRrYY+RsFVWWcU7IuaWw/Fee+3lrf7YY4/1Bl68SP2Sl7xk8NGPfnSAhTTsCofecu63a6SCLgLpu9/9bm99D3jAAwZ4n+sLX/jC4IgjjhjgiTES0fL9au9xhLhu0/tlwiUWE37fp//j7ma5fvGtqlqKxV+a38ko/OLFiwe77bbbAB8gxzuxG2200QhP4N7wLuvVV1/tvb2u+ULjW7Rjk002yb6puOWWWw5x2ktf+tKRduMbWvj+4pVXXjm48cYbs7ZrePgSLiwFjyXhRbeyxwfksVBGeesaB1y/TnvL7Rn3t9wLE65xKAX+bZYJrwtoeP9MeLqwo6bXSNn+JADUwQ4vNyO5kHPb7LfZZptiNKzcBnwE1LdyVZX60Jnx6bWLQIrVFDfddNNG948n7L524d5DXLfp/TLhKltjuL81ewhX4/CVZ7l+4YLhOxr/Vwz+0vwOqxT6VvaT+yjvfaNbcndd84VdHnzw4Ac/uDKvPeMZz8hmMOD7fOV2y98Y4cem4eFLuFAeC5z4Fk7Ce2blrWsccP267S23SftbcGHCpSEUQT7LhNcFPLx/Jlxd2FHTa6RsfxIA6mKHOfx4L8k3giPXHLfHk148BS2vIlhuB5522u9vDfDy9rjryW94unrkkUeWL1P83VUgxRQgjK6hPql70h6LeshUy6JBpYOur9v0fplwlRQT8M+U+Qewtrl/8bm66gnNX5rfYfEHjIBjWrG0XdtLsjLu3rrmiwsuuGCAd8a0NokcyZZwN0bsRV7eyz1oeGgJF+4Zy9GXr4e/y9PPUbZrHJq0F+2YtMn9MOGahFTA39sQThfNYv1MeLqwo6bXoP31Z38SAJrq7oYbbsimz+HJqG9BDbk+9ngSuvnmm2dLy+OpZJ0N02rsB4YHWL3QVw86CfbjmYNvfetbYy/bdSDF9dD5WHvttb2dg3vc4x6DXXfddYDlnutsXV236f0y4aqjrXZlyX/N+U/4pakGQvGX5nfyTilGcDDluTyKA77A6DmSsjpbV3yBOpGMom2CrbsHz2OJenflV3D5fvvtN/LwDXz/yU9+MrsNDY9xCdef/vSnAaaPu/XjeK211hrgHV/f1hUOTdrra09ZJveSYsK1AGBYAGb6S+tof9st2pemlYay/r8b+wRfQSe8mPini79NXjIDy6mwlbHZKYDmD3/4g/n9739vfve73xkbVMz97nc/s84662T/7GITra4vJ9sOqrEfRzZ2Pr+xQd3Ylb3MIx/5SLPSSitJkV729omvsQt6mOuuu87Y99yM/U6ZWW+99Vr7dqjrhgRJ7Ao2MGmzq48Z+8S/KAadxtzIf7PLf2Jn08ZfF198sbEPl0bM2CYYxn7DsJCDL+0Ux4wv7ZLxxn4UfsgXioI1Drrii6VLl2Yca7/DZew7Z8YuwZ7xrGBebhL82CZrxn6X0dgZDGaDDTYwNqEsF4v2d1c4dNlgwc7lxTL/afWF4sVY/MeEK9dsLMA1Q2L9sxvwNJ3WkVP//elfAkAXHZY6OmfZ+UZA7MrtWGh3XO5whOpYaPWTf/rjH+ikDf5iZ9PGX1UTLs0mKZ9PBMReXV4s859256F4sY3/aW31yZlw5ajEAtynBMhY/+wGPE2ndeTUf3/6lwAwbR2WOvbDstOHgNiV27HQWlnucITqWGj1k3/64x/opA3+YmfTxl9MuDRvS1su9uryYpn/NIRC8WIb/9Pa6pMz4cpRiQW4TwmQsf7ZDXiaTuvIqf/+9C8BYNo6LHXsh2WnDwGxK7djobWy3OEI1bHQ6if/9Mc/0Ekb/MXOpo2/mHBp3pa2XOzV5cUy/2kIheLFNv6ntdUnZ8KVoxILcJ8SIGP9sxvwNJ3WkVP//elfAsC0dVjq2A/LTh8CYldux0JrZbnDEapjodVP/umPf6CTNviLnU0bfzHh0rwtbbnYq8uLZf7TEArFi238T2urT86EK0clFuA+JUDG+mc34Gk6rSOn/vvTvwSAaeuw1LEflp0+BMSu3I6F1spyhyNUx0Krn/zTH/9AJ23wFzubNv5iwqV5W9pysVeXF8v8pyEUihfb+J/WVp+cCVeOSizAfUqAjPXPbsDTdFpHTv33p38JANPWYaljPyw7fQiIXbkdC62V5Q5HqI6FVj/5pz/+gU7a4C92Nm38xYRL87a05WKvLi+W+U9DKBQvtvE/ra0+OROuHJVYgPuUABnrn92Ap+m0jpz670//EgCmrcNSx35YdvoQELtyOxZaK8sdjlAdC61+8k9//AOdtMFf7Gza+IsJl+ZtacvFXl1eLPOfhlAoXmzjf1pbfXImXDkqsQD3KQEy1j+7AU/TaR059d+f/iUATFuHpY79sOz0ISB25XYstFaWOxyhOhZa/eSf/vgHOmmDv9jZtPEXvmF10UUXjZjcFltsYdZYY40ROQVpICD26vJimf80JELxYhv/09rqkzPhylGJBbhPCZCx/tkNeJpO68ip//70LwFg2josdeyHZacPAbErt2OhtbLc4QjVsdDqJ//0xz/QSRv8xc7IX5p1Uz5NCIi9urxY5j+tvaF4sY3/aW31yZlw5ajEAtynBMhY/+wGPE2ndeTUf3/6lwDADksdi2XZSQiIXbkdC+2ccocjVMdCq5/80x//QCdt8Bc7I39p1k35NCEg9uryYpn/tPaG4sU2/qe11SdnwpWjEgtwnxIgY/2zG/A0ndaRU//96V8CADssdSyWZSchIHbldiy0c8odjlAdC61+8k9//AOdtMFf7Iz8pVk35dOEgNiry4tl/tPaG4oX2/if1lafnAlXjkoswH1KgIz1z27A03RaR07996d/CQDssNSxWJadhIDYldux0M4pdzhCdSy0+sk//fEPdNIGf7Ez8pdm3ZRPEwJiry4vlvlPa28oXmzjf1pbfXImXDkqsQD3KQEy1j+7AU/TaR059d+f/iUAsMNSx2JZdhICYldux0I7p9zhCNWx0Oon//THP9BJG/zFzshfmnVTPk0IiL26vFjmP629oXixjf9pbfXJmXDlqMQC3KcEyFj/7AY8Tad15NR/f/qXAMAOSx2LZdlJCIhduR0L7ZxyhyNUx0Krn/zTH/9AJ23wFzsjf2nWTfk0ISD26vJimf+09obixTb+p7XVJ2fClaMSC3CfEiBj/bMb8DSd1pFT//3pXwIAOyx1LJZlJyEgduV2LLRzyh2OUB0LrX7yT3/8A520wV/sjPylWTfl04SA2KvLi2X+09obihfb+J/WVp+cCVeOSizAfUqAjPXPbsDTdFpHTv33p38JAHX0xbJEoCoCbsdCO6fc4QjVsdDqJ//0xz/QSRv8yV+aVVM+zQi4vFjmP63doXixjf9pbfXJFyxbtmzg+4EyIkAEiMAsIbBw4UKzfPny2k1eaaWVap/DE4hAVQRuvvnmqkWLcosWLSqOeUAExiFA/hqHDn+bVgRS5EWOcOXWGCvD1Yyf9c/uE0ZNp3Xk1H9/+pcnxJySU8diWXYSAmJX7pNc7ZzyE95QT3K1+sk//fEPdNIGf7Ez8pdm3ZRPEwJiry4vlvlPa28oXmzjf1pbfXImXDkqsQD3KQEy1j+7AU/TaR059d+f/iUAsMNSx2JZdhICYldux0I7p9zhCNWx0Oon//THP9BJG/zFzshfmnVTPk0IiL26vFjmP629oXixjf9pbfXJmXDlqMQC3KcEyFj/7AY8Tad15NR/f/qXAMAOSx2LZdlJCIhduR0L7ZxyhyNUx0Krn/zTH/9AJ23wFzsjf2nWTfk0ISD26vJimf+09obixTb+p7XVJ2fClaMSC3CfEiBj/bMb8DSd1pFT//3pXwIAOyx1LJZlJyEgduV2LLRzyh2OUB0LrX7yT3/8A520wV/sjPylWTfl04SA2KvLi2X+09obihfb+J/WVp+cCVeOSizAfUqAjPXPbsDTdFpHTv33p38JAOyw1LFYlp2EgNiV27HQzil3OEJ1LLT6yT/98Q900gZ/sTPyl2bdlE8TAmKvLi+W+U9rbyhebON/Wlt9ciZcOSqxAPcpATLWP7sBT9NpHTn135/+JQCww1LHYll2EgJiV27HQjun3OEI1bHQ6if/9Mc/0Ekb/MXOyF+adVM+TQiIvbq8WOY/rb2heLGN/2lt9cmZcOWoxALcpwTIWP/sBjxNp3Xk1H9/+pcAwA5LHYtl2UkIiF25HQvtnHKHI1THQquf/NMf/0AnbfAXOyN/adZN+TQhIPbq8mKZ/7T2huLFNv6ntdUnZ8KVoxILcJ8SIGP9sxvwNJ3WkVP//elfAgA7LHUslmUnISB25XYstHPKHY5QHQutfvJPf/wDnbTBX+yM/KVZN+XThIDYq8uLZf7T2huKF9v4n9ZWn5wJV45KLMB9SoCM9c9uwNN0WkdO/fenfwkA7LDUsViWnYSA2JXbsdDOKXc4QnUstPrJP/3xD3TSBn+xM/KXZt2UTxMCYq8uL5b5T2tvKF5s439aW31yJlw5KrEA9ykBMtY/uwFP02kdOfXfn/4lALDDUsdiWXYSAmJXbsdCO6fc4QjVsdDqJ//0xz/QSRv8xc7IX5p1Uz5NCIi9urxY5j+tvaF4sY3/aW31yZlw5ajEAtynBMhY/+wGPE2ndeTUf3/6lwDADksdi2XZSQiIXbkdC+2ccocjVMdCq5/80x//QCdt8Bc7I39p1k35NCEg9uryYpn/tPaG4sU2/qe11SdnwpWjEgtwnxIgY/2zG/A0ndaRU//96V8CADssdSyWZSchIHbldiy0c8odjlAdC61+8k9//AOdtMFf7Iz8pVk35dOEgNiry4tl/tPaG4oX2/if1lafnAlXjkoswH1KgIz1z27A03RaR07996d/CQDssNSxWJadhIDYldux0M4pdzhCdSy0+sk//fEPdNIGf7Ez8pdm3ZRPEwJiry4vlvlPa28oXmzjf1pbfXImXDkqsQD3KQEy1j+7AU/TaR059d+f/iUAsMNSx2JZdhICYldux0I7p9zhCNWx0Oon//THP9BJG/zFzshfmnVTPk0IiL26vFjmP629oXixjf9pbfXJmXDlqMQC3KcEyFj/7AY8Tad15NR/f/qXAMAOSx2LZdlJCIhduR0L7ZxyhyNUx0Krn/zTH/9AJ23wFzsjf2nWTfk0ISD26vJimf+09obixTb+p7XVJ2fClaMSC3CfEiBj/bMb8DSd1pFT//3pXwIAOyx1LJZlJyEgduV2LLRzyh2OUB0LrX7yT3/8A520wV/sjPylWTfl04SA2KvLi2X+09obihfb+J/WVp+cCVeOSizAfUqAjPXPbsDTdFpHTv33p38JAOyw1LFYlp2EgNiV27HQzil3OEJ1LLT6yT/98Q900gZ/sTPyl2bdlE8TAmKvLi+W+U9rbyhebON/Wlt9ciZcOSqxAPcpATLWP7sBT9NpHTn135/+JQCww1LHYll2EgJiV27HQjun3OEI1bHQ6if/9Mc/0Ekb/MXOyF+adVM+TQiIvbq8WOY/rb2heLGN/2lt9cmZcOWoxALcpwTIWP/sBjxNp3Xk1H9/+pcAUEdfLEsEqiLgdiy0c8odjlAdC61+8k9//AOdtMGf/KVZNeXTjIDLi2X+09odihfb+J/WVp+cCVeOSizAfUqAjPXPbsDTdFpHTv33p392WOpYKsvWRcDtWGjnljscoToWWv3kn/74Bzppgz/5S7NqyqcZAZcXy/yntTsUL7bxP62tPjkTrhyVWID7lAAZ65/dgKfptI6c+u9P/9Jh4ZScOhbLspMQELtyOxbaOeUOR6iOhVY/+ac//oFO2uAvdkb+0qyb8mlCQOzV5cUy/2ntDcWLbfxPa6tPzoQrRyUW4D4lQMb6ZzfgaTqtI6f++9O/BAB2WOpYLMtOQkDsyu1YaOeUOxyhOhZa/eSf/vgHOmmDv9gZ+UuzbsqnCQGxV5cXy/yntTcUL7bxP62tPjkTrhyVWID7lAAZ65/dgKfptI6c+u9P/xIA2GGpY7EsOwkBsSu3Y6GdU+5whOpYaPWTf/rjH+ikDf5iZ+QvzbopnyYExF5dXizzn9beULzYxv+0tvrkTLhyVGIB7lMCZKx/dgOeptM6cuq/P/1LAGCHpY7FsuwkBMSu3I6Fdk65wxGqY6HVT/7pj3+gkzb4i52RvzTrpnyaEBB7dXmxzH9ae0PxYhv/09rqkzPhylGJBbhPCZCx/tkNeJpO68ip//70LwGAHZY6FsuykxAQu3I7Fto55Q5HqI6FVj/5pz/+gU7a4C92Rv7SrJvyaUJA7NXlxTL/ae0NxYtt/E9rq0/OhCtHJRbgPiVAxvpnN+BpOq0jp/77078EAHZY6lgsy05CQOzK7Vho55Q7HKE6Flr95J/++Ac6aYO/2Bn5S7NuyqcJAbFXlxfL/Ke1NxQvtvE/ra0+OROuHJVYgPuUABnrn92Ap+m0jpz670//EgDYYaljsSw7CQGxK7djoZ1T7nCE6lho9ZN/+uMf6KQN/mJn5C/NuimfJgTEXl1eLPOf1t5QvNjG/7S2+uRMuHJUYgHuUwJkrH92A56m0zpy6r8//UsAYIeljsWy7CQExK7cjoV2TrnDEapjodVP/umPf6CTNviLnZG/NOumfJoQEHt1ebHMf1p7Q/FiG//T2uqTM+HKUYkFuE8JkLH+2Q14mk7ryKn//vQvAYAdljoWy7KTEBC7cjsW2jnlDkeojoVWP/mnP/6BTtrgL3ZG/tKsm/JpQkDs1eXFMv9p7Q3Fi238T2urT86EK0clFuA+JUDG+mc34Gk6rSOn/vvTvwQAdljqWCzLTkJA7MrtWGjnlDscoToWWv3kn/74Bzppg7/YGflLs27KpwkBsVeXF8v8p7U3FC+28T+trT45E64clViA+5QAGeuf3YCn6bSOnPrvT/8SANhhqWOxLDsJAbErt2OhnVPucITqWGj1k3/64x/opA3+YmfkL826KZ8mBMReXV4s85/W3lC82Mb/tLb65AuWLVs28P1AGREgAkRglhBYuHChWb58ee0mr7TSStk57LDUho4njEFAOhY333zzmFL+nxYtWuT/gVIiUEKA/FUChH9ONQIp8yJHuHLTjJXhap7A+mf3CaOm0zpy6r8//UsAYMJVx2JZdhICYlfuk1ztnPIT3lBPcrX6yT/98Q900gZ/sTPyl2bdlE8TAmKvLi+W+U9rbyhebON/Wlt9ciZcOSqxAPcpATLWP7sBT9NpHTn135/+JQCww1LHYll2EgJiV27HQjun3OEI1bHQ6if/9Mc/0Ekb/MXOyF+adVM+TQiIvbq8WOY/rb2heLGN/2lt9cmZcOWoxALcpwTIWP/sBjxNp3Xk1H9/+pcAwA5LHYtl2UkIiF25HQvtnHKHI1THQquf/NMf/0AnbfAXOyN/adZN+TQhIPbq8mKZ/7T2huLFNv6ntdUnZ8KVoxILcJ8SIGP9sxvwNJ3WkVP//elfAgA7LHUslmUnISB25XYstHPKHY5QHQutfvJPf/wDnbTBX+yM/KVZN+XThIDYq8uLZf7T2huKF9v4n9ZWn5wJV45KLMB9SoCM9c9uwNN0WkdO/fenfwkAdfTFskSgKgJux0I7p9zhCNWx0Oon//THP9BJG/zJX5pVUz7NCLi8WOY/rd2heLGN/2lt9cmZcOWoxALcpwTIWP/sBjxNp3Xk1H9/+meHpY6lsmxdBNyOhXZuucMRqmOh1U/+6Y9/oJM2+JO/NKumfJoRcHmxzH9au0PxYhv/09rqkzPhylGJBbhPCZCx/tkNeJpO68ip/9nU/2233VZHzWrZqgFHvUDLH1j/7WbFFVdsiWLz08v4h+pYaC0k/8wm/2j6rCoX/irbX9XzuyrH+qeLf7rSa9XrVNV/KF6MxX9MuHKLiAW4ZoCsP82AJ/ZA/c+m/qXDInpsuq8acJpef9J5rH+6OjyhOhaaHZB/ZpN/NH1WlQt/0f+ny/+r6q+rcrOi/1C8GIv/mHDlFhsLcM1BWH+aAU/sgfqfTf1Lh0X02HQ/KwGv6f1NOo/3P9zhC9Wx0PRA/plN/tH0WVUu/EX/G/a/qvh1VY74V8M/FC/G4j8mXLnHxAJcc1DWn2bAE3ug/mdT/9JhET023TPgVgu4TfGddN604R+qY6HhQP6ZTf7R9FlVLvw1bfZftf1dleP9zwb/huLFWPzHhCv32FiAawTB+tMMeGIP1P9s6l86LKLHpnsG/NkI+E31O+m8sv5DdSy0dpB/ZpN/NH1WlQt/le2v6vldlWP95L8q79CG4sVY/MeEK2eMWIBrBMX60wx4Yg/U/2zqXzososeme3Y42OFwOxyhOhaafZJ/ZpN/NH1WlQt/kX/IPy7/VLWfrspVtb9QvBiL/5hw5RYTC3DNQFl/mgFP7IH6n039S4dF9Nh0XzXgNL3+pPNY/3R1uEJ1LDQ7IP/MJv9o+qwqF/6i/0+X/1fVX1flZkX/oXgxFv8x4cotNhbgmoOw/jQDntgD9T+b+pcOi+ix6X5WAl7T+5t0Hu9/uMMXqmOh6YH8M5v8o+mzqlz4i/437H9V8euqHPGvhn8oXozFf0y4co+JBbjmoKw/zYAn9kD9z6b+pcMiemy6Z8CtFnCb4jvpvGnDP1THQsOB/DOb/KPps6pc+Gva7L9q+7sqx/ufDf4NxYux+I8JV+6xsQDXCIL1pxnwxB6o/9nUv3RYRI9N9wz4sxHwm+p30nll/YfqWGjtIP/MJv9o+qwqF/4q21/V87sqx/rJf1XeIQvFi7H4jwlXzhixANcIivWnGfDEHqj/2dS/dFhEj0337HCww+F2OEJ1LDT7JP/MJv9o+qwqF/4i/5B/XP6paj9dlatqf6F4MRb/MeHKLSYW4JqBsv40A57YA/U/m/qXDovosem+asBpev1J57H+6epwhepYaHZA/plN/tH0WVUu/EX/ny7/r6q/rsrNiv5D8WIs/mPClVtsLMA1B2H9aQY8sQfqfzb1Lx0W0WPT/awEvKb3N+k83v9why9Ux0LTA/lnNvlH02dVufAX/W/Y/6ri11U54l8N/1C8GIv/mHDlHhMLcM1BWX+aAU/sgfqn/hctWiTmEH1P+6P90f7of9GJJ6+Q/EP+SYF/mHDR4TMESHgkvBQIT+tQ0P5p/7R/JhwaP4SWk3/IP+Sf+ecfJlw5k5LwSHgkvPknPK3jRP+n/9P/6f8aP4SWk3/IP+Sf+ecfJlxMuDIESPgkfBL+/BO+1nGk/9P/6f/0f40fQsvJP+SfFPiHCVfOJHR4OnwKDq8FTto/7Z/2zw63xg+h5eQf8g/5h/wTmme068fiHyZcuQZiAd63wlm/HwHqnwGfAZ8B388O4aXkH/IP+Yf8E55p/DWQf+LwDxOu3P5ocHEMzu/uxhB/4s8OBzscGj+ElpN/yD/kH/JPaJ7Rrk/+SYN/mHDlHkCDT8PgSXh+BGj/tH92ONnh9LNDeCn5h/xD/iH/hGcafw2x+IcJV45/LMD96uYID/FnwGXAZcDV+DG0nPxD/iH/kH9C84x2ffJPGvzDhCv3ABp8GgZPwvMjQPun/bPDyQ6nnx3CS8k/5B/yD/knPNP4a4jFP0y4cvxjAe5XN0e4iD8DLgMuA67Gj6Hl5B/yD/mH/BOaZ7Trk3/S4B8mXLkH0ODTMHgSnh8B2j/tnx1Odjj97BBeSv4h/5B/yD/hmcZfQyz+WbBs2bKBvwmUEgEiQARmB4GFCxea5cuXz06D2VIiQASIABEgAkQgCQQ4wpWrOVaGq1kV6+cTPj7h4xM+jR9Cy8k/5B/yD/knNM9o1yf/kH9S4B8mXDkD0OHp8Ck4PAOeHwH6P/2f/s+Ew88O4aXkH/IP+Wf++YcJV86lJDwSHglv/glP6zrR/+n/9H/6v8YPoeXkH/IP+Wf++YcJFxOuDAESPgmfhD//hK91HOn/9H/6P/1f44fQcvIP+ScF/mHClTMJHZ4On4LDa4GT9k/7p/2zw63xQ2g5+Yf8Q/4h/4TmGe36sfiHCVeugViA961w1u9HgPpnwGfAZ8D3s0N4KfmH/EP+If+EZxp/DeSfOPzDhCu3PxpcHIPzuzs//Ez7o/2xw8UOl8aPoeXkH/IP+Yf8E5pntOunwj9MuHILSEXhqRs879+PAO2fHS52uNjh8rNDeCn5h/xD/iH/hGcafw2x+IcJV45/LMD96uYID/FnwGXAZcDV+DG0nPxD/iH/kH9C84x2ffJPGvzDhCv3ABp8GgZPwvMjQPun/bPDyQ6nnx3CS8k/5B/yD/knPNP4a4jFP0y4cvxjAe5XN0e4iD8DLgMuA67Gj6Hl5B/yD/mH/BOaZ7Trk3/S4B8mXLkH0ODTMHgSnh8B2j/tnx1Odjj97BBeSv4h/5B/yD/hmcZfQyz+YcKV4x8LcL+6OcJF/BlwGXAZcDV+DC0n/5B/yD/kn9A8o12f/JMG/zDhyj2ABp+GwZPw/AjQ/mn/7HCyw+lnh/BS8g/5h/xD/gnPNP4aYvEPE64c/1iA+9XNES7iz4DLgMuAq/FjaDn5h/xD/iH/hOYZ7frknzT4hwlX7gE0+DQMnoTnR4D2T/tnh5MdTj87hJeSf8g/5B/yT3im8dcQi3+YcOX4xwLcr26OcBF/BlwGXAZcjR9Dy8k/5B/yD/knNM9o1yf/pME/TLhyD6DBp2HwJDw/ArR/2j87nOxw+tkhvJT8Q/4h/5B/wjONv4ZY/MOEK8c/FuB+dXOEi/gz4DLgMuBq/BhaTv4h/5B/yD+heUa7PvknDf5hwpV7AA0+DYMn4fkRoP3T/tnhZIfTzw7hpeQf8g/5h/wTnmn8NcTiHyZcOf6xAPermyNcxJ8BlwGXAVfjx9By8g/5h/xD/gnNM9r1yT9p8A8TrtwDaPBpGDwJz48A7Z/2zw4nO5x+dggvJf+Qf8g/5J/wTOOvIRb/MOHK8Y8FuF/dHOEi/gy4DLgMuBo/hpaTf8g/5B/yT2ie0a5P/kmDf5hw5R5Ag0/D4El4fgRo/7R/djjZ4fSzQ3gp+Yf8Q/4h/4RnGn8NsfiHCVeOfyzA/ermCBfxZ8BlwGXA1fgxtJz8Q/4h/5B/QvOMdn3yTxr8w4Qr9wAafBoGT8LzI0D7p/2zw8kOp58dwkvJP+Qf8g/5JzzT+GuIxT9MuHL8YwHuVzdHuIg/Ay4DLgOuxo+h5eQf8g/5h/wTmme065N/0uAfJly5B9Dg0zB4Ep4fAdo/7Z8dTnY4/ewQXkr+If+Qf8g/4ZnGX0Ms/mHCleMfC3C/ujnCRfwZcBlwGXA1fgwtJ/+Qf8g/5J/QPKNdn/yTBv8w4co9gAafhsGT8PwI0P5p/+xwssPpZ4fwUvIP+Yf8Q/4JzzT+GmLxDxOuHP9YgPvVzREu4s+Ay4DLgKvxY2g5+Yf8Q/4h/4TmGe365J80+GfBsmXLBpoRUE4EiAARmBUEFi5caJYvXz4rzWU7iQARIAJEgAgQgUQQ4AhXrmg+YUjjCYPm19Q/9c8n3HzCrfFDaDn5h/xD/iH/hOYZ7frknzj88/8ByN3kmxm95ksAAAAASUVORK5CYII=\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 19,
"metadata": {
"image/png": {
"height": 400,
"width": 400
}
},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='ATMClassDiagram.png', width=400, height=400) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The diamond arrow is a \"has-a\" relationship. For example, the Controller has-a ATMInput. This means that a Controller object has an instance variable for an ATMInput object."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Interaction Diagram for the ATM System"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"An interaction diagram specifies how components interact to achieve a use case. \n",
"\n",
"Interactions are from one object to another object, indicating that the first object calls a method in the second object.\n",
"\n",
"Rules for drawing lines in an interaction diagram:\n",
"- The calling object must know about the called object.\n",
"- The called object must have the method invoked by the calling object."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABmAAAAKECAYAAAAQZ/XGAAAMFGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdUk8kWnr+kEBJaIAJSQm+CFOkCofciHWyEJEAoERKCih1ZVHAtqFhAVHRFRMW1ALJWLFhYBOz1gYrKyrpYsKHyJgV0fe28e8788+XOvXe+O7kzZwYAZVt2bm42qgJAjiBfGB3ow0xMSmaSegEOMEAHJoDA5ohyvaOiwgCU0f7v8u4mQCT9NWtJrH8d/6+iyuWJOAAgURCnckWcHIiPAIBrcnKF+QAQ2qHeaHZ+rgQPQqwuhAQBIOISnC7DmhKcKsMTpDax0b4QswAgU9lsYToAShLezAJOOoyjJOFoK+DyBRBXQezJyWBzIb4P8YScnFkQK5MhNk/9Lk7632KmjsVks9PHsCwXqZD9+KLcbPbc/3M5/rfkZItH5zCEjZohDIqW5AzXbU/WrFAJpkJ8XJAaEQmxGsQX+VypvQTfzRAHxcntBzgiX7hmgAEACrhsv1CIdSBmiLPivOXYni2U+kJ7NIKfHxwrx6nCWdHy+GiBIDsiTB5neQYveBRX80T+MaM2afyAYIhhpaFHCjNiE2Q80XMF/PgIiJUg7hRlxYTKfR8WZvhGjNoIxdESzsYQv00TBkTLbDDNHNFoXpgNhy2dC9YCxsrPiA2S+WKJPFFi2CgHLs/PX8YB4/IEcXJuGKwun2i5b0ludpTcHqvmZQdGy9YZOygqiBn17c6HBSZbB+xRJjskSj7Xu9z8qFgZNxwFYcAX+AEmEMOWCmaBTMDvGGgagL9kIwGADYQgHfCAtVwz6pEgHRHAbwwoBH9CxAOiMT8f6SgPFED9lzGt7GsN0qSjBVKPLPAU4hxcG/fE3fEw+GXBZo+74K6jfkzl0VmJ/kQ/YhAxgGgxxoMDWWfDJgT8f6MLhT0PZifhIhjN4Vs8wlNCF+ER4Qahh3AHxIMn0ihyq5n8IuEPzJkgHPTAaAHy7FK/zw43hawdcR/cA/KH3HEGrg2s8UkwE2/cC+bmCLXfMxSPcfu2lj/OJ2H9fT5yvZKlkqOcRerYP+M7ZvVjFN/v1ogL+9AfLbHl2GGsDTuDXcKOY02AiZ3CmrF27IQEj1XCE2kljM4WLeWWBePwR21s6237bT//MDdbPr9kvUT5vDn5ks3gOyt3rpCfnpHP9IanMY8ZLODYTGDa29o5AyA522VHxxuG9MxGGJe/6fJOA+BaCpXp33RsIwCOPQWA/u6bzug1LPc1AJzo5IiFBTKd5DgGBEABynBXaAE9YATMYT72wAm4AxbwByEgEsSCJDADrngGyIGcZ4P5YAkoAWVgDdgAtoBtYCfYA/aDQ6AJHAdnwAVwBXSCG+AerIs+8AIMgndgGEEQEkJD6IgWoo+YIFaIPeKCeCL+SBgSjSQhKUg6IkDEyHxkKVKGlCNbkB1IHfIrcgw5g1xCupA7SC/Sj7xGPqEYSkXVUV3UFJ2IuqDeaCgai05H09E8tBAtRlehm9AadB/aiJ5Br6A30B70BTqEAUwRY2AGmDXmgvlikVgyloYJsYVYKVaB1WAHsBb4P1/DerAB7CNOxOk4E7eGtRmEx+EcPA9fiK/Et+B78Eb8HH4N78UH8a8EGkGHYEVwIwQTEgnphNmEEkIFYTfhKOE83Dd9hHdEIpFBNCM6w32ZRMwkziOuJG4lNhBPE7uIj4lDJBJJi2RF8iBFktikfFIJaTNpH+kUqZvUR/pAViTrk+3JAeRksoBcRK4g7yWfJHeTn5GHFVQUTBTcFCIVuApzFVYr7FJoUbiq0KcwTFGlmFE8KLGUTMoSyibKAcp5yn3KG0VFRUNFV8UpinzFxYqbFA8qXlTsVfxIVaNaUn2p06hi6ipqLfU09Q71DY1GM6WxaMm0fNoqWh3tLO0h7YMSXclGKViJq7RIqVKpUalb6aWygrKJsrfyDOVC5Qrlw8pXlQdUFFRMVXxV2CoLVSpVjqncUhlSpavaqUaq5qiuVN2rekn1uRpJzVTNX42rVqy2U+2s2mM6Rjei+9I59KX0XfTz9D51orqZerB6pnqZ+n71DvVBDTWNSRrxGnM0KjVOaPQwMIYpI5iRzVjNOMS4yfg0Tnec9zjeuBXjDozrHvdec7wmS5OnWarZoHlD85MWU8tfK0trrVaT1gNtXNtSe4r2bO1q7fPaA+PVx7uP54wvHX9o/F0dVMdSJ1pnns5OnXadIV093UDdXN3Numd1B/QYeiy9TL31eif1+vXp+p76fP31+qf0/2BqML2Z2cxNzHPMQQMdgyADscEOgw6DYUMzwzjDIsMGwwdGFCMXozSj9UatRoPG+sbhxvON643vmiiYuJhkmGw0aTN5b2pmmmC6zLTJ9LmZplmwWaFZvdl9c5q5l3meeY35dQuihYtFlsVWi05L1NLRMsOy0vKqFWrlZMW32mrVNYEwwXWCYELNhFvWVGtv6wLreuteG4ZNmE2RTZPNy4nGE5Mnrp3YNvGrraNttu0u23t2anYhdkV2LXav7S3tOfaV9tcdaA4BDoscmh1eTbKaxJtUPem2I90x3HGZY6vjFydnJ6HTAad+Z2PnFOcq51su6i5RLitdLroSXH1cF7ked/3o5uSW73bI7S93a/cs973uzyebTeZN3jX5sYehB9tjh0ePJ9MzxXO7Z4+XgRfbq8brEcuIxWXtZj3ztvDO9N7n/dLH1kfoc9Tnva+b7wLf036YX6BfqV+Hv5p/nP8W/4cBhgHpAfUBg4GOgfMCTwcRgkKD1gbdCtYN5gTXBQ+GOIcsCDkXSg2NCd0S+ijMMkwY1hKOhoeErwu/H2ESIYhoigSRwZHrIh9EmUXlRf02hTglakrllKfRdtHzo9ti6DEzY/bGvIv1iV0dey/OPE4c1xqvHD8tvi7+fYJfQnlCT+LExAWJV5K0k/hJzcmk5Pjk3clDU/2nbpjaN81xWsm0m9PNps+ZfmmG9ozsGSdmKs9kzzycQkhJSNmb8pkdya5hD6UGp1alDnJ8ORs5L7gs7npuP8+DV857luaRVp72PN0jfV16f4ZXRkXGAN+Xv4X/KjMoc1vm+6zIrNqskeyE7IYcck5KzjGBmiBLcG6W3qw5s7pyrXJLcnvy3PI25A0KQ4W7RYhouqg5Xx1ec9rF5uKfxL0FngWVBR9mx88+PEd1jmBO+1zLuSvmPisMKPxlHj6PM691vsH8JfN7F3gv2LEQWZi6sHWR0aLiRX2LAxfvWUJZkrXk9yLbovKit0sTlrYU6xYvLn78U+BP9SVKJcKSW8vcl21bji/nL+9Y4bBi84qvpdzSy2W2ZRVln1dyVl7+2e7nTT+PrEpb1bHaaXX1GuIawZqba73W7ilXLS8sf7wufF3jeub60vVvN8zccKliUsW2jZSN4o09m8I2NW823rxm8+ctGVtuVPpUNlTpVK2oer+Vu7W7mlV9YJvutrJtn7bzt9/eEbijsca0pmIncWfBzqe74ne1/eLyS91u7d1lu7/UCmp79kTvOVfnXFe3V2fv6nq0Xlzfv2/avs79fvubD1gf2NHAaCg7CA6KD/7xa8qvNw+FHmo97HL4wBGTI1VH6UdLG5HGuY2DTRlNPc1JzV3HQo61tri3HP3N5rfa4wbHK09onFh9knKy+OTIqcJTQ6dzTw+cST/zuHVm672ziWevn5tyruN86PmLFwIunG3zbjt10ePi8Utul45ddrncdMXpSmO7Y/vR3x1/P9rh1NF41flqc6drZ0vX5K6T3V7dZ675XbtwPfj6lRsRN7puxt28fWvarZ7b3NvP72TfeXW34O7wvcX3CfdLH6g8qHio87DmHxb/aOhx6jnR69fb/ijm0b3HnMcvnoiefO4rfkp7WvFM/1ndc/vnx/sD+jv/mPpH34vcF8MDJX+q/ln10vzlkb9Yf7UPJg72vRK+Gnm98o3Wm9q3k962DkUNPXyX8274fekHrQ97Prp8bPuU8OnZ8OzPpM+bvlh8afka+vX+SM7ISC5byJZeBTDY0LQ0AF7XAkBLgneHTgAoSrK3l1QQ2XtRisB/wrL3mVScAKhlARC3GIAweEephs0EYirsJVfvWBZAHRzGmlxEaQ72slhU+IIhfBgZeaMLAKkFgC/CkZHhrSMjX3ZBsncAOJ0ne/NJhAjv99ttJKiz7yX4Uf4JEL9tBtKO/vwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGeaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIj4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjE2MzI8L2V4aWY6UGl4ZWxYRGltZW5zaW9uPgogICAgICAgICA8ZXhpZjpQaXhlbFlEaW1lbnNpb24+NjQ0PC9leGlmOlBpeGVsWURpbWVuc2lvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+Cs7GCv0AAAAcaURPVAAAAAIAAAAAAAABQgAAACgAAAFCAAABQgAAuvgGoFDoAABAAElEQVR4Aex9BdwFRfn1IiAgSnd3SHeJII3AJ5IiiISUf0CUkFBCWgRpkVJKUgHpkhBFkJCS7g4REAUJ95tz9bl37uzM3Znd2d173z3z+73vbEw8c+aZc2fnmRjnrX+maRLRvf/++8lEE00UMcWwpJg/8af+sf2FsUa80OQf8g/5h/wTj1HCUiL/kH/IP+QfYY2tz/3v1WXby5Mwf/1T/xv+F1v4xSP/kH/IP+QfP7aIH4r8Q/4h/5B/4jOLX4rkH/JPCP+MQwOMX8PyDcUGyAYY0gB99co3HPWP+kf9YwfUly9ihyP/kH/IP+Sf2Lzimx75p59/aIDx1Zw44ah//foXB1X/VIg/8Wf/g/0Pf8aIG5L8Q/4h/5B/fFmFBhhfpDzDkYBJwCRgErAnXUQPRv4h/5B/yD/RicUzQfIP+Yf8Mzz8QwOMJ3FFCkb+I/+R/4aH/yI1a+9k2P7Z/tn+2f69CSNyQPLPaPHPOF/5edwtyCLrE5MjAkSACBABIkAEiAARIAJEgAgQASJABIgAESACRIAIEAEiQASIwMghQAPMyFUZBSYCRIAIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASJABIYdgXGUgOmwC0n5iAARIAJEgAgQASJABIgAESACRIAIEAEiQASIABEgAkSACBABIjBKCNAAM0q1RVmJABEgAkSACBABIkAEiAARIAJEgAgQASJABIgAESACRIAIEIGRQGCcVLmRkJRCEgEiQASIABEgAkQgMgLjjIO5KGo5cMnu0L/+9a/kM5/5TGTp/JNj/sSf+sf2588YcUOSf8g/5B/yT1xW8U+N/EP+If+Qf/wZI25I8g/5J4R/aICJ2/6YGhEgAkSACBABIjBCCNAAE6ey+AHCD5CQD5A4WtdLhfpH/aP+cQCuxwj1XpF/yD/kH/JPvazTy438Q/4h/4wO/9AA0+MuXhEBIkAEiAARIAItQ4AGmDgVzg9AfgDyA3B0PgDjtPpeKmz/bP9s/2z/PUao94r8Q/4h/5B/6mWdXm7kH/JPCP/QANNrO7wiAkSACBABIkAEWoYADTBxKpwfIPwACfkAiaN1vVSof9Q/6h8H4HqMUO8V+Yf8Q/4h/9TLOr3cyD/kH/LP6PAPDTA97uIVESACRIAIEAEi0DIEaICJU+H8AOQHID8AR+cDME6r76XC9s/2z/bP9t9jhHqvyD/kH/IP+ade1unlRv4h/4TwDw0wvbbDKyJABIgAESACRKBlCNAAE6fC+QHCD5CQD5A4WtdLhfpH/aP+cQCuxwj1XpF/yD/kH/JPvazTy438Q/4h/4wO/9AA0+MuXhEBIkAEiAARIAItQ4AGmDgVzg9AfgDyA3B0PgDjtPpeKmz/bP9s/2z/PUao94r8Q/4h/5B/6mWdXm7kH/JPCP/QANNrO7wiAkSACBABIkAEWoYADTBxKpwfIPwACfkAiaN1vVSof9Q/6h8H4HqMUO8V+Yf8Q/4h/9TLOr3cyD/kH/LP6PAPDTA97uIVESACRIAIEAEi0DIEaICJU+H8AOQHID8AR+cDME6r76XC9s/2z/bP9t9jhHqvyD/kH/IP+ade1unlRv4h/4TwDw0wvbbDKyJABIgAESACRKBlCNAAE6fC+QHCD5CQD5A4WtdLhfpH/aP+cQCuxwj1XpF/yD/kH/JPvazTy438Q/4h/4wO/9AA0+MuXhEBIkAEiAARIAItQ4AGmDgVzg9AfgDyA3B0PgDjtPpeKmz/bP9s/2z/PUao94r8Q/4h/5B/6mWdXm7kH/JPCP/QANNrO7wiAkSACBABIkAEWoYADTBxKpwfIPwACfkAiaN1vVSof9Q/6h8H4HqMUO8V+Yf8Q/4h/9TLOr3cyD/kH/LP6PAPDTA97uIVESACRIAIEAEi0DIEaICJU+H8AOQHID8AR+cDME6r76XC9s/2z/bP9t9jhHqvyD/kH/IP+ade1unlRv4h/4Twzzjjjjtu2lOf/15dffXVyRprrGE+5j0RsCJw9913J8suu2zmHfUoAwkfEIEOAnfccUey4oordtG48sork7XWWqt7zws7Apdeemmy8cYbd1+CexZddNHu/Vi9aGu566pPGmDiIM0PEH6AhHyAxNG6XirUP+of9Y8DcD1GqPeK/EP+If+Qf+plnV5u5B/yD/lndPhnHNV0MwaYa6+9NllzzTV7rZpXRGAAAhgEXWqppTIh2q5HJ598cvLSSy91cVlkkUWSTTbZpHs/6OIf//hHcsQRRwwKUvjdl770pWS11Vbrxj/rrLOSxx9/vHuPi6222iqZe+65+56F3hx77LHJG2+80RftwAMPTMYff/y+Z743ZfD0zaOucDDALL/88t3sYKxce+21u/e8sCPwm9/8Jtlwww27L++7775WGGDaWu5uRVd8QQNMHID5AcgPQH4Ajs4HYJxW30uF7Z/tn+2f7b/HCPVekX/IP+Qf8k+9rNPLjfxD/gnhn6E1wLz55pvJxx9/3NFsFGiSSSbpaTmvKkcgBH8aYLLV8dxzzyVzzDFH8p///Kf7csopp0xefPHFZMIJJ+w+c1288soryQwzzOB6Xer5D37wg+Tggw/upoGBfxjLdLfzzjsnJ5xwgv4o6Pqpp57qGHDStN++ix+oiSaaKCgtBC6LZ3CGFUegAaYYwG01RLS13MW0JDwWDTDhmNli8AOEHyAhHyA2HSrzjPpH/aP+cQCuDIeUiUv+If+Qf8g/ZTikTFzyD/mH/DM6/DOUBpi33normW666ZKPPvqow0U77LBDcsopp5ThJcYNQCAUfxpgsuDCyHHooYdmXpx77rnJ5ptvnnluPmjaADPFFFMkL7/8cjLBBBOYonnd77///n1GHomEDkIRA0xZPCX/qv2VV165Y2Tbeuutk/3228+ZHQ0w/dD44gZD3C233NKNvN566yXQ1VF1bS33sNUXDTBxaoQfgPwA5Afg6HwAxmn1vVTY/tn+2f7Z/nuMUO8V+Yf8Q/4h/9TLOr3cyD/knxD+Geedd97pn6KudAkJjDfeeD2tqvnqtNNOS7bffvturjTAdKGo5SIU/08++ST55z//mZGtaT3KCFTTAxgOZ5llluTVV1/t5Dj//PMnjzzySOca537cdtttuZJgC7LDDz88N9zll1+e/PWvf+2G++53v5u7wgZbkK2++urdOPoKGAxEyqqVCy64INl000274XwvEH/22WfvrFrR00N8/ECFGmBi4Okre5lwWDU29dRTd5L4zne+k2ALNpejAaaHTAhuvVijf9XWcg9jzdEAE6dW+AHCD5CQD5A4WtdLhfpH/aP+cQCuxwj1XpF/yD/kH/JPvazTy438Q/4h/4wQ/6jB0qFzaoAYRqHunzLADJ2MY1kg4l+udi+66KKu7n72s59Nb7zxxu499Prhhx8ul4EW++tf/3pf2m+//bb21u9SHf7eTWPxxRfvXq+xxhp+CRihbrrppm4a6oD07jXKrjoIRuj82zrxzJfGHeKKK67ollUZYNwB1Zs//vGP3bDARZ0BMzD8WH4ZgttYwqGt5R7GOpT+RlnZ1ESEskmUis/8iX8pBSoZmfpH/SupQqWiU/+of6UUqGRk6h/1r6QKlYpO/aP+lVKgkpGpf9S/kipUKvqo6R9muw+VU9sepZ/61Kf6BidpgKmvioh/eaxXWWWVrv6qFSSpOgcmnXXWWbvP8gbnQySIbYDZbbfdUrXtWEdWtEO15VOIOJ2wW2yxRbesu+++e/e6qAGmTjyDC6tFUFuOdcuaV8c0wPSAC8GtF2v0r9pa7mGsORpg4tTKqHWA45S6lwrLzw/QnjbUf0X9o/7Vr3W9HKl/1L+eNtR/Rf2j/tWvdb0cqX/Uv5421H9F/Rst/RtHHZaNQcM+N/3001u3CXrvvfeS119/vS/s+OOPn8w888x9z5599tlEDTAm8D/96U8nCy64YLLQQgslM844Y184ufn73/+e4A/uvPPOS3B+hO7UIHPfeRKTTDJJMtVUU+lBrNcffPBB8thjjyVqxUFHljnnnDNZbLHFkrnmmitRg8vWOPpDn/I++OCDyV133dU5LwPl/OpXv6onkblWKxSSRx99tHNOxAsvvJC8//77ncPaIRP+Jptsskwc3wfYCuzJJ5/slBd5TD755J00Ue7ZZpvNWeay+P/73/9OXnrppYyYLj3KBNQe/O1vf+tsqYUtu3A999xzJ/PNN1/H9z2PxKfekCX0M0RPNTGdl9A3yCvut7/9bYJzKvbdd9/ulmKoF5yvMuGEE0qwwj7Ok/nVr37VjQ/9mnTSSbv3Phf6FmTf//73O/pz5ZVXdqIedNBBmfY4KM133303Qb1jKey4446bXHbZZZ3ySxw8D9mCLDae2NrtjTfeEHE6W8XlbbeofkaTZ555phsHZ45IO9XT22qrrZLf//73nXA4Awbn1ojT4+BZ3hZkDzzwQHL//fd3eAJ6Am6QtiBphvjQi4ceeqjzB5kXWGCBDi9jqzwfp37Yk9dee60TFNs1YYs53UHe++67r6vXefIWxU2XA/nPNNNMnd8YXRbbNbgWMgIDtSqtgyfaqTKM2oIPfIatw/CbAs7DH3gXeOAPdYT27XJ1lxu6DlmxTSF4cd55502wJeIcc8zhtc2ojneMenfh0vRzlA0Obb2M4xYA3AKAWwCM0BYAZRq7JS7bP9s/2z/bv4UaanlE/iH/kH/IP7WQjSUT8g/5h/zjzz8YdciMOFx77bXJmmuumWlel1xySbLxxhv3PcdgEw5th3vxxRcTNYO+M+iKQSnTwZBy8sknZwaIXQd2m/HlPu9MGMi/xx57dAwdNjkmnnji5Itf/GJy6qmndgbwJF3Tt5UXA6kwDGCgZs8990yOPvrobjQMLIOAbA4DfzgTAgYmGIZsDkYhDNwecsghyXTTTWcLYn12zz33JLvsskty7733JjCG2NznP//55IADDujUnww2Sbiy+N99993JUkstJcl1fZcedQP87wL6AyzVljx9g+N6OGCDQUMYMoDRIGertxh6OihPefe9730v+elPf9q5hZEQhhYYKTEAikFvcWeddVay5ZZbym1hP7YBBmfILLLIIgmMCXAYVFZG2sTUmc5Ly78zzjgj+da3vtV5o1audIwQ8MWhfYQYYGLjiTYP/hD39NNPZ4wJ8k58yAzOEIezefbee+/O7emnn55st9128srpH3HEEQmMW+JMA4zapi5ZddVVkz/84Q8J6uDPf/6zBO3zcX4POFQ38vUFMG7OPPPM5MADD0xggLA5GLPB6eAmGCZcDobEr3zlK93XH374YUevIS+4B8YXm1tppZWSU045JSNvUdx+85vfJBtuuGE3K+Srtrnr3usXH3/8cfLDH/4w+fnPf9418Ovvcb3uuut2+BY6n+fuvPPO5IQTTkguvvjiBOW3ObR16Bc4Vc4D0sPVUW785kFHjzvuuATGIpvDxIiVV165gw2M8y4Xu95d+TT9XPgNBic6IkAEiAARIAJNI4BJTLZv2KblYv5EgAgQASJABIgAESACxRGAAabvTw2cW9dOXXfddX3hEE8NXKSqg5iqmeqpmk2deW+mja2Ynnjiib701SBZbjw9HdeWZO+880667bbbeqelBsjSG264oU8W/QY46PniGtsyYUsptTIg804NLOvRu9dHHXVUJqyZrn6Pc0OUoaYb33WhDidP1eBqqmbwe6evBhpTNWu7L8my+KvBYmv+Lj3SM8f5HtNMM401vo6Jfo0zah5//HE9mb7rqvS0LxPLjRqoT5Whp1sWcxsqZaTqvlthhRUsKYQ/ir0F2c4775yqFVGpGkjuyoozXXwdyiV1pYwdnbNN5B4+MPJ1VeCpBuO78kEeZYDJFUcNyvbFUYPb3TinnXZa3zu9rPq1MsB04+DC3IJMrZxJL7jgglQNjOemhzDK2NqXnnmjBt5TtRovNy2RUa3cSJUh1Uyme6+f64M4ymiaqpVX3vIqI3E3LVwUxe3Xv/51X5mUAaYvXblRq9vS5ZZbri+slNX08RumDFAS1er/8pe/7PzWmXFd95/73OfSW2+9NZNW1eUGLy677LJe5YbskBMyuVzsenfl0/RzqceycoArmnTMn/hT/5pDgO2P7a857UtT6h/1j/rXHAJsf2x/zWkf+Z/tj+1vlNqfGnfoN77g3jVwjgElW3i1LVmqtjWxvrOF32ijjfowKmsAQGJq66NUzdZ3yqAPKOsywaCiZiX3ySM3t9xyizU9tR1RqmbEZ97ZDDDmgK+e96BrpG8aqkQu+DC+LL/88hkZBqUp7xZeeOEUxipxZfEvaoDZZpttCsmPcqhtmdLf/e53UoQ+vyo97cvEcoNBWsEYvtqeri+UqQtqVVTf+yI3sQ0wYtxU26Z1y4I8fBwGf6X8OEcGg/SXXnpp9xnehRhgqsDTrIOyBhi1vVOqVkV0/nTjiVpd0H2O96ZxwzTAwOAKnQZGalVGqlYvpDfffHN64YUXpmrlTKpWvPThqFYoOqsEbVttzdUXfo011kiB51/+8pcOr1x++eWpWl3UZ7wFR8IQZHNmm1IrdlLwHeRVK2M68oIvIbNa8ZKCY0QX4JvyFsXNxwADA7NuCIWBBb85MITjtw2GI5xNJPJDPvwOIG2bU6tAUjUTtVseGC1gXMVzcN+f/vSnjsEcOOhlxu+R2nKsL8kqy237XVp//fVT6LzaJjNV21OmagVRqrbGS2Hk12X9yU9+0ien3MSud0l32HzBoqxc/ADgB0BZHSoTn/pH/SujP2XjUv+of2V1qEx86h/1r4z+lI1L/aP+ldWhMvGpf9S/MvpTNi71L0z/1LiDvwHGHDSUuBiMkmu1TVSKAVusUrAZKRAOA2IYuBKnzptIMfMef/rAmaSptm7qvkeY888/X6J2fbUlUFcGiYdBs0MPPbRzkDhWrWAACvHlvfhqq6hU7Y/fTUsu1PY6mbCIo7Y3sz43DTAwTNlWp6gzczoDYa+88kqKmdonnXRSd/BVZIKP1QSQ2+YwqKuHlet55pknVVuNpWo7r87MZgwEyzvd1wdEy+JfxAAD+XR55BqDwN/85jc7mGCA8+CDD071lSMSDj6MfmoroAw8VelpJiPjgT7zfOmllzbeph2jl9ofsVtutXVTJkzog9gGmO23374jgm44gWEAq2LynNoerlu2TTbZpBMcA756nYUYYKrAM7YBRsdEH9RWWzHqrzLXpo6qc3NS6IbaMiwTFg/U+SspVg/qWJqrSiQiBtglHLgWg+suHkEaM8wwQzc8eNvmYJiRNOHDwAN51VZ6tuAdeU0jkEveENx8DDD/93//15UVuouVRTYHg8W0007bDQs5TIMJ4ul6iN8016obhMVKGh2nvfbaC4+tLna51baB3bxhUDryyCOt+eIhDHF6/eA30Fb2KuvdKVwDL6TOymbNDmhYB7Qs3mZ84k/8TZ2o8576R/2rU9/MvKh/1D9TJ+q8p/5R/+rUNzMv6h/1z9SJOu+pf9S/EH1T4w7+BhjMorWFxyAfjB3q/Ie+vNXZESm2trHFUecc9IWVG3VWSSb8jjvuKK+tPmaxY8a9mY9rZYvNWKPOcsmkrfb8z6SJPNQh553nmFUOI4E65yNVh8ZntjM7/vjjrfFtK4wwWGbKj/vnnnsuIxcGw6eccspM+IUWWihVhy73hcfAqzozIRMWaZsrNBCxCP6hBhgMwttWK6mDzVPMrDcdjCyureUwq910deipmScGZfX6w/ZbNqcPkqK8IQYJW3pVGWCAub41nDp3xJZ99xm2IdQHdK+55prOu6IGmKrwHFYDDHTHpstdgNWFubXeOeeco7/uXMOoqxv5vvGNb2TCmA/OPffcPt3FqgfT2YzRrlUTEhfcqLeJs88+W171+TENEeBLfSWSufVbX8bqRjc0QlZTRvy26GWQFWJmOnKvzp1J1UH33TjYBs3lYpb70Ucf7Vulk/ebCZmwglAvm761nshcZb1LHsPgCw5lZWEHnB3wsjpUJj71j/pXRn/KxqX+Uf/K6lCZ+NQ/6l8Z/Skbl/pH/SurQ2XiU/+of2X0p2xc6l+Y/qlxB38DjGugHWnA2GBz5hYmkh+2RrG5IgaAzTbbrG8gCXnA8IPBMJvDFj3mShvMQH///ff7gg8qL2b4YxuwQW7XXXdN1QHR6VxzzdWZaY3Z09i+xibX888/nykDynH11VdnssDWQYKj7sPwYHPY/kgPJ9fq4PtM8CL4u3CyGZqQoWvLM9fsf8SBIQmrq0R28YEnVhrpziUP4sTSUz0/XGNgVmRCPWNLPJu7/fbbu+EQ/he/+IUtmPezqgwwEADbNEmZllxyyYEyXX/99d2wM844Y1fHixpgqsJzWA0w6iD09IMPPhiIMX7cYOyWOsHqPtNhVZW8x+qPF1980QySuUfbwtlQEm+11VbLhDFX7MDYZvKlGQltQJf3kEMOMYN07mMaInbaaaduOTApwDzvyhQAhkYYQrF6ESsTzXObYOyGoQLblv30pz8duPpF0ta3VoSx3uVilhuGNqk/+INW6Yg8qHfoncSDUR+GVN1VWe96Pk1fCwZl5WAHNKwDWhZvMz7xJ/6mTtR5T/2j/tWpb2Ze1D/qn6kTdd5T/6h/deqbmRf1j/pn6kSd99Q/6l+Ivqlxh/IGmOmmm27g4KE+I1jyw4CfzRUxAMB4IumK/+1vf9uWfPcZzlmQsOJjxrbuXAP52FbshRde0IN6X2PQy+ZglNHPGRCZfvzjH2eC2wwR2HpskMPKC2wvhLM9MGiPraZsM+6L4O/CyWWAseUxxRRT5K4GgbyCi+771ltMPdWxxkCzPpi69dZb668z1/p5HoNmyGciWh5UaYDBeRU6zvfff79Fgv8+0o2g++yzTzdcEQNMlXgOqwEG22b5uEkmmaRbJ7JdnB5viSWW6L7HGVG+DisSpa5huDF5yhyIh6HDx8FAKuna5EUaetvJ27otbwsy3ZC0yiqr+Iho3cbQK6Ij0I9+9KNumVH2V1991RoyZrn1M9gWX3xxa362h/q2gZDVNNhVWe82eZp4BiOb6GjZ/NkBZwe8rA6ViU/9o/6V0Z+ycal/1L+yOlQmPvWP+ldGf8rGpf5R/8rqUJn41D/qXxn9KRuX+hemf2rcobwBxpw1bFaibQssrECxOdvg/KDtVHB2i60MmK08yNm2ITNXR7gMC67VO4Py83knW5vp5cEqBN1hxrbNUBPjPBHkE4o/4rhwshlgYGjStwiSsn5TnfuS5x577DFrXZvbx7nkiamnuqzYnkvKAR+rXAY505D0wAMPDAo+8F2VBhhkrJ9/4cLv7bff7jvDCPUkrogBpko8h9UAg7NDfJx+Xgvq3nT6yj6XwcOMg3tzGzKcOaM7cyDeZrzVw8t1nrwIF9MQoXPot771LRGjVv+4447r4wPbNpKxy61vO7fFFlt4lxcr8HTuQj3rrsp61/Np6hrGF6xSBQauSSEhsrEDGtYBDcHWJyzxJ/4+elJVGOof9a8q3fJJl/pH/fPRk6rCUP+of1Xplk+61D/qn4+eVBWG+kf9C9EtNe5Q3gBjGi5MAWwH32PQzeZCDQCYlW8rA2ZxIw/Xn+3MmD322KNPJNdA/kEHHdQXzucGZzNgG5vDDjss3W677dI111wzXWmlldIVVlghxYHtmLVsM6yYBpjHH3/cWl7X9j4+sulhQvFHXBdONgPME088YZUfB4fnOayMsNW1aaBzyRNTT3VZF1544a5cWN2S5zC4Pf7443fj+K5+sKVbtQHmtNNO68qJLYr+/e9/Z8Q45ZRTumGgz7orYoCpEs9hNcBcdtllOmzOa2yTJW3ANMDoM/kRBivesMLB508/mwhxze0MzYH4Sy65xCmj/mKQvBIulgEGhkDBBr6+EkvyKuvj8HqcLbbffvulm2++eYpVRjh7C+0eW01iSy9saabLUbUBBlsw6vmZvxmDynzVVVf1xb3gggv6gldZ730ZNXBjGl9wX9axA84OeFkdKhOf+kf9K6M/ZeNS/6h/ZXWoTHzqH/WvjP6UjUv9o/6V1aEy8al/1L8y+lM2LvUvTP/UuE15A0ze4CEGq8x8YhlgzAFeM5+Qe5zrojvXQD4GpX0dziDAygEYhEJkkbA470V3OBNG3um+69B3Pa7PddUGmCuvvNIq/0knneQjXt8B41L+VVddtS+uq95i6qlkaB5S7bsyYIMNNujigFn7RYmragMMjF767PqLL75Yit719VUyGJzWndk+//Wvf+mvM9dV4zmsBhjbWU8ZcNSDQQaNe++9t6tT0jaK+qaBxRyIjyGvlC+WAQbGEb28easgJX8fH2eZwWiup+97/eyzz1qziFVuGMt0WXw5CEKZXGlueVllvVtBqelhFcYXiF6Ux2MVm/mHdYBj4S7pEH/iL7rQhE/9o/41oXeSJ/WP+ie60IRP/aP+NaF3kif1j/onutCET/0bLf1T4zblDTC2lQ668mF1g5lPLAOMOaBq5hNyj4Fk3ZmDU5LWFVdcoQdzXmPgDWebSLwivmmAcZUXq2tiuKoNMDAU2XDwlV/f0kjSWWCBBfqK7qq3mHoqGZqHX8PQBoNF3p++AgblOOOMMyTJIL9qAwyEwfZwgvVaa63VJ98jjzzSfTfxxBOnMNjoLtQAUzWeZvt5+umndXGt1/hRk/LDP/zww63hQgbUqxjYvvHGG/vk1GUOvTaNF1XIKyCG4DboDJgbbrihr/yxjNKobxM/rFbEypfVV1893XjjjdMtt9wy3XbbbVOsxltxxRX7wldtgDGN8iHlNldUfv/735dq6fhV1ntfRjXeVGV8QRHYAR6tDnBstWP9s/5j61RIetQ/6l+IvsQOS/2j/sXWqZD0qH/UvxB9iR2W+kf9i61TIelR/0ZL/9S40mgbYK655pq+wS4pz0YbbZTiMOSQvxNOOKFP14sO5CMRbNWErcVEHt3HAB0GODE4ffPNN6e///3vUwx06QOREt40wODAeXmn+6bsfQUJuKnaAHP99ddb5ce5CXkOB4Pbzo9Zd911+6IWrbcQQyEyfPPNN1PbVnZ6vfheL7PMMn1l8L2pwwBz2223devsU5/6VPrCCy90xcOArZQRg9CmCzHA1IHnWDbAmIPpe+21V4rzhYr8YVsr3VU5EK/z3m677aZnm7keZIB5+OGHu7oIncR2j2UdVr7oW0PiGltQ/uMf/3AmXfcZMObKH5eB0CawWa/mNo3m+5grn2zyVP2sSuMLZGcHeLQ6wLH1jfXP+o+tUyHpUf+ofyH6Ejss9Y/6F1unQtKj/lH/QvQldljqH/Uvtk6FpEf9Gy39U+NUo22AMQcdpTw+A/p5il10IB/pmodai1w77LBD+sknn2Sy/vDDD63GBXM/f33FgaQJf//998+kWeRB1QaY559/vm+QVMqw995754r7xhtvWOP6nt0TewXMT37ykz55sOoFq0B8/0zjDQZSQ10dBhjINPfcc3fLKgPbH3/8caqvSIIx0XQhBpg68CxigMH5TaKn8F0D3CGGhCoGtj/44IN0nHHG6cpqtguzbkLuq5BX8g/BbZAB5r333uuWHfW06667ShaF/cUWW6ybJlatwSCT54444ohuHMhR9Rkw5tk32PLS11166aV9ssLAr7sq613Pp47rqo0vKAM7wKPVAY6td6x/1n9snQpJj/pH/QvRl9hhqX/Uv9g6FZIe9Y/6F6IvscNS/6h/sXUqJD3q32jpnxofGm0DDFaaYFa+WQ7M/i7ryhhgMPhpyoT7J5980irWn/70J2t4cwWMq7xbb721NV15iK2WMHh4zz33pI899liKs2kwcGe6qg0wWMWinykiGJnn75hy4d4860DimmfyFK23kBUwKAcO3RYZcDaHzbBmK4c8e+KJJ/oGzHfaaSd55e3XZYCB0UXKuuSSS3bk07e8mmOOOVJgYjpfA0xdeJoGGBhw85x5Lo0YoMx4IYaEqga2dYOYT5syy+C6r0pe5BeC2yADDNKaaqqpunq66aab4lFhB67Vtwr84he/6JUWjOzSVuBXvQUZhJp88sm7eYaU+5RTTunGg6xYLaW7Kutdz6fq6zqMLygDO8Cj1QGOrXesf9Z/bJ0KSY/6R/0L0ZfYYal/1L/YOhWSHvWP+heiL7HDUv+of7F1KiQ96t9o6Z8acxl+A8x22203UAdnnXXWvkEklGnllVceGMfnZdGBfKS92mqrZWSC4cHlzNn/Ui+mAQbxZ5999kzaGHj86KOPXMmnm2++eSYOzqcxjQY2A0we/qE4LbroohlZgI3NIKQXaOedd87EA07Ywk13ofJI3BADjHnexAEHHCDJBPnQU6nrSSaZJMUs/hBXlwEGBjvZigmrLHD/7W9/uys7tvqzOV8DTF14XnjhhV2Zgfvdd99tE7vv2dlnn90XZ5gNMCussEJX1vnmm6+vHGVuqhyIj2mAWWKJJbrl9zWKnn/++Sn4F+cwXXXVVV2Y7rvvvm5a0BWXjncjqAusCkO+0qbh12GA0Vfq4PfBZgzV5ZTr7bffvk9W8wynKutdZKjar8v4gnKwAzxaHeDYusf6Z/3H1qmQ9Kh/1L8QfYkdlvpH/YutUyHpUf+ofyH6Ejss9Y/6F1unQtKj/o2W/qnxoeE3wKy33noDdXCXXXbpG0SSMrm2dIKhYsMNN0zXWWedFCtHsP3VMccck5n9W3QgH8KutNJKVpkefPDBTFmwOmWaaaaxhscAmelglJEy6r65fYzEg2FDnxkucYCB6WwGmDz8Q3E68cQTrfKbB3/rsqEMn/vc5zLxFlhggRTbt+kuVB6JG2KA2WCDDbqyYAWWa5shSdvlm1vVmat5XPHkeV0GGOSH9iK684tf/KI70AyDjKv8vgaYuvC84447umVAWSBfntONZIjjY4DJ2waqqoHtgw8+uK98ukFhUDmxKu7KK690DiBXJS9k0g0webjlrYDRzyRCXeVtOwhDxXTTTdfFTOc6GHZF3+GfddZZgyDsvDNXWCEe+N3mYpYbv2G6rFidludg7NU5FYZx01VZ72ZeVdzXaXyB/OwAj1YHOLbOsf5Z/7F1KiQ96h/1L0RfYoel/lH/YutUSHrUP+pfiL7EDkv9o/7F1qmQ9Kh/o6V/asxmuAwwyy+/fN9AEuTDQNXLL7/s1EOcDYLVA2ZZsFUSzm8wHVYrmGEnnHDCzCBy0YF85Lfjjjtm8kCe++23X584r732Wjr//PNbwyL8qquu2hceNxhUshlUYMTBQdS6wzY62IrILC/ur7/+ej1o57oI/qE4YdXN4osvnpHp05/+dHrxxRdnZHrxxRdTfYa3lAUD/+bqF0QOlUcy9DXAYPXHeOON15V/7bXXliSC/ffff79v+yDZ3ss3oToNMLoxZZlllumWH6u9XE6Pg3r717/+lQlaJ57IS/QH/rbbbpuRR3+AAXw9PK5dBphJJ520G3bLLbfUk8lcVzWwjcPhdWMuVsSYq9xMYWCEAM+gbODB3XbbzQySViUvMgrBLc8Ag98C3bCx1lprDSy/eQbK6aef3i07uFmv+z333LP7znaB1VVYJaafw4P4LmNIzHK/+eabfcaU9ddf3yZi3zNz+7Grr7667z1uqqz3TGaRH9RtfIH47ACPVgc4ssqx/v/J+o+tUyHpkX+ofyH6Ejss9Y/6F1unQtKj/lH/QvQldljqH/Uvtk6FpEf9Gy39U+NDw2WAwcClTSYMDG6xxRYpBsltA2E4GNsWb6aZZkpxHgy2mcEWMliZIlsp6eH32WefjJ4XHchHQieffLJVHuQJY8K+++6b4kwBXRZb2THQj7APPfRQCkOEOFf6OAvgG9/4RopVJvvvv38677zzWuVYd911Jak+3yYDZB6EfxGccOaNOVCJfLCaBIOmqKujjz463WyzzdKpp57aWoZtttmmT3a5KSIP4voaYA466KA+eTAoXMaZW6vde++93snVaYDBSiNbXZx33nlOeX0MMHXiCWOEfk4KdO6SSy6xyg/ZJ5tssnT66adPsV0fwuLvkEMOsYbHaiwJg22gzJVZeqQqB7aPO+64rhyQZ4011kj/9re/6dl3r/GDjTYmcsPHdnCmq1LeENzyDDCQG3ypl2ejjTZKP/jgA7NIKc720Y0gMGrDkKE7Xd9h5Het9Lrooos6RlmcGWPif+yxx+pJdq9jlxt8r5f7W9/6VmdLtG6G2sWZZ57Zd74Nfhdtrsp6t+UX61kTxhfIzg7waHWAY+mbpMP6Z/2LLjThU/+of03oneRJ/aP+iS404VP/qH9N6J3kSf2j/okuNOFT/0ZL/9R4zXAZYMxZuTb5sE2W6bCSQN//3xbP9Wz11Ve3DpwUHciHbJjprx/S7spbnsPogK3R9Nnb8k58/ZwRnDWAgVV5F+Jj0N7VUIvgXxQnDGTrBqiQMiy11FKZwVLRiaLy+BhggDuMeiLrtNNOO3CgXWQa5GOrPEkPPg7x9nV1GmAgk7n9HQawbataRP48A0wTeJo6jvOHsBLmZz/7WYot4bBKTW9bWAUz99xzd+sIBiObw5Z+ej1iQB91CQMbtknUXZUD21j1Zq4ww7kkWJWHLbKuueaaFAPwWOmiH94O2XFWlM1VKW8Ibj4GmLfeeitzTtYss8zSKRu2mgSPYtWaXlcwnNxyyy2Zoh9//PF94YAXjMOXX355Z/s6nB2z9NJLd8MceuihnRWKunF5yimnTI844ogU29/phrDY5cY2jfPMM09XFpQPPAl9vuyyy1JsUYkt6mB818sO/b/zzjszZceDKuvdmmGEh00ZXyC663c1QrG8kmD+o9UB96rUgECsf9Z/gLpED0r9o/5FV6qABKl/1L8AdYkelPpH/YuuVAEJUv+ofwHqEj0o9S9M/9Q4zHAZYGCEWHDBBfsGiEwZbQYYaBJmnGMWsL49lBnXvMeAo2umetGBfNFqDOhNNNFEA8sCeWB8kQPosRLHlFHudQMM8sDWQSeccEKKATQJM8gHLoPOWUGaRfAvgxMG/vSZ4IPkxzuUFYOeGLh3uaLy+BhgMPCqy4jVVTEcth6TdHEuA7aS8nF1G2CwEkvkhJ9nLMozwDSBJ3Rcx1svj36N1VgYsIdbeOGFu+X+4Q9/aK0ac7BaT2uhhRbqi2OGtW3/1Bfhfzf6Ae+oe5eDEQa6iTLocgy6hnHNtV1ZlfKaaesymrj5GGCACfh044039io7jN6u813AM7ZtGXUZ5RqGDnAynCtv3chTRblxrgvONROZ8nyU7YknnujIbPtnyhhbT215lnnWpPEFcrMDGtYBLVPXtrjEn/jb9KKuZ9Q/6l9dumbLh/pH/bPpRV3PqH/Uv7p0zZYP9Y/6Z9OLup5R/6h/IbqmxmeGywAD4XFOgzk7GHJiMHHWWWdNt9pqq4FlxAA8jBrmVkNSVsx2xrY7t99+e246Ekf38w521hPFAczmjGNJCytksD2NPuiJlTw4iNpcGYJBQtcB7RhAwzY72PZIn3kt+cAI9JWvfCW97bbbdNGc16H4FzV4iAAYLMaqAswkt60AguFovvnmSzHg/NRTT0k0p19UHh8DDPRKcIX/+OOPO+UIeWGuysBKBR9XtwEGMunnv2AruUEuzwDTFJ4wwmBVwsQTT9xXn1K3ODvluuuu6xbtC1/4Qjec7YwUCYiVJfrB5kgPvGWe5VTXwPatt96afulLX7KeGQXZwA3Y2lE3DEhZdL9qeX1x8zXAiOxoR1gZiS0UpW7Fx5lTO+20U/rqq69KcKsvumIzdINvV1lllfTKK6/si4s011lnnT4+hgxYBaO7qsp9wQUXpMstt1xGF1H2CSaYoGNQPOqoo/p+e3S55Lrqepd8YvhNG19QBnbA2QGPoctF06D+Uf+K6k6MeNQ/6l8MPSqaBvWP+ldUd2LEo/5R/2LoUdE0qH/Uv6K6EyMe9S9M/8YB6GpQZijd66+/njz66KPJO++8k8w555ydPzV4FCSrmgmdqIPpk2effTZRh1MnagZ5orajSdRgWlA6ZQOjDGqwPnnyyScTtW1TogxJiVrJk6gBPGvS6syCRBlvEjWjOVFbGSWzzTZbogZyrWH1h6oBJI888kgnL2XMSNT5FZ181ECzHszrOgb+XhlpgaCOL7zwQqfO1NZWyfzzz5+o7Z8SZTTTQvGSCMRBQBk/k+effz5RRsxEHeCeTDfddIkyjHbaZ9Ec0HbBW0gP7RxtVw32F00uWjy0Z3Dhyy+/nKit8xJloO7IVjcXugpUJW6oZ9SxWsGVgAvVVl2dsitDt0uczHO1GqbDyY899lgCnp1xxhk7ugKOdTmEg36Bw9V5MtZgVZYbfIr8H3zwwQTyq9WGyRxzzJGElNsq9JA9xO+8MjQmajvHZJFFFkmUQTFR5zfVLiV+s5psT8yf+FP/6u3b6yTD9sf2x/bH9qdzQp3X5B/yD/mH/FMn5+h5kX/IP+Qff/4ZagOM3rB5TQSIABEgAkSACBABHQHd+KK2rEvUSs9GjC+QiR8g/ADhB4j/B4jejmNcs/2x/bH9sf3F4JIiaZB/yD/kH/JPEe6IEYf8Q/4h/4wO/9AAE4P1mAYRIAJEgAgQASJQKwK68QUrX9QZNZ2VXbUKoWXGDyB+APEDaHQ+gLSmG+WS7Z/tn+2f7T8KmRRIhPxD/iH/kH8KUEeUKOQf8g/5x59/aICJQjtMhAgQASJABIgAEagLAdP4gm3HsNUfO4D+HcDYdcUPMH6Asf2x/cXmFd/0yD/kH/IP+ceXL2KHI/+Qf8g/5J/YvOKbHvlntPiHBhhfzWY4IkAEiAARIAJEoHEEbMYXnPnCDuhodUBjKxLrn/XPARAOgMTmFd/0yD/kH/IP+ceXL2KHI/+Qf8g/5J/YvOKbHvknjH9ogPHVLIYjAkSACBABIkAEGkXAZXyBUOwAhnUAY1ck8Sf+HADgAEBsXvFNj/xD/iH/kH98+SJ2OPIP+Yf8Q/6JzSu+6ZF/Rot/aIDx1WyGIwJEgAgQASJABBpDYJDxBUKxAzpaHdDYisT6Z/1zAIQDILF5xTc98g/5h/xD/vHli9jhyD/kH/IP+Sc2r/imR/4J4x8aYHw1i+GIABEgAkSACBCBRhDIM75AKHYAwzqAsSuS+BN/DgBwACA2r/imR/4h/5B/yD++fBE7HPmH/EP+If/E5hXf9Mg/o8U/NMD4ajbDEQEiQASIABEgArUj4GN8gVDsgI5WBzS2IrH+Wf8cAOEASGxe8U2P/EP+If+Qf3z5InY48g/5h/xD/onNK77pkX/C+IcGGF/NYjgiQASIABEgAkSgVgR8jS8Qih3AsA5g7Iok/sSfAwAcAIjNK77pkX/IP+Qf8o8vX8QOR/4h/5B/yD+xecU3PfLPaPEPDTC+ms1wRIAIEAEiQASIQG0IhBhfIBQ7oKPVAY2tSKx/1j8HQDgAEptXfNMj/5B/yD/kH1++iB2O/EP+If+Qf2Lzim965J8w/qEBxlezGI4IEAEiQASIABGoBQHd+LLQQgsl1157bTLZZJPVkjczIQJEgAgQASLQJALjjjtu8sknnzQpAvMmAkSACBABIkAEiAARiIgADTARwWRSRIAIEAEiQASIQDkEdOPLIossktxyyy1exhfOwAmbgVOulrKxiT/x5wxMzsDMMkM9T8g/5B/yD/mnHrbJ5kL+If+Qf8g/WWao5wn5Z7T4hwaYetoFcyECRIAIEAEiQARyEChqfEGy7ICOVgc0RxWCX7P+Wf8cAOEASDBxRIpA/iH/kH/IP5HoJDgZ8g/5h/xD/gkmjkgRyD9h/DOOwj2NhD2TIQJEgAgQASJABIhAaQRCVr5IZuwAhnUABbdYPvEn/hwA4ABALD4JTYf8Q/4h/5B/QnkjVnjyD/mH/EP+icUnoemQf0aLf2iACdVwhicCRIAIEAEiQAQqQ6CI8QXCsAM6Wh3Q2ArE+mf9cwCEAyCxecU3PfIP+Yf8Q/7x5YvY4cg/5B/yD/knNq/4pkf+CeOf6FuQsQLCKsBXsX3DEX/izx9g/gD78kXscOQf8g/5h/wTm1d80yP/kH/IP+QfX76IHY78Q/4h/5B/YvOKb3rkH/IP+Yf848sXscORf8L4hwaYyBpIBQxTwMjwcwb0v4g/OyDsgMTmFd/0yP/kH/IP+ceXL2KHI/+Qf8g/5J/YvOKbHvmH/EP+If/48kXscOQf8g/5h/wTm1d80wvlHxpgfJH1DBdaAZ7Jegdj/vwB4g8Qf4C8CSNyQPIP+Yf8Q/6JTCveyZF/yD/kH/KPN2FEDkj+If+Qf8g/kWnFOznyD/mH/EP+8SaMyAHJP2H8QwMMFTAqAmyAYQ0wKvgqMeJP/NkBYwcsNq/4pkf+If+Qf8g/vnwROxz5h/xD/iH/xOYV3/TIP+Qf8g/5x5cvYocj/5B/yD+jwz80wERmQBIgCZAEODoEGLn50wDGLfAStn+2/9i84pse+x/sf5B/yD++fBE7HPmH/EP+If/E5hXf9Mg/5B/yD/nHly9ihyP/kH9C+IcGmMgtkA2QDTCkAUZWPxoAaACgAeAz7IDG5hXf9Pj7x98//v6Rf3z5InY48g/5h/xD/onNK77pkX/IP+Qf8o8vX8QOR/4h/5B/Rod/aICJzIAkQBIgCXB0CDBy86cBjAYwGsBoAItNK97psf/B/gf7H+x/eBNG5IDkH/IP+Yf8E5lWvJMj/5B/yD/kH2/CiByQ/EP+CeEfGmDYAKMiQAIiAYUQUFTlU4lR/6h/1D92wGPzim965B/yD/mH/OPLF7HDkX/IP+Qf8k9sXvFNj/xD/iH/kH98+SJ2OPIP+WeU+IcGmMgMQAIgAYwSAURWfxpAuAKEK0C4AiQ2rXinx99f/v7y95cDAN6EETkg+Yf8Q/4h/0SmFe/kyD/kH/IP+cebMCIHJP+Qf8g//vxDAwwJKCoCJGASMAnYn4CjNj6VGNsf2x/bH9tfbF7xTY/8Q/4h/5B/fPkidjjyD/mH/EP+ic0rvumRf8g/5B/yjy9fxA5H/hkt/hlTBphxxhkntj4zPSIwZhFI0zR62fgD0NwPAPkvujozQSIQDYEq+NYUjvxL/jV1gvdEoA0IgF/Jf+S/Nug6y9g+BHz6j+S/4vzH7+f2tSmWmAiYCPjwrBlH7kP5lwYYQY4+EWgZAmWIxgVVKAG50in6vM35swNZVGsYjwhUj0AVfGtK3Wb+AxZNlp/8a2oj74lAfQiAX5ts/yhpm/Mn/9Wn68ypfQj49B/bzD/QiDLlJ3+1r02xxETARMCHZ804ch/KP2PSAFMGQAGSPhEYqwhIR6OKdhJKQLExbnP+VdZr7HpiekSgLQjU2S7bzH/QpybLX2c9t6XtsJxEIA8Bvd012f4hZ5vz1+shr874nggQAT8EQtpVm/kHaJYpfwjOfjXHUESACIwKAjHafyj/0AAzKtpBOYlAJARiEI1LlFACcqVT9Hmb86+yXovWB+MRgbYjUGe7bDP/Qc+aLH+d9dz2NsXyEwFBQG93TbZ/yNPm/PV6kLqhTwSIQDkEQtpVm/kHKJcpfwjO5WqUsYkAERg2BGK0/1D+oQFm2LSA8hCBihGIQTQuEUMJyJVO0edtzr/Kei1aH4xHBNqOQJ3tss38Bz1rsvx11nPb2xTLTwQEAb3dNdn+IU+b89frQeqGPhEgAuUQCGlXbeYfoFym/CE4l6tRxiYCRGDYEIjR/kP5hwaYYdMCykMEKkYgBtG4RAwlIFc6RZ+3Of8q67VofTAeEWg7AnW2yzbzH/SsyfLXWc9tb1MsPxEQBPR212T7hzxtzl+vB6kb+kSACJRDIKRdtZl/gHKZ8ofgXK5GGZsIEIFhQyBG+w/lHxpghk0LKA8RqBiBGETjEjGUgFzpFH3e5vyrrNei9cF4RKDtCNTZLtvMf9CzJstfZz23vU2x/ERAENDbXZPtH/K0OX+9HqRu6BMBIlAOgZB21Wb+Acplyh+Cc7kaZWwiQASGDYEY7T+Uf2iAGTYtoDxEoGIEYhCNS8RQAnKlU/R5m/Ovsl6L1gfjEYG2I1Bnu2wz/0HPmix/nfXc9jbF8hMBQUBvd022f8jT5vz1epC6oU8EiEA5BELaVZv5ByiXKX8IzuVqlLGJABEYNgRitP9Q/qEBZti0gPIQgYoRiEE0LhFDCciVTtHnbc6/ynotWh+MRwTajkCd7bLN/Ac9a7L8ddZz29sUy08EBAG93TXZ/iFPm/PX60Hqhj4RIALlEAhpV23mH6BcpvwhOJerUcYmAkRg2BCI0f5D+YcGmGHTAspDBCpGIAbRuEQMJSBXOkWftzn/Kuu1aH0wHhFoOwJ1tss28x/0rMny11nPbW9TLD8REAT0dtdk+4c8bc5frwepG/pEgAiUQyCkXbWZf4BymfKH4FyuRhmbCBCBYUMgRvsP5R8aYIZNCygPEagYgRhE4xIxlIBc6RR93ub8q6zXovXBeESg7QjU2S7bzH/QsybLX2c9t71NsfxEQBDQ212T7R/ytDl/vR6kbugTASJQDoGQdtVm/gHKZcofgnO5GmVsIkAEhg2BGO0/lH9ogBk2LaA8RKBiBGIQjUvEUAJypVP0eZvzr7Jei9YH4xGBtiNQZ7tsM/9Bz5osf5313PY2xfITAUFAb3dNtn/I0+b89XqQuqFPBIhAOQRC2lWb+Qcolyl/CM7lapSxiQARGDYEYrT/UP6hAWbYtIDyEIGKEYhBNC4RQwnIlU7R523Ov8p6LVofjEcE2o5Ane2yzfwHPWuy/HXWc9vbFMtPBAQBvd012f4hT5vz1+tB6oY+ESAC5RAIaVdt5h+gXKb8ITiXq1HGJgJEYNgQiNH+Q/mHBphh0wLKQwQqRiAG0bhEDCUgVzpFn7c5/yrrtWh9MB4RaDsCdbbLNvMf9KzJ8tdZz21vUyw/ERAE9HbXZPuHPG3OX68HqRv6RIAIlEMgpF21mX+Acpnyh+BcrkYZmwgQgWFDIEb7D+UfGmCGTQsoDxGoGIEYROMSMZSAXOkUfd7m/Kus16L1wXhEoO0I1Nku28x/0LMmy19nPbe9TbH8REAQ0Ntdk+0f8rQ5f70epG7oEwEiUA6BkHbVZv4BymXKH4JzuRplbCJABIYNgRjtP5R/aIAZNi2gPESgYgSEaP7xj38E5/TZz352YJxQAhqYWIGXbc5f6jVN0wLIMQoRIAJVICDtsgq+NeVtM/8BiybLL/VM/jW1kvdEoDoEpN2BXz/44INkwgkn9M4srz/rndD/AjbJPxChyfylHsh/oVrD8ETAjYC0K5/+o8l/sfnNLeV/3zTJP5CgTP6CM/krr5b5ngiMPQSk/fvwrFl64dlQ/qEBxkSS90RgjCMQg2hcEIUSkCudos/bnL/UKzuQRbWH8YhAfASkXZbp2PlK1Wb+A0ZNll/qmfzrq60MRwTKIyDtjgYY8l95bWIKRGC4END5LU8yGmD+lXzmM5/Jg8n6XnBm/80KDx8SgTGNgLT/Mt/pod+f4/zzn/8cM9OlJ5544o6CkEDHdDth4UoiIETzxhtvBKdUtHMTnFGDEcYdd9zkk08+aVCCYlmT/4rhxlhEoEoEyLdVojs8aZN/h6cuKEl7EBjL/DpKfVHyX3vaHEtaHwJjmd/qQzE/J/JXPkYMQQTGKgJN8CxXwIxVbWK5iIADASGaMpZeR9KNzkCGTKEWaFc5ij5vMn+pVxqgi9Ye4xGB+AhIu6yCb01pm+QfyNLm/KWeyb+mVvKeCFSHgLQ7roBpln+lHsh/1ek6U24fAtKufPqPXAHDFTDtayEsMREoj0AIz5q5cQsyhYgAyA6gqR68JwI9BKSd+HToerH+eyVEYz6X+zYPwAGDJssv9Ur+E22kHxOBu+++O1l22WUzSV599dXJGmuskXkeGj6TwBh5IO2yCr41IWqSfyBLm/OXeib/mlrJeyJQHQLS7miAaZZ/pR7If9XpesyU2T+LiWZ1aUm78uk/0gBDA0x1msiUh9pafQAAQABJREFUicDYRSCEZ00UZFw09PuXK2BMJEfo/vLLL0/uuuuujMS77bZbMvXUU2eeux789a9/Tc4777zM6y9/+cvJCiuskHnOB6ONQAyicSEQSkCudIo+b3P+Uq91fgC/++67ye23357ccsstyf3335/87W9/6/x9+OGHyQwzzJDMNNNMycwzz5zMNttsySabbNK5L1q3jNcsAvhgX2qppTJCXHvttcmaa66ZeR4aPpPAGHkg7dLnA9ossnTszOeu+zbzHzBpsvxSz3XyL8qMQZdDDjkkseWLLUP3228/BMt111xzTYfLcwMWDHDooYd2Yj788MPJr371K2cqMOautNJKzvfmi3feeSf58Y9/bD7u3i+66KLJxhtv3L2XC5cc66yzTrL88stLMPpDjoC0Oxpgxib/udqpqZaf+tSnks997nPJ5JNPnkwxxRTJ/PPP3/kT/TDDt/2e/bPR0ADRX5/+Iw0wo2eAYf+tWP9tUOvFFvL33XdfcvPNNyd//OMfk1dffbUzLoG+4iSTTJJMNdVUyTTTTJMst9xyySqrrJIsscQSCbb7pGsvAiE8a6Ik3+nB35/qoy2qw5kyTTkFCs6zaSr72vPdYYcdOuWVcouvDCpBslx66aXWdI455pigdBh4NBAQPVEdujT0L6+ETbZ/yNbm/KVe8+ooxvvnn38+3XnnndMJJ5zQyh0ii+6rDk761a9+Nb3xxhvT//znPzHEGPo01DlL6SuvvNL5U52/oZd3kIB//vOfrXWtDDDWaKHhrYmMgYfSBkK5FuFDXZv5D1g1WX6p59A6Kxv+wgsvtLZLkQft0MftvvvuA9OR9Ir6IsOvf/3rgfmstdZaEtTLV5OHBqa3+eabW9NxyXHsscdaw/OhPwJ1/u6JPoIvkW8Iz/qXyC9kk/wDCZvMX+rBDyn/UK52KvkN8pUxJlUTCVNw5Mcff+yfacUh62wfrqKwf+ZCZriei3778JrJf3WXpEn+QVnL5C84140Z+2/F+m+2elLGrPSkk05KZ5llloF9Qqlr8Wecccb0+OOPT99//31bso0/G4bfiyZAqLPcogs+PGuGEWxC+Se6tSJUABE8hi8AxkhrFNKgAWYUamn4ZJR2YpKIz31eaZps/5CtzflLvebVUdn3J598cvrpT386qIMjsomvZiSn//73v8uKMtTx1WqgdPzxx+/iBL4eZRf6wR4afpSxGSS76LwPv5phBqVre9dm/gMeTZZf6tlWL1U+W3fddbscIzLo/q677uqV/bAYYPDb8vbbb3vJjED4LdHLa17TAOMNZZSAdf/uSX2DO80BSJNPzfsoBdYSaZJ/IEaT+Us9aHBEuSxjgBGZ4GNQ7vTTT48iU5lE6m4fLlnZP3MhM1zPRYdN7rLdm/xXd0ma5B+UtUz+gnPdmLH/Vqz/ZtaT2g0o2PAidS6+2rEjVStmzKQbvR+W34u6Qai73KIDNl7NeybYhPIPDTCC3Aj6NMCMYKUNgcgxiMZVjFACcqVT9Hmb85d6LYpdXjysWtlpp50GDnaJDD6+2momfe+99/KyHdn3p556ah9WNMD8d4Wqa8XMyFZ0juDSFvI6cbb3OUlnXreZ/wBGk+WXes5USoUPXn/99XS88cbr4xmRQ3y11UL60Ucf5UoxLAYYyH3uuefmyosAmPGoth0aWH4aYLygjBao7t890XPwpzkAaeNU/Vm0Qv8voSb5ByI0mb/UQ2xMYxlgRL6NNtoo/fvf/x5bTO/06m4fLsFogHEhM1zPRW913nJdm/xXd0ma5B+UtUz+gnOdmLH/Vrz/ptfTOeecE7Qbh9S1zccEoF/84hd68o1eD8vvRd0g1F1u0QUXtw56LtiE8g8NMILcCPo0wIxgpQ2ByDGIxlWMUAJypVP0eZvzl3otil1evMMPP3zgQBfyx5YPK664YrrFFlukX/rSl9JZZ511YJyVV145L9uRfY/yS53ApwGGBphBnTjbu1DlbzP/Aasmyy9tPbTOyoQ/7rjj+jgGMuir7kSmK6+8MjebH/zgBx3+Boe7/mxpI49JJ53UGUfSEgF8BlQ32GADCT7Qv+qqqzLllzKLTwPMQAijv6z7d0/qGfxpDkDaOFV/FrvwTfIPytJk/lIPsTF18cVEE03UxzlqH/ZcLhAZ1Z7/jWFVd/tw1QcNMC5khuu56KzOW65rk//qLkmT/IOylslfcK4TM/bfivffpJ5uuOGGFNubS/3ZfPxWqPNL069//evpMsssk6qzEQeGV+eBpD59ZpGhSn9Yfi+qLKMt7brLLXrj4tZBz0X+UP6hAUaQG0GfBpgRrLQhEDkG0biKEUpArnSKPm9z/lKvRbEbFO/22293dnLQWdlzzz3TF154wZrEH/7whxQDaiKf6V922WXWeKP88OWXX07VobB9ZaYBhgaYQZ0427vQNtBm/gNWTZZfeC20zsqEX3LJJfs4BjKAi0UW8TfddNMy2XTjbrLJJpm0kQfOufJ1tgFVdTBqX7r4QFYHWuYmud122/XFs62GoQEmF8ZoAZr43RMdB3+aA5A2TtWfRSv4/xJqkn8gQpP5Sz3ExtTGF8jLdlYTZpTfdttt6WmnnZa6uErkXH/99VN1WHNscQem10T7cAlEA4wLmeF6Lvqq85br2uS/ukvSJP+grGXyF5zrxIz9t+L9N9QTzqKdaqqp+vqAUo/wsdrxkUceyfA8eB/PN9xwQ2fcySabLH3qqafqVIdMXsP0e5ERrsIHTZRb9MbFrYOeCxSh/DMOIqqMozn10ZSoj6do6YUkpAYCO8EjFylEhFrD7rjjjsnPf/7zTJ5//etfk/nnnz/z3PVADYAm6nDszOtjjjkm+e53v5t5rj946aWXEkVSyYsvvpioAdgE9a8OtOr8zTHHHEFy6OniWm0vkTz22GPJww8/nDz77LPJnHPOmSy22GLJXHPNlajBTTN45l5tb5SoDnnfczWDM5l55pm7zx588MFE7R2ZqAafLLjgglYcuoHHyIW0E0UowSVSs8wGxmmy/UOwNucv9VoF/6nZCMktt9ySqftpp502OfvssxO1nVjmnfnghBNOSL7zne/A6N/3atFFF03uvffeROTve2ncqH1BE/Cb6jwluJ577rmT+eabr+NPMMEERmj7rQ8vICY4R+0H2/HVsuQOPyy00EIdbrOlrLa1SPAHpw6GTvbff/++YGr2TXLwwQd3n6lBx0R1Hrv3PnIV5asYuN19992JmkXUlVcu1JZiyZprrim3XT80fDeicTHqvwOi11XwrQFVq/kPWDTJ/1LPJr+ZdRTrHhz4+c9/vi85td1Y8sQTTyTw1Rlb3XdqBmDy6quvJuCcMk4ZcpKLLrook4QywCTTTTdd5rntwW9+85tEffj2vQJ/XHfddX3PLr300kQNkvY902/UlpjJDDPMkLz22mvdx6uvvnqiZkR273GhDDCJ2tKs7xlubHLguRrY7fxO4Vp3PvyM8KG/G5KHLX3o1Oyzzy5BOv4dd9yR3HfffZ0+98QTT5wsu+yyHV7Oq1v990kSRD96ttlmk1urj779hx9+2PdOGbqSqaeeuvNMT7fI715fwgVupN2BX/FbMeGEE3qnktef9U7ofwGb5B+I0GT+Ug+x+S+0nep1duONNyZq29zkySef1B93r8EL4Ic8p86kSh599NHud646rDnB9y2+RfGnBuucSVTRPsrII4L69s8ef/zx5J577ul832NsR80gTxZZZJEEfeJQF0NuW57DPA5hkzfkmbQrn/6jyX+x+S1P7ib5B7KVyV9wjs1fLszYfyvXfwOu22yzTaK2C8tAjD4Axi/B/XnuxBNPTNT2u5k+DuKp8wWt/V2803kd93DD0J9iP/K/dRH6X9q/D8+aaQvPBvOPIpuoLtQCFDNzBUrHmhkzzWFOq8kVMFj2t9Zaa6VKaTuYC/amv/jii3cOPlSK6Q3lNddcky6wwALOGffqozNde+21nTPuJaOLL744I9sUU0zReY3zLMw9z7FMsQ1O6kgRTRr6l4dPk+0fsrU5f6nXvDoKfe+aKYf81GBQUHLKAJFpk5jtfOeddzrTwWFsqqOVqgGfTFwpM1abqA/h9Mwzz3SmIy9svIBtcsRhJQ9mxriWNWMZs+2Q6B/+8IdO+URO3TdXxNjkKsNXsXFz6YHrTJfQ8IK/+GPld0DqPJRrET7UtZn/gFWT5Zd6Dq2zouH32WefDN9sv/32neRsB7ueccYZRbPqxnPNKi+7AgYrdBZeeOG+8nzjG9/o5mu7wMpKwVz8Aw88MPMs1goYGz/H+N2QstnSR7nUB3UnCLbEUJMNMuVDGPz+YZWphJU0dX+//fbLxFUDFXoQ6/W8886biYctRsWV/d2TdIr6UvfgS3MGeB7nFs3TFa9J/oFMTeYv9eDCpujzkBUwtjyUsaSzLa7Ip/tqAs/A87HUhJd02223HXi+ANoewrg4MGb7iCGPYOTqn11//fWdIHi/0korZdo+8FOTnVLwKrD1cTHl1vMbhXEIXd4i16KveVxm478i+ZWJ0yT/QO4y+QvOZcofEpf9t3L9t+eee8663S7q8Ve/+lVIVaRnnXWWlefA7crwbk1rWPtT7Edaqyv3obR/H541w0jiofzDLcgEuRH0mzDAfPzxx+l6661nJStRYJu/9NJLp2+99dZAlN95551OR9YW3/YMA7LogLkcBgbNeCBUGF8OOuigzDsaYPINMi6s5XkoAUm8WH6b8xddj4WlpLPLLrtk2gryghE01KF+1EzpFIbZvffeO/3d736XqpnazmTUbOsUh0hL2Xx87B2qZu0501QzrTPpwZCMZclqxV06yyyzZN6b+eJsGzXTvC+Psh/aMfmqCtxcH+yxDTBj7XdAdMfstPnc9ymYx02b+Q/wNFl+qWePaiodBH0YtZI3w1PSH4KxReQRP8Z5W1UZYNZZZ530+9//fp/MMG6olRdOrMyt1tQK6fSUU07pSwNlj2WAqep3QwpoSx/yq9n7ne2W0HeVunT52NLENRA8rAMGUv6ivmABPqUB5p9FYSwdT+qhdEJGAmUNMEjuoYceSscbbzxr+1Er7Ywc/3t71FFHWcNLOU1fzYJN1QqwTFpl+4WSYCx5JD1Xf06tdE+BCb6HzTKa98stt1ynzUmaNj+23MhjlMYhbJiEPBPMffqLJv+F5BMjbJP9L8hfJn/BOQYOeWmw/5ZmtsoN7b+pHSas/KRW53XG+PLqQH+Pb3+1A441PbVrhx60ez2s/Sn2I7tVFHQh7d+HZ80wklEo/9AAI8iNoN+EAUZte2YlKVHeQT6IEYNrNvfuu++maqsFZ9quw1/xUXr66afbkkzRkbTJ88wzz6RYRWO+owGGBhirIgU8DCXggKRzg4o+5wYMDKC2/cu0FeSFD7gibpDBRU8Pq16kTKE+ZvbCuGNzt956qzVd7B+utm60vrPlj/1ldVf2QzsWX1WFm+uDPaYBZiz+DojumJ02n3tdv3yum+QfyNfm/KWefeqpbBhwm+QnPiakYGAKDqvfzD4TjMyYNVjGVWWAgdHcxn/4mHQ5rHiUssNH3/SnP/1p3zM8j2WAqep3Q8qHsyv08sg1VnW6VmNKGN1X29Jl9jxHHsM6YCDlL+pL2cGn5gBkHscWzdMVj/wXfUghjWGAQX2ZOx6I3nz729/OVKfa2tvaFiWOy8d3ZeyJORAupjxSWFd/7oILLkhhTHKV0XyOgUvXWTpVyA35R2kcQvAu6gveeVxm47+ieRaNN8r8JzgXLXtIPPbf0s6OFYI5/ND+24orrmjlKKwULuJwFq0uj1yrbcetyQ1rf4r9SGt15T6U+vbhWTOMJB7Kf9F7S6ECiOAxfAEwRlqjkEbdBhgcxC0Yi48PQ3VOTHrTTTd1DrVC5xPhDjjgAGsnDh/INofZ8JKm+Ej70EMP7QwaYMYAZgLuvPPOmXA4hMu29YJtiwqkvccee2TSwHMaYGiAselmyLOxxn8YELcN/mD2dZXuiiuusLZRDCp+85vfTE866aT0t7/9bYotzdS5JNawMKbYZlCrc12s4THTRbhH7e+dYqsxDAzajLUIhwFN3QiFjh/4CX+YvS1piY9tFeU9/PPPP78Pwhh8VSVurg/2mAaYsfg7IPVvdtp87vsUxOOmSf6BeG3OX+rZo5pKB9l6660z/KL2u+5LF6tKRCbxDzvssL4woTdVGWCWX375Dlerc0z6ZDa3aRR5MaNdyiT+5Zdfnh5xxBGZ57EMMFX9bkiZXOkLJjPNNFNn1Sg4/mc/+9nAlegYTDBdVQMGZX/3TDlD76X+wac0wHAFjEt/YHwWXdH9eeaZpy8KJuLYVsugz6vOo+msMFPnPHX6oJjoo6eF6xVWWKFvBnbZ9hFbHimsqz8nEyGx8hzGqXPOOSfFKhZ1TlemrFJ2cK/pqpJ71MYhTFxC7wVjn/6iyX+heZUNP8r9P8G5LAY+8dl/K9d/w5EG6gyqDB9hLLCMw5bfogfi4zsf7cp0w9qfYj/SrCm/e6lvH541w0gOofxHA4wgN4J+3QaYH//4xxlywjJAlzv66KMz4bGftOmefvrpzp6y0gDEd61ssQ3SIS/T4VwJSUv3J5100s5zdXB4ZxD35Zdf7hiPZPsOM52xdi9YmCTic5+HRSgB5aUX+r7N+Uu9hmI2KPz9999vbUNf+MIXBkUr9Q6dK/kIlDLBVwedpupQ1UzaMLJgD249rFzjw9F0d911lzUsOlowNplnJTz11FMp9gqXNHUfxmebwyxkPRyuMcNnkCvLV1Xj5vpgj2WAGau/A6IHPvxqhhmkL7Z3beY/4NFk+aWebfUS8xnauToEPcMvWEGiOwyciUzig5fKuKoMMDCiw+EcE5EVPrartM2uPuSQQ/rCYSAUdX/44Yf3PUcasQwwVf9uuNJHGbDlJQZ9TWdu2ybY4ewG01U1YKDnU+R3T49f5FrKDO40ByBNPjXvi+Q3KE6T/AO5msxf6mEQPkXexVoBg0l8tm210O/76KOPuqIdf/zxGQ5B2Wz9nCOPPNIa1rXSsEj7qEoeV38OZYWxyVzJA4D23Xdfa3kxUcl0Vck9auMQJi6h99KuTO6y3Zv8F5pX2fBN8g9kL5O/4FwWg7z47L+ladn+m20CDuoPRx2Uca7JnFhVYrph7U+xH2nWlN+9tH8br+Y9kxxC+YcGGEFuBP26DTDYckeUVHx0slwOnVrMoNlrr706e1jjcChYZ2WbDIm32WabZdLFgKcZTsJjGzNzhvn000+fORBwUAcTAwl6p1vSboMvdZdHKrb3efiEElBeeqHv25y/1GsoZoPC27aFQT76IbyD4hd559rKC1uxuBw+rrFqRTAQHwOVmImnu0G84OIz1/Yz66+/vp5097rIh/YguXz4qincbAMTAMJVHlf4sfo7ILpo49O8Z12F8rxoM/8BoibLL/XsWVWFg+GAUclL/BlmmCFjqMDqRdsM7bvvvrtw3lUbYE477bRM2TDj2XQ460TKDl/OI6vSAOPiM+Qf43djUPo2DAQT228NZMLkCd0N64CBLmORa9EDcKk5ABmbX/Pka5J/IFuT+Us95GEU+j6WAQb5YjsZkVP3X3vtta5Yu+66a7rooot2tsiZdtppOyug0Y+0fY8+//zz1vSuvvrqbnr6ha2t5k3MqUqeQXxjG3CUcmArcR07uX7wwQclSMevSu5RG4foA6XAjeCbx2U2/iuQXakoTfIPBC+Tv+BcCgCPyOy/pWnZ/ptrm62vfe1rHjXgDrLppptauc12Ttiw9qcG8Tr7ke66l/bvw7NmGEk1lH9ogBHkRtCv2wCz4YYbZsgJ2yKYA5yhUMJ4Isovvm1fXj3dddddNxMHWxLpzkVEWF7+wgsv6EFbdS0YmyTic58HVCgB5aUX+r7N+Uu9hmI2KDy2XJB0dR+dj6qc7SMVS4Mxc2iQcx326csLmG39wQcfOLPA6j0dA1zjY9TmbGXI+9Auy1e2POvAzWVQcZXHFX6s/g6IzvjwqxnGpluDnrWZ/4BLk+WXeh5UPzHewdggeYm/2267WZM2V5QgvOtQUWsCxsOqDTAYCDUPm//e977XJwX6blJu8U899dROmCYMMLF+N1x8aVs1rgNi23YNuPzyl7/Ug1V2Boyeie03KO93T49f5Fp0ANxJAwy3IBukQ7ZvWOjPww8/PCha35ZiekAYZWxb9GKVhs3Fah+YcGRzIfIU5RtXP9vkG5t8MeS21eEwj0PYcAh5pvOb2T80703+C8knRtgm+1+Qv0z+gnMMHAalwf5b+f4bDCJSX7qPFXpl3D777GNN17Ybz6gZYNiPHKwZokcmp/rcS8qh/EMDjCA3gn7dBhgb4UBpP/OZz6SwHOPAvUceeSQISZzdIoqv+66zYiRx2zZk5ixEVwfTNWtd0h7rvuDsQyxmmDxsQgkoL73Q923OX+o1FLNB4bFqTdLV/R/96EeDohV+hw9I296uOPclzz322GNWWc3tCV28kDcwafvww0o8myvyoe2Sy4evmsTNZVBxlccWfiz/Dki7MbnU596mW4OetZn/gEuT5Zd6HlQ/Zd+98sor1gG/O+64w5r0RRddlOFEzOouuvq3agMMCoHtswRL+NiOUncnnnhi33sMgMokoCYMMLF+N1x8+YMf/EAvfub6L3/5Sx8egh22+dCdrf+OFVJ5zjbxwLUCtsjvXl7+ee+lvOBTcwAyj2Pz0g593yT/QNYm85d6CMUsL3zMFTCuGc6h3626zLKltZQf/u67764H6V7X0T585SnKNw888IAX33QL7XnhK7eNx4D5sI5DeBbfGUz0Ko/LbPznTLSiF03yD4pUJn/BuSJoOsmy/5amMfpvrnGJgw46qFT1HXjggVZuw8ps09l4aBj6U0V5nf3IpFP3PjxrhhHdCOUfGmAEuRH06zbAPPPMM9aPf/nhEn/qqadOv/rVr6YY+EScQc51xgSI7LOf/azzb4IJJsgQ5R577NGXlYuIypJ0XyYjeCP1ZJKIz31ecUMJKC+90Pdtzl/qNRSzQeFvuummTDtDPttss82gaIXfYd9pKYfu5w1CIUNsuaPHkWtzBq6LF0wDrlmInXfeOZM+OMrminxou+Ty4asmcbMZVICJqzy28GP5d0D00IdfzTA23Rr0rM38B1yaLL/U86D6KfvumGOOyXDQbLPN5kwWqwbBUSKb+FdddZUzzqAXdRhgwMMip/j33ntvV6zVVlut7/3KK6/cfdeEASbW74aLL20f/90Cq4tXX321Dw/BzPzdG9YBA70sRa6lvOBOGmC4AmaQDi2xxBLWtoK+o81hwBRbBh122GHpdttt1zmIHgbiFVZYoXPewOKLL279Jq7KABNTnqJ8A2O3tDndN/lGxzOm3KM2DqHjUORaMDb7hrZ7k/+K5FcmTpP9L8hdJn/BuUz58+Ky/5amMfpvrnEJn4mag+poq622snKbbUvJYe1PFeV19iNpgBnUNnLf1UGguULUGKBuAwyKhu18bB/0gr3pYzsJbBcGArMtP3ZtcWSm43OPwQHdFSUiPY2xeC1Y2jpwec/y8CjTAcpL2+d9m/OXevXByTfMfffdZ+2QrLrqqr5JBIW78sorrfmddNJJXulgFpzgIL4pq4sXLrvssoF52DpcdRhg8gbgIHSTuNkMKpDJhbMt/Fj+HRA9zONW23vgGOLazH/AqcnySz2H1FdoWJxNIPmIjwOQzzrrLOffwgsvnIlTdK/sOgww2GIMB2NL+eCLEfrvf/97ii1k9Xe6AaQJA0ys3w0XX15xxRUD1QSrH81t24AP+t26s/1+DcOMTV3GIteiC+BPcwDSxqn6syL5DYrTJP9Aribzl3oYhE+RdzFXwEw22WR93AGZcb6L6V566aXOVo1oH1KuEN/cNlHSLzIxB3GrkKco33zyySdefFOV3Eh3lMYhIG8ZJ3qn85br2uS/MvkWidsk/0DeMvkLzkXK7RuH/bc4/TfXao0VV1zRtyqs4TCZR/RA983z9BB5WPtTRXmd/UgaYKyNwvehNBjf8KMebqeddrKSReghqzjcWrDT/eOOO84KEQ7bw6xLPazPtW2GDLYt84nrE2bZZZftk7coEfUlMgZvBEtXJ27Q8zw4ynSA8tL2ed/m/KVefXDyDYMOvaSr+3POOadvEkHhsJe/no9cYxaij8Nh1BJH/AUWWKAvqosXbIYBPSJW4Uia4tdhgMkbgIOMw4hbCM5j+XdAdGUQr7re6frnc91m/gM+TZZf6tmnnoqEQb9L8ijrTzTRRJ0Vg6Fy1GGAgUzLLLNMX1mXW265jqjm1hMw1Lz44ovdYjRhgIn1u+Hiyz/84Q/d8rkuJp544j68oB/mYMSwDhi4yuT7XNoCONQcgHTxqjz3zcM3XJP8AxmbzF/qwRcr33CxDDBvvvlmpo1AZnNv/GeffTbF2XlSniJ+TANMVfKU4RvbJMwvfOELfVValdySyaiMQ4i8RX3RP+GsQb7Jf0XzLBqvSf6BzGXyF5yLlj0vHvtvaRqr//bWW29lJumg/maccca8ahj4ftZZZ7XyPn47TDes/akyvM5+ZJIO4lfXO9GNUP7hFmSC3Aj6Rx55pJUssO93iHMdPHXeeec5k8HWFsgHh7xiBpH8eOX55n7Z11xzjTXuRhttlOKciZC/E044oU9eFxHlfTD3JTIGb6SOXGQy6HkeHKEElJde6Ps25y/1GopZXnjbHvCYhfzyyy/nRbW+xwxn/Nnc9ddfb+UDlzFYTwMr7Gznx5gzgYvyQlMGGB++GkbcQnAey78D0i4H8arrna7fPtdt5j/g02T5pZ596qlImL322svKjZJvqI+JN6GuLgMMDrHWy4PfG7SRbbfdtu+5OelmLBpg8gzwH3zwQR8mgpu5Itw2YICtfPMcDriWNMXnGTB21JrkH0jUZP6iG3Zkij+NZYCxbW0ImfXtdP/97393thaTsug+DJo4mxSrdW+++eb097//ffrHP/7RuiNELANMlfK4+mdYTT3I+fBNlXLrso3COIQub5Fr0UFXH1F/TgNM8S0YBecideQTh/23uP23hRZaKNMvwYSchx56yKc6MmFgMMZ5gqIH4sMoY3PD2p9y8Tr7kbZa7D2T+tb51PdaUgntf9EAI8iNoI8GJUqj+/gIDXEbb7yxNR0M6vk4LEnGkkBsE7T55pt3rNC6PPo1CBLWa3GPP/64NW+fAVdJw+W7iMhnQNOV5lh4LvXhSy56uLzyhxJQXnqh79ucv9RrKGZ54bH3taSt+7vsskteVOv7r3zlK50tDNZYY430/PPPT99///1uuOeff96a1957790N47pwrdbxPRsqjxeG2QAzjLiF8O9Y/h2QNqPzqO+1S9ddz9vMf8CkyfJLPbvqpsxz9LEwu0/yiOFj67JQV5cB5sknn8yUFdvYmsYAGGp0NxYNMFjdOMi5uN88h8I2YAA9eu+995zJf/jhh9bthmiAsUPWJP9AoibzF06yI1P8aQwDzDvvvJPibFKRUfdhTBF37rnnWsNgu29wsOnQPmyTfsy2J/FCtyCrUh5X/yxvy1tMntLxk2u9zFXKLVia/rCOQ5hyht4Lvj59RhpghtMAw/5b0jmGIGb/zXYmK9oKzp8u4szJPdLu9t13X2tyw9qfcvE6+5HWauw+lPr24VkzjCQS2v+iAUaQG0H/6aeftnaEll9+ee/S4HA82woW7CltW3bnm/ADDzyQfv3rX7fKp8+wwUwZ2/7VmC1Q1rmIKG+gtWy+wx4/BtG4yhhKQK50ij5vc/5Sr0Wxc8W77rrrrO0Ys2ddK1lcaWHGoMgpPvblFoMrVrHYznExZ/Pa0r/rrrsyaSMP84OyKC8MswFmGHELwXks/w6InpudNp97m54PetZm/gMuTZZf6nlQ/RR9d8MNN1i5DYN/4OG8v/HHHz8TH/0uDN6HuLoMMJBpkUUW6ZP5y1/+ct898H7qqaf6xB+LBhisUB/kbr/99gwuwObYY4/ti3bwwQdbw8HY5XKPPPKINQ4NMHbEmuQfSNRk/lXxXwwDjK3vBnlnmWWWvrNJMVlHyqH7rjbypz/9yRo+1gqYKuVx9c8wsDjI2frwwAqrg8RVKbfk4eMPwziEj5yDwoge+vQXaYAZTgMM+29JGrv/5uIhtBeMBYS4J554InO2oLQ79IFsblj7Uy5eZz/SVou9Z1LfPjxrhpFUQvtfNMAIciPouwbdoEjYa9HHbbXVVtYO5NJLL+0TPTcMZruLYotvWpRt+y7iMKyyzkVENMCUP2zKVTehBORKp+jzNucv7asodoPi2Q4PRH7oVGF2oY+DwXjmmWfO8AHSwSCSOFteMMq8/fbbEsTqu2bEYKsI3RXlBdtHfMgZMFhJNMgVlUvSHDbcQsszVn8HpF2anTafe6lbX7/N/AeMmiy/1LNvXYWE23LLLTO8GXKOi2uyTuhq6ToNMNh+VjC1+eA7041FA8wcc8zRN0hslhmDvTZ8MHCtu7PPPtsaDqtQXW633XazxsFKd5uzzfDP+92zpRPyTMoOPjUHIPM4NiQfn7BN8g/kazJ/qQcfnELClDHA4Bv5sMMOs24tA3nxTnerrbZaRt/R93S5n/zkJ5nwSDfEADOofVQpj6t/Ntdcc7mK23nuMq5ccskl3XhVyt3NJOCiyXGIADGtQaVd5XGZjf+sCVb4sEn+QbHK5C84VwEP+2//HXMSjOGX7b+hnr74xS9a+Rfbkz3zzDNeVYmJ5iuttJI1HXOLWz3BYe1PuXid/Ui99rLXops+PGuGkdRC+YcGGEFuRP1NN93UShzTTjttqq80MYuHvVPRkcKWYKJ4un/66af3RcG+iphRt9NOO6WrrrpqZyBVn/HSF1i7OeCAAzLpo9OqO2xlpOct19jWzOY++uijdMMNN0zXWWeddOutt06xPdExxxyTYraL7lxERAMMDTC6nsS8DiXgmHlLu4mZpqTl+ghGnnPOOWeKtjbIwcBiG2BH/K997Wt9UU888UQrHwziGxhnbCv5FlhggRTbROiuKC+UNcCst956uhiZ66JySULDhltoecbq74C0S7PT5nMvdevrN8k/kLHN+Us9+9aVbzhsEWU7HBNbx4Y4fEyKjOKDH0NcnQYY9DlFTpsPA43pxqIBBmXHKlSbw2/b9NNPn8EJxrnXX3+9LwomIthwdE12gtHOpndII8QAk/e71ydkgRspE/iUBpjiM8ALQN8XReqh72GEG1ff01zhZWaFMwrXXHNNq85D1uWWWy7Ft6TuXANxOEDbdGgf00wzjTX97bff3gzeubcZKAe1jyrlcfXPgM1NN91klR98Y9sKE3yDtieuKrlHcRxCMCnqS7vy6S+a/Fc0z6LxRrn/JzgXLbsrHvtvWeMLsC7bfwPe2D7SNYY5+eSTp3nnnmBcwtwWTfRgwgknTG28L/U8rP2pQbzOfqTUXtaXevfhWTOMpBbKfzTACHIj6uMjy7W3LRQKH+mnnHJKeuutt3YOp8IBgoccckg699xzWzuOiDP//POnH3/8cR8it912WyY8PvzQCXU5/PAstthimXh33HFHXxR0GiaZZJJMuCWXXDLFFmmmsxl1QJbPPfdcX1AXEdEAQwNMn6JEvAkl4IhZd9tPzDT1tFxnwYAzsBUOZpntv//+KWbC3X///SnOkPrZz36W4qwB+XEzfXy4mdvgYL/cxRdfPBMHedhW9r344otWnkHHzFz9gvIU5YUQAwy2gTTLitUyGBRwuaJySXrDhltoecbq74Dogdlp87mXuvX1m+QfyNjm/KWefevKN9w555yT4RLkhb5ciMOApcio+/fcc493MnUaYCDUvPPOa5UZ8j/88MMZuceqAQZ9fHOCEQZD/9//+39WfHbccccMNvjt0etdv4bxWx+MvvPOO7uGHfSt9bC43myzzTLp40GR3z1rQgEPRTbwqTkAmcexAdl4BSX/RR9SSF0GGOj+UUcd1fd34IEHphtssEE622yzZXRW9AQ+vjdt365oN3o4uTa35Xrttdc638ny3vQxSdHmQttHlfKgjZtyyz0MS+Zh1uAHYCthdN/km6rkHsVxCJsehDwTnPO4zMZ/IfnECDvK/Cc4x8BBT4P9N7sBpmz/TTDGmIPUneljDACr8TBJ+6KLLkrvu+++zvgEvuXXXXdd57ZjSOeEE06QLKz+sPanXN/dKBP7kdaq7DwU3fHhWTOMpBrKf9F7S6ECiOAxfAEwRlqjlAYGJaXsZf1JJ53UafXFtmRm+lNOOWWKrX+wHO+qq67qDLpecMEFnYFYm5FnuummS7Hfv+lsH87IC9ZpnAeDbRJgMcfMmnHHHTcjh21/QxcR0QBDA4ypf7HuxzL/vf/++51ZgyYHFL2HQcI1IwN7a9tmtuDcgrXWWqvDBUcffXRnIMhlgN5mm22s1VqUF0IMMLYl58AJg1nYPx9p7bnnnn3yFZVLT2SYcCtSnrH4OyDtw+y0+dzrdetz3ST/QL425y/17FNPIWFWX331TH8HA4gffPBBSDKdySy28/awzZSvq9sAg+1qBVfdn2+++awi2/jDtVrDNbDrmllfhM8gpO/vhiv9qaaaqoMB+uY4V/H4449Pv/vd76ZYvaRjIteoY+xpbnMugw3iYrULVgXMMMMM3XQxEcK2yt510G2R3z2bnCHPpNzgUxpg2rMCRuo91Mc3K85ksLmTTz65q/tmuphMCD7Ctjf6N6hN58cbb7xOWBgxMEFInC0s8nH1C6uUx3WGwhRTTNHBAGczwtCK8xmxWwa29TExwT345rHHHpMidvwq5R61cYg+YArcCOY+/UWT/wpkVyrKKPf/BOdSAFgis/+WNcDE6L8J1Jh4uP7661u5Seo01Hf1GSVP8YexP8V+pNROmC864sOzZhjJKZT/aIAR5Ebc/7//+7/SBIQtgmwzxgUaDO6hUyaKGupj0AAWaJvD4O4SSyxRKG38wNkU30VENMDQAGPTwRjPbHoYI12fNKQ9+oQtGgbtFINAkldRH4bYvJnXWKmnf+iG5LXUUkul2NvV5orygu9AGvLEqsM8ebEdhe6KyqWngethwa1Iecbi74Dogdlp87k36zbvvkn+gWxtzl/qOa+OQt6/9NJLnQEuSVv8b37zmyHJdMOussoqGV7CdrXmiuduBOOibgPM3XffnZEXGJjnCIqYY9EAc+qpp3ZWmErd5/nmbHTBBj621LAZ4WxpIhxWq2+77baZOlh77bX1ZLvXRX73upELXojs4FNzADKPYwtm6YxG/os+pOBcASP1HuLDwGiuuNYrE1tz4wwU3zQxGQgrQzCZyBUHOzaIC20fVcpjW02CMpx77rnpBBNM4CyPWc4ddthBitf1q5R71MYhuqAUvBC887jMxn8FsywcbZT5T3AuXHhLRPbfquu/6XDDCLP77rt7c5bUteljlw0YnH3dMPanXN/d7EcOrlXRBR+eNcNIyqH8F723FCqACB7DFwBjpDWKafzhD39IbbNDBBeXj5l1Rx55pNeMSmyDYNtz2pW2PMfh2zer/RoHOWypgOWEmD0k8fJ8WKoRz+ZcREQDDA0wNn2J8awt/HfmmWems88+u3c7lXYMgwrOb7Jt/2DDH9skuGb6Spq6jwNTccbUoAHForwQYoDBR/mCCy44EJ+qDDDAcRhwK4rzWPsdEP00O20+97Y2MehZk/wDudqcv9TzoPoJfYctdiRd3S/ahznttNOs6V199dVeotVtgIFQtu2EXMb7sWiAwXkMWAFu2wpM1wlc64O9rgrF72NeHxsDERdeeGEnCduh265zY4r87rnk9H0uGIBPaYDhChjRB93H6g0MrLm+FXVdu+WWW1JsjavHt13D+IKzB+GwA4MtDJ7pbbJI+6hKHvyG2GR+/PHHO9v1+GCA73WXq0pu5DdK4xAufHyfSx359BdN/vPNI1a4Ue7/Cc6xsEA67L9V13+z1dPll1/uXKkn9evyMQEc382hbtj6U67vbvYjB9es6IUPz5phJOVQ/qMBRpAbI/5//vOfzgwWfCBh+y7bNj5QNCzDXmaZZdLvfe97nY+WkOK/88476RlnnNHZDsyVPvLAOxz8ii3J0PH0dSAQdG71rRCkccAff/zxO0ujcYDWIOcioqKDF4PyGqV3gqVJIj73eeUMJaC89ELftzl/qddQzIqGR5vG1oMbbbRRKtukiAymDy7CrOUXXnghODtsWXjQQQd1jMu2mYYYTMKSZqzMeeqpp3LTL8oLIQYYCIHZTzA2mVhgZjFWG2611VZ9shaVqy8R7aZp3MqWB/HHwu+A1L8Pv5phtOr0umwz/wGgJssv9exVUZ6BbNu+YMvFkP6UntVbb71lXU3hOtNDj4vrJgww6KMKtvBh+He5sWiAwVlqcDA6Yd9ycwUL+sMYPICRxtdhoMGmW+izg3OxPZG4ww47rA9/1AH69S4X+rvnSsf3uegGuNMcgDT51Lz3zcM3XJP8AxmbzF/qwRcr33CurQIlP9NHX3TRRRdNcbg9uOOuu+7yzaobDhOE0NbMtHGPFTLYphCzrsVh5e53vvOdzIpt9Fdh9NZdkfZRhTw4E8FWPrQRuHvvvXcg32ClTJ6rQm7Jc1TGIUTeor7UkcldtnuT/4rmWTRek/wDmcvkLzgXLbstnu03lv23OP03G954hjFQ/GZgPAA7bUi92nycdYUteHFmbRk3TP0p13c3+5GDa1j0w8arec8k5VD+GQcRVcbRnFp6mqhZyNHSC0lIfTx0gkcuUogIQxdW7ROeqE5QogYmE1zPMccciepAJmrVSxRZ33333eSVV15JXn/99UQdTJiogYFEDbZ2/macccZEzaQrlY+aYZSow7qSZ599NlFkmaiVNMkss8zSmI6VKsyQRJZ2okglWCL1QTEwTpPtH4K1OX+p1yb4D3mqfec7PKC2/kqgW2prm0QZGjrtVc2mG6g3vi+RjzLidDgBdT3//PMn6qypRA1C+SZRezhw46OPPpqoD8Zkzjnn7PypLR5qlWMUcdMBGuXfAWmXVfCtjhGu28x/TZdf6rkJ/jX1gPejh4Dabi1RW2dmBFcThpI111yz+/zVV1/t/J6oQ2A7/Xk12Jyo1THd9yEX6L+rcyo6/Wu1sj2ZZ555EvTbY7i6fvek3YFf8Y0TgkVefzYUhzbzr9TDWOI/9NnUipDkySef7Hwzoz+rVi4nUlZTP+R7+7333kuUIShRq/cSZTA1g3Xui7SPKuWxCqkexuCbquUey+MQoms+/UeT/2Lzm0tH5Pko85/gPJb4S+qlzT64Gxwm4xIYR5QxyljjoILvMPSn2I+U2gjzpf378KyZsvBsKP+NA4uNmdio3qtDJDuik0BHtQYpdx0ICNGo2TLB2TVlXA0WtEQEtU1Woma3lUihmajkv2ZwZ65EYBAC5NtB6Iydd+TfsVOXTZTE98O5CdmGOc+xzK+j1Bcl/w1zK6Fso4rAWOa3YaoT8tcw1QZlKYoA+5HFkGuCZ7kCplhdMRYRGFkEhGjKWHpdhQ+1ALvSKfq8zflLvdIAXVR7GI8IxEdA2mUVfGtK22b+AxZNll/qmfxraiXvfRDgh7MPStkw0u7Ar+YM8Gzo/icyc7H/afG7JvkHUjeZv9QD+a+4/jAmETARkHbl0380+S82v5mymfdN8g9kKZO/4Ez+MmuV96OEAPuRxWpL2r8Pz5o5CM+G8g8NMCaSvCcCYxyBGETjgiiUgFzpFH3e5vylXtmBLKo9jEcE4iMg7bJMx85XqjbzHzBqsvxSz+RfX21lOB0BfjjraPhfS7ujAYb85681DEkERgMBnd/yJKYBpvgRCIIz+295Wsb3w4wA+5HFakfaf5nv9NDvTxpgitUVYxGBkUUgBtG4Ch9KQK50ij5vc/5Sr+xAFtUexiMC8RGQdlmmY+crVZv5Dxg1WX6pZ/Kvr7YynI4AP5x1NPyvpd3RAEP+89cahiQCo4GAzm95EtMAQwNMno7w/dhGgP3IYvUbwrNmDlwBoxARAPkBbKoH74lADwFpJ1UMCDY5AIYStjl/qVfyX0/XeUUEmkZA2mUVfGuWrc38ByyaLL/UM/nX1Ere+yDAD2cflLJhpN3RAEP+y2oHnxCB0UZA57e8ktAAQwNMno7w/dhGgP3IYvUbwrNmDjTAKEQEQH4Am+rBeyLQQ0DaSRUDgk0OgKGEbc5f6pX819N1XhGBphGQdlkF35plazP/AYsmyy/1TP41tZL3Pgjww9kHpWwYaXc0wJD/strBJ0RgtBHQ+S2vJDTA0ACTpyN8P7YRYD+yWP2G8KyZAw0wChEBkB/Apnrwngj0EJB2UsWAYJMDYChhm/OXeiX/9XSdV0SgaQSkXVbBt2bZ2sx/wKLJ8ks9k39NreS9DwL8cPZBKRtG2h0NMOS/rHbwCREYbQR0fssrCQ0wNMDk6Qjfj20E2I8sVr8hPGvmQAOMQkQA5AewqR68JwI9BKSdVDEg2OQAGErY5vylXsl/PV3nFRFoGgFpl1XwrVm2NvMfsGiy/FLP5F9TK3nvg8A777yT/P73v88EXWaZZZKpp54685wP/ouAtDsaYMh/bBNEYKwhoPNbXtlogKEBJk9H+H5sI8B+ZLH6DeFZMwcaYBQiAiA/gE314D0R6CEg7aSKAcEmB8BQwjbnL/VK/uvpOq+IQNMISLusgm/NsrWZ/4BFk+WXeib/mlrJeyJQHQLS7miAIf9Vp2VMmQg0g4DOb3kS0ABDA0yejvA9ESACWQRCeNaMTQOMQkQA5AewqR68JwI9BKSdVDEg2OQAGErY5vylXsl/PV3nFRFoGgFpl1XwrVm2NvMfsGiy/FLP5F9TK3lPBKpDQNodDTDkv+q0jCkTgWYQ0PktTwIaYGiAydMRvicCRCCLQAjPmrFpgFGICID8ADbVg/dEoIeAtJMqBgSbHABDCducv9Qr+a+n67wiAk0jIO2yCr41y9Zm/gMWTZZf6pn8a2ol74lAdQhIu6MBhvxXnZYxZSLQDAI6v+VJQAMMDTB5OsL3RIAIZBEI4VkzNg0wChEBkB/Apnrwngj0EJB2UsWAYJMDYChhm/OXeiX/9XSdV0SgaQSkXVbBt2bZ2sx/wKLJ8ks9k39NreQ9EagOAWl3NMCQ/6rTMqZMBJpBQOe3PAlogKEBJk9H+J4IEIEsAiE8a8amAUYhIgDyA9hUD94TgR4C0k6qGBBscgAMJWxz/lKv5L+ervOKCDSNgLTLKvjWLFub+Q9YNFl+qWfyr6mVvCcC1SEg7Y4GGPJfdVrGlIlAMwjo/JYnAQ0wNMDk6QjfEwEikEUghGfN2DTAKEQEQH4Am+rBeyLQQ0DaSRUDgk0OgKGEbc5f6pX819N1XhGBphGQdlkF35plazP/AYsmyy/1TP41tZL3RKA6BKTd0QBD/qtOy5gyEWgGAZ3f8iSgAYYGmDwd4XsiQASyCITwrBmbBhiFiADID2BTPXhPBHoISDupYkCwyQEwlLDN+Uu9kv96us4rItA0AtIuq+Bbs2xt5j9g0WT5pZ7Jv6ZW8p4IVIeAtDsaYMh/1WkZUyYCzSCg81ueBDTA0ACTpyN8TwSIQBaBEJ41Y9MAoxARAPkBbKoH74lADwFpJ1UMCDY5AIYStjl/qVfyX0/XeUUEmkZA2mUVfGuWrc38ByyaLL/UM/nX1EreE4HqEJB2RwMM+a86LWPKRKAZBHR+y5OABhgaYPJ0hO+JABHIIhDCs2ZsGmAUIgIgP4BN9eA9EeghIO2kigHBJgfAUMI25y/1Sv7r6TqviEDTCEi7rIJvzbK1mf+ARZPll3om/5payXsiUB0C0u5ogCH/VadlTJkINIOAzm95EtAAQwNMno7wPREgAlkEQnjWjE0DjEJEAOQHsKkevCcCPQSknVQxINjkABhK2Ob8pV7Jfz1d5xURaBoBaZdV8K1ZtjbzH7BosvxSz+RfUyt5TwSqQ0DaHQ0w5L/qtIwpE4FmEND5LU8CGmBogMnTEb4nAkQgi0AIz5qxaYBRiAiA/AA21YP3RKCHgLSTKgYEmxwAQwnbnL/UK/mvp+u8IgJNIyDtsgq+NcvWZv4DFk2WX+qZ/GtqJe+JQHUISLujAYb8V52WMWUi0AwCOr/lSUADDA0weTrC90SACGQRCOFZMzYNMAoRAZAfwKZ68J4I9BCQdlLFgGCTA2AoYZvzl3ol//V0nVdEoGkEpF1Wwbdm2drMf8CiyfJLPZN/Ta3kPRGoDgFpdzTAkP+q0zKmTASaQUDntzwJaIChASZPR/ieCBCBLAIhPGvGpgFGISIA8gPYVA/eE4EeAtJOqhgQbHIADCVsc/5Sr+S/nq7zigg0jYC0yyr41ixbm/kPWDRZfqln8q+plbwnAtUhIO2OBhjyX3VaxpSJQDMI6PyWJwENMDTA5OkI3xMBIpBFIIRnzdg0wChEBEB+AJvqwXsi0ENA2kkVA4JNDoChhG3OX+qV/NfTdV4RgaYRkHZZBd+aZWsz/wGLJssv9Uz+NbWS90SgOgSk3dEAQ/6rTsuYMhFoBgGd3/IkoAGGBpg8HeF7IkAEsgiE8KwZmwYYhYgAyA9gUz14TwR6CEg7qWJAsMkBMJSwzflLvZL/errOKyLQNALSLqvgW7NsbeY/YNFk+aWeyb+mVvKeCFSHgLQ7GmDIf9VpGVMmAs0goPNbngQ0wNAAk6cjfE8EiEAWgRCeNWPTAKMQEQD5AWyqB++JQA8BaSdVDAg2OQCGErY5f6lX8l9P13lFBJpGQNplFXxrlq3N/Acsmiy/1DP519RK3hOB6hCQdkcDDPmvOi1jykSgGQR0fsuTgAYYGmDydITviQARyCIQwrNmbBpgFCICID+ATfXgPRHoISDtpIoBwSYHwFDCNucv9Ur+6+k6r4hA0whIu6yCb82ytZn/gEWT5Zd6Jv+aWsl7IlAdAtLuaIAh/1WnZUyZCDSDgM5veRLQAEMDTJ6O8D0RIAJZBEJ41oxNA4xCRADkB7CpHrwnAj0EpJ1UMSDY5AAYStjm/KVeyX89XecVEWgaAWmXVfCtWbY28x+waLL8Us/kX1MreU8EqkNA2h0NMOS/6rSMKROBZhDQ+S1PAhpgaIDJ0xG+JwJEIItACM+asWmAUYgIgPwANtWD90Sgh4C0kyoGBJscAEMJ25y/1Cv5r6frvCICTSMg7bIKvjXL1mb+AxZNll/qmfxraiXviUB1CEi7owGG/FedljFlItAMAjq/5UlAAwwNMHk6wvdEgAhkEQjhWTM2DTAKEQGQH8CmevCeCPQQkHZSxYBgkwNgKGGb85d6Jf/1dJ1XRKBpBKRdVsG3ZtnazH/AosnySz2Tf02t5D0RqA4BaXc0wJD/qtMypkwEmkFA57c8CWiAoQEmT0f4nggQgSwCITxrxqYBRiEiAPID2FQP3hOBHgLSTqoYEGxyAAwlbHP+Uq/kv56u84oINI2AtMsq+NYsW5v5D1g0WX6pZ/KvqZW8JwLVISDtjgYY8l91WsaUiUAzCOj8licBDTA0wOTpCN8TASKQRSCEZ83YNMD8f/buYMmtHNfWsBWeVFRFD/v9H7Cn7RN34shbdlnZFizm3gCoTJH+zsTJrQ1SWMD6SSddp/9W5CpgFMeYAhT4VYFH/ELwI38B9i3D33l9/Pu1xz2hwLMo8Ajextx+Z/590+Ij88ff2I3GFHg/BVzA4N/7dZuVKPC+Cpw5P7qA6V/AvG9VrUYBCjyTAmc4G7+vC5i/FfEX4NgWxhQYK9ABzWjWj/wF2Lfv9Duvj3+jrvScAh+vwCN4G7P6nfn3TYuPzB9/YzcaU+D9FPjG1/gLyKPVr39xPnrv7OcfyZ9v3/Ej18e/s13iPQrkFThzfoz8m823o2/9kfz59t066+PXUXV9ToH9FTjD2ajClbNZ/lz+/n+X8BIn64yzX6Cz1r3Y6vr//e9/702XfhY3wPQEzQDr/79Pf/zxR1PFevju+l9BMzrH7ksAADqsSURBVFKo6r/RfNnn1q/9CyD8y3ba/fd39//9rP/3VP5z958j3v5P+X9+wr8a/6KO1XFVf/ytKn4bhz9z+XOr7vFoNf2zfD1SoOr/o3nPfr7q+vh3tsJvv7ea/97OJv+p/G/5P5tvRxVZlT9HeR19fuWX/rvtvyPdZn9Of/p/xO9/r5zN8u/y5cuXqRcwsw31XvN9E87/PU6Bf//7398n/89//vO4Rcz8cAX+/PPPh6/x0Qt8/vz509evXz/6a7zr+vj3rnKfXgw3T0u15Yu/A2+3LFwyKfxNCvag1/H2QcI+6bTPztff5SyKfx9jELz7GN3fa9Vn59t76fDodfDr0Qq/7/y4+L56r75albP+C5gflb/eYHcbwQ3s/RvYf/3rX9+lrfznXZma0P++/hkN33r3etM7eufbQaQKo9GcmefWr+mPf5kuG787mz9Zbs5ef5zp/U+sP5e/R7yNVcC/Gv+ijtVxVX/8rSp+G9flT5a3t6t/Sv+/wIrx3XE3/99t/Sxfj/Sp+v9o3rOfr7o+/p2t8NvvZf3f5V38Ntn1Y3x3bP3b8+dsvh3VZ1X+HOV19PmVX/rvtv+OdJv9+Sz9q1yctX5VF+t/TP9dOZvlnwuYH51+BWi18a9xDHDfAFWgXXU9+yf97+t/Vr+j966gGb2XBdBonupz69d+AYl/1Y67jZvNnyw3Z69/m93xyPpz+XvE21gR/KvxL+pYHVf1x9+q4rdxXf5keXu7uguYrv5Rz+w4u36Wr0ffp+r/o3nPfr7q+vh3tsJvv5ft/y7v4rfJrh/ju2Pr354/Z/PtqD6r8ucor6PPr/zSf7f9d6Tb7M9n6V/l4qz1q7pY/2P678rZLP9cwPzo9CtAq41/jWOA+waoAu2q69k/6X9f/7P6Hb13Bc3ovSyARvNUn1u/9gtI/Kt23G3cbP5kuTl7/dvsjkfWn8vfI97GiuBfjX9Rx+q4qj/+VhW/jevyJ8vb29VdwHT1j3pmx9n1s3w9+j5V/x/Ne/bzVdfHv7MVfvu9bP93eRe/TXb9GN8dW//2/Dmbb0f1WZU/R3kdfX7ll/677b8j3WZ/Pkv/KhdnrV/Vxfof039Xzmb55wLmR6dfAVpt/GscA9w3QBVoV13P/kn/+/qf1e/ovStoRu9lATSap/rc+rVfQOJfteNu42bzJ8vN2evfZnc8sv5c/h7xNlYE/2r8izpWx1X98beq+G1clz9Z3t6u7gKmq3/UMzvOrp/l69H3qfr/aN6zn6+6Pv6drfDb72X7v8u7+G2y68f47tj6t+fP2Xw7qs+q/DnK6+jzK7/0323/Hek2+/NZ+le5OGv9qi7W/5j+u3I2yz8XMD86/QrQauNf4xjgvgGqQLvqevZP+t/X/6x+R+9dQTN6Lwug0TzV59av/QIS/6oddxs3mz9Zbs5e/za745H15/L3iLexIvhX41/UsTqu6o+/VcVv47r8yfL2dnUXMF39o57ZcXb9LF+Pvk/V/0fznv181fXx72yF334v2/9d3sVvk10/xnfH1r89f87m21F9VuXPUV5Hn1/5pf9u++9It9mfz9K/ysVZ61d1sf7H9N+Vs1n+uYD50elXgFYb/xrHAB9jAPr/o8Cj++8Kmqve8c8sgGJ8d2z92i8g8a/bef/EP9p/R9/S+nvtP0e8jf2AfzX+RR2r46r++FtV/DYO//bi3211j0fZ+mf5evQNqv4/mvfs56uuj39nK/z2e9n+f3u2/KfWfy7+zubbUUesyp+jvI4+v/JL/z9X/x/Vbfbn6v971v/K2Sz/XMD8cOAVoF1DMuDvacBr3+xe/ytorvnGP7MAivHdsfVrv4DEv27n/RO/u/+PVJL/3P3viLexHvhX41/UsTqu6o+/VcVv4/BnLn9u1T0eraZ/lq9HClT9fzTv2c9XXR//zlb47fdW89/b2eQ/lf8t/2fz7agiq/LnKK+jz6/80n+3/Xek2+zP6U//P/74Y3ZbHc535WyWfy5gfkh7Beih0gcvAAAAfAQArm356P67gua6XvwzC6AY3x1bv/YLSPzrdt4/8Y/239G3tP5e+88Rb2M/4F+Nf1HH6riqP/5WFb+Nw7+9+Hdb3eNRtv5Zvh59g6r/j+Y9+/mq6+Pf2Qq//V62/9+eLf+p9Z+Lv7P5dtQRq/LnKK+jz6/80v/P1f9HdZv9ufr/nvW/cjbLPxcwPxx4BWjXkAz4exrw2je71/8Kmmu+8c8sgGJ8d2z92i8g8a/bef/E7+7/I5XkP3f/O+JtrAf+1fgXdayOq/rjb1Xx2zj8mcufW3WPR6vpn+XrkQJV/x/Ne/bzVdfHv7MVfvu91fz3djb5T+V/y//ZfDuqyKr8Ocrr6PMrv/Tfbf8d6Tb7c/rT/yP+AfyVs1n+uYD5QYArQLtAAAAA+AgAXPv20f13Bc11vfhnFkAxvju2fu0XkPjX7bx/4h/tv6Nvaf299p8j3sZ+wL8a/6KO1XFVf/ytKn4bh3978e+2usejbP2zfD36BlX/H8179vNV18e/sxV++71s/789W/5T6z8Xf2fz7agjVuXPUV5Hn1/5pf+fq/+P6jb7c/X/Pet/5WyWfy5gfjjwCtCuIRnw9zTgtW92r/8VNNd8459ZAMX47tj6tV9A4l+38/6J393/RyrJf+7+d8TbWA/8q/Ev6lgdV/XH36rit3H4M5c/t+oej1bTP8vXIwWq/j+a9+znq66Pf2cr/PZ7q/nv7Wzyn8r/lv+z+XZUkVX5c5TX0edXfum/2/470m325/Sn/0f8A/grZ7P8cwEzmQDZAkxe/tOzrn+5XL6n+vLyMjvlm/meNf+bL/nAgfzX/AXcrJZQ/73qn+Wm+u9V/ywX1F/9//zzz2zbTHt/9f7L8jYKt3r+MZ/sWP74gz/r8LfLu8gH/ud//l/H/9G/3fEu/q9ycZf8q30g/xz/XcBUO20QpwHvN2AVaAOZh4/pf1//oWCTP6A//R3A5x3As9zkP/7jv3n+y26P/Le2/7K8jf2h/mvXP9YzO1Z/9V9p/+3yLvpD/+v/lfo/9m93rP/36P8qF9V/j/pXOZCtvwuYqtKDuGwBBtOUHz/r+lWgZYV41vyzeVTfl78NwAF4n1/AZrnJ//zP//v4P3sO4P+e/7O8jfWhf0//qGd2TH/62//O739d3kV/8h//8d95/0X/dMf8N8d/VS7Sf47+VR+spr8LmGqlB3GrNcAgjfLjUf5VoGW/yGj97DzV960PwA6gDqBVfsS4LDfxB3/wB38iR95rvDp/sryNuq6ef8wnO5a//cf+s87+0+Vd5AP/8z//r+P/6N/ueBf/V7m4S/7VPpB/jv8uYKqdNojTgPcbsAq0gczDx/S/r/9QsMkf0J/+DuDzDuBZbvIf//HfPP9lt0f+W9t/Wd7G/lD/tesf65kdq7/6r7T/dnkX/aH/9f9K/R/7tzvW/3v0f5WL6r9H/ascyNbfBUxV6UFctgCDacqPn3X9KtCyQjxr/tk8qu/L3wbgALzPL2Cz3OR//uf/ffyfPQfwf8//Wd7G+tC/p3/UMzumP/3tf+f3vy7voj/5j//477z/on+6Y/6b478qF+k/R/+qD1bT3wVMtdKDuNUaYJBG+bH8AcgBzAGsDJBmIP7gD/7gTxMj5XD8wR/8wZ8yQJqB+IM/+IM/TYyUw/EHf/AHf8oAaQauxh8XMM2Cx/DVGiB+/+5Y/jZgG7ANuMuRajz+4A/+4E+VH904/MEf/MGfLkeq8fiDP/iDP1V+dOPwB3/wB3+6HKnGr8YfFzDVSg/iVmuAQRrlx/K3AduAbcBlgDQD8Qd/8Ad/mhgph+MP/uAP/pQB0gzEH/zBH/xpYqQcjj/4gz/4UwZIM3A1/riAaRY8hq/WAPH7d8fytwHbgG3AXY5U4/EHf/AHf6r86MbhD/7gD/50OVKNxx/8wR/8qfKjG4c/+IM/+NPlSDV+Nf64gKlWehC3WgMM0ig/lr8N2AZsAy4DpBmIP/iDP/jTxEg5HH/wB3/wpwyQZiD+4A/+4E8TI+Vw/MEf/MGfMkCagavxxwVMs+AxfLUGiN+/O5a/DdgGbAPucqQajz/4gz/4U+VHNw5/8Ad/8KfLkWo8/uAP/uBPlR/dOPzBH/zBny5HqvGr8ccFTLXSg7jVGmCQRvnxKP/L5fJ9zpeXl/LcZwJH65+JnfGO9R1AHEAcQGaw5NscWW7iD/7gD/7M4k92ntX5k+Vt1Gf1/GM+2bH87T/2n3X2ny7vIh/4n//5fx3/R/92x7v4v8rFXfKv9oH8c/x3AVPttEGcBrzfgFWgDWQePqb/ff2Hgk3+gP70dwCfdwDPcpP/+I//5vkvuz3y39r+y/I29of6r13/WM/sWP3Vf6X9t8u76A/9r/9X6v/Yv92x/t+j/6tcVP896l/lQLb+LmCqSg/isgUYTFN+/KzrV4GWFeJZ88/mUX1f/jYAB+B9fgGb5Sb/8z//7+P/7DmA/3v+z/I21of+Pf2jntkx/elv/zu//3V5F/3Jf/zHf+f9F/3THfPfHP9VuUj/OfpXfbCa/i5gqpUexK3WAIM0yo9H+VeBlv0io/Wz81Tftz4AO4A6gFb5EeOy3MQf/MEf/Ikcea/x6vzJ8jbqunr+MZ/sWP72H/vPOvtPl3eRD/zP//y/jv+jf7vjXfxf5eIu+Vf7QP45/ruAqXbaIE4D3m/AKtAGMg8f0/++/kPBJn9Af/o7gM87gGe5yX/8x3/z/JfdHvlvbf9leRv7Q/3Xrn+sZ3as/uq/0v7b5V30h/7X/yv1f+zf7lj/79H/VS6q/x71r3IgW38XMFWlB3HZAgymKT9+1vWrQMsK8az5Z/Oovi9/G4AD8D6/gM1yk//5n//38X/2HMD/Pf9neRvrQ/+e/lHP7Jj+9Lf/nd//uryL/uQ//uO/8/6L/umO+W+O/6pcpP8c/as+WE1/FzDVSg/iVmuAQRrlx/IHIAcwB7AyQJqB+IM/+IM/TYyUw/EHf/AHf8oAaQbiD/7gD/40MVIOxx/8wR/8KQOkGbgaf1zANAsew1drgPj9u2P524BtwDbgLkeq8fiDP/iDP1V+dOPwB3/wB3+6HKnG4w/+4A/+VPnRjcMf/MEf/OlypBq/Gn8uX758eakmK44CFKDAbgp8/vz509evX3dLSz4UoAAFKEABClCAAgso4Cy6QJF8RQpQgAIUoAAFKJBQwH8BkxDrzKur3cCdySnzjvz9Cwj/AsK/gMgwY+a7+IM/+IM/M5mSmQt/8Ad/8CfDjJnv4g/+4A/+zGRKZi78wR/8wZ8MM2a+uxp/XMDMrP7fc63WAJPTl///2YBtwDbg2Vw5Ox/+4g/+4M9ZXsx+D3/wB3/wZzZXzs6HP/iDP/hzlhez38Mf/MEf/JnNlbPzrcYfFzBnK3vyvdUa4GRap1+Tvw3YBmwDPg2MyS/iD/7gD/5Mxsrp6fAHf/AHf04DY/KL+IM/+IM/k7Fyejr8wR/8wZ/TwJj84mr8cQHzmzfA5PSH/wXM5XL5vtTLy2P/J4dWM+B76T97ndF89HcAcwCbdwDLcpP/+I//5vlvtM+NnvPf2v7L8jb2gfqvXf9Yz+xY/dV/pf23y7voD/2v/1fq/9i/3bH+36P/q1xU/z3qX+VAtv4uYKpKD+KyBRhMU378rOtXgZYV4lnzz+ZRfV/+NgAH4H1+AZvlJv/zP//v4//sOYD/e/7P8jbWh/49/aOe2TH96W//O7//dXkX/cl//Md/5/0X/dMd898c/1W5SP85+ld9sJr+LmCqlR7ErdYAgzTKj0f5V4GW/SKj9bPzVN+3PgA7gDqAVvkR47LcxB/8wR/8iRx5r/Hq/MnyNuq6ev4xn+xY/vYf+886+0+Xd5EP/M///L+O/6N/u+Nd/F/l4i75V/tA/jn+u4CpdtogTgPeb8Aq0AYyDx/T/77+Q8Emf0B/+juAzzuAZ7nJf/zHf/P8l90e+W9t/2V5G/tD/deuf6xndqz+6r/S/tvlXfSH/tf/K/V/7N/uWP/v0f9VLqr/HvWvciBbfxcwVaUHcdkCDKYpP37W9atAywrxrPln86i+L38bgAPwPr+AzXKT//mf//fxf/YcwP89/2d5G+tD/57+Uc/smP70t/+d3/+6vIv+5D/+47/z/ov+6Y75b47/qlyk/xz9qz5YTX8XMNVKD+JWa4BBGuXHo/yrQMt+kdH62Xmq71sfgB1AHUCr/IhxWW7iD/7gD/5EjrzXeHX+ZHkbdV09/5hPdix/+4/9Z539p8u7yAf+53/+X8f/0b/d8S7+r3Jxl/yrfSD/HP9dwFQ7bRCnAXMNOJCx/Jj+9HcAdAAsA6QZiD/4gz/408RIORx/8Ad/8KcMkGYg/uAP/uBPEyPlcPzBH/zBnzJAmoFZ/riAaQoew7MFiPHdsfVtQDYgG1CXI9V4/MEf/MGfKj+6cfiDP/iDP12OVOPxB3/wB3+q/OjG4Q/+4A/+dDlSjcefHH9cwFQ7bRCnAXMNOJCx/Jj+9HcAcQApA6QZiD/4gz/408RIORx/8Ad/8KcMkGYg/uAP/uBPEyPlcPzBH/zBnzJAmoFZ/riAaQoew7MFiPHdsfVtQDYgG1CXI9V4/MEf/MGfKj+6cfiDP/iDP12OVOPxB3/wB3+q/OjG4Q/+4A/+dDlSjcefHH9cwFQ7bRCnAXMNOJCx/Jj+9HcAcQApA6QZiD/4gz/408RIORx/8Ad/8KcMkGYg/uAP/uBPEyPlcPzBH/zBnzJAmoFZ/riAaQoew7MFiPHdsfVtQDYgG1CXI9V4/MEf/MGfKj+6cfiDP/iDP12OVOPxB3/wB3+q/OjG4Q/+4A/+dDlSjcefHH9cwFQ7bRCnAe834OVy+a7Yy8vLQLk5j+l/X/856h7PQn/6OwDOOwBmucl//Md/8/x3vOPdvsF/a/svy9vb6n/6pP5r1z/WMztWf/Vfaf/t8i76Q//r/5X6P/Zvd6z/9+j/KhfVf4/6VzmQrb8LmKrSg7hsAQbTlB8/6/pVoGWFeNb8s3lU35e/DcABeJ9fwGa5yf/8z//7+D97DuD/nv+zvI31oX9P/6hndkx/+tv/zu9/Xd5Ff/If//Hfef9F/3TH/DfHf1Uu0n+O/lUfrKa/C5hqpQdxqzXAII3y41H+VaBlv8ho/ew81fetD8AOoA6gVX7EuCw38Qd/8Ad/Ikfea7w6f7K8jbqunn/MJzuWv/3H/rPO/tPlXeQD//M//6/j/+jf7ngX/1e5uEv+1T6Qf47/LmCqnTaI04D3G7AKtIHMw8f0v6//ULDJH9Cf/g7g8w7gWW7yH//x3zz/ZbdH/lvbf1nexv5Q/7XrH+uZHau/+q+0/3Z5F/2h//X/Sv0f+7c71v979H+Vi+q/R/2rHMjW3wVMVelBXLYAg2nKj591/SrQskI8a/7ZPKrvy98G4AC8zy9gs9zkf/7n/338nz0H8H/P/1nexvrQv6d/1DM7pj/97X/n978u76I/+Y//+O+8/6J/umP+m+O/KhfpP0f/qg9W098FTLXSg7jVGmCQRvnxKP8q0LJfZLR+dp7q+9YHYAdQB9AqP2Jclpv4gz/4gz+RI+81Xp0/Wd5GXVfPP+aTHcvf/mP/WWf/6fIu8oH/+Z//1/F/9G93vIv/q1zcJf9qH8g/x38XMNVOG8RpwFwDDmQsP6Y//R0AHQDLAGkG4g/+4A/+NDFSDscf/MEf/CkDpBmIP/iDP/jTxEg5HH/wB3/wpwyQZmCWPy5gmoLH8GwBYnx3bH0bkA3IBtTlSDUef/AHf/Cnyo9uHP7gD/7gT5cj1Xj8wR/8wZ8qP7px+IM/+IM/XY5U4/Enxx8XMNVOG8RpwFwDDmQsP6Y//R1AHEDKAGkG4g/+4A/+NDFSDscf/MEf/CkDpBmIP/iDP/jTxEg5HH/wB3/wpwyQZmCWPy5gmoLH8GwBYnx3bH0bkA3IBtTlSDUef/AHf/Cnyo9uHP7gD/7gT5cj1Xj8wR/8wZ8qP7px+IM/+IM/XY5U4/Enxx8XMNVOG8RpwFwDDmQsP6Y//R1AHEDKAGkG4g/+4A/+NDFSDscf/MEf/CkDpBmIP/iDP/jTxEg5HH/wB3/wpwyQZmCWPy5gmoLH8GwBYnx3bH0bkA3IBtTlSDUef/AHf/Cnyo9uHP7gD/7gT5cj1Xj8wR/8wZ8qP7px+IM/+IM/XY5U4/Enxx8XMNVOG8RpwPsNeLlcviv28vIyUG7OY/rf13+Ousez0J/+DoDzDoBZbvIf//HfPP8d73i3b/Df2v7L8va2+p8+qf/a9Y/1zI7VX/1X2n+7vIv+0P/6f6X+j/3bHev/Pfq/ykX136P+VQ5k6+8Cpqr0IC5bgME05cfPun4VaFkhnjX/bB7V9+VvA3AA3ucXsFlu8j//8/8+/s+eA/i/5/8sb2N96N/TP+qZHdOf/va/8/tfl3fRn/zHf/x33n/RP90x/83xX5WL9J+jf9UHq+nvAqZa6UHcag0wSKP8eJR/FWjZLzJaPztP9X3rA7ADqANolR8xLstN/MEf/MGfyJH3Gq/Onyxvo66r5x/zyY7lb/+x/6yz/3R5F/nA//zP/+v4P/q3O97F/1Uu7pJ/tQ/kn+O/C5hqpw3iNOD9BqwCbSDz8DH97+s/FGzyB/SnvwP4vAN4lpv8x3/8N89/2e2R/9b2X5a3sT/Uf+36x3pmx+qv/ivtv13eRX/of/2/Uv/H/u2O9f8e/V/lovrvUf8qB7L1v3z58uWx/6Mc1UzEbaXAX3/99T2fv/ttq7wks58Cnz9//vT169f9EpPRcgrg5nIl84UpQIFFFcDbRQu36dd2Ft20sE+SFt49SSF8DQpQ4GkUwMWnKcXWX8R/ATO5vNkbsMnLP+3/CGj1RjmrD/3dQPsXOP4FeJYbs96fzZ8sN2evn9XF+viLv/ib5cas97v8yfI2fu/u+nG+7Nj6+Iu/+HuWG13exXXwB3/wB38iF95rPIs/VS7OWr+ql/XX4q8LmGqnD+IYYC0DDMpYfqz+6u8A6gBaBkgzEH/wB3/wp4mRcjj+4A/+4E8ZIM1A/MEf/MGfJkbK4fiDP/iDP2cB4gLmrFIn3wNgAAZgAD6Ji+mv4Q/+4A/+TAfLyQnxB3/wB39O4mL6a/iDP/iDP9PBcnJC/MEf/MGfk7iY/hr+rMUfFzCTLcAAaxlgcvmf9v8F3Ow8R/Ppf/3vAOoAOuLDo5/jD/7gD/48mjOj+fEHf/AHf0Z8ePRz/MEf/MGfR3NmND/+4A/+nOePC5gRSYrPAQiAAOg8gIo2G4bxH//xH/8NAfHgD/AHf/AHfx6MmeH0+IM/+IM/Q0A8+AP8wR/8wZ8HY2Y4Pf7gz0r8cQEztHLtAwAAgJUAUOvycZT+1//63wF8TIjHfoI/+IM/+PNYyoxnxx/8wR/8GRPisZ/gD/7gD/48ljLj2fEHf/DnPH9cwIxZUvoEgAAIgM4DqGSyN4L4j//4j//eQMRDP8If/MEf/HkoZN6YHH/wB3/w5w1EPPQj/MEf/MGfh0LmjcnxB39W4o8LmDfMXPkIAO4D4HK5fJfz5eWlIuvpGPrf1/+0gM0X6U//lTbAZrv/Ej67/7PcnL3+LwkePLA+//O/v4AfYOJhH3f5k+VtTKS7fpwvO7Y+/uIv/p7lRpd3cR38wR/8wZ/Ihfcaz+JPlYuz1q/qZf21+OsCptrpgzgGuG+AKtAGMg8f0/++/kPBJn9Af/o7gM87gGe5yX/8x3/z/JfdHvlvbf9leRv7Q/3Xrn+sZ3as/uq/0v7b5V30h/7X/yv1f+zf7lj/79H/VS6q/x71r3IgW38XMFWlB3HZAgymKT9+1vWrQMsK8az5Z/Oovi9/G4AD8D6/gM1yk//5n//38X/2HMD/Pf9neRvrQ/+e/lHP7Jj+9Lf/nd//uryL/uQ//uO/8/6L/umO+W+O/6pcpP8c/as+WE1/FzDVSg/iVmuAQRrlx6P8q0DLfpHR+tl5qu9bH4AdQB1Aq/yIcVlu4g/+4A/+RI6813h1/mR5G3VdPf+YT3Ysf/uP/Wed/afLu8gH/ud//l/H/9G/3fEu/q9ycZf8q30g/xz/XcBUO20QpwHvN2AVaAOZh4/pf1//oWCTP6A//R3A5x3As9zkP/7jv3n+y26P/Le2/7K8jf2h/mvXP9YzO1Z/9V9p/+3yLvpD/+v/lfo/9m93rP/36P8qF9V/j/pXOZCtvwuYqtKDuGwBBtOUHz/r+lWgZYV41vyzeVTfl78NwAF4n1/AZrnJ//zP//v4P3sO4P+e/7O8jfWhf0//qGd2TH/62//O739d3kV/8h//8d95/0X/dMf8N8d/VS7Sf47+VR+spr8LmGqlB3GrNcAgjfJj+QOQA5gDWBkgzUD8wR/8wZ8mRsrh+IM/+IM/ZYA0A/EHf/AHf5oYKYfjD/7gD/6UAdIMXI0/LmCaBY/hqzVA/P7dsfxtwDZgG3CXI9V4/MEf/MGfKj+6cfiDP/iDP12OVOPxB3/wB3+q/OjG4Q/+4A/+dDlSjV+NPy5gqpUexK3WAIM0yo/lbwO2AduAywBpBuIP/uAP/jQxUg7HH/zBH/wpA6QZiD/4gz/408RIORx/8Ad/8KcMkGbgavxxAdMseAxfrQHi9++O5W8DtgHbgLscqcbjD/7gD/5U+dGNwx/8wR/86XKkGo8/+IM/+FPlRzcOf/AHf/Cny5Fq/Gr8cQFTrfQgbrUGGKRRfix/G7AN2AZcBkgzEH/wB3/wp4mRcjj+4A/+4E8ZIM1A/MEf/MGfJkbK4fiDP/iDP2WANANX448LmGbBY/hqDRC/f3csfxuwDdgG3OVINR5/8Ad/8KfKj24c/uAP/uBPlyPVePzBH/zBnyo/unH4gz/4gz9djlTjV+OPC5hqpQdxqzXAII3y41H+l8vl+5wvLy/luc8EjtY/EzvjHes7gDiAOIDMYMm3ObLcxB/8wR/8mcWf7Dyr8yfL26jP6vnHfLJj+dt/7D/r7D9d3kU+8D//8/86/o/+7Y538X+Vi7vkX+0D+ef47wKm2mmDOA14vwGrQBvIPHxM//v6DwWb/AH96e8APu8AnuUm//Ef/83zX3Z75L+1/ZflbewP9V+7/rGe2bH6q/9K+2+Xd9Ef+l//r9T/sX+7Y/2/R/9Xuaj+e9S/yoFs/V3AVJUexGULMJim/PhZ168CLSvEs+afzaP6vvxtAA7A+/wCNstN/ud//t/H/9lzAP/3/J/lbawP/Xv6Rz2zY/rT3/53fv/r8i76k//4j//O+y/6pzvmvzn+q3KR/nP0r/pgNf1dwFQrPYhbrQEGaZQfj/KvAi37RUbrZ+epvm99AHYAdQCt8iPGZbmJP/iDP/gTOfJe49X5k+Vt1HX1/GM+2bH87T/2n3X2ny7vIh/4n//5fx3/R/92x7v4v8rFXfKv9oH8c/x3AVPttEGcBrzfgFWgDWQePqb/ff2Hgk3+gP70dwCfdwDPcpP/+I//5vkvuz3y39r+y/I29of6r13/WM/sWP3Vf6X9t8u76A/9r/9X6v/Yv92x/t+j/6tcVP896l/lQLb+LmCqSg/isgUYTFN+/KzrV4GWFeJZ88/mUX1f/jYAB+B9fgGb5Sb/8z//7+P/7DmA/3v+z/I21of+Pf2jntkx/elv/zu//3V5F/3Jf/zHf+f9F/3THfPfHP9VuUj/OfpXfbCa/i5gqpUexK3WAIM0yo/lD0AOYA5gZYA0A/EHf/AHf5oYKYfjD/7gD/6UAdIMxB/8wR/8aWKkHI4/+IM/+FMGSDNwNf64gGkWPIav1gDx+3fH8rcB24BtwF2OVOPxB3/wB3+q/OjG4Q/+4A/+dDlSjccf/MEf/KnyoxuHP/iDP/jT5Ug1fjX+uICpVnoQt1oDDNIoP5a/DdgGbAMuA6QZiD/4gz/408RIORx/8Ad/8KcMkGYg/uAP/uBPEyPlcPzBH/zBnzJAmoGr8ccFTLPgMXy1BojfvzuWvw3YBmwD7nKkGo8/+IM/+FPlRzcOf/AHf/Cny5FqPP7gD/7gT5Uf3Tj8wR/8wZ8uR6rxq/HHBUy10oO41RpgkEb5sfxtwDZgG3AZIM1A/MEf/MGfJkbK4fiDP/iDP2WANAPxB3/wB3+aGCmH4w/+4A/+lAHSDFyNPy5gmgWP4as1QPz+3bH8bcA2YBtwlyPVePzBH/zBnyo/unH4gz/4gz9djlTj8Qd/8Ad/qvzoxuEP/uAP/nQ5Uo1fjT+XL1++vFSTFUeBswr89ddf31/9u9/OhniPAh+iwOfPnz99/fr1Q9a2KAV+VgA3f1bDzxSgAAUepwDePk5bM+cVcBbNaybivAJ4d14rb1KAAr+HArj4e9T5o7P0X8BMrsBqN3CT0/80yv9yuXxf6uXlsfd9o/Vn5zmaz/r+BYh/AeJfgIz4kH2e5Sb+4A/+4E+WM7PeX50/Wd5G3VbPP+aTHcvf/mP/WWf/6fIu8oH/+Z//1/F/9G93vIv/q1zcJf9qH8g/x38XMNVOG8RpwPsNWAXaQObhY/rf138o2OQP6E9/B/B5B/AsN/mP//hvnv+y2yP/re2/LG9jf6j/2vWP9cyO1V/9V9p/u7yL/tD/+n+l/o/92x3r/z36v8pF9d+j/lUOZOvvAqaq9CAuW4DBNOXHz7p+FWhZIZ41/2we1fflbwNwAN7nF7BZbvI///P/Pv7PngP4v+f/LG9jfejf0z/qmR3Tn/72v/P7X5d30Z/8x3/8d95/0T/dMf/N8V+Vi/Sfo3/VB6vp7wKmWulB3GoNMEij/HiUfxVo2S8yWj87T/V96wOwA6gDaJUfMS7LTfzBH/zBn8iR9xqvzp8sb6Ouq+cf88mO5W//sf+ss/90eRf5wP/8z//r+D/6tzvexf9VLu6Sf7UP5J/jvwuYaqcN4jTg/QasAm0g8/Ax/e/rPxRs8gf0p78D+LwDeJab/Md//DfPf9ntkf/W9l+Wt7E/1H/t+sd6Zsfqr/4r7b9d3kV/6H/9v1L/x/7tjvX/Hv1f5aL671H/Kgey9XcBU1V6EJctwGCa8mPrA4ADkF/AlQHSDMQf/MEf/GlipByOP/iDP/hTBkgzEH/wB3/wp4mRcjj+4A/+4E8ZIM1A/MnxxwVMs+FiuAbMNWDUrzumP/0dQBxAuhypxuMP/uAP/lT50Y3DH/zBH/zpcqQajz/4gz/4U+VHNw5/8Ad/8KfLkWp8lj8uYKpKD+KyBRhMU35sfRuQDcgGVAZIMxB/8Ad/8KeJkXI4/uAP/uBPGSDNQPzBH/zBnyZGyuH4gz/4gz9lgDQD8SfHHxcwzYaL4Row14BRv+6Y/vR3AHEA6XKkGo8/+IM/+FPlRzcOf/AHf/Cny5FqPP7gD/7gT5Uf3Tj8wR/8wZ8uR6rxWf64gKkqPYjLFmAwTfmx9W1ANiAbUBkgzUD8wR/8wZ8mRsrh+IM/+IM/ZYA0A/EHf/AHf5oYKYfjD/7gD/6UAdIMxJ8cf1zANBsuhmvAXANG/bpj+tPfAcQBpMuRajz+4A/+4E+VH904/MEf/MGfLkeq8fiDP/iDP1V+dOPwB3/wB3+6HKnGZ/njAqaq9CAuW4DBNOXHz7r+5XL5ntPLy0s5tzOBz5r/me8+4x35O4A4gOxzAMlyk//5n//38X/2TMD/Pf9neRvrQ/+e/lHP7Jj+9Lf/nd//uryL/uQ//uO/8/6L/umO+W+O/6pcpP8c/as+WE1/FzDVSg/iVmuAQRrlx6P8q0DLfpHR+tl5qu9bH4AdQB1Aq/yIcVlu4g/+4A/+RI6813h1/mR5G3VdPf+YT3Ysf/uP/Wed/afLu8gH/ud//l/H/9G/3fEu/q9ycZf8q30g/xz/XcBUO20QpwHvN2AVaAOZh4/pf1//oWCTP6A//R3A5x3As9zkP/7jv3n+y26P/Le2/7K8jf2h/mvXP9YzO1Z/9V9p/+3yLvpD/+v/lfo/9m93rP/36P8qF9V/j/pXOZCtvwuYqtKDuGwBBtOUHz/r+lWgZYV41vyzeVTfl78NwAF4n1/AZrnJ//zP//v4P3sO4P+e/7O8jfWhf0//qGd2TH/62//O739d3kV/8h//8d95/0X/dMf8N8d/VS7Sf47+VR+spr8LmGqlB3GrNcAgjfLjUf5VoGW/yGj97DzV960PwA6gDqBVfsS4LDfxB3/wB38iR95rvDp/sryNuq6ef8wnO5a//cf+s87+0+Vd5AP/8z//r+P/6N/ueBf/V7m4S/7VPpB/jv8uYKqdNojTgPcbsAq0gczDx/S/r/9QsMkf0J/+DuDzDuBZbvIf//HfPP9lt0f+W9t/Wd7G/lD/tesf65kdq7/6r7T/dnkX/aH/9f9K/R/7tzvW/3v0f5WL6r9H/ascyNbfBUxV6UFctgCDacqPrQ8ADkB+AVcGSDMQf/AHf/CniZFyOP7gD/7gTxkgzUD8wR/8wZ8mRsrh+IM/+IM/ZYA0A/Enxx8XMM2Gi+EaMNeAUb/umP70dwBxAOlypBqPP/iDP/hT5Uc3Dn/wB3/wp8uRajz+4A/+4E+VH904/MEf/MGfLkeq8Vn+uICpKj2IyxZgME35sfVtQDYgG1AZIM1A/MEf/MGfJkbK4fiDP/iDP2WANAPxB3/wB3+aGCmH4w/+4A/+lAHSDMSfHH9cwDQbLoZrwFwDRv26Y/rT3wHEAaTLkWo8/uAP/uBPlR/dOPzBH/zBny5HqvH4gz/4gz9VfnTj8Ad/8Ad/uhypxmf54wKmqvQgLluAwTTlx9a3AdmAbEBlgDQD8Qd/8Ad/mhgph+MP/uAP/pQB0gzEH/zBH/xpYqQcjj/4gz/4UwZIMxB/cvxxAdNsuBiuAXMNGPXrjulPfwcQB5AuR6rx+IM/+IM/VX504/AHf/AHf7ocqcbjD/7gD/5U+dGNwx/8wR/86XKkGp/ljwuYqtKDuGwBBtOUHz/r+pfL5XtOLy8v5dzOBD5r/me++4x35O8A4gCyzwEky03+53/+38f/2TMB//f8n+VtrA/9e/pHPbNj+tPf/nd+/+vyLvqT//iP/877L/qnO+a/Of6rcpH+c/Sv+mA1/V3AVCs9iFutAQZplB+P8q8CLftFRutn56m+b30AdgB1AK3yI8ZluYk/+IM/+BM58l7j1fmT5W3UdfX8Yz7ZsfztP/afdfafLu8iH/if//l/Hf9H/3bHu/i/ysVd8q/2gfxz/HcBU+20QZwGvN+AVaANZB4+pv99/YeCTf6A/vR3AJ93AM9yk//4j//m+S+7PfLf2v7L8jb2h/qvXf9Yz+xY/dV/pf23y7voD/2v/1fq/9i/3bH+36P/q1xU/z3qX+VAtv4uYKpKD+KyBRhMU378rOtXgZYV4lnzz+ZRfV/+NgAH4H1+AZvlJv/zP//v4//sOYD/e/7P8jbWh/49/aOe2TH96W//O7//dXkX/cl//Md/5/0X/dMd898c/1W5SP85+ld9sJr+LmCqlR7ErdYAgzTKj0f5V4GW/SKj9bPzVN+3PgA7gDqAVvkR47LcxB/8wR/8iRx5r/Hq/MnyNuq6ev4xn+xY/vYf+886+0+Xd5EP/M///L+O/6N/u+Nd/F/l4i75V/tA/jn+u4CpdtogTgPeb8Aq0AYyDx/T/77+Q8Emf0B/+juAzzuAZ7nJf/zHf/P8l90e+W9t/2V5G/tD/deuf6xndqz+6r/S/tvlXfSH/tf/K/V/7N/uWP/v0f9VLqr/HvWvciBbfxcwVaUHcdkCDKYpP7Y+ADgA+QVcGSDNQPzBH/zBnyZGyuH4gz/4gz9lgDQD8Qd/8Ad/mhgph+MP/uAP/pQB0gzEnxx/XMA0Gy6Ga8BcA0b9umP6098BxAGky5FqPP7gD/7gT5Uf3Tj8wR/8wZ8uR6rx+IM/+IM/VX504/AHf/AHf7ocqcZn+XP58uXLS3UxcRSgAAV2U+Dz58+fvn79ulta8qEABShAAQpQgAIUWEABZ9EFiuQrUoACFKAABShAgYQC/guYhFhnXs3egJ2ZM/OO9f0LAP8CwL8AyDBj5rv4gz/4gz8zmZKZC3/wB3/wJ8OMme/iD/7gD/7MZEpmLvzBH/zBnwwzZr6LPzn+uICZ2X1/z6UBcw04WX76/x/9HUAcQGZz5ex8+I8/+IM/Z3kx+z38wR/8wZ/ZXDk7H/7gD/7gz1lezH4Pf/AHf/BnNlfOzpfljwuYs8qefC9bgJPTnn7N+jYgG5AN6DQwJr+IP/iDP/gzGSunp8Mf/MEf/DkNjMkv4g/+4A/+TMbK6enwB3/wB39OA2Pyi/iT448LGA04VYGRAS+Xy/d1Xl4e+z85NFp/apJvTGb9HIDekLL0Ef3pv9MBNMtN/a//d+r/7Cag//V/p/+zvI39qf/0X6f/Yj9lx/pP/2X6r8u72J/6T/9l+i/2T3es//TfjP6rclH/6b9M/7mA6RI/xDPgfQNWgRbkPRzS/77+h8JNeoH+9M9sQJPa7nWa3fovy83d8n8t7Mkf5I8/+ONfAJ7ExS+vZXkbJ8Af/MEf/IlceK9xlj9d3sW8suvH+O7Y+viLv/jb5UiVi/iDPxn+uIDpOjXEM+B9A1aBFuQ9HNL/vv6Hwk16gf70z2xAk9rudZrd+i/Lzd3yfy3syR/kjz/44y/gJ3Hxy2tZ3sYJ8Ad/8Ad/Ihfea5zlT5d3Ma/s+jG+O7Y+/uIv/nY5UuUi/uBPhj8uYLpODfEMeN+AVaAFeQ+H9L+v/6Fwk16gP/0zG9CktnudZrf+y3Jzt/xfC3vyB/njD/74C/hJXPzyWpa3cQL8wR/8wZ/IhfcaZ/nT5V3MK7t+jO+OrY+/+Iu/XY5UuYg/+JPhjwuYrlNDPAPeN2AVaEHewyH97+t/KNykF+hP/8wGNKntXqfZrf+y3Nwt/9fCnvxB/viDP/4CfhIXv7yW5W2cAH/wB3/wJ3LhvcZZ/nR5F/PKrh/ju2Pr4y/+4m+XI1Uu4g/+ZPjjAqbr1BDPgPcNWAVakPdwSP/7+h8KN+kF+tM/swFNarvXaXbrvyw3d8v/tbAnf5A//uCPv4CfxMUvr2V5GyfAH/zBH/yJXHivcZY/Xd7FvLLrx/ju2Pr4i7/42+VIlYv4gz8Z/riA6To1xDMgA2YMGNqnPdR/+k//OYC2QVKcAH/wB3/wp4iPdhj+4A/+4E8bJMUJ8Ad/8Ad/ivhoh+EP/uDPOvxxAdNG3u0EAAiAALgOAG/d2x/xP//zP//3SVKbAX/wB3/wp0aPfhT+4A/+4E+fJLUZ8Ad/8Ad/avToR+EP/mT44wKm77mbGRiQATMGvGmeCQP9p//0nwPoBJSUpsAf/MEf/CnBY0IQ/uAP/uDPBJSUpsAf/MEf/CnBY0IQ/uAP/qzDHxcwE6D38xQACIAAuA4Af/bujJ/5n//5n/9nsKQyB/7gD/7gT4UdM2LwB3/wB39msKQyB/7gD/7gT4UdM2LwB38y/HEBM8N1P83BgAyYMeBPrTPlR/2n//SfA+gUmBQmwR/8wR/8KaBjSgj+4A/+4M8UmBQmwR/8wR/8KaBjSgj+4A/+rMMfFzBTsPe/SQAQAAFwHQD+z7lzfuJ//ud//p9Dk/ws+IM/+IM/eXLMicAf/MEf/JlDk/ws+IM/+IM/eXLMicAf/MnwxwXMHN+9zsKA9w14uVy+a/Ty8vKq1SN+oP99/R+h9b056U//zAZ0r4c6z3brvyw3d8s/2wvyxx/88RfwLDeu72d5e427/ok/+IM/+HPlwXv/meVPl3cxv+z6Mb47tj7+4i/+djlS5SL+4E+GPy5guk4N8Qx434BVoAV5D4f0v6//oXCTXqA//TMb0KS2e51mt/7LcnO3/F8Le/IH+eMP/vgL+Elc/PJalrdxAvzBH/zBn8iF9xpn+dPlXcwru36M746tj7/4i79djlS5iD/4k+GPC5iuU0M8A943YBVoQd7DIf3v638o3KQX6E//zAY0qe1ep9mt/7Lc3C3/18Ke/EH++IM//gJ+Ehe/vJblbZwAf/AHf/AncuG9xln+dHkX88quH+O7Y+vjL/7ib5cjVS7iD/5k+OMCpuvUEM+A9w1YBVqQ93BI//v6Hwo36QX60z+zAU1qu9dpduu/LDd3y/+1sCd/kD/+4I+/gJ/ExS+vZXkbJ8Af/MEf/IlceK9xlj9d3sW8suvH+O7Y+viLv/jb5UiVi/iDPxn+uIDpOjXEM+B9A1aBFuQ9HNL/vv6Hwk16gf70z2xAk9rudZrd+i/Lzd3yfy3syR/kjz/44y/gJ3Hxy2tZ3sYJ8Ad/8Ad/Ihfea5zlT5d3Ma/s+jG+O7Y+/uIv/nY5UuUi/uBPhj8uYLpODfEMeN+AVaAFeQ+H9L+v/6Fwk16gP/0zG9CktnudZrf+y3Jzt/xfC3vyB/njD/74C/hJXPzyWpa3cQL8wR/8wZ/IhfcaZ/nT5V3MK7t+jO+OrY+/+Iu/XY5UuYg/+JPhjwuYrlNDPAMyYMaAoX3aQ/2n//SfA2gbJMUJ8Ad/8Ad/ivhoh+EP/uAP/rRBUpwAf/AHf/CniI92GP7gD/6swx8XMG3k3U4AgAAIgOsA8Na9/RH/8z//83+fJLUZ8Ad/8Ad/avToR+EP/uAP/vRJUpsBf/AHf/CnRo9+FP7gT4Y/LmD6nruZgQEZMGPAm+aZMNB/+k//OYBOQElpCvzBH/zBnxI8JgThD/7gD/5MQElpCvzBH/zBnxI8JgThD/7gzzr8cQEzAXo/TwGAAAiA6wDwZ+/O+Jn/+Z//+X8GSypz4A/+4A/+VNgxIwZ/8Ad/8GcGSypz4A/+4A/+VNgxIwZ/8CfDHxcwM1z30xwMyIAZA/7UOlN+1H/6T/85gE6BSWES/MEf/MGfAjqmhOAP/uAP/kyBSWES/MEf/MGfAjqmhOAP/uDPOvxxATMFe/+bBAABEADXAeD/nDvnJ/7nf/7n/zk0yc+CP/iDP/iTJ8ecCPzBH/zBnzk0yc+CP/iDP/iTJ8ecCPzBnwx/XMDM8d3rLAx434CXy+W7Ri8vL69aPeIH+t/X/xFa35uT/vTPbED3eqjzbLf+y3Jzt/yzvSB//MEffwHPcuP6fpa317jrn/iDP/iDP1cevPefWf50eRfzy64f47tj6+Mv/uJvlyNVLuIP/mT44wKm69QQz4D3DVgFWpD3cEj/+/ofCjfpBfrTP7MBTWq712l2678sN3fL/7WwJ3+QP/7gj7+An8TFL69leRsnwB/8wR/8iVx4r3GWP13exbyy68f47tj6+Iu/+NvlSJWL+IM/Gf64gOk6NcQz4H0DVoEW5D0c0v++/ofCTXqB/vTPbECT2u51mt36L8vN3fJ/LezJH+SPP/jjL+AncfHLa1nexgnwB3/wB38iF95rnOVPl3cxr+z6Mb47tj7+4i/+djlS5SL+4E+GPy5guk4N8Qx434BVoAV5D4f0v6//oXCTXqA//TMb0KS2e51mt/7LcnO3/F8Le/IH+eMP/vgL+Elc/PJalrdxAvzBH/zBn8iF9xpn+dPlXcwru36M746tj7/4i79djlS5iD/4k+HP5cuXL4/9H+XoOkH8Fgr89ddf3/P4u9+2yEcS+yrw+fPnT1+/ft03QZktowBuLlMqX5QCFFhcAbxdvICbfX1n0c0K+mTp4N2TFcTXoQAFPlwBXPzwEvwWX8B/ATO5zG5A79+AVm+Us+Wh/339szpW36c//TP/AqDaZ6O43fovy83d8h/VefRc/viDP/4F5IgPR8+zvI3z4Q/+4A/+RC681zjLny7vYl7Z9WN8d2x9/MVf/O1ypMpF/MGfDH9cwHSdGuIZkAEzBgzt0x7qP/2n/xxA2yApToA/+IM/+FPERzsMf/AHf/CnDZLiBPiDP/iDP0V8tMPwB3/wZx3+uIBpI+92AgAEQABcB4C37u2P+J//+Z//+ySpzYA/+IM/+FOjRz8Kf/AHf/CnT5LaDPiDP/iDPzV69KPwB38y/HEB0/fczQwMyIAZA940z4SB/tN/+s8BdAJKSlPgD/7gD/6U4DEhCH/wB3/wZwJKSlPgD/7gD/6U4DEhCH/wB3/W4Y8LmAnQ+3kKAARAAFwHgD97d8bP/M///M//M1hSmQN/8Ad/8KfCjhkx+IM/+IM/M1hSmQN/8Ad/8KfCjhkx+IM/Gf78fwAAAP//x/ExIgAAQABJREFU7d3dctxGkgZQM3Q3fv9H5dwpuLOKUJssAkT+NUeFOXtjollZLSTyO4AGduzL23/+76/B//v3v//917/+9a/BHXNb+X79N3/yl1NjbjV/+MMf/syJktuJP/zhD39yasyt5g9/+MOfOVFyO/GHP/zhT06NudX84U/GnxcvYObC9/87CaAAZgI4O33mT/7kT/48gE+7Gt2PP/zhD3+iXkyv4w9/+MOfaVei+/GHP/zhT9SL6XX84c9O/ngBMywAAI4BeHl5+dXp4f/g6tPV0//j/n9q1JM+0H/93+kGOB2D6fnPujn9/dn++H75l39/Ac+6MbW+60/W2/XP3f3+db/sse/nL3/5G3Wj6936PfzhD3/4s7rwXcdT/lRdnPr+ar98/17+egFTnfSTOgE4DkAVtJM2n36s/8f9P23Y8C/0X/89gM89gGfdlD/5k7+5/GVvj/K3d/6y3q7z4frvff3X65k9dv1d/53uv13v1nyYf/O/0/yv89s9Nv/3mP+qi67/Pa5/1YHs9fcCptrpk7rsBTjZpvzxn/r9VdCyjfhTzz97HtX1zt8NwAPwff4H2Kyb8i//8n+f/GefA+S/l/+st+v10f9e/9d+Zo/1X//d/+L3v653az7lT/7kL56/NT/dY/mbyV/VRf2f6X81B7v13wuY6pU+qdttAE5Oo/zx2flXQcv+Qc6+P7tPdb3vB7AHUA+gVT/Wuqyb/OEPf/izOvJdx7v7k/V27evu57+eT/bY+bv/uP/sc//perf6IP/yL//75H/Nb/f4LvmvuniX86/OgfPP+e8FTHXSTuoM4PEAVkE7afPpx/p/3P/Thg3/Qv/13wP43AN41k35kz/5m8tf9vYof3vnL+vtOh+u/97Xf72e2WPX3/Xf6f7b9W7Nh/k3/zvN/zq/3WPzf4/5r7ro+t/j+lcdyF5/L2CqnT6py16Ak23KH/+p318FLduIP/X8s+dRXe/83QA8AN/nf4DNuin/8i//98l/9jlA/nv5z3q7Xh/97/V/7Wf2WP/13/0vfv/rerfmU/7kT/7i+Vvz0z2Wv5n8VV3U/5n+V3OwW/+9gKle6ZO63Qbg5DTKHzt/AHkA8wBWBqRZyB/+8Ic/TUbK5fzhD3/4UwakWcgf/vCHP01GyuX84Q9/+FMGpFm4mz9ewDQv+Fq+2wCsf/7usfN3A3YDdgPuOlKt5w9/+MOfqh/dOv7whz/86TpSrecPf/jDn6of3Tr+8Ic//Ok6Uq3fzR8vYKpX+qRutwE4OY3yx87fDdgN2A24DEizkD/84Q9/moyUy/nDH/7wpwxIs5A//OEPf5qMlMv5wx/+8KcMSLNwN3+8gGle8LV8twFY//zdY+fvBuwG7AbcdaRazx/+8Ic/VT+6dfzhD3/403WkWs8f/vCHP1U/unX84Q9/+NN1pFq/mz9ewFSv9EndbgNwchrlj52/G7AbsBtwGZBmIX/4wx/+NBkpl/OHP/zhTxmQZiF/+MMf/jQZKZfzhz/84U8ZkGbhbv54AdO84Gv5bgOw/vm7x87fDdgN2A2460i1nj/84Q9/qn506/jDH/7wp+tItZ4//OEPf6p+dOv4wx/+8KfrSLV+N3+8gKle6ZO63Qbg5DTKH5+d/8vLy689397eyntHCs++P1I7scb3ewDxAOIBZMKS/98j6yZ/+MMf/kz5k91nd3+y3q792f381/PJHjt/9x/3n33uP13vVh/kX/7lf5/8r/ntHt8l/1UX73L+1Tlw/jn/vYCpTtpJnQE8HsAqaCdtPv1Y/4/7f9qw4V/ov/57AJ97AM+6KX/yJ39z+cveHuVv7/xlvV3nw/Xf+/qv1zN77Pq7/jvdf7verfkw/+Z/p/lf57d7bP7vMf9VF13/e1z/qgPZ6+8FTLXTJ3XZC3CyTfnjP/X7q6BlG/Gnnn/2PKrrnb8bgAfg+/wPsFk35V/+5f8++c8+B8h/L/9Zb9fro/+9/q/9zB7rv/67/8Xvf13v1nzKn/zJXzx/a366x/I3k7+qi/o/0/9qDnbrvxcw1St9UrfbAJycRvnjs/Ovgpb9g5x9f3af6nrfD2APoB5Aq36sdVk3+cMf/vBndeS7jnf3J+vt2tfdz389n+yx83f/cf/Z5/7T9W71Qf7lX/73yf+a3+7xXfJfdfEu51+dA+ef898LmOqkndQZwOMBrIJ20ubTj/X/uP+nDRv+hf7rvwfwuQfwrJvyJ3/yN5e/7O1R/vbOX9bbdT5c/72v/3o9s8euv+u/0/23692aD/Nv/nea/3V+u8fm/x7zX3XR9b/H9a86kL3+XsBUO31Sl70AJ9uUP/5Tv78KWrYRf+r5Z8+jut75uwF4AL7P/wCbdVP+5V/+75P/7HOA/Pfyn/V2vT763+v/2s/ssf7rv/tf/P7X9W7Np/zJn/zF87fmp3ssfzP5q7qo/zP9r+Zgt/57AVO90id1uw3AyWmUP3b+APIA5gGsDEizkD/84Q9/moyUy/nDH/7wpwxIs5A//OEPf5qMlMv5wx/+8KcMSLNwN3+8gGle8LV8twFY//zdY+fvBuwG7AbcdaRazx/+8Ic/VT+6dfzhD3/403WkWs8f/vCHP1U/unX84Q9/+NN1pFq/mz9ewFSv9EndbgNwchrlj52/G7AbsBtwGZBmIX/4wx/+NBkpl/OHP/zhTxmQZiF/+MMf/jQZKZfzhz/84U8ZkGbhbv54AdO84Gv5bgOw/vm7x87fDdgN2A2460i1nj/84Q9/qn506/jDH/7wp+tItZ4//OEPf6p+dOv4wx/+8KfrSLV+N3+8gKle6ZO63Qbg5DTKHzt/N2A3YDfgMiDNQv7whz/8aTJSLucPf/jDnzIgzUL+8Ic//GkyUi7nD3/4w58yIM3C3fzxAqZ5wdfy3QZg/fN3j52/G7AbsBtw15FqPX/4wx/+VP3o1vGHP/zhT9eRaj1/+MMf/lT96Nbxhz/84U/XkWr9bv68vL6+vlVPVp0ORDvw999//1r6n3mLllinA/+VDvz48eOvnz9//le+25fqwPsOcPN9N/ysAzqgA8/rAG+f11s75zvgWTTfMxXxDvAu3isrdUAH/jc6wMX/jev83z5L/wXM8BXY7Q3c8On/dXb+Ly8vv77q7e257/vOvn/6PM/28/3+DRD/Boh/A+TMh+znWTf5wx/+8CfrzNT63f3Jerv2bffzX88ne+z83X/cf/a5/3S9W32Qf/mX/33yv+a3e3yX/FddvMv5V+fA+ef89wKmOmkndQbweACroJ20+fRj/T/u/2nDhn+h//rvAXzuATzrpvzJn/zN5S97e5S/vfOX9XadD9d/7+u/Xs/ssevv+u90/+16t+bD/Jv/neZ/nd/usfm/x/xXXXT973H9qw5kr78XMNVOn9RlL8DJNuWP/9Tvr4KWbcSfev7Z86iud/5uAB6A7/M/wGbdlH/5l//75D/7HCD/vfxnvV2vj/73+r/2M3us//rv/he//3W9W/Mpf/Inf/H8rfnpHsvfTP6qLur/TP+rOdit/17AVK/0Sd1uA3ByGuWPz86/Clr2D3L2/dl9qut9P4A9gHoArfqx1mXd5A9/+MOf1ZHvOt7dn6y3a193P//1fLLHzt/9x/1nn/tP17vVB/mXf/nfJ/9rfrvHd8l/1cW7nH91Dpx/zn8vYKqTdlJnAI8HsAraSZtPP9b/4/6fNmz4F/qv/x7A5x7As27Kn/zJ31z+srdH+ds7f1lv1/lw/fe+/uv1zB67/q7/TvffrndrPsy/+d9p/tf57R6b/3vMf9VF1/8e17/qQPb6ewFT7fRJXfYCnGxT/tj3A8ADkP8BrgxIs5A//OEPf5qMlMv5wx/+8KcMSLOQP/zhD3+ajJTL+cMf/vCnDEizkD85f7yAaQ7cWm4AcwO49q97rP/67wHEA0jXkWo9f/jDH/5U/ejW8Yc//OFP15FqPX/4wx/+VP3o1vGHP/zhT9eRan3WHy9gqp0+qctegJNtyh/7fjcgNyA3oDIgzUL+8Ic//GkyUi7nD3/4w58yIM1C/vCHP/xpMlIu5w9/+MOfMiDNQv7k/PECpjlwa7kBzA3g2r/usf7rvwcQDyBdR6r1/OEPf/hT9aNbxx/+8Ic/XUeq9fzhD3/4U/WjW8cf/vCHP11HqvVZf7yAqXb6pC57AU62KX/s+92A3IDcgMqANAv5wx/+8KfJSLmcP/zhD3/KgDQL+cMf/vCnyUi5nD/84Q9/yoA0C/mT88cLmObAreUGMDeAa/+6x/qv/x5APIB0HanW84c//OFP1Y9uHX/4wx/+dB2p1vOHP/zhT9WPbh1/+MMf/nQdqdZn/fECptrpk7rsBTjZpvzxn/r9Ly8vv87p7e2tfG6Rwj/1/CN/9ok1zt8DiAeQ+zyAZN2Uf/mX//vkP/tMIP+9/Ge9Xa+P/vf6v/Yze6z/+u/+F7//db1b8yl/8id/8fyt+ekey99M/qou6v9M/6s52K3/XsBUr/RJ3W4DcHIa5Y/Pzr8KWvYPcvb92X2q630/gD2AegCt+rHWZd3kD3/4w5/Vke863t2frLdrX3c///V8ssfO3/3H/Wef+0/Xu9UH+Zd/+d8n/2t+u8d3yX/Vxbucf3UOnH/Ofy9gqpN2UmcAjwewCtpJm08/1v/j/p82bPgX+q//HsDnHsCzbsqf/MnfXP6yt0f52zt/WW/X+XD9977+6/XMHrv+rv9O99+ud2s+zL/532n+1/ntHpv/e8x/1UXX/x7Xv+pA9vp7AVPt9Eld9gKcbFP++E/9/ipo2Ub8qeefPY/qeufvBuAB+D7/A2zWTfmXf/m/T/6zzwHy38t/1tv1+uh/r/9rP7PH+q//7n/x+1/XuzWf8id/8hfP35qf7rH8zeSv6qL+z/S/moPd+u8FTPVKn9TtNgAnp1H++Oz8q6Bl/yBn35/dp7re9wPYA6gH0Kofa13WTf7whz/8WR35ruPd/cl6u/Z19/Nfzyd77Pzdf9x/9rn/dL1bfZB/+Zf/ffK/5rd7fJf8V128y/lX58D55/z3AqY6aSd1BvB4AKugnbT59GP9P+7/acOGf6H/+u8BfO4BPOum/Mmf/M3lL3t7lL+985f1dp0P13/v679ez+yx6+/673T/7Xq35sP8m/+d5n+d3+6x+b/H/FdddP3vcf2rDmSvvxcw1U6f1GUvwMk25Y99PwA8APkf4MqANAv5wx/+8KfJSLmcP/zhD3/KgDQL+cMf/vCnyUi5nD/84Q9/yoA0C/mT88cLmObAreUGMDeAa/+6x/qv/x5APIB0HanW84c//OFP1Y9uHX/4wx/+dB2p1vOHP/zhT9WPbh1/+MMf/nQdqdZn/fECptrpk7rsBTjZpvyx73cDcgNyAyoD0izkD3/4w58mI+Vy/vCHP/wpA9Is5A9/+MOfJiPlcv7whz/8KQPSLORPzh8vYJoDt5YbwNwArv3rHuu//nsA8QDSdaRazx/+8Ic/VT+6dfzhD3/403WkWs8f/vCHP1U/unX84Q9/+NN1pFqf9ccLmGqnT+qyF+Bkm/LHvt8NyA3IDagMSLOQP/zhD3+ajJTL+cMf/vCnDEizkD/84Q9/moyUy/nDH/7wpwxIs5A/OX+8gGkO3FpuAHMDuPave6z/+u8BxANI15FqPX/4wx/+VP3o1vGHP/zhT9eRaj1/+MMf/lT96Nbxhz/84U/XkWp91h8vYKqdPqnLXoCTbcof/6nf//Ly8uuc3t7eyucWKfxTzz/yZ59Y4/w9gHgAuc8DSNZN+Zd/+b9P/rPPBPLfy3/W2/X66H+v/2s/s8f6r//uf/H7X9e7NZ/yJ3/yF8/fmp/usfzN5K/qov7P9L+ag9367wVM9Uqf1O02ACenUf747PyroGX/IGffn92nut73A9gDqAfQqh9rXdZN/vCHP/xZHfmu4939yXq79nX381/PJ3vs/N1/3H/2uf90vVt9kH/5l/998r/mt3t8l/xXXbzL+VfnwPnn/PcCpjppJ3UG8HgAq6CdtPn0Y/0/7v9pw4Z/of/67wF87gE866b8yZ/8zeUve3uUv73zl/V2nQ/Xf+/rv17P7LHr7/rvdP/terfmw/yb/53mf53f7rH5v8f8V110/e9x/asOZK+/FzDVTp/UZS/AyTblj//U76+Clm3En3r+2fOornf+bgAegO/zP8Bm3ZR/+Zf/++Q/+xwg/738Z71dr4/+9/q/9jN7rP/67/4Xv/91vVvzKX/yJ3/x/K356R7L30z+qi7q/0z/qznYrf9ewFSv9EndbgNwchrlj8/Ovwpa9g9y9v3ZfarrfT+APYB6AK36sdZl3eQPf/jDn9WR7zre3Z+st2tfdz//9Xyyx87f/cf9Z5/7T9e71Qf5l3/53yf/a367x3fJf9XFu5x/dQ6cf85/L2Cqk3ZSZwCPB7AK2kmbTz/W/+P+nzZs+Bf6r/8ewOcewLNuyp/8yd9c/rK3R/nbO39Zb9f5cP33vv7r9cweu/6u/0733653az7Mv/nfaf7X+e0em/97zH/VRdf/Hte/6kD2+nsBU+30SV32ApxsU/7Y9wPAA5D/Aa4MSLOQP/zhD3+ajJTL+cMf/vCnDEizkD/84Q9/moyUy/nDH/7wpwxIs5A/OX+8gGkO3FpuAHMDuPave6z/+u8BxANI15FqPX/4wx/+VP3o1vGHP/zhT9eRaj1/+MMf/lT96Nbxhz/84U/XkWp91p+X19fXt+qXqdMBHdCBu3Xgx48ff/38+fNup+V8dEAHdEAHdEAHdEAHNuiAZ9ENLpI/og7ogA7ogA7ogA4kOuC/gEk0K7I0+wYssmdmje/3bwD4NwD8GwAZMybX8oc//OHPpCmZvfjDH/7wJ2PG5Fr+8Ic//Jk0JbMXf/jDH/5kzJhcy5+cP17ATE7ff/YygLkBHG6//v9b/z2AeACZdiW6H//5wx/+RL2YXscf/vCHP9OuRPfjD3/4w5+oF9Pr+MMf/vBn2pXofll/vICJdja4LnsBgtuGl/l+NyA3IDegMBjDC/nDH/7wZ5iV8Hb84Q9/+BMGY3ghf/jDH/4MsxLejj/84Q9/wmAML+RPzh8vYAzgaAfOAvjy8vLre97envv/cujs+0dP8ovNfH8OoC9aWfqV/uv/nR5As26af/N/p/nP3gTMv/nvzH/W23U+zZ/568zfOk/ZY/Nn/jLz1/VunU/zZ/4y87fOT/fY/Jm/ifmrumj+zF9m/ryA6Yq/1AvgcQCroC3tvTzU/+P+XzZuaIH+63/mBjQ0do9t7jZ/WTfvdv6PCxv8wfnzhz/+DcAgF5+WZb1dN+APf/jDn9WF7zrO+tP1bj2v7Pev9d1j389f/vK360jVRf7wJ+OPFzDdpC71AngcwCpoS3svD/X/uP+XjRtaoP/6n7kBDY3dY5u7zV/Wzbud/+PCBn9w/vzhj7+AB7n4tCzr7boBf/jDH/6sLnzXcdafrnfreWW/f63vHvt+/vKXv11Hqi7yhz8Zf7yA6SZ1qRfA4wBWQVvae3mo/8f9v2zc0AL91//MDWho7B7b3G3+sm7e7fwfFzb4g/PnD3/8BTzIxadlWW/XDfjDH/7wZ3Xhu46z/nS9W88r+/1rfffY9/OXv/ztOlJ1kT/8yfjjBUw3qUu9AB4HsAra0t7LQ/0/7v9l44YW6L/+Z25AQ2P32OZu85d1827n/7iwwR+cP3/44y/gQS4+Lct6u27AH/7whz+rC991nPWn6916XtnvX+u7x76fv/zlb9eRqov84U/GHy9gukld6gXwOIBV0Jb2Xh7q/3H/Lxs3tED/9T9zAxoau8c2d5u/rJt3O//HhQ3+4Pz5wx9/AQ9y8WlZ1tt1A/7whz/8WV34ruOsP13v1vPKfv9a3z32/fzlL3+7jlRd5A9/Mv54AdNN6lIvgAKYCeAyPu1D82f+zJ8H0DYkxQ34wx/+8KfIR7uMP/zhD3/akBQ34A9/+MOfIh/tMv7whz/7+OMFTJu8jxsAEIAA3AfAj+ntH8m//Mu//Pclqe3AH/7whz81PfpV/OEPf/jTl6S2A3/4wx/+1PToV/GHPxl/vIDpZ+7DDgIogJkAfhiegQPzZ/7MnwfQAUpKW/CHP/zhTwmPgSL+8Ic//BmgpLQFf/jDH/6U8Bgo4g9/+LOPP17ADKD3fgsAAhCA+wD4PrsTP8u//Mu//E9YUtmDP/zhD38qdkzU8Ic//OHPhCWVPfjDH/7wp2LHRA1/+JPxxwuYidS920MABTATwHejM/Kj+TN/5s8D6AgmhU34wx/+8KdAx0gJf/jDH/6MYFLYhD/84Q9/CnSMlPCHP/zZxx8vYEbY+2cTAAIQgPsA+E9yZ36Sf/mXf/mf0SS/C3/4wx/+5OWYqeAPf/jDnxlN8rvwhz/84U9ejpkK/vAn448XMDO5e+wigMcBfHl5+dWjt7e3R6+e8YP+H/f/Gb0+2lP/9T9zAzqaoc5nd5u/rJt3O//sLDh//vDHX8Czbvxen/X2d93vf/KHP/zhz28PvvufWX+63q3nl/3+tb577Pv5y1/+dh2pusgf/mT88QKmm9SlXgCPA1gFbWnv5aH+H/f/snFDC/Rf/zM3oKGxe2xzt/nLunm3839c2OAPzp8//PEX8CAXn5ZlvV034A9/+MOf1YXvOs760/VuPa/s96/13WPfz1/+8rfrSNVF/vAn448XMN2kLvUCeBzAKmhLey8P9f+4/5eNG1qg//qfuQENjd1jm7vNX9bNu53/48IGf3D+/OGPv4AHufi0LOvtugF/+MMf/qwufNdx1p+ud+t5Zb9/re8e+37+8pe/XUeqLvKHPxl/vIDpJnWpF8DjAFZBW9p7eaj/x/2/bNzQAv3X/8wNaGjsHtvcbf6ybt7t/B8XNviD8+cPf/wFPMjFp2VZb9cN+MMf/vBndeG7jrP+dL1bzyv7/Wt999j385e//O06UnWRP/zJ+OMFTDepS70AHgewCtrS3stD/T/u/2Xjhhbov/5nbkBDY/fY5m7zl3Xzbuf/uLDBH5w/f/jjL+BBLj4ty3q7bsAf/vCHP6sL33Wc9afr3Xpe2e9f67vHvp+//OVv15Gqi/zhT8YfL2C6SV3qBfA4gFXQlvZeHur/cf8vGze0QP/1P3MDGhq7xzZ3m7+sm3c7/8eFDf7g/PnDH38BD3LxaVnW23UD/vCHP/xZXfiu46w/Xe/W88p+/1rfPfb9/OUvf7uOVF3kD38y/ngB003qUi+AApgJ4DI+7UPzZ/7MnwfQNiTFDfjDH/7wp8hHu4w//OEPf9qQFDfgD3/4w58iH+0y/vCHP/v44wVMm7yPGwAQgADcB8CP6e0fyb/8y7/89yWp7cAf/vCHPzU9+lX84Q9/+NOXpLYDf/jDH/7U9OhX8Yc/GX+8gOln7sMOAiiAmQB+GJ6BA/Nn/syfB9ABSkpb8Ic//OFPCY+BIv7whz/8GaCktAV/+MMf/pTwGCjiD3/4s48/XsAMoPd+CwACEID7APg+uxM/y7/8y7/8T1hS2YM//OEPfyp2TNTwhz/84c+EJZU9+MMf/vCnYsdEDX/4k/HHC5iJ1L3bQwAFMBPAd6Mz8qP5M3/mzwPoCCaFTfjDH/7wp0DHSAl/+MMf/oxgUtiEP/zhD38KdIyU8Ic//NnHHy9gRtj7ZxMAAhCA+wD4T3JnfpJ/+Zd/+Z/RJL8Lf/jDH/7k5Zip4A9/+MOfGU3yu/CHP/zhT16OmQr+8CfjjxcwM7l77CKAxwF8eXn51aO3t7dHr57xg/4f9/8ZvT7aU//1P3MDOpqhzmd3m7+sm3c7/+wsOH/+8MdfwLNu/F6f9fZ33e9/8oc//OHPbw+++59Zf7rereeX/f61vnvs+/nLX/52Ham6yB/+ZPzxAqab1KVeAI8DWAVtae/lof4f9/+ycUML9F//MzegobF7bHO3+cu6ebfzf1zY4A/Onz/88RfwIBeflmW9XTfgD3/4w5/Vhe86zvrT9W49r+z3r/XdY9/PX/7yt+tI1UX+8Cfjjxcw3aQu9QJ4HMAqaEt7Lw/1/7j/l40bWqD/+p+5AQ2N3WObu81f1s27nf/jwgZ/cP784Y+/gAe5+LQs6+26AX/4wx/+rC5813HWn65363llv3+t7x77fv7yl79dR6ou8oc/GX+8gOkmdakXwOMAVkFb2nt5qP/H/b9s3NAC/df/zA1oaOwe29xt/rJu3u38Hxc2+IPz5w9//AU8yMWnZVlv1w34wx/+8Gd14buOs/50vVvPK/v9a3332Pfzl7/87TpSdZE//Mn48/L6+vrc/6cc3SSov0UH/v7771/n8Z95u8X5OIn7duDHjx9//fz5874n6My26QA3t7lU/qA6oAObd4C3m1/Am/3xPYve7IL+YafDuz/sgvjj6IAO/Nc7wMX/+iX4n/gD+C9ghi+zN6DHb0Crb5Szl0f/j/uf7WN1vf7rf+bfAKjO2Vnd3eYv6+bdzv/sOp997vz5wx//BuSZD1efZ71d9+MPf/jDn9WF7zrO+tP1bj2v7Pev9d1j389f/vK360jVRf7wJ+OPFzDdpC71AiiAmQAu49M+NH/mz/x5AG1DUtyAP/zhD3+KfLTL+MMf/vCnDUlxA/7whz/8KfLRLuMPf/izjz9ewLTJ+7gBAAEIwH0A/Jje/pH8y7/8y39fktoO/OEPf/hT06NfxR/+8Ic/fUlqO/CHP/zhT02PfhV/+JPxxwuYfuY+7CCAApgJ4IfhGTgwf+bP/HkAHaCktAV/+MMf/pTwGCjiD3/4w58BSkpb8Ic//OFPCY+BIv7whz/7+OMFzAB677cAIAABuA+A77M78bP8y7/8y/+EJZU9+MMf/vCnYsdEDX/4wx/+TFhS2YM//OEPfyp2TNTwhz8Zf7yAmUjduz0EUAAzAXw3OiM/mj/zZ/48gI5gUtiEP/zhD38KdIyU8Ic//OHPCCaFTfjDH/7wp0DHSAl/+MOfffzxAmaEvX82ASAAAbgPgP8kd+Yn+Zd/+Zf/GU3yu/CHP/zhT16OmQr+8Ic//JnRJL8Lf/jDH/7k5Zip4A9/Mv54ATOTu8cuAngcwJeXl189ent7e/TqGT/o/3H/n9Hroz31X/8zN6CjGep8drf5y7p5t/PPzoLz5w9//AU868bv9Vlvf9f9/id/+MMf/vz24Lv/mfWn6916ftnvX+u7x76fv/zlb9eRqov84U/GHy9gukld6gXwOIBV0Jb2Xh7q/3H/Lxs3tED/9T9zAxoau8c2d5u/rJt3O//HhQ3+4Pz5wx9/AQ9y8WlZ1tt1A/7whz/8WV34ruOsP13v1vPKfv9a3z32/fzlL3+7jlRd5A9/Mv54AdNN6lIvgMcBrIK2tPfyUP+P+3/ZuKEF+q//mRvQ0Ng9trnb/GXdvNv5Py5s8Afnzx/++At4kItPy7Lerhvwhz/84c/qwncdZ/3pereeV/b71/ruse/nL3/523Wk6iJ/+JPxxwuYblKXegE8DmAVtKW9l4f6f9z/y8YNLdB//c/cgIbG7rHN3eYv6+bdzv9xYYM/OH/+8MdfwINcfFqW9XbdgD/84Q9/Vhe+6zjrT9e79byy37/Wd499P3/5y9+uI1UX+cOfjD9ewHSTutQL4HEAq6At7b081P/j/l82bmiB/ut/5gY0NHaPbe42f1k373b+jwsb/MH584c//gIe5OLTsqy36wb84Q9/+LO68F3HWX+63q3nlf3+tb577Pv5y1/+dh2pusgf/mT88QKmm9SlXgCPA1gFbWnv5aH+H/f/snFDC/Rf/zM3oKGxe2xzt/nLunm3839c2OAPzp8//PEX8CAXn5ZlvV034A9/+MOf1YXvOs760/VuPa/s96/13WPfz1/+8rfrSNVF/vAn448XMN2kLvUCKICZAC7j0z40f+bP/HkAbUNS3IA//OEPf4p8tMv4wx/+8KcNSXED/vCHP/wp8tEu4w9/+LOPP17AtMn7uAEAAQjAfQD8mN7+kfzLv/zLf1+S2g784Q9/+FPTo1/FH/7whz99SWo78Ic//OFPTY9+FX/4k/HHC5h+5j7sIIACmAngh+EZODB/5s/8eQAdoKS0BX/4wx/+lPAYKOIPf/jDnwFKSlvwhz/84U8Jj4Ei/vCHP/v44wXMAHrvtwAgAAG4D4Dvszvxs/zLv/zL/4QllT34wx/+8Kdix0QNf/jDH/5MWFLZgz/84Q9/KnZM1PCHPxl/vICZSN27PQRQADMBfDc6Iz+aP/Nn/jyAjmBS2IQ//OEPfwp0jJTwhz/84c8IJoVN+MMf/vCnQMdICX/4w599/PECZoS9fzYBIAABuA+A/yR35if5l3/5l/8ZTfK78Ic//OFPXo6ZCv7whz/8mdEkvwt/+MMf/uTlmKngD38y/ngBM5O7xy4CeBzAl5eXXz16e3t79OoZP+j/cf+f0eujPfVf/zM3oKMZ6nx2t/nLunm388/OgvPnD3/8BTzrxu/1WW9/1/3+J3/4wx/+/Pbgu/+Z9afr3Xp+2e9f67vHvp+//OVv15Gqi/zhT8YfL2C6SV3qBfA4gFXQlvZeHur/cf8vGze0QP/1P3MDGhq7xzZ3m7+sm3c7/8eFDf7g/PnDH38BD3LxaVnW23UD/vCHP/xZXfiu46w/Xe/W88p+/1rfPfb9/OUvf7uOVF3kD38y/ngB003qUi+AxwGsgra09/JQ/4/7f9m4oQX6r/+ZG9DQ2D22udv8Zd282/k/LmzwB+fPH/74C3iQi0/Lst6uG/CHP/zhz+rCdx1n/el6t55X9vvX+u6x7+cvf/nbdaTqIn/4k/HHC5huUpd6ATwOYBW0pb2Xh/p/3P/Lxg0t0H/9z9yAhsbusc3d5i/r5t3O/3Fhgz84f/7wx1/Ag1x8Wpb1dt2AP/zhD39WF77rOOtP17v1vLLfv9Z3j30/f/nL364jVRf5w5+MP17AdJO61AvgcQCroC3tvTzU/+P+XzZuaIH+63/mBjQ0do9t7jZ/WTfvdv6PCxv8wfnzhz/+Ah7k4tOyrLfrBvzhD3/4s7rwXcdZf7rereeV/f61vnvs+/nLX/52Ham6yB/+ZPzxAqab1KVeAI8DWAVtae/lof4f9/+ycUML9F//MzegobF7bHO3+cu6ebfzf1zY4A/Onz/88RfwIBeflmW9XTfgD3/4w5/Vhe86zvrT9W49r+z3r/XdY9/PX/7yt+tI1UX+8Cfjjxcw3aQu9QIogJkALuPTPjR/5s/8eQBtQ1LcgD/84Q9/iny0y/jDH/7wpw1JcQP+8Ic//Cny0S7jD3/4s48/XsC0yfu4AQABCMB9APyY3v6R/Mu//Mt/X5LaDvzhD3/4U9OjX8Uf/vCHP31Jajvwhz/84U9Nj34Vf/iT8ccLmH7mPuwggAKYCeCH4Rk4MH/mz/x5AB2gpLQFf/jDH/6U8Bgo4g9/+MOfAUpKW/CHP/zhTwmPgSL+8Ic/+/jjBcwAeu+3ACAAAbgPgO+zO/Gz/Mu//Mv/hCWVPfjDH/7wp2LHRA1/+MMf/kxYUtmDP/zhD38qdkzU8Ic/GX+8gJlI3bs9BFAAMwF8NzojP5o/82f+PICOYFLYhD/84Q9/CnSMlPCHP/zhzwgmhU34wx/+8KdAx0gJf/jDn3388QJmhL1/NgEgAAG4D4D/JHfmJ/mXf/mX/xlN8rvwhz/84U9ejpkK/vCHP/yZ0SS/C3/4wx/+5OWYqeAPfzL+vLy+vr7NjJ5ddOC8A3///fevX/5n3s4X+Y0O/AEd+PHjx18/f/78A/4k/gj/6x3g5v/6BDh/HdCB7+oAb7+r074n0gHPopEuWVPtAO+qnVOnAzpw1w5w8a5X9s86L/8FzPD18Ab0+A3oy8vLr06/vT33fZ/+H/d/eMxPt9N//c/8GwCng1T8xd3mL+vm3c4/OwbOnz/88W9AZt34vT7r7e+63//kD3/4w5/fHnz3P7P+dL1bzy/7/Wt999j385e//O06UnWRP/zJ+OMFTDepS70AHgewCtrS3stD/T/u/2Xjhhbov/5nbkBDY/fY5m7zl3Xzbuf/uLDBH5w/f/jjL+BBLj4ty3q7bsAf/vCHP6sL33Wc9afr3Xpe2e9f67vHvp+//OVv15Gqi/zhT8YfL2C6SV3qBfA4gFXQlvZeHur/cf8vGze0QP/1P3MDGhq7xzZ3m7+sm3c7/8eFDf7g/PnDH38BD3LxaVnW23UD/vCHP/xZXfiu46w/Xe/W88p+/1rfPfb9/OUvf7uOVF3kD38y/ngB003qUi+AxwGsgra09/JQ/4/7f9m4oQX6r/+ZG9DQ2D22udv8Zd282/k/LmzwB+fPH/74C3iQi0/Lst6uG/CHP/zhz+rCdx1n/el6t55X9vvX+u6x7+cvf/nbdaTqIn/4k/HHC5huUpd6ATwOYBW0pb2Xh/p/3P/Lxg0t0H/9z9yAhsbusc3d5i/r5t3O/3Fhgz84f/7wx1/Ag1x8Wpb1dt2AP/zhD39WF77rOOtP17v1vLLfv9Z3j30/f/nL364jVRf5w5+MP17AdJO61AugAGYCuIxP+9D8mT/z5wG0DUlxA/7whz/8KfLRLuMPf/jDnzYkxQ34wx/+8KfIR7uMP/zhzz7+eAHTJu/jBgAEIAD3AfBjevtH8i//8i//fUlqO/CHP/zhT02PfhV/+MMf/vQlqe3AH/7whz81PfpV/OFPxh8vYPqZ+7CDAApgJoAfhmfgwPyZP/PnAXSAktIW/OEPf/hTwmOgiD/84Q9/BigpbcEf/vCHPyU8Bor4wx/+7OOPFzAD6L3fAoAABOA+AL7P7sTP8i//8i//E5ZU9uAPf/jDn4odEzX84Q9/+DNhSWUP/vCHP/yp2DFRwx/+ZPzxAmYide/2EEABzATw3eiM/Gj+zJ/58wA6gklhE/7whz/8KdAxUsIf/vCHPyOYFDbhD3/4w58CHSMl/OEPf/bxxwuYEfb+2QSAAATgPgD+k9yZn+Rf/uVf/mc0ye/CH/7whz95OWYq+MMf/vBnRpP8LvzhD3/4k5djpoI//Mn44wXMTO4euwjgcQBfXl5+9ejt7e3Rq2f8oP/H/X9Gr4/21H/9z9yAjmao89nd5i/r5t3OPzsLzp8//PEX8Kwbv9dnvf1d9/uf/OEPf/jz24Pv/mfWn6536/llv3+t7x77fv7yl79dR6ou8oc/GX+8gOkmdakXwOMAVkFb2nt5qP/H/b9s3NAC/df/zA1oaOwe29xt/rJu3u38Hxc2+IPz5w9//AU8yMWnZVlv1w34wx/+8Gd14buOs/50vVvPK/v9a3332Pfzl7/87TpSdZE//Mn44wVMN6lLvQAeB7AK2tLey0P9P+7/ZeOGFui//mduQENj99jmbvOXdfNu5/+4sMEfnD9/+OMv4EEuPi3LertuwB/+8Ic/qwvfdZz1p+vdel7Z71/ru8e+n7/85W/XkaqL/OFPxh8vYLpJXeoF8DiAVdCW9l4e6v9x/y8bN7RA//U/cwMaGrvHNnebv6ybdzv/x4UN/uD8+cMffwEPcvFpWdbbdQP+8Ic//Fld+K7jrD9d79bzyn7/Wt899v385S9/u45UXeQPfzL+eAHTTepSL4DHAayCtrT38lD/j/t/2bihBfqv/5kb0NDYPba52/xl3bzb+T8ubPAH588f/vgLeJCLT8uy3q4b8Ic//OHP6sJ3HWf96Xq3nlf2+9f67rHv5y9/+dt1pOoif/iT8ccLmG5Sl3oBPA5gFbSlvZeH+n/c/8vGDS3Qf/3P3ICGxu6xzd3mL+vm3c7/cWGDPzh//vDHX8CDXHxalvV23YA//OEPf1YXvus460/Xu/W8st+/1nePfT9/+cvfriNVF/nDn4w/XsB0k7rUC6AAZgK4jE/70PyZP/PnAbQNSXED/vCHP/wp8tEu4w9/+MOfNiTFDfjDH/7wp8hHu4w//OHPPv54AdMm7+MGAAQgAPcB8GN6+0fyL//yL/99SWo78Ic//OFPTY9+FX/4wx/+9CWp7cAf/vCHPzU9+lX84U/GHy9g+pn7sIMACmAmgB+GZ+DA/Jk/8+cBdICS0hb84Q9/+FPCY6CIP/zhD38GKCltwR/+8Ic/JTwGivjDH/7s448XMAPovd8CgAAE4D4Avs/uxM/yL//yL/8TllT24A9/+MOfih0TNfzhD3/4M2FJZQ/+8Ic//KnYMVHDH/5k/PECZiJ17/YQQAHMBPDd6Iz8aP7Mn/nzADqCSWET/vCHP/wp0DFSwh/+8Ic/I5gUNuEPf/jDnwIdIyX84Q9/9vHHC5gR9v7ZBIAABOA+AP6T3Jmf5F/+5V/+ZzTJ78If/vCHP3k5Zir4wx/+8GdGk/wu/OEPf/iTl2Omgj/8yfjjBcxM7h67COBxAF9eXn716O3t7dGrZ/yg/8f9f0avj/bUf/3P3ICOZqjz2d3mL+vm3c4/OwvOnz/88RfwrBu/12e9/V33+5/84Q9/+PPbg+/+Z9afrnfr+WW/f63vHvt+/vKXv11Hqi7yhz8Zf7yA6SZ1qRfA4wBWQVvae3mo/8f9v2zc0AL91//MDWho7B7b3G3+sm7e7fwfFzb4g/PnD3/8BTzIxadlWW/XDfjDH/7wZ3Xhu46z/nS9W88r+/1rfffY9/OXv/ztOlJ1kT/8yfjjBUw3qUu9AB4HsAra0t7LQ/0/7v9l44YW6L/+Z25AQ2P32OZu85d1827n/7iwwR+cP3/44y/gQS4+Lct6u27AH/7whz+rC991nPWn6916XtnvX+u7x76fv/zlb9eRqov84U/GHy9gukld6gXwOIBV0Jb2Xh7q/3H/Lxs3tED/9T9zAxoau8c2d5u/rJt3O//HhQ3+4Pz5wx9/AQ9y8WlZ1tt1A/7whz/8WV34ruOsP13v1vPKfv9a3z32/fzlL3+7jlRd5A9/Mv54AdNN6lIvgMcBrIK2tPfyUP+P+3/ZuKEF+q//mRvQ0Ng9trnb/GXdvNv5Py5s8Afnzx/++At4kItPy7Lerhvwhz/84c/qwncdZ/3pereeV/b71/ruse/nL3/523Wk6iJ/+JPxxwuYblKXegE8DmAVtKW9l4f6f9z/y8YNLdB//c/cgIbG7rHN3eYv6+bdzv9xYYM/OH/+8MdfwINcfFqW9XbdgD/84Q9/Vhe+6zjrT9e79byy37/Wd499P3/5y9+uI1UX+cOfjD9ewHSTutQLoABmAriMT/vQ/Jk/8+cBtA1JcQP+8Ic//Cny0S7jD3/4w582JMUN+MMf/vCnyEe7jD/84c8+/ngB0ybv4wYABCAA9wHwY3r7R/Iv//Iv/31Jajvwhz/84U9Nj34Vf/jDH/70JantwB/+8Ic/NT36VfzhT8afl9fX17f+2NlBB3RAB+7RgR8/fvz18+fPe5yMs9ABHdABHdABHdABHdiqA55Ft7pc/rA6oAM6oAM6oAM6cNkB/wXMZYtyC7wB9QY08wY0N13Xq82f+TN//g2gaymes4I//OEPf56jy/Wu/OEPf/hzLcVzVvCHP/zhz3N0ud6VP/zhzz7+eAFzbVpqBQABCMB9AEyFO7BY/uVf/uU/QMVTlvCHP/zhz1NwCWzKH/7whz8BKp6yhD/84Q9/noJLYFP+8CfjjxcwgVBllgigAGYCmJmtyFrzZ/7MnwfQiBXPWMMf/vCHP8+wJbInf/jDH/5ErHjGGv7whz/8eYYtkT35wx/+7OOPFzAR1RJrAAhAAO4DYCLaoaXyL//yL/8hLJ6wiD/84Q9/nkBLaEv+8Ic//Alh8YRF/OEPf/jzBFpCW/KHPxl/vIAJxSq+SAAFMBPA+GTFVpo/82f+PIDGtJhfxR/+8Ic/87LEduQPf/jDn5gW86v4wx/+8GdeltiO/OEPf/bxxwuYmGvhVQAEIAD3ATAc7OBC+Zd/+Zf/IBfjy/jDH/7wZxyW4Ib84Q9/+BPkYnwZf/jDH/6MwxLckD/8yfjjBUwwWNFlAiiAmQBG5yq6zvyZP/PnATTqxfQ6/vCHP/yZdiW6H3/4wx/+RL2YXscf/vCHP9OuRPfjD3/4s48/XsBEZQuuAyAAAbgPgMFYh5fJv/zLv/yHwRheyB/+8Ic/w6yEt+MPf/jDnzAYwwv5wx/+8GeYlfB2/OFPxh8vYMLRii0UQAHMBDA2VfFV5s/8mT8PoHExZlfyhz/84c+sKvHd+MMf/vAnLsbsSv7whz/8mVUlvht/+MOfffzxAiZuW2glAAEIwH0ADIU6sUj+5V/+5T9BxuhS/vCHP/wZRSWxGX/4wx/+JMgYXcof/vCHP6OoJDbjD38y/ngBkwhXZKkACmAmgJGZyqwxf+bP/HkAzZgxuZY//OEPfyZNyezFH/7whz8ZMybX8oc//OHPpCmZvfjDH/7s448XMBndAmsBCEAA7gNgINKpJfIv//Iv/yk0Bhfzhz/84c8gKamt+MMf/vAnhcbgYv7whz/8GSQltRV/+JPxxwuYVLyuFwugAGYCeD1RuRXmz/yZPw+gOTXmVvOHP/zhz5wouZ34wx/+8Cenxtxq/vCHP/yZEyW3E3/4w599/PECJufb5WoAAhCA+wB4GejkAvmXf/mX/yQbY8v5wx/+8GcMlORG/OEPf/iTZGNsOX/4wx/+jIGS3Ig//Mn44wVMMmBXywVQADMBvJqn7O/Nn/kzfx5As25MrecPf/jDnylPsvvwhz/84U/Wjan1/OEPf/gz5Ul2H/7whz/7+OMFTFa4i/UABCAA9wHwIs7pX8u//Mu//KfhGCrgD3/4w58hTtLb8Ic//OFPGo6hAv7whz/8GeIkvQ1/+JPxxwuYdMS+LhBAAcwE8Otpyv/W/Jk/8+cBNC/HTAV/+MMf/sxokt+FP/zhD3/ycsxU8Ic//OHPjCb5XfjDH/7s448XMHnjvqwAIAABuA+AX4a58Ev5l3/5l/8CHSMl/OEPf/gzgklhE/7whz/8KdAxUsIf/vCHPyOYFDbhD38y/ngBUwjZVyUCKICZAH41S5XfmT/zZ/48gFbsmKjhD3/4w58JSyp78Ic//OFPxY6JGv7whz/8mbCksgd/+MOfffzxAqai3Bc1AAQgAPcB8Isol34l//Iv//JfwmOgiD/84Q9/BigpbcEf/vCHPyU8Bor4wx/+8GeAktIW/OFPxh8vYEoxOy8SQAHMBPB8kmq/MX/mz/x5AK3p0a/iD3/4w5++JLUd+MMf/vCnpke/ij/84Q9/+pLUduAPf/izjz9ewNScO60CIAABuA+Ap0Eu/kL+5V/+5b/IR7uMP/zhD3/akBQ34A9/+MOfIh/tMv7whz/8aUNS3IA//Mn44wVMMWhnZQIogJkAns1R9XPzZ/7MnwfQqh/dOv7whz/86TpSrecPf/jDn6of3Tr+8Ic//Ok6Uq3nD3/4s48/XsBUpTupAyAAAbgPgCcxLn8s//Iv//JfBqRZyB/+8Ic/TUbK5fzhD3/4UwakWcgf/vCHP01GyuX84U/GHy9gylE7LhRAAcwE8HiK6p+aP/Nn/jyA1gXpVfKHP/zhT0+RejV/+MMf/tQF6VXyhz/84U9PkXo1f/jDn3388QKmbt1hJQABCMB9ADwMceND+Zd/+Zf/BiGtUv7whz/8aSHSKOYPf/jDnwYhrVL+8Ic//Gkh0ijmD38y/ngB0wjbUakACmAmgEcz1PnM/Jk/8+cBtGNIp5Y//OEPfzqGdGr5wx/+8KdjSKeWP/zhD386hnRq+cMf/uzjjxcwHe0OagEIQADuA+BBhFsfyb/8y7/8txBpFPOHP/zhT4OQVil/+MMf/rQQaRTzhz/84U+DkFYpf/iT8ccLmFbcPhcLoABmAvh5gnqfmD/zZ/48gPYUqVfzhz/84U9dkF4lf/jDH/70FKlX84c//OFPXZBeJX/4w599/PECpufdp2oAAhCA+wD4KcDND+Rf/uVf/puMlMv5wx/+8KcMSLOQP/zhD3+ajJTL+cMf/vCnDEizkD/8yfjjBUwzcGu5AApgJoDr/HSPzZ/5M38eQLuOVOv5wx/+8KfqR7eOP/zhD3+6jlTr+cMf/vCn6ke3jj/84c8+/ry8vr6+dUOvXgd0QAfu0oEfP3789fPnz7ucjvPQAR3QAR3QAR3QAR3YqAOeRTe6WP6oOqADOqADOqADOhDogP8CJtCkzBJvoL2B9gZ6nzfQmWxH1sq//Mu//EeseMYa/vCHP/x5hi2RPfnDH/7wJ2LFM9bwhz/84c8zbInsyR/+ZPzxAiaSqsQaARTATAAToxVaav7Mn/nzABrC4gmL+MMf/vDnCbSEtuQPf/jDnxAWT1jEH/7whz9PoCW0JX/4w599/PECJsRafBEAAQjAfQCMJzu2Uv7lX/7lP6bF/Cr+8Ic//JmXJbYjf/jDH/7EtJhfxR/+8Ic/87LEduQPfzL+eAETy1V4lQAKYCaA4cEKLjR/5s/8eQANcjG+jD/84Q9/xmEJbsgf/vCHP0Euxpfxhz/84c84LMEN+cMf/uzjjxcwQdiiywAIQADuA2A019F18i//8i//US+m1/GHP/zhz7Qr0f34wx/+8CfqxfQ6/vCHP/yZdiW6H3/4k/HHC5hosoLrBFAAMwEMjlV4mfkzf+bPA2gYjOGF/OEPf/gzzEp4O/7whz/8CYMxvJA//OEPf4ZZCW/HH/7wZx9/vIAJ0xZbCEAAAnAfAGOpjq+Sf/mXf/mPizG7kj/84Q9/ZlWJ78Yf/vCHP3ExZlfyhz/84c+sKvHd+MOfjD9ewMSzFVopgAKYCWBoqBKLzJ/5M38eQBNkjC7lD3/4w59RVBKb8Yc//OFPgozRpfzhD3/4M4pKYjP+8Ic/+/jjBUwCt8hSAAIQgPsAGMl0Zo38y7/8y3/GjMm1/OEPf/gzaUpmL/7whz/8yZgxuZY//OEPfyZNyezFH/5k/PECJpOuwFoBFMBMAAMjlVpi/syf+fMAmkJjcDF/+MMf/gySktqKP/zhD39SaAwu5g9/+MOfQVJSW/GHP/zZxx8vYFK8XS8GIAABuA+A14nOrZB/+Zd/+c+pMbeaP/zhD3/mRMntxB/+8Ic/OTXmVvOHP/zhz5wouZ34w5+MP17A5PJ1uVoABTATwMuBSi4wf+bP/HkATbIxtpw//OEPf8ZASW7EH/7whz9JNsaW84c//OHPGCjJjfjDH/7s448XMEngrpYDEIAA3AfAqzxnfy//8i//8p91Y2o9f/jDH/5MeZLdhz/84Q9/sm5MrecPf/jDnylPsvvwhz8Zf7yAySbsYr0ACmAmgBfjlP61+TN/5s8DaBqOoQL+8Ic//BniJL0Nf/jDH/6k4Rgq4A9/+MOfIU7S2/CHP/zZxx8vYNLEfV0AQAACcB8Av05z/rfyL//yL/95OWYq+MMf/vBnRpP8LvzhD3/4k5djpoI//OEPf2Y0ye/CH/5k/PECJp+xLysEUAAzAfxymAq/NH/mz/x5AC3QMVLCH/7whz8jmBQ24Q9/+MOfAh0jJfzhD3/4M4JJYRP+8Ic/+/jjBUwBua9KAAhAAO4D4FdZrvxO/uVf/uW/YsdEDX/4wx/+TFhS2YM//OEPfyp2TNTwhz/84c+EJZU9+MOfjD9ewFRS9kWNAApgJoBfjFLpV+bP/Jk/D6AlPAaK+MMf/vBngJLSFvzhD3/4U8JjoIg//OEPfwYoKW3BH/7wZx9/vIApMXdeBEAAAnAfAM+TXPuN/Mu//Mt/TY9+FX/4wx/+9CWp7cAf/vCHPzU9+lX84Q9/+NOXpLYDf/iT8ccLmFrOTqsEUAAzATwdpOIvzJ/5M38eQIt8tMv4wx/+8KcNSXED/vCHP/wp8tEu4w9/+MOfNiTFDfjDH/7s448XMEXozsoACEAA7gPgWY6rn8u//Mu//Ff96Nbxhz/84U/XkWo9f/jDH/5U/ejW8Yc//OFP15FqPX/4k/HHC5hq0k7qBFAAMwE8GaPyx+bP/Jk/D6BlQJqF/OEPf/jTZKRczh/+8Ic/ZUCahfzhD3/402SkXM4f/vBnH3+8gKkQ+9IAABu2SURBVClTd1wIQAACcB8Aj1Nc/1T+5V/+5b8uSK+SP/zhD396itSr+cMf/vCnLkivkj/84Q9/eorUq/nDn4w/XsDUs3ZYKYACmAng4RA1PjR/5s/8eQBtENIq5Q9/+MOfFiKNYv7whz/8aRDSKuUPf/jDnxYijWL+8Ic/+/jjBUwDu6NSAAIQgPsAeJThzmfyL//yL/8dQzq1/OEPf/jTMaRTyx/+8Ic/HUM6tfzhD3/40zGkU8sf/mT88QKmk7aDWgEUwEwAD0ao9ZH5M3/mzwNoC5FGMX/4wx/+NAhplfKHP/zhTwuRRjF/+MMf/jQIaZXyhz/82ccfL2Ba3H0uBiAAAbgPgJ8T3PtE/uVf/uW/p0i9mj/84Q9/6oL0KvnDH/7wp6dIvZo//OEPf+qC9Cr5w5+MP17A9PL2qVoABTATwE8D1PzA/Jk/8+cBtMlIuZw//OEPf8qANAv5wx/+8KfJSLmcP/zhD3/KgDQL+cMf/uzjjxcwTfDWcgACEID7ALjmt3ss//Iv//LfdaRazx/+8Ic/VT+6dfzhD3/403WkWs8f/vCHP1U/unX84U/GHy9guolb6gVQADMBXManfWj+zJ/58wDahqS4AX/4wx/+FPlol/GHP/zhTxuS4gb84Q9/+FPko13GH/7wZx9/vIBpk/dxAwACEID7APgxvf0j+Zd/+Zf/viS1HfjDH/7wp6ZHv4o//OEPf/qS1HbgD3/4w5+aHv0q/vAn48/L6+vrW3/s7KADOqAD9+jAjx8//vr58+c9TsZZ6IAO6IAO6IAO6IAObNUBz6JbXS5/WB3QAR3QAR3QAR247ID/AuayRbkF3oB6A5p5A5qbruvV5s/8mT//BtC1FM9ZwR/+8Ic/z9Hlelf+8Ic//LmW4jkr+MMf/vDnObpc78of/vBnH3+8gLk2LbUCgAAE4D4ApsIdWCz/8i//8h+g4ilL+MMf/vDnKbgENuUPf/jDnwAVT1nCH/7whz9PwSWwKX/4k/HHC5hAqDJLBFAAMwHMzFZkrfkzf+bPA2jEimes4Q9/+MOfZ9gS2ZM//OEPfyJWPGMNf/jDH/48w5bInvzhD3/28ccLmIhqiTUABCAA9wEwEe3QUvmXf/mX/xAWT1jEH/7whz9PoCW0JX/4wx/+hLB4wiL+8Ic//HkCLaEt+cOfjD9ewIRiFV8kgAKYCWB8smIrzZ/5M38eQGNazK/iD3/4w595WWI78oc//OFPTIv5VfzhD3/4My9LbEf+8Ic/+/jjBUzMtfAqAAIQgPsAGA52cKH8y7/8y3+Qi/Fl/OEPf/gzDktwQ/7whz/8CXIxvow//OEPf8ZhCW7IH/5k/PECJhis6DIBFMBMAKNzFV1n/syf+fMAGvVieh1/+MMf/ky7Et2PP/zhD3+iXkyv4w9/+MOfaVei+/GHP/zZxx8vYKKyBdcBEIAA3AfAYKzDy+Rf/uVf/sNgDC/kD3/4w59hVsLb8Yc//OFPGIzhhfzhD3/4M8xKeDv+8Cfjjxcw4WjFFgqgAGYCGJuq+CrzZ/7MnwfQuBizK/nDH/7wZ1aV+G784Q9/+BMXY3Ylf/jDH/7MqhLfjT/84c8+/ngBE7cttBKAAATgPgCGQp1YJP/yL//ynyBjdCl/+MMf/oyiktiMP/zhD38SZIwu5Q9/+MOfUVQSm/GHPxl/vIBJhCuyVAAFMBPAyExl1pg/82f+PIBmzJhcyx/+8Ic/k6Zk9uIPf/jDn4wZk2v5wx/+8GfSlMxe/OEPf/bxxwuYjG6BtQAEIAD3ATAQ6dQS+Zd/+Zf/FBqDi/nDH/7wZ5CU1Fb84Q9/+JNCY3Axf/jDH/4MkpLaij/8yfjjBUwqXteLBVAAMwG8nqjcCvNn/syfB9CcGnOr+cMf/vBnTpTcTvzhD3/4k1NjbjV/+MMf/syJktuJP/zhzz7+eAGT8+1yNQABCMB9ALwMdHKB/Mu//Mt/ko2x5fzhD3/4MwZKciP+8Ic//EmyMbacP/zhD3/GQEluxB/+ZPzxAiYZsKvlAiiAmQBezVP29+bP/Jk/D6BZN6bW84c//OHPlCfZffjDH/7wJ+vG1Hr+8Ic//JnyJLsPf/jDn3388QImK9zFegACEID7AHgR5/Sv5V/+5V/+03AMFfCHP/zhzxAn6W34wx/+8CcNx1ABf/jDH/4McZLehj/8yfjjBUw6Yl8XCKAAZgL49TTlf2v+zJ/58wCal2Omgj/84Q9/ZjTJ78If/vCHP3k5Zir4wx/+8GdGk/wu/OEPf/bxxwuYvHFfVgAQgADcB8Avw1z4pfzLv/zLf4GOkRL+8Ic//BnBpLAJf/jDH/4U6Bgp4Q9/+MOfEUwKm/CHPxl/vIAphOyrEgEUwEwAv5qlyu/Mn/kzfx5AK3ZM1PCHP/zhz4QllT34wx/+8Kdix0QNf/jDH/5MWFLZgz/84c8+/ngBU1HuixoAAhCA+wD4RZRLv5J/+Zd/+S/hMVDEH/7whz8DlJS24A9/+MOfEh4DRfzhD3/4M0BJaQv+8CfjjxcwpZidFwmgAGYCeD5Jtd+YP/Nn/jyA1vToV/GHP/zhT1+S2g784Q9/+FPTo1/FH/7whz99SWo78Ic//NnHHy9gas6dVgEQgADcB8DTIBd/If/yL//yX+SjXcYf/vCHP21Iihvwhz/84U+Rj3YZf/jDH/60ISluwB/+ZPzxAqYYtLMyARTATADP5qj6ufkzf+bPA2jVj24df/jDH/50HanW84c//OFP1Y9uHX/4wx/+dB2p1vOHP/zZxx8vYKrSndQBEIAA3AfAkxiXP5Z/+Zd/+S8D0izkD3/4w58mI+Vy/vCHP/wpA9Is5A9/+MOfJiPlcv7wJ+OPFzDlqB0XCqAAZgJ4PEX1T82f+TN/HkDrgvQq+cMf/vCnp0i9mj/84Q9/6oL0KvnDH/7wp6dIvZo//OHPPv54AVO37rASgAAE4D4AHoa48aH8y7/8y3+DkFYpf/jDH/60EGkU84c//OFPg5BWKX/4wx/+tBBpFPOHPxl/vIBphO2oVAAFMBPAoxnqfGb+zJ/58wDaMaRTyx/+8Ic/HUM6tfzhD3/40zGkU8sf/vCHPx1DOrX84Q9/9vHHC5iOdge1AAQgAPcB8CDCrY/kX/7lX/5biDSK+cMf/vCnQUirlD/84Q9/Wog0ivnDH/7wp0FIq5Q//Mn44wVMK26fiwVQADMB/DxBvU/Mn/kzfx5Ae4rUq/nDH/7wpy5Ir5I//OEPf3qK1Kv5wx/+8KcuSK+SP/zhzz7+eAHT8+5TNQABCMB9APwU4OYH8i//8i//TUbK5fzhD3/4UwakWcgf/vCHP01GyuX84Q9/+FMGpFnIH/5k/PECphm4tVwABTATwHV+usfmz/yZPw+gXUeq9fzhD3/4U/WjW8cf/vCHP11HqvX84Q9/+FP1o1vHH/7wZx9/Xl5fX9+6oVevAzqgA3fpwI8fP/76+fPnXU7HeeiADuiADuiADuiADmzUAc+iG10sf1Qd0AEd0AEd0AEdCHTAfwETaFJmiTfQ3kB7A73PG+hMtiNr5V/+5V/+I1Y8Yw1/+MMf/jzDlsie/OEPf/gTseIZa/jDH/7w5xm2RPbkD38y/ngBE0lVYo0ACmAmgInRCi01f+bP/HkADWHxhEX84Q9/+PMEWkJb8oc//OFPCIsnLOIPf/jDnyfQEtqSP/zhzz7+eAETYi2+CIAABOA+AMaTHVsp//Iv//If02J+FX/4wx/+zMsS25E//OEPf2JazK/iD3/4w595WWI78oc/GX+8gInlKrxKAAUwE8DwYAUXmj/zZ/48gAa5GF/GH/7whz/jsAQ35A9/+MOfIBfjy/jDH/7wZxyW4Ib84Q9/9vHHC5ggbNFlAAQgAPcBMJrr6Dr5l3/5l/+oF9Pr+MMf/vBn2pXofvzhD3/4E/Vieh1/+MMf/ky7Et2PP/zJ+OMFTDRZwXUCKICZAAbHKrzM/Jk/8+cBNAzG8EL+8Ic//BlmJbwdf/jDH/6EwRheyB/+8Ic/w6yEt+MPf/izjz9ewIRpiy0EIAABuA+AsVTHV8m//Mu//MfFmF3JH/7whz+zqsR34w9/+MOfuBizK/nDH/7wZ1aV+G784U/GHy9g4tkKrRRAAcwEMDRUiUXmz/yZPw+gCTJGl/KHP/zhzygqic34wx/+8CdBxuhS/vCHP/wZRSWxGX/4w599/PECJoFbZCkAAQjAfQCMZDqzRv7lX/7lP2PG5Fr+8Ic//Jk0JbMXf/jDH/5kzJhcyx/+8Ic/k6Zk9uIPfzL+eAGTSVdgrQAKYCaAgZFKLTF/5s/8eQBNoTG4mD/84Q9/BklJbcUf/vCHPyk0Bhfzhz/84c8gKamt+MMf/uzjjxcwKd6uFwMQgADcB8DrROdWyL/8y7/859SYW80f/vCHP3Oi5HbiD3/4w5+cGnOr+cMf/vBnTpTcTvzhT8YfL2By+bpcLYACmAng5UAlF5g/82f+PIAm2Rhbzh/+8Ic/Y6AkN+IPf/jDnyQbY8v5wx/+8GcMlORG/OEPf/bxxwuYJHBXywEIQADuA+BVnrO/l3/5l3/5z7oxtZ4//OEPf6Y8ye7DH/7whz9ZN6bW84c//OHPlCfZffjDn4w/XsBkE3axXgAFMBPAi3FK/9r8mT/z5wE0DcdQAX/4wx/+DHGS3oY//OEPf9JwDBXwhz/84c8QJ+lt+MMf/uzjjxcwaeK+LgAgAAG4D4Bfpzn/W/mXf/mX/7wcMxX84Q9/+DOjSX4X/vCHP/zJyzFTwR/+8Ic/M5rkd+EPfzL+eAGTz9iXFQIogJkAfjlMhV+aP/Nn/jyAFugYKeEPf/jDnxFMCpvwhz/84U+BjpES/vCHP/wZwaSwCX/4w599/PECpoDcVyUABCAA9wHwqyxXfif/8i//8l+xY6KGP/zhD38mLKnswR/+8Ic/FTsmavjDH/7wZ8KSyh784U/GHy9gKin7okYABTATwC9GqfQr82f+zJ8H0BIeA0X84Q9/+DNASWkL/vCHP/wp4TFQxB/+8Ic/A5SUtuAPf/izjz9ewJSYOy8CIAABuA+A50mu/Ub+5V/+5b+mR7+KP/zhD3/6ktR24A9/+MOfmh79Kv7whz/86UtS24E//Mn44wVMLWenVQIogJkAng5S8Rfmz/yZPw+gRT7aZfzhD3/404akuAF/+MMf/hT5aJfxhz/84U8bkuIG/OEPf/bxxwuYInRnZQAEIAD3AfAsx9XP5V/+5V/+q3506/jDH/7wp+tItZ4//OEPf6p+dOv4wx/+8KfrSLWeP/zJ+OMFTDVpJ3UCKICZAJ6MUflj82f+zJ8H0DIgzUL+8Ic//GkyUi7nD3/4w58yIM1C/vCHP/xpMlIu5w9/+LOPP17AlKk7LgQgAAG4D4DHKa5/Kv/yL//yXxekV8kf/vCHPz1F6tX84Q9/+FMXpFfJH/7whz89RerV/OFPxh8vYOpZO6wUQAHMBPBwiBofmj/zZ/48gDYIaZXyhz/84U8LkUYxf/jDH/40CGmV8oc//OFPC5FGMX/4w599/PECpoHdUSkAAQjAfQA8ynDnM/mXf/mX/44hnVr+8Ic//OkY0qnlD3/4w5+OIZ1a/vCHP/zpGNKp5Q9/Mv54AdNJ20GtAApgJoAHI9T6yPyZP/PnAbSFSKOYP/zhD38ahLRK+cMf/vCnhUijmD/84Q9/GoS0SvnDH/7s448XMC3uPhcDEIAA3AfAzwnufSL/8i//8t9TpF7NH/7whz91QXqV/OEPf/jTU6RezR/+8Ic/dUF6lfzhT8YfL2B6eftULYACmAngpwFqfmD+zJ/58wDaZKRczh/+8Ic/ZUCahfzhD3/402SkXM4f/vCHP2VAmoX84Q9/9vHHC5gmeGs5AAEIwH0AXPPbPZZ/+Zd/+e86Uq3nD3/4w5+qH906/vCHP/zpOlKt5w9/+MOfqh/dOv7wJ+OPFzDdxC31AiiAmQAu49M+NH/mz/x5AG1DUtyAP/zhD3+KfLTL+MMf/vCnDUlxA/7whz/8KfLRLuMPf/izjz9ewLTJ+7gBAAEIwH0A/Jje/pH8y7/8y39fktoO/OEPf/hT06NfxR/+8Ic/fUlqO/CHP/zhT02PfhV/+JPx5+X19fWtP3Z20AEd0IF7dODHjx9//fz58x4n4yx0QAd0QAd0QAd0QAe26oBn0a0ulz+sDuiADuiADuiADlx2wH8Bc9mi3AJvQL0BzbwBzU3X9WrzZ/7Mn38D6FqK56zgD3/4w5/n6HK9K3/4wx/+XEvxnBX84Q9/+PMcXa535Q9/+LOPP17AXJuWWgFAAAJwHwBT4Q4sln/5l3/5D1DxlCX84Q9/+PMUXAKb8oc//OFPgIqnLOEPf/jDn6fgEtiUP/zJ+OMFTCBUmSUCKICZAGZmK7LW/Jk/8+cBNGLFM9bwhz/84c8zbInsyR/+8Ic/ESuesYY//OEPf55hS2RP/vCHP/v44wVMRLXEGgACEID7AJiIdmip/Mu//Mt/CIsnLOIPf/jDnyfQEtqSP/zhD39CWDxhEX/4wx/+PIGW0Jb84U/GHy9gQrGKLxJAAcwEMD5ZsZXmz/yZPw+gMS3mV/GHP/zhz7wssR35wx/+8Cemxfwq/vCHP/yZlyW2I3/4w599/PECJuZaeBUAAQjAfQAMBzu4UP7lX/7lP8jF+DL+8Ic//BmHJbghf/jDH/4EuRhfxh/+8Ic/47AEN+QPfzL+eAETDFZ0mQAKYCaA0bmKrjN/5s/8eQCNejG9jj/84Q9/pl2J7scf/vCHP1Evptfxhz/84c+0K9H9+MMf/uzjjxcwUdmC6wAIQADuA2Aw1uFl8i//8i//YTCGF/KHP/zhzzAr4e34wx/+8CcMxvBC/vCHP/wZZiW8HX/4k/HHC5hwtGILBVAAMwGMTVV8lfkzf+bPA2hcjNmV/OEPf/gzq0p8N/7whz/8iYsxu5I//OEPf2ZVie/GH/7wZx9/vICJ2xZaCUAAAnAfAEOhTiySf/mXf/lPkDG6lD/84Q9/RlFJbMYf/vCHPwkyRpfyhz/84c8oKonN+MOfjD9ewCTCFVkqgAKYCWBkpjJrzJ/5M38eQDNmTK7lD3/4w59JUzJ78Yc//OFPxozJtfzhD3/4M2lKZi/+8Ic/+/jjBUxGt8BaAAIQgPsAGIh0aon8y7/8y38KjcHF/OEPf/gzSEpqK/7whz/8SaExuJg//OEPfwZJSW3FH/5k/PECJhWv68UCKICZAF5PVG6F+TN/5s8DaE6NudX84Q9/+DMnSm4n/vCHP/zJqTG3mj/84Q9/5kTJ7cQf/vBnH3+8gMn5drkagAAE4D4AXgY6uUD+5V/+5T/Jxthy/vCHP/wZAyW5EX/4wx/+JNkYW84f/vCHP2OgJDfiD38y/ngBkwzY1XIBFMBMAK/mKft782f+zJ8H0KwbU+v5wx/+8GfKk+w+/OEPf/iTdWNqPX/4wx/+THmS3Yc//OHPPv54AZMV7mI9AAEIwH0AvIhz+tfyL//yL/9pOIYK+MMf/vBniJP0NvzhD3/4k4ZjqIA//OEPf4Y4SW/DH/5k/PECJh2xrwsEUAAzAfx6mvK/NX/mz/x5AM3LMVPBH/7whz8zmuR34Q9/+MOfvBwzFfzhD3/4M6NJfhf+8Ic/+/jjBUzeuC8rAAhAAO4D4JdhLvxS/uVf/uW/QMdICX/4wx/+jGBS2IQ//OEPfwp0jJTwhz/84c8IJoVN+MOfjD9ewBRC9lWJAApgJoBfzVLld+bP/Jk/D6AVOyZq+MMf/vBnwpLKHvzhD3/4U7FjooY//OEPfyYsqezBH/7wZx9/vICpKPdFDQABCMB9APwiyqVfyb/8y7/8l/AYKOIPf/jDnwFKSlvwhz/84U8Jj4Ei/vCHP/wZoKS0BX/4k/HHC5hSzM6LBFAAMwE8n6Tab8yf+TN/HkBrevSr+MMf/vCnL0ltB/7whz/8qenRr+IPf/jDn74ktR34wx/+7OOPFzA1506rAAhAAO4D4GmQi7+Qf/mXf/kv8tEu4w9/+MOfNiTFDfjDH/7wp8hHu4w//OEPf9qQFDfgD38y/ngBUwzaWZkACmAmgGdzVP3c/Jk/8+cBtOpHt44//OEPf7qOVOv5wx/+8KfqR7eOP/zhD3+6jlTr+cMf/uzjjxcwVelO6gAIQADuA+BJjMsfy7/8y7/8lwFpFvKHP/zhT5ORcjl/+MMf/pQBaRbyhz/84U+TkXI5f/iT8ccLmHLUjgsFUAAzATyeovqn5s/8mT8PoHVBepX84Q9/+NNTpF7NH/7whz91QXqV/OEPf/jTU6RezR/+8Gcff7yAqVt3WAlAAAJwHwAPQ9z4UP7lX/7lv0FIq5Q//OEPf1qINIr5wx/+8KdBSKuUP/zhD39aiDSK+cOfjD9ewDTCdlQqgAKYCeDRDHU+M3/mz/x5AO0Y0qnlD3/4w5+OIZ1a/vCHP/zpGNKp5Q9/+MOfjiGdWv7whz/7+OMFTEe7g1oAAhCA+wB4EOHWR/Iv//Iv/y1EGsX84Q9/+NMgpFXKH/7whz8tRBrF/OEPf/jTIKRVyh/+ZPzxAqYVt8/FAiiAmQB+nqDeJ+bP/Jk/D6A9RerV/OEPf/hTF6RXyR/+8Ic/PUXq1fzhD3/4UxekV8kf/vBnH3+8gOl596kagAAE4D4Afgpw8wP5l3/5l/8mI+Vy/vCHP/wpA9Is5A9/+MOfJiPlcv7whz/8KQPSLOQPfzL+eAHTDNxaLoACmAngOj/dY/Nn/syfB9CuI9V6/vCHP/yp+tGt4w9/+MOfriPVev7whz/8qfrRreMPf/izjz8vr6+vb93Qq9cBHdCBu3Tgx48ff/38+fMup+M8dEAHdEAHdEAHdEAHNuqAZ9GNLpY/qg7ogA7ogA7ogA4EOuC/gAk0KbPEG2hvoL2B3ucNdCbbkbXyL//yL/8RK56xhj/84Q9/nmFLZE/+8Ic//IlY8Yw1/OEPf/jzDFsie/KHPxl/vICJpCqxRgAFMBPAxGiFlpo/82f+PICGsHjCIv7whz/8eQItoS35wx/+8CeExRMW8Yc//OHPE2gJbckf/vBnH3+8gAmxFl8EQAACcB8A48mOrZR/+Zd/+Y9pMb+KP/zhD3/mZYntyB/+8Ic/MS3mV/GHP/zhz7wssR35w5+MP17AxHIVXiWAApgJYHiwggvNn/kzfx5Ag1yML+MPf/jDn3FYghvyhz/84U+Qi/Fl/OEPf/gzDktwQ/7whz/7+OMFTBC26DIAAhCA+wAYzXV0nfzLv/zLf9SL6XX84Q9/+DPtSnQ//vCHP/yJejG9jj/84Q9/pl2J7scf/mT88QImmqzgOgEUwEwAg2MVXmb+zJ/58wAaBmN4IX/4wx/+DLMS3o4//OEPf8JgDC/kD3/4w59hVsLb8Yc//NnHHy9gwrTFFgIQgADcB8BYquOr5F/+5V/+42LMruQPf/jDn1lV4rvxhz/84U9cjNmV/OEPf/gzq0p8N/7wJ+PP/wGDdru7gvbzcwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 20,
"metadata": {
"image/png": {
"height": 800,
"width": 800
}
},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='ATMAuthentication.png', width=800, height=800) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Look at Objects/ATMDiagrams.pdf for a solution."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What Else in Design?\n",
"- Other diagrams: state diagrams, package diagrams, ...\n",
"- Object oriented design patterns"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Complex Example of Class Hierarchy"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAkQAAAQkCAYAAACcxAE6AAAMFGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdUk8kWnr+kEBJaIAJSQm+CFOkCofciHWyEJEAoERKCih1ZVHAtqFhAVHRFRMW1ALJWLFhYBOz1gYrKyrpYsKHyJgV0fe28e8788+XOvXe+O7kzZwYAZVt2bm42qgJAjiBfGB3ow0xMSmaSegEOMEAHJoDA5ohyvaOiwgCU0f7v8u4mQCT9NWtJrH8d/6+iyuWJOAAgURCnckWcHIiPAIBrcnKF+QAQ2qHeaHZ+rgQPQqwuhAQBIOISnC7DmhKcKsMTpDax0b4QswAgU9lsYToAShLezAJOOoyjJOFoK+DyBRBXQezJyWBzIb4P8YScnFkQK5MhNk/9Lk7632KmjsVks9PHsCwXqZD9+KLcbPbc/3M5/rfkZItH5zCEjZohDIqW5AzXbU/WrFAJpkJ8XJAaEQmxGsQX+VypvQTfzRAHxcntBzgiX7hmgAEACrhsv1CIdSBmiLPivOXYni2U+kJ7NIKfHxwrx6nCWdHy+GiBIDsiTB5neQYveBRX80T+MaM2afyAYIhhpaFHCjNiE2Q80XMF/PgIiJUg7hRlxYTKfR8WZvhGjNoIxdESzsYQv00TBkTLbDDNHNFoXpgNhy2dC9YCxsrPiA2S+WKJPFFi2CgHLs/PX8YB4/IEcXJuGKwun2i5b0ludpTcHqvmZQdGy9YZOygqiBn17c6HBSZbB+xRJjskSj7Xu9z8qFgZNxwFYcAX+AEmEMOWCmaBTMDvGGgagL9kIwGADYQgHfCAtVwz6pEgHRHAbwwoBH9CxAOiMT8f6SgPFED9lzGt7GsN0qSjBVKPLPAU4hxcG/fE3fEw+GXBZo+74K6jfkzl0VmJ/kQ/YhAxgGgxxoMDWWfDJgT8f6MLhT0PZifhIhjN4Vs8wlNCF+ER4Qahh3AHxIMn0ihyq5n8IuEPzJkgHPTAaAHy7FK/zw43hawdcR/cA/KH3HEGrg2s8UkwE2/cC+bmCLXfMxSPcfu2lj/OJ2H9fT5yvZKlkqOcRerYP+M7ZvVjFN/v1ogL+9AfLbHl2GGsDTuDXcKOY02AiZ3CmrF27IQEj1XCE2kljM4WLeWWBePwR21s6237bT//MDdbPr9kvUT5vDn5ks3gOyt3rpCfnpHP9IanMY8ZLODYTGDa29o5AyA522VHxxuG9MxGGJe/6fJOA+BaCpXp33RsIwCOPQWA/u6bzug1LPc1AJzo5IiFBTKd5DgGBEABynBXaAE9YATMYT72wAm4AxbwByEgEsSCJDADrngGyIGcZ4P5YAkoAWVgDdgAtoBtYCfYA/aDQ6AJHAdnwAVwBXSCG+AerIs+8AIMgndgGEEQEkJD6IgWoo+YIFaIPeKCeCL+SBgSjSQhKUg6IkDEyHxkKVKGlCNbkB1IHfIrcgw5g1xCupA7SC/Sj7xGPqEYSkXVUV3UFJ2IuqDeaCgai05H09E8tBAtRlehm9AadB/aiJ5Br6A30B70BTqEAUwRY2AGmDXmgvlikVgyloYJsYVYKVaB1WAHsBb4P1/DerAB7CNOxOk4E7eGtRmEx+EcPA9fiK/Et+B78Eb8HH4N78UH8a8EGkGHYEVwIwQTEgnphNmEEkIFYTfhKOE83Dd9hHdEIpFBNCM6w32ZRMwkziOuJG4lNhBPE7uIj4lDJBJJi2RF8iBFktikfFIJaTNpH+kUqZvUR/pAViTrk+3JAeRksoBcRK4g7yWfJHeTn5GHFVQUTBTcFCIVuApzFVYr7FJoUbiq0KcwTFGlmFE8KLGUTMoSyibKAcp5yn3KG0VFRUNFV8UpinzFxYqbFA8qXlTsVfxIVaNaUn2p06hi6ipqLfU09Q71DY1GM6WxaMm0fNoqWh3tLO0h7YMSXclGKViJq7RIqVKpUalb6aWygrKJsrfyDOVC5Qrlw8pXlQdUFFRMVXxV2CoLVSpVjqncUhlSpavaqUaq5qiuVN2rekn1uRpJzVTNX42rVqy2U+2s2mM6Rjei+9I59KX0XfTz9D51orqZerB6pnqZ+n71DvVBDTWNSRrxGnM0KjVOaPQwMIYpI5iRzVjNOMS4yfg0Tnec9zjeuBXjDozrHvdec7wmS5OnWarZoHlD85MWU8tfK0trrVaT1gNtXNtSe4r2bO1q7fPaA+PVx7uP54wvHX9o/F0dVMdSJ1pnns5OnXadIV093UDdXN3Numd1B/QYeiy9TL31eif1+vXp+p76fP31+qf0/2BqML2Z2cxNzHPMQQMdgyADscEOgw6DYUMzwzjDIsMGwwdGFCMXozSj9UatRoPG+sbhxvON643vmiiYuJhkmGw0aTN5b2pmmmC6zLTJ9LmZplmwWaFZvdl9c5q5l3meeY35dQuihYtFlsVWi05L1NLRMsOy0vKqFWrlZMW32mrVNYEwwXWCYELNhFvWVGtv6wLreuteG4ZNmE2RTZPNy4nGE5Mnrp3YNvGrraNttu0u23t2anYhdkV2LXav7S3tOfaV9tcdaA4BDoscmh1eTbKaxJtUPem2I90x3HGZY6vjFydnJ6HTAad+Z2PnFOcq51su6i5RLitdLroSXH1cF7ked/3o5uSW73bI7S93a/cs973uzyebTeZN3jX5sYehB9tjh0ePJ9MzxXO7Z4+XgRfbq8brEcuIxWXtZj3ztvDO9N7n/dLH1kfoc9Tnva+b7wLf036YX6BfqV+Hv5p/nP8W/4cBhgHpAfUBg4GOgfMCTwcRgkKD1gbdCtYN5gTXBQ+GOIcsCDkXSg2NCd0S+ijMMkwY1hKOhoeErwu/H2ESIYhoigSRwZHrIh9EmUXlRf02hTglakrllKfRdtHzo9ti6DEzY/bGvIv1iV0dey/OPE4c1xqvHD8tvi7+fYJfQnlCT+LExAWJV5K0k/hJzcmk5Pjk3clDU/2nbpjaN81xWsm0m9PNps+ZfmmG9ozsGSdmKs9kzzycQkhJSNmb8pkdya5hD6UGp1alDnJ8ORs5L7gs7npuP8+DV857luaRVp72PN0jfV16f4ZXRkXGAN+Xv4X/KjMoc1vm+6zIrNqskeyE7IYcck5KzjGBmiBLcG6W3qw5s7pyrXJLcnvy3PI25A0KQ4W7RYhouqg5Xx1ec9rF5uKfxL0FngWVBR9mx88+PEd1jmBO+1zLuSvmPisMKPxlHj6PM691vsH8JfN7F3gv2LEQWZi6sHWR0aLiRX2LAxfvWUJZkrXk9yLbovKit0sTlrYU6xYvLn78U+BP9SVKJcKSW8vcl21bji/nL+9Y4bBi84qvpdzSy2W2ZRVln1dyVl7+2e7nTT+PrEpb1bHaaXX1GuIawZqba73W7ilXLS8sf7wufF3jeub60vVvN8zccKliUsW2jZSN4o09m8I2NW823rxm8+ctGVtuVPpUNlTpVK2oer+Vu7W7mlV9YJvutrJtn7bzt9/eEbijsca0pmIncWfBzqe74ne1/eLyS91u7d1lu7/UCmp79kTvOVfnXFe3V2fv6nq0Xlzfv2/avs79fvubD1gf2NHAaCg7CA6KD/7xa8qvNw+FHmo97HL4wBGTI1VH6UdLG5HGuY2DTRlNPc1JzV3HQo61tri3HP3N5rfa4wbHK09onFh9knKy+OTIqcJTQ6dzTw+cST/zuHVm672ziWevn5tyruN86PmLFwIunG3zbjt10ePi8Utul45ddrncdMXpSmO7Y/vR3x1/P9rh1NF41flqc6drZ0vX5K6T3V7dZ675XbtwPfj6lRsRN7puxt28fWvarZ7b3NvP72TfeXW34O7wvcX3CfdLH6g8qHio87DmHxb/aOhx6jnR69fb/ijm0b3HnMcvnoiefO4rfkp7WvFM/1ndc/vnx/sD+jv/mPpH34vcF8MDJX+q/ln10vzlkb9Yf7UPJg72vRK+Gnm98o3Wm9q3k962DkUNPXyX8274fekHrQ97Prp8bPuU8OnZ8OzPpM+bvlh8afka+vX+SM7ISC5byJZeBTDY0LQ0AF7XAkBLgneHTgAoSrK3l1QQ2XtRisB/wrL3mVScAKhlARC3GIAweEephs0EYirsJVfvWBZAHRzGmlxEaQ72slhU+IIhfBgZeaMLAKkFgC/CkZHhrSMjX3ZBsncAOJ0ne/NJhAjv99ttJKiz7yX4Uf4JEL9tBtKO/vwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGeaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIj4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjU4MDwvZXhpZjpQaXhlbFhEaW1lbnNpb24+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj4xMDYwPC9leGlmOlBpeGVsWURpbWVuc2lvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+CvXGX1AAAAAcaURPVAAAAAIAAAAAAAACEgAAACgAAAISAAACEgAAljFaWiepAABAAElEQVR4Aex9CdzdRL32tEWWFqSVgihIyyYIslQWZdFSRWWRTURRUIqAslxp0Q8ordy2LiyilEUW2auAKCoU2S54bUvhgoBKUUBZWzYRF6hQKULJN09gQpIzkzMzSc57Mnnm93vfJJOZTP7Pf8lzJjOTQZFMokT697//LYYOHVriCuWqsn3iT/uj/5WLIv61GX8Yfxh/wok/g0iI/IMhajIgMiAyIIYTEF2jAf2f/k//D8f/SYhcI2CuPAMiAyIDYjgBMefeXQ/p//R/+n84/k9C1DXkFRdgQGRAZEAMJyAWe3vnWfo//Z/+H47/kxB1xjinHAZEBkQGxHACopPzy8L0f/o//T8c/ychco2AufIMiAyIDIjhBMSce3c9pP/T/+n/4fg/CVHXkFdcgAGRAZEBMZyAWOztnWfp//R/+n84/k9C1BnjnHIYEBkQGRDDCYhOzi8L0//p//T/cPyfhMg1AubKMyAyIDIghhMQc+7d9ZD+T/+n/4fj/yREXUNecQEGRAZEBsRwAmKxt3eepf/T/+n/4fg/CVFnjHPKYUBkQGRADCcgOjm/LEz/p//T/8PxfxIi1wiYK8+AyIDIgBhOQMy5d9dD+j/9n/4fjv+TEHUNecUFGBAZEBkQwwmIxd7eeZb+T/+n/4fj/yREnTHOKYcBkQGRATGcgOjk/LIw/Z/+T/8Px/9JiFwjYK48AyIDIgNiOAEx595dD+n/9H/6fzj+T0LUNeQVF2BAZEBkQAwnIBZ7e+dZ+j/9n/4fjv+TEHXGOKccBkQGRAbEcAKik/PLwvR/+j/9Pxz/JyFyjYC58gyIDIgMiOEExJx7dz2k/9P/6f/h+D8JUdeQV1yAAZEBkQExnIBY7O2dZ+n/9H/6fzj+T0LUGeOcchgQGRAZEMMJiE7OLwvT/+n/9P9w/J+EyDUC5sozIDIgMiCGExBz7t31kP5P/6f/h+P/JERdQ15xAQZEBkQGxHACYrG3d56l/9P/6f/h+D8JUWeMc8phQGRAZEAMJyA6Ob8sTP+n/9P/w/F/EiLXCJgrz4DIgMiAGE5AzLl310P6P/2f/h+O/5MQdQ15xQUYEBkQGRDDCYjF3t55lv5P/6f/h+P/JESdMc4phwGRAbENAXHcuHFav3jttdfE4MGDted6kcn23fA/4IADxPjx4ytTDeMf419I8Y+EqGRoYEBgQAgpIJjcYdCgQaZTzG8QAlOnThXTpk2r7I4Z/xj/Qop/JEQlQwMDAgNCSAHB5A6KEKGHYfTo0aZizO9TBC655BKxcOFCQUJUrYIY/8OK/4MWL14cVWsivFrTEBgyZIhYunRp026b99tDBIYNGxa3Nnv2bLHDDjv0sGU2VQUC0NncuXPF5MmTxZQpU6q4JK9BBIJDgD1EJVXKXwhh/UJwNYe26F/1EJEQuVpIf5RXhIg9RNXqoy3+b0ItNPlJiEyatswPzSAsxU6KUf52EEISosTkG7lDQlSP2hj/wop/JEQl/YQOEZZDuJpDW/RPQuRqGf1VnoSoHn20xf9N6IUmPwmRSdOW+aEZhKXYSTHK3w5CSEKUmHwjd0iI6lEb419Y8Y+EqKSf0CHCcghXc2iL/kmIXC2jv8qTENWjj7b4vwm90OQnITJp2jI/NIOwFDspRvnbQQhJiBKTb+QOCVE9amP8Cyv+kRCV9BM6RFgO4WoObdE/CZGrZfRXeRKievTRFv83oRea/CREJk1b5odmEJZiJ8UofzsIIQlRYvKN3CEhqkdtjH9hxT8SopJ+QocIyyFczaEt+ichcrWM/ipPQlSPPtri/yb0QpOfhMikacv80AzCUuykGOVvByEkIUpMvpE7JET1qI3xL6z4R0JU0k/oEGE5hKs5tEX/JESultFf5UmI6tFHW/zfhF5o8pMQmTRtmR+aQViKnRSj/O0ghCREick3coeEqB61Mf6FFf9IiEr6CR0iLIdwNYe26J+EyNUy+qu8IkTHH398/MV717uD/gcPHtxRrS323yH4GxmUP6z4T0JksnTLfDpEWA5hqfakWFv0T0KUqLyRO4oQHXfccfEX712FABkaOnRoR7W22H+H4G9kUP6w4j8JkcnSLfPpEGE5hKXak2Jt0T8JUaLyRu6QENWjtrb4vwm90OQnITJp2jI/NIOwFDspRvnbQQhJiBKTb+QOCVE9amP8Cyv+kRCV9BM6RFgO4WoObdE/CZGrZfRXeRKievTRFv83oRea/CREJk1b5odmEJZiJ8UofzsIIQlRYvKN3CEhqkdtjH9hxT8SopJ+QocIyyFczaEt+nchRI888ojAX91po402EmuuuWbdzQRxfRKietTYFv83oRea/CREJk1b5odmEJZiJ8UofzsIoQshmjp1qvjGN76R2EhdO+ecc4449NBD67p8UNclIapHnYx/YcU/EqKSfkKHCMshXM2hLfonIXK1jP4qT0JUjz7a4v8m9EKTn4TIpGnL/NAMwlLspBjlbwchJCFKTL6ROyRE9aiN8S+s+EdCVNJP6BBhOYSrObRF/yRErpbRX+VJiOrRR1v834ReaPKTEJk0bZkfmkFYip0Uo/ztIIQuhOjqq68Ws2bNSmzEtHPTTTeJp59+uuP0+uuvL7bbbruO/HzGF77wBTFu3Lh8No81CJAQaUCpIIvxL6z4R0JU0inoEGE5hKs5tEX/LoTIFsOPfexj4uabb+4ofvDBB4vzzz+/I58Z/giQEPljV1SzLf5vwiA0+UmITJq2zA/NICzFTopR/nYQwn4nRA899JC2t2mrrbZKvsH117/+Vdx4443irrvuEi+++KLYfPPNxcSJExNbNu0sXbo0Xkbg/vvvF/fdd5/485//LJZbbjnx9re/Pb7Gxz/+cbHSSiuZqlvlP/XUU/G1VRuvvPKKWG211QR6y3bZZRexxhprWF3HVIiEyIRMuXzGv8DiX1QyLV68uOQVylVn+8S/nAWVq90W+5OPjQh/s2fPLgdYqvZHP/rR+Jrq2more4hSpex2JbHRXuu2226LL/DHP/4xkqQiU0Z+rLTw4i+99FL0ta99LZLkJ1NP3afaLrvsshHu+dlnny28nu7kRRddFI0cObLw+pKMRh/+8Iej+fPn6y5hlTd27Ni4Dflx1+iFF15w/jPZuSnf6qYqKMT2Gf8rMKPkEiLZ89yhQdIgPU2nkmq0v97Yn3r49yshOv7447Wk4tprr42Jytve9raO80WE6I477og23HDDjjoKB912xIgRkSJg3Yxb9ghFu+66q9P1hwwZEp155pndLq09T0KkhaV0JuNPb+KPSVFV409CZELaMr9qhVg2mxRj+2E5ZKJYy51e6V8RgH4lRCeccIKWXFx++eXRhAkTtOdMhOjcc8+NQD6UzC5b+eosuvvuuwu1d+edd0YgTy7XTZf9wQ9+UHh93UkSIh0q5fN65X+mO2X71cZ/EiKTpVnm0yCrNUhL2JNixL83+KsHcr8SolNOOUVLME499dQIJEXdf3qrI0TPPPOMsfyee+4ZXXHFFdG9994bXXPNNfFrsvT11D5eb5nSa6+9Fm299dba+9l0002jCy64IPrtb38b/frXv46++c1vRrhHdV21HT58eLRo0SJTE9p8EiItLKUzGX96E39MiqoafxIiE9KW+VUrxLLZpBjbD8shE8Va7vRK/+ph3K+EaMaMGR3EAfe88cYbJ/mbbbZZPCYIpEN+WiQ67LDDOlA+6KCDkvJKZmz/+7//u6MsMi699FJtedOrsx/96Efa8jvttFOk0+Uf/vAHbW8SesRcEgmRC1r2ZXU6s69dviTbrzb+DwKg0uGZWoyAfD0gMJOGiQiYEBg2bFh8ShIigRlLVaQqp93LsTXiyCOPNN7Wl770JXH22WcL2Lop3XPPPWKLLbYQshcnU2S99dYTf/rTn4x1d95553j2WroSZoZdd9116SyBGUkbbLCBePLJJzP5uCfMXFt33XUz+erg5JNPFpMmTVKH8XbVVVcVCxYsSGbQZU5qDtQss6OPPlocc8wxmhLFWZhluMIKKxQX4lki0HQEynJUMtRqGaqrPog/8Xe1GZ/yMs7FPRv92kN0xhlnaHtecN9Fr7DSWBxyyCHaa3zve99LF+vYl1P5tfUkwcqUNfUm7bbbbply+QO5RIB2TNPpp5+eL2o8Zg+REZpSJxh/w4q/fGVWyh0ibTd3yUs6VadDhuWQTsqXhXul/yYToquuusoKVkUalKxqC8JTlDDuSJVNb88777xMtalTp2rLyd6fTDndgW7G2+c+9zldUW2eko3T7rXweGf2yv9MN8j2q43/XJhRRrAyiQtzBbYwl6MxtEX//b4wo+mVmRyALP7+978bX3el1b3mmmsKLJCYT3Lcj1hrrbXy2ZljvCKTD6dM3te//nUhB0Ynefvvv7+47LLLkmO1I9c6Ervvvrs61G4nT54s5LikzLntt99ezJs3L5NnOlCvzCQhEriWaxo8eLD29Vxb7N+EF+UPLP6bmKdtPhlqtQzVFndVjvgTf2ULdW7lAyHu3WjaKzPM3LJJ8sEWYQFEJWcVW/mttUzT73//+yu9viRpmesXHbCHqAgd/3OMv2HFX74y8/eFuCYdIiyHcDWHtuhfEYSmESL5WQ0rlWI2l5Kxqq3slcm0vcoqq1TaBtZKevXVVzNtmA5IiEzIlMtvi/+bUApNfhIik6Yt80MzCEuxk2KUvx2EUJGEphGiAw44ILHVop1bbrmlUrICvNZZZ52kSaw/tMwyy1TexuOPP560UbRDQlSEjv85xr+w4h/HEMnIVSbxHXJg75AdjaEt+m/qGCK5rpCQ6w511eoTTzxhHCf0la98xWvKOT4AK9c7StrGtPpHH300OVY7e+yxRzwdXx27bLHUgM2HXzmGyAVV+7Jt8X8TIsHJ78+NX69JhhwWQ3a1B+q/HfqXATHu3WhaDxEWWrRJch2uCB9pVXKmtw888IDNJbqW2XHHHbXXP+ecc7rWLVuAPURlEdTXZ/wLK/7xlZnezq1z6RBhOYS14t8o2Bb9K4IQKiGCOuWiiVrC8qtf/crVLLTlv/zlL2uvL2ejactXmUlCVCWab16rLf7/psTZvdDkJyHK6tf5KDSDcAWA8reDELaBEMkVp7WEpaoeHLnitPb6n/nMZ1zdzrk8CZEzZFYVGP/Cin8kRFZmby5EhwjLIcya1p9pi/7bQIiwQKKSM7193/vep1f+G7lynaPoyiuvjObOnRvh9do//vGPCIOo88m0orUcaxQ9++yz+eLJMa6F6998883R/PnzIywEaTu7TF2EhEghUe22Lf5vQi00+UmITJq2zA/NICzFTopR/nYQQkUQQn5lBlLy1re+VUuKrr/++sTm8zt77713R523vOUt0eWXX54vGm2zzTYdZYGt/L5YR1mVIRed7KgjF0rUfpxW1clvSYjyiFRzzPgXVvwjISrpF3SIsBzC1Rzaov82ECLoHl+RV7Kmt/LDptFPfvKTjHn861//ivCds3Q5tb/xxhtre3HkatPa8qgnP7waYXC3Sv/5z3+im266KULb6rpqi16lxx57TBXtuiUh6gqRV4G2+L8JnNDkJyEyadoyPzSDsBQ7KUb520EI1YM45B4iGLWcRhzJT3h0EBAl/+qrrx7Jz2xE2267beG6QkXfP9P1KKnrr7TSStG4ceMi+SmQaMUVVzTeh833zxInlTskRGk0qttn/Asr/pEQlfQNOkRYDuFqDm3Rv3pgh06IoP9f//rXEYiPktlli9Wjzz///EIzwmKKW265pdf1cS9f/OIXtb1PRY2SEBWh43+uLf5vQig0+UmITJq2zA/NICzFTopR/nYQQkUK2kCIYNwYKP3pT3/aibSgd2fWrFmJbxTtvPLKK9H06dMjjDVS2HbbYtyQ7xR9EqIibfifY/wLK/6REPn7QlyTDhGWQ7iaQ1v0rx7WbSFEyg6uuOKK+BXWaqutZiQuWL/ojDPOiBYtWqSqWW9/97vfxa/g1l57bePHZUeOHBkde+yxTmOG8jdAQpRHpJrjtvi/Ca3Q5OenO2SkL5OCW7rcEQzK345Pl9Tx6Q5HUxvw4rLXSNx3333i4YcfFsOHDxfvete74j/5ek0ofMrcpHy4CDltX9x///1Cfvcsub4c0xQfl7k2P91RBj1zXca/sOIfCZHZ1q3O0CHCcggrpacKtUX/6oEve4gEHq5MzUKAhKgefbXF/03ohSY/CZFJ05b5oRmEpdhJMcrfDkJIQpSYfCN3SIjqURvjX1jxj4SopJ/QIcJyCFdzaIv+SYhcLaO/ypMQ1aOPtvi/Cb3Q5CchMmnaMj80g7AUOylG+dtBCEmIEpNv5A4JUT1qY/wLK/6REJX0EzpEWA7hag5t0T8Jkatl9Fd5EqJ69NEW/zehF5r8JEQmTVvmh2YQlmInxSh/OwghCVFi8o3cISGqR22Mf2HFPxKikn5ChwjLIVzNoS36JyFytYz+Kk9CVI8+2uL/JvRCk5+EyKRpy/zQDMJS7KQY5W8HISQhSky+kTskRPWojfEvrPhHQlTST+gQYTmEqzm0Rf8kRK6W0V/lSYjq0Udb/N+EXmjykxCZNG2ZH5pBWIqdFKP87SCEJESJyTdyh4SoHrUx/oUV/0iISvoJHSIsh3A1h7bon4TI1TL6qzwJUT36aIv/m9ALTX4SIpOmLfNDMwhLsZNilL8dhJCEKDH5Ru6QENWjNsa/sOIfCVFJP6FDhOUQrubQFv2TELlaRn+VJyGqRx9t8X8TeqHJP0h+YTkyCcv8diAwZMgQsXTp0nYISym9EBg2bFhcjx939YJvwCspQnT00UeLY445xvl+QIhXWGEF53qsQASahAB7iEpqKzSG7AoH5W9HDxl7iFw9o7/KK0J03HHHicmTJzvf3ODBg8XQoUM76tH/2+H/HYp/IyM0/ZMQmTRtmR+aQViKnRSj/O0IiCREick3coeEqB61Mf6FFf9IiEr6CR0iLIdwNYe26F8RohkzZogxY8a4wsTyA4zAhAkTxPz58wV7iKpVRFv834RaaPKTEJk0bZkfmkFYip0Uo/ztIIQgRPiLIg45TIy/YTvQ36RJk/jKrEK9Mf6FFf9IiEo6Bx0iLIdwNYe26J+EyNUy+q88CVH1OmmL/5uQC01+EiKTpi3zQzMIS7GTYpS/HYQQD1MkzjJLTL9ROxxDVI+6GP/Cin8kRCX9hA4RlkO4mkNb9E9C5GoZ/VWehKgefbTF/03ohSY/CZFJ05b5oRmEpdhJMcrfDkJIQpSYfCN3SIjqURvjX1jxj4SopJ/QIcJyCFdzaIv+SYhcLaO/ypMQ1aOPtvi/Cb3Q5CchMmnaMj80g7AUOylG+dtBCEmIEpNv5A4JUT1qY/wLK/6REJX0EzpEWA7hag5t0T8Jkatl9Fd5EqJ69NEW/zehF5r8JEQmTVvmh2YQlmInxSh/OwghCVFi8o3cISGqR22Mf2HFPxKikn5ChwjLIVzNoS36JyFytYz+Kk9CVI8+2uL/JvRCk5+EyKRpy/zQDMJS7KQY5W8HISQhSky+kTskRPWojfEvrPhHQlTST+gQYTmEqzm0Rf8kRK6W0V/lSYjq0Udb/N+EXmjykxCZNG2ZH5pBWIqdFKP87SCEJESJyTdyh4SoHrUx/oUV/0iISvoJHSIsh3A1h7bon4TI1TL6qzwJUT36aIv/m9ALTX4SIpOmLfNDMwhLsZNilL8dhJCEKDH5Ru6QENWjNsa/sOIfCVFJP6FDhOUQrubQFv2TELlaRn+VJyGqRx9t8X8TeqHJT0Jk0rRlfmgGYSl2Uozyt4MQkhAlJt/IHRKietTG+BdW/CMhKukndIiwHMLVHNqifxIiV8vor/IkRPXooy3+b0IvNPlJiEyatswPzSAsxU6KUf52EEISosTkG7lDQlSP2hj/wop/JEQl/YQOEZZDuJpDW/RPQuRqGf1VnoSoHn20xf9N6IUmPwmRSdOW+aEZhKXYSTHK3w5CSEKUmHwjd0iI6lEb419Y8Y+EqKSf0CHCcghXc2iL/hUhmjFjhhgzZowrTCw/wAhMmDBBzJ8/Xxx33HFi8uTJznczePBgMXTo0I56bbH/DsHfyKD8YcV/EiKTpVvm0yHCcghLtSfF2qJ/ECL8RVGUyM6dZiEA/U2aNImEqEK1tcX/TZCFJj8JkUnTlvmhGYSl2Ekxyt8OQkhClJh8Y3dIiKpXHeNfWPGPhKikj9AhwnIIV3Noi/7xMEWaPXu2wHgUpmYhwDFE9eirLf5vQi80+UmITJq2zA/NICzFTopR/nYQQhKixOQbuUNCVI/aGP/Cin8kRCX9hA4RlkO4mkNb9E9C5GoZ/VWehKgefbTF/03ohSY/CZFJ05b5oRmEpdhJMcrfDkJIQpSYfCN3SIjqURvjX1jxb9DixYs5baQeX2nMVYcMGSKWLl3amPvljfYegWHDhsWNcgxR77GvokVFiI4++mhxzDHHOF8ShHiFFVZwrscKRKBJCLCHqKS2+AshrF8IrubQFv2zh8jVMvqrvCJEXIeoWr20xf9NqIUmPwmRSdOW+aEZhKXYSTHK3w5CSEKUmHwjd0iI6lEb419Y8Y+EqKSf0CHCcghXc2iL/kmIXC2jv8qTENWjj7b4vwm90OQnITJp2jI/NIOwFDspRvnbQQhJiBKTb+QOCVE9amP8Cyv+kRCV9BM6RFgO4WoObdE/CZGrZfRXeRKievTRFv83oRea/CREJk1b5odmEJZiJ8UofzsIIQlRYvKN3CEhqkdtjH9hxT8SopJ+QocIyyFczaEt+ichcrWM/ipPQlSPPtri/yb0QpOfhMikacv80AzCUuykGOVvByEkIUpMvpE7JET1qI3xL6z4R0JU0k/oEGE5hKs5tEX/JESultFf5UmI6tFHW/zfhF5o8pMQmTRtmR+aQViKnRSj/O0ghCREick3coeEqB61Mf6FFf9IiEr6CR0iLIdwNYe26J+EyNUy+qs8CVE9+miL/5vQC01+EiKTpi3zQzMIS7GTYpS/HYSQhCgx+UbukBDVozbGv7DiHwlRST+hQ4TlEK7m0Bb9K0I0fvx4MXr0aFeYWH6AEbjkkkvEggULBL9lVq0i2uL/JtRCk5+EyKRpy/zQDMJS7KQY5W8HIVSEKFE8dxqJAAlRtWpj/Asr/pEQlfQPOkRYDuFqDm3RP1656NJrr70mBg8erDuVyUO5KIoyeVUc2LZf1NbTTz8tnnrqKbHVVlsVFdOeq6J97YUtM13b32+//cT+++9vefU3i0HHQ4cOfTPjjb222H+H4JQ/RiA0/ZMQmSzdMj80g7AUOylG+UkIdQ/KxEDe2HnllVfEyy+/nM8ufbxkyRKx/PLLl7rOuuuuK5599llx5ZVXip122snpWlW079RgrnCv2ichygH/xiHjX1jxj4RIb+fWuXSIsBzCWvEMiDECtvbfr4To2muvFZ/97GdjWXbccUdx1VVXOZlArwiJ6aZ61T4JkV4Dtvavr10+l+1X+/whISppkzTIag3SVR3Evxn49ysh2mWXXcS8efMSs3vyySfFyiuvnBx32+kVITHdR6/aJyHSa4DxpxnxR6+9zlwSok5MnHLoEGE5hJPyZWHq307//UiI7r33XrHddtvFKgcJWrRokTjppJPEEUccYW0GvSIkphvqVfskRHoN0P/t/F+PXvncqvEnISqpk6oV4no7bD8shwxV//1IiA499FBx2WWXibFjx4rNN99cnH766WLTTTcVt912m7UaekVITDfUq/ZJiPQaYPwNK/6SEOnt3DqXDhGWQ1gr/o2C1L+d/vuNEKE3aM0114y1ePHFFwvMolt77bXjYxAiECOb1CtCYrqXXrVPQqTXAP3fzv/16JXPrRp/EqKSOqlaIa63w/bDcshQ9d9vhOiEE04QJ554ohg1alS8YCFwBymaO3euwNT0c88910oVvSIkppvpVfskRHoNMP6GFX9JiPR2bp1LhwjLIawV/0ZB6t9O//1GiNA7hF6iqVOnimnTpsXaxGrOBx54YDyo+r777rMaXN0rQmKyy161T0Kk1wD9387/9eiVz60afxKikjqpWiGut8P2w3LIUPXfT4To0ksvFYcddlhMePA5i+HDhyewYx9E6ZxzzrFawLBXhCS5wdxOr9onIcoB/8Yh429Y8ZeESG/n1rl0iLAcwlrxDIgxArb230+ECDPLMMPsgAMOEOgVSid8q23mzJnWg6t7RUjS95je71X7JERp1N/ct7X/N2tUu8f2q33+kBCVtE8aZLUG6aoO4t8M/PuFEGHNIaw9hPTYY491fKj2nnvuEWPGjInP47XZWmutFe+b/vWKkAx0+yREeg0w/jQj/ui115lLQtSJiVMOHSIsh3BSvixM/dvpv18I0b777iuuu+66eKr9nDlztOrGFPz58+eLww8/XJx88snaMiqThMhO/wqvqrf0P+Jv8+kgW7sjIbJFylCODkmHrNIhDWZmzG6K/fUDIXr88cfFxhtvHGM5e/bseFaZDtj04GqsXF2USIjo//T/zo/+FvlMleeqjn8kRCW1U7VCXG+H7TMgNyEg9wMhOvbYY8XZZ5+dmWqv87fnn38+fpVmM7iahIj+1wT/09l5FXmhPX9IiEpaRWgG4QoH5ecDoQkPBJAcLLyILRZixODpoqQGV2NtIvQmmRLtn/bfBPs32W/Z/NDsn4SopEWEZhCucFB+PhCa8EA47bTTxFFHHaWdaq+zeYwvGjduXHxKN/ha1aH90/6bYP/KXqvehmb/gxYvXhxVDRKv1ywEhgwZIpYuXdqsm+bdEgEHBDbaaCOxcOHCzEKM3aqPHj06rjN58mQxZcqUbsV5nggQgYYjwB6ikgoMjSG7wkH5+Qu5338hX3311WKvvfaKTbuotydv+6pXCcQI9XSJ9k/773f719ltVXmh2T8JUUnLCM0gXOGg/Hwg9PsDAa++8ApMtxBjkb1jvNGIESPiIldddZXYc889O4rT/mn//W7/HUZbYUZo9k9CVNI4QjMIVzgoPx8I/fxASC+0WDTV3mT3anD1HnvsIdDTlE+0f9p/P9t/3l6rPg7N/kmISlpIaAbhCgfl5wOhnx8IitCMHTs27iVyte9ur9to/7T/frZ/V3t3LR+a/ZMQuVpArnxoBpETr+sh5ecDoV8fCOlXXjZT7U3GrgZXz5gxQ0ycODFTjPZP++9X+88Yak0Hodk/CVFJQwnNIFzhoPx8IPTrA2HatGli+vTpXRdi7Gbz6jq6wdW0f9p/v9p/N7uu4nxo9k9CVNIqQjMIVzgoPx8I/fpAwIBo9BJNnTpVgNT4pgULFsSLOqJ+fhwS7Z/236/272vvLvVCs38SIhfta8qGZhAaEQuzKD8fCP34QEh/jwyEZvjw4YV23O0kZpjNmjWrY6Ya7Z/234/2382eqzofmv2TEJW0jNAMwhUOys8HQj8+EMaMGSMww8x1qr3J/tODq5977rmEYNH+af/9aP8mO646PzT7JyEqaSGhGYQrHJSfD4R+eyDYfnbD1dbRy4QPvqYHV9P+af/9Zv+udl2mfGj2T0JUxhpk3dAMwhUOys8HQr89ENTrLd+p9iYfwAyz008/XWy++ebi97//fVyM9k/77zf7N9lvHfmh2T8JUUkrCc0gXOGg/Hwg9NMDoWgAtKtt58unrw1CBGJE+6f995P952227uPQ7J+EqKTFhGYQrnBQfj4Q+umBoHpxRo0aJUBgqk477LCDmDt3bjI2ifZP++8n+6/a3rtdLzT7JyHqpvEu50MziC7idpym/Hwg9MsDAVPs11577XiqfZmFGDuMPJWhZq9hPBE++LrsssuKfpE/dZs926X/0/9Dsn8SopKhgwGBASGkgODqDv1k/+rr9CuvvHLcO1R2qr0JCzW4GqTr05/+NAnR0KEmqGrP7yf7q11YTQOUv9rnDwmRxshcsmiQ1RqkC/YoS/yJvyKk6B3Ca7KyCzF2s0H1fTSMIbrttttIiEiIuplMbecZ/6qNfyREJU2VBlmtQbqqg/gTfxCi9DpBeJWFz2zUlbC+EdY5Qrr99tvFBz7wgbqa6npd2j/tX/0g6GosNRQIzf5IiEoaSWgG4QoH5WdA7oeAPG7cuPhr9lUtxNjND9A7NH/+fHHEEUeI73//+92K13ae/kf/6wf/q83Au1y4avsnIeoCeLfTVSukW3v582yfAbHtAfHBBx9Memzy3xrL+0tVx+nB1Vi5eqAS/Z/+33b/r1J+EqKSkYwBiQGpSod0NUfa37/F4YcfLmbOnCmqXoixSBeY0YbXcli5uq4ZbUXtq3PUP+MP4091g/pJiFRk8dwyIDEgMSBVF5Bc3fDpp58Wa6yxRlyt18REDa7G2kTomRqIxPjD+MP4U138ISEqGcUYkBiQGJCqC0iu7jhlyhRxwgkniLoWYiy6n/Tg6roHcpvug/GH8Yfxp7r4Q0JkijSW+QxIDEgMSNUFJEu3S4qNGDEiXoix7qn2SYO5Hbw2W7hwoZgwYYLAOki9Tow/jD+MP9XFHxKikhGMAYkBiQGpuoDk4o5qYHPdCzEW3ZNaDBLECL1EvU6MP4w/jD/VxR8SopIRjAGJAYkBqbqA5OKOWAsIr616NdVed28YXI1eKqSrrrpK7LnnnrpiteUx/jD+MP5UF39IiEqGKgYkBiQGpOoCkq07zpkzR2DtIaSBGr+j7lUNrt5jjz3iBSJVfi+2jD+MP4w/1cUfEqKSUYsBiQGJAam6gGTrjuiJmTVrVk+n2pvubSDJGeMP4w/jT3Xxh4TIFOUs8xmQGJAYkKoLSDZuh++V4btl+YTp7y4JH2nFitMuCWOF8JdPIGh4fdbrwd2MP4w/jD/VxR8SonxkczxmQGJAYkCqLiDZuN/EiRPF6aefblO0p2UwuBv3Nm3atJ61y/jD+MP4U138ISEqGboYkBiQGJCqC0g27oiB1OiNQVqyZIlYfvnlM9XQg4Q/m4SZapg2v8EGG4jVV1/dpkpSZu7cuck+dnq5UrZqmPGH8Yfxp7r4Q0KkIovnlgGJAYkBqbqA5OqGZf0Pr9lAbGbMmBH37vS6fdf28uXLyp+/nusx22f8Cyn+DVq8eHHk6gQsHxYCQ4YMEUuXLg1LKEpDBCwQ2GmnncS8efPEDTfcID70oQ9Z1GARIkAEQkWAPUQlNctfSPyFFNIvJFd3aLr9qx4ifIvMdVA2sGq6/K76zpen/Ix/IcU/EqK8hzseMyAwIIQUEBzNv/GEADPN8MV6EiJXzb9envGP8S+k+EdC5BcHkloMCAwIIQWExLAtd5pu/4MGDYolJSGyVHiuWNP1nxPH+ZDyhxX/SYicXSBbgQ4RlkNktdv9iPpvtv5JiLrbeFEJ2n+z7b9ItzbnQtM/CZGN1gvKhGYQBaJqT1F+BsQm95CREGnd2jqT/k//b7L/5w2dhCiPiOMxAwIDQkgBwdH8Gz+GiITIVePZ8ox/jH8hxT8Soqx/Ox8xIDAghBQQXB2g6fZPQuSq8Wz5pus/K437EeUPK/6TELn7QKYGHSIsh8go1+KA+m+2/kmILIy8oAjtv9n2X6Baq1Oh6Z+EyErt5kKhGYRZUv0Zys+A2OQeMhIivV/b5tL/6f9N9v+8nZMQ5RFxPGZAYEAIKSA4mj/HEP2b9k/7b+6na1z9PV8+tOcfCVFew47HoRmEo/iNfyC6ypsvT/03mxCwhyhv0W7HtP9m27+btjtLh6Z/EqJOHTvlhGYQTsLLwpSfAbHJPQSKED322GNi9OjRruZP+2cPmWiy/TsbfK5CaPGfhCinYNfD0AyC8rshQP03mxAqQhRFft+4pv6brX83b+8sTf2HpX8Sok4bd8qhQ4TlEE7Kl4Wp/2brn4TI1eKz5Wn/zbb/rDbdj0LTPwmRuw1kaoRmEBnhLA4oPwNiU18ZzJkzR4wbNy62cvYQWTi7pgj9n/7fVP/XmLMgIdKh4pDHgMCAEFJAcDD9uGiT7Z+EyFXbneWbrP9OadxzKH9Y8Z+EyN0HMjXoEGE5REa5FgfUf3P1T0JkYeBditD+m2v/XVRrdTo0/ZMQWandXCg0gzBLqj9D+RkQm9pDRkKk92mXXPo//b+p/q+zcxIiHSoOeQwIDAghBQQH04+LNtn+SYhctd1Zvsn675TGPYfyhxX/SYjcfSBTgw4RlkNklGtxQP03V/8kRBYG3qUI7b+59t9FtVanQ9M/CZGV2s2FQjMIs6T6M5SfAbGpPWQkRHqfdsml/9P/m+r/OjsnIdKh4pDHgMCAEFJAcDD9uGiT7Z+EyFXbneWbrP9OadxzKH9Y8Z+EyN0HMjXoEGE5REa5FgfUf3P1T0JkYeBditD+m2v/XVRrdTo0/ZMQWandXCg0gzBLqj9D+RkQm9pDRkKk92mXXPo//b+p/q+zcxIiHSoOeQwIDAghBQQH04+LNtn+FSHabLPNxD333OMqeuPl9xI4V6nJ+s+J4nVI+cOK/yREXm7wZiU6RFgO8aZm7fao/+bqXxGisWPHCuz7JOq/ufr30Xe+DvUflv5JiPIW7nhMhwjLIRzVz4+7/ru5+r/66qvFXnvtJUiIXK3+zfKMf821/ze16L8Xmv5JiPxtIa4ZmkG4wkH5GRCb+spw2rRpYvr06SRErk6fKk//p/831f9TZpzskhAlUPjtMCAwIIQUEFy9oMn2T0Lkqu3O8k3Wf6c07jmUP6z4T0Lk7gOZGnSIsBwio1yLA+q/ufonIbIw8C5FaP/Ntf8uqrU6HZr+SYis1G4uFJpBmCXVn6H8DIhN7SEjIdL7tEsu/Z/+31T/19n5oMWLF0e6E8xrDwJDhgwRS5cubY/AlJQISAS+/e1vixNOOEF88IMfFDfeeCMxIQJEoOUIsIeopAHwFxJ/IYX0C8nVHZps/+whctV2Z/km679TGvccyh9W/CchcveBTA06RFgOkVGuxQH131z9kxBZGHiXIrT/5tp/F9VanQ5N/yREVmo3FwrNIMyS6s9QfgbEpvaQkRDpfdoll/5P/2+q/+vsnIRIh4pDHgMCA0JIAcHB9OOiTbZ/EiJXbXeWb7L+O6Vxz6H8YcV/EiJ3H8jUoEOE5RAZ5VocUP/N1T8JkYWBdylC+2+u/XdRrdXp0PRPQmSldnOh0AzCLKn+DOVnQGxqD5kiRFOnThXY90m0f9p/U+3fx97zdUKzfxKivIYdj0MzCEfx+S2vBn/Ly1XXuvJNtn8SIp1G3fKarH83SfWlKX9YhJiESG/n1rl0iLAcwlrxbxSk/pur//Hjx4uZM2cK9hC5Wv2b5Wn/zbX/N7Xovxea/kmI/G0hrhmaQbjCQfkZEJv6ymCHHXYQc+fOJSFydfpUefo//b+p/p8y42SXhCiBwm+HAYEBIaSA4OoFTbZ/EiJXbXeWb7L+O6Vxz6H8YcV/EiJ3H8jUoEOE5RAZ5VocUP/N1T8JkYWBdylC+2+u/XdRrdXp0PRPQmSldnOh0AzCLKn+DOVnQGxqDxkJkd6nXXLp//T/pvq/zs5JiHSoOOQxIDAghBQQHEw/Ltpk+ychctV2Z/km679TGvccyh9W/CchcveBTA06RFgOkVGuxQH131z9kxBZGHiXIrT/5tp/F9VanQ5N/yREVmo3FwrNIMyS6s9QfgbEpvaQkRDpfdoll/5P/2+q/+vsnIRIh4pDHgMCA0JIAcHB9OOiTbZ/EiJXbXeWb7L+O6Vxz6H8YcV/EiJ3H8jUoEOE5RAZ5VocUP/N1T8JkYWBdylC+2+u/XdRrdXp0PRPQmSldnOh0AzCLKn+DOVnQGxqD5kiRDNmzBATJ07UG3iXXNo/7b+p9t/FtK1Oh2b/JERWajcXCs0gzJLqz1B+PhCa+kBQhGj27NkC+z6J9k/7b6r9+9h7vk5o9k9ClNew43FoBuEoPj/uyo+7iqY+EEiIXL29szzjHwlhU/2/05qFICHSoeKQx4DAgBBSQHAw/bhok+1/+PDhYtGiRYI9RK5af7N8k/X/phT+e5Q/rPhPQuTvC3FNOkRYDuFqDtR/c/U/aNCgWN0kRK5W/2Z52n9z7f9NLfrvhaZ/EiJ/W4hrhmYQrnBQfgbEpvaQkRC5entnefo//b+p/t9pzXxlpsPEKY8BgQEhpIDgZPyycJPtn4TIVdud5Zus/05p3HMof1jxnz1E7j6QqUGHCMshMsq1OKD+m6t/EiILA+9ShPbfXPvvolqr06Hpn4TISu3mQqEZhFlS/RnKz4DY1B4yEiK9T7vk0v/p/031f52dkxDpUHHIY0BgQAgpIDiYfly0yfZPQuSq7c7yTdZ/pzTuOZQ/rPhPQuTuA5kadIiwHCKjXIsD6r+5+ichsjDwLkVo/821/y6qtTodmv5JiKzUbi4UmkGYJdWfofwMiE3tISMh0vu0Sy79n/7fVP/X2TkJkQ4VhzwGBAaEkAKCg+nHRZts/yRErtruLN9k/XdK455D+cOK/yRE7j6QqUGHCMshMsq1OKD+m6t/RYgee+wxMXr0aAttdxah/pur/05tuudQ/2Hpf9DixYsjdzNgjZAQGDJkiFi6dGlIIlEWItAVgWHDhsVlZAzsWpYFiAARCB8B9hCV1DF/IYT1C8HVHKh/6p+vTIe6uk1l5el/9L8q/Y+EqKRrNtEh1Ve+S4rO6kSACBABIhAAAmPHjhVz5sxxlqSJz78iIUmIitCxONdEgyAhslAsixABIkAEWoIACdHriiYhKmnwTSZEBxxwgBg/fnxJBFidCBABIkAEmojAJZdcImbOnClIiF7XHglRSStuMiGaOnWqmDZtWkkEWJ0IEAEiQASaiADi//Tp00mI3lAeCVFJKyYhKgkgqxMBIkAEiMCAIEBClIWdhCiLh/MRCZEzZKxABIgAESACfYAACVFWCSREWTycj0iInCFjBSJABIgAEegDBEiIskogIcri4XxEQuQMGSsQASJABIhAHyBAQpRVAglRFg/nIxIiZ8hYgQgQASJABPoAARKirBJIiLJ4OB+REDlDxgpEgAgQASLQBwiQEGWVQEKUxcP5iITIGTJWIAJEgAgQgT5AgIQoqwQSoiwezkckRM6QsQIRIAJEgAj0AQIkRFklkBBl8XA+IiFyhowViAARIAJEoA8QICHKKoGEKIuH8xEJkTNkrEAEiAARIAJ9gAAJUVYJJERZPJyPSIicIWMFIkAEiAAR6AMESIiySiAhyuLhfERC5AwZKxABIkAEiEAfIEBClFUCCVEWD+cjEiJnyFiBCBABIkAE+gABRYg++MEPiv/93/91viM8/1ZeeWXnelVVqPr5S0JUUjNVK8T1dnza32GHHcTcuXMFv3bvijbLEwEiQATCQUARou23317ccMMNzoItWbJEjBw50rleVRV8nn9FbZMQFaFjca5qhVg0mSni0z4JUQZCHhABIkAEWokACVFW7SREWTycj3wIiXMjBRV82ichKgCUp4gAESACLUGAhCiraBKiLB7ORz6ExLmRggo+7ZMQFQDKU0SACBCBliBAQpRVNAlRFg/nIx9C4txIQQWf9kmIzIBecskl4r//+787Cuy7777iO9/5Tkc+M4gAEagXgS9/+cva8S2nn3662GuvveptPPCrkxBlFUxClMXD+ciHkDg3UlDBp/26CNFrr70m7rnnHnHrrbeKJ598Uvzzn/8U//jHP8SQIUPEmmuumfy9613vEltttZVYdtllCyQbmFNnnnmmOPLIIzsaP+igg8QFF1zQkc+M/kTgpZdeErfffrv4zW9+I/72t7/Fdgh7fOtb35rYIWxynXXWEZtttll/CsG7ihHYe++9xS9+8YsONH70ox+J/fffvyOfGfYIkBDlsIpKpsWLF5e8QrnqbN8d/7Fjx0bSDCI5y6wc+G/U/v3vfx/JHpRo+PDh8XVx7W5/q622WjRlypTo8ccfr+QeqrrIGWecob13SYiqaoLXqQkBScijWbNmRePGjYsk2dbqUWeXG2+8cXTWWWdF//rXv2q6M162DAKf/OQntbqUhKjMZVlXIoBnAHxCzjKLXnjhBec/+WNjQHGs+vkvykpT9Q253g/bHzhCtHDhwugTn/iENljpHjy6PNl7FO2zzz7Rc88956r6WsqTENUCa+0XnT17drTpppuWssWVVlop+vrXvx6BWLU1TZ8+Pdp1112Tv4ceemjAoSAhqk8FJERZbPnKTD6lyySfV1Zl2svX9Wm/ildm8+bNE+jKxuuIKhJeW/zP//yPePvb317F5byvwVdm3tANWMXvf//74qijjhKvvvpqJfeA1zAXX3yxWGaZZSq5XlMuglgie26F/JGZ3PJdd90lttxyy+R4IHagi3vvvbejaehpiy226Mhnhj0CfGWWwyrLj9yP2EPj3kPjjrK5hg/+ZV+Z3XjjjdFb3vKWUr/GpRl21F9vvfWiRx991CxsD86wh6gHIFfYhBwA32FHOttyzUPPpyQIFd5p/1/qiiuu6MBSEqL+v3HeoTcC7CHKQsceohxBdD306aFxbaOovE/7ZXqIMFh6zJgx4u9//7vxtrBy6eabby422WST+G+VVVYR8vWakGRH/PznPxdPPPGEsS6u/dvf/lYMGjTIWKbOE+whqhPdaq99/fXXC0lc8NrfeOG1115byFdpiS0OHjxYPPbYY+KBBx4QV155pXjxxReNdSdOnChmzJhhPB/aiT333FPIMVgZsfqhhyhzQzyoFAH2EOXgzPIj9yOfHgr3Vsw12L57D1WZHiJVV5pRx69J5B1++OGRnOFjVNgrr7wSXX755ZGcaaatj2tI0mSsX/cJ9hDVjXA115eEPJJE22hDK6ywQvSDH/ygsDGMWzvppJOi5ZZbTnud5ZdfPnrqqacKrxHKyeeff16LA3uIQtGwXg72EGVxYQ9RjiC6Hvr00Li2UVTep33fHqJbbrlFSEKkvZ0RI0aIiy66SOBXpk1CT9PHP/5xcf/993cUR8/S/PnzrXqJFixYIH7961+Lhx9+OO61kgRZoFdggw02EBtuuGG8xVRr2+TTQ4QeBzlbrqOJUaNGidGjR3fkpzNQD/XzCVPC11133Uy2JJPi//7v/zJ5OFh11VXFRhttlORLFxe//OUvxZ133ikeeeQRseKKK8bTy+XsK/GBD3wgKZffQQ/eVVddFd8PegBxTfTYbbPNNlbfK8J4Mp0+119/ffHOd74z09xtt90Wf08P+oPO0Bb0jvEq+bKZim8cfOMb34i/xac79973vlf85Cc/yWCiK6fy5syZI/bYYw8hZ5mprGR7xBFHCIxRsklV2yJ6Z+Df6SRfVYttt902nSUWLVoU93Y9+OCDsR1iHB4wAJ5Y3gLLXujSH/7wh3hpDJyTg9KFHFDdUUySytiH1Il3vOMd4t3vfrc6NG6x3IEckB0vv4EeYWALX4BNy1fj8VIHchC7sX76xH333aftkX7Pe94Tj3lKl1X7aPvpp59Wh8kWeAwdOjQ5xriza665Jl4uBPrDUiAKu6233lrY3mNywTd2li5dGvse/AH3/+c//1lI4h2PkUTvOWKfzbVtfR76u+OOOwR0itjxuc99Lu6lz99X/pg9RDlE0MPCv3ZhIL9sHP8ixq8Dl7Tbbrtpf0lLk4p++MMfulwqLvvMM89E8mHdcU359eRIPsyN15NBLMKUW/kQ7aiLe8n/ycAZ/epXvzJeL33Cp4do8uTJHW3iHrCsQLf0rW99S1tXDhLuqCoffNqyH/3oR5OykjBFmEaex0Ady0AcyQdUUh478P/Pf/7zEWb8qXLprSS7kfzwY6aO7gBT3tP11P63v/3tpLh8UEbyQaMth/LolZEL7hXO9EIPJJZtUNdPb+VA6EiSwKQ9253rrrtOez2MawM+plSnLUoy2nFPGLunEnpbjznmGK0PKUwkeTKOy9t55507rq/qmbYHH3ywar5jC73ItboiSSi6Xle+Vo8k0YwgQ7fkM8sM/qOTQRLxpLmZM2dGa621lrYc6q6xxhrWcUNdFBh87Wtf0/a2pe8Hy0IAy2effVZV1W7Rc5eup/aVz2NGpE5WuYis9nr5TNVDBDvBFHqfv5D4A6fd5y3E8bgoWDpeyqu4T/vqtZcLIcIrCjmuR+ucsjcmwoPBJ4FM4EEMh5S/ViIErKJrYaq/7kGhAkXR9oADDoggR1HqZ0Ikf3VqdfC+970vFkn+QowwdbwIA5zD9HS15o7sgYg+/OEPd60jx95EsvesCLpI/krVXuerX/1qXO+mm26Khg0bpi2Tv+eddtop+s9//qNtTy7SZ7xG0QNbe7FU5nbbbRffH6adg5TJcUaps527ddui8tM8NtAdHry77767EYd0HdgECF8+VUmI/vKXv0SyJ9DqftL3Jntxoz/96U/5W8sc+xAi9aBPt4V92RsUXxskPX9Od4yYh6UIbBL8D/LormPKw4+NNEnLtwOf19WVPalxUSwToTvvSoi4DtHryJMQ5S3Q8diHkDg2UVjcp30VaF0IEQKJzvGQhzFBvgn3j19BNkl2PRt7Bkz3ls+Xr5eiu+++29hcPxMi3LRuvIt8DREvqCZflRh1lMdBkZQJEyZY15GvGuJfkCbw5MrQ2mthUUv02qD3J38fRcdnn322tincu64eek/kaw9tHZtM/Dp++eWXbYpGvbBF9Obp5EQP35e+9CXtOV155KEnZMmSJRnZqiJEcjV6q14h073J11iFPUU+hOjEE0/U4oOeZcQr073o8vFj4I9//GMGu/zBueeea+xh1V0znQfCWhSTdIuMyteWkXwlGGGsXPpaap+EKK8hu2MSIjucjKV8CInxYh4nfNr3IUTomlfOlt7iFz9+xdSd0DWMXqR02+l9dG/L8UsRepw+/elPR3K8grEsArDpnvudEOl6WPD6KP2LGK+NTK+UFGY4j4d6evkE/Fo1BVhVD79ITQkDcFW59Bb6yC/gufrqq2vJXbqeHK+ifV1leuWGB3wvUq9sET1VaTzUvvzeXqanEA9MYKXOm7ZyxlwGHvmNsPi1M149m/Qux+MlZVAOyxzk06c+9Slt27DV4447Ll49/Oqrr44mTZpkXEFcjgnLXzY59iFEp5xyivaeTj755AxW6AGSY24yeOrwk2PMkvvJ7+DVv6lnFjEJyxnIdZTi3in0YOquj15aU9L5PPQNzHTXQh4JkQnN4nwSomJ8up71ISRdL+pQwKd9H0Jk+rWKINmLdOGFFxqdHyRIt7pwmiTkA8d5552nve1+J0S6z6PggaiCJh4EqscNhKfoNQYeBMAFZBLd9iCJ6CHB2ArTeKK3ve1tWtyQKb9jp9VRejYYxjvIQeTxNdCWXIwzQq9dXj/q+Pzzz4/Lpv/peslQHjMce5F6ZYt4mCoc0luFJ3p9br755mRWJ3oMvvjFL2rroD70bEp4XZhuQ+13m2Umvw9nJDlyYH9Hc6aeZhAy048UH0J02mmnaeVR2MGGYFvo3ULC+Dy8EjbZPfAwrdqNHlCFV3qrI49o69JLL9WWN706w5jK9HWxDwKmxj9hHCZ+dIDwIn6hB/Xaa69FU12TipF8ZfY6VCREXU2muIAPISm+ottZn/Z9CBHeWeedEse77LKL2w17lEbQwiBMXfvpAbu6S3/zm9/U1sP1EMzzqd8JEQiJDgfknXDCCXlx4gG1RUEewVQX6E2vHNCOaRwWfgWb7g35+HWuSxirY7pHDFBNJ7lukLEN21/F6eu57vfSFk1EAFhisLecqam9/f3228+IEb5XpUu+hAhLG+h0jp4lU8IkB10dnR3iGiYcir5lZvJjtItXt3Jmofb28ENJd2/I0xE8fMcRr9TydaCforGQGCOXr2OKpUU+j55euW6bVhabTBKiLEokRFk8nI98CIlzIwUVfNr3IUQYp5J3YBwfdthhBXdXzSnTasRyOn08dqaoFaw1g7Evuns/9dRTO6qaAmnRx117NcsMN2sKjuhlMY1/wYwUnfzI+6//+q8ODJCBQbK6QI86v/vdiGNKKwAAQABJREFU77R1iggRZr7pevHUhfBKQnePeBimE8bP6MohT061TxetZb+XtmgiApD1pz/9qVE+PKRNGEFHuuRLiORU/7iXD2uHoWcRH8kF8S0aV4gPQevuTy75oLu1yglRUU8ifMjUY4nYkE+HHHKIVpbvfe97+aKZY6z2r8MAvaz5ZPJ51J87d26+uNMxCVEWLhKiLB7ORz6ExLmRggo+7fsQItXVnHdiXa9Ewe16nTK9OvjKV75idb0DDzxQG3wwMDWfmkqIjj766LwoyfF3v/tdrfzQpVy3JCmX35HrpWjrYTyILhURIjwsixKWbcjbFo4xozCdcL+6csjDkgN1p17aookQoffB9HpJyb/OOutoccLSCLrkS4h01+qWp5smDv2hV1KXTDj49BChJ7Lb54FMrx1x3/mkYmneJkF4ihLGHeXr4Fj3Kt9EiOT3H4uasDpHQpSFiYQoi4fzkQ8hcW6koIJP+8qJ4Qy2SY03yTvxsccea3sJ73KmqawYrGiTTCRHLlTYUd1Utt97iH72s591yKIy8ODI6w3HGFDt2q2PerpxPWiriBDJBSjV7Wi3cnFN7T3KRRoz5eUCnNpyuC+btZIyF/M46KUtmogAHtjd0oc+9CEtTroHLq5VFyFCryB6XfCqE2Pb8LoVP2R09mgac2PCwYcQgSh2S6ZeQLnYYUdVjMvSyYJ7Q+9N0Z8a95eur5u0YCJE3XqhOm5Wk0FClAWFhCiLh/ORDyFxbqSggk/7PoQIa9ekHVftf+Yznym4u/KnsHBbeiaUahdbuXK2VQN4vZCup/ZB8vKpqYQIU95NydQ9j56GooTFGhVW6a3poWoiRNBftx4NjCNKt6H2MZsmnTDuS53Lb88555x00cr3e22LJiJQNCNLCQ2/zOODY9PnTKogRCA86I38whe+EIGQ4fM8pteuuns7/vjj1e1ntiYcfAhR0Wwu1SjsSHd/n/3sZ1WReIs1vExrs+nq2+QBu3wyESKsx1U2kRBlESQhyuLhfORDSJwbKajg074PIZKf+9AGCfkpiIK7K39KLnmvbRfBxTQIM9/qvHnztNdAMMvj11RCpGZu5WXHMYijLhhjxfKihGnZunquhEh+wqSomfgcepB0beUJEYiV6SGLad11pl7bookIXHzxxV3FNL32qYMQgQjhwaqbAanTqSmvF4QIi7N2S6bXt3lCVPT61iRjt3zE2XwyEaKiH0H5a5iOSYiyyJAQZfFwPso/UJ0vULKCT/s+hAiBROfMWE+mzmR6mONeui17r+5LfhdNe++4BlYbTqemEqL85zjSMpkwhB0UpaoIEQbkd0u2hAjXAcHS2SIG69aZTDjWZYsmQlTUM6Lk7xUhwmri8lt3Wn3odFSU1wtCVPTqW2FnS4iK7KFIzqJzuld6JkJU9CNIydJtS0KURYiEKIuH85EPIXFupKCCT/s+hAjjRnSOjF6WMqsDQ7SipfvxtXFdu8jrtnqsgg2fjNBdA2uR5MfQ9JoQ4XtnunvTDeCEPKbg2CZCZJpWbjPYWNmEbgtbKOp17LUtNoEQmQZIw6bx2gwDpbHuDsZ34XuCmO5u0l/TCJGJxEN2jJPCYraufzoMfHxeZ9+6PBKiLCokRFk8nI98CIlzIwUVfNr3IURFrwvKfD8K03axsjIeZvjQqW7wrWkVWCxKZ5Owsq+OdOAjlPlUJSEqmt6r2jU9HEiIXv9Ib/6VGXAzrX0DHePh65vwKgrXwHgafKRUfe8tfb1e2mK/EyL8kNH5FfJMA6SB5ZFHHqmtZ6rjg4OPHys92/YQ4fWt7rMakL/bd/BUWzZbEiIzSj7PP/PVooiEqAgdi3NVK8SiyUwRn/Z9CBEaBWnRBUDfL4zjmvnBnxgfgnVz1EcYUWaLLbbQtguiY5OwNIDuvvHJgXzyCaSmWSl77bVX/vIdx6bBrCREZkKEHknTQo74xlO+168DdE0GvvOlVv5VtoL1qzCwPL12Ty9t0YcIKNF68crssssu0/oVvqlXlDDuUGGc3up6R3AdHxx8/Fjdsy0hQnl82Dotg9pHb1hViYTIjKTP8898NRKiImyszlWtEKtGU4V82vclRKbZFwgCIDZFC++lbjnZxUJ6plka+FiiSqZeFKwJY5Pe//73a4OWboqrTyDFIGMVCNNbzMwrShi/BDKZrqP2SYjMhAiY5om0wg1bLA7omo444gitHkC80q9me2mLPkRAyd0LQoS1r9K4q/0iv3zppZeMvSpNJESmD+RWOeORhEhZdefW5/nXeZU3c9hD9CYWXntVK8T1Jnza9yVECGZFHw392Mc+FmHBMZuEdXNMZABEIv0rH+RIBdv0FvUxrqMomT44iuvgO1r55EOI8OoufV/pfawabEqm9VhQn4SomBDhcwVpnNP7INn45AcG/NokYJ2un94HUUqnXtpiPxCiotfS++yzjxY3kFVTMo1FBOamNc18cPDxY3XPLj1EmNmYthe1/773vU9dTrvFekxXXnllvE4RXq/hkzCmH5QkRFoI40yf55/5auwhKsLG6lzVCrFqNFXIp31fQoRm0aujnF63xawzLOOv+04Y6mOqKgKmaeo0rolF+tIJ5Airsuraw8wirA+jSxgDYlouYLfddtNViT+OqGunaHZK0WKB+GK57pMaeN1gWl8J7ZMQFRMiKA9jtHS6Unlbb711hKnJIPK6dN1110Wm1ze4xogRI5KPf6r6vbRFHyKg7tO1h8i0kGPR4n+mHiK8Wk//oFH3hAHVpjE3wNs0FtEHh14RIsx0xSeElM2lt9dff70SvWO79957d9RBPNB98oSEqAO+JMPn+ZdU1uywh0gDiktW1QpxaRtlfdovQ4jQpmlQZDoYYB8Ls4EQYPo2upYxvsP0ikzVxZgNXcKXoE118R0sfOlbJfzSwrgPE4nC2BDTzDifQApCVtRzBlKGHjHMYEKQRM+QksX0eYx8z4SSzSc4mqYHww6KUr9Ou1f3DKK51VZbdTxYlC2pLV57YYVpfBEcRAH6MK0wrOpgi6/a61KvbNGHCKj7dSVEpkU4sXhpehZoutftoosuMmKP2VWKFOHVMF5jpm0XMzzTWGMf8UH348EHBx8/Vti59BChjmmM4gorrNDxfT38SAPJzMuOY3zvT2Gm7gXbNG7pekUzS9P1i/Y5yyyLDglRFg/nIx9C4txIQQWf9ssSIgRFU3d52mFd9w899FBtQFDim4K8amf06NHxVN+VV15ZG3BUuZNOOkldsmPrG0hN9VSbui0eNtdee632Xk09Uj7BMVRCBOXhoYDZgjp8ffPwKrbbgP1e2KIPEVAGbbo/08KM06dPN2IIQonBw1j/Cb0/KqkZoiacsVDj+uuv33FdrMaMP109tDFt2rTMito+OJj80eRXSiZsXQkRVqw2fdoIMqLXfPfdd4+23XZb4zABlDN9/8zH59PyFO2TEGXRISHK4uF85ENInBspqODTfllChNtBLwyCqOrp0AU3lzxMue+W8OV6U9e+bVsYFJv+lZtv0zeQ4pctCJntfQA3fN3bNMZJ990k3KtPcAyZEAGTF154IX7g2GJfVG7FFVc0PpjQlkq9sEUfIqDuz5UQYaxb0WtshVl+4cDJkydb2zyugUU60UtSNJYI5RCjVPLBwdeP0aYrIUIdvOYH8VE4uWxBOE3fB8S1fXwe9WwSCVEWJRKiLB7ORz6ExLmRggo+7VdBiNQt4fUBBlO7BIB0WRAc9JLYJpAZvHIyDchOXzu9j/VjisZDqPbLBNK7775b+4s4fR/Yx1gBjCFCMo0/wkNAl3yCY+iECDiBoAPT97znPV62CJ2AhGKMm22q2xZ9iIC6d1dChHqHHXZYV+zyhAjjs7bffvuu9WD3GK/1l7/8Jb5FLHOAV2R531DHTSNEEAoDpfFaVslgs0VcmjVrVoyJ6Z+Pz5uulc8nIcoiQkKUxcP5yIeQODdSUMGn/SoJkbq1O+64I5o4cWI8bqdbr9Eqq6wSfelLX8qs76KuY7sFkcAYl6KuagQkvJfHdF4EK5tUhhDh+viq9yGHHBJh/EA+IOIXOMY7ASuV0NOQL4djjLnSJZ/g2AZCpLDCYnkYrzV+/PiOdYXyOMNO0auHnk71oFbXcdnWZYu9JkQYC3fKKadEuq+wgzDi9RdwzSeQUSw9Ab/OY4xj9ArhuiBB6YQxdTvuuGNHHYwvgm+r5INDGT/26SFS94rtFVdcEY0bN65wXCFeQeIeFy1alK6q3ffxee2FNJkkRFlQBuFQGq13ku9PhRyk6l2/bEW2746/HFQq5s6dK6QzCPm+vqwKOurLKaRCPiQEtviTgVDIQaxCjg8QcvE7IX8VddQpkyHHMohHH31USNIjJCERcnaQGDlypJBjS4RcJK7Mpb3ryoeEeOSRR4TscRAy6An54BVyYK+QKy97X5MV3RGQA3qFHGeU2KIkpbENwhYlmRby4et+0YIa/WiLBberPYWYCjnwJ2dQCUmEYt+VvbLa8ioTNg+85ar2MebyFVJcb5NNNhGSfKpiHVv4B+IF4oQkVUISKCEJWEe5JmYgJt13332xfHJMlZATTeI/YFOESa9kRfyXPwiE7OUT8vMqzs1CZ4i1A5Wqfv6TEJXUZNUKcb0dn/brJkSuMrA8ESACRIAI9B4BEqIs5iREWTycj3wIiXMjBRV82ichKgCUp4gAESACLUGAhCiraBKiLB7ORz6ExLmRggo+7ZMQFQDKU0SACBCBliBAQpRVNAlRFg/nIx9C4txIQQWf9kmICgDlKSJABIhASxAgIcoqmoQoi4fzkQ8hcW6koIJP+yREBYDyFBEgAkSgJQiQEGUVTUKUxcP5yIeQODdSUMGnfRKiAkB5iggQASLQEgRIiLKKJiHK4uF85ENInBspqODTPglRAaA8RQSIABFoCQIkRFlFkxBl8XA+8iEkzo0UVPBpn4SoAFCeIgJEgAi0BAESoqyiB2Gl42wWj0JHYKeddhLz5s2rbWHG0PGjfESACBCBEBBQhEh+eFbIT4h4iTSQCzN73XBBJfYQFYBjc8qnh8bmurZlfNpnD5EtuixHBIgAEQgXAUWIuFL16zomISpp6z6EpGSTmeo+7ZMQZSDkAREgAkSglQiQEGXVTkKUxcP5yIeQODdSUMGnfRKiAkB5iggQASLQEgRIiLKKJiHK4uF85ENInBspqODTPglRAaA8RQSIABFoCQIkRFlFkxBl8XA+8iEkzo0UVPBpn4SoAFCeIgJEgAi0BAESoqyiSYiyeDgf+RAS50YKKvi0T0JUAChPEQEiQARaggAJUVbRJERZPJyPfAiJcyMFFXzaJyEqAJSniAARIAItQYCEKKtoEqIsHs5HPoTEuZGCCj7tK0I0duxYMW7cuIKr8xQRIAJEgAiEisDs2bPF3LlzBafdv65hEqKSlu5DSEo2manu0z4I0S233CKiiGtyZsDkAREgAkSgZQgMGjRIbLfdduKGG25wlnzJkiVi5MiRzvWqquDz/Ctqm4SoCB2Lc1UrxKLJTBGf9lUP0ahRo8To0aMz1+MBESACRIAItAOBBQsWiIULF7KH6A11kxCVtHsfQlKyyUx1n/YVIZo6darAO2QmIkAEiAARaB8CHEOU1TkJURYP5yMfQuLcSEEFn/ZJiAoA5SkiQASIQEsQICHKKpqEKIuH85EPIXFupKCCT/skRAWA8hQRIAJEoCUIkBBlFU1ClMXD+ciHkDg3UlDBp30SogJAeYoIEAEi0BIESIiyiiYhyuLhfORDSJwbKajg0z4JUQGgPEUEiAARaAkCJERZRZMQZfFwPvIhJM6NFFTwaZ+EqABQniICRIAItAQBEqKsokmIsng4H/kQEudGCir4tE9CVAAoTxEBIkAEWoIACVFW0SREWTycj3wIiXMjBRV82ichKgCUp4gAESACLUGAhCiraBKiLB7ORz6ExLmRggo+7ZMQFQDKU0SACBCBliBAQpRVNAlRFg/nIx9C4txIQQWf9kmICgDlKSJABIhASxAgIcoqmoQoi4fzkQ8hcW6koIJP+yREBYDyFBEgAkSgJQiQEGUVTUKUxcP5yIeQODdSUMGnfRKiAkB5iggQASLQEgRIiLKKJiHK4uF85ENInBspqODTPglRAaA8RQSIABFoCQIkRFlFkxBl8XA+8iEkzo0UVPBpn4SoAFCeIgJEgAi0BAESoqyiSYiyeDgf+RAS50YKKvi0T0JUAChPEQEiQARaggAJUVbRJERZPJyPfAiJcyMFFXzaJyEqAJSniAARIAItQYCEKKtoEqIsHs5HPoTEuZGCCj7tkxAVAMpTRIAIEIGWIEBClFU0CVEWD+cjH0Li3EhBBZ/2SYgKAOUpIkAEiEBLECAhyiqahCiLh/ORDyFxbqSggk/7JEQFgPIUESACRKAlCJAQZRVNQpTFw/nIh5A4N1JQwad9RYjGjh0rxo0bV3B1niICRIAIEIFQEZg9e7aYO3eu2H777cUNN9zgLOaSJUvEyJEjnetVVcHn+VfUNglREToW56pWiEWTmSI+7YMQ3XLLLSKKosy1eEAEiAARIALtQmDQoEFiu+22IyGSah+0ePFiPhXbZf9ip512EvPmzROjRo0So0ePbpn0FJcIEAEiQASAwIIFC8TChQvFtttuK2bNmuUFytChQ73q9WMl9hCV1IpPD03JJjPVfdpXr8ymTp0q8A6ZiQgQASJABNqHAMcQZXVOQpTFw/nIh5A4N1JQwad9EqICQHmKCBABItASBEiIsoomIcri4XzkQ0icGymo4NM+CVEBoDxFBIgAEWgJAiREWUWTEGXxcD7yISTOjRRU8GmfhKgAUJ4iAkSACLQEARKirKJJiLJ4OB/5EBLnRgoq+LRPQlQAKE8RASJABFqCAAlRVtEkRFk8nI98CIlzIwUVfNonISoAlKeIABEgAi1BgIQoq2gSoiwezkc+hMS5kYIKPu2TEBUAylNEgAgQgZYgQEKUVTQJURYP5yMfQuLcSEEFn/ZJiAoA5SkiQASIQEsQICHKKpqEKIuH85EPIXFupKCCT/skRAWA8hQRIAJEoCUIkBBlFU1ClMXD+ciHkDg3UlDBp30SogJAeYoIEAEi0BIESIiyiiYhyuLhfORDSJwbKajg0z4JUQGgPEUEiAARaAkCJERZRZMQZfFwPvIhJM6NFFTwaZ+EqABQniICRIAItAQBEqKsokmIsng4H/kQEudGCir4tE9CVAAoTxEBIkAEWoIACVFW0SREWTycj3wIiXMjBRV82ichKgCUp4gAESACLUGAhCiraBKiLB7ORz6ExLmRggo+7ZMQFQDKU0SACBCBliBAQpRVNAlRFg/nIx9C4txIQQWf9kmICgDlKSJABIhASxAgIcoqmoQoi4fzkQ8hcW6koIJP+yREBYDyFBEgAkSgJQiQEGUVTUKUxcP5yIeQODdSUMGnfUWIRo8eLfDHRASIABEgAu1DYMGCBQJ/22+/vbjhhhucAViyZIkYOXKkc72qKvg8/4raJiEqQsfiXNUKsWgyU8SnfUWIMhfiAREgAkSACLQSARKi19VOQlTS/H0ISckmM9V92r/kkkviXwWZCzkcvPbaa+LVV1+Na2C7zDLLONSutuiLL74o/vnPfxov+te//lXgVwzS4sWLxbBhw+L9d7/73eLtb397vF/m30DL3/T277rrLvGrX/1KrL/++uJTn/qUsyqaLr8S+MQTTxRbbbWV2HHHHVWW1TYU+a2E1RSi/NXE37XWWkvsv//+GoSLs9hDlMPH54Gcu0SpQ7b/bzF06NBSGLpWXrp0qXjppZfianCI5Zdf3vUSHeUXLVokDjvsMPH88893nFu4cKF4/PHHO/J9M/bbbz9x7rnn+lbP1KtK/sxFHQ6a3P4BBxwgfvGLX8TSnnzyyeLwww93kPz1ok2WPy3sSiutFB+uueaa4o477hArr7xy+rRxPxT5jQJ2OUH5q4m/XWA2ngb+fGWWgoeEpPeEJAW/GAj8qyZEIEO77LKLuPfee9OildrHA2XzzTePr3HPPfcItIGEX+BXXXVVvF/FPwZkv4C82WabiUcffTRRwaRJk8SUKVOSY9udUPDfaKONxBNPPBGL/da3vlVcccUV4oMf/GBXGEKRv6ughgKU38//DHA6ZwN/EqIUbAPxQE41PyCEoO3tV0mI8mRowoQJYvjw4QnEGO9kSjaDwvF68MADD4wvsc8++4iLLrrIdDmvfAZkt4CMnr5tt902IagK9Jtuuklss8026tB6Gwr+e++9twAG6TR58mRx3HHHpbM69kORv0MwywzK7+Z/lrBaFwP+JEQpuEiI2EPk+8osTYbQo3P11VeLIgKUMjurXfQMjRs3Ln4Nt8kmm8SzKGxfRVg1IAsxINsH5J///Ofi0EMPTcZ04ZXZzJkzY6hfeOEFW8gz5ULB/4QTThAYR4SeM/wgmDt3biznbrvtJs455xzjK7RQ5M8o1eGA8tv7nwOs1kWBPwlRCi4SIhIiH0KUJ0Nz5sxJXnGlzMt7txdkCDfHgGwXkM8++2xx7LHHxvoEKUXPHR78IKxIbSdEZ511lsBrw7Fjxwr4glofBthgwOuPf/xjsemmm+Iwk2h/dvaXAa3CA+JPQpQxJxIiEiJXQoSxQhhAjS0ejk0lQ3AEBsTuD6QjjjhC/PCHP4zjxqhRo+KeQIzvQo/gXnvtFQ/K/9vf/paJK7YHoeA/b968eBwd5I6iKBYf+IwfPz55vYieovxMoFDkt9V3vhzl7+5/ecyqPAb+7CFKIUpCRELkQohAgjCAGj1EdZAhLDI2ZsyY+DXZu971LnH77bcbXzekzNh7lwG5OCCnB09jH+RXjRFTvSAYRPzUU0956SAU/OEX2223XYzBc889l2AEe95zzz3F/Pnz43MgRCeddFJi06HI76V8WYnyF/ufL6629YA/CVEKLRIiEiJbQlQ3GcKUfbyCwesyPGSx8qruNUPKfEvvMiDrA3J+8DTGC+E1WTqREKXREEJNvZ89e3bHWDr0FKnxVrBp9BZhS/vT218W2fqOiD8JUca6SIhIiGwIUYhkCI7AgNj5QMoPnp4xY4aYOHFiJm7gQD3kfVfJxTVCwl9NvceyEOgVyicQSuCoelexlhaWkbDxv/y1qjoOCX8fTCg/CVHGbkiISIi6BeRQyRAcgQExS4h0g6d1D3dghxmFmE1FQgQ0hNh5553FrbfeKqZOnRoPqn49N/sfvZ8gkuoV2pe//GXx3e9+N1uoh0e0/6z99xD6uKl+wJ+vzFJaJyEiISoiRGkyhDEk+JWrFkxMmVGpXYwZwoMC6frrr7da0K5Ug6nK/RCQivBP3Wotu2n504OnbXStCNEnPvGJeBaVzw2m2/epX7ZOle1jSYLLLrtMYC2u0047zXhreDUMUjRr1qy4DF6dwe6rXlLCeAOpE1XKn7qs9S7bH3hCFhQhkt93en1Kg7UJsmBoCAwZMkRgsUXbhLIvv/xy1+J//OMf465/dPHnB9R2rWxZAIsugmQhnXnmmWLfffeN9/mvtwhsvfXW4rHHHosbxdRxzJBSg6dNdzJixIh48Pu3vvUtgZ6OtqfvfOc74pRTTkmm3nfDA6TpqKOOiouBDGGMkRqY3a0uzxOBqhDo9aejqrpv3XX4cVcdKg55bewhs1mpGtOIP/vZz8bjHXpBhnRTkh3U6F207b9QH3rooXggO0gvkm7wtAncQYMGxad8v2OGyiHhf+2118Y+gxXYFbk0Yafy0TOKnjaFv83q1qpuFduQ8PfBg/JzDFHGbtpICNIAtFF+fO0egQAJH3ldYYUV0pCIH/3oR/GKxMjsBRnC4NLPf/7zmXvo1YFO/l61jXYGsv2f/exncc+OsoWLL744fpVjK78iRDfffHP8OQ/beulyAyk/7qPK9m+55ZZ4HBGuq9Yiwn63hFdoGKelVrfGN9B+8pOf9OQVWpXyd5NTd57td8ZfHU515QH/VVZZpa7Ld71u5c9f6XilEl65DWRi+/2Fv3wo4hVs/CfJUCTXVKncPOSg06QNOW6l8uu7XLCt9idnjkWS0MR6kK9rIjlV3AW2uLyyE6eKucIh4Q9fUZjIHqKcpN0P034B3+tFCgl/H7wof389f3x0mK6DXyKlEg0iLINwNYa0/ntBhtJtyNczUbp913uvonwb2z/ooIOSBzcevL///e+doQSBUg9/58qpCqHhrzBxJZgKEjllPwJBla/dIvhK3Sk0/F3xovxhPf9IiFw9IFeeDvG6Q6SJSl09Q+k2QIaQiH9vA9J6662XEBk5eNq7B1DpUs6Qi/Xo+y80/cN3QIqAj29SPUXQT90pNPxd8aL8vY0/ef1UjT8HVcvoUyZV/g7T8Wb6of2f/vSnArO9kPbYY4941le3GUY6MTFAVA0OxT7GRiCpfXz2ASk9cLcf5B/IWRa9kn/hwoXxcglKJ2kdxEpx/KdWqcbsKHVNx0vExXslv+neqm5fLUVQtBaR6V5UvvpGnMvgbFXXdVu1/GzfDQHiX+2yNyREbvbXUbrtBnneeeclU6bzD0l8hwkPUiTs4y+/r8hOfKLLP/nrOS6R/h5W2/HvhfwYoAvCiwGUSLL3wmnwdFwp94+EKAfIG4cKF/ywALHxSfAprM2FlP4ums+1utXphf0V3QPbr5YQFGGtOxca/iREOi075IVmEA6ii0MOOURccMEFSRX8uk0Tn+SE4w56DdTijehpUvu4Pv7Sqc34A4e65cdaN1/96lfjWU/QCx7SeR2k9WG7j1lRWFgQaxapnj/buulydcufbku3X3X7ihCVxUXN4JNjkSrRl0525FUtv6kdUz7bJyGqsoeehMjkaZb5bXNIvN44/fTT488FvPjii5YoifjBpwqrB2qa7KT3VTmbbdvwz2NSp/wHH3ywuPDCC+Mm0TuHBTAVOc3fh+sxbADTxMs++OuU30amqtsHOcQHiuEP6N3xTQrfMq/ebNquWn6bNtNl2D4JEQlRyiPoEL1xCPT8gAjhoajGfGCFa6xBseuuu4q11lor1ooiOzhI76dUVuku9V+P/tdff33x8MMPx7oCabFZedpFseqBjZ4ifMzUN4Wmf0WIgIccQOoLS/xKEytX519je1/QUDE0/A1iGrMpfz3xxwh47kTl+OdHbbseVz3Km+27IVA3/phSPX78+GRmkbTHeFovZrJg3ZS62++GBtuvdpaHJL6R7J1I9C0fqN1U4HUedoQ/rGdUJoWof4WNz3IGCkvgiuvIHj2VVcs2RPxdgKL81cYfF+xRtmr8Oe3eVQO58lUrJHf5rod1tY91UOSv+OTBiOA6atSojunAdbXfVfA3CrD96gLSFVdcEclVxxOdl5n63U1/6qFPQtSJFNYRAj6+axHhiqirMO5soboc+l91/uejFeJfLf4kRD5WmKoTmkHKV2Lxom4qmGIrX5lEWPBNl0KTXydjUV4o8k+aNKnUytNFGOXPpVdklt+8y592Og4F/7TQ8Df4HXp3gJVPSmNcpqepW9sh4t9N5vR5yl8tIUlja7NfNf4kRDaoF5SpWiEFTWlPVdE+gqec3dJBhPC6pNuv1Cra1wpmmcn2ywekT37yk0lvAhYGrPMBCrVW2XsRov7RM6d6ifD60lcf6NEFsaqzpy9E/C1DT1yM8pePPy5458tWjT8JUR5hx+OqFeLYfKl3qPhe0sSJEzNjRhCIQYRsv6XUZPldsdaVb7r8Va08rcPGlEdCZELmzXyQoDQpMvXQvlmjc0+uZRQTIoz3qys13f7L4kL5SYgyNkSDaJ5BINgWDZTOKLjLAfXfPP1DpRg8nR4vVNfgaZ35oMcCPRdlP9uBa4dsf/hRoj7lAbzkmlA6OI15IEKoh1dwdaWQ8bfBjPI3M/6ZdMseIhMylvlNcgj8MrcZKG0pelysSfK7yGVbtonyY/D0MsssEz8s636losNRPajRA1I2NRF/F5nxOluNKYKu8EPGNqFXCXXw2q2uFDr+3XCj/CREGRuhQfS/QbgOlM4ouMsB9d//+k+rsJeDp9PtpvdJiNJo2O2jBw/kBn/4UWMz2Bo9TKqOTXm7O8mWov83y/+z2it/FJr+2UNU0ib61SDKDJR2gaRf5XeRoUzZJsnf68HTJlzV2JYqXuU0CX8THrb5am0hkBzMQLMZ56cIEXqH60htwl+HH+UPixCSEOms3CGv3xwCQbLsQGkH8YMew2GDQ7/p33TPeICqhyO2ruNRTNf1yVevgEiI3NHDa7D0YOtuM9AU1nUNrG6K/bsjbVeD8pMQZSyFBtEfBlHlQOmMgrscUP/9of8uaooHUauHoyJGo0ePNq4v1e16Zc6r+5Cf7ShzmbhuG+0vPwOtaFr9hAkTYiJc16D5NuKfNlrK34z4l9ZZ0T57iIrQsTg30A5xww03VD5Q2kLspMhAy8/23QISFkJcd911M71FGJNS1yuVxFBSO4qQlV2lGpdsq/7xStxmBpp6zVbXJzzair8yZ8rvFn8UblVtq8afhKikZqpWiO3t1DlQ2vYeUG6g5Ff3yPb9AtJAEiMSImW95bYgRZ/4xCcScqubgQaiq/Au15q+Nv3Pz//0aLrnEv9q8SchcrfBTI1eGmSvBkpnBOxy0Ev5dbfC9ssFBBAjNSZFPTjxKstmwK5OH93yYMOqHayFVDZR/4uj9Aw03ec+FN7dxhv56IL4l/M/H8zTdYh/tfiTEKWty2O/FwZZNFD6/vvv97jr6qr0Qv6iu2X71QQEvFrJEyP0OFRNjKrusaD+X9e/WuwS5AekKE1+6vyEB/Gvxv+KYlzROeJfLf4kREXWZnGuToO0GShdZ/sW4vOV2eJqHdIG83SZqvVvIkbo2akikRBVgeKb10jr3zQDTS1zgAHWVad0+1Vf2+Z6bD+s+GOj83SZqvVPQpRG12O/aoXgFvDQsF1Ruo72XWBg+2EGpIMOOigaMmRI8noLqx3jA8BliZHqyahilWrYKe0va3/4EaV6hNBbBLzVQphVLHOQjw3EP4t/Hp+6j4l/tfiTEJW02CoN0megdJXt+0DB9qt1SFcd1I1/1cRIPZxJiFw1rS+v0z9Ia3oGmvpxVccnPHTt6++0nly2H3b86WY1VeufhKgb4l3Ol1UIghd+eWNNGDX4EVsMlERPUbdUtv1u1+92nu23IyDtu+++GfvEw9VncUdFiFZfffVupmV1nvantz/ElfRgaxVbqh4TRvz1+FsZbwWFiH+1+JMQlTRKX4MsGijtErR82y8pdlKd7VfrkAmwlju9wl8tpqgerGoLIo+eTdukxrNU9fqmV/Kb5Ov39tXCjEpfv/zlL02ieOX3u/xeQjlUovxhxT8SIgfj1xV1dQibgdK6dkx5ru2bruObz/bDCgg6O8DU/EGDBsU9RHiFhunyeYJkS4xUPRIiHdLueTb+d9ZZZyW9e3iVVmWyab/K9vLXYvvhx5+8ztPHVet/EC4ofz0w1YzALbfcIk488USBrUprrbWWmDJlith///1V1oBs5eBZsXTp0gFpm432PwKbbLKJePTRRwXs5F//+ldywwsXLhRyYcD4nMqU41WEfC0msNUl5M+dO1fI1zni7LPP1hVhXg0IHH/88eLUU0+Nr3z77beLTTfdtIZWeEki0HAE0mzLZ79qhuZ6D01oH2OBpJkkf/h1jCmyVaQmyF+FnKZrUP56fyGid0jZLnqH8gn4u6x6ra5VxWc7cC/Uv73+t9hii1iXkpTm1eh9TPzt8fcGuaAi8a8Wf74yKzA2m1O2BqkGk+KBkF40zaaNojK27Rddo8w5tl+tQ7rqom781XfPMAVfl9LtgxhhsLQiPdji4ZseE6fOkRDp0HTPS+PfrXb6hxl/kHVDy+68C/52V3Qrxfarjb8kRG7211HaxSDVVFiMtyi7nou6EZf2VZ0qt2y/Wod01U2d+Kd7hyZNmqS9NV37psUd8UNAEaIqPtuBG9K1r73RmjKb1r6aeVZVDGqa/FWbAeUPK/4NgoHIIOWd/v3vf4uhQ4d61y9bsUnty4eAkMvqi0WLFgn5WQQhF00rK75okvylhdVcgPLX538jRowQzz//vJBrBsVbDfyF9ien5Qu5pERs7/m6JcNOcjnq303/0KckQ7FOMNYL+imTiL8b/mWw1tUl/hXjX5YxkyG7MWS1Uq807krGERF/N/zL2nu+fqj4o5cHNoq/otdbNvKjvlr1ernllouWX375PIzexzbte1/comIT21ev77GWVPp1poW4HUWaKH+HECUyKH9Y8Zc9RDra7ZDnw9DROzRz5kwhA5KQrxHiX2wOTWaK+rSfuUDJA7Zf8S8UR33Uhb9N7xBu1aX9gw8+WKy66qrxbEtHMY3FXdo3XqTEiaa2j14izBLEbD+5jpQ3Ak2V31vgXEXKH1b8IyHKGbjroY9DoNsar84QkDANWQ52dG02Ke/TflK5gh22H1ZAgEngVddRRx0VW4fs3RETJ040Wgr130z9X3311WKvvfaK9Yr4gzjkk6j/ZurfR9e6OqHpn4RIp2WHPF+DuOeee8SYMWPilsq8y/dt30HEwqJsP7yAaNs7BMOg/purf5AgrAmFre+PMuq/ufovDOyWJ0PTPwmRpeJNxcoYBAY0Tp8+Pb6076+0Mu2bZHLJZ/thBcTjjjtOnHTSSbEJyFlmYvvtty80B+q/ufpP/yjDBA+8yndN1H9z9e+qa1350PRPQqTTskNeWYNQv9LwTh/jiTCuyCWVbd+lLV1Zth9WQHzLW94iXn31VSHXHxIPP/ywTuWZPOq/2frH69DTTz89jjtygDXjT8a6ux/Q/ptt/3kNkxDlEXE8LusQ6an4e+65p5ALpjndQdn2nRrTFGb74QQEDHq+8MILYy3b9A6hIPXfbP2XnYZP/Tdb/5qQ7pQVmv5JiJzU31m4CoNID3B07bquov1Oqexz2H44AdG1dwhWQv03X//pQfToJUJvtW2i/puvf1td68qFpn8SIp2WHfKqMgjfqfhVte8gcqYo2w8jIPr0DsEQqP8w9K+m4bv2UlP/Yeg/E9QdDkLTPwmRg/J1RasyiPRUfEzJx3gim1RV+zZt6cqw/eYHRCz/sPbaa+MzPkJ+eFjMmTNHp2ptHvXffP1DsdD5uHHjYh27TPCg/sPQv9a5LTJD0z8JkYXSi4pUaRDpWR+2U/GrbL9ITtM5tt/8gKgG9kPHGNM2atQok7o78qn/5utfKVXZAX+QKUS6b2n/4dg/tE1C1N3mC0tU7RDp9/k2v9Sqbr9QWM1Jtt/sgFCmdwjmQP03W/9plwYZRk8hku1YRuo/HP2nbcF2PzT9kxDZat5Qrg6DUL/UbKbi19G+QVRtNttvdkBUtgbluvYOoQ7132z9Q4fp5DoNn/oPS/9pW7DZD03/JEQ2Wi8oU4dBpKfCdhvkWEf7BeJ2nGL7zQ2I6d6hbnbWofg3Mqj/5upfp9N07JkwYUL8GRddOZVH/Yelf6VX221o+ichstW8oVxdBpGeil/0Pam62jeI25HN9psbENdbbz3xyCOPCPkl+ngxxg7lWmRQ/83Vv0m9+NjrgQceGJ/uNg2f+g9P/ya70OWHpn8SIp2WHfLqNIh09zXGE2GwYz7V2X6+Ld0x229mQLz11lvFBz/4wVilBx10kLjgggt06u2aR/03U//dFItYM3/+fIFXqog9pkT9h6l/k77z+aHpn4Qor2HH4zoNAt3XCEgITKaZH3W2bwMF229mQKyidwj2Qf03U//dfNt2Gj71H6b+u9mHOh+a/kmIlGY9t3UbRHoqvu6dft3td4OF7TcvIFbVOwTboP6bp/9uPq3OY1zZrFmz4pWr8epMl/pJ/w8++KC45pprBMbGPfPMM2Lp0qXiHe94R7yMxO677y423HBDnQil8qqW/4EHHhBPPPFEfE/4EbzaaqsV3l/V7Rc2pjkZXPtyMbZSafHixaXql63chvblGKJI2mL8J7uvM5C1Qf6MwLkDyu/uf/LDrbEtLb/88jk03Q+Jvzv+7iiba9SJvyRBSdxBDNKlOtvXtZfPQ/uS4EdjxoxJ7lXFyvx2iy22iO644478JUodVy2//NGbyHHdddd1vbeq2+/aYK5AaO1jddpSKTRAXMHolfxyBeHYUYYPHx4999xzyW32qv2kwdwO22/WAzFNrk0PuZyKCw+p/2bpv1CZmpNygVht3FFFB1r/U6ZMiQYPHpyQiDwJyh/LCQTRySefrG6/9LZq+SdPnpzIIl9bdr2/qtvv2mCuQGjt85WZ9JgyqVddhunpsOkp0r1q34QR22/WK5MRI0YI2NLKK68cb016tc2n/pulf1u9qnKwFby6wWuoAw44QGAGWjoNpP7PPvtsccQRR6RvR+ADxbInSGy//fZi2WWXFbfccou48847xX/+859MuR/+8Ifi85//fCbP56Bq+b/97W+Lr3/96/Gt3HXXXWLLLbcsvK2q2y9sTHMyuPZzhM/5MDSG6ApAL+XH6zJpk/Gf+nXfy/Z12LD95vQQVN07BHug/pujf53/2uTJVauTuCO/sZipMlD6v++++yL09qh4iO1+++2ntUf50I4kmcuUXW655SK8EiybfOV/5ZVXopdeeqmj+VNPPTW5z/vvv7/jfL6Ob/sdF/bMCK19vjLzNARVrdcGod4x49UZglOv21dyqy3bb84DETaDB4fsHVLqK72l/puj/zLKVq/s5azXzGUGSv/77LNPQhxg03vssUcEkmFKOLfrrrtm6sjlJkzFrfN95ZeD1aO3ve1tkVxaJUoTn3PPPTe5x8cffzy+Dzk4PLrhhhuivffeO5KDxDNy+rZvLWCXgqG1T0LUReHdTg+EQWy22Wax08iu7Oipp57qdou1nh8I+dMCsX27B3K6d+iKK65IQ1hqn/jb4V8K5ILKvcI/3Tt91VVXJXfUq/aTBuWOXEw0GjRoUEIc5BIS0ZIlS9JFtPvoKVprrbWSessss0z09NNPa8vaZvrKj96sdO+WXBMsuvTSS6Pzzz8/yf/d734XTZVjuNL3jDogRyr5tq/ql92G1j4JUUmLGAiDQM8QfuXDOeQ79JISlKs+EPKn75jt2z2QEfxhL5hhVmUi/nb4V4l5+lq9xF+9dpLfWExuoZftq0bT5B42fcopp6hTXbfTpk1LCAfqnnfeeV3rFBXwlX+bbbbJ3AfuBX/p14Bp0qfOY2bod7/73eSWfNtPLlByJ7T2SYgaahDpoJD+xVZSHOfqoTmEKwBNkB+vBlRAnTdvnquIheWbIH+hACVPtkl+jLlRP8TQc4E0EPJ/5CMfSewZdv3QQw/F92LzTy5ym6kr1yeyqWYsU0Z+uVZSdPnll0fwz7XXXjtzX8pf8UNm2223jeRA6wi9dPmesDLtG4VyOBFa+5xlJi2vTBrIUfZq4TQ5NkTIYCWw7XUaSPkhK9vvPssJM29effVVIXuHxMMPP1ypiRD/7vhXCnjuYr3GX/awiOnTp8exBjEHM7mGDh2au6v6DuWzWqy44oqx36MVLFz417/+1brB1157LZ5h+eKLL8Z1MOvyn//8p3X9fMEq8ZevzDIz39Zcc834KwVyrFG+2eS4yvaTizrshNb+IDA8B/lZtI8QwJTYjTbaSCxatEh86EMfEvLdstfd4eOeWNWVKTwEDj/8cDFz5sxYsJtvvlnIX5vhCUmJeoYAYo583SPkgF8hx8EI+cqpZ22joSeffFJssMEGSZsf/vCHxS9/+cvk2GYHdX7zm98kRRcsWCBWXXXV5Hggdv72t7/FvinHNImRI0eKv//97/Ft4OsEJ5xwwkDcUjvbdOgd0xYNrctMK2RB5kDLjwF20nLjP7xG63UaaPnZvnkMiwz0kRo7hFlCdSTib8a/Drzz1xwI/PGKXsWc9ADf/L3VcSxJfdI27kGuJeTcTH6GGla69k1V4I9ZZB/72McSua699troU5/6VHyMcUQ4NqUq2jdd2yY/tPY5hshG6wVl+sEg1FR8BIj8OiEFt17JqX6QvxJBPC/Sz/KrqdKwC5CjOlI/y1+HvPlrtlV+ZVuyZzoPSa3HF154YUIcYNeTJk1ybu+oo47KXOOyyy5zvoaqUIX+0wO95TCI+NIYr4UB1JBR9hhFsmdMNZnZVtF+5oKOB6G1T0LkaAD54v1iEOmp+OlPe+Tvt+rjfpG/arlsr9ev8oMAqVkqdfUOAaN+ld9Wf2XLtVV+/PDCwxp/WLixV+mMM85I2kXbcmVn56YxIFzdO7Y/+MEPnK+hKpTVP3q81KdHhg0bFskVwdWlo+OPPz65TxBPOQ4wOad2yravruO7Da19EiJfS3ijXr8YRHoGCHqMepX6Rf5eyZtvp1/lV7/gEfDr6h0CFv0qf15PdR23Wf70NPxe/Qg78cQTE5IA2/7e977nrNr8NbA6tG8qo385wDvzUdqTTjopcxu4thxYncirWz+sTPuZxjwPQmufhMjTEFS1fjKI9BL7vZqK30/yK530ctuP8veqdwg496P8bdd/r+QHCcpPw6+7bUw/T/funHXWWc5NppcswbW++c1vOl9DVShr/y+88EL0//7f/4vQwy+/t6Yum2x//OMfR+uss45xHFHZ9pOGPHdCa5+EyNMQVLV+MwgsYQ8nx2ca0GtUd+o3+euWN3/9fpRf9Q5hkbc6e4eART/Kn9dRncdtl199nb1X8Sb/uuvMM890Vi8WNkyTKjmLy/kaqkJV+i/67Ej++2WqbWyraj99TZf90NonIXLRvqZsvxkEfrWNGjUqdvj8d4c0t186q9/kLy2Q4wX6TX4svKiCfRXfauoGR7/J3+1+qz5P+Rcn8UYNCK4a4/T1sCq1sm9sXVapVtf51re+lbkGxiX5Juo/rFmWJES+nvBGvX50iPR3h9SKsiXFNFbvR/mNN1vDiX6TH5/mwIMCvUO9SP0mfy9kTrdB+RfHKygrkoLYU2c6++yzM2TG53XXlClTMte46KKLvG+Z+ichyhgPDaI/DSLdtVznVHzqv3/03+veIQQC6r9/9J8JzD06UPpXr2nxwek6E8bUKPKF7ZFHHunc3MEHH5y5Rpnxlkp+55uoqALbr9b/+OkO6VVlUj8vXS6DU7z0u/wYo5CkqJZPe/Sz/GX0alu3n+SXX/0W8kvgAiuP41MdvUj9JH8v5M23Qflf/3SJHKsm5Pe4Ynjk5A4xfvz4PFSVHP/2t78VW265ZXKtT37yk+LnP/95cmyz8/GPf1zcdNNNSdH7779fvOc970mOXXao/8A+XVOWqJKhVstQXfVRhH96Kr4MUK6Xtipf1L7VBUoWYvuv2x+m5MpAHv/1csVy4t+//l/Stayqp/WvFojFAOu6puFjVpayc2zHjBljdZ/pQpi1pa6Bldx1s7vS5Yv20/IXlavrHNuv1v/YQyQ9o0zq918Il1xyiTjwwANjEWXXsMAHYatM/S5/lbLqrtUv8uMjlfjOlJwGHW9191pHXr/IX4dsNtek/G/2EMD+0BuNbyvKV/YCH4KtI6EnCj1SSPhwMdq1/cAsPgS7+uqrx3Xx773vfa/4wx/+kBy77lD/b+rfFbsqyleOf1nmSoZaLUN11YcN/moBtTqmxtq07yqTS3m2vzhKr6vSy94h6In497//u/iTa9m8/tO2WNeyH4cddljSwyMfqhFWe7ZN+TFIxx57rG1Vbbm8/NpCNWay/Wr9jz1EJWlq5QzV8X5s2scvKIwnksvCCzkVX8iZII6tmIvbtG+uXf4M2/+3WGONNQakdwjaI/6B/UJ2dEmd/tFLhFiD3mj0SledbrzxRrHzzjsnl91vv/3EpZdemhwX7ciPqApJoJIit99+u/jABz6QHLvu6OR3vUaZ8my/Yv8rS17JUKtlqK76sMU//e2hKqfi27bvKpdt+ba3f/LJJye/lnvdOwQdtR1/yt8Z/9LLftQxDf/ll1/OfNJiueWWi+66666uIeP6669Pvu8nSUi00UYbRfh8RplE/XfqvwyernWrxp89RGXouazbJIaOd/rTp0+PJUYvEXqLyqYmyV9WVl39gZZ/hRVWEEuWLBFy/SHx8MMP626x1ryBlp/tV/wL2dFaTPijd2jWrFnxmCL56szxqt2Lyw+yikMPPTQpuOqqq4pbb71VvPvd707y0juSMIlx48YJ+QBNsjE7DbPUTEmu+i+WLl2anJY/OMT666+fHGMnL79NncwFSh7k2y95OefqwbXvysjy5atmaPnrdztm+24MXa0XIru1K5kJQvzd8O9mzy7nsRK1jGDxH9YgGohE/Q+c/qHvfsUf44eUbdbRc4mZYZtuumnSBtrCCv2XX3559PTTTyeugE/XYOFFSZgyZT/ykY8kZUw7mIGmZMD2zjvv7Ciax9+mTsdFSmTk2y9xKa+qobXPHiJp6WVS0xgyZmdgPBFmglTxjr9p8pfRta7uQMqPGTZYb2igeoeAx0DKz/b7G3/VIy0ncwj0EmFbZXr88cfF1ltvLTBzLJ/QUwTfePTRR/OnxAYbbCAwdggzM4uS8i9VRhIisdVWW6nDeJu3f5s6mQuUPMi3X/JyztWDa9+LFqYqhcYQU6JZ7TZRfqzMKi0//pOLqFnJaSrURPlNsvjkD5T8/dA7BLwGSn6lK7bfvz1UWItILgMRxxmsUVRHuvvuu+Mvxat41m0rhwlETzzxhNWt2PT25O3Ppo5V45aF8u1bVqusWGjt81tmJU2jqQZR1VT8pspfUu1J9YGSXwVeLDI3kGmg5Fcys/3+JUTQEX5wKZKC12hVJ+gfg6wxuQCDpFVb+a3sSYrOO+88p0HUysfUtfjKrFN7ofkfX5lJay+TmtplmJ6Kj1do+LSHT2qq/D6y6uoMhPx77bWXuPrqq+PbKfPZAZ08rnkDIX/6Htl+fw6qTutIfUKo6iU/0EZe/3/+85/j13NyHFH8CZt3vvOd8UBrOb4ofUuV7efbr+zClhdi+9XaPwmRpeGZijXZIO+55x4hl76PRfNdWbbJ8pt06pLfa/mxvgtW6pW/1YQcIC/kVGLrVXpd5LIt22v58/fF9qt9IOTx7XZsg/+cOXPiGV64VtWr5du0302GMufZfv/bn4t+W0mIHnzwQXHNNdfEi4c988wz8dTKd7zjHQK/InbffXex4YYbWmM4UA7xwAMPCPkuXMjuYvH+979frLbaatb3nC542mmniaOOOirO8pmKP1DyKxna1j5+Zc+dOzcWHwPkMd3Y9rMFCrMqt23DP48d5bd7IOJjrzNnzqx8Gj7xt8M/b7dVHQeHf+dbQbecJr1DlOtUxB8DlMZgfNeMc1tssUV0xx13WAExUPKrDynifq+77jqrezUVKjMVf6DkV7K0qX1MIR40aFBsu9AZUpvkjwXO/aP8/T2GSKkL44fUAGsuDKtQKb+l/Vdr/60ZVC2ngEaDBw8uJEJpojRkyJB4oF43kx0og5w8eXIii+yS7nabhefTs0HkVPzCsvmTAyW/uo82ta+IK+wU5AipTfIrnae3lL/aB0IaW5t9F/xBhGC7+Kbi/2fv2kO1KNr4mFQHS0LLkhKzMi0rL2lF4CmyjhQSkRYSBVYEGfSHdCHrFB9djiVdSMuuFt2LokgQThRZWiioWJlGYcckTcjKMouyo2e/+a3NNmd2Z3dndnbPu/M+A++7u3N75rnMzG9n54I2x4Uzoe+CnpoH0a+P/am6S3puCkC0aNGiCDwI0MP3iwj4GTbBLbfcEgBcTJ48OTjooINi8V566aUkuUV+fVUh7rvvvqisebatjwqsuZGX4ptspNZX/As2moU+Nl4Uo0NYci9cs/Av+FWvxH99OiSAIGyeiDYYq1xdONJ/ffTvQt9qHq717z0g2rhxY4DRHgGEcOWHASa+WfPvoWFFlePinJy05aKuFaIqvLu7O/jrr79U7+CRRx6JeOIrjWLhSWlikRQP8RkOb3A4+yyPK5v/rDI0C32++WKob9iy7JqFf5ln+Z74r1eHKC/Dz9vGyIaydjQAABXlSURBVPpW70n/9dK/qr+iz6717z0guvzyyyPgAKDDz5oJADJ0DmHTpk3rlUZ+I1fTuVaImj8/DygYPHhwMGfOnEAGPk899VRURr5ja5iMn7sTdHZ2BjNmzAj4JPFUPlU6eMYb3Lhx48J8+VLZpCgxv7L5jxFUPJqBPkaHBEhXbbEZ+FdU3uuR+K9fhyg+/WKTxKKO9F8//RfVuZzetf69BkRdXV3RZwZ0KCNHjgz4QZiyPBPvMVI0fPjwqBPCBl3y+ThyItcKkfPGPUazRGeIa2tra/DKK68Ezz77bOS/bt264H/8+7xcZsQFODJ1eGsT9PLsLls2/1nlbwb6utEhyKYZ+E+zAeK/fh0iX80atTH4VF/Ekf7rp/8i+lbTuta/14AIc2FE547rgw8+qMpT+4xJ2HJa7HKa5FwrRKVx9tln9yqHKJP8GVDMLRFhuLa0tAQPPfSQml2uZ1luaLzSXNn8p9FGmO/05dGhuXPnxsThO/8xhhUP4r+eHaLYKb/oIdOk/3rqX6nG1o+u9e/1PkQXXHAB+/DDDzk+2O82bdrE+CiReEy9rl+/nvHPR1Ec7E/EP19Fz+Kmin0YcHjhsmXLQl5w5XOaBPnoykexwoMOp0yZwvhJzowDKcbnP0Xhpjdiv5usgxmr4D+t7L7TxwGU2FWcL1kOr6osfOdf5Vd9Jv7ruQ8NbJqDofCQaT66zfgLqKraXM+k/3rqP5dyc0Ryrf9+QFg56NYuCoec4WaFEBgcNi5MAhI6xnp6ehg2a/zjjz/CKOiYtm3bpoteqf/rr7/OrrvuuojmMcccw/i+SYzPNYr8TG74aFO4OaWcBg0WPxsobLAuvvhi9sYbb8jBdF+BBB5//HF22223hZT4WU3sxhtvrIAqkSAJVCOBjo4ONm/ePIaXrpUrV4Yb41ZDmaiQBDQSsB6r+jeh6yEr0/Lo6GOiMWc5+rW1tZlmHaifq3bs2BHLQ0c/FtGRB8rAAVDI1xFHHBHxd/PNNzui8F828rd+3VL8qvn/r3T773ymj9V+sGFsaKdzPvOv41n2J/7r/cmk6DJ80n+99S/XZZt71/r3dg7RBx98EIEFdCrXXHONsbzVFWrY6Vp1rhWi5i8/YxXZ1KlTI76WLl0a8IM+w2fMI8Kza5e1FL9K/pN485W+PI9LB0YhD1/5T9J1kh/xX+8OUd7/LGu+Iuk/LgGyf7f27y0geu655yLgAEB01113xa0pw4ef8dUrj1dffTWWokqDlCd6ix2lsRQfE6jBI0aM+Ge9WBmLeshL8dUdZqvkP4kPX+nnGR2CPHzlP0nXSX7Ev9sOIUnGaX4u5F9kGb4L+mn8ZYUR/frbn6xjbwHRwoULe4EZkxVmQkBYyg6gIX5PP/20CIquVVUIjHiJo0cOOeSQgJ96HpYB9AH2RBnPOeecYO/evVH5XNxgKb44h0hdil8V/zo+fKSP1WRCn1hlluZ85D+NXzWM+K9/hyRv9YGNG00c6b/++jfRtxrXtf69BUT3339/1Kmgc3nsscdUWWY+q3lgd2jVuVaImj+e+QTvXofSPvDAA1E00Mdv2LBhEb98AnQU7upG/oQj7x1SBf9pPPhIH/tewWax/1CW85H/LJ7lcOLfjw5R/jSvjkLL+lbvSf9+6F/Va95n1/r3FhDdeeedEUBA54KNDE2dDAKQx7333hvLwrVCYgT+9di9e3d47ho+X/3zzz9RNEGfrzwLjj/++FLmEQli2OUbcsDnHNFoCfoiTtVX3+hjJ2rIGL+s0SHI2jf+Te2H+PejQ0R7IkahMTKf15H+/dB/Xn2r8Vzr31tAlOdzlypc9RkbG4rOCVe+RFSNUnmHpB47IhuEzfllMYZSPORGS2y7L9NPSVpakG/0TUaHIFTf+Dc1FOLfnw5RfgFNOz9SthHSvz/6l/Wa9961/r0FRJgzJIOZBQsW5JVxFE8+UR55YV6S6lwrRM0/67lq+upS/Krpq/Lwib7p6BBk4RP/qm7zPBP/fnWIYhm+WDSSZQOkf7/0n6VvNdy1/r0FRE888UQvQCTPu1GFqntub2/vlcfzzz8fi+paITECGR59QV987wdIXLVqVUYJyw3uC/5ljlzR37JlS3TuHlbd5HWu6Oelp8Yj+tQhqTZR5Fl+4cqzDJ/sj+yviL2pab0FRJhTI48Q3XTTTSrvmc98N+heeciTiUXiZq2QYin+2LFjo/lEQiZVXn2Rv1h6DJsFOMrrfOE/L79qPOLfvw5R1IXx48er6o49k/79039MySkervXvLSBau3ZtLzCDTRZNnbwJIjoq7PmjOtcKUfPPeu4r+vjGLyZBqkvxs8rsMryv+Bc8uKBvOzqEMrigL3ixuRJ96pBs7CYtDdoW8TKbtQyf7I/sL82WTMO8PdwVZ5ANHDiQ16v9buLEiYyDJPGY68qXPbPNmzeHcXF4Ks5FO/DAA3uldX24XK/Mczz0Jf0XXniB8R3Aw1Ly0TPGv/vnKLHbKH3JPzhxQV8cpIv8ODgyOtPJBX3QtXVEnw7XHDBggK35aNPNmTOH8Xmf4TlnHCCF16TIZH9kfy7tz1tAhMpz3HHHhR0M7gFkcGBpXuHhhPmhQ4ciaehOPfVU9uWXX4rH6NrsFRIHv/IjQ8IGi2+wFp5gHQmngpu6y59vsBnaKX+TCQElgKWJqzv/JrwmxSX+/ewQ0VaPGDEiPFyaj0CzRx99NEn9Tl5IEjPO6Un255n9mQ4pqfEbecjyhhtuiIZeuX0H2O05r1PnIPFTxxOTNjL/iQV27PnDDz8EYmWIWIrvmERqdnWXP+ZJwDb79++fyqcusO786/jK60/8+/vJBJ/LUDfww2e0JEf691f/SfpW/Vzr39s5RBBcZ2dnVKFQqa688kpVntrntra2Xml1q6lcK0RbIE1AI9CXV4aYbKqmYcnIuxH4NyqwFBkbL4oGH0vubVyd+bfhV01D/PvdIYrFG7qXLdK/3/pX67v67Fr/Xn8y4zs6M8wD4gee8n6HsYMPPpjxE+vZpEmTwmfdHwdSbNq0aQCLYZQxY8awDRs2MH6ifCwJDZnuHzLlB8+yu+++O5QPPp3xkY+YrMrwqLP8R44cybq6uhgfHWL8/Dkr8dSZfyuGlUTEv2efLBT9fvzxx+y8884LffmLF8N8O9mR/v3Wv6zrpHvX+vcaEEGA/EBWNnv27EiWQ4YMCUHRqFGjIj/5Zs2aNWEF5Mgz8n777bfZ9OnTo2f5Bgq54oor2L59+yJvvuMqO/HEE6PnpBt+DIZxmqR8XBtEEo00P5k+QNAXX3wRfvsHKOJHfKQldRIm03eSoWEmtvQBzFtbW0NqfHSILV682JDy/ui29K2IJSQi+tQh5Z2XmWA+ubywWGPJkiVhu4IJ1rIj+yP7c2p/6hCU6bPrISvX9HHuF/bK4ZUo+mHOy2uvvRZs3749IsdX9wTYeJEDpige0px//vlRnKQb8C+OWxA0Vq9enRS1l59Nml4Z/PvQSPLHd36xFP/qq69OKq5zv0bi34Q5HNwKe2lpaTFJFotbV/5jjFh6EP/+fzJBuyLaVhzvITvSv//6l/Wt3rvWv9dziITw+EqegK8YiyqVqFy48pGi8FBU2U/cjx49Oti5c6fIJvEKhdiAG5s0SQVwbRBJNNL8VPryRMikjSzT8rIJU+nb5FEkjQ19+cwmtYE3LYsNfVMaafGJPnVIafbhKkycTSkfLI28yf7I/lzZGPJpCkAERjdu3BiICXoC8KRdMYlv69atSJrqUCFtwI1NmqSCNGKDMGvWrBB8ovHC212ZrhH5z+IXcoHtYTStqKsj/0V5ltMT/83RIeJgabGaFe2LcKT/5tC/0Ld6da3/pgFEEOSePXuC+fPnB3ySdOJoETqpM888M3jmmWeCnp4eVfaJz1CIDbixSZNUANcGkUQjzS+Jvtx46VaHpOVpEpZE3yR90bim9F2ODqHspvSL8qumJ/rUIak2UdazPPrM5yiGZMj+yP5c2pv3k6o5yEl033zzDeOjF4zPIwpX+Rx99NEME635W0hifJ0nTepLntT3+eefswkTJoRi4yCAYefZMlzd5D9o0KBwg1A+OhRei8qkbvwX5VdNT/wn1z9VTmU9Vy1/rDJbvnw5wxWrzqqmr8qR6Ptlf00LiFTDtn2mCqGvEFiKzyerh7vMlrXirG7yx+oyPuGcdXR0sJkzZ9qaXZSubvxHBXd0Q/zr658jEadmU7X8sQwfu1bjN4LvZF01fVUYRN8v+yNApFq44XMdKwTOIMORES5cd3d37Hw3F/nmzYPou5c/RkkB2vK4Otp/Hr7yxmkk/vHy8eKLL+YtupN4VP/c1z8TxTSb/M8999xwdFDIyHX9I0AkJGt5da0Q02LY0BfDzqa0KH5zSACNDt7E8zgb+8uTb944RP+/N3R5E8O88qN4JIE6SYCvNmT48iCc6/pPgEhI1vLqWiGmxbChLwARRgIw7EyOJAAJYIQBI4cEiPLbg039y597dkyZvgyIoENyJAFfJIA5qbt27WIEiDI0KjcIGVFLCa4jfQGIVOMqRUCUaW0kII5fIUCUX2WNVP9lQMRX3uRngmKSBBpcAro+y3X9oxGigobgWiGmxbGhrzMuU9oU3y8JECAy16dN/TOnok8h0ydApJcThdRbAro+S7Z/FxwSICooRdcKMS2ODX2dcZnSpvh+SYAAkbk+beqfORV9Cpk+ASK9nCik3hLQ9Vmy/bvgkABRQSm6VohpcWzo64zLlDbF90sCBIjM9WlT/8yp6FPI9AkQ6eVEIfWWgK7Pku3fBYcEiApK0bVCTItjQ19nXKa0Kb5fEiBAZK5Pm/pnTkWfQqZPgEgvJwqptwR0fZZs/y447Ietz11kRHnURwIXXngh++STT2Iz9uvDAZW0DAkIQNTa2sree++9MkhQniVKYMWKFeyiiy4KKdCk6hIFTVlXLgEBiO644w7W3t5eGn0aISooWtcI1bQ4NvSFcdEqM1Np+x1fACJaZZZfzzb1L3/u2TFl+jRClC0vilFPCej6LNn+XXBGgKigFF0rxLQ4NvR1xmVKm+L7JQECROb6tKl/5lT0KWT6BIj0cqKQektA12fJ9u+CQwJEBaXoWiGmxbGhrzMuU9oU3y8JECAy16dN/TOnok8h0ydApJcThdRbAro+S7Z/FxwSICooRdcKMS2ODX2dcZnSpvh+SYAAkbk+beqfORV9Cpk+ASK9nCik3hLQ9Vmy/bvgkABRQSm6VohpcWzo64zLlDbF90sCBIjM9WlT/8yp6FPI9AkQ6eVEIfWWgK7Pku3fBYcEiApK0bVCTItjQ19nXKa0Kb5fEiBAZK5Pm/pnTkWfQqZPgEgvJwqptwR0fZZs/y44JEBUUIquFWJaHBv6OuMypU3x/ZIAASJzfdrUP3Mq+hQyfQJEejlRSL0loOuzZPt3wSEBooJSdK0Q0+LY0NcZlyltiu+XBAgQmevTpv6ZU9GnkOkTINLLiULqLQFdnyXbvwsOCRAVlKJrhZgWx4a+zrhMaVN8vyQgANHkyZNZZ2dnLub+/vtv1tLSEsU99NBDo/sqbmzs32W5Gok+ASKXmqW8GkkCos+6/fbbGTZnFE5tf4S/ej3ggAPYgAEDVO/YMwGimEjMPBqpQcxbcmFctDFjXok1RzwCROZ6bqT6T4DIXH+Uoh4SEH0WAaIMfTVSg5RR1FKCbfgXxkWAqBSV1DZTAkTmqrOpf+ZU9Clk+gSI9HKikHpLQPRZBIgy9Cg3CBlRSwmuI31hXASISjGJ2mZKgMhcdY1U/wkQmeuPUtRDAqLPIkCUoa9GapAyilpKsA3/wriaGRCNHTuW/fbbbzGdrF69mg0dOjTmb+tx/fXXJ87HWbBgAbv00kttsy0lHQEic7Ha1D9zKvoUMn0CRHo5IaSqOp9eCgq1kYDoswgQZUhPbhAyopYSXEf6wrjyAKJff/2VrVmzphTZyZkChKDBqsodfvjhbOfOnTFyW7duZcOGDYv523rMmDGDvfPOO7HkL7/8Mrvqqqti/n3pQYDIXPqNVP/LBES//PILW758OVu/fj3DPerO77//zoYMGRLWF9QZ/MaMGcNGjBhhLsgKUlRV5ytgpelIiD6rbEDEgoLuzz//LJhDseRE31z+/DTzgNeogAOiTOEvW7YsjIv4Zf5mzpyZWRaXEQYPHpzIDwdELskE06dPT6TDAZFTOi4ygz1Ax3yVWbB79+5cv59++qlXPBflMMmD6v9/9f+jjz6KbM1Ehrq4HOwFCxcuDE477bSgX79+Ud5p7QDitbW1Be+++26wd+9eXdZ94l9Vne8T5jwnKvosDoh6tTdq+6Nrt/K2EwSIChpSXkEXJKNNbkNfGBcBojjII0BEgEhb2RICbOpfQjbWXjJ9l4DoySefDI466qhcIEgHkIYPHx68+eab1ry5TkiAyLVEq8tP9FkEiDJkLjcIGVFLCa4jfWFcBIgIEMmVgkaIZGnku2+k+u8CEPF9XYJZs2YVAkIyQOL7vwSLFi3KJ8ySYxEgKlnAJWYv+iwCRBlCbqQGKaOopQTb8C+MiwARASLZKAkQydLId29T//LlnC+WTL8oIMInrilTpjgDQzIwuueee/IxVGIsAkQlCrfkrEWfVTYgoo0Zea0t4hppUmVePsQENd4BMkykTXNff/01mz9/flqUMAyTLdetWxeLN3DgQIaJxVnurLPOYrNnz86K5iy8qgmWNKnamcoSM6pj/UtkxNJT5r/opOq5c+em1vX+/fuzU045hfE5ReHv5JNPZrt27WJbtmxha9euZUuXLmU9PT1aTvi8InbJJZdow8sOqKrOl81HM+Yv+iwOiErdqZrmEBVEtvIbWsGsrJLb0BdoO88IUd5CdXR0JL5Zjhw5Mm8Wlcar6m2RJlWXq1Yb+3dZokaiX2SECIsn0iZOYz7Qp59+miq6rq6u4Nprr01sB3gnHowbNy7ggCk1jzIDq6rzZfLQrHmLPotGiDLgsPyGlBG1lOA60hdoO88IUV6hzZs3j7W3t8eic0DENm3aFPM39dizZw9bsWIF+/7779m2bdsYlsfjbfSEE05goIHf+PHjGd5i87i8b4sbNmxg77//fkjv559/DpcVYzTrjDPOYBj9ynIuR4iwBcJXX33FNm7cGF75Cgt25JFHhsudp06dGr61Z5UnLZyW3adJJzmskep/kREi/qmMcUCVyCQH9Wzx4sVs0KBBieGq58MPP8xuvfVWvGyrQeytt95il112Wcxf9cAZVatWrQp/O3bsYKh7OCdv9OjR7KSTTgp/xx57LMMZVXld3jov8kN9w8i36g477LCwrVH95WdsSfDZZ5/JXuE9eJg4cWLMH23k9u3bY/5oZ+QzuND28Ynq7Ntvvw23P4AMRo0axfgqXW17tG/fPobROZQHo3lot04//XQ2YcIENmnSpBhN1aO7u5utXLlS9Q63XMA2C7LbvHkzW7JkCfvuu+/Yjz/+GLbPGFFE24wRRVsn+qyyR4j+DwAA//8iDvuRAABAAElEQVTsfQn8HsP9/yRxJBEiKHVUKKF1q6OIK+oIWhFVR/k7qu7WUcTRFvFzVlu0RdC6qapK4gptUYmzjkQIpY6EONtKHCGOZP/z2WSe7zy7M7MzuzPPd4/3vF7f7+7O9Zn5XPN+ZmdnWFQwzJo1q2ANxYqDvjv/t9pqq4gxFp122mnFmC+VPuuss+I6qV75b9VVV5Vyud++8847cTuXXnrptnplGuJ+zTXXjO6++24rIksssYSyvjfffDMu/9RTT0WDBw9W5iF6PXv2jA466KDos88+M9LbbbfdlHVcd911xnJy4sMPPxxR30Q/ddfVVlstGj16tFzU6Z70gerefPPNow8//NDq7z//+U9bPieCHjLD/rvs//7772/piAtrn3zyyVa5pG4NGjQo+uKLL1yqi/OecMIJqTp79OgR7b333sa6XnnlldiuevfunSqfbBvlOfLII6MPPvjAWKdI1Nn866+/LrK0Xf/6178q20B+ISs8+OCDyrLrr7++suixxx6rzP/QQw/F+T///PPoqKOOihZaaCFlviWXXDK65JJLUnXfeeed0corr6wsQ/z83ve+F9tvqqAU8f777yvLb7fddq1c5Ke/+93vxn4xKSfxTP7yo48+apVxuRFj1sknn9zmb5L+R+e3bP0Ec2mUKq8tIVVZH3Gg3+UQbfkplKvsgOiBBx6I+vbtqzRGYWSq60477RR9/PHHRnbonON///vf6Pbbb48WWWQRK7rkFMhh6EIRQDR79uyIBhYCX6p+6uL22WefiByoawAgcuVYFJXJ/+QFRDTQ6nTp+uuvd2cKL0F2tOiii0Zf/vKXo//3//5fRD8A3nrrLWNdv/rVr6IFFlhA2xZdG5dffvlozJgxxropUWfzZQBEwvaSfbztttuiOXPmRHvttZcVX66++uoWH8iP6QCUTId+bBGg0QWiT2BWLkP33/jGN+IiU6dOjQg4J9NVz5SPQK9rEGMWAFEG58rkkDKaGiQ5T/+FcpUZED3++OPRYostZmVkKsM75phjjPzWOcdnnnnGGgwJuvSrT/crOi8gIpC1xhpr5O7/97//fWP/VYnCKWOGSMUddVwe+1PXlC9Wpp8XENHAJnRZvn7ta1+LB+N8LYsimm2dO3euVXGa6ZFp57n/wQ9+YKSls/kyAKJzzjlH2X8Ckueff74yTcWjhRdeOKJZk+nTpzv9mBwxYoSRd1Rvkt4qq6wS//Cymb2Wy+6xxx5GWqpEMWYBEKm4I8XJDkGK7thtFekL5SorIKLZjWWXXTZlgGRUK664YnThhRfGr8ZuuOGGeApeNjZxT79o/vGPf2j1QOcct9lmmxbdgQMHRvvuu2904IEHRquvvrryV5Kgd/PNNytp5QVEqlcORIva/ctf/jIaP3589M9//jMaNWpURO0U7ZCvlMclABC5cGte3jLZfx5ARK+bevXqpdSf8847z50hOUrcc889SvqkyzTDsfHGG0dHHHFERD9yCKybXqfRrIgu6Gy+DIBIB3poKcKAAQNa/PnSl74ULbjggq1n2d7F/UUXXRQdcMABrTw0w6zzp6IMzea99957OtYpfyTSMgbyRaIOuvbv3z9afPHF2+LkdLon30xLElyCGLMAiDK4ViaHlNHUIMl5+i+Uq6yA6I477lAaFM0YvfHGGyk+/uQnP1Hm32GHHVJ5RYTOOQqDvfzyy0XW1vXGG2/UTulvttlmrXzyTR5A9NJLLymnugn4qKabyZHRoJF0PNtvv73clMx7AKJMFqUy5LG/VCUFImT6eQDRI488ktIboUc6kF+guami9FpY97qF1r48//zzqTIvvPCCtsxXv/rViOpUBZ3NlwEQ0Y88wXf5Ktq89tprR5MmTYq7RetwdGs2qexyyy3Xes1OvpFeX1J47bXXYkAp1y/f/+Y3v4nzqf6pQA6B1X79+sXtph+SEydOjGcUaVZwypQp0UYbbaTsE9Gk1/ouQYxZAEQZXJMdQkbWIMlVpC+Uq6yAiBZeyoYq7mmmRhVoal61zobWFuiCcDSibvlqcgwXX3yxsm1UnmZskiEPIBo+fLiShrw+IElHN7A99thjyazaZwAiLWu0CWWy/zyASPfjQ6fPWkbkTBg5cqRS18l23333XW2t//vf/yKaLZHtVtyfccYZynI6my8DICKfI9qfvNKsuGr9Fb0iTOaVnw877LAUH+hVvI5vP/rRj1L5RYSOd0Rv2LBh0aeffiqytq4E3HRgd4MNNmjls7kRYxYAUQa3yuSQMpoaJDlP/4VylRUQEbC46667IvqFeuWVV0bkLOgXkfjiQsVIWrwpOwNxP2PGDFV27QLLpZZaSmncohLit/hVJGiI6/HHHy+yta6ugIje/Yv65CtNm2ctlN5kk01SZQlc2QYAIltOdeXLY39dpYvfyfTzACJaoyLrmXxvWmhbvOVR/OGD7vWXDtTIdGlwlNsr7um1jSroBvWyA6ILLrhA1Z3YH4o+J6/0Wk18MZssfPjhhyv5tssuuySztp51vKNZIvJZukBtT7aNnqk+lyDGLACiDK7JDiEja5DkKtIXylVWQJRHULSwWWV4NHOiCjoDz1qMTXXRuiIVLdViQVdAJA9qMg0CO1mBfhHKZeieps9tAwCRLae68pXJ/mXd6Wqh+e63v/1tSmdIb2gRbehAr4CS+krPNJi//fbbmeTp6yZVeYpTgQGdzZcZEJEcaDZMFejVFK39UfGAPoHXBfoiT1VmvfXW0xXR/oDUzdqLiug1nYoWxZm+zhXlxVWMWQBEgiOaa5kckqaJQaPz9F8oV1UBEX3RResEaM8JmgGiqXWaglUZ3n333afkv8450meuWUG3AFK1jsgVEF1xxRXKftA7etqGwPRHU95JHtCrRNV0tqqPAEQqrpjj8tifuUa3VJl+HkD0+9//PqUzQoeytq5wa2k690033aSkTV+32QadHZOdJIMub5kB0VprrZXsRtszfekl5CVfTTNsjz76qLJMniUG1157bVt7kg/kq1XLGaitL774YjK79lmMWQBEWhbNS5AdQkbWIMlVpC+UqwqAiBYY//SnP41o9oUWDuvef8vOQL6/9957lXLXOUfVOqBkBbSWR6Yh7uldfzK4AqITTzxRWbegkeeqWoidbCc9AxCpuGKOK5P95wFEt956q1bfVAuazdxwS9WtHyLwbxt0W1MQ0EsGnc2XGRCZPgyh/qlek5OPMO0f9fLLLytlbppN1vHO5kvWZZZZRkmPFsfbBjFmhQZEPcigOQMRGsSBoUOHsgkTJjA+ALLTTz/dS8/PPvtsxoFLqi6+UzX797//nYrPiuBGy84880zGDZvxXxlZ2bXpHBAx7mBT6XxnV8a/zkrF8yle9pWvfCUVL0eMGzeO8c0f5aj4nk/1Mz5zxfgvolYan7pmfNBpPYsbvnaD8Vdv4rF13X333dlf/vKX1rOPG779AOMOJbMq0gU+SDE+08XGjh2bmV+VgW+kqYpGXAc4wAcntuOOO8aU+EBjRZHPpLCtt95amZfv+s74gKxM8xHJ98pif/zjH1NV8S+QYrtPJSgitt12W0Y2ngx8Xx3Gtw1oi9bZPAdEbIUVVmjLSw9/+9vfGP9SMxXPd6pmfCfqVLwcwdc7Mr5FgBwV3/NX+4x/cp6K568uGd8gMxW///77M/4DLBUvIr71rW8xPgsuHltXnd+jDPx1JOOf4bfyihsOiBj/ilc8tl11vHv11VfZSiut1JY3+cBnsRj/UZaMZhwQMb67fipeFUE6SrrKtyNhJFvXwD/1Z3369MkuZovQdPnK9AtJ18aQ8VXsv0DbZZ0hmjZtmvadNddo5a8NXbzrDBG9hssKNB2vo5fUB9cZIvp1rKs7b3zWtLboL2aIBCfsr0l525f0k1Omn2eGiA9oWn2jPa5CBp2u055DtkH3RaZqbYtulqPMM0R03IUp6HhIuqAL9MWaypfkmSHS8U6mTVshqOiVcYYIR3fIkstxLzukHMULF8lDv8yAiM4G++Y3v6k0IHoXTVvY08Zj9AUabehGgIcAim7q3BUQERjLCrfccouyfbRXRzK4AiLdp7S0aJx2k83zR/yxCQBENlxqz5PH/tprKPYk088DiIg6rR1RDVhZOz9ntZx2TBZ74KjyHnzwwUq6fJZUlV0ZR+v2VG3ns8up/J0ERLpz0MiOVUH32T0A0TxuiTEr9CszACKVdjrEyQ7JoZi3rHnoC+Uq4wwR/SpVOTg608y0C+0666yjLOe6qJoWHGaFSy+9VElLtQDSFRCRI1f1f88998xqVuF0ACJ3FuaxP3cq+hIy/byASLfvF33tRTNIeQN/3RNvMEpfPNF+R8njbZK7HAu9tzk8VbSJv65R2gv9aEkGX4CIfnxlBd3HEQBEXTP8mCHK0qIc6bJDyFG8cJEq0i8zINL9ajQBAtoATHcopOsMES0yzQoCOAgHLq58/UaqqCsg4msqlA6ejiwIHUS/cJaZPafLZP95AREtwBU6nLzmnSV69tlnU18X0V5hdCQNzRxRoB84SXr0TCDHJtBn56oztqgOop8MroCIfkyp2kd7gmUF+hBEVRaACIAoS3cKpZfJIRXqSM7CefpfZkCk2+6dtrbXBQI9KudDca6AyGYA0E3TH3LIIakmugIi2lla1Rc6i4hOnQ4ZAIjcuZvH/typ6EvI9PMCInpNzRcVK/WOfmg8/fTT+gYoUmgdnu61N4GdTz75JC7FP7ZQ0iT9F8dUKKpvRfGPG5Tl6Ww21fEdroCIPgtX2SLF6fYGosaRndLZh6qyAEQARC0FDnEjO4QQ9WfVWUX6ZQZEus/q6TWVLug2SiSHRE5TFXTOkXahphknXdB9skq0VEd+uAKimTNnag+vzNojiQZE2uH7iSeeiM8tUg0Kun5RPACRiTvqtDLZf15ARD379a9/rRzASa/JJmwX5pPt0AyjCgxQ3J///OcWI+kVmg6I0W7KWWHnnXdW0tl0002VRXU2r1sYTPt36fbQ0e0eTYT5V6LKdlH/AYgAiJTK6SuyTA7JV59c6snT/zIDIt0MkeqrEeLTOeeco3U+5IB0+3HonCOVOfbYY5UioCl6Hfiig2dVO6+6AiIifNJJJyn7RGsrdMd3PPnkk8pTsGltVXLthrJzPBKASMcZfXwe+9PX5p4i0y8CiAg8f+Mb31DqHdkE/dGaoH/9619KfaLyl1xySTSQH0As8iev5HeSgQBSMh89Ewgzrefj20IowQoBmMcffzxJJn7W2bwOEFEhHWCjmS7VkRU0m2Y6WR6ACIBIqZy+ImWH4KtOl3qqSL/MgGi//fZTOkiaupfX99DJyvTFAd9fIs6vW0twwAEHKMVJ5x2pHLGII1BEszUi0I7Y9MWHSE9ejzvuOJG17ZoHEBGwojPVkjTome87EtHp9nKg9RJrrrmmMj+tSbINAES2nOrKVyb7LwKIqEc0+6k61Typh3w/l2jDDTeM6EcK30sofj2WVY4Aju7VG20+mKRBz4ssskg0evToiF7pifDBBx9EtFO8bubmyCOPFFlT1zyASGe/1D7aiJXOWiT7o3MW6ceZ8Ct0DIaqT2SnqoCvzFRc6YoTYxa+MuviifKuTA5J2cDAkXn6L5SLBkBfgQ5fVTkAvjGjE4mrrrpKWY+omz4RVn0mTI6JHJTIJ19pCp3aR5/CikDOVs4j7imvuCenu+6660Y0y6JzwJSXwBqd2aMKOodKh2qagu6MKaJHX//QUSX09Y7p16ju1YGOLgCRjjP6+Dz2p6/NPUWmXxQQEXVaSJwFboR92F5pp2KawdQFWquj+0FDNAiA0ewoHekhfgCpaNOibflHTJJeHkBEa5lMNFXtIF9Br61V5eioDVUAIFJxpStOjFkARF08Ud7JDkGZIXBkFekL5SojIKLXUqY1CCoHJA5V5TvctsCMKp/cX50Dpl/J9GtWVV4VR06P1l/oQl5ARK/Gsvqjao+Io1/wdMabSwAgcuHWvLxlsn8fgIh6RQBFtyhY6Jftle9EHNkcHXPjjTcaQVEWPb6TcpR1jEQeQET8oFmwLPpyunjlrvrRpdv8EICIOK0PYswCINLzKE4pk0PKaGqQ5Dz9F8olA4SijfM1Q0TtoHUKqlkg2emIe/pMX0yp09lLCy20kNZ5if4S2BDl5SsBIQrkWHWLu+X89MtVtd9JXMn8f3kBkaiDFmjatEVuFz9WJD74VtRhewUgsuVUV7489tdVuvidTN8XIKJW0ZdiZNMENGTdsr0n8EGf2Js2Zkz2/uGHH44GDRrkTI9mj2xAV15ARD8sdK/1kvz48Y9/HNGPOgqq9UfUBlUAIFJxpStOjFkARF08Ud7JDkGZIXBkFekL5RIAwQeLfAIiag85ZFqXQ6+Hkk6HnskJyl+siD7w84eUTpX2DqHXahTok1lVnfSrWISpU6dGP/zhD+N1DMm8VNd2220X2RwEWxQQUXveeeeduC20/kDHD5rxogXfjzzyiOiC8xWAyJllUZns3ycgEpwgO7z44oujYcOGZb5KE69y6WDVjz/+WFThdKUPAOjw5C222EKr62SP9BHDLrvs0vYaPItQXkBE9RLIoR3ydXXQK+zkej163Z70HfQjShUAiFRc6YoTY1ZoQNSDSHKh5Q5c8Vl3HugI+u78Fwfl8QHQ2+GuuRUooyD/9JXxE+/jgwD5wub44FX+K5KtvPLKxpJ0gOGr/OBB/korPsiQry+K742FFIl8ESebPHkyo0NfKfCv4BgdWEv1dkfgA0Z8WO6UKVMYH6xiftBhtNQ/7mwLNUkc7spfWTI6wNYm8K+LWO/evVtZ+Sxb674TN7D/LvunQ3yHDBkSs72gW1eKjoMCxmdvGQfojP+oiA9HXnTRRRn/sizWPzoclK+fUZbNE8nBZnwQKt/IkfGZJsYBF+MfGzCiw8EG42v38lRbuMybb77J+ELq2CfwmWxGh5faHlJamHhDKxBjFgdE7JRTTmlxIel/WgmJG9JLG5wCQJRgnOtjFR2yUK4qACJXeSB/fg4AELnzrkz2HxoQuXMHJcABPxwQYxYAUQY/y+SQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/0m5xo8fz6IoCtImVFpdDvTo0YMNHjyYjRs3zqoTs2fPZr17927l7devX+u+Ezd59N9nu8pEnwDRNttsA7v2KWDUVRoOkG866aST2CmnnNJqU9L/tBISNz179mR9+/ZNxKYfe8yaNQujYpovtY4ZOnQoe/DBB+E4ay3lfJ0jp7PpppuysWPH5qrAxunkqhiFMjlAP3J22mkn2HUmp5Chihwg33T88cezESNGODefyvbp0yezXA8+S1AIEJXpF1JmbwNkqGL/xfQjXpkFUIgKV4lXZu7CK5P945WZu/xQohocEGMWXpllyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0hfKBcAURCVqGylAETuoiuT/QMQucsPJarBATFmARBlyKtMDimjqUGS8/RfKBcAURCRVLZSACJ30eWxP3cq+hIyfQAiPZ+QUm0OiDELgChDjrJDyMgaJLmK9IVyARAFUYnKVgpA5C66Mtk/AJG7/FCiGhwQYxYAUYa8yuSQMpoaJDlP/4VyARAFEUllKwUgchddHvtzp6IvIdMHINLzCSnV5oAYswCIMuQoO4SMrEGSq0iflGv8+PEsiqIgPEGl1eVAjx492ODBg9m4ceOsOjF79mzWu3fvVt5+/fq17jtxU0X788kXuf8EiLbZZhvYtU8Go67ScIB800knncROOeWUVpuS/qeVkLjp2bMn69u3byI2/diDD4qFRkXZINPVh48B/Y+tBC1LAoBI5gbuZQ4AEMncyL4vk/8BIMqWF3JUlwMARBayK5NDsmiu9yx5+i+mH/HKzLs4Kl0hXpm5iy+P/blT0ZeQ6eOVmZ5PSKk2B8SYhVdmGXKUHUJG1iDJVaQvlAuAKIhKVLZSACJ30ZXJ/gGI3OWHEtXggBizAIgy5FUmh5TR1CDJefovlAuAKIhIKlspAJG76PLYnzsVfQmZPgCRnk9IqTYHxJgFQJQhR9khZGQNklxF+kK5AIiCqERlKwUgchddmewfgMhdfihRDQ6IMQuAKENeZXJIGU0Nkpyn/0K5AIiCiKSylQIQuYsuj/25U9GXkOkDEOn5hJRqc0CMWQBEGXKUHUJG1iDJVaQvlAuAKIhKVLZSACJ30ZXJ/gGI3OWHEtXggBizAIgy5FUmh5TR1CDJefovlAuAKIhIKlspAJG76PLYnzsVfQmZPgCRnk9IqTYHxJgFQJQhR9khZGQNklxF+kK5AIiCqERlKwUgchddmewfgMhdfihRDQ6IMQuAKENeZXJIGU0Nkpyn/0K5AIiCiKSylQIQuYsuj/25U9GXkOkDEOn5hJRqc0CMWcEB0axZswrtVF1tNjez9UOHDmUTJkxgAETNlL+u1wIQbbbZZmzs2LG6bMZ4m+3xjRUgMTcH6DieHXfcMS5f8ACC3G1AQXAgBAcEIDrhhBPYiBEjnEnQLtd9+vTJLIejOzJZZM4g/0Iz5wyTmoe+UC4AojAyqWqtAhBtvvnmOMvMUoh57M+yaqtsMn3MEFmxDJkqyAExZgWfIcJZZsW0Q3ZIxWrKVzoPfaFcAET5eF7XUgBE7pLNY3/uVPQlZPoARHo+IaXaHBBjFgBRhhxlh5CRNUhyFekL5QIgCqISla0UgMhddGWyfwAid/mhRDU4IMYsAKIMeZXJIWU0NUhynv4L5QIgCiKSylYKQOQuujz2505FX0KmD0Ck5xNSqs0BMWYBEGXIUXYIGVmDJFeRvlAuAKIgKlHZSgGI3EVXJvsHIHKXH0pUgwNizAIgypBXmRxSRlODJOfpv1AuAKIgIqlspQBE7qLLY3/uVPQlZPoARHo+IaXaHBBjFgBRhhxlh5CRNUhyFekL5QIgCqISla0UgMhddGWyfwAid/mhRDU4IMYsAKIMeZXJIWU0NUhynv4L5TrggAMY/SGAA8SBq6++Ov7DZ/f2+pDH/uxrz84p05cBEd0jgAN14cAxxxzDJk2axACIMiQqO4SMrEGSq0hfAKIgDEGllecAAJG9CMtk/zIgsu8BcoID1eEAAFGGrMrkkDKaGiQ5T/8BiIKIojaVAhDZizKP/dnXnp1Tpg9AlM0v5Kg2BwCIMuQnO4SMrEGSm0h/zpw57JNPPon5OXv2bNa7d+8gvLWp1Af966+/nh1++OFsn332YaNGjbIh28rjg36rshw3ZaPfr1+/HL3IX6SJ9idzy3f/qb65c+fKJIz3ZdM/Y2M9Jb7//vtszTXXjGt78skn2TLLLOOpZvdqmsh/mUu2/e/ZsyezOVYIR3fI3M1x79shuTahO+jXDRCtssoq7N1332W9evVi06ZNY/3797cWg61BWlfomLFs9AGIHAVYMLtv+wcgyhbImWeeyc4777w4429/+9tuXYdZNvvP5p7fHLb9ByDyy3dtbb4dkpaQJqE76NcJEE2ePJkNHjy4xd1LL72U7bvvvq3nrBtbg8yqJ2962egDEOWVZL5yvu0fgChbDuIHFOUk33H33XdnFwqUo2z2H6ib2mpt+w9ApGWh3wTfDsm1dd1Bv06A6LDDDmM33HBDi+3rrLMOe+ihh1rPWTe2BplVT970stEHIMoryXzlfNs/AJFZDuL1upxrypQpbMUVV5SjOnZfNvvvWMfnE7LtPwBRhyTj2yG5Nrs76NcFENFagBVWWCFmOe3JNHLkyPj+rrvuYltssYWVKGwN0qqyHJnKRh+AKIcQCxTxbf8ARGZh0IwQzSrvv//+jBax0yv25EJfcw1+U8tm/357l12bbf8BiLJ56SWHb4fk2qjuoF8XQHTxxRezk046iQ0cOJBNnTqVia/vXBZX2xqkq1xt85eNPgCRreT85PNt/wBEerlMmDCB7bTTTnGGV199Nd6zi35E0ewQzRJ1Ryib/XeaB7b9ByDqkGR8OyTXZncH/boAIvpS5LXXXmNix+4xY8aw4cOHxyKYPn261eJqW4N0latt/rLRByCylZyffL7tH4BILxcCQwSKttpqq3h2iH5ErbzyynEBl1llPQX3lLLZv3sPipWw7T8AUTE+W5f27ZCsCc/P2B306wCI7rjjDrb33nvHXKRfeyuttFJ8T1eXaXBbg5wvLu+XstEHIPIuYmOFvu0fgEjNbvrhJD61v//+++PZZMqZZ1ZZTSFfbNnsP18v8pey7T8AUX4eO5X07ZCciPPM3UG/DoBor732YnfeeScbNmwYo5khEcR5XrbT4LYGKer3fS0bfQAi3xI21+fb/gGI1PwWH1+su+668RESIhcdd3PggQfGs8n02sxlyw5RR5Fr2ey/SF/ylLXtPwBRHu7mKOPbIbk2oTvoVx0Q6X7tEe/lafA//vGP7Nvf/rZRJLYGaaykQGLZ6AMQFRBmjqK+7R+AKC0E2V9cddVVbfsOzZw5M55dpg80XLfsSFNyjymb/bv3oFgJ2/4DEBXjs3Vp3w7JmvD8jN1Bv+qA6MQTT2SXXHJJazF1kud04O0111wTf2lGawNMwdYgTXUUSSsbfQCiItJ0L+vb/gGI0jI4++yz2TnnnOPFX6RrLxZTNvsv1hv30rb9ByBy522uEr4dkmsjuoN+1QERfWpPv+guuOACRqcoJ4N8JlTWHiO2Bpmk4eu5bPQBiHxJ1q4e3/YPQNTOd3FMhy9/0V578aey2X/xHrnVYNt/ACI3vubO7dshuTakO+hXGRCJjdXoXT+9Hlt88cWVLBeLq4844ojWNv2qjLYGqSrrI65s9AGIfEjVvg7f9g9A1M57sTWHrb/o9J5EZbP/du6Ff7LtPwBReFnEFHw7JNdmdwf9KgMi8eksbaxGCyJ1QV4sSZ/g64KtQerKF40vG30AoqISdSvv2/4BiNr5n9yaoz2168n1Y4yuksXuymb/xXrjXtq2/wBE7rzNVcK3Q3JtRHfQj6KodSJ2d9CXeeRCf9KkSWzDDTeMi0+cOJGtt956clVt9/JiyT/84Q/xzrRtGeY/uNBXlS8aVzb6dEBuJ0PZ+t/JvhMt3/2nk+7Jvm2Db/q2dEW+kPRpHeFBBx0Uk5K35hC05av8Mca9994b71Ukp4e6D9l/mzZXhX6PHj0YgaLMwJW/UJg1a1ah8kULgz74b6tDfFaIPH3EP521KiLyc+CkzQ/9g/5plaMDCdC/cPpHdk/+gvyATeAbNjrlt6kzKw/k71f+PYjhmajJkKEqCNHQhUJJ6P/HrG/fvoV4WKSwLf9pxod2laVr8tNZHX35V59uRsmWvo5G0XjQr4b+FZWzrjzkH0b+8ocVWbNDQjbiNTutS6QyuvWJIr+PK+TvV/4ARAW1EgrpVyFdxWHL/wsvvJAde+yx8cZpBIpsg9iJlv9KVK45sqVvS881H+hXQ/9c5WqbH/IPI/8hQ4bEx3OIYzps5CG/Zrf90WVTrykP5O9X/gBEJm2zSINC+lVIC5a3ZbHlP80O0YzP0UcfzQgc2Qbxq4/yz5gxI/Wrz5a+LT3XfKBfDf1zlattfsjfv/zlmWH5mA4bmYg9zOiHFJUNHSB/v/IHICqosVBIvwrpKg4b/ueZ/pbbQVPfun1IbOjLdfm+B/3y659vmcv1Qf7+5S9ATfKYDpnvuvuivkZXry4e8vcs/6xFW1npWNTld1FXFr+T6eB/Nv/F4mh+blmSfVbPp512WrxYku9NlMoP/mfzP8U0jxHgP/jvUZ0ivvYntnUOQCL+2itX1QMHDozrIL8ROkD//ep/D2KoDn0ivhkcoE+laW+hOgY6uX6NNdaIuzZ69Gi26667OndTnkIfN24c23LLLZ3rQAFwABwoPwfOOussRkd1cFATv2LP02KxJxHV8dxzz+WpAmW6iQN4ZVaQ8Ziy9Dxl6SiPLP7LzomATd5AQGrs2LGMzzKxMWPGtKrJot/KGOgG9Mutf4HE3qoW8vcnf/lLVN2xPi3GG27kH1Cua5AM1SqTIH9/8icGAxAp1cw+EgrpVyHtOT8vZxb/xWLqIg6OKOnWBmTRd+2Pa37QL7f+ucrTNT/k70/+BIgGDBgQiyDvbLKQH236SusOqR7TBrAif94r5O9P/iQDAKK8mji/HBTSr0K6isPE/6wvxFxpifPN+NoARjNPFEz04wyB/4F+efUvsOjj6iF/v/IXM8G6bTZsZCrPNIX+/B7y9yt/ACIbDTfkgUL6VUgDq5VJJv6LvUSKODeZqNjLiL46o0/wKZjoy2VD3YN+efUvlMzleiF/v/IXP6JkG5f5bXMv6qADYQkchQyQv1/5AxAV1FYopF+FdBWHjv8h3uPLU+ril5+Ovms/8uYH/XLqX155upaD/P3KX7Zx3e70WTJaf/31GZ2b6LrnWVa9qnTI36/8AYhUWuYQB4X0q5AOrI+z6vh/zDHHsIsuuojl2UvE1AaxR4nYeE1H31SHzzTQL6f++ZSxqS7I37/8xe70eQANASECRBRsj/wwyTcrDfL3K38AoiyNy0iHQvpVyAx2p5JV/A/5Dl92ePQLcrXVVqvEWW4pxnmKUPHfU9VW1YB++ezPSnCeMoWQv3g1TmsGCdS4BPGDyeXID5f6k3lD9D9Jw/RcN/oARCZpW6TVTSEsutyWpYz9l9/h06sz34cs0lcjTz/9NKO1SZdccgkAUQUO921TWo8PZdR/j93LrKqO/Zdft7u8Ngv5Q0wniDryX9dXVbzv/gMQqbjsEOdbIA6k46ygn/6FHPodvgBcBLSmTJnClltuOVexecsP+afl7425FhWB//Xkv/jR4/LaTPgFWkwd4oeYSh2hf371D4BIpWUOcVBIvwrpwPo4a5L/uv2CXOvNyk9giPYZueyyy9ghhxySlT1YerL/wQhpKgb9cum/RkzBousqf/HajIARzRLZBPFDzNdXrTY068p/m75THt/9ByCy5bwmn2+BaMhoo0G/fUDq1Dt8sWi7yBb/WqE6JED+7fJ3YJ2XrOB/PfkvvzazWRydXFsYcjNGWXGhf371D4BI1q4c91BIvwrpKgKZ//Ins+KzeNf6bPPLDjP09vymNsn9N+ULlQb65dH/UDI21Vtn+YuNWG12uRc/kHx/1WriPaXVmf9ZfQ/S/6Kn8eK0Xb+n7brKA/zv4r84lZ5Om+5E4Oeaxada8ynyTpBT0oD8u+SvZFDgSPC/vvzn64di++azPZlaxF+hx3n5D7HMvD4zQP/86h9miGxgqCEPEHp5fiGLc8vkozUMoiucRIe8Dh8+PK7HZlq9MEFFBdC/8uifQjzBoyD/cPKXX4OZ7Ls7FlMLxYL8/cofgEhoVs4rFNKvQrqKQfC/u8CJmFbvFAhL8kf0PxnfqWfQL4f+d0reSTp1l7+wb9NrM99HBCV5bHquO/9Nfac07/0vOn2HKTu/U3au8gD/5/G/u15fidd03HG6is5Lfsgf9udFkXJWUnf9E6/NyL+oAp85il+V8bE54l+jqbIEjas7/7OY57v/mCHKgqAZ6d4Raga9ZDLof8zeffddRq/LKHR6gbO8kHv06NGMTsvuZID8MUPTFxtjBjM5eRsPOtA5uclrdy2mFh2G/fu1fwAioVk5r1BIvwrpKgbi/ymnnBKfW9Zdn8CLT/3F+WaufSiSH/rX/foHQNK3iAoXKtsJ/Rd7jqm+XB0wYEB8or3plVqhDmYU7kT/TU2oG30AIpO0LdLqphAWXW7LUob+L7/88t3qlORfkabFl22M8/RQBv4DENQbEJhUtQn6J37w8NdmjNYqiiAWU9OzavZI5At5bQL/Tfzz3X8AIhO3LdJ8C8SCZFuWptO//PLL2aGHHso6uV1+mwDmP+TZ6l9Vj2tc0+WP/mOGLDQglz/YkIEPvR4fO3ZsfKYhgaPuCNB/v/oPQFRQi6GQfhXSVRy0EdrkyZO71SlRm8WvRZpep1mi5FoD137Z5of+da/+gf/N4L94bSbWCWJj1nkeqm76D0BkO/Jo8tVNITTd1EZ3Z//lfUJcTqXWdqZAAi2upk906Xwz1VqDAlUbi3Yn/6lhoN8MQKBTwqbIX7w2E+eUnX766WzkyJFsxRVXZNOmTdOxJ3h8U/ivY6Tv/gMQ6ThtGe9bIJZkW9maTF84Kfr1Rl97dHegWSL65ehyIGTRNjdZ/sQ79B+ALPQrM9IzeQaYXpuJTWDPO+88NmLECMrSLQH671f/AYgKqjEU0q9C2oqDZmTIKdG1bIHvXcLotOxOBOhf9+ifkC343wz+y9tr0CzRNddcE6vAG2+8wZZbbjmhDh2/Qv/86h8AUUEVhkL6VUhbcdBCRwIdc+fOZT179rQtpsxHszo07U0Ls11PqVbRp6/OOhWgf92jf0K+4H9z+C8WUQvZEzC65JJLWCdmqATN5BX651f/AIiSGub4DIX0q5CO7PfyykSsB9hqq62YK5iB/Ksvf1edk/ND/s2Rv3htJuRPC6y33357AKIabQwKQCS0O+cVDrH6DhGAKKfy82LQ/+rrf37pN0v+8mszmk2mZ+h/vfQfgKiIN8CAUAuHAECU3wgwINRrQHDVhKbJv1+/foyfn8XEbHLT+p/Uj7r1H4AoKWHH57ophGP3AYj40SFYQ4Cdml3txld++J/O2t+qq67KXn75ZSY+nAD/O8v/pN345j8AUZLDjs++BeJIvhaAxLXPcn4f/McMkcxRt3sf/Hej2J4b9Os1ILVLN/up0/LfZJNN2GOPPcbE2WWdpp/kCOj71X8AoqSGOT5DIf0qpCP7vQBCACJXrnflh/5XX/+7pOl+1zT50wHODzzwALv//vsZ3Tet/0kNqVv/e/D3oVGyk3huFgd69erF5syZ06xOS70966yz2Nlnn8222GILdvfdd0spuAUHwAFwoIsD4iDpcePGsS233LIrAXe14ABmiAqKsW4I2ZUddeg/Zohcpd6Vvw7y7+qN+x3636wZsh49esRKghmiebZSN/0HIHL3gW0l6qYQbZ2zeKhD/wGILAStyVIH+Wu6ZhWN/gMQ4aOK+nxUAUBk5fb0meAQq+8QAYj0+p2VAv2vvv5nydiU3jT5Y4aoXRvqJn8Aonb5Oj/VTSFcGVCH/gMQuUq9K38d5N/VG/c79L9ZgBCAqN1G6qb/AETt8nV+qptCuDKgDv0HIHKVelf+Osi/qzfud+g/ABFemeGVWctzwCE0yyG0BD//pg7yByBKStX+uQ7yt+9tOif63yz/J2aIZsyYwRZffHF8dl+zjWkxQ5T2cU4xcIjVd4gARE4q35YZ+l99/W8TqONDk+Qvn2UWRfN2q2lS/1WqUbf+AxCppOwQVzeFcOh6nLUO/QcgcpV6V/46yL+rN+536H9zAOE//vEPNmTIkFhJAIjm2Urd9B+AyN0HtpWom0K0dc7ioQ79ByCyELQmSx3kr+maVTT6D0CENURYQ9RyFnAIzXEILaFLN3WQPwCRJFDH2zrI37HLbdnR/+b4P8wQtal+/FA3/ccMUVrGTjF1UwinzvPMdeg/AJGr1Lvy10H+Xb1xv0P/AYgwQ4QZopbngENojkNoCV26qYP8AYgkgTre1kH+jl1uy47+N8f/YYaoTfXjh7rpP2aI0jJ2iqmbQjh1nmeuQ/8BiFyl3pW/DvLv6o37HfrfPEA0cOBANnXq1FhZIP96yR+AyN0HtpWAQVTfIACI2lTa6QH6X339dxJ4InOT5C9miLbaaitG9xSa1P+4w4l/des/AFFCwK6PdVOIJvYfgMhV6l35of8ARE1ZQ6PyE9D/euk/AFGXb891B4OovkGoHJ2tMkD+1Ze/raxV+SD/5shf5Scg/3rJH4BI5eUc4mAQ1TcIlaOzVQHIv/ryt5W1Kh/k3xz5q/wE5F8v+QMQqbycQxwMovoGoXJ0tioA+Vdf/rayVuWD/Jsjf5WfgPzrJX8AIpWXc4iDQVTfIFSOzlYFIP/qy99W1qp8kH9z5K/yE5B/veQPQKTycg5xMIjqG4TK0dmqAORfffnbylqVD/JvjvxVfgLyr5f8AYhUXs4hDgZRfYNQOTpbFYD8qy9/W1mr8kH+zZG/8BOnnXYao3sKkH+95A9AFKt1/n8wiOobhHB08v4ithoB+Vdf/rayVuWD/Jsj/wMOOIBdc801DICoyxLqpv8ARF2yzXVXN4VwZUId+g9A5Cr1rvx1kH9Xb9zv0P/mAKKtt96aPfDAAwBEkpnUTf8BiCTh5rmtm0K48qAO/QcgcpV6V/46yL+rN+536D8AUVM2plRZR930H4BIJWWHuLophEPX46x16D8AkavUu/LXQf5dvXG/Q/8BiACIcNp9y3PAITTHIbSELt3UQf4ARJJAHW/rIH/HLrdlR/+b4//wyqxN9eOHuuk/ZojSMnaKqZtCOHWeZ65D/wGIXKXelb8O8u/qjfsd+g9AhBkizBC1PAccQnMcQkvo0k0d5A9AJAnU8bYO8nfsclt29L85/k/MEF111VWMvjijAPnXS/6YIYrVOv8/GET1DQKACPqflwOw/+rbv63s119/fTZp0iR2//33MwJHFCD/eskfgChW6/z/YBDVNwgAIuh/Xg7A/qtv/7ay79GjR5w1NCCaPXs2GzduHPvnP//J3n77bfbf//6XDRgwgC233HJsww03ZDvvvDPr06dP3JYy69/DDz/MPvroo7id22yzDVtggQVsWW2dz3f/AYisWa/O6Fsgair6WNAv7pABiPT6lZUC/Suuf1k8NqWD/53jf2hA9Mknn7Cf//zn7LLLLmsBCZXs+/Xrx4444gh2xhlnsDlz5rCyrmFab7312NNPPx13YdasWUHa6Vv/e/CGRiqmI645HOjVq1dsWM3pcXtPzzrrLHb22WezLbbYgt19993tiXgCB8ABcIBzYJFFFon5QLM3W265pVeevPLKK2z48OHspZdesq53jTXWYKNHj2YrrLCCdZlOZvzWt77FHn30UUZA8sMPP4yvnaSfhxZmiPJwTSrjG6FKVVvdgn7xX4iYIbJSNWUm6F9x/VMy1jIS/O8c/0PNEM2YMYNtuumm7IUXXmiT+rLLLhv/SKO1S88++2y8S/b06dPb8qy99tqMXk3RrFF3BJP+bbfdduzvf/97DCTFqzPfbTTRz0UrKhhohqk7A+iD/0X1j59NRLOkET/LzLkq6B/0z1lpPBaA/nVO/8hH0B9fQ9SSoA/+77333nG9ov5FF100mjBhQouGfPPII49Eiy22WFv+Qw45RM7S0XvqP5/9iebOnZuiu8suu8TtXHrppVNpFMFfESrjXSJ98F+mx+SHPPe+G+TaBtDvnENQyaYO/AcgUknWLq4O8rfrqToX+t8c/yMAy8SJE1vKUFT+zzzzTMRnnloAhy+Wjvh5aa36VTcEyBZeeOFWmQUXXDDir9xUWYPHUf+PPfbYaNVVV43OO++86N13323R3GuvveI2fvWrX23F8Zmi6Morr4w222yzaNiwYa34vDdF+Z+kC0CU5Ijjs2+BOJKPQL+4QwYgctW6rvzQv+L618VN9zvwv3P8F4BIllJR/u+3334tYEP1//73v5er197/7ne/ayt35JFHavOGTCCAw9cwtdqy0EILRXvuuWd07733Rj/4wQ/ieP5aL+JfzEU0k0WzX4KPBOpmzpxZqHlF+Z8kjjVEXDpFgvd3mI6NAf3iawiwhshR6aTs0L/i+iex0/kW/O8M/2n/IVrLQ4EPoi05FeE/fSHGXyex9957L65vySWXZLRGqHfv3q36dTe0JofWGIm1Ocsvv3xcVpc/VPxzzz3Htt9+e/bGG2+kSIiPdWjtlcwzkZH6e+uttxZaoF6E/6Id8hWASOZGjnvfAnFtAugXd4gARK5a15Uf+ldc/7q46X4H/neG///4xz/YkCFDYgHJg3sR/j/44IPxomkh9X322Yddf/314jHzuttuu8VfmYmMTz31VAu0ibjQV9F/WhDOZ4XYfffdF29cKUCeTJ/PDsXgh/Ykor9111238Jdngr5Mp9B9csrI9dn3lBXou3EA/C8+ZY5XZm46J+eG/hXXP5mfrvfgf2f4T+t2+EAb/8kyKsL/c889t1Un1X3xxRfLVWfe05od0Sa6XnTRRZllfGdQ9Z/PfEUHH3xwW9togfXnn3/um7z3JSNYQ1RQRCqFKFilU3HQL+4QAYicVK4tM/SvuP61MdTxAfzvDP9DACKxxkaAmoceeshJ+vfcc08b6OCbNTqV95FZpX/jx4+P+K7UcduWWmqpVhtvu+02HyTb6lDRb8vg+ABA5MiwZHbfAknWn/UM+sUdIgBRlpbp06F/xfVPz93sFPC/M/wPAYgGDx7cAgsEiqZNm5YtcCnHlClT2spvu+22UmpnbpP6984770T8iJG4XbQ9AN9oMvrKV74SP/M1Q9Hrr7/utWFJ+kUrxxoirolFgvd3mI6NAf3iawhofQD9rbTSSq1TrG3FAP4X578tr1X5wH/wvxNHV4RYQ7TiiisyDhBite7Zsyf79NNPnc77+uCDD1j//v1bZjFo0CD24osvtp47cSPbH9+LKF5gTWuJKFx44YXs6KOPZn/6058Y/wQ/jtt8881jX0sLrn0Emb6P+gCICnLRt0BMzeGfKLbOhhH56CBAm68SRH7fV9AH/4voH98Ms5BKdtL+VA0F/WYAMgGIaCEwfXEmQhH501dWYvExHQsivhgTdWdd+WwIIyAlAn119uabb4rHjlzl/p966qns//7v/2K6dI7ZE088wQTwITvnr9LitJ/+9KfszDPP9NI+mb6PCgGICnLRt0BMzRFGacqDNHCgShwgp14kdNL+VO0E/WYAoquvvpodeOCBjAZ28sMiFJE//ZCgWSEKBI7oVHvXINfBX1Gx999/37WKQvlF/+mz+9VXX53xV1jxl2N0nMgmm2zSqptA5AYbbMBoFonvPxQfUzJw4MBWet4bQT9v+WQ5AKIkRxyffQvERB6AyMQdpFWRAwBExaTWSf+jamlT6Ou25sjbf9qDiC88brE07z5Ciy++eAsE0WzMF1980aqzEzdy/6dOnRq/IqO9la644ooU+cMOOywGQvxrOkYH0/oIMn0f9QEQFeSib4GYmiMDoqIDiYkO0sCB0BwQB2UW1eNO2p+KJ6DfjBki34CI9J4AjND/vK+7aG8f8aqN7xLdmnFS6WqIOJX+88/rGT9OJEUuxPIKFf0UYYcIACIHZqmy+haIioaIAyASnMC16hwAIPIjwU76H1WLm0LfNyAiXtIJ9fSKicKAAQNa64niCMt/BDzErNASSyzB/ve//1mW9JOtbvIHICqoF51UCACigsJC8dJwAIDIjyg66X9ULW4K/RCAaJlllmH8MNSYrbQWiJ/+rmKxNo6AkDwTQ1+t8U/3tflDJNRN/gBEBbWkkwoBQFRQWCheGg4AEPkRRSf9j6rFTaEfAhB97Wtfi9fUCL7SZ/T0Csw20EJmfrBqK3vyC7hWQsCbuskfgKigsnRSIQCICgoLxUvDAQAiP6LopP9Rtbgp9AUg2n///Rl9cSZCkf5/5zvfYXfccYeoivGNFp0WGz/yyCNss802a5XfY4894j1/WhEduCnSfx/N806fL+oqFHzvFOnamCbR1+2W6soz5AcHupsD3BnGu9cWbUeT7F/FK/S/MztVi93s6SqHIvw//vjjYxsQtnD77bfLVWfeX3vttW3lk23LrMBDhiL990AeZ5klmVg3gST7Jz8DEMncwH2VOSAGgaJ9aJL9q3iF/ncGEPH9h2LwkQQdRfjPZ5raAM0pp5yiErE2jn/G3lb+lltu0eYNlVCk/z7a5Js+XpkVnLfzPmVnaA9emRmYg6RKcQCvzPyIq5P+R9XiptDfeuut2QMPPMA4IGL0+kyEIv1/++23GT/3q/XpPT/bjD344IOi6syrvAaJPrn/z3/+w2hzxk6GIv330U7f9AGICkrFt0BMzQEgMnEHaVXiAACRH2l10v+oWtwU+iEAEfGTdnN+7LHHYtaSTbzwwguMziTLCrQTNAEoEXbYYQd29913i8eOXesmfwCigqrTSYUAICooLBQvDQcAiPyIopP+R9XiptAPBYguueQSduSRR7ZYu/vuu7Obb745Pv6iFZm4+eyzz9h2223XOhuMkm+66Sa25557JnKGf6yb/AGICupMJxUCgKigsFC8NBwAIPIjik76H1WLI/Qo6wAAQABJREFUm0I/FCAicLPaaqu17R901FFHsYsuukjF7vj12ve///0YAIkM9Ln9xIkTtSCKTpu/7rrrRHa20UYbxa/+WhGKm+eff56dcMIJrRTaJ4mvUWo9i5vayb/owibfi5pc29Mk+lhU7aodyF9WDnCHGi8ILdq+Jtm/ilfof3UXVQt5csDStjiabOOII46I+GuxiAOmOBs/9iIi/7/vvvu25eXHf0T33XefqEp55SfLt5XZaaedlPnkSL6Wqa1M37595eTWfd30jxBnoVA3hrgyo5P9ByBylQ7yl5UDAER+JNNJ/6NqcVPoi6/MyAfLwVf/Tz755DYAIuxjkUUWifiMTtSnTx9l+gUXXCA3R3kPQKRkizISgEjJFvtIXwZhQxGAyIZLyFMFDgiHX7StnbQ/VVtBvzMzNCreU1yn+M9PlY8BSShANHfu3GjkyJHRAgssoAQ+wl7ElYDSqFGjrPoPQKTTnnQ81hBxDSsSOvkOFWuIikgKZcvEAbGGiA9ouZpFnxnzwYN10v5UDQX9Zpx2L/SVAyJG64lE8C3/J598kp1//vnstttuU55txoEZ++53v8tOOukktuqqq1rp/1lnncV+9rOfiSYz/sqM3Xnnna1n1c1DDz3ENt9881YSf2XWOoi2FclvfPdfrtvm3jd9ACIbrhvy+BaIgRQDIDJxB2lV4oAYYD788MNczV544YXjgy07aX+qhoI+ABGBBd/ho48+Yk8//TR788032Xvvvce+9KUvseWXX56tt956jHRfBOifX/0DIBKalfPaSYUEIMopJBQrHQcAiPyIpJP+R9XiptAX+hp6hkjFY1NcU/iv44Hv/gMQ6ThtGe9bICayAEQm7iCtShwQAwxmiIpJrZP+R9XSptAX+gpA1K4FdZN/D1qU1t5FPJWVA+PHj2c77rhj3Dy+HKyszUS7wIFMDogBho4byBMWXHDB+JVZnrIoAw64coAvYo6LjBs3jm255ZauxZG/IhzADFFBQXUSIWOGqKCwuqH4oYceysiJJgNtvDZ8+PBkdO7nf/3rX2z77bdPlR84cCCbMGFCKr67IwQgwgxRMUl00v+oWtoU+kJfZ8yYwWhhswhN6b/ob/Jat/4DECUl7PjcSYXIC4iee+45Nn369FTPllxySbbBBhuk4rMiXnnlFfbSSy+lstGvKPl8HcpAZ/NMmzYtlZecysYbb9wW//jjjzNyOKEDtVH84gtNi74IufXWW1NkaOdYvslaKj5vxDPPPMPWWWedVPFVVllFKatUxg5HiAEGgKgY4zvpf1QtbQL9mTNnsgEDBsTdT87MN6H/KrmLuNr1P/0lvltMp/aB0LWqSfRpDwyuiPGfjh+q+B/+8IetcqI8XbfddltV9sw42i9Drkfc89OXU2WPPfZYZd5vfvObqbx8KlqZV9Tv68q3pU/RDhWx2267KfvEAZFXkpMnT1bS4YDIKx1flQlZckAU5fkTO/g2yf5VvEf/w++DZPK74H94/qv0XsT55j82ZhSczXn1LRBTM0yGaSoHQDQPRIpBGIDIpC2dSROyyAOGqAwA0Tw5ddL/qDSjCfRNfrcJ/VfJXcTVrf8AREKyOa+dVAiTYZqaD0AEQGTSj+5IAyDyw/VO+h9Vi5tA3+R3m9B/ldxFXN36D0AkJJvz2kmFMBmmqfkARABEJv3ojjQAIj9c76T/UbW4CfRNfrcJ/VfJXcTVrf9YVM09c5HQyUVleRdVH3zwwez3v/99qpt8DRH729/+lorPijjjjDPYaaedlsrG1xAx/jqqLf4nP/kJ4wcQtsXRA19DxB599NG2+HPPPTdehN0WqXi49tprGT/7J5WyxRZbMFpEnBXOPvtstuyyy2Zl85KORdVqNmJRtZovrrGd9D+qtjWBvsnvNqH/KrmLuNr1XyC9vNe6IURXPnSy/6ZfKqZ2V2WGyNQHOY3vQaNcQHz99dfL2Upxj0XVajFwhxrLEGuI1Pyxje2k/1G1qQn0hd/t379/igVN6H+q01JE3fqPGSIBdXNeO4mQTb9UTM2vygyRqQ9yGh3s+fnnn8tR8T0HRGyfffZJxbtGPPbYY+zf//53vFXB66+/zj744AO20korxbNPdKDiuuuuyxZddFGram1niN555x02evRoNnXqVPbGG2+wr3zlK/EsGm1NYDOb5fOz+zlz5rCXX36Z0XYNU6ZMiWft6PykZZZZJj5LaYcddrDuv45JmCHSccYtvpP+R9WyJtAXfnerrbZidC+HJvRf7m/yvnb9l8Bertu6IURXJnSy/+KXCldKp2ZihiibXZ988knEXytGa621lnL2iXgu/pZaaqnod7/7XcRBWWbFuhmiG2+8MS773//+N9prr70i3awX0dxkk02it956y0jLx2f3xIPjjjsu4uCn1VfRZ/nKAWlEOvXuu+8a22RKFPVhhsjEpey0TvofVWuaQJ8vD4jtgQOiFAua0P9Up6WIuvXfbWSVGCFu68YQ0S/bayf7D0A0Tyo68JD3lRmBjUGDBhlBgBjA5Svtu8R3iDaqig4Q3XLLLdGLL74Y8RknK7p8hiriMzZaWkUBEV/PFVF/5P5l3fPN6qKHHnpI2yZTgqgbgMjEpey0TvofVWuaQB+ASCX5eXF1kz8AkV7WVimdVAgAonki8QmI/ve//1nNCokBPHndaKONjDNFOkDEd6+O1ltvPWcAwncIV+plEUA0atSoqFevXk5tEXzgrw6jJ554QtkmU6QoD0Bk4lJ2Wif9j6o1TaAPQKSS/Ly4uskfgEgva6uUTioEANE8kfgERLvvvrsSCPCjPaKTTz45Gjt2bDRmzJjopJNOiuhVkRjI5Sv/6k6rKzpAtM0227TqWmKJJaLvfOc70ZFHHhnxNUPG12dHHHGEklZeQPT2229HBGrk/oj7XXfdNbrpppsiqvu2226LX5OJNPlKfXENojwAkSvn2vN30v+0U5731AT6V111VUSvy44++ugUC5rQ/1SnpYi69R+ASBJunttOKgQA0TwJ+QJE7733nhbk3H777Sl1IFAgBnL52qdPn4gvRE7lpwgdIBLl999//1RZvkA64guYlbQIqPHz3lK08gKigw46SEnn1FNPTdGgCHotKdouX11fnYmyAERKNltHdtL/qBoF+vU6ukIlY1Nc3eQPQGSStkVaJxUCgGieQHwBossuu0w5uK+88spayX/9619XluFfpSnLmAARzU7pgBSBop49eypp/eIXv0jRygOIJk6cqKRB65q++OKLFA0RMXTo0FS7dtppJ5FsdQUgsmJTZqYQ/odmQ4R8cO36mAK8SPMihP5lKr2UwTd9ACKJuXlufQvE1AYAonnc8QWIaFHzPffcE/3lL3+Jrrnmmujiiy+OzjvvvEh8AaaSBX0RpnKM/JN5VXbjDNFTTz2lLCMihwwZoqS14YYbiiytax5AxLdjUNb/q1/9qlWv6ubuu+9Wlps0aZIquzJO8BAzREr2WEeG8D8AROmBX+grru28CaF/1srPM/qmD0Dkwn1FXt8CUZBoRQEQzWOFL0DUYqzDzbHHHqsEA+ecc46yFt0MES2ozgq0DYDKAS+99NKponkAkW7gI8BjCrTuSNWuyy+/3FSsLU2UByBqY4vzQwj/I/SCFhMjgANJDsjjUAj9S9IzPfumD0Bk4rZFmm+BmEjKimjKl0zDPkRJjtg98+NBok8//TT66KOPopkzZ0a0Z9CPf/xjJRjQrbnRASJ+pElmIx5//HElLb6pYdwuuYI8gGj55ZdX1n/ddddFDzzwgPGP1jIJUCOuP/vZz+QmGe9FGQAiI5syE0P4HwCiTLY3OoM8DoXQPxfm+qYPQOTCfUVe3wJRkGhFyYrYirS4ASDKZhIBnl/+8pfRfvvtF2255ZYR3ylaub5GDOTJ689//nMlER0gUq0DSlbAd61OgQ5B95VXXmnL7gqI+A6zEQErUZ+PK/HONgh6AES2HFPnC+F/AIjUvEbsPA7I41AI/XPhs2/6AEQu3Ffk9S0QBYlWlKyIrUiLG9+A6PTTT1cOpLSxXzLoXjHxw12TWa2ffb4yIyBErwYWX3xxZZ/EwJ11dQVE/IDazP4SaNHRnTBhQlt5V0BEi7Z1deeN33rrrdvaZHoQNACITFzKTgvhfwCIsvne5BzyOBRC/1x465s+AJEL9xV5fQtEQaIVJStiK9LiRrd4lo6EyBN+9KMfKQfTtddeO1VdmQHRZ599Fm266abKvogB2/bqCohUn/UnmUev7HRfmt15551t2V0B0fjx4730W+bPV7/61bY2mR5EOQAiE5ey00L4HwCibL43OYc8DoXQPxfe+qaPw125Zy4SOnm4nThkkNrLlca62SNGjGDnn39+Kj9fnMvoUFHXsOOOOzK+8DZVjM8QMG4sbfF8rQy74IIL2uLogc8QMX5cRCreJsLX4a66tlEb+GszRv2kQ1aXXHJJxmel2AILLMCuuOIKdsMNN6SayQER4xs0puJ1h7vyr9oYf8WUyi9H8F20GT83TY5q3fMvuuJDZkWE6+GudGjtiiuuKIq3Xfk6Kcb3VmqLs3mgA2BVPFCVxeGuKq64x4XwP2THfA0Z4zOnjM8GuzcKJWrNAXkc4oCE9e3bt9v6613/XdCYKq9vhKaiYYprEn0ZmZt4kkyjT8m5xir/6Be6a1hllVWUdX3ve99LVVXWGSI6g0zHE90CaercUUcdpSynK6NbQ3TuueemeJWMeP7555W0qN20wFsOrjNEtP+Rbudtohs6CN5jhqgYp0P4P8wQFZNJ3UvL41AI/XPhn2/6eGXmwn1FXt8CUZBoRcmK2Iq0uKHjF8QAlLyOGzfOooauLM8++6z2Nc7IkSO7Ms6/Kysg4rM8Sp7QDtGmQK8ZkzykZ9dXZgSssoIsb5km/0WWKuoKiKiC1VdfXdmXv//976n6fUeI/gAQFeNsCP8DQFRMJnUvLfulEPrnwj/f9AGIXLivyOtbIAoSrShZEVuRFje6fWNoUKL9cHS7Jauq3nbbbZWDKNVFJ6YnQ1kB0QknnKDsB53fpQuffPKJdlbFFRDRLButETKFU045RdnG1VZbLVUsDyDirwSV9V966aWp+n1HABD54WgI/wNA5Ec2da1FHodC6J8L33zTByBy4b4ir2+BKEi0omRFbEVa3phOVqfPzW0C7eQsBrLkdYUVVlACq7ICInq9l+wDPe+5555aVvD1Q8oyVO7EE09UltO9MqMy/F28sgxFElgaOHCgkh7VmQx5ABEdWKviwTe+8Y1k9W3P9Lruz3/+c7xPEb1e42udMsFdWwX8QdDFDFGSM27PIfwPAJGbDJqWWx6HQuifCz990wcgcuG+Iq9vgShItKJkRWxFWt7oXhGJgWnYsGHRm2++qaxt+vTp0c4779waxEQZ+fqHP/xBWbasgEg3Q6Q7x4vAi27NDfGBtjZQBRMgGjx4sHbredr1WeavfE96kAx5ANG7774bLbbYYko6d911V5JE65kvFE+Voa0QTEeetArPvxH9ASBKcsbtOYT/ASByk0HTcsvjUAj9c+Gnb/oARC7cV+T1LRAFiVaUrIitSMsbei1mmiWiAYp/RRWvK6HXRvRp/be//e2IPqXWffotBjU6W0t3GGhZAdGVV16ZGtRFf/hXea3+TJs2LT7jbIkllmjl519Tte5FGXqNRbtaJwMBTZFHdaXB57XXXmsVmz17djRq1CgtzzfYYINWXvkmDyCi8meffbayffwrs+hPf/qTTCL64IMPIjrnTNWPNddcs8WztkKaB1EHAJGGQZbRIfwPAJEl8xuaTR6HQuifC1t90wcgcuG+Iq9vgShItKJkRWxFOtzQ7sZ0DpYYjHxc6WT4t956S9uKsgIiOtiVAKCOB7RR46BBg1LptBsz/anK0Ssu2rTysssua/FDN7OW3P9opZVWijbbbLNIBbZkWrpZmLyAiDZ/pNedMg35/stf/nK0yy67xG0z8Svr/LMWQ+bfCBoAREnOuD2H8D8ARG4yaFpueRwKoX8u/PRNH4DIhfuKvL4FoiDRipIVsRXpeEMnrK+77rraAVAMVDbX73znO9Grr75qbEFZARE1WrdoWdd3WghNsySmtURUlgYUEXbYYQclr++5555o/fXXV6bp6O++++7R559/Lqpuu+YFRFTJfffdFxHw0dE1xffq1SvmR1tjLB5EnQBEFswyZAnhfwCIDAxHUiSPQyH0z4XFvukDELlwX5HXt0AUJFpRsiK2InPc0OszOkk97yBIi26pLTahzICIvhrbfPPNrYAAfW4vZsLotRa9IhODevIqAyJaJ5RMp+cnnngi4psjRvQKTJWejKMF0Kav0ooAIpIjLZTeY489rNoi2rboootGY8eOtVGDVB5RBwBRijVOESH8DwCRkwgal1keh2bMmBGRP3T9c/my2cRg3/rfgyrkzgmhAhzgxy3EuydTU7mSFG4xP8U93sH63nvvZS+//DLjn+cr66SdofmrMcZnSNhee+3F9t13XyZ2GlYWkCJ1u0GXYadqaibxkYNDdvLJJzPaGToZqM+HHXYYo92baSdmEV566SV2+OGHM75nj4iKr5TngAMOYHwdUPy8zjrrMNpFOhk4uGIckDIOyhjfODPeAZsvam/LRnXxWaSYTtau1q47VbcRkh74uiHGX/mxKVOmML7oWkrpuuX7F7EjjzyS7b///owvyu5KcLgT+vOf//zHoVRXVto5nP4Q/HNg6NChjJ+Vh52q/bO2FjXKO1XntV/ybXx2uXT8wNEdBUXifetwQ3tkRfQBiJKkODiOgREN9hz5t0AQHV/BF1Yns9fqmc++ML6Amr3wwguMjrUgsMLXBDF+PpsR/L3//vuM+MV/IcVHfBCAyjNQ80XpjI7j4AusGdVJQIr+8tTlSzB81igGRtQ/vqYqPsaEdIF4IwBNXlqiPJ8hylUFOVTiTSftT9XQOtLH0R0qSSNOcEAehwgQ9e7dWyRZX+loIB+AyLf9ARBZi1Cd0bdA1FTmxcqKGAIQmWgjDRzwyQEAIj/cDOF/AIj8yKautcjjEABRQsohDDJBwvjYJPqyIgIQGdUCiSXnAACRHwGF8H8ARH5kU9da5HEIgCgh5RAGmSBhfGwSfVkRAYiMaoHEknMAgMiPgEL4PwCiLtnQa+uZM2d2Rcy/++c//xm/Ok4lNCBCHocAiBICD2GQCRLGxybRlxURgMioFkgsOQcAiPwIKIT/cwFEb7zxRrzOTNUb+nCif//+qqTMOBpoJ06cqMy30UYbsQEDBijTfEcuueSS7L333ktVS+sM+f5dqfgmRMjjEABRQuIhDDJBwvjYJPqyIgIQGdUCiSXnAACRHwGF8H8ugIifZcfWWGMNZWf42YfsiCOOUKZlRfINTtnIkSNT2fr27Rt/Dcu3fEilhYgAIEpzVR6HAIgS/AlhkAkSxscm0ZcVEYDIqBZILDkHAIj8CCiE/3MBRNSLjTfemD3++OOpDn3rW99KbUuRyqSJ0G1X8f3vf5/xcxk1pfxHAxCleSqPQwBECf6EMMgECeNjk+jLighAZFQLJJacAwBEfgQUwv+5AiKaCeJnH6Y6xI96iWdzCFS4BNrmgR+boyzCd3hn22+/vTItRCQAUZqr8jgEQJTgTwiDTJAwPjaJvqyIAERGtUBiyTkAQORHQCH8nysgog1Nl1tuOfbZZ5+lOnXVVVfFG5WmEgwR559/PuMHLKdyEA3ap8vH/jWpyjURAERpxsjjEABRgj8hDDJBwvjYJPqyIgIQGdUCiSXnAACRHwGF8H+ugIh6sttuu7HRo0enOsXPO2S33XZbKt4UwQ8+Zo8++mgqywknnMB+8YtfpOJDRgAQpbkrj0MARAn+hDDIBAnjY5Poy4oIQGRUCySWnAMARH4EFML/5QFEY8aMYcOHD091inYxpkGzX79+qTRVBH21Rruhq/wbHU+z1lprqYoFiwMgSrNWHocAiBL8CWGQCRLGxybRlxVR5TCMjEIiOFAiDgAQ+RFGCP+XBxB9/vnn8WszOu4lGeh8PH5wcDJa+axbj0Rn+j311FPKMsnIxx57jP373/9m06dPj4/h+eCDD9hKK60Un8W46qqrsnXXXZfZfqXmCojIL9OZk6qw5ZZbZh55Q2VVvp0fQm39qpCOEfrXv/4Vb4dAZxLSkUR09A4dubPFFlswqovWd+UN8jhUN0BEzC8UfJ8269qYJtGXTxl25RPygwNl4gB3xnQ6cYTT7otJJYT/y3vaPT8AOZapkK247rnnntad5F+mKeu44IILjHXwQ5IjfkhzxGeQlOVFW+i61FJLRb/73e8iDuKMdVLiEkssoayP70OkLMvXUSnzE10behyoKMvz8w2V9ORIDgCjnXfeOeLnTirrEDzgezhF/EDp6NNPP5WLW9/L4xAHRLlsmJ/daE3PlNG3/uMsM64lRUKIX2i69sjInCuJLhviwYHScwAzRH5EFML/5Jkhot488cQTjDZNTAaajaGZBDqQ1xRocTbNYtBBx3Kg2Qx6lbb00kvL0a37t99+m9HsC80KuYSvfe1rjF71rb766tpirjNENFO20EILKeujtKyZGTqwONl/qowOfF5sscWU9VLkNddcw4455hjlrtq6QrS1wV//+le2zDLL6LIo4+VxCDNECbjmG6Elqs98bBJ9GZlnMgYZwIESc4B72vhXLGaIigkphP/LO0NEPeGbNCpnJ26//fbMjvIv0pRladZDFziIspoVEvqWvHIAZ5y5qcIM0T777KPkW7Kvquevf/3rET+aRMdeZbw8DtVthgivzJQit48M4ZB01GVF1OVBPDhQBQ4I5wxAVExaIfxPEUBEr2KEbOXrgQcemNnRXXbZRVmWr0HSlt19992VZRZZZJHo5JNPjsaOHRvxWaDopJNOivjMjTLvGWecoa2/7IDozjvvVPaJb00QHXfccRGlT548OeKbWUZ85k+Z19R/FWPkcQiAKMGhEAaZIGF8bBJ9WRGNTEEiOFByDojBEoComKBC+L8igIjWsajWsPBXT8aZGNID/kVaasDmi4EjWh+kCvyMMS3IUc1I8c//U/WTHvbp0yeaM2eOikSp1xDRmiT+2i/VJ1qHxDewTPWH1u0ceuihqfwE+oj/tkEehwCIElwLYZAJEsbHJtEnReRrL1IKLQYXXOe9hgEfqsMHACKje8tMDOH/igAiajDfSVrpo+69915tf26++WZlmYMPPlhb5rLLLlOWWXnllbVl6BWRyj/w9UfKMmWeIbrooouUfTnggAOUfaFI/sVd9KUvfSlVju/vpC2TTAAgSnJEeg5hkFL1mbdNog9AVJ2BXuV0EZeWHwBRposzZgjh/4oCouuvvz414JLuH3nkkdq+7L333soyEyZM0JZ58cUX45mQv/zlLxFfVBzxT/bjr6duvPFGbZm99tpLSYdvKqksU2ZAxLcQUPblySefVPZFRNLrw6Qv4gurrb86qzMgwldmXDOKhBBfeejaI6/u50qpy4Z4cKD0HBgyZEjcRg6IcrWVvliiL3I6aX+qhtaRft6vzAR/iCf0tVhStnT0Bu0NJL4wFPn559/xF2S0X5AcVlllFUbnmvkMP/nJTxj/hD9V5TnnnMM4UEjFl/UrM/oSjb/qS32RRrwl/tOGmLpA+0JxYJhK5gBTe4acnFkeh+r2lRkAkSzpHPeddIiyInK0n6O1KAIOlIMDYlBMDpq2rQMgmsepEP6nKCCilh100EHsyiuvTInzkUceYZtssklb/F133cX4l2RtcfRw2mmnsdNPPz0VbxtBPpI+dac/AhD0N3LkSPbb3/42VcWpp54apyUTygqIdAfg8hkt5REqcr9oe4If/vCHclR8//e//53xfaBS8ckIeRyqGyDCV2ZiHjHnNcSUta4p8lSlLg/iwYEqcIA72XjaHq/MikkrhP8p+sqMesQHzdRrGZI5P48s1WE+OKfy0lpJPuin8uoi6NPxX/7yl9F+++0X8T2JIn78h3Jxt9C75PXnP/+5suqyvjIbN25cimfJPrk+cwCr5EEyUh6HsKg6wZ0QBpkgYXxsEn1ZEY1MQSI4UHIOCGcNQFRMUCH8nw9ANHfu3Igfl5EatPlrsLYO05dPqkW+gwcPbsuneyAgxGeSIvoaTehUnmvVABGf5SrUXxWP+Gycjs1t8fI4BEDUxpooCmGQCRLGxybRlxXRyBQkggMl54BwyABExQQVwv/5AETUK/4aSjloP/30061O62aSLr/88lYe3Q0dk7HpppsqaQj9sr1WDRDR3kG2fbPN94Mf/EDH6rZ4eRyqGyDCGiKuLUVCiHf4uvbI7265huqyIR4cKD0HsIbIj4hC+B8fa4iod7p1LrSOh9bsUFAtcqYFwW+99VZ8IGmcSfNPVVZkpaM8dtxxR8ZfnTFaB0QL8OnYjCuuuILxTQpFttaVAyLGQUbrWdx0cg0RB3jxYmiVb08e3XHdddcx/npQNLN1pfbS+q08gW9JwPgn+5lF5XEIa4jasCJmiEL8QkuwuPUoI/NWJG7AgQpygHvd+BcuZoiKCS+E//E1Q0Q9o1dfQtbi+s1vfrPVadXGgnvssUcrXXfDT3NP1Svqp5kpXTjqqKOU5XRlfK4hevfdd3XNiuNpLyTRh+Q1ebjrgw8+qMxLn8+HDvI4VLcZIiyqLqg9IRySrkmyIuryIB4cqAIHhMMHIComrRD+xycgUm2eSDtZ00A6depU5aB+xx13ZDKFjqIQOiRfswAB/8JNWc7XKzNaE0ULwuU2iXv5VaGqg3/729+U5ah8EhDxGTRlXqJNrxJDBnkcAiBKcDqEQSZIGB+bRF9WRCNTkAgOlJwDYpAAIComqBD+zycgmjFjhvJIjj/+8Y/RpZdemhrUCdDQkRRZgb5WEzokX3fddVdtUToCRHeemS9ARMT5fkvKtt16663atlEC7cot90W+TwIiyt+3b19l/ueff56SgwV5HAIgSrA5hEEmSBgfm0RfVkQjU5AIDpScA8LZAxAVE1QI/+cTEFHv9txzz9TATQt4VQezHnPMMVYM+d73vpeqk3SKaOkCXz+kLEPlTjzxRGUx11dmVInqNSHRGDZsmJIGRb755psR31tL2z4VINLNdvG1VVo6lDBlypT4wNuHH3443tqAbNAlyOMQAFGCcyEMMkHC+Ngk+rIiGpmCRHCg5BwAIPIjoBD+zzcgUp3ITvsELb300ikA8NRTT1kxRjdDRMdZ0GurZKCv2XSzQ6SLtBeSKuQBRPvuu2+qX0SDTqB/4IEHUmTokFodiBJ2ogJEd999t5LOYostFtErNVWgs8xU2yEsuuii0SuvvKIqkoqTxyEAogR7QhhkgoTxsUn0ZUU0MgWJ4EDJOSAcPWaIigkqhP/zDYgIoPCjPJSDt9ADuq699trWzKBNBOWy8v2IESNaoGjatGnxGWcysFHNxKy22mrKs7zkcjKN119/XdvW3/zmN9q2EW1+TEj06KOPRs8880w0atSoaI011ojz9+/fP6KDaWU64p6AhyroDtIdOHBgNHny5LYib7zxRqQ7M+7QQw9ty2t6kMehugGiHmRQnOkIFeDA+PHj409JqalcYSvQYjQRHFBzQHx2zx2qOkNGLH1GTX8I/jkwdOhQxg9VLXx0htyy448/nv3qV7+So1L3/MR1xmd+UvGqCDp+ggOJ1FleIi/fqJHxDR8Z5ZOD+FT92muvlaPjew4i2IEHHsiWXXZZdsghh8Rxrp/dU6HZs2czPlPFOACJ67D9d+GFF7IxY8Yw+qw9GTgAYyussEIymnHQw9Zff33GN8JMpZGNDRo0iK2zzjqMvyZjfG1RKg9FcCDG6BwzPmOnTE9GJj+7T6bbPNPRO3zGzCZrZ/OYkKBNWohfKDZ0RZ4m0ZeRueg/ruBAFTnAvVz8SxgzRMWkF8L/+Z4hoh7SF1ZC5qorvU6iGQyXcMoppxjrTNKhXbLplZFpLRGVof6LkGeGiMrSxpJJ+qbnjTbaKJ7V4me6KctxwCKalLpyIGV8HWiiu9RSS0WPPfZYqk5ThDwO1W2GCJ/dmyRvkRbCIenIyoqoy4N4cKAKHBBOGoComLRC+J8QgIh6ud566ykHe9IFevXjGuirsc0331xbp9AxutICZLGuhs/gRPSKTE6X730AInpNeNxxx2k/wZfp0foh+hqPgm79UfL1V5JXlG7ir0xP3NN6qxdeeCFZVeazPA4BECXYFcIgEySMj02iLyuikSlIBAdKzgHhlAGIigkqhP8LBYh+/etfa0HI9ddfn4sRdGYazcbwV1vKumlW6Pzzz48IBMmBNkHcdtttU2VojY+8nibvDJGgde+990b8tVWKDun/8ssvH5177rkR321cZI+OPvpoZV6bWRzaf4iO9Nh4442jfv36KeshukOGDIluueUWq+0NWg2TbuRxqG6ACEd3cA0pEkJsna9rj/zuluunLhviwYHSc0CsIeKAKFdbaQ0CrSHqpP2pGlpH+r6O7lDxK1QcraHhC6gZn/FgtN6GL+JmtCaIL9RmQtdUtPnXW/ERI7Tuh9YLcQAVZG0a0Xn22Wfj9g0YMIDxL73YWmutFYQW9ZPGh9dee40999xzbPr06fG6KDrGZMUVV2REv0iQxyFaA0hHrbiGPn36eFlD5Nv+AIhcJZnI71sgierbHmVFBCBqYw0eKsYBMUgBEBUTXAj/U0VAVIyLKO3CAXkcAiBKcC6EQSZIGB+bRF9WRAAio1ogseQcACDyI6AQ/g+AyI9s6lqLPA4BECWkHMIgEySMj02iLysiAJFRLZBYcg4AEPkRUAj/B0DkRzZ1rUUehwCIElIOYZAJEsbHJtEnRdxmm22wB5FRI5BYJQ7glVkxaYXwfwBExWRS99IARAYJhzBIA7lUUpPoAxClxI+IinMAgKiYAEP4PwCiYjKpe2kAIoOEQxikgVwqqUn0ZUXknz6meIEIcKAqHOCf/sZNBSAqJrEQ/g+AqJhM6l5aHofwyiwh7RAGmSBhfGwSfVkRsYbIqBZILDkHsIbIj4BC+D8AIj+yqWst8jgEQJSQcgiDTJAwPjaJvqyIAERGtUBiyTkAQORHQCH8HwCRH9nUtRZ5HAIgSkg5hEEmSBgfm0RfVkQAIqNaILHkHAAg8iOgEP4PgMiPbOpaizwOARAlpBzCIBMkjI9Noi8rIgCRUS2QWHIOABD5EVAI/wdA5Ec2da1FHocAiBJSDmGQCRLGxybRlxURgMioFkgsOQcAiPwIKIT/AyDyI5u61iKPQwBECSmHMMgECeNjk+jLighAZFQLJJacAwBEfgQUwv8BEPmRTV1rkcchAKKElEMYZIKE8bFJ9GVFBCAyqgUSS84BACI/Agrh/wCI/MimrrXI4xAAUULKIQwyQcL42CT6siICEBnVAokl5wAAkR8BhfB/AER+ZFPXWuRxCIAoIeUQBpkgYXxsEn1ZEQGIjGqBxJJzAIDIj4BC+D8AIj+yqWst8jgEQJSQcgiDTJAwPjaJvqyIAERGtUBiyTkAQORHQCH8HwCRH9nUtRZ5HAIgSkg5hEEmSBgfm0RfVkQAIqNaILHkHAAg8iOgEP5PAKKVVlqJ0R8COCBzYObMmWzSpElxFACRzBl+H8IgEySMj02iD0BkVAUkVogDAER+hBXC/xEgGj9+PMOPLj8yqmMtZL+kHwBECemGMMgECeNjk+gDEBlVAYkV4gAAkR9hhfB/YoZoq622YnSPAA7IHJg6dSq75ppr4igAIpkz/D6EQSZIGB+bRB+AyKgKSKwQBwCI/AgrhP8TgOi0005jp59+up+GopbacEAehwCIEmINYZAJEsbHJtGXFRHT2Ua1QGLJOQBA5EdAIfwfAJEf2dS1FnkcAiBKSDmEQSZIGB+bRF9WRAAio1ogseQcACDyI6AQ/g+AyI9s6lqLPA4BECWkHMIgEySMj02iLysiAJFRLZBYcg4AEPkRUAj/B0DkRzZ1rUUehwCIElIOYZAJEsbHJtGXFdHIFCSCAxXhwIcffpirpQsvvDBbcMEFsYbx449Z3759c/FQVwiASMcZxBMH5HEIgCihE00CJImux4+d7L+siKq2IA4cqBoHAIiKSSyE/wEgKiaTupeWxyEAooS0QxhkgoTxEfTdfiESv+bOnWvkqUvi7NmzWe/evV2KeM3rk/5rr73G1lxzTbbzzjuzm266yaqdPulbEUxkaip9zBDNU4QQ/g+AKGFkeGzjAABRGzvaH0IYZDsF8xPoAxD5AmRHH300u/LKK2OFmzJlCltxxRXNysdTmwpIBGO6q/8ARPMkEML/ARAJ7cZVxYFaA6JZs2ZFqk4jrp4c+OSTT1I70Pbs2dPrrFFVOUfHFHB7iJt/wgknsBEjRlS1K7VvN60foj8E/xwYOnQomzBhAsM+RP55W4cak4AoT5/oB02vXr3yFA1apgf/WqkQIArxC8Wlx6CPGSIfM0TXX389O/zww1uq179/fzZ9+vTWs+6mu2ZIRHuaSh8zRPM0IIT/wwyRsC5cVRxIAqI8/rdPnz5eAJFv/QcgUkncIc63QBxIx1ld6VN+rCFKc3mnnXaKfxUPGzaMkcG///777NJLL2X77rtvOrMU01RAIljQXf0HIJonAVf7F3IzXQGITNxBGgCRQQdCGKSBXCoJ9DFDlOcXiqxIkydPZoMHD46jJk6cyC688ML4rJ4tttiC3XXXXXLW1H13AQLRkKbSByCapwEh/B8AkbAuXFUcACBScWV+XAiDNJBLJYE+AFFRQHTYYYexG264ga277rps0qRJ8d/6668f69pDDz3E1llnnZTeiYimApLu7j8A0TwJhPB/AERCu3FVcQCASMWV+XEhDNJALpUE+gBERQARvRqjT+3petVVV7EDDjgg1rH11luPPf3002yfffZho0aNSumdiAAg6p5tFwCI5mlgCP8HQCSsG1cVBwCIVFyZHxfCIA3kUkmgD0BUBBCJxdS0iHrmzJkt/br66qvZgQceyCiePsGnqyoAEAEQ+d4pWqVnurgQ/g+ASMdtxBMHAIgMehDCIA3kUkmgD0BUBBDR7BBtyEh7ENHaITksvvjimYurAYgAiACIZKvBfd05AEBkkDAAiRsgMbAyV5Ir/yk/vjKbx2raa4W+LqPw6quvMtqHSA7HHHMMu+iii+INGmmWSBUAiACIAIhUloG4unIAgMggWdcB2VBVriTQdwNkAERdaiYWU9On9mPGjOlKmH83depUtvLKK8dP9LUZfXWWDABEAEQAREmrwHOdOQBAZJAuAIkbIDGwMleSK/8BiOaxWZxbRk+jR49mu+66q5L/FD927Fjt4moAIgAiACKl6SCyphwAIDII1nVANlSVKwn03QAZANE8NTv77LPZOeecwwYOHMhoJkgXaOZo+PDhcbLqfDMAIgCiugIieoWcfI2ssxPEN4cD9PEJbU9CAafdJ+QOQOIGSBLsK/zoyv8vvvgidZZZkUa40i9CS1U2L/1BgwaxadOmWZ3XRIMC5f3Zz37GTj311LZm5KXfVkmBh6bSp3OQ6Ay+pvZfqEyI/tNXZuPHj/fqJ0R7ca0HB3r06BHrBwBRQp4hDDJBwvgI+tUCZEZh5kjMI3951mfGjBmMviYzhdNPP52NHDmSETCixddyyENfLl/0HvSh/75nqMRn91tttRWjewRwQOYAzahfc801cRQAkcwZfg+HDIfs2yEnVMz4mEf/hgwZwug9+P77789ov6GsQFPEAwYMiLPJmzdSRB76WfRc0kEf9ufb/gQgwmn3LpbYnLxYQ2SQNRwyHLJvh2xQt1SSq/7JX47df//91r+AaQdr+lVEgwWVE8GVvijn6wr6sD/f9gdA5Ms661kPAJFBrnDIcMi+HbJB3VJJrvon9hYS55alKtREyE5A3rPIlb6m+tzRoA/7821/AES5zbERBWVfiFdmCZHDIcMh+3bICRUzPrroH736on2F6Jp89WUkMj9RnG8m72rtQt+Ghmse0If9+bY/ACJXK2xWfgAig7zhkOGQfTtkg7qlklz0Tz6fjF6dZS2mThIT5akczRLR1YV+sj4fz6AP+/NtfwBEPiyzvnUAEBlkC4cMh+zbIRvULZXkon/rr79+vH+G7WLqJDGaWaIvzd5///3WDJML/WR9Pp5BH/bn2/4AiHxYZn3rACAyyBYOGQ7Zt0M2qFsqyVb/aCMxAkQU5DVAqQozIsQaJHp9NnHiRMwQ8bPxqiD/DLHmTrbVv9wEMgqGoA9AlMH0hicDEBkUIIRBGsilkkAfA5LNgCy+EqO9Vcig84bkV2obb7wxAEHfvnnZWbgc7N+//QMQFVbLWlcAQGQQLxySf4dkYHcqCfzP5r9pH6EUQy0ixIBBr94uueQSACIAIgutCZMlhP0L/cY+RGFkVvVaAYgMEgxhkAZyqSTQzwYEKaZ5jKgC/y+88EJ27LHHZp5bZssWsbia8r/xxhtsueWWsy3qPV8V+O+901KF6L9/+wcgkhQMtykOABClWNIVAYfk3yF1cTf7DvzP5j99ak+vunz+4qXF1XS+2XnnncdGjBiRLahAOSD/bPkHYn1cbR35D0AUUmOqXzcAkUGGdXQIhu6mktD/cg9I8rllRRZTJwUvzjcbOHBgDLaS6Z16hv6VW/9C60EI+QMQhZZatesHIDLIL4RBGsilkkAfA4JpUfWuu+7Kxo4dy4YNG8YIHPkK8uLq0aNHM6LTHQH6D/036X8enQQgysO15pQBIDLIGg4ZDtm3QzaoWyrJpH8yaHE5tyxFRBMhvlzzDbY05JTRpv4rC3iOBP362T8AkWcjqVl1AEQGgcIh1s8hGsSdSiqz/MWeQaFea8mOwefruBSTDRFl5r+h2d6S0H///geAyJt61rIi2e/hLLOEiOGQ/DukBIuNj+C/nv8DBgyIzy274IILGIGjEEEsrpbPNwtBR1cn5K+Xv45nPuPryH8AIp8aUr+6AIgMMq2jQzB0N5WE/pdzQBKfxvfv3z9e9Ox6bllK0JoI8Uk/1T9jxgxNrnDR0L9y6l84ibfXHEL+AETtPMZTOwcAiNr50fYUwiDbCGQ8gD4GBNUapiFDhjAy3LznlmWoXStZdb5ZK7EDN9B/6L9K/4uongBERepA2WZwoHavzGbNmhU1Q3TopY4DvXr1YnPmzNElVy5+8uTJbNNNN43bTeeN0bljIYNYXL3OOuuwRx55JCQp1A0OBOfA0KFD2YQJE4LTAYHqc4AAUZ6w8MILMxp3yhZ6RDwUaRR+oeIXqu9fqC76qNI/AVCKnltm2w754NhOADC5Xar+y+mh70G/fvZP+kwznzZh9uzZrHfv3m1Z586dyz799NO2uFAPn332GVtooYVCVZ9Zb9Ppb7TRRin5ZzKNZ+jTp48XQOTb/wAQ2UjPkMe3QAyklEmg3z4gkSOnnanpetVVVzECR50I4jVD6Fd0yb5A/u3yT/In9DP4n+Y/zTZ/8sknoVkf168CZB0hPJ8I6KcBsQ3/AYhsuJQjDxxS2iHlYGPuImXjv1jkTIupbX/l5u68VFAs4qbF1fQJfqhF3BLJ+LZs/E+2L/Qz+l8++wcgCq31XfVXFZABEHXJ0OsdHGL5HKJXAWdUlpS/OLesOz6DJxD0/vvvs5Cf+SfZkex/Mj30M+jD/pKvzAGIQltdV/0ARH7tD6/MunQr1x0GBL8K6SoEmf/y56DdsVGi2AiS9iYi+p0Icv87QS9JA/TLo/9J2XTiWSV/AKJOcH4eDQAiv/YHQFRQd1UOoWCVTsVBv8sgxGLq7jpKI/RRISrFgPy75K/iT+g48D/NfwCi0FrXVT8AUVr/urjjfgdA5M6zthJwiH4Vso25Fg+C/zIY6c7DVkMdJqtjhei/Lj10POiXQ/9Dy1lXv0r+AEQ6bvmPByDya38ARAV1VOUQClbpVBz05xnE6aefzkaOHMlCnVtmK5QxY8aw4cOHx9k78doO8vfrEG3lLPKB/2n+AxAJ7Qh/BSBK618RrgMQFeEeLwuH6FchXcUh+C8WU3dyQbOureJ8s9NOO40RUAsZRP9D0jDVDfrl0H+TjEKmqeQPQBSS4+11AxD5tT8Aonb9cn5SOQTnSgoUAP2P2c0338wOPPDAmIs0Q9OpT951YqNP8OmvE4urIX+/DlEnU108+J/mPwCRTlv8xwMQpfWvCJcBiIpwj5eFQ/SrkK7iIP7vvPPO8bllrmVD56fXd/TlGwGjUAH61/36l/zsPJSsVfWWUf4ARCpJhYkDIPJr/wBEBfW0jA6pYJecind3/59//nm2xhprOLW5U5nvv/9+RjtYhwzdzX/Q9+uQXXWljPwHIHKVYv78AER+7Q+AKL8uxiXL6JAKdsmpeJ36L+9jZHvEX5367yT4+ZnRf78O2VUGZeQ/AJGrFPPnByDya38ARPl1MS5ZRodUsEtOxevUfwAiJ9FD/zkH6qT/7tJX9x+AKA8n85UBIAIgatMcOCS/CtHGXIuHOvEfgMhC4IksdZJ/omtWj+h/2v/Qafeff/65Ff+KZqJDZOlcrO4KoJ+P/wsuuCDr2bNnYbH5tj/MEBUUiW+BuDYH9NMO2ZWHIj8AkeCE/RX650//7LnelRP8B/+xqL9vl0EUvAMgKshAOKT6OCQAIndjgP7XR//dpa9+ZZannrxloH/QP5+AEIAoryXOLweDrI9BAhC5GwP0vz767y59ACLof730H4AojxeQysAg6mMQAESSYlveQv/ro/+WIm/LBvlD/j5naNqUy+LBt/4BEFkw3ZTFt0BMtFRpoO/PIQEQqTTMHAf986d/Zk6rU8F/8L9OgESt5fpY3/oPQKTntVWKb4FYEZUygb4/hwhAJCmW5S30z5/+WbK8LRv4D/4DEGFRdcspwCHAIfhyCABELbOyvoH9wf582Z+10kkZoX/QP5/6hxkiybjy3MIg62OQAETuFgD9r4/+u0sfi6qh//XSfwCiPF5AKgODqI9BABBJim15C/2vj/5birwtG+QP+fucoWlTLosH3/oHQGTBdFMW3wIx0VKlgb4/hwRApNIwcxz0z5/+mTmtTgX/wf86ARK1lutjfes/AJGe11YpvgViRVTKBPr+HCIAkaRYlrfQP3/6Z8nytmzgP/gPQIRF1S2nAIcAh+DLIQAQtczK+gb2B/vzZX/WSidlhP5B/3zqH2aIJOPKcwuDrI9BAhC5WwD0vz767y59LKqG/tdL/wGI8ngBqQwMoj4GAUAkKbblLfS/PvpvKfK2bJA/5O9zhqZNuSwefOsfAJEF001ZfAvEREuVBvr+HBIAkUrDzHHQP3/6Z+a0OhX8B//rBEjUWq6P9a3/AER6Xlul+BaIFVEpE+j7c4gARJJiWd5C//zpnyXL27KB/+A/AJHHRdWzZs2K2iwMD43jQK9evdicOXMa1+9kh8ePH8923HHHOJrbRTIZz+AAOAAOgAM15gBmiAoKF7/Q6vMLDTNE7sYA/a+P/rtLH4uqof/10n8AojxeQCoDg6iPQQAQSYpteQv9r4/+W4q8LRvkD/nX6ZUdAFGbebs/wCHUxyEAEEH/XTkA+6+P/bvKnvJD/vWSPwBRHiuQysAg6mMQAESSYlveQv/ro/+WIm/LBvlD/pghkkwCBgGDqItBABBJhm15C/uH/dfF/i1Vvi0b9L9e+o8Zojb1dn+AQdTHIACIoP+uHID918f+XWVP+SH/eskfgCiPFUhlYBD1MQgAIkmxLW+h//XRf0uRt2WD/CH/Os0QAhC1mbf7AxxCfRwCABH035UDsP/62L+r7Ck/5F8v+QMQ5bECqQwMoj4GAUAkKbblLfS/PvpvKfK2bJA/5I8ZIskkYBAwiLoYBACRZNiWt7B/2H9d7N9S5duyQf/rpf+YIWpTb/cHGER9DAKACPrvygHYf33s31X2lB/yr5f8AYjyWIFUBgZRH4MAIJIU2/IW+l8f/bcUeVs2yB/yr9MMIQBRm3m7P8Ah1MchABBB/105APuvj/27yp7yQ/71kj8AUR4rkMrAIOpjEABEkmJb3kL/66P/liJvywb5Q/6YIZJMAgYBg6iLQQAQSYZteQv7h/3Xxf4tVb4tG/S/XvqPGaI29XZ/gEHUxyAAiKD/rhyA/dfH/l1lT/kh/3rJH4AojxVIZWAQ9TEIACJJsS1vof/10X9Lkbdlg/wh/zrNEAIQtZm3+wMcQn0cAgAR9N+VA7D/+ti/q+wpP+RfL/kDEOWxAqkMDKI+BgFAJCm25S30vz76bynytmyQP+SPGSLJJGAQMIi6GAQAkWTYlrewf9h/XezfUuXbskH/66X/mCFqU2/3BxhEfQwCgAj678oB2H997N9V9pQf8q+X/AGI8liBVAYGUR+DACCSFNvyFvpfH/23FHlbNsgf8q/TDCEAUZt5uz/AIdTHIQAQQf9dOQD7r4/9u8qe8kP+9ZI/AFEeK5DKwCDqYxAARJJiW95C/+uj/5Yib8sG+UP+mCGSTAIGAYOoi0EAEEmGbXkL+4f918X+LVW+LRv0v176jxmiNvV2f4BB1McgAIig/64cgP3Xx/5dZU/5If96yR+AKI8VSGVgEPUxCAAiSbEtb6H/9dF/S5G3ZYP8If86zRACELWZt/sDHEJ9HAIAEfTflQOw//rYv6vsKT/kXy/5AxDlsQKpDAyiPgYxadIkdswxx8TSJXBkEyD/+sjfRt7JPJA/5F+nGZKkfmc9103/AYiyJJ6RXjeFyOhuKhn9x4CAAaFvyi46FQH7g/3B/vzZX60BUY8ePTrll0AHHAAHwIGYA1EUdYwTAEQARABEHgHRrFmzOme9HXMT8wgtssgiHaYIcuAAONB0DnCf2nQWoP/gQCU50IgZok7+YqukFqDR4AA4UIgDeRbkFyI4vzBmiDBDhBkijzNEHCwUmiEqs0GKV2YFu+jDb6EOcAAcqDEHAIi6R7hlHn86wRH03y8gxgxRJ7QWNMABcKDWHAAg6h7xAhD4BQSuUqwb/wGIXDUA+cEBcAAcSHAAgCjBkA491m1AdmUb+u8XEAIQuWog8oMD4AA4kOAAAFGCIR16BCDwCwhcxVY3/gMQuWoA8oMD4AA4kOAAAFGCIR16rNuA7Mo29N8vIAQgctVA5AcHwAFwIMEBAKIEQzr0CEDgFxC4iq1u/AcgctUA5AcHwAFwIMEBAKIEQzr0WLcB2ZVt6L9fQAhA5KqByA8OgAPgQIIDAEQJhnToEYDALyBwFVvd+A9A5KoByA8OgAPgQIIDAEQJhnTosW4Dsivb0H+/gBCAyFUDkR8cAAfAgQQHAIgSDOnQIwCBX0DgKra68R+AyFUDkB8cAAfAgQQHAIgSDOnQY90GZFe2of//v73zjrWiaMP4XK6UCypiBYEPsFdEECso2MAYS2LDgrFFNMaKojEK6h8aey+gMaLRqEHF3lBjBxvYsKKooCCgKBI6+8273j3ueXdmz77nzO69zH0muTk7s+/uzDwzO/O7s7MzboEQQCStgbCHAlAACjAFAERMkIK8AAK3QCAtNt/0BxBJawDsoQAUgAJMAQARE6Qgr28dslQ25N8tEAKIpDUQ9lAACkABpkAciJYuXcrOZvO2bt1atWrVKptxoxU6RLcdokh8bQz9/dIfQCR9AmAPBaAAFGAKxIFo0aJF7Gw2b0NDg6qvr89m3GiFDtmvDllU+NoY5e+2/AFE0hoIeygABaAAUwBAxAQpyAsgcAsE0mLzTX8AkbQGwB4KQAEowBQAEDFBCvL61iFLZUP+3QIhgEhaA2EPBaAAFGAKAIiYIAV5AQRugUBabL7pDyCS1gDY567AZpttplauXJmIZ/r06WrttddOhCOgWAV69+6tFi5cmIj0gw8+UJ07d06EVxvwwAMPqNGjRycuHzZsmLruuusS4U0ZACBqGvV965ClKiL/boEQQMRq4KpVq9Rrr73GQrN71113XdWjR4+wY6irq8t+ISxLCtDXNiYg+uuvvxfqgHMAAB51SURBVBTpuya5V155Jffktm3bVu2zzz65xxNFsMEGG6g//vgj8pZ+f/nlF9WtW7eSv9aD22+/XZ1zzjmJ25x66qnqvvvuS4Q3ZQCAqGnUBxC4BQJpKfqmP4CI1YC///5bdezYkYXKvdRJde/eXfXs2VMdd9xxavjw4WqttdaS36gFXuELEAVBIP6Mupri3mSTTdScOXOqubSqawBESdkARElNigjxrUOWaob8uwVCABGrga6AiN1W9erVS11yySXqpJNOUm3atOGn4Y8pACCKiZHhEECUQaScTQBEOQtsuT2AwC0QWGS2BvumP4CIFXVeQBRFQ682Jk2ahNGiSBDDL4DIIEpKEIAoRZyCTgGIChKaReNbh8yyV9GL/LsFQgARq3J5AxFFN3LkSHXDDTewmOGNFAAQRUpk+wUQZdMpTysAUZ7q2u8NIHALBHalzWd80x9AxMo5DYgGDx6sunTpwq74z7tixQr166+/qp9//lnRBNM0N2HCBHXEEUekmbTYc74AERXgySefXLEcf//9d/XCCy8Y7Y466ijVoUMH47kokOa83XLLLZE391/MIUpKDCBKalJEiG8dslQz5N8tEAKIWA1MA6IXX3xRDR06lF1h9r7//vvq8ssvt36xRq/OqBGFSyrgExAlc5cMee+999Ree+2VPKFDZs2apbp27Wo811SBAKKk8gCipCZFhAAI3AKBtMx80x9AxGqAKyCi2y5fvlwNGDBAffjhhywWFX7J9ueff6osn+bTZpFff/21+vLLL8O/n376Sa233nrhp/0DBw4M48jyBRuNYFHny91GG22ktttuu7LgH374QT399NPqxx9/VHPnzlWbb7652nHHHVWfPn3UtttuW2abxUNfXH3zzTeK1qohPf7555/wK7yddtpJHXLIIWUTzWnSOaWVO8ln90Vr9sYbb6jJkyerzz//PPz0nL4sJK2yuCKAaMqUKeq7774LAYtGL6me0xeQVK5bbLGFonJYZ511siRXZQWiL774QtGyAxTf/Pnzwzq22267qf79+2eKy+Vn967qg00gAJFNmXzDfeuQpWoh/46BUHdUNbnFixfXdH2tF6fFrytXQH8Spzvd8Jro2vivHiGS3Cq01a9CrPebMWNG6v306EBw8MEHB3oHbOs9KH2dOnUKrr322mDZsmWp97Pl7YADDihdp+En0K/yUuPU68AEGmhK11Q6mDhxYpjGuJbx4w033DDQr3xKt9FLFhjzS+mv5FxrphcgNKYl0mz16tXB+eefn7DRCwdWSmrp/Lvvvpu4PtKH8lOtW7JkSaDX6wl22GEH6/2jeKgM7rjjjkCDaMXo1l9/feP99Ovi8NpPPvkk0CNeRhuKj+oz1SH9D0NqXLfddpvxHnRtVue6Ptji1UBcSqve3DWo5k+vvWW7vTU8rf2zXuTwBOJvvv2fw2K23sq38pfRgkGW5ixI1Ngbkm0NskED3asaIJo9e3apoYzSE/0+9dRT1nToVXoDPQpkvTa6R/xXryAc6PVorPfUi04GekQqcc++ffuG18ycOTPYcsstE+fjcUTHZKdHkaxxRScI1CoBXXTPE088MSDAaN++vTENlYAoL82i9MV/d9lllzCLl112mTGtTQ1Ev/32W+ayjOdrm222CfRoZFR8xl8bEOlRoODZZ58N9JwnoybxeOiYoDKtTGsFojzqg1EQHQggsimTb3hz7n/yzfm/d0f+3QIpgIjVWtdARB0T7wgi/+uvv85i/9d7/PHHW6+JrrX96tdZAY1q2Jxp9EW/NglHBrbffntRvEcffbQtmjD8wgsvFN2P8nTXXXcF+tWN8bq0zjNPzfQrvER6ttpqq4BGRBoaGhLnKB9NCUQLFizINCpkq0P6lVbqSJENiPTrwswwFMW98847B7aRkVqAKM/6YKr0ACKTKvmHAQjcAoG0xHzTv44ypBsnL130dY4u5Mz5czmHiCKlORRDhgwxxq9Hj9Smm25ado6+NtKvycrCyFNfX6/OO+88te+++4Zzb2iuyr333qto7gJ3V111VTihm4eTn/YC02VedmrjjTdWo0aNUhpgSuH05RLNbzLtWRUZ0fmPP/5Y6U4tCir96lcVivYkM80FIiO6hiYS01yod955J5x/Q/M8aB6LfvUXzr8q3azxQAORceuOptCMvjY888wzjXttUXJpr62LLrqIZ8Hodz2HiL5Mo68YuaPngbbC2H333ekfoVDzm266yah1Wh2yzSGiuqkhP4yWtq+h+W00QZ7y9+2334Zx8jSR//HHH1eUZu6qnUOUd33g6SR/fA7RvHnzTCYVw2h1e3rO4aAAFGgiBaREyO2bMyFqScP/3nma0/wuR4joFdWgQYOMIwj0Oow7mr9BryyidEe/esJ08PLLL3Pz8D/rESNGJOzpP3iaw2ByptdwNAKiQSm8j+7UgqlTpwaUdnp9pSdyBzRiEKWF/9J/4iaXNjp08803Jy756KOPAtvIQxSnaYSoCM00HCbyT6NY//vf/8Jw0o5GyyhfNKpxwQUXBM8991wij7YAl3OI9B5jgWlEizSk11ncPfPMM4m8kS2NfFEdMLm0cqJXsuPGjUtc9sgjjwRUj6OyjP/uueeeCXsKqGaEqIj6YEosRohMquQf1pz7n/xzHwTIv9sRMrwyY7XWFRDp/xLDiaPxhj9+fMUVV7CYg+DWW281dhh6u4+EbRSgR7QC/ZVY4jrbK5u0zuywww4zTsymCdS2uUX9+vWLklL6pVd2ttdeBEo2p78+S+QjrpkJiJpaMz26FuhRMluWMoW7BKKxY8caNdRbx1jTQq9Z4zpHx/qrNOM1aXWIIMbm7rzzTmM8FJ/++jBxWTVAVER9SCRUBwCITKrkHwYgcAsE0hLzTX8AEasBaUB01llnBdSo2/6oAb/44osDPfxvBQJq/KkTNY3g6M+fjR1GpQ5X75GWuE6vXmyEG1tnRqMKaV800ehH1FHGf+l+3NFk1rhN/Pj777/n5mV+vT6T9VoTEDWlZpSvN998syz91XhcApF+NRWOJj7xxBPB+PHjw7pKE9tphMbmhg0bZtTcNunfVofoS7W0Lx2p8YxGIuN1go5NoFwNEBVRH0w6AohMquQf5luHLFUM+XcLhAAiVgPTgIg34tX427VrZ3ydQkP9plcK9AqCPp9Oc48++qixQ6POkTtbZ6ZXVOamZX69+rYxDtKAg8qYMWOMtnoNmrJ7mjzUidt05fE0tWZ67R5TFsRhLoFIHLm+wLRsAJXBNddcY7ydrQ7pOW5G+3jgCSecYCxf0wR9KRAVVR/i+YmOAUSREsX+AgjcAoG09HzTHwsz6pY/7tImVcftqjnW6wUpPWcjXEiRX69HTpR+LcWDle58lP5PPREeD6AF90477bR4UHhMm8jut99+ZeG2CbEPPvigGj58eJlt3KPnk4SLJ+p5RfHg8JgmzMbTrteJUffff3/C7owzzlB33313IjweQIs36nlU8aDSsQaisknVTa3ZjTfeqPR8oVL6qj1wPak6LR26wQsnumt4UPrrrvDvyiuvVDSBmbvRo0crOsedrQ5R3aZFNtMc7eFnmmyu5xEpDYZll0onVRdVH8oS2eiJT6rWo78mk4phet6WeFI1FuZzvDBfxVIqN4D+nukvJUJu35wJUVfd8L9RnuY0fx4jRPQqQXcCAa3zY3O0xlGUXle/GkoS0dn+u3/rrbcStjyAXsOZ0qYhpsyU1pcx2emtTMrsTB7bQoh0Pz5C1NSaPfnkk6YsiMPyGiEiLTWABLS+09577x10794985pQpLetvGx1yDQPiIthe51KE9S5k44QFVUfeDrJjxEikyr5hzXn/if/3GNStevyxyszVmtdA1Hnzp2N84VYtIH+b9gIESawyBpmmrht68z0Fh08SQm//ozemEYORKYv5SjNlMcsjl4rmvLIgaipNdP71WXJTkUb10BEIESvLU1fFJp0tYVJgYheq1ZytpXb9ef5ia/apEBUVH0w5RFAZFIl/zDXHaI0xYjfr1d2ACL2BKQBEX1irl8jGP/OPvtsYydOnc3VV1/NYkl69bov1uttHVal8FNOOSURkQ2I9H5TCVsekBWITF+9UVppdCCL069kjFpwIGpqzbJAZJb8ugQi2g5jjz32MOpXqb7w81IgMn0owPNPk9B5PJGfdy5SICqqPvA8kR9AZFIl/zBeZ/KPsTwGxO8XEGEOkW6N4y5tDpEekk/d7f7II49U+uue+O3CYz3ioT799FOlVzdOnIsCHnroIaVfbUTe0i/N16A5OdU42oRVf7Jfdqlt/gdtwNmtW7cyW+6hjUBp01fuaN5PPG+0CSxt7MkdLQKoJ/Dy4DI/zW2hBep0s1MWTh4NRGVziNYEzRKZMAS4nENEc5r0F4GGWJTSr83UQQcdFC7sSfWAFk2kTYFpgc+HH344cY0GIkULNHJnq0O06bB+9cXNy/z0fNBzwh0t0EmbHcedHvEJF5KMh9ExPQ96jzYerIqqD4mIdQDmEJlUyT8Mc3g8m8MjrDLOy7+cd+W+5kzIWtvwv1FJrtJGiGiOQpqjURbbZ8U0h4MWOrQ5vVqz8T9nmrfj0hUxQjR06FBjXmh5gEqONIzKjf/yEaI1QbNK+aXzrkaIaA8yrlnkp5FNm9OrVxuvs11jq0OTJ0+2RVEK15PqjXHRBrTcSUeIiqoPPJ3kxwiRSZX8w5pz/5N/7jGHyHX545UZq7W1ABHdiiaxRp0Q/73nnntYbP95bXue0Wf3lXYF/+8ulY9snZnLV2b6izejBpU+7afU07wcrlvk50C0JmhWuUTcAZEe5TFqVwmq9VYexuukr8yyTDK3LcmgR64SUkmBqKj6kEioDgAQmVTJP8x1hyhNMeL365UZgIg9AbUCEa2Fol8ZGTuYddddN3XxQ9su71999RVLZfXeIoCIJnNHEBP/7dmzZ+ooGeUqbcsPDkRk39w1ozRWcq5GiOhLxrje0fHhhx9uTQKtcWXb6kMKRKY5azxi2qYjSlf89/TTT+emVW3dUUR9SCRUBwCITKrkHwYg8QtIpDXGdfkDiFgJ1ApEdLu33347oJGdeIMfHR966KEsxv+8tv/UaW+sNEf7jU2cODHQc1ECWgk6bXJrEUD02GOPGfNOGqR93k8jYbSKd6QV/zUBUXPXLK3conOugIhWSOeakf+YY46Jokr86vlDxmvoOlp13eRsdYheF9M2LzY3Y8YMa1w0GsSddISIri+iPvB0kh9AZFIl/zDXHaI0xYjfLyADELEnwAUQ0S3p9ZCpc6IwAgaTe+mll4zX0MgSvQ4wOdrLjEZeeFy0l5ieAJ24xNaZuXxlpnetD2xrFg0ZMsT6CpBGJHg+4n4TEDV3zRIFYAhwBUS2ESLazkIvwpiIWU8Eto4Oke706tPkbHWIrqFVr02O5s/ZVqmm+m0q22qAqIj6YMofgMikSv5hABK/gERaY1yXP4CIlYArIKLNXW0dB8HCggULWMz/eg888EAjFPTo0SP47LPPyq6ZPXt2cOyxxxrtR4wYUWYbeWxpcglEFJdtrgh1mrSJLOkTOdL80ksvNeYjDkTz58+PLin7bc6alSXU4nEFRLQQZ1yv+PGoUaNKUKS/Bgv3OIvXBf1lX+Ja/eWgcW+yjh07JmzjcREU0VpIkdNfj6VudDxy5MjItOy3GiCiG+RdH8oS2egBEJlUyT/MdYcoTTHi9wvIAETsCXAFRHTbcePGWTsO2w72+vN862rC9BqOOin92XJg26GcOibqsObOncty9q833gnGOzHXQDRnzpzU0QeKm/LQr1+/oL6+vqQT7XdmW1DQlsbmrJmxEFigKyCivetM++FF5Uy66i1WSlpH4bSSNf1F/vgvgTjNCRs7dmwp1R06dDDaxtc/atWqVUB7vfXu3dtanykeSq9tQcdqgSjv+lASInYAIIqJUeAhgMQvIJFWHdflDyBiJeASiOg1gW1OA3UGr776Kov9X+8tt9xSESbinVb8mLYJmTJlivG+FFgUEFFcet0h61yqeJqjY5rcq9cvCnr16mXscPWebXRbo2uumhkTywJdARHdNstIW6Q3/eq1pQJ67Zo2l4js9tlnn1KqTaNJZENzhGzLTsTjjI4J8KmO2Fy1QET3y7M+mNILIDKpkn+Y6w5RmmLE7xeQAYjYE+ASiOjWU6dOLRsBiToD+qWO3/ZA0euxPn36GMEgfo/4Mc0V4dtosOwVCkQUt14sL6BtGeLpNB3TqNbzzz8fJrdv375Ge/7KkOetOWrG02jyuwQi+mpswIABRv247gTr0dw0mvdFo4/cJvJHQERfUUZh8V8CIXI0ad62UnncXm9kGkyYMMEkRymsFiCim+RVH0oJjB0AiGJiFHhoaz+LSgLiBxCV1bXmXCGiBrgswRU8roGIojv33HONnQilL+0LMvrqirYj2HXXXVP/8x48eHDYuVBnVckVOUIUpWXSpEnBwIEDA+oEozKJfqkjpQno9LoncvQlXnQ+/ps28hVd29w0i9KV9usSiCgeGpmk17V6RWmjjjQqdP311wcEQXFHI3D7779/4hoaEYrmpNHct3iZRMdbb7116Va0iTFNyDa9WuvUqVNAm/9m2Qi2ViCiBOVRH0oZjR0AiGJiFHjYnPufImRA/t0CGbbu0C36muD0w6X0XAs1ffp0NWvWLNWlS5dwCwbaKkF3MmtCFpT+0incwoS2MdFfFqmuXbsq2uZDQ1Eu6fdBs1qE0WCkaDsN2lpFz79SeqNhpecEhZrr11XWW+t/CpRevkFpYFK0TQdt2ULbfEgdbYOjR2nCekvX9u/fX+lRTJUWtzQOiX2e9QFbd0hKwp2t860bhElD/H5tHQIgEj4AMIcCUAAKcAUARFyRYvwAEr+ARFprXJc/gEhaArCHAlAACjAFAERMkIK8rjtEabIRv19ABiCSPgGwhwJQAAowBQBETJCCvAASv4BEWm1clz+ASFoCsIcCUAAKMAUAREyQgryuO0RpshG/X0AGIJI+AbCHAlAACjAFAERMkIK8ABK/gERabVyXP4BIWgKwhwJQAAowBQBETJCCvK47RGmyEb9fQAYgkj4BsIcCUAAKMAUAREyQgrwAEr+ARFptXJc/gEhaArCHAlAACjAFAERMkIK8rjtEabIRv19ABiCSPgGwhwJQAAowBQBETJCCvAASv4BEWm1clz+ASFoCsIcCUAAKMAUAREyQgryuO0RpshG/X0AGIJI+AbCHAlAACjAFAERMkIK8ABK/gERabVyXfx1tDidNxJpirzeXDJNKexjBQQEoAAXyUiAORPPmzasqGr2Jrqqvr6/qWlwEBaBA7QpghKh2DXEHKAAFWrgCcSBatGhRVWo0NDSIgcj1f8jShCN+jNC0b99eWm2c2buufwAiZ0WDG0EBKNBSFQAQNU3Ju+4QpblA/H4BIYBI+gTAHgpAASjAFAAQMUEK8gJI/AISabVxXf4AImkJwB4KQAEowBQAEDFBCvK67hClyUb8fgFZiwCiQYMGSes57KEAFIACmRVYuHChmjZtWmiPOUSZZavZEEDiF5BIK4Tr8m8RQCQVGfZQAApAAakCdXV1ir5oBRBJlave3nWHKE0J4vcLyFoEEI0ZM0Zaz2EPBaAAFMiswMyZM9X48eNDewBRZtlqNgSQ+AUk0grhuvxbBBBhHSJpNYM9FIACEgUwh0iiljtb1x2iNGWI3y8gAxBJnwDYQwEoAAWYAgAiJkhBXgCJX0AirTauyx9AJC0B2EMBKAAFmAIAIiZIQV7XHaI02YjfLyADEEmfANhDASgABZgCACImSEFeAIlfQCKtNq7LH0AkLQHYQwEoAAWYAgAiJkhBXtcdojTZiN8vIAMQSZ8A2EMBKAAFmAIAIiZIQV4AiV9AIq02rssfQCQtAdhDASgABZgCACImSEFe1x2iNNmI3y8gAxBJnwDYQwEoAAWYAgAiJkhBXgCJX0AirTauyx9AJC0B2EMBKAAFmAIAIiZIQV7XHaI02YjfLyADEEmfANhDASgABZgCACImSEFeAIlfQCKtNq7LH0AkLQHYQwEoAAWYAgAiJkhBXtcdojTZiN8vIAMQSZ8A2EMBKAAFmAIAIiZIQV4AiV9AIq02rssfQCQtAdhDASgABZgCACImSEFe1x2iNNmI3y8gAxBJnwDYQwEoAAWYAgAiJkhBXgCJX0AirTauyx9AJC0B2EMBKAAFmAIAIiZIQV7XHaI02YjfLyADEEmfANhDASgABZgCACImSEFeAIlfQCKtNq7LH0AkLQHYQwEoAAWYAgAiJkhBXtcdojTZiN8vIAMQSZ8A2EMBKAAFmAIAIiZIQV4AiV9AIq02rssfQCQtAdhDASgABZgCACImSEFe1x2iNNmI3y8gaxFANGjQIGk9hz0UgAJQILMCCxcuVNOmTQvtFy1alPm6uGFDQ4Oqr6+PB1U8RofsV4dcscCZAcrfbfm3CCBidQheKAAFoIBzBerq6lQQBApA5Fxa6w0BBG6BwCq05YRv+rcIIBozZoylOBEMBaAAFKhdgZkzZ6rx48eHNwIQ1a5n1jv41iFnzXdkh/y7BcIWAUT0XxscFIACUCAvBTCHKC9l0+8LIHALBOlqJ8/6pj+AKFnGCIECUAAKiBQAEInkcmbsW4csFQb5dwuEdYsXL/Z2+KRDhw5h/cIIkfQxgz0UgAISBeJANG/ePMmlJdu2bduKJ1WXLsYBFIACNSuAEaKaJcQNoAAUaOkKxIEIc4iKqw0YIXE7QiItOd/0BxBJawDsoQAUgAJMAQARE6Qgr28dslQ25N8tEAKIpDUQ9lAACkABpgCAiAlSkBdA4BYIpMXmm/4AImkNgD0UgAJQgCkAIGKCFOT1rUOWyob8uwVCAJG0BsIeCkABKMAUABAxQQryAgjcAoG02HzTH0AkrQGwhwJQAAowBQBETJCCvL51yFLZkH+3QAggktZA2EMBKAAFmAIAIiZIQV4AgVsgkBabb/oDiKQ1APZQAApAAaYAgIgJUpDXtw5ZKhvy7xYIAUTSGgh7KAAFoABTAEDEBCnICyBwCwTSYvNNfwCRtAbAHgpAASjAFAAQMUEK8vrWIUtlQ/7dAiGASFoDYQ8FoAAUYAoAiJggBXkBBG6BQFpsvukPIJLWANhDASgABZgCACImSEFe3zpkqWzIv1sgBBBJayDsoQAUgAJMAQARE6QgL4DALRBIi803/QFE0hoAeygABaAAUwBAxAQpyOtbhyyVDfl3C4QtAoiklQz2UAAKQIFqFcBu99UqJ78OQOAWCKQl4Jv+ACJpDYA9FIACUCBFAQBRijiOT/nWIUvlQf7dAqHXQETD2LW4FStWqJUrV6beYvny5apNmzapNnmeRPzQH/WveT1/AwcOrOqRb2hoUPX19aJr0SG67RBF4mtj6O+X/l4DkbRyc/tly5YpgqI0t3TpUtWuXbs0k1zPIX7oj/rnx/MHIJI3lQASv4BEWgNclz+AKKUEAEQp4jSeApAByABkboAMQFS5veEWrjtEfv9KfsTvF5ABiFJqPIAoRZzGUwAiABGACEBUuaXIxwJA4heQSGuJ6/IHEKWUAIAoRZzGUwAiABGACEBUuaXIx8J1hyhNJeL3C8gARClPAIAoRZzGUwAiABGACEBUuaXIxwJA4heQSGuJ6/IHEKWUAIAoRZzGUwAiABGACEBUuaXIx8J1hyhNJeL3C8gARClPAIAoRZzGUwAiABGACEBUuaXIxwJA4heQSGuJ6/IHEKWUAIAoRZzGUwAiABGACEBUuaXIx8J1hyhNJeL3C8gARClPAIAoRZzGUwAiABGACEBUuaXIxwJA4heQSGuJ6/IHEKWUAIAoRZzGUwAiABGACEBUuaXIx8J1hyhNJeL3C8gARClPAIAoRZzGUwAiABGACEBUuaXIxwJA4heQSGuJ6/IHEKWUAIAoRZzGUwAiABGACEBUuaXIx8J1hyhNJeL3C8gARClPAIAoRZzGUwAiABGACEBUuaXIxwJA4heQSGuJ6/IHEKWUAG3sunr16hQLpZYsWaJoD6Kmcogf+qP++fH8tW7dWrVq1UrUlLjuEESRa2PEDyBp3769tNo4s3dd/+oWL14cOEsdbrRGKlBfX69WrVq1RqYdiYYCUAAKQAEo4EIBjBDVqKJrQpUmB/HjPzSf/kND/ZcpgOcfzz+ef3cjVAAiWfuTsEaDhAYJDZK7BinxgFUIwPOH5w/PH56/Cs1E5tMAosxSmQ3RIKNBRoOMBtncOuQfivYH7Q/aH3ftD4CoxjYLDRIaJDRI7hok6eOI5w/PH54/PH/SdsNmDyCyKZMxHA0yGmQ0yGiQMzYXzs3Q/qD9Qfvjrv0BENXYRKFBQoOEBsldgyR9HPH84fnD84fnT9pu2OwBRDZlMoajQUaDjAYZDXLG5sK5GdoftD9of9y1P/8HeqxadZ1Y1OIAAAAASUVORK5CYII=\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 21,
"metadata": {
"image/png": {
"height": 30,
"width": 300
}
},
"output_type": "execute_result"
}
],
"source": [
"from IPython.display import Image\n",
"Image(filename='SciSheetsCoreClasses.png', width=300, height=30) "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.7"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-2-clause |
SIMEXP/Projects | NSC2006/labo8_filtrage/labo 8 Introduction au filtrage reponses.ipynb | 1 | 760682 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#Laboratoire d'introduction au filtrage - Corrigé"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"> Cours NSC-2006, année 2015\n",
"\n",
"> Méthodes quantitatives en neurosciences \n",
"\n",
"> Pierre Bellec, Yassine Ben Haj Ali"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Objectifs:\n",
"Ce laboratoire a pour but de vous initier au filtrage de signaux temporels avec Matlab. Nous allons travailler avec un signal simulé qui contient plusieurs sources, une d'intérêt et d'autres qui sont du bruit. \n",
" - Nous allons tout d'abord nous familiariser avec les différentes sources de signal, en temps et en fréquence. \n",
" - Nous allons ensuite chercher un filtrage qui permette d'éliminer le bruit sans altérer de maniére forte le signal. \n",
" - Enfin, nous évaluerons l'impact d'une perte de résolution temporelle sur notre capacité à débruiter le signal, lié au phénomène de repliement de fréquences (aliasing). \n",
"\n",
"Pour réaliser ce laboratoire, il est nécessaire de récupérer la\n",
"ressource suivante sur [studium](https://studium.umontreal.ca/):\n",
"\n",
"- labo7_filtrage.zip: cette archive contient plusieurs codes et jeux de données. SVP décompressez l'archive et copiez les fichiers dans votre répertoire de travail Matlab.\n",
"\n",
"De nombreuses portions du labo consiste à modifier un code réalisé dans une autre question. Il est donc fortement conseillé d'ouvrir un nouveau fichier dans l'éditeur matlab, et d'exécuter le code depuis l'éditeur, de façon à pouvoir copier des paragraphes de code rapidement. Ne pas tenir compte et ne pas exécuter cette partie du code:"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Starting Octave on ZMQ socket ipc:///tmp/pymatbridge\n",
"Send 'exit' command to kill the server\n",
"..Octave started and connected!\n",
"Starting MATLAB on ZMQ socket ipc:///tmp/pymatbridge\n",
"Send 'exit' command to kill the server\n",
".MATLAB started and connected!\n"
]
}
],
"source": [
"%matplotlib inline\n",
"from pymatbridge import Octave\n",
"octave = Octave()\n",
"octave.start()\n",
"%load_ext pymatbridge"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Section 1: Exemple de signaux, temps et fréquence"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 1. Commençons par générer un signal d'intérêt:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%matlab\n",
"\n",
"%% Définition du signal d'intêret\n",
"% fréquence du signal\n",
"freq = 1; \n",
"% on crée des blocs off/on de 15 secondes\n",
"bloc = repmat([zeros(1,15*freq) ones(1,15*freq)],[1 10]); \n",
"% les temps d'acquisition\n",
"ech = (0:(1/freq):(length(bloc)/freq)-(1/freq)); \n",
"% ce paramètre fixe le pic de la réponse hémodynamique\n",
"pic = 5; \n",
"% noyau de réponse hémodynamique\n",
"noyau = [linspace(0,1,(pic*freq)+1) linspace(1,-0.3,(pic*freq)/2) linspace(-0.3,0,(pic*freq)/2)]; \n",
"noyau = [zeros(1,length(noyau)-1) noyau]; \n",
"% normalisation du noyau\n",
"noyau = noyau/sum(abs(noyau)); \n",
"% convolution du bloc avec le noyau\n",
"signal = conv(bloc,noyau,'same'); \n",
"% on fixe la moyenne de la réponse à zéro\n",
"signal = signal - mean(signal); "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Représentez `noyau` et `signal` en temps, à l'aide de la commande `plot`. Utiliser les temps d'acquisition corrects, et labéliser les axes (xlabel, ylabel). Comment est généré `signal`? reconnaissez vous le processus employé? Est ce que le signal est périodique? si oui, quelle est sa période? Peut-on trouver la réponse dans le code? "
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7d09qOzofcfx/7XX2GEXjHCxhhQGFSkM2QR0ijTBa5DS\n",
"pHAaHRbcpJJwUhuJVCE4YdSlMIRRbrlwzYgULsM8xb0xJDaM2OAYYtg9Ym+1XFjug1kwuzG7J8Vz\n",
"PHdGo5nRaEYavXw/xbJXZx7puXN1fvPM86ZH9/f3AgCYki9duwIAgK4R/QAwOUQ/AEwO0Q8Ak0P0\n",
"A8DkEP0AMDlEPwBMDtEPAJND9APA5BD9ADA5RD8ATA7RDwCTQ/QDwOQQ/QAwOUQ/AEwO0Q8Ak0P0\n",
"A8DkvNbZlZRSaZpqrR3HiaLIsqxm59Fap2mqlBIR13WDIKg8VRzHpSOu67qu2+yiADAmj7p5QGOa\n",
"pmmazudz27bTNM2ybLVaNTiP1vr29tZxnCAIzGmVUsvlcjf9Hz16tFwuN4/Ytm3bduO/AgCMRhfR\n",
"r7W+ublZrVbrgI7j2LZtE98nCcPQdV3f99dHkiTRWs9ms9IrHz3q6FMNAAani77+LMt8399smAdB\n",
"kKZpg1PZtr2Z+yISRVGe5+dWEQCmpIvoL4rCcZzNI7Zta60bnCqKot2THx42UEo1uxYAjFUXw7xF\n",
"UeyOr16q2/329na3t8fwPE9rbVmW1tq27fl8Xn9s+fvf//5HH32076dvvvlmk7oCmLwXL17s+9G3\n",
"v/3tH//4xx3V4759rusul8vdg+efOQiC+Xxe+aPZbHZ3d7f+43w+932//pk7evcB4Pdee+21czOx\n",
"tgHP6w/DcD3VZ1cURZtfLIIg0FoXRVH//N/97nc7+2cYliiKdj/LYSyXyyiKrl2LnuLNOSCKoi99\n",
"qbtA7uJKpY7+85kpQwdyf181Top+ABirjj5kdifhNJ6Wo7X2PC8IggZzQwEA0k30+75vFt+umeme\n",
"+16vlDKz9Xd/VJn7NdvyWZZd/PsHAAxRdx0+64n8WuskSfa12fM89zwvjuMwDEs/Mkt5oygqlb25\n",
"uSm90vO8LMs2j4RhWFpbAACT1dEePovFwvO8PM8ty1JKBUGwrwG+TufdmM7zvCgKsyfE5vHd7weL\n",
"xSKO4yRJzKRS8yVj3xxQAJiajqLfsqzVapXnudb68N5ttm3f3d1VLgVwXffu7q7m5ebzudbajCic\n",
"s1scAIxPdzt3Su2pPpfaZ82yLLbqBIBdA57X37Y33njj2lXoKdd12QN1H9u2aXDsw5tz2Fe+8pXO\n",
"rtVpq39YXn/99WtXoaf47T2AvcEP4M057Gtf+1pn16LVDwCTQ/QDwOQQ/QAwOUQ/AEwO0Q8Ak0P0\n",
"A8DkEP0AMDlEPwBMDtEPAJND9APA5BD9ADA5RD8ATA7btwFol9aSJOWDvi9HN3FvXBBHEf0AWqSU\n",
"pKlE0VZem0zPMjnw6DylJMskimRzr09TUCmJohbrPAV0+ABoS1GIUrJYlNvpliWzmThORaPeyHPJ\n",
"MpnPpbTHsyloWXsLoiaiH0BbkuRQ89z3RWvJ8+qCB74QBIEUhRTFBWo4WUQ/gFYoJa4rh5+KHUWS\n",
"ZRUFff9IwdlM0vTcGk4Z0Q+gFXl+fDy2Mt/NZ0aDgqiPYV4ArSiKck+91vI3fyPf+tbWwWfPJI7L\n",
"R0o++0z+6I/kBz9ooZZTRfQDaMVuwzxJ5B//sfx5EIblbv04rujoL3084Ex0+ABoheOIUq/+qLWI\n",
"lHO/km1vFdzHnBDNEP0AWuE4W0O4SSJBUH5NllWMB7ju8eivLIj6iH4ArbBtse2H9K9s8mstWVbx\n",
"eWBediD99xVEffT1A2hLFEkYiojkufj+1o+KorpP35jN5PZWtC6XMqc6POsfdRD9AFo0n8vf//1D\n",
"/4xliWVJnj+06OfzQ3M0FwtJEglDcV1xHPnsM1GqVkHUQfQDaNcf/IHM5yIiWSZai+NIENQa7zUr\n",
"gc1mPj//ufzlX0oUEfqXQfQDaFdRPIT40YValVxXXFe0blgclRjmBdCiNK3or8fV9S76lVK3t7ee\n",
"58VxrM+YuKu1TpLE8zzP85IkOedUABrL84u11tmv7YL6Ff1pmsZxHEXRYrGwLMvzvGbn0Vrf3t5q\n",
"refz+Xw+11p7nkf6Ax27YJPfdYn+S+pR9Jt2+nK5dBzHsqwoilzXTRvtzhfHcRAEs9nMtm3btmez\n",
"me/7CTt8A926YJMfl9Wj6M+yzPd9a2P8PgiCZtFv27a/3diIoiiv3BccQDvSlAW3/dWj6C+Kwtm+\n",
"U2zbbtZLE+08HqIoCotJYUCHLrvgtrQjEM7Ur+jfTWe7zuzfGm5vbwPWfQNdybILT+yh5XZZPZrX\n",
"394wbBiGQRC4J3Y6Pn36dN8483K5vES9gNFS6mEZF0r2pcoHH3zw6aefdlaNHkV/S8IwdBynQZP/\n",
"7bfffvLkSRtVAsZNqVZ6+ccxR29fwzGO48ePH3dWjR51+DiXvlm01jc3N81yH0BjLW2rSZ/PBfUo\n",
"+kVkdxJO42k5Zi5/EATkPtCllpr8uKweRb/v+2p7CN9M96x8sVLqwBrdytwvWBACtI+d9AehR9Fv\n",
"OnzWE/nNCq/KNnue52anh9DsBb7NLOWNoqhU9ubmpoVaA3hFqVpbcuLq+jXMu1gsPM/L89yyLKVU\n",
"EASVAwDrOaCVU/XzPC+KIk3T0nIwNnIA2pamTOwZhn5Fv2VZq9Uqz3OtdRRF+xZh2bZ9d3dXFEXl\n",
"fE3Xde/u7lquKYCyohDbZjB2GPoV/UadqT5mc54OKgOgpjSVnXX0l2TbohSbAl1Gj/r6AQyXmUXR\n",
"apOfxt4FEf0ALqDtJj8ui+gHcK4Omvzm/MzQvhSiH8C5umnyOw7RfzFEP4CzFIVozcSegSH6AZwl\n",
"SejlHx6iH0BzZqEkc28Gh+gH0BxN/oHq45IuAP2U56KUaP3Quf9nfyZCk3+YiH4Ax2ktSSKWJb7/\n",
"kPVFIX/7t/KlLz3s39BZNXARdPgAOEJriWPxfYmiVylvWfInfyLvvitJIk0fq3Ey5hFdCtEP4Igk\n",
"kSAoP4DFHLQsmc0kSa5UMzRF9AM4JM/Fssq5r/Wrfh7LkiDoKP1Z0HspRD+AQ5SS3WflmSb/mut2\n",
"1AvPgt5LIfoBHKJ1xSjuixdsnjxsRD+AQ3ab8//8z/K9712jKiLCJJ8LIfoBHLLbvf6//yt/9VfX\n",
"qYzjdDebaNyIfgCHuK4o9eqPaVrR9V8UHU27ZHLnpRD9AA4x0b/uZsnzil7+0qgv+o/oB3DEbCZx\n",
"LFpLmlbkvlntRXt8WNjIAcARti1BIGEod3dbXe1FIUkivs9sn+Eh+gEc5zjiuvL55xLHrw6apby0\n",
"94eI6AdQS57Lv/3btSvB5M4Loa8fwHFKlfdyuBa+ZFwE0Q/guCxjDs+oEP0AjuhPkx+XQvQDOKJX\n",
"TX7H2VpihmaIfgCH9K3JT1//RRD9AA6p3LkBQ0f0A9grz8W2+9XQtix2cLsAoh/AXlkmUXTtSmxz\n",
"HKb2X0B3S7qUUmmaaq0dx4miyDqvIZFlWVEU0f67Mt5cdCgiIq7ruqw3B2ozezX3qsmPS+ko+tM0\n",
"TdN0Pp/btp2mqed5q9WqwXnM50dRFLZta60PRH+SJMvlcvOIvfuoIQD7pWnvmvy4lC6iX2udJMlq\n",
"tTIt/SiKtNZpmganzxezLCuKIsdxlFLJsedA08YHGqPJP25d9PVnWeb7/mYPTxAEaZo2OJXjOE6v\n",
"JpoBI0WTf9y6iP6iKEp5bbprOri0iCilOrsWMA40+Ueviw6foih2+1466Hn3PE9rbVmW1tq27fl8\n",
"ftLY8i9/+cvdsWJjNptdqI5AHyUJTf627EuVZ8+e/e53v+usGh319XdwlZLZbOb7/voDJk3TMAwX\n",
"i0X9M7z55puMFmCCTJOfWREt2Zcqz58///Wvf91ZNUa7X39p8k8QBGY+aP1vG0Q/pole/lbtSxWl\n",
"1Je//OXOqtFFX39PBmYdxylMewbAHuYres+b/CzoPV9Hq3nznX+o3SMAri5JerRJ5z4s6D1fF9Hv\n",
"+77a3mXVTPfc93ozZ//iIwRZlvXk+wfQT4No8uMiuuvwWU/kNyu89q3nyvPc87w4jsMwbHxFz/Oy\n",
"LNs8EoZhaW0BgJJBNPkNWv1n6miYd7FYeJ6X57llWUqpIAj2NcDX6VwZ00mSmC8QWuuiKDzPM8dL\n",
"ezYsFos4jpMkMSMq5ksGMzKBA7QWrYfR5HddiWO2kj5LR9FvWdZqtcrz3Gy8c6D1bdv23d1d5VIA\n",
"EYmi6MC+PZuXm8/nWmszonD+bnHA6CUJYTohnU7urNnVbtv2RRZ8WZbF7EygpqIQfl2mg/36AUia\n",
"DqaX36Cv/0xEPzBFWotSotRDhub5wJr89OCeiegHpkUpub2VJHkI/SSR73xH3nzz2tVCt0a7kQOA\n",
"XWbrsM29rFxXwlBef13CUObza9ULXaPVD0xFkojjSGmSc5qK70sUie/Lnj0lMUJEPzAJRSFFUTF9\n",
"M8seevnNf9nmaiKIfmASsqxiDo9p8q9FkTR6et51MMnnHEQ/MAlFIbvrapTa+jwY0LQZx2HzzrMQ\n",
"/cAk7Mb6u+/Kn/7pNapyCQP6lOonZvgAE/WznzGlZ7po9QOTYNtbPSRKVfT/DKj3vPTXwamIfmAS\n",
"XHdrCLdy1HdAmzbb9pA+qHqI6AcmwbbFtsU8xkKpis2ZzeOUBrFpM85HXz8wFVEkcSx5LkVR7uU3\n",
"+zrwSIvpIPqBCZnN5N135ac/fVjZKyJ5LlqL7w9s+zaciegHpuVXv5L//E+xrIceHlr600T0AxNi\n",
"9mkwk+Jp5k8Zw7zAhKSp1HjCKcaP6AemYrPJj4kj+oGpGNC0fbSN6AcmwTT5xzRtnwW95yD6gUkY\n",
"Xy8/C3rPQfQD42cickxNfpyJ6AfGb6y9/DxTrDGiHxi5sTb5XZfob47oB0ZurE1+nIPoB8ZMaymK\n",
"ETb5cSaiHxizNKXJjwpEPzBmRcFePahA9AOjlabi+9euBHqpd9GvlLq9vfU8L45jffaCjSzLkiS5\n",
"SMWAwcnzkTf5WdLVWL+iP03TOI6jKFosFpZleZ7X7Dzm8+Pm5ibLMmV2JQcmZgpNfraia6xH0a+1\n",
"TpJkuVw6jmNZVhRFruumm0+Srs0UX61WASNcmCqlRt7kxzl6FP1Zlvm+b218jgdB0Cz6HcdxzNPn\n",
"gElK06nkPn0+zfQo+ouiKOW1bdvnd/cDE6TUJOZ0ui6bdzbUowc0FkXh7jRU7OutRXnx4sW+cYLd\n",
"egL9QVdPn+1LlefPn3/++eedVaNH0d+3Bj7Rj4HKMpnPr10J7LEvVT788MMvvviis2r0KPr75q23\n",
"3prNZteuBXAapWQ641yOI0kysK84+1IljuP333+/s2r0qK+fgVngfFk2iV5+g8mdjfUo+kUk3xmy\n",
"2T0CYJ9JNflxjh5Fv+/7pV4wM92z8sVKqSRJ+jY8AFzXFJZxlZABzfSor990+KRpatZhmRVe86rh\n",
"qjzPzULfPM8Xi0XH9QR6Ikkegs/89//+T/7wDyfXBzK1v++l9Cj6RWSxWHiel+e5ZVlKqSAIKgcA\n",
"1su+rD3/7EmSmC8QWuuiKNYbQiyXy3YqDnQqzx92Y978/fjBD+TDDyXLJtfwRwP9in7LslarVZ7n\n",
"WusoivYlu23bd3d3lesAjCiKoihqs6bA1RRFxfTNopCvf13+5V8kjsWyBjbpBd3rV/Qbdab62LZ9\n",
"xdVewBUliezOD0xTMa2d2UzCUByHnhAc0qNhXgBHmZW6pVg3TydfH4wiabT3FSaE6AeGpHKThiSR\n",
"zQ5O2374MAD2IfqBgSk1+f/7v+WTT6bbvWPbwiM5GiD6gWH7yU/kRz8qH5zOJwFDfs0Q/cCQWNZW\n",
"Z46Z0U/84VREPzAkrrs1hJskFTv2ZNmEPgxKn4WoiegHhsTMfDZbW1U2+bWe1g5ujkP0N0H0AwNj\n",
"5m7meUWTvyjk9rZi1j9Q0sclXQAOsCyZzeQf/kGePn21Z0NRiFKS57JYTGiMF40R/cDwWJZ89asS\n",
"BJLnkmUPR1x3Qv08OBPRDwxSUdCxg+bo6weGx2zbCTRG9APDk+fszYmzEP3AwEzwUVy4OKIfGBia\n",
"/Dgf0Q8MCU3+XSzobYDoB4Yky2jyl7GgtwGiHxgMmvy4FKIfGIw8Z05nNbOdEeoj+oFhUEpqPLV6\n",
"ihznYT871Ef0A8Mwqf04T8KeRQ0Q/cAA0OTHZRH9wADQ5MdlEf1A3yk1oaduoRtEP9B3bNaGiyP6\n",
"gV4rCrFtRjKPYHLnqYh+oNfSVKLo2pXoPT4aT0X0A/1l9icg13BxRD/QXzT50RKiH+gpmvz1OY4o\n",
"de1KDEp3z+ZVSqVpqrV2HCeKIuuMO7rOqeI4Lh1xXddlz0MMR5Lw9N26+IA8VUfRn6Zpmqbz+dy2\n",
"7TRNPc9brVatnipJkuVyuXnEZmo0hoMmP1rVRfRrrZMkWa1WpnkeRZHWOk3T4PS5yiedijY+hote\n",
"/pNYlijFkwxO0EVff5Zlvu9vdssEQZCm6XVPBfSWmaXO19T6HIep/afpIvqLonC2t56ybVs3+odq\n",
"cCqlVLNrAdeSJCzfRbu66PApimK376VZz/tJp/I8T2ttWZbW2rbt+Xx+ztgy0B6lHnacd5yHHTpp\n",
"8qNVHfX1d3+q2Wzm+/76UyFN0zAMF4tF/Ws9ffrU87zKH5UGkIHGkkSKQhxHXPehw/qHP5S/+Itr\n",
"Vwut2ZcqH3zwwaefftpZNbqb3NmxaHuMLAiCLMuKoqj/bePtt99+8uRJC1UDHtzeiu9vDef6vhSF\n",
"uK6EocxmzPAZoX0NxziOHz9+3Fk1uujrdy73jIlzTuU4TmFmzAE9EMcSReXHrCeJuK64rgSBJMmV\n",
"aoYJ6Gg1b77z6MzdI92fCrgW0wjZbcmYJv/6R9zaaEkX0e/7vtpeZG3maO57vVIqSZLKbv1TT1V6\n",
"5QW/fwDnqNyCv3QwiiTLuqwUJqS7Dp/17HuzLGvfeq48zz3Pi+M4DMPGp/I8L9v+pQnDsLQgALgi\n",
"rSvm8OT51qIk7la0p6Nh3sVi4XlenueWZSmlgiDY1wBfp/O+mK5zqsViEcdxkiRmJqj5ZjBjPxT0\n",
"xu7d/U//JH/+59eoylhYluQ5D6+vq6PotyxrtVrlea61Prx3m23bd3d3lfP365/Ksqz5fK61NsMA\n",
"Z+4WB3Tg+XP5u7+7diWGjAW9J+l0cmfNrnbbto9OwaxzKsuy2MYH/WTbW03UNC1P9RGRoqDPB21h\n",
"v37gCnx/a+5mllVsPRbHbOdwGlr99RH9wBVY1qv0r2zyJ4n4Pq3+E7guc2FPQPQD12HiPgzlv/5r\n",
"q3WvtZjnDNWbtAw0MdqNHID+iyJ5913513+V0jPlgoDt29Auoh+4pp/9TJ49E/l9PzU9POegr78+\n",
"oh+4GqVeTfIh9M/He1gfff3A1WQZc3hwHUQ/cB1K0UrF1RD9wHUoxYPXcTVEP3AFZtNmWv24FqIf\n",
"uII0pcnfCib51ET0A12jyd8Sx2FBb11EP9A1mvwt4dO0PqIf6BRNfvQB0Q90KkmYy98WsxU26iD6\n",
"ge5oLZbF/jxtsW2Geesi+oHu0ORHTxD9QEdMg5QmP/qA6Ac6QpMf/UH0A12gyY9eIfqBLiRJxdN3\n",
"gWsh+oEuFAXRjx4h+oHWpSm9/OgXoh9oXZ7T5Ee/EP1Au9JUfP/alZgMFvTWRPQD7aLJ3yUW9NZE\n",
"9AMtSlNyH3302rUrAIxZlslyee1KTIzZGxWH0eoH2pJl9PJ3zXWJ/lqIfqAtSjGnEz1Fh89l5Llk\n",
"WflgFB1/IodSolSTgo2vmOeSpiIbTwvRWmazugU3X1azYFFImj7sV3xSVU3BkiA4vh1CZcFWr6i1\n",
"JMnWkefP5Y//+EgpjMbuDSAivi+Oc43a1HE/Xsvl0vd913WjKHr58uVJZUXknXfeqfniKLqPovLB\n",
"u7v7ILhfLk8uuFrd+36tgqW/U/0r7hb0/fvFopWCs1nzgkFQLvjy5X0Q3M/nJ1/RFDx8xfm84RUX\n",
"i4qCf/3X91F0P5sdKog27P5OtW25vPf9+9Wqoib1KxNF0Te+8Y3LVuyA0Ub/fD53HGe1Wr18+XI2\n",
"mzmOc1Lx+tEfRYcCJYru7+72/mj3XlkLgkMFD19x32lns0MRdrjggSsGwd6C8/mRK+77oFosDoXm\n",
"bHaoYEtX3PcOLJcVv97L5UM15vMjnze4uI6j3zS59qm8PSoR/Rfw8uVL27Y3W/pRFM0Pt9y21Yz+\n",
"1erIv6tpMzYr6PuXLHj4BjUqX3B31+IVfb/cWD5wwk27rez7/e/2Ra54UsHNg5VVRXs6jv7KG2PT\n",
"4Ubexss6jf5xDvNmWeb7vrXRsxsEQbrbiXuBC0kUHXqBZYnjVPTmZ5nMZkcKum7FusQ6V/T9iium\n",
"6ZEriojrVhds74qNCwZBxVBHkhyp6r4rHn1XRSSKKq6oVMUcHqW2xgaiqKIXGO3pckmXWa93eAwp\n",
"iioGkK5unNFfFIWzPbxi27Zu5444OnLoOA1Xlu8r2OyKpVHWSpXRX/OKzQr6fnVVjw6rOk7FHL46\n",
"BSuvmOfHh+Mq39U8r47+zQ8S1pd27Ohdd0F17hzL6rRKNY1zhk9RFO7OGkr7xMdkPH361PO8yh8t\n",
"96/Sefdd+dWvygefPSv/8j97JnG8deT5c/nWtyoKlgKuZsF///fyFf/jP8oFf/Mb+drX5KtfPXL+\n",
"3SMvXsibb5av+NOfVtSh5De/ERH5+tdPvmLNgr/8ZbsFd1+2r6qlX/Ue/ubjIoqiPH9Xa3n8WH74\n",
"w71F9qXKBx988Omnn160dgd11rXUJdd1lzvDea7r1j+D1Ovrr9Or+PJlxcvqFKzsZD/al73v/LXH\n",
"mrouuPs3Gt/fsfs5J1O2O7+ry2vN5xVTCercAPT1j03l7l11egAqC9ZpPyrVcDZxnjd8guA5V9wt\n",
"aFnH35/GKzaLovo9PHrFyhdYFmtHe6dykKyzaw1lt75xRr/T1ToK264Y+ivJsop0s+3qzvE6BZtd\n",
"0XGOjzVlWcVdW+eKldHvOMeHNyuv6PvHC1buhOy6DQvWuWKSVBc8+q7yaMYRc5zyb8duw6I07N8T\n",
"44x+Ecl3Pvd3j5zPzDM50GDMMrHtirvBDPofKGiCZrdgzSvu3mpmePNAE9V8FO0WrHNFy6q+YlE0\n",
"uaL5FDnwz2V+tPthY/Zv6fKK5lQHPsVNfYj+sTIz8dbpv9vq0lqyrJf7eXTWtdSl1WpV6tlfLBZB\n",
"zS7k+/v7U5Z0mYWplfN25/NDfXxm1W7lui2zHrXBFReLQwXNtPd9BQ9MbO/+ima+fOXyK7Nycl9n\n",
"rinY5RXv7/euTDb/xEzq79jRlSgXt162XbquWdqyb23mzkk67et/dH9/f+1Pn1Z4nuf7fhAEIqK1\n",
"9jzPrO+tWfzRo0fvvPPOkydP6rx4vX2H6z5MOszzhy6/wxs3ai1x/NBwWBc0U8WPFty8otYPBetc\n",
"sbKgbR+Z2N64oMjDHJhmBbV+KCjyUNCyjs/6N1d0nFcF81wsq8UrJoloXb6iyPGCaEMcd/3OZ5lk\n",
"mXzyifzoRw9PCjPfBevsHGXEcfz48eOPP/641XqujTb6Tdw7jmNZllIqCILglC9dJ0X/76/4Kikc\n",
"54Tv+BTsVUERUepVD0+DgusPD+Z0Xkv30S8iWSb/8z/y+usNbwCi/5LyPNdamw+Akwo2iH4APXGV\n",
"6A/DWhvZ7tNx9I9zSddaZ1N9AExcP1ft7jPaGT4A0JnGa2KuhegHgHMN7mGcRD8AXMCAenuE6AeA\n",
"Mw2ut0eIfgA40+B6e4ToBzA+dfbIuqB9ewL2GdEPYGy67H4piobb1l4X0Q8AzQ2xt0eIfgDj0+Vz\n",
"FIpieGO8QvQDGJ/KRze3YaC5L0Q/ADQ20N4eIfoBoDFa/QAwLUOc07lG9ANAE+apSgNF9ANAEwOd\n",
"0W8Q/QBwMq2vXYPzEP0AcLLhzu0xiH4AONmge3uE6AcwVu2t6tKaDh8A6B/XbTH6lRLXbevk3SD6\n",
"AeA0eT7sjn4h+gFggoh+ACPkOG09rSXLhj3AaxD9AEaovS0WRtDbI0Q/AEwQ0Q8AdWXZULfqLCH6\n",
"AaCucfT2CNEPACcZ7kbNm4h+AON08QW3eT6S3h4h+gGM1cWb50Pfsm3Ta51dSSmVpqnW2nGcKIqs\n",
"M/5Z6pwqjuPSEdd13aEvvgZwVePo7ZHOoj9N0zRN5/O5bdtpmnqet1qtWj1VkiTL5XLziD2ar2oA\n",
"Ojem3h7pJvq11kmSrFYr0zyPokhrnaZpEAStnoo2PjBlZkHvpWIgy+T0xOqvLvr6syzzfX+zWyYI\n",
"gjRNr3sqAON22c4ZrUfV6u8i+ouicLb3vLBtWzcafW9wKqVUs2sBgFEUo8p96abDpyiK3b6XZj3v\n",
"J53K8zyttWVZWmvbtufz+Uljyy9evFB79n+iKwnoP8u6WIfPBef27EuV58+ff/7555e5Rg1nRb/W\n",
"Os/zyh9ZlrVunl+w0V3/VLPZzPf99adCmqZhGC4Wi/rXIvqBQXMcybLLnOqCrf59qfLhhx9+8cUX\n",
"l7lGDWdFv5lkWfkjy7JOytmLi6Jo849BEGRZVhRF/W8bb7311mw2a6FqAIbksr09+1IljuP333//\n",
"Ypc55qzo933fr/EtyLnc5tbnnMpxnJOiHwBEJMsG/zjGXR2t5t3tF9rXU9TlqQDgqKIYw7NZSrqI\n",
"ft/3S91bZo7mvtcrpZIkqezWP/VUpVde8PsHgCnQejwreDd1Ef0mcNejAmZZ1r71XHmee54Xx3EY\n",
"ho1P5Xletj2+E4ZhaUEAABw1pn17NnW0kcNisfA8L89zy7KUUkEQ7GuAr9N5X0zXOdVisYjjOEkS\n",
"MxXHfDNgzBaYmvNnFxbFqBbxrj26v7/v7GJ5nps91w63vouiqJy/f+qp1nNPj15x16NHj955550n\n",
"T56cVApAH2gtaSpay7Nn8p3vPBwJglpd9kny6gPjs8/k5z+XH/+4i77+OI4fP3788ccft34lEely\n",
"506pPT/Htu2j83DqnMqyLCbgA1OT55KmD0Efx2K+7WstSSJKyfas73LBJJEgeDWfJ03le9+TLJMs\n",
"k5H1GrBfQRxsEwAABlZJREFUP4DxKApJU5nPH9rpliVF8fA/s5nYtiRJdUHz2TCfb83jzHN5+22Z\n",
"zR4+RcaE6AcwHutmvuE4D9Fv+L5ovXWkVHBfx7AZ6R3TNHKiH8BI5Lm47pG5mFEku1sQFIVYVnnJ\n",
"bmklVxRdbFuIPiD6AYxEnleMx5Ym+VR+MJjPjN2Dm9M6RzYzvNNhXgBoT56XJ2K6rjhOuaPm2bNy\n",
"x72ZCFTaV+3583Zq2Q9EP4CRsKyKxbe7HfSl8QARSRLx/bHtyH8YHT4ARmK3gd92weEi+gGMRJ0N\n",
"+pWq6LV33XJvz648H1V3P9EPYCRsW2z7UPqbVb6Vq7pc98jHxr6CA0X0AxiPKBKlqkO8KCQM98a3\n",
"70ueVxfUWsJwbDv5MMwLYFTmc0kSCUPxfXGchyf0KiVay3x+qNNmNpM0lTB8mBdk26KU5Lnk+ZGC\n",
"Q0T0AxibKBKtH/bkERHHkSCoNYEnCB4KmmVfti2uO6p+njWiH8AIWZa4bpMHKzYuOCz09QPA5BD9\n",
"ADA5RD8ATA7RDwCTQ/QDwOQQ/QAwOUQ/AEwO0Q8Ak0P0A8DkEP0AMDlEPwBMDtEPAJND9APA5BD9\n",
"ADA5RP9eL168uHYVeiqOY3X0SaZTpZSK4/jategp3pzDPvnkk86uRfQDwOQQ/QAwOb2LfqXU7e2t\n",
"53lxHGutzzxblmWJeUQbAOD3+hX9aZrGcRxF0WKxsCzL87xm5zGfHzc3N1mW0SsNACU9in6tdZIk\n",
"y+XScRzLsqIocl03NU9HPpEpvlqtgiC4eD0BYOh6FP1Zlvm+b1nW+kgQBM2i33Ecx3EuVzUAGJUe\n",
"RX9RFKW8tm37/O5+AEDJa9euwCtFUbiuWzpo2/ZVKiMiv/3tbxknqPT8+fP33nvv2rXoqffee+/5\n",
"8+fcOZV4cw7ouJnbevRrrfM8r/yRZVmbzfxeNfC/+c1v/uIXv2g8zjx6P/nJT65dhV7j/TmAN2ef\n",
"N954o7NrtR79Sql9/fWWZS0Wi7Yr0MxHH3107SoAQFtaj37f933fr/NKBmYBoBs9GuYVkd2uoX2d\n",
"RQCAxnoU/b7vl8Z/zHTPyhcrpZIk6dXwAAAMRY+i33T4rAcGzAqvyjVZeZ6bnR7CMOy0igAwCj2a\n",
"3Ckii8XC87w8zy3LUkoFQVA5ALBe9rW5/mtTkiTmC4TWuiiK9USd5XLZTsUBYEge3d/fX7sOZXme\n",
"a63Ndg77XlMUReU6AADAUX2MfgBAq3rU1w8A6AbRDwCTQ/QDwOQQ/QAwOUQ/AEwO0Q8Ak9OvJV09\n",
"YXYbNWsLoig6sLxgauI4Lh1xXXfKqyuyLCuKIoqifS+Y8r10+M2Z7L2ktU7T1Kw5dV03CILKu6Lt\n",
"O4d5/WVpmqZpOp/PbdtO0zTLstVqde1K9cWjR49KK6Jt277i43SuxfxaFkVhHiS3b5X4NO+lmm/O\n",
"NO8lrfXt7a3jOGaLGvMZsFwuS8nexZ1zjw0vX760bfvly5frI1EUzefzK1apV7hhjNVqtVqt7u/v\n",
"l8ul67qVr5nsvVTnzbmf6r0UBMFisdg8MpvNoijaPNLNnUNf/5YLPhoeI+Y4ztHHS0z2Xqrz5kyW\n",
"bdul3YijKCptTd/NnUP0b+HR8DUppXhbDuNeqmlS99LuyEdRFKXenm7uHIZ5t/Tt0fA95Hme1tqy\n",
"LK21bdvz+XxSQ5f1cS8dxb0kIre3t7PZbPNIN3cO0b9lOq2PZmazme/767swTdMwDHv7gOXr4l46\n",
"jHtJRMIwDIKgFPTd3Dl0+OAEURRttj6CIDBPRLhilTBQ3EthGK6n+nSP6N/C8NSpHMeZ1K9rfdxL\n",
"p5rOvaS1vrm52Zf73dw5RH8Zj4bHpXAvYZfW2vO8IAgOtPc7uHOI/i0nPRoeIpJlGc3bStxLp5rC\n",
"vVSZ+6XvOt3cOUT/lvqPhp8gz/OyLNs8EoZhaQIy1riXDpjmvWSW8kZRVLoNbm5uNv/YzZ3DRg5l\n",
"5mPZPBnYPBqeX1dDax3HcZ7nZkKCaYmU5qVNRJIkpl1mRibXbdXSzgTTvJfqvDnTvJeUUmEY7k7T\n",
"VEqVcriDO4for1bn0fDTpLU23Y68OTVxL+3DvXRYq3cO0Q8Ak0NfPwBMDtEPAJND9APA5BD9ADA5\n",
"RD8ATA7RDwCTQ/QDwOQQ/QAwOUQ/AEwO0Q8Ak0P0A8DkEP0AMDn/D3EMMAQ3atOKAAAAAElFTkSu\n",
"QmCC\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7d0/kuM4ni9w1IuetiZiA+2UO4E6AtIei7zBUrt1ATL6\n",
"BOQBxpCOIEY9v0ZyxhcO0IYwfYESO9qbiuhIxMQ4OevkGnjNp5JEJf9AIH7g92NVZWWJIER+CQIg\n",
"+O719ZUBAMCS/J+5CwAAAL4h+gEAFgfRDwCwOIh+AIDFQfQDACwOoh8AYHEQ/QAAi4PoBwBYHEQ/\n",
"AMDiIPoBABYH0Q8AsDiIfgCAxUH0AwAsDqIfAGBxEP0AAIuD6AcAWBxEPwDA4iD6AQAWB9EPALA4\n",
"iH4AgMVB9AMALA6iHwBgcb6buwDE/O1vf/vrX/86dykAIEIfPnz4y1/+4mdb715fX/1sKQ4fP378\n",
"/Pnz3KUAgAh9//33//73v/1sCx0+g/3pT39KkuSVoMPhUJbl3KUYoyzLw+EwdynGSJKEbsnnLsJI\n",
"REtelqXPHEP0AwAsDqIfAGBxEP0AAIuD6AcAWBxEPwDA4iD6AQAWB9EPALA4iP4xsiybuwhjCCGS\n",
"JJm7FGMkSSKEmLsUY2RZRrfkcxdhJLol/8Mf/uBtW3iad5iPHz/+9NNPv/zyy9wFAYCoVFX16dOn\n",
"3377zc/m0OoHAFgcRD8AwOIg+gEAFgfRDwCwOIh+AIDFQfQDACwOmehXSq1WqzRNq6oyxjj5wKIo\n",
"0jRdrVZa6+kfCABABY0XNNZ1Xdf1drsVQtR1nabp8Xic8oFFUTRNk+d5lmVN07gqJwAACQSi3xiz\n",
"2WyOxyPnnDFWlqUxpq7rPM/HfeBqtZJSbrdb+1eiD1sCAIxGoMNnv99nWWZz38rzvK7rcZ9m/6Pn\n",
"d6EBAASFQKu/aRop5flPhBCju/vrut7tdi7KBQBAFY3ov150bEovjRCiaRrb/M+y7OK68qavX7+m\n",
"aXrzn9br9dBPA4BF6UqPL1++vLy8eCsGgeh3Mp/HUkpxzuu63mw2ZVlyzouiyPN80LDB+/fvD4eD\n",
"qyIBwKJ0pYddvs1bMQhEv1vGmP1+3w4aZ1n29PREd01gAIARCAzzOuxCkVJqrbfbratBYwAAighE\n",
"P2Ps+pGrcQ9hcc6llBcNfLT3AWBpCER/lmVKqfOf2OmeXb+vlNpsNl0jBFLKi0/TWiP9AWBRCES/\n",
"7fBp+2TsE15dA7Naa7vYQ1EUN3+hLMvzC4Od6kP3jW4AACPQGObd7XZpmmqtOedKqTzPuwYA2k78\n",
"8978c0KI9Xr99PRk414ptdvtun4ZACBKNKKfc348HrXWxhg7KbPrN4UQp9Pp5qMALSnl6XSy3T7r\n",
"9fohJQYACBiN6Ld6TvURQvTpu79zbQAAiBuBvn4AAHAL0Q8AsDiIfgCAxUH0AwAsDqIfAGBxEP0A\n",
"AIuD6AcAWBxEPwDA4iD6AQAWB9EPALA4iH4AgMVB9M+vqrxuruOl0I/iee+i35y7N1X32ty377Z4\n",
"LKV8b26/97o5z0fLfYj++Y164RjcFn1lxr2DPi9sLPbKvA/RD4/ls2E1C58NVf+QxbFC9C+O56hq\n",
"Gq+b88x/VEWcxXFfRFlgFzZE//yiP+I9i7s+g4oP6pZcmYj+mcXdKGaMSRlzFgux6PiAQTzfsd2H\n",
"6J9Z0zDPrwvznMWeX3vs+VLKudfzOfqGgk9a+87ioF4BjuifX9xZ7FmWRX6TAa4Y47vVFRRE/7L4\n",
"v+WMu8MHYJBw+nwQ/cuiNUsSZDH0Ek5OPY63fWwaJmVAI0OI/vl5bhdL6W9bQNosfYM+rzdJ4i+L\n",
"bfSHA9E/v7g736MXfdM41iz2z/OkgPsQ/QCT+L9y+5znE3cWswVXJqIfHkgp3NM4liSRT/H0nMVx\n",
"V+YdiH54rKD6Nx8knLv4R0AWOxTOoYLon5nWaBe75/ME8z9tA1ns0GKf6kL0z8wYtIudsSHlOYt9\n",
"nsz22W9ksRO2GsPJYs8Q/QsV5bQNO3/O/8nsrTKX8DSvt69vCZV5B5noV0qtVqs0TauqMi5OtaZp\n",
"qqqq63r6Rznhs10c1EwDt2xwRHlhA3CIRvTXdV1VVVmWu92Oc566eMdgVVWMsX0YbxLx3C72D1lM\n",
"Udw9S56FVpkEot8Ys9lsDoeDlJJzXpZlkiQTW+tKKc55ssjVm9Auhp4W3iXilq1MzkO5BhCI/v1+\n",
"n2UZP+sCzPN8YvRXVbVerycXzSVkMYB/nHs9F6RE9PfWNI38tpNCCDGlu7+qqotryeyiz+JwpjM7\n",
"FMg5HA17kPjP4igPzjfRiP7rmBZj70WNMUqpsiwnl4s2P4d7u5WQrrPOtAMncWeHtyy2B0ncWez5\n",
"wnbHd3MX4G1O5vO0pnf1fP36tWuceb1ey7GjqFE+WqI1y3MfG7rgrTJtNUZ5YWtFn8VK+Xtni5Ts\n",
"P//zs1L/9/qfvnz58vLy4qkcJKLfIaWUMWbi6O779+8Ph4OrIsXdLmYzDRXGWpmWfSFwrE8C+s9i\n",
"z7P8/uu//nu9/u/rn1dV9enTJ2/FINDhM7odfa2u6yRJ1O+01sYYPesNWNwhtRB+pm0o9f+uo0J4\n",
"bYZ7fvW8t5uMiG9l+iAQ/Yyx63Qel9dJkjRN00Z/0zS2699FGWF+7UHheQqdt2kbs9xCeb7SeLPw\n",
"VheBDp8sy+zzXO1P7HTPrt+3zfk8z68Hh/NvO55t+i9qyHeuSSk2ix+dXO2Ltm0Wxzot3XOXCESJ\n",
"QPTbDp+6rm1w2ye8ttvtzV/WWtsxWK31brfzWc6JkoRV1e1/MoZ17O5gbRr62Vwry1jXkxhNw5x/\n",
"UUKwur792kutmbuRmnk2Z7unb359xrAsc3NVuHjXwsXm/ud/2Pffu9zcOSE6D07OmfOm2p3NMcZc\n",
"Pf/Ttrq6NvfPf/7gZkv9EIh+xthut0vTVGvNOVdK5XneNQDQtvTvT9vXWtu1gJqmKYqi60LiU5J0\n",
"nkJ3jksqmxOi8xTyvzljHN/s39lcXT9kSLZrc0q57Jxpi921OWPYZuM++u/MCnvE0eJnc22rq2tz\n",
"VfXsbGM90Ih+zvnxeLSjsmVZ3ol1IcTpdGqa5v40Himlw1k6MIWfvqCWfXrOW2+J545yezPX3Rvq\n",
"2MK7y0mjMcxrSSmTJHnzKVwhRHyL83ie0eFz5Nv/o+2uKrPPVAPPlUlXIA86XYhyfNuiFP2L5XmZ\n",
"B8+jo55n4ziszHZU+Y5Yh5qd61OZ/kV8W4Pop4Foq79PscNZ0OpBIm45LkGsByeinwC6rf6ejaa4\n",
"w9FVy7FnLfmvTIrPl/Usc8Svw0T0w/wivq12qOdMIc+V6flNyK6GzftXJqIf4FHibvU71CfWPa+7\n",
"wDnJVj/rV5kR90Yi+mlwdXaFeRx77hJhfutBSq+TfFy1i3t+CNFWv2cBlhnRT4OrcAx2womTLO5Z\n",
"S547cP13ZznZO617HS3orOujZ2X6hOiH2zw/iBTm7YgrRCsztLQiLbTKRPTDDZ7v4uOGyoQAIfpp\n",
"8D92FzFXldmzcR13ZbpysVocPBqinwaio1v9+ezwcVWZod3Ct4geKrG+dyxMiP45hdzBTbR7Ghju\n",
"M6AHRP+cmibEdUuYu+5pBLpDwbblgy3YHYOOTIo7+CZEPw2eF4CMfi4pxZM52LZ8sAW7o3+rK9ZR\n",
"ekQ/DU4ylGLePQjFtAKLaDMoNIj+BQnwuRK3cG1bAorHcIBHJqJ/WSieNv3F2kALHOdxdom0pgf3\n",
"I17SORGin4wAGw50oTIdkjLm+nS1ZHpo7RJEPxmhHTpuec6OuCsz7ma45+XwYoXoh9uQxW8aVEWe\n",
"1wol1wzvX2CKh0qAEP1wG06wN/WvouifWZu+dyEfb+Suo30g+ucU8V154NBp4FD0F7aQL0ujIfrn\n",
"ZEygT/M6ofWAc8Zz9zTFk3lQlwhaFfdF2ZAfBNEPnSY25YwZMKGNYvf0ID67RKKvzOkoXvvdQvRT\n",
"giXVHEJlQk9RXkcR/WRMX0sk7vQZtHexLsziUJR5N870W4QAKxPRT8b04y/YhUKtiVemQXsX/f3+\n",
"9KwJuYoCTNL7AqxMRD8EAV0ibgWYNQ7FvXd+IPrhNs6Rxfegctwi15CnDtEPt0mJdLunaYJbkIs0\n",
"NOQ9IxP9SqnVapWmaVVVZkILwRiz2WzSNE3TdLPZTPkozzBZ2624e8M9o3MajRHlqUcj+uu6rqqq\n",
"LMvdbsc5T9N03OcYY1arlTFmu91ut1tjTJqmM6b/0EkpcZ9gniG4HYq7MqM89QhEv22nHw4HKSXn\n",
"vCzLJEnquh7xUVVV5Xm+Xq+FEEKI9XqdZdlms3Fe5p7iXj1fqWE7GN/Z5RAq89z0Znjc9dMHgejf\n",
"7/dZlvGzdkWe5+OiXwiRZdn5T8qy1PHdywVjUFrF3XKcDpXZmt4Mj7t++iAQ/U3TyG8H1IQQ43pp\n",
"yrK8/nCOo6ADWkYOoTIhKDSi/zqdhaO+ktVqlee5k4+KD61r4qDV4vwLuWzXAq9McgK88H83dwHe\n",
"9rhh2KIo8jxPBj7h+vXr165x5vV6LR85429iTcQ9WXPQanEsyLMxHEMr03a+Rzzb1WH/Uld6fPny\n",
"5eXlZdJmhiAQ/Q9SFIWUckST//3794fD4RFFetPEhljco8pDoVXrUJRzYFpSss2GfTtKOF5XelRV\n",
"9enTJzfb6IFAh4/zdrQx5unpaVzuw+PQyo7Ab6FoTUUfUZk+j5YoWwkEop8xdj0JZ/S0HDuXP89z\n",
"5H5oaJ1gga+FR6sZPrQysfDqdASiP8sy9e3L9Ox0z67fV0p1PaZ7M/ebwNtv8yGUHeETAq+EdIZW\n",
"KyFMBKLfdvi0E/ntE15dbXattV3soSiKi3+yj/KWZXnxf5+enh5Q6l4Cz1acYA5NHGgJ/FChBZXJ\n",
"qAzz7na7NE211pxzpVSe510DAO000Ov5oFrrpmnqur54HGzGhRyGZisOWYdsMzzkTptzWrOrh1IC\n",
"IgSra0qVGfFkpJ5oRD/n/Hg8aq2NMWVZ3nkISwhxOp2aprmespkkyel0enBJHwvNcIfIzXcK+duP\n",
"vjLja3XRiH6r51Qfuz7PowsDztFqhgeOVjM8fCFfd8ch0NcPC4HecIcmVubQ1eLgjjArE9EPnWhN\n",
"Sgm8XUarMhnBPpyQBViZiH7oFODxShcqE4KC6KdESmItx5BNrEz0LzmE1eL8Q/RTgtPDoYmVie/C\n",
"oaGrxfkX35Ue0T8bPER8Afc0EKz4rvSI/tk0TegtHTatsTP0/8Z3djkUX6tzoikVglYXcxX9WAZn\n",
"nMDDbuIiWYHvHS2ozAtTKiTwpff8cBP91wvmwINgrVoAmG5Y9Kdp+u4WhT5aL7BWLQA5YXbWDW71\n",
"Hw6H1zPPz89JkhyPx0cUDi6gGQ5ATpirxQ2LfiHExdJpnPPtdltVldNSwUKF2T4iCpXp0MSHsQNs\n",
"tA2L/u12e72Gmr0ejH5tFvhB4vsJ8AyhC5XpUHwPY7sZ5hVCzLjqPfRhzJhZDfhWu4yoGVRml3E1\n",
"g3mFU7iJfvsSFScfBUHBt9plRM2gMruMqBkpEf2TDFuvv67r6yn8TdNwznsupg+tMAd/AEjAdXSi\n",
"Ya3+/X5/3bGTZdlut3NXpKUY1wNDBYmhBUI9MOG3cDmn8aUzCpXpwbBWvxAiy7Lrdx8CXCBxYSPU\n",
"cgx/mFFKMpfS8CvTg2HRv91uH1QOAADwBsu3QUBGNxtxC39tylR0Ku13b+KrTEQ/BGR0DwwW5Lo2\n",
"pVuDUFeYH/FVJqIf7gmzwUIX7k4cQmVOgehfCqXGtFzCbLDMblxlJgnS6rYRLQxU5kSI/gXBxAaH\n",
"UJkOoYXh39ToN8YURYHl20aIuy+FxN5NXJPLG1QmODdscue1uq7rumaMJUmC+f6DjGvpULnJ1ZqV\n",
"5dyFeAuVljuJB7+pVCZYU1v97foNAt+8F4Sqedy1jUQL1z9UJrg1Nfrte1qOxyOiH6Yb/RoyrdFf\n",
"fAmVCXdM7fBhZw1/gIlGJ44xBLpEPENlBiLMey/M8IF7CK3JFT5UplthRuq1MG+hlhj9SqnVapWm\n",
"aVVVy3nDzLgdJbQml0/j5vWjMm8aV5ks1EilYnHRX9d1VVVlWe52O855mqZzl8gTnCc3jc5ijG05\n",
"hMr0z030X7+/JUzGmM1mczgcpJSc87IskySxk1PBLRLNWyFo9MAQOb1ofOlUKvPR3ER/URROPufR\n",
"9vt9lmXn75LM83yu6CdxnoxG4iaDSmOTyuJ0JL50KpX5aINn+Cil1NVDe1Ra/U3TXMxHmvGF8uPO\n",
"E/vMZMTHLpFDiYa4mxeeRVaZw1r9SqmqqqSUSZIopZIkkVIqpai8wsW+Rvjih7SeSCBV2MFGr8kV\n",
"2WnpyrjmBeb13xRZnQx+Lft2u5VSaq3tBYAx1jSNvQw8poQuOWngf/36tWtweL1e4ymHWUR2Ws4L\n",
"8/odum7KdKXHly9fXl5eHl6g3w2LfqWUfQO7MaZtPpdl+fT0dP6TuL1///5wOMxdCk84Z/t9zP1L\n",
"nqE765oxMa9n1TSX19Gu9Kiq6tOnTz7KxBgb2uHTFe5JkmgKUyXQJB8KFeZW3P1144xenI5KZYbZ\n",
"JB4W/barx/6ZytDuhetLFImLFkDEwgzHuA2Ofju9J0mSpmnarnOtNYnB0izLLqYn2emec5UnYhh3\n",
"dQiV6RDNJqt7w6I/z/N2OLcsyzRN67ouikIIQSL6bYdPO5HfPuGV57n/kkR//KEd5xAq0yHM67eG\n",
"DfNyztvu8izLhBD7/V5KOUt6jrPb7dI01VpzzpVSeZ7PMgAw5fiL+7KBFq5DqEy3mobMAMObJi3a\n",
"LKUkN3DKOT8ej1prY0xZluRmJSUJi/ttmHgniUOoTIfsQyeIftrIXbHgPmpX8KChMpdgcSt3LtOU\n",
"PiK0Aa+NrhNU5rUpi6eG/yJ4pQK9lCL6F2HK0EKYB+68RtcJKvPa6Dqh0vcSZhcDoh8WDc1wt+Ke\n",
"gxATRD+4R2j9LxLlpHJ9Gr36nk9UKvPREP3gHtb/covE9YkKVKaF6J/H6PeRRm9EowztuDvCb4YT\n",
"ElNlIvpnMzr64066EY2y0et/RY9EDwwVkVUmop8e3LFeQ50ADILoXwRC467hm1iZcd+0jTClQlCZ\n",
"oyH6F2HKuCvOrgtTKlNKhjXCL4y+jqIyp0D0wxtwu+AQKtMhVOYUiH5wD/OXHEJluoW7WAvRDw9B\n",
"Ja1IrAODynQI9woWon8eaHo4NGXKHZVU9QaVuRCI/nmg6eEQ3rvkECpzIRD9i0DrJiPwaRu0nutB\n",
"ZTpEq7T3IfrpGXH8EbrJSJLQL1SE2sWoTLdG9GgFW/+IfnrC71EN9nCnKKaW5gIF2+pC9IN7wR7u\n",
"IRga5bTaxZ4NbWRgpmwL0T8PWu3iwEsbePHOhb8EWODFuzCikYHotxD98yDULhYi9KFCQpUZPtxk\n",
"LASifxGmtIujbyUNrRxCNxnho3WTERNE/yKgXdxlxBJgqEyH4r7JCHloAdEP7hFqF4ef44QqE64h\n",
"+mFBws9TQlCZDuHFFS1E/wymH38RtwQ5H7wEWMS1Md3QzvS4K3PKuxZYXCMTiP4ZTDz+wp9yM8WI\n",
"mkE77o6hHQ6ozDuC7b0ZAdFPz9DjDze5bsXdLvYs7soMee8Q/fGbeJMBF9BZ51Dclal1uKceoh8c\n",
"w03GfUMrJ/B0m1f4R1qwJfxu7gL0pZSq69oYI6Usy5KPrVFjTF3XSinGWJIkeZ6P/qjlGDS6hZsM\n",
"t3B4wiPQaPXXdV1VVVmWu92Oc56m6bjPMcasVitjzHa73W63xpg0TY33ZhWtdnHgy85gupRbE2sD\n",
"lUkFgeg3xmw2m8PhIKXknJdlmSRJXdcjPqqqqjzP1+u1EEIIsV6vsyzbbDbOy3wf2sUOTa9MQpdh\n",
"DybWBiqTCgLRv9/vsyw775bJ83xc9Ashsiw7/0lZljrimZKMMWo3GYFDZbqFu4S5EIj+pmnkt+06\n",
"IcS4XpqyLK8/PPq+ftxkOITKdIvcyRfNtYpG9F+ns3D0cMVqtcrz3MlH+YTO94VAZQYlpqcp55zh\n",
"Y4zp6mzhnLct/ccNwxZFked5MnDlwK9fv3aNM6/Xa/n4NqGUg5c68Amd7w6hMoPipMHZlR5fvnx5\n",
"eXlxsIF+5ox+O1/z5j9xzne73UO3XhSFlHJEk//9+/eHw2HKpidey3Ayn1OKEbxtC1TIiww7EcI9\n",
"UFd6VFX16dMnb8WYM/qzLLsYdL3JeTvazunM83yurh5kt1u00iqE9LmDVmUKwZQasOI/Tr0Wgb5+\n",
"xth1v9DoaTmz575/gWcNLdPbxUif1vTKDPxCFfKpRyD6syxT3/Zt2+meXb+vlNpsNjdHCG7mfhPy\n",
"mKkLyBq3Ao8bWuKuzJBPPQLRbzt82lEB+4RXV5tda52maVVVRVFc/JN9lLcsy4v/+/T09IBSR2VQ\n",
"4yXkls5NIReYXOc75/HMgYkbjTV8drtdmqZaa865UirP864BgHYa6PV8UK110zR1XV+MLftfyIGc\n",
"QY2XkFs6NwVeYFrRL2XQl1Jo0Yh+zvnxeNRaG2Pur90mhDidTk3TXE/ZTJLkdDo9uKS94NxwCJXp\n",
"UNzTpfAk9jka0W/1nOpj1+d5dGGm8Hz8kQvHQQVGZb6paQbcOvg8dZrG66PRTp7E7j8yGPihQqCv\n",
"H64NGpkm19IJucAhl+0mKcN99ttz9E83qDK1HjDr1D9EP0lh39VAQMhdq0IWU2Ui+n1TilhLB5wL\n",
"vCuAlv6VqTXaTP8fon8GPtsOONxDE9MSYLMbVJnG+B7JCBmiP3I43EMz6OvA/cF9ITdrmgZ9/XAm\n",
"7pPZ8+Eed2WyuDqXISiIft+0Rl+/M04q0y4BBk6EXJnRNxQGQfTPwGdTzslKACGfM9Mrs3/9kFtW\n",
"wb+Q6we3UOcQ/fGbfjb2P2eaJvITzPPASdyVCTNC9INLrh7S6TlcHPLtyHSuKrPnHJi4K9OVaCYy\n",
"IPpJiub4uylJ+u5g4A9MhiBJ+mZ69JXp5NoWco/WIIh+kvoff2jKOYS+ftKw3NM5RH/kcLi75ST6\n",
"+9/TRNzX7+phw2APucC/O0S/b8EeqU7gSvOm/kuAOVlpsj/PvYiuHjYMPGGDhej3DUeqQxQrM9gy\n",
"B/706URYO+sCoh+A5N0DDOV57axgr/EWoh96iTgcpcR6ajOI+6kFz511IyD6vSJ6uMcdjhS/kQj4\n",
"f0UXnEP0e+X5cHc1iaJnOOLsgmB5fmoBHT7wDc+tfs8rNntemY7oLZR/uCQ71LMy0eED33DV6u+5\n",
"PqLn97QY4yaLOe/Vv0T0Fqonh3mNC6RD0dwBI/pJ6plBRFv9UvY6c3AL5VD4UTWR5x0M/3KL6I+Z\n",
"//PZ5xHvudXvcBWHPg9PubqF6onuayR6PokWfhZ7huiPGQ53t1xFf5/P8b+YmufXSLi60vSpzLiX\n",
"OxwH0R+z6O/ifYq7Mj0/7Or5nsbzg8qeh4XGQfT743++V9ytfodZ3Oej4q5M5m4H+1Rm3JPBPA8L\n",
"jYPo98fzfC+37bg3b5lJjytEH+tv8j+hKOJhIRKt/u/mLgBJdT2y9zDLXBeFsaLoPItcbS5JWFX5\n",
"29y5drvn/vlP9h//8ZCz6+bmrAg2d+e4fUQQK+X1Fe1as/3+9j89ol1yf3OI/jjl+dwlOMM5W6+j\n",
"3ZwxbLv1tznGvO6d5801jdfNKcXK0l/r3nboe+vTN8br5pxDhw9VtiET/ROtce+dHzMOUMc3P7V9\n",
"mpL6sD+Z6FdKrVarNE2rqjIuar1pmqqq6rqe/lH+teupee7EjP5KE6XlfGUe9rTtyaH+KmMa0V/X\n",
"dVVVZVnudjvOeZqm0z+zqirG2L6ruy5sc53M3q40C7mnAZgLgeg3xmw2m8PhIKXknJdlmSTJxNa6\n",
"UopznpC+ajPG4g1Hu1Ox3tPgCSOHOPc6mBwNAtG/3++zLONnJ2We5xOjv6qqtefhvMeINRxn4a0y\n",
"w5/+QQjR9SdmRyD6m6aR3369Qogp3f1VVV1cS6AnXGkcwttiYUY0ov86psXYhpMxRilVluXkcsHD\n",
"ebvS2B4Y/1caz481eRPxO91a1Gf4zDmv3xijO44Rznnb0ncyn6c1vavn69evXePM6/VaRtqQs18C\n",
"9cO9i21INE1YT2y45W0dmyRhxkR7qLRGX7a70uPLly8vLy/jCzTQnNGvlOrqsuec73a7R2zRGDNx\n",
"dPf9+/eHw8FVkaiwB7rnRnHc8aH1Q55/DoTnuY+ERs670qOqqk+fPnkrxpzRn2VZ1uPYd9iOrus6\n",
"SRL1+4QArbW986DbVI87HOO+0vh83N8Y1jQxDy/7XJvTViZ1BPr6GWPX/UJdPUX3JUnSNI36XdM0\n",
"tuvfRRl9szkVdzh6FuuQsn0A0PPCxRGE402zVOYjEFjDJ8sy+zxX+xM73bPr95VSWus8z68Hh/Nv\n",
"u3Jt+hMd8p0lp3CloWiWQ8XzwIm3e5po2gcEWv22N6YdFbBPeOUdh5XW2i72UBSFvyLOhMTasOPM\n",
"ck8DdPm/p6F+cBJo9TPGdrtdmqZaa865UirP867e+balf3/avtbargXUNE1RFFvPi0M64v9F4d42\n",
"R/28uq9dAgymE4L5X4grgslgNKKfc348Hu2obFmWd2JdCHE6nZqmuT+NR0q5wFk6E0V8pfEs1v2a\n",
"BSpzHBrRb/WchyOEGP3AFy1xzw70fKWJ4BYeoD8Cff3QBc1wVzhndY1lFdzAemokIPqhF/t8ZqxX\n",
"Gv+hH/FNBq6gJCD6oRf/OeX5SuN5Iqn/F4XHeqWZRQTTjhH90FcEh/sdETykc4fnK40xMV9p4tg7\n",
"RD9V/oMYz3M55LPDJ0l8P1sb9+LeEeQ+Q/TTxXnk4Rj3lcYYdPg447ky4xinQfQTFnc4xg1XGofi\n",
"rswHQfRDX57vqT2fzz73TspoVzez/IdjBM1wzxD9hEXQ9OgiZcwnM+e+v7tYH8iwUJ8jIPoJ8xyO\n",
"EV9pWBQn8x2e9y7uymRR7CCiH/qK+EojhO+9iyA77vA8TTbuynwQRD9hPsPRf5PfZxb7z464rzQR\n",
"v92exXKleff6+jp3GSj5+PHjTz/99Msvv8xdEACIin0372+//eZnc2j1AwAsDqIfAGBxEP0AAIuD\n",
"6AcAWBxEPuVdvAAACjhJREFUPwDA4iD6AQAWB9EPALA4iH4AgMVB9AMALA6iHwBgcRD9AACLg+gH\n",
"AFgcRD8AwOIg+gEAFgfRP0aapnMXYQylVFVVc5dijKqqlFJzl2KMNE3plnzuIoxEt+T/+te/vG0L\n",
"0Q8AsDiIfgCAxSET/Uqp1WqVpmlVVcYYJx9YFEWapqvVSms9/QMBAKj4bu4C9FLXdV3X2+1WCFHX\n",
"dZqmx+NxygcWRdE0TZ7nWZY1TeOqnAAAJBCIfmPMZrM5Ho+cc8ZYWZbGmLqu8zwf94Gr1UpKud1u\n",
"7V9FHG9ZBgDojUCHz36/z7LM5r6V53ld1+M+zf7HsizdFA4AgCACrf6maaSU5z8RQozu7q/rerfb\n",
"uSgXAABVNKI/SZKLH07ppRFCNE1jm/9Zll1cV9708vLy/PxMcbL2zz///Ouvv1Is+a+//vrzzz/P\n",
"XYoxnp+f6Zac4qHCyJbcyeyV/uaMfmNM19QaznmbyA5rRCnFOa/rerPZlGXJOS+KIs/z/sMGf/7z\n",
"nz9//vyPf/yD7mMjnz9/nrsIYxAtNmPs73//+9xFGInuQU605H/84x+9bWvO6FdKdXXZc84f1C1j\n",
"jNnv9+2gcZZlT09PSZL0vI348ccff/zxx0cUDADAmzmjP8uyLMve/LWhHTL3P0prfTqdrgeN1+u1\n",
"q60AAASOwAwfxth1v9C4h7BsP9JFAx+TOwFgaQhEf5ZlF4M2drpn1+8rpTabTdcIgZTy4tO01kh/\n",
"AFiWVwqSJNlut/bPz8/PUsrj8XjzN9unfLMsu/kLp9MpSZLn5+f2r0KI9q8AAEtAYHInY2y326Vp\n",
"qrXmnCul8jzvGgBoO/HPe/PPCSHW6/XT05O9b1BK7Xa7rl8GAIjSu9fX17nL0JfW2hgjpbyf1E3T\n",
"3HwU4ILt9nnz1wAA4kMp+gEAwAkCw7wAAOAWoh8AYHEQ/QAAi4PoBwBYHEQ/AMDiIPoBABaHxiNd\n",
"4bCrjdrHC+yyz3OX6Iaqqi5+kiTJ9RMMIezLfr9vmub+S9P6lNP/vrxZ8gC/Bftm0/aJljzPp1Rm\n",
"aCXvWeFsvpILIcqyvLlszAx1PvfjxJRst1u7hsTz8/N6vZZSzl2i2xhjh2+dTqeL35l3Xw6Hg31J\n",
"TpZlSZLc+c0+5fS5L/1LHtq38Pz8nCRJWZan0+l0OpVlKaW8XsKkZ5ECLHmfCvdc8tPpZF8Dbkuy\n",
"2+1uLkIzS50j+vt6fn6+WO2nLMt2ZaGgvHlFn31fjsejPQEOh8OdAO1TTs/70rPkr+F9C3me73a7\n",
"85+s1+uyLEcUKcCSv/ao8Nf5jpbzn1wsLzZXnSP6+9putxdHm72kz1WeO948B8LZl/sB2qecc+3L\n",
"9Oj3XPL1en39w4td6FmkAEv+2i/6QzjyhRAjiuS85Bjm7cvt2+H9UErdLCGVfelTzvD3JZBv4XpY\n",
"ommai87inkUKsOTnuiqcBXC0KKUuhh/mqnMM8/bl/O3wD5WmqTGGc26MEUJst9vzU4XKvvQpZ8j7\n",
"Evi3sFqtLl5O17NIAZbcul/hbL6S26UnlVJa64tXz85V54j+voJqSN63Xq+zLGsPi7qui6I4P+Co\n",
"7Eufcga7L4F/C0VR5Hl+kSY9ixRgyVmPCmfzlVxrrbVWSl1Py5mrztHhE6GLCWR5nhtjmqaZsUgL\n",
"FPK3UBSFlDLP87kLMtidkodc4Xme23k+WuvrSaizQPT35fDt8P5JKc/PASr70qecVPaFhfEtGGOe\n",
"np660rNnkQIs+U0XFc4COFq2263WesRh4LzkiP4BXL0dPgRU9qVPOansyzXPJTfGpGma5/md9OxZ\n",
"pABL3tPsR8v1BWmWOkf09zX07fBB2e/3560GKvvSp5xU9oXN/S3cTM+LDOpZpABLftNFhbMwjhb7\n",
"otmhRXJf8tHTQheo/9vhZ5QkycXzL3meXz//Esi+vDk7vk85Z9mX+yUP7VuwD8ReFOn19ZVzPq5I\n",
"oZW8Z4W/+j1asiy7+HA7Fj2uSG5Ljhc0DmBbH/blwPbt8AEOlBljqqrSWtspELZpcD0Tbt592Ww2\n",
"tgljB+LaptnhcBhRTp/70rPkoX0LSqmiKK7nAiqlLhKgZ5FCK3nPCvdZcsaYHdQ1xthS2Un9Nyf5\n",
"+K9zRP9gPd8OPy9jjO0HvF9OEvvC+pUzwH2h+y30LFJoJe9Z4cxvyZumsd1TTg4DVyVH9AMALA6G\n",
"eQEAFgfRDwCwOIh+AIDFQfQDACwOoh8AYHEQ/QAAi4PoBwBYHEQ/AMDiIPoBABYH0Q8AsDiIfgCA\n",
"xUH0AwAsDqIfAGBxEP0AAIuD6AcAWBxEPwDA4iD6ASjRWl+8nru/uq7dFgbo+m7uAgCMVNf1fr/v\n",
"+tfr1/zGoSiKm6+c7cNWV4AvlAb/8IJGoKqqKs65fTG61nq/37eZmKZplAe2vdqNvqpprVer1el0\n",
"clsqoAitfiBMSpkkif2zUqr9c6w2m83oJj9jTEophKjrGg1/QF8/UJXnuW3yX7to2CqlVqvVhw8f\n",
"fvjhh9VqddFXvtls0jRVShVF8e7du6Io7A8/fPjw9PSktbafkKZpmqaMsf1+n6bpu3fvnp6eqqoy\n",
"xlwXwLavf/jhB7vF/X4/vZ9dKWWMybJsyuayLEOPPzDG2CsAfYfDIUmSm/+03W6TJDkej/avx+Mx\n",
"y7KyLNtfOJ1OeZ4LIXa73evra1mWUso8z+0vCyHs7xwOByllWZZ5np9Op/bDhRDth7cf2H5a+/ld\n",
"xevPbvr654M2Zy+Kz8/PEwsD1CH6IQZd0X86naSU1z9PkuRwOLR/LctyvV63H3X+X84/NkmS6/C9\n",
"3vR6vT6/tLy+vj4/P99M7UGSJLn42HGbY4yd7zssEzp8IGZ1XZdlef3zsiwvZged9x1xzrs+8PrT\n",
"kiQxxjRN0/4ky7L9fr/ZbNqeJc75drsdUf5zWmshxPXPh24uSRLbiwVLhuiHmNlO8HdX0jQ9D+v+\n",
"boYv5/z802wXEPt9VODDhw9FUYzb3JubHre5m+MTsCiY4QMxs732N4dGx2ma5jqCjTEXA86c8/P7\n",
"AxvKx+Pxzv3Emy4uMKM3p7XGDB9Aqx9iliSJ2wktVVVd/KSuayHEeche/06WZUKIid0sUsqbrfVB\n",
"mzPGXF+oYIEQ/RCzJEmEEHa+5rm6rjebzbgPTNPUjhNorauqquv6omNda31xvWma5ubtwtBN31zC\n",
"YdDm9vu9nd0/pSQQAXT4AG2r1cq2ZJumsfPuy7I8f7Zru91WVfX09GR/aIzRWksp22ejqqra7/dK\n",
"qTzPbU+IHSHY7Xb2F9I0Xa/XtqVsp4G2E+ftTKGLfhXbM9NusWkarbWdBjplT+2nXT+5NmhzSimH\n",
"3V9AFxZygEWwiW//PPqh3zRN+y+i0G6xXW1iujsLOfTZnL1CnE6nKUMOEAdEP0Bfg6L/QT58+GAf\n",
"Uhvxf4uisOPezksF5KCvH4CSthtqBCEEch8stPoB3naxQHSWZchQIA3RDwCwOOjwAQBYHEQ/AMDi\n",
"IPoBABbnfwHGetk46b119wAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"%% représentation en temps\n",
"% Nouvelle figure\n",
"figure\n",
"% On commence par tracer le noyau\n",
"plot(noyau,'-bo')\n",
"% Nouvelle figure\n",
"figure\n",
"% On trace le signal, en utilisant ech pour spécifier les échantillons temporels\n",
"plot(ech,signal)\n",
"% Les fonctions xlim et ylim permettent d'ajuster les valeurs min/max des axes\n",
"xlim([-1 max(ech)+1])\n",
"ylim([-0.6 0.7])\n",
"% Les fonctions xlabel et ylabel permettent de labéliser les axes\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A partir du graphe du noyau, on reconnait la fonction de réponse hémodynamique utilisée lors du laboratoire sur la convolution. Le signal est généré par convolution du noyau avec un vecteur `bloc` (ligne 18 du bloc de code initial). On voit que bloc est créé en assemblant deux vecteurs de 15 zéros et de 15 uns (ligne 7). Le signal est donc périodique. Comme la fréquence d'acquisition est de 1 Hz (ligne 9 définissant les échantillons temporels, on voit un pas de 1/freq, avec freq=1, ligne 5), la période du signal est de 30 secondes, soit une fréquence de 0.033Hz. On peut confirmer cela visuellement sur le graphe."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Représenter le contenu fréquentiel de `signal` avec la commande `Analyse_Frequence_Puissance`. \n",
"\n",
"Utilisez la commande `ylim` pour ajuster les limites de l'axe y et pouvoir bien observer le signal. Notez que l'axe y (puissance) est en échelle log (dB). Quelles sont les fréquences principales contenues dans le signal? Etait-ce attendu?"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fjOTGfedrdndm5ZVWMxxJiP4sVgIHdmAD8QXmINJC\n",
"CBIZZIxA0NOanRXkhX0vbAFBACdAUESM09sB5Bm+REmAhNTmcIEDGCCBQwA/5IGMfUJedAFpxU9n\n",
"RG7Kyh/kBqewfMnuJjuzNu+hRhSX3c2p6ibZVeTvA0Ho7fl18Vf16/6x+K1/W0VRIAAAAGBMnNu0\n",
"AwAAAEDfQOoHAAAYHZD6AQAARgekfgAAgNEBqR8AAGB0QOoHAAAYHZD6AQAARgekfgAAgNEBqR8A\n",
"AGB0QOoHAAAYHZD6AQAARgekfgAAgNEBqR8AAGB0QOoHAAAYHZD6AQAARgekfgAAgNEBqR8AAGB0\n",
"QOoHAAAYHZD6AQAARgekfgAAgNEBqR8AAGB0QOoHAAAYHZD6AQAARseFTTsAANJg2zZCSNd1Xdc3\n",
"7QsrhmFomuY4zqYdAcQCev2jgxAynU4PDg62trYmk0kcx67rbtopJIIPZ6LrOiEkjuMuCp9MJkaF\n",
"yWRi23aWZV1cCwC2iqLYtA9AfxBCDg8PMcaWZSGEsiyzbTuO4zzPN+uYYRhRFG3WBxZox7+LTnQc\n",
"x2EYIoRM06TvZFnm+75lWTRYq5GmqaIoqqq24yUwFEDwGRe+75umWaYSVVWDIDg4ONisVwBCSNd1\n",
"+jxRVZNM0zw8PDRNU1GU1YrVNK0d/4BhAYLPuCCEzOcCjHH5Oo5jKjgghMIwNAxja2vr8PDQtm1C\n",
"SO2DcRxPJpODg4P9/X2qHS27qG3b1aLSNC2Np9OpYRhpmlbljul0Ol+O67r0r2malu4ZhkE7y7xe\n",
"sUCL2t/fPzg4mE6n8y3Q+hVrKIpimiatL/qorXzfLw3oOzReVbIsKxUk+qSykDRNaQWp52EYVgtn\n",
"NyOEuK5LG6EUEmuF+L5PnaellV+G+cs1f2FKumv2UVAAYyIIAtM0Gwxms1kURZqmUVFoNpvR9z3P\n",
"U1U1SZLS0vM8XdfLd5IkMU0TY1wrMM9zTdM8z8vznP7T8zxFUUrLKIroFaMK1QuVJElCLYMgsCwL\n",
"YzybzWazmWmaVT9ZvGLB8zxN08qiaMkY41ppLV5xvvCiKCzLKguPoohWvPwrbZOFP2Tako7j6Lq+\n",
"8HKz2Yw+9pX/tCxr3pjFLEkSx3FKP2ezGQ1orRz6wfJ7led5rToFwxeG0mKzjxNI/aPDcRya2T3P\n",
"W5hhi6Kgv8/am1EUlT94+tte+MHaD37+naIoPM+r/UqXpaeFl1AUxfO8+T+xe3UmtCiafUqSJEEI\n",
"VT1v8YrFotQ/n7gX3h4a+nDVqNVwHGc+7c7HndGsRhAE835ijGvNlee5oijVd1i+MO02+zgBwWd0\n",
"YIyTJKGTVXzfPzg4WPiMX1WBKPQjdM6J7/vzBvRTVfklyzJCyPxUSNM0y8HMFXAcZ+HIJ6NXLNDx\n",
"1ZrCrmla7botXpFSqliGYRwcHGRZFgTBCuWwYJpmGIau65ZSCb2nrmaGEIo/go4tL7xo7cugKEpV\n",
"RmP8wrTe7CMEhnlHSjk5nRBCp37XxgAWzglRFCXLMlVV0zRdNh2z+rvNsmzhFHhFUdYZflw2X4XR\n",
"KxbSNF3meUdXLD9V5riuVw9QBc/3fZrZabAwxrXmZTELw9C2bU3T6JuEkGUN2AzjF6b1Zh8hkPrH\n",
"RRiGte62oii6rodhWMvFNMXXPl6OEtP+L0vPvc+Z6exesRTV8xUpNBxtlcZyuWr3mT5zJElSu8M1\n",
"m2VZ5rpu7VO0+7+CSyxfmNabfYSA4DMulvWV5h/P56de+L6vqiq11HV9oUxUQ9f1NE0XTozp4pbA\n",
"6BULmqYtlA5qb7Z4xZVZNu/oTOZDbJomfaTjMlsojq3mFeMXRoRmlx1I/eMiTdPaLzlN0/lHAYSQ\n",
"ruvlvEn6Kd/3S4VX13VVVeenYPq+X7u7YIwnk0ntx+y6bu2zWZbVbgZxHPPeHti9OhPTNOmKquqb\n",
"0+m0luBavCIjmqZVm4VO4lytqDRNaxWkUag97Z1pNn+3cF23YUZpMyxfmP6bfXjAat5xQWX9OI6p\n",
"qpBlWZqmQRDU9A26tpauL6WJhs75qSU+uhK4HDNI05RuF1Mzoz9IOjOHboSg63rNjIrF9A600CbL\n",
"MvpTT9O0fPhACGGMawoJo1dnQmeXl5p1HMeWZWVZFoahqqrVtcetXNEwDNrUNKU2bLwznU6zLKP3\n",
"AEKI4ziHh4e6rtMJuGVpZS2oMf1ndUHfZDJRVbX2ZaCTJquXYzErXaINRUeSptOpqqqlV9PplEpA\n",
"dHou9Y3Ox685z/KFaavZRwuk/jFCfydo+XAr+7YKZVHorBG2UvldZsZeVItenUn5ONJcTotXZIGq\n",
"ImuOllPO/DIwmpUNpWlaK8n3zC8M6r3ZhwSkfmABsuyoAwDAaoDWDwAAMDqg1w88AJ2+Xf6zKg0D\n",
"ADAYIPUDAACMDhB8AAAARgekfgAAgNEBqR8AAGB0QOoHAAAYHZD6AQAARgekfgAAgNEBqR8AAGB0\n",
"jDr1p2la23EQAABgDIx0SRchhG4riBDq9Aw8AAAAARlp6rdtuzyhkB4ntGyDXAAAgOExUsGnenAo\n",
"PRhos/4AAAD0yUhTf23DcTjbAQCAUTHG1D/fx58/fxwAAGDAjDH1AwAAjJwxpv754+V4j/8GAACQ\n",
"mjGmfjSn+RBCNuUJAABA/0iZ+sMwdF23wSCO48lkYhiGbdsL07qmaeWhz3Ecr3+2NQAAgETINK8/\n",
"jmPf97MsU1WVELLs3HDf933f9zxPVVV63GCSJDWb2pIuz/Ngkg8AAONBptRPVRraYXddd2HqJ4Qc\n",
"Hh4mSVKmctu2VVVdeMBsWWCXXgMAAIhHISFRFOm6vvBPnudhjKvvzGYzTdPauvQXv/jFTUcMAIBh\n",
"srW11VamOpMLm65sy2RZVuvFU3WorfJ/+MMf7uzs/OZv/iaL8be//e2f+Zmf+YVf+AVG489+9rPP\n",
"Pvssi/Gf/dmf/eIv/iKj8R//8R+//vrrLJbdGX/wwQd/8Rd/wW78V3/1V1/60pdYjP/6r//66Ojo\n",
"lVdeYTHmikh3jfynf/qnX/7ylxmNBQnfsCPSnTF7rNM0/e53v8tYbAv0dpNpkYZev2maURTV3lxm\n",
"vALXrl179NFHGY1ff/31b37zm+zG854v48aNG+zGn/vc5xgtuzOOoojL+MaNG4zG3/zmN19//XVG\n",
"Y66IdNfIL774IruxIOEbdkS6M2aPNcb4woUL7CWviZQzfBroeprmQw89tLW1xWi8u7v75JNPshuz\n",
"u8HY8aHs7+9LZ8xewSeffJK96bgi0l0jf+ITn+ioZIhIiSDtxhXrc+f6S8hDS/1dc/v27Z/+9KeM\n",
"xkdHR++99x67Mbsb3//+99mN//Ef/1E6Y/YKvvfee+xNxxWR7hr5X//1XzsqGSJSIki7ccX6Jz/5\n",
"CbvxmgxN6+96us6FCxfYe/1f+cpX2Ls/X/nKVz772c8yGr/22mvsNf2N3/gNRkvE2UlhL1nTNC7j\n",
"1157jdH42rVrn/nMZxiNH3roocuXLzMad9fIv/M7v8NuLEj4OooI129kb2+P0RJxtlt3xlyxZs8t\n",
"LdCbtNQiDVo/xthxnNqbiqK0demXXnppd3e3rdIEpMVxEQHBGLOLxTIC4ZMXjPHOzk5vlxua4GOa\n",
"ZrlMlxKGoWmabZXPJfhwHQDJdWaA7/sdGXM9zHbnBrsxVyNzyQvd1a67WIsQPt6vPbsxl+AjwpcT\n",
"cca6T8FnaKmfPqGXsSGEuK67cD0XAADAaJFpNa/rurRHTwipzt+vLeslhBiGoWmaoihxHFuW1WLq\n",
"//znP/+9733vxz/+cVsFioZhGMt2yBgA1YM5BwmET15s2/7d3/3de/fu9XS93qSlnkmSJIqiPM/b\n",
"LfaVV165cuUKo/FsNpvNZuzG7G5wKZ7DNuZtZHbj7mo37FjLGBERYo0xZl8ztD5Dm+FT0tFUn+Pj\n",
"Y3atn2uRAZcx1wEDwzaWsZEFcQMi0oMxVwX71PplEnxE4NVXX33nnXfef//9TTsCAMCgsG371q1b\n",
"H374YT+XG9owb9fcuXPn/v37jMZZlrF3ELi6ErVZTGM25m1kduPuajfsWMsYEUFifXJywm68JpD6\n",
"+bh9+zakfqGMZUw0w461jBERJNZ9pn4QfPgAwQcAgC4AwUdoTk5OuIZ52Qd5Bj/e1d2gIlcjsxsL\n",
"MvQnQiNzGcsYEUFiDUu6xCXP8+PjY0bj5pWKWYaq3wpBVvNKZ9zd2lFBVniK0MhcxjJGRJBY9zep\n",
"HwQfXloUfGwb6Toa6PIUAAD4AMFHaEDwEc1YRnlh2LGWMSKCxBoEH3FpUfCZN2Z3Q5CHWRGMZZQX\n",
"hh1rGSMiSKz7FHwGu5FDR1y/fv3q1auMxnmeN+wkgXFRXRDOtecE104AwzZubuR1jLur3bBjLWNE\n",
"RIg1xnhvb4+95DUBrZ8P0PoBAOgC0PqF5ujo6N///d8ZjeM4Zl/9wbVOxLZtMKbwNjK7cXe1G3as\n",
"ZYyIILG+e/cuu/G69PZ8MQzaFXyC4AFjdjcEeZgVwVhGeWHYsZYxIiLEGgQfoWlX8EEIOc76JQEA\n",
"ID0g+AgNCD6iGcsoLww71jJGRJBY9yn4DHa//o545JFHLlxgbTRVVdlL5jLmOqho2MYyNrIgbkBE\n",
"ejDmquD29ja78ZqA4MMHCD4AAHQBCD5CQwiBJV1CGcu4gGjYsZYxIoLEml1MXh8QfPjY2dk5d471\n",
"fqkoCnvJXMbdPVNLZyxjIwviBkSkB2OuCp4/f57deE1A8OEDBB8AALoABB+haVHwIQQ2bW7BWEZ5\n",
"YdixljEigsQaBJ9RwPMgCAAA0CYg+PABgg8AAF0Ago/Q3LlzB45lF8pYxkPAhx1rGSMiSKz7PJYd\n",
"BB8+jo+PuY5qYS952Md3dGcsYyML4gZEpAdjYY9qAcGHDxB8AADoAhB8hAYEH9GMZZQXhh1rGSMi\n",
"SKz7FHxGnfrjOOYKDELo9u3braT+OEaK8sDkzmGng+6MZUw0w461jBERJNZ9pn5uwYcQQqfiEkJ0\n",
"XVdVlWttmyCkaTqdTuk2TFmWeZ7HuOiuLcGHfnniGAQfAAAQElnw8X3/8PBwf3/fMIw4jtM0NQzj\n",
"4ODg8PDQ932u0YzNQghxXTdJEsdxHMfBGLuuy/jZk5MTrmFe9mYZ/HhXd4OKXI3MbizI0J8Ijcxl\n",
"LGNEBIl1n8O8TKnf9/2Dg4MwDC3LoifURFEURVFRFLPZzLKsMAwPDg64FrltEEIIxrj8p6Zp7J/N\n",
"8xy2bxPKWMa1o8OOtYwRESTW9+7dYzdek7MFH9/3wzB0HKc5RWZZ5rquqqrVrCoFWZbZth0EAYsx\n",
"CD4AAHSBcIKPZVlRFJ3ZNVZV1fM86fI+IWQ6nXqex2gPgo9oxjLKC8OOtYwRESTWwgk+0mHbtjHH\n",
"/LFqhJDJZOI4DvvGqiD4iGYso7ww7FjLGBFBYt2n4IN6OwBeNPI813U9SRKuT12/fv3q1avsl8jz\n",
"fOGfHKdIktP/l8bsbtARFzAuGht5TePuajfsWMsYERFijTHe29tjL3lN+CZ3xnEs6WzOGmma+r5v\n",
"WRbXGC9qT+u3beQ4p4o/z0mfnZNlSP7wAoB8CKf1V3Fdl3cN1GqEYdg84TKO48lkQmUc3nmlaZra\n",
"tl0duJ7XgpZxdHTEvqd2HMfsqz+41omwO8xr/Npr/1MEN9iNeRuZ3bi72gkSa4hID8Zcsb579y67\n",
"8bpwPSM0H0WvaRqd8bkyURSZpqlpmmmauq4vM/M8T9O0JEnyPKcZnOsqGGNN0/QKiqIwfrYtwQfj\n",
"oiiKKCrKBhNEBHjxxTsiuDFseUGQWENEejAWVvDh1voty8IY0/rkeY4xxjSNFcVsNlsz+ydJQsX3\n",
"KIqWpf48z1VVrTYoxtjzvJUvysWNGzeee+659cuZT/2CsPyGCwBAh2CMH3vssd4ux5f6q4m+xDTN\n",
"IAjo6yRJTNNc362G1E+nkFbfobec9S/KwksvvbRV4dy5c7qu7+zs7O7u0qeH559/viiK559//okn\n",
"noii6NOf/vQTTzxRFMUbb7xx8eLF8gWtwc7Or968+d+Lorh48eLNmzeLonjiiSdoCeULWlT1xRtv\n",
"vHHhwoVqmbSEN954o/qiLOHSpUsNRVW9KorioYfuNBRV8wpj3FBUzasXX3yxiwpGUbS3t8dYQboU\n",
"kbGCly5dam6ragkXLlxobqvqi5s3bza3VbUojHFzWz34vcLNX4YeKki/9rWi6IuaVxcvXvz0pz8d\n",
"RVG1zFoFn3/++bKE6rdivqiaV5cuXWooquYVxrihqJpX9GvPXsFaUTs7O7qu7+7u7uzsXLp0aetB\n",
"ir7gS/2aps0/v9TSfYNQw05D6scYl3eaElVV178oC6+88sqVK1cYjWez2bJnw/leP9dTJNejFZcx\n",
"lwTYnRvsxg2NvKZxd7UTJNYQkR6M2WuHMX700UfZS14TvtS/bGygmqa7Tv2mac43fSsXZaEtwcey\n",
"iqIooqjoS6liBaGCR4gGAKAdehZ8+Gb46Lo+P8MnDMM+p3tudp84QkgrS7roGjJdR2VzCrLM59ln\n",
"/y+7IyKsmpFxAZEgsYaI9GDMFWv22YPrw5f6LcuqTWyiu2Caplm+4wx6V5qdnZ1z51gbTVEU9nXC\n",
"7JYIIa57LbsxIeixxzi+Eh25wWXM28jsxt3VToRYd2csY0QEifX58+fZjdeF9zEBY6zrehAEURQF\n",
"QaBpWheza5q1/gEIPuVA9dyo+SaJogJj4SYdAcAYEFrwQQjRDe7TNHVdN03TIAgsy+rintTA/DMU\n",
"11PVOrQl+Cw0Zneju+fT73//b0RwY9jygiCxhoj0YCys4HNhhc/QZVCtu8KIaZq2bVe3CA3DsKo4\n",
"AWsiz6E7AACsSm/PF1w0CD5FUei6XqpMeZ7Tlb39ODZ4wScIxHIJAEaC6IJPp7iuW26wTA+ApNTM\n",
"giDwfX86ndLNmVfYhW1l7ty508qx7AuN2d3o7EBt9KMffW/jbnAZy3gIuAix7s5YxogIEus+j2Vf\n",
"RfDxfZ9uuqSqqq7rGGOuUewG6GrhM80URUmShB4N3+LVWTg+PuY6qoW9ZBGO78gypKrJP//z5zbr\n",
"BpexdI0sjhsQkR6MhT2qZZU9fEzTLJeo0Z3UuLajkpphCz7UGaFcAoCRILTg4/s+ISQIgnJmq2VZ\n",
"juNMJpMO7koiMmzBR0ZjGeWFYcdaxogIEus+BR++1B/H8fyKLV3XCSH97OO/cW7fvg2pXyhjGRPN\n",
"sGMtY0QEiXWfqZ9P8Fm2r/3CZVaDBAQfAAC6QGjBZwBHM67JyckJ1zAv+yDP4Me7uhtU5GpkdmNB\n",
"hv5EaGQuYxkjIkis+xzm5Uv9mqYtXMkWx/EGF3n1SZ7n66/mXfhlGPYKz+6MZVw7OuxYyxgRQWJ9\n",
"7949duN14XpGmM1mqqrW1k/Rc7tafRYRl1YEH7pyikJ3bxYEYQUfnv3tAUBKRBd8giCga6noyekH\n",
"BweKogx7t84qbQk+5VKE8sWwRYB1jOMYNXSzZJQXhh1rGSMiSKzFFXzQR2eva5pGH2SiKBpP3kct\n",
"CT7LjNndEORhVgRjGeWFYcdaxogIEmtxBR/g+vXrV69eZTTO83zhYrfquYylusK1LI7rhD+eI+KK\n",
"2WzGLvh05EbNmG4lvYxljby+cXe1EyHW3RnLGBERYo0x3tvbYy95TVbZyGHMbG9vcx3Vwl7ysI/v\n",
"6M5YxkYWxA2ISA/Gwh7V0s72bVxPQFJzdHTEvqc23emI3ZjdjdpZaa0bM+qTXbtBIaTJH95GZjfu\n",
"rnZCxbp1YxkjIkis7969y268Lq08O/R2SNbGGbDgM5udCj5BwHpQVz/P1BiD4COTsYwRESHWPQs+\n",
"Ym3aLD68gs/Cx704RuUjo6oi2i3Y+JNvliFdR6qqsjsiwjO1jCfBbjzWnRrLGBFBYi2f4DMe2hJ8\n",
"qqm/NGZ3Q5CHWRGMZZQXhh1rGSMiSKz7FHzOHub1fT8Mw2ab3o7G3TiPPPLIhQusY+PddSW41k4P\n",
"21jGRhbEDYhID8ZcFdze3mY3XpOtoiiaLWzbVhSl+Rgs27aTJGnVMUF59dVX33nnnffff3+dQmwb\n",
"lWshaJ9AhF0wSk/iGBGCxDnteDpFCCHP27QfANAltm3funXrww8/7OdyTIKPpml6I32ek7VZCCFD\n",
"XdKVpkhRkO/7moYYfeln1YyioIbvl4wLiDYe606NZYyIILFmF5PXB+b187GzszPUef2EIE1DhMg3\n",
"zMtebIuNnGWo+ncY5i2R62vftbGww7xnT+5kmX01nsmdrWzfVp2qWJ3ouVmqXgm1g1vz5M5NIaBL\n",
"gNQIt30by+yrKIpauhOJTiuCT3WBkqKcqivDFgG6M96UvFBbZQaCTwkIPlWEFXxgcucGqN5JNY11\n",
"6exooe0jWitlGeKZtgcAgtHb88UwaF3wmf/nphBZ8BFHFivRdeFcAqRGOMEHqHLnzh04ll0oYxkP\n",
"AR92rGWMiCCx7vNYdpjhw8fx8THXUS3sJQ/7+I7ujGVsZEHcgIj0YCzsUS1nCz5JkkRsT7bslvIC\n",
"gk//CCv4OM6mnQAGhIiCj23bhmE0PObEcTyZTCaTyeDXdg1Y8KG9E0Eek0vjcqu7ZZ2nTckLtfF5\n",
"EHxKQPCpIrHgo2lakiS+70+nU4QQXbtL93VI05QQQhsCYxwEQdfubpzbt2/T1M+yg9MHH5xDCD37\n",
"7BlmaYpsG33wwblnn0Wq+sBCIU1bvJA1jmP2jUQYjemFuih5TWNVRZqGXHfx3hL0p8W8OymHcXe1\n",
"y7KMfVmQgBFpRsaICBLrPlP/2Xv4VAnDkM7DjeNYVVVVVTVN0zTNFGfDl44p9/Cp7sPTItX+BCEP\n",
"bKhAyGl2Ll+U94lldwguqjXqqHYrUO4sJI5LFHrvF8olQGp63sOHb5jXNM2BZfnJZBLHcZ7njPYn\n",
"Jye8w7yMIhghRFGUWmdiWWPTrkR5n3DdBTb0fqDrfP0O6Yx5G5nduMGHLEOKgqqP8ly1o7FmNOYq\n",
"+e23/+6XfulqFyULHhFhjbli3ecw76gnd/q+r+t686akNfI8F2f7Nl0//c9xFvynKIgQZNvotdf+\n",
"zrYR/S8MUbP2KMgayNL4zPkRG1k7mmX1Jy1BVvO+/vqPOyoZVvOuZswV63v37rEbrwmf4DMkCCG2\n",
"bXueZxgG+0YUXQs+nUIVpDT9OJ8qCtI0pOsoTVEcI4xP3xendraNMEaKIpBL6CMZKo4FcoliGGg0\n",
"m6oMDRE3bR4krutalsX7KV7Bh31Wbw8TnKn+g/HHTwamibLs9GmAPvxQY01j2qWgn6nT5QjHQngb\n",
"md1YkLneXCX/7d9yjBN2N69fuogIEmsQfDrnowTHIfVQhBJ81jdWVWRZp7cBOsxAjRUFxfEZ0lCL\n",
"brAYL9NLNyIvzG8rJILgk2Xo7/6O45gnEHx6MBZW8Bnmal7btudbXNM056Pncyr1rFDy/v7+zs4O\n",
"ozHXrYXLmOt5ZQVjXUeKgsLwNLupKj2xvW83WNhII6cpwviBByOu2nUU6yxDL754F6FLrZfMZSzv\n",
"174LY64KXrx4kd14TYaZ+p1GCTZN0yzL3I+mxdDXuNS5G9ne3h7qUS01Y01D5Zc2TU/HhxUFmebH\n",
"7/fgxpmPy5tq5FpJghzV8olPsOZ93pLhqJbVjIU9qmWMgo+qqo7jVE+XZF+gcXR0xL6ndhzH7Av/\n",
"uJYI2iwrytoz1jSEMfI8hPHpAjTbpi86d+PMHw5vI7Mbd1e7jmJNCPrww//FXnZHFaw1cpY1KYeC\n",
"RESQWN+9e5fdeF162zKCiyAInMYdUqIoMk1T13WM8ZmHiDXDdcTY9evXr169WrDtcsNywFnVmN2N\n",
"2Wy2WeM8LzyveP11gnGRJB26UbazZS3zhK+R2Y0bHKZeOU5RmnDVrqNYY1z84R/+H/bNjjr6FtUa\n",
"uXn/pbYiIqwxe+0wxnt7e+wlr4lYvX66F9Dh4WEYhg13S9/3bdumW0coimIYxmqXC8PQMIw0Teke\n",
"FSzwCj7sj3tyPfkqCrIs9Ed/tEefAyYT5LpnDAuv6cay5uFtZHbjMx3WtI+rLIjg87M/+zMdlcwl\n",
"+FQrSOcTMxq35YM4xiD4MKEoCsY4SZKGgRRCiOu6URRpmkbtdV3nGnMvMU0ziqI8z9mHfMcp+DQY\n",
"03tAECDTRL6PbHvprNB+5IUWjQURAbhK/pM/ucU+87CfiBDSNGAjSEQEiTUIPkUURct0GM/z8INq\n",
"y2w20zStF7+KV155ZWtr69y5c1tbztbW1vb2tq7rly5devzxx3Vdv3Llyssvv1wUxcsvv6yq6mw2\n",
"e+mll1RVLYrizTffvHz5cvVFURSXL19+88036Ys33nijKApVVWkJ5QtaVPXFm2++eenSpYai6Iuy\n",
"hKeeeqqhqJpXURQ1FFXzKoqi+aJ+7df+cnv7f3hekecPePXrv/7rK1RwZ+e/0QpevPhfF3o1m82u\n",
"Xr3KWMHZbDabzRgr+NRTTy0r6uLF/1oURRQVly69Qku4dOlSc1tVX7zxxhvNX4ZqUVEUNbdV1aso\n",
"ijBu+jIwVnDeK/YK0q991SuMT8useXX58uWXXnppNptVy6xV8OWXXy6Lqn7t54uqefXUU081FFV9\n",
"8eabb9a+9rWial7Rr/2youYrWCvq0qVLuq4//vjjly5d2t3d3dra+iilbG1tbRV9IV/qpzpP7U0a\n",
"mB4o9+sXakd7AUmSAuMC44JHF11A2c5CNTh1JooKz9u0KxWoV0I1VFEUGC8dpwGqiLhfv1BkWTYv\n",
"n3Gpb+tACBnSkq7ujDUNOQ6yrFMVKMtaWNK1sIU2uKRL1z/W+kVY0iWI8XwjN8jdsKSrCruYvD7y\n",
"zevnWhjdOjs7OyOZ19+Ksaoix0FZhlwX/cu//Ippsm4uPV9y7WiUko008nwxIgzzEoJUVWVPNTCv\n",
"vwdjYYd55Uv9m+Xhhx++cIG10br7PrEvRBDBWFWR56Ese46uoqPbsbXlhoyN3JEbioJ0XWcfVuyo\n",
"gjJGRJBYBkCK6QAAIABJREFUb29z7MOxJvIJPitsvNMiIPisbBzHPpWAXBfZ9hnLdGnJ5emMDWx2\n",
"x5iyFiD4lNQauXmGDwg+Ve7evcZuvCbypX60qDW52hfYIFQCMk00nSKWX1BfgzgrIs5Z1GV63agg\n",
"ugBFEaiVBOcnP3mpv4v1NqDMRcMMnyRJan8KgsDqaw4BzPBpkSAoLKtpMXB1IWiSiDKdpjqxR5yv\n",
"QRQVdOKbOC5R6EQv4Exu3Hjr8uX/2Nvl5Ov1U8GncooTWW3n/dW4c+cOPZadhSzL2Lf25toEnGud\n",
"iLDGpokcB4XhAv1n3ri6dLYKbyOzGzfUbv5ZhKspOoq1oggR62oj07DWDrNcZtyiD+IYc8X6pz/9\n",
"Z3bjNVllmDeO4zAMsyyjh1vRzMs1kL0M13VpsxJCsiwrd2ionaIVBAHdgEFRlDiOLcvqbQDg+PiY\n",
"92zeLowFOYZifWNFQY5zuiWcrn98FjE1Lg+gb0DGRhbEje6Oailfp+npSZZZtli7G3ZTIM4KsueW\n",
"FuB9TPA8T9f1IAjKz3qe15veUiVJEroNQ58XBcGnOxynsKyiGk+M6/8UgaoMJYhLRWUvOc9r2i6t\n",
"Z2hbNe/gBlBeeOG7+/s9LU0teAUf2t+nu2aWb1qWtZFRVk3T6JbLfV4UBJ/ujOnJkdMpiuOPjc8M\n",
"b/+CDz23gNF4mRvsxowlE4JUFcVxzD4w3oPgU3WP3Xh9H840rl1TEMHn/v2eDuZFvDN8fN9feAqK\n",
"pmlczSEvt2/fhtTfnbGioCBAcYz+039aIEUuTB8bSf3z+uLGU784xtVGTlOkKEjTlm7euanUX9ur\n",
"V5DUf3LCcbTyunA9IyiKUr6ufhZjHI3jiQ4En36IosI063u/CNLmVTdqktQGKdtKqJ2FxNyCqSgK\n",
"TRNOg3rhhe+Ku4dPz+qKgJycnHAN87IP8gx+vIvLWFUzxo20eRuZ3ZjF4bI/u/FhXvrTzLKsurNQ\n",
"KyXzGm82IozGivLAQ6Qgw7w/+clP2I3XhC/1a5q2UNaP43izi2x7I89zWM3bj7GiIJbsv9nVvGVf\n",
"CFbzlixs5GUJcCOredMUmeYDGpQgq3nv3bvHbrwuXM8I1ZVW5Wcty8KiPc51Bgg+G0SQNq+6Ic7c\n",
"lZoMJQhiCj5BUESRWC4Vggs+uq6bpkkPUEQIhWE4mUwQQgvHfgcJCD6iGW9cXqDlLTOO4wX//fmf\n",
"/2v5+syLrNBujFUcakTONKarDbooeZ6BCD4IIcuygiBI01TX9TRNLctiP91wAIDgs1nj+bc3K/iU\n",
"Wv8f/ME34/h0Z7rp9OP/L8wS7733XvmaLmaufcr3Pz7ncoV2YxyS61PwacW4RYdrWv/GBZ8sQw89\n",
"9G99Cj5bRVH0drEB8Oqrr77zzjvvv/++baPRPOoIhO+jNGUaA+iOWugPDxHdxFfTkKoumPe5AvRp\n",
"oHLmO9K0M0queiXOl7P0RByX0EfO2DbT/uH9EMfoT/7kVhTZH37Y09R+2K8fkAnLQmmKDAMFgSg/\n",
"2iRpv8zahvBpitIUhSFCp5vy128DafrANgmibd4pJvSJjWfv/UHBvZrXtm3btsunGLrTzmZPzuqT\n",
"o6Mj9kPU4jhmX/3BtU7Etu3RGmsa8ryPtRTeRmY3rvlANxqiew1xObzQDXZj27Y1DVkWcpzT/a7j\n",
"+NQTejNAHy3lLd1gvCl2FL7eIrKacfVZqnzd3TeZsXZU8Ll79y57yevCNSicJImqqp7nVXfOcRxn\n",
"I3v4bITr169fvXq1YJuxkOc5+xZDXJsRzXgOOx+kcZ4XplkkCXcjsxtTH/K8cJzCNAvPa1q9xVW7\n",
"VmKd50UQnG6JjPHpRCNqzDh3paPwVRu59GTZzkIrRGRN44VbMHX3TWasHcYFxnhvb4+95DXhE3zC\n",
"MMQY13ZIxhgfHh62ej8Sl+3tbTibVwRjuuXDdIo0TWHfsZurkbNM9X1ECMIYYXyGcf9n8yoKMs3T\n",
"vU7D8LTXL0L4ytrF8cfC1LJP9/+1p5P6uyh5IcKezcst+JjzzTamPXxA8BHK2PPQD37wv1999UeM\n",
"xTJGJI7RdIr+83/+C4yR5zGdFNap4HOmjWk+IPio6sda0Jolr2BcbeQz817/gk8pjrVe8kK4Yi2u\n",
"4LPMfjx7+IDgI5pxnuff/e7/M82C5RNnRsTzTrUdLh94jbuOdZ4XGBeWdXpuV4sls1A2clVaWbaz\n",
"UP+Cz8K1bxuPteiCj67rhJD5R5jxDPOC4COasaIov/zL6D/8h/phL8uMl/2JThs1TRQE3D7wGncd\n",
"a3oADkLI99F0ilQVWdaCDnjXgk/1eBZdRwv7yis0RXXa63LLpQ7XchU9DkiQWIsr+GiaFs49SRJC\n",
"4jjWxzFJihACS7qEMqaNXG74M5025YX5iBDycX70vAdm72x8mc/6blgW8jxkmsh10XRaV4G6XtKV\n",
"ZWdPnVz4G8kyFMfI908nMpX//eqv/g1d78bg7anx/H/VVKzrpyvyBIk1u5i8Pny9foyxYRiqqpaJ\n",
"nhAymUzwmaNgQ2FnZwd6/UIZV9vNND/uXWK8QNKtGqcp8v3TwdKFA8WC9ATXd0NVTx8CwhBNp0hR\n",
"kGU19YvXdIP3a//3f38hDB/YTI1u8U+ntFaJ4w8Ze5i6zmSsqsj3URiif/mXX6En8NB1ec11HUav\n",
"n3s1L831hBBd17MsS9N0fs7PgIHVvFKQZad9Q1VFpvlAR4/unEMI0rT6n0ZC2Ti63u2CptpvpPwn\n",
"XaFWPpzRhCuCakClpDR9QBRqcZF2A7aNELJv3brV22pe7rN5KbPZLIqikQztVvnCF77w9NNPF2zD\n",
"vEmSJEnCWDK7ZVEUHs9hHMM2bm7kJDmd9m5ZBcbFV77yT1/72o8YhxW7q50Isc7z4ktfeps2C8uw\n",
"5QoRqa32odfCuPC8omwArt/IRr5vdIC6XD+BcWFZEXsAWWoXRXSJBn744YdZy12bFTdyUFWV66ln\n",
"MIDgI5pxc7vVtr7JsruIebHrYASfJT6gL3/5mJ7rQh8CaNd7mWu8EaHDp1UW7rwkQlM0G88/jnz9\n",
"6/vlvhqUhicDxgpSK6EFn5EDgg8wVKgURllNC4rjUyWHJjLT7FwnEYTqdnv0nkdVLPp/lo8jhOK4\n",
"V8Gnne3bsiwbyUPAnTt3uI5lR8y9D6425JpSNWxj3kZmN+6udmLGukz3hJxuE0Sh+evdd7/3+c9/\n",
"TtNOc9zt2+iRRxbI4qaJEJIvImsaz3+Utkwco1u3fvzTn+7RPaLLWwKlHE+OY4QxiuNej2VvJ/VP\n",
"p9MoilopSnCOj4+5jmphLxmOalnNWMZGFsSNZcbVLSLQR4Of//RP/0RVjmryKlcRV0lT+SLSujFt\n",
"Il1HaTqrHl5bXZRQnSNKn5P6PKqFW/Cxbdv3/fmAjUQ4AsEHAIAusO1eBR++JV22bRNC5tcxj2Q9\n",
"F+IXfNh7E1z9Dq6NQYZtzNvI7Mbd1W7YsZYxIoLEWlzBJ47jKIrmx6zHc0YjCD6iGcvYyIK4ARHp\n",
"wVjYs3n5BJ+trbHPCALBBwCALhBa8DFNk+uOJwVcO+2cnJxw9frZ7/mD7/5018fkamR2Y0F6giI0\n",
"MpexjBERJNZ99vr5Uj/GeOFe1ZPJpCV/eiUMQ8MwwjAMw5BRv8vzHLZvE8qYt5HZjQXZ0kuERuYy\n",
"ljEigsT63r177MZrwifg+L5Pq10b1w3DcDabtexax7iuSwhxOFWbUvCZTD7e3RcAAGBNhBZ8wjDU\n",
"NG0A83noxnO8eR9VBB+WxzgQfHowllFeGHasZYyIILEWV/AxTRNj7Mwh3c3A9/3VNpouBR+WnTlA\n",
"8OnBWEZ5YdixljEigsRaXMFnMBiGEQTBdDql92TLshaeOTwPzPABAKALehZ8hrmHj23b8zdbTdOq\n",
"Co9t247jULcnk4mmaUJVAQAAoDv4BJ9lTKfTVsppC8dxojmqeV9RFNM0y1xvmub8wZMLOTo6Yj9E\n",
"LY5j9oV/XEsEF86zGqcxbyOzG3dXu2HHWsaICBLru3fvshuvCXevf2GoWp/sH4ZhlmUNcnwcx3Qr\n",
"IU3TMMZcu34jhDRNq36E/eP7+/s7OzvsV+Fyid2Y61i0YRvL2MiCuAER6cGYq4IXL15kN14XroNd\n",
"oijSNC0IAvoiiqIgCOiLFo6NKYooikzT1DTNNE1d15eZeZ6naVqSJHmeO46jaRrvhfI8typnCJmm\n",
"Ob8x0UJu3Ljx3HPPFWyndAEAADCCMX7sscd6uxyf4OP7vud5pmkqikJneZqmaZom10NNA4qiYIyT\n",
"JGm4rxJCXNel9x5qr+s615g7+kjwmUwmtm1PJhNd1xmFfhB8RDOWUV4YdqxljIggse5T8OHr9SuK\n",
"Ql9EUYQr/V5N03LGA0/ZiKJoWa/f8zz8YJd7Nput0PEviiLP8yiKGPv7lOvXr1+9erVg6/Xnec7e\n",
"LFwNyOXzsI15G5nduLvaDTvWMkZEhFhjjPf29thLXhO+1K+qKn1RS/0Y43aPaG9I/RjjIAiWOdY1\n",
"N27c2NraunDhwvnz/2Vra+vhhx/WdX13d/fKlSu6rv/cz/0c1ZEsy3rhhReqL771rW8988wz1RdF\n",
"UTzzzDPf+ta3qi9eeOEFWkL5AoqCoqQryrKsWlH0Ra2oZ555plbUCy+8MPiidnd3dV2/cuXK7u7u\n",
"U089df78+a2tLXro97lz54q+4Ev9pmnSA+apKF++32fqN01z/loNAwPt8oUvfOHpp58u2Hr9SZLQ\n",
"5mKB3bIoCs/zwJjC28jsxt3VbtixljEiIsQaY/zwww+zl7wmfFq/pmlUutJ1Pcuyco1ymqa9TYrn\n",
"WhjdOvTmzGisKAr73CGuSUpcrT1sY95GZjfurnbDjrWMEREk1ufPn2c3XheuG0We5+VNjM7t8TzP\n",
"sqzqbJlWaOj167q+wV4/zPABAKALhJ7hQyf20NemaXqel2UZvQF0cFdaDNc82dYhhMCmzUIZy7hj\n",
"zLBjLWNEBIk1++zB9VlrIwdN0zaSiNM0rW0Yx9W+68Ar+LCXPGwRoDtjGRtZEDcgIj0YD0Tw6Y0G\n",
"wSdJktqfgiBoXXFaBgg+AAB0gdCCjwjQ54zymYuu8OJaWr0Od+7cuX//PqNxlmXsW1xwbYbBtU5k\n",
"2Ma8jcxu3F3thh1rGSMiSKxPTk7YjddkLcGHEJKmaW0/nHVwXZc2KyEkyzLDMOj7URRVzYIgMAwj\n",
"TVNFUeI4tiyrN93p+PiY62xe9pKHfXxHd8YyNrIgbkBEejAW9qgWvv36aWpWVZUO8B4eHmqalmWZ\n",
"53n9n9aSpindvq2tGw8LsF8/AABdIPQBjaqqqqpKdz92XZfujUzPPOnGvSboJkJ95n0Ego94xjLK\n",
"C8OOtYwRESTW4go+YRg6jkOzbRzHdE4nnedDlZ9OfBQJEHxEM5axkQVxAyLSg/FABJ/9/f08z+lr\n",
"wzBKCd62bV3XpTuhdwVA8AEAoAuEFnxKqOLfritScHJywtXrZ7/nD777010fk6uR2Y0F6QmK0Mhc\n",
"xjJGRJBY99nr50v9uq7Tgwxrh/HGcTwGtQchlOc5rOYVyljGtaPDjrWMEREk1vfu3WM3XhM+wSdN\n",
"U8MwLMsKwzBJEir6+76fZZkzDvkDBB8AALpAaMGHHouoKEoURTTv27ZNz9Htxj3hAMFHNGMZ5YVh\n",
"x1rGiAgSa3EFH4SQqqoY41LtKed3tu2YoIDgI5qxjPLCsGMtY0QEibW4gg8Agg8AAF0gtOADAAAA\n",
"DIC1Uj8hJI7jzR6b1TNHR0fse2rHccy+8I9riaBt22BM4W1kduPuajfsWMsYEUFifffuXXbjdeHa\n",
"59NxHF3X6Q7Js9lMURRd11VVbfdgXpG5fv361atXC7ZNm/M8z/OcsWR2y6IoZrMZGFN4G5nduLva\n",
"DTvWMkZEhFhjjPf29thLXhM+rT8MwziO6V4O0+lU0zTLstI0nUwms9msu/uTOIDWDwBAFwit9Ydh\n",
"iDEu9/Chu+SXe/h04qBggOAjmrGM8sKwYy1jRASJtbiCj6Io5evqUVkY45FoPiD4iGYso7ww7FjL\n",
"GBERYt2z4LPiUS2j3cNne3sbzuYVyljGRhbEDYhID8bCns0Le/jwQQiBJV1CGcu4gGjYsZYxIoLE\n",
"ml1MXh++Xj/GmJ6MSPfwoW/6vt//kSmbYmdnB3r9QhnL2MiCuAER6cFY2F4/92reLMvCMDRNk9bf\n",
"tm16Ru5I9nKAGT4AAHSB0DN80Oj38AHBRzRjGeWFYcdaxogIEmtxBR8ABB/RjGVsZEHcgIj0YDwc\n",
"wWfkgOADAEAXiC74jJw7d+7cv3+f0TjLMvatvbk2AedaJzJsY95GZjfurnbDjrWMEREk1icnJ+zG\n",
"a9JO6ucSv6Tm+PgYjmoRyljGg0GGHWsZIyJIrPs8qqUdwccwjCiK1i9HfEDwAQCgC0DwERoQfEQz\n",
"llFeGHasZYyIILHuU/CBGT588Ao+7CUPWwTozljGRhbEDYhID8YSCz50mzrLslRVpQu45m3SNM3z\n",
"vBMHBQMEHwAAuqBnwefsXj/N9fTelaapruvz2/Vw7WIqNScnJ7y9fsaJvYQQ9inAtT2UxmzM28js\n",
"xt3VbtixljEigsS6z17/2Vp/FEVRFJXpXtM0fQ5JN/DhWklIyfMcVvMKZSzj2tFhx1rGiAgS63v3\n",
"7rEbrwnfDJ/JZGJZlq7rtfelm+GTZZlt2/TWnaZpEASMdy8QfAAA6AKhZ/jQs3k7cqVPXNf1PM9x\n",
"HMdxPM+bTqeMH+QVfGBef9fGMs4iH3asZYyIILEWS/CpskzhkqvLjxDKsqzs5nPtyAGCj2jGMsoL\n",
"w461jBERJNbiCj6DYTqd0sPlEUJpmvq+73keywdB8AEAoAuEm+HDAteQtwg4jjOdTqnPhBAHsjgA\n",
"AGOindW87Fp5P9i2bcxRnYEahqGiKHR6EuJZnnd0dMS+p3Ycx+wlcy0R5JpNO2xj3kZmN+6udsOO\n",
"tYwRESTWd+/eZTdeF65D3BvGeFs/ML5TTNOs/lPXdcYPXr9+/erVq0VRYHy2cZ7neZ4zlsxuWRTF\n",
"bDYDYwpvI7Mbd1e7YcdaxoiIEGuM8d7eHnvJa8Ld64+iqPr5PM91XS/P6W2LMAxd120wiON4MpnQ\n",
"vjzXGDqlJk+xr0vY3t7mOqqFveTBn1nR3cEgXI3MbizI8R0iNDKXsYwRESTWfR7Vwj3Dp1YTRVE8\n",
"z2trNS9N6IeHh2EYNjwo+b5v2zbGmM7HNwyD90JpmpY3DK47Bwg+ohnLKC8MO9YyRkSQWIsr+CzD\n",
"NM0kSdYvJ0kSWk4URctEmDzPVVWtPkZhjD3P472QrusYY4wxfWph/CAIPqIZyygvDDvWMkZEhFj3\n",
"LPi0k/oxxjUhaE0aUr/nefjBvDubzTRNW+0qvHesGzduPPfccwVb6gcAAGAEY/zYY4/1drl2Zvik\n",
"adrbNj5ZltX2j1NVdQW5HyG0cCu6ZgghH3zwwe7u7u///pvb29tPP/20YRhPP/30pz71KcMwXn75\n",
"5a9//esIoa9//es3b95M0/SrX/3qzZs3EUJvv/32tWvXqi8QQteuXXv77bfpi7feegshdPPmTVpC\n",
"+YIWVX3x9ttvHxwcNBRFX5QlXLt2raGomle+7zcUVfPK9/2Gompe/fZv/3YXFUzTtNbsDRWkC4gY\n",
"K0g/yFjBg4OD5raqvnjrrbea26palO/7zW1VLYquNtpsBenXvlYUfVHz6tq1a1/96lfTNK2WWatg\n",
"6WftWzFfVM2ra9euNRRV86r2ta8VVfOKfu3ZK1griiaNT33qU08//fRnPvOZhx9+eHt7+/HHH/+9\n",
"3/u9H//4x6g3uG4UtMddwzTN2oSZ9Wno9ZumOf+EwT5FZ01eeeWVK1euFGy9/tlsxv5syPUUyfWM\n",
"NWxj3kZmN+6udsOOtYwRESHWGONHH32UveQ14VvNaxjG/EivpmmmabZ7Q4rj2HXdhftDGIZBBfra\n",
"m/1sJgGreQEA6AKht29TVdU0TedBWs/7IkMIgT18hDKWcceYYcdaxogIEmv22YPrw7eRA+NGN53C\n",
"q863y87ODte8fvaShz3XuztjGRtZEDcgIj0YCzuvX9Dt2xoEH9u2FUXBGFff3N/f7+eESCr4/OVf\n",
"vu/7IPgAANAaQgs+ImCaZm2VRBiGvYlOd+7cuX//PuN+3VmWsW/tzbUJONc6kWEb8zYyu3F3tRt2\n",
"rGWMiCCxPjk5YTdeE47UTwiJ45j3RMPWoYJPKbcRQlzXtSyrn6sfHx/DUS1CGct4MMiwYy1jRASJ\n",
"dZ9HtbAKPr7v+76v63qWZYQQ9hMNuXBdl95RCSHV+fs15YcQYhiGpmmKosRxbFlWb6mfCj5vvfU+\n",
"IWhMw9sAAHRLz4IP07z+2WxW3TvBcRwswGLWJEmiKOJaE78+dF5/FBUsU3thXn8PxjLOIh92rGWM\n",
"iAix7nleP9MMH9/3McZlNx9jfHBwsPHjTTYy1YdX8GEvedgiQHfGMjayIG5ARHowFlbwYer1zy+g\n",
"1XW9+o4IDwH9QPfwYez1AwAAMCLiHj5n3rg2PvbbGycnJzDMK5SxjIOKw461jBERJNZ99vrlm9y5\n",
"WfI8h9W8QhnLuHZ02LGWMSKCxPrevXvsxmvCNMNnfuueMAx1XS/fCcNwNpt15aNIlDN8EELLT6sE\n",
"AADgQ44lXaZp9rZLs1CA4COasYzywrBjLWNEBIm1cIKPoijzu7ZV4drUQmpA8BHNWEZ5YdixljEi\n",
"gsRaOMEHKAHBBwCALpBD8AEAAADkBVI/H0dHR+x7asdxzL7TE9eeULZtgzGFt5HZjbur3bBjLWNE\n",
"BIn13bt32Y3XpbcVBMPg+vXrV69eZVzSlec5+z4TXDtScO0EMGxj3kZmN+6udsOOtYwRESHWGOO9\n",
"vT32ktcEtH4+QOsHAKALQOsXGhB8RDOWUV4YdqxljIggsQbBR1xA8BHNWEZ5YdixljEiIsQaBB+h\n",
"AcEHAIAuAMFHaAghsKRLKGMZFxANO9YyRkSQWLOLyevDtF8/ULKzs3PuHOv9kmuvCy5jruXTwzaW\n",
"sZEFcQMi0oMxVwXPnz/PbrwmIPjwAYIPAABdAIKP0IDgI5qxjPLCsGMtY0QEiTUIPuICgo9oxjI2\n",
"siBuQER6MAbBZyCA4AMAQBeA4CM0d+7cuX//PqNxlmXsW3tzbQLOtU5k2Ma8jcxu3F3thh1rGSMi\n",
"SKxPTk7YjdcEBB8+jo+PuY5qYS952Md3dGcsYyML4gZEpAdjYY9qAcGHDxB8AADoAhB8hAYEH9GM\n",
"ZZQXhh1rGSMiSKxB8BEXEHxEM5axkQVxAyLSgzEIPgMBBB8AALoABB+hOTk54er1s9/zB9/96a6P\n",
"ydXI7MaC9ARFaGQuYxkjIkis++z1Q+rnI89zWM0rlLGMa0eHHWsZIyJIrO/du8duvCajFnxoVDRN\n",
"Y/8ICD4AAHQBCD7tkKapbduGYSwcjieETCaTMAzDMJxMJuzFguAjmrGM8sKwYy1jRASJNQg+LRDH\n",
"sWVZGOOFf3Vd17Isx3Ecx7Esi/3ENRB8RDOWUV4YdqxljIggse5T8Bn4AY1RFEWLjlLUdb3hnw28\n",
"9NJLu7u7jAc0ygh7U8gIxnjh92EwQPjkBWO8s7PT2+UG2+tvpqbvc+2uBwAAIDtjTP3zj2Dsu7AS\n",
"Qtj1uDiO2Rf+cS0RZFeoeI1/+MMfiuAGuzFXI3/wwQfvvvtu6z7wGncXaxHCx/u1Zzd+++23GS2R\n",
"GF9OxBnrPrV+WVfz2rY9n8E1TXMcp9PrXr58mX2/fq65Q1zGlmV1ZPzMM8+I4Aa7MVe7Pfnkk5/8\n",
"5Cdb94HXuLtYixC+7r72P//zP89uLMKXE3FWkD23rI+sqX+dFK9pWhiG1XfYh+wvXLiwtbXFaEwI\n",
"YZeS6EwALntGY645Bp/4xCfYjTuayMHlMOJpiosXLz7yyCNdlMw7aYc9IwgSPvZiEWe7sX/nd3d3\n",
"uXwQwZgr1uy5ZX02JviEYei6boNBHMeTycQwDNu2eb95Z1J7YuD6DbA/lH3ta1+7desWuzH7ZIDX\n",
"XnuN3fiLX/wioyXiVAzYS07TlMv4tddeYzS+devW1772NUZjLsGnu0bm6jYKEr6OIsL1G+ESfLja\n",
"rTtjrlgPeXInTeiHh4dhGDaoYL7v27aNMQ6CQFEUwzDadUPTtPLqcRyz35a5BB8ueeHJJ59ktESc\n",
"T75cIoAgxuwV/OQnP8nedFwR6a6RH3300Y5KhoiUCNJuXLEesuCjKArGmGbeZb1+QojrukmS0CdB\n",
"jDEhxPd9rvsnvVtUVZQoisq/Yoyn0ynN/lmWeZ7HWCyX4MMlL1y8eJHREnE++XKJAIIYs1fwkUce\n",
"YW86roh018gXLnD87iAiK/iAhGk3rlj3Kfj0nfpZ+tdhGJqmWVUALcuaTCZcqb+a6OdRFCUIghU2\n",
"crh9+/bJycm7734PIYRQ3mz87rvv/tu//Rtjye++++5jjz3GaPyd73yH3fi9995jn2bQkfG7777L\n",
"Zfyd73yH0fjb3/72D37wA/aS2SPSXSP/wz/8w8YjwmU8+Ih0Z8weay4xuQV6W0FQI4qiZctPqM5T\n",
"e1NV1e6dOpvf+q3fQgghpCLEOh8UAACAhYsXL/aWykSc4ZNlmT63NRr71PtO+cY3vvGNb3xj014A\n",
"AACshYhLulqfzwMAAABUETH1AwAAAJ0iYurnGncFAAAAeBEx9aNF2+xw7X0KAAAANCBi6jdNszYd\n",
"ik733JQ/AAAAA0PE1E8Fn/I8BLrCi2tSPwAAANBA32fzuq5Le/SEkOrGRrUVWIQQwzA0TVMUhZ63\n",
"BakfAACgLYQ+lj1NU0IIvQFs2hcAAIDhIHTqBwAAALpARK0fAAAA6BRI/QAAAKMDUj8AAMDogNQP\n",
"AAAwOkTcuVNY4jj2fZ9OOsIYSzTvqF3PwzDMsgxj3JZ7a9JW7eiJQHTysa7rlmUJEuIuKqiqKsZY\n",
"hA1xW/9ZZVnm+76qqoLMCG+rgrZt197RdX1+k2NWetseWnY8z9M0LUmSPM8dx9E0bdMesdKW51EU\n",
"maZDWrWMAAAIdElEQVSpaZppmsvOWuiftmqX57mu6xjj2Ww2m83oWXJ5nrfr7Qq0VcHZbKZpmud5\n",
"s9msKIogCGixrTrLTRc/K9M0McaCfEVbrCBCKHoQGsoVS1v5k6Miz3NVVauJAGPsed4GXWKkRc+T\n",
"JKGZouGYnZ5psXaWZdUOCHIcB2O8rovr0UX4qu+Yprmui2vQxc8qiiLLsgT5irZbwXZ76pD6mfA8\n",
"r5YFaB9qU/6w04XngvyuilZr5zjO/Jsbr2bXX7zNHn7XRe3os5ogX9F2K9hu6odhXiaqe05QVFWV\n",
"4kgZeT1nocXazQ9dZFm2ca2/0/DFcby6UtwGrdfOtu3asd6bpaPwxXG8fiEwzMuEyGdGNiOv5yx0\n",
"WrvJZOI4TitFrUwXFaT7o8RxnKZpEATrFLUm7daOVipJkrX9ao3Ww2cYBiFEURRCiKqqnuetfJ+D\n",
"1M+EvN1keT1nobvaTadTy7I22ylG3VQwTdM0TeM43vgstXZrZ9v2xm/VNdqtoOM4pmmWdw7f96fT\n",
"6co3bxB8AKDOdDrVNE2QqYGtY1kWneeTpun8fEFJoRrIxm/VnVKbjGtZFt3/eLXSIPUzIe+ZkfJ6\n",
"zkLrtSOEHB4eipP3Ow2f53lpmq6cO9anxdr5vq/revwRVNTa+NF+Xf/6NE2D1N858p4ZKa/nLLRY\n",
"O3pKhGiHQ3QavnVyRyu0VTtd17MsK1N/lmVU+m/Dx7UQ99fX4myhAZMkSW2uWBAElmVtyh92uDyP\n",
"oshxnDPXMQkyc67gj0tDBfM8pyueqm+us2SmFboIXxVd1ze4qqvF8M1bivAV7Tp8tUUDXEDqZ0XX\n",
"9TIv0DSx8ZWQjDB6Xk6NOHOZjyC/Kwp7XBoqSJfy1pZ0FUWhKErrDvPSVvhM06x9kA4btu4wF62E\n",
"bx5xvqJthW/++2lZ1jpLDmGGDytBEBiGkaZpeWakLDI6o+flZI9lsz5qh2sahkHfrx2u2TPscWmo\n",
"IJW8fd8vT4SmiDA/qq3wYYxt2y7HQumkfs/zuvOchVbCV4WOXdOv6HQ6laWCZ9YuCALbtl3XpeEL\n",
"w9A0zXVmNMEpXXzIe2Yki+dZli2ciSw+jHEZdgVZakdtEEJCfYchfIitduXY9frhg9QPAAAwOmCG\n",
"DwAAwOiA1A8AADA6IPUDAACMDkj9AAAAowNSPwAAwOiA1A8AADA6IPUDAACMDkj9AAAAowNSPwAA\n",
"wOiA1A8AADA6IPUDAACMDkj9AAAAowNSPwAAwOiA1A8AADA6IPUDAACMDkj9AAAAowNSPwCMgjRN\n",
"6fmaHVE72xIQHDibF+iQyWSy7HhbTdPWOVkU4GU6nVYbPI5j13URQoqiBEGAEArDkKZvVVVXONI2\n",
"DEOEkGVZrXkMdAmkfqBDLMuiGcE0zdqfaN4B+sH3fUVRque+apqmqiqqhEbTNIyxYRhJkqxwCcdx\n",
"JpMJpH5ZgNQPdIiu61RkmD9sGlJ/n7iuW3vGUhSFnutdhkZVVXoz0DRthUvQe4nv+5D9pQC0fmAz\n",
"VPOL67qGYRiGkaYpQigMQ/pP+sRQJY7jyWRycHCwv78/mUwWitfUZn9//+DgYDqdZlnm+75hGNPp\n",
"lBpMp1PDMKraNH3HMAzey9GSfd9P03QymWxtbR0eHtq2Pe8VIcS2bcMwSpuF4jtLBXmJ45gQMv/g\n",
"xQitY42FdTRNExR/aSgAoEswxhjj8nWSJPM2SZJEUaRpWhAElmVhjGez2Ww2M01zNpuVZp7n6bpe\n",
"lpAkiWmaZeHlJao2QRBommaapmVZURTRN6MoolepOVD7ObBcbjabWZal67plWdTVPM9rhdM3NU3z\n",
"PC/Pc/pPz/MURamZsVxxBTDGlmUtfH++8PmcQD8eVaDS0HyBs9kMIUTrCAgOpH6gW2gupllG1/Uy\n",
"/86j67qiKJ7nLfzrbDbTNG3hp6o5Xdf1+Q/OJ9kzsx7L5cqiapZ5niuK0vypoig8z6v6wH5FXmj7\n",
"z79fDU3JfOp3HMdxnOqnFt5IKAihNb0F+gG0fqBzVFWlgvKy2T4ljuMsU4p936eJqQbGOAxDWn4c\n",
"x/MfV1V1BfWZ5XIltX8qilKtaZZlhJD50Q7TNLMsW+2KXKRpukztKUNTMj8GU/XK931CSMP8H13X\n",
"0zRdx1ugHyD1A51Tzi3JsowOLS6DDjMuJE3TZSPDZaJpMemwXI6RLMsWfkRRlOqAR4tXrNHQqrVp\n",
"P83Q2Z9UGWvgzBs8IAIwzAv0h2VZq80eQQjRkYCFj65lMtI0rdqPLlkhGbFcjp2FXnV6xSqKorA4\n",
"0EyapjTvN9+80zRdOcRAn0DqB+RA1/UzZ49YlkUVieqbNGedWX7tUyyXY4RqIAtvP9WM3OIVa2ia\n",
"tmZPnM5fokPT9J0wDOfLJIQQQiD1SwGkfkAOdF1XVbWcoFni+36pk1BZn84KJYTQaZ22bc9r6LXn\n",
"gyzLJpMJ7+XYwRjPL2x2XbdafrtXrFKurlgNOi01CIKqcETns9YswzAsV4oBggNaP9AhhmHQDEvT\n",
"xMLNG7Iso/kuTVPbtst+JZ1/UrX0PM+27cPDw3LQmMoL1TLpVEvXdWkPmqoo86nTNM04jg3DoPcA\n",
"QojjOIeHh4ZheJ5HkxfL5abTKc2qWZbR7RAIIfQuUi2KjjPTouggcBzHuq7Tj3BVcAXKMfBqe5ae\n",
"p2kaBIGiKL7v04UUhmFYllWODLuum2VZbSL/fN6nl1h59QDQM1tFUWzaBwDggCZE+ppxiJKmrfkE\n",
"SnWY2nDr+pdroOx9NxTV7hUpNK2vOWbQTJZlh4eHdCptd1cB2gJSPzB8lqX+UXFwcECXjHVU/nQ6\n",
"1TQNdnGQBdD6AWAU1MSl1llt/QSwKaDXDwyZ2rY8nSoeACARkPoBAABGBwg+AAAAowNSPwAAwOiA\n",
"1A8AADA6/j+4HZFtMhQZmQAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"%% représentation en fréquences\n",
"% Nouvelle figure\n",
"figure\n",
"% La fonction utilise le signal comme premier argument, et les échantillons temporels comme deuxième\n",
"Analyse_Frequence_Puissance(signal,ech);\n",
"% On ajuste l'échelle de l'axe y.\n",
"ylim([10^(-10) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Comme attendu, étant donné le caractère périodique de période 30s du signal, la fréquence principale est de 0.033 Hz. Les pics suivants sont situés à 0.1 Hz et 0.166 Hz."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 3. Répétez les questions 1.1 et 1.2 avec un bruit dit blanc, généré ci dessous."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%%matlab\n",
"\n",
"%% définition du bruit blanc\n",
"bruit = 0.05*randn(size(signal));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Pourquoi est ce que ce bruit porte ce nom?"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7d09j+tKeuDxusZ4PG/AgDfYAwe7MHhswOmanRjOLsho\n",
"AWfUNeDEwAJUupssGUzoQHK0qYjjwNmMlExgbCIC8wVUmGQDB0dcTHiSLgzG8BzDY/cGdW7dOnwT\n",
"SVGi2PX/Rd1qNfnw7WHxqSL5xcvLiwAAuOT35g4AAHBvpH4AcA6pHwCcQ+oHAOeQ+gHAOaR+AHAO\n",
"qR8AnEPqBwDnkPoBwDmkfgBwDqkfAJxD6gcA55D6AcA5pH4AcA6pHwCcQ+oHAOeQ+gHAOaR+AHAO\n",
"qR8AnEPqBwDnkPoBwDmkfgBwznfmDmBhfv7zn//sZz+bOwoAr9Dbt2//9m//9j7z+uLl5eU+c3od\n",
"vvrqq1/84hdzRwHgFfrud7/7r//6r/eZFwWfwX784x+/LNDxeEzTdO4oxiDy+1tu5C8vL2EYzh3C\n",
"GGma3jOPkfoBwDmkfgBwDqkfAJxD6gcA55D6AcA5pH4AcA6pHwCcQ+of5kc/+tH3v//9uaMYw/f9\n",
"MAznjmIMIr+/5UYuhIjjeO4QRvr93//9u82LBzkM88Mf/vB73/ve3FGM4fu+7/tzRzEGkd/fciMX\n",
"QiRJMncII90zt9DqBwDnkPoBwDmkfgBwDqkfAJxD6gcA55D6AcA5i0n9RVGsVqsoirIsU0pNMsH1\n",
"eh1F0Wq1klJeP0EAWIpljOvP8zzP891u5/t+nudRFJ1Op2smuF6vy7JMkiSO47Isp4oTABZhAalf\n",
"KbXdbk+nk+d5Qog0TZVSeZ6PvnFjtVoFQbDb7fSvy711BQDGWUDB53A4xHGs876WJEme5+Ompv/x\n",
"zu9CA4CHsoBWf1mWQRDYn/i+P7rcn+f5fr+fIi4AWKplpP76k6SuqdL4vl+WpW7+x3FcOa9c9OHD\n",
"hyiKGv+02WyGTg2AU9qyx/v37z9+/Hi3MBaQ+icZz6MVReF5Xp7n2+02TVPP89brdZIkg7oN3rx5\n",
"czwepwoJgFPaskeWZe/evbtbGAtI/dNSSh0OB9NpHMfx09NTGIZ09gJwxwK6eScsoQRBIKXc7XZT\n",
"dRoDwBItIPULIeq3XI27CcvzvCAIKg182vsAXLOA1B/HcVEU9id6uGfb94ui2G63bT0EQRBUpial\n",
"JPsDcMoCUr8u+JiajL7Dq61jVkqpH/awXq8bv5CmqX1i0EN9lvtGNwAYYRndvPv9PooiKaXneUVR\n",
"JEnS1gFgivh2Nd/m+/5ms3l6etLpviiK/X7f9mUAeJWWkfo9zzudTlJKpZQelNn2Td/3z+dz460A\n",
"RhAE5/NZl302m81NIgaAB7aM1K/1HOrT843SHecGAHjdFlDrBwBMi9QPAM4h9QOAc0j9AOAcUj8A\n",
"OIfUDwDOIfUDgHNI/QDgHFI/ADiH1A8AziH1A4BzSP0A4BxSPwA4h9QPAM4h9QOAc0j9AOAcUj8A\n",
"OIfUDwDOIfUDgHNI/QDgHFI/ADiH1A8AziH1A4BzSP0A4BxSPwA4h9QPAM4h9QOAc0j9AOAcUj8A\n",
"OGcxqb8oitVqFUVRlmVKqesnWJZllmV5nl8/KQBYlmWk/jzPsyxL03S/33ueF0XR9dPMskwIcTgc\n",
"rp8UACzLAlK/Umq73R6PxyAIPM9L0zQMwytb60VReJ4XhuFUQQLAgiwg9R8OhziOPc8znyRJcmXq\n",
"z7Jss9lcHRoALNICUn9ZlkEQ2J/4vn9NuT/Lssq5BACc8p25A7isLMt6Zcb3/XFTU0oVRXE6na6O\n",
"CwCWagGpf5LxPMb1pZ4PHz609TNvNpvKBQoA2Nqyx/v37z9+/Hi3MBaQ+idUFIVS6sre3Tdv3hyP\n",
"x6lCAuCUtuyRZdm7d+/uFsYCUv+E7eg8z8MwLIpC/yqlVEpJKWmqA3DKAlK/EEJKWWmqSylHTCcM\n",
"w7Isy7LUvyqldOmf1A/AKQtI/XEc6/u5zCd6uGfb94uikFImSVIfw5MkSeWbZVnaUwYAFyxgcKdu\n",
"kpuB/PoOr0oSN6SU+mEP6/X6fiECwKIsoNUvhNjv91EUSSk9zyuKIkmSthKNael3D9uXUupnAZVl\n",
"uV6vd7vd9EEDwKNaRur3PO90Oule2TRNO9K67/vn87nxVgBbEASM0gHgrGWkfq1nZ6zv+6Nv+AIA\n",
"Fyyg1g8AmBapHwCcQ+oHAOeQ+gHAOaR+AHAOqR8AnEPqBwDnkPoBwDmkfgBwDqkfAJxD6gcA55D6\n",
"AcA5pH4AcA6pHwCcQ+oHAOeQ+gHAOaR+AHAOqR8AnEPqBwDnkPoBwDmkfgBwDqkfAJxD6gcA55D6\n",
"AcA5pH4AcA6pHwCcQ+oHAOeQ+gHAOaR+AHAOqR8AnPOduQPoqyiKPM+VUkEQpGnqed646Sil8jwv\n",
"ikIIEYZhkiSjJwUAC7WMVn+e51mWpWm63+89z4uiaNx0lFKr1UoptdvtdrudUiqKIqXUtNECwINb\n",
"QOpXSm232+PxGASB53lpmoZhmOf5iEllWZYkyWaz8X3f9/3NZhPH8Xa7nTxmAHhkC0j9h8MhjmO7\n",
"LJMkybjU7/t+HMf2J2maSimvDREAFmUBqb8syyAI7E983x9XpUnTtD5xav0AXLOM1F/Pzr7vTzLx\n",
"1WqVJMkkkwKApVjACJ/bdcOu1+skScIwHPRfHz58aOtn3mw2lQsUALC1ZY/3799//PjxbmEsIPXf\n",
"yHq9DoJgRJP/zZs3x+PxFiEBePXaskeWZe/evbtbGAso+EzejlZKPT09jcv7APAKLCD1CyHqg3BG\n",
"D8vRY/mTJCHvA3DWAlJ/HMf65ltDD/ds+35RFNvttrGHoDHvl2U5YbQA8PgWkPp1wccM5Nd3eLW1\n",
"2aWUURRlWbZeryt/0rfypmla+d+np6cbRA0Aj2sZ3bz7/T6KIiml53lFUSRJ0tYBYIaB1seDSinL\n",
"sszzvHI7GA9yAOCaZaR+z/NOp5OUUinV/ew23/fP53NZlvUhm2EYns/nG0cKAAuwjNSv9Rzqo5/P\n",
"c+tgAGC5FlDrBwBMi9QPAM4h9QOAc0j9GCnL5o4AwFikfozBgFhg0Uj9GIPX2wCLRuoHAOdMk/p5\n",
"DA6cteh9f9R7TvEaTJP66w/MARyx6Oy56PMWrjHsbt4oiioP0YSzKPcLIaRcdvZkIzprcKv/eDy+\n",
"WJ6fn8MwPJ1OtwgOD0tKMdfb7MtS/PmfzzPrOqUY7IRFGpb6fd+vPDrN87zdbpcxxtsxSom5npNU\n",
"luKP/mieWfe06BIQHDEs9e92u/oz1PT5YPRrs4BFq7f6F10CmspDrQSq1HXTdPP6vs9T7w0afe4o\n",
"ClF7OviS3OioLcvHOgq22znn/pg1kWlSv36JyiSTegUeqr0DcftGX2WL32EHmKp7WcqbZP+yfKAu\n",
"kNmPx4c6CxrDRvjkeV4fwl+Wped5PR+m/+q97kvLLBObzdxBDHfTtnkYirL8rOfjcLjVvOxZhOEE\n",
"3S1hKKScfuWQ+o2imG1ARLdhrf7D4VAv7MRxvN/vpwsJ6KKU+M1vBnz/VZ6M79yzptSwpmvlXDiv\n",
"ougbjFK9zhODTu0PWxIc1ur3fT+O4/q7D2F7tA7vCXe+R1g0KcWf/MncQVh8/1Mb/J7u3KaW8iE2\n",
"/a1tt8L3RZJc/loQDDidvIZW/263I+8vzo36uGa8jv6DPxj2/ZuG6vv3TsRl+alQczc9m8OVf3kc\n",
"fZKvDrjPYgbBg5bvB+HxbWN07B8z3ut0B/aC92n1jMu5ZTlxleah0tD1dHX+ngslpRjUl/cITd2h\n",
"6yfPL7f3xTeL1n/inic87xGvmUj9Y3S0o2e816mNUpNl0qGpfNywNikfpUBflvOPD6mbtmP2Fgs4\n",
"e94XQmy3YrsVh0PfYHoeuXrlD1rAIHjExgepf4xxR0tRPEpGu5txe/y0TaTuGJTqOj+NG58+tJUX\n",
"RcOmP2EeCYIBO3PP+Uo5oPVzONzwoNC1uDSdYFL6SvQBM/hopP77mSvv6xbKhG3//sYdKtcfYPYY\n",
"jO5ixeRX4krdvJU3VZu6f5BKDehdMMMK+pxUbnqFF8cXajhF0bcnLM+FlJ9OVHp3esDLwUFI/YP9\n",
"7nf/ueOv3YfTLMk3CERRDDjG2tq5I9LZLUqcF5+YVpZivb53L6jRvyxeFDPf59k/VNN66ENXTvTt\n",
"Do+jLXjz+cWlS9NPS+R5rUt3h1s6pnJt6ldKrddrpx7f9rvf/Rfzc1FUN3ZHi2yWq0VTF+4/SKMs\n",
"m/Pm0L6+ccryQqtW95t1T2G/F4fDBMdh98nSDBi/dWn7di2GPpHrxbzdmKIgGL+lej45NQg+C95O\n",
"V+bz6zdiPRs8coHo2tSf53me59vt1s3n+Cs14Hi4XYLoc+RUKrDdHZj2Lmtv2MZFyPPLk+ouqdv0\n",
"yMVr6Evyzabvprnm+JykS//ioXM4zNmCHjRyYVChX4vj8ScVXYS5qLLf2rObMDvXl8K0lh7qAki7\n",
"NvWb5zf4jzau5ZbM7tK9y+b5ZO01XbEZMSO9z5n8a3/ev3RbmWD9kTWNe3ZRiCT5NJf+z5zRbcw+\n",
"B2RHB6w+1H3/8vqf6j77m/Zq2Gt46Ojhiy/QuxjDoFsC7S9PNUi3eyJXZtVBK7N7z2wc0tpRHZrX\n",
"talfv6fldDo5lfp77i6V7X1N+0JfS7YdA7qa3xaDGYtmh90/9dtf0wNCzDQvHthmjh0Ja7utTsf3\n",
"e63hi4fTrXdJs1D1YkifbW0edHPxFGWXNXTnjejd/ri4lqa9GDWXCDrfXX/rU/e4uBGnFnvP19co\n",
"fQ4EvbaD4HI1cikm6OYNgsCpZ7f99rd/YeeU7lbAxWpJf2n62dSKQqzXIsu+LY73STfmO90ZofLX\n",
"xgPMbPM+LXq7gm8/FUD/PO56v/G/GldCz8N7KJOFKyqV5TbmQTcXT1H2qcUsoFmfegB7h2uW3X4a\n",
"T+Nq7N70kzwZdET8HTMty2+3mlIijntFqNd2EHwaMmSfrc3pzQypWARG+IxhJ/F6Qje7hf2nesll\n",
"kMZrSb3X6npidy+cabP0PIr08dyzOt82Ntx+bJZ9A6RS39ZnDwex2w1bLebL9WMsz8V2++14PjO+\n",
"vk8FqVKdaFuiPs3YQef4i8XxSr93vbPd9y88KfOaaoNdwGnMax3FRr3TXn/StRetT7+uro72LFIN\n",
"Tdb1s7VeQH2OHHSj77xcTP1FUaxWqyiKsiy7xRtmGo9k+ybAEeOh6u16fTzr0REX9/J6weciczzY\n",
"hYWhFy72qrBb/fXYDD27jpShv9+YzspSbDbfznTQ+Ho9cNssdWOJvG2U1KAEZ588dCK7OGCpkusb\n",
"GwEdq+ua5GufabrXZ32vvua5gfZ6rpz5uhfncGg4PduN9Mq5trIyzZVN//Ol/qbeTBfHQT3OicG5\n",
"1J/neZZlaZru93vP86Khd1IKIb45nC4O4W+sBnQU2S92i1WK9WEo4vjbscbd+5x+1uCgBo7Z+80l\n",
"S+NwhY71oKOqlKTsolNjt5i4lGVu1G/WeNzaVY62NWxHe/ERwXaK7HMqraSqymrR67Bj63cEc3Ed\n",
"breXc7e54NAB2OHpIaEjmGKmZi9dfbxDpdneeBVVWYEdLX1zgaibAmaaHVuq50g5Pc16k2JUBprA\n",
"NKm//v6Wx6SU2m63x+MxCALP89I0DcMwH9gV9R//8WN9qNcvve3DvvLIcrNHNh6iei8fMSLC88Ru\n",
"J8Tn2cfeGqYj0fOqh8TFJxzoL9QTYmX8ZdtRYe5rbWsQmbPj6KbQtPtd5Xyjz+4jHszZnfr1Q577\n",
"s8dW2jlIn5P0uu1zfaNUtUvg4jhaXQqvBF/ZiCYMzd4Z7Im3XemaUqS95+e5MG8A0UdZpeZjs2ss\n",
"JozuHaP/85bNDx29mabVXw/PThF2G6jy77PcCDZN6l9fHEH2GA6HQxzH9rskkyQZmvp/7/d+rX+o\n",
"XKrrwdd26rd3F30A68e9VnajKwdC1HfKersySRoO8u4mZ+MNXH2qB41ZoG0WOqoRHeBSiiRpOMnV\n",
"6TU/9JyqG7MmsAkPzjBsaKX27BbO82+fSKPPSf3fQ3I4TFB2j+PmfbUx1aap8LxPa7ItFzeOPbOH\n",
"eCklkqSh/Gh+tXuwzMns+rtDLtKRmPVv5lgp99sLUn/um96NZ+kZHpz6i6LIapbS6i/LsjIY6ZoX\n",
"ypvkaC54LyYIvVtUZmj3THbHMmgg2sWp9VGZQr11Wbm+3m5FljXcCqCLEuYmg0outn/tP96xfhQ1\n",
"Hu31y53KdBrpvlMTf6VtU+9W7f61jV7MJLn8fc/79HbMxmEFF/9Xd2OYb/bpLG2bVGPfTNvU9BCA\n",
"i9VRu0lRz9p2Mq3MXcdT2eHb+lo7OsPNblyJpDtmrbL+28r9Zse2/6obiLM81XlY6td5PwiCMAyL\n",
"ogjDMAiCoih2uujw8PRrhCsfXnNHgud91ug4Hqsl9fquVh8aXGnydOhffNDTuf7RC41TqFx9Vwqp\n",
"5lEndjC6KGG6JXxf5Pm3xYR6t1vbNulY/BH3kYrPG2XCOjJNtGH4KVT7VLRaVc80Hdu0Y6aNAa9W\n",
"DS1rvV8NvTzSBaI0rV5rtjVTOuoqdiT2/+qQRgwBsNenblLUi0L1jN8Ylcn1eqN0DDnTK7aeas1u\n",
"bBo39pXKoF2rrSNBx1Y5hPWH+s7HX//6y77zmMLg17LvdrsgCKSU+gQghCjLUp8GbhPhlCYZz/Mv\n",
"//Ivafq/fvvbP/ztb/9Qyr9/fv6vQogvv/zl+/f/PY7/JAgCu0uznhEq+6X988XjR99F1WdNm9JT\n",
"4wR1kb2jt7ljCIT5RAdTOTHoC/DD4cIpSh9g9qjBPj2KovNkpq57U4I55ZhKnW6PCyHKUhyP1UL5\n",
"xQ2hW9aNIXW38nR2qCxp44sDLxYKTJFat81012XHowXW68+K7I0LGMciyz6NKbKX7uIQ1Upg67U4\n",
"n7uWpbH5XBnto2cax+Jw+Gz91JdOp3J9sdjnqUGVkdltS1efUfchHATiz/7sp3/8x3+vf/2nf/of\n",
"Uv5v/fP79+8/fvx4IazpDG7164KJUso0n9M0LYriFqMkH9MPfvADKf/uL//yf3799V8dj8ft9u+2\n",
"2787Ho9ff/1XdjWpcQ8wt4QY+vJWtxTa9jBzSujuzavXeRq7lTrC0+yGScfsTF+3XUawR3CaxFGf\n",
"mueJzaZXMG2R6/LFuMtkpUQUNS+afUY0laIk+ew8p7PM4XAh2elRhpWWrN6UbX3yhs5lNt+vzk7v\n",
"M3bp32TPomierF3FsplrxP6PpD8cxHZbrXmKlh2mfhbRz8+w2zqbzeVzf6W4ZDfV7T1BN64r9JVB\n",
"4yxGdAUZuqHQP/l5ntB5Q/vrv/5v5uevv/76e9/73sg4hhuW+uvVEi0MQ3n/YtVwt7jruDEB2Umw\n",
"frBVjtKLd4fbAww6djIzEXP9Wx8S3jiR+rgIr+X5BI2T0llJj7ozs7MvCOzAzNwvBqar24aU4u3b\n",
"zwYd9SmRN05Z5+4s+5S+7c1hyhd27tBnKV1v0bPWwxYr+aVS0dY3GVRmrT4fIFt/u7epO/V5AMPx\n",
"2FA70hm5cUSNSZH2xM1I2aIQu92nU45uI7ftln/6p+If/uGzy8rKJq4skaq91FDKTzU0sxuYpNxx\n",
"7at3sMa/9mk9eJ6I48/aHNqgkW/1r+m1urim77DUr0s9+ueldO1W1E9RV560zEALO5eZnNs4Al3v\n",
"am09V9363JF78TuVVph59Ga9xFwfWtfIDHKwl2XEBYd98rBfriTlpwF/ba2ztnxh305s2tE67+jU\n",
"o1N/vZNWD8eyJcmnT3SQle4t3XtRTwFJ8qlSZI8TN3tFvYRtNo3pIO1YXfafzAmsLEWaijRteLqD\n",
"3SaoU+rTbSL6bQdt7QYhxN/8jfjHf+zbWDYXrPXx+JV15X1zu0xHC61S8GlbORffzFXf4t1nr45I\n",
"6oOUehrXOzWVwalfP5w5DMOyLE2RR0q5iMe3xXFcebi0Hu45ycQ7emsbd53ttnmcXHeerZcCKv87\n",
"4oxs/qvxhFEZ1NExlMWMzRh0CVyfXX36263Y7bpOaW2FaXNX0WbzKU+Zs4t9Vm7rQrB3aj0yr1Km\n",
"MJLkU2dd5U/mvNJdS6lP0LQle16p6hmZfhpzR0XHjBpvBlS9H0Rj7iQ3EXbse409RpXvV3Yb+9Si\n",
"f66MZLVXjr74Nv/e8/52c41VH3LdHbwdQ+P3+xyGV/ZOXWlY6k+SxHTnpmkaRVGe5+v12vf9RaR+\n",
"XfAxA/n1HV5J9zvcPvdv//ZD/UOlxl3fKe2dry2zVIZ5qZbX4LXd1F6h/7fPfTqNBZ/Kk+ba7v5t\n",
"HMpS6TcLguqtQObL/W99FN8sUVF8OzWzaJUw2pqo9nlLD6i3t4X91IfGbF7fqfVQpUaVzFWpv1UW\n",
"3Fwm1u8KNGemoZejnify/LOt370z2CcJsz/vdp+6oy6evM3ymvJgd76rdEFdbB809iG3pRl95us4\n",
"OiqDF7SO4WR9BjuJluOxbYhRRdsN//cxuNZvyuVxHO92Oz1SfimDO4UQ+/1en66yLIuiKEmSQR0A\n",
"//zP/+mHP/w/4vMzdn0Hshsj9Ue5mVZVHH922JjvVG7unfD+FJ1Q6vtrvf3ldQ6HN8zBb6d137qD\n",
"3z5s9II3Hi0do6HtNWM6A3veBmxnat2Otk8S9VK7HXPb4ve8tLfnkucNp0z9Sb303HGN1U1fEY7L\n",
"Jqo2SLfPYpqbmC7O1N6+ZhMMWrrunuQ+N4IMap32KV0O0nbTyVyuups3CILNZjOo1Tw7z/NOp5O+\n",
"fDkej0OD97z/993v/l/xeXOyXoSxU79ouvVcC8OGoqRSIs8/XUnocRR1bcfMoGOpPoZdWN2PdpvU\n",
"++aeTNH+9Ku2ERqVQ6hjdKY+1VVqLN3XMYOOnD59p1r3/RBm+GM3uwOznpF7pqFBd2a0XWxdVO+s\n",
"6rli9aow8x1avNbd5ra2DWR3pbZ16nSfrupDpCp/bdO9UG0Fn44rtp71tFtz7vFtmr4poW3AUu+J\n",
"fPtDZQ+unFD6H8DmBiKd8na7hoNBf6exFmHftNmnb9b+jm6Pl+W3RW1h1QTspreZdWW52k6j9opq\n",
"O7ZNuWBE4bB/xmnLGvWRmlc2x+zbbvUPepuaS67+0x8UiX0NMWjEoahdmI7Q1rKuRGK2V/0+2I7n\n",
"PVQmXq+WdNdPuq9i226/0C2exr/q6ww92UpHTr2WZY8Hm7Glb3M09U+uPt7D6GiqNNKlbbt40nh/\n",
"Slvh0sy97Z6jytT0cdhW4tBTaLuabqyf1vWsYNQ7ITrYV0s9w2ij1/BN+6p0H7VeQJ2e/JZbcycc\n",
"I9i2y3VXTrTRqb9PJGbvHXSNUmln1DdZ9xasF9bsA6FxeXVLpe2MYg4Ke5Brhd3t/GidoaT+kfoX\n",
"3xuv7zpaKPoawuyX9bcI9ewAbBz00vgqwbY0JMS37yRqVB8BeVH3UMX68dmm0ovec3P4Yx8jfKX6\n",
"WjJDRSumbRK29ZyLWhO78k3fH7AtzJR7dvPa/9JfpTpU79jv2I3rKtF2L2zHnQRt/9jd4Ou+beI+\n",
"SP0jXRw4bNQf1ydqIyZtp5MQ1nHSmK2uuaeiUjrvOSm796LSk9Gt3t5pO+Abn002rcYnmFYEPe7y\n",
"73DNpqkX3K+5CBi0Mm+35jvGyzdqW+SLjYyOwVd1vi+229Y6j/5Td9dxEHSdMDoWtj7cYBak/ptr\n",
"a2l2b3g7QddPM205t88NX5W56BmZRkrbv8fxpysA+6TVZ9+tpP4R/ZB3bqf3HNo0+f+KWhGj5xjB\n",
"NoP+/Xap3x4y0P8WMM0+DZg867W8KGnQiI2OKp8uzZlu4clvXdULOPsdsaT+e2i8ROg+2NrGHZr/\n",
"batOavoFXo1MJ5t9zWuG53c0M+tdcyPGdg39lzi+R5F0qrNL97nwYhP+Pi1BM4jLHqI2yRpoe3mA\n",
"GTIwNN/VhwCJb/bS689VffarzWbMTi76bet5n3hJ6p/HxUKqfbdRXVtZ03xu32NZUTmpDC0p3Hko\n",
"b/cpMI7FajXBucFembc70wzNVh0bcfTs7GdImCUdVCrp1jhSwH40xSQm6QzvP+juovrg3e5t/QgP\n",
"/CH1z6O7zX5Rx5mj56hzrT7WcN7nigwVBGK/HzmY3dZ44+iV02nUccw3ltquOdEGlx4LOPmGvlsz\n",
"tn/HfocJa1yDepinnfVopP4Hcp8dotLHq88i5qwz73NFxrl+vVUy7Og1cHEEUVuo+m0q9b9euS26\n",
"/32WezEvjmy52+7XNshqaIdZI99veAP7Qxn2qha8AnbHg7kdQRdVRzw35nWopJv+w7fqxrVGPe+q\n",
"mbZpvDqcpFA+ThCILLtwyql0dDeGWhSDx57Wta0Ez/v0/OprXDytzl7zIfU7zX5PFoxZrnvuNtOy\n",
"nKBENs7Q/uTGOCdplV90080x49nXIPU/iqHlQmC0G+W1PhWk63fyPk+Le3CPcKST+h/Foh6CBzS4\n",
"/mLiYte0duvUOfTU2DgItdvs7zIn9eMzS29P4aJHaHK26XnyuPVeOjT1L25khGCEDyqWuBMvyOyd\n",
"e+JVbOLr+3jn9QhPc6PVj8/Mvke+bg/S4mYrdxt6VTG0Wjt7tUfQ6kfFI+yUr9WDFNO6X1oCMfyq\n",
"Yonrk9SPz5D6b+dBmvwMKIAg9QOAg0j9AOAcUj8AOIfUD9zJXK+HBOoY3AncCUNr8Dho9QOAc0j9\n",
"AOAcUj8AOIfUDwDOIfUDgHNI/QDgHFI/ADiH1A8AzlnMLV1FUeR5rpQKgiBNU2/sUxCVUnmeF0Uh\n",
"hAjDMEmS0ZMCgIVaRqs/z/Msy9I03e/3nudFUTRuOkqp1WqllNrtdrvdTikVRZF6hDcnAcAdLSD1\n",
"K6W22+3xeAyCwPO8NE3DMMzzfMSksixLkmSz2fi+7/v+ZrOJ43i73U4eMwA8sgWk/sPhEMexXZZJ\n",
"kmRc6vd9P/78xc9pmkoprw0RABZlAam/LMvg81fb+b4/rkqTpml94tT6AbhmGam/np39iR6BuFqt\n",
"El5YB8Axc47wUUq1FVs8zzMt/dt1w67X6yRJwoHPUP/w4UNbP/Nmswke5N3bAB5SW/Z4//79x48f\n",
"7xbGnKlf99cQxwAADdtJREFUj9ds/JPnefv9/qZzX6/XQRCMaPK/efPmeDzeIiQAr15b9siy7N27\n",
"d3cLY87UH8dxpdO10eTtaD2mM0kSSj0A3LSAWr8Qol4XGj0sh7wPAAtI/XEc65tvDT3cs+37RVFs\n",
"t9vGHoLGvF+W5YTRAsDjW0Dq1wUf0yug7/Bqa7NLKaMoyrJsvV5X/qRv5U3TtPK/T09PN4gaAB7X\n",
"Mp7hs9/voyiSUnqeVxRFkiRtHQBmGGh9PKiUsizLPM8rfcs8yAGAa5aR+j3PO51OUkqlVPez23zf\n",
"P5/PZVnWh2yGYXg+n28cKQAswDJSv9ZzqI9+Ps+tgwGA5VpArR8AMC1SPwA4h9QPAM4h9QOAc0j9\n",
"AOAcUj8AOIfUDwDOIfUDgHNI/QDgHFI/ADiH1A8AziH1A4BzSP0A4BxSPwA4h9QPAM4h9QOAc0j9\n",
"AOAcUj8AOIfUDwDOIfUDgHNI/QDgHFI/ADiH1A8AziH1A4BzSP0A4BxSPwA4h9QPAM4h9QOAc0j9\n",
"AOAcUj8AOGcxqb8oitVqFUVRlmVKqesnWJZllmV5nl8/KQBYlmWk/jzPsyxL03S/33ueF0XR9dPM\n",
"skwIcTgcrp8UACzLAlK/Umq73R6PxyAIPM9L0zQMwytb60VReJ4XhuFUQQLAgiwg9R8OhziOPc8z\n",
"nyRJcmXqz7Jss9lcHRoALNICUn9ZlkEQ2J/4vn9NuT/Lssq5BACc8p25A7isLMt6Zcb3/XFTU0oV\n",
"RXE6na6OCwCWas7Ur5SSUjb+yfM809KfZDyPcX2p58OHD239zJvNpnKBAgC2tuzx/v37jx8/3i2M\n",
"OVN/URRtJXvP8/b7/S3mqJS6snf3zZs3x+NxqpAAOKUte2RZ9u7du7uFMWfqj+M4juOLX5uwHZ3n\n",
"eRiGRVHoX6WU+sqDpjoApyyg1i+EkFJWmuptlaJuYRiWZVmWpf5VKaVL/6R+AE5ZQOqP41jfz2U+\n",
"0cM9275fFIWUMkmS+hieJEkq3yzL0p4yALhgAYM7dZPc9AroO7wqSdyQUuqHPazX6/uFCACLsoBW\n",
"vxBiv99HUSSl9DyvKIokSdpKNKal3z1sX0qpnwVUluV6vd7tdtMHDQCPahmp3/O80+mke2XTNO1I\n",
"677vn8/nxlsBbEEQMEoHgLOWkfq1np2xvu+PvuELAFywgFo/AGBapH4AcA6pHwCcQ+oHAOeQ+gHA\n",
"OaR+AHAOqR8AnEPqBwDnkPoBwDmkfgBwDqkfAJxD6gcA55D6AcA5pH4AcA6pHwCcQ+oHAOeQ+gHA\n",
"OaR+AHAOqR8AnEPqBwDnkPoBwDmkfgBwDqkfAJxD6gcA55D6AcA5pH4AcA6pHwCcQ+of5sOHD0qp\n",
"uaMYoyiKLMvmjmIMIr+/5UYuhIiiaO4QRvrNb35zt3mR+gHAOaR+AHDOYlJ/URSr1SqKoizLJim5\n",
"FEWxXq+jKFqtVlLK6ycIAEvxnbkD6CXP8zzPd7ud7/t5nkdRdDqdrpnger0uyzJJkjiOy7KcKk4A\n",
"WIQFpH6l1Ha7PZ1OnucJIdI0VUrleZ4kybgJrlarIAh2u53+1ff9yWIFgCVYQMHncDjEcazzvpYk\n",
"SZ7n46am/zFN02mCA4AFWkCrvyzLIAjsT3zfH13uz/N8v99PERcALNUyUn8YhpUPr6nS+L5flqVu\n",
"/sdxXDmvXPTv//7vRVGMnvtcfvnLX/7qV78i8nsi8lk8Pz8vMfI73zA0Z+pXSrUNrfE8z2TkCddI\n",
"URSe5+V5vt1u0zT1PG+9XidJ0r/b4KuvvvrFL36x3HtGfvrTn84dwkhEfn/LjXyhR+iPfvSju81r\n",
"ztRfFEVbyd7zvBuVZZRSh8PBdBrHcfz09BSGYc/LiJ/85Cc/+clPbhEYANzNnKk/juM4ji9+bWhB\n",
"pntSUsrz+VzvNN5sNlPNBQAe3AJG+Agh6nWhcTdh6TpSpYHP4E4ArllA6o/juNJpo4d7tn2/KIrt\n",
"dtvWQxAEQWVqUkqyPwC3vCxBGIa73U7//Pz8HATB6XRq/Ka5yzeO48YvnM/nMAyfn5/Nr77vm18B\n",
"wAULGNwphNjv91EUSSk9zyuKIkmStg4AU8S3q/k23/c3m83T05O+biiKYr/ft30ZAF6lL15eXuaO\n",
"oS8ppVIqCILuTF2WZeOtABW67HPxawDw+iwp9QMAJrGAbl4AwLRI/QDgHFI/ADiH1A8AziH1A4Bz\n",
"SP0A4Jxl3NL1IPSjRvW9BfqZz3NH1CDLssonYRjWb194hGU5HA5lWXa/Ma1PnPdflouRP+BW0K81\n",
"NbezJEnSNrsHXOd9gu+5zsV8q933/TRNGx8b0zOkKSOf+3bixdjtdvoBEs/Pz5vNJgiCuSNqJoQ4\n",
"fu58Ple+M++yHI9H/YacOI7DMOz4Zp8477ks/SN/tK3w/PwchmGapufz+Xw+p2kaBEHj80sebZ33\n",
"D77POr9z8OfzWb8GXEey3+8bH0LTM6RpIyf19/L8/Fx51E+apuaxQg/l4ul89mU5nU567z8ejx0J\n",
"tE+cd16WnpG/PN5WSJJkv9/bn2w2mzRNR0R1//2nZ/B9GrJz7TD2J5XHi/UMafLISf297Ha7yq6m\n",
"z+dzxdPh4gHwOMvSnUD7xDnXslyf+u8c+WazqX9YX4THXOc9g++T+h9h5/d9f0RIk0dON28v074a\n",
"/j6KomiMcCnL0ifOx1+WB9kK9W6JsizrleLHXOc9gzfa1rl4gB2mKIpK90PPkCaPnG7eXiZ/NfxN\n",
"RVGklPI8Tynl+/5ut7OPk6UsS584H3lZHnwrrFar+pvplrLOG4MXl9a5mC94/ejJoiiklJVXz/YM\n",
"afLISf29PFRDsttms4nj2OwTeZ6v12t7b1vKsvSJ82GX5cG3wnq9TpKknkoWsc7bgr+4zsV8wUsp\n",
"pZRFUdSH5fQMafLIKfi8NpXRY0mSKKXKspwxJAc98lZYr9dBECRJMncgY3QE/8jrPEkSPc5HSlkf\n",
"hDoLUn8vE74a/v6CILAPgKUsS584l7Is4jG2glLq6empI+8/8jq/GHxdZZ2LB9hhdrudlHLEnjB5\n",
"5KT+vqZ6NfwjWMqy9IlzKctSd+fIlVJRFCVJ0p06H3Od9wy+j9l3mPoJqWdI00ZO6u9l6KvhH8rh\n",
"cLCbDEtZlj5xLmVZxNxboTF11oshj7nOewZfV1nn4jF2GP2i2aEhTR/56GGhrun/avgZhWFYufkl\n",
"SZL6zS8PsiwXR8f3iXOWZemO/NG2gr4bthLSy8uL53n1Lz/aOu8ZfM91/nLf4OM4rkxc90WPC2na\n",
"yHlBY1+66aHfDKxfDf+AHWVKqSzLpJR6/INuF9SHwc27LNvtVrdfdC+caZcdj8cRcd5zWXpG/mhb\n",
"oSiK9XpdHwhYFEX98H+0dd4z+J7r/M7B605dpZSOSg/qbxzk0yekaSMn9Q/T89Xw81JK6SJgd5yL\n",
"WBbRL84HXJZFb4XXvc7FfYMvy1KXpyZZn1NFTuoHAOfQzQsAziH1A4BzSP0A4BxSPwA4h9QPAM4h\n",
"9QOAc0j9AOAcUj8AOIfUDwDOIfUDgHNI/QDgHFI/ADiH1A8AziH1A4BzSP0A4BxSPwA4h9QPLImU\n",
"svJ67v7yPJ82GCzXd+YOABgpz/PD4dD21/qbfl+H9Xrd+MrZPvTqesB3SuP+eEEjlirLMs/z9LvR\n",
"pZSHw8HkxCiKXuWOrc92o89qUsrVanU+n6eNCktEqx8LFgRBGIb656IozM+v1Xa7Hd3kF0IEQeD7\n",
"fp7nNPxBrR9LlSSJbvLXVRq2RVGsVqu3b99++eWXq9WqUivfbrdRFBVFsV6vv/jii/V6rT98+/bt\n",
"09OTlFJPIYqiKIqEEIfDIYqiL7744unpKcsypVQ9AN2+/vLLL/UcD4fD9XX2oiiUUnEcXzO7OI6p\n",
"+EMIIV6A5Tsej2EYNv5pt9uFYXg6nfSvp9MpjuM0Tc0XzudzkiS+7+/3+5eXlzRNgyBIkkR/2fd9\n",
"/Z3j8RgEQZqmSZKcz2czcd/3zcTNBM3UzPTbwutPz7r++aDZ6ZPi8/PzlcFg6Uj9eA3aUv/5fA6C\n",
"oP55GIbH49H8mqbpZrMxk7L/xZ5sGIb15Fuf9WazsU8tLy8vz8/PjVl7kDAMK5MdNzshhL3scBMF\n",
"H7xmeZ6naVr/PE3Tyuggu3bkeV7bBOtTC8NQKVWWpfkkjuPD4bDdbk1lyfO83W43In6blNL3/frn\n",
"Q2cXhqGuYsFlpH68ZroI/kVNFEV2su6vMfl6nmdPTZeAxDe9Am/fvl2v1+Nmd3HW42bX2D8BpzDC\n",
"B6+Zrto3do2OU5ZlPQUrpSodzp7n2dcHOimfTqeO64mLKieY0bOTUjLCB7T68ZqFYTjtgJYsyyqf\n",
"5Hnu+76dZOvfiePY9/0ryyxBEDS21gfNTilVP1HBQaR+vGZhGPq+r8dr2vI832634yYYRZHuJ5BS\n",
"ZlmW53mlsC6lrJxvyrJsvFwYOuvGRzgMmt3hcNCj+6+JBK8ABR8s22q10i3Zsiz1uPs0Te17u3a7\n",
"XZZlT09P+kOllJQyCAJzb1SWZYfDoSiKJEl0JUT3EOz3e/2FKIo2m41uKethoGbgvB4pVKmr6MqM\n",
"mWNZllJKPQz0miXVU6vfuTZodkVRTFj+wnLxIAc4QWd8/fPom36jKOr/EAUzR/O0iet1PMihz+z0\n",
"GeJ8Pl/T5YDXgdQP9DUo9d/I27dv9U1qI/53vV7rfu/Jo8LiUOsHlsSUoUbwfZ+8D41WP3BZ5QHR\n",
"cRyTQ7FopH4AcA4FHwBwDqkfAJxD6gcA5/x/jY8SRJGUs/gAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b19rOTGdeBbdz7uyCON7uWVZI2keWOFd+WFjcTRhhe2\n",
"BkYQT5ZcAysoiTFmewxFiBcx2MYaxrMN5JGJsHp5WGTBhmE4wnuLuGkBXq/lJ7iJBNk1FC9ARraQ\n",
"BPALmpL9kIcEGTctZR1Y43Wa8npmopmruN8f504Nb/Gjq7pJdpF9fjCsnr6ni6fqkIdVp05Vbcxm\n",
"M4IgCIKsE0dWrQCCIAjSNOj6EQRB1g50/QiCIGsHun4EQZC1A10/giDI2oGuH0EQZO1A148gCLJ2\n",
"oOtHEARZO9D1IwiCrB3o+hEEQdYOdP0IgiBrB7p+BEGQtQNdP4IgyNqBrh9BEGTtQNePIAiydqDr\n",
"RxAEWTvQ9SMIgqwd6PoRBEHWDnT9CIIgawe6fgRBkLUDXT+CIMjaga4fQRBk7UDXjyAIsnYcW7UC\n",
"CNIaHMchhOi6ruv6qnXhxTAMTdNc1121IohcYK9/7UiSpN/v7+7ubmxs9Hq9MAwHg8GqlSIy6DAX\n",
"XdeTJAnDsI7Ce72ekaLX6zmOE8dxHddCkI3ZbLZqHZDmSJJkb2/Ptm3LsgghcRw7jhOG4XQ6Xa1i\n",
"hmEEQbBaHXiAjn8dnegwDH3fJ4SYpgnfxHHseZ5lWWCsxYiiSFEUVVWr0RLpChjwWS88zzNNk7oS\n",
"VVVHo9Hu7u5qtUIIIbquw3giHU0yTXNvb880TUVRFitW07Rq9EO6BQZ81oskSbK+wLZt+jkMQwg4\n",
"EEJ83zcMY2NjY29vz3GcJEmYH4Zh2Ov1dnd3d3Z2IHZUdFHHcdJFRVFEhfv9vmEYURSlwx39fj9b\n",
"zmAwgL9GUUTVMwwDOsuiWvEARe3s7Ozu7vb7/WwLVH5FBkVRTNOE+pKbbeV5HhWAb8BeaeI4phEk\n",
"GKnkEkURVBA0930/XTi/WJIkg8EAGoEGEplCPM8D5aE0ejNkL1d+w1Dqa/a1YIasE6PRyDTNEoHJ\n",
"ZBIEgaZpEBSaTCbw/XA4VFV1PB5TyeFwqOs6/WY8Hpumads2U+B0OtU0bTgcTqdT+OdwOFQUhUoG\n",
"QQBXDFKkL0QZj8cgORqNLMuybXsymUwmE9M003ryaMXDcDjUNI0WBSXbts2UVuEVs4XPZjPLsmjh\n",
"QRBAxelfoU1yH2RoSdd1dV3PvdxkMoFhH/2nZVlZYR6x8Xjsui7VczKZgEGZcuCH9L6aTqdMdWYc\n",
"NwxQYbOvJ+j61w7XdcGzD4fDXA87m83g+WS+DIKAPvDwbOf+kHngs9/MZrPhcMg8pUXuKfcSiqIM\n",
"h8Psn/i1mgsUBd6HMh6PCSFpzSu84izP9Wcdd+7roaQPl7Yag+u6WbebtTunGMNoNMrqads201zT\n",
"6VRRlPQ3PDdMtc2+nmDAZ+2wbXs8HkOyiud5u7u7uWP8dBQIgJ9AzonneVkB+FU6/BLHcZIk2VRI\n",
"0zTpZOYCuK6bO/PJqRUPML/KRNg1TWOuW+EVARrFMgxjd3c3juPRaLRAOTyYpun7/mAwoKESeKcu\n",
"JkYICW8Cc8u5F2VuBkVR0mE0zhum8mZfQ3Cad02hyelJkkDqNzMHkJsToihKHMeqqkZRVJSOmX5u\n",
"4zjOTYFXFGWZ6ceifBVOrXiIoqhI85quSH9FfVzdqwcggud5Hnh2MJZt20zz8oj5vu84jqZp8GWS\n",
"JEUNWA7nDVN5s68h6PrXC9/3me62oii6rvu+z/hicPHMz+ksMfR/eXruTWam82vFU1TDVwTAHFWV\n",
"xnO5dPcZxhzj8Zh5w5WLxXE8GAyYX0H3fwGVeG6Yypt9DcGAz3pR1FfKDs+zqRee56mqCpK6rueG\n",
"iRh0XY+iKDcxpo5XAqdWPGialhs6YL6s8IoLU5R3NJesiU3ThCGdkFhucGwxrThvGBmave2g618v\n",
"oihinuQoirJDAUKIrus0bxJ+5XkejfDquq6qajYF0/M85u1i23av12Me5sFgwPw2jmPmZRCGoejr\n",
"gV+ruZimCSuq0l/2+33GwVV4RU40TUs3CyRxLlZUFEVMBcEKzGhvrlj2bTEYDEoySsvhuWGab/bu\n",
"gat51wsI64dhCFGFOI6jKBqNRkx8A9bWwvpScDSQ88M4PlgJTOcMoiiC7WIYMXggITMHNkLQdZ0R\n",
"g2AxvIFyZeI4hkc9iiI6+CCE2LbNREg4tZoLZJfTmHUYhpZlxXHs+76qqum1x5Vc0TAMaGpwqSUb\n",
"7/T7/TiO4R2QJInrunt7e7quQwIuLY3WAoThn+kFfb1eT1VV5maApMn05XjEqErQUDCT1O/3VVWl\n",
"WvX7fQgBQXou6Ab5+IzyPDdMVc2+tqDrX0fgOSHF06382yrQosi8GTYa+S0S4y+qQq3mQocj5eVU\n",
"eEUeICqy5Gw5MPdm4BSjDaVpWiXOd+4NQxpv9i6Brh/JoS076iAIshgY60cQBFk7sNePHALSt+k/\n",
"06FhBEE6A7p+BEGQtQMDPgiCIGsHun4EQZC1A10/giDI2oGuH0EQZO1A148gCLJ2oOtHEARZO9D1\n",
"IwiCrB1r7fqjKGJ2HEQQBFkH1nRJV5IksK0gIaTWM/AQBEEkZE1dv+M49IRCOE6oaINcBEGQ7rGm\n",
"AZ/0waFwMNBq9UEQBGmSNXX9zIbjeLYDgiBrxTq6/mwfP3v+OIIgSIdZR9ePIAiy5qyj688eLyd6\n",
"/DeCIEirWUfXTzIxnyRJVqUJgiBI87TS9fu+PxgMSgTCMOz1eoZhOI6T69Y1TaOHPodhuPzZ1giC\n",
"IC2iTXn9YRh6nhfHsaqqSZIUnRvueZ7necPhUFVVOG5wPB4zMsySruFwiEk+CIKsD21y/RClgQ77\n",
"YDDIdf1Jkuzt7Y3HY+rKHcdRVTX3gFlaYJ1aIwiCyMeshQRBoOt67p+Gw6Ft2+lvJpOJpmlVXfqD\n",
"H/zgqi2GIEg32djYqMpTzeXYqitbMXEcM714iA5VVf53v/vdzc3NT33qUzzCX/va1+699953v/vd\n",
"nMLvete73va2t/EIP/vss7/4i7/IKfz5z3/+Yx/7GI9kfcKvvvrq17/+dX7hP/uzP/v1X/91HuG/\n",
"/Mu/vHz58mOPPcYjLGSR+hr5S1/60m/8xm9wCktivm5bpD5hfltHUfSNb3yDs9gKaOwlUyElvX7T\n",
"NIMgYL4sEl6Ac+fO3XnnnZzCH/vYx7785S/zC2c1L+LixYv8wr/wC7/AKVmfcBAEQsIXL17kFP7y\n",
"l7/8sY99jFNYyCL1NfJ73/tefmFJzNdti9QnzG9r27aPHTvGX/KStDLDp4S60zRvu+22jY0NTuGt\n",
"ra3Tp0/zC/OrwdnxAXZ2dlonzF/B06dP8zedkEXqa+S3vOUtNZWMFqFI0m5Ctj5ypDmH3DXXXzdX\n",
"rlz56U9/yil8+fLlS5cu8Qvzq/Gd73yHX/jv//7vWyfMX8FLly7xN52QRepr5J/85Cc1lYwWoUjS\n",
"bkK2/qd/+id+4SXpWqy/7nSdY8eO8ff6P/KRj/B3fz7ykY+8613v4hR+/PHH+Wv6iU98glOSCHZS\n",
"+EvWNE1I+PHHH+cUPnfu3Dvf+U5O4dtuu+3UqVOcwvU18u/8zu/wC0tivposIvSMbG9vc0oSwXar\n",
"T1jI1vy+pQIaCy1VSEms37Zt13WZLxVFqerS58+f39raqqo0CalwXkRCbNvmDxa3ETRfe7Fte3Nz\n",
"s7HLdS3gY5omXaYL+L5vmmZV5QsFfIQOgBQ6M8DzvJqEhQaz9anBLyzUyELhhfpqV5+tZTCf6G3P\n",
"LywU8JHh5iSCtm4y4NM11w8jdGqbJEkGg0Huei4EQZC1pU2reQeDAfTokyRJ5+8zy3qTJDEMQ9M0\n",
"RVHCMLQsq0LX/8u//MsvvfTS66+/XlWBsmEYRtEOGR0gfTBnJ0HztRfHcT73uc9dv369oes1Flpq\n",
"mPF4HATBdDqtttjHHnvszJkznMKTyWQymfAL86shFPHstrBoI/ML11e7btu6jRaRwda2bfOvGVqe\n",
"rmX4UGpK9blx4wZ/rF9okYGQsNABA90WbmMjS6IGWqQBYaEKNhnrb1PARwY+/OEPf+tb3/re9763\n",
"akUQBOkUjuM888wzP/rRj5q5XNemeevm6tWrb775JqdwHMf8HQShrgSTxbTOwqKNzC9cX+26bes2\n",
"WkQSW+/v7/MLLwm6fjGuXLmCrl8q4TY6mm7buo0WkcTWTbp+DPiIgQEfBEHqAAM+UrO/vy80zcs/\n",
"ydP5+a76JhWFGplfWJKpPxkaWUi4jRaRxNa4pEteptPpjRs3OIXbuJq3dcL1rR2VZIWnDI0sJNxG\n",
"i0hi6+aS+jHgIwoGfBAEqQMM+EgNBnxkE25jeKHbtm6jRSSxNQZ85AUDPrIJtzG80G1bt9Eikti6\n",
"yYBPZzdyqIkLFy6cPXuWU3g6nfLvJCG054TQTgDdFhZtZH7h+mrXbVu30SIy2Nq27e3tbf6SlwRj\n",
"/WJgrB9BkDrAWL/UXL58+Y033uAUDsOQf/WH0DoRx3FQGBBtZH7h+mrXbVu30SKS2PratWv8wsvS\n",
"2PiiG2DARzbhNoYXum3rNlpEBltjwEdqMOCDIEgdYMBHajDgI5twG8ML3bZ1Gy0iia2bDPgc/d3f\n",
"/d3GLtYB/vAP//CHP/zhpz/9aU55RVEUReEX5tdEVVUUBkQbmV+4vtp129ZttMjKbR2G4UsvvfTb\n",
"v/3b/CUvAwZ8xMCAD4IgdYABH6lJkgSXdEkl3MYFRN22dRstIomt+YPJy9PZAxprYnNz88gR3vel\n",
"0KC+2xGA+oTb2MiSqIEWaUBYqIJHjx7lF14SDPiIgQEfBEHqAAM+UoMBH9mE2xhe6Lat22gRSWzd\n",
"ZMAHXT+CIMjagQEfMTDggyBIHWDAR2quXr2Kx7JLJdzGQ8C7bes2WkQSWzd5LDtm+Ihx48YNoaNa\n",
"+Evu9vEd9Qm3sZElUQMt0oCwtEe1YMBHDAz4IAhSBxjwkRoM+Mgm3MbwQrdt3UaLSGLrJgM+a+36\n",
"wzAUMgwh5MqVK+j6pRJuo6Pptq3baBFJbN2k6xcO+CRJAqm4SZLouq6qqtDaNkmIoqjf7+u6TgiJ\n",
"43g4HHIuusOAD4IgdSBvwMfzvL29vZ2dHcMwwjCMosgwjN3d3b29Pc/zhGYzVkuSJIPBYDweu67r\n",
"uq5t24PBgPO3+/v7QtO8/M3S+fmu+iYVhRqZX1iSqT8ZGllIuI0WkcTWTU7zcrl+z/N2d3d937cs\n",
"C06oCYIgCILZbDaZTCzL8n1/d3dXaJHbCkmSxLZt+k9N0/h/O51OcTWvVMJtXDvabVu30SKS2Pr6\n",
"9ev8wksyP+DjeZ7v+67rlrvIOI4Hg4Gqqmmv2griOHYcZzQa8QhjwAdBkDqQLuBjWVYQBHO7xqqq\n",
"DofD1vn9JEn6/f5wOOSUx4CPbMJtDC9029ZttIgktpYu4NM6HMcxMmSPVUuSpNfrua7Lv7EqBnxk\n",
"E25jeKHbtm6jRSSxdZMBH9LYAfCyMZ1OdV0fj8dCv7pw4cLZs2f5LzGdTvmF+dWAGRcUnok3Mr9w\n",
"fbXrtq3baBEZbG3b9vb2Nn/JSyKW3BmGYUuzORmiKPI8z7IsoTlegrF+BEHqQbpYf5rBYCC6Bmox\n",
"fN8vT7gMw7DX60EYRzSvNIoix3HSE9fZWFARly9f5t9TOwxD/tUfQutE+BXuvLBoI/ML11e7btu6\n",
"jRaRxNbXrl3jF14WoTECrIEqQtM0yPhcmCAITNPUNM00TV3Xi8SGw6GmaePxeDqdggcXuopt25qm\n",
"6SkUReH8LQZ8ZBNuY3ih27Zuo0VksHXDAR/hWL9lWbZtQ32m06lt27Ztw58mk8mS3n88HkPwPQiC\n",
"Itc/nU5VVU03qG3bw+Fw4YsKcfHixQcffLCZayEIsj7Ytn3XXXc1djkx15929BTTNEejEXwej8em\n",
"aS6vVonrhxTS9Dfwyln+ojycP39+I8WRI0d0Xd/c3Nza2oLRw3ve857ZbPae97znnnvuCYLgHe94\n",
"xz333DObzZ566qkTJ06kP8xmsxMnTjz11FPw4YknnpjNZvfccw+UQD9AUekPTz311LFjx0qKgg+0\n",
"hJMnT5YUxWhl23ZJUYxWtm2XFMVo9d73vreOCgZBsL29zVlBWIrIWcGTJ0+Wt1W6hGPHjpW3VfrD\n",
"E088Ud5W6aJs2y5vq3RR8GistoJw2zNFwQdGqxMnTrzjHe8IgiBdJlPB97znPbSE9F2RLYrR6uTJ\n",
"kyVFMVoxtz1TFKMV3Pb8FWSK2tzc1HV9a2trc3Pz5MmTG4eZNYWY69c0LTt+Ydx9SaCGnxLXb9s2\n",
"fdNQVFVd/qI8PPbYY2fOnOEUnkwm/GNDoVGk0NCq28KijcwvXF/tum3rNlpEBlvbtn3nnXfyl7wk\n",
"Yq6/aG4g7abrdv2maWabvpKL8oABHwRB6qDhgI9Yho+u69kMH9/3m0z3XO0+cUmS4JIuqYTbuICo\n",
"27Zuo0UksTV/9uDyiLl+y7KYxCbYBdM0TfqN67rVqCYlm5ubR47wNpqiKPzrhPklCSFC79puC4s2\n",
"Mr9wfbXrtq3baBFJbH306FF+4SUR3q/fcZwoiizLUhQF/L5lWZZlVatWGIaDwSAIglwFICMz/aVh\n",
"GLnClYNLuhAEqQOpl3QRQmCD+yiKBoNBFEWj0ahyvz+X7BhKaFS1DBjwkU24jeGFbtu6jRaRxNZN\n",
"BnyOLfCbbKe7SUzTdBwnvUWo7/vpiBOCIAhSjnDApxlKAj6EEMMwTNOE0UaSJIZhwPreBhTDgA+C\n",
"IHUge8CnVgaDAd1gGQ6ABBix0WjkeV6/34fNmRfYhW1hrl69iseySyXcxkPAu23rNlpEEls3eSz7\n",
"IgEfz/Ng0yVVVXVdt21baBa7BFgtPFdMUZTxeAxHw1d4dR5u3LghdFQLf8ndPr6jPuE2NrIkaqBF\n",
"GhCW9qgW4YBPv99PksR1Xchw8jzP87wgCJr0vysEAz4IgtSB1AEfz/OSJBmNRjSz1bIs13V7vV4N\n",
"uskIBnxkE25jeKHbtm6jRSSxdZMBHzHXH4ZhdsWWrutJkjSzj//KuXLlCrp+qYTb6Gi6bes2WkQS\n",
"Wzfp+sUCPjs7O9PpNPt97jKrToIBHwRB6kDqgE8HjmZckv39faFpXv5Jns7Pd9U3qSjUyPzCkkz9\n",
"ydDIQsJttIgktm5ymlfM9WualruSLQzDdejyE0Km0ymu5pVKuI1rR7tt6zZaRBJbX79+nV94ScQC\n",
"PnEcG4YxGo3SefT9fl9RlG7v2kbBgA+CIHUge8BnNBrBWio4OX13d3d9/D7BgI98wm0ML3Tb1m20\n",
"iCS2ljfgQ26eva5pGgxkgiBYH79PMOAjn3AbwwvdtnUbLSKJrZsM+Agfy77mXLhw4ezZs5zC0+k0\n",
"e55liTC/GkIn/HVbWLSR+YXrq123bd1Gi8hga9u2t7e3+UteEkm3b5MWjPUjCFIHUsf6ixAaAbWa\n",
"y5cv8++pDTsd8Qvzq8GclbbOwqKNzC9cX+26bes2WkQSW1+7do1feFkqGTs0dir6ysGAj2zCbQwv\n",
"dNvWbbSIDLZuZcCnsfMRVw4GfBAEqYNWBnzWBwz4yCbcxvBCt23dRotIYusmAz7z9+v3PM/3/XKZ\n",
"xo7GXTl33HHHsWO8hxwI7XshJCy0drrbwm1sZEnUQIs0ICxUwePHj/MLL8n8gI/jOIqilB+D5TjO\n",
"eDyuVDFJwYAPgiB1IGPAR9M0vZQ1OaeFEJIkCS7pkkq4jQuIum3rNlpEElvzB5OXZ5EDGteZzc3N\n",
"I0d4J0iE3ohCwvWNqVsn3MZGlkQNtEgDwkIVPHr0KL/wkswP+MAeFOUVwAwfBEGQZZAu4KMoytwX\n",
"15r4fYIBH/mE2xhe6Lat22gRSWzdZMAHkzsRBEHWDtzDRwwM+CAIUgfSBXyQNFevXsVj2aUSbuMh\n",
"4N22dRstIomtmzyWHTN8xLhx44bQUS38JXf7+I76hNvYyJKogRZpQFjao1rmB3yiKEqShGcBG79k\n",
"e8GAD4IgdSBjwMdxHMMwSoY5YRj2er1er9f5tV0Y8JFNuI3hhW7buo0WkcTWTQZ85rt+TdPG47Fp\n",
"mv1+f3d3lx7M6/u+4zj0S13XJ5NJ+X4PHeDKlSvo+qUSbqOj6bat22gRSWzdpOsXy/DxfR/ycMMw\n",
"VFVVVVVN0zRNM02zPhWlAgM+CILUgYwBH4ppmq7rBkEwm80mkwmcyd5qv9/r9XZ2dvjl9/f3haZ5\n",
"+Sd5Oj/fVd+kolAj8wtLMvUnQyMLCbfRIpLYuslp3rVO7vQ8T9d1oSDVdDrF1bxSCbdx7Wi3bd1G\n",
"i0hi62vXHucXXpL1XdKVJInjOMPhUGgDIgz4IAhSB5/61P8xHG5fu/a/NnO59e31DwYDy7JEf4UB\n",
"H9mE2xhe6Lat22gRGWz92msPHDnyMn/JS7Kmrh+Mt0A+EgZ8ZBNuY3ih27Zuo0UksfWbb/4PfuFl\n",
"aewA+CaxbTt7noxt21TANM3pdAqfdV3nL/nChQtnz57lFJ5Op/QqPML8akwmExQGRBuZX7i+2nXb\n",
"1m20iAy2/rVfe/aOO36Vv+QlWcdYfxRFsBAB/un7vmVZtm3z/BZj/QiC1MG5c9+8dOmDkiZ3dgNV\n",
"VV3XTZ8uyb/5xOXLl/n31A7DkH/1h9A6EcdxUBgQbWR+4fpq121bt9Eiktj62rVr/MLL0tj4QojR\n",
"aOS6bolAEASmaUIYR2j4nAUDPvzCw6EUaqRpY3ihFbZeWLiNFpHB1g8//K3t7W3+kpdELtcPDh2W\n",
"B5d45OFwCNtLTKdT13U1TVvscqPRCHr9lmVx/uTixYsPPvjgYperD5FbcSlE3pLIutPYbdkNHnnk\n",
"G3fddVdjl5PL9Y/H4/F4PJvNgiAocv3T6VRV1fS71LbtIdMdrY3z58+fPn2aUzgIAlj5zJCrbK5k\n",
"Eekp69lsputljxkjLFQyAzNKrLDkhYWLGnl54fpqt4yt5Remjazrs3SXN/cWlcQiywiXv+H4a/fI\n",
"I994y1vewq/Gksjl+iklrn84HGaafrJwx1+Uxx57bGNj48iRI0eOHNnY2Dh+/Liu6ydPnrz77rt1\n",
"XT9z5syjjz46m80effRRVVUnk8n58+dVVZ3NZk8//fSpU6fgw7FjL0Bpp06devrpp+HDU089NZvN\n",
"VFWFEugHKCr94emnnz558mS6TE2b3XbbJ2hR8IGWcN9995UURbWCD0EQpLViiiJkdv78b9ISgiAo\n",
"KQpK+NCH/nQ8np06derjH//4whVk2iqt1WQyOXv2LGcFJ5PJZDIpqWBaq/vuu6+8rdIlnDx5sqQo\n",
"RqunnnqqpChGqyAIVFX9V//qQ9Pp/AqCo1ltBeG2P3XqlK7PPvShP4WiXPfzx469wGh16tSp8+fP\n",
"TyaTdJlMBR999FGqVfquyBbFaHXfffeVFJX+8PTTTzO3PVMUoxXc9rSE48f/qESr8+fPM0WdPHlS\n",
"1/W777775MmTW1tbGxsb4FI2NtyNjY1ZU0ia4ROG4WAwyF1k6zhOdsO43d3dyWTSgGKVZPjs7pJq\n",
"lYVpJ9ctk0kS4vtEVYmikIX3VzUMYttE6EQGxyGKQvjyp5BCwpBEUcua0XFIHJPR6OBzkpDhcNU6\n",
"1cDGBqnEiWKGzxziOM6eCqCqajNXT5JkySVdSUJyFwMuvMwnikh57UHY9+k/eUtmALXTixM517bA\n",
"Dzu2gIj5Y91LusKQ8CwLlWEdEzQyaKtpB9YvWgAr1ZKuOCY8uqRLzj4UDFA7x7n1AJbAnz24PO1z\n",
"/UKL4Ctnc3PzyBHeRlMUJfuWiiKiaYfuFeizC51yk37VxfFBX77o6QLhKCKWRXSdqGrZ/V3yEo1j\n",
"YtuHfkuFw5A4DhkM8n8INRN6PfML5zZyJcLlOsQxSaftCdVuYVtzCsdx4c0wt+SixEVRi0QR0XVi\n",
"msTziOcRyyK5lS63iOfl3288LNZuPA6aefqYh4KB1q48yTOKyPb29OjRo1zqVkH7XP9quf32248d\n",
"4z3QGEKE2e91/dC9Ap+F7tT0QgR4xnS98N7SdR1eD4Cmld2pQudrgjCM5S2rsO8Dr6UFSuahqJGX\n",
"Fy7XIUkONbim5Qvnvg4XsDW07dxuDwiDt+3358hnK5gkhYPCxSwC//X9wiBhiUU8j/j+oSrUdAul\n",
"hXlememSk6Ss10VSti4XSxKyvT09fvw4l7pV0D7Xv9qDwJYP+Nws5+ADdR8LB3yYkXWusOcROjmi\n",
"6zmSvn/wzC82pjbNspGHppEwbE3Ah3b9ynVQlENe6dd+7a+zdY+ifE+6gK0VJf/tzjh3qrPrEtsu\n",
"7MIzwhTfJ6aZ3zMQtQiNQ6oqKTnRo8gi0N9n5jYaCGfxuH4m3GrbZb+itbOs+UMKDPjMIXuvCD1L\n",
"zZO+M6CTTvVdPnzFGTwo72hGUf7tm/Y1cTznWrrO3txQu9yXjZw4DhtkKCHdGlevnsi6miQ5iHhU\n",
"Qu5wzXEO/pf9E7yMhQhDYpoV3JOEkCQ5uOUsi4jvkEuiaAVzwnPv8GVQ1bKnIAzJ9va0rmvn0T7X\n",
"b5omszba9/3GTgpTFGVzc5NTGE6vJIenBJPk0OAXQv9EcDSTu920ouT7LEWxGL9f8mwzJafjFXHM\n",
"pgaBMC2NmcMgN99zJTpzqlECbeTlhR2H6PqtRKm5OtAGjyJiWQfB4jRg66xRFrN1kVdy3Vtd9WUa\n",
"OWtfkqpRJRbJ3nhFwrmVXaB2cTxn6MMI59prGTWgdnRoXhLx39qa3nbbbfwlL0n7XP9NZ3rgTZMk\n",
"WWzn/cW4evXqAsey88wdLXZUd7qfUhTu/6M/eoVpHmamN50jlH6tFg0FUtGqkHAPO/74j7/JJZdR\n",
"o5xqDwFPv5Xn6kDdhO+Tt771m9kAC7z5st29XB3CMH9ioFwNaHwa7gvDkP8+YkqGqKCqHrqLBoOD\n",
"fy5vkdxRS64wvauZEOICh6dzDuBoySWB0xI1SvpSUDuojmnOmext8lj2RVx/GIb9ft8wDPjnYDCo\n",
"KutmMBgYhmEYhuM4URQZN2HERqOR53n9ft9xHMMwLMtqbALgxo0bCxzVwvM0LnZ8R7qnlu10A6+/\n",
"/jrzDfMQ1qHhhwAAIABJREFUpmfh0s9henKYku4WwWObdv2M4wjDA/V0nXz967yvTCLyIqzjYBDo\n",
"nc3VgTZjkpAf/vBvFYWtPmBZbMyH6pC+QlFmYRzHtBnLs7PITYtwTnBmK6iqrMUV5aBGy1skt4uQ\n",
"K0zvasYRL3CgCqfrpyWXJ0EUqVHS+0nXbm4nSeqzeT3PGwwGuq7TV5+iKEJb2ZVg2zYs7Ib9eYKb\n",
"MGKKoozHY8uydF0PgqCxLj9ZNOBDOGL6iwUBwnBOEJ8Q8vM//zDzDRN8h7As9LDSjUmDUQy0LpZl\n",
"MVGCbL+GdksVRSDjwjSbDvhQ90puhmV57itoNFU9ELbtQ9WHhso+8DQMmH4l5L5oyU1b02Ysd0yW\n",
"ZaVvifJXRbqC5fdnkggHfDhfx7kWKfptTTFDwhFVKy+5pJ01TUt3j8rzfOQN+IRh6Ps+bLJGv7Qs\n",
"ayWzrJqmweZrTV50gYAPM69bIpz7fa+X82V6yDnX9b/66islf4XsNHKzh5UdzDJ6pesShmEUHXpa\n",
"iqyhKOSv/ur7cxS9SRiSD3zgctFCgSQ51JhVBXzC8FZnuagpcoE4CY19pd1WUWsUhQHTHiQMb0Va\n",
"aESuxPXDb8MwpPOr8GWJC2aCe0VjBdMkvi8c8OF8LnMtUtTnWCDgIyTM+bqiJadHY0W/hfrR6pQk\n",
"YROZAz6e57l52wVomibU0O3lypUroq4/SXLu45sPKnSHIaqe75JyH3Wh1n7llVdK/gr5fCmVbpUM\n",
"s5SlaQlhbu1yH4N/+Ifvciocx+RnfmYEN1puHmraaZa7fmbtNCOc1pO+Aik8jQxJTapKUoPgHDGm\n",
"VxjHcTrdliqQ9gtp15/25kUuFd4KYRgyAkVtkyTkP/7HyyVVS5cchk3PvuRWs1wHOi3BI5xbMufr\n",
"Kl3yzeWKha9kpnbl4zZ5XX8YhgXT8Y12vVfIvffeyz8og6NgSN4oD7oJ4G4gRk/XiaTvDBi8Zx+N\n",
"3BdwEb/0S+/LfknfPUzPhZacdYVZCvoB+f2aXDVyiWPyxS9+guRli5KcUYhesnhnMDhUAiMcRQcD\n",
"i2xl001RgqYdZC6WCzO9Ql3XfZ9NeYSpguzGACUlp2M7MFJhhIve3FFEHIe89a2P029y8xrpl5pG\n",
"TJP3ltN1XVH07GA0NwMt13xFPejyRob7mcaeXdedu8dJbsnlMZm0MG3/kl6/ruv8apw8eZJLrgrE\n",
"XP/6uPgi9vf309O84L6LgCksmHZjbia4vdIDWzodxMyb5I4Q6RRWdlIu+3T9+MfsNC8hRNMOlkoy\n",
"2dO0k0IjACWPQW5/rSi6latGecnZiWu4ICgPlMzcZnePYYRhTzQ6/EqjKGWTivSZpzvTZQcTaaWY\n",
"6d8//uOfFGUjwxM2GNx6MTBqMHVlboBvf/uVIp0p4Pddlxw5cssiRZmd8KVlkc9+9n/OLfmmhsl/\n",
"/+8/yTq73DSEXPOVB8pygb0iXJfo+sETBMMJTp+bLnlukk9amJZf5Aegfmk1sq8W+lt5p3k1TcsN\n",
"6xeNBrrHdDpNr+al3cZcYKVi7kMFt1e6s1k0X5J7I9Id2RgPkn26wpC89trzucVCPjjzmNGsWfCG\n",
"5QGf3AWTtEBGk29/+9uFBR0mSdLJu4f+BJ3l9IrTkgW64EDTFcwKj0YHgQKmJVWV/Pt/n9NuaYE0\n",
"VGH65ku/1xnhr371H4rmIGHMRJ1FuimA8t7XYBDOTe/xfTIaEUURsIiikO997yXOUHgURS+9xLu1\n",
"bdEWh7kwTeH7h6ZGoOK6fvBzz/NKJjBKSs4OWz3vYN0cPOzltz1DtnbZvhHV8/r161zqVoGY67cs\n",
"K5vMA0ecr8mAgAn4RFFZrz87mGXyatJtlhu1yA7/ARhyZsMUuWPVj3/8cfarYjgDPqBSyQAcJmPT\n",
"dfo3/+Z9PNkA0FOjJTMxn2w/TlH03NwhCFYwwrnhBdfNaWFVJf/6X39ivrq3CnFv6nPLBEUNeOed\n",
"DxaVo+uk37/lxcJQILinquTOOz/K088FxUpCcNAg6cHQV77yvpJeThpd12/ceBdnVzDXIsWL1w41\n",
"BQxfYNCWLgMGha7rUrPOfWkxAZ+0PKxucV3iukTTSL9PNE0g3JqtXUnSh7wBH13XTdPc29vzfZ8Q\n",
"4vt+r9cjgqHnVpMN+JSn9DLD2XTONb3DIBoAcswqKpBn7kVCSBzHuVti5Q4RXnvtB1x1I0RVyX/9\n",
"r9+n6hVBu0XPPvuD3Cc8N0h18uQPeLqN0FmmY+p0Bz/tieDxjiLy7LNvPPtszs4nnncQiklPweWG\n",
"F1T1YE95pgovvCAcoSIpE5REeE+ePFA4+6qGuR8YgsCUIP+UqaaR//bf9stdv+/fasMf//j1XIuk\n",
"pyJTt0FMhX//98l/+A+Fl0iS5Pr1Nzi7glmLCAUYR6ODvTfSoyjIMKZZRguk6qeVpzcSIUTXyXBI\n",
"Xnjhdf6URp51JPTi8gZ8CCGWZY1GoyiKdF2PosiyrGEnz18ogAn4lJsVBrMlzwBNDyA3B4ZMWBDI\n",
"elLP87IxilzCkPzFX3x5vhw50OSLX3wx90/pJE6qz/PPP59bO+jXMAH0559/Pttc2c1nYKyQHVMn\n",
"yaEAF2Qc+j559NE/v3SJPd0CnqXsky+01xt/PITkbaiXa0pCSBiSU6f+Fj6nVuHeaiv6PIH+Tz75\n",
"AmfAWtPIkSOvlMtE0a02fO215wt2/jhUEcDzPNiPaDAgJ0+S/1kc+Y+i6LXXXsv9U/YGyFqkZEla\n",
"9q5QFDIa5UyYp4V5XkJMydC7TxIyGOQERbe23GzIpyi7Ye4GjiRVZXkDPoCqqq7rBkHguq7Qzqgd\n",
"gAn4QB8tbxqWkHnJJ+RwCLhEMjtCtG2XP8D2B3/wv3FK6jr55//8cUJypj3TSZy01m9720fLx/Vp\n",
"JZ977qNMLSCSw3j/bChJUQ62IGYC96YJ03r6z/7sGea66Z5aeiSUJPnRoVxK4iHZlXSMwrlA1eKY\n",
"/Oqvvov5Mv0r5ue/+ZuFMZysGn/6pw8xMiX5KiWRwOxiNNd1dZ0MBkRR5mzHpuv62972YO6fsi0z\n",
"9xkpSnaityjsacqgaYQQl3/+kYlbmCaxbdLv57+HXNe1LNLrMQHb/P1acmtXFPORN+CDZMlN6c1d\n",
"h0Uyz2r2kWaSQ4pGFdkJXqaEZYCthsvf6XRzgrnzASV/9X3iugcTrVkPSDFNEsdkNGLfRrQFGO+W\n",
"7vIzpC/EQxwf5As6DtnbO3QV0XPh6OCD2XuDbgWRC+yjwGyVkb7fGDVy82qo2uloT7YoSkkwejw+\n",
"8Ptzt5QQhfajmW5H8fRp2TmjMCikWVgLqAphwKJItqYRVWX1zN3Gg4eK9sERQziv33Ec2GAHvonj\n",
"2DCM1Z6c1SSXL19m9tTOTaq5+SGkqz/obUEfTstKZ3be2m0qHd0uuu+/+MVvFt332Z8IbbPxX/7L\n",
"/0szQMqxLPLVr14q+ms2NYhRw3EOIhuKQobDg/NeaEumhVW17NjhMAyPHHkp/Wynu/xpoojcccfl\n",
"P/mTvy4s6zCvvvoM9ONs+2CWryQMPbeR0xM22fVfRbkomka+9KXvM/665GnLVYPKp6M9hBDPc7J5\n",
"qOUlp4N+RZsShmEosnI7hDVracWL7r107coTNxWFvPWt36QbAc2toOM4uSsbcjUBNWDWN41t52zQ\n",
"/eyzf5GrXvpeole5du3aHEWrQziv3/f9w6fwqLquV7WHj/zs7OzQPXyK5vEg3yCOD+1PkpVMb6eu\n",
"KKREEkjfvg8/zG7LUyRJBDcz+fznt3P9LLNhAyFE10mvt1NUjq7n7/AMxDFbfdsmvd6tVA2hHWM+\n",
"+tGfSe0od1BgGnjSfJ/8p/90Yjb7Gc6Sf+/3fhnOoBfd1yU3BpjuSqczocu9kq6T115jw1mcalBl\n",
"igYWlmXBl9kXT65w+p8lblfTtIceuptTYXhG4J00t8ssdCd/5Stn+YWzu1HxqJE7QmW8/x13vIsz\n",
"HYMQcuLECS4NqkDM9fu+b9u2ZVnpVE7btiU/KaVCjh8/Ts/mLZrHIzf7vIqiEJLKkCjN1CjPjmWy\n",
"FLa2tosks6N1oeMAf+mXch4Y6I9nH4zB4K6SophXSFqN7GgduvaOQ5dHLng2b26Xn/riBx/cPnGC\n",
"dzE2o0P5Is+0cDYji3Izhq6khcvJHcHwqMGUn00JU1W1ZM8lpmdTYhFmVyVCFP5GBvOFIbvzXS5U\n",
"B56l5nUf5JsLBCfT3HHHKf6S5T2bNwzD3ENR1mcPn3TAhz4buSl6sP/XM8+8RHctLnf96SBA9k3K\n",
"3OgvvvjNkqIYvyM0JssKl0R+Fy45N76haSQIDpqUv2QaMSBlO2UepGqEYVi+mV2RwmTeIs+0MGRA\n",
"5fomqLjgw7KU+UgqSZ9pcyqcG+tgejbZkunqs37/UFf33/7bV972tv8nV730ndnvg1YHQdHSHdBY\n",
"HcoD/UUKr0T4q1+9xJ+RIW/AJ4qi3M7pmqznIocDPvTZSHfJYZIK3ISmaQ899BBn29AgAE9osiTg\n",
"k/XUDWx1yy9cXrXURIjYFsFgguyeaACkJGka0TTt9OnT8OXc/a6XaYpsihS52TtWVSK09D2rRkkW\n",
"QNHxbVm/nxbOjXXMDRvCG24wILZNNO3A+8cxOX369MWLb8+ty+GV1eDBb+3wnLtdVbrPlN6rfG4T\n",
"SnLb33HH/1Kuavq9K2/AR9f13Bnd9ZnmTQd8KIf3MT54xpKEKIrCP9wrf30yQ4Gf/rQw4JNl+cFs\n",
"0VZFoiXzbF4tWjJEDG6ufir0CDenlA/FIsovktWh5DZnhHNLVhQ6ySHQVWJKLlhvlS9Mye4WVyIM\n",
"MCOz3FAS7ehY1oFWnkc+8YnbeCoIgwZFUZJEgbLnnmOcDvjMvUFEb87sbNZiJTMzPXNjX+mbVt6A\n",
"j6ZpfmZeP0mSMAzXJME/SZL0ki5Kdr5eUUgURV/5ymucPbzsfEm6TGYo8Hd/x7XaCO7m3C1HisgK\n",
"g6/JfSoWKzk3vLBwybAmCHqdJU0NV4yi6PLl/NVGPDqUqJ3daSerTCqf55at52ZJCu3hU9RuRebj\n",
"z9HMLTkIDi2ygxhOknCtm4MZkSiKfD+me8fmrlEv16Eq4dzZrAVKZsYu/PcbIYTJHqwVMddv27bn\n",
"eYe3dE96vZ4tNBXVZjY3N9PTvBRIUMlE/JXbbruNsyuR7SiVLGvc3ubq9cPdvGSvv0R/0ZLB0fAE\n",
"aheY5qX7J5cL0xV5c0eqy7Qbs/oM0DTaLbj1t/JkzSXVAHQ9f64YLJJ79eyEU27JzJomyNRiJt5z\n",
"oa//o0fveuWVHXqfly9Qf+tb3z4YkH6fax37SqZ5SWZOaO4e7+nAY5O9/mNC0oqiBEHQ6/Ucx9F1\n",
"PY7jKIog56cm/WTj9ttvP3bsoNHSt7emkeGQvSlVVd3a4i2Z/+ZLElK0WjIXoQFZ3cIQ75675xN/\n",
"ybTdeLofaYvMVYN/H/mscK76ys3t5Bhbl886LG+RogJ0XQ/D/LnrbH4qjxrQnopSWBl4o9ycCSOE\n",
"kEuXHkw/I+UW+da33meavH1z0Xbjn3oXKrkkGY8uTaDWP378OH/JSyK8mhe8/2g00nXdsqzJZLI+\n",
"fp+kAj7ZxxW2E6GuX9PIH/zB3zLDvZLO0De/ybtjTBSRJCm7T+lzC32rSobJuV6v1gE4pyTdBIbn\n",
"1QkBH86ZqWUCPrnQcUk6HgLzHyXK19rIcxPPFii5ZKMkJm6p6+RP/uS1S5f+R0lp6SWy3/nOt/kn\n",
"yFd4c6bn4YsCPrktL2/AhwIrudYkvp8mHfAp9zWKQk6dOpUe7jErv9NoGvn+9+9NbTVDSN4qKso/\n",
"+2eFa6lIans16FtVMpjN1WSxknk878J5/XOF/+W/nFU+1SwqzCi8cMAnb6/panTO3qvVWoQGfK5f\n",
"P1nuzdOX5Yxz3vzhrV8W7a2WFuZPVZnbFHRhh++TD3yA9zxXIvM0L0IDPnPTyzSN/NVf3Zce7tFQ\n",
"bxZFIadP30eD+yBWMu/0L/7FL5RcOrPsVqKAD+eaSaGAD79XUlX19On7OIWzOpRMigo1BaNw+QRj\n",
"Scm5u6Hxq0FDcHkasmGiai1Cb4MPfODO97//Hs6SF45zzu0b6LrOn3U1tynS+zX9yq/kL8bOXb4j\n",
"dcAnF/4txdvO1atXf/jD/3PuzmXw1x//+PW/+7tbm9tCGlwRc3fVp49oHJNLl/KXzOT+ZIHzqesT\n",
"Lhn6LFay6CHgr73GdWxArg7qzROVeYTL1WCKLbmX6rZIUTYB82VNFtG0WFF4hfmX4xE+hWFdAqcw\n",
"f8nQRYBbpagpaOwrfTvJeyx7EX3I6loDbty4sb3d5+wgvPHGGydO8C7P+8lPfpL+Z9a/0IvGMTl6\n",
"9Dvlpd1MmgZ5gRdzkXBulRcoObu3j5AaWUrO5s0VPnPmMmfAp0iH3KXIQk0htA6mEvOVCHPezFVZ\n",
"JLM3rYD5Xn99kcNzbv6zTJ9qGxncOizxmVu7dPtLfVSL4zg7Ozsbh1mTXRwIIYqibG5uwk7xc9nc\n",
"PH3vvaf5iiVHj76dTh3PPVdo7tR6+nSXSlYq5vrrBUrmDBuIrublF37f+8p2vivXoWRXXqGmYBQO\n",
"AjE1qhUuH3MsUHKJReiNTa/IYz7qPH/+53ltRw4rXDSbXe0zwgB70pXULvtSmJsJWiFirt9xnCRJ\n",
"JpPJ7DDrM9979erVN9/knbc5cuT12ewfeCQ1jbz88uvk5qRW0aOY3fW3iHQJyw9mi+5eGUJJogEf\n",
"Kjy3r5kb8OEXLleDX7juRuYch1VikeyNzWM++qvKAz5pYf6RWFW2psuhKU0GfMTy+sMwDIIgO32/\n",
"Pmc03rhxI302bznHj1958MFrhJRtb0l54403yhcBQI8JXrJ1BwEYit7sDauRi1DwJC08t6tbX+2W\n",
"DPjQ7diyr6LFQnCLqVEET+3SAR/OYsOQ3Hnndwl5kFOeU2Ea8OGf5uUsGXy6tAEfMddftH2bUEpZ\n",
"q4GAD6fwJz8psNN6OjQE3QHmnkk3PM+Qkw6ulx/MFj0VMuyQJbQVGggXnTHCo0OS5B8SskzAR1QN\n",
"ao4l1VihRdIBH34dTFMgusAoXHIOGgjzb8fJ0xQ0IFxeQSbhTd6Aj2ma3UvmETqqe39/n7/XryiJ\n",
"ovB2aq5fv7WaA6aJSrohPFbQ9dUMERoWFp3mBWGeX+TqAFuwdWmat3LhxSzCw9wsuDSMwkVPEyRE\n",
"rGqEx7h+ead5bdvO3au6V3QWrdz4vm8Yhu/7vu9zxu+m02nu9m25CL1ULl36UbkATQROEq7Fh8rN\n",
"46plWHNbn7BQI1PhogMRF9NBVFjoaCMZGllIuNwidOdqHuE0YUiiqHqF4ZWwEltnj/S5fv06f8lL\n",
"IhzwieN4b2+Pmddt4yldg8EgSZKgPLsiw7333vu9732PU1ho9vtnf3ZOdEjTDiIVikJcngSjm3Rb\n",
"eIFFTJyzdPXVTkhnGRpZSLi8duDvqOsXaorPfe5/5xdmFC7qfN88xsfln7utytb0iaacPHmSv+Ql\n",
"ET6gUdO0DuTzwMZzQiYEhAI+QoPZdMCHFB/8C8gwrpdEuL7wgrTTvKTYkaFFioSzXWx4xKDX/9d/\n",
"/QP+SYcKbc2EoeQN+Jimadu2m6F1LwPP8xbbaLq+gM9rr7HbPK1qS692CS8Q8IHe1sJnBiy/k92S\n",
"AR/Y8S03w6cVFlks4COkQ1bYsgiz8DQ9+Hj++ecXLrmcktplzddkwIfM1hJd16fTqWmasAndaDTi\n",
"/OHFixcffPDBOlSy7ZltpzWcBUGOTBDMhsM6rr9GBMFM1xf87Wi0+G+rIghmQXDobmkRzH3O+RP6\n",
"/8swHs8s69Y/R6ODRwweq+zj1gDpStm2fddddzV2abFYfxFxHEuV3+k4TvZlq2laOsLjOI7ruqB2\n",
"r9fTNE2qKpQekNKgHshh1uYU6rooT12rFdhEy/cPdlbnOTeibla44X039/BxXTfIkPb7iqKYpkl9\n",
"vWma2YMnc7l8+TL/ntphGPIv/Hv11VfS0cbybc5y86zWU1iokUF47ha+ojqICgstB5WhkYWEyy3C\n",
"+H0e89HctuUVtqx80/+7f/dN/h5VhbZmLnrtGu+WX8sj3OvPNVXlyf6+78dxXBKOD8PQ87wkSTRN\n",
"s21b6JxrQoimaemf8P98Z2eHf0mX0HKV06dPp7XI3VkF9gJUFClW7kgivMCSLnpa1gI6FF2tySVd\n",
"kgsvYJF5MgfzK5UoTB8rOmej6+TP//zd/K6/PlufOHGCX3hJxHr9YRg6jgNJPnAUu6ZpYRhWtZFD\n",
"GIa9Xm9vb6880d7zPMdxbNsejUaKohiGIXohy7LSczWe55k8x30Scvz4cXpUy1yEThE5ceLQQr7c\n",
"uwu6P7q+snNHJRQWPaoFhHmKLzqNdvlTa4R6KrmnJRfNHbbXIuWAm67q0CHoqdLLKgr5wQ8Esirr\n",
"s7W8R7V4njccDk3TVBQFXgCmaZqmWdXOnYqi2LY9Ho9L3qtJkgwGgyAIoOdu27au60Jz7uRmwAcO\n",
"Ge71erquc5qzvoDPXXe9VNOQs9vCCwR8CJ/rL9Ih995sMuADveDcRKP2WqQcONG3EoXTm9oCzEHq\n",
"C5eci5Ctmwz4iGX4KIoCH4IgsFOT05qmTafTCmefgyDQCxIphsOhfXiyfzKZaJq2wFWm02kQBNmN\n",
"SEu4cOHC2bNn+cvnbxYeSZodIaRzt4VFGxmEeYqvr3ZCD0tuyUV5MvJbhNGcx3yQzhQElSkMeT5p\n",
"Nba23qyk5Cz8trZte3t7m7/kJRFz/aqqwgfG9du2HVSaG1Xi+iHOU6RY3Vy8eHFjY+PYsWObm5sb\n",
"Gxu33367rutbW1tnzpzRdf3nfu7nLMuazWaWZT3yyCPpD88999wDDzyQ/jCbzR544IHnnnsu/eGR\n",
"Rx6BEuiHdFHvfOcnNK2aoirUCotqvqiHH/76Aw/8Z9m0Sn9gioIPzz333Gg0O3Xq/6JlMkU98sgj\n",
"2aLuvvtDljV78skXmKIY9XiKghJ+5Vf+vwceeMC2bxVlWQsWla3gXK22trZ0XT9z5szW1tZ99913\n",
"9OjRjY0NOPT7yJEjs6YQc/2maY7H49lsFgSBaZr0+yZdv2ma2WsVCVfO+9///vvvv59TeDweQ3Nx\n",
"Cs+VoQnpQ5Hc/m4LizYyv3B9tePXoajkol6//BZhFqZwWoSQ2XRamcK2PRuNZukO5O/93v9dSclZ\n",
"+G1t2/btt9/OX/KSiMX6YVKXEKLrehzHdI1yFEWNJcULLYKvHHg5cwqLznfxqyHDbJ4kwnVMKorq\n",
"ICrcbVvPbeR0SfwWUZTKFIbl0OnLvvvdvEfDl5ecRdppXrFe/3Q6pS+x0WikadpwOLQsy0ovkquC\n",
"kl6/rusr7PXXt5qXh8lk9UtJERlYYE1sq6l82wFFmYkMvZqg4dW8Yr1+SOyBz6ZpDofDOI7hBVDD\n",
"WykfoTzZykmSpKY9fHgk6TovGbZqkUR4sU2bq9VBVHidN21eTLjy255ZMimJrfmzB5dnqY0chE7E\n",
"rpAoila1a7RowIe/ZE5hqLcM43pJhOtoZFEdRIUlUaNFFgGpChVmVotKYmt5Az6NURLwGY/HzJ9G\n",
"o1HlEaciVhvwQRBg3QI+61BZqQM+MgDjDDrmghVeQkurl+Hq1atvvvkmp3Acx/xbXAhthiG0TqTb\n",
"wqKNzC9cX+26bes6LAL7b8lQO1FhIVvv7+/zCy/JUgGfJEmiKGL2w1mGwWAAzZokSRzHdIcG5iyt\n",
"0WhkGAacER+GoWVZjcWdbty4IXRUC3/J3T6vtT7hNjZyJUe15D5zaBHZhIUq2ORRLRuz2YxfGlyz\n",
"qqowwbu3t6dpWhzHw+Gw+dNaoiiC7duqevHw8OEPf/hb3/oW/xmNCFIHsJXAyvccRirEcZxnnnnm\n",
"Rz+ac0Z3VYgFfFRVVVUVdj8eDAawN/JoNFrJps2wiVCTfp9gwEc+4bUN+OTONaJFZBPuSMDH933X\n",
"dcHb0g07Ic8HIj+16CgTGPCRTbiNjVyJGrmuHy0im3BHAj47OzvT6RQ+G4ZBQ/CO48BJh9UrKBkY\n",
"8EFkwHGIrpM1eODWCKkDPhSI+FerSivY398X6vXzv/M73/2pr48p1Mj8wpL0BGVoZCHhNlpEEls3\n",
"2esXc/26rsNBhsxhvGEYrkO0hxAynU5XuJqXIsOiTUmE13M1b1G/Cy0im7CQra9fv84vvCRiAZ8o\n",
"igzDsCzL9/3xeAxBf8/z4jh21yPbAAM+iAxAv3MtB96dReqAj6Zp4PGDIAC/7zgOnKNbj3rSgQEf\n",
"2YTbGF5Y3taqKvU0b+ssIomt5Q34EEJUVbVtm0Z7aH5n1YpJCgZ8ZBNuY3ih27Zuo0UksbW8AR8E\n",
"Az4IgtSB1AEfBEEQpAMs5fqTJAnDcLXHZjXM5cuX+ffUDsOQf+Gf0BJBBxbyo7B4I/ML11e7btu6\n",
"jRaRxNbXrl3jF14WoX0+XdfVdR12SJ5MJoqi6Lquqmq1B/PKzIULF86ePcspPJ1Op9MpvzC/GpPJ\n",
"BIUB0UbmF66vdt22dRstIoOtbdve3t7mL3lJxGL9vu+HYQh7OfT7fU3TLMuKoqjX600mk/reT/KA\n",
"sX4EQepA6li/7/u2bdM9fGCXfLqHTy0KSgYGfGQTbmN4odu2bqNFJLG1vAEfRVHo5/RRWbZtr0nM\n",
"BwM+sgm3MbzQbVu30SIy2LrhgM+CR7Ws7R4+x48fX+3ZvIAMR7BKItzGRpZEDbRIA8LSns2Le/iI\n",
"kSQJLumSSriNC4i6bes2WkQSW/MHk5dHrNdv2zacjAh7+MCXnuc1f2TKqtjc3MRev1TCbWxkSdRA\n",
"izQgLG2vX3g1bxzHvu+bpgn1dxwHzshdk70cMMMHQZA6kDrDh6z9Hj4Y8JFNuI3hhW7buo0WkcTW\n",
"8gZ8EAz4yCbcxkaWRA20SAPC3Qn4rDkY8EEQpA5kD/isOVevXn3zzTc5heM45t/aW2gTcKF1It0W\n",
"Fm1kfuH6atdtW7fRIpLYen9/n194Sapx/ULBr1Zz48YNPKpFKuE2HgzSbVu30SKS2LrJo1qqCfgY\n",
"hhElNpo9AAAV10lEQVQEwfLlyA8GfBAEqQMM+EgNBnxkE25jeKHbtm6jRSSxdZMBH8zwEUM04MNf\n",
"creDAPUJt7GRJVEDLdKAcIsDPrBNnWVZqqrCAq6sTBRF0+m0FgUlAwM+CILUQcMBn/m9fvD18O6K\n",
"okjX9ex2PUK7mLaa/f190V4/Z2JvkiT8KcDMHkrrLCzayPzC9dWu27Zuo0UksXWTvf75sf4gCIIg\n",
"oO5e0zQ9Q0s38BFaSQhMp1NczSuVcBvXjnbb1m20iCS2vn79Or/wkohl+PR6PcuydF1nvm9dhk8c\n",
"x47jwKs7iqLRaMT59sKAD4IgdSB1hg+czVuTKk0yGAyGw6Hruq7rDofDfr/P+UPRgA/m9dct3MYs\n",
"8m7buo0WkcTWcgV80hRFuNrV5SeExHFMu/lCO3JgwEc24TaGF7pt6zZaRBJbyxvw6Qz9fh8OlyeE\n",
"RFHked5wOOT5IQZ8EASpA+kyfHgQmvKWAdd1+/0+6Jwkieu6q9YIQRCkOapZzcsfK28Gx3GMDOkM\n",
"VN/3FUWB9CQisjzv8uXL/Htqh2HIX7LQEkGhbNpuC4s2Mr9wfbXrtq3baBFJbH3t2jV+4WUROsS9\n",
"ZI638gPja8U0zfQ/dV3n/OGFCxfOnj3LKTydTqfTKb8wp+RsNptMJigMiDYyv3B9teu2rdtoERls\n",
"bdv29vY2f8lLItzrD4Ig/fvpdKrrOj2ntyp83x8MBiUCYRj2ej3oywvNoQNMeIp/XcLx48eFjmrh\n",
"L7nzZ1bUdzCIUCPzC0tyfIcMjSwk3EaLSGLrJo9qEc7wYWqiKMpwOKxqNS849L29Pd/3SwZKnuc5\n",
"jmPbNuTjG4YheqEoiugLQ+jNgQEf2YTbGF7otq3baBFJbC1vwKcI0zTH4/Hy5YzHYygnCIKiIMx0\n",
"OlVVNT2Msm17OByKXkjXddu2bduGUQvnDzHgI5twG8ML3bZ1Gy0ig60bDvhUk9zpOA6dMq2EMAwH\n",
"g0HucgHP8+I4TufkxHHc6/UWCDqFYagoSnZLohIwuRNBkDqQejVvEVEUNbaNTxzHjLNWVXWBcD8h\n",
"JHcrunKSJHn11Ve3trbuvvvu48eP33///YZh3H///W9/+9sNw3j00Uc/85nPEEI+85nPPPHEE1EU\n",
"ffKTn3ziiScIIS+++OK5c+fSHwgh586de/HFF+HDF77wBULIE088ASXQD1BU+sOLL764u7tbUhR8\n",
"oCWcO3eupChGK8/zSopitPI8r6QoRqvf+q3fqqOCURQxzV5SQVhAxFlB+CFnBXd3d8vbKv3hC1/4\n",
"QnlbpYvyPK+8rdJFwWqj1VYQbnumKPjAaHXu3LlPfvKTURSly2QqSPVk7opsUYxW586dKymK0Yq5\n",
"7ZmiGK3gtuevIFMUOI23v/3t999//zvf+c7bb7/9+PHjd9999+///u+//vrrpDGExgjD4dDOYJom\n",
"kzCzPCUBH9M0manmmUiKzpI89thjZ86c4RSeTCb8Y0OhUWS2BdZWWLSR+YXrq123bd1Gi8hga9u2\n",
"77zzTv6Sl0Qs4GMYRnamV9M00zSrfSGVBHwMw4AAPfNlM5tJYMAHQZA6kDrgo6qqaZruYSr3+zKT\n",
"JAnu4SOVcBt3jOm2rdtoEUlszZ89uDxiGzlwbnRTK6LR+WrZ3NwUyuvnL7nbud71CbexkSVRAy3S\n",
"gLC0ef2Sbt9WEvBxHEdRFNu201/u7Ow0c0IkBnwQBKkDqQM+MmCaJrNKwvf9xoJOV69effPNNzmF\n",
"4zjm39pbaBNwoXUi3RYWbWR+4fpq121bt9Eikth6f3+fX3hJBFx/kiRhGIqeaFg5EPCh4bYkSQaD\n",
"gWVZzVz9xo0beFSLVMJtPBik27Zuo0UksXWTR7XwBnw8z/M8T9f1OI6TJOE/0VCIwWAAb9QkSdL5\n",
"+0zkJ0kSwzA0TVMUJQxDy7Iac/0Y8EEQpA4aDvhw5fVPJpP03gmu69q2XVu+KS/j8TgIAqE18cuD\n",
"ef2yCbcxi7zbtm6jRWSwdcN5/VwZPp7n2bZNu/m2be/u7q78eJOVpPqIBnz4S+52EKA+4TY2siRq\n",
"oEUaEJY24MPV688uoNV1Pf2NDIOAZrh48eKDDz64ai0QBOkatm3fddddjV2Oa5p37otr5XO/jbG/\n",
"v4/TvFIJt3FSsdu2bqNFJLF1k73+9iV3rpbpdIqreaUSbuPa0W7buo0WkcTW169f5xdeEq4Mn+zW\n",
"Pb7v67pOv/F9fzKZ1KWjTGCGD4IgddCOJV2maTa2S7NUYMBHNuE2hhe6bes2WkQSW0sX8FEUJbtr\n",
"WxqhTS1aDQZ8ZBNuY3ih27Zuo0UksbV0AR+EggEfBEHqoB0BHwRBEKS9oOsX4/Lly/x7aodhyL/T\n",
"k9CeUI7joDAg2sj8wvXVrtu2bqNFJLH1tWvX+IWXpbEVBN3gwoULZ8+e5RSeTqf8+0wI7UghtBNA\n",
"t4VFG5lfuL7addvWbbSIDLa2bXt7e5u/5CXBWL8YGOtHEKQOMNYvNRjwkU24jeGFbtu6jRaRxNYY\n",
"8JEXDPjIJtzG8EK3bd1Gi8hgawz4SA0GfBAEqQMM+EhNkiS4pEsq4TYuIOq2rdtoEUlszR9MXh6u\n",
"/foRyubm5pEjvO9Lob0uhISFlk93W7iNjSyJGmiRBoSFKnj06FF+4SXBgI8YGPBBEKQOMOAjNRjw\n",
"kU24jeGFbtu6jRaRxNYY8JEXDPjIJtzGRpZEDbRIA8IY8OkIGPBBEKQOMOAjNVevXn3zzTc5heM4\n",
"5t/aW2gTcKF1It0WFm1kfuH6atdtW7fRIpLYen9/n194STDgI8aNGzeEjmrhL7nbx3fUJ9zGRpZE\n",
"DbRIA8LSHtWCAR8xMOCDIEgdYMBHajDgI5twG8ML3bZ1Gy0iia0x4CMvGPCRTbiNjSyJGmiRBoQx\n",
"4NMRMOCDIEgdYMBHavb394V6/fzv/M53f+rrYwo1Mr+wJD1BGRpZSLiNFpHE1k32+tH1izGdTnE1\n",
"r1TCbVw72m1bt9Eiktj6+vXr/MJLstYBH7CKpmn8P8GAD4IgdYABn2qIoshxHMMwcqfjkyTp9Xq+\n",
"7/u+3+v1+IvFgI9swm0ML3Tb1m20iCS2xoBPBYRhaFmWbdu5fx0MBpZlua7ruq5lWfwnrmHARzbh\n",
"NoYXum3rNlpEEls3GfDp+AGNQRAEQZD9Xtf1kn+WcP78+a2trQo0kxX+pmgjtm3n3g+dAc3XXmzb\n",
"3tzcbOxyne31l8PE94V210MQBGk76+j6s0Mw/l1YkyThj8eFYci/8E9oiSB/hEpU+Lvf/a4MavAL\n",
"CzXyq6+++vLLL1eug6hwfbaWwXyitz2/8IsvvsgpSeS4OYmgrZuM9bd1Na/jOFkPrmma67q1XvfU\n",
"qVP8+/UL5Q4JCVuWVZPwAw88IIMa/MJC7Xb69OmHHnqoch1EheuztQzmq++2f/jhh/mFZbg5iWAF\n",
"+X3L8rTV9S/j4jVN830//Q3/lP2xY8c2NjY4hZMk4Q8lQSaAkDynsFCOwVve8hZ+4ZoSOYQUJiJN\n",
"ceLEiTvuuKOOkkWTdvg9giTm4y+WCLYb/z2/tbUlpIMMwkK25vcty7OygI/v+4PBoEQgDMNer2cY\n",
"huM4onfeXJgRg9AzwD8oe/LJJ5955hl+Yf5kgMcff5xf+IMf/CCnJBGMGPCXHEWRkPDjjz/OKfzM\n",
"M888+eSTnMJCAZ/6Glmo2yiJ+WqyiNAzIhTwEWq3+oSFbN3l5E5w6Ht7e77vl0TBPM9zHMe27dFo\n",
"pCiKYRjVqqFpGr16GIb8r2WhgI9QeOH06dOckkRw5CsUBJBEmL+CDz30EH/TCVmkvka+8847ayoZ\n",
"LUKRpN2EbN3lgI+iKLZtg+ct6vUnSTIYDMbjMYwEbdtOksTzPKH3J7wt0lGUIAjoX23b7vf74P3j\n",
"OB4Oh5zFCgV8hMILJ06c4JQkgiNfoSCAJML8Fbzjjjv4m07IIvU18rFjAs8dWmQBHYg07SZk6yYD\n",
"Pk27fp7+te/7pmmmI4CWZfV6PSHXn3b0WRRFGY1GC2zkcOXKlf39fc5Z+5dffvkf//EfOUt++eWX\n",
"77rrLk7hF154gV/40qVL/GkGNQm//PLLQsIvvPACp/DXvva1v/mbv6nDIvU18ve///2VW0RIuPMW\n",
"qU+Y39ZCweQKaGwFAUMQBEXLTyDOw3ypqmr9Ss3n05/+dHO2QRBknThx4kRjrkzGDJ84jnVdZ77k\n",
"T72vlc9+9rOf/exnV60FgiDIUsi4pKvyfB4EQRAkjYyuH0EQBKkVGV2/0LwrgiAIIoqMrp/kbbMj\n",
"tPcpgiAIUoKMrt80TSYdCtI9V6UPgiBIx5DR9UPAh56HACu8hJL6EQRBkBKaPpt3MBhAjz5JkvTG\n",
"RswKrCRJDMPQNE1RFDhvC10/giBIVUh9LHsURUmSwAtg1bogCIJ0B6ldP4IgCFIHMsb6EQRBkFpB\n",
"148gCLJ2oOtHEARZO9D1IwiCrB0y7twpLWEYep4HSUe2bbco76hazX3fj+PYtu2q1FuSqmoHJwJB\n",
"8rGu65ZlSWLiOiqoqqpt2zJsiFv5YxXHsed5qqpKkhFeVQUdx2G+0XU9u8kxL41tD912hsOhpmnj\n",
"8Xg6nbquq2naqjXipSrNgyAwTVPTNNM0i85aaJ6qajedTnVdt217MplMJhM4S246nVar7QJUVcHJ\n",
"ZKJp2nA4nEwms9lsNBpBsZUqK0wdj5VpmrZtS3KLVlhBQkhwGDDlgqUt/Mu1YjqdqqqadgS2bQ+H\n",
"wxWqxEmFmo/HY/AUJcfsNEyFtbMsizkgyHVd27aXVXE56jBf+hvTNJdVcQnqeKyCILAsS5JbtNoK\n",
"VttTR9fPxXA4ZLwA9KFWpQ8/dWguyXM1q7R2rutmv1x5Neu+8VZ7+F0dtYOxmiS3aLUVrNb14zQv\n",
"F+k9JwBVVVtxpEx7Neehwtplpy7iOF55rL9W84VhuHikuAoqr53jOMyx3qulJvOFYbh8ITjNy4XM\n",
"Z0aW017Neai1dr1ez3XdSopamDoqCPujhGEYRdFoNFqmqCWptnZQqfF4vLRelVG5+QzDSJJEUZQk\n",
"SVRVHQ6HC7/n0PVz0d5ucns156G+2vX7fcuyVtspJvVUMIqiKIrCMFx5llq1tXMcZ+WvaoZqK+i6\n",
"rmma9M3heV6/31/45Y0BHwRh6ff7mqZJkhpYOZZlQZ5PFEXZfMGWAjGQlb+qa4VJxrUsC/Y/Xqw0\n",
"dP1ctPfMyPZqzkPltUuSZG9vTx6/X6v5hsNhFEUL+47lqbB2nufpuh7eBIJaKz/ar+6nT9M0dP21\n",
"094zI9urOQ8V1g5OiZDtcIhazbeM76iEqmqn63ocx9T1x3EMof8qdFwKeZ++CrOFOsx4PGZyxUaj\n",
"kWVZq9KHHyHNgyBwXXfuOiZJMudm4nYpqeB0OoUVT+kvl1kyUwl1mC+NrusrXNVVofmykjLconWb\n",
"j1k0IAS6fl50Xad+AdzEyldCcsKpOU2NmLvMR5LnCuC3S0kFYSkvs6RrNpspilK5wqJUZT7TNJkf\n",
"wrRh5QoLUYn5sshzi1Zlvuz9aVnWMksOMcOHl9FoZBhGFEX0zMi2hNE5NafJHkVZH8zhmoZhwPfM\n",
"4ZoNw2+XkgpCyNvzPHoiNCBDflRV5rNt23EcOhcKSf3D4bA+zXmoxHxpYO4abtF+v9+WCs6t3Wg0\n",
"chxnMBiA+XzfN01zmYwmPKVLjPaeGcmjeRzHuZnI8sNpl25XkKd2IEMIkeoeRvMRvtrRuevlzYeu\n",
"H0EQZO3ADB8EQZC1A10/giDI2oGuH0EQZO1A148gCLJ2oOtHEARZO9D1IwiCrB3o+hEEQdYOdP0I\n",
"giBrB7p+BEGQtQNdP4IgyNqBrh9BEGTtQNePIAiydqDrRxAEWTvQ9SMIgqwd6PoRBEHWDnT9CIIg\n",
"awe6fgRZC6IogvM1a4I52xKRHDybF6mRXq9XdLytpmnLnCyKiNLv99MNHobhYDAghCiKMhqNCCG+\n",
"74P7VlV1gSNtfd8nhFiWVZnGSJ2g60dqxLIs8AimaTJ/Ar+DNIPneYqipM991TRNVVWSMo2mabZt\n",
"G4YxHo8XuITrur1eD11/W0DXj9SIrusQZMgeNo2uv0kGgwEzxlIUBc71pqZRVRVeBpqmLXAJeJd4\n",
"nofevxVgrB9ZDWn/MhgMDMMwDCOKIkKI7/vwTxgxpAnDsNfr7e7u7uzs9Hq93OA1yOzs7Ozu7vb7\n",
"/TiOPc8zDKPf74NAv983DCMdm4ZvDMMQvRyU7HleFEW9Xm9jY2Nvb89xnKxWSZI4jmMYBpXJDb7z\n",
"VFCUMAyTJMkOvDiBOjLk1tE0TYz4t4YZgtSJbdu2bdPP4/E4KzMej4Mg0DRtNBpZlmXb9mQymUwm\n",
"pmlOJhMqNhwOdV2nJYzHY9M0aeH0EmmZ0WikaZppmpZlBUEAXwZBAFdhFGAeB57LTSYTy7J0Xbcs\n",
"C1SdTqdM4fClpmnD4XA6ncI/h8OhoiiMGM8VF8C2bcuycr/PFp71CfDzIAWEhrIFTiYTQgjUEZEc\n",
"dP1IvYAvBi+j6zr1v1l0XVcUZTgc5v51Mplompb7q7RP13U9+8Osk53r9XguR4tiJKfTqaIo5b+a\n",
"zWbD4TCtA/8VRYH2z36fNg0l6/pd13VdN/2r3BcJQAhZUlukGTDWj9SOqqoQUC7K9qG4rlsUKfY8\n",
"DxwTg23bvu9D+WEYZn+uquoC0Weey1GYfyqKkq5pHMdJkmRnO0zTjON4sSsKEUVRUbSHmoaSnYNJ\n",
"a+V5XpIkJfk/uq5HUbSMtkgzoOtHaofmlsRxDFOLRcA0Yy5RFBXNDFNHU6HT4bkcJ3Ec5/5EUZT0\n",
"hEeFV2QoaVUm7accyP6EyFgJc1/wiAzgNC/SHJZlLZY9QgiBmYDcoSt1RpqmpfvRlAWcEc/l+MnV\n",
"qtYrplEUhUeBcqIoAr9f/vKOomhhEyNNgq4faQe6rs/NHrEsCyIS6S/BZ80tn/kVz+U4gRhI7usn\n",
"7ZErvCKDpmlL9sQhfwmmpuEb3/ezZSZJkiQJuv5WgK4faQe6rquqShM0KZ7n0TgJhPUhKzRJEkjr\n",
"dBwnG0NnxgdxHPd6PdHL8WPbdnZh82AwSJdf7RXT0NUViwFpqaPRKB04gnxWRtL3fbpSDJEcjPUj\n",
"NWIYBnhYcBO5mzfEcQz+Looix3FovxLyT9KSw+HQcZy9vT06aQzhhXSZkGo5GAygBw1RlKzrNE0z\n",
"DEPDMOAdkCSJ67p7e3uGYQyHQ3BePJfr9/vgVeM4hu0QkiSBt0i6KJhnhqJgEjgMQ13X4SdCFVwA\n",
"Ogeebk+qeRRFo9FIURTP82AhhWEYlmXRmeHBYBDHMZPIn/X7cImFVw8gDbMxm81WrQOCCAAOET5z\n",
"TlGC28o6UIjDMNOty1+uBNr7Limq2isC4NaXnDMoJ47jvb09SKWt7ypIVaDrR7pPketfK3Z3d2HJ\n",
"WE3l9/t9TdNwF4e2gLF+BFkLmOBS5Sy2fgJZFdjrR7oMsy1PrREPBGkR6PoRBEHWDgz4IAiCrB3o\n",
"+hEEQdYOdP0IgiBrx/8PdFJ/eteDWYoAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"% Ce code n'est pas commenté, car essentiellement identique\n",
"% à ceux présentés en question 1.1. et 1.2.\n",
"%% représentation en temps\n",
"figure\n",
"plot(ech,bruit)\n",
"ylim([-0.6 0.7])\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"%% représentation en fréquences\n",
"figure\n",
"Analyse_Frequence_Puissance(bruit,ech);\n",
"ylim([10^(-10) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Le vecteur `bruit` est généré à l'aide de la fonction `randn`, qui est un générateur pseudo-aléatoires d'échantillons indépendants Gaussiens. Le spectre de puissance représente l'amplitude de la contribution de chaque fréquence au signal. On peut également décomposer une couleur en fréquences. Quand toutes les fréquences sont présentes, et en proportion similaire, on obtient du blanc. Le bruit Gaussien a un spectre de puissance plat (hormis de petites variations aléatoires), ce qui lui vaut son surnom de bruit blanc."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 4. Bruit respiratoire.\n",
"Répétez les les questions 1.1 et 1.2 avec un bruit dit respiratoire, généré ci dessous. "
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%matlab\n",
"\n",
"%% définition du signal de respiration\n",
"% fréquence de la respiration\n",
"freq_resp = 0.3; \n",
"% un modéle simple (cosinus) des fluctuations liées à la respiration\n",
"resp = cos(2*pi*freq_resp*ech/freq); \n",
"% fréquence de modulation lente de l'amplitude respiratoire\n",
"freq_mod = 0.01; \n",
"% modulation de l'amplitude du signal lié à la respiration\n",
"resp = resp.*(ones(size(resp))-0.1*cos(2*pi*freq_mod*ech/freq)); \n",
"% on force une moyenne nulle, et une amplitude max de 0.1\n",
"resp = 0.1*(resp-mean(resp)); "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z2xr+Q4fuf1PDPrveAAs70GFjjAt1CvHWzWq4cLD4Yh\n",
"HQxcrIfNB1CF50wC7h8o5ZuUMPMPlBYOFwaKgfcSJ6VpBw4Mbz9hOtjAcM+j1zCwDQxm3gX0aNWS\n",
"yCIpSqKk7yfqVtWjWBT15Y8//vjj3fPzswcAAGBP/MHSFQAAADA3kH4AANgdkH4AANgdkH4AANgd\n",
"kH4AANgdkH4AANgdkH4AANgdkH4AANgdkH4AANgdkH4AANgdkH4AANgdkH4AANgdkH4AANgdkH4A\n",
"ANgdkH4AANgdkH4AANgdkH4AANgdHy9dActQSouiYIwFQZCmKSHErBzGWFEUlFLP88IwTJLEuCgA\n",
"AHCNTVn9RVFkWZam6fl8JoREUWRWDmPs4eGBMXY6nU6nE2MsiiLGmN3aAgDAUtxt5mxextj9/f31\n",
"em3M8yzLfN9PkkS3qMPhEIZhHMfNlTzPGWPH49FadQEAYDm2Y/WXZRnHcdstkyRJURQGRfm+39Z9\n",
"z/PSNK2qamwVAQDADbYj/XVdB0HQvuL7vpmXJk3TfuHw9QMANsN2lnnrug7DsHPR930rhT88PGh5\n",
"e+I4/uqrrwY/+t73vodRBIDd8i//8i+ij37yk5/8/Oc/n6ca25H+6ZZhD4dDkiT9cUXCL37xi4kq\n",
"AwDYKlVVzSb923H4TMThcAiCwGCt+HK5pGl6uVyenSEMw6Wr8HvQOBLQOBK22jhpmn7yySdTiNgg\n",
"25H+jqN/PDxkyEz3AQDAZbYj/Z7n9YNwjMNyeCx/kiTQfQDA9tiO9MdxzDffNvBwz8EvU0p5qP7g\n",
"p4O6X9e1xdoCAMCCbEf6ucOnCeRnjOV5PmizV1UVRVGWZYfDof8p38qbpmnnb+/v7yeoNQAALMB2\n",
"Inw8zzufz1EUVVVFCKGUJkkyuADQxFYOBllWVVXXdVEUne1gSOQAANgMm5J+Qsj1eq2qijEmyd3m\n",
"+/7j4+PgPgDP88IwfHx8nLimAACwJJuSfo5KqI/v+7Z2ewEAwOrYjq/fQcIwdGqAES16LwIaRwIa\n",
"RwIaxwrbydzpFHd3d5fLRWsDMABgz2RZ9tlnn717926e28HqBwCA3QHpBwCA3QHpBwCA3QHpBwCA\n",
"3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHp\n",
"BwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3QHpBwCA3fHx0hVQhVJaFAVjLAiCNE0J\n",
"IWNKK8uyrus0TUVfyLKscyUMQxyzDgDYBuuQ/qIoiqI4nU6+7xdFEUXR9Xo1KIePH3Vd+77PGJNI\n",
"f57nl8ulfcX3fYM7AgCAg6xA+hljeZ5fr1du6adpyhgriiJJEt2iCCFpmgZBQCnN81z+Zdj4AICt\n",
"sgJff1mWcRy3PTxJkhRFYVBUEARBENirGgAArJIVSH9d1x295u6aee5OKZ3tXgAAMA8rcPjUdd33\n",
"vczgeY+iiDFGCGGM+b5/Op201pbTNH3x4kX/ehAEx+PRXjUBAGsiiqLB62/evHn//v1s1ViB9C9i\n",
"dB+PxziOmwGmKIrD4XA+n9VLyPMcqwUAgA6d+JGGLMs+++yz2aqxAofPIqRp2p5YJEnCGKvresEq\n",
"AQCALVYg/Y4szAZBAOkHAGyDFUi/53lVVd28AgAAQJEVSH8cx5TS9hUe7in6Po/Zt75CUJalI/MP\n",
"AAAYyQqknwtuE8jPd3iJ9nNVVRVFUZZlh8PB+I5RFJVl2b5yOBw6ewsAAGC9rCDCx/O88/kcRVFV\n",
"VYQQSmmSJCIDvFHnQZnO85xPIPiabRNl1VlzP5/PWZY1ITp8koGITADAZrh7fn5eug6qVFXF07fJ\n",
"re+6rge3AujCGOMrCjfv2Ofu7u5yuSC4EwCgCA/ufPfu3Ty3W4fVz1F0tfu+b2XDFyEE2g0A2CQr\n",
"8PUDAACwC6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6Qf\n",
"AAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2B6QfAAB2\n",
"B6QfrJuqWroGAIyGMe+3v30x5x0h/WDdZNnSNQBgNFXl/cM//I8577g16aeUPjw8RFGUZRljbGRp\n",
"ZVnmeW6lYqBDUbhlsGMIAWastOdsSvqLosiyLE3T8/lMCImiyKwcPn7c39+XZUkptVtJwKlrb/TQ\n",
"bBOnxiGwIlbac7Yj/YyxPM8vl0sQBISQNE3DMCyKwqAo/ufX6zVJEuv1BACAxdmO9JdlGccxIaS5\n",
"kiSJmfQHQRAEgb2qbY26XroGrsIYGmc1rNRat8V2pL+u645e+74/3t0P+hiNp7ugqtA4q2GlPnpb\n",
"fLx0BaxR13UYhp2Lvu8vUhnP816/fj14nRCCKQUAu2Vw+fD16xf//u///s0338xWje1Iv2sG/hdf\n",
"fPHVV1/1r/u+D+kHYLcMSv/btz/+7W//8Ntvv52tGtuRftf49NNP+7MQAMDOOR6P/YuUel9++Xe/\n",
"/vUns1VjO75+mNI3seKGRrDrDLi26cEp0DhW2I70e55X9XpE/8qe2WrwyfZ+l2ubHpxik40zfx/e\n",
"jvTHcdxxovFwz8EvU0rzPHdteWAt2BpPrTR/Vdl5bdAXgAG2uk1de//2b8jhYwR3+DSB/HyH1+Ce\n",
"rKqqeKaHw+EwaxVBi7q2M4RY8fNVFXwIwASLPeeP/ujJTkFqbGqZ93w+R1FUVRUhhFKaJMngAkCz\n",
"7au9/6tNnud8AsEYq+u6SQhxuVymqfgNsswbWhnSxinHyHJhtwMw5m1yST6KvIX67ACUepTa6clO\n",
"sdJFxk1JPyHker1WVcUYS9NUpOy+7z8+Pg7uA+CkaZqm6fj6cHPAnZ4BnwYww5bxAdxhOw6fhiAI\n",
"wjAU6T7H9/0ZIi8Zc0tt3Q/OkbeYeoSS/JvTzX4odeuJ22KT3rC6nvCNkPQxR7yLG5R+sF6qSvY2\n",
"qku2fCFh0lwLUpMDOMSkLkdJH3PEPoD0rwAXbIQxaCVLcSp8aOdpXkAHK/3BBd33IP1rwX1fzQxp\n",
"y6yMClreHskdp562OyIQbjJd48itdXXcf3yQ/mlZu8HeR/SLylL4J7Zeg/mlX8KkCzmMbbDn2GLS\n",
"xrHVPZyKphsE0j8hYbiCwV/CoGHLmHbMkkW1VUdusI9HqzK6UyIsGEgwaByt9rfyzlpZspoUSP/e\n",
"kXREi4at+mTZQJcHf8LUg65WPd0XgrUj76tavpqp51uD9ZzfRoT07x3JsfNTd0et8ikdCMmoay8I\n",
"9NRT8uXBj6zMHqxErBowafyiLpNGtsiXXtTvKw/K1Pq+VrckxHv//r9o/MFoIP17YVA6Pf2+Lilf\n",
"hMjM0Z25i6Rfi8E/kQwhEtVw35tnJX7RVpYkbw2OLN3HLeo5YajdaN///u/0/mAckP5tMhiFZiAE\n",
"Via/gy+8LRUQlaOlywZDiC3UBYJS2Vr6dDC2WNaNVYQFW5x3zgmkfwUM9sUs0+6jhGi/HjMbtrby\n",
"8RpMKawMRaL6y30R6logKWe9WxAkNVfvrpKeM1hIVXm+P/BREGi/I7o9Jwic8MJB+ufGYD1Kq09L\n",
"rvu+tjDNTF0L06hVlcY7ZtGxoGWj+f7wreXj2cxmoFx3tLZMSz6a+UfJoxUGL8axnp2hG/Ug+rIj\n",
"iQsh/XMjz1Uw+NGgeSLBVh/VKsH39cYts1vMjO5cfkHU21ku/VYSJWlJ/1pamBANk8Jg9jAzkP5p\n",
"0Q0aGSQItAV05tepqjzBoTheVTmUu9RBRDapbgigrnEwKerly80U0cK7+wvsItypOaR/WnQNVa0X\n",
"eBFzaeq+K5o9rJe6lq2yiNbAB6/bCscSfdlW/Lt6ZeTfHPy9WtY3v4U7guuOJQTpdwutd08kBJRq\n",
"dC9ChDcdfGGmjs8TDZbuvL261LWXJA7VX662VkLgPZeyTrl2Do8jEa6Q/gVwygkomZdo9dGpff2O\n",
"vDB2sbhZuj/Yi4JY5EznozfwYoHpgPQ7BPcMTFf4pKWJhpAZZrjza4fFhHTqjSNfO+33HFEQi2Q8\n",
"EC1NDf4JIdobVrV2ePDXYS2LwCNBIoddo7WxyGDboa1pr+5ORcm7PfhliVt8cGIxWL4kelpUeS0P\n",
"tVZjGuyo6FPXwrV0LQgRdp7BHigaQqYOf+KOsvG3mFRVdeM4RM7Y+Se1kP4FsNIXJX3F1u4ki92x\n",
"8zLwFhicKEjCmfrvDKXCSkoqP3jfSdOsGsRoaTHpfHFqpjbtJ20Z3pc6D1e+uiCqz/e//7uvv/6f\n",
"9qp2A0j/3Ihy6dj6vhyt7ZG6jhqRuvVVlfsQrKBVSVFjmiXq6QsW/7KWu9zWOK3Vnu4Ed3qe5/t2\n",
"pF9rCOHf7NdTEjohamGRA023kX/4w9/o/cE4IP0LIOpDou4l2oWr27emPj9Ad1l4EQbvqzuFEs1a\n",
"CNHzhumOrwbLtoNYGW8kLjUr5evaB1oOKN7y/XoOWvHtj9SvOz4Pg/RPi645o+W+sNW3NhliMen+\n",
"AF1fv2cpA6jICNgkU+/fFr0+YehWDN5EfLx0BVShlBZFwRgLgiBNUzJC9lSKyno5pcIwDPXXSUXu\n",
"bEodijUebEsDdZsOA71zJFNKg6jDBoGX5x+s3/JsRbq7cx23MSVovQ68cXYS9jMp67D6i6LIsixN\n",
"0/P5TAiJomjqovI8Dz/Et6clM7ylVuIibPn61ZHE3mhVRpLwTv0x8kKsBOdIGAzKDAK9oUu3R1lM\n",
"rNRHd3VKq/K8cQb/xJY3bBCt7IGcSesznhVY/YyxPM+v1ys3z9M0ZYwVRZEkyaRFGdj4M8N9Gp1q\n",
"SoJnrCCKHDVLWtnB1v4ySRJ/9Zbh44RTPhY+RRB1zI7tzx+KKILWCqJyBu/L69MZxS3OVyw+qX45\n",
"fMjROlLNqZ7TZwVWf1mWcRy33TJJkhRG59pZLGoMkhmrJK1Cn0EVM9hCpWXYinLLiG5q8GJPapNq\n",
"sRavER/SOg+R7+QY/xO4Oo83YH1fGOs1nUQaxFBJfP3jRyl3BoMVSH9d18GHuuL7PjNqQoOiKKVm\n",
"95IgCUWwsvFV3frmF61EnVv0Yk1tk86MZPOBLQjRdmSpR6YSMtBDJD9KFDcpQjRftEITyeNITiFH\n",
"+qS3CodPXdd934uZ512rqCiKGGOEEMaY7/un00lrbTlN0xcvXrx582lVfd6+/h//8X897y8G/8RA\n",
"f9V9+qK1XIOG5C9S3+0w6ICyAqWyjZ1aKYINGL9wEgTLnK04SBOB2nn0uvNFUXAn34XriNRyxltU\n",
"Bj1H9JpEUdSRhd/97oe/+c3/fv/+777++utx1dRgBdJv0ehWL+p4PMZx3IwKRVEcDofz+ax+L75Q\n",
"nGXe8fiz9nXJcXS6kTZhOFCaQai4LiIh6xclX/HjbgTF2ko2/tg6vWuw/MFGXoQZwlrcsUkbFok0\n",
"6+uEwRHQotfkcrl0ZIFSjzHvb/7mP375y19q19WUFTh8FiFN0/ZsIEkSxli9REyZKNJGKw2L/K8m\n",
"DYGXSL/E0aQ4Rsu/pmsz2PLsi5Jdj+w+ujsBV4T6PnBdzNp8oqNAb2bf+/bbH2kUN44VSH9gxf89\n",
"uqggCMykfzB9zXjMDDRRVFyfSdej5O5vyeF2nScgbwTJp51fZ2VM5xIsCunrL/BYbGFd6R/01Rh4\n",
"/5zaXTyIKGshb3xbj0DxycpTKP7wh7/55pv/bqdCCqxA+j3Pq3r9q39l/qJU6Jstol6udb7KDBi8\n",
"jZKd/YN5H9Vv3SxHW9HovmDZspq59Cty05UxXXZ7USCAgfRPZCKMX9eRw1vAYlxpG7MltD/8w9/Z\n",
"qY0aK5D+OI7ph4rCYzRF36eU5nk+6NbXLarzTYvzj0GsdMQFo8f69W/egZE/bdIXVZdGlSby//HZ\n",
"g2jq02+EbWxt7fwKkYHcbLaYwkXZTEa3FxbcZwXSzwW3ib7n27JE+7mqqoqiKMuyw+FgXFQUReWH\n",
"CzSHw6GzIcBZ7I4fI2XFOA2LO6H9fRpV0v1p6o2pFe84j09DhGL58vFSK+ed1tRK9+dz626iF92d\n",
"oH5vFdLved75fOYxNlmWRVGUJInIAG/UWSTTKkWdz2dK6f39fZZlWZa9fPmSEHI8Hi3+oj5O2W5N\n",
"4E3nHZshRN2T+vq1cCoPV1/dmt1GEymCramSZAhRb2E+Pk13ukuTdUNrNWhm3DmT3VtFcKfneYSQ\n",
"6/VaVRVjTJ67zff9x8fHwfh99aIIIafTiTHGlwFGZosT0d92bzEaWhRTrFXCIDP03YleV6cGV++7\n",
"J+7p56iYWUEsetvUCzE4B837bjXIHWeLepDo/KxD+jmKrnbf929u+FIpihAyXRofbi6JvJnjbzt4\n",
"zJ6EiQxP3WKtVEMSHWTWsP1woAXFZXxErIP4vleWHzwdg+yBdmk/ZePwWfmG5z6ffPIrz/s/JnfS\n",
"Zx0On/3QjwiyZatqxUHakmxdG8fWQoWVIbvxbnVqZWsIsYtinKWkOzXVU6mn6MtNoJrWzozpIoXM\n",
"iu1755poBSvzctFA8skn/89C6WpA+l2n6SWijUJTuLNvuhQUI1aN0X1jBxVNEmyqiBXDs/ktk072\n",
"Fc3Sm4n2FBdaJLFbWg4iu23SH/+a8q2YUBNNRBZxRUL6J2fwRdKNTpNsFGqr5M2s4upJuIx3S6kj\n",
"aQSt8kXxIUtlsR9ZDTnjd1HZerLuuNQbRLOHiZaXbe2jNjgHezyQ/mkR7UQ32DvTRrLhRd6H+i92\n",
"E802fzCMYiPYCiu6OS6q7/6Vlz+REceLteUb6QTDGNe575+0O9TZOrF9sFjFbi9pcHkfVncQzb/8\n",
"C+mfGytdue1utiIEVvI295HsaNdCNJ5p1Vk0Lt58+Ts+EMkq62BErDGD7mZbdAxh4wWM/kKIXQO2\n",
"86tt7TjhxYq6fWc+enN37qQ52CcC0j83ct+9LrZC4DtMvbZsS8XmWRbu3MX4ploL+Fq7nLTuuwh2\n",
"EzBIHDjtGxk7ZPp/JS/HQd/XTSD9izFFoLStYWCNXdl9Og/LuJHb6nZzeBhpHDReLJF2//a3quVo\n",
"BQ7If5fk3bHVyJsH0r8pbMU1ilh8c6wtQ9jWD1nEoO7sBNRd3WmutxtB1CCNF0tUzo9+pOQNk5Qw\n",
"+OmqJdu1zYODQPp3wZi+2H6Zpx5abmJFEcZngefYSlk8ErPpY8fNbfxkO+W4s1vVAFsRO6sYt+xI\n",
"/yJnmOwEKyJlvIjniLq5yaRHuwB1LKaWWoVqW8GO9A+myQRmWNktZSurre6bYCtI1OXMndZZtaXs\n",
"CC7H0jQ41Rv1pD+Korsh6HTn+60flRlRe6Y5KAS6O8iXkmxbQaK21BCqCtzBqd6obfVfLpfnFk9P\n",
"T2EYXq/XKSq3DRRVWP413eN2JYi2OzplkujSHl/H/JBVN4LivjMr37F1r803uMrfLtIIetLv+34n\n",
"fTHPb5xlmdVaAQ20TAmX9wEYL7J1QuDNjsfzeo2j+6Ns7TYyRqUn3FzOVVwDv3kvW+VMwZin3AmL\n",
"MnM0dZbQFmkEPek/nU79dMd8PJj0hFvQwdhM6O+9tIKtg90HyzFYxBss5+aPlcQXqsQvNn+umHVD\n",
"hPUDIFdtWXcwbpzOvJCPf5J9c4ObJ9SP2m4+HfTTurCYbGeZ1/f9wbNwQQeLYemTRqHZyptvq/xB\n",
"20q3MY0r03nhjceh9tq7JKFQ+/sNulOi5vsjY7Saeo7MV2yWEbr//cHGEf1tu9EMVr/6N5Ugyh3r\n",
"LHakv6qqVZxbuzjGQZZ9bBnag0wdKmelfFuNOduhV+3WMDiKRDQlEjVyI/0iVHYFN/WU1FZrSiQZ\n",
"8NrjYnO7kUc+zGNfT3fw5HTondJVFEU/hL+ua0KI4hFaYFKmHn+3OrVbtd1irG66hu0gYfjBbMC4\n",
"JTsVWNcTWVdtOXpWf1mWfcdOHMfn89lelcDvsWVK2NrzssYuDgDoo2f1+74fx/F0J9aCDhZT4GJW\n",
"BgBo0JP+0+k0UT02jOKWrjge/qgxtNfibJGksx8/aXBtl+9aHgoAHZC+TQil9OHhIYqiLMvGxC8p\n",
"rrPdtMpFumlLfURDlFZ8iGjfgEGcyeD3dQcP0Y+ydcCklZBmW4d97xZb/sxJDQLXot8h/cMURZFl\n",
"WZqm5/OZEBJFkfVbiFRSt//ZOoF2cIiSbMzROg5XdxXRYnLN6bBVOHxx47HShpOmD1k8620HSP8A\n",
"jLE8zy+XSxAEhJA0TcMwLIrC7l3MzkMfiS1D1VY0m2uOF1vr6qsL9VsEKzlIZrjvWsrRAtI/QFmW\n",
"cRy3dyokSWJd+hfBqZMRXStn5JmIzQs8ZlwckzK+rSDtLWNap3p5goRIHa+Uytbo9vfb5TTGh+7O\n",
"xPb3x8ilrZ0cTvVeXSD9A9R13dmmgO3KC+KCRd/UQeJW1t21ZOwca6uqaJtxe8uYKH5fNCS0v9P8\n",
"bUcr299p/rb9ozrfb19v33cwW4ZK46icPmZ8ZJi3g4SAehE+fRhjWZYRQo7Ho5UKuUBd1/0AVl/T\n",
"GHv9+jX/x9u3P6b0Df/3L3/53/7szz4Kwz8fXUO961rl6BqeIg8SpV6SDFwXvQwiW0yyvj34kagR\n",
"dK1pkapqGYwiSdXdzdv+se0/HGMwWtnS1f5bgy3KDe2tYZ1ytGLD2kNLZyzUYnD8k5RzcxtzA6X0\n",
"9esX//zP/9Xz3vIrXCLevn37zTff6NVyBGOlvygK7gkJw3Az8f5WDPwvvvjiq6++8jzvyy8/bs4z\n",
"+Pu//6s//dMvPU9V+kWdXr53Xx0r5UjWrwbLEU3zddfBqmp4aBkj8W1sZZuw4luoKi9NLZSzOng0\n",
"xHhpmdQ54/teUQjjsztwNfjHf/yrP/7j/5QFLhFffvnlt99+a6eWCoyV/sYxomsUb55PP/2Uj4VZ\n",
"5h2Pf8EvZpn313+tUYhrL7yt2autzmKlnKk9rav2CC/OKn61Vj/kDpKOLByPf5Fl2a9//esJajfM\n",
"WOlvzmnZkvRbz0d0c1lJ4qhxakvXKt5DAMBNLCzzBkGwvdxt/eMHjA8kkISoN9dVxk2J7LowKgAA\n",
"VgQifAaI47hz2jAP97R7F1sHZtkK1UdIOwD7AdI/AJ/ENIH8fIdXMrikOIKpc+KvvZxV75cBoINr\n",
"/RDSP8z5fC6K4nA4ZFkWRVGSJLM5tWxldNGNQtNl0pwkFncdL5I7RbeRRaHoxlOoKcLSjSvTidM3\n",
"fiKdCix+GLIWs50IpIgd6e+f37J2CCHX6zVJkjAML5eLdZNfgq3+YStRxKBw6ObYkYxnonRvIrQS\n",
"H4l+rMqJrFq0t3rpjlvtxmwLhGR38c0XThSW3qbZ/aQSZeCJH0p7S9cg7Th9lZ4jSRvVRHm2B/Ux\n",
"4bxjxkjRthitV28p7bQj/YfDwUo5rhEEQRiGOz970sqvF41nukOI6PtWzm2XlKNytGzzG1VytY7Z\n",
"aKp4mPhNmt1PnaMudaW5vaVLKwB/zI6KMbt5ReNZp0zeyBJpFj1o3U1/i2yI0g7upJTSnv22Pat/\n",
"jYxJ/9Kmrmc60VQRKx6qkY3TiMLInRY3kz2Mgc825Dqi0pg366bou7h5L9GmvDEEgVeW//nvMY3M\n",
"EzH5/thNea65+Bv0rH5KaZZl3BamlIZhGAQBpRRHuEzEmN3nxuXYMkNs2QOurYc7OwkcGSKsxRjD\n",
"vI1TRkabduVtZctwCj3pL4ridDrxrJZ8AIjjuB8KCTrc9PwqznxV3AUq5XB0pVn3QAzRW23rYA1b\n",
"Q4uzdlmbVVRyIlbhU1hFJdtoW/080IUx1njA0zSllCKxpQgVd7aKFLbXtWxJp651PzjzleRZ1CpH\n",
"l0mteFvd2dY456zxODUjM2k3TH0UmrPTFxF60i9a8AzD0HizK1BEZV1rEcbka+yUYwUrSqGbSl6C\n",
"UyF9u8W1p7C4qawn/UEQNBKPpV1H6CRAN2bxE2Jd8+mvzo4DK2LxaZy29HO3fhiGdV03Tp6qqraU\n",
"vm2f2DKLFjdngNd7Cmbzwo4rb8yWrjboIS6gJ/18ixP/d5qmURTxLa++70P618LUs7XFzZlV0zkf\n",
"xnge1n4KktUm+ZaujitP8orLQ+A78f7GPaRTPnzMY9D29Tf5DOI4Pp1O/CxDBHfaZeocCVaYeghZ\n",
"lxdLlGNAF8XjwHj5BgvsbZohYWQ4b7MSO7JrNW0oar12+bqbAdtYmRLp4pqDfNRu3iAIjsfjnEkO\n",
"9oBxn+7/lftDiESadUVt8NXS9WKNyZmjYtiKwnN178vLt7XA7gg3z90V0WlM/l/JJj7FKZEcW7HO\n",
"607kACZCq1t09liOMYuM66DLTeVS/Ak3QwAVy5GIBR+iBlVGHdFuXrhLx9BpzHYyJXU6/acJnJNI\n",
"vOK4K+8kSyVygPTPgfzZS6btnb5rtj9AN4eBKEPLSMyGkH6Qpdl41i9Hqz7NSy5SGUe4qTKKyOeL\n",
"irPJdS3ndhI2tAPndHPytLGVg9Y6kP45kAuE4rR9TP5hLfkW1Vb37v13wIz2H455kdrl8AwtG+Nm\n",
"4yimo7l5rpximrab46JrY4OtnZKKa+PLAumflTF9vZ1BzGKx6ujmZZzCuWl9B++WBoCmceq6m5zS\n",
"bB84pV1D2K4B69qcaQyd0Cz3gfTPilafUAyV0y3W+66bLqV6Th3jtZSnVRGz00j6hqeViKOlFM04\n",
"ddWcrELu20D658Csy/ZVyUrkTxj+Ppq7IxDrysK3upfNALMVy41hK9M1Hz5dHj/mBNI/B3Nmyu0j\n",
"ya6ucgaTCIlB6ua6FugjV8POdUm2KPdVtVnd6bwOBqtHLv9MdSD9u2AKA1lkkBoHlY50QFnxYjVT\n",
"H1sZNydCvnu246OXwJ+d4oGComxRTWStYosFgXB+WddT+SFFnitdb1gzVIw8/Gfx8QPSPxMGHdrW\n",
"qVsdCHF0bXPMjxV5scbUYf7dUupywOspWahwedwS1Y0PIaIfpT6eTUon3syYxR8QpH8OdHOONxKg\n",
"FdKuKBxrDIOGIgAAGkBJREFUiWs03gwhOt9mkOkEZfC+fFYhqvzN4xV3jqJc8u4tspwmMrclU5lJ\n",
"72sMpH95+kKgKGpan1pn6mVhK5shbpaj8oXmjuqfNrOQDlyM5k/AsKDu9DfTTT3vbG43KP398dVW\n",
"tqiRX5gZSP/CMCYUgpE90jhzmSSotM08MZoza5Zo0a8JaVc8SlMXyc+0dUbVUjDW7Spm807Rn4xv\n",
"n6kbxzV7n/Px0hVQhVJaFAVjLAiCNE1F54XZKirLss6VMAxD09m473tlOTCXl++RGdkjg8ArS5M/\n",
"7Gs6Yx4hdt6Q/msgL7aqvDSd5L6DiBb9bMUXiuDF1vXAmnn/4j6pa6+fKJKvDbiwBiAiCLw89+J4\n",
"6Xr0WIfVXxRFlmVpmp7PZ0JIFEVTF5XnefghYw4kuCko6uUMGvKTGs5muRMk7mzdF9XKmfI3U2ka\n",
"Y9EanXR/WV2rPsdmQULU5dUbraom9O3oRhZxRJW3FRvWwTU/T8MKrH7GWJ7n1+uVm+dpmjLGiqIw\n",
"SBatVZSxjS9ifMRO4ynWSiI2svOJ6uz7XlEIparvxWpeOVuZUqwkCx8/tRqUjDD0evPG+eirG1dJ\n",
"xVQcTTdTSXosgYf5Dj6pJhfQ/PQr34QFj7HNVzczW4HVX5ZlHMdtt0ySJEVRLFuUGWMyaDZYPDFc\n",
"8Y6DN9Wtg0QvdLMUjMfWES6No2Yia91syqU+ntmSYC7x6vAaOmIRm3nzJpo9zMYKpJ8fBNa+4vs+\n",
"M+qtBkVRSs3uNZ7Bjsjroi67WnWXdH2JDTgS3cjX8V4Ib4mYfRX6P4G7Cgf3l1mMS9FyqQ1e50E7\n",
"Vsa//u8S1WTZHSqKidblTLR3R4UVOHzquu77Xsw871pFRVHEGCOEMMZ83z+dTlpry2mavnjxovnv\n",
"mzefXi5feJ4XRX9wPB716+55Rm6E+UPF5Y4gSu0s2/YxMyGdir6Q/ITOWMUDBAYrP6iG/KFoMeio\n",
"0R2nPUELizY98Ep27it613kggzueFsW+xNcX37z5tKo+f3p65XleWb72PO/Nmzfv37+fsoIfsKT0\n",
"M8YqwWy2fQiwRaNbvajj8RjHcTMq8NPnz+ez+r1+9rOfvXr1qvnv55//+Kc//XPP8/7yL59V/ryT\n",
"d9dNRC+wHKd+l62wpemWkQeRW+v9cXdBfRys5OBFeTz+eCSD1jyh/Zw0TT3P+/zzH3/66Q9ev37h\n",
"ed6rV//L87zPP//8b//2by3UQ40lpZ8HWQ5+RAjR0lnrpB+apkmSlGVZ17X6bOPVq1ftGUZZeq9e\n",
"/cgbcjWIbDddp4RW99Xt65QO2ICNp3skTpneBpWpKk80kesfxFgUHiHYtTshfCFn0Hs2iGj/nQTJ\n",
"ZvKbcFmg1AvDHzUV8DyPUvrRRx8ZFqrPktIfx3GssKYe2PPLjikqCAIt6e8gsQonzes56PAx6Oue\n",
"NNRnDNyLNV4KbZ2ER7478XwKltrNa4DcJzOynEnhbTvdDgy+R8fKE6yqxUL+V7DM63le3y8k8hTN\n",
"WdR4RFu6LL4tuioz9YuqHrakmyhCtCIq3yirnjODMb2hZampjK2VQ7lPZnw5ixwOoWWtD6ZHNVP8\n",
"/kNppiZL+eJWIP1xHNMPuwmP0RR9n1Ka5/mgW1+3qM43Lc4/OBLd0U0rZmv80oocNVA3yYs3Mni0\n",
"odNu8qBS9UYmRO+IygWXNNxZ+RShW0NbkTxaSVN4JW01Zj+bxbKsQPq54DarAnxblmg/V1VVURRl\n",
"WXY4HIyLiqKo/DAHwuFw6GwI0P8V2maO+t1EKfIlCWckQ4V6X3dqwdYW8saZDqcWPFxDEjk6vt0M\n",
"zhwe4+t3hBUEd3qedz6foyiqqooQQilNkkRkgDfqLJJplaLO53OWZTyXg/fdzMA4IvO7+oz569+j\n",
"tTbADdU+xul91Jk/qNTWLi3RgSSTEgT/ufw7HoMF/MFC5Js8+lcGcw1JJq9WDHnuhRu5r9ug2W2t\n",
"1iw43q9D+gkh1+u1qirGmDx3m+/7j4+Pg/H76kURQk6nUxN7OjJbXIOVJR3diljZoGhgBU+UjlSC\n",
"wXg2aWY0LXe2rjdJXpSIvtqGIQ810Shk8FO+u6ojwXz+NPijbCW64DVRf4iDgWoWsZVaagbWIf0c\n",
"RVe77/s343BUiiKE2E3jYyvF4HTqOdgRuToMYrBYZ6Wv21rJtJIISDQuWvQR99WZT3F0hWbmNQB5\n",
"bx+0hCTGh61IGCu7wQcx2O+2ICvw9W8Di91iEbfAILpvkcVBazoV00oPwFdZJp22D/5S7pXSagSR\n",
"928QgwSrg8h3JvbrL8oNPnUkjMUY67UA6V8e3eQzFqPXJ0IUzyequS3p1CpHpO8GB4nYykUqKsdK\n",
"wj7d32XrR4mGEPWHJek5ttL4WHwdJt1ZaRFI//JodTuJOuiyyAFYgxJmZUFCt5ypvR+imC5RkkvJ\n",
"yuGC0d/Tof6wRMddeII1edFuXm+WbStWXucZgPTPx9QzVt2FCd3Uvn10ff1WJIwvHro/PZds2tBq\n",
"BFvzPF3UN7u5hmQ376SVX+pJmQHpn4/p9liKsJUDThRVvZQpOnUiBF3HkagdrDhqbKmVbouJvq9V\n",
"jq3HtNR4o3hONcf9QbENpN9FRItdnuBdkiSE0H33DPa2jFc3kTPX4hZlLUQrjYORRZKpjNYsx5Yv\n",
"QjT5W0SY1NNQm2ErcZOo8KKw4KL0BD1w2U18kH4XCQK9F8PuIpWu40hd3UQG8qAz11bwjFmuur65\n",
"pxtCrovkIU6q2kuNr1pIzkWZTkBFiRwMTiwYfK1shVGZAemfj6VS9I1H4jjSeg0kVrDIfS85qkx0\n",
"iz4GOyrm985JmM5tItrSJemrYTjQOFNPNZxa5bZ1NOmyEaWQ/vlQ3z0kt/rVe56kHJHvftB2k0in\n",
"qDIGIXdamdR0P7IVRNRnqTVnUQtLuod6LhJ5X1XvyZI7OqXmWkGiVuYZBjHEdoH0u4jE1+953umk\n",
"V5Q6Ft9G3d1GToVG6I4T461y3zdJZtm/7/EoK2d+tZXcMUnsJK6wUohW4iYrpxAvviYM6V+YFe38\n",
"Ho9kF5UtS8qpIUR9SPB9vV2v3i37YGNIhhCtcdepw9F0E7PbZU05fDaJraRdg0im21qqoet9Ejkx\n",
"p7Y6tX7Uggck6aI1z9seTum1HGzpAqrYGvZ1Pc5BoOGxlbx782+cscgi7mbRbt5JM0pumMF2s5UB\n",
"W5e19HwP0r8ZDDzOTq2zOYWWmZmmeoWLdvPicZghSm+n6whar+PIDDh8NsKk5oatPPKSSlq5hWvq\n",
"CUPeKcLQLcletrvC6t8IthxHg8utkhdG/b5BMHlf1ypfvrI6iO4askHcDpgOA9032Aeu/sSX7Ruw\n",
"+sEo5l8ptbi/SXeOPygE4w7uXB5dh9UgkvN81kL/OYahF0Xe5aJRyOKHrasDqx98wKSOI10zZ1Bq\n",
"dYMaDQ5uHNywCgBnhtnDDED6we+ZWu8kvm/R7EHXjBIdG9svR/5j3XfTGzis3GcVP0oyTxq0S5xK\n",
"qNcAhw/4PRalX3ermkhq+6+HfDAQuV/65bgv7nJ0HVarYO2TLa0nsqyrENK/MK5FHdhikQyXk953\n",
"q9jqfpvsxpOCCB+bUEofHh6iKMqyjI1ODlCWZZ7nViomAi8MWBZI/z7ZlPQXRZFlWZqm5/OZEBJF\n",
"kVk5fPy4v78vy5KuJHDBKWt3e44Ii6zCnb120Mg32Y7DhzGW5/n1eiWEeJ6XpiljrCiKRN+nSwhJ\n",
"0zQIAkrp1Fa/LayE6NkCb50EW4P02tcqBlkqcneHbMfqL8syjmPSUp0kSYqiMCgqCIJgbR3HKasf\n",
"zMAmn/iu0pEuy3akv67rjl77vj/e3Q8AANtjU9JPegaDv0nTaEpgc4mA+3iHrG3yr4Hrvn7GWCXY\n",
"CUcIaZv5rhn4aZq+ePGifz0IgqPDe/836UG2gq2EPLBGZsDlsCVR+MmbN2/ev39v/34CXJd+SqnI\n",
"X08IOZ/PM9dHnTzPwxXGuzlVZVtWtlPWOqR/Bpzqxt6HPfAiyAqUZdlnn302U4Xcl/44jmO1DGGr\n",
"W5gFN/F9O+8wpjJgQdzMbbcdX7/neX3XkMhZBAAAe2Y70h/HcWf7FQ/3HPwyD9h3bXlgMxCymmNv\n",
"tYCvZm9s+Im77vBRhzt8mj1cfIfXaehA66qq+EpLVVUurxasl6363uA42hsbfuLbkX7P887ncxRF\n",
"VVURQiilSZIMLgA0MaD9YFBOnud8AsEYq+u6WZEXrc8AAMC6uHt+fl66DpapqooxFgSBSNk9z6vr\n",
"uq7r6SJw7u7uLpfLGiN8nKKu7cy4bZUDgBkqPZBH+Lx7926WGm3L6ueohPr4vo/dXu5j6xHhUYNl\n",
"cbAHbmeZFwAAgCKQfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA\n",
"2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2QfgAA2B2Q\n",
"fgAA2B2QfgAA2B2QfgAA2B2QfgAA2B0fL10BVSilRVEwxoIgSNOUEDKmtLIs67pO01T0hSzLOlfC\n",
"MAzDcMxNAQDAEdYh/UVRFEVxOp183y+KIoqi6/VqUA4fP+q69n2fMSaR/jzPL5dL+4rv+wZ3BAAA\n",
"B1mB9DPG8jy/Xq/c0k/TlDFWFEWSJLpFEULSNA2CgFKa57n8y7DxAQBbZQW+/rIs4zhue3iSJCmK\n",
"wqCoIAiCILBXNQAAWCUrkP66rjt6zd0189ydUjrbvQAAYB5W4PCp67rve5nB8x5FEWOMEMIY833/\n",
"dDpprS1//vnnlNL+dd/3DVxVAIBt0A8h4fzqV7/6+uuvZ6vGktLPGKuqavAjQkhj6S9idB+PxziO\n",
"mwGmKIrD4XA+n9VL+OlPf/rq1av+9ZGxSQCAVSNaRHz79u0//dM/zVaNJaWfx9sMfkQI0dJZ63SC\n",
"f5Ik4fGg6rONV69eYaEYANBBJAuU0o8++mi2aiwp/XEcx3F882uOLMwGQaAl/QAA4CwrWOb1PK/v\n",
"FxJ5igAAANxkBdIfx3FnvZSHe4q+z2P2ra8QlGXpyPwDAABGsgLp54LbrArwHV6iIJmqqqIoyrLs\n",
"cDgY3zGKorIs21cOh0NnbwEAAKyXFQR3ep53Pp+jKKqqihBCKU2SRGSAN+o8KNN5nvMJBGOsruso\n",
"ivj1Ts6G8/mcZVme53xBhk8yjsejxV8EAAALcvf8/Lx0HVSpqoqnb5Nb33VdD24F0KWJPb15xz53\n",
"d3eXywURPgAARbIs++yzz969ezfP7dZh9XMUXe2+71uJwyGEQLsBAJtkBb5+AAAAdoH0AwDA7oD0\n",
"AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA\n",
"7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0AwDA7oD0T0iWZfwUeEdojqF3ATSOBDSO\n",
"BDSOFSD9AACwOyD9AACwOz5eugKWoZQWRcEYC4IgTVNCiFk5jLGiKPi8MgzDJEmMiwIAANfYlNVf\n",
"FEWWZWmans9nQoixD44x9vDwwBg7nU6n04kxFkURY8xubQEAYCm2I/2MsTzPL5dLEASEkDRNwzAs\n",
"isKgqCzLkiQ5Ho++7/u+fzwe4zjO89x6nQEAYBG2I/1lWcZx3HbLJEliJv2+78dx3L6SpmlVVWOr\n",
"CAAAbrAd6a/rOgiC9hXf9828NGma9guHrx8AsBm2s8xb13UYhp2Lvu9bKfzh4eF4PGr9SVVVb9++\n",
"ff36tZUKWOHp6cmdgGg0jgQ0joStNs7Mq4l3z8/Pc95PF8aYyNNCCGmb+VEUcf9++ztRFF0ul5F1\n",
"OBwOQRAkSaL+J3/yJ3/y7t27kfcFAOyKH/zgB//6r/86z71ct/p5sObgR4SQ8/k8dQUMdN/zvNme\n",
"HwAAGOC69Mdx3FlxFdFx9I+Hx3QmSaKr+wAA4DjbWeb1PK/vGjIOy4HuAwA2zHakP47jzmILD/cc\n",
"/DKlNM9z0brKoO7XdW2xtgAAsCCuL/NqEUVRHMdcr7l8n06nviOoqqr7+3vP8+I47q8W8K28SZJ0\n",
"ho0XL148PT1NWX0AAJgJ1339WpzP5yiKqqoihFBKkyQZXABoIvQHQ/WrqqrruiiKzvIyEjkAADbD\n",
"pqx+TlVVPH2bZBNWXdeD+wAAAGAPbFD6AQAAyNnOMi8AAABFIP0AALA7IP0AALA7IP0AALA7IP0A\n",
"ALA7IP0AALA7IP1TQSl9eHiIoijLsjm3g/GDKqMoiqJIkqxi5urVdZ1lmeTQtJnrQyk9HA5RFD08\n",
"PPQTPc1WmaIoVG40XX3KspSfPKp4ays1vFmZmfv2zfpwXOvbqjyDCeAJJK7X69PT0/F4DIJgnvs+\n",
"PT2FYZim6ePj4+PjY5qmQRA8PT0tXr04jvlpCoOfzlyfJEnCMDyfz8/Pz7yhFqkMTxL1+Pj49PR0\n",
"Op183+/UZLr6XC6XOI6DIIjjWPRQ1G89soaKlZmtbyvWp8Gpvq0OpN8+T09Pvu+3O2WapqfTaYZb\n",
"J0nCFa3heDymabps9S6XS5Ikl8tl8PWYuT5xHB+PR9Gns1Xmer12WoO30jz1uV6v1+uV31SkWYq3\n",
"Hl9Dlco8z9i3FevDcapvawHpt8/pdOr0yMfHx3lG+0FR63TK+avHrTPR6zFnfU6nUxzH8i/MU5k0\n",
"TTs3en5+9n1/5vpI1E3x1hZrKJfa+fu2ivS707d1ga/fPhYPiNdF5UD5mauXZVkcx/J8SrPVpygK\n",
"+RnLs1Wmn1iwf+s569NH8daz1RB92y6Qfvv0e6Rn74B4XXgC6vaVOavHGKOU9l/aperDS+brclmW\n",
"9Rd4Z6tMHMd1XTeriHVdHw4HFXWbqD59FG+9YA3Rt8cA6bePI6O653mHw4EvabYvzlm9LMvkVrY3\n",
"Y30opYSQoiiiKPJ9PwiCw+GwYGru8/lMKb27u7u7u3v58iVft+x8Z8G+pHjrpWqIvj2STeXrB23M\n",
"DpS3CKWUMeZUZmzGWFmW1+uV22JxHN/f34dhuIghdjgcwjC8XC6e51VVlWUZIcT6EdObBH17PLD6\n",
"7bP428sYu7+/F70bs1WvKIowDOl38HMU+j6W2eoTBEFVVafTqT0HT5KkbfjP2TiEkMZdEATB+Xx+\n",
"eHjofG3BvqR465lriL5tC0j/JFg8IF4XlQPl56leGIZ1XTevR13X3D26VH24Td0x8Pv2/jyVoZR2\n",
"bEZCyODkY8G+pHjr2WqIvm2TpUOMNkg/ZPt8PvdDtqfg6ekpCIJO4HBno9BS1RMFwM1ZHx6C3b5y\n",
"PB7bzTVbZdI07USpPz8/98P+pq6PJH5R8dYWaygPppy/b6sEd8q/uaAU3ATSPwlhGDZ9lHdZvklk\n",
"Uvh2x76gEEJcqJ7kRZqtPo+Pj2EYNltsHh8fOztuZqsMj+/ubPbpR/pPXR+5uine2lYN5fvL5u/b\n",
"46Xfbn3sggMaJ4HPTPn5wPyA+BmWpHhemr7TgFLaecozV4+vYTLG6rqO4/h0OnW+MGd9qqp6eHiI\n",
"49jzPEop32e/SGUopVmWNTcKw3AwYmSK+uR5zr0T/KE0LcDXnHVvPbKGKpWZs28rNg7Hqb6tBaR/\n",
"QlQOiF8Q16o3Z334uy2J0JitMrwmvu/Lo4wWfFiKt3aqOzlVGc+9+niQfgAA2CGI8AEAgN0B6QcA\n",
"gN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B\n",
"6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6QcAgN0B6Qdg3VRVxY/6MqAoCruVAWvh46UrAIA1iqIo\n",
"y1L06eDZqhvgcDgMHuqrAm8uR06LBXOCAxrBdsiyjBDCz9Guqqosy0YToyjaZFfno53xqMYPqX98\n",
"fLRbK+A+sPrBpgiCoDlsnVIqOXh9G+R5bmzye54XBIHv+0VRwPDfG/D1g+2QJAk3+fv0DVtK6cPD\n",
"w8uXL1+8ePHw8NB2l+d5HkURpfRwONzd3R0OB37x5cuX9/f3VVU1JURRFEWR53llWUZRdHd3d39/\n",
"n2UZY6xzO25fv3jxgt+uLMvxfnZKKWMsjuPBTxXvGMcxPP575BmALXK5XMIwFH16Op3CMLxer/y/\n",
"1+s1juM0Tfl/Hx8fkyTxff98Pj8/P6dpGgRBkiT8m77vN1+7XC5BEKRpmiTJ4+NjU7jv+03h/JtN\n",
"aU35kuopwu87+JH6Hfmg+PT0NLIyYF1A+sE2kUj/4+NjEAT962EYXi4X/u80TY/HY1NU+/udYsMw\n",
"7Otv5+7H47EZVzhPT08i1VYnDMNOsWZ39Dyv+eFgJ8DhA3ZHURRpmvavp2naDhBq+44IIZIC+6WF\n",
"YcgYq+ua/zeO47Is8zxv3EqEkNPpZFb/hqqqfN8f/EjrjmEYNl4ssBMg/WB3cCf4XY8oihqx1mJQ\n",
"fwkhTWnc/+N9tyTw8uXLw+Fgdq+b9zW7Y39xAmwbRPiA3cEd96LVUQPquu6rMGOsM29oTw64Il+v\n",
"V/l8Qk57dBn8VPGOVVUhwmdvwOoHuyMMQ7sxLVmWda4UReH7fiOy/S/Ecez7/kg3SxAEImtd/Y6M\n",
"sc4oBfYApB/sjjAMfd/nIZttiqLI89yswCiK+DpBVVVZlhVF0XasV1XVGWzquh6cK+jeV5TCQf2O\n",
"ZVny6P4xNQGrAw4fsDUeHh64JVvXNQ+6T9O0s7frdDplWXZ/f8+vM8aqqgqCgG+PyrKsLEtKaZIk\n",
"3BPClwfO5zP/8yiKjsdjYynzSNAmcJ5HCrX9Ktwz09yuruuqqngM6Jhfyksb3LmmfkdKqUXfF1gL\n",
"SOQA9gtXfP5v432/URQp5lFobtdkmxiPPJHDzTvy4eHx8XHMkgNYI5B+AEahLv0T8fLlS75DzeBv\n",
"D4cDX/S2XivgOPD1A7BuGjeUAb7vQ/f3Cax+AAzp5IiO4xgyCtYCpB8AAHYHHD4AALA7IP0AALA7\n",
"IP0AALA7/j/BPhXjhGkUiQAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1frOTGfedb5/j80Z8ZzeGMFMuauTMyT7xYOZavEp7N\n",
"SBAMRwZ7HUMYY+0xO2PLgJUHs7XIRkjyUkS0MHxfDLYuvF7jZi9CRg82PAsDzYdk18h6d0nI8g2w\n",
"0GZJy8l1sLkrNXXtODeZWEva8cw4M0cS78PvDIeHZPNUdZPsIvv3gSD08Pz6x2L92MXit35VtZYk\n",
"CUEQBEFWifVlFwBBEARpG2z6EQRBVg5s+hEEQVYObPoRBEFWDmz6EQRBVg5s+hEEQVYObPoRBEFW\n",
"Dmz6EQRBVg5s+hEEQVYObPoRBEFWDmz6EQRBVg5s+hEEQVYObPoRBEFWDmz6EQRBVg5s+hEEQVYO\n",
"bPoRBEFWDmz6EQRBVg5s+hEEQVYObPoRBEFWDmz6EQRBVg5s+hEEQVYObPoRBEFWDmz6EQRBVo6N\n",
"ZRcAQTqDYRiEEFVVVVVddllYGQwGiqKYprnsgiBigb3+lSOO49FotLu7u7a2NhwOPc8bj8fLLhQR\n",
"oQxHoqpqHMee5zXhfDgcDjIMh0PDMMIwbOJcCLKWJMmyy4C0RxzHe3t7lFJd1wkhYRgahuF5XhRF\n",
"yy3YYDBwXXe5ZWABOv5NdKI9z3MchxCiaRocCcPQtm1d1yFY8xEEgSRJsizXU0qkL6Dgs1rYtq1p\n",
"WtqUyLI8mUx2d3eXWyqEEKKqKrxPZNUkTdP29vY0TZMkaT63iqLUUz6kX6Dgs1rEcVxsCyil6WfP\n",
"80BwIIQ4jjMYDNbW1vb29gzDiOM490XP84bD4e7u7smTJ0E7mnVSwzCyroIgSI1Ho9FgMAiCICt3\n",
"jEajop/xeAx/DYIgLd5gMIDOMm+pWABXJ0+e3N3dHY1GxRqo/Yw5JEnSNA2ul9yqK9u2UwM4AvHK\n",
"EoZhqiDBm0opQRDABULJHcfJOmc3i+N4PB5DJaRCYs6JbdtQePCW3gzF01XfMCnNVftKkCCrxGQy\n",
"0TStwmA6nbquqygKiELT6RSOW5Yly7Lv+6mlZVmqqqZHfN/XNI1SmnMYRZGiKJZlRVEE/7QsS5Kk\n",
"1NJ1XTijmyF7ohTf98FyMpnouk4pnU6n0+lU07RsOVlKxYJlWYqipK7AM6U0563GMxadJ0mi63rq\n",
"3HVduPD0r1AnpT9kqEnTNFVVLT3ddDqF1770n7quF41ZzHzfN00zLed0OoWA5vzAF9P7Koqi3OUk\n",
"DDcMUGO1rybY9K8cpmlCy25ZVmkLmyQJ/D5zB13XTX/w8Nsu/WLuB188kiSJZVm5X+ms5qn0FJIk\n",
"WZZV/BN7qY4EXEHrk+L7PiEkW/Iaz5iUNf3Fhrv08VDRh8tGLYdpmsVmtxh3RrMck8mkWE5Kaa66\n",
"oiiSJCl7hOWGqbfaVxMUfFYOSqnv+5CsYtv27u5u6Tt+VgUC4CuQc2LbdtEAvpWVX8IwjOO4mAqp\n",
"aVo6mDkHpmmWjnwylooFGF/NKeyKouTOW+MZgVTFGgwGu7u7YRhOJpM5/LCgaZrjOOPxOJVK4Jk6\n",
"nxkhxLsFjC2XnjR3M0iSlJXRGG+Y2qt9BcFh3hUlTU6P4xhSv3NjAKU5IZIkhWEoy3IQBLPSMbO/\n",
"2zAMS1PgJUlaZPhxVr4KY6lYCIJgVskbOmP6rbSNa3r2ACh4tm1Dyw7BopTmqpfFzHEcwzAURYGD\n",
"cRzPqsBqGG+Y2qt9BcGmf7VwHCfX3ZYkSVVVx3FybTE08bmvp6PE0P9l6bm3mZnOXioWVy2fEYBw\n",
"1OWN5XTZ7jO8c/i+n3vCVZuFYTgej3Pfgu7/HEViuWFqr/YVBAWf1WJWX6n4el5MvbBtW5ZlsFRV\n",
"tVQmyqGqahAEpYkxTTwSGEvFgqIopdJB7mCNZ5ybWXlHR1IMsaZp8ErHZVYqjs1XKsYbRoRq7zrY\n",
"9K8WQRDkfslBEBRfBQghqqqmeZPwLdu2U4VXVVVZlospmLZt554ulNLhcJj7MY/H49x3wzDMPQw8\n",
"z+N9PLCX6kg0TYMZVdmDo9Eo18DVeEZGFEXJVgskcc7nKgiC3AVCFHJve0eaFZ8W4/G4IqO0GpYb\n",
"pv1q7x84m3e1AFnf8zxQFcIwDIJgMpnk9A2YWwvzS6GhgZyfXMMHM4HTMYMgCGC5mJwZ/CAhMwcW\n",
"QlBVNWcGYjE8gUptwjCEn3oQBOnLByGEUppTSBhLdSSQXZ5q1p7n6boehqHjOLIsZ+ce13LGwWAA\n",
"VQ1NasXCO6PRKAxDeAbEcWya5t7enqqqkICbekuvAozhn9kJfcPhUJbl3M0ASZPZ07GYpUWCioKR\n",
"pNFoJMtyWqrRaAQSEKTnQtkgHz9XeJYbpq5qX1mw6V9F4HdCZg+3si+rkLoiR42wpcrvLDN2VzWW\n",
"6kjS15FqPzWekQVQRRYcLQeOvBkYzdKKUhSllsb3yBuGtF7tfQKbfqSErqyogyDIfKDWjyAIsnJg\n",
"rx85BKRvp//MSsMIgvQGbPoRBEFWDhR8EARBVg5s+hEEQVYObPoRBEFWDmz6EQRBVg5s+hEEQVYO\n",
"bPoRBEFWDmz6EQRBVo6VbvqDIMitOIggCLIKrOiUrjiOYVlBQkije+AhCIIIyIo2/YZhpDsUwnZC\n",
"sxbIRRAE6R8rKvhkNw6FjYGWWx4EQZA2WdGmP7fgOO7tgCDISrGKTX+xj1/cfxxBEKTHrGLTjyAI\n",
"suKsYtNf3F6Od/tvBEGQTrOKTT8paD5xHC+rJAiCIO3TyabfcZzxeFxh4HnecDgcDAaGYZQ264qi\n",
"pJs+e563+N7WCIIgHaJLef2e59m2HYahLMtxHM/aN9y2bdu2LcuSZRm2G/R9P2eTm9JlWRYm+SAI\n",
"sjp0qekHlQY67OPxuLTpj+N4b2/P9/20KTcMQ5bl0g1mU4dNlhpBEEQ8kg7iuq6qqqV/siyLUpo9\n",
"Mp1OFUWp69Sf+MQnlh0xBEH6ydraWl0t1ZFsLPtiayYMw1wvHtShuvy/9tprW1tbv/3bv81i/I1v\n",
"fOOd73znL//yLzMav//97z937hyL8eXLlz/wgQ8wGv/+7//+M888w2LZnPH3v//9b37zm+zGf/In\n",
"f/LpT3+axfhP//RPr1y5cuHCBRZjrog0V8lf/epXP/OZzzAaCxK+fkekOWP2WAdB8K1vfYvRbQ20\n",
"9pCpkYpev6ZpruvmDs4ynoPHHnvsnnvuYTR+5plnvva1r7EbF0s+i0uXLrEb/9Iv/RKjZXPGruty\n",
"GV+6dInR+Gtf+9ozzzzDaMwVkeYq+fHHH2c3FiR8/Y5Ic8bssaaUbmxssHtekE5m+FTQdJrmHXfc\n",
"sba2xmh84sSJ+++/n92YvRiMHR/g5MmTnTNmv8D777+fveq4ItJcJd95550NecaIpAhSb1yxXl9v\n",
"r0HuW9PfNFevXn377bcZja9cufLqq6+yG7MX48/+7M/Yjf/6r/+6c8bsF/jqq6+yVx1XRJqr5J/+\n",
"9KcNecaIpAhSb1yxfuutt9iNF6RvWn/T6TobGxvsvf6nn36avfvz9NNPv//972c0fuqpp9iv9Dd/\n",
"8zcZLQlnJ4Xds6IoXMZPPfUUo/Fjjz323ve+l9H4jjvuOH78OKNxc5X8u7/7u+zGgoSvoYhw/UZ2\n",
"dnYYLQlnvTVnzBVr9ralBlqTlmqkQuunlJqmmTsoSVJdp37iiSdOnDhRlzcBqXFcREAopexicRfB\n",
"8HUXSunW1lZrp+ub4KNpWjpNF3AcR9O0uvxzCT5cG0By7Rlg23ZDxlwvs80Vg92Yq5K55IXmrq65\n",
"WIsQPt7bnt2YS/AR4eYknLFuU/DpW9MPb+hpbOI4Ho/HpfO5EARBVpYuzeYdj8fQo4/jOJu/n5vW\n",
"G8fxYDBQFEWSJM/zdF2vsen/0Ic+9J3vfOfHP/5xXQ5FYzAYzFohowdkN+bsJRi+7mIYxpe+9KUb\n",
"N260dL7WpKWW8X3fdd0oiup1e+HChTNnzjAaT6fT6XTKbsxeDC7Fs9/GvJXMbtzc1fU71l2MiAix\n",
"ppSyzxlanL5l+KQ0lOpz8+ZNdq2fa5IBlzHXBgP9Nu5iJQtSDIxIC8ZcF9im1t8lwUcEPvnJT778\n",
"8suvv/76sguCIEivMAzjhRdeeOONN9o5Xd+GeZvm2rVrb775JqNxGIbsHQSurkQui2mVjXkrmd24\n",
"uavrd6y7GBFBYr2/v89uvCDY9PNx9epVbPqFMu5iQ9PvWHcxIoLEus2mHwUfPlDwQUTGMIhpLrsQ\n",
"yFyg4CM0+/v7XMO87IM8vR/vam5QkauS2Y0FGfrj8vyTn3CkHWNEWjAWdpgXm34+oii6efMmo3EX\n",
"Z/N2zri5uaOCzPDk8vzd7363Ic/9joggsW4vqR8FH15Q8EFEZjQilrXsQiBzgYKP0KDgI5pxF+WF\n",
"5mL9F39xvSHP/Y6IILFGwUdcUPARzbiL8gIu3zafsQj3G6+xsIJPbxdyaIiLFy+ePXuW0TiKIvaV\n",
"JLjWnOBaCaDfxryVzG7c3NU1F+vHH7/WkOd+R0SEWFNKd3Z22D0vCGr9fKDWj4jMYED6u3pbz0Gt\n",
"X2iuXLnyD//wD4zGnuexz/7gmidiGAYaA7yVzG7c3NU1F+vXXmPdjYDXc78jIkisr1/nGKpZlNbe\n",
"L/oBCj6iGXdRXkDBZz5jEe43XmMUfHoCCj6IyKDg011Q8GkDwzD29vYGt2AfskfBRzTjLsoLKPjM\n",
"ZyzC/cZrLKzg09v1+o/ENM05tvs5duzYxgZrpcmyzO6Zy5ir5P027mIlN1eMkydPNuS53xERJNab\n",
"m5vsxguyooLP3Du9oeCDiAwKPt0FBZ+WCIJgPB4bhsH1RhbHMU7pEsq4ixOImpzS9cOGPPc7IoLE\n",
"ml1MXpwVFXxkWQ7DEHr9oDaabGvdbm1tra+zPi8lSWIvEpdxc+/UnTPuYiU3V4w777yzIc/9jogg\n",
"sX7HO97Bbrwg/RR8DMMoPmwVRZnVvo9GI0opS0RR8EFEBgWf7oKCTw2YpukWqOjXS5LEuCQTCj6i\n",
"GXdRXmgu1jziJUakDWNhBR9Bm37HccbjcYWB53nD4XAwGBiGwbU23iy43ssQBEE6jViCj+d5tm2H\n",
"YSjLchzH7ox3V9u2bdu2LEuWZdu2HcfxfZ/rLHEca5oG/4zjeDAYMHpAwQcRAejdFzPU1tZI8QeN\n",
"uzZ2gpUWfCRJopT6vq/r+iybOI7H47HruoqigL2qqlyvYKqqBkEwHA4NwzAMYzgcWszbW1y7dg23\n",
"ZRfKuIubgDcXay4wIi0YC7stu6Br+Liuq6pq6Z8sy6KUZo9Mp1NFUeY7i+/7XF/58Ic/vLa2tr6+\n",
"vr6+vra2trm5SSl94IEHHn74YUrpI4888vTTTydJ8vTTT58/f973/QsXLpw/fz5Jkq985Svnzp3L\n",
"fkiS5Ny5c1/5ylfgw+c///kkSc6fPw8e0g/gKvvhK1/5yqlTpypcwYfUw7vf/e4KV7lSWZZV4SpX\n",
"KsuyKlzlSpXzUNcF+r7/vve9j/ECfd/3fZ/xAt/97ndX11XWw6lTp6rrKvvh85//fHVdZV1ZllV0\n",
"9eEPP//QQ/+iWCr4QedcUdrqBcJtn3MFH3IXeO7cuQsXLvi+n/WZq6unn3469ZC9K4qucqV697vf\n",
"XeEqV6rcbV+8V7Ou4LZnv8CcqwceeIBS+vDDDz/wwAP33nvv2toaNCnw/6QtxOr1sxCGoaIo2SOg\n",
"Ds3hSlXVnKsj4RoSUBTl1KlTjMYPPvggu+djx46xG//cz/0cu3HF+9aCxr/yK7/Cbsx+gYqi3H33\n",
"3ezG7BHnqjeuiHDFurSS/+f/5PAwi4YukOu2P3XqFHtEunjbs1dF27T2kOGiotevaZrrurmDs4xr\n",
"58KFC2fOnGE0nk6n7Iv8cS0HWKyBlTXmrWR24+aubvFYU5qUnrD0B01pUnpCjEgLxuxXRym95557\n",
"2D0vSPd6/bXk88zN1atXUesXyriLynJDsa7wWvonjEgLxsJq/dwZPnEcQypuHMeqqsqyzDW3jRHP\n",
"82Ast/inwWAAQ7u5g7PSgeoFM3wQETAMoqr5DB/PI6MRmU6ZjBHREDfDx7btvb29kydPDgYDz/OC\n",
"IBgMBru7u3t7e7Ztt9YZ51Xn62V/f//tt99mNI7jmL1auCqQqyvRb2PeSmY3bu7qmov1u97Fseov\n",
"RqQFY65Yv/XWW+zGC8LU9Nu2vbu76ziOrusgXcH82CRJptOpruuO4+zu7nJlWC5CcYIc15S5RYii\n",
"CGfzCmXcxbmjTS7f9tcNee53RASJ9Y0bN9iNF+XI0QDLslRVPTIJEp4BpmnWMQJRNczr+37uT5PJ\n",
"RNf1Ws57JJcuXXrwwQfbOReCzKJ0mNd1k9IfzawxYUQoKKWQvdoOR/f6dV2H+VPVZrIsQ8Z9TY+k\n",
"mUBJ0gcvzPDiSrdaBBR8RDPuorzQXKx/9jMUfMQy7rbg0xrj8Rh2TISlN9MNFHNmk8nEtu3RaGQY\n",
"xmAw0HW9tQEAFHxEM+6ivICCz3zGItxvvMYdFnyExfd913XZN7yvhYsXL549e5bROIoi9uJxXQhX\n",
"Yni/jXkrmd24uatbPNazBJ/HH7/GaDzLM1cxSuliRESINaV0Z2eH3fOC8G3V4nleQ9mcc7CUVJ/N\n",
"zU3cqkUo4y5WcpNbtdzVkOd+R0SQWLe5VQuf4DMej7l0rv5x5coV9jW1Yf8vdmP2YhiGgcYAbyWz\n",
"Gzd3dc3F+rXXXi0enPWTxYi0YMwV6+vXOYZqFoXrHaF6H3NFUbimOHcRFHxEM+6ivFCL4GNZ+YOz\n",
"BB9VRcFnacY9EXxc1x2NRrBUsiRJkF1DCIENsMIwHA6HpmlWPyE6DQo+ohl3sZJrKUZpXx4FH9GM\n",
"eyL4GIYhSZJpmnA98DkMQ8dxyK38ztYmdi0FFHxEM+6ivNCy4FOL535HRJBYtyn4cA/zFpfKoZSO\n",
"x2PY9EpRlOUur9Y0x44d29hgrbTmuhJc71X9Nu5iJTdXjJMnTzbkud8RESTWm5ub7MYLwrd829pa\n",
"uX129bTWVlJbCrh8GyIC0O/MbbvoeWQ8JpTmV2obDEoOIqIh7vJthBBVVYsZPo7jCJLu2QJxHOOU\n",
"LqGMuziBqLlYb2x8tyHP/Y6IILFmF5MXh6/p13U9p3PBSG+6xTm5NeTbV7a2triGedkHeXo/3tXc\n",
"oCJXJbMbCzL0x+V5Z2enIc/9joggsW5zmJd7vX5YYkHX9TTDR9f11pbQWToo+CAiMEvw8bySpflR\n",
"8OkEQgs+hBDTNCmlQRCMx+MgCGDVzCZKJiYo+Ihm3EV5oblY/9mfoeAjlrGwgg9fhg+gqmqPM/cR\n",
"RHzCkHCNr632HHykBG7BZ8VBwQcRAS7BZzQikpQ3RkRDdMFnxbl27Rpuyy6UcRc3AW9uW/bvf///\n",
"LR6fNdCIEWnBWNht2edp+m3bHg6HJ0+e3NvbMwyju3O4uHRG4ObNm7hVi1DGXdwYpKFYhyHZ2PhB\n",
"E565jLsYEUFi3eZWLdyCz2g0iuPYNE3IcLJt27Zt13W5cphaIAgCx3GCIKCUFkcm4jgejUZwCWEY\n",
"TiYTRrco+CAiUCr4GMaB1JO730uNEdEQWvCxbTuO48lkkma2wn68w+GwgbIthOd5uq7P2jASclJN\n",
"0zRNszhZoQIUfEQz7qK80FysX3nlOw157ndEBIm1uIKP53nFGVuqqsZxLNo6/pTSipkXQRCkrwKq\n",
"qrLLPlevXsWmXyjjLjY0zcX6O9/Bpl8sY2Gbfj7B5+TJk1EUFY8bhiFmxicEqVgwwzCyz7DhcMio\n",
"+aDgg4gACj79Q2jBpx9r9RT7+OzXtb+/j8O8Qhl3cVCxuVj/7d/+TUOe+x0RQWLd5jAvX9OvKErp\n",
"TDbP81ru8huGMSjAtY72fERRhLN5hTLu4tzR5mL9x3/8xw157ndEBIn1jRs32I0XhWtPr+l0Ksuy\n",
"7/vZgzCaWtOuYTXjum7pnpG5Amuaxujw0qVLDz74YA0lQ5AFoDQp/uYoTVy3ZC9GXS8xRkSDUnrq\n",
"1KnWTsct+Ewmk9FoZBiG4zjj8Xh3dxf26uJ95MDXKww8zxsOh9CXr33qQO5RzO4fBR/RjLsoL9QS\n",
"69LDpYLPrLxrjEgLxj0RfMitvdcVRYHW03VdrnYfGvS9vT3HcSoGym3bNgyDUjqZTCRJGgwGvOWs\n",
"RlGU9Oye5ymKwvhFFHxEM+6ivFBLrEvHp1DwEc24J4LP4vi+D3qR67qqqpbaRFEky3J2J3tKqWVZ\n",
"XCeCjCNFURRFgc+5U2iaRimllGqalj1XNRcvXjx79iyjcRRF7J7ZLZMkmU6naAzwVjK7cXNXt3is\n",
"Zwk+X/va/1cUfEqNZ3nmKkYpXYyICLGmlO7s7LB7XpB5Vu5cBJb+teM4mqZlpwfruj4cDrlWh67e\n",
"JFKSpMlkAg9k9i4/IWRzc5NrqxZ2z7hVy3zGXazk5opx//3vashzvyMiSKzb3Kqlnl4/b5c8qez1\n",
"g86TOyjL8jwlq5snnnhiLcP6+rqqqhsbG3fffbeqqnffffdDDz2UJMlDDz10/Phx13XPnTt3/Pjx\n",
"JEmeffbZjY2N7IckSTY2Np599ln48LGPfSxJkuPHj4OH9AO4yn549tln19fXK1zBh9TD9vZ2hatc\n",
"qSilFa5ypaKUVrjKlWpvb6+JC3Rd96677mK8QBj2Z7zA7e3t6rrKelhfX6+uq+yHj33sY9V1lXVF\n",
"KS26uvfeP9je/le5Uq2vjy9d+gPXzbuiNNne/letXSDc9jlX8CF3gRsbG+fOnXNdN+szV1cPPfRQ\n",
"5gLXK1zlSrW9vV3hKleq3G2fc5UrFdz27BeYc7WxsQFtxcbGxtbW1tphkraop+mf1YhXUNH0a5pW\n",
"TMuZ4xRNgIKPaMZdlBcaFXxKj6PgsyxjFHw4EHkpUBR8RDPuYiU3V4xPf/pd7JNbMCItGAsr+OB6\n",
"/XxcuXKFfRM1z/PYl/vgWhiEa/Jav415K5nduLmr63esuxgRQWJ9/fp1duMFObrXb9u24zjVNryr\n",
"3lfDNe7aMseOHdvYYH1Vaq4rwTV3ut/GXazkRovB3tRgRFow5rrAzc1NduMFOboVC8MQsiQrbGpf\n",
"QSG7smZ6pN5TzAcMzjAa42+gBeMuVvLixYjj8olas5r+Ug0VI9KCsbBNP5Pgk6bGz6LefVo0Tcu9\n",
"JUG6Z42nmJs4jnFKl1DGXZxA1O9YdzEigsSaXUxeHBG1fnjDSOs3jmPYWWWphTpga2uLa5iX/aHY\n",
"+/Gu5gYVuSqZ3ViQob9Sz7MczCpGqT1GpAVjYYd5j16vH/Jtqi9gMBhUT6FKGY/H0KOH3V1SHSn3\n",
"9TiOB4OBoiiSJMF+W4I0/bhePyICs9brN82D/x9pjIiGcOv1szyWGdt9QgilFKbV+L4fRZF7i+JJ\n",
"fd/XdV1VVdd1BWn3CQo+4hl3UV5oKNZhiBERzlhYwUfEvP4UkVN9EEQ0erGREtISfBs0Iij4ICKA\n",
"gk//EE7wQbJcu3YNt2UXyriLm4D3O9ZdjIggsW5zW3ahBR8BuXnzJtdWLeyecauW+Yy7WMmCFAMj\n",
"0oKxsFu1HC34BEEQxzHLLAZ2y+6Cgg8iAuyCj+cR6KSi4CM4Igo+sAd6xWsO7L01HA7rndslICj4\n",
"iGbcRXmhlliXZo6UGs/qjGFEWjAWVvA5uulXFMX3fU3TRqPR7u5uujGv4ziGYaQHVVWdTqe9z8m5\n",
"evUqNv1CGXexoakl1qU/NYyIaMbCNv18GT6O40Aerud5sizLsgw7IAqyykILoOCDiACX4AP/R8FH\n",
"cEQUfFI0TTNNE/ZRmU6nsCf76rT7hJD9/X2uYV72QZ7ej3c1N6jIVcnsxoIM/YlQyVzGXYyIILFu\n",
"c5gXkzv5iKIIZ/MKZdzFuaP9jnUXIyJIrG/cuMFuvCA4pYsPFHwQEUDBp38ILfggKPiIZtxFeaHf\n",
"se5iRASJNQo+4oKCj2jGXZQXGo01e7uEEWnBWFjBh7S2AXw/uHjx4tmzZxmNoyiKoojdmL0Y0+kU\n",
"jQHeSmY3bu7qFo81pQmlJQen02nuuOsmrltiPMszVzFK6WJERIg1pXRnZ4fd84LgQg58bG5ucm3V\n",
"wu4Zt2qZz7iLlSxIMTAiLRgLu1VLbwWfIAgqJiEbhrG3tze4Bfsb3JUrV9jX1PY8j332B9c8Ea7N\n",
"kPttzFvJ7MbNXV2/Y93FiAgS6+vXr7MbL0pr7xctY5omzDyAWQg5YMeYOdyi4COacRflhQVjDQIO\n",
"l+Cj60yeuYoxiy5GRIRYo+BTD5RSwjkWzwIKPqIZd7GSFy+GqpLS3qQge/OyuxUkIoLEGgWfNgiC\n",
"YDweG4bB9UaGgo9oxl2UF/od6y5GRJBYtyn49LbXX40sy2EYwvrScPOZbDNejh07trHBWmnNdSW4\n",
"Vsbut3EXK7nRYrA3NRiRFoy5LnBzc5PdeEG6OpvXMIxiwqyiKLkWHB65R4ZqNBpRSlmChLN5kaUz\n",
"a4LucEgmE5zN21VwNi8TsIpcDsaeexFJkhhHBeI4xildQhl3cQJRQ7GWZYyIcMZcsWYXkxdnRQWf\n",
"IoyjMVtbWzjMK5RxFyu50WKwZzZgRFowFnaYd2mCj+M4YRhCHk4pnufZth3HsaIolNL59v8qFXw8\n",
"z4vjOF1rOo7jwWDg+z6LQxR8kKUzS8MpXb7Ntokso+DTAXou+MBWjnt7e47jVIx927ZtGAaldDKZ\n",
"SJI0GAx4TwRztQzDgIldWQ+qqgZBMBwO4a/D4dCyLEa3KPiIZtxFeaGuWBfdFI3DkMzqpGJEWjBG\n",
"wecASZIopYqieJ43Ho9LbeI4Ho/Hvu9DT59SGsexbdu6rrOfyHXdir/CqIDneZIkzT1CgCBLRFUJ\n",
"46KQPPoEsjK0Nnksh+u6qqqW/smyLHp4SiLs+ttKuY7g0qVLa2trGxsb29vba2trd955J6X0rrvu\n",
"euCBByilp06dOn/+fJIk58+fv++++7IfPve5z21vb2c/JEmyvb39uc99LvvhvvvuAw/pB3SFrnKu\n",
"XDd56KF/sbNz0XUPudrY+N+TJKH0kKvHH/+/kiS5664vt3mB58+fz7mCDzlX29vbOVf33Xdf713d\n",
"ddddlNIHOlYC9AAAIABJREFUHnjgrrvu2t3dXV9fX1tb297eXl9fX19fT9pCxKYfdJ7cQVmWmy/U\n",
"0Vy4cAHCCXz0ox/NphjlJm1Pp1P2Od9cs8O5VqHotzFvJbMbN3d1C8Ya1maA/7JQmrium1vIAf5Z\n",
"unInRqQF47J1OG7zG7/xG2ljcvr06fSJ2wLzCD6e58EgLYgq4/FY1/X5hmFLSSdbZeEaVW+Omzdv\n",
"njp16uWXX2Yx5tqlod/bdzRn3MVKFqQYGJEWjIsXmG3csp8Nw/i93/s9ds+LwvussCxLVdXJZJJ+\n",
"17IsvXR1qEoqev2qqhafq7OMW+bSpUsPPvjgskuBrDQVvf6k0MGv6PUjQgGKcWun48vwgf6+67pp\n",
"ZiQhRNd1rlHsTnPt2rU333yT0TgMQ/YOAldXgmthkH4b81Yyu3FzV9fvWHcxIoLEen9/n914Qfia\n",
"ftu2S/NhIGOnpiIRRVHqclU7V69exaZfKOMuNjT9jnUXIyJIrNts+vkEH0mS0s/Z786x/H31MK9p\n",
"mhWnXiIo+CBLBwWfXiK04FPjWG4FmqblnquO42QlpiWyv7//9ttvMxrHccw+itX78a7mBhW5Kpnd\n",
"uKPDvOzmGJEWjLli/dZbb7EbLwhf068oSqms73lejSoNuEqnzMEML675XM0RRRHO5hXKuItzRxuN\n",
"NXsqHEakBWOuWN+4cYPdeEH41vCBKbiQ07m2dvDd0WjEPid2PB5Djz6O4zAM0wdGbvItrKujKIok\n",
"SZ7n6bouSNOPa/ggSyf7SpzNgi5dwyc9SGn5Xl2IIAi9ho+qqpqmwQo8hBDHcYbDIbm1LgILMCrg\n",
"uq7v+1EUpVMbcmaSJPm+r+s6JHoK0u4TFHzEM+6ivLBgrCu+PasYslyy4A9GpAXjngg+hBBd1yeT\n",
"SRAEsAiaruvsa5/xoiiKqqrtDDAwgoKPaMZdlBcWjHUQzOy/zypGqQqEEWnBuCeCD4KCD7J0QMMB\n",
"2YdR8CkaI6IhtOCDIAiC9ADu2bywxn36FhOG4WAw4NKzOs2VK1fY19SGDd/ZjdmLYRgGGgO8lcxu\n",
"3NzVNRFr+AliREQz5or19evX2Y0XhWsWgO/7sixblpVdotI0zTnW8OkoFy9ePHv2LKNxFEW5tTyr\n",
"jdmLwbX0Y7+NeSuZ3bi5q1sw1jA/Kzely3UT00ym02nplK7i/K9Sz1zFmEUXIyJCrCmlOzs77J4X\n",
"hG/lTsdxKKW5fBtK6d7eXq3PI3HZ3NzEvXmFMu5iJTdUDEXBiAhnLOzevNyCT+ms2nrX8BEZFHxE\n",
"M+6ivFBXrItJhkXjikREjEgLxj0RfGbZz7GGT0dBwUc04y7KC7UIPlF0aGUekHRQ8BHNuCeCj6qq\n",
"cRwXX2FWZ5gXBR/RjLtYybUUo9QHRkQ0454IPoqiwDzeLHEce55X3Ferl8RxjFO6hDLu4gSifse6\n",
"ixERJNbsYvLi8PX6KaWDwUCW5bShj+N4OBxSShsom4hsbW1hr18o4y5WcqPFYF9lACPSgrGwvX7u\n",
"DRqjKFJVVVEUSqmmaZDr2YQUJSa4Xj+ydFI1v6j1JzPW6y/V+hGhEHq9fkKIJEmu604mE1VVdV2f\n",
"TqfirK3WAij4iGbcRXmh37HuYkQEibW4gk+KLMtcbz29AQUf0Yy7WMko+MxnLML9xmvcH8GnW7iu\n",
"W5GJ5fu+7/tcDlHwQZYOCj69RHTBpxSuBazbIQiCvb09z/Ns2x4Oh7n0Uxiddhwn3XKAkWvXruG2\n",
"7EIZd3ET8H7HuosRESTWbW7LPqfgk2M0GhW3W1kisKej7/vwzyAIxuNxdj8Z2PER8pRgTTrG3WZu\n",
"3rzJtVULV5nZjQXZhkIE4y5WctPFiGOmDbkwIi0YC7tVC7fgQyktVa+aeCWZm+l0mlNy6OHXYFVV\n",
"K/5ZAQo+yNKpFnxM85C2g4JPVxBa8DEMI47jonou2nwuWZaz28QXXypzm8izD8Wg4COacRflhUZj\n",
"ffjWvk2x94kRacG4J4KP53mu6xYbyub2aFycOI5Ho9FkMkmPFNOt2IfsUfARzbiLldxoMUrvZUki\n",
"nkdySy9iRFow7ongw2vfHJRStUBO1UluTUDLiT++7+csi1+cBQo+yNJJd8coFXxy2k6pOoQIiNCC\n",
"j6ZpgiTzmKbpFsgN1UIaj2maOXlHKbwSs1/U/v4+V6+f/Znf++5Pc31MrkpmNxakJ1j0XCFPYkRE\n",
"Mxa218/X9FNKS9eq5sqPBBzHGY/HFQae5w2Hw8FgAAMMvP6DIIC8nWJDTwqaD7v/KIpwNq9Qxl2c\n",
"O9rvWHcxIoLE+saNG+zGi8L1jmBZlqIosIBPFlmWGT24rqtpmqIomqZV5NXAiXzfj6IImm+ucvq+\n",
"r6pqdqXsosKTbjDgui4KPkiHqM7wQcGnowgt+DiOoyjKIvk8kiRRSn3fr1j5B7LyXddVFAXsVVXl\n",
"etI6jgNqz+AWua9TSm3bhi3mbdtmX3kUBR/RjLsoL/Q71l2MiCCxFneY17Ks0nUR5tiW3XXdWb1+\n",
"y7Jy3fDpdMrb8WdhjoUcnnjiiTvuuOPJW/z6r/96drAhtyMPHGT0zLXNGftrSu+NeSuZ3bi5q1sw\n",
"1qUdeUoT14XX2UO9fk0rMZ7lmasYs+hiRNqMdbbFeO6559LG5Od//ue3trbYPS/I0jJ2Kpp+Sulk\n",
"MskdZNeUGuXSpUtra2t33HHH8ePH19bWdnZ2YFu13d1dSunZs2effPLJJEmefPJJKHD64ctf/vLx\n",
"48ezH5IkOX78+Je//OXsB1mWwUP6AV2hq5wrSg8+6PptD6r63+CD6yZ33XUhdaWq/w087O46rV3g\n",
"k08+mXMFH3Kujh8/nnMF60L22xU0Gru7uzs7O4888sjm5uba2trx48c3NjbW19eTtqin6efarBKo\n",
"aPo1TSs+Ktkn3DYKav3I0pnV6wdQ6+8oQmv9sxiNRrX4AUTe6ffKlSvsa2p7nsc+8Y9rimBpntVq\n",
"GvNWMrtxc1fX71h3MSKCxPr69evsxgvCvXxbaagESfZvgZMnT25tbTEal+aV1mLMtT1Ov427WMmN\n",
"FoP9t4gRacGY6wK3t7fZjReEr9cPi1xCkg9sxa4oiud59S7kwFVZLbO5ucm1VQv76kC937OiuY1B\n",
"uCqZ3ViQ7TtEqGQu4y5GRJBYt7lVC1/Tb9u2ZVmapkmSBA8ATdM0TeN6qWGhOA+Ca2ZEc6DgI5px\n",
"F+WFfse6ixERJNZtCj58w7ySJMGH3DQoRVFyeY1HUjHMCxOyskcmk8kc+aNNcPHixbNnzzIaR1HE\n",
"Xi1cFcg1rt5vY95KZjdu7uoWjHXFMO90OmUf5sWItGDMfnWQK8jueUH4ev2zXl5UVa2xVw6CTzoJ\n",
"C2Z4CbL5Owo+ohl3UV7od6y7GBFBYi2u4KMoStrEzze0Ox6PYXqtYRhBEKSzbXNmk8nEtu3RaGQY\n",
"xmAw0HVdkAGAOI5xDR+hjLu4Yky/Y93FiAgSa3YxeXH4MnxgUBdUflhVDZ5pQRAw9sphzZ8jzSRJ\n",
"8n0/CII4jmftC7YUtra2uHr97J773RNszriLlSxIMTAiLRgL2+vn0/qjKEpXPphMJoqiWJal67og\n",
"QnwL4JQuZOnglK5eIvSULkjsgc+aplmWFYYhPAAaeCqJCAo+ohl3UV5oOtaMcyIxIi0Y90TwyQEL\n",
"ONdVlE6Ago9oxl2s5EaLUboXYy2eGS27GBFBYi2u4IOg4IMsnWrBZ9bndAlPREyEFnyQa9euvfnm\n",
"m4zGYRiy50FxZUxxzRPptzFvJbMbN3d1S4l1sauKEWnBmCvW+/v77MYLspDgE8dxEASwoUpdBRKc\n",
"mzdvcm3Vwu6539t3NGfcxUpesBgV6jFGRDTjnmzVYpqmqqqQzzOdTiVJUlVVlmWurSc6DQo+yNKZ\n",
"T/DBDB/BEVrwgS0LTNMkhIzHY9M0XdedTCb1LtosMij4iGbcRXmh37HuYkQEibW4go/jOKZpgryT\n",
"LtgJeT6g/DRSRpFAwUc04y5WcmvFqD4PRqQF454IPunybcnhbbMopSui+aDggyyd0qSdWdO7TLPE\n",
"ABEQoQWfFM/zuJJbe8P+/j5Xr5/9md/77k9zfUyuSmY3FqQnWOE5+xOEsd+iccWrOEakBWNhe/18\n",
"Tb+qqo7jEELCMMw2/bCwT81FE5IoinA2r1DGXZw72kSs4feHERHNmCvWN27cYDdeFK53BN/3JUmi\n",
"lMqynK5DbVkWXZmXSRR8kKXDnuGTXc9nZX6jXUVowUdRFGj9XdeFwV7DMBzHWZ29eVHwEc24i/JC\n",
"v2PdxYgIEmtxBR9CiCzL0OuHf6b5nXUXrB48z6v3sYSCj2jGXZQX+h3rLkZEkFi3KfisJUnS2sna\n",
"JAiC0WikqiohJAxDy7KyU44Nw/A8Lz2iaRrjfgOf/OQnX3755ddff72JMiMIC4ZBTPPQh1mfIQFd\n",
"VfMGiIAYhvHCCy+88cYb7ZxuoYUchAX2dPR9H/4ZBAFMQMvawMzkZZQOQRBkySy0fFscx57ncYlZ\n",
"7QB7e6X/rDH76MqVK+xranuexz7xj2uKoGEYaAzwVjK7cXNX1+9YdzEigsT6+vXr7MYLwtfrH4/H\n",
"kNEPm7Ts7e0pigJyilA96Nycg9LJ4iAyxnGsqip74U+ePLm1tcVozPXI4TLm2qS+38ZdrGRBioER\n",
"acGY6wK3t7fZjReEr+kvruGj63oQBMPhcDqdNlPCRYnjeDQa5QaiZVkOwxBafOh3mGw66ObmJm7V\n",
"IpRxFytZkGJgRFowFnarFj7Bx3GcdJN0z/Pg6Zeu4dNIAWdgGMagQPFFLI7j4XCYrjuUous6aP2q\n",
"qpqmGccxYyIQCj6iGXdRXuh3rLsYEUFi3abg0+c1fKIoUlU13Ue+AvbyX7x48ezZs+wFSCe+sRgz\n",
"WiZJMp1O0RjgrWR24+aubsFYV0zpAmPGKV0YkRaM2a+OUrqzs8PueUHmzPARfw2fIAhs2zZNk1Fr\n",
"Y3wvQ8FHNOMuVrIgxcCItGDcE8GnxjV8HMcZj8cVBp7nDYdDkHF4k4iCIDAMI9vuZ9/RPM+DqwAg\n",
"T4mx/HEc45QuoYy7OIGo6ViXipfFgxiRFoy5Ys0uJi8OX6+fUjoYDIIgcBwnzZq3bVtVVcaHm+d5\n",
"tm3DkyOXgpnFtm3bti3LkmXZtu3BYJCejgXHcUDlT48EQZAO5KqqCutPwNMrCALYeICFra0t7PUL\n",
"ZdzFSm66GKXfKB7EiLRgLGyvn0/rT5JkOp2appmqXZRSVVW17MLhlfi+D+K767rZ0YIsURRll4eD\n",
"s1iWxVvUI3Fdl2UkIAsu34YslyjC5dv6ScvLt3E3/XVR0fQXlwKdTqeKorRSriP48Ic/vLa2trGx\n",
"sbW1tba2dvfdd6uqeuLEiTNnzqiq+vDDD8PGxbquP/roo77vf/zjH3/00UeTJPn6179++vTp7Ick\n",
"SU6fPv31r38dPnzhC19IkuTRRx8FD+kHcJX98PWvfx3G22e5gg+pB1mWK1zlSmVZVoWrXKksy6pw\n",
"lSvVZz/72SYu0Pf9XLVXXCD0PBgvUJbl6rrKepAkqbqush++8IUvVNdV1pVlWVlX733vb5rmgStK\n",
"b3v46Ef/4vTp09BDOn7898DDvff+2nPPvQiuHnnkm+1cINz2OVfwIXeBp0+f/vjHP+77ftZnrq50\n",
"XU89ZO+KoqtcqWRZrnCVK1Xuts+5ypUKbnv2C8y5OnHihKqqZ86cOXHixLve9a53vOMda2trICes\n",
"r68nbSFi008pnUwmuYNwmy6dCxcunDlzhtF4Op2yJwNwpQ1w5VP125i3ktmNm7u6RWI9qyMPn8GY\n",
"sdePEWnBmP3qKKX33HMPu+cFEXENn3SyVRZBEoruvvvujQ3WSmtOQOSaO91v4y5Wco3F8DyS/XvO\n",
"OAiqdunCiLRgzHWBm5ub7MYLstAaPg0h4KJAKdeuXXvzzTcZjUsXkKgwZi8G1zyRfhvzVjK7cXNX\n",
"V1esi01QzjiOq5p+jEgLxlyx3t/fZzdekHqafq5sp05z8+ZN3KpFKOMubgzSZqwrEkwwIi0YC7tV\n",
"Sz1a/yzVvoJqrb+ops1xiibADB9kuWTl++zn7O/jyBQgRECE3qCxNYrzIFpeI2gWKPiIZtxFeaGJ\n",
"WIOwgxERzbjngk+9aJqWq1zHcTRNW1Z5sqDgI5pxF+WFfse6ixERJNZtCj5Hb9AISyBAFrBhGKW9\n",
"7yAIoijiOrHneePx2HXd0r8OBoN008Q4jgeDgWVZNe64Mje4QSOyXLJ7Ls7af/HIHRwRARFug0Zo\n",
"6+HZFQSBqqrFJph9FVPY7AUchmE4GAzgeO4ZMJlMYMUISZJgdWgR2n1CyP7+PlevnzDP5I7jmH3O\n",
"d24NpVU25q1kduPmrq7fse5iRASJdZu9/qMFH9d1XddNW15FUdQC7NcGQ7iwgkIURe4tcmaSJPm+\n",
"r+u6qqqu63Jti9MoURTh8m1CGXdxsbB+x7qLEREk1jdu3GA3XhSuQWFN00pnsgmSftMCmOGDLJdZ\n",
"GT6lyTyY4dMhhM7wgZ2tGnoIdQJewQeHeZs27uKgYr9j3cWICBJrsQSfLLMUrlmjtf0DBR/RjLso\n",
"L/Q71l2MiCCxblPwOTrDB8mCGT7IcsEMn77ScoZPPXn9XG9ACIIgyHKpp+kfjUa1+BGfK1eusG+i\n",
"5nke+8Q/rimC7Nm0vTfmrWR24+aublmxzsnOGJEWjLliff36dXbjReEaFK4Y421mFFo4Ll68ePbs\n",
"WUbjKIqye40dacxeDK4F3/ttzFvJ7MbNXd0isa7O8AFjXT90EDDNJJedhxFpwZj96iilOzs77J4X\n",
"hLvXn0vujKJIVVWujXM7zebmJtfevOwzHnq/SWlzO8FyVTK7sSD7tdZVjOKcSIxIC8bC7s3LneGT\n",
"uxJJkizL4noD6jQo+Ihm3EV5oelYM7Y2GJEWjHsi+MxC0zTe/c07Cgo+ohl3UV5YJNZZ3WaW4FM6\n",
"pStrPEeZ+x0REWLdsuBTzwaNsiyLvLVWjfAKPuyeUfCZz7iLlbxIMXIbbwXBob26MCKiGfdE8JkF\n",
"rLNWiyvBieMYp3QJZdzFCUQLxjr9qSlKPmknZ1zdH8OItGDMFWt2MXlx+Hr9tm0XU/jDMJQkSZCV\n",
"NZtma2sLe/1CGXexkusqRtFNzrj6PBiRFoyF7fXzzeYdDAbFkV5FUQTZR6UFcDYvslxyk3KrJ+5m\n",
"D2an/iICIvRsXlmWNU0zDyNyu+95XsULF9fLJoCCj2jGXZQX+h3rLkZEkFiLK/hYltVQOWrHcRzb\n",
"tkGGMgzDNM2sJBXH8Wg0ghe38Xg8mUwY3aLgI5pxFyu59mKkzQtGRDRjYQWf3s7CNU0z/RxFkZ5O\n",
"cEySJElgxxj47LouZV7LHNfrR5ZL7laFf7puMpmU2FQndyJCIfR6/R2CUpp+liQpl3sKO03CZ1VV\n",
"2V/Krl279uabbzIah2HIvrAd1xJ4XPNE+m3MW8nsxs1dXROxhs4lRkQ0Y65Y7+/vsxsvCIfgE8cx\n",
"JHF2LpnHtu3cO1ruEthfym7evMm7N28TxoJsQyGCcRcrWZBiYERaMBZ2qxZWwceyLEVRKKWapqmq\n",
"yjUdcYlYliXLck7t8X0/p/Cg4IN0hVmCT1bMQcGni4go+IRhOB6PXdc1TXMymaiqOh6Pm34mVWMY\n",
"xqBAcW0NXden06ksy3WtMoSCj2jGXZQX+h3rLkZEkFgLJ/jYtk0pTVURSunu7q651C1/uM5OKTUM\n",
"IwgC0HkURXEcJ2vAHh4UfEQz7mIlC1IMjEgLxt0WfDRNy63VrKpq9gi7YJIymUyySThFXNcFcYlS\n",
"uri+lE3pSZJEVdXsX3P/rAAFH2S5oODTV0QUfI58cLFnyHieNxwO9/b2HMepeG+ybdswDErpZDKR\n",
"JGkwGDD6T8uTLVIcx57nZfeZURQlPbvneewD1/v7+1y9fvZnfu+7P831Mbkqmd1YkJ6gCJXMZdzF\n",
"iAgS6zZ7/W0nd0qSRCn1fV/X9Vk2cRzD0IKiKGCvqirXDDpZlm3bHo1GhmEYhjEcDnOT0Sil8HQx\n",
"DAPkLEbPURThbF6hjLs4d7Tfse5iRASJ9Y0bN9iNF4Xl1UBVVV3XaQZIm8n+k/d1w3XdWTKLZVk5\n",
"BWk6nSqKwnuKKIpc163YSMD3fd5tBi5durS5ufmLv/iLjz766Llz5z74wQ9SSi9cuPCpT32KUvql\n",
"L33ppZdeSpLkpZdeunz5cvbD66+//vzzz2c/JEny/PPPv/7669kPly9fBg/pB3SFrrKuLlz4XtbV\n",
"P//nP37++eddN7l8+W9SV0888TJ4SD9cvnz5i1/87mTS0gW+9NJLOVfwIefq+eefz7m6fPly711d\n",
"uHCBUvqpT33qwoULly5d+oVf+IVz5849+uij999//x133JG0xZzr9Te6bk8YhjkFZr79ACRJqthM\n",
"mBSy+1nY39/f3Nz81V/9VUmSvv3tbz/22GPnz59fX1+/99573//+9+eWdYvj+OrVq4ye//7v/569\n",
"GFEUsRv/6Ec/OnPmDKNxc2++f/VXf/Xggw8yGrNfYBzH7Hsbcd1FP/rRj9iNuSLCFWveiMxaZuD4\n",
"8TeDgDz88O0jDV0g121/9epV9qDw3vb33Xcfo3Fzt32xKt73vvd96EMf+vM///M33njjve99ryRJ\n",
"P/jBDz74wQ/+0R/90Xe/+112z4vC8nwoDvPmYB8mTano9Zeebo5TNMETTzxx//33Mxq7rltdbzlj\n",
"9mJwjav325i3ktmNm7u6RWJdPcwLxpQmsJFUqfEsz1zFqKCLEREh1pTSO++8k93zgixtDZ+Kpj+X\n",
"PpQebL5QR4MZPshyYcnwsaz0SVD1XUQoRMzwQRBETErFEp6VJZEVRcSmX+Q1gq5cucK+prbneewT\n",
"/7imCHJNTu63MW8lsxs3d3WLxLo6YWQRY65iVNDFiAgSa/ZRq8WpZ1v22smurJkeWVZhspw8eXJr\n",
"a4vRmOsZxmVckRq7asZdrORFipH7am7hwdQY3gaqzyNgRMKQSNLMfSVFuN94jblqY3t7m914QUTs\n",
"9WualntUOo4jyF5gm5ubpVu1BAExDGIYZDi83dWSJIl9TdDe71nR3MYgXJXMbizI9h0sntOUEzBW\n",
"FHJ4pZL5Pc9hPHdE4Ec0Gs0svAj3G6+xsFu1iNj0w3MynTcBM7y4nrTNMUvwsW1CKTFNYlnEcQi8\n",
"EaLg04JxF+WFGmMtSQc3G3QuwViSiK6TI5dYrP0C4YxpJbO8qKfGtk1sm0wmZDIhcUxKzybC/cZr\n",
"LKzg03aGj2maqqqqqgozddVb5MyiKFIUBWaNKYpiWVbL5ZzFxYsXz549mztoWYf2SEpupVJEUQSr\n",
"D1UUP4puGydJMp0mLKlMU8jdq8T3DzL8WIy5PAtlnFZy7cbNXR3XmlQ5z9VZOlljSo/I8Kn3AqfT\n",
"RFES1z2o5ChKNC3R9YTSgwSk7OzJKEp0PYmiA2PXzZet+JuqvcDtGLPHmlK6s7PD7nlBhN6g0fd9\n",
"13WF2hugNLnz8HYASZIklnXoRleUJF2qzvcTVT34K/wATPP2s0HTkuzPIIoSzunGB04oTUwz0fWS\n",
"3w/SadgTNKMo3+doNLkTJhOkp0h/AlF00PRn73NdTywr7fQkmlbiEJ4NqwMmd95GURRVVbnEsqaJ\n",
"4zi3hk8cl4xKqSrxvIP1SRyHUEriGI4Q2yauSxyHjMdkOCSmSSglYUj+7b/97+Mx0TSiqkSSiG0T\n",
"zzvQPQ3jQMwNw4MPFauIjEYH0hOlxLJIGJKPfIRjiqAgK5/0e8WYdtbwAdmHxRjuMdDZZ0nt1cWA\n",
"21KWSRyTl176LlQzaFCSRFSVqCqBhbJsmxgG0TSi60RRyLPP/nA4jA+vsHVAUbMS4X7jNeaKNXv2\n",
"4OIImuEjLFtbW7lhXschxRFoWYZcBYkQEgSEUqJpZDgkcUwmE0IIMU3iOMQ0Dx4blJJPf/p/efjh\n",
"A1eUEsO4bRzHB78BSSJxTExz5kCTbRNFOZTXQSm5dm19PCaMK9QJMjjGNajI7laQsXRBigHGwyHR\n",
"NELp7R6MYRBZzmcHgXGuo7O3R1SV6PrBWBchRNfJf/pPp9/3vhulBQFLWSaQvqdp5MUXj/2zf3aj\n",
"tD5gsNrzSJrrJ8L9xmss7DCv0IKPgBQFn6LakzueVW8qXmB9n+n1tuKd3fdn/pXSeYQjpFEq4lXB\n",
"IqJN8bumWSIJpkJ8kexx100s68A461nX69RqiiMWy0LXm93wAAUfockJPpCGXIosk3//7//vl166\n",
"LbZUJCwTQggJWPoHsgyqUf6VM45v97xy2LZNKbHt8pmfReOjjXiM05Mu7rk0V2JZgs9weDsLJY7J\n",
"Rz7yXfZFvaAMEJEjg5ItxnhcfQvxVfIXvvD1MCx5Z00ThEACynpOX0AJIZ5HNI1IErEskt007777\n",
"vn/z5t8ydnaPjIhpElU9eGNmvDqo2Frut9HowNtgcKDizjKehbCCDzb9fOQEn/F4ppyqquR737v/\n",
"v/yX05WLh96G8cUQ7r/iKyeUpNSHLMuM2X4k817P8pxgefMdjw9+MAu+U0PCX7H1XySvHwZU2MuQ\n",
"AiqEqh4o46MR+dCH3gaNjrEYoJxQenRQ0mIYxsFXWIxZ+M//+UOz9jlVFGKaB81uGr5Uvo/jA3G/\n",
"tOI/8YnkYx9j3b+aJXyqSiyLjEbkrbf+1yMdBgEJQzIek299658yloHMqDfHIZZFZJmMx2Qyuf2M\n",
"RMFnFckKPvCqW0FD76rFXfeyuROMX6zGNBNKE11PeNLYZp40e97pdE6fUJjqCucC9Jb5YpRmpPj+\n",
"odytaldRdPvasyusVWsjkK9Vi2SnabedMDpMk4+TW0k7EIV0cdA2YZFc0oKZ5jwlzMlZRefzAYl8\n",
"1aDgIzTXrl17882DHs2RY6c/+cmPf/KTHzN65loEHOaJeN5Bj0xRqnI50kklikKOfFUFYxhMNs0j\n",
"+qSf/eyrjAUOQ+J5HvTcIZ+kuiS5iTAgrMnygd51+E8he9WlxiBcQCqUopRPIJo1Gcfzbq+PpigH\n",
"94CCBsilAAAUSklEQVTneTDAXjHdx/MOhIswDNPRS3gbC0PiOAdvIdkLtG3yT/7JdyAWLCsCVE8g\n",
"gvmGUP+aRuL46NlGkFkAnqHXD9cexzMXiZsvIix85CMvHTlLOS3Y+vp32LUWqLfRiKSvbo4z8zfF\n",
"NUsrDMPRiOj6QY5fNfv7++yeFwQzfPi4efMm7M0L90f1m9/mJuzSsMPimX3DClkmL73096p68EJ6\n",
"JOlPS9NuS7dHGhNCJOkgy6J0EQ3PI//u373zD/6gylsQHKRz2DaR5dDzID2JEHKg3pSqYZ5HHOfQ\n",
"n7IJJOPxoUbwX//rrZ/+dOOd7yRhSCzrCCk8reTR6LaxphFZPjiSJdckxfFBo2zbJdUOxppW9fMO\n",
"AuK6xDDII4+8mV6CLB/k8kJSLyHEcUgcH1x+EBBF8Qn5paqrml3mHJJETPOg3VcUYttMbS60/mEY\n",
"pnVrmqTiPFz74XAZ/93f/Q9F+RXbntkoZ8feTpzwg+CX0lsXHq5wtqLMFYYhZMdpGjGM27EoKzBT\n",
"Lw26ZYpC/sN/uOuxxw7y7kajg9/ULNrcmxcFHz5SwYflhbc6pWduptMDhWeOOc4sb8G+f8hzTq5J\n",
"gfli1S/g6ekoTSaT/PuyppXUD4gbMN8HKhCmp2UNsrIJu96SvYri23fWVRHXPZhtl5uVWiQ3DTV7\n",
"gekMJkk6WuSBCVmNppQw4rrJZHJI+VkuFelDuamU2QKnAlfpfZI9GEWJqpaf4sgbPvUAESzOYYbb\n",
"u3SiZcuCDzb9fFy4cOHMmTMJm+o3nU7Z53xzzQ5/8sm/Yle9s/veHDk+4bpu7vGQ/tJ8P1GUQ7+f\n",
"P/zDb1XXQ/pX103+0T/6Se6v2cmfSZJY1u15zq7rwrTn4nhDmk0I056zlVw6KRSAHxsYm2Z58w0P\n",
"J0rT3+1BvcHIRzXZSk6NJ5Pby3JMJrd/8EfGGlofiBTXll4NGVOaPP98wGjOe9uzG0OBi6s+pBwe\n",
"BnOzt3r2T8XW/8kn/4qllwa9oiPrLds7Kb269E47XEJ6zz33HF2ImkCtn49U8GEhjmP291muN9+f\n",
"/vSn7CuZ5jQcSapaVysMw5yMq+sH0zvH4wO9At6dKSV/93f/g7HUqko+85k/zh2EeUPpPFJCiOse\n",
"vA6HYagoxHUPUiyyQDahrhOQj7KVDDOGiozHaSblgXnpS7emHYxwWBYxDPK97/0wjsloRGS5RCLI\n",
"UVSH4vhAtgIJKAhu62ZHxhqUGbBvbttYLuMXX1xnXH6Y97ZnN4YCgxR2ZNnDMExHhhznUMRhxCKV\n",
"5oKAbG//NUsmjqLAjPqqc99KiDr4Z+nVpXeaJB26EBR8xCUr+CyRBZMrZr3PAsXXAkgyya47lF5+\n",
"RYJKNvulNYqFhx5WWhhG4QL63Zo2T1WDoJS+r0CRBFFL5gPehMQh+/I6mRzkzxSnp6VZOqV3aeqB\n",
"awJaMY6KcujrXBWVffHFDB+h2d/ff/vtt7M5HhU01+snZKHO3WRChkNCMjlCKZcv/02xcwdH0iVZ\n",
"dP1gnC0MQxhtLiU3ittQhzRXybmhbEiYgfSYMCRxHH/1q9dYZlpIEvmX//IHkwnrZofZAkOPEvKR\n",
"CDl4s8nWKlesRej1axrZ2Ph7RuOme/3k1rpA8DIXBMSyDt6Qcvebqh70qUsX2oIeN/wpjtnvt0P1\n",
"FoZEVW+ndRlGPuuv+urSdClCyI0bd+7vn2EsxuJg089HFEUwm5elReCdaMpejAVnKqaZHqBLDIe3\n",
"3zr/zb/5f4oto64fUjzSDD/btrO/Lpi9lV5HTldpZ/k2WFImXfYORKG02C+88Pp//a8/Ypxk981v\n",
"/p9zFxiWzwNAMcsKdG3GuhZjRSEnTvw+o3E786s17eDGg/jK8qFliLLGYVj+awV5EEQ59qqQpEPG\n",
"MKU5fQ4V1z468uqg8xTH5D/+x4/dvHk3YzEWZy1JktZO1j6e50mSVONmv5/85CdffvnlX/u113P3\n",
"WaeBVjvtGR2pa+eA1b48L30VuP0wYMk9bQJY1qI4vRmy63gvsJby9OZu6RYwBVpVy0d3RqPbiyQy\n",
"klshMc0Jho7UfDc8vIKfPv2/fe1r/8cbb7wxjwt+etvrdxxnMBh4ngcfcs9ewzD29vYGt2B/5oPg\n",
"Q2ZMYc/RnOBT73s9tIawEouuc3tWFCJJZDI5WNsAXhHAYXNlTimtZFjwoBiju+76h3/8j6/WXoYj\n",
"jXMl6Zzgw2XcguDDbgydkll9P5jfwOVZlsnLL19J/5md61Da7rNcna4TyyLb2z9rc5i3t01/GIau\n",
"65qmaZrmZDIpNu6mabq3YN/9MRV8WBBW8KnXWNPK53y1UwyuSv7gB1/e2fFrLwOvcXdjzYJQOyik\n",
"4mQpmV0EWD2rKrl8+b/DZ5ixWA3L1aUzyG7cuMFYjBpobUB5uWiHx90ppVwZ0ClPPPHEiRMnalxJ\n",
"RjSKm2X2ibnj3hUwfK0U4/aHGhcyopRubW3V5u4oVmIhB9u2i4vtQXcjjmPYHJjLIeq2CLLKpItJ\n",
"8CziKRa9FXwA27Z3d3eDIDAPD+3JshzHMWwA6XmeUbHm1mHiON7ff5ix6fc8j32lJ641odgLzGv8\n",
"2muviVAMdmOuSv7+97//yiuv1F4GXuPmYi1C+Hhve3bjb3/724yWpMnwEWLAutAscMUap3QdDaVU\n",
"LUBnTJsxTXPWnwBd1xlnk3/gAx+4++6PMr50RlHEvqc81+7zXKs+cBk//vjjIhSD3Zirkn/rt37r\n",
"D//wD2svA69xc7EWIXy8tz278TPPPMMu+DR9czKusMR+dZTSzc1N9mIsSFcFH5MnQY9SahhGEASz\n",
"sjwlSQrDkGUHho2Njbfe+kXGt7w4jtk3aoBMAC57RmOufJI777yT3bihRA7O2W0cVbG9vX3s2LEm\n",
"PPMm7bAnHAsSPna3hLPe2O/5EydOcJWhUWPG1BCuWK+trbEXY0GWJvg4jjOufGXyPG84HA4GA8Mw\n",
"eO+8UqqdsN+pb799D2PT/9xzz73wwgtMpoQ899xz7KkOTz31FLvxJz7xCUZLwqkYsHsOgoDL+Kmn\n",
"nmI0fuGFF5577jlGYy7Bp7lKZs8o4/XcXPgaigjXb4RL8OGqt+aMuWLd5+ROaND39vYcx6lQwWzb\n",
"NgyDUjqZTCRJGgwGXGfJZYzFcex5XjqWC8n+ub8yPpmPHz/O/mS+//773/Oe97AbM1oSQh555BF2\n",
"49OnT3fOmP0C3/Oe97BXHVdEmqvke+65pyHPGJEUQeqNK9bZzV+bpm3BR5IkSqmiKJ7nzer1x3E8\n",
"Ho9934eeOKU0jmPbttmfn7Isw7gNeAiCwMpMt1BV1TAMx3FA4cn9tZqNjQ1CWJt+Lnlhe3ub0ZJw\n",
"vvlyiQCCGLNf4LFjx9irjisizVXyxgbH7w4jMkcZiDD1xhXrNgWftpt+ls614ziapmUVGF3Xh8Mh\n",
"e9MvSZJlWXEcB0EgSVJxYACOwDIPXMMGV69effvttxhH7V955ZWf/exnjJ5feeWVU6dOMRq/+OKL\n",
"7Mavvvoqe5pBQ8avvPIKl/GLL77IaPyNb3zjL//yL5uISHOV/MMf/nDpEeEy7n1EmjNmj3UcxyuR\n",
"4eO67qzpJ6Dz5A7Kstx8oY7md37ndwjhmwSAIAjCwvb2dmtNmYgZPmEYFudYsaTftMAXv/jFL35x\n",
"2YVAEARZDBGndNWSz4MgCILMQsSmH0EQBGkUEZv+GpfXRxAEQYqI2PSTspVOuda5RRAEQSoQsenX\n",
"NC2XDgXpnssqD4IgSM8QsekHwSfdPAFmeHHNh0YQBEEqaHtv3vF4DD36OI6zCxu5rps1i+N4MBgo\n",
"iiJJkud5uq5j048gCFIXQm/LDlupwANg2WVBEATpD0I3/QiCIEgTiKj1IwiCII2CTT+CIMjKgU0/\n",
"giDIyoFNP4IgyMoh4sqdwuJ5nm3bkHREKe1Q3lG9JXccJwxDSmldxVuQuq4OdgSC5GNVVXVdFyTE\n",
"TVygLMuUUhEWxK39ZxWGoW3bsiwLkhFe1wXC9lNZVFUtLnLMSmvLQ3cdy7IURfF9P4oi0zQVRVl2\n",
"iVipq+Su62qapiiKpmmz9lpon7quLooiVVUppdPpdDqdwl5yURTVW9o5qOsCp9OpoiiWZU2n0yRJ\n",
"JpMJuK21sNw08bPSNI1SKsgtWuMFEkLcw0Ao5/Q29zdXiiiKZFnONgSUUsuyllgkRmosue/70FJU\n",
"bLPTMjVena7ruQ2CTNOklC5axMVoInzZI5qmLVrEBWjiZ+W6rq7rgtyi9V5gvT11bPqZsCwr1wpA\n",
"H2pZ5WGniZIL8rtKar060zSLB5d+mU3feMvd/K6Jq4N3NUFu0XovsN6mH4d5mciuOQHIstyJLWW6\n",
"W3IWary64tBFGIZL1/obDZ/nefMrxXVQ+9UZhpHb1nu5NBQ+z/MWd4LDvEyIvGdkNd0tOQuNXt1w\n",
"ODRNsxZXc9PEBcL6KJ7nBUEwmUwWcbUg9V4dXJTv+wuXqzZqD99gMIjjWJKkOI5lWbYsa+7nHDb9\n",
"THS3m9zdkrPQ3NWNRiNd15fbKSbNXGAQBEEQeJ639Cy1eq/OMIylP6pz1HuBpmlqmpY+OWzbHo1G\n",
"cz+8UfBBkDyj0UhRFEFSA2tH13XI8wmCoJgv2FFAA1n6o7pRcsm4uq7D+sfzecOmn4nu7hnZ3ZKz\n",
"UPvVxXG8t7cnTrvfaPgsywqCYO62Y3FqvDrbtlVV9W4BotbSt/Zr+tenKAo2/Y3T3T0ju1tyFmq8\n",
"OtglQrTNIRoN3yJtRy3UdXWqqoZhmDb9YRiC9F9HGRdC3F9fjdlCPcb3/Vyu2GQy0XV9WeVhh6vk\n",
"ruuapnnkPCZBMucS/rhUXGAURTDjKXtwkSkztdBE+LKoqrrEWV01hq9oKcIt2nT4cpMGuMCmnxVV\n",
"VdN2AZqJpc+EZISx5GlqxJHTfAT5XQHscam4QJjKm5vSlSSJJEm1F5iXusKnaVruizBsWHuBuagl\n",
"fEXEuUXrCl/x/tR1fZEph5jhw8pkMhkMBkEQpHtGdkVGZyx5muwxK+sjt7nmYDCA47nNNVuGPS4V\n",
"FwiSt23b6Y7QgAj5UXWFj1JqGEY6FgpJ/ZZlNVdyFmoJXxYYu4ZbdDQadeUCj7y6yWRiGMZ4PIbw\n",
"OY6jadoiGU24Sxcf3d0zkqXkYRiWZiKLD2Nc+n2BLFcHNoQQoe5hDB9hu7p07Hrx8GHTjyAIsnJg\n",
"hg+CIMjKgU0/giDIyoFNP4IgyMqBTT+CIMjKgU0/giDIyoFNP4IgyMqBTT+CIMjKgU0/giDIyoFN\n",
"P4IgyMqBTT+CIMjKgU0/giDIyoFNP4IgyMqBTT+CIMjKgU0/giDIyoFNP4IgyMqBTT+CIMjKgU0/\n",
"gqwEQRDA/poNkdvbEhEc3JsXaZDhcDhre1tFURbZWRThZTQaZSvc87zxeEwIkSRpMpkQQhzHgeZb\n",
"luU5trR1HIcQout6bSVGmgSbfqRBdF2HFkHTtNyfoN1B2sG2bUmSsvu+KooiyzLJhEZRFErpYDDw\n",
"fX+OU5imORwOsenvCtj0Iw2iqiqIDMXNprHpb5PxeJx7x5IkCfb1TkMjyzI8DBRFmeMU8CyxbRtb\n",
"/06AWj+yHLLty3g8HgwGg8EgCAJCiOM48E94Y8jied5wONzd3T158uRwOCwVr8Hm5MmTu7u7o9Eo\n",
"DEPbtgeDwWg0AoPRaDQYDLLaNBwZDAa8pwPPtm0HQTAcDtfW1vb29gzDKJYqjmPDMAaDQWpTKr6z\n",
"XCAvnufFcVx88WIErjFH6TVqmoaKf2dIEKRJKKWU0vSz7/tFG9/3XddVFGUymei6TimdTqfT6VTT\n",
"tOl0mppZlqWqaurB931N01Ln6SmyNpPJRFEUTdN0XXddFw66rgtnyRUg93NgOd10OtV1XVVVXdeh\n",
"qFEU5ZzDQUVRLMuKogj+aVmWJEk5M5YzzgGlVNf10uNF58U2Ab7uZgBpqOhwOp0SQuAaEcHBph9p\n",
"FmiLoZVRVTVtf4uoqipJkmVZpX+dTqeKopR+K9umq6pa/GKxkT2y1WM5XeoqZxlFkSRJ1d9KksSy\n",
"rGwZ2M/IC9R/8Xg2NCnFpt80TdM0s98qfZAAhJAFS4u0A2r9SOPIsgyC8qxsnxTTNGcpxbZtQ8OU\n",
"g1LqOA749zyv+HVZludQn1lOl5L7pyRJ2SsNwzCO4+Joh6ZpYRjOd0YugiCYpfakoUkpjsFkS2Xb\n",
"dhzHFfk/qqoGQbBIaZF2wKYfaZw0tyQMQxhanAUMM5YSBMGskeG0oamx0WE5HSNhGJZ+RZKk7IBH\n",
"jWfMUVGrubSfaiD7E5SxCo58wCMigMO8SHvouj5f9gghBEYCSl9d08ZIUZRsPzpljsaI5XTslJaq\n",
"0TNmkSSJpQDVBEEA7X71wzsIgrlDjLQJNv1IN1BV9cjsEV3XQZHIHoQ260j/uW+xnI4R0EBKHz/Z\n",
"FrnGM+ZQFGXBnjjkL8HQNBxxHKfoM47jOI6x6e8E2PQj3UBVVVmW0wTNFNu2U50EZH3ICo3jGNI6\n",
"DcMoaui594MwDIfDIe/p2KGUFic2j8fjrP96z5glnV0xH5CWOplMssIR5LPmLB3HSWeKIYKDWj/S\n",
"IIPBAFpYaCZKF28IwxDauyAIDMNI+5WQf5K1tCzLMIy9vb100BjkhaxPSLUcj8fQgwYVpdh0aprm\n",
"ed5gMIBnQBzHpmnu7e0NBgPLsqDxYjndaDSCVjUMQ1gOIY5jeIpkXcE4M7iCQWDP81RVha9wXeAc\n",
"pGPg2fpMSx4EwWQykSTJtm2YSDEYDHRdT0eGx+NxGIa5RP5iuw+nmHv2ANIya0mSLLsMCMIBNIjw\n",
"mXGIEpqtYgMKOkxuuHXx01WQ9r4rXNV7RgCa9QXHDKoJw3Bvbw9SaZs7C1IX2PQj/WdW079S7O7u\n",
"wpSxhvyPRiNFUXAVh66AWj+CrAQ5cal25ps/gSwL7PUjfSa3LE+jigeCdAhs+hEEQVYOFHwQBEFW\n",
"Dmz6EQRBVg5s+hEEQVaO/x9e+taR25jfhwAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"% Ce code n'est pas commenté, car essentiellement identique\n",
"% à ceux présentés en question 1.1. et 1.2.\n",
"\n",
"%% représentation en temps\n",
"figure\n",
"plot(ech,resp)\n",
"xlim([-1 max(ech)/2+1])\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"%% représentation en fréquences\n",
"figure\n",
"[ech_f,signal_f,signal_af,signal_pu] = Analyse_Frequence_Puissance(resp,ech);\n",
"set(gca,'yscale','log');\n",
"ylim([10^(-35) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Est ce une simulation raisonnable de variations liées à la respiration? pourquoi?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On voit que ce signal est essentiellement composé de fréquences autour de 0.3Hz. Cela était déjà apparent avec l'introduction d'un cosinus de fréquence 0.3Hz dans la génération (ligne 7). L'amplitude de ce cosinus est elle-même modulée par un autre cosinus, plus lent (ligne 11). D'aprés wikipedia, un adulte respire de 16 à 20 fois par minutes, soit une fréquence de 0.26 à 0.33Hz (en se ramenant en battements par secondes). Cette simulation utilise donc une fréquence raisonnable pour simuler la respiration. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 5. Ligne de base.\n",
"Répétez les les questions 1.1 et 1.2 avec une dérive de la ligne de base, telle que générée ci dessous."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%matlab\n",
"\n",
"%% définition de la ligne de base\n",
"base = 0.1*(ech-mean(ech))/mean(ech);"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAABxqSURBVHic7d1BbuvIncdxvqATYIBsqjfeBUG9I1DrrMgjUEBfoIg+\n",
"AXmALKgjkPABXqRN9qoDZKFKX8Bi0LOKgcC1CAbjzsazqBmOQkm2RNGiSvX9IAieZZn6S1b/VP5X\n",
"sfjl7e0tAgCE5FdTFwAAuDaiHwCCQ/QDQHCIfgAIDtEPAMEh+gEgOEQ/AASH6AeA4BD9ABAcoh8A\n",
"gkP0A0BwiH4ACA7RDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6ASA4\n",
"301dgGf+/Oc//+lPf5q6CgB36OvXr3/84x+v81hf3t7ervNI9+GHH3749u3b1FUAuEO/+c1vfvnl\n",
"l+s8Fg2fs/3+979PkuTNQ+v1uiiKqasYoiiK9Xo9dRVDJEnib+VTlzCQp5UXRXHNHCP6ASA4RD8A\n",
"BIfoB4DgEP0AEByiHwCCQ/QDQHCIfgAIDtE/RJZlU5cwhJQySZKpqxgiSRIp5dRVDJFlmb+VT13C\n",
"QP5W/utf//pqj8XZvOf54Ycf/vKXv/ztb3+buhAAd6Usy8fHx3/84x/XeThG/QAQHKIfAIJD9ANA\n",
"cIh+AAgO0Q8AwSH6ASA43kS/1no+n6dpWpaltXaUA+Z5nqbpfD43xlx+QADwhR8XaGyapmmauq6l\n",
"lE3TpGm62WwuOWCe523bKqWyLGvbdqw6AcALHkS/tXaxWGw2GyFEFEVFUVhrm6ZRSg074Hw+j+O4\n",
"rmv3pacnWwLAYB40fFarVZZlLvcdpVTTNMOO5n7wytdCA4Cb4sGov23bOI53b5FSDm73N02zXC7H\n",
"qAsAfOVH9O9vOnZJl0ZK2batG/5nWdb7XPnQ8/NzmqYHv1VV1blHAxCUY+nx9PT0+vp6tTI8iP5R\n",
"1vM4WmshRNM0i8WiKAohRJ7nSqmzpg0eHh7W6/VYJQEIyrH0cNu3Xa0MD6J/XNba1WrVTRpnWTab\n",
"zfzdExgABvBgmnfEFkocx8aYuq7HmjQGAB95EP1RFO2fcjXsJCwhRBzHvQE+430AofEg+rMs01rv\n",
"3uKWex67v9Z6sVgcmyGI47h3NGMM6Q8gKB5Ev2v4dD0Zd4bXsYlZY4zb7CHP84N3KIpi94PBLfXx\n",
"94puADCAH9O8y+UyTVNjjBBCa62UOjYB0DXxd7v5u6SUVVXNZjMX91rr5XJ57M4AcJf8iH4hxGaz\n",
"McZYa92izGP3lFJut9uDpwJ04jjebreu7VNV1adUDAA3zI/od05c6iOlPKV3/85nAwDcNw96/QCA\n",
"cRH9ABAcoh8AgkP0A0BwiH4ACA7RDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO\n",
"0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCCQ/QDQHCIfgAIDtEPAMEh+gEgOEQ/AASH6AeA4BD9\n",
"ABAcoh8AgkP0A0BwiH4ACI430a+1ns/naZqWZWmtvfyAbduWZdk0zeWHAgC/+BH9TdOUZVkUxXK5\n",
"FEKkaXr5McuyjKJotVpdfigA8IsH0W+tXSwW6/U6jmMhRFEUSZJcOFrXWgshkiQZq0gA8IgH0b9a\n",
"rbIsE0J0tyilLoz+siyrqrq4NADwkgfR37ZtHMe7t0gpL2n3l2XZ+ywBgKB8N3UBH2vbdr8zI6Uc\n",
"djRrrdZ6s9lcXBcA+MqD6B9lPU/n8lbP8/PzsXnmqqp6f6AAwK5j6fH09PT6+nq1MjyI/hFpra21\n",
"F87uPjw8rNfrsUoCEJRj6VGW5ePj49XK8CD6RxxHN02TJInW2n1pjLHWGmMYqgMIigfRH0WRMaY3\n",
"VDfGDDhOkiRt27Zt67601rrWP9EPICgeRH+WZe58ru4Wt9zz2P211sYYpdT+Gh6lVO+ebdvuHhkA\n",
"QuDB4k43JO8W8rszvHoh3jHGuM0e8jy/XokA4BUPRv1RFC2XyzRNjTFCCK21UupYi6Yb6b+/bN8Y\n",
"4/YCats2z/O6rscvGgBulR/RL4TYbDZuVrYoindiXUq53W4PngqwK45jVukACJYf0e+cOBkrpRx8\n",
"whcAhMCDXj8AYFxEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6ASA4RD8ABIfoB4Dg\n",
"EP0AEByiHwCCQ/QDQHCIfgAIDtEPAMEh+gEgOEQ/AASH6AeA4BD9ABAcoh8AgkP0A0BwiH4ACA7R\n",
"DwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcL6buoBTaa2bprHWxnFcFIUQYthxrLVN02it\n",
"oyhKkkQpNfhQAOApP0b9TdOUZVkUxXK5FEKkaTrsONba+Xxura3ruq5ra22aptbacasFgBvnQfRb\n",
"axeLxXq9juNYCFEURZIkTdMMOFRZlkqpqqqklFLKqqqyLFssFqPXDAC3zIPoX61WWZbttmWUUsOi\n",
"X0qZZdnuLUVRGGMuLREAvOJB9LdtG8fx7i1SymFdmqIo9g9Orx9AaPyI/v10llKOcvD5fK6UGuVQ\n",
"AOALD1b4fN40bJ7nSqkkSc76qefn52PzzFVV9f5AAYBdx9Lj6enp9fX1amV4EP2fJM/zOI4HDPkf\n",
"Hh7W6/VnlATg7h1Lj7IsHx8fr1aGBw2f0cfR1trZbDYs9wHgDngQ/VEU7S/CGbwsx63lV0qR+wCC\n",
"5UH0Z1nmTr7tuOWex+6vtV4sFgdnCA7mftu2I1YLALfPg+h3DZ9uIb87w+vYmN0Yk6ZpWZZ5nve+\n",
"5U7lLYqi97Oz2ewTqgaA2+XHNO9yuUzT1BgjhNBaK6WOTQB0y0D314MaY9q2bZqmdzoYGzkACI0f\n",
"0S+E2Gw2xhhr7ft7t0kpt9tt27b7SzaTJNlut59cKQB4wI/od05c6uP25/nsYgDAXx70+gEA4yL6\n",
"ASA4RD8ABIfoB4DgEP0AEByiHwCCQ/QDQHDGiX62wQEAj4wT/fsb5gAAbtZ5Z/OmadrbRBMA4J2z\n",
"R/3r9fptx8vLS5Ikm83mM4oDAHyG86JfStnbOk0IUdd1WZajVgUA+ETnRX9d1/t7qLnPg8GXzQIA\n",
"XNk4O3dKKdn1HgAGsDYyJvrll/+45oOOE/3GmHeumAgAcBHftlHbRtZGu73z0zakH9N50d80zf4S\n",
"/rZthRAnbqYPAPfNhbsx0X4rJEmiOI4OXl7WmP++Qm2d86J/tVrtz/RmWcaQH0BoXLi7/++N4pPk\n",
"f1P+Zp0X/VLKLMv2r30IAPfKhfv+GU1SRlJGWRb5eFXA86K/rutPqgMApqX1/47ie4SI4jgqiuj4\n",
"RcH949O1eQHgQq4R7/7XE8eREFFVTVHW1RH9AO6Q68/sL6dxQ3gpD8+1hoPoB+CxY3OtrhF/bDkN\n",
"iH4AHnCj+G6utUt5N4q/8eU0N4joB3Aruv7M/lyra8Qr5eVymht0afRba8uyFEJUgUyOALhY159x\n",
"/+g14sOZa53QpdHfNE3TNFEUJUnCen8Au1yy7y+ncY14In5Cl0Z/t3+D5M8wIFS9RnzHjeKZa71B\n",
"l0Z/d50Woh+4b7sr4v/1r+i//uv/GzWuS3NnJz3dtxGmedm4Dbgnu8sld7Ei/p6wwgcI1LGTnrze\n",
"mgYnCjH6tdZN01hr4zguikLwNyru2rFGPCc9hSy46HdLkuq6llI2TZOmKdeUxx3oWjTHVsTTiMeu\n",
"caK/bVsvpnmttYvFYrPZuJF+URTW2qZpFMMeeMKF+8HLgLAiHqcbJ/rzPF+v16Mc6lOtVqssy3Y7\n",
"PEqp+XxO9OPWHFsRH0VRktCIx6XOjn6ttd7rGu5ftfE2tW3bW4/EBeUxrd3LgOyf10ojHp/kvOjX\n",
"Wpdl6aZGy7Ksqsq1UHy5hEvbtvunHHvRqoLvjl0GxM210ojHlZ19Wfa6ruM4NsbEcexitG1brbUX\n",
"uziMMsB/fn5O0/Tgt6qq4iyHkL0z10rEwzmWHk9PT6+vr1cr4+xR/3K5jKLIWtt1zIuimM1mu7fc\n",
"t4eHBy8mNvB5XLjvNuK7Xk2SMNeK9xxLj7IsHx8fr1bGedF/LNyTJDHG3P7AnyE5zrK7dcFuIz6K\n",
"OK8Vfjsv+rtWT+TP1G7P/keU2f/jHIF5f+sC5lpxf86Ofq216/KXZdk1eYwxXqyPzLLMTVN3t7jl\n",
"nhOWhKvpWvDHzmtlxSTCcV70K6W6wX5RFGmaKqWMMVJKL9bJuL9XunO4/FqehBPtzrW6Ls1uIz6K\n",
"mGsFzu/1d+3yLMuklKvVKo5jL4b8znK5TNPUGCOE0ForpZgA8NRuI76HrQuA9110Nm8cx97lphBi\n",
"s9kYY6y17N3mBdef6S7pJ0T0n/8Z/e537CEMDBfc9m2Od59Yd+/DFfE04oERBRr9mEq3imZ/rpUV\n",
"8cDVEP34FMca8W4IHzHXCkyK6MdFdhvxjmvH04gHbhnRj4/RiAfuDNGP/9f1Z3b3EHb/TyMeuCdE\n",
"f4jeWRHPSU9ACIj+e/b+1jQ04oFgEf33YPdKT7tcxNOIB9BD9PvEhfux3cfo0gA4EdF/c/YvA9Jh\n",
"axoAoyD6J+PCfb8RH0XsEQ/gcxH9n25/rnV3D+EkidhPCMCVEf3j6F0GZPdifpz0BODWEP1DGBOt\n",
"Vv0bXSNeKSIewK0j+gdirhWAv4j+IejOA/Dar6YuAABwbUQ/AASH6AeA4BD9ABAcoh8AgkP0A0Bw\n",
"iH4ACA7RDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcLzZtFlr3TSNtTaO46IoxNDN8q21\n",
"TdNoraMoSpJEKTX4UADgKT9G/U3TlGVZFMVyuRRCpGk67DjW2vl8bq2t67qua2ttmqZ2/7LoAHDX\n",
"PIh+a+1isViv13EcCyGKokiSpGmaAYcqy1IpVVWVlFJKWVVVlmWLxWL0mgHglnkQ/avVKsuy3baM\n",
"UmpY9EspsyzbvaUoCuOupw4AwfAg+tu2jf/9iohSymFdmqIo9g9Orx9AaPyI/v10llKOcvD5fK6U\n",
"GuVQAOCLKVf4WGuPNVuEEN1I//OmYfM8V0olSXLWTz0/Px+bZ66qKuaS7QCOO5YeT09Pr6+vVytj\n",
"yuh36zUPfksIsVwuP/XR8zyP43jAkP/h4WG9Xn9GSQDu3rH0KMvy8fHxamVMGf1ZlvUmXQ8afRzt\n",
"1nQqpWj1AAiTB73+KIr2+0KDl+WQ+wDgQfRnWeZOvu245Z7H7q+1XiwWB2cIDuZ+27YjVgsAt8+D\n",
"6HcNn25WwJ3hdWzMboxJ07QsyzzPe99yp/IWRdH72dls9glVA8Dt8mMPn+VymaapMUYIobVWSh2b\n",
"AOiWge6vBzXGtG3bNE1vbpmNHACExo/oF0JsNhtjjLX2/b3bpJTb7bZt2/0lm0mSbLfbT64UADzg\n",
"R/Q7Jy71cfvzfHYxAOAvD3r9AIBxEf0AEByiHwCCQ/QDQHCIfgAIDtEPAMEh+gEgOEQ/AASH6AeA\n",
"4BD9ABAcoh8AgkP0A0BwiH4ACA7RDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO\n",
"0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCCQ/QDQHCIfgAIDtEPAMHxJvq11vP5PE3TsiyttZcf\n",
"sG3bsiybprn8UADgFz+iv2masiyLolgul0KINE0vP2ZZllEUrVaryw8FAH7xIPqttYvFYr1ex3Es\n",
"hCiKIkmSC0frWmshRJIkYxUJAB7xIPpXq1WWZUKI7hal1IXRX5ZlVVUXlwYAXvIg+tu2jeN49xYp\n",
"5SXt/rIse58lABCU76Yu4GNt2+53ZqSUw45mrdVabzabi+sCAF9NGf3WWmPMwW8JIbqR/ijreTqX\n",
"t3qen5+PzTNXVdX7AwUAdh1Lj6enp9fX16uVMWX0a62PteyFEMvl8jMe0Vp74ezuw8PDer0eqyQA\n",
"QTmWHmVZPj4+Xq2MKaM/y7Isyz6824jj6KZpkiTRWrsvjTHuLw+G6gCC4kGvP4oiY0xvqH6sU/S+\n",
"JEnatm3b1n1prXWtf6IfQFA8iP4sy9z5XN0tbrnnsftrrY0xSqn9NTxKqd4927bdPTIAhMCDxZ1u\n",
"SN7NCrgzvHoh3jHGuM0e8jy/XokA4BUPRv1RFC2XyzRNjTFCCK21UupYi6Yb6b+/bN8Y4/YCats2\n",
"z/O6rscvGgBulR/RL4TYbDZuVrYoindiXUq53W4PngqwK45jVukACJYf0e+cOBkrpRx8whcAhMCD\n",
"Xj8AYFxEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByi\n",
"HwCCQ/QDQHCIfgAIDtEPAMEh+gEgOEQ/AASH6AeA4BD9ABAcoh8AgkP0A0BwiH4ACA7RDwDBIfoB\n",
"IDhEPwAEh+gHgOAQ/UOkaTp1CUNorcuynLqKIcqy1FpPXcUQaZr6W/nUJQzkb+X//Oc/r/ZYRD8A\n",
"BIfoB4DgeBP9Wuv5fJ6maVmW1tpRDpjneZqm8/ncGHP5AQHAF99NXcBJmqZpmqauayll0zRpmm42\n",
"m0sOmOd527ZKqSzL2rYdq04A8IIH0W+tXSwWm81GCBFFUVEU1tqmaZRSww44n8/jOK7r2n0ppRyt\n",
"VgDwgQcNn9VqlWWZy31HKdU0zbCjuR8simKc4gDAQx6M+tu2jeN49xYp5eB2f9M0y+VyjLoAwFd+\n",
"RH+SJL0bL+nSSCnbtnXD/yzLep8rH3p9fX15efFxsfZPP/30888/+1j5zz///NNPP01dxRAvLy/+\n",
"Vu7jWyXytvJRVq+cbsrot9YeW1ojhOgSecRXRGsthGiaZrFYFEUhhMjzXCl1+rTBH/7wh2/fvv39\n",
"73/397SRb9++TV3CEJ6WHUXRX//616lLGMjfN7mnlf/2t7+92mNNGf1a62MteyHEJ7VlrLWr1aqb\n",
"NM6ybDabJUly4p8RP/74448//vgZhQHA1UwZ/VmWZVn24d3Obci8fyhjzHa73Z80rqpqrEcBgBvn\n",
"wQqfKIr2+0LDTsJyfaTeAJ/FnQBC40H0Z1nWm7Rxyz2P3V9rvVgsjs0QxHHcO5oxhvQHEJY3HyRJ\n",
"Ute1+/fLy0scx5vN5uA9u7N8syw7eIftdpskycvLS/ellLL7EgBC4MHiziiKlstlmqbGGCGE1lop\n",
"dWwCoGvi73bzd0kpq6qazWbu7wat9XK5PHZnALhLX97e3qau4VTGGGttHMfvJ3XbtgdPBehxbZ8P\n",
"7wYA98en6AcAjMKDaV4AwLiIfgAIDtEPAMEh+gEgOEQ/AASH6AeA4PhxStftcLuNutML3LbPU1d0\n",
"QFmWvVuSJNk/g+EWnstqtWrb9v2Lpp1S5/Wfy4eV3+BvwV3ZtDujRSl1yYt5a5Wf+IJH01UupSyK\n",
"4uC2MRO85lOfTuyTuq7dHhIvLy9VVcVxPHVFh0VRtP532+22d59pn8t6vXYXycmyLEmSd+55Sp3X\n",
"fC6nV35rv4WXl5ckSYqi2G632+22KIo4jve3MDmxpBus/JQX/MqVb7dbdxlwV8lyuTy4Cc0krznR\n",
"f6qXl5febj9FUXQ7C92UDz/RJ38um83G/QewXq/fCdBT6rzyczmx8rfb+y0opZbL5e4tVVUVRTGg\n",
"pBus/O2EF/xtunfL7i297cWmes2J/lPVdd17t7mP9KnqeceH/w3cznN5P0BPqXOq53J59F+58qqq\n",
"9m/sPYUTS7rByt9Oi/5beOdLKQeUNHrlTPOeatyrw1+H1vpghb48l1PqvP3nciO/hf1pibZte83i\n",
"E0u6wcp3HXvBoxt4t2ite9MPU73mTPOeavSrw3+qNE2ttUIIa62Usq7r3f9UfHkup9R5y8/lxn8L\n",
"8/m8d3G6E0u6wcqd91/waLrK3daTWmtjTO/Ss1O95kT/qW5qIPm+qqqyLOveFk3T5Hm++4bz5bmc\n",
"UufNPpcb/y3kea6U6qXJiSXdYOXRCS94NF3lxhhjjNZ6f1nOVK85DZ871FtAppSy1rZtO2FJAbrl\n",
"30Ke53EcK6WmLuRs71R+yy+4Usqt8zHG7C9CnQTRf6oRrw5/fXEc7/434MtzOaVOX55LdBu/BWvt\n",
"bDY7lp4nlnSDlR/Ue8GjG3i31HVtjBnwNhi9cqL/DGNdHf4W+PJcTqnTl+ey78qVW2vTNFVKvZOe\n",
"J5Z0g5WfaPJ3y/4H0iSvOdF/qnOvDn9TVqvV7qjBl+dySp2+PJdo6t/CwfTsZdCJJd1g5Qf1XvDo\n",
"Nt4t7kKz55Y0fuWDl4UG6PSrw08oSZLe+S9Kqf3zX27kuXy4Ov6UOid5Lu9Xfmu/BXdCbK+kt7c3\n",
"IcSwkm6t8hNf8LfrvluyLOsd3M1FDytp3Mq5QOMZ3OjDXRzYXR3+BifKrLVlWRpj3BIINzTYXwk3\n",
"7XNZLBZuCOMm4rqh2Xq9HlDnNZ/LiZXf2m9Ba53n+f5aQK11LwFOLOnWKj/xBb9m5VEUuUlda62r\n",
"yi3qP7jI5/qvOdF/thOvDj8ta63rA75fpxfPJTqtzht8Lv7+Fk4s6dYqP/EFj65bedu2rj01yttg\n",
"rMqJfgAIDtO8ABAcoh8AgkP0A0BwiH4ACA7RDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANA\n",
"cIh+AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP2AT4wxvctzn65pmnGLgb++m7oAYKCmaVar1bHv7l/m\n",
"9z7keX7wkrOncC/XDV5QGtfHBRrhq7IshRDuwujGmNVq1WVimqZ3+cZ2n3aDP9WMMfP5fLvdjlsV\n",
"fMSoHx6L4zhJEvdvrXX373u1WCwGD/mjKIrjWErZNA0Df9Drh6+UUm7Iv683sNVaz+fzr1+/fv/9\n",
"9/P5vNcrXywWaZpqrfM8//LlS57n7savX7/OZjNjjDtCmqZpmkZRtFqt0jT98uXLbDYry9Jau1+A\n",
"G19///337hFXq9XlfXattbU2y7JLHi7LMjr+iKIoegP8t16vkyQ5+K26rpMk2Ww27svNZpNlWVEU\n",
"3R22261SSkq5XC7f3t6KoojjWCnl7iyldPdZr9dxHBdFoZTabrfdwaWU3cG7A3ZH645/rLzTuYfe\n",
"v/2sh3Mfii8vLxcWA98R/bgHx6J/u93Gcbx/e5Ik6/W6+7IoiqqqukPt/sjuYZMk2Q/f/Yeuqmr3\n",
"o+Xt7e3l5eVgap8lSZLeYYc9XBRFu88dYaLhg3vWNE1RFPu3F0XRWx202zsSQhw74P7RkiSx1rZt\n",
"292SZdlqtVosFl1nSQhR1/WA+ncZY6SU+7ef+3BJkrguFkJG9OOeuSb4lz1pmu6G9ekOhq8QYvdo\n",
"rgUU/d+swNevX/M8H/ZwHz70sIc7OD+BoLDCB/fMde0PTo0O07btfgRba3sTzkKI3b8PXChvNpt3\n",
"/p74UO8DZvDDGWNY4QNG/bhnSZKMu6ClLMveLU3TSCl3Q3b/PlmWSSkvbLPEcXxwtH7Ww1lr9z+o\n",
"ECCiH/csSRIppVuvuatpmsViMeyAaZq6eQJjTFmWTdP0GuvGmN7nTdu2B/9cOPehD27hcNbDrVYr\n",
"t7r/kkpwB2j4wG/z+dyNZNu2devui6LYPberruuyLGezmbvRWmuMieO4OzeqLMvVaqW1Vkq5Toib\n",
"IVgul+4OaZpWVeVGym4ZaLdw3q0U6vVVXGeme8S2bY0xbhnoJc/UHW3/zLWzHk5rPWL7C/5iIwcE\n",
"wSW++/fgk37TND19E4XuEbvdJi73zkYOpzyc+4TYbreXTDngPhD9wKnOiv5P8vXrV3eS2oCfzfPc\n",
"zXuPXhW8Q68f8EnXhhpASknuw2HUD3yst0F0lmVkKLxG9ANAcGj4AEBwiH4ACA7RDwDB+R9OmxoA\n",
"oYASlAAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fiOXYfedP9Z9qT8/0VKmmh8yfpjOosIMNMSYqMtOY\n",
"PHSQNoSms4G2btpMmvhJd0gI2IZwFA80YR+CtMYks+Qh0gyE4IBBwpsHL8mChJMhS8gGybN+SEgY\n",
"S97J2g8VjI4Hd3fcVZ1oH05bo9G9pTrnXkn3HOn3YRhu3/rdo3PO996fpK/On62yLBEAAAAwJc5s\n",
"ugIAAADA0EDqBwAAmByQ+gEAACYHpH4AAIDJAakfAABgckDqBwAAmByQ+gEAACYHpH4AAIDJAakf\n",
"AABgckDqBwAAmByQ+gEAACYHpH4AAIDJAakfAABgckDqBwAAmByQ+gEAACYHpH4AAIDJAakfAABg\n",
"ckDqBwAAmByQ+gEAACYHpH4AAIDJAakfAABgckDqBwAAmByQ+gEAACbHuU1XAACkwbZthJCu67qu\n",
"b7ourBiGoWma4zibrgggFnDVPzkIIfP5fH9/f2trazabxXHsuu6mK4VEqMOp6LpOCInjuI/CZ7OZ\n",
"UWM2m9m2ned5H8cCgK2yLDddB2A4CCEHBwcYY8uyEEJ5ntu2HcdxURSbrZhhGFEUbbYOLNAL/z4u\n",
"ouM4DsMQIWSaJn0nz3Pf9y3LomKtRpqmiqKoqtpNLYGxAIbPtPB93zTNKpWoqhoEwf7+/mZrBSCE\n",
"dF2n9xN1N8k0zYODA9M0FUVZrVhN07qpHzAuwPCZFoSQxVyAMa5ex3FMDQeEUBiGhmFsbW0dHBzY\n",
"tk0IaXwwjuPZbLa/v7+3t0e9o5MOatt2vag0Tavg+XxuGEaapnW7Yz6fL5bjui79a5qmVfUMw6AX\n",
"y7y1YoEWtbe3t7+/P5/PF3ug8yM2UBTFNE3aXvSTvvJ9vwqg71C96uR5XjlI9E5lKWma0gbSmodh\n",
"WC+cPYwQ4rou7YTKSGwU4vs+rTwtrfoyLB6u/QtT0V+3T4ISmBJBEJim2RKQZVkURZqmUVMoyzL6\n",
"vud5qqomSVJFep6n63r1TpIkpmlijBsFFkWhaZrneUVR0H96nqcoShUZRRE9YlSjfqCKJEloZBAE\n",
"lmVhjLMsy7LMNM16PVlqxYLneZqmVUXRkjHGjdI6POJi4WVZWpZVFR5FEW149VfaJ0t/yLQnHcfR\n",
"dX3p4bIso7d91T8ty1oMZglLksRxnKqeWZZRQRvl0A9W36uiKBrNKRm+MJQOu32aQOqfHI7j0Mzu\n",
"ed7SDFuWJf19Nt6Moqj6wdPf9tIPNn7wi++UZel5XuNXelJ6WnoIRVE8z1v8E3utToUWRbNPRZIk\n",
"CKF6zTs8Yrks9S8m7qWnh5ZruLpqDRzHWUy7i7ozhjUIgmCxnhjjRncVRaEoSv0dli9Mt90+TcDw\n",
"mRwY4yRJ6GAV3/f39/eX3uPXXSAK/Qgdc+L7/mIA/VTdfsnznBCyOBTSNM3qYeYKOI6z9MknY61Y\n",
"oM9XGw67pmmN43Z4RErlYhmGsb+/n+d5EAQrlMOCaZphGLquW1kl9Jy6WhhCKP4J9Nny0oM2vgyK\n",
"otRtNMYvTOfdPkHgMe9EqQanE0Lo0O/GM4ClY0IURcnzXFXVNE1PGo5Z/93meb50CLyiKOs8fjxp\n",
"vApjrVhI0/Skmvd0xOpTVY7re/YAdfB836eZnYqFMW50L0tYGIa2bWuaRt8khJzUge0wfmE67/YJ\n",
"Aql/WoRh2LjcVhRF1/UwDBu5mKb4xserp8T0+pflyn3IkenstWIpauAjUqgcXZXGcrj65TO950iS\n",
"pHGGaw/L89x13can6OX/ClVi+cJ03u0TBAyfaXHStdLi7fni0Avf91VVpZG6ri+1iRroup6m6dKB\n",
"MX2cEhhrxYKmaUutg8abHR5xZU4ad3QqixKbpklv6bjClppjq9WK8QsjQrfLDqT+aZGmaeOXnKbp\n",
"4q0AQkjX9WrcJP2U7/uVw6vruqqqi0Mwfd9vnF0wxrPZrPFjdl238dk8zxsngziOeU8P7LU6FdM0\n",
"6Yyq+pvz+byR4Do8IiOaptW7hQ7iXK2oNE0bDaQqNO72Tg1bPFu4rtsyorQdli/M8N0+PmA277Sg\n",
"tn4cx9RVyPM8TdMgCBr+Bp1bS+eX0kRDx/w0Eh+dCVw9M0jTlC4X0wijP0g6MocuhKDreiOMmsX0\n",
"DLQ0Js9z+lNP07S6+UAIYYwbDgljrU6Fji6vPOs4ji3LyvM8DENVVetzjzs5omEYtKtpSm1ZeGc+\n",
"n+d5Ts8BhBDHcQ4ODnRdpwNwq9KqVtBg+s/6hL7ZbKaqauPLQAdN1g/HElZViXYUfZI0n89VVa1q\n",
"NZ/PqQVEh+fSutHx+I3Ks3xhuur2yQKpf4rQ3wk6+XEr+7IKVVHotCdslfN7Uhh7UR3W6lSq25H2\n",
"cjo8IgvUFVnzaTnl1C8DY1jVUZqmdZJ8T/3CoMG7fUxA6geWIMuKOgAArAZ4/QAAAJMDrvqBD0GH\n",
"b1f/rFvDAACMBkj9AAAAkwMMHwAAgMkBqR8AAGByQOoHAACYHJD6AQAAJgekfgAAgMkBqR8AAGBy\n",
"QOoHAACYHJNO/WmaNlYcBAAAmAITndJFCKHLCiKEet0DDwAAQEAmmvpt2652KKTbCZ20QC4AAMD4\n",
"mKjhU984lG4MtNn6AAAADMlEU39jwXHY2wEAgEkxxdS/eI2/uP84AADAiJli6gcAAJg4U0z9i9vL\n",
"8W7/DQAAIDVTTP1owfMhhGyqJgAAAMMjZeoPw9B13ZaAOI5ns5lhGLZtL03rmqZVmz7Hcbz+3tYA\n",
"AAASIdO4/jiOfd/P81xVVULISfuG+77v+77neaqq0u0GkyRpxDSmdHmeB4N8AACYDjKlfurS0At2\n",
"13WXpn5CyMHBQZIkVSq3bVtV1aUbzFYF9llrAAAA8SglJIoiXdeX/snzPIxx/Z0syzRN6+rQn/nM\n",
"ZzatGAAA42Rra6urTHUq5zbd2I7J87xxFU/doa7K/853vrO9vf2FL3yBJfgb3/jGT/3UT/38z/88\n",
"Y/AnP/nJn/7pn2YJ/rM/+7Nf+IVfYAz+4z/+49dee40lsr/g99577y//8i/Zg//mb/7m13/911mC\n",
"//7v//7w8PDmzZsswVyK9NfJf/qnf/obv/EbjMGCyDduRfoLZtc6TdO/+qu/Yiy2AwY7yXRIy1W/\n",
"aZpRFDXePCl4Ba5du/b0008zBr/22mtf/epX2YMXa34St2/fZg/+uZ/7OcbI/oKjKOIKvn37NmPw\n",
"V7/61ddee40xmEuR/jr505/+NHuwIPKNW5H+gtm1xhifO3eOveQ1kXKETwt9D9P8yEc+srW1xRi8\n",
"s7Pz3HPPsQezV4Pxwoeyt7cnXTB7A5977jn2ruNSpL9OfuKJJ3oqGRSpEKTfuLQ+c2a4hDy21N83\n",
"9+7d+4//+A/G4MPDw3fffZc9mL0a3/72t9mDv//970sXzN7Ad999l73ruBTpr5N/9KMf9VQyKFIh\n",
"SL9xaf3v//7v7MFrMjavv+/hOufOnWO/6v/c5z7Hfvnzuc997pOf/CRj8Kuvvsre0t/+7d9mjESc\n",
"FynsJWuaxhX86quvMgZfu3btE5/4BGPwRz7ykUuXLjEG99fJX/rSl9iDBZGvJ0W4fiO7u7uMkYiz\n",
"3/oL5tKaPbd0wGDWUoe0eP0YY8dxGm8qitLVoa9fv76zs9NVaQLS4XMRAcEYs5vFMgLyyQvGeHt7\n",
"e7DDjc3wMU2zmqZLCcPQNM2uyucyfLg2gOTaM8D3/Z6CuW5m+6sGezBXJ3PZC/21rj+tRZCP92vP\n",
"Hsxl+Ijw5UScWg9p+Iwt9dM79EobQojrukvncwEAAEwWmWbzuq5Lr+gJIfXx+41pvYQQwzA0TVMU\n",
"JY5jy7I6TP2/+Iu/+K1vfeuHP/xhVwWKhmEYJ62QMQLqG3OOEpBPXmzb/oM/+IOHDx8OdLzBrKWB\n",
"SZIkiqKiKLot9ubNm1euXGEMzrIsyzL2YPZqcDme4w7m7WT24P5aN26tZVREBK0xxuxzhtZnbCN8\n",
"Knoa6nN0dMTu9XNNMuAK5tpgYNzBMnayINUARQYI5mrgkF6/TIaPCHz2s5/9u7/7u+9+97ubrggA\n",
"AKPCtu233nrrBz/4wTCHG9tj3r65f//+o0ePGIPzPGe/QOC6lGiMYppyMG8nswf317pxay2jIoJo\n",
"fXx8zB68JpD6+bh37x6kfqGCZUw049ZaRkUE0XrI1A+GDx9g+AAA0Adg+AjN8fEx12Ne9oc8o3/e\n",
"1d9DRa5OZg8W5NGfCJ3MFSyjIoJoDVO6xKUoiqOjI8ZgGWfzShfc39xRQWZ4itDJXMEyKiKI1sMN\n",
"6gfDhxcwfAAA6AMwfIQGDB/RgmW0F8attYyKCKI1GD7iAoaPaMEy2gvj1lpGRQTRekjDZ7QLOfTE\n",
"rVu3rl69yhhcFAX7ShJca05wrQQw7mDeTmYP7q9149ZaRkVE0BpjvLu7y17ymoDXzwd4/QAA9AF4\n",
"/UJzeHj44x//mDE4jmP22R9c80Rs24ZgCm8nswf317pxay2jIoJo/eDBA/bgdRns/mIcgOEjWrCM\n",
"9sK4tZZRERG0BsNHaMDwAQCgD8DwERowfEQLltFeGLfWMioiiNZDGj5nf+/3fm+wg42Ar3/96//6\n",
"r//6xS9+kTFeURRFUdiD2WuiqioEU3g7mT24v9aNW2sZFdm41nEcf+tb3/rd3/1d9pLXAQwfPsDw\n",
"AQCgD8DwERpCCEzpEipYxglE49ZaRkUE0ZrdTF6f0W7Q2BPb29tnzrCeL7lu6sftAPQXLGMnC1IN\n",
"UGSAYK4Gnj17lj14TcDw4QMMHwAA+gAMH6EBw0e0YBnthXFrLaMigmg9pOEDqR8AAGBygOHDBxg+\n",
"AAD0ARg+QnP//n3Yll2oYBk3AR+31jIqIojWQ27LDiN8+Dg6OuLaqoW95HFv39FfsIydLEg1QJEB\n",
"goXdqgUMHz7A8AEAoA/A8BEaMHxEC5bRXhi31jIqIojWQxo+k079cRxzCYMQunfvHqR+oYJlTDTj\n",
"1lpGRQTResjUz234EELoUFxCiK7rqqpyzW0ThDRN5/O5rusIoTzPPc9jnHQHhg8AAH0gruHj+/7B\n",
"wcHe3p5hGHEcp2lqGMb+/v7BwYHv+1xPMzYLIcR13SRJHMdxHAdj7Lou42ePj4+5HvOyd8von3f1\n",
"91CRq5PZgwV59CdCJ3MFy6iIIFoP+ZiXKfX7vr+/vx+GoWVZdIeaKIqiKCrLMssyy7LCMNzf3+ea\n",
"5LZBCCEY4+qfmqaxf7YoCpjNK1SwjHNHx621jIoIovXDhw/Zg9fkdMPH9/0wDB3HaU+ReZ67rquq\n",
"aj2rSkGe57ZtB0HAEgyGDwAAfSCc4WNZVhRFp14aq6rqeZ50eZ8QMp/PPc9jjAfDR7RgGe2FcWst\n",
"oyKCaC2c4SMdtm0bCyxuq0YImc1mjuOwL6wKho9owTLaC+PWWkZFBNF6SMMHDbYBvGgURaHrepIk\n",
"XJ+6devW1atX2Q9RFAV7MHs16BMXCC75O5k9uL/WjVtrGRURQWuM8e7uLnvJa8I3uDOOY0lHczZI\n",
"09T3fcuyuJ7xIvD6AQDoB+G8/jqu6/LOgVqNMAzbB1zGcTybzaiNwzuuNE1T27brD64XvaCTODw8\n",
"ZF9TO45j9tkfXPNE2Cs8+mDeTmYP7q9149ZaRkUE0frBgwfswevCdY9A50CdhKZpdMTnykRRZJqm\n",
"pmmmaeq6flKY53mapiVJUhQFzeBcR8EYa5qm11AUhfGzYPiIFiyjvTBurWVURAStBzZ8uL1+y7Iw\n",
"xrQ9RVFgjDHG9E9Zlq2Z/ZMkoeZ7FEUnpf6iKFRVrXcoxtjzvJUPysXt27dfeumlYY4FAMB0wBg/\n",
"88wzgx2OL/XXE32FaZpBENDXSZKYprl+tVpSPx1CWn+HnnLWPygL169f36px5swZXde3t7d3dnbo\n",
"3cPLL79cluXLL7/87LPPRlH08Y9//Nlnny3L8u7duxcuXKi/KMvywoULd+/epS/u3LlTluWzzz5L\n",
"S6he0KLqL+7evXvu3LmWouiLqoSLFy+2FNWoFca4pahGrTDGLUU1avXpT3+6jwZGUbS7u8vYQDoV\n",
"kbGBFy9ebO+regnnzp1r76v6izt37rT3Vb0ojHF7X9WLoj+NzTaQfu0bRdEXjVpduHDh4x//eBRF\n",
"9TIbDXz55ZerEurfisWiGrW6ePFiS1GNWjW+9o2iGrWiX3v2BjaK2t7e1nV9Z2dne3v74sWLWx+m\n",
"HAq+1K9p2uL9SyPdtxg17LSkfoxxdaapUFV1/YOycPPmzStXrjAGZ1nGfm/IdRfJdWs17mDeTmYP\n",
"7q9149ZaRkVE0Bpj/PTTT7OXvCZ8qf+kZwP1NN136jdNc7HrOzkoC2D4AADQBwMbPnwjfHRdXxzh\n",
"E4bhkMM9N7tOHCEEpnQJFSzjBKJxay2jIoJozT56cH34Ur9lWY2BTXQVTNM0q3ccx+mmakKyvb19\n",
"5gxrpymKwj5PmD0SIcR1rh13MG8nswf317pxay2jIoJoffbsWfbgNeFer9+27TRNLctSFIXmfcuy\n",
"LMvqtlpxHLuuG0XR0grQEZn1Nw3DWBrcOTClCwCAPhB6ShdCiC5wn6ap67ppmgZB0HneP5XFeyiu\n",
"u6p1AMNHtGAZ7YVxay2jIoJoPaThc26FzyxedA+JaZq2bdeXCA3DsO44AQAAAO1wGz7D0GL4IIQM\n",
"wzBNk95tEEIMw6DzeweoGBg+AAD0geiGT6+4rlstsEw3gKQ0woIg8H1/Pp/TxZlXWIVtZe7fvw/b\n",
"sgsVLOMm4OPWWkZFBNF6yG3ZVzF8fN+niy6pqqrrOsaY6yl2C3S28KlhiqIkSUK3hu/w6CwcHR3R\n",
"rVpsG506lIlrHOq4t+/oL1jGThakGqDIAMHCbtXCbfjM53NCiOM4dIST7/u+70dRNGT+3SCV4WMY\n",
"aJAhRQAATAKhDR/f9wkhQRBUI1sty3IcZzab9VA3EakbPqfe9oHhM0CwjPbCuLWWURFBtB7S8OFL\n",
"/XEcL87Y0nWdEDLMOv4b5969e1XqP/VODlL/AMEyJppxay2jIoJoPWTq5zN89vb2iqJYfH/pNKtR\n",
"Uhk+dFLzqGcuAwAwHEIbPiPYmnFNjo+P6WNeFggh7A95Rv+8q7+HilydzB4syKM/ETqZK1hGRQTR\n",
"esjHvHypX9O0pTPZ4jiewiU/QqgoCpjNK1SwjHNHx621jIoIovXDhw/Zg9eEz/DJ89wwjCAI6uPo\n",
"5/O5oijjXrWtAgwfAAD6QHTDJwgCOpeK7py+v78/nbyPPmz4qCpqP6OD4TNAsIz2wri1llERQbQW\n",
"1/BBP9l7XdM0eiMTRdF08j76sOGjqqj9OwCGzwDBMtoL49ZaRkUE0XpIw4d7W/aJc+vWratXr5Zl\n",
"SbcHXtio+EMURbG4n2VLMHs1uHb4G3cwbyezB/fXunFrLaMiImiNMd7d3WUveU1WWchhypw/f55r\n",
"qxb2kse9fUd/wTJ2siDVAEUGCBZ2q5Zulm/jugOSmsPDQ/Y1telKR+zB7NVo7JU25WDeTmYP7q91\n",
"49ZaRkUE0frBgwfswevSyb3DYLuibxwwfEQLltFeGLfWMioigtZg+AhNw/BRFJSm6KQVo+HOd4Bg\n",
"GTtZkGqAIgMEj9zwmQ4Nw0fT2gb5gOEzQLCM9sK4tZZREUG0HtLwOf2q3/f9MAzbYwbbGnfjPPXU\n",
"U+fOfdBpuo5sG520O2R/lxJcc6fHHSxjJwtSDVBkgGCuBp4/f549eE1On81r27aiKO3bYNm2nSRJ\n",
"pxUTlPpsXjqfgWXPFgAAgHZEnM2raZreykT2aUEIEUIW1/A5yfOBKV0DBMs4gWjcWsuoiCBas48e\n",
"XB94zMvH9vZ2Y1y/aaI4Rpa1JBiedw0QLGMnC1INUGSAYGEf855u+NA1KNobYBhGNI3tChcNHwSe\n",
"DwAAayOc4aMoyqknronkfXSC4XMSYPgMECyjvTBurWVURBCthzR8YHBnB9DR/QAAALLAt14/sNTw\n",
"yXMUhgjjjdYMAACZEc7wAercv3+/2pa9QlWXb9EO27IPECzjJuDj1lpGRQTResht2WGEDx9HR0cn\n",
"7c2b56jx5J9rl4Zxb9/RX7CMnSxINUCRAYKF3arldMMnTVNCCMsENvZIeVlq+CDwfAAAWA8RDR/b\n",
"tg3DaLnNieN4NpvNZrPRz+1aavigE3bsAsNngGAZ7YVxay2jIoJoPaThc3rq1zQtSRLTNOfz+f7+\n",
"frUxbxiGtm1Xb+q6nmVZ+3oPI+DevXtLUz9CSNNQ4ysBqX+AYBkTzbi1llERQbQeMvXzjfAJw5CO\n",
"w43jWFVVVVU1TdM0zTxpAbPRcZLhgxAiBLkuzO0CAGAVRDR8KkzTdBwniqKyLLMso3uyS533Z7PZ\n",
"3t4ee/zx8fFJj3mp11V/qEMIYX/IM/rnXf09VOTqZPZgQR79idDJXMEyKiKI1kM+5p304E7f93Vd\n",
"5zKpiqJomc1rmsh1P/gnzOYdIFjGuaPj1lpGRQTR+uHDh+zBazLdKV2EENu2Pc/jWoCoxfChzGbI\n",
"89DYn3YDANAxQhs+Y8J1XWvpeputtBg+FMf54MIfDJ8BgmW0F8attYyKCKI1GD69Q8VbYTxSu+GD\n",
"0ONZXVRuMHwGCJbRXhi31jIqIojWQxo+aLAN4IcEY7y4nwzGuAowTbMoCvpa13X2km/dunX16tWy\n",
"LGuFNcmyx38tiqI6yqmwR5ZlmWUZBFN4O5k9uL/WjVtrGRURQWuM8e7uLnvJazJFrz9NUzoRgf4z\n",
"DEPLsjDbTNxTvX6KbSPLaq7rAAAAcBLg9feOqqqO49R3l2RffOLw8JBlTW2MkeuiOI7ZZ39wzROx\n",
"bRuCKbydzB7cX+vGrbWMigii9YMHD9iD12Ww+wsugiBwHKclIIoi0zSpjcN1+7xI54YPxXHKP/mT\n",
"H4Hh03ewjPbCuLWWURERtB7Y8BEr9dOETqcHt2Rkz/Po8hJFUTiOo2naaocLgoBe9VuWxfiR27dv\n",
"v/TSSyVD6i/L0rLK9c5KAABMBYzxM888M9jhxDJ8FEXBGCdJ0jLskhDium4URZqm0Xhd17meuVeY\n",
"phlFUVEUnucxfoTR8KF86lP/+zd/8/8yBo/bBOgvWEZ7Ydxay6iIIFqD4VNGUXTSVb/nefjDl9x0\n",
"2bhB6lXevHlza2vrzJkzW1vO1tbW+fPndV2/ePHi5cuXdV2/cuXKjRs3yrK8ceOGqqpZlv3Mz3zl\n",
"2We/VJblG2+8cenSpfqLsiwvXbr0xhtv0Bd3794ty1JVVVpC9YIWVX/xxhtvXLx4saUo+qIq4fnn\n",
"n28pqlGrKIpaimrUKoqilqIatfqt3/qtPhqYZdnVq1cZG5hlWZZljA18/vnn2/uqXsLFixfb+6r+\n",
"4u7du+19VS8qiqL2vqoXRRdZ2WwDsyy7fv16oyj6olGrS5cuXb9+PcuyepmNBt64caMqof6tWCyq\n",
"Uavnn3++pahGrRpf+0ZRjVrRrz17AxtFXbx4Udf1y5cvX7x4cWdnZ2tr6ycpZWtra6scCvlSP8Y4\n",
"CILGm1SYAeAyfCgYl0nSY5UAABgBkzZ8WMjzfHFXAHWocZSEkPYpXXXodBWMke8v38GxEcxeDUGm\n",
"q4gQLOMEonFrLaMigmjNbiavj3wbNHJNjO6c7e3tM2dYz5f0FKUoyLKQbaP2Bwpcu9xwnerGHczV\n",
"b4J0siDVAEUGCOZq4NmzZ9mD12Ww+wsuWgwfXdepodl4s/9KleVKhg8lirg/AgDAdADD5xQ2uxHY\n",
"CoYPfa3rSFVRy53iuE2A/oJltBfGrbWMigii9ZCGj3ypHy3rTa7+3RSWhdK0LfsDAAAMxGD3F1y0\n",
"GD5JkjT+FAQB+5ysNVnZ8KmAAT8AACwChs8pUMOnuueiM7xWWHl/Ne7fv3/StuyLLN1y2nFQGDY3\n",
"cEdj36q7v2AZNwEft9YyKiKI1kNuy77KCJ84jsMwzPOcbm5FMy/Xg+yTcF2XdishJM9zwzDo+41d\n",
"tIIgMAwjTVNFUeI4tixrsAcAR0dH7Vu11DlpMJLjoPkc5Tmqn7DGvX1Hf8Fc/SZIJwtSDVBkgGBh\n",
"t2rhXrTZ9326yvFsNqOf9X0/TVP2tRC6Ik1TQghdzmGwgzIu2swC3cyLba1oAABGjtCLNtPrfbrI\n",
"WvWmZVkbecqqaRpdfG3Ig65v+FRgjBQFVcuBjNsE6C9YRnth3FrLqIggWg9p+PClft/3nWXXupqm\n",
"cXWHvNy7d6+r1I8QsixkmsgwUJ6PPB30Fyxjohm31jIqIojWQ6Z+PsNnb2+vKIrHn9z64LO2bdNt\n",
"T7qvoGB0aPhUEILmc2SaqHYrBQDAtBDa8BnYXRGQ4+Njrse8LA95FAUFAfrbv/0x+1qwgjzCEiGY\n",
"sZNXCBbk0Z8IncwVLKMigmg95GNevtSvadpSWz+O481Osh2MoihWm817Kjdu/C/TRLMZYvmEIDMV\n",
"RQiWce4ozOZdLViE1vEGc2n98OFD9uA14TN84jim26SgmuEzn88VRVn6DGB89GH41CEEuS5SFBj5\n",
"AwDTQmjDR9d10zQPDg7CMEQIhWE4m80QQhPJ+6gfw6cKRggpCnIcpKpoNkMtt5WC3MyKECyjvQCG\n",
"z2rBIrSON3gkhg9CyLKsIAjSNNV1PU1Ty7KGH9G/QfozfOqRpok8D/k+su3lC/0LcjMrQrCM9gIY\n",
"PqsFi9A63uCRGD5A34ZPA7rcm6ahoRaqAABgMwht+AADo2nI85CioPl8ybI/AAAAq8E9m9e2bdu2\n",
"q7sYutLOZnfOGpLDw0P2NbXjOGaf/dESaZrIcVAcP175ByFks48DHXswbyezB/fXOq45QSJ0Mlew\n",
"jIoIovWDBw/Yg9eFa53PJElUVfU8ryiK6k3HcQZbM3nj3Lp16+rVq2VZsmwLVhRFvaNODWaIKTEu\n",
"MS7/+q/fYyy2LMssy0YczNvJ7MH9tY69Dr1WAxQZIJi9dRjj3d1d9pLXhM/rt21bVdXFFZIPDg6S\n",
"JOn0lCQolddvGOjDy4kOBx0AihAyTTSN2RQAMH6E9vrjODaXrTYwnTV8NmL4NFAUhJCN8WML6NTP\n",
"CXLnC/ZCqTr+TgAAIABJREFUvRo9lSxCsIyKCKK1uIbPSfEY48Wt0kdJZfiw7NLVueFTUb/l9LzS\n",
"skrPYwrmKlmKYBntBTB8VgsWoXW8wcIaPnxbtei6TghZXMlnOo95z58/f+YM660S15JHXMGqqlav\n",
"qf0Whmg+R4qCLAvV/tgM5ipZiuBhOrnbYEGqAYoMEMzVwLNnz7IHrwn3Gj50Hm8dQkgcx1NYthMh\n",
"RAgZYErXqSxOKqGzwCwL+T6az1FdJUHmtsAEono1eipZhGAZFRFEa3YzeX34rvoxxoZhqKpaJXpC\n",
"yGw2w5NZcWZ7e1u0q/4Pv/94ohmdCYwQvQkQ4vIHrjFFqwYoMkCwsFf93LN5aa4nhOi6nud5mqYY\n",
"48F2Rd84A8/mXZM8R2GI8hypKjLNphEEAIA4CD3CByGkKEoURUEQ6LpuWVaWZdPJ+0hgw2cpqoow\n",
"RprmmyYKQzSbIdddvigQb8niBMtoL4Dhs1qwCK3jDR6J4VOhqirXXc9oENzwOSmYngMQQmn6eE4A\n",
"vQ9YPKYgt8njthcEqQYoMkDweAyfiSOX4dNCmj5+FKyqSNfBCwKADSO64bMUrgWspeb+/fsdbsve\n",
"CGavxvq7SGsachzkOEjTHg8Ksm2UpqJsZj3uTcBhW/bVgkVoHW+wsNuyr2j4NJjP59GmljUYlqOj\n",
"I66tWthL3tT2HZr2eDUIQlAYoj//88txjDQN6foSO6i/aqwcLEUni1kNUGSAYGG3auE2fGzb9n1/\n",
"sT0TMY5GY/i0E8cfrA+h62gaczYAYJMIbfjYtk0IWZzHPJH5XGhEhk97sK4/toMwRoQg20a2jVy3\n",
"uWW8CPfUMtoLQmndebCMigiitbiGTxzHURQtPrOezh6N4zN82oMVBZkmokv25TmK4w/mCWsa+v73\n",
"v8d+0gd7QbRqgCIDBI/E8NnamvqIoIkYPixQU4gQpChI15Gmnf5sAACAkxDa8DFNc3yDebgmlRwf\n",
"H3Nd9bOf86W7/NF1ZFm55z2eMeC6j30h216+jnR/15hcncweLMiVoAhacwXLqIggWg951c+X+jHG\n",
"S9eqns1mHdVnUMIwNAwjDMMwDBn9u6IoJJrNO0wwveqnzwYcB1nWB48H6BMC2rUwd7RejZ5KFiFY\n",
"RkUE0frhw4fswWvCZ+D4vk+b3XiuG4ZhlmUdV61nXNclhDicrg0YPrzQJwTVdZKqfjCcFACACqEN\n",
"nzAMNU0bwXgeuvAcb95HYPjwB6sqsix6N5A7DlJVlKbNe4LFpo/bXhir1hQZFRFEa3ENH9M0McbO\n",
"AtKdDHzfX22haTB81gzW9cdnAvqfaT7eaphOJ7Zt5PsojkduL4xbaxkVEURrcQ2f0WAYRhAE8/mc\n",
"npMty1q65/AiYPj0TZqiPP/QBAJVfbzQEACMmIENn24WcsjzXKiFPG3bXjzZappWd3hs23Ych1Z7\n",
"NptpmiZUEyYLfRJQPxHTk0F9eIGiIE17fEoAAGAVOtnhV9f1TsoZDNM06/vIB0HgOA7LB69fv/7c\n",
"c8+VbNuyR1HEvls91772mOXw4w1OkjKKSscpMS5v3/7ujRv/D+PSccooKts3weZSpL/WjVtr3q+9\n",
"CIqIoDXG+IknnmAveU24r/rjOF4cB9n5YP8wDPM8b7Hj4zimSwlpmoYx5loUGyGkaVr9I+wf39vb\n",
"297eZj8KV5XYg7m2xxlfMO0qagERsoMQUhSUpo8fG9Sh9wf0/0iYThakGj0Fw9e+DlcDL1y4wB68\n",
"JnxefxzHtm3TVEsNE0KI67pdPemlCZ3aR4SQk1YDpWNMPc9TVdX3/TAMkyThOhAhxLbtav2J2WxW\n",
"mT/tgNcvF3n+wX916LcVnh8A4jCw189n+JimmSRJWZZJkliWRd90HIfrDqiFJElo+VEUnWQiFUWh\n",
"qmpRu7HHGHuex3usKIrogCXTNNk/DoaPaMEr2AtZVkZR6Xklxh/8Z1ll5RolSY8VLseuNRg+dYQ1\n",
"fPhSv6Io9EUURfX2a5pWtJusnLSkfs/zGl2fZZmmaSscpSiKKIoWFyJt4datW1evXi3ZUn9RFOzd\n",
"wtWBXHUedzBvJ7cH158ifPaz79fPDZ5XRlF5Ur24WjdurbtVZLU6iBPM3jqM8e7uLnvJa8KX+lVV\n",
"pS8aqR9jzHUhcyotqR9jHATBSRXrm9u3b29tbZ07d+7s2f+6tbX15JNP6rq+s7Nz5coVXdd/9md/\n",
"lt4MWZb1yiuv1F987Wtfe/HFF+svyrJ88cUXv/a1r9VfvPLKK7SE6gUUJUhRv//7//Py5V9znPJX\n",
"fuUfnnzyq/R8cOnSH/3Kr/yD45SXL//a669/M0kkbmCHRVmW1SiKvmgU9eKLLzaKeuWVV0Zf1M7O\n",
"jq7rV65c2dnZef7558+ePbu1tUU3/T5z5kw5FCsaPtQtqd4fMvU3BudQBhti9Eu/9EsvvPBCyXbV\n",
"X/lXLLBHlmXJZXCNO5i3k9mDeepQfuEL/6O6XaDeUf1FEJRR9MEApHFrLYIi4gSztw5j/OSTT7KX\n",
"vCZ8I3w0TYvjmK7lQLdtoWNj0jTleuq9DlwTozuHnpwZg7nGHXEFc01BGHewCJ2saYiQCy3bmVVj\n",
"4ugApPff36+2PagXQmvXWP5ahE7mChZBEXGCuRp49uxZ9uA14RvhQwjJ85wOVwrD0HVdy7Lo5Klu\n",
"d2uJ49h13aUjfAzDwBg3BhQZhjHM5sAwwgfoCXp6IKS5FVqd+lkBNkgYGUIv36YoSjVMlQ6MoWeC\n",
"IXfp4hon2zmEEFjDR6hgGVeMWVoHetNgmh8scET/U1W/2iyznuvrGyRU//3yL/+f+lJI9L+TZt2A\n",
"IgMEc/2uf/zjH7MHr8laCzlomraRRJymaeOqn6t/1wEMH9GCZezk1apB90WoWGouxfEP6Pt0ghul\n",
"ylR0S7WK9977T/WzQn1hjMXCx62IIFqLa/gMRovhk6apbdv1P9GNVoa58wDDBxgr1QOJxRlwjXMG\n",
"Quj999HOzuPXi9YTmFErIOXybUNC7zN836cPlul04sEcp/v37z969IgxmK5vwXiNwLUEXhzH7NOn\n",
"xx3M28nswf21Tkyt2z93UsmLDyf++Z8Pv/71Czs7uyx1eP/9HyKEaPBJFahuR0T4vvEGc2l9fHzM\n",
"GLk+a6V+Qkiapo31cNbBdV26QBB9nmwYBn2/cfkfBIFhGGmaKooSx7FlWYP5TkdHR1xbtbCXPO7t\n",
"O/oLlrGTBalGJ8ENGwohpCjfe+UV1mdyaZohhDRNa3m+HYaPzatvf/tyff2wxXuR+p/+5V8ut2y6\n",
"2lj29S/+gmmhfLoY1Di2auEzfGhqVlWVPuA9ODjQNC3Pc8/zht+tJU1TunxbVyceFsDwAYARwLYV\n",
"d5P6E5TOefvtv/7Hf/xv77//3/s6QAOuWQBBEFiWRacmW5ZFpzYkSTLYZNqNc/PmzStXrpRsU7qy\n",
"LGOf8801O5xrAt24g3k7mT24v9aNW2sZFRFBa4zx008/zV7ymvAZPmEYOo5Dr7KrJ6t0nA91fno5\n",
"O4kEGD6iBcvYyYJUAxQZIHgkhs/e3l5RFPR1fRaVbdu6rku3Q+8KgOEDAEAfCD2lq4I6/t1WRQqO\n",
"j4+5rvrZz/mjv/zp7xqTq5PZgwW5EhShk7mCZVREEK2HvOrnS/26rodhiBZGLNGFfTqumpAURQGz\n",
"eYUKlnHu6Li1llERQbR++JBpoFEn8Bk+aZoahmFZFt0Yi5r+dF8tZxr2Bxg+AAD0gdCGj6ZpNONH\n",
"UUTzvm3bdB/dfqonHGD4iBYso70wbq1lVEQQrcU1fBBCqqpijCu3x3GcKIqCIOi6YoICho9owTLa\n",
"C+PWWkZFBNFaXMMHAMMHAIA+ENrwAQAAAEbAWqmfEBLH8Wa3zRqYw8ND9jW14ziOmSeMs0cihGzb\n",
"hmAKbyezB/fXunFrLaMigmj94MED9uB14Zr76ziOrut0f+EsyxRF0XVdVdVuN+YVmVu3bl29erVk\n",
"W8ihKAq66AUL7JEl50oA4w7m7WT24P5aN26tZVREBK0xxru7u+wlrwmf109XxqdrOcznc03T6AaN\n",
"s9ksy7L+zk/iAF4/AAB9ILTXH4Yhxrhaw4eumF+t4dNLBQUDDB/RgmW0F8attYyKCKK1uIaPoijV\n",
"a13Xq9cY44l4PmD4iBYso70wbq1lVEQErQc2fFbcqmWya/icP38e9uYVKljGThakGqDIAMHC7s0L\n",
"a/jwQQiBKV1CBcs4gWjcWsuoiCBas5vJ68N31Y8xpjsj0jV86Ju+7+u6PuRWWRtke3sbrvqFCpax\n",
"kwWpBigyQLCwV/3cs3nzPA/D0DRN2n7btukeuRNZywFG+AAA0AdCj/BBk1/DBwwf0YJltBfGrbWM\n",
"igiitbiGDwCGj2jBMnayINUARQYIHo/hM3HA8AEAoA9EN3wmzv379x89esQYnOc5+9LeXIuAc80T\n",
"GXcwbyezB/fXunFrLaMigmh9fHzMHrwm3aR+LvNLao6OjmCrFqGCZdwYZNxay6iIIFoPuVVLN4aP\n",
"YRhRFK1fjviA4QMAQB+A4SM0YPiIFiyjvTBurWVURBCthzR8YIQPH7yGD3vJ4zYB+guWsZMFqQYo\n",
"MkCwxIYPXabOsixVVekErsWYNE2LouilgoIBhg8AAH0wsOFz+lU/zfX03JWmqa7ri8v1cK1iKjXH\n",
"x8e8V/2MA3sJIexDgBtrKE05mLeT2YP7a924tZZREUG0HvKq/3SvP4qiKIqqdK9pmr6ApAv4cM0k\n",
"pBRFAbN5hQqWce7ouLWWURFBtH748CF78JrwjfCZzWaWZem63nhfuhE+eZ7btk1P3WmaBkHAePYC\n",
"wwcAgD4QeoQP3Zu3p6oMieu6nuc5juM4jud58/mc8YO8hg+M6+87WMZR5OPWWkZFBNFaLMOnzkkO\n",
"l1yX/AihPM+ry3yuFTnA8BEtWEZ7Ydxay6iIIFqLa/iMhvl8TjeXRwilaer7vud5LB8EwwcAgD4Q\n",
"boQPC1yPvEXAcZz5fE7rTAhxIIsDADAlupnNy+6VD4Nt28YC9RGoYRgqikKHJyGe6XmHh4fsa2rH\n",
"ccxeMtcUQa7RtOMO5u1k9uD+WjdurWVURBCtHzx4wB68LlybuLc84+18w/heMU2z/k9d1xk/eOvW\n",
"ratXr5ZlifHpwUVRFEXBWDJ7ZFmWWZZBMIW3k9mD+2vduLWWURERtMYY7+7uspe8JtxX/VEU1T9f\n",
"FIWu69U+vV0RhqHrui0BcRzPZjN6Lc/1DJ3SsKfY5yWcP3+ea6sW9pJHv2dFfxuDcHUye7Ag23eI\n",
"0MlcwTIqIojWQ27Vwj3Cp9ESRVE8z+tqNi9N6AcHB2EYttwo+b5v2zbGmI7HNwyD90BpmlYnDK4z\n",
"Bxg+ogXLaC+MW2sZFRFEa3ENn5MwTTNJkvXLSZKElhNF0UkmTFEUqqrWb6Mwxp7n8R5I13WMMcaY\n",
"3rUwfpAaPlEEho8owTLaC+PWWkZFRNB6YMOnmxE+qqqu4Lossrg60CJhGJqmWb/5sCyLTjPmOlAU\n",
"RXEcK4rCNbyH1/BhL3ncJkB/wTJ2siDVAEUGCB6J4XMSaZoOtoxPnueNM8TKJ56lS9G1Qwh57733\n",
"fvVX//Mf/dF/OX/+/AsvvGAYxgsvvPCxj33MMIwbN258+ctfRgh9+ctfvnPnTpqmn//85+/cuYMQ\n",
"evvtt69du1Z/gRC6du3a22+/TV+8+eabCKE7d+7QEqoXtKj6i7fffnt/f7+lKPqiKuHatWstRTVq\n",
"5ft+S1GNWvm+31JUo1a/8zu/00cD0zRtdHtLA+kEIsYG0g8yNnB/f7+9r+ov3nzzzfa+qhfl+357\n",
"X9WLorONNttA+rVvFEVfNGp17dq1z3/+82ma1stsNLCqZ+NbsVhUo1bXrl1rKapRq8bXvlFUo1b0\n",
"a8/ewEZRNGl87GMfe+GFFz7xiU88+eST58+fv3z58h/+4R/+8Ic/RIPBdY/geR5ewDTNxoCZ9Wkx\n",
"fEzTbDxqLnmG6KzJzZs3r1y5EkXlQhWWkGUZ+70h113kYg9MNpi3k9mD+2vduLWWURERtMYYP/30\n",
"0+wlrwnfbF7DMBaf9GqaZppmtyekOI5d1126PoRhGNSgb7w5zGISdDbvm29+FyE0itWMAAAQAqGX\n",
"b1NV1TRN58N0nvdFhhACa/gIFSzjijHj1lpGRQTRmn304PrwPeZlXOimV3jd+W7Z3t6Gx7xCBcvY\n",
"yYJUAxQZIFjYx7yCLt/WYvjYtq0oCsa4/ube3t4wO0SC4QMAQB8IbfiIgGmajVkSdLjnMEe/f//+\n",
"o0ePGIPzPGdf2ptrEXCueSLjDubtZPbg/lo3bq1lVEQQrY+Pj9mD14Qj9RNC4jjm3dGwc6jhU9lt\n",
"hBDXdbkG9a/D0dERbNUiVLCMG4OMW2sZFRFE6yG3amE1fHzf931f1/U8zwkh7DsacuG6Lj2jEkLq\n",
"4/cbzg8hxDAMTdMURYnj2LKswVI/GD4AAPTBwIYP07j+LMvqayc4joNZ1jHomSRJoijimhO/PjCu\n",
"X7RgGUeRj1trGRURQeuBx/UzjfDxfR9jXF3mY4z39/c3vr3JRob68Bo+7CWP2wToL1jGThakGqDI\n",
"AMHCGj5MV/2LE2h1Xa+/I8JNwDDcvn37pZdeYrzqBwAAYARj/Mwzzwx2OKbHvKeeuDb+7Hcwjo+P\n",
"4TGvUMEyPlQct9YyKiKI1kNe9cs3uHOzFEUBs3mFCpZx7ui4tZZREUG0fvjwIXvwmjCN8FlcuicM\n",
"Q13Xq3fCMMyyrK86igSM8AEAoA/kmNLVWDF/OoDhI1qwjPbCuLWWURFBtBbO8FEUZXHVtjpci1pI\n",
"DRg+ogXLaC+MW2sZFRFEa+EMH6ACDB8AAPpADsMHAAAAkBdI/XwcHh6yr6kdxzH7Sk9ca0LZtg3B\n",
"FN5OZg/ur3Xj1lpGRQTR+sGDB+zB6zLYDIJxcOvWratXrzJO6SqKgn2dCa4VKbhWAhh3MG8nswf3\n",
"17pxay2jIiJojTHe3d1lL3lNwOvnA7x+AAD6ALx+oQHDR7RgGe2FcWstoyKCaA2Gj7iA4SNasIz2\n",
"wri1llEREbQGw0dowPABAKAPwPARGkIITOkSKljGCUTj1lpGRQTRmt1MXh+m9fqBiu3t7TNnWM+X\n",
"XGtdcAVzTZ8ed7CMnSxINUCRAYK5Gnj27Fn24DUBw4cPMHwAAOgDMHyEBgwf0YJltBfGrbWMigii\n",
"NRg+4gKGj2jBMnayINUARQYIBsNnJIDhAwBAH4DhIzT3799/9OgRY3Ce5+xLe3MtAs41T2Tcwbyd\n",
"zB7cX+vGrbWMigii9fHxMXvwmoDhw8fR0RHXVi3sJY97+47+gmXsZEGqAYoMECzsVi1g+PABhg8A\n",
"AH0Aho/QgOEjWrCM9sK4tZZREUG0BsNHXMDwES1Yxk4WpBqgyADBYPiMBDB8AADoAzB8hOb4+Jjr\n",
"qp/9nD/6y5/+rjG5Opk9WJArQRE6mStYRkUE0XrIq35I/XwURQGzeYUKlnHu6Li1llERQbR++PAh\n",
"e/CaTNrwoapomsb+ETB8AADoAzB8uiFNU9u2DcNY+jieEDKbzcIwDMNwNpuxFwuGj2jBMtoL49Za\n",
"RkUE0RoMnw6I49iyLIzx0r+6rmtZluM4juNYlsW+4xoYPqIFy2gvjFtrGRURROshDZ+Rb9AYRVG0\n",
"bCtFXddb/tnC9evXd3Z2GDdolBH2rpARjPHS78NoAPnkBWO8vb092OFGe9XfTsPf51pdDwAAQHam\n",
"mPoXb8HYV2ElhLD7cXEcs0/845oiyO5Q8QZ/5zvfEaEa7MFcnfzee++98847ndeBN7g/rUWQj/dr\n",
"zx789ttvM0YiMb6ciFPrIb1+WWfz2ra9mME1TXMcp9fjXrp0iX29fq6xQ1zBlmX1FPziiy+KUA32\n",
"YK5+e+655z760Y92Xgfe4P60FkG+/r72n/rUp9iDRfhyIs4GsueW9ZE19a+T4jVNC8Ow/g77I/tz\n",
"585tbW0xBhNC2K0kOhKAK54xmGuMwRNPPMEe3NNADq4KI56uuHDhwlNPPdVHybyDdtgzgiDysReL\n",
"OPuN/Tu/s7PDVQcRgrm0Zs8t67MxwycMQ9d1WwLiOJ7NZoZh2LbN+807lcYdA9dvgP2m7PXXX3/r\n",
"rbfYg9kHA7z66qvswZ/5zGcYIxGnY8BecpqmXMGvvvoqY/Bbb731+uuvMwZzGT79dTLXZaMg8vWk\n",
"CNdvhMvw4eq3/oK5tB7z4E6a0A8ODsIwbHHBfN+3bRtjHASBoiiGYXRbDU3TqqPHccx+WuYyfLjs\n",
"heeee44xEnHe+XKZAIIEszfwox/9KHvXcSnSXyc//fTTPZUMilQI0m9cWo/Z8FEUBWNMM+9JV/2E\n",
"ENd1kyShd4IYY0KI7/tc5096tqi7KFEUVX/FGM/nc5r98zz3PI+xWC7Dh8teuHDhAmMk4rzz5TIB\n",
"BAlmb+BTTz3F3nVcivTXyefOcfzuQJEV6oCE6TcurYc0fIZO/SzX12EYmqZZdwAty5rNZlypv57o\n",
"F1EUJQiCFRZyuHfv3vHx8TvvfAshhFDRHvzOO+/827/9G2PJ77zzzjPPPMMY/M1vfpM9+N1332Uf\n",
"ZtBT8DvvvMMV/M1vfpMx+Bvf+MY//dM/sZfMrkh/nfy9731v44pwBY9ekf6C2bXmMpM7YLAZBA2i\n",
"KDpp+gn1eRpvqqraf6VO54tf/CJCCCEVIdbxoAAAACxcuHBhsFQm4gifPM/1haXR2Ife98pXvvKV\n",
"r3zlK5uuBQAAwFqIOKWr8/E8AAAAQB0RUz8AAADQKyKmfq7nrgAAAAAvIqZ+tGyZHa61TwEAAIAW\n",
"REz9pmk2hkPR4Z6bqg8AAMDIEDH1U8On2g+BzvDiGtQPAAAAtDD03ryu69IrekJIfWGjxgwsQohh\n",
"GJqmKYpC99uC1A8AANAVQm/LnqYpIYSeADZdFwAAgPEgdOoHAAAA+kBErx8AAADoFUj9AAAAkwNS\n",
"PwAAwOSA1A8AADA5RFy5U1jiOPZ9nw46whhLNO6o25qHYZjnOca4q+qtSVetozsC0cHHuq5bliWI\n",
"xH00UFVVjLEIC+J2/rPK89z3fVVVBRkR3lUDbdtuvKPr+uIix6wMtjy07Hiep2lakiRFUTiOo2na\n",
"pmvESlc1j6LINE1N00zTPGmvheHpqnVFUei6jjHOsizLMrqXXFEU3dZ2BbpqYJZlmqZ5npdlWVmW\n",
"QRDQYjutLDd9/KxM08QYC/IV7bCBCKHow1ApVyxt5U9OiqIoVFWtJwKMsed5G6wSIx3WPEkSmila\n",
"ttkZmA5bZ1lWY4Mgx3EwxutWcT36kK/+jmma61ZxDfr4WUVRZFmWIF/RbhvY7ZU6pH4mPM9rZAF6\n",
"DbWp+rDTR80F+V2VnbbOcZzFNzfezL6/eJvd/K6P1tF7NUG+ot02sNvUD495maivOUFRVVWKLWXk\n",
"rTkLHbZu8dFFnucb9/p7lS+O49Wd4i7ovHW2bTe29d4sPckXx/H6hcBjXiZE3jOyHXlrzkKvrZvN\n",
"Zo7jdFLUyvTRQLo+ShzHaZoGQbBOUWvSbetoo5IkWbtendG5fIZhEEIURSGEqKrqed7K5zlI/UzI\n",
"e5ksb81Z6K918/ncsqzNXhSjfhqYpmmapnEcb3yUWrets21746fqBt020HEc0zSrM4fv+/P5fOWT\n",
"Nxg+ANBkPp9rmibI0MDOsSyLjvNJ03RxvKCkUA9k46fqXmkMxrUsi65/vFppkPqZkHfPSHlrzkLn\n",
"rSOEHBwciJP3e5XP87w0TVfOHevTYet839d1Pf4J1NTa+NZ+ff/6NE2D1N878u4ZKW/NWeiwdXSX\n",
"CNE2h+hVvnVyRyd01Tpd1/M8r1J/nufU+u+ijmsh7q+vw9FCIyZJksZYsSAILMvaVH3Y4ap5FEWO\n",
"45w6j0mQkXMlvy4tDSyKgs54qr+5zpSZTuhDvjq6rm9wVleH8i1GivAV7Vu+xqQBLiD1s6LrepUX\n",
"aJrY+ExIRhhrXg2NOHWajyC/Kwq7Li0NpFN5G1O6yrJUFKXzCvPSlXymaTY+SB8bdl5hLjqRbxFx\n",
"vqJdybf4/bQsa50phzDCh5UgCAzDSNO02jNSFhudsebVYI+TRn00Ntc0DIO+39hcc2DYdWlpILW8\n",
"fd+vdoSmiDA+qiv5MMa2bVfPQumgfs/z+qs5C53IV4c+u6Zf0fl8LksDT21dEAS2bbuuS+ULw9A0\n",
"zXVGNMEuXXzIu2ckS83zPF86Ell8GHUZdwNZWkdjEEJCfYdBPsTWuurZ9fryQeoHAACYHDDCBwAA\n",
"YHJA6gcAAJgckPoBAAAmB6R+AACAyQGpHwAAYHJA6gcAAJgckPoBAAAmB6R+AACAyQGpHwAAYHJA\n",
"6gcAAJgckPoBAAAmB6R+AACAyQGpHwAAYHJA6gcAAJgckPoBAAAmB6R+AACAyQGpHwAmQZqmdH/N\n",
"nmjsbQkIDuzNC/TIbDY7aXtbTdPW2VkU4GU+n9c7PI5j13URQoqiBEGAEArDkKZvVVVX2NI2DEOE\n",
"kGVZndUY6BNI/UCPWJZFM4Jpmo0/0bwDDIPv+4qi1Pd91TRNVVVUk0bTNIyxYRhJkqxwCMdxZrMZ\n",
"pH5ZgNQP9Iiu69RkWNxsGlL/kLiu27jHUhSF7utdSaOqKj0ZaJq2wiHoucT3fcj+UgBeP7AZ6vnF\n",
"dV3DMAzDSNMUIRSGIf0nvWOoE8fxbDbb39/f29ubzWZLzWsas7e3t7+/P5/P8zz3fd8wjPl8TgPm\n",
"87lhGHVvmr5jGAbv4WjJvu+naTqbzba2tg4ODmzbXqwVIcS2bcMwqpil5jtLA3mJ45gQsnjjxQht\n",
"Y4OlbTRNExx/aSgBoE8wxhjj6nWSJIsxSZJEUaRpWhAElmVhjLMsy7LMNM0sy6owz/N0Xa9KSJLE\n",
"NM2q8OoQ9ZggCDRNM03TsqwoiuibURTRozQq0Pg5sBwuyzLLsnRdtyyLVrUoikbh9E1N0zzPK4qC\n",
"/tPzPEVRGmEsR1wBjLFlWUvfXyx8MSfQj0c1qDW0WGCWZQgh2kZAcCD1A/1CczHNMrquV/l3EV3X\n",
"FUXMScfIAAAC7klEQVTxPG/pX7Ms0zRt6afqOV3X9cUPLibZU7Mey+GqohqRRVEoitL+qbIsPc+r\n",
"14H9iLzQ/l98vy5NxWLqdxzHcZz6p5aeSCgIoTVrCwwDeP1A76iqSg3lk0b7VDiOc5JT7Ps+TUwN\n",
"MMZhGNLy4zhe/Liqqiu4zyyHq2j8U1GUekvzPCeELD7tME0zz/PVjshFmqYnuT2VNBWLz2DqtfJ9\n",
"nxDSMv5H1/U0TdepLTAMkPqB3qnGluR5Th8tngR9zLiUNE1PejJcJZoOkw7L4RjJ83zpRxRFqT/w\n",
"6PCIDVp6tTHspx06+pM6Yy2ceoIHRAAe8wLDYVnWaqNHEEL0ScDSW9cqGWmaVr+OrlghGbEcjp2l\n",
"ter1iHUURWGpQDtpmtK8337yTtN0ZYmBIYHUD8iBruunjh6xLIs6EvU3ac46tfzGp1gOxwj1QJae\n",
"fuoZucMjNtA0bc0rcTp+iT6apu+EYbhYJiGEEAKpXwog9QNyoOu6qqrVAM0K3/crn4Ta+nRUKCGE\n",
"Duu0bXvRQ2/cH+R5PpvNeA/HDsZ4cWKz67r18rs9Yp1qdsVq0GGpQRDUjSM6nrURGYZhNVMMEBzw\n",
"+oEeMQyDZliaJpYu3pDnOc13aZratl1dV9LxJ/VIz/Ns2z44OKgeGlN7oV4mHWrpui69gqYuymLq\n",
"NE0zjmPDMOg5gBDiOM7BwYFhGJ7n0eTFcrj5fE6zap7ndDkEQgg9i9SLos+ZaVH0IXAcx7qu049w\n",
"NXAFqmfg9f6sap6maRAEiqL4vk8nUhiGYVlW9WTYdd08zxsD+RfzPj3EyrMHgIHZKsty03UAAA5o\n",
"QqSvGR9R0rS1mECpD9N43Lr+4Vqorr5biur2iBSa1td8ZtBOnucHBwd0KG1/RwG6AlI/MH5OSv2T\n",
"Yn9/n04Z66n8+XyuaRqs4iAL4PUDwCRomEuds9r8CWBTwFU/MGYay/L06ngAgERA6gcAAJgcYPgA\n",
"AABMDkj9AAAAkwNSPwAAwOT4/10VWX5h49ZuAAAAAElFTkSuQmCC\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"% Ce code n'est pas commenté, car essentiellement identique\n",
"% à ceux présentés en question 1.1. et 1.2.\n",
"\n",
"%% représentation en temps\n",
"figure\n",
"plot(ech,base)\n",
"xlim([-1 max(ech)+1])\n",
"ylim([-0.6 0.7])\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"%% représentation en fréquence\n",
"figure\n",
"[ech_f,base_f,base_af,base_pu] = Analyse_Frequence_Puissance(base,ech);\n",
"ylim([10^(-10) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Le vecteur `base` est une fonction linéaire du temps (ligne 4). En représentation fréquentielle, il s'agit d'un signal essentiellement basse fréquence. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 6. Mélange de signaux. \n",
"On va maintenant mélanger nos différentes signaux, tel qu'indiqué ci-dessous. Représentez les trois mélanges en temps et en fréquence, superposé au signal d'intérêt sans aucun bruit (variable `signal`). Pouvez-vous reconnaitre la contribution de chaque source dans le mélange fréquentiel? Est ce que les puissances de fréquences s'additionnent systématiquement?"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%matlab\n",
"\n",
"%% Mélanges de signaux\n",
"y_sr = signal + resp;\n",
"y_srb = signal + resp + bruit;\n",
"y_srbb = signal + resp + bruit + base;"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1fcCRHnt/3G3I4BHbnDxIkNRjO3g6UxHD/eOUbsqAT\n",
"bZ9u6Yiq0EkKOxSnKNxuyAqFYy+qvfckP0hVssPv3eF/54sLn7uC6wcrHKfttjY2JPPMCKS1y73T\n",
"LS+EnNnTcY/cAVAEvByicUsiMcQs0bMccvyQmEKhqrrRVZWVXdX9+zxMYBqN+mVWZX3zl7/8ZeaZ\n",
"hw8fAoIgCDJNPDbuAiAIgiC6QelHEASZOlD6EQRBpg6UfgRBkKkDpR9BEGTqQOlHEASZOlD6EQRB\n",
"pg6UfgRBkKkDpR9BEGTqQOlHEASZOlD6EQRBpg6UfgRBkKkDpR9BEGTqQOlHEASZOlD6EQRBpg6U\n",
"fgRBkKkDpR9BEGTqODvuAowKY8z3fSGEYRiu6xJCcl/K933GmJJLIQiC1JF6eP2+73ue57pup9Mh\n",
"hFiWlftSjUaDc95sNjudDqV0eXk5CAKFRUUQBKk+Z6p/Nq8QYnl5eW1tLXTPPc+jlDqOk/VSnHPP\n",
"81ZXV8NPGGPdbrfdbisrLoIgSOWpgdff7XZt246GZRzH8X0/36UMw4h+YpomY6xoEREEQWpFDaQ/\n",
"CIKYXlNKhRA5LhW7TurFEQRBJp4aTPMGQWCaZuxDSmmOS9m23e12W62W67ryyo1Go9lsjn6F7373\n",
"u7/7u7876Lfz8/NPPPFEjoIhCDIl7O7uDvrVl7/85d/7vd/TVI6Hlcc0zdXV1eSHRS4YVj955eF8\n",
"7Wtf0/RgEASZMi5evJhb1rJSg4CPWhqNRthtrK2ttVotznmmKywuLhbpeMaI67pZu7qKUNMbvrq6\n",
"6rruuEuRB2wqmlldXX3ppZd0xgxqIP0KY/G+7xNCZLRHXrnT6aysrKi6PoIgSC2ogfQDQNIxz+qq\n",
"SxhjsWkDQki+aQMEQZD6UgPpt207ln8p0z0HfZ8x1mq1UlOAUlOD8iULIQiC1JcaSL8M+ISJ/EKI\n",
"Vqs1aD0X59yyLM/zGo1G8reO48R6Bc/zkulDCIIgk00NkjsBoNPpWJbFOSeEMMYcxxk0ARCu/Erd\n",
"mYdS2mw2LcsyDENeyjTNTMmdCIIgE0A9pJ8Qsra2xjkXQgzfcI1Surm5mboUQGKa5tramowgOY6D\n",
"gX4EQaaQeki/ZMRUH0rpqYKOQR4EQaaZGsT6K8iQSeYqY5pmTUc5Nb3hlNKaOhnYVDRDKV1cXNRp\n",
"sQY7d1aKr3/962+88cY777wz7oIgCDJReJ73yiuvvP/++3rModePIAgydaD0IwiCTB0o/QiCIFMH\n",
"Sj+CIMjUgdKPIAgydaD0IwiCTB0o/QiCIFMHSj+CIMjUgdKPIAgydaD0IwiCTB0o/QiCIFMHSj+C\n",
"IMjUgdKPIAgydaD0IwiCTB0o/QiCIFMHSj+CIMjUgdKPIAgydaD0IwiCTB0o/QiCIFMHSj+CIMjU\n",
"URvpZ4ytrKxYluV5nhBCyQUbjYZlWSsrK5zz4hdEEASpC2fHXYCR8H3f9/12u00p9X3fsqy1tbUi\n",
"F2w0GkEQOI5j23YQBKrKiSAIUgtqIP1CiFartba2RggBANd1hRC+7zuOk++CKysrhmG02235X0qp\n",
"srIiCILUgRoEfLrdrm3bUvcljuP4vp/vavIPXddVUzgEQZAaUgOvPwgCwzCin1BKc4f7fd/vdDoq\n",
"yoUgCFJX6iH9pmnGPiwSpaGUBkEg3X/btmP9yqns7u5alpX6q2azmfVqCIJMFYPUY2Njo9/vaytG\n",
"DaRfST6PhDFGCPF9v9Vqua5LCGk0Go7jZJo2uHz58urqqqoiIQgyVQxSD8/zXnnlFW3FqIH0q0UI\n",
"0e12w0lj27aXl5dN08TJXgRBpocaTPMqDKEYhsE5b7fbqiaNEQRB6kgNpB8Akkuu8i3CIoQYhhFz\n",
"8NHfRxBk2qiB9Nu2zRiLfiLTPQd9nzHWarUGzRAYhhG7Gucc1R9BkKmiBtIvAz5hTEau8Bo0Mcs5\n",
"l5s9NBqN1C+4rhvtGGSqz5COBEEQZPKoxzRvp9OxLItzTghhjDmOM2gCIAziR6P5USilzWZzeXlZ\n",
"yj1jrNPpDPoygiDIRFIP6SeErK2tcc6FEDIpc9A3KaWbm5upSwFCDMPY3NyUYZ9ms1lKiREEQSpM\n",
"PaRfMmKqD6V0lNj9kL4BQRBksqlBrB9BEARRC0o/giDI1IHSjyAIMnWg9CMIgkwdKP0IgiBTB0o/\n",
"giDI1IHSjyAIMnWg9FcAnfuGCqHVHOcTbq7b1Wru5PZTpZvLtUkimhu/uRFA6R83QQBBoM8c51rN\n",
"CTHh5nS+z0JolX4htHZs+s1pvpko/cgJgkB3m9ApjgCg7pA1BFGJ5pap+b07DZT+6WOyW7zmfnSy\n",
"zaGXoIqKufyA0l8JNLf408wpjpZP8Ps8Ap437hIUQeezOy3yqThazpjW2lXvLUDpHz8fzZyyZbRi\n",
"LT5th2qFrt5ODz48UHa1U7m9DiKoVj9aX3Pv/iv+8zt6pX/orovq53GGvghqe5reLvR2lV1NCSj9\n",
"Y+b2Oty5c8orrVaLP9g75Tsqze3A7i/0nYVw7x68/6m+fnT7+8GHZ4eZUzuPuPUt9u7CsM1r1WYA\n",
"PfiZWL+mb3fbrW3Y+vCUZ6dTi4VQ2c/u70O/r+xqSkDpHzP37sGdBWN4o1bY4nd24M/PGcBYTN/D\n",
"/waBYs9yb44Or4BCLb5wm+/N0eF9l8KO7eFmcPOMAUIMupnK2fiADHk8apNW9vdhf3/YF9T6xf2+\n",
"VnHs9U43p7Kn6Z1yM/WD0l911Arx7M6RLMXOrwz1V61sfeZP2J0FQ9uY5ufvij//oj3kimprt78P\n",
"G4smcB4L6Ldaxz+rlY9TvQSF7O/DnQVjSGeitqfp9eAv+hQ4j10zvLdqh1D7+7B1l0AQxJ5d9EVQ\n",
"++rt71cryQelf8x8/Aa/ecYY0uLVvul3bwWhOEbbYUl60uvB9uPD3HD1b9fQi6p9n0M/LnbNkl7w\n",
"fh8OZwgkuu3y0tMPT5uFUj9AFCLacUKZqTEblwwIgtj1w6UFyh/ixqKJ0o8cc/ie+Mtfs2WLj75I\n",
"Jb3P/T68ec5ISn958rH7FROCwLJOfBj6VsoXOW5cS3HDo/9V+/aFfnFYi1Lfbhk9i5kItVL5HPDu\n",
"LwgEQcxcuQuhgiB6/fJu5lG0Rwit5hLhzTHmfKL0VwMh4GQ7KK9NhHkNYUPnfHhuhRo0dGwhsbtX\n",
"0s3s9+G9jwicnBKMDiw4PzWdKht7lygIEc11id5VtdXs9+HgupEMiYQ9jfKHuHEt7heXp8UzM0de\n",
"gh5zBIT0EmILlseY+4vSXw3IkYJINGgxpSfkIzRXXvagho4tOnEXCpPyoG3IzMyRshvGCa8/lPvo\n",
"jVWGEISc6LZLYmYmxUR54jjbF/IxGcaJZxftOxU+x9m+AID+/WHmFHI4Qw6fJKDLvRsFlP7xE7b4\n",
"sCnEtLiM942Q9J5GuaMaEtaOsbJMhGoVlfvo+1xSnxq9mUEAxrAMTAXGotJf3hZQUhwBgJAT4lgS\n",
"hzOEEPjZuqA0/dnB6StSMiCAAECvB6Z5wlypPlD//okB4niXedVG+hljKysrlmV5nidU3LMgCDzP\n",
"83Vu9DiAZINm7IQW27YyW1G/OOqcRstQhqNqGOnvc7SmCs3Z9nFPE5X7WE0L8tjdlHZY3vscanF0\n",
"xBYEKptHlMMZIusS8xKiKK/sz8+R6LNT+7yihF5CzOUKa1SG3V4PHOeED1SulzCUeki/7/ue57mu\n",
"2+l0CCFWbNIwF57nAUBX52aBWSi7xYNOp+NkOCvmFyus6ZE4nrxiefLx6SUCAL3dE71XzJbCmyzz\n",
"bXq7ZcVAkhAC+3fj4ljSs0u9ZkkPboi5si3GAq1jpAbSL4RotVqrq6uGYRBCXNc1TbOgt84YI4SY\n",
"pr7FioOQbvhHM+Tq7gmHKjqoV4gUx94u/PLFINboy4g8SnP7d2FhRgx6qcoQxyEjCVXmwuv0+yfM\n",
"Ra9fRq/T75cuvlH290+EREpCXj9ppSS7jMHCQilXHs7ZA2EYx++1ho5tCDWQ/m63a9s2idwnx3EK\n",
"Sr/nec1ms3DRFEBAEALf+9D4D3/pRDOPNhFVcA5PLhAAeO/L5heeOJHfaZyy7ionUov/7Bnz1z47\n",
"sGNR/gK8M28s32WDqqPKHOdH8nF4hV5YP65dSU4r5zA3BwDw8XlyYZ3rdBhne8deQkl2OYfFRSAE\n",
"ej1NXv/MDAgBW1s6ctuC4Gi0vfEB0WBuRGog/UEQGCdDYpTSIuF+z/NifckYOZwhhgE7O0BAGGlr\n",
"JxW+bEIcyYfELHmJSTh9vb5+9ElojtKjmiqXEsOAH79HICHBZYxp5Pt8eIU+cU9ApC6pz7Eg4bM7\n",
"eN544t7AIZQqwifFwHzm4LiVlG1XADHg6FHF2obaFwEACIHDGULhqHaxBAeF5oLgeJBBiVB+/XzU\n",
"Q/qTMk3z9p5CCMaY67q5y9Pv99kAsnZInD9yB66ZF9d56nslP1TYUCiFf/2eMX9zmDgpMRe6cntz\n",
"9MJtHu1pwqen3C8mBDbeJ3/lpzzsXaCcMU14wdu34am7QTQgXqo+3rwJzz9zQj6iNVVVzSCAxUUw\n",
"Tbh9G56/Hv9teTczuu0H50ehLdlsyLDti7LBOSxee2TuUaMsdRrj7IEAONr2Y3t7izH2yis3z537\n",
"9/Jnyfb29ieffKLS6vAiabOUGyX5PCHFQz2Hh4dsgFNHKc00mBAClhZgQw4JPzvwa1JWik9MRJSC\n",
"aDAXsrpB/6khtpVdLx0hYGkO3gfgYHzuM13Zu5S6TMG+BpTCt7j5tae8dQJQZs4G57A8B6YJrZb5\n",
"W297ADY8EsdSIyTrFw1gLQATIrULm4dCLbYvCgA4OLnFNyFHY1P5NFXWTsj0zjhygCirqbDxPLhA\n",
"DAP+1f8Bv/UN2NraYoxtby8BwNbWUigmW1tbn376qTKTp1ED6VeIdMwLzu4SQpTPE3AOCza8OdCi\n",
"MivWHACAELBAhDSXjPmU4rRGXDmdkbbwNS6J5OCzpNoJAXOXTlgJfeHodxRal47qTw9OXDF2fZWV\n",
"JcQ04Z982/ivH/U05UIIIfD6H9Pf4t2ouegAUVXtGINfXQBC4MLnCXD21a+6zebLUvA5B9N8WTZR\n",
"z/PWw9ho+dQg4GOoe3d93zdNMxxhcc6FEHzcZ6eFkRDpcchU95IyfI7lgxB4tCBIrQcXwhjMzT0K\n",
"Rzx6jWLD6vDD4iRXxklK7GnGcU6LbBWpWQAKa8oYnP+lR1MmQkRjSqXy9BIBAHrKPt9qMAzozdLo\n",
"XS2PmScBANYvxCOPJaVXjEI9vH7OecxVz6fXpmkGwfF+VEIIGfpX2LvkRwhDsFs/gvnHYB7gRQG3\n",
"vgdA4fKbMPsVerigMjMgCAAMMIG98j2YvwsAcP06fPs7AESxublLMEePtP7z62x9Ha5cAQA4f/5o\n",
"7ndpG579Vco5LR5fOgoakCNz87dStGppGx58nnJO1TzwR90nGAPNffavUcYU1C40J8cZg8zdWTAg\n",
"NZCRnblLMr4EQMjyXQa3jn/1WP8jgM+oNXeMEMt3GfwbeOIALlw4+mynp7h2UXMrS2z/X8L9Hbh+\n",
"He7dAwC4vQ43PoCfnC/F3N/8LLv538P7t+GrX4WdnUefa080r4H027Yt13OFn8h0z0Hfl+684zjJ\n",
"sLvjOLFvBkFQZMq3IJzDEgDI527bwNjSFszL330AS1sADF74AK79C/H2P26rMSnEUZq2aUbNXYiY\n",
"u/oqbHxDZUSLEADDeJ6z934I84sAAIvX4L0fApyDpS1YBNj4giJz4ROn9MtvsTfegMVFAIC5OfjR\n",
"j45u6SLAhlBWO0KAUgBKn/0h6/WOknBmZqDXi5j7FWXmjnosSue/xwCg3z9KE+j3j8wtbTEA1c/u\n",
"kbleDxYXod+HMx//An5+bmkLrvY4gOrXxzCkuQ+34MsvQa8HAHAfwAR460flmnv+HGw9mpJ6CeDc\n",
"uwGAM+xvs9kBwwAg9D/4EYMdWNiCK0/BfWnuA5T+NKRL7vu+FG65wqvdTpdCzrlc68s573Q6OsuZ\n",
"AyFg8eKj8Z5pgmm+5h21gUUTXvPg5Sa85sF/ta1ufz9CQCqIHnMhtg22/Zp3NC1ZqjlCABxnBuA1\n",
"72iecNEoy9yRFjvOggO/4wEhYNuwQOF3PLhRgrmjrs1xNigAAGPQbIIQ8L+1oNmE1zz4e3/qqZ3e\n",
"cBwA84Q5GZO0bfhTAn/ju6XczNDcy03YiAxvZv+7ElrmYHPzSs0deQmOK01EzS2OY2lpDWL9ANDp\n",
"dHzfbzQanudZluU4zqAQTejpD8+0kT2E53mc80bs5AvNEAKndfkzM1o3+Tt7ED9xsCDREVrZ864A\n",
"EO3xk1MLcvayJErZqvMk8vrRaDh5lFxEKSwsKI4dy5YZXRghw9NyN465OZVzAISktI3oNIMqc/IW\n",
"mWZ6Uwwbf7iZqCqctCHEuI5vqYf0E0LW1tYcxzFNc3V11Um9hQAAQCnd3NxcXV0dNCyQGIaxurq6\n",
"tra2t7c3/Jt6CGNOQqTkwCx8kZzZKquBJM197itk5y2VTT72uKL7aOrM9pHi+OCCYpODqlDKznSP\n",
"+tHo9pYh5fU6g2YjoysElZDs2KKVUmXu2c/EKxPqb3T1yaVFosTlurp7oqFHMzjKXlY5hHpIv8Qw\n",
"DNM0T02cp5RWYXOefMh1K6EzcrTJpWHM76tsIFEtjpo70mLTvNorZZSRXJ9pGPGNEEqFUvXmBvsh\n",
"QCl8fJ7M9lQ+u1Ob9tl7ZQ1rystFuffnR7dI3sxkx6bW9NXe0dhTmpP6Gzv0htITex0WYf+dE2PP\n",
"MvZoyUGdpH8KOdrkktKlLZW5dalz5HLHWmmuJOlP7bUfv053/m3pr0L4Yof7LqhiuBYfPG/M7iio\n",
"3ez9kcr84XXjooqOLeaoSqIfSKfkw+tGaq5RVm5cDIbfR7mI7PAKVWIO4ES6VOSDI2TgTpWXILPa\n",
"hjCWs7pQ+uuAlj2fjps+peHW8MpJ+lbPf82Y2yzd65fRakph3jI+/I4C+Zi/Gxf0VM/08Ar9+A0F\n",
"tbu4fsokiYwvHV6hanqaftr6i0eEsf4HF4gScyNyeIWWOlWTNKezdppB6a80JcWLB6E2+J7qqCZ9\n",
"KyBESU+T6qhGkeYWb6ip4RM/jTuqMeNy24P/5L+gh+8pqN2FCynnEMSgFA6uG/ffUqBWsQ0VYoQF\n",
"2XvB1COOsrJ7L5hKxjQjomoIVU1Q+itH7JVWKP1JRzVpWmH6TRhRPRW5t3NBhjuqyglXGw2h1Ens\n",
"1IubJtzvKeppRoBS2Noqbi2FQcceRI+ZK4nQ9IPzldjctyRQ+sfJqRFVtczvxx3V6Il0cPL4ETWc\n",
"5qgiylHSj45IeUPS1D3pDONohVcZJLfukecHlM24XgqU/nGi2VFNEjuRLvxZSW5DMmhQ6smCx2vi\n",
"I2BnUwZ3747nhCnNoyjD0DHICE6Z4S4LlP4pIlUcQ2IjgOIMDxocLW5UR2oeRfR4qXGdzVPenHlI\n",
"tHYlmYu2jf39Y49FQ+2UM7zMRxnV6ljaYsOvOJaWidJfOVL1d29OwWaGw5PMoiOAw5lyNg49ic4Z\n",
"7NSVonrQEIGJnnRfkrmoPL3zzvGzU2JueDKx8hXgw2ehojNeyjq2k+Ziq77H0jJR+qtFbHVfOBLc\n",
"m0tbvqma8PWOnl5UHidafPm109nTRLVYCcM1yDCOa6ckRpHqqIYmrl9XfDNn+yI5CxVFvV88mhte\n",
"Xj8a3sDBG1GWC0r/OEmNwJR3SlyS2KkAZXsf0eo0m8f/lQfXlWraNI9ftjsLCg7PHe6oyhMXJO+e\n",
"UzBiG+6oUnpcu4dzikZsCXOhiX/+z0/+ooRuO9byNfvFOs0NWQ1eKij942R4BMZxjpvgwUEpL1jU\n",
"WwTVPU3SUY2dJqiWpa34Iojo/lxRn1JZLunQ6bljN/xZRSO2xL0LaxeVj5JGbIMeXHnddngDo83m\n",
"9nkF3XbqwCh8mNGnqqTbriYo/dUlqmO7X1Hwgg13VKM9jTK/OOE+DfSnlIhjIgwxrqnd6CCjPHTW\n",
"zjR138zwBkaPQ33saQWFGJ7AFj2/Q0m3nexpooPCcYHSP06u9uJ5/aU2iOGOalSqDp9UVI6T9YnG\n",
"JaL8eCZxrKIKBpnbmyvrvMGBg4wSajdsyFGC13900kg57O+XdeUqkOxpom7WuEDpHyfJvH7DGE+S\n",
"rx4GafGTl0vp8QZK/6VSHPJBfvGdy6UcwDqodv/uotaNgJUMEJO7MQ/ygZSkuo2OnlS3sVCDU7qm\n",
"jYHSP45DwJHiCKHghNekXzwooKQ5kqBsgHiSQXkve5dKSXWz7cHddtAtePFqLn1A6a8N+48R1Qdj\n",
"DA1Jjz0YWSolBHAHDeEJUWBO+aEolSIpjjozcWHws1PSbevcWmN0MOBTD0yzrHho6jtGCPR2SzE3\n",
"iP59reaKd2zJAG5sVwy15jSTzVEt3LFlE0eN41El3XY1QemvDTp3Kteze0nUXPF9snQWGKo6ildF\n",
"Ni3W3LFNtjldoPTXBuWHypbN6MMUJS8XgVG12DBga7uouWqO4iX7dyfZHKIElH6kLDSHp0fXYv1e\n",
"o05xNE2491N9IxLN5hBVoPRPEY/dxVd0DBiG7rx1zQNEzeZ09qOEwM/WJ/OtQekfJ6PHiymFXq/o\n",
"jNOnl6obo9AcqUdqSnn5DqkYBvz8XHXfmiLURvoZYysrK5ZleZ4nCiigEKLValmWZVlWq9Uqcqni\n",
"iJETxyiFzblSlrwOMvdWr5Q1qKkcTfNO6NoZpGponqKvZkZAPaTf933P81zX7XQ6hBDLsvJdRwix\n",
"srIihGi32+12WwhhWdYY1T/TYViaD967s1DKGtRUCIGNRX1rUA0Dbu6XtZdDKh+f17co9OhYQY2t\n",
"urgbrlMchdD6Kmk2Nzo1kH7pp6+urhqGQQhxXdc0Td/3c1zK8zzHcZrNJqWUUtpsNm3bbrVaysuM\n",
"VBlCYG9O65Kh2xeK7qY5ujgahoIB4ujmTBN2+kUHiJnFscDN5FxrAoJmc6NTA+nvdru2bZNIWobj\n",
"OPmkn1Jqn1wh7roun9BNWZFSySaOQ4/GHIVM4ljczcx0hYIDRMayDX+3rxcdII6uxYTA278oOkBE\n",
"6c9JEATGyXXWlNJ8URo3uh/ro4uTGi3Z0BubOrhXyGCmUXzyDPdSzRUnq7y++oeTuvG7AhYWRv2m\n",
"YcD6Oty8VWZpTpp795zePSV0UYM9fIIgMBNbmlFFe3ysrKw0o9uBj8Du7u6gyYZms2mUthnrxjXz\n",
"R/+79z6x9Wzt+c4Z+uP/xb93PnnvRyWTOJ59hgBnRbYtzezq6u1Hd3bgybwGNfcZjMHTlXRU4dGa\n",
"jJs34UWNRm/eghfVvXSD1GNjY6OvMdGtBtJf3jRso9FwHCertl2+fHl1dbWkIg1HZ1rbJ5+n/Xf0\n",
"mbtz2QBRdIvEDOYWjO//T60HeftRxuB8lhjF3hyd/3+78I2c+iEELC1m+P7BAbz1h8GXCqhVphjF\n",
"wQHs9GDoiXOKuX0bgkDfFm+vvw4v/hNlVxukHp7nvfLKK8rMnEYNAj4l0Wg0DMNwxnUyJgBkj1EU\n",
"3+imyua+/7o+9/bwSVKwHx09RgEAe5eozi2Ydr9i/uT/CbRlMH38S/TP/kd96VKHM+TSB4HOTODd\n",
"t6qYnVmQGki/8hCKEGJ5eXnsug/ZYxSaF4UWMZdjqLa1lT8Gw1jmyTTNNzPTTGZxdNZu7xLt9fTl\n",
"yt65bDx3Jr/wz/ay/e2PZ4yF9/LngszfYodXqjhbUAPpB4Dkjc/9KGQuv+M4Y9f9HGhOFShijvNs\n",
"fnEQZPt+kkylLW4uE0Jolf6sN7+4ucXF/H9+YZ1/fD6DD5Sjm48yuxPsZYncv/kuuXGj0MQQSn9O\n",
"bNtmJz0Kme456PuMsUHLdFN1X+vQsQBSrbQVtrh8ZBI7x4EvfrGQuUwIAQu5Z12zEwTF1CqjowpQ\n",
"SIuzOqqGUcjcE/fEwfMZRvaE6B5CVTM7syA1kH4Z8AkT+eUKr0E+O+dcbvbQaDRiv5JLeV3Xjf3t\n",
"8vJyCaVWD6Vw44Y+6ScEFhb0jeI1n0jsODD3V/Mn9WZ1VAHg8rn8PU1WR7XZhPMfF+rYMkl/xhQ5\n",
"BRTpabJCyGRKfw0yfACg0+lYlsU5J4QwxhzHGTQBECbpJ7P1OedBEPi+H1sONt5tfEbHNGFO31wa\n",
"UApFvPAcjmoRsjqqtg1b38lvLqujCgCzzxJt3bZhwFbdTncYHc3rcNpt+Pk/rIdEZKIe0k8IWVtb\n",
"45wLIVzXHbIIi1K6ubmZuhTANM3Nzc2SS1oipglQQPqz5iM2mwBefnPSUV3M+FeaI6qcaxptNJuw\n",
"2MXt6dTQbAL8t/rMEQJ3J7EfrUHAJ8QwDNM0T118SynNvwxJI/rXdmaO3esdDy0saL0ni9f01a+0\n",
"dX7TiEznz/3siq8bz8TNm3D+vFaLI1In6Z8whNAasswTgdE7tJ55Uqe1iT1uWzIzo3Nn0kLk0OIi\n",
"XsL6OlzRuPxsti+ev67P3Oig9I+N+Vss61RhEbJOFU4+Ndq7KTsLBWaVc/DZX4jcPU0OLS7iJczv\n",
"B1eyp67l7mmu9ri+ZcdZQOkfJ1mnChFkVAp0bP/fn4msMYpnruc3t7TFrnxJXzc8vx9kneFZvFgs\n",
"FwSlH0GQHGz9m0BnvHhukz//t/SqVcUnQyZxgIjSXysMY2lbYwSXkAvrWiejZ+/ndK507pADAB9+\n",
"h80+q9VRff6beoN1lXRUEYWg9NcKzd6HYeReiDS7k31W2TSv9nL2NB/9Ef/wekbPkdKru/k7ti/9\n",
"g8yO6vxdzO5EqgJKP1IKd28Fey/oc1T7fXj572XsFyl98DONYwXTfOKnGqWfUq0DROzY6gZKP1IK\n",
"/b7uvRlycOHC5JrTHLExzfl97NjqBEo/gkwmmtcuaYXS4scdZ0Bzx6YFNdJfl80vK0W+mcncJ9DO\n",
"36zovuFISWge02juaXIvy8r3Bk1eP6pG+pPbZCKncnE9+8ykYeSeCAWAw4WM0k9IEXM50Hy0OqKQ\n",
"3D2N5oee4jIy4AAAIABJREFU+QxnANDej2ogm/RblnUmDVaXNeMV40HW1bzaM3y0vpbFOrbM1Kdj\n",
"m+weMZ8W1wWNB61nI7PXv7q6+jDC3t6eaZpra2tlFA5Jkrsl5TtoV2vDrU/HlucPC3RsecRRe8eG\n",
"pKL5VJnRySb9lNLYxpmEkHa77XkFtvedVra28mhd7paUL+Umtzl0VOPUp2PLA6VLW3pTbvLOu1bW\n",
"DddMNulvt9vJM1Jkf5D/3OIppuLL14sw2aP4fNRFdPKUs0AuaR5zBVJu8ngz2js2DaiZ5qWU1uWs\n",
"KwQZF5Ud+8fQXM4a3JZJ3NZCjfTLoxOVXAoZjuapwsmO29SF/f08f1WXQUY+ctdOc5Ou7BuU7YBG\n",
"3/eTKfxBEBBCBh2WiwwiX5vIHUjJ94ea4za53xPNMpdPi3OT71hwzd60Zi3OXTvNTbqykc9sXn+3\n",
"200Gdmzb7nQ66oo0LVS2TYyR3PdEs8zl0+LJTu6sixYjkmxeP6XUtu1anHyLjJfJjjbUYsSmmVr0\n",
"T0hINulvt9sllQMZkZkZ4FxrapAQefISCUyyENRCizUz2fdk8jq2ady+jTG2srJiWZbnebVLTFpY\n",
"0HqceO7zrydbCJBpY/La89RJv+/7nue5rtvpdAghlmWNu0TZ0Hwclf7EO8198WSbQ8ZMEFQ28jld\n",
"0i+EaLVaq6urhmEQQlzXNU3T9/2xFOaxu3lk4MGFnN5HvhGr5p7m8+eFzqWBucc0tTBXDzRv+svY\n",
"3pzGJP0gePeLFZ0ZnS7p73a7tm1HlyA4jjMu6f/0Ug2SzHL3NPl47Gmt5s5/rLVjy2mugDjm+VPG\n",
"3j2nVRxvPZVTHPMNobRKf4WZLukPgiC2/gDXIU8zmju2nObyiuPSUyJfr9F/No84ygSEHOTbDxmH\n",
"UAXJluGTRAjheR4hpNlsKilQqQRBkMxMpRlXaff7/UGbVMs4Us7CIbnR3HlrDhrkFUfNHdvCAmxo\n",
"fA6aZ6EunxOMqTlzdJB6bG9vf/LJJwoMjEZR6fd9XwZMTNOsfr6/Egf/8PBw0MNL7mw6pXCuNSOC\n",
"8zsLWheTbz+OQYPpYvZZZe15kHpsbW19+umnqqycSlHpD+MnWX3n+jL2Ic67bwowq93BCKFZizXn\n",
"3k3emU1IKQgBEG+Zg9TD87z19fXyy3RE0Vi/PKdlbW2tFtJfoY2G8o4/Fn/DePCn2WOced3ws8+Q\n",
"t/5PrSHVs/dw6mWa0Bysm/Tx6OgomOY1DKNCknoayXMFxnPSQO42kS+glNcN/9x/rvXEjw+vG2du\n",
"6j00sac3ubD6aM621CyOQty5rM/c1jZc+VJFB+jTleFj23Ys0CbTPcdSmL/8uKJtYoz81ReJxiEv\n",
"PPl3zbde1ad0Z56jW9/KfuIHY/nE8ePzJEfH1n8r2LimddLu8MlJfhEqGw2ZLumXo5MwkV+u8HIc\n",
"ZyyF0RwvPjjQai4fF85rNXdlQau5ay/nlIF84njwvPHgdmbp7/VyqtXhFTp/K3PH1tvNf3Jljo5t\n",
"a7u6WqyZotO8taPT6ViWJc+WYYw5jlOjaFURJnlmMggANL7QjO3N6XMX+vcBnszzh1euwM2b8NXs\n",
"f5hb+nP8Vb+fcy/CvRfN2Z08z71Qx1b5JMbRUSP9QRDUYpoXAAgha2trnHMhhOu6mItZCpwfzmh8\n",
"SYJg45rWodveJX2tvdcD4zfy/KHmMc358/CDH8CLGi3u7Oizla9jqzJqAj6NRkPJdbRhGIZpmrXU\n",
"fUKu9rJPhBbIo8gzzat3Mq23q83UeKhFO33+ulZz169rlf58aN4CKxOZvX7GWHJJQvLURuQUcvvF\n",
"hjHb7+Ywd2fBzWfuaq8FkG0mPHeMAgi52mMA2e5Mv59/IJ6jY9vaBnIjpzkkRm5x1DwtlG9Mo3lB\n",
"dSayef2MMc/zpMvMGDNN0zAMxhge4ZIZvX4x5M6jyOVw9np5D5MxtOaSgmHkGUJB3trlGrEV8Ryr\n",
"f8BIlcUxiuYxjQaySb/v++12W25+KTsA27aTGZMIUosYhe5S5urY8otj3o4tN/P7OPo/Qa9X3Rch\n",
"s9cv82GEEGGg3HVdxhjuf5mJ/v1xlwCZeHKpTv6jRUxTs/Rr7thykDt/SQPZpH/QvKhpmuNZE1tb\n",
"8odEAPb3s//J3Zy2aoHmybQqz90VJ3defz5yNOYjTDPHEKrXy2uO0qWtiYptZJN+wzBCicep3YLk\n",
"HgnOzWX+k/39/BOhOdxAzeJYj23364Nm6deZK58/IyDXTanyXEtm6ZdhfdM0gyAIgzyc87rk9VcE\n",
"zXN3Rczl2Bi9iDjmdwMnlK2tSV6AqlkcNZur8mHu2ZI7HccJnX3XdS3LchxH6j5KfyaKiGOO9lTE\n",
"nOa3JceYpgjV72lm+0LnuzXZ4lhlLdZMNumXiT3yZ9u2KaXdbtcwjHFtg4NooPpvy9ZW/ujZlRmt\n",
"SpcjeobiiJRBoY0c6rVdM6IN/a507maYQ+mKZOwR0NrTVH9Mg4yL6dq5E9HD/n51c9qKUyRjT7NP\n",
"rTl69tjd6s5qjoX8mbLlg9I/HjS3Cc0pN7N9UdmVLEh5fHqp2k9d+yk0D+eqe0NQ+sfD3S2h0y/W\n",
"nI+I8eK6IoRWp4Sxd8/ln8LOPCMdBBuLGjNJtZ9QnQmU/vFwOKN129DJThCcZBjbm9P45Dj/YFGr\n",
"WvWfzV+7nT56GPlB6a8f+dLvUPpryvbjWp9cjUZsmmcyqhy4zwFKf/3Q/HJWfU8u7QFcrW74ZB+v\n",
"VityrG2sMij940DzVnecF+ktMiud5hhFsQBu5iGUEJqlf5Kp1YuQGc0vQkZQ+scB50Xmf7Ima7/y\n",
"P+iebtLc4oucOJ9VC179w/y2IPsQ6uatQuaqTrEXIROMwdtv6D4kQ+dBnllB6R8PRbyPrCHO27dz\n",
"mwLIHuK8eauQFueIqGoLiQQB3L5dqHaZOsUggN0/1O2oFtHiTEMozuHtn+Q9QSgX+bftzEuVd7JH\n",
"6R8D//Pv6LMVBHDvXqErZA1xvvpqIS3Oam5H4/scBLCzo7Wnubul1VHdv1tIizP1UkJo1WIhtM7T\n",
"cg5b29U9pwVQ+sfCD35QyHPMRBDAeY2nmAYBBFyrq/N//bNCfnHW6NmX39MawNWpVozB97+v1VHV\n",
"Kf2ca52nFQLeflufuRyg9OtGCPjyTFDQE8/ES0/wf/1jTWoVBPCbS/zf9jU5qpzDE/fEH/08v7ms\n",
"0bOZGdj8NP/NzNrTaM4q2d/X56hyDhce6A6IFOnYMoWzgmAM8aVM1Eb6GWMrKyuWZXmeV+QwSCFE\n",
"q9WyLMuyrFarpf9cSc7BNoIfPFFsVWGWjMb5M+Kjy/oc1YUFePeeJv0QAl5+WaujurBQKJs0a0+z\n",
"sAA6j7+7cUOfLSHgqSXdAZEiHVumwWUQwEsv5belgXpIv+/7nue5rtvpdAghlmXlu44QYmVlRQjR\n",
"brfb7bYQwrIs/eo/N1foZKKNRTOT/Cws5LcFcmaSZTiabm6u8PKxLE9kZgY6nWLmRkYIrcuIggDm\n",
"Hmrd8OPpx0Wzmf/Ps4anCrbMrCwuajX3xS9AlTezr4H0Sz99dXXVMAxCiOu6pmn6vp/jUp7nOY7T\n",
"bDbl2TLNZtO27VarpbzMp+K6mgwFQdGgQY7Qdrud39ydBSOro1s0RjFyP8o53PjlYrayEARw4+U6\n",
"nT2ZtaUtXtO6yFz/mqwqL6GvgfR3u13btqNb3jiOk0/6KaW2bUc/cV13sg+UDwJYvAYnK12uuYK7\n",
"hGadsy1oLusQCop121mHUABQxA0HyDCEYky3Gw6gzy8WAhYuaz0HuNKpnbWQ/iAIYgfCUErzRWnc\n",
"xFsbBIHWfdQAhNC9hTJofMGCAD73FX33kzE4/0u648VF5EPzYresQ6iZJwubzNSPahRH+ZZrlf4q\n",
"p3YWPKVLD0EQmIknpuoo4JWVlWZGt2p3d3fQZEOz2Tz12DLO4T+7Xuk2US/mLo27BBVG83ZPG4vm\n",
"y0GQIcxRTBxregbZIPXY2Njoa0zmHaf0CyEGBVuihwCXNw3baDQcx0n2K8O5dOlScvQgGbFDUuBb\n",
"IVOAEACanYRqxyhi1HTnzkHq8a1vfeu1115TY2MExin9jLFBIXtCSKfkvI1Go5HvQPmZmZmsvQUy\n",
"OWiPUWil2jGKFDINMoqhapZ4kHowxh5//HE1NkZgnNJv27Y9wvyj8pPfZU6n4zg5dL8KnD8P69/m\n",
"1yvZ/QgBUPjk8YN7UN2NimsnjpNLpvjS7H0BxUbbR1P0o713V3c5fLHSTaUG07wAkIwL5U7LqYTu\n",
"F/Mcn/5N84l7+nzPz/41uvWtUZNSCCkqjleuwLs/qPYJAYgKlraZzuTHi+u84CRvpin62b4AnSsy\n",
"slMD6bdtm53Mh5PpnoO+zxgbtEw3VfcDzWd9QM08x2d+RWtSymd/zZjd0fpEPvrjSc7urSwHB1rz\n",
"3vHEmxg1kH4Z8AlnBeQKr0E+O+dcbvbQaDRiv5JLeV3Xjf3t8vJyCaVGcvLgvNZ+8dJvmH/5E31D\n",
"qEx5/bP3VRRsZM/m6i7X6ZSgFo+XGiR3AkCn07Esi3NOCGGMOY4zaAIgTNJPZutzzoMg8H0/Nres\n",
"fyMHnRQPcWZi/m4Ai/rk4+ouh/+okOeYSesuv8ngHxUaxe9dovt3YcTMlKs9Dt8oFKP44Ia59T1v\n",
"cbTQ5oOfCfgHhWp3OEOAjxoN18xsX2u+1Px+AFDhtbx1kX5CyNraGudcCOG67pBFWJTSzc3N1KUA\n",
"pmlubm6WXNLTWdpm8Bv6goAX1zn8Y32v4hM/DeDv66vdbF/oDhoU84sNA/a/M6r0F8cwAH406peL\n",
"u+F3Lhu9t7sjrghe2mJA9c23Xe1xMHRtnyKl36x0Fkk9pF8yYqqP3J+n7MLk5uBAa6xf87AaR/HD\n",
"yfTkx+CokkLdtmlC/1tZ/kDXe3o0sK/VHFvZ1CDWP2GUJI6el/555mPHi5H17NmCXO1pDU8vbZWS\n",
"lDJoP6qrPa4zS2R+P9Bmrrwga+qLwLnWbTv1J47kAKVfN0rkI7kL0KBk15LkY5Baze8HOkO9JaXQ\n",
"DdsbsATpT1WKyXZUOYfPny8q/6lz5oM6FTUbZ43WZQWB7g2ic4DSPw4Ky0e2zXULy0fytel2C14y\n",
"mznNpGoxY2XtHJBqjnOt+2iWd37hoH70saeLNsu9Synv0SCPu+B+1DBgL7xcOwhXApT+PIySnpf3\n",
"OBkFhK2fczVqNeJrU/xsgEHmUm+4qmH16EOokqR/UD9akhanhkSEKKun0Rz9CM0Jodh06oH1GXfg\n",
"rhAo/XnI/bz1vAbhkgb9p0qVJB+p4qhqWJ3saaLSr/zdHj6mUe5Fjn0IVepxGP378U+ifo/ym5k0\n",
"V9/McJR+rZQXBGRMayuMvs8rK6Wb0+w5Ru+kcukfMoTiXH1Nk+Y0B+vCGxjT4uJ9EqWjHn2uJJw1\n",
"urla9Aco/YUQ4sRjDoL0V3dQ+k0+CIGtrfiHpnksxxqOHYtWXG1DT61d7CZrgzGtp6ILocNc9Abq\n",
"7NiiERjO4ewzRYPvySmzWFMMb6Y8oku5OYjcQMYgPOlV8zxNPlD6C8H5CR+q200PNap9n09NaVGr\n",
"xZSmaLFhlNXTpNYuakLPxFr0OcY+0WOuvFnlEMZOuOQajq5Vq8Wp14+2H83ed9Rc9c/kQOnPQ9Th\n",
"jSpC9NkTcvwrzXNBhKiU41RnJ5o0pOcFk1aC4IR8KCE5ijcj5/WGNZWnHCuHc7DtFHOg5QCysrV4\n",
"0DOavxuUlLeaetWru7yMrFx2Mk87vJlL26zi23YCSn8+wuYVU1jOB7Z1tfo4ZKGWEGAYR+Y0uHJC\n",
"HPc05Tmq4SAjCI7v5F/8iSg+rDbN+OlLPLFKTFqcv1uK2y8SW1FIc6o2U4udYigvngzWlaRW0g1P\n",
"jmlULR9LThiErTEIgJAji+Vt+BG96ol3vPILMlD6VUJpursdKtfNfxkoEcfYmavS+wjlPnzZPvM2\n",
"X1BxXkSsp4k6O5yD4xyZXtpmcy8oeMGSHVv0PQp/vtrjM/+xerWKaXH47FStVht+zl9oTslqNcOI\n",
"Sz/n4LrHrfSEQKlQq2TtYkMotT5QcmohfBGCABxHcTRyyNR0UNYwpixQ+lUSPvuobxX1Pub3g7m/\n",
"X8pi1+g0b/iyqVrsmjzdO/oOn4gvqfCtUju2EMOIBNBUvG2n7nWhMMpvGMOyRKQhheZOvT3KY4ND\n",
"ascY2LbWafMTXr8KUnsa2RqD4Pi907y/SD5Q+nMSFT75vDk/4QuHrTwITvhZJZEaoyhvA5/oNG8Y\n",
"XyrPXHoEZl+No5Xs2OCR/gqh+H0mJP0uhaLfbEbMlby7mRwgHo3YVOwvcuoFwvHo0lYp8aWklyBb\n",
"6VNbRY/oSiXm6Ye1q/4RXYDSn4+Y8IXvbbTZpQZwS2rxSWSLvNorpcXDAC0uzxyNbNYSjm/K224s\n",
"lPtoxkhJQ6iotyhRG54ePi3kOJEhVDnbE6WKI0BZ0fBoJUILJc14BSdDgDTDMTzjB6U/D9FGG8b3\n",
"+dB90o7/RONIUNu2nWXXKTqcUj6KjxGb5g1/Hh6jz02QmEFQezOT0TPTPFYo5Q8u9lCCAGz7hCCO\n",
"MeGybCq8VXwKKP1FCaeVYHyz+smkFElqKKM40WF19NUqSRyjtZP5S489BlBa7cQA556AShUZ476+\n",
"pe6smnwoMUEs4x2Jdi0x11vzK1mLdbwSlH5lRJ961DmN/vaxuyqbRrgkJ5rQGc32UavFnB+HuaJu\n",
"eCiUJQ2rk1p8qYSE91O1WG1PU98dHxWgWiBj0h83UqYep/Q0QVCSU6IWlP48xJ63bFqxVU6GcfSJ\n",
"1GJCAIT49JKaNnE4Q4DzmFqFBTgyFwQqtViIQdsEHdnV3OI535tTOcCOaXG8pqrNwfBV0IzdWdA4\n",
"T6ja3Cn9KOcbi2qGHjLbMnWV3/H7qM6cJGwqyTUZAABBoPXZ5QWlPw9Zx7BH31fXBO8sGCBEdH1T\n",
"CkGg0hznpzhP6lr8/j5AEJwyYyaEci0eFigIArXmwmeXvKtCAAihth8Nd5FKf4iqaxcVxxQ4V1W7\n",
"MNtSqn/6m6iu25aLJE6ZKWFMecssgzqdzVshOF/aFsDg8psADJa2R/yX7c2pOal5Z+foh7/4EwGE\n",
"l20ufFHf/GNhwgBz3e6dhaYSc+/fMCEIGKNPnxU3HvDkTf7S5kcgXlVlTg6hAIyz9wSwE+aOfxZs\n",
"41pbiTmJECDN/fUP47X76x8CMMXmAGDrR2Lx/RRzS9sAgr95TuUZ4kLA/paY20gxd/lNgKvBm+cU\n",
"eAlyp79FAAA4+KkAkdIypbk9okCLDQP+bB8gUrv0F+GiUGKubFD6c8H50lYADF74AIDB0lb838+9\n",
"nfb5tfRzhXJw5crRD1d7HLrdz71NSjUX9jTnf8JhZ4C5r5JD1WeIf/rvOGx0X/iAxG7sc9u/gOfI\n",
"e0KNOTmE4hxWnoqbO36+X1Ufy7q4zmGju7SVfjPVBqg5h72n+OJgc2qrFwQQdPmLaeZe+ADgb1Ki\n",
"onaGAd9/9PP8TQa7bJA5JTP00Xu087vduZ/z9Jv5XxpQh7N5ayP9jDHf94UQhmG4rksKt9UgCHzf\n",
"p5Q6TnZ/x3H+gMPLTXjNg5eb8AeN+M/fB/j1R5/If2/78IAClJH2a9vfJ2bM3GsefN4BUDSXGPY0\n",
"UXPRWr/mwS+7AK2BV8jH2QMBtv0aMUND3wf49Sb83x78ahOIoq2ww47t3r8P4B+dMBf9VzSGXmVk\n",
"5CCDEOPjNzj8N85rXSPVnKrahVy4zeGfua/5NNUcqDY3f5PB/9p8rUVSzLmKzQkBF9c5/EE7Wa8y\n",
"zAHA7E4w0Jyj3lwZ1CPW7/u+53mu63Y6HUKIpeLwQ8/zAKCb99yK1NRvSAv/SfdNhvuV5xokl5hK\n",
"E7FVQqqIrvmMLdVRvlxZCPjoj9LXiKldOyM7NsOATzcG7tIjd6lTghxkEAKH7+lY8xmeXf7J+2Vt\n",
"YRZHe7IzpUdR+GROXRnUKINzCDWQfiFEq9VaXV01DIMQ4rquaZp+seQ4xhghxCw1w/kRwzuGgiSX\n",
"mJb6uvX76QtX1Bo9ODi65qDkVM1rZ8ro2FKXQ0vUdmxyyjF176DQKVFoTmYEEAK7bx9XKaaVyqWT\n",
"UrjfE1DyuxYyfCOmulAD6e92u7ZtRyM8juMUlH7P85rNopOEk9H5Z0LDaR4AcOHC0Q/aViND2j7G\n",
"IRqcV2kiOkDUgDSq1pzMCKD0xDKIsgeIMHTVhcLhr/RFhjglhECrVf39ewBqIf1BEBgn7yWlVBTQ\n",
"Xc/zYn1JPqKrmWLraVP9KYVNcPcXJHrpsjuhg4PxdHQCTshHqVvghe+ztvWfSfkY12pwpmDrtiPk\n",
"iG0IcrtDVTU9nCEH3x02ZonuaFucmZmjF2G2n65AcmVl5XftBKiL9CdlmuZtqkIIxpjruoXLBfDo\n",
"XTUM6HaPu4Hw2Uf3eFAbfD+4bkAipho7LUChVn94PcVVO7F5svKdCTgHgJmZ4/1Qw+XKAEBIKftk\n",
"RbdqkApVan+ndmeIUWCPNg+MPTtQ5/uHIzaI9CjRE+sAIFC37d6dBWN9HQwD+v2BD4ur21TwzoKx\n",
"8yoHgMMZMnzPruozzgwfIQQf0CMTQkJPv4iDn6R4qGd3d9eyrDt3/s63v31lfv7m/Pytvb0X9vZe\n",
"XF296fu/CWB0u0dNzTCOT2ouA+mohrcn2tOoNX345FHXO9sX4fgmulOFaao8ev7T/9Ts/ZDBZYDI\n",
"fqjRGhkGeB4o6r7hcIYA6wKYhzMkKo5R51TtgOPmLTAMOHydRDu2qBYrdMOjhE5J7LgFtd32wb1j\n",
"c2HtSt2z6JknBMyolPhBHM6QnR349ZcEvH7iZjKWwdMflKWysbHRL2kbrDTGKf0yXzP1V4SQTqdT\n",
"hkUhRMHZ3cuXL6+ursr9c0zza3IfRPmz9EzDEUA0gAtKs0Qohd4PAS4f+cXSHKXHZ8SrHXISAvtb\n",
"AJfgcIY8EMfiGO1d5BEFSqAU+t+D2fui3z86VQrKDIZ89EWj93Z3dk4AxN9niaypqp5G8uz94MMZ\n",
"8kAc+8UhlKZs51mE2+vwK2f53hzlHKTbY5rQaKQMp5Swvg5/+xz7YI5Gn100k06hORlfurjO31ow\n",
"zon04a9yLq7zm4vmxqObKbvt0Z/X6upq6uee573yyiuKyng64wz42La9OoCo7hvqhlW+75umyR7B\n",
"OR8y8hhObLYq2ppj49nwrVb4PlN6HCmOxZeGTFfmJnrOX+ioJrVYraN6tcc/WDRSDanFMGBrC5bP\n",
"8I1FM+xHY/El5czuBG9/1kj1+qOjt+Jcvw4/+AEsXorve8HKOTni/Hm4fRsuXIC9ORq2TPmyyMav\n",
"NvIZxpdkBEaakD6Qttly2VVLSprELoMaxPoBIKnO+fTaNM0gCELpD4JAhv5zXEp6haEIhkEeGBz1\n",
"Vjvm3d+HpW0mXbloj1JGTwMAvR7c+IDdWTDSt6xSjUyei6VtlJe13e8fL1sru6d59lfph99hZw/E\n",
"hQvHIRHlh9aGXLgA8/tB8lDZkh7i88/DvXswuxMczpyYoStv1uT2bbj2Pn/nzHF9pBaHfapaLT44\n",
"gPmbLGlOEpWFilMD6bdtO6bOMt1z0PcZY61WK3WGwHGcZgTbtimluad8TTN9yDzowStsEJTC22/D\n",
"iy8e+VZlQwj0evD883A4Qwbpr9oDbLe24Kvn+bO/eqJ2JWVtyymT+Zuadt069wW6vw9/5ac8tttd\n",
"SaHqD68b8/vBxXW+cc0cdDMVjgA+Pk+u9vjsTnDn8sDlJgpb7JUrsL4OT50Rn3z+hBaXNGK7fh1e\n",
"fRUWFiBqLglKvxpkwCecFZArvAbtvsA5tyzL87xGQ9G6+8EMalXRt6ikHADZtmZ3guvXdQwyZAbF\n",
"7E6weINELxuLUKtCXvaJe+LcF2gsJTw1klaQMJwV2/Ko1EHGwuXjyXNJSaONB+dJrwczM4+28n5E\n",
"9HmZpjLrB9eNu1tiYSH+efT6CnNjrlxJzzwuySmR8aWZJ+Of1yKbM0Y99vDpdDqWZXHOCSGMMcdx\n",
"Bk0AhIPM4Wn7nHPP84QQQRA0Go12O88uiam9DyHpp4Mq58IDMbsTfPwNB36Y/gXlrsfsTgB/x6En\n",
"pb/UMQelJ25y7Jkr7Fb7fTh7IKInF0LiUarCMMDfSvk8akuhWpkmtLZg4TJQGj+yvIzGSSnwLZh5\n",
"Ekxz4FCYEHV5/Vfoi3t+8nLRD9RGPi88OKpV7GaG/61LN1AP6SeErK2tyVnZ4Xu3UUo3NzeDIBie\n",
"xmMYxqB59tGJWghlKOaZmmZZCWc/e0BipuFk2FEt4axyzA0vSfof7gkAElPe8sbRuz14+jqBRO3C\n",
"/ypUq/A6yZ4mhFL148VYO1SVjhUjfEax8kfHHAqr9uW/S//4Hw4rhlrmLePcP23B347fPccZWPHK\n",
"Ug/pl4yY6kMpzb3gKzej6LthqOwGZmZgYQE2Tn5YnvTPzMDiNfiUnmj0sQeisHZn5kkyaBBF7Qv2\n",
"lc+JmSdJrNsub5ABcBSSGDJArIvzOIhY+XNsjzuilWuLAIm2V1IocvEGubwAkNax1Y46SX+VGcuz\n",
"l8Pq2OCjVKdjyPFkyu/AzEfDBhRqzR2cjbv8yk1E+RsvAZB4T6N23UCUJ0/beUltm7k0p/JqIxJ7\n",
"WNH3Qu1zPHUbq7p0Ayj9ahjFqVEb+VlYSJndimmxQotzp73P6r3UoVcsyYvUg7yZ2vz6GzdO+ULh\n",
"nQxP8MKiANWH9gzhV54KgBhJ6S+Ja58EQIddvaRImnJqkOEzMahtji9/9RTxUKssv/63TvmC+o5N\n",
"I6eKo1q/+Mbt7vArqn12S3fL3+IgwtX7p8yrqhVHSnQcexDy/DOnLGzReKcLgdKPjMZp87mKO7bz\n",
"WjfH+uK9U8RR8ft82qyx2jHN5+5rPTDwc1dP+YLiEdtpLVNtP/rUfh1OXxwBlP7actoSIMUvmNoU\n",
"uVGo0kSnZulXbC6W11k2CnfmHIXTXgS14awxvAjlgNJfW057mesy3VQVNPc0mnMAdbaG2OIxDeYK\n",
"/X57OJOOAAANxklEQVRKQemvLSWtOBpE2clDMQjR7VvVJR87B5p7Nc3mNLeTWicYREDprzOa/Zkq\n",
"uXL1NjfBLr9+c5PdsZXGmYcPH467DHXi61//+htvvPHOO++MuyAIgkwUcr/+999/X4859PoRBEGm\n",
"DpR+BEGQqQOlH0EQZOpA6UcQBJk6UPoRBEGmDpR+BEGQqQOlH0EQZOpA6UcQBJk6UPoRBEGmDpR+\n",
"BEGQqQOlH0EQZOpA6UcQBJk6UPoRBEGmjtpIP2NsZWXFsizP88RpR7KNeMFGo2FZ1srKCue8+AUR\n",
"BEHqwtlxF2AkfN/3fb/dblNKfd+3LGttba3IBRuNRhAEjuPYth0EE3LYJoIgyIjUQPqFEK1Wa21t\n",
"jRACAK7rCiF833fyHpezsrJiGEa73Zb/pXiAG4IgU0YNAj7dbte2bRI5HMdxHN/3811N/qHrumoK\n",
"hyAIUkNq4PUHQWCcPNCOUpo73O/7fqfTUVEuBEGQulIP6TcTJy8XidJQSoMgkO6/bdtGxoNShRCe\n",
"56X+ynEcDB8hCDKEQerx+uuvf/zxx9qKMU7pF0IMSq0hhISKrCSfR8IYI4T4vt9qtVzXJYQ0Gg3H\n",
"cTJNG8zOzia7IgmZlCObEQQpiUHqsb29/fbbb2srxjilnzE2KGRPCCkpLCOE6Ha74aSxbdvLy8um\n",
"aY7urc/MzAx6eAiCIMMZpB6Msccff1xbMcYp/bZt27Z96teyBmSGX4pzvrm5mZw0bjabqqwgCIJU\n",
"nBpk+ABAMi6UbxGWjCPFHHyMziMIMm3UQPpt22aMRT+R6Z6Dvs8Ya7Vag2YIDMOIXY1zjuqPIMhU\n",
"UQPplwGfcFZArvAaNDHLOZebPTQajdQvuK4b7Rhkqs8ocScEQZCJoQbJnQDQ6XQsy+KcE0IYY47j\n",
"DJoACIP4g5JtKKXNZnN5eVnKPWOs0+lgZg6CIFNFPaSfELK2tsY5F0LIpMxB36SUbm5upi4FCDEM\n",
"Y3NzU4Z9cHYXQZAppB7SLxkx1YdSOkrsHhM0EQSZWmoQ60cQBEHUgtKPIAgydaD0IwiCTB0o/QiC\n",
"IFMHSj+CIMjUgdKPIAgydaD0IwiCTB0o/QiCIFMHSj+CIMjUgdKPIAgydaD0IwiCTB0o/QiCIFMH\n",
"Sj+CIMjUgdKPIAgydaD0IwiCTB0o/QiCIFMHSj+CIMjUgdKPIAgydaD058GyrHEXIQ+e58kTiWtH\n",
"TW84Y8zzvHGXIg/YVDTDGHv99dd1WkTpRxAEmTpQ+hEEQaaOs+MuwKgwxnzfF0IYhuG6LiEk96V8\n",
"32eMKbkUgiBIHamH1+/7vud5rut2Oh1CSJFwXqPR4Jw3m81Op0MpXV5eDoJAYVERBEGqTw28fiFE\n",
"q9VaW1uT7rnrukII3/cdx8l6Kc55EASrq6vyv47jUEpbrVa73VZcaARBkApTA6+/2+3ath0NyziO\n",
"4/t+vksZhhH9xDTNmmYyIAiC5KYG0h8EQUyvKaVCiByXil0n9eIIgiATTw0CPkEQmKYZ+5BSmuNS\n",
"tm13u91Wq+W6rrxyo9FoNpuZLtLv9/f29uo4Vtje3r5169a4S5GHmt7wW7dubW9v17Hk2FQ0c+vW\n",
"rX6/r9PimYcPH+q0F0UIwTlP/RUhJHTGLctyXTem/pZlhSH7rFiWFTaO1dXVZL8yhN///d//7d/+\n",
"7Xx2EQRBhvD000//7Gc/02NrnF6/zNdM/RUhpNPplGG00WiYpim7Dc6553nRbuZUvvnNb37zm98s\n",
"o2AIgiDaGKf027Zt2/apX1MYi/d9nxAioz3yyp1OZ3l5eXNzU5UJBEGQ6lODaV4ASMaFBkWKhsMY\n",
"i4V3CCH5pg0QBEHqSw2k37bt2LyNTPcc9H3GWKvVSk0BSk0NypcshCAIUl9qIP0y4BPOCsgVXoPW\n",
"c3HOLcvyPK/RaCR/6zhOrFfwPC/TNC+CIMgEUIPkTgDodDqWZXHOCSGMMcdxBk0AhCu/UnfmoZQ2\n",
"m03LsgzDkJcyTTNrcieCIEjdGWdyZ1Y453LPteEbrgVBkLoUIIqMIFFKMdCPIMgUUifpRxAEQZRQ\n",
"g1g/giAIohaUfgRBkKkDpR9BEGTqQOlHEASZOlD6EQRBpg6UfgRBkKmjHku6qoPC0+FLwvO82Cem\n",
"aaaucqhCXbrdbhAE4YZ6SUYspOa6nFrsEZ+CzmLLY03lihbTNB3HKXIzq1byCjb7aLEppa7rDlpF\n",
"NJ4b/hAZmXa7bRjG2tra3t5es9k0DGPcJUoBAFZPsrm5mfzaeOuyurpq27ZhGLZtm6Y56GsjFlJb\n",
"XUYs9sPRnoLOR7C3t2eapuu6m5ubm5ubrusahrG3t5f85iilqmDJq9bsNzc3DcNot9uyGJ1OR9rN\n",
"V6Qyio3SPyp7e3uU0mibc1233W6PsUipjNKdj70ua2tr8jWQR+WkfmfEQuqsyyjFlpz6FDQ/Asdx\n",
"Op1O9JNms+m6bo5SVbPkVWv2YVOJfmLbdo4ilVRslP5RabfbsQYnO/ZxlWcQo7wD1anLEA0dsZBj\n",
"qUtx6ddc7GazmfwwWYVRSlXNktei2VNKcxSppGLjNO+oKDwdXg+MsUHFq0VdRixkxesy6CloLnZy\n",
"WiIIgmS8eJRSVbPkIZVt9snDQkYsUknFxmneUVF4OnzZWJYlhCCECCEope12O/aq1KIuIxaysnUZ\n",
"/hTGXuyVlZXknrWjlKqaJYeqNnu56SRjjHOePHR2jDccpX9UquNIDqfZbNq2HbYM3/cbjUaszdWi\n",
"LiMWspp1OfUpjLfYjUbDcZykoIxSqmqWvLLNnnPOOWeMpabljPGGY8Bn0ojlkDmOI4QIgmCMRZpC\n",
"qvwUGo2GYRiDDjuqMkNKXtkb7jiOzPPhnCczUMcISv+oKDwdXjOGYcTegVrUZcRC1qIukHgKYym2\n",
"EGJ5eXmI7o9SqmqWPEnVmn273eac5yhSScVG6c+AqtPhq0At6jJiIWtRlySaiy2EsCzLcZzh6jlK\n",
"qapZ8lEYb1NJ9kapBdBzw1H6RyXr6fDVodvtxhyHWtRlxELWoi6QeAqai52qnkkZGqVU1Sx5kgo2\n",
"e3nEbNYilVXsgsmhU4VpmuFKir29vUHL88aIaZqx9S+O4yTXvzysTF2GJ8iPWEj9dTm12KM8BW3F\n",
"lgtiY0V6+PAhIST55VFKVbWSV7DZ27Ydu7KciM5XpDKKjQc0ZkA6IOGR7kpGoGoRQniexzmXKRDS\n",
"O0jNhBtvXVqtlnRk5Fxc6J2trq7mKKS2uoxe7FGegrZiM8YajUYyHZAxlnz9RylV1UpewWYvJ3WF\n",
"ELJIMql/UJLPWG44Sn9mRjwdfowIIWQo8NRCVr8uMHIhq1aXEZ9C1YotGaVUVSt5BZt9EAQyNqWk\n",
"SGqLjdKPIAgydeA0L4IgyNSB0o8gCDJ1oPQjCIJMHSj9CIIgUwdKP4IgyNSB0o8gCDJ1oPQjCIJM\n",
"HSj9CIIgUwdKP4IgyNSB0o8gCDJ1oPQjCIJMHSj9CIIgUwdKP4IgyNSB0o8gCDJ1oPQjCIJMHSj9\n",
"CIIgUwdKP4LUCc557JDu0fF9X21hkPpydtwFQJCc+L7f7XYH/TZ2Xu7E0Gg0Uk+dHQV5u6p2oDQy\n",
"FvCARqSueJ5HCJFno3POu91uqImWZU1kw5a9Xe5ejXO+srKyubmptlRIHUGvH6kxhmGYpil/ZoyF\n",
"P08qrVYrt8sPAIZhUEp930fHH8FYP1JXHMeRLn+SmGPLGFtZWXnuuefm5+dXVlZisfJWq2VZFmOs\n",
"0WicOXOm0WjID5977rnl5WXOubyCZVmWZQFAt9u1LOvMmTPLy8ue5wkhkgWQ/vX8/Ly02O12i8fZ\n",
"GWNCCNu2i5izbRsj/ggAwEMEqT+rq6umaab+qt1um6a5trYm/7u2tmbbtuu64Rc2Nzcdx6GUdjqd\n",
"hw8fuq5rGIbjOPLLlFL5ndXVVcMwXNd1HGdzczO8OKU0vHh4wfBq4fUHFW90pOnk55nMyU5xb2+v\n",
"YGGQuoPSj0wCg6R/c3PTMIzk56Zprq6uhv91XbfZbIaXiv5J9LKmaSbFN2m62WxGu5aHDx/u7e2l\n",
"qnYmTNOMXTafOQCI1h2ZTjDgg0wyvu+7rpv83HXdWHZQNHZECBl0weTVTNMUQgRBEH5i23a32221\n",
"WmFkiRDSbrdzlD8K55xSmvw8qznTNGUUC5lmUPqRSUYGwc8ksCwrKtajkyq+hJDo1WQICB7NCjz3\n",
"3HONRiOfuVNN5zOXOj+BTBWY4YNMMjJqnzo1mo8gCJISLISITTgTQqLjAynKa2trQ8YTpxLrYHKb\n",
"45xjhg+CXj8yyZimqTahxfO82Ce+71NKoyKb/I5t25TSgmEWwzBSvfVM5oQQyY4KmUJQ+pFJxjRN\n",
"SqnM14zi+36r1cp3Qcuy5DwB59zzPN/3Y4F1znmsvwmCIHW4kNV06hYOmcx1u12Z3V+kJMgEgAEf\n",
"pN6srKxITzYIApl377pudG1Xu932PG95eVl+KITgnBuGEa6N8jyv2+0yxhzHkZEQOUPQ6XTkFyzL\n",
"ajab0lOWaaBh4rzMFIrFVWRkJrQYBAHnXKaBFqmpvFpy5Vomc4wxheEvpL7gRg7IVCAVX/6ce9Gv\n",
"ZVmjb6IQWgx3myjOkI0cRjEne4jNzc0iUw7IZIDSjyCjkkn6S+K5556Ti9Ry/G2j0ZDz3spLhdQO\n",
"jPUjSJ0Iw1A5oJSi7iMS9PoR5HRiG0Tbto0aitQalH4EQZCpAwM+CIIgUwdKP4IgyNSB0o8gCDJ1\n",
"/P/qOJV7iXVYrAAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1frOTGdedfd2buHWlGo7m8khD9GYwEXtg/2Nh4A/Mi\n",
"0sAIsDLINQJBT2N2RpAH9u+FLSAI4AQIiogRvS3AXsObaPdhQ2p2sYECGGgCi8UaQR7I2CtkH4Qs\n",
"aa2f1oDcVPTb+GcMViGNZGaSmTs296FGFIfdzXuq+aeryPOBIPT0PV08Vaf7kPyy6tROnucEQRAE\n",
"GROntu0AgiAI0jeY+hEEQUYHpn4EQZDRgakfQRBkdGDqRxAEGR2Y+hEEQUYHpn4EQZDRgakfQRBk\n",
"dGDqRxAEGR2Y+hEEQUYHpn4EQZDRgakfQRBkdGDqRxAEGR2Y+hEEQUYHpn4EQZDRgakfQRBkdGDq\n",
"RxAEGR2Y+hEEQUYHpn4EQZDRgakfQRBkdGDqRxAEGR2Y+hEEQUYHpn4EQZDRcWbbDiCINNi2TQjR\n",
"dV3X9W37AsUwDE3THMfZtiOIWOBV/+jIsmw6nR4eHu7s7EwmkzAMZ7PZtp0iIvhwIrquZ1kWhmEX\n",
"jU8mE6PEZDKxbTtJki6OhSA7eZ5v2wekP7IsOzo6opRalkUISZLEtu0wDNM03a5jhmEEQbBdHyCw\n",
"C/8uLqLDMPR9nxBimiZ7J0kSz/Msy2LB2ow4jhVFUVW1HS+RoYCCz7jwPM80zSKVqKo6n88PDw+3\n",
"6xVCCNF1nd1PlNUk0zSPjo5M01QUZbNmNU1rxz9kWKDgMy6yLFvOBZTS4nUYhkxwIIT4vm8Yxs7O\n",
"ztHRkW3bWZZVPhiG4WQyOTw8PDg4YNrRuoPatl1uKo7jwng6nRqGEcdxWe6YTqfL7cxmM/bXOI4L\n",
"9wzDYBfLvF5BYE0dHBwcHh5Op9PlEWj9iBUURTFNk/WXfDJWnucVBuwdFq8ySZIUChK7U1lJHMes\n",
"g8xz3/fLjcPNsiybzWZsEAohsdKI53nMedZa8WVYPlz9F6agu2EfBTkyJubzuWmaNQaLxSIIAk3T\n",
"mCi0WCzY+67rqqoaRVFh6bquruvFO1EUmaZJKa00mKappmmu66Zpyv7puq6iKIVlEATsiEGJ8oEK\n",
"oihilvP53LIsSulisVgsFqZplv2EeAXBdV1N04qmWMuU0kprLR5xufE8zy3LKhoPgoB1vPgrG5OV\n",
"P2Q2ko7j6Lq+8nCLxYLd9hX/tCxr2RhiFkWR4ziFn4vFggW00g77YPG9StO00p0c8IVhtDjs4wRT\n",
"/+hwHIdldtd1V2bYPM/Z77PyZhAExQ+e/bZXfrDyg19+J89z13Urv9J16WnlIRRFcV13+U9wr06E\n",
"NcWyT0EURYSQsuctHjFflfqXE/fK00PNNVw5ahUcx1lOu8txB5pVmM/ny35SSivDlaapoijldyBf\n",
"mHaHfZyg4DM6KKVRFLHJKp7nHR4errzHL6tADPYRNufE87xlA/apsvySJEmWZctTIU3TLB5mboDj\n",
"OCuffAK9gsCer1YUdk3TKsdt8YiMQsUyDOPw8DBJkvl8vkE7EEzT9H1/NpsVUgk7p25mRggJP4E9\n",
"W1550MqXQVGUsowG/MK0PuwjBB/zjpRicnqWZWzqd+UZwMo5IYqiJEmiqmocx+umY5Z/t0mSrJwC\n",
"ryhKk8eP6+arAL2CEMfxOs87OmLxqSLHdb16gCl4nuexzM6CRSmtDC/EzPd927Y1TWNvZlm2bgDr\n",
"AX5hWh/2EYKpf1z4vl+53FYURdd13/cruZil+MrHi6fE7PoXcuXe58x0uFeQpno+IoOFo63WIIcr\n",
"Xz6ze44oiipnuHqzJElms1nlU+zyfwOXIF+Y1od9hKDgMy7WXSst354vT73wPE9VVWap6/pKmaiC\n",
"rutxHK+cGNPFKQHoFQRN01ZKB5U3Wzzixqybd3QiyyE2TZPd0nGZrRTHNvMK+IURYdhlB1P/uIjj\n",
"uPJLjuN4+VaAEKLrejFvkn3K87xC4dV1XVXV5SmYnudVzi6U0slkUvkxz2azymeTJKmcDMIw5D09\n",
"wL06EdM02Yqq8pvT6bSS4Fo8IhBN08rDwiZxbtZUHMeVDrIoVO72TjRbPlvMZrOaGaX1QL4w/Q/7\n",
"8MDVvOOCyfphGDJVIUmSOI7n83lF32Bra9n6UpZo2JyfSuJjK4GLZwZxHLNyMRUz9oNkM3NYIQRd\n",
"1ytmTCxmZ6CVNkmSsJ96HMfFzQchhFJaUUiAXp0Im11eaNZhGFqWlSSJ7/uqqpbXHrdyRMMw2FCz\n",
"lFpTeGc6nSZJws4BWZY5jnN0dKTrOpuAW7RW9IIZs3+WF/RNJhNVVStfBjZpsnw4iFnhEhso9iRp\n",
"Op2qqlp4NZ1OmQTEpucy39h8/IrzkC9MW8M+WjD1jxH2OyHrH7fCyyoUTZGTnrAVyu86M3hTLXp1\n",
"IsXtSH07LR4RAlNFGj4tZ5z4ZQCaFQOlaVoryffELwzpfdiHBKZ+ZAWyVNRBEGQzUOtHEAQZHXjV\n",
"jzwEm75d/LMsDSMIMhgw9SMIgowOFHwQBEFGB6Z+BEGQ0YGpH0EQZHRg6kcQBBkdmPoRBEFGB6Z+\n",
"BEGQ0YGpH0EQZHSMOvXHcVypOIggCDIGRrqkK8syVlaQENLpHngIgiACMtLUb9t2sUMh205oXYFc\n",
"BEGQ4TFSwae8cSjbGGi7/iAIgvTJSFN/peA47u2AIMioGGPqX77GX95/HEEQZMCMMfUjCIKMnDGm\n",
"/uXt5Xi3/0YQBJGaMaZ+sqT5ZFm2LU8QBEH6R8rU7/v+bDarMQjDcDKZGIZh2/bKtK5pWrHpcxiG\n",
"zfe2RhAEkQiZ5vWHYeh5XpIkqqpmWbZu33DP8zzPc11XVVW23WAURRWbypIu13Vxkg+CIONBptTP\n",
"VBp2wT6bzVam/izLjo6OoigqUrlt26qqrtxgtmiwS68RBEHEI5eQIAh0XV/5J9d1KaXldxaLhaZp\n",
"bR36q1/96rYjhiDIMNnZ2WkrU53ImW13tmWSJKlcxTN1qK32f/KTn+zt7f3u7/4uxPh73/ver/zK\n",
"r/z6r/860PgLX/jC888/DzH+sz/7s9/4jd8AGv/Jn/zJG2+8AbHszvijjz76i7/4C7jxX/3VX33t\n",
"a1+DGP/1X//1zZs3X331VYgxV0S6G+Q//dM//frXvw40FiR8w45Id8bwWMdx/IMf/ADYbAv0dpJp\n",
"kZqrftM0gyCovLnOeAOuXLny+OOPA43feOONd955B2687Pk6rl27Bjf+4he/CLTszjgIAi7ja9eu\n",
"AY3feeedN954A2jMFZHuBvlLX/oS3FiQ8A07It0Zw2NNKT1z5gy85YZIOcOnhq6naT7yyCM7OztA\n",
"44sXLz799NNwY7gbwAsfxsHBgXTG8A4+/fTT8KHjikh3g/zoo4921DJGpECQceOK9alT/SXkoaX+\n",
"rrl169Yvf/lLoPHNmzc/+OADuDHcjR/96Edw45/+9KfSGcM7+MEHH8CHjisi3Q3yP/zDP3TUMkak\n",
"QJBx44r1L37xC7hxQ4am9Xc9XefMmTPwq/5vfOMb8Mufb3zjG1/4wheAxq+//jq8p7/zO78DtCSc\n",
"FynwljVN4zJ+/fXXgcZXrlz5/Oc/DzR+5JFHLly4ADTubpD/4A/+AG4sSPg6igjXb2R/fx9oSTjH\n",
"rTtjrljDc0sL9CYttUiN1k8pdRyn8qaiKG0d+uWXX7548WJbrQlIi89FBIRSCheLZQTDJy+U0r29\n",
"vd4ONzTBxzTNYpkuw/d90zTbap9L8OHaAJJrzwDP8zoy5rqZ7c4NuDHXIHPJC931rrtYixA+3q89\n",
"3JhL8BHhy0k4Y92n4DO01M/u0IvYZFk2m81WrudCEAQZLTKt5p3NZuyKPsuy8vz9yrLeLMsMw9A0\n",
"TVGUMAwty2ox9X/5y1/+4Q9/+POf/7ytBkXDMIx1FTIGQHljzkGC4ZMX27b/6I/+6O7duz0drzdp\n",
"qWeiKAqCIE3Tdpt99dVXL126BDReLBaLxQJuDHeDS/EctjHvIMONu+vdsGMtY0REiDWlFL5mqDlD\n",
"m+FT0NFUn3v37sG1fq5FBlzGXBsMDNtYxkEWxA2MSA/GXB3sU+uXSfARgddee+2999778MMPt+0I\n",
"giCDwrbtGzdufPzxx/0cbmiPebvm9u3b9+/fBxonSQK/QOC6lKjMYhqzMe8gw427692wYy1jRASJ\n",
"9fHxMdy4IZj6+bh16xamfqGMZUw0w461jBERJNZ9pn4UfPhAwQdBkC5AwUdojo+PuR7zwh/yDP55\n",
"V3cPFbkGGW4syKM/EQaZy1jGiAgSa1zSJS5pmt67dw9oXL9SMUlI+VshyGpe6Yy7WzsqyApPEQaZ\n",
"y1jGiAgS6/4m9aPgw0uLgo9tE10nA12egiAIHyj4CA0KPqIZyygvDDvWMkZEkFij4CMuLQo+y8Zw\n",
"NwS5mRXBWEZ5YdixljEigsS6T8FnsIUcOuLq1auXL18GGqdpWlNJgtK8vCCcq+YEVyWAYRvXD3IT\n",
"4+56N+xYyxgREWJNKd3f34e33BDU+vlArR9BkC5ArV9obt68+U//9E9A4zAM4as/uNaJ2LaNxgze\n",
"QYYbd9e7YcdaxogIEus7d+7AjZvS2/3FMGhX8JnPHzKGuyHIzawIxjLKC8OOtYwRESHWKPgITbuC\n",
"DyHEcZq3hCCI9KDgIzQo+IhmLKO8MOxYyxgRQWLdp+Az2Hr9HfHYY4+dOQMdNFVV4S1zGXNtVDRs\n",
"YxkHWRA3MCI9GHN1cHd3F27cEBR8+EDBB0GQLkDBR2iyLMMlXUIZy7iAaNixljEigsQaLiY3BwUf\n",
"Pvb29k6dgp4vFUWBt8xl3N09tXTGMg6yIG5gRHow5urg6dOn4cYNQcGHDxR8EATpAhR8hKZFwSfL\n",
"sGhzC8YyygvDjrWMEREk1ij4jAKeG0EEQZA2QcGHDxR8EATpAhR8hOb27du4LbtQxjJuAj7sWMsY\n",
"EUFi3ee27Cj48HHv3j2urVrgLQ97+47ujGUcZEHcwIj0YCzsVi0o+PCBgg+CIF2Ago/QoOAjmrGM\n",
"8sKwYy1jRASJdZ+Cz6hTfxiGXIEhhNy6dauV1B+GRFEemtw57HTQnbGMiWbYsZYxIoLEus/Uzy34\n",
"ZFnGpuJmWabruqqqXGvbBCGO4+l0ysowJUniui5w0V1bgg/78oQhCj4IghAisuDjed7R0dHBwYFh\n",
"GGEYxnFsGMbh4eHR0ZHneVxPM7ZLlmWz2SyKIsdxHMehlM5mM+Bnj4+PuR7zwodl8M+7unuoyDXI\n",
"cGNBHv2JMMhcxjJGRJBY9/mYF5T6Pc87PDz0fd+yLLZDTRAEQRDkeb5YLCzL8n3/8PCQa5HbFsmy\n",
"jFJa/FPTNPhn0zTF8m1CGcu4dnTYsZYxIoLE+u7du3Djhpws+Hie5/u+4zj1KTJJktlspqpqOatK\n",
"QZIktm3P53OIMQo+CIJ0gXCCj2VZQRCceGmsqqrrutLl/SzLptOp67pAexR8RDOWUV4YdqxljIgg\n",
"sRZO8JEO27aNJZa3VcuybDKZOI4DL6yKgo9oxjLKC8OOtYwRESTWfQo+pLcN4EUjTVNd16Mo4vrU\n",
"1atXL1++DD9EmqYr/+Q4eRQ9+H9hDHeDPXFB47x2kBsad9e7YcdaxoiIEGtK6f7+PrzlhvBN7gzD\n",
"UNLZnBXiOPY8z7Isrme8pD2t37aJ4zxQ/Hl2+uycJCHyhxdB5EM4rb/MbDbjXQO1Gb7v10+4DMNw\n",
"MpkwGYd3Xmkcx7Ztlx9cL2tB67h58ya8pnYYhvDVH1zrROAO8xq//vp/E8ENuDHvIMONu+udILHG\n",
"iPRgzBXrO3fuwI2bwnWPUL8VvaZpbMbnxgRBYJqmpmmmaeq6vs7MdV1N06IoStOUZXCuo1BKNU3T\n",
"SyiKAvxsW4IPpXme50GQFwMmiAjwpS/dFsGNYcsLgsQaI9KDsbCCD7fWb1kWpZT1J01TSillaSzP\n",
"F4tFw+wfRRET34MgWJf60zRVVbU8oJRS13U3PigX165de+GFF5q3s5z6BWH9CRdBkA6hlD7xxBO9\n",
"HY4v9ZcTfYFpmvP5nL2Oosg0zeZu1aR+NoW0/A475TQ/KISXX355p8SpU6d0Xd/b27t48SK7e3jx\n",
"xRfzPH/xxRefeuqpIAg+97nPPfXUU3mev/nmm2fPni1esB7s7f3m9ev/Kc/zs2fPXr9+Pc/zp556\n",
"irVQvGBNlV+8+eabZ86cKbfJWnjzzTfLL4oWzp07V9NU2as8zx955HZNUxWvKKU1TVW8+tKXvtRF\n",
"B4Mg2N/fB3aQLUUEdvDcuXP1Y1Vu4cyZM/VjVX5x/fr1+rEqN0UprR+rh79XtP7L0EMH2de+0hR7\n",
"UfHq7Nmzn/vc54IgKLdZ6eCLL75YtFD+Viw3VfHq3LlzNU1VvKKU1jRV8Yp97eEdrDS1t7en6/rF\n",
"ixf39vbOnTu38zB5X/Clfk3Tlu9fKum+RqiBU5P6KaXFmaZAVdXmB4Xw6quvXrp0CWi8WCzW3Rsu\n",
"X/Vz3UVy3VpxGXNJgN25ATeuGeSGxt31rrtYv/POf++o5WFHRIRYU0off/xxeMsN4Uv9654NlNN0\n",
"16nfNM3loW/loBDaEnwsK8/zPAjyvpQqKITkPEI0IhZL9+SINPQs+PDN8NF1fXmGj+/7fU733G6d\n",
"uCzLWlnSxdaQ6TophlOQZT7PP/9/4I6IsGpGxgVE3cX6v/7Xv+2o5WFHRJBYw2cPNocv9VuWVZnY\n",
"xKpgmqZZvOMMuirN3t7eqVPQQVMUBb5OGG5JCOE618KNs4w88QTHV6IjN7iMeQcZbtxd77qL9aOP\n",
"PtpRy8OOiCCxPn36NNy4IXx785qmyWo1W5alKArL+5ZllSd98i6S4qXr9us5f/78mTPQQevu+1Q/\n",
"y3Zj4zgmhvHE1t3gMpZukDt14+Bg++GTMSKCxHp3dxdu3BDuGj6swH0cx7PZLI7j+XxuWVYXntWw\n",
"fA/FdVfVhLYEn5XGcDe6uz/90Y/+pwhuDFte6C7WP/0pCj5iGQsr+PBd9TPYMqjWXQFimqZt2+US\n",
"ob7vlxUnpCHybLqDVLlz5+y2XUAkobcHylzUzPDJ81zX9WINV5qmbGVvP461u6QrF2xKRhDk87lY\n",
"LiFciPqDRk5G6Bk+XTObzYoCy+yhAqNiNp/PPc+bTqesOPMGVdg25vbt261sy77SGO5GZxtqk7/5\n",
"mx9u3Q0uYxk3Ae8u1lxgRHowFnZb9k0EH8/zWNElVVV1XaeUcj3FroGtFj7RTFGUKIrY1vAtHh3C\n",
"vXv3uLZqgbcswvYdSUJUNfq7v/vidt3gMpZukLtzI47J+fN3CYFqPhiRHoyF3aplkxo+pmkWS9RY\n",
"JTWuclRSM2zBhzkjlEsInCDAEkwSI7Tg43lelmXz+byYsWRZluM4k8mkg7OSiAxb8JHRWEZ5obtY\n",
"p+nfddTysCMiSKz7FHz4Un8YhssrtnRdz7Ksnzr+W+fWrVuY+oUyljHRdJn6045aHnZEBIl1n6mf\n",
"T/BZV9eeUtqwUr8soOCDCAsKPlIjtOAzgK0ZG3J8fMz1mBf+kGfwz7u6e6jINchwY0Ee/XG1vLd3\n",
"C76ECCPSg7Gwj3n5Ur+maStXsoVhuMVFXn2Spmnz1bwrvwyCrOaVzljGtaPdxTpNI3iqwYj0YMwV\n",
"67t378KNm8J1j7BYLFRVrayfYvt2tXovIi6tCD5s5RSDVW8WBGEFH5769uPFcXJKhdv3DQEiuuAz\n",
"n8/ZWiq2c/rh4aGiKMOu1lmmLcGnWIpQvEDBZ51xGJKayywZ5YWOYp1l5J/9s5910TKnG/JFRJBY\n",
"iyv4kE/2Xtc0jd3IBEEwnrxPWhJ81hnD3RDkZlYEYxnlhe5i/ed//ucdtTzsiAgSa3EFH+Tq1auX\n",
"L18GGqdpunKxW3lfxkJd4VoWx7XDH88WcflisYALPh25UTEOgjoNat0gNzfurncdxZrS/J13/n+4\n",
"4NNRB2WMiAixppTu7+/DW27IJoUcxszu7i7XVi3wlkXYqkVGYxkHuTs3nn76mY5aHnZEBIl1n1u1\n",
"tFO+jesOSGpu3rwJr6nNKh3BjeFuVPZKa90YqE927QYjy+r84R1kuHF3vesu1v/hP9yAC9EddVDG\n",
"iAgS6zt37sCNm9LKvUNvu6JvnQELPovFA8FnPofOEunnnppSFHxACKLXyRgREWLds+AjVtFm8eEV\n",
"fFbe7oUhKW4ZVZWwy4Kt3/kmCdF1oqoq3BER7qll3Am2o1hnGUZEOOOBCz7joS3Bp5z6C2O4G4Lc\n",
"zIpgLKO80FGsFQUjIpyxsILPyY95Pc/zfb/epretcbfOY489NuBt2WU0lnGQO3UDnmowIj0YC7st\n",
"+06e5/UWtm0rilK/DZZt21EUteqYoLz22mvvvffehx9+2KQR2ybFWgj2QxWhCkbhSRiSLCPi7HY8\n",
"nRJCiOtu2w/hYd+r8rcLkQjbtm/cuPHxxx/3cziQ4KNpml5Ln/tkbZcsy4a6pCuOiaIQz/M0jQB9\n",
"6WfVjKKQmu+XjAuIth7rTo1ljIggsYaLyc3Bef187O3tDXVef5YRTSNZJt9jXnizLQ5ykpDy30V4\n",
"zMuM4ZM7BxYRMY2Ffcx78uROyOyr8UzubKV8W3n6XXmi53YpeyVUBbf6yZ3bQliXhCoIiMARrnwb\n",
"ZPZVEAQtnYlEpxXBp7xASVEeqCvDFgG6M96WvFBZZSaO4AO/yhxYRMQ0FlbwwcmdW6D849Q06NLZ\n",
"0cLGR7RRShLCM20PQQSjt/uLYdC64LP8z20hsuAjjixWoOvCuSTsdgsIBOEEH6TM7du3cVt2oYxl\n",
"3AR82LGWMSKCxLrPbdlxhg8f9+7d49qqBd4ybtWymbGMgyyIGxiRHoyF3arlZMEniqIAdmcLt5QX\n",
"FHz6R1jBx3G27cTDoOAjNSIKPrZtG4ZRc5sThuFkMplMJoNf2zVgwYddnQhym1wYF6Xu1l08bUte\n",
"qDyfF0fwgbeNgk8PxhILPpqmRVHked50OiWEsLW7rK5DHMdZlrGBoJTO5/Ou3d06t27dYqkfUsHp\n",
"o49OEUKef/4Eszgmtk0++ujU888TVX1ooZCmrV7IGoYhvJAI0JgdqIuWGxqrKtE0Mputri3Bflrg\n",
"6qQcxt31LkkS+LIgXjdUdcvhkzEigsS6z9R/cg2fMr7vs3m4YRiqqqqqqqZpmqaZ4hR86Ziihk9H\n",
"lVLK1xNZ9lBBhSx7kJ2LF8V5Yt0Zgotyj8SpA1NUFhLHJQY794vjUhiSJCGWJdxAIUB6ruHD95jX\n",
"NM2BZfnJZBKGYZqmQPvj42Pex7xAESzLMkVRKhcT6wabXUoU54nZbIUNOx/oOt91h3TGvIMMN67x\n",
"IUmIopDyrTxX71isgcbwllWVXUSPMSLCGnPFus/HvKOe3Ol5nq7r9UVJK6RpKk75Nl1/8J/jrPhP\n",
"UUiWEdsmr7/+/9k2Yf/5PqnXHgVZA1kYnzg/YitrR5OkeqclzmrerRvjat4yXLG+e/cu3LghfILP\n",
"kMiyzLZt13UNw4AXouha8OkUpiDF8af5VFGIphFdJ3FMwpBQ+uB9cXpn24RStgmJKC6RT2SoMBTO\n",
"JQGVMQSIiEWbB8lsNrMsi/dTvIIPfFZvDxOcmf5D6ad3BqZJkuTB3QC7+WHGmgaqUtDP1OniCcdK\n",
"eAcZbizIXG9B5qdzzeuXLiKCxBoFn875JMFxSD0MoQSf5saqSizrwWmAPWZgxory4LFhP25AjNfp\n",
"pVuRF5bLCgkl+ACzDQo+PRgLK/gMczWvbdvLI65pmvPJnTCTejZo+eDgYG9vD2jMdWrhMua6X9nA\n",
"WNeJohDff5BEVJXt2N63GxC2MshxTCh96MaIq3edxpppepDJh0OKiLDGXB08e/Ys3Lghw0z9Tq3Y\n",
"GcdxkiSzT6bFsNe00Llr2d3dHepWLRVjTSPFlzaOHzwfVhRimp++34MbJ17AbmuQKy1tfasWlu5x\n",
"qxbRjIXdqmWMgo+qqo7jlHeXhC/QuHnzJrymdhiG8IV/XEsEbciKsvaMNY1QSlyXUPpgAZptsxed\n",
"u3HiD4d3kOHG3fWui1izTdZ6/mKspDLISVKnHAoSEUFifefOHbhxU3orGcHFfD53aiukBEFgmqau\n",
"65TSEzcRq4dri7GrV69evnw5h1VKgWxwVjaGu7FYLLZrnKa56+ZvvJFRmkdRh24U47xu8yneQYYb\n",
"1zjMvHKcvDDh6l0XsWYuLRYLeL2jjr5FlUGu96etiAhrDO8dpXR/fx/eckPEuupntYCOjo583685\n",
"W3qeZ9s2Kx2hKIphGJsdzvd9wzDiOGY1KiDwCj7w2z257nwVhVgW+ff/fp/dB0wmZDY74bFwQzfW\n",
"DQ/vIMONT3RY0z7t8tYFH3GMK4PMnj0AjdvyQRxjFHxAKIpCKY2iqOZBSpZls9ksCAJN05i9rutc\n",
"z9wLTNMMgiBNU/gj33EKPjXG7BwwnxPTJJ5HbHvtrNB+5IUWjQURAcSJNdCyMshZVvfARpCICBJr\n",
"FHzyIAjW6TCu69KH1ZbFYqFpWi9+5a+++urOzs6pU6d2dpydnZ3d3V1d18+dO/fkk0/qun7p0qVX\n",
"Xnklz/NXXnlFVdXFYvHyyy+rqprn+VtvvXXhwoXyizzPL1y48NZbb7EXb775Zp7nqqqyFooXrKny\n",
"i7feeuvcuXM1TbEXRQvPPPNMTVMVr4IgqGmq4lUQBMtN/dZv/eXu7n923TxNH/Lqt3/7tzfo4N7e\n",
"f2QdPHv236z0arFYXL58GdjBxWKxWCyAHXzmmWfWNXX27L/J8zwI8nPnXmUtnDt3rn6syi/efPPN\n",
"+i9DuakgCOrHirWg6//jwoULQRCUvdq4g8tewTvIvvblsaL0QZsVry5cuPDyyy8vFotym5UOvvLK\n",
"K0VT5a/9clMVr5555pmapsov3nrrrcrXvtJUxSv2tV/X1HIHK02dO3dO1/Unn3zy3LlzFy9e3NnZ\n",
"+SSl7Ozs7OR9IV/qZzpP5U0WmB4o6vVjVfR6oiinNKc059FFV1CMs1ADzpwJgtx1t+3KJxTjE0Vi\n",
"bSRA6drnNEgZEev1C0WSJMvyGZf61oQsy4a0pKs7Y00jjkMs64EKlCQtLOlaOUJbXNKl659q/Vtf\n",
"0sVc8jyv6whEhwAAIABJREFUspFA85Z5jZcHuUbuxiVdZeBicnPkm9fPtTC6dfb29kYyr78VY1Ul\n",
"jkOShMxm5O///l+aJrS49HLL6zLaVgZ5uZmtP+b9pI739r8Y+LUvI+xjXvlS/3Y5f/78mTPQQevu\n",
"+wRfiCCCsaoS1yVJ8gJbRcfKsbXlhoyDLIgbHRnLGBFBYr27uws3boh8gs8GhXdaBAWfjY3D0GMS\n",
"0GxGbPsEUYK1XOzOWMN2K8YUvehZ8JnNVs+kEiHWlUGun+GDgk+ZO3euwI0bIl/qJ6tGk2t8kS3C\n",
"JCDTJNMpgfyC+nqIsyHb2os6y04uricIirK1UZKOX/zi5f4O1tsDZS5qZvhEUVT503w+t/qaQ4Az\n",
"fFpkPs8tq24xcHkhaBSJMp2mPLFnW18DNnuq8s7K13mes4m222LZVWQl1669feHC/9vb4eS76meC\n",
"T2kXp2yzyvubcfv2bbYtO4QkSeClvbmKgHOtExHW2DSJ4xDfX6H/LBuXl86W4R1kuHFN75bvRbiG\n",
"onms10kozLjy13XraTuKdXmQmSeVzSzXGbfogzjGXLH+5S//Dm7ckE0e84Zh6Pt+kiRscyuWebke\n",
"ZK9jNpt98t3NkiQpKjRUdtGaz+esAIOiKGEYWpbV2wOAe/fu8e7N24WxINtQNDdWFOI4D0rC6fqn\n",
"exEz42ID+hpkHOTmbqwbFmZc+WuSrD5VdLdVS/E6jh/sZJkkq7U7QSIiSKzhuaUFeG8TXNfVdX0+\n",
"nxefdV23N72lTBRFrAxDnwdFwac7HCe3rIekCUqr/xSBsgy1FZeY9gUXfLYoubCxgleUGzMvvfSD\n",
"g4OelqbmvIIPu95nVTOLNy3L2spTVk3TWMnlPg+Kgk93xmznyOmUhOGnxieGt3/Bh+1bADRe5wbc\n",
"eLnl4gp6uRkRYr1ykNdd+25L8KkcUxDB5/79njbmJbwzfDzPW7kLiqZpXMMhL7du3cLU352xopD5\n",
"nIQh+cM/XCFFrlMt+k/9y/pin6mfqSjltcT1xutOnz2kfnZ0TVtbvHNbqb9Sq1eQ1H98fAw3bgrX\n",
"PYKiKMXr8mcppcE47uhQ8OmHIMhNs1r7RZAxr0gr/U+e+aQ0/0O1etYJPkxs2eJMpMoLQdA04TSo\n",
"l176gbg1fHpWVwTk+PiY6zEv/CHP4J93cRmragIspM07yHBjiMPF9WzPj3kJIaq64jZo2TiO166N\n",
"6O4x7xYjAjRWlIdGT5DHvL/4xS/gxg3hS/2apq2U9cMw3O4i295I0xRX8/ZjrCgEkv23u5q3uBbq\n",
"czVvTTJZabwu9fdWvo2s93krq3njmJjmQxqUIKt57969CzduCtc9QnmlVfFZy7KoaLdznYGCzxYR\n",
"ZMyX5ZQ+SdPVKkr5dVkoY+/P59vRN8QUfNhoCOVSLrjgo+u6aZpsA0VCiO/7k8mEELLy2e8gQcFH\n",
"NOOtywusvXXGYbjiv//yX/6heH3iQSotxzFZrh5WFDtaOa9/5Ts1PkPcqGHrETnRmD0n76LlZQYi\n",
"+BBCLMuaz+dxHOu6HsexZVnw3Q0HAAo+2zVefnu7gk+h9f+7f/dOGD6oTDedfvr/lVnigw8+KF6z\n",
"xcyVT3nep9XZKm6UZ+yUV8my1L/OZ01bUe6tT8GnFeMWHa5o/VsXfJKEPPLIP4or+CAo+GwX193+\n",
"lk+V0GvagzVT83ldPSIuWJkg1iyluet+2vJKuamiOxU269Sh3hBT8GHObGV21jqCIL927e0+BR+s\n",
"14/IhGWROCaGQeZzUepBRlH7bVYkHVaEx/cJeXgtkqoS31+h/5Q/WPx1q1sciQi7Y+OpvT8ouFfz\n",
"2rZt23ZxF8Mq7Wx356w+uXnzJnwTtTAM4as/uNaJ2LY9WmNNI677qZbCO8hw44oPrNAQqzXE5fBK\n",
"N+DGtm1rGrEs4jjEcch8/umflud3VtwonyeWz5Qdha+3iGxmXJbIitfdfZOBvWOCz507d+AtN4Xr\n",
"HiGKIlVVXdctV85xHGcrNXy2wtWrVy9fvpzDbmDTNIWXGOIqRrTg2ex8kMZpmptmHkXcgww3Zj6k\n",
"ae44uWmeUPqYq3ctxroQhZjgw4xXyizLv9GOwlce5MIB1109xWiDiDQ0XlmCqbtvMrB3lOaU0v39\n",
"fXjLDeETfHzfp5RWKiRTSo+Ojlo9H4nL7u4u7s0rgjEr+TCdEk1T4BW7uQY5SVTPI1lGKCWUnmC8\n",
"rb152dw633/wmJcZsy3sK5NYGu4nvMHevGH4qQ/rPt3/155N6u+i5ZUIuzcvt+BjLg/bmGr4oOAj\n",
"lLHrkh//+H+99trfAJsFRiQMyXRK/tW/+gtKieuCdgrrVPA50cY0HzjJjFfubaCq1UI6PQg+J+a9\n",
"/gWflWvcti74MPoUfPiu+lmJ/OX3x1Pg4eDgYG9vD2jMtcKZy5hra5phG//hHz79ox+dnkyI45yc\n",
"o08cZDarUtfZPvL/D/x7zdW7rmOtaSs2711+MNBRRNb1buU818F/7bk6ePbsWbhxQ/hSv67rWZYt\n",
"J/rxPOZFwUc0Y0VR/sW/IP/8n1c3e1lnvO5PnvdACiieowoiAmzgBtsAh5w0Hahrwae8PYuuk5XX\n",
"yhsMRZKcvA5OVdc6XMlVbDsgQWItruCjaRpbx1smy7IwDPVxTJLKsgyXdAllzAa5KPgzndblheWI\n",
"ZBnxPDKdElUlrvtQZtz6Mp/mbpRzVHlCS/OWaygGOUlOnjq58jeSJCQMiec9mFJV/Pebv/k/2Xo3\n",
"gLcPjJf/K6diXX8gggkSa7iY3By+q35KqWEYqqoWiT7LsslkQk98CjYU9vb28KpfKOPyuJnmp1eX\n",
"lK7Qf8rGcUw8jygKMU2y8g5ekCvBFt3QdTKdEkUhllV3XdzQDd6v/f/+32d8/6HnEKzEP5vSWiYM\n",
"PwZeYeo6yFhViecR3yd///f/ku3Ao2lsZOo/NYSr/p08z7k+wHJ9lmW6ridJEsfx8pyfAfPaa6+9\n",
"9957H374oW2T0RQuko8keXBtqKrENB+60GOVc7KMaFr1TyOhGBxd73ZBU+U3UvyTrVArbkFYwhVB\n",
"NWBSUhw/JAqxk0HXhYltmxBi37hx4+OP+9qoa7M5oYvFIgiCkWzPUuYrX/nKs88+m8Pm9UdRFIGX\n",
"9sMt8zx3XReNGfWDHEUPpr1bVk5p/o1v/Oxb3/ob4Dzy7nonQqzTNP/a195lwwKZp75BRCorCdix\n",
"KnUpuH4jW/m+VYpqUJpbVgAPIKR3QZDP5zml9Pz589B2G7NhIQdVVbnuegYDCj6iGdePG9MNCpLk\n",
"DgHMOOT1gddYhFgrCvn61++xXR7ZTQC79F7nGm9E2OPTMivLPIowFPXGy7cj3/72QVFXg1FzZwDs\n",
"ILMSWvAZOSj4IEOFSWGMzbSgMHyg5LBEZpqd6ySCwIpvMwmLnfOYisX+D/k4ISQMexV82infliTJ\n",
"SG4Cbt++zbUtOwFffXCNIdeUqmEb8w4y3Li73okZ6yLdZxkJw0/nYrL89f77P/zyl7/IFoslCbl1\n",
"izz22ApZ3DQJIfJFpKHx8kfZyIQhuXHj57/85T6rEV2cEhjF8+QwJJSSMOx1W/Z2Uv90Og2CoJWm\n",
"BOfevXtcW7XAW8atWjYzlnGQBXFjnTGb9VSskGC5/mc/+xlTOcrJq1hFXCaO5YtI68ZsiHSdxPGi\n",
"vKqrvCihPEeU3Sf1uVULt+Bj27bnecsBG4lwhIIPgiBdYNu9Cj58S7ps286ybLlw3UjWcxF+wQd+\n",
"NcF13cFVGGTYxryDDDfurnfDjrWMEREk1uIKPmEYBkGw/Mx6PHs0ouAjmrGMgyyIGxiRHoyF3ZuX\n",
"T/DZ2Rn7jCAUfBAE6QKhBR/TNLnOeFLAVWnn+PiY66offs4f/OVPd9eYXIMMNxbkSlCEQeYyljEi\n",
"gsS6z6t+vtRPKV1Zq3oymbTkT6/4vm8Yhu/7vu8D9bs0TbF8m1DGvIMMNxakpJcIg8xlLGNEBIn1\n",
"3bt34cYN4RNwPM9j3a481/V9f7FYtOxax8xmsyzLHE7VphB8JpOHdklFEARpgtCCj+/7mqYNYD4P\n",
"KzzHm/dJSfCB3Mah4NODsYzywrBjLWNEBIm1uIKPaZqUUmcJ6U4GnudtVmi6EHwglTlQ8OnBWEZ5\n",
"YdixljEigsRaXMFnMBiGMZ/Pp9MpOydblrVyz+FlcIYPgiBd0LPgM8waPrZtL59sNU0rKzy2bTuO\n",
"w9yeTCaapgnVBQRBkO7gE3zWMZ1OW2mnLRzHCZYo531FUUzTLHK9aZrLG0+u5ObNm/BN1MIwhC/8\n",
"41oiuHKe1TiNeQcZbtxd74YdaxkjIkis79y5AzduCPdV/8pQtT7Z3/f9JElq5PgwDFkpIU3TKKVc\n",
"Vb8JIZqmlT8C//jBwcHe3h78KFwuwY25tkUbtrGMgyyIGxiRHoy5Onj27Fm4cVO4NnYJgkDTtPl8\n",
"zl4EQTCfz9mLFraNyfMgCEzT1DTNNE1d19eZua6raVoURWmaOo6jaRrvgdI0tUp7CJmmuVyYaCXX\n",
"rl174YUXctguXQiCIEAopU888URvh+MTfDzPc13XNE1FUdgsT9M0TdPkuqmpQVEUSmkURTXn1SzL\n",
"ZrMZO/cwe13XuZ65k08En8lkYtv2ZDLRdR0o9KPgI5qxjPLCsGMtY0QEiXWfgg/fVb+iKOxFEAS0\n",
"dN2raVoK3PAURhAE6676XdelD19yLxaLDS788zxP0zQIAuD1PuPq1auXL1/OYVf9aZrCh4VrALl8\n",
"HrYx7yDDjbvr3bBjLWNERIg1pXR/fx/eckP4Ur+qquxFJfVTStvdor0m9VNK5/P5Ose65tq1azs7\n",
"O2fOnDl9+l/v7OycP39e1/WLFy9eunRJ1/Vf/dVfZTqSZVkvvfRS+cV3v/vd5557rvwiz/Pnnnvu\n",
"u9/9bvnFSy+9xFooXmBT2JR0TVmWVWmKvag09dxzz1Waeumllwbf1MWLF3Vdv3Tp0sWLF5955pnT\n",
"p0/v7OywTb9PnTqV9wVf6jdNk20wz0T54v0+U79pmsvHqnkw0C5f+cpXnn322Rx21R9FERsuCHDL\n",
"PM9d10VjBu8gw427692wYy1jRESINaX0/Pnz8JYbwqf1a5rGpCtd15MkKdYox3Hc26R4roXRrcNO\n",
"zkBjRVHgc4e4JilxjfawjXkHGW7cXe+GHWsZIyJIrE+fPg03bgrXiSJN0+Ikxub2uK5rWVZ5tkwr\n",
"1Fz167q+xat+nOGDIEgXCD3Dh03sYa9N03RdN0kSdgLo4Ky0Gq55sq2TZRkWbRbKWMaKMcOOtYwR\n",
"ESTW8NmDzWlUyEHTtK0k4jiOKwXjuMa3CbyCD7zlYYsA3RnLOMiCuIER6cF4IIJPb9QIPlEUVf40\n",
"n89bV5zWgYIPgiBdILTgIwLsPqO452IrvLiWVjfh9u3b9+/fBxonSQIvccFVDINrnciwjXkHGW7c\n",
"Xe+GHWsZIyJIrI+Pj+HGDWkk+GRZFsdxpR5OE2azGRvWLMuSJDEMg70fBEHZbD6fG4YRx7GiKGEY\n",
"WpbVm+507949rr154S0Pe/uO7oxlHGRB3MCI9GAs7FYtfPX6WWpWVZU94D06OtI0LUkS13X7360l\n",
"jmNWvq2tEw8ErNePIEgXCL1Bo6qqqqqy6sez2YzVRmZ7nnTjXh2siFCfeZ+g4COesYzywrBjLWNE\n",
"BIm1uIKP7/uO47BsG4Yhm9PJ5vkw5acTH0UCBR/RjGUcZEHcwIj0YDwQwefg4CBNU/baMIxCgrdt\n",
"W9d16Xbo3QAUfBAE6QKhBZ8Cpvi364oUHB8fc131w8/5g7/86e4ak2uQ4caCXAmKMMhcxjJGRJBY\n",
"93nVz5f6dV1nGxlWNuMNw3AMag8hJE1TXM0rlLGMa0eHHWsZIyJIrO/evQs3bgif4BPHsWEYlmX5\n",
"vh9FERP9Pc9LksQZh/yBgg+CIF0gtODDtkVUFCUIApb3bdtm++h2455woOAjmrGM8sKwYy1jRASJ\n",
"tbiCDyFEVVVKaaH2FPM723ZMUFDwEc1YRnlh2LGWMSKCxFpcwQdBwQdBkC4QWvBBEARBBkCj1J9l\n",
"WRiG2902q2du3rwJr6kdhiF84R/XEkHbttGYwTvIcOPuejfsWMsYEUFifefOHbhxU7jqfDqOo+s6\n",
"q5C8WCwURdF1XVXVdjfmFZmrV69evnw5hxVtTtM0TVNgy3DLPM8XiwUaM3gHGW7cXe+GHWsZIyJC\n",
"rCml+/v78JYbwqf1+74fhiGr5TCdTjVNsywrjuPJZLJYLLo7P4kDav0IgnSB0Fq/7/uU0qKGD6uS\n",
"X9Tw6cRBwUDBRzRjGeWFYcdaxogIEmtxBR9FUYrX5a2yKKUj0XxQ8BHNWEZ5YdixljEiIsS6Z8Fn\n",
"w61aRlvDZ3d3F/fmFcpYxkEWxA2MSA/Gwu7NizV8+MiyDJd0CWUs4wKiYcdaxogIEmu4mNwcvqt+\n",
"SinbGZHV8GFvep7X/5Yp22Jvbw+v+oUylnGQBXEDI9KDsbBX/dyreZMk8X3fNE3Wf9u22R65I6nl\n",
"gDN8EATpAqFn+JDR1/BBwUc0YxnlhWHHWsaICBJrcQUfBAUf0YxlHGRB3MCI9GA8HMFn5KDggyBI\n",
"F4gu+Iyc27dv379/H2icJAm8tDdXEXCudSLDNuYdZLhxd70bdqxljIggsT4+PoYbN6Sd1M8lfknN\n",
"vXv3cKsWoYxl3Bhk2LGWMSKCxLrPrVraEXwMwwiCoHk74oOCD4IgXYCCj9Cg4COasYzywrBjLWNE\n",
"BIl1n4IPzvDhg1fwgbc8bBGgO2MZB1kQNzAiPRhLLPiwMnWWZamqyhZwLdvEcZymaScOCgYKPgiC\n",
"dEHPgs/JV/0s17NzVxzHuq4vl+vhqmIqNcfHx7xX/cCJvVmWwacAV2oojdmYd5Dhxt31btixljEi\n",
"gsS6z6v+k7X+IAiCICjSvaZp+hKSFvDhWknISNMUV/MKZSzj2tFhx1rGiAgS67t378KNG8I3w2cy\n",
"mViWpet65X3pZvgkSWLbNjt1x3E8n8+BZy8UfBAE6QKhZ/iwvXk7cqVPZrOZ67qO4ziO47rudDoF\n",
"fpBX8MF5/V0byziLfNixljEigsRaLMGnzDqFS65LfkJIkiTFZT5XRQ4UfEQzllFeGHasZYyIILEW\n",
"V/AZDNPplG0uTwiJ49jzPNd1IR9EwQdBkC4QboYPBK5H3iLgOM50OmU+Z1nmYBZHEGRMtLOaF66V\n",
"94Nt28YS5Rmovu8risKmJxGe5Xk3b96E19QOwxDeMtcSQa7ZtMM25h1kuHF3vRt2rGWMiCCxvnPn\n",
"Dty4KVybuNc84219w/hOMU2z/E9d14EfvHr16uXLl/M8p/Rk4zRN0zQFtgy3zPN8sVigMYN3kOHG\n",
"3fVu2LGWMSIixJpSur+/D2+5IdxX/UEQlD+fpqmu68U+vW3h+/5sNqsxCMNwMpmwa3muZ+iMijwF\n",
"X5ewu7vLtVULvOXB71nR3cYgXIMMNxZk+w4RBpnLWMaICBLrPrdq4Z7hU+mJoiiu67a1mpcl9KOj\n",
"I9/3a26UPM+zbZtSyubjG4bBe6A4josTBteZAwUf0YxllBeGHWsZIyJIrMUVfNZhmmYURc3biaKI\n",
"tRMEwToRJk1TVVXLt1GUUtd1eQ+k6zqllFLK7lqAH0TBRzRjGeWFYcdaxoiIEOueBZ92Uj+ltCIE\n",
"NaQm9buuSx/Ou4vFQtO0zY7Ce8a6du3aCy+8kMNSP4IgCBBK6RNPPNHb4dqZ4RPHcW9lfJIkqdSP\n",
"U1V1A7mfELKyFF09WZZ99NFHFy9e/Lf/9q3d3d1nn33WMIxnn332s5/9rGEYr7zyyre//W1CyLe/\n",
"/e3r16/HcfzNb37z+vXrhJB33333ypUr5ReEkCtXrrz77rvsxdtvv00IuX79OmuheMGaKr949913\n",
"Dw8Pa5piL4oWrly5UtNUxSvP82qaqnjleV5NUxWvfv/3f7+LDsZxXBn2mg6yBUTADrIPAjt4eHhY\n",
"P1blF2+//Xb9WJWb8jyvfqzKTbHVRtvtIPvaV5piLypeXbly5Zvf/GYcx+U2Kx0s/Kx8K5abqnh1\n",
"5cqVmqYqXlW+9pWmKl6xrz28g5WmWNL47Gc/++yzz37+858/f/787u7uk08++cd//Mc///nPSW9w\n",
"nSjYFXcF0zQrE2aaU3PVb5rm8h0GfIpOQ1599dVLly7lsKv+xWIBvzfkuovkuscatjHvIMONu+vd\n",
"sGMtY0REiDWl9PHHH4e33BC+1byGYSw/6dU0zTTNdk9IYRjOZrOV9SEMw2ACfeXNfopJ4GpeBEG6\n",
"QOjybaqqmqbpPEzreV9ksizDGj5CGctYMWbYsZYxIoLEGj57sDl8hRyAhW46hVedb5e9vT2uef3w\n",
"loc917s7YxkHWRA3MCI9GAs7r1/Q8m01go9t24qiUErLbx4cHPSzQyQTfP7yLz/0PBR8EARpDaEF\n",
"HxEwTbOySsL3/d5Ep9u3b9+/fx9YrztJEnhpb64i4FzrRIZtzDvIcOPuejfsWMsYEUFifXx8DDdu\n",
"CEfqz7IsDEPeHQ1bhwk+hdyWZdlsNrMsq5+j37t3D7dqEcpYxo1Bhh1rGSMiSKz73KoFKvh4nud5\n",
"nq7rSZJkWQbf0ZCL2WzGzqhZlpXn71eUnyzLDMPQNE1RlDAMLcvqLfUzwefttz/MMjKmx9sIgnRL\n",
"z4IPaF7/YrEo105wHIcKsJg1iqIgCLjWxDeHzesPghwytRfn9fdgLOMs8mHHWsaIiBDrnuf1g2b4\n",
"eJ5HKS0u8ymlh4eHW9/eZCtTfXgFH3jLwxYBujOWcZAFcQMj0oOxsIIP6Kp/eQGtruvld0S4CegH\n",
"VsMHeNWPIAgCRMQaPieeuLb+7Lc3jo+P8TGvUMYyPlQcdqxljIggse7zql++yZ3bJU1TXM0rlLGM\n",
"a0eHHWsZIyJIrO/evQs3bghohs9y6R7f93VdL97xfX+xWHTlo0gUM3wIIet3q0QQBOFDjiVdpmn2\n",
"VqVZKFDwEc1YRnlh2LGWMSKCxFo4wUdRlOWqbWW4ilpIDQo+ohnLKC8MO9YyRkSQWAsn+CAFKPgg\n",
"CNIFcgg+CIIgiLxg6ufj5s2b8JraYRjCKz1x1YSybRuNGbyDDDfurnfDjrWMEREk1nfu3IEbN6W3\n",
"FQTD4OrVq5cvXwYu6UrTFF5ngqsiBVclgGEb8w4y3Li73g071jJGRIRYU0r39/fhLTcEtX4+UOtH\n",
"EKQLUOsXGhR8RDOWUV4YdqxljIggsUbBR1xQ8BHNWEZ5YdixljEiIsQaBR+hQcEHQZAuQMFHaLIs\n",
"wyVdQhnLuIBo2LGWMSKCxBouJjcHVK8fKdjb2zt1Cnq+5Kp1wWXMtXx62MYyDrIgbmBEejDm6uDp\n",
"06fhxg1BwYcPFHwQBOkCFHyEBgUf0YxllBeGHWsZIyJIrFHwERcUfEQzlnGQBXEDI9KDMQo+AwEF\n",
"HwRBugAFH6G5ffv2/fv3gcZJksBLe3MVAedaJzJsY95Bhht317thx1rGiAgS6+PjY7hxQ1Dw4ePe\n",
"vXtcW7XAWx729h3dGcs4yIK4gRHpwVjYrVpQ8OEDBR8EQboABR+hQcFHNGMZ5YVhx1rGiAgSaxR8\n",
"xAUFH9GMZRxkQdzAiPRgjILPQEDBB0GQLkDBR2iOj4+5rvrh5/zBX/50d43JNchwY0GuBEUYZC5j\n",
"GSMiSKz7vOrH1M9Hmqa4mlcoYxnXjg471jJGRJBY3717F27ckFELPiwqmqbBP4KCD4IgXYCCTzvE\n",
"cWzbtmEYKx/HZ1k2mUx83/d9fzKZwJtFwUc0YxnlhWHHWsaICBJrFHxaIAxDy7IopSv/OpvNLMty\n",
"HMdxHMuy4DuuoeAjmrGM8sKwYy1jRASJdZ+Cz8A3aAyCIFi1laKu6zX/rOHll1++ePEicINGGYEP\n",
"hYxQSld+HwYDhk9eKKV7e3u9HW6wV/31VPR9rup6CIIgsjPG1L98CwavwpplGVyPC8MQvvCPa4kg\n",
"XKHiNf7JT34ightwY65B/uijj95///3WfeA17i7WIoSP92sPN3733XeBlkSMLyfhjHWfWr+sq3lt\n",
"217O4JqmOY7T6XEvXLgAr9fPNXeIy9iyrI6Mn3vuORHcgBtzjdvTTz/9mc98pnUfeI27i7UI4evu\n",
"a/9rv/ZrcGMRvpyEs4Pw3NIcWVN/kxSvaZrv++V34I/sz5w5s7OzAzTOsgwuJbGZAFz2QGOuOQaP\n",
"Pvoo3LijiRxcDhOeoTh79uxjjz3WRcu8k3bgGUGQ8MGbJZzjBv/OX7x4kcsHEYy5Yg3PLc3ZmuDj\n",
"+/5sNqsxCMNwMpkYhmHbNu8370QqdwxcvwH4Tdm3vvWtGzduwI3hkwFef/11uPFXv/pVoCXhVAzg\n",
"LcdxzGX8+uuvA41v3LjxrW99C2jMJfh0N8hcl42ChK+jiHD9RrgEH65x686YK9ZDntzJEvrR0ZHv\n",
"+zUqmOd5tm1TSufzuaIohmG064amacXRwzCEn5a5BB8ueeHpp58GWhLOO18uEUAQY3gHP/OZz8CH\n",
"jisi3Q3y448/3lHLGJECQcaNK9ZDFnwURaGUssy77qo/y7LZbBZFEbsTpJRmWeZ5Htf5k50tyipK\n",
"EATFXyml0+mUZf8kSVzXBTbLJfhwyQtnz54FWhLOO18uEUAQY3gHH3vsMfjQcUWku0E+c4bjd4cR\n",
"2cAHIsy4ccW6T8Gn79QPub72fd80zbICaFnWZDLhSv3lRL+Moijz+XyDQg63bt06Pj5+//0fEkII\n",
"SeuN33///X/8x38Etvz+++8/8cQTQOPvf//7cOMPPvgAPs2gI+P333+fy/j73/8+0Ph73/vej3/8\n",
"Y3jL8Ih0N8h/+7d/u/WIcBkPPiLdGcNjzSUmt0BvKwgqBEGwbvkJ03kqb6qq2r1TJ/N7v/d7hBBC\n",
"VEKg80ERBEEgnD17trdUJuIMnyRJ9KXSaPCp953yne985zvf+c62vUAQBGmEiEu6Wp/PgyAIgpQR\n",
"MfUjCIIgnSJi6ud67oogCILwImLqJ6vK7HDVPkUQBEFqEDH1m6ZZmQ7Fpntuyx8EQZCBIWLqZ4JP\n",
"sR/oZZ2BAAAJT0lEQVQCW+HFNakfQRAEqaHvvXlnsxm7os+yrFzYqLICK8sywzA0TVMUhe23hakf\n",
"QRCkLYTelj2O4yzL2Alg274gCIIMB6FTP4IgCNIFImr9CIIgSKdg6kcQBBkdmPoRBEFGB6Z+BEGQ\n",
"0SFi5U5hCcPQ8zw26YhSKtG8o3Y9930/SRJKaVvuNaSt3rEdgdjkY13XLcsSJMRddFBVVUqpCAVx\n",
"W/9ZJUnieZ6qqoLMCG+rg7ZtV97RdX25yDGU3spDy47rupqmRVGUpqnjOJqmbdsjKG15HgSBaZqa\n",
"ppmmuW6vhf5pq3dpmuq6TildLBaLxYLtJZemabvebkBbHVwsFpqmua67WCzyPJ/P56zZVp3lpouf\n",
"lWmalFJBvqItdpAQEjwMC+WGrW38yVGRpqmqquVEQCl1XXeLLgFp0fMoilimqNlmp2da7J1lWZUN\n",
"ghzHoZQ2dbEZXYSv/I5pmk1dbEAXP6sgCCzLEuQr2m4H271Sx9QPwnXdShZg11Db8gdOF54L8rvK\n",
"W+2d4zjLb269m11/8ba7+V0XvWP3aoJ8RdvtYLupHx/zgijXnGCoqirFljLyeg6hxd4tP7pIkmTr\n",
"Wn+n4QvDcHOluA1a751t25VtvbdLR+ELw7B5I/iYF4TIe0bWI6/nEDrt3WQycRynlaY2posOsvoo\n",
"YRjGcTyfz5s01ZB2e8c6FUVRY79ao/XwGYaRZZmiKFmWqarquu7G5zlM/SDkvUyW13MI3fVuOp1a\n",
"lrXdi2LSTQfjOI7jOAzDrc9Sa7d3tm1v/VRdod0OOo5jmmZx5vA8bzqdbnzyRsEHQapMp1NN0wSZ\n",
"Gtg6lmWxeT5xHC/PF5QUpoFs/VTdKZXJuJZlsfrHm7WGqR+EvHtGyus5hNZ7l2XZ0dGROHm/0/C5\n",
"rhvH8ca5ozkt9s7zPF3Xw09gotbWt/br+tenaRqm/s6Rd89IeT2H0GLv2C4Rom0O0Wn4muSOVmir\n",
"d7quJ0lSpP4kSZj034aPjRD319fibKEBE0VRZa7YfD63LGtb/sDh8jwIAsdxTlzHJMjMuZw/LjUd\n",
"TNOUrXgqv9lkyUwrdBG+Mrqub3FVV4vhW7YU4Svadfgqiwa4wNQPRdf1Ii+wNLH1lZBAgJ4XUyNO\n",
"XOYjyO+KAY9LTQfZUt7Kkq48zxVFad1hXtoKn2malQ+yx4atO8xFK+FbRpyvaFvhW/5+WpbVZMkh\n",
"zvCBMp/PDcOI47jYM1IWGR3oeTHZY92sj8rmmoZhsPcrm2v2DDwuNR1kkrfnecWO0AwR5ke1FT5K\n",
"qW3bxbNQNqnfdd3uPIfQSvjKsGfX7Cs6nU5l6eCJvZvP57Ztz2YzFj7f903TbDKjCXfp4kPePSMh\n",
"nidJsnImsvgA4zLsDkJ6x2wIIUJ9hzF8BNa74tl18/Bh6kcQBBkdOMMHQRBkdGDqRxAEGR2Y+hEE\n",
"QUYHpn4EQZDRgakfQRBkdGDqRxAEGR2Y+hEEQUYHpn4EQZDRgakfQRBkdGDqRxAEGR2Y+hEEQUYH\n",
"pn4EQZDRgakfQRBkdGDqRxAEGR2Y+hEEQUYHpn4EQZDRgakfQUZBHMdsf82OqOxtiQgO7s2LdMhk\n",
"Mlm3va2maU12FkV4mU6n5QEPw3A2mxFCFEWZz+eEEN/3WfpWVXWDLW193yeEWJbVmsdIl2DqRzrE\n",
"siyWEUzTrPyJ5R2kHzzPUxSlvO+rpmmqqpJSaDRNo5QahhFF0QaHcBxnMplg6pcFTP1Ih+i6zkSG\n",
"5c2mMfX3yWw2q9xjKYrC9vUuQqOqKjsZaJq2wSHYucTzPMz+UoBaP7IdyvllNpsZhmEYRhzHhBDf\n",
"99k/2R1DmTAMJ5PJ4eHhwcHBZDJZKV4zm4ODg8PDw+l0miSJ53mGYUynU2YwnU4Nwyhr0+wdwzB4\n",
"D8da9jwvjuPJZLKzs3N0dGTb9rJXWZbZtm0YRmGzUnyHdJCXMAyzLFu+8QLC+lhhZR9N00TFXxpy\n",
"BOkSSimltHgdRdGyTRRFQRBomjafzy3LopQuFovFYmGa5mKxKMxc19V1vWghiiLTNIvGi0OUbebz\n",
"uaZppmlalhUEAXszCAJ2lIoDlZ8D5HCLxcKyLF3XLctirqZpWmmcvalpmuu6aZqyf7quqyhKxQxy\n",
"xA2glFqWtfL95caXcwL7eFCCSUPLDS4WC0II6yMiOJj6kW5huZhlGV3Xi/y7jK7riqK4rrvyr4vF\n",
"QtO0lZ8q53Rd15c/uJxkT8x6kMMVTVUs0zRVFKX+U3meu65b9gF+RF7Y+C+/Xw5NwXLqdxzHcZzy\n",
"p1aeSBiEkIbeIv2AWj/SOaqqMkF53WyfAsdx1inFnuexxFSBUur7Pms/DMPlj6uquoH6DDlcQeWf\n",
"iqKUe5okSZZly087TNNMkmSzI3IRx/E6tacITcHyM5iyV57nZVlWM/9H1/U4jpt4i/QDpn6kc4q5\n",
"JUmSsEeL62CPGVcSx/G6J8NFomkx6UAOByRJkpUfURSl/MCjxSNWqBnVyrSfetjsT6aM1XDiCR4R\n",
"AXzMi/SHZVmbzR4hhLAnAStvXYtkpGla+Tq6YINkBDkcnJVedXrEMoqiQByoJ45jlvfrT95xHG8c\n",
"YqRPMPUjcqDr+omzRyzLYopE+U2Ws05sv/IpyOGAMA1k5emnnJFbPGIFTdMaXomz+Uvs0TR7x/f9\n",
"5TazLMuyDFO/FGDqR+RA13VVVYsJmgWe5xU6CZP12azQLMvYtE7btpc19Mr9QZIkk8mE93BwKKXL\n",
"C5tns1m5/XaPWKZYXbEZbFrqfD4vC0dsPmvF0vf9YqUYIjio9SMdYhgGy7AsTaws3pAkCct3cRzb\n",
"tl1cV7L5J2VL13Vt2z46OioeGjN5odwmm2o5m83YFTRTUZZTp2maYRgahsHOAVmWOY5zdHRkGIbr\n",
"uix5QQ43nU5ZVk2ShJVDyLKMnUXKTbHnzKwp9hA4DENd19lHuDq4AcUz8PJ4Fp7HcTyfzxVF8TyP\n",
"LaQwDMOyrOLJ8Gw2S5KkMpF/Oe+zQ2y8egDpmZ08z7ftA4JwwBIiew18RMnS1nICZTpM5XFr88PV\n",
"UFx91zTV7hEZLK03fGZQT5IkR0dHbCptd0dB2gJTPzJ81qX+UXF4eMiWjHXU/nQ61TQNqzjIAmr9\n",
"CDIKKuJS62y2fgLZFnjVjwyZSlmeThUPBJEITP0IgiCjAwUfBEGQ0YGpH0EQZHRg6kcQBBkd/xfl\n",
"0fKyOGVwtQAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"% Ce code n'est pas commenté, car essentiellement identique\n",
"% à ceux présentés en question 1.1. et 1.2.\n",
"% notez tout de même l'utilisation d'un hold on pour superposer la variable `signal` (sans bruit)\n",
"% au mélange de signaux.\n",
"\n",
"y = y_sr;\n",
"% représentation en temps\n",
"figure\n",
"plot(ech,y)\n",
"hold on\n",
"plot(ech,signal,'r')\n",
"xlim([-1 301])\n",
"ylim([-0.8 0.8])\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"% représentation en fréquence\n",
"figure\n",
"Analyse_Frequence_Puissance(y,ech);\n",
"ylim([10^(-10) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On reconnait clairement la série de pics qui composent la variable `signal` auquelle vient se rajouter les fréquences de la variable `resp`, à 0.3 Hz. Notez que les spectres de puissance ne s'additionnent pas nécessairement, cela dépend si, à une fréquence donnée, les signaux que l'on additionne sont ou non en phase. "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1xcCXHfef3W3JXBMTFEg3RWsBLkUgTu5Z9tETuQLbs\n",
"sy2WM5NznapSqVMGsi+pVFJWzYucP3JXFddMKnf/JP+8V07lHJerXJii6pKKL7LfOzuuq9IdXeg6\n",
"iTz7JCfoXcqST9QCaAKyVsCK5GtwdyWA3CU3fzR2MJh57+HNTE+/mfd+nz9I7MPDdPdMz7d//etf\n",
"//rMgwcPAEEQBJkkHhl1BRAEQRDToPQjCIJMHCj9CIIgEwdKP4IgyMSB0o8gCDJxoPQjCIJMHCj9\n",
"CIIgEwdKP4IgyMSB0o8gCDJxoPQjCIJMHCj9CIIgEwdKP4IgyMSB0o8gCDJxoPQjCIJMHCj9CIIg\n",
"EwdKP4IgyMSB0o8gCDJxnB11BYaFMRaGoZTSsizf9wkhuS8VhiFjTMulEARB6kg9rP4wDIMg8H2/\n",
"3W4TQhzHyX2pRqPBOW82m+12m1K6vLwshNBYVQRBkOpzpvpn80opl5eX19fXI/M8CAJKqed5WS/F\n",
"OQ+CYG1tLfqEMdbpdFZXV7VVF0EQpPLUwOrvdDqu68bdMp7nhWGY71KWZcU/sW2bMVa0igiCILWi\n",
"BtIvhEjoNaVUSpnjUonr9Lw4giDI2FODZV4hhG3biQ8ppTku5bpup9NptVq+76srNxqNZrM5/BX+\n",
"7M/+7Pd+7/f6/XZubu7cuXM5KoYgyIRw69atfr/6mZ/5md///d83VI8Hlce27bW1tfSHRS4YNT99\n",
"5cH8+q//uqEHgyDIhHHhwoXcspaVGjh89NJoNKJhY319vdVqcc4zXWFxcbHIwDNCfN/POtRVhJre\n",
"8LW1Nd/3R12LPGBXMcza2tqnP/1pkz6DGki/Rl98GIaEEOXtUVdut9srKyu6ro8gCFILaiD9AJA2\n",
"zLOa6grGWGLZgBCSb9kAQRCkvtRA+l3XTcRfqnDPft9njLVarZ4hQD1Dg/IFCyEIgtSXGki/cvhE\n",
"gfxSylar1W8/F+fccZwgCBqNRvq3nuclRoUgCNLhQwiCIONNDYI7AaDdbjuOwzknhDDGPM/rtwAQ\n",
"7fzqmZmHUtpsNh3HsSxLXcq27UzBnQiCIGNAPaSfELK+vs45l1IOTrhGKd3a2uq5FUBh2/b6+rry\n",
"IHmeh45+BEEmkHpIv2LIUB9K6amCjk4eBEEmmRr4+ivIgEXmKmPbdk1nOTW94ZTSmhoZ2FUMQyld\n",
"XFw0WWINMndWit/4jd/4xje+8cYbb4y6IgiCjBVBELz00ktvvfWWmeLQ6kcQBJk4UPoRBEEmDpR+\n",
"BEGQiQOlH0EQZOJA6UcQBJk4UPoRBEEmDpR+BEGQiQOlH0EQZOJA6UcQBJk4UPoRBEEmDpR+BEGQ\n",
"iQOlH0EQZOJA6UcQBJk4UPoRBEEmDpR+BEGQiQOlH0EQZOJA6UcQBJk4UPoRBEEmDpR+BEGQiQOl\n",
"H0EQZOKojfQzxlZWVhzHCYJASqnlgo1Gw3GclZUVznnxCyIIgtSFs6OuwFCEYRiG4erqKqU0DEPH\n",
"cdbX14tcsNFoCCE8z3NdVwihq54IgiC1oAbSL6VstVrr6+uEEADwfV9KGYah53n5LriysmJZ1urq\n",
"qvonpVRbXREEQepADRw+nU7HdV2l+wrP88IwzHc19Ye+7+upHIIgSA2pgdUvhLAsK/4JpTS3uz8M\n",
"w3a7raNeCIIgdaUe0m/bduLDIl4aSqkQQpn/rusmxpVTuXXrluM4PX/VbDazXg1BkImin3psbm4e\n",
"Hh4aq0YNpF9LPI+CMUYICcOw1Wr5vk8IaTQanudlWja4ePHi2tqariohCDJR9FOPIAheeuklY9Wo\n",
"gfTrRUrZ6XSiRWPXdZeXl23bxsVeBEEmhxos82p0oViWxTlfXV3VtWiMIAhSR2og/QCQ3nKVbxMW\n",
"IcSyrISBj/Y+ohc0JJDqUwPpd12XMRb/RIV79vs+Y6zVavVbIbAsK3E1zjmqP6IR3COIVJ8aSL9y\n",
"+EQ+GbXDq9/CLOdcJXtoNBo9v+D7fnxgUKE+AwYSBEGQ8aMey7ztdttxHM45IYQx5nlevwWAyIkf\n",
"9+bHoZQ2m83l5WUl94yxdrvd78sIgiBjST2knxCyvr7OOZdSqqDMft+klG5tbfXcChBhWdbW1pZy\n",
"+zSbzVJqjEwwmAwQqT71kH7FkKE+lNJhfPcDxgZEF4wBYzDy4TUIRl8HBKkUNfD1I0i90LcHEUHK\n",
"AqUfQTSDDh+k+qD0I+NP2VqMgfxI7UDpR8afsj0wnU651x9tcchYgtKPjD9lW/0n9wiWThjirjGk\n",
"KCj9SIkY1kTDcA5hOIJFXULG/MYiBkDpR8YHIY4M/CAwUZyURyXGo44N2OOU4koyUhSU/gpgcpVQ\n",
"SpPFXbrFn/u6ueLe/HO+809CMBVjM7PBH/83HSkhvsVQCChrxwjnytpPlFgWnBsdYfoUV1ZvrUbr\n",
"RghK/6gRwqjjlnOTxU0fyqfeO6U4je/2ubtybv+ouOhF47wsoTx3V/7E9zjn4LpGPDBSqmLMpB25\n",
"87fy8A87YGxVWcqeJZV1Yx/eTENIidKPnCRyUpgs0SDTh6f4wkuqTuSClxJKOjTz2jX4+MdBCBht\n",
"4teSFGxjA/b2jq6/slJKEcNQ4lLKyUsLUeJ8+Np12P5qtZbmUfoni909eHvL6LpkZIbHKc/eurTH\n",
"AYAQQ+Ppz77HjS3z3tiA21/r0aryrPLbrwkAIMTU2DaKbdDRslCpNtjMjWqZ/IDSXwkM9vhr1+Dg\n",
"B0ZfsJ5WfyT9jOl8365dg/v3AQAoNXRTPzJ3yhc0DnJ370K32+Pz8mZxp87YdGLY88mY6iLx7lde\n",
"+W9vSjWFqg4o/RXAYMro3V04mBrnDNUz981ajlKurvb4OBIRvfObs3fMte7sN7lJ6d/7unjzglnH\n",
"Weq9K0/6Dw/h8LCsi+cDpb8aSNlqjboO5aBGGsc5YYaX5/DpN7CV8VbP7QsghFKg9ESLLOuoOL0z\n",
"j9t/ym7OW4wBpccerfJs5e6W3Fw0l9328BB+9CECqcDcUmcCiRknpab3ypmJQu4JSn8FsCzg3EC4\n",
"gRBw/jzcnLdMxjZ0ZylwTsiJNbSSnKqX9nh3lv7lH4q4w0dFW5Yl/ZYFUvZzhWtv5sEUOXtXUqqK\n",
"BQBDi8yJsa0MIn9IfOkiPrBJqd+Jp3ZmRERjtjFGGPWD0j9BCAGfnDnu2mW8SwmWttnN+SNxNNDL\n",
"pw/lv7/kTu8KZRcrhCgrwgcAwLYTDSsvlhQAbs5bFzbMqcXNeeva7zDLMjG6HB7C985S4FyI5LCt\n",
"0B8ZT8j0noiaxhjYdokj3OFhtU5tRukfNWozqJHRXwiY3hXf+rgLQkgJKyvHxZbXJ3cePZpF95xN\n",
"axfKmZkjh7ixIJ8EiVhSjXU4POzhzip18FbFJR5QeQFFN+5TkDI1mB6jWZct629fEfFRzbZLvJ/f\n",
"/3hy7jnabBwo/aNGSkZckNKADS4EzM/Dtz9kgRCtFsRPti8vovnWc0c9vqfXRUrNFuXmM7ayiyOX\n",
"SLlY5rxnU1PQnaWJMMFEGgm93HqPTO+eeGalbwYXwmSaivffkomBbXJO6UbpHzHbO8AYpOPM4mhc\n",
"C5p67Lhzj6qXC1Fu0Xt7hpp2eHh8E3sOM9rHnu4T9EffNxR1c3gIdy5b737HnKG6+YwNQhBiKtrZ\n",
"ttUuEAPFTR9Kw2tsp4LSXw3IgKPmTWDSN1Kq851S2N4u07kfY2rq+Oeej0+7SS4lvLsn0zmC1HSK\n",
"MdAYJ6Zat79/IiVRvEV6ne+md30/1Hsz3taDKXLwWLKLqGCtUYHSP3p69rx4RzfQNQ2bI+U54tPv\n",
"0jidlEtID3d/3JOmsbFxLe7p1uqTdCcnR+3q3wDN0v9wrI7GbDP9xHF61mIE1Eb6GWMrKyuO4wRB\n",
"IHU8JSFEEAThqM/WUybq/jvJz6N6VSkoIC+p5xUFX5bxvqldXdHokni7NA5yRje7poorW6oOpgil\n",
"RzGX5vTx5NNi7MSoU2rp6X6i3R46fFfzBYtQD+kPwzAIAt/32+02IcRJDJ25CIIAADrVOOxufz/p\n",
"GYgUv77Sf/yi9rdt9Fo9ShzfvE+g/zKvxvfZ8L7oeHFm3BSUwv7+8T/T6am1k7aB4u4mkzay3tap\n",
"rbzb2zqvWZAaSL+UstVqra2tWZZFCPF937btgtY6Y4wQYpeVWD0z986Tj/+Yx1/msoakh3I4985x\n",
"1y4pFJ1zePr8UXHT78qo8MRLpXG7kDJU4y54RTQD0CiXnJ8oqGxzmHOYnT3+Z08zvAyvXbzQ9KE0\n",
"elstZXJpoVSEgKmpvr5HIXTez6kpsG344XeTAUUjpAbS3+l0XNeNL4N6nldQ+oMgaDabhaumAWWo\n",
"3rlifeJjWvxYp6Fuo22rhJqR16WkddFHniQAcOMZ+9IejwzVxGEmele6KIWNC0nPdDQDSOzeLIKU\n",
"MD//sEjOE1ocJXLQ9UylhNlZsG34fzdOaFV5UnKccyZ2y0oKhWQM5udPXM3Au9BqwfPPmwoCBgCA\n",
"HxyMOJojTg2kXwhhnVQmSmkRmQyCIDGWjBA1i9/dhdkPjltU6o7Q6M6ZcRpYFrz6Kly9WvpsPWrX\n",
"nbODStL/np9ME0rI8borIfpb/dYzPbSqDPGamgLLgmtz5STB6FUcANw7T2Y2uIGeqTxLU/Mk0bpS\n",
"h4H9ffjJD58owECGjH6cHU2xWRBCpD0zNK+tKKVkjK2vr+euz+HhIevzuJRLKusFLQt+N7TXPhQA\n",
"uA8reSKETi+EAFjW0j9tEWJiak0IvDFLZ250AMotjnNYWgQAuHuOAGdg2+nXuKwXu3xxPFHzh/9Q\n",
"/7csaLXAdfUXSggsLBz/k/Oj6Vp5J0TeuWKduyvJ5VIuHmdvD9z/DgBU1h4KD29mSe2aPpR3AAS1\n",
"r+wdZ+va2Vn6yEe6168DQBcAdnZ23n///VKK70UNpF+vH6S4q+fg4KCf9FNKc0j/4L8oxRtzskjO\n",
"y40v7j5Bz+0kjZ0wLMur+z/83xaEHeh1Y0vZ+2rbBhIwcg7uM7AJcH3OBh4opVfNifuatCvXC1+w\n",
"gLXUo1JdUR1pEo0BWuAcfu5Mj2uVZ4O/sy1tGyD2Hpc6zz6YIrYN31oAAFDqcevWpb29e9eu3QSA\n",
"t9/eBIDt7e0PPvigrEqkqIH0a4QxJqUsuLpLCCl7nUDFtJVKPFJQSYb2HJBCwNLDn+OJ5rUnb0hg\n",
"ZpsMY7AcWwJVM/eylyjTvSIuWGWES734nxH4RuklSgkXniYAcPuytfjHre4Ldvz6ZQwAR+FSlELH\n",
"xHz0qXkAgF/8LOm22Re+3ISTa/Kq2wRBsLGxUWpN4tTA12/pU8EwDG3bZg/hnEspuQGHdx+iCXvP\n",
"KhjIzBVRRlpjlTJIcX/muLj0UmHFDqwelvjyTM/xRvMTlEbjQ457iMFNcffPJ1tYrt+/z3Fu2ufB\n",
"aiXj579oEZAV6e31sPo55wlTPZ9e27YthBAPRU5KqVz/GkeXTCj3NCFgWQBSLt1maga6tAOXL8Mb\n",
"LwF5AZZ2oDtLlTtSY7mzswCMLe0AMFjagbnrx7/93jn69Gf0FDf1GACAlDA1daK4+H8tQjtSQ3FC\n",
"wMfjh1gxtrQDd/4sWZzOmxlT4rnrR1ZcvLhP3YbuI5qLO+qqjF38Nsx9BBKF/s2UBaBhfDgRS0rI\n",
"0bMDAAZz1+GRwx8DfHhpB27O6ykuQko4e0f+nT32la8AACztAOHHrbs5b0mpOz7j4XsXf3BnrsMy\n",
"wHduaW4dADz1uPzhv2UgT7xxAGAupvUhNZB+13XVfq7oExXu2e/7ypz3PC/dR7x4skoAxpgQIn7l\n",
"UeK6S//0ofRvwzPqw7fhqdfhZ0EC9DoGMAdSAgEpYe5XbWBsaRuAwVOvw9zD4g7fhX/7R/Bf7+r0\n",
"aAkB854FjD31OgADVejxf0MA0FCcEPDUcw+fOKWquLf/GGw4WRzoKe4ElM59lQEAvJ1qne7iPA+A\n",
"UWDshbfhw/8epqZOFLoETEtxUsJSJP2UHnUVAGAwtwNn7r0HP/rQ0jb87HucMV+janEOf9+2Hv82\n",
"S95GBkvb8HOPcs41FHdiT4ZlLf1ztv8n8NzecVmPfBPm5+GX9wSAN+A6OThYoHPXGLwNczsAALOz\n",
"8NprAG+j9PdCmeRhGCrhVju8VnueiArAOVd7fTnn7XbbZD3zoZzgtg1g2y8z+8UmAMDLwVFPWLTh\n",
"awC/9oq+VURCQAWkvGCDbb8cwItN+BrA2YfF/QWD2ZcD/Wc/uS647tcAfq0JqtCXA7hvg6Dwoihh\n",
"jdTzAOBrAN+jYFmwaB0XqvNmxorbpAAAizZ8uXFUkPrvr38z0LsGQOlR614OAAB8H4CU3rqouBeb\n",
"sMlASnjGhZcD+G93gju6S3v8Hx0VF7+NLzbhyw34H28HP9RRhJSw9NAVCZ73ZQ73PwcAAPZRWX8U\n",
"QLMJc7+g/2bufN4HgEUbNhkAgP2wRPPUwNcPAO12OwzDRqMRBIHjOJ7n9XPRRJb+4GmhGiGCIOCc\n",
"NxoN/TUeGuUET0w8SnKuqssOdusLAZ94SurdS5xwzsVbV/aSbJQlNCq0vMQ7PaMD47thy8Ck9z++\n",
"NGU+KZ7GlqodZBH9lhN0dZXETuyoDiNM2wm1sPoBgBCyvr6uVmV93x8g65TSra2tnlsB4liWtba2\n",
"VkJNsxGPgYGYPCXaN/2T5C//UPzd/7JoT0nftvQLLARQixzuSV1ezvTJR+WFbaRJ39KSEu+kg+vr\n",
"m3ypH+oeqv8exXd+qZaJUafflWoVSuG64Dg9oqd0dZUPv85nP350qXhY82ilvx5Wv8KyLNu2T13l\n",
"oZRWJznPYOIxMNBfE8992koclqSL3oPBwyMsSkWFkxICQOlMaefNphvYnaXf/1f6i0sXpPJV3DtP\n",
"pveMDgLbr5kT4/l5PeE38YxSin4jipaR5tLeif0diXBV7RE404fHe3N6yn3520J6UCfpH0vi1oci\n",
"2i8TcbQ0pI8Be3+UFuuV/n5lHXljKF38wNDABgCLv0p/+N3SxfE4q8QVPcO2yn83AOVAmHOs7pqG\n",
"Z/edf8Fnnj7d5p36RWtpR0PPnNsXiU7fM0XoT/w8fedPNb0IJzuH5x19EE/p0501eFakcVD6K0o8\n",
"ucfBvOaZYfqcrBPGDqVn9nWKY+KY8qQiW1ZJk4yeebBvX7a0jKNpQzXOsX9pIXmabj4ShmpPKIWD\n",
"BapnpDmUH3GSxcXLP9p1SIjKA1gqkaX8+HO0pKUazzvROqX+3VlqOkWHQVD6K4faTmLYD6iMnejU\n",
"3HTe4xykDVWVyTKpYIRoeZ8v3eqR9C6RZNi2e2waykfaUO3JwTw9d1fTy93f1Xk8ybhclm8wnjHi\n",
"uDoPU8Dqop8OHlkMmlyRd04LS1ItvTlvIsHhqNJIovRXjvLyHAw2VEH3qblpQ7VfL9eynhb3qCos\n",
"q8Ro6d3d5CdSnsjAEf18nP24NAiBTueo28RzZmiE0t6PT2PrbPtEeoP4llq9maxmZob6Wvo03XwM\n",
"HmnKy4U3GJT+UZIwVNMZXPVOBpWhmljIKjVBdPrSJmPaEjmT9e7Oj6e0jIqD1JphdMZhqdg2NJtH\n",
"rYvnzNCIZfUWXy0TxIj4A9K/uWREDB5p9Npbw4PSP0oShmo6oYha8iVEp3wkzqYo75yWfozqfVbT\n",
"KUqNnpNnprGqk6jiKnUKYBHS8Q7jykjeCJT+CpGY8EZYlgmnAejOGBq5RPol3YjKMtC6aLQr9TWL\n",
"30ADm8jSUGqiuHdjx4sbPpteS1cxXOelbTZ4Zo3Sj/TtIXrjzAYYU6oCB1PJ04tyELlEvD55UKLG\n",
"anEapJ3vPcsqm6igsjeR9cNAcXt7xyOcluKGX7zV0lWGCZdS3P6epkEiVlxiZj+qg2JR+qtF4njS\n",
"yD3dne2dXbYg/eT95rxlIKztxNtXuHVp5/s4USlD9fCwhLMB+tsjGk9UPmZgA6KUJ90H+sfRRMkj\n",
"yhqM0l8xXPd49kfImJxqEidS+GgTDQBsLtoGouiixt6cT57bnoOehmrP8UvLjG14Q1XLjG1/f5Am\n",
"xa1+AA3Ddk83Tnz+ZOAYnHhZ1Ti3u1xQ+qsFpX3dIyXt/YhUQgXdR9wofF5Q2lCNViOhhFFnafuU\n",
"4KHol9piSVNq1FMytM3YhhMkLTO2wVnn/sE/OK7L9Y9oGLaVGyfePts+Hl2i4CXQNGwPIDHeHSzo\n",
"39A7wqPY46D014PNZzS8YD0NVfFwZ1I8FHLp89aHXtVhFw8/m9UijgOlv9bhImm7+OiEn1Hw2799\n",
"/POQMfLDEN81ZtsnnlfkEDe9cLKg39FakYhVlP5Rcmlv2KB6Ld0vMlRPFUFdW16HbN3dn7L2/nW5\n",
"Dp/4Ylp3tiy7K3pM8Zj0gykNKcHSy5vp7bXH1DZrqBlZNBMvN4AqpDtF6R8l6Q2o/dDifNzfP/ph\n",
"hOeS9Rx1nvslYvJt7D5RlsDE3VnHPoqLlsl3ffOZEs5Z7k/ZHpgEWhZOhg8Tundew8JJAtvEwtbp\n",
"1CNf/7gSafFQFJaPTMeGlJEPoNYul6pREb+BrmwHQ9J9opRQt54QAuy29fOy6LlF6UWvUSVviINW\n",
"/ygZrMVJa8NsZykpH0AVkLKUoBTbPiHHJx5XCWplPsdfeUTieGqQuwHZj4qI9r0XtPvT6xNV2KiM\n",
"0l9dzLzYVXA7GoYQDeNoT6dB/JGd8OSN3MbLSLZtBIX70PCLt4SU3mVFIiWrlGGouYgqdAd0+FSa\n",
"E+pfTo+vQi+sI2lxjGv9yG26gmTS4r1bZP70L+rDcJcd0zcErf5Kc0L6S+iC/Q6kNk/xZV7D+13T\n",
"4hiPjq279A+PsQRTxkibWGpffT4Y6+HXHVVUbhyU/johhOZwg0TeiPhIk20JuhfDK4JlaUhNajji\n",
"u9KY9eKVdEJAdRCi0B3NFF5hDJT+ShNpMaWwvQNhWEj6B9vFKrm8wrZhfz+5vzcrw4fQ6Q1dPRXL\n",
"gu0dDSVWE8uC7dtFb2gmQ75gREDVNiEk7KEyxtFERMBIQOkfJYO12PNOSD8A3Cp2nnhWu5ixqriD\n",
"hmF426p2zttM4qOldXoPYBmMELC4aK64TGiJCEiD0p8BxtjKyorjOEEQyALjsJSy1Wo5juM4TqvV\n",
"KnKp4gzW4kS4yF8eWtP/wZwSH0yRsnfYJqma+VcZOK+o06COMAazD7K99QVFopoOsXpIfxiGQRD4\n",
"vt9utwkhjuPku46UcmVlRUq5urq6uroqpXQcZ7TqPySEwMEUOX9e/5X7rTjdnLdMLpxuLhrdg3qw\n",
"YDSH1o8LZ9PMLP1me3XBR2dYHGf/o1MM+fR5O0Wo5haZGki/stPX1tYsyyKE+L5v23aYK9Q2CALP\n",
"85rNJqWUUtpsNl3XbbVa2utcBteulZ6SfkLiUggBAebm25YFrz9eNJtmJnHc/cmikVvDj/qEwPY7\n",
"5Cv/S6HiMotjyVZC4ryd2nkIh6EG0t/pdFzXJbHb73lePumnlLonTwv0fZ/XxJ99/ny50p9OFn3n\n",
"TonFjbAsyzrlSK9hyCSOxRleHG0b/uYHRYscflnIsmDzCWv60Nzk+YbZJEVA6Qvd/BNEzo0unAxP\n",
"DaRfCGGd9EpQSvN1ND+Vt0wIQWoypn/mM/BzS7I8L0V63amgPmbyFxXP/TvyuP5J5sYNQxEBtg13\n",
"75oo6BhKocA0Q0qYv6izOrqowW5eIYSd8kRQTQvkKysrzYyHY966davfYkOz2bRK263x2f/NhiAA\n",
"6HPGuW66s/RqNwTI7wPKJI4HUwR4oaOYMmtxHdZ4kNFCKfzRH8NnPgP/Tt80o596bG5uHhrcHVcD\n",
"6S9vJtloNDzPS48rg7l48eLa2lpJVTLMgKZvfUCfNiiPNy9aUDhFYobi5i3gLXBzjqOMwfkss/iD\n",
"Bfr2WucRyzY3wzQbLmXaEjcFpbD9VbhyBeBtbdfspx5BELz00kvaijmNGjh8SqLRaFiW5fU9DtEE\n",
"j7xjzvDsNx/vp/6EwNRUneL6M/GDH5P9dwoNbPNZ0tb84DH6rVelsZv5/10w6g3vztJfec9cuFQZ\n",
"OfTjpO2BakZnFqQG0q/dhSKlXF5eHrnuA8AHT5jzF0uZeePMGMeSEwKvvWZoYDOfKMnw6lV5R9/0\n",
"5M7lQuFS03un/G1CFW7OWxc28j+/pZ1TjoweFTWQfgBIB+HkDstRsfye541c95E45h3v29uGClJC\n",
"XDwnUiZe/vNCK5OZKBjE8v1/xe/pOhB0CO7fEN2rw/p4LQv+9/+TFLWBUPrz4bouOxnXosI9+32f\n",
"MdZvm25P3Re4ibQCGDZUhYCnPmx0tCmygPfedzN30e3t/NL/xkts5hPZ1KqION5/U17+vLlUlhsb\n",
"GYKkCQEpYfaJMis0Imog/crhEwXyqx1e/Wx2zrlK9tBoNBK/Ult5fd9P/O3y8nIJta49QhR6nxnL\n",
"ZgkSAvvv5C8uq8xJCU9eyT/azGxkNlRn7ucfaX7wF+Kxz2YIRuAcPvOJQgPbmaUqGqq6WDB6vEBF\n",
"qUGEDwC0223HcTjnhBDGmOd5/RYAoiD9dLQ+51wIEYZhYjtYLRI5mEdKmH0y/59P74lMC6G2Ddv/\n",
"BJ7PW9z+n2QzVFdX4ZH/Cd7KW9y5u/LOlWyG6pv3yVN5i4OMatVswvT/anQaNTub/2ZWnKNzwcZu\n",
"F0c9pJ8Qsr6+zjmXUvq+P2ATFqV0a2ur51YA27a3trZKrilyxPSu6F61F4f+vmXBy8VS9mcyVCmF\n",
"7UKlZcbklk7LMt06Y9JPKYQhPPnN/FZCVmx7PDM51EP6FUOG+qj8PGVXZlSYXJgwHNNWzf3uWsCJ\n",
"pS7Um21yzXxctaQGvn4kTu6OeGpMW5rzHzPtNDAZBHn2jjQ2jgqRbR9AvVATbMPDm7G8qxk3+ycx\n",
"nF9keFD6RwdjJvPAKA/M8N+3LNOBDbOzRuXjqefIGMd2mZyx+T7MnTG3YQ2g0HGec/tGn/qlPV7N\n",
"iQNK/yi5OV+B45kRIxh2ZxXJEZ9j2LjwdP7ilraZSWf63L7InCqqoEmC0o/UCBUBi07qnuTIaVrE\n",
"4WPYUL2w2AWVYgAAIABJREFUwQ8WzKpVaUkP9VBgZDKYkC0bKP21wrKWdgz5OCkFIOS594ymIDh7\n",
"N+dQY3hF+vGvs6VPZZODqan87uk8hmqxYftgvoqGakQRPTWsxZUNXkDprxWGg8ys/Gc0Tu9mNlS7\n",
"V+3cyVIubPDblzNajpReupV/YLvwYobimk2Yvwhz75gz3ousmRsWxxzhOkX0tLJabBiUfqQUpndF\n",
"94XMhmqRs7ruZ80DQ6mx6AvLArBtk36b2Rdo7gni3l4e73Tuga0WWQLHz/OJ0j8y7oxpivPcXL4M\n",
"GxujrkQlyWOGF1tazPzXBgc2IeD2R+hbf2wuTTQAPPvIuEWDofSPjExppIpT/DTaspk5P+oaVBX0\n",
"UcQRApY/T40eDmN2xmYGPdKPyS9zcPaOzCH9H7yVc+b5+NfZs465tTvDOYrzuaerPxwiaQoueFV2\n",
"j5Vh9Eh/Ok0mcip5ViYt68rd/CuTTzyfUfoJubSXs7j9/TwBe7lfy3zuaZOzLqQfhrXY5D7KKpNN\n",
"+h3HOdMLZmxX9XiReWWyPhE+kKOylpV7pIEc7ukCA1s+8odLjbWhmkOLL18uoyKTRWarf21t7UGM\n",
"brdr2/b6+noZlUMmi/oMbHn+sMDAlsdQNT6wmaQuy0JVdoRnk35KaSJhMiFkdXU1CAKttUJqDxqq\n",
"SeozsOWB0idfMzr1r8W6qxCZD8Q2RjbpX11dTWdOVuNB7sNykSqTe3dPPo9qZXe9I6dAae7w/KwP\n",
"nRAA2/5w9ky0+aH0uT02ZgqnZ5mXUopnXY0lhsMKMYpRI4aDrHKT9aGr7FK5u0q+TRLz8+O2q0uP\n",
"9KujE7VcChmM4aXC8fbb5KYWqlqLXbI5yJ7N6AQEjHZpw9mlhifbKV1hGKZD+IUQhJAhj9BCIvL1\n",
"idyhafn+0HAkXF1GGsOqWotNErkZ7+DOItmzSyWb1d/pdNKOHdd12+22vipNCpXtEyNkvGOuc2vc\n",
"wtQ4n5Q53g+9smSz+imlruumTzxHjDE7C4wVnfMiBckn4oZnbIapy4wNUWST/tXV1ZLqgQzJ7Cy8\n",
"Neo6DMN4C0EttNgw431PKuuyz80kpm9jjK2srDiOEwQBBiaVxHgLAaKLurx/+dyznFc3aG3ipD8M\n",
"wyAIfN9vt9uEEMdxRl2jbIyf9REH4/onDc4LHV1Zcc5si/mLo65EH7I5fOqOlLLVaq2vr6tQVN/3\n",
"pZRhGHoqVNgs+2/kEfHci8OGgzvziXjuwLtaRFsiaab3hFG7mLHurLn8tXP7Aj5X0XW5ybL6O52O\n",
"67rxLQie54VhOJLK7J8hJldrcwd35puS53ufc7uJ8kVbGl6QyFmc4UQwZsVxeld0rxoVx9ytq3JC\n",
"nhxMlvQLIRL7DyZnH3I+M7zIEa/Vx/CCRM7ihNhczCOO93+Ys2PnE8daTLxu5D0GbnZ23KS/qMNH\n",
"ShkEASGk2WxqqVCpCCHSkak0Y7bfw8PDfkmqLcuq7K7mfGZ4PQKK8g7eU1PAefZzBczaxbkP8jz7\n",
"0ZxdMd8JybXYPHz3Lly9mucPZz/QZiD2U4+dnZ33339fVymnUlT6wzBUDhPbtqsf76/FwD84OOj3\n",
"8NKZTScUzo0a1JzfnM+zmXx+HjZz9YidR81Jv+GDPAFgZsZocfVA33vdTz22t7c/+OADXaWcSlHp\n",
"j/wnWW3n+jLyKc7ZuxKg2gOMlPm0ODeGXTeGxRFPE6sp04c9XtV+6hEEwcZGXodUdor6+tU5Levr\n",
"67WQ/golGso7/5j+JWvzj7N73/Oa4ffOk5kNs87+8V16qYU33DDdfNOuh9vaszJzg9/LejReAS7t\n",
"5fAnGkLDMq9lWRWS1NNInyswmpMG8vooLv5Uro6b1wy/c8U6dzfPy5nPX7z/rHXjj8wemmgw7Xst\n",
"vOGGVzPP/jW/+oU8PTPfzTx3V97JeiB2Afb3jR/RMzSTFeHjum7C0abCPUdSGZM+it09Y0Udkc8l\n",
"8vQnyd28q5o56F61p3fNKV13luawVOeusdu51OpgiuTRcSE2nzG7aFdVcSxOlQf7yZJ+NTuJAvnV\n",
"Dq+R7OcyzO5uzsAGRCO544Lu5/JR3Jy3TJrw+Qa2IpicsY0fk7WbFwDa7bbjOOpsGcaY53k18lYh\n",
"vRFid9fgUhNj3dnxNxeyYjLgFY5nbKYKpXTpqwyg6kGMw6NH+oUQtVjmBQBCyPr6OudcSun7PsZi\n",
"lgLnB1MGXxIhfvTpnFqcb02i+0Q9ensO9t8BeGLUlagglMJXR10Hrehx+DQaDS3XMYZlWbZt11L3\n",
"Cbm0l3khtEjSt3f3sv+tlDcv1mAutbAABqPpRkCONZ79fTwNQhtVTl2e2epnjKW3JKRPbUROIbdd\n",
"bFnTh52sf3Rhg29/3s9R2pxjbX+xBWBoJfzeeTJ3zdy0emG+0i+nInc208uXYXcXKr4lwPD9394G\n",
"k+6JKqcuz2b1M8aCIFAmM2PMtm3LshhjeIRLZqT89ofM2cV7ezDzsTy9cPF5o333zuWcsaQ5sawc\n",
"U6i9WzlLO5giOTIivbMt861GzcyYTvGdI0OOzLs58fx5uHEjzx/WxDNdOtmkPwzD1dVVlfxSDQCu\n",
"66YjJpFhMOltOjw0urNk71bO1lEK29uaKzOIXLU8PMzpErl50cqxYe1gKqdj8vZl64LB7XhXr8L7\n",
"G5ln/7kzNl+5DCbjgMePzFa/ioeRUkb90fd9xtiE5L9EhiH3SIMWmUbyhYTmpvuC0U0SoPbKGiRH\n",
"RECVjx7KJv39zA/btkezJxZBwHTuh/E+KK022LbRdQJKX3g7s2+jsqczQlbptywrknhc2h0V1U8F\n",
"Y1oczUZq5T4oDQAO39VYEcQguSakVQ4iyCz9yq1v27YQInLycM7rEtdfEW5/L3+fWJjK/LeGu2AR\n",
"cRxjKIU94xk1smLYR1GPg9LyUuUIn2zBnZ7nRca+7/uO43iep3QfpT8T3Qf5T2fM0Z9yx1FAtS0X\n",
"RV12IVEKObYFGb7/uQOK8lGPg9LGkWzSrwJ71M+u61JKO52OZVmTkAan1hTxOVb/bdnfB/tzOf/2\n",
"kXeqPrCZF8c67nREslIokUO90jUjxqhyYEOCD54wqnOGV0Fq9CAQw0xW5k4kBznkY2+vsgdUjJgc\n",
"qyC55duyTC8tVD/2yeRYyBgmbUZS7O2ZC0vpdODih/K/kzmcRdOHMnfrKm6ohqHpGuZ21pn321R9\n",
"eV8Ik9GWMxv88aeqe0NQ+kfDmX1zi2mMwU//Qm0W06ocCg0AQsDe3vhuPSu2QyLzoMhYkVTPmRfA\n",
"hdhcNJea7txdeedKdSe/KP2jweTaHa7a6SLKV2JO+ouJY2bynhsKufxLu3vw3lP5W1ckbg1B6a8f\n",
"1Y+2HGPMb2Q0fARKbqMkh4WxuwtXruQrDaDyE8SKg9JfPwxH+83tV3vbtlkxfvJ73LAWGybf2TXV\n",
"R0q4Yzbd27VrsFDhlNko/aNASmNLhVLCpVu8iNMns9IZ9lEI0b2a34GbdQp1/p4cb+mfmTFX1ve+\n",
"KY2JI+fwxr/kJs2mpW228IvV7Soo/aOA87cXDa3/cA6f+Jg0GWv5z34Xdh412uN3d/P/rWF/seHc\n",
"lhVndosvfNZcz+xuGT88rsLxACj9I+DadfjhPXOKY9KOA4Br10yXuLub/0zBrP7igjni3ziTUQt4\n",
"IUM1R8hN7mVeyLcKVZ8ghIqHHWcFpX8EvPIK/ON/lP/Pq9wFpYS7d8fZX3z+fP4/t+3sz67YKcdZ\n",
"B7b9d+DgsfxaXOWcHyoqtwhjtqqM0m8aIYou/lS5C3IO//l/LIt4YDKLYzG7OGNR8Pc/ZHYlo8zD\n",
"CKSEIDj+J2Pw2muFLlhlo0QImJ8fdSWqBEq/aYSAT84YdfjO3OAmfY5/d4q/+bQ5Q7WgXZyD7hNG\n",
"pb88j0j6dCXDdrHh3HmHh4XCwcYsqLo20s8YW1lZcRwnCIIih0FKKVutluM4juO0Wq2RnCs5vSvy\n",
"O6cVWbrwubvS8HLTP/9/qjvxL8jiIoThqCtRGoZPATKcO29qqtB7UGV3Vg7qIf1hGAZB4Pt+u90m\n",
"hDiOk+86UsqVlRUp5erq6urqqpTScRzD6s9Y0Ynn5qJtMpi9O0uPt7GaodrnPBvNTGf2Vnzs/Dif\n",
"sV3lZGrmqYH0Kzt9bW3NsixCiO/7tm2HuUyvIAg8z2s2m+psmWaz6bpuq9XSXufBTD1mrqzi6QMN\n",
"u7Zvzls9PBGlMuqjRgeUv32bmBxpHn/KXLJ+zov2zKxLCyj9cWog/Z1Ox3XdeJf0PC+f9FNKXdeN\n",
"f+L7vuED5c1bVbNmT7AqmLk387S62A2twhRqQF/e3y/sqxv6/ghhVBylLFpc1qUFw/ERFV8bqIH0\n",
"CyESB8JQSvPNS33fT1/c8KFEhFTdoVEExuD8x8y6RA0+Pilh8ZlCV8i62W1/v5B/6cb5U6ZQ8V8K\n",
"Ac9/EooeuJdlHDWc33/+otE1r4qvDRQ6pcsMQgg7tSiq6yjglZWVZrOZ6U9u3brVb7Gh2WwOdWxZ\n",
"fbax5MDwJAOKjaQLC3DtOgyZCaL4czO82e2RJzPXuMiLtblovyjEkJcQApaM5/evwkmy/dRjc3Pz\n",
"0GB47CilX0rZz9kSPwS4vIWnRqPheV56XBnME088kZ49KEZ4Nj1jRYOG6ksRRT51j8XQUlYKpiPl\n",
"i71rmfZzCFF0CnXq9UXhSLoy6KceX/rSl15++WVj1Ril9DPG+rnsCSHtdrvU0huNRr4D5aemprKO\n",
"FgZotUrs5bt7YCwF4fnzGcxwA4QhnJgWyvwHkPWj04F+M0/T2/eKtW0EiSr7j8xCjNIeGuD36qce\n",
"jLFHH320rAqlGKX0u66bWHTtifaT31VMp+d5OXS/IFxtriq+rMi5sU599Srs7maR/mKW4zAJ3H/n\n",
"d+C3f/vo59e/C/BTRQrMCCHe6X02G/1kgjF4EoNS+nOqfyneE6fflVAssu5oiX649+7NP+eXnqu0\n",
"X7cGy7wAkPYL5Q7LGaHuA4BUm6sKBqU8Yw9/heLesoMFOnctS1x/Yav41PSWf/qnRz8wBq+/XrC0\n",
"QfTcz2DSkBzjeMSL32ZluNLijyw+pl7aK2otZYpyrvjpjFAL6Xddl518BVW4Z7/vM8b6bdPtqfvC\n",
"fFh3YXHcf8dYUXAwn6HHFx9pbl+2hs9szJgGl8jMjWFjYMaPEW5pmJkpJadxP+kviag4zk1vfCxI\n",
"DaRfOXyiVQG1w6ufzc45V8keGo1G4ldqK6/v+4m/XV5eLqHWJWJZpjfcpwmC3ipffKS5fz7bJZ5/\n",
"vpA6d1+wz901N4V640yGrdHf/7bU4Ovvr3/8ZG6ngkf6VIR4c7WPLLupHEfRw5SyZtJfg+BOAGi3\n",
"247jcM4JIYwxz/P6LQBEQfrpaH3OuRAiDMPE2nLttq73fD05773iVdzF2RMpodXqsTg5946ARXPy\n",
"cekWn/8FapkyXT91m4FdaBb//tMZ1Oj+X/H53yzko3j7eXvv68F8H9emPHmEz/Rh0SN9DqYI8BGH\n",
"mkVvM+dgWUf/BYAP3pJQ7Fiey5d7LHr1G1gfbIozS9U9pwXqIv2EkPX1dc65lNL3/QGbsCilW1tb\n",
"PbcC2La9tbVVck1PQUp4dpuVkQXGsnpL/6U9DsXkoyf9nsDcvig7x02UAIAx+MTHJFDaNLlqUyu7\n",
"2LLgsFge5kzcvGgd7nWmhgs1fup1BrTEJycl2LFFsSt3OVi9oyqHpOeejH52452/Fi+uVmATQX9q\n",
"4PCJsCzLtu1TN99SSisYfKngHBYWaiYfVSOeAEDLDqnB3rMRzgkNZwKY2xcFe6ZlHaV9Hsb1MTVV\n",
"1COj4oATxL1/NOFdK/m9q9eyUJ2kfzxYMHteRHnyQUiPvj63b8L5Em0dmrlR1D1t2xkWTpa2SwlK\n",
"6celPW4yTWjxGZthk6ZnHHB8qDa5F69ubmOUfvMwDfIxfPKTj2yXJR+W1aO7z+0X3UBJyCkHhkh5\n",
"tHVICDh3t/QT55NypltOGBuomOWraRmadar9K6UGo2SYsOOodVpsoAHvHTd6HpIGUPpHQeE+cn/o\n",
"5CdTU0XlgxDYf8OcSWNZcGZ/UHGcwzPPAIzRkXuuO7LgEKu0DNmDL8s5PFE4HCAddpw2q6K+XzyZ\n",
"2u3L1oWNQa2qlx8XpX8cUAu8Jb3DlgX7Z4x26uHfUi0nHwxpD3JeVlqFEUpGeUWfOpko6WZG0q99\n",
"NhOFHcejeurl34+D0l8IFcwbdQXOR9MVhADXrZ+3sSIMGGmEOF7SkFLDJINS+P63jT4nw4mRq0N8\n",
"VNO7tys620nKGr90KP2FUFof7RMQosZdoQhBMOoalIMQ4Hk6nymlGZx1xSEEvv+joYrTNacZcqQR\n",
"wtCYpJ6dELC4qO2acVMvvtJkWXXa1YXSX5T4s49M/nGVwp6Maq4z3hQ/vxBUXP9waZ+1zGkA4K33\n",
"CQxhZQsBT5WW3Sw+VJftTItfH339E0TaHlSfhGHv3j+Wc4IwLD0EcaKGUkXx8wvNE0XKjirWRe1P\n",
"HokhUrtXG6U/D5GHJx3Rpbqd6/Y+cNWwXWCmO0aNKm8hFGcVJdFzc4YWBve9uXeKbh/rCe8TyTyz\n",
"wQ8WtA1HPe8YITGHD2M35yudthNQ+vMR9+n3NHBKlXhC4NbrEmKeln7za87LDX+M3gF1N3Q5DYZk\n",
"+l09I9tgl0i0I/S975ayW63fs5vZ4PcyZrLLirKR1bObu85uX9amVqea3roSfqQXDBKvnnp85+5K\n",
"jdIP/dU/ouIH8wJKfz5sGzqdPH84944G+bCso44VBRikD6JTgjKzwR/NfjprmkT4oyo0niBFdfq5\n",
"60zLC3b/h6dourJVL2zo2a02eKYSDe0/+Avxkc/rTxAi+mjgt16V8581t1vtzh2j68+6uHvu1LQu\n",
"OotTI03PzYy1A6U/D7Y9aCFL9J/LFt/sOiTKOa7rvIiECdNvWg0AWqT/7EfTWVdP/FO9ezMzeqZX\n",
"amAbJv5v5nzx0nrkjejXCC3FDcnGhrbjFY3JIqWnbPyO0BVNpBaxB3DUds7R6h9bevbvyAa3rBOR\n",
"Xo5TSh0Y6z3x5PyoJrp6fNol0lOtygvXI+ToZsZve/F0Ywr1lobhKZp1aU9DOnvbhnf3evgooufo\n",
"OEeD0KU9o5kBlrbZwi/qKW6AZRDx1Osa8tcOf3u6a3z2c0VNLnVOBotVnKd6xNE/pbx5EX39Y0pP\n",
"ETg10mtJd8bmnmoVpYW5sMG7L2iYZAy5eKuruDTRSx4/k1h7gujB7uni6ewVaXswciAoo0EFCEwf\n",
"Si3S/8g7Q4/HOopTVkK886+s9Pha8fwiPUm/DpEFVrxx6fqq81bThQ5/iN4IQekvkWjx80TnKG0J\n",
"OCpFPhQNA7tm4oaP4bPDyktKOqqNOek1m+J88IRRzwOBEw/F8J4PQpIxS2XH1EUJVOLv+P7+aI+r\n",
"GQqU/kIMcBHY9lGfiIvjkPtr8pHu5QYW7uInPRnu8eW5U+M79SMymM8TTPRQ1K3rdE6EAxig7DXY\n",
"xJpQNJmo134uQOkviHreqqtFWQMHLBgmbKLiDO7le3vmeqTe9y1xteSZG+UQPTghjoqL3z3D5nOp\n",
"VoIBolfDdVOGv25tTveNeApPXUHAitNnZkKUHZWrBZR+DUQCEUm/6hyqh6ttX0IASKnLUD2YOprW\n",
"DlJ2IQ4P9TnDB76ulgX/4StCV+sWF0+IRfy0v6gWMxu8O6tnWVKJrJTH0t8jLJ1rK+5UpARg7O1F\n",
"ncsYpwycWrcgxSPclAcmaQxxvrmoZ3qopmI9WxdJ/49e5T/6BZ2z0SjooDdCaAmrKxuU/hKJGz5C\n",
"6OzxN+eHmNYKobM4zgGAMeh0TiwqKAiB6V2hUT6m906oRXzDsBrMzt2VurRYLWLHi0j4KKQEEKIk\n",
"6U/PEQnRaSWogY2xgf1FiO1HtLUu2qmgxgB1avQJ9MU+qqnY4OWEK3f47FWdz+4Uc4qxvQ/X4NCW\n",
"ehzLXjk4/+X35LXfgaUdAHb033f/NSwswNIOAAAwADj+7Zw6QfRt1p3VfFLz9LsSGI9X46hcAGDa\n",
"ivvhvaMX9fvflvf/igPAr30egMGnbj9sGsBHX+ncvNzUUtx7v2L/7StC/CKlRALnqoiojYTDk9/4\n",
"8ZPf+Mrf/ISe4h5OoSx1M89ch2WAR2K39FO3ARjbfGZVS3HHnhwpgfP/5NHjgo5bKrUVpwY2KeGb\n",
"r8gXz5/QyONuI/mdy3q6yuzskdBPvyv3/4Q7jwAwuPhtAAbXrsO1a/CF3wQQQn/so5TAuSro+I0D\n",
"AICFA/Ezn9WjxbOz0OlAs3n83kUFHd/MC/JVoP4/1FJgiaD054Lzv7MrYBeWtgHY0X8f/zpc/Qzc\n",
"3gaAIwl+6vWj39JZeP11gJ+H7hM6zQEpYek2h05naZsAg+V92PsXMDUFS6oOz2grLjr9/P5f8Z99\n",
"vXMwRWa+AQCwtA1zD79zf4b84Md6TLkrl+HVVyEM4b9/ji/8u87cbaLKim71wt++98aPyGOaUj9G\n",
"U6hLexw6nUe+R+bn4XasuKVtgM9o894eR8ry42enCvrwdx8+Pn3FKYSACxscNjtxF2EZrZudBfkW\n",
"AMClPf7Rjc79GQJvwwtvAzCY2zkqESjVveYFImRUsBfePrqZR93ybQCA/Tmqa8Vrfh7ofQCAn329\n",
"Az/mS9skKuj4Zv43FpSSoEgztZF+xlgYhlJKy7J83yeFb60QIgxDSqnnZbd3PG+TqlrBi014OTjx\n",
"XwB4sQkA8DWAX3v4+Z8F8OkmgNYMlIQA3AZw3ZeJ/WIT3mLwlvrF544qprc4xbc+7m4+Y6sGvhwA\n",
"pbEgB60rsYzBP/yQXHDdTbDh5K2+CPDPSmja3L6A33T/iNnNJvxuAJ/04WU4LlQ29JRyNMlQ6wme\n",
"93LHior4PwLwfXi5pf/ZEQK3v8rh9/14fPuXG/Bi8+i/2rvK0jb7l3+v+Z/+VwToURGbDFqto1dD\n",
"b3FCwCOvcfjyavQOqsUh5e/8L/RMDgEA5i8CfB9AdZV/sxoVtAkgKLzowcsBvOiV8t5ppx6+/jAM\n",
"gyDwfb/dbhNCHB27Y4MgAIBOvlw8DznV317SOT537hz9oLaY9ixC78lEiqVt9saZEzOJfilotHBh\n",
"g4Ntl9GQnsTTbESxuYoByTmyoiYZUp4IjE1kQ9J45k93lgJjlB5v94iWKFVZeu3T2VnYXD+q+t4h\n",
"UQNNVERJYZfp7Vrpfba6WO3jh4taWpcsszWQfillq9VaW1uzLIsQ4vu+bdthz5zIQ8MYI4TYhaPQ\n",
"VfdSoYfpbu150GqdWD/U1R0jD8z0oZTUSl+2x9qaJt5/OvmelfGO3bgBtn3kFo+H05Uast0vnnJw\n",
"yqZ8tFqwvXP8z/g9VMXpuqvdWXrn7on71mqVeP7B7K9avzTNodeGu1KH8MTuRaln53UPBu8KrlFm\n",
"txpIf6fTcV037uHxPK+g9AdB0GxqmwcmTJvE5xEldcd4boOE8ai3FwrRN6OD9rj7mRnwfXhn+5SU\n",
"vHop6bCBfrz2mgmZuHwZNjaO71upszQAAEJUGrh4DI+yhdUQXlKT788QY7PDBHUx8xPUQPqFENbJ\n",
"3koplQV6UBAEibEkb8VO/47nHQ0Aenv8wdRRaPHsLLRaR0UoH0UZp9MtLMBfvyqF6JuOX3uesS98\n",
"AQgxl/R8N5UAUqlVqdL8/PM5U39nIpogKuKGQhyNLb1yJflJZAsn3GjFOZgiu3/IIi+ZidmhlBDb\n",
"2m14r7JG6iH9aZmmecVGSskY832/YK36OQESu4EoBbWKrNdcjWLjZmePM/YohsmbmJXHf8W6sMFP\n",
"Heo0vgMLN82ZUlevwu4uAMD0oYyOXVNqVcYk4/z5o5Fm8YLU6NMfEiX9UeaZCI0tvXp10G/12uYf\n",
"/mXrK18B24bt7RNFlDWzefh6D97aXYvBYJQRPlJK3scGIIRYxytgOm9kcVfPrVu31Drz5uZvAgDn\n",
"X+p2XwCAbveq616OVfwEak9jGVl40y+tdsG6f/7orO3FC4OehbZybbun/6ikN+reeXLx1Q48Yz82\n",
"T347gHY7+QXLgpUVyBEI1pMrV45GGrU+3/Om6W3pjRtAPwXwyvEniXyTeuX46gt9f2XbEAQnsiwU\n",
"RM1prnzUkKM/4Ujtl7l98IvQL0plc3Pz0GD6jlFKv4rX7PkrQkg7/QrqKFFKWXB19+LFi2tra/Dw\n",
"OJRm89eVTKlE3v1c3upXeqVf9byyj0Q/gclw5ZMvWMKdpdEkv3PZuvhqZ/pdOTsLcqPvUKq36XPv\n",
"CFhMXjJqqeOA62or6+5d+OT7/Gaf3chlLGIDY4c/eaK4RKib3hfhwgb/zrx18eE/1RbiEuF8c9F+\n",
"MdYlGDuyDCzrOPdfP5R6pAmC4KWXXtJXy1MYpfS7rusO0cF7W9G5CMPQtm32UJ4552rmobGIfhCi\n",
"32glBGYfOaERJfkoEiSTHJQE5yozRBRG1emcWK7UZYYrLu3x7lXbff74k/Ju5p07R4cN2Cfzz8SL\n",
"0yWOCwtw4wZcvSof+2m6vAz6ghtO4aOfpuSDo5+VIJZ0M3d34fx5OJgikf6WYDSeTr9Yj8pSA18/\n",
"AKT9Qv08RYOxbVsIwR4ihFCu/7y1OjIulCoNpoxoy6UdNvsCjQ9b8Z5XRnFgWQkjsdS+Hl/mTfso\n",
"tBd99QWIrwGV1LRnHbr7f7GfuywBwLZLT3O9MA8LB+LsHbmwAK5rKqu2EPfOk6hnltdJFhbg2jW4\n",
"cvsouZ6hY80YG5DQiRs9XS0/NdjN67qu2s8VfaLCPft9nzHGOfc8L704nNi4q9S/yJJvZJAKAade\n",
"ppTgs1Qvi5wGQaDNJKcUtrcBFge9xPptZM67s32fsva3a2mbAe07j9D47J54noLarfaPfYDytdiy\n",
"3vsOe/pNmP2fm1ePPzvdL5ETldZSyit+75upd5q4MA937wBIqTdFyqkkikvnGK8+NbD6lTcmWhVQ\n",
"O7z6ZV/gnDuOEwRBo6Fp331/+kX49HNEUKr5PZ/b71GDUw+JzIHqyrrOwh0W4+/zgFdW78u8twez\n",
"syeUzoD3AAARPElEQVQeT0I7dOojIQAw+0T6s3J4GMip0jX3qY5uRh1SUyM/T0QNrH4AaLfbjuNw\n",
"zgkhjDHP8/p55yNLf3DYPuc8CAIppRCi0Wis9tudPZCectCvx+tHyrl9AbbmVKADmNsXYHmkj6dt\n",
"mHlPVtLL5iXd2/3904971Dhsv3toUIuHQHsAQpr4pFBnqBuln5sNRxJ90M/lOKqdZVmph/QTQtbX\n",
"19Wq7ODcbZTSra0tIcTgMB7Lsvqts+djmCQNeteS9x8ZjVoYCiiSEkjyOZfkG7EseGUb5ufN3c9n\n",
"Fk/5AiE6tfixXruUo71dyvlTtt8pepS2Da1W30w4maG03zbDUoh5yvrtHtA+uS+Jeki/Ysg4HEpp\n",
"7g1fuRkmlFhjRIptw/6XtF0tKybuLiHqP53OcXElvVGEwLm70qT0z8+f7qPQeJOff77Hh1GPHcmE\n",
"Q2PrZme1Xep0YjcrGjvNhNVpp07SX3f0Kub2ttlOHyMRTloWUlqWoUnGnbO9391osNFbjRc/AwA1\n",
"VAsdaE/39OJndF5teEY7dhanBsu8VSZ+Bql5nnzU3OpWfJthJIiUltnwUb9S8UmG3j0Ehulp9Zd4\n",
"d3uZA9Fn+qeMQvTLW14KqZWKhNN/1N12WFD6CxEZgxr3Xg7P/ZlkL4t3O70vw/5+j0nGaIPYTG5j\n",
"1tzSTmdw7fUWN7vZJ2dbScTzqD2EkNKqICVYPfKWl0UiZ1bK2Wts01xBUPrz028vlQEohb1Uskk4\n",
"WSW9KYNm7svB/iXL0vpuD5GFTuM9v3KHd68ma1+iuykVB6ZSPEVojpWqWNCJ5jHAcGTnaTezFkH9\n",
"gNKvC8Nr+pT2Vqv013SxcCBOLU4zA6XdwFhbYpxu6tKJzd6a5SN+imYvNG+NLv1MgJP0y0NdEn3m\n",
"NLUDl3nzE3+bzIdz7U7TBdNlVgi94njvHsB5s69vShzLNV5T9ytePqVatfq0JSDN3tFRmNmJNP1G\n",
"UyhqAq3+/Ix26e/OWXKw0OOsxJJ64Y0Zi7qDLq35bpToG+7B/ftw5/IoX1/tZ5icwLBR2qs4dUiA\n",
"QnNXedhPDA0Bnge6N16MBLT668r+Pjw538OUK0n6Z2dhdnGQguj3URhkf47+tMkCez0kzksLFjCs\n",
"Ur2KK3Ecf7gFxFArCYHUnKmOoNVfV/5kuWmyz33t7/UOXCjrlT4tTkJvHMXvfnzV6Avcq/YlneTT\n",
"r7gSGUVx5lwuqdZp25lsFrT6a4xJter5Otdiw3pdMGw81nFlcgA1Nb1HCEo/glQCw1qsPdfeaEHp\n",
"zwo6fMYWY1kQEC2MULzGbBhAhgGlv64MI+tjNqlHSgIddxMIOnzqCs5wxwzXxaEaMQdKf12pdUKx\n",
"qlGFcRS9c4hJ0OEzttQljVQVqGl8HoLkBqUfQRBk4kDpRxAEmThQ+hEEQSYOlH4EQZCJA6UfQRBk\n",
"4kDpRxAEmThqI/2MsZWVFcdxgiCQOk61YIw1Gg3HcVZWVniJudIRBEEqRz22dIVhGIbh6uoqpTQM\n",
"Q8dx1tfXi1yw0WgIITzPc11XVOzkUgRBkLKpgfRLKVut1vr6OiEEAHzfl1KGYejl3c+6srJiWdbq\n",
"w208tApbOREEQQxSA4dPp9NxXZfE8pt4nheGYb6rqT/0MVchgiATTA2sfiGEdTK/CaU0t7s/DMN2\n",
"u62jXgiCIHWlHtJvp7LKFvHSUEqFEMr8d13Xypg3S0oZBEHPX3meh+4jBEEG0E89XnnllXv37hmr\n",
"xiilX0rZL7SGEBIpspZ4HgVjjBAShmGr1fJ9nxDSaDQ8z8u0bDA9PZ0eihQEs+4iCDKQfuqxs7Pz\n",
"+uuvG6vGKKWfMdbPZU8IKcktI6XsdDrRorHrusvLy7ZtD2+tT01N9Xt4CIIgg+mnHoyxRx991Fg1\n",
"Rin9ruu6rnvq17I6ZAZfinO+tbWVXjRuYo5jBEEmhhpE+ABA2i+UbxOW8iMlDHz0ziMIMmnUQPpd\n",
"12WMxT9R4Z79vs8Ya7Va/VYILMtKXI1zjuqPIMhEUQPpVw6faFVA7fDqtzDLOVfJHhqNRs8v+L4f\n",
"HxhUqM8wficEQZCxoQbBnQDQbrcdx+GcE0IYY57n9VsAiJz4/YJtKKXNZnN5eVnJPWOs3W5jZA6C\n",
"IBNFPaSfELK+vs45l1KqoMx+36SUbm1t9dwKEGFZ1tbWlnL74OougiATSD2kXzFkqA+ldBjfPQZo\n",
"IggysdTA148gCILoBaUfQRBk4kDpRxAEmThQ+hEEQSYOlH4EQZCJA6UfQRBk4kDpRxAEmThQ+hEE\n",
"QSYOlH4EQZCJA6UfQRBk4kDpRxAEmThQ+hEEQSYOlH4EQZCJA6UfQRBk4kDpRxAEmThQ+hEEQSYO\n",
"lH4EQZCJA6UfQRBk4kDpz4PjOKOuQh6CIFAnEteOmt5wxlgQBKOuRR6wqxiGMfbKK6+YLBGlH0EQ\n",
"ZOJA6UcQBJk4zo66AsPCGAvDUEppWZbv+4SQ3JcKw5AxpuVSCIIgdaQeVn8YhkEQ+L7fbrcJIUXc\n",
"eY1Gg3PebDbb7TaldHl5WQihsaoIgiDVpwZWv5Sy1Wqtr68r89z3fSllGIae52W9FOdcCLG2tqb+\n",
"6XkepbTVaq2urmquNIIgSIWpgdXf6XRc1427ZTzPC8Mw36Usy4p/Ytt2TSMZEARBclMD6RdCJPSa\n",
"UiqlzHGpxHV6XhxBEGTsqYHDRwhh23biQ0ppjku5rtvpdFqtlu/76sqNRqPZbGa6yOHhYbfbreNc\n",
"YWdn5/r166OuRR5qesOvX7++s7NTx5pjVzHM9evXDw8PTZZ45sGDBybLiyOl5Jz3/BUhJDLGHcfx\n",
"fT+h/o7jRC77rDiOE3WOtbW19LgygD/4gz/4rd/6rXzlIgiCDODJJ5988803zZQ1SqtfxWv2/BUh\n",
"pN1ul1Foo9GwbVsNG5zzIAjiw8ypfPGLX/ziF79YRsUQBEGMMUrpd13Xdd1Tv6bRFx+GISFEeXvU\n",
"ldvt9vLy8tbWlq4iEARBqk8NlnkBIO0X6ucpGgxjLOHeIYTkWzZAEASpLzWQftd1E+s2Ktyz3/cZ\n",
"Y61Wq2cIUM/QoHzBQgiCIPWlBtKvHD7RqoDa4dVvPxfn3HGcIAgajUb6t57nJUaFIAgyLfMiCIKM\n",
"ATUI7gSAdrvtOA7nnBDCGPM8r98CQLTzq2dmHkpps9l0HMeyLHUp27azBnciCILUnVEGd2aFc65y\n",
"rg1OuCaE6LkVII7yIFFK0dGPIMgEUifpRxAEQbRQA18/giAIoheUfgRBkIkDpR9BEGTiQOlHEASZ\n",
"OFD6EQRBJg6UfgRBkImjHlu6qoPG0+FLIgiCxCe2bffc5VCFtnQ6HSFElFAvzZCVNNyWU6s95FMw\n",
"WW11rKna0WLbtud5RW5m1WpewW4frzal1Pf9fruIRnPDHyBDs7q6alnW+vp6t9ttNpuWZY26Rj0A\n",
"gLWTbG1tpb822rasra25rmtZluu6tm33+9qQlTTWliGr/WC4p2DyEXS7Xdu2fd/f2tra2tryfd+y\n",
"rG63m/7mMLWqYM2r1u23trYsy1pdXVXVaLfbqtx8VSqj2ij9w9Ltdiml8T7n+/7q6uoIq9STYYbz\n",
"kbdlfX1dvQbqqJye3xmykibbMky1Fac+BcOPwPO8drsd/6TZbPq+n6NW1ax51bp91FXin7ium6NK\n",
"JVUbpX9YVldXEx1ODeyjqk8/hnkHqtOWARo6ZCVH0pbi0m+42s1mM/1hugnD1KqaNa9Ft6eU5qhS\n",
"SdXGZd5h0Xg6vBkYY/2qV4u2DFnJirel31MwXO30soQQIu0vHqZW1ax5RGW7ffqwkCGrVFK1cZl3\n",
"WDSeDl82juNIKQkhUkpK6erqauJVqUVbhqxkZdsy+CmMvNorKyvpnLXD1KqaNYeqdnuVdJIxxjlP\n",
"Hzo7whuO0j8s1TEkB9NsNl3XjXpGGIaNRiPR52rRliErWc22nPoURlvtRqPheV5aUIapVTVrXtlu\n",
"zznnnDPGeobljPCGo8Nn3EjEkHmeJ6UUQoywShNIlZ9Co9GwLKvfYUdVZkDNK3vDPc9TcT6c83QE\n",
"6ghB6R8WjafDG8ayrMQ7UIu2DFnJWrQFUk9hJNWWUi4vLw/Q/WFqVc2ap6lat19dXeWc56hSSdVG\n",
"6c+ArtPhq0At2jJkJWvRljSGqy2ldBzH87zB6jlMrapZ82EYbVdJj0Y9K2DmhqP0D0vW0+GrQ6fT\n",
"SRgOtWjLkJWsRVsg9RQMV7uneqZlaJhaVbPmaSrY7dURs1mrVFa1CwaHThS2bUc7Kbrdbr/teSPE\n",
"tu3E/hfP89L7Xx5Upi2DA+SHrKT5tpxa7WGegrFqqw2xiSo9ePCAEJL+8jC1qlrNK9jtXddNXFkt\n",
"ROerUhnVxgMaM6AMkOhIdy0zUL1IKYMg4JyrEAhlHfSMhBttW1qtljJk1FpcZJ2tra3lqKSxtgxf\n",
"7WGegrFqM8YajUY6HJAxln79h6lV1WpewW6vFnWllKpKKqi/X5DPSG44Sn9mhjwdfoRIKZUr8NRK\n",
"Vr8tMHQlq9aWIZ9C1aqtGKZWVat5Bbu9EEL5prRUSW+1UfoRBEEmDlzmRRAEmThQ+hEEQSYOlH4E\n",
"QZCJA6UfQRBk4kDpRxAEmThQ+hEEQSYOlH4EQZCJA6UfQRBk4kDpRxAEmThQ+hEEQSYOlH4EQZCJ\n",
"A6UfQRBk4kDpRxAEmThQ+hEEQSYOlH4EQZCJA6UfQRBk4kDpR5A6wTlPHNI9PGEY6q0MUl/OjroC\n",
"CJKTMAw7nU6/3ybOyx0bGo1Gz1Nnh0HdrqodKI2MBDygEakrQRAQQtTZ6JzzTqcTaaLjOGPZsdVo\n",
"l3tU45yvrKxsbW3prRVSR9DqR2qMZVm2baufGWPRz+NKq9XKbfIDgGVZlNIwDNHwR9DXj9QVz/OU\n",
"yZ8mYdgyxlZWVp599tm5ubmVlZWEr7zVajmOwxhrNBpnzpxpNBrqw2effXZ5eZlzrq7gOI7jOADQ\n",
"6XQcxzlz5szy8nIQBFLKdAWUfT03N6dK7HQ6xf3sjDEppeu6RYpzXRc9/ggAwAMEqT9ra2u2bff8\n",
"1erqqm3b6+vr6p/r6+uu6/q+H31ha2vL8zxKabvdfvDgge/7lmV5nqe+TClV31lbW7Msy/d9z/O2\n",
"traii1NKo4tHF4yuFl2/X/WGRxWd/jxTcWpQ7Ha7BSuD1B2UfmQc6Cf9W1tblmWlP7dte21tLfqn\n",
"7/vNZjO6VPxP4pe1bTstvumim81mfGh58OBBt9vtqdqZsG07cdl8xQFAvO3IZIIOH2ScCcPQ9/30\n",
"577vJ6KD4r4jQki/C6avZtu2lFIIEX3ium6n02m1WpFniRCyurqao/5xOOeU0vTnWYuzbVt5sZBJ\n",
"BqUfGWeUE/xMCsdx4mI9PD3FlxASv5pyAcHDVYFnn3220WjkK+7UovMV13N9ApkoMMIHGWeU177n\n",
"0mg+hBBpCZZSJhacCSHx+YES5fX19QHziVNJDDC5i+OcY4QPglY/Ms7Ytq03oCUIgsQnYRhSSuMi\n",
"m/6O67qU0oJuFsuyelrrmYqTUqYHKmQCQelHxhnbtimlKl4zThiGrVYr3wUdx1HrBJzzIAjCMEw4\n",
"1jnnifFGCNFzupC16J4pHDIV1+l0VHR/kZogYwA6fJB6s7KyoixZIYSKu/d9P763a3V1NQiC5eVl\n",
"9aGUknNuWVa0NyoIgk6nwxjzPE95QtQKQbvdVl9wHKfZbCpLWYWBRoHzKlIo4VdRnpmoRCEE51yF\n",
"gRZpqbpaeudapuIYYxrdX0h9wUQOyESgFF/9nHvTr+M4wydRiEqMsk0UZ0Aih2GKUyPE1tZWkSUH\n",
"ZDxA6UeQYckk/SXx7LPPqk1qOf620WiodW/ttUJqB/r6EaRORG6oHFBKUfcRBVr9CHI6iQTRruui\n",
"hiK1BqUfQRBk4kCHD4IgyMSB0o8gCDJxoPQjCIJMHP8/EQzhMPUqVtsAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1/rOTWded5X/943epW92s+SVFLarc0fJFhC7BHEd9G\n",
"ahgZRwEJwyMIwWybhRZkIR5kwHJsBGsH8F5uDAjYAWaGtYYmFhaIQ1r/eO2NMsXFYGAjYxgknFGC\n",
"CZSkGFkJFvCOVJSltWG/HZlsW91t9Xtt1f5xXrP5SBbr3iqSdck6HwhCdb1Tl4f3kIeX3/trbTKZ\n",
"EARBEGSVOLRsBxAEQZCmwdSPIAiycmDqRxAEWTkw9SMIgqwcmPoRBEFWDkz9CIIgKwemfgRBkJUD\n",
"Uz+CIMjKgakfQRBk5cDUjyAIsnJg6kcQBFk5MPUjCIKsHJj6EQRBVg5M/QiCICsHpn4EQZCVA1M/\n",
"giDIyoGpH0EQZOXA1I8gCLJyYOpHEARZOTD1IwiCrByY+hEEQVYOTP0IgiArB6Z+BEGQlePIsh1A\n",
"kNZgmiYhRFVVVVWX7QsrmqYpimJZ1rIdQcQCW/0rRxzH/X5/a2trbW2t1+v5vj8YDJbtFBHBh5mo\n",
"qhrHse/7dRTe6/W0FL1ezzTNMAzrOBaCrE0mk2X7gDRHHMfb29uUUsMwCCFhGJqm6ft+FEXLdUzT\n",
"NM/zlusDC9Dwr6MR7fu+67qEEF3X4ZswDB3HMQwDgjUfQRBIkiTLcjVeIl0BBZ/VwnEcXdeTVCLL\n",
"8nA43NraWq5XCCFEVVV4n0irSbqub29v67ouSdJ8xSqKUo1/SLdAwWe1iOM4nwsopcln3/dBcCCE\n",
"uK6radra2tr29rZpmnEcZ37o+36v19va2trc3ATtaNpBTdNMFxUEQWLc7/c1TQuCIC139Pv9fDmD\n",
"wQD+GgRB4p6madBY5vWKBShqc3Nza2ur3+/na6DyI2aQJEnXdThfcrOuHMdJDOAbiFeaMAwTBQne\n",
"VAoJggBOEDx3XTddOLtZHMeDwQAqIRESM4U4jgPOQ2nJxZA/XPkFk1Bfta8EE2SVGA6Huq6XGIzH\n",
"Y8/zFEUBUWg8HsP3tm3LsjwajRJL27ZVVU2+GY1Guq5TSjMFRlGkKIpt21EUwT9t25YkKbH0PA+O\n",
"6KVIHyhhNBqB5XA4NAyDUjoej8fjsa7raT9ZvGLBtm1FUZKioGRKaaa0Co+YL3wymRiGkRTueR6c\n",
"ePJXqJPCGxlq0rIsVVULDzcej+G1L/mnYRh5Yxaz0WhkWVbi53g8hoBmyoEfJtdVFEWZ05kwXDBA\n",
"hdW+mmDqXzksy4LMbtt2YYadTCZwf2a+9DwvueHh3i78YeaGz38zmUxs287cpdPSU+EhJEmybTv/\n",
"J3avZgJFQfZJGI1GhJC05xUecVKU+vOJu/DxUNKGS0ctg2VZ+bSbjzujWYbhcJj3k1Kaqa4oiiRJ\n",
"Sn/DcsFUW+2rCQo+KweldDQawWAVx3G2trYK3/HTKhAAP4ExJ47j5A3gV2n5JQzDOI7zQyF1XU86\n",
"M+fAsqzCnk9Gr1iA/tWMwq4oSua4FR4RSFQsTdO2trbCMBwOh3OUw4Ku667rDgaDRCqBZ+p8ZoQQ\n",
"/ybQt1x40MzFIElSWkZjvGAqr/YVBLt5V5RkcHocxzD0O9MHUDgmRJKkMAxlWQ6CYNpwzPR9G4Zh\n",
"4RB4SZIW6X6cNl6F0SsWgiCY5nlNR0x+leS4umcPgILnOA5kdggWpTRTvSxmruuapqkoCnwZx/G0\n",
"CiyH8YKpvNpXEEz9q4XrupnmtiRJqqq6rpvJxZDiMz9Peomh/cvScm9yZDq7VyxFNXxEAMJRVWks\n",
"h0s3n+GdYzQaZZ5w5WZhGA4Gg8yvoPk/h0ssF0zl1b6CoOCzWkxrK+Vfz/NDLxzHkWUZLFVVLZSJ\n",
"MqiqGgRB4cCYOh4JjF6xoChKoXSQ+bLCI87NtHFHM8mHWNd1eKXjMisUx+bzivGCEaHa2w6m/tUi\n",
"CILMnRwEQf5VgBCiqmoybhJ+5ThOovCqqirLcn4IpuM4macLpbTX62Vu5sFgkPltGIaZh4Hv+7yP\n",
"B3avZqLrOsyoSn/Z7/czCa7CIzKiKEq6WmAQ53xFBUGQOUGIQuZtb6ZZ/mkxGAxKRpSWw3LBNF/t\n",
"3QNn864WIOv7vg+qQhiGQRAMh8OMvgFza2F+KSQaGPOTSXwwEzjpMwiCAJaLyZjBDQkjc2AhBFVV\n",
"M2YgFsMTqNAmDEO41YMgSF4+CCGU0oxCwujVTGB0eaJZ+75vGEYYhq7ryrKcnntcyRE1TYOqhpRa\n",
"svBOv98PwxCeAXEcW5a1vb2tqioMwE1KS84CjOGf6Ql9vV5PluXMxQCDJtOHYzFLXIKKgp6kfr8v\n",
"y3LiVb/fBwkIhueCbzAeP+M8ywVTVbWvLJj6VxG4T8j07lb2ZRWSosisHrZE+Z1mxl5UhV7NJHkd\n",
"KS+nwiOyAKrIgr3lwMyLgdEsqShFUSpJvjMvGNJ4tXcJTP1IAW1ZUQdBkPlArR9BEGTlwFY/cgAY\n",
"vp38My0NIwjSGTD1IwiCrBwo+CAIgqwcmPoRBEFWDkz9CIIgKwemfgRBkJUDUz+CIMjKgakfQRBk\n",
"5cDUjyAIsnKsdOoPgiCz4iCCIMgqsKJTuuI4hmUFCSG17oGHIAgiICua+k3TTHYohO2Epi2QiyAI\n",
"0j1WVPBJbxwKGwMt1x8EQZAmWdHUn1lwHPd2QBBkpVjF1J9v4+f3H0cQBOkwq5j6EQRBVpxVTP35\n",
"7eV4t/9GEARpNauY+klO84njeFmeIAiCNE8rU7/ruoPBoMTA9/1er6dpmmmahWldUZRk02ff9xff\n",
"2xpBEKRFtGlcv+/7juOEYSjLchzH0/YNdxzHcRzbtmVZhu0GR6NRxiYzpcu2bRzkgyDI6tCm1A8q\n",
"DTTYB4NBYeqP43h7e3s0GiWp3DRNWZYLN5hNCqzTawRBEPGYtBDP81RVLfyTbduU0vQ34/FYUZSq\n",
"Dv2JT3xi2RFDEKSbrK2tVZWpZnJk2SdbMWEYZlrxoA5VVf7rr7++vr7++c9/nsX4W9/61t133/3r\n",
"v/7rjMYf/vCH77//fhbjb3zjG7/xG7/BaPwnf/Inn/70p1ks6zN+8803v/3tb7Mb/9Vf/dUnP/lJ\n",
"FuO//du/3dnZefLJJ1mMuSJSXyV/7Wtf+53f+R1GY0HC1+2I1GfMHusgCP7iL/6CsdgKaOwhUyEl\n",
"rX5d1z3Py3w5zXgOLly4cPr0aUbjT3/601//+tfZjfOeT+PSpUvsxo888gijZX3GnudxGV+6dInR\n",
"+Otf//qnP/1pRmOuiNRXyR/5yEfYjQUJX7cjUp8xe6wppUeOHGEveUFaOcKnhLqHaR4/fnxtbY3R\n",
"eGNj4+zZs+zG7G4wNnyAzc3N1hmzn+DZs2fZq44rIvVV8m233VZTyRiRBEHqjSvWhw41l5C7lvrr\n",
"5sqVK++99x6j8c7OzmuvvcZuzO7Gq6++ym78ox/9qHXG7Cf42muvsVcdV0Tqq+R33nmnppIxIgmC\n",
"1BtXrH/5y1+yGy9I17T+uofrHDlyhL3V/6lPfYq9+fOpT33qwx/+MKPx008/zX6mv//7v89oSTgb\n",
"KewlK4rCZfz0008zGl+4cOGhhx5iND5+/PipU6cYjeur5D/8wz9kNxYkfDVFhOseOXPmDKMl4ay3\n",
"+oy5Ys2eWyqgMWmpQkq0fkqpZVmZLyVJqurQjz/++MbGRlWlCUiF/SICQillF4vbCIavvVBK19fX\n",
"Gztc1wQfXdeTabqA67q6rldVPpfgw7UBJNeeAY7j1GTM9TJbnxvsxlyVzCUv1Hd29cVahPDxXvbs\n",
"xlyCjwgXJ+GMdZOCT9dSP7yhJ7GJ43gwGBTO50IQBFlZ2jSbdzAYQIs+juP0+P3MtN44jjVNUxRF\n",
"kiTf9w3DqDD1/9Zv/dbf//3fX758uaoCRUPTtGkrZHSA9MacnQTD115M0/yjP/qj69evN3S8xqSl\n",
"hhmNRp7nRVFUbbFPPvnkuXPnGI3H4/F4PGY3ZneDS/HstjFvJbMb13d23Y51GyMiQqwppexzhhan\n",
"ayN8Emoa6rO7u8uu9XNNMuAy5tpgoNvGbaxkQdzAiDRgzHWCTWr9bRJ8ROCpp556+eWX33jjjWU7\n",
"giBIpzBN84UXXnj77bebOVzXunnr5urVqzdu3GA0DsOQvYHA1ZTIjGJaZWPeSmY3ru/suh3rNkZE\n",
"kFjv7e2xGy8Ipn4+rly5gqlfKOM2Jppux7qNEREk1k2mfhR8+EDBB0GQOkDBR2j29va4unnZO3k6\n",
"399VX6ciVyWzGwvS9SdCJXMZtzEigsQap3SJSxRFu7u7jMblMxXDkKSvCkFm87bOuL65o4LM8BSh\n",
"krmM2xgRQWLd3KB+FHx4qVDwMU2iqqSj01MQBOEDBR+hQcFHNOM2ygvdjnUbIyJIrFHwEZcKBZ+8\n",
"MbsbgrzMimDcRnmh27FuY0QEiXWTgk9nF3KoiYsXL54/f57ROIqikpUkKJ2kJ4RzrTnBtRJAt43L\n",
"K3kR4/rOrtuxbmNERIg1pfTMmTPsJS8Iav18oNaPIEgdoNYvNDs7O++++y6jse/77LM/uOaJmKaJ\n",
"xgBvJbMb13d23Y51GyMiSKyvXbvGbrwojb1fdIMKBR/DmKT3E+u2CFCfcRvlhW7Huo0RESHWKPgI\n",
"TbWCDyHEshYvCUGQ1oOCj9Cg4COacRvlhW7Huo0RESTWTQo+nV2vvyZuv/32I0dYK02WZfaSuYy5\n",
"NirqtnEbK1kQNzAiDRhzneDRo0fZjRcEBR8+UPBBEKQOUPARmjiOcUqXUMZtnEDU7Vi3MSKCxJpd\n",
"TF4cFHz4WF9fP3SI9XkpSRJ7yVzG9b1Tt864jZUsiBsYkQaMuU7w8OHD7MYLgoIPHxUKPv0+IYTY\n",
"9uIlIQjSelDwEZoKBR9JIukGQbdFgPqM2ygvdDvWbYyIILFuUvDB1I8gCLJyoODDB47wQRCkDlDw\n",
"EZqrV6/ituxCGbdxE/Bux7qNEREk1k1uy44jfPjY3d3l2qqFveRub99Rn3EbK1kQNzAiDRgLu1UL\n",
"Cj58oOCDIEgdoOAjNFUJPvmvuy0C1GfcRnmh27FuY0QEiXWTgs9Kp37f97kCQwi5cuVKVak/sxBI\n",
"t9NBfcZtTDTdjnUbIyJIrJtM/dyCTxzHMBQ3jmNVVWVZ5prbJghBEPT7fViGKQxD27YZJ91VJfjA\n",
"xeP7KPggCEKIyIKP4zjb29ubm5uapvm+HwSBpmlbW1vb29uO43D1ZiyXOI4Hg8FoNLIsy7IsSulg\n",
"MGD87d7eHlc3L3u1dL6/q75ORa5KZjcWpOtPhErmMm5jRASJdZPdvEyp33Gcra0t13UNw4AdajzP\n",
"8zxvMpmMx2PDMFzX3dra4prktkTiOKaUJv9UFIX9t1EU4fJtQhm3ce5ot2PdxogIEuvr16+zGy/I\n",
"bMHHcRzXdS3LKk+RYRgOBgNZltNZtRWEYWia5nA4ZDFGwQdBkDoQTvAxDMPzvJlNY1mWbdtuXd6P\n",
"47jf79vMi6hVLvgk747dFgHqM26jvNDtWLcxIoLEWjjBp3WYpqnlyG+rFsdxr9ezLIt9YdWqBJ8g\n",
"IJJEVPVW6u+2CFCfcRvlhW7Huo0RESTWTQo+pLEN4EUjiiJVVUejEdevLl68eP78efZDRFFU+CdK\n",
"J5PJxPMmnnfLmN0N6HFB40lpJS9oXN/ZdTvWbYyICLGmlJ45c4a95AXhG9zp+35LR3NmCILAcRzD\n",
"MLj6eEl1Wr9pEsvaV/x5dvpEEKSbCKf1pxkMBrxzoObDdd3yAZe+7/d6PZBxeMeVBkFgmma64zqv\n",
"BU1jZ2eHfU1t3/fZZ39wzRNhd5jX+OMf/48iuMFuzFvJ7Mb1nZ0gscaINGDMFetr166xGy8K1ztC\n",
"+Vb0iqJ4iX4xF57n6bquKIqu66qqTjOzbVtRlNFoFEURZHCuo1BKFUVRU0iSxPjbzgs+Tz31MxHc\n",
"6La8IEisMSINGAsr+HBr/YZhUErhfKIoopRSSGOTyXg8XjD7j0YjEN89z5uW+qMokmU5XaGUUtu2\n",
"5z4oF5cuXXrggQcWLyef+gVh+gMXQZAaoZTecccdjR2OL/WnE32CruvD4RA+j0YjXdcXd6sk9cMQ\n",
"0vQ38MhZ/KAsPP7442spDh06pKrq+vr6xsYGvD08+uijk8nk0UcfveuuuzzP++AHP3jXXXdNJpNn\n",
"n3322LFjyQc4g2PHPvCRj/zlZDI5duzYM888M5lM7rrrLigh+QBFpT88++yzR44cSZcJJTz77LPp\n",
"D0kJJ06cKCkq7dVkMjl+/GpJURmvKKUlRWW8+shHPlLHCXqed+bMGcYThKmIjCd44sSJ8rpKl3Dk\n",
"yJHyukp/eOaZZ8rrKl0UpbS8rg5eV7T8YmjgBOGyzxQFHzJeHTt27IMf/KDneekyMyf46KOPJiWk\n",
"r4p8URmvTpw4UVJUxitKaUlRGa/gsmc/wUxR6+vrqqpubGysr6+fOHFi7SCTpuBL/Yqi5N9fMum+\n",
"RKhhpyT1U0qTJ02CLMuLH5SFJ5988ty5c4zG4/F42ruhYex/SJ5iXG+RXK9WXMZcEmB9brAbl1Ty\n",
"gsb1nZ0gscaINGDMfnaU0tOnT7OXvCB8qX9a30A6Tded+nVdz1d9JQdloVrBJ/1BEFZ4uG8XEO1y\n",
"QthpWPDhG+Gjqmp+hI/ruk0O91zuOnFxHHd7DR8uRJg108YJRPXF+pvf/GFNJXc7IoLEmn304OLw\n",
"pX7DMDIDm2AVTF3Xk2+sTq9Ks76+fugQa6VJksQ+T5jdkhDC9axlNw4C8sgjP2UfjVaTG1zGvJXM\n",
"blzf2dUX69tuu62mkrsdEUFiffjwYXbjBeHbm1fXdVir2TAMSZIg7xuGkR70yTtJipe6yy/n5MmT\n",
"R46wVlp911P5KNu5jeOYaNodS3eDy7h1lVyrG2tryw9fGyMiSKyPHj3Kbrwg3Gv4wAL3QRAMBoMg\n",
"CIbDoWEYdXhWQv4diuutahE6L/i8+ur3RHCj2/JCfbHmug8wIg0YCyv48LX6AZgGVbkrjOi6bppm\n",
"eolQ13XTihOCIAgyg8Y6lLkoGeEzmUxUVU3mcEVRBDN7m3GsqhE++cGdImDbE0qFm2WGMDIaTZin\n",
"pSPCIfQIn7oZDAbJAsvQqQBkzIbDoeM4/X4fFmeeYxW2ubl69Wol27Ln+35E2Ko7DMn99/8N+xuq\n",
"CDtft3ET8JpiHcfkn/yTn9ZRMpdxGyMiSKyb3JZ9HsHHcRxYdEmWZVVVKaVcvdglwGzhmWaSJI1G\n",
"I9gavsKjs7C7u8u1VQt7yYJs33H48Ktx/OjS3eDaGIS9WEEquT431tZ+FoZ3MPYsYkQaMBZ2q5Z5\n",
"1vDRdT2ZogYrqXEtR9Vquj2lC5wRyiWEHc9Dva7FCC34OI4Tx/FwOExGLBmGYVlWr9er4akkIlUJ\n",
"PoXG7G7U9H4ax6K8JndbXqgv1m+++YOaSu52RASJdZOCD1/q930/P2NLVdU4jptZx3/pXLlypdrU\n",
"n7wOipD6JUmUG6bbiaY+rf8HP/hBHSVzGbcxIoLEusnUzyf4TFvXnlK64Er9bQEFH0RYKJ0Mhyj4\n",
"tBWhBZ8ObM24IHt7e1zdvIWdPL5P8hXZ+f6u+joV2auOy1iQrj+ukn/lV95ib5JiRBowFrably/1\n",
"K4pSOJPN9/0lTvJqkiiKKpnNm0/9gszmbZ1xG+eO1hfrb3/7j2squdsRESTW169fZzdeFK53hPF4\n",
"LMtyZv4U7NtV6buIuFQi+KQ35xKq5lDwaTUYvlYjuuAzHA5hLhXsnL61tSVJUrdX60xTieAzzZjd\n",
"DUFeZhszLvlpG+WFbse6jRERJNbiCj7k5t7riqLAi4zneauT90l1gk+hMbsbgrzMNmPs+6Tkp22U\n",
"F2qKdRwLEb42RkSQWIsr+CAXL148f/48o3EURYWT3dKCj2VNQD/jmhbHtcMfo3EUTSidjMfjZH2h\n",
"pbiRN4aZStOYVsmLG9d3djXFGsLHLvjUdIJtjIgIsaaUnjlzhr3kBZlnIYdV5ujRo1xbtcy0UZT9\n",
"of1L36olCIiiEFmW2R0RYTcMrnpbeiUL5QZGpAFjYbdqqWb5tvq2ABSNnZ0d9jW1YaWjou8LRvhw\n",
"zRPJ7JVWlbEk1VXygsYlL83TKnlx4/rOToRY12fcxogIEutr166xGy9KJe8Oje2KvnQqEXzSr+SJ\n",
"+LN0wQc8EUExmOQEn5Lrq43yAgo+8xkLouGg4LOKVC74zGcsyMtsM8bl4ynaWMm1usE+ogQFnwaM\n",
"Oy74rA6VCD7TjNndqOP91PeJouwbM45ea+adOgwL9LGENsoLtcaaPdWg4NOAsbCCz+xWv+M4ruuW\n",
"2zS2Ne7Suf322zu8Lbsk7RuXZ9u63cgbl6Sz1lVy3W6wpxrclr0BY2G3ZV+bTCblFqZpSpJUvg2W\n",
"aZqj0ahSxwTlqaeeevnll994441FCjFNksyFCEPiOESEqRGJV5A7xFmYA9pYIlSR4EAE01cX0iJM\n",
"03zhhRfefvvtZg7HJPgoiqKW0uQ+WcsljuNqp3QlbQKc0jWfcRsnEHU71m2MiCCxZheTFwe7eflY\n",
"X19fvJu3sCNu6f1d4JUgnWMZY0nan3aQp42dirW6IUnE95le2rCbtwFjYbt5Zw/uZBl9tTqDOytZ\n",
"vi0z/G7x9baGw0VLSLuRnmwsAoYhnEsCMhpNLGsyES98CCPCLd8mSdLMB5fneRU9iUSncsEnbczu\n",
"RuaVs/wFlPdlVlEIY1dhM+/U5VdfG+WFOgSfOCaKIoTK0caICBLrJgUfHNwpOizjLMOQNVmzsDId\n",
"NwgiFjdu/MvmDtbY+0U3aFjwGY0mijKx7RkFqmoFmk/aDaHWfKd0f2k5pIRE5/G82RcMIiCU0ttu\n",
"+3Jjh8NWPx9Xr16tdlt2II6LFwF3XTIcEnJzgGNCep5IGBJFmbHKDZO7AhuXvIi0cRPwmrZlJ/v7\n",
"5bHOyMNt2RswZj+7n/1sk30vkMXB1M/H7u5u5Vu1GAYZDIq3dICpVYYBMm76+zBtUz6cQ5A9K+Y2\n",
"Lq/CNm4MUsdWLVCkCOFrY0REiPXly5uHDn2XveRFmfleMBqNPLYRA+yW7SURfEajSX4RJ0r3/9P1\n",
"ycFdLPcB4SL/Pk5pgX0yZgOYtow+rPg/hx4C6+Cr6r4/6RLYl+xvAHBMKJcEBGSx5DPSOi5d+urp\n",
"0/+iscMxtfpN09Q0reQ1x/f9Xq/X6/U6P7crEXxcl7guMc1bjXFoClgWsSwyHBLXJd/85g8zzXPT\n",
"JLpODCNbLKXkued+nvnSdYmu3/pneuBNOhYwtCPdtuj3D+g/+cDFMen3SRgSyyKeR+KYmOa+qALG\n",
"jGFs8p16mkttlBdqEnwkSQiVo40RESTWYm3QqCjKaDTSdb3f729tbSUb87qua5pm8qWqquPxuHy9\n",
"hw5w5cqVROunlFjWrdE1pkkovWVpWeTFF2/89V//OPnGdQml0+YlkbNnf5TR6zML6eh6cepPSkiI\n",
"YzIY3PpnxjgISL9PKL31BKKUyPK+Y4LcMOInmswAPxFSf2LMqDF0LCJiGrOf3eXLm+z9iBXA9Y4w\n",
"HA4ppbB6kSzLqqpSSoeVTChqCYngk5FHLKtAxhmPDyg25a/hmUEsGbUnKaFQZZpMJpa1/ycop2RT\n",
"QxY1YJqNbRc4UDfgjGgihmgClLADtBBGHnvsL8Sa0pVG13XLskDQH4/HsCe7nlYl2kav19vc3GS3\n",
"39vby3fzQts/L+NIUvz977Pvs3ygqZZRewDoECZFvaCKsq84BQFR1f2OX3iNqKoLK45JEBDHIaa5\n",
"fywRetKW1amYmUux9G5ecYwzlew4ZVMOsZs3jViCT4dxHEdVVS6RKoqi/GxeSSK2XWAcBMG77/64\n",
"4A9FBEEgy/vJ+uZyOlkb+CYMCya7Jr+FZfcJIZZFYLHtqmYqwsowlkUo3X8CgXG/P2M68cySS4wL\n",
"N7NM08a5ozXN5uV1o5nZvEFQNthUkIgIEuvr19lbigvT2PuFaERRZBjGhHMBokLBp4REovG82bOu\n",
"Es3HtqcuwzIeZ/d3TIrNCyN5J1ncKPxh5svhcF+Psu2JbU8Moy4hKJmpJJqIoapiLZUjpuBj25Ph\n",
"8MDoI2QaDz/8sriCT5cYDAZGXqOZRaHgM404jh977J1MY7zEOOmqBdGmEGgCv/TSWzd/lR36kn+/\n",
"zKhD5aN3GF9mdZ2EIfnGN34cBMQw9peJL2fxd+rCV+dlCT6wmCijcd4NdmNBhIv5BB/QLXWdTNvt\n",
"CQWfhOPHf4GCT+1A8OYYj1Qo+EwjCILbb/+bRMOZKVwQQmSZmOaMhwSlxDTDm786YJwZFAQqUPr9\n",
"tOShAkx7mc1fwJZFvvCFX8KuIJIEXs1TMqPxtBnLyxJ8ZPlAnSxd8BHHOKnkpL8q6YgqMa7WB3GM\n",
"hRV8urlev2ma+RpXFMW6uX2RaZp2oTw/i83NzfX19TBkGvkOjxboDJxpD8a6Tra3yXhcZilJ5OGH\n",
"H07WZE+XnHkSQLrkermZZuy62WeGJJH/+l93k6MrCnHd7FtFHO9/qSjk4x//zCJuTKtAruc3l3El\n",
"9SayGzUZJ2cXBAf2Cyvc9bPbVUE4T/DYsWPsxgvSzdRvle5QFwRBGIaDm0Pf4TNNj8mfztGjRw8d\n",
"OgTL5swkmeDG8s4HxpJEWBbA/spXzvT7BTdS5maD5R8Mo4JtKAqHMGWMdZ04zq3JDfASoKpEkkgc\n",
"kz/90/Mf/Si3GzN3CV7KxiD5gIqzVcvSjQsve9B88jdZB6qifEdM9hN8993bmtyqZRUFH1mWLctK\n",
"7y7Jvs/yzs4O+5ravu/7vi/LxHFm75qUzBNhuQhN07QsWPnn1peF6+xLEjFnyvAHSwYfWKatZEpO\n",
"v9fDvGXLIqpKFIWoKnnrrf/IPhUmKTm9QlGhaACVzFgsl3FJveV1M65K5poTNEf4CNta3/OVPJOk\n",
"ktNJLzPhPG9crQ9NGpfLP+xnd/z4L65du8buxoII2up3XTcMw5KWuO/7juPEcawoCqWUt+mXzvUz\n",
"N51PA4IPozEUK8uzNRzC/+YrScQwDiRoSSp+F5njZTbz+JkmcOVLBtkHfp5x5t/9u0f+7M9Yd3vP\n",
"l6yqxX0Jqj6FBAAAIABJREFUKPjkjXV9v8dI18taErUKPkHA1IgRJCJzG898xAor+IjV6oe1gLa3\n",
"t13XLXlaOo5jmiZMJJYkSdO0+Q7nuq6maUEQ9Pt9xp+A4MNoDBucyTKR5dla/xxvvopy4A1aVQtm\n",
"gSkKCcP9W3DmKCMy5c132g/zxvA0cpyCV+CHH36AsLVGp7lRCMsucrzG4KQg+7XO4YaikOFw/wFQ\n",
"IjbWJ/hIkpQf1zBtS2r22hBQ8IG30pKuXGH35hUr9UuSRCkdjUYlD+E4jgeDged5iqKAvaqqXH3u\n",
"Cbque54XRRF7ly8IPowtmuRlFtbcn2nM6AOZ/n6ab1MrCvk3/+bb8HnmyM6k5Ix2NG1d6EI3FKWg\n",
"VwCMKWWa/DWt5EIqF3xgbbtyH/IXwLIEn0x9po1lmYAqOF/Jcxv7+2SrqPDamxaRXm8hHxozBumv\n",
"5PnKGGtobTQp+Ag6pcvzvGkzrWzbpgenrMCycY34NXnyySfX1tbW1qxDhw6tra0dPXpUVdUTJ07c\n",
"eeedqqqeO3fuiSeemEwmTzzxhCzL4/H48ccfl2V5Mpk8//zzp06dSn+YTCanTp16/vnn4cOzzz47\n",
"mUxkWYYSkg9QVPrD888/f+LEiZKi4ENSwu23/+/wYWvLzReV8crzPCiB0ltFnT79p4VeeZ5XUlTG\n",
"q89+9rMlRU07wWPH/n1SlKr+Xf4Ex+Px+fPnS4pKezUej8fjcUldybL86KNfVJTJE088cc8990wr\n",
"CrxKV9GJEyfyRU3z6tlnny2vq3RRnudNK2o0mtx55+VTp943mUxU9e9OnToFi6yki1LVv/O8Yq9K\n",
"TjDvFfsJwmUPVZSptMwJnjp16vHHHx+Px+kyoaijR99JykxKSF/2+aIyXt1zzz2Zak8Xlf7w/PPP\n",
"J5d9YVGJV+nLHkpQ1b87efI3bHuqV48//vhkMrnjjsGjj34Rijpx4oSqqnfeeeeJEyc2NjbW1tbW\n",
"1tYOHdLW1tS1tbVJU7Qv9RcuGAeBaQCYzSvObEkWkoXGuNyuafl+2F0gQ8lic+lDN1PtlM4+3wZW\n",
"lIui2TNgYZ0+qNL8Yn8Jul6ta0zkK6dw8cFCYF/S5hcKnAPGKwH28CgJqOdNLl36Ks7mLSMMw7x8\n",
"xiXVLUIcx1xTurhmG7G7wSlw+eyvs4UlT5OJ5pgIkx/pEYZZ1SKOyb/9ty+WHzqh8ildIIvF8eyz\n",
"S8tilU/zgQ0hSkqOYxLH+0IzzJyYZjxNjC40nnapzL2GT9qNfE9PoXFyXnP7II5xcnbJylclsI8e\n",
"XJz2pX6uSfCVs76+ztvNy27M7gbXow6GeTBerknJkrR/o5YsoDZH51hm/QPYJSbT1RIE5B//8QJj\n",
"sXV080LemXl26ZIq7+YNwwO9zZDo0wwG+538qnrrCVToRmbicYnPsNMDo/E0Fo+I7xNKC1L/HNdb\n",
"HDMNU26gS//mfhjFZhDr1e3mFZ+TJ08eOcI6IhYkQnZjdjfYJyKAsWGUDUIoLDkZpF8yqYrXDZJr\n",
"9cMUsHyiOH36gXwJikL6/QM7oxH+Sk4bu272iQgnC4+9Oc6O3Y38l0FwKy+kqwhKzi99nAyhSe/h\n",
"U+hGsqrrTJ8hHIzG05BlWZLmjEhC4bNjjog4ztTlgxYsmRASBPt+Mg6jShbTzROG5P77Xz969Ci7\n",
"GwvSvtS/3I3A2ij4gLFtFw+8mVZyomaUbPs+32ty+j5J5kVnvgyCgkGguk5se393hIRFBB/4mJY4\n",
"YCUMeOzNPLt0Sl1c8EnvrZberQFKDsPsIzMJSno+R6Eb01r9eeOSJZ64BJ8/+7P/VjjYLN/mrXsN\n",
"H8Y1V+a+kqHmSw6RObtyZ1DwmUH+WuHKmysLV4dIco1WLrClr/7kc/rLMCR33fXzkqOnv/zRj9a/\n",
"//0T83kSx8Qw9pfMA5Lcx3LW01LqfMBTJ3ncwhMokyuTwwXBgTkctj1jrhyLn7Aq1LRXBC5+9KOC\n",
"qUm8+3bP7UlysjNXAWFkWlM9rYUuVYeeh/alfl3XM0NlXddtbKcwSZK4ZvOyv6O0fVoju/G0myT9\n",
"/T/9pw/Dhykv/rfuxj//8w/94z9+kNGHTESgcPArk2Qlad/hOC4eY54hUxWwaF2JG/kv43hfEEh+\n",
"mKy+l7yLgJMlJU+LCMtkbN/f7xYqLJ9rNu+NG/czKigl90h+rVYWHxyH9PvwUDccZ/8BOTMvl5ec\n",
"6Z5NG0PqL5nVlTm7ac8z8PD48eMzHK2O9qV+qMrUO1c838r783H16tUbN24wPuF596dmd6PJLadL\n",
"GmvzlZzeliD5nLl5fvrT10rqQ9dvbWd26NDlt976OaMPmYgkcaS0oGUHDvs+Y5P5QFUEQdlwjpJY\n",
"K8r+8keEEFmGbSB9aI8nmn5+FdVpbnD5XD7jj2tb9p/97DK7caY20k++TD1lfPD97AM7CEgQ7I+l\n",
"8X0fukPKZ9sWlpwh8/NC42kXSebsIKZ5oOb39vZK3aySeVK/7/v9fj9ZPmEwGFQ16mYwGGiapmka\n",
"rLqs3SRjNhwOHcfp9/umaWqaZhhGYx0Au7u77733HuOrK+8uIuxuNLMNhSQRxyl7ZZ6v5GSQTyKV\n",
"5jl16r+xlO265MMf/v9KVjmHzYQTvvzl9e9850byz7TcBGsEHdSdQpJbB5tMucnzVSFJU4dzlMTa\n",
"MG71f5D9cVZh0qML7mXUnnI3StzOGFeyhw8hJI5jds06uUeSuirpb8j44LokDPf3B/V9Eob7o8Wg\n",
"9r7ylVPwgUU4SkouqqVsCfmqKHm6ZHJA+XNI6K1aHMcZDAaqqqYacRLXNOgSKKWe53meNxqNoijy\n",
"bpIxkyQJFntQVdXzvMaa/GTFBB944658/a9kkE96aaDM3fX000+Upxp4fgQB+b3fe/+DD941zSyO\n",
"DzSyrl8/9+ab74fPmUGr8CaR+KMoRJaLzy7/MCBFVQFvEoVJHmKd8S0hc73r+q2SSx4n09y4ecSC\n",
"jJM2Tr+BcZVcdCxlff0su7GiKEFwq7ulpGM247AsE8Mgtr0fR8e5tWKKZZGf//zR5OWJUfDx/YJ3\n",
"tTAkun6gBN6l+govmELEFXx833dd1/O8tLZuGMZSelkVRYEll5s8KAg+jMZtF3xmLjc9t+CTXC9J\n",
"9DL3Zxz75fWh62QwAE0gfN/7dhJHfP9Ajss4eOjQ5bQWkXmqwRLTiWN/+Zf/AC7ll7DOX3Tpqkge\n",
"adPWLEreJ9J/LUxPqko+85kfJH7CimxzRAQmqZUYl7yBlZecJwzDQ4dmCz5w7nCPwIgmCFz6pSdT\n",
"82kfHOfWiDVVJapKLOtAXCj12XMDlJzsLHTwT9mLE4yntYpyMxZDwtzFLa7g4zhO4S4oiqJwZYH2\n",
"cuXKlZVK/eUDJOYredrS7Xnj0tlk+82xMAw3Nl5P0n0yCTZPHJPLly9fvnz55iGyyS6zwZnnRcmg\n",
"l5mkqyJp5U1rbxbKC9M6tP/Tf/qVJNcnA/lZ3MiUk2+e1XQVfec7//22234802wwAMUm/Id/eCuO\n",
"i/fvzbid9kGSZuTTOc4uCIhtFzT8M9NiwLhw+JDvk4w+zXVfi5v6fd8v1CUabnovkbvvvvvQoW3G\n",
"04WtYBhL5ppUUr4NWYXG5UuaLujGlL07iKLcMi5Ju8MhaPTqJz/5kaSo/Cb1ScvR98nv/u4D99//\n",
"wDTjNJJEPvrR38wMrQEKtZH02c3chzmJNUtaePLJE+nSao0IUCiOs5f84IOP/vN/PnvMFfRaK4r6\n",
"8su/SWnxYzLzZeIDy95HGYfLWxuJMaw2wWJc2CcBjmVm5GUaGZkJ7WlOnJhzmPIc8KX+1Unx09jb\n",
"27tx4zSjctf2bl5StAp0VSWXjCdJ+jbLgYSYruT8Ozj038KdFgTkV3/18gc+cIVRnvzZzy6Dk/nH\n",
"Sf4C4KqKpGMz8bZkKwXLOlBy+bVXyYWRTriJCXvJV668c+XKO7MODcNnyb/+1+/u7FyHepg2+iXv\n",
"cElXcN6YFL30ZA6UNjaMGYvtTKuKwYAYxoF1NcjNWLNsWEZE7uZVFKVQ1p/2NtA9oii6cYP1pUyo\n",
"2byiGU+7e+G2chyHsZmRruTCUY/pRPb666MjR15lrOnvfe97M31IXghKFlkr9Bk+FM5uy1BVRBJP\n",
"BgNimsQ0yZe+9H8VWibLNxFC+v39pMnuxmuvvfbaa69NKzkt6CsK+clPfvLQQ/83/DU9XaPQ87kn\n",
"6ObfYzKyDBjDgcrX388YJ0BHOvQ6HHxHzF5tJTP1SsaqVQ5f6jcMIz+Yp9/vN9/duizuvvtu9hE+\n",
"HRB86jOe1ksG60aAMUtDEyoZVB0WpSWtDpXz0Y/+5sz2THLVJ2eXSUzla9GkU+G0G6iqiCSrzYQh\n",
"sSxCKdnY+J+Tv6ZVrMyAeshT7G488MAjv/ZrjxT+KWnwJuf74osPfOELjyR/zffupDMp+OC6TEuS\n",
"pB3O9dMWGKdfQ5MBUYW9TZZl5QftKMqtnenSoczf1/lAJ80gcQUfVVV1XYcNFAkhruv2ej3CeXW2\n",
"mr29vffemzAad0DwqckYMnX5jAGWmTjkZiVD1ihdSgVGuexHhGWftY9//C32x3Fai5j5wEhinU6F\n",
"035VVUSgLZ+sDiRJJD0VrlDFggkENz0MCdvD+K//+l1FmXExp9ZuOnCPKEpB6k8ug8QHlo73kqqA\n",
"h0f672EYpgOX9DkXNiYyxkB6TET6tYnrvhZX8CGEGIYxHA6DIFBVNQgCwzDYdzfsAFEUXbt2gXFh\n",
"EBR8phkX9ulB+obvwRgG2JQDlQzbwU8b+qIo+/1vSURmvh8QQr797T9OP0umLGW8v1z+7/7u/wMG\n",
"GSFr2ppl6Z+XU1VEoC2fdu+NN/6+vDTogUhHhGUb7J/85CclFzOUllqM6MA9QmnZg9NxHPZlefJV\n",
"kX7hyLzZQMn5FaWm9OU6JY9qclC54rqvmxR8BN2lS1guXbq0sfHHy/ai9YzHBVtHeV52uy6uyzP5\n",
"YbIRmOdNYD+38fhAUbY9Y8ukPMPhxPOyBwIUZWIYk9FooqqTKMr+FU6qxGH4f4X7oE0Dtr5Kb3CX\n",
"djXjdtq35Nw9b6LrU09nWlGFf517wzjLmnP3riiaqOpkNJoYxiSKCuKSccm2J6PRrS/hn9OMy33O\n",
"BzdzFlDDlFLcpQvpODAPMw+PtpElER3TIyig+ZY5HCi5XJ1T6SlRmeb/aLS/eIBlFS/0Nu2k0u3f\n",
"BnrKoFrmWOcwUdt9n1gW084n1ZJ+N5p7MU5JIp5HXHf2hAAg0+e8yCqt+cNl3jlYBixVDve4ftM0\n",
"YYEd+CYMQ03TlrtzVpPs7Oyw63E+rLzFbMzuBtfKGWIa56/19AZ+YMxyPxRWcvJqnwCqJBgrCtPN\n",
"n3Y4UZynpR7TNCH756XqfOoHh8GHmZ5UGJGMNPvSS/+lxDhxGx57n//8/8qikhFC3nzzB1yX/Uzj\n",
"RDT7vd/739jzfmFVWNZ+EyEjxOWNIdcfnGG+/+Gpp16Y2Z2Tmk3CcV9fu3aN3XhBuMf1u66b3lhH\n",
"lmVVVataw0d8Njc3Dx1i3USt7Wv4tMI4X8nJ8Iz8JjOJMcu4hEIf0usH5I0VhWnwybJinamNhx9+\n",
"OPmcb7ylR8pKEnn33f+J0ZGzZ8+Wn2C6j53lHoGAmiZ5663PsL+1lFdF5olbaAz7tQHp3ubz5//F\n",
"zAAm9nfe+T/kn+7pfuA0x44V7HNQE6x7DQKu61JKM9VEKd3e3q7UK3E5evTo2hqrMdeA1/r25m2R\n",
"cbImJRjnFu4rIF9vpXN09//G8j6Rdxhu18LyefdrLWxOMrpRlfHGxpmUSwf+BOuYwt6/N/955itf\n",
"IeRmexkqsHA407FjxyWpbBmy9NsD42V/c12221mMAc6IFBhPe8ysrd0xs+xEIHr77Y18FcGohDzi\n",
"7s3r+37hpiirs4YPCj51G8NNxV4ybyWzG2d8iOP9rWtZjGe6kSRNGH1UkgDri0i54JNGVcn73vd/\n",
"Jp+TrcQKB/zMFHwOTmOePyIVGn/mMy8UTgYsTPHf+c7fsJQJqf+VV2YMo0rTpODD1+oPgqDwKb0i\n",
"87kIv+DDXjIKPvMZN1bJIHmzrCfM4kbSzwzFlryF1FfJacEn52HWpeeeuwAfkhqAdQvynD17VlE2\n",
"ppUMdZgWfNgdrq8qPvSh32bMYY5D/tW/eoDFEtaluOuu98+0TF77mhR8uKd0Ffbork43L6/gw/5Q\n",
"RMGHpDIOe8m8lcxunPFBkqY2+fPGM91IPs+cuVar4DPtxpWkbHdIpmTX3W8U552/du14SSVn/rJI\n",
"RCo0/vnP72KYiEcIIUFAPvvZu1nKhNej73//9pnqYlIB4go+iqK4OY0qjmPf97nWIWgvcRzfuHGK\n",
"0RindPEaJw019pJ5K5ndOOMDrC7JaMzgBtPabbwlcxnHsc9+0aVL/sAHyNe+RqYtt7m7WzalK8Mi\n",
"EanQ+NVXvzfTBvpmZZm1ZBjBubPzE3Y32Hc3Wxw+wYdSqmkajOqBb+I47vV6tKQ51C3W19cPH2bd\n",
"CRa7eXmNExOuVj+7D0upZFio5+CyvVK6q1NVy7T++iLyq7+6mXxmWCf1Vsm//dsEtCLYNSzT6jt+\n",
"vKzVn0GQy/7MmTOzjQgZDIhlkSDgKHnmxlvpRkCTrX6+1C9Jkud5vV7PNE1VVcMwDIIgP+anw5w8\n",
"eXKNWfGp70rlesfqtnFhvcly8QiKpVRyfpHejBvlUkN9lZxeZG1mBk6XnMyKKhypsrFxRpanZtLM\n",
"ysyCXPb33//ATBtQt2CLCPaS33tvxkMl3Qg4evQoe8kLwj2bF7L/cDhUVdUwjPF4vDp5nxASx/F7\n",
"773HaIyCTwPGhZUMd2n+DhVEXsj4UD7JoD43/vN//vPKS45jsrNTJvjI8oFHnSARYRF8VHVfkGQv\n",
"WVHIq6+yigREZMEnIT2ra6VYX19nb/WLr0V0wFj8SlYUMhgceA4JEut77rmHfXwGY8lBQLa310pO\n",
"MPM8XmJVJNp9EJAPfnD20Jo51EhVJc8/X5xjk6P7/q3hA00KPrh8Gx8f+9j/srlpLdsLZDaSNOc6\n",
"X3WQX+2La/2ymkgvNje3P+zL1YlG4mqtPqcXfSs8eioELVy+jWtJ8VZz48Z/P3bsm4zGbd+WvRXG\n",
"0yp52krr7PVcucOOs7/znyCxDoJaSv7JT37MddkvMSJAEJDXXmOapTWHG5I04+zSL17ibss+jX6/\n",
"X0k54nPkyP+7tvYDRmPcqqUB42mVXPhSzhWRah123Vv7fYsW6/Jtc2aWnDmbd955h+uyX1ZEUj6Q\n",
"w4dfraNkMj3WyTI+acWrya1auAUfSmmhPFfHK4mAXLp06YEHHli2F8hsRFBUEgwju069IO6BG4so\n",
"HumdDCaTiW23RvBJ9K5lxSJ3SQgs+JimGcfxOKehrsh8LkLI1atXb9y4wWiMgk8DxtMquXDYzLLk\n",
"BVne78qDMf5dinWmHRiGRJb5LvtlCT5pz+urN65YNyn48I3w8X3f87x8q3919mjc3d1lH9zJ9V4v\n",
"mgjQFuNWVHJ6CcwgIL/85Q32sSoiVHKJcX78UisictCHGutN2L15+YQaXvvugYIPsiCUCjQMZnHB\n",
"Z1K60aPgoODDiq7r3RvMwzWpZG9vj6vVj928dRvzVvLSOxUJIVeuvFNTySIYtysiNzd0W06rP7N8\n",
"U5Otfr7UTyktXAW7V7gnqfC4rqtpmuu6rusy6ndRFO3u7jKWj7N5GzBubPm2qowlifyH//BT9plM\n",
"DVRy+fpxXCXHccsiArO+G5u5nSa/LfP169fZS16Qtclkwm7tOA6cdqZf13Xd8XhcsWs1MxgM4ji2\n",
"WHbqS/HUU0+9/PLLb7zxRk1eIZ3H90m/TwS5Xfp9YtvENJl2rCwvBFiwqIYxTQIbNS9lnIpp7i98\n",
"DUc3TfOFF154++23mzk6X6vfdV1FUTowngcWnuPN+wQFH/GM2yUvkCkbtTfvBhizv3yUlJwppF0R\n",
"gVb/sgSfzPbR4go+uq5TSq0crXsYOI4z30LTKPiIZtwueQF45JGf1lTysozTybCNEVmK4JPfnL1J\n",
"wWdFR+yoqhpFka7rqqqqqjocDhl/iCN8kC5RyRCX9ACh1o3wWaLDnjdRlLQzjY7wmXPlzgxhGAq1\n",
"kKdpmvmHraIoaYXHNE3LssDtXq+nKIpQp4AgLSJRNdq1VWu+3d28A8uim2v4WJbl5UjnfUmSdF1P\n",
"cr2u6/mNJwvZ2dlhX1Pb9332iX9cUwQLx1mtpjFvJbMb13d2QsWaMfeVlJzeXliS2hQR6OOto+SE\n",
"krPL5/1r166xl7wg3K3+wlBVPtjfdd0wDEvkeN/3HceJ41hRlGnLCpWgKEr6J+w/39zcXF9fZz8K\n",
"l0vsxlzb43TbuI2VLIgbhmGEIWvqLy853dhvY0SWEmtFyY6pPXZs9rYBlcElD3mepyjKcDiED7Bd\n",
"F3yoRH7yPE/XdUVRQIWfZmbbtqIoo9EoiiLLspS0YMZGFEWGYST/1HU9vzBRIaj1I10CZPrF9W7R\n",
"lqVjZDRa8rTqdNYRejav4zi2beu6LkkSjPLUdV3Xda4X2BIkSaKUjkajkudqHMeDwQCePWCvqipX\n",
"nzu5KfjAJsO9Xk9VVUahHwUf0YxbJC+k3aip5OUaQ9u/RRFRlFtj6qstOWHmun5pmhR8+Fr9kiTB\n",
"B8/zaOr5rihKFEUVPpE8z5vW6rdtmx5sWozH4zka/pPJJIoiz/MY2/vAxYsXz58/z14+e7VwVSCX\n",
"z9025q1kduP6zk6cWLO3+stLhqWbPW8yHLYyIiLEmlJ65swZ9pIXhC/1y7IMHzKpn1JaleaTlD8t\n",
"9VNK82MxE8fq5tKlS2tra0eOHIFNek+ePKmq6sbGxrlz51RV/dCHPgQ6kmEYjz32WPrDiy++eN99\n",
"96U/TCaT++6778UXX0x/eOyxx6CE5AMWhUXVV9RoNPln/+zr9933fyxY1K/92v9oWZMnnvj3Dz30\n",
"+/BNpij4kCnqvvvuyxT12GOPZU6we0VtbGyoqnru3LmNjY177rnn8OHDa2tr6+vrhw4dOnTo0KQp\n",
"+FK/ruuj0WhyU5RPvm8y9eu6nj9WScdAtXzsYx+79957GY1Ho9Fo2tacRcbsbti2jcYAbyWzG9d3\n",
"dkLFmnFs+8ySkxVJ2xgREWJNKT158iR7yQvCp/UrigLSlaqqYRgmc5SDIGhsUDzXggeVAw9nRmNJ\n",
"ktjHDnENUuKq7W4b81Yyu3F9Z9ftWLcxIoLE+vDhw+zGi8L1oIiiKHmIwdge27YNw0iPlqmEkla/\n",
"qqpLbPXjCB+kY1Q1o9Uw2rQ7o4AIPcIHBvbAZ13XbdsOwxAeADU8lYrhGghcOXEc4xo+Qhm3ccWY\n",
"TsZalveXQmtjRASJNfvowcVZaCEHRVGWkoiDIMgsGMdVv4vAK/iwl9xtEaA+4zZWsiBugHEcMy0n\n",
"MLNkRSEwjrGNEREk1k0KPnzr9TeG7/sweD//pyAITNNM/wk2WmnmzQPX60c6Rr9PJKmCRfbjmGxu\n",
"EiHTSTsQer1+EYD3jOSdC2Z4cU2tXoSrV6/euHGD0TgMQ/YlLrgWw+CaE9RtY95KZjeu7+yEinVm\n",
"yfi5S5ak/beHNkZEkFjv7e2xGy/IQoJPHMdBEGTWw1mEwWAA1RrHcRiGmqbB95nm/3A41DQtCAJJ\n",
"knzfNwyjMd1pd3eXa6sW9pJxq5b5jNtYyYK4UbkxPELaGBFBYt3kVi18gg+kZlmWoYN3e3tbUZQw\n",
"DG3bbn63liAIYPm2qh48LKDgg3QMTSOULmeHQiSN0IKPLMuyLMPqx4PBANZGHg6HS1m0GRYRajLv\n",
"ExR8xDNuo7wgVKwZb6BuR0SQWIsr+Liua1kWZNukZxXG+YDyU4uPIoGCj2jGbaxkQdwAY8bhKt2O\n",
"iCCxFlfw2dzcjKIIPmualkjwpmnCTofVOygYKPggHcM0iaqi4LN8hBZ8EkDxr9aVVrC3t8fV6md/\n",
"5ne++VNfq5+rktmNBWkJNlDJLHm/2xERJNZNtvr5Ur+qqrCRYWYzXt/3V0HtIYREUYSzeYUybuPc\n",
"UaFizTguutsRESTW169fZzdeED7BJwgCTdMMw3BddzQagejvOE4Yhtbic0LaAAo+CILUgdCCD2yL\n",
"KEmS53mQ903ThH1063FPOFDwEc24jfJCt2PdxogIEmtxBR9CiCzLlNJE7UnGd1btmKCg4COacRvl\n",
"hW7Huo0RESTW4go+CAo+CILUgdCCD4IgCNIBFkr9cRz7vr/cbbMaZmdnh31Nbd/32Sf+cU0RNE0T\n",
"jQHeSmY3ru/suh3rNkZEkFhfu3aN3XhRuDZ2sSxLVVXYk2s8HkuSpKqqLMvVbswrMhcvXjx//jyj\n",
"cRRFURSxG7O7MR6P0RjgrWR24/rOrtuxbmNERIg1pfTMmTPsJS8In9YPK+PDWg79fl9RFMMwgiDo\n",
"9Xrj8bi+55M4oNaPIEgdCK31u65LKU3W8IFV8pM1fGpxUDBQ8BHNuI3yQrdj3caICBJrcQUfSZKS\n",
"z+md0CmlK6L5oOAjmnEb5YVux7qNEREh1g0LPnNu1bKya/gcPXoU9+YVyriNlSyIGxiRBoyF3ZsX\n",
"1/DhI45jnNIllHEbJxB1O9ZtjIggsWYXkxeHr9VPKYWdEWENH/jScZzmt0xZFuvr69jqF8q4jZUs\n",
"iBsYkQaMhW31c8/mDcPQdV1d1+H8TdOEPXJXZC0HHOGDIEgdCD3Ch6z8Gj4o+Ihm3EZ5oduxbmNE\n",
"BIm1uIIPgoKPaMZtrGRB3MCINGDcHcFnxUHBB0GQOhBd8Flxrl69euPGDUbjMAzZl/bmWgSca55I\n",
"t415K5nduL6z63as2xgRQWK9t7fHbrwg1aR+LvGr1ezu7uJWLUIZt3FjkG7Huo0RESTWTW7VUo3g\n",
"o2ma53mLlyM+KPggCFIHKPgIDQo+ohm3UV7odqzbGBFBYt2k4IMjfPjgFXzYS+62CFCfcRsrWRA3\n",
"MCINGLdY8IFl6gzDkGUZJnDlbYIgiKKoFgcFAwUfBEHqoGHBZ3arH3I9PLuCIFBVNb9cD9cqpq1m\n",
"b29Tu6t8AAAVWUlEQVSPt9XPOLA3jmP2IcCZNZRW2Zi3ktmN6zu7bse6jRERJNZNtvpna/2e53me\n",
"l6R7RVHUHC1dwIdrJiEQRRHO5hXKuI1zR7sd6zZGRJBYX79+nd14QfhG+PR6PcMwVFXNfN+6ET5h\n",
"GJqmCY/uIAiGwyHj0wsFHwRB6kDoET6wN29NrjTJYDCwbduyLMuybNvu9/uMP+QVfHBcf93GbRxF\n",
"3u1YtzEigsRaLMEnzTSFq11NfkJIGIZJM59rRQ4UfEQzbqO80O1YtzEigsRaXMGnM/T7fdhcnhAS\n",
"BIHjOLZts/wQBR8EQepAuBE+LHB1eYuAZVn9fh98juPYsqxle4QgCNIc1czmZdfKm8E0TS1HegSq\n",
"67qSJMHwJMIzPW9nZ4d9TW3f99lL5poiyDWattvGvJXMblzf2XU71m2MiCCxvnbtGrvxonBt4l7S\n",
"x1v5hvG1out6+p+qqjL+8OLFi+fPn2c0jqIoiiJ2Y0bLyWQyHo/RGOCtZHbj+s6u27FuY0REiDWl\n",
"9MyZM+wlLwh3q9/zvPTvoyhSVTXZp7cqXNcdDAYlBr7v93o9aMtz9aEDGXmKfV7C0aNHubZqYS+5\n",
"83tW1LcxCFclsxsLsn2HCJXMZdzGiAgS6ya3auEe4ZM5E0mSbNuuajYvJPTt7W3XdUtelBzHMU2T\n",
"Ugrj8TVN4z1QEATJA4PryYGCj2jGbZQXuh3rNkZEkFiLK/hMQ9f10Wi0eDmj0QjK8TxvmggTRZEs\n",
"y+nXKEqpbdu8B1JVlVJKKYW3FsYfouAjmnEb5YVux7qNEREh1g0LPtUM7jRNM+kyrQTf9weDQeF0\n",
"AcdxwjBMj8kJw7DX680hOvm+L0lSfkmiEnBwJ4IgdSD0bN5pBEHQ2DI+YRhmkrUsy3PI/YSQwqXo\n",
"yonj+M0339zY2LjzzjuPHj167733app27733vv/979c07YknnvjSl75ECPnSl770zDPPBEHwuc99\n",
"7plnniGEvPTSSxcuXEh/IIRcuHDhpZdegg9f/epXCSHPPPMMlJB8gKLSH1566aWtra2SouBDUsKF\n",
"CxdKisp45ThOSVEZrxzHKSkq49UXvvCFOk4wCIJMtZecIEwgYjxB+CHjCW5tbZXXVfrDV7/61fK6\n",
"ShflOE55XaWLgtlGyz1BuOwzRcGHjFcXLlz43Oc+FwRBuszMCSZ+Zq6KfFEZry5cuFBSVMarzGWf\n",
"KSrjFVz27CeYKQqSxvvf//577733oYceOnny5NGjR++8884vf/nLly9fJo3B9Y5g2zbNoet6ZsDM\n",
"4pQIPrquZ7qaJzxDdBbkySefPHfuHKPxeDxmfzfkeovM18DKGvNWMrtxfWfX7Vi3MSIixJpSevr0\n",
"afaSF4RP8NE0Ld/TqyiKruvVPpBKBB9N00Cgz3zZzGISKPggCFIHQgs+sizrum4dpPK8LzJxHOMa\n",
"PkIZt3HFmG7Huo0RESTW7KMHF4dvIQfGhW5qhVedr5b19XWucf3sJXd7rHd9xm2sZEHcwIg0YCzs\n",
"uH5Bl28rEXxM05QkiVKa/nJzc7OZHSJR8EEQpA6EFnxEQNf1zCwJ13UbE52uXr1648YNRuMwDNmX\n",
"9uZaBJxrnki3jXkrmd24vrPrdqzbGBFBYr23t8duvCAcqT+OY9/3eXc0rBwQfBK5LY7jwWBgGEYz\n",
"R9/d3cWtWoQybuPGIN2OdRsjIkism9yqhVXwcRzHcRxVVcMwjOOYfUdDLgaDATxR4zhOj9/PKD9x\n",
"HGuapiiKJEm+7xuG0VjqR8EHQZA6aFjwYRrXPx6P02snWJZFKa1tvCkro9HI8zyuOfGLg+P6RTNu\n",
"4yjybse6jRERIdYNj+tnGuHjOA6lNGnmU0q3traWvr3JUob68Ao+7CV3WwSoz7iNlSyIGxiRBoyF\n",
"FXyYWv35CbSqqqa/EeEloBkuXbr0wAMPLNsLBEG6BqX0jjvuaOxwTN28Mx9cS+/7bYy9vT3s5hXK\n",
"uI2dit2OdRsjIkism2z1t29w53KJoghn8wpl3Ma5o92OdRsjIkisr1+/zm68IEwjfPJL97iuq6pq\n",
"8o3ruuPxuC4fRQJH+CAIUgftmNKl63pjqzQLBQo+ohm3UV7odqzbGBFBYi2c4CNJUn7VtjRci1q0\n",
"GhR8RDNuo7zQ7Vi3MSKCxFo4wQdJQMEHQZA6aIfggyAIgrQXTP187OzssK+p7fs++0pPXGtCmaaJ\n",
"xgBvJbMb13d23Y51GyMiSKyvXbvGbrwojc0g6AYXL148f/48o3EURezrTHCtSMG1EkC3jXkrmd24\n",
"vrPrdqzbGBERYk0pPXPmDHvJC4JaPx+o9SMIUgeo9QsNCj6iGbdRXuh2rNsYEUFijYKPuKDgI5px\n",
"G+WFbse6jRERIdYo+AgNCj4IgtQBCj5CE8cxTukSyriNE4i6Hes2RkSQWLOLyYvDtF4/krC+vn7o\n",
"EOvzkmutCy5jrunT3TZuYyUL4gZGpAFjrhM8fPgwu/GCoODDBwo+CILUAQo+QoOCj2jGbZQXuh3r\n",
"NkZEkFij4CMuKPiIZtzGShbEDYxIA8Yo+HQEFHwQBKkDFHyE5urVqzdu3GA0DsOQfWlvrkXAueaJ\n",
"dNuYt5LZjes7u27Huo0RESTWe3t77MYLgoIPH7u7u1xbtbCX3O3tO+ozbmMlC+IGRqQBY2G3akHB\n",
"hw8UfBAEqQMUfIQGBR/RjNsoL3Q71m2MiCCxRsFHXFDwEc24jZUsiBsYkQaMUfDpCCj4IAhSByj4\n",
"CM3e3h5Xq5/9md/55k99bUyuSmY3FqQlKEIlcxm3MSKCxLrJVj+mfj6iKMLZvEIZt3HuaLdj3caI\n",
"CBLr69evsxsvyEoLPhAVRVHYf4KCD4IgdYCCTzUEQWCapqZphd3xcRz3ej3XdV3X7fV67MWi4COa\n",
"cRvlhW7Huo0RESTWKPhUgO/7hmFQSgv/OhgMDMOwLMuyLMMw2HdcQ8FHNOM2ygvdjnUbIyJIrJsU\n",
"fDq+QaPneZ7n5b9XVbXknyU8/vjjGxsbFXgmKuxV0UYopYXXQ2fA8LUXSun6+npjh+tsq7+cjL7P\n",
"tboegiBI21nF1J9/BWNfhTWOY3Y9zvd99ol/XFME2RUqXuPXX39dBDfYjbkq+c0333zllVcq94HX\n",
"uL5YixA+3sue3fill15itCRiXJyEM9ZNav1tnc1rmmY+gyuKYllWrcc9deoU+3r9XGOHuIwNw6jJ\n",
"+L777hPBDXZjrno7e/bsgw8+WLkPvMb1xVqE8NV32T/88MPsxiJcnITzBNlzy+K0NfUvkuIVRXFd\n",
"N/0Ne5f9kSNH1tbWGI3jOGaXkmAkAJc9ozHXGIPbbruN3bimgRxcDhOeqjh27Njtt99eR8m8g3bY\n",
"M4Ig4WMvlnDWG/s1v7GxweWDCMZcsWbPLYuzNMHHdd3BYFBi4Pt+r9fTNM00Td4rbyaZNwaue4D9\n",
"peyLX/ziCy+8wG7MPhjg6aefZjf+xCc+wWhJOBUD9pKDIOAyfvrppxmNX3jhhS9+8YuMxlyCT32V\n",
"zNVsFCR8NUWE6x7hEny46q0+Y65Yd3lwJyT07e1t13VLVDDHcUzTpJQOh0NJkjRNq9YNRVGSo/u+\n",
"z/5Y5hJ8uOSFs2fPMloSzjdfLhFAEGP2E3zwwQfZq44rIvVV8unTp2sqGSOSIEi9ccW6y4KPJEmU\n",
"Usi801r9cRwPBoPRaARvgpTSOI4dx+F6fsLTIq2ieJ6X/JVS2u/3IfuHYWjbNmOxXIIPl7xw7Ngx\n",
"RkvC+ebLJQIIYsx+grfffjt71XFFpL5KPnKE477DiMzhAxGm3rhi3aTg03TqZ2lfu66r63paATQM\n",
"o9frcaX+dKLPI0nScDicYyGHK1eu7O3tMfbav/LKK7/4xS8YS37llVfuuOMORuPvfve77MavvfYa\n",
"+zCDmoxfeeUVLuPvfve7jMbf+ta3vv/979cRkfoq+Yc//OHSI8Jl3PmI1GfMHmsuMbkCGptBkMHz\n",
"vGnTT0DnyXwpy3L9Ts3mD/7gD5qLDYIgq8SxY8caS2UijvAJw1BV1cyX7EPva+W555577rnnlu0F\n",
"giDIQog4pavy8TwIgiBIGhFTP4IgCFIrIqZ+rn5XBEEQhBcRUz8pWmaHa+1TBEEQpAQRU7+u65nh\n",
"UDDcc1n+IAiCdAwRUz8IPsl+CDDDi2tQP4IgCFJC03vzDgYDaNHHcZxe2CgzAyuOY03TFEWRJAn2\n",
"28LUjyAIUhVCb8seBEEcx/AAWLYvCIIg3UHo1I8gCILUgYhaP4IgCFIrmPoRBEFWDkz9CIIgKwem\n",
"fgRBkJVDxJU7hcX3fcdxYNARpbRF446q9dx13TAMKaVVubcgVZ0d7AgEg49VVTUMQ5AQ13GCsixT\n",
"SkVYELfy2yoMQ8dxZFkWZER4VSdommbmG1VV84scs9LY8tBtx7ZtRVFGo1EURZZlKYqybI9Yqcpz\n",
"z/N0XVcURdf1aXstNE9VZxdFkaqqlNLxeDwej2EvuSiKqvV2Dqo6wfF4rCiKbdvj8XgymQyHQyi2\n",
"Ume5qeO20nWdUirIJVrhCRJCvINAKOcsbe5frhRRFMmynE4ElFLbtpfoEiMVej4ajSBTlGyz0zAV\n",
"np1hGJkNgizLopQu6uJi1BG+9De6ri/q4gLUcVt5nmcYhiCXaLUnWG1LHVM/E7ZtZ7IAtKGW5Q87\n",
"dXguyH01qfTsLMvKf7n006z7wlvu5nd1nB28qwlyiVZ7gtWmfuzmZSK95gQgy3IrtpRpr+csVHh2\n",
"+a6LMAyXrvXXGj7f9+dXiqug8rMzTTOzrfdyqSl8vu8vXgh28zIh8p6R5bTXcxZqPbter2dZViVF\n",
"zU0dJwjro/i+HwTBcDhcpKgFqfbs4KRGo9HCflVG5eHTNC2OY0mS4jiWZdm27bmfc5j6mWhvM7m9\n",
"nrNQ39n1+33DMJbbKCb1nGAQBEEQ+L6/9FFq1Z6daZpLf1RnqPYELcvSdT15cjiO0+/35354o+CD\n",
"IFn6/b6iKIIMDawcwzBgnE8QBPnxgi0FNJClP6prJTMY1zAMWP94vtIw9TPR3j0j2+s5C5WfXRzH\n",
"29vb4uT9WsNn23YQBHPnjsWp8Owcx1FV1b8JiFpL39qv7rtPURRM/bXT3j0j2+s5CxWeHewSIdrm\n",
"ELWGb5HcUQlVnZ2qqmEYJqk/DEOQ/qvwcSHEvfsqHC3UYUajUWas2HA4NAxjWf6ww+W553mWZc2c\n",
"xyTIyLkJf1xKTjCKIpjxlP5ykSkzlVBH+NKoqrrEWV0Vhi9vKcIlWnf4MpMGuMDUz4qqqklegDSx\n",
"9JmQjDB6ngyNmDnNR5D7CmCPS8kJwlTezJSuyWQiSVLlDvNSVfh0Xc/8ELoNK3eYi0rCl0ecS7Sq\n",
"8OWvT8MwFplyiCN8WBkOh5qmBUGQ7BnZFhmd0fNksMe0UR+ZzTU1TYPvM5trNgx7XEpOECRvx3GS\n",
"HaEBEcZHVRU+SqlpmklfKAzqt227Ps9ZqCR8aaDvGi7Rfr/flhOceXbD4dA0zcFgAOFzXVfX9UVG\n",
"NOEuXXy0d89IFs/DMCwciSw+jHHp9gmynB3YEEKEuoYxfITt7JK+68XDh6kfQRBk5cARPgiCICsH\n",
"pn4EQZCVA1M/giDIyoGpH0EQZOXA1I8gCLJyYOpHEARZOTD1IwiCrByY+hEEQVYOTP0IgiArB6Z+\n",
"BEGQlQNTP4IgyMqBqR9BEGTlwNSPIAiycmDqRxAEWTkw9SMIgqwcmPoRBEFWDkz9CLISBEEA+2vW\n",
"RGZvS0RwcG9epEZ6vd607W0VRVlkZ1GEl36/n65w3/cHgwEhRJKk4XBICHFdF9K3LMtzbGnrui4h\n",
"xDCMyjxG6gRTP1IjhmFARtB1PfMnyDtIMziOI0lSet9XRVFkWSap0CiKQinVNG00Gs1xCMuyer0e\n",
"pv62gKkfqRFVVUFkyG82jam/SQaDQeYdS5Ik2Nc7CY0sy/AwUBRljkPAs8RxHMz+rQC1fmQ5pPPL\n",
"YDDQNE3TtCAICCGu68I/4Y0hje/7vV5va2trc3Oz1+sVitdgs7m5ubW11e/3wzB0HEfTtH6/Dwb9\n",
"fl/TtLQ2Dd9omsZ7OCjZcZwgCHq93tra2vb2tmmaea/iODZNU9O0xKZQfGc5QV5834/jOP/ixQic\n",
"Y4bCc9R1HRX/1jBBkDqhlFJKk8+j0ShvMxqNPM9TFGU4HBqGQSkdj8fj8VjX9fF4nJjZtq2qalLC\n",
"aDTSdT0pPDlE2mY4HCqKouu6YRie58GXnufBUTIOZG4HlsONx2PDMFRVNQwDXI2iKFM4fKkoim3b\n",
"URTBP23bliQpY8ZyxDmglBqGUfh9vvB8ToCfeylAGsoXOB6PCSFwjojgYOpH6gVyMWQZVVWT/JtH\n",
"VVVJkmzbLvzreDxWFKXwV+mcrqpq/of5JDsz67EcLikqYxlFkSRJ5b+aTCa2bad9YD8iL1D/+e/T\n",
"oUnIp37LsizLSv+q8EECEEIW9BZpBtT6kdqRZRkE5WmjfRIsy5qmFDuOA4kpA6XUdV0o3/f9/M9l\n",
"WZ5DfWY5XELmn5Ikpc80DMM4jvO9Hbquh2E43xG5CIJgmtqThCYh3weT9spxnDiOS8b/qKoaBMEi\n",
"3iLNgKkfqZ1kbEkYhtC1OA3oZiwkCIJpPcNJoqkw6bAcjpEwDAt/IklSusOjwiNmKKnVzLCfcmD0\n",
"JyhjJcx8wCMigN28SHMYhjHf6BFCCPQEFL66JslIUZR0OzphjmTEcjh2Cr2q9YhpJElicaCcIAgg\n",
"75c/vIMgmDvESJNg6kfagaqqM0ePGIYBikT6S8hZM8vP/IrlcIyABlL4+Eln5AqPmEFRlAVb4jB+\n",
"Cbqm4RvXdfNlxnEcxzGm/laAqR9pB6qqyrKcDNBMcBwn0UlA1odRoXEcw7BO0zTzGnrm/SAMw16v\n",
"x3s4diil+YnNg8EgXX61R0yTzK6YDxiWOhwO08IRjGfNWLqum8wUQwQHtX6kRjRNgwwLaaJw8YYw\n",
"DCHfBUFgmmbSroTxJ2lL27ZN09ze3k46jUFeSJcJQy0HgwG0oEFFyadOXdd939c0DZ4BcRxblrW9\n",
"va1pmm3bkLxYDtfv9yGrhmEIyyHEcQxPkXRR0M8MRUEnsO/7qqrCT7hOcA6SPvB0fSaeB0EwHA4l\n",
"SXIcByZSaJpmGEbSMzwYDMIwzAzkz+d9OMTcsweQhlmbTCbL9gFBOICECJ8ZuyghbeUTKOgwme7W\n",
"xQ9XQtL6Limq2iMCkNYX7DMoJwzD7e1tGEpb31GQqsDUj3Sfaal/pdja2oIpYzWV3+/3FUXBVRza\n",
"Amr9CLISZMSlyplv/gSyLLDVj3SZzLI8tSoeCNIiMPUjCIKsHCj4IAiCrByY+hEEQVYOTP0IgiAr\n",
"x/8Ph8Pk+ta7u1EAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"% Idem au code précédent, y_sr est remplacé par y_srb dans la ligne suivante.\n",
"y = y_srb;\n",
"% représentation en temps\n",
"figure\n",
"plot(ech,y)\n",
"hold on\n",
"plot(ech,signal,'r')\n",
"xlim([-1 301])\n",
"ylim([-0.8 0.8])\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"% représentation en fréquence\n",
"figure\n",
"[freq_f,y_f,y_af,y_pu] = Analyse_Frequence_Puissance(y,ech);\n",
"ylim([10^(-10) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"L'addition du bruit blanc ajoute des variations aléatoires dans la totalité du spectre et, hormis les pics du spectre associé à `signal`, il devient difficile de distinguer la contribution de `resp`."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1fbCTJfef565keDSk3uxkcyc12z2noHPZYsmVb08lb\n",
"yzZOmjMyV7sSdtfQIbkW7uEO8CLr5Ke9AxaZ+3Qvt0DVPR0M43yVGO3LAXt2FQ5n7GEWg2MAlrS7\n",
"9ljH6B57tfDskEyRklpkSzMMTrNvyJ7pmb6HKCaT+acq/0RGZlb9Pg8z7GIxIjIz8hu/+MUvfnHp\n",
"yZMngCAIgswST9XdAARBEEQ1KP0IgiAzB0o/giDIzIHSjyAIMnOg9CMIgswcKP0IgiAzB0o/giDI\n",
"zIHSjyAIMnOg9CMIgswcKP0IgiAzB0o/giDIzIHSjyAIMnOg9CMIgswcKP0IgiAzB0o/giDIzIHS\n",
"jyAIMnOg9CMIgswcl+tuQFYopZ7ncc51XXcchxBSuCjP8yilUopCEARpI+2w+j3Pc13XcZzBYEAI\n",
"MU2zcFGdTocx1u12B4OBpmlra2u+70tsKoIgSPO51PyzeTnna2trm5ubgXnuuq6mabZt5y2KMea6\n",
"7sbGRvAJpXQ4HPb7fWnNRRAEaTwtsPqHw6FlWWG3jG3bnucVK0rX9fAnhmFQSss2EUEQpFW0QPp9\n",
"34/otaZpnPMCRUXKSSwcQRBk6mnBMq/v+4ZhRD7UNK1AUZZlDYfDXq/nOI4oudPpdLvd7CX82Z/9\n",
"2R/+4R+m/XZpaemZZ54p0DAEQWaE+/fvp/3ql3/5l//oj/5IUTueNB7DMDY2NuIflikwuPx4yeP5\n",
"vd/7PUUPBkGQGePq1auFZS0vLXD4yKXT6QTDxubmZq/XY4zlKmFlZaXMwFMjjuPkHeoaQktv+MbG\n",
"huM4dbeiCNhVFLOxsfHFL35Rpc+gBdIv0RfveR4hRHh7RMmDwWB9fV1W+QiCIK2gBdIPAHHDPK+p\n",
"LqCURpYNCCHFlg0QBEHaSwuk37KsSPylCPdM+z6ltNfrJYYAJYYGFQsWQhAEaS8tkH7h8AkC+Tnn\n",
"vV4vbT8XY8w0Tdd1O51O/Le2bUdGBdd14+FDCIIg000LgjsBYDAYmKbJGCOEUEpt205bAAh2fiVm\n",
"5tE0rdvtmqap67ooyjCMXMGdCIIgU0A7pJ8Qsrm5yRjjnI9PuKZp2s7OTuJWAIFhGJubm8KDZNs2\n",
"OvoRBJlB2iH9goyhPpqmTRR0dPIgCDLLtMDX30DGLDI3GcMwWjrLaekN1zStpUYGdhXFaJq2srKi\n",
"ssYWZO5sFN/4xjfeeOONH/zgB3U3BEGQqcJ13VdfffWdd95RUx1a/QiCIDMHSj+CIMjMgdKPIAgy\n",
"c6D0IwiCzBwo/QiCIDMHSj+CIMjMgdKPIAgyc6D0IwiCzBwo/QiCIDMHSj+CIMjMgdKPIAgyc6D0\n",
"IwiCzBwo/QiCIDMHSj+CIMjMgdKPIAgyc6D0IwiCzBwo/QiCIDMHSj+CIMjMgdKPIAgyc6D0IwiC\n",
"zBytkX5K6fr6ummarutyzqUU2Ol0TNNcX19njJUvEEEQpC1crrsBmfA8z/O8fr+vaZrneaZpbm5u\n",
"limw0+n4vm/btmVZvu/LaieCIEgraIH0c857vd7m5iYhBAAcx+Gce55n23axAtfX13Vd7/f74p+a\n",
"pklrK4IgSBtogcNnOBxaliV0X2Dbtud5xUoTf+g4jpzGIQiCtJAWWP2+7+u6Hv5E07TC7n7P8waD\n",
"gYx2IQiCtJV2SL9hGJEPy3hpNE3zfV+Y/5ZlRcaVidy/f980zcRfdbvdvKUhCDJTpKnH9vb26emp\n",
"sma0QPqlxPMIKKWEEM/zer2e4ziEkE6nY9t2rmWD69evb2xsyGoSgiBTj9Aw4bROUw/XdV999VVl\n",
"TWqB9MuFcz4cDoNFY8uy1tbWDMPAxV4EQSpCRI/HnBd10oJlXokuFF3XGWP9fl/WojGCIEgbaYH0\n",
"A0B8y1WxTViEEF3XIwY+2vuIXCituwVIw6C0cb2iBdJvWRa9eNtEuGfa9ymlvV4vbYVA1/VIaYwx\n",
"VH9EIk17yZEsMAauq7pS9TUGtED6hcMn8MmIHV5pC7OMMZHsodPpJH7BcZzwwCBCfcYMJAiC1EjV\n",
"4+hwOPqBc1C/r7/GDDLtWOYdDAamaTLGCCGUUtu20xYAAid+2JsfRtO0bre7trYm5J5SOhgM0r6M\n",
"IEi9DIfVro56HgSG30yldGmH9BNCNjc3GWOccxGUmfZNTdN2dnYStwIE6Lq+s7Mj3D7dbreSFiMz\n",
"DCYDlIhKOVZsAdbrGGyH9AsyhvpompbFdz9mbEAQZBaIjCuaBoxBFZsyOVc9rkykBb5+BEHCBO5p\n",
"pCS+f67+Qp0rmmQ0TfcBpR9BpFP1RN7zQN4O91kncBAwBo5TobMu/sgorXNIQOlHkJZBiArDP7CI\n",
"19dVxCAG1UXs7koHOd+/IL6VCrEoPHIna4wqR+lHpp+qN2sr3gwuXNJV4/uj6YsaeQqkP3Izgyvl\n",
"XP4w4Puqxbc5IQAo/cj0U3WUiPo8IGocBeK+qXEuBZoYvpmUXnDINEc3i9Go9qP0I0hZGvVKS0fN\n",
"MBPeURUeqsNWeRWLKLquIshSrCE3aps3Sj8y/VRk9TMGw2HUKFa/AFuRI179eCYek67XE8sfeXBy\n",
"JxmEjMaY5hzngdLfAFT6CzhXWd2P/zX72/9B4dUxlnh1FUnJ4++xD/7VkLEL200rCgwHgAffZsd/\n",
"lmA3VqTRn3yLLWyNiiak8pFgYYvdvM9AlRkel/bI5Mb3ZY7iN++zhS0WX67QtNqmAij9dRMOLVYA\n",
"Yyqr++l/4vf/UuHVpeRhqUi2nnnIn36TxSusyEOy/f/ynb46nZg/5b/9k6GIgdH1ymcz1z/Bf/Wt\n",
"cXFLkrst50DpmIuS+6LMn/KrWwxifQMjfGYY31c9tVabqWT+dJpD0E9PwffBthXZbkdHKmoJ4/vR\n",
"SUxdG8qkd9vTA07IuAmN3BpvnPhh3a89XxBK/+yh1hu9dKS2jzMGqvzUd+7Ab88xxhQthL79Ntw8\n",
"YIyBpp2vGVYa9xJ/dpX6C+NWgri3FV3gG2+AZaVOaCS+Jb4PNw/Y4rULg6jv13xoF0p/A1C8Mqi2\n",
"OpVW/9tbcP+nAArToC8tTfiCxNnAw4cAAJyDpp2LCOcVrhw+8zBBiyti6chPHGlsu5oOS+lT7/H4\n",
"rQvqkjic+z58bpkDgMgV2ZCd2Cj9DUDxbu4G5hORxMOH8OFPRy9W8IJVapU/d4mPL1yuI0jlOLr0\n",
"A7bwmItJRkA4RoVSmTOApSP/cFFT5gbZ3YOf/6WEJ5cW8CMLXW9KKDBKfzNoiCUgm/19OJlTOtIE\n",
"1YV3gVZkFy8d+UDIYDCqJSAI25ArZKu79N5y9EoiqQgksnSJb68YYpIR7B+O9FO5F8iBKHOD7O7C\n",
"ysq4L1R0VyPFKgpnSgKlvwEotgQUdrf9fThcVJJ2AAAAFt5mh4sa+L6aE5eWjnzhKo48wOD1lt6G\n",
"kzly+aITRk0qAk0biX5FgkgpLC7C3Nz5J1U/vtNTmHs29bfKJh+Yvg1RhdrAgpGhOnZOI3EY+ugd\n",
"/hc3LfB9w1B1oYYBjCmL3Li3rF+6kzqOii1mElky9Y83Uh+PXPthcREOFzWxk0DB45ubgzE5msXk\n",
"Q/5UPFSdsuiANFD660ZsAVJm9fs+WJbKAWDvaW18dRIV5OAAFhZq9p5FXBZyH+zJHNnaivqvghgY\n",
"ziVX93iBiLVlQdWbUQ8XtfjCcoVM2jcsS5rFnEYMaMFwE/ZD1hLoidJfN5yDZSlVK7U75e9/XpkF\n",
"DgCw/YKRqH9VNUGts/ZwUbt5wOL+4oq6z4dXyK2nL9y4igxV3x95e+b3VXSV89t19lPEBpc+yC1e\n",
"G/2Q+PKpT/8HKP1NYUqXedMI+noVG9qO3gMI3VGxKakq6R+rhdKf6uE1LQjyqbrLnJ7C5b+j3zhR\n",
"ocW+D8vXYfsFIy79VaQ6YAyWl0fOOjhLBx2fS8lEVNCk/G0o/c1gSgMuT0+TP0/M0SiLoyMwjAtr\n",
"rRUFjaRdXUAV+XyE9Cf6COUOonNzFxovVs7FXa1k1OHR5WtBZBFbStW+D889dV6QCoer2DfcJFD6\n",
"kQoJx2yoR8VSoSoCyRPRq4kyIleRxRizvDz6p3BS63plQkkIAJz8hEP6Mq+R7MzLje/Dp2+d30HL\n",
"msXjjlsj/ZTS9fV10zRd1+Uy+rjv+67rerW42WYNzk3zgjD1ehXWdvl4nHxIROUGK8Zg9Tmu6/DW\n",
"W4pqFGPMF74Q/bxS4/X+ByRtnlSdg4uQ87mFslSaYYdkLUnc2iH9nue5rus4zmAwIISYplm+TNd1\n",
"AWA4Y8P90Xt1+BsJUXOcrNDih88omlkr3q32eIEQAouL0c8rzagcrE/GqUiL04aWSoccyxrpr/iv\n",
"uDRZF5hYTnjbMEp/MpzzXq+3sbGh6zohxHEcwzBKWuuUUkKIUW/+pDAKEqIDAMDhNh9Jv5Kom8Au\n",
"/pWbPHHIkSsfQosPDhp0IEalBGebyJWqjAjxqrQfKbuiQPoF4tJkDTbn5aRcD0p/MsPh0LIsEnoO\n",
"tm2XlH7Xdbsil1LtiN6gICE6AAD88CEBUOINAQCAkznCOYBh3DxgiWE20hdCDQP+7fs6YefjTEX3\n",
"NYhHjJySHlZhiSeJMzay9x8+c24lRFawJdrFo1D0oJoUqu5H8SuqPddxKVKeEEp/Mr7v6xflQdO0\n",
"Mu5+13UjY0mdVJ0vqlZOT8+vT8F2AhFyc3x5VKWoLvKcZS3u+P7ZEmiQ5QBG1QULoRLDOjiHxWug\n",
"afD2giIrYST9Z+oerlN6/RcWsWPT3+C3skaa8/anb+ititi929hQWn/A5XqqzYPv+3HPjFZ0oOSc\n",
"U0o3NzcLt+f09JSm+MuFS6pIoYYBrguWVbhVWTjvdboOvZ6CRFmBXXzzYAgwqi6SDFJudY9HdjE1\n",
"HCMxdXMlb7qvYt8TBOZhuvRWuhYqEH1H12VeZlBUYtoP6ffzvEBhjyiwusVFGQYwtre3Sum2+G/4\n",
"K3t7ex999FHlLTmjBdIvJZ4noLyr5+TkJE36NU1rymQiCcZgdQUARn2f0pGJWjmaNn/KH5/9S6xr\n",
"cV6VRH7vsQ78wpqyONjEMKpZ4hbDtiqeMg1gLljW+MVDacSshMDFL9Rf3FgJcA7pjZef8aaWhREA\n",
"ANjd3aWU7u5ejsjI7u7uxx9/rKxFLZB+iVBKOeclV3cJIVWsE+zuwYr0Qi8S7u0/2+I9Bo4z+qfr\n",
"QqVrH/On/Dj0T+ESqWLWEd7MFa4uiC+qbjW9usEsjGEAUAAAQqqtUcTIjq8gfGPLQggA/PtT/Z/Q\n",
"0UgTcTFJtlHEdWkaDIdjOqLkO0wIUPq7v+tY1isA0O2+Ev6l67pbW1vyKptAC3z9urxn7nmeYRj0\n",
"DMYY55w14+iEN9+svAqxVCjeKOYT2668xgDFcZAKYAyWLk3YESrZsuSj/QrhNlTktOMcHi+MW4Wq\n",
"wmg2DPju35z3k+qu7pyL6zQRZG1eu+Bo5VxtDq1U2mH1M8YipnoxvTYMw/d9/+zGc86F61/i6FKY\n",
"Zx7yVH+EOCxDBovXRrPquTn4+V0Ku6PPr39/ZEvKrS7M0l169gOs7sHSXQCA1T14/BmNMa38E/B9\n",
"WHwSeo0pFRe1unf+30f/BpZPNAAJV8c5XP3MuU69eHYzw9X95w/g8Ck51QFcNMApXd0TP1yo9N6y\n",
"DmP8JplhDP7B2T5eYauu7sGtW6PqPrfz/nt7n7R+H4DLqS5A0wA4F8/unXfhy18eXZfoLaBLrg5g\n",
"VF3wr6W7cHw8up+ffkZ/LKO6C/MGzsWLIKo4R3mgeQuk37IssZ8r+ESEe6Z9X5jztm3H3e72RUOX\n",
"Uur7frjkGvnOz1tfS5N+zqHfl1PNmUd1e8Uw7lAAgHcBAD54DeDzoa/J8P4E8YgAcG9ZX7lDj44A\n",
"3oUP/grW5mDxDsC7sLoLKwDbXEJ1vg+rv0hA6IOmAaUvvwtAYXX3/L8/95fw+wAAsn1bmrb056Ob\n",
"Ga5udRcAgPOuZLeMpgGlovCR9J9Vt7pLZVV3fpKJpgGla0ewuAXwAQCAtvfBR09/AigAY5zLfn10\n",
"ffTs3oUbzwF8H1Z3YXQEsscAKqku+NcvP4I33oBVAKBw/QP/3ldlT4017Zd/QoMqzkHpjyNMcs/z\n",
"hHCLHV79FClkjIm9voyxgTg6r+GczQbvLhnQTX78u99wV2RVd6YK2y8YK4YBACsGAIDbAyfQQ0mL\n",
"lpzD6uLoh//wS9Z/3bVcF77QhT9zwTDgHYAVA1534b/bk7xG2u0CgA0Ar7vwSjf637/3nQqWZG17\n",
"WwM4u6Jwdf/tf3LlOy7s0dUBwCtdED8vWPBXBP7RG1VV9xGDdwFWdACA14KqXVf+YkPS1YkrWqGV\n",
"PLvwv+ZCVc9/o4LqHGfu4tXVRQt8/QAwGAw8z+t0Oq7rmqZp23aaiyaw9MdH2ogRwnVdxlin05Hf\n",
"4sycfpKISHOe7u/Z3VXYIJDsxyVkFAvYEJ56r9rQjsjNk5XibeIzEQuh1WWUE4nbakHNcZtxRgvd\n",
"FVD1oTdZaIHVDwCEkM3NTbEq6zjOGFnXNG1nZydxK0AYXdc36tpKcZGDA/CfBRgbSXHvfVJp9HH0\n",
"vZIaOyLm0/HC1ATXRWrhHD6+VsmCc5CJo6KDecc/jWncDniOuLe2fdFDUoL5RxzSD+YNOF/oLsfN\n",
"+ww+e6GoJqRwbofVL9B13TCMiYHzmqY1KDlPUcLC8deXq40JiGa0l5UbN51w7MTJjdGJrCVhLGrz\n",
"igMLw+YVIVUdEx8P2xB39cMrZP6gcpNViKN4My5Xf8bho0eSC1x6L+GElqBPOo5koby6lTV/iJTX\n",
"bv5UemiqBNok/VPJ6WmyEAX5BiiF/fmqMskma6BWiTiGCb/JJze04zclvGGcw/L1aC3x2cvh4rh4\n",
"PlkENRy/pEs5dHD+0YQ2i915D27pV2WMozfvj9tDdXBwpsu6vronoWc+8yMfDCNcYTifGiFnYQea\n",
"JqW6hYVMm99W/kvt0V8yKDcAJPa1WpL2REDprxmRZpLSaG8Ia+/BvMyeEs6IkqyBY4Ods0NpJtfz\n",
"7X+iX/6bqkaaYM0zuKB7y3LOyYsbqmECYTm5oS28LUOLD8YZqo4zWq1cWtN++oaMkWasofrOO2c/\n",
"EbJ0JKG6hQUAuJAcIpxD/xxNU3BGwnmiEU0TV1cm7xNjcONG9MPavT2A0t8cIomkqsuqrywb4vwj\n",
"LszwCeMIIVLe5/GG6rkWPyvntVs6ynTw48my9owsD0yGq3v+H+pzP6ncv/Tw4dmlG8YnpbqzJpjD\n",
"hnHzQMUGzFEzdF1KdXHp17T61R+lvykoyKOcZqiKfCzSvSCBoZp2Om5w1quUvb4ZPaqaBrt75WtL\n",
"JpxqJojimHiEr1ykjKPHx+N++/Wvn/9c7xmc1XL2LMWikURsu37nP0p/rTCWqHoV5bYcY6hWeuBq\n",
"GmLIqZT4eCbrxu7vJ9QVSTUj/O8HB3JqzIiUcVR4YNL4Z/+sfA0FOTqqvIr4i+D7UxhDhdJfK5zf\n",
"W9YhFucbPrMtMTJSOuEqpJ+kGI+wjH9YBZFUbnKzP2Z04NY+r28XE3eRx8+nlE7t9rgaUPpr5vh4\n",
"FEs5RiOkzwDiq8oBnEvOQByfT8g9/W484cuUn/0xRuDCgtDYpvL0dqh+z1oExVcnBcVtXrqjxHzL\n",
"CUp/zSTOrBM2+8kOuEyTfhES8+P3pZ1eNKbPV72nMRwbroawC+t8YVlt1tKK9qylIeXq1CzeXqgu\n",
"W88Tg4SEGWrzphIo/Y0gsW9d0F5JAZcJJcd+ZVnw+s8UJZadeGJ1GSIZSOtad5XCg72Es6uq05PV\n",
"XaWG6vwpVzZKj/r12KuLDNtl7kR8p2FDQOmvk/0DuHIloc9zXknAj1iZHF9yWjROGcIFhi39QO23\n",
"VyrfPwxnx24YBjCQENofN1TTBi8p+4dvP4kaqmlHJJ7MSZqxZR5Yjnbb5PM5P1Q5HYljanynYUNA\n",
"6a+T/X146SWAmFmRbGWUtovjK5PxIiUa33GPKr947pNcs3J1N30F4+JxS9JiSS8OkmmXI23/cLb7\n",
"dW9Z6VEgl0zDH5Ya2HLdGyk78rKb4RWl/WgCKP0tQUZenbihGhcT8YmUFyzuUR2nXVLEMV36a1xm\n",
"Gx8jX5i0A3Uqqi6N8WGgWWBsshkeoHjhJBi2m3CullxQ+utk4W324RUCABNPi5GWRsow4GIgSmIV\n",
"P3lf0gsWqyZw+ISl/t6yhG0F2T34h4tV5UQKLio8ybj8aVKF5Zgm/QsL7ROqZnrDAeDKFfiTPwXb\n",
"bt0dnQxKf50885Af39Jh0hE90v3+8TBHUUUwJFRqIwdVBLVIGWkmykdwyYfXqsqeFfZlBdXdu17B\n",
"Vul0tl+ofl94iAe39KU7lWUdiaHYA/OLt8knfuw3LzJTAij9dZK4zzNxA1TCLyrgwvba0tUFZnja\n",
"olk8DrJS4hH3SBrZN80+vqJUFxdf1nbfrPb5hXvj8S1dQn66RnY4lP46OT1NkMUgxXxkUbQigUzt\n",
"lqWrC8zwtC2aKo2pcIw/IVXFkqbSyJd/DAo2zYbJfh6WgnTHMs6lPofzhm7pRumvmbTd/1Ul1Rkd\n",
"sn3+T5Z1d4v8Zqis144cr13B2xjZQXbBiafw5ZeSny7XfteP3+Eld4DnOg+runMTBeHRRdfh7Td4\n",
"mfGmkbIPgNLfQERSh4QeI8lyjPfjcLLJqq2q4CKiWtw24vkSwk+txrM4pFSdPZBG1+GHD5XKm6xz\n",
"E7NACHAgTThZRToo/Y0jNdWMEvuh0l4eyacmF8WJWeL5EsIHl7d9YMuOeKC+X+EJE3KZvlidYqD0\n",
"NwgSCwIM0rrJ9RU38Ojio/fKlqA44lsleV1/VbtEIsyf8hatZfg+rLyQ4/vPNjXwtCQo/Q0ifl6K\n",
"mAHI8vs3IcliotVvGCrysLcXzmFlJcf3Hz7TvgxujeXzv1D/W1MFKP11EtFiPWULrawcZ+Nf0XDZ\n",
"1R1l1bwMhtOG+sNhoFzHbLgH5vLPT+fA1hrpp5Sur6+bpum6bpnpJee81+uZpmmaZq/Xq3emGtFi\n",
"QtKD+qGqk7SCpd2wPa5p8OEV+XtQDWOsr6nhGtASagkpKVNplnxqksnz1r/yZaXVKaMd0u95nuu6\n",
"juMMBgNCiGmaxcrhnK+vr3PO+/1+v9/nnJum2Sg/ZeRokQuRl5W908mpYF5Sugf18La6PaiEwM+u\n",
"VpXLIZF3n0g7/yArCp9d+STYc+/naK2EnNsKh0eM6y+OsNM3NjZ0XSeEOI5jGIbneQWKcl3Xtu1u\n",
"t6tpmqZp3W7Xsqxerye9zYUxjHMhri6nQgOXeVWi6/CjZ9TF6xkG7H2qbDbNXCu35XMi5VoW2nqH\n",
"/MPny00QM/dy4c76n7/ZmgliI2UfoBXSPxwOLcsioVto23Yx6dc0zbKs8CeO47AmJWXV9QrjAoOl\n",
"1InZ4tRTPt+k4gNYFK+Z5wpm/+mHpfTG9/Ot3P7o53Vld4MQ2F4xlo58dZMoTekEURktkH7f9/WL\n",
"i4OaphXz0jgxzfN9nzR2XI5TbhaveHd+djnQddjaKlsdAaVa3OSwloUF2C+x0lvA+X7lSvHqCnB8\n",
"rNB/NpUbugAu192Ayfi+b8Q8FJqk57G+vt7NmbPj/v37aYsN3W5Xry6ExTDAdeHirKU6Tm5oQL0y\n",
"vqHs4kgInMwRYFRNdSOatMYjnT/5E/hHv1VctfJmUX7pJTgsWFUR9vfhVxVWJ5c09dje3j5VOHVt\n",
"gfRXtwzb6XRs246PK+O5fv36xsZGRU1ST9rdPVnW4PulSs4Vqn/vug58WKq+zOg6/OFr+u13eyrH\n",
"0b/64+FlYiiLbX3/+77vT6vBWgrOAfJP2CSKUJp6uK776quvSqtmEi1w+FREp9PRdd2udcd9E/ZY\n",
"VWf7KvYvZYcQOHm2lLsm7/LQf3xfO/mJulCyP33H+Nrn1C2EPvNLmsqU/Sdz5Nq7xa+uiH+X8xZ5\n",
"hTPSAumX7kLhnK+trdWu+wCwf5p1j1VFGEbywVKETOXKljRyba8tf9JO3j/vdpWOu//iX2lzc+o6\n",
"zL3r+s1HxW/o0ns5/7bcfprVvepzIhaiBdIPAPEgnMJhOSKW37bt2nUfJtnFig2N8MFS4oej93CX\n",
"lTTK7LDNm3ZG/Zbp5evF//bmfZa3r5c50HHpyM+3pFT+PUTpL4ZlWfSiRSHCPdO+TylN26abqPsK\n",
"w8RyU2/ag7feUif9Nay5tmeZN7ehWrK6u/Tkhjq1evyztFy142jF02tS3HiUFki/cPgEgfxih1ea\n",
"zc4YE8keOp1O5FdiK6/jOJG/XVtbq6DVcogYHKePlPZ4lZHy6n2p3/4bUthHsbDFPsx5MOGTw+JP\n",
"LrehWjp5p0rpX1jI931KYWWl0aoawDncvl13I1JoQYQPAAwGA9M0GWOEEEqpbdtpCwBBkH48Wp8x\n",
"5vu+53mR7WCNSuQwBt+Hn74JD5nkvbhVTUYVz6UoPVzMdyW7u/B80dqeeciPX8pnqF5amtrzTBRD\n",
"CCx/Sm2VnBcICmo47ZB+Qsjm5iZjjHPuOM6YTViapu3s7CRuBTAMY2dnp+KWSiYY4MRS4eUKzPDw\n",
"vZTpX/L97RXjFXnlTSSv9JfxF+elJdYFksL0xfe0RfoFGUN9RH6eqhujgPBWM3GKy9UDqM7ciR+h\n",
"9finU6tYjMHvrsBDVdVx3txQ1zjHx7mdMFOPiHmbpuRXLfD1IwCg6+D75Zzvkzww8W79zsdTaOwI\n",
"DAOe/zl1AxvnSicZQaXF2NqCGzekNkU2ueKdpFB4Qqz4xLTsoPTXB6W5cg/4fjnL0fe3V6bIaLlI\n",
"3pQ1jjPN3nAAuDHHyyyE3sibQL89Lq2Pt5SuQl3dYhjciUS5t5zDlqjCaTCmT4p3ucGBrxfY34db\n",
"t+puxFgUn0by7PXiA1uRTeYlvOGru1SlM/2lZ3KHS5Ud2FD6kTJomvyYNk1LzRFNCMzNKZX+kiez\n",
"F3BPqzRVy9zMpSOlI/DNA+WGah5/iviu0mnGNC7zovS3hn4fVr6uP/dmwVj0NJfImHf82WVy837B\n",
"oSavB8ayBLP6cwAAIABJREFUYHe3+AtdwKO6vFx8HP3kX9C8cf3Ly8Wl/5MH+Q3VkiiU/rwrWCL8\n",
"oRVqzFgNazwZQelvFSX6ewGXyL3l4kdwHN3xc1Wn6/DnTxuFxfjqFntwK99K3NzntMID28EBfPor\n",
"Oarb2IC5Z4tvym2sfIQpPLC14uqKwXmpFBeVgtI/Q6iM2Jvf9z/8Uj5DtWTzHuc0w0HTymROzW0W\n",
"G4ZSv42mre4pzcC39lxL1oUQAEDpR9JgTPXC6Y0bcOeu0hqnGcXO+mkf2OYPpm1gQ+mvk/39ulsw\n",
"FsX7ehoeS440COUD2/w+Sn8STU5+2Vw4LyB2hX0US3eUpmNEkGZS+A1qRcK47MiR/niaTGQyjOWK\n",
"6wcA0PWbB8U74MlyPun/8AopU10BGrv1EamOYlp8fFywutxnOAMAwK1bLdq1lol80m+a5qUkKB7p\n",
"VIjcxwQqjGgjBH7jm8UjfArw4JZ+dUvhSENUD2yFb6ZicVSZrBuKarFib+TCFaXVKSC31b+xsfEk\n",
"xOHhoWEYm5ubVTQOqRH1OxBzh+iURNcvHSnU4hIztiLiSMhn/7+C1amMtlQc+U5pm/LoVUo+6dc0\n",
"LZIwmRDS7/dd15XaKiSVoyOl1RU2AIu5bhRfXWHRKabFBSsrhq50xgaatrpbZOrPecEUF4UDilRK\n",
"f5PXQPNJf7/fj2dOFuNB4cNykVwo67hiz2RhcSyQHM0wiku/Yh8FEmXaY0mLnTrfyOQ9I+Qs82qa\n",
"1pazrpCp5OCg0a8Z0m6msW/JkX5xdKKUopDxFJ7FF/PAKHUalKP5r6didxaSiOoosqbaxPlO6fI8\n",
"Lx7C7/s+ISTjEVrIOYUO/CwWDgFFD2stXF0x2jLSFBPx6V5gLDywFdZi3y8y3qs+p6GpNnE+q384\n",
"HMYdO5ZlDQYDeU2aGZraJ6Swu1vk+hSPNIUpJuKKgzsVU3hgK6bFKyuNXkRtPvmsfk3TLMuKn3iO\n",
"IHGmeB5YTIsLD2ytGBGL3ZOmukOmn3zS3+/3K2oHUjWKY2BaYagWphVaXJhiXaXYPWEM/oHa88sK\n",
"Usg922RmMX0bpXR9fd00Tdd1ZycwSXEMTDEhaMuuhVZQ+OoUJ9Cfe1ZpdQWZOvfszEm/53mu6zqO\n",
"MxgMCCGmadbdonwoTTGvHMULoVN8SAhM+9UVQ/HywNM/bO5yRD6HT9vhnPd6vc3NTRGK6jgO59zz\n",
"PDvtgNoqeXSfQ/4TfApPO4uNGYr9NtPtJkLiLL3nwzV11T315/TTv6HOAvrFJ8pP1szMbFn9w+HQ\n",
"sqzwFgTbtj3Pq6Ux+6ekgBmuNPdAiZGmGNMdS1qsuh9+R63lSOnhojpxXDpSLY4/9/mCVzdlAUWz\n",
"Jf2+70f2H9S7D7n5HpjpdhooHmmKVffO9/yrXy8ijoUHNpXSXwbFL27z39ZclHX4cM5d1yWEdEXO\n",
"l2bj+348MlXL+UhPT0/TklTruo67mmtAsQaotYsLM91hSMvLwBhYlqr65EX4pKnH3t7eRx99JKeO\n",
"DJSVfs/zhMPEMIzmx/tLMfBPTk7SHl48s+mMwphS3Slw6E05WiH9raDwoQKq44Lkvddp6rG7u/vx\n",
"xx/LqmUiZaU/8J/ktZ3bS/1THM6bHmrGuWIt9rnSG1JYsJrP/oHS6hSfuKKY+VMOsclCmnq4rru1\n",
"tVV9o0aU9fWLc1o2NzdbIf0NSjRUdP5xb1kvckhoUTP8ZI6oPJP09LTgnSl8pHuxtbspFqz9fbh9\n",
"u+DfFugpilfabx4wZWYTY/DiEWvspnYJy7y6rjdIUicRP1egnpMGGHtwq8hNK+hIKWqG31vWVXrS\n",
"310pNLAVZWUF9v9iuuI2SjO/X/CGrKwU6Sk3D5SK4/wpV1bd6BSapk7QZyvCx7KsiKNNhHvW0hjV\n",
"GQTVUswlonhl8vC2UVjpilS3WOTEj6U7tLCVUCAwdH7fP3xZ7aJdU8Vxupkt6RezkyCQX+zwqmU/\n",
"19QzxS6RwhReHC52avH1r+rvfE/dwHZyQ1u6W+Qoq8IsvYcztuLM1m5eABgMBqZpirNlKKW2bbfI\n",
"WwUAV67Anbtwu+mxVGrxfQCFS02UHi6iuRDl5IbyMxq/lfu5F8/apGmrf04BpufFkyP9vu+3YpkX\n",
"AAghm5ubjDHOueM4rYvFfOmluluQBcZO5hS+JL6//YJSLT68pq63H6gNuZluim9R1DT483x/wRis\n",
"NfhwHjkOn06nI6UcZei6bhhG63QfAD68Qhbezr8QWmKp1mf5/5bze9fbNJdqMqenjU0DI4EpTp7K\n",
"OSx+3NycVLmtfkppfEtC/NRGZAKMfXi1yAt9fEu//t1hgeruLTsFqlv9x/pTf9oDULQSfjJHgFGV\n",
"Uqf6pNbGo1iLCUz1/W+wcZnP6qeUuq4rTGZKqWEYuq5TSvEIl9xwflwobKMwJ88W6YXFFhgL8+xv\n",
"6rtvqtOCB7f0q1vqYkmLbZIoE/leYGA7OFAaiV4mpmt/X2JDZo580u95Xr/fF8kvxQBgWVY8YhJB\n",
"ilF4wajYtPMzv0Z2d3P/1emjInUBwL3rRTZJFBbHwgNbYVNVZaQs5NzHxzkeBnmB3Fa/iIfhnAeO\n",
"csdxKKWzc9yVLGrZSaaMVmRVLPZXiu3iwiiesR2+rHSTBIjtYJlhrMCeigvknWQ0XBHzSX/auqhh\n",
"GPXsiW0znE/z8p1SJ6fal+zyMW+wC7dO8q4TUArLhQ/mNYy8rrBSEqVp/8WjfENHwztJPunXdT2Q\n",
"eFzaRVJRbPCofcnKbMM+uC+xIZNRedaxrheJQ23NgRDFZogNtvxzS79w6xuG4ft+4ORhjLUlrr8p\n",
"lOgTRYJSplqL24JhKI2f0XWl0l/gmXOuLsKKMfB95SeANvhFyBfcadt2YOw7jmOapm3bQvdR+vNR\n",
"tE9oGmy/S57P+VennyzeBTH8sV4Kq1WxLqZSHBkD6/OKxJFz0DQ4+VFztVgxuX39QdoDy7L6/b44\n",
"8hCDO5WhfmVScZo5xXHlzT8Ifv+0BadItoUp3kGWl1KJHNqVrnnGafDU8xxdh78+gM8qrFGx0hWY\n",
"Qi2qTQagUhx5wkEm1dKapYXqma3MnUgBCqzdFY58b8X4VIbmZ+ouI455p1CKHzf6pMOg9M8Ehf31\n",
"xVYm39nibZkNogdAIg13Fv3KJ9VuO7iv7kSwAqD014TakBvFxubjBaWZ8Y7eK/636AG4QLlumXcc\n",
"vf59WsYUzzvJ0MDfXlG0lYZzpSeCFQClvybUmgPTbdseHanbHOe6cHCg8OlRWviAlwLsv8aKHeQp\n",
"yDuOLiyU8sLwnAsFN5aLHzucF8bg1i1FdRUDpb99FAhKOTiY5p3DyhCBzaenSo25SqU/nNuAMXjt\n",
"NXVOm/Lz3gIzttsvl600Ow0/qA6lv30o9qguHTV727bCXeW+DzfvM5VmeKX4/gXp5xzefltd7YxV\n",
"a4NzrrJrtA+U/jpQvLeWsTKjRW6lo1TpWX2+f1jivMq8U6gf/Q2fJumP8PCh0gZUuluQMTg7hDv0\n",
"kWxXXXAPKY1Wt3Sn1EpG1aD01wFjoOvq9J/zMg7cApSRfsXLEoqnUE/vNdoQvXIFjo/VVXd1iyn1\n",
"nXH5665huU+YZKD0I1FIG0+HzEqZMzSmOORG02DnSU4tYOz+B+o6ylc/QR+UOEEo1xSKUlhcrDbe\n",
"QXo24XiBaQZcqaSkSkDpbx8FcnKpNOUAYH9/aleVy7hEipiACk9z4xwWFwue5ibIO4VavFa4qlQm\n",
"mOElWFlJEPpwFZHfzj0rs3bpoPS3jwI7+8sEG+QeaZSvZHyo8EySL32gNNqyasLPijH47GdLjdlN\n",
"iCEOa7Fid0u7VpVR+utAcR9hpYJSco80rFRseG4U2sWMwdwcHF5TpyiFU2JkJNIT554tJf25nXUV\n",
"WAmBT8b3gZDzCyxf1fhF6XbpPrRI+iml6+vrpmm6rlvmMEjOea/XM03TNM1er1fPuZK+72vlHCK5\n",
"OhrnKtUKih4BXxhlb51wiahkyjdkVOno932w7fO+Ub6q8Vvifb/Ja7oJtEP6Pc9zXddxnMFgQAgx\n",
"TbNYOZzz9fV1znm/3+/3+5xz0zRrUX/fL/5Kb68YudSuTJ4DEMGdJU81zUvOJ1LmZuZlcVH+4uGY\n",
"u3v0A65UUBp8qlQBCFF6Ana7AjdaIP3CTt/Y2NB1nRDiOI5hGF40ZDcTruvatt3tdsXZMt1u17Ks\n",
"Xq8nvc2N4s03wbaL/7li1/a9ZV31ifV5xtHFRfnyOE76LxGl0t8u9Up6dOGbqeuVj2XtPZK8BdI/\n",
"HA4tywrHQtq2XUz6NU2zLCv8ieM4U3+g/Omp2qloubctd6B9ueryTqGgnDz++BPNnUK1zuJfXp78\n",
"6Kq4KNdNLf9Ce5p9Q1sg/eIgsPAnmqYV89I4jhMvvIYAe7V9QnGk/OvfI0qvr1WG6ukvNHcKJedG\n",
"5lyFKlNVvGPHy6uidwR3lF7crmtErIhm98xSp3Spwfd9I+bKlXUU8Pr6erfbzfUn9+/fT1ts6Ha7\n",
"mY4tI8T3m5zPtRRvvQXkK3U3ojKWlwHekVxmdSPlxCmU3Kq3Vwz9b/wFTfO8bD5G2eLI1O4OhkLx\n",
"o2nqsb29faowPLZO6eecpzlbwocAV7cM2+l0bNuOjyvjuXbtWnz2IMg+IInwg+nD92Furn2Bbhnh\n",
"HKrI+zAcQuLh1pTC81XuCKXxHDPl3rUbN2BrC27XGumYOJooaI+4cxdiSVO6Spp6fOtb33r99der\n",
"aFsidUo/pTTNZU8IGQwGldbe6XR0XbfzC/Dc3Fze0aJG1K+YfvGL8H822slZHEIqMdHHFFm1sy4q\n",
"/eXM8Bs3Rj9MvEki6B5K38v5Ax9gnL0VKLJhAEhaZEm8OkLAMM6XAcbcyDT1oJQ+/fTT5ZuXkTql\n",
"37KsyKJrItJPfhcxnbZtF9D9psBYxnhGzmF1pVRVeRPyfOpprv96qRpVcuMG3LkLY1J/RuO1m+3A\n",
"jTDx6ipiopU9cniW0+LD28b8/gTpDx7X5Ydlx5mTG9rSXQqGwRhwPqEj3LzP4LON7iotWOYFgLhf\n",
"qHBYTiN0v2RQyguGyoXiZz+XLyjl8QLJuXoSQ6G/IDBU04jPS5V5kxkru4Ns4tVVx8Qus3S3qpzG\n",
"id3n6lZWaymNIB+tnmHtvOGnM0IrpN+yLHqxH4lwz7TvU0rTtukm6r6v3jFJ1MbAlEPxTuB7y3pe\n",
"6S95MxfezmdGlB3YMsN5JQnOGoRs6ReTiapf6DH2fove6xZIv3D4BKsCYodXms3OGBPJHjqdTuRX\n",
"Yiuv4ziRv11bW6ug1RMo4zZoUfcqQIEkEGVu5uHLxjPprgDpIfg/uJRjCjX/SMKTnt8fJ4Th/a43\n",
"78s/ySQNxuDKFfnFxvd1a5q05a4rV+DOnbNVirPqIohfteINbUFwJwAMBgPTNBljhBBKqW3baQsA\n",
"QZB+PFqfMeb7vud5kbVl9Ykcjt4D/nHxP8/1epZ3ceZi/sBXmUcTGANNgyqtvLBwrO5R+HqpWfxH\n",
"n8lh517dYvBPS/koDl82Vu+4Y74Q3u9a3kfx4RWydIcCTG4z5/BSxe4QcV2aNvrh8nF6zE02XroF\n",
"3/3uhbUfMcmI+/0Zg5evTliEqJ12SD8hZHNzkzHGOXccZ8wmLE3TdnZ2ErcCGIaxs7NTcUszQOm/\n",
"/Gu9+5qi2q5uscPbxoqi2uBvX/O1r5V9p08fQdbAFs7f/kjdC3Z8rHSZt+Hnesc5vqU/+6+HkNHs\n",
"pbTSAOfIg7q6xeC/T46qLIOYVRix1bfnHvhgNDqKpAUOnwBd1w3DmLj5VtO0Jgdf7h/A1RfU7SBW\n",
"fEgLANwoF4qu63BwMOE7v/mbox/e3oLXVA2iUI0Wj1HJvOcGl8H3YenILzmwGcbodIesxZTz9QsP\n",
"TBaqOxEsuIJWRX4BtEv6p4P9fbh9W111P/4P/NYtddUtHZV1vuR6hX7yf7Otd9S9c6u78oNShMsq\n",
"cQC4eaBuc6rvw+1FmVvMFQRPvJShY2tnayuyFswT9sGFaIWXX4DSr5qlO7TMqeUjMnexmwds4cvq\n",
"gsyWjhQmUAYAzr/+P+mVbluL3ukK4hEtK30pspwxqWmwu1umgIJkCrMpL5Oatrp7Yc1cFBku+Pxx\n",
"yVBlMQ/TtNSra5Htj9Kvmt1duPFbpeUjVxcr3R8f3VdqzIw/DinM6SkYRllTdfwJlC16meNkGadq\n",
"M1TL39nY5RGSHnRfvjpdf26XQTxNW4yRf6nZoPTXQLtO89E02D9Vqn/jj0MKpCrY8VQm0N4w4NGB\n",
"UvEreXKORDjPtDupQLFSvlMMofCVuJsImZvL2vLmb8hA6UcmkGugUpB5kDFYWQEA4ByWZWQ3y3hC\n",
"gBS1Mgx4+KNMBcmyHMesFRNSVU7j8DxsOEyuWiJxoQ8H+I/3zudiZeXCSNkiz34clP4pYX297hYA\n",
"gKqzAdSHLQEAY3JGmvFzmjBSpD/jwCZOnC/PU+9xCCk75xcONrmAPOEcf24TIdKkf3n5wqAV/Cxx\n",
"dFEGSv+UoNgAMc06E/OKIEsFlyy2bgaGnuJDb1TCOSxfl1DOx9cujDTDYbomyrP8J/qsZAUuzT2b\n",
"ejnic10HStsxG0Dpn3Iq8sDo+gRTqwzj2xy4+MtnN5uIOFahlje5FfIxEd8fG7+kBLl+rcSTFcJ1\n",
"QUtCA1D6p5zWGaqaNmFLF+dw7WwNrfmLaRNJmzzJ8i8pJj5sJ+5aWHqv7PaxCGPmoIPB2e6JaogP\n",
"bKt7tOFpOwGlXzHiEKvyPPhhI2zCKizT7G+olOxm2Zk/qMTDFc84Jrh5n80tSxDHidM+8RBlqdXc\n",
"HLCLWeCEDyTC0pGc7WNiEZvzC9LPeaxnci5X+oPy4ykcRjTe8kfpV8r+X/jlTTldh8Mn0Y6VbPUw\n",
"lnGVbzyJgfYJcYGUHi5KeMEyJjBQudkVAOb3/cPKDj0J5CNwo8lK+D7R1DjXKElqxc8aLhY/w2uh\n",
"wZKvrIV6npSRTSzPVNI1zp5T44V9Mij9SpEiH4ndjpCkZMCc31uW8AYkBqUkNkOK9OcYrmS8guNH\n",
"msBozXtaWSKJ22uDxMKcX9DHNrK4eMEKSTO1ZWVDEgNb2htxjqz56cWaglKDH8Soc/NAXfrrwqD0\n",
"TwnJPU1Sj4/vd00uWO3SZPl0Y4LxI01Qw1N32e3fKVudpiWMNIE+MgbBEUQ3Dyp0T8d5/i058YmL\n",
"iwmCGN6FJ1jdle8NHxdylvlA01wEfSOYZIgczs0/ogtQ+hWzdIc+uKWwTzC2/ULZHq/rCdKfLLky\n",
"qksk0RCW5S/OiKz3OeNIM38qxz0tRpqJM4m5Ocm7zDk/F8RwmP85kuziQPHTVk3UEL7GVsRWoPSr\n",
"5rHKk0y4hHNosryhiTs2JZIYHSg3p3F1sar1Eow0aiIsly5x4R+Lhzn6koN6AAAWF2E4BMu64O2s\n",
"xsTPiu+3IzQLpV8pu7tqfYBExcEAvl+Dbvp+niWBbAWmeQzE8Kkse34VbjPGUouVW93Vz5BgahQu\n",
"Wdxe6QfnCv9SfLrSeHdL/aD0K2X+lFfRKcU7Vtf22nE7NqtBKIj03WrjM/HKHWnGUNFoHZd4cb3S\n",
"qwsKDH4IUl2Ofqh4TciyqlnjzcYn76s9o7QoKP0K4VyWfHx4hYQn8IyBbceUS+5QkP7+jCbyvv/j\n",
"94mUMSCu6RFnBSGwsMXeX65qwAkSIp1fNGM//kQl1SXfV0qlhGYFhCNxA9/I+cOSWt0Y44YQ8H04\n",
"/g7bXpHjkbl8zIOjcenZynH02McKHEAJWwfOuPnIv6LwhIzCoPQrhEnr8ccv6ZGul2C7yVv2urc8\n",
"LrcvIcA5gO//9D/TpUj/3Fx03ApCV4PtQs885FICSRMJnD/nd9X3T39BTnWRgS0tNKu6SYbnQadz\n",
"8SPfl3gzg04XF0cxXTt4ja18Qc7VXf40GQ7PB5u06APp01IRxJl4pV/6gEo4kKN62nEse+MY4zod\n",
"A6WHi7JPauYcGFu6CwCwugcQDu2Xd+z1uQyJuA2A1T34lYPRubirewAAMBw++PslEueH2F4xXvH9\n",
"UQYAxgDgv1oEcY2X7oL5FDz1xvufeuO1e7fkVHcyJ6ZQ+r9/jRvAAOB3nsDf/hFoXx3d0tU9AE63\n",
"XxibvSUz5+EfnANj51VQeOdP4fZt+dWJUXv+EQfKjh/C330a4MF5pat7AJzduy6tZwpBnH/EVx8w\n",
"0SHFs7v+fQAK178P8+DDP5ZjFy9fP1uJecRvHjCIb20BANGXpDL/iD/6N+zGDYCg/59VvfBY8s7h\n",
"ikDpLwRjxdwph9dk9wnGYDhcekAAYHUXol1fehdkDIbDo6fI6i7c+P6oxtVdAAD4MpEfvMQYDIdA\n",
"yO1DWLoD8C4s7QEAPPXhB48XyMmzcqrbfKL/fc45h9UHDIbD00+Sr34C4C8BPjG6wOffAvhKNYnt\n",
"h8PVXTK6hxSWvw8vPQc/2YXTLxJZDurlZdjmAGKjwHD47gNiAOzuQlDp6i7Al6VVF/DKApv79hAo\n",
"AQDtPXjzTXgZACi8/C6cfF6+Mq7u0tVdKqqLUoEQ/+pbw08dsNtfIef9/+zVe3tB/5r0+iqgNdJP\n",
"KfU8j3Ou67rjOOUjV3zf9zxP0zS7gGmc8ifi/RnXtCo2alrWNhgAQCm8ctEOrmTh17I2weC/A2DB\n",
"6y680oXXXQCAV7qxgac8nINlgWF8i8Gnfh9WDNi+MK2RU4mw3QiBpR/68PvWvwMDvja6meICvw3w\n",
"97rSnt1okiG877b9+lB/pQv/R+e8uscU/h0AkX0zbx4w+BfO/+ZpjgNvD+GxBhTOKyWye+YLW/Tb\n",
"/033N/4pAYBFOO8kr7uSHe/idbt5wP7l3+n/hpx54GSWjvz/6yuj6v7XdTAMeOVMEj5owRIvQFt8\n",
"/Z7nua7rOM5gMCCEmKZZvkzXdQFgWC4inXPwvPN1M8aU56cN5cpKDOGQ8pqdZ1w5O5NCUYjqmT9V\n",
"05LSVMhGzZny95Z14Nx14eCt8z1i1d3PkxvaM9+lENojFjm6RP69PeuIz39eRS+Z4Oivnkh0qePU\n",
"04y8tED6Oee9Xm9jY0PXdUKI4ziGYXjlIskppYQQo/R7Lnz+wZsT/JDWOinTakLgzp1RdbtvctD1\n",
"SJ4skG3vX8i4cnH6HIndlvL63bgBb2+d/5OG9vwrCGANqqs6JvCNN1SEHZ7c0La2xo1okt0hZ7FE\n",
"K1e5mn1V4mEp23UxNbRA+ofDoWVZYQ+Pbdslpd913W6Zw7xDJIaydTrJb7UUZUysMfICK0sBFk6R\n",
"6EtKrHDjBjx8CADn6htcnZrN+oRciIYkpJLJ3Be+UPkuaIGYtM3NgetWv9cpHtUf+73cmymcr8p2\n",
"XSTShmXdKC2Qft/39YsdVtO0MgkKXNeNjCWFibdCGP62Db1e+eJTOZkjQGnaPSgWfzSB9BKrmGiP\n",
"XEzpRY8JrJZCJOO83LqOHwIArLwAvp9cssTqbr88yjm6vDxaOpFeRS5EJlRpIxAhmk+hstPoEuAc\n",
"AD5zhYd7CEp/Jfi+H5dprejN5pxTSp1yDrlwJsJwJw7nbq301bp3XRe1xzMAQwWHRI+P6wfZ/uJb\n",
"t+D9f8si87rw/RQmufQhR43T4PZt2BLuLH7hBPOzD0aHX0p8goH0BxPdhLMW1CLt2Z29fooypp3d\n",
"uKc+RdqeK6LOCB/OOUvpgISQwNKXkIEsRHlXz/3793/t11777Gf/FwDY3v59xr4l/gsAzz//vwOM\n",
"UjfVmK9b+qhzHkaZUrTckWbhd435HqUU/u7TsHL2Yfh+yr23J3ME6BDAiDgN0kxyaRASMRHCKc8k\n",
"3tKDfTAMAApzKc6YKsbRNBIP7SqLsimMuE2cLy/DtTPpzzsGpEWpbG9vn6qbvNQq/SJeM/FXhJDB\n",
"YFBFjZzzkqu7169f/+f//GsAX7NtcF3odn9P/BfOPOzxpciqzgxKIdjaLp3dB+T/8c7Pua500fVn\n",
"Wxw+C1Dl5Qje/6x+8NbwEYyO+hMYBrjueb1yr/T4GJbe82GFGIYid/+YHa3C+S5p898ZsYln8BAr\n",
"eZSMyc17MbG6ua8ZwTia15Lc2NhI/Nx13VdffbVcy3JQp/RblmUFrsd0dHmq6XmeYRj0zOpgjImZ\n",
"R94qhOinIZYiReSPGGVcF1IetxwiRk/4SDwprzTnIA7COzoaiaBwmEXERKLtdXoKv3ONibMNGAPH\n",
"qTC4U9fh9E34FWDbK8ZfeRDvkroOvZ60oL0rV+C11+BLX/JB16WvIqQSy28ZHAtTVRsuVkfI+fp8\n",
"Fepf7zJvG2mBrx8A4n6hNE/ReAzD8H2fnuH7vnD9y2gjACRM3itldW90Fu6YuqT4DUblU/of58bF\n",
"oUu85KMj+NKX4HtbRHrJY7h1CzwvYX4mt/aXvqLd2qMERn1FQcDSKy8kuK4qyG5wsfT0uyZ/BszY\n",
"4WLh5b/8SF9Mq4MW7Oa1LEvs5wo+EeGead+nlDLGbNuOLw5HNu4K9S+55Bsm4roVP4fjbaSbV9Wl\n",
"MEvkpx9Gb6mYWEj3/KyswBd/jv3V4uRJoSxWd+nlr9kqQtE17eAAXvkRA/2840U6hsz7qeu/fYMC\n",
"izomqtIukWmPc9kupLFwvviyQumHdsb0XKQFVr/wxgSrAmKHV1r2BcaYaZqu63aiyQkVEc5RHpy1\n",
"PSnWuSBLR2oz9Pv+5U8nXEAVb8EXfwOAc/kpj8Zy47c0NXr16BSWr1/oDZGOoWny7iohi4uSispC\n",
"Bv+RpB01IThvvxSrpgVWPwAMBgPTNBljhBBKqW3bad75wNIfH7bPGHNdl3Pu+36n0+n3C2ZJDFtn\n",
"wc9VL0sG1Swd+d/79QtaFaQarsR76/tp+R2DpMqVUumq8vzpOPmQez+vZzjAT6KWfeHXpRVVGMM4\n",
"vyKZDh9NA88DIuegiEzUtSFCNu2QfkLI5uamWJUdn7tN07SdnR3f98eH8ei6nrbOnotwhxOru5SO\n",
"liXhrJOIDSzBkq80CIGL/TA4C6mS+DmAo/eArCT3fF2XHakSGj9FjeLqwjsqMoQI5GDiaekSh/OV\n",
"leSzkV1WAAAQ+ElEQVTP61IVBfVW5Uk7ewMVSb9Y8Z8K2iH9goxxOJqmqXX7JRCJY6vOg3wWZ5zw\n",
"K4k2MiFw8Bacnk4YVGQqSMwZIl664OPEE1kLc/n4LIYpHYm26he+kHyzVO4FidTV9g1Kiqhxt45s\n",
"WuDrnw7kGlZp0ZwBERu5JLoOp6eT98pLfi8mHkMmj3c+UvpKL16bcD0KFCY8cMqd0yCtAKW/IPEs\n",
"VMKxk6i2wZKvxNrhLPHAmOPn5L7PBwfR6UvVm12L/jIfhgG7u6oyAWRDZXSMfBT7rWQljM1eXd1O\n",
"BSmg9BckUeUVW0/CPR0EGYtEOirfu6pTFSnj9BSWk5Ze9aKb9ScQPk/2rPywJ02yh7CCc8nHoSa9\n",
"agDnqvfKo/QjEwknmKwiQCW8gCw6ZEVJIy4fn2u8ip1rjIGua9qF2VJ1I+tLx+zwdlStDOO8Osnx\n",
"iLErqdZiUHDKQY2on2RMBSj9pQjv1Yr3QJG6OZwHRqYoM7a9YiTa3VXoyPy+f/c5A0JxRBHkv4CE\n",
"iIPZg5J1fVpWI2PSHxnkJJO0TaDarbwqn9N0z2kqo00RPg0kCD5JzH0olKuqlJOaBg9G/68aQuD4\n",
"GBZeqryiOMOhikApAPgwdqZ8tTc2egRFxS7r2MWElxMkX2nkxLiqmQr3i3pQ+iUwpp93u5XtdSLk\n",
"8Clt5WLPr2g3ma7Dt5/TxydH9H2pp5ISAoZhKElxIzi+Fb06xZJCKRTdWTiJSX1Ccr2Ko4UU2+Dt\n",
"XoI/B6W/OIkuDk27sLmJEMk7j8IcXtMM40LPr+54XjjL2q9IEDNUI/Mwk3ntWWmFZSDJH1LhjVU8\n",
"iCmuTvFIMy1hsOjrL0j8nCMxEqRlX5G/wzZl5TFx72t5Xv9yN7hAFWRYV5XYkv/xekX2dgrys9hg\n",
"dVNaXWWg9BckPvaPz9GmzFao7jSroLTEMymRkkzJCjbSElD6FVH7aagSSXMxqUSuUBKCyovMFij9\n",
"cpho/KrZ/VRdFZE8cZEfpoDaXbgYqIKoBKW/OMHmKZG3cuKrK3fXYeIqbnX6NXH7uqZN1UigHtvG\n",
"G4ioA6W/FEGGzmB39xgFlBjuLD0pUBbGS/90R/QhyJSBwZ3FSQvuTJNIuTP6ihI2tAWUfgQpA1r9\n",
"xclr50oP8B/fAMW5RlCLEaRFoPTLQWRsHo8CcQxXIT2h4fjSUPoRpEWg9EtDcdqSLL5+iU1Ky5o5\n",
"HXEp03EVCJId9PW3EvVSlVjjmIWNdlFV8hwEaSoo/aVI3OBaLxVNPhK3r0+H7iPIDILSX4pA8Rvi\n",
"6Y5kc0MQBEkEff3FqdfSn5bDghAEqYHWSD+ldH193TRN13W5jHwFlNJOp2Oa5vr6Oiu9P0p9Em9N\n",
"a5CXCUGQdtEOh4/neZ7n9ft9TdM8zzNNc3Nzs0yBnU7H933bti3L8ovaz2FPdy1e7/Fu/dqT0iAI\n",
"0lhaIP2c816vt7m5SQgBAMdxOOee59lFLe319XVd1/tnUR1aUdlu+HE9mFQHQZA0WuDwGQ6HlmWR\n",
"kBFr27bnecVKE3/oyDxLEEEQpGW0wOr3fV+PnmGtFXb3e543GAxktKtm0NGPIEhh2iH9RsxzUdhL\n",
"I/7W931h/luWpecUUc6567qJv7Jtu0zDcjHRmYPeHgRpIGnq8Z3vfOfDDz9U1ow6pZ9znhZaQwgJ\n",
"FFlKPI+AUkoI8Tyv1+s5jkMI6XQ6tm3nWjaYn5+PD0UConBpFaUfQdpImnrs7e299dZbyppRp/RT\n",
"StNc9oSQitwynPPhcBgsGluWtba2ZhhGdmt9bm4u7eEhCIKMJ009KKVPP/20smbUKf2WZVkZEhnn\n",
"dciML4oxtrOzE1807iZmKkAQBJlGWhDhAwBxv1CxTVjCjxQx8JV55xEEQRpCC6TfsixKafgTEe6Z\n",
"9n1Kaa/XS1sh0HU9UhpjDNUfQZCZogXSLxw+waqA2OGVtjDLGBPJHjqdTuIXHMcJDwwi1CeL3wlB\n",
"EGRqaEFwJwAMBgPTNBljhBBKqW3baQsAgRM/LdhG07Rut7u2tibknlI6GAxURuYgCILUTjuknxCy\n",
"ubnJGOOci6DMtG9qmrazs5O4FSBA1/WdnR3h9sHVXQRBZpB2SL8gY6iPpmlZfPcYoIkgyMzSAl8/\n",
"giAIIheUfgRBkJkDpR9BEGTmQOlHEASZOVD6EQRBZg6UfgRBkJkDpR9BEGTmQOlHEASZOVD6EQRB\n",
"Zg6UfgRBkJkDpR9BEGTmQOlHEASZOVD6EQRBZg6UfgRBkJkDpR9BEGTmQOlHEASZOVD6EQRBZg6U\n",
"fgRBkJkDpb8IpmnW3YQiuK4rTiRuHS294ZRS13XrbkURsKsohlL6ne98R2WNKP0IgiAzB0o/giDI\n",
"zHG57gZkhVLqeR7nXNd1x3EIIYWL8jyPUiqlKARBkDbSDqvf8zzXdR3HGQwGhJAy7rxOp8MY63a7\n",
"g8FA07S1tTXf9yU2FUEQpPm0wOrnnPd6vc3NTWGeO47DOfc8z7btvEUxxnzf39jYEP+0bVvTtF6v\n",
"1+/3JTcaQRCkwbTA6h8Oh5Zlhd0ytm17nlesKF3Xw58YhtHSSAYEQZDCtED6fd+P6LWmaZzzAkVF\n",
"ykksHEEQZOppgcPH933DMCIfappWoCjLsobDYa/XcxxHlNzpdLrdbq5CTk9PDw8P2zhX2Nvbu3v3\n",
"bt2tKEJLb/jdu3f39vba2HLsKoq5e/fu6empyhovPXnyRGV9YTjnjLHEXxFCAmPcNE3HcSLqb5pm\n",
"4LLPi2maQefY2NiIjytj+OM//uM/+IM/KFYvgiDIGD71qU/97Gc/U1NXnVa/iNdM/BUhZDAYVFFp\n",
"p9MxDEMMG4wx13XDw8xEvvnNb37zm9+somEIgiDKqFP6LcuyLGvi1yT64j3PI4QIb48oeTAYrK2t\n",
"7ezsyKoCQRCk+bRgmRcA4n6hNE/ReCilEfcOIaTYsgGCIEh7aYH0W5YVWbcR4Z5p36eU9nq9xBCg\n",
"xNCgYsFCCIIg7aUF0i8cPsGqgNjhlbafizFmmqbrup1OJ/5b27Yjo4LrurmWeREEQaaAFgR3AsBg\n",
"MDBNkzFGCKGU2radtgAQ7PxKzMyjaVq32zVNU9d1UZRhGHmDOxEEQdpOncGdeWGMiZxr4xOu+b6f\n",
"uBUgjPAgaZqGjn4EQWaQNkk/giAIIoUW+PoRBEEQuaD0IwiCzBwo/QiCIDMHSj+CIMjMgdKPIAgy\n",
"c6D0IwiCzBzt2NLVHCSeDl8RrutGPjEMI3GXQxOuZTgc+r4fJNSLk7GRiq9lYrMzPgWVzRbHmood\n",
"LYZh2LZd5mY2reUN7PbhZmua5jhO2i6iem74EyQz/X5f1/XNzc3Dw8Nut6vret0tSgAANi6ys7MT\n",
"/1q917KxsWFZlq7rlmUZhpH2tYyNVHYtGZv9JNtTUPkIDg8PDcNwHGdnZ2dnZ8dxHF3XDw8P49/M\n",
"0qoGtrxp3X5nZ0fX9X6/L5oxGAxEvcWaVEWzUfqzcnh4qGlauM85jtPv92tsUiJZhvPar2Vzc1O8\n",
"BuKonMTvZGykymvJ0mzBxKeg+BHYtj0YDMKfdLtdx3EKtKqZLW9atw+6SvgTy7IKNKmiZqP0Z6Xf\n",
"70c6nBjY62pPGlnegeZcyxgNzdjIWq6lvPQrbna3241/GL+ELK1qZstb0e01TSvQpIqajcu8WZF4\n",
"OrwaKKVpzWvFtWRsZMOvJe0pKG52fFnC9/24vzhLq5rZ8oDGdvv4YSEZm1RRs3GZNysST4evGtM0\n",
"OeeEEM65pmn9fj/yqrTiWjI2srHXMv4p1N7s9fX1eM7aLK1qZsuhqd1eJJ2klDLG4ofO1njDUfqz\n",
"0hxDcjzdbteyrKBneJ7X6XQifa4V15Kxkc28lolPod5mdzod27bjgpKlVc1seWO7PWOMMUYpTQzL\n",
"qfGGo8Nn2ojEkNm2zTn3fb/GJs0gTX4KnU5H1/W0w46azJiWN/aG27Yt4nwYY/EI1BpB6c+KxNPh\n",
"FaPreuQdaMW1ZGxkK64FYk+hlmZzztfW1sbofpZWNbPlcZrW7fv9PmOsQJMqajZKfw5knQ7fBFpx\n",
"LRkb2YpriaO42Zxz0zRt2x6vnlla1cyWZ6HerhIfjRIboOaGo/RnJe/p8M1hOBxGDIdWXEvGRrbi\n",
"WiD2FBQ3O1E94zKUpVXNbHmcBnZ7ccRs3iZV1eySwaEzhWEYwU6Kw8PDtO15NWIYRmT/i23b8f0v\n",
"TxpzLeMD5DM2Uv21TGx2lqegrNliQ2ykSU+ePCGExL+cpVVNa3kDu71lWZGSxUJ0sSZV0Ww8oDEH\n",
"wgAJjnSXMgOVC+fcdV3GmAiBENZBYiRcvdfS6/WEISPW4gLrbGNjo0AjlV1L9mZneQrKmk0p7XQ6\n",
"8XBASmn89c/Sqqa1vIHdXizqcs5Fk0RQf1qQTy03HKU/NxlPh68RzrlwBU5sZPOvBTI3smnXkvEp\n",
"NK3ZgiytalrLG9jtfd8XvikpTZLbbJR+BEGQmQOXeREEQWYOlH4EQZCZA6UfQRBk5kDpRxAEmTlQ\n",
"+hEEQWYOlH4EQZCZA6UfQRBk5kDpRxAEmTlQ+hEEQWYOlH4EQZCZA6UfQRBk5kDpRxAEmTlQ+hEE\n",
"QWYOlH4EQZCZA6UfQRBk5kDpRxAEmTlQ+hGkTTDGIod0Z8fzPLmNQdrL5bobgCAF8TxvOBym/TZy\n",
"Xu7U0Ol0Ek+dzYK4XU07UBqpBTygEWkrrusSQsTZ6Iyx4XAYaKJpmlPZscVoV3hUY4ytr6/v7OzI\n",
"bRXSRtDqR1qMruuGYYifKaXBz9NKr9crbPIDgK7rmqZ5noeGP4K+fqSt2LYtTP44EcOWUrq+vv7i\n",
"iy8uLS2tr69HfOW9Xs80TUppp9O5dOlSp9MRH7744otra2uMMVGCaZqmaQLAcDg0TfPSpUtra2uu\n",
"63LO4w0Q9vXS0pKocTgclvezU0o555ZllanOsiz0+CMAAE8QpP1sbGwYhpH4q36/bxjG5uam+Ofm\n",
"5qZlWY7jBF/Y2dmxbVvTtMFg8OTJE8dxdF23bVt8WdM08Z2NjQ1d1x3HsW17Z2cnKFzTtKDwoMCg\n",
"tKD8tOZlR1Qd/zxXdWJQPDw8LNkYpO2g9CPTQJr07+zs6Loe/9wwjI2NjeCfjuN0u92gqPCfhIs1\n",
"DCMuvvGqu91ueGh58uTJ4eFhomrnwjCMSLHFqgOA8LUjswk6fJBpxvM8x3HinzuOE4kOCvuOCCFp\n",
"BcZLMwyDc+77fvCJZVnD4bDX6wWeJUJIv98v0P4wjDFN0+Kf563OMAzhxUJmGZR+ZJoRTvBLMUzT\n",
"DIt1dhLFlxASLk24gOBsVeDFF1/sdDrFqptYdbHqEtcnkJkCI3yQaUZ47ROXRovh+35cgjnnkQVn\n",
"Qkh4fiBEeXNzc8x8YiKRAaZwdYwxjPBB0OpHphnDMOQGtLiuG/nE8zxN08IiG/+OZVmappV0s+i6\n",
"nmit56qOcx4fqJAZBKUfmWYMw9A0TcRrhvE8r9frFSvQNE2xTsAYc13X87yIY50xFhlvfN9PnC7k\n",
"rToxhUOu6obDoYjuL9MSZApAhw/SbtbX14Ul6/u+iLt3HCe8t6vf77uuu7a2Jj7knDPGdF0P9ka5\n",
"rjscDimltm0LT4hYIRgMBuILpml2u11hKYsw0CBwXkQKRfwqwjMT1Oj7PmNMhIGWuVJRWnznWq7q\n",
"KKUS3V9Ie8FEDshMIBRf/Fx4069pmtmTKAQ1BtkmyjMmkUOW6sQIsbOzU2bJAZkOUPoRJCu5pL8i\n",
"XnzxRbFJrcDfdjodse4tvVVI60BfP4K0icANVQBN01D3EQFa/QgymUiCaMuyUEORVoPSjyAIMnOg\n",
"wwdBEGTmQOlHEASZOVD6EQRBZo7/H3fGpXyyo6mlAAAAAElFTkSuQmCC\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1/rOTWded5X/943eqW+j22ZKslNdoC38qGDceQxQdb\n",
"DW3gUUBOMBAEzKLNSntkIf6LJcNjrJNJcAkbEPavASte/9A/65AWMMg6Mw6KQIAdT2AY5NhRAowd\n",
"pyjJO17EWLloKeOs9MYyaY+62+p+bXP/OK/ZfCSLdW8VybpknQ/6j+p6py7PvYc8vPzy/thIkoQg\n",
"CIIg68SRVTuAIAiCtA2mfgRBkLUDUz+CIMjagakfQRBk7cDUjyAIsnZg6kcQBFk7MPUjCIKsHZj6\n",
"EQRB1g5M/QiCIGsHpn4EQZC1A1M/giDI2oGpH0EQZO3A1I8gCLJ2YOpHEARZOzD1IwiCrB2Y+hEE\n",
"QdYOTP0IgiBrB6Z+BEGQtQNTP4IgyNqBqR9BEGTtwNSPIAiydmDqRxAEWTsw9SMIgqwdx1btAIJ0\n",
"BtM0CSGqqqqqumpfWNE0TVEUy7JW7QgiFtjrXzviOB4Ohzs7OxsbG4PBwPf90Wi0aqeICD7MRVXV\n",
"OI5932+i8MFgoGUYDAamaYZh2MSxEGQjSZJV+4C0RxzHu7u7lFLDMAghYRiapun7fhRFq3VM0zTP\n",
"81brAwvQ8W+iE+37vuu6hBBd1+GbMAwdxzEMA4K1GEEQSJIky3I9XiJ9AQWf9cJxHF3X01Qiy/J4\n",
"PN7Z2VmtVwghRFVVeJ7Iqkm6ru/u7uq6LknSYsUqilKPf0i/QMFnvYjjuJgLKKXpZ9/3QXAghLiu\n",
"q2naxsbG7u6uaZpxHOd+6Pv+YDDY2dk5e/YsaEezDmqaZraoIAhS4+FwqGlaEARZuWM4HBbLGY1G\n",
"8NcgCFL3NE2DzjKvVyxAUWfPnt3Z2RkOh8UWqP2IOSRJ0nUd6ktutZXjOKkBfAPxyhKGYaogwZNK\n",
"KUEQQAXBc9d1s4Wzm8VxPBqNoBFSITFXiOM44DyUlp4MxcNVnzApzTX7WpAg68R4PNZ1vcJgOp16\n",
"nqcoCohC0+kUvrdtW5blyWSSWtq2rapq+s1kMtF1nVKaKzCKIkVRbNuOogj+a9u2JEmpped5cEQv\n",
"Q/ZAKZPJBCzH47FhGJTS6XQ6nU51Xc/6yeIVC7ZtK4qSFgUlU0pzpdV4xGLhSZIYhpEW7nkeVDz9\n",
"K7RJ6YUMLWlZlqqqpYebTqfw2Jf+1zCMojGL2WQysSwr9XM6nUJAc+XAD9PzKoqiXHUShhMGqLHZ\n",
"1xNM/WuHZVmQ2W3bLs2wSZLA9Zn70vO89IKHa7v0h7kLvvhNkiS2beeu0lnpqfQQkiTZtl38E7tX\n",
"c4GiIPukTCYTQkjW8xqPmJSl/mLiLr09VPThslHLYVlWMe0W485olmM8Hhf9pJTmmiuKIkmSst+w\n",
"nDD1Nvt6goLP2kEpnUwmMFjFcZydnZ3SZ/ysCgTAT2DMieM4RQP4VVZ+CcMwjuPiUEhd19OXmQtg\n",
"WVbpm09Gr1iA96s5hV1RlNxxazwikKpYmqbt7OyEYTgejxcohwVd113XHY1GqVQC99TFzAgh/i3g\n",
"3XLpQXMngyRJWRmN8YSpvdnXEHzNu6akg9PjOIah37l3AKVjQiRJCsNQluUgCGYNx8xet2EYlg6B\n",
"lyRpmdePs8arMHrFQhAEszxv6Ijpr9Ic1/TsAVDwHMeBzA7BopTmmpfFzHVd0zQVRYEv4zie1YDV\n",
"MJ4wtTf7GoKpf71wXTfX3ZYkSVVV13VzuRhSfO7n6Vti6P+y9NzbHJnO7hVLUS0fEYBw1FUay+Gy\n",
"3Wd45phMJrk7XLVZGIaj0Sj3K+j+L+ASywlTe7OvISj4rBez+krFx/Pi0AvHcWRZBktVVUtlohyq\n",
"qgZBUDowpolbAqNXLCiKUiod5L6s8YgLM2vc0VyKIdZ1HR7puMxKxbHFvGI8YURo9q6DqX+9CIIg\n",
"dyUHQVB8FCCEqKqajpuEXzmOkyq8qqrKslwcguk4Tu7uQikdDAa5i3k0GuV+G4Zh7mbg+z7v7YHd\n",
"q7noug4zqrJfDofDXIKr8YiMKIqSbRYYxLlYUUEQ5CoIUcg97c01K94tRqNRxYjSalhOmPabvX/g\n",
"bN71AmR93/dBVQjDMAiC8Xic0zdgbi3ML4VEA2N+cokPZgKn7wyCIIDlYnJmcEHCyBxYCEFV1ZwZ\n",
"iMVwByq1CcMQLvUgCNKHD0IIpTSnkDB6NRcYXZ5q1r7vG4YRhqHrurIsZ+ce13JETdOgqSGlViy8\n",
"MxwOwzCEe0Acx5Zl7e7uqqoKA3DT0tJagDH8NzuhbzAYyLKcOxlg0GT2cCxmqUvQUPAmaTgcyrKc\n",
"ejUcDkECguG54BuMx885z3LC1NXsawum/nUErhMy+3Ur+7IKaVFk3hu2VPmdZcZeVI1ezSV9HKku\n",
"p8YjsgCqyJJvy4G5JwOjWdpQiqLUknznnjCk9WbvE5j6kRK6sqIOgiCLgVo/giDI2oG9fuQQMHw7\n",
"/W9WGkYQpDdg6kcQBFk7UPBBEARZOzD1IwiCrB2Y+hEEQdYOTP0IgiBrB6Z+BEGQtQNTP4IgyNqB\n",
"qR9BEGTtWOvUHwRBbsVBBEGQdWBNp3TFcQzLChJCGt0DD0EQREDWNPWbppnuUAjbCc1aIBdBEKR/\n",
"rKngk904FDYGWq0/CIIgbbKmqT+34Dju7YAgyFqxjqm/2Mcv7j+OIAjSY9Yx9SMIgqw565j6i9vL\n",
"8W7/jSAI0mnWMfWTguYTx/GqPEEQBGmfTqZ+13VHo1GFge/7g8FA0zTTNEvTuqIo6abPvu8vv7c1\n",
"giBIh+jSuH7f9x3HCcNQluU4jmftG+44juM4tm3LsgzbDU4mk5xNbkqXbds4yAdBkPWhS6kfVBro\n",
"sI9Go9LUH8fx7u7uZDJJU7lpmrIsl24wmxbYpNcIgiDikXQQz/NUVS39k23blNLsN9PpVFGUug79\n",
"0Y9+dNURQxCkn2xsbNSVqeZybNWVrZkwDHO9eFCH6ir/xz/+8ebm5h/8wR+wGH/jG9+49957P/Sh\n",
"DzEaf+ADH3jXu97FYvznf/7nv/3bv81o/Kd/+qfPPPMMi2Vzxq+99to3v/lNduO//du//fjHP85i\n",
"/P3vf39vb+/JJ59kMeaKSHON/Gd/9me///u/z2gsSPj6HZHmjNljHQTBd77zHcZia6C1m0yNVPT6\n",
"dV33PC/35SzjBbh48eKZM2cYjZ955pmvfe1r7MZFz2dx+fJlduNHHnmE0bI5Y8/zuIwvX77MaPy1\n",
"r33tmWeeYTTmikhzjfzYY4+xGwsSvn5HpDlj9lhTSo8dO8Ze8pJ0coRPBU0P0zx58uTGxgaj8dbW\n",
"1rlz59iN2d1g7PgAZ8+e7ZwxewXPnTvH3nRcEWmuke+4446GSsaIpAjSblyxPnKkvYTct9TfNFeu\n",
"XPnNb37DaLy3t/fKK6+wG7O78YMf/IDd+J/+6Z86Z8xewVdeeYW96bgi0lwjv/XWWw2VjBFJEaTd\n",
"uGL961//mt14Sfqm9Tc9XOfYsWPsvf5PfOIT7N2fT3ziEx/4wAcYjZ966in2mn76059mtCScnRT2\n",
"khVF4TJ+6qmnGI0vXrz4vve9j9H45MmTd911F6Nxc4382c9+lt1YkPA1FBGua2R7e5vRknC2W3PG\n",
"XLFmzy010Jq0VCMVWj+l1LKs3JeSJNV16Mcff3xra6uu0gSkxvciAkIpZReLuwiGr7tQSjc3N1s7\n",
"XN8EH13X02m6gOu6uq7XVT6X4MO1ASTXngGO4zRkzPUw25wb7MZcjcwlLzRXu+ZiLUL4eE97dmMu\n",
"wUeEk5NwxrpNwadvqR+e0NPYxHE8Go1K53MhCIKsLV2azTsajaBHH8dxdvx+blpvHMeapimKIkmS\n",
"7/uGYdSY+n/nd37nxRdf/MUvflFXgaKhadqsFTJ6QHZjzl6C4esupml+6Utfun79ekvHa01aapnJ\n",
"ZOJ5XhRF9Rb75JNPnj9/ntF4Op1Op1N2Y3Y3uBTPfhvzNjK7cXO163esuxgREWJNKWWfM7Q8fRvh\n",
"k9LQUJ8bN26wa/1ckwy4jLk2GOi3cRcbWRA3MCItGHNVsE2tv0uCjwh87GMf+973vveTn/xk1Y4g\n",
"CNIrTNN8/vnn33zzzXYO17fXvE1z9erVmzdvMhqHYcjeQeDqSuRGMa2zMW8jsxs3V7t+x7qLEREk\n",
"1vv7++zGS4Kpn48rV65g6hfKuIuJpt+x7mJEBIl1m6kfBR8+UPBBEKQJUPARmv39fa7XvOwveXr/\n",
"vqu5l4pcjcxuLMirPxEamcu4ixERJNY4pUtcoii6ceMGo3H1TEXfJ9lTSJDZvJ0zbm7uqCAzPEVo\n",
"ZC7jLkZEkFi3N6gfBR9eahR8TJOoKunp9BQEQfhAwUdoUPARzbiL8kK/Y93FiAgSaxR8xKVGwado\n",
"zO6GIA+zIhh3UV7od6y7GBFBYt2m4NPbhRwa4tKlSxcuXGA0jqKoYiUJSpPshHCuNSe4VgLot3F1\n",
"Iy9j3Fzt+h3rLkZEhFhTSre3t9lLXhLU+vlArR9BkCZArV9o9vb23n77bUZj3/fZZ39wzRMxTRON\n",
"Ad5GZjdurnb9jnUXIyJIrK9du8ZuvCytPV/0gxoFH8NIKD1kzO6GIA+zIhh3UV7od6y7GBERYo2C\n",
"j9DUK/gQQixr+ZIQBOk8KPgIDQo+ohl3UV7od6y7GBFBYt2m4NPb9fob4s477zx2jLXRZFlmL5nL\n",
"mGujon4bd7GRBXEDI9KCMVcFjx8/zm68JCj48IGCD4IgTYCCj9DEcYxTuoQy7uIEon7HuosRESTW\n",
"7GLy8qDgw8fm5uaRI6z3S0mSqg2yc7znGmdp7pm6c8Zc7SZIIwviBkakBWOuCh49epTdeElQ8OGj\n",
"RsFnOCSShIIPgiCEoOAjODUKPrneQL9FgOaMuygv9DvWXYyIILFuU/DB1I8gCLJ2oODDB47wQRCk\n",
"CVDwEZqrV6/ituxCGXdxE/B+x7qLEREk1m1uy44jfPi4ceMG11Yt7CX3e/uO5oy72MiCuIERacFY\n",
"2K1aUPDho17BJ46JbS9fEoIgnQcFH6GpS/AJAiJJhwb59FsEaM64i/JCv2PdxYgIEus2BZ+1Tv2+\n",
"73MFhhBy5cqVWlJ/HBNFyRuzuyHIaS2CcRcTTb9j3cWICBLrNlM/t+ATxzEMxY3jWFVVWZa55rYJ\n",
"QhAEw+EQlmEKw9C2bcZJd3UJPnDy+D6O8EEQhBCRBR/HcXZ3d8+ePatpmu/7QRBomrazs7O7u+s4\n",
"DtfbjNUSx/FoNJpMJpZlWZZFKR2NRoy/3d/f53rNy94svX/f1dxLRa5GZjcW5NWfCI3MZdzFiAgS\n",
"6zZf8zKlfsdxdnZ2XNc1DAN2qPE8z/O8JEmm06lhGK7r7uzscE1yWyFxHFNK0/8qOeWlkiiKcPk2\n",
"oYy7OHe037HuYkQEifX169fZjZdkvuDjOI7rupZlVafIMAxHo5Esy9ms2gnCMDRNczwesxjXLvhQ\n",
"ml/RAUGQNUQ4wccwDM/z5naNZVm2bbtzeT+O4+FwaDMPsaxX8FEUkvYJ+i0CNGfcRXmh37HuYkQE\n",
"ibVwgk/nME1TK1DcVi2O48FgYFkW+8KqdQk+xcGd/RYBmjPuorzQ71h3MSKCxLpNwYe0tgG8aERR\n",
"pKrqZDLh+tWlS5cuXLjAfogoikr/RGmSJInnJZ5325jdDXjjgsZJZSMvadxc7fod6y5GRIRYU0q3\n",
"t7fZS14SvsGdvu93dDRnjiAIHMcxDIPrHS+pT+s3TWJZB4o/z06fCIL0E+G0/iyj0Yh3DtRiuK5b\n",
"PeDS9/3BYAAyDu+40iAITNPMvrguakGz2NvbY19T2/d99tkfXPNE2B3mNf7kJ/9EBDfYjXkbmd24\n",
"udoJEmuMSAvGXLG+du0au/GycD0jVG9FryiKl+oXC+F5nq7riqLouq6q6iwz27YVRZlMJlEUQQbn\n",
"OgqlVFEUNYMkSYy/7b3g88wzsQhu9FteECTWGJEWjIUVfLi1fsMwKKVQnyiKKKUU0liSTKfTJbP/\n",
"ZDIB8d3zvFmpP4oiWZazDUoptW174YNycfny5QcffHD5ctLU35bjrMy+4SII0iCU0rvvvru1w/Gl\n",
"/myiT9F1fTwew+fJZKLr+vJuVaR+GEKa/QZuOcsflIXHH398I8ORI0dUVd3c3Nza2oKnhw9/+MNJ\n",
"knz4wx9+xzve4Xnee9/73ne84x1Jkjz77LMnTpxIP0ANTpw48dhjfwMfnn766SRJ3vGOd0AJ6Qco\n",
"Kvvh2WefPXbsWLZMKOHZZ5/NfkhLOHXqVEVRWa+SJNnefrOiqJxXlNKKonJePfbYY01U0PO87e1t\n",
"xgrCVETGCp46daq6rbIlHDt2rLqtsh+efvrp6rbKFkUprW6rw+cVrT4ZWqggnPa5ouBDzqsTJ068\n",
"973v9TwvW2augh/+8IfTErJnRbGonFenTp2qKCrnFaW0oqicV3Das1cwV9Tm5qaqqltbW5ubm6dO\n",
"ndo4TNIWfKlfUZTi80su3VcINexUpH5KaXqnSZFlefmDsvDkk0+eP3+e0Xg6nc56NjSMgw/pXYzr\n",
"KZLr0YrLmEsCbM4NduOKRl7SuLnaCRJrjEgLxuy1o5SeOXOGveQl4Uv9s94NZNN006lf1/Vi09dy\n",
"UBbqFXyyHwRhjYf79gHR9EOEnZYFH74RPqqqFkf4uK7b5nDP1a4TF8dxv9fwIYSwN7AIs2a6OIGo\n",
"uVh/+cs/bajkfkdEkFizjx5cHr7UbxhGbmATrIKp63r6jdXrZYg3NzePHGFtNEmS2OcJs1sSQrju\n",
"tezGQUAeeeTn7OdqQ25wGfM2Mrtxc7VrLtZ33HFHQyX3OyKCxPro0aPsxkvCtzevruuwVrNhGJIk\n",
"Qd43DCM76JN3khQvTZdfzenTp48dY2205s6n6lG2CxvHMdG0u1fuBpdx5xq5UTc2NlYfvi5GRJBY\n",
"Hz9+nN14SbjX8IEF7oMgGI1GQRCMx2PDMJrwrILiMxTXU9Uy1C74pOqKIILPD37wsghu9FteaC7W\n",
"XNcBRqQFY2EFH75ePwDToGp3hRFd103TzC4R6rpuVnHqFrhiM4IgK6C1F8pcVIzwSZJEVdV0DlcU\n",
"RTCztx3H0hE+hfGlfBQHd4oApYltL1s1ZFVMpzhAq8MIPcKnaUajUbrAMrxUAHJm4/HYcZzhcAiL\n",
"My+wCtvCXL16FbZld5z5I2EqtpwudvYF2ar7ne/8a/YnVBF2vu7iJuANxToMySOP/LyJkjnd6F5E\n",
"BIl1m9uyLyL4OI4Diy7JsqyqKqWU6y12BTBbeK6ZJEmTyQS2hq/x6CzcuHEj3aolCOYsusk1DlWQ\n",
"7Tv++3//fwn5Zyt3g2tjEPZiBWnk5tzY2PhlENzN2BHCiLRgLOxWLYus4aPrejpFDVZS41qOqtOk\n",
"gg+lS2k1Yk7pAmeEcglhx/MSSpPlVlBEVobQgo/jOHEcj8fjdMSSYRiWZQ0GgwbuSiKSCj4s8D75\n",
"srshyMOsCMZdlBeai/Vrr73aUMn9joggsW5T8OFL/b7vF2dsqaoax3E76/ivnCtXrqSpfxmtv9SY\n",
"3Q1BTmsRjLuYaJqL9auvvtpQyf2OiCCxbjP18wk+s9a1p5QuuVJ/V8gKPradLDywCAUfpHZwgFan\n",
"EVrw6cHWjEuyv7+fvuZVVVJ9+4/juPQlj++TYkP2/n1Xcy8V2ZuOy1iQV39cJX/oQ6+yD9DCiLRg\n",
"LOxrXr7UryhK6Uw23/dXOMmrTaIoSmfzyjKpPgcqZioWU78gs3k7Z9zFuaPNxfov/uJPGyq53xER\n",
"JNbXr19nN14WrmeE6XQqy3Ju/hTs21Xrs4i4ZAWfZFFtJLsvo1Ath4JPp8HwdRrRBZ/xeAxzqWDn\n",
"9J2dHUmS+r1aZ5as4EMIkaSqjj/vky+7G4I8zLZmXCGsdVFe6HesuxgRQWItruBDbu29rigKPMh4\n",
"nrc+eZ8cFnzIPLmf5WFWkg6W3Fq54APnsyCPyVlj31+2kRczFkQEYC85jmH4df0lcxl3MSKCxFpc\n",
"wQe5dOnShQsXksxjdboaT5Eoikonu2UFn/Qz17Q4rh3+GI3Bk+l0yq4YNOFG0RhmKs1iViMvb9xc\n",
"7RqKNaVChK+LEREh1pTS7e1t9pKXZJGFHNaZ48ePc23Vwl6yCFu1dNG4i40siBsYkRaMhd2qpZ7l\n",
"23i3AOwue3t7b7/9dhDcXn9NVYnrlhvDSkdl35eM8OGaJ5LbK633xhUPzbMaeXnj5mrX71h3MSKC\n",
"xPratWvsxstSy7NDa7uirxwQfLKKTTJ7TMWsh9msvTiCj2Ulk8mBYsDoS2uCT8X51UV5AQWfxYwF\n",
"0XBQ8FlHeiz4xDFRFEKIrCjzFyVtzo2ise+TiqUou9XIQrmBgk8Lxj0XfNYHEHxyX8pyuebD++TL\n",
"7kajD7Ps52prz9QVo1a6KC+IE+smjLsYEUFi3abgM7/X7ziOO0vMvkVrW+OunDvvvLO4Lbuuk9GI\n",
"FPeIZOkdyDJxHKKq/d+fehnjirtRFzcBb9QN9lSD27K3YCzstuzzU38YhqqqVm+DxXUb7DSnT58u\n",
"pn5JIpJEBgNiGId0EsbUz26c0sSZCj1rEXIHl3EXEw2m/sWMRTjfeI2FTf1Mgo+iKGolbe6TtVri\n",
"OM5O6UqhlIzHJAhI9ibIO7eF3Y3ckKrqWTyM468ghmDMOC2otVkzFbOmuziBqNHpe7JcNSBqmZIZ\n",
"LbsYEUFiXRSTmwO1fj42NzePHDkyKzPC5pJpkpIkqfSmWPrzZd53DYccxnNLhte8C7jRnLGizEz9\n",
"sxp5eWNBXv3xuiHLrHfu5l7zdi4igsS6zde88wd3soy+Wp/BnbB8W8Xwxyiqmt8L5IbfVYzGm04T\n",
"VZ2/K4CiLL5zQKkbQi0BBpsOrsd+EIszmSSWlSQJtlVXEW75Npbbsud5Nd2JRCcVfGY1iSQRWT5Y\n",
"c2Z5wcdxiGWR0SjfDS/qIRUdPUGefFFeyLpRe8kwNhcjIpoxV6yvXbvIbrwkKPjUD6VkNCpZcSwM\n",
"yxN05dqfRFHIeExct0Lsnr9pTNdRlJ5XsF54FotEBOLXv368vYO19nzRD1LBZy6UJjldyLISXT/4\n",
"U5bxODGMEgVpMkls++BzFM0UYcbjxPPmq0yzKN05QDTBJxHMJQERdhMIhJHPfOZ/u+OOL7d2OOz1\n",
"83H16tV0W/ZqLIu8//2vW9bP02/CkBgGKY6D1XVCKfn4x6/k+vWOc3uuAOhLqUF2ngj0+rMClOMc\n",
"6veVTioJQ2KaZDgkYUgGg/KS5yKCcRc3AW9uW3YRjLsYERFi/cYbD2xsvMhe8pJg6ufjxo0b2a1a\n",
"qnnve/+/F188aOEwJLJ8MOq/eDLIMhkOf5KTEGG6QAqlt28b1eeT7x8a85MzDkMyHJLRiBgGsW1i\n",
"GMSyyHB4sFiCIBtcFI1niRhd3Bikia1awEqE8HUxIoLEOkkiduNlmftcMJlMPLYRA+yW3YVd8AFs\n",
"++Ax3LKSdNGn8bjcOCsQ2XaJGYx1KX6ZFOSaijXuDSMpLj8VRYcUJ6EUAxR8WBBWr0MYuXz5q2fO\n",
"/C+tHY6p12+apqZpFY85vu8PBoPBYND7uV0g+DDeyMMw/NCHXoVmg14/UFzygRzMmj5YCyiOie+X\n",
"mFF6YFCMRfoiFBY7AwlolnFxXHL6hFH9MJsbayTCM3UX5YWmBR/G8xMj0oIxV6zF2qBRUZTJZKLr\n",
"+nA43NnZSTfmdV3XNM30S1VVp9Np9XoPPeDKlSs3b95kvMGFYfjmmz8mhARBSbYtGqcDdUajg9lh\n",
"OSQJBvDdPvnC8CBlp/Ndff9AVqL0IE1nz9TsHaiUitM6jkkYkiAgg8HMm8piJS9jvKpEk1PnhEr9\n",
"jOdnzyIipjF77V599X/6zW/+nr3kZeF6RhiPx5RSWMJClmVVVSml41n6RR/hFXySJJlMEkUp0VhK\n",
"se2E0oO5ObPIDgcqjuvIDvUpDvthnO9TWkHbvj1xLKsaUXp7JFLteN6B8CWaiLHwkKqGEFbwyWmJ\n",
"yCweffQ7Yk3pyqLrumVZIOhPp1PYk10v1S86wmAwOHv2LLv9/v4++2teeIWlKERR5vf64XWQYZA4\n",
"Lu/ypxgG+exnfwGfi2vZZ3t8MNUr2++oXvueVHZSwvD2by2LmCYJw9A0ia6TIKianTC35Grj6j7s\n",
"ql4qhuGhqQYrf80rjnGukU0z/4RUYVyXD+IYc8VaLMGnxziOM3dR0hxRFJUu31ZKOlPRtpmM4cNc\n",
"Y0UhL7/8cqq5ZzNjTlkCBak49beCWTMVcyewJBHDIIqyBTc2uBNUg3NHs27UXjIESITV97KNDIJk\n",
"RXUFiYggsb5+/Tq78bK09nwhGlEUGYaRcC5AtIDg0xCGcaAOpYDwklvMh329oGqzYslJckjFmkwa\n",
"0RlSharUgRUiy2ItlSOm4KPrSRQJFzsxEVrw6ROj0cgwDN5fLSD4sBuzuxGGoW2XaCyles5iD7M5\n",
"d4KgVCm6XbKiHLwHzhRFHIcMh8Q0iWkSSn9e/P1cN1JmLUi5KsFH11HwKSdtZDgbJYno+kzNBwWf\n",
"LCj4NA4Eb4HxSIsJPozG7G7AI6dlHXoroKrlyTF9PmUZaATGjOs25558Lev2Fe77xDSJLBPbJpZF\n",
"LIv8zd/8V/arIC3Z9+f4jIKPaMZpI/v+wfmZm5xYalyvD+IYCyv49HNbdtM0iy2uKIplWamBzSLA\n",
"Fzh79uzm5iZjCuO6tXAZp88r2StKlkumAigKuX79f4XPc0d2piXnLlTXLd+lPffYBL8KAiJJxHHI\n",
"eHzI2LJk02R67ZErOfW5tLPVQiMXKXrC9QRZlxtiGpfWTlGI65aen51viuGw6qzmquCJEyfYjZel\n",
"NWlJHCaTiaIo9BayLFvVoykziKP1M5Jd943d7XTx9/SHjOPzoijR9QOFt0jpROJqxJSw4Q2EOP4k\n",
"hweblk4Fb59c+4g2HLYu6kqiDz/8PdT6mwVyfXZ3SfbNNvf29tg3UfN9n332B9c8EfbNkCWJfOtb\n",
"fwefWR5WoGQQ7nPlsLgBwi6lJfamaWYVIRY3WOBtZBZj6NRz7TjNZdxErKHBwRiG25omGY1qKJnX\n",
"2D+gathx+tsQ9wAAIABJREFUzrh2H1ozniuistfu5MlfXbt2jd2NZWntJsPFeDyu7ol7nqfrOswp\n",
"m7uJWDVcI3wuXbp04cIFxu4eywZnWWN2N6Y8nednnolhyhWL22nJLN1tLjfAeFZRudqzu8HbyCzG\n",
"cEZU1A6GrGT94WqKJmINzuSMLauq+79A+FiARoa1xIselhqXHW4pH1ozhhXXK8Yvscf60Ue/s729\n",
"ze7GkojV64e1gHZ3d13XrbhbOo5jmiZMJJYkSdO0xQ7nuq6maUEQDKs3t81w/PjxI0dYG413k1JG\n",
"S8K5O+hXvrIty4SxkbIlQ8c/XStiSTfAuHTTFcfJ90/Tkuc+qdS+E2zqXkXtsrPb5hqXusFuXF1y\n",
"rreaM4ZFn2a1YaN788Ja4ozGxe9Lr0hBttvNGkM1K85SYffmFSv1S5JEKZ1MJhVvXeI4Ho1Gnucp\n",
"igL2qqpyvXNP0XXd87woithf+XZO8AFjVSWeR1heZaUlp4N8KiYAL/CYXNxL0nHy+5fFMfnkJ/8E\n",
"Ps+9cGoXfFJnxBd8HIf4/qGmKxrbdnkarS55GWNoZPYl5IqtEcflA8wEFHzIvOFwUDvXnTNkzvfJ\n",
"9naEgk/ied4sHca2bXr40RGWjWvFr+TJJ5/c2NjY2LCOHDmysbFx/PhxVVVPnTp1zz33qKp6/vz5\n",
"J554IkmSJ554Qpbl6XT6+OOPy7KcJMlzzz131113ZT8kSXLXXXc999xz8OHZZ59NkkSWZSgh/QBF\n",
"ZT8899xzp06dqigKPqQl3HfffRVF5bzyPA9KiKLkxIkvPvfcc5TO9MrzvIqicl596lOfghJ2dty0\n",
"qPE4uXDhm7IsU3rbq0996i+PH//foagTJ76YFqWqf1+s4HQ6vXDhAmMFp9PpdDqtaCtwj9Lkn//z\n",
"37vvvvtmFQVeUXq7hFOnThWLmuXVs88+W91Wzz333Hic3Hvvp5544gnP82YVZRjJH/3R10+e/HSS\n",
"JKr693fddRcsspIryrKSCxc+UvSqooJFr9grCKc9NFG2zJMnP/1Hf/T1nHuPP/74dDrNlinLsucl\n",
"99zz0oMPPgxlpiVkT/tcBO+6666cV/fdd1+u2bNFZT8899xz6WlfWhR4lTvtoQRodkpnevX4448n\n",
"SbK9/ZX77vtbKOrUqVOqqt5zzz2nTp3a2tra2NjY2Ng4ckTb2FA3NjaKOachupf6SxeMg8C0wOXL\n",
"l8+f/22hhnY0R0ML5ZfK99kvx+ODnSyLxvCvrtXiJpMSlZbSpKhTF22SZL7ZMkBNK0i3gjCM24vc\n",
"lcK4Zl963FpYeOnAJElsO7EssSZLz6K4ZuIss+rp7p6XXL78VRzhU0UYhkX5jEuqW4Y4jt9++37G\n",
"AUFNT+nqq3EQkLfeern4PaUHs8Oyw+qXmdLluuVP4qBKzXX48KaYbU/pSsV0WK8bnCk1luVytaFo\n",
"HMdkNJozMXAuQRD89V+/zChxl4YvDA8GKS3sQ2oMG5EyGnOVTDIvoioqC7WL44OJzbDa+SzYxeTl\n",
"6V7q55oYXTubm5sbGxuMxoK85l3YGM7Uil/X6EYuPR09eg98yEa7tIUkSTp69G5GH3IRgUVSTTOf\n",
"ZVQVBu011cilsfb923nBcW6/X4GSg+CQk9l9mw1jzqvpWWtgFI1HI2Lb5fcJrte8P/3pvcXuUekd\n",
"aNY1UurzAhFhTOmLxZrlVTbUDqqYbqFRBLT+9X3NKz6nT59mDw9IhOzG7G6wT0RYxhi2hamYjbhY\n",
"ydldZTIJ7tCl/v73n0+Ni2STSBDI3//+g4w+5CICCwyMx7cTRDpMO45vOzwYlJeWHa3E1RSlsYb+\n",
"KTRCEBBdPygfSoYHlJRs0pHl249BS54YcTzzPsFesizL167dVwzcrGzOfua3c9oXyb2HTo1ZVkZh\n",
"r93WVnT8+HFG4+XpXupf7UZgcRzfvHmT0bjrgg90fivae7GSFeUgVWULz3UJ47hqFEy6nRkh5C/+\n",
"4mff/e4bjD78+3//D//xP/7X3JdwA0hHssKlKkkHDueG0OR+mJJriuGwagOD0liHIfG8A70FSi5d\n",
"c7sUw6gSfGaRM3ZdAktwM6pDswiC4LvffYPxMq19DZ84PlB4HMep7riwl5wbeZwVfNKzZVa4U8GH\n",
"BRR85lA8V7jyJsLOQgsdzUGWDxJ3euWQQpfw9OnrFVdLahzH5MyZqsUOc4uJ+r70/e+fgc+w1hCg\n",
"6wd96uKtLmsGVEx0yFKt6pYCrTEaHYg56VGgdynLB2UWl1QyDNYcV4Hv376FrJDcMN8KcmOCgVt5\n",
"n5DDD0/LMPfnaW9mFmmrpif/yule6td1PdchdF23tZ3CJEk6dox1zTtFUdifUcRcx6q6XRcredYT\n",
"cJrNCSFf/OITbEuHkn/9r8/de++5WQZBcEjtvffeczdvvgs+Z6dlZS/d9CoFh7P3p+IPU4or2VXk\n",
"gopYgxyc/bthGKDsp8tEQ0YrZVZESv0pXX1vFlzLt1VEpGgMrZFe06mWBQ+dFT6MRmQ0gt3ibn+j\n",
"qulAAAMCx7IMbeVEovnGFeHOxTqrzhWPcvLkyTmO1kf3Uj80ZeaZK15s5f3FuHr1Kvua2rz7U7O7\n",
"IciW0/Uapwt/quqBccWKzSAQhSGRpPDMmZ+l1zbMcsqSvez/8R//xy9/+Yv0+4q7rSSRr3zl79L/\n",
"zn1gz9YOjGdd5KQy1pJEPO/2f2WZfP7zL5LKdY9nuZGltFuaNZ579nFty542MotxGIawxHfqCdS0\n",
"+Fo46wM8CVkWMYyDbSEch8TxwU3Rssh/+A97kBUqAlFacg640WY9KRpX9PpzOUBVyy2hyvv7+3Mc\n",
"rY9FUr/v+8PhMF0+YTQa1TXqZjQaaZqmaRqsuqzdImc2Ho8dxxkOh6ZpappmGEZrLwBu3Ljx9tv/\n",
"M+Obm0a3aum0cRyXTBLO9vpT41lNrarEcUD5id/1rjezfcbsVZqVa4KAyHL89ttvpwfKLXmdvaIV\n",
"hbzyypvgRa77WSr4ZGsHd69URCoCsc49kcyq5r/7d+9M5R1FIcNh1avFWREpHV2TNQ7D2yJS6ZnI\n",
"Husf/vAqi2YN77ThGnFdYhgHHqYPVcXXwlkf4CdgZlkHymR2+4p/9a/+rzRMc++aFbUrvvoG41y/\n",
"JDXIvRiI4zjbttW0uVUL95Qu27ZVVR2Px+lvbds2VrEe62QygWUY2jzo5cuXt7b+jzaP2EsoTSwr\n",
"v0RXbgYZzFSqmNcjy7cXfctODStuWgmFwBHT2U+5+TWw3HS6ZuB0erD2GfiQnTA1d0W5tGrVl0V2\n",
"2efs2to5shPVoyiRJNYFtHNUz9XKNvWSs7oqopYtWdcP/ut5iW3fbgG2dQP5nFymRpSW1yg3oQ8O\n",
"YdtJcXZp7uelzlCaUErFndLl+77rurBqZvqlYRgrecuqKAosudzmQa9evZokCaMxCj6zjGHjjlzv\n",
"NSuY+r4/N7C2DT+53cgwRiVH2mcPQ0JIKMth6dkKg3yyI45efvlV6L+ziMU5wQeqNktqSB3ODFGd\n",
"qT793u+9mHUSas3ixlxmGZc+IrCX/MYbr7/xxuvVNtBEskz+7b/92Ze+dGXW6+Vcrz/1wXHmL0iV\n",
"dXjWpLZS4yI5KR+MSwf1B0F+8D5PDhBY8HEcJ93oKouiKFznXHe5cuUK+968mPpnGZcq11nB1Pf9\n",
"uWMh4MLLNrLvl7z/TJ/Ws/eJ4rgdQoiuH7ob/ehHe6m3FUDhpU0xS/MBH3IDVGYd5ec/P7TbWfWL\n",
"94Ujkj37Sgfgs5f8+uuvv/56eepPUzDkTcMg/+W/XH/Pe/4b/FWSSBDk2yT731w2rybX1WBJ/bCb\n",
"dLHuOSl/VlOAhpkLOpxx2ZtExX1I3NTv+36pqt5y13uF3HvvvexTumArGHZjdjdKb8AdMgYpPEe2\n",
"b2VZFlwhc69waGQYwFc8DdPL+JZqfxCRGaN0Dh3ud3/3w3Pfv6Q5JVu79FfV06NguYLi7LYctUck\n",
"namQNc6mp9LcxO7GBz/4yAc/+Ejpn9IGSd+X/Kf/dP6LX3wv/BV2b88GUVUPpVHwofTZrkjW4bmD\n",
"L8EYWsY056z9MKsp4PVD7nZVvK4rXjufOnWq6sC1wpf61yfFz2J/f59Z78HXvFXGxQf27PUZhiFk\n",
"87mpHxoZJh4XjdOxIo4D66rfNp57q/3lL38xN8WkF0Rau9zb49KoprEuHVSao8aIwHMGjIeJ46p3\n",
"wkW32d24cuWtK1femufnQfrOXiNwy8m2eXbuXupDxdjWxRzOlkxpKiTylayqhyappCbFHFDxCNLm\n",
"a16+1K8oSqmsP+tpoH9EUfSb37CGp+uzeds3Ti8Yx3G41v+CrDErI8BwIFU9MJ41wC7Hj3703dKT\n",
"Onclw3/T2uWSV2kt0lizzDaqq5Gh1qMRsSxCKRmNmor1X/3VG1eu/N+lf0qfJ9I2zF0juQcvcjj7\n",
"L+lwRVODcRqs9KClnQ/HcYqCoSzf7s1kNZ8gCHKWxVMifbq9fv36TBdrh+ulcHYt5fS3hmHQulZ6\n",
"FR4c4dMoqnpoLATP1pm3B+Fkx9WkJ2a6CnTue0YqhuLk/gt7N7IcKLvebwsX0GRye1BNkiTjcZLd\n",
"ArW6UnO/Z7dZYCXwbEDH48V3nK9eBzsX2XT0EZyQuR/OXa+79CSc9Q0cRegRPqqq6roOGygSQlzX\n",
"HQwGhFOO7DQo+LRpzNLxTxs57fKX/mo8PmTMcsJmHYY3kITAemo5s0PGpW8Rij5nSyaVU8bqamTQ\n",
"GdKK6zr5wQ/+x9wC0x2+oGSW1SmuX3+b67Sfa5zKL2EYMqo9pKwpLIvo+oGUn5ssBNPKihpg6TsY\n",
"cKM6yqniz3Vdiyv4EEIMwxiPx0EQqKoaBIFhGOy7G/YAFHwaNVaUg8sPjMfjOfZkufX6q8k6rCi3\n",
"19Qsrp9jmsuu119xk6uxkbPzhAkhP/nJizMMDwhD4vsH9zzHceDd7FyF6o033qhu5OycOJaIgDzF\n",
"soNCllJjRTnY8iENaGqci2yqTRVDk1OHSkklo9LazXqXIK7gg6DgIz4sc4J4mUwOtgYrnaUFs35K\n",
"j1jhABRl2wf/2qeioShNptODWXWpLgQa0VxX5wo+XLuGAdPpgVq1sNqTo6jY5NyGOX2lu8gV/1sk\n",
"Kx8VjXMtYFmwh5fAgg+CiE8qztS4qQ8MxZm1ZqdlEcc5UBLYt13IrlTT1i5zrKSdVlXNvpIllDK9\n",
"Ia+mYiTrLGSZjMflY4IXY66WyLLyT3X52YVJimQLz84lbA3ucf2macICO/BNGIaapq1256w22dvb\n",
"Y9fjfN9nnwjDNRnHZNl0bj2Mi42cFWdyVxRXRHI+wLpDs1KPLJugJLAsJJj1AYauV2Si5hr5hRf+\n",
"uuKvo9GhJXHSkrPXeukmNj/84U8Zl+oj3NdIbU2R9g+Aj33s+WLyzQYlOxbrk5/8E5a3UGDz/PMv\n",
"Fl8hzBpjdu3atfnl1gT3uH7XdbMb68iyrKoq1wnXac6ePXvkCOuUrh4s2iy+cXUj5y5RroiUrsM8\n",
"69cVqyUXxV5FUbKjA2W5qtPXXCM//PDDs/6kqrcHqsNzSWnJpW99H3roHq7TfuGILGOc0/q3tz9a\n",
"TNCwmy6QPZEee+xpFpfhhHnooYfY/CWEkBMnTrAbLwnr0vOA67qU0lybUkp3d3dr9Upcjh8/zrw1\n",
"L98MOAH35u2EseCNnEsxqRvZZ/zqyWXNNfIHP7hdOqwFSMcCwXOJrsvQeJkOe7lOdeLESUmqWnf+\n",
"8FINQpz2W1vbpQt7lPLDH973xBPzy7w1desudjfE3ZvX9/3STVHWZw2fvb29/f07GY1R8GnBuNjI\n",
"6eI/pSvULyz4kEqBmKt2OR+qR5o218jf+c7z8KH0HUb2oSQMyac+9ZfpWsrZdXiKvPbaqxWNLMuH\n",
"jrVkROoy/ta3/q7aILu4xbe+9XcsNyxYN/Av//JV9iVa2hR8+Hr9QRCU3qXXZ4GHs2fPHjt2hdGY\n",
"S8NBwWcx42K7pb29MMwr78s0siRVdc9ZHI7jgxUrFUUpLly6TMmLGT9xq+/KMhfhwQd/B6oPdwJ4\n",
"moG3wblmOXfunKJszSonl/oFOe0fffQ91QbZxS3mGmc5d27OhmXZDkqbgg/3lK7SN7rr85qXV/Bh\n",
"vykK8uTbOWPeRmY3zvlAaVV+nOVwdv3RdG8WSZLYt+9orpGfeOI+xg63LJPf/GYbPqeLYOdWK0o5\n",
"ceJkRSPnRuksE5G6jIOAPPjgNqNxHJOtLQ7jEyfm7LmYPRPEFXwURXELb3biOPZ9n2vhye4SxzH7\n",
"os04pasF43amdC1snMs/t4YeCRFr12U1VlXyj//4cvabMJz51PLKKz8TOSJF4pjs7f0Vo7Hvkzhm\n",
"VahkmQRBebc4HTKUVdtYdjerC77UTyl1HOfwrhTxYDCg2VFgvWZzc3ODuduPvf4WjFvr9S9vnF43\n",
"osV61nyFFEUh/+bfvJn9JtV5ig/873zn8a5E5NZeC+SRR1g78kFA/sW/YNXJVZX86lflGk5mzdfb\n",
"T5Pi9volSfI8bzQa7e7umqY5GAx2d3d1XW9tV/SVc/r0afbUnx0Fy2LM7gbXM1a/jXkbmd24CYdv\n",
"TeMSK9YsWn+uZJgzkdu1GNja2u5ERLLOf/zjj7GX/C//5T9jtFQUcscd5Uvwl26KcPz4cXY3loR7\n",
"Ni9k//F4rKqqYRjT6XR98j5BwUc8Y8EFnyJh2PlYSxI5Mjtz7O3NWcMniwgRYTSGt/S8JVtWee1K\n",
"N0VoU/DhG+GTwnWv7hMbGxKX4MNesmgiQFeMu9XIMI1TlkWJNftaBdmS3/Me8vLLMy1Pnqx6zZtj\n",
"hRFJN/BhLBmWrlNVQgiHG1wVbFPwWTD1ry3Xr7//5Mn/h9G4uYtWBKVFEOOKdiv2qlbeyLJMXJeo\n",
"qsw+Jq7RRmafTJIt+SMfIR/5yEzLra1tWWaVzlcYkeyRGUu+teo1hxvVFcydBkILPqVwLSneaY4c\n",
"efXo0dkdnsPgtuwtGFc0crG/xRWRJhyGx/wwDNn7giI0cs5Ykma+FvZ9cubMz7hO+9VGBNbOa67d\n",
"qmuXmxYn7rbssximGzr0nWPH/tvGxquMxrhVSwvGvI3Mbtxc7YSKNeMv2EuWpC5FBCbZsRinb8Jr\n",
"jHWupDa3auFer59SWqpeNbGitIBcvnz5wQcfXLUXyBxgl0RBtg1Nt/qDle4pTSaTQ5sjrpBbWwMu\n",
"XkLpXoNdAbZsjCIm4+k0mU7rPLpl5fZxFHi9ftM04zieFhpgTeZzEUKuXr168+ZNRmMUfFowLm1k\n",
"mENbVFlXKy+k/vzDP7zOvn5BC43M0u1mL/mNN17vkOBDDt7fMoUPIliX4JNdCBoQV/Dxfd+yrGKv\n",
"f332aLxx4wb74E4UfFowntXI8CDPaLykD3ONs9u8KAr5z/+ZeTGQhhsZFhZmefHAXvJbb73VIcGn\n",
"aePq2uVO0TYFn42EfZdxQjY2+Oz7x8c+9rHvfe97P/nJT1btCFKF7x+MwxPhcRR6dr5/sEKn7x/s\n",
"giKCb4QQWOCSZZ/6WT/P/jbd26sTwJa/C9d9eYZDknabTdN8/vnn33zzzcpf1AZfr1/X9f4N5uGa\n",
"VLK/v4+9fqGMSxv51lLpTMbL+8BlXLraZftuNGTs++See37ZlV7/Ym9ua+z151bAabPXz72GT+kq\n",
"2IPSjdqEx3VdTdNc13Vdl1G/i6Loxo0bjOXjbN4WjEsbGWbfFAUfQeaO3ncfx7LsTTey7zMJPrNK\n",
"LgrWb775912ZzStJB9m/uUaurl3uFL1+/Tp7yUvCJ+A4jgPVzr3XdV13Op3W7FrDjEajOI4tzoc9\n",
"FHy6wsYGEUSbDAJY7vG2sKBpxPNW6lMGTVtKfcopPDn9B2FHaMHHdV1FUXownicMwyAIePM+QcFH\n",
"PGPxx/UX92gcj/sca/Ej0qYx13UtruCj6zql1CrQuZuB4ziLLTSNgo9oxrMaufSUFETwESrWjCsp\n",
"VJScS26dW1CvUWOuWLcp+KzLVKwcqqpGUaTruqqqqqqOx2PGH+KUrq4gyHwuQNdFmcNVBKaYLVlC\n",
"6WeEi5andNWzfFsYhkIt5GmaZvFmqyhKVuExTdOyLHB7MBgoiiJUFZAlEepBtLhLsDjI8vzF+pH+\n",
"0c81fCzL8gpk874kSbqup7le1/XixpOl7O3tsa+p7fs++8Q/rimCpeOs1tN4ViOXpn6uiNTocG4I\n",
"jVCxZrwnLR+R5Y1FON94jblife0ax9CvJeHu9ZeGqvbB/q7rhmFYIcf7vu84ThzHiqLMWlaoAkVR\n",
"sj9h//nZs2c3NzfZj8LlErsx1/Y4/TbuSiNnb0X9jnVXItKOMVcFT5wo382xEbjkIc/zFEUZj8fw\n",
"Abbrgg+1yE+e5+m6rigKqPCzzGzbVhRlMplEUWRZlqIovAeKosjIrJyk63pxYaJSUOtHFmD2udwH\n",
"UOuvBaGXb3Mcx7ZtXdclSYJRnrqu67rO9VBTgSRJlNLJZFJxX43jeDQawb0H7FVV5XrnTm4JPoPB\n",
"AHYYVlWVUehHwUc0407IC7lRxP2OdSci0pqxsIIPX69fkiT44HkezdzfFUWJGFc+ZcPzvFm9ftu2\n",
"6eGuxXQ6XaDjnyRJFEWe5zH294FLly5duHCBvXz2ZuFqQC6f+23M28jsxs3VrmexzvX6uxgREWJN\n",
"Kd3e3mYveUn4Ur8sy/Ahl/oppXVpPmn5s1I/pbQ4FjN1rGkuX768sbFx7Nixzc3NjY2N06dPq6q6\n",
"tbV1/vx5VVV/67d+C3QkwzAeffTR7Ievf/3rDzzwQPZDkiQPPPDA17/+9eyHRx99FEpIP2BRWJTg\n",
"RT388DfToh544P+89eGBYpm5oh544IFcUY8++mjOq/4VtbW1parq+fPnt7a27rvvvqNHj25sbGxu\n",
"bh45cuTIkSNJW/Clfl3XJ5NJckuUT79vM/Xrul48VsWLgXr53d/93fvvv5/ReDKZTJiHTLNbJkli\n",
"w64faMzfyOzGzdWuZ7HO9fq7GBERYk0pPX36NHvJS8Kn9SuKAtKVqqphGKZzlIMgaG1QPNfE6NqB\n",
"mzOjsSRJ7GOHuAYpNbfhe+eMeRuZ3bi52vU71l2MiCCxPnr0KLvxsnDdKKIoSm9iMLbHtm3DMLKj\n",
"ZWqhotevquoKe/04wgdBcuAIn1oQeoQPDOyBz7qu27YdhiHcABq4K5XDNU62duI4xjV8hDLu4oox\n",
"PYt1bt3mLkZEkFizjx5cnqUWclAUZSWJOAiC3IJxXO27DLyCD3vJ/RYBmjPuYiML4kZdxmltQIvt\n",
"YkQEiXWbgo+gGy76vg+D94t/CoLANM3sn2CjlXaePHC9fgTJkS7ZD9sS6PqqHeomQq/XLwLwnJE+\n",
"c8EML66p1ctw9erVmzdvMhqHYci+xAXXYhhc80T6bczbyOzGzdWuZ7GGvd0zn7sXEUFivb+/z268\n",
"JEsJPnEcB0GQWw9nGUajETRrHMdhGGqaBt/nuv/j8VjTtCAIJEnyfd8wjNZ0pxs3bnBt1cJeMm7V\n",
"sphxFxtZEDdq3Ismu/hhFyMiSKzb3KqFT/CB1CzLMrzg3d3dVRQlDEPbttvfrSUIAli+ra4bDwso\n",
"+CBIEdiXMbdZI8KF0IKPLMuyLMPqx6PRCNZGHo/HK1m0GRYRajPvExR8xDPuorzQy1invdsuRkSQ\n",
"WIsr+Liua1kWZNv0zSqM8wHlpxEfRQIFH9GMu9jIgrhRozG84yWESFInIyJIrMUVfM6ePRtFEXzW\n",
"NC2V4E3ThJ0O63dQMFDwQZBSYDlLSvP70iCMCC34pIDiX68rnWB/f5+r189+z+9996e5Xj9XI7Mb\n",
"C9ITFKGR2Y2h19+5iAgS6zZ7/XypX1VV2Mgwtxmv7/vroPYQQqIowtm8Qhl3ce5ov2PdxYgIEuvr\n",
"16+zGy8Jn+ATBIGmaYZhuK47mUxA9HccJwxDK7cbRU9BwQdBSnFd4jikbBYmwoTQgg9siyhJkud5\n",
"kPdN04R9dJtxTzhQ8BHNuIvyQi9jrSgEOrhdjIggsRZX8CGEyLJMKU3VnnR8Z92OCQoKPqIZd1Fe\n",
"6GWsZfngBW8XIyJIrMUVfBAUfBBkFq6LC/gsjtCCD4IgyCww73eIpVJ/HMe+769226yW2dvbY19T\n",
"2/d99ol/XFMETRhEjcb8jcxu3Fzt+h3rLkZEkFhfu3aN3XhZuDZ2sSxLVVXYk2s6nUqSpKqqLMv1\n",
"bswrMpcuXbpw4QKjcRRFURSxG7O7MZ1O0RjgbWR24+Zq1+9YdzEiIsSaUrq9vc1e8pLwaf2wMj6s\n",
"5TAcDhVFMQwjCILBYDCdTpu7P4kDav0IgjSB0Fq/67qU0nQNH1glP13DpxEHBQMFH9GMuygv9DvW\n",
"XYyIILEWV/CRJCn9nN0JnVK6JpoPCj6iGXdRXuh3rLsYERFi3bLgs+BWLWu7hs/x48dxb16hjLvY\n",
"yIK4gRFpwVjYvXlxDR8+4jjGKV1CGXdxAlG/Y93FiAgSa3YxeXn4ev2UUtgZEdbwgS8dx2l/y5RV\n",
"sbm5ib1+oYy72MiCuIERacFY2F4/92zeMAxd19V1HepvmibskbsmazngCB8EQZpA6BE+ZO3X8EHB\n",
"RzTjLsoL/Y51FyMiSKzFFXwQFHxEM+5iIwviBkakBeP+CD5rDgo+CII0geiCz5pz9erVmzdvMhqH\n",
"Yci+tDfXIuBc80T6bczbyOzGzdWu37HuYkQEifX+/j678ZLUk/q5xK9Oc+PGDdyqRSjjLm4M0u9Y\n",
"dzEigsS6za1a6hF8NE3z1mNnNhR8EARpAhR8hAYFH9GMuygv9DvWXYyIILFuU/DBET588Ao+7CX3\n",
"WwRozriLjSyIGxiRFow7LPjAMnWGYciyDBO4ijZBEERR1IiDgoGCD4IgTdCy4DO/1w+5Hu5dQRCo\n",
"qlpcrodrFdNOs7+/z9vrZxzYG8cx+xDg3BpK62zM28jsxs3Vrt+x7mJEBIl1m73++Vq/53me56Xp\n",
"XlEUtUBHF/DhmkkIRFGEs3mFMu7i3NF+x7qLEREk1tevX2c3XhK+ET6DwcAwDFVVc993boRPGIam\n",
"acK0sSYcAAAU8ElEQVStOwiC8XjMePdCwQdBkCYQeoQP7M3bkCttMhqNbNu2LMuyLNu2h8Mh4w95\n",
"BR8c19+0cRdHkfc71l2MiCCxFkvwyTJL4epWl58QEoZh2s3nWpEDBR/RjLsoL/Q71l2MiCCxFlfw\n",
"6Q3D4RA2lyeEBEHgOI5t2yw/RMEHQZAmEG6EDwtcr7xFwLKs4XAIPsdxbFnWqj1CEARpj3pm87Jr\n",
"5e1gmqZWIDsC1XVdSZJgeBLhmZ63t7fHvqa27/vsJXNNEeQaTdtvY95GZjdurnb9jnUXIyJIrK9d\n",
"u8ZuvCxcm7hXvOOtfcP4RtF1PftfVVUZf3jp0qULFy4wGkdRFEURuzGjZZIk0+kUjQHeRmY3bq52\n",
"/Y51FyMiQqwppdvb2+wlLwl3r9/zvOzvoyhSVTXdp7cuXNcdjUYVBr7vDwYD6MtzvUMHcvIU+7yE\n",
"48ePc23Vwl5y7/esaG5jEK5GZjcWZPsOERqZy7iLEREk1m1u1cI9widXE0mSbNuuazYvJPTd3V3X\n",
"dSselBzHMU2TUgrj8TVN4z1QEATpDYPrzoGCj2jGXZQX+h3rLkZEkFiLK/jMQtf1yWSyfDmTyQTK\n",
"8TxvlggTRZEsy9nHKEqpbdu8B1JVlVJKKYWnFsYfouAjmnEX5YV+x7qLEREh1i0LPvUM7jRNM31l\n",
"Wgu+749Go9LpAo7jhGGYHZMThuFgMFhAdPJ9X5Kk4pJEFeDgTgRBmkDo2byzCIKgtWV8wjDMJWtZ\n",
"lheQ+wkhpUvRVRPH8Wuvvba1tXXPPfccP378/vvv1zTt/vvvf/e7361p2hNPPPH5z3+eEPL5z3/+\n",
"6aefDoLgM5/5zNNPP00IeeGFFy5evJj9QAi5ePHiCy+8AB+++tWvEkKefvppKCH9AEVlP7zwwgs7\n",
"OzsVRcGHtISLFy9WFJXzynGciqJyXjmOU1FUzqs//uM/bqKCQRDkmr2igjCBiLGC8EPGCu7s7FS3\n",
"VfbDV7/61eq2yhblOE51W2WLgtlGq60gnPa5ouBDzquLFy9+5jOfCYIgW2augqmfubOiWFTOq4sX\n",
"L1YUlfMqd9rnisp5Bac9ewVzRUHSePe7333//fe/733vO3369PHjx++5554vf/nLv/jFL0hrcD0j\n",
"2LZNC+i6nhswszwVgo+u67lXzQnPEJ0lefLJJ8+fP89oPJ1O2Z8NuZ4iiy2wtsa8jcxu3Fzt+h3r\n",
"LkZEhFhTSs+cOcNe8pLwCT6aphXf9CqKout6vTekCsFH0zQQ6HNftrOYBAo+CII0gdCCjyzLuq5b\n",
"h6k974tMHMe4ho9Qxl1cMabfse5iRASJNfvoweXhW8iBcaGbRuFV5+tlc3OTa1w/e8n9HuvdnHEX\n",
"G1kQNzAiLRgLO65f0OXbKgQf0zQlSaKUZr88e/ZsOztEouCDIEgTCC34iICu67lZEq7rtiY6Xb16\n",
"9ebNm4zGYRiyL+3NtQg41zyRfhvzNjK7cXO163esuxgRQWK9v7/PbrwkHKk/jmPf93l3NKwdEHxS\n",
"uS2O49FoZBhGO0e/ceMGbtUilHEXNwbpd6y7GBFBYt3mVi2sgo/jOI7jqKoahmEcx+w7GnIxGo3g\n",
"jhrHcXb8fk75ieNY0zRFUSRJ8n3fMIzWUj8KPgiCNEHLgg/TuP7pdJpdO8GyLEppY+NNWZlMJp7n\n",
"cc2JXx4c1y+acRdHkfc71l2MiAixbnlcP9MIH8dxKKVpN59SurOzs/LtTVYy1IdX8GEvud8iQHPG\n",
"XWxkQdzAiLRgLKzgw9TrL06gVVU1+40IDwHtcPny5QcffHDVXiAI0jcopXfffXdrh2N6zTv3xrXy\n",
"d7+tsb+/j695hTLu4kvFfse6ixERJNZt9vq7N7hztURRhLN5hTLu4tzRfse6ixERJNbXr19nN14S\n",
"phE+xaV7XNdVVTX9xnXd6XTalI8igSN8EARpgm5M6dJ1vbVVmoUCBR/RjLsoL/Q71l2MiCCxFk7w\n",
"kSSpuGpbFq5FLToNCj6iGXdRXuh3rLsYEUFiLZzgg6Sg4IMgSBN0Q/BBEARBugumfj729vbY19T2\n",
"fZ99pSeuNaFM00RjgLeR2Y2bq12/Y93FiAgS62vXrrEbL0trMwj6waVLly5cuMBoHEUR+zoTXCtS\n",
"cK0E0G9j3kZmN26udv2OdRcjIkKsKaXb29vsJS8Jav18oNaPIEgToNYvNCj4iGbcRXmh37HuYkQE\n",
"iTUKPuKCgo9oxl2UF/od6y5GRIRYo+AjNCj4IAjSBCj4CE0cxzilSyjjLk4g6nesuxgRQWLNLiYv\n",
"D9N6/UjK5ubmkSOs90uutS64jLmmT/fbuIuNLIgbGJEWjLkqePToUXbjJUHBhw8UfBAEaQIUfIQG\n",
"BR/RjLsoL/Q71l2MiCCxRsFHXFDwEc24i40siBsYkRaMUfDpCSj4IAjSBCj4CM3Vq1dv3rzJaByG\n",
"IfvS3lyLgHPNE+m3MW8jsxs3V7t+x7qLEREk1vv7++zGS4KCDx83btzg2qqFveR+b9/RnHEXG1kQ\n",
"NzAiLRgLu1ULCj58oOCDIEgToOAjNCj4iGbcRXmh37HuYkQEiTUKPuKCgo9oxl1sZEHcwIi0YIyC\n",
"T09AwQdBkCZAwUdo9vf3uXr97Pf83nd/mutjcjUyu7EgPUERGpnLuIsRESTWbfb6MfXzEUURzuYV\n",
"yriLc0f7HesuRkSQWF+/fp3deEnWWvCBqCiKwv4TFHwQBGkCFHzqIQgC0zQ1TSt9HR/H8WAwcF3X\n",
"dd3BYMBeLAo+ohl3UV7od6y7GBFBYo2CTw34vm8YBqW09K+j0cgwDMuyLMsyDIN9xzUUfEQz7qK8\n",
"0O9YdzEigsS6TcGn5xs0ep7neV7xe1VVK/5bweOPP761tVWDZ6LC3hRdhFJaej70Bgxfd6GUbm5u\n",
"tna43vb6q8np+1yr6yEIgnSddUz9xUcw9lVY4zhm1+N832ef+Mc1RZBdoeI1/vGPfyyCG+zGXI38\n",
"2muvvfTSS7X7wGvcXKxFCB/vac9u/MILLzBaEjFOTsIZ6za1/q7O5jVNs5jBFUWxLKvR4951113s\n",
"6/VzjR3iMjYMoyHjBx54QAQ32I252u3cuXMPPfRQ7T7wGjcXaxHC19xp//DDD7Mbi3ByEs4KsueW\n",
"5elq6l8mxSuK4rpu9hv2V/bHjh3b2NhgNI7jmF1KgpEAXPaMxlxjDO644w5244YGcnA5THia4sSJ\n",
"E3feeWcTJfMO2mHPCIKEj71Ywtlu7Of81tYWlw8iGHPFmj23LM/KBB/XdUejUYWB7/uDwUDTNNM0\n",
"ec+8ueSeGLiuAfaHss997nPPP/88uzH7YICnnnqK3fijH/0ooyXhVAzYSw6CgMv4qaeeYjR+/vnn\n",
"P/e5zzEacwk+zTUyV7dRkPA1FBGua4RL8OFqt+aMuWLd58GdkNB3d3dd161QwRzHMU2TUjoejyVJ\n",
"0jStXjcURUmP7vs++22ZS/DhkhfOnTvHaEk4n3y5RABBjNkr+NBDD7E3HVdEmmvkM2fONFQyRiRF\n",
"kHbjinWfBR9JkiilkHln9frjOB6NRpPJBJ4EKaVxHDuOw3X/hLtFVkXxPC/9K6V0OBxC9g/D0LZt\n",
"xmK5BB8ueeHEiROMloTzyZdLBBDEmL2Cd955J3vTcUWkuUY+dozjusOILOADEabduGLdpuDTdupn\n",
"6V+7rqvrelYBNAxjMBhwpf5soi8iSdJ4PF5gIYcrV67s7+8zvrV/6aWXfvWrXzGW/NJLL919992M\n",
"xt/+9rfZjV955RX2YQYNGb/00ktcxt/+9rcZjb/xjW/86Ec/aiIizTXyT3/605VHhMu49xFpzpg9\n",
"1lxicg20NoMgh+d5s6afgM6T+1KW5eadms8f/uEfthcbBEHWiRMnTrSWykQc4ROGoaqquS/Zh943\n",
"yhe+8IUvfOELq/YCQRBkKUSc0lX7eB4EQRAki4ipH0EQBGkUEVM/13tXBEEQhBcRUz8pW2aHa+1T\n",
"BEEQpAIRU7+u67nhUDDcc1X+IAiC9AwRUz8IPul+CDDDi2tQP4IgCFJB23vzjkYj6NHHcZxd2Cg3\n",
"AyuOY03TFEWRJAn228LUjyAIUhdCb8seBEEcx3ADWLUvCIIg/UHo1I8gCII0gYhaP4IgCNIomPoR\n",
"BEHWDkz9CIIgawemfgRBkLVDxJU7hcX3fcdxYNARpbRD447q9dx13TAMKaV1ubckddUOdgSCwceq\n",
"qhqGIUiIm6igLMuUUhEWxK39sgrD0HEcWZYFGRFeVwVN08x9o6pqcZFjVlpbHrrr2LatKMpkMomi\n",
"yLIsRVFW7RErdXnueZ6u64qi6Lo+a6+F9qmrdlEUqapKKZ1Op9PpFPaSi6KoXm8XoK4KTqdTRVFs\n",
"255Op0mSjMdjKLZWZ7lp4rLSdZ1SKsgpWmMFCSHeYSCUC5a28C/XiiiKZFnOJgJKqW3bK3SJkRo9\n",
"n0wmkCkqttlpmRprZxhGboMgy7Iopcu6uBxNhC/7ja7ry7q4BE1cVp7nGYYhyClabwXr7alj6mfC\n",
"tu1cFoA+1Kr8YacJzwW5rpJaa2dZVvHLlVez6RNvtZvfNVE7eFYT5BStt4L1pn58zctEds0JQJbl\n",
"Tmwp013PWaixdsVXF2EYrlzrbzR8vu8vrhTXQe21M00zt633amkofL7vL18IvuZlQuQ9I6vprucs\n",
"NFq7wWBgWVYtRS1MExWE9VF83w+CYDweL1PUktRbO6jUZDJZ2q/aqD18mqbFcSxJUhzHsizbtr3w\n",
"fQ5TPxPd7SZ313MWmqvdcDg0DGO1nWLSTAWDIAiCwPf9lY9Sq7d2pmmu/Fado94KWpal63p653Ac\n",
"ZzgcLnzzRsEHQfIMh0NFUQQZGlg7hmHAOJ8gCIrjBTsKaCArv1U3Sm4wrmEYsP7xYqVh6meiu3tG\n",
"dtdzFmqvXRzHu7u74uT9RsNn23YQBAvnjuWpsXaO46iq6t8CRK2Vb+3X9NWnKAqm/sbp7p6R3fWc\n",
"hRprB7tEiLY5RKPhWyZ31EJdtVNVNQzDNPWHYQjSfx0+LoW4V1+No4V6zGQyyY0VG4/HhmGsyh92\n",
"uDz3PM+yrLnzmAQZOZfwx6WiglEUwYyn7JfLTJmphSbCl0VV1RXO6qoxfEVLEU7RpsOXmzTABaZ+\n",
"VlRVTfMCpImVz4RkhNHzdGjE3Gk+glxXAHtcKioIU3lzU7qSJJEkqXaHeakrfLqu534Irw1rd5iL\n",
"WsJXRJxTtK7wFc9PwzCWmXKII3xYGY/HmqYFQZDuGdkVGZ3R83Swx6xRH7nNNTVNg+9zm2u2DHtc\n",
"KioIkrfjOOmO0IAI46PqCh+l1DTN9F0oDOq3bbs5z1moJXxZ4N01nKLD4bArFZxbu/F4bJrmaDSC\n",
"8Lmuq+v6MiOacJcuPrq7ZySL52EYlo5EFh/GuPS7giy1AxtCiFDnMIaPsNUufXe9fPgw9SMIgqwd\n",
"OMIHQRBk7cDUjyAIsnZg6kcQBFk7MPUjCIKsHZj6EQRB1g5M/QiCIGsHpn4EQZC1A1M/giDI2oGp\n",
"H0EQZO3A1I8gCLJ2YOpHEARZOzD1IwiCrB2Y+hEEQdYOTP0IgiBrB6Z+BEGQtQNTP4IgyNqBqR9B\n",
"1oIgCGB/zYbI7W2JCA7uzYs0yGAwmLW9raIoy+wsivAyHA6zDe77/mg0IoRIkjQejwkhrutC+pZl\n",
"eYEtbV3XJYQYhlGbx0iTYOpHGsQwDMgIuq7n/gR5B2kHx3EkScru+6ooiizLJBMaRVEopZqmTSaT\n",
"BQ5hWdZgMMDU3xUw9SMNoqoqiAzFzaYx9bfJaDTKPWNJkgT7eqehkWUZbgaKoixwCLiXOI6D2b8T\n",
"oNaPrIZsfhmNRpqmaZoWBAEhxHVd+C88MWTxfX8wGOzs7Jw9e3YwGJSK12Bz9uzZnZ2d4XAYhqHj\n",
"OJqmDYdDMBgOh5qmZbVp+EbTNN7DQcmO4wRBMBgMNjY2dnd3TdMsehXHsWmamqalNqXiO0sFefF9\n",
"P47j4oMXI1DHHKV11HUdFf/OkCBIk1BKKaXp58lkUrSZTCae5ymKMh6PDcOglE6n0+l0quv6dDpN\n",
"zWzbVlU1LWEymei6nhaeHiJrMx6PFUXRdd0wDM/z4EvP8+AoOQdylwPL4abTqWEYqqoahgGuRlGU\n",
"Kxy+VBTFtu0oiuC/tm1LkpQzYzniAlBKDcMo/b5YeDEnwM+9DCANFQucTqeEEKgjIjiY+pFmgVwM\n",
"WUZV1TT/FlFVVZIk27ZL/zqdThVFKf1VNqerqlr8YTHJzs16LIdLi8pZRlEkSVL1r5IksW076wP7\n",
"EXmB9i9+nw1NSjH1W5ZlWVb2V6U3EoAQsqS3SDug1o80jizLICjPGu2TYlnWLKXYcRxITDkopa7r\n",
"Qvm+7xd/LsvyAuozy+FScv+VJClb0zAM4zguvu3QdT0Mw8WOyEUQBLPUnjQ0KcV3MFmvHMeJ47hi\n",
"/I+qqkEQLOMt0g6Y+pHGSceWhGEIrxZnAa8ZSwmCYNab4TTR1Jh0WA7HSBiGpT+RJCn7wqPGI+ao\n",
"aNXcsJ9qYPQnKGMVzL3BIyKAr3mR9jAMY7HRI4QQeBNQ+uiaJiNFUbL96JQFkhHL4dgp9arRI2aR\n",
"JInFgWqCIIC8X33zDoJg4RAjbYKpH+kGqqrOHT1iGAYoEtkvIWfNLT/3K5bDMQIaSOntJ5uRazxi\n",
"DkVRluyJw/gleDUN37iuWywzjuM4jjH1dwJM/Ug3UFVVluV0gGaK4zipTgKyPowKjeMYhnWaplnU\n",
"0HPPB2EYDgYD3sOxQyktTmwejUbZ8us9YpZ0dsViwLDU8XicFY5gPGvO0nXddKYYIjio9SMNomka\n",
"ZFhIE6WLN4RhCPkuCALTNNN+JYw/yVratm2a5u7ubvrSGOSFbJkw1HI0GkEPGlSUYurUdd33fU3T\n",
"4B4Qx7FlWbu7u5qm2bYNyYvlcMPhELJqGIawHEIcx3AXyRYF75mhKHgJ7Pu+qqrwE64KLkD6Djzb\n",
"nqnnQRCMx2NJkhzHgYkUmqYZhpG+GR6NRmEY5gbyF/M+HGLh2QNIy2wkSbJqHxCEA0iI8JnxFSWk\n",
"rWICBR0m97p1+cNVkPa+K4qq94gApPUl3xlUE4bh7u4uDKVt7ihIXWDqR/rPrNS/Vuzs7MCUsYbK\n",
"Hw6HiqLgKg5dAbV+BFkLcuJS7Sw2fwJZFdjrR/pMblmeRhUPBOkQmPoRBEHWDhR8EARB1g5M/QiC\n",
"IGsHpn4EQZC14/8HEbr8PnQbLPAAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"% Idem au code précédent, y_srb est remplacé par y_srbb dans la ligne suivante.\n",
"y = y_srbb;\n",
"% représentation en temps\n",
"figure\n",
"plot(ech,y)\n",
"hold on\n",
"plot(ech,signal,'r')\n",
"xlim([-1 301])\n",
"ylim([-0.8 0.8])\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"% représentation en fréquence\n",
"figure\n",
"[freq_f,y_f,y_af,y_pu] = Analyse_Frequence_Puissance(y,ech);\n",
"ylim([10^(-10) 1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Section 2: Optimisation de filtre"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.1. Nous allons commencer par appliquer un filtre de moyenne mobile, avec le signal le plus simple (`y_sr`).\n",
"Pour cela on crée un noyau et on applique une convolution, comme indiqué ci dessous."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%matlab\n",
"%%définition d'un noyau de moyenne mobile\n",
"% taille de la fenêtre pour la moyenne mobile, en nombre d'échantillons temporels\n",
"taille = ceil(3*freq);\n",
"% le noyau, défini sur une fenêtre identique aux signaux précédents\n",
"noyau = [zeros(1,(length(signal)-taille-1)/2) ones(1,taille) zeros(1,(length(signal)-taille-1)/2)];\n",
"% normalisation du moyau\n",
"noyau = noyau/sum(abs(noyau));\n",
"% convolution avec le noyau (filtrage)\n",
"y_f = conv(y_sr,noyau,'same');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Représentez le noyau en fréquence (avec `Analyse_Frequence_Puissance`), commentez sur l'impact fréquentiel de la convolution. Faire un deuxième graphe représentant le signal d'intérêt superposé au signal filtré. "
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"err = 0.030706\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fjOTGfedr9s+stdJqhiMpXkmLicCBDchwDCc1iLQw\n",
"8rABiVwgKEBuzcY6G8F+YgsIAjgGjGJiRMnLBSQMwxGQB5PWwwX2wQCJvMQPPoA8O4s8XC4gLSQB\n",
"DgFkMifDAW6SgOVLdjfamY37HmpNUeyenqpukl1F/j7Yh96eXxer6tv9I/ll/dmazWYIAAAAGBPn\n",
"Nl0BAAAAoG8g9QMAAIwOSP0AAACjA1I/AADA6IDUDwAAMDog9QMAAIwOSP0AAACjA1I/AADA6IDU\n",
"DwAAMDog9QMAAIwOSP0AAACjA1I/AADA6IDUDwAAMDog9QMAAIwOSP0AAACjA1I/AADA6IDUDwAA\n",
"MDog9QMAAIwOSP0AAACjA1I/AADA6IDUDwAAMDog9QMAAIwOSP0AAACj48KmKwAAyuA4DkLIMAzD\n",
"MDZdF15M08QYu6676YoAcgFX/aODUjqdTg8ODra2tiaTSZIknudtulJIhjqciWEYlNIkSboofDKZ\n",
"mDUmk4njOEVRdHEsANiazWabrgPQH5TSw8NDQoht2wihoigcx0mSpCzLzVbMNM04jjdbBx7YhX8X\n",
"F9FJkkRRhBCyLIu9UxRFEAS2bTOxViPLMk3TdF1vp5bAUADDZ1wEQWBZVpVKdF0Pw/Dg4GCztQIQ\n",
"QoZhsPuJuptkWdbh4aFlWZqmrVYsxrid+gHDAgyfcUEpnc8FhJDqdZIkzHBACEVRZJrm1tbW4eGh\n",
"4ziU0sYHkySZTCYHBwd7e3vMOzrtoI7j1IvKsqwKnk6npmlmWVa3O6bT6Xw5nuexv2ZZVlXPNE12\n",
"sSxaKx5YUXt7ewcHB9PpdL4HWj9iA03TLMti7UU/7asgCKoA9g7Tq05RFJWDxO5UFpJlGWsgq3kU\n",
"RfXC+cMopZ7nsU6ojMRGIUEQsMqz0qovw/zhln9hKrrr9lEwA8ZEGIaWZS0JyPM8jmOMMTOF8jxn\n",
"7/u+r+t6mqZVpO/7hmFU76RpalkWIaRRYFmWGGPf98uyZP/1fV/TtCoyjmN2xLhG/UAVaZqyyDAM\n",
"bdsmhOR5nue5ZVn1evLUigff9zHGVVGsZEJIo7QWjzhf+Gw2s227KjyOY9bw6q+sTxb+kFlPuq5r\n",
"GMbCw+V5zm77qv/atj0fzBOWpqnrulU98zxngjbKYR+svldlWTaaM+P4wjBa7PZxAql/dLiuyzK7\n",
"7/sLM+xsNmO/z8abcRxXP3j22174wcYPfv6d2Wzm+37jV3paelp4CE3TfN+f/xN/rc6EFcWyT0Wa\n",
"pgihes1bPOJsUeqfT9wLTw9LruHqqjVwXXc+7c7rzhnWIAzD+XoSQhrdVZalpmn1d3i+MO12+zgB\n",
"w2d0EELSNGWDVYIgODg4WHiPX3eBGOwjbMxJEATzAexTdfulKApK6fxQSMuyqoeZK+C67sInn5y1\n",
"4oE9X2047BjjxnFbPCKjcrFM0zw4OCiKIgzDFcrhwbKsKIo8z6usEnZOXS0MIZT8FPZseeFBG18G\n",
"TdPqNhrnF6b1bh8h8Jh3pFSD0ymlbOh34xnAwjEhmqYVRaHrepZlpw3HrP9ui6JYOARe07R1Hj+e\n",
"Nl6Fs1Y8ZFl2Ws07OmL1qSrHdT17gDl4QRCwzM7EIoQ0upcnLIoix3EwxuxNSulpHbgczi9M690+\n",
"QiD1j4soihqX25qmGYYRRVEjF7MU3/h49ZSYXf/yXLn3OTKdv1Y8RfV8RAaTo63SeA5Xv3xm9xxp\n",
"mjbOcMvDiqLwPK/xKXb5v0KVeL4wrXf7CAHDZ1ycdq00f3s+P/QiCAJd11mkYRgLbaIGhmFkWbZw\n",
"YEwXpwTOWvGAMV5oHTTebPGIK3PauKMzmZfYsix2SycUttAcW61WnF8YGbpddSD1j4ssyxq/5CzL\n",
"5m8FEEKGYVTjJtmngiCoHF7DMHRdnx+CGQRB4+xCCJlMJo0fs+d5jc8WRdE4GSRJInp64K/VmViW\n",
"xWZU1d+cTqeNBNfiETnBGNe7hQ3iXK2oLMsaDWQqNO72zgybP1t4nrdkROlyeL4w/Xf78IDZvOOC\n",
"2fpJkjBXoSiKLMvCMGz4G2xuLZtfyhING/PTSHxsJnD1zCDLMrZcTCOM/SDZyBy2EIJhGI0wZhaz\n",
"M9DCmKIo2E89y7Lq5gMhRAhpOCSctToTNrq88qyTJLFtuyiKKIp0Xa/PPW7liKZpsq5mKXXJwjvT\n",
"6bQoCnYOoJS6rnt4eGgYBhuAW5VWtYIFs//WJ/RNJhNd1xtfBjZosn44nrCqSqyj2JOk6XSq63pV\n",
"q+l0yiwgNjyX1Y2Nx29UnucL01a3jxZI/WOE/U7Q6Y9b+ZdVqIpCZz1hq5zf08L4i2qxVmdS3Y4s\n",
"L6fFI/LAXJE1n5YzzvwycIZVHYUxbiX5nvmFQb13+5CA1A8sQJUVdQAAWA3w+gEAAEYHXPUDH4AN\n",
"367+W7eGAQAYDJD6AQAARgcYPgAAAKMDUj8AAMDogNQPAAAwOiD1AwAAjA5I/QAAAKMDUj8AAMDo\n",
"gNQPAAAwOkad+rMsa6w4CAAAMAZGOqWLUsqWFUQIdboHHgAAgISMNPU7jlPtUMi2EzptgVwAAIDh\n",
"MVLDp75xKNsYaLP1AQAA6JORpv7GguOwtwMAAKNijKl//hp/fv9xAACAATPG1A8AADByxpj657eX\n",
"E93+GwAAQGnGmPrRnOdDKd1UTQAAAPpHydQfRZHneUsCkiSZTCamaTqOszCtY4yrTZ+TJFl/b2sA\n",
"AACFUGlcf5IkQRAURaHrOqX0tH3DgyAIgsD3fV3X2XaDaZo2YhpTunzfh0E+AACMB5VSP3Np2AW7\n",
"53kLUz+l9PDwME3TKpU7jqPr+sINZqsCu6w1AACAfMwUJI5jwzAW/sn3fUJI/Z08zzHGbR3605/+\n",
"9KYVAwBgmGxtbbWVqc7kwqYb2zJFUTSu4pk71Fb5P/jBD7a3t3/nd36HJ/jb3/72hz/84V/8xV/k\n",
"DP7EJz7xsz/7szzB3/zmN3/pl36JM/hrX/va66+/zhPZXfC77777ne98hz/4L//yL3/zN3+TJ/iv\n",
"//qvj46OXn31VZ5gIUW66+Q//dM//exnP8sZLIl8w1aku2B+rbMs+973vsdZbAv0dpJpkSVX/ZZl\n",
"xXHcePO04BW4fv36k08+yRn8+uuvf+Mb3+APnq/5ady6dYs/+Bd+4Rc4I7sLjuNYKPjWrVucwd/4\n",
"xjdef/11zmAhRbrr5E996lP8wZLIN2xFugvm15oQcuHCBf6S10TJET5L6HqY5oc+9KGtrS3O4J2d\n",
"natXr/IH81eD88KHsbe3p1wwfwOvXr3K33VCinTXyY899lhHJYMiFZL0m5DW5871l5CHlvq75u7d\n",
"uz/5yU84g4+Ojt555x3+YP5q/M3f/A1/8D/+4z8qF8zfwHfeeYe/64QU6a6T/+3f/q2jkkGRCkn6\n",
"TUjr//iP/+APXpOhef1dD9e5cOEC/1X/5z73Of7Ln8997nOf+MQnOINv377N39Lf/u3f5oxEghcp\n",
"/CVjjIWCb9++zRl8/fr1j33sY5zBH/rQh65cucIZ3F0n/97v/R5/sCTydaSI0G9kd3eXMxIJ9lt3\n",
"wUJa8+eWFujNWmqRJV4/IcR13cabmqa1degbN27s7Oy0VZqEtPhcREIIIfxmsYqAfOpCCNne3u7t\n",
"cEMzfCzLqqbpMqIosiyrrfKFDB+hDSCF9gwIgqCjYKGb2e6qwR8s1MlC9kJ3retOaxnkE/3a8wcL\n",
"GT4yfDmRoNZ9Gj5DS/3sDr3ShlLqed7C+VwAAACjRaXZvJ7nsSt6Sml9/H5jWi+l1DRNjLGmaUmS\n",
"2LbdYur/5V/+5e9///s//vGP2ypQNkzTPG2FjAFQ35hzkIB86uI4zle/+tUHDx70dLzerKWeSdM0\n",
"juOyLNst9tVXX7127RpncJ7neZ7zB/NXQ8jxHHawaCfzB3fXumFrraIiMmhNCOGfM7Q+QxvhU9HR\n",
"UJ/j42N+r19okoFQsNAGA8MOVrGTJakGKNJDsFAD+/T6VTJ8ZOAzn/nMX/3VX/3DP/zDpisCAMCg\n",
"cBznrbfe+pd/+Zd+Dje0x7xdc+/evYcPH3IGF0XBf4EgdCnRGMU05mDRTuYP7q51w9ZaRUUk0frk\n",
"5IQ/eE0g9Ytx9+5dSP1SBauYaIattYqKSKJ1n6kfDB8xwPABAKALwPCRmpOTE6HHvPwPeQb/vKu7\n",
"h4pCncwfLMmjPxk6WShYRUUk0RqmdMlLWZbHx8ecwSrO5lUuuLu5o5LM8JShk4WCVVREEq37G9QP\n",
"ho8oYPgAANAFYPhIDRg+sgWraC8MW2sVFZFEazB85AUMH9mCVbQXhq21iopIonWfhs9gF3LoiJs3\n",
"b+7v73MGl2XJv5KE0JoTQisBDDtYtJP5g7tr3bC1VlERGbQmhOzu7vKXvCbg9YsBXj8AAF0AXr/U\n",
"HB0dvffee5zBSZLwz/4QmifiOA4EM0Q7mT+4u9YNW2sVFZFE6/v37/MHr0tv9xfDAAwf2YJVtBeG\n",
"rbWKisigNRg+UgOGDwAAXQCGj9SA4SNbsIr2wrC1VlERSbTu0/A5/4d/+Ie9HWwA/Nmf/dk//dM/\n",
"feELX+CM1zRN0zT+YP6a6LoOwQzRTuYP7q51w9ZaRUU2rnWSJN///vd/93d/l7/kdQDDRwwwfAAA\n",
"6AIwfKSGUgpTuqQKVnEC0bC1VlERSbTmN5PXZ7AbNHbE9vb2uXO850uhm/phOwDdBavYyZJUAxTp\n",
"IViogefPn+cPXhMwfMQAwwcAgC4Aw0dqwPCRLVhFe2HYWquoiCRa92n4QOoHAAAYHWD4iAGGDwAA\n",
"XQCGj9Tcu3cPtmWXKljFTcCHrbWKikiidZ/bssMIHzGOj4+FtmrhL3nY23d0F6xiJ0tSDVCkh2Bp\n",
"t2oBw0cMMHwAAOgCMHykBgwf2YJVtBeGrbWKikiidZ+Gz6hTf5IkQsIghO7evQupX6pgFRPNsLVW\n",
"URFJtO4z9QsbPpRSNhSXUmoYhq7rQnPbJCHLsul0ahgGQqgoCt/3OSfdgeEDAEAXyGv4BEFweHi4\n",
"t7dnmmaSJFmWmaZ5cHBweHgYBIHQ04zNQin1PC9NU9d1XdclhHiex/nZk5MToce8/N0y+Odd3T1U\n",
"FOpk/mBJHv3J0MlCwSoqIonWfT7m5Ur9QRAcHBxEUWTbNtuhJo7jOI5ns1me57ZtR1F0cHAgNMlt\n",
"g1BKCSHVfzHG/J8tyxJm80oVrOLc0WFrraIikmj94MED/uA1OdvwCYIgiiLXdZenyKIoPM/Tdb2e\n",
"VZWgKArHccIw5AkGwwcAgC6QzvCxbTuO4zMvjXVd931fubxPKZ1Op77vc8aD4SNbsIr2wrC1VlER\n",
"SbSWzvBRDsdxzDnmt1WjlE4mE9d1+RdWBcNHtmAV7YVha62iIpJo3afhg3rbAF42yrI0DCNNU6FP\n",
"3bx5c39/n/8QZVnyB/NXgz1xgeCZeCfzB3fXumFrraIiMmhNCNnd3eUveU3EBncmSaLoaM4GWZYF\n",
"QWDbttAzXgRePwAA3SCd11/H8zzROVCrEUXR8gGXSZJMJhNm44iOK82yzHGc+oPreS/oNI6OjvjX\n",
"1E6ShH/2h9A8Ef4KDz5YtJP5g7tr3bC1VlERSbS+f/8+f/C6CN0jsDlQp4ExZiM+VyaOY8uyMMaW\n",
"ZRmGcVqY7/sY4zRNy7JkGVzoKIQQjLFRQ9M0zs+C4SNbsIr2wrC1VlERGbTu2fAR9vpt2yaEsPaU\n",
"ZUkIIYSwP+V5vmb2T9OUme9xHJ+W+suy1HW93qGEEN/3Vz6oELdu3XrhhRf6ORYAAOOBEPLUU0/1\n",
"djix1F9P9BWWZYVhyF6naWpZ1vrVWpL62RDS+jvslLP+QXm4cePGVo1z584ZhrG9vb2zs8PuHl56\n",
"6aXZbPbSSy8988wzcRy/+OKLzzzzzGw2e+ONNy5dulR/MZvNLl269MYbb7AXr7322mw2e+aZZ1gJ\n",
"1QtWVP3FG2+8ceHChSVFsRdVCZcvX15SVKNWhJAlRTVqRQhZUlSjVp/61Ke6aGAcx7u7u5wNZFMR\n",
"ORt4+fLl5X1VL+HChQvL+6r+4rXXXlveV/WiCCHL+6peFPtpbLaB7GvfKIq9aNTq0qVLL774YhzH\n",
"9TIbDXzppZeqEurfivmiGrW6fPnykqIatWp87RtFNWrFvvb8DWwUtb29bRjGzs7O9vb25cuXtz7I\n",
"rC/EUj/GeP7+pZHulxg1/CxJ/YSQ6kxToev6+gfl4dVXX7127RpncJ7n/PeGQneRQrdWww4W7WT+\n",
"4O5aN2ytVVREBq0JIU8++SR/yWsilvpPezZQT9Ndp37Lsua7vpWD8gCGDwAAXdCz4SM2wscwjPkR\n",
"PlEU9Tncc7PrxFFKYUqXVMEqTiAattYqKiKJ1vyjB9dHLPXbtt0Y2MRWwbQsq3rHdd12qiYl29vb\n",
"587xdpqmafzzhPkjEUJC59phB4t2Mn9wd60bttYqKiKJ1ufPn+cPXhPh9fodx8myzLZtTdNY3rdt\n",
"27btdquVJInneXEcL6wAG5FZf9M0zYXBrQNTugAA6AKpp3QhhNgC91mWeZ6XZVkYhq3n/TOZv4cS\n",
"uqtaBzB8ZAtW0V4YttYqKiKJ1n0aPhdW+Mz8RXefWJblOE59idAoiuqOEwAAALAcYcOnH5YYPggh\n",
"0zQty2J3G5RS0zTZ/N4eKgaGDwAAXSC74dMpnudVCyyzDSAZjbAwDIMgmE6nbHHmFVZhW5l79+7B\n",
"tuxSBau4CfiwtVZREUm07nNb9lUMnyAI2KJLuq4bhkEIEXqKvQQ2W/jMME3T0jRlW8O3eHQejo+P\n",
"hbZq4S952Nt3dBesYidLUg1QpIdgabdqETZ8ptMppdR1XTbCKQiCIAjiOO4z/24QMHwAAOgCqQ2f\n",
"IAgopWEYViNbbdt2XXcymXRQNxkBw0e2YBXthWFrraIikmjdp+EjlvqTJJmfsWUYBqW0n3X8N87d\n",
"u3ch9UsVrGKiGbbWKioiidZ9pn4xw2dvb68sy/n3F06zGiRg+AAA0AVSGz4D2JpxTU5OToQe8/I/\n",
"5Bn8867uHioKdTJ/sCSP/mToZKFgFRWRROs+H/OKpX6M8cKZbEmSjOGSHyFUliXM5pUqWMW5o8PW\n",
"WkVFJNH6wYMH/MFrImb4FEVhmmYYhvVx9NPpVNO0Ya/aVgGGDwAAXSC74ROGIZtLxXZOPzg4GE/e\n",
"R2D4yBesor0wbK1VVEQSreU1fNBP917HGLMbmTiOx5P3ERg+8gWraC8MW2sVFZFE6z4NH+Ft2UfO\n",
"zZs39/f3OYPLspzfz3JJMH81hHb4G3awaCfzB3fXumFrraIiMmhNCNnd3eUveU0kXb5NWsDrBwCg\n",
"C6T2+k9D6A5IaY6OjvjX1GYrHfEH81ejsVfamINFO5k/uLvWDVtrFRWRROv79+/zB69LK/cOve2K\n",
"vnHA8JEtWEV7Ydhaq6iIDForafj0tj/ixgHDBwCALlDS8BkPYPjIFqyivTBsrVVURBKt+zR8zl6v\n",
"PwiCKIqWx/S2Ne7GeeKJJy5c4N3kQGjdC6FgobnTww5WsZMlqQYo0kOwUAMvXrzIH7wmZxs+juNo\n",
"mrZ8GyzHcdI0bbVikgKGDwAAXSCj4YMxNpYykn1aEEKUUpjSJVWwihOIhq21iopIojW/mbw+q2zQ\n",
"OGa2t7fPneN9QCJ0RhQK7u6eWrlgFTtZkmqAIj0ECzXw/Pnz/MFrcrbhw9agWN4AGOEDAACwDtIZ\n",
"PpqmnXniGkneR2D4yBesor0wbK1VVEQSrfs0fGBwJwAAwOiANXzEAMMHAIAukM7wAercu3cPtmWX\n",
"KljFTcCHrbWKikiidZ/bssMIHzGOj4+FtmrhL3nY23d0F6xiJ0tSDVCkh2Bpt2o52/DJsoxSyjOB\n",
"jT9SXcDwAQCgC2Q0fBzHMU1zyW1OkiSTyWQymQx+bhcYPrIFq2gvDFtrFRWRROs+DZ+zUz/GOE1T\n",
"y7Km0+nBwUG1MW8URY7jVG8ahpHn+fL1HgbA3bt3IfVLFaxiohm21ioqIonWfaZ+sRE+URSxcbhJ\n",
"kui6rus6xhhjbFlWd1WUCjB8AADoAhkNnwrLslzXjeN4Npvlec72ZFc6708mk729Pf74k5MToce8\n",
"/A95Bv+8q7uHikKdzB8syaM/GTpZKFhFRSTRus/HvKMe3BkEgWEYQiZVWZYwm1eqYBXnjg5baxUV\n",
"kUTrBw8e8AevyXindFFKHcfxfV9oASIwfAAA6AKpDZ8h4XmebduinwLDR7ZgFe2FYWutoiKSaA2G\n",
"T+cw8VYYjwSGj2zBKtoLw9ZaRUUk0bpPwwf1tgF8nxBC5veTIYRUAZZllWXJXhuGwV/yzZs39/f3\n",
"OYPLsqyOwhPMX408zyGYIdrJ/MHdtW7YWquoiAxaE0J2d3f5S16TMXr9WZaxiQjsv1EU2bZNCOH5\n",
"LHj9AAB0AXj9naPruuu69d0l+RefODo64l9TO0kS/tkfQvNEHMeBYIZoJ/MHd9e6YWutoiKSaH3/\n",
"/n3+4HXp7f5CiDAMXdddEhDHsWVZzMYRun2eBwwfpYNVtBeGrbWKisig9agNnyRJgiAoikLXdUrp\n",
"aWMugyAIgsD3fV3XgyCIoihN0xUOF0VREARZllmW5fs+z0fA8AEAoAtGbfhomkYISdN0ybBLSqnn\n",
"eXEcY4xZvGEYQs/cKyzLiuO4LEvOvI/A8JEvWEV7Ydhaq6iIJFqD4TOL4/g0H8b3/fpYndlsxpaN\n",
"66Ves1dffXVra+vcuXPnzp3b2tq6ePGiYRiXL19++umnDcO4du3aK6+8MpvNXnnlFV3X8zy/ceOG\n",
"ruuz2ezNN9+8cuVK/cVsNrty5cqbb77JXrzxxhuz2UzXdVZC9YIVVX/x5ptvXr58eUlR7EVVwrPP\n",
"PrukqEat4jheUlSjVnEcLymqUavf+q3f6qKBeZ7v7+9zNjDP8zzPORv47LPPLu+regmXL19e3lf1\n",
"F2+88cbyvqoXFcfx8r6qF8UWWdlsA9nXvlEUe9Go1ZUrV27cuJHneb3MRgNfeeWVqoT6t2K+qEat\n",
"nn322SVFNWrV+No3imrUin3t+RvYKOry5cuGYTz99NOXL1/e2dnZ2tpiKYW9mPWFXIZPRZIk7NJ+\n",
"/k+O48wvGHdwcJDneQ8VA8MHAIAuGLXhw0NRFPO7Aui63s/RKaUwpUuqYBUnEA1baxUVkURrfjN5\n",
"fdTboFFoYnTrbG9vnzvHe74U2rhGKFjoVDfsYBU7WZJqgCI9BAs18Pz58/zBa6Ke4WOaJnu023iT\n",
"fwm2dQDDBwCALgDD5ww2uxEYGD6yBatoLwxbaxUVkUTrPg0f9VI/WtSbQv0LAAAwctQzfLIscxyn\n",
"/qcoipIk4R+bvw5g+AAA0AVg+JwBM3yqey42w2uFlfdX4969e7Atu1TBKm4CPmytVVREEq373JZ9\n",
"lRE+SZJEUVQUBbv0ZplX6EH2aXiex7qVUloUhWma7P3G5X8YhqZpZlmmaVqSJLZt9/YA4Pj4+J//\n",
"+b+ZJtI0dOZz/qOjywihD3+Yq+T797d/7dcW/wlj1OhdSbahkCFYaMSXJHukSFINUKSHYGm3ahE2\n",
"fNiaObZtTyYT9lm2DE4/fkudLMsopWw5h94O2p3hk2Vo4ZeEUrTkQQalzbNC/Twxf84AAEBOejZ8\n",
"xK762fV+4xrctu3Dw8NWa8XFRob6iBo+iHsUsKYVGC+O/ODMZYQQSpLktIWmq5tRSpHnIYTQu+/+\n",
"nyeffKE6B1RnC01DrAurF8tLXnSszQcLdbJQcHetYwsUdlGyDMEqKiKJ1vIaPkEQuK47/z7GWKg7\n",
"1OXu3bsdpf620kH9bXbOcJyvLVStus9IEhRFCCFEKfrbv72QJGecHniqIVTndYJVTDSQ+lcLlqF1\n",
"osHSpn4xw2dvb68sy0ef3Hr/s47jsG1P2q+gZIxthE91ejjNj2KeEjhLALAmUhs+fbrqcnJycvKT\n",
"n/yEM5g94eHsNEopf/cKXUqsE1xd6S88rRdFURQ6Qo+cpQaNs0JHdRbtZP7g7jpZTq3bClZREUm0\n",
"7vMxr9jgTozxwslTSZJsdpJtb5RlCbN568GGgQwDuW7zHyFI0x49b3Ac5Djo9u0fshdRhJin1Eo1\n",
"VJw7qqjWnJEqKiKJ1g8ePOAPXhMxw6c+06oyfKbTqaZpC93k4TE2w6d12ICl+WFLuo50HYwjYLxI\n",
"bfgYhlEUxeHhISEEIRRFURRF48n7aHyGT+vBmvbIO2oMW2Lng8o4+uEP/3V//0me84GK9sKwtVZR\n",
"EUm0ltfwQQjZth2GYZZlhmFkWWbbdv8j+jcIGD4dBWP8AeNof/+PXPfRk4bKMnIc5HlNs0hFe2HY\n",
"WquoiCRay2v4AGD4bJaiQEWB6hPp2W3BOJ40AUNGasMHADYLs4Dqw42yDGXZ+/MS2JlgBMOMAWAt\n",
"xAyfJEkcx3Ecp7qLYSvtbHbnrD45OjriX1M7SRL+lZ6E1oRyHAeCGZQmup4wm8j3kWUhSh+5Q9Pp\n",
"owFF1ddTSJHuWjdsrUW/9jIoIonW9+/f5w9eF6FN3NM01XXd9/2yLKs3Xde1bbudXeKl5+bNm/v7\n",
"+5zBZVnWO+rMYP5q5HkOwYzlnVyWszieEfLo3x/8wb3vfe//tV4H0eBhay36tecPlqF1osH8rSOE\n",
"7O7u8pe8JmJev+M4uq7Pr5B8eHiYpmmrpyRJAa9fadhzgmrhRfaQQGSnVQDoCqnX60+SxJpfS+yn\n",
"a/i0VCWpAcNHtmChTi6K990h10WahqLokTsUBKixFq8kJoAMnSwUDIZPnYEYPqfFE0LiOG7hJkR6\n",
"wPCRLbgteyFNZ677yBfy/VmeS2ECiJYsQzAYPnUGYviYphmG4fwMhel0alkWLN8GDIMse+QLsTWI\n",
"DAPmGAOdI7XhgzGO2DC6GpTSkazYjBCilMKULqmCu5hAhDEiBGEcEIIQQp73aLDQko/ClK4KmNJV\n",
"R0hrfjN5fcTG9RNCTNPUdb1K9JTSyWTC1nUYA9vb2+fO8Z4vhRY6FQrmn0c++OBOO1nTkGU9WnOC\n",
"PSIOgsW33NN7gwAAIABJREFUAkKtG7bW8LWvI9TA8+fP8wevifBsXpbrKaVsPZ8sywghve2KvnHA\n",
"8AEQQknyaD0JXUeWBWOEgBaQ2vBBCGmaFsdxGIaGYdi2nef5ePI+AsNHvuCN2AtsuSE2gyyK0HSK\n",
"bt78X/wCDltrMHzqDMTwqdB1XeiuZzCA4SNb8GY7WdcRMzu/+c2HWfbIDrLtM+4Dhq01fO3rDMfw\n",
"GTlg+ADLKQoURagowAsCxJDd8FlI0ZgMM1zu3bsntC07f88I9aHQPJFhB4t2Mn/wahVm9wHMCwoC\n",
"NJ2iuTFxA9daNkU2G1wUBXsyVP9XLUJe/3fnzn96771P8Ze8Ju2s3DmdTtnWXYPn+PhYdKuWLoKF\n",
"csewg6XtZF1HbAcj9jCgbgQNW2tpFWkxmC0ejtD764dT+v6Ir/rro6PL1683b/4WWoKO89//7u/+\n",
"B3811kTY8HEcJwiCecFGYhyB4QOsBtuDjFKEMRrTwAiFWbiZaJXW2fh2top4K0ht+DiOQymdn8c8\n",
"kvlcCAwf+YJVsRc07dGgIE1Dv/Eb/+o4zSWD+qlGD8GqKNIIZpM2qrW+2ZZw6KfCVf98HxlG4rrI\n",
"MJBhnJ33hX7XJycn/MFrImb4JEkSx/H8M+vx7NEIho9swcp1smUhXX9H0zAbIsgySP/V6C5YCUWK\n",
"4tEmP+z4P/zh07/+60jXuW7IhKoh1MA+9+YVM3y2tsY+IggMH6BFKEVRhLIMWRbsLNYtLNHXk7Zh\n",
"IIwlWp1JasPHsqzhDeYRmlRycnIidNXPf86X4YJUxWDRTuYP7q51VR3Ys1/fR0WxeCxQp9UYvCJJ\n",
"gjzvkXuTJAjjD1g39aU4etCahz6v+sVSPyFk4VrVk8mkpfr0ShRFpmlGURRFEaczWJYlzOaVKljF\n",
"uaPzdWAnAEqRaTZPADJ0slDwZhUpikfL7d2+/UNKkWU9SvSEIIzXKnm1YKHf9YMHD/iD10TMwAmC\n",
"gDW78Vw3iqI8z1uuWsd4nkcpddn4O27A8AG6JgjAAhKD+WbsWpytuKfiTDqpDZ8oijDGAxjPwxae\n",
"E837CAwf+YLlsRf4g5fXgd0BJAmaTlFRSNHJQsG9KVJd4Hve+2YOIY/yvgxdgSQ2fMR26fJ9f+EO\n",
"Ncpty04ISdN0hQ/euHHj6tWrnMFxHPNvXia0zRkhBIIZop3MH9xd6zjrUJYzQmYvv/w9/l2hxqBI\n",
"ns9cd2bbM9edLekZGbpiJvK7JoQ89thj/CWvyUhH7LDtxqbTKTsn27a9cM/hecDwAXqmKBDzlsXv\n",
"UQfF4BdH6tnwaWchh6IopFrI03Gc+acrGOO6w+M4juu6rNqTyQRjLFUTAIDBFoRg/s84HwAEwSMf\n",
"/8wlUQEBWrl3MAyjlXJ6w7Ks+o1YGIau6/J8EAwf2YIHbPjMl8x2jV+y0feQFGF+l23PwlC4DvIE\n",
"S2v4CF/1J2zK8wdpfbB/FEVFUSzZ9zFJEraUEMaYECK0KDZCCGNc/wj/x/f29ra3t/mPIlQl/mCh\n",
"7XGGHaxiJ69cDddFWYamU2Tbiy//h6EIe36L0PvPbEXrIE+wUG9cunSJP3hdhE4UcRxjjMMwZC/Y\n",
"dl3sRSsnojiOLcvCGFuWteROwvd9jHGapmVZuq6LMRY9UFmW9UfTlmUtfHw9z61bt1544QXRwwFA\n",
"u7DL/+ERx2ff2QwVQshTTz3V2+HEUr9lWWxgTJqmVep0XVfoDmgJaZqy8uM4Pi31l2Wp63pZ+2oQ\n",
"QnzfFz0WO80QQizL4v84GD6yBY/K8PlgITPLag5xUVeRPJ9ZlgJ2lmiwtIaPWOrXNI29iOO43n6M\n",
"cdnqaXpJ6vd9v9H1eZ6vcOE/m83KsozjmPN6n3Hz5s39/X3+8vm7RagDheo87GDRTuYP7q51bWld\n",
"lh+wwkWrIYkib7/9Y84rfRlaJxrM3xWEkN3dXf6S10Qs9eu6zl40Uj8hpC3Ppyr/tNRPCAnrX/YP\n",
"Vqxrbt26tbW1deHChe3t7a2trccff9wwjJ2dnWvXrhmG8XM/93PsZsi27Zdffrn+4lvf+tbzzz9f\n",
"fzGbzZ5//vlvfetb9Rcvv/wyK6F6AUVBUcuL2tn5L4TIVSvbthtFsReNop577mOf/OR3CJn9/M//\n",
"56rM1Yp6/vnnG7WStqidnR3DMK5du7azs/Pss8+eP39+a2uLbfp97ty5WV+saPgwt6R6v8/U3xic\n",
"w+htiNGv/MqvPPfcc5zBlX/FGcxfDSGDa9jBop3MH9xd61rXOgxntj0rS5UUYXX+5jf/twyKyKA1\n",
"IeTxxx/nL3lNxBZywBiz4T2GYRRFUc1RzrKst0HxQhOjW4ednDmDNU3jHzskNEhJqLeHHSzayfzB\n",
"3bWuda0tC9k2mk7Rz/zMR9steYXgMzuZ0kdrVPg+un79kgyKSKL1+fPn+YPXRehEUZZldRJjY3t8\n",
"37dtu/WFHJZc9RuGscGrfhjhA0gLs/5FjOgNEIYLnk4Ds95H+Ihd9WuaVg1TZQNjiqJgJ4AOzkqL\n",
"ERon2zqUUli0WargYSza3ErJmoZefPG/TqeIs/ieFaEUsW0pw/D90fqSKCKJ1u+99x5/8JqstZAD\n",
"xngjiTjLssbqoUL9uw6ihg9/yWD4rBasYid3V42Pf/zaZz+LJhPkusuWp1+h5DUVyTIUBMi2m7WS\n",
"RBFJtJbX8OmNJYZPmqaNP4Vh2NvSoWD4APJTljPDmK20NG0nxPGjp9DAEqQ2fGSA3WdU91yUUs/z\n",
"hKZWr8O9e/cePnzIGVwUBf8SF0KLYXDuKTaGYNFO5g/urnVda61pKAwfuSvtlsxDo5ODACUJ8v3F\n",
"u+BKoogkWp+cnPAHr8lahg+lNMuyxno46+B5HutWSmlRFKZpsvfjOK6HhWFommaWZZqmJUli23Zv\n",
"vtPx8bHQVi38JcNWLasFq9jJPVSjyv6ue+rO4z0oMp0+2kSFJ7jFOsgTLO1WLWLr9bPUrOs6e8B7\n",
"eHiIMS6Kwvf9/rfuyrKMLd/W1omHB1ivH1AIttt7GJ6a/TvFcRDGiG8jDEDuDRp1Xdd1na1673me\n",
"67psBbfpdNpN9ZbBtorsM+8jMHzkCwbDZ0kwW+ufrYLZbslLYJ3sOMiyzs77kigiidZ9Gj7Ce/NW\n",
"KyQzpwX9dJxPb2NsNouo4QN783YdPLy9edutBsZI19HC4YjdKfLFL16xrLOHGCFpFJFEa3kNn729\n",
"vbIs2WvTNCsL3nEcwzAGsF37mYDhA6gIuwbv54mY4yBdR30NvBgOUhs+Fczxb7cqSnBycgJX/VIF\n",
"w1U/TzCzfRqH7aKBQYCuXr1nWYopIonWfV71i6V+wzCiKEJzm/EmSbLZSba9UZYlzOaVKhhm83IG\n",
"E9I0/VtvYJahLEMf//j/VE4RSbR+8OABf/CaiBk+WZaZpmnbdhRFaZoy0z8IgqIo3CUDuAYEGD6A\n",
"ujgOMoyuNnYvCuQ4KAw7KXwMSG34sG0RNU2L45jlfcdx2D663VRPOsDwkS0YDB/+YNdFUfS+7dNu\n",
"Az0PsaW8VFREEq3lNXwQQrquE0Iqt6ca39l2xSQFDB/ZgsHwEQqu2z4tlsweI7OB1ioqIonW8ho+\n",
"ABg+gOo4DrJt1OIojSxDUbRsyi7Ag9SGDwAAqkPI4mH+K+N5iJA2CwR6YK3UTylNkmSz22b1zNHR\n",
"Ef+a2kmS8E/8E5oi6DgOBDNEO5k/uLvWbVZrZsskSTsls6WY63PqVVREEq3v37/PH7wuQut8uq5r\n",
"GAZbITnPc03TDMPQdb3djXll5ubNm/v7+5zBZVmW3CvV8kfOZrNcZJejYQeLdjJ/cHetk0Fr226h\n",
"5LKc1bbort5UTxEZtCaE7O7u8pe8JmJefxRFSZK4rqtp2nQ6xRjbtp1l2WQyyfO8u/OTPIDXDwwD\n",
"z0MYrzvQs89JwoNHaq8f1vABw0e2YBXtBRm0tm30+7//F+uUzIY4zud9FRWRRGt5DR9N06rX9a2y\n",
"CCEj8XzA8JEtWEV7QRKtX3+d8ofPl/yZzyzeeEtFRWTQumfDZ8WtWka7hs/Fixdhb16pglXsZEmq\n",
"8Ud/tOs4j+ZhiZZMKdrfX7wNgIqKSKJ1n3vzwho+YlBKYUqXVMEqTiCSROsoChBqrunGWbLnnbo2\n",
"p4qKSKI1v5m8PmJX/YQQtjMiW8OHvRkEQf9bpmyK7e1tuOqXKljFTpakGrquY4yCgGtU/vxV/2mH\n",
"UlERSbTu86pfeDZvURRRFFmWxdrvOA7bI3ckaznACB9gYEwmwmuuBQHS9a6WgRstUo/wQaNfwwcM\n",
"H9mCVbQXpNIaY8SzHFm95CRZlvdVVEQSreU1fAAwfGQLVrGTJakGC7YsFEVnez5VyUVxxkB+FRWR\n",
"RGupDZ+RA4YPMDymU95xPgghz0OW1ebqbwBDdsNn5Ny7d+/hw4ecwUVR8C/tLbQIuNA8kWEHi3Yy\n",
"f3B3rZNNa10/2/OpgovijLyvoiKSaH1ycsIfvCbtpH4h80tpjo+PYasWqYJV3BhENq0t6+y1PFlw\n",
"USwey19HRUUk0brPrVraMXxM04zjeP1y5AcMH2CQOA7XgvuehwwDFu3pBDB8pAYMH9mCVbQX1NWa\n",
"0rPzvoqKSKJ1n4YPjPARQ9Tw4S9ZNhNAlWAVO1mSatSDMT5jyGZRFJy1VlERSbSWy/Bhy9TZtq3r\n",
"OpvANR+TZVlZlp1UUDLA8AEGCaXI887wfIIAYQxuT1f0bPicfdXPcj07d2VZZhjG/HI9QquYKs3J\n",
"yYnoVT/nwF5KKf8Q4MYaSmMOFu1k/uDuWieh1mdWpyiKotBPW7enjoqKSKJ1n1f9Z3v9cRzHcVyl\n",
"e4yxMYeiC/gIzSRklGUJs3mlClZx7qicWi93JoatiCRaP3jwgD94TcRG+EwmE9u2jTlHULkRPkVR\n",
"OI7DTt1ZloVhyHn2AsMHGCpn+jmco4CA1ZB6hA/bm7ejqvSJ53m+77uu67qu7/vT6ZTzg6KGD4zr\n",
"7zpYxVHkcmptGGjJ0JU///MfcZocKioiidZyGT51TnO41LrkRwgVRVFd5gutyAGGj2zBKtoLcmqt\n",
"68s8n69+9e84H/CqqIgkWvdp+Iht0DgYbNuuNk5L09S2bc4P3rp164UXXuisXgCwSQg59U/cPxFg\n",
"RQghTz31VG+Ha2dcv9AjbxlwXXc6nbI6U0pdsDABACFNQ1m22O5XcyQHcCrtzObl98r7wXEcc476\n",
"CNQoijRNY8OTkMj0vKOjI/41tZMk4S9ZaIqg0GjaYQeLdjJ/cHetk1ZrjE/1fO7c+QvOYlVURBKt\n",
"79+/zx+8LkL3CEue8XZ0V9IRlmXV/2sYBucHb968ub+/zxlclmVlK/EEc0bOZrM8zyGYIdrJ/MHd\n",
"tU5ardN05vsLIuN49id/8n85i1VRERm0JoTs7u7yl7wmwlf9cRzXP1+WpWEY1T69bRFFked5SwKS\n",
"JJlMJuxaXugZOqNhT/HPS7h48aLQVi38JQ9+z4rutmoR6mT+YEm27+izk0/bsSvL0K/+6oc5i1VR\n",
"EUm07nOrFuERPo2WaJrm+35bs3lZQj88PIyiaMmNUhAEjuMQQth4fNM0RQ+UZVl1whA6c4DhI1uw\n",
"ivaCclpTioJgyIpIorW8hs9pWJaVpun65aRpysqJ4/g0E6YsS13X67dRhBB/4W3q0gMZhkEIIYSw\n",
"uxbOD4LhI1uwivaCzFovHORDyMAVkUHrng2fdkb46Lq+gusyz/zqQPNEUWRZVv3mw7ZtNs1Y6EBx\n",
"HCdJomma0PAeUcOHv2RpTQDJg1XsZEmqAYr0EDwQw+c0sizrbRmfoigaZ4iVTzwLl6JbDqX03Xff\n",
"3dnZefrppy9evPjcc8+Zpvncc8999KMfNU3zlVde+fKXv4wQ+vKXv/zaa69lWfb5z3/+tddeQwjd\n",
"uXPn+vXr9RcIoevXr9+5c4e9+PrXv44Qeu2111gJ1QtWVP3FnTt3Dg4OlhTFXlQlXL9+fUlRjVoF\n",
"QbCkqEatgiBYUlSjVl/84he7aGCWZY1uX9JANoGIs4Hsg5wNPDg4WN5X9Rdf//rXl/dVvaggCJb3\n",
"Vb0oNttosw1kX/tGUexFo1bXr1///Oc/n2VZvcxGA6t6Nr4V80U1anX9+vUlRTVq1fjaN4pq1Ip9\n",
"7fkb2CiKJY2PfvSjzz333Mc+9rHHH3/84sWLTz/99B//8R//+Mc/Rr0hdI/g+z6Zw7KsxoCZ9Vli\n",
"+FiW1XjUPBMZorMmr7766rVr1ziD8zznvzcUuouc74HRBot2Mn9wd62TWWvXnTVqV5YzQgauiAxa\n",
"E0KefPJJ/pLXRGz5NtM055/0Yowty2r3hJQkied5C9eHME2TGfSNN/tZTAKWbwOGDXsqWf95zb8D\n",
"dIHUy7fpum5ZlvtBWs/7MkMphTV8pApWccUYybVeOL5z2IpIojX/6MH1EXvM6/t+R/XgR9Sdb5ft\n",
"7W14zCtVsIqdLEk1FgYbBmqMXaQUadrAFZFE6z4f84oZPr2xxPBxHEfTNEJI/c29vb1+dogEwwcY\n",
"PNMpql/jwTL9/SC14SMDlmU1Zkmw4Z79HP3evXsPHz7kDC6Kgn9pb6FFwIXmiQw7WLST+YO7a53k\n",
"Wi+8Th22IpJofXJywh+8JgKpn1KaJInojoatwwyfym6jlHqeJzSofx2Oj49hqxapglXcGGTYWquo\n",
"iCRa97lVC6/hEwRBEASGYRRFQSnl39FQCM/z2BmVUlofv99wfiilpmlijDVNS5LEtu3eUj8YPsDg\n",
"aTg8YPj0Q8+GD9e4/jzP62snuK5Lluzp0BdpmsZxLDQnfn1gXL9swSqOIpdca0Jm9V8V+60PWxEZ\n",
"tO55XD/XCJ8gCAgh1WU+IeTg4GDj25tsZKiPqOHDX/KwTYDuglXsZEmqcVqwYaAsaw7kH7Yikmjd\n",
"p+HDddU/P4HWMIz6OzLcBPQDbNAIDJ44noXh+/8dzY97w/S8QSPXY94zT1wbf/bbGycnJ/CYV6pg\n",
"FR8qSq41u+pfuWQVFZFE6z6v+tUb3LlZyrKE2bxSBas4d3TYWquoiCRaP3jwgD94TbhG+Mwv3RNF\n",
"kWEY1TtRFOV53lUdZQJG+ABjoBrVkySIUjSmtVo2hhpTuhor5o8HMHxkC1bRXpBf63oF2Q992IpI\n",
"orV0ho+mafOrttURWtRCacDwkS1YRXtBfq01DTVS1rAVkURr6QwfoAIMH2AMRBHStEdLuRGyeGkH\n",
"oF3UMHwAABgwuv7+0s2Q9wcJpH4xjo6O+NfUTpKEf6UnoTWhnMa6uiMOFu1k/uDuWie/1hg3V+0f\n",
"tiKSaH3//n3+4HXpbQbBMLh58+b+/j5ncFmW/OtMCK1IIbQSwLCDRTuZP7i71imhNZvJZdvCJauo\n",
"iAxaE0J2d3f5S14Tsa1agIsXL8JWLVIFq9jJklSDJ7iq6bAVkUTrPrdqAcNHDDB8ZAtW0V4YttYq\n",
"KiKJ1mD4yAsYPrIFq2gvKKF1GM7iGAyfdYOlNXxgcKcYMLgTGAlJgooCFQUs1t8TMLhTaiilMKVL\n",
"qmAVJxApobVhfGCQz7AVkURrfjN5feAxrxjb29vwmFeqYBU7WZJqnBmcJKja/m7YikiidZ+PecHw\n",
"EQMMH2A8mCYipLlnC9ARYPhIDRg+sgWraC+oonV9H7xhKyKJ1mD4yAsYPrIFq9jJklTjzGDDQFXI\n",
"sBWRRGswfOQFDB8AALoADB+puXfv3sOHDzmDi6LgX9pbaBFwoXkiww4W7WT+4O5aN2ytVVREEq1P\n",
"Tk74g9cEDB8xjo+PhbZq4S9Z/u075AxWsZMlqQYo0kOwtFu1gOEjBhg+AAB0ARg+UgOGj2zBKtoL\n",
"w9ZaRUUk0RoMH3kBw0e2YBU7WZJqgCI9BIPhMxDA8AEAoAvA8JGak5MToat+/nP+4C9/urvGFOpk\n",
"/mBJrgRl6GShYBUVkUTrPq/6IfWLUZYlzOaVKljFuaPD1lpFRSTR+sGDB/zBazJqw4epguvT1c8C\n",
"DB8AALoADJ92yLLMcRzTNBc+jqeUTiaTKIqiKJpMJvzFguEjW7CK9sKwtVZREUm0BsOnBZIksW2b\n",
"ELLwr57n2bbtuq7rurZt8++4BoaPbMEq2gvD1lpFRSTRuk/DZ+AbNMZxHMfx/PuGYSz57xJu3Lix\n",
"s7PTQs1khb8rVIQQsvD7MBhAPnUhhGxvb/d2uMFe9S+n4e8Lra4HAACgOmNM/fO3YPyrsFJK+f24\n",
"JEn4J/4JTRHkd6hEg3/wgx/IUA3+YKFOfvfdd99+++3W6yAa3J3WMsgn+rXnD75z5w5nJJLjy4kE\n",
"te7T61d1Nq/jOPMZHGPsdryH9JUrV/jX6xcaOyQUbFf75rUd/Pzzz8tQDf5goX67evXqRz7ykdbr\n",
"IBrcndYyyNfd1/6Tn/wkf7AMX04k2ED+3LI+qqb+dVI8xjiKovo7/I/sL1y4sLW1xRlMKeW3kthI\n",
"AKF4zmChMQaPPfYYf3BHAzmEKoxEuuLSpUtPPPFEFyWLDtrhzwiSyMdfLBLsN/7v/M7OjlAdZAgW\n",
"0po/t6zPxgyfKIo8z1sSkCTJZDIxTdNxHNFv3pk07hiEfgP8N2Vf+tKX3nrrLf5g/sEAt2/f5g/+\n",
"9Kc/zRmJBB0D/pKzLBMKvn37NmfwW2+99aUvfYkzWMjw6a6ThS4bJZGvI0WEfiNCho9Qv3UXLKT1\n",
"kAd3soR+eHgYRdESFywIAsdxCCFhGGqaZppmu9XAGFdHT5KE/7QsZPgI2QtXr17ljESCd75CJoAk\n",
"wfwN/MhHPsLfdUKKdNfJTz75ZEclgyIVkvSbkNZDNnw0TSOEsMx72lU/pdTzvDRN2Z0gIYRSGgSB\n",
"0PmTnS3qLkocx9VfCSHT6ZRl/6IofN/nLFbI8BGyFy5dusQZiQTvfIVMAEmC+Rv4xBNP8HedkCLd\n",
"dfKFCwK/O1BkhTogafpNSOs+DZ++Uz/P9XUURZZl1R1A27Ynk4lQ6q8n+nk0TQvDcIWFHO7evXty\n",
"csL51P7tt9/+93//d86S33777aeeeooz+Lvf/S5/8DvvvMM/zKCj4Lffflso+Lvf/S5n8Le//e2/\n",
"//u/70KR7jr5Rz/60cYVEQoevCLdBfNrLWQmt0BvMwgaxHF82vQT5vM03tR1vftKnc0XvvCF/rQB\n",
"AGBMXLp0qbdUJuMIn6IoDMNovMk/9L5TvvKVr3zlK1/ZdC0AAADWQsYpXa2P5wEAAADqyJj6AQAA\n",
"gE6RMfULPXcFAAAARJEx9aNFy+wIrX0KAAAALEHG1G9ZVmM4FBvuuan6AAAADAwZUz8zfKr9ENgM\n",
"L6FB/QAAAMAS+t6b1/M8dkVPKa0vbNSYgUUpNU0TY6xpGttvC1I/AABAW0i9LXuWZZRSdgLYdF0A\n",
"AACGg9SpHwAAAOgCGb1+AAAAoFMg9QMAAIwOSP0AAACjA1I/AADA6JBx5U5pSZIkCAI26IgQotC4\n",
"o3ZrHkVRURSEkLaqtyZttY7tCMQGHxuGYdu2JBJ30UBd1wkhMiyI2/rPqiiKIAh0XZdkRHhbDXQc\n",
"p/GOYRjzixzz0tvy0Krj+z7GOE3Tsixd18UYb7pGvLRV8ziOLcvCGFuWddpeC/3TVuvKsjQMgxCS\n",
"53me52wvubIs263tCrTVwDzPMca+7+d5PpvNwjBkxbZaWWG6+FlZlkUIkeQr2mIDEULxB2FSrlja\n",
"yp8cFWVZ6rpeTwSEEN/3N1glTlqseZqmLFMs2WanZ1psnW3bjQ2CXNclhKxbxfXoQr76O5ZlrVvF\n",
"NejiZxXHsW3bknxF221gu1fqkPq58H2/kQXYNdSm6sNPFzWX5Hc1a7V1ruvOv7nxZnb9xdvs5ndd\n",
"tI7dq0nyFW23ge2mfnjMy0V9zQmGrutKbCmjbs15aLF1848uiqLYuNffqXxJkqzuFLdB661zHKex\n",
"rfdm6Ui+JEnWLwQe83Ih856Ry1G35jx02rrJZOK6bitFrUwXDWTroyRJkmVZGIbrFLUm7baONSpN\n",
"07Xr1Rqty2eaJqVU0zRKqa7rvu+vfJ6D1M+FupfJ6tach+5aN51Obdve7EUx6qaBWZZlWZYkycZH\n",
"qbXbOsdxNn6qbtBuA13XtSyrOnMEQTCdTlc+eYPhAwBNptMpxliSoYGtY9s2G+eTZdn8eEFFYR7I\n",
"xk/VndIYjGvbNlv/eLXSIPVzoe6ekerWnIfWW0cpPTw8lCfvdyqf7/tZlq2cO9anxdYFQWAYRvJT\n",
"mKm18a39uv71YYwh9XeOuntGqltzHlpsHdslQrbNITqVb53c0Qpttc4wjKIoqtRfFAWz/tuo41rI\n",
"++trcbTQgEnTtDFWLAxD27Y3VR9+hGoex7HrumfOY5Jk5NxMXJclDSzLks14qr+5zpSZVuhCvjqG\n",
"YWxwVleL8s1HyvAV7Vq+xqQBISD182IYRpUXWJrY+ExITjhrXg2NOHOajyS/Kwa/LksayKbyNqZ0\n",
"zWYzTdNar7AobclnWVbjg+yxYesVFqIV+eaR5yvalnzz30/btteZcggjfHgJw9A0zSzLqj0jVbHR\n",
"OWteDfY4bdRHY3NN0zTZ+43NNXuGX5clDWSWdxAE1Y7QDBnGR7UlHyHEcZzqWSgb1O/7fnc156EV\n",
"+eqwZ9fsKzqdTlVp4JmtC8PQcRzP85h8URRZlrXOiCbYpUsMdfeM5Kl5URQLRyLLD6cuw24gT+tY\n",
"DEJIqu8wyIf4Wlc9u15fPkj9AAAAowNG+AAAAIwOSP0AAACjA1I/AADA6IDUDwAAMDog9QMAAIwO\n",
"SP0AAACjA1I/AADA6IDUDwAAMDog9QMAAIwOSP0AAACjA1I/AADA6IDUDwAAMDog9QMAAIwOSP0A\n",
"AACjA1I/AADA6IDUDwAAMDog9QPAKMiyjO2v2RGNvS0ByYG9eYEOmUwmp21vizFeZ2dRQJTpdFrv\n",
"8CRJPM9DCGmaFoYhQiiKIpa+dV1fYUvbKIoQQrZtt1ZjoEsg9QMdYts2ywiWZTX+xPIO0A9BEGia\n",
"Vt/3FWOs6zqqSYMxJoSYppmm6QqHcF13MplA6lcFSP1AhxiGwUyG+c2mIfX3ied5jXssTdPYvt6V\n",
"NLq0uwfFAAAEJUlEQVSus5MBxniFQ7BzSRAEkP2VALx+YDPU84vneaZpmqaZZRlCKIoi9l92x1An\n",
"SZLJZHJwcLC3tzeZTBaa1yxmb2/v4OBgOp0WRREEgWma0+mUBUynU9M06940e8c0TdHDsZKDIMiy\n",
"bDKZbG1tHR4eOo4zXytKqeM4pmlWMQvNd54GipIkCaV0/saLE9bGBgvbaFkWOP7KMAOALiGEEEKq\n",
"12mazsekaRrHMcY4DEPbtgkheZ7neW5ZVp7nVZjv+4ZhVCWkaWpZVlV4dYh6TBiGGGPLsmzbjuOY\n",
"vRnHMTtKowKNnwPP4fI8t23bMAzbtllVy7JsFM7exBj7vl+WJfuv7/uapjXCeI64AoQQ27YXvj9f\n",
"+HxOYB+PazBraL7APM8RQqyNgORA6ge6heVilmUMw6jy7zyGYWia5vv+wr/meY4xXvipek43DGP+\n",
"g/NJ9sysx3O4qqhGZFmWmqYt/9RsNvN9v14H/iOKwvp//v26NBXzqd91Xdd1659aeCJhIITWrC3Q\n",
"D+D1A52j6zozlE8b7VPhuu5pTnEQBCwxNSCERFHEyk+SZP7juq6v4D7zHK6i8V9N0+otLYqCUjr/\n",
"tMOyrKIoVjuiEFmWneb2VNJUzD+DqdcqCAJK6ZLxP4ZhZFm2Tm2BfoDUD3RONbakKAr2aPE02GPG\n",
"hWRZdtqT4SrRtJh0eA7HSVEUCz+iaVr9gUeLR2ywpFcbw36Ww0Z/MmdsCWee4AEZgMe8QH/Ytr3a\n",
"6BGEEHsSsPDWtUpGGOP6dXTFCsmI53D8LKxVp0eso2kaTwWWk2UZy/vLT95Zlq0sMdAnkPoBNTAM\n",
"48zRI7ZtM0ei/ibLWWeW3/gUz+E4YR7IwtNPPSO3eMQGGOM1r8TZ+CX2aJq9E0XRfJmUUkoppH4l\n",
"gNQPqIFhGLquVwM0K4IgqHwSZuuzUaGUUjas03GceQ+9cX9QFMVkMhE9HD+EkPmJzZ7n1ctv94h1\n",
"qtkVq8GGpYZhWDeO2HjWRmQURdVMMUBywOsHOsQ0TZZhWZpYuHhDURQs32VZ5jhOdV3Jxp/UI33f\n",
"dxzn8PCwemjM7IV6mWyoped57AqauSjzqdOyrCRJTNNk5wBKqeu6h4eHpmn6vs+SF8/hptMpy6pF\n",
"UbDlECil7CxSL4o9Z2ZFsYfASZIYhsE+ItTAFaiegdf7s6p5lmVhGGqaFgQBm0hhmqZt29WTYc/z\n",
"iqJoDOSfz/vsECvPHgB6Zms2m226DgAgAEuI7DXnI0qWtuYTKPNhGo9b1z/cEqqr7yVFtXtEBkvr\n",
"az4zWE5RFIeHh2wobXdHAdoCUj8wfE5L/aPi4OCATRnrqPzpdIoxhlUcVAG8fgAYBQ1zqXVWmz8B\n",
"bAq46geGTGNZnk4dDwBQCEj9AAAAowMMHwAAgNEBqR8AAGB0QOoHAAAYHf8fagDORQ7N/64AAAAA\n",
"SUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7b1/bBzHmeddkmWbsimLJdsRaTkSXRFlK+sfEptJbCcX\n",
"yYvuszfGZn0JehwneF+8vl30xLjs4hwc0P0uErx7iA+YORySPcA5Z/qUyyJYJ+sZbDa7CzsW2Eis\n",
"bM6n9bFI2bmNZf5oU/7FkX+wKJO2xj/1/tHSeMThkN1VNVXd7OfzFzWa6af617eeeuqppzacOXMG\n",
"AQAAAHlio+4GAAAAAKoB6QcAAMgdIP0AAAC5A6QfAAAgd4D0AwAA5A6QfgAAgNwB0g8AAJA7QPoB\n",
"AAByB0g/AABA7gDpBwAAyB0g/QAAALkDpB8AACB3gPQDAADkDpB+AACA3AHSDwAAkDtA+gEAAHIH\n",
"SD8AAEDu2KTMUhAEvu8zxgzDcF0XY8x9KN/3gyCQcigAAIAcosjr933f8zzXdavVKsbYsizuQxWL\n",
"RUppqVSqVquEkJGRkTAMJTYVAABg3bNBwd68jLGRkZGxsbGme+55HiHEcZykh6KUep43Ojra/CQI\n",
"glqtVqlUpDUXAABgvaPC66/VarZtt4ZlHMfxfZ/vUIZhtH5immYQBKJNBAAAyBMqpD8Mw2V6TQhh\n",
"jHEcatlxVjw4AAAAsDoqpnnDMDRNc9mHhBCOQ9m2XavVyuWy67rRkYvFYqlUin+En//85z/4wQ/e\n",
"fffdFf+3t7f30ksv5WgYAABAHE6ePNnpvz75yU8++OCDitpxpvuYpjk6Otr+ocgBm+1vP/Lq3Hbb\n",
"bYquLAAAQBI2bdrErYpJyV5ef7FYbHYbY2Nj5XKZUpr0IMqub5dwXTdpn5dCRLr/lLAObsTo6Kjr\n",
"urpbIcqK/mW2cF1340Z1gqzCksRYvO/7GOMo2hMduVqtFgoFWccHAADIA4o6mXbHnMNVRwgFQbBs\n",
"2gBjzDdtAAAAkFtUSL9t28vyL6N0z07fD4KgXC6vmAK0YmoQX7IQAABAblEX8Gkm8jPGyuVyp/Vc\n",
"lFLLsjzPKxaL7f/rOM6yXsHzvPb0IQAAAGAVFNXwqVarlmVRSjHGQRA4jtNpAqC58mvFyjyEkFKp\n",
"ZFmWYRjRoUzTTJTcCQAAACiSfozx2NgYpZQxtnrBNULIzMzMiksBIkzTHBsbiyJIjuNAoB8AACAp\n",
"6ip3otipPoSQNQUdgjwAAADcZC+vX5De3l7dTZCAaZrrYLizylR/VlgHN4IQsg4cKdu2s34jEEIX\n",
"XnihMlsqKneminvuuedv/uZv8nbWAACkHM/zDh069Prrr6sxlzuvHwAAAADpBwAAyB0g/QAAALkD\n",
"pB8AACB3gPQDAADkDpB+AACA3AHSDwAAkDtA+gEAAHIHSD8AAEDuAOkHAADIHSD9AAAAuQOkHwAA\n",
"IHeA9AMAAOQOkH4AAIDcAdIPAACQO0D6AQAAcgdIPwAAQO4A6QcAAMgdIP0AAAC5A6QfAAAgd4D0\n",
"AwAA5A6QfgAAgNwB0g8AAJA71El/EASFQsGyLM/zGGNSDlgsFi3LKhQKlFLxAwIAAOSETWrM+L7v\n",
"+36lUiGE+L5vWdbY2JjIAYvFYhiGjuPYth2Goax2AgAA5AEV0s8YK5fLY2NjGGOEkOu6jDHf9x3H\n",
"4TtgoVAwDKNSqUT/JIRIaysAAEAOUBHwqdVqtm1Huh/hOI7v+3xHi37ouq6cxgEAAOQPFV5/GIaG\n",
"YbR+QgjhDvf7vl+tVmW0CwAAIKcokn7TNJd9KBKlIYSEYRi5/7ZtL+tX4uB53oqfm6bZ3lQAAABZ\n",
"dBKfI0eOvPfee8qaoSjWL+tQQRBgjH3fL5fLrutijIvFouM4SacNOuk7TBsAANBVOonPiRMnjh8/\n",
"rqwZijJ8JMIYq9VqzUlj27ZHRkZM00yk2uDaAwCghU7iEwTBBRdcoKwZKqZ5OQIyqxyKUlqpVGRN\n",
"GgMAAOQQRUu62pdc8S3CwhgbhrHMwYcoDQAAQCJUSL9t20EQtH4SpXt2+n4QBOVyudMMgWEYy45G\n",
"KQX1BwAAiI+6gE8zJhOt8Oo0MUspjYo9FIvFFb/gum5rxxCl+qzSkQAAAADLUDTNW61WLcuilGKM\n",
"gyBwHKfTBEAziN8azW+FEFIqlUZGRiK5D4KgWq12+jIAAADQjiLpxxiPjY1RShljUVJmp28SQmZm\n",
"ZlZcCtDEMIyZmZko7FMqlbrSYgAAgPWL0uTOmKk+hJA4sXtI0AQAAOAD6vUDAADkDpB+AACA3AHS\n",
"DwAAkDtA+gEAAHIHSD8AAEDuAOkHAADIHSD9AAAAuQOkHwAAIHeA9MsgDDUYZQzJ2wMnAVpOFq7w\n",
"ejUKV1gTIP0y8H0NTzCl6PwKporosL1cd9GyHwOliKu0uCharnCHaondxff1XGEtj1PK9hQB6ZeE\n",
"lidYi1EtbhqlGuwypm20AXQVLbdVy9vaGZB+ICFahhpIx5tDadoG6d1FV6euHuhcQfqlkR+vH+g2\n",
"+elckQ4VDgJtEwxp8iRA+mWgZT5Q42Ok/mQJ0SaIwPpDy/YehID0rzu0PElhiLRsS2maGtzD/GzF\n",
"E4YIYw0agTEMInMFSH+WyY8g5ocwRI6jR/rzEwHX0s8RkqrOFaQ/42iJvaTpCQbkoMWN0NXZEKLB\n",
"dMo6V5D+LGMYqlWYUj2vjUbUO+D5mdiAYas+QPqzjPo3hzEUb5dN+Xa1YJp6pD8/aJnYMIy8dK6d\n",
"AemXhJYnOD+xF10T6UC3MQw9Exu5B6RfElqe4FzFXtT3c4SAe6gCxc9wEGgYV0XikKa3FaRfBtEd\n",
"1XJf0/QwdRddU3NAV1E/X4V0hNTCEJlmqh4nkH4ZYKzhCY50ME0PU9fJQz+nMcqkZYiTqwcYpegZ\n",
"BumXQ8jY7IkTSk1ijBBSbRQhhNCxp59W/wRTjGd/9jPFRpH6KxyGyDSPP/ecUqOUIozHZ2fn6nWl\n",
"dhFCCIU65qu0vDgPP/dceibn1El/EASFQsGyLM/zmAzhCMPQ8zw/HaVQgyA4fvy4YqNhGD7++OOK\n",
"jSKEDk1MzD36qGKjtVptdnZWsVFK6dGjRxUbRQg9/vjjp44dU2ePMWQYvzh6dOrwYXVGEUII1Wq1\n",
"Z156SbFRhJCWF+d//u53R379a/V2V0SR9Pu+73me67rVahVjbFmW+DE9z0MI1Wo18UOJE4ZhT0+P\n",
"YqNBEAwODlKVfgSlL7399r7bbjty5Ig6o4whhBhjjUZDnVGEEEJBEPT09EjxVOJDKe29667f/PjH\n",
"Ko0ihF644ooPp6eVmmSMUtrX16fUKEJBEHzs2muDclml0cWlJWwYb//TP6k0ugoqpJ8xVi6XR0dH\n",
"DcPAGLuua5qmoLceBAHG2DRNWY0UhDHW09MTqg3UhmH4qX/9r5988EF1Jhl7+NlnP3PPPRf99rfq\n",
"jFJ68uMfJ4SoV+EwDPft26fYvajVanfeeefc3JxKo+MTExreJowRQv39/YHaOYYgCG75xjdmVY6r\n",
"EBofH7/t3/7bzcrdl06okP5arWbbNm6Zz3EcR1D6Pc8rlUrCTZPD8eeeM01zcHBQpUY03nkHIXS5\n",
"Zb3/2mvKjCKEGGM3fPGL2zZsUKnCvzp2LLrCKjVi4dQpjPHgrl0LExPKjCKEGGMDd965W210a3x8\n",
"3DTNvr4+lYPI+smThBDFtzVioL9fsQpPTU2Zptl35oxiB7ETKqQ/DEPj/CWghBAR4fA8b1lfopd6\n",
"vW7bdv/27SrVsF6vR1f1YxdeqNJuZGtnb6/K13VpackwjMFdu1QK09KLL5qmiUzzwhdfVGYUIYQx\n",
"Rhir94UxxopV+Pjx46Zp9vT3bzt1SpnRs5jm7zUa6h6nc3Lfv3ev+n5uRRRJf7tME97UWsZYEASu\n",
"6wq3Sz6Kn2CMMTLNz/b0qHyYolt51fXXK51j0MFLb70VPaUDAwPqPbWrNm9WrxF9W7cqDqkRQpBh\n",
"bFtYUGY3Gi4jxYGmMJzetQsh1L99e0q8/k0KbMi9qVJCPZ3mmW3bdhwn2bGCYP7MGYQQMs2djzxC\n",
"KTWUVLlZWFiI/hjctesHlNq2rcBok56LL1Zp7iwYb5udZYypGfA1Go1I+j+3efNjQZD4weCDsSgC\n",
"ftnOnSrMpYOhoSFKqZrJhnq9bnzpSwghxcP0Jo888siKbtP09LTKRAYV0i+RIAgYY+KPyOjoqJT2\n",
"RMxfc030x/Dw8BMKpT89s9yKMAxz48YgCJT2c4Rcfcklyjy12TffNNTf1iA4+e67CCGE8U0ffKDM\n",
"fTkLIZ959NG/CAJlz3PTddAi/V//+tdt224Pe3ied+jQIWXNUBHwkfgY+b5vmmZwDkopYywtkQdC\n",
"9rz5ZqtGROmnCmh9govFYveGsfWTJ5uvDSGkaYhSqmaBxfD+/a23W0tqb7FY7Ooj17zCGOPm40Qp\n",
"7erJLg4NIYSQYRzcubN5WxljXTV61sklZNkgUtbSnzXBGDcN+b6v4hnG+ItXX63sCq+Corz+9leF\n",
"7+UxTTMMw6b0h2EYhf5ltFGY84vMFItFxHuaSTEMIzLkeV6rIktnw/PPn+3IMf5Cf39kNFpb18Uz\n",
"bV7V8ysNFAoF3/e7pxHLRt+RCnueZxiGmkcu8nLQOd1X8ywN9PezcwspCoVCF4WJsRWXwhSLRYxx\n",
"9+w2I6Wo5QpHl7d7Y7vmBAMyjL3nwv2MsWKxqEv6VQR8bNuO1nM1P4nSPTt9P3LnHcdpD+kui7dG\n",
"6q99yndxcfHsX5R+ZdOm+r33NhqN+xYWrrvkkqPf+AY6cAAhdGLTpl0PPNClBhQmJo796EfowIE7\n",
"jhw5eODAE0eOIM9DCB17+ultnrfzwAFZhk4PDJz9yzCurtWu/fWvEWOThw//48GDx44dW7jvvr6t\n",
"WxFCyDSRxME7pS/39yN0dl+9u95/f+G++2ZnZ/9zX1/P1Vef+OpX8U03IYReu+yyK//8z6UZRegj\n",
"YWLM27jx+B//8VX79t1x9OhBhJ44ciTqkI49/fS+X/xCotGP+htCDN9/7amnUBi+dvhw6fbbnzhy\n",
"pHH//T0XX9x45513/+iPLjt4UKLdsxgGKhTuWFpauO++E7Oz//2KKxqNxm+/+tUbookHw0ASQ23N\n",
"24oQYuz/efXVY3/wB4ODg/dOTt6M8RM//3mUFXP0n//55l/9SprR8yOlZhA8ceQIonTL4cOV229v\n",
"vjgLp05tKBa37tsny2hzggEhhGq1O555pnH//U8fPerv2zc7O1u/997+7dtl2YqJuoBPczAVrfDq\n",
"NGlGKY2KPURecybYsmXL2b9GR3f95Cd/uX37D3bt2veLX/R873s/vfFGattFxib+9m+7Zb5U6nvo\n",
"occPHKgZxmvf/CYqlR4/cCAyOtbX9/pTT3XFqGmiSuXV+++vGcYTt9/e873vfeyHPyxt3eoh5CH0\n",
"xLe/Ldfa6WZAYHT02p/9rLR160M7dw7+9Kf9P/rR39x0k0+IhxDtnvdUqfQ99NB3r7zyx3v3bnnw\n",
"wegKM9cthOG/9PRMPvSQRFPNnF3kOKhSeeL22wPTfOL221GptOXBB3+8d6+H0P+7sPC7//gfZRpt\n",
"xvEwRqOjOx9+uHmFr/u7v3twy5YiYx5CT3z3uxKNIoRONzvXSuW6v/u7h3burAwOfuyHP0SlUvTi\n",
"FMKw3r2yQqVSdCsD03z6K19BpdJr3/ymT0ghDEvT06/IXk199gqbJqpU3v/Od368d+9Pb7yx76GH\n",
"dv3kJ//fRRch5auUFE3zVqtVy7IopRjjIAgcx+k0AdAa6FzlgJTSKCAYhmGxWKxUKvIbzcWyZhNC\n",
"arVapVJ54pZbmskb3cAwjHK5PDY2hs4Ns6rV6u8effQSqV1OvV5vnZ5yHOcTn/hENGdOCKGUlkol\n",
"wzCeuOUWiUYXTp1C0WACIXTuCi+bJSuVSo/LrT/TNvY3TbNWq0Uui2EYhUKhWq0+f+hQQ/ay29ZH\n",
"yHXdbdu2zczMREajR136FW40Gq3vY3Qrm+Pyt9566/Of/7zjOHKNtoMxppRGg3jDMKJn+Fdf/SoK\n",
"ApmDyPOxbbtQKDRfnE984hPVapUQ8vQXvrBXnpXN5z8kpmmOjIxEmYoYYy1LlBRJP8Z4bGwsmpV1\n",
"XXeVUyWEzMzMhGG4+nS/YRhys3QkYppmU5iaYavpwcGDlHb1CW7Ggg3DiGolffLOO5/+/vevk2el\n",
"me/YpFKpND/p0h1ZWFgwv/zl1k9aEySamb5n+voQpdL2jwzDicsvP3i+0WYs2DTNqCoJ3b//6u9/\n",
"X47FlcAYR0oU/TNSKAVEXXj091//9V9/9B/ddF8cx2kGvm3bjpZtXv6pTz3z61/f2LUXxzCM1vWh\n",
"Y2Nj0d9y1/qytosWdeESTSRFadFmwzBM01yziyOEZChtcamt7mCr9DdPdnDfvmcfe6yrLWld7hDZ\n",
"VeBNaLlTkewu+/Dl/v5FqctuP4rjIYQQwhg3rzDGOLrFpmnKjUhsa5mEjFC8YiNiRVV6ub+/qzWH\n",
"CSHNebumL/ze5z9/2dRU94yilV4c1BqMksFHcbxz6NV9BPX6xXn98OHdd9+99vcMY7PEyEDsVISN\n",
"6pfIIzR/5oz6LUd23333G488otiodOaVl7FECC08/3wcL2G+r++1Lk0ddYYQsvD884qNdoP0FJ6J\n",
"AOmXwPu9vWt+hxAi0z0Mw+nBwThf/LAlSq6M+WuukSj9C22O8IrEuQvdQH0paYTQZG+vxB21FjZs\n",
"iOOE7v3a196SV7F1cmqqN96Ls7BhgyyjyUhHxYUuAdKvCELIhngSJpfTPT0SB+kxA6DzfX1v/+Y3\n",
"sozGXLdsGIbEvVwWl5ZifrOnp0f9nmUbr7hCy1Z/Evu5paWlPXv2yDpafGKewvTgoDLpj+a31dhq\n",
"AtKvDrnRw5i83N8vUSNinsLwl7/8quItBhHCGEucmpuamhoeHo7zzcneXomda0xhemPfvoVf/lKW\n",
"0ZjIndjYMjkZ85une3okqnDMLZXmo6wBJRiGob6kBEi/KLOzszFnbCQ+TOMTEwPN1VWr8nJ/v4a9\n",
"tjWhpXPdeMUVEo8WU5gMw4gZB4uDlpjVhUtL8/v3x/nmy/390qQ/tsL27d9fV77lqkpA+iUQcwJn\n",
"vq9PogMeU/oH9u6tnzwpy2hMjZAbe4mP3OhWTHR1rhL1Wv3eoij2FI5kWpcQrwohROIVTs/mXE1A\n",
"+tc5cp/gmBqhK5nh+KWXyupcNz399Hvx5o0/eeutsydOSDEaH+lJpTGRGHuJX3pWYuc6OTXVd67O\n",
"7upgjCV2TlrGo6sD0q8WHTkDp195Rb1RLTGEZZn4IszPzOz5ylfifFNiP/fSP/xD9xZMSeH4pZeq\n",
"f4Yldq5LS0sxh8tyQ2opBKRflPhDua1f+tKspEJUk5OTMZ9g0zTPlmJXi5YYAkIJgrlrEl/TP3z9\n",
"dSkWX33uuctuuy3ml7WEIyR2rvFJW0a8dCDDJ5PEH8pJfIL7/8//Gbj1VllHi0kQBH06FhzF58Pb\n",
"bpv92c8UGzVN84XYmaASkdi5pjAckSsgwwdIAu/mxtxsm5i4eG/cklZaJj+5N3wGYrJ07bX1hx9W\n",
"bFRi1sD4+HjM4fK6B6RfKVrC7hI5Hfu1yZUjqSV/Y76vT33nev3nPqd+FkduwGcgXoaPRNI5XAbp\n",
"V4eusHuukCVMiY4ja6z+0Z4/MdBS7UciifpLWZ1re3W8VZDYuYL0AxqQuxgyJioXQzaRmPKYKJIu\n",
"K+w+NTU1FO2Rm2I2JemfViHRuFBW57ptYSF+WW9ZneuWqamYicIqAekXRUsWYyKjMhdDxuaa3//9\n",
"2WPHFBuVSCI3U2LnuiW2RsjqXBOFIwzDmH7jDXGjSZGZMKY8X+jCpaXFtaoVwTRv9kj0UMrqJ7Sl\n",
"TsZGV0KerMhAIp9UVrb7jno9vjD17d8vq3ONL/068yzX9chV/YUF6RclkdZok2wZr834+HicKrtN\n",
"pEQGknpDGqpZyst239xoxA9HyEpnSmc4Yhkq62g2OTM4uI7L+ID0i6IllSVRfzO9a1fj2Wel2N0T\n",
"OxKNMX7prbfELVJK+5OkZGS6c02KlM41TjiiFS0T6VowDCP9jeQGpF8psrLdE/U3hmFImfxMlB0h\n",
"8bVJf3RretcuLdL/+gcfqDcq63YkPo6MaPg6lvKkgPQrRcsQQVYYcdvCQve2le9odGIiUThCS7a7\n",
"YRhaKrit7yIzrUzv2iUl7J60v5HSVSTK2VUGSD+QdhKFI05ccIEUo4ne+azPaSdC1uRnosYTQqTU\n",
"Hk9kVFaucDpzdkH6laKloDzGWEuBXy3ImnFNf5QJaRpEnrjgAimxl0SNl1V7XNci8/g5u8oA6ReC\n",
"UppII17evr2hXIXX92zVCsgQpkTuodza7opJGo7QUrwz0+yenVVfcWtNQPqFYIwlyj/RtcOGFnTt\n",
"mdV48knx4ySdSJci/VoCOOkMR7ST3c4VIQ3FFtcEpF+IzbnRcQ7k7ggfk0/eemt2O1eecISMK5w4\n",
"HKE8nSlXc9pqUCf9QRAUCgXLsjzPE1m1zBgrl8uWZVmWVS6X1S+AbmXz3Nz88LAGu7kJ4MzNzSX6\n",
"fq5mXF/u7xcfVyUNR0jZcSjUkQsLtKJI+n3f9zzPdd1qtYoxtiyL7ziMsUKhwBirVCqVSoUxZlmW\n",
"XvVPBMZ44fnnxY+Tn5LIc3Nzw/v3627F2mi5I9KMJpF+KZ1rGIaDg4Pix0kKz9BBibwQQk6ozQ9W\n",
"If2Rnz46OmoYBsbYdV3TNH3f5ziU53mO45RKJUIIIaRUKtm2XS6Xpbe5SxiGsbBhg+5WcMLh2C4K\n",
"b1/FYRQiA+sSKeOqpMWTpYyr4mCapuLCziqkv1ar2bbd6iw4jsMn/YQQ27ZbP3FdV/22lplDS2Lc\n",
"VZ/73BuPPCJodEe9Hr+sDZIUFE7n3hrpQfxx2jYxEX/bnwgpQ5yk/YcUo3EeSELI1q1bxW3FR4X0\n",
"h2FonP/2EkL4ojSu67YffN3v2izO2zq2S7zo2mvlHEjH/dUi/Ukltbe3N1Tu9xiGcUrGdolJpV8K\n",
"WuJy6XQjNimwEYah2VYAQFbdwUKhUCqVkv4q6KCDURwp/nEmJyeHE07zintMHL1m1nd0UgxH4laj\n",
"0UCMCfZSSdeRXXH33Rt/+EMRixxgjPMz1SSFZUONTuJz4sSJDxQWZVIh/d2bhi0Wi47jtPcra9Lp\n",
"6pummUj6l5aW4hezjBBfJkopvVr5/qIZQrxzjRK3BpP85I3BQUSpYI0jLWlC+Vrul5CBgYHxiYlh\n",
"sdu6rKfsJD6zs7MffvihiKFEqJD+LlEsFg3DcByH47ccA4UVSVTMUiIc/cfi0pLiVZiGYTz97W8P\n",
"qjWKNNVgkOIIa/GmM1Gy4ixhqHhtVN/w8LZHH5V7zE7i43ne1NSUXFuroCLWbySZposDY2xkZIRb\n",
"9yWipZglx94aQ0ND4k9VUvcQ5mC6jZTqTFqGGkmXayBNu7WcXr/Da0V5/e1JONxpOVEuv+M42nWf\n",
"D/HxddK9NRBCPQMDWyYnBe1qcQ+zkqnZ29s7qdBli5BSnYljqCHeW2hZrpG04tb6RoX027a9LLwV\n",
"pXt2+n4QBJ2W6a6o+9laGdgjbwvv+CwODV0onGKvBY7sCC3B6z179ixl8wpzIB6Y4us8BJeJJK24\n",
"hdZ11Vt1AZ9mIn+0wquTz04pjYo9FIvFZf8VLeV1XXfZb0dGRrrQ6m6hZdyaXThmU8Q9u8nJyUS7\n",
"ECOE3hwa2jY+Lmg3P+yo15NG7YeHhwWDlhyJW+u46q2iad5qtWpZFqUUYxwEgeM4nSYAmgHi9kgx\n",
"pTQMQ9/3ly0Hy1AhB10QQur1+qByu+KRAY601LMVQwVmmDgSt94XLsgeBMEVGRniyCH5hK3gXsQc\n",
"iVtIxjOcznukSPoxxmNjY5RSxpjruqtMABJCZmZmVlwKYJrmzMxMl1uaDI6bGgWF96idHCaEvKDj\n",
"+dOSsiJeMZQvcUt8WoIjuqUteC28iCEp8/v371a+iAHJeIbTOcGgtGizYRimaa6Z+EEI4UjV1wLH\n",
"TRUPCo+Pjw8kXwmZn2KfCKE5sfgsR+KWeAEJjsQtXSirbLM+SOerB/X6heC4qe/19oon2wwkzznT\n",
"4oBrGeoODw9z5A5qhyNxSwoc90jLs2QYxqyMAhLqSefiZ5B+IThuqniyzY56XUtZGw7SOdTtEul0\n",
"7taE4x5Fa1xFjHL0N7BMRC4g/aqJZlxFjrC50RCZw+SDLydayx6NpwcGtCTbpNO5WxOOHosj3rgM\n",
"LT4BR+IWymyPviYg/aohhKRzxn91OHKikaY9Gk/392fxCuuCr8fanMGQGkfiFspsj74mIP15QdB5\n",
"4ZuEFI8McGCapuC4KkM9x8s6ynHP79+vRfoF7wtf4laGHoZEgPRrQMsQUtB54ZuEFI8MaLlWWsIR\n",
"fIlbF1xxhWA6EweEEC0zroL3ha/ilqDR1K46AukXgs8jWK9DyG6g5Vrx9TfivRRH4taePXvUpzPJ\n",
"2mwjD1BKOSKlCgDpF0KLe5ihEehpGWXj1MPX3wj2UhlK3ModApVXNi0tpTPPDaRfiPyEI/jo2bv3\n",
"jelp3a3IBloSt7JV+lDL6zY9ODj35JPcP79saurN5HPLCgDpFyJD4QgtrOPqVylBcIVgGIaDg4Py\n",
"mtNdtLxu4isE39+ieJOkWID0Zw/+cAQsvl93LA4NvfXSS9w/35SbQtMoO3s/qAGkPy98uH//+C9/\n",
"yf1zvvwTQbIVjtCCYO2g1IYjugFHdbx1DEh/XhAXbo78E0F0hSP4E7cy2FelMxzRDTIUKVUASD8Q\n",
"i92zs4p3xEZce2uc/aHYS843kX5q9+7Jw4e5jcKkSLeBpOpWQPr5CYIgX0NILukXUeHNc3N84QjB\n",
"VTR8bRYsx52hxC2dqN+ZXawkFF/hIAWA9AuhRfqz5R4KqjBfOEJQRrW4h3xlBnKFYJ4lHz1794rU\n",
"BeErHKQAkH5+dO2twa1rgvvb8QHObEw4tqKMEBlXpdYnXREtOzEIJiindqUeSD8/3HtrCOZZ8r3q\n",
"8/v3X/Tb33IbBVKLyLiK2ycVUcNcRUq1rNSLA0i/Bk7t3j351FPcP+cLRxiGITJu1RJlytxmW5kb\n",
"V3FHmQQHCa1nDgAAIABJREFUcxAp1Q5IvwbEt+flQHCTIy1xm7m5ueH9+zl+KDKu4i61+ObQ0GVT\n",
"U3y/1QVfMUtRoxMTp5WvEUEQezwfkH5+FnW4eLrQkhPN7ZO+3N+/+OKLfL/lLrW488YbRUoZ52qt\n",
"qRbp52ZdLggA6ednampqKJVz992AO+lF5LXh9kmHh4eneB3wzfU6n3soWMo4P+FvbmDrTYmA9POz\n",
"udHYojw7gm+PXI2kdKOKzmyem5sfHtZgN3OupfIU+4Fbb9WyRcy6BKSfnx31OvfcPff+dosvvsi9\n",
"8wOUmE4zWsZV3DOf04OD3NLPPXsPW8RIBKRfDK65U5GtTUXqbWXOAQfiIBKO4O6Ye3t7J3lDatyz\n",
"94BEMin9QRAUCgXLsjzPS+3Wl6sguLUpd72tzDngItl4WvIs84NIlpqWVU65WkwQh+xJv+/7nue5\n",
"rlutVjHGlmXpblFisjhuzVawSCTPUiRxCzLH46BlldOmpSWQ/lYyJv2MsXK5PDo6ahgGxth1XdM0\n",
"fd/X0phcvedCSQ68IzPu/mbLxz/OvX5NJHGLu6+CnQliwv1I6NqZILUqkTHpr9Vqtm23rk5yHEeX\n",
"9GcufqKFl/v7uVdXcfc3InVXdtTrWz7+cb7fcpOtjRI1IuKCcEdKReQ7tSqRMekPw9A4f6hICNEV\n",
"7tcSAxGpt6Wlwad7euYECkioR0s4QtcCVxFR405VyBwi8p3anN1NuhuQjDAMzbY1Phyh804zBLZt\n",
"O44T8yAiDgj3A/HB669z14DVuKt1ltZuaoJb+uf7+lAQ8K194xa1+f37d/OurkptDKQbtL90ncRn\n",
"enpa5ZXJmPTLcvBHR0elHIcb7tMQWUzA/WBlbh2ZLrS4ePN9fYtLS3yxDO4GY4zr9fog129z/ix1\n",
"Eh/P8w4dOqSsGRkL+KwbhJ5+3sQ4bqMi68h0oSu6pd7o0NAQd9UKLbMpWsjWzgQKyJj0G6msfL3u\n",
"0ZUdISLfWlRYixpuyc2+6iJc9NJL3JHSsyG19UXGpB8hRNvSRdo/UUO2vB5BuLMjkMDqqszJN/+4\n",
"ChagdRmR8tTcG6ileR1ZxqTftu3g/O43SvfU0pg07rq2JsqzoTJXxV7Lbc1VFVgRtPhbAwMD4xMT\n",
"HD/cXK+D9MshCvg0E/mjFV7xc3LkoiXDR+TRF0mx5+b93t5sDY+0DDV2z85uufFGxUYFfdJsLfAW\n",
"YYA3+UpXFdg4ZCzDByFUrVYty6KUYoyDIHAcJ4sTANz6IvLoRyn2HE/x4uIid0DZMIyn6/Xr+H6c\n",
"K3jLe5weGNjx6KMcPxT0SddlFfv8kD3pxxiPjY1RShljrusK7juoCy2OMHeK/dTU1N13381nlPsG\n",
"CWaUavFJX+7v506x5+Y0dxHvubn54eFBXrvcz3BqVznliuxJf0QWPf1WspXarCUc0Xj22R0CGaVa\n",
"fNLTPT3cKfbcRIVgB9UaRQLPcOZm79F6XLqcsVh/eshdvS3l1UYF46RaxlUiKfbcZLEQLDfceZYi\n",
"wQHuDTa4N6VRAEg/Jy888wzU24pJtuYDRfoMSLHvNtx5loJDjYWFBZ5fPf98ajelAennRNcqJxHe\n",
"6+3dMjmp3m625gMzOXfERRYXE3DnWYpgmiaf9IuUXek2IP38iKxy0rI+cHFo6ELenZXyQ7Y6KhEE\n",
"FxPwDeYEI6XceZbaSGseCki/HrjHrSLBk6jkFscPs5WYn0P4ngrB2Xu+PnLuySd3XH89t1FAFiD9\n",
"euDe1VrEJ+UuuaXFbxkfHxdd4Kp86XL2Qmo6Zu8X9+xRbBRoB6RfDyK7Wqsniwtc5/v61C9d1hVS\n",
"g2HZmsAlWgZIPydQA1YFAj4pd0hNEO49gUXI1jIRLQiOXPlCamnub0D6Odk6Pb3n05/W3QqgI729\n",
"vRypIIKTkKZppvltXwecHhjYxrU7mODIle/nKZ3hRQiB9HOjZQfXjKIlr38PV0B54W//dvstt0hv\n",
"zJpo6TCy2EtxV60QhO9apTlbDKQ/S+jaKFFQI9L8ArSjZXt0LbdVi0/67JNPiszec2epCbL+Qmog\n",
"/drg2MBkwy9/uVVscSCfA57mcSvAjYQuOXl8bEe9vuWuu7gNZm5jyNQC0q8H7g1MBH1Svrddi9sO\n",
"9R3jo+VaTQ8Ocki/FoIgyNzm0t0GpF8P72vKDsqQx6Slv5GwmCA54nE8XSG1xYwkKG+bmDhzzTW6\n",
"W5EuQPr1EBXaTfor8YxSDokJwzCjgU6Oaos76vUtH/94NxqzCosvvijok2aoTKku50PLFE6aAenX\n",
"A1+h3Q9ef32Pcp80DEMtg2VBjeArtKslceuyqSnBbfz4+mbBMBFfmdKsuhHZGS7HBKQ/S2gpBLhl\n",
"auo9HeEpcY3Q4mDylXjUQrYyr0QQj+NxXKuUb+kB0p81lBcCvHBpSULRFeWvgWEYWrIAOXa7nZyc\n",
"zF5BykyxudHYIua+cLgRYRimeUsPkH5gDebm5gQnGLSkgmRo0+alpaUB5SG1IAhE9mTnRstQTHy4\n",
"nNE41SqA9OcLjpDl3Nyc+ARD0lQQprzoZoSWkO62hQUtVd3FpZ9jNkVbHE/5Fd42MZHm3ZxA+rXB\n",
"oTLiwqQlvMuRCkIp1TJY1nJ9ti0sCPqkp3t6ku78s1k4Gsa9Y60gGXLARXZz6jYg/TxQSsU9Jg6V\n",
"0VU8WbCqO+xY221eTh4vEtz1PoLDAV9/qTKdGB8fT/MUDkg/D4wxLXFSbSjf0ENXWpE4uqQt6c4/\n",
"c8IOO99EeoZXhicPQqqfwokPSD+QRqSkFW3TkWepRdqGh4eT7vwzNzc3LFYPimMiXVdBBfGb8nJ/\n",
"v/qdf7qKOukPgqBQKFiW5XmeyCQeY6xcLluWZVlWuVzWMh+4bWICFgd2FSmD5aS7teRqblkXGYrU\n",
"t8LReYhHSruKIun3fd/zPNd1q9UqxtiyLL7jMMYKhQJjrFKpVCoVxphlWerf2Lm5OZD+RHDMB4oP\n",
"lpNGoiml4j4pR/g7wzEQHWhpOd/OP3mX/shPHx0dNQwDY+y6rmmavu9zHMrzPMdxSqUSIYQQUiqV\n",
"bNsul8vS27w64oNlDrKbiJ2hVBBxnzQrXq2uleHiPpOWnpJv5580o0L6a7WabdutkUHHcfiknxBi\n",
"23brJ67r0vUVg1sFLdIvRcuS9h9awvS5otFoiKe6J3XAnx8fv0B5qjtjLLtDnO6hQvrDMDTO9y8I\n",
"IXxRGtd12w+eoXWb2uFIABeHIxXkknodmWaX2tOJd597TrFFWbzX25t0x1opPXpSB3xpaUl9/UFK\n",
"6dYUF1TQhSLpb1dnvtKV7RQKBcdxpBwqPjvqdfUekxQ4EsDF4eibtYRNXvnNby6/+27FRiml2y+6\n",
"SPAgiyleNZoGtDxOKR9qbBL5MWOsU7AFY9z09Ls3DVssFh3HMZO7h53mmW3bjtORbBBefomSe0zP\n",
"PvzwTTfcIGgUITRXr8ePtoZhmPInWC6CRb44YIxdftVV4sep1+uD4kcBOpN0R9VOL3gn8ZmenlZZ\n",
"4EhI+oMg6BSyxxhXq1WRg69JsVg0DIPP5R8dHRUxrSX8vbnRuPLTnxY0Ojw8PDc3l0j6d193naDR\n",
"XDHf14eCQHG0yjTNJ7797UQ/0dKjSxkuJ0WK6/nm0NDgI4+IHwd1Fh/P8w4dOiTFRByEpN+27WWT\n",
"ritiyE4kiHI6HcdRH+qRSFZSQbSgpb7jYkK3bkWSLibQhbaMUuVpRfXHHhu87TbBg+jaUbV7KMrr\n",
"b48LcaflrA/dzxtJM3a09IvXvfWWFJ80UZnS//noo/kqCqKczY2GeH49xjjRjqq6lgfGR4X027Yd\n",
"nJ9VEqV7dvp+EASdlumuqPsp3w0n04jvGB6hxRfmCKmJ+6RJy5TuqNf7fv/3BY0mJf3CtApnQ2pq\n",
"SRq60FV6Nj4qpD+6as1ZgWiFVyefnVIaFXsoFovL/itayuu67rLfjoyMdKHVqWP37Kz6wfIlx4/3\n",
"ZzbWr2XowFOmVHn4W8q6ZaRp+UVWQmopRyjWH59qtWpZFqUUYxwEgeM4nXrRZiJge0YgpTQMQ9/3\n",
"l80tZ9qFSYYMjUiUqKAlOBsEwdUpLnmYTpJO2/a+9564UV0qnChLLVcpavFRJP0Y47GxMUopY8x1\n",
"3VUSvQkhMzMzYRi2p2yapjkzM9Pllq5NEARXyHriwzB+FFLKzKfERIWukp85cFnClHTaNs27iKxO\n",
"0iy1HTqWBwZBMJLu0Yki6Y+IGS+L6vN0uzEiXHHBBeIHmR4cPJhE+qWoYdJEBSlJL8AqyKqlk8gz\n",
"oJSqFyZZ80aZYMfJk33pjpRCvX4esusxYYwT1VTY/8Yb6gM+WjQiDENZRpOu/ZESx0vU+EuOH+9T\n",
"PgnJGLv60ksVG0WaEoW1REoTAdKfGFka0dvbm3RnJXEMw0j8JiifhNwwOyttbjl2DnEYhlJmPt8c\n",
"GrpM+W1Nii5h0uIz5WeokQiQ/sQsTExIEaY9e/bE31kp64PlRBFt8W3KI6YHBzk21RMkaUgtP5OQ\n",
"WU/HSOQzbVtYUO8zJQKkPzGyhCkRjDEtO9vJQsvaUZRkdZVEYVpIkvKo5cpoScr83ZNPDu7aJeVQ\n",
"8bd/kHhbE/leWlQiESD9gAoSe0wyGBgYiL+66ndPPimlczVNM5H0a2HbwoKUpJfTPT3xQ2qyJrQT\n",
"7fwjawXD+gOkPzH5GaFLJLHHJEOYEu3uu6Ne77n1VnGjiaCUyqrioK0GeCK3WkcMJNOR0u4B0p8Y\n",
"LWnCEiu9xNeI3FXI0FFUUtZtTRQ4kpj0kqhgkRSSZqkBKwLSr43TAwPxd1baUa/3ffnLcuzG1ogw\n",
"DFNehwRokkjNZTnCiQoWyapEkihLLXfuS2xyKv1p2M73NIQg08Tu2Vnx+o4ayUbBIuXjqo2/+pV4\n",
"xeaI+MPlTOTj5VT605BnRghJVAYW4CDZ6ipJ0h9fI559+OErP/MZKUbjI3HxWiK0LK1CSNptjS8Z\n",
"mcjHy6n0p4FExSq0+KTTo6ObrrxS1tFmjx2L8zWJI/RtlvX2P/2TrKPFJ35IbXOjcen113e1Me3I\n",
"WryWlPQ7wquT9fYvA6Q/Gbo8JoSkOS/x2fTCC1d/8YtSDrXNsubjbYopcYJhcN8+bZ5mPujt7Z2L\n",
"nWephZ5XXlFvVKdKxAakPxlhGGqpQ5J1slv1qKtIzMjs6+sL4m1gIjGjdM+nP71xYiKmUS1qePW7\n",
"76rPx9v4q1/133KLYqNJyan0c0cVGGNaVExL1rYWo0EQqA9HSFTDREhMFO7r69scL+Xx8mPH+vbv\n",
"l2IUGUbMh0RX+FvusC+mbiwuLqY/ZQCkPxmUUlmL0ePDGJO43D++oMtafhkRs/7zjpMne/bulWU0\n",
"5psvMb8+vlG5vDk0FH+Nq3ph0pVYIXGoMTg4GFM3PnbhhbKMdo+cSj83u0+ckKiGMVVY7j6fyXoR\n",
"Sdl48RPApWyi3STmmy83+1tLZCP+YHRHvS4xyTJmP/f8L38p0WeKaVRXUr9cn6lLgPQno+eVVyS+\n",
"NrqKmql/JbbErmepZQvid/7X/5KV/R0fueHv3t7eycnJON+UW7E55inIKs6RyGgYhrsvv1yWUYRQ\n",
"zJAaQnpKViQCpD8ZWmaN5GZ/xxy3BkGw/aKLZBmNT6PRkPjaxBxXyR1qbG404sQ35Ia/9wwNxa8B\n",
"rp5tzz+vRQ0lzszNDw+/H69zzQQg/cnQMvO5bWFBffY3QmjzVVepNyo3WhJzXCV3qLF1cDDOcvHX\n",
"nnrqvYTF/cUJw1DPM7xhg/rB3OwPf3jF7bfLOlrMoKWWPAUOQPqToSVEoyV0+Pojj2z+3OekHQ7j\n",
"bc8/L+1o3UCeTxqz93rrt78duvtuWUZjEobhdql7xsYMu8vtb7ZfdFGcTNZtCwu9N9wgy2jMoOWm\n",
"paX0J/UjkP5VaH+2GGPSPaZlkYFisbhyA6QK07KAT61Wa37SbM9FL720/dprZRlFhrFtw4Zln7Vf\n",
"YQUeU7lcbv6tbM6jXC43bTX/kD6r0Z5DtYI+Uno6SS3rNWl/LluvcPNxkusztY9HPc9rXtjmkKvb\n",
"+6VQStuv8PQjj1x8553dMyqLXEt/GIYjIyPNpzMIAsuymn83VTgMQ8uyGGNPHzmyVWoly8HzIwOM\n",
"MUqp7/vRPz3Pa32LZNG/ffsyyaOUNg2Vy+ViscgYkzsv107rFaaUFgoFxtiWqakz11wj11Br5xqG\n",
"oe/7zWtuWVZ0tbvdo7feVt/3Pc87a1Rq+HtZMTXf95u3tVarRbf15NGje7/wBYlGl2l6GIblcrl5\n",
"+pZlqSmVSCmt1WrR3+dd4W5Sq9Wa0h8ZZYztqNcHlG/8wEGupd/3fdd1IwEKgqBWq5mmGclirVZz\n",
"XTd6XWu1WqlUKpfLj33nO29386b6vl+tVqMGhGFo2zbGOHqIZYLxjpMnm/+K3lKMcfQHY8xxHM/z\n",
"ur3VVHSFozenVqs5jvOnf/qnTz76aN/wsEQr/f39rdITXeFIIyilruuGYVgsFuX6pIO7drUapZQa\n",
"htHaGdi2XSgUJCe6Y7zj/PyTIAhM04xaQimNbusFx451tUcvl8ujo6PNF8d13Vqt9o0779z2iU90\n",
"z2itVrNtO3pxGGMYY8MwCoWC9PDssnFVdE9bX1jP805lpATsJt0N0ICD0B1HjiDPu+PIkYMIDS0u\n",
"zt5zz6bZ2f96882N2dljX/vaJdddd8/x4wcxfvzwYRSGNx0+bDBmIIQsC0kqmh/xUV3JIEC12rW/\n",
"/jVh7I4jRxbuu+/V48eL113Xx9jCqVPhl74k0SgyjM3NSmqW9dz77//7wcFGo3Hiq1/dMDh47+Sk\n",
"UatVMH6rJfQkGc+rnzx57+zszRj//HvfQ3/0R9GNMG+6Cb3xBpI6WP4o6lqroSC445lnDIQWjxxp\n",
"3H//4tGj//fNN/dcfPHCxo2n/92/k2j0PCxrcWmpuG9f/dVXj/+bf4MQ+kqjsQ+hKiFUbsZL68La\n",
"YnH2zTf/fHHxunr9iT/5E3T77XccOWIgVMEYyZ5d6Ovri/o25HmNd96555lnjFrttcOHEWNXHjly\n",
"8MABGyF0ww3IcSQa7e/v/0EQmKaJKEW+v+Wpp/7w4MFPv/BC/d576/X6v+/v76f0D3fs+N2nPiXR\n",
"KGodVxUKx997736E+jduPPa1r1118813HD169gp//etyjXaJPEq/j5Dz4IOFctm8996DjrOLMc/z\n",
"8IEDB0ulHoT+W6HAXnqp+thjCONNplnwfeMrX7nDdbvRkve3bDkbe2Fs7l/9q6MY31Uq7QxDu1gk\n",
"e/ZUHnoIIdSHkEw3GCHU6rwYxo8Yq1QqCKFouOr8l/8ShUe7WqjoL7dvd7/7XYRxr2kWfD+6Ed00\n",
"iBClx+65Z9IwDjrOFkr/0POMAwcOlkoIoT6EulXDgVJk24+H4cFSqQ8hy7IwxpX/8T+iOE8Xg9AY\n",
"/wDj0k9/ihB6wfdHfN91XWTb3TDV19c3fW5A84+33orvvBOZ5ibTLNZq6MYboyssnZ6LLz77F2PI\n",
"tp/A+I5SKXqR0c6d0fPc04UX5yMI+SuESqUSQmjS9/9bENjf/GaXrnCXUCf9QRD4vs8YMwzDdV0s\n",
"7PJEcVtCiJNcNQzDKJVKURswxhjj5kEcxzEMI/ov0zQJIeJN7cTgrl1npZ/S3xiGaZoIIUJIqVSK\n",
"WYqLj7POSxAgw0DnDJVKJc/zDCWpRNGoHHX/Cm9aXGxGWg7/8z9HVzi6+12MQROy/R/+ASGEGFv8\n",
"2MfQuZmVarVaLpe7d7Ir4jgOIcRUshgliqGhc7dVRfEGxubeeaf5IkeB2W7Zwnj3ShtsOI6DMbYz\n",
"pftIWaw/mgNxXbdarWKMm7OpIkRB8ObcTlJaFadUKjWr55um2fpydlWYWqGUNt/PqHdUYHTy9ddb\n",
"tb7UHR9tOed0P6KrV/jq669vSnzkdkR/G4bB4THEhZCznStj4+PjTaORNnXLaAuNd95p/aca3Y9o\n",
"3kpCiAo3gtJ/fPttRVe4uTFkELx22WWtD23mdB+pkX7GWDT5E3nTruuaptlMeOAjCAKMscpnurto\n",
"KW4VhuPj4yqvYeQG1t99N9E2NXKtK4XSX7z7ruqnNAgmNm5UZrS1WLTKK7zt1KnojzAMlZ1sc+ro\n",
"qddfz7r4qJD+aP69tZN0HEdQ+j3PU+Sidpmzb4uWih9heOzyy5Wp8O7LL6eUojA88eabasJKrTTO\n",
"hQXUo97uv7zyijrp//DD6I/6yZPqbqtpbosy0LT4TIzNzc2pf4blokL6wzBcdpkE44Ce5y3rS7JL\n",
"dBb1kye1OMIqOVtNJQx/e9FF6l+b2dlZDW6aWmGKkm2Q4tp8517D2dlZDT36JZcotsgYQ5ROK6/c\n",
"Lh0V07wrjsi4lY4xFgTB2NiYSJM6TaISQrRI8PHjx81vf1uRMYw/fcEFtVrtUydOEIXlKs8m5BlG\n",
"zML9sjgbZarXVUr/wMAApfTSV181FBodHBysBMHv1euKhSlSw1d6er6kUPp7e3vDMHzz+HH7gQeU\n",
"Gb3uuutqtVrh1CkssLSzk/icOHHigw8+4D5sUoSkP1p9uuJ/Rasqml8TsbIMKaGeTlc/ykwQPHgC\n",
"CPmDl176+V/9VU+joc6uYdx49dXfD4IrZ2dVTk/1XHwxY6z+2GNYrfdtGMbkQw/Nq92E6/Of//x/\n",
"qtUOqr3CfR9+yBibnZ01u7dMYSUwxosvvnjiggtUGh0eHg6CYM/CwkGF/U3/9u2U0hsnJ80/+RPu\n",
"g3QSn9nZ2Q/PRc8UICT9Ub7miv+FMa5WqyIH72SRMSbuvqVlnoCQA4R854EHbvi931NsGWPcaDQU\n",
"B80wxsePHPm8svENQggh0zT//s/+bI+8nb/isKW3NwzDOxSX8cIYIXT8+PG71Haupmn+1POGpdaH\n",
"WJM9Q0MPPfzwHpUmEULnXpybBfqbTuLjeV7M7YykICT9tm3HcWokRgB93zdNs9ltUkqjkUemp1wW\n",
"Fxc/c8cdio0SQtTXF7Rt+39XKgfVhtQIQq8/9dQf/4f/oNAkQb5vGEaf2tAWQsg0zaW//3v1Rv/y\n",
"X/7lgFgMloOdr7228667FBs1DKNx+LBio91A0ZKu1qT15iccx4lq7LSWmYxC/5mW/j/77GfV13uy\n",
"bXvDxIRio4ZhvLdvn1KTponC8P/67GcvO3hQnVFCEEL33HzzpfPz6owihBAyTfOY1AqDMTmo8vKe\n",
"48477yRDQ4qN2rZ9/Cc/UWy0G6iQ/qiqUesapSjds9P3gyCIqk21hyOWLcMJgiAMQzWrn7rH1Zdc\n",
"or7eEw5DpEMjbt6jfoyOrpNYfTo2O997D8lYupiUfTfdlAujYbjnzTe1FErT8jhJR0VyZ+SSN2cF\n",
"ohVendZSUkoty/I8r9i98mEAQogx1du/aFzBAHQPjJGSssznYZooDBFjGqQ/DNfHM6wo4FOtVqPK\n",
"3RjjIAiiOjkrfrPp6a8+A0kpjcqNRUV3o4JNQAIYU/0Er4sXJgFBgNSPRylVrYaGoWddlS7CUP2W\n",
"ed1AkfRjjMfGxqJZ2dVrtxFCZmZm1lycbRjG6OhoF1qqHE3LERGlGoQpKhiXH9T3dloc4Vyh3mfq\n",
"DkqLNsecjNW1rkoDhCCxghacRM+ulid4Xbw2KYUxFIYg/d1Fi8/UBXK9S5d+8vaWUgrS30UwRmHY\n",
"1U24ViYI9DzJugJN6+IZBukHFKJ+bhkhVKtpMJqr8DfS5MSsCwnWBUi/bijVE/7OiTZFqSDqNQJU\n",
"aV2iuDReNwHpTwEQc+8q6+h1TSmUaogyaRnMEbJufCaQft2slzTh9KIl/K1rulW9MGnJ60cIEQI+\n",
"kwgg/brRkiasJcq0Xt6ZWOhKslR/kQ1D253N1RMlG5D+XIKxHo3QQt7SqNSj6wpreaLWy8IUkH7d\n",
"dG9z8FXQNVjWgi5h0rJ3a8Y3jM0A6+XFAenXja4nSYvzAsLUVXL1LOnq0deL9CtdzQusgBavX4tR\n",
"XSNlLfWdtOwFpOW26rKrZUmt46yb+CFIv260PEk5mYGM0HKyWvq5XF3h/BjtDhDwAQAAyB0g/QAA\n",
"ALkDpB8AACB3gPQDAADkDpB+AACA3AHSDwAAkDtA+gEAAHIHSD8AAEDuAOkHAADIHSD9AAAAuQOk\n",
"HwAAIHeA9AMAAOQOkH4AAIDcAdIPAACQO9RJfxAEhULBsizP85iMzaODICgWi5ZlFQoFqmVjaAAA\n",
"gGyiqF6/7/u+71cqFUKI7/uWZY2NjYkcsFgshmHoOI5t22EYymonAABAHlAh/Yyxcrk8NjaGMUYI\n",
"ua7LGPN93+Hd3KdQKBiGUTm3+xJZR/snAAAAKEBFwKdWq9m2jVu2EHIcx/d9vqNFP3S1bM8GAACw\n",
"LlDh9YdhaJy/Xx0hhDvc7/t+tVqV0S4AAICcokj6TdNc9qFIlIYQEoZh5P7btm0k3wfVsqwVP7dt\n",
"mzsMBQAAsCadxGd6errRaChrhpD0M8Y6pdZgjJuKLCWfJyIIAoyx7/vlctl1XYxxsVh0HCepXo+O\n",
"jspqEgAAQHw6iY/neYcOHVLWDCHpD4KgU8geY9ylsAxjrFarNSeNbdseGRkxTRMmewEAAGIiJP22\n",
"bdu2vebXOAIyqxyKUjozM9M+aVwqlWRZAQAAWN8oWtLVHhfiW4QVxZGWOfjg7wMAACRChfTbth0E\n",
"QesnUbpnp+8HQVAulzvNEBiGsexolFJQfwAAgPiokP4o4NOcFYhWeHWamKWURsUeisXiil9wXbe1\n",
"Y4hSfeLEnQAAAIAIRYUcqtWqZVmUUoxxEASO43SaAGgG8Vuj+a0QQkql0sjISCT3QRBUq9VOXwYA\n",
"AADaUST9GOOxsTFKKWMsSsrs9E1CyMzMzIpLAZoYhjEzMxOFfWB2FwAAICmKpD8iZqoPISRO7H6V\n",
"vgEAAABYBajXDwAAkDtA+gEAAHIHSD8AAEDuAOkHAADIHSD9AAAAuQOkHwAAIHeA9AMAAOQOkH4A\n",
"AIDcAdIPAACQO0D6AQAAcgdIPwAAQO4A6QcAAMgdIP0AAAC5A6QfAAAgd4D0AwAA5A6QfgAAgNwB\n",
"0g+qWzQVAAAHB0lEQVQAAJA7QPoBAAByB0g/AABA7gDpBwAAyB0g/QAAALkjd9J/8uRJ3U2QgOd5\n",
"QRDoboUolmXpboIo6+BGBEHgeZ7uVohiWVbWbwRCaHFxUZmt3Ek/AAAAANIPAACQOzYpsxQEge/7\n",
"jDHDMFzXxRhzH8r3/SAIpBwKAAAghyjy+n3f9zzPdd1qtYoxFgnyFotFSmmpVKpWq4SQkZGRMAwl\n",
"NhUAAGDdo8LrZ4yVy+WxsbHIPXddlzHm+77jOEkPRSkNw3B0dDT6p+M4hJByuVypVCQ3GgAAYP2i\n",
"wuuv1Wq2bbeGZRzH8X2f71CGYbR+YprmOpjZBwAAUIkK6Q/DcJleE0IYYxyHWnacFQ8OAAAArI6K\n",
"gE8YhqZpLvuQEMJxKNu2a7VauVx2XTc6crFYLJVKSY+T9YHCiRMnJiYmdLdClPn5ebgR2pmYmDhx\n",
"4kTWb8T8/HzWbwSfN8zNhjNnznD/mDFGKV3xvzDGTWfcsizXdZepv2VZzZB9UlqXb4yOjrb3K6vw\n",
"wAMP/MVf/MUHH3zAZxoAAKBL9Pb2KlvVJeT1R/maK/4XxrharYocvBPFYtE0zajboJR6ntfazazJ\n",
"t771rW9961vdaBgAAEBWEJJ+27Zt217zaxJj8b7vY4yjaE905Gq1OjIyMjMzI8sEAADAukdRXn97\n",
"XKhTpGh1giBYFt7BGPNNGwAAAOQWFdJv2/aySaQo3bPT94MgKJfLK056rJgapHh6BAAAIOuokP4o\n",
"4NOcFYhWeHVaz0UptSzL87xisdj+v47jLOsVPM9LNM0LAAAAKKrhU61WLcuilGKMgyBwHKfTBEBz\n",
"5deKlXkIIaVSybIswzCiQ5mmyZHcCQAAkGeEkjuTQimNaq6tXnAtDMMVlwK0EkWQCCEQ6AcAAEiK\n",
"UukHAAAA0gDU6wcAAMgdIP0AAAC5A6QfAAAgd4D0AwAA5A6QfgAAgNwB0g8AAJA71G3LngYkbg2v\n",
"AM/zln1imuaKyx3Sdl61Wi0Mw2aVvXZiNljjea15CjHvjpZTiDZAjda+mKbpOI7IFdZ1F2KeRZpv\n",
"BDr/LAghruuuuBRJwxtxJjdUKhXDMMbGxubn50ulkmEYulu0Bgih0fOZmZlp/1p6zmt0dNS2bcMw\n",
"bNs2TbPT12I2WMt5xTyFM/HujpZTmJ+fN03Tdd2ZmZmZmRnXdQ3DmJ+fb/9mnObperrin0Vqb8SZ\n",
"M2dmZmYMw6hUKlGTqtVq1Ay+5sk9i7xI//z8PCGk9dFxXbdSqWhs0prE6ZhTdV5jY2PRYx3tn7Pi\n",
"d2I2WNd5xTmFiDXvjq5TcBynWq22flIqlVzX5Wiexqcr5lmcSfGNONPyOLV+Yts2R/Okn0VepL9S\n",
"qSx7bqIOWVd74hBH+tN5XqvoZswGaz8vcenXdQqlUqn9w/ZzidM8jXch5lmcSfGN6AQhpPWfut6I\n",
"vEzzStwaXj1BEHRqaubOK2aDM3Rene6OrlNon58Iw7A9KByneRrvQsyzaCVtN2JF2ncc0fVG5GWa\n",
"V+LW8CqxLIsxhjFmjBFCKpXKsqc/c+cVs8GZOK/V7056TqFQKLRXt43TvPScAupwFhHpvxFR5cog\n",
"CCily3au1fVG5EX60+kwrk6pVLJtu3l3fd8vFovLnpvMnVfMBqf/vNa8Oyk5hWKx6DhOu2rEaV5K\n",
"TgF1PguUkRtBKaWUBkHQnpaj643IS8AniyzLA3MchzEWhqHGJgFNMnF3isWiYRidtkXKCqufRSZu\n",
"hOM4UZ4PpbQ9G1ULeZF+iVvDa8QwjGXPdObOK2aDM3deqO3u6D0FxtjIyMgqihmnedrvwppnsSKp\n",
"uhHLqFQqlFKO5kk/i7xIP5K3NXzayNx5xWxw5s6rHV2nwBizLMtxnNUVM07zNN6FmGcRh1Q9S+0O\n",
"nJY3Ii/Sn3Rr+HRSq9WWdf6ZO6+YDc7ceaG2u6PrFFZUzPYASJzmabwLMc9iRVJyIzoR7VPb/Ke2\n",
"N4I7LTRzmKbZXAExPz+/4rK69GCa5rIlLY7jrLikJYXntXpSfMwG6z2vNU8hzt1RfwrRIthlbTtz\n",
"5gzGuP3LcZqn5S7EP4vU3ogI27aXGYompfmaJ/cscrRBY+RHNPdzlzKQ7B6MMc/zKKVRVkPUw6+Y\n",
"3Jae8yqXy5FjEs2zNT2v0dHR1q/FbLCW84p/CnHujvpTCIKgWCy25/wFQdD+psdpnpa7EP8sUnsj\n",
"IqJJXcZY1LwoqX/FJB/1b0SOpD8i5tbwKYExFoXz1mxwts4LxW5wms8r5t1J8ymgeM1L+Smk/EaE\n",
"YRiFqqQ0T9ZZ5E76AQAAgLxM8wIAAABNQPoBAAByB0g/AABA7gDpBwAAyB0g/QAAALkDpB8AACB3\n",
"gPQDAADkDpB+AACA3AHSDwAAkDtA+gEAAHIHSD8AAEDuAOkHAADIHf8/FTxy9N/QEuYAAAAASUVO\n",
"RK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"%% Représentation fréquentielle du filtre\n",
"figure\n",
"% représentation fréquentielle du noyau\n",
"Analyse_Frequence_Puissance(noyau,ech);\n",
"ylim([10^(-10) 1])\n",
"\n",
"%% représentation du signal filtré\n",
"figure\n",
"% signal aprés filtrage\n",
"plot(ech,y_f,'k')\n",
"hold on\n",
"% signal sans bruit\n",
"plot(ech,signal,'r')\n",
"\n",
"%% erreur résiduelle\n",
"err = sqrt(mean((signal-y_f).^2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On voit que cette convolution supprime exactement la fréquence correspondant à la largeur du noyau (3 secondes). Il se trouve que cette fréquence est aussi trés proche de la fréquence respiratoire choisie! Visuellement, le signal filtré est très proche du signal original. La mesure d'erreur (tel que demandée dans la question 2.2. ci dessous est de 3%."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.2 Répétez la question 2.1 avec un noyau plus gros.\n",
"Commentez qualitativement sur la qualité du débruitage."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"err = 0.076207\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fjOTGfedr9s+stfozw5EUS9rNxuCcfbAPMYxwYHlh\n",
"+GETEg4gLBBgzYYMRYif2AKCXBwDvqKjYOHkISBhOLEOSRDSerjEPjhoXpIHP+QAEsoJwSFGQFr2\n",
"AQESyKQjOwFuEh9LSXY33hnFvIdaUVx2N7uqm2RXkb8PDKPV++tiVf04P5Jf/qp+O0VRIAAAAGBM\n",
"nNl2BwAAAIC+gdAPAAAwOiD0AwAAjA4I/QAAAKMDQj8AAMDogNAPAAAwOiD0AwAAjA4I/QAAAKMD\n",
"Qj8AAMDogNAPAAAwOiD0AwAAjA4I/QAAAKMDQj8AAMDogNAPAAAwOiD0AwAAjA4I/QAAAKMDQj8A\n",
"AMDogNAPAAAwOiD0AwAAjA4I/QAAAKMDQj8AAMDogNAPAAAwOiD0AwAAjI5z2+4AAEiDbdsIIV3X\n",
"dV3fdl9YMQxD0zTHcbbdEUAs4K5/dBBCptPp4eHhzs7OZDKJosh13W13ConQh5Xouk4IiaKoi8Yn\n",
"k4lRYTKZ2LadZVkXxwKAnaIott0HoD8IIUdHRxhjy7IQQlmW2bYdRVGe59vtmGEYYRhutw8s0Bv/\n",
"Lm6ioygKggAhZJom/SbLMt/3LcuizlqPJEkURVFVtZ1eAkMBBJ9x4fu+aZplKFFVdTabHR4ebrdX\n",
"AEJI13X6PFFVk0zTPDo6Mk1TUZT1mtU0rZ3+AcMCBJ9xQQiZjwUY4/JzFEVUcEAIBUFgGMbOzs7R\n",
"0ZFt24SQ2g+jKJpMJoeHhwcHB1Q7WnZQ27arTSVJUhpPp1PDMJIkqcod0+l0vh3Xdem/JklSds8w\n",
"DHqzzNsrFmhTBwcHh4eH0+l0fgZaP2INRVFM06TjRW/Ple/7pQH9hvqrSpZlpYJEn1QWkiQJHSDt\n",
"eRAE1cbZzQghruvSSSiFxFojvu/TztPWypNh/nDNJ0xJd9M+CgpgTMxmM9M0GwzSNA3DUNM0Kgql\n",
"aUq/9zxPVdU4jktLz/N0XS+/iePYNE2Mca3BPM81TfM8L89z+p+e5ymKUlqGYUiPGFaoHqgkjmNq\n",
"OZvNLMvCGKdpmqapaZrVfrL0igXP8zRNK5uiLWOMa621eMT5xouisCyrbDwMQzrw8l/pnCz8Q6Yz\n",
"6TiOrusLD5emKX3sK//Tsqx5YxazOI4dxyn7maYpdWitHfrD8rzK87w2nILhhKG0OO3jBEL/6HAc\n",
"h0Z2z/MWRtiiKOjfZ+3LMAzLP3j6t73wh7U/+PlviqLwPK/2V7osPC08hKIonufN/xN7r1ZCm6LR\n",
"pySOY4RQtectHrFYFPrnA/fCy0PDPVzVazUcx5kPu/N+ZzSrMZvN5vuJMa5NV57niqJUv2E5Ydqd\n",
"9nECgs/owBjHcUyTVXzfPzw8XPiMX1WBKPQnNOfE9/15A/qrqvySZRkhZD4V0jTN8mXmGjiOs/DN\n",
"J2OvWKDvV2sKu6ZpteO2eERKqWIZhnF4eJhl2Ww2W6MdFkzTDILAdd1SKqHX1PXMEELR29B3ywsP\n",
"WjsZFEWpymiMJ0zr0z5C4DXvSCmT0wkhNPW79g5gYU6IoihZlqmqmiTJsnTM6t9tlmULU+AVRdnk\n",
"9eOyfBXGXrGQJMmynnd0xPJXZYzrevUAVfB836eRnToLY1ybXhazIAhs29Y0jX5JCFk2gc0wnjCt\n",
"T/sIgdA/LoIgqN1uK4qi63oQBLVYTEN87eflW2J6/8ty595nZjp7r1ia6vmIFOqOtlpjOVz19pk+\n",
"c8RxXLvCNZtlWea6bu1X9PZ/jS6xnDCtT/sIAcFnXCy7V5p/PJ9PvfB9X1VVaqnr+kKZqIau60mS\n",
"LEyM6eKSwNgrFjRNWygd1L5s8YhrsyzvaCXzLjZNkz7ScZktFMfW6xXjCSPCtMsOhP5xkSRJ7S85\n",
"SZL5RwGEkK7rZd4k/ZXv+6XCq+u6qqrzKZi+79euLhjjyWRS+2N2Xbf22yzLaheDKIp4Lw/svVqJ\n",
"aZp0RVX1y+l0WgtwLR6REU3TqtNCkzjXaypJktoAqRdqT3srzeavFq7rNmSUNsNywvQ/7cMDVvOO\n",
"CyrrR1FEVYUsy5Ikmc1mNX2Drq2l60tpoKE5P7XAR1cCl+8MkiSh28XUzOgfJM3MoRsh6LpeM6Ni\n",
"Mb0CLbTJsoz+qSdJUj58IIQwxjWFhLFXK6HZ5aVmHUWRZVlZlgVBoKpqde1xK0c0DINONQ2pDRvv\n",
"TKfTLMvoNYAQ4jjO0dGRrus0AbdsrRwFNab/WV3QN5lMVFWtnQw0abJ6OBazskt0ouibpOl0qqpq\n",
"2avpdEolIJqeS/tG8/FrnWc5Ydqa9tECoX+M0L8TtPx1K/u2CmVTaNUbtlL5XWbG3lSLvVpJ+TjS\n",
"3E6LR2SBqiIbvi2nrDwZGM3KidI0rZXgu/KEQb1P+5CA0A8sQJYddQAAWA/Q+gEAAEYH3PUD90HT\n",
"t8v/rErDAAAMBgj9AAAAowMEHwAAgNEBoR8AAGB0QOgHAAAYHRD6AQAARgeEfgAAgNEBoR8AAGB0\n",
"QOgHAAAYHaMO/UmS1HYcBAAAGAMjXdJFCKHbCiKEOq2BBwAAICAjDf22bZcVCmk5oWUb5AIAAAyP\n",
"kQo+1cKhtDDQdvsDAADQJyMN/bUNx6G2AwAAo2KMoX/+Hn++/jgAAMCAGWPoBwAAGDljDP3z5eV4\n",
"y38DAABIzRhDP5rTfAgh2+oJAABA/0gZ+oMgcF23wSCKoslkYhiGbdsLw7qmaWXR5yiKNq9tDQAA\n",
"IBEy5fVHUeT7fpZlqqoSQpbVDfd93/d9z/NUVaXlBuM4rtnUlnR5ngdJPgAAjAeZQj9VaegNu+u6\n",
"C0M/IeTo6CiO4zKU27atqurCArNlg132GgAAQDwKCQnDUNf1hf/keR7GuPpNmqaaprV16E984hPb\n",
"9hgAAMNkZ2enrUi1knPbHmzLZFlWu4un6lBb7X/nO9/Z3d39lV/5FRbjr3/96+9+97s//OEPMxp/\n",
"8IMf/Imf+AkW469+9asf+9jHGI1///d//4UXXmCx7M74jTfe+LM/+zN247/4i7/4+Z//eRbjv/qr\n",
"vzo+Pr5+/TqLMZdHupvkP/iDP/iFX/gFRmNB3Ddsj3RnzO7rJEn+/M//nLHZFujtItMiDXf9pmmG\n",
"YVj7cpnxGly9evWRRx5hNH7hhRe+8pWvsBvP93wZzz77LLvxT/3UTzFadmcchiGX8bPPPsto/JWv\n",
"fOWFF15gNObySHeT/NGPfpTdWBD3Ddsj3Rmz+xpjfO7cOfaWN0TKDJ8Guk7TfNe73rWzs8NovLe3\n",
"98QTT7Abs3eD8caHcnBwIJ0x+wCfeOIJ9qnj8kh3k/zAAw901DJ4pESQeePy9Zkz/QXkoYX+rrl1\n",
"69aPfvQjRuPj4+PXX3+d3Zi9G9/+9rfZjf/hH/5BOmP2Ab7++uvsU8flke4m+V//9V87ahk8UiLI\n",
"vHH5+t///d/ZjTdkaFp/1+k6586dY7/r/9SnPsV++/OpT33qgx/8IKPxc889xz7SX/qlX2K0RJw3\n",
"Kewta5rGZfzcc88xGl+9evUDH/gAo/G73vWuhx9+mNG4u0n+1V/9VXZjQdzXkUe4/kb29/cZLRHn\n",
"vHVnzOVr9tjSAr1JSy3SoPVjjB3HqX2pKEpbh7527dre3l5brQlIi+9FBARjzC4Wywi4T14wxru7\n",
"u70dbmiCj2ma5TJdShAEpmm21T6X4MNVAJKrZoDv+x0Zcz3MdtcNdmOuSeaSF7obXXe+FsF9vKc9\n",
"uzGX4CPCyYk4fd2n4DO00E+f0EvfEEJc1124ngsAAGC0yLSa13VdekdPCKnm79eW9RJCDMPQNE1R\n",
"lCiKLMtqMfT/9E//9De/+c0333yzrQZFwzCMZTtkDIBqYc5BAu6TF9u2f/u3f/vu3bs9Ha83aaln\n",
"4jgOwzDP83abvX79+uXLlxmN0zRN05TdmL0bXIrnsI15J5nduLvRDdvXMnpEBF9jjNnXDG3O0DJ8\n",
"SjpK9Tk5OWHX+rkWGXAZcxUYGLaxjJMsSDfAIz0Ycw2wT61fJsFHBD75yU9+4xvf+O53v7vtjgAA\n",
"MChs23755Zd/8IMf9HO4ob3m7Zrbt2+/9dZbjMZZlrHfIHDdStSymMZszDvJ7MbdjW7YvpbRI4L4\n",
"+vT0lN14QyD083Hr1i0I/UIZyxhohu1rGT0iiK/7DP0g+PABgg8AAF0Ago/QnJ6ecr3mZX/JM/j3\n",
"Xd29VOSaZHZjQV79iTDJXMYyekQQX8OSLnHJ8/zk5ITRWMbVvNIZd7d2VJAVniJMMpexjB4RxNf9\n",
"JfWD4MMLCD4AAHQBCD5CA4KPaMYyygvD9rWMHhHE1yD4iAsIPqIZyygvDNvXMnpEEF/3KfgMdiOH\n",
"jrhx48aVK1cYjfM8Z99JgmvPCa6dAIZtzDvJ7MbdjW7YvpbRIyL4GmO8v7/P3vKGgNbPB2j9AAB0\n",
"AWj9QnN8fPzDH/6Q0TiKIvbVH1zrRGzbBmMK7ySzG3c3umH7WkaPCOLrO3fusBtvSm/PF8MABB/R\n",
"jGWUF4btaxk9IoKvQfARGhB8AADoAhB8hAYEH9GMZZQXhu1rGT0iiK/7FHzOfv7zn+/tYAPgj//4\n",
"j//xH//xM5/5DKO9oiiKorAbs/dEVVUwpvBOMrtxd6Mbtq9l9MjWfR1F0Te/+c3Pfe5z7C1vAgg+\n",
"fIDgAwBAF4DgIzSEEFjSJZSxjAuIhu1rGT0iiK/ZxeTNGWyBxo7Y3d09c4b1esn1UD9sBaA7Yxkn\n",
"WZBugEd6MOYa4NmzZ9mNNwQEHz5A8AEAoAtA8BEaEHxEM5ZRXhi2r2X0iCC+7lPwgdAPAAAwOkDw\n",
"4QMEHwAAugAEH6G5ffs2lGUXyljGIuDD9rWMHhHE132WZYcMHz5OTk64SrWwtzzs8h3dGcs4yYJ0\n",
"AzzSg7GwpVpA8OEDBB8AALoABB+hAcFHNGMZ5YVh+1pGjwji6z4Fn1GH/iiKuByDELp16xaEfqGM\n",
"ZQw0w/a1jB4RxNd9hn5uwYcQQlNxCSG6rquqyrW2TRCSJJlOp7quI4SyLPM8j3HRHQg+AAB0gbiC\n",
"j+/7R0dHBwcHhmFEUZQkiWEYh4eHR0dHvu9zvc3YLoQQ13XjOHYcx3EcjLHruoy/PT095XrNyz4t\n",
"g3/f1d1LRa5JZjcW5NWfCJPMZSyjRwTxdZ+veZlCv+/7h4eHQRBYlkUr1IRhGIZhURRpmlqWFQTB\n",
"4eEh1yK3LUIIwRiX/6lpGvtv8zyH1bxCGcu4dnTYvpbRI4L4+u7du+zGG7Ja8PF9PwgCx3GaQ2SW\n",
"Za7rqqpajapSkGWZbduz2YzFGAQfAAC6QDjBx7KsMAxX3hqrqup5nnRxnxAynU49z2O0B8FHNGMZ\n",
"5YVh+1pGjwjia+EEH+mwbduYY76sGiFkMpk4jsO+sSoIPqIZyygvDNvXMnpEEF/3Kfig3grAi0ae\n",
"57qux3HM9asbN25cuXKF/RB5nrMbs3eDvnEB44J/ktmNuxvdsH0to0dE8DXGeH9/n73lDeFL7oyi\n",
"SNJszhpJkvi+b1kW1zteBFo/AADdIJzWX8V1Xd41UOsRBEFzwmUURZPJhMo4vHmlSZLYtl19cT2v\n",
"BS3j+PiYfU/tKIrYV39wrRNh7/DgjXknmd24u9EN29cyekQQX9+5c4fdeFO4nhHoGqhlaJpGMz7X\n",
"JgxD0zQ1TTNNU9f1ZWae52maFsdxnuc0gnMdBWOsaZpeQVEUxt+C4COasYzywrB9LaNHRPB1z4IP\n",
"t9ZvWRbGmI4nz3OMMcaY/lOaphtG/ziOqfgehuGy0J/nuaqq1QnFGHuet/ZBuXj22Wff85739HMs\n",
"AADGA8b40Ucf7e1wfKG/GuhLTNOczWb0cxzHpmlu3q2G0E9TSKvf0EvO5gdl4dq1azsVzpw5o+v6\n",
"7u7u3t4efXp4+umni6J4+umnH3/88TAM3//+9z/++ONFUdy8efPChQvVD0VRXLhw4ebNm/TD888/\n",
"XxTF448/TlsoP9Cmqh9u3rx57ty5hqboh7KFixcvNjRV6xXGuKGpWq8wxg1N1Xr10Y9+tIsBhmG4\n",
"v7/POEC6FJFxgBcvXmyeq2oL586da56r6ofnn3++ea6qTWGMm+eq2hT909juAOlpX2uKfqj16sKF\n",
"C+9///vDMKy2WRvg008/XbZQPSvmm6r16uLFiw1N1XpVO+1rTdV6RU979gHWmtrd3dV1fW9vb3d3\n",
"9+LFizv3U/QFX+jXNG3++aUW7huEGnYaQj/GuLzSlKiquvlBWbh+/frly5cZjdM0ZX825HqK5Hq0\n",
"GrYx7ySzG3c3umH7WkaPiOBrjPEjjzzC3vKG8IX+Ze8GqmG669Bvmub81LdyUBZA8AEAoAt6Fnz4\n",
"Mnx0XZ/P8AmCoM90z+3uE0cIgSVdQhnLuIBo2L6W0SOC+Jo9e3Bz+EK/ZVm1xCa6C6ZpmuU3juO0\n",
"0zUh2d3dPXOGddIURWFfJ8xuiRDiutYO25h3ktmNuxvdsH0to0cE8fXZs2fZjTeEe79+27aTJLEs\n",
"S1EUGvcty7Isq91uRVHkum4Yhgs7QDMyq18ahrHQuHVgSRcAAF0g9JIuhBDd4D5JEtd1kySZzWat\n",
"x/2VzD9DcT1VbQIIPqIZyygvDNvXMnpEEF/3KficW+M38zfdfWKapm3b1S1CgyCoKk4AAABAM9yC\n",
"Tz80CD4IIcMwTNOkTxuEEMMw6PreHjoGgg8AAF0guuDTKa7rlhss0wKQlJrZbDbzfX86ndLNmdfY\n",
"hW1tbt++DWXZhTKWsQj4sH0to0cE8XWfZdnXEXx836ebLqmqqus6xpjrLXYDdLXwSjNFUeI4pqXh\n",
"Wzw6CycnJ1ylWthbHnb5ju6MZZxkQboBHunBWNhSLdyCz3Q6JYQ4jkMznHzf930/DMM+4+8WAcEH\n",
"AIAuEFrw8X2fEDKbzcrMVsuyHMeZTCYd9E1EQPARzVhGeWHYvpbRI4L4uk/Bhy/0R1E0v2JL13VC\n",
"SD/7+G+dW7duQegXyljGQDNsX8voEUF83Wfo5xN8Dg4O8jyf/37hMqtBAoIPAABdILTgM4DSjBty\n",
"enrK9ZqX/SXP4N93dfdSkWuS2Y0FefUnwiRzGcvoEUF83edrXr7Qr2nawpVsURSN4ZYfIZTnOazm\n",
"FcpYxrWjw/a1jB4RxNd3795lN94QPsEnyzLDMGazWTWPfjqdKooy7F3bSkDwAQCgC0QXfGazGV1L\n",
"RSunHx4ejifuIxB8xDOWUV4Ytq9l9IggvhZX8EFv117XNI0+yIRhOJ64j0DwEc9YRnlh2L6W0SOC\n",
"+LpPwYe7LPvIuXHjxpUrVxiN8zyfr2fZYMzeDa4Kf8M25p1kduPuRjdsX8voERF8jTHe399nb3lD\n",
"BN2+TVhA6wcAoAuE1vqXwfUEJDXHx8fse2rTnY7Yjdm7UauVNmZj3klmN+5udMP2tYweEcTXd+7c\n",
"YTfelFaeHXqrir51QPARzVhGeWHYvpbRIyL4WkrBp7f6iFsHBB8AALpASsFnPIDgI5qxjPLCsH0t\n",
"o0cE8XWfgs/q/fp93w+CoNmmt9K4W+ehhx46d461yAHXvhdcxlxrp4dtLOMkC9IN8EgPxlwDPH/+\n",
"PLvxhqwWfGzbVhSluQyWbdtxHLfaMUEBwQcAgC4QUfDRNE1vZCR1WhBChBBY0iWUsYwLiIbtaxk9\n",
"Ioiv2cXkzVmnQOOY2d3dPXOG9QUJ1xWRy7i7Z2rpjGWcZEG6AR7pwZhrgGfPnmU33pDVgg/dg6J5\n",
"AJDhAwAAsAnCCT6Koqy8cI0k7iMQfMQzllFeGLavZfSIIL7uU/CB5E4AAIDRAXv48AGCDwAAXSCc\n",
"4ANUuX37NpRlF8pYxiLgw/a1jB4RxNd9lmWHDB8+Tk5OuEq1sLc87PId3RnLOMmCdAM80oOxsKVa\n",
"Vgs+SZIQQlgWsLFbygsIPgAAdIGIgo9t24ZhNDzmRFE0mUwmk8ng13aB4COasYzywrB9LaNHBPF1\n",
"n4LP6tCvaVocx6ZpTqfTw8PDsjBvEAS2bZdf6rqepmnzfg8D4NatWxD6hTKWMdAM29cyekQQX/cZ\n",
"+vkyfIIgoHm4URSpqqqqqqZpmqaZptldF4UCBB8AALpARMGnxDRNx3HCMCyKIk1TWpNd6rg/mUwO\n",
"Dg7Y7U9PT7le87K/5Bn8+67uXipyTTK7sSCv/kSYZC5jGT0iiK/7fM076uRO3/d1XecSqfI8h9W8\n",
"QhnLuHZ02L6W0SOC+Pru3bvsxhsy3iVdhBDbtj3P49qACAQfAAC6QGjBZ0i4rmtZFu+vQPARzVhG\n",
"eWHYvpbRI4L4GgSfzqHOWyMfCQQf0YxllBeG7WsZPSKIr/sUfFBvBeD7BGM8X08GY1wamKaZ5zn9\n",
"rOs6e8s3bty4cuUKo3Ge5+VRWIzZu5GmKRhTeCeZ3bi70Q3b1zJ6RARfY4z39/fZW96QMWr9SZLQ\n",
"hQj0P4MgsCwLY8zyW9D6AQDoAtD6O0dVVcdxqtUl2TefOD4+Zt9TO4oi9tUfXOtEbNsGYwrvJLMb\n",
"dze6YftaRo8I4us7d+6wG29Kb88XXMxmM8dxGgzCMDRNk8o4XI/P84DgI7WxjPLCsH0to0dE8PWo\n",
"BZ8oinzfz7JMVVVCyLKcS9/3fd/3PE9VVd/3gyCI43iNwwVB4Pt+kiSmaXqex/ITEHwAAOiCUQs+\n",
"iqJgjOM4bki7JIS4rhuGoaZp1F7Xda537iWmaYZhmOc5Y9xHIPiIZyyjvDBsX8voEUF8DYJPEYbh\n",
"Mh3G87xqrk5RFHTbuF76VVy/fn1nZ+fMmTNnzpzZ2dk5f/68rusXL1587LHHdF2/fPnyM888UxTF\n",
"M888o6pqmqbXrl1TVbUoipdeeunhhx+ufiiK4uGHH37ppZfoh5s3bxZFoaoqbaH8QJuqfnjppZcu\n",
"XrzY0BT9ULbw5JNPNjRV61UYhg1N1XoVhmFDU7Ve/eIv/mIXA0zT9MqVK4wDTNM0TVPGAT755JPN\n",
"c1Vt4eLFi81zVf1w8+bN5rmqNhWGYfNcVZuim6xsd4D0tK81RT/UevXwww9fu3YtTdNqm7UBPvPM\n",
"M2UL1bNivqlar5588smGpmq9qp32taZqvaKnPfsAa01dvHhR1/XHHnvs4sWLe3t7Ozs7NKTQD0Vf\n",
"iCX4lERRRG/t5//Jtu35DeMODw/TNO2hYyD4AADQBaMWfFjIsmy+KoCqqv0cnRACS7qEMpZxAdGw\n",
"fS2jRwTxNbuYvDnyFWjkWhjdOru7u2fOsF4vuQrXcBlzXeqGbSzjJAvSDfBID8ZcAzx79iy78YbI\n",
"J/gYhkFf7da+ZN+CbRNA8AEAoAtA8FnBdguBgeAjmrGM8sKwfS2jRwTxdZ+Cj3yhHy2aTa75BQAA\n",
"GDnyCT5Jkti2Xf2nIAiiKGLPzd8EEHwAAOgCEHxWQAWf8pmLrvBaY+f99bh9+zaUZRfKWMYi4MP2\n",
"tYweEcTXfZZlXyfDJ4qiIAiyLKO33jTycr3IXobrunRaCSFZlhmGQb+v3f7PZjPDMJIkURQliiLL\n",
"snp7AXBycvJP//Tf3+4XQgg1HPn4+OKHP/wv730vQggpSpMlGnr5ju6MueZNkEkWpBvgkR6MhS3V\n",
"wi340D1zLMuaTCb0t3QbnH70lipJkhBC6HYOvR2US/AhBJXvILIMzZ8wqvrO/wAAGDM9Cz58GzlU\n",
"91eo/ra3fRS2zvXr1y9fvsxoTLcNaDCI4yIMC8cpMC5eeIFgXGBcOE4RhkUcN7VM1+szMmzjlZO8\n",
"tnF3o+Pa+lGESeYyltEjIvgaY/zII4+wt7whfFq/7/uO48x/r2kal/4lL7du3WpR69c0pOsIY+Q4\n",
"6MaN2HGQ4yC6RUWSINu+9z/XRVGEqg+OguiYIhjLqCyD1r+esQij4zUWVuvnE3wODg7yPL/3y513\n",
"fmvbNi170n4HBWMrGT5ULKLnGyFIVe9dMwAAGAxCZ/j0qaqLyenp6Y9+9CNGY0II+0ueBktVRbqO\n",
"6DOB5yHTRH/7t8flM8HKWxBB3nd191KRa5LZjQV59SfCJHMZy+gRQXzd52tevtCvadrCxVNRFG13\n",
"kW1v5Hm+9dW8qoq+//3fplcCjBEh7+hCC9sQZFkjrB2tdqOjlkUwltEjgvj67t277MYbwif4VFda\n",
"lYLPdDpVFGXhO4DhIfKSrixDQXAvj0jTkGmi0T+kAYA0CC346LpumubR0VEQBAihIAgmkwlCaCRx\n",
"H21J8Jln4SOnqiKMkechz0Oahlz33qPAq69+b8OWRTaWUV4AwWc9YxFGx2s8EMEHIWRZ1mw2S5JE\n",
"1/UkSSzL6j+jf4uIIPgghkdOTbv3bkDX0ec//9fTKXJdxHISCvKYPGx5AQSf9YxFGB2v8UAEH0Bk\n",
"waeZJEFBgBBCqgpaEAAIR8+Cj3ylWoD10LR7O0lEEXJdhBDSdcgQBYCRwif4RFFk27Zt2+VTDN1p\n",
"Z7uVs/rk+PiYfU/tKIrYV39wrROxbXttY5onijHKMjSZ1IWgTVreijHvJLMbdze63ny9FWMZPSKI\n",
"r+/cucNuvClca3/jOFZV1fO8PM/LLx3HsSyrxRXGInPjxo0rV64wGud5Xp2olcbs3eDaCWDlZhJ0\n",
"Awlq1WLL/RjzTjK7cXej25av+zGW0SMi+BpjvL+/z97yhvBp/bZtq6o6v0Py0dFRHMetXpIERV6t\n",
"v5ksQ/TdlWXBXnIAsAWETu6MosikW8zcz3j28BmA4LMQVb2nAj333P+aTFavEO6oG2sYyygvgOCz\n",
"nrEIo+M1Hojgs8weY8y1m528DE/wWWjseYVlFStdKsIztYzyglC+bt1YRo+I4GuhBR/DMGaz2fxO\n",
"PtPp1DRN2L5tYPg+iiKE8YoiMwAAbI7Qgo+maXQdbxVCSBRFY4j7CCFCiBRLuloxtizkeSgIkG0v\n",
"qDPTWzeakXEBkYC+btFYRo8I4mt2MXlz+PL6McaGYaiqWgZ6QshkMsEYd9A3Ednd3T1zhvV6ybXR\n",
"KZexyvMqdhNjRUGOc2+HOPp5K91oQMZJFqQb4JEejLkGePbsWXbjDeFezUtjPSFE1/Usy5IkwRj3\n",
"VhV964xK6mPEggAAIABJREFU8KkRRcj3kWXBQjAAaB+hBR+EkKIoYRjOZjNd1y3LStN0PHEfjUzw\n",
"qaHraDZDUYRs+94qMBGeqWWUF8T39SbGMnpEEF+LK/iUqKrK9dQzGMYm+MzjOCjL0HSKTFOIZ2oZ\n",
"J1mQboBHejAejuAzcsYs+NRwXZRlyHFgJzgAaAHRBZ+FcG1gLTW3b99usSx7zZi9GyKUnMYYfexj\n",
"/5t9/RcUAa92o6OWRTCW0SOC+LrPsuzthP7pdNpKO+JzcnIibKmW/o3v3PnrMLyn/m+rGzIWBpHR\n",
"18P2iCC+7rNUC7fgY9u27/vz4xmJcASCz0KCAEURiD8AsD5CCz62bRNC5tcxj2Q9FwLBZ4mxaSLL\n",
"Qra9uC58p92QUV6Q2tcrkdEjgvi6T8GHL8MniqIwDOffWY+nRiOv4MPesuwiAC0JOZ0u3fihO3mB\n",
"vVlBJlmQboBHejAeiOCzszP2jCAQfFZi20hV0ZgWewBACwgt+JimObxkHq5FJaenp/Cat9mYJv7P\n",
"r3qBl4rVbnTUsgjGMnpEEF/3edfPF/oxxgv3qp5MJi31p1eCIDAMIwiCIAgY9bs8z0e7mpfdmG71\n",
"U/vHQa4dTRIURSiK0IsvvkI/0P81H2RIvp4HVvNW4fL13bt32Y03hE/A8X2fDrv2XjcIgjRNW+5a\n",
"x7iuSwhxahuSrQIEH3bKsl+yQ8i9EF/9hr7wUpTFLzaS5L6Kx9SeGmsa5EEBC+hZ8OF7zRsEgaZp\n",
"XEuTxYRuPDebzXh/yCv4IOaV3IQQ9onNsox9Nfm2jC0Lue69Hd+66wbvJDMaJwmazf7fm28+Sm11\n",
"HWHcFLJrHV6Y8pYkKMuQ66Lj47vvfvcFarYyOU4KX1fpyCNcfRDHmOvvuk/Bh69Kl+d5CyvUSFeW\n",
"HWMcx/EaP7x27doTTzzBaByGIXvxMq4yZxhjWYwtq/C8DrvBO8nNxrNZYVkFxoXjFJ/61H9lbLbg\n",
"HB3tQ54Xs1mB8b3/LTsfJfI1pV2PrNcHcYy5RvfAAw+wt7whI83YoeXGptMpvemwLGthzeF5QPBZ\n",
"A9tGpil0qS8q0COENA2xnQgtQwgKgnv1cASfK6AjhBZ8lsH1BNQDtm3Pv13RNK2q7Nu27TgO7fZk\n",
"MtE0TaghDAnHQYaBPA8JOMG0COVKPadrFOWeLEavAbQUHlwDgA5p5dlB1/VW2ukN0zSrD2Kz2cxx\n",
"HJYfguCznnGeFx/60DfYq5H3IC+sLD2/XREgzwvHKUyz+Nmf/eOOugGCTw/Gwgo+3Hf9URTN50G2\n",
"nuwfBEGWZQ11H6MoolsJaZqGMeZ981x7Wc3+84ODg93dXfajcHWJ3ZirPI4IxoqCfv3XL9k2Ylz3\n",
"zd7yGpMcRch171UebqUPvMYsfVYURE//3/3dj06n91bJrTxPRfA1nPZVuAZ44cIFduMN4dP6oyiy\n",
"bZuGWiqYEEJc13Ucp5VtfGhAp/IRISQMw4VmNMfU8zxVVX3fD4IgjmOuAxFCbNsu95+YTCal+NMM\n",
"aP2bsPV0zyxDto10Xb6U0/JtxHaFqS1CU2zp/7P/hM4V/aCqSFXFTa7tWevnE3xM06SJMXEcl1k9\n",
"juNwPQE1EMcxbT8Mw2UiUp7nqqrmFe0AY+zRJBIewjA0TRNjbJom+89B8NnQuCGVZb2W2SfZ84pn\n",
"nvn+n/7pnzO2LIIIUGs5TQvTLBq0SRF83ZbgU82AomlXP/dzX2WfufkOh2ERhvdas6zCcd6R+0Tw\n",
"dc+CD1/oVxSFfgjDsDp+TdNydh2XgYbQ73leberTNNU0bY2j5HkehuHCdNVl3Lhx48qVK+zts08L\n",
"1wRy9Vko4zwvTLPNllkmOc8LjAvP4/NId1Oxoa/DcOlbChF8zXva14zjuHCce7E+DIvqP7bb4TR9\n",
"59LywguEPdm7I19jjPf399lb3hC+0K+qKv1QC/0YY64bmZU0hH6M8Ww2W9axrnn22Wd3dnbOnTu3\n",
"u7u7s7Pz4IMP6rq+t7d3+fJlXdd/8id/kj4MWZb1kY98pPrha1/72qVLl6ofiqK4dOnS1772teqH\n",
"j3zkI7SF8sPwmnrmmd/CuL9e/diP/axlFb/5m/9TxrlqaOrSpT/EuHj55f8hVK8q3bs032atqUuX\n",
"LpVNffKTv4pxcenSH1658jtpulFT5Qf2XqVpoSj/5Wd+5nXLKg4Opps0tbJXe3t7uq5fvnx5b2/v\n",
"ySefPHv27M7ODi36febMmaIv1hR8qFpSft9n6K8l51B6SzH6+Mc//tRTTzEal/oVozF7N7gELgGN\n",
"MS6a75zYW26e5DguLOudO0cuj3Q3FW35Ok3rt/8i+Jr3tH/xxb+j8svKm+keRpfn91K/Gk7RjnyN\n",
"MX7wwQfZW94Qvu3bNE2j6T26rmdZVm5KlyRJb0nxXDvhtQ69ODMaK4rCnjvElaTENdsCGmOMXLed\n",
"lhsmmSbIe947r/W4PNLdVLTla1VFnoeS5J0CmSL4mnGSCUG2jW7e/I9PPvkuz0MYr1720cPo6AIL\n",
"z0OWhXwfTacLSk935+uzZ8+yG28K14Uiz/PyIjabzTRN8zzPsqzWN3JouOvXdX2Ld/3PPvvse97z\n",
"nn6ONWxms4L/3TwHVBAfCXFcmObqu2ZBoK9eVj75CYLnFbre7blKwRg/+uijnR/mbfju+hVFKdNU\n",
"aWJMlmX0AtDBVWkxXHmyrUMIgU2bWzE2zfr2luu1vHCS6Uab82elIFsEt+5rTUOeh1wX/dqv/Um7\n",
"La9h3DzJtn1vUYXjIFUVxSMNxpaFaJK5Ydx7AujO1z/84Q/ZjTeEL/TXoFsjcC1waIVFf+oc87sJ\n",
"IPi0aGyaS2WfTeSFJEGuixbuxj0wwef+NpHnoW9968PscalnwSeK0GSCdP1e0G823rAPrRvTC0CW\n",
"ockEXbz4n9hbHojg0xsNgk8cx7V/ms1mvW0dCoJPu2BctJoVXOT5fe91R4jj9KFOcFEqPAOgu7EI\n",
"LfiIABV8ymcuupy4tyeP27dvv/XWW4zGWZaxb3HBtRkGY00x8Y3pnv6btFybZComLLvT4vJId1PR\n",
"qa/p9g8s9/4dDbA2yUmCplNkmoufwwTxCLuxoiBdj3QdTSZM64q5fH16espuvCEb7dxJCEmSpMXi\n",
"La7rUh8QQrIsMwyDfl/b0WE2mxmGkSSJoihRFFmW1dsLgJOTE95SLV0YC1J3dHNjVUWEvLPgfo2W\n",
"q/PmuvfKYLEYr0SQeq1rdINmp9j24mi7Scss1DxCCGooiSSIR3iNLQvpOrJtFEVo+U5jCAlcm5dP\n",
"8KF79VB1JU1TRVF0XVdVtd2kfkbiOA7DsN1VxCsBwad10rSdx+e22hkMnrdN5adcQT1saG2fVoKQ\n",
"0IKPqqqqqtJd7+mubWEY0pon3VyYmtA0Tdf1nqtFguDTurGqovmhryEv2PaK+y8kjLzQj6+pCNqg\n",
"/HQn+HzrW383mSDTXL1NniAeWduYjtG2l4o/wgo+fKE/CIJyh2SqtCCENE3TNK23HJvtwiv4sD/u\n",
"Sfrk24oxFSjWa5lOchAgXV+9IyOXR+QVfEosq15Qvq2WG/je9/7ls5/dcxymOjOCeGQTY01DjoN8\n",
"f3H0H4jgU27fVty/iqr1jRyEBQSfjthkTR7jlnCjpc/VXmPOsNpQ4BJa8CmJomic5QxPT0/hrr8L\n",
"Y9O87+aU667/N37jh83vM6vGItxj9uxrz3tnp4d2W65BCJpM0Oc+9yZCHKe9CB5pxdhxUJLUn1+F\n",
"vevnC/26rgdBgOaK8UZRtN1Ftr2R5zms5u3C2DTvFaTlbfnVV7/9+us/YLwPEWTtaM++pgW/5qN/\n",
"6wOcTpHjoO98J+Y67UXwSFvGdEul6oC4fH337l12403hekaI41hRFIxxtVjK/Ab6AwYEn+5Yb1me\n",
"5zXV1wVK6Pb3nbbPsyHpkLGsdaZCaMFH0zQa/cMwpC97bdumdXS7uTAJBwg+3Rlr2js3/uwt/+Vf\n",
"3tU0yeSFrfiavoqsHrnFAfr+vdqHiP+0F8Ej7Ro7DrLte1M9EMEHIaSqKr3rp/9Z5ne23TFBAcGn\n",
"O2O6oRtXy76PfvzH/1Y6eWFbvq7tld1Wy0mCsuydPE7e014Ej7RrrChoNkM0411YwYevLDsAZdk7\n",
"ZeUC1BqTSdNKUWAeWpVe19tsk0r8YtY63yJRhKKI43zuuSy7fHv4AAOmqvmsJMuYMseBKo7DMcMs\n",
"2DYyTYj7C6ALTdqd7RbZKPQTQqIo2m7ZrJ45Pj5m31M7iiL2VYJc6wnthcl68huXmg+LcRDQlFC+\n",
"SWY37m4qtuvr8vq6ectU9K49Q8jokY6MMUa/+7vH7AHyzp077N3YFK6XwkLt4bMVbty4ceXKFUbj\n",
"PM/Ztxji2owo5VmiI5cxTRZjMaYZQbyTzG7c3VRs3dd0BdzmLZvmgtVbMnqkO+PXXnuTMXUNY7y/\n",
"v8/e8obwhX66Mz51lWVZtDxxHMeqqnbSO/GA5M6uYSnPXRRFmhaO031vBkoYtrCx2u/93vB3Z2sF\n",
"x2FKqxU6uRP28AHBp2tjTUNRtNqYqj1ITnlh677WdVrMfaOW/+RPFu/OJqNHOvU1xigIltYirSKu\n",
"4AN7+IDg04MxxquNy4doGeUFEXztecXv/M7/Xbvlhh2hZfRI174Ow9U7ivcs+KxZqmW0e/icP3+e\n",
"qzYve8sjrM27tnGW3Vfclb1ZQSZZhG5YFppO3712y0GA7q+f9A4yeqRrX+s6iqIFJYlq9FmbF/bw\n",
"4YMQAku6ejD+0pf+W8O/0i2aKTIuIBLE19/73rfYF7FWW/b9e2rbQmT0SA++XlaLtAq7mLw5fHf9\n",
"GGNaGTEIgjiO6Ze+7/dfMmVb7O7uwl1/18aahv7u7z7YYEDIOxn9Mk6yIN2YTt90XeR53C033PIj\n",
"OT3Sg6/pj5pv/Pu86+fT+ouiSNPUcZxS7cIY67pujma7dMjw6QFa26+B0ewW2DkYc++tH8eQ2LMm\n",
"zTVEhc7wQaPfwwcEnx6MFQV9+9vfYjSWUV4Qx9e1vbJZWi5zq5Yho0f68bWqrsjz6VPwgY0c+OAV\n",
"fNifZwf/5MtlfPbsY8v+KYru27+Bd5LZjQcv+KiqqmlLi8oua3nlu0oZPdKbr3W9qVpyn4IPbN/G\n",
"B2zf1g++jzRt8RY9to0sC/H89QFNcG2ZRx8Rmu/6gWam08XvV2D7NqG5ffv2W2+9xWicZRn7PuBc\n",
"O4ZzrQmS0fif//mby+aDkPviPu8ksxt3NzqhfM24ZR41TpLVcV9Gj/Tpa0VBy0Z8enrK3vKGtBP6\n",
"ucQvqTk5OYFSLT0Ynz//f5YJETV5QMbCIEL5ulomodmYEKYlqTJ6pE9fW9ZSzafPUi3cGT4Lqa7s\n",
"HTaQ4dMbC3MhVib/AGvAuL+Y50EJxnZYOOGiZ/iMHBB8tmucJPUtgmWUF0TzNcvL3iiKGAskyOiR\n",
"nn1NF/fOI5/gMx5A8NmucS29B8kpL4jma5YUT/aWZfRIz75eFvr7FHxWZ/jQbeosy1JV1bbthUm4\n",
"SZLked5JBwUDMnx6Y2HmybLsCGBDVub5ZBkKAoRxXx0aOvNncs8ZPqs3cqCxnl67kiTRdX1+ux6u\n",
"XUyl5vT0lOuuHzEncRNC2BOca3soDdIYoQXG8zPEO8nsxt2NTkZf/9Ef/dPHP/44i6WMHunf14qy\n",
"YIVEn3f9qwWfMAzDMCzDvaZp+hySbuDDtZKQkuc5rObtx5hu3F9j/ulZxrWjAvpaVVfI/UGQMe7Q\n",
"KKNH+vf1QpHt7t277C1vCtdLYdM0F+7LL12GT5qmpmlijOkeROw7hkOGT2+E4YLaRpDe0xErd+Zh\n",
"zAIC2KmdzEJn+NDavB1dhPrEdV3P8xzHcRzH87zpdMr4Q17BB17zrm2sqotfhdWQ8aWigL7WtKXr\n",
"jBBCWYbOnHmTsVkZPbIVX8//i1iCT5VlClfYsIWrkGRZVtlMlWNPABB8ejOed0sULdi/QUZ5QTpf\n",
"Jwl6883/wWwsn0e24uv5nFpxBZ/BUBaXL4oijmOL+WkWBJ8+qT0RL5SAgLZo3E+4x36Mhtoezj0L\n",
"PmsWaKzB9cpbBBzHmU6ntM+EEId9/yoAGCj0Te84qu0JwXZDZjtLuti18n6wbduYo5qBGgSBoig0\n",
"PQnxLM87Pj5m31M7iiL2lrmWCHJl0w7GeKHgwzvJ7MbdjU5MXzev6WVvWUaPCOLrO3fusBtvCtcz\n",
"QsM73o6eSjqiVlaMPUPpxo0bV65cYTTO85w9d4jdsiiKskrasI3nUiAWWPJOMrtxd6MT1tcN+yax\n",
"tyyjR7bl65rgs7+/z97yhnDf9deSO/M813W9rNPbFkEQuI01jKMomkwm9F6eK1+CUpOn2NclnD9/\n",
"Hkq19Ga8MtkcyVkYRC5f032T2FuW0SPb8rWi3HeG91mqhTvDpzYSRVE8z2trNS8N6EdHR0EQNDwo\n",
"+b5v2zbGeDabKYpiGAbvgZIkKS8YXFcOEHz6NF5Z0A7JKS/I5WvqAhB81jNuHl0tp1ZcwWcZpmnG\n",
"bWznGscxbScMw2UiTJ7nqqpWH6Mwxh5noeg4jnVdL5d0sXceBJ8+jeO4cJx3vgTBp2vjhdsy02kH\n",
"wWc94+bRVTch71nwaSfDR1XVNVSXeeZ3B5onCALTNKsPH5ZlTSYTy7K4DhSGYRRFiqJwpffwCj7s\n",
"LcslAvRjzFJASsZJFqQb88YNj1lcgg97H4SdiraMVwo+VcQVfJaRJElv2/hkWVa7Qqx94Vm4FV0z\n",
"hJA33nhjb2/vscceO3/+/FNPPWUYxlNPPfW+973PMIxnnnnmC1/4AkLoC1/4wvPPP58kyac//enn\n",
"n38eIfTqq69evXq1+gEhdPXq1VdffZV++PKXv4wQev7552kL5QfaVPXDq6++enh42NAU/VC2cPXq\n",
"1Yamar3yfb+hqVqvfN9vaKrWq89+9rNrDPCrX/1K2dT3v/+9+V4lSVKb9oYB0gVEjAOkP2Qc4OHh\n",
"YfNcVT98+ctfbp6ralO+7zfPVbUputpo7QH+8i//5/le0WlnHyA97WsDpB9qvbp69eqnP/3pJEmq\n",
"bdYGWPazdtrPN1Xr1dWrVxuaqvWqdtrXmqr1ip727AOsNUWDxvve976nnnrqAx/4wG/91hfPnz//\n",
"2GOPfelLX3rzTdYl0y3A9YzgeR6ewzTNWsLM5jQIPgv3EeptE6Hr169fvnyZ0ThNU/ZnQ66nyIU7\n",
"KQ3S+P4UiAWWvJPMbtzd6IT1dZrep7BR6LSztyyjR7bo66rg88gjj7C3vCF8gk8QBPNvemnob/V6\n",
"1EQrytLaPPjgg+fOsU5ad0+RXDspDdtYxkkWpBvzxg2Cz7A9skVf0yrt1Or8+fPsLW8Id4aPaZrO\n",
"/fQZ97cOIQT28OnZmAajJFm8+lHGHWMk8nV5JeDZ8Ec+j2zR19UkH/bswc3hu+v3BKiQxKvOt8vu\n",
"7i685u3TWNfv5ZUTsjj0yzjJgnRjoXHtrr8shgyvedczXjlATUOue2+S+3zNK+gq3AatH2PszOmR\n",
"iqJ036migO3beqfM74S92/qh9kJlNoNp7xw650Lv1y8CpmnWVknQdM9+jn779u233nqL0TjLMvat\n",
"vbk2AedaEyS1saatEHx4J5nduLvRSeTr8q6fvWUZPSKIr09PT9mNN4Qj9BNCoijirWjYOlTwKeU2\n",
"QojrulxJ/ZtwcnICpVq2YrxM8JGxMMiwfS2jR7br69Kkz1ItO0VRsNj5vu/7vq7rWZYRQugOCq33\n",
"xnVdekUlhFTz92ulYAghhmFomqYoShRFlmX1Fvo/+clPfuMb3/jud7/bz+EAhJBtI8e59/9A19Tm\n",
"Gaa9B94+w+2XX375Bz/4QT8HZbrrz7LMdd0wDB3Hmc1muq437622NhhjWgU+juM8z8O3qZkpikLr\n",
"q+i6HoZhb3EfgeAjnrGM8sKwfS2jRwTxdZ+CD1OGj+/7GOPyNh9jfHh4uPXyJltJ9eEVfNhbHrYI\n",
"sImxpjUV6ZVxkgXpxkLjapr5ei3L6BFBfN2n4MOU4TO/gJbebpf/iUdTwA0yfPonDAvPgxqBPVHN\n",
"pKpuLgZ0h7gZPisvXFt/99sbp6en8Jq3Z2NdRw0/lfGloiy+LtN7uFqW0SOC+LrPu375kju3S57n\n",
"sJpXKGMZ144K7usyslWj1rA9Ioiv7969y268IUwZPoZh1LbuCYJA1/XymyAI0jTtqo8iARk+W4HW\n",
"xtj226WxUGb1QHpPP4ib4TNPbcf88QCCz7aMly2el1FeGLavZfSIIL4WTvBRFGV+17YqXJtaSA0I\n",
"PlsxVpSloV9GeWHYvpbRI4L4WjjBBygBwWcr0DunUT5nbgEQfHpmK4JPOwUaAaBTIOj3T5LAtA8Z\n",
"yPDh4/j4mH1P7SiK2Bf+cS0RtOl7TzDmn2R24+5GJ4WvswxVF00O2yOC+PrOnTvsxpvS2wqCYXDj\n",
"xo0rV64wGud5nuc5uzF7N7gq/A3bmHeS2Y27G53gvn57hVFR7eawPbJdX5dLuvb399lb3hAQfPg4\n",
"f/48lGoRyljGSRakGyy1A9doWUaPCOLrPku1gODDBwg+ohnLKC+I7+v5jMRhe0QQX4PgIy4g+Ihm\n",
"LKO8ILivaWWu2u49w/YICD7ACkDwEc1YxkkWpBvLjOnmnbU+DtsjgvgaBB9xIYTAki6hjGVcQCS+\n",
"r2vpPVwty+gRQXzNLiZvDtz187G7uwt3/UIZyzjJgnRjmbGmIcNAGK/ZsoweEcTXfd71w2pePmA1\n",
"LzAGDg5Qnm+7E6NBpu3bRgsIPqIZyygviO/r+Qp4w/aIIL4GwUdcQPARzVjGSRakGw3G81v3DNsj\n",
"gvgaBB9xAcEHAIB2AcFHAm7fvv3WW28xGmdZxr61N9cm4FzrRIZtzDvJ7MbdjW7YvpbRI4L4+vT0\n",
"lN14Q0Dw4ePk5ISrVAt7y8Mu39GdsYyTLEg3wCM9GAtbqgUEHz5A8AEAoF1A8JEAEHxEM5ZRXhi2\n",
"r2X0iCC+BsFHXEDwEc1YxkkWpBvgkR6MQfAZCCD4AADQLiD4SMDp6SnXXT/7NX/wtz/d3WNyTTK7\n",
"sSB3giJMMpexjB4RxNd93vVD6Ocjz3NYzSuUsYxrR4ftaxk9Ioiv7969y268IaMWfKhXtPlF68sB\n",
"wQcAgHYBwadNkiSxbdswjIWv4wkhk8kkCIIgCCaTCXuzIPiIZiyjvDBsX8voEUF8DYJPC0RRZFkW\n",
"ru08+zau61qW5TiO4ziWZbFXXAPBRzRjGeWFYftaRo8I4us+BZ+BF2gMwzAMw/nvdV1v+M8Grl27\n",
"tre310LPRIV9KmQEY7zwfBgM4D4ZKQs07u7u9nbQwd71N1PT97l21wMAAJCdMYb++Ucw9l1YCSHs\n",
"elwURewL/7iWCLIrVLzG3/nOd0ToBrsx1yS/8cYbr732Wut94DXuztciuI/3tGc3fvXVVxktkRgn\n",
"J+L0dZ9av6yreW3bno/gmqY58xuNt8rDDz/Mvl8/V+4Ql7FlWR0ZX7p0SYRusBtzzdsTTzzx3ve+\n",
"t/U+8Bp352sR3Nfdaf+hD32I3ViEkxNxDpA9tmyOrKF/kxCvaVoQBNVv2F/Znzt3bmdnh9GYEMIu\n",
"JdFMAC57RmOuHIMHHniA3bijRA6uDiOeqbhw4cJDDz3URcu8STvsEUEQ97E3izjnjf2c39vb4+qD\n",
"CMZcvmaPLZuzNcEnCALXdRsMoiiaTCaGYdi2zXvmraT2xMD1N8D+UPbiiy++/PLL7MbsyQDPPfcc\n",
"u/EnPvEJRkvEqRiwt5wkCZfxc889x2j88ssvv/jii4zGXIJPd5PMddsoiPs68gjX3wiX4MM1b90Z\n",
"c/l6yMmdNKAfHR0FQdCggvm+b9s2xng2mymKYhhGu93QNK08ehRF7JdlLsGHS1544oknGC0R55Mv\n",
"lwggiDH7AN/73veyTx2XR7qb5EceeaSjlsEjJYLMG5evhyz4KIqCMaaRd9ldPyHEdd04jumTIMaY\n",
"EOL7Ptf1k14tqipKGIblv2KMp9Mpjf5Zlnmex9gsl+DDJS9cuHCB0RJxPvlyiQCCGLMP8KGHHmKf\n",
"Oi6PdDfJ585x/N2BR9boAxJm3hh9TR8v+xR8+g79LPfXQRCYpllVAC3LmkwmXKG/GujnURRlNput\n",
"sZHDrVu3Tk9PGd/av/baa//2b//G2PJrr7326KOPMhq/8sor7Mavv/46e5pBR8avvfYal/Err7zC\n",
"aPz1r3/9b/7mb7rwSHeT/Pd///db9wiX8eA90p0xi6/feOM/vPJKziUmt0BvKwhqhGG4bPkJ1Xlq\n",
"X6qq2n2nVvOZz3ymP98AADAKdIRUhNCFCxd6C2UiZvhkWabreu1L9tT7TvniF7/4xS9+cdu9AAAA\n",
"2AgRl3S1ns8DAAAAVBEx9AMAAACdImLo53rvCgAAAPAiYuhHi7bZ4dr7FAAAAGhAxNBvmmYtHYqm\n",
"e26rPwAAAANDxNBPBZ+yHgJd4cWV1A8AAAA00HdtXtd16R09IaS6sVFtBRYhxDAMTdMURaH1tiD0\n",
"AwAAtIXQZdmTJCGE0AvAtvsCAAAwHIQO/QAAAEAXiKj1AwAAAJ0CoR8AAGB0QOgHAAAYHRD6AQAA\n",
"RoeIO3cKSxRFvu/TpCOMsUR5R+32PAiCLMswxm11b0PaGh2tCESTj3VdtyxLEBd3MUBVVTHGImyI\n",
"2/qfVZZlvu+rqipIRnhbA7Rtu/aNruvzmxyz0tv20LLjeZ6maXEc53nuOI6madvuEStt9TwMQ9M0\n",
"NU0zTXNZrYX+aWt0eZ7ruo4xTtM0TVNaSy7P83Z7uwZtDTBNU03TPM9L07QoitlsRptttbPcdPFn\n",
"ZZomxliQU7TFASKEwvuhrlyztbV/OSryPFdVtRoIMMae522xS4y02PM4jmmkaCiz0zMtjs6yrFqB\n",
"IMdxMMabdnEzunBf9RvTNDft4gZ08WcVhqFlWYKcou0OsN07dQj9THieV4sC9B5qW/1hp4ueC/J3\n",
"VbQ6Osdx5r/c+jC7PvG2W/yui9HRZzVBTtF2B9hu6IfXvExU95ygqKoqRUkZeXvOQoujm391kWXZ\n",
"1rW1HTCiAAAHjklEQVT+Tt0XRdH6SnEbtD4627ZrZb23S0fui6Jo80bgNS8TIteMbEbenrPQ6egm\n",
"k4njOK00tTZdDJDujxJFUZIks9lsk6Y2pN3R0UHFcbxxv1qjdfcZhkEIURSFEKKqqud5a1/nIPQz\n",
"Ie9tsrw9Z6G70U2nU8uytntTjLoZYJIkSZJEUbT1LLV2R2fb9tYv1TXaHaDjOKZpllcO3/en0+na\n",
"F28QfACgznQ61TRNkNTA1rEsi+b5JEkyny8oKVQD2fqlulNqybiWZdH9j9drDUI/E/LWjJS35yy0\n",
"PjpCyNHRkThxv1P3eZ6XJMnasWNzWhyd7/u6rkdvQ0WtrZf26/qvT9M0CP2dI2/NSHl7zkKLo6NV\n",
"IkQrDtGp+zaJHa3Q1uh0Xc+yrAz9WZZR6b+NPm6EuH99LWYLDZg4jmu5YrPZzLKsbfWHHa6eh2Ho\n",
"OM7KdUyCZM4V/H5pGGCe53TFU/XLTZbMtEIX7qui6/oWV3W16L55SxFO0a7dV1s0wAWEflZ0XS/j\n",
"Ag0TW18JyQhjz8vUiJXLfAT5u6Kw+6VhgHQpb21JV1EUiqK03mFe2nKfaZq1H9LXhq13mItW3DeP\n",
"OKdoW+6bPz8ty9pkySFk+LAym80Mw0iSpKwZKYuMztjzMtljWdZHrbimYRj0+1pxzZ5h90vDAKnk\n",
"7ft+WRGaIkJ+VFvuwxjbtl2+C6VJ/Z7ndddzFlpxXxX67pqeotPpVJYBrhzdbDazbdt1Xeq+IAhM\n",
"09wkowmqdPEhb81Ilp5nWbYwE1l8GP0y7AGyjI7aIISEOofBfYhtdOW7683dB6EfAABgdECGDwAA\n",
"wOiA0A8AADA6IPQDAACMDgj9AAAAowNCPwAAwOiA0A8AADA6IPQDAACMDgj9AAAAowNCPwAAwOiA\n",
"0A8AADA6IPQDAACMDgj9AAAAowNCPwAAwOiA0A8AADA6IPQDAACMDgj9AAAAowNCPwCMgiRJaH3N\n",
"jqjVtgQEB2rzAh0ymUyWlbfVNG2TyqIAL9PptDrhURS5rosQUhRlNpshhIIgoOFbVdU1StoGQYAQ\n",
"siyrtR4DXQKhH+gQy7JoRDBNs/ZPNO4A/eD7vqIo1bqvmqapqooqrtE0DWNsGEYcx2scwnGcyWQC\n",
"oV8WIPQDHaLrOhUZ5otNQ+jvE9d1a89YiqLQut6la1RVpRcDTdPWOAS9lvi+D9FfCkDrB7ZDNb64\n",
"rmsYhmEYSZIghIIgoP9JnxiqRFE0mUwODw8PDg4mk8lC8ZraHBwcHB4eTqfTLMt83zcMYzqdUoPp\n",
"dGoYRlWbpt8YhsF7ONqy7/tJkkwmk52dnaOjI9u253tFCLFt2zCM0mah+M4yQF6iKCKEzD94MULH\n",
"WGPhGE3TBMVfGgoA6BKMMca4/BzH8bxNHMdhGGqaNpvNLMvCGKdpmqapaZppmpZmnufpul62EMex\n",
"aZpl4+Uhqjaz2UzTNNM0LcsKw5B+GYYhPUqtA7U/B5bDpWlqWZau65Zl0a7meV5rnH6paZrneXme\n",
"0//0PE9RlJoZyxHXAGNsWdbC7+cbn48J9OdhBSoNzTeYpilCiI4REBwI/UC30FhMo4yu62X8nUfX\n",
"dUVRPM9b+K9pmmqatvBX1Ziu6/r8D+eD7Mqox3K4sqmaZZ7niqI0/6ooCs/zqn1gPyIvdP7nv6+6\n",
"pmQ+9DuO4zhO9VcLLyQUhNCGvQX6AbR+oHNUVaWC8rJsnxLHcZYpxb7v08BUA2McBAFtP4qi+Z+r\n",
"qrqG+sxyuJLafyqKUh1plmWEkPm3HaZpZlm23hG5SJJkmdpTuqZk/h1MtVe+7xNCGvJ/dF1PkmST\n",
"3gL9AKEf6JwytyTLMvpqcRn0NeNCkiRZ9ma4DDQtBh2WwzGSZdnCnyiKUn3h0eIRazTMai3tpxma\n",
"/UmVsQZWXuABEYDXvEB/WJa1XvYIQoi+CVj46FoGI03TqvfRJWsEI5bDsbOwV50esYqiKCwdaCZJ\n",
"Ehr3my/eSZKs7WKgTyD0A3Kg6/rK7BHLsqgiUf2SxqyV7dd+xXI4RqgGsvDyU43ILR6xhqZpG96J\n",
"0/wl+mqafhMEwXybhBBCCIR+KYDQD8iBruuqqpYJmiW+75c6CZX1aVYoIYSmddq2Pa+h154Psiyb\n",
"TCa8h2MHYzy/sNl13Wr77R6xSrm6Yj1oWupsNqsKRzSftWYZBEG5UgwQHND6gQ4xDINGWBomFm7e\n",
"kGUZjXdJkti2Xd5X0vyTqqXnebZtHx0dlS+NqbxQbZOmWrquS++gqYoyHzpN04yiyDAMeg0ghDiO\n",
"c3R0ZBiG53k0eLEcbjqd0qiaZRndDoEQQq8i1aboe2baFH0JHEWRruv0J1wDXIPyHXh1PsueJ0ky\n",
"m80URfF9ny6kMAzDsqzyzbDrulmW1RL55+M+PcTaqweAntkpimLbfQAADmhApJ8ZX1HSsDUfQKkO\n",
"U3vduvnhGijvvhuaaveIFBrWN3xn0EyWZUdHRzSVtrujAG0BoR8YPstC/6g4PDykS8Y6an86nWqa\n",
"Brs4yAJo/QAwCmriUuust34C2BZw1w8Mmdq2PJ0qHgAgERD6AQAARgcIPgAAAKMDQj8AAMDogNAP\n",
"AAAwOv4/E9CZ3HHl0UIAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fjBzHfedLFmUtJdJkSba1azkhXRYVOn8QibW5yLmz\n",
"KSPdB8HGxbKNXttJcJcAh54ckOSSe+m+wMEZQR5mYOD84pwzfTLy5xD/mXmInIN9cqYQaP1gW8EW\n",
"KesMROZy60g7MpeWvEWKjLWSKfIeajg7nL/d1dVV3dO/z4vE2Zmu6q7qb/3qV7/61W03btxAAAAA\n",
"QJ14g+sKAAAAALYB6QcAAKgdIP0AAAC1A6QfAACgdoD0AwAA1A6QfgAAgNoB0g8AAFA7QPoBAABq\n",
"B0g/AABA7QDpBwAAqB0g/QAAALUDpB8AAKB2gPQDAADUDpB+AACA2gHSDwAAUDtA+gEAAGoHSD8A\n",
"AEDt2GetJMZYkiRSSkppFEUYY+1LJUnCGDNyKQAAgBpiyepPkiSO4yiKOp0Oxtj3fe1LNRoNznmz\n",
"2ex0OoSQ1dVVIYTBqgIAACw8t1k4m1dKubq6urGxMTDP4zgmhIRhmPVSnPM4jnu93uATxli32223\n",
"28aqCwAAsOjYsPq73W4QBMNumTAMkyTRuxSldPgTz/MYY3mrCAAAUCdsSL8QYkSvCSFSSo1LjVxn\n",
"4sUBAACA2dhY5hVCeJ438iEhRONSQRB0u91WqxVFkbpyo9FoNpvpr/Dkk0/++Z//+WuvvTbxrwcO\n",
"HLj77rs1KgYAAJCGixcvTvvTz/7sz37mM5+xVI8bxeN5Xq/XG/8wzwUH9R+/8mze9773WXqyAAAA\n",
"Wdi3b5+2KmalenH9jUZjMGxsbGy0Wi3OedaLWHu+BRFFUdYxr4TkGf5LwgI0RK/Xi6LIdS3yMtG+\n",
"rBZRFL3hDfYE2UZJBn3xSZJgjJW3R1250+msra2Zuj4AAEAdsDTIjBvmGqY6QogxNrJsgDHWWzYA\n",
"AACoLTakPwiCkfhLFe457fuMsVarNTEEaGJokF6wEAAAQG2x5/AZBPJLKVut1rT9XJxz3/fjOG40\n",
"GuN/DcNwZFSI43g8fAgAAACYgaUcPp1Ox/d9zjnGmDEWhuG0BYDBzq+JmXkIIc1m0/d9Sqm6lOd5\n",
"mYI7AQAAAEvSjzHe2NjgnEspZydcI4RsbW1N3Aqg8DxvY2NDeZDCMARHPwAAQFbsZe5EqUN9CCFz\n",
"BR2cPAAAANpUL64/JwcOHHBdBQN4nrcA050ZS/1VYQEaghCyAIZUEARVbwiE0B133GGtLBuZO0vF\n",
"xz/+8S9+8Yt1u2sAAEpOHMdPPPHESy+9ZKe42ln9AAAAAEg/AABA7QDpBwAAqB0g/QAAALUDpB8A\n",
"AKB2gPQDAADUDpB+AACA2gHSDwAAUDtA+gEAAGoHSD8AAEDtAOkHAACoHSD9AAAAtQOkHwAAoHaA\n",
"9AMAANQOkH4AAIDaAdIPAABQO0D6AQAAagdIPwAAQO0A6QcAAKgdIP0AAAC1A6QfAACgdoD0AwAA\n",
"1A6QfgAAgNphT/oZY2tra77vx3EspTRywUaj4fv+2toa5zz/BQEAAGrCPjvFJEmSJEm73SaEJEni\n",
"+/7GxkaeCzYaDSFEGIZBEAghTNUTAACgDtiQfillq9Xa2NjAGCOEoiiSUiZJEoah3gXX1tYope12\n",
"W/2TEGKsrgAAADXAhsOn2+0GQaB0XxGGYZIkeldTP4yiyEzlAAAA6ocNq18IQSkd/oQQou3uT5Kk\n",
"0+mYqBcAAEBNsST9nueNfJjHS0MIEUIo8z8IgpFxJQ1xHE/83PO88aoCAACYYpr4rK+v/+QnP7FW\n",
"DUu+flOXYoxhjJMkabVaURRhjBuNRhiGWZcNpuk7LBsAAFAo08Tn/Pnzzz//vLVqWIrwMYiUstvt\n",
"DhaNgyBYXV31PC+TaoNpDwCAE6aJD2Ps9ttvt1YNG8u8Gg6ZGZfinLfbbVOLxgAAADXE0pau8S1X\n",
"epuwMMaU0hEDH7w0AAAAmbAh/UEQMMaGP1HhntO+zxhrtVrTVggopSNX45yD+gMAAKTHnsNn4JNR\n",
"O7ymLcxyzlWyh0ajMfELURQNDwwq1GfGQAIAAACMYGmZt9Pp+L7POccYM8bCMJy2ADBw4g9784ch\n",
"hDSbzdXVVSX3jLFOpzPtywAAAMA4lqQfY7yxscE5l1KqoMxp3ySEbG1tTdwKMIBSurW1pdw+zWaz\n",
"kBoDAAAsLlaDO1OG+hBC0vjuIUATAABAD8jXDwAAUDtA+gEAAGoHSD8AAEDtAOkHAACoHSD9AAAA\n",
"tQOkHwAAoHaA9AMAANQOkH4AAIDaAdJvAiEcFColMncGTgac3Cw84UUtFJ6wI0D6TZAkDnow5+jW\n",
"DKaWmHK8XLE4OY+Bc6SVWjwvTp7wlGyJxZIkbp6wk+5UsjNFQPoN4aQHOynUiZnGuYNypXQ22wAK\n",
"xUmzOnlbpwPSD2TEyVQDuXhzOC/bJL1YXA3q9oHBFaTfGPWx+oGiqc/gilyoMGPOFhjKZEmA9JvA\n",
"yXqgw25k/2YJcSaIwOLh5HgPQkD6Fw4nPUkI5ORYSs9zYB7W5ygeIRDGDjQCY5hE1gqQ/ipTH0Gs\n",
"D0KgMHQj/fXxgDsZ5wgp1eAK0l9xnPheytSDATM4MSNcDTaEOCi6ZIMrSH+VodS2CnPu5rVxiH0D\n",
"vD4LGzBtdQdIf5Wx/+ZIidKdsmm+XCd4nhvprw9OFjYorcvgOh2QfkM46cH18b24WkgHioZSNwsb\n",
"tQek3xBOenCtfC/2xzlCwDy0geU+zJiDeZUShzK9rSD9JlAt6qRdy9SZisXV0hxQKPbXq5ALl5oQ\n",
"yPNK1Z1A+k2AsYMerHSwTJ2pcOowzjn0MjmZ4tSqA6MS9WGQfkPY78Fu3xn7PdjJVjL7KPPQMpwj\n",
"jJ31qNKoYeE4meJMwZ70M8bW1tZ834/jWJpobCFEHMdJyVKh1oIy9eCFxab5rwK3nIQqINdGjE3K\n",
"dKeWpD9JkjiOoyjqdDoYY9/3818zjmOEULfbzX8pIC1OzMP6WIUDnASV2g9VcNiytd/Qa0P6pZSt\n",
"VqvX61FKMcZRFHmel9NaZ4xhjD37U+OyYbkHK/PQcg/m3M1mAqBoHFrBlLrZCV8aO8aG9He73SAI\n",
"8FAzh2GYU/rjOG42m7mrVn1q0oPdzpRhz9FCUu+QPBvSL4Sgt1pthJA87v44jkfGklpT7x5cIOoe\n",
"nfheatW3nawxWI4aGNxgaVrWkvSPyzTRDa2VUjLGoijKXa8CWPgePKA0PbhA6hZD5Qon2yEt4yRw\n",
"ayb7LJRhJJ5ngBFXz7R15iAIwjDMdi3GlEZ88Uc/uvD7v3/3r/1a5ivkgHN+ZX39TJLYnAapQp+K\n",
"4yiKbM69/s8zz3z+3/yb//DJT9pc4/m/P/7xP3/6089xHoahjZuVEiHEGNv33HOWn7CU8tvr6/9j\n",
"bS2KImpxcWX961/f3Ny8LoTNF4cxtm99/ZlWy1KzIoQQEkI89+Uv/97f/M2RI0f2798/8tezZ8/u\n",
"7u7aqQmqXFw/Y0xKmf/N701Bs/NRyhg7ePDgH/7BH6hJSc7qpSdJkkceeYQQouKd7NDtdh955JEw\n",
"DC0Xetd73vO/PvlJxpiwaCR+5itfed9DD1FKW62WjfIwRggxxtQTbjQaNgplDGHcarV+4b3v/Z9/\n",
"9EdJkpg112YghHjmxRf/45EjCCFLTxghdLMPB0Fg6QkjhBBKkuSxxx577rnn3va2t3U6nRHx+ehH\n",
"P7q0tGStMjak36AFkSSJ53nsJpxzKSUvQbwU5/wXPvhBxHkURdZ6MOecUrp0552e5xFCrA05Usql\n",
"O+8khHieZ/NmT5w4gRCKosjakMMY8zxPPWH1TzvlDp5wEASWnjClCKF7ff/QSy9Z7sMnPvIRhFAY\n",
"hlJKa4M6xtj2E0YIIbS0vIyFsPmEp2HJ6h9XZz299jxPCDGQfiGEZSt7GlLKnz55Us3WwzAc7DYo\n",
"1EQVQgyWTKIoGhTKOS9qp5sQCCGsQvs5D4JANcGg3EIKvXn9gydPIsYwxpTSQVmFDvxqcFX/32w2\n",
"h5u1uA0lw2tj6gkP/mRnF4vqVINyi5oBSIlufcJRFA36bZIkxbUsY2zw4gRBMChISln4FlFKkZTq\n",
"lq1NrSZiw9cfBIHazzX4RIV7Tvu+Mucn+uBGHDJKWEu05Ms5iuMAoafX1xHnT6+vX9vdfcPx4+jI\n",
"EUQIMu3K5Jw3m03EGIpjhNDHn3tu9w//cHt7+8q5cz+9u9tfOgtDk8mqCOGcE0IQIShJEMb/9eWX\n",
"z//6r+8/fvypp55CCNEPfhAhhDzP5KIW5yiK+msqnKM4/s+vvvqt3/1ddPLkk1/+8tLS0rnjx48W\n",
"84SllERFst58wiiOn//ud/dtb79FVQwhZDrIWAjhqbCiRgNh/J++973nP/Sh5eXlp59++vXd3X6h\n",
"QVDIXgdK0doaYiy+fPnZ3/gNcvLkU1/72rmdnY+9//2HDx1ClKLpr21m1HYNzrE6viqOMUKPra+j\n",
"OH56ff1BhH7yhS+gX/5lhAp5wkQdkh7HCKH/8uKL27/920tLS+tPP/3g4cOFvDjDdLvqCT//4Q8/\n",
"om7QBTakXw1xSZIo4VY7vNrt9sQvc87VGiznvNPpWKieSXo99d+n4via5zGE1Myu2WyiAnwUfavh\n",
"5otxkPO/5rz7ne/0vvnNOI4fU6OC6dPb+6/NTXE/ilCj0cB33hl+5StJkpxUy5JxbDieYWAE9HoI\n",
"oSWEnorjZzAmf/InP0XI33MehmERT7jPzb76YrebSMmlbP/t38Zx/GizqV5jszfLOQ+CYHDNI1LG\n",
"cYyuX29+4xutVutjzSaSErVaZqW/P9XAWD3hwwh9odF4BmP6qU89gNAGQp7noTg2Kf1oqFlvPuEz\n",
"SfIixhyhZrMZx/Ejxbw4Qi0p33zCbxXir7pdznn7G9/oNyvniDGzlgRjjFI6eHEOI/QXjcYjw6Oa\n",
"xZUzZM3h0+l0kiRpNBpxHPu+H4bhtAWAgaU/e9ldjRBxHHPObS7UTOTC9vbIJ4OJzi13YXp+N/KI\n",
"1FLkLXOgAo7645yPLLOrubNy/Rc0Se9PNYZQSz5BEFBKC3GpCYHGpuSe56k9JXsfFXDgan+qsVcC\n",
"Vj4ujDEhhKtcGqYZ33yjWtPzPEqpNZ+qWne9ZXJf/HGVap3M8zz1qKXasm62Uwkx7J5VDPst7WPD\n",
"6kcIYYw3NjbUquzseDVCyNbWVn/OOx1Kae+mie2cCxcujNSWUtput2+5TRWAX3BUokqSof5fSokL\n",
"mLGOOygHrjlCSLfbLSLycvy1USvbt3xJuYNM2cJCXPj5nycvvHBrCbjdbt9yg0XYwmOEYTgYX8c1\n",
"2gjje2WCIFB3Omq+mBt4Tp0+PdKIGONer3fLh1a2jjebTfVUBwOe4UIJEWPRq57ndbtdm3G0w1gN\n",
"7qSUqqF19teU/WinSgaQ8tSpU+PtN/qJ6S2L586fHy900LeKM8DHm2/wSc5N2jMYn2qg8V2BpnNa\n",
"XLhwYfwJD0z+vgFunKFl8wGDOy2uWdHMlu1jOmPrxCc8/ImU0s6mxUGhGOP+EzY9tZrYrA5XeisW\n",
"119GOH9heXnGeIYxFkIYnkIOIm2msCdMBbgj5n9pIc7avnDhwuwnXIijiZDZtlEhYpHymmpp1BwT\n",
"pX/A3jhnUR8ppQXJcdkSz4D0G+AHP/7xjL8W4owW4vyxYzP+vmdQmO5wqYTJ7tb8vjPa9J2mFSa7\n",
"9J+/2XEuxUScK2eaxWbdM1+Mtuy58+fTZpFZ6PQSIP0GmK2Ge6tkRq2Jzc3NVF5Cs1md591C/1HY\n",
"zepclO9lHnvmobmW3b54MZV5WMDy8gyKmuLMK7QgA3y29EuHafssAtJfOHtvsl0DvI9RD/juXXfN\n",
"K40yxixndd6bpNv1nO4Z4OYGnt3d3dkjet9/aDdtXyFTnPQXtOs/dGK+2Aek3yLWO1M/TM2cZ2B7\n",
"e3v2CnxB5mFa68+JO9VuoUUFs9pHyrNHjqT6pkFHk5RzU6T1J5FlOlalCED6DZBWmKzbwgXFgM8u\n",
"tAhhSrtEZvfMsr0FfIupRFx5txYEzvm8rGJFmC8vbm5qp6kvCJB+A5Rt7V7hxD/rGIPeLc5fmZdG\n",
"sT/OmV2EPHdutkYU4QFPu8CAbPte9paXzQ2urywtzb7ZIrxb//LGN05s1r1YUuuA9Ntgb6XXbtxL\n",
"X/oNLkJub9s3Xi5dvjz3O30D3CBSvnDffbO/Yj5bKuevLC3Zf8JzFxgUxre5zh3D+uOcddPKWrh9\n",
"cbGkcwHpz02KlttbmrNrhhuP79zd3XUg/Zcuzd3iV8Q4l0aYBl81VeQLy8spvmVYLPZduTL3O0Vk\n",
"HZg71bCZQ2IY4/N4m2ewpASkPy/br702t6OoXNMmS2Vs5/Dhud9y4olyMoftG+BG414yPD1zz/lK\n",
"ChU23qzXDh5MU6h9/2E5XakaTIuPcDW2IZD+/KScLBtn59Ah20WmG2/6c1jri5/WyiqUgylU2Lhe\n",
"nDt3bm4f7psvdpvVIXbGOYdjG0i/XawHnps1wFNKv9m9tXNXPt1jvVmFysVtToXTaJBZt3vKXbVO\n",
"XOHmp+nlA6TfEgWlVZiNk0WkIgwZ+9KfMuiloBwSs+kLk/VnYrZl9125kqZZ+4Wa6sZCpHSpmR1c\n",
"wde/gGxvb6d5Jcy+Nruvvprma32r33oyNSll1TdDpvTjLYwzOg1mt0ynWWBAg/hOU89ZiJdnJr9S\n",
"9KMGTA2unN9IMV22DEh/XlJqhFn/7NxdtYNCCzl3Yh4YY4P719JbTAanOGmCXtCw1W/fP2B9cO2P\n",
"c3ZHO+P7GF65806DV0tFusAty4D0W6JW5qFZluZtrVL0d+LYtUn30vgYkf4U+8j2sJ5pwOzSUZq1\n",
"ZTS8e9nEE045XR6UbeeoACdBPiD9edmfziZ1GMWFkKP0s9aXGQyuQ6b04yGjU43d7e25+8jMk3q8\n",
"Mb50lOYJ961+Q3tiUk6XB2Vb6MP9IyGtA9Kfl5SNZtbqv/7SSxm+bX0rWX+VzPrip0GbNH3Mbr9l\n",
"DQlTtkBhI5Ih5fN3353mi66yDjg8ysoCrg5+AOnPS0p3RB9DYdHfu3rV/hmW//TVrx5LsUSGFim7\n",
"ZErMDa4pTYT+FjZDg2uazQTIXdYBw0E+qVnsIQek3y4uPP6mVHj/hQs/ee97LReKGMvg/kbIbLR7\n",
"aSn7RgfjGNqnnd6PZ9AYP7O5eeDAASOXMghI/4LjZHOK2UKzRUdY10SDWZQvXbqU3uo3taZ95erV\n",
"bD8wtPiZcpHMLLddumR/7/3Vq1cffPBBy4XOBaTfKi/v22fktcm0Q8SUCpdwW0oZMBh9eCm1MBlM\n",
"abm5uZnSjzco28iQk34yZzBEwkmh5QSk3x6U0n+8ds3Ia5N+gcGgAZ55EdIEp06fXllZyfYbE084\n",
"k01adadwSl+/WdJbEq6yEJq61D2nTr0yrw/b70Ig/fZYgND+bLdg6MysTNJ/7s1vNlJoJvPQlMPH\n",
"iQ/EFdniIwzhZOa6vb299K53zfiCkyAfkP5cXH72WddVKDFGT4RPg+d5ZzOFvZrA4IiebUFbkfsJ\n",
"p8lpM4r1WGFTyphpvDFlibtK7jsbe9LPGFtbW/N9P47jPM9UStlqtXzf932/1Wq5nWtv9Xpv+vCH\n",
"7ZdbK/OwGjjph5Tmn+Lc6PXe6fspv4wx5tazVjgOKrVSkP1YDEvSnyRJHMdRFHU6HYyxn7qrjSCl\n",
"XFtbk1K22+12uy2l9H2/Qp5WIYTlJbKqc+rUqcy+fic48eYZKvTQQw+l/KYpFeacO3H46FC8vDjZ\n",
"B2ND+pWd3uv1KKUY4yiKPM9LkkTjUnEch2HYbDYJIYSQZrMZBEGr1TJe5yLor7hW1uPvZKqxf3d3\n",
"xXrqq6zqViHjoyRIKZezNmtl51XlxIb0d7vdIAiGZ09hGOpJPyEkCILhT6IocnWkPULozJkzJdys\n",
"URCZpxomdlfdv72NUvtJTTmFOedHjx5N//0FWMC3zD2nT88NehnFxEPOHLhlq2UXM8JHCDGyyqEd\n",
"Ch1F0fjFHb54V69efTBTTLQJGGOZLSYne1xN7a5K3b6unMIucXK/RpyWLvx4mcwXm8JiX8T2WShD\n",
"CDGecMbUTvS1tbVms5n1V9M2ayg/Uu5KFU7mQAUXe1wZY/nTDDmJxtu/va3zM4tGYh/PQ3GMbp0H\n",
"FwohJEkSL/dtnjp16gMf+ICRKqVHCOFkgWFkqjFRfM6fP48Qev311y3VyY70F2eINRqNMAw1EplN\n",
"k37P8yoh/ZlwMisy9RidvKvfX19/S+psRX2UUzhHTj0hRNbVFCGE5c5q8O2wv4QjhHjAxZEpI1ON\n",
"ieJz7tw5hND169ftVAnZkf6CaDQalNIwDDV+qzFRmMjSD35g5DqZqJ1Pwzo6frzc46sQ4oHjx9N/\n",
"X0UNLJqdMhv7JxITgpIkz4g+zkTxieMYIbS5uWmwoNnY8PUb384gpVxdXdXWfYO8/bXXzHaLNGx/\n",
"9atHU0fjmaIq401V6lkeKrNHxPqxE5RSZqtEjPHly5ftlKWwFNc/HnehHYmhYvnDMHSu+67Yv7ub\n",
"PuhFkT9tHOc809qyqV0qWX39EGyTFSdbiJ3AGDuc5Xh0m30pDEPLvk0b0h8EwYh7S4V7Tvs+Y2za\n",
"Nt2Jul+9U0HsVtjzPCNp4zJ1TVO7VJz4+nVyG+RGY5eTsylObk10NdU4fOiQ5RJTri1jjO+0e168\n",
"PYfPIJBf7fCaZrNzzlWyh0ajMfIntZU3iqKR366urhZQ68KwPm+tNPdcumS/0KyZLAkhz+7blzN8\n",
"Vkq5nOVgXiNp41wNHvdvb9uPOrvHrkdFIYTIHIptBUvLvJ1Ox/d9zjnGmDEWhuG0BYDBJGt8tsU5\n",
"F0IkSTKyHQzcuxbQfMi5m2Ynywy9j8oYajFhFiHkpWvXrBWnMOKO4Jy/3YUw7e7uZpX+K1evHvzJ\n",
"T/IUes+lS+gjH0n/fSVW3oLKiyXpxxhvbGxwzqWUURTN6LWEkK2trYlbATzP29raKrimwGQ45/9O\n",
"QyPyyRPnPJNztk/ujKFOphqu0HSp5dvEkLVQz/OeQchjzOYmBkppt9utbuaV2VhN2kwp9TxvrrVC\n",
"CLF/5rgGVVlj6B/hnd/Xb9cXiRCSUupIf27uuXTJfuDW/RcvVkJlpJQLnNnGOEKIu197zXUtJgD5\n",
"+vURQjxw772Zf2boAJP09LfhVEFWqkt+O0AjcCu/q1PjChhj6EvpEUK8xXqulzSA9OfiWvb1QCZl\n",
"TgP8/u1tePdKRT8nq3WncH53f9aYXSNUKWPz4gLSbxUj++A1zENn5Jvi6Pn6v3fHHQ5y1aGqzquW\n",
"fvxjyyVqZGzuOy2dsKDLvCD9+lTF148cBkHlW3GVUmYNxPY870y+OBCdxKiVRm/Estv5XWbWyjei\n",
"lzb+EKRfHyHE0SNH7BeqMVnGGOf1MlVkEdIIVXFH9Fdc7ZrDTs5oNIKTwK3Sbi8H6beNzOfr198h\n",
"kq8LOvMyldVoGsHZ4bHWlSX/oQiufP1OArdKC0i/Vfo7MMtqCJQRF89qX/ZEDvnnVfUh675lI2RN\n",
"4LPwgPTroxkYVysIsR8Ant8mPfBTP6XzyxyNK4R44PJlsAkKRV/6c3i3Xr14Ufu3hQLSr48TQ69C\n",
"a8uEEGY95NHzvJyZbTTWlvMjhDh66FBlArdc4WRelS/p1s+VNR4PpD8f1s00IcTRN73JcqF6dvTi\n",
"nXdWRqzvEEQO7Y+KzopKWW2Q/gqi15NyaATn/FgpdyTWnPw7BPe/+mrWn/T3r1UN2Ec2Aki/Pnq2\n",
"cEVD7LPmMa4bOZvV1bzq/u3tcrojjONkbbnMYyRIvz56a7a1W+mtB/04S91X3UlChT716ZBacRln\n",
"cpyXK4Q4ceKE9s8LBaQfmI+U8p5TpzTO1shpC+udrZFz54Q+lOZZD7SfGJUxViE/noHpcvZBjlJ6\n",
"9erVvOWWEpB+YD59mzSj9Pc3Mei+sZzzn9u/X8MdYWCjU20i9Cvkx+tPl3UHV+2R45WVFTcpoQoG\n",
"pF+TMnvxxiGEnDp9Os8VNGzS/ruqq8JSypWVFTfuCCeFavUoJ0tHztarcsRZajtaX8nhiCuzSoD0\n",
"ayKE+NCRI1Xxk/bXA2tjzFYOKaWGP62/iaGCyaJrghDixPXr5VQJkH597rh6VcMdIdXJdrpxltqO\n",
"7J2HH4aTlYoj53pgLjHV/a0TXz9jrF4bPlSKvfIB0m8bjHGeOMv6nJHEOV9ZWXFdi7T01wOrNq86\n",
"+MMf2i+0WtJfZqdNHkD6NVnUDmGWPE5hKeWKlps1z7wqT4VfPnasevMqIewns7zn9GkN71bOeZUe\n",
"OfevlTZZPwLp10YIceLhh13XwiJanTivU1jrrcszr+KcU93p+bUDB/R+iMqtEYWQXfpdxlnmmaOX\n",
"FZD+KqFtgGCMcyY10/cy5RE1Fzbp27LnNsiPtkZULsKHc35Ad4x0FmdZYgXXBqQ/By7SdnpaUpjz\n",
"eI1c+lK112b/hQtuDvRwMq/SIk+IvZTyQd215TxxlsAIIP054Fxj7b4fYq9rv+/LM+et1Ly1cj6Q\n",
"vMs/TuZV2uRLZWyZyvUlC4D05yP760oI2Xn4Ye3X5k2bm/qxYpUywPOMN1esO4Vd5rOsVLM6Ic8S\n",
"zqJSSelnjK2trfm+H8exq/HcpR1RnVfdyVOilG5ubmov82p7orWpnU2qe0ZpnsEVZq4jVE/6kySJ\n",
"4ziKok6ngzH2fd9JNcq8dl8IlfJEa8dZ5vFEa1NFmzTXvEprl1POeVUuT6kuZVaJikm/lLLVavV6\n",
"PUopxjiKIs/zkiRxXS9L5LFJtQ2Q/g/zdGJt20f3h3niLJ3gJMJH+7ee523qhtjnNYR1f57LU7qI\n",
"VEz6u91uEATD70kYhpWT/jwqrG2TaotLXpuUUv2NTk6MJl13hBPy2JUuo4Ny/N7NbxeOikm/EGJE\n",
"hgghzhxqWuXmPzdcHycRPpWKWFcF2zcP9Ta4OqY6ET4u996X1d2/z3UFsjExsF0jJci0FYIgCMIw\n",
"THsVVz4Q7XJdWD1Xrl49qOV+yTPeVDLNhrb0E4IYs7wXYefhhyuUxV4IETrZq4EmvHTTxOfs2bO7\n",
"u7vFV6hPjey5/QAAIABJREFUxaTflCXY6/UM1MTJ3JNzFEX65dpFBdtYznjheV4cx3q/zdusWv1T\n",
"CHGPfpE5xgxUXpu0PGh3Cc45xnj8CU8TnziOn3jiCY2C9KiYw6c8uFy7t160dnSEy6fkJCRJN2Yx\n",
"z+iYK9hG93xpZ05L6+RZgS9z4FbFpL/Mj9ICTtzfQghn0RF1SiChR38TQ3b6NqluoXkDxuyTxweo\n",
"XGqLRcWkHyE0bm6AAVIofZvUycJGPeQ7D5WzSZ1NBPOkAqzcCnwKKib9QRCwW4dfFe7ppjZV9JNa\n",
"r7Pe7qo8NmleqtiswExcTTX2b287KTcNFZN+ZacMAvnVDq8MMTlmcWII5yFPiL0uZ7TOgcppkzpJ\n",
"NZqrUMaqZ1pWZ4x0ZUY4ywKbgopJP0Ko0+kkSdJoNOI49n0/DEP781YDNqmTvmi9UFdJzaq1Wak/\n",
"ZuhKv3YW+7w2qfWH7MR4J4TonQ7mJB9Ueqon/RjjjY2NMAw9z+v1ek5M/pKv3QMIuZtXZVfhPAMV\n",
"IeR/f+c7er+t1skEyNGITgjROx3MST6o9FRP+hWUUs/zypwdaQau8lmeOn1a44dSSifuiMrZpE4K\n",
"1T7iXAjhLEdpFV/bKm4SnElVpb/SVMsd0f+hfekvsZ90Ik7ODddGCFHJHKXacZY57K08B2yUFpB+\n",
"TZzkgK0q2d+6KmZicHlueHXIafdcuOsu7YL1fkcIYdpB/SVeCQfp16SKOWB3rl+3H+GDkM5bl3OD\n",
"qx798abEr+tEKncyuzae5124cMFyodouNYQ0z3C1A0i/Dn2NyGFH/NNrr1neH0gpZVJWTtds0k8O\n",
"WLXAFWf+Q+hLMyn5wgZIvw45bVJCyCsrKxqFIlSx6AhXYIy3L160XCgh5MyZMxo/NNA0er0i5+q9\n",
"VrX3b2+XVg3NUvI3DqS/Mri0SV0cBZUHSunu7q5ls5QQ8uK1a1VxqeXcTKDN/gsXtH0gGGP7Dh9U\n",
"7iN2tQHpB+aAMc4z3ujbPvls0ldWVuyr8Av33VcVN0hOm1RvXsUYW8k+3x1AKXUi/SW33/UA6XcA\n",
"pfTUqVOua1Fq8tukGi41ID39eVV2VpaXjVdmNowxQkjeIbkiI3p6QPp1yXGC60IaEWbJb5NquN3z\n",
"5+fQ8AwspDOhOHYOH9aIjyCE5PWU6v28xI0L0q9D3/1d1rCtsvGq9RVXvRB7KSWVMs9UQ2PkMLDL\n",
"qU5sXb9uv1D94bnERh5Ivw5OzHYneYzz26Se512weOKoAayvfFY0PbXmQbIVjWRdOED63ZHxHchv\n",
"k2oU2rdJSzxvBQgh586f1/llDkXzPG97e1snvQHn1crPsaiA9LvhheVlzfiTnNKf/W3PGeGjT77x\n",
"5sqVK6YqUnIIIftc3OzZo0ezSr+rE0btF1p+QPrd8Mqdd7quQunJN94cPHgw60+qu+J6LfvNOsHV\n",
"CaMeymUz6c+rSgxIvw7V1YhLly9bLpEQcu7cOcuF9slo7mGM8wRu6cE5f+DNb7ZZYk3JJ/1Zf1J+\n",
"iQDp18GJ8ZJzVy1CyPO8S5cuZS40H7myX+Xg7JEjOp7o3IFbu6++mrFAefSll/K4vzHG23pnG4BL\n",
"LTVZXWqcc6/cSxog/ZWhb5PaDQTknP+rffvKHKNWKiilmiqcr9CswTb9XU7WXWrVpSoutfSA9FcN\n",
"6yr8pmvXDIw3WQzw6q7LVSgK0NVsLCcabvf802WXTsvCAOl3RlbPgBGyOnyMkDUUpJ+oDgDG0Bix\n",
"8k+XKzpMzgakPzP9yXI+nHgGPM971XqhFSP32obORichck7mNHdX5adC8zO7EzLG2M9tb5d5wz9I\n",
"vw75pR9jrBOLnVuYXllaylhg2QMVpkEI0UnZn08gNEd0IXJqxI2MmW2EEHlPvc++kF7dvqTHyvJy\n",
"mRfJQPqdobNwZL0nYYzzHujhCEKIfVvYla//hYzpMIUQ/3p52fKuWiM7wxfS7e4EkH5nOJmkaxaa\n",
"T/qzRgEyxuyHFQkhjAj3/molLLJL/p3hmhNuIxOOxZq1gPRnxohGOPH1I4SWMjp8jKARBWgkrGh/\n",
"lmM9hBBGMmhmdakZwUmIPaW0Mntcc7+w+plXyoo96WeMra2t+b4fx3Eer5+UstVq+b7v+36r1bLv\n",
"QBRC5E+jVqEowIqCMf5/t93muhbpyN2HnYTY16oP64zo5faUWpL+JEniOI6iqNPpYIx939e7jpRy\n",
"bW1NStlut9vttpTS9303y0d2G9VIWJEGpp7tv3znO0aukx7tY6QcUMHseBqYyjr+BuvJSPSpufQr\n",
"O73X61FKMcZRFHmelySJxqXiOA7DsNlsEkIIIc1mMwiCVqtlvM4lxIj0Z1VDI+/qoQ9/+MVnnkn/\n",
"fSdjed3iT4zsDM/UnaSUFBlQw+uHDuW8AoDsSH+32w2CYFhEwjDUk35CSBAEw59EUcQXywdXKE58\n",
"/VnHD4yx/YDxSp+WdezYsVOnT2f+Wb5x3fO8y1mDbfIfOJERMwfzLiI2pH98AY0QomdkRVE0fvFa\n",
"+Rxz8srSksbRpg4QIn/oYeYpjot1IyPXWVpZuefUKSOXyoSTNe2sGDiYF6GVlZUzm5tG6lMSLEn/\n",
"uDqb8lyvra2FYWjkUhkwkdo3UxSgKXdE1gBwI2CMnSSQyDzFMTHeZCxQeJ6X3ya9cuyYkfoA01hZ\n",
"Wcl82nO5pxr78vxYSjnN2YIxHlj6xXlRG41GGIYa+V6mrTMHQZBqIDFxJnsmi4lz/kePPWZksnxh\n",
"e3sl3TcZY5TS/LMESunTLqS/MpiYtlZpm0g1ybz9fkqzThOfs2fP2nyeuaSfMTbNZY8x7nQ6eS4+\n",
"l0ajQSnVM/l7vZ7x+hTNm65dyy/9J06cuHDhQkrpRw5PZ7SOKQNl5/DhK08+efDxx41cLSWe5z39\n",
"x398PNNvTNxv5nmV9YN5pZRGHMIvHzu2/Fd/lf86aLr4xHH8xBNPGCkiDbmkPwiCkUXXiRhfPVMx\n",
"nWEYOnD1ANUhkw1lasXo3l/6pc3NzRNGrlUoriJKrR84YWS6/IsnT3671Uo5uPbXlsud285SXP+4\n",
"X0g7LAd0v4rcUwlfv4klnEy7qzjnb96Xy/zSoLrHISgOHz6cST2MTJezWgblz/NsQ/qDIGC3+otV\n",
"uOe07zPGpm3Tnaj7Ve/KaTC4XnIhdXoDg4XuHD5s6lIFYt0mlVI+ZOQknCwYPA7Bia//zne967Z/\n",
"+Af75S4YNqRfOXwGqwJqh9c0m51zrpI9NBqNkT+prbxRFI38dnV1tYBaF87y8jJLvYLaz6CZWyNO\n",
"PPxweunnnHvWff2u9i0bJHNGncquprzNhfS/spJ+rcokC7ambWmy2el0fN9XO7kZY2EYTlsAGEys\n",
"xmdYnHMhRJIkI2vLNvdhGvTi6eyusp9a0rohjNRk2dATtr9R69ixY1/60pdO2iwSIZSlWYUQpnY5\n",
"VWYyZ+LFSf/CMsaiKCr5BhpL0o8x3tjY4JxLKaMomuE4I4RsbW1NnJN6nre1tVVwTedjcAEn/3EZ\n",
"maH0/nIf1GUqgyZCaHl5+Ww6gTNoPRw8cCDbDwwJU/pYYSFEGIamhCllCI1Bm2llZWV9fT3DQjrn\n",
"qNnMX24myr/P1GrSZkqp53lzHwohpLRHs3LOjVlMJ05kyipshtL3SIPSnx5XWRyklEZy6aAs7giD\n",
"49zy8nL6FVdTfryV5eX0u6ucpWYyETJQKJCvPxtSSiP7wpHKu5Ju831/vHGCiQWGSmDQTEvve+kX\n",
"atcd0T+m3G6hBm2mTBhs1my+fhee0kyA9DsjvWegP964wtDLkyEQK/cx5YrDhw//89/9XZpv9vct\n",
"GyG1S81l+ikXsUymbKb0mGxWR6kPi6Om0p8r2achYUqPk6AXs1ONB+69N5v0m3hjD3/kI9defDHl\n",
"l42pcOrr9F1b5c70Mhu1kJ7mm64ScTsbXK2rRFZqKv3aHVFKaUqYUJYoQIMqnHLeanaqoXMGvUWc\n",
"CFPf6jckECljhft3aihOYfm++1I+OoyxwUEu5Q5BJ0s4/amGOZUoiJpKv7bVb9aIcHKuXsp5q8v4\n",
"eut79MwKU0rMLminbFbOued5xnKUYnz/xYtpv2xoQRt5XvrN4QZf2PS7iMsf3oNqK/16Vl7/V1We\n",
"oWfCoPQvLS2lcfjshQDaD/EyJUyOSJlX0vD8htJs20QMaaKT3VWHDx9O8/TMLjAUB0h/BvoWk/Xs\n",
"gwiZHG/27+6muX2zGrF8330pff0LsKDthGsHD6Zpsn4ftotxf1rJV1zB6i8vem1juAcT8kCK8+36\n",
"hZobbw4dPZpm3uqk+5o6uTtroVVPHYEyhthbpj/e1CZQuBLUVPr1MGwxpZMb42ZamS0mKaX9yXI/\n",
"sQFjpo6NPXz4cPrsTKZYuvNOyyWmZy+M1eK43jcjzDXrPbfdZr9ZiwOkPwNO4kCc2KRF3KmTp5fG\n",
"E70XB2LoOb/59tvnfqfvEebc8jHlxkkTpWZ8h3aaoNI9M8LQE37TT/+0keuUBJD+DBThi5griP0g\n",
"S3PGS5oV1704EHO3/La77jJ1qbSk3l1ltmXTRLL2Q86lrLr0O4lSW15envviOFludblNLyM1lX6M\n",
"cRmy/GfzzxrSiDQrrv0ebDA22UnaOHcv4VxhcrLcugAJsTPR78MWcZKBSo+aSj+lNKv0743n5hwX\n",
"pXW7m+/B6ZM7GiXToQimOHrkSNoR3a4TzHxGEIxLngjWcqBw3z1rbo5eHDWVfg321NDVoaYVL3Su\n",
"U7iIVEVzB1fHkz+jgcL3XL48rzROKTUpTJSuLC3NHlwXZkRPw14fBukvJxjjrJFwRfTguW73PX+l\n",
"wfFGyrQrrkZ3Oc11Cu9tm7D42hg8rdAxlN7x/e/P/speThtzT/jwvNNaChnR54UzOcvVfLN4l6Wn\n",
"o6bSTynV6Bz9qZw5NVx+4xtnS38hq0YYZ7im/SmO6ZXP2U+4oAAqB9KD8dzBtd/udlPJ74UMWMTJ\n",
"Uspw8eXfwVBT6dfHbEK+eZdyYpO6ilK4rPwVRgfXo0eOzJb+vk1qeqox+wE63utvOmNzqnHOtM99\n",
"dqF7ewONjsFzXWp7lD7Op77Sn9Uu20t56CS9jF0fSF+YjL42x44dm+2fPXToUP//jHq30n7N4BOe\n",
"V2h/E5ldCpqIpF3TNj3VmD247gX1Gyx0Xtq4am0Lr6/0ZzJs995V0+9PWovJYpcqZIFhnq+/qNcm\n",
"5S2YzTGQYjLXz+tr9AkfOHBghgrv+UBchQzYn+jYTR3hZETXpr7Sn4niwntSjUDWXYf9HfBG1fCt\n",
"3//+DN+Le4vJ/gzddEr3Bx98cIYlsRenYPFOiwiJVldzYjOtrKzMH1yrsMaL6iz907rOsDwNvrNn\n",
"CBffrpxz5Ri5pYZGX1dK6bjvpdvt3vJvszYppW+/665x6R98UtyqxnhDc85VucX53Mf3DEopR5+w\n",
"aZt0ZWVlvFmHb7+IVY2Jb8SgGkXZTJNCFYQQE/qw6Sc83ocHT9h4psVCqa/0D7rOQGoVa2trg4F9\n",
"dXV18Kf+tvviczl0u90kSVCRUQqEkBHjpdvttlqtW2piZVWj0Wjc8i4VsKoxrhHqZtFwsKPpEZ1S\n",
"Ov6EVbPuYbo7rUxKb7C6unrLEzbuPJx0C61WS91scYMrIWRknBt+cQpq1hMPPzzSrEKId77zneqx\n",
"7wVQVcHtU1/pVwghkiThnKtOE8dxFEWDDjT4/z4FjOee541PIVW3LiqDMcZ0bLzhnLfb7VarZTO8\n",
"hzHmeZ5S4T4F5LQZ1wh00yrfG1xN3/K49AshoihqtVoFLaUgjNFYh0mSJIqiOI73PiqgD49McdQE\n",
"jjEmpewPrgUcVEsIGTHAhRBhGCZJUsga701GXpwkSTqdzi1PuCJ5mfa5roADQoRQHP/Wd7/7rfe9\n",
"DyHUOn78sJRPP/nk9je/+djzzz+K0Fueew7F8ZX19X//yCO/dvfdX3zHOx5bXkaqdcPQZFWkJIR0\n",
"u10PIdTtIoy3L1782Pb28ePHn/q93/sZhKiUqNs1/K4OHwXu+2pG/Nj6OkXo9m9/+x9/9Vc/+sgj\n",
"KI4L7L4335N96+vRyZPnXn75qYcffmxpCX3qU+hHP0JRZLa0vkZ0u4gxhPGz3/72by0tHT169KkP\n",
"fOChQV7PAtSw/3++jyjdffXVx771rUcR2re+fukv//I9jzxi3jakFA3cHY2GUr0H19cfPXny395+\n",
"+5Pvetfjgz5sGpUWhdw0kn74zDON48fRvfc+/Su/8qGlpUJeHIQ8z4vjGHGOkgRhfOny5d8+c+YR\n",
"jJ9eX9/e3n788ccRYwVOW9fWVPM9+rWveQi9/Yc//OI73vFbDz2E4rj8YZ2KOkp/glC72TyOUKPR\n",
"kFJ2PvtZhNBTcfwFKZtf/SrC+BpjMWPo5MlHm81lhD6mXNLFxJ8QQqSUSEoUBMjz/luj0fz855cw\n",
"fvzTn261WsZ1cBRKUbOZJAmmFAXBQwi9zvkhQgrqvmqNwUMINZtCiKcQerTZPIrQ0eKe8EAjEELN\n",
"JsL4s41Gu91GCD3+6U93u10UBEUU2odzFAQoDP86Sehv/iai9FGEut3ucmGFKgOcYIyaTc758BOW\n",
"xbgrEUKEkCRJVLMihP6i0Wh/9rMIocfVIdiFRSgMvzjNOA4/9zlEyKMIxXH8sWazoEL3tkM3m4yx\n",
"7xGCwvA4Qvcpc6oiuo9sSj9jbDAXi6Iov1dB+WoIIaGuQdFsNgeugCAIBr4Oz/NGnOyFB59wrt5V\n",
"PLR+FRWs+1eefPIgpVJK5e1RHxa61Wh4jSGO40GhqLgnLCUaqB7G3W53+AaDgiRY7fpG/bm/esKD\n",
"XlpUoQihgQGOEEKo1WoNP+Hi/HjDbRfH8fANFr5zTUqEsXLCDKrRLEj3MUbd7p75ctPbc/OPlRF9\n",
"hSVff5Ikyo3e6XQwxr7v57+mMuVG1/SzgDEedFNKaaHv5GzOnT/POW+1WkX12jE8z/vKV75y5Y47\n",
"4jjWHjuz0o8skrLVagVBYONtuVmEesKMMRs3SwhCiFL6N3/2Z2c2N1utlu0njFCj0QjD0JoeSSkv\n",
"Xb6sxnVr+88xxs9//vMcY0t9mFKEECHk3Oc+9y/Ly+oJF15oYdiQfillq9Xq9XqUUoxxFEWe541G\n",
"O2SEMYYxXozEW1EUvfKDH3DOrek+QohS+rbd3S996UtRFNlMKhCG4Rf//u+HB10LNJvNS5cuMcaK\n",
"nkgNEwQBRehvX345CAJrTxhj/J7XXvvvX/96GIY2345ms/nss892u117T1gI9b6o4dzaphBK6crK\n",
"SsKY5SdsHBsOn263O2LihWG4traWZ8yM47jX65X2HOpMYIzxu9/9LrsWBMb4vfff/16Lg43yvXiE\n",
"oN/5HeOLfrPBGONf/MWHLOq+4vjP/Mxx64V+4P3v/8D7329vD+DNuMZHT5581Fp3UvngCDn+1rc6\n",
"eMLvfrfVJ1wMNqz+8XM/+mubuih/YuWca3VHtZfpXTalxsnGTssnELh9DZ2UXpFNW7OxYfVP3Kip\n",
"PUGTUjLGNjY28lRpWh4xQkiFsnBoopI0uOq7hcWZlBEndyqE5UkVQpXZx1QGponP+fPnX3/9dWvV\n",
"yCX9KnRh4p8wxgNL32zKwDiO8/vEpz19z/OsSr/pAwBSMRwAbh/OC49YHacKB+YZwGH2mIrsYyoD\n",
"08Tn3Llz169ft1aNXNKv4jUn/gljPAh7MojaIph/dcXmguos1NtShYMdTOLEFq6DMDmcTtlNLtun\n",
"IonSRpgmPnEcb25uWqtGLukPgiBNnIbB8IYkSdQecfVPzrmaebg8+MII9fGB2EcI2wsMhKAkWQB3\n",
"cAZceZmq/uK7w1Jc/7hfSC84x/M8IQS7iRBCuf5N1NEd4CctDhUKYl/6kenUp8BE4AnrYmOZNwgC\n",
"tZ9r8IkK95z2fZW5bOKGlJF4UKX+NoO1C8GJn9TuAa17VHOSrkOtYpnsI0Q/iwOghQ2rX3ljBqsC\n",
"aofXtKB+zrnv+3EcNxoNC3WrL/ZPTapakhMgFRgj+9tr1GTOic20KJM5Szl8Op2O7/sqR43afTfN\n",
"Oz+w9GeH7XPO4ziWUgohGjcTcgEZsB9kuRAvTAYYcxDLZN95OJwItg4symTOkvRjjDc2NtSq7Ozc\n",
"bYSQra2tuWc2UUp7vV4BNbWOq4NSXQVZLsRrkxb7ox0EWRbNomxMsZq0OWUcTi32VSlUKIh9VN91\n",
"0oMX4rUpKVK6CbKsFU5spgKo+yldjqnbW+pqbbkmqPOw7AeVutox58rRtBB9GKQfsIj9tWWEULfr\n",
"oNBaub+RIyNmISTYFSD9rnG1LaUm2qRCQexrBKjSQmI5NV6RgPSXAPC5F8oCva4lxUkmSyeTOUIW\n",
"xmYC6XfNooQJlxcn7m9Xy632hclJXD9CqLATpOewKG8rSL9rnIQJO/EyLco7kwpXQZb2HzKlzlq2\n",
"Vj3KNCD9tQRjNxrhhLqFUdnH1RN20qMWZWMKSL9rnJzs7Gqy7ARXwuQkc2et0oU6YVFeHJB+17jq\n",
"SU6MFxCmQqlVX3I1oi+K9FvdzQtMwInV76RQVzNlJ/mdnJwF5KRZXZXrZEttGC6M/xCk3zVOelJN\n",
"ViAVTm7WyThXqydcn0KLARw+AAAAtQOkHwAAoHaA9AMAANQOkH4AAIDaAdIPAABQO0D6AQAAagdI\n",
"PwAAQO0A6QcAAKgdIP0AAAC1A6QfAACgdoD0AwAA1A6QfgAAgNoB0g8AAFA7QPoBAABqhz3pZ4yt\n",
"ra35vh/HsTRxeDRjrNFo+L6/trbGnRwMDQAAUE0s5etPkiRJkna7TQhJksT3/Y2NjTwXbDQaQogw\n",
"DIMgEEKYqicAAEAdsCH9UspWq7WxsYExRghFUSSlTJIk1D3cZ21tjVLavnn6Elmg8xMAAAAsYMPh\n",
"0+12gyDAQ0cIhWGYJIne1dQPIyfHswEAACwENqx+IQS99bw6Qoi2uz9Jkk6nY6JeAAAANcWS9Hue\n",
"N/JhHi8NIUQIocz/IAho9nNQfd+f+HkQBNpuKAAAgLlME5+zZ8/u7u5aq0Yu6ZdSTgutwRgPFNlI\n",
"PI+CMYYxTpKk1WpFUYQxbjQaYRhm1eter2eqSgAAAOmZJj5xHD/xxBPWqpFL+hlj01z2GOOC3DJS\n",
"ym63O1g0DoJgdXXV8zxY7AUAAEhJLukPgiAIgrlf03DIzLgU53xra2t80bjZbJoqBQAAYLGxtKVr\n",
"3C+ktwlL+ZFGDHyw9wEAADJhQ/qDIGCMDX+iwj2nfZ8x1mq1pq0QUEpHrsY5B/UHAABIjw3pVw6f\n",
"waqA2uE1bWGWc66SPTQajYlfiKJoeGBQoT5p/E4AAACAwlIih06n4/s+5xxjzBgLw3DaAsDAiT/s\n",
"zR+GENJsNldXV5XcM8Y6nc60LwMAAADjWJJ+jPHGxgbnXEqpgjKnfZMQsrW1NXErwABK6dbWlnL7\n",
"wOouAABAVixJvyJlqA8hJI3vfsbYAAAAAMwA8vUDAADUDpB+AACA2gHSDwAAUDtA+gEAAGoHSD8A\n",
"AEDtAOkHAACoHSD9AAAAtQOkHwAAoHaA9AMAANQOkH4AAIDaAdIPAABQO0D6AQAAagdIPwAAQO0A\n",
"6QcAAKgdIP0AAAC1A6QfAACgdoD0AwAA1A6QfgAAgNoB0g8AAFA7QPoBAABqB0g/AABA7aid9F+8\n",
"eNF1FQwQxzFjzHUt8uL7vusq5GUBGoIxFsex61rkxff9qjcEQujKlSvWyqqd9AMAAAAg/QAAALVj\n",
"n7WSGGNJkkgpKaVRFGGMtS+VJAljzMilAAAAaoglqz9JkjiOoyjqdDoY4zxO3kajwTlvNpudTocQ\n",
"srq6KoQwWFUAAICFx4bVL6VstVobGxvKPI+iSEqZJEkYhlkvxTkXQvR6PfXPMAwJIa1Wq91uG640\n",
"AADA4mLD6u92u0EQDLtlwjBMkkTvUpTS4U88z1uAlX0AAACb2JB+IcSIXhNCpJQalxq5zsSLAwAA\n",
"ALOx4fARQnieN/IhIUTjUkEQdLvdVqsVRZG6cqPRaDabWa9T9YnC+fPnT58+7boWednZ2YGGcM7p\n",
"06fPnz9f9YbY2dmpekPoWcPa3Hbjxg3tH0spOecT/4QxHhjjvu9HUTSi/r7vD1z2WRnevtHr9cbH\n",
"lRn86Z/+6Sc/+cnXX39dr2gAAICCOHDggLVdXbmsfhWvOfFPGONOp5Pn4tNoNBqe56lhg3Mex/Hw\n",
"MDOXT3ziE5/4xCeKqBgAAEBVyCX9QRAEQTD3awZ98UmSYIyVt0ddudPprK6ubm1tmSoCAABg4bEU\n",
"1z/uF5rmKZoNY2zEvYMx1ls2AAAAqC02pD8IgpFFJBXuOe37jLFWqzVx0WNiaJDl5REAAICqY0P6\n",
"lcNnsCqgdnhN28/FOfd9P47jRqMx/tcwDEdGhTiOMy3zAgAAAJZy+HQ6Hd/3OecYY8ZYGIbTFgAG\n",
"O78mZuYhhDSbTd/3KaXqUp7naQR3AgAA1JlcwZ1Z4ZyrnGuzE64JISZuBRhGeZAIIeDoBwAAyIpV\n",
"6QcAAADKAOTrBwAAqB0g/QAAALUDpB8AAKB2gPQDAADUDpB+AACA2gHSDwAAUDvsHcteBgweDW+B\n",
"OI5HPvE8b+J2h7LdV7fbFUIMsuyNk7LCDu9r7i2kbB0nt6AOQFV7XzzPC8MwzxN21Qop76LMDYFu\n",
"vQtCSBRFE7ciOXgjbtSGdrtNKd3Y2NjZ2Wk2m5RS1zWaA0KodytbW1vjXyvPffV6vSAIKKVBEHie\n",
"N+1rKSvs5L5S3sKNdK3j5BZ2dnY8z4uiaGtra2trK4oiSunOzs74N9NUz1XvSn8XpW2IGzdubG1t\n",
"UUrb7baqUqfTUdXQq57Zu6iL9O/s7BBChrtOFEXtdtthleaSZmAu1X1tbGyobq3Oz5n4nZQVdnVf\n",
"aW5BMbd1XN1CGIadTmf4k2azGUWRRvUc9q6Ud3GjxA1xY6g7DX8SBIFG9YzfRV2kv91uj/QbNSC7\n",
"qk8a0kh/Oe9rhm6mrLDz+8ov/a5uodlsjn84fi9pquewFVLexY0SN8Q0CCHD/3T1RtRlmdfg0fD2\n",
"YYxbB3P4AAACw0lEQVRNq2rl7itlhSt0X9Nax9UtjK9PCCHGncJpquewFVLexTBla4iJjJ844uqN\n",
"qMsyr8Gj4W3i+76UEmMspSSEtNvtkd5fuftKWeFK3Nfs1inPLaytrY1nt01TvfLcAppyF4ryN4TK\n",
"XMkY45yPnFzr6o2oi/SX02CcTbPZDIJg0LpJkjQajZF+U7n7Slnh8t/X3NYpyS00Go0wDMdVI031\n",
"SnILaPpdoIo0BOecc84YGw/LcfVG1MXhU0VG4sDCMJRSCiEcVgkYUInWaTQalNJpxyJVhdl3UYmG\n",
"CMNQxflwzsejUZ1QF+k3eDS8QyilI326cveVssKVuy801jpub0FKubq6OkMx01TPeSvMvYuJlKoh\n",
"Rmi325xzjeoZv4u6SD8ydzR82ajcfaWscOXuaxxXtyCl9H0/DMPZipmmeg5bIeVdpKFUfWncgHPy\n",
"RtRF+rMeDV9Out3uyOBfuftKWeHK3Rcaax1XtzBRMccdIGmq57AVUt7FRErSENNQ59QO/unsjdAO\n",
"C60cnucNdkDs7OxM3FZXHjzPG9nSEobhxC0tJbyv2UHxKSvs9r7m3kKa1rF/C2oT7Ejdbty4gTEe\n",
"/3Ka6jlphfR3UdqGUARBMFKQWpTWq57Zu6jRAY3Kjhic525kIlkcUso4jjnnKqpBjfATg9vKc1+t\n",
"VksZJmqdbWB59Xq94a+lrLCT+0p/C2lax/4tMMYajcZ4zB9jbPxNT1M9J62Q/i5K2xAKtagrpVTV\n",
"U0H9E4N87L8RNZJ+Rcqj4UuClFK58+ZWuFr3hVJXuMz3lbJ1ynwLKF31Sn4LJW8IIYRyVRmpnqm7\n",
"qJ30AwAAAHVZ5gUAAAAGgPQDAADUDpB+AACA2gHSDwAAUDtA+gEAAGoHSD8AAEDtAOkHAACoHSD9\n",
"AAAAtQOkHwAAoHaA9AMAANQOkH4AAIDaAdIPAABQO/4/Yb8tGgzxHS8AAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"% taille de la fenêtre pour la moyenne mobile, en nombre d'échantillons temporels\n",
"% On passe de 3 à 7\n",
"% ATTENTION: sous matlab, ce code ne marche qu'avec des noyaux de taille impaire\n",
"taille = ceil(6*freq);\n",
"% le noyau, défini sur une fenêtre identique aux signaux précédents\n",
"noyau = [zeros(1,(length(signal)-taille-1)/2) ones(1,taille) zeros(1,(length(signal)-taille-1)/2)];\n",
"% normalisation du moyau\n",
"noyau = noyau/sum(abs(noyau));\n",
"% convolution avec le noyau (filtrage)\n",
"y_f = conv(y_sr,noyau,'same');\n",
"\n",
"%% Représentation fréquentielle du filtre\n",
"figure\n",
"Analyse_Frequence_Puissance(noyau,ech);\n",
"ylim([10^(-10) 1])\n",
"\n",
"%% représentation du signal filtré\n",
"figure\n",
"plot(ech,y_f,'k')\n",
"hold on\n",
"plot(ech,signal,'r')\n",
"\n",
"%% erreur résiduelle\n",
"err = sqrt(mean((signal-y_f).^2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On voit que ce noyau, en plus de supprimer une fréquence légèrement au dessus de 0.3 Hz, supprime aussi une fréquence proche de 0.16 Hz. C'était l'un des pics que l'on avait identifié dans le spectre de `signal`. De fait, dans la représentation temporelle, on voit que le signal filtré (en noir) est dégradé: les fluctuations rapides du signal rouge sont perdues. Et effectivement, on a maintenant une erreur résiduelle de 7.6%, supérieure au 3% du filtre précédent."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.3 Nous allons maintenant appliquer des filtres de Butterworth.\n",
"Ces filtres sont disponibles dans des fonctions que vous avez déjà utilisé lors du laboratoire sur la transformée de Fourier:\n",
" - `FiltrePasseHaut.m`: suppression des basses fréquences.\n",
" - `FiltrePasseBas.m`: suppression des hautes fréquences.\n",
" \n",
"Le filtre de Butterworth n'utilise pas explicitement un noyau de convolution. Mais comme il s'agit d'un systéme linéaire invariant dans le temps, on peut toujours récupérer le noyau en regardant la réponse à une impulsion finie unitaire."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%%matlab\n",
"\n",
"%% Définition d'une implusion finie unitaire\n",
"impulsion = zeros(size(signal));\n",
"impulsion(round(length(impulsion)/2))=1;\n",
"noyau = FiltrePasseHaut(impulsion,freq,0.1);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Représentez le noyau en temps et en fréquence. Quelle est la fréquence de coupure du filtre?"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAABzeSURBVHic7d3BjuPIfcfxGmccr+FBnBoE2N1rzc0XI2a/gA3y5DMF\n",
"5AXIJzDIwz4AlaPhi4jN3RAvvqsA5xgkqvgBdkV4geQwCNB1sAEPsFh3DjXWaESpm6IoidX1/RwG\n",
"PWo19Sel/rG6qlh88fDwIAAAIfnerQsAAFwb0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCCQ/QD\n",
"QHCIfgAIDtEPAMEh+gEgOEQ/AASH6AeA4BD9ABAcoh8AgkP0A0BwiH4ACM7LWxfQl9a6rmtrbRRF\n",
"RVFIKQdvqq5rrfUomwIAH/nR6q/ruizLoiiWy6WUMkmSwZvK89wYU1XVcrlUSt3d3bVtO2KpADB9\n",
"L6Z/b15r7d3d3Xq93jbPy7JUSmVZduqmjDFlWa5Wq+0jWuumaRaLxWjlAsDkedDqb5omTdPdbpks\n",
"y+q6HrapKIp2H4njWGt9bokA4BUPor9t2728VkpZawdsam87BzcOAM+eB8O8bdvGcbz3oFJqwKbS\n",
"NG2aZj6fF0XhtpzneVVV/bfwu9/97te//vWx775+/fr73//+gMIABOLt27fHvvWTn/zkN7/5zZXq\n",
"eJi8OI5Xq1X3wXM2uN397pYf9/Of//xKbwy8FwnBH5Q4wcuXLwfH2qk86PAZV57n29PGer2ez+fG\n",
"mJO28OMf//hqb8+IVqtVURS3rmIITytfrdb/+q+1j5U/eHvMnXPahTdUFMX3vne9QPYg+kfsi6/r\n",
"WkrpenvclpfL5Ww2G2v7AOAFD6JfCNFtmJ/aVHe01nvDBlLKYcMGAOAvD6I/TdO9+Zduuuex52ut\n",
"5/P5wSlAB6cGDZssBAD+8iD6XYfPdiK/tXY+nx+7nssYkyRJWZZ5nne/m2XZ3lmhLMvu9CEAeN48\n",
"mNwphFgul0mSGGOklFrrLMuODQBsr/w6uDKPUqqqqiRJoihym4rj+KTJnQDwDPgR/VLK9XptjLHW\n",
"Pr7gmlJqs9kcvBTAieN4vV67HqQsy+joBxAgP6Lf6TnVRyn1ZKDTyQMgZD5F/xS8evXqhz/84a2r\n",
"GEIp5ekJz9/KP//883/+Zy8r9/eYCyEemQMycddcC4DoP82PfvSjTz755NZVDNHnj6Fp8rfyzz77\n",
"PI4/v3UVQ/h7zIUQA9b0nYhrZosHM3wAAOMi+gEgOEQ/AASH6AeA4BD9ABAcoh8AgkP0A0BwiH4A\n",
"CA7RDwDBIfoBIDhEPwAEh+gHgOAQ/cBFcN9PTBnRD1yEMbeuADiO6AeA4BD9ABAcoh8AgkP0A0Bw\n",
"iH4ACA7RDwDBIfoBIDhEP3ApbXvrCoAjiH7gUoh+TBbRDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIf\n",
"AIJD9ANAcIh+AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCCQ/QDQHCIfgAIDtEPAMEh+gEg\n",
"OEQ/AATHm+jXWs9msyRJyrK01o6ywTzPkySZzWbGmPM3CAC+eHnrAnqp67qu68VioZSq6zpJkvV6\n",
"fc4G8zxv2zbLsjRNW26eDSAwHkS/tXY+n6/XaymlEKIoCmttXddZlg3b4Gw2i6JosVi4/yqlRqsV\n",
"AHzgQYdP0zRpmrrcd7Isq+t62NbcDxZFMU5xAOAhD1r9bdtGUbT7iFJqcHd/XdfL5XKMugDAV35E\n",
"fxzHew+e00ujlGrb1jX/0zTdO6886e3bt0mSHPxWVVWnbg1AUI6lx9dff/3u3burleFB9I8yn8fR\n",
"Wksp67qez+dFUUgp8zzPsuykYYNPP/10tVqNVRKAoBxLj7Isv/zyy6uV4UH0j8ta2zTNdtA4TdO7\n",
"u7s4jhnsBRAOD4Z5R+xCiaLIGLNYLMYaNAYAH3kQ/UKI7iVXwy7CklJGUbTXwKe9DyA0HkR/mqZa\n",
"691H3HTPY8/XWs/n82MjBFEU7W3NGEP6AwiKB9HvOny2fTLuCq9jA7PGGLfYQ57nB59QFMXuicFN\n",
"9XnkRAIAz48fw7zL5TJJEmOMlFJrnWXZsQGAbSf+bm/+LqVUVVV3d3cu7rXWy+Xy2JMB4FnyI/ql\n",
"lOv12hhjrXWTMo89Uym12WwOXgqwFUXRZrNx3T5VVV2kYgCYMD+i3+k51Ucp1afv/pFzAwA8bx70\n",
"9QMAxkX0A0BwiH4ACA7RDwDBIfoBIDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6\n",
"ASA4RD9wEUduEwdMAtEPXETb3roC4DiiH7gI7vyGKSP6gYvocbsg4GaIfgAIDtEPAMEh+gEgOEQ/\n",
"AASH6AeA4BD9wKUwtR+TRfQDl8IFvZgsoh+4FKb2Y7KIfuBSuKAXk0X0A0BwiH4ACA7RDwDBIfoB\n",
"IDhEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCC\n",
"Q/QDQHC8iX6t9Ww2S5KkLEs7xj1P27Yty7Ku6/M3BQB+8SP667ouy7IoiuVyKaVMkuT8bZZlKYRo\n",
"mub8TQGAXzyIfmvtfD5frVZRFEkpi6KI4/jM1rrWWkoZx/FYRQKARzyI/qZp0jSVO7e4zrLszOgv\n",
"y7KqqrNLAwAveRD9bdtGUbT7iFLqnO7+siz3ziUAEJSXty7gaW3bdntmlFLDtmat1Vqv1+vB9bx7\n",
"905rffBbrktq8JYBPHvH0uObb7757rvvrlaGB9E/ynyerfO7ev7yl78ce/OUUkQ/gEccS48//vGP\n",
"f/3rX69WhgfRPyKttbX2zNFdKSXjBACGOZYeZVl+9dVXVyvDg+jf6+g/R13XcRxvz7rGGGutMWbE\n",
"lwCA6fMg+oUQxpi9proxZsB24jhu27ZtW/dfa63r+if6AQTFg+hP09Rdz7V9xE33PPZ8rbUxJsuy\n",
"brd7lmV7z2zbdnfLABACDyZ3uib5diK/u8JrL8S3jDFusYc8z69XIgB4xYNWvxBiuVwmSWKMkVJq\n",
"rbMsO9ZFs23pPz7Txhjj1gJq2zbP88ViMX7RADBVfkS/lHK9XrtR2aIoHol1pdRmszl4KcCuKIpW\n",
"q9UFKgUAD/gR/U7PwVil1OALvgAgBB709QMAxkX0A0Bwxon+7Ux5AMD0jRP9zKQEAI+cNsybJMmx\n",
"tYcAAL44udW/Wq0edtzf38dxfM4ayACAKzst+ruLEkspF4uFu88tAMALp0X/YrHoTq5354Nh66kB\n",
"AK5vnGHeM++YCAC4pnGi362uM8qmAACXdtoMn7quu1P427aVUrLkPQD44rRWf9M03Y6dNE2Xy+V4\n",
"JQEALuu0Vr9SKk3TM+9tCwC4rdOin3XtgZ6MEXSCYrJYvg0AgkP0AxdBkx9TRvQDQHCIfgAIDtEP\n",
"AME5N/qttXmes3wbAHjk3Nuy13Vd17UQIo5j5vsDgBfObfVv129QSp1dDADgGs5t9W/v00L0A3tY\n",
"yByTdW70i52GPwDAC8zwAS6FRhEmi+gHgOAQ/QAQnHGiv3v/FgDAZI0T/Xmej7IdAMAVnDzDR2ut\n",
"td57kFY/AHjktFa/1rosyyiK4jjWWsdxHEWR1ppbuACAR06+LftisYiiyBjjTgBCiLZt3WngMhUC\n",
"AEZ2cqvfXcBlrZVSugeLotBad2/XDgCYptOifxv3e+I4Nly0DgCeOC36XVeP+5qhXQDw1MnR76b3\n",
"xHHctu22k8cYw/JtAOCL04Z5syzbNvaLokiSJMsyl/tEPwD44rTol1Ju1+lM01Qp1TRNFEVZll2g\n",
"NgDARZy1aHMURazYDADeYfk2AAgO0Q8AwSH6ASA4RD8ABGeEe/Neh9a6rmtrbRRFRVEcu674Sdba\n",
"uq63VydkWTZ4UwDgKT9a/XVdl2VZFMVyuZRSJkkybDvW2tlsZq1dLBaLxcJamyQJqw8BCI0H0W+t\n",
"nc/nq9UqiiIpZVEUcRzXdT1gU2VZZllWVZW7Bq2qqjRN5/P56DUDwJR5EP1N06Rputstk2XZsOhX\n",
"SqVpuvtIURQsPAcgNB5Ef9u2exeOKaWG9dIURdHdOH39AELjR/R303msJYNmsxmrUAAIjQczfC43\n",
"DJvneZZlp95f7O3bt8fGmauqYmULAI84lh5ff/31u3fvrlaGB9F/IXmeD1t47tNPP12tVpcoCcCz\n",
"dyw9yrL88ssvr1aGBx0+o7ejrbV3d3csOAogWB5EvxCiOwln8LQcN5c/yzJyH0CwPIj+NE3dxbdb\n",
"brrnsedrrefz+cERgoO5z50mAYTGg+h3HT7bifzuCq9jbXZjTJIkZVnmeb73LXcpb1EUez97d3d3\n",
"gaoBYLr8GOZdLpdJkhhjpJRa6yzLjg0AbKeBdueDGmPatq3reu9yMBZyABAaP6JfSrler40x1trH\n",
"125TSm02m7Ztu1M24zjebDYXrhQAPOBH9Ds9p/pwj3gAeJwHff0AgHER/QAQHKIfAIJD9ANAcIh+\n",
"AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCCQ/QDQHCIfmB8LASOiSP6gfENvX8ocCVEPwAE\n",
"h+gHLqJzryBgQoh+AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP3ABbXtrSsADiH6gQsi+jFNRD9wKVLe\n",
"ugLgCKIfuJQounUFwBFEPwAEh+gHgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6ASA4RD8ABIfo\n",
"B4DgEP0AEByiHwCCQ/QDQHCIfmC4thXz+ck/VZbC2gtUA/RG9APDlaVo29Ny3D2/LC9WE9AD0Q8M\n",
"VNciy0SaiqY57aeKQigljLlYZcBTiH5goLYVcSzi+OS7MCp18gkDGBfRD1zPtmtIqZvWgeAR/cAQ\n",
"xnwU3z27+4356K6NDPbiVkKMfq31bDZLkqQsS8svHwbRWsTx+6+jqG/Hfdt+OGFEkdD6IrUBTwou\n",
"+uu6LsuyKIrlcimlTJLk1hXBS9Z+CHGl+nb3t+2HVn+aMtKLmwkr+q218/l8tVpFUSSlLIoijuO6\n",
"rm9dF6ZI674dMlF08kjvk6zlxIALCiv6m6ZJ01RKuX0kyzKiH3uMEUkijBFleTh/9zr6z3Hw7GKM\n",
"yPP3/9IliUt4eesCrqpt22h3lE0IpRTd/UHZtqa3PfV7jBFNI5ZLIaWwVuS5WC73n6O1SNMRionj\n",
"A5uyVszn71/UWjGbvS+m68l9AY4JLvrjzm+JOrH99n//99N/+ZcvD37rl7/85WeffT6wOByxOxYq\n",
"pYgi8ec/i1evPnqOMcJaYe2HiIxjodSHtnnbiqYRbSukFHH84XraovgoVV1Lf7X68HJZJuZzURQf\n",
"vdxuR39/7tV3RZGYz/ejfz4XVfWhgOVSlKWoqo9+tm2F+2N1d1/c5QLbp7WtaNv9keTdY7Jr72nP\n",
"6VzS/bTc1r/92+H02Gz++9tvv71aGWFF/ygN/B/84O9/9rOfHfzWq0l9xJ6L3XR2cdaVpvtTLV3j\n",
"ffuGS7n/nDQVbSvKUkj5/iW0FnW938aPY1HXH51UBtsd491Wtbc77r+7dUopqkqUpUjT90HvVg3a\n",
"PSzu5GHMRwsKudNk99x28Jcgyz46TY4+dIGtY+nx7bf/8dVX/3W1MsKK/lH8wz/8169+dfjNw6Ud\n",
"a7TucU37J5uuSonFQmj9PjGVOtC3I4TIMtE0Isve/7dp9hPc/ezudM/+3MTQ7Qa7f2GIv6V/Xb8f\n",
"eXbrQBzcVLew7nOe1PMgY5g4PpweZflP//7vf3e1MsKK/qjPBx+BefIkEcfvh1td89mYA+ncJyuN\n",
"OTBCkKairt8ncrfJv+X+NAHGEtYMHyGE6czY6D4C7HE9/uJvE3KODbo+7uAIwe41AXX9oZcfuKiw\n",
"oj9NU/3xeJab7nmreuAL1yp3XUMHPy9xPHwaflGIsnx/ajl/RAHoI6zodx0+24n87gqvbNuJCxxX\n",
"Ve+X6hy919D10StFkx/XE1ZfvxBiuVwmSWKMkVJqrbMsYwAAPT3eSDhn+hh/eeLKgot+KeV6vTbG\n",
"WGuLopD8gY2R8FGCR4KLfoeWPoCQhdXXDwAQRD9wHVpznRQmhOgHRvP4+gdEP6aD6AfG8fj92Vkf\n",
"FpNC9APXYMyzWg4TviP6gdGw4CV8QfQD43i8wweYFKIfAIJD9ANAcIh+AAgO0Q9cA5M7MSlEPzC+\n",
"7tr9LO6GSSH6gfHRxsfEEf3ARewu22AMqzhgWoh+4CJ2s/7gXXmBGyL6gdEoJT6+9zMwUUQ/MJpj\n",
"Tfu2ZZgX00L0AxfXtuPfzB04B9EPjEapA9M6gQki+oHRKHV4WidzPTE1RD9wQW7Ul45+TA3RD4yJ\n",
"Bj68QPQDY9pt4G8n/HA+wNQQ/cClbKOfDh9MDdEPjIkGPrxA9ANj6jbwuWsjJojoBy6rbUUc37oI\n",
"4GNEPzAmKbmqCx4g+oExRdF+dz+9/5ggoh+4LGPo8MHkEP3AmKRkXBceIPqBMUUR0Q8PEP0AEByi\n",
"HwCCQ/QDQHCIfgAIDtEPAMEh+oELMubovdqBGyL6gZHt3aGX6McEEf3AyHazvm1ZrB9TRPSf5u3b\n",
"t9bPNVm01mVZ3rqKIbyrfNvq11q3rYiiWxd0Ou+O+a4kSW5dwkB/+tOfrvZaRD8wMqVYsg1TR/QD\n",
"49t28nz22f/ctBDgsJe3LqAvrXVd19baKIqKopBDO1CttXVda62FEHEcZ1k2eFPAMdtOnk8++ctN\n",
"CwEO86PVX9d1WZZFUSyXSynl4L48a+1sNrPWLhaLxWJhrU2SxNO+e3jhH//x/tYlAAd4EP3W2vl8\n",
"vlqtoiiSUhZFEcdxXdcDNlWWZZZlVVUppZRSVVWlaTqfz0evGYFL0/dffPbZ/960EOAwD6K/aZo0\n",
"TXe7ZbIsGxb9Sql0+0sphBCiKArD/fQwtix7/8VPf/qfNy0EOMyD6G/bNvp4fpxSalgvTVEU3Y3T\n",
"1w8gNB4M87ZtG3ducKdGukRyNptVVXXSj3z33XdulNgvf/jDH7755hsqvyYqv4n7+3sfK7/yoOMt\n",
"o99ae6yzRUq5belf7ojkeZ5lWfe88ohf/OIXv//97/29ZuS3v/3trUsYiMqvz9/KPf0NffXq1dVe\n",
"65bR7+ZrHvyWlHK5XF701fM8j6Io23bK9vPFF1988cUXFyoJAK7jltGfpuneoOtB0dgXwrs5nVmW\n",
"nZr7APA8eDDMK4To9gsNnpZD7gOAB9GfpuneoI2b7nns+Vrr+Xx+cITgYO63bTtitQAwfS8eHh5u\n",
"XcPTkiRJ09TltYvvxWJxsCPIGHN3dyeESNN0b7TAXcqbZdneaeP169f391xyCSAgHkzuFEIsl8sk\n",
"SYwxUkqtdZZlxwYAtpP0u7P1jTFt29Z1vTe2zEIOAELjR6vfMca45dsevwirbduDlwIAAByfoh8A\n",
"MAoPhnkBAOMi+gEgOEQ/AASH6AeA4BD9ABAcoh8AguPHJV0TMdat4S+qLMu9R+I47l7lMIV9aZqm\n",
"bdvu/XN29anz+vvyZOUTfBestXVduzVR4jjOsuzYy03wmPcpvucxF7c77EqpoigO3mukZ0ljVv6A\n",
"ftzSEev1+v7+vqqqKIpuXdFhQojVxzabzd5zbrsvq9UqTdMoitI0jeP4kWf2qfOa+9K/8qm9C/f3\n",
"93EcF0Wx2Ww2m01RFFEU3d/fd585tWPev/g+x/zKxW82myiKFouFq2S5XLqXHlbSuJUT/b3c398r\n",
"pXY/bUVRLBaLG5Z0zJOn85vvy3q9dp/+1Wr1SID2qfPK+9Kz8ofpvQtZli2Xy91HqqoqimJAVdf/\n",
"/PQsvk9D9lYfmN1H0jQdUNLolRP9vSwWi72Pmjuf36qeRzz5CzCdfXk8QPvUeat9OT/6r1x5VVXd\n",
"B7u7MM1j3rP4PtE/hQ+/UmpASaNXzjBvLyPeGv5qtNYHK/RlX/rUOf19mci70B2WaNu221M8zWPe\n",
"s/itY8dcTOADo7XeG37oWdLolTPM28tFbw0/uiRJrLVSSmutUmqxWOz+nviyL33qnPK+TPxdmM1m\n",
"VVXtPejLMT9YvHjqmIvbFe+WntRaG2P2FpPvWdLolRP9vUyqIfm4qqrSNN1+Juq6zvN899Pmy770\n",
"qXOy+zLxdyHP8yzLulHixTE/VvyTx1zcrnhjjDFGa92dltOzpNErp8PnudmbPZZlmbWWO5Fd2ZTf\n",
"hTzPoyjy9AaljxQ/5WOeZZmb52OM6U5CvQmiv5fRbw1/TVEU7f4C+LIvfer0ZV/ENN4Fa+3d3d0j\n",
"uT/lY/5k8V17x1xM4AOzWCzcPaO2j/QsafTKif6+Rrw1/M35si996vRlX7quXPnBG1MPq+r6x7xn\n",
"8X3c/APTPSH1LGncyon+Xk69NfykNE2z22TwZV/61OnLvohbvwsHo7PbGTLNY96z+K69Yy6m8YFx\n",
"N5o9taTxKx88LTQ0cRxvL6C4v78/eFXezcVxvHfxS5Zl3YtfJrIvT86O71PnTfbl8cqn9i64q2H3\n",
"Snp4eJBSdp88tWPes/iex/zhusWnabq3cTcWPaykcSvnBo19uaaHuzOwuzX8BAfKrLVlWRpj3PwH\n",
"1y7oToO77b7M53PXfnGjcNt22Wq1GlDnNfelZ+VTexe01nmedycCaq27v/5TO+Y9i+95zK9cvBvU\n",
"tda6qtyk/oOTfPqUNG7lRP9pet4a/rasta4T8PE6vdgX0a/OCe6L1+/C8z7m4rrFt23ruqdGOZ5j\n",
"VU70A0BwGOYFgOAQ/QAQHKIfAIJD9ANAcIh+AAgO0Q8AwSH6ASA4RD8ABIfoB4DgEP0AEByiHwCC\n",
"Q/QDQHCIfgAIDtEPAMEh+gEgOEQ/AASH6Ad8YozZuz13f3Vdj1sM/PXy1gUAA9V13TTNse927/T7\n",
"POR5fvCWs324wzXBe0rj+rhBI3xVlqWU0t0b3RjTNM02E5MkeZYfbHe2G3xWM8bMZrPNZjNuVfAR\n",
"rX54LIqiOI7d11rr7dfP1Xw+H9zkF0JEUaSUquuahj/o64evsixzTf6uvYat1no2m7158+b169ez\n",
"2Wyvr3w+nydJorXO8/zFixd5nrsH37x5c3d3Z4xxW0iSJEkSIUTTNEmSvHjx4u7urixLa223ANe+\n",
"fv36tXvFpmnO72fXWltr0zQ95+XSNKXHH0II8QD4b7VaxXF88FuLxSKO4/V67f67Xq/TNC2KYvuE\n",
"zWaTZZlSarlcPjw8FEURRVGWZe7JSin3nNVqFUVRURRZlm02m+3GlVLbjW83uN3advvHyuvPvXT3\n",
"8ZNezp0U7+/vzywGviP68Rwci/7NZhNFUffxOI5Xq9X2v0VRVFW13dTuj+xuNo7jbvh2X7qqqt1T\n",
"y8PDw/39/cHUPkkcx3ubHfZyQojdfUeY6PDBc1bXdVEU3ceLotibHbTbdySlPLbB7tbiOLbWtm27\n",
"fSRN06Zp5vP5tmdJSrlYLAbUv8sYo5TqPn7qy8Vx7HqxEDKiH8+Z6wR/0ZEkyW5Y93cwfKWUu1tz\n",
"XUDib6MCb968yfN82Ms9+dLDXu7g+ASCwgwfPGeu1/7g0Ogwbdt2I9hauzfgLKXc/fvAhfJ6vX7k\n",
"74kn7Z1gBr+cMYYZPqDVj+csjuNxJ7SUZbn3SF3XSqndkO0+J01TpdSZ3SxRFB1srZ/0ctba7okK\n",
"ASL68ZzFcayUcvM1d9V1PZ/Ph20wSRI3TmCMKcuyruu9jnVjzN75pm3bg38unPrSB5dwOOnlmqZx\n",
"s/vPqQTPAB0+8NtsNnMt2bZt3bz7oih2r+1aLBZlWd7d3bkHrbXGmCiKttdGlWXZNI3WOssy1xPi\n",
"RgiWy6V7QpIkVVW5lrKbBrqdOO9mCu31q7ieme0rtm1rjHHTQM/ZU7e17pVrJ72c1nrE7i/4i4Uc\n",
"EASX+O7rwRf9JknSfxGF7StuV5s43yMLOfR5OXeG2Gw25ww54Hkg+oG+Tor+C3nz5o27SG3Az+Z5\n",
"7sa9R68K3qGvH/DJthtqAKUUuQ+HVj/wtL0FotM0JUPhNaIfAIJDhw8ABIfoB4DgEP0AEJz/B7MU\n",
"5vYUyLwDAAAAAElFTkSuQmCC\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1PrOTGfefrzZ830ujPGz5JyEgajAU+2IANxDDCB0uz\n",
"gg+TJTcHQYfFiI0JFCE+sRUEARQDQTE2IOS27DW8iYA9hLT2EDiAgSYCAzGSHFiwIeSQwCGtzWkD\n",
"yGSihYPNBAHLu5mZZOYp6T2URVPsfv2qukn2r8jfB3Po6fftYlX9un8kv6w/e4vFgiAIgiBj4tyu\n",
"K4AgCIL0DaZ+BEGQ0YGpH0EQZHRg6kcQBBkdmPoRBEFGB6Z+BEGQ0YGpH0EQZHRg6kcQBBkdmPoR\n",
"BEFGB6Z+BEGQ0YGpH0EQZHRg6kcQBBkdmPoRBEFGB6Z+BEGQ0YGpH0EQZHRg6kcQBBkdmPoRBEFG\n",
"B6Z+BEGQ0YGpH0EQZHRg6kcQBBkdmPoRBEFGB6Z+BEGQ0YGpH0EQZHRc2HUFEEQbfN8nhNi2bdv2\n",
"rusii+M4lmUFQbDriiCwwKv+0cE5n06nR0dHe3t7k8mEMTabzXZdKQKhDmdi2zbnnDHWReGTycSp\n",
"MZlMfN8viqKLYyHI3mKx2HUdkP7gnB8fH1NKPc8jhBRF4fs+Y6wsy91WzHGcJEl2WwcZxIV/FxfR\n",
"jLE4jgkhruuKd4qiiKLI8zwRrM3IsswwDNM026klMhTQ8BkXURS5rlulEtM05/P50dHRbmuFEEJs\n",
"2xb3E3U3yXXd4+Nj13UNw9isWMuy2qkfMizQ8BkXnPPlXEAprV4zxoThQAiJ49hxnL29vePjY9/3\n",
"OeeNDzLGJpPJ0dHR4eGh8I5OO6jv+/WisiyrxNPp1HGcLMvqdsd0Ol0uZzabib9mWVZVz3EccbGs\n",
"WisZRFGHh4dHR0fT6XS5B1o/YgPDMFzXFe0lH/dVFEWVQLwj4lWnKIrKQRJ3KivJskw0UNQ8juN6\n",
"4fIyzvlsNhOdUBmJjUKiKBKVF6VVX4blw63/wlR01+2jYIGMifl87rruGkGe50mSWJYlTKE8z8X7\n",
"YRiappmmaaUMw9C27eqdNE1d16WUNgosy9KyrDAMy7IU/w3D0DCMSpkkiThiUqN+oIo0TYVyPp97\n",
"nkcpzfM8z3PXdev1lKmVDGEYWpZVFSVKppQ2SmvxiMuFLxYLz/OqwpMkEQ2v/ir6ZOUPWfRkEAS2\n",
"ba88XJ7n4rav+q/nectiGVmapkEQVPXM81wEtFGO+GD1vSrLstGchcQXRtBit48TTP2jIwgCkdnD\n",
"MFyZYReLhfh9Nt5MkqT6wYvf9soPNn7wy+8sFoswDBu/0tPS08pDGIYRhuHyn+RrdSaiKJF9KtI0\n",
"JYTUa97iERerUv9y4l55elhzDVePWoMgCJbT7nLcJWUN5vP5cj0ppY3uKsvSMIz6OzJfmHa7fZyg\n",
"4TM6KKVpmorBKlEUHR0drbzHr7tAAvERMeYkiqJlgfhU3X4pioJzvjwU0nXd6mHmBgRBsPLJp2St\n",
"ZBDPVxsOu2VZjeO2eERB5WI5jnN0dFQUxXw+36AcGVzXjeN4NptVVok4p24mI4SwjxHPllcetPFl\n",
"MAyjbqNJfmFa7/YRgo95R0o1OJ1zLoZ+N54BrBwTYhhGURSmaWZZdtpwzPrvtiiKlUPgDcPY5vHj\n",
"aeNVJGslQ5Zlp9W8oyNWn6pyXNezB4SDF0WRyOwiWJTSRvfKyOI49n3fsizxJuf8tA5cj+QXpvVu\n",
"HyGY+sdFHMeNy23DMGzbjuO4kYtFim98vHpKLK5/Za7c+xyZLl8rmaJ6PqJAhKOt0mQOV798Fvcc\n",
"aZo2znDrZUVRzGazxqfE5f8GVZL5wrTe7SMEDZ9xcdq10vLt+fLQiyiKTNMUStu2V9pEDWzbzrJs\n",
"5cCYLk4JkrWSwbKsldZB480Wj7gxp407OpPlELuuK27plGQrzbHNaiX5hYHQ7bqDqX9cZFnW+CVn\n",
"WbZ8K0AIsW27GjcpPhVFUeXw2rZtmubyEMwoihpnF0rpZDJp/Jhns1njs0VRNE4GjDHV04N8rc7E\n",
"dV0xo6r+5nQ6bSS4Fo8oiWVZ9W4Rgzg3KyrLskYDRRQad3tnypbPFrPZbM2I0vXIfGH67/bhgbN5\n",
"x4Ww9RljwlUoiiLLsvl83vA3xNxaMb9UJBox5qeR+MRM4OqZQZZlYrmYhkz8IMXIHLEQgm3bDZkw\n",
"i8UZaKWmKArxU8+yrLr5IIRQShsOiWStzkSMLq88a8aY53lFUcRxbJpmfe5xK0d0HEd0tUipaxbe\n",
"mU6nRVGIcwDnPAiC4+Nj27bFANyqtKoVQiz+W5/QN5lMTNNsfBnEoMn64WRkVZVER4knSdPp1DTN\n",
"qlbT6VRYQGJ4rqibGI/fqLzMF6atbh8tmPrHiPidkNMft8ovq1AVRc56wlY5v6fJ5ItqsVZnUt2O\n",
"rC+nxSPKIFyRLZ+WC878MkjKqo6yLKuV5HvmF4b03u1DAlM/sgJdVtRBEGQz0OtHEAQZHXjVj3wC\n",
"MXy7+m/dGkYQZDBg6kcQBBkdaPggCIKMDkz9CIIgowNTP4IgyOjA1I8gCDI6MPUjCIKMDkz9CIIg\n",
"owNTP4IgyOgYderPsqyx4iCCIMgYGOmULs65WFaQENLpHngIgiAAGWnq932/2qFQbCd02gK5CIIg\n",
"w2Okhk9941CxMdBu64MgCNInI039jQXHcW8HBEFGxRhT//I1/vL+4wiCIANmjKkfQRBk5Iwx9S9v\n",
"L6e6/TeCIIjWjDH1kyXPh3O+q5ogCIL0j5apP47j2Wy2RsAYm0wmjuP4vr8yrVuWVW36zBjbfm9r\n",
"BEEQjdBpXD9jLIqioihM0+Scn7ZveBRFURSFYWiapthuME3ThqYxpSsMQxzkgyDIeNAp9QuXRlyw\n",
"z2azlamfc358fJymaZXKfd83TXPlBrNVgV3WGkEQBB4LDUmSxLbtlX8Kw5BSWn8nz3PLsto69Guv\n",
"vbbriCEIMkz29vbaylRncmHXjW2ZoigaV/HCHWqr/B/96Ef7+/u/+Zu/KSP+7ne/+3M/93Nf/OIX\n",
"JcWf//znP/WpT8mI//AP//BLX/qSpPj3f//333zzTRlld+IPP/zwz/7sz+TFf/7nf/4rv/IrMuIf\n",
"/OAHd+7cefXVV2XEShHprpP/4A/+4Fd/9VclxUDCN+yIdCeWj3WWZd///vcli22B3k4yLbLmqt91\n",
"3SRJGm+eJt6AGzduPPnkk5LiN99881vf+pa8eLnmp3H79m158S/8wi9IKrsTJ0miJL59+7ak+Fvf\n",
"+tabb74pKVaKSHed/PLLL8uLgYRv2BHpTiwfa0rphQsX5EveEi1H+Kyh62GajzzyyN7enqT44ODg\n",
"6tWr8mL5akhe+AgODw+1E8s38OrVq/JdpxSR7jr50Ucf7ahkjEgFkH5TivW5c/0l5KGl/q65e/fu\n",
"v//7v0uK79y588EHH8iL5avx13/91/Liv//7v9dOLN/ADz74QL7rlCLSXSf/8z//c0clY0QqgPSb\n",
"Uqz/7d/+TV68JUPz+rsernPhwgX5q/4vf/nL8pc/X/7ylz//+c9Lil9//XX5lv7Gb/yGpJIoXqTI\n",
"l2xZlpL49ddflxTfuHHjc5/7nKT4kUceeeKJJyTF3XXyV7/6VXkxkPB1FBGl38iVK1cklUSx37oT\n",
"K8VaPre0QG/WUous8foppUEQNN40DKOtQ9+8efPg4KCt0gDS4nMRgFBK5c1iHcHw6QuldH9/v7fD\n",
"Dc3wcV23mqYriOPYdd22ylcyfJQ2gFTaMyCKoo7ESjez3VVDXqzUyUr2Qnet6y7WEMKn+rWXFysZ\n",
"PhC+nEQx1n0aPkNL/eIOvYoN53w2m62cz4UgCDJadJrNO5vNxBU957w+fr8xrZdz7jiOZVmGYTDG\n",
"PM9rMfX/4i/+4g9/+MOf/OQnbRUIDcdxTlshYwDUN+YcJBg+ffF9/3d/93cfPHjQ0/F6s5Z6Jk3T\n",
"JEnKsmy32FdfffXatWuS4jzP8zyXF8tXQ8nxHLZYtZPlxd21btix1jEiEGJNKZWfM7Q9QxvhU9HR\n",
"UJ+HDx/Ke/1KkwyUxEobDAxbrGMnA6kGRqQHsVID+/T6dTJ8IPDLv/zLf/mXf/m3f/u3u64IgiCD\n",
"wvf9d99995/+6Z/6OdzQHvN2zb179z766CNJcVEU8hcISpcSjVFMYxardrK8uLvWDTvWOkYESKxP\n",
"Tk7kxVuCqV+Nu3fvYuoHJdYx0Qw71jpGBEis+0z9aPiogYYPgiBdgIYPaE5OTpQe88o/5Bn8867u\n",
"HioqdbK8GMijPwidrCTWMSJAYo1TuuBSluXDhw8lxTrO5tVO3N3cUSAzPCF0spJYx4gAiXV/g/rR\n",
"8FEFDR8EQboADR/QoOEDTayjvTDsWOsYESCxRsMHLmj4QBPraC8MO9Y6RgRIrPs0fAa7kENH3Lp1\n",
"6/r165LisizlV5JQWnNCaSWAYYtVO1le3F3rhh1rHSMCIdaU0itXrsiXvCXo9auBXj+CIF2AXj9o\n",
"7ty586//+q+SYsaY/OwPpXkivu+jWKDayfLi7lo37FjrGBEgsb5//768eFt6u78YBmj4QBPraC8M\n",
"O9Y6RgRCrNHwAQ0aPgiCdAEaPqBBwweaWEd7Ydix1jEiQGLdp+Fz/nd+53d6O9gA+KM/+qN//Md/\n",
"/MpXviKpNwzDMAx5sXxNTNNEsUC1k+XF3bVu2LHWMSI7jzVj7Ic//OFv//Zvy5e8DWj4qIGGD4Ig\n",
"XYCGD2g45zilC5RYxwlEw461jhEBEmt5M3l7BrtBY0fs7++fOyd7vlS6qR+2A9CdWMdOBlINjEgP\n",
"YqUGnj9/Xl68JWj4qIGGD4IgXYCGD2jQ8IEm1tFeGHasdYwIkFj3afhg6kcQBBkdaPiogYYPgiBd\n",
"gIYPaO7du4fbsoMS67gJ+LBjrWNEgMS6z23ZcYSPGg8fPlTaqkW+5GFv39GdWMdOBlINjEgPYrBb\n",
"taDhowYaPgiCdAEaPqBBwweaWEd7Ydix1jEiQGLdp+GDqV+Nu3fvYuoHJdYx0Qw71jpGBEis+0z9\n",
"yoYP51wMxeWc27ZtmqbS3DYg+L7PGKsm2rmu63mezAfR8EEQpAvgGj5RFB0fHx8eHjqOwxjLssxx\n",
"nKOjo+Pj4yiKlJ5mQCAIguRjJPM+IeTk5ETpMa98twz+eVd3DxWVOlleDOTRH4ROVhLrGBEgse7z\n",
"Ma9U6o+i6OjoKI5jz/PEDjUiYy4WizzPPc+L4/jo6EhpkpumlGWJs3lBiXWcOzrsWOsYESCxfvDg\n",
"gbx4S842fKIoiuM4CALLstbIiqKYzWamaVJKW61hJ/i+L9weYVvZti35QTR8EATpgp4Nn5EO7oyi\n",
"qCgKkfHFQ5sgCGQ++Nprr/3VX/3Vhx9+KCMW93qSS/dxzuUX+SuKQv4RS2/iLCNr7m7/4R/+z9Wr\n",
"z0qWLC++e/efCSGPP/5E6+KOKiyqIVmHTquxjfjuXfL446uVOkYEQqz/x/9490//9L//3//7PyVL\n",
"3pJhjvDxfd9Zor6tmud5QRCI6/0gCDjnkv7dmA0fzkkcE9//2b/XX//f9f/GMWGMnDb84U/+5E/k\n",
"qyEv/uCDDz744IMuxB1VWFSjo5IhiHWMCJBYy+eWFuhtA3jIUErFo4szuXXr1vXr1yWLLcuyLEt5\n",
"saRysViIJy79iNN0QelP/zU6qc9qnIZqJ8uLu2sd2Fi3ItYxIhBiTSm9cuWKfMlbomb4MMY0Hc25\n",
"Ht/3Xddd/zBDMCqvnzESRcSyiOcRlQ0nEARRBu7gTkLIbDZTGti0MXEcz2azNQLG2GQyETaO6rhS\n",
"xlgcx9V/OeeMMZm8Twi5c+eO/JrajDH52R9K80Tq5lUX4qIg0ynJMjKfE0pPzftdV0MG1U6WF3fX\n",
"OlCxbl2sY0SAxPr+/fvy4m1RukdYPxLGsixJ2+Q0kiQRV9+u69q2fZosDEPLstI0LctSDD1SPRCl\n",
"1HVdSiml1LbtNE0lPzgGwydNF7a9kKkOhHtqHe0FOLHuQqxjRCDEumfDR9nr9zyPUiraU5alyJ7i\n",
"T3meb5n90zQVWThJktNSf1mWpmnWO5RSGobhBodLkkQ+6Qtu3779wgsvbHAsXUjThedJ5X0EQVqE\n",
"UvrUU0/1dji11F9P9BWu687nc/E6TVPXdbev1prUH4Zhow7ilLP9QWW4efPmXo1z587Ztr2/v39w\n",
"cGDbtmEYL7744mKxePHFF5955pkkST772c8+88wzi8Xi7bffvnTpUv3FYrG4dOnS22+/LV688cYb\n",
"i8XimWeeESVUL0RR9Rdvv/32hQsX1hQlXlQlXL58eU1R9Vql6eKll76/pqhGrSilpxW1XKuXX365\n",
"iwYmSXLlyhXJBoqpiJINvHz58pqiGrW6cOHC+r6qv3jjjTfW91W9KErp+r6qFyV+GrttoPjaN4oS\n",
"Lxq1unTp0mc/+9kkSeplNhr44osvViXUvxXLRTVqdfny5TVFNWpFKV1TVKNW4msv38BGUfv7+7Zt\n",
"Hxwc7O/vX758ee+TLPpCLfVblrV8/9JI92uMGnnWpH5KaXWmqTBNc/uDyvDqq69eu3ZNUpznufy9\n",
"odJdpNKtlaS4LBeuu/jOd76/22qoilU7WV7cXet2HutOxTpGBEKsKaVPPvmkfMlbopb6T3s2UE/T\n",
"Xad+13WXu76Vg8owVMNH5H30eRBkV/Rs+KiN8LFte3mETxzHfQ733O06cZzzQU7pms1+OpIHyMon\n",
"w14xBv70vW3EOkYESKzlRw9uj1rq9zyvMbCJcz6bzVzXrd6RXBFBU/b398+dk+00wzDk12aQVxJC\n",
"lM61Z4oZI4ZBxOjWdkvuQazayfLi7lq3w1j3INYxIkBiff78eXnxtqjeJojRkPP5PEmS+XxuWdZm\n",
"o2vWs97rR8OnRcpy4Xm7rgSCjB7Qhg8hJAgCSmmWZbPZLMuy+Xwuv9h9WyzfQyndVW3D8AwfYfV0\n",
"UXI/Yh3tBTR8NhNDaJ2qGKzhc2GDzyitctw6ruv6vl9fGjqO47rjhMgjZhoObmEOBEHOorf7CyXW\n",
"GD6LxcK27cplKstSzOztp2IDM3xw9haCAAG64dMps9msWmBZbAApaMjm83kURdPpVCzO7Hme5Ao8\n",
"23Pv3r3BbMsex8SymuvzANnMetibgOO27JuJIbROVQx2W/ZNDJ8oisSiS6Zp2rZNKVV6ir0GMVv4\n",
"TJlhGGmaiq3hWzy6DA8fPlTam1e+5P73a2WMhGEnJfcpBt7JkKuBEelBDHZvXuVduqbTKec8CAIx\n",
"wimKoiiKkiTpM//ukMEs2hxFxDTJ7h7ZIAjyCUAv2hxFEed8Pp9XI1vFdleTyaSDukFkMIZPlq3O\n",
"+0Buk4dtL6Dhs5kYQutUxWANH7XUzxhbnrFl27b8Boe6c/fu3QGk/igipw2JAvKDGXaiwdS/mRhC\n",
"61TFYFO/muFzeHhYluXy+77v73bEZ28Mw/CZTle4/AiC7BDQhs/wtmZU5eTkROkxr/xDnt6ed625\n",
"5N+y5J2IVTtZXgzk0R+ETlYS6xgRILHu8zGvWuq3LGvlTDbG2Bgu+QkhZVnqPpv3NJd/+5J3ItZx\n",
"7ijO5t1MDKF1qmKlWD948EBevCVqhk9RFI7jiKV7qjen06lhGMNeta1Cd8MniohhrLvqRxBkJ0A3\n",
"fObzuZhLJXZOPzo6Gk/eJ/obPll2Rt4Hcps8bHsBDZ/NxBBapyoeiOFDPt573bIscSOTJMl48j7R\n",
"3PBhjJw56xnIbfKw7QU0fDYTQ2idqhis4QN0DR+w3Lp16/r165LisiyX97NcI5avhtIOf5WY0rNX\n",
"7Nms5B2KVTtZXtxd63qI9Q7FOkYEQqwppVeuXJEveUuUZ/OOHH29/qIgUUTGdIeGIDoB2us/DaU7\n",
"IK25c+eO/JraYqUjebF8NRp7pcmIo4jIbKywQcm7Fat2sry4u9Z1HevdinWMCJBY379/X168La3c\n",
"O/S2SdbO0dfwkdyKC8ht8rDtBTR8NhNDaJ2qeOCGj+M4SZJsXw58NDV8cLE2BAGOlobPeNDU8Fk/\n",
"jWubkncu1tFeQMNnMzGE1qmKwRo+Z6/XH0VRHMfrNb1tjbtzHn/88QsXZDc5UFr3QkmsNHf6U5/6\n",
"z/IraiuVDEEMpJOVxECqgRHpQazUwIsXL8qLt+Rsw8f3fcMw1m+D5ft+mqatVgwoOho+vk8obe7G\n",
"hSAIKCAaPpZl2WsZyT4thBDOuV5Tujgnf/EX/0s+PkAmwgx7AhFO6dpMDKF1qmKlWMubyduzyQaN\n",
"Y2Z/f//cOdkHJEpnRCWx/F1kFJHbt/9fFyUDEUPoZFUxkGpgRHoQKzXw/Pnz8uItOdvwEWtQrG8A\n",
"jvABy2RC5vNdVwJBkLMAZ/gYhnHmiWskeZ/oZvgwRmwbyp0v2gv1anRUMgSxjhEBEus+DR8c3Dlk\n",
"GMP1mREEWQGu4aOGRoYP52Q2w0V7EEQPwBk+SJ179+7psi17tREjkP2pcRPwejU6KhmCWMeIAIl1\n",
"n9uy4wgfNR4+fKi0VYt8ya1v35FlhFJZsVLJoMS77eTNxECqgRHpQQx2q5azDZ8syzjnMhPY5JX6\n",
"oovhk2Uky6SW6kQQBAIQDR/f9x3HWXObwxibTCaTyWTwc7t0MXzi+GcPeIHc+aK9UK9GRyVDEOsY\n",
"ESCx7tPwOTv1W5aVpqnrutPp9OjoqNqYN45j3/erN23bzvN8/XoPA+Du3bvwU7+4xazOwkB+A5ho\n",
"6tXoqGQIYh0jAiTWfaZ+tRE+cRyLcbiMMdM0TdO0LMuyLFfPIYRiyK3S6UoLwweXaEYQ7YBo+FS4\n",
"rhsEQZIki8Uiz3OxJzvMvJ9l2RqfinM+mUzEvctkMpEv9uTkROkxr/xDnhafdzWWaAbyvKu7h4pK\n",
"nSwvBvLoD0InK4l1jAiQWPf5mHewgzsZY57nUTHGZYnZbOZ5XhAEQRB4nie/AHdZlsBn8xYFaSwx\n",
"AmRaI84drVejo5IhiHWMCJBYP3jwQF68JQOf0iUu+ZcHHTUWHZJfgwi+4eP7xPOa2R9BEOCANnwG\n",
"Q8Pflx+YBN/w4byZ94Hc+aK9UK9GRyVDEOsYESCxRsOnW5ZvweRXYQVu+DBGlh9aA7nzRXuhXo2O\n",
"SoYg1jEiQGLdp+Gj62xe3/eX+9SyrKDjNWsODw/39/clxUpjh5TE3imTtRgjy083ThMrlQxW3H8n\n",
"by8GUg2MSA9ipQZeunRJXrwluqb+bVK8ZVmN3Ybl7+AuXrwIfKuW5WKA7FmBG4NAqwZGpAcx2K1a\n",
"xmj4kKW7MHk/7s6dO/JrajPG5Gd/KM0TWTkkKYpWuD2niZVKhixW7WR5cXet2z7WkMU6RgRIrO/f\n",
"vy8v3pbFjpjP50EQrBEkSeK6rm3blNKyLDc7SpIkYhZCA0pp9X6SJJRSyQJv3bp1/fp1SXFZlvI1\n",
"V2pjnufLb3qeglipZMhi1U6WF3fXuu1jDVmsY0QgxJpSeuXKFfmSt6TvwZ2MsSiKiqIwTZNzftqQ\n",
"yiiKoigKw9A0zSiK4jhO01TpQI7jkE/uLlk/Fud8Op2KG7eiKMIwlLwvAzu4k3Pi+yQMd10PBEE2\n",
"oufBnX1f9adpmqbpYrFIksS27ZWasixN06yfLSmlYRh2Vxl5bt68efXqVUnxafccp4nlq7F8mxKG\n",
"i9OaIn9Po6NYtZPlxd21bstYAxfrGBEIsaaUPvroo/Ilb8nODJ81qT8Mw0bnioXheqnXGbz66qt7\n",
"e3vnzp07d+7c3t7exYsXbdu+fPny008/bdv2tWvXXnnllcVi8corr5immef5zZs3TdNcLBbvvPPO\n",
"E088UX+xWCyeeOKJd955R7x4++23F4uFaZqihOqFKKr+4p133rl8+XKjqEuX/ltVlHhRlfDss8+u\n",
"KapRqyRJ6rVqFNWoVZIka4pqNPDXf/3Xt2ngabXK8/z69euSDczzPM9zyQY+++yz6/uqXsLly5fX\n",
"91X9xdtvv72+r+pFJUmyvq/qRYlEs9sGiq99oyjxolGrJ5544ubNm3me18tsNPCVV16pSqh/K5aL\n",
"atTq2WefXVNUo1aNr32jqEatxNdevoGNoi5fvmzb9tNPP3358uWDg4O9vT2RUsSLRV/sbDYvY2w2\n",
"m600fHzfX14S7ujoKM/zvmp3KjANH9yLEUF0B2fzkqIolp13pQFV3cE5Bzilq9qLUUasVDJ8sY4T\n",
"iHBK12ZiCK1TFSvFWn704PZAHNevNPW5Z/b39wGO66/2YpQRK5UMX6zjKHIg1cCI9CAGO64fotdv\n",
"2/bys5HTxD1z+/btF154Yde1+ARluVB57IQgCEQopU899VRvh4No+EDe6gug4VPfi/FMsVLJWoh1\n",
"tBfQ8NlMDKF1qmKwhg/E1E9W9ZdSD46Kolg9iRdBEORUeru/aLDG8EnTtPGn+XzunTZXtV+gGT7o\n",
"9iDIMEDD56eGT3VXxTkXm2rttFI/5d69e6C2ZT/T7SFg9qfGTcDr1eioZAhiHSMCJNZ9bsu+yQgf\n",
"xlgcx0VRiFH5Ii9LPsiezWai4zjnRVGI5RbIJ1dZIITM53PHcbIsMwxDbLUI5AHAw4cPlbZqkS95\n",
"s+07ioKceU4EsmdFdxuDyBcLZI8UINXAiPQgBrtVi/KULrGijud5k8lEfDaKoizLwg6Wj8myjHNu\n",
"WZbSAKlOATWlC2dyIchgAD2lS1zvizU1qzc9z+voGaxlWbZtw8n7BJjhE8dSD3iB3PmivVCvRkcl\n",
"QxDrGBEgse7T8FFL/VEUrdwjxbIspe7Ql7t378JJ/UVxttFPwPwGMNHUq9FRyRDEOkYESKz7TP1q\n",
"hs/h4WFZlj/95N7PPuv7vm3btm23X0FggDJ8fB/dHgQZCKANH1Dey044OTlReswr/5BH9XmXpNtD\n",
"wDzv6u6holIny4uBPPqD0MlKYh0jAiTWfT7mVUv9lmWttPUZY0BG4HRNWZZAZvMyJuX2EDDTGnHu\n",
"aL0aHZUMQaxjRIDE+sGDB/LiLVEzfOorLVeGz3Q6NQxjm33SNQKO4TOd4p5cCDIcQBs+tm27rnt8\n",
"fBzHMSEkjuPJZEIIGUneJ2AMnz/+4x/L32UBufNFe6FejY5KhiDWMSJAYg3X8CGEeJ43n8+zLLNt\n",
"O8syz/O62FRmdgAAIABJREFUGNEPFiCGz3/5Lz+SdHsImDtftBfq1eioZAhiHSMCJNZwDR8EiOGD\n",
"bg+CDAzQhg8CgaIgMLYsQxBEV5Rn8/q+7/t+dRcj1uGBvK9Wu9y5c0d+TW3GmPzsD3llHJO/+7v/\n",
"KikmhPi+P2CxaifLi7trndKcIAidrCTWMSJAYn3//n158bYorfOZpqlpmmEYlmVZvRkEAZAVlXvg\n",
"1q1b169flxSXZVnvqDPFkkrPW+R5LileLAYuVu1keXF3rZOvQ6fVwIj0IJZvHaX0ypUr8iVviZrX\n",
"7/u+aZrL6ycfHx+nadrqKQkoO/f6cck2BBkkoL1+xpi7amTJeNbw2bnhIxboB3IzC0Gso72Ahs9m\n",
"YgitUxUPxPA5TU8pXd5IfZDs3PAR1hqQm1kIYh3tBTR8NhNDaJ2qGKzho7ZVi23bnPPllXzG85j3\n",
"4sWL587J3iopLXkkKRYqU2WIz7DFXXSyah1UxUCqgRHpQazUwPPnz8uLt0R5DR8xj7cO55wxNoZl\n",
"OwkhnPMdTuli7KdLtgGZrgJBrOMEIpzStZkYQutUxUqxljeTt0ftqp9S6jiOaZpVouecTyYTSmkH\n",
"dYPI/v7+Dq/6GSOip4Fc0UAQ63iNCaQaGJEexGCv+pVn84pczzm3bbsoiizLKKVA9kzvgd2O8MEF\n",
"+hFkqIAe4UMIMQwjSZL5fG7btud5eZ6PJ++TnRo+RUGqCwggN7MQxDraC2j4bCaG0DpV8UAMnwrT\n",
"NJXuegbDDg0fxkj1PAXIzSwEsY72ApBqYER6EA/H8Bk5OzR80O1BkAED3fBZidIC1lpz7949ONuy\n",
"o5jouQn4sGOtY0SAxLrPbdk3NHwaTKdTsXXX4Hn48KHSVi3yJa8XV8M6BUC2oYAgbrGTN66DqhhI\n",
"NTAiPYjBbtWibPj4vh9F0XJ7RmIc7crw8X1CKVGxDREE0QnQho/v+5zz5XnMI5nPRXZq+NTzPpCb\n",
"WQhiHe0FNHw2E0Nonap4IIYPYyxJkuVn1uPZo3Enhs/yX4DczEIQ62gvAKkGRqQH8UAMn729sY8I\n",
"2onhE0XENMlo7qwQZIyANnxc1x3PYJ6VnJycKF31y5/z1yiLopn3gVzRQBCrdrK8GMiVIIROVhLr\n",
"GBEgse7zql8t9VNKV65VPZlMWqpPa2RZ5vu+4zgrjTnf94+Pj52PkZ+eV5blDpdvqwAyUxGCWMe5\n",
"o8OOtY4RARLrBw8eyIu3RM3AiaJINLvxXDeO4zzPW67adsxms+oeZfkptO/7tm1v8HS6f8Mny362\n",
"ahuCIEMFtOETx7FlWVqM56GUdrHURP+GD2NkeWM0IDezEMQ62gto+GwmhtA6VfFADB/XdSmlwRJa\n",
"nAwaZFk2m81831caqtW/4cM5WT6FAbmZhSDW0V5Aw2czMYTWqYoHYvhoh0jry2emKIqKohDvC00g\n",
"tz5O/4YPLt2DIGOgZ8OnnYUciqLoeSFP3/eXT6eWZUlm8PpC07ZtT6fT/psgA2MrLvkRBEG2pJ3l\n",
"26bTaSvlyBMEQbKEZN5fxjAMSf/uzp078mtqM8bk3aSVyvpCzXVWjrM6jWGLVTtZXtxd65Q8Rgid\n",
"rCTWMSJAYn3//n158ZYoX/WvDNUGg/3jOC6KYs3OjowxsViQZVmUUqVlrzdAsvzDw8P9/X3JMq36\n",
"imsbiVca/eSTdy1nMmzx9p28fR1UxUCqgRHpQazUwEuXLsmLt2WhQpIklmXN53PxQmzXJV7Il+C6\n",
"rmVZruvatn2aLAxDy7LSNC3LMggCy7KU6lk/3HLdRLWr/5ZlKV/+7du3X3jhhc0qswGe19uhEATZ\n",
"JZTSp556qrfDqaV+13XTNF0sFmmaeh+npSAIKKWSJaRpKkpIkuS01F+WpWmaZVlW71BKwzBUqqoY\n",
"tm9ZlhiN2jgWpVSMVqKU2rYtqiTDzZs3r169KileeeJZI156Z3Fao+U7fPBi1U6WF3fXOvk6dFoN\n",
"jEgPYqXWPfroo/Ilb4la6jcMQ7xIkqTefsuy6plahjWpPwzDRufmeb7xhf/6OsgnfcGtW7euX78u\n",
"KS7LUr5blpWULk779PLiqWsYtli1k+XF3bVO6ccCoZOVxDpGBEKsKaVXrlyRL3lL1FK/aZriRSP1\n",
"U0qVLmQWa1M/pbRuyDQOvVtu3769t7d34cKF/f39vb29xx57zLbtg4ODa9eu2bb98z//8+JmyPO8\n",
"l156qf7i29/+9vPPP19/sVgsnn/++W9/+9v1Fy+99JIo4aWXXvrCF/6sraJarBUWhUWdWZTneY2i\n",
"xItGUc8//3yjqJdeemnwRR0cHNi2fe3atYODg2efffb8+fN7e3ti0+9z584t+mJDw0dY9tX77aZ+\n",
"13WXS1vzYKBPfumXfum5556TFFfulqS48c6a20ol+2vYYtVOlhd31zqle00Inawk1jEiEGJNKX3s\n",
"scfkS94StcGdlmVVk6SKoqjmKGdZ1uKgeKWpzz0jTs6SYsMw5AcmNZSNHRkbKPX2sMWqnSwv7q51\n",
"SsPVIHSykljHiACJ9fnz5+XF26J0oijLsjqJibE9YRh6nuepj0RZc9Vv2zbYq/7eRvisMfoRBBke\n",
"PY/wUbvqNwyjGqbqum4YhkVRiBNAi2cjpZGwPcM572cNH87X7cQLZH0SCGIdV4zBNXw2E0NonapY\n",
"Kdby00W3Z6uFHMTQybaqUifLssbCO0o92B2qho98yQ3x+o8CuZmFIN6mk9uqg6oYSDUwIj2IB2L4\n",
"tMgawydN08af5vP5Bp5SF/Rj+KTpIgi6PgiCIIAAbfj0g7iTqO6qOOez2Uxp8nR33Lt376OPPpIU\n",
"F0Uhv8RFXZllZ+zEq7QwyLDFqp0sL+6udUoLn0DoZCWxjhEBEuuTkxN58ZZsZfhwzrMssyxL/qZm\n",
"NpuJjuOcF0XhOI54P0mSumw+nzuOk2WZYRiMMc/zgDwAePjwodJWLfIl18VFQdaf6YBsQwFBvHEn\n",
"t1gHVTGQamBEehCD3apFbb1+kbhN0xQPeI+Pjy3LKooiDMMudmvJskws39b12m3y9LNeP67RjyBj\n",
"A/QGjaZpmqYp1kaezWZi5eT5fN7Ros1i+R04eZ/0YvjIXCUAuZmFINbRXkDDZzMxhNapigdi+MRx\n",
"HASByMWMMTGmU4zzEc5PJ3WERA+Gz5lGPwFzMwtBrKO9AKQaGJEexAMxfA4PD8uyFK8dx6kMet/3\n",
"xeqY7VcQGD0YPr5PKD1jcCeCIAMDtOFTIRz/dquiBScnJ0pX/fLn/LryzLwP5IoGgli1k+XFQK4E\n",
"IXSykljHiACJdZ9X/Wqp37btOI7J0ma8jLExuD2EkLIs+5nNux4gMxUhiHWcOzrsWOsYESCxfvDg\n",
"gbx4S9QMnyzLHMfxPC+O4zRNhekfRVFRFBvvi6sXXRs+WUay7IyRnQiCDA/Qho/YNNEwjCRJRN73\n",
"fV/ssttN9cDRteGTZesW7KwAcjMLQayjvYCGz2ZiCK1TFQ/E8CGEmKZJKa3cnmp8Z9sVA0rXho9k\n",
"6gdyMwtBrKO9gIbPZmIIrVMVD8TwQbo2fHAyF4KME9CGD9IpgLeoQRBkUGyV+jnnjDHIm2q1zp07\n",
"d+TX1GaMyU/8Y4xJuj2EEN/3JYsdvFi1k+XF3bVOaToohE5WEusYESCxvn//vrx4W5TW+QyCwLZt\n",
"sX5ynueGYdi2bZqm6sa8+nLr1q3r169LisuyLKW32irLUn5nrjzPJYsdvFi1k+XF3bVOvg6dVgMj\n",
"0oNYvnWU0itXrsiXvCVqXn8cx4wxsZbDdDq1LMvzvCzLJpNJnufdnZ/g0KnXP52SVrc7QxBEG0B7\n",
"/XEcU0qrNXzEGvrVGj6dVBAYnRo+8os3ALmZhSDW0V5Aw2czMYTWqYoHYvgYhlG9rm+kRSkdiefT\n",
"neHz/vs/kd+ZC8jNLASxjvYCGj6biSG0TlUM1vDZcKuW0a7hc/HixY725v3BDw7kl78Dsu8oBLGO\n",
"O8ECqQZGpAcx2L15cQ0fNTjnHU3p+ou/+Af5LgQyXQWCWMcJRDilazMxhNapipViLW8mb4/aVT+l\n",
"VOybKNbwEW9GUQRtQ5Xu2N/f7+iq/5FHHpEXA7migSDW8RoTSDUwIj2IwV71K8/mLYoijmPXdUX7\n",
"fd8XO+iOZC2H7kb44DxeBBkzoEf4kNGv4dOR4ZNl5MKFD+WrAeRmFoJYR3sBDZ/NxBBapyoeiOGD\n",
"dGT4ZBn54hcV7vWA3MxCEOtoLwCpBkakB/FwDJ+R05Hhg24Pgowc6IbPyLl3795HH30kKS6KQn5p\n",
"b6VFwJXmiQxbrNrJ8uLuWjfsWOsYESCxPjk5kRdvSTupX8n80pqHDx92sVUL5wPfvqM7sY4bgww7\n",
"1jpGBEis+9yqpR3Dx3GcJEm2Lwc+XRg+WUYYI5S2WCSCIJqBhg9oujB8xFrNwzYBuhPraC8MO9Y6\n",
"RgRIrPs0fHCEjxqqho+MrCiI55EsG7IJ0J1Y6YYaiNMCpBoYkR7EGhs+Ypk6z/NM0xQTuJY1WZaV\n",
"ZdlJBYHRheGDw3sQBOnZ8Dn7ql/kenHuyrLMtu3l5XqUVjHVmpOTE9Wr/jMH9orLAs65/BDgxhpK\n",
"YxZLdvIG4u5aN+xY6xgRILHu86r/bK8/SZIkSap0b1mWvQTYBXwYY2vuzpRmEgrKsmx3Nm9REPEt\n",
"GvYMz+7EOs4dHXasdYwIkFg/ePBAXrwlaiN8JpOJ53n20uLCAEf4ZFk2nU5FVYuiCMOwfn7inE+n\n",
"U3HqLopCfiGK1g2fOCaGQeSXa0YQZJD0bPiobdVy2h4F9W1bIFCWpeu61X/TNKWU1gX1vWWSJGn8\n",
"dQ2tb9VSHXnY23d0J9ZxY5Bhx1rHiECIdc9btagN7jzN4YJ2yc85p7Vx8ssPJ8RDC/Hatm35m7LW\n",
"DZ+6WFJJwNzMQhDraC8MO9Y6RgRIrPs0fNSu+jUlz/P6TcBisWhc5jf+uobbt2+/8MILrdWsdtWP\n",
"IMiYoZQ+9dRTvR2unSldSgNde0bY+mEYVu8sn4d3tdkk4G5DEGTItJP6p9NpK+XI4/u+s8TyGFPO\n",
"+WQyCYKgrTFId+7ckV9TmzG2fuJflv3sAa/SFEGl0bTDFp/ZyRuLu2vdsGOtY0SAxPr+/fvy4m1R\n",
"ukdYHtuzWTn9UJalbdtpmi7/aWPDp93HvJQuqr8P+9Ffd2IdHyoOO9Y6RgRCrEE/5iWEVANjBFV6\n",
"VS0njuPZbLZGwBibTCbiWl5pMrQgyzLf94MgWLlffMPzkS//4sWLSlu1nHm3Uf198HtWdLcxiHzX\n",
"KYmBbN8BoZOVxDpGBEis+9yqRXmET6MlhmGEYah0MziZTI6Pj+M4XnMrFEWR7/uU0vl8bhiG4zhK\n",
"9VzO+40aWpZVHZ0xtvL0sJJ2DZ+GWFJJwNzMQhDraC8MO9Y6RgRIrOEaPqfhuu5KX2WZNE2FMkmS\n",
"02YDlGVpmmb9RolSGoahfH0opY1Zx4ZhNA7hui6llFLquq78TVmLhk9ZfmJ4z7BNgO7EOtoLw461\n",
"jhGBEOueDZ921uv3fV9kWPmPMMZms9nKCQFRFBVFEdSWNCuKYjKZbGArrUfYPvKX/KTV2bziagDn\n",
"8SIIQjRdrz/LshaX8SmKopGOTdPcwO4/E8uylPI+IYRz/uGHHx4cHDz99NMXL1587rnnHMd57rnn\n",
"PvOZzziO88orr3z9618nhHz9619/4403six766233njjDULIe++9d+PGjfoLxshXv/qf3nvvPULI\n",
"jRs3vvnNbxJC3njjDVFC9UIUVX/x3nvvHR0d1YsSJVRFiRdVCTdu3FhTVKNWURStKapRqyiK1hTV\n",
"qNVv/dZvddHALMsa3b6mgWICkWQDxQclG3h0dLS+r+ovvvnNb67vq3pRURSt76t6UWK20W4bKL72\n",
"jaLEi0atbty48dZbb2VZVi+z0cCqno1vxXJRjVrduHFjTVGNWjW+9o2iGrUSX3v5BjaKEknjM5/5\n",
"zHPPPfe5z33uscceu3jx4tNPP/17v/d7P/nJT0hvKN0jhGFIl3BdV36ETMUaw8d13cbD5AWYtSJe\n",
"ffXVa9euSYrzPF9zb9iYzKV0F7ncP6MVr+/kbcTdtW7YsdYxIhBiTSl98skn5UveEjXDx3Gc5Se9\n",
"lmW5rqt6yllj+DiOQylt2EdAVohr0fDBZfoRBKkAbfiYpum6bvBJNsj7+sI5xzV8QIl1XDFm2LHW\n",
"MSJAYi0/enB71DZorC+H0B2q/nuf7O/vK43rly952GO9uxPr2MlAqoER6UEMdlx/OyN8NmCN4eP7\n",
"vmEY9aU3CSGHh4cQ9oBEwwdBkC4Abfj0g+u6jXkQcRwDsZXu3bv30UcfSYqLojhtYTvGSOPeRmkJ\n",
"PKV5IsMWr+nkLcXdtW7YsdYxIkBifXJyIi/eEoXUzzlnjKnuaLgBwvCpDDXO+Ww28zyv6+PK8PDh\n",
"Q6W9edeMSW3cCCqNXlX6Pg1bvL6TtxF317phx1rHiACJdZ9788oaPlEURVFk23ZRFJxzsb7CBseb\n",
"zWbinMk5r4/fbzg/nHPHcSzLMgyDMeZ5HpDU35bh4/uE0mb2RxBktEDcoDHP8/rKCkEQyO9ouA1p\n",
"miZJojTrvWvaGte/3H/DHuvdnVjHUeTDjrWOEYEQ657H9UuN8ImiiFJaXeZTSo+OjoLun1ECHOqj\n",
"avjIlzxsE6A7sY6dDKQaGJEexGANH6mr/uXptbZt19/p5yYAAm1t0DiaDkMQRAqIGzSeeeLq4dkv\n",
"EE5OTtp6zLsslq8GkCsaCGIdHyoOO9Y6RgRIrPu86oc4uBMyZVluP5t35Zdh2DM8uxPrOHd02LHW\n",
"MSJAYv3gwQN58ZZIjfBZXronjmOxCH713zzPu6ojJFoZ4cMY4ZzAmKiAIAgI9JjS5bpui6s0a0Qr\n",
"hg/nK4Z1DtsE6E6so70w7FjrGBEgsQZn+BiGsbxqWx2lRS20phXDJ8tW7NAybBOgO7GO9sKwY61j\n",
"RIDEGpzhg1S0Yvjg6j0IgjTQw/BBEARB9AVTvxp37tyRX1ObMba80tNp1p/SmlC+76NYsLKTWxF3\n",
"17phx1rHiACJ9f379+XF29LbDIJhcOvWrevXr0uKy7JsrEIxny88b5Gmq8Xy1VBaCWDY4uVObkvc\n",
"XeuGHWsdIwIh1pTSK1euyJe8Jej1q7GN1z+dEtMkn9yGAEEQhBD0+oGzseETRcSy1uX9YZsA3Yl1\n",
"tBeGHWsdIwIk1n0aPnjVr8Zrr72WJP/x137t12TEDx78KyHkP/yHRzgnRXHGqB7OufxUiaIo5AfU\n",
"Dlssxk1Ldp2SuLvWDTvWOkYEQqx93w/DUGkewDZg6ldD1fDhnDBGigJ9HgRB1oGGD2g450pTuooi\n",
"c12pvD/saT7diXWcQDTsWOsYESCxljeTt0dqvX6kYn9//9w52fOl0loXSmKl6dPDFuvYyUCqgRHp\n",
"QazUwPPnz8uLtwQNHzXa2qARQRCkDho+oFE1fJTufOWrAeRmFoJYR3th2LHWMSJAYo2GD1zQ8IEm\n",
"1rGTgVQDI9KDGA2fgYCGD4IgXYCGD2ju3bv30UcfSYqLopBf2ltpEXCleSLDFqt2sry4u9YNO9Y6\n",
"RgRIrE9OTuTFW4KGjxoPHz5U2qpFvuRhb9/RnVjHTgZSDYxID2KwW7Wg4aMGGj4IgnQBGj6gQcMH\n",
"mlhHe2HYsdYxIkBijYYPXNDwgSbWsZOBVAMj0oMYDZ+BgIYPgiBdgIYPaE5OTpSu+uXP+YO//Onu\n",
"GlOpk+XFQK4EIXSykljHiACJdZ9X/Zj61SjLEmfzghLrOHd02LHWMSJAYv3gwQN58ZYM3PBhjJmm\n",
"qTT7bj1o+CAI0gVo+LRDlmXHx8eMsSiKJpNJ47bL9/3j42PnY+RP42j4QBPraC8MO9Y6RgRIrNHw\n",
"2RbO+Ww2S9M0CIIgCCils9msoQmCIPkYz/MkS0bDB5pYR3th2LHWMSJAYt2n4UN62wC+T/I8T9O0\n",
"/g6ltPHfJEk2KPnmzZsHBwdbVQ42tm3vugodsnHcdQHDpy+U0v39/d4ON8xx/Q1zf+W0EXG5wTm3\n",
"bdu27R5rhyAIsmOGafjU4ZxPp9MwDOtvmqbJObcsy7Ztxpjv+/KlyftxjDH5iX9KUwTlK6wq/tGP\n",
"fgShGvJipU7+8MMP33///dbroCruLtYQwqf6tZcXv/fee5JKAuPLSRRj3afXr6vhQym1l2i4OovF\n",
"oixL27Yb5s8ynufleS5z3C996UtPPvmkZCXLsizLUl4sqVwsFpK13UD88ssvQ6iGvFipk996663v\n",
"fOc7rddBVdxdrCGET/VrLy9+88035Q0fCF/OhUqsKaUXL16UL3lLdDV8giA4U8M5n0wmQRBYlrVe\n",
"aRhGURQyY0AvXLiwt7cnWUnOufxGDWIkgJJeUqw0xuDRRx+VF3c0kEOpwkSlKy5duvT44493UbLq\n",
"oJ0zv5Obldxd+OSLJYr9Jv+dPzg4UKoDBLFSrOVzy/bszPCJ43h51E0dxthkMnEcx/d91W8eISTL\n",
"Mt/3ZfK+QP6bKn9T9rWvfe3dd9+VF8sPBnj99dflxa+99pqkkig6BvIlZ1mmJH799dclxe++++7X\n",
"vvY1SbGS4dNdJ8uPKFMtubvwdRQRpd+IkuGj1G/diZViPeTBnSKhHx8fx3G8xgWLosj3fUrpfD43\n",
"DMNxHKWjLOf9uj3HGIvjuPov55wxJnmGeOKJJ+Q3aLx69eqnP/1pebGkkhDyhS98QV78/PPPayeW\n",
"b+CnP/1p+a5Tikh3nfzkk092VDJGpAJIvynFWj63bE/fho9hGJRSy7IYY6dd9Vej8sWVOKWUcx5F\n",
"kfz5M45j4fZU72RZVnlEtm37vh/HsXB4sixrPAReg5Lho2QvXLp0SVJJFO98lUwAIGL5Bj7++OPy\n",
"XacUke46+cIFhd8dRmSDOhAw/aYU6z4Nn75Tv8zFdRzHruvWHRjP8yaTiXzqP/NJgBAwxgzDkHls\n",
"UHH37t2TkxPJp/bvv//+v/zLv0iW/P777z/11FOS4u9973vy4g8++EB+mEFH4vfff19J/L3vfU9S\n",
"/N3vfvdv/uZvuohId5384x//eOcRURIPPiLdieVjrWQmt0BvD5QbJEly2vQT4fM03jRNs/tKnc1X\n",
"vvKV/mKDIMiYuHTpUm+pDOIIn6IoludYtbgE2zZ84xvf+MY3vrHrWiAIgmwFxCldG4znQRAEQeSB\n",
"mPoRBEGQToGY+uVnQCAIgiAbADH1k1UrnSqtfYogCIKsAWLqd123MRxKDPfcVX0QBEEGBsTULwyf\n",
"aj8EMcNLaT40giAIsoa+9+adzWbiip5zXl/YKEmSuoxz7jiOZVmGYTDGPM/D1I8gCNIWoLdlF1up\n",
"iBPAruuCIAgyHECnfgRBEKQLIHr9CIIgSKdg6kcQBBkdmPoRBEFGB6Z+BEGQ0QFx5U6wMMaiKBKD\n",
"jiilGo07arfmcRwXRUEpbat6W9JW68SOQGLwsW3bnucBCXEXDTRNk1IKYUHc1n9WRVFEUWSaJpAR\n",
"4W01sL7VoMC27eVFjmXpbXlo3QnD0LKsNE3LshRbP+66RrK0VfMkSVzXtSzLdd3T9lron7ZaV5al\n",
"bduU0jzP8zwXe8mVZdlubTegrQbmeW5ZVhiGeZ4vFov5fC6KbbWyynTxs3Jdl1IK5CvaYgMJIckn\n",
"EaHcsLSNPzkqyrI0TbOeCCilYRjusEqStFjzNE1FplizzU7PtNg6z/MaGwQFQUAp3baK29FF+Orv\n",
"uK67bRW3oIufVZIknucB+Yq228B2r9Qx9UsRhmEjC4hrqF3VR54uag7kd7VotXVBECy/ufNmdv3F\n",
"2+3md120TtyrAfmKttvAdlM/PuaVor7mhMA0TS22lNG35jK02LrlRxdFUezc6+80fIyxzZ3iNmi9\n",
"db7vN7b13i0dhY8xtn0h+JhXCsh7Rq5H35rL0GnrJpNJEAStFLUxXTRQrI/CGMuybD6fb1PUlrTb\n",
"OtGoNE23rldrtB4+x3E454ZhcM5N0wzDcOPzHKZ+KfS9TNa35jJ017rpdOp53m4vikk3DcyyLMsy\n",
"xtjOR6m12zrf93d+qm7QbgODIHBdtzpzRFE0nU43Pnmj4YMgTabTqWVZQIYGto7neWKcT5Zly+MF\n",
"NUV4IDs/VXdKYzCu53li/ePNSsPUL4W+e0bqW3MZWm8d5/z4+BhO3u80fGEYZlm2ce7YnhZbF0WR\n",
"bdvsY4SptfOt/br+9VmWham/c/TdM1LfmsvQYuvELhHQNofoNHzb5I5WaKt1tm0XRVGl/qIohPXf\n",
"Rh23Au6vr8XRQgMmTdPGWLH5fO553q7qI49SzZMkCYLgzHlMQEbOLdTjsqaBZVmKGU/1N7eZMtMK\n",
"XYSvjm3bO5zV1WL4lpUQvqJdh68xaUAJTP2y2LZd5QWRJnY+E1ISyZpXQyPOnOYD5HclkI/LmgaK\n",
"qbyNKV2LxcIwjNYrrEpb4XNdt/FB8diw9Qor0Ur4loHzFW0rfMvfT8/ztplyiCN8ZJnP547jZFlW\n",
"7Rmpi40uWfNqsMdpoz4am2s6jiPeb2yu2TPycVnTQGF5R1FU7QgtgDA+qq3wUUp936+ehYpB/WEY\n",
"dldzGVoJXx3x7Fp8RafTqS4NPLN18/nc9/3ZbCbCF8ex67rbjGjCXbrU0HfPSJmaF0WxciQyfCTj\n",
"MuwGyrROaAghoL7DGD4i17rq2fX24cPUjyAIMjpwhA+CIMjowNSPIAgyOjD1IwiCjA5M/QiCIKMD\n",
"Uz+CIMjowNSPIAgyOjD1IwiCjA5M/QiCIKMDUz+CIMjowNSPIAgyOjD1IwiCjA5M/QiCIKMDUz+C\n",
"IMjowNSPIAgyOjD1IwiCjA5M/QiCIKMDUz+CjIIsy8T+mh3R2NsSAQ7uzYt0yGQyOW17W8uyttlZ\n",
"FFFlOp3WO5wxNpvNCCGGYcznc0JIHMcifZumucGWtnEcE0I8z2utxkiXYOpHOsTzPJERXNdt/Enk\n",
"HaQfoigyDKO+76tlWaZpklpoLMuilDqOk6bpBocIgmAymWDq1wVM/UiH2LYtTIblzaYx9ffJbDZr\n",
"3GOhIZ82AAAEMElEQVQZhiH29a5CY5qmOBlYlrXBIcS5JIoizP5agF4/shvq+WU2mzmO4zhOlmWE\n",
"kDiOxX/FHUMdxthkMjk6Ojo8PJxMJivNa6E5PDw8OjqaTqdFUURR5DjOdDoVgul06jhO3ZsW7ziO\n",
"o3o4UXIURVmWTSaTvb294+Nj3/eXa8U5933fcZxKs9J8l2mgKowxzvnyjZckoo0NVrbRdV10/LVh\n",
"gSBdQimllFav0zRd1qRpmiSJZVnz+dzzPEppnud5nruum+d5JQvD0LbtqoQ0TV3XrQqvDlHXzOdz\n",
"y7Jc1/U8L0kS8WaSJOIojQo0fg4yh8vz3PM827Y9zxNVLcuyUbh407KsMAzLshT/DcPQMIyGTOaI\n",
"G0Ap9Txv5fvLhS/nBPHxpIawhpYLzPOcECLaiAAHUz/SLSIXiyxj23aVf5exbdswjDAMV/41z3PL\n",
"slZ+qp7Tbdte/uBykj0z68kcriqqoSzL0jCM9Z9aLBZhGNbrIH9EVUT/L79fD03FcuoPgiAIgvqn\n",
"Vp5IBISQLWuL9AN6/UjnmKYpDOXTRvtUBEFwmlMcRZFITA0opXEci/IZY8sfN01zA/dZ5nAVjf8a\n",
"hlFvaVEUnPPlpx2u6xZFsdkRlciy7DS3pwpNxfIzmHqtoijinK8Z/2PbdpZl29QW6QdM/UjnVGNL\n",
"iqIQjxZPQzxmXEmWZac9Ga4STYtJR+ZwkhRFsfIjhmHUH3i0eMQGa3q1MexnPWL0p3DG1nDmCR6B\n",
"AD7mRfrD87zNRo8QQsSTgJW3rlUysiyrfh1dsUEykjmcPCtr1ekR6xiGIVOB9WRZJvL++pN3lmUb\n",
"hxjpE0z9iB7Ytn3m6BHP84QjUX9T5Kwzy298SuZwkggPZOXpp56RWzxiA8uytrwSF+OXxKNp8U4c\n",
"x8tlcs4555j6tQBTP6IHtm2bplkN0KyIoqjySYStL0aFcs7FsE7f95c99Mb9QVEUk8lE9XDyUEqX\n",
"JzbPZrN6+e0esU41u2IzxLDU+XxeN47EeNaGMo7jaqYYAhz0+pEOcRxHZFiRJlYu3lAUhch3WZb5\n",
"vl9dV4rxJ3VlGIa+7x8fH1cPjYW9UC9TDLWczWbiClq4KMup03VdxpjjOOIcwDkPguD4+NhxnDAM\n",
"RfKSOdx0OhVZtSgKsRwC51ycRepFiefMoijxEJgxZtu2+IhSAzegegZe78+q5lmWzedzwzCiKBIT\n",
"KRzH8TyvejI8m82KomgM5F/O++IQG88eQHpmb7FY7LoOCKKASIjiteQjSpG2lhOo8GEaj1u3P9wa\n",
"qqvvNUW1e0SBSOtbPjNYT1EUx8fHYihtd0dB2gJTPzJ8Tkv9o+Lo6EhMGeuo/Ol0alkWruKgC+j1\n",
"I8goaJhLrbPZ/AlkV+BVPzJkGsvydOp4IIhGYOpHEAQZHWj4IAiCjA5M/QiCIKMDUz+CIMjo+P8i\n",
"kpvwP+eSRgAAAABJRU5ErkJggg==\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"\n",
"%% représentation temporelle\n",
"figure\n",
"plot(ech,noyau)\n",
"xlabel('Temps (s)')\n",
"ylabel('a.u')\n",
"\n",
"%% représentation fréquentielle\n",
"figure\n",
"Analyse_Frequence_Puissance(noyau,ech);\n",
"set(gca,'yscale','log');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On observe une réduction importante de l'amplitude des fréquences inférieures à 0.1 Hz, qui correspond donc à la fréquence de coupure du filtre."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.4. Application du filtre de Butterworth.\n",
"L'exemple ci dessous filtre le signal avec un filtre passe bas, avec une fréquence de coupure de 0.1. Faire un graphe représentant le signal d'intérêt (`signal`) superposé au signal filtré. Calculez l'erreur résiduelle, et comparez au filtre par moyenne mobile évalué précédemment."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"err = 0.061297\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fjCTHXcfLf3I+5PP5CmNubSm5U4VzTGQpiWsfAIEQ\n",
"VrWQEgkFRA+JyIsl1CPEUx5Q94ODkABp5iUgESSm5YjHhBkRoUhEiqaEuTxAIFO+JCDieL2lW1vK\n",
"7WH76uy7WHuXnI+H2p3Mzb/trqqu6p7+fV7sm53pqu6u+tavfvWrX9139+5dBAAAALSJ+0NXAAAA\n",
"APANSD8AAEDrAOkHAABoHSD9AAAArQOkHwAAoHWA9AMAALQOkH4AAIDWAdIPAADQOkD6AQAAWgdI\n",
"PwAAQOsA6QcAAGgdIP0AAACtA6QfAACgdYD0AwAAtA6QfgAAgNYB0g8AANA6QPoBAABax4PeSuKc\n",
"53mulKKUpmmKMTa+VJ7nnHMnlwIAAGghnqz+PM+zLEvTdDgcYoyjKDK+VLfbFUL0er3hcEgI2d7e\n",
"llI6rCoAAMDGc5+Hs3mVUtvb25PJZGqeZ1lGCEmSpOylhBBZlo3H4+knnPPRaDQYDJxVFwAAYNPx\n",
"YfWPRqM4jmfdMkmS5HludilK6ewnjDHOuW0VAQAA2oQP6ZdSzuk1IUQpZXCpuessvTgAAACwHh/L\n",
"vFJKxtjch4QQg0vFcTwajfr9fpqm+srdbrfX6xW/wj//8z///d///e3bt5f+9dSpUw8//LBBxQAA\n",
"AIpw9erVVX/66Ec/+qUvfclTPe5WD2NsPB4vfmhzwWn9F6+8nt/6rd/y9GQBAADK8OCDDxqrYlma\n",
"F9ff7Xanw8ZkMun3+0KIshfx9nwrIk3TsmNeDbEZ/mvCBryI8XicpmnoWtiy1L5sFmma3n+/P0H2\n",
"UZJDX3ye5xhj7e3RVx4Oh51Ox9X1AQAA2oCnQWbRMDcw1RFCnPO5ZQOMsdmyAQAAQGvxIf1xHM/F\n",
"X+pwz1Xf55z3+/2lIUBLQ4PMgoUAAABaiz+HzzSQXynV7/dX7ecSQkRRlGVZt9td/GuSJHOjQpZl\n",
"i+FDAAAAwBo85fAZDodRFAkhMMac8yRJVi0ATHd+Lc3MQwjp9XpRFFFK9aUYY6WCOwEAAABP0o8x\n",
"nkwmQgil1PqEa4SQ3d3dpVsBNIyxyWSiPUhJkoCjHwAAoCz+MneiwqE+hJBjBR2cPAAAAMY0L67f\n",
"klOnToWuggMYYxsw3Vmz1N8UNuBFEEI2wJCK47jpLwIh9IEPfMBbWT4yd9aKz372s1/96lfbdtcA\n",
"ANScLMtefPHFt956y09xrbP6AQAAAJB+AACA1gHSDwAA0DpA+gEAAFoHSD8AAEDrAOkHAABoHSD9\n",
"AAAArQOkHwAAoHWA9AMAALQOkH4AAIDWAdIPAADQOkD6AQAAWgdIPwAAQOsA6QcAAGgdIP0AAACt\n",
"A6QfAACgdYD0AwAAtA6QfgAAgNYB0g8AANA6QPoBAABaB0g/AABA6wDpBwAAaB0g/QAAAK3Dn/Rz\n",
"zjudThRFWZYppZxcsNvtRlHU6XSEEPYXBAAAaAkP+ikmz/M8zweDASEkz/MoiiaTic0Fu92ulDJJ\n",
"kjiOpZSu6gkAANAGfEi/Uqrf708mE4wxQihNU6VUnudJkphdsNPpUEoHg4H+JyHEWV0BAABagA+H\n",
"z2g0iuNY674mSZI8z82upn+YpqmbygEAALQPH1a/lJJSOvsJIcTY3Z/n+XA4dFEvAACAluJJ+hlj\n",
"cx/aeGkIIVJKbf7HcTw3rhQhy7KlnzPGFqsKAADgilXic/HixZ/85CfequHJ1+/qUpxzjHGe5/1+\n",
"P01TjHG3202SpOyywSp9h2UDAAAqZZX47O3tvfLKK96q4SnCxyFKqdFoNF00juN4e3ubMVZKtcG0\n",
"BwAgCKvEh3P+wAMPeKuGj2VeA4fMmksJIQaDgatFYwAAgBbiaUvX4pYrs01YGGNK6ZyBD14aAACA\n",
"UviQ/jiOOeezn+hwz1Xf55z3+/1VKwSU0rmrCSFA/QEAAIrjz+Ez9cnoHV6rFmaFEDrZQ7fbXfqF\n",
"NE1nBwYd6rNmIAEAAADm8LTMOxwOoygSQmCMOedJkqxaAJg68We9+bMQQnq93vb2tpZ7zvlwOFz1\n",
"ZQAAAGART9KPMZ5MJkIIpZQOylz1TULI7u7u0q0AUyilu7u72u3T6/UqqTEAAMDm4jW4s2CoDyGk\n",
"iO8eAjQBAADMgHz9AAAArQOkHwAAoHWA9AMAALQOkH4AAIDWAdIPAADQOkD6AQAAWgdIPwAAQOsA\n",
"6QcAAGgdIP0ukDJAoUohd2fglCDIzcIT3tRC4QkHAqTfBXkeoAULge7NYOqJFcfLVUuQ8xiEQEap\n",
"xW0J8oRXZEusljwP84SDNKeanSkC0u+IIC04SKFBzDQhApSrVLDZBlApQV5rkN66GpB+oCRBphoo\n",
"RM8Rom6T9GoJNaj7BwZXkH5ntMfqB6qmPYMrCqHCnAdbYKiTJQHS74Ig64EBm5H/myUkmCACm0eQ\n",
"4z0IAenfOIK0JClRkGMpGQtgHrbnKB4pEcYBNAJjmES2CpD+JtMeQWwPUqIkCSP97fGABxnnCKnV\n",
"4ArS33CC+F7q1IIBNwQxI0INNoQEKLpmgytIf5Oh1LcKCxGm2wTEvwHenoUNmLaGA6S/yfjvOUqh\n",
"Yqdsui83CIyFkf72EGRhg9K2DK6rAel3RJAW3B7fS6iFdKBqKA2zsNF6QPodEaQFt8r34n+cIwTM\n",
"Qx94bsOcB5hXaXGoU28F6XeBfqNB3mudGlO1hFqaAyrF/3oVCuFSkxIxhjCWUmZZltcgnw9Ivwsw\n",
"DtCCtQ62SpvaMM4F9DIFmeK0qgEjJL71LcaYlFKFbswg/Y7w34LD9hn/DTfIVjL/aPPQM0IgjIO1\n",
"qNAi6A9KxTe/yRijlPLQjkR/0s8573Q6URRlWeZkxKvP1Ck4nHPhUxYpRUJIKUejkb9CEUIIKaX6\n",
"/b7nQhFCeZ5Lz/a4lJxzTwKhA7cwRlIqpXz3KYz1a/X9hBHK89yrBB8NrnEce+2wy/Ak/XmeZ1mW\n",
"pulwOMQYR1Fkf80syxBC/tWnbmRZJqXM89zHFPLIPOSXLulu46MFz9xXt9vFGGd+M9pnWea7UMby\n",
"L32Jcz4ajfxpBKXy0qVut+tvfD16s91ulxDi9QljnD3/PCFkNBr5G3IIQfv7nso6Dh/Sr1vSeDym\n",
"lGKM0zRljFlaFpxzjDHzPzVei5Zgr0VijK5eTZIkSRIf3VWbh4Twb3yj1+sNBoN+v1/5kCOE3kzA\n",
"9/biOE6SBCHk2WiK4zhNU5/aJK9c6fV6vV7P5yyHX76cJEmapkopH4KIMUJI3bpFCNFv1t8TphQd\n",
"HDDGer2et0IlQlOfGiEkrOHvQ/pHo1Ecx3jGk5gkiaVEZlnW6/Wsq+YY/+ah+shH0MEBQohqcfQz\n",
"eyVEF4oQStPUhzZhjBDily/r29SC6GehTFy9Sk6fRkdP2FN3pVS98gpCCGPsUxDl9evanPI5zon9\n",
"ff1sddH+bPCDA4QQxjiOYz8WmxCCPvyw/n/GWFh3vw/pl1LSe7eAEkJs+m2WZXNjSR0Y/fCH8RGd\n",
"TseTMO3s0Cef1P/f6/XyPPekTUfSTyklhHib65CjsDwfQ45SCCGBMT1qafoJe9AmhRA+eVL/vxZE\n",
"z45NPeR0vZzayPf32YUL+v/TNNUep6oLFRiTozYcx3HlrkspEUJCCPbMM/oDSw20x5P0L8o0MQ2t\n",
"VUpxztM0ta6XY8RRC6aUarM0y7Jut1tpp+Vvv83ef3/6z8FgMBqNqtZEzjk9f376T+2B6XQ6Ppfp\n",
"KKV6iK3QdMIYISSvXKFHwoSOJhxVD3Wcc/bYY7OFCiFcxUesYu7ijDH9hCt/rVtb+K239P9ijIfD\n",
"YdW9BuknPNOGK+84QQK31uLJ1+/wak5cPdEKTLo054cL9+fPT1swIUQ7ageDQdXTOvzQQz/7f4x7\n",
"vR6ltNLZOuecbm3NfpIkifaZVqdNUkp08uRs2DulVD/eap/wmTOzQaUY48FgUKFbT081ZsxDTa/X\n",
"q9oMF0LMvVbG2GAw+LM/+7NKLWJ148bsP7X66/i96gqVUpJHH50ttNfrEUI8THSmavO1r33tV37l\n",
"V6b//Md//MeDo4mIBxoW1885V0rZr+6OV6AN2NJQukby4jiuzppYWm7VPlOl1Gy30RBCKl1qllKy\n",
"T35ybseT7rHVWoiPProYeB7HMXJt0xyy2o2pn3AlEw7OEcacc/axjy0+4b/927+ttAHjD35wcStZ\n",
"mqaV7nta6i7WbuSqbbWp2nzlK1/53d/93ek//+AP/uDkkZfPAz6kn7rL9ZjnuV4e0QghlFLBI2SR\n",
"NtM+9amle44YY55bMKrYFb6qUL1NsaJCpZT41Kmlf6pug8yaF+c1HOUIxlhVrZ1ShBD+9V9f3E6M\n",
"MSaEVPSEhRD0ueeW/qnS6KZVbzZN02q9eTOnxFBK/W9lmOLJ6l9sr2YtWIvLVPq1XRB8XxzSJvbW\n",
"lud9iUsXUTRVrYFPW+qKc44qiVtQCulggc98ZmmmgSRJqhOmVVNM48UqSwgh/vUiTdOKXita3VYr\n",
"fcJrOk61b5bSWZUIGKvyoIcy4jjW+7mmn+hwz1Xf1+Z8kiSLz2XOIaPVvw5LvlLKJElQv4+WWoIX\n",
"L6I8R2bepLWFUp13ZVmh5NVXxfPP0y98wWWyqumlKEV5vuidoFev8q98hSHkclFLCJSmh2sqQvh8\n",
"wocotbRQ/P3voyxDFQUZE4K63SVPeG9PfPvb5IUXKjk4gVLU6cyPr6dP43ffRRcvotEIre62pREC\n",
"USqEiON41RNGFy9W8YR/ZvIvK5T+8If8s59lf/VXVWV5G42mT5h873vi+efp2bOVFLQWH9KvHT55\n",
"nmvh1ju8BoPB0i8LIfReXyHEcDj0UD2XjMdLPyZ5zl96ibkWJqUUxnhVx6Ccy299i1Z0ejtjS8Wd\n",
"IjTKMsS543iGqQKueMIoy6pIfMY5T5IErWirdDTi//3fzPXNHhr1K1oLQyj7/Ofj0agS6cd43RMW\n",
"wqX0o8MUDoSQVU8Y9/vy8mXnzfdwMrfirVEpR3/zN4xzt5bE4Wu9t1wm5Wg0otp49es/9OTwGQ6H\n",
"eZ53u90sy6IoSpJk1QLA1NJfPxXSI0SWZUIIP9HHNlBK5fXrzt1BQog16yiMMfHmm85zMa7xMoVF\n",
"vvOO08sdDiRrpv+UUnHlivPXKqVcH8ig3nvPbYm1hVIqf+7nPOcTJYTIW7ccWxJSLn2tQdx3Gk/S\n",
"jzGeTCZJkjDG1gfSEEJ2d3fH4/GqaYGGUjoejyeTybVr19Z/sw5QSuW9MYKuOEaFF+Jw7FncoFcH\n",
"GGPypz91+YQLBGITQtRjj/nPJxpk6KWU8r09z6tZlFJeweAqhFj/DLHzI9RXGxChMjp4De6klDLG\n",
"jm24hJC6JedZR8Emcm9M+gZDCBFXr3oulFLKb97chPS/Ugohjl1pVLduuS72mMkcIUSePu15nMMY\n",
"qwoKVUodb764Hl9XPeGqAnaPo2Fx/XVECPVLv3T8186edSn9xS6FMZavv+6sUIQQQpzz9cJEKRXv\n",
"vut2nDs2OhZjjLa2NuEwRUIO3d+rYYwJtwkglTp2MkcplbdvOzdfCr1Z7yM6IYTv7bm95qonjDHG\n",
"GPtP6gDS7wDx2mu+pylSogLbBSil8u5d54UfK/3yxAm3GrEmyPJnzOxq9gbG2PEaQwEIIeKBB1yO\n",
"cwUtXLfmy2HJBYr27uA6bOG+pumek8JqQPodUHTEdj2wF+o2p065nC8rVehmq1nYWE+QZFgVLeCv\n",
"hxCi7txxWyjn3P8Sjtzfr2fIACGEI3/SjzGmlN5y7cRbD0i/A9ZH2mgwxvJ+30+bEOLYA45xob66\n",
"LPmBDUWEyblnQOzsFNrdc+FCgJMjz51zXqhvFRZCXrly7GslhIj33vO8TkYI8Wy+JEnykN9pK0i/\n",
"G47tNodhau4aE790qUi32RAPeAjPgLp581jpJ4TwnR2HhaJA05cAhSqlZnJnroIQoj74QWfSX/w2\n",
"XZsvdQOk3yNPPOG2MRVSQ9emRBGNcK4jRS5IKeVvv+3ZAK9icA3iAylYqNvIoiLTZbSQ2tOyyEq2\n",
"wh1L/UYRkH5PUEr5yy+HroUDimiEc/EqWuhTTznrY0Lw//3fQg6fEMvLQaCUips33fpejn2zjDFx\n",
"44bDwVX6dakfUr8lDZB+Txw2cXfdRrz6alGFrZ/FUQUYY3nlirPLKYXOnvWdo00I5TFtb1kOB1f/\n",
"21OcDq7yypUi8Xhhj9DyAEi/NcWbyLlzDruNunmzaEhGiNi4ILu6ZAU7PwvhqlClxMMPB9gsXSxw\n",
"C2MsXn3VQ3XmCKLC9Qw9cghIvzUhtmMgztGZM74LRYjv7RUxhAkhyul5Q0WfcAVxL4VwKhNFRMfx\n",
"4FoscItSqm7edFZoYTZAhZ3vvrYHpN8BYZpmBfl5joFz9MQTRX0gFy449M8GecJ1nvI7H1yLEiJg\n",
"zO2LKOgpPcxZ5KrQ/f26Zb4C6feHUsqhO6Jgf3BsHj7xRJFvUUqdhzz6p8R44+61yitXigbbnD7t\n",
"SoVL2KSBtkw7vFpBT2mQUAWfgPT7A2Ps0DNQsCW5NQ8LhtnVrZVXCiGEv/uuq6sV2eWEpomSHBHG\n",
"Ji01XroaXMsstskHH9yMPTFLAem3paD7WxPE5aceeMDV8rLY2SmYrUjdd58rt3upJ+yfIHULaZO6\n",
"UuHCJVJKnQ2u+iDVAhymAXeCEOqBB9xcyh0g/Q4o2PndJ1wsAKVU3LnjPyAPf+hDDt0gAeS1YLYi\n",
"zalTAUIeQyRKQihAwJjjcc6/z0opcecO+PoBNxQUplb5XjDGwtUaQ8FsRdOjApxIvxCoeFy/u0wD\n",
"8vp1J9eploYPrnXriSD9tqi33gpSbrmWFOSUGEfCVHytglKqTpxwUmhxXHZppZD/E7qFkAcHxbOO\n",
"u3JaFr8OIUQEmVdtdBofkH5bRPGtVWVU7LgLlWmRTreSFUQp5cozUMPAuCU0d3BVqqD7G2n/oSOn\n",
"ZfHXSggJsp9gswHpd0Bxz4BAyE3MQJDJYxl1czu99T9ZLre2HGJwRajxbvdyV9tcAzwIIP3+wBiX\n",
"8OSuRVy9GsB1KCU6d853oZwXf2gYY4cBeXUOK2odofZpby4g/Y1EHRzU3wfiLJK1jDvCWUBeIwiS\n",
"2d/ROelhFslg6nAESL9fTp5sifHi0CkMrMT7zO9wK5kLAS21SOYKcft23SJtQgHS75ezZ1tid4Ts\n",
"YC6eMH/lFf8On1InvBNCHCaZKUjTl3DCTJcDJVtcD0h/IxEhzrMu7cBxeyJ8Qba23BR68mQA6X/j\n",
"jeJBlq1aigiSSs9l/iv/yRaPA6TfDimDJFAsa7w4cbuXDbKUjzwSYIrT6DOzHnmk9E+CTCL9bw4P\n",
"MYkMlh7VC/6kn3Pe6XSiKMqyzGYMV0r1+/0oiqIo6vf7gTPrSomffjpAuWVapEO3e/EeyBhzeWZW\n",
"/Qmy4vrkkw6mOGXdEaEiWV3AL19u1WxpDZ6kP8/zLMvSNB0OhxjjKIrMrqOU6nQ6SqnBYDAYDJRS\n",
"URTVOa/6HM7yNpcJEoV1LQNKmXuEEHH7tn2hpRIqUErFj35kXyhCdXRHVEcp6VcHB/Ydtp75B31I\n",
"v7bTx+MxpRRjnKYpYyzPc4NLZVmWJEmv1yOEEEJ6vV4cx/1+33mdK8Jt3mbfFMvY7JiSHc+VHYDL\n",
"DK6uPAPy+vXivn5XI3qYPSIlcZmdqTCHezBdLB21VPpHo1Ecx7PNK0kSM+knhMRxPPtJmqaiHeGS\n",
"NjjJzyXv3Cn1fXXffQ52VwlRPK4fwRSnPI0IenGWnanMCO1wD2YN8SH9Usq5tkUIMbPO0jRdvHjA\n",
"3s4vXSLFDq4KCGNMIgcJJErZpEjnbbaG7+3RX/s1++tUTZjV/hs3GnwMfZB4x82V8rI86KEMKeWi\n",
"ZLiaAXU6nV6vV/ZXfIUOaj9SqUuVkn5CiPiP/wiwDbd+YcXFCZOyogyU0v7+fuwuY11B8DPPICHQ\n",
"vfNgLwW3ZWpV8Fi6Y7j3IqvEZ29v707JibUNPqS/umXYbrebJEkpU1Sz6ukzxir1yhFC1EsvVXd9\n",
"ACEk33nH9hVKqR57rPjXMcaH+wnKN8VZVJktXa2CEJJfvmz1cI3ABuG2C4gf/5jNDJarxOfy5cvv\n",
"v/++fXEF8SH9FdHtdimlSZIY/NZgorCcK1cKnlQeFjfGS9lCvVvBSHu3vvxl+9G7dJ934UnAISJt\n",
"xP4+q70Vf2iQSYk8r5eeOYM4tx3R711NWSU+WZbteFzK9uHrd76IpJTa3t421n2HyB/8AH3iE75L\n",
"LXWWE0LIkfFS1p3dqhXXYIOr/UWuXy/VQyml/hNIIITQ+fNhTmvZUDzF9S8G4RiH5ehY/iRJgus+\n",
"Mlj5xNjB7qoyZ2sc4iJtXKl4R1c0ZQ+Ok8G1dKFOBteyZgTG9mG+oeIjypovDdozVBYf0h/H8Zx7\n",
"S4d7rvo+53zVNt2lui+bs7eQUqoODgIYL01OG1dW+u2DbeBMqGOwH+du3Cgr/U7mVWXNlw2eufpz\n",
"+EwD+fUOr1U2uxBCJ3vodrtzf9JbedM0nfvt9vZ2BbWujCDz1hC4yX5VckeCk6wVYmeHPftsud9s\n",
"bdmHz25wxph5dnbKLpI5mFcF6nf1fK2elnmHw2EURUIIjDHnPEmSVe7F6TC7ON4KIaSUeZ7PbQfb\n",
"4EnZUsTOTv03EyAdzvT1r9tepWRY6uE2HCGQ521KLtLGGbjU1K1bnu1SjDHf33cQbFPWaYms9xNI\n",
"ic6f911oIE/psXiSfozxZDIRQiil0jRdM40ihOzu7i7dCsAY293drbim5QizkefmzUZIP0IuPAMG\n",
"bG3ZdteGBG5RSsXXvuY55JFSOtKZbSycIergoPSP9RmNsInBEV6DOwsGEhjsqwqFiZkWJBMOaurR\n",
"dGEmy1euoE9+0nehBoFboVTJehOD2N9P/R/RVX66jDEWr7xiW9FaOnwgX78d5V8qfvzxMGc0hpAJ\n",
"e+EOMlkOcxLOG2+Y+ECC4GQTQ8knbO/XNZguH8ZlWFJLhw9Ivx0GL9U62EZ973vo1KnSv3J1SHph\n",
"mns8r2FGM7vXKnZ26IULNlfYbDY42CYIIP1WBHFHiN1d+pnPlPpJEBX+2YqrZ/QOTP9Ya1PZIBaM\n",
"sX1OVoPsEcGclkGwvtl6RviA9FsRau2+rAVkbzEZTrftV1wNCLQDs9Sh6k6glNpLv0H2CPzII5aB\n",
"kvVUw+VYhyrUM8IHpL812Bkv4qtfpR/+sKu6FKcpGsEYc3IoQmlc7CcojfUZjWF2hv/rv5Z1qTmZ\n",
"V9UTkP4QBAm2sTRebt7EH/tY2R/ZewYMZisO1gNDjDeGRxnX0qKsAgc7BK9fx5/+dKlfOJlX1ROQ\n",
"/hDYuV/MhCmInDnYgVle2uy9W4a/txvn5JUrzH8qwObg6hRMQAPSb44QgoQ4AsVgshws2ObMmTCR\n",
"rJaYmdKW49z+voFNYDmvattOeEMsvFvi3/4NfP2bhlKKPPCAwQ/9rwcGC4x79NGGbiUzwNYzcHBg\n",
"kHzCcl4lhGAGuQ2sMbTfLcc5s0Ltkm6p73yH/sZvGP+8OkD67Sjf8RysB4aY9vKXX/YfdS6EMLOY\n",
"/G9iCLbMGyR81hpDQ9hunDNsS/aRrEHSmRwHSH8DMes21hqBy+8js0QpRctvcG3oVjJDm9Ryh2Bz\n",
"0lO7OevCoNxaCrc9IP2tIUiIfQgauu0zjEd4ZweVn8xhjB2k4y6Jm5wKwBEg/eYYuyOAzeTkycad\n",
"xKBu3DBwRzRVhRsUs1s9IP3mKKXo2bNlfxVq3mrL5cu+T8RGCBk/qCAn5T78cOOkP0jiIM55kNC4\n",
"IHsgahuzC9Lvm4ZaTOrgwEz6lYVnQFy8iD/+cYMfyjt3jAtFyNA8bKhT2P8SDkLIXPq9D67qvvvC\n",
"pISqGJB+oBBmri1KqbAY59TNmwYZNC2DbTjnJETyZPV//+e/0GahHnvMv/TjD33Ic4l+AOm34OrV\n",
"hp3g432Zt6ErrmF26v3iL5r8CmP5+uvOK7MeQgi/fNlzoaih8yqjnXoeAOk3R735puEBsBZxlpxz\n",
"ajRDV6dPNzEAHFgPpVTeveu50KYcolcLjHbqeQCk3xxjG0Q9/LCNAY5/4RdMflVL02PTaFz4bIht\n",
"aKEyoACzgPQHoInzVuOl6RbtcdUn1jaL69dtjtg1Q333u8R70ItNKLb/zCseAOkHCmE2ZbBNb2D8\n",
"W4v9a9J4IfGhhwx/2EK8u4zMdoYj3YbfeMN5fYID0g8Uwzgm2iaSNYRNKi9dYufOeS7UONS9qdtE\n",
"zAh19GYDp+nHAtJvjnrrLf+FGs9bCSF8b895fY6ncRueQ4w3CCGzLLAht4n4378W6OjNjQSk3xx8\n",
"86bZ2r26ccO426j9fYMtxEhHZbTqNO0QWGUMNTYtg0i/XSpjIDgg/XYYhc3gZ54x7zb7++axYqbi\n",
"EmznfaMIljG0cfOqENgcStPE7ffH0kjp55x3Op0oirIsa+MxQyHCNI2lP1i3gf1rtcVil5NxsI0Q\n",
"wniZdyNXU5on/XmeZ1mWpulwOMQYR1EUukbtwNRZFCa5qUWcpYOjOcpjHlYUCKunZLrLySpg7NYt\n",
"DCFYMzRM+pVS/X5/PB5TSjHGaZoyxvI8D1IT/4XaYLv53ibIwfhZGc8YLDp5kF0XUkr/YUU2bTjY\n",
"3hTjIcfGU7qJNEz6R6NRHMezM+skSYJIv/H8EQUKtgm2+d5mo1OQGYOFO6JZTmGbNmyD1VOyGXK8\n",
"e+Q450GecBEaJv1SyrlUjoSQUAY4/slPzH4YTIVNu5zVMq/xFkoLH4jVMVKm7girZd69vQDHIVi6\n",
"40xfUKsOODJWiap5MHQFyiGlZAsx1wZKumqFII7jJEmKXsXGADGet9pYTBZdjpiGVBs7haWU7Px5\n",
"s99SStV3v2v2W2Nsl3mNpV9vdPK8F+HcuSDBnca+/iBLOAgtUYlV4vPaa68deJw1Nkz6XRn44/HY\n",
"yXXMMR42muaybFzCIit3RBCHj03crYUgqlu3PDtQGGPZF75g9tv6tMNV4pNl2YsvvuitGg1z+AAI\n",
"hQjutNmpJXPc8gAAIABJREFUFIogIUmmv7WxSY1/q5QyNkGCbWIAHNEw6Tc4s6kibNzfhBDjbhNm\n",
"ITHUVMNmkl4bK68INjap8W9tlnmNvVs2GTStsEkjaJo7qM57IRsm/QghsRAusviJH4zd34QQYwUP\n",
"0m3UjRtWUw0jN52U0li+25XUzAL/oe7GGTRtsUnNZCHfxipRNQ2T/jiO+b3Drw73DFObpoX2I2RY\n",
"Zys/qWlwp02ou1VSs0YFaLaNZoXPohon+m+Y9GuHzzSQX+/wKhGT4xYbQzhICw5xlgj55V8OkzHU\n",
"mCDuiMuXgwR3WhEiZqZhgaGBssAWoWERPgih4XAYRZEQAmPMOU+SpD4LACUI4rcJEWJMCEEvveS/\n",
"XDNCOWfVwYFNcKf6l3/BBhLzzjvGaZAxxvzHP66pqgEFaJjVjxDCGE8mkyRJGGPj8TiUyW8ZZmo2\n",
"b7UstD7xbT4wnVdZSf/Wltl6oI0xS597znBhw8ImNXapCSHw7dtmhQIOaZ7Vrwlu6Vvu3zHr6kII\n",
"411ONqhXXglwot7rr6MPfcj85w6rUpwQk7lmZQxVStELF0LXojTqf/7HZF5VY5pn9QP+wSdP+pd+\n",
"fPeujZ+0YU5hoBjqxAmDeZVSymZ1jf7e74n//E/jn9cTkH5TmrjLKRDyRz8KXYWiNC4ha9vATz5p\n",
"8CshBHv6afNCjedVNY5HAuk3pWkJFRBC+PHHxde/7rlQxphsjm9XCEG9TxeC7XICqqbGKgHSb4GF\n",
"j9Vs3mqpEfR3fke9+WbZX7XNEMZGRx/bYLnLyXj/mm1GsxChCs1CHRwEOVOvCCD9YTCbtyql6IkT\n",
"ziuznmBZ3Rt4iDx54gl+6ZLnQimlyihLAX77baslHCMrBN9/f23V0Dl1nsyB9DeNEN0mSM5xB6Go\n",
"3g1McuECevVVz4UiZBFZ5H8f2fXrlj4QdfNm2Z9YTpdtT7irJSD9QAGCbAiw3OB65ozB1mVbd8SF\n",
"C6i8MAHFYc8+K3Z2yv5KKUUt/HjBzlaqEpD+FtG8pGaW0l+eIDHydT7Gb3OwHNRrHKtjBki/KRYn\n",
"uCKE8KlTsrwKW9qkZjswpZR1dlluBpYZNA1eq33KCsMd6ZZLOE88gV5+2eSHloN6+S4ghCDeV+aK\n",
"A9JvghACI2TjsqRPPSWvXCn7qyA2qZTSZrKMkInF5CQOxGBwtTwjN5RT2GxstpR+s0Jtl3CaMz1S\n",
"ShGjaA4/gPSbECzneEMxspgsnzB79lmDwRUhKy9Tw5zCQWKorD0nBrONVkWUFgSkPxwGHc/OJkXI\n",
"tOOFyFXXHi9TMGGyX703OJl9f98mP4fZwZDNSnPkB5D+QFy4gMoHKiBkHY1npqchctWFsUlD4ECY\n",
"gixCnj+vvv99z2WCiLsCpD8Qp05Jm8NCPdJgm7Q9lB9c7Zd56YULZeMspcEswQn20+XyCCFqezAv\n",
"Auk3w14NGWNNkf4gdpabZV4Dm9QucMuQQKkALY+NNViwlVIGyTqOkO102WyBobYH8yKQfjNC5TbY\n",
"vODiVThY5v3TP5WvvVb6ZwcHAfJt2bm/zYHFz8JsnpsJpN8Qy0BsQ4IkArx61d7XL8pvrPX/hENt\n",
"rQqWrQj85sXZuKADkP7GcLi1yq67mgTbWBvCdGtL/eAHNlfwRpCwIicHZwZZkjEMn/VPa6bLxQHp\n",
"D0ZZFZZS2tukYSImn30WNUUjmgnd2io7r3KwXvWJT5SV/mDLvDXOmx8KkP5ghFHhNpk/JlMca9+L\n",
"SaHXr/sPn3Wzel8yVEFKyc6dc1BuyULtp8smTsu9vTqPNyD9JriZXIcQps1zWa6hrCBKKe0jSk1G\n",
"dOs8xujUKVT2nIB33rEqESHEWFnpD4KT6TLd2jLp9TVeTQHpN8GNxWSgEU1MnqwPMDFLueWXIDap\n",
"fXw9Qgg99VTpn1y/DmFFbQakvzG40YiS/tbDL1tKv4HNZR1WFIzykzk3r7UpqylBXquTGKrNOokB\n",
"pD8YBk5h+x0i7Pz5stIfZg+Ok/j6IO6IEC41gxXXIBGlDd4ZXj7zSs1PGPUn/ZzzTqcTRVGWZTYt\n",
"QCnV7/ejKIqiqN/vh2lMLvaFtyc9mQFuuk2IbfQm64EhNMJJRGnpQgOdhGM/ryJPPVXWaWl79HHF\n",
"eJL+PM+zLEvTdDgcYoyjKDK7jlKq0+kopQaDwWAwUEpFUeRf/dWNG3V+qXWkpAEeRJicUHY9UAiB\n",
"H3+8uvqspLmxXiGmyyZOSxTi6OPC+JB+baePx2NKKcY4TVPGWJ7nBpfKsixJkl6vRwghhPR6vTiO\n",
"+/2+8zqvJ4gwBZnfuCm0IaEgQbA8NtacUDvDrdWQbG1xzp1Up834kP7RaBTH8excL0kSM+knhMRx\n",
"PPtJmqYGSQKaiKvJclmb1H/QC0KB3PRNppSL7NAH4j1ZtHrzTQfSb+C98W421TxtJ/Ij/VJKeq99\n",
"QQgxMyfTNF28eHNTePs35NnHPy6+9jXPhZZFCIEPDvyHHqrXX/dcojMwxm+/XeoXboSp5HpVsOmy\n",
"d4lQSoH0L1dnV0fZdTqdJEmcXKogUkr8zjv2jYk99liA+UqNtxdOcXj+ZanBFd+9az/e4JMnS8VQ\n",
"KaUc2KRNeK2hCGYa1jvC50GbHyulVokXxnhq6Vdn23a73SRJWPnuumqdOY7jYwcSKSV99FEHna2s\n",
"BXT1KvrVX7Ut1AAXr8/sjEZLdGYbg+ZhVejZs6My0h/qOISmzpQDUqYNK6VWTXFWic9rr7124LGb\n",
"WEk/53yVyx5jPBwObS5+LN1ul1JqZvKPx2Pn9amcg4MwAQMutClMRswg4bOEoJdeClBuGYQQqaOH\n",
"I6UsOIPnnJPbt+2bEzlzJufc84iOKEVlzgQWQvRWLJKtEp8sy1588UWTuhlhJf1xHM8tui6Fup6N\n",
"6pjOJEk8u3oAP3DOE+9+UiEEPnXKwYUCSX/ZeRV2EVakdwgWd96SEyfsp8tlIzXVzg767d+2LLSp\n",
"e8tX4ymuf9EvZOzmDq77Dv1XwXLY+qdkxI7/k+2UUhSF6OGOTmeEHYKrwCdOOJkuB3FaVocP6Y/j\n",
"eC4OV4d7rvo+53zVNt2luu9ZQF3FO7Jz54rXXErpxiYNxZkz/sOZyJkz5SyMmzfDnM7ovdAG7xFB\n",
"CBGC9vbcXKoMpQbXYCkrCuND+rXDZ7oqoHd4rbLZhRA62UO32537k97Km6bp3G+3t7crqHW9kFLS\n",
"IMLkKI0aO3/efzgTefTR+vdAhAJMNVytLeO33ipuvjg70brGW2Sn1D/i3MrXX5zhcBhFkRACY8w5\n",
"T5Jk1QLA9JEtPjshhJQyz/O5teVmdG8nuGhP6q23Snw7yDHlIQiywOAQcuIEL7X46aLXUErLhTOF\n",
"OG+ZnD7tudBG4En6McaTyUQIoZRK03TNkEgI2d3dlVIuNmLG2O7ubsU19Yv9cRlloRRvVu5Zh/hf\n",
"YJBS4gcecHIp8uST5X5Qe7PUFeTdd51sD9Q7NlxtSAqOJ+nXFAz10fl5qq6MMc4mGYyhL3+54Hel\n",
"lNTJOl6ZDu92OtWiyVlhpJT0zp2WzKuC7Kp1CN3aKiH9V6+ip5+uuEZWQL7+0mCM/bdgKaX/JF9C\n",
"COrI4cPOnSvu62/8IFE2FMS/IIY4CQdj3KIjumrvKQXpbx3kzJniiQ/tz7M2AN9/v7NCr151c53i\n",
"lNz744pSrzWYMHlvS/VPoxYKkP7yuEjgE5AwPaGUuWd/TLmGsQBZ6TEuflqLlNJVphf/CxWNQCnl\n",
"8MkUDGeSUmIX+5YrBaS/NOqNNyAQuzT17gZuKX5ai5SSPfNM1fWZg3NOQwS9KIczsOvX/W+HLL4R\n",
"R0pJXexbrhSQ/tJswMl2BYXJWSB2GYQQ5EGv0Qcal8JUe7CjoBeEcXGXGnblZWKMnTnTop3w1QDS\n",
"Xx6nPgT/LVjnsyz4Zf+B2Eop8tOf+k/W70yYQqFUgKkhpeW6Qzsmf42IUwDpL8/+vithYs8+W1T6\n",
"HWV6QQjh994r+M1GtOD14FOnSuwidiRM5VZcXYFxwakh5zzIZK7ZmUgQQmWmy2HOtisDSH85pJTO\n",
"8mQRgl5+ueiX3Y03xQUuyGZ0t8JEn3qqSHcVQpAnnnBVaP1XXN1O5oqYL0oph5lIii+ku6X+6RmK\n",
"A9JfDimlM2EKt22t5uZ8GC/TlSuNSA5TN0rMXJGzeRU9e7ZoG97bc/Za691rytJS6a/JGlHB1JKc\n",
"c3rhgsNyCxovNR8hClEsdPLwTv1rxNWrDsebOr+vIF6mQ1w94Q0y+RFIf1nc9q7iqSXxzo5/m9Tl\n",
"1irkcrmiKJSSN98s4nZ3HMtUfGR1evJazd0RQXK3ubWZ6jy4lqWl0m+8ChdkAedwgcGv9Esp8U9/\n",
"6izohVK0v++752Bc3O3uX5iEEOzZZz0X6pxyC+necZussOaDaylaKv1WeB/5nSfwKSLBUkr61FPO\n",
"isSYXrhQRCMav3mtFI628gYDY/ruu7W1hYUQWCnPgcJSSpcLDJUB0l+eICO/095V1HhxKkwFt8IF\n",
"MayCFCqEIG++6VCYyOnTxw6uQgj89tvOhInSOi9+KqX8Jz2UUrJnnwXp3zSCGTgOtanYLXDO6Y0b\n",
"bnc5FXp6Tlc+64zb9DKIUvKBDxz7hJVS9Kmn3D7hIq/VeccJ0hMxxscOrkqpRkzmQPrLgd9916Ua\n",
"BhlIMCaEFFntwA895HDIKeLw4ZzTD36wPdLv8nIYF7mmUgq9+qrbmWuRORO+37HUBJmoUUqPfcJC\n",
"COc2UxW0VPoppWu0T58mtvxv16+77DaBVo2CnIRTcDMn3tkJcwSx02eyvoFpnIsX+8Qnijh86KlT\n",
"AZ7w9ev+k3Mg5Nq6Khaq4NZmqoiWSj8hZFV8Z5Zlo9Eoy7LlvwzSgl0LE8a4UHir90nJYb/y7t1y\n",
"G2SJlKpzKEiYIMsHHnCrhkUGV4SctiXGWJn8VzWnpdJPKV2qffrDXq+HVsX+u87/TghZ35iklPgn\n",
"P3FukxaS/hAHaziOnS3gBuGcuzqMbFrosa8VoUoOfijkRAoxomPX51AeO7gqpdDeXv0dL6FoqfSj\n",
"FZ0kz/M0TRFCaZrmeb7kZ64S+BxBCFnfXYUQ/o9vdd9tMEaBIjsppetV+HA/l1MVPva1Ot42cUSh\n",
"2UYFI/qxbZi5PSFAqWNnrkIIevp0gHUj/1sXjWiv9C+ilFJHU/Wl3vDD7ZcVlLvmr4eGsF8D/LDb\n",
"OCw0XBRgEfPQf8I1IYTDdGYlcB5ApRRj7PgpjtsGjPGxM1chBL3/fs9PmHNOH3kkzKpGSdor/YuK\n",
"MBqN4jie/WROlMXFi+zpp91W49huEySI7bDb+G3BSil8+7ZzM63Qwob3h3xoCPsd0Tnn9Od/3vET\n",
"LnALobbpkfff91yoEILeutWIELX2Sv9igKOUks2IHWNsfh1pZwd533nvfsGwgO+lIkN4fVCpEIJ9\n",
"9KPOu02hhY0gq7KuDWH9WtforBCCXLvmfERfH+0upXScDOqI40cU769VKUXuu68R0h/gJLzgJAih\n",
"LItv3er/wz+wIyVSt26hb38bzQT2MISyixfjmTYtv/c98od/6LIq07bLORqNFlvqYa3+4i9cFjrr\n",
"e4mi5TPiixfR88+7LBQhNHWjrYie4v/1X+nHPob+6I+cl4sQQqMR4nzxCfO9PXpwgP7kTyopFK18\n",
"wuqb30R//McuC6IUjUZ6YYMta0sIIXXxIv3N33RZ6GHJdDQarXqtcm+PIYTunU87AevRLs+XS/zF\n",
"i447ziydznJ9v3gRffrTVRXqlDZKf47QoNfDCKEsQ72e/nCU5/HnPjffS2e+gBCSWZZ87nMuqzJt\n",
"skqhOF40xwTn7FOfqsjxIqUklM7e4BTV7aIkcV7iz8zDZYXe+vzn8V//tfNCDxEC9XqLGiH6fcZY\n",
"VR5hIVAcL32SGKGKnrD+z9InPNee3bPs4jzL0jStygBf0XE455TSKjqOnrkyQhZvlnNOCKnitVaB\n",
"P4cP57zT6URRlGWZE9+flDLLsuVxOIWZ1kQIQZdaZ37clEIsbaaHLbgCGGPyn/5pqeTlec6qGWzW\n",
"+F6klFerOBh99vUtUx8ppfsnTAjiHGMsf/CDpbZhlmUVPeE1QaWhAtJVpbscVnRPzrn7J4wx0uK+\n",
"gjzPk4boPvIm/XmeZ1mWpulwOMQYR1Fkf02962o0GhlfYborREq5tHUucfd7RKtkdd1G3bixVA2F\n",
"EHEF0/PDQpVa2l3zPP+7v/s79+WtfXpVjayEID3Ovfrq4h91IFl10r/KWOn3+zpw2Sd5nlfXlhBC\n",
"6t//fdFmqqrjUKovK7/xjcURPcuySu/UOT6kXynV7/fH4zGlFGOcpiljzNJa55xjjC37TxzHeuTo\n",
"9/tLh+tCUWvWEELEzs7ch1LKSvsqY0x85ztzHyqlut1upS0YY7wox/1+H1WclUW+887cJ5zz0WhU\n",
"nZlGCOHj8ZwwKaW0DVRRoQihpRsytDB53mPMOa/E+tZIyRgT+/sLH8tut1vdE6aUyoWzPLMso5SC\n",
"9M+jgyZnm12SJJbSn2VZz4XXMk3TD3/4w5TSY9ParJoZ2MMY49euzX6SZZnW/Wr76r1JKTjn3W43\n",
"SZKq+qq2Rt95R81si5NSdjodQoiTt7mKRY3IsoxzPhgMqit0sUXpBCFpmlaeQ2mm2egnzBirSpiU\n",
"QnoCvbc385nKskwIMRwOKymUMSQlpZS/8srsx3me53muXQuVlKu5d3OPtpaapfvIzzLvojv12L2O\n",
"63FowlBKx+Px+q6ojrYOVuR2J4SomcakHcFV6e8Ms4VqE7iqjqrBGCHECBEI6XvTAjEYDKq2Rhlj\n",
"2Re+MO2a3p7wrEaMRiMhRKWDjQbfvi3393WD1hPuap8wxgghSmn+xS9OH6i2uyvqLzMl49nd9f1+\n",
"H2NcqQ2hUZcvT20mvbRb9Z1WgSfpX+xmxoaPUopzPplMbKq0GNE/rdVcxbRTKEkSznl1zoGpCud5\n",
"TgipVpUwRpwjxujWll7cVkppW6nCQo+gjz/e/+Y39e31+/1er+ffC2HvKizKyZPablBKVT6yHkFP\n",
"nODvvadbqp5keHjCRCl05oz+/36/H8exHzWcdhwppZTSw8iKEJp2HITQaDQqW+iq5cO9vb07d+44\n",
"qF8xrKRfKbXKFY4xnr57t0EyTlw9q54+Y2xO+g9jlhFCVeQ6JgRxjiglZ87oJymlrNxsoRSNRmim\n",
"BftcAMSvvIK2ttDRK/CUPppzLUw+BzmEEDt/nnMex7Er/+QxKIUQYufOZVIihEaj0aIpU2HRZ86g\n",
"Iwn21pymbVhPHz0Xmue5wQi3SnwuX778vsftx1bSzzlf5bLHGFfRwTjnTqIjyvZDmziidehuKUT8\n",
"+7/fz3OllLfmixCiZ8/2OVdHvlpv5aKHHsrznHPuTYIRQuy553RUsQ8JPoJubXVHIyHEoklRCUfW\n",
"vfbzeLOCEUJISvLEE1mWeS1UKXb+fD/PMcY+F7Hp2bMjKRFCZh68VS0wy7KdhXCP6rCS/oKLGw5l\n",
"RYecT4dNfabKqpB8VyRJ0ul0LF1M6yEf+cigug2lqxkOh9Nkpd7o9Xqcc38SLCWSkj33HMFYSulD\n",
"gglBeY4Yww89NBgMtOFfeaEzDAaDSoOXliBl8sUvSimrjeKfQwjy3HM9xhazb1UNpTSKIv/Bsg7x\n",
"tJtXGz5znxhchzGmZ5T6nzpEurp9TxpCSKW6f7jnMxBBNqF4crWjw1AQJCVKEuLNv6RLkRJhrA1S\n",
"H4XeS5BCA5z+hjHG2H8bbmJIzxw+pF/7OmdHyPWjNOdcCJEkyaL5MPeOOec+HYtVoVSAfE9ChMlZ\n",
"Fupce/9ICeeEVIiUh1kcACN8xPVrk3y6KqAdkasGaiGETvbQ7XY91K29KOVbmJwfvgjUgWKH8DhG\n",
"T+aC2ExSbkYb9uTwGQ6HURQJITDGOkpylYtmaumv9xgKIfSqnd6853N1dENQyncL3ogOUwLOkf/5\n",
"qBC+1TDcITxh2JTJnCfpxxhPJhO9Krs+0JgQsru7u3QrwCx6K1YFNfVOkG6jFBIigDBxvhndpij+\n",
"R7sghnCr8G8zVYPXpM0FF2P9BSMHR4eC+Gea2jdU0UAVKIWkBOmvliA2UwW095SuWtC2Xhpqbbkl\n",
"YIykDHAwLOdhWnIoR9NGtGGQfsAj/teWEUKjUYBCW+X+RoGMmI2Q4FCA9IdGiDDu75Zokw4F8a8R\n",
"oEobybGHPDcHkP4aAD73Stmg7lpTVpwxVy1BJnOEbIzNBNIfmk0JE64vQdzfoZZb/QtTkLh+hBAh\n",
"YDPZANIfmiBhwkG8TJvSZwoRKsjS/0OmNNibbVWLcg1IfytZdkpi5YSK6G9bGJV/Qj3hIC1qUzam\n",
"gPSHJkT2tGCT5SCEEib/XqZQhbaKTek4IP2hCdWSghgvIEyV0qq2FGpE3xTp97qbF1hCEKs/SKGh\n",
"ZspB8jt5PBDmZwR5raHKDbKlNkk2xn8I0h+aIC2pJSuQmiA3G2Sca9UTbk+h1QAOHwAAgNYB0g8A\n",
"ANA6QPoBAABaB0g/AABA6wDpBwAAaB0g/QAAAK0DpB8AAKB1gPQDAAC0DpB+AACA1gHSDwAA0DpA\n",
"+gEAAFoHSD8AAEDrAOkHAABoHSD9AAAArcOf9HPOO51OFEVZlikXh0dzzrvdbhRFnU5HBDkYGgAA\n",
"oJl4ytef53me54PBgBCS53kURZPJxOaC3W5XSpkkSRzHUkpX9QQAAGgDPqRfKdXv9yeTCcYYIZSm\n",
"qVIqz/PE9HCfTqdDKR0cnb5ENuj8BAAAAA/4cPiMRqM4jvHMEUJJkuR5bnY1/cM0yPFsAAAAG4EP\n",
"q19KSe89r44QYuzuz/N8OBy6qBcAAEBL8ST9jLG5D228NIQQKaU2/+M4puXPQY2iaOnncRwbu6EA\n",
"AACOZZX4vPbaawcHB96qYSX9SqlVoTUY46kiO4nn0XDOMcZ5nvf7/TRNMcbdbjdJkrJ6PR6PXVUJ\n",
"AACgOKvEJ8uyF1980Vs1rKSfc77KZY8xrsgto5QajUbTReM4jre3txljsNgLAABQECvpj+M4juNj\n",
"v2bgkFlzKSHE7u7u4qJxr9dzVQoAAMBm42lL16JfyGwTlvYjzRn4YO8DAACUwof0x3HMOZ/9RId7\n",
"rvo+57zf769aIaCUzl1NCAHqDwAAUBwf0q8dPtNVAb3Da9XCrBBCJ3vodrtLv5Cm6ezAoEN9ivid\n",
"AAAAAI2nRA7D4TCKIiEExphzniTJqgWAqRN/1ps/CyGk1+ttb29rueecD4fDVV8GAAAAFvEk/Rjj\n",
"yWQihFBK6aDMVd8khOzu7i7dCjCFUrq7u6vdPrC6CwAAUBZP0q8pGOpDCCniu18zNgAAAABrgHz9\n",
"AAAArQOkHwAAoHWA9AMAALQOkH4AAIDWAdIPAADQOkD6AQAAWgdIPwAAQOsA6QcAAGgdIP0AAACt\n",
"A6QfAACgdYD0AwAAtA6QfgAAgNYB0g8AANA6QPoBAABaB0g/AABA6wDpBwAAaB0g/QAAAK0DpB8A\n",
"AKB1gPQDAAC0DpB+AACA1gHSDwAA0DpaJ/1Xr14NXQUHZFnGOQ9dC1uiKApdBVs24EVwzrMsC10L\n",
"W6IoavqLQAjduHHDW1mtk34AAAAApB8AAKB1POitJM55nudKKUppmqYYY+NL5XnOOXdyKQAAgBbi\n",
"yerP8zzLsjRNh8MhxtjGydvtdoUQvV5vOBwSQra3t6WUDqsKAACw8fiw+pVS/X5/Mplo8zxNU6VU\n",
"nudJkpS9lBBCSjkej/U/kyQhhPT7/cFg4LjSAAAAm4sPq380GsVxPOuWSZIkz3OzS1FKZz9hjG3A\n",
"yj4AAIBPfEi/lHJOrwkhSimDS81dZ+nFAQAAgPX4cPhIKRljcx8SQgwuFcfxaDTq9/tpmuord7vd\n",
"Xq9X9jpNnyjs7e1dunQpdC1suXbtGryI4Fy6dGlvb6/pL+LatWtNfxFm1rAx9929e9f4x0opIcTS\n",
"P2GMp8Z4FEVpms6pfxRFU5d9WWa3b4zH48VxZQ1/+Zd/+ed//ud37twxKxoAAKAiTp065W1Xl5XV\n",
"r+M1l/4JYzwcDm0uvoput8sY08OGECLLstlh5lheeOGFF154oYqKAQAANAUr6Y/jOI7jY7/m0Bef\n",
"5znGWHt79JWHw+H29vbu7q6rIgAAADYeT3H9i36hVZ6i9XDO59w7GGOzZQMAAIDW4kP64zieW0TS\n",
"4Z6rvs857/f7Sxc9loYGeV4eAQAAaDo+pF87fKarAnqH16r9XEKIKIqyLOt2u4t/TZJkblTIsqzU\n",
"Mi8AAADgKYfPcDiMokgIgTHmnCdJsmoBYLrza2lmHkJIr9eLoohSqi/FGDMI7gQAAGgzVsGdZRFC\n",
"6Jxr6xOuSSmXbgWYRXuQCCHg6AcAACiLV+kHAAAA6gDk6wcAAGgdIP0AAACtA6QfAACgdYD0AwAA\n",
"tA6QfgAAgNYB0g8AANA6/B3LXgccHg3vgSzL5j5hjC3d7lC3+xqNRlLKaZa9RQpWOOB9HXsLBd9O\n",
"kFvQB6DqvS+MsSRJbJ5wqLdQ8C7q/CLQvXdBCEnTdOlWpAA94m5rGAwGlNLJZHLt2rVer0cpDV2j\n",
"Y0AIje9ld3d38Wv1ua/xeBzHMaU0jmPG2KqvFaxwkPsqeAt3i72dILdw7do1xliapru7u7u7u2ma\n",
"UkqvXbu2+M0i1QvVuorfRW1fxN27d3d3dymlg8FAV2k4HOpqmFXP7V20RfqvXbtGCJltOmmaDgaD\n",
"gFU6liIDc63uazKZ6Gatz89Z+p2CFQ51X0VuQXPs2wl1C0mSDIfD2U96vV6apgbVC9i6Ct7F3Rq/\n",
"iLszzWn2kziODarn/C7aIv2DwWCu3egBOVR9ilBE+ut5X2t0s2CFg9+XvfSHuoVer7f44eK9FKle\n",
"wLdQ8C7u1vhFrIIQMvvPUD2iLcu8Do+G9w/nfFVVG3dfBSvcoPta9XZC3cLi+oSUctEpXKR6Ad9C\n",
"wbuYpW4vYimLJ46E6hFtWeZ1eDS8T6IoUkphjJVShJDBYDDX+ht3XwUr3Ij7Wv926nMLnU5nMbtt\n",
"keqSMfOPAAACbElEQVTV5xbQirvQ1P9F6MyVnHMhxNzJtaF6RFukv54G43p6vV4cx9O3m+d5t9ud\n",
"azeNu6+CFa7/fR37dmpyC91uN0mSRdUoUr2a3AJafReoIS9CCCGE4JwvhuWE6hFtcfg0kbk4sCRJ\n",
"lFJSyoBVAqY04u10u11K6apjkZrC+rtoxItIkkTH+QghFqNRg9AW6Xd4NHxAKKVzbbpx91Wwwo27\n",
"L7TwdsLeglJqe3t7jWIWqV7wt3DsXSylVi9ijsFgIIQwqJ7zu2iL9CN3R8PXjcbdV8EKN+6+Fgl1\n",
"C0qpKIqSJFmvmEWqF/AtFLyLItSqLS0acEF6RFukv+zR8PVkNBrNDf6Nu6+CFW7cfaGFtxPqFpYq\n",
"5qIDpEj1Ar6FgnexlJq8iFXoc2qn/wzWI4zDQhsHY2y6A+LatWtLt9XVB8bY3JaWJEmWbmmp4X2t\n",
"D4ovWOGw93XsLRR5O/5vQW+Cnavb3bt3McaLXy5SvSBvofhd1PZFaOI4nitIL0qbVc/tXbTogEZt\n",
"R0zPc3cykawOpVSWZUIIHdWgR/ilwW31ua9+v68NE73ONrW8xuPx7NcKVjjIfRW/hSJvx/8tcM67\n",
"3e5izB/nfLGnF6lekLdQ/C5q+yI0elFXKaWrp4P6lwb5+O8RLZJ+TcGj4WuCUkq7846tcLPuCxWu\n",
"cJ3vq+DbqfMtoGLVq/kt1PxFSCm1q8pJ9VzdReukHwAAAGjLMi8AAAAwBaQfAACgdYD0AwAAtA6Q\n",
"fgAAgNYB0g8AANA6QPoBAABaB0g/AABA6wDpBwAAaB0g/QAAAK0DpB8AAKB1gPQDAAC0DpB+AACA\n",
"1vH/kbYkcRAEIJoAAAAASUVORK5CYII=\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"y = y_sr;\n",
"y_f = FiltrePasseBas(y,freq,0.1);\n",
"\n",
"%%représentation du signal filtré\n",
"plot(ech,signal,'r')\n",
"hold on\n",
"plot(ech,y_f,'k')\n",
"err = sqrt(mean((signal-y_f).^2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Avec une fréquence de coupure de 0.1 Hz, on perd de nombreux pics de `signal`, notamment celui situé à 0.16Hz. Effectivement dans la représentation en temps on voit que les variations rapides de `signal` sont perdues, et l'erreur résiduelle est de 6%. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2.5. Optimisation du filtre de Butterworth.\n",
"Trouvez une combinaison de filtre passe-haut et de filtre passe-bas de Butterworth qui permette d'améliorer l'erreur résiduelle par rapport au filtre de moyenne mobile. Faire un graphe représentant le signal d'intérêt (signal) superposé au signal filtré, et un second avec le signal d'intérêt superposé au signal bruité, pour référence."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"err = 0.014540\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fkCRHfefTRkIdeLidtJE1QyBplTAridNJ2s1B/Anw\n",
"CK7qdLFEYBlFjUScHo6TozrEvRw4HFUPOMIh63zdcYe5B5/XXSFbLwZEd4CBCCluY/KExjhkISZ3\n",
"VpIdWmZ20rPG1rRAbM7GLjDIiL2H3Gn19kzPVmVlZVZN/T4vu9vbXb+sf9/85S9/+ctfuXjxIgIA\n",
"AADqxK+6bgAAAABgG5B+AACA2gHSDwAAUDtA+gEAAGoHSD8AAEDtAOkHAACoHSD9AAAAtQOkHwAA\n",
"oHaA9AMAANQOkH4AAIDaAdIPAABQO0D6AQAAagdIPwAAQO0A6QcAAKgdIP0AAAC1A6QfAACgdoD0\n",
"AwAA1I6rrFlijCVJIqWklEZRhDHWPlSSJIwxI4cCAACoIZa8/iRJ4jiOoqjb7WKMfd/XPlSz2eSc\n",
"t1qtbrdLCJmdnRVCGGwqAADAvudXLOzNK6WcnZ1dWloauOdxHBNCwjDMeijOeRzHCwsLg08YY71e\n",
"r9PpGGsuAADAfseG19/r9YIgGA7LhGGYJIneoSilw594nscYy9tEAACAOmFD+oUQI3pNCJFSahxq\n",
"5Di7HhwAAADYGxvTvEIIz/NGPiSEaBwqCIJer9dut6MoUkduNputViv9Eb7xjW/8+Z//+euvv77r\n",
"/05MTPzar/2aRsMAAADS8Oqrr477r/e+971/+qd/aqkdF4vH87yFhYWdH+Y54KD9O4+8Nx/96Ect\n",
"XVkAAIAsXHXVVdqqmJXq5fU3m81Bt7G0tNRutznnWQ9i7foWRBRFWfu8EpKn+y8J++BGLCwsRFHk\n",
"uhV52dW/rBZRFP3qr9oTZBuWDMbikyTBGKtojzpyt9udn583dXwAAIA6YKmT2emYa7jqCCHG2Mi0\n",
"AcZYb9oAAACgttiQ/iAIRvIvVbrnuO8zxtrt9q4pQLumBuklCwEAANQWewGfQSK/lLLdbo9bz8U5\n",
"930/juNms7nzf8MwHOkV4jjemT4EAAAA7IGlGj7dbtf3fc45xpgxFobhuAmAwcqvXSvzEEJarZbv\n",
"+5RSdSjP8zIldwIAAACWpB9jvLS0xDmXUu5dcI0Qsra2tutSAIXneUtLSyqCFIYhBPoBAACyYq9y\n",
"J0qd6kMIuaKgQ5AHAABAm+rl9edkYmLCdRMM4HnePhju7DHVXxX2wY0ghOwDRyoIgqrfCITQ1Vdf\n",
"bc2WjcqdpeJTn/rUE088UbezBgCg5MRx/Nhjj7322mt2zNXO6wcAAABA+gEAAGoHSD8AAEDtAOkH\n",
"AACoHSD9AAAAtQOkHwAAoHaA9AMAANQOkH4AAIDaAdIPAABQO0D6AQAAagdIPwAAQO0A6QcAAKgd\n",
"IP0AAAC1A6QfAACgdoD0AwAA1A6QfgAAgNoB0g8AAFA7QPoBAABqB0g/AABA7QDpBwAAqB0g/QAA\n",
"ALUDpB8AAKB2gPQDAADUDnvSzxibn5/3fT+OYymlkQM2m03f9+fn5znn+Q8IAABQE66yYyZJkiRJ\n",
"Op0OISRJEt/3l5aW8hyw2WwKIcIwDIJACGGqnQAAAHXAhvRLKdvt9tLSEsYYIRRFkZQySZIwDPUO\n",
"OD8/TyntdDrqn4QQY20FAACoATYCPr1eLwgCpfuKMAyTJNE7mvphFEVmGgcAAFA/bHj9QghK6fAn\n",
"hBDtcH+SJN1u10S7AAAAaool6fc8b+TDPFEaQogQQrn/QRCM9CtpiON41889z9vZVAAAAFOME5/F\n",
"xcV//dd/tdYMS7F+U4dijGGMkyRpt9tRFGGMm81mGIZZpw3G6TtMGwAAUCjjxOfMmTOnTp2y1gxL\n",
"GT4GkVL2er3BpHEQBLOzs57nZVJtcO0BAHDCOPFhjL3lLW+x1gwb07waAZk9DsU573Q6piaNAQAA\n",
"aoilJV07l1zpLcLCGFNKRxx8iNIAAABkwob0B0HAGBv+RKV7jvs+Y6zdbo+bIaCUjhyNcw7qDwAA\n",
"kB57AZ9BTEat8Bo3Mcs5V8Uems3mrl+Iomi4Y1CpPnt0JAAAAMAIlqZ5u92u7/ucc4wxYywMw3ET\n",
"AIMg/nA0fxhCSKvVmp2dVXLPGOt2u+O+DAAAAOzEkvRjjJeWljjnUkqVlDnum4SQtbW1XZcCDKCU\n",
"rq2tqbBPq9UqpMUAAAD7F6vJnSlTfQghaWL3kKAJAACgB9TrBwAAqB0g/QAAALUDpB8AAKB2gPQD\n",
"AADUDpB+AACA2gHSDwAAUDtA+gEAAGoHSD8AAEDtAOk3gRAOjEqJzO2BkwEnJwtXeL8ahSvsCJB+\n",
"EySJgyeYc3R5BVNLjNlerlic7MfAOdIqLZ4XJ1d4TLXEYkkSN1fYyeNUsj1FQPoN4eQJdmLUiZvG\n",
"uQO7UjobbQCF4uS2OnlbxwPSD2TEyVADuXhzOC/bIL1YXHXq9oHOFaTfGPXx+oGiqU/nilyoMGPO\n",
"JhjK5EmA9BtA/NM/2X+YxPPPi5/9zLJRhFAbOXhd2TXX2BdEce6cOHfOslGEUM++SYTi06ftG2Vn\n",
"zji5wuziRftGESEg/fuN5B//0f4TLF56KfnJTywbRQglb3ubffew9y//4uAKb272Tp2ybBQJkVx9\n",
"tX2N4D/7mf3bytbXeb9v2ShCKPmXf7Fv1Ennugcg/WZw8gSLrS0HRn/6UwdGNzftX2He70v7V1gI\n",
"/pa3OHAPr76anTxp26irF+f11+33c/wXv5B/+7eWje4BSL8ZnDzBvN+3H3uh117LvvpV20anpuxf\n",
"YQe6v21XWD9ZPDEhNjctG0UurjBfXRU/+5mDcP9VV/Hvf9+20fGA9BvAiUaIzU1yww22nRfOyfS0\n",
"+Od/tmoUIeROiO074N6tt4onn7RslExOOpD+RsO2RYTkhQvBLbew5WXLdnGjwdbXLRvdA5B+A2AX\n",
"T7DY3Ax/+7dtP8FSkve+14l76OQi49tu48eP27Qo+n16xx2l0ohiaTSk9UAT+bf/Vjz9tG2jk5OW\n",
"Le4NSL8ZMMZicdGyUfrv/z3/9rctG3VDo4EQkpYH6Zub9NAhsbFh06bY2PCOHLFpUeFqUOUdPcoX\n",
"FiwbpXfc4cB9cThy3Q2QfjPQj36U/7//Z9komZuzLUz9PnL0BHsf/CB/4gmrJicnvd/9XfvC5ATs\n",
"onOVW1tkepq/8IJNo+jECTQ9bdUiuhQ2xLat7gVIvwm2tujMDH/pJfuWLT9MYmODzszYj73IrS08\n",
"M8NPnLBsF+FSva3F4h08yO1OHeFGg3z843JtzaZRhBCamrJtUQh08CA9eJC5Wq+3A5B+EzQaeG4O\n",
"Wc7KUK63dRXGb387mZy0rxF0Zka+9ppNo26G53aHcZcxMyP/5m9sG61T54obDekiRWJXQPoNYf8J\n",
"djHtqSCTk/IHP7Bt1fOk3clPJxPLaGMDHT5Mp6asuoeco0bD+63f4qur9owOsNvFsvV1QghuNIT9\n",
"3K1PftJy1sAe2JN+xtj8/Lzv+3EcGwkpCiHiOE5KUArV4eyNfQccIUQ+/GH7qf3IlRa7ADca0mYO\n",
"uJRoagphLF95xZ7RAdZvKyGETk3ZlH6+uoonJko1xLEk/UmSxHEcRVG328UY+76f/5hxHCOEej0n\n",
"JU8uw4kkqf6GTE5anZpbWUETE+Tmm+1ZRI7rLFruXHm/jzH2HnqIW1z5KS9cQAghSvHrr1szipCb\n",
"JV0KfO214plnrJmTFy7QQ4cQIbbDwuOxIf1Syna7vbCwQCnFGEdR5HleTm+dMYYx9jzPVCONYNOP\n",
"UP0NueEG/q1vWTOKLlxAMzO2n2DOHczLbWO5c5VbW5RShJA8f96aUb66SmdmrJl7k0YDIWQ7uoUQ\n",
"Qoh+4hPC/vQyIQ57uxFsSH+v1wuCAA8NdsIwzCn9cRy3Wq3cTTOJd/Cg/egh8X35ox9ZM3cpG9r+\n",
"E9xoIIScxGfJ5KSD/E5K8Y9/bNMgfvvbbZpTqJGrszieExWulfQLIZQjM4AQkseTiuN4pC8pA06E\n",
"CSGrD5PY3Lw00rJo9FKcFCHL8Vl1juS+++Q//ZM9owpHzzZuNGxGt5To05tvZl/7mjWjl/A8qyPX\n",
"7cQtPDnpRiV2YEn6d8o0IUTvaFJKxlgURbnbZRh63XXCemEQ20/wgEbDWhjkUpzUfue67Y3ajL28\n",
"iQv3kE5N2V4yjRD+8IfRvl9bu7GBDh9G9t2X8VxlwYbZh8lIqGfcPHMQBGEYZjsWY5c0wvPk//7f\n",
"ORtWFdTyH8tzLfSWW3oWO9dL0kAItrkvwrYe4clJzvnIcLloyORkz/ptdYWTQBOZnPyPn/nMjTfe\n",
"OPjkF7/4xVVXXYUQOn369JbF3qhief2MMSll/kdzYQyZdV9lR2xPQg4HTFUCkgWGfWGbRgeRgV6v\n",
"ZylKQOnAPZRSFn2yl6SBEDnkkxZ+hbf1aNg9NJUPPZYTJ9DEBEKIHDwotssqCCHa7XaBRgcQgoZW\n",
"bFh7hoenl4s2qhYTIITIgQOf/OQnhwXn2muvVX+///77GxZ7IxvSb9BzSZLE8zy2DedcSmk/sX2Y\n",
"N7MjhvJeVPMG3yniwRoMV+nU1OAKDNstVC/oddcNDs45H6TYJkli53YMn6lKISvO1nB+Z5IkhXa0\n",
"g9vq3XjjwKgQYpAW0W63jUcM5NYWUs8wpXh788Jerze4wsMNMA8haDs2oAzZcWWGXxzO+fAVLuLF\n",
"uRTixhi9+qr6RAjBOXc1Z2nJ698pB3oC4XmeEGIg/UIIFfo30UZ9Ljn7hNDJSdUYxtggi6nX6wkh\n",
"jK8/GAxXBxrBOQ+CQDVASqmWvJk1+mZMdugJHn5POOfm35xBqJ1StL6uDq6usDpxNewo7jEYFLfp\n",
"9XqtVkvdVvXsGb/Cw1GIwWUkhAzUUN1Ws1eY9/s7/TM1vFZ2VTdguFMfOoXBFWaMdTod9bJwzgt5\n",
"hrchBw6os1N5KMPdQLPZLMptonQQ0+v1emEYEkKcOK82Yv1BEKj1XINPVLrnuO+rhywMw5394UhA\n",
"Rql/eaZ86Y9+1Pvv/91jTB4/Ht5zT7y4iITgi4vdubn4L/9yj1POiTx+HCHEvvvd4JZbkpMn5Wc/\n",
"2zt1KpqaEj/8Ifurv/IefNCYoYEwUYqeeALFsTh3jqys4Eaj9zu/4x08iF98MbrzzvZnPtP6yldM\n",
"GUWrq+j++xFCCGPv9df5Zz7j3XgjfvHF4G1vaz/+OJ2bE+oKf+ELBQWp6Vvf2nv8cXUrow98IH7m\n",
"GYRQ77vfjW65JVlcFEJo5yzsBSH42DEUx+zMGbq1Jbe2+Kc/jRsNsrJCp6Z6X/hC+OijBq1detco\n",
"pb/3e+xTn/JuvBEtLgZ33tl76KHI90Wv17n77vajj9K//mtjJoeWa9BGo/0Hf+AxJhYXW3Nz89/8\n",
"JpKyt7jY+cAH2kXWQscvvojimL3wgjc5ydbXxcMPy60t7/x53GjwJ580+OIMQ155hX/60/S66+Ti\n",
"IpHSe/VV9n//L33/+4uwtQf2Aj6D8ZQano+LqnPOVbGHZrNpoW1mIX/7t+LQIRlF+J57UKuF5uZ6\n",
"lKK5OdRqFZjD0Gopc/L97yfHjoVf+lL7mmvEHXfQxx/HH/qQ2XJgb/qknocfeIAHQe/gQe9//a/g\n",
"y19mv/mbydSU90d/RI4dQ0aL7bD1dXL77ervlDF2440iDPG99+IvfhHNzTHPK/wKdzrKhLz9dvzF\n",
"Lwb/83/GCPFrryXHjnm+LwpKTAxDdM89MorYjTd6f/mXwZe/3P7JT5IDB4K/+Avvz/5MFFQhHGP6\n",
"13/N77yTeR793OfIsWP82mu/ddtt5IEH8Be/aDaXjC0vk5tuumT28ccv3cS5OdRqBY880sYYzc3h\n",
"L37RoMVRts3xG27wvvKV8Etfin/849511wVf/jL99Ke5wU5uGM+jf/In/IMfHFinjz8uDh1C1lcp\n",
"WQr4dLvdJEmazWYcx77vh2E4bgJg4OnvHQIb9BBqdGa+xbpgjNvttnLwW61Wr9d780yLnKkb9KyE\n",
"kIETSu66iz/1VEEWKaVq1KUWaasAl/K7jafNDc4IYyylTJJEXeEoitQiD7PmENplX8YkSdQzqc7x\n",
"UpPe/nZUWOqnWvQupcQYq2XwnHNCSKFZ/yq41G631Wl2Op0//uM/LmjASi6vm58kibqqQRBIKS/N\n",
"i77nPfzYsSKsI4QIIcMvThRFqkwA+cQnDJczGvJLKKUqAmw5fWsEGwEfhBDGeGlpSc3KRlG0h6wT\n",
"QtbW1oQQew/eKaULpdxDA2NMCBnc1E6no06WfPCD/Ikn6MMPF2E0CAIVhlb/DMNQRSrJ3Fxxycue\n",
"5w0bpZQuLS2pvxeaNocxDoJA6QLGeGFh4dLj1GggzpGh10k8+yw6eHDwT/W6Dk621WqpK0x/93fb\n",
"R496jzxixOgIhBDG2PAV7na7RRgaAWPcarXUVcUYP/fcc2/+n5QFdTzqhg6CAYMrTG6/XRZWyJpS\n",
"2uv1Op3O4J9vqorZF+fy3RkxxiN27dcisyT9ipS93LDfWgHOn0dDOZ0jEw+DTo7MzMjCKuJSSkeu\n",
"rZ20gcGza9PoyKqOgVH6kY+wp5/2TEn/5Rsl7nR7B8poxNybDLmHhJBxJ1soY9fNTE3JxUV8771F\n",
"GN0ZAb50hT/2Mf75zxdhEe394hTpvoyoRBiG1lJaB1Qsr7+EsIUFkqIQKb7rLvHyy6aMZtjJ2knN\n",
"kEZjZ8CkaPCRI8j+Nl6mkekUx+xgTp47l+Zr3n/4D9z6Xi6UUlGaapeF8vOf/9ymOZB+A5A777zi\n",
"dyilBneC5gsLNGXhaye1saam5IsvWrZJbr+dV18jUsbK8MGDyFwyKz5wINX3ZmbcbCLmqii6RfdF\n",
"YzFpTkD6LWLUU0tZalFevIjMZQ2ndA/phz/Mn3zSlNGUEEKc7Zljf0cBF1v9UUqZ3Y3SHIJvucWm\n",
"9BNCrrnmGmvmEEi/VVw4L/immwwKU0r3EN98M1K7f5ggg6A7kf6pKYOda0q8hx6yv9Wf2ZkGMTx7\n",
"vDdO4oc33CBKmUhiCpB+i0xO2tcIfPPNRSWej4cQYjD2kiFfyEl0qzbbRppFvPKK9/u/n+qrU1Om\n",
"pF+kniSjvi/sF+u2CEi/RSYn7UcG6Ic/bHCOISWuYi8Go1vpCzWT97+ff+lLRoymhxBSn9iLQcTC\n",
"gmdid9ispIyU2gSkH9g/GIxu8e98h77vfWm+SW67zVQ/l75ujKvsZ3nxov3Yi+HONd0kmdmJjbQT\n",
"6RYB6c9L+teeTE+zwtbWjoNSyk6dsmx0P7C1he++O+V3TUk/f+IJ+u53GzlUJtK3H990kwPpN9e5\n",
"pqdsmwAaB6Q/L+kfEHL0qKncOL6yovYsvCIY4/oEo+nMDLOeeO55HjflHl64gO+4w8yhspBJ5KS5\n",
"CfyUYIztBy2R5W28rAPSn5sswmrqCZZ///f0nnuMHCo9nHNnO2inA//Wb6HClkzvRbkvy5VJ3X7v\n",
"yBFu/QqbXROTnpI/7TkB6beH53kmn2Dr0V759NP08OG0356aMrjmKCWu3MMaMTOzD5ZMAwik3zZO\n",
"8l4MGr281OIe4He8oz7uoZv1BJOTDjrX66+v9JJp4WQ1cikB6beK9UWfCDkat9JDh+wHhV3h5LaS\n",
"W2910rka8yQyHceQUfHyy176kauhztX4hppGAOm3ipvooYvFkGh6Wm5v8F1FMgmcqduafjEBQohM\n",
"T7vpXE1Jf6aLZurF2dxMX9abvu99bHk5v01x/Lh32235j2MWkP79D/3IR5j1Bb3egw/ytTXLRg2S\n",
"LbOv0chQS3U8fHWVqu3RU4BvvjlDLQSDVH3yM3XWZsoyWVfmwgV06JCZQ5kDpH//Y+wJrgQufFLv\n",
"6FFupN5Lv4+vvz7ld+knPiFM7CTFGCOXbyRSQnCjIYrcpHdXyF138W9/27JRa4D056b0yb9kepo7\n",
"cQ9dbRVQXba2TO0yloHVVfKud6X/upNsd3r0qHj+ectGydxc+vXVlQOkPzdZtIZMTnIjRWayvH7k\n",
"wQeNbDTKTpwgqTN8EDKjwuWcIhuBTE+zp592YNiICmcMR7jKds80EWLMaOkdO21A+q1C3vc+aUQj\n",
"Mr5+Zp7gzU0yNWXZqBDCG9oj94rQqSlmPeWRPPggcpJU6kqFTfjCmR4POjPDX3opv9Gs7ONVXSD9\n",
"dnn72504L2ae4M1N5Hm2jS4vo3QlKy4ZvekmZCIroxK4ib1MTRkZuWZ6PPC99yIT6wn2sRefFZB+\n",
"q3iHD9vPxa48mbIjMoWkKo6TAmP4ppvMVMvIqMJGVDvrFTNiNH3FLZuA9NsFYyPOS1WwH6kn09N8\n",
"ZcWyUVNkFhon4YjpaTNbsGVsvJlBpAuj8sKF9Dm71gDpz0XmimaUlj8jyBTewYMOpH9qSr72moED\n",
"ubhNVYksOwlaVpj1dfsVt64ISH8upJQ0y8ynMbuV6D8mJhzU0aTUzLjKiQpnvK1kcjL/nHbWxC06\n",
"MwNBy8yA9O83squMmZBlJdzDQ4cMbs6elkrvsJHxtpLJSSNXOFPiFp6YcJPOBBjFnvQzxubn533f\n",
"j+M4T3KYlLLdbvu+7/t+u912vOZiYwMdOZLpF2ZUu+oVQNMbrUpswck4bGbGwLgqazjC8/JLv8Zr\n",
"6+TxMzKuKieWpD9JkjiOoyjqdrsYY193Z2Qp5fz8vJSy0+l0Oh0ppe/7FVtxZ+QJduH1Z+20jMy4\n",
"Zipr4xIn4zBTJTqshyM451kjpWZmXLOH1ByMXK1gQ/qVn76wsEApxRhHUeR5XpIkGoeK4zgMw1ar\n",
"RQghhLRarSAI2u228TYXiAuNMOO8ZH1tpqYMlJbc2iphYlx5qO4a18xS7sSokXFVKbEh/b1eLwiC\n",
"4W2OwzDUk35CSBAEw59EUWSmNMK+xkx9rqyvDSEo/6a1/b79sjZ6W1HaH326WiZiwAFfXs68AsNJ\n",
"pNTEuKqcSRk2pF8IQS9/ewkheu9JFEU7D47dzexVJhI9Pe1gjaupMIL1+6uRuGVkjauORjiRFSNG\n",
"nSy+q0Kk1A5XWbAhhPB2FAAghnRhfn6+1Wpl/dW46IeKI6U/Dl9dje6/P6v1nOj0mnVa42rAycqe\n",
"uIUbjfxB4cwa4XnoD/4gp1EdHAmoEMKUbqSEzsy0v/rVDNVLduXyB3Kc+Jw5c+aNN97IaSo9NqS/\n",
"uIFws9kMw3Bnv3JFxl19z/OyPlv2I9EaU2S1woCTlT1xy0xQuDaJWxrQqSn70m/m7b78gRwnPuvr\n",
"67/85S8NmEuHDekviGazSSkNw1DjtxoDhd1xlOCskWyTPPlkXucF2AMjyTYaEwy5hbuc4YjdsV8E\n",
"xch81eWME584jlctztzYiPVT09N0UsrZ2Vlt3TdJxmKWCCHcaOQNCq+uZipmiTKu2RlHVdxDV1S1\n",
"JquL26pT0ezIEbSxUUxzxlO+VbimsJTXv1PstOVP5fKHYehe97WgU1N5I2AaW32aKBtXJffQOhWu\n",
"yapxW3P3Fk4qmlViK0pr2JD+IAhGwlsq3XPc9xlj45bp7qr7ldjI6TLsj1sdlY1zVVA+5yKGyiRu\n",
"ucLFUANPTORfIQjSP8BewGeQyK9WeI3z2TnnqthDs9kc+S+1lDeKopHfzs7OFtDqwnAybnWEgYFC\n",
"9tmU/EZ1lhBTmjMoXCEPRiXb5DpEv581lkJnZvKuEHRUL12UsuSRpWnebrfr+z7nHGPMGAvDcNwE\n",
"wCBJf2e2PudcCJEkychyMIeFHCD8fQXyXx8NN01VDM2e9zVM5kh07sUHWbeidIiZZBuNn+d8nDQS\n",
"t/IbLetQw5L0Y4yXlpY451LKKIr2WIRFCFlbW9t1KYDneWtrawW3NBsaDmb+TGG+suJpPMFOcDI9\n",
"kL9iqJabVi8/wH5lmzotYrCA1eTOlKk+WddVVYv8mcKaU2SOhElKaX+5tcgZUsueuIXyB5qyJ24Z\n",
"QafH2r+VbQqhlD4B1OvPh8ZNdbVHowvnxdQW3pnwDh/OK/1O0EjcMoFOj2WqYmhGqjquKuW4AaQ/\n",
"Hxo3NX+yTb9vv6yNXkWzeuWDOtrT0X7nSqan2YkTlo2i3I9TJR2CwgDpd0Be52Vry34xS82tKHPv\n",
"0ahzrQpYgZkKR+OqvGkO2a+wkRWC9hEbG97hw5l/VtGhxpUA6XdAjXzh3DOuOtcq90SRXt9cr3BE\n",
"KRMWC2Gfvq0g/bUhpzDpTkI6GWXnVGG9vjlnj551e/RLzMw4KMdtYo9GB7hoc2mXEIP050JTYpy4\n",
"hzmdF61JSAMzrlrXqqLjKp1AiqMZVyfkHVdpJW7l3+EOpH8foikx+YSpqoEFPZyIeIV6dEc4eQid\n",
"9OjlFO78gPRXjyq5tIS4Wj2fCxc9ul7iVs5kG+16DFV6CPOT5xku667uIP35qI6jZ2Zn9sxWSYUu\n",
"kWO0ErdyJtu4qh5RpUhpzqJbq6vIeo3SNID056M64Yic41bIiS4prlYI5qNekdJSzseA9FcQvRcg\n",
"X4q9Zk50PkqbHTEOB9U3c64QLGs4ogjqFaS6EiD9tSF/UTMX6Em/E//OO3gwj/S78UnLGo4Aigak\n",
"X58KFVh3SH1SQdDERJ7YizOftJThiELQfRTzRDs1l2sUD0i/PhWbIsvJ+rreKtlciqatpE4u0aFD\n",
"9dmExwl5CxZpPYr516aUs+4FSH/1cOYe6hVIyKPCGxua4Yiclwiykq6Eq6035csv27bqqiRUwYD0\n",
"1wg3WTo5VdhJOMJJ56pbZiCPCvOVFb0NJNz4H042N92ne4eA9OdAt6yNk0K7dGZG/OM/WjYKZEA3\n",
"lylP/W7NbX/yUbnErVy4KLGeBpD+HOjurUHf8x75/PP6dvXK2tx7b55JSCcDfHn+vH2j1aOCOYtO\n",
"pN/NJJmLEutpAOl3Qc48SxevupMBPl9dte+TaoMnJvgLL7huRUaqWIBTF8jrHwakHyg1epFo8s53\n",
"smPH9CxqhyPoAw/ItTU9o87QKmaZl+VlVMp8xyIobbFFkH592IkT+fdYrwxOnmBdn5R84AN5xlWa\n",
"4YhShnRLiq70O4kBih/+UPu3pR1qgPTnwn44Iu9ufNpoP8F5+gwnPmkFS+LUBOr7fGHBvl3ym79p\n",
"32jRgPTnIYQS4gAAIABJREFUwIUjzDnX2SPXIWX1esaysYGOHHFgt6yRgXHIkyctW8R33mnZ4j4G\n",
"pD8H/b7+3L12evKFC9pDSHnunKZRwAKVuq15HHCoAlsGQPrzoRXeJffdx/7u7zQt5qi3hQ8c0DQK\n",
"lBgntxXnWGrnpAosMEIlpZ8xNj8/7/t+HMfOYt85IDnXB9am3lau7AhYE1BaXKxyqtc6shRUT/qT\n",
"JInjOIqibreLMfZ933WL6kG1CnDOzIjvfc9oWwBzOFnldOECSP8wFZN+KWW73V5YWKCUYoyjKPI8\n",
"L0kS1+2qAXlma7VHZrr9jXfvvUI3MdRJld0qDl7doO2CONqZQPs5LJqKSX+v1wuCAA+NFsMwBOkv\n",
"NVNTSLtgkZPsoH6f3HqrZZucc/BJ05Crh3QRKS3tba2Y9Ash6OVDRUKIM4+patl4ThpMbrqJLS/b\n",
"t6uPk3DE8rL9/iYvLhJ1SrtCaixlVYmrXDcgG0IIb8caH41Z03EzBEEQhGGY9ih5nkLdB4I9+2x4\n",
"332aRl28NuXcoqiMaF+oyUnEmN7aN/2J9MOH0YkTmr+tFTteunHic/r06S2L/UTFpN+Ug7/gYk3g\n",
"MPqn0e+Tj3/cYEsAkzhx8SYnRb+vlzSmnWdDCEnW1/VWWpe2rI0dxolPHMePPfaYtWZULOCzb8g1\n",
"brWeGMefeQYG2qlwcZXozIz+IindBudJUK7es7QfqZj001JWvt73yO99j37kIw7s5lmn6kJf3OxB\n",
"X5t1Hnngzz2nX2xRhdT2FxWTfoTQzv2t7O94VUfy6Ivu6qo861TdqDD4s2VFvvIKffhhzR+XNUsn\n",
"DxWT/iAI2OXdr0r3dNKYSpbEsZ8NNTODVldtG82hwpW8rUCR4IkJrvUMs7/6q9J6AxWTfhXwGSTy\n",
"qxVeGXJyjJKrdoqTSHSeFHttqralgZOSOOzrXyd33WXfbi5qM1tLDx2Sets/bGzQo0dNN8cMFcvw\n",
"QQh1u13f9znnGGPGWBiGlZwAcOILONnZEeOebipIrSBzc5q/nJ5GTz6p80MhNC0qyurPAmmonvRj\n",
"jJeWljjnUsooinDNtkbKE8JW41Zqd/MTSmnPpr0BrsZVuin2uYxqwb72NfLBD5ptSxogpFYGqif9\n",
"ikp6+kNoK3ie0KH2uFU++yzWXkemTRV9UkeOsPbjlGfBnf4zXMXi4ftuj4GKxfr3DaWd/NkV3u9T\n",
"6+vIxLPPooMHLRutIpRS7mJTSTfPsHaeZZ5R4OHDIP3ANjUrtZgrsKb11omNDS/HRolOkjvJ9LT9\n",
"gkX1innq5lm6eV1LvGkESL8unGvHWJ0xMYFWVhzYdTK97GIfeShYVFpyjlH0PAn50ktOKkWnAaRf\n",
"E766it/xDv3fO1kfODOD9HLU6kS9RnN5cJTcKaxHt7RDarzfJ7ffbrw9RgDp10ReuEAPHdL/vfb6\n",
"wNokU7vCSQg7b3hK7+cnTuiXC0W6gzkh8owCvSNH7O/qnieklnc31sIA6a8aTubW8gmTs0qN9udj\n",
"dENqefsbrZ+LzU0HQUshqhcp3Y+A9DtDM88yTySaELa+rvPLfMKkqWs5fdLJSQdLlysVUhObmzt3\n",
"vygatrwMMyJlAKTfDXRmRq8qSB73UHvs6cxtz+Me7seSW6XCyWICfZyE1EoMSL8uKyt5qtNUq9Cu\n",
"k/A3W18vbZx0D+qzD4mbvP7pac3dwVyE1MrcYYD063LhQmnTtkqHtnuYT/p1xlWM5RkuuFpdVSN0\n",
"B4JuuuQSr9wE6QeKx8UL4B05olltMYf0V2x1lRM1dLTKyU1eP3j9+w8D4QiNdyCfT4qQ7tte4ifY\n",
"LJq9RUXJ3yVr1FlaXUWHD+eyubmZ5+d66PUcZa7XAtKvTy7p197AJKf06z2LFcwo1YOvrlIXcTw3\n",
"ef05OXgwb4m97Hie50T69x8g/Y7QmiIGn9QCTmbgneT1OwlHuBHu/MPlfQdIvzM0Xrz8Pun+C1nu\n",
"hcayz3yJW5o4KgWYPxyh4Ys4WUyAECT7jgLS7wbNVJDz53P6pPsvZDkWvUK7ThK3OM9Znlqzb87X\n",
"o2uvTbGPgeFyRb2f8YD0u0EzFWR11Y0wVVH6tajo+Eazb865SLs6a1MMTOFUJ6SWEpD+quEkHJG/\n",
"6Ir1+UCkFVbm/X7ODeD04ni4apvXV4zcw2U9yjxcBumvEmJz037muIHBcqVSQXJeYY23PW8VWF3K\n",
"7JMaxslwudyA9FcJsbmZd1NiF3PLVcKJGm5sOBjMGfFJXWxbqNlj2b/CjJW5RilIvzs0nuD8wqQ3\n",
"zZtzbnlioirzgW5mNTY28vqkjUbmnX/yj8Mc7Vir0WPxft/NQmsI+AC7oPFYOHmSchZPRogeOlSv\n",
"FQkZMRB40fAuhXCz672LcZXc2so7XM6O/d3EMgHSXy80Vcb+uLW6aUUaIbXcc8vIxXI/jLFOgnJ1\n",
"V4ZnXH4hNja8I0cM2C0GkH5naKhwfvewMoNlI2lFThaO6oXU8l1hjRT7/FumUEqdPMM65O9vpqYc\n",
"7PxTJPaknzE2Pz/v+34cxzLH8kUpZbvd9n3f9/12u53nUPqYWBeuocKuto2t6mC5Kgs48/foWpMx\n",
"TrZMKXO+415oNDt3pLRQLEl/kiRxHEdR1O12Mca+7+sdR0o5Pz8vpex0Op1OR0rp+74b9a+KrJSE\n",
"jPOBRgbLThxMHaNO1NBR8WQDuLitmqkKNc/wUX76wsICpRRjHEWR53lJkmgcKo7jMAxbrRYhhBDS\n",
"arWCIGi328bbvDcln8ApHdVJBXESUnODq5Xh+X0mF1dYI1Wh5BVGbUh/r9cLgmA4mhmGoZ70E0KC\n",
"IBj+JIoibj0G52oCp7prcDK33EVXgSok3EbIn+qe9bZK6Wa47KhGqZtCdemwIf1CiJFgMSFEL0oT\n",
"RdHOg1dsa6QcGBAmjQTw3OjUqtvYyLmhhw4uqk2YYWIi6461bH3dwBROxgfSWcmKWvXo6bAk/TvV\n",
"2dSO2/Pz82EYGjlUBoyU9nXiwrsIPmr0zW4Gy9VNddcK3TgpCuKkZIUbyj1GvyrPj6WU44ItGOOB\n",
"T1HcNGyz2QzDUGNUNW6eOQiCVB2JkdK+WT0RE3FSNVtFM10xR4Pl0Ppg2dkUTm6fFGPM+v3yBhf2\n",
"B1knxsfc1nHic/r06S2L71ou6WeMjQvZY4y73W6eg1+RZrNJKdVz+RcWFvKYFpub+ccsmcPfJuKk\n",
"OgtrazNYNjOFMzmJGEN2+y1KaS/r4+TEJ11ZQSVe5bQXMzPoq1/N9ItxL/g48Ynj+LHHHsvcMF1y\n",
"SX8QBCOTrrtiPCtc5XSGYegg1IMQMuSTZg3c51+DA9igKlm/Tnp0Vzvh5L8pExNZfbWSpwxYyuvf\n",
"GRfSTstxrvsOqbD0lzvR7RImpnDwxARbXs7wA0e7MzrB2crw/MNlvW31SowN6Q+CgF2eVaLSPcd9\n",
"nzE2bpnurrovqpuYUR8yvntu0lhN+KSZpzE5L/PCH7OYWRmuQmqpMTJc3n9phDakX93swayAWuE1\n",
"zmfnnKtiD81mc+S/1FLeKIpGfjs7O1tAq8vHiRPV3Z2xEoNl3u+bSjxLj+j3Kzyb4mQwNzmZdb6q\n",
"wsPlwsgV609Pt9v1fZ9zjjFmjIVhOK7zH/SuO7tZzrkQIkmSkbll+4UcXFUIMJMTnSlRwUgZtdLH\n",
"PRVya8uB9JtaHuhkmtfFxIaqVZdhqu38eeRid8aSL8C0JP0Y46WlJc65lDKKoj1GT4SQtbU1IcTO\n",
"lE3P89bW1gpuaSqMCZkQKLXW8H6/lT9vJGOiAswtF44pYcr6TLoYzBkhc6261VX00EPFtGUvSu7u\n",
"WJJ+Rcown6rPU3RjcmHkiVc71lo+04mJrKulnEh/yT0mk6yuovvvd90ITUqubgre7wf29aT0G05A\n",
"vX4djASYnGxbmHmzcicTDBXRlLFkCamx9XVy++3FtWV3XAmTo0ipfVdS/uAHJZ+9B+nXwYgwVWLb\n",
"Qra+TufmbFsVwpgw2d9eY2YGZezR7QsTf/55Yr9EkiGfyRWZRqJ8dbXMW3QhkH4dDApTFTCT1pbl\n",
"tWFf+xr9yEcMGD14UP7gB+m/biTKhK+/PlMCuDx3Lr/RrMgLF2Cflqxka/zGhoEyX0UC0p8ZY8JU\n",
"KzK+83rbTo1ApqczhdTMDOYybluIDxzIbzQr4sUX7VfQlOvrxo7lqKZ3etjf/R194AHXrdgLkH4d\n",
"jAgTMA7+3HNGfNJMBxEnT1baJ82EOH2aPvywgQM1GulDarzX83S357uMjDv/uEoZKPkqMJD+zPAX\n",
"XrA/WHazCaUj5CuvkAcftGxULCw4GcwZEyZHNcAzhdSMpLESQliWAUR9evRMgPRnRq6t2Rcmvrjo\n",
"mSolX/q8STcr5hwt/DElTE5cA7W6KuWX2YkT1ES2WKZZ8Vr5TJkA6XfH9HSGnZVWV01Vuy3/q+Cm\n",
"isPqqmc96cWgMDm5aNkin+vr2Hq2GOecukiyLP/CFJB+Z5APfSj9uJWvrJiKMqXXCCFEjQbL6+u2\n",
"l9chxDk3NpjLgqtKJMh++Ht5Gd90k5lDZZq9L/2LA9LvjGzj1gsXiHXnRQjhxGMySerVVXJry5j0\n",
"p9eI1VVUmyRLN4O5lRVsak1iFp/JjMUiAemvCC58UtTvm8xNth51xe97H//Od9J+2aAwpT4UP3GC\n",
"WF/4U6vBnLxwwcgEQyaEEE4Gc5kA6a8O1qWfPfkk/fjHjRwKv/vd/Ikn0nyTc04M1YOkd99d8pAr\n",
"DOYKx0VZ6UrMLYP0Z4MxRt76VtetsIephT/0jjtSVq2QUpqS/grgJOZuUJgmJuQLLxg7Wmoy9Oib\n",
"m5b3SUYI8a9/3fvoRy0bzQpIf2bIO99p36iT5f6VF6ZyG0UIoX7foDDJkyfTfM2gMNEHHuDp6qgz\n",
"xgz26BUIWJW89nBtpZ9l2eBtGIPhiEwYXO6foRfp91H+7fQywp96yr7H5CoF0CD0Qx/iCwtpv21I\n",
"mDItWIXBXKmoqfRrI0+eJB/7mLGjpVNhzrlBNydbL2I/G89gpk0WKuBI7glO33X1+/Zvq3j++apf\n",
"4Qy48JmyAtKfkc1Ng69NShWWUlbdJ02PPHXKwVDjW98i/+7fWTbqjK0t+1dYvPQS/U//ybJRzrnB\n",
"mTncaPBvfSv1t0tdwAfVVvr1Y7suZo3EM8/Yz/6WUjoZt+JGw+Brk3JcJX/0I3LXXaaMprxujLH6\n",
"9OhOhhpSSoMzc/ToUfn975s6mnNqKv18u9xgHMfZfulCDcU//IN39Khlo5xz75ZbDB5QZtoO3hBp\n",
"o1vr6yYd4ZSRjX4fv+Mdxoymx0kk2slQ46mn8J132jZakWUTNZV+hdomPpv6O7mpTkKHy8sGt2ak\n",
"WVZXucG6T8oXF4n1mjZCCGx0ujVtnqXR/iblYE68/DK1P0Z/8cVKDOZqLf1SyiAIsv2mSI/J9/3h\n",
"JeCXLQcvTJjiOB7OdxqEwtjTT1NzC03x3XcPX7okSUZ6XAtr36WU8/Pzw7E+Owvu5+fn+VBR+4FR\n",
"+fd/TwytmNtJu91ut9uDf0op1YmL48ep0Sp1w88l57zZbO56hc0mz44M5prN5q5XGG1uFuczJUnS\n",
"6/UG/xxcYXnihKlKi4VSU+kffjoxxsPPTZIkw/87fIPZN75BC1ufzTn3PG8giJxz3/eLyDfHjQa/\n",
"fHuNXq83+MT3/Uvnu7mJ773XuHWFEGL4ZOM4TpIEIcSOHaOF7VG+6xVWfy902QQhJEkSpUeq+7l0\n",
"tY2WM8MTE3xlZfBPKSUhZKD+g55Anj5teN5oaBzMOSeEDK5wr9ebn5+/1LyCh8uD11YI8aYLVaSj\n",
"xjnnnKvnFiHUbrfVi8O/8x3vvvuKs2uKmkq/ykdmjBFCPM8bCJ/yWeI4Vo/RJT1ibNCf4w99qKAm\n",
"KWEKgkD54O12O4oi7fUHe0Df8x75/PPDn7RaLfXUxnHc6XS4la3MPc9TV7XX672ZHn7hAn7Pewqy\n",
"yBgLgoAQIoSQUg5f4eJ2SRRCYIzDMFRXuNlsdrvdS52rUTWkd90lT58e/FONaAdXmBCi/s6ffdb7\n",
"/d83aHcYIUQURRhjKaUQgnMeBIEQQp48WVyklHNOKR28OOoZLuIKj4AxbrVaqo9RV/jN/qb067kQ\n",
"Qle5boADQoTQ4iKKY7S4qG5Rb3ERCREvLtLJyRBj/vrr7aNHwzvvFCdPtubm+Ouvxx/7WOeee3rf\n",
"/Gb3ySdNNmXglTAmjh0L77mH/Pzn7eeek//n/wQIBapJTz+NzA41Dh1C2zUVGKX0hhtwuy2PH0cI\n",
"ocVFqq5GHKPiFuDEsbr+ZGVFPPwwP3myNTeXvPAC/2//jX33u8H/+B+FGO310PHjGKHg3LneQw/h\n",
"RiOamiIvv9x+/HH8pS/h224za00IoSqz8t/5Hfre91Ipe4uLYn2d/uhHJEnQ4qL87GcNX2FKB4+T\n",
"/PSn8alTg+vc++Y3u7/92+2VFfHwwwUWNdo2R7//ffZf/gvv98M770TnzvUeeohMTnoPPVSIUc7Z\n",
"f/2v3q23UiHixUXy1FPe+fMeY2xxUfb7hl+coVQF8fGP45/+FMWxenHY8eOde+6JFxflZz8rL140\n",
"a7Qg6ij9CULR3BxqtVAco1YLIYTiOCGEEBKGIUKIIsTa7SZj3aeeQhhThGiSzDMWPPKI4f584JVI\n",
"iW65BbVaGCHZbDKEOp2Oalhbytaf/ZlJo0Pwf/Nvgi98ARGCEWpj7P3RHyHPo72enyRRFBVkVJw7\n",
"h++9F0WRx3nS66G5OdRqBVJ+7nOfe+vtt9O77zZo602l4xzdfTdqtQhCMo65EOHjjyOEZLPZlvLS\n",
"1TaEd/DgJennnL/zna2vfEUZSg4cCP/iLxAhuN1uch49+qhBo8PwrS36uc+hIKC9Xsw5/c//GUVR\n",
"IESz2fQK3Stc3UqVOHfzzaTVQggx38dXX90taGM7KcU73kEffxwhhOK4h1D0J3+CMEZx3BSipd5u\n",
"Q9CZmfZXv6rmBvlb30o/+1nkeZSQtpT04YdRGAacz8dx+Hu/Z9BocdiTfsaYisdRStWoMOcBhRBJ\n",
"kgz0Ov/Rhh+UKIoopYNGKhOZ54TTwzm68Ub11+ErQyklhBS1vzNjcnJSOacqCK7k3vM8FYsvxChC\n",
"vN+n992HEKKUzs/PLywsIIQwxtdff/0jjzxi1tZlF+6aa9SfKg6u/k4p9TzP8BWenkbLy8jzkJQD\n",
"197zvHa7rZ6xIAgwxrSwGUi2vh55njI6Pz9/9uxZhJCKbRbbo2972SrUo/4eBEERL46UEmOMpBzs\n",
"FEYI4ZyrW6nuaaYtMa4Ivv56tL23Eu/3W9tXeHZ2Vl1h9SwVqBJGsST9SZIkSdLpdNSUl+/7S0tL\n",
"OY8ZxzEhpNfraUg/xng4uyMMw51PyYj2GelgxjH82gw/OoU/RtvDjuFHFmNchECI7fK5fH092la9\n",
"4StvXPcRevME2Zkz9JOfVH9XEf9BA8wbHcyjDs3SDz9OpvyVPVAKiDHudDqDjq2I2zoYVw16dIRQ\n",
"EASDEyziTOnUlJobG/aZPM8b3NZCHJdBV83YoEcnhAwPGYvrWY1jQ/rVlNrS0pJ6BKMoklImSZLn\n",
"mWCMYYyHZ2gzQSkdln6z3oEG4gc/GLw2xTmDO6xeltpY9FM7qN4lh0Y21l4VsblJto0WN6AZQT77\n",
"7PBgzpI/yBgayisvvI/Z7lx5vz/coxdutN9HCLEzZ8h2sT9CiL0XeWiepipu/gg2Mnx6vZ4a4Q4+\n",
"CcNwkBSlRxzHeQJ5amyYpwGmuJR38ZOfWHtqyfQ0O3ECISSWl62udVTuoeklRSkRm5vWFH8A7/ft\n",
"deTD2Fx4ODRvXFRkcidHjqCNDYQQOn/egd9WhZ1YrogN6RdCjLwAg1QzPeI4HulLspKzAaZQ41aE\n",
"kNzasif92y6h2Ny0KkxKj4RAVVjraAT52mv21HCA5Y1hnRYtYD/+sf3OlT/1FCn9TixXxEbAZ9c5\n",
"Q22lk1IyxnJOFTDGnnvuuZmZmZHEeatjxqHBstV9BDFWg2WxuUntC1MJelwLiI0NhBC/cCGyLkzs\n",
"298ezGrYg3PpaPc6+51rTkdt3GKdM2fOvPHGG9qHzUou6ZdSjgubDCcwmPWvc4Z6FIyxM2fOTE9P\n",
"j9yG4ZkiG6hUEEqt1nvaTgAXm5uhfWH6+tfJ+99vzRyZnGSMeQjZFCbv8OH4xAn1d6vCtO1AOBhq\n",
"SIld7F5nGeWi8X4/KED619fXf/nLX2ofNiu5pF/la+76Xxjjbreb5+DjLEop8wdtVefheZ79+O9l\n",
"qFQQzusTA0EIEdPrp/aytT2vUAdhUrEXNpRAZQ3x/POmtnFOiTx/3v4IUrloOb3+cZ5rHMerq6va\n",
"h81KLulPmbFrMBiXJInneYNuU5XeVCu5sx7KcmxnD+SFC24DpnZQHpMDYer3+alT5N3vtmeRkEEC\n",
"uBNsev2qJJR86SVa0Hrd3bi0uqpmPpNZLOX1X0rCvfwTjeOo1UZvlgOUUoX+NaS/6Pyz9PAnn/QK\n",
"q+BYHgZBLavhiCNH0MaGXFsjFoXp0pJvIerQo9OpKSkl7/c9m/3NxARCSPT7dbjCBWFD+oMgGKwU\n",
"Vah0z3HfZ4xxzsMw3KkRI3rNGFMVo8w22CZiYwO/9lqGjVVNILe2EOduXhsX+4Q4iYHUK5dpa8t2\n",
"ps3mplhcrIPPVBA2kjvVMzGYFVArvMY53aqUbhzHzWbTQtvc4h0+LDY2eL9vecoBNxri5ZeLq5G5\n",
"O0r0Hblp9mc+2fIyNbfXTRqs5okNmJhAFiPUl/A8tLkp/vmf8a232ja9XwZzlgI+3W7X931VYYMx\n",
"FobhOB9h8Iru/a5yzlVpZSFEs9k0W36rDoiVFXrokFWTjl4YJxtDyq0t8fTTxK77ghsN+cwzBZZc\n",
"3ZWhQrCWcZKixo8fJ0b3unGFJenHGC8tLalZ2b1rtxFC1tbWrlg+jFKqyn5VHkcbpbKFhegrX7Fs\n",
"lh87RgrbiWVX1HygTYsK3GiIzc2wsL1uxsG/9z3vYx+zbLQ+yK0tfvIktb7fbxFYLdqcMhpYntyb\n",
"wiFEra6yTaMht7ZwYTuOjYOvrlp+bSxnHDpma4s9/XRkPVLKV1bsb0Qut7bsG8WNhnjxxdBoLWhX\n",
"1HSXrrJAiNjcJC5q2th/bRBCYnmZ3nWXZaN8ZaUS22QboNGQ/X5x22ruCp6YYIyZ3e83ld1Gw82I\n",
"GRW4UbZNQPod40r67UMmJ9mpU8Vtkz0O/g//QK0v3Ct0s989sN+j05kZtr7uHT1q2S7v94vbKLsO\n",
"gPQ7hvf7nv2KKwhR65EQMjnpwPv2PPnzn5Obb7ZsVvzsZ15thMmV7+LA7vaeE/sAkH7HhO96l5Px\n",
"I3nXuxwYdaER3tveZt8oQshJlMmJUfKWtyD7BVF++ENqfaiBJie93/gN20aLoY5785aK4I037Eu/\n",
"d/Agve46y0bJ5KQT6Q9++lP7whT8xm/YTzlX26BbNoowjl5/3bZRhKJbbnHz4uyXeSOQfsd4Gxv2\n",
"w9/ea68h61EmcvCgk4rNTup1hBgj61lq5MABdOCAZaOIUu/aa20bRcj79V93IP3be67tAyDgU0sw\n",
"dhBlcrJfFUL2Jbh2uLrCTp4oV4+xaUD6XeOkihwh+yNBLRWuhMlJPXC3RcjrwH55cUD6XePqSXLi\n",
"vIAwFUqtniVXPfp+kX6I9bvGidfvxKirkbKT+k5OFny6qkPuxK6Ter1huG/ihyD9rnHyJDkx6spd\n",
"cnKyTvq5Wl3h+hgtBgj4AAAA1A6QfgAAgNoB0g8AAFA7QPoBAABqB0g/AABA7QDpBwAAqB0g/QAA\n",
"ALUDpB8AAKB2gPQDAADUDpB+AACA2gHSDwAAUDtA+gEAAGoHSD8AAEDtAOkHAACoHfaknzE2Pz/v\n",
"+34cx9LEHq2MsWaz6fv+/Pw85zz/AQEAAGqCpXr9SZIkSdLpdAghSZL4vr+0tJTngM1mUwgRhmEQ\n",
"BEIIU+0EAACoAzakX0rZbreXlpYwxgihKIqklEmShLqb+8zPz1NKO9u7L5F9tH8CAACABWwEfHq9\n",
"XhAEeGgLoTAMkyTRO5r6YeRkezYAAIB9gQ2vXwhBL9+vjhCiHe5PkqTb7ZpoFwAAQE2xJP2e5418\n",
"mCdKQwgRQij3PwgCmn0fVN/3d/08CALtMBQAAMAVGSc+p0+f3trastaMXNIvpRyXWoMxHiiykXwe\n",
"BWMMY5wkSbvdjqIIY9xsNsMwzKrXCwsLppoEAACQnnHiE8fxY489Zq0ZuaSfMTYuZI8xLigsI6Xs\n",
"9XqDSeMgCGZnZz3Pg8leAACAlOSS/iAIgiC44tc0AjJ7HIpzvra2tnPSuNVqmbICAACwv7G0pGtn\n",
"XEhvEZaKI404+ODvAwAAZMKG9AdBwBgb/kSle477PmOs3W6PmyGglI4cjXMO6g8AAJAeG9KvAj6D\n",
"WQG1wmvcxCznXBV7aDabu34hiqLhjkGl+qSJOwEAAAAKS4Ucut2u7/ucc4wxYywMw3ETAIMg/nA0\n",
"fxhCSKvVmp2dVXLPGOt2u+O+DAAAAOzEkvRjjJeWljjnUkqVlDnum4SQtbW1XZcCDKCUrq2tqbAP\n",
"zO4CAABkxZL0K1Km+hBC0sTu9+gbAAAAgD2Aev0AAAC1A6QfAACgdoD0AwAA1A6QfgAAgNoB0g8A\n",
"AFA7QPoBAABqB0g/AABA7QDpBwAAqB0g/QAAALUDpB8AAKB2gPQDAADUDpB+AACA2gHSDwAAUDtA\n",
"+gEAAGoHSD8AAEDtAOkHAACoHSD9AAAAtQOkHwAAoHaA9AMAANQOkH4AAIDaAdIPAABQO2on/a++\n",
"+qrrJhggjmPGmOtW5MX3fddNyMs+uBGMsTiOXbciL77vV/1GIITOnz9vzVbtpB8AAAAA6QcAAKgd\n",
"V1mzxBhLkkRKSSmNoghjrH2oJEkYY0YOBQAAUEMsef1JksRxHEVRt9vFGOcJ8jabTc55q9XqdruE\n",
"kNnZWSGEwaYCAADse2x4/VLKdru9tLSk3PMoiqSUSZKEYZj1UJxzIcTCwoL6ZxiGhJB2u93pdAw3\n",
"GgAYo5yeAAAGLUlEQVQAYP9iw+vv9XpBEAyHZcIwTJJE71CU0uFPPM/bBzP7AAAANrEh/UKIEb0m\n",
"hEgpNQ41cpxdDw4AAADsjY2AjxDC87yRDwkhGocKgqDX67Xb7SiK1JGbzWar1cp6nKoPFM6cObO8\n",
"vOy6FXk5e/Ys3AjnLC8vnzlzpuo34uzZs1W/EXresDa/cvHiRe0fSyk557v+F8Z44Iz7vh9F0Yj6\n",
"+74/CNlnZXj5xsLCws5+ZQ8effTRP/zDP3zjjTf0TAMAABTExMSEtVVdubx+la+5639hjLvdbp6D\n",
"j6PZbHqep7oNznkcx8PdzBX5/Oc///nPf76IhgEAAFSFXNIfBEEQBFf8msFYfJIkGGMV7VFH7na7\n",
"s7Oza2trpkwAAADseyzl9e+MC42LFO0NY2wkvIMx1ps2AAAAqC02pD8IgpFJJJXuOe77jLF2u73r\n",
"pMeuqUGWp0cAAACqjg3pVwGfwayAWuE1bj0X59z3/TiOm83mzv8Nw3CkV4jjONM0LwAAAGCphk+3\n",
"2/V9n3OOMWaMhWE4bgJgsPJr18o8hJBWq+X7PqVUHcrzPI3kTgAAgDqTK7kzK5xzVXNt74JrQohd\n",
"lwIMoyJIhBAI9AMAAGTFqvQDAAAAZQDq9QMAANQOkH4AAIDaAdIPAABQO0D6AQAAagdIPwAAQO0A\n",
"6QcAAKgd9rZlLwMGt4a3QBzHI594nrfrcoeynVev1xNCDKrs7SRlgx2e1xVPIeXdcXIKagNUtfbF\n",
"87wwDPNcYVd3IeVZlPlGoMvPghASRdGuS5EcvBEXa0On06GULi0tnT17ttVqUUpdt+gKIIQWLmdt\n",
"bW3n18pzXgsLC0EQUEqDIPA8b9zXUjbYyXmlPIWL6e6Ok1M4e/as53lRFK2tra2trUVRRCk9e/bs\n",
"zm+maZ6rpyv9WZT2Rly8eHFtbY1S2ul0VJO63a5qhl7zzJ5FXaT/7NmzhJDhRyeKok6n47BJVyRN\n",
"x1yq81paWlKPtdo/Z9fvpGywq/NKcwqKK94dV6cQhmG32x3+pNVqRVGk0TyHT1fKs7hY4htxcehx\n",
"Gv4kCAKN5hk/i7pIf6fTGXluVIfsqj1pSCP95TyvPXQzZYOdn1d+6Xd1Cq1Wa+eHO88lTfMc3oWU\n",
"Z3GxxDdiHISQ4X+6eiPqMs1rcGt4+zDGxjW1cueVssEVOq9xd8fVKeycnxBC7AwKp2mew7uQ8iyG\n",
"KduN2JWdO464eiPqMs1rcGt4m/i+L6XEGEspCSGdTmfk6a/ceaVscCXOa++7U55TmJ+f31ndNk3z\n",
"ynMKaMxZKMp/I1TlSsYY53xk51pXb0RdpL+cDuPetFqtIAgGdzdJkmazOfLcVO68Uja4/Od1xbtT\n",
"klNoNpthGO5UjTTNK8kpoPFngSpyIzjnnHPG2M60HFdvRF0CPlVkJA8sDEMppRDCYZOAAZW4O81m\n",
"k1I6blukqrD3WVTiRoRhqPJ8OOc7s1GdUBfpN7g1vEMopSPPdOXOK2WDK3deaMfdcXsKUsrZ2dk9\n",
"FDNN85zfhSuexa6U6kaM0Ol0OOcazTN+FnWRfmRua/iyUbnzStngyp3XTlydgpTS9/0wDPdWzDTN\n",
"c3gXUp5FGkr1LO104Jy8EXWR/qxbw5eTXq830vlX7rxSNrhy54V23B1Xp7CrYu4MgKRpnsO7kPIs\n",
"dqUkN2Icap/awT+dvRHaaaGVw/O8wQqIs2fP7rqsrjx4njeypCUMw12XtJTwvPZOik/ZYLfndcVT\n",
"SHN37J+CWgQ70raLFy9ijHd+OU3znNyF9GdR2huhCIJgxJCalNZrntmzqNEGjcqPGOznbmQgWRxS\n",
"yjiOOecqq0H18Lsmt5XnvNrttnJM1DzbwPNaWFgY/lrKBjs5r/SnkObu2D8Fxliz2dyZ88cY2/mm\n",
"p2mek7uQ/ixKeyMUalJXSqmap5L6d03ysf9G1Ej6FSm3hi8JUkoVzrtig6t1Xih1g8t8XinvTplP\n",
"AaVrXslPoeQ3QgihQlVGmmfqLGon/QAAAEBdpnkBAACAASD9AAAAtQOkHwAAoHaA9AMAANQOkH4A\n",
"AIDaAdIPAABQO0D6AQAAagdIPwAAQO0A6QcAAKgdIP0AAAC1A6QfAACgdoD0AwAA1I7/D6yRGbpO\n",
"DX9qAAAAAElFTkSuQmCC\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAf4AAAF/CAIAAAAn4TwPAAAJNmlDQ1BkZWZhdWx0X3JnYi5pY2MA\n",
"AHiclZFnUJSHFobP933bCwvssnRYepMqZQHpvUmvogJL7yxLEbEhYgQiiog0RZCggAGjUiRWRLEQ\n",
"FBSxoFkkCCgxGEVUUPLDOxPn3vHHfX49884755yZA0ARBQBARQFSUgV8Pxd7TkhoGAe+IZKXmW7n\n",
"4+MJ3+X9KCAAAPdWfb/zXSjRMZk8AFgGgHxeOl8AgOQCgGaOIF0AgBwFAFZUUroAADkLACx+SGgY\n",
"AHIDAFhxX30cAFhRX30eAFj8AD8HABQHQKLFfeNR3/h/9gIAKNvxBQmxMbkc/7RYQU4kP4aT6edi\n",
"z3FzcOD48NNiE5Jjvjn4/yp/B0FMrgAAwCEtfRM/IS5ewPmfoUYGhobw7y/e+gICAAh78L//AwDf\n",
"9NIaAbgLANi+f7OoaoDuXQBSj//NVI8CMAoBuu7wsvjZXzMcAAAeKMAAFkiDAqiAJuiCEZiBJdiC\n",
"E7iDNwRAKGwAHsRDCvAhB/JhBxRBCeyDg1AD9dAELdAOp6EbzsMVuA634S6MwhMQwhS8gnl4D0sI\n",
"ghAROsJEpBFFRA3RQYwQLmKNOCGeiB8SikQgcUgqkoXkIzuREqQcqUEakBbkF+QccgW5iQwjj5AJ\n",
"ZBb5G/mEYigNZaHyqDqqj3JRO9QDDUDXo3FoBpqHFqJ70Sq0ET2JdqFX0NvoKCpEX6ELGGBUjI0p\n",
"YboYF3PAvLEwLBbjY1uxYqwSa8TasV5sALuHCbE57COOgGPiODhdnCXOFReI4+EycFtxpbga3Alc\n",
"F64fdw83gZvHfcHT8XJ4HbwF3g0fgo/D5+CL8JX4Znwn/hp+FD+Ff08gENgEDYIZwZUQSkgkbCaU\n",
"Eg4TOgiXCcOEScICkUiUJuoQrYjexEiigFhErCaeJF4ijhCniB9IVJIiyYjkTAojpZIKSJWkVtJF\n",
"0ghpmrREFiWrkS3I3uRo8iZyGbmJ3Eu+Q54iL1HEKBoUK0oAJZGyg1JFaadco4xT3lKpVGWqOdWX\n",
"mkDdTq2inqLeoE5QP9LEado0B1o4LYu2l3acdpn2iPaWTqer023pYXQBfS+9hX6V/oz+QYQpoifi\n",
"JhItsk2kVqRLZETkNYPMUGPYMTYw8hiVjDOMO4w5UbKouqiDaKToVtFa0XOiY6ILYkwxQzFvsRSx\n",
"UrFWsZtiM+JEcXVxJ/Fo8ULxY+JXxSeZGFOF6cDkMXcym5jXmFMsAkuD5cZKZJWwfmYNseYlxCWM\n",
"JYIkciVqJS5ICNkYW53txk5ml7FPsx+wP0nKS9pJxkjukWyXHJFclJKVspWKkSqW6pAalfokzZF2\n",
"kk6S3i/dLf1UBiejLeMrkyNzROaazJwsS9ZSlidbLHta9rEcKqct5ye3We6Y3KDcgryCvIt8uny1\n",
"/FX5OQW2gq1CokKFwkWFWUWmorVigmKF4iXFlxwJjh0nmVPF6efMK8kpuSplKTUoDSktKWsoByoX\n",
"KHcoP1WhqHBVYlUqVPpU5lUVVb1U81XbVB+rkdW4avFqh9QG1BbVNdSD1Xerd6vPaEhpuGnkabRp\n",
"jGvSNW00MzQbNe9rEbS4Wklah7XuaqPaJtrx2rXad3RQHVOdBJ3DOsOr8KvMV6Wualw1pkvTtdPN\n",
"1m3TndBj63nqFeh1673WV9UP09+vP6D/xcDEINmgyeCJobihu2GBYa/h30baRjyjWqP7q+mrnVdv\n",
"W92z+o2xjnGM8RHjhyZMEy+T3SZ9Jp9NzUz5pu2ms2aqZhFmdWZjXBbXh1vKvWGON7c332Z+3vyj\n",
"hamFwOK0xV+WupZJlq2WM2s01sSsaVozaaVsFWnVYCW05lhHWB+1Ftoo2UTaNNo8t1WxjbZttp22\n",
"07JLtDtp99rewJ5v32m/6GDhsMXhsiPm6OJY7DjkJO4U6FTj9MxZ2TnOuc153sXEZbPLZVe8q4fr\n",
"ftcxN3k3nluL27y7mfsW934Pmoe/R43Hc09tT75nrxfq5e51wGt8rdra1LXd3uDt5n3A+6mPhk+G\n",
"z6++BF8f31rfF36Gfvl+A/5M/43+rf7vA+wDygKeBGoGZgX2BTGCwoNaghaDHYPLg4Uh+iFbQm6H\n",
"yoQmhPaEEcOCwprDFtY5rTu4bircJLwo/MF6jfW5629ukNmQvOHCRsbGyI1nIvARwRGtEcuR3pGN\n",
"kQtRblF1UfM8B94h3qto2+iK6NkYq5jymOlYq9jy2Jk4q7gDcbPxNvGV8XMJDgk1CW8SXRPrExeT\n",
"vJOOJ60kByd3pJBSIlLOpYqnJqX2pymk5aYNp+ukF6ULMywyDmbM8z34zZlI5vrMHgFLkC4YzNLM\n",
"2pU1kW2dXZv9ISco50yuWG5q7uAm7U17Nk3nOef9tBm3mbe5L18pf0f+xBa7LQ1bka1RW/u2qWwr\n",
"3Da13WX7iR2UHUk7fiswKCgveLczeGdvoXzh9sLJXS672opEivhFY7std9f/gPsh4YehPav3VO/5\n",
"UhxdfKvEoKSyZLmUV3rrR8Mfq35c2Ru7d6jMtOzIPsK+1H0P9tvsP1EuVp5XPnnA60BXBaeiuOLd\n",
"wY0Hb1YaV9YfohzKOiSs8qzqqVat3le9XBNfM1prX9tRJ1e3p27xcPThkSO2R9rr5etL6j8dTTj6\n",
"sMGloatRvbHyGOFY9rEXTUFNAz9xf2pplmkuaf58PPW48ITfif4Ws5aWVrnWsja0Latt9mT4ybs/\n",
"O/7c067b3tDB7ig5BaeyTr38JeKXB6c9Tved4Z5pP6t2tq6T2VnchXRt6prvju8W9oT2DJ9zP9fX\n",
"a9nb+aver8fPK52vvSBxoewi5WLhxZVLeZcWLqdfnrsSd2Wyb2Pfk6shV+/3+/YPXfO4duO68/Wr\n",
"A3YDl25Y3Th/0+LmuVvcW923TW93DZoMdv5m8lvnkOlQ1x2zOz13ze/2Dq8ZvjhiM3LlnuO96/fd\n",
"7t8eXTs6/CDwwcOx8DHhw+iHM4+SH715nP146cn2cfx48VPRp5XP5J41/q71e4fQVHhhwnFi8Ln/\n",
"8yeTvMlXf2T+sTxV+IL+onJacbplxmjm/Kzz7N2X615OvUp/tTRX9KfYn3WvNV+f/cv2r8H5kPmp\n",
"N/w3K3+XvpV+e/yd8bu+BZ+FZ+9T3i8tFn+Q/nDiI/fjwKfgT9NLOcvE5arPWp97v3h8GV9JWVn5\n",
"By6ikLxSF1/9AAAACXBIWXMAABcSAAAXEgFnn9JSAAAAHXRFWHRTb2Z0d2FyZQBHUEwgR2hvc3Rz\n",
"Y3JpcHQgOS4xMJremEEAACAASURBVHic7Z1fjCTHfd+LJnm3jPZ8V7Yi7tGhblXJSrRBW+TVgVGA\n",
"RISBHgSQHiLQ6AUE5MVw0IMgL0lsoxuIBAiQBczk2XG8DfLNAuQZSBBsyACxBcUXCIYlbfEuFIFQ\n",
"t9zyrhX7dmXqao+3YobHkJeH2uvt7T8z0931Z3r794FA7c3OdlV3V33rV7/61a8eefDgAQIAAAC6\n",
"xC+4rgAAAABgG5B+AACAzgHSDwAA0DlA+gEAADoHSD8AAEDnAOkHAADoHCD9AAAAnQOkHwAAoHOA\n",
"9AMAAHQOkH4AAIDOAdIPAADQOUD6AQAAOgdIPwAAQOcA6QcAAOgcIP0AAACdA6QfAACgc4D0AwAA\n",
"dI7HrJXEGIvjWEpJKQ3DEGNc+1JxHDPGtFwKAACgg1iy+uM4jqIoDMPRaIQx7vV6tS/V7/c554PB\n",
"YDQaEUKuXbsmhNBYVQAAgDPPIxbO5pVSXrt2bWtrKzHPoygihARBUPVSnPMoijY3N5NPGGPj8Xhj\n",
"Y0NbdQEAAM46Nqz+8Xjs+37aLRMEQRzH9S5FKU1/4nkeY6xpFQEAALqEDekXQmT0mhAipaxxqcx1\n",
"Ci8OAAAATMfGMq8QwvO8zIeEkBqX8n1/PB4Ph8MwDNWV+/3+YDCY/wrf/va3//iP//j+/fuFv11e\n",
"Xv7IRz5So2IAAADzcHBwUParX/u1X/vDP/xDS/V4YB7P8zY3N/MfNrlgUv/8lafzm7/5m5aeLAAA\n",
"QBUee+yx2qpYlfbF9ff7/WTY2NraGg6HnPOqF7H2fA0RhmHVMW8BaTL8Lwhn4EVsbm6GYei6Fk0p\n",
"tC/bRRiGv/AL9gTZRkkaffFxHGOMlbdHXXk0Gq2vr+u6PgAAQBewNMjkDfMapjpCiDGWWTbAGNdb\n",
"NgAAAOgsNqTf9/1M/KUK9yz7PmNsOBwWhgAVhgbVCxYCAADoLPYcPkkgv5RyOByW7efinPd6vSiK\n",
"+v1+/rdBEGRGhSiK8uFDAAAAwBQs5fAZjUa9Xo9zjjFmjAVBULYAkOz8KszMQwgZDAa9Xo9Sqi7l\n",
"eV6l4E4AAADAkvRjjLe2tjjnUsrpCdcIITs7O4VbARSe521tbSkPUhAE4OgHAACoir3MnWjuUB9C\n",
"yExBBycPAABAbdoX19+Q5eVl11XQgOd5Z2C6M2Wpvy2cgRdBCDkDhpTv+21/EQihxx9/3FpZNjJ3\n",
"LhRf/OIXv/GNb3TtrgEAWHCiKHr55ZfffvttO8V1zuoHAAAAQPoBAAA6B0g/AABA5wDpBwAA6Bwg\n",
"/QAAAJ0DpB8AAKBzgPQDAAB0DpB+AACAzgHSDwAA0DlA+gEAADoHSD8AAEDnAOkHAADoHCD9AAAA\n",
"nQOkHwAAoHOA9AMAAHQOkH4AAIDOAdIPAADQOUD6AQAAOgdIPwAAQOcA6QcAAOgcIP0AAACdA6Qf\n",
"AACgc4D0AwAAdA570s8YW19f7/V6URRJKbVcsN/v93q99fV1znnzCwIAAHSEx+wUE8dxHMcbGxuE\n",
"kDiOe73e1tZWkwv2+30hRBAEvu8LIXTVEwAAoAvYkH4p5XA43NrawhgjhMIwlFLGcRwEQb0Lrq+v\n",
"U0o3NjbUPwkh2uoKAADQAWw4fMbjse/7SvcVQRDEcVzvauoPwzDUUzkAAIDuYcPqF0JQStOfEEJq\n",
"u/vjOB6NRjrqBQAA0FEsSb/neZkPm3hpCCFCCGX++76fGVfmIYqiws89z8tXFQAAQBdl4nP9+vX3\n",
"33/fWjUs+fp1XYoxhjGO43g4HIZhiDHu9/tBEFRdNijTd1g2AADAKGXis7e39+abb1qrhqUIH41I\n",
"KcfjcbJo7Pv+tWvXPM+rpNpg2gMA4IQy8WGMPfroo9aqYWOZt4ZDZsqlOOcbGxu6Fo0BAAA6iKUt\n",
"XfktV/U2YWGMKaUZAx+8NAAAAJWwIf2+7zPG0p+ocM+y7zPGhsNh2QoBpTRzNc45qD8AAMD82HP4\n",
"JD4ZtcOrbGGWc66SPfT7/cIvhGGYHhhUqM+UgQQAAADIYGmZdzQa9Xo9zjnGmDEWBEHZAkDixE97\n",
"89MQQgaDwbVr15TcM8ZGo1HZlwEAAIA8lqQfY7y1tcU5l1KqoMyybxJCdnZ2CrcCJFBKd3Z2lNtn\n",
"MBgYqTEAAMDZxWpw55yhPoSQeXz3EKAJAABQD8jXDwAA0DlA+gEAADoHSD8AAEDnAOkHAADoHCD9\n",
"AAAAnQOkHwAAoHOA9AMAAHQOkH4AAIDOAdKvAyEcFCol0ncGTgWc3Cw84bNaKDxhR4D06yCOHbRg\n",
"ztHpDKaWKDlezixOzmPgHNVKLd4UJ0+4JFuiWeLYzRN20pwW7EwRkH5NOGnBTgp1YqZx7qBcKZ3N\n",
"NgCjOHmtTnprOSD9QEWcTDWQi57D+aJN0s3ialC3DwyuIP3a6I7VD6QQJsaG7gyuyIUKM+ZsgWGR\n",
"LAmQfh04WQ+coxnFccxM6Ij9myXEmSBOBQ6FNk2v19N/USfHexAC0n/WEL8w+zHq1wgh0KzU1iZs\n",
"0vFv/IZ98zD+27+1XOL8aH7IQiCM7WtELCVMIhM45/UOD59C/Hd/p/eCDQHp10B88+bM72hXYXH3\n",
"7jxDjnactODxm2/O/I72+Q0/OOAHBzO/pl36o099arr0CyG0N6fxwYH9yVx0/fo8T1g7M8c5KWXZ\n",
"2eC1EefPL9TgCtKvATmZyPfes1yoODwUh4cOfC9PPDGzBTtxg4zHY80XfPNNOZnoveY88P396V8Q\n",
"Quj34z02+9Sm4XCoudDJxP4TFvv74vHHp3ccI9Pl3d2FWl4G6deAODyc2V21qyHb3eWPPoo4j06H\n",
"gZvy7ys4R088Mb0FM8ZM9JyZg6uRFVeEkBCZJxxFUeIN0O4W4Nvb6IknZi5saL/ZmQ0YGZhXoaUl\n",
"9f+Z2zFqOojbt5NS0qZ92tI3Ma8Sh4d6L9gQkH6dZIQgLRna548IIfnBB+rK6XJNKSBCCCH23e+K\n",
"oyNz1y9D/vzn82iTdsTly0iIvL6beJvHVz46Qk88gRBijKXLlVIafbPO5jfLy0iIjNabbs/83XcR\n",
"Y+L0m834940+7UUApF8Ty8t581C7SZjl0iXEuRAiY7ykK6BdpMjly6hoHcxoV8Ef+UhhKUbNQ/nT\n",
"nyYWYuapmis0gTGWKTS5WRMVwEtLTtzu4sIFJETGlZR+y5nm3Rx+6xZ5+mn1c/rKmQeulwUcSED6\n",
"NSAnE3n5MspNEo2/74sXkZQY4zJrhVJqSKcy7ua0MJni8uW8dyvt39fujsAf+xhaWUGMZeZV5gQC\n",
"IcRv3cIXLqif03eUfq3aKyClpCsrcjKRUmaecBJbaeKu6cqKuH077z9MP3DtbVi+8QZ++mmUmy4j\n",
"k4O6+Ku/8lZX5cEBYyzvPzRU6HRA+jXgrazw7W2Um5Kbln4pJZKSEFJm9WtH3L6thCkzn0j/rN1M\n",
"Oy5ieVn87/9ddmVTj/r8eYQQxjhdLjYZFS6PjtS8KoPRtsQ5pysr6oeygkzIopxM0MoK4pxSmh7n\n",
"0g/cyNO+eHH6lfU34Nu36Wc+w3NeNROLCnMC0q+DpSW0ssK+9S1KafIiOedJ2zLydicTjHF+cwoh\n",
"xKDxcvt2IkyZyfLJd4TQ210ZY97qKt/eFrdulc3QhRCe52ksFKXc32nDMyMKGGPNs42Hi4FGh/Bi\n",
"1tbQjRtlr9VElfDSUn5w1d5+8sy8EXMVkP/n/2Tm6A5eNEIIpL85x7J+/jxCyPO8ROWllMlIIITw\n",
"fV+zIj+MjshUhlJqtDGRy5fZ3h56771M9zBaKF1ZQVeuoO3ttEZIKY1qBC56wpxzSmnyTzJrV11l\n",
"Dg/RlStolvpoftrb22hpSSIk792zNoNM4NvbnuclvUMIof+pnsb00JKH37pFLl9Ga2v81VfT7Ydz\n",
"bvpmy7An/Yyx9fX1Xq8XRZGWJiWEiKLI+U56IYS3uqp+TlvcnHPf95ORIOOWMVeZdMMygWrBcns7\n",
"87md7pQ2wDMqbAh+cJC+NfUSbUzS795N/yuzyUjv0xbb297nPsd/8hP+wx+mzZfME9ZcaGIknTuX\n",
"UcOkoPTP2kk/0nzf1Ntbj/14D1dx0qXYH4cUlqQ/juMoisIwHI1GGGMteTnU8oj2jTz1kFLKySSt\n",
"71JKc+P5FJe32ZakovEuXFAefztWoXjjDfUD291NC5NRGGPk0iWEkJxMMsI0GAzMhjNhzK9cQakw\n",
"cCUQ5t6suH3be/559OST6PCw7Alrb1pCCO+Xfzn/uZouJz+b6kQY4/v302NMxmGo/WmTy5f522+j\n",
"/X1CiMGdN3NjQ/qllMPhcHNzk1KKMQ7D0PO8htY6YwxjrN29WxuMMd/fT2uE2TgQzunKipRSLi2h\n",
"gwOUskbNGsKTCVpbQ5cvo/19c+FDGcT3v++99JL6ebow6a2Pkn77UErl0ZH6QWmEnfmNomytyIgf\n",
"JmcFo6KOY2SgpRRNJsnNWjBiyMqKfOQRdNpAdIgN6R+Px77vp0fRIAgaSn8URYPBoHHVNMA5TzQi\n",
"fY95L4Fe8NISxph/5CP06aenqLCJosW778rDw8TtbsMML3qYmbCiIAhMRD0ihND+Pip6kgbdEWtr\n",
"aHc3ubhNt0Bm5mquoOTifH8/03HSdrHeeZ66FMaYb2+nVThv9ZtiMkkvbDjEhvTnTdGG414URZmx\n",
"xCFSSnLx4vTvaLfaTrl9p05O9T4lOZmorogRSlpwPrrGkGSokJvkjjIaoRfGGHnkEYyxXFtDt28X\n",
"dte0a0Izy8votNWffsKmHm/usvnGo7Hok5krQvR0QeY8pWpljlLKH320bEQ3QuK+S8UOuN3nZUn6\n",
"822o9tuVUjLGwjBsXC+dKF//lISLmdjwhnDOvStXEELo+edRbsVVFcQY096FToJeiqJfTr6md7y5\n",
"dy9b+kOMRkeQj38cIcS3t+na2pSv6X2tagYphDgO3i3CkNGTuWx+TqPdxYfPn8cYo5UVVOKvM7q9\n",
"9ngMsGOAHx4iz8vcjomI5PmZna6vOXrfnxZXT9k6s+/7QRBUu9beHnruOYwQeuaZjPQTQuI4Vm+X\n",
"UjocDn3fr1njIlRvUWZnYfgHIcSCZZG3SfVqU7KkjJeWkidsz2K6dAn/+McotfCYrZ6+m5VSkkcf\n",
"VU0leBg2lv6troJmVgM9nNOojB1qcmN0nl0YlMw5D8NQ48Qu6S8Ka56D9IS11+u99dZbnPM7d+4g\n",
"hO7cuaOGn7feemtiMZOSDenXiNrF03yo3Nzc1FKfYyhNp1pMtC9tk5poZMca8eyzyMC4kkcIoexu\n",
"znmYEialEUmolUGbdGUlLf2WLKaLF1FuWDWowhcuqCLSUxxVnEGd2t09Xk1ZWkKn5+jmtolIKY8L\n",
"vXQJMYZK3qbmGaSU3pUr00cSNd3Re9fpt7m5uansVzWkMcaULRtF0csvv6yx0OnYcPho9IcqI5o9\n",
"RKUTWIQ1E4SOk6kpQ4kxZi0k43jWjBAyncVBCLXdfwFzUSGEMMbaK5bZapQuC1l5DsZFP0E119Tg\n",
"apqTRvvhh3ZKTCCEFAaFp6c7JsrlnHvPPoseJkFRY4yrWE9Lcf15da6n12qNMZF+tQ16EYJkMcby\n",
"ww9RytfhZBXaeKG3byM1m1letnfkUDILXllRs6vCXGbpLBrNyUS5FMaZmJt5JBOs/As1sYST4F29\n",
"mvxs3L/03ntovgAe7TVRjtDj1bIUNvrsJz+ZqIQaY1zt5rXh8PF9X+3nSj5R4Z5l31fmfBAE+TeR\n",
"ccQr9V+EJd/jeTHnaG/v5FPG0PXrKIrQ9evIzK7j416hijj9X/7973urq5qPD3uYwId+/vMojtHr\n",
"ryfF4e9/n//2b+OlJXTzJlpd1RkGvr+PKCUq0RXn3kc/Kv7LfzmuxsrK8K//2udc+xM+NYRLWfiE\n",
"j/9rACEEDUPU76ef8PF/9/YIQmLqMnt91tbQcIiOjlAU8evXBy++yPb20D/6R8ct+dw5+eu/rq2s\n",
"/X30cLsGkhJ//etsdxd//et4dxdFkXz1VYTQcdMyp8iFL1R1YX27OpKx7XgyMR6feq2qOOv2qw3p\n",
"Vzccx7ESbrXDa2Njo/DLnHO1Bss5H41GFqqnk83NU6/Q81AUocEARZGJefTxeKMWvZOCHv5XRhH1\n",
"PPzKK9rLRQjhL3wBfeEL6eIoYxIhiZD3W7+FXnlF8w4gjI+vNhighx7SIAgwIUaf8DGqreaeMIoi\n",
"RCn61rd0lZMsQnqeh5SVky+UMXR0hLSflahYXkabmySOuRKpwUAdaYKCQPb79N69Iec6l5QSTd/Y\n",
"oAiNo0h6HkUIeR5GCA0Gst/XVlaeko6DGEPb2+jP/kxXOYmnFCHk/f7vZwtViqG0wiKWHD6j0SiO\n",
"436/H0VRr9cLgqDMmzanw0SNEOqovL7R9lGLwk0xUvdRGDgRxExByc+EoN1dvYW6AmOc3x1isLy7\n",
"d/NFFOzhwhjpi8pQi5CFn6vKHPs2l5eRgZUGz/OU/yq97SZxyGCM8fnzektUTHGsY4wRIadm0pqY\n",
"Ii+cc/zCC0jreYr4odsw+SSTlMk+lqQfY7y1tRUEged5m5ubUwIoCSE7Ozubm5tl0wIFpXRzc3Nr\n",
"a+vOnTvTv2mHRJhU/yyIh/M8rFUj8hUo+NmMODp54JTSGYtvGCONg+vhIfK8jPQXLAB6HjJwcmRm\n",
"RE8HjB2vPayumpD+2V/S6z+cJwaEEI2Da8IUCTp+y3oLvXwZpZ6wCgY5DuXSnYBkTqwmbaaUep43\n",
"03NHCFmc5DyzmUwQQpRSNRFOOm02kQPGGu2IwmdoLQGsq4WphGLVo1T+wz9oL6tQmwzaa0IghJLl\n",
"q/yLtpbPp+AeKdU+zs3OxGVmcC2rzIkKLy2Ze8t2wmenA/n6G7O/j2Z1RYwxolTnFPJhRt+04zWT\n",
"5vC4PZnfJJL2bh3Hnywvm+uuygVRKEz4Zz/TXlyheWhw4ZEQNGtw1Vs65zzfSDL78o6fNiF63SCK\n",
"RPpLfSAG2nDhttC0CtOVlUWJGjcDSL8O7MdxHh6qLTBT5q042aRjDJVkRhWU7IknhKBPfhI9PNDc\n",
"EAXyZ+YtOJ/iFLO2hm7c0HIlKaX3zDPpT/LpDY6nGnrNlxzHu9NzhpRpk7gwDR9eWrI220AIDYfD\n",
"A91rgdMB6TdC8aKrSQO8dM64tCT/8i+1FCGEQA/T6SjKMpWSF15gf/EXWgqdB5sb6IqxkuHyFBcu\n",
"ZN6FRvLnr9lMHZqfbRQel6aRzBLO8QO/etWo+ZJxWkopn3zySXPF5QHpN0K6+Z4YMiZbcFnPpP/q\n",
"X/Ef/lBLEUKI6YnMEsiLL1pwNCWcCJPhQou3U62smNvdpnJ1qPZz6uzyorR9ekmGHGWM619+m8Om\n",
"Ppm5WtxAflzo5cvo1i1DRVg7cWgKIP1mSVtM8tw5oztgk76a3hqOr15Fr72mq4h8eJ/pFarCHpIp\n",
"9ESYTA6uSYRl9hfmR/T0f5PPuWF3hOkDJ8T+flneHsXJQKsvvYT48Y9nfuf4ZldW0NGRlkIXE5B+\n",
"s6QtJvzUU0Y9A8n0Qu1TP+66y8vmSsQYm3a2pLfDpMstdqktLZkbXDPzquTG8ac+xb/+dUOFlkEp\n",
"lRb9hya8PfMcgqZ9oYUsLaHc7pB0JhhTR5wa887VBqTfODYjt5JWa+F8dvQwbU5SqKH0MoWu3uIT\n",
"rFZWtA2u+/vT142TG6f/8l8aVeFMoXaWnUvlz7DvJd1ZTqyKh7mb9FB+LIxKDXmyqULja80dRWnt\n",
"VZYB0m+Ewuz5CCFr3eaUINqyONK7i62hPb+uQh4eTonZ9TxvPB7rH1wPDqaPN9LcMeXlnIo8MZza\n",
"MzPkHP/z/HnNqahOkw4rSp4wpdSoSy0t/faOh0wB0t+YWTHRJ1y5Yq7bZBaOTln9RYdfG8KIxTSL\n",
"U09b0zBQONUodYPoGlwnk8x443lessyLzO3ay9U/LUaTycTJFst0TlZrCxvJE9Z7As+UEgv/aQGQ\n",
"/sbkNMLGW9zdnZ6kwZqXKRMTfbKZ2fyKa8LJIHflilFff/ECA9I2uIqSaML0sWtGpH9q/ff39+1P\n",
"NdIpuG3Kool5VXLuZhmEEPvRySD9xkk3XPFwF64Gcg00f5YIUqtYujK47e3lC0232lO2oV7/7Gky\n",
"u//tCFNmw72Rlc+HObGn1EF7oYWk7+5zn/vcyRM2+VrR6YhSOzebWeY1NMyQixen/NZJ2nmQfrOk\n",
"k455nid+8hNzZSX9kxCSln69ZWQ+SHeVUy3Y8DachEwWWKNO4TSnhMnWasqphMnqXEMzpJvN76s8\n",
"wwozyTsVTqLdMx3EpvWdmC9O1ntB+htRluUjeZee551qTJo8A9M96abcAgtJ+k4tOIULK8AM5A4q\n",
"5NS8St9ZIoUYb0JFbTjdWYwMrkWJKErNF5ODq+P95yD9DZFSeqkDyhPS+TtNTCHznvRMSzqV28fu\n",
"ZshjLl2yd4LjQ6w5hQkhiQFuWiKnpGnSQuGyUJn1gDHmunYRT50Xep53KjXh44/rKbQocCvdd4wM\n",
"rkWBW86NM5B+/TgJh8Dl0cpGA/JKheniRXP717xcJn39FNmkaTfaqbHW5OBaOp5pGlw55/lNc2Wv\n",
"lVIqz51rXmglPM/TOZmzn2wxF7iFzI/oMwHp10+n/C06j+ubm2nSr8szkLNJpxWqa3At2kdWakno\n",
"G1wNHb+lGWODa+lrdTFztQZIf2NyWlMm/TqDbYqYNt7o6DZloYelODl/zuImBv0UmYfGJ5Gz9pGZ\n",
"oNDLNG1wXV01J/2lbneTM1fngPQ3Zm6t0TkVKHJHlBrgmraSzQw9zKJDUCptUDCd1KxMheW9ew5W\n",
"U5CmwbVovDFNWai78YWNoo7j3PfiBJB+u+gKiy5aIjNuHlY8pkPLJoaZ22HSmE5qVvaE8bPPupF+\n",
"+25rhISm01rmf63H6BjnTKf+bxEg/XZpdct7eDTYPHiep0cj9vZIUQxVKSYD8gBtr7UqJvdpdxOQ\n",
"/rOPk0OfdVLJHaEjIK8tT0zaPdLvGF2Ln07yGFtMLbXggPRbRd6/f4aj3c8MlbxMrvA8jzsRskuX\n",
"9KwxOFmQb/W0Wysg/VbBa2tnOGZgEZD37ml5wuTRRysUqumduvGlAIYRN29OT7boBJB+wBTCyRRn\n",
"bU1PoVVsUl3zKgI26SJBCGF7exquc+kSSP9ZQ85x1Gc38TxPnDvnYIrTit1JZdSQfieTSOvhTE5W\n",
"X872xkx70s8YW19f7/V6URQ1eZFSyuFw2Ov1er3ecDh0uyLHv/c98vnPWy6UMYYfPKj0J9byWXYX\n",
"F+1Q/OIvapjizDr7IYvJE4fKgPUq7ViS/jiOoygKw3A0GmGMe71evetIKdfX16WUGxsbGxsbUspe\n",
"r+dW/Uku/8kMdNSWfuIT839ZcwoUoBDr2uR5nnjnHT3XOtPmbVPO6OKcDelXdvrm5ialFGMchqHn\n",
"eXEc17hUFEVBEAwGA5UsYTAY+L4/HA6119kQUkon23D04CSepCXReO2dV7VmbdmJBOtaOlo8bEj/\n",
"eDz2fT89ZQuCoJ70p5PlKsIwLEuav4C0e95a0RMtH3lEw+6q/f1Kcf1OpoCtnle5CWO9cQO5yAtS\n",
"yZIghDBdGaoXDxvSf+qIcIQQQoSQel00f5KZEKLdemqHy5ft73HFH/+4pgtVeL8OGwNzsovYiS3c\n",
"uFB5714l6ccY84MDDWd4VTFfzvYy72MWyhBC5JOf6Hqs6+vrg8Gg6l+V9VI7+ZYZY5Zz+svl5fgv\n",
"/iJoVqjR9DiLRS0Tfvi1r9l+rWqZ137e7MbjK9/eDqrER1BK5c2b4ziu0dkT7J/+eMzpjlMmPnt7\n",
"ex988IGVCiFkR/rNzcH7/X4QBDX6W9nTt3EGCELD4dCmRlBKh6+8wm/dapif0Enqq3qe6OFw2Oio\n",
"69u30dWr1f5kbU2+9lr9EhUVB9dWz3crx0cgFDeW/vyhNDOJXnklaGgRnu44ZeKzu7v74Ycf1i+l\n",
"Ijak3xD9fp9SWi/hapMGdIrqwqRlk0gllEDIoyPL5SKExN27kvMmx5DW8ESLu3cZ542kvzoSIX7r\n",
"VtOrVB9c4//1v4j9SeR7743j2H6u4+ZGZGXz5dIl8Zd/KYTQaBGWiU8URdsWlxZs+Pq1H0Aspbx2\n",
"7Vpt3ddJlWSWCCHP8zSc1rK9jZaXq/6RBmGqzvjNN8fjsc0SMcbxzZsNLyIrZhajlGo7sbYiGpaX\n",
"q/vxxm++ad95wmqcGNEY+eGH7V3An46luP58EE7tsBwVyx8EgXvdrwXf3286Fh4doU9+stJfiLff\n",
"Jr/8y/ZDoewHDlJK2e5uwyfMt7crqQzGmN+65VX1EemA7e42tYWrTzXGb7xhX/rlvXv2pR9jvPiJ\n",
"/OphQ/p938+4t1S4Z9n3GWNl23QLdd/Z6k0t5GQifvQj24Ui5K+t2Q98rOFabY6WNYmqnmhx+zZu\n",
"loqSc1615kKI4LnnLI/onufRf/JPmjpAKk41PM+Lv/MdWtHiaU7hmfVVWcz4CHsOnySQX+3wKrPZ\n",
"Oecq2UO/38/8Sm3lDcMw87fXrl0zUGtT4KeeIr/4i5YLlVLaV2Hf94NPf7rpVarPG5yMN+L2bfLe\n",
"e02skBrviBDiP/NM7RLrQQgJnnuu6VX29x1sIa7lumlu9S/m0WCWlnlHo1Gv1+OcY4wZY0EQlE3J\n",
"k6CFfPQC51wIEcdxZjuYw0QONcZz+5YLQghjbL/9UUpRHDcNBKzY8QghwWc/G1s/wwRj7K2u6l0P\n",
"nMlgMEBRZK04BSEEXbyo5UKVvu5dvdp0a3eNwK2K6btbhCXpxxhvbW1xzqWUYRhOCUojhOzs7BRu\n",
"BfA8b2dnx3BNq1FVTwkh3tWrrFkUIL91q+r44fs++h//o0mhNbEefUgIQb0eeuWVRlepPtXwfR/p\n",
"yqjTCuwnrvilX6pntjdhc3OTffGLlgu1g9WkzZRSz/NmBiMTQiwHq1mDEOI9/3zDi8ijo6oXCYLA\n",
"zXl4LaVi4BYq2mdemVqBW26g1L4Kb2xsIEcLe039Cp319Z9larxUjO13G4QcnYfXGTT4eaoHbmmh\n",
"ThSWi61kt9u9EgAAIABJREFUhBDlUrNcLl1ZabqQvpC+fpD+ZtR4qZQ2tQL291uU/rMtR5xroJ3z\n",
"qrMavKgL3OrDf8oB6W8hk0mlZJYJDibLGOP7920XSghqvm+uBi2dV7lwRyxmvGMxZ9R2Ael3g/3d\n",
"Vd6VK02kv+bfNp/i1OBMJ1zMY39LF0JINNu97CTeseom7WPaM8OuBEi/A7zVVQdukGYlildfpf/0\n",
"n+qqy/y0yTx04t2iFNuPLPI88vjjtgttDP/hD+3vB15YQPpd4MQp3NB4OTrCzfdnVadFFpeG9cAa\n",
"nFGb1AiHh+Tf/lvXlVgUQPpd0FKnsBOcREfUmmrgd9/VXhEAMARIP2ASQpxEspJLl5qcmVXTa9PQ\n",
"AL91qzVx/e5wEzB29279v13UVWKQ/ma0yhPtAEKcPKKGAYtOFiHZG2/gF16wX26LoEtLDlxqnid/\n",
"8pP6f845cpFUaiYg/c1ojzsCWHzq5Jp2tUPQBfjJJ92U28BDy27cwB/9qMbK6AKkvxH289EjVHe8\n",
"wRhZT2qG2hai0z4ahs8uqjviLOEkY+NMQPobUdux0MRlWVNMnYTYL2rGWuCYBu6IDu3TPouA9Dug\n",
"YRQgiOmCgnGj9cC6NJ161mpObiJZGwIT0BQg/Q5oZVaQ115D9rfD1N5+7GTnBKWN1gPr0mRNW9Rd\n",
"J2il/dHGOhsDpB+Ym3qegSamlhA1C224c6JunRue0Wgfcfs2XVtzXYsq2J9XuUoJZRiQfsAwDU2t\n",
"Wn+Ol5aaxPW7MQ+dhAw4Gq5qrld5noOndEZTQoH0N4Dzlk0hO+PrpI6iABtR22/Twtda218kbt/W\n",
"W5N5aBSltqg79UD6GyBlTXdEwzjL2hZTgwBwtrs783g1wA3tsj+a0ST/Wm0Fb7SwcXSEFtKlBtLv\n",
"goZxlo66ep0NRwihBucEsBs38EJaTKW0zgB3YUS7opVL08YA6e8QTjag0ZWVJucE1NwO42T/mosT\n",
"a5ty+zZqfFh0ZRir790CNAHS74aap0Y0o1FmGyeT5do2abN5Vc0xsmMOsUaHvrVL+ls3mZsDkH43\n",
"tC4KsL6Xqckg58QmFaL+Jm37403zcKZaNDz0rSau4izPoqcIpL8+nPOWeaKd0LpBTgi0ulrvT5tM\n",
"cUjdv6WuEkM6CbFvG2x3lyxktUH66yNv3qSf/3zNP67tdm+SOOUszlvLcOJSa4STeVVtnITYtxOQ\n",
"/rNIPau/SbfhXDzySM2/PYvz1jLa51KrTYM7bV1eVVcVduDdMkwrpZ8xtr6+3uv1oijqYPpAcuWK\n",
"6yq0gbaJmhP4/n7tmN0GpdbfC+kkQNNbXQXpd08cx1EUhWE4Go0wxr1ez3WNukG7lLSNcZaOsL9T\n",
"j928iZ95xnKhcDJBhpZJv5RyOBxubm5SSjHGYRh6nhfHset6tYbaxkvtfoOXlvj3vlfvb8Xf/33d\n",
"UrsVZ9k66k81apsgi3pQoitaJv3j8dj3/bSdEgRBG6Xficuyyby19kSbfu5z8sc/rve34v59z/Pq\n",
"/W19WpeaqVM0eTXwWlO0TPqFEBl7gRDizN3fILLCzZ5yJ6EgbTPA5f4+sp/9rYUbXGXtOVmnWFRP\n",
"6WOuK1ANIUTeDKwRO1W2QuD7fhAE81bmgw/qB23VbhBNxrnuBL00gO/v05deqve35NIlxli9mYr4\n",
"v/+3ZqG//uvxK6/Ynh55Hv7yl62W2E5ErqeXic9bb701sThOtEz6dRn4m5ubzS8iDg+D2v2tttUP\n",
"Lsv5aOJSq73ySR59tHahtXNSkhdeQD/6Uc1SF9UmPTPkd4aXiU8URS+//LL5Gh3TMocPgBBC9s93\n",
"bGF0hBs3U+vmVS10fztx8J69IPKWSb+DGOQFg+3tOcib72qq0cLU1oBR6h8H3yR97D//5/xb36r9\n",
"54tJy6QfIZR/8TWbQmtxM/41UdLaCg7yfRbh+/u1zZf68RFCoLp7IfGzz9YsdIFpmfT7vp9JUqjC\n",
"Pd3Upo1+0qOjen9X/2C8Brur3Ozab13yn7YhJ5OuTN8XeA9wy6RftZgkkF/t8Jo/JkczTgzhBuDn\n",
"nmN/+qf1/rb+wXgYN0lHXLPQJjjx17cwuLNdpo987z0HpTbIAmualkX4IIRGo1Gv1+OcY4wZY0EQ\n",
"tNKCWFoSQlhO6UcpHd+8abNERaMjYrrDxYs1/7B2FvuGNmmr3HFNYnbPJO2Tfozx1tYW51xKGYah\n",
"w7PCm7gj1LGFi5nN9YxQ9+3IyaR+k1pbQzduIMsh9rVbkSub1NF0wYlWLGzy8PZJv2IRLP0m7oiW\n",
"nRDtxB3hyCbl+/th7dZV11nEDw4cbCFuRn3Tp12NX1Hbabmo8b4t8/UDzqjtjqiNOz9pE/OwnpUn\n",
"J5Mm23GdrIe7MV8uX0Y3btT5wybW91k8lwakvy5nbouHQVq1HtgEcvky3962X27LJpFNqB1u4MT6\n",
"XmCVAOmvi6NdTk1iohHGbrLYOxKmmhs+GgxUBHJszEHrjgarzwKnXQHpb0ATRas7b20UE01pPV0T\n",
"9g/gRgg1WyLzVldrbr7vjgXdkLoK3qE5CnKRdmU+QPodUXve6sJiEoeHDvLmL/AS2cJRr1U0XL2v\n",
"p+BCtHFwPXszFZD+ttGdRP/Nqbt1uT6tc6k5Wb1v5gOpt7G8oXafvZkKSD8wB23c4Hr5MrK/4lrX\n",
"pQbMCV1bqyf9Tg6g5wcHDjceTQekH1hgmtiktV1qwAKDl5dr/uVk0kiFa43oi5ytCKS/LnCC69zU\n",
"zuHjBCdeXe7CTeQmrU1DametaNhb6/35AntKQfrrImXrtl+6grRojGQMu4jGa7ilqx5OfCBNaVfu\n",
"kwWOUwDp7xZuDPAWST9C7cugWZt79xx4ohd4l1OnAOl3hnjrrcp/w5g8d65JofUMcPn2200KrYer\n",
"zQQdorFNyv/sz6r/Da99ZAqgEZB+N1DfF6+/XuMP8VNPNSq4lvTzoyP7ngHxk5842UzQRsRPf2q/\n",
"UO+ll+SPf2y/XEALIP1uwIt6gEMZDjwDC+wnXTTIxz7mugqLTRtPwjEMSH9NWhkd0TVqBIA7CdwC\n",
"97cFXEi/k8CtOQHprwnf33dw0ApoxPw8/3wd6W8cuFVnIZ1zN+mpFzj0UDtNj0ypG9e/sE5LkP76\n",
"OJB+J4kA27mDAWPM6gWAN6NFp1HKxx93XQV7NMwHdfZsLpD+tmE/EaCUGsabhkduVaf2unTNfJ/N\n",
"cHKMXyvj+uvR+J1CDh/AGYwx11Woy+qqfemvjZOkK65ylC5shhmNSCnlX/3VwubNdwVIf2tgjLG9\n",
"vaZXaU9yMfu7z6Iosr+aIoQQP/hBG11qCNVZSGd7e5Y9pePxmO/vO5guM7bI4w1Ivzuqq7B8+21h\n",
"97Byzvn4f/7PRiUihBAS1UMdnBwSwN55x3KJQoj4z/+8aVKQpSVUdVLYfB5WfSF9fX0dNV4kq5pk\n",
"SQjhZNUHoYXexw7SXwfVgptSvVnwoyPLFpOUkv35nzcMjKuRaNeJd0tK6STRhYaEcdWtS/7qq/bD\n",
"iqSU/G/+puFF2uJ2j155xXUVpgHSXwcp5SJH7OqF7e42PNCjhiN7+KUv2beYMMYapL+ijrtawln/\n",
"6lftF4oxFk42xGjxc1Z0Bsbf+Y6T1fs5AemvAyFk+Nd/7SC40wVOohWllOPmSQKq67gGA7z6iOXE\n",
"jMUXLoyvX294kaqPixDixmZq/oRXVhDnlf4CLy/XO1XGDvaknzG2vr7e6/WiKGoSPyelHA6HvV6v\n",
"1+sNh0MnoXjo7/4OX7jQRumvatVKKenKCq/Y6JvjXb2q4SrVBy03KvzgQdMlHIRkxdMomz9hZzpe\n",
"i6ZCUbFhCCH8K1fQE080KtQklqQ/juMoisIwHI1GGONer1fvOlLK9fV1KeXGxsbGxoaUstfr2Vd/\n",
"fOGC98ILlgvVQlUTnnMefuYzGgqubv5s/tf/qqHcNkA/8YmGbZhcvsyrnkY5mWz90R81KrS66aMs\n",
"iSaFIlTZeyOlJJcuWQ5jFUJ4q6vhV75is9BK2JB+Zadvbm5SSjHGYRh6nhfHcY1LRVEUBMFgMCCE\n",
"EEIGg4Hv+8PhUHudZ7LxH/9jwyvU8C1o6DbVwefPb2xsNLpErZwKxPrNKo2wP5nzrlxpKEyk4mmU\n",
"Qgi0v49ffLFJoTXA9+9rOAmnogGOMXa1xXphszggO9I/Ho9930837iAI6kk/IcT3/fQnYRjad0do\n",
"oYZvwVVsgwPXlotIG4wxXVmxvMFV2ftBENgsVNmkqLkhXNV8mUwGv/u79gWRtiQoyCY2pF8IkelO\n",
"hJB6M9wwDPMX78KORISQlNK7cqWpRtQIALcOY4wghOxbTHfv0ieftCz9qvU2VcPlZfTaa3oqVImW\n",
"SCp+8snBYOC6FouFJenPq7MuQ3J9fd2yxcQYI/fv27eY1DNs+twWeHthGjcz9MPD5uNNnRih5otV\n",
"a2tNrwDMotJqCucc379vrjLNeazJH0spy5wtGOPEejK3DNvv94MgqGExla0z+74/z0BCzp1DzW3D\n",
"qhbTwQH6F/+iaaE1aG2maA2RmtWp45TrxrRVCIGXl13Xoibe1auyynqVlJKWjMdl4vPWW29NLLbY\n",
"RtLPGCtz2WOMR6NRk4vPpN/vU0rrmfybm5va62OcyQQ5CSdtrTBVUuHm4ZXHXLqEGHPgraqCEIJa\n",
"t0mFEBS1tjmtraE//VMtVyoTnyiKXn75ZS1FzEMj6fd9P7PoWoh256mK6QyCwLKrB6hNJQNcSmlf\n",
"HoQQrjYT2EcIETjxER0daZguV0XLdLm185UyLMX15/1CtcNyQPdbByGEv/nm/N/nnDsJY0W3bjmw\n",
"SeGkT9O4mi4vNjak3/f9TKISFe5Z9n3GWNk23ULd1zZVnw/GmP1FSMZY1djtxYEQUtUWxvZT7CJH\n",
"Nun+voNC2wy/e3fxo9TcZBmogg3pVw6fZFVA7fAqs9k55yrZQ7/fz/xKbeUNwzDzt9euXTNQ62mQ\n",
"ZunMahZ6+7Z9jZDb2211zraI9j7hKtsvdJlo9NOf1nIdoyx+xHkjX//8jEajXq/HOccYM8aCIChb\n",
"AEgeWf7Zcc6FEHEcZ9aWF3+A1YaW9lTlcWEtsUxtQAjRbqdAlSSRurpMJS0XQgRXrmgpt1KhLTqe\n",
"yCaWpB9jvLW1xTmXUoZhOGVIJITs7OwIIfIhm57n7ezsGK6pXYSw7YVUCQjnWJzvGk6ECSFt56bx\n",
"n/98/qAiXTbp4p9BL4TwlpYWPODKCVaTNlNKPc+b2ewIIYuc+wIhTaHuTk6sPX9e3L1ru1CgBCml\n",
"Fl+/53lONjEApRwcLLgfD/L1V0ZKaf+lavOTUlotb/PubkccPjqZ2zLgnOvJpVMVV8LUHd/sZLLg\n",
"HQekvzK6JsuFJ/iUSbwQwtPhjqhTefsacfeutkLtp/YrOtPDchDabFwIk1GbqV46yC4D0l8dTcJU\n",
"eGxhPq7JAkKIQm1ijGmLr6/kjjg81CNMq6t5M9P4gYhFYalxHJeqv4sz/JwcHGg06GXhBtfDQ3D4\n",
"nDl0CdPCwBgr6zna0kRXuY5RYXJ1Fm6pNlU/uLg5+IMPzF289E41bl4rKqIwbEnXLhyMMdvdzZdY\n",
"Giu18CoB0g8snMVkVJhKt5HrEya5+Bt0deQoRQihpaW8d6vU96Jr89qVK3np55yXvVktu3AKg9Gn\n",
"FLr4gPSXUnqKpK1QivF4bKcgV5RqhCZhqjZ70CRMlU6s5Zxri48sapZRFOm5eBkrK9VWbq34QGxO\n",
"7IxONYwC0l+d/X2jYcKJHZFWRnlwoK2AqcvLQggTW+QKw4pMzzYKV1PSZlp27NEhTIUHKqTvNIqi\n",
"5J9SSm07w3MutTKD1PQWyDLltbbAYE36p2StB+kHylHZfU9T5j3Ek4m28aZIEBMxiuM4ac2cc12+\n",
"/sKe4GSynH681uZVUsq0+tvxsJVJvOnseGWDK/7Zz+y4v6WUdtQ/fafT/P4LSdelP9MJy7TAyMS5\n",
"yNzLREE4WZNMWrCUkj75pKFSMreWnnYYKjGhuIvu7prbWU0ptS/9KKVNmSAua4c8Z0d3Kw6fU493\n",
"b0/ba53q6eWcu4ogqEfXpT8z5U/+qfIFJZ+3dzGnBvZvNn3mz/GJ4brIqTylNLnB7IRdl0bM8myc\n",
"NK2DAzuZPFTyKwsFZTBUaH5HukoOpn4mhJxSYV1PeNZ42S6V6LT0Zxbo01ovpUyctmn3t0YfyEwo\n",
"pSct2KRNWorGrVVoxk5OI92maHdVZl5lZJI+NV7zVIkmU8lnbs2OO0KlaDRabuGO9PQSi82smWll\n",
"SD60qRK16bT0z+mBTR8rL6U0fYpIeg3w1C9MSn9x/9QYmzxrj6sRYcrtruKcpzUiPQOwRlqYNK58\n",
"5nP4cM7TIYnWFhgopcnb9DxP+xOupuyV0pZUJ60MyYdGPaW66LT0o9PGAmOsMDwDIYQxPuk5xgIV\n",
"OOee5yUF2TReTumRCRUuij9JC5Odm5VSpgvCGLtdmsOPP67tUlPNzPQipE6btCiuPzOgqvbs7Dnr\n",
"2sFQCY0LDMbouvRjjNPNNNGFjIlECDn5xNj2S2UxFf9O32aC6enb0uIo335bV6GFBWUm6dYWPzMG\n",
"mp1Ci9EbKFz+AJVVoX6WN2/S5mfVKp58crofL1nfdnbopitA+hccQkhh51cHBiSjAiHEcSSiJjON\n",
"UipyG47STwBjnNwstnVgoRoGjs1DzpHJoygzLggnpykZGedWVqbnAD+1dGRrbTn9T9Pu73RkmtGC\n",
"yjh5wm1IoN1p6VeKUxaSlXZZnowQN26gtTUtpWOM2RtvzPyOlrJOXTDXAzOlnBoOrSgj5zwIAvUi\n",
"+M2b9LOftVBoGsvbLzOxnnrIvdaMAp7MXPf3zb3WtNf01IFLc+9wroG6r8wBf/Y3T5z4D9tw3nJH\n",
"pf9YZTgvOyI4zanVyLfe0uXwoZTOcyk7Jky6lCnDoV7SBZ04f3Z38YsvGioxLUynlna2t8mv/qqh\n",
"QjMol5qFSWRmRD8ZbwxnbC6eSd++ja5eNVRi/lC/kzUzfQa4nEzy86r0Mm8yoZSTyYKn7USdlf48\n",
"jLEyP3u6YfHXX6f/7t8ZqkPeTjluTJwjwzZpWiZOBNHwvDWzqH7//v2kNtrKyGlQutCTn4+OdHqZ\n",
"TgcCZP0eGKcnlKaxn5uvOG7q1i20vGy5Jghp85QihPAzz0xxqZ0KH1j4yE4E0p8GY5yYY/meefzJ\n",
"ZKLdCZPeyJqMMaeGIiFMS38x+lqwuH175nfOnTunq7iTcn+hoIUXBLy/9pouPx5Cx4EAyQZa9VoL\n",
"tF4I+eCBtkKLSAeMJUjDJ3QWd5CjI51PGCE0z153xpDdteUW5XIA6T9FYo6p1c502zpu0AbG87Id\n",
"jyfhRt/9rvYWnGxnK7UKtXYb8olPzDwwy9zen7zdnf7OsYmqySZNErtncyfkBVEI/IlPaCm0kLLn\n",
"iXUljKtSqOZosXv3EEKMsSnBWlJKOzZT9i23RP07Kv2ZvEuF3ymO8TfgA5np9hWHh97nP6+3UCml\n",
"SliU95M+LFXI99/XVl5JFKB6+Mlwq604hNIXnHL2mfZCk7nabG++YZu0+Na0Ow+lRCn5Sxea7OwV\n",
"QvCjo9LA5Ro8XCTLB2upmhyP6EIg3VurpJRpW61gXsU50piJxBgdlf684kzZz5X+MxNWP1qMeWK2\n",
"BQuBn31WeynJREptYjiOIk30gnNpwO2TUPqcDWzTm54/UkqJpCw8zbEhU1INGjGEMUYlM1f1ihNx\n",
"1D7KpjepZcKKjssy0K2S7F6lbcn8ypwWOir9inxQY/Jz4URSfOc7hsbzMgvxVCy2LpaWUO50oUKn\n",
"sAmGw6H6Qa2sZH8tJX7qKXOlZ2zS5I3zn//c2nbik5roLbFoY23BjkXO0ZUrusrEGLO9PTRzirO/\n",
"b8JmOnXsQeExCUUrPbrIbEc/UQwp5YcfmitXF4+5roADAoTQ9esoigr+u7cnJxPEGH799eRD9bO3\n",
"tyf29uQjj+isSmJs3riBxmOUKhTt7SGEMGPo+nX00ks6C11ZQcm2/l4PffSjJ79Sxak6/PZvT98i\n",
"VB9lluYf/g9+cFw9A4j/9t/I66+rJyxffRUhJK9fJ1KKvT05mciVFZ3uiDS9Hjs6Cp57juzusi9+\n",
"ESFEJxMTT1j8/OdISsYY5xz1+whjdP06RWh8/TqS8uQ5aw2cpZSimzeRkv6y17q3hxBCzzyjsdwk\n",
"YZHkvLDjqJYsXnrJe/55jeUqhBBofR09+ujJ0J1WjC98YdHjOhFC3bT6Y4Tkb/wGGgzQiy+q/8ow\n",
"VD/TP/oj/qlPpX918t/f+R30O7+DP/5xnVW5cAEpe+HePeT76eL4c8/h3/u9438aaL7H5VKq7uv4\n",
"f+lbnmPHQ50SFUVPmP77f888z4QPRAghvve9pCD8r//1SaHqjeszhE9xcKBeK/nv/5387u8eN6H/\n",
"8B9U6UJrbplTZi/GzPPof/7PyW2mG7wJ7+LxNU8XlO44hadT1CM5ApNSym/eTHccGYanWrK5jkPI\n",
"8dv8vd/jzz136pbD0ESh2rEn/Yyx9fX1Xq8XRZGWxieEiKKoXkLw9Ow+vbPf1bZ++aMfZXK5TMvn\n",
"o6vcd95BlBYuchhae+CcqyvnU/siQw//3j2UyGLR9Y0Umpy/NjUnc+kCuyYyieoKf9ZYFj84KLy4\n",
"9v1rp5prKuwis59AfxteWkKMZfqLzS0aerEk/XEcR1EUhuFoNMIYl554XgW1nNXkjL3SQDS775JS\n",
"Ov0gb4NeeIwRQoQQlVUmUWTVXTVqBKVUOYVV9FtmYDP4wE/vl7b0ZpNVPhe5XKa0FnP7tCml+azR\n",
"6mmbE0cpZTr/Xaa56h/hHgYL4XfeQSW5v1qEDemXUg6Hw83NTUopxjgMQ8/zGh7fwxjDGDc0msoa\n",
"R2YBR6G922CMTxQ/1W3yBek1D09yxKdSeKpd/mlF1jvtOPWop9r7GntU4hlIHrXtWV15Yk4jXpf3\n",
"3mOMeb/6q6hkWJ0dw1YR9WBLNxAYfdqpUzTSzBWq1xxCClUCLUa03jzYkP7xeOz7fvo9BUHQUPqj\n",
"KBoMBo2rVkpejLS3p1OGUir+wXTDxQ8NYak3Y/BM7t1DCNF/9s/Yz35WXDHdUw1CiJxMhBDqh/Sv\n",
"0iev2aEsPbgukrkjvnABpZ6kUf2llMrDQyWC05OBa2Z1FZWn6DEu/Q8LzZ/TQilt4oewiQ3pF0Jk\n",
"hseyVMlzEkVRZixpQsbKTh9qoTDaefSKXSVsZxq5cIExRv/xP0af/GShaWbIM1CW28v06TRSyown\n",
"WkX6GxKmk7yV9++L/X0La0XHLC0h9UgPD6ckwtLLycx1ahvW3rnke+8hVDCZS2YAynFqdAlHFzaC\n",
"OwufRe0OoPrP1tZWkyr97Gc/+5M/+ZO9vT0l+nt7e/fu3VPdUllnakqRz6uuXSNUF2Xf/rbRUk5R\n",
"FACeKVQ9BI3dmFI6/PKX0ZUr+GG/TRqA0ZtNG/tThMnQymehMJm2Sem5c2JlBaXygacV0NTYs72N\n",
"Ll1KzvnJm1N6nzAuSnlLKU12jaDUSoOuQiml/FvfUsFgTQzEMr/x3t7eBx980LCS89NI+qWUZWv3\n",
"Kj1h8rUmpWTQ4uo5Ojr65je/ub+/r17D7u4uQogxlhmiMnnVtbdgdOlScgBA0ic9z5uyIVMDJTkV\n",
"MplttC9sHF/53r0hOjk118TZrafKVeJ744Zaek2EyeasvKz9p0/O0oL4+7/PR6mmR3EljkZs0qMj\n",
"dOkS5zwMQ5Qb3kyMrOzGDUKIuH69rBRzeUG81dUm84mynrW7u/uhxb1gjaSfMTYl9dhoNGpy8bIS\n",
"VV7shtf52te+FkXRV7/6VXUpJbVqREm/GEJI+gb1t2AVCrK9rfYxFZpj+scbNW89fx7lokFMlJUB\n",
"nz+PTm9qjeM4bSWYqsClS4yxRJhsOvrL7ijvCG2C53nRl7+sfk7fHU3F7xp6tpxz/6G5qopQY4zp\n",
"h0w+9jE+mWQ23tt3nyrfwPxzqTLLNYqi7e1tffWaQSNfv+/7myWkdV9j+47j2PM89hAVJ17DbMx0\n",
"/moZ3PSRuCzl+++n8wqkwbqPDk/WA73V1YwBknby6HX4ZDiZBFCa7jYm+i3f3CTvv698L5Z04dIl\n",
"8c1vqrLS5mH6PZrLnEFXVtI9wsLZolJK8s476QlHfoXZyDCwvY1XV9OTJ+2dJU06nCkzuCavsvis\n",
"goXEUlx//nHUe0CqwyTSr+I06rkmyhLq5lO/mtMLfOECe+018vbb+Omny/KQIN2Clb5aehlGtVrT\n",
"e39UoZk6JD+XjX/1WV2Vf/u35J138lnhzGkEef75+OZN+iu/Qp56Kr3AYGfgwefPp9XQ5hRnSkGm\n",
"7n1pyZrVr0LyMMZ4aSntHE4PrvnVwYXFhvT7vp9RZxXuWfZ9xljZbDEIgkEK3/cJIWGtndNpiUkr\n",
"DsY4k8fNdNACeeQRdPHiPLMQXbDdXfzuu2h5Od1V0haTwRac28+V0XrTATBTPtHF8S3cvk0+85n0\n",
"aKp9X2sG+dD7MWUIN9e0bDpb6Noa++530a1baoGhbHA1dLP0ySfVviL1T7WmndShLRE+NqRfPZTE\n",
"aa52eJUdiss5V8kepuRY11irhOJz+8rTeeqpw9oav3VL/WzB3FZ4nsf39+nTT6sgy+Q5pFdcjZwb\n",
"roJtHi60Jh9bikF0RHqcM56ZY2kp8bSky0pbMxnLRgNLS+hhCgdr0o8/+1n+5pt0eZk8/3xmcE06\n",
"qfIM6y/77l2EcWadRm1W1V+WSSw5fEajURzH/X4/iqJerxcEwcwwu+mPMhkhOOf1BglCSFkfKLNJ\n",
"Mz2qOYUxasjOJP3ePe/5523uYEjm5mqulnysAmrVz9rF0bt6lb32Wv5z0xud2O6uOvRxyghq5BUf\n",
"HCBCMlPqTFPXLP0rK/If/kH9mBlvdJaSQ04m+Pz5TE/JmCzaZ5ByMkGHhygn9K3TfWQtaTPGeGtr\n",
"S63KhmE45UkRQnZ2dmZOmiilm5ubTaqUnnakm2xm/T3Ti/QH2xweopyFQghJLxw13PmcR9y5g7a3\n",
"0X/j2w2VAAAM2ElEQVT6TxmptZEwzvOC04+0bP6nl/QAgwwdhPAQtR5IV1b48nJafTzPSwLPTUUQ\n",
"TCaIkOB03zG67927enX4jW+gZ5/NP2Fz5ouauaqfbcquODwM19ZQThbS/2yFtwdZTtqsjuyZ+aoI\n",
"IYvz+IxOY73f+i307ruFhRb+rAvyS7+kLp0RoCkueG3Yj71bXkYIUUozE7jkZ0MDHj5/fkprzwil\n",
"FuTdu/j+fWQhk0ERmam853lT1vM0kinUeHnb24jSjY2N9Gd2zBe9dPGolkLceJwJUXuOCCGZWUgm\n",
"Pk97yd6VKwihTAtOm4dG5GN/37L007W14x9y8xujgTfew9PcMmJULyRhTvDFi/Tcuel5mYy81jt3\n",
"puSmRmbc7nhpCRUtLBsd9ojaiNNC904ekH6EEAqCYJ7+b86myLfX9Eigf1/iHNl7TIyFZGkJTb1s\n",
"EAR6uy5eXkY//en0Qo3w//6f+v+MPeh8Oqt97CGXL5NLl6ZLPzJw48FzzyGM00O4IrFmTDRgVx3H\n",
"BCD9CM1tKZjot/4TT9gXJm911cSJ1bMLnYV+k83z8Pvv2zfTfAMn2mtB+xMmKyu28wAihOZoTkb8\n",
"tIeH3qwD3YyurGgEpN8xwa/8ynRhMjGBDT796dnf0e2+dCIQCKHRRz5iv9B5nrB2/GeecaPC9+9P\n",
"9zKZMIS9H/xg5pnV2vvO4N/8G/s2kyFA+l0jhH3pnwf95xM8POTINkLMFCb9D3lWoSi30NIcWpKY\n",
"zywYe3/zN7O+YsAAJ2TmZM5IuWfC0Y+6eSz7YiHETIeP/ikk5w7c34vaZ/TvckIIqZO7p2JkULf/\n",
"kCl19mZnldsW34sTQPo7CcZuNMIJjqZNHcLVE3bSolqyijsTkH7XOIkInmOyfHZwJUxOgnlcRxCd\n",
"fc5KxwHpd42rluTEeAFhMkqn2pKrEf2sSD8s87rGidXvpFBXM2Xdq6lz4cTL7GpPqZNyTW6OKyUI\n",
"zoz/EKTfNU5akpNCXZlLTm7WyTjXqSfcnULNAA4fAACAzgHSDwAA0DlA+gEAADoHSD8AAEDnAOkH\n",
"AADoHCD9AAAAnQOkHwAAoHOA9AMAAHQOkH4AAIDOAdIPAADQOUD6AQAAOgdIPwAAQOcA6QcAAOgc\n",
"IP0AAACdw570M8bW19d7vV4URVLH4dGMsX6/3+v11tfXOefNLwgAANARLOXrj+M4juONjQ1CSBzH\n",
"vV5va2uryQX7/b4QIggC3/eFELrqCQAA0AVsSL+Ucjgcbm1tYYwRQmEYSinjOA7qHu6zvr5OKd14\n",
"ePoSOUPnJwAAAFjAhsNnPB77vo9TRwgFQRDHcb2rqT8MnRzPBgAAcCawYfULIejp8+oIIbXd/XEc\n",
"j0YjHfUCAADoKJak3/O8zIdNvDSEECGEMv9936fVz0Ht9XqFn/u+X9sNBQAAMJMy8Xnrrbcmk4m1\n",
"ajSSfillWWgNxjhRZC3xPArGGMY4juPhcBiGIca43+8HQVBVrzc3N3VVCQAAYH7KxCeKopdfftla\n",
"NRpJP2OszGWPMTbklpFSjsfjZNHY9/1r1655ngeLvQAAAHPSSPp93/d9f+bXajhkplyKc76zs5Nf\n",
"NB4MBrpKAQAAONtY2tKV9wvV24Sl/EgZAx/sfQAAgErYkH7f9xlj6U9UuGfZ9xljw+GwbIWAUpq5\n",
"Gucc1B8AAGB+bEi/cvgkqwJqh1fZwiznXCV76Pf7hV8IwzA9MKhQn3n8TgAAAIDCUiKH0WjU6/U4\n",
"5xhjxlgQBGULAIkTP+3NT0MIGQwG165dU3LPGBuNRmVfBgAAAPJYkn6M8dbWFudcSqmCMsu+SQjZ\n",
"2dkp3AqQQCnd2dlRbh9Y3QUAAKiKJelXzBnqQwiZx3c/ZWwAAAAApgD5+gEAADoHSD8AAEDnAOkH\n",
"AADoHCD9AAAAnQOkHwAAoHOA9AMAAHQOkH4AAIDOAdIPAADQOUD6AQAAOgdIPwAAQOcA6QcAAOgc\n",
"IP0AAACdA6QfAACgc4D0AwAAdA6QfgAAgM4B0g8AANA5QPoBAAA6B0g/AABA5wDpBwAA6Bwg/QAA\n",
"AJ0DpB8AAKBzdE76Dw4OXFdBA1EUMcZc16IpvV7PdRWacgZeBGMsiiLXtWhKr9dr+4tACN27d89a\n",
"WZ2TfgAAAACkHwAAoHM8Zq0kxlgcx1JKSmkYhhjj2peK45gxpuVSAAAAHcSS1R/HcRRFYRiORiOM\n",
"cRMnb7/f55wPBoPRaEQIuXbtmhBCY1UBAADOPDasfinlcDjc2tpS5nkYhlLKOI6DIKh6Kc65EGJz\n",
"c1P9MwgCQshwONzY2NBcaQAAgLOLDat/PB77vp92ywRBEMdxvUtRStOfeJ53Blb2AQAAbGJD+oUQ\n",
"Gb0mhEgpa1wqc53CiwMAAADTseHwEUJ4npf5kBBS41K+74/H4+FwGIahunK/3x8MBlWv0/aJwt7e\n",
"3o0bN1zXoil37tyBF+GcGzdu7O3ttf1F3Llzp+0vop41XJtHHjx4UPuPpZSc88JfYYwTY7zX64Vh\n",
"mFH/Xq+XuOyrkt6+sbm5mR9XpvAHf/AHX/nKVz744IN6RQMAABhieXnZ2q6uRla/itcs/BXGeDQa\n",
"Nbl4Gf1+3/M8NWxwzqMoSg8zM/nSl770pS99yUTFAAAA2kIj6fd93/f9mV/T6IuP4xhjrLw96sqj\n",
"0ejatWs7Ozu6igAAADjzWIrrz/uFyjxF02GMZdw7GON6ywYAAACdxYb0+76fWURS4Z5l32eMDYfD\n",
"wkWPwtAgy8sjAAAAbceG9CuHT7IqoHZ4le3n4pz3er0oivr9fv63QRBkRoUoiiot8wIAAACWcviM\n",
"RqNer8c5xxgzxoIgKFsASHZ+FWbmIYQMBoNer0cpVZfyPK9GcCcAAECXaRTcWRXOucq5Nj3hmhCi\n",
"cCtAGuVBIoSAox8AAKAqVqUfAAAAWAQgXz8AAEDnAOkHAADoHCD9AAAAnQOkHwAAoHOA9AMAAHQO\n",
"kH4AAIDOYe9Y9kVA49HwFoiiKPOJ53mF2x0W7b7G47EQIsmyl2fOCju8r5m3MOfbcXIL6gBUtffF\n",
"87wgCJo8YVdvYc67WOQXgU7fBSEkDMPCrUgOesSDzrCxsUEp3draunPnzmAwoJS6rtEMEEKbp9nZ\n",
"2cl/bXHua3Nz0/d9Sqnv+57nlX1tzgo7ua85b+HBfG/HyS3cuXPH87wwDHd2dnZ2dsIwpJTeuXMn\n",
"/815queqdc1/Fwv7Ih48eLCzs0Mp3djYUFUajUaqGvWqp/cuuiL9d+7cIYSkm04YhhsbGw6rNJN5\n",
"BuaFuq+trS3VrNX5OYXfmbPCru5rnltQzHw7rm4hCILRaJT+ZDAYhGFYo3oOW9ecd/FggV/Eg1Rz\n",
"Sn/i+36N6mm/i65I/8bGRqbdqAHZVX3mYR7pX8z7mqKbc1bY+X01l35XtzAYDPIf5u9lnuo5fAtz\n",
"3sWDBX4RZRBC0v901SO6ssyr8Wh4+zDGyqrauvuas8Ituq+yt+PqFvLrE0KIvFN4nuo5fAtz3kWa\n",
"RXsRheRPHHHVI7qyzKvxaHib9Ho9KSXGWEpJCNnY2Mi0/tbd15wVbsV9TX87i3ML6+vr+ey281Rv\n",
"cW4BldyFYvFfhMpcyRjjnGdOrnXVI7oi/YtpME5nMBj4vp+83TiO+/1+pt207r7mrPDi39fMt7Mg\n",
"t9Dv94MgyKvGPNVbkFtA5XeBWvIiOOecc8ZYPizHVY/oisOnjWTiwIIgkFIKIRxWCUhoxdvp9/uU\n",
"0rJjkdrC9LtoxYsIgkDF+XDO89GoTuiK9Gs8Gt4hlNJMm27dfc1Z4dbdF8q9Hbe3IKW8du3aFMWc\n",
"p3rO38LMuyhkoV5Eho2NDc55jeppv4uuSD/SdzT8otG6+5qzwq27rzyubkFK2ev1giCYrpjzVM/h\n",
"W5jzLuZhodpS3oBz0iO6Iv1Vj4ZfTMbjcWbwb919zVnh1t0Xyr0dV7dQqJh5B8g81XP4Fua8i0IW\n",
"5EWUoc6pTf7prEfUDgttHZ7nJTsg7ty5U7itbnHwPC+zpSUIgsItLQt4X9OD4uessNv7mnkL87wd\n",
"+7egNsFm6vbgwQOMcf7L81TPyVuY/y4W9kUofN/PFKQWpetVT+9ddOiARmVHJOe5a5lImkNKGUUR\n",
"51xFNagRvjC4bXHuazgcKsNErbMlltfm5mb6a3NW2Ml9zX8L87wd+7fAGOv3+/mYP8ZYvqfPUz0n\n",
"b2H+u1jYF6FQi7pSSlU9FdRfGORjv0d0SPoVcx4NvyBIKZU7b2aF23VfaO4KL/J9zfl2FvkW0HzV\n",
"W/BbWPAXIYRQriot1dN1F52TfgAAAKAry7wAAABAAkg/AABA5wDpBwAA6Bwg/QAAAJ0DpB8AAKBz\n",
"gPQDAAB0DpB+AACAzgHSDwAA0DlA+gEAADoHSD8AAEDnAOkHAADoHCD9AAAAneP/A3+0JKa9NZ5Q\n",
"AAAAAElFTkSuQmCC\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%matlab\n",
"y = y_sr;\n",
"\n",
"%% filtre de Butterworth\n",
"% on combine une passe-haut et un passe-bas, de maniére à retirer uniquement les fréquences autour de 0.3 Hz\n",
"y_f = FiltrePasseHaut(y,freq,0.35);\n",
"y_f = y_f+FiltrePasseBas(y,freq,0.25);\n",
"\n",
"%% représentation du signal filtré\n",
"figure\n",
"plot(ech,signal,'r')\n",
"hold on\n",
"plot(ech,y_f,'k')\n",
"err = sqrt(mean((signal-y_f).^2))\n",
"\n",
"%% représentation du signal brut\n",
"figure\n",
"plot(ech,signal,'r')\n",
"hold on\n",
"plot(ech,y,'k')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"En combinant une filtre passe-haut et un passe-bas, de maniére à retirer uniquement les fréquences autour de 0.3 Hz, on peut restaurer le signal de maniére trés précise, et obtenir une erreur proche de 1%, meilleure que le 3% obtenu par moyenne mobile."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
sdpython/ensae_teaching_cs | _doc/notebooks/sklearn_ensae_course/01_data_manipulation.ipynb | 1 | 177897 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 2A.ML101.1: Introduction to data manipulation with scientific Python\n",
"\n",
"In this section we'll go through the basics of the scientific Python stack for data manipulation: using numpy and matplotlib."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*Source:* [Course on machine learning with scikit-learn](https://github.com/GaelVaroquaux/sklearn_ensae_course) by Ga\u00ebl Varoquaux"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can skip this section if you already know the scipy stack."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**To learn the scientific Python ecosystem**: http://scipy-lectures.org"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"# Start pylab inline mode, so figures will appear in the notebook\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Numpy Arrays"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Manipulating `numpy` arrays is an important part of doing machine learning\n",
"(or, really, any type of scientific computation) in Python. This will likely\n",
"be review for most: we'll quickly go through some of the most important features."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0.93806505 0.88546824 0.72716304 0.04025777 0.89691774]\n",
" [0.54692084 0.56108889 0.77577327 0.62409764 0.17180018]\n",
" [0.96342087 0.60346547 0.16957905 0.58235256 0.22502235]]\n"
]
}
],
"source": [
"import numpy as np\n",
"\n",
"# Generating a random array\n",
"X = np.random.random((3, 5)) # a 3 x 5 array\n",
"\n",
"print(X)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.9380650481256236\n",
"[0.54692084 0.56108889 0.77577327 0.62409764 0.17180018]\n",
"[0.88546824 0.56108889 0.60346547]\n"
]
}
],
"source": [
"# Accessing elements\n",
"\n",
"# get a single element\n",
"print(X[0, 0])\n",
"\n",
"# get a row\n",
"print(X[1])\n",
"\n",
"# get a column\n",
"print(X[:, 1])"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0.93806505 0.54692084 0.96342087]\n",
" [0.88546824 0.56108889 0.60346547]\n",
" [0.72716304 0.77577327 0.16957905]\n",
" [0.04025777 0.62409764 0.58235256]\n",
" [0.89691774 0.17180018 0.22502235]]\n"
]
}
],
"source": [
"# Transposing an array\n",
"print(X.T)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0. 3. 6. 9. 12.]\n"
]
}
],
"source": [
"# Turning a row vector into a column vector\n",
"y = np.linspace(0, 12, 5)\n",
"print(y)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[ 0.]\n",
" [ 3.]\n",
" [ 6.]\n",
" [ 9.]\n",
" [12.]]\n"
]
}
],
"source": [
"# make into a column vector\n",
"print(y[:, np.newaxis])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There is much, much more to know, but these few operations are fundamental to what we'll\n",
"do during this tutorial."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Scipy Sparse Matrices"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We won't make very much use of these in this tutorial, but sparse matrices are very nice\n",
"in some situations. For example, in some machine learning tasks, especially those associated\n",
"with textual analysis, the data may be mostly zeros. Storing all these zeros is very\n",
"inefficient. We can create and manipulate sparse matrices as follows:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0.41799001 0.20034867 0.60892716 0.25861014 0.63509755]\n",
" [0.65058502 0.0098216 0.13038958 0.03960645 0.55062935]\n",
" [0.94271976 0.28736949 0.21038553 0.49161759 0.11113543]\n",
" [0.80481651 0.09016237 0.40425573 0.56510904 0.53661611]\n",
" [0.079217 0.15374011 0.76457524 0.1097451 0.91216209]\n",
" [0.21447349 0.7089186 0.70915116 0.44892699 0.80017261]\n",
" [0.67488076 0.02466962 0.67453018 0.00671606 0.21792525]\n",
" [0.61421541 0.41031706 0.05108445 0.18081791 0.9790548 ]\n",
" [0.91433767 0.15576258 0.07304524 0.53041295 0.46649357]\n",
" [0.83730157 0.89792046 0.7531655 0.05661956 0.13875142]]\n"
]
}
],
"source": [
"from scipy import sparse\n",
"\n",
"# Create a random array with a lot of zeros\n",
"X = np.random.random((10, 5))\n",
"print(X)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0. 0. 0. 0. 0. ]\n",
" [0. 0. 0. 0. 0. ]\n",
" [0.94271976 0. 0. 0. 0. ]\n",
" [0.80481651 0. 0. 0. 0. ]\n",
" [0. 0. 0.76457524 0. 0.91216209]\n",
" [0. 0.7089186 0.70915116 0. 0.80017261]\n",
" [0. 0. 0. 0. 0. ]\n",
" [0. 0. 0. 0. 0.9790548 ]\n",
" [0.91433767 0. 0. 0. 0. ]\n",
" [0.83730157 0.89792046 0.7531655 0. 0. ]]\n"
]
}
],
"source": [
"# set the majority of elements to zero\n",
"X[X < 0.7] = 0\n",
"print(X)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" (2, 0)\t0.9427197583439572\n",
" (3, 0)\t0.8048165053861909\n",
" (4, 2)\t0.7645752378228468\n",
" (4, 4)\t0.9121620939410845\n",
" (5, 1)\t0.708918601388826\n",
" (5, 2)\t0.7091511593075851\n",
" (5, 4)\t0.800172608559929\n",
" (7, 4)\t0.9790548029613194\n",
" (8, 0)\t0.9143376669464592\n",
" (9, 0)\t0.837301565304061\n",
" (9, 1)\t0.8979204572473508\n",
" (9, 2)\t0.7531655008508734\n"
]
}
],
"source": [
"# turn X into a csr (Compressed-Sparse-Row) matrix\n",
"X_csr = sparse.csr_matrix(X)\n",
"print(X_csr)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0. 0. 0. 0. 0. ]\n",
" [0. 0. 0. 0. 0. ]\n",
" [0.94271976 0. 0. 0. 0. ]\n",
" [0.80481651 0. 0. 0. 0. ]\n",
" [0. 0. 0.76457524 0. 0.91216209]\n",
" [0. 0.7089186 0.70915116 0. 0.80017261]\n",
" [0. 0. 0. 0. 0. ]\n",
" [0. 0. 0. 0. 0.9790548 ]\n",
" [0.91433767 0. 0. 0. 0. ]\n",
" [0.83730157 0.89792046 0.7531655 0. 0. ]]\n"
]
}
],
"source": [
"# convert the sparse matrix to a dense array\n",
"print(X_csr.toarray())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Matplotlib"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Another important part of machine learning is visualization of data. The most common\n",
"tool for this in Python is `matplotlib`. It is an extremely flexible package, but\n",
"we will go over some basics here.\n",
"\n",
"First, something special to IPython notebook. We can turn on the \"IPython inline\" mode,\n",
"which will make plots show up inline in the notebook."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"# Here we import the plotting functions\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYYAAAD8CAYAAABzTgP2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xd4VPeV8PHvGVUkhIR6RwJEkQABlsEYV0x1AZc4tmPHJU68Jd7kdXaT2NndZF8n2Ti7aW+ycRLHJbaTuMYYjMEgY9wwGGTTJNFBoF5RQV2a3/uHRl4JSxTNaO6U83meeTRz5965RzCaM/f8mhhjUEoppfrZrA5AKaWUZ9HEoJRSahBNDEoppQbRxKCUUmoQTQxKKaUG0cSglFJqEE0MSimlBtHEoJRSahBNDEoppQYJtDqAkYiNjTUZGRlWh6GUUl7lk08+qTPGxJ1rP69MDBkZGRQUFFgdhlJKeRUROXE++2kpSSml1CCaGJRSSg2iiUEppdQgmhiUUkoNoolBKaXUIC5JDCLytIjUiEjhMM+LiPxaRI6IyF4RmTvguXtE5LDjdo8r4lFKKTVyrrpi+BOw/CzPrwCyHLcHgN8BiEg08ANgPjAP+IGIjHdRTEoppUbAJeMYjDHvi0jGWXZZBTxn+tYR3S4iUSKSBFwF5BtjGgBEJJ++BPOCK+LyBcYY9pU3UVzRTI/d0NNrZ2xoEFdOiSMuIsTq8JQaVQerWjhe10pDaxcNrZ0kRo5hfmY0qePHICJWh+ez3DXALQUoHfC4zLFtuO2fIyIP0He1QXp6+uhE6UFKG9p4aWcpb+yt4ER92+eeF4G56eO5bmYSd16STkhggAVRKuV67V29rN1Tzp+3n2RfedOQ+yRHhrJydgr/ePUkxoUGuTlC3+euxDBUajdn2f75jcY8ATwBkJeXN+Q+vsBuNzy3rYSfvnWQzp5eFk6O5etXTWbBpBhCgwIItAkVTe28XVzDpuIqHl1XzF8+PsFjt8zi4oxoq8NXyimb91fz7Vf30tDaRVb8WP7vyhwumjCe2LEhRIUFUVLfyo7jDXxwuI4/vH+UVwpK+eelU7nt4jQCbHoF4SruSgxlQNqAx6lAhWP7VWdsf9dNMXmc0oY2/uWVPXx8vIErp8TxnzfPJCVqzOf2Gx8eTE5yJN9cnMWWgzX82+pCbv39Nu6cn873b8jWqwfldTp7enlswwGe2VpCdtI4Hr9zLvMzoz9XLpqWOI5pieO4e0EG+8qa+OG6Yr63eh+vfVrGH+/OY3x4sEW/gW+RvrK/C16or41hnTFmxhDPXQc8CFxLX0Pzr40x8xyNz58A/b2UPgUu6m9zGE5eXp7xtbmSDlQ1c+cfP6arx86/X5/NrXmp511Dbe3s4Rf5h3jqw+NcnhXLE1/OY0ywJgflHepOd3LvMzsoLG/m3kszeOTaaef95cYYw+pd5Tz82j5Sx4/h2fvmkRYdNsoRey8R+cQYk3fO/VyRGETkBfq++ccC1fT1NAoCMMb8Xvo+4f6HvoblNuA+Y0yB49ivAN9zvNSPjTHPnOt8vpYYiiuaueupjwkKEF742iVMjBs7otd5uaCUh/+2l7wJ0Tx1bx4RWntVHq6xrYvbn9hOSX0rv759DktzEkf0OjtLGvjqswUEBdj4030XMyMl0sWR+ga3JgZ386XEUFjexF1PfcyYoABe+NolZMSGO/V6b+yp4KGXdpOTPI4/f3W+JgflsU539nDnkx+zv6KZp+7N4/Ksc84GfVaHq1u45+kdtHX38vo/LnT6b8kXnW9i0JHPFqpu7uDeZ3YQHhzISw8scMkb+YbcZH5/10UUVjTzzy/vwW73vsSvfF9Hdy/3/2knheVN/PbOuU4nBYCshAheeOASAL76XAHNHd1Ov6a/0sRgke5eO1//y6e0dfXy7FcuJj3GdXXRxdkJfO/a6Wwqrubxd4+47HWVcpUfv7mfj4838Isv5rIkO8FlrzshJpzf3XkRJXWtPPjXXfT02l322v5EE4NFfrL+AAUnTvHTW2YxOT7C5a//lYUZrJqdzM/zD7HlYI3LX1+pkdqwr5Lnt5/ga5dnsmr2kMOWnLJgUgw/vHEG7x+q5T/XH3D56/sDTQwWWLe3gqe3HufeSzO4ITd5VM4hIjx28yymJY7jmy/sorTh84PklHK30oY2vvO3veSmRfHtZdNG7Tx3zEvnngUTeHrrcT44XDtq5/FVmhjcrLq5g0f+to+56VF879rpo3quMcEB/OGui+i1G763eh/e2NFA+Y7uXjvfeHEXGPjN7XMIDhzdj59Hrp3OxLhwvvvqXlq0veGCaGJws/9YW0RXr51ffHH2qP9hAKTHhPGd5dP44HAdq3eVj/r5lBrOHz84xq6TjfzklpkubVMbTmhQAD+7NZeq5g7+c/3+UT+fL9HE4Eb5xdVsKKziG9dkubUr3ZcvmcDc9CgeXVdM3elOt51XqX5lp9r49ebDLMtJ4PpZo1M+Hcrc9PF87fKJvLCjlPcPaUnpfGlicJPTnT18f00hUxMieOCKiW49t80m/PSWWbR19vLoG8VuPbdSAP/3jWIE4fs35Lj93A8tmcKkuHAeeW0f7V29bj+/N9LE4CY/23iQquYOfnLLTIIC3P/PnpUQwdevnszaPRW8p9+clBtt3l9NfnE131ycNeTcX6MtNCiAn9w8i/LGdp784Jjbz++NNDG4weHqFp7bVsKd89OZm27dOkT/cNUkJsSE8ZP1++nVgW/KDdq7evnB2iKy4sfylYWZlsUxLzOa5TmJ/O69o9Q0d1gWh7fQxOAG/73xIGHBgXxryVRL4wgOtPHtZVM5UNXCa5+WWRqL8g9Pbz1O2al2Hl01wy2dLc7m4RXT6O618/NNhyyNwxtoYhhln5w4xabiav7uiolEe8CUwNfNTCI3NZJf5B+io1vrrWr0NLV384f3jrJ4ejwLJsVYHQ4ZseHcsyCDlz8ppbii2epwPJomhlFkjOGnGw4QOzaE+y+37jJ6IBHhkWunU9nUwTNbS6wOR/mwP75/jOaOHsuvlAf6p0VZRI4J4sfri3Vcz1loYhhFWw7WsKOkgW9eM5mwYHetiXRul0yMYdG0eB5/9winWrusDkf5oLrTnTy99Tg35CaTnTzO6nA+ExkWxD8tymLrkXq2Hzvrsi9+TRPDKLHbDf/11kEyYsK4fZ7nrVH98IppnO7s4QntpaFGweNbjtLZY+ehxVlWh/I5d85PJ3ZsCL9557DVoXgslyQGEVkuIgdF5IiIPDzE878Ukd2O2yERaRzwXO+A59a6Ih5PsKm4mgNVLTy0ZIol3VPPZUpCBNfOTOL5bSdoatfpApTrVDS28+ftJ/jC3NQRLzo1mkKDAvj7Kyfy0dF6Ckr0qmEoTn9iiUgA8FtgBZAN3CEi2QP3McY8ZIyZbYyZDfwGeG3A0+39zxljVjobjycwxvC7946SHh3GdTOTrA5nWP941SROd/bw/LYSq0NRPuSJ949hMHzDA68W+n1pfjrR4cH8+h2dln4orvgqOw84Yow5ZozpAl4EVp1l/zuAF1xwXo+17Wg9e0ob+bsrJxLogVcL/XKSI7l6ahxPby2hravH6nCUD2ho7eLFnSe5cXaKJYPZzldYcCBfvTyT9w/Vsru08dwH+BlXfGqlAKUDHpc5tn2OiEwAMoF3BmwOFZECEdkuIje6IB7LPf7uUeIiQrhlbqrVoZzTg4sm9/0x7yg9985KncPz207Q0W13+7QvI3H3ggwixwTxP9rW8DmuSAwyxLbh+oHdDrxqjBnYgT7dsQbpl4BficikIU8i8oAjgRTU1nrulA57yxr58Egd91+WSWhQgNXhnNNFE6KZnxnNE+8fo6tHV7tSI9fe1cuz20pYPD2erATXLz7lamNDAvnKwkze3l/DwaoWq8PxKK5IDGVA2oDHqUDFMPvezhllJGNMhePnMeBdYM5QBxpjnjDG5Blj8uLinF8fdrT87t2jRIQGcud8z+uJNJyvXz2ZquYOVu/S0dBq5F79pJSG1i4euGLI73Ye6e4FEwgJtPHM1uNWh+JRXJEYdgJZIpIpIsH0ffh/rneRiEwFxgPbBmwbLyIhjvuxwELAa6f/LKlr5a2iKu5eMIGI0CCrwzlvl2fFMj1pHM9sLdFBP2pEenrt/PGD48xJj+LiDOvmA7tQ48ODuXluKqt3ldOgY3o+43RiMMb0AA8CG4H9wMvGmCIReVREBvYyugN40Qz+5JkOFIjIHmAL8JgxxmsTw3PbThAgwj0LMqwO5YKICPddmsGBqhYd9KNG5K2iKk42tPF3V0xCZKjqsuf6ysIMOnvsvLDjpNWheAyXDMc1xqwH1p+x7ftnPP6PIY77CJjpihis1trZwysFpayYmUT8uFCrw7lgK2cn85MN+3n2oxKPmNdGeZdnPyphQkwYS7ITrA7lgmUlRHB5VizPbSvha5dPtHyyP0+g/wIusnpXOS2dPdx76QSrQxmR0KAAbp+XzqbiKspOtVkdjvIi+yub2VlyirvmTyDA5l1XC/2+sjCT6uZONhRWWh2KR9DE4ALGGJ7bVsKMlHGWrrfgrLsu6Utqz28/YXEkyps8v/0EIYE2bs3z/O7Zw7lyShwTY8N56sPj2s6GJgaX2HasnkPVp7l7QYbX1VcHSokaw7KcRF7aWapLIKrz0tzRzeu7ylmZm0xUmPXTyo+UzSbctzCDvWVN7NIBb5oYXOHZj0oYHxbEylz3LXI+Wu65NIPGtm7W7C63OhTlBV77pIy2rl7u9rIOF0O5cU4KYcEBvKiN0JoYnFXR2E5+cTW3XZzuFQPazmV+ZjRTEyL4q/5xqHMwxvD89hPkpkUxMzXS6nCcFhHa9+XujT2VNHf498SSmhic9EpBGXaDVw1oOxsR4fZ5aewta6KoosnqcJQH23a0nqO1rdx9iXd2uBjKHfPSae/uZc3u4cbo+gdNDE6w2w0vF5Ry2eRY0qLDrA7HZW6ak0JwoI2Xdur8SWp4f9lxkqiwIK6b5bkzCF+oWamRZCeN468fn/TrRmhNDE7YerSO8sZ2brs47dw7e5GosGBWzEhk9a5yXRdaDelUaxf5RdXcNCfFJ0qo/USEO+ans7+ymb1l/nvFrInBCS/uLCUqLIilOd43qOdcbrs4jZaOHu3XrYa0Znc5Xb12br3It74UAayancyYoAC/HgmtiWGEGgZ8YwoJ9J1vTP0uyYxhQkwYL+h03GoILxeUMTMl0qPWc3aVcY5G6LV7Kmjx00ZoTQwjtHpX3zcmXysj9bPZhNsuTmPH8QaO1Z62OhzlQQrLmyiubOaLXjyg7Vxun5dGW1cv6/b65xWzJoYRMMbw8s5SctOimJboe9+Y+n1hbioBNtFGaDXIKwWlBAfaWJk75HpcPmF2WhQT48J57VP/nIpeE8MI7Clr4mB1C7fl+ebVQr/4caFcPTWO13eX02v33x4a6n91dPfy+u4KluckEhnmPVPLXygR4Za5qewsOcWJ+larw3E7TQwjsPrTMkICbVyf6zvd9IZz05xUqps7+ehondWhKA+QX1xNU3s3X/TxL0XQ121bBF771P9mAdDEcIG6e+28sbeSxdkJjPOixXhG6prp8USEBvrlH4f6vFc/KSMlagyX+sHU7MmO3/O1XWXY/eyKWRPDBXrvYC0NrV3cPMd366sDhQYFcP2sJN4qrKK1s8fqcJSFals6+eBwLTfOScbmpdNrX6hb5qZS2tBOwYlTVofiVi5JDCKyXEQOisgREXl4iOfvFZFaEdntuH11wHP3iMhhx+0eV8QzmlbvKicmPJgrpnjuutOudvPcVNq7e3mrsMrqUJSF1u2twG7gxtn+8aUIYPmMRMKCA/jbJ/7VCO10YhCRAOC3wAogG7hDRLKH2PUlY8xsx+1Jx7HRwA+A+cA84Aci4rELGjS1d5O/v5obcpMJCvCfi628CeNJix7D6l1aTvJnr+8qJyd5HFkJEVaH4jZhwYGsmJHEm/sq/WoWAFd8us0DjhhjjhljuoAXgVXneewyIN8Y02CMOQXkA8tdENOo2LCvkq4eOzf5SRmpn4hw05xUth6to6qpw+pwlAWO1Z5mT1mT3733AW65KIXTnT1sKq62OhS3cUViSAEGdnQvc2w70y0isldEXhWR/i4N53usR3htVzkTY8OZ5QNTDF+om+akYAy8rus0+KXXd1cgAjf4wJojF+qSzBgSx4Wy1o9mXHVFYhiqFerMJvw3gAxjzCzgbeDZCzi2b0eRB0SkQEQKamtrRxzsSJWdamPH8QZHFzb/aHgbKDM2nDnpUbyu5SS/Y4zh9V3lLJwUS8K4UKvDcTubTbh+VhLvHaqhsa3L6nDcwhWJoQwY2Kk5FRiUWo0x9caYTsfDPwIXne+xA17jCWNMnjEmLy7O/Q2/b+zpGxp/ox9eSvdblZvMgaoWDle3WB2KcqNdpY2cbGjz6/f+ytnJdPcav+mA4YrEsBPIEpFMEQkGbgfWDtxBRAaOBFsJ7Hfc3wgsFZHxjkbnpY5tHueNPRXMSY/yqXUXLtS1s5KwCbzhp/PH+KvXd5UTEmhjmQ/OIny+ZqZEkhkbzto9/lFOcjoxGGN6gAfp+0DfD7xsjCkSkUdFZKVjt2+ISJGI7AG+AdzrOLYB+CF9yWUn8Khjm0c5UnOa4spmbpjlf/XVgeIjQrlkYgzr9lT49SIm/qSn1876fZUsnp5AhB8M6ByOiHBDbjLbjtVT0+z7HTBc0ufSGLPeGDPFGDPJGPNjx7bvG2PWOu4/YozJMcbkGmOuNsYcGHDs08aYyY7bM66Ix9XW7e1rePOllapG6obcZI7VtVJU0Wx1KMoNPj7eQN3pLm7wg+lfzmVlbjLG4BczrvpPZ/wRMsbwxp4K5mVE+2XD25mW5yQSaBPe8JNLan+3bm8F4cEBXDU13upQLDc5fizZSeNY4wfvfU0M53CgqoWjta1+2U1vKOPDg7k8K5Z1eyv9bv4Yf9Pda2dDYRWLsxN8avlOZ6ycncye0kafn3FVE8M5vLGnggCbsGJGotWheIyVs5Mpb2xnV6l/zR/jb7YeqaOxrZvr/bxtbaD+L4i+Xk7SxHAWxhjW7a3k0kkxxIwNsTocj7F4egIhgbbPuvAq37RubyURoYFcMSXW6lA8RkrUGOakR/GmJgb/tbesiZMNbVpGOkNEaBBXT43nzX2VuoCPj+rs6WVjURVLsxN9ck1zZ1w3M4niymZK6ny3nKSJ4Sze3FdJUICwLFvLSGe6dlYStS2dfOJn0xH7iw8O1dHS0eMXi1FdqBUz+/5N3tznu1cNmhiGYYxh/b5KLpsc69NLGI7UomnxhATaWO/Dfxz+7M19lUSOCWLhJC0jnSklagyz06J8+r2viWEYheXNlJ1q/+zbgRpsbEggV06JY0Oh9k7yNZ09vbxdXM2ynASCA/UjYijXzUyiqKLZZ3sn6f/6MNYXVhJoE5Zm++80AOdy3awkqps7tXeSj9l6pI6Wzh79UnQWK2b2lZd9tZykiWEIxhg27KtkwaQYosKCrQ7HYy2aFk9wgI039/rHxGL+Yv2+KiJCA7WMdBap48PI9eFykiaGIeyvbKGkvo1r9RvTWUWEBnHFlFgtJ/mQ7l47+cXVLJmuZaRzuW5mIoXlzZysb7M6FJfT//khbCisxCZoGek8XDszicqmDvaUNVodinKBbUfraWrvZrkO6DynFTN8t3eSJoYzGGN4c18ll0zUQW3n45rpCQQFiM9eUvubDYVVhAcHcMUU96954m3SosOYlRrJxiLfK6VqYjjDoerTHKtt1Ya38xQ5JojLs+JYv69Kp+L2cr12w6aiKq6eFq9zI52nZTmJ7C5tpLKp3epQXEoTwxk2FFYigl8vSnKhluckUt7YrlNxe7kdxxuob+3StrUL0F9y2+hjK7tpYjjDW4VV5E0YT3yETrF9vhZnJ2ATfPKS2p9sKKwkNMjGVVO1jHS+JsWNJSt+LG/52HvfJYlBRJaLyEEROSIiDw/x/LdEpFhE9orIZhGZMOC5XhHZ7bitPfNYdzpR38qBqhaW5WjD24WIDg9mXma036yH64vsdsPGoiqunBJHWHCg1eF4leUzEvuutk53nntnL+F0YhCRAOC3wAogG7hDRLLP2G0XkGeMmQW8CvzXgOfajTGzHbeVWKj/G68mhgu3PCeRwzWnOVp72upQ1AjsLmukurlTeyONwLKcROwG3t5fbXUoLuOKK4Z5wBFjzDFjTBfwIrBq4A7GmC3GmP7OvtuBVBec1+U2FlWTnTSOtOgwq0PxOksdyVTLSd5pY1EVgTZh0VRtW7tQOcnjSIse41NXzK5IDClA6YDHZY5tw7kf2DDgcaiIFIjIdhG5cbiDROQBx34FtbW1zkU8hJrmDj49eUq/MY1QctQYclMj2VjkO9+a/IUxhk1F1SyYFKMTRo6AiLA8J5GtR+pp7ui2OhyXcEVikCG2DdlvUUTuAvKA/x6wOd0Ykwd8CfiViEwa6lhjzBPGmDxjTF5cnOsbxzYVV2OMlpGcsWxGInt8sOuerztcc5rjda2fXfWpC7d8RiJdvXa2HKixOhSXcEViKAPSBjxOBT63WraILAb+FVhpjPmslcYYU+H4eQx4F5jjgpgu2MaiKjJjw5mSMNaK0/uE/qS6Sa8avEp/V0sd6T9yc9LGExcR4jOlVFckhp1AlohkikgwcDswqHeRiMwB/kBfUqgZsH28iIQ47scCC4FiF8R0QZrau9l2tJ6lOQmIDHUBpM7HZ133fKjW6g82FlcxJz2KhHHaRXukbDZhSXYC7x6spaO71+pwnOZ0YjDG9AAPAhuB/cDLxpgiEXlURPp7Gf03MBZ45YxuqdOBAhHZA2wBHjPGuD0xvHOgmh670TKSCyzLSeTj4/U0tHZZHYo6D2Wn2igsb9b3vgsszU6grauXj47WWR2K01zSYdkYsx5Yf8a27w+4v3iY4z4CZroiBmdsKqomPiKE2alRVofi9ZblJPI/W47wzoEavnCRR3Y+UwP0l/00MTjv0kmxRIQEsqmomkXTvLss5/cjnzu6e3nvUC1LcxKw2bSM5KwZKeNIigxlk4/UWn3dxqIqpiSMJTM23OpQvF5woI2rpsXz9v5qer18Gnq/TwwfHa2jrauXJdn6jckVRPpqre8frqW9y/trrb6sobWLnSUNLNX3vssszU6g7nQXu05696qGfp8YNhVVExESyIKJMVaH4jOWZifS0W3ng8OuH2+iXGfz/mrs2kXbpa6aGkdwgI1Nxd7dM8+vE0Ov3fD2/mqumhavq1W50PyJ0USEBpLv5X8cvi6/uJqkyFBmpIyzOhSfEREaxKWTY9hY5N3T0Pv1p+Guk6eoO92l/bddLCjAxjWOWmtPr93qcNQQ2rt6ef9wLUuytYu2qy3NTuREfRuHqr133jC/Tgz5xdUEBYhOMzwKluYkcqqtm09OeHet1Vd9eKSOjm47S/RLkcstzo5HvHwaer9NDMb0TTO8YFIsEaE6P4yrXTEljuBA76+1+qpNRVVEhAYyP1Pb1lwtPiKUOWlRXl1K9dvEcKTmNCX1bVpGGiVjQwK5bHKs19dafVGv3bD5QA1XT9W2tdGyJDuRfeVNXjtvmN++K/q/yeql9OhZkp1A2al2DlS1WB2KGuCTE6doaO1iqS5fO2r6P1fe9tKrBr9ODLlpOj/MaLpmel+t1ZsvqX1RfnEVQQHClVO0bW20TI4fy8TYcK8tpfplYqhu7mBPaaOWkUZZfEQos7281uprjDFsKq7um75B29ZG1ZLsBLYf8841GvwyMfQvwadlpNG3JDvBq2utvuZwzWlO1Lfpe98NlmQn0N1reO+g9w309MvEkF9czYSYMLLide2F0bbUy2utviZf29bcZk76eGLCg73yitnvEsPpzh4+OlLPkuk6sMcdJsX1TdDmrbVWX7OpuJrc1EhtW3ODAJtwzfR4thysodvLBnr6XWJ4/1AtXb06sMdd+ifV89Zaqy/pb1vT9777LMlOpKWjh4+PNVgdygVxSWIQkeUiclBEjojIw0M8HyIiLzme/1hEMgY894hj+0ERWeaKeM4mv7ia8WFBXDRh/GifSjl4c63Vl/xv25pOmucul02OJTTIRn6xd42CdjoxiEgA8FtgBZAN3CEi2Wfsdj9wyhgzGfgl8FPHsdn0LQWaAywHHne83qjo7rXzzoEarp4WT2CA310sWWauF9dafcnbxdWkR4fpuuZuNCY4gMuz4sgvrvaqgZ6u+HScBxwxxhwzxnQBLwKrzthnFfCs4/6rwDXSV+BfBbxojOk0xhwHjjheb1TsLGmgqb1bu6m6WYBNWDTNO2utvqK1s4etR+t10jwLLJmeQEVTB0UVzVaHct5ckRhSgNIBj8sc24bcx7FGdBMQc57Hukx+cTXBgTYuz9KBPe62JDvBK2utvuL9Q7V09dhZPF2/FLnbIi8c6OmKxDDU148zr5mG2+d8ju17AZEHRKRARApqa0dWq+7otnPNtHjCQ1yy1LW6AJdnxREaZPuszq3cK7+4mqiwIC7O0LY1d4sdG8JF6eP9LjGUAWkDHqcCFcPtIyKBQCTQcJ7HAmCMecIYk2eMyYuLG9k3/p/cPJPH75w7omOVc8YEB3DZZO+rtfqCnl477xysYdFUbVuzypLsBIormylv9I6Bnq54l+wEskQkU0SC6WtMXnvGPmuBexz3vwC8Y/o+HdYCtzt6LWUCWcAOF8Q0LK2vWmdJdjzlje0UV3pPrdUX7Cw5RWNbt3ZTtZC3TarndGJwtBk8CGwE9gMvG2OKRORREVnp2O0pIEZEjgDfAh52HFsEvAwUA28BXzfG6AryPmrRtASvq7X6gv62tSt00jzLTIwby6S4cK9577uk2G6MWQ+sP2Pb9wfc7wBuHebYHwM/dkUcyrPFRYQw11Fr/T+Lp1gdjl8wxpC/v4qFk2K0bc1iS7ITefKDYzS1dxM5xrMnMNSCo3KrJdkJFFV4T63V2x2sbqG0oV0HtXmAJdkJ9NgN7x6ssTqUc9LEoNzK22qt3i6/qO/fefH0eIsjUXPSoogdG+IV5SRNDMqtJsWNZaIX1Vq9Xf7+amanRRGvk+ZZzmYTFk+P572DfWNKPJkmBuV2/ZPqNbXQRCdtAAAXTUlEQVTrpHqjqaqpg71lTdobyYMsyU6gpbOH7cfqrQ7lrDQxKLdb6kW1Vm+W7xhMqFPAeI6Fk2MJCw5gk4dPqqeJQbnd7LTxxI4N0TUaRll+cTUZMWFM1gWpPEZoUABXZMXxdnGNRw/01MSg3C5gQK21s0eHrYyGlo5uth2t00nzPNDSnASqmjvYV95kdSjD0sSgLLE0J4HTnT1sO+rZtVZv9d6hWrp7jXZT9UCLpsUTYBM2FXnuFbMmBmWJSyf11Vq1d9Lo2FhUTUx4sC5I5YGiwoK5OMOzJ9XTxKAsERoUwJVT+ibVs9s9t9bqjTp7etlyoIbF0xMIsGkZyRMtzU7kYHULJ+pbrQ5lSJoYlGWW5iRQ09LJnrJGq0PxKduPNXC6s4elOdobyVP1dyH21KsGTQzKMldP7au1euofh7faVFRFWHAACyfHWh2KGkZadBjTEiM8tp1BE4OyTFRYMPMzo7XbqgvZ7Yb84mqunBJHaNCoLZ+uXGBpTiIFJxqoO91pdSifo4lBWWpJdgJHak5zrPa01aH4hD1ljdS0dGoZyQssy0nAbmCzB65qqIlBWWppTl93yo0eekntbTYVVxNgExZN1cTg6bKTxpE6foxHvvc1MShLpUSNYWZKJBuLPHuKAG+xqaiKSyZGExnm2fP9q77VJJflJPLh4TpOd/ZYHc4gTiUGEYkWkXwROez4+blO0yIyW0S2iUiRiOwVkdsGPPcnETkuIrsdt9nOxKO807KcBHaXNlLV1GF1KF7taO1pjta2slQHtXmNpdkJdPXaPW7eMGevGB4GNhtjsoDNjsdnagPuNsbkAMuBX4lI1IDnv22Mme247XYyHuWFljnKSfkePrGYp+u/6tLZVL1HXkY0MeHBHldOcjYxrAKeddx/FrjxzB2MMYeMMYcd9yuAGkAXn1WfmRzft0aDp/1xeJuNhVXkpkaSHDXG6lDUeeqbNyyBLQdqPGreMGcTQ4IxphLA8fOsy0SJyDwgGDg6YPOPHSWmX4pIiJPxKC/UX2vdfqyepjZdo2Ekyhvb2VPWxLIZWkbyNstmeN68YedMDCLytogUDnFbdSEnEpEk4HngPmNM//JFjwDTgIuBaOC7Zzn+AREpEJGC2traCzm18gLLchLpsRs2H9CrhpHY5CgjLc/RxOBtLp0US3hwgEddMZ8zMRhjFhtjZgxxWwNUOz7w+z/4h2xBEZFxwJvAvxljtg947UrTpxN4Bph3ljieMMbkGWPy4uK0EuVrZqVEkjgulLcKtZ1hJN4qrGJKwlgmxunaC94mNCiAq6bGk19cTa+HzBvmbClpLXCP4/49wJozdxCRYGA18Jwx5pUznutPKkJf+0Shk/EoL2WzCctyEnj/cC3tXZ5Ta/UG9ac72VnSoFcLXmzZjETqTnfyyYlTVocCOJ8YHgOWiMhhYInjMSKSJyJPOvb5InAFcO8Q3VL/IiL7gH1ALPAjJ+NRXmxZTiId3XbeO+RZXfc83dv7q7EbtH3Biy2aFk9woI0NhZVWhwJAoDMHG2PqgWuG2F4AfNVx/8/An4c5fpEz51e+ZV5mNOPDgthQWMXyGUlWh+M13iqsIi16DNlJ46wORY3Q2JBArsiKY2NhFd+/PtvyVfd05LPyGIEBNpblJLJ5v2d13fNkzR3dbD1Sz7LsRMs/TJRzVsxIpKKpgz1l1i/5qYlBeZTlMxI53dnDh4frrA7FK2w5UENXr53lWkbyeounJxBoEzbss76cpIlBeZRLJ8UyLjSQ9fu0d9L5WL+vkoRxIcxN1yU8vV1kWBCXTo5lQ2EVxljbO0kTg/IowYE2FmcnkF9cRVeP/dwH+LHWzh7ePVjLihlJ2HQJT5+wYkYiJxvaKK5stjQOTQzK41w7I4nmjh62HfOckaCe6J0DNXT22FmhZSSfsTQ7AZtg+XgeTQzK41yWFcvYkECPqLV6svX7KomLCCEvI9rqUJSLxIwNYX5mDBs0MSg1WGhQAIumxbOxqIqeXi0nDaWtq4ctB2tYMSORAC0j+ZRrZyZypOY0h6pbLItBE4PySNfOTORUWzfbjzVYHYpH2nKglo5uO9fO1PEevmbZjERsAuv2WnfFrIlBeaQrp8QTFhzAm1pOGtL6fZXEjg3hYi0j+Zz4iFDmZ8awbm+FZb2TNDEojzQmOIDF0xPYUFhJt5aTBmnv6uWdAzUsn5GgZSQfdX1uEsdqWzlQZU05SROD8ljXz0qisa2brUd0sNtAWw7W0N7dq2UkH7Y8p6/taN3eCkvOr4lBeawrp8YRERJoaa3VE63bW0Gso/eK8k0xY0O4dFIM6/ZWWlJO0sSgPFZIYABLchLYWFSlcyc5tHR0s3l/DdfPStIyko+7bmYSJ+rbKKpw/2A3TQzKo92Qm0xLRw/vH9JyEkB+cTWdPXZuyE22OhQ1ypblJBJoE96woJykiUF5tMsmxxIVFmRZrdXTvLGngpSoMcxNj7I6FDXKxocHs3ByLG9aUE7SxKA8WlCAjeU5ibxdXO33K7udau3ig8N13JCbrFNs+4nrZyVRdqqdXaWNbj2vU4lBRKJFJF9EDjt+DjnFo4j0Dli9be2A7Zki8rHj+Jccy4AqNcgNucm0dvWy5aB/r+y2vrCSHrvhhlztjeQvls1IJCTQxppd5W49r7NXDA8Dm40xWcBmx+OhtBtjZjtuKwds/ynwS8fxp4D7nYxH+aD5mdHEjg1hzW73/nF4mjf2VDApLlxXavMj40KDWDw9gXV73Tuex9nEsAp41nH/WeDG8z1Q+q6FFwGvjuR45T8CA2yszE1my4FaGtu6rA7HElVNHXx8vIGVuSlaRvIzq2YnU9/axYduHM/jbGJIMMZUAjh+xg+zX6iIFIjIdhHp//CPARqNMT2Ox2VAipPxKB9189wUunrtfruAT9/0CGgZyQ9dNTWeyDFBbi0nBZ5rBxF5Gxhqwvd/vYDzpBtjKkRkIvCOiOwDhuqcO2zTu4g8ADwAkJ6efgGnVr4gJ3kck+PH8vqucr403//+/1/7tJzc1Egmxo21OhTlZsGBNq6dmcSa3eW0dfUQFnzOj22nnfOKwRiz2BgzY4jbGqBaRJIAHD+HbB00xlQ4fh4D3gXmAHVAlIj0/5apwLB9Eo0xTxhj8owxeXFxcRfwKypfICLcNCeFHSUNlDa0WR2OW+2vbKa4spmb56ZaHYqyyI2zk2nr6iW/uNot53O2lLQWuMdx/x5gzZk7iMh4EQlx3I8FFgLFpq9j7hbgC2c7Xql+q2b3Deryt0bo1bvKCbSJDmrzYxdnRJMcGcrrbionOZsYHgOWiMhhYInjMSKSJyJPOvaZDhSIyB76EsFjxphix3PfBb4lIkfoa3N4ysl4lA9LHR/GvMxoVu8qt3yxdHfp6bWzelc5V0+LJzpce3P7K5tNWDk7hfcP11F/unPUz+dUscoYUw9cM8T2AuCrjvsfATOHOf4YMM+ZGJR/uWlOCo+8to/C8mZmpkZaHc6o23q0ntqWTm6Zq/0y/N1Nc1Iob2ynrauX0Z4+UUc+K69y7cwkggNt/O3TMqtDcYvXPi0jckwQV08brsOf8hdTEyP4zR1zSIsOG/VzaWJQXiVyTBBLsxN4fXe5z8+42tLRzcaiKm7ITSIkMMDqcJQf0cSgvM5tF6fR2Nbtth4aVtlQWEVHt117Iym308SgvM7CSbGkRI3hpZ2lVocyql7eWcrE2HDmpOlMqsq9NDEor2OzCV+4KJUPj9RRdso3xzQcqm6h4MQpbp+XplNgKLfTxKC80q15feWVVz/xzUboF3eUEhQg3KJlJGUBTQzKK6WOD+OyybG8UlCG3e5bYxo6unt5bVcZS7MTiRkbYnU4yg9pYlBe64t5aZQ3tvPR0XqrQ3GpjUVVNLZ1c/u8NKtDUX5KE4PyWkuyE4gKC+KFHSetDsWlXtxRSlr0GBZOirU6FOWnNDEorxUaFMCtF6WysaiK6uYOq8NxiZK6VrYdq+e2vDRsNm10VtbQxKC82l2XTKDXGP76sW9cNbyw8yQBNuHWPC0jKetoYlBebUJMOFdNieOvO07S1eO+pQ9HQ3tXLy/tLGXJ9AQSxoVaHY7yY5oYlNe7e0EGtS2dbCzy7tXdXt9dTmNbN/ctzLA6FOXnNDEor3fllDjSo8N4ftsJq0MZMWMMz2w9zvSkcczLjLY6HOXnNDEor2ezCV++ZAI7ShrYXznUirGeb9vReg5Vn+a+hRk60llZThOD8gm35qUSEmjjuW0lVocyIk9vLSEmPJiVukqb8gBOJQYRiRaRfBE57Pg5foh9rhaR3QNuHSJyo+O5P4nI8QHPzXYmHuW/osKCuXluKn/7tJyaFu/qunqyvo3NB6r50vx0QoN0em1lPWevGB4GNhtjsoDNjseDGGO2GGNmG2NmA4uANmDTgF2+3f+8MWa3k/EoP/Z3V0ykp9fOM1tLrA7lgvzpoxICRLjrkglWh6IU4HxiWAU867j/LHDjOfb/ArDBGOObU2IqS2XEhrNiRhJ/3n6Clo5uq8M5Lw2tXby48yQ35CZrF1XlMZxNDAnGmEoAx89zrT94O/DCGdt+LCJ7ReSXIjLsjGEi8oCIFIhIQW1trXNRK5/191dOoqWjx2sGvD2z9ThtXb3841WTrA5Fqc+cMzGIyNsiUjjEbdWFnEhEkoCZwMYBmx8BpgEXA9HAd4c73hjzhDEmzxiTFxcXdyGnVn5kZmokCyfH8NSHxz1+6c/mjm7+9FEJK2YkkpUQYXU4Sn3mnInBGLPYGDNjiNsaoNrxgd//wV9zlpf6IrDaGPPZNb4xptL06QSeAeY59+soBf9w5WRqWjpZ/Wm51aGc1fPbTtDS0cPXr55sdShKDeJsKWktcI/j/j3AmrPsewdnlJEGJBWhr32i0Ml4lGLh5BhmpkTy+LtH6e71zGky2rp6ePKDY1w9NY4ZKZFWh6PUIM4mhseAJSJyGFjieIyI5InIk/07iUgGkAa8d8bxfxGRfcA+IBb4kZPxKIWI8NCSLE42tHnsutB//fgkp9q6eXBRltWhKPU5gc4cbIypB64ZYnsB8NUBj0uAlCH2W+TM+ZUaztVT47k4Yzy/3nyYW+amMibYc8YHtHR08/v3jnLppBgumvC5oT9KWU5HPiufJCJ8Z/k0alo6+dNHJVaHM8gf3jtG3ekuvrt8mtWhKDUkTQzKZ12cEc3VU+P4/XtHaWr3jHENlU3tPPnhMVbmJpObFmV1OEoNSROD8mnfXjaNpvZu/vDeUatDAeDnmw5ht8O3l021OhSlhqWJQfm07ORx3Dg7mSc/PE5JXaulsRRXNPO3T8u4d2EGadFhlsai1NloYlA+75FrpxMcYOPf1xRijLEkBmMMP3qzmMgxQXz9Kh23oDybJgbl8xLGhfIvS6fwweE61u2ttCSGVz4p46Oj9fzzkilEhgVZEoNS50sTg/ILX16QwcyUSB5dV+z2hujq5g5+uK6YeZnR3DlfZ1BVnk8Tg/ILATbhP2+aSf3pTn628aDbzmuM4V9XF9LVY+ent8zCZtPV2ZTn08Sg/MbM1EjuvTST57efYPP+arec8429lby9v5p/WTqVzNhwt5xTKWdpYlB+5TvLp5KdNI5vvbyHslOjuyzIyfo2vr+mkNy0KL5yWeaonkspV9LEoPxKaFAAj985F7vd8OBfd9HVMzqT7LV29vC15wowBv7fbbMJ0BKS8iKaGJTfyYgN57++MIvdpY38ZMN+l7++3W741su7OVzTwv98aQ4ZWkJSXkYTg/JLK2Ymcd/CDJ7ZWsLj7x5x6Wv/+p3DbCyq5nvXTufyLF1USnkfp2ZXVcqb/dt12TS0dvFfbx0kyGbja1dMdOr1jDH8dssRfvX2YW6em8L92q6gvJQmBuW3AmzCz2/Npcdu+PH6/dhsMuIPc7vd8KM39/P01uPcPCeFn94yi771p5TyPk6VkkTkVhEpEhG7iOSdZb/lInJQRI6IyMMDtmeKyMciclhEXhKRYGfiUepCBQbY+NVts1kxI5EfrivmoZd209xxYQPgWjq6+dbLu3l663G+sjCTn92aS1CAVmmV93L23VsI3Ay8P9wOIhIA/BZYAWQDd4hItuPpnwK/NMZkAaeA+52MR6kLFhRg4zd3zOGhxVNYu6eCFb/6gG1H6895nDGGNbvLWfTz91izp4JvL5vKv18/XQexKa/n7Apu+4FzXTLPA44YY4459n0RWCUi+4FFwJcc+z0L/AfwO2diUmokAgNsfHNxFldMieWhl3Zzxx+3k5sWxa0XpXJDbjKRY/53fqOT9W28d7iWtbvL2VlyilmpkTx5d56ur6B8hjvaGFKAgQvvlgHzgRig0RjTM2D755b/VMqd5qSP581vXM4LO07ySkEZ//Z6If++ppCxwYGEhwQiApVNHQCkjh/Dj26cwR3z0nWcgvIp50wMIvI2kDjEU/9qjFlzHucY6i/GnGX7cHE8ADwAkJ6efh6nVWpkwkMC+erlE7n/skwKy5t5e381zR3dtHb20NVjJzctiiunxJEZG64NzMonnTMxGGMWO3mOMiBtwONUoAKoA6JEJNBx1dC/fbg4ngCeAMjLy7NmUn3lV0SEmamRzEyNtDoUpdzKHV0ndgJZjh5IwcDtwFrTt2LKFuALjv3uAc7nCkQppdQocra76k0iUgYsAN4UkY2O7ckish7AcTXwILAR2A+8bIwpcrzEd4FvicgR+tocnnImHqWUUs4Tq5Y6dEZeXp4pKCiwOgyllPIqIvKJMWbYMWf9dBSOUkqpQTQxKKWUGkQTg1JKqUE0MSillBpEE4NSSqlBvLJXkojUAidGeHgsfYPr/In+zv5Bf2ff5+zvO8EYc87Vo7wyMThDRArOp7uWL9Hf2T/o7+z73PX7ailJKaXUIJoYlFJKDeKPieEJqwOwgP7O/kF/Z9/nlt/X79oYlFJKnZ0/XjEopZQ6C79KDCKyXEQOisgREXnY6nhGk4ikicgWEdkvIkUi8k2rY3IXEQkQkV0iss7qWNxBRKJE5FUROeD4/15gdUyjTUQecryvC0XkBREJtTomVxORp0WkRkQKB2yLFpF8ETns+Dl+NM7tN4lBRAKA3wIrgGzgDhHJtjaqUdUD/LMxZjpwCfB1H/99B/omfVO8+4v/B7xljJkG5OLjv7uIpADfAPKMMTOAAPrWefE1fwKWn7HtYWCzMSYL2Ox47HJ+kxiAecARY8wxY0wX8CKwyuKYRo0xptIY86njfgt9HxY+v6a2iKQC1wFPWh2LO4jIOOAKHGuZGGO6jDGN1kblFoHAGBEJBMI4y+qP3soY8z7QcMbmVcCzjvvPAjeOxrn9KTGkAKUDHpfhBx+UACKSAcwBPrY2Erf4FfAdwG51IG4yEagFnnGUz54UkXCrgxpNxphy4GfASaASaDLGbLI2KrdJMMZUQt+XPyB+NE7iT4lhqFXbfb5LloiMBf4G/B9jTLPV8YwmEbkeqDHGfGJ1LG4UCMwFfmeMmQO0MkrlBU/hqKuvAjKBZCBcRO6yNirf4k+JoQxIG/A4FR+8/BxIRILoSwp/Mca8ZnU8brAQWCkiJfSVCheJyJ+tDWnUlQFlxpj+q8FX6UsUvmwxcNwYU2uM6QZeAy61OCZ3qRaRJADHz5rROIk/JYadQJaIZIpIMH2NVWstjmnUiIjQV3feb4z5hdXxuIMx5hFjTKoxJoO+/993jDE+/U3SGFMFlIrIVMema4BiC0Nyh5PAJSIS5nifX4OPN7gPsBa4x3H/HmDNaJwkcDRe1BMZY3pE5EFgI329GJ42xhRZHNZoWgh8GdgnIrsd275njFlvYUxqdPwT8BfHF55jwH0WxzOqjDEfi8irwKf09b7bhQ+OgBaRF4CrgFgRKQN+ADwGvCwi99OXIG8dlXPryGellFID+VMpSSml1HnQxKCUUmoQTQxKKaUG0cSglFJqEE0MSimlBtHEoJRSahBNDEoppQbRxKCUUmqQ/w8jsU4otldS8QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# plotting a line\n",
"x = np.linspace(0, 10, 100)\n",
"plt.plot(x, np.sin(x));"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJztnX+MHOd537/P7Q3JParQ0jBRWyueqTgGGcu0eNXBZMECDR3XVCVLOYu2GVVqg+YPokAKhKxwCBUJIZnKFQvCloAmQCHARlJYUU4y5bNkCqBskIVbAZJ97B1NMyILK9avldEwEY+JeEtyb+/tH3fvcnb2fd95Z+bd+bXPBzAs3s3NvPPOzPM+7/OThBBgGIZhysNQ1gNgGIZh3MKCnWEYpmSwYGcYhikZLNgZhmFKBgt2hmGYksGCnWEYpmSwYGcYhikZLNgZhmFKBgt2hmGYkjGcxUU/+tGPio0bN2ZxaYZhmMJy+vTpvxNCrA87LhPBvnHjRszMzGRxaYZhmMJCRG/bHMemGIZhmJLBgp1hGKZksGBnGIYpGSzYGYZhSgYLdoZhmJLBgp1hGKZkZBLuyDBFZXq2gaMnLuD9+SZuqVUxuWsTJsbqWQ+LYbpgwc4wlkzPNvDIC2fRbLUBAI35Jh554SwAsHBncgWbYhjGgunZBh5+7kxHqEuarTaOnriQ0agYRg0LdoYJQWrqbU3j9/fnmymPiGHMsGBnmBCOnrjQo6n7uaVWTXE0DBMOC3aGCcGkkVe9CiZ3bUpxNAwTTmLBTkRriOgnRHSGiM4R0WEXA2OYvKDTyCtEeOL+Lew4ZXKHC439GoDPCyHuALAVwF1EtN3BeRkmF0zu2oSqV+n6WdWr4Btfu4OFOpNLEoc7CiEEgA9X/umt/E/tZWKYAiKFN8evM0XBSRw7EVUAnAbw6wD+TAjxuovzMkxemBirsyBnCoMT56kQoi2E2ArgVgCfI6LPBI8hor1ENENEMxcvXnRxWYZhGEaB06gYIcQ8gP8J4C7F754WQowLIcbXrw/t7MQwDMPExEVUzHoiqq38dxXAFwCcT3pehmEYJh4ubOwfB/AXK3b2IQDPCSF+4OC8DMMwTAxcRMX8DMCYg7EwDMMwDuDMU4ZhmJLBgp1hGKZksGBnGIYpGdxog0kVlx2IuJsRw6hhwc6khssORNzNiGH0sCmGSQ1VXfO4HYhcnothygZr7Exq6Oqax+lAFPVcbLZhBgnW2JnU0NU1j9OBKMq5pNmmMd+EwA2zzfRsI/J1GaYIsGBnUkNX1zxOB6Io52KzDTNosCmGSQ2Xdc2jnMulCYhhigALdiZVXNY1tz3XLbUqGgohzk2ombLCphim9Lg0ATFMEWCNnSk93NqOGTRYsDMDAbe2YwYJFuzMwFKE2PYijJHJHyzYmYGkCCUJ8jZGXmSKAztPmYGkCLHteRojJ3kVCxbszEBShNj2PI0xT4sMEw6bYpiBJCy2PQ9mhzzF3+dpkWHCYY2dGUhMse39MjtMzzaw48hJ3HbgOHYcORl6vjzF37us88P0HxbszEAyMVbHE/dvQb1WBQGo16p44v4tmBir98XsEGexMI0xbfK0yDDhsCmGGVh0se39MDuYFguToM5L/D0neRULFuwME6Aftu0y2Kjzssgw4SQ2xRDRBiI6RURvENE5IvoDFwNjmKzoh9khzEYd1f7OMCZc2NgXATwshPgNANsB/D4RfdrBeRkmE/ph287CWcsMLolNMUKIXwH41cp//yMRvQGgDuCvk56bYbLCtdnBZKPeceRkLPs7w+hwamMnoo0AxgC87vK8DFMG0nTWMoONM8FORDcBOAZgnxDiHxS/3wtgLwCMjo66uizDFB6TszYPiVJFZxDn0EkcOxF5WBbqzwghXlAdI4R4WggxLoQYX79+vYvLMkwp0Nnfd25ez7b3hAyq/yKxxk5EBOBbAN4QQnwz+ZCYsjOIGpQJnf09bux7nvA/65urHoiA+YVWas+9DHMYBxemmB0A/i2As0Q0t/KzPxJCvOzg3EzJyFsp2rygsr/vn5pTHlsU23vwWc83W53fpfXcB9V/kdgUI4T430IIEkJ8VgixdeV/LNQZJVwl0J481meJEm+vetZ+0njueZzDNOBaMX2Ek0566acGVbb5zlt9lqj2aptn2m/NOW9zmBZcUqBPsMlBjS4CZIgItx04Htv2mnS+82j3z1t9lqj2at2zDh7TT/I2h2lBQojULzo+Pi5mZmZSv26a7DhyUvlS12tVvHrg8xmMKB8EBbCKqleJnOmZZL5VY7IZQx4Xg35y24Hj0EmLp/Zs7bn3sGcd5zkPOkR0WggxHnYca+x9oqxOm6TCLKhBDRGhHVAu4kQt2M63avxxIicGcUdm0sBV9x581llExQwqLNj7RJ6637jClTDzR4BsPHBceUzUBdBmvnXj12mUpjHEXQyKrOFP7tqknS/dvauifeQ87J+aw9ETFwo3D0WAnad9ooxOG9cRLdOzDZDmd1EXQJv51o2/QupRmMZgu0N4bPosPvnIy9h44Dj2Tc0VOlFGFkfTYbMYD2rCUNqwYO8Teep+4wqTMIsTkXL0xAWlzZYA5QJouobNfOvG3xYi8iJsE0b32PRZfOe1d3pMTZIihnlOjNVRTxBCyOGu6cCmmD5StsYEN1e9riQTyRpvKJaJRidoheLvbMxAYfOtM9fUfbZ2WzOJyiwRXAyeff1d7d9Liuhzsbl3HWX1PeUNFuyMNRqLBa4tLmEpoJTaOEBNgjaITtPbF8FOaxJIURdhmzA6nabup4g+lyQhhGX0PeURFuyMNfMLvdo6gB6hLgnTwqJofqZz2e4QksY0q5yfplDKiiLix0+RfS5xd6NJtH3GHhbsjDU2CSfB401EEbRh17YNkbQVSEEhvnPzehw73Yhkbnpg2wZ857V3lL+rFzAqxgWDmjCUNpyglDFFCoFTJZwQoHWAPqlIWkly7cnvnkGrrX9fCcAvj9zj5Fq291khwpIQ2mf32PRZPPv6u2gLgQoRHti2AY9P6CNLGMYEJygVgKIluai0LZ0WrXKAAgkXshAdxJWdVmXP111amlp0z+7xiS0syFOgSApSGrBgz5Ai1ooOmjJMqfxBkixkR09cQEtnzF/BlZ02boRG3p9dWXGpIJVlgeA49gwpQ+hXlESsJDHMYXNSq3rOPsAkmn+Rnl1ZcBUbX6bkKRbsGVLUWtH+RKGjJy5g9511q0SsJAuZaU6qXgWH7rvdevxhTO7aBG+oN7ZziIB1Ix4IiJWt6qdsJYazxJWCVKbkKRbsCUnygRax7IBKqzl2uoHJXZvwyyP34NUDn9dqzkkWMtVcAcua+u476zh64oIzITkxVsdNa3qtlEsCGFk1jF8euQff+Nod2mcX9k6USTPMA64UpDLsoCVsY09AUtteFqFfSW2ISRKFksQwy3MeevFcJ/t13YiHez77caswxOnZRs/fHrz3du1YL2li9uVHrnt2AHreicnnz+DwS+c6VQ2vXFssnG8lz6jeKwKwc/P6SOeJmjyVZ3s8C/YEuHB+pll2QLUQ7Z+aw76pOeu46iSJQi4WsmuLS53/vrTQwjOvvdMTsdJstfHwc2c615yebWDy+TNdztdLCy1MfvfGMX5kcTKVq9b/kaue3Y4jJ3veidaS6CwUplj8LDXDPAupMCbG6ph5+4Oud0EAOHa6gfFPfMT6PqIoHnmPaGNTTAKKtnUzhfHZmgPCtrdhNsmJsTomd23CLbUq3p9v4uiJC9YmiKhhiPJ+dBE1rbZQjjVqcTI/SZ59HN+KC1t9XNNQnvwEp85fVC7wUezjUQr35d0ezxp7AuLWvchKOwoTOja7DVNNbpvrJNF0ogpNeT9huwzb6+hi8/1Ezc6VxPGt2M5l2PvW70YjabzvumcW9VnY7qDzrtSxxp4AnQ3PZNvL0nFmoxGGvZh+rSbOdZJoOnE0WilMdKiiW3THm+5ZonPyBlk34iUu6WwzlzbvWxwhZfscH5s+i/0p1KHXPTMC+vJt5T2ijQV7Ak6dvxjp50C2WzgboWPzYkpzSq3q9fwuTPNMounowhArQ2Rs2GEaj6pIV9JopdXD4Z/VwXtvx6sHPh8aSWTCZi5Nzm5pPokjpEwashSk07MNrQ/E9fs+uWuT8h0QQF++rbxHtDkR7ET0bSL6WyL6uYvzFYU4QirLLVxQ2w5+CLYvptQCg7XZ1414oZpnEk1HF4bYXhKojXg9H5o3RFi4voj9U3NQrAcA1Fp43CYpunkJsnZVxYkpwmYubZzdOzevd9ZoBECXb0PnA3H9vk+M1VO7lrxenhvpuLKx/zmAPwXwPxydrxDEsbFnXY/ab0OMa/tUaYHAcox3mG03adlWXeng+YUWntyztatx8pXri51oFFWtO9N140Qr6eYlyJf/WfTqkqpnYzOXNlUxT52/iCfu35K40Yj/nGG+jX687/WUv608N9JxVt2RiDYC+IEQ4jNhx5aluqOqCmDVqxhX7jh/kwZRhPxtB45rtaP6SrSLFKz+aozyPoFoIY/+sQ1papzXa9Wu2uhbD7+i1JzDqjEmwTQvfrwK4ehX7nDyjoQ9N9W5gsStijk928C+qTntOXWLiuvKn/7x5PHbcglXd0yBOHHZeaxHHTVSxfTByp+rhKrU5KLYlINjUwn1oJY6PdvQmkOWhEhU2tcvSG+ueiBCJ/FI1zowSKstcPilc9o50NnFD72o/xsd/vdNp7nH1Wgnxura88r3WpU49OD20b6873n8trIiNcFORHsB7AWA0dHRtC7bd+Jsx/K2hTv80rlI4W66D9ZGW3VRvwNYbtMnZXzQWWlyliXZlgcXGb8QjxpWd2mhhdsOHFcKH90czTdbmJ5tdJnSbBZk+b7ptPcr1xa7zmvL9GwDC9cXe37ubzcIpCto8/ZtZUVqgl0I8TSAp4FlU0xa12XMTM82QtPng0Spyx7EVf0Ov+I+32x1CTTT4pEkasHWhm6LP/wPuDGvpvn0L7ZR48/lzw6/dK7rmQfnL4jK3ANAuUjUqh4O3XejVAML2mxgU8yAE1e7ta3L7kdlMgnT5mwXDb9A0/3NupHu0r6q9nenzl/UjqdfkUvBWjuTuzZpbdf+MdhGWAXvUzcG1YKg2xWsHh5SLnJrVw+zIM8BTgQ7ET0L4DcBfJSI3gNwUAjxLRfnZvpLFO3WJIhV5hlviHDTmuGODdp/vK0ZwSbTNXgvumiRg/feKO2rur6/P6mqjk7crFJb5DUf3D6KdSOeciflF8y68dRGPOw4chLvzzdRG/Hw4dXFTkmFqLVqdLsC3fNQnb/IdWiKihPBLoR4wMV5mPTRCodqr3ZrEsRR7am2ZgTVeRd8YYzBe9H9jU0afZBgHZ3dd9a7Kkn2AwHgO6+9g7WrKvCGqKvGTXDHs3PzemWz7MsLrc786MxsKlTafNRdisz0jLqAM25hU8yAo9Nug40rdILYX0XR76Q7euIC9k3N4eHnzqAtRE/1yCiJWkGzjy6szS/0wmy7cerOyHhveU9Rqa+Ye6Z+8m5om78r19vwKoRa1cPlZu+OB9BnOC8pf2pGF9NvMmvNL7R6HOYy0zOuH0AFa/zRYcE+4Nhq2jpBKKsoynPpwhODmlqSRK040RZB4VD1hrDQiiYCG/PL1SijCvWHto92NbQ+/rNfWWnSrbbA2tXDmDv4ReXvk9j8a1UPa1cP98yfyu8Q3KVIs5ZLP4AO1vjjwYKdsYpcMNmX/RqYycThPy5pBmqUaAuVcIhLY74ZGtoZlgSly55VEZa9GbeSpD9yRaKap2OnG9h9Z13pVDbFsIeN0TY6qogN3/MAC3bGijAnphRAYZqY/MjTjHHuR5iiTrjbZDpGEch+R6jKYa3Tmk1ErTF+6vzFrqxeic3inHQBz3t53LzCgp2xQgqC/VNzSoF280qlxzCh5XeupRXj3A8hIHCjNkllpcyBbRcq20gfr0L48OpiV/eloMM6GJMeRr1W1Y4vqhC1WZyTLuBZ11YqKizYE1AUp46rcZoEiSxrHia0gs61NOhHmGKFCO/PN62FuUQ+i2ar3bUg7Ny8Hj8486uunqxC9JZmCJohTLbuIF6FcOXaojbjNY4QtVmckyzgUdvVFeF7TINCCfY8PbiiOHVcj9NUXdF/TlNtkrS30Ts3r1fWBffjL1Fgg84pbOKx6bNd42gLgapXUToor7aWQs1e8pr+Jt1BhlbuS8azy+NU4zYJ0ay+PVuN3+V7nic5Exdn1R2jEKe6Y94qt+kyLYNVBrNGN85a1dNGW8Q537oRDyOruqMsdMI9OEf9/JBsqxuGafUVTVVJiS7KxD8OnRkr7NxBVPNn0tqfWilnHPdZAL3lA1TfXloCUXUd2/uzOXee5EwQ2+qOhemglLfmsUVx6oQVlLLB37R44fpiTxcjaQsOtj+zaeDQ71aBNo7Tm6ue8bnVa1W8+cTdxtZ4882W8R5MTSeiCHWVGWJirI51I73drCQPP3fGevc0MVbv6ezkqgWfCdvG2LrruNod5k3OxKUwgj1vgjTvPQ8lYf1Hwwh+SJcWWgAta6iyc8zaVcM9CTf+hB5TlxnTh2T7sZuweT+uXF/sOH+DEG6UVojyrjVbbRx+6Vxn/EaHsq6vXwBTlx5/uYQgbSGMrQPDsBGaSQRilEVBdx1V71rAXdG5vClsYRTGxp4373jSMC4dNtvZKFte24JSOlQfUjBx5rYDx7Xnj5sBKj/upDZTG8dpqy1wWWOj9vfMjOqEveRL7TdBAIYr1NWURHWMyaQQZmtXhWjavK/Tsw1taKdNC76475guVt2UKFf1Kom/x7zJmbgURmPPW/PYiTH3PQ9tNJeoW17TNt3mZTV9sFKj1omjWuC6Kg1cN4YKkZMtsU0Db8CccGQyLRGAVRVLlVvDkgDWrho2mnpsntWh+2433qsM0ZTv6+47l80sph2RzoTk38mYxpf0HbM9n/z+kn6PeZMzcSmMxp5mQkuUMbm8vqlzjqk1XFgm3sF7b4+9uzBVEAxzSvqHqYtaUBXWCmpefqJuiYPvja61Xhiq3qCyg1KUOHIdl5stzB38olUdHB3yXnW1bNaNeB2t3zaKRFsPP3Ccbge7c/N6bYKVJIqWbNopu/ge8yhn4lAYwQ6Uv2i/ydEpt9g6oWQSeEleVt2HJARCnZJ+84Zu0Xr29XfxwLYNPSnrNunqOlSmKp1Ai4LftJTkPCqiVKY00Qld/O6ZHtPOh1dvdEqyNX/ohG5wd6EadzCMM0ppZt1ilobgLYOcKZRgLztJEmn62Ykd6P2Q9lskxdjYYNtC4NjphnLbHEdz1WmiM29/0Fk8bq56uLrYjhS3Hrwf12UKFq7fELomwWLyr/h/p/KWtpZEpxqnrfkjTOg+Nn0Wz77+LtpCoEKEB7Zt6BQ823HkZOzSzCZhXQbB229YsOeIKE0l/IQJvKTJG6oPyZSApBqTbREx/zVn3v4Af/n6O7gRcBMuiXWaqD8xaL7ZglchQCC0fK7qfqZnG4kyWb0hglehruqSlxbM7enkdXXPEQgshJrbktU4axaNPPxjUQndx6bPdtWDbwvR+ffjE1sSlWZmklEY5+kgoHLI6hyfFSJrJ5GplvrGA8fxyUdexsaIIYUmpyQB2H1nvWe7bXLsqdq5Tf30XfjlbrO1hH1Tcxj7k1e04zTZhP202gI3rRnWhsmNeEOd31WIOvcjhast9VoVD20f7XqmR796B9atXd1zbJhz2GQ+ibKDaLaWdys6J2HQyQ2gJ7YdAJ59/V3l+eXPixISXEZYY88ZQc3FRSacTruU9vqw9HjT9l/lqJNdgE6dv9jl1Jp5+wNlxx+g+2Ofnm0Ym1mYtNso5qz5hRae3LNV2dKvtSS65ufY6QbGP/GRSAJUl/Vo0vhltJFqvk2hoVG53Fy+97AsU9PuTvd85M/7FRLMhMOCPQFppFC7cBZFSVkPmkXCzDgmW3vwWF3HH3/onLxe2HiD3ZskKmFiisNWza+q9Z6cF9uoHFOhKpPGf3PV0863y2Jm8t6D75HOLu6PzJLvoO69kjudskSYFBEW7DHpZxEwU1RHHKKG99lmFE6M6TshqY61CZ2LohEHuzf5/9+mC5AUvEEBZ0q4MvWINdWKkZjujwC02r3Fv+QiJjNIk1Z3MmnNNpFZ8l3f/mvr8OqbH/Qc+8C2DZ3/trGdx1GQylCoq5+wYI9JPzq7TM82esriulgw6hE1vSgZhTYOX3msTehcnF6kKsdrcK6kGcVUpCss1l3+na5HrM3zMd2fwHKvUxVyPKYmHxICjPH6Qf+HH9tdQbPVxlt/38RD20e1UTE2xFGQilJZNUvYeRoT1zUl5MuqilRIWoQoik1TFc2iwh93LR2+OuSxNll9cRxrjRW7tAlVcStJMJtXJRD9STBJMhxdOA4FoHX61mtVPLlnq3GXdux0Qztftpm6wPK7/vjEFrz5xN1468g9ePOJuyMJdSBejZmyFOrqJyzYY+La4x9mgtAtGDaFsibG6hjxwh+1SkjZCGMpNJ/as9V4rI1QnNy1SVuwykSSipC6uddFHpkWiTCiCE4TsjaKH5npGRa1YxKC8hnVfEXRhjQPxMUiFUdBKmKhLhcF7aLgRLAT0V1EdIGIfkFEB1ycM++4rikR9lIGP6Lp2Qa2Hn4F+6bmrOrGNH0x0yr8Yw+GutlqqDaCe2JsuZH1LbUq3p9vdqo4+n8fZmZQkURjMyVPPblna2ThbUIlOOOgq41y6vxFKx9FmLnl2uKN90UV6u8quiWOglS0MMp+l6ZWkdjGTkQVAH8G4F8BeA/AT4noRSHEXyc9d55x7fHXJYwA+hrmqg9YZ+e3cXIeevEcri0u9dgud99pf09++7a0W++fmosUTqfzCcg2dEmqVaowzU2/bLd+wenHxjnqNwsBN97BsKSx4HVkpitg52OoEGFJCKfOyjghkUULo+yHPy4MF87TzwH4hRDibwCAiP4KwG8DKLVgB9xmy+lMooTervJxzDY2Tk5Vyddg1qatc0vnBF49PBT6kod9uLowu7gam2lu/GNzFYlhMv08sG1DTwSPN0S4ac0w5hdaXddVORFto2b8vWeD59HZ55eEwC+P3GN1j7ZzFUdB8v+NbCbu37HlzYGahenIhWCvA/CnoL0HYJuD8w4UunrgQO+LGtVsI89hShAyEfzMm6029k3N4eiJC8roEpOQtKnaqAtZNNUb94YIC9f1jZpNyONMOwGVEN03NYdDL56zjohR3aufJSHw+MQWYwSPfxek0qxtomaC47ANMbVdOKNGrcRRkOTxRYiOyaLGuwvBrjJ79rxXRLQXwF4AGB0ddXDZchHl4ZtMB6YtqS5BCFh+iCZzkArVhxS3ONbNVa+nvGuUioytJdEZe9gHrtMmdaaM2oinzYSdb7Yw+fwZHH7pXI9GrUP3/IaIjAuTrWYt667L+7tybVG5IMp3y0ZzjGLqSMv04PI6/YyLz8J05MJ5+h6ADb5/3wrg/eBBQoinhRDjQojx9evXO7hsuYjijNVFVqwb8Yyhd6YP+MHtozh4r7lRg4qg0zJMSKwb8Xqu4Q0Rrlzv7ZkqnUtxFgudM9XkyFLNq+znagoflIuKrWNM9/zaQhjPYTsPspSBjNpRNeDwv1umZify/+V8hjn8wsoluMSViaPfzs2kIbJxcKGx/xTAp4joNgANAL8D4N84OO9AEcXWGNdxa8qa9McfR3HCAcsfwo4jJzvRLqbdhOzNaZvCb8pYDUP1dyYtT+4Q/GPTabsmdFqjv8TtEAFVbwhXW0va5imHX+pO47d5JoTl5/HJR15GW4iOw9nfICT4vug0ymATFJudkCnU0rXpwZWJI40dhkt/nA0kYnST6TkJ0d0AngJQAfBtIcTXTcePj4+LmZmZxNdlohGloNiOIycj1yVRCQNJreppbdG3HTiutQmHZVGaUBXh2qgpFwAAbykcg6axmSCgy9EYLHEreWj7aJdzOuycquOkM1n3e5uicSpThG6B1xU3M70zUQvX2eCiQB6gf8bBZ5gHiOi0EGI87DgnJQWEEC8DeNnFuZj+EUXTj1MbvtnqbR+XxOYMQJsJGoYqRNQU527qch+n8FZQa9SVuP3Oa+9gnaVvQ+UYJaCTzq+bJxvtU6VR6gq8NeabSl+AaWfVD9ODq5DjsjSw9sO1YgYM2y2hPMZUPleFv31cEJ2DynYR8cdRqwp7SaFXr/VGkoSdX3ePqrHJ8EOdMA42ejadH1huWedVqKeVnQp5f8HQxrBnFMecFbbg+iODvnTHx7U7q7qviqZrXJg4ihYXbwMLdkbLxJi5LK8KnZZjEwInhb5ORAXjqMMKe0lsnI6qWjdyIWq22h2NWC4aAJThl4RlR3Qw7t1Ea0l0VYc0iWhpBolqKoujfdouuPPNljaM1qtQ7gWk62TDPMCCnTGiC4Fcu6qCpUBDa5OWE+ag8mteOqGlatuWtKKibtzTs42uhtBtIbqElErgrV1VgVcZwjOvvYMXTr/X1foujMvNFuYOfhGA/v79O4EoGrhqB2GD7YJrotUWmHn7g9wLybSdm/3GifM0Kuw8tSMPNae3Hn5FGRUinaHBJCLZMDo4XpMT0sZ0EsUpFpw3VdSN7tqSsT95Rfk360Y8jKwa1greuF+TjZnpwe2jXY2io2js/rj2uO9RHIc6sDz2J/dsLZXgzIpUnadMdMKEdl5qTusyYi83Wz11YSafP9NpDt2Yb2Ly+TOd402RLap785ceWN4dCOybmsO+qTmsG/Fw8F51hI1q3mTzaL8NOygog+gWgksLLcxrfpdERfK3Jzx2uoHdd9a1iyQQzbktQyDl+eO+Rzs3r4+dudyvuih5UH7yCAv2DLC1N6ddOEiFbcTAoRfPdYS6pLUk8J+m5iAQLvT8CUVBgRVsPnFpoYXJ7/a2xQPU8xYcF1bGI/uYyr8L9v7U4bJFnQoZXWTqmhWsl2JCVRLC9j0KFgeLSz/qouRF+ckjXI89A2waBbgsHJSkFrRtRqwuiWcJ9pqsrFBoo4W22kIZvhhlfmQSkCrr0ISrmuomwu7DL3BrVU9bMz3u+eU1whqQSB7aPop1I/pSxP0IHeSGG3pYsGeAjdB2VXM6abp0munQska7LTI30S7uAAAWkUlEQVTj1X8vUefn0kJLKRxMHHrxXKRSxnEw3Ufwmc43W8qa6XHPLzn04jnrEgaPT2zB7B9/EQ9tH+0pHtWv0MEiNtxICzbFZICNecNVbK0Lk45NxIBtko0k6GiU9xannIF/+z25a1OXrb8fzDdbOHa6gVrV0+5UalUPROgUBjPdU9WrRHrOcQutBc8vtX5Z+taf6GS6N9W5JGHVKV1SxsQiV7DGngG27eZcaMppaTWyBowN0nGpurc4Zo5gLe6b1tjpK1WvEruTUbPVBhGUz/Gh7aNYu7q7frquJ6yuExIApfnMVGTLFnl+qfUDN8ws8v9NQl3XMlAyMRa/dWAUXHcxKxOssWeAbUKEi9jafmg1ukgEm3rvYdEoALDGuxERU6t6+NIdHw89r3+h0kWtyOv7s1MBdUy6DfMLLTy5Z2tXohJB4NmfvIu2Lzpo39Qcqt6QMjKnseJXMIV7ynNMPj8HfXNAeybG6thx5GRsrf8bX7sjF87JMiYWuYIFe0aklRDhOl3aFIkghXWwqJUu1V917qAZ5cq1RYx/4iM4df6iUVP1L1S6xaxCpBVKuiYbJuQ1/W3udElJzdYSvCHqmKz8pqigOUlnalk+dTITk9w5xN2xrRvxciU4XX1HZQubZFNMyXHt/AyLRHh8Ygue3LO163pP7tmKtyy25Y+88DNlyOS+qTksXF+Epwn9CC5UOzer6/1v/7V12jLIOlMJAGXEid8nYKv5tpYERlYNo16rakMQgf45/2xqsIf9fRSTW1HIotl0v2GNfQBwuTvQCR2/hhznetOzDTQNKfiXFlrwKtRx6hHd6BO7erhbP9F1inr1zQ+w8cBx5c5Bt7ORi6C/lnqFCLvvrMeqpWMS2vJ3LuPkdQ2oo1bvNCWFFZ285Iy4hAV7TjFFLISZNJJe07Qd1QmdYNf7qNjEHrfaAmtXD+PQfbd3CaX5ZqvLlBGm8aoSWYL22ptXolr2r1QvvHJ9scvBKJOborYTrBlKEkgtenLXJuxfSexKiq4BtfSJyMUqjJFVw4UVcmGUMWySTTE5xL81BHojFvqxVbTdjk7u2qRtcpskMcT2I5LORpM5yMbMoEpkkdEcT+7ZimuLS512d/PNVk9J3WarjUMvnsOHVxetxi358Ooidm5eb4zmmBir48Ht6r7AQ7QSSonl//cqZmeqqdrmsdONLqGuM3UBxRZyYbjKGckTLNhziI3d1kWGnT8j9eHnzlhl8U2M1bWapPz442S62n5E/ronuuvbOoZV55mebSjnQsV8s6WMl696Q1qbfWtJdJqRmPwej09swVN7tnZlc9aqHr75ta04dN/tuKVWxeVmC2tXDXeOiZIYpCu9YGo4UlbKGDbJppgcYqsdJdGibDveq65R15hjbqlVret3BM0+qoqGKgSg7RYkhc/EWB2Pfu9sT42ZIEHzkRx7nI5Nfq62lvDqgc9rK1qampH4UR0TnN/5ZgtVr4Kn9mzFzNsf4JnX3+n4HshgzNG9O20hIidMFZ0yhk2yYE8R25AqW+dZEi3KNpqjNuJ1le5dN+Lhns9+vEcIm6JEgo4olfBXVTTUzYFK8AaFT5hQB3qrDkaJcKl6FazxhpT2dflcbtZkb7p+btIsdOXaIvxTs9Ba0hZL082v9N+UScjZYOvwL0pYJJtiUiJKSJWNdpRUi7LR9r0K4fJCq0s4XVpoYeqn72L3nXWlKcHGEaUTTrKiocxYNIUg+lk34nWZMqZnG9ZpPP5xmeZExqD77/fgvbf3bOG9IcLC9UVsPHBcKdS9oWQdhXRj1JmFWu3lcNGgScxkfpAZwLJ2z9ETFwod+ueKIoVFssbuAJtVPEpI1cRYXdl2TZIkKkaOVbdJ94fHXbm2qBxDqy20ZWVtMl1toxBsQ/KCERum+zONy5TYdPSr+mxLfyTNFUNTDwC4aU2y6JK4oZBBk5jJ/JB1Odw4WnEamnSRwiJZY0+I7SoeNaTq0H292qC0pcatvxGMtglS9Sp4YNuGjqZmqheiG7eNI8o2CsGfXGWiMd/sctTa+h5sE5se2LZBO9/+uihrVw+HNqQ2lTuwQTe/ppK5kqAzXFfTJctyuKrvaf/UHB6b1pdSTkuTLlJYJGvsCbFdxaPWbOmHQ8dkQ65HcGAmHXeUMgfy78I0d/8HbYotr1U9XG62lOPSJTbpfh7E5gMXWC7upXqWXTXWRzwIgZ6x6uYXsCuLYDPGpAIsifasekcFlstUjH/iI8rzpKVJF6maJAv2hCQxK4TZyV3Xk9GNlQC8euDz1oWhwjrPh4076qIVxanZbLWxenhI23907erhTtPoIFEFWlCA2SYrSS105u0POvV1guYP/3lUZpS49W5shFASAaYy40w+fwaHXzrXVe1S96x1c21qr5eWJu267lI/SWSKIaKvEtE5IloiotAGq2Ukjlmh3w0rdISN1fZDOPqV5NX9opR2jfqBXm62QmPt/ci4e93fqOZNtf3/8OpiT8KQzokrtVBpLghbvMJMITYOY1shlCSuWxcfL5O9wswkpsVD9x6klWCUh2/YlqQ29p8DuB/Ajx2MpZBE+QhshFmSNnZJx2rzIdRr1dRf5Kgf6C21qtYuHzyXjd9B9Sx1AmztSpEvfwE0k3CPUvjLdEyYwziKEAoKsFrVwxpvCPsV0TVRxigxLVK6zGZA/x6kmWCUVq35pCQyxQgh3gAAStDktui4tIUHy9bKbaz/Ov0ca1gUSlbbzigFq/xjtNk2m9q/jXhD+C8aYagTYJebrR5Tj6krVJTCX7qdQ1jXqbcUtWLCkOaeqBEytlE7uvmTNWxUpZ91zu0yJhglJTUbOxHtBbAXAEZH1XUwioorW/ihF88py9YeevGcs5fUNFZdISwb26grTI43+XOTZhrUSk0f+/Rswxj5Y6o2GSX5yFTUy1/4a/K7Z7RRNapFKSh0VbgozhbFMWm7CJt2Yaq6/gLoFF7TlV4eZEEeJFSwE9GPAHxM8atHhRDft72QEOJpAE8DwPj4eP8aUhYYnZCx6T3piiw/EJ12OPP2B10ZqTrhXiHqGnvYvYSF7+kcdtOzDVy53lv8S5d8pNNCg4W/TLkLwfZ/cvw2JRiSRIdEdUyqlIMr1xe7Fiybnd+p8xe1NetZgIcTKtiFEF9IYyBMNuQpRVqnHfoFYmO+icoQdVrP+Xlg24ZI14tr1z780jmlZm1KPrJp8nw5ZAEPmkHSqCkUJ0ImuKDGeceKFDOeRzjcMUes04TL2SSfxCHrDMMgplA3P+0lgbWrKrjaWurUqX9g2wZjH1UVtnZtv2DSmWCA8OSjsB2EzXj8WmsaNYVchPjF2QXGDbm0WUTypMz0i6Thjl8movcA/HMAx4nohJthFZu4kS0H7729J1zOq1Df2pGFZRj2M0JHdf5ahAVs4Xobbz5xN946cg/efOLuyEIdWBZapnrmQwDmF65j39RcJ6zRZBYbIko0V6roDhX+8sQ2xydxeE+M1bH7znqnnK+/e1Q/iRPpYpOBWqR6L0lIJNiFEN8TQtwqhFgthPinQohdrgZWVJK8OBNjdRz9yh1d4XIuYsZ1mLa7/f4AbOPAdTiLUTZ4e5ZgVyVS0hYi0VwFwwzDaqPL400kbT4dbMghu0f1WxDGiRm3KYWQZbmENGFTjGOSpje7dl6atp2m7a7rNO3gOK5cW1TGgdeqHtauVreOk7gKuzx64oKyIqILdHMVZgbwP39V1Evw3ifG6jj80jltxmvS3V6Wha+ifgs2dvlBsd1zETDH5OnFCdO6Tdtdl/ehGofOpHG52TKW7K0QOcv26/czaazsfCSqedg3NYeth19RasC2WquuL0jVG0o8T3l6n8OwyUAtYxs8FSzYI2Bjc87TixO27TQJDpf3EaXWiz+uW7XofONr7kxTcZ9JsDa7ybm9f2oOG1fel8MvqZOhZDNunXAPy3TURdNcNcTh25Kn9zkMG7t8GdvgqWBTjCW2ESR5KhRko23ptru296EyLQDdiUG29cODcd3B87iOXtAl06xdVUHzehsqsVirejh03+094Xy6pBx/mKaJJOaNflYdzNP7HIbNOzMoWaokEvZ3jMP4+LiYmZlJ/bpJ2HHkpLaVWLDhRF7CqaKMWUXYfagEmjdEAKErzltXaXHdiIeRVcOZzpPqHnUp+gTgyT1bu2zgNmGQthCAX8ZI/9fZ4l2ZrPLyPjMAEZ0WQoQWXGSN3ZIotsa8pDcn1bZsMjdVDtAgAr3CvepVcPDe23MhyIOL3H5N+VsBdHZpQHctmvlmS7uA2RJXw+63FpqX95mxhwW7JUUqsi/p9wcfxYEmsLxTaMw3USFSpsj3G5U5bf/UHPZNzXW1GzSZj/zjVjWECBPutZX6O8EolqTmDRa+ZgZt18GmGEv6vd0tIjpTjwopOINzSAAe3D4aK8EoKmHjlc8TMHdsktHlpr6xbSGUuxT5vgQFzc7N67vq4ZRd8KSJ7bdbBOFva4rhqBhL4iRMlB1VhIE3RMpmEzs3rze2PUsj8y9sh+F3YD5x/xZtglBtxMOQoVR1WwhUvQoe3D6qfV/80S6Tuzbh2OlGX5LB+p09XARskpLKlpHKppgI8HZ3mWBvztXDQ129OYOVDGXJVZ0GnLQCoS02ETpS+Mux9DiHK4QPry52MjF1NFttnDp/0cpJHTUJyFazzFstoKyw8Y9lmYjVD1hjZyIR1GwuLbRwudnCg9tHO3HWupKrOg0YSCfhxaa2it9notqlrV01bJ2tmrT6oq6Nn61mOSjp82HYxOIXKRHLBhbsJSKNbbeNOUX3MUi7s4o0nNDBglZBVA7MYIJQWGldP7b3FCUJKIqwLpuwiotNUlKRErFsYMFeEtKyEYZ1kQf0H0O9VsWD20d7hHtaCS/BglbADUeorc9Ed29J7ilKNqRu/qNEbBVVWMXFxj9WtoxUFuwlIa1tt00XedNH8vjEFjy5Z2smTmjdbkMmbNmMQXdvJkdpGFFK45oWluAiXjZhlYSw0gxlC45g52lJSGvbbdO/Myx+PisntIs56kdugK40rqq/p27+VQ7oQUmfd0WZgiNYsJcEVwlUNmVlw/p3yuPy9JFMzzYwtBJfHiTqHLm+tygRGRNjdezTZMbmOQuaSRc2xZQEF9tuWzt9luaUOMj7Ugn1PJgmou4kdCWNXdnOOfa9+LDGngH9yHBzse2Oqjm6EuSu5yN4voXrvU09ALe13ZMQdbeVpPJm2L1y7Hs5YMGeMv38cJIK2yzC41zPh+p8OpaEyIWwilqszWYRjzuvZUvUGVRYsKdMnj+cLAqduZ6POE09/GRRLyTObitO5U2beeXY93LAgj1l8vzhuGyqYCsgXc+H7d/pTBdZmSFcOzmjxLv7KWIVU6YXdp6mTJ6TRlzF8kZJlnI9H7q/q1W90PsqUwp+lHh3Pxz7Xg5YY08Zk1ach7KhLjTHKGYA163XdOcLtrNTkdZuyqYzVdL3IEq8ux+OfS8HiQQ7ER0FcC+A6wDeBPDvhRDzLgZWVnQfDoDSRCNE7TYFuBMkSc6XhhkizNzjyhwUNd49+LdFe+eYbpJq7D8E8IgQYpGI/iuARwD8YfJhlRvVh7PjyMncOlUltppkVAHpWpDEPV8/GjfbhF76n7NLZ3Kd7eUDSyIbuxDiFSHE4so/XwNwa/IhDSZ5dqoC0ezmRbXTuq4XopqzYEs8iXzOLt+Doj6HOHBSVTcubey/B2BK90si2gtgLwCMjo46vGw5yHs0QtTkJfk3RbPTutw9xAm9dPkeFPk5RIGTqnoJFexE9CMAH1P86lEhxPdXjnkUwCKAZ3TnEUI8DeBpYLnnaazRlph+mAFssTGxRNUk2U4bL/TS9XswCM8hz7khWREq2IUQXzD9noh+F8CXAPyWyKIzdknISruy1XbyvqPII7o5q1U9rF09rK18CZRfy3ZJ3s2YWZA0KuYuLDtL/6UQYsHNkAaXLLQrW20nyx1FEVDteuKGXg6Clu0SVjp6SZqg9KcA/gmAHxLRHBH9dwdjYlLEVtspWyMCl+gcywCs54ydf/EZJCexLYk0diHEr7saCJMNUbQdlSaZh6SqrDHtemw6M7HzLxlsvuqFM08HnCQmFhZIyyS18bLzLzlsvuqGa8UMOElMLGWqrZKEpPVu2PnHuIY1dia2tsMCaZmkjmV2/jGuYY2diU2eK1WmSVLHMjv/GNewxs7EhkMgb5DExsvOP8Y1LNiZ2LBAcgc7/xiXsGBnEsECiWHyB9vYGYZhSgYLdoZhmJLBgp1hGKZksGBnGIYpGSzYGYZhSgYLdoZhmJLBgp1hGKZksGBnGIYpGSzYGYZhSgYLdoZhmJLBgp1hGKZksGBnGIYpGSzYGYZhSgZXd2RyDzfMZphosGBncg03zGaY6LAphsk13DCbYaKTSLAT0X8mop8R0RwRvUJEt7gaGMMA3DCbYeKQVGM/KoT4rBBiK4AfAPhjB2NimA7cMJthopNIsAsh/sH3z7UARLLhMEw3k7s2oepVun42qA2zGcaWxM5TIvo6gH8H4DKAnYbj9gLYCwCjo6NJL8sMCNwwm2GiQ0KYlWwi+hGAjyl+9agQ4vu+4x4BsEYIcTDsouPj42JmZibqWBmGYQYaIjothBgPOy5UYxdCfMHymn8J4DiAUMHOMAzD9I+kUTGf8v3zPgDnkw2HYRiGSUpSG/sRItoEYAnA2wD+Q/IhMQzDMElIJNiFELtdDYRhGIZxA2eeMgzDlAwW7AzDMCUjNNyxLxcluohlm3wYHwXwd30eTlaU9d7Kel8A31sRKdt9fUIIsT7soEwEuy1ENGMTs1lEynpvZb0vgO+tiJT1vsJgUwzDMEzJYMHOMAxTMvIu2J/OegB9pKz3Vtb7AvjeikhZ78tIrm3sDMMwTHTyrrEzDMMwEcm9YC9rlyYiOkpE51fu7XtEVMt6TK4goq8S0TkiWiKiUkQkENFdRHSBiH5BRAeyHo8riOjbRPS3RPTzrMfiEiLaQESniOiNlXfxD7IeU5rkXrCjvF2afgjgM0KIzwL4vwAeyXg8Lvk5gPsB/DjrgbiAiCoA/gzAvwbwaQAPENGnsx2VM/4cwF1ZD6IPLAJ4WAjxGwC2A/j9Ej2zUHIv2MvapUkI8YoQYnHln68BuDXL8bhECPGGEKJM3aY/B+AXQoi/EUJcB/BXAH474zE5QQjxYwAfZD0O1wghfiWE+D8r//2PAN4AMDDdWRJ3UEoD2y5NBeb3AExlPQhGSx3Au75/vwdgW0ZjYSJCRBsBjAF4PduRpEcuBHtYlyYhxKMAHl3p0vQfUZBmHjbdp4joUSxvG59Jc2xJse2sVRJI8bNS7BzLDhHdBOAYgH2B3X+pyYVgL2uXprD7IqLfBfAlAL8lChZ3GuGZlYH3AGzw/ftWAO9nNBbGEiLysCzUnxFCvJD1eNIk9zb2snZpIqK7APwhgPuEEAtZj4cx8lMAnyKi24hoFYDfAfBixmNiDBARAfgWgDeEEN/Mejxpk/sEJSI6BqCrS5MQopHtqJJDRL8AsBrA36/86DUhRCk6UBHRlwH8NwDrAcwDmBNC7Mp2VMkgorsBPAWgAuDbQoivZzwkJxDRswB+E8tVEP8fgINCiG9lOigHENG/APC/AJzFsuwAgD8SQryc3ajSI/eCnWEYholG7k0xDMMwTDRYsDMMw5QMFuwMwzAlgwU7wzBMyWDBzjAMUzJYsDMMw5QMFuwMwzAlgwU7wzBMyfj/b9j86tP6ZuQAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# scatter-plot points\n",
"x = np.random.normal(size=500)\n",
"y = np.random.normal(size=500)\n",
"plt.scatter(x, y);"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(100, 100)\n"
]
}
],
"source": [
"# showing images\n",
"x = np.linspace(1, 12, 100)\n",
"y = x[:, np.newaxis]\n",
"\n",
"im = y * np.sin(x) * np.cos(y)\n",
"print(im.shape)"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP4AAAD8CAYAAABXXhlaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJztfV2sbNlR3ld7d/e5c+6dmesx/hlmRthIDgEhESOLGIgihEEBgjAPJjIgNEKO/EKCIUhgkweIRCSQEDYPkaVRHOREKIYYK7YcBELGPOTFYQwogAeDY5A99oCN7Pm7955zunuvPOyq2rVqrbV7d59z+5xLr086Wmfv3j9r7+peX1WtWlUUQkBFRcVhobnsDlRUVOwf9YdfUXGAqD/8iooDRP3hV1QcIOoPv6LiAFF/+BUVB4j6w6+oOECc64dPRN9FRJ8kok8R0dsvqlMVFRV3F7RrAA8RtQD+EsB3AngawB8C+MEQwicurnsVFRV3A7NznPtNAD4VQvg0ABDR+wC8EUDxh9/euB5mL33oHLeciIsKRjzPdS4rIJIu8fzz3ntXnPddX4Ss9i3vwrtefelLWN+6tVES5/nhPwLgs2b7aQD/1B9ERG8F8FYAaB+6iYd/5m0X/wXxLz0nhOSYvhMUCp+bfcVj/DW27dN5UHqHZn/wx0hH3f7oOML4MbmHLZyT69OFYBt5u5eQlaU7PzkmeZGZ17BveWfeaSDgc+9656TLneeHnxNn8rghhCcAPAEAR1/1WMgfVbhaDmMvdMrLzghxMuRUdx97Sf1C+GMnva0N9z3vMReB7MPKZ4W+nEfepfNL+wvHZgfnqbAn8/PLa7gr8i6dX9i/y1f6PM69pwE8ZrYfBfD5c1yvoqJiTzgP4/8hgNcQ0asBfA7AmwH80OgZARerAm3FBAWVb8pt/OjuL2Ku7UffCyfiwgVHR/3Cw46e45gr86jpsVNQ0JpGsenYCfLeCbm+uhdRZP6LuncB2cfb4ku98w8/hLAion8D4HcBtAD+Swjhz3e9XkVFxf5wHsZHCOG3Afz2BfWloqJiTzjXD38nbKOe73yPsp600Rs7BcnlyxcJYzrbRdoBY2reBd4n8nMVLzzSl7sx7XXB8h5V33VffKFROWtnNh8yGefyVtaQ3YqKg8TeGZ86uhC/S3TNXQa/Hc5JHHdTHDrqDNr+fpOwxbvc6b0nDk3zb1F7ix1fF42t5H2O95516han2QpTmxeFC36XlfErKg4Ql2Ljn9M8uTLYitEuK5z1orGF7O4ZOW+YYtxJc7ni8q6MX1FxgNgv4weAuunHRrigEfRCWfqCR/WiD+HcF747x15I/+6SnPXy24Q77yk0eqxP536nE/tXGb+i4gCxfxu/owu3/YojaOZGJU/8Vswwdk7p4XZgikmvaXTRkriludlhTnvSORte3t7knblZsl7oouRcuF/xxhNRfFVT5LwFKuNXVBwg9m/jr4fN85pLCXkna5bTOwyDY7w2fXQRCrnP/CifW89e2o76sj0VUml0z60zdzEEPrrMv4r4PoXPzP2L2sAFBxEW3QBZWbkYAhdpp7sndCQr703yzS6b3V3lSeSd1bi2v35l/IqKA0T94VdUHCD2quoTWGsaUy03IEoAk7uBaSMNKPZzGbU3VvlH7+lTV2WmgRK1bpupogkISfof19pbS8f1GP6n28XTSHzN8r0T0+Ecco5PKmxnHLXyiOS/C1PkXTLpcqacHlu43kXLe8TJGsm5TudVVFSUcDnOvXMwQbRCssC8OouVc7TIAN1Il0pzXSiP4v5+zZjzZzPDbAXPpiPeqtCJQysfGSTPPposVJi+c/vNrdFFl93ATpl7bcIGOURaYMEX5l9TJo1e2knZ39hjC1pf6dxcv6eg6Dh1qisATZEfcifmURm/ouIAsf9luWsqM4PFhCWv5Ef80ZGaPxKm79z22P0Ko7wyPY0cmztGjy3cx3c62udb59Cwl2h4aos/o86xRe6ZvYvC2/EZG99rA+T6lvULeIy8/4TFvbwtfals4svpbYsJFMc0SHOsp0ov3zG/gMfoHLJ0akMLDD6bLTSKyvgVFQeIS7HxpxSxSDDGmNryPzKchXSkVmLxTD8FJabP2fgFJojYa8wetL2NGFNYPD5EW+ux72IaDdoHx3q5oBw3I5B47DEw/cD4eX/A2EzAKEq2vciX4j4Cg2yU6R21bZMXReUcaRQF2Tfx51k563Zyp+y//baTd8bXothitqYyfkXFAeISUm/lPcS7Xcy1yvSynTFenUmcesXL3v3UoyujfcYGlJHfMT816fVzsw8WkVaitnz8ICE72vM+Yf7GMeQUgvA2vllWPTC+3McdM8b4u6Dkm2jSg4KTd6Ic5PqxyWNv97UFuYrGkQnz3SRni0Gjc/KW5+gy3+1SnzOojF9RcYCoP/yKigPEfkN2R5x7u4TsJiqZqvjJ5Qc9qwv5c8buVVL9mnR/ovKp6ifdyKn64w8fbIkuOUc0QFGrUz+XvUPf8MpIdfKN6IWJ1psL4Cmo+FNU/V1KmOkU3dpt506SnV18ja2cijnnbUm+Iybd4Hue/tAicz1D5Sz3sd8Jb+NuRmX8iooDxOU49/zUBLZggBzjC8MLA+Ty+pW0A8Tbk7rhRv0cI3gmaCilujEtIOqaZXw33dZRzLrZmSHvDNMbj942Plede3a6UPZxy0ycBP1YeWzB+D70WrUcoSthc3OO9k7X5TvBTrrvyPSbfMcSOcttZXt46KlyjvrgpvGE1UNOdREHL6g69yoqKsq4lCy7WXtx4ohsp0SCM23kGl3L25Zp1E5083m72Hyujew5z/Q88mtskT1Wgz22YXxmen42IZYuZ+b5ijYFX0V2qXNBI6KMzJTxPcN7mx/T5QwgE5Ltzs3QlidEf7/R2yYBQ2MPzU2B6a2cm9wUXwEJ08t3Gk7Qjf1ObKOu8unTD62oqPiHgssN4NmGCfzob8/x4bjOC2w/lHv7UM7kmiNd8UyQY3yx6Zsmbu2o37hgHs8IfvTv/48fWl7hwPwjTOCDfLaw8bPy8d77AtOP2vj+Jef6lJk9KZ7jZzmaWAXQrWh6qGDTZzSkxLZ3TN+2ZTlP0fAGmYtmFz90wvwYtI4asltRUTGKS2H8nWy/nH2a2GTcdunnflGLOnvH7isJK7yt50MwMzayn7/PMr5oBQUG0NdjPu+Cf8h+7F6H9Nihf87DPYXqE2ZOAwUSE9jb/LswvoWz15OltrkZmk1ynoLS98r87z31Xr6xjd9FlynJGzBKlFdn/XHBypnl24Tq1a+oqChjI+MT0WMA/iuAV6IfkJ4IIfwqET0E4DcAvArA3wD4VyGEL49eLPRX8F5gAJG933/m7F0e1Ua9+iNRWtssx5yMzBJMb8cNXv2U3Rt3rLf9yNl7EXRZsdwHskMPWfsJ8G1WiRQwusTWK0YjjD8cm5dzdIyTc3DXx8h34kKWAUdaVN6/4305jZnHbzfIObqll3kTa3a6PzPT0L+6ad/wKYy/AvBTIYSvBfB6AD9GRF8H4O0APhJCeA2Aj/B2RUXFPYCNP/wQwjMhhD/i/18A8BSARwC8EcB7+bD3Avj+u9XJioqKi8VWzj0iehWA1wL4GIBXhBCeAfrBgYhevvF89FpJPmR3XBcn/sCWgUqCM0YcR/4zUZlIwx0noBjIU1K7Mk6gaJqHgz0KGniX6VWScoBVy5wKmElQ447J3Lj0/kdU5pKTL6tmexXfXS9S/TXWimXlTLmc+bbRpNvKyZeacurck82CGh+d4s2/EYvLy1xU//Q+5nfA7TaPNtm5R0Q3APwWgJ8IITy/xXlvJaIniejJ1Z1bW3StoqLibmES4xPRHP2P/tdDCB/g3X9HRA8z2z8M4Au5c0MITwB4AgCOX/FYmV49a+Q/Vubvr12itMuDZ3jPAKOOHfdZw2flmL9YPDN74fzuKctzpyWnK7S5rjim968j+1hOQUlYfUQL2aGe5CSU5JjT7DzTj30HvMzlOvoKxhyEW3wlNjI+9TrFewA8FUL4FfPRhwA8zv8/DuCD029bUVFxmZjC+N8K4EcA/CkR/Qnv+1kAvwjgN4noLQA+A+AHtr25n8o5N7aZurkCmMIA58I2ATt38/ZbPF42ZHqb7t8jsr9I0A5y3vjDDyH875ErvmHynSoqKq4M9h6yC2Dw1kaeSWfLiI22zWhfWHa6T3glJhtwwdDkt4g9t+PX5wCPSZ25XB9Itobhhr5kU6ttg7Fw20uC/w4E56nPBWj5fdkgrgmflVBDdisqDhB7ZfwAHtEzTKCVWx3zp0kjciti4ja49sJQYqvRETt+ntzorB5c97CiEdhzuoQJ4nabh540M+DeZfaMYnyDa2FCr+W9+EnozLEluSYJOgwuRPYaPms89E4mpdZGKeuqWacOqgc/873S62y4T3zSpgdK+1RRUXFA2L+Nbxg/HzhWoJYce7gkm6MpphKWcIyzDQoRg/aCwhJDIgVJmWQWb8gpmiIrHrL9qG9v3XXxoo0cEyRawBStYNP7GH2n3PrwQquk6eIiyh+T+074RBx+O9ISCp9dkP9n8LGIfR7vV3nnKJVlJrb9egLTD4zv7p+Z/QhWnd6AyvgVFQeI+sOvqDhA7FfVJ0S57qL8ecl6/PQYuYae71V9pwKGzLG5z4rQhTy8OehU8UWM3qVqeTH/2fACgg/rLUzV5bPsxq0UUYyO7ZxauEOY7zAlJ6ZRxrkqmXF8wE6uolEhqCcrby+rgryj/IkFR+8klEKPoy8Svwd5t5L7kOJ185F7z78H+V6520RdSeTcRNvB5NzTApqhcLEMKuNXVBwg9u7cCy2G6TwzKPqROSljjXTb11STYUzy6mfz812E00eYWTPApCyoTOBSC1lGTpdayjEonuOZQEb7zvep70TU31SVSJ4shWf+TOZinxNPP1ZtoXyO7s7Ju+A8LDp1M5/5PInTAp9cG31PY+ezvlqRgxxnXoY4epMMSwV59/ucnGV77SvqGO2jZtmtqKgYw/5tfMP42bz3hSE5G6zhR11vx7fDoQMTxAyQBgjlbu5an7s9k8tuOIRHaMk/F9VUY1uv8ND5UE5u/XSeJKnoUiZI6uoV7Ot4p2tdjr9+I0+jCdNbv07Bl5NDaWrOM33kNyr4ctJr5Wi20IGQOUaTgvC0LT8kZdi962KNblpe/bgPnXuQbm2+GypnqjZ+RUVFGfu38Zs8q25MrjDmpS0xvmUCrnCS2Ify+Zh5VPLyZqryJqTBo7Hm2bdqiLf5NlzL3lsZ3s0ihEw1W2WEJJAnd4NCHzLsXZJRohGZ48j7AUrXsMd4rWxEzoOfJ0Tb21DckOmWrxHJOWZkseV91Vzr2BjqG+TlPSpn70fJyjn+DkxBZfyKigPEfhfpENDNMvO99t8SC40xfcEGtCNsaa5/zObz8/cpE5TpyfsSgvPcRzcoDdTZCd68DTjYnhnGdxoKde6c8m0SO90FFfNBvMWZRTQpZsZvkzD8mNbh5Vq0+Y2cfX99vwu+nejkzsnFqhy6cip+h8rETSrnpILRFO3S9Sl4+drjqo1fUVExBfWHX1FxgNj7dF43D/kpnF2WyfkVdiXVMLcv5xgqwamA5NX5KPaYW1/eSQobZvq/FTYF40TRLHGbqPiZayUhupIYUKcjM13RkF0+x983mg7bXc7JJTJqe+L4kw/8dO7IbULpfWWur2q2K1MWf/d2kLPesOCQzb3HjLO5hMr4FRUHiP0H8MwzDh4Ak70Shetmr5RhfD3GO/Wyzp74o+BGd81gk72PjPw+Wmak49sgCcIZcdgV2GKUiLRrjvlzwSyyWXiVsbzvgpxzxyQanne2jtyn5OSD0QLGtMukr4Wbjc7n+T65U0ua3USNqjJ+RcUB4hKm884x4k/FhEFvl+Waw6zM5pMHZeAcrL4DJpmTUwJ3HKNtU2PwblWvKeKi5J34JCZMv+mhV1DOI6iMX1FxgNi/V3+xBzoYGd6TkXKsO4ldNe04wJrIe2KCMQoodGEs/NlvbzURc7cqA5VwXnkXupuffSodu1/G31hkcgMq41dUHCD2zPgB4W4yvno3ndfdHpIsUXUe7hx7dxuONec4Z3jSt/OSYdl7nNqjpTDVIamGi4PIXHcIgc247PWYwszF3SZBJ28gnd3wMQUqw8ycdyrXzOyHj1Eo7M9edwcU5W18CpGcK+NXVFSUsHcbH/MuzwQXEcXmFjJkk0ZIlJkubGDW69LRnQos4ZkhYo/kmBGNYhcm2DBPbSMRNbWTS1yh+/kilFnkkjB9LvLNz5EX0l3FWsIFyjkXeeiZ3C9M0rn5CRGOXpbRMflzRisEb/PoJV+LytRoOUbOU5WsyvgVFQeI+sOvqDhA7FfVbwKaxXrwQ42ogMVoxijjbHxQcJlmoiwla2676JQhwCaX5tU55LR11yJzH/lMH0eP8Q8yYaopo7cli4xUJednzuWfE7VQkv+4ElfRbUsqfuteAgC4LDdqMuiadG5z9CKfud1ZbditSQ9u8Uw2G806flFS8krkHWUFcvfxKr7KG8bc8+aAl/MUJ1/mK+e74js55JUwB1gzrDr3KioqStgr4xMB7XytTN9EDgrH+IUCkrmikL66yJCD3BxLngl4v9xvLF9Zl2+bFTt0sowQtzlHUaIFFBh/dHmxqyUQ+axaafl9yIKbojqVuY9jcWV5AMT/U9s/iDB708QP22QcUb6mgPY5m1mY+1+sJWDkzPIN0hmVzUgkkhzhfZKivZnvzLCP24K8I9l6ZWkXzW6kepD+31Jl/IqKijImMz4RtQCeBPC5EML3EtGrAbwPwEMA/gjAj4QQzsavEbBYrJUR7EDXNl1yrEWO8dfKBFJXrL/Gei3liIdxrSNhPZ+UXW7oWnOMfiRMv46Z3jJ+4xmhwAzRvZUR3DO7qi32fx35henX8TYwzFxp3/jkzgfu5FjCvw+x2y3jz/qHEUZvmPlb11pZtkn1oDLjl0pGC/OLnKW6DAB0FNeyCy5ZoNY3iFjWfRc8e1v5rtxnftvJO/rfxznJwqfcAp8S07dxG+0L02dLt2H8twF4ymz/EoB3hhBeA+DLAN6yxbUqKiouEZMYn4geBfAvAfxHAP+O+hIw3w7gh/iQ9wL4eQDvHr9OwGK2wkwYwbB847y8st05m29tGZ+Zfs0MsFr3Q58w0Coa/mSI7OLr5urfebigDc/mwgL2/4Tx1yG6RvR/cZT2caE5BmBNiB/Psryv26qvTp5DmMLeUX0Iedte7HnAMPssZvh52z+0aHZzc44wfDuBmuSIQc5O3m2/vVoN9LdayVn9PqliM8xwZLQoB++5j3w4Tubp9gQ5p1NV5uC4DerDER8Vb5tfrsp8C4/dVMZ/F4CfxvAdeimAZ0MI8pV/GsAjuROJ6K1E9CQRPbl67vb0nlVUVNw1bBwjiOh7AXwhhPBxIvo22Z05ND8FG8ITAJ4AgBv/6JXhvsUS86bM+G1uwhuDvbcy7kxhgKW0zE5LwwDpdfpH1gUqMv+tGofx4BZCOXWUzzC+2HwNM0+iAYwwwRQbf2AA3taQY72qHuuVGe2DaAk6MR45NuLLaIWY1MYXm3426y8sTL/g7VkTawB2XyPz6iM2fsedWDnGF3m3rOHlvoyrEGtCoSt/J0qLrrIyk30qZ2lD/PnYTM9IphKRudfs5L2rbZ+Z/ejsM2zAFOXgWwF8HxF9D4BrAB5ArwHcJKIZs/6jAD4/7ZYVFRWXjY2qfgjhHSGER0MIrwLwZgC/H0L4YQAfBfAmPuxxAB+8a72sqKi4UJwngOdnALyPiH4BwB8DeM+mE4iAa7MV5k2sCgLAjPWgRttYZ+lU1TeOHFX9+n2nEjCScRxpsM+anXvq5BG9ruzt8UE4iSoYTfdwH5ayHR/TrM10WKLquz5nMgBroA5PKYqTJ6e1q4rfuHYkjHg4OW5F1W+szGaxKn807x/2qI1Vf5E3MMh8xi+kJOf+f3becbtk1b7ll3CWk7Oc64J8xOkWRuStj+ym9RorX2feeXln5eyndEfU8eCmWtVpq8/D148cgpsdlh5b/fBDCH8A4A/4/08D+KZtzq+oqLga2GvIboOAo3aFa20/PC6s08cxvscw+g/nCOOfrOeFc9Jgn7UElXDQR1KVxSJx7rk2y/i+9U6+lPGLzJsJ2RUHo5aBlqAcub+lkyZ2cI2uFdcb+Kgfce71m61x7olzVqZnhemPWmb+Wd8ujPdz0cRMX5I3AKyY2YXxz6j/urZdfE4k5y6WswT3dJsKlAKpE9dreshMz25w8gED+2+evh36p05c7QtfQ77H9hRdDEV3JYCnoqLiHwj2vEgn4Fq7xDVhhHZgAmF8aw9aCGOvzLTMKeW7Lwxgg31WPPKv3PQUXC21XP65UsadgflTe84zfZYJJNhkw3ReFJ5ZZI14Gsj2S/wBpaWjWZZwZb2FVSIbX6bvnE0vTC+anbQAMOebz1jOY4E8S8f4qiWInyYXxs1a4Iq1Ai/vUQ1P4ENrM4xftPXddn+Om+obm85zWtqQOzCedm5yy3LHfDYOlfErKg4Q+7XxKeBau8J9zAAx4zNrUIHxeYxameG36Plv2AtMA1W26pWOQ4OH/HObQQXGt0pKGs4bopZssI8wgWoUcS+0b2YkHxjdrbCRY+1SZB+AUghUGYXaj/GCHGB4pxqowy9CbHph+iPzgo74M2X8kRKvM5bfaZf/moq/Z23UHAnqaSmWd+qyz2CDZtf/H7N349h80OxMoJPX9sZKDbmZF+nL4MNJNTvoTE+oy3IrKirKuBSvvjC99fbOHeP7RTrC+DmGUKZvY8//6dosKJGlwI7B8nmhGMoATi1w87yR17eUmCHj1R/YIrb1k3z1rbHnxDWh3t+C/W73eQYbs+315LjV5Cl2ia0LyV00cXuk7SDnI57wFi1B5JlblNWEfFzG2ml2Z1azKyz7pSm2vRzi3k/2nSZan3juYw0PAMhpAcnsihWvZEuesV/Da3ReI8AwC7FNFt/K+BUVB4j9JttE773P2fPCCrJIx490S3FzmqFqzbOZMx4GZ118ro0MLCV+GA6YPlwOjOBGcBgbcEMLGAaQfd6bLAO52a/mrl86qtvmYL/0eAtGGPoQvzfLvuplRzwnL/b7XBl/8OqLnOWzxnWqsxF1TrlbMbOLn6fJ9Ek1CZfw08s3rv5DuUPyvpCCH2AsmtMv1SWfIcVqIfL8q4772cTXFXu+pIVUG7+ioqKE+sOvqDhA7D2Ap6FOVTOr6ouKX5rOE1jnjziGdOrGL/RBqpb6abxJ/d6kAob02PIab6PqOxU/CeDJZIaV6wZVNZ2ZYN5P0XqZ4tSbgOFdxip3m5gAZfPA51+IVs1LotxOAnhiFX/mtm1fNnZ6DCOXKMk3UeOjQp7xZ0kAj93UmgdxqK4E8OQsl12qklXGr6g4QOzduQfkp+S8k8dvix6QY4/kWtsMgVsw3C4YXfoqx+iaYbdfgk+sv06dSXe54w4+dDeHbd574sRldBmB+Cm/KfdNpvEuE6XXolE5m48lX+kpc9w2X/vK+BUVB4hLYfx1ZryRkb5128lxUaKGzcdsxA720TbQgIvcZy6BAiULhig+DkizxO6J0TTRx8i73ea9r3ORKIjDb3Uff1/89eU7krvvUIdhcpfOBw26Ylt8JHOufpStKei3M9+B3HHYTgmsjF9RcYDYK+OHQFh1LToO4lhGZV+4lfprPCzKqC5MYLUF+V8r6oQmbpFqB+qM3YIJSpVLc6w75KV3n7k8+ICx29Rsi9ncZ1zNXXfQGuRYKh6b9D+Hbd6LtK7SjchjKYFVRs5NyNv0Xt6AWZbbxXJdhVgDsIw/9GVDp8cw8r68fDUbrpeLlYNbYuurFcfXl2W5wvTuuv77ZfoAyvS9gMr4FRUHiP0yPnoWyC6zdHO23vMv2oHVEs74OkMbJ24QprDXDcmQnRlCNz2HG9WDsc2Dq1OfVDc1Q628hiFBQ+E+rWUPZrRZ/j7RiO/2efN5yiP7moW5Skb6vlk2Ig9JumGXUqtcJbWUr5RkXpAmUw3x8lyvCay79Jyk1qK7D2UevliTnjL7CvINmZBa7YMkRnWLpaLr6/cnZv6ivM351cavqKgYRf3hV1QcIPas6hPOulk2z5o4bmaFnHu5vPqn61nUnnEr+delBYbsq5K1dNJ0jzpWxAm3QY0HkjLGnQu4iUZaKW0ta+oLqn5sHjjnj6iCcj+bn69gBmRmzFK4kNSg7y81n6Q94/ctmXNmmZyI4rybhel59UXFP5V8+l1sUkRl1cQk0dLpTs4TnHvecRfXNWBZ+RJsmaKlAvW/uhWVua4MMuNjxDzQ71Us9+izZrquXxm/ouIAsVfG7wLhZDXXUX3ZDPSk1XW6fIyrnmNGd3XqrT0TxM4fYCih3ZWcfCNIGKDg0AFMpZuZztHxDncNmFx9fm034mOjqSE3LSgOwkETsH3Z4AAcndbjc11FGmFQYMhcfCp57ngtvK9z0Bl2EvnNMwtsPLSCjpOrXF81vtXwNVY5u/6GboK8/dSrOlfNMU7m6qDVx0ivnzJ+uQuevTW//szJu82c02Zvn0Vl/IqKA8TeGf/Oaj5M/5hcbDNm/xIDqI1vWVymj3iUFwY4WYmtn7FH18IA/IFfXpkmZklaz/SRvTXjQBTHAEGz/KZTc0lGFvlc75syvtr0ngmMRL2/oWjzb8H8a/NOJcfh2Sovu5xfRvIs5rLneKw0R37M+ForcRVrfLYv0s8g3xefly53W/8+MlqaMu1M/DL9hdYi58w79VlzRhP9+qli9d3Ecg5GzqrZtZNcGAAq41dUHCT2zvi3lgvMO86C2wy3bzfYfLmqKb6Kqtr6q9Srv1qJl1eYgK8zJUNpKWjD2Xn2YM2WKmtRRNOwkxYF294ja+NL62y+bm61j7ifk5heKSdeKqy2vmV8fs9+qa7Iat4IQw8PLdWPcjn8PIYQ4FjOy85tr4ycpWKSytvZ+BPkrRVrhUltMI6rTixM3zh5R6HZPkBr0nfN2fh+tmg2XL+byz5UG7+ioqKMvTP+7bM5Zm3sBQbS1Fi5POtAPmRU5ujFo6uhpCtj4zMrBGVeGUr7ZiyEcxjFeVR3tcojiAfXjdhix9tJC3Jz/MV5fNO1VOs5Ao5cAAAgAElEQVRwtqC18Z02MNiLfCPVADIPIruEMfm92Sy4a61JMONni7WqFVestTa41jdwt8vJW7sQvHxjf89qldHs1rG8Rwr2JGUTNLuxj8WwB8mxOtPDMlzLd8Qco/UX4qfOhuyW/EmF2Rz7f6iMX1FRMYb9z+OfzbWema286pk+dy4QD7i6BNN5nLtMlFnHTKAMIK0f7nMoePP12rZPatNzqwtxUlbfWC89Z4tv8DdElXVLn8n+3C3VDnX2rTB+LomK2OJ8zJq9/U2m3h4VNLsc/LLboryN36FzGkoQrc8zf+623ncjlXxsNKGczsdKLMawOCfVMBJv/pTvmp9RmBA7EpoNMzQGlfErKg4Qk374RHSTiN5PRH9BRE8R0TcT0UNE9HtE9FfcvuRud7aiouJiMFXV/1UAvxNCeBMRLQAcA/hZAB8JIfwiEb0dwNsB/MzYRUJHODud58tZOZUvVz6q32GcPz6rTmnqBhkV36tkORVQpmikM6ICQvrP6rsZPn2pIx8YRCOOomQ759zzzp+CSmj3qVOyoPJnHUKd+0xUZiMQUauJr99xEcu1lK9yJckBJCWtfCq57KIpn2nHmSEhknPstPXyppHQ3cSZ6uQNmDLVcm8x7Zz5F5W4Kqn4mQw8w0lxn8YWWkWyvyhVn4geAPDPAbwHAEIIZyGEZwG8EcB7+bD3Avj+abesqKi4bExh/K8G8EUAv0ZE3wDg4wDeBuAVIYRnACCE8AwRvXzjlTrC+qQtjHATGd+iVL7aF4vMHJs4YXJekczoGu8PadcTR45z6kXeSXfZ0nRe5t5peGkcQJLrf0lbiG/KrTCk2x/JQ9hPSkLrfeQluz6bfrpLDLcfYXyFl1n0/vPHenlnfYqyU6Zidf9wyJq1m6RYZjddzv52ow65ooYXkmPCRTI++sHhGwG8O4TwWgC30Kv1k0BEbyWiJ4noyfWLt6aeVlFRcRcxhfGfBvB0COFjvP1+9D/8vyOih5ntHwbwhdzJIYQnADwBAEdf9Vigk8EYCiNTOVMWGyRBN5tsZruvEDQTHcqX16QLqoXENj+Nje4jKsvEwTm+3KaLZS7qtQJ/TlbZETbyTJkLNnHZgccezMt8JzmPnVy0p0cYWXb5gCZ1awz31/eS9MF/MGAXOSeXH7tYzge0ARsZP4TwtwA+S0Rfw7veAOATAD4E4HHe9ziAD067ZUVFxWVjqlf/3wL4dfbofxrAj6IfNH6TiN4C4DMAfmDjVTqguUPTh6WpmFI0rEQaE+yrNHTWLUqZ8ji7lDSdggnvsljtN3u9uE2VhZxKsXvfdsJFy9srjiPy9m6k8v0vWN5T5TzxlU/64YcQ/gTA6zIfvWHabSoqKq4S9hqySx3Q3qH8YDiVHTIn+xp0o6GufjR3dl3WK67HxjQY3Hbch8xnybE7sMKmmYzoWG78TIb33GcWsCQLiDJxDkmN+KRPbn+pn5vg/QIFeQOZ+W75QOe6U7mkiTdiGz++fkmuIzMZ/pgpKPmvRuQduun3qCG7FRUHiPrDr6g4QOxd1Z/doYIK6I4tBTfY/HNeGyqsZLL/a/iqfCb30YwpxpHjVPzg17Hrtum8D1fV1j0YMtqiV2lz6py0Tm1PwpWBwevo8wzK1Jxe1ExXuYAX8ueYDEJ6zNqf6zprUJpOGw1m0VLRss3HZuQ8yF5kxttORVZZGqgar6HNmS+q+w5oaXMv74xJV5L3mJy1v8n0qvkdWDlfYABPRUXFPzDslfERgNkdmDDK4aONa5XHHHZ+3fnYmmXJWCPZcOUNeGcfhmATHfml5XNlcQrNTCYhyTXQxmvRW962rO7Xopey1EaKkVuT3rnswTYHgc82FFb8kLrghhsrB705b69duxoEIEmSqXRsLo98yRGYg5evk5HPLBQdq3LmY2fOMRt9kQpO2yaWNzDIumHZa84BJ2+bg6BxWYem5CBQ/6urCKRtlINA8hLQZCqvjF9RcYC4hOm8MFSQGctS4jCaf87lHlfmN09Hkom0k1uzfZqbxvNwNr2O+vO+FTYHgPm8fzjJLbeYxduzTJ5BzTdYsPFtHjpfG05qB0g+ulUmC+56Jc/MzB/Etuz3U/RSZR+3LKtmye9rKIWgjK/Mr9shOpcycs76eRw2MX2TyT+nDC/ylvto3UPncwHKU37M9M18cGy0LHtpZyzfecuVoPi7YPNJSq1Ikb2Xs4XIXEuAO3mLfOMM0iLnZvTaFpXxKyoOEHtn/PltaCbSHBMMtp93+8qIPexK6opJQggZ7dcpk0HKuok9J9VshAWje0ob2/gNM4GM9ovFQINHsm/W77vGrdQGXLQDe8worhhbrERjCqUltQSkygxvnywHkZ4xc53JK/CeYXk/ufJB3rsvbL4cjpT/2zPuf8L83K6NjZx4/vNyBkysUkGzE7udTKm+zgcpLbhdxdcImUcOTs7k2B0A5ixr0eSO5rzNcj1y8gaAhdSFbPIVgi2E6aVS8JTqQVKf4pRmNYCnoqKijP3P458EYwMaJlB7sDBi6eg/MMJQNy7E25LtdZEZ1pXp4/tml3M621K8+K3YdWz7XZsPjH8872nw2qxvj2c9315r+2OO2uFYqSMnNmDjF/9wB5YZxr/DFWNPVn17h9s2mjXgR3L179TjraGvafyq99Q3ausPhyrTn8k2t0vRAOLWXk/lPGrjxz6bUp3AtZnTHr4/sYYoNr1kO7aeeoWLA2nEjjc2vjD98RHLlRn++lzkvIxaADjilydagJezhchcKwFLRWj+DtxuexVG5A34maLipSNUxq+oOEDsmfEDZnc6NMwItDIe7nXMAORsv6GWWMr4YSYMz57QXDotl1ZpqGMvfct1WDonc/POtufRXlgeAG4sTvt23rfXmQavz/rtI1MhWP6fMw22rhNaM85MVAsD3Fn3I/8tZoAFtzmvrjCi5KHXSrJjw77Iwc3NN9arzww/O2VNSJmfZz3OUs1OZc/MnMg5qgwcs3Y3536LvI/EPzOcv3LVif18fmntlAXpnHzsuQeAawvW5Fjm11mjU3mznO8zjH/ML0oYf27DHx1E1qLl3e6Y4VnDU39B5gsbAlWvfkVFRRn1h19RcYDYb8huB7R31miXHMiwNCW0WO0vTecNjp5hrGpmPPWxiHOpa442E6WhxQZlSk5CXL1zz97T6YWi+knAjjj1xJEHDCrfg/M7AIAHZif9/rbff8wtAFwjUfX7tjSddxIGR84pz1WKk+doddSfyw8QFZ3k/2XqZ7nuH3a5lAiYVO8d8v/H02LDdN7Qx1an87g95fdzKk4/UfkH1VanctkeS5y5VtVvY5l37CRUeWdslWEK0IXs+qCxnEYsgVQaZt23czMFq848VvEfWIicT7ntt29YObNH9Ihbr+pHAVrMxSpnVvVvNws+N1XxxSG47ppRx6FFZfyKigPEfp17IaA9WSsDRIzPbKSOoITxeYyaGRaf98xFulpDLtYf05qFEhrmOYuZ3hV2yffbLbmU0EsJ2pApO2Bw5gnTP8gM8GDbt8fNwATX+f9Nzj3L+CfMBC901/rn4YcWpugMfZ+xI3Cx6q9/2sROq/WIh8tX/mmckw8w03WsBQjTt6c8bSWtZfzlWh6Or+8YLMv4LOcjbk3wSr/DfCfEeatML/eJpymzcIqiaHYL49yT6ViRuTD9zfltAMCDs769vznRc0TmwvwLx/hro7msuRMnyvi9RvccHUfnWDnLFO/paladexUVFWXs38Y/XYPO+lFTWgDAShhfipK5kavVYdic03e/SbQDbtthVGzmPOL7hSPqU3ChnkASsitLLWUhhkytXDNBOTKdIzaeMP2DbV9M5IF2YIJrtIzaxtFRl2H8W9QzgNcOhAHOzIoVCSI5mvXn32r6ltxzRXNbLpDJJ+KIpvOE6dWW51YZn30XJ+akpawYYht/XWZ8kTnN+2eSxUW68kZNfStn8eHw5daO6TOBWskCMJV3f9LcLLgRWct0ncj7fparyPuB5o6ecz/vEzmnNn7K+CJnrx0I7BTvnZa1g9lqNBzYojJ+RcUBYu82Pp2tQCf9yEfLMhPA2X4kTD+zWRfikV8qmbZix8/NDMA69ub7ZCCjA6Xz6ouXV1obrCH/i/deRnth+vsNE1wnDvMsePWXzATXwnD9Bnk/wCmz+X3N4G+4xp5/DRxxySJ83boIjvE14Mbc3tv9zTL24ivTnw39V5mvxNZ3jNYMMiORtdMCtUqxLI+2iVBk+fA61vByyV8SuMVSEv5svfoLx/gSnHOD5StMf7O9reeojc+Mv+DOyH2sV/+Mv8ze7yM+nCVPUxy3g5ylL4tmNRqYZFEZv6LiALHn1FsBtFwPo75hAqz6fWG10mMBDLQkNqGx50nr1nMop3h/xds8sgjI543Pz+vKfWIbX0ZVWWQzM0swxXMrTCCj/TGxBmC8vdd1Hp81CZmL58/XJPP4ubnb2P4/0rliGxIsy0HjBBC+Rn0OSc589e7bdypefb6+xGKI557lHGl2p/17CcL4IWZzNINGJzM9mLOPg2150f6GOA7Tp87Z+AWmH9fwYhvfhseKX0fet8hbZmiOXQsAD7Dsj/hLuODrCeva/KhnrMG18l3gKYYlL709Yc3uuFnoOfI9XDTr6tWvqKgoY7+MD/T2mozkq4EJwpLZXz5Tz62uLe0bcykSe1BnBOTcGW8bJtAsFPHCjkkDpGN+YVCx0Ww0ldhmcx3d2fMvDGG8tPL/kSgu7rZLfdrhnI61AD8jIK1l/EaZJbZZyXnzx6oWJ+/JHJrY/2KLy3sXP81q6L8yvcg+sfHNsWzPqk0vMzt8TuhkXt90yiX4ICfvUbhVyo2Te78vTqHmo/G8PICB6a+JZufkbd+A+HA63rv0cs5E/8n/s2YNqpF7FRUVJdQffkXFAWLvzj10narxwQZviPom+0RNZGeH+j/sHJQLAhE/0RAENByqzr2MyrotyE37NBlVf+EW4CxYdWvNjb3KN/fza0HCce05oi7mF/i0UV/EJHFTo1PmfPx7yplGhc/IB+dYdV5ipVXeTtU3wSzE/Q5Sk0DMNVngo+G41qRz/fRrgLaQu5czMJhLLavkIk+Rg7z/hZl21WlBfu8LFoAmb47uysdC5Cym4yq6r5WpnX6s03kVFRVF7N+5B6ThuGMQ5p9AUz6by91GKTvu6DkZVaOdRMHjaF1gT/beu5TlHkHyvu/2+y/lY8z14S51ZdOy1zYnX7dvCtvmrlM+drPsPSrjV1QcIPbM+NQzt58vAXQt5FDZxo1JOrdi9muufZc1NpNqdDS/3JbwFW7iSjdNvmXryy6nlFkoteEd82cKDul1hmW4TbRtl3h2zuLrwg6axcgpQ5ZeOZbybZPKbJimjQVD9h1IwE46vxbdP66n6Pvk+1x+ninw71Tl6uS8tnJW2fdyXgaxyflYoymJrM/89UIs57gPQ9WdqXpCZfyKigPEJMYnop8E8K/RW05/CuBHATwM4H0AHgLwRwB+JIRwVrwI0I++baMLbcgsIQ3OfksGZlmiaVJv6VJdYRRJ3OCys9oLJjXWt2CAEtOvzBJJzZKq7SxqT4IJsBlqovbdd+O1aARn5kFO3PXP3HasUcRspI7uKTMb/r3k3pfuk4QZcasyixbezKJbk4+ltdqahO+2vo3lDbP82tfb8+0UqJvA1a0Dhneq71sq3vC2hFCfmIVV8yDylVJD4GukApDMZktdlMPyhf9emVoLUfWdaQ+6kfGJ6BEAPw7gdSGEr0c/+/BmAL8E4J0hhNcA+DKAt0y6Y0VFxaVjqo0/A3AfES0BHAN4BsC3A/gh/vy9AH4ewLtHr0LUL6RRxjept+QfWXDjRkNljZnREjhBAyRRA6fikuSMwaTp6kraQMEWjOAZwNW0s5VuJO/9MPJzEozQL6posgtueBmre2Zh7xMzuuv1OCWTpGaS5IySsgkYknJIaiZhruDojzJ0mDBmJr+lr2sQ/GIpkY9PtoHBbg+tjzEwfRGGF/ny90blLIt0jBaY1F+YIl89WVph+tQvI+9U5CzJME9YvieybUJ2W5c4ZJ75DghOVXPory9yllbke2rkrNpf106a+DBdKSOE8DkAvwzgM+h/8M8B+DiAZ0NQvfVpAI/kzieitxLRk0T05Nnq1rReVVRU3FVMUfVfAuCNAF4N4CsBXAfw3ZlDs2NNCOGJEMLrQgivW8yun6evFRUVF4Qpqv53APjrEMIXAYCIPgDgWwDcJKIZs/6jAD6/6UKBgHDUglhdteWSSFaVyYorvzqvEfXdBDiyCtgtuGUVUEst2WQ96njibacKZp0/TsWXEsyiMkshw9OMqn973atmL7DKlwuykLXWJxqO6Zx7quqbnHus8r3Q3Rdvr/usu1JqCRgKL0pJben3UEp6s/7rVXybxzBIWXKX8Uiy4QYNuzZ1rHVNPR87UiZbZa6mXGzSdaLqz4dz5H+Vs8pbrs/bWXnzuc6ptzRZfaVGwSDnXrV/senfv4RqW6z5Oc7YQSfh2xJ2a3PuyTFDNuVezi+s+1ZMO7kvMJRTO1vPMDVod8p03mcAvJ6Ijqk3wN4A4BMAPgrgTXzM4wA+OOmOFRUVl46NjB9C+BgRvR/9lN0KwB8DeALA/wLwPiL6Bd73no13I0J3NNNRnYzzDT6/mkfGYacjvzD+kWyzM2sxHKt51h0DDEyQsVR0ti1m/CUXnRRGvb0aRt8X235ElvXaPhvumXXUSTFFt8BDMJ5Xv2eA51Z9vvUXWcO4xZV1AOBESi1zu1rHjC9lsyOOkI0mbrUSkSkvrUy/YIZcC4vHy06i6Txx2Pm8C4Imw/gs8yByXrCcj2INr++T61tJ3rZ/qtlJG0/XLs103glrVPKetfBpE7O4DaQS55vkTpxntILhWHYOd7ET97n1Mbe93EXefV+Y8bs2cdyWMMmrH0L4OQA/53Z/GsA3TbpLRUXFlcJeQ3ZDQ1jfN9NpH5oPzNBIyWzNsisfcCvTP5bxpaaaMDwzgJRPXi9MMIvYfjM5l9sksCdlfk3nzoy2EjuP8/pLHTtgyMnWuuvIqH/cDCP17Q2VdM40+Mf6EJjx2aaXkf/5Vb99y9h+oomccn8l0CMIg40E8vhpPGFOE3Ol73TIaMvvhz+XkNTGTLfRkmUvF9KXywdYRmbGF1teZL8+4v3SGjmLja+Xd76d0ek9YXxdTcy2+Wp46NOZaHm9HOZs28sCKM163A5a2u1GtIPY39OOaAfC/DJdKPIWOb/Abd8XLqW9michxSXUkN2KigPEfhfpNMDqvhYN22SNqZ2nNc4KDBDcghxgCByRUV5s+mHbMgGiz5QRfCCPgQS2BLXxhfF5VBfGNxlPNVc6xD7sR3CpdmJz8Pv8aX7Jp17D+gX4Qe44W/MFbl9cGo1iyYy/ZBt/xTaxePVdRVyL0MhiqZgxxXYGgPUizmsnaDWQhxl/ZRh/Fc/aRPnygIiKtA6esPYsL99Is1vId0L6i6j/Y/KGk/dqJXIe3v/tZX9hv8RZgrrOWCOwsysic6/ZaYXjKMya7+kChe4w8z+/ZE1vmdr4J6vZ5IVYlfErKg4Qe7fxV8fNkI/dlGsVRyf5RArJQhBzPa15328rE8zjUR9ImSCx9XNDoPfqc3+lvvyJVqQxnm4N52X7kO1rqWpzZOrsSb529QhnGADwIcESnsneX7Y173B7a2nmd5npxUZdM4MFV00oemRnAyvT83uzbgh5bKnfMlSqZflKHTtbb28Vy7ckb3s97YPOLMSyXNt5fH78RN46OxGi2+UQZPaDZbdcDkefOKYXeYs8xN629RSPXP0F8f/kGT8OB9cQ8LW0sbyBQQs5OZtP9upXxq+oOEDsmfGBs+ukTB/lvd9Qw857mfv/PSPwfpnLjSK6+lac3nrsmLdX+sL9DcyYa14ueiZ9MqOs2P8y9yt29tEsnaufZSq1WAgTWLtNNAnRAiSqTCPKloNIz1bCWDzbIYy/UsdJ/JyACsC/W33HC9iD+Vg+hpme5mLbcxvJOb7nWDawZImt0/BUzuZb3DltL7H1x2z8oYRRv8n9X5Hxscihwsz83k/Ytl+wZrcw9QFakXMT2/Y5iMxFzj5KVOQczTSonGeD/2YDKuNXVBwg6g+/ouIAsV9VvwVW12lQ8Y0KO1XVj50/0hbUUvN0fp8691g9HVukoy2rfrK4RvxUEtgDACuechKVu21jNa9tTI52V8wyuX0mp9+wgMSphBI8Y6aeOnVS8XWWEi7rnHu59fgSuDOLZRUy71/eqaj2Q4HSuI3+n6LqO/NOp3JdUFHIydk5JVXOOWeu9EVCmaWep5h29lB5/+Lo5VDzk7bvhKrzjcmr38TZmMcKW3qZq5zXbbTfyln60q3byYmOK+NXVBwg9u7cW95IHTz2/20Y3y+xTJZe2qk/P53jnXvOkWQ3hMG0a8ExaTt0WhxoJFN9rrQ2GSYYktGOM368j1uXTUerTRvnjv6/dq0szpE2cu5xqw47PoWfnuw7FSetHOPZXLU48xxblKtOZO41gJzD18mz8/IeW5TVuXYpIc5muo211Y7DiddS5Yevm5QiN/faJG/AyNNlA1KtT7bX9p2KpkJAde5VVFSUsH/Gvx7yo/zUNKi5RTQlZhjRDjx75K6ryzXXjhklmEh8Fdbu1fuknyXbu1S28VNwjhniY+M20bQympdeRkJ2ZQm17I+IzAfjFO4baXYT5WwhU4yld5nxO8A/mvoJCnKBeT8SeyPXMuwadLpTrt9GfRxdBLSNvP3DTpF3B4xGJhlUxq+oOEDs36t/ozQk7cB+dxtio8r2Oh5laXJt0nsIiX9kc4jrdriCci5pRhlceZlXG7+ioqKEPS/LDehurFN7yKI0YGX9AtJOsHsn2ru5RSjw3m8fc5A6cDPHZDzopefRi2UOSexcZ/82mWNd3g1v7+YWKOk+sYnVk2466c+j+Njsw475PJJOFLZL8s58lsrZ7Y+Oja+RjS1JjnX7M9+95DWMfQe8aa8+AyfnnP+qme5GqIxfUXGAqD/8iooDxF5VfWoD5jfOhqAWo5dMCW4A4qAWzRZbCGqxQQ7BBbH4bT0ypwL6EFTeHlYZmmcshauOqY0b1LPstKQPV86sOktCmCWYRaQuFzYd0Oto4Iuo79yaLLvkPmvaWK6k4avbyxlIg1mGYKU4qCVYOWswi8s9oLJyATIwM3DO3NMcETZvxNq1Xb6NzL8N4eg5pEFp3G+XKzLa1yCbYyGHyvgVFQeIvTJ+03S4/8YdzFtZsGIWMkhWksKw6EtTAyZbiWSRlYUqkhvPLmSQBRfc6oIVgbJfuk9G7GZJ3PKhwvxDGj3NNqOf8Uoery301+d9OSeV6UvE+C4/fOcrBNm16W69OknmGqY7XcCSCeDRQBdh9Tmz99zIbNY/zGzG8mS5zlveP0HOXt5WvsrovD1UtomzHa/sIimWuSxa6iTsVlpIll9zU7doSZjeyxtIZT7IWbZjedv/c9pAgkSjc61mIRpOsXkJqnOvoqKiiL0y/qzp8LLrtzQf2SKTf24T46/M3JMwu+Qhk4oxkv321GQpOZH8c2eccVYG+SB13nikNpTvR+pGmaBv2zPePhv62XB+NjlGz2Hmb6w/oEvZwSI3deMZ3i8/tXkGh2y0vC22soThtrrDdoo7zNts07cLXl48H2S2WPT/X+N91zjLkGQbkvyCC5N0b9HG+QVL8gYGWWv+QqY5yUIj+QZPTW27k7N+n2QfOkO/La9dF9zYuo1O89LMQSJDI1+VuZezyjsjZ6cFbLUU2eeV1OxSwzlDdimqNn5FRUUZe2X8RbPGI8fPaZ7xI2M8SSZSYQBfVUZzzEVVZSSHeU9pkl9cMp2+YHKPt5z7XrzJ6ikWL6/YgJGN3zdaKYaJS0f9vhAOZifDEN6ehfiYpWzz8s3VcGzKBDEVDLUEzD7JLZ/UFIhbAFgfOUb3bCK2f46BZOZlFjP90WJg7xvX+hdwPO/leP+8z0h3POu3r8/6z20tAa01V6geZKvKiJbnc8sPNQW4Uq2R84vsT7jFzD/MDDDzryRoyT608+Y7u721jM+ybk/ls5BtrZwl5+Ag7zLlD0llxJaP5ewzSQND5SjqCgvgMqiMX1FxgNgz46/w6H1fxo2WmcEYT9ekjrxWGXGMn6kjd9vVhpe6Ys+v+oqiM2NoaYUbTZ0kXn628Zt0qFQT2zGA2vin/TmW8eX/9oQ92qf8PMz4zXLoE0m9QF9FiCGMD1MvsFRHruV2dZ+pWuMWbAx5793nuUltmZtnxp/P+34fHw0yu3/R097NozsAgAfnfXuT2/tZziJvYJCzVBHycu4MF0ntQKkXWKoj92x7n54za9z1XGqyrs1odgIXt+Hl3P/ft/M7wvwsZy9vUyWKWObElaCT6kG2C+rD4X5qRWiRd7/dHFlf1JCZpOQv8qiMX1FxgNgr489pjUcWX8bN9hYA4LoYyQCuU1wr3kPrhpta8VI7/FmpHd727eAvSIc/yUO/lFzkPNfcaYKGdFI78eqzHTfLMf5ttonvcB+kPe1bOjPPt+R9a8mb5ZhAKwSbqsLz/j1IrfhmKVVyJHuovQCzhqttL15ruS1Sc1cpQebmF+ypF3seAB5Y9Ez+0OI2AOBlixcAAC+Z9fJ9qH2xP84w/jH1Mr/mKscK1oaLRLsTOd928v5ScwPA4C+wGOoP8IwAy3vVsoYX5RDjR/c2vvPYA4OsZ3dYzrfZV3HCsxUn/cF0ajS7M9634n3dCC03otFxPxdcq+8ay5tnpWjVpudSU238ioqKMuoPv6LiALFf5x6t8Mj8S7jZ9KrhTaPqX2P9SnwWosiIwiR1C0/MdM8LrPbf3/TOJDEdciq+L2qo5Y5bF7Bi4RfpeKcP+7nEsQMMKn57i51Xt/uD6A4/69mgNwb+P6xY/Q+u35K6dTaIiY54WpJVQOKpLMrl/3NFLGWqL1loghSykGpQ9fuDr88H596DPH330B8wFDYAAAVUSURBVLxX7V8+fx4A8LJZ376UVf2bLB8AOGZT7rqWk+oh8jZatcr8Fpt5z3a9M++Y5ZxT8cU88MUlb7tsuDnoIh15L6t4is7+395hFV/lLXLm9tTMAfL/YclPtxaVXyKGjATYFKE5y5flHc5Y7sc8dWlMXtgpwOrcq6ioKGG/IbvU4ZXt83iIp/FuNsO4c9wccYf6Ea91Q/OSy5vcDsNI+kLHjiIXDCIOIjv19+Kap/5mfbtoe/ZolQky03nO36eLNzSwI57KAYwzT5j+Vs924XbPjuFkcHSFk77/YcVMUHDu0WKoVNkc8Yh/X99/6hxztmaRC/8vAR6y6EQZLecIctN58n6OONT2eDa8/wdm/bN9xbx36gnTv3L2XL+tmt3wfu5v+q/cEfXPMafYSbU2Ws9p6N/l7cABQdRrEDIlqOcY/jpl7eDWqr/+8yznGfefvFAtnJPPT98CdvqOv3O32XF3u5clvdg/s8gWAMId/g6wZqcaXgbE2p3InFjedMxTlkFCnQc5tzz1180pmRIuoTJ+RcUBgsLUYlsXcTOiLwK4BeDv93bT8+ErcO/0Fbi3+nsv9RW4d/r7VSGEl206aK8/fAAgoidDCK/b6013xL3UV+De6u+91Ffg3uvvJlRVv6LiAFF/+BUVB4jL+OE/cQn33BX3Ul+Be6u/91JfgXuvv6PYu41fUVFx+aiqfkXFAWJvP3wi+i4i+iQRfYqI3r6v+04FET1GRB8loqeI6M+J6G28/yEi+j0i+ituX3LZfRUQUUtEf0xEH+btVxPRx7ivv0FEi03X2BeI6CYRvZ+I/oLf8Tdf1XdLRD/J34E/I6L/TkTXrvK73QV7+eETUQvgPwH4bgBfB+AHiejr9nHvLbAC8FMhhK8F8HoAP8Z9fDuAj4QQXgPgI7x9VfA2AE+Z7V8C8E7u65cBvOVSepXHrwL4nRDCPwbwDej7feXeLRE9AuDHAbwuhPD16JcRvBlX+91ujxDCXf8D8M0AftdsvwPAO/Zx73P0+YMAvhPAJwE8zPseBvDJy+4b9+VR9D+WbwfwYfTBtn8PYJZ755fc1wcA/DXYp2T2X7l3C+ARAJ8F8BD6kPYPA/gXV/Xd7vq3L1VfXqbgad53JUFErwLwWgAfA/CKEMIzAMDtyy+vZxHeBeCnMazHeimAZ0MIEgh+ld7xVwP4IoBfY9PkPxPRdVzBdxtC+ByAXwbwGQDPAHgOwMdxdd/tTtjXD38kw9nVAhHdAPBbAH4ihPD8ZfcnByL6XgBfCCF83O7OHHpV3vEMwDcCeHcI4bXow7YvXa3Pgf0MbwTwagBfCeA6ehPV46q8252wrx/+0wAeM9uPAvj8nu49GUQ0R/+j//UQwgd4998R0cP8+cMAvnBZ/TP4VgDfR0R/A+B96NX9dwG4SUSy4vIqveOnATwdQvgYb78f/UBwFd/tdwD46xDCF0MISwAfAPAtuLrvdifs64f/hwBew57RBXpnyYf2dO9JICIC8B4AT4UQfsV89CEAj/P/j6O3/S8VIYR3hBAeDSG8Cv27/P0Qwg8D+CiAN/FhV6KvABBC+FsAnyWir+FdbwDwCVzBd4texX89ER3zd0L6eiXf7c7Yo9PkewD8JYD/B+DfX7ZzI9O/f4Zeffu/AP6E/74Hve38EQB/xe1Dl91X1+9vA/Bh/v+rAfwfAJ8C8D8AHF12/0w//wmAJ/n9/k8AL7mq7xbAfwDwFwD+DMB/A3B0ld/tLn81cq+i4gBRI/cqKg4Q9YdfUXGAqD/8iooDRP3hV1QcIOoPv6LiAFF/+BUVB4j6w6+oOEDUH35FxQHi/wOgowbu8rukGgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# imshow - note that origin is at the top-left by default!\n",
"plt.imshow(im);"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD8CAYAAABn919SAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXWUXdXdsJ9zznUdd8/MRCcycYWQQHACBNfiHxTa0pZSe9u+pcULfaGlSFvcXYITiBObuI5l3OW6nv39cScDhWTm3pmJFOZh3bVYmW333H1+e++fbUkIwTDDDDPMMP/9yEd7AMMMM8wwwwwNwwJ9mGGGGeY7wrBAH2aYYYb5jjAs0IcZZphhviMMC/RhhhlmmO8IwwJ9mGGGGeY7wrBAH2aYYYb5jjAs0IcZZphhviMMC/RhhhlmmO8ImiPZWVJSksjLywPhgFANSCaQ40C2HYahCBAuUB2Rj2wBJTumFtyhdgKqhzhdJlIfa19YqNR7Okg22DAqukOWa3G7AUgxmw9ZxuMP0trlIis5DkWWDllOVQX1tR2YzHoSkyxRfJuvaKhowuPwYok3Y0u0YrQYkKRD9zUQQsEwnm4P3e1OvC4fmYVpmO2mqOuHwyp1tR3YbEbiEw79vAC63F48viDpCdZDfo+QqtLocpJgNGLWHvo3avc7CYowaYa4PvsMql66g43YtRloZUP/X6iXMAT3gKSNzH3JBpI+hvpRInygdoHoAiFAOwqI/jcOqB6cwWbsugw0/YyvwduJSdETpzv079vt9+Hw+8m22Q9ZJhRWaepwEm81YjYc+jcCaG1xEPCHyMhKIJap29XSTWtdOyabCWu8GUucGVkZ2n2tqgrc3W6cHW7c3R7iUmwkZyXG1EZzYzeqEKRnRObhxo0b24QQyf3Vk45k6P+UKVPEhg0bEOEW8L6B8L0LoT2ADJoxoJuCpJsc+X8lHUmKXsgL1QHBXRDcighuhsBqEG6QzKBfgGS6FEk3Mer2NrW/worWRxljX8TCtJ8iSYf+0V+qXs39u9/lmVk/ZKQt45DlLnn9ZUKqyktLLjxkmd21LVz85+f42XnHcfEJpYcsp6qCv9z5Lh++t4XLr57HZVfPi+6LAXvWl/P+Pz9j2Ysr8Ti8GEx6So4bQ+mCEoqnjCB7VCZxybaohXw4HKaxsoWqrfvZu7GSDR9uprysCoCMEamceu2JLPrB8cQlH/pl/jpOh5fbbnmO/dWt/PGeC5g8reCQZYUQXPTn55CA5391ySHHXOfoZt6TT3DPwkUsGTPukO39Zdd7vFqzlneP/wUJ+kMvlM5gC6/W3Io/7ObcnPtINoyI6rsJEQDfUoTnBQiWRf5RyQLdPCTteNCOBs0IJKlvgfYfbaouCO+H4HZE4EsIfAlqK6AB/XFIxnNAfzySpI2qvf2u9bxT/zvidBmck30fJs2hF7cKZxMXrfo/bh55MpflH3oOPrB2FQ+vW0vFLT89ZJlAMMTJv3qCSYWZ3H/9GX2OcenbZTxw13vMO2E0t/9uMVqt0v8XAxqrmnnn7x/yxStraKlpQ9EojJszitEzihkzs5iiyQUkpMUhy9EJeSEEXS3dVG7dz87Ve9m+ejc7V+3B5/GTkBbH3HNncOq1CykYnxtVe6oq+PuDH/LWqxu49Kq5XHHNcQBIkrRRCDGlv/pHdId+AElJAcv1SJbrEcE9CN8HEFgPnhcQnid7SikIOQ2U9MjuWjJFPggQfhCByE4/3AJqc0R4H0DJAcOpSIaTQDczppfDH3bzRfPD7HJ8TJF1HgvSbu1TmIfUMC/XrGGMPatPYR4to7JTKMlP54XPylgydzw67cF/IlmWuPWXpyOE4Ol/Lqe1xcEPbz0Znb7/n3Tk1EJGTi3khr9cwcaPtlD26TY2fbKVR98v6y1jtptIyUnCmmDBmmDBZDMiSRJCFahhFXe3h65WB92tDtrqOwj6g5FxKTJjZ43k6j9fzNRTJlEwPjem3X9VRQt//p83qK/r4Pd3ndenMAdYv6eWvXWt/OriBUNyyjgneyov7l/FyzVruKHoxEOWs2pTOCf7Xl6tuZXXan7KCWk/pth2fL/tS5IOjIuRjIsR4Sbwf47wfw6+NxHe53tKyQg5CeQkkBN7TrAKSBpAAtUFwtlz+mwEtf2rDuQk0M1A0k0H/UIkJfqdoRCCLZ1vsqLlURL0uZyTfQ9GTd+L8NNVy9HLGs7I7FfW9ItOq+HMmWN47tNN1LV2kZV86IXk1DMn4XH7efShT2hp6uaXv19MRlZCv32k56dy3b2Xc+09l7F3QwXLX1lD2bLtvHLf24RDYQC0Og1JWYkkZydiiTOjM2jRGXXIsozP48fv8eN1emmt66Clpu2ruS9L5JXksOgH85l77gzGzR2FokS30AB0tLu4+3/fYtP6Ks69cDqXx7BJO8BREehfR9KORNKOBHp2L8EdECpHhOshXBcR1uG2iMAWbkAGSdfzsYCmCJQ5SHIqaItBW4Ik9//DHox6zzY+arwbZ7CFaYmXMj3pMmSp7x/k7boN1Hraub/0sgH1eTCuP30GP3zoDV5evpVLFxx6l35AqCcmWXnh6VVs31rLT35xGiUTc6Lqx2DSM3vxNGYvngZAW0MHVVv3U7e3kdo9DXQ0duDocFG/rxGPw9vbJ5KE2W7CnmwjszCNxPR4skdnkTc2i7xxORhMsasQQqEwLz27hmf/tRyzxcAd919I6ZT8PuuoquDB11eQlmDljBljYu7zYORZUliYVsLz1Ss5N3s6yQbbIcvadeksyfkL7zfcwfsNd1DhXMnxaTdjVKI7iUhKGpguRDJdiBDhnl32TkSoIjLv1bbI3A/XAGEQKqD2bHBsICeAdjSSkgua3J53IX9AC5sz2MLnzQ9R6VpDvnkGJ2X8AoNi7bPOru563m/YzBX5x/WpbomFS04o5aXPN/PIu2v40w9O6bPskotmkJJq54G73+OGK5/gpp8s4qRTx0f1/SVJ6t3YAPg8fvZtrKRiSzWtte201rXRVtdBU3ULAW8AvzeAGlYxmA3oTToMZgMjJuYx84wppOYmkz0qg1HTizDbBvYcvlxdzn1/egeP28+PbjuF084qHdDveNQF+teRJB3oJoFuUgzavsHT6qtgQ8eL7HN8gU2bynm5D5Ju7F9AtPi6ebT8EybE5zInedSQjWfWmDxmjM7l8ffWcmJpEanxh36xFEXmqhvmUzIxh7/es5Rbb3ya+SeO5fJrjiMrO7aFLSkjgaSMBKaePGmwXyFqwiGV1Sv38vQTX1Bd2crxC8Zw062LiIvvW28O8Obq7eyubeGOH5yM/hAnmYFwU/EiPm/eycN7P+AP48/vs6xdl875uf/HhvaX+LLtaWo9m5mSeCFj7SejV6K3bUiSApoC0BQc0bnvCzvY2PEKmzveAARzk69nUsK5fZ5KIXIyvXfn28RpTVxRcNyQjSc5zsIlCybzrw/Wcdr00cwak9dn+XknjGbU2Azu/t+3uO9P77D0rTIuvmI202YVxiQQDSY9JXNHUzJ39CC/QWxs31LDs/9eycZ1leQVJHPvQ5eSV9CvqvyQHFMC/UiiijC17k2Udb7Bfvc6tLKRSQnnMj3xMnRK/6tsQA1xe9nz+MNBfjl28ZAbFX9xwXwuufM5fvnPpTz2k/PQ9GO4mTpjBI8/dz3PP7WSN19ez7KPdzB5WgGnn13KzNnFKJpjy6HJ4fDy/ttlvP3aBlqaHWRkxvP7O89j9nEjo6q/r76N+1/9ginF2Zw8ZegWU4BMUwJXFMzjnxXLmBifx9nZ0/osL0sK05IuJt8yneUtj7Ci5R+sbXuKsfaTmRC/mDhd5pCOb7AIIWjy7WJ711L2OT4nKPwUW49ndvLV2HRpUbXx0J4P2N5dy58mXIhFG4tRuH+uPmUay7dV8ut/vc+zt19MZlLfJ56UVDv3/N+lLH27jBefXsVvfv4SBUWpnHP+NOYePwqT+TAYnQeB3x9k9fK9vPPGRrZtriEu3sy1Ny1g8ZKpUalM++KIGkXHTioUK9Z+SrwuZ8gFYDT4wy7qvdupcq2l0rkKT7gToxLHxPhzGB9/Rr9HzAOEhcod217nvYZN3DXxYk5IO7SR7etEYxT9Oh+s382v/vU+p08fzW8vOxFtlPq4jnYX7721ifffLqO1xUlCkoWZs4uYPK2ASVPysViH9gWMloa6DtatrWDdmnI2b6gmGAwzsTSXs86bGtOiU9PSyQ0PvkZYVXnm9otJiet/JxytUfQAYaFy68anWddezj2TLmVuSvSLRrNvL2Udr7HP8TkqYVINI8m3zCDPMp1k/Yh+1XiHg5AaoNG7gxr3Rqpca2kPVKOVDBTb5jMx/mySDH3bKr7OG7XruHPHm5yfM5OfjenbeHmAaIyiX6empYtL73qejEQbj/54CXZzdHM2FArz2UfbefGZ1dTub0ev1zBtVhEz5xQxYVIuKWnRqcOGmo52F1vL9rNuTTmrlu/F4/aTkmrj3AtncOpZkzAY+jZYR2sUPaICPWecTfz01WmYlAQyTONI1o8gSV9AkqEAqya532NeLPjCDtr9++kI7KfVV06Ddwft/mpAoJWN5JqnMtI2nzzzdDRyLEbTIP+77VU+btrGdYULuKZwQdR1YxXoAI8vXcsj76xh+qgc7rn2NKym6IVxOKSybm05Hy3dyqZ1lXg8AWRFomBEKkUj0ygamc6I4lQysxKw2Y1DtsiGwyotTd3U1XZQvreJPTsb2L2zgfY2JwCZ2QnMmFXEotMnkD8iJaa2t1Q08JNH3gJJ4u+3nMOo7OjqxyrQAVxBHzeuf4J9ziZ+OXYxZ2bFZvhzBdvY7fiUCucKmnx7ODD3Ug2jSDeOJllfSLwuizhdVkxzsD+CqpeuQCNt/gpafeW0+stp8u4mJPzIKKQZxzDavpBi6/yoTqMHUIXK3/Z+xDNVy5mZVMx9pZeilaPbUcYq0AFW76zmJ4+8TV5qPA/8v7PISDy0PeObCCHYtb2eTz7cxqov9tDR7gIgJdVGyYQcRhSnkVeQTF5BMknJh3Z3jRUhBN1dHqoqWqiubKWyvJntW2upq+kAwGI1MHNuMSeeXMKE0ryITSoKjkmBPmnyBPHMp3dS59lMo3cnjmBT799kNFi1yVi1qZg1iRgUKwbZik4xo5F0KJIWRdIiEAihohImpPoJqB4Cqhtf2Ik71I4r1I4r1Iov7OhtWyebSDOOJsNYQoZxLOnGsQN6gfY6Gvjfba+x19nYr5vWwRiIQAd4e80O7njuE7KT47j7mtMozEyKqT5Edi67d9SzYV0lu7bXs29PE84eQyeAyawnIzOexCQLcfFm7HEmLFYDer0WvV7TexQUQiAEBAIhfN4APm8Ql8tHZ4ebznYX7W0umhq7CAbDvW1nZicwanQGo8ZlMmX6iJh1+xDxUX5z1Tbue+ULUuOtPPTDs8lJ6dtX/OsMRKADuEN+bi97ni/b93FB7kyuLzxxQCoGT6iTGvcmGr07afLtos1XgcqBZyRh1SRj0SZh1iRiVhLQKxa0sgmtbEAj6ZEkGannv5AIEBYBQqofv+rGG3bgDXXhDrXjCDbhCXf29quR9CTp80kzjibbPJks4/iYhPgBugIe/rT9db5o2cm52dP56ejT0cjRnzQGItAB1u7az22PvYuiyPz64gUsmFQUs/BVVUHlvma2balh25ZadmyrpaPN1ft3g0FLUoqV5BQbSSk2bFYjZoses8WATq+g0SgoiowkSYRCYUKhMMFAGI/bj9Ppw+X00dHuoqW5m5ZmB15PoLdtm93ImHFZjJ+Uw/iJuRQWpw1I/XlMCvQDfugH8IfdtPuraQ9U4Qg04Qg2905IX9hJQHX30dpXKJIOvWzGrEnEok3GokkkTptJgj6XBH3uoHf/nQEXj+37lDdq12HTGvmfkiXMieEIfoCBCnSADXtrue2xd3F4/JwybRTXnzajT7eu/hBC0NzUTVVFC431ndTXddLY0Elnu5vODjeObs9/COW+MBi1xMebSUiykJBoJSMznqycBDKzEsgtSMZmMw5qnKt2VPPX11dQ0djOlOJs7r72NOItsbU5UIEOEFRDPLh7Ka/WfEmczsR1hQs5K2tKTALt22366AzURj7+WrqCDbhDHXhC7bhDHfhVN9D/uykhY1BsGBU7Jk0Cdm0adl06Nm06SfoC4nVZg1LxuII+Xtq/muerV+IJB7hl5ClcmDsrZqE6UIEOERXbLx5/jz11rcwck8uPz5lH0QA2NV+nu8tDdVUr1ZWtNNZ10tLioLXFQXurA5fL/x9CuS8MRi0Wi4H4BDMpaXZSUu2kpdvJzU8mf0QK8QnmQe3+9zd34vYFGJuXduz6oR9Ar5jJMI0lwzT2oH9XRZiA6iEsgr0fCQkZBUlSUCQtesWMEmXARCwIIdjrbOS1mi95v6GMkFBZkjOD64oWYtMOXEANlCnF2bz2+yt58sP1vPzFZj5cv4czZo3h3DkljM5JjXnSSJJEWnocaekHXxSEEAQDYfz+IH5/kIA/1FsPCXQ6DQajDoNBizLEkXYAvkCI5dsqePmLLWzaV092chz3Xnc6J0yMzXthKNDKGn4+5kzOyJzMA7vf4+6db/F89UqW5Mzg5IwJxOtii9SNtGkgxVBEiqHooH8XQhASPgKqj7Dqj5xMEQhUNJIOjaRHkXVoe3bvQ02Dp5P3GjbxYvUqnCEf81JGc33RQoqs6UPeV3/kpMTzzO0X89Lnm/nHu2u44I5nmDkml4vnT2LGmFyUKIOAvo49zsSESblMmHTwgJ9wSMXt9hEIhAmHwoTCaiTgViOjaBS0WgWTWR91QFMsCCHYXNHAc59uYtmWckoLs6Kue0x7uciSErWhcigIqCE2d1Szpm0vq1v3UOVuRS9rODVjEhflzSbPEpu+d6iJtxj5ybnzuHRBKf/8YB1vrNrOGyu3k5loY+HkYmaPzWNcXjoG3eB/VkmS0PWoWqwcmQWspcvF+j21rN5ZzRdbKvD4g6Qn2Ljt/OM5d+54tJojb0z8OqPsmfxj2rV83rKTZyqX88Du9/i/Pe8zLbGQWUnFTE0aQb45ZUgWHEmS0EpGtPKRefZhoVLpamZ1614+a9rOLkc9APNSRnPNiBMYZT+6njoaReaSBaWcPmMMry7fyoufl3Hz394kwWpi9tg8Zo/LY+bo3JhsTH2haGRsMaSqGCzeQJD1e2pZvrWSFdsqae12YzXquWrRNC6cP5EnojzYHNMC/XDiCweo83RQ7mxiZ3c9uxx17O5uwK8G0UoKExPyOC93Jiemjcc+REETQ0VynIXbLzyBG8+YxbItFXy8cS/PfbKJpz7agEaRGZeXxviCdIqzkinMSCI3NX5I/bQHixCCLrePysZ29ta2sruuha0Vjexvieh+7WYDi6aMZNGUkUwuzhrQDuxwIUkS81PHMj91LOXOJj5s2MJnzdu5f/e7ACTprZTE5TDSlsFIWwYjLKmkGGzIh2EXPVBCapgGbyeVrhbKnY1s76pla1cNrpAPgDH2LG4eeTInpI4j0zSwIL3Dhd1s4OpTpnHZwlKWb6vks7JyvthawTtrdyJLEgUZiYzNTWVsXhrFmcnkpcZji9JD5kjh8vqpaemkvKGdHdVNbKtqory+jZCqYtJrmTkml+MmjGDBxCKM+ti0D0f0La9ytfCzTc+QarCTYrATpzMTrzMTpzVj1Rowa/SYNQaMijbmF0AIgV8N4gkF8IT9OIJeugMeuoMeugJuWvwOWn2RT52nnRb/V0ZTvayl2JbO4uwpTE8sYnJCAUbN0HkdHC5sZgNnzRrLWbPG4vT4KKtooKy8no1763hh2WaCPaHMkgQpcRbSE2xkJNpIibOQYDOTaDURbzViM+mxGA1YTXqMOi16rRLzLjOsqnj9QbyBIE6PH4fHh8Pjp8Ppob3bQ7vDTUuXi/q2burbunH5vtJRJlhNjMlN5dy5JUwZmU1xZnLU1v+jSaE1jcKRadw0chENnk7Wd1Swvr2cXd31LGve0VtOJ2vIMMaTaUogRW8jUW8l2WAjTmfGrjVi05qwagwYNXpMii5m3XxEPRPGGw7iCvpwhbw4gz46g246/S46Ai5afA6afF00eSOfoPjKPlJgSeHEtBImxOdRmpBPmnHgtpkjhU6rYWFpMQtLiwmFVbZXN7Jm5352VDfz+ZYK3lr91fOPMxvISo4jLcFKst1CaryFeIuRuJ6P1ajHbNBhNugw6rUxz30hBL5ACLcvgMcfwOX10+ny0eXy0uny0trloqnTSUunk/q2btocnt66ZoOOMbmpXHbiZKaOzKa0MPOQ6T6i4YgKdI2sUO/pYFNHVe9u4FBoJQWdokEna1AkGVmSUXpi6FREzyRWCaohAmqYoBpC7cOIpJUUkgw2UvQ2JieOIMeUSLY5kQJLKnnm5EEZuI4FrCYD80oKmFcS8ScOhsPUNHdSXt9OVXMHje0OGtodbCqvp63bTSisHrItSQK9VoNOo6BRFDSK3LtLFggQkeyFoXDkEwiGCIT6NqBajHqS7GaykuxMLMwkM8lOfmo8xdnJJNtj10Efa2SY4jnLNIWzelwbXUEfe52NVLtaqPN2UO+JfHZ119EZ8ESe4yHQSAp6WYNGVtDKCrIkIwHSgfkvVEJCJSxUAmoIfzjY59yXkEjQW0g3xDHSlsHxqWPJMyeTb0mhwJKCSXNsBd7EikaRmTgik4kjImohIQT1bd2UN7RT09JJTUsXda1dlDe0s3pHNZ6e3CuHQqdRIh+tBkWWkGWpd4MphCCsqqhCEAiGCYRC+PtxHtBrFVLjraTEWZk5No+81HhyUuIpSE8kJyVuSE+gR1SgZ5sSeWHOjwDwhgJ0Bd10Btx0Bdy4Q37cIT+ukA9vOEAgHMKvBvGrIVQReYBhoUaMoj0rqEaS0coRoa+VFUw9OxyjosOqNWLXmbBrTcTrzNi1pqMSzHS00CoKIzKSGJHxbW8AIUTv7rnT6cHp9eP0+nF5/PgCIbyBIL5AREiHwhGDUDisfvX8JNDIcq+w12kVjDotRr0Wo06D1WjAatZjMxmItxhJtJmHRK//34RFa6A0IZ/ShG/nowmpYdoDLroDbrqDXhxBD85gZN57wn58oSABNURIhAmqYcJC7XHXjSyoGllBkWQUSUIna9HLGgyKDoOixaoxYNYasGgMxOvMJOgs2HUmlGNI5XO4kSSJrOS4Q3qBRXbQXrrdvt757/EFcPuCePwBAqFwr7BWVUFYFT3uugJZlpGliJDXayNCX6eJzH+zQYfJoMNi1BFnMUZOAWYjVpP+iMmeo/aWGTU6jBod6cb4ozWE7y2SJGE3G7CbDeSnHVs60u8DGlkh1WAn1XB0oha/71iMeixGPdkDT5lyzPL9WbaHGWaYYb7jDAv0YYYZZpjvCEdU5dLkcnHXquVHsstjig6vlw6vl99//il6jeZ7pdM/qghBuzeS5qDR5eTuVcujiMEcZigQQhAIh9nYUI+A7/X7P1BKklOjLntEQ/+NOTki7xexh/5+FwiLiFdJvMFIIBzGHw5xBB/99x6DRoNVr8MVCOD0+//rvZr+W5Ak0CsatIpMu8eDIsvfKwPtULB41GjuWrjo2M/l8n1iV2sLp73wDLfNmssNU/rOrz3M0COE4Jp33mRV7X7euOASRid9By1ixzCfVJZz3btv8ezZ5zErO7obtYb5imiTcw0vlUeI0ckpjEtJ5Yv9VUd7KN9LmlwullVXcuOU6cPC/CiwvaUFgCkZx9ZlH981hgX6EcSq06EO61mOCgdUXhnWI5cbaJivEAgkQBfDpcnDxM6wQB9mmGGG+Y5wxAOL/MEQTR1OmjudtDs8tPdEKzo8PlzeAE6PH48/gC8Qwh8MEQiGCKuRcNuwKpCkSGCMLEkosoxeq6DVKOi1mt58DGaDDps5EqUYbzGSYDORFm8lNd6K3Wz43nqXCCHoDnpo8XXT6nfS5nfS4XfhCHpwBL04gt5IpGI42ButGxLh3jDzrxOJ0lV6UjRoMSq6SJSuRodNG4nQtWuNJOgtpOjtJBtspBhsGJRjP0fO4SIUVmnrdtPc5aSl00W700OXy0uXy4vD7cPtD+A5EK0YDBMIhQmGwoRUFcRXyQIUOZKKQaNE5r9Bp8Wg02LSa7Ga9NhMeqwmA4lWE4l2M0k2M6nxFpLtlv+KHDmHC28oQJOvi2ZfNx1+F50BFx0BN46gpzdK3RPy41dDBMKRKPWQUCPh/kIFBPKBNCSSjE5W0Mta9IoWk6LDrDFg0RqwagzE6ywk6MyR+W+wk2aMw6I5/EnCjqhA31ffxsxbHvr2IBQZm8mA1ajHYtRh1OtIsusx6CJhtYoio5Hl3smoCoFQIRSOTPpAKIwvEMLjD9DucOPyBuj2+PAeJGeD2aAjNzWeERmJjEhPZGR2CiV5aZgM3y1B4w752eNoYFd3PXudDex3t1HjbjtoDh2DosWmMWLVGjFp9BgVHfE6c28+EY0UCTU/IAoEERVGUA0TUEME1BDecICuoId6b0fv4vDNRQAg1WAnz5xMrjmZUbYMxsRlkWdOPqayEQ4FTR1OtlU1sru2haqmDqoaO6hr6yKsflvlZjPpsZkNmPWR0PEEq6k3l45Wq6CRZZC+lstFFb0pGQKhcG+qhuZOJ/vq23B6fP+R/OwAOo1CdnIcuanxjMxOZlR2CqNyUr4TuXS+TkgNs8fRwG5HA5WuZsqdTVS7W+kMfPvCHK2kYNeZsGgiyQFNGj12rak3j5RGUiKh/kggSb1pSA7kkfL3CH53yE+LrxtXyI8j6MGvhr7Vl01rJNecTKEllUJrGkW2dEbbMtErQ3efwxEV6GaDjhtOn0lGko3UOCuJNhNJNvNhy3XgC4TodHlod3ho7nDS2Omkoa2bysZ21uyo5p01OwFQZInirGQmFWYyt6SA0qLMqC9kPlYIqiG2dtawtm0fa9v3sdfR2JsAKllvI9+SwskZE8g2JZFmsJOot5FssJKgswzphDqAEAJXyEe739mb6bLJ10WNu41qVyvv1m/k5Zo1AJgVPePjc5mVXMyc5FHHXMrWaOhyeVm5o4qV26rYXNFAS1fkijONLJOdEseIjEQWlBaRkWgjNc5CSryVJJsJq8mA5jBcEBIWgNMfAAAgAElEQVQKq3Q6PbQ53JFTQaeT2tbunrStbXy2uby3bFaSnemjc5gxKpdpo7KHLKf4keLAZTQrW3azqbOKbV01+MKRzZxZ0VNgTWVeymgyjQmkGeNINdhJ0tuI15sxK0Mve4QQeMMBOgNu2v1Omn3dNHq7qPd2UONu5dPm7bxRtx6ILChj47IpTchnZlIxJXHZg9rcHFGBnpFo47rTZhyx/gw6DekJNtITbIzLS/vW37tcXnbsb2ZLRQObK+p5bcVWnv+sDKtRz8LSIi44fiLFWce2R8R+Vysv16xhaUMZ7pAfRZIZH5fDNYUnMMaexShbBon6I28IlCQJqzay6z/YxSCqUKlxt7G9u44dXbVs6Kjg/l3vcv+ud8m3pLAkezqnZ04+ptMYq6rg860VvLisjE376lGFIMlmYkpxNuML0inJj+SkPxoXc2gUmeQ4C8lxB999u7x+9ta1srOmhQ17avlg/R5eW7ENjSwztySf84+bwLRROce0erLV5+CN2nUsbSijwduJhEShNY0zM6cwMSGPsfYs0gxxR/w7SJIUSRSo0R90cyKEoNXvYI+jgbKOajZ2VPJkxef8q2IZSXorp2RMYnHWVLLNiTH3/f1KgfcN4izGyG0nY/MA8PqDrN21n882l/P++t28sWo7CyYVcu2pM445wb6jq5bHyj9lTdtetJLCwvQS5qeOY0piwRHR1Q0WWZLJs6SQZ0nh9MxSAGrd7axq3c1HjVu5d9c7PFr+CUtyZnBB7swBXfN2uAiGwixdt5unPlpPdXMnmYk2rj5lGvNKChidk/pfoae2GPWUFmVRWpTFpQtKCYbD7KhuYtnmyGURy7ZUkJ+WwPWnz+DE0uJjSrB3+F08XbWc12rWElDDTEscwQ9GzGdeyqhjap4cCkmSSOm5E2Juymggkm55VesePm7ayvPVK3muagWnZEzi2sIFZJiiT2D4vRbo38So1zJ/YiHzJxby8/OO57nPNvH8Z2V8WlbOyVNG8suLTjjqx1Fn0Mt9u97l/YYyEnRmri9cyOLsqUdlFz7UZJsTudA8mwvzZrO1cz/PVq/g3xWf8/L+Nfxo1KmcmTn5qAuWLZUN/O6pD6lp6WJkVjJ3Xn0qCyYVHRa1yZFEqyi9OcVvPHMWH2/cy9OfbOT2J5byfEEZv71k4UFTMR9JwkLl3xXLeKZqBf5wkNMyS7lqxPz/ShXdN7FoDSzKmMCijAm0+hw8V72SV2vW8mHjFs7PnRl1O8esQPf5gnS2u+ju9uD3hwj0fCQJFI2CRiOjN2ix2YzY7EasNuOQXlZsMxv4f2fM4uITSnn2k4089dEGdtW08MD/O5O8o5Rydmd3Hb/a/ALNvm6uLDiOKwqOx3wYLicQQsUb7sYb7iaoegmoHkI9FxVLyCBJaCUDesWMXjZjUOzoFfOQjmF8fC73xOdS5Wrhnp1v86ftr7O1cz8/H3MmhsOg84+GV1ds5Z6XlpEaZ+GvN57FnHH5h2WB8fuDdHd5cDl9OJ0+fN4gQghUVYAQ6PQajCYdBoMOe5yR+HgLimbo5r5eq+H0GWM4Zdoo3lm7k4feWMlld73A7RedwJkzD36h++HGFfTxmy0vsrptLwvSxnFD4YnkWob+1CyEIKB6euZ/FyHV33tBvUCgSNrIJd2yHoNiw6TEoZPNQzoPkg02fjzqVC7Km80T5Z/GFLty1AV6a4uDbZtrqKpsoa6mg9r9bbQ2O/B4vm2l7wtZlkhOsZGeGU9GZjz5I1IYOz6LghGpg5rsdrOBm86azcwxufz8sXe5/O4XuPOa03rVNEeKNa17ua3sOeJ1Zh6ddh3j4wcfPh0WIVp9+2j27aXdX0WHvwZnqAVXsA2Vb1vp+0Inm7BqU7Fp00jQ5ZBiKCLNOBqrZnCXJudbUnh46lU8Uf4p/6xYxj5nE/835UridEO7gPRFWFW568XPeG3FNmaOyeXOq04dknsqnQ4vu3c2sGdXA9WVrTQ3dtHU2E1X57e9MfpCliXiEsykpNjIzksiNy+JEUWpjC3JxmgauA1CkWUWzxrHnLH5/Prf7/P7pz+ipcvFNadMH3CbA6He08GtG5+ixtPO7WPO4pycwfcfceFtpMGzjTZ/JV2BerqCDTiCjYRF3zcafRNF0mLRJBOnyyJel0WCLocMUwkJusHZIFINdn497hyEEESbAeuIC/RQKMzGdVWsWbmXzRurqa/tAEBRZDKy4snOSaR0agEJCWbiEszExZvR6zXo9Vp0Og0CQSikEg6F8XqDOB1eHN1eujrdNDZ00lDfxcovdrP07TIAjCYd48ZnM+e4kcyaN5K4+IEJgtKiLJ65/WJu/cfb3PqPt3nsx0uYMCJjyJ5LX+xzNvKLzc+Ra07ir1OuHJR6xRVso8q9lv2u9dR6ygiokfsNdbKZRH0e6caxWKxJWLXJGBU7WtmETjahkfVISD0356iEVB9+1Y1fdeMNdeIMtuAIteAINrLftb53QbBqUsm3zKDAMoNM0wQ0cuwCRpFkri86kTH2LH61+QVuL3ueh6dedcQSbD3yzhpeW7GNK0+awk1nzR7wlWFCCMr3NrF6xV5Wr9hL5b5mIJLAKj0jnvTMeGbPSyUlzU5cvBmr1YDZasBo1EWuQevRzfv9IbyeAD5vgO5uD+1tLtpbnTQ1drFpXRUfL90KgEYjM6Yki8nTCpg5p5j8Ed82TkdDkt3Mwz88mz888xF/f3s1yXYLZ806Mjv1zoCLH67/F86Ql4enXMXkxIIBtxVS/VS711HuXEGdZwvuUDsAGkmPXZdBgi6HAssMTEo8Bo0do2JDJ5uQJQ2KpEVCIiyChESAkOrHF3bgCXfhCXXiDDbTGaijwbOVoIi4BhuVODJNJRRYZlJgmT3gU2wsi8IRTc6Vk10sppfcQFeXB5NJx/hJuUycnMeE0lzyCpLRDKE3QEtTN9u31rJjWx0b1lbQUN+JLEuMn5TLKWdM5LgTxgxo597t9nHZXc8TCIV54VeXEG81RV33ktdfJqSqvLTkwqjrdAU8XLnmbwTUEE/PvIkkgy3mMYdFiErnKnZ0v89+90ZAYNWkkGuZSo5pMqnGkYPeSf9nf0Ha/FU0eXdR495IjXsTIeFDJ5sYaVvA+LgzSDIM7MV8v6GM3219hQtyZ/LT0WdEXa/O0c28J5/gnoWLWDJmXNT1Pt20j58//i5nzxnHby85cSBDprPDxXtvlfHBO5tpbupGliXGlmQxefoIxozLZOToDEzmoVOdORxe9u1upGxDNRvXVVK+twmAwuI0Tjp1PAtPLsFqM8bcbiiscvPDb7CpvJ7HfrKECQXRb2geWLuKh9etpeKW6LOtqkLlRxueZHNnNY9Mu5ZxcdkxjxmgzrOF7V3vUelaQ1D1YlTiyDZPItM4nszenfTQqKwO7PzrPVuo92yl1lOGK9SGIunIt8xgtP0k8s3TY37Xok3OdUQFut2aJX72o7+y4KRxTJ1ZiFZ7ZHZYQggqy1tYsWwXyz7ZQUNdJ1k5CfzguvnMnT8q5oe7u7aFK+95kRMmFvLnq0+Nut5ABPqvN7/A5807eXT6dTFPaCEEFa6VrGh5FEewCYsmmTH2RRTb5g/6OBgLIdVPrWczex3L2Of8grAIMsIym1nJV5Ogj1119Jdd7/Hi/lU8NOUHTE8qiqrOQAR6p8vLWf/zb/JS43ni1vNivo3d0e3hxWdW8/ZrG/D7Q5ROzWf+iWOZMbtowCfFgdDZ4eKLT3fx0dIt7NvThNGk47Kr5nL2+dNi3kQd2NCEVJXXf3dl1HfFDkSgv1G7jjt3vMkvxy7m7OzYM5S2+spZ2fo4Ne6N6GUrhdY5FNuOJ8s0EVk6crKn0buTvY7P2Ov8Am+4izTDaOam3ECGKfpTzjEp0EtLJ4tNmzYesf4OhqoK1qzYy78fW8b+qjbGjs/iZ78+k6zs2Aydf3trFf/8YB3P/OIixh7Ex/1gxCrQt3Tu59ovH+XawgVcW7ggpvF1Bxr4vPlhqt3rSNIXMDPpSvIs04/YRD4UvrCDzZ1vUtbxGmERYGriJUxJvABFit7QGVBDnL/iAYyKjmdn3xxVfu2BCPS7X1rGq8u38NJvLqMgPXqfYCEEyz/bxcP3f4DD4WXBonFcfMUcsnJi9yseasr3NvHU41+wdtU+cvOT+OGtJzNxcl5MbWzYW8t1D7zKLWfP4cqTpkZVJ1aB7g75OXf5/WSbEnls+nUxbT78YRcrWh5lR/cHGGQLU5MuYXzcGWjkoXcgiAVVhNnV/TFr2v6NO9ROkXUex6XehFnT/7w4JtPnHgv+ubIsMfu4kTz69HXc+svT2F/Vxv+74nHWrtoXUztXLppKgtXE395edZhGCk+Uf0aCzsKleXNjqrfPsZxnq66l3ruNuSk3cFHeIxRYZx11YQ5gUGzMSLqcywueZIRlNmvbnuTl/T/CFWyLug2drOHmkSdT4Wrmo8Yth2WcDe3dvLp8C+fMGR+TMA8Gw/zlzne547evk5xm55Enr+G23551TAhziKhd/njvBfzx3gvw+0P8/OZn+ecjnxHLxm5KcTazx+bx5Ifr8QZiMyBGyyv719ARcPGjUafGJMy7Ag28UH0jO7s/pDRhCVeOeIbShCVHXZgDyJLC2LiTuaLgSWYkXUGV60ueq7qeFl9ssqfPPqIpJEnSTyRJ2iFJ0nZJkl6QJMkgSVK+JElfSpK0T5KklyRJOnZD+g6CosiccsYkHn/2OrLzkvjd7S/3GlKjwWzQceH8iazdVUNta9eQj6/B08mX7fs4N2d6TNGSu7s/4f2GO0g2FHJZ/r8oTVhyTAjyb2LWxHNK5m84LfP3dAZqeWn/zXQHGqKuf0LqOLJNibxVe3guTHl95XaEgKtOjm4HChFX29/87EU+eHcLF18xm4ce+wEFhdFfH3YkmTG7iCeeu55Tz5zEi8+s5m8PfBhxi4ySK06agsPj59OyoRNGB1CFyht165mSUBCTmrHFt4+X99+CX3WxJOcvzE25Hr1y7AUaaWUj05Mu48K8v6ORdLxW81Pq3JuHpO1+BbokSZnALcAUIcQ4QAEuBO4GHhBCFAGdwNVDMqIjTFKyjfsfvozSKfk8cNd7fPz+1qjrnjVzLIos8eaq7UM+rvcaNiEhcUbm5Kjr7HMs58PGu8k0jefs7Luwao+t6NaDUWidw5KcvxBSfbxW83O8oe6o6klS5Nls6qyi3tMxpGMSQrD0y13MHJNLanx0HkWqKrjjN69RtqGKn/36DH5w/fwh9Q0/HOj1Wn78i1M598LpvPXqBh558KOo604uyiIr2c7bq3cO+bg2tFfS6O1kcXb0i2mbv4rXan6KImk5L+dBMkzRG76PFon6XM7L/SsWTTJv1v2S2iEQ6tHOOA1glCRJA5iARuAE4NWevz8FLB70aI4SRpOOP957AeMn5fDQ/R/Q2NAZVb3kOAulRVms3D70txCtat1DSVw2aca4qMp3Bxr5pOk+0gwjOTPrDrRy7F4MR4sUQxFnZd+JJ9zBJ033R338PzF9PBB5VkPJvvo2mjqdLCwtjrrOm6+s48vV5dz4k0UsOm3CkI7ncCJJEtffvJBzLpjGm6+uZ9nHO6Kud9LkkZSV1+Hy+od0TMtbdqGXtRyXMiaq8mER5MOGu1AkHefn/nVAhvajhVWbzJLcv2DXpvNR4134w65BtdevQBdC1AP3ATVEBHk3sBHoEkIciD6pA/6r75bSaBRu+82ZSJLEvX98O2qhMn1UDvvq22h3xBYM0hfdAQ+7uuuZEaUHhxAqHzT8CZA4JeM3aOVjP5fLN0kzjmJW8tVUulazo3tpVHUyTQlkGhP4sm1oj/3rdtcAMGN0dIKhurKVJ/7+GTPnFHPWuf3arY45JEni2psWMKYkiwfvWUp7mzOqejNH5xJWBev31A7peNa1l1OakB91FtB1bc/S5q9gYdqtWLUD87U/mhgVOydl3I471MEXLY8Mqq1+fY4kSYoHzgLygS7gFeCUgxQ9qASUJOk64DqAnJzYVk5VVanZVU9DeRP15U00VTWj1WmwJdmwJ1nJKExj3JxRaHVDEwqemh7HdTct4MF7lrJ+bQXTZhb2W6e0KLKO7djfzLySgQc9fJ2d3XUIBJPi86MqX+VeR5NvNyem/RybLjqPm2gQIgihfRDcjghVEknKrQG0SJp80E1FUoauv0nx51DpXM2a1icZZVsYlSGrNCGfVa27h2wMANuqGslMtEWtbnn6n8vR6TX85PbThtQV1NnpYusXO6nd04Df48fn9hMOhcksSie/JIf8khys8UOjI9ZoFH7+mzO5+qJHeOPl9Vxz4wn91hlfkI5GkdlW1cj8if2/K9HgCvqodrdySsakqMp7Q91s6niVYtt8CqyzhmQMENkkEdoOof2gtiDCzSACkfmuZICSBdpxDJXpMNVQTGnCEjZ2vMLUxIuI12UNqJ1onEgXAlVCiFYASZJeB2YBcZIkaXp26VnAQS1aQojHgMcApkyZEtW2t7vNwesPvscnzy6npeYr7wdLnDkSIer66pIGk83I1JMnMv/COcw6a+qgX6iTTpvAc0+u4MVnVkcl0At7EhaV17cNmUDf54wEghTZ0qMqX9bxGhZNMiPtsbk2HgoR2IBw/QMCa4EDKRh0gASEgHDv6i2ULNDNQbLchKQMzgAoSTIzki7ntdqfsdvxKePi+vfxL7Sm8U79Rtr9ziFLULavvi3q7Jq1+9tZ+fkuLrp8NvEJg/ct93n8vHLv23y5dCP7Nlb+h6HSYNIjydJ/zP+RU0ew+OZTWXDJ3EHP/azsBGYfN4r33trEJVfO6TdtgFajUJCeyN666D2U+qPCFYmeLbJGt1HY0vUWIeFnWuKlQ9K/CJUjPM+D72NQm7/6g2QEdAjxNRuPZEcYTkIyXYKkjU491BeTEs5jc+cbbOp4lQVpPx5QG9EI9BpghiRJJsALLAA2AMuAJcCLwBXAWwMawTf48Mll/OPWp/A4PEw+aQKX/e588ktyyBiR2rsbCfgCdLc5KS+rYs3bG/jyvY188fIaFl05nx/949pB7di1WoXF503j8b99SmNDJ+kZfaeutBj1pMVbqWoaOsNctbuFJL0Vm7Z/Pbgr2Eadp4yZST9AkQaXyUEIP8J5P3ieBDkFTJcgaUtAOw6Ur6LphAhBaA8E1iMCG8D7BsL/EdjvQ9LPGdQYMk0TSNDlsidKgV7Qk2u92tU6JAI9FFapbe3ihEnRqbs++3g7kiSx+LzYA1++SUNFE3849z6qttUwZlYxF//6XCYtKKGoNB9Dz9WJQgjaGzqo3FpDeVkVnz2/grsvf4iPnvqcnzx6PekFg1tUzz5vKiuW7WLtqn3MP7H/wJcR6YlsrojeO6k/qt2tQCSHT38IIdjV/RG55ikk6nMH1a8QAjz/QjjvBbSgn4dkOCky9+VUkCIJuITqAbURQhUI30fgW4rwvoowXY5kvR1pEB5lZk08I20nsMfxKcen/nBA73O/NYQQX0qS9Cqwicj2rIzIjvs94EVJku7o+bd/xtz7N3jpnrd44vZnGX/cGG752zXkjjm4y5LOoCM5K5HkrERmnjGFcDjMc398jWf+9xWaqlv43Ws/G9RRdOacYh7/26dsWFvJGef072WSGm/pvaFmKGjxOUgzRGcMrfVEXC3zLYNLWCTCLYjOqyC0F0wXI1luQ5IPntZAkjSgHQvasUjmKyO7mq4fITqvRphvRLL8cMATW5Ik8izT2NL5JiHV36/aJdVgB6DV7xhQf9+kw+khrArSEqJbHDZvrKZ4VPqgd+fr3i/jzkv+iiTBn5b+iqmLJh60nCRJJGUmkpSZyLRTJnHh7Yt577FPeOIXz3JD6c+568PfMnp6dIvRwRhTkoXZomfThqqoBHpqvIXWbheqKoYkzqTFF9kBp0SR4qIrWI8j2ERpwnmD6lMIFeG8K7KR0Z+MZP8DknzwjZwkm0AeAZoRSIaTEKoD4foLeJ5CqC1gv3dQaph8y0x2dn9Ik3cXmaaSmOtH5eUihPidEGKUEGKcEOIyIYRfCFEphJgmhCgUQpwnhBiUqXvn2r08cfuzHH/BLO7+6LeHFOYHQ1EULv/9+dz+zC3sXL2Hh28e3NqSlZNAUrKVHVujM/Ykx1lo7R46o2ib30GSITqB0uDdgV62kKQfnLpHOP8E4Vqk+CeQbb8/pDA/GJKmECnhFTCcBe6/gW9wh7VM43jCIhhVwMWB3DZDJdDbuiMLc7KtfwEdDqvs3lFPycTBeVU0VjXzu8V3k5KbxN/W331IYX4wZFnmjBtO4rGt92NPsvHnix4gHA4PeCyKIjN+Yi47tkQ59+0WQmGVbrd3wH1+nXa/kzitCa3c/+60wbMNgBxT6eA69b4ZEeamK5DiHjykMD8YkmyLvC/WX4DvfXD/e1BDyTZFfvt6T/Tu01/nmHGUfeOv72G2m7j18RvQxJgz4wALLpnL2T86jc9fXEV9eeOAxyJJEukZcbS2RickTHodXn9s6X77whMKYFai81RxBluwa9MHlVxIhNvB9wkYL0DSzxtQG5JsQrLfDUoOwvvGgMcCYNdFbAfOUGu/ZU1KZDfkDQ3N83f7eu6iNPa/y+rscBMKqaRnRi8ADsa7j3yEEPCnd385YJVJam4yV995CU3VrWz4cHDRsxlZ8bQ0d0fl6XXgOXkOciH7QPCEApijvHHLEWxGQsami87WdDCEUBGeJ0AzCsn6qwG/R5L5atDNQXieQYiBz0W9YsGoxOEMtQyo/jEh0L1uH8tfXcuJlx+H0TI4/+klt56OJMssffzTQbUTn2ihoz06NYpBp8EXiC1/eF/4woGoL3HwhNoxaQZ54Yb/EyCIZDxnUM1IkgSGMyHwJUKNzpf/YBzIbXEgvWlfyJKMXtb2Xgo8WHw9oeyGKOwwB+ZHYuLgPE1Wv72e0oUlJGUOLj3ArLOmYEu0suyFlYNqJzHJit8fwu3q/9Bt7HlO3iES6D41+rnvDrVj0sQPznYU3AyhciTzDwZtVJZMl4HaAv7BPX+LJimmVBhf55gQ6DqDFkWR0ekH735oMOsJh8KYrIMPrIkpD/GgextovzLSYHuXenZEMSTIOmRTB14uaQiefyzTc4h+gFievTxELoo6ow5lCFJHa3VaJAn0UZwuoiEWnfhQeWvGOpcHnVywd54OQa4XqacNKXp15cERAz4pHBMCXVEUMgrT2LuxYtA/0M41ewHIHTswP84D+H1B9FEuMGFVRR7gpQcHQ5FkQiI6PahG1vcm1B94hz064ODgIy5FaB/IyUjSwIObgmrk+0R7GUZYqChDNJUPXF4RDqv9ltXpI4uXzze43WlaXgr7d9ahqv332Rdt9e10tznJKBy4CgLA54uoDKKZ/+GeMQ/V/I9l7mtlI6HBzn1NASAjgkOQSyXYo+rSRBc/cshmVB9aaWALzDEh0AEWXDKPzct28PHTXwy4jY6mTu676u+k5iYz6YTB5XJoauwiKSU6w6TbG8BkGLp7Lo2KDk8oOhuzRZscU1Krg6IdE9F9u/6CEAM3bgn/yohhyDCwiyAO4AhG7B9WTf+ua75wkJAIYxqiu1VNPULMHYVNJCk5Mj8a6weuXgKYc850GiubeexnTw+4DSEEf73xcbR6LbMXR58D5WA01neSkBTdPaWuHuFvNgzNqSAy96PTQVu1KQRUD+7QwJ+/JOnBcBp4nkb41wy4HRHcg3A9ArpZEZffARIWQZyhlgFHvB4zAv38285k/HFjeOiHT7Dli+jySXydjqZOfnf2vbg63fzhzdsw2wfuRhbwh6itaacgyiu7utw+4sxDlzslTmemK+iJqmySvgBnqAVfOLpw7YMhSXok+58hXIPovBERqoupvhAC4fsI0XUTaIqRLNFfYnAw2vyVAFF57nT3PKc43WCPuRHsPXeFdrn6X9hMZj3pGXFUVgzMgHWAhZfOY/HNp/Dag+/x5P+8SCgYmz3G6/Lyr189z9p3NnL1ny8mq3hwVyNW7GtmRFF0xtkDz8k+BHesAth1JrqDnqhO6sn6SOBf6yDTz0q2P4CSh+j6MSK4K+b6ItyA6LoFZCuS/b5B6eI7/DWERZBkw8Aib48Zga4oCrc/cwv2JBs/m/97bj3+f1j3flm/P2x9eSP//NXzXDPuVio2V3Pb0zczYkLeoMay4csK1LBg3ITo3NFau1wk/n/2zjs8yir74593es+k9w4JhNAhVKUKiKKCKPaCXde6zVVXd11dy9r7b9fuqmBDARVFeu8QSEhCSe9lkkmml/f3xwCyLsKEzGQCm4+PTx5g3vuezNw577n3nvM9hsA4FIAopZ5Gu38ZNglqX65whaVrjUMERR6C4Qlwbkdsmo7X/DSi9+TFUqLoRXTuQjTdgtj6G1/xUfg7CJKuFfiUW3agk0X7Jfx/9H0KVJVo5JFAwN+6gv65iezZWY7HffrbJYIgcPsL1zP12nP5+IkvuWvkg6z5bCM2y8m3E5x2J1+99C3X9bmbBc98fSTLy/8OWieiqdFM6aEGcnL927JsbO1Ar1aiPM3MtF8SpdTj9Loxu079QI1VZSEV5JRbtnXpnoJEhxD+OggyxOa5eFsf8FVLn8L3iK5CvG0PIjaeB94GX8qjNKpLtpRZtgIQrz69nq3d3iT6ZEQnRfKvvc/z/dsr+eKFJTx8wd9J7pdIzugsUnOSMMaEIVPIaG/poK3JzO5V+8hfU4hEIpA3cxg3P3MNqf27tncOsOLHfRiNGoaOSDvla0VRpLqpjdE5XatUO55EdQTrG4p8e8OnOByJVw9AI42gxLyaLMPELt1X0FwOynMRO14C63uI1vcRZTmgHI0gTfEdIIkewInoygfHKvA2+6ro9H8CzTUIXTxYdXgsVFi2M9A4y69Ip8rqy4RJVHcx0+cIerUSo05NdZN/Mr7jJ/Rj5Y8F7N5ZxvC8068FkEql/PGDuxk/exRv3PceT1zxIkq1grwLhuqZABMAACAASURBVNFnSDrGmDBUGgWCREJVcQ2Fm4sp3FSC1WxjyORcbvzb78kZk33a9z/K2pVFiCJMmOxfKXtlYxvJMf4VwfnD0c+x2tZC2ClWXQqphjTtKErMqzkn5vYu6f4LskyIWuKTvLB9iWhfCrJsRMVYn36LJBrwgLcN0VMFrnxw7fR9JzSXI2jmI8hOr+fp8ZSYVxGvzsEgP7301R7l0AHUOjVz7ruAWXdOY9WnG1jx8Vq2fLeTH95fdaz0+ShJWfHMf/Iqzrt+AlEJgflC11S1sGFNMRddOsKvfou1Le3YXW5SAzipU7RRuEQPNVYTydqTR6kSQUqWYSL5psWYXfWnPRGOIkjjEMKeRtTMR7Qv8+m5WD5AxAMcF4UKOl95tHIKKCcgSDrfvPpE7G1dgkd0kW04tTgU+ErFpYKERE1gPn+A1Bgjh2v9k3IYNbYvhjA1n328qUsO/SjjLslj9Kzh7FtXxJrPN7Fh0RY2L9mB67i0QEEQSB+YwuQrx3PuZWMYOrnzFYUnwuP2smTRdvpmx5Gc6l8KZWldM8P6dj2IOkqK1hfhlnY0kBN26nH7h53HoY71FJtX0j+sa2c3giQCwfAQou4+sH+LaPsMrJ8i8suVkgpkGb5iIvVcBElYl+57lArLTpoch5kUe89pj9HjHPpR5Ao5066fyLTrJwI+5TnTkWIHQ6Qefbj2tAuQTsb7/1qDTCbh8qvH+PX6/eU+AZ/+KYHrTJMT5lNwLGyrOqVDBxgWMZd802I2N33ItPjfB8QGQZ6FIM8C7kEUHeBpADyA1JfeKIn6OUUxQFjdrWxr/oR07Wji1P38umZ/WzXpuhi/c5f9oX9KLN9sKsDj9R7Levk1FEoZV98wnjdfXs72LYcYMSqzy/eXSqUMnjiAwRMH8JtX59NhsmC3OnBYHXjcXmLTolEHaM/6eFb8uJeqihYe/ftcv17f2NZBvamDnADO/RRtFGqpgv1t1VyQeOoK0AzdGKKVfdjc9AFZhomd6k37awgSDWguQ9Bc5gsgxTbwHskLl0SAEB7wBuuiKLKx8d0jjdxnnPY4PWYP/VTow3Wk9EsktX8S4TFhQXHm2zYfYtXyAmbPyzuWwXAq8ktrkcuk9E3s2t7Z8WToYlFJ5eS3lvv1er08hqERc9jf9gOHOzYHzI6jCIISQZaMIEvz/ZTGBdyZi6LI6vpXcHntjIu5xa9r3F4PBW2VfkVynWFAWhw2h4sD1f4Vd1w4ezhxCUZefW4Zlo4uptH9AolEgiFST0xyFMnZiaQNSA6KM2+oa+Nfr62gb794xk/wb+tmzxFRrlw/m6T7g1SQ0M+Q4PfcFwQJ46JvwuyqY2vTxwGz4+fxBQSJ0SdvIevji+ID7MwBCtqWUW8vYlTUdX6n656IM8ahB5umxnaeffwb0jKiueZG/5sybygoZWhmAooAPmBkEikjIjLZ2Fjid17+6KjriVH25Yeap2h1VgfMlu5it+krDrSvZVz0TX4r5xW0VWF22fxuBOIvo/r5DsM3FpT59XqFQsYf/3wRdXWtPPf3pV0vdulmnA43f33oC5xON3967BK/Hdb6fWXo1UoGBNChA4yJyqLIXON3YkCqbiT9DdPY1vwJ5Zbg9JgNJnW2ItbUv0aSZigDwqZ3aaxehw7U17byx3s/xu5w8cgTl/pdUFRW18Lh2hbOCZAO+vGMi86m2tZyTB/6VMgkSi5IfAwJEhZXPXLapcOh4GD7OtY3/JNM3TiGRVzu93VrG/YjFSSMigxMc4WjRIVp6Zccw5r8w35fkzs4hZvvmML61UX836s/darhcihxOt38/bFFlBTV8sfHLvF779zl8bB+XyljclKRSQPrRsbH+Lbb1jT43690YtzdRCrT+Lb6r1RYdgbUnmBSby9hcdUjaGThnJ/wcJc0maDXoXOguJZ7bn2f5qZ2nnjuClLT/N86+Wr9XmQSCdNHdD274JdMjhuATJCyuMr/dESDIo4Lkx6nw93E5xX30Wj33yGFAlEU2d68kG+rHydG1Zfz4v/gd3To9nr4vmYXY6Ky0PuhG99Zpo/IZm9pLYdq/H8wzr1yFBfPHcGXC7bwt0e+7HIFabBpN9v48+8XsmFtMXc9MJ2x5/jfQ3Xd3lJa2q2cn+ffWUdnyNTF0kcfxzdVp04dPIpCoubipL9jkMfxTeVDFLV1TcupOyi37ODLit8iE5Rckvw0GlnXEyv+Zx26x+Nl2dLd/Pauj5DKJLz01g0MHup/6qHV7mTJ5kImDckkqgtFTL9GuELHxNgcvqvZ2SklwUTNQOYk/wOP6OKz8nvYY/oar5+l1N2Jzd3G9zV/Y0Pjv8jST2BOynMopf6/j6vqC2hytHNxUnB6eF40Jge5TMqnq/wvCRcEgbvun84d957HhjVF3Hfb+5QdPrViZCjYvuUQd974Nvm7yvntQxdyydzOVZd+sTafGKOOcQO6VuZ+IgRBYE5yHsXmGva2+t+vVCeP4rKUF0nQ5PJD7VOsrX+zy02Xg4Hb62Bz04csrnyYMHk8l6e+fNot537J/6RD37m9lLvmv8Pzf19KZt9YXvnnjaRl+Ndy7Cgf/bSDNoudq6ecugHG6XJF6ljMLhsLyjd26ro4dT+uTHuTBM0AVte/xufl91F9RDs61Li9Tna2fMFHpfM51L6RsdE3MSPh4U41tnZ7Pbx1YDnpuphjy/NAE67XcPGYASzeWEB5vf+l5YIgMGfeKP727DyaGtu5/fp/8fI//G+8HGwa6tp46i+L+NP9nyKVSXn+jeuYcaH/+usAew7XsHl/OfMmDg74dstRzk8YSrhCy5sHfuzUmYRSquPipL+Ta7yQXaav+ODwDexr/bZHBDWiKHKwfR0fHp7PlqYP6aMfz9yUF9DJA5dQ0a1pi6WHGljw0UamzRxERBclRzuLy+Vh26aDLP16J9s2HyI2LoyH/jqbiVNzOn1q3djWwYc/7WDK0D4MyuiaENLJGBSeyoSYHD44vJqZiUOPdefxB60sgkuSnqbYvIK1DW/xRcX9JGmGMjR8Dmm6vC4VYZwONncbReaf2NnyOR3uJlI0wzkn5jaiVJ0/f/iiYjOV1mZeGHbdKQuvusKtF4zm2637eXnROp6/zb9Cp6OMGteXtz++jY/eXce3X+9k+Xf5XHTpCKZfOKRT23qBoriwhsVfbWfFD/uQSASunX8OV1w77pjAmL+4PV6e/3wNUQYN8yZ07kHQGbQyJfMzJ/H8/qVsaCzu1INbJlEwJe4+co0zWVP/OivqXmS36WsGGS8iyzARlTQwVcX+4vLaONi+jr2tS6m1FRKpTOfShOdJ0gwO+L261aHL5VLeeXMl7/1zFXmj+5A3tg95ozOJjQ9cUc7x2GxOCvIr2biuhDUrCjG32TCGa7n5zsnMviyv05MZfE/Zv364HK/Xy92XdK1/pj/c2+98rt7wKn/es5A3Rt6ETOK/IxYEgX5hU8nUj2dv61J2tnzOkuo/o5YaydCNIVM/jmTNsC6lSZ0Mi7uFwx0bOWBeS5V1NyJeEtWDmB7/IEna03MGB9vreL3kB8ZEZTEuOvBnF8cTFabllvNH8crX6/lmUwGXjO2c4JsxXMvdv53BpfPy+ODtNXy5YAuff7KZjL6xTJqSw5hzs0lJjQxKGpzH46W4sIZNG0rYvO4AZaWNqNRyLpw9jMuvHkNM7OkVw7y5ZCP7yup4av5MNAES5Po15iTn8WXFFp4u/IZ/G1M6rdcTq8rispSXONC+mq3NH7Oq/mXWNrxBhm4sGbqxJGuHoZV1rTnJr2H3tFNp2UWZZQsH29fh9FoJkycyKfZeco0zgxZQdatDT0qJ5N1P72DZ0t2sWVHI5g0+UZ3k1EhycpPI6BNLemY0SSmRRET4p/Z2FIvFQVVFM5XlzZSXNVKwp5L9BdW43V4UChljz81i6oxBDM9L96sC9Nf457eb2VhYxoNXTCYlJjiT4XiSNJH8acAlPJr/GW8dWM5vsjtfdCCXqBgWMZfB4ZdwuH0jB9vXcqB9DQVt3yMVFMSqsohT9ydamUm4MgWDPBaVxOC3o/GKHjpcjbS6amh1VlNnL6LGuo82ly99MkyeyPDIeWTpJxKtOv3CG6vbwUO7P0UnV/PowEuD4gh/ybXnDWfT/nKeXbCKAalxp1VvkJAUwZ/+MptbfzOVtSv3s/qnQt55axXvvLUKo1HDgMHJ9OufQGpGNIlJEcQnhiOX+z9HbVYnDfVtVFe2cOhAPcX7a9hfUI25zYZEKjBocAp3z5nBlOm5aHWnn8O+bu9h3vthG7PH5TJ9ZHAfpgByiYy/DLqMWzb/Hw/t/oSXR9zgV2u64xEEgSzDJPrqJ9LoOEhh2w+UmFdxoN2n6hqlzCBRPZBIZToRylSMiiQ00jC/s01EUcTuNdPqrKbZUU6zo5Q6WyH19hJEvCgkGjL15zAgbAYJ6tygz1mhO3NmR4wYIW7f7ssTFUWRyvJmtm85xPathzmwv5bW1p8VBiUSAWOElogIHWq1HKVKjlIpRxRFXG4PHrcXq9VJq8lCa4vlPzIKpFIJmX1jGTI8jSHD08gdlIxa07VoQhRF3lq6iX99t4VZo3P4y3XTOv3hXP3VZ7i9XhbOvaLT939q3yIWVW3j3uyZXJ3e9ZWB2+ukyrqbcst26u1FNNgP4BF/fg/lggqNLBKlVItCokEh8WWSiPhEuVxeG3ZvOw5PO1Z3K15+VghUS8OIVw8gQZ1LinY4UcqMLk/kVqeVB3Z8wH5zNa+MuJGRkZ17MFSZ2zj3/bd5dup05uZ0LtJubOvg6qc+we328OpvZgck77q+tpVdO8rI313B3t0VNNS1HUt1lEgE9AY1BoMag1GNRqNEIhGQSCQIgk9/3WpxYLU6MTV30N7+czGTIEBKWhTZ/RMYnpfByNGZ6A1dzwLacaCKu19bRGpMOO/9/gpUis451hc3b+C1rZs5dE/nlTiXVu/k8b1fMCYqi2eGXoVK2rXvslf00Gg/SIV1JxWWndTbi3B5fxYDkyBFIwtHI4tAIVEjFRRIBTkCEtyiE4/owOW1Y3WbsHpM//G9kQkqolWZJGuGkaodQZy6X0CicUEQdoiieMoMgJCV/guCQEpaFClpUcyZNwpRFGlp7qD0UAN1ta00NbbT3NiOqcWCw+6io91OU2M7EomATCZFJpei0ShITAzHGKElPEJLUnIkSamRJHQywjkVXq/Ic5+vZsHq3Vw0ZgCPXD21W6LD4/l9zkW0uay8XPwd9fY27sme0antl18ikyhI0+WRpssDfDrMJmcVbc4azK46zK56rB4TTo8Fh9eC2eU71BOO/CeXqDHKE1Cq9GikRsIU8YTJEwhTJKCXxQT0/am1mbh3+/vU2Ez8fciVnXbmXSU6TMc7v72cO1/+ktte+oLnb7/oWPHR6RIbb2TGhUOOHUia26xUVbZQXdlCTbWJVpMFc5sNc6sVc5sNr9eLxyuCKKJSKdDqVETHGBg8LJWY2DBiYg3EJRhJz4jpcvDyS37YVsxjH/5AQlQYr909u9POvKtcmDgMt9fDUwVfc/f293hh2HVdSlWVCFJi1dnEqrMZGXklouil3d1Ii6OcNlctHe4mrO4WLG4TLq8Nl9eMR3Qh4kUmKJEKClRSPeGKZLSySLSyCAzyOCKV6RjksQHdTrF7XHS4/a8+7jFaLoIgEBmlJzKqew8sTkVJVSNPL1jJ7kM1XD1lGPfPObdTrbkChUwi5ckhV/Jy0XcsKN/AvtYKHht0GanawBywSQU5Ucp0opSBT0M7XURRZHldPs8WLsYrirwy4kaGRYTGvuRoI+/+bh53vfoVv3n1K+bPyOOG6SOP9dTsKoYwDTlhGr9la7sDs8XOPz5fzbdb9jMkM4Hnb5tFuD5wMtGd4ZLkkWhlSh7N/4x561/i/n4XMDVuYEACB0GQYJDHdlnYLtBsbTrI04VfEyb3/z3vMQ69p9FutfPmkk18tmYPBq2Kv1w3jVmjO58RE0ikgoQH+l9IrjGZZwsXc82GV7gsdQzXp084pdTomUZhWxUvFn3LHlM5OWFJPD7o8mNKfKEi2qjj3d/N45mFq/jXd1tYsqmQe2aPZ/qI7JDOi0Dj9nhZsqmAN5duwtRu5ZaZo7j5/FHIA9D3tCucFz+IRE0ETxd8zcN7FrCkege/73+RXwJ2ZxJNjnZeLV7G9zW7SNZEcmfWdN7389peh/4Liisb+Gr9Pr7fuh+Lw8nccwZz50VjA9aRJRBMix/M0PB0Xiv5gY9L1/NVxRYuShrJ7OSRpOtOv/1VqHF63WxsLOGbqm1saCwmQqHlwZyLuShpRJe2lwKJTq3kbzfM4JJxuTz/+Roeevd73vthG3PGD2T6iGyMusBXrXYXpg4bizcWsHD1bupM7QxMj+flOy8OqJJoV8kJS+K9MXfyRflm3jqwnMvWvcD4mH5cmjyKUVF9kAQxjTWYiKLI3tYKvqjYwoq6vYjA/MxJ3JgxEWUnlET/5x26KIocqmlmfUEpK3YeoKC8HoVMytRhfblm6nD6JfdMBxmtMvDXQZdxbfo5fHh4LZ9XbGJB+Qb66OKYGj+QybEDSNVG9/jI0eFxscdUzor6fayo24vZZSNCoeO2vlOZlzoWnaznPEiPZ3jfJD568Eq+31rExyt28szCVTz/xRomDMpg6tAsRvVPOSOce7PZwqo9h/hpRwk7DlTh8YqMyErmwSsnc05ueo+cP1JBwry0sUyOy+Wz8k0srt7O2ob9JKjDmRQ7gPHR/RgcntpjgoBfwyN6KWitYn3jftY07Ke0owGtTMns5DzmpY49rZVHtzp0l9uD1yuGZA/6KBa7k6LKBvaX17O/ooFdB6upM/kO/Polx/D7yyYyc1T/HhWRn4w++jgeH3w59/Q7nxV1e/mpdi9vHVjOWweWE6M0MDg8lQHGZPoZEumjj8MQBN0TfxFFkRqbiZL2Wg6Ya9ltKmNvayUOrwulRM7E2BxmJgxlZGRmj/8yAkglEi4cncOFo3MoqWpkyeZCvtuynxW7DiIIvvk0KCOBAamxZCfHkBYXjlwaut/L7nRTWtdMSVUT+Ydr2H2ohtI6XyOPlBgj108byfQR2QGVgg4m0SoDd2VP59a+U1hdX8iS6h18Vr6Jj8vWo5OpGByeSn9DIgOMyWQbEohU6EL6gGp1Wilpr6GgtYqCtkr2tlZgclqQChKGhKcyL+diZiQM6VLD82516Adqmhh//2ukxUaQEmMkLkJPXLie2HA9EXoNRp0ao06NTq04ZWOBXyKKIlaHC7PVTrvVQZPZQmOrhcbWDmpNZirqW6loMNHYZjl2TVy4ntz0OG6ZOYpxuenEGLu3ejWQRCn1zEsdy7zUsdTbWtnYVMKO5sPsbi3np7p9iPhS4mKUBpK1USSow0lQhxOrNhKp0BGu0BKu1KGXqVBLFZ2e+G6vhw63g3aXDZOzg2ZHO83ODupsrVTbWqi2mqi0NmFxOwCQINDXEM/s5JHkRfZhWER6lyZyqMlKiua3cydw35xzKCirZ1NhGdtLqliyybeFAaCQSUmMCiMpOoykKCPxkQaiDVqiwrREGDQYNEr0amWnpZhFUcTh8tBhc2DqsGFqt2Jqt1FrMlPb3E5ti5nyehNVTa0czVLWq5UMzkzgglH9GZ+bTt/EqB4ZjfuDXCLjvPhBnBc/CIvbwdbmg2xsLGZva4VPgvrI3NfJVKRqo0jRRhGnMhKtMhCjCiNSoSNMocEg16CTKTu9bSOKIhaPgzanlTaXFZPTQoO9jQZ7G/X2NiosTZRbmo41NAdI1UYxOiqLMVF9GRudHbBAq1sdenyEgTnjB1Ja10JheT2r9hzC5T6xxoJKLkOllKNSyJBJJcikUmQSAVEErygey0d3uNzYnW5sTpcvresEhOvUpMQYGZ2TSkp0ONnJ0fRPiSHSEHhRrZ5ArNrI7OQ8Zif7UhIb7G0cbK/jUEc9B9vrqbI2s6mphCbHifVFJAioZQrUUgVyiQy5IEV+JGIWj3w93F4PTq8bp9eN3ePC5jmxgJhMkJKgDidRE8FAYzJ99fH01ceRqY/tcj5xT0QqkTAoI55BGfHchu+AsaLBRFFlAyVVjVQ2tlHV2Mq24krsTvcJx1DKpagUcpRyGQq5FLlUiiCA5IjDdXu8uD1enG4PdqcLq92F23viJtUGjZL4CAPZydGcn9ePPgmRZCZEkRoTHtKVcrDQypRMih3ApFhfk2Wr20GRuYYScw0VVp9j3dlSSpOjHY/43++ZgIBKKj/yvwKZIEEmSJAIEgQEPKIHt+jFI3qxe1zYPU5sHtexh8Yvx4pS6knWRPq2QHXRZOpi6R+WFLSVcrc69HCdmt9dNvHYn71eEVOHlXpTO6YOO60dNlo7bFjsTqwOJzaHC5vD56jdHg9ujxcEAalEQCIISKUS1Ecmvkohw6BREaZVodcoiTRoiA7TERWmDVhH8jOVGFUYMaowxv6iVN7hcdFgN2NydtDitGBydtDhtmNxO7C47dg9LlxeDy6vG5foQcDnAAR8aZRKiRyFRIZSKkcvU6GTqdDKVUQqdEQqdUQo9YQrtEHVW+npyKQSMuIjyYiPZGZe/2N/L4rizyvJNgstZivtNgftVgdmqx2Hy43T5QtYXB4Poigiir7rZDIp8iNBjlopR6OUo1Up0KmVhOvUhOvVhOvUxIbr0anP3FVPINDIlAyLSP+vdFeP6KXF0UGDvY0WpwWzyxddt7ts2I5z1B6vBw8+By6Kvv17mSBBKpGgkvicvlqmQC9TYZBrCFNoMMo1xKjCiFLqu33rMKSeTiIRiDRoz9pIuaejlMpJ1kaedWlfZwKCIGDQqjBoVWTE977/3Y1UkBCtMhCtCkxz857C/27o1EsvvfRyltHr0HvppZdezhJ6HXovvfTSy1lCr0PvpZdeejlL6NZD0WablQ/2nDkduQON3e1mb0M91yz6nLFJKWgDJOzUy8lxejz8eOggAG12Bx/u2XXCNLNeAk+H08X2miq21VQjk0j+p7//p0tGeITfr/VLD10QBCPwNpCLTxJ7PlAMLATSgDLgclEUT9p8UZmSLCb+7j6/jTvbUEqlzO4/gJ011ZS0NIfanP8p0o3hnJOSyuKSIlrt/suR9tJ1+kZEMiQunkVFhb+aL9/Lr3Np/wE8N+38gOqhvwwsE0VxriAICkADPASsEEXxaUEQHgQeBP54skFyoqJZecudft7y7KLRamH2wo9xuN0su+YGzA4Hnt7J3S0IAsglUia8/zZqmYyPr7qOOO2ZWxV8JiGXStEpFHyUv5vPC/fx2dwryOxExNkLKKRSnvPztad06IIgGIBzgRsARFF0Ak5BEC4GJh552QfAak7h0KUSCeHqni9YFAzC1WoGx8ZTZW4DwKD83y746G6qzG202G08NWUa/aOiQ23O/xxNVgsCMCIhMdSmnNX4cyiaATQC7wmCsEsQhLcFQdACsaIo1gIc+dkzZQl7EGeoVMZZhbT3Q+jlLMYfhy4DhgFviqI4FLDg217xC0EQbhUEYbsgCNsbGxtP08xeeumll15OhT8OvQqoEkVxy5E/f4HPwdcLghAPcORnw4kuFkXxn6IojhBFcUR0dO9St5deeuklWJzSoYuiWAdUCoJwVNlpClAILAauP/J31wPfBMXCXnrppZde/MLfLJe7gY+PZLgcBm7E9zD4TBCEm4AK4LJAGSWK4rFu11aPE7fX7VP9O6L4JxEEpIIEuUSKRqpEI1OikSrOiKYIZwIer5cOmxOL3YHD5cHpcuM8InMsCD7NRbnMJ/GqVsjQqBRolPIzVk+7p2H3uI6pXdo9TpxeDyKiTzYaEbkgRSGVoZDI0EiVGOTq3rkfILxeEZvThdXupMPuxOX2qbx6vD61RZlU8El5SyVolAp0agUapaLHSBH75dBFUdwNnCgHcsrp3NTt9VBhbaLS0kyFtYkqSzMNDjNNjnYa7WbaXNYTahWfCoNcTbhCS4RCR6zKSKImnER1BMnaKDL1sT22nVl302FzUFZv4nBtMxUNrdSb2qk3ddDQ2k5rh412mwM/yhP+A5lUcqxBSVy4nvgIPfERBpJjjPRJiCIpOqzTTUvORkRRpMFh5lB7HZWWZmpsJmrtJuptbbQ6LZhcFuweV6fHVUsVGOWaYwqCMcowkrWRpGmjSdPFhLxbT0/B6XJTWtdCeYOJqsY2Kht987/ZbKXZbMXUYe303AcI06qIOtKsJDpMS3KMkeRoIykxRtLjI1F3UxFht1aK1tvbmL/pTQ601+Lw/izub5RriFUbiVLq6W9IxKjQoJWp0MtUaGRKFBIZMokU2RFdbY/oxSOKuLxurB4n1iP63SanhRZnB82ODvaYyvixdg/e4yoCkzWRZBniGWxMZXhkBn10cWf9JBdFkZKqRnYfqiH/cC17DtdQ02w+9u9SiUC0UUdcuJ5+yTGE632dc8K0KjQqBSq5DKVcdqzjuyj6aixdLg92lxu704XF7qTN4tOzb2m3Um/qYG9pLW2Wnwt4lHIpGfGRDMlMYEhmIsP6Jv5PyCbb3E7yW8vZ2VJKfms5B9rrMLtsx/5dJZUTrw4nVhVGmi7G1zlKoUUrU6KSKlBJfZrzkiMrUwDXkeYiDq8b65EuUWaXjVaXhQa7mQPmOtbbi3F4f34wGOUaco0p5BqTGWhMYUh4KnLJ2d8noK6lna3FFew+WENRZQMHa5p8fRWOEGXQEBdhIDEqjIHp8UToNb6oW6VAq1SgkEuRSSTIpD7f4/b6mou43V6sDl8U32Fz0Npho8lspdlsYVtJJUu37D92D4kgkBEfQf+UWAamx5HXL4WUmPCg/L7d+om2Oi1IJRLmJI8i25BAmi6aZE0k+iB173B53dTZ2iizNFLSXsMBcy2FbdWsqNsH+NqxTYwdwCXJI+mjjwuKDaHgqBNftr2YH7eXUNvic+DRYVoGZyYwZ/zAI00XIkiIDDs2WQONxe6koSAyuAAAIABJREFUvN7EoZomDtY0s7+igUUb9vHpKl9LtiGZCcwc1Z9pw7IwnCE9XP3B5XWzobGEb6t3srGxGJfoQSpIyNLHMyVuIH10sfTRx5GqjSZcoQ1KUHF0JVDW0UBZRyPF7TXsa61kfWMR4GvHNiEmh6nxAxkV2ees2rJpbOvgm40F/LTzACVVvsy6MK2K/ikxXDNlGNnJMaTHRZAUFYZGFZyuWXanm+qmVsobWimubGB/RQMbCspYsrkQgLS4CCYP6cPFYweQHG0M2H39Kv0PFMNHjBB3bN/ebff7NepsrWxrPsS6xv1saPB94XLDkpmdnMeMhMFBi1yu/uoz3F4vC+deEZTx3R4vy3eU8NFPOyiqbEAmkTCqfwrnDc9iZHYyceH6kK9IXB4PxZWNbN5fzrJtRRyubUEukzJpcCY3TB9Jv+TglDNUmds49/23eXbqdObm5AblHg32Nj4t28C31TtpdVmJUOiYFj+YsdFZDDKm9IieqWaXjT2mMlbVF7C6vpAOt51YVRjzUsdySdJIdPLgPFhf3LyB17Zu5tA9vw3K+KIosq24ks/X7mHNnsO4vV6GZCYwcXAmY3LSyIyPDPk+tyiKVDa2srGwnNW7D7LjQBVeUWRsThqXTxjMuAHpv2qjIAh+lf53q0MfMWKEuL0HOPTjaXVa+K5mF99UbqPU0kiCOpw/5lzMmOisgN8rmA591e6DvPjlWqqa2kiLDefKSUOZOjyLcF3PrcwVRZGiygaWbt7Pkk0FdNidTBnahwfmTiA+IrCdZILp0O0eF+8dWsW/S9fhRWRCTA6zkob3+MjX6XWzqbGEBeUb2dFyGK1UyQ2ZE7k6bXzA7Q6mQ69oMPG3f//EjgNVGLUqZo0ZwKXnDAzatkagaGzt4Kv1e/ly/V6a2ixkJUXzl+umnTCo8dehn/2baKfAqNByVdp4rkwdx+amA7xQtJR7d7zP+QlDeaDfBYQpNKE28aRY7E6e/WwVSzYVkhkfyQu3X8S5AzNCHo34gyAI9E+JpX9KLLfPGsOnK3fx/g/b2FBQxh/mTeLiMQNCvqI4Ffmmch7N/4wam4nzE4Zwa5+pJGrODK0ShUTGhNgcJsTmUGyu4V8HV/B6yQ+sa9jPXwdd3uN/D4/Xyycrd/HG4g3IZTL+dMVkLho74IzpIRxt1HHbhWOYf34ey3eU8NKXa7nu6U+56fw85p+fh1za+YfqmfGbdwOCIDAmOot/R9zNe4dX88HhNexuKeXVkfNJ0UaF2rwTUtFg4p7Xv6aqsY1bZo7i5pmjTmsS9AT0aiW3XjCaC0fn8NePfuTxj5aTf6iWh6+e0mOzY76u3MYzhd8QpzLy5sibGR6ZEWqTTptsQwLPDbuWZTW7eabwG67Z8Cp/GXQZE2JzQm3aCbE5XNz/5jdsLa7k3IEZPHzVFKKNZ6bgmlwqZWZef8YNSOfZz1bxf99uZk3+YV6/ezbh+s4FlD3zmxJClFI5t/c9j3dG347N4+Sube9QazupKnBIKKtr4ebnP8NsdfB/983ljlljz1hnfjwJkQbeuGcON83I4+uN+3jsgx96pCrl4qrt/L1gEXmRffhw7F1ntDM/nhkJQ/hk3D2k6qJ5cPcnrK4vDLVJ/4XD5eaBtxazvaSKR685jxfvuOiMdebHE6ZV8eSN5/PcbbMoq2vhrlcX0W7tnNRzr0P/FXLCknht5Hysbgd3bXuHZkd7qE06hqndym9eW4THK/L2A5cxPCsp1CYFFKlEwl0Xj+Oui8bx3dYinl6wMtQm/Qc/1u7hyX2LGBXZl2eHXh20LK1QEa8O542RN9HfkMif9ywg31QRapOO4fWKPPTOd2wpquCxa8/jknG5PX5brrNMHtKHf9w2i4M1Tdz7xjc4XO5TX3SEXod+ErIMCbw84kYa7Wb+tvdLuvMA+WQ8+9lqGtssvHzXJWTER4banKBx0/l5XD9tBF+u28u6vYdDbQ7gq6V4at/XDDKm8I9hV6OUnp1dpzQyJS8Mv44opYHH8j/D7nGG2iQAPlm1i1V7DvG7yyYwa8yAUJsTNMYNSOOJG2ew+1ANby7Z6Pd1vQ79FOQak7krazobm0pYUb8v1Oawdu9hfthezE0z8shNO3ty53+NO2eNJSM+gqcWrMRqD71Tea5wCW7Rw2OD5qKSBieHuadgVGj588A5VNtaeOvAT6E2h+qmNl7/Zj0TBmVw5aShoTYn6Ewbns3scbksWu+/3+l16H4wN2U0ffXxvFnyI97TkCQIFF6vyEtfrSMjPoIbp48MmR3diVwm5c9Xn0ddSzsLVu8OqS35pgrWNBQyP3MySZqzd2V0PMMiMpidNJKF5RupsYb2LOnt77cgIPDgFZPPum2WX+P+S8/l04ev8fv1vQ7dD2QSKdeln0ultZnNTQdCZsfGwjLK6lq4acaoY6X4/wsMzkxgVL8UFq7ejcvjCZkdC8o3oJOpmJc6JmQ2hIL5mZMAWFDu/9I/0Jg6bHy/tYgLRvcnNlwfMju6G51aSUKk/zUZPTpt0epupcKyg1ZXNa3OasyuOqSCDJU0DLU0DKMikXTdaMIVwT8UnBKXy8vF3/FV5VbGRmef+oIg8PnaPcQYdUwd3jfo9/J4vFSWN1O8v4aSoloqypoQBJDJpMhkUpJTIxk0JIXcwclodcEv279q8lDufeMb1u0tZfKQPkG/3y8xOTtYVV/AFalju6Xi0yO6qbcVUWHZgclZhUu04/LaEUUPRkUiUcoMolWZxKqykUmCa0+s2siU2Fy+q9nJPdkzQlIs9e2W/TjdHq6YOKRb7mdqsbBpfQlVFc00N7XT1NiOy+khJi6MmFgDcfFGRo7JJD6hZxUv9TiH7hFdlHVsZX/bj5R2bMaLBxDQy2IIU8TjFT00O8qweVqxe8ysa3iLCEUqmfpxDA6/BK0sOMUQMomUibE5fFu9C6fXjaKbhY2cLjfbiiq5ZFxuUNMTO9rtfL9kF998sZ36Ol//U7VGQWp6NBJBwOJ24HS62bb5IJ99vAmJRKB/biKXXzWG0eOzglbQNCYnDZ1aybq9h0Pi0Dc3HcAjejkvflBQ71NvK2Z7y0IqLNtxeq0ISDDI41FI1MgkSgQEDnVsoKDtewCUEj05YdMZFD4LoyJ4/Tonxg3gx7p8CtuqGBSeGrT7/Bob9pWSER9BZkLwakJsNic/LdvL2hWF5O+uwOsVkSukREXpiYzWo1LLOVhSx8Z1xbicvpViTm4Sk6YNYPJ5AzCEhb4IsUc59A5XE19V/h6TsxKNNJwhEXPINkwmQpGKTPLfB1BtzloOd2zicMcmtjcvYLdpEecnPEy6bnRQ7BsTlc0XFVvIN5UzIjIzKPf4NfYcrsXucjM6J3hfpuXf5/Pq88uwWZ0MGprCtTedS78BiSSn/LcOhsPhYv++avJ3lfPTsr089uDn5AxM4tEnLyUyKvBLYplUwpicVDYWlAV8bH/Y3HSAcIWWfoaEoIzvEd2sqX+dva1LUEn0ZBsmk6IdTpJmCCrpf76foihicTfTYD9Akfkn9pgWscv0BQONFzIx9m4kQuAf+HmRfZAgsKX5YLc7dLvTzc6D1cybMDho96iqbOFP931MXW0byamRXHn9OM6d1J/0zJj/2q/3ekXqakysXVXEquX7eP2FH/jwX2t44vkryMkNbQpxj3HoVreJryr/QIe7iZkJj5KpH3fKiRmmiGdoxByGRsyh1VnN9zVPsrTqMc6L/wP9wk5Lqv2k5Bp9H9aB9rpud+gHqn2qcbmpwcls+X7JLl546lsGDU3hjnum0Sf75PdRKuUMGZ7GkOFpXH3DOSxfls/rL/7AXfPf5ZlXriY1LfCR1MD0eJbvKMHUYet2jZoScy25YclIhMAfOzk8Fr6rfpwK6w6Ghs9lVNS1KKW/Li0sCAI6eRQ6eRQZ+jFY3M1sb17IbtNXiIhMjr0v4IeGBrmaZG0kB9prAzquP5TXt+ByexiYHh+c8Usb+cM9H+PxeHnu9WsZNCTlpO+fRCKQkBTBFdeO5Yprx3KwpI6/PfIlf7rvE5568SpyBobOqfeIQ1GP6GZR5YO0uxq4OOnv9DWc2+kow6hIZE7yP0jQ5PJD7dOUmFcF3M5whQ6jXENpxwnbpwaVsjoTBo2ScH3gHdm+/EpeevY7RozK4JmXrz6lM/8lUpmEGRcO4ZV/3ojX6+XRPyzE6fC/GMJf0mJ9+5VldS0BH/tkuL0eKixNpOuCowT5U91zVFl3MzXud5wbe/tJnfmJ0MoimRB7JyMir2Rf67fsbPk8KHamaqMp6+j+Ru+Ha32fd3pc4LdTG+rb+O1dHwHw/OvXMnhoaqcfhn2y4nj+9WsJj9Tx4P2fUF7WFHA7/aVHOPRKy06aHIeYEnc/iZqBpz2OUqrl4qSnCFckk29aEkALfyZObaQpBFWjzWYLMUGSv/3um51oNUr+/MSlyLqQPZOeGcO9v59JTZWJPbvKA2ihj5gj5d0tZmvAxz4ZZpcNl+ghRhUW8LFtnjYOtW9gaMRcBhhndGmssVHzSdYMZY/p66AUwcWqwmhxdgR83FPRbLb47h8R+K287xbvwtxm5dlXryE1/fSb2EdFG3jutWtwuz0sXbQjgBZ2jh7h0A+0r0Eh0dBHf06Xx5JJFGToxlBrK8TptZ36gk6ilSnpcHdOXyEQtNuc6IIgxu/xeNmy8SB5Y/ug0XY9W2LE6AyUShlbNgY+vVOn9v3+Hd1cYGRxO3z3D0ILw0rLTkS8ZOrHdXksQRDINkym3d1Ao+NgAKz7T7QyFRa3o9srptttvvdfqwz8/N+0/gADh6QEZIswKtrAqLF9WbOiEI8nNPUqPcKhd7iaMMjjTnjweTro5TF4cWP3mE/94k4iE2S4vd2fC+32eJAFIbvF6XDTbraRkBiY9CulUk5EpI6WpsBHckeze1zuwG/nnAy36Pu8ZUFQfbS4fcU6BnlsQMY7munS4Qr8sl8ukeIRvf/R1rE7cHu8yCSSoGRQtbZYiI0PXMegpJQI2lqtQdly9Ice4dATNLk0OUoD5oAb7QdRSfToZYHf87R7nKhCoN+hUsixOzvfPPhUHE1J3F9QHZDxzG1Wamtayeof+GwQm9P3JVEpu/f9P/p5OzyB/5LGqHw1BfX2wKxoamwFAMSp+wdkvOOxe1woJDKkQTgYPhlqhRy31xuUorLMvrGU7K8J2Hh7d1fQNzsetSY0shA9wqGnakcCIhsa3+3ycq7RfogD7WuIVwenOYLZbUMbhKX3qdCpFbRbHUEZe+iIdHZtL6NwX1WXx/rqs60ADBqS0uWxfkmHzbfVpVN1byu3o5/38c2dA0WMqi8yQUW+6WvELspKWN2t5JsWE6XMRCMLXNR5lHaXDW0I2uhpj2w1tlsCP/9Hjs6kvLSJxV92vZPampWFFORXkTemezPgjqdHOPQ4dT9GRFzBvtal7DYtOu1xTM4qFlX+EYVEy8S4uwNooQ+v6KXGagpJJ5eESAM1LWa83sAvd6+dfw7RMXqe+PNXtJospz3Oyh/38ekHGzhv5qCgpG5VN/lWcJ0phQ4EepkKvUxFta054GPLJSrOibmVcst2ltf+A694elGoV/SwrOZJbJ5WpsYHp29nta2FBHX3V0YmRvsOo6ua2gI+9kVzRjB6XF9ee2EZ61YXnfY4+/ZU8Mzj3zBgUBJXXNv185DTpUc4dICx0fPJ1I1jbcOb/FT7PM0O/7MkPKKLva1LWVj2GwDmJD8bsD3J46mzteHwukgOgTBTcrQRl9tDTXPgJ7XeoOaRJy6l1WRh/pVv8emHG7B2Ihqqrmrh8Ye+4Km/fM2gISnc/UDXsjV+jfJ6335zYlTgs01OhiAIJGujKA1Syt6g8IsYHXU9+83LWVj2G6qte/2+1it6KDav4pOy26m07mJy7H3EqgLfDxeg3NIUElGylGjfaqM0COmqUpmEh/82h345iTzx5y95582VmFr8P/8xt1lZ8NFG/nT/p8TGhfH4M5ejUIauvKfHFBYJgoQZCQ+xvvFf7Gv9loK270nWDGOg8UJiVVno5TEIx+3deUQ3tbYCis0rOWBei8PbTqJ6EFPiHwiatsue1jIABhqTgzL+yTgqlZtfWktSdOCX09n9E3jlnzfy3v+t5t23VvHFp5s5f9ZQBg1NISc3CZ3+P7eZGura2L7lENu2HGbTuhLkCinX3Xwu864eG7QJvfNgNX0SIo8twbuTgcZkvq7cjsvrRh4E2YdRUdcSrkhiXcM/+aLifuJU/cnQjyFDN5YIxX/mRru9ThodB6m1FZJvWkKbq5oIRQozEh4i2zA54LYB1NlaabC3kRvW/XM/JSYcg0bJnkM1XDw28BroKpWcp168kjde+pEFH23k8082M2psH6ZfMJiBQ1LQ6VX/8f6bzTYOldSxbOlu1q0qwuXyMHJMJg88eEHIy/97jEMHkEmUTIz9DXmR17Cv9Tv2ti7hu5rHAZAKCpQSLTKJErunHafXtzUgF1Rk6MfRzzCFVO3IoMpqbm8+jF6mIlPf/TrkfRKj0KkU7CipYmZe4A+8wFcg8eTzV7C/oJp/v7uOLz7dzMJ/b0QQQKNVotUq8XhE3G4Pba2+XPDoWAOz5gznyuvGEREZvDZgDpebPYdrmDU6ND0uh4Wns7B8E3tbKxkWkR6Ue2QZJpGuG80e02IOtq9lY+O7bGx8FwC11IhMUCIIAu2uBkR8++0xqiwuiPkLmbqx/xHwBJqdLaUADIlIC9o9fg2JRGBon0S2FVcgimJQvuNanYrfP3IRl18zlh+/3cNPy/aycV0J4HP4xnANTqcHu82J1epLm9VolZx/0VAuvGQY6ZnBKTrrLD3KoR9FIzOSF3UVIyLnUWsrpMVZTquzGoenA4/oQinVoZLoiVCmkq4bhVwS/DJwh8fF6voCxsf06/ZTfvC1ZRuXm87K3Qf547xJKILY2bz/gESefP4KbDYnRQXVFOytwtRiwW5zIpVKkMokJCVHMmJUBilpUd2iTb0m/xA2h4uJg0Nz4JQX1RelRM6PtXuC5tAB5BI1IyLnMSJyHh2uJsosWzC76rF5zHi8Drx4yDZMJlaVTawqG528exqYr6zfR7TSQN8QBDMAEwZlsib/MIXl9QwIYmOX1LQobrlrCvNvm8TO7aWUlzbS1NhOq8mCXC5FrVESHWMgKSWCIcPTUKt7VpOTHunQjyIRpCRqBnapejRQrG8sot1t5/yE0HVKmTUmhx+2F7Mm/zDnDQ/OPunxqNUKho5IZ+iI4Dkwf1myqZAYo46R2d2/5AdfQdnE2Bx+qtvLff0u6JbUVZ08ilzjBUG/z6locrSzobGYK1LHBkXLxh+mDO3DUwtWsnTL/qA69KNIZRJGjs5k5OjQZaycDj3mULQnI4oiHxxeS4I6nBERoevuPqpfCsnRRt5dtjUo2S49lf0V9WwoKGPO+IFIg1Dc4y+zk/Mwu2wsqtwaMhtCwYeH1wAwJ3lUyGzQa1ScN6wvizcVYOoIfPpoT8Xpcneq9WKvQ/eD9Y1FFJmrmZ85KSTi/keRSiTcesFoiqsa+WlXScjs6G7eWroJvVrJlZND20dyWEQ6wyMy+ODwGmzu0Pc37Q7qbK18WbGFCxKHkawNbdu9+TPysDtdvP/DtpDa0Z18tmYPFz/2nt+v73Xop6DNaeWZwsWkaKKYGcLtlqPMGJlN38QonvtsNa3/A5HKil0HWLe3lBunj0Sv7v6ill9yR9/zaHF28NaB5aE2Jeh4RS9P7vsKqUTCzZnByZ7pDBnxkVw0ZgAfr9jJnkOBq+7sqZTWtfDG4o30S/b/wLXXoZ8EURR5qmARzY52Hh98eUij86NIJRIev346rRY7T326otuFkrqTelM7f/9kBf2SY7h66rBQmwPAoPBU5qaM4tPyDaxrOP1ClDOBz8s3s6X5IPdlzyROHfhU2dPhgbkTiIvQ88h73x8T7Tobcbk9PPzu96gUMh695jy/r+t16L+CKIq8WrKMlfUF3Jk1jZyw0HYiOZ7s5BjumDWG5TsP8NJX685Kp95stnDHK1/hcLl54sYZQW2711nuyZ5Jlj6eR/YsYI8p8DLBPYF1DUW8XPw946KzmZ2cF2pzjqFXK3ly/vnUmdr57VtLcLhCI4IVTLxekUc/+IGiygb+fM15RBv9TwfudegnQBRF3jm0kn+XrmNuyiiuSeu6rG+guWHaSC6fMJiPftpx1jl1U7uV2176groWMy/fdQkZ8aHdu/0lKqmcl4ZfT5RSz33b36egtTLUJgWU1fWF/HHXx/TRx/HXQZd3S1pqZxickcBfr5/O9pJK/vCvpdidZ49Td3u8PP7v5fywvZh7LhnPpE72z+116L/A7LLx8J4F/PPgCmYmDOV3/Wf1uAkNvnL0P86bdMypP/L+MmxBUGPsbvZX1HPjcwupaTLzyl2XMLxvz1kZHU+UysAbeTdjVGi5a9s7LK3eecY/VEVR5KPStfxp9yf0MyTw+sj5GOTd2+rPX2bm9eehKyezfl8pN/xjAYdrA6+z093Um9q5/eUvWLypgFtmjuL6aSM6PYbfDl0QBKkgCLsEQVh65M/pgiBsEQThgCAICwVB6FkZ9qfB9uZDXLXhFVbVF3BH32k8OvDSkOXd+sNRp37HrDEs21bEvCc+YlvxmRktutwe3lyykeue+RSrw8Ub985hRFZocs79JVYVxv+NuoUsQwKP7/2CP+z6mBZH93f0CQTV1hbu2/EBrxYvY0JMf14dOR99D3XmR5l77mBeuuNiGlo7uOapT/hq/d4z9qG6Zs8hrnzy3+yvaODxG6Zzx6yxpxVIdqaw6F5gP3BU6u4Z4EVRFBcIgvAWcBPwZqct6AEcbK/j/UOrWV63l2RNJO+Mvr1H7ZmfDEEQuGXmaIZkJvK3j5dz20tfMH1ENnfMGktKTM84yDoZHq+XNfmHeWPxBg7XtjAzrx+/v3wSYdrulyg+HWJUYbyZdzOflm3gzZIfmbf+JW7ImMDFySOD0uEo0JhdNj46vJYF5RuRCAK/6z+Ly1JG98hV6Yk4Z2AGCx+5hkff/4EnPv6Jrzfs49YLRjNuQNoZ8TvsOljNP7/dzJaiCrKTonn65gtIjT19RUu/HLogCEnABcCTwAOC752aDFx15CUfAH/hDHLoXtHLblM5n5StZ23DfjRSBdemn8NNmZNRy868xcbI7GQWPnIt7y3bxr9X7ODHHcWMz03n8nMHMyYnLSjdXrpCh83BNxsLWLBqF9XNZpKiw3jx9ouYEKLS/q4gFSRck34OY6L68vz+pbxc/D1vH1rJ7OQ85qWOJTYIvUi7Som5lkWVW1lWsxurx8m0+EH8Jms6sT0km6UzRIfpeP3uOXy9cR/vfL+Ve17/mv4pMVw7dTgTB/dBpehZBfEut4d1+0r5bPVuthZXEqHX8MCl5zJv4hDkXejpC/5H6C8BfwCOdmmNBFpFUTx6GlEFJJ5qELPLSpOjnShl4Ju9+oPb66GgrYo19YWsqN9Hrc2EQa7m1j5TuCxlDGGK0CqldRW1Qs6dF43lsgmD+GJtPl+t38vdr39NYqSBSUP6MC43nWF9Ers8aU4XU4eNDQWlrMs/zPqCMmwOF0MyE7h3zjlMHNwHmbTnbm/5Q6Y+jjfybqawrYqPS9fxSel6Pildz9CINCbE5HBOTP+QaOmDL4A50F7H5qYDrKkvZF9bJQqJjKlxA7kqbTxZhviQ2BUoJBKBOeMHMmtMDt9u2c+7y7by0Lvfo1MrmTykD5OGZDKsb1LIahlsDhe7DlWzNv8wy3eUYOqwERWm5YFLz+XScwehVgRGSuKUDl0QhAuBBlEUdwiCMPHoX5/gpSfcvBIE4VbgVgBN3zhmrnqKTF0swyLSyTYkkKWPJ0MfiyLAkqRe0UudrY1DHfUUmavZbSpjb2sFdo8LmSBlZGQmt/edysSYAWdkRH4yosN03DFrLDefP4qVuw/yzcYCFq7Zw79X7ESjlDMoI4HctDgGpMbSLyWGGKMu4MtTh8tNRUMrRRX15JfWsre0joPVTXhFkSiDhvNH9uOScbnHZIHPJnLCknhyyJXcZTWxtHoHK+v38ULRt7xQ9C1xKiODwlMYZEylnyGRdF10UPaqzS4bxeYaiszV7G+rZmdLKS1O3/5+tiGB+/rN5IKEYWd8EPNL/r+9O4+Purr3P/46s2cySSY72QOYAAnIYpSIVKyguBU3vKLWcnt7tVe7eX/aVnvv71f7a3sf19ZHF5ffVeraat33pe5oBQFZBQETwhYCIXsySSYzmeX8/pjRurAkkJlJvvN5Ph48kpn55ntOvpx553zP93vOWM1mLpozlUW11ayr38cra7bzzqYGXly1FZNSTC7N46SKYqaU5nFCYQ5l4zJH/JbYUDhMU1sP9U1t1DW1sWFHEx/vOUgwFMZhtTB32ni+UVvFqVXlI96JGUqKngYsUkqdBziIjKH/AXArpSzRXnoxcMipW1rrZcAygKkzT9Tfq1zIuo6dvLx/A081rgYip6z5jgwKUzIpdGaRa08j3eokw+okzerAZrJgNVmwmSxoNGGtCekQ/lCQ3uAAfQEfnsAAbX4PLb4eWn09NPa34w1FpmcrFBVp41hUVMOMrHJmZ58w6i/4jASrxczCmkksrJmE1zfI2vp9fLB1Dx/taubB1z8kFF0PxmGzUJLrpiTXTa7bRXaak8y0FFwOO06HlRS7FZsl0lQ0Gq01/kAIr28Qrz9A74Cf9p5+Ojz9tHb30djSxYFOD59en3Kl2JlaPo5rzpvN3KnjmVKaP+qGgGKh0JnJtRULuLZiAU3eDla21vFR9142de7hjebNn22XZXNRlppDniODXHs6WXYXbqsTp8VOqsWO3WzFhEIphUIxGA7gDwXxhQbxBH10D/bTNdhPu9/Dfm8nTd5OegLez/ZfkJLJydkTqc2pYHZORcLOkOPJZFKcMrmUUyaX8h+BIJt2HmD9jibW72ji8XdX4fo6AAAYAElEQVQ3EQhGP/jbbKIk101BVjrjstLIc7tIT3WQlmIn3WnHbrVgMZuwmM2YTIpAMEQgGGIwGKLX68fj9dHr9dPW009zp4fmDg/723vwRe+PN5sUU0rzuXrBSdRUljBjYiEpMfxM3KMGutb6FuAWgGgP/Sat9VVKqaeAxcDjwFLghaPty2G2sXTCPJZOmEdYh2nydlLnOcCO3oMc8HZyYKCLFa2f0DXYjz6GTxZ3WRzkOzLId2QwPbOMCa58JrrymeDKx2Ud/ReoYsnpsDHvxInMOzEyRj0wGKBuXyv1Te00tnaxr62bXQc7WVu375hm4JlNiqw0J7luF1PHF3BBbRXl+VlUFOdQnp+VFAF+JMXObC4vn8PlzAEia6Ts6D3Inv5W9vS10ehtZ0t3I+3+XgLh0LDbv91kJdvuosiZxZn51RQ5s6lML2ByehFug/XCh8tmtXwW7hAZw959sJOGA+007G+nsbWb5k4P2xtbjnnhr3SnnYKsdEry3NRWlXFCYQ6VxTlMKMjGHsOlrr/seEr6KfC4UupXwEbg/uH8sEmZKE3NoTQ1h7MKTvzCa2EdpjfgoyfgpS/oYzAcZDAcJBAOoYj06M3KhM1kwWV1kGZJIc3qwGE21tBJLKXYrMyYWMSMiV+99DEYCNLd78PT78MXCOIbDOCPTt5Qpkgv0W4143TYcNqtuBx23K6UpA/t4RiX4mZcipuvMfkLz2ut6Q366A0M4A356Q/68YcC6OhrYTQ2kwW7yYrDbMFlSSHTlmq4YcNYslrMVBbnUlmc+5XXAqEQfV4/nmjvezAQIhgKEQyFCWuN1WKO/DObSXPayXA6SHPaE3Zd6suGFeha63eBd6Pf7wJiMifYpExk2JyGG98bK2xWC3luF3nDmHIsRoZSinRryqid0GN0VrOZzDQnmWljM3vG9m0FQgghPiOBLoQQBiGBLoQQBiGBLoQQBiGBLoQQBiGBLoQQBiGBLoQQBiGBHkfhMbpWs5H4Q6FEVyFpfTo5SsROXNeV9Pj9vNawI55Fjho9vgHWNx/gsqqpePx+1u5vIhAOJ7paSUEpqMrNo8Dl4rYVf0cBWSljc+LIWGMzmzm5sIjCtMjHKDz00UYKXMZfS2YkFaYN/XipeP7FtJeW6KKbbohbeaNNnjOV6fnjeK9xD4PSU4wru9nCBRWVfNzWSl1He6Krk1RsJjO1xSVsOtiMZ3D46wQlu0unVHP72eeu11of9TPp4tpDr8jK5qkrvxXPIkeVX723nJVNjSypnsa5J1SS7kjuBcPixRcI8JfNm3jmk23cNn8h0/Lzj2HpN3Esenw+3tm9kxfrP8EbDPBKEr//j1WG3c7tQ9w2roHusFiYkvPVBXGShoLq3DxuPWN+omuSdHJTU3m+bjtKweRkboMJUFtcQorVyl0frk7u938cyEVRIYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwCAl0IYQwiLgun3ssvL5BOnu9dPUN0N03gMlkwmm3kuqwkZXmJDvdiVIq0dU0rL6Aj4O+bjr8vQCYlAmzMpFtc1HozMRqGvVNaMwKhcMc7Oyl3dNPMBhmMBgirDVZaSnku9Nwu1IwmaTtx4onMECHv5e+oI++gI+QDpNuTSHNmoLb5sRtTR112TPq3o2BYIh19U28t3knH2zdQ1N7zxG3d7tSmDZ+HKdMKuW8UyaTmSYfLXY8+gI+lrds5bXmTWzv2U9f0HfYbU0oClIyOTGzlPOLZlGTNQGTkpO+47FjfzvPr/yYjQ372dXcwWDw8J9sZTGbqCzOZcHMCs46qZKinIw41tR4fKFB3m3Zxpr2BjZ07qLZ133E7bNsLmqyJnBqbiVzcyeTYUt89oyaQB8MBHl25cc8+NqHtPX047BaOGVyKRedNpWcjFQyXSm4XSmEw5qBwQBef4CWzl7q97exqeEA72/ZzV0vrOCC2iquOnMW5eOyEv0rjSl7+9r4U8PbvNu6jcFwkBJnNucUTqcgJZNxDjc59jSUUoS1JqTDtPk87PO2s6e/jZVtdfztwCaKnVksKqphcVktLot8GtNQBUNh3t6wgyf//hEbG/Zjs5iZMbGQy8+YQXl+JnmZadgsZmwWMwAdvV5au/to7eplXX0Tdzy/gjueX8GMiYVc9405nDypJMG/0djSGxjg6cY1PL53JV2D/WRYndRkT+DS9FryHRm4rA7SLA7MyoQnMBDpuQ/2Uuc5wJr2HbxxcDNOs41LS2u5qnwuWXZXwn6XURHoyzc18Jsnl9PS1cesiiJ+dsV8Zk8pw2EbevV2NXfw6DsbeGnVNp55fwsXzqnmZ1fOx2o2x7DmY19Ih7m7/nUe27MSh8nKRcUnc07hDKoziod8OukLBXi3ZSvP71vL/9vxBk80ruLWaYuZnVMR49qPffvauvnxspepb2qjODeDGy75GotOrcbtShnyPva39/DmhnqefPcjvvuHp5k7dTy/WLqQzGHsI1k9tmcly3a8RX/Iz5ycSq4efzozs8qHfKYZ1mG29+znsb0reXT3+zy5dxVXlp/GdysWJORsNeGB/s6mBn687CUmFedx67cWcsqkkmMal5pQkM3/vuosrv/GHP785nr+8tZ6wlpz69Vnj7pxrtEiGA5x65aneKN5M4uKa7i+4uxj6l04zFbOKZzBOYUz2NbTxC+3PMONG/7Cb2d+k1NzK2NQc2No7vTwb394Bq9/kNv+9Xzmz6w4pjHxopwM/vnsk7ni6zN5fPkm7nn5A75z+xPcc8Ni8tyJ6y2Ods/t+5Dff/IKp+VO4rqKs6hMLxz2PkzKRLW7hF+5l3DNCQv4U8NbPLjrXTSa6ysXxqDWR6lP3Ev8nLp9rfzng3+jumwcD9x0ObMnlx53+Ganp/Lvl57Od8+v5aVV27jz+RUjVFvj+e32l3ijeTPfq1zIf069ZEROFasyivmfU66hLDWXn2x8hLUdO0egpsbT6fFy3R+fodfr4+4fXMJZJ1Ue9wVOu9XC0rNruPsHl9Da3ceN97zIYCA4QjU2lpVtddy29QXm5FTy25nfPKYw/7Ky1Bx+eeLlXFx8Mg/teo8Xm9aNQE2HJ6GBvuyV1aTYrPzu3xYNa3hlKK49v5YL51Tz0BvrONjZO6L7NoKWgW6e2/chS8pOY+mEeSO6b7fNyd0n/ws59nTuqnttRPdtFI+8vZ4D7R7u/P7FVJXlj+i+Z1UU83+uPoute1t4d7P8Qf0yrTV3fPIq5a5c/mvGFVhMIzcsq5Tix1WLOClrPHfWvUYwfPiL2rGQsED3+gb5YNseFtZMIicjdcT3r5Ti2wtPBuDNDfUjvv+xbkVbHQAXl5wck/27balcUDyL7Z79dPr7YlLGWKW15q0NO5g9pZTpE4+/Z3go82dW4E518N7mXTHZ/1i2s6+F3f1tLC6txWmxj/j+LSYz/1Q2h56Alw2du0d8/0eSsEDfvq8VfyDE7CmlMSujNC+TsrxM1tXvi1kZY9XH3fvIsqVSnpobszJmZo4HYFtPU8zKGIs8Xj9N7T2cVFkcszLMJhMnVRazeeeBmJUxVm2MhuycnEkxK6M2O3JDwMauURboSqkSpdRypdR2pdRWpdSPos9nKaXeVErtiH7NHE7Bn16s6eobOKaKD4XWms5eL+My02JWxliVbXfhCfgIo2NWRs9gf7QsOf6fl5Zix2ox09N/+Hv8R0JX30BMzn7HujxH5H79rsHYnTl2Rdt+vsMdszIOZSg99CBwo9Z6ClALfE8pVQXcDLytta4A3o4+HrLC7HRsFjObGmLXg6hvaqN3wM/4guyYlTFWlaTmENQhdniaY1bGdk/k/7bYKXMCPs9kUhRlp/PRzgNoHZs/qAP+AA372ynNH1Y/KymUu/IA2BDD3vNH3XuAyIXSeDpqoGutm7XWG6Lf9wLbgSLgQuDh6GYPAxcNp2CzycTFc6fx8uptbG9sGV6thyAYCvPLR98i05XCwprYnVqNVfPyqkizOLi7/vWYhMquvhYe27MiUo5V7of+ssvPmMGmnQd45v3NMdn/Q2+sxeP1c9GcqTHZ/1hW6sxmdnYFDzQsp2XgyLNBj0Vf0Mddda9TmVbANHfshpQPZVhj6EqpcmAmsAbI11o3QyT0gbzhFn79N04lMy2FX/zlTbp6vcP98cPSWnPHc++zbW8LNy85UyZYHILb5uTaigWs6WjgzvqRvRrfPNDFLRv/itNi56fVF47Yfo3kstOnUzullN898/cRv8azfFMDf35zHefUTGLmCUUjum8jUEpxc/WFBHWYW7c8xUBwcMT2HQyHuG3rC7T7e7ml+qIRvYNmKIYc6EopF/AMcIPW2jOMn7tWKbVOKbWura3tC6+lOR38/Oqz2X2wk8X/98+8s6lhyBU/nA5PPz+97xUeeXsDl50+nQWzZLbi4VxWWsvFxSfzyO73+d7a+2nzDfm/9bDWduzkWx/cTavfw6+nLyFHxs8PyWRS/OJbCxmXlc71f3yWJ97ddNxnSr7BIP/117e58d6XGD8um/+1eGRvRzWSImcWN1dfyMbOPXxn9T1s7T7+P6o7ew9yzZp7eb35I75bsYBqd/yXYBjSzd9KKSuRMH9Ua/1s9OkWpVSB1rpZKVUAtB7qZ7XWy4BlADU1NV9psXOnjueRm6/k5w+/zk33vsRZJ1VyxddncOL4wmFNtOj0eHl2xRb+/OY6fIEgP7x4LkvPqpFZokdgUiZumXoxM7LK+e+tL3DVyju4esLpLBg3jYKUoY+9hnWYTV17eH7fOt5o/oiy1Bx+M+vquI8fjjW5bhcP/2QJ//HA37jtieW8smY7V82fxdenT8RmHfq8jN4BP+9v2cWDr61lZ3MHVy84ie9feBpWiyx7cSTnF80i05bKrz9+jn9ZfQ8XFtdwZflpn42xD1XLQDdPNq7msT0rcVns/Gr65ZxdMD1GtT6yo7YaFUnE+4HtWuvffe6lF4GlwH9Hv75wrJWoKMrh4Z8u4cHX1vLXdzbw5vp6ctKdzKkeT+2UUopyMsjPTCM73YnW0Dfgp3fAz96WLjbsaGJjw3627m0hGAozd+p4blw8jzK5GDRk5xbOZEp6Eb/++DnurHuNO+teY5q7lJmZ5VRlFFOWmkuxMwuTUoR0mEA4xD5vB/WeZuo8B1jVXs+BgS5SzXaWlJ/GNSfMJzUG9/caUVqKnd9ft4iXVm/jvlfXcMv9r2KzmDlj+kSqy8dRXZZPeX4WdpsFm9WMQtHc6aGxtZvGli5Wbd/Lmk8aCQRDFGSlc9cPLmZOVXmif60xY07uJJ742g3cu+NNnm38kOeb1lLqzKEmewI12RMpT83FbXXitkWWyu0Z9NIx2EvzQDfrOnbxYccOdvW1olCcUziDGyafS6YtccstqKOd5iml5gLvA1uAcPTpnxEZR38SKAUagcu01p1H2ldNTY1et+7I02F7B/y8t3knK7bsZtW2vfQO+D97zRRd7e/zLGYTVWX5nFRRzAW1VYwfxassXvXskwTDYZ5YvCTRVTms/d5O3jq4hfdbt7O5u/Go27ssDqa6SzivcCZn5FfhMNviUMvha/L0cPpD9/GbBQtZXDU6LxSGw5o1nzTy1sZ6Vm3bO6QZzoXZ6cyfWcGZM09gWnnBqF0f/ferV3LXh6vZ+cMbE12Vw+rw97K8ZSsr2+rY2Lkbb+iLY+sm1Bdu87WbLMzILGd2TgVn5FdR7Izd3XRKqfVa65qjbXfUHrrWegVwuFYyf7gVO5q0FDsXzK7igtlVBENhdjV3cLCrl9auXlq7+7FaTKSl2HE57YzLTKO6fBwpNutIVyNpFTmzWDphHksnzMMb9LO3v529/W0cGOjChPrsAy4KUtxMSi+kMCVThrVGiMmkOLWqjFOryoDI9aBte1vY3+EhEAzhHwwSDIcpyEqnJDeDkjw3Oemj70MWxqpsexqLS2tZXFpLMByiznOAg75uuge9dA/2MxgOkm1PI9vuIseezqT0Qhzm0ZU9CV9t8Ug+XcC/sjh2sxnF4TktdqZkFDElQ+6USITs9FS+Nm1CoquRlCwmM9XuEqoZW2vLy8fLCCGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigCyGEQUigx4nWms6BASwmOeSJYDWZAWjo7EhwTZKTSSk04AsGEl0VQ7PEszBvIMCmg83xLHLUaOjsoK6jnZ/PO5MDvR7avF601omuVtLIS03loklT+NOGdUzMyqYiKzvRVUoKJqXIdjo5MX8cAI9/vIUZ4woSXKuxJdORMuRtVTxDxV5aootuuiFu5Y02TqsVXyBAONEVSVKpViv5qS52dXcluipJyawUIenEDNulU6q5/exz12uta462bVx76OVuN/cuuiSeRY4qd364itb+fq6rOYX8VBdmGX6Ji7DWfNLexu2rVvDtGbMoTs9AYiU+guEQ7V4vL9V/wqqmfTyQxO//Y5XvcnH7ELeNa6Cn2eycUT4+nkWOKn/asJbCtDSunDY90VVJOpXZ2dy+agV2i4V5SdwGE6W5r5fVTfuS+v0fD9JFFEIIg5BAF0IIg5BAF0IIg5BAF0IIg5BAF0IIgziuQFdKnaOUqlNKNSilbh6pSgkhhBi+Yw50pZQZuBs4F6gCrlBKVY1UxYQQQgzP8fTQTwEatNa7tNaDwOPAhSNTLSGEEMN1PBOLioB9n3vcBMw+vuoYW7k7k1BYJv4ngtVkZmpu3rDWxRAjJ9eZSnVefqKrYXjHE+jqEM99ZUa1Uupa4NroQ79S6uPjKNMQbot8yQHaE1qR0SUux+OlWBcwcgzZPtQVVx/LjxnyWAxT2VA2Op5AbwJKPve4GDjw5Y201suAZQBKqXVDWWAmGcix+CI5Hl8kx+Mf5FgM3fGMoa8FKpRS45VSNmAJ8OLIVEsIIcRwHXMPXWsdVEp9H3gdMAMPaK23jljNhBBCDMtxrbaotX4VeHUYP7LseMozGDkWXyTH44vkePyDHIshiusHXAghhIgdmfovhBAGEZdAT/YlApRSJUqp5Uqp7UqprUqpH0Wfz1JKvamU2hH9mpnousaLUsqslNqolHo5+ni8UmpN9Fg8Eb3QnhSUUm6l1NNKqU+ibeTUJG8b/x59n3yslHpMKeVI5vYxHDEPdFkiAIAgcKPWegpQC3wvegxuBt7WWlcAb0cfJ4sfAds/9/g24PfRY9EFfCchtUqMPwKvaa0nA9OJHJekbBtKqSLgh0CN1noqkRsulpDc7WPI4tFDT/olArTWzVrrDdHve4m8YYuIHIeHo5s9DFyUmBrGl1KqGDgfuC/6WAFnAk9HN0mmY5EOnA7cD6C1HtRad5OkbSPKAqQopSyAE2gmSdvHcMUj0A+1REBRHModlZRS5cBMYA2Qr7VuhkjoA3mJq1lc/QH4CfDpOgjZQLfWOhh9nExtZALQBjwYHYK6TymVSpK2Da31fuB2oJFIkPcA60ne9jEs8Qj0IS0RkAyUUi7gGeAGrbUn0fVJBKXUBUCr1nr9558+xKbJ0kYswCzgf7TWM4F+kmR45VCi1wouBMYDhUAqkeHaL0uW9jEs8Qj0IS0RYHRKKSuRMH9Ua/1s9OkWpVRB9PUCoDVR9Yuj04BFSqk9RIbfziTSY3dHT7EhudpIE9CktV4Tffw0kYBPxrYBsADYrbVu01oHgGeBOSRv+xiWeAR60i8REB0jvh/YrrX+3edeehFYGv1+KfBCvOsWb1rrW7TWxVrrciJt4R2t9VXAcmBxdLOkOBYAWuuDwD6l1KToU/OBbSRh24hqBGqVUs7o++bT45GU7WO44jKxSCl1HpFe2KdLBPw65oWOIkqpucD7wBb+MW78MyLj6E8CpUQa8mVa686EVDIBlFJnADdprS9QSk0g0mPPAjYC39Ra+xNZv3hRSs0gcoHYBuwCvk2ks5WUbUMp9QvgciJ3h20E/pXImHlSto/hkJmiQghhEDJTVAghDEICXQghDEICXQghDEICXQghDEICXQghDEICXQghDEICXQghDEICXQghDOL/AwXp2BMUOQmsAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Contour plot - note that origin here is at the bottom-left by default!\n",
"plt.contour(im);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are many, many more plot types available. One useful way to explore these is by\n",
"looking at the matplotlib gallery: http://matplotlib.org/gallery.html\n",
"\n",
"You can test these examples out easily in the notebook: simply copy the ``Source Code``\n",
"link on each page, and put it in a notebook using the ``%load`` magic.\n",
"For example:"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEKCAYAAAD3tSVSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXeYHNWVt99bXZ17ctJIGmmUhRICBJhoRDDBBoyxjTEYbGOzzhHjtb34s73eXYf91vZ+9jqsYR2WbGyyyDkKSaAEytKMpMmhe6ZzV9X9/ugZaWY6VXVXA8L96qlHmqrbdapH3adunXvO7wgpJRUqVKhQ4Z2J8lZfQIUKFSpUKB8VJ1+hQoUK72AqTr5ChQoV3sFUnHyFChUqvIOpOPkKFSpUeAdTcfIVKlSo8A6m4uQrVKhQ4R1MxclXqFChwjuYipOvUKFChXcw6lt9AWZobGyU7e3tb/VlHCJpaOwa7aPBHaDFU10WGyOpCD3xIQCcipN2fwsCYauNqB6jJ9536GcFQYunGa/DY6udUS1EMDl46GchFKrUaqqctSg2zzMSRoS4PoohNQxp4FTcuBQfbkfA9t8fQMqIoMs4hkwBAkWoKMKJUwkgbH5vUqZIGUEMGcWQScAABAInDsWLIrw4hA8hnCXbMowQutGPlJECIwWK8KMoTShKEd8FGQd9P8iE9deKAKgzgMnvd/369QNSyibrJzzMuav9cnBILzhu/abEw1LK80qxVW6OCCff3t7OunXr3urLOER/fJRzHv8JC6pauPP0L5TFxqM96/jRG7cc+vmTc87nivZzbLXxYPdj/Lnjjkn7nELl+sVfYlnNYltsJI0kN2z5NEkj80tc46zjQzM/xdKa42yx9XDXz9gceijrMafwsKTmLE5r/gQeR1XJtg6En+TVgf9LVOsFAhnHHcLNTP9q5lRfTLP3OIQo/gaT1PvZO/R9BqMPAQ4g1/XrQIR671lMr/4U1Z7jLdvS9QGGg98gFn8I8I5tZhjF5VpEXc0PcbmONvUKmXgOOfxZoMXydR5CqULU/R7hPPx5FUJ0FH/CNINDOmsfnlVwnKN1Z2OptspNJVxTBFXO9Ex312gfoWS0LDZqnP5JP9/W+QTBZNhWG0qWmW1KavzHjv9if/SgLTYGE71ZHTxAKDXM7/f+lKf6HijZTmfktZwOHiAl42wMPsBNuz/NttBTJdnaNvy/PN9z/ZiDz44uE3SEH+Kprs/yQMcl7B25ryhbo4lXea3rPAajD5KeuRfCYCj2KFt6L+ONvk8TS+01bUvTDtDbf96Yg7dOMrmO3v6LCYf/WHCsTK5DBj8PFDGDn4jRhxy6ApnaWdp5piABw8SfI4GKky8Cj8OJx+FEItkwVPKkISvTPPWTfo7qCe4++JytNhrdDVn3x/Q4v9p1I5qhlWxjVAsWHHNP1595pOevJdnZMWrudxPVh7m/69+4q/MGRlP9lu2EknvYNPhLS6+JaAdZ2/cDnun6MjFtwPTrYqm9vNH3KTRj2OplAjAce5zXus6nP3JPwbGGEaR/4MPoeqk39wTDoX8kNPKTnCOkMYoMfgVkrERb4yccRQa/gDTsm3BJJCmpF9yOBCpOvkhqnT4A1g/tK8v5p3kbcArHpH33d71IygbHO85sf1vOYx3RA9x54N6SbdS7mk2NW9NzBw9031a0naiJm8lE9kbWcvO+LzOQ2GfpdftG7kdS3Je7O/oCj+y/kv7Ya6bG7x36XtEOfhxJkp0DX6N79E95xwVHfoSmm5/1F2Jk9GeMhv+Q/ZpG/y8YfVmPFY2+Fxn5la2nrMzk/86pc6XDKZuG95fl/C5FZX7VzEn7hpOjPN230TYbTe4Gapy5F8vu73qEHaO7S7LR4GrG5/AXHgg81ns3j/cWd2NJGXHLrwlrg9zWcR29MfOP+gPxTZbtTCSuD/LUwc9yMPx03nHR1C6C8WdLsnUYyd6h73Ew9NusR1OpnUQif7bJ1mGCoe+STG2bfCX6AMTuyPGKEonegjRCtpxKItFl4e1IoOLki2SGrxaA3eE+yqXJv6xmTsa+uw/a9cVPc0L9sTmPGRj8Zvcf0Et4LBVCsKBquenxD3bfxq7RrZbttHgWWH4NQFwf5S/7v8NQwtzNOmUUyjYpjIHGS73fJZjYlXPMSPyVku1MpSP4U4Kx5zP2R2N3YS7eb5UUwdANk3fF7wHsexqdhIxA7C+2nc5AFtyOBMrm5IUQNwkh+oQQW7Icu04IIYUQb/uV6VzM8qfj2REtQVfMWqjALMtq2jP2vTHSyZ5wl202Tmk8Ie/x7ngvT/SVthawsvZdpscaGPyp4/8R0UYt2ZjtP8bqZR0ipoe4s/PbJPTCDtzjqC84xgyajPJ8zzdI6iNZj8e1fbbYmYzBzsGvoxuTF/DjcXvXeiaSSDxHKrX90M8y/ljZbAHIROZNrKjzADqy4HYkUM6Z/B+AjPxRIUQbcA7QWUbbZWfcyQPsHrU5vjjG0iwzeYCn+szFdM2wMDCPphwLsOP89cB9JI1k0TZW1JxAs3u66fGjWpC/HLjRko2ZvmVUqcXPGUa1Pp7p+33BcbXuhUXbmEo4dYAXer6NkeVJSVB6rns2UnofXSN/mLRPN7rLYmucSHTC7FrbnnugHaTW23aqyky+AFLKZ4ChLId+BlwPR8hvKAdtvsOOcedoT1ls1LmqWBCYmbH/KRvj8kIITm7IP5sPpkZKms0rQuHslvdbes1rwZfYNmL+fQqhsLLuQquXNomNwTUciG7OO2aG/4ySbEylN/YynaMPZ+x3qeYWrIuhJ/znSSFGw8j+NGEXyWS6xkUaYZD2pgFnYFPGjgRSUhbcjgTe1Ji8EOIi4KCUsuC3VwhxrRBinRBiXX+/9VS3cjN7wkx+b7h813dy49KMfQdj/eyL2HdjObvldBxTMnmmcn/XwyXF5o+tO4UGk5k24zzce5el8asaPkiju93SayYjeaT7F2h5nlqavEdT5z6qBBuZbAtmLnrWuE+y1cZEUno/0QkLog5HCcVIJtC0sTRjGypx3yykiVBNJVwzBSGED/gO8F0z46WUv5NSrpJSrmpqKqlCuSw0eqoOpVF2RrI9sNjDaU0rsu5/YSBjqaNoGt0NnNaYP24+mBxmU/D1om04hINzp33Q0mv2RXaw08IirEOovKf1KyXJCQwl97MxmL84a0ndx4s+fzZCyV0MxCc/QfhcC/Cqc221M5HRxKuH/q2W0Q6AlOnMJyHcHCFF9iBBN7EdCbyZM/l5wBxgoxBiHzAT2CCEmPYmXoNtxLQU86rSM9P90cECo4tnTqCVdn/mr+jV4dyZGcVwyYz3FpzNPz+4tiQbx9efzpLq3Nk82Xik11qR1HTvUayse5+l10xla/DRvMdnBs5kXvWlJdmYSn9sQ8a+GTWfsdXGRPQJWUJej71yGVNRJi5Wq/PLagthLl23EOmK18LbkcCb5uSllJullM1SynYpZTtwADhWSlmegHaZueKpPzEnkH7CGE5GGUnZVL03gf/c9ih/3P0cZzZnOsY3RjrQpT0fs+7YIFVqFWc1n5533Pqh10jopZWhX9Z2LVVqjenxu8JbORizVlV8WvMnaXbPs3pph+hL7CaYzL8YeWzTdTR5is/omUoomVmP0OS/hCq3Pbo+UxHi8Iza570Igb2idBNRJzp2l/lMq6JwmtPNKYxAN7EdCZQzhfJW4EVgkRDigBDimnLZerPRpcHrwR7CydShfZ0Re2fzmqFz894X+Nm2h+mOJjKqX2N6wpZUyt/vfoArX/oXPvzC94hpLqrUTLGtceJGgnXDxS369icGufvgGtZ0P8mKmjMthVTeGHm18KAJuBQvH2j7IdXO4h8S90fzFz0pQuXk1h/jU+15EJVZbthCOFjY+HNUxfxN0SwB17JD/1aUGgKBT9luYxyv59xD/xZlfmoQ3otsOU964VUU3I4Eypldc7mUslVK6ZRSzpRS3jjleLuU0ryQx9uI8Wq3vSOH8+P74vZmKByIDpEYkzC4ee/LLK3JfMzdGiq9DP2+rheAtDbOXQeeR5A/D3xj0Hqh0mBiiG9t+mdu3/837u5aw10HHyesmZ857g6/YXpsR2Qnv9r1z/yfrV9kezhGyijuI25G10YRXhp9FyNxF2VjIrny793qDI5qvtFWR+9UGgi4J6/1VFd9FdXRbpuNcRzKNHwTHK9wHQ9OayE704gqcNuj+pvOk6/M5P9ucSkOHEKwdagPjyOdMRC0WY1yYnxcItkVyryJbBstTVKhPxEkrE0OM+0aHcIlcjuUvRHrgmxreh4nok/+/YxqKiMpD2ay0Lpi5koq9kV28MtdP2BXeCsGOgYKA6kqkkb+tYZs+AqElPrj+/jTns/y/OCddKW8xI3SFhSn+3OHylzqXBLKseg2zRxn1HwORUy+MSmKj8aGP6ModbbYGKem5rsoyuQ4uQh8FcrgIEXV1xCKz7bzGVIU3I4EKk6+SKqcHhKGTrs/HZe328nXuSZ/WDsiI7RMKVrqjpUWInKK7I7pYFRDFa6sx3rifRgW1wI6ogey7o/qLka0wo4+YVKX5r6uW9BkatI+A4X+VBUhzYthIRui1pm7eCucGuSOzusJproO29CrGNZ9lmyM0+hZSbM3e+xdM2I83fUlumKb6NVqSJR4M2n0XUhr1cezHnOobYSYbVvWSMD/Cfy+SzL2C/eJSO9H7TEyhqEuBO/ltp2vMpOvQI0rHW7wKem/gyl7nXzA6SGgTg5phJOTv+D9idLkFGqcftxKZu6yRNAXc6BmuQloUmMkZa2gZTTP+JjuIpTy5nX0Da7CKbSakWJvJFc1pSCse+hLVpuacTe4ZuWVSXhx4H+J6VOFsARhw0OPVsOI7jE96653L+Hkaf+Ws6nI+v4fM5xIh6t0HPTp1QxqATRp9asrmFb1MeY3/jSnrf3BXxBMbqdX95CwfP7JRKnBH7gu5/GQHiJqpHIet0JK6gxoIwhhnzuTCHSUgtuRwJFxlW9DalzpjjmhRPqDGtFKbH6QhQVVk4tUOiNhFlbNPvTzSIk3FiFE1vRMAE06CCW9OKcUsCgoBFRrj8QtnvxyA3HDyUDSnzOssqi6cMbEcGoQWaA4RcfBYKqKwZSfmO7MemNpds/nkrbv53QYhtTZNvJMXhshw0eXVsuAFiBmZLfjU2ewsvGrnDnz93hzyDGEknvYN/rglL2CqHTTPXb+uKHmfXqQEqKGk0GtkVrfZSg5ntDiqU66Rm4aew+CPt3FkO5EsxiS0CT06y4GtSSdoeya8pq2n0jsNoZlnHAJchkASakzYMRI6TuJx58q6VxTeaeEa46QyoS3Hy3edAu2jtERqjwekob9DQRW1LXx6vDkGLim+fA4XMT1JNXO0uOPy2vnsj1HbD+iSVo9M/CKQUbGBMPafNNRFWsfmzn+2awdyp8ho0sHQ0k/fofk6No2hpI9xPQYS6qP4dwWe3PS44aLuOFCIHEJjRqnj3OnXU6rdy6t3vxtD8PaIAnDzJOMICZdxHQXIFGQOMYyqzUcVFPDOVUX4shTBbo//Di51T8EMekmprsBiYqOS+g4RNqGJH2jTkoVAwUweKn3u7yn7X9RlcxF757wLUiSk84fkSoR3YFP6PiEjlsYKFn8miEhKRUi0kFUOhiPt/eF/8KM6mvxOicXW6W1bNLvKyQTJHSNGsWDamEmLqUkLJOMyMPXHI7cjMdzhulz5D0/gqS0vpbzdqTi5ItkdiCdDRFKxrmgfSk1TvvzjI+uy2zqsW5wPz857sP8fMcdzPaVXo5+RtNK/rI/t7b5rvAA1y++jLgxREf0AO9ttZ4Ct6R6kemxEV2wJ5LkR8t/htthPmul0dWC1+EnZkJJchyJICGd9CVTPNn/LF9ZeG7B1ySL6j4kMBBjzjZNKNXDAwd/wgfafpAzfDIYM6tdL9BQ0aSaVxFqNNXB68M3saLhcxnHhqOP5zx3VKpEpQpIHIAqDARjcWsp0BBkX0g16I/czazar03aG4tPriiOoxM3IviEE59QceHI+TvRpUFEpojIVIZAWCL5co73YJ10MdQ7I9DxzngXbwGzA4ezEFbWtLMii0MulRW1meeUSDrCo/zquK/wlUXWZAKycVTNbFo9+dMm/7zvMd7X+h6+tODTzAu0W7axsGoebb4Zpsf3xPu4pdOabo0QgoUWdOunciC2l2f6p4ZGMqm2UThsb2QtLw3emvN4wqYGGBPZFbqD1JQblZQaMc1MOm56sTEhHcSlg4R0oKGQL1NmKPrIFFsJUlMaiYwTlSkGjBg9RoQBPUrQiBMy4gSNOENGjB49TI8RYVQmsypAGkY/mmZfE5/KwuvfOe2Bw45xKBHnnNZleUYXR6OnirmBzEXHR7o20+6fRksB52yWdzevzHu8Oz7IY72ZZfdWuHi6tfzlR3ufZl/E2hfWim59Nh7q+QvDyfylGy6Hj1pna0l2JrJ24PacOvZKGR60U0aE7shkRdGkPkC5ivRjqT3ICcJ2mnYACrRPNJAk0InIFOGxWXtMaqYEwQzDnqJEKQW6VApuRwJHxlW+DZk9wcnvGilfTdcZLZmKhztGezkYLa3350TOaz0BpcCs5LbOXI/z5jip4Xia3eb13iWSe7vWWLKxouYEZnqLF9tKGgn+dvCPBcctrj6jaBtTSck4W0PZtXKq3eURDpvawlAU0CwqBYlGSp/4/ShTV6hxe9J6G8hcGIfCbLm3I4GKky+SVl81Vc50zLgjXD4VyjOnZZe1fbLXfBVoIdp8zTnVLsfpjPbxRsh6IdQ4ilC4yOJs/uXBDfTEzTdkUYTCh9quQZTw5dsceoWeePa8/nFW1F1QktLlVHaMZu9m1OSxS4dlMuHU5PfnVBrL1qQEgAk3ESHKp5GTPr/XlvOkF17Vglvh6xFtQognhRBvCCG2CiG+PLa/XgjxqBBi59jf9lahTaDi5EtgQXU6lNIRtm9WPZVltTOZ6cv8/18/uM9WO1e2n1NwNv9kiR2pVjefyuIq871YDQzu78psqJGPWb55nNJYmj7KxmD+BbxqZzMnNHyoJBsTGUxkv3nODKxGtUlVcTKTwx5CCPyuzL4FdiBw4lQOF/EpShNQricHgapm76ZmlfGF10KbCTTg61LKo4B3AZ8XQiwB/hF4XEq5AHh87OeyUHHyRRJNJVlYk16E64+HiWil5fvm44LpmTO6TUH7FpgA5gamc9a0/IqHz/RvLKlpuSIUPjPv43gd5mdzzw+stdys5ILWj1huUDKRXeHC+jynNF1dUl/ZicT0UNYWgE4lwMLaj9hiYyIeNXOdp973HtvtAPhdR03KlFEUH06nvU1XxlHV+ShKtW3n06UouBVCStktpdww9u9R4A1gBnAxMB4b/CNgrXWaBSpOvkg+/eRfafYcVmzsLMNs/t7OLXzpxbt4T+vyjBziwUTYtrh8VzTI5uABrplzAX41twPuTwTZGtpXkq0WTxP/MPdq0+PjRoK9YWthIq/Dx2fmfZsqtdbq5QGYkjZWhIP3Tv8WVVkcplWcihclR1x8Sf0nqXHZq8He6MkMzTX7L8nQs7GDel9mWqrHfartdgB8Xvv8ZDkqXoUQ7cAxwMtAi5SyG9I3AqBs/R4rTr5I9oSG2DF0OBY/ELe/d+Vtuzew5sAbfOGFv/LulswinY3DpfdC3zjcycVP/5yPPf9brn3pj5zVlD9D5fWR4uLySUPj5n2P8o3Xfs2DXZuY4zOfO59L+yYfcd3gxPoLcRURo3Up5pydT63h4pnfxaNUWbYxkRZP7hCWQ7g4qeWHuJXiblhTcSp+ZvrPzNjvUltorbJXDVxVamgJZD6J+P1XYb9AmQO/z96iOUMqBTegcbxN6dh2bbZzCSECwF3AV6SU5W2qO4VKMVSRpAyddT0H8TmcRPUUoaR9q/rjbA+lFx13jw7QXp2pirjHht6yj3e/TmqsWndvZIB9uwc5pnFmTsfaUWRv2Z++cStP9E2uevWrbvzOwnIQA0nzC9thLcJvd//hkO69QziocyqoivkUwTqXuSwgQxpsHXmD/lQNbhHFpRRX9by8Jn+opMY9j9UzfsOjBz6FXmIj7KX11+JyZO8Z0Fb7RULxFwgnS1t7OXS+mq/idGSuJznVOXg95xGLW8ueykfAfxWqOrvwQJOkBcpMzYEHpJSr8g0QQjhJO/ibpZTjrc56hRCtUspuIUQrYD7DwCKVmXyRuB0q3dEwi2vTVaehpP2doVTl8H/PEwd3s6hqcn52T6z0YpmNU2L7EsmrA0P4HdlnwAMJ6zb7E8EMBw8Q0ZyMJN15qzQBGlzmEw9+vuO3kxqb6FJhIOknrLlMyRoDLK85vuAYXWrcuPen3N99KyNahP5UFaOa27SNcWb7j2VJzdkFx708dD8Hkg5SJeRmz6m6kEW1udUfFeFmUdNvkZS+2Nvoez/Tqj6W83htzQ8QtrXq81JTfb0t5zp8TkFKOgpuhRDpBYkbgTeklP8x4dC9wHjc8mrgHlvfwAQqTr5IqlzpR/paNf1BHUnZP5OvdR12tBLQUs5J6YF2tByc2nEqbUvQFRZZhciUHOXm+dg+knuROK47CSY9yDzOa66/3ZSdraFtbB3JVk0pCGseBpJ+Enr+L+Ys3zxObSy8CPlg9+28PqljlWBE99GXqiKsu00tyi2pOZv3z/xezhL+cdYO3sGm4INoOOjRagjqXkviWBJYVPtxjm/+p4Jj94yuoSvlKkkfP2K40BzL874vVZ1J3LHS8k1xKoaEXk2SzFAFLQ0psasY6hTgY8CZQojXxrYLgB8B5wghdgLnjP1cFirhmiKpHpMaDo+pUCZ0+4s8pvtq2DN6uIJv01AvF89ZymO9W4DiHO5UWrzZsxE0KYglfTR7XfRNkDSeG8its56LWIG+sElDZSDuoNqlE1B1UhM04c9oOoW5AXOP4TvDe/Ie16WD4ZQfVdPxOFK4FB2XYuBz+Kl3NXN07Qmc1nhewZh8TI/ybH/21E5NqoQ0lRBePEoKr5LEKQyUMeEwXSoIEeCyWd9mbiB/pTFAKNnD8/1/mrBHMGp4CRse/EoCv5LAiU62j4IhIWq4GTU8JEa2sKw+d58AgLg2yOtDN47p41dTJeNUKzEUYc4TG1IQ1H1EpIfQ8E3Mqb4wp8JmNLmDvvireIWLBiWZ9foL24MBw0UKQW/4dmbX2Tmbt6fYSUr5HLkXIM4q2YAJKk6+SOrc6Vn2juEh5lU34lNzf3mKZVndNJ7rney4dN3JsfWz2TDUwcLq0vuLZpNNGKcvHmVx1XzOaF7Jg90v41c9XDTjFMs2zMgvSAShpIph+Pn64g+gyySt3hYWVZnPLOmK9Zoap0kHYe3wjH6Ofxafm3+d6dTObSOvkZKFUmbFIbXLbDzUcz+fmbcCpYDy4obhe9Blpu66HNOvDxseQOJERxX6mHCYQJMKKQ4rQvYn9vDS4K2c2pQ7s2l78BY0Oa5rk76ZRAw3fiWBTyRwisybiZSQwkHUcBM23Mix4IAu4+wM3saKxi9ktdUfuRuQxKSDPt1FvSOF0+TNBCApBYO6a0w7B/oj99jq5NPia++MQEc5G3nfJIToE0JsmbDvp0KIbUKITUKIvwkh7EkZeAuYGUjPgPtjEa6Yd9wkmQO7OLo+U9Tr4f3b+MGKS/n0/Hdz4YzS87RPaVqY9/gz/btYVn0U95z2L9xy0g20eKwX5i0IzChYaDXOqJbg5n3Pcmrjuyw5eAC/Wly1495IJ7/c+XvT44Op0iucd4a38Fjv3wqO2xdZb+JsghQqMekmKt3EpIsUKlMnkK8M3kk4lVvbpTOcKa9goDBqeOnVazmo1dGTqqFfq6Jfq6JXq+agVkevVsuo4T3k4Mc5EHkqp63B6OFF1yQOenQ3w7qzYHPspBQM6C56dfchBw+Q1LtJ6qUnIkyk0jSkMH8AptaxPwosk1KuAHYA3yqj/bLSXnXY2c0LNHPuzPw65MVwdEOmk09Jg0cP7uDzi86mzV/6jWVxTSttvvzn+cW2h0sqgvKqbpbUtJsevzN8gJs7suu55GOWb6bl14yzIbiJdUPmskoiY9r6pfJwz13si+zMeVyXKQYTpafJTjzfllD2MFM01UNU6877eolCCpW4dBGXLpLSmeHYJzKa6iCqZT5dpfRB4trUVFxBWKr06B56NDdDupMRQ2XEUAnpKoO6ky7NQ6/uITZBs34ikeTrea/fCpLCDUOOlKYhZXPyUspngKEp+x6RUo4Hr18Civ9WvsW0Vx928tuD9s4gxmnyBCZJGo/z4H77PswAZ7fmL2nfMdpbslbOpTNzN6rOxi0dj9MXt1bstaKmtNL8P3fcQdJES7paV0PBMWYwMHh24KGcxzUjScHUI4t0RLI3b4kUcPDFEkllptzGUvnXTlIoRKRKyHASMpyMSCdRqRaU9tVNNXMxhwRSUi24HQm8lc8bnwTsS5R9k2mvPjz73REsnwrl6tbMQpmNQwfpjdkzmwS4YHp+cTKA/9n9bEk2Tm1aznSveeeoSZ2/HbBms8Fdx7Lq4p+o+hIDPNhd+Alint++svzNwbUkc7TAcwinrUJoAP2J7LrxSb089TnJLJr4mmHfZ3ciMsvaRfEU1pKv6MnnQQjxHdLCPTfnGXPteBVZf395ZsqlMNNfjU9NK/ftGymfQNk5MzIrQyXwZHfux3yrLKiexilN+YXDNgcP0BkpXqtbEQqXzny3pdc80PUSEc1aaupV7ZfhKKGh85N9zxUc0+pto9Uzq2gbE0nJFJ3RXVmPqYqLOpe9D7tJPXtnK6ejtKrdXLiyVAMreVoeloJDyV7kVQwS0xWvb3ve9KsUQlwNvA+4QuYJ9EopfyelXCWlXNXUVLo+iN0IIVhQm04P6xgtn5Nf1TiLFk/mF2Vdv32xWoBrF5xRcMxj3YWFu/Lx3unvYq7ffMONiB5nTbe1lm5tvhmc03KGxSs7TF9igG4TWTqnN1mTTc7HYCJ3seNsf+E0SyuoOdJDfWrprSSznzfz/9uhlENZEzzOdlvPV5nJF4EQ4jzgm8BFUspimmW+rVhcl775dEdGiZchTx7SufAXzs7sOrVxqMtWO0fXzeKMLPo4E3mspzQn71RU/nHJR7MWYOVi7aD1tYCHs04LAAAgAElEQVQPzryIWmfxaoSdJrRy3tVwpqnKWDP41dyz6BW159tiY5wmd3Yp3oBzBn7VfItGM3jVZvzOzDRfn3MRdrseh1KN1yaZYUh3hqrM5AsghLgVeBFYJIQ4IIS4BvglUAU8Olb59Zty2S83kVSSRbVpJy+BA2H7+3GOc+W843BMSVDuCA/ZLqXwtaPOw+vIne//eqiLwURpi1vzAjP4/IJLTI/fMWpdUtmv+rh+8ZcsSRpPZCRlLmb8kbZ/oM5pvttVLqqduTOJmzxzTckemGW2/9icx2b4rYXTCtEWyH7dDsWP1znPVlsNvvNs7XCVXngtXdbg7UA5s2sul1K2SimdUsqZUsobpZTzpZRtUsqVY9tnymW/3NzwzGOoE+7kwYT92jVvDPVx6YP/S8dIiPfMmDzLlsDmYXsyIkLJGPd0bEZKwTeXvjfv2N2jpesoXTjjZC6ZYU5udlSLEbUYl4d0gdP1i76IL4cGTz5aveZCFz41wNXtX8aZp4q0EHXORmZ6889AV7f8A4EclaNWUIWbo+suyHl8Ye1HUGzqEOUQHhbVXpHzeKPvQlvsjNPkt1uOvdLj9e+efcEgD+3aSZUz/QUfSRZWU7TKPXtfZ33/Qa569A6W12Q+SndHS396kFLygcdu4rq193D2mv/i9l2bOa0ptwxwT7x4m491b+WSp37BeY//Ow8f7GCWt/DipSKUglWh2dg+sp9XhvYScMzCSiciVaiW8u1n+xdwzZxv4lYydX7MsLr5fQXfn9dRzYdn/Ri/WlpdxOnN1+Q9h9/ZyuK6q0qyMc5RdVfhU3NLpLcEPoSwqeC+xnMSNZ7SmrhPJb3wWsmT/7smZei83HWAY5rSWi6jZXDy24bTWUWaNPjN5lc4tWVyY+ehROnLGq8OHqAzcnjheN3Afl7q7mWGN3tla0IvLk3tpYHdfGPD7eyNDNATD7E/OsSrg4NEkvl1Ytp9LXjyhJCycWfnU3xh/c/5w96H2BI6SH/MQyTlNCWG9Z5pq6l2ms80eWlwHT/a9hs6owox3dos+Pi60zm1MbOpRjbq3TNZXvvRomePK+su5Nj6iwuOW1Z/LdO8pTnMWvdyjqr7ZN4xLrUlr0qlWaSEmTXXlXyebFQqXv/OcTtUdCkPZb7Ei3R++ZgYhx+MRwngx+s47EhShnmN9Fy8OngwY18wGaN7RGOOPzOraXltcSl9D3dtRmYp7IlrKqG4B5Xszv79M0+zZOf5/i38Zve9GBNsSQQRzc1QwkdCd2R19gLBWc2ncXmb+fWCFwbW8p87/5u4kUCiEEp5GUz4iGpOjDw3lCq1lktmXM1HZ3+uoALlONtGNvK3g7fSm6wibEHSWEqodx/L2dOya8hMRQiFGu85xIziwjYxQ2VPLELSKDwBmVX7dSSlpT0O63764valE4/zTqp4PTJKtt6GBFzp2WUiYeAQoqTc7FzUuCYvHK7Zt4NvHH8a/77lCQAW1tjRei57KGM0lUSm6rhwxkoe7t5C0tBo89WzqNp8CuREnu/P/UXUDAe9UUmLt55jG6YR1WM4hMI501ZxfuuJluw82vtKzmO6VAglvQgkTkVHVQxaPXV8sO1sltcsNh2Lh/Ti7O/3/m/GjSslVVKayojmwa1ouBT9kIqjIQUpw4FPaeOkBvOLqWFthD93/D8MDEAhpPsI6278jgReRwoHRoZwmCbTTxZh3UNXci+P997DWS2FZ/JxPcxzA38irgeoljGqlDiKCV8mJYwYHkYMLxBk/dDdnNKUf6YeSu6jO6XSrCqowvqEZUT3EpEe9o2uYUHthy2/vhAmG3W/7ak4+SIZd/Kv9XTz3vbFtAXs11qbVTX5nJo0GAjH+fcTLubm3es5vrH0gpwWb+7QxNZgL8c3zeaxs69n3eBejm+Ya3rmOZXx7lO5EfTGEmwYGObWUz9Hvbu4XOpNwfwl85CepSUNlaQBu8MRHut5g9XN1tQ1n+5/gZieb0FYkDCcJLLMiPdEO7ht/918bPaHTNl6ou8+ovrkrCYdByO6jxEdQKIKHQcSg3Tq39RQwgPdt7G05jimefI/ia0bvIu4PgoIRgwfEcNNlRLHpyRxZFGJ1KRCzHAyanjQJ6x9bBp+kJMbr8z7edk7+gA6Dvq0ahoco7hNdtaSEoYNPxEjPQkaSmwhpvXjtaHf7kQbKeOd4eTfGe/iLaDJl3ZCnSMhvnnMGRzXbG+OMcDyhswc41t3bmR160LuOPPj1LmLW+ybyOLa/P2D/7BzLbtHBjlz2hKqnMWlJAK0eMzlrffGR/jWa3cWJYjWnwgSSkUsv2798A5+vctaY56toWzNScyzpvsxNofMaRCtGyok7yDQpEpCOklJNWusWCJ5LocG/qExUrIl9MikfToOgoafLq2W7lQNfVoVA1qAPq2K7lQN3VotQcM/ycEDRPQhBpO5C/aklBwMP3nIRp9eQ1D3oeUJgUgJEcNNt1Z7yMGPE0xkrxouFkklT/7vntnVh2fZXeGRSa367GJFY2ZoJJxKcv++0sTCJjI7UM/86vzpeT/Z9HjJdqyEeV4e2M3tHdYqXQFqnYFJnbOscF/Xi+yz0L+2P1G8xAOkne5vd/8RQ+YPU3TH9jOqBfOOMcurwRfz2utP7CGs5dJhEmg4SEgnMekiIZ1oBbKWumO5b4ThVCexSdLAaf36bq2Ofq2KkO4lYriIGG5GdQ8DWoCDWh1DeiDjhgIwksquyVMKlYrXv3Nm1xx28tsGyyNQ1uT1M8OfOQO+b699Th7gnOm5UyYhnXHzQm9pX6Jzpy+3NP6X2x8jolnLWHIqKm2+/E8muTCkwW923Wt6fFi3/sQwlcHkMK+P7Cgwxr7+zlE9zFAytw7UYGKq/G9pxPOIno0k9+U4IohLFyOGjyG9iiE9QNDwE5PuvLLGumFvdlslhbICc2oPpxjuGCqfCuUZM+Zm7Fvbu5/huH3FV+8xoYX/++0vlmTj5Kb5ebtQTSWsJbh3f3ZZ3HwcW5dfaC0frwxtY+Owucf+md7iFqCnsjG4Je/xpGFv7+DhPE4+lDLXWcssWh5VyJhu93fGXklmKuGaCm1VNbgd6XXrfcEyqlDOynRaupQ8dbDwAqNZltW1sqqxLe+YF/r2EixRRuGy2dYyZW7reMlybP5DbWfgVIrPJ3hp0Fyc/Kiq/B21zNIRzS/bUKXau6Cv5Cn9LzbUlYuAmk9a2l6nXA4VTWOsz2u+7Uig4uSLxKEoLKhPf4j3jdgTM83Gqa3t1LszS/PX92fmt5fC547KLzOgS8kTXflDC4W4qO0YZvrMtw/siAyyfmifJRvTvPVcMsNabv1Eto2YU/c8sWFV0TYmUkgvfprH3gX9KrUm5zFXkVW7uahz5W76ble16zjVTnPN3s2Szq5xFNyOBCpOvgQW1acXLLtGR0jp5tK/rKIqChfNXZKxf9OAvZ18Tps2j3c15f+iPHawNCfvdbj4/ooPmO73Cmkde6tc0X42Nc7iUjB7E+aeytp801ndbE5/Jx9N7vxSBVXOWtp9xYegJlKt1tHsye14mzz2qTg6FS/TPLnXegJO+25eAgd1bnvbb76TiqEqTr4EjmpMx5h1KemN2td6bCqfPGpVhgrltuF+kjbfWG445lw8jtwzrA2D1h3uVI5raOczC1ebHn8waj0UFlC93LD0qqLCNk1u8+GRq2ZfxjRPcQu948z2F651OKXxPSXZGGd5bX5p5GmeRagliK1NZEHVKahK7nPVuDLXmoql2XscLkfx0tK5qIRr/s6JpVIcP+3wbGQ0kb2Fmx3MqqrlvFmTY8BJQ6fT5mYlC2ua+c7K3A5lMBEhYYNu/qfnn8FFM48xNbZYuYhj6hbwT0s+ZtnRr6g1L4Hrcbj5wvxPFV3t7HV4OKXhhILjjqk7ibn+0maqqnByZnN+5UdVcbGw2lov3mwoOHhXw+V5x3jUBmpc9jyhzKqy5yY4kUp2TQV+8/JaNhzoos6TjpdHUvY7+biW4sN/u41/e/FpPrXk+Ix5w5BN8saGlPx19xZu2fEapzXP571tmeGhcSJaae9TSslQIspnF5zNVXMKV5keW198rPXUpuX8y/Jr8FuQGz6h3poznRdo5/pFX8LvsB7P/uisS/Gpha/NIVSumXMdLe7iQxyXzLiaelfh7KYTGy5DKTFefnTd+6h3F9Y4ml1Venctn9rK7Krc8sml8E7JrqnIGhTJ7qEh1h/s4uS5bTywewfRlP0CZU937mNt9wHWdh+gMxTkQ/OXc8euzYeO2xWu+fGGp/ntlsPFR1csPJoTm2bzcv/kvOlal5fqEqpeO8PDfPWlv7FpON3VyiEEi+pa6Ur0kZKZ70UgOL05fw5/LrpjQX6740me79/JQELgdap4VC1D42UiV7efy/Ja62GE+YG5rKw9haf7n0RVCj/pCASXtb2fs1vMN+nwqQGunfeP/HzHPzGqWZN7PrP5Ik5uNKeV0+CexSlNV/Fs/02WbIwj8XFq0ydMjZ1bfRFvDN9Eyii+5mCa/xwcZegZK6VAO0KceCHeGe/iLSClG/RFIsyvyZcmVhrbBg/nNK/Zs5Ol1dMmFUdN85eeNqYZBndNuHEA3LxjI6m4g4tmTW47uLp1QUmVvdc+d/shBw/ptYzXh4YIRR20eZsnKWz6VTc/PPoDNGbpb1uIfeF+rnjuN9x9YAP9iVEkgmjKTTDuJZ5S0Y3Dnt7v8HBi/VF8Z8mVXDXHnOzvRLpiA3z85R/xtwMvMpTwEEx4iGtqVhVKKaHe2cwNS67j4hnW2/olDcmoVktcNzc3M6QglPTS7LZ2ozyh4UPM8llvbZg0HPQknDw78EjhwYDbUcvSuk9btjNOxHCxL2ZvG8yJvFPCNZWZfJG41HT6VDJpMM0fYHpVebrdT+Rna1/glvd/mK8+dx8pw7DlBtMdGWEgnikL+3Lvflp8R/HXsz7JmgNvkDR0Pl8gzTIfm4e62D2avQBGSsG2wRCrGmfznWPOxudw0uAOUOMqLqXvug23MZTMnB0aUiGSckMKQKIIybtaj+H7yy9BzaHGmY+knuI7m25kMHm4sjMtfKZCKq106ZigQKlJhf54lL/sf5EbllqLR6eMFD/e9p/0xIcBH05Nx6cm0iqXyENPKFKmRcPiupOo7kIi+PXu/6HZ08QcE4u8ADE9yrbwMLrhIeCI5336GSequwhqPiSCp/sfZHXz+3CYaMfX4D2FqPFf+BRrYcCkdDCs+xmKbCCqBfHZXE8wHpN/J1Bx8kXic6ZnnS90dPLr8y5mTo35/G+zVLunijDFea6zg3vfd7VtNhx5Zub37n2DVc0zuX7FWSXbeaqncCXpuoH9fPPl+7njrE/gV4vL8tgz2scuUy0K0zOxB7o2IpH8y8oPWlbYvLnjMTqjuapEBSlDJVsQ76m+1zi5cSlntRxn2taD3Y/REz/8vlLSQSg1fhOUKGM3LV0qyCmrNwkjyS0df+E7S75mytbT/Q8ynBoEvEQNF9WOGB4lleHsDQkJIy1nnJSHXUlYC7Er/DqLqgpLWawdvINB3Y9A4lXMhTzjhsqAHjj0PoeTB2138vDOcfLlbOR9kxCiTwixZcK+eiHEo0KInWN/2+8Z3ySq3OkmF6/39bG4vjGvsyyW+XWZOdQ3blqPQByqti2VBo8vbyLYD195gh3DuUvhTWOywHHHSD/fWXd/0Wae7bOey/9g1yb+tOd5y697qu81y68Z55c772Yoaa5huGZorOnJJxInMFDQpCPDwY+zdWQ7Q8nC2ViGNFg79PRh29LBkBagO1lLf7KKwZSfwZSf/mQVPclahrTAJAc/zs7R/HINaVs6O0afBQQDeoBh3Yeex7HqUjCk+enXqybp2Awn7Q/ZVPLkzfEHYOry+T8Cj0spFwCPj/18RDKzJh0bN6Rkx0B5tGuWNWU2seiNhFmzu7SipIm4HWpWSeNxkobOjzY8nfO4WZq95jsAPbD/de7v3FqUnYOx4tJKf7/raUZS5rOVIlqcg7Hi/99HUhFu6zCn7rkxtJVQKrfYlxkkkq2h7QXHdUZ3E0xlKmxKBEmpEjdcxA0XSanmvKEApIzC4Zf+xF40OT5OEDY8dGu1DGp+IoaLuKESM5yEdTf9WoAurZaIdMMUu8EyOHmo5MkXREr5DDA0ZffFwB/H/v1HwO4W628ak1Qo+8vj5Os8XmYEMmP99+y0V4XyzJn5c8OfOLC75Arb5fW5Ky2z8ZNNj6MXkOHNRr2ruErXUS3OH3Y/Z3r8rtEDWdsZWuHlQXP/jwMlyhqP0xktXMxmZgZuBoPCmV998d0Z+ySCqHQzpAfo16sZ0KsYNvzEpYupzn2cYKoMM3kJmqEU3I4E3uyrbJFSdgOM/V1aueBbyKzaw06+XDN5gJNmZi6WPbe/g3DSvrz8s9rmFxzzu61rS7KxpHYaS2tzPzFMpTs2wtPdmU6gEAurzduYyq37XjLRwSpNtpRPqxyI9RPTC0vkBkucxY/jNVEvMJi0R4lSN/H7GU3ZEAYEVJG/GXyxVMI1ZUYIca0QYp0QYl1/vz0fBjuZVVuDcywOv2+4fAJlZ7dnOuCkofPc/n222VjeMI0l9fnvt08e2FNyXv5H5h1rafyte9ZbtrGqYQ4Btbhc/pieZPeoOSc3q0jd+qkMJgo78FDSHidf58otTjaOIuxZ63GYOE9Em/qgXxxVzvxNb4qhEpMvnl4hRCvA2N850yCklL+TUq6SUq5qarKvd6NdOB0O5tanF0Y7Q+Vz8mfMmkOVKzPT5LU+812MzPD55SflPR7Rkrzca06hMRcXzVpGk8d8bP7Znt2WZRSqnV6unmutX+tEzGrlNHvqmO4tLYXVqahM8+QXKAPwmqiKNUOts7CTt6sh/Vx/4dx8r016M7V51C5LQUpRcDsSeLOd/L3AeP7f1YC1xppvMxY3pWcQB0IjGEX0JDWDR1W5cP5RGfu39tvb4OGC2YtYkWcBFihZw96nuvjBseaLgHQp2R+xfgO9Ys5JRcfmNQvrAOdNK6w7k4+5/lZT+fkLA6WLealCZY6/sEREPr15syg4WFC1rOA4u5xzax61y1KoLLwWQAhxK/AisEgIcUAIcQ3wI+AcIcRO4Jyxn49YlrWks1+Suk4obm8Hn4lce8wqlClJylsH7GsLByCE4F9OOhdXHqezb6R0QbSzZyziY/PNa7FbbQEI4FPdfGfZhZYkjSEtN3B8g3mHetmsM5kXKN5RHVVtTpfn6NqluJXS4s4nNayi1lV45tzgKj0MtaR6JQG1sC07nLzfUU+dq7BOjlWkrMTkCyKlvFxK2SqldEopZ0opb5RSDkopz5JSLhj7256g3FvEKbMPL4rGyqBdM057TR3nz51cITkUj9muYb+8YRrfPSF34dNo0p4+mt86+hzOnVFYCMwhBNN9hUMM2TirdSnfXn6hpW5HS2qmU+82/wSgKg6uX3x5USEOn8PNR2afaWqsx+Hh3U35w2n5cAonH5x5kamxy2uOL7lD1KlN5uQh6lyla8of1/ABy0Vs5hDohlJwOxI4Mq7ybUhK12mvq6MlkHYKkWT5nDzAl48/+dBC7zgxrXTZ36lcuegYLp2X/VG7ymVPFoNTcfD/TrqUzy7OHzs/sandUgx/Kh+cdTw/OuZD+NXC1+0QCp9daM7pTmR+1Qy+edTlliSNBYLrFl9mSbv+itkfYp6/3fL1AXx09qU0e8wtTta5Gk2FWnJxeuP5LKpaYWqsX62jxll8NpRbCbCyLr98cinYFZPPURj6PSHEQSHEa2NbeaQ0qTj5orl74+v885onOWNu+vG+XDH5bz38CB+57XaEIfjiqsOzOZfiwKPap0rxwsFOvvfsE9z2+iauO+Z0PrYoU+/9ve32dN/ZNtzPw507melp4OtLz2S6L/PR3udw8rklpXdeOqVpIZ+ffx5zfa0oOT7uHsXJv678IKc2F9e39ayW4/jFMV9khrdwgkCju4ZvL7mSdzevtGTDpTj5+qLPUe8yf2OQEs5ufg/nTbN287qw9aMoFKHlYzhQFWtO+9j6iy3bGcflmIlLKV4VNR8268n/gczCUICfSSlXjm0P2nXtU6lo1xTJ9r4B7nptK7+6/CJu37SZBp+9/TEBukZGuHPzFiRw2W23cdcVH2X/SIg7t23hlJmzcDns6TG5sbebj95zx6Gfq1wufnj6OZxyxmxu3bmRV3oPcNr0OZw/u7QFLs0wuOHlR7h1x8ZJ++dX1/OJeUuIynQ4yK+6uHzucbRXFc48yWfrXzc+yu17NpAcy30XQsXhMFAUg0aPj+V107lw5kpOappPtbP4DJakrvFo93beGI4jhBuXQ8Pp0FEm+ABDCpKai/PaVnNmi7mGKVOpc9XyjUVf5Ptbf0bcyN+JzJAQSnq49+CrXNC6mlYLmUAzfXM4v/XDPNB9q+nXGFIQTHq5t+shzp12Ji7FnPzv8trzeXngdqK6tQV2XQr2RAaJ6VG8RWj5F0Smb5K2nErKZ4QQ7faczToVJ18kKd3AkJLu4RG+e+ZqGv32f9B2DAweqqkMxRN8Y81D3HH5R3j/wqOYV1u8A5zKHze/Ounn0WSSLz/2ADecspo/nv1hpJS2xD1v3fFahoMH2DUyxK7NQ1yzZBXfPm51yTpAUkq+/vLdPHjg9Sn7BZrmABx0JVN0jXQw1zeTc6cXFtLKx/c2/Y0HuzaN/aSS1FVATlKgHJcA+MX2R4kbWlGhISklv9v1EJ0RiUvx4FNTqIqOAIQYbz6tkNBV4roTiSBlxPjnrX/iP4/9kiWlzXc3XcCankfRjYGCKpRJw0Ew6cVAIaxFWDf0Kic3mss8cileVtZ9iOf7/9uU2iWkb2CDqQApqbF9dBMra99l7oUWeROyZ74ghLgKWAd8XUppb6u3MSrhmiIZlxp+auderj62uJlZIaaGgF7t6ubB7Ts4ZeZspmWROyiW13Nk6vzrC0/x7P59ti1s3bwjv6DXja+v4+OP32m66jQXDx3cluHgc/HrN57nx5vMachk46+d6yY4+IkIdKlkVYW8cdcz7DallDmZR3rW8fLQG4AgaagEk14G4gH64wH6Yn76436CSR+xMYnhcbaP7mfdUGHdmonc1/UIXbEkQ0kfSSP7zSFlKIRSHoaSPowJrmRj0Jru0I7IAUZ1c2GXww4+PT8NJu2RfJiKNL/w2jhetDm2XWvSxK+BecBKoBv4v2V5I1ScfNG4x0Ila/cdsL2h9ji13swP/n+99DLS7vh/DieuS8kXH7mfrtHSKy4HYhG2mVCzfLZrHz985YmSbD1gUdzs99tfZM0B63pACT3Fz7eZa5AxEU3q/OuW+yy9Rjd0/mfvmjwjBLm0XQBeGjR304O0EuWTfc8CkJIqQ0k//YkAw0kvoZSH4aSX/oSfwWSAmJ6pKdMR3W/aVlyPsjm4llHdy1DKl7XZyqGxhkpfspqkPBwKGk6VT1JEysIbMDBetDm2/c7cuWWvlFKXUhrAfwOlFV3koeLki6RxLKsmrmns6S9PJuiChsw46vaBAZ7cs9dWOy3+3GmDwUScn7z0bMk2rCxM/3HbBp7r2leUnYSu8bQJ7fqp/HLrM5ZvnpuDBywpV05k/dA+to+YF317un8T/YniK6t3hQuLk42zbXQnA8nJn2ldKiQMJzHdRcJwosvcoR8rKZj7o3sxSBegxQw3PckaQpqXuKGmQ0+GSlh3jckcV6FPWRAu10weylvxOl75P8YlgD3KcFmoOPkimVl3OH97W295tHWq3G5mVGdmnvxtq/lZmRlOnpG/Y9A9O99g11BpX6Z6jy+joCsfP93wTFF24nqKuEUpBEjr2D/aZS2k8epQR+FBedg8bN7xvja8syRbwSydsnJhNdwyFTMdocY5EJs8YZEohHUPg6kq+lI1DKSqCGn+rJr1AKFUWcLYYzN121IosxWG/kQIsVkIsQlYDXy1LG+EipMvmlkTnPz23vI9Mh47vTVj35N79pCwMUf+tLb2vMclcNOmDSXZUBWFk6aZaz8HsHGwm51B679Xv+rGWaT+ygOd1m6eW0MHi7IzTk/cfEPu7nhpT4stHvP9eXaOliZfoVj4/Q8lS6vcdjvKk0IJ9qVQ5igM/ZiUcrmUcoWU8qJxdd5yUHHyRdJeX4tjbGa6b6g8swmAM+dlar3HNI2X9puPexZiSWMzc2vzO4EnO0r74gN8cJ61LJa/7Lb+BKsqCnOri1Ml7Ahbc6ReR3EtCsexUinbEy/tSWqa13w2VtJEw498BFTzVcOlhlvqnKX3Oc6FyZj8256Kky8Sl6rS3pB2jAeC5mdkVjlr3tysRU9be+3VrvmHlfnXfbojoyWHbM6fvZAal/mZ1+aB4pQ2PzrPfO/UicR0a1XLs/ylOZhj6s1p1wAMJ/PnxRdiusmKV+BQjLxYltVYKZorLXOr0Z35pGsHEoFhKAW3I4Ej4yrfpixuSVc47h8un5P3u1y8d1FmEZLd3aguXby0YO79+p7SOvB4VCffWbXa9PhQsjjRt0vbj6bFaz3FdG6VNad9XH27ZRvjqELh6No20+NLkTUWCE5vNic1ABTVkWsiK2vNP7HVukq7Uc7yla7QmQtpYjsSqDj5Ejh6ZrqEO5bSypZGCfDZE0/IWLTcM2RvRo+qKPxk9bkZ+jgTCSVKV9r88IIVXNieKZ2cjYCzuHCI26Hy9WXmbybjnN+2xNL4ExrncqIF1cqJnNa8CK9q/v2ZVazMxkmNS2mz0ORELUFueEFgLtO95qUNap3FF/U5hZNZvvytK4vGxoXXt5qKky+B0+fPOfTvZBnEwsaZU1/HBYsm66pEy6B6eVzrDP7PqbkrMe2SUfjJKedzVoG+sgDvM3kzyMYl7Sv44pLTTI+vc/k4a7p17ZpvL7sQlwVxMoCA6uGbS99r6TWnNhZXlasKB9fOe5+l1yyqKtwOMhfvbT3H0vhSZvLH1Z+GpxySBuO8Q6byFSdfAnMa6jf2v8oAACAASURBVGivTwtGafmqOGzgW+8+nWr3YTVFt2qPw53KlctW8g/HHJ+xX1A4C8csXtXJ78+8lC+tODlnRLbe7eWSedZm1lP50tJ3808r34PHkd8J+1UXvznlQ/gtzKzHmR1o5Lol55vWrleFg58eexnTvNYklI9vWMwpjdbUIRUEX154qaVZPMCqOmviaeMsrlrMiQ3W1kOaSoipr26ydvOySmUm/3eOlJJIIsmFyxfjEAKfs7wyQNOqqviPC84/NJs+eZb5dESrfOukd/OLc95LveewaNdFC45iXp19ejlCCL52zGncef4VnDdrIe4JjvjYpuncef4VBJylSxtfveAEnrrgi1y76OQMJ+51ODlv5lHcfubHObbRfHx8Kh+efQK/OP5Kmtz51wGOrp3FHad9jpOaipspX7/4clpNtAuEdOaHpgdYWrOg8OApLKlZxHSPNTVJ3RC8OjTAcHLU0utm+eYV5ehThotal/29XceRgGGIgtuRQEWgrEie29HBbx57iV9/8v10Dodw2Sj7O5Fb1m3kt8+t5ZqTVnHVicdw95VXcNumTVyzynx3JTN0BoP8+uW16IZk+bQWPrx8Ge+bt4htQwOEkwlOaLWv+87+kSD37drO/pEQmmFwzvSF/PBd70EIQY3Lg1qiQNlE+qJh/rJ7C2t272ZkVOJQnDR6/Zw+o52vrjidaVlkjovhtOaF/OK4j/G1V+5kf2wQh2IcEg0zDAVNV9jaH2J7aJC5VcV1Xwo4vXx/+Sf4/pY/cTCWuwDPkBBOuknpBje8dhf/c/KnLDc2+eScj/Jv236BLguvNUkJIykPKSPOE70buLTt3ZZsndxwNvd0/dn0+LQ9lVeHN1t+cjBvBDhCZuqFqDj5Itne3c9rnd1s3t/LT96fTSq6dHTD4FdPv8RAJMq/PPwU0WSKz5x2Av/nLOsKhvnQDIOr77yLzlA6S+iurVv5n/Ub+OVF72Npc+nt4CayZvcOvvr4g8QnrGHcuW0LNW4PP1l9LufOtT7zzMVDHTv4yrP3TaqANXToDke4fftW7tu9gxuOP5PLFxYXnpjIPR2b+af1D4zZyi6zG9LjfPnFu9BPvIT3zVpalJ15gRmc3vgufr/7YdyqhiLSmTAC0MYUKBOaynhq4qbgfv605zk+Me90S3aW1izmmjlX8rs9f8w7TjcEoaQHbUzm4Ln+zdadfOPZPN53H2HNnGxDWHOTkiqvj2wvn5PnyMmDL0QlXFMkSS09w3lk846y2RiOxhiIRA/9/J9PvcCmg8Xljufjwe3bDzn4cTqCQa668y/sG7av0CuUiPONJx6a5OAnHvuHh+7hB889aYsA27Nde/nC0/fklTiIaim+9eLD3PT6upJsrRvo5Fuv3GdKTkECP970GHGLOfnjvNC/i19uf4K45iQU9zIc8zMc8zMU8zOS8JLQnEzNPb/vQH71z1wMJjSCCQ96lrCElBDVnAwlfIccPMCO0QPoFlVEXYobtzLLlFONak4iejqMF0qVLpyXl8rCa/EIIb4qhNgqhNgihLhVCFG+2uQy4RjrCPHk63swyrTomtIn5yvrUvKLp16w3c72HDn3w7E4n/7b3YzY1KT85q0bCafyV1PetGk9v1z/Usm2fvjKE2gm871/uO4JNg4UV1Ue11N8c+19pCzklvfERvmfHS9btmVIg39/3XoDoT3hfkZT1v4PDWnwl/1PkzRUBhM+hhNeRpJuRpNuhuJe+uN+wil3hoxy3EgyqlkTbRtKBnl9pIPhPCqU6RCNmxHtsKsYSZVWIJafwouulYXXHAghZgBfAlZJKZcBDuAjb/Z1lIrXmX4kHwxH2TdQHlmDhoDvkHTCOM/t7uDV/aUVJU1FM3I7qD1Dw/zH8/bcWDaYLKb6+SsvsKmv+CeW1/q72G5B98aQkv/eurYoW/d2bKEzYv3//4ku64JjT/a8wZ5wcWJ4PTFrCpavDu+aoHopSBkO4rqTmO4cm7nndnAei3IPu8J7kEiShspAIkBYc6EZCoYUpAyFiOZiIBkgqrsn2R3RrC3yWqYyky8JFfAKIVTAB9jrtd4EptcdXrDb1lUeFUqXw0FbXWaq3e0bNttqp70uv27NrRs30TVS+qOx2WYgupT8ar31me44D3dad6APdeygJ2LdaTzds9vyawA6wtZvDHftLz6s5LTQFQrgxYHilG8VBG6Trf/G2RvpPPTvdHcpDwPJAH2JKgaTAUY1D7rMdFWjWhln8hKkIQpuRwJvupOXUh4E/h3oJN0RJSSltN554S1mZv0EFcru8jh5gEUtmc2hH9u2O+/s2yontuXPnNEMg1s2Zut+ZI0WX8D02Kc69xJOFieUFU4lLL9GkwZbhnqtvcYweLGvOG3/RBEx+W2h4kJKLkWlzaLOzvrh4taa3A6X5U5i3TFrv/dxAuUshAION2LJt739eSvCNXXAxcAcYDrgF0JcmWXcteMttfr7y+dEi2VWY+0hqYFyhWsATp/fnrFvNJHgNRtDNnPr67Pq1k/k+Y7StNMBzrOQOZPQNZ7ZX5wDrXIVl19v9eYwkAgzWsQNBWB+TebNOx/DyQhDFjThJ9Lub7CcQtkbL+4zPc1kHv9EBpPFSXQ0usunQAlUwjUlcDawV0rZL6VMAX8FTp46SEr5u/GWWk1N1r4QbwY+l5O2hvRs/uBQ+Vb5z148P6uezPY+ezvifOK4Y/Me39rbV/TMepzT2tqpcZtfY++PFufUVjUXl9NvRSETwFeC1PC7p1nTXNkzWvxEZ3HNdEvjDWmQMIrL/llVnymmV4ioxYXacaZ5Wop6nWkqTr5oOoF3CSF8Iv1cdxZgvcHm24BFrembT1ewfE6+1uvhvKWZmip7BuwVKPvo0SuYXvX/2zvP6Liqqw0/R733almy5CoX2ZZ77wUXsMEQaigOJYRQkgCBBEIKIYXyQQKhlxCqselg44IL7r13y7Ksalm9Tzvfj9GozUjT7tVY4j5rzbJm5nr2HZV3zt1n73e337FplJK8Cvfep6+3N/eOHOfw8QHezuV2LUxP6k3vMOdWlOF+AYxPdM4ELMwvgEi/QPsH2mBKgnNdryY3FOWaXs6ND603uv5hPsFJ6wWAUF/H03gt6R3summbXSzNUPZuXQBP5OR3AMuBvcChxnNwaPjtpcbo3uYVY4NePXMygHumjLOqsimuVnbTyd/Hh6fnXdahC6Wvt/u/LkuHjWRyT/t/nF5CMCoxyaUYQgjuHOycsC3uPciux40t5iQ5451uZlpiX4ZHO/fekgIdn+zUkrExfciIcO7Kpt7FVXyPwGgywtPsH9iGMB/nbaEB+oeq5EDZiDY0xA2klE9IKdOllEMax2C5ltj0MNMHmX/JlNwEtUVadCRLMlt3SKphozAuJZk/z55p87mIgAC7eXtH8BKCF+dczhQ7Zmdz0vq65ZVzXf9hXN9vmEPHJgWHcc/Q8S7FuX/IVIKcuOKIDQjhLyPnOx2nR1CEXW+ctvgILx4c6Hw3drhvsNNlkADXpsxwetMVIMzXeZEfFNafxECV0zUmYf/WBdA6Xt0gMSKU4SmJNic3Kc0jc6bSP655o2lQgrJ2AxZ+kpHBP+bOIci3tXD9bNRI/BV6n+EBAfx34RIeGjsZPxulfYNi4jq0PHaUp8bP5d6h423GsNA7LIoP5lxHXKBrKYPYgBDuH+JYG39iYBivTPwJCYGufVhemex4C79A8MehV9IvzDmjMTCPJUwPdc4AT0h/psVmOh0LIMLX+e/H9FjHbaRdRUj7N1XjC6GIsZLmXeMmv5wznjc27FI9TrCfH2/ftISn1/5Adkk5V2e65n3iCFdnDGFSai++On6CrNJShiYkcO1Q1/zM20MIwT0jx3L9oAxWnz3NkYsXiA4MIi0ikvm9++OrgHe9EILfZE7hlvSRvH9yP1+fPcaFuhq8hWBYTCLX9hvKzOS+TteQt2Vp/3GE+gbw1/2rqTHYzmfPSOzPU6MWEB3g+PzTttzRbxobLxznRGXHjWJSQr3Om5eP7GBmwmACfZzf25gUm8H+8tMOHSsllNV78dLJdU775AMMCR/IiryvHT7eaBLoTK7t1zjMpbGxuk8I8Xsp5UfuvIhQwidEbUaNGiV373bPX0QNKmvrCQsKQGcw4qeSv7uGMtQb9Kw/d5bCmmq8BIxO7MmgGGWvhorqqvg+/yTLsw5yuKwQg8mENAlMBi+QgpSQCJ6dtIDR8a47ep6uKuKO7W9T1k45pckEOr0PRqP59/Hu9In8OsP5KVkV+hpu3/lPSu1YB0sJNTo/Goy+xPiHsGbmw06nbKSU/HLfI5TqHCvbrNb7MSVmEg8NtN0oL4TYI6V0y6bVv1eyTPzd/XaPO/fzh9yO1R5CiF7A80AIcLeU0rFP3TZoK3kXOV1wkbtf+pTlj95MeLB61jv7svO5990vGZaSyGOLZ5AY4domlT1qdXr+s2k727LPExscxGWD+rNo6ECXcqz2qNHpeG3nLnbk5nKmpJTooCAm9ErhjtGjSOygwscVKhsaeHXfTj44epCy+talehmx8Tw4dhJTU5zfLLSFF158m3WaPfkXMGdCW2dDc6rLuXH1RyyfdyNDY1wbltE3NJ7Pp97Hk4e+ZnXBYSSyaVSdweiFwdDacuCNk9u5rs8IegQ5N6Qk3DeYxwffzIP7X2535qtstDTWGc0ycrGhmpyaEnqFOOfzLoRgbsJ0Psz51O6xOqMXtQZfTlTl2D3WbTy8/pVSngOuFEJcBmwRQuyC5inrUsorHHkdLSfvIkdziiiuqOHTrcpaDLTlpTXbKKupY8OxLG5/fQWVdcqYhbXlmXU/8PrW3RzOL2L9qbP89ovvuO29FdTqlB0zeKG6mqve+4AXt+9gV24epXV1nCop4b979zH/nXf57MhR5WLV1nDNZx/y0t4dVgIPcKi4iKXffMpXp467HetiXQ2Lv3mXH/KzOzxOZzLywoEtbsUqrKtmTU42tXV+1NX5U1fvT32DH4YWFsMW9CYjuy+edynO0Ig+XJYw2aZpmMHoRUV9YJPAW3DVW2d2/DS86Xiz12gSVOoCAEGNQZ2/g1aYHLipjBBiAPAw8APwbJubQ2gi7yI6vdmHZdXeE6rGOVnYbLSVfbGM51e5JxC2uFBVzUe7rW0Ltp09zwPLv1G0eujZzVs43c4Q8sqGBh5cuYqPDrpvoWAwmVj6zaecKO3YqMwoJb/5fiUXalwvSZVS8stNX5JX41gfwbrcM5wsc7256U97V7Wb+7dFjgs+OWBuivou7yRldUFUNfhTo/OjusGPsrpAKhoCbfrJuNpEVdJQRVG9j01bYwCDSVCuC8TUKFk1RpVF/hKokxdC/B34DHhaSnm1lHK9lHKj5ebo62gi7yKy8VruRG4xBSp2vFp86y2s2HmYcxedcxS0x5mLpRjb2ZvZePos/9nkvvUvwPnyCodW6n/+fj1n3fSx/+bMCQ4XO+aJojMaWXHiiMuxPjx1gO2FzqUPjrko8hsLTrPronOxXPHyAdhxMYui+kpAoDP6UG/wpcHoi8mGuFuI8HNtY/lg+RlM0ouyhkDqDD6YGuvQDSZBlc6P0oagVh8qdQb1q649XV0DGIERUsqV7ryIXZEXQvyy0W9GowWRIc3mSEdzXDNYcoTEyNY5aoPJxLub9yoaw2jHD//NrXsobTG8xFWOXChq98OkJQ0GI+/tc23QhYW3Duxx6vgv3EjZ/O/4Pqf/T53BtRXvGye2Of1/koMjXIq1usB5J8oIX9dMw05V5wFmF8oqfQAX60Morg+mtCGYOqMfbdNQJiQNbnTmOoSHbQ2klL+XUjZdsgghXCqpc2QlnwDsEkIsE0JcJtTYieuCJEU3l7CeyFPPQC01xvrzdfXBk4oOKkmP73ijrN5g4LMD7ufKq53I76/Pcs2cDMxTpg446Ud/0UWfnOzKMo6VXXD6/znj4WOhSl/PjmLnjeKGRLm2ybu12HnL5gg/10Q+p8bWQqljz3p/N7yDuiiOD8JtgV2Rl1I+BvQD3gRuBU4JIZ4SQqjbU3yJkxzTvDo6d0E9F8oxfZKtHiutqVPU3jgmJJikiI77LvYq4HrZP9px18Bz5eVUuDiRypX/F+LnmmCsPe+8EPp5eTMxMdXp/3e4rMDpxaOv8CI93PnO0Av1lY2pGseJ9AsiLsC16qiieue8mOL91U8uXALpGqtTcuU/OZSTl+Zi+sLGmwGIBJYLIf7pStDuQEigf9NqPq9ERRfKwX2aLI1bcrZY2Q+WJcM7vhI8XOB+SiojIZ7YYMdztq42KQW7INgjEpxzarRQXOf8FcCExF6EuWCHfLDUeT/5MXG98HfBk6e9OvyOGBfTFy8nLY0tlOic+xtKDlKn47sJySVhayCEeEII8QchxBNAfOPXfxBC/MHR13AkJ3+fEGIP8E9gC5AhpbwbGAkscfXkuwMDk82/aBcrXbvUd4TYsBDmDrV2ocwtrbBxtOvcMjaTqKD2HRXt5e0dQQjBdQ52zvYMCyPIz7WuxujAIMYkOtdwtHSo45YBLXHlg+iavq51D5+tct5eeml/x10/W1Kuc34PZlbCIJdiAfg5OU2qX6jrDWUOc2lYDWcD5xr/1Td+bbk5hCMfuzHAVVLKuVLKTxo94JFSmoCFTp5wt2LS4N6dEufeORPwaeMAKRX+DQvx9+fZq+a160LZK8q1zbu23D12DBnx9tMHd411zkWyLdcOdFxIZ/TqzZBY18yuUsOcSxtMT+rNglTnnSsBp10yR8UkM8VJ33oLzop8uG8gU+Kd95K3EOTt3B7FoDAVbYYbuRTSNVLK/1puQEmb+w7hSE7+D42dV7ae65I+8EoxY2gffH28rQRYaXrFRHD3zNYrspRoZUS3JRN69+Lvi+faFPrbJyjTue3v48MbVy1mcmr7f6Qjk3rwkwznfclbcuWAQcxOs+/ZPjQ2nudnOe+3YmFh2kBiAx1LQfUMCee5Sa6vi5zpWvXz8uax4XNcjuUs16WOw9fL9Qb6IB/H01cx/uEMj3TOj98lLo2VfEvUy8lr2CYsKIDF4wbTO8F1S1xH+fnMsdw5Ywx+Pt6kxUYya4g6v+QLh6Sz/I4bmN6/N3GhwUQFBfLrGROZ3l+5q5aY4GDeuXoJT86eRXpsTNO0zJSIcO4eO4b/XXM1Ph342juClxD8Z87l3DxkOH42zM6CfHy5JSOTjxZfS5i/a+MCwby6vnuI/ZTI6LieLLvsBiIDXBsyApAZ7ViKQgA39R7DoAjnHSgtpDphTWAyCfKrXJvuZCHYiZV8r6Bkl3P/TuFhkRdCtK26mNniOYdtODWDMjep0+kpqayhZ4zyK2tbVNTWE+jno4qfvKeoaRwr6MqGqSOU19fxxaljnCwtwcfLi7TwSK7sP4jwAOU8h/51YAv/OrAVQxufFz8vb342aBQPZk7B280PLoC7Nn/M9wUdV/QYGryRRi8WpKbz0tRFLsUxmIxMW/M3qh1oOqqr90VIb9bM+wXJwa5VvTx3Yhnf5NtvupMSBgQP5uWxP2v3GCUMygJ6Jsue9//K7nFnHv6NmgZlWcArwHNSSkPjY/GYLQ0GSClHO/I63UcpPESgn2+nCTxAeJB6ZmieQi1xtxAREMgtGR3PsHWX+4ZNZEFqOjuLznOuqpyC6iqKqqo5dqGEl3fs5s3d+xgel8hT02bTN9L1AdSPZ85lR/E5m7YGUoJRZxZ4gG+yj3Nr+kiXXC99vLyZHDeAlfkdW0zo9d6YTF6AZFdxjssiPzoq3SGR15u8OV6pXl9KKzw/FGQk8HfMlsP3AxnArzEXwdzs6ItoIu8GlTX1hKnoQNkSk0ni5eXxXzrFKa6uoaCiip4RYUQFu9ZI4wiV9fW8s3cf685kkV9ZSai/P7P69OGajCH0i3FddFvSJzyaPuHRfHDkAG/t2ofO1GxJoTMa2VmQy5JPP+T7G5YSHejae+0ZHMHXc+7k+cMbWF9wmipdA0YTSGOjpXGbtO2rh3e4bG38wMC5bL5wkqp2zMD0ei90+uZU2OnKjn2COmJMVDohPoFUdzDU22JrbJI1VOhqCXex8cpRPFAH3wopZRlwV6PArwXygXFSylxnXkcTeRcpqajhqkfe4rVHrmVAL/Vqdkuravnpsx+iN5q4e/54rhzv3oZkR6zYeZg3N+6itkFPcnQ4t00dxYxB6vS8fbLvMG9s2UV2abMPz9jUZJ6YN50+scqIroW39+zlha3bqGpoTj2U1tXx5p49fHDgAK9ftZjxKc5NQrKF0WTisU1r+fBo+6vfioZ6Pjl+mJ9nul491DM4gt8Pm8uuvCJK6owdHnum0vmySwvxAWE8lXkND+75qJXxmJRmz3qzrXEzxfWum7z5e/uxoMc4Ps5Z3+4xZoE3X6U0mNSdqwx43GpYCBEB/AMYC1wGzAdWCiHul1J+7+jraBuvLnL83AVq6/W8881OVeO8sXoneSWVXCiv5k8frOGrHcpZ8bZkw7Es/rBiDecullNcVcPe7Hzu/e+X/GetMuZkLfnLyvU89tWaVgIPsCP7PItefY91J84oFuvvGzfx5PoNrQS+JXUGA/d//a0iTpv/2L6pQ4G38PlJ94vSHtv+Heeq7BvV1ejds4qeENsXf1MYDTpvdHpv6ht8qK3zsxJ4wKWmq1axojLRG21LUp3ebI5mQW/q+MPNbRwon+yElf5e4BQwSkq5Wkr5APBT4EkhxIeOvohHRF4IESGEWC6EOC6EOCaEcG2KsgepazD/8Wzad4bqWvUc8U7ktvZFeebTjVTUKG+z+vyqzTYff2nNNpZtd9/618K2rBze29W++ZjeZOKRL76juNr9BrMVh4/w+i77G/YltbXszHXqCtiKTTnZvLbfseKAqgb3fn57LuTxzTnHLK793RyjuLXoLAW11RgMPuibJk7ZThu6OrvWwu7SbKoaAmgweGOpBzGYBJX1AdTqW+/bGNQWeVCsukYI8ZYQ4oIQ4nCLx6KEEGuEEKca/7W1mTFFSvmMZdMVQEq5X0o5AbjkV/IvAKuklOnAMKDL1dtbrAZ0BiMHTuV1WtyK2nr+u07ZSiOdwcDpovYv6/9v1WZqGpRx/Ht+/Va7x1TWN/DtEfd8+vVGI89vsR/Lwp5c13+GJil5bNMah48PdcGcrCX/Puj4+3J1ApWFr3Icd6JMDHJP5I9X5iMRVOsCKKsLorQ2iIr6IPQm6w+qtlVMaiBM9m8O8g7mdEtLHgHWSSn7Aesa77eio9y7lPJ1R4N3usg3TiCfgtnwDCmlTkqprEF6JxAf1WzEdCJHvd3+OBvj/r7d7f4ko5YIITos76usa2D1QeeNuNpiNJkc9sDZk+PeB+fnR4+RX9XxfNKWBPi6Phh6a24OOZWO20wMdmO2bHZlGRvyshw+fly8tcGdo5ikZEOB46mzRDdX8meqmq9aJQLZQe9PrItGaJ5ASrkJaOvAtgiwdK3+F1isVnxPrOR7A8XA20KIfUKIN4QQVi2DQog7hRC7hRC7i4s7qWTKCXrGNXcfns13fXPLHoOSrQWhsKyKnGLlPhd9vb3pZaeD9niB83a6bWkwGDE6mPuuqHMvBbbjvHPpl35OOGS2Zflx53zXlwxwyRYcgC0FzlkNj3FD5I+WF1LmoL2Br/BiaJRrJm8WcmsdM90L8QkgzNf1pjKHcSxdE2PRqcbbnQ6+eryUsgCg8V/Vqjc8IfI+wAjgZSllJlCD7UuV16SUo6SUo2JjYzv7HO0SHhLYtJovUNGFcsawvthy8M8vUdagbOrAjjtaCytcr5ywEOTnS784x8S0d4x7XcTFNY7n9FMjIzq0WbDHxvPZDh+bFBrG+CTXhXdnkePzWgdHxTMg0vW/newqx+1/R8YkE+Lreudwma6GOgeHgDjTjesyjm+8XrToVOPtNfVPzjk8IfK5QK6Uckfj/eWYRb/LkdHHnO9Uc+M1KTqc2cOtXSgr3VzptuXWKSMJDWj/j7RnpOO+KR0xrZ99ewQvIexaH9ujR5jjl/O/HDfO5W5UvdFoc0h4e/xq9ATcmbvjjMj/fMhYl+MAFNY5vniZl+y6AyXg8BUewIAw1+0anEJdW4MiIUQiQOO/7l8qt0Oni7yUshA43ziFHMx+DOrUBarMrNFm8fX3U7fd4IHFkwloE6PtWEB3iQ4J4rkbF+DnY73J5ePlxcJM15wT23LXpDGkRXfcFXnDqGEM6eGaK6SFOX0d8/aZP6A/iwYNdDmOM4I9N60fV6e71+fgqH/90OgEFrrodmmhsM6xPQ1fL2/muynyzlg2Z0S4fiXkFOqK/JfALY1f3wJ84dardYCnqmvuBd4XQhwEhgNPeeg83GJKZh/iIkNIjHZvw8kePaLCeGbpQgJ8zUI/KDmOQSnuiaAtJvTvxcu3LSY5qnnV7u0l+M38yQxMUiZlGOLvx9s3LWFavzSr57yE4JaxmTw6d6rbcSal9mJ0z6QOj1k0MJ3n5s+zOZTFUXy8vBjpwMCRQTFxPDtznstxLDhyxRHg7cNfx89164oBoKTesQ+UviFxRPi5lyP3c9DB0gvBjATXP5QdRaBcdU1jTfs2YIAQIlcI8TPMdgWzhRCngNmN91XBIx2vUsr9gCqmPp2Jr483T997hdt/TI4waXAa3/7pZ2w7fo5xA1IUMbuyxbi+KXzz0K0cyCmgul5Hn7gokqKUSdVYSAwP5dXrF7PtbA47snMpq61jYEIs41KTSbWzyncUX29v3rjqSp5Yu45VJ09Rb2jukByZ1IP7J4xnYi9lPMlvHDyMPYXtj0dc2HcAT0+/jEA3KngsxAeGkFPd/qa7AH7abwRGg/udOo4It5RwsLCYHYXnGZvg+grbx8GVvJ/w77RNV6WanaSU17fz1Mx2HlcUzdbATQaldVJ+EIgKDWLBaPVXMd5eXoxI7XgVrATj01IYn+a+nUB7hPj58ez8eTw5exa7cvMQAlIjIkmOUPZDa1G/gewuyOeDQvP/IAAAIABJREFUowdaPR4XFMw9I8cqao62qPdA/n1wW7vPS53g9T17eH3PHn47bjJ3j3A9L98z2L7xnklv9st578Q+t0Te18ubcN9AKvQd729U1Buo0tcT6tsJnlGXvkGvQ2gir9HtCfT1ZUpaqmqv7+3lxVPTZnP9oAzOlJdSXl9Pn8goxiT2ZEPWWX71zbfU6vVEBwXxq4kTnJpz25bbB4/hv8f3UqlrvfEuANkgwNB8hffGgd38bNgom376jjAkquNGKlOTKRqcqnDdnKwpXkRPthS3348hJRiMXpypLGF4tPqLEE3kNTS6IOV19ew+l0tueSV9Y6PJTE5UzOo4Iy6BjDjzld2J4mKuev8Djhe3Fr9dubmsvu1Wl1N84X4BfDDnOp7avYHDpYUkh0SQVVpGXa0BZOvXLKmrY3veeaakpLoUa3RMCoMiEjhaXmj1nDSBsaHZ4uBinfMzYdsyJrp3hyKv0/sAggv1jje5uYOnXSiVQhN5N6isqiMstBPyg0C9Tk+Ai4OtnaWuQY/BZCI00PW6Z0eQUnIkr4itJ3Oo1xtIi43ksmH98XXTb8UW1Q0NvPLDTv67Yx86Y7PvSXRwEG/deBXpCcr1YmzOPsc9X35Ftc667jurtIxDhUUMTXQ9zTckOoEP5l6HwWTihi+XUVdjpD0/mWq966W2XkLwxxGXcevG96k1NhudmYyilcAD6BRwhZyVOJgXjq/GZGMJbTQKDI1XDcK1KXjOo4n8j5u6ej0/ufdN7rt1OvOnuVfT3RF6g5H7nvuUvcdzGTM4hSduv4yYcNcv9zviUHYhTy1bx7Hz5pLdwSnxPLhkKpm9lb80PpxbyO+XrbbyzHlxzVaevn4+Q1Pc81xpycG8Qn7x8RcUV1uvNktqann867V8cnt7e2POseb0ae798mv0HdR97y8ocEvkLfxz+yZ25nfc2Rvk695VSmZ0T5bNuJXr175Pua4eaRRIk/Wmf1xgiFtxAJKCIpmTkMGqwtaGeFJCg84Xy4dKp0i8dMqb5pJGsxp2kezcEqpqGnhz2VZMJvU+8r/YdJjdx85jkpLth89x/3OfYjAq/9uXX1rJva981iTwAEdyirj7xU/Zeixb0Vi7snK5+eVlNk3Rcksrue/drxQzRDuUX8it/1thU+AtHCkoahpB6A5ny8p48NtVHQo8QKgbM2UtnC4r4a2De+0e1zPU/fLe/OpqSmv0mPTeNgUeIDVMmaqoKN/IphU7mFfwdfV+yBapqM6oZgM8PuNVKTSRd5HKarNdbGFxJQeOuWdT2xHHslvnQ0/mFLNs7T7F47y1eiflNiyM6/UGnnhvNTq9MkMaKuvqeeSjVTQY2reKLa6qYXeW+9/TOr2ee5d9bVfAjVJSVe9eB7FJSh76dpXNFE1b+rrhk2PhuZ1b7HrgJ4WEujVq0MLnWfZ7FdNClRH5ExXFNOh8qa0z3+obWgs8gHdnDPHmkvCTVwRN5F0kJLh5NXb0tPXGlFL42uhAXbFBOX93C4fPte8OWVxZw/YTOYrE+WTHIQor7G+cZV9034Dtza27Kai0HysiMID4UPfSDatOnmJfQYHd43pFRDAk3r3GsqzyUlZl2XcFnZJi3XDmLHqTke9zT9s9rne4e15DFk5UmK8kpfRCStvyFB/YSQ6U2kr+x02Pli6U59VzoewRY13TnVNYRkmF+0M1WhIc0HHuNk8hQ7TdZx2zEE4Id090GwwG3ty6x6Fj5w7q53YK4N19jl1d/TRzuNuxPj95DJO0rzAzetn3CbLHrqJcqvT2r04mJqa6HavOoKfIASuFZAfq993GEYHXRL57ExkeREykWYgulKhX0jUl0/aM1bIqx02xHCG9Z8fVJYH+ypQZejswjDzE348J/dzrRj2YV0itA6Pvgv38uG+qe4PJThQXs8uBoSNh/v5cPcT9TfqNOWftHtMrLEIRkd9/0f7VSd/waFJC3Rfe3Br7V2/xgaFuuV06ikBL12gAI4eob5SUmhjF7DEDrB4PCVRGdC3cOH1EkzdOWwJ8fZg4UBkLgPRE+6WKv1883e3yzaIqx6yRH5g+gZgQ96qVHPWuf2z6NLc3XUvqajl4wX568J6RYxWxvsiutG83fHmaMl3Y5Tr7C5f0cOU9m9pDE3kNFs8ZBkB0pDoljRZ+c8M0kmKb0zYZfRJJUNgUrUdUGP+6a5FV2kYIePz6WcS6mT6xcOPETOLC2v9+3T5tNFeMcM/REGBAnH3P8Z+NH8nNYzPdjpVbad+Sd/GggSxRYBW/r6jAbpZgQFSM226XFrIrOx7kIYDFae7/vACkA/mPYW4OJnGKbpKu0erk3WBoehK3XT2OkUPU818BiA4P5p3Hb2DZun0Ul9fws8vHqRJnzIAUlj1yEyu2HCKnuJywIH8WjxvC0DTlatYjgwP5393X8q/vtrLywAlMUuLv483YvincPCmT8W6maSz0jY1mQHwMJ4qs2+3DA/x5YMZEbhg1TJFY9mwDZvTuzV9nz1IkVkltx52l/t4+PDvTPWfNlmRXdZxC8ZM+7CssoJcCJZSOaObYuFS34zhMFxFxe2gi7ya3XzuxU+JEhAZy5+IJqsdJig7nvismqRqjZ1Q4/7x+Hn9aMouymjoiggMJUribVwjBmzdexZOr1rP97HnK6+pJjgxn9oC+3DV5DBGByhlcTUtL4+UdO20+d9PwYfxhxnTFXEONdgZY/2XKTHqFRVBUXU18iPtXX/XGDvY1JDTUmXh+11YW91dgNW9nM1mawKCAu6Zj59J10jH20ERew2ME+vkSqKJVQ2xIMC9cvRApJTqjEX8fdX7dRyT1YFafPqw90zz0Oi0ykgcmTmBhuvV+ijukRrS/Yr42PYMdZ3P543ffYzRJXl28iGm93SujDPLxtTJDa8IgQAqyK8o5evECg9wYUA72B4eYjF6cqShlQqIyV3t20UReQ6NrIIRQTeDB7PHy6pWL2Hk+l1q9nojAAIYlJDSVSuaWV7D3fD5V9ToWDxvoliHa+B7JpIZHkF3RnEbxEoLbMkaw/vhZzpU3P/7V8eNui3xicBiFtTY2sU2Arjkl5MwIxPboFdJxrb00Corr3J817CjdxdZAE3kNDYUYk9yz1f3qBh3Pr9/Ch7sPNnWnbjubw4s/udzlGEII/jF9Lr/bsIYqXQNjeyRzVf9B/GnNes5XtO5lOHrB/bGhExJ6sa+4zUAUCTSYfeSbHlJg1RsdEExsQAjF9dZCbmr0zKlyw3DNWbR0jYZGFyS7uIy3N+1m47Gz1Or09EuI5p/XzVN8+tXF6hpue+9TTl5oYzV8zn27hrE9kll3w9Km+7/44ksrgQdlPHJuGTiCd47tocbQ2BBlEXhT641dJaZegdne+Nvc1jYKUlqGk0CAd+c4sXal6hl7aCLvBhWVdYSFBnSKYVJFVR0hQf54e6tf9VpUWsX5ojKCA/1J7xWn6vvbl5XHF9uOsPdMHnqDkXHpvbh9zhiSbHT6uoPeaOSN9bt4bf1OdC18c/afK+DFNdv427WXKRaroKKKW99bQXaJdflhrU6PSUrFql8+2H+A707Zth1IDnf/exgXGMIHc6/jnWN7WJ99lvKqemz5QPbpYK/AGX7ab5SVyJsMXk3GaP4q2FC3iyby7iGE8AZ2A3lSyoWeOg9XMRhN3H7PO4wb3Zvf3DdXtThSSp55fR2frzlAoL8vd90wiWvmKzdOriXlVXU8+fZqNu5r3kDs2zOGf9xzOSkJyvwRW6isredPH6xh3YHWAvXZtsPsPZPH8t/9VDFf+Tqdnvve/ZKtp2z77+SWKmPZAGYRv/2DT20KPED/+BjFBL6oupqnNmxs9/mRPZSpKR8Wk8jC5IF8dug4tgQ+PjiEiABl5iqMikmhd3AsWTXFABj1Xk2reIAAn85ZyVs6XrsDnmyGuh845sH4bpGXX0bxxSq++e4guXn2uwJdZcf+bD5fY54dWteg5/m31/PDLvuGUc5Sr9Nz//992krgAU7nXuRXz3+G0Y7joTPUNuj42QufWAm8hXMXyrhQpswGm95o7FDgARIjlGss+9O36zhd3P7vw5Q+qYrF+tfWbdQZbLuDegnBnH59FYv1+cn2/1TTo+03njlDgAzEUO+Nvs4Hk771cJKgThJ5AGGSdm9dAY+IvBCiJ7AAeMMT8ZWgttacozSZJDt22/cScZXjWdbukG8u26p4nG+3HOPoWdtOlDlF5ZzMKVYs1p8+WMOp/I5ngjrS/egIr6/f1aHAA8waoowYfn/iDJ8fbF8M/X28uXG0Mg1Y+ZWVrDh8pN3nRyb1IMaNWbItqTcYWJd9pt3nh8QoZzVgkpJT5RfN6RlpfdWQFKxsp3e7aAZlbvM88DDmQiybCCHuFELsFkLsLi5WTmCUIi622e40K1u98/PztU5ZnMouVszf3cLRsx37oej07fu/O8OJ3GK+23uyw2P6J8XSM8Z9w6usC6W8vt52k5KFockJzBqsjMi/sGFbh88vGT7EbZ8cC2/v2dvhcJJFA5XxkwHYmnuOWkP7TVHTFTBCs1BQU9VhLCU6ax1F865xESHEQuCClLJDH1gp5WtSylFSylGxscrN31SK6KgQIhs9a8rKlLX9bcmoDGvLBCFAKnypGBLUfiVGeEgA6anuNbpY2H7iXIfP+3h58fCSaYrEemvj7labrFaxvL3489Wz8XLAGdMe609mcbyo/Q/7sAB/fj55jNtxwLxP8+2J9j8o44KDuWqwMn4yAJvOt/8ziw4MZESCcn4y56ra98rx9fKilwJulw6jreRdZiJwhRAiG/gImCGEeM8D5+E20yebuxkjwoNUi9E/LZ55U1sbW2UMSMLfX9nc5KIpQ2wOKPH2Evz+1tn4t+NQ6SwdvY4Q8PDV0xjVr2e7xzjDxmNZHcb685LZ9EtQJp/83s79HT7/xPwZbg8msbC/oIDC6vb3LO4eO0bR5q+jJe3X28/vM0CxjWSAIluNV430CY+22xWrJNpK3kWklI9KKXtKKVOB64DvpZQ3dfZ5KMGN144juWcUkyf2VzXOQ3fO4pr5I4iPCSVjQA+euG++4jHSekTz6iPXkNajeVxc/5RY/u+BK5k+sp9icaZl9LFpIxwbHswLdy7iJ5OVyVlLKdudE+vj5cWT18xh0UhlVrt6o5FdOe3Xv98wahgLh6QrEgtot2QSIDUyguuHDVUsFsCJkvb3TxTxrGlBXQdeOT2DlC2rtUs3WclrdfJuEB0Vwv9ev131OP5+Pjxw23QeuG26qnEy+vRg2V9vobyqjsAAX8VW7y1JiAzlw4dvYNnmg2QVlBIZEsj0oX2YPDjN5pWEqwgh6BMfzdG81qvQjOQE/rRkFgMc8LV3lLzyynZn1l6TOYTH5yn7cztcZHuD3NfLi+fmz1Os9BQgv6qSigbr2b8AGTHxPL9pK7+dOpkh8cpsvta3Uy0EWDVgqYrUbA0UQUq5AdjgyXPQsCYiVJma5/boGRPBrxdPUTUGwDM3zOff320lt6ySHhGhzMnox5yM/ork4FsSExKMwHphd8vYTB6dM1XxZrK8Ctv+9Q9MnMCwRLMttJRSkbjnq9rvIcgqKqO+oZhVJ08pJ/LGdkRegl7XearbnerktZW8RrelV0wkz9y4QPU4If5+jE9LYetZc6lmanQkv501mRkDbI9udBed0fqqYWaf3tw1ZjSFlVX8c80PbD6TzYo7biQ50r0UR3sr6wAvH+przc8dV7D6TW9qZ6PcBNU6+7NmFUUJQ55LAE3kNTQU4LUbFrP3fD4xIcGkRkVY+ccbTSZOF5XQJy4aHzetKTJ7JLLy5Kmm+3P79eX5hQvIr6jipv8uI7/CPHP4eFGx2yLvY8MHXwC6WiOisUlJKa98gHC/dnz+jaLjVI4KaCt5DQ2NJny9vRmbanvm77LtB3n+uy1U1Nbz85ljuXeOe8Nfbhw+jO3nz5MQEsp1QzO4cfgwqhoauP2Dz5oEHswbwu6SGBJq9Zi/9GlVox8VqFx6LyHIRgWSBPSic/c5u9DGqj00kdf4UbIvK49Nh7IwSsnS2aOJCFZ+H0JvNPLox9+x8sCJpscuVLhv1zA+JYWdv7i7VeniX1auJ+tiazuFPjHRbf+r0/SOiCIjNp5DxebN3kFRcRzPLW5axQMkhlp/ELhK33Ab52wQgCBcAVdNZ9A2XjU0FKS0spZjZwvx9fVhWL8eqlT2AOSVVPDH99ew69T5psciQwK5bdZoReMYTSYe/nAlqw+davV4crQyzTwtBf77E2f48tDxVs+H+vvTL859kQf4/YRpvLR3B1f0TeeVrTtbCTxAhkKbrgBpYVEkBYeRV9O4udy4igcI91duZKMjaCKvQV2tDgQEBro+6cdRKqvqqKyqJzE+XHW74ZKyGnYfOkduYTk94sOZPTEdHwXLG1tyOvcib3+9g3W7T2E0mv+qMvok8tZj1ysea/W+k/z5w7VU17UePBGgwgfKY5+sthJ4gBmDld2Mrapv4A/frLN6fOaA3oo1KY1LSmZcUjLrzpwhu8x6sLelokcJvL28uGPwGP64c22zd32jh02YXyeu5CXaxuuPHSklP1/6Bn5+Prz0xlL8/NT7Vn74yQ7e+O8PGI0mknpE8M+/XENSD+U9PEwmyasfbubjr/egb1H3/cWag7zypPKi++63u3j50y0YjK2XTGfzlXf1/GTzAZ5a9r3V362PlxfTMpQV3ve27OPLvdZGZaN796RvvDKrawuvb9lFcbW1rcbioco2KQF8duSo1WPJ4eFEBSmb6rp14Ehe3LWdi3W1rWrjIxWyM3aU7rLx6kmr4S5NYX45+bllZGcVs35t+26A7nL8ZAGvvrWxaZWbl1/O359bqUqsP//7W977fGcrgQc4dCKf0nJl/Xme/2gj//7kByuBBxjWTzkvFIBvdx+3KfAAi8YPJjFKOWfDEwXFPPPNDzaf+/W8SYrFASipqeXdnfusHk8MC2Vsmu1NYFep0elYn2XttjoySdmfFUCdXk9pTb1V81NymNbx6gqayLuITwt3yBNH8zs40j1On7H2DTltw37YXXYcyGbN5uM2n4sKDyJcwQap5d8f4P3vbPvT+fv58MurlRPDcxfK+MuHa20KfHJsBL+5UrmmLCklj3+y2mZVy+whfRmaolxaA+DtbXuos+FGet3IoYr6yQD8kJ1ts4RxVh/lewHOlJdisvEDS1No+pQjWJqhNO+aHzGxcWFERpldKBt06tXvpqVat9/3tvGYu5xuxy7Z20vw69tnKrYPUFOn4z8rNtuO5e3F3+5eSN9kZd6flJLf/XcldTprP5RAP1/+fus8gvyV209ZeeAkR/KsP5TDgwL43SJlrQ10BgPL9h6yjhXgz01jlPH/acm6M9Zmb/4+3kxOS1U8VnaFbSfKPhFRisdqF2l/YIg2NORHwM1LzavA4Zm9VIsxeGAPbrlxQlMrfnxcGA/er9w8Ugsjh6RYeddHRwTzt4cXMX2ccgZsp84XU1XbYPV4ZGgg/3f/YiYPV86bfMOhLI7kWF/1BPj58MKdVzA4JUGxWAajiX+t3mLzuT8vmU1cmDIOlBa+P5lFRb319/H2iaMJUaHUcHduntVj09LSCPFTvuggp9LaSiHE148EGzX7qqJQukYIkS2EOCSE2C+E2K3OybaPtvHqBgsXj2Dk6DQSk9S9jLztpklcMX84pWU1pPWKUaXSJb1PPO8+ewtrNh/HYDDSv3c84zPT8Fd4QzkmIhh/P5+mq5/gAD8WTRnCLQvGEBWmrGXzmn3WnuuJkaH847YFDE1TNnXyw4mznC+xFqc7Z4xRbPJUS2xNoEqKCOPmMZmKxyqprSWnwvq9LR6k/OYuQHl9ndVjeoWG1jiDwumY6VLKjsehqYQm8m6itsBbiI4KITpK2dVgW5ITI1l6zXhVY/SMi2D5U7dx4FQeYcEBDO3bg2CVSlBr21gNzxuVzqPXTCcsSPl663VHrMfj3TRxOPfPnah4rDq9ns2ns1s9JoCnLp+jSjnowQLrqWEp4eHM6tuHf2/Yxs1jMwkPVO57WtFgfYWi05kor6sjQsHu2g6RQBdJx9hDE3mNTichOpSEaOX81dvjjsvGEhUaRFhQAPNHpdM/Sb0JY9kXW+eRb5o4nEcun6ZKrIN5hVaj/64fNYxxClfUWDhkw9r4lpGZvL5lFy9u2s6MAb0VFnlra2PRaFDWaSIPSlbPSGC1EEICr0opX1PslR1AE3mNbsvglARF8+4dER0S1PTvo1dMY96wAarFOl1c0up+enwsD82a3HT/WN4Fnv5mE2/esUQRu+H8ytbWxqH+/kxITmHJax8AoLdRBusOlW1X8pIOpkGrh4Ppmpg2efbXbIj4RCllvhAiDlgjhDgupdyk1HnaQxN5DQ0F+Os1c7hj+mgG9Yhv169eKY/3lq6PKZHhvHb9YoL8zOMgj+YVcfPLy9CbTIr52JfVtV5Z/3zMaN7dvq/J8jgxXNkNUdl2CW0CgSDAR9mRl/ZwsHrmopRyVEcHSCnzG/+9IIT4DBgDdJrIa9U1GhoKEBLgz5CeCe0K/Ko9J1jwx7dYbWMz2FkGJ8bh5+3NwiHpvHfrT4hvrNyprm/ggf99TZ3eQGqMcntFLf3r+0RFsbD/gKaN34jAAMVm11oIbCPmwmD+ngb7daLIO1JZ48BngBAiWAgRavkamAMcVuWc20FbyWv8aKlr0HP0bCGD0xIIUHgwekteXbmdl7/dBpjN0Nwlo0cCex+5x2rM31+/WE9emTm1Mql/qttxLPSPiWZTdjZBvr48M+8y3tu1v6nhKz1e+X2OiIAW+X0JwmjeWA5QcDi5PczNUIok5eOBzxqvqnyAD6SUq5R4YUfRRF7jR4eUks82HOI/KzZTUVPPiw8uYexgdXod/v3VFt5cvROA2LBgMnsnKfK6bQV+9aFTrfxyLhumXG/DvAH92ZOfzx9nzqB/dDRL933a9NyghDjF4ljoHd7c9CQM5lRNRGCA4mMU7aLAPoCUMgtQvjvNCTpd5IUQycC7QALmb+NrUsoXOvs8NC4tss5f5Mu1h9h/9DyD+iby8F2zVYlTWlnL71/+ht3HzVbDIYH+DO6tzubsBxv2NQk8wM0zR7o9FcoWOoORZ79tTvEmR4WTkazcexqemMjyG8wGdWuOn6aqxcboiBTlvWvm9+3PMzs3E+Dlg66xPj4lXBmLZmdQaCXvcTyxkjcAv5FS7m3MVe0RQqyRUlpb3F3iNNTrqavVEdFob6Am9fV6ThzNJyjYj779E1Rd1dTV6/hu7RF27TlLcUkVI4b14uc/m6ZKrMrqev71zgZWbmw2eUuKV+cPurCkknueXk5OUbNd7p2LxxMSqHyH6P6sfJ77vFl4o0KDuHrSUMXjAHy8/QC5pc0VMEvGDFElDsBXLXzr/by9mdhb+Sug3hFR/GXKTJ7buBV943K6V2Qni3wXMiCzR6eLvJSyACho/LpKCHEMSAK6lMibTCbuvf5livLL+ecbSxmQ0VO1WF99voc3X1lPTbV5BTVrbga/ffwKVWJ9891BXn97E+UVtU2PFRZVctfSqYp/sBw+kc9jz31FcWnztKSgQD/uvF75BqL8ixXc+bdlFJU2j8cb1q8H185SvkO0rLqOh976upXD5gOLJhGowsZhdX0Dr37ffLUQGuDP9ePVyQ5UN+jYcKrZw2ZsanJTVY/SzE3txx9XrW+6nxLeyQ6UdB1vGnt4NCcvhEgFMoEdnjwPVygtriYny2zqtX7lQdVE/vSpQv71TOt9mtMnrTsQleD1dzbx/sfbrR5XQ+DXbjnOky+uamVr7OPtxR/vn0+vJGU91y9W1HDP08tbCXyP2HD+dvfCdqth3OGvH6+juKLZmnlaRh+uGDtY8TgAH247QFlNsw3A9ROGERKgznCNjafO0tDi5zW9v3I+Q205VdK6FyAlovPTNd1laIjHSiiFECHACuABKWWljefvFELsFkLsLi627ZDoSaLjQumRYt4gio5Vzzipvra1g6K/vw9336d8vvro8XwrgQ8J8efhBy5jwVxl0wyHTuRZCXxUeBD/euIaJo5U1rrWYDTx6+c/J/dCs/dKdHgwLz24hNhI5W0ivt19nLX7mydCRYYE8vh1MxWPA1CvN/DuD3ub7gf5+XLzpBGqxAKzKZoFLyGYNUB5m2EL59pMoOob3YkOlGCu6jHZv3UFPLKSF0L4Yhb496WUn9o6prFr7DWAUaNGXXIfqUII/vH6Ug7symLqZRmqxRkyLJl/PH8D+/ZkExMTypQZA4mMVH4PwGg0ERzkR02tjrjYUObOGsKSK0YSEaGsaZiUkr/8u7XATx7dh4fumE20Cu/rnW92ciy7uS0/MTqMFx9cQs845VeGtQ06nl6xoem+lxD87ZZ5RIeps2ezfOchSlus4m+bOopIFQaSAxhMJn443Tw0ZFRKUlN9vhqcK28WeS8h6NnZA0Og26zkPVFdI4A3gWNSyuc6O76SxCaEM+ty5XO6bRkxKo0Ro9JUjZExuCeff3QvRqOJgAD1asbLK+soLK7A20swelgqS+YOZ8JIdS77Cy5W8tZXzZnAvj1jeOHXVxIXqc6V10cb91NW3Sy6d88fz7h09Wyo39+yv+nr6JAgbp0yUrVYe3PyW1kbLxiinm0D0Mr1smdYGM+u28xTV8xRNaYV3UPjPbKSnwj8FDgkhLD8lv5OSvmtB85FowW+vt74+qozsNtCZHgQK9++ByEEQSoPQF+3+yR6gxFvby9umTea2xeNw1elgeT1OgP/W9+cOlk4ZiC3zx2jSiyAI7lF5JQ0r3Z/OXu8apugANuzc5q+9vXy4rJB5jr8Q+cLFS3XtNAyXRMdGIT0wKpamLpIPsYOnqiu2Yy5oUzjR0pwkDobg20ZmBrPPVdPYsbIfqQkqGsJvfHQmaZV/JXjh/D4dbNULXNdefBE09fj+6ZwzVj1UoYARwub98VmpvchIjCABr2Bxz40+UDnAAAM70lEQVRZzRe/vlnxeMU1zRvX0igJVWkzuV08ZIqmBlrHq0a3ZWR6MiPT1bHfbcuZwhL8fLxZOns0d80bp3p35sZj5vx4eFAAf/3JXKt4n287zOLxytXLHytsHmt410TzFcoXe4/SI1K5IegtqdU3FxyUV9cpamXsCAKpNUNpaGg0c82koSyZOJT4CHUHu4C5qibrQileQvDUT+YSH9465vLNB9mfla+YyFfU1VNYae5lmNSnF4MSzVYG723ex2VDlbNPsGCSsmloeKi/P3mllcSFqN9waEU3EXnNhVJDQwFiw0PsCvzbX+8gu6DU7Vg6g8E8iPy6y5g2sPWmdUFpJc99vokFYwa6HcfC+bLmTdBfTB4LwJ6zeZy5UMqo3sr3h7RcxadHxyAlxHpK5O3dugDaSl7jR43RaMLLS6ieXnn9i22s33OKWxe4vxkbFhjAD4/fZbOD9ukVG4kIDmRs/xS341gwNG5Azh/cn5EpZoO15TsP4e/jzfBeys7KBTC22PCM9jeXhMYpbGdsl26Uk9dW8ho/Wg4ez+PmB9+ltLzW/sFu8PnGQ7z2+TbuuXqyYh8mtgR+85GzfH/wNNdMHqpoJ298aAgjk3vw5OXmJrzq+gZWHzrF8F498FPB/tev0WHT18sLk8G8Wu4RoU7uvyOEyWT31hXQRF7jkuLYiQLWrlffxuiTlXv55R+XsWjWUFWasCzsPJrD3/+3jqmZfZg4VL1eB6PJxLOfbSLA14crFdxwBfPkpw9uu5ZgP3PJ6/dHz1CvNzB5QKqicSwE+vqSFBbGdUMzyCktJyIwgIhO3ngFB1I1XSRdo4m8RoeUXKzi6OFc1eNkn7vIbx9fzi9/8z6hIer9QUspee7NdTz/1npmjOvPTxaoZwNwoayKx175Bj8fb35zw3TV4gB8tfMYZ4tKuXLCECJU6nq1sOqgebrVjMF9VYtx5+hR3D12DOdKykmNUrf81SaSbiPyWk7eDXQNBi7klZKUFqt6TtdoMHJ47zmyT18gLjGc8dOV21izimU0sWn9MT5dtpMTx/KZNnMwg4aoY8BmMkk+XrGTt97dDMATj17B2NHqdMCaTJJ/vLKar9cfZlC/RB69W70OSqPJxGOvfEtZVR2/u3UWiTHqpRv0BiOvrtyOn483t84arVocgMq6eraezKFvfDS9YtQzDbspczgnL1xEbzKRGu0BczLoNjl5TeRdpKFex52z/sGFvDJu+tVcbrxvrmqxvvp4B++/sp7yUnODyE+WTlZN5PfsyuKVf60l+2wxPj5e/PS2ydx462RVYpWV1/CXf3zN3v3niIoM5olHr2BYhjp17VJKnvrPd6zceIT+aXE89/ur8Fdx5N/rX2xj38k8pmb24cqp6vjIW1ix5RAFpZVcM0n9Es71R7PQG43MGKyeOZmF08VmJ8rUaA+s5NGGhvzo8fXzYfqiEdRU1jPnmrGqxck6UcD7r6wnMNif8dMHMmfxCAYOVUcI33x1PR+/txXhJZgxezC33D6VHknq/IFlnS3m4cc/4WJJNaMyU3n0wflER6knUE+/vpaVG4/Qt1cs//fYEkKD1UsJHTiVzztf7yQ2IpjHblPXb0WnN/DW2l34+3pz+xz1bBQsrD18GoA5Q/qpHivrYhkAfWOVtZ52GE3kf9x4eXlx60MLVI/Te0AiH61/RPU4Z7MucOZUEUvvms60mYNISFTvEvnU6SJ+/ejHmEwm7rt7FldenqlquuudFdv5Ys1BBvZJ4LnHlhCmYs6/tl7HE6+vBODJny8gIlTd/Pjn249wobyan04fQbxKxmsW6nR6tp46R6+YCAYmKT/btS3nSj0o8lKCsXvkazSR1wAgrXccTz1znepxpJQ8+c+vmTdnCDdcM05xK+O2bN59hjc+3sL4zDT+9MAC1X1zXv18G3nFFfxiyURGDFBvWhiA3mjk7TW7CA7wY2knrOK3njpHvd7AXBW6XG2RXVKOn7c3KZEesBkGbSWvoeEKQgjeeXWp6hvVAMWl1fzt5e+4afEY7rxukipToFpyOvciH6/dx9xx6Yo0Pdnj+/2nKSir4hcLxhMZou4VA8CGo+ahIWpYGdjiXGkZvWOi8PbyUBGgJvIaGq7RGQIPUFJWw5O/vpzMwZ1jUvbCxxsZ2jeRPyyd0ynv8aNN+0mOCeeWmaNUjwWw7XQOAxJjGZAYq3qs8rp6KuobmNLPU/l4QJvxqqFxaZPeJ77TYh04lU91bQP/fnAJfr7q/1mdzr/Ivqx8Xvz5Yvw7IV5OSTkF5VUsndo5HyhFjYZoGT0672fYGglSy8lraGg00jMunJceupqgAHUHoVj4audR5o1KZ9JgdSeGWdh55jyBvj5cnqlef0ZLLlSZRX54kvLeOA4h0TZeNTQ0mokO71yXxKM5F3j29oWdFu/AuQLmD08nNLBzhndcqK7Bz9ubgYnqV/G0SzfJyWu2BhoaXZCX7l5MWFDn+bkczivilsnqWUC0pbSmlsGJcU1mZR5BszXQ0NDwFJ2R929JZq8e9InvvE3QqvoGxqZ2zoa5bbqOiNvDIyt5IcRlQogTQojTQgj1O300NDTc4g9XzuzUeFUNOsanKeeJ7zQSMJns37oAnS7yQghv4CVgHjAIuF4IMaizz0NDQ+PSZWrfVEam9PDsSWjpGpcZA5yWUmYBCCE+AhYB6puIa2hodAmm9VfHidRxNFsDd0gCzre4nwuo5/CloaGh4SwSpFYn7zK2WgGtrnuEEHcCdwKkpHgwN6ehofHjpJt0vHpi4zUXaLlt3hPIb3uQlPI1KeUoKeWo2Fj126g1NDQ0WqHl5F1mF9BPCJEG5AHXATd44Dw0NDQ0bCNll6mesUeni7yU0iCE+CXwHeANvCWlPNLZ56GhoaHRIV1kpW4PjzRDSSm/Bb71RGwNDQ0N+0ik0ejpk1AEreNVQ0NDoy3dyGpY867R0NDQsIU02b85gKc7/LWVvIaGhkYbJCAVWMm36PCfjbmycJcQ4kspZac1f2oreQ0NDY22SKnUSr6pw19KqQMsHf6dhraS19DQ0LCBQhuvHu/w7xIiv2fPnotCiHNO/JcY4KJa5+NBtPfVtdDel2fo5e4LVFH23Vq5PMaBQwOEELtb3H9NSvlai/sOdfirSZcQeSmlUy2vQojdUsrOGUbZiWjvq2uhva+ui5TyMoVeyqEOfzXRcvIaGhoa6tHU4S+E8MPc4f9lZ55Al1jJa2hoaHRFLoUO/+4q8q/ZP6RLor2vroX2vjQ83uEvZDfxZ9DQ0NDQsEbLyWtoaGh0Y7qdyHu6hVgNhBDJQoj1QohjQogjQoj7PX1OSiKE8BZC7BNCfO3pc1EKIUSEEGK5EOJ4489tvKfPSQmEEL9q/B08LIT4UAgR4Olz0uiYbiXy3XhIuAH4jZRyIDAOuKebvC8L9wPHPH0SCvMCsEpKmQ4Moxu8PyFEEnAfMEpKOQTzRuJ1nj0rDXt0K5HnEmghVgMpZYGUcm/j11WYBSPJs2elDEKInsAC4A1Pn4tSCCHCgCnAmwBSSp2UstyzZ6UYPkCgEMIHCKKTa741nKe7ibytFuJuIYYWhBCpQCaww7NnohjPAw8D3WMMj5neQDHwdmMa6g0hRLCnT8pdpJR5wDNADlAAVEgpV3v2rDTs0d1E3uMtxGoihAgBVgAPSCkrPX0+7iKEWAhckFLu8fS5KIwPMAJ4WUqZCdQAXX5/SAgRifnKOA3oAQQLIW7y7Flp2KO7ibzHW4jVQgjhi1ng35dSfurp81GIicAVQohszKm1GUKI9zx7SoqQC+RKKS1XW8sxi35XZxZwVkpZLKXUA58CEzx8Thp26G4i7/EWYjUQQgjM+d1jUsrnPH0+SiGlfFRK2VNKmYr5Z/W9lLLLrwyllIXAeSHEgMaHZgKd5h+uIjnAOCFEUOPv5Ey6wYZyd6dbdbxeCi3EKjER+ClwSAixv/Gx3zV20mlcmtwLvN+42MgCbvPw+biNlHKHEGI5sBdzxdc+tO7XSx6t41VDQ0OjG9Pd0jUaGhoaGi3QRF5DQ0OjG6OJvIaGhkY3RhN5DQ0NjW6MJvIaGhoa3RhN5DW6FI2OnGeFEFGN9yMb77s9vFlDozuiibxGl0JKeR54Gfh740N/B16TUp7z3FlpaFy6aHXyGl2ORouHPcBbwB1AZqPrqIaGRhu6Vcerxo8DKaVeCPEQsAqYowm8hkb7aOkaja7KPMx2t0M8fSIaGpcymshrdDmEEMOB2ZinZP1KCJHo4VPS0Lhk0UReo0vR6H74MmZP/RzgacyDLDQ0NGygibxGV+MOIEdKuabx/n+AdCHEVA+ek4bGJYtWXaOhoaHRjdFW8hoaGhrdGE3kNTQ0NLoxmshraGhodGM0kdfQ0NDoxmgir6GhodGN0UReQ0NDoxujibyGhoZGN0YTeQ0NDY1uzP8DgZh3QVzDS6MAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# %load http://matplotlib.org/mpl_examples/pylab_examples/ellipse_collection.py\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from matplotlib.collections import EllipseCollection\n",
"\n",
"x = np.arange(10)\n",
"y = np.arange(15)\n",
"X, Y = np.meshgrid(x, y)\n",
"\n",
"XY = np.hstack((X.ravel()[:, np.newaxis], Y.ravel()[:, np.newaxis]))\n",
"\n",
"ww = X/10.0\n",
"hh = Y/15.0\n",
"aa = X*9\n",
"\n",
"\n",
"fig, ax = plt.subplots()\n",
"\n",
"ec = EllipseCollection(ww, hh, aa, units='x', offsets=XY,\n",
" transOffset=ax.transData)\n",
"ec.set_array((X + Y).ravel())\n",
"ax.add_collection(ec)\n",
"ax.autoscale_view()\n",
"ax.set_xlabel('X')\n",
"ax.set_ylabel('y')\n",
"cbar = plt.colorbar(ec)\n",
"cbar.set_label('X+Y');"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.0"
}
},
"nbformat": 4,
"nbformat_minor": 1
} | mit |
aleaf/pest_tools | Examples/Interactive_Plotting.ipynb | 2 | 441039 | {
"metadata": {
"name": "",
"signature": "sha256:831cd0b4a3842d3674b7e201d31b3199f3c303c35a53d0dd7990b51b7417c80b"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"import pest_tools as pt\n",
"import matplotlib\n",
"%matplotlib inline\n",
"from IPython.html.widgets import interact, interactive, fixed\n",
"from IPython.html import widgets\n",
"from IPython.utils.traitlets import Any, Bool, Dict, List, Unicode\n",
"from threading import Lock\n"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"MultiSelect Widet"
]
},
{
"cell_type": "heading",
"level": 4,
"metadata": {},
"source": [
"MultiSelect Widget from: http://nbviewer.ipython.org/github/abarto/embedding_interactive_charts_on_an_ipython_notebook/blob/master/embedding_interactive_charts_on_an_ipython_notebook.ipynb\n",
"\n",
"\n",
"Needed for some interactive plotting. For example selecting multiple groups."
]
},
{
"cell_type": "code",
"collapsed": true,
"input": [
"class MultipleSelectWidget(widgets.DOMWidget):\n",
" _view_name = Unicode('MultipleSelectView', sync=True)\n",
" \n",
" value = List(sync=True)\n",
" values = Dict(sync=True)\n",
" values_order = List(sync=True)\n",
" description = Unicode(sync=True)\n",
"\n",
" def __init__(self, *args, **kwargs):\n",
" self.value_lock = Lock()\n",
"\n",
" self.values = kwargs.get('values', [])\n",
" self.value = kwargs.get('value', [])\n",
" self.values_order = kwargs.get('values_order', [])\n",
" \n",
" widgets.DOMWidget.__init__(self, *args, **kwargs)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": true,
"input": [
"%%javascript\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
" var MultipleSelectView = IPython.DOMWidgetView.extend({\n",
" initialize: function(parameters) {\n",
" this.model.on('change',this.update,this);\n",
" this.options = parameters.options;\n",
" this.child_views = [];\n",
" // I had to override DOMWidgetView's initialize to set model.views otherwise\n",
" // multiple views would get attached to the model\n",
" this.model.views = [this];\n",
" },\n",
" \n",
" render : function(){\n",
" this.$el\n",
" .addClass('widget-hbox');\n",
" this.$label = $('<div />')\n",
" .appendTo(this.$el)\n",
" .addClass('widget-hlabel')\n",
" .hide();\n",
" this.$listbox = $('<select/>')\n",
" .addClass('widget-listbox')\n",
" .attr('multiple', '')\n",
" .attr('size', 6)\n",
" .appendTo(this.$el);\n",
" this.$el_to_style = this.$listbox;\n",
" this.update();\n",
" },\n",
" \n",
" update : function(options){\n",
" if (typeof(options) === 'undefined' || options.updated_view != this) {\n",
" var values = this.model.get('values');\n",
" var values_order = this.model.get('values_order');\n",
" \n",
" var that = this;\n",
" _.each(values_order, function(key, index) {\n",
" if (that.$listbox.find('option[key=\"' + key + '\"]').length === 0) {\n",
" $('<option />')\n",
" .text(values[key])\n",
" .attr('key', key)\n",
" .appendTo(that.$listbox)\n",
" .on('click', $.proxy(that.handle_click, that));\n",
" } \n",
" });\n",
" \n",
" var value = this.model.get('value') || [];\n",
" \n",
" this.$listbox.find('option').each(function(index, element) {\n",
" var key = $(element).attr('key');\n",
" \n",
" if (key in values) {\n",
" if (value.indexOf(key) != -1) {\n",
" $(element).prop('selected', true);\n",
" }\n",
" } else {\n",
" $(element).remove();\n",
" }\n",
" });\n",
"\n",
" var description = this.model.get('description');\n",
" if (description.length === 0) {\n",
" this.$label.hide();\n",
" } else {\n",
" this.$label.text(description);\n",
" this.$label.show();\n",
" }\n",
" }\n",
" return MultipleSelectView.__super__.update.apply(this);\n",
" },\n",
"\n",
" handle_click: function (event) {\n",
" var value = $(event.target).parent().children('option:selected').map(function() { return $(this).attr('key') }).get()\n",
" \n",
" this.model.set('value', value, {updated_view: this});\n",
" this.touch();\n",
" }, \n",
" });\n",
" WidgetManager.register_widget_view('MultipleSelectView', MultipleSelectView);\n",
"});"
],
"language": "python",
"metadata": {},
"outputs": [
{
"javascript": [
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
" var MultipleSelectView = IPython.DOMWidgetView.extend({\n",
" initialize: function(parameters) {\n",
" this.model.on('change',this.update,this);\n",
" this.options = parameters.options;\n",
" this.child_views = [];\n",
" // I had to override DOMWidgetView's initialize to set model.views otherwise\n",
" // multiple views would get attached to the model\n",
" this.model.views = [this];\n",
" },\n",
" \n",
" render : function(){\n",
" this.$el\n",
" .addClass('widget-hbox');\n",
" this.$label = $('<div />')\n",
" .appendTo(this.$el)\n",
" .addClass('widget-hlabel')\n",
" .hide();\n",
" this.$listbox = $('<select/>')\n",
" .addClass('widget-listbox')\n",
" .attr('multiple', '')\n",
" .attr('size', 6)\n",
" .appendTo(this.$el);\n",
" this.$el_to_style = this.$listbox;\n",
" this.update();\n",
" },\n",
" \n",
" update : function(options){\n",
" if (typeof(options) === 'undefined' || options.updated_view != this) {\n",
" var values = this.model.get('values');\n",
" var values_order = this.model.get('values_order');\n",
" \n",
" var that = this;\n",
" _.each(values_order, function(key, index) {\n",
" if (that.$listbox.find('option[key=\"' + key + '\"]').length === 0) {\n",
" $('<option />')\n",
" .text(values[key])\n",
" .attr('key', key)\n",
" .appendTo(that.$listbox)\n",
" .on('click', $.proxy(that.handle_click, that));\n",
" } \n",
" });\n",
" \n",
" var value = this.model.get('value') || [];\n",
" \n",
" this.$listbox.find('option').each(function(index, element) {\n",
" var key = $(element).attr('key');\n",
" \n",
" if (key in values) {\n",
" if (value.indexOf(key) != -1) {\n",
" $(element).prop('selected', true);\n",
" }\n",
" } else {\n",
" $(element).remove();\n",
" }\n",
" });\n",
"\n",
" var description = this.model.get('description');\n",
" if (description.length === 0) {\n",
" this.$label.hide();\n",
" } else {\n",
" this.$label.text(description);\n",
" this.$label.show();\n",
" }\n",
" }\n",
" return MultipleSelectView.__super__.update.apply(this);\n",
" },\n",
"\n",
" handle_click: function (event) {\n",
" var value = $(event.target).parent().children('option:selected').map(function() { return $(this).attr('key') }).get()\n",
" \n",
" this.model.set('value', value, {updated_view: this});\n",
" this.touch();\n",
" }, \n",
" });\n",
" WidgetManager.register_widget_view('MultipleSelectView', MultipleSelectView);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x41c17b8>"
]
}
],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Adjust some matplotlib defaults. \n",
"Change figsize so plots are larger in the notebook and change the defualt cmap.\n",
"Use ggplot style"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"matplotlib.rcParams.update({'figure.figsize': [14,8], 'image.cmap' : 'cubehelix_r'})\n",
"matplotlib.style.use('ggplot')"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 6
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load some example data. Assumes this notebook is in the same directory as the example data included on GitHub"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"res = pt.Res(r'example.res')\n",
"jco_df, par_names, obs_names = pt.load_jco(r'example.jco')\n",
"pars_dict = pt.load_pars(r'example.pst')\n",
"obs_dict = pt.load_obs(r'example.pst')\n",
"par_sen = pt.ParSen(jco_df, obs_dict, pars_dict)\n",
"ob_sen = pt.ObSen(jco_df, obs_dict)\n",
"par_groups = []\n",
"for i in pars_dict:\n",
" group = pars_dict[i][5]\n",
" if group not in par_groups:\n",
" par_groups.append(group)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"0.0 Percent; Record 0 of 1036222 \r\n",
"96.5 Percent; Record 1000000 of 1036222 \r"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"C:\\Anaconda\\lib\\site-packages\\pandas\\io\\parsers.py:615: ParserWarning: Falling back to the 'python' engine because the 'c' engine does not support regex separators; you can avoid this warning by specifying engine='python'.\n",
" ParserWarning)\n"
]
}
],
"prompt_number": 7
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Interactive example of measured vs model plot. When first loaded all groups will be selected. Use Ctrl click to select multiple groups"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"interactive(res.plot_measure_vs_model, groups = MultipleSelectWidget(value = res.groups, values = dict(zip(res.groups, res.groups)), values_order=res.groups), plot_type = ('scatter', 'hexbin'))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA+kAAAI7CAYAAACQvNrvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXuUHOV55/95q/o6F0lz0Q3JuiEhWwKEQCBAyEiyDcGX\nHwlLbMxiYzteZ/HG2bXxrr0xNsSxnfhs1sTHTuINXtbm5CQnthMcEzBxjATGECMkgRACJCEkbkLS\nzGhGo5m+VFfV+/ujp1rdPX2pmanpqZ55Pudw0HS//X2f+tbz9Ntv1VtVSmutEQRBEARBEARBEARh\nyjGmOgBBEARBEARBEARBEPLIJF0QBEEQBEEQBEEQQoJM0gVBEARBEARBEAQhJMgkXRAEQRAEQRAE\nQRBCgkzSBUEQBEEQBEEQBCEkyCRdEARBEARBEARBEEKCTNIFQRAEQRAEQRAEISTIJF0QBEEQRnj0\n0UcxDINjx441tN+77rqLVatWFf7+wQ9+QDQabWgM5ZTHNBl87GMf4z3vec+k9iEIgiAIzYZM0gVB\nEARBGMV//+//naeeempS+1BKoZSa1D6mGw899BAXXXQRiUSC5cuXc/fdd49q853vfIc1a9bQ2trK\nOeecw8c+9jFOnjw5BdEKgiAI40Em6YIgCIIgjKK1tZXOzs5J7UNrPan6041du3Zx/fXX8773vY+9\ne/dy11138Ud/9Ef8n//zfwpt/v7v/57bb7+dz3/+87z44ov8+Mc/Zvfu3Xz0ox+dwsgFQRCEsSCT\ndEEQBGFS2bJlC5/85Ce54447mDdvHh0dHXzlK19Ba82dd97JggULmDdvHnfccUfhM//3//5f3va2\ntxX+PnLkCIZh8JGPfKTw2j333MOiRYvGFMtbb73FTTfdREdHBy0tLWzdupXdu3ePardnzx4uu+wy\nkskkF1xwATt27Ci8t3nz5pJY77zzTgzD4JFHHim8tmnTJv7oj/6o8Pe//du/sWnTJlpaWli8eDGf\n+MQnOHXq1Jhi98Phw4e58cYb6erqorW1lXXr1vHggw8C8La3vY3vf//7hba33norhmFw+PDhwmuL\nFy/mnnvuAca33H2sfUB+on733XezaNEiWltb+eAHP0h/f7+v/gYHB/n4xz/OwoULSSQSLFmyhNtv\nvx3IXzLQ0dFBOp0u+cxXv/pVzjvvPODs5Q2//OUveec730lraytr167l4YcfHtN2A3z/+9/nHe94\nB8lkkq6uLq6++mrefPNNzpw5Q3t7O3//939f0v7o0aMYhsETTzwBwLJly7jzzjv5r//1v9LV1cWC\nBQv43Oc+h+M4hc9861vfYuPGjXz9619n9erV3HrrrXzmM5/hz/7szwptnnrqKS688EI+8YlPsGTJ\nEjZt2sSnPvUpdu7cOeZtEgRBEKYGmaQLgiAIk85PfvITHMfhySef5Fvf+hZf+9rXuO6668hms/z6\n17/mz//8z/nGN75RmBxt3bqVN998k0OHDgGwfft25s6dWzJZ3r59O9u2bfMdg9aa3/7t3+bgwYM8\n+OCD7Ny5k/nz5/Oe97yHvr6+kraf+9znuOuuu3j22WfZuHEjH/jABzh+/DgA27ZtY/v27SVxzJs3\nr/Da0NAQu3bt4l3velfh/d/+7d/m5ptvZt++ffz0pz/l6NGj3HDDDeNwsjrHjx/nyiuvZHBwkAce\neID9+/fzjW98g0gkUjHuHTt2lMR94MABjh07VuLpWJeij6ePnTt38thjj/GLX/yChx56iGeffZbf\n+73f89XfHXfcwTPPPMPPfvYzXn75Zf7hH/6BNWvWAHDTTTehlOLHP/5xob3rutx77738p//0n0p0\nPv/5z3PHHXfw3HPPsXHjRj70oQ8xMDDge7t3797Nbbfdxpe+9CUOHjzIY489xq233gpAe3s7//E/\n/seSAxOQPxC1Zs0aNm3aVHjtO9/5DosWLWLnzp185zvf4bvf/S4//OEPC+8/8cQT/NZv/VaJzrXX\nXsurr75auI/Cddddx4EDB3jsscfQWnP8+HF+/OMf8/73v9/39giCIAhTjBYEQRCESeTqq6/W69ev\nL3lt7dq1+sILLyx5bd26dfrzn/984e9ly5bpv/7rv9Zaa33zzTfrO++8U8+aNUsfOHBAa631ggUL\n9L333us7jl/+8pdaKaVffPHFwmvZbFYvXLhQf/WrX9Vaa71jxw6tlCrRtW1bL126VH/5y18utIlG\no3poaEgPDw/reDyuv/Wtb+nLL79ca631Qw89pOPxuM5kMoXt/5//83+WxPLqq69qpZTeu3ev1lrr\nO++8U69cubLw/v/7f/9PRyIR39umtdZ33HGHXrhwoU6lUhXf/8EPfqDnz5+vtdb64MGDuqWlRX/t\na1/TN910k9Za67/6q7/SS5cuLbQvj8kPY+3j1ltv1e3t7XpwcLDw2i9+8QutlNKHDx+u29/111+v\nP/axj1V9/w//8A/1VVddVfj74Ycf1rFYTPf09Gitz+7v+++/v9DmxIkTWimlf/GLX/jbaK31P/3T\nP+nZs2eXbEcxe/bs0UopfejQIa11PqcWLVqk/+Iv/qLQZunSpfr6668v+dx1112nP/zhDxf+jsVi\n+p577ilp8/zzz2ullN61a1fhte9///s6Ho/raDSqlVL6Ax/4gM5ms763RxAEQZha5Ey6IAiCMKko\npVi3bl3JawsWLODCCy8c9VpPT0/h761btxaWkD/66KNce+21bN68mUceeYT9+/dz4sSJMZ1J379/\nP11dXbz97W8vvBaLxdi4cSP79+8vaXvFFVcU/m2aJpdddlmhzRVXXEEkEuHRRx/l8ccfZ9myZdxy\nyy3s2bOHoaEhtm/fzhVXXEE8Hgfg6aef5u6776a9vb3w39q1a1FKFVYKBMHu3bu58sorSSaTFd/f\nsmULJ0+eZP/+/Wzfvp3Nmzdz7bXXFlYnbN++na1bt04ohvH0sWbNGtrb2wt/X3nllQC88MILdfv7\n9Kc/zU9+8hMuuOAC/tt/+288/PDDJde5//7v/z5PPPEEBw4cAPKXSFx//fV0d3eX6Fx00UWFf8+b\nNw/TNDlx4oTv7b7mmmtYsWIFy5cv58Mf/jD33HNPyeqM9evXs2HDhsKlAD//+c/p6+sruU5cKVUS\nB8DChQvHFAfAz372Mz772c9y9913s2fPHh566CGOHDnCJz7xiTHpCIIgCFOHTNIFQRCESaf8cWJK\nqYqPGHNdt/Dvbdu2sWPHDl588UXOnDnDxo0bC8upt2/fzrJly1i6dOmEY9Na113WXdwmHo9z5ZVX\n8sgjj7Bjxw62bdvG3LlzWb16NY899tioZfhaa774xS+yd+/ekv8OHTo0aunyRFBK1bwR29KlS1mx\nYkVJ3BdffDHZbJbnn3+exx57bEwHPYLqo1bM9bjmmmt47bXX+NKXvkQmk+GWW25h27ZthTxas2YN\nV111FX/zN3/DyZMneeCBB/jUpz41SicWi416rTgX69Ha2squXbu4//77Oe+88/je977HypUr2bNn\nT6HNf/7P/5kf/OAH2LbN97//ff7Df/gPdHR01IxDKVUSx8KFC3nrrbdK2niT+IULFwLwjW98g1tu\nuYXbbruN888/n9/6rd/ir//6r/m7v/s7XnnlFd/bJAiCIEwdMkkXBEEQQkH5RHnLli2cOnWKb33r\nW1x99dUYhsG2bdt49NFH2b59e+Gab7+sXbuWvr4+XnzxxcJr2WyWp556ivPPP7+k7b//+78X/m3b\nNjt37ixc6wz5s/zewQIvjm3btvGTn/yEvXv3lkxEN2zYwPPPP8+KFStG/dfa2jqmbajFJZdcwpNP\nPkkqlaraZuvWrfzyl7/k0Ucf5V3veheGYXD11Vdz991309vbO+FJ+nj68A7CeDz55JMAJX7XoqOj\ng5tuuonvfe97PPjggzz22GMl+/j3f//3ue+++/ibv/kbFi9ezLvf/e4Jb2MlDMNg8+bN/PEf/zG7\nd+9m4cKF/N3f/V3h/Q996ENkMhm+973v8dBDD426Lt4PmzZt4l//9V9LXnv44YdZtmwZ55xzDpA/\n6GGa5qjYvPcEQRCE8COTdEEQBGFS0VqPmhz4eW3x4sWsXLmSH/7wh4WJ3bp163BdlwcffHDME8p3\nvetdXHbZZdx88808+eSTPP/883z0ox/Fsixuu+22krbf/OY3+fnPf86LL77IbbfdRl9fH5/+9KcL\n72/bto3nnnuOvXv3FpZvb9u2jb/9278lmUxy+eWXF9p+9atf5Z//+Z+5/fbbefbZZzl8+DAPP/ww\nn/zkJ8lkMmPahlp8+tOfxnVdrr/+ep588kmOHDnCv/zLv5TcqXzbtm38/Oc/x7IsLr744sJr9913\nH6tWrRrz3fIrMdY+lFJ89KMfZf/+/fzqV7/iv/yX/8L111/PihUr6vb1pS99ifvvv58DBw5w6NAh\n/vZv/5b29naWLFlSaHPjjTcC8LWvfY1PfvKTE96+SvzsZz/jL/7iL9i9ezevvfYa999/P6+//jpr\n164ttGltbeWWW27h9ttvZ8WKFVx99dUlGn4m0J/97GfZuXMnd9xxBy+99BI//OEP+e53v8sXv/jF\nQpsbbriBe++9l/vuu48jR47w+OOP85nPfIZ169Zx7rnnBrfRgiAIwqQhk3RBEARhUlFKjTpL7ve1\nbdu24ThOYUKulGLr1q0lr3ls2bKl7jXVP/3pT3n729/O+973Pi677DJOnjzJv/3bv5U8D1wpxZ//\n+Z/z5S9/mfXr1/Pv//7v/PM//zMLFiwotLn00ktpa2tjzZo1hc96k66rrrqq5Ezmli1b2L59O889\n9xzvfOc7WbduHZ/73OeYNWtWYcl/NT+KMQyDr371q1W3bcGCBfz617+mvb2d9773vZx//vl8+ctf\nLmnjeXf11VcX9Ms9Lu6/OAbvkWH33Xdf1RjG08fGjRu56qqreM973sN1113HunXruPfee2v24ZFM\nJvnKV77Chg0buPTSS3n++ef5+c9/XnKNezwe55ZbbkFrXfG6bD93sK+XWx0dHTzwwANcd911rF69\nmi9+8Yt8+ctf5uMf/3hJu0996lPkcrmKZ9ErxVG+DzZs2MBPf/pT/uVf/oWLLrqIu+66i2984xsl\nS/j/x//4H9x555386Z/+Keeffz433XQTa9as4YEHHqi7nYIgCEI4UFrWPgnCpLN///6SMyqCIATP\n0qVL+fSnP80XvvCFQPTCVLevvPIKq1at4te//nXJTe0ayfbt23n/+9/PCy+8wLJly6YkhvHywQ9+\nEMdx+Md//MdxfT6o3HrooYe44YYbeOONN0bdvE4IhjDVrSAI/pHaLUXOpAtCAyi/c7QgCMHy3HPP\nkUwmuf322wPTDFPdPvjgg9x6661TNkH3YvjiF7/YVBP0/v5+/vVf/5Wf/vSnfPaznx2XRhC5lU6n\nOXr0KHfddRe33HKLTNAnkTDVrSAI/pHaLSUy1QEIgiAIwkS58MILeemll6Y6jEnjM5/5zFSHwP/+\n3/+74X22tbVVXY7+pS99qeRa7EqsX7+eU6dO8YUvfIGrrrpqXDEEkVvf/OY3+frXv87GjRv55je/\nOSEtQRAEYfojk3RBEARBEELJc889V/W98seXVeLo0aMBRjN+7rrrLu66666pDkMQBEFoEuSadEEQ\nBEEQBEEQBEEICdPuTPqxY8emOgRBGEV7e3vJc4AFQQg/UreC0HxI3QpCczLda9d1XQ4ePMiePXuY\nO3cul156KXPmzOGcc86p2H7aTdIFQRAEQRAEQRAEYarRWnP06FF27dpFMpnk3e9+N/Pmzav7OZmk\nC4IgCIIgCIIgCEKAHDt2jKeffhrbtrn88stZvHhx1ZuhliOTdEEQBEEQBEEQBEEIgL6+Pnbu3Mnp\n06fZsGED5557ru/JuYdM0gVBEARBEARBEARhAgwODrJr1y6OHTvG+vXrefvb345pmuPSkkm6IAiC\nIAiCIAiCIIyDVCrFM888w+HDhzn//PPZvHkz0Wh0QpoySRcEQRAEQRAEQRCEMWBZFvv27WP//v2s\nWrWK3/3d3yWZTAaiLZN0QRAEQRAEQRAEQfCB4zi88MIL7N27l8WLF/M7v/M7tLe3B9qHTNIFQRAE\nQRAEQRAEoQau6/Lyyy+ze/duOjs7ee9730tnZ+ek9CWTdEEQBEEQBEEQBEGogNaa1157jV27dhGN\nRtm6dSsLFiyY1D5lki4IgiAIgiAIgiAIZZw4cYKnnnoKy7K49NJLWbJkyZgfpzYeZJIuCIIgCIIg\nCIIgCCOcOnWKXbt20dfXxyWXXMLKlSsxDKNh/cskXRAEQRAEQRAEQZjxDA0NsXv3bl5//XXWrVvH\ntm3biEQaP2WWSbogCIIgCIIgCIIwY8lkMjz77LMcPHiQNWvW8MEPfpBYLDZl8cgkXRAEQRAEQRAE\nQZhx5HI5nn/+efbt28e5557LjTfeSEtLy1SHJZN0QRAEQRAEQRAEYebgui4vvfQSzzzzDAsXLuT6\n669n9uzZUx1WAZmkC4IgCIIgCIIgCNMerTWvvPIKu3btor29nWuvvZbu7u6pDmsUMkkXBEEQBEEQ\nBEEQpi1aa958802efvpplFJcddVVLFq0aKrDqopM0gVBEARBEARBEIRpSU9PDzt37mR4eJgNGzaw\nfPnyhjzrfCLIJF0QBEEQBEEQBEGYVgwMDLBr1y5OnDjBxRdfzOrVqxv6rPOJ0BxRBoRSCtM067Yz\nTbPu0RW/Wn6eq2cYhq+E8aNlmmagWkH60MyeBhV7M+eWeJqn0fWqlJqSeq2HYRih9TQoH5RSTZtb\nYfW02etVfBBPPeS3W56ZMBY0c241s6eOAzm7dhsN5FDosteHh4d5/PHHeeCBB+ju7uamm25i7dq1\ndb2YCh+qamity7erqclms9i2TTqdxrIsotEoyWSSaDRa+BJ0HAfbtslms2QyGQASiQTxeJxIJIJp\nmriui+M45HI50uk0uVyOWCxGMpkstFFK4TgOjuOQyWTIZDIYhkEymSQWi2GaJqZpFtp4Wo7jjNIC\nCnFlMhmy2SymaRZij0Qihdgdx8GyLNLpNK7rEo/HSSaThf6KtVKpFJZlEYlEaGlpGeWD4zhks1nS\n6fQoHwzDQGtd0Cr2tKWlpcQH13VHeer5MF5P0+k02Wy2oqdef8WexuNxEomEb0/L90+xp4lEgkQi\nUWhTzQe/udXa2gpQ4qlfH7z9U82H4tht2y7kQ7kP5Z56+eDt62JPU6lU3dzytCKRSElc1fI0mUwS\nj8fH5Gm13Gp0vY41t8ZSr2PNLU+rXr2mUqmqPlSr1+L9U83T4tqvllvNXq/NMBaMtV79jgWZTAat\ndajGgsmu16nIrbGMBeWeKqUKWpXqNZVKBTYWFHvqdyyo9x042fUK+ecdhyG3JvrbrZoPk/3bzc9Y\nMJ7fbjOhXifzt1sQY0FxvY5lLGjEb7dYLEFPb4ozw1FyOQPbMdAaIqYmGnFpacnR2mKjDUWKCFkM\nbAxcwEATQaOzaV7Zu5uDL73I2rVrufLKK2lvb59wvU40t2r9dqs2UZ92k3QP13XRWqOUqnnUxHGc\num38aGmtC4NDraMinpZhGFWPwnhafmOvdbbHb1yO4wDUjGssPvjx1CMIT6H2Wa8gPQ1zbkEwPvjV\n8r4+wuapRy1Pvf8amVteTPV8gHDVq5/+pF5LY4fGjgVQf//4yfmgcsvTauaxwIspCB/8xB5UbgX5\n26DZxwI/nvodC8L4281PXDIWnO0vrGMBBPfbzU+ehrVen92XZjjlAtXOUmsis1wic1y0KtVybJtX\n9z/Lked2M3/pCj7wnm10d3aELregdv0UM20n6ZA3zc8Sj6C0/Pbnp53jODWLeqriCmN/YdbyirZR\n/U333PLjZ5D9hVkrjLnV7Fph9LSZ67XZ80Fya2rikrFgarSaOfagtaReg9XyW6979g4znKo9LY3M\ndjDnlPb/5sEXeHnPb5g9dwHnXXolbXM6WTevjXiktl9hzS2PGX/jOO8oil/D6lHPfL/HRJRSgWkF\nGVdQ/QWpFVYfio+OBoHk1lmtsHkatJafvhpZY0FqhdVTbywIirD6IGNB8Fp++gqjDzIWlOo1sw9B\n6s10T+W329i1auE4mlP9OZSh6JwTwTBG96m1JpXWWLnafZomdM6K4EZdzlgOx48e5uCuJ4gnW1n/\n7vcxZ95CAFqiBhW6qUiYx4Jpdya9fOlc8d+QT/LiH2Pe/z0bvGUi5baMR6va56ppFX+u/O9GfG48\nPnjt6vkwlrjG42mxfnEBFP/bz76YzHyYKbk1Uzwt1xqrp2ON3U+9lk80x+vDVHz/SG5V9mI6eTrW\n7ZmsscBPDJJbE//cVHlaHF8zjAUT/VwlH+qNBZPx222inxtLPki9Bv+5ID0dGnY5cTLHcMohm6Uw\n+Y7FFPEYtLWadHVFSA27nBqwyWY1WUvjugql3JH+ABSz2k0WzDNpSZrE44po1ODIkSM88sh2cnaO\nSza9k9YFb2N2PMKseIS4aRA1DAxj9HZ729HIscBPvVabtE+7SXottNYFQ2rh5+y6Z1utNp6Wn2Ug\nQWn5XRkQlNZYPG2kD83uKQTnQ1D7J8y5JfU6NfU63XPLz76Wes0jY0HwWlKveWQsCF4rrPUaZh+k\nXv378NSuYXJ2TSmU0mhdO6Z4DC5e10Ikko/r+PHjPPLII/T19bF161bOP/98lFI4rovZxHlarU1D\nlrtblsVdd91FLpfDtm0uvfRSbr75Zn70ox+xfft2Zs2aBcCHP/xh1q9fD8D999/Pjh07MAyDj3/8\n46xbt27CcVQ6YlKrbb33y49UNiIuv3pB4OcLIsjYg/TU0wuKRmrNhNzyoyX1Ojamol6D1JLcCra+\ngtRr5rFAPA1ey9NrlFaY6zWMnjZ7vTZzbgXpaZA02tOq930rIu9VvYb59/v7+9mxYwdHjhxh8+bN\n3HTTTSXX5/vZurDWa61JesPOpGezWeLxOI7j8JWvfIWPfOQj7Nu3j2Qyyfvf//6Stm+88Qbf/va3\n+dM//VNOnTrFn/zJn/Dtb3+77pdOPbxlCLW+BLyjV1D7rodBaRW3qaVVvITCj1YjYve0PI1GeDpW\nH/xohSkfpkLL24e1Bnavv3oDaDPn1kyp10ZqjSW3/Gg1Mvby5WgT1Zqq70AZC6Re/WrJWOBfazrk\nVqPrtZnHgjBqhTm3dj2TImvVmoRr8tem55e4V0MxzOlTu9m//3k2btzIFVdcQSwWG3NcYa/XKT2T\nDhCPxwGwbRvXdQvPja50jODpp59m06ZNRCIR5s2bx4IFC3j55Zc577zz6vZTfj1AMZ4JrutWPOrn\nDTzF7fxoVdoGz3TvugU/Wt5t/qtpeV9w1dqVx1WvP79xTcRTIHBPx+pDkFr1Yg/a06Byy48PUD0H\n/cbufRkF6Wkjc8vzdKbmFkxOvULt7zfviHi9uCbD00paxWOBUkrGghDnVrPV62T9zghKa6z1Wo1G\njgWT4YPUa+PHgrHE1ez1GubcCkLrkotaOdWfo7fPJp1xCxP2eBxaEgbz5kaZPcska8HxExZnhhyy\nWY3tQDQCpmnx+qu7eenFZ1i37kJuu+22wryxuO/p9NutEg07k+66Ll/4whc4ceIE11xzDbfccgs/\n/vGPefTRR2lpaWHFihV89KMfpbW1lXvvvZdVq1axefNmAL73ve9x0UUXcfnll4+5z1obH7SW3/78\ntGvmRy00ur8wa3lf8I3qb7pr+fEzyP7CrCW5FbxWGD2VsWB6aEluBaslY0HwWs0ce9BaYazXZtbK\nZl0MQxGN1lp9oxkattj//B6eeOIJVq5cyZYtW5gzZ05Zu+b1Afx/d0EDz6QbhsH/+l//i1Qqxde/\n/nX279/PNddcw4033gjAP/zDP3Dfffdx2223Vfy83w0SBKE2DTouJwiCIAiCIARAM/92i8XqXx6z\nb98+duzYwfz58/nIRz7C/PnzGxhhOGn4c9JbWlpYv349hw8fZu3atYXXt23bxje/+U0AOjs76evr\nK7zX19dHZ2fnKK39+/ezf//+wt8f/OAHgdJrprylUZWSo3jZVLVrAsaqVavNWLS8pRtQ+QBFuVYQ\nsQepVes6i6A99TyqdRSrOC6vfb24gojd+3eYPDUMY0x5OpNzq54P5XHBzM6toOu10Xnq/TtMnspY\nIPVaKfZGjQWeR5Jb4c2tZvXU80jGgupaWmvSGc2JkxZDwy6mCd1dUTo7IkTM0Zd91PJBa83QkMPJ\nXpvhlEssqpjbHaGjwrPLG5VbWmsOHTrEI488QiwW43d+53d429veVlEna7v0pLIMWQ6Ggo5ElI5k\njIgx2gdovnnBj370o8K/165dy9q1axszSR8cHMQ0TVpbW7Esi3379nHjjTcyMDBQWMawc+dOlixZ\nAsCGDRv49re/zfvf/35OnTrF8ePHWbly5ShdbyOKcd38un9v470d4L3uGVncxmtXqY1SqkTLdStf\ny+Cnv7FqeZ/3tIqppFWJanGVaxXHOBGt8qRrhKdjid37/GR7Ohm55TEZnk6WDxPNrbDVa63Yvc9P\nlafFsZdrhSm3gvqumainfnKrXn+N8tT7fNjrtVrs0JixoFnrNcxjQZD12qixoLzdTM6tsfrg0Wy5\nNdljQaPrNWdrDh3OkMloLEvjFN1cre9Uhmg0/7zxpUtizJkVqelDOuPwylGLTCb/LPLix5719NmF\nZ5efuzxOa4tZ+Pxk1GuxD6+99hrbt28nk8mwbds2Vq9eXfiM54OjNUf6U2Qcl5wDTpHOQNbm9cEM\nMVOxsDVORzI6rti9eKeyXk3TLJxoLqYhk/SBgQH+8i//smD6O9/5Ti644AK++93vcvToUZRSzJ07\nl0996lMALF68mCuuuILPfvazmKbJ7/3e75V84dSi0lGOYmNqHVXxXvfTpla7sfYH1a9RCDL2sWrV\nul7Nj9Z4fAhKq5qf49EK0tOpyK2gtBrlQzN4GtZ6bdbcCmu91oprpuVWs44FtZhqT5u1XmUsCH+9\nNmtuhXUsaLQPOcth4LQ7MqEu90ORy0EuBxHTqKt15ozNwGld+Gy5lmWBZYFpqkn3VClFT08P27dv\n5/jx42zitDmaAAAgAElEQVTZsoULL7xwVNuCD7bLGcstmZwXx25rsG1N1EfsEM56te3qD5RvyCR9\nyZIlhaXsxfzBH/xB1c/ccMMN3HDDDZMZliAIgiAIgiAIgjCJnD59mkcffZRDhw6xadMmbrjhhlGP\nUxNKadjd3RuF61a+pmMiS1EmolWrTSWt8v6qxTWZWvWWaVTrr5bWWD2tFXut/sLqg9curLkVpFbY\nc8tvXFNdr8Vt/HgapA8zvV4nW2uqc8uvltRr9f7CWq8yFjRXbslYMD6tZswt23XJOS62qzEUxEyD\naNkKJU/LymkOHMqQyWpylkaXnQFXThayZ1i6EDrnthCbNYtoPFEau+NgD2cZ7E3z8pEsbjSGE41T\nfjZdKRdQrFweZ1a7QSxmEImUxu4UxQ5e7IYvHzKZDI8//jh79+5lw4YNXH755SQSCV+eOq7m5f4U\nWccl5472wQBiJixqSxSWuzdjvVZdqTbdJukwukArGeB3p1V6Tl6lneYdHKjWpjwub8f5SQA/WoZh\nVEy44gSZqFY5QfgQtFalfRi0p35iL+6v0Z7Wyq3xaIU1tybyYyCsuTXVnoalXoPM03JtGQsmrlVO\nM+VWI8eCILWmeiyA6t+5k5VbYa3XSrHPtNwKWisM9er3t9tYcsvVkLZdhnI2vSmbjHM2jqih6EyY\nzI5HaYtFUIyuV9fVnB60OdFjM9h7Gqu/F3qOoF97FpU5XWgXn9PB3IsvZc7yc4nGZ2OdGmJg7yuk\nXu+DkYm1NgxyXd3kFi4iN7sDHYuPbG9p7MmEYv7cCO2zDIwYpG2H3nSO4dzZ2A0Fc+ImnckY7VET\n0xg9EbUsi9/85jf85je/Ye3atWzevJm2traa+1CpszdyK26nteZM1qY3bZHOORhK0RYzmdsaJxEx\nK2p5hCG3/GqVMy0n6R61rgWYDC2//flp18zPL210f2HWKv/xMtn9Tffc8uNnkP2FWSuMudXsWmH0\ntJnrtdnzQXJrauKSsWBqtJo59qC1gqrXt85keP1Mtm5/F85tJRGtfQXywX/6ESd376yjpJjTfgnK\nqR3X0PoNWB3zaitFNLGFTn5GXoN3dLXQHo8W/nYchz179vCrX/2KZcuWsXXrVjo6OnzVa1C++20X\n1tzyaPgj2ARBEARBEARBEMKG6+qRVRy1J1K2o4nVmZPltaDWnExrcBwN0eptAJRp5oXqnFvVERPl\n1Dn/agBoRt9IrkSptsYITtHS7v3797Njxw46Ojq4+eabWbhwYeE9YexMuzPplZYdeHhHOKpdNwGj\n78rnR6t8aU95m1paxf1NRKt86USlJWgT0apGUD4EqVXuabV9HZQP5Uvy/MQ12T6UL3Ns9tzysw8r\nLUGrpBXW3GqWeg0yt0DqtVLsQddrvdiD1JrJY8FkaYWlXqc6TyeyDytpSW7N7Hr1xgKtNam0y/ET\n+WeRZ7MaDcRjivZWg3nzorS1mjgO9Pbl6DuVy18rnoNoFBIJRXdXlK7OKKYBg2fyy9NTww4ZS2Nr\njYqAEdeoVlARwAU3pdFpA22DoRXxmCKZMJg3N1p4dnmxp65jkxsaItt/ioFXXubknqexTp+GtlmY\n71iHuXg5tM9BReKotIUxMIR54A3MEwNgKJxzunBWnYM7qxXdmkQrE20rnBQ4KQPcfGxmm4sZ1xAB\nZeaPMOjChN7bt2f3jaGh/63XeHHnE0RNk/e8+92sPHeF1OsYtSrGPd0m6dV+6JbvlGpLEoqNrHQd\nw3i1qrUp1qrWX5BaU+1Ds3kqPgSvJZ5Obuxh1RJPa7eRsWD8WpJb/rVkLJDcmmqtsHn6zHNpMhkX\nV1fuz1DegS7I2dXOPmsipjdx01W1lHILH9dutdPwmrY2gwvekcQ0q/uQy2Q42HOGYReIVrlLuutC\nzkYBOhatfEpfa/DsUtRY3j6yb/Bu4KYY6DnOwZ1PkBkeYtWGK1mw/FyihsH5c9uIGNUfizZTcsuv\nVrX3p90kvR6u27zXKDQ6drlezX+bmaDVzLEHrSX1GqxWWOt1KuKS3Apeyw/iaXj7C7OW1GuwWlPx\nnbtz9xBZq16rekvD8yjlonXtPpXS6CqTeI/WVoN1axOYZm2t/ScHGbbrTeP8xe6vnQsYDA/0c3DX\nk/SfOMbKiy9n8eq1JV5fNK+NWKR2Dkq95rFtm0ik8tXnck36BPDzRdLMTPftE4TphNTr1DHdvZ/u\n2zcV+PVUvBfGiuTM2HCDPFVZZ/INdS8pL+BnN/qK3e8c3QeZoWFefuYpjh89zPILLubCLddgRkZf\nTC8p6J8Ztdy9fKlCrWsPvDblnyvHW85Qq02t/oqP3IxXy9OYSi2vzVg9rXTkqlp/5W0b4YOfuOpp\nVWsDeR+8mMuZrrkV5DaWt4Hx5Zbf/sLm6XjjGku9hu27ppZWpW2cjNzy9Is/M91yazLytLwNTJ+x\noFI7P/t6Jv/OCHIby9tAZU+Lt2E6eTreuCY6FlTSaubcct38M7+zjmY4Z/NGj0XuDGhboe2zy9CV\n4aIiI9eQJzTKBtcaaWPnl3srpYnFFImYor3dIBY1GBi0yWQ0WUvjOArQKOXNlPNn0fN/M7I9I9d6\nK41h5m8gZ8Zd5s+P0ZGMEI/kn0keGfEhl3PJZDWplMPrPRZOzMWIaTABg/wM2XVRFuishn4HTAWz\nDYgriKqRJe0aNTKD9645V0Uzem9xO64ml8pyeO8u3jj0PItWrGXFukuJt8bzfaq8Vkwp4hGD1qjJ\ngrY4EaP0+xumz3dg0GPBjFvu7hnlmVuNetcDBK3ltQlSy0/sQWqF1VPxQXIraK2p8jRsPki9Bq8l\n9Rq8lp82QWqF3QfJreb3NGw+NPtY0Jey6E3nOGM5Fe9drh1whvMTVbNlZII+SgfcjKZLxZjfHWVW\ne6SiF5msy+FXMpwacKh9KltjtLkYbRojpqhkayJi0KGjDJ126e93KXrc+lmUxki4RHM29LiQqTK9\nawFWRSGpasalbY112uHV/Xt57ZVddM9byfJzryCRaC/ErWIuC5ZEmNsepT0exaiSE2HMrSC1goy9\nmGm73L38SEg1/BjlV8uPnncUr56W1rruNUWeVi282P3G5UcrCB8mw1M//TXSB++oWhBanl6996d7\nbtX7AhyLlhdbvff9eDoWrVqENbekXsem5enVe3+616un1ygtP7EHqSW5lUfGgvFp1WIsuTWd6zXo\n3OpJWZzJ1Tiba0JkVv7McLUJrFJgJhWLuqO0xqo/Ny0RN5g92+TUQL3vJEV0toZIdU8ztsvrfVmc\noRr1qhVuyoAeB5wa3aWArIZk7YnpGwde4OU9v2HWrIVcfNmHaG3tGhW3tkzmxmPMTtR+fpzfei3+\nfy2m81hQzLSdpNdaFlOM3yMkfrQ8PT9a9VBK1dXym4Bev358qKfhR8vTa5SnYfWh+Mj7RLU8vZme\nW97RyrDVqx+tmZBbfrTCmlth9bSZ69XTC2O9Sm41d25N97GguN8w1qsfJuqD1pqM43IqZdESNZmd\nqH+mtp5eVzKKJsdQlYl6RCnmJCMooD9jY1e56Ls1ahAdmXDV8rSt1WBut8mpfgen0sRZa1TWhmMu\nzDUgoSpe0B03FfPmRhmOagZOu1TcXNfFPJPGSGVwIzGocgAu0W7S0ZVg2HQ4Y7klKwq01pw4epiD\nu54gnmhl3RXvoy2xCJxK25g/k96btVAZaI9XXlHg6fqpVy+/JjtPtdZkHZfelEVLxGBOMjbh3PL+\nP9GxoJhpt9y92MxKRz+8ox3FfwOjXiu3xc+RFO8ISfHOKj9q4h1NGq9W8ZHc8Wp5nx2vVqU2xYlZ\nrb9G+lCpUIL2wc82FsdS7Si85NZZrXq55adeJ+qDH63y/GqEp7XiqjYwjCe3/PTnVyvMuVVvLKiU\nD9W06sUu9Rru3GpEvRb7EGS9zpTcqqTlxVzcxvPWe32yPQ3bWFBLqxnGAsd16cvYDGRyWLaL5Wrc\nkWu5o4YibihaYhEWtMaIGmpcnjqui+1oso7DGcshlXPoSERJRAzipkFk5I7qtutiOS5p26U/naMl\natIWM4mbJlFTYY7BU+868nTa4c03LLK9FqbtgqMhN3LW3gRi5CfqsxVdS5J0tkaJmwaxkbi01liW\nSybrkkq5vHk4BSfOYGZyqJyDskbiMRWYCtcw0fEYnatnMWdBnHirSSxhYkZGrs13NVnbYTjn8NzB\nw7y089c4tsPbL7uSrsXLUMrI353OBtdW2MNgRMBMgopoMAAjfy171FDETYO2mMn81jimGn12fCp/\nu7la05fOMZDJkXVcLIeRJ89pokoRMxUtI9fTx8aZW+Otn2oHHKbdJL0e9Y6++G0DwRyV9HRg4keO\n/LaZCVriafBa3uA60z1t9twK6nsryLjC6qkfr/y2a2YfmllLPA1eq9nHAqnX8Gr1py0O9aeottTc\n44K5rSSjtRcDh9WHFx/v50xPrmabljkma7Z01NU6cP8RMr3Zmm3mrJrF0i3nVH3/+PHjPPLIIxw7\ncZJVG65k4bmrq+e01hXP9Jezfn4b0TqX0jR6/wxmcrx0aph6uXV+dystscblVq1HJk7b5e6NwO8P\nuHqUH2kJC2GMaSwEsW+EUsTT5q/XoL63giaMMflFxoLwEta8amZPIby++kHqNez4OTDagDAmCWX4\nCV5R8c52o7TGH0d/fz87duzgyJEjbN68mTVbriOnak+sKdylvjah3D8+a177MT5AatXrBHZvOKm2\nsVrrwvKCWksW/LQp1qpl7li0ypdIjFfLazNRLe9IeS0tL/Z6y0CmwtNiXyeq5bUJwtN6WpORW0Fp\n1Ys9SC2p17FpjaVe/Wj5iX0m1Gu9uCS3SmMP41jgum4oc6uZ69VrI2NBc9erHy0/sQfpqam8+6fV\nmihpbK1x6sTuaE3OcSYcl+NDy68PjuOiIkZ+aXtVNG7Owc66NeOyczagas/kFORyLpZ1NvahoSEe\neugh7rnnHrq6uvjMZz7Dhg0biEajI49gq8LIsndluzVm4fl9iApfbhloIip/6UQ18rul9jgWZL06\nrotT46DHtFvuXssMb8lB8Q+KYrzrGrzXJ6JV3MavlrfDx6tVvPzMb+yVdn+5D47jVD3qPFmeVkvL\nej54/hV7Wq+/WlpB5sN49k+QWuP1dDz9VWsXpKeNrtdKudXoep2ID1qfvZNzWHIrrPU61WPBRLWm\n01gQhnqditwKY72Op79q7aZTvU7H325BxlXcpppWcb06rmYgbXEqkyNj559n7qK9p4zjzUoTEYPu\nZIS2qEk8YqKgcA15b9piyHIxFMyOR+hKnr22u+jx3RV90Frj6LzWcM6hN51jOOcSMRQdiQgd8fyz\ny2OGUXJytrJWfpKctTRnzric6HFIpV1wXMy0jZlzUI5G2S5Ku2A7GGkLw8phmIq2c1qYc94sErNj\nRFsiuLbGGrIYPp6m/8Ag1pmRZfMGhRPc2lDoWAQnFsGa1YLTmsCIKNpbc7z+2m6e37eHCy+8gKuu\nuorW1tZC7FprUpad317LJutobMtFWxqV0ugTDgyRn8l2Kug0IaEw4opYRBGLGMyJR+lqiREduX4+\nbPXqak1/2uJUOp9bOVdjKIibBu2xCHNb48QjtX+PTOS3W3FupXIOPSO5ddk5syv3Nd0m6cW4rr9r\nBoLS8tufn3a1rlGYyrjC2F+YtaoN3JPV33TPLT9+BtlfmLXCmFvNrhVGT5u5Xps9HyS3piYuGQum\nRiussb/Ue4ZBq/pkCPLzU6U0rq6dE2/vTDIrEavZ5kzW5sCpobpaa7tbaj6CDeDNt7IceTVX/cQz\ngNa0HT6BkbFrahlJAzfj1lxkoIHh1fNxo2fjcl2bN19/jlePPEVn1zKWr7ySDevn0dlRO/bhwRz7\nH+uH2pfPs+qds5jTFa9Zj37rNajvSb/tLNshahoN+24esmxe6hudW9Um6XJNuiAIgiAIgiAIoaPa\no7GK0dRYgV3Wzg9Vnrw2ZrT2EZdStZeZezFZtSfoeS3A9M7guhx/6yWOvPwErW3dXHTJjbS1zy3E\nVQ9DKZSPLiM+biIZViJG42MfS25NyzPplZYeVTq6Ub5MwU+bSu0qLcOop1W+3GOytMp3r59trHTX\nVj8+VGo33v7C6ulU5JaffVi+rK0RnhbHVbw0s5pWtbgmK7fKl7sWvx7G3BpvvU52bjV7vZYTtrEA\npF7rxR7G3Brvvp7uY8FEtJqhXqfjWOBHy3Y1p1IW/RkL24V4xKArGS15drnWmiHLpjdlkc7l83B2\nPEJ3a5yYeVYv57j0pSwGsjkcF5IRg+6W2KjnbHue5lxNxnbpz9qjnl0eMxVdiQizRj6byjn0pnKk\n7LPbo4BZcZPuZJT2WITIyHr34m3UWpPOaI6ftDg9aJOyXYyYRrWBipy951h++bxJVzJGe8zEVJW1\nhoYcTvTkOD3okE7rkmX6HpEIdHWadHdGiNk21uks/QdPM/xWGj0SvgbcOVH0kiRuWwTlaIyeLMab\nGVS2KJfiBu7iBO7cOHYyxsnXj3LomScxzRjnrtrMnI7FgEbFXSLtkGiFZMxgTiK/PD1SFH/Gdukd\nzjCYsRkecNDDLpx0IFWUHybMmhela0mCWd0xzOhoHzzGkqdKnX3UYjPVq18tV2tSOZfhnE1v2iY9\nkqczZrm7Z1R5oVfazHITK32ZhUmreHI40f78aBW3CTL2ID3180Nmoj741Qoyrlpak71/JLfqb+NY\n42rm75rJrNfJyC2/WkHG1WgtqdfxeTpdc6uZxwK/Wn5iD6tWo30IMh96hrP0pHNYTv5mbaV39s4/\nGzumQCuF7Wpyrh65evwsJhAz82dmXQ2Wm78ut2SbR55V3RozWT6nBUNVjj3nuuQcF0fnz+DGTEWk\n7ICj47j5dm4+kqipiJpmyRn5Yh8OvJxheNjFsjSOWxq7Ui4qAt3dJosWxoiZxqjl0Z6W62peOpgh\nndFkLY3Wo7UAFsyPsmBulFhcEY2UarmOi52xSZ2xeGUgjRMz0DEDyvaPyjmorIvOuaiogY4b6KhJ\n/4ljHHjq1+SyGc67dBPzFi0H18ifqTdHdoYq3YcRpUaeC87IDfLAoQxXQ04zyzBZNCtBPGEQjZso\nIxx5WuJNk4wFjutiOS6ZnENHS3xUe5iGk/R6NPpaGr9axUnRiP78tJPr1fy3mQlazRx70FpSr8Fq\nhbVepyIuya3gtfwgnoa3vzBrTfd6PdB7htN1rgfPUz6BH1+b2XGT1V1tdXsL0tOdu4fIWrXbrF4V\nY1537WvZcznNrmeHsO3a23j+2+N01Lse3HLY33sGv56eOdXHwV1PMNjXw6pLLmfRynegCtvuZ9/4\na/e29jgL2xN1laRe/bezbZtIpPLV53JNuiAIgiAIgiAIQhORHhrk0O6n6Hn9KCsu3MBF296LWWXC\nJzQf0+5MehDL3Se6BKPasolyrUrLJqZCa6qXX4XFBz9aYVgi00yeTrUPUq+jtar1V6zVDD5IvUpu\n1YpLPJ147NPJBxkLRmtV669Yqzdl0ZOysBxNTpeeaVXecncjf9sz29VYo5a7n11ObRr5VdPZCkvn\nFZqYkV/uvmx2srA0vRFjwaFXsgwNOViWxnbKluqbmnhMMa87wqJzYlX7y7matGVz8LBFLqvRNmhd\n6mnE1MTjikULo8ztjlbUchwXK6cZTjscGUijTZ2/lN0o9TSXSfHys7t48+CLLHnHBaxYdzGRWKLE\nU1wNLuiRM/sqoisud4+q/GUDSoHjVr4cgZG92hozWdwWJx4xiRql1427riaXccimHdAQiRnEkgaR\naOmqjrCOBTknv/zccTURQxEzDSJllzZMVr1WO9s+7SbpkDfFm6xrXflCfxhtdiWTXPfsjcKC0CqO\nsZJWpaSrpFV+c5hKbYp98BtXLa3iuMqLYCxaU+FpkD4U55ZSo29uMRat4kKebB/GowXB3XioWpty\nLcmtYHMLJu5psa4fT7Ue/43JwuxpkONKsW6zjQVSr9NrLAhjvVbrz6+W/HarHNd4PfWeXd6XzmFr\nPfKM8tKbvWmdv8Fbz3CWoZyDqWBOIkpnS4xokZ7tak6lLQbSFraGlpEbx7XGKt84rlH1ms26nOix\nOD3ooDXMnmUyf16MRNwYpaW1Jm07pHJnn8muC+8DNrjDYOQMWqIGnXMizO2OEotVnqgND7sMDTsc\nP2kzNFycRxoVdTHbwExqbJ3j6P5nOLrvGRauOI9zL95IoqW10BYNOqtwLXCGDHQOzk7cNSrmYrZD\nS5uiJW7QkYjSkYxhFh0EsEZu7NefyTGccyre9E4BbbF8DsRzCuuMTe+rGc702oWb3gHEkgZdS+N0\nLIjTMidSdf949WoYRmGJeCPGAsvVpG2XU2mL01mn5OBExFB0JCJ0xCP5PK/SX5B5Ws60nKR7+L1m\nICgtv/35aSfXq00PreKjaI3ob7rnlh8/g+wvzFphzK1m1wqjp81cr82eD5JbUxOXjAVTo9XMsQet\n5Se/9p0YJD36lHMJ81oiLJvTWrMNwNN7hshkq7/vug4nBvbyygs76VywiFUbrqR19pzRcbuQO6bQ\nTu1tXLM6Tldn7evi0zmH53vOjLoRYDnqhSx6sGYTZi+IsvrKjtqNCO570m+7Q31D9GdH3SavhIih\nuGBuK9E635VB5lahb1+tBEEQBEEQBEEQBKKGqjtJN3zMxVyt0YanM/qM78kTB3jl5SdomTWLi6/5\n/5gzd35tQUNXuD372ONytPb1XPlY3CBL7ZsLaiO/giLip+MGYiqFgprbqfB3273JYNqdSS9fTlCM\nd4Sj0tIE7/XiZRF+tIqXVAWhVQ1viVK12MeiVc+H4v7GolUplYL0IWhP/fgQpNZYPZ1obhUvYfSb\nW7W+Dry4ypfrVWpTq8aKl5lJbs2MevWbW83s6URzazz1Otk+jCcfpF4np16D/M1SifHUq4wF0yO3\nxNPxeao1WK5L1nY5nc1xKuNgu7rwTPZExCBmGoVnqXs+AGSckcsCLAfLdsk5Gu3krx+3U+CmDE71\nvMrhg4+DUqw87yo6u5agRh6jpmIa1aoxYgqlNIzcmV3pkUe/OeDmFM4wuGmDiKkKz2RPxBWxuFEy\nUTcMA601Z7I2ven8c+6zjsYp5IZ3rwFF1FB0Jkxmx6PEIwYRFI7lkh12GTxp0fd6FivjQrtCzTfQ\nCYWKK8yoQdxUJCIm3S1R2uPR/GP5pjC3NGA7LllHlzy7vCVqMDcZpSVqEjNVyeUafuIqbuM3tyox\n7SbptfDMrGVK8RdWrWULfrSKd141reL+wqpVz4fi68fGqzUdfKjXn+TWaK1G5FZxXGH1IUx5Kj4E\nrzVTPJ0pY4EfLcktqdep1ppovc4UH+r151fLdhxAYRiq5Jns5f290p9iIGvjVjk/O3DyLQ489SSZ\nwSFWrNzE3PnnVZngaaLzXVS89CZ8ZcEzOxZhxZwWIpHanr7QO0Tadmssb9csaI1zTlts1LPpi8lZ\nDvt6hrDRZTepK9VaPjtJVzIaqtxyXBd35F59ptm4saBa3DNqubthGDWPugGFo8i1CtGvltemllbx\nWZEgtMYSez0t13XrXq8WVFyeD0F5Wvz/yY69WCuMuRWUVpC5NVVaUq/hzK3i/09UK8h6HUtcklvh\nHAvq7b8gYy/WqpdbzVyvYfz+lrHgrFZQ9Spjwdi0IqaZj6uOD7arK07Qhwf6ObjrSfpPHOPcCy9n\nXtv5GEb1aZrW3ln0Gn4pRcRURKP1fXBG3Zl/lBhRQ9WcoANEY2Z+lqtra5lG5Zttng09+LGgXr2a\nhoFqcG45jiOT9KCpt6PHqhUkQcXmJ6GDJKw+BK3lp68wanl6zerpTKjXRhJWH4LWamRfYfV0KsaC\noD0NW2750ZCxIHhmQr1WP3s5OQSbpwDTPLfKmmSGh3h5z284fvQwyy+4mAu3XINyIuROmNS7KFxr\nVf966ZGztfVi87sXA9Py0Wgm1GvNAwI66KinmPJlD+XXC5QflfH+79ngHR0pt6WaVnG7iWiV432u\nXL9ef5USphE+NEqrmg/e52oxnn1YKabxxO69F9bcKv/cRD0d6z4cr5ZfHyq1m0hclXyYifVavh1h\nqdep+N6a6rGg2NPpkFtB7mu/PjRiLPD+H4Z6na5jQbHmVOTWVIwF3jOe07ZLX9oiETGYM3LNcMw0\nMA0Dx823ydouA9kcGVvTlYySHGkTNc9eQ1vuqR8fxjsW5BwHy3HJ2C6nMjkAuhIxEhFF1DSIjpyh\nLvehkqf564vzWn3pHFFT0ZmIEh/Zvog59WOBraFn2KLvzBD7d+/k6IvPs3j1Wlas20AskRhpB25K\noVMq/8x1G7RrgHeuW+n8AY2IItLmYsZ1/rTryHPQVc5BZVwYtjGPpelsizF7eTvx2TGiLVEiMbPw\nTPZMxuX0oMPxUxY6qTFjOq9jAor8c+5NRdK7ljxWen7XKMut09kcJ1M2kF86rzh7ht57JnsyajKv\nJUZL2TPUp+K322SO535zq9pkf9pN0ovxjKl1pMMztNaRDO8Lt97SBj/9hVXLjw9eu7DFHlYtya2z\nbcBfbomnU1Ov9bTC6oPUa/BaklvBa8n4erYNyFgQpFbasjk2lGUga1PtRuOJiMHsmMlpyyFjV560\nmAoWtceY1xJvqKevD6bpS9vk3MrBRw3Fqo7kqGeol2M5Dm8OZunP2NhVpjVx0+C8jiSJqDmluZXL\n5di5cydPPvkkq1evZsMVm3grF6l5Q3btQK5HobOK6svb889UT/YPYB7LoqzK+zraFiG5fj4DllH2\nTPYilCberlm6NE5XS6zmXdnfOpOhN50jXSW3AFoiigWt8VHPZC+JPqQ1NhXfgR7Tfrl7LbPAn1GV\njtCMtz+/Wn4SIsi4/BxxGgtB+dDMWpWOtE1mf9Mht/xsY7PmQ6Nzayw0Mh/CqiX1mifosUByK/h6\nnQm5JWOBPy2tFKcyuZrXEmdsl6zt1GzjaBiyHBa0NbZe+1I5cjXkcq7GcjRtdbRAcSqdqznRzTou\nlvJbNgkAACAASURBVOuSVLWnPpM1Friuy7PPPstjjz3GokWL+PjHP053dzcAPcdP49QoDWWCEdU4\n2Vr7R6GzBpE3s5CrLpYbshl8I0OuNVldSisMy6A7Ga06qfY4lbZI27W9iJoG3a3xmm3q5ctY2oa1\nXsc6FkzbSbpnQr0j036OatRbQljedqJa3ntBaY0lrlp4bfwe7W9U7N5jYPxoOY5T84Yqk+Gpn6Nq\nMz23/Gr5OaI5GbGHVctPboWtXsOaW1KvpVq18Ks1lv5kLJDcGotWUGNBcdtm/A400Sxqj9ObsslU\nmOVpF9wM6LRCJcFIgKoil7Ic3hhMM7clTjxSuVHQPixqj9OTzjFcZVLZGjVIRGvfGMxyXE4OZXAL\nFzmPjksB7TGThHdztypa6YzLyR4LrWH+3BiJxOiDQY6rGUhbDFo2cxJRZieio24Wp7Umc8ah59UU\nZlRxKvMav3riUdra2vjd3/1dFi9enNfK2Jw+3Is60oexeDZudxujHmKuNeq0RezVDI6KkpvVgo6M\n/u5StkP09DC1ZvsasFti2NHIyF9V6sJxcQdsXt/vMH9ZC4n20asPXK05ncmRdXRNrbhp0JmIjun7\nYSaPBcVMu+XuxQZ4O8jbxEoGe2aWDx7FbStpVWIsWvUGq0rXNfntr5jJ9mGqPK20jWH2tPhI3GTn\nlh+tSrGPNU8nmg9Bas3k3CpG6rV6f2HwIYixoFK9hsEHya3m9DSIsaCWlp/Yi5HcKu3Prw+265Ib\nuSa4Z9Cip8dBWyr/vGzbWyKtMSK68Jxtc5aLiqiRd8CbZBlA3MxPrrpb4syOm5PqqePF7rgMWTag\naI+ZxEyTqKkwK3h6OpN/nnfGdrFcXbTU/2ybiAELW+O0RSP5Z12bJoYx2tPeUw69vTkyWU3W0jhO\nfltNUxOLKRJxxew5JnbCIZVzsBxNTnuTUk3UUMSN/HXW0R6XoZ4c2WEHK63pPf0mB47/Bo3D+cuv\nYMni5cyZ5ZJ7o5dsX4rcmSzOcG7ENIVuiaJbozidrTiJFszTNirtQNqhsEwgqnBjJk4sip2IEsnk\nMK0chuVQWJZgFHYnWimy3e24rTHcWATXNEYaaM7eHV5DyiGStTEcne9rpD9lQiypiLeatC2IYnca\npHIOWVePXKaQ/7wamahrNF3JGF1l9wKolA8ztV7LtapN7KfdJL0eQRz5nwytSjtzMvub7lp+/Ayy\nv5mg1cyxB60l9RqsVljrdSriktwKXssPYY09qHwIMq5mz4cw7p8gYz94OM2Jk7UWfgNo4oud/MXo\nNVjVkaQjGQskriC/c587MUim2kX4I5zTFmXxrJa6Wk/tHsKyareJdjsYrXWEchq110LbMJju5cDx\n3zCcHeC8BZexcPaqwnYle17HGB6uKaWNCE5bJ3XvgG5CzTX+gDUnSWZxVx0hiPekwK7TaJkJC+ov\nwr5oXhuxCmf7i5F6zVPrTP60Xe4uTJwZdvxGEJoaqVdhspDcCh6/nvqdtAhCgRlQrirAjQyyulLW\nIAfe2Mmp4Tc5d+7FvG3pdRhG6QSs5uPDp5KwxjXNqXkWv4FxNIRqG6u1LiwvqLVkobhNI7Rc1y28\nX01rqmL3loo0o6eeXtg8DZtWeZtanoYt9qnQknoNXivM9eq1DWtuNapemzm3iv8LU+xh83Q8uRU2\nTxupFeaxIJk0iEWh+mxdE4uBqRRGjcmuAdhu474DHccll3OxLAenynXVWmusrA02qBp3EwdN1tFk\nbQe3yp3jtdZYtpNf/m/UWMqMi5sDbA1VYs8OD/HCb3bwxEv/SGtiDu8872aWdl8waoKuGLmBX60V\nDAYj7+vas7TIyGUMkdpaynEw7Pwj0SqjiUbAjBmY0epSyoSIA1GV/0xVLZV/V+rVn1atM+3Tbrl7\nrWsLio2oZpqfNt61BxPV0rr0+XjeTq101LyRWpXalB/N9/4OwtNKsfvZh96NIeppTcSH4n0tuRV8\nbk1HT7XWJUuX/OZWM9er5NbEtJrJ03KtIHMLxvedO5GxYLz1KrkV3nqtphVGT8vjCspTx9H0D+To\n6bVJZ1ysHMSikEwYzO2O0DEnimFAxnHpHc5yxso/q1wBMdOgPR4puYHcZP12s21NJusyPOxy/KRd\neCRYe5ti/rwIbS0GsaiBk3PJDjn0H8vSf8zCyWmIAt0K5piQUBBTI2eDNd7sVgHtMYOuZKzwPPic\n65K1NX0Zi9NZB1eDzoEzrCFr4NqAk59p6iItlEYlXCJtFK7tz6WzHNn3DK8e2MuChe9g2fKNxI0k\nZiaHabuQczHsHCqXw0gNEzkziOGMrClX5G8Sp8ifXjdNXMPEVQkwo+DlQPE83zTQhokTjeBE4mAY\n4LqYdhYzZ6McJ3/jOO9GAyO7TQNOMobd3YKTiEI8SjxpkEgoujqjdHdGiUQUVsqh57UUg705rJSD\ndiHWYtDWEWXushYSbSYaOJ3J0ZfOkck5WG7+uvxExKAzGWVO4uxj1sZaY9513d6/g/jObZbfbhX7\nmm6T9GLqHaEIWstvf37a1bvb4FTFFcb+wqxVPlma7P6me2758TPI/sKsFcbcanatMHrazPXa7Pkg\nuTU1cclYELyWbTtE6lwj7DhOyWRmIv35jX3n7iGyda4Hj51Oo1J1pioxYF0UzDqTHnTNR9EBOGmw\nTxrUWv/tujZvvvEsr77yNJ1dy1i+8kqSydmj2sXfOkHL0TfrriR3ZnWhde39Y7cncaKJs5P3yoER\nHxyoe536kmsX0bGkvWYbrTWu42LWyRvbcYjU+R7xW69BfU/6bRfWscBDrkkXBEEQBEEQhGmKUedZ\n1+Dv2fNB4+c0odbBXS7t56xkLQu0djn+1kscefkJ2tq7ueiSG2lrn1tDzGfsStUPTqnawZW0qS3m\nIx3y+eCjYfnj54TgmJZn0istKyg/ulG+RKF8OcRYtYptnIiWnzZBalVaqlHpi7rRnlZasjveuILc\nh5WWVUpuVY89jLnVaE8r9Ve+PHgsWkH6EGS91msTpJbkVvBaYfC0fLmh10bGAsmtalph8NRxNf1p\ni/5MjqzjYihFW8xkbmuchFmqV0/LdjWnUhb9GYucozENNWrpudaaIcumN2WRyuVPmSYiJl0tUWbF\nzz6zO5dx6XsjzcCJLLmMSzRhMHt+nK7FCWKJs3UWlKeOozk1kKO31yaTdTEMRVurwYL5MVqSlX1I\npV3SGZeeXpv+ARevC9OEzjkG3V0RElGFm3U505ej99Us2eH8NmvAjSh0awQdMyCpUDGNaiX/PPiR\n7rQDbgp0WuE6+WurjbiL0apQ3qlKV6MGsphvZlCDNuTAiUexZrfgtMTRQF/vEQ6//DiRWJTVl1xF\n58JzwFE4KXBSBrj5DpWC2bMM5s81aYmCSmfInBxiYN8JMieHznoQiWLPmo2bTOKaMZTWGGkLw8qh\nRvJSG+DOi+MuSua3EwOGXDihIXM2dxPtJt3L4rR1RDFxsc7k6H/5NEOvp9Ajd8E3YgazlrYxe3kb\nLXOTREZyIEz16i13rzQWBBlXkL/dghwLypl2k3TPhInstOIfBPV2GkwseZtFy88AHtbYa2n52dfF\nbSbT02bKh0ZrTXQfTmXsU6E1Xeu1UVrNHHsYtJqxXmUsaF6tqcoty3E53J8qe2520efQxAzFsjlJ\n2mKRmlpDls2rgxlyjsauqJV/drkG3P+fvTf7kSW50vx+ZuZLLLkv99a+sopVZBWLZDeJ7p5Go3sE\narpnIGgE9AACBg296X/QG/WuFz3oQe96FAQIkARBDbRITI+mF5LdXVWsroVVrL3uzX2Lxd3N7OjB\nIzIjIz08PO/1mxmZNw5AsOpeq89OfH6Omx+zc+wIZL4obVsIlcLse/jGkfU8riCV3EQQNTWv/v4K\nYUM/NA+ZFf75gz5JKqRpge5KiGLFS89HrK5M5iHNPFmW/6owVIThxSDGZo607/nwoz6dnsdrBRdu\nV8v7wQuDA2oP4tQFvZT2qACan+1i+hn0PBfuVtOw63b5decdUp3x6u/+C+688NJ5vUTAg/Lw6lqb\nOFREkbmQveCsw3ZSvnr3mL1vEkSHedA9prtSAkbglQAaJt+AGA/mvIcUnl2IWWmFRA2DCcY49ULW\nt9i+RaEImoagEczXghr0qnstmJQmf+vS3Sf90OGfl9UMVBkz+jDqxBo/KXhQrGk1EZfBmlavNsuc\nlvF5Waw6Ob0O26oL66p4qIo199fzWHN/rd+2yvSa29blsK7TX8tkFjmdrwWXw7ouHjLr6VhPHvxd\ntDWPou9Bq4unb+NY3czTs8NAoggLeg7yML14PlBkAtmehcPJ528uhb71KP1w38xntuzpdD3eT+BB\nFP0+BEE5D3FkiMLytSAIDUFocDrB60nvJIW3CvAFQfCZiNdICvokg+RiUHWUHfLe8dscZge88saP\neep3v4cq0l8pMGACRaulCSf4tQkMZrlJSg8/US2FiMovwVsMmZiXrjU0YHE5pBkXX8mutCJqhQQN\nM/fXGV5frbWPT5A+l7nMZS5zmctc5jKXucxlLpeVru3w/vG73Eu+4dWF1/nR6h/gn13HlwRll5Ib\nnL98g1W/kXLrgvRhisHorsRo2sGwLgAu7q4M0w5Gx5RhTZpvEtb4zv44VlHaw3iaRhWsy+o+iYeq\nWLPK6ejvuApO6+ThsljTbGsapw/LQxWsq+ChDKsKD3N/nfvr+HyT9HqU/jq3rfP/Xoe/Fs133bZ1\nkzm9irXAeU/mPInzeBFCnbfQCk1x268h1jA7ZxwrdZ7EegQhMkOs87XZl+Eh1oqVyJA4T+IYy5TO\nU90jo3B+OtZSZFiONIn1pF7wIyfSirzFVWw0WuV16xdT7OW06xYbGlIHCZAIw1ppAGUgairilsH7\nh3s+NnPYbkZykBF2E6zW+MAg50645bRd2c5JioogDjSh1oymg9vMkfY8SdehFEQtQ9TQBOFISyzn\nsJ0e6cEx0e4RqYvxjTY+bIzwANguJEf47iFKa1RrDeIl0OE5vZQXtPO4KMKQkaU9Pjj4NZ93P+XF\n9rf4yZ0/y+3D91AffQksIYttpNnMi+ZHsACcCAd9Syv0REYT6PN2mmaeJPGoxQA5cigr+S3so5Gv\nARWDNMnT6EesYHS+SCsirU772I8/Q6jXX7OhL1pBq/wZRkZjbth7azj2QXgAyDJHkgpJkt89EceK\nKNIEwYPzUJY5cutq0ocyJGX4oi4iYfzBFaUbjL70J415lFiTUvZGH/r4YlQ0rg4eRp1hEtb4BQpX\nwamI1MrDVXI6ysO0Z30ZrIexrUfB6TTdq9jW3F8vzidy8XKVIt2v2rbKsKra1mhK2Sz66223rTLd\nb8NaAHN/HcpVrgVVsLqZp5NZtnsZ3ez8bzYKVuKAjVbEYlR88dVQF+89Xes5Ti07PUvfnscKtGKt\nYdhsxTQHH9kPymliPTvdhOPUEmp94RK3cR6GMo4lIqe9yzuZIzKajWbEYny+lnh4Wd1OL+UoHfbb\nGuNdBLoedjytTLOwZNh4vkl7JbzwjC5jW73tPp37PfY+OCQ9zM7jBBq72iTbaMOiObvEbQROcda7\nPOzA8XbK7ucJae+8DlFLs/F8zGIrwR3usver9+l+fg9GfUob7MZTZE+/QKL6uK33sV/+EtKTc1hq\n4Q7hC39AcOf7aN1CdSx6UP9ufcanO2/z6c7bPLn4Aq+1X6WVdKG3DZ1tlNiz+QC/vor/7rdwLz4H\ncQgFKfWBVqw2AlaCAJsotrYzDg4952gWQaWOILFoI7CoYDPIe75fEE+sNa0oYLMZstS4aFt1+6sX\n4SR17CeW/b7F+vPhYjNQbDQj1pshRlHLWqC1rvz+noZV1/rqvXB84tnbt2zv5vcmjEqzobhzJ+Du\nRkAQTOahylowLrc2SAdOH/hVYVWdr8q4m9y/9Krnm2Ws4Qvzqua77bZVhc8655tlrFm0rZuONYuc\n3mR/ven2MLet69Hrva0jTmz5p+lSZHhtY2HqfO/cP6LnyrGebIc8u9yaijWLttXNHL/ePp7a+/v1\n9RaLE2qXLzMfwD//rx+T7melY+x3F3EvTH8+/CqBaX3Sv/xb9N6XpWOcpOzKR3iblI5b/O5/i2k+\nD4AXxxd7/8zHW79krf0Ur9z9Me14GdXZIf7451NVT//8X+PXVsr1OhLs/vSk5fhpC0H5M3xxOWaz\n3ZiKVZdt9TLHuzXZVtVvt7rek1XHVRmTZsIv//EEa8v1euP1mNWVch6gOhdwC9Pd5zKXuZRL1ZfD\nXOYyl7nM5fbKrK4FcaDpWFda/xpUafQ8wOq7cizrhcx5QlPPoc40ybwntY5WWO1ywzJRQGQ0yZSN\niMR62pE8dE9r5wRrDEI2MXTLb6DXyKDd2STxSRfX3SIwd1GqmHsRz4G9z6KkhCqaiNWXPl3pEaNQ\nEzVT6EyQyHHv+Ld8eP/vaEVL/M4L/5rl5lmvc+UcqBBk8kaEKI0kCrxMvtwtnxL0+ZKDC+IHGQ+L\nOr+EboJcdT/yNBV8BgST1VKU//zbIo1YcWLLxzyK18etO0kfT4UYymhax6QxQxmmW4ymSxSNKZuv\nbqxhKsZ43cRlsS7LQ1W9roKHUd3rxPL+Yh/eh8EqkyEPVZ5hUe/FIqzbaFtX7a/D5/8o7PQqOX3Y\n+cax6rStOv11mu51Yj3ua8FoWt58LZivBVWw6vDXzHtSJ3RSx04v7z++HBvWmhENo4mMuhC0TOI0\n80JiHSeZY6dr6TvPsBB4iKBVXuPbCDTrzZCVZoQa6PWw9iDAYT9jt5fRzxyJF0Qg1PkmwnIcst6K\niIx+IE69kNfbO89+P2OvZwf18R5QqMGN8OGgjrkdBWy28xT/aSGAUoqjY8v9bUu340hSyDKPch6d\nWkwnJdzrIE5wq03sYgOJAnxoQIMKQIV573IVOrJvPiL56O+xe/dwJ3v4pE8QLWPiNcL2KzRWf0gi\nKV8e/ozdzrt0k/v0kl0iHdFWCyyxwvP2eVZYY1tt8bn5jBOO6PgTrGQ0dUxDIlZdmw23QMus0W6/\nShTdIdBttrIu7yafgNJ8Z/VNVldexocRJukQ9o7RNkNlGYgDsYhP8ckBkhzhG4v4zZeQ1gqELbyJ\nINIQAwsaNk2eqj4wF8WgrFwACz5T2A5IT6ESj0ksxgq4vIUbETnWooaNgLClWWsYluPwtAZcjT2b\nOv3Ve9jbz9jetfT7niQVnJP8GQagmoJuQTPWbDQDFkJDPLgjYtxmHnQtGP6ey+j+qL7dRrG8hzTz\n9PvC3r5lZ9djAri7aVhaNDRiTRSpQqyq78AiuXVBepkMiZpUewDn6+3KiKsTazimbBEerTUpGzfU\n66p0H3euh8WaNmbUXKfxMI2rKpxehz08Cqy6OK0636zaVhW9qvhYHbY1qtfctqZzOus81GnzN9W2\nrtpfhzJfC273WuCG89WA1beWd7c6+NNWZoVofHutxWIU1OKv722f0LGuZD7YbAY8v9yshdPPDnts\nddPS+TTCW3cXz11uVoT1wUc9dvccXkqOSyW/5k4mnIYPBnHyd/8jdudDxE0+kjw2ng/0N2SuO3GM\n0SEag5MUL5MDoDea/5Lvtf4ULYY9d8S7ySd0fZ834pd4OtjMf7dRgAJXHkgl63ewi8tASWpACLwV\nDtLWJ/AlAh9keYu8kuiruWJ47Y9WCIPJ89Xtr796u0ev5yfrjvDcsyFPPxURzNhacNXfbpn1aAWm\n5Pj8MrpP4uBqcntmRIYklBE//LtpNQp1YpVhjI+pMrYu3csMZxSr7ORhdJ6qepXJUK9pPExzsFG9\nZs0eHgVWmVTl9DLz1aV73bZVBWsaD1U5rYJVBa9uf62CdRm9yqROf70OH1Nqcl/fR6lXmcyybV21\nv1axreFpRplcx1pwk/31MvPVobvR+QliLTyo4Wlk2W+sn9Py+fK/rotTX2E+QSEyHcs5KQ/QAZSG\nqTajUN6XBugA1vdKA3QA5zMwqjRABwhMg45L+E+9d/n/eu/wTHCH/7z9Y54J75z9bjc86i4XCQJK\nA3RymKm2pVQ+cMqUCoWp8N6q1V+n2o0i0Ko0QB9i3fZvN6PLA/TR+ab6a8lJ+2MVpF8maWDa2KqO\nURWrzoSGKvNVkbPF5eGxqup1lZzWrfusYlXltK75ZhVr7q+za1s33V/ntnWzOb0O25plTuuarxoO\neH91POSRaRWk6c9nWB4xHarCQQzD4HqyiEilPtV6GAiWg1WJTYEKWFTTa1qADqCUZlJ9+nksN2VE\nzNeZ8P92f8WqXuRP27/HS9FT6CLsCs9QSYVgXqj2rCv5YTVOq0ql92QlnJv9HfiwGHXPB49Zuvto\n7VZeY3Hxuv7RPxuOHaWh6L8bXVBHUyHKaimqYo3WSdSFNZ4Gc1msSWOqcvog8w1/+yxyOpoCUxVr\n1LZGT06qcFrETdF847WKV8FpmV4ief1q1d8zyuncX4u5qoI1aczcXx/MX8vmG/2zUdt62Gc4y7ZV\n9b97HGxr+M+X+Y0PYluT8G/KWjAJC9Rpv+iTE8/9HUscKe5sBDSbeV1nFF5cQ+pcC7qZY7ub0s3c\nab9xBYO+5prFOOBOO75w2bZSiszl/dZ71rPTS/ECm82QVmhOe7iP82AFdroJR4k97YMuQKjyPuqt\n0LDRimiH5sJ8zsu5evNO5lhrhCxEhtgYwkFt/rk5lWKvm7Lfz+gP5nMCynlIQPoCO46G1Ww+36C9\nGhC3DWGsEYEsE/qJ5/DIcW/LkqaS17WfHgIrlOR9xlXmoWNRHmQhQEINBrzSIA6VnEB3H9n+GP/Z\nL7F2n0xneBzOZ4jLIAxweFLJOLAHHKseWWiwSrDiSW2fyMQ0dZOWNNhwy6z4NjvBMXv6iK706fku\nXhyN+C6Behnrlrm79DxvrP6YdpZgsgxlM8hcnuI+3Hvwg80KDac3oA02jaQVIu0It94ifW4drIE9\nn/eeTwALJoKoqWksBqw9HROtGXYTSze1JF7IfG5bwz73i1HAahhyci/h4F5K0sn7w3srqFAhMaim\nQtY17Y2QzVZUalt1frtlVnH/fsrhsaOfCGma350QRYpGpFhY0NzZDGm3zgeVj/Lb7VG8v6/7HVj0\n7TZJbl2QPireV2vpBNN3tqpgVal3uAxWFd1HjWVWsOrm4SZzCrNpW9Ow5rZ1eay5v958TmE2/XVu\nW3NOR8fcVE77fcdvfptwcOiZ9OUZhoo3vxPTbpU3H6rLX70IB72U0GgWoqAU7+O9DgeJZdJF6lrB\nK6tNlhuTbyEXETqpJXWe5UaEKbka+8vDLjt9S1pyc/taw/DiSgtT8htT53nvVwek9yxMuLBcKWg9\nHZE1Q45PysOC4LCP7nnUhGEC2JP38F//PRzfL0xcEBE8lt/qT+n4Y2QCmEdY0Xe549dp0yy8uV0Q\n9o3j/vp32T7e4+7SC3zr7o9ohmMt4JylufU5Oinv+eaWItIfPI2/u8jEq8sT4RkVsvlEk7BRzL0X\n4bCfEujJtiUiJB3Hrz87wi3qiW3YtIKXV5qsNC72uB/Hq+NdIyIcHVusFVZXQnSJndb5rhndXH9Y\nrJu8FgzlsW/BNu0hXxdelb2Tol2bB5U6sYZ4s4hVZa7bzmmVF8Ss8lDlxXxZvKuSunmoU+aczra/\nVpnrtvNQN1aVuW67v17mY7GW+VAcHTmkpMY5ywSbVeO9Dh60Uqw0wko8HKeTA3TID2CzKan7SikW\n4nDwQV+u/8ngpL9MelP6yUPeoi3sCGlJa3MRONq12JXpYYHJfGnmtwL00RZyfH/yGKUwhGTGlfqZ\nRrGp11nwxX3sPXBPR3yiY1Z8yO+99G9ZaKxOUDyAIIApQTpRgH9isTx1PVYsb0SE0WS70UqxHJfb\nllKKxkJAsG5K767zAnbkBLgMr473llKK5aVqdloVb74WXF5v89Of/vSntcw8YzKejlgkwx2NaTuy\nVbGmjamKNdwlqopVh+5FaXHjMkynq8pDHXpNG1MVq8qY0XF16F6F0yFW2Q7cdXJax3yX4eGm+utl\nsOrQvU5OR/9/zmk9WJfRfb4WzG1rFGtW14I6OBXxNBoaa4W0IBAPDGxuaDY2QrQq/n3DE74vvkrZ\n27eEoSKKLgYAmfNsdRK2OglWhDgwF1q2eS8cHFq++Crj8NASx5owuIiVWM+9kz6HiYMJt8IrYDk2\nbDSjPJt6gu69vvDF1wnbOxatIY4vXmzoMs/eVz12P+7jex5iPbiF/BwYdDzytSXZsphQETXNBSzb\nTdh/5zNO3vkNkmb4IAZdcAHaAvCUQS+AOCHv630eS2WO6OCE8KALCKLMhUDW+Yzto3/iw73/gwO/\nTcOHhAQXTsC79PgsuM89vwPkV7KNj9E6ZnXlR2w88WcErSeR5ABckv98YFsFvBM26IUx3/3uW7z8\nO/8ZkWpAQQxuQsXaMxF3v7NM2A7JDvv47HxULIBfbZK9fgdZjAc/f5I9exIreF9sW3A5f40DgyCk\nblJteP53iXXEgcZMCHpndS2o+u12mXXltq4Fo3Lr0t2HRI3u2lysiTqT0RqFaWPGCR6VSfONP7Ai\nrHHDfRis8XGXxSrjYYg1rvu4oT0op+NYN43TSb9x9MUzCetR2tasclr0G+e2Vd97q4ptTcK66bZV\nJ6ejWPO14PxvnPtrfbb1OPmr9540lbwuvesIjKLVMsSRIgx1IQ9ffp1ycOhIBrWywxvHtRKiSBHH\nioUVhWvk9duJk5FTbyFQef13w2jkSNPtCP1EyFJBTm9zF+Ih1qoiC90AC0Z+1WnfcaWEZxabtEND\nZBShOQvWRnnY3snY3rGndb7Oq1Os4XzNUNDHluTYkfQ8tj/yMR8CEUhD5b20e5LXRCfDYBqUhrCh\niNqGdpygvv6UdO+E7KiL7ySnWEQREsXYsEn21qvIRgNiladZj9Zke5BMIVsp4ZcddGrRmYPRzZVA\nIUaTKc+7B/8bB/2P6aZbdJMdvM+P7SPToKmbNKVB2zfo6oSu6tOXHontDexHEwUxAZqGXuT1vG/M\nzQAAIABJREFUJ/897dYLRNE6gV7k7I7rFLITdg8+4YPD9/CB4ds/+DEbL72KCqOh0eU6JkKYwDPL\nDZpLAVFLE0Znmxi2n5KdpKT7Pb745pBkqYm0Q3wjzK/uHjyfMxlaiQKGNqPO2VYzMDy7FJ/efv4g\nPja88+AktXx5nAw63Y/Ol7MRGYiN5sl2zEIcFGLVtRbMv90e/VowaWP21gXp06SuGoW6sYqM+lHO\nd9uxqvBZ53yPA9ZN1r1urLm/1os1q/56HXrNbat+rCoyq7rPIlad8znvS+uph/K3vzgpTdcGCDcd\nujgr+lTEQvaNQnz5nPFdB41yrIXQ8NpGu/AUdVR+9U8ndMq7imG6KcHh9NvP0WeB+SSJtz4k2P26\ndIxoRe+//mMknlw/DxD+Yg99Pykdc5R9w19u/ZTMlv/IMGiQ2X7pmLuLv8sfvPLfF8/T2+GDe39D\nJzng1R//Pk++/nrpu/Kpdsgzy1MMAvjHbw5Jp0ZCxRkUoxIoxZt32oSmvFVbFb/opI5f7xxPnfM7\n6y0W4vCh56s67qZjzeL66pzDTLCZx74mfS6T5THbv5nLXG60zP11Lo9K5rZVv8w5zWX6Ftj1yPSQ\nLJdKY674R9ZpWVV1L7rQ7SJWhQ21AphuesSH9/6Ovc5XvLz5Q559/s/QLzamKzerxjWXuYxI2Vpw\n64L0SbsWo6kFw/Tj8d2U0VSG4fgqWEVjxrGK5hvHEim+xOWyWGW6XwZLKXUpHqpwWoWHujgdjp0F\nTq/bturCqsu2pmHNum0N/5tZ4vSy/jprtnVV/npZ2yrTa25bF3WfVX+dpPt1rQVX6a/OezLnUSiM\nOIKCU5tZXQtOdQ9AeY+4s7TfkRlRIkhPIBAI1YQATvJcYaNQ+Amn6YJ2Dul6NILEF+uuc6WFLPP0\nEk8UKIKg6BkKWeJQHrS4vC1ZUT278ohREAIO8BeG5L8Rn/+dUuSX7xVgYRETQqDJ09YLAgCtwGhU\np59jRQUnsSKQdLGqgyFB0+Qs7XxkmLJo7YgIIWiQFpyUKzTNoAXeE4QL9G0XLxd/ZLO5RKMdEzQc\n3hp6vS4fb/+Srw9+w/Prb/LG039EEISoSCE+52M0DXxUjALrBOd9fpFdiY+FRuOdx0rR1oxglEKj\nUCq/GFAKo3/BD+rGwRWepg/T2b2A8o5Qa4ouZfPeo5XQMJrMCcUd4YVQKbzITPnrTVgLZmV9HY4p\nO2m/denuMmKwo3+m9fnLOcYX76GMklU3VhHV4w9nHGu4mI+OqzLfJKxZ4GEcCy7e/FgFy3tfWvtS\nhvUg8xU9wyIexvvVTsK6btsqGncdnD4oDyJyLkWoTtua++tkrCq6F42bVX+drwWX030W14KHsdPb\nuhZkPr9k6iRz7PQsfZv/95FRrDcDlqKAZmAIRoKE6/bXIQ920Bu8mzm2exmdwQVf4sB3QXoKyYBU\nUFZQPXu+JdiCQt3VSEtDUw1iy2EAluslFnxH8IlGEkH3HTq1BAc9gqM+yguiwa9HyDNNZDHI65Ud\nuEThTjRiARSNWHFn07C8ZIhDhc88vWPL7ucJR1sZ4kEU+FgjrQAZ1HKjhpuAekgCygqmn2Gsh8Sj\nvUNZh+omaGvzKmil8HGIb0SI1iifobI++miH8GAL5UbqAozO4T1n/z9yjbg0IrKXnsA/t4lvxzjf\nxx/ukn78DtnHbyNJD9CEjWdorbxJEG+ACrH+iF7/C/b2/4Y02wIgxXIUODo6IxVLqEOaErFhF1jz\nbQwGh2dfd9gJTuipFL3QYnXtGZ5/7k1++P1/w/r6M/T7ff7Dz/8jv/zVL3juzrd58c4PMFEz7x++\noWHJnNXPD/IGFHkv8obRLMUBG+2YaFBbXsVfM+/Z66Yc9DMS50EgCjQrcch6KzrtUX6cWHZ6Kb3M\n0bMeAWTMtkKtWGsYluOQOMh7z/edZ6+XcpC4PEgHFiPNejOiGWiaoTkN/Uf9IrGe7U7C8aBtn1aK\nRqBZa4asjLTwe9C1AGbr202ps/ubrvrbra71/EGxiuTWBemjMmnn5VFhVZ2vyriyGoXr1GsW55tl\nrKKPnEc53223rSp81jnfLGPNom3ddKxZ5PQm++tNt4ebbFv/dO+QZPL9RQA8vxRzd2FK4XXNelUZ\n997WESfTWosdWHi/+IxxVNRbIdIsn898fETwfmcq1snrT+BNeQJqeJD3EC8TUZA90UAKTqZHpf35\nNuaovB6crEdw+DFMCALOFDOQlfPVdffY779TjgMchx2yrLz+fCFYJbLTk3X/6L/7H2gsLgNgreUX\nv/gFf/3Xf83LL7/Mn/zJn7CyssKHuyccJOW6h1rx5ma7MEtkVOr013fuH9Gb0iLvbHekXL632aYR\nlvN1k9eCqt9udb0nq46b1bVgKLcu3X0uc5nLXOYyl7nMZS5zmcvsi/eed955h5/97GfcuXOHv/iL\nv+Du3bvXrdZc5nLtcitP0ovSCh4kPfNhsMbTNB40Ha8obaJOrIdJaXsQTutMS6yb06KUlfFdywdN\nFSqqR3kQTh+1PTxqTqtgVR0zPu5h5rtJ/lokdXBalE49qzxctW09DNZNsq2rXguqPMOilPGbvBZU\n0ethdB/ykDohcY6jxLLbs6SD2uRAK1YbAatxQDM0hFrNnL8OU/U7g1T93iBVX6u8F/l6IyLWChKh\nf+LY/aLP0f0MPzhsbS4ZNp5v0F4NCBYMFs9x6tjpZSTnTj4H/2wF3bOoY4v6sofeTVF5xjPeGKQd\nI4HBhyESKFxkcI3grFWXFkzLY1qgtKAyDz1B7js4OccOSg9mNWoEKzxN39a9HvHWl4SH+5hOF4XC\nmyY+XIGgmdfHi0dlJ6jsAG2T097h+EHN+oDzVI45kM/osUfmugSmRZM1VtRzxGppkFrsEWVBZYjP\nsNLHSUIn2yJ1h2ccASoIQWm8ZHglZD6h747xg0kVili3iU0TIxqlAhAQO9q4XBHGT9JaeQsTrXMY\ned7dfYe4GfOTf/UTXn71JQCS1LO1nXFwaOn0PQ5BhYJqCzrO68NPOR2km8dGERvNaiNirRWdK+V4\nFP46tNPctmyeJp8/WlbigLVmSDRIk+9bz04v4zh1p4y2Qs1mM6QVGlqBOf1N170WPMx3+sOuBaPp\n7o/jWnAB57YF6ZPSDcYJKgqaih7IVWPNku6jH2w3Wa+brPtV6zWrfjGrWLOk+6zbVlWsWdL9OrFu\nsu5z26pf94fRK3MO6/PrroxWBGMfo1X1ug57cD7vG61QaJVf8nUBa3BBmxsE4HHToM1FLOs8/czx\n4X4XJxMuHRNBJQ4+zeBABinpBampBmgCr0Z5TmrBBWB4ASvwkYXOMIAeHydgFLp3QHT/N+g0QRX1\nmjMagijHVAJZSuE17oFmL/2YXfcBme/iCi5yM0GDULd5zvyAUMdIVtD6TYE3wkn2FT0OwDvEFaSc\nBwFCvqOhlAZbgKU1SgcsrP0RjfbLaNViN9njvaO3SX3Cd5a+xxPxU5imgcWI/rPrWA/WFnCqBGWE\ncEPQ8aSL4/Le5WvNgGeXmlMvjjuFfgh/tW5wwaECrVShnXoRMusGvc9zWy5qPzj/dnv0WLOke1Hg\nP5Rbl+4+aVdi+OdlNQNDEqfVFTwKrKITjOvW3Tl35TzUhVXG56zrPmtYN1n3R4U199fHw1+vQ69Z\nta2yWshZtq1p8jj4a2gMobmZa4HRmqbW5VhaETWDqViB0USACJPrwZVCGgHIlHp3B6DyG9knvSO0\ngkjlE07sba7Age52MCcnE8aQX/bm+vmt7VlJ/bn19GWffro3Gcr28SSolioO0AEEtFV45ZE0LR4D\nMLjMTpkAKQrQAbxHfErUuMtJ5njv+D9ymB3w2uIbPNd8nmFrNt/3ZEbop5PfuYhCrEJpW1LTr7CS\nZ40UBcFDqdNOA6MJTLmdaqWIw+l2WmUtmFV/nXWsWVxf7SS/4RYG6XOZy1zmMpe5zKU+KduomMtc\nbprMZPporUpVBKuUSFuPYgmGfzx8n630gFcXXudHq3+AUdMvQXvEas1lLjMtty5IH6YYjO5cjKYd\nDOsV4Hz6wWgKw+iYB8EaT3MowhpPmRjd3ZmENUmvcd1H6zYehodJuj8IVp2cVuFh+O9DeVhOZ4WH\nKljjY0ax6+Shis1fJw9Vsa7bX+viYZLuD4JVRa+6bWs0EHyY51M3p6P/fNNsa3QtqIJ10/y16low\nKo+Tv173WlCGlTlP4jz9zGO0Ig4UkdHn+ktXs4e8X3k/8fT6njBQNJuGKDzfu/z02xBhvRnQzRyp\nEzIZts8ChRDqvK45eqFBds+SdBxpT0YO1kfqyhMPOxpaChWrvNf58D3mBTxIpvDNAG0dyslYH3RB\nSZbXleMgMHkqu+dcmzRvPH16dP0Bie3S1is01SKRNFDDYQrECCKWRX+HJNzHqgTrE+xIyrsOIrQy\nKFGcuC2awQqGGOOGPwpEg9WWhC69rEcWegICtFcwkvKugwilDEoG/2kUIuLx2dmN9JkO+CpYYIsW\nT2bb/IvVt2jHd/LqgFEXDTU+MkjToHCgNCCc7wcvp/TaY4VpgwokLz1QZ2NCpYiMQoTTPunw6N5b\nmXOkzpNYwYsnDgyRUUTGXMr3q64Fznkyn/tPYj1xoImNJtQaU9B2br4WXKwrf1isOnko2wS/dTXp\nQ5lE3qiMkzSJqCpYkxash8ESuXiRwaju3p9djlBFrzIe6sK6Dh4mfUSPyqQX1INgzW2r+nx1Y10l\np+Mv5EnpvlWxZpHTm25bc3+dXduaVX+drwXnx1ylbTnnOUodO72UozTvFz0qoVasNwxPLDQItCrF\nSlPHwaHn/rbl6Ngz/iU77F3+1BMhxhRjOS/s91L2+xlGKzaaEYtxcI4LEaF37Nj+tMvWb/uIOwvq\nz4kB1hSyGeDRuBOQTJ8fK4LKHKaXEW1vYw63CI53Ub4gtV4rDv0We/IVn/ffpiMH5/5aoVk1T/Fi\n9H3W1CYuO8a7DowdMWeS0NFHHPktlFJo59FjaeIKRcOs0TKbpCpjO/stJ35n0P/7TAICFoNVFv0S\ngYoJnGKYqj7Kl9OOHn2+1A3u60UW/T7r9h4BZ2m9cfgEq6u/x8Ldf4FdXiRbap1dxHdO/EBDmZDe\nLqjIEy3ByqphrRmy2jzrH34OqWZ/PUkdB/2U3b4jGzNmrWApMjy5ENMKDFo/vL/2rOc4tex0M7rW\nXxjTCjSbrZCNVjSxDr/qfNe1Fih1dpHltPmuai246vV1VG5tkA7ltQCPAqvqfFXG3eR+iFc93yxj\nje6EXsV8t922qvBZ53yzjDWLtnXTsWaR05vsrzfdHua2Va9efet4d+sYXxTkjshray2WGmHpmL39\njF+/P6WHOPCD7zVYaJcnjVbl9B//723Sbvkns10N89vaS0RlGSt/93NUUlLrDfzS/V/cT35TOqbN\nIr8b/CFqfMdjTPbMVyTpYemYRFuOfPkYgJejNwkK7raDPKT+Wod8YkIa/ogN+zURk3/nU3/6P6HC\n5SkzepjSazyKFD98q0kYXJ2/VumTfqcV8MJKe+p8VfT6eK/Dbn9y/TLkW0Jv3VkgCurpF3/V3251\nvSerjpvVtWAo9USwN1jK0uKuU6o+wLnMrsyiXcHNt61Z5fWqZc5DvTKrfN50f51LfbYlIpykll7m\nasGsy7a8CEeJJXUXT/fOzQe0wumbAp0sw/pyLGOg1SrXPwjyDPIyERGOjh3dni/lNHUe11KFh+in\nWN6S7X+C7+6XzqlSi9eN0rJqKxldd3LhNHtc945k3PN7pbo7sfRs57RVWiEWQubLA0AAh2ffHeA4\nf/ovwH0d8Ddhm20d8Kz9irv2k9IAPVQtgoMjKMokOAUe3LZfZlsikHk6eykyZbNimogIxyeW45Ny\nH7PeYyvMFRVmB1xevBeyAwtJ+ZyRUYWNBmZBZnWNnWW5dSfp4+kLoz9vmM7gp7z8tdYXgvdRrNH0\nsCpY42OqYI3rXgVrVPfRlIrx+ZRShViTeJiENfz3y/AwXmPzqHgYrft4WKwqnE6zh9EUnttqW2VY\nRbrXaVsPwumD8DCahnVVtlWXv85ta74WzAqndawFwzTGOteC8T68j2ItGMeaZlupE7Y7Ccdp3oc5\nG7RSC7UiDjQrcch6K8KMfZg/6vW1k1q2u+m52m6jFJFWNALNaiNPO1ZjQabAaT36SerY7qakXgbp\nzOr0/4MhVmjYaIb5yfqYriJ5P+0kEfb3LTt7nmZT8cSdgEZD04jzuvRxHvqJcO9+ytGxI0mENJP8\nIvZI0Wgo1lYC1tZDTrKM/X5G33pSLzgvqEyQVOBEkPsWv7dFuv8P+O5X+PQA1z9EhQ10cwXV3kDf\nfRO9/jpRzxOe9DCpQ2XDoNOhfIpKO3C8y372GV+oDziSXbr+iK49JDARSmmUCFiLFceR0RxpSBH6\n3oIIi2aBFdXmab/Oa+4JAmU5CPZJ6ZFKnzTrEgQxRhuMN4RWoYHMgNUOh8e5FJRC6Xxnw3uHdymJ\nEtIQLB4rHmsTGmGbBg0WpEns7vK1WcYpxwrfYNgldX2UNhgVYEQROEXsQ1ai51iJXiTWiwQ00WLw\njQa+0cQuLJPceQoftzCpx2QenIAlLycw4I3CxQE+NJjU5nwOxwBRQxG3DQtrIZvPN4nbZup7K8uE\n+4Oe7P1ESBMBBVGoiGPFyrJhcyMkEcduL6OXOVIvWLlot5HJe58vRmZwx4K+sK9TZS1QSpGceLY+\n69LZz0i7nrQ3qL+PgIaCVY1ZM6y0Q9aaYX6XgtEYfXPWggd5n96UteAy326T5NYF6WUyXBCrpCwM\njaxsDJSTW2QcDzrfUPe69KqLh+vgtG4ebiKnl9H9OmyrTr1m0bbm/lovp9dl87PGw9y2Lq/7rGLV\nwYN1nre3jrGlX2nCK6stVhrhldnWbjfhk4P+lAu2hTc3F2gEphTri8Mu33RSSo+oEX5wd/HcpXJF\n4pwffBhPxuonjn94u1fYznt0vviuh8aE+vOB2G8+p/O//8+ILUu7V6w9998QmvVS3T87+Tnv7P0v\nOD8hjxxQSvMRGb2SMQBv6jWeoYmUnYwrjVYaP+X0/MCkdCVB5GKgIWoZzKugmiz5LwjcvdKn+MPW\nf8UyT5TOZxfXSJ59A6TMfyS/KE7Kn8+T327y9Ovtqf7697/qMKXygHDDodvl8xkFb95ZICqx06o+\ndrKf8v5/OKD88Qiv/8kqCyvTfR9u7rfbrH7DVsV6mDT5xyrdvYzwy46tUncw3FWpC6uKXlXwqvJQ\nRffr4LQK1nAHqw6sKrrVyUMVrKq6D3f76sAa4tWFdVNta+6vuVwXD1dpW9MWapjb1mWxqoytm9NZ\nXAvq41TlfaqvcC0QGb+erFivPJaagjUcOwWrShazUpQG6PmYiydnRfNV08sjrjxgBkGr6cp7XGmA\nDiDiMaa83h3AaFMeoAOIPz0xLxOlgwsButBCgu9D8EPw99DZXxOxO5UtXUF3PFMCdAAFqjxgBlC6\n3m+3qfMNfLHKfFN9H8WUA9h8VAUfg9lcX6uMrfO9NTyVrwNriFcFa5qUnbQ/VkH6ZZIGpo2dlr4w\ninGVWFXwqmIpNT1dpYo+dfNQbZGtj4fLYFWRuW1dDquKXKVtzSqnV637aJrXw2IN08bqwBrqVgVr\nmgx3wh9mrtH5brJt3dS1wHt/LbZ1Vf7KoGr5Kv01h5nGVZ4yPA3LKHUhJb4Iq8rnrpe8drcUqZLv\nS95qrEIwr8yUTsZK42W69oaAQEelY7QyiCup3x6I8x6ty/VSylTZacH7jOEN7kKMmO9C+PvgjyD7\nOcp/kZ/IF5y0j83I1CGQRyVq2kABUUz7AS4T/JR7EkRk+l7M6LxT/n5amF55TUSosFdZycdg/u12\nGawqelXBq4r1WKW7T6pJH6YcVPnYeBS1naO75uPGNDytuao6xKL5roKH8Q/eh+V0Gg/ARE6Hz+Oq\nanCG4+viVOSsBueqbavsGQ45Ha/nGZfbbFtlWJN0n/trddu6iZxep7/WaQ831bbg5vpr5gc16Ule\nk57XbysiA7HRrDRC1loRwWDOyzyfy/CQeaFvHZ3Msd3JSLwnD1rO6nFHa9LXmyErzQiZsjmglOJk\nUN/eG6lvD1Te67oZGDZaIYvxxZp07yHNPP2+sLdv2d33NBt5TXqzqYmjvCbd+rwGvps5tnsZnZ7H\nnQgkGm9BLCjv0EkP3T3G3PuMcPtL5IkN/KsvISuLSLuFBAGq30eddFHbO+hf/wa/v0VfHWJVF+sT\nnEvQURPVXEW11lFPfh+z9iph3xMd9dCZRafDmnSb16QnHTjZ5TD7ki/UhxzINl05opcdEpkGDdWg\nRZONbIWmNPitOeAzvc8RPY58F0FY0kusqEVe4Ele98+jJWHP3KPHMYl0yWyHKFwiMss0zQYb+rvE\neold/wFH9jNSd0BiD/F4vIYMz5HvceQ7KBURBq+AeholXyP2Y5SBVCmOveWrrIugeDFYZN1ENEUR\neE8YNInjdaLoCVaWf8TqwltE/R7hyTY666OyPliHb8T4ZpNscYXkzjNI3MT0LcZ6sHK+Jj3Q2Ngg\noUGnliAZ6T/vBIVHeY9KM0wvpbUWsvbaCo31mGghJGwE5y7jU0qRWWF7O2PvwJIkQpIKCESxohEr\nVlcCNtcD+uLY6Wb0bG6nVs56sjdDw2YrYiEKSoOyqmsBQNr1bH/a43gvI+060r5gDERNTbxgWHsq\nZvWpBmNd8ObfbiU8wGyuBZPk1gXpo1KW5/8osKrOd9uxbrLudWONvoSvYr7bjlWFzzrnexywbrLu\ndWPNor/OW7DdDqw6bEtEOEkywsAQm/LUzTrfuR/sdjhKy09wn16IuNOOCafcZj1tTufz39iOQ4KS\n1PXDw4yPfpvS603+hDUGVp4TuuInpsuLgHr3Y6J//DW6dzIRS5oN/MoS+v4OasJHt4hw/K1X8M98\nB9WY3FZMd/ssvv336O7xxHNXJ5avs18SW0tIcZq4iHCEJQw3ucvaRHtwktFvLdI2z2B0PBHro97P\n+Yfe/0mGH5wua4x+gUC/jJP7WPchSJ+vlWHHJaXnyn/2xL/j+3f/LXG0MXGMyhLskscurTLx2FgE\nlVokCLhwO+IoVj+j9fkuOrUTOVVG8a3/8jla682JOCJCr5cHX+325PsUrBc6ScZCHBb2ZB9KXe8a\n8cLxXkKjHRI1H7692qx+u9W1BlcdN6trwVCm5OnM5brkFu+dzOWaZW5bt0OqvuTnMpe53A5RStGO\ngtoOH6quBb1seop1KzRTA/QqYrRiMQ6YVlvuPKUBOuQZ6yeJg7DsJB+M65UG6ACq18dkWX58PxFL\nESw9SVYSoAP5KbBLShOjjQpYNRtkdrd0vlXaLJgNyor2jQpZip8BXxygD7HCcIms7wGFUc8QmFfx\nckBq/xPCgB8FiTHIFJPQjc3SAB1Awhi33ODCUfB5xZDYMDUn3ShMWSs3QJzg0vJTTaUUrZZCpPw+\nkqCindYlSivaq2GlDdu53B4xP/3pT3963Uo8ChmmIJTtWAzTTYb/KxsH5bsfo2Og+AN6NDViGtYw\nRWKYLvGwWGVjRtNNroKHqnrVzenovHVgzRKnozZcp22V7QyOcjVNryq/sQ57uCxWnfYwDasue5h1\nf71KTut6Bw7XgiHuVfnrNKxh6uF8LXg81oK6eKh7LWiGBq0gcRe7dodasdkMWGmEp/2Zx7G8Fw63\nU7765xP2vkwQ74lbBl1wMjqNB+eE3f2Mr7/JSE8Drovjmg3F00+GPLkeEQeK1AmuMI4VpN1GNtcg\nSVCd3jk0AdziKskrb5E+/TISN9DdE5Q7fzGbDyPSZ17C3nkOouHJ95heIpjjE1r37hF0s/yvCwJL\nEY+oBOXBBDHepciFHueaINqksfBtgnAjL9F2RVeUa1TUQnkFSkD0xaBYPEif2Cm0vkNHPQeqQebf\nxvnfwqDX+bK5y/cW/xVvRL/HSrDGrt0mkfM328fBAm888xNee+4ntBZWEScozwVOfaDwSyE+1AzL\nJi6qLpi2J1gG3RDECnh1bqxSsLSoee7ZiI1nm6AgO7EX+qX70JBttDk0Md1EiGNNEFy01Wn+KiIk\nzvPNcZ/7nZS+dcTGFGZ91Omvj2otmKbXJB6KsOZrQT1rwajcunT3IVGjgcXwz+A8MaMPpYy8q8Aa\nlVGsSfONYl237leB9SA8DDHKsEblJvBwnZyOy23hoQpW2Zi5v9ZjW6PjLvuefFQ8jMt8Lbh+rPla\ncH2c2kF/88R5FBAHetAL+ux0bxTrm4+6HN5Pzno8j7hV2FBETc3i3Yinv92a6vu//Szh+MSRpJCm\no0GdoAa3py8tap55KqbR0ERhXo8+lMw5Mif0rOPTwz5O5LSW/hTLe1SvjzrpIPc7OGnjmwv4qImo\ns9+oXYLq91C9Y5QIvrWIxC18EJ3Xi/xfo3vbxPsH6H6KTrLzp94GEIe3XSTZQilBvONcjzijEOXx\nkiHBKkG8itJNtETnOMU48BZJT8DnfcoRxbndicCANgxuaAPlwTu200Pecds4PG+YO6wEhi7HHEuX\nRrzJol6nySLan/GQ6JQjOWRH9jh+7klWlp5hsbFJHC6d58ELyuX15SpQiFF4rQueoQLtCVZBh5Jz\no8kjcch58yCZ4k4jZG0hJI41UaTO22nPknYyDrYSvvgmw4cBPjDIyG32WgtxlNecv/RCbjMw2ceO\nkoz7nZTEelLPuS0TA4QGGkbz/HLzNKNkvhZcP9aDrAXXwemkDIlbF6RPk5tco3DVut/kWsgqfNY5\n3+OAdZN1rxtr7q/1Ys2qv16HXrNoWzcdq4rM/bX++d7+yx36x+Xpxc+80eKpVxemYv3tL05Ip3Q7\ne+2ViM2N8hvSU+d5+/7xhXPpccnug+9XSS2ecAo8Isu/fh9z1C0d4+0e0v1m6mxm5dvgp1SqumNI\nO1OxCDQHWZd3/BYnkvJdvcmzaun8+6e1BlLOqWvEHL312rkguEgUHpnSVEo1HNHd6aoGv2CqAAAg\nAElEQVS/sdGmFZXz8Onnfb74akorOuBHP2zSiMt1/2j3hP2kPJ0+UIo377TPbVoVyXwtuD6sWeTU\nWksQFNvyvCZ9LnOZy1zmMpe5TJTHbC9/Lrdcpm+7UaHjdc1S53QVsE4k5b10hy1/wmt6g5f0Krow\neKmoWDVSmdrFbC5zmcup3LogfdKuxWj6waT6g9H0g6K0+UeNNdzhGccan68I67p1v0osEanEw/D/\nb4ru16HXcExVTm8rDw+iV1V/vYk+VgfWZW1rFv31uvSaZltX6a+Z8zgv4Cyh0QQFl4PNor+OzjeU\nub9e7VrQWDQ4K2T986nuAzRUpOh0Ld00IzKm0Las9WQ9h/aC9n4sTfoMS3vP8YFloaGIGgYTFGBl\njqTnUGmeXi2BOkulPlMelVhUCibT+CBECi42Uy6BtJf/S9hAgviiXuIxNkOUym8mlzxd+4IEGlQb\nGgt5XXlWUFseBBC18DpAhSEqzYoD3tBAFkPswGVgz5/+9sXyz2qPL/whL0eb/CR8njgpwFIKwggQ\nCAPwjqKift0ICJZCGmHeKS2zRZkFggoGqcZ4xKk8DX9sTBiACRSREiyF06EQIq1wIlP9YqGtaTUh\nSQXnLu4iDFPexZdjpaknFA2ZHaTgX8QyQKglf8S3dC2Yf7s9Gt3LTvZvZbr7KDlDGSfR+/M9Cof/\nXDSuCtaoiJz19hv9s+GDui4suPiRUvQhUxXrQeZ7UKxZ5nSabUF9PBRhVX2G4/0vq/JQVC9z3bb1\nuPhrlcDjQbEe5TO8SZw+yrUAijl9lDw8rL+KQOI8fevZ7accJu60hDYyio1mwGIU0AoNZvDfP4ju\nk/S6zbb1sFjjctVrQRW9xrG8F462U3a/6NE7svQyj8QK1jSsmtO2WqO2FXqF7XpOdjN2Pkvon+SB\npgA+1kjbIIEGAeU8qmPRiZyGho0Fw8YLMQtrIUGsyfqeo62U3c8T0t5AXwOsKlg3EAo6S9GHfcwn\ne5jtTn7HGmBbTbInN3ALLRwZqn+Evv9b9FcfoNI8hV3CBv6pb+OfeAlprqIxmE6X6Jtdgk73fMhq\nVB7DqrxG2usIMfHZZW4uQSX3IT0An+bYzRXs8gtIvJgHz+LR/Q5h7xidJSjrQBu8jgdYgxltgs4O\nUK5LKhkf+h0+6d3jiSde4/lX/5AoauWbb7vbNHa+wXRO0JnHmxgJl5FwIddLBLxDSx/tLUFTEy03\naD+3wuprdwkX81vjrRW2dzP29jI6fSETjwoF1RZ0rHLVBXwqSEchqSJWOu9FvhpwZyMiHNzEnznP\nbjflIMlInWBU3kFgsxXRjoJz7+tpdtpPPPe3Ug6PHGkqhKFiccHwxN2IZuN8XXLuP4pe39PrebZ2\nLAeHntzMBRWAWfCYWAgbikaoWYwCNtsx8cjG0Cz46038dlPq7EK727QWVOV0XG5lkD4U7+f1anXr\nNYvzzTLWtF2yuue77bZVhc8655tlrFm0rZuONYucXrW/djPHe9vH+Cn5q6+vt1iMi/s3X2a+quNu\nOtbctqBvHe9uTbct3kvgaJpW02vBAZQWxJePC493iHZ3pmL1Or9A0vLa8nj5Oxg9pfUYCr+8jvhy\nvrLVRbwu9zFlLdHxUfEJPeDE8WnnYz7ofcDaxgu8+K0/oNksbhEXHnRofrlfOh/Aq//uBZorjdIx\nnx10ud+dcokA8P07C0RBPTXcddnp4ZHj7V93mWZf33+zweJCeULyTfbXOrGqfrvV9Z6sOm5W14Kh\n3Lp097nMZS5zmcv1yC3e853LXB5bqdOvr/wNIRWC+Tp/X0WsSqMeQi8Rzxe9z3n/+F0Wg2V+583/\ngubGM1OVqrL1Uas9VMC6yevKTdZ9Ltcvt+4kfVLKx3gaQ1F6ApxPPagT62HS3oqwHkR3uJjWctU8\nFKV8PAyn08bUiTUrnI6nMNWp11U/w7m/TtYdboa/9q1ju5NwkjoS5zEKYqNZa0asNiOMPkslnDZf\n1XFz27qc7kXL/LhtDVMqhTzVNLGew9Sy27Nkg3z3dqjZbIa0QkMjyHtnz9eCM5mFtaDKs56ml/PC\nfi9lv5/Rtx4nQmQ0C5Fhsx3TMPo0LbXoGY6ms1ov7HVT9vt5+6pkYEt5x/UzHtqhZqMZ0g4NgShs\nz9M7sux81udk1+bxaghsKFgxEA9+TyKw72BH8qJoEVSWYWyK9g7lPGI03gS4IESCEJRCZX2C43sE\nvUNU0kN5D8qAjoCR9HM4TVEXlyKS4O0xWecrxI+cqudNt1GiUEEDpRoYs4EJVlHKIEpj2wu4xUUk\njBAVoMSjUovpJfn8IpAdo5ItcCdgUySM8PEibvEZ/MId0IYgUqw+FbH6VEzU1mgvpCcZJ1922Pvo\niK/2v+C9o7cxOuS1J37E2tLTeBNAqPGBwsYBEpk8Ld55TN9iUoeygrIO5RwqSTH9DCWCKLDtGLvW\nwschph0SNxTttuHuZsjigjmXMg7gJb9Jv+88e72Ug5GymeEWhSK/ET0ONAvhwLYGKeM969nuJHQy\nR+o8RikagWa9GbLSjE4vuXsUPiaS17H3E8/evmVn15NlglJ5m7+7m4ZWy9BsaLS+iJU4z04n4Six\npM6jBmviaiNirRUSDHSbhW+3ovnG0+snYT2K74zR98rjthYUya0L0ielG4wb5yRiRokcJ7lozCSs\n8fluI9ZN1v26sW6y7teBdZN1nxWsuufLnOf9vS7WCcWNaYRAKV5aabIUBzPDw3wtuBxW5hze50FV\naDRmvhZcCdZ16f7JQY/jxJJJ8ZmqBpYjzUurbZQqx/pwr0s3c9gJWCCsN0OeXogn25bzZInnvd0O\nVnxei35xQpQT9IcnBF928xvHir6JNaAEs/8xyqX5RWBFEgQQLkLQADvhE1kLzh2RnLwH4sEVvQUV\nKmogz/9LWLiLYAp5UMqjDu8Tff2P4JJiLK0hbvLiv/83NDZXCKKLdzx88cUX/OX/85ccH3Z4ee13\n2Vx8EVVw6R0KznVCK3yB55fr2XaAbwV4M0l3odXSvPl6E2Mm20PmPJ/sdznO7Pne9KM/EUGjUDrf\n3JEJNhMqxStrLVqhuZp3YDZ4BwrnerKPz+e88P5uh3TKmvjcUoO1Zjgz75r5t9v1Y036Drl16e6T\nfuiQoGk1A1rrSmOgvP7gMvNBeY1CnbpfBmta/cuj4KEurDI+L4tVJ6fXYVt1YV0lD1WwrosHmPur\n1hrvhNT5CR9SAAorYHTxR80o1qz66zS9HgfbCo3B4TBm8ufCLL+3psnj4q9VsRLryAQmJT17AK0w\nBTexj2Olzg1i3MnviGagaYQltmU0cUvDIYhMmFMpJFDoxDJQvlg84CzKpmBL+mdbC7GZHKADeAVO\ngbMlaemCpD2ImkjJ57aIRtsulNW7ew+9DlE7JBzr6b21tcVf/dVfce/ePf74j/+YBfc8e5+V1IML\n4KbV6ytEFBIH+Sn8RN0V3jFxwwZye4gCgxcp7ZPuB53U8cVB/FCvTECr6etKbe/A0FTzaTyZnxSg\n57pbgaDCmgiztxbMv93OsOrk1Fr7+ATpc6lPyj5O5zKXucyWXI+/zt8Rj4PM14L65fHgVHGlVeiV\np6owUCbcxPYgUHVSMGI3h4eH/OxnP+PDDz/kD//wD/nzP/9zgiDgk18dVoKqoldl1R8Hc64gVfia\nUzWXUSk9oLiN6e5wtosxqQZjKKM7NZOkCKuspnAUa3zc6G7OJKzRtIjLYo2PuyzWOA9FWA/C6Wi9\nyU3goQrWZexhOH5c5rb18LZVBatOHq6a03HfKeNhVB61bTnv+eYkpZM5EutJR1JaDXm73thonmjH\nLMZBKVYVHsr0epS2NSpzf30wTp33pIM6905qaYSGRqCJjCbQF+ub6/bXIcbDYlXhYVb9tSqnB72M\nnV5K33kyN5oJLSjyFGSj4OnFBu3QEBlFZC7WJAPsdFP2+ln+fhhJX1YIoVbERrMch9xth4Wc2sSR\ndTL6Bylfbp2QLgRIK0AiDcOTfOfR/QzVSTGfHmHupxCEubajt6cHKq9N1xrd2cakx6i0j0qT/JQa\nEAOeFOu7JL77/7P3ZjGyJde53hcRe8ih5uEMPbFHTi2RtNSkfKWrwdPFxYUsEYZAwBIESA96NgRD\nrzIFgdCDHiTC0JNf/WJZlmjYgA35WhSvJVxKJMUWW02yyWZP7D5T1akxhz1ExPLDzqzKysrcuetU\nVp2s6lzAwTmnauUfa/+xIncMa8Uiqt0iMEsYVUf549NrrzPEd8nzXfLuu0WYvmhw/mjlq4IAlEFh\nYPFZZPNFiBaQoDZwqi4oPMp7VKdFuP0G2DbYBLLk2PYoRqIGPl5g5bM/Re12nX967eu8/t3XeOWV\nV/jZn/1ZwjDEdhxZK2Pn7Q7bP06RwCBaI9I/mRZUqJAYqBWcqK4gKZD1T7ApQuENiFHk9QDq5ujz\nx9EMQhQqogiaTcOzz0QEpnyM7Sc5W52M1HlSN5iRUNQ+j7SiHhpEirtOUicn0i6MgkgXOexPNCMa\n0aO9Vx5ljA3LKCzvPffaOYeZJXXFqfqgz/dtv9EIWalFpbZf13fBfO42moexkQJSxuoVlkECxj38\nIOGDBJ8Xqyy04SKwzmv7NLEeJ6dXkYfBCzrmvlXYNy4EdD5eT7c3Kzx4EQ7SnJ1OTmhU7wKg0f14\nlcfrdfets2JNGq+pdewllq1uRndE6HCgFWs1w1OLdbS6HB5mdbzO4rsgtZ4H7YR77bx30dtp27WC\npcjwzFKdyIwO4xURkt5FYFaEjXrEYhyM5MJ7T+tuh723Djl4+xCXDk3qAb8UIE/FqDwleGsHvZec\nskyUwkcxrrmKq9XwYXTiFLpQ8ujuAer+v5B33qKT/Bgrp0POta7TbLxErNfJ0jvY7AGjkt6VDon0\nEkbXMT5AqdNjw0dN3MZzsPgMKsnR1p5m1VvIdhC7j1tcwy0+DWEN63Pe2f4O72x/h9vLL/Dy85/j\n6RdXCbxl9/v7dB8mp45yRSl8HGJvL8CmKWrTB8M8CLQc/p4gqcLVQiRQp/kqjGNtJWBzI2B9LcSY\n0zpVfWurk5I6z3otZKkWHl0Gd9SSCHvdjN3EUg80G82YaEyaxayNVxHhMLVsdzMCpY4uxRvn82ex\n6yq+C6q+X/uL9Fn5DhzEuizfGpRru0iH8jyGi8Cq2l4VvatcD/Gy25tlrFG7tBfZ3nX3rSp8TrO9\nWcaaRd+66lizyOlVHq/bnZS39pJSHYCf2GieOBV71Paq6s19q5AqviUivHrvoDTVG+Cl1Tqr9ahc\nqaJdP/w/36Fzt9xvVJ5ikslh3d1nnsPruFQnuf81kh//9USsRrgGdnzGMUA9foLQ10t1RAXw5L8C\nKff5fp10L44f73yPHz34FmvNJ3jp5udoxkWt80l10o+w/vU6frm8f1wb7Pbk75qf/nSNRmM+Xmdx\nvD4Ou6Y5d5sW71X1ZtW3+vKhz0kfFY5wXrxpYPV3k8qwprm/Mu29mmnxUAVrVnno75rNfWv6WLPG\naRWsD4NvVcGadd+aJt6HfbyGWrEYaVqZH5urGRt9VKavim1XkYdZHK/OC7uJpRZ4mtHoU20RoZXm\nuAlUBFoRVOjDKpzmrRS33y4WnXrMgkQ85K3iJnQ94oT8SC1D7X4AS7chHL1wFpfhOlsT7dKEaG/w\neE4dV/fEi6djH1JjhUg1S/pIo5JDJFwa+4yiFM4L9w7e5Af3/5F6tMhPP/vvWK5vHusAPtLkzZig\nlaLG0Cs1jQ/L+0cEfNZHHacrqAD2MksYa8Ixp9pFCb+8KK02xreKNqczxkSEg0NLlglrq6NP98+K\nN02Zvwuqz92muZg/i22zOne7difpwyEHo+L+B3/WJ2qQhiqf63+2H57R//8wneM+N6g3mMdwHqx+\niMiwE1TBGuZhEOtReBjE6n9uuPbiIFbf3mlzOvyz83Ba9rl+qM84Tge/XB+V00e1HabnW/1/j9I5\nK9a0+vW6jddH+d66iPE6yfZpjdfH5Vvzd0E1Hs47XkWE3Beh763c8bBrWQg1K7WQmikm+oG5eE6n\n6Vtl43XSu+BRbJiGPwC0c892J6Pby/e1UmTMRloRGc1SHLBSC9lPcvZ7NZ6LXHKO8tH7fy9FARv1\nkHr/bgFzdh8REfBw+NZDDn64RbabkLdSfNcWIdnaIMrgdYR4Qbt9tO2CyyHPirWkCXoL3QCRCJEO\nSBvxGbjeLe5RjER1JFrALj5FpnPyve/gk/v4dA+X7oPSqP4ppffgPFGwTGSaGAyqn3MeGFCCF0ue\nd8h9mzy0OOXw3uJsgjIhoa4TqBo1lmjKJkG0jDYRKA1egReIQjAR3tRwwQq+uYw0YiQwPGjd4Y27\n/4BSio/d/hnWF58CT5FXv2DwkUaMRvp+6Bw6d+huhtlpo1cD/JM1aARIzfRK153sH5eCtBWSKXDg\nbc/HAJQgAiiFbnqCBqhAigtHtDrKD68FmrVaQGA0D7s53dyR9XLJFRzdPbAYB9xoxqci7R/1XZDl\ncO9+xsGhI0mFLCvsjUJFHEOjYbi5GbC4cHIT5FHfBZc5XgdtmMV54DTnbmXrgsHPzuq7oOxzZ3kX\njFu0X7tFepn0X65VQhbKSDsrVpUwkGlhTdv2y8aCyTtt0+JhmliPg9MqfM196xgLpuNbl+2nHwZO\nZ3W8XvYY+zCMV+c9ej5eLx2rk1m+u92eFBV9tAgvk9Wa4YWVJrrk9Lyq7ff//h22//G9cYfTx5Jt\njalFfizOt8GVh8k7ch66H+BdWqq3EN4m9OXh4Rlddvy7yISb4J9u/pdELJTq5KtPkN16if3OFm/c\n+zrdvMVHb/0Mt5aeH+hXIbtRR0rK3wEEKw6zJGMjDKDon/wDg7jyvg43HbpejnXceeVYn1hvsBiH\npTpV3wXferVNp1vuNE8/GfCRp+OZG6/zudvZsOD6vwvG6Xyowt1H7ZiU6U4L67xtTRuvqu1VnGva\nnA7ulp1HqnzJnxVv0u8v27em3T9VZBZ5qIo1Td+aRU7n4/Uk3qTfz98Fj8e3VEW7pulb05RZ5LSK\nXSg19vK3R5GyBXrfnko8eD95gV4AVjBKUVKkutegVIPSwcQ8b0R6nE4QM9muQ9/hu+/9P+y27/Hi\njZ/mqbWPo09dPKdQqkKLhgp8KcpD23ta6ixY5VLFlau/C2ZznjHNsT9NmUUeqmJd97lb2SJ9cob7\nNZLB0Opx0v/dcKjDZWCVyWCYxbTam4TVHxyTsCY54uOwq7+DNY32BnWvKlaZ9Dmt+nKp0t60bL9s\n3zoL1mW3N63x+jjsmuQ3szpeRWQilnNFvvU07LLe4/xkrgb/Pk97zhe2+0t8F3gvOHe5Pj/Jt5z3\neAFfwv30v2sUroI/TMu3EMGoCYspkaI8+CS+HFg7eVx4V4HTQBd/yiRQR2HdY0VRhJIH5WdPygQU\nJcnKlDTe5TDpZK4oSVCOpTXOZYxrsis533J3+budb7JcW+MXP/bf8sz6yyMW6ICmZ3tZ/whYipD9\ncuuH/h6towA9YUFc6FSwS03206rvAj3JlxG8v9pztyrvzVmdI82qXZPkcfhD2YbNtQt3LyOtv0M3\nidjBvLMynart9Sd643ZdJmH1O3HaWP0vgUfFqqrT1zuv7XBxnI7ra5HjshLT8q1JWFVsV0pNhdPr\n5FtVxutw/tOgXLZvnRVr7luPZ7yOai9zQuocrcyx3bVY71mtBazWQmJT5OgOHjSO8y0BcudJnWc/\ntTzsWgRYqxlW4pC4l+97FOw6BU5z78mc0M4d252crvUsRYaNRnhUu9wMYZ7Ht5wT0kzodj0Pti17\n+55aTXHrRsBCUxPHmigc3d5FjlfrhdR5urljq5vTyT2LkWajHlEL9KkL7c7rW06E3AmJ8zzsZuyn\njshoNuoBC6Eh7uV1Wy8k1tHOHVudwreW44D1+mnfOut4zZ3nYSdjLx2oXe4o8pEzhW2BpAoVC8EC\n6Eh6p7KFjliF64DraKJAc2Nds7ISUIs1YajwuSfretp7OVvvJHQPHIsbARsfqVFfDAjrBq0h63rS\ntmPng4S9Oxm+mxF29jFZF2VzlLX4KMTHEbbZIN1Yx4UB4c4Wte17mG4HlXZBQOp1XL1BsnGbfG0D\n3Tkkvv825uAhuttGJV3QmqIcmkH5EMHT9VukPMRKF+u6vTW+QYtGWTBi0CrAhA2MDkEUXjy5ykno\nsuMfcNe+h5OclWCFBdUkJMB4QCscnoyc/XyfnJyV4AmeqP0ETb1GTAMvhjfcQ952uzyrV/i4WicI\nG7i1W7iFVSSs4U1U1IM3ChdqXGyQ0IACpfqn4FKsf52AE3THohOPihXcVLCgIVa9HP8jbwY04sF3\nwXcU5CAOjFLEsaJe02ysB6yuBCTOsd3J6OTHdxkc5ZpHAZvNGK1gp5Oxm+Zk1pP5IrAhMop6YFhv\nhCzFIQqm8i4Qgb19y4OtnG7iSdLid1GkqMeK1dWAzY2IMCj/np/P3WZr7ja8uL8uc7cqnI58tuu2\nSB8U7+cl2KZt1yy2N8tYZQPzItq77lhV+Jxme7OMNfet6WNV4fQH2y32svLY1ScXQp5cakxs73tb\nhxzm5ROZF1dqrDXKS0hBtWd8a7fNTmIpO6xfCA0fW29gpsDp9sOMN9/OyUvqdylVlHSq1y+vpNM7\nu222J/AQG8XLG02CCe/hKu21M8sPd9pkJV2tgFqgSGx5OPPthYinl8pLfFWxS0R44+0uWw8cY495\nAZSgjCBWURYavZhn2F2LLxkaQaTQIWTt8tN8tyjYZqP0lFqlXUAhcW08lncs/+PfottJ6bhu2/dI\n0zsoVd6P3zM/Ys+V3AQvsGgWeifnYzYS0Vj9HEnwLE+oBT6pN2mo03naArQ+8zPkq2vl4ea5J9pN\ni0X6OFHATwbQKPflZWN4brVBFI3nwYvQzS2NsPzW9m7uiAIz8db/aX1/57mQ525qpeHm79fpYlWd\nu02L96p6szrP6MuHKid9LnOZy+SQ9bnMZS7jJZ0Qqg1MDFk/E9YUx2vufOnC9Ki9KTXpPaULdCgi\nqyvSNTXJvVTgYWo0IEDm+yef43W61pfqQBEBMA1RSmFElS/Qofi9K7cdIG071IS8a5sJRcH1sk0B\nha/Hk0PN49pEm9AGFcYoVX5JnNHRxAU6QKqT8txyBVb7kQ4tKFJ9k655llDa/Hz4FKsyfiNPAWiZ\nmA+uADXJJwRUBX82IaULdACtipPxskWGUsWt75PuLZimhKHCTLhQ76rLfO724ZNreZI+GPIwGHIw\nLINhCoOhbOfFgtHhC8PhE+N2XKpgVdEZ1JuG7dPkYTAk5Tw8PArWuItJztqHZTyMKitRZvss+tag\nXZOwzsvpRYzXadh1Fk7P24fTxJrV8Toc9nUVx2vXelqZY6ub0bUnX5+hVqzVDOv1iEZoJtrVyhyt\n3LLdsSRDC/bIKDbqAev1iLg3+TzveE2sL8Lcu9mp2uVGwXJclNVaioOJPJT5VpYLW9sZW9uWVsv3\nLtc6jbW4UIS9r6+HGH2x41WkCG/faqc87Obk3vcybodC7RUsx0UfLsdBkW/7iL6VW2H7Yc7Ww5xW\n5lB1QTdgON24GWo26kW6QWI9W52czsicb0+gNAuhYbUeslaPToTkexEO0pyHneL5GoFhsxlTC07b\n5r0nSYV22x2lIZygWQSVWoLEgRd8pHG18GT+uAg6s4R77aJON2CDGAnDEYtLOUn18OaACDpLCLoH\nKJ/jGjHJxhpuYeEklhdMkqPTYrXsagYfh5zILxHBdFKigw7hwx101obDhyiXnDAh8222eYd9+y4i\nOU2/wIJvnMgHd3i21D4fBA954LcJlSa2FoNCDaCFYlgN1qj5EGU0h/aArnQRBZnaoBs8hxbL7TDg\nuZXPsqqfQdsE1d5B+fwkF8pArYlrrOAWF0jW17CLiyef0Qs6tZiuRfdDNEZsuDRWDJvP1qjdCEnw\nR6kdgxIMfG81x3xveREO05ztTk424Fv1Mb41KOd9F/S/a2btXXDV526PY54xae7WD4H/sM7dhuXa\nLdL7JAw+/LCDjJrADw/gcYN0XP7BoM44rGGnOyvWoFwGVlUezsrpeW2fJU7nvjV9rDmn1bEehYdx\nE6P5eD3NaRmW877IJ7fFIjTs5QuHAxOQqjzYASyAyBzXnr4oHjJX/HFSbC5EvZrlj8qpiPDmWxnt\njiPNBGvheFUm9HNo11YNT94KiXt5zIOnXxfhW7nzvLPfJXWezDF0YbcclRy7vRAV9wA8Ig+Ddr31\nbsrhoSNNi4X6CR60oAJYXtU8fTsiDor2BtMLnPPk3pNYx9t7CVYEEOTERocQKEVsFEYpPBzVNR9c\nDSuESCvqoea55cbRon7Y9izzJKnn/Tc6tB9kxem5PYlFkdaNeEfYTdC5RWW+d9J+1CAEGtGavFFH\ngmKjo6hSNmCXLj6jki7R/kO0zVE2P4llFD4O8XFMun4LtClOst1JTjGqsM1agiTB5I5Tna0EJRbv\nWry79b+Q+B1S3yLP24NKRGGDUIXs+4xdk9AmoW1beDk+Qg9MTKgNsTd8TG5RU1ERlVA4ff8BOQwa\nfKDWUKbJR5c+xhON5whZOLG4R3mU5JB1MVm7eEbRJ23XfR4i0rWbEIbF5XBDEQ59TptrIU9+vEnc\nNIQ1fWKMHX1v9aJqIqNKv7d2ujlbnay4w0BG+1Yt0Dy/Mt63rsO74MM8z6iKNee0Otaw7ePSm69d\nuPuonYnhjh+lM0heWV7BRWENO+ujYpXpnBXLOXfpPEwLaxyfj4L1OPxhFrGm6VtXmQeYnfE6qDMf\nr9P3rTK7jC4WVrXw/DwEWhNoTT28HN/SWlObYPsgVtkdKYN9uLfvyHI4HYas6N+ofWMzYHl5dK3k\ni/CtNPfsj00GV0c1wddqIc2o3K6q43Vnt1ig99s40Z5XSAabiyHL9dF1uI0pFlahMXiSkSf+oLAC\n1grFik4d/XxQBEXqQTvQWo3lNI4NcWx4v20hlZFY9C6ZM5nFHI4JIRcg9yh8cZPryMYAACAASURB\nVGmZVyPDrMUX2GG3hWm3R2jQuwgtQ3cysqWbAwfFJznt2xW2u+gkP40DIAohJBfNvnufPDscaXyW\nt8mAu3HKXn4wEsq6FOsglBpNApCTMfAdFXMn2CBVEbftNi/f+ndE5sYYuzRCjNIOJBsdTu8F3c3Q\n3Yx8+eZAxMNQX/c43Xg6ZvnG6Hsszvq99bCbDdybMdq31ATfug7vgg/zPKMq1pzT6liDOnZwc29I\nrt0ifS5zmctc5jKXuczlOsjo5cpcLl7OznxKyN1gg0Pd4JZ9yLr/AA1jF51zmctc5lIm126R3s+P\nGP5SHAxRGBUSP/jzfm7EKJ3hMIbztDeMNS4P46xYg3kp58FSSo3FGsXDKKzHyWn/7zKsqnZNi9PH\n5VvTwpoWD9PAmvXxelm+Nfj5s4zXWfOtKuO1Kta0OB2066J5yHJPnnsQRRgqwvD0xUuXzYNznjwX\nrBPAEkWKcCgHVUSw3pNah44ELYIfcRO4VkV5pCy73PEaKmgEitwJ+VC4LhRR0qEB76fH6UJDoZDi\nWYfyhFWPhzSRo/zXceNVRKgHemSoMRyHG2ulASFzIw5iRcBDbj3tjicKhWiEb1nrybsOEyiUFooI\n++HFpaBihcQG0QEq9ZCMiFIwqvjjfZHDPg5LLF6bojyYcDLU/QgLwKGTFhLX8DqCU/cbOHBdnGuh\nJUOZOuKHp7eCU10s+4DBBDHe54g/ab8xMbFpsOYTgqhO2x/StSdP+hWahXCZJZYIZAWL58e+xq5e\nYNPt8XR2D4NgghqBaeDTPagvgwqKUPaTYFDXeFVH1V0RCdA5fbImkUHiCNFSzNwdMEy9Kvja37E0\nNi1xrAhGjNezzN2W4oDM5WReRnRPkXIRaMF7QXH95m6zPs+oinUZc7ersC7o/3+WfGvciTxw/XLS\nYXQ9vVFE9zu9/3+tJ1+AUQULJnfaOCzvT9fTG9WBw1iP2t5F8nBerGHXnMRDn7eyCXdVLLh8Tkfl\npTxu3zoPp6O+GEfx8DjG61l9a5zeVfGty8C6zPFa1bdmfbx2u55u4tnatuzsHV/cpTUsL2lubAYs\nLRiiSI20fZRd5/UtUHS6nnbbce+B5bB1zHMQwPqaYWMtIKqDFWE3zdlN3NGt4yLgU0HaCmWLm6Cb\nDc3NGyGLCydvhb7M8eq8sNfN2ElyUucxSh3VeI6Dch98FE5FhMOW4/6DnHbHI0KPh4ClxaCUh2Hf\nEhEOUsvDTkbXFsvwZlRc8teMjrGy3sV4h6nlsOtxGbg2+K4+WiQrVfjWzRsB9Ughqae1k7P9bkrS\nGlriq95lbzWFaihkXcOy4egCM+vRWwnmboLat+AVLghwQQwnxoYU62oRdJ6h8xSzv4dJuie3HTQF\ntuvFr9sEsi791agArraI23gCH9XxkqG6O8j970J3+xhLx+ilj2Aat8mUJ3W77By+ym7rVZzvDj4g\nJozQElDXizTUChvuCWpq8YjTlhzyln6He+o+mWQs6lWe46M8pZ4FDD/wO/xIdrhNwG0OUL6FNhGx\nWmWRJwl188h2TIwsrCFRE7+8iCyF2Nt1ZD0uNjUAcof5YJ/wg304yBETkC0tkq6tIXHUdwhU7jCp\nQ+ceRJBQY+MAiUzRyRTjdWPNsL4WsLigMWb090iV78DMebbbKQeZxfpic2i1HrFaj06UWfswvl/n\nc7dyrLNwqtRxnfQP49xtWK7lIr0v3s/rpE/brllsb5axhr9YL7q96+5bVficZnuzjDWLvnXVsS6b\n02/8U4ukvDoUH30h5OaY/NKLsKvdcbz6Wgfvy3mIb1mIy3VWa4aX1hZKdaraNfets7X3jW+3SJJy\nneAgxbQn1E0D1E+HSDihzR9ksFM+nVR5RuP+OzDy5voB8XuQlhtvXZss/6AcB3jTvE4n2ynVeTJ6\nmSd4aSKWqa0Xh/bieUv2+L7f5qZa4GW9QVP1FtBGw4TSihIFdH/t548X3WMkf6CKDZaJcjrKYlg+\n/RMxS4uj71zoy1UfY1d5vM7nbtX1Pgy+1ZdrF+4+l7nMZS5zmctVkIrv6ZkU1YtQnstsilRYuFVK\nuxYpwtDL13fgpdAtc2oRRPzEZuXk/efnkipITjweQZfYXqR15HzgO7zut1hSMT9vnmFF1U7q9TDK\nWhWqjp1qWkoV1JeJn+J5nBcZUVBxLnOZy7Tl2p2kjwoL6cvgDseo8IQqOsMhJKNCWs6CNRjuMG2s\ncV07DR6mjTUYQjLLnD4qVtX2hn2rSh+OCjmCi+V0lF3DIV9V+voyxuss+sN8vHL02Yvi9HG8C846\nXq0V0lTodB33txwHh0VY9EKvfnizoanFmiAYHeZ4Ub6V5UKaeA5bnvtbjk7XozWsLGtubATU65ow\nUljxpFZ4mGTspw4vUAs0G/WAhdBQC8yJUNjr4luXPV6rtGe9sNPJ2E0yUudJM0Ec+FxhD0HSQk9F\nHrMIJhTQUuQ2pwJ7DrYFcsB7TJ5ibI5yvii71jD4hQD3VB1ZiUBA7aSYO110y6I6HgREG2wQ4sOo\nyNvIWqj9H0LrHmQHKJujTYzSTYy+gTZNUAoJQqg1EN07OxILLkW191DpAUo8KANxE0yRly7iEElx\n+T628wHii9N3bWoYU0crgxNLrjK6/pCt/G0O3H08jn1y7gZwqBwdcdRUnRW9xLNyk0/J8yyrBTJJ\nuKPe5566wwGGjjyBUYpN1eGjPMu6fgKlgqMQfKk18SZCiUflCfpgm3DvAcrl+HqMffE2/qkNZKGO\nNGqg1cBmSt8vj8sC4gWcQnKF7YDvaBBFHCtubhqWlwxxrFFAmvbHq6XTFVCCqnmCBdCBYCJFZIpy\naau1kNV6dFQybZKfWi/sdDP2uhmJ8zhflG2shYaNeshSLUT3wpRncbxe9LtgWO88c7dZ/t4anruN\nk/ncrRrWsM4ouXaL9HEDcZjIccQMEjkq92AWsK6y7ZeBdZVtf9xYV9n2WcG6yrZfJNZVtv2yvrfy\nvHh/GcOJ2sbjsC7Ddud8kSKMEIajc+hEhNx5lCraC2aE00Gsq+YPZ8F6d7/LbmJ79dRHnOFKcXlc\nAcTY025lPcG3dtG7+ehL3PqfD3v/yD2nLi/rS6DI730NyfchH5PTYQLMwguYlZc5daHasfEo5dCt\nXRQyvj3tcd274A7GhtOLgpbu8D9lf0WbjMxlI/WawQLPSciKDug4A+ZjxUO7H4A8QAFaB6w2XuKV\nF/8HlKn1iDktCou8ZFCLBhlT4u/0ifn4PvzExgL1UBMEo9uzznNnP+FeOyvpayFUipc3FwjGlE6D\nwrfeO0jY6ebjfQuhbjSf2FhAq/nc7XFhXWXbZwXrcdo+7vfXLmJlFFn9n/dJKNu5GNS5TKxBzElY\nl2X78I7RebCmadckrEE+r5rtjxvrKts+K+P1cdk+6+O1TGdWx+tl2qW1Jo4NYajGLtCHsc7TXlXb\ni5rdQhSZUqwoMJiSBfq07ToL1iz61jTHa+Y8VmBskLVSvRvXKQ1Hl0CjvIxfoEOxSE6BtGSBDmAF\nJBu/QAdwFoJayQIdQCESoLQqb8/r4vFL8t2VgFghV4xdoAO0bQtMjQ4vQfAZ8O+D/TtUb4EO4L3F\niYeSBTqAEEA9LFmgF8/IqRP1YZWiD8OAsQt0gMBorJKiv8f2ter5y2TfSq0r9y1UkZ5QskAfbGc+\nd7va64KrjjWLc7eyqIR5Tvpcxso455vLXOYyezIfr3O5KJn71vSlKqdV9GSa1dT99IIrxU++lI6q\nwZxV1GTChXQ9cSV6IXWeCD5ByG3wPwL/Kqp0d6CKVOmf6flDVW+o5oLzsX8WmX9XzuWsUuYz1y7c\nvb8j0Q9BGAw5GBUK39/hGN7JGNQdhTVKzoJVtnPSx5rU3qNinYWHUe1Nk4cqWKNsnwano7AelYdJ\nnPb1z8PDKLuus29d9ni9aN+qgnVeHiZhVeGhL7PqW5cxXgc/O5i7dlZOc+fInCexnv3UshAZGoEh\nMprQ6JnhdJTt0/St3Dly50mssJfmNENDIzTEQzzkXkiso50XJd2WooA40ERGYy75XTDr43XQt+61\nUzq5o38iK70TWYUQakVsNM2wiChoZbaou+57eiIo61Fdh2pZ1JuHmM6Anf11tuL4wNj1/t1/TKF3\nyi1Y1SG3e3TSO+zv/gNLqk5NNQgkQvePb41B6QCFRqsmeukFqC2DrlHE0vdOllWGuA4+3UVaW4Tx\nKlrXUDoCVxhjdU5XDjjwW3zQ+g4rqsa62aAuDSIboihUD1XOtm/zg+wBX7X/RBQ6QuVRWKzLMEQ8\nEX6SVfUkW/I+d7If8XRgWNKaGoKyKSAEJqYRrNAwa2yYF3j2xn+NNJeQIMIr0yNGUKFCYlB1hdw2\nqMbxKbkcETrYz/1/D/pOoROqIp+8HhpuD5UMHOVbmXXc7+S0M0vmhczLEVakFZFWNKOAW82I0JRj\nJbnjfiejkzsyJ+S9sPe+b0VGsxgZbi/UGLh+4trM3QZlPncb395lc3rd3gVjT/ev2yK9L4NElYUa\nTMoHGNTpd8JFY53V9mlilen0sS6Lh2liXQQP08CadR7mnF5dHubjdfpYVXk4THN2ujk7iSUfcTKp\nFSzHhueW65iSkLlZH6+TeOhkOdvdnIfd8TwsxYalMGAnyWnloydBtUDzkaWYxSiYSR6miTWJ01aa\n87DEt3porNdCNhsRi3FwCk9EaGeW994+IHn3EH03ReUlU8Hh9eQI2e9+l4ftb7HXeg0vp0PcA0LW\ng2e4rV/ASIzitN8LCuIVfH0Z17mDJPdHno4rHZPES7zHu/wo+QYdv3dKx2C4rZ/G+af5u+47fN8+\nwJ16CKGmNJ9a+AhPBs9yx97hh9mbpEP2B8ATQcAvNz/HC+ErrAZPoZQeQgIfxaQvPoncrsOqgWBc\nP45akJ/WWY4D1ocueRuWSb7lRThIcvaSnJXa8SVvj4LlvLDbzWjljrVaONK3qmIN6lzF8Trr78RZ\nexdcB04vy7cG5dqGu/d3NCYRUYWofs5AmdNUxauC1d+xmVQPsSpWVR4m7TgN7y5NwqvS3mVyOm0e\nqmBN2gOb+9bZsCZ9eQ+292H3rfl4PTvWtMZrK7Pc7+Rjf+8FdhPH04tCYK7ueJ3EQ8d67rXLedhL\nHHuJpWzBklhPO3cs18rrSl9l36rKaTtzpb7VQ+OJxZh6OHqKp5RiIQ5Z3M7I35tQTB2Kw+EJkevb\nnX9g9/DVsb+35OzZuzxV/0n0GCyFQLqLtx8gWXcslviUvc7rvMZ/HKvjcLzv3+Hr+Q4P7OlnVCie\nj5/ik/Xn2fX7/F3n7+lIZ4zt8J61vNT8r1iRxTG2g8lS9IrFbU6aWisUfkKaguJmI2KlXs3nx/5e\nKVbqEUtx+QbXIN44MVqx0YxZ89XqQc/fBce658W66u+CqnO3y5yzzKpvndCvrHlFZRIZ3vuJ5J+F\n0Glh9Tt8WnZV4aEqRpV2p8nprPFwFqxp2n6dfasqlojM5Hitovu4fGs+XqtjlemICIdpzt1WSjd3\nY3Vz52lljslJtMJWJycpuegKZnO8VvEt64VWapnEQzPU3GpG1Eouywu1oh6UT5S8CHtJxv12SjqB\n00m2OydsbWfcvZ+TZaOxRIRu7rjbTjlM87F4Lvdsvddh650udgzWoD1ldlXxLRFwiXDvnqXbHe/T\nmfO0VwLcZjT23jYRh+vew+3/ELGjF7AAeb6LTg8JSoqpawKWw2fQKmbchoyIkPsunfwhuU/H2p5K\nxgdskdMvYTYaq+0FQ5dAeQY5ezq6yb9d/lmejG7w9da3uZN/m7ruoMdgaW346FOfwXz0CXxz/KJZ\nlEY/yFFbyYTcfpmwQIea0UTB5An9fO5WyHzudna7ZnHuVtX+6zx3G5RLCXfPsowvfvGL5HmOtZbP\nfvaz/Pqv/zqtVos/+ZM/YXt7m83NTX73d3+XZrMJwF/91V/x1a9+Fa01v/3bv82nP/3pSm0Nkjlq\n96O/GzWYawAnv8RG7XSM20kZ3PWpglUlt6Hf3rDDjrJ9FNbwTtSj8ND/WRUehvXOy2kZD5fN6bhd\nvbNyOrjbWJXTafjpKPvH8fConF7kGJu2bw3y8bh9qwxrPl6rczps+zTGa/9vB2y1Mw5SS+aO83hV\nL7czDjRLUUBkNLtJseDOvOB6GKp3Y/NxLeT+30dWYIDQQGw0q7WI9frJENLzjNfLfhccZpbtTk7X\nFvmrdoCHPm9Ga240Qhaj4Cgn3WiN9Z7ceVLr2U0t1nnW6iG1Xk56aMwp38o9PGintHJHav1RvqwG\nIlMsdFbrEWu1yZx2up6793PabUeaFrXiQREYIY4V9Zpmbc0gNc9easl6fe2Hcr8Xo4Bmqtj9cUL3\nwJF2PDYt2gliRVTX1BcNm8/VWVg7uagdxelBj9Mkd6QjfAsEbxW+pfCpQiyILfKfi1v5FbVYsbps\nCJdgLz3OSXcCiKBSh0ocai+H79+H3R9BvovYDpJ3wHtUWIOwjjILEN+g6/dJ0h9g7R4uP8DlHdAa\njMYh5JLiXcCtxk/S0OvEqoFxUeH9RoESRCw2PSTxD8hUG0uKcynicpQJ0DpCK0MgMTuuzTvhPfY4\npC1tWvYQUERBjFEaJYLLU9omItGG1HsSb8ldTmAiUAENWedJ8xJKhBZvYtQuEQ5xCSiNMhEZmpaD\n/WiZf/WZ/4bnb3+S1aWbLDRW0NqgrEN1c1Qrxby3j77ThagGyiBKg1fF8VdNI3WDXw6xzzagblCn\n7gzwRz2pFazVI9bi43ERmPm7YBRW/7OX9X696HVBGdawzlV5F8x9azxW3+ZhW0fJpeWkp2lKHMc4\n5/j93/99fvM3f5NvfvObLC4u8qu/+qt85Stfod1u8xu/8Ru8//77fPnLX+aP/uiP2NnZ4Q//8A/5\n8pe/XCm8ZpL4CmE6VXRg/ITwrFj9LpgGVt8ZpoVVhYdpYfUHyrSwYM7pNDm96jzAdPxh7luFzPJ4\nnRYPb+602UnsRKzTi+9H02mGmk+sN6/keBURvn3v4Ki00zh5caXOWqM8hLeqb31363BsHntfFiPD\nx9ebE3n41qttOt1y482SI1gRmIClvp0yIi37hDz3ygKbzzRKdZwXXr1/UFoRDSB/oPDdCalCoSe6\n7Sfb/r/9r/DgXqlOVw7Z8z8uNwp4ZuHfEEr5M+7bH9FK35qI9dfB63T8+BB4gB0CDtzp8dpUKzwd\nfJJINbhjv8ua2QZfnjLwX/zqn3Dzyc+U6qidlOjrOxODZrJf2EAWy0qwwWYj5Nnl+sx9B171d8Fl\nv1+nuS6Yz90+HHM359zYNIZLC3eP4xgAay3ee5rNJt/85jf5xV/8RQB+6Zd+iW984xsAfOMb3+Dn\nfu7nCIKAGzducOvWLd58883LMrWyTGt/Y1InPy68S9q/OZJZ5WHaWJcps8zpZcqo3d/zYE1T5uP1\nYvAuU1SF+lDVnm42Oa3qW5Vaq6D0OHxLqYrjpwKWVHnGaq1N0SMqIpXU4D6Wiv5QYTKvxlyINixa\nl+fiFjonc8FrqsmL4Wf5aPQz7Pg7vJb9v+z6O5gKdhlVgYeKflrl+wGq5eJWkfm74GKwqsg05xlX\nmYdpyYd97nZpi3TvPb/3e7/H7/zO7/Dyyy/z9NNPs7+/z8rKCgDLy8vs7+8DsLu7y/r6+tFn19fX\n2dnZqdRO2cMOhjBP+nxZWIOIVMLq61TBGg63eFSsvs40sKqEd/R3k6bFQ//f58Ua5PW8WH2daWKV\nybR9a1pYfZ3L5GEWfeuqj9fBts/T3nUYr5N0jJowwRYB6xHb+/cYUb1g7wn7/EVYuJTb5bzHS/H3\neLMe17ugeI5xohC8L89NFBFyVzyjn2B7oNXYPOIeGojgJvBgracoIVb2jILupSeUPaOmuGCrdI2n\nhDQVcld+G5sX37uJu+QZvUd5jyqtES7gPORS6qdYW1Aw4XIqpQ3KlF+O5oOA1HVxuqQPFWReyIPy\n9vLAkHt7ahE+KFoHiLfEQUxIjWeDT/PJ6Bdo+z3+Of33PHDvIAh1E4MXdEkHBSYi7x5AXhIOIYIS\ngUl7BxokEygdP4LzhT/M525Xc+72YZlnTNLp/34WfWtWOS07ab+029211vzxH/8xnU6HL33pS/zL\nv/zLid9P2pGoumNR1gF9IkQE59wpzD5Zfb0yYgexRun1sfptVMEq6/BJ7T0q1igeoOD7rDyUcTqJ\nBxE5Cvfw3h8N8lF2XQSn42wf5uGyOb1M35om1iz51rDto3zrssfrsG+N42oYa1a+t4bH6zgeLnO8\n9tt7VCyhCC/OnKdjHdudfkkwBfT/BpygcpBUYNfBthQ3Xy8p1A2N1BQqVgShJjKKRmjYaEQsRAGp\n82y1U1qZI3UeJxDqInd6pR6x1iu1NGi7CFgRUuto5Y7triWxnnqg2agHNMOilng4dCJ52ePVGMOn\nbi5xkOY8HMhLV3BU43mjflwSbBDLi5A7IXGevSRnN3E4EZZiw3o9oN6rLW8G7FNK8dJak2SA08x6\nHBDpIsd/rR4dla86wakXbCYkHUf7Yc72uyl5yxEECmkGSKRBgw71UT765kbA6kqIV8JOO2MvzUmd\nJ3fF4XNkNItxwGYjJvo3isOdjO33ukd56c5LUTe7ppANwwf1nAdbjrWaYTkOj+rBD/ZAaAyfurnI\nQVKUXevaIvfep77IId/PUe91ifZzJDTk63Vcs4YPA0QrtHOo1BLsdwn3E3gd/GaEf7IOzQCJFdgM\n1eqgtrYx3/0R7CTAAj60iPKId3jJ8dphfUbHPSS1B8U9C9oUC3al8OLIlKdDzra0eMs+oO2+ww11\ni/+k/llu6FssqkUQzR5t7rqH/H3nVb6fv0uE4lPBJh8LVlklpo4mxbNHxptun28n9zkkY0ErbkV1\n6loR4ItNLaXJRdjLE7wEPGGeZy1+jl35gB/4v8epjJWwRhPDDR9w22lCr2hry2EgZMqT+ZxABdRU\nyIKP2Mxr8H/9z2wt/zWNl/810e3nMYvr6GgRlQmqY9F3EvT9tLj6HTiqGz+Y1SKAh/DrO/jFAHmm\njqyESM0UTqqP76vYSRz7aZvVmmG1FhIbTWz0icP6WXy/zurcbfideJ3XBdPEmiXfGrb9us/dRslj\nqZP+F3/xF0RRxN/8zd/wxS9+kZWVFXZ3d/mDP/gD/vRP/5SvfOUrAHz+858H4Etf+hJf+MIXeOml\nl07gvP7667z++utH///CF75w4vd9MqchVbC8v9yclap6VXmYll2X3V5VrKp2XfYzzn1rujpV9ea+\nNf32rrKfHqSWH+y0yy9lBvh+BnvlSjc+WuPpTy6OrW3ctyl3nmjCKeI7e222Orb0vNgo+NSNBcIJ\nJ6CX3de5K06Cy3gA+N7WIYcTcsufWYq5tVArt0kEW4HTt/9pn+1309JDZRMrPvmfrVFvjMcSKTZ1\nIjO+1j3Afifnje12Sd3sQn5io0kjKj87uf+9He7+xy1USaK6AMQalZZzSv4ObL+LKpnYeu+5yz+T\n21Yp1KvhNu/kD0pD/b0E7LDIjj0sxdoMF9nKy3XqyrFm+ktczbp5gQ3zEgf+Lg/s97AkiMDPRrdZ\nysZPpAFis0DThZiyWBeleepj/z0mrZfahaY8IAPwocL+5zeQCakFH19rsFQrz2WH+dztLG3O527V\n25umXXPfmqz353/+50f/fvnll3n55Zcv5yT94OAAYwzNZpMsy3jttdf4tV/7NV555RX+9m//ls9/\n/vN87Wtf47Of/SwAr7zyCl/+8pf55V/+ZXZ2drh37x4vvvjiKdz+Q4yTy16kTxNrmnsn0xwcs9he\nVayr7A/TxJpV37rqnF5322f1GafZXhFePSGqy44r+nQs2jNxYaqUIqiQj+s8FYq5MVmJy+9ro0BX\neMZ8QvgklIe+90VX5NTmvnSBDoUXBBNmSEopQj05d9QEqlLcYpVnNELpAh16HlyhDJ1K8glh2L2c\n0EmrTsDiJ+biWyxtJtyoB7TUhKLsgOsloqzqZ7gRfJyO3+Pt/P8jlePFvVJQw6BUuf0hunyBDiAe\n0iqXSE4WJTDRAanmDzCfu027vVnFmtW526zKVfOt4YNmuKST9Pfee48/+7M/Owox+IVf+AV+5Vd+\npbQE21/+5V/y1a9+FWMMv/Vbv8VnPlN+y+agiJwOeR+1AzIcylBFZzBk5zxYwyEagz8fDum4TKxx\nOoNYw+EeZ8WqanuVPhwMIbksHua+Ned08OeDPIjIyFs6q9g1TU7737Xz8Vrdt7wIndxxmDm2uznp\nwEJIK1iKDOv1kChVpC3L9rsJh9uWfiqwABIofNNgGgGNJcPKSsCNzZA4Om7TemGnm7HXzbACtUCf\nCAMf5iH3kFjHbmrZ7dqjsmYD1qNQNAJNsxda34xGY10GpyJyIqwfOAoDjwdODp0XdrsZO0nOQeoQ\n/FFpqkGpB4qNesRyHFDrfX7YrtwK2w9zHu7kOAv1hubmZsDS4hhOE0/3wLF7J2X3TobLj59HNPiG\nQWqGxmrI4oLmxmbIQtMcYXkv7B9Y7m9ZksQTRYr1tYCNtRBjTtp/7Fu+KFHXtaTumGcFLMeFby3F\nAab33TBsd+I8W62Ug1ZGspuit1L0+8mJ03LRCrtUI1+pI1pjckuw3cF0s+MIbBEk20OS9/DJA5TP\nUBJgfIAayNP2YknUPimHpG4frzy57ZxYsHuEPZVwP+jyQA7ItJA5SzZ0c7oTcEFEJpquB4/mME97\nSP3vA0iyGnm6TJpDFEIcHhLFHQa7WwTCIGZD3+DF4EUsGffy75Cxe6QToHhKrfCCWWddIrSCtj0k\nJzthV0yDjfBpGixglCH1h3TsDp7jxbjSMY3mJ1hYepk4fgalwyK9ZUAEcLUQu9HERQFaBHPQJdzr\nnthQkUjjn6jhb8b4tah3K9RJn1fAQlR8JyzFwVEay/xdUM2ucTrXaZ5x2VjjdC6C00E//TDO3Ybl\nsYS7X6T0iRp+wY16zGGC+gQO7oZcJNa43InhCU+/vbNildk+iDXO9qpYKSw9rQAAIABJREFU42wf\nxJomp2V2nYfTi+RhlN5V9q2qWHPfmg4PV43Tq+5b1nky57G990m/bvFJ24U8cSRtyxtvpuS+WCTJ\n0IlcEBS1quNlgYYM1A8fnJgXdbbrgeH5lfrRKfwwD3273jtIaOUOBmouD2JFWrEQmaOSTpfhWyLC\nW3vdXi766YhfTVG7PFDFCWjm5Kiu+bEUNmkFL6w0jmqkD9/G3bfrg7sZ2w8taVos1E/woAreF5ua\nl16Ij070T3GaOtLE86O3ElodQczpPtRKiGJFEBQtZBlkWZ/7Y9vDUFGL4aXna9TrozcUrCvqwVvv\nQSkiowiN6V0Qd5JT3+M0yd1RTfYTfZF7VOqwOx6fGCQweGOGOPVo59HtFuE//zXkraL2+VCpMhWG\nKGXouj1yErxPcTY5oYMxoDUt3+GfzXskWLq+i/WDWIowiEEptqzDaoP1nsSePEEPTYTShr1OwIOD\nFXKr6aTuxIWIRivqcUAUCCsre0QhLMoSLwQvoNG8kb3BltuiFkSEWvNx6vynwRoNQsLe+DjuRA1a\n44EV9QSRrhNIcCoqQQKNVw5pPEO4+BzGLKKldpJTBWjwRpM8tYqPQnyg4YTfCNp7lHUECxa9oJGa\nRsLhhUDRfj3QfGSpRhwYQq0e+3fgVZoPXwYP08Saz93mc7dhrHEL9ku7OO6yZNSDDhJYllfQ/3mZ\nzjSxhh1k1K7R47S9rHbfrHM6js/HZXtf73H41ji9We3DWcWaj9fqWGdtb9bGa2A0gdGldmmtiBsB\nKjS4IMfb0XrWKqwFu+hRR2uZoZ14FJmHUIqFyThOw8AQBgYn3ZGnzn2s1MOiUlPzhyq+JSK0Mkd+\nel5VtAMkrv+vvt3D9hf/D7RiMQoITLldO7uOVvvkZ/siokhTqMWKYEyOulKKsBYQ1sCZDD8m/dyL\nIkn6tvdtOm17nkOegzGj+xCOfasSp77gtKg9P6KvQ42EGtdReBl3KqPxRiNYgu6D4gb3ESJ5jpCT\nmw55NiYf3DlwjgPdYcvujtZByHuLe2satLLOSK3cZeCgm2yyc+g4dTxNEW3R6han8k+vLfCifpYF\nvcAb2RvcsXeO9BKbkQAv1G6ynCtgxDN6D94TENCMl3rpAKedVVmPQREuvIDSG6NUekfn4KMA2xha\nwB8j4bWByBCsa3w0+vuh/9mFyLBUi0ZrXOF3QVWsWX0XzOcZVx9r1jm11n54Fulzmctc5jKXucxl\nLnO5+rIYxnxu40k+Ulvkh9kP+WbyTSbfCjGXucxlLldfrt0ivUq4ez/EoCz0YDA/4jxY/VyFKlj9\nf5eFYEzL9ipY/ZPfy+bhPM84nIvSl8vgtMz2Qb1Z5PSyfWtWeSizazjMaT5eq2GVPeOo8TpLvlVm\nlxcht44k9+hY0EoQq5Ch27MCU4RdR1qjgtHh7iBEShGo4vQQTts1aPtSFCBiybwwfIdYP9xdRHCu\nqF1+0b6VuaI0WL/9HmMnDfNSnD46hdZS1JfWgBriQStqpuB3nF157kgzITBFWDtIj/fT4e6BEax1\njA13d57UeYI66F7Ne/FDpxpK0EYQDUr54jnscCRDoUMAB4nFayHqnZo/Cqf9PwuRodsLd5dT4e45\nqpMStBw+Mfi4jg/Ck3aJw+f72Owe3qSEKIw3qKEyBj5QOGWxtijnplCQnzyR9lpzqGDfh6R6gUh7\njGR4P3RyreskPqCdeJRZxOgc606Gzhsd432IVo5GtAgIqc2Pwt3rJuCVjSd5cWmdN1pbfLX1DwSh\nIzQhmTuZW94MYhZ1yK5PIGygUfg8Z/AYXGlDbXmN+uIGNX0D6eZkBwdIdjJ/nnodFhZwTY+pBajE\nQzIU4qpBQoPEuqhPrzVyKtpBCAOKsW8MYmTkeNW9VBfxXN54zTxpVvw+MJ4o0gTB7L0LhrEe97tg\nvi54fDxc57nbuFN04PrlpMPoXIZRJAx3XBWd4c541PZErtYFEd4fXz4yDaxBGcfpRfEgcr4LIi7C\nt/rcTgtr7luFnKcPL+pimzKsuW/N/njtWk83Ly6XO8zc0TJABCQH3waTa+qhZmXZcHMzIo6P8awX\ndjoZu0mGk6JG+kZj/MVxZZzmzrPdydhPc7wUea39muxnxToLDyJC6oSudTzsXfx2unSdB6eQXOES\ncG0NgykBStB1j2lCc0HRiAzrjZClODyVn+29x1podz27u5bth57sVFx9cYFes6lpNjQ3b5RcHOeF\nxHp2ezXZBy/jEwu+I/hEgwcVCaop6Egd7SeIgE9A2iBWgQHdEHQdBu5eIzKKjXrAchzSCE2RyvwI\n41WksPdBO+XwsEu6dYC5+xDzwzvo9vHi15uA7MZN7M1btHWLpHOH3Xf+PcnO90COw8nrNNmInqEm\nDVCKjt/l0D7ADV6YhiI2C0S6xt3c8oHP+Q+dB7zr0iOfVwhrgefZpibGkfuQ91sB7x0a8oHw+9A4\nbi45lmOL90KSRby/HZBkAccLW8EYxUKtxsura3xi6QZvJ/f4bvImGfmRjgIWayE1JdwyAU+okI/5\ngBV18swpUBGhiVnafIqlm0/z1Gd+jo3nP4kJwiNOO/fus/3qaxy8f5dEKXjySeSFj8HCwjFQ5tH3\nu5gHKdLy+DgkW2rgGvGpDSalhCjUNOqK1dWAGxsRYXiskznPw6HxunnBFz32x2uSCJ2u58G2ZW/f\nM/jRek1x80bAyrKh2dCV25vP3cbbPk2sD9PcTanxF8d9GOZuw3ItF+l98b5aLb1pYVVtr4peWU7R\n47RrFtubZazhL7CLbu+6+1YVPqfZ3ixjzaJvXXWsKpy+dv+A7oQSWLcaAc+sNCe2d5XH6+sPDmjb\nch5cG+z2ZNt/6tM1mo3ywL633014/87kElif+6k6cVze5g8ftthNJ5f5Upw+vT4tw1ERp6UZGj6x\n0Tyx+TBKqvD+8Ftvcu///qcJNsF38v+dTrZdqlMPFtC2nAcnwpeThJ0sKdUzbonDTnn/iIfI1Uny\n/NTvtFL8xNomP7V5my2/x3c636ftx7f5vAn5zfpyaXsA//a/+x9Zufl0qc4H+10+aGelOgDZBwqx\n5f3zsRcjbmyOzi0flMser6++1uKwvNQ9m+uGj390Qh34iu19GN4F87lbdZ2qc7dp8V5Vb1Z9qy/X\nLtx9LnOZy1zmMpeLEqMUTMiJ9U7wXqhSI/wyJfeeaMQJxVlFRPC2OFGeCKWE8gLagj19DH9KfAUd\nKG55j+MJWG6y7YqiryfsQ0BiIQ5KwcQJLvfoaPwEW0TIE09UL+8f50FUL8y6BEtk8iaEFUeIFKHt\n49oTwVU4y/GZTCbVCzK0waWAl1bW+NzNJ9lJuvwf77yBWTkkV0kplIHeFkq5AzpXYVO34llVEKjh\nDIBTcs6hdSEiIog6jn8YJ1M605rLXOYyJbl2J+nD4QSD0t/hGBXm0P/5YCjDOKzBkJtRYQ5nwRq0\nq4rOOL3hELnL4OGysQZ1qmJVbW/cMBgMuRkMoXkU2wexzmPXo/rWuN27i+J0mjxc9Hh9FLvOO15n\ncYxdJ986z3gt48GLkLuiFni/dnnuBZ8I0i7Cu3HFLd5xBAtNw83NkIWFos72Zb4LbK8W+W43I3FF\nzXWjIDb6RO3yKjxkubC1nbG7a0lSIc0FdJGDrWse3VQoA0VIcu8EWgS8AgsuV7hDkEyDAdP0mDqo\nQNCBIjKFXau1iLVGhAb29i33t3K6XU+SyvFCXfqBz317j23XGuJYUa9pNtYC1teK8OaHOznbO5Zu\n4klTwStBBRT3CTRBhcc12ZuhITYKrRSZ83StP05vyCzB+/sEdw7QrQyV5Ehk8M0Id3MB+8waUg+g\n5VDbHjoCabHgjxua+pJh45k6i+sRNhO23++yfz8lbTtsJoSRImoGrNyKWH+qjgkVB9sZD9/r0j10\nZG2HTzKUTVBJi2D7DjptkfkWD3mbA7lP6ov/o4o+cN6CdwhCqoQ0AKcE63OMMoQqIBbDQm4IRPPQ\nC//sFR94Ycc5Dp1Da40g5DbDiQMH5v9n782aJFmu/L6fLxGRS+1dvd0N9wIX+zpYBjMUt+HMkBLN\n9EK+0mSk+K4nyvSKB30LfQE9SJoxUpKRZqKRNiNhZjADDADiYrkb7ta3l+rac4nF3Y8eIrMrKysj\nMqo7u7q6Oo8Z0H27vP5+4h/Hw/24n+Nn16IeRpAq3CCgIwMthe9CuuEgUdAX2scxZqAIaUCCoBND\niOH6S6v87uuvUITA3+x9yp4forQQ8Fij0CagVE7QA4wWbhnNNzstrhnDCoGW0lhlSzMshAiDSTZZ\nee3v0brxDUxnG9veJGlZWolia8NyfTvGWDhKCx4OC9LCkwUhSBjZ1DgyQpEYxXY7YjU2xEajURS5\nMEwDO7uO/f2AABvrmhvXLe2WppWoU5tzz2rtVoxC6w+ygswFcieIL9Mz/AD8QKNEsbqiuXXD0Gkb\nkkRh7eww4cs6Fzzttdvjzq9XzS+A5drtPLpPYjXlYZZcOSe9LoxgksyqkIQmbSaNZVbexIuGNf7Z\n86j7RWI9z7pfVqznWfenhfU8636ZsJr2l2aen/4ixRXVYc9KCV/+QovNDXNhPOwPcz44TGdcUnci\nGvja9W7pgNRgfXwn487dYlS9q+IZtSd+aXQhXNVpnQiPKrBVRhkI2iuKe7q2v3E0Q7khUHUEWOY5\nA3hf934CX/9qm5WuOVOTfSxBhL237nH/z94f15KbLYlhcPt1RNtyg2KW6HIzQWnwNVHWOio19o6a\n4A3Pnd/+Lxwd/i3OzS53BhCM4aHq4YJDKk7hrUn4f44iHgRDv5itmFYata8Ib2nyQUHVCrLVSfAI\nCk2enQ5vv7G9yvd/5w1aScSPP/mEOys9UldNRDuO+dc3BqwZYPqSurFe2vLSl/811177QzBVIduC\njSC6HQiqLk1B+NxGm/UkqiwDKCI4VxqztZfnuyUi3DlOud/Pz1xSNynKC1+/uUpsq8sFPs/f7+U6\n49liKaUeOaHPm+7PAqvq51cuuKVuR2JMQl3OQJM2kztTT9rfGKvuRZ8Ha9xmEVhNdnm0rq8lfJ7+\nFsnpJK9PijVu87za1qKwxm0uE9ZyvJ5g1X3oJ3Wf7PtJ+nsRxuvkc1b1Z4wpnc+aMFIRhdYXa1su\nUFlfeyyB0vebh5Xlgjtzm/lpObkRvboNSo1uda9pg8KHeqd63E6pOgd9hFWW9q7FEtEYrSoddACt\nFGFQ1DvoAJlHCdUOOkAACVLroAOEokydqM+uMHhJax10AO9zgkilgw7gfIY3ttJBBwgSCLmQ9asd\ndIB0kBGb6JSDvrHW4R///S/zR3/3S/zmvfv8b//Xj/m0f1TroAMM85zE2EoHHSAER9zZrnHQAcpx\nEeaMV1BYrSoddCjHRRSZWgcdns1ckPtQ66ADYOZ/k5Zzwfn6exHWGU2x5q1HlpyeYNWdxi9z0p9A\n6l7OeWTRwQzznOamsqjne1ayKB6ehVx123oWctU5vej3cll5eCZSm3NdSpMnW3xg2/xLzebl9MIc\nn/ppiVJznNNy82O+zM/FXbRIGEcU1LSZ6yiOsQLzwCTMzz8HEKoXg2PJ/PzL+ZqaaTFK4O52Yr77\njc/w2stb/PStT/iP/++vR6UGwflmutPgGUPNBsR5ZZHjtemoXtg3sGGHi/rcLueCE7nq64znWS5r\n4Hjde7ly4e7T4QXTOxTjE6fJ/wbO/Ns0LbOwpmW8ezT+3fFO0jT29M7JrMEzjTX+3enw8nm7MOfB\nmuShLq/ovJzO4qEKa57uTTltgjX+3cfldBYPVZyOOTqPbU2+gyacPi4PY6ynaVuTWEvbWqxtTbZp\nwkOTsb9o22qCNW0XF8HpIuYCEWFv37Oz60hH+c7OK0CII0UcQ7djuH0relTeqEr3Rc4FXoTdQcFB\nVpC7QB4YuWiTzyN0IsuNTkTHlnm30ej0cPIdeg/3HhQcHnnSVMhyGUUHlM+YJIr1NUN3U3OQl3m+\neZBHpc2sKvN7W9aw2YroF45e7sl8WQ6tvP6rrJGeWM16bFGpZm/fl5w+Oskvy1yd8FX+3tijGtdK\nVwSUF5QXGLoy07htEaPK/6FPYwm024aXblm6XU0Sa+K4PCVxaUHRy8j3hxz88j693+6V3o0aUenL\n3HwvKV76ZNl9BnJMcut3MO0b6GgddHm6qwhoX6DyHH10BK0E3+kgNiaoceF4h3eHFNkug8O3KNId\nVq99l6h9CxNtoNUIK+QoN0QND3H3fs5e/gv6ckAmfXLfJwSHNhFKl1eseecYkpOP89HFU7gUlKbQ\nCQNveJAr/ubAE+LWKE0gkPmcEAItnaCcIQwh/dQjO4oYDSIE70nTHGsNkTVowDuHeM93v/cF3nzj\nBm+//4Af/+Ij8tzR7ibolkYSGK457LVxWLnCB0/mClrWshEZNi28Fnm+3c5IYosohUjAufLm9yRa\nJVEdOqxyw3yR1ht/h3DtJr61QohboAxKCcpO3J+wAkqPzUYe2UOkFLFRtCPDzU5MOzrZHBmPMecD\nuQ/lnRRpGU2w1Y5IjCY2Gms0IQiF9+Re6BWew8yx2bJ0IkNsyrrpSqlRm0DmhL00x2rNRmJJbDkO\n7Tm+30UeKIaeYc+x81HKsQ6woct7ASI12mk7PfbX4ojtdkTbnug+Pfafxfz6LOaCRc2v0/o/zXXG\nRazdJnlYrt2enm1VOepXzkkfy5j0uoeHE6e+LhzhaWDVtRljLaK/RWI9Kx4WibXktBnWkofzYy1t\na8kpQJ4Hdh4W2EixvRU9yomuwroI3UWE1Afe3u2R1YSRawXXOxGvrrZqsXo9z96BY3PDsjq6EG9a\nihDYG+Qopdhqx9gZx/EiwnHmOM4dW+2Ylp0dPpjlgbffHXJwOE5orxLB9ArMwJcO+qwWRlFsRkhk\nKrG0hs2usLn7gKNf7+BqynP18/foD96hcA+ZeYRpEtpb32N15ZvYfg81a1EPhDhhR7/H4e4PyYd3\nZmJpu8r1a3/IulzDHN1DzQj/DhLohV3e48c4X13CzBH4WSH8rAcfpxo/kwvBatAPNNldgWxGGxEQ\nIcodPk0R57DW8PVvvMHXv/4G771/l5/8+B2Ggwy92kJ/tkuxIRBXv8fvrxm+mRS8HM+O4hCEWK9y\ny7zJNV4iUmdLngkKv3aN7B/+A9RWgoqqT45XI8X1TsJmO8ZUhI2IlLneu0NH5mcv1mOj2GpZBkUo\nLxmc0UYrWIsNidHspeWlk7OkZTVvbrZp29njayxpr+DeO0P27mS4vGI53wG+GJUOe4XNW614eSXm\neidezgWXeH5d8nD1OZ2UKxvuPt7FqSMLmhHVFKsJ3qzduFnSxLia7DhN9vukWM+Ch0VjLYKH82DN\n0+tZ2da8WpuX1bbmfQAnsZrI0rZO8JpgNZEXndM41ty+FV2quUApRdsaWkZXOhgAQeAo88hKvd6r\nq+WJc51ekdZzF/xKKdZaEStx9YV6AEmsWekaDg7n8aWwQwc1kdHKCzpQ4ZSWEgLs7TrCf7mHyuvD\nrFP3MYXbqW7gM9z+r4nkdaocJAWYPKPf/yH58JNqvdwxxd7fYtWXKttopVkz14lo1zrpFs3DIuGD\nNKvWHUXhof0wgayinVKgFJEpT8G//JXX+PZ3Ps+9u3v86Z/8fxwdneTKe5djb2+AP1snfVK+u2a5\nRXUbhaIlLW6p12vaCPboIaGVEuL6mnwrsWW7W99GKcXDQU5e87nJvXCvn1O3kRQEDjKPoqi9TyF1\ngdwFOlH9Mj042PkwpTbSfwDKCZJU9+eCcJw7bq60avtbzgUnGEu/YPFrt6ZylW1rUswPfvCDHzRu\n/RzJrDCLWRJCdcmI82JN7ijV9TcPa15oyTRWE90XidWk3SJ4WCTWktOzeC86D0vbOmm35HQ+VvDC\nwf2MB78dojTE7eoTrsvKg9aKgJB7mXnKZ7Viu21ZTSy6SqcgHN/p8/Ct/fJEcyVGzTh9zFzgfj+j\nnzsSa2aeUHov7O4V3H/gMEZI4uqLeJQSlKIsnzZrvaQE3QmYLlAIM308EZRzmGEKIRAiO/uoNghm\nmKNzQRUFhHDG7RLAJy382jYBIWQHMCPnWxPRsTeIVBtUhFJnN0iDOPbd+9xN/5YgBRo1866AQKBQ\nAa8cCW2MOuvAFeL4SH3M2/5tkEA0QpuigZ0CfnSsGQSDlzDzlFk82DTGHSt8EZjILDjFhFoRPve1\nbf7ov/oWnXbCn/3nn/PWLz4km7g0LmoJr3zZsHnLM3AKJ2cX2Qb4SqvLH3Q2SRQ4ZkcwxKrLrfir\ndO12uaMyw5qVNay8+RrXvvEFvNbkFSfWiSk3kxIz/wRMK0XhpfL0u20Vt7pl1Ejmw8wxZpTiWtuy\n2Y4oguAqsGBcn15IjKkcj0EEbSAbBHwxgwcFq9uWG6+3QZdjf5bERnGjG9My9ZdhLeeC01hN2i15\nWK4zzoM1KVcu3H2SgPFOSt0jjndj5p1CNMWabDN+WZMvbYz1ODkX0y91kViL5mEW1iJ4WCTWRXJa\ntav3InC6tK3Tz7jk9Ml4OC/Wk/CQDz333h0yOCjIBoEildIf0BC3FHHHsLIVcfvzHUykTmFd5rmg\nGOXV9gtPL/dstCytUV5qNIqymcRyQ8fOL/YZ7qRkxzlu4Et/VEPUsUQrls52C/vFNQ6DJ/WB3J+4\nrEZBrBUtq1nRht4+9PueLIN8VLpOqTK/vdVSrK0aXnkpZvKwZKy7c2Xe/2Do+WQnJ7cBHcvo1nhK\nryRI6ahnAnse/eEA6wqUD+DDiWKxJsQGH0fkK220KLQL5Un8KC1AEVDBoVyO7vfBGEK7Q7ARoiyl\n2xogDAj5Ia5/h3D3x7TpYHULjUWNo9KtBROjVESmFJ+GX3Ls75KGA9LiAAkepQ1Wxxil0UEReQ22\nrFEexONHN6FHUZdYdWjRIQrrfGgesK/2OZZjjosjhIDVEYmOSTC0guHDwza/zWP2PezngUFROtHt\nJMEoRSCQDXPiYRvtNKGAwaDsL4ki7Ihbn+fYLUe8pbm5tsI31l4lSOAnxx+wn/dRQ/CHntbuMa+9\nqemuK6KOJ6jyZN+YFkWIGDrDUT/m+9FrfLG1wnUTsYpChwBK4S04HEPpEyTmWutNWnqNmA7aj4zD\nKkCQ4DFdxfbvfY3OS9eJ1lew3fajU7AiCKkr7b3wwkbLkozuYLCm+Xj1PlCEMif9KHPIKLc7GY0f\nMzXGhi5wlBWsJxEtq0lG/SmlcCFQ+EDmAntpzsNhweltkPLZxrnynchwu5sQ25OBMf5uucKTDwNZ\n33NwLyNZMaxsRiQdQ9TSIx7KXPnMB3qFJ3OBjdbpfPrpsT/JxyQPz+NcUIc13Qaezvx62eaC5Trj\ncnBaFRlw5Zz0eRJCaJRX0CQMfpFY83ZfFt3fVcdqwuci+3sRsJ5n3ReNtRyvi8W6rOP13R8dsPdJ\nfXkoGyu+8U+uYaOra1uf/PAeu28d1LYRoPjjG0hcn0rjdhR+UN9fkii+8802pqYEFsBbD47puznh\nmLsZ8V/u1bYByLfWRk53nYx2JuZI8pv/G5UNa9v8Rn7MffdePZBAx3SQOTeu/zYasuePa9sc5pY/\nv3eTvCbdASDZb5P26vuL1j03X9d8d/WzdE3CT45/ywfpwzPtfu/aEEM9D7+vv8S3wiu1bQDWV76D\nDvW29co//33Wv/TqXKyLngt8CLXl/QDuHad8dFyXelDKN2+skNh6HrwPc8cOLOeCp4G1qO/3IrGe\n57XBorEuI6fe+8oU1Cubk76UJ5cXbP9mKUt5rmU5Xp+dXHXuGz9fg2ZNmWrSZcOIwUaiVAPdGjVi\ndKP6vDaN1EIpg1DvNKuGYGW7eifdGgM1/a23E37/s7e5ud7lZ70PeXtwj9nJE5QLzzmV04w281QC\nmoaHLtAgFiiL1KrZWLza36PLLE03GZaylLHURiBcoB4XIlUPKyKPwgvqQhYm21wk1rxQkWeh+zi8\n47JyWiVjLuv6a4r1rOzhWWE9z7ovx+vVHa/PSvekY7BJ/YJLx4A8uV4hCLnzOB/wFzReC+fxQXA1\np6s+BOxqBK16Hmy3zDtXNQ6CBmwE5V1Y1bm4RpdOet0zFt6jVRmOXimhDFVHe1A1jotRiKe+DR5c\nBiGt1Z0wwIeijPGv6S8JbRLbpdqFU4iNyUMBpvo8JZiYwgXGZd5mIimDUQkaiGqw2joizzLaUXTm\nZ5044h986VX++fe+yN5gyL97+FPeTe9XOugbcYJ4T2KrLyKLbZshgoq7tTsuqrNG0Aai6s0PFVvc\nIHtu54LYKMqMmWrbsuo0ZhXWci64OuuM5dptcbZ1WddutZerXrVw9zFps3ayJomoIq1Jm8l24xfx\nuP2Ncx2eFEukvPVxEmvWqxU5fbN3E72a8lBlSk10V0othNNZPCwKa2lb9bb1OFhNeKhrd1Vsa5Hv\nepHj1Xs/U6cXybZcEdj/NGX/04ys7ylyIUoUSddw7ZUWG7daGKseiwcfhGyUt7o7zDnOy8umViLN\n9qh2eWL0qUvXnoTTIELhy3JsB2nBfupxIiRGs922rMSGxBjU6HK5fuHZGeYMnYAL6J0UczdFDzw6\nD0RtS7IWsf76KuufWUVHmqEL7PQz+oV7dElVbDSrsWG7m9AyGufh4W7B3l5BmgmFgziCdktzfduy\nuVGWrpvkNEh5ydY4F3g3dROXYAXGzq7KClQ/RR/0ML/5BHP/AESQqAMr20jUQnQMxiJG422EjxIe\nJcCPLqgTQBUpuB4MdpH7v4ThQ1AG1l5BbX8BWuuIbSF+iM92yXffotj7BeJTDAnd5CaRWcVINDo6\nd7iQkmd7BAo8niN9zJE5JidnIEMyJQzEcdcNeChDArCK5XW7wbqKiUVTeM2B1/x2IPzVfsGeU8Q6\n8Jl1x6trBV3rMcqT+4ijoeWdBxH3ezFBQBuh3Y3RFnxw6EJQqcc/GJB/eIjKAmIN8fYmer1L1I74\n6mdu8sXbW7zzcJ+/fvAJqXaghCgWOisGYwStPOtWs6nhsybwBeN3yO1cAAAgAElEQVTpaMUQz0Mb\nONSeVDzatFmPbnAj+gxfbv09bsafAfG49A4u/S3ijghhCK0VpLMJN7+M3PgC2AQ96NG69wm2d4hJ\nh0SRIlrv0nlpi81vvEF8bbUyP3aRcwE8nW9gEOEwLdgdFqSFJw9lCbzEaDZaEdc6MXZOnvBFzgWX\ndU5crt149LuXfX6t6+95WLst0rZmyZVz0idl3g7ForGa9tekXV2OwrPU6zL2d5mxqgbv0+rvqttW\nEz4X2d9lxrqMtvW8YzXhtMg90Zy866b9/ezeIVnNQTDAG+sJ17v1ZZGa9vn2w2MO6mpIjUQhyJwg\n3S+ut1ifU7bKeY/WuvJm6rEUhSeqOSUF+PhwwN1+fekugPaf/Dn6YFDbJn31q/judn28fDGAd/8E\nlfZrsXr2mCKrz3nXGFp6dW4M//9uf8YnRU05N2Cvv84vH3TnvB+hKx2OB/V8dT/tk334cCaSMZqv\nfuNzfPN3Ps9H2TF/+eAT+q4a71++Zvh8NKwdP7HZ4kuv/hti1a3Vq//GOr67WttmYwW+9pUOak7u\n9WX91jRpV3j/6CLHi9DrsvJwWeeC5dqteZuma7dF8d603WW1rbEsc9KXspSlLGUpS2koxjabXJvI\nRe+QN84Hb9BG2/mLEa3UXAcdwNSFhp9DJ6C8wX1uIxoltCuZk1ANIPX54ucRabIBCXM3UEARZpQ4\nO9NKzgbbK6X4wpde4zu/+yV2Hhzwb//0zxl8a5uh1Dv8duL0r7I/pbA6nvsylTkbbn9GtJ7roD/v\nYpa5zUtZygstV/IkfVZYwfTuxnS4w3QIw5NgzWrztLHUjAmyaX+TJlDFw6xQp6fN6bRpzuNhOjzm\nPP3NwlqUPVwm2zovp/D4tjXd7ipyOivU6TKO1+k0l/G/TfOwKL1mtZnGepJ32ATLBWFvmHMwzEdh\no4qNpAwZjSYW901sq/CB3UHOQVbgghBrxUY7Zqtd1kSuwpqne+oCQ+fZTQuOMs+4ZLKCMjy8E7ES\nGeKRvk9qW7kPpC5wmBXspX6q3rOM/jcKG390mj7xfB7CAGSoiNC0E8XWpuX6tZgoqubhcd91CMLh\nkeP+jqM38GQhoBNBdUHZEz9b9YbY9z/F3ttHPyjD25l167tJIOkgpo0kbVzSxnXWERs90pNsj3Dw\nFtL7FAY7ZcVyp9GYR/o7cezqXXb1DoPQwyrNSuiw5ttEo7MPQegx5EHUp6eGKNGs0eW222KD1Ue1\ny4+D48f+mJ/5Hh/5Q5TxrOgBq2aA1eNSPpCKIVUd+k6Tuogit+wfCd6Zk3ekhE7bEMXlDd9KDOmR\nkKUKZMy9YCOhtWIRX2CzgN/NSN874I1bN/je732F4TDjrZ/+ktduFbz8ssWsGg59xM/24YO+xo+w\nWjrmd298iT9++bt8trtOW6ccDn7Nw8O/ovCHj2hPWi9x7dY/otP9PJ34ZXQQ1CBHO/fIusQqwq2E\ncLtFWI0RDH5AWQkgnOiu4oBZAduCTrssS3a9E9ON7Sn7Ws4FpTwvc8Fy7VaP9aKs3cbpKk2wmuhe\n1e5ZjNcmPEzLlXPSxyRMf5RmPWbVB2HyxTXBWuTHrA5rUq8nxarTa1abRXL6NHW/rJyOsc5rW7Ow\nngYPF4W1tK3FYy05PY11lDk+OU7JveDkxOkctcIoRawVb252SOxs53fc38NBzv1+6eT7GVhWKRKj\n+PxmF2vUE/FQ+LJmMqo8lYysOXMKvUhOC+/JfeD9/SHDR6fP0wuGUS77APyhRjyIV5zhwUISK77y\nxRZxXM9pk3fonPCrt9MyXz0/G3qvVEBZaH/wDvHD+6heCtnUibYCjAY0xBugDfgZCyKrkSii3/sF\nvthB8mOkmCqFpTXKWI7lmI/Ux2RkpEXvET9jiW2bSMX0JMMpYSgpzp8u4Wd1TNu0+WQQ8U7eYddn\n7OVnw/NXkphYB1o2RWnN0HlcOP2MkYlREjHINBISAp7UndZdK0VsEoJX+NygjCL3+anLCW+31vi9\nrc9glSY9eo/b8T6dtqCYKj+oNLlK0OolvnLtv2Mz2WDNdB5tOIwlqIwiHJK1YnRrFWvXUcRTTygo\nArIK6jULiUEifTrCQaQMHfAgolBGwHAmCkJRbpzd6MbcHKVgXNW123IueDbr4eXabWlbi9Zrsr8X\npgTbrJ2QSQLrcgbG/17X5mlhTe/oPC7WvJyIJljjf6/Lf7nsnNbxeV6sRXDaBOuyc7pI23qeeYDl\neL3M4/U49wzceBKdxlR4gaEXtD57cjPd31HuGfpqLCdAKO8Ee1IeYmuIrbkw24qMITKGIIMZz3by\njAAhhZBXYSmcA+fKvhf1rekPAv7MhkApIhopwDw8QO32ZqsllKfp2oLY6lJgLqBchqT3CWlFbnkI\nSMg5NkccurP1wMeSuyE5QwaxJitm1wd3Iec45LznN3hnuF+J1ctyQLi+asjydGabwudAjjHrHM1w\n9AGCCKlLkQBat8mLE0d/K+7w/a3X2Ija/PX+x7zbe8i/fAW6VNTrlkAsQ251r/F65+VK3bUkJOoG\namUdoSqHVpU/29LIakV4u1KlU24YVQ2YbaeCIgvlBYXLuWA5F1yVNctltK3l2m3xnDpXnTJ15Zz0\npSxlKUtZylKW8pzLBcf4NemusUoNGj7LEMZVm/C9zVd5ub3OTw7u8B+OfkNY1tZeylKWspRLJVfO\nSR+HD0zuXEyGJ4zzAuDs7sq8NpP4T9rfLKxZeRjToRVNsCb//iRY492iWViT/z75jIvgYVFYk896\nWTid1H0a61lyetE81GFV8bAcr4vhdPK/r+J43WgZerkm94EiCGEqNDtWithqQgPb2mpF5D48wpoM\nux6H2MZGlVG5l8S2nAtkeSDLAkorkliRxBpjZmNttCKOczczPUCNSpvpjiCFQtwo3F1Oc6qtoCwc\npo6uCsRGn7qVWqSsxZ6NeDQKEmuIpqIZgvMU/ZxsPyXupRTG4qMY0eZ0f86h85wQdyDugfjyKH/S\nzzQKlIDkwAB0BERMllUXBKdT8nDIIAxQkcdKhJ7KZ3dW0VcFfR9IbUysFCYExJ9cpqa0QYzFIxSS\nYaI2SMBPh5/bhKAUN3zKQadN5suydbk/OU2JjMWqCBHIsow46oL25O70iXpi2ogY+rnQth1Q4Uwo\ne2wiDBFBwISE379+i9c7m/zi8C5//vB9CglopVhPItqRsOMGrLYTIkBcAXKCFSWrJCvb6NV1/LbG\npApSD5MHQYoyhUBrCAGsRjGGmbAtFVASCA8EHQekY5BYj1IUxlBCpFV5Qg4UQWaknpQpLIlW5D4Q\nwkne54s6FyzXbufj9LzrjGmsF8m2Lusa9nnmtC5y5MrlpMPJyxqHzmg9Ozl/+sXNCklYNFbVx+e8\nWI/T37SBnBfrvDyIzM6zmMR6Ur1COH35wzxOx22fhNMXxbYm9ZqHddG2dRFYz8K2JiecKt2nLwK6\naNu6yPH6JP2JCP3csTPISV0oa4F3YlYTewavCdZx5ng4yMl8oGVLrJX4/FhjvEWOVxE47nkOjjwP\ndjxZdnpa77Q1N68btrctcTQ7d94FYW+QszfMOS48ggDTPEDIBBkopFAoK6iuoBPFJJzViq2WYT0p\nw5gna7KPRQErsWa7HdM6TMnu9zj4L/fIHp4ueebjiPzmNdzqCkoC0c4+8d4hapIbEZAMyJG8h1Ag\n+YBTHjmAjlHtLTI8Q/Z50P85h/n7yISXqdCs6k1WzQaHwXFH7fML9xHHUyHgbTQvRyt0BNCa/aJP\nijsVka2ARMdEyuBE6Itw4NNTkfci0HeWY1nn4cDiQ0S/XxCCZhJM68DaCsRxASiGQ01/qJBTt7gL\n1iraLYN3AeUjjg89Nlh+5+Ytvn7jOr/Z3eNvHtxFJ0LSytjsBLbjYzbjk4vqxrqvEbNlO9y6+RU2\nX/oaN774j2iv3z6lvOo5zJ0B6n4BHpyNkSiGM2NWQAmq8JgiR6c5auLiQgHCmkU+0yF5pUunY2eO\n18lLHBWK9ZblWvv0ZZClas9ufl3kXADV38CnNRdc1rXbZVkbXPa123mwLtvaTWv96M8Xce02LVfS\nSR/L+EVfFFbT/pq0e57rIV50f5cZa/JDcRH9XXXbasLnIvu7zFiX0baed6zLyGmT8eq98KOf9KlJ\nbQPgK19MuLZVX95qUHh+uXM8FYFwVprUUqcmj3hSOv/hN6j92XnXj8RQnVc+IX74Lkxf/DYl7/O3\n7OYf1rbJ8PyV7TNws3PLx3Ij6SAV+edjKUQ4QhMk1Lb7zd5rPDiuf4mxtRR+fr34VrHKMM352vVt\nvnPrFh8dHfGjT+9ynJ9cBvfd1/vcXK3OsQdQyvCv/tWfkLTX6zt8O4e9OctJ70mOD+e+x8/9t6+y\ncqu+lvpyLlg81vOs+6Kxnte54Fnotci126J4b9rustrWWK5cuPtSlrKUemn6cVjKUq6CiAipC7Si\nZjW7FyG5D1jA1kzYYaRXO5p9knEe8UHAyCjsuApLKCQQRGp5cEGmz5/PIglleXA748D0nCICPoow\npLXufGhHqMyjimrtRBwhZKiaRZCIlOHxc0Sj6Yhl9nVsIywgDwE7Z9ElE/9f2UbA45i3sVGeq9S3\n0Qhvbnb5xtab7A1T/u0777I7PLuR0AWMKLyq1i1SLdRQoCXVL1sEfIPzHguSaNSgxsIUKLuYw5Wl\nLOUqyXLt9uLJlTtJnw5NmJTxDkddm6btmrQZh5FMhwidF2syfOJJsRapV1Pdx2Ek02E9j4O1KB6m\nsZ5EryZtpkPHr6JtXTSni8a6aE4nQwqb6DUdwvU4z/g03uF0CFcV1kXaVuYCO/2M49w9yoMe57Z2\nI8ONbkLL6lqcJnqN20zWZE99IPegFcRa0YoM2+2I1cQyLDw7g5xB4cm94AUiDYnVrCeWa52E2Oi5\nPACPwu+HzpN5wXkpS1U5dVJfWoHpBkybMjTdlKHoiSnrS293YtqR4Shz7A4L0sKTBSGInHIpRRQ4\nCH0IWZmbjqe8ddsyVbu8/E3FiXOqRv8lKEQUIR+FzOclrjjQRYFOM+xhj/j+LloC7tU1/KvryEqC\ntCwEQQ0L9GGKeW8P/aCHLw4o/Cf40CP4AeJzlI7QymKkRSRthEBf7ZFyiCOl8CmihUDAiaPvDnF4\nYlqs2U1iFaOlvLdgqD1HpLznH/J+2CHDo02M1hZB8MFhtcUqhZVA5NLyPnNl0DYuC42JL7P7lcFL\nIHUFWfDkohjICikRuYfMCwqLBEOew2EPQlDEkSGODVqBl3K8aaUJQUizAu8DsfVc34BX2ut8Pn4D\nL45389+ym/U46lke7kYkYvjepuWbm5btBFa0R2nIVOCYjA+LXQ7JudX6PN/Y+CO2k9dYMVskZhXV\nNkjH4K8n+FvtsqTBroPDABmQC2NfX4DRA8OqQt3QSFuhktH4Tz1q4NCfpuj7GUnbsvmFNbq328Qr\nMVHHntqDWM4Fi9Wrqe7nXbtdxrmgDqtpm0ViLddu9e3GOpwH6zJyOqlX07XbTIyr5qTXyZjMqhwM\nOJ1bUEfcRWNdZt0n85MuQq/xn030qtt5vMycXiTWmKs6Tsf9XTSnF21b59FraVuLGa+Ltq17vYw7\nx1ntabBC+OaNVSIzO3esqe4AufO89bBHEepONwU9ChCvCxHvWM2Xt7voOeP117t9+oWvxhIZOUmU\nuwUVokYOdKg9mRXcgSIcTec/T2EpT/yyMPJQq7EeKsKgAdZtD1ZXn96GgPt3/yvh7ofgq0PEnQ70\n2CNM1Ss/JdoQ00KjoWbR9V/0Q/5C3RmVPpstkYlZY3QpWkV4u0LzUd5i17dIXQ2WTjjuxzgfkIqT\neKM111cH3G53+Zz9PJGKeSf/FTv+/ql213SHf2au06qLItCGV27993Rbr6OlOqzWtyPc6srsuvOP\nHlLgazF0VO0J/K1WzEtrCTaq7u8yzwXzsJ737/fzPBdcVh6Wa7dny+lleodjrCqcFyqmaExCnaGO\nfzYvr2DRWPMG0LPQfd7idIxVt0P0rPSax+d5+ptsexWxxu+wdjdvzgf3PP2dR/eLtq3zYF10f4sa\nr5dNr/FYXZRtNQrXHlddXgAPSinK+6/q9J/voI+x1By9tNajk+46B0mVznKNgw4lD/UOOuXPArVO\nNUz+fA4PUu+gA4jR5S3fdTahNahQ66ADiC/qHXSA4NEmqnXQAYKm1kGH8ufGRLX550IAHdU66AC5\nz7DGVDroAKsm4fsr3+Sr0Te54z7mh8P/fMZBL5XPSeaMMYIntu1aB71sR72DDiAKZah/h0phY1Xr\noMPlngue57XbZdNr0XPBZNvnEauJbS3Xbufn9CL7a4JVdxr/QuWknydoYJ6Bzfv5eWRyp2tRePN0\nbyLjj+oisJrqtSgOFo130TwsShYdKPM8c7pIvRcpy/F6otci8Eq/dJ7juUAeFlhfWhqjKeY+Q6A8\nzZzrmNFwu34xnKomWA3tNLj5F6iVz6/mYvrgmHclk4SAGm241GLN2Tgo28zPi1eoynZdE/Odjdd4\nrb3JB8WH/Nz/FaFue0oppgsSzhIJ42iIedLgUsAmw1mWc8Ek3nIuWNxcMMZ7XtduF7neWiTWZbet\nRcmieHihwt0ndyS0Pp3bN95xmnzkMcHT/zadizCNNavdLKyq35sV+jOtw/SraYrV5Pem/21a9/Ng\nPS4PTbHOy0OVDi8ap5MhTk/K6aTukx+mJlhPm4fzPM/Sti73eF2EnaIU+8OCvbQgc2FUVxkYnT2P\nEVtWc70d040MiVFExqDU480F/VGu+XCUa16MMMY12Vdjw2Y75jhzHGYnepVuztjZKU/HV2PDdjum\nbfWo3vjZ9+oEHvQzjrOTnHsRRiecEHKF6wEabBd0NHK8jIIgp3LXQ64wHcEkUm7bm/Gzj7UTJCjC\nsAxTpwDxIEGjdECN8tJVR9AdQenTOejAqJ58eR/AVhJzdODZ33ekmZDngg9l0L3ygnJS5ivbgL5p\noK0gUYhVEDxueEh+vEP/019x8PP/SDczdPU6MREmaPABbROUtmgijG/jSBmYfQoZ4iTFF0PEGDId\n6OO4K0d86g74nL3FTbXGCjGJ16gQyCPNQBXsS59fFnd4oIZgI1AaHwKZS7EmIWDJg2Y/U/Qzz2td\nw1okJMqjQlZ+O2mTFhEHPcPbdy3SsnQ3AiYKiHHkPiMxCQSLc5r+kWYwEFZWY0wEogJI4FtrL/P5\nlRu8O3zA28OPyThkra1pGY1Wgoij8DndqEVXGboKbnrPa0SsR+vEyqKDAlegdURkOsS6TVs2WFev\nYdfegPYm5WUGEYiGlkbamrBicbfbYAxqT2AokIMUgjKKuK1Iuob1mwmrLyXsFzm93Jc2P7LjSCli\no2hHhuudcgzWjfOqtZsIFL4cc73Cs5vmdK1hsxWPxrTGzrjjYTkXVPMw/Twvwtpt0Toswi942mu3\npW3NbtME62mM1ypn/8o56ZMSQrOyADB/164JVpNc1fFAmYflvZ8bmtEUqykPi8JqwsMisc6j+yKx\nlpwueXhaWEtOF4eV+8Cvdo7J6g4ZgRvdiFdXW0/MqQ/C/jAnNnpmTfax3kMX+OVOrzY03yh4c7PN\nWhJV8iAiHA0LfvneENfXIBV8aUG3ApLr8uK3mcecgu4Goi2pDZUXByEFnZQ+XJV0rOKVtRZrSTTz\nRnkRYZgKv/yLA/yRP1U3+7TucCh/zc7H/57h/XcqT8UTWnwh+n1iVtBq9nGwl4Ifhr/gLf8+h2Qz\naVAC23RZ1R0+Crs4NfstBYF7RZf7qSKfqmv+CAthLYDbb3P/ICZUhPrryNPZFAZ9CP6s7lZrvnnj\nBt+6eYOPsvv8Kn2XjFnh8oJWwt/tWF4i0Kpc/CnetF/llnyGtl6fbacA8SrFH/wDwksr5S2Hs6QQ\nbuSWGzdbtFdNpc0fZ47cBzbbMabGvpp8a46znDvHOce5r4xrSIzmS1sdkjnh9Mu120mbqzwXNNX9\nReF0ycPl5XQsL1S4+yyZZzCLxpu1a3MRWE36WuR+zSJ5fZ45XaQsCq/JB+Ky2laTj/x58eb9fGlb\ni8W6aE5jU55IZzV5XwIMiuqbXM8jRiu22lF9CJsqb1e3GvIaL91LuclQp5dSipUkgjSvjzgPChno\nOXnxCsk18wpZKwt2ZX6OfWI1G624VvdOWxGHQFrloAMESO9+yPDe27X9ZaRY20XPcHLHYlTEgREO\nQ3UtdVGwQ58D43E1ueVaQU6bPFSH3QuK3dyQHXZq89RDYSBLCP50vXgNfHl7m+/dus2nvR7//s5b\n5CsPKnFAEUTxsk1IfHXteVFCbNfphI0aJJCih9yMqx10gEixfiOm065eUiqlWGtFo4Xsk48zH+Ao\nr7fTzAecBJIG8fuL+m41maMu6/w6xrsorOX8ej55EdZuTbl6UWzL/OAHP/jBQnq+ZDIOL6jb2Rjv\naMw7TR+XlZgMFZmFNf6z7iXMCnt4mljToc9PG+u8ui85fX45fRY8TIdsPQnWonR/3jk9T3/PG6fe\nCzu7BQ/ue7yTMix7xnTQtoqbnZiW1bUXt83jQUTo5Y67vYxe7kisxlQsTkIIxEbjg5DPqDGtgNVY\ns91JsKpap8wF7vZSet6V+cReceZEVwmqHTDrgjKCOFV94s4oHN6U4cvT3UqAMAB3pCGMQt2noURQ\nRznq3R7F/ZS4G2FaZ09Yi0K4v5Pz8CAQwijU/QyUZ9B7h72d/4z3x0id02wi8tBHY4lpoaZedhDP\nEQ85Cp9gNQxCPrNGuAbWTEI0yvIOM3Y/fID9vMPdfgJEBNxZrgRCoaG3As6U9exnSRDiYAjHHq0V\nQQVQijc3N/mvP/s5OlHMf/rwA355eBe9khHFmhBKB3W6z9Vknb//5j/l22/8N2iBdHif6brwCsPG\nyle5deufEnVvobIBasZGQ7TWZev7X2Prc6/iFRQVdroeG651IkyNncJiv1uKcgOuCAE3wySMUlxr\nW7baUe2Yvozfrck2y7lg8Zw28QuaYj2PnC7XbovHWiSnk3Llwt3HBIx3baYH3LSMB+p0HsGkzMKa\n9SJmYU23m8w/r9JrcsepTq8qrMk+q3Qf/6xO96ZYj8PDk2A15WFSzsvpeXmYpf8k1uRO3CI5HWNU\n8VDFe1MemtjWLL0WYVt1ej0t27qI8fo4Y2z8s0VgPY5tNcF6UtualCexrSwLfHynoD/wZHnpCI7O\nBFFGyhzqSLj1kmWrG5GMcr/NY84FIQTuDYrT+eEjV1MDsS5PlG90YtZbJ7Hhj3QXofBlrfNB7gGh\nExkSa4i0mvmMh6ljZ5A9qsn+6CdSOtg48LkCBSaWUT46pUcnwqPc9UJR7IPyekzRyem4KvnSFiQK\nKFFIocp66Y82AiY4tYHosEe0n6MGHob+0YG8ihRRxxKvRcQvr9BLWqRpIM0E9yj0XtASyt/Jcvbe\n/j8Y9t8hz3YospMSatrGI+db8N5hdLlLIBIIo9vSlTIkdoVYt2nJKgoYqh55GJC5HjJ2Wm1EpmBA\nwSfhGEzp3CEB77LRe7IobQlKcZgH3u53GbiEoVf0MkcY2UE7jjFGAQHXD6isRXCaIocsLx3gOLJY\nXd59UKSOKFeYoAkuMBxmI93hjZev8Z3P30YQ/vb4Iw6iQ5QOBAqKkTMd2xiry8J+r258ln/ylX/G\njbVX2Gxvk9juyCACLj8kT3foH7yPPuyz2v0srfg61qyjRifMigLlUsh6bHT7bH/1JZKtdaLVLnYU\nCRFCaduZ8/QLj1ZlNEg8us9BP+Z4nW533rnAh0DuA5kL9ApHyxjakSHWCmvO1n6+THPB87J2m+zz\nRVu7VcnTXmc8z2u3pV9wftuq2jS6ck76PGma79AkX2CRWPN2Xxbd31XHasLnIvt7EbCeZ90XjbUc\nr4vFWuR4/eCjlI/vzL9d+3e/3SZJ6sNgm+hV+MDPHxwz45DxlHxxq816Tej3efr8xYMjBm5OhyIz\njrjPSn5HIW5eCGVgXtk0RFh95y6qLn4fGL5+jWKlXdumGNznoz/7H/FFv7adtgnBVYetn0fejwf0\nXX1/7w3W+cn+/Hdo9ldJ0/qb59upIT8+nVN+fb3D97/yCivthB/96hPef7DHte/n5FL/jP/mD/9n\nvnzr27VtVBGId4c1ERSlfPkfrrO6ldS2eZ6/NYvGWs4Fi8Vart1OZGlbi8e6jJx67zFm9lrkhc9J\nX0q1vGD7N0tZynMty/F6PrnybM1f55bN1MVy0bhkXQP9myzmm4qelQdxpsNmWHWXoj3qb6LNejfh\nd7/0Cre2Vvibtz/lNx89LE/ozegZ51DWmIdGL3txnC7l2chyLljKUp4fqRuvV85Jr9q1mA5PrNrZ\nGIcgjEOUZ01+k2EKTftrgiUy+1KI82KN/3xSLKVUbZsmnD4OD4vCGre9aE4vo20tCmtRtnVerMvI\n6XK8nvz9Mo3XdkuTxJAXgsw8NRTiuCzf1MS2xjvvlbqLEGkFXiquWxOsUjgvC7OtxGhy73EyDuWf\nBhuFtCNlzP0sp3EUGi+o0Un5OIT9tChdZmQrE8pc9opb4ZUERCmUVWWNuFmSKHQIaBsIVVgSsGKI\nzCrKgqs43Y5sB4Jgog55kcKMe/K1iUY9lKXkgp91uq1wUUThe2jbIrjZl60pkxBpTyeOcEHI3dlo\nDaM1sY5JvacdxwzzWbevQzuJKZxja6vL11+7zus3N/j5e/f5Tz/9Lc6XzxFHhtWuIgopURTTK2Zj\nbcQtDg4/xm++gYnXmFX0XolH+wIVHKCRGW0AbEsRXDM7fdHnAh8CzgsosFo9Spd5HKzlXHAaa7l2\nu7zrjPNiLTmdz0PdSfuVC3cXOZlgJmWa7MkXNimTZM3KZRi/3HlYInIqfKGqv8fRq6nu0zyMF5uL\nwmrCwyysx+V0Gutx+3sSrEXa1qI4DSGcCeF52py+qLZ1keP1cftbNKeLtNMm/TUZr+PLPKvaiAhH\nx477Dxz9gacoIIqg3dbc2I7YWLePTjIXZVuZC+wMTmqXa7vqe8oAACAASURBVFWWgNpoRWx1YqIR\n3qzxCud/125U6m1/mJP6QJoLUihCBr43LrMGKgqY1Ync9AChKOuoS6Ynwp9DWd9cAaNcdNUK6K5C\n2dKnD5kg/TI3XTLKuuZFQPUcuhhls/uAKTKMLyAEVKyQjsFfj/G3O5CYEisF6VPmuQ89OsuxvQHR\nvYfY/hAFpH6fh+4tev4T0mIPhScipus7dMMKRhmCePq6T88MKFROEVKUMmgB7fyoZnt5gh+sISjI\npSBVcCwFv3U97soAT+nebpiIdWuJULggpGLZzRXvDQKDoBEBCYpIdwGDKwQdLCGH4aHHDcebD0Ic\nR1g7sklVcuq1R4zj29dv85X1G/x6d4dffbSLGwrGOzY6sNFxvHHjiFvrOVpDP8DH0mYnWHpOiJRh\nUyte18KbSuhohdIxnevfYOO1PyBeeYk4vo4tPKY/ILq7ix0MSz1shFtfJ7Q6kCTEKxFJ17D5csLW\n7RYmOrHTxx0X03PBvPE6/r3LMBfUrd1ckFHuu+fhMGc42oxqWc1227ISGVrWYCc2xa7SXHAZ126P\na1tw8ZzOsq1FzAVPqvtlWrspdZLX/bRsa5FYi7StWXLlnPRJmbdDsWispv01aVeXo/As9bqM/V1m\nrFkf4KfZ31W3rSZ8LrK/y4x1GW3rsmI1tflFcdqkVvJ5sObp7r3wo5/0cK6+P0WoPEV9JFaIb3mU\nmTPOfpnBUX0TNoEvxHNz49v/4Tfo/epyYQCD9Ndk/foSbAB39R28H9a2+aE+4l2/X9vGBcW9bItB\nUZ9bzs42R/v1pcAwAbMlaISvb97kW1u3+aB3wF8/vEPfnZyQ/4s3ctbUcS3Uiuqw5u1c2/rW9f+B\nlqzWtrn5h2+y/c2X6nXnco79ZzEX/PTeYW3JRIDPbrTY7tTn9C9ar+XabfFYl3F+fRHWbovivWm7\ny2pbY7ly4e5LWcpSlrKUpUxK0wlxkf1ddJ/Nconnt1Gq0X1z48vgFwLWSPOGfDZq1/jVNNG9Gadf\nWt/mu9du8yDt86cf/YqD/OymRCPVG9pWM04bNFrKUpaylKU8E7mSJ+mzwgqmdzemQxRmhVY0xZpu\nMwurKnRnGms6dKcKa1Z4RZNwjlk8NNHrcXiA2QuKRXL6ODxcNKdP27YWibVoHhaFNSss7DLY1nK8\nzm7TlIfp8L8meokIx5nj4SBn6DxBIDGKrXbMZjs+dWnX8zwXzMMSKWuy7wxyhoWnPxSkADeAMDgJ\nY48ixfY1zdamJYnK3Pjj48D9HcdgKGNwVO6xqUP7UG7ftxRc07Bu4NSpehkWL7lAJnAU4EGA0QXk\nAoREIV1LiDSqpVCRoLqgWydV4MSV4e4hU6jjAp1mRPtHxA/20ePTawkgGZAjLiUwxPshaXoXH3qP\neEgZ0rN9Mp2R+WHJkxdMkEdOdIbnrs55YHL2QkquFV4C/SIdZbOX9xQM0oReukmaxwwLhbaAHSI2\nZXy3nAQwuo2SCJeD8hafQX/fwzjXXgQtii9c3+I7n7nJsHD85JN7fFIc4mP/CCuxjlc2PeudglWb\ns2I0HRHWnCcZvWujYm52v8Vrq3+Hrr2BAYb5PXYOfkgvfQ8ZPUG88iqbb/wxrc0v0IpvY10g2jsk\n3tlHF2X+g0Qa9+o6/tV11GaHZCWmHRmud2JWYvso3LSXl2NsUJRjLDaKzVbMVic+Fc7d5DvyvM8F\n4/GajUq97WeO/dThTtW9L/9ulSIxZXm6652YbmxPjdnlXLC4uaAKq4les9rMWrtNh4I3xVqu3arb\n1NnW+PvTBOt59guq2k3LlXPSq8INpkmcZSRjEicngCfFmpQmL63OeOv0atLfeXW/KB6aYj0uD487\n2Sw5XXx/V42HpW1VYz0NTt/bH9DPPbnMujBNiJRis215da2NegLdn8b7qcM6Lw8fHAw5yt2pmuwT\nYBCgawyvb7SJIkUcnQ2RdC6QF4F3//KQ9NiDF86W55Iyp/y6glfs6Oh1xvGrD0gGbkdDgKD1jHaC\ntuXd7kqNnPQZZd10cOjhgNWf/RjlCyhmlNPTIMrzQfaXHIQ7uJDiZ1wKZ2zCEM9POSQj0HeDM22s\nidDa8qu76/TSNoNcKNzp8HUFtFsxmALbFkSYeSlcYmIMhuwjw0srK3z7MzcxWvGX79zho4dlboDW\nmlYrYuvmEa98po81DufPnqq3bEJbJfyLm/8T6/FNIumeObUXAp4eg60Ev7mCSTZBny0Rp4ND+YLo\nhkDLIJE5c4yuKC9AVKNL9mba1ugSxJXI8NnNNnqGAwPP/rtVFW2wyO+WC4F+7nl3f4Aw5uosp7FW\nvLHRYSU2lVjLuWA5v54Xa7l2O93mebetF6YEW9WuxPjf63IGxiTOyytYFNbkS5veGb4Muo/zKheB\ntQi9ztNfHZ/PQvfLivU86/6seIDleH1W43XoPLnA7GBeRSHVNy0/Tb0uei4YOD/KjZ3RTikw5SV5\n3U71FG+txlqNFAFcBRYKyYFIQ12JMqOhDRhFqMx5VwSnUISaNhC0BW2rHXSAAApDqgZkRXUOt3cZ\nx+Ts0ats43wBviB3tzgczO5PgEGa0+5qBll1zfLM52xFHf7hl99gtRXzo3c/5Z27e6dVD4HBIOON\n1QLo4SrS2VOXIUqzGt8mls7MNgqNZQ27cQ3a1bXng7aoxCCrvjLGXVDkYXxvQcVmDAonpSnYmtzY\nF2EuiIzBmHEMw+x2giILoFX12nQ5F5zub7l2O8G6jOuMy4Z1FdZubkalkLFcOSd9KUtZylKWspSl\nNBUFc7PLFxdwt9DQvUUGAjbBqmmyahO+u/EaL7fX+fmHD/npu/fKWuePA7aUKyXVLudSlrKUpVTL\nlXPSxyEGkzsXk2EH4xwDOLu7Mg5hmGxzkVjj35/Eepa6T//OZed0us3kbllVf5P/fdnsYVFYVc9Y\n1d8k1uPYQ1V/z5qHix6vF83D9O9cdk4fZ7xut2MOMkfmAoVMhrzLo1zQEE7fFfCknE7+/bLY1nY7\nYi915D5MhSWXPMSjsGXvw6OD06r+tl5JON7JyQeBPJUJ31FQUqBdBh/k4CNktYN0EsSeLB2UD5B5\nVM9jjhTamrLUmTFMvh+lxjxw6u+TLowKBToboI8P8TiMpQzB9xM2riFVQ47lkEMcw9iQiEZ7gXBy\nIuF0wnHQPCgihghJFIh0gQ8nN79rFRFcQjY0SM/RpY0YIReHCydH3O04QaNwhadl2mgLgUDqMlo6\n4tsbr/Bmd5u3Bzv8n7u/IB0IK1sRPlMMB+4R30YrrnUTrrcsL+cR123Ekco5DinpRMh7J1ljbfU6\nm6svU1w3JEWEGnpIJ74vGqKOJVqxdFYV6YoiTYUsF2QibcFaIY4VrZbGxooiBPIguInxMw51T4zG\nKoUTIZthW0YpEq2wNbblC4frp+QHfVw/JVrrEq93sN0W2swe+1XjwrlAngfSTPA+EMeaVqKJ49N3\nM+Tek3shcx6rNS1riMzpiJqnMV4TrdhMLKkrOfUVnLqwXLvVYS3XbtXPOP6d5dpt8fPrZeGhLnLk\nyuWkjyWE8Ch0pirUYPqlNGnXpM3ki5iU8cvSWjfSa9ymDmv8jFX5DE31qlqIVmE9Cafj/pq+nyY8\nNOF0MkRlHqdNn/Gq29Y8vZpw2tS2Fjler4JtXfR4ndffPE7HjvFFcBpEOMoKdgcFQYT1VsRW+/SF\nVo/LQ9N2l2G8ipxcoudEWE/sqZrs01jj9zNLr+CFo52MB+/36L3/AHPwAHO8iwqn47HDahv3+Zfx\nN2+i+sL/z96bxkiWXXd+v3vvW2LPyK323veN3RKbEoeiZsSRxpQpWJBgQxxBA1ASbIsQ9MmAAcEG\nBAgC9EGAJAxk+Qs/iJQhwCRljy2NR8aMSFG2SMmUyCa7m81uslnd1V1dXVm5R8b23ruLP7yMrMhY\nXrysisqMrIoDkF1dfeJ/z/u/c9/dzrlHvttBtMyh00InBboSEq9UsKUgI3w6Da9W2+t4m9fw37uM\n7A7mjQvwQpoiYo01Xou+xfv2HSx978xByfmc8xfYavm8GUm+uatp2cNt+tJwYcFQcxG2E3DlsqS5\nGxyyzQGyJPGXfEzgcBaS2AzZ73uCD91/jqfqK1yJNvlW800iF9NPq7NAMyDcK/OYKvKjywHPLvoU\nVH97jl0ivu812D6zzIVLz/PME/+KxYWLh2nQFrnWJVyPqBZ9Fh+tUb1QPlj4QuoPzZbhxo2ETuRY\nqCnOrPiE4WF/SKxlqx2z29V4UrBSCqiGh8u6HfhWJ0ZbRy30WC4G+Gq0b0U3dmm/t8nOS5fpru0c\nfoNSUnpwhfoPPULt0QsgR+ey97CaLcvurmFtXdPpDuZ/Qn1BcuaMhwgdW92E3cgMxSX0apevlkJU\nRrj5tPprYiyb7ZjdWONLcegivlFYszx3m9ZYMAlrPnc72bnbuLGgh3Wc64JBu07z3O12eeiXu3aR\nDtm5AHcCK297efROcz3E425vlrEGd4XvdHt3u2/l4XOa7c0y1iz61mnHmkVOj7u/dtd3ufwnf41L\nsmt/mzOP4RifBw2Q1Ap07l/J1AGo/sO/R+5m1y3/R/ES30j+cSLWV9buY7uTXdu8uF6gsz588Vu/\nOAnhfSU6yWE9KQTPrq7wwQvneGe3wQ/cu2y5rTEoqTyoCvz31QcQE6ZbtX/93yFXsuuWr5Z8HqqP\nzlHvl+P2rSt//nc037iWqePXyzzy33wcFWQHcX771RaNvWyuRMEQnM1UAeCZlRLlwM/UOe3frfnc\nbfpY87Fgulh5527T4j2v3qz6Vk+ms4Kdy1zmcmok78dhLrMtd/H+6j0hibU0Y5OZt+yco9lMQ36z\nJDaWVmIyfcJax17TkCTZftNNQJfKmRnTzhl0dx1nxy90nXN0u9eIm9cy7eome7wbXSVx4y/Psc5x\nbS+hHWVPULuRJGqlt69ngGFaEZhsTrEO29W9mHwE8PjyEr/03NPct1DjL954ky+//TYRe8gJ+eWr\n3iKeWshuTwYQ+YdC+0eJPyJaZFCSJH3X1mb7Vltb4kk85JRgsYIqDt8s3y9GBbT39MRvV7EombQW\nKYaSwohT/X5xFlpNh8ng1FlH+/oa0c7OWJ284pyjlZipcTqXufTLfO5278ldd5I+GGbTnz/QC2cY\nDDkYlF6IRH+Iw+1i9dPcj9XTgeFQiFFY02ivF95yEjyMwzqqXdYerpWah9NB24UQR+L0dnjoD+E5\nzb41iHUafOuoWLfiW1lYeWzP018Ha7KPwzou3zpqf52kA9n99SS/39PAQgh2uwmbnYRuYoj2c1gD\nKQiUpLxfVxkjWLuR0NgzRJEjThxKQbifV7y67LGw4NGIE7a7yUE+rHU3c2CrgWK5FGITuL4W02zZ\nFCt2KE9QCNOF0JkVn0pZsbmt2dpK6EZpTrPVFhlHyG4bf2Md/9p72O4midjBuA7WRlgTIf0Swqsg\n/UW8wiNYVWAneplG9w1ivUmU7ICU+MUV/NJZSmd+mOKZF3m/eZk3rv1HtppXaHTWaHe3qakqdVnl\nnFvmBfswRCX+dmudVxrbXO92WO+0UR6UQ0upkHC23mC5ssfuXonr6wu0Oj7ttqQdWYKCQgQCGxg6\nhQ4klvK2QzYdrq1JWjG+7yN9D6skXSkxSuIrRSAk0oExFmsNKvS5eL7OC09cILKGb66/jaruUC5p\nfE9j6aJUgHGK2MBm26JcmR9feJ4PV5/mnL/EoqjgI7F00XaPbvcq7fZbiNIq4bkfwSudQ/o1kCVE\nICAEVxKwIvFrHktFj4XQJ/QkgZIjEgcEO7uaGxsJ7Y4lisDoNBc9DAWVsuTc2QDpw0Y7ohmbg5xz\nKdI7DAqeZLHgs1gMEBM2HcZ9A02UkDQ6xJsNdl5+i9Y7WySVZczCKi4o4lQAyiMoCoKSYmHVZ+X+\nEn5BHupjINDaEsWOVstw/Yam24WVZcnSokehIAh8CSLd7OrVLt/qaOKOhZbEJqRl/oxIeQigXFac\nXfUJTYuNl19l760rRNs7JI09hKcIajXCpUWWnn6C+pOPo8Jw4pwlMpb11j6n+3dl9DgNlWS55FMv\n5ON01saCXjj+nRwLbmXudtrHgvnc7c5g3e66YBDrOG0fJ3fdIj1Lep1iXA5GXh24+ZKzyD0K1iSd\nk7JrEtZxt5cXq6c3a3adBKdz38qP1ZM5p7Nn+3Fj9U+ipsHp9zZb7MaarLueXezQawprx+uAI7xg\nwe+/OG+EVguSTYkbqn1+GEtKSB8h4/Ka1/4TvP0PYMeHwDuheEt8j8QM1yLvl295MddsE20zQtKT\nIq++coFmd/zpuhSCwICOHCZjEuRbg9zYQccZWFKi6jWM5VBkw5nlKj/6woOEocc/fvsK7fINzj7T\nxrrxtivp8T8s/Y8sycXMW727y6uYah3IKGXmwQc+vkwQjtdxzvHdNzpsbg/nzR/C8i3BeUemO+B4\nerlMeUQudb/k+tYYyyv/aYOone2nF58ucv7xciaWMb32svvrG292Wd/I7mMiblH46p/hOtl++viv\n/BtqDz2QycNelPDGZpvsKbjjmZUKJV/N1DdwVucZszh3m/ZYMJ+7zedug1jjcO6pcPf+3Y7b0YGc\nCf8ngJUHLy/WpA9lnraO0t6s8nDcWNPmdNI+3L3CQx6s/l3Y47ArD9690F+FGH+R1FGx8tiWdyzI\nY9dRfCtr8QDgnGDSgTyI/RDsSXl7TFigp1hu4Ib10aIzF+hpgzqzlHpPHDZ7gQ50TYKd9HzO4Sk/\nc4EO6aVvWQt0SCdJge8fLNDrtSL/2Y8/xU/92BO8cXmN/+2vXuLKe1v4nshcoAMYq/GUmsio8Dyy\nFuj7WpNxhNi3e4JvIXATy76l571T+X4riVByol0i4xK5niglEWJyf03D+yfwYB0uIw2gD3AyDyKt\nKj9BKde4Aqd7LDit84yjrAtO6/iaB28+dzuaXXnw8mJlnbTfdSXYsuQoQQOTXngerB7GJKzDYV7Z\n7eVxxEmXF+TlIY/t0+R0mjzk3Y3Ng5W3vbxyWjnNozOrPEy7v0L2h/ckOD3N/bWHN2v9tac3iYc8\naK63uM60PR+ScyK9hCwLSwLCkX106nJVSUd4IFX2Ql1IXJ5cXGuQQmLdeF0lFcZN2BQA4jiZaL9S\nEqXkwWnsKBFCEMcJ5VLAi889wP0XFvnWd9/jS199HdO3oDPWokS2bVLshyZMmuNZt2/5pA2sCTip\nFmAnYDnExKDrfN9AmGIfs+l9CTIj1z4vVvr5yOZUyHRjYPLSOse3xjkkYuJJujxmTk/zWDCfu6Uy\nq+uCPO1Nm4c8GEfBmrW52z0V7j6tnPSs3IZxWP06g1j9Mgqr9+dJWIO5SIN6k/IksuwaxUN/mM8o\nrN5p0+3mIt0pTm+Fh6Ny2vOTLE57+pM4vRU/ncTDNDjt/TvcGqejbJ/kp0f1rVnsr7frW1lYo3iY\ntf7qXJrTeCd9607010lYiUkv3Opoy0YnJjGwXPSoBopApTWanYU4sXS7jq1tzcaWwXgGVQHpu/QQ\nVQAm/Z+JBXoPSPZPT0WPQ0Gvrjhuf1ktQZYsXhFEP9bB0OBwTmIjh2sJXCL2D8MFnnczv31l2aO6\nn5O+vaPpRo44SvPbpbbIRKOaEd7mHq75HrpzGat3cEkTG7eQXoiQHhIfz5YwzrItr7Mntohti8i0\nQICSPgqJbxXCwBoRV/w2DRL2XExbd5GqQGI8WrHHezuSRsunkBQRicJpiLsaT0iktYhYo7d2iTe2\nCapVvHodEQQYIYiNIZCAjkiau+xc/QEi1iwuX8QPSgjhEceWIPBRUmCtQWJ49gOP8MTTD/L9t9Z4\n7ftrdBONsZZiVRGUHP5CTHhul0LNUfBClJA4LHESU/ELVEXAAj6P6AIPimUWy09TCu/Hl1UURYRU\n2NDHhiFJrUy0tIRD4UUGqe2BH3ihIChJilXF8n1FaqsBg9sQjvSywEhbdqOEzbZJL8xrizQPW4Oz\ngsAXhCGUSoozK4qgKFlvx7QSTWwcsXUoBL6CUEkWCwFLpWDoIrxb7a8mhs2rHXbWIqKWIe44cOAX\nBGFZUVnyWX2gSFhWUxkLQLC1nbCxaWh3DFHs0Bp8P81JL5UUZ1c9wniXjW+/QvPd94i3d4j39pBK\n4S/UCOt1Fh5/lOVnn0IVD1cvGPUdaSeGjU5CO9ZE1pH0cVpQknoxYKkYINzhRdd8LBhvF8zuWHCc\nc7fen8c937R4yMIaZftpn7vNom+Nk7tukd4vk3aOIN9JSV6sPDr3AlaevI9ptjerWHPfmj7WnNNU\nepOFeX89ft+6vNViO9KZl3AXY0m0I+l0MpSUQ/oWG8kJp92WiZlpviU8ZyHrNNLChSDgbD0kCEbj\nOefYuR7x1t9cQ7biseeRzkSYjb9HJRopRodsO+fYMG+zY9/CwxsbuN1B80e7Dd5uOqwbZxd4b0Xo\nNzdh//R8pJ7nkYgmra219IFHimBp6SGckXie5LkXHuO5H3qcy9+/yje//hrtdhcAWVLc9/EKwWI3\nI4zf8THvAk/YEiUxPjCxUH+Oygu/jKlUxh+NW8djlxQr5wt4Y94PwGY74lozpqMzLvzS8GC5wEo9\nQKnR7Vnn2OsmhL6i4GWH3U+jjznn6O4Z4khTWw4RGb46rf4aJ45mM6FW9fG80XrOWBrvvEtQKVNY\nWc7Em2SXdY5GN6Hoe4TedL7N87FgdseCWbR9VrHy+laeE+zTzEPe/tqTeyrcfZRMcoaTktO+dzKr\nvB6njNqhmwWZRZuOInPfmj4Hc07z99dWYiZVyaLZNejOBE6NwJkcObv7UfKZosXEmHUhoVJVYxfo\naVuCYijwojgTTqgQP6iDHl/bXAhBSdZo2ewa1UU8nK1gXSsDC3wMJs7OBxdag2lmLNABHJ4Hjz39\nED/8oad5/9o6/8cXvkxjt3kYyxkqy44JLXJOVSiN2VzoSUITUylNSE8QlJeDzAU6gDYuc4EOaXZC\nrabGLtDT5gSVQOWquzwNEUJQrHmEVmYu0I+KmSWBL6gveGSF0gslqT5wX+5Jc5ZIIaiF3lSw8sq0\n5xnzsWA+d7sTkmeBfi/IUTm4a0/S+8MLxn0w+0NXshwoD9ZgKMadxhoMs8iDdRw83AlO+0Nebhdr\nku3T5LR/5/A4fasXVjZJZxyngyFd4+zqT73I4w9ZendLfz1tvnWcnDrnaMeajU5CbCz1gs9SMUAN\nTKC1dWy1Y3ajhFBJVsshBW/YV0/Kt/Ziw043ZqtrSEZeQOVwCdiuSNeL8eBC3CE8UBWL8MB0wbYl\njLzRfd8m3H72+LBOuSQ4d0YR1gRbUcJuZBgyK3GwZSi3BbUFn9UH0xDj/ud0ztFoaN6/FrP7ThO1\n3cZrRogBrD29xRvdf+Bq4+tcYJGn7MPUROWQTuwML0eb/E3zCjENPhRKHgkUaoDX9Zbhn9YcX1pr\nE1cEcSUB/7COTTRmbZvo9ffw2yBtAU8Vhmw3NkF6Ce32FiCI43joPQohef6HX+SffeRHaLW6/P3/\n8y021oc3GmqrgkdeKFB7GJo4msbu839TKqLCj5Q/yI8Hz+HbPRqt76Dt3mEgKfHPP0L5uZ/CP/cs\npilx0YiNGeVQZUt9RVIveayUQoIRNcCdc0Ta0IgM652YVjK8WA+VZKXocbYcIsXtja/zseDWseZj\nwfHO3abpW7M8d8vCulPrgmliTeKht0FyL/fXfrnrFuk9ovpJ6ievX/pJGnTIfhmHNZhH0fvzuPb6\nsQbby4M1GAYyCmtQ53bsGtdeXh7ycDrYXg9jGjxMEysPD/0yjofb5XTuW3e2v+bhYZpYef20X2bF\nt/LavtVJ2OjERPv1vG8udhyeEIRKHNR+7hpLbBzaOXoLGcl+/W9PcqlaoOTfnMTc6f46jgeAxJg0\nLz0xXGlE+zdsDyymnQMDTgtsDNIH4e3nkMs+HUualx4JzHbv9+kFcfTx1Xus1WXFmVWfQigJAoFS\nN3no5cvv7sVce60NXQcRuKSPUw+CoiQsK+RSQFtzUJP95o3wDmkMMjHsbHyPb1z+X9jRazT0Jq14\n54CHslehKissuCrXdpd4N4lZS9qsRy2S/YvmQqVYDAJWPMlyC5rrsNF2bLUT9trxAVaxHCIDgfU1\nO9ffwDXbJM02nd09jNnHCkPCoIinfKRLT0mtTUiSmG63c/A+i8UiUkqsFVSq57n/wfv4oQ8+ibWO\nr//Dd7n23gZhGKTcOce5R2IuPKIo1kCF5uAWdyEkUgUYJCEL/PPyf8FZ7wx1uUBow4O3Y6XBuDaJ\n2aX9WAX/0iVkbRlZrIJUh/wBAyYRCNl3P0HfZpUSHNQuv79WwN9/v/1+aqwlMY7YGDraEipJqCS+\nknjq3h4LRk3078axIAtrFseCafrWfO526zzMWn+9VayTXhfkweqXLN8atzlz1y3SJ8ks5ijAsFPc\n6fby6BljcoXCzSKneficZnv3AtZptn3aWPP+ml/vtRsNmnrSMHNzAZklz66UKQXZWVrTtD3Pe06M\n5eUbexND4HEuO9wZsBEk10ectA7I888WqFWzebjxVpu3X2pm6gAkZwvYCTz8/Wv/lm9f/mKmjnPw\njfX72Iuyy50V3wvo3IgydXTcpnn1m3Ta40PgAerVOp1Wdr3ri/c9xL/8Vz9FpVLkH/+/13nr8vsj\n9T72r338cicT68OVj/PR8GcydQDaP/skrhRmKznLpJp1UsDzqxX8KeSM59Wb1W/urGLNx4LpYs3n\nbjdlFn3rtGPNIqdZ/fWez0mfy1zmMpe53Dm5p3aBM0SI6XExeQp7FDnefNYcKqleDh2ZAba0tMQ/\n/9i/4NL99/Gtb17m9dffyayPLfIUec/J/ORSZ9P1h7nMZS5zmcvplKyz8rGL9LW1tVzgZ8+ePbpF\nd1DG7Vr0hx/05wT0S3/4waiw+TuNNRieNQ7ruGwXQpwID5OwnHNjdfqxeu1Oq71Zw+rXz4OV5Vt5\nOZ1FfzgprFnrr7OKVfIUidHEbvRpuRIgEQgBxqbRX2+pqwAAIABJREFUwMOS2tTRFiU0vqeGFmh3\nioes74hODEkrQXYNVoLz5PAq1O2HvDtA7Ic2j1pcGovQIB04IXAjb3R3COdoNzWBAj+UyBG5y7qr\nkVikMDgEbsTFZo6E2OwStXxkWMAPFmCgTYejk+whvWVQZRQJxsRDWEqGxCbAGUvRL9BNukMLUIkg\nRKFtTClQaCeIk+FT9zDwCAjoSI9KuUKzNRwN4HkexUIZbRyVSo0o6pIkqV2VSoUf++cf5cmnnuSl\nl77F337tHyiWLhGWQrrN7hBWEHgs1HxclFBaKNHVEXZEHfRKuEwkE0zooYyFUZe3eQJX8nHWIrBj\n7hFwfXcM9Fga4Q/WQgxRx+AChx+oIT+11pEkFmMdQjgC/2bqQ79oY0msRQDKOfwRpzbWWhK7X37P\npikmWf1nFr81WTp30q75WJAP67jnbtO0/aSwbse3+rFOOw/HwelJzeWzNrfHhrt/8pOfHPujfvn8\n5z+fS+84pZ+cngwSNEoHDpM9Lndi8IUM1i7vOcDg3/VeVBbWoF3jsPLYlQcrDw/j9PLoDOrdKg8w\n/A5PE6ejOuitcNrr0NPg9E77qbV25AfoVt71NPvr3eZbebDy6gzqTau/OudoRJqNdkxXG4xzBEqy\nEHos912SFRnLRitiL9K0tcW44TxvAVQDxUrJp+hJCp5KlztuOK/rTviW7miiRkJ7rcPWG7vEjTR3\n2fkCez7Enitgyz54CpsIdBNctxfC7hCBRVVB+Q6cQ8QOt2thPV2UATgJtqSwocKptHiZSCyiqZHJ\nPhsCKsseKw8UKNYUSkDSTGi802T38h66Y/axJKYY4AKf2HXoJDdotN/iytr/TaP9JuCQMmRp9UNc\nuP+nKJQv0XKKjdYaX3/77/ind75KJ2kBjoK0XCxJar5DWIvWAdstj8trPq3IP3jGoCgJChIwiCiB\nliZ+ext9rcFBXoAfUFxdRYUFjAPpLLq9R3t9DXTKqXUGlMEIjTYJSnkoGSCtjxIFhEhr1RoXUyxK\nXnjxWZ5+7mle/8EP+Oa1K3SWq8higX3norht8Boav5uwWJYs1eHRBzTnV0HKdFndxtHyJIkA319m\noXCR+6of4qH6Ryl6C6kPJTF+excVdwANZR9TL6AfXMQu9t/iPu6EZHBSZtO/ix1EDpoW1lx6nwCg\nfEH9QsDShZCgonBC0O5a1jc0O7uWngtXyoJzZzzKZYkXChJracSazU5aFx3Ak4KlgqIe+gSexNr0\ntviNTkwztgeJJ5VAslIMKHqSoq8OLJ7WWHBc/XWcDgzP3Ua1N8tjwa2Or3f73G0WfOtenbvdrm8J\ncfNm/Vn0rVvFyjt3G5RcOelf/vKXeeWVV/iFX/gFVlZW2NjY4Itf/CLPPfccH/vYxyb9/MTE2nw5\nA9PCytteHr3TnFN03O3NMtakXbJpt3e3+1YePqfZ3ixjzaJvTRPrext77MSjB7aeBErw7Erl4KKs\n27UrD6dv/LvLdDeGT5P7JV6t0D1bn9heuNFmQo0vhHS4kTe/94lzhI0dmJD7//XNP+L9vW9k6uwY\nwV93S3R1tmFu5wy7jWwdtdWEV9/N1AEoFjyazez8+VKlShQNn3ArpXj2+cd44cWnePvye7wSttnQ\nwyfm/fJf3ad5MMhuz/cW+NHn/2cUxWzjn/aglqeMWY57F16NYMI1AqYk0QuFia2FFzWMqQ1+UyyD\n0ROj5IUzFYIZy4ufjwXTxzrNtk8baxbH13th7jYt3vPqzapv9STXCvYLX/gCn/70pzl//jy+73P+\n/Hl+7dd+bSZP0ecyl7nMZS5zmcvdLUIInnj6YX7xl3+GcxdW+D+/+CX+9q+/TnvC5sJc5jKXucxl\nLqdBcl0c55xjfX2dS5cuHfzd+vr62OP7k5TB8IRe2MathB4Mhk30fpMVItP/56wQmZ7euLAJIURu\n2ydh9f58q1ijeJiElcXDKE4n2T4O6yic9v95UpjTNDkdFbozbd86Cqf9vjUYfjUY5nQcvpWnv/aH\nJfbrz30rn2+dhv7qnCMylvVWRDNOy0odzt9NbZACFkLFciGg4KW57KOwWrFms5PQijXxfo5t0Ves\nFAOqoYcQ4qAm+3Y3JjIpRqgk9YLPcinA68Pr8fDQx+8j3otpb0Rsf3eX7nZ6U7n1JLpeRFcL2NDf\nz0lm3+6b4c8itHgVkIGDc34a4tywsH4zvDkoSpYfCKmtBAQlidGOblOzeSWisZ7gLGmofBLj6Rhp\nDNj9fHdHekC6b3c3ucFW559oxVcI4jUu+KvETrOXNIlIQIDF0ZWSrpQknuOH/A6Rk2xEgve7jsRJ\nnAOjJZ6t4qxHIgyVhQBjHN1WxEG5OOsItYenFcg64skyJAl6e4d4ZxvRe1d+QLFaR/k+2lrqtRV0\n1KW5swFmP1fd8wjPncVbWMR6HkUhcHHChaLHi88/SrfT5T/+1VdpeQ2Wf7TM6uIyrryFxafV9ljf\nkWiTTnPO+UV+ZuUhPlBe5rwX4Hualt3l3eR7bNnrOCxKBCyXnuNi7SOUg7MUdjsIL8EoHxOEICUO\ncJ7AlhUukLgdiWiD8B2i7JChuBntPhTuPpyDXvIlq0Wfkq/wf7xM0ja0djQbb3dp76aRA14oWLoU\nUj8XEJTTcPdO17KxqdnasRiTRthXK5JzZxSlksILILGWZmLYaGu6+/4dSMFy0aMWegRKYp2jqy0b\nnYRGZA7O+2uBYnk/pUTJ8ffTzMeC8VjHORbM525Hw8o7vg6Gzs/nbuNtn4SVp7/2njGP7eOwTotv\njcIalFzh7n/xF3/BX/7lX/Kxj33sINz9K1/5Cp/4xCf4uZ/7uUk/P1axdvLFcTA6R3hU/kEerFE6\ng1ij2ptVrFvl4V7ldM7D9LHmnI7WOe7+elw8tGPND3a66cVVQxrQW6w/slim4it8JcdibXcTrja6\nAzXZb4rYr7vuAOc4VJO9vz1PCM5XQs6Wg7HPaLQlaiW88loHbQVWjgpFTC/1UnWHKmVfHBcieXyp\nhB9IPH/U5V6OJDJc+fI1OutdSMZslEvY67zJO1tfJDENdDJcpkxIhVOKV90mXeHo6i6jcqilKnJl\nt8Dl3TpaOyI9fNlb4HkoFPaqQ1lJpzNcYk0IKHgebreJrw2JtugRWGHgg4RkuYL0fTp9l8tdWKzw\n4ccv4inJSz+4TqfyNtUVjQn0yMvefBWy6ur8t+FPUVcFwhF0OQGJSjD1J1GFJTxXRowKS/cESaVA\ndL6OU+Mv9pOewztjkf7hzaV+HQGcKfmcLYf4SqLG+FYSpQtSqQReMOzzzvUujktbCYLRl71pa9HG\nIhBIyeiL45wjMQa3XynQV8OXM8Lp+AbOyvf7pHk4Caw5p8dj+6xizTkdrTOJh3GL9Vwn6T/7sz/L\n/fffz9e+9jXefvtt6vU6v/7rv84LL7yQ5+fHKuMetPf34xbxcJPELJ07hdW/A3Y7WJN08mD1dCbl\nv8wyp1l8HhXrJPxhFrGm4Vt5sWaZBzi+/noU209zf40dRBnlsdKltaCgZGZurJSSdmKJbPqbUeIQ\npKnuvcX5KD2BdumpepbtypN4pQDrxVg97nsjcE4gA5OdI6zShXlYVBnjmCAseqDN+AU6gIVIb9Lp\nXh+r4qwBa7CBpJuMT4S2pkOka7S648PIY63BaUouHLlAh3RDpJNoqp5Hpzm+HnkUJzgl8fyATpK2\nuVwt8uHHLlIvF/j6m9f4/vtbADx+v0fit0btLQCQmIiyFJwVBcbs/iAcBNrHhSvgSmPtQjtcoLCZ\nOaECqwVC2DGL+FTHAWXfo+CPn4IpT6K87G+EEIIgUBP7mCcl3oTvjRSC0PPmY8F8LDiy7dPEms/d\nZnNdkBdrzunRbdda394iHeCFF16YyUX5XO6cZH0o5zKXucyWzPvr9GVimFlPL6/ilMRlrM9vKuXE\nymG8ywlmc2DZzM2Yw21WiwE/+ugFLi3X+Mbl9/mrl35wqA2bi4i5zGUuc5nLXGZTsuZuuRbpcRzz\n53/+53zta19jb2+Pz33uc3z729/m/fff56d/+qenZug0ZFRuwbi8Aji82zFJZ1SIxqT2erkWWVi9\nf/Z+f7tY/TlbR+Vh8BlHYQ2219t5ut328mIdN6eDv7kV3+rxBoc5PS7fmhZWHt86Lk4n6ZyG/gqj\n+9itPuPt9FezX0s5MpZ2Ygg9RUFJfCUOwmOdcyTGEhtLR1usS+ugB0ocql1+VB7KnmSl6NFJDLFx\nJIdC0G8+3/VWlyUTEHqSoC9MuB9rpejt25di9YezK5Hm5BY8iScFXZ0+b3IoNP5me+83I8BR2G+v\nnwcdG6KOpdNIUB2NkwKnJE705887glBQCAXlgo8ODF1jSUxfPXjn0vJqHUPc0mxuJRQXA4JKgF/w\nEDLF0okhaSfEjQShSMPme+ba3h8thhax2SFxTZRXYL8+HUbfPOH2vAK+CPAJeMrVuO432aNDy3aI\nTbT/njyE9DEIliotzhmPRAdEWtDsO1Uv+iHSSWxisQGUVQFnHXGs0Tp9ysD38DwFQqCFoCCrSOuw\niabbuXkTe7FSRIQeXsXn2Scv8shqne9e2+R//eprdPfD3ouhR6UIlaJm2Tq8sEDkBF1r6e4/oxSS\nJX+BJbXAg+IMxg/whABncclN22UhwK9VCBZr+BdrRO2AuJGQtDUu2fcDCX7Jw696LCz7dJclna4l\niiDRN31LSIvwQHjgbHqO3hc4uf//aapFqCTaumMZC3r9tb3/Loq9/qpuvb/O+ljQ++6dprFgmnO3\n3mn6cc7dZpHTwd/cq/OM4+6vg77Vj3U3rQtup78OcjhOcuWkf+Yzn2Fra4uf//mf53d/93f57Gc/\ny9bWFr/zO7/DH/7hH076+YnIqMFvUAY/auOI6ne8cSFER8XKsiuPTr/e7bY3TdvvFFYeHrL05pzm\n15km1qzyMO+vN7G62tCINOvthLYePpkMpGCp6FHyFTtdzW6kD0pd90SQ1i6/VA0p+ePDtfPYZaxj\nuxNzda9LbC2MCRsueoIzpYCVYoCUo3nQ1rLZjmlEmkqgDtVk7+egGWuuNyO2o17+8zCWv19futJR\n7F6L2Hk/RseHiXCADQTBakB9NeDMGZ9KWQ3ZFmnLejvixuUGvNdBrkWIAVKFElQulag/VCVp6UM1\n2QfFCcNO6xU29v6RRud1nBvO9UYqipSoygUquowvggHbHZvs8Zp6n+/YNRrG0HV2iAttJO1ulevr\nFUzXJ25qcAN8OYe04FsFBpJe7vngOzKWonUYG+MWAmzV44UL5/nAmVXe2NziG9ev00kSpBYsKcuF\nesx9K9vUynoIquugIUNW3cO86D/NM+oBwsFndA6HpnCuROWRiyw9/yThUm1IJ9qO2fzeNrprqD9S\no3qhjBzwm0Q7NjcT3rkRYTyDLAvEyGMPhxKCxYJ36NLCQZl239+NNJudmJ3IMBi8IEgvhrtUCyl6\nt9dfp237fO6WH2tWx8SjzN0GN1RmyfbT7Fu3i3VSnE7yh3thXdAvuU7Sv/71r/NHf/RHFAqFA9Cl\npSW2trby/PxERKnJeVp5SerlH2Tl+ExyrEGsSbkMeeoh9rCynuGo+SjTwJoWD9PmdJJOv960OO3t\nAt4u1kn51u1yOm3f6v/n7WLNfSvF2osNVxqj84gBYuu43kqAmNH52+nitBEb9mJDJfTHYuWxS0nB\nSjlkqxMTZ5Qj72jH+62Y5WIwlgdPSs5WCqyWsvPCqqGPQ7AdNRn3jIl1rLU1N15t4cakcAtAxY7V\nouD+h8fX1w49yaVakcYb75E0RiyoAWcce1da7F1t9R27jxZrNO/u/DviaCdLiVX/AkUdjHxEgWCF\nGk9qyd+LDbpOM0rRU5ZaeZfmWp31PTNSByGwCrRwuNgOL857oiQdBeVLyzy0UOGD58/xTqPBF777\nOnu9ly8E1oeH7495tL4+9vEKAgou4t9UPk7RjK4jLoRA4LP60RepP3nfWJ3CUsjFD5/L9FPfE5w7\nG7AtI/aSrG+SoOApHqyXRl7E1pNpf7fe2e3s380wLA7YjQ312FAObq+/HsX2PGNB3rlb/z8n2XWc\nc7eTGAvu9bnbtHk4yvg6q+uCWeO0/59ZWJP4uhv66yTfOoSbR8n3fYw5PEtoNBrUarUxvzg9MipU\n5XbxpiF5X+C0ZJocTBtv2rYdV1uzyulp9q1Z7a/H3dY0efCloOxnDwWBEtRDDzXBdTqJpp2YsbY5\n5+gkhp1ugpmQm1wOPEKVbVdxvwTb7Yqzlu7VdeT1LbBjVjaA6CTI3b2bJcJGKkHXczSjZOI7qpwr\nITO4d0KQlENM6I3NCnfOoeNNfC1H30q+LxbHlt2iQ3e8jnO8q9u0EsgyXVtBrGJQ47kChwgNomBh\njPUCeOqBOv/lkw9x/0KVv/j+m3zp7Ss3F+j74gvBA7LMgiuPgwKg5p1D+nWcyOBUKRqRotOxmX66\n19Rs72gm5dBXAkUgs51QW8NeN8mVs59H8vT9ajC5v7YTk9lfpy2zOiZOG+s4Zc7p9NuaVU7nc7fD\neMclJ8lDrnD3P/3TP+X69et86lOf4jd/8zf5gz/4Az772c9y7tw5fvEXf/G2DJ62DOYIDD5eb7cj\nS0bpDGL12hj8uzzt9ev17wj179TcLtbt2tWv07/rkwfrVtvrtTFNHm4Xq9+u2+G0f/dvku1CiKlw\neqd8axqcnpRv5XmH/d+QO8nDneqvWTqj9IQQ++WX0vzsRqzZ7mpKnmK56BMqSaAESkr0vk5nP1y7\nmaQLsHRx6A7+FEhB6EkWQo96IWC3m7ATJcTaEu+XWfOFIFA3a5dXAjXkD8Y64v02t7sJzdhQL3gs\nBB6hJ/GlRMpbe9d6t832y2/RvrpJvNtC73XAgSuHuEoRs7pA8tAF5F6Cf3UXuRchOgl0DfgK5/sY\nzycp1LBL5bTmeUUgAoHzBVKkGyCBktRCj9VyOHS5uxAC3dXErYTuVszmG7vs7Wr0chlb9LFeepu4\ncA6pDSLWqL0uan2DuPU6cfcKRu9ikj2ciXGexGCJXcSu3qBJROILtHBoZ4h1h8ArUhAFChRYMQtI\nXeKfXJPv2xbrJmJLd9HOUPA9fOnwhEa5PYwN6ZoK2iliLWjFMQWvgDQSnUB3B+K2o1T38AoSJy2J\nS0jPrj3QAtNyRJsxKyuaJx6o8nD1QazQvJO8Slt0MNqn3fW4tuFRTyp84uwZHi4VWPE9qjichEga\nWnS4bje45ra4UHuRB8ofouafoSgWUc5DCAMugaQLe5uYckhy6RKmUsOGBawXoGRasqxQECwteixU\nPbZ2NDu7mm7XEccO61KdMIBKWXF21adSUUO+pa0lMY6usWmIedeQevnhFx4IQeBJKoHiTDkcWtxP\n+xvYf39Env5aD32WS8HQ4v5OjwXOuVvCGpT5WJBfZ5TeaZm7OecOIi7y2HUcnM7nbneHbx0Va1q+\nNU5yLdKTJOHP/uzP+NKXvkQcxwRBwE/+5E/yS7/0S/h+dqjULElvB2NSaEPvBWbtWvVom7SzlRdr\nkl3Ttn1WsWA6nJ52Hk6C00nt5cGaZR6mhdX74N7N/dVYi5yA1Y4139loTbz3WxzcDT4eayFQPLZU\nmsipdW5kTel+ycvD9/6nf49ujC8FBkBxEUSYeXrrQkX7Z56CIDsM8YmlIrXQz7Srsad5+TttnMt6\nRkf8d/8Ws30ls7112eAyV3Ej6offFMF/aJfYSsaXVwMQLiRKROZt6gIJOiAx2bH5P3xW8UTpITwC\nrurX2LbDZeIWRIn/Wv4zwgnOFV74BH5wPjOCQJd92g+uQsbpOjikBGuzv5MXz3s8eH+IzDg5d87x\nrbVGZoU8gAcXCqyWxqdq9LCm1fdbccJrG62+CxJHy9PLJcrB6Lz5o7R32r+B98JYANObw04L6zT7\nw6zO3e4VHk6zb43TyZWT7vs+v/zLv8ynPvUpGo0G1Wp1YqOzKKN2ObJ0J/33STkKR8HKgzFN2/Ng\n5XGuWeZ0WjzkbW9WsfJyOklOwh9mEat38nNc7Z1EfxU57eKg1ngexOz/nMd2MUVOydMnhMhcoN9U\ny1ekLJddg5ewDWtBzvE3e4EOsH/p0YRFupIKO+oyuj6xzhIoNXaRXveL/MjyfZwvlnjPvMaGeSfD\nLIuSgqEbCgfEU17mAj0VOWGBDpC3X7jMBTrs++lEpDTX8Hi/gTl9JgdWvvZm8/s9HwtuYk1zvjWf\nu50c1nG3N6tz2NPaX29pkb62tjYWsNu9mdN29uzZiQbMivR2PfvDNAalR+ik3amjYGXp9OtlSV6s\nnm3TsL3XOabFQ16sLOm1k5fTPDrHyelJYWXJNHnIg3UU2ye965PgYd5fDxRRQqAz6UgDat2kxbwD\na7MXQNbaNIB4Cpwaa3Muqh0oiRtx6/2BSAFM2LBwDmMc1tihW8IPqRmzz1bW81kwNl14ZpxsSwSe\n9NF2/AJcSI/ExEgEWYxoowmUR5yRi+8rnyQe/u9lFfDi0iUeKC/y7Z1rvKNfolLMjmDwpT+5n0mJ\ndfv0Z6kKx+TNpN4mS7aedmmpQpXxDm9OKIfD3fvbs+54xwKcQwoxYd/D7Vfsm72xYNpYWTIfCw7b\nPp+7Hf+6oId1Wnk47rnbUXxrElY/ZpZMi9NbCnf/5Cc/mWlcTz7/+c/n0jsuGfdCe0T0Pl5ZMipH\napROVnvTxurtLt4u1q3wMM6x+7EGc7fGYd2u7UKIiXblxToKD9PEmmXfmnM6XU6ttZkf6Gnx4Fx6\nIjrpHfbsmlZ/jY1lsx2xG2kibYltumgK93Ncl4s+tYJPM9ZstpOD2uXGuTQPVkmqocdKOSRUw7lb\nej8nvaMtG52YdmKphorlgn9Qu1wN2DeO08RaYuNoJ4b1TkK7FaHeuYH/zg3kXgfR6iCEwK8VCeoV\nqo9fpPb4BaLdiJ3vrNHdaKIbEbqT4AoerhxgFoskDy3jauHBeixd5JCWVIvBdR1sGNh1VOoeKw8U\nKC14BEWJ5wmSdkyyG9G6tsPuqzfodgzxmSV0vYYtBFjPQxiDjLuoVhP/vat4W+vEZpMO62jXxtgO\nxsYgSXPSbZeO2SMmoeUZutKQOENsI5xSaAQdZ1jTbfasoWULtG2J2Cki49AuPT13DmJt6SYJzgmK\nfgFB6meJMfgqLS9nnaWTpJv3vghR+PjC55nyGR4tr3Cls8770XucCxqc89to4Wh6AZGQRM6ijaGm\nStRFhYuuzgfsBZZcCedZrLCAxVkDfgjFBSgvY889AysPozqGYK+NijQyMekGRkHiSh5mKcBcKOIC\nD9N0EEmsBmcEQjqEAuE7RNmldwlE4NrgEoHTgCMtq+aBLFhkWVAMJStFj4qvCD2FJ2+enPf6q3Ww\n1YnZ7sRExhKZ1C98BaGSLBYClvZzv7P6WP93JEuO0l832hGNg/6aLtxDKSj46R0UCwX/YKGe1d6o\nPtaTkx4Lbsf2Qaz5WDDbc7fj4LSHNavzjOOeu+VdF9wKD4Onz0f1rdPaX8faM26RfjfIxJ3lKWPl\nbS+PXp5SCydh1yy2N8tY09iNO0p7dztWHj6n2d4sY82abznnaMeawFP4GSeN2lq6iZmY9/r2TpvN\nTpJ58lfyJU8ulfEm3AJ/ebvFVlcP1Yvul0oU8Ui9RLhYGatjE8N33lynUwkhq80bCbxrISOKXHqC\nevsa0fu7Y0+CHWBCg2zuIPV4sMS2uBx/idiMqQ1Helb8DbXNu6ZB1tSpkSje6tT3w9bH7f5D6IV0\nk5jBV+gJydOlSzxTucSN6AZlXqfsjT85N87xovdj3G+WUWNCsp1z6Eeexzz0IxCOfz8YS2Epwi34\nY9MZnAOXOIQnMqPgnQGsg4wKAgJ4crlEdULZwUhbrHMU/ewxfRb763HblVdnPhZMH+s02z5trFkb\nX087Vt7+Oi3e8+rNqm/1JFdO+lzmMpe7R+7ifbm5nKAIkd7UPmmQ8qSk5E/O54q1mZSSjJ5QHqsn\n6SIpW0dUSwT1cqaO9BUslSbmSmPIXKADWO3obrbTaOxxNgFepwUZC3QAKQKcJLOeukBgpYedkKbu\nS4cUEjKW8kKApxSiL7pdIHi8dI7nKw9wI97l/9p4ibrX4seq2aHtSgjOqAWUzQj5EwIR1rIX6JCm\nJlTHL9B7tosgGwZIT9lVdiS9g1xl1UJvci7kcYsQgoInM0P35zKXucyOzNo3ZC53XsaepP/Wb/3W\n5B8LwW//9m9P3ahpSC+8oD/kYJxOT0ZNLgfDJ8ZNQO8UVi/0YhRWfx7GJKy8PGSFXuSx6yR46O1e\nTeKhP08ry/ZpczruGQdDhsa1NxiOlsVpHh56cty+Nc72aWKdZH/Nsv24Oc3rW7PYX6P9clEb7ZjE\n2v0s2cNYAlgIFStFn3rBn2hXOzE0E8NGO6E9Mr/coRBUQ8ViwWepGKQXl42wva0te7Fmo6PpjsEi\nctBysJ6GuQ+vdx1Cgui08aIOqrE7dFLuhMQGBZyUSBdDawsRtxB9y0bjNGvuXd7mDbaSK5RdwILx\n8Dn8Dd80lpeN4NW4jfAsVblL2deH1rLGCHa3K2yuV9mNFbJmMJVOGu7dZ3coLecr4AuNdj7XmpZz\n/nl+uPoQTdPlG423aJgGlwrwUDFhxbcIaxHODF3yVqfOI95jXHTn8aQHengHwQVF7MUn0fc9A5Wl\nkf4ADhFavArIkgPpSK9mOyyBFCwXPaqBR2IdG52YZjwqG78/j300VkFJloseK6UATzATY4Fzjr1I\ns9GJiY2l7CtWywUK3jDetMeCWRxf52PBsN587jabvjXLc7fjXBcchYdpYc1af+2XsYv0r3zlKxN/\nDPATP/ETufSOS3ok9D/8oLP15z70/tw/SA6GIhwHVr/064zL/RjsDHmwxumcNh7GtXcrWP0ySzyc\nNk5Pg28dFetO+VZerFnhIQtrnO1H5TTWhncaXbrGkpjBA+GbfJ4vB9QLPoES+Eohj2i7MZbEpnXX\n39rpEFvXd1Fb7zcOTwhCJVgs+JyrhCOx0tr4MHDTAAAgAElEQVTYaej+W7udg8P1/WuPekQgdLpo\nd9c07PQp9d3iLrAImyDiGK/VQgiFExL6S4IJh0CDTfj+9n/gavwKLbdLK9k9dPN66BXxhUc3EbzU\nKrFjYVtrmkl8oBMoj6IvKSiLvi4wzZBOR9FsaWxfyEGpHKBCKNZbXHqoRagsAo0xEQBVscpF/1kc\ngneTNxF2m5ovKAgDpv8EXRB4IVJIzttVnlCPUXYlAusj+0MclAIpcVKin/mXuOoyrlDBqcIhfxD7\n4Qei7PDLLo0JVAycoKc6nhQ8uFCkoCT+vt/0xFpLYh2RNrzb6NLSdqQ/iP0Fe0EJLtV6WPJQmsVJ\n9tfNTsJGO81/T+zhiwcVaS580ZM8VC8d9Jm7eSwYNaGez92GsWZxLMiL1S/jbM/CupfG17w89Mus\n8nC3zt3GbYKMDXeftcV3Xhm1MzFI3iidfvKy8gruFNags94q1jRtN8YcOw/TwhrHZ16sk/aHWcQ6\nzbZPG2veX6eL1TaanXhcePVNnpeLAaVgeNjK255SaXhvwQfnOoAYcZN6emO91o7z3vjwfU/Kg/85\nuqPDooXA+QJ8wOrDi+4+cUicDBGeApHgege5h5QEDh+EzxX7OuvR5ZFYke4QAW/HRV5ptUfqxEYT\nG9gFvM06rd2YEcf9tFsxtODChQSfvYNQ+ZKoc8F7hoAS1/R32LHXAHgkLGJ1NPIJY51eLPeg/yDL\nSe3g7w+JMWAMrljDnnkYJ0flegvc/gaHX9EQjua05zdFT7FUHB3fLqUklBB6CrvbZZw/9P5uoeCz\nmIHVk+Pur1udmL2DwuyH7TektAqR/uZeGQsGv8/zseDWsOZzt/k846R5uNs51Xp81ZRcOenWWr78\n5S/z1a9+lUajwe///u/z2muvsbOzw0c+8pE8EHOZy1zmMpe53LMiGF53z4KMW+KO0glFhQvqKcpy\nmev6dTbsFQ4/1WS0PO3llWlizWUuc5nLXOYyS5Jrkf6FL3yBl19+mU984hN85jOfAWBpaYnPfe5z\nM7dI7+WJDO6U9IcfjNPphR8450aGzffrHLW9PFj9oVq3g9XTuV0sIcRYnVFY0+JhWli9f94uVr8/\nTPP9nEZOp8VDVh8bhTXvr3d3fw2loKgEiXVo18sFvikSCGR6E/jt9lcda5KWRrU1WoALFAzVZ0+f\nbzfSFDyBr+ShMOlDz46j6MmDUONR+dIAriIRscVFjLjgzSGcRpguuAghFM6pYSyhsbZN1VXp+DUi\nG5GYwZNrCV5AwcJCwUM7SSuKGZSCH+ApQTeMqSz4xG1HnBze0feUpFpRSB3ycPBBKpxlzbzJ2/E3\ncX0PUfaKlAkoOIvwKnRsF2sHsGRARS3QcQkyKOFsghtxIZ4olxG1KkJqhKewWozg1CKtwzYdyjlc\nAAz5fJq2IHFoY5D7vjDOT0u+wjpNPBAu3sPyhUAbizH24FR6VvprJfCITDwiVeQmD2m5N5emVszQ\nd2s+FszHgkGsk5q7ZflWVnt5se4G35pGf+3pzPtrijXuRB4yctL75dOf/jS/93u/R61W41d+5Vf4\nkz/5E6y1/Oqv/iqf/exnJ/382KWfnJ6MIqf30nv/LuVwsv9xY+Vtb9RrG9QbVf9yku0w2eHy2jVN\nHo6D08F3KMRwaOBJ+Nad4nSUzjSxpu1b0+xj/SFP8/5689/z8ODccP7UqPZuxS5tHVudmJ1OTGQc\nSgoqgeLMfh31/nd2lP6atDVRI6b5Xoud7++RtNIFpBNg6z7u/iJ2IcBVPIQYzElOLxxbKnosBB7l\nQI3M67XOsdtN2OwktGJNZPsvHxM98iAC1jU0LXK7jYg6qN11vN0NhO3ZJXFhDVeuY4XA2BZx933a\nO9/GJJupDo4mHdb9Fnuiy5pt0kFwLYnZMOYgeN1agbZFElsgNgIl5X5IfRsp3YFZuunBzgK27VHA\nUi0bLpzZ4/6lS5TVQ3TsFRrme8QKEqHwnKQqCpy3RR40RcqkoekWx47osuG3aWMIZIVFscqj7inO\nyAv7N8eDdQmGJpYIU/JgYQEeeBD30CNQLKZ2WbBd0trlHSAGEVtESyN131K6IOCsgIqkUPMo+ILF\nYjB0AeAk/3PO0Yo16+2YdmJwpHXNl4ppmLsU+bF6eMc5FnS1Yb0V0YwN2joCJQ5qsnsTeLjV78h8\nLDia7ffCWNDP6e3YNZ+73Xp7t4t1Uv1ViJt10mehv94p3+o966Dtg5LrJN05R6FQOPR3URRR3B9I\nZ03y5AwIIXLVIT8KVpZOXqze32fVSe9/sVlYvd/n5SGPXZOweju40+LhuLAGeRjH/VGxsnbJTorT\nLN86KtZx+pZSamjwv1O2TxPrTvXXLC5Oa3/1pOBMOeRMOZxqf333b9+ndW24FJhwoLYT2E6wSwHJ\nh5dwI27yjq3jeivheivhmZUS5WA4V1qKdGG4WAx4f6/Du3sxwyfhAgrAfenvC//71xG7w3njwllE\ndwe6OzTM67S77w7rIKhSopqUiJ3hb+QP2E1aIzhwBLJNQJuyrLAXRQem9JvlVzVUNykJy4sVSYFL\nlOXzRO46m/pvsHSQAgoWCiR81HuKyvABPRLBkiuyFBcpexc5539oWAmQwkeyCEDnEx/F1obL3wkJ\nqgSUgHcTWB+eDAHQdXDFAZYn/vMaYXH01GaS/wkhqIQ+lf2659P8Bh7HWFDwFPctlHLbPh8L7o6x\nYD53m8/d8vrWrPfX2+U9r95J+9akxfkBdh6lF154gc997nPEcXxgyOc//3k++MEP5mpkLnOZy1zm\ncvfLuN38UXrH2t5UWrvZ5kQd69Lj6WlgOYeb8ASO6bQnEFz0L7Ik/wW+WGJL/780zEtYRtQ6z0Oq\nELnUZjFXfy5zmctc5jKXk5Rc4e7tdps//uM/5lvf+hZaa3zf5wMf+AC/8Ru/QalUOg47c8uoSduo\nEIVR4QlALp3BEIVbxRoM1RgVDtH7+/4dnDx2jcPKY9egzjhO+23Pi5WHh2liTZuHaWGNCgmDO+tb\n47p6P9aoMLs7zemd7K/3om+Ne9d3wrd64cEHId7GoQQEnqRe8FkuBvhKoq1lq52w3U3LRBkLgRKU\nfMVqKaAceAd4k3iIjWWzHbMbJUQ6rXEdKEnFV6yWQwqexAGNKGGzndDRhm7XQMdASyOvtpHrMcKC\nX/FYfKxG+UKJoBpAIc0t79VBj407HHKdCKQThIGgVJScWfGpL3gIAd2mYf1Km+aWptsyaByEwIKE\nZQ8CAXGCfOcq3ttXEY09RKOFQAIKjIfYL0oe2V2avEdMg1jvgbAIBNIIhE0X0x0S3pJN3lF7NIjY\nsV2skCTWsRtHmINb0CWeFyKERFuDFB7GOWKtiY2hd6Xdg4ULPBE8SkLMW/r7aLFHCUPVtglFekK+\nLCrcr1apiJCi9VBCAQ7bV95N1VYoPf0RgouP4VWWkSJENruoa5uoN68hW12cpzCXVjCPnMculLCV\nEig5VP6s6ElWih5l3yOUAhs7opZh53rM1tUIHTmUL6hfCFi6EBKWFWFZIcTp6a/zseAmdh67bvX9\nzPJYcJxzt8H28mLNx9dsnfm6YDpzt9484F70rVGSa5Hek52dHTY2NlheXmZxcTHvz45VxoURDDrU\nOGIGneVOYw2+uFFYg+1NE2tWeMiDNefhaFhz35o+1p3i9DTyEBvLG5ttYmtHXLQF4FAiXYI6GHkh\nHIDEUQ0Ujy6VEWPs6tn+xlabdmIOapKPwpIIhIBkTHs4h4gNT69WCQOJN6KkG4A2litXI67fSMZc\nXpY+Y+CBv9HFJg47ppKK8EFdewlv7zo0R5dFQ0oSIm7oV9EuwpnhS9UApBf+/+y9WZBkyVX3+XP3\nu8SSe2Yt3dX7LrVQSyDUWqabYfkGG6QxG7APGGE2gDAMAxM8Y7wIGXrAeAAzmSRDDxhmM/a9SDMm\nwccDPPAhCbSANAjRUkvd6pa6u7qruir3zMhY7uJ+5uFGZEVGxr1xsyoyM7IqjllZVWV6/P3E/x6/\n7sf9HD/8D3eZNd2hkR4ObwfwjE/bKnZcgHWOdIhiCkXghywwx2PBo2jRvBC/wJpdO9Cu4gX8uJrh\nGW8F3wIyZLGhNNrzWfrlP8SbXQI/PNwGUEkCaXbxmguDgzH3+yJ4WvGW5RkC082hH2whQho7nBOU\nAj800/FaUvc8rOlccDSsKaflsaY8HA1ralvjx5r0uSDv97k56cO8/rm5Oebm5koBn5YMI6v3c6XK\n5YeMajNOrN7v8jYXTlP3UflqJ63XUfor4vM0dD8NrN7vxsXpWeVhOl7Hr5fWGrFS4KADKKyAGzgd\nHRSHAjXcGRvUPbH5DnoPy+FAdG5/KIWEHl7F4Hn5fHlGE0fg0qI5ThFHgopl2LXa+yIJmHYr30EH\ncA7nOqSujbh8MJdGdAKhEQ930AFSm+AIiNIhSeNdmdUzPOE9wZyZ5YXoBa6mV4e266QxS2EVP83J\nBwcQh0tidHUm10EHEN8Hf9jt6f2i0Erh63ybUErhh+XvgSmSO2W8wnQumM4Fp6PXdO12NKxJtq2z\nijXJnKZpenQn/UMf+lAuaL989rOfLdVuKmdPil6UU5nKVCZLTme8ju7zxPONcw7Qj73PUU2cK6VW\nmeC2YSfjh3GG/7yqqjwRPs6KWeal+Id8J32OKB0s43Z0nSA7nR8pTjhc8m4Y1u0t0/l1KsclU9ua\nylTOjhRuSuWFu6+uru7/+1vf+hb/9m//xi/+4i+ysrLC+vo6f/M3f8PTTz/Nz//8z49f41uQ3gl/\nbxejP+Rg2A5K/w5zv/S3vVWsfhmGNUx6O4rH0d9p8TAKK4+HslhFPPSwbra/frkZHnrt83Q/adsa\nhXUS/R23bTknJNYSW6GZWFJxzPgeoacJjN4/pZuO15vDciJca8Y0opTYugP1pRUOuHFpmNr3nG+c\nqisEXytCo5kNDHfNhEP7S60jso5O6rjS6HRLm+0zRlcZcFnOuO2AMmBCAUP2R6kszD0ViATawhIe\nSxdCKnWDX9F4/o1bXHvS7liuXE1ptixRDEly43uYNEFHMXqvjbfdRipVxPNx2oPunayKFJVGqLiN\nt/Yaun0dwaGcRdJuuTUNHR2zR4NVe40t+zrzukpFvCy8vKuP9QwdZWkQ8d30GhvGIkqTit13sj3t\ng/axKJqppe18lNIZ61bxkP8g9/iXeCN9g+tyGUOCLzGxCkjQxE5od7Fqfo1Ff4lz3nneHj7Kk8qQ\nxKuk6Q5pvNMNe1f4fh3P1AmYpf6Wn0E9eC8yW0WqIeJl5wAqTVGtCNVooa9uIEtzuMU6Uq8igd8N\ne5e+nHThYj1kPsjGq681xmScJoklioV2x7G7a5md1VQrhkqo8Dx9pLkgtVnaRjt17CWWucAj9BSB\n0fjdk0jrHIl1RKmjkaQYld1/EBiFbwxan43xmsfDKKzbYS44rnk/D+tOmwvyeCiLdVLrmkni9Li+\n41nj4bjH6yT7BcN+fgg3z0nvlz/4gz/gT//0T5mZmdn/2d7eHn/0R3/EJz/5yVEfPxXpJ6Ao1KBM\n2P6g4z9M+h9MEVbvMpZxYI1Tr6PwME6sSeVhyunZ5mGrk9U6bsR26CFn1VPcN1dlNjDT8ToG2xIR\n9uKU13Y6tNIUCguHOFaqASvVgNnQy8XbiRI22wnbHdvNZx8i1mFbGtsASYaFuAuq4giMhS0LW5kz\nPyhh3XDX4xVW7q2izXDdrRXWNxNe/9Yq5uo6/nYDNaCXAM4PsTM1SJp4W9fRQ06pRRyiEn6YfocX\n0u9xXd48fIO7wKxUOa8X2FUJl+0GsTocBu8ErPFZt4rdxBHLwdQCg+Hh4CEeDB5gzV5lx75EyB5m\niAnGAlav8Gj9/bxv9lnuCu4+9HycS+h0fkS08y2qLFHT59DqYFCeADJfJ33kbnAO76Wr6L3DN8SL\nb0jvO0/ynrcggcfh55dJzdMsGp+oIaxtOOL4sD14HqwsGR68P8SY4jG220nZjBK2OimpO4zla8VS\nxRAYw3o7pp0OuXwLmA0MD8xXCIw+U+MVJnd+nVQepnPBwTYnzYPI4Zrsx63XrXI6qWNsalunj1XU\npl9K1UlvtVr75dd6EscxrVZBft0pS5mcgV67slh5DwfY30EZhderpz4Ky7n8mnzHoVcPq0ybspyV\nwRqn7pOINWoP7DQ4Pcu2VfSS7Me62mjTLsgRbqdCI06Yrxyud90vZcfrnW5bSilmQ5/ZIKFVlLuc\noXHPbIWgIB9cKcXqXsR2XIwlorFbCpE8/RXSMbAVZ7W0cyRqWjZeizl3f361EmMUF84FNNavE20N\nzwdXgEkizMYWRLu5WEppFCHfVs+xLas5jaCh2mwaSyvt5MZ/awViE1oySyw3NgQ0mvv9+3gkeJh1\nu84/N7/C/dWUmsrPZQ8ULHkVfvHcL2Mkr9a4T632OHPWh/ZenuqonSbBv7+U2xeASiz+D98kfcfD\n2Yl6jrRSR2M9It3Jt5k0hWurlvvuETyvOFdwtRWxFeW/IBInXG+lKJLc/HkBdmNLZB0Vv3gpNWnj\nFU53LijCGvdccNJrt9Nas5Rpc5bXbidtp+MYr+Pm4U5Yuw07fR7Eud39gn4p5aT/1E/9FB//+Mf5\nwAc+wPLyMuvr6/z93/89zz77bOmOJlWOuqsxSkYZWNmH03vg48Aqo9eogXhUOUndJxWrf/dtHHJW\nbesoWGX6gmJORYTFaoBrJ0Q5t4wZpagYM7E8nKRt9XaAi3aIm3HKXmxZrAaEBQ5Q3TfMBpa92A1P\n0xaBhmWj3WHlUhW/ko81X/FJJKGZDH83iYDtQFZmrEA8QZY1atNBe/gz0AbqK95IHqK1LZKt64gL\nUDrI71MZMAHY4Re3iQgNt0aQxhhRWDVcL0EQl6KVwuXYjxJYpkpIwAsktHFc8i7xRPgYDbfHv7a/\nQcM1WFJ13s4jrPMGa2wMxTLK557wLagiTkVALOBl31OGO7tiDPHKOZR1+JvrqCFzjABucQYXFC88\njVIszhvaothtOPKG0uyMQg8LEeiTuBu6TsHlBdkpucY3mu2OxeZ0GBiFX2JhOZ0Ljo5Vpi+YPE5P\nGmu6dhs/1qSO10nGKtMXjF67jdKpv+0k8jBu2yoV7u6c4x//8R/5+te/zvb2NgsLC7z3ve/l537u\n58bm3I5LBkMvBl9gvd2oHkG9v3s09HZCBmnJw+pvN4g1rE0e1qAMazP4s1vpb9w8nCSnZbgZJncq\np732eVhleMh78dzMM+zpPrgzOW4eevmmkXVsdhJS51iqBFQ9TWg0XjeseWpbh7GswForZrebb544\nwXUreocGQqNZrAYsVf0Dbk7v+yROiFLLXmJZ3YqJ30xgz0FEFlPtFCaAoKqpzBiWLlVYuCs4ZA/7\n+cDd2uXXthPiBkisIKVbGg2U6jlcWdC4rgleDZQvWU66VllceCxZTvq2pRZpzt1foTbvE9Y0fmgO\n8SBRwuZzL9J4+Q2S7V2S3SYSJ1lstfFRygc9g/LmUMbrqQBWsn/rrkPrEqLWda7JC+zINTqyS8c2\nsDZGeQFOQYxlO22yS4L2A0DhxJGkHbT2MNpDlCJ1FpVYHvCWWdBVqmLwrCDOsestsq4vkGJ5PXqJ\nmqrzdPgw5/UcC1QJrcZqaOkOu9Lgsnud12WTtyz+LOfDB5g1K1SYyZ50v9+cOpSN0C5GiQVrs++o\nAeXAWUg7JBWf+N57sTNzuLCC87KNDJNE6KiDaeziXbsC98zj7llBZqq4agjGdIm7IXOBx0rVp9I3\nXkWEOBGiyNFoONa3LIvzmvk5QyXU+L7CmIM270TY7qRsdRI6aXZ3QrZ319+fEBqP87VuTfZuHrxS\nHLgTYaOd4GnFUtUnNNndFp45/fF6knNBnkzSXNDf73TtdnJYd/rabZg936ptnfTabWpbp2NbeU77\nkeqk3w5SJiyjTJvejs+4sGD0zkpZ3ZUaHVYyLqxJ5WGSOT1p2xoX1knb1lGwpuN1vOP1Bxt7bBeE\nAwNUjOLJczOFpdMAnv/SBs3NYqz5CwGPvW9+JA/f/I89Op3CJpg5i7cgMALrqXMzhH7xCe5rn/8f\n7Dz3g+IOlcHMPQa5IfeZ/Ofef2MzKg7/bmN5TbdwOafTPXmXupeavdFfW9VY8y5hMazYN5lxO8yb\ne7hknhx5S7q962m0zg/zB9DxHjoqTm8TYPsnfwzxilNI/OUUPVOsVWAUbzs3gzfCtqx1+xfK5clO\nJ+HFzSa5+QJdeXKlTj0oDi48jfEK45sTp3PBnbPOOKu2NcmcTtdu0/Ha3+YkeCgV7i4ifPGLX+Rf\n/uVf2NzcZGlpiWeeeYaf/umfHqng7SrDdlEmAauHNw4p84IYNw+DO+q3ijcuOUk7vxNsa9xYZfq6\n3Tkd53gt9f3K6l2mmSoX4laiclemVhndyuglJUNJeyfoRU1G5BJ2OyyFpY0P1hKpCuvmLjq6xkr6\nJnNuc/9raaVLfcVS0XA54fiHmjFSdVSZh0gJIEo+5swgxtMhJz9exzUnTup7a9xYZfq63Tmd2tbx\nYJXpa5zrjHHKWeb0drfTIie9VKz6F77wBf72b/+W97///Xz4wx/m/e9/P3/3d3/H5z//+bEoeFLS\nC0Moeki9340KkSiD1WtThCUiOOf2d81uFavXpgzWKB56g6NIeoNn0jjt5/VWsUa16f/9pPEwTqxe\nm5PkdBJt6zjGa5GMe7yWwfK0HjE5CE4c1hXzYJ3LPGtdNDFm4cdJagux0rSXi1yMJY7RzrUTnAM3\n5Gbv/SZO0GEF/ILcc4AgQJQu9ANFO7CSOdcFoo2PyWLIc9v4JiBK4Zp/P6/7j1CVJg/G32O+z0EH\nheAYeoX7ATA/uxit6GErcNogI6IO8HT30RQ/HzeyzY1vP8q2nHRtLK83ycq6ZTTkY/VKBJ7V8TpK\nr6PMBaP0ms4FN/o763PBJHI6XbtNtl8wqr/e7yfRtiZ1vBZtqJUKd//IRz7Cxz72Mc6dO7f/s7W1\nNT760Y/yl3/5l6M+fqJSRFqPiKKH1B++UAYrr02P+HFg9evVM7S8HZwyWP08DMPqveTHhTUuHvqx\nRg20HlavbMrN6F5Wr7JYN2NbvWfRL8fJ6UnwcDNYkzJeRW7cMjtJ4/Vm7KHItgA61rHejNiLLVHq\nSKS/SJgAGq1gPjQsVwIqnsI3GidCbIVWYllrJ7RiCy0H6w6aDhWR3TUWABUFixoWDZ6vWawYFio+\nFaPxjMKmEHUcjT3H9bWUVlsAQfWf7CpQXvdPTdBVUBro1mqn908HkipcBOmeRlnF3KzmwjlDrWYI\nA4USIWo7Oo2U9dc6NNZT6DTRO5fxWhuouAk2RsIKrjpDvHSR5MKDiF/B396hsrmFiSLoRFjbIpId\n9pLrXGl+g930DUAwXohSGhGHwyFKY3E0XUTTtrBKsNog2sMpcGIJ8KmqgBlXw3f3sWeWWLZbrKht\ntMpwlCh8XcWnyqysMMMKRnnZJkkvJFzUvu7p/ArxXQ/hqrOYdkyw08LECSq2KBFcYLCBTzxbxc5U\nUUlCuLFJ0GigOzE6ThGjES8gDauktXmc5+MChdQ9xNeIUWBAmex+AFUXdEV1T8BvPB9NVvYs9DTz\noc9yLSAYyPUWwDohto5mYllvZ5cKVj3FSjXoq11+cMGjtSZ1wmYrZqsTE1lHYjNKAq2od3Pfa91Q\n9+lcMJ0LzvJccNS122nY1qSu3cZpW7fbeL1Zv2AYp8fFw6h2kzZe+/vL1aeMk/7bv/3bfOpTn6JS\nqez/rNPp8Pu///v81V/91aiPn5o4V67kxLiwyvZXpp21dmSphdPQaxL7m2SsYS/q4+zvdretMnyO\ns79JxjpJ2xIR/vPaLkPKUx8QXwtWFAUH1OAEEoFwRDjmtibaVRTOUFoILlqUX8xDsgauNeKE2jr8\nrQ42KQASIZ1LsfW5wljrzZf/O1df+L+wDL/dfb+dZ2mn7cJT+AfUXazYOhtmmVWzyKLb42K6jk9/\n3rrirspPELpqYX/tt7+P+MKDUPS8rUOJQ7yCbDgRKqu7iPUKeZAlBY8E3U2TfHl8scpcxS+05zd2\nW1xrJoW2pYC3n58hLCjvB9BJUgLPoE/w3TydC8aLNZ0Lxo91lnUfN9YkjtezjFV2vI6L97LtJtW2\nelLKg33HO97BJz/5Sa5cuUIcx7zxxht86lOf4qmnnirVyVSmMpWpTOXsSrbbO7pd4qTYQYfsZDcc\nDRYnUuygQ3aKXibV243OS05TwSajEssVUp0ZmQxtjRvpoAOIViPUUkT6Ai8GD9NWIY8ll7k3vT7g\noINC4etKDkZff2G12EEHMBoZ4eSiFOIHI3lQMNJBB/BN/u22PXHCSNsqm20YGD3SQZ/KVKYylUmS\nEmeqU7nNpNRJeqvV4q//+q/52te+tr/z+t73vpff+q3fol6vn4SeR5LB0IK8cILBMIVhOyD94RqD\nYRVHxToQujdGrCLdB0MsxoV1K5z2hwKV5aE/VKWov2F6DQu5GQcPt/oMp7Y1HOssjdfjtK3+0LJb\nxbpVHkSEdnowzLhfKp5mpepR9w1WYLuTsNVJ6S9TrxUshIalaoBRilYXq50OhotlIe2SKCRR2D1w\nHQ19tbtVavEbLfxGBxUIsuiTXqpBffD0N8tJdnGGle6BdA6eqKuoQ7B6lWBzHR07bG2BdPYC4od9\nMA7daeK3G4DF1UI6y8ukswcd9rR5nfaVr9K6/u9Ee68TSUzbthDVnyggiNKIMUSS4BTspW0s7oDD\nXvefxOiHqZsZHq/fjdd6ldbeC4hEN3Q3VSpLT1FdegehXsREu+i1V1BR40ZeN4A/g5q7Bzt7AVev\nEc3VsDOVgw67FUwnwcQWBGygsRU/yzUf5FRl0RA6dahmio7lwF5DUNUs3xcyezGAmmInStjsWJI+\nL1sBc4FhueaxEAYoDtupiOynXWy1Ezr7nx/mYGe/q3uGemBYqfrUA+8QXpnxOhhqexLjdToXTOeC\nfqzj4HSSbStv7Ta1rZvDKtJ9UjntnQPs58gAACAASURBVET3/p4Ev+Ck54JBKXTS19fXDynRaDSY\nnZ3dJ3BlZWVkJycpPRL6v/zggOoRPkhQ77P9bQYf7iDJPSnT36Ri5fHQL4P95eWaTDm9edsqw+lZ\n46EM1tS2joZ12uO1v3a5IjsF9Y0+UC5LRPbrS6dO8LQi6LYbxIqtoxGlvLbb4aALtw8GDkhBf7+B\n2Y7RsYWBjQJ8BRVNei7EPjHb5zwPYFnAgv+V7+Ft76CiDioaiHH3fSQIcd4Myq+h0gQVJweParXC\nhT5poHmj8Q8k0Tq2vYmN9w5AKT9AEHZck45JERxJEtEPpo0H2mB0nUuz/5U32usoDE/OPcX58GJP\neZzqYO0usQeqNo/2F1C6evA7kqJsB91q4rXbYEJQPoMl4iTQSGBIavUsQbvLywEx2Z80MLhZn94V\nawf7E5QIyjoeeyikPmvwKwY/OLh4Sqwlto7ECkarbv74wZDznv1ZJ/xou0WUOmKXPf4D/SHZhXcI\nqvt39v++zRekm3NueGC+ut/PpIzX6VxwspxOiu6301wwKTyctm3dqeN1altHwyoar3kOe6GT/qu/\n+qt5v9qXz372syPbTJKc5RyFk9Z9mq9Wvs2dgHWWdR831nS8jhdrsx3z8lZ7ZH/hv6zCbnEN8fTx\nGewjsyOxav/vP6MaI/qsLYEU3+6euhYvNf4babJX2G4ziGkmu7m/t2oO8d+Gby7w1rm3c3flnlwb\nS5bmcKq4gqqOOvh7xbXNAeLleYRiu0nnfWyt+GZ6gHf/eJUwLMYqYw9R6vjOaoPhy6F+EUalMcwG\nhreszIxEmo7Xye1vkrGmc8F4saZrtxsyibZ11rEmkdM0TfFy7oApnOXvv/9+4jjm2Wef5dlnn2Vp\naWnoLslUpjKVqUxlKlM5ujhqJOZhnF5glh1+6vz/iVGjHeKpTGUqU5nKVKZy+8rInPTLly/zpS99\nia9//evcc889PPvsszz99NMEwYjasackvbyA4wrBOCpWv5TBGmyTp9dphzlNCqeDbSaV0167SeV0\nnDyctJ0eF9ZZsS1rHVHssFZAIAg1gX84t3dsYWgi3dDlLMDY01nZKzOAlXZikr02LkrRgYc/W8Wr\nHJw3nHUkkWO3mfDqdgfxycLW+znthbtbMN/dRe90w93Tge+jAQV20cc9MYtUDBKYw1hRG/YahF/6\nNrqVovGGhHlr0Aa8Knj17MDWHuxPEKzu0LHbXN79OxwxOIfY9CCW5xErYVP2iHWKAVwSIQQk5mFS\nfZ7Avc6s3mLGLPJjy7+N58+BCg6FqOMrnG9I6nXwzPAQdSXZhXpJit9qo8RB6g6G6kN2eV/VEM/U\nAYPEQ7C0QKhwVY2dDcCCswfDykHwfUUYwBOPVQiDTOdbeW9ZJ7y81crKpbleKHufWkBoss+LQOxk\n8PFkeqks3P2hhSzcfRLG6+0+v05qaPadMBfc7raVp9dZ4/Soep0UD7cLp2fRtvIiX0pdHNcDe+65\n5/jSl77Et7/9bT760Y/y0EMPlfnoiYtzh2sUDgs3GCS7TJth7URu7iKGYUZyM1gi+ReZjEuvmx0I\nw/rrv4ih95zGwek4ecjDmtrWjZ+XedZlOR2UO5HTQdvKe3E753BOaLYce3uOa2sprdaNZ2E0LC1q\nVpY95ucMxgyfbI46Xtupo51a1lsJjdge8PnqvuZc1admLWztsffKKjvfeZW0L5zcm6kw97b7mHno\nImp2gXbTsf5qh73NlH01FDAL6rxBajqrId4C29JkN7R3m8UpwU4Trxlh2t1b1AccTNHgzofIpSrW\nayGtLexL38P96AWIb1y+plWFsHoRX89hzDxoH6iQFffue0YK0Iq23aDjNllrPsd29DKOG/nsGkXg\n1RGEjnLsSJsrdpOOuuG4G/FZ9N6CUfdSkw3Oqz0u2hUWZBG9fxW6QoVLmPmHoX4Bqc+R1EOSuTri\n99mEdZh2ikksKu7maruesvsPGpXEeGmMMgJ1gz0fYi9WoetQZ5sXwFoKe12HvqZhRUNd7/MgDlwb\npKUI0FRDxcqSz/KSj+cVL1LKjIvBuUBE2ItT1lox7cSilWI29DhXCwn7LrSLrWOjFbMTJViXXWS4\nXPOZC/0DOe+TMBfcyvw6ie+t6Vxw81jjmAtG6XXW127jtK3p2m3yx6tSav+7nlW/4FbG66CUdtKv\nXLnCl7/8Zb7yla9w4cIFfvd3f5cLFy6U+eipSdmcgXFhjTNH4SznFJ10f5OMNTgpHHd/t7ttleFz\nnP1NKtbenuXb320hUszFU2+rMDdbnLtcVvf/vLZDNCJJOPjGC/jPvzYSq/XE+xBVHI2VLAe4oFh3\nFafM/uj64VP1AWmv/wPp3huFbTxvidn5/6mwDcB3m/83e+3XC9usewmvua2Bn2pq+iHq+lEiucae\nfYFfDv4Xaknxd0zf+fOkd72lWCknhOvtwyfhg/KEBwtlataNzvV+y3KN2bA4LP8sj7FxY03ngvFi\nTeeC8WOdZd3HjTUdr+PFKjtex8V72XaTals9KVwdNBoNvvrVr/LlL3+ZdrvNs88+y5/8yZ9M3I3u\nU5nKVKZympI6wVflX7zjwNIa7CinrIRYERAZWTdal/hqojWiFKpg71eAEXsLABijRl8cJpId745w\nKBlxMVomerRrKoIugaVFoUR1S68pKupeZswTJLLNZvoVLA0AlBQ76ABYl33PoucjQlZEfAQPt26e\nN9SKLDJQ4mwqU5nKVKYylamMRwpP0n/t136NCxcu8Mwzz/Doo49mHxiYkN/2trcdr4ZHlGHhFz3p\n7XAMC3Po/bw/lOFWsPrbHAUr73GUweoPnSjTX167sjz0h3QU8XBUvW6F02G65+1ajYuHsrqfJA/D\nsM6SbQ3qPgnjtT+8z4mw00nYaCd0EkvsBKMgMPpQOO4oHqwTttoxm52EKM1ycI2C0NMshD7LtQDf\n6EO5Y2kKUexoNh3XVlP2moLnwfKiZnnJo1LRhKE+4FxrneE0opT1dhZCHFtBKbrlqjzO1UOqnt4P\nO+uJFSG2jigVNjoxO5HN/MK+kljKOugk6L0W+voW3g+uohotXKVKfPc9pEtLuEoV54VZ6nRyo862\n1jB/wWf53pDKrIdfMVgHncixtZ2ytuGII4fuRITrG/h7TXQUoxMLWuO0wakKGD/TyUZoF6PEIjZG\nXIRzLeLOm8TtNxCJ0cESwcJbMeEKysygtZ+Fh6cJdNool2Y53dIBiUEs1kUktOi4XdbjH7IVv4Il\nIaDCnLeIrwK0KBIcq9rnTeaJpcWO/Q6BcjxRe5r7wrcwq5eoU0dJirNtkvY1XLwJCNrU8IIFjA5B\nBUhYwVVrJHOLRBcu4ao1VJQS7DbxWhE6tijrEKMRrUm9EPF9MAoWFKwYVEVBCGJ6BiFk2d37Vg+o\n/SJrDJY2Sxz6ehtzPcpy+WPBrxqC2YDZ++osPjiPVzET8w4cDMc9jblg2Dt3EGuwDm8e1nQumJy5\nYBjWzXJ6nLZ11tYsU9sajnWWxuuk+gX9c8G4fYwyupcZr8Ok0En/yEc+kvvBnnz6058e2eYkJW8S\nHiQpLyShn/C8fIGbwcpr049VlJ9w0lhTHspjTW3raFjHxUMZrHHw0IpTfrDVIik4udTAE8t1ar4u\nxNpoxVze7ZBKPpZR8OTKDIE5nKPVE2sdzmWYvj/8pS8iWOd4fr1JbN2hy7h6ohAeWqixWPEKdW/G\nKS9stHAF588qTUmugUs0ovNCo4XZuuatj1fwfI3OObJPEssrn3uOZLN5uEZ6T3T2DVAqO4HO61Gn\n2OpS5tBLzsm4Bt24io62IM0PWYh1m7XWv4FY6NrQjgq47M3jUNxnd5lTCfMz76YW3ofvisL8IyTa\nQgkcuuitJ4FHuvBQdqldXpi/AnshJH37Angq9xRe0W8HeQsFwfyoifdKEzr5nJqq5vFfehBTMbfl\ne2s6F4wf6zTngrJYU05PTvfpeC2v+2lgnfW12yRi9drk/b4w1m7SHPAykkdWj8hROQNa65FtjgMr\nb3PhqFi9nZkiKYOltR6Z/3JcnI6Dh/6/bxVrFKeTblvj4nSctnWWeXCoQgcdumeSarTdJE66flY+\nlu2eVmudPxaN0cDo8aq1xg65LbtfBIVW+ZNGD8tojYwIEBfPQzyF2CK7UXi+IhhRX9v3DcrZfAcd\nMuINhQ46gHIemCG3pw9gaWyhgw5grEFrD5ckNJXPZTNHW/vcm+6w4tr77FT9+REOOuA0CpWFr+dJ\nnGZn3EV5+EJ2S75fPF4F3W1c9K5UqE5a6KAD2Ha2XTNp43XUPHAUrHHOBWd5fr0d5oLp2m0ybav/\n71vFOutrt0m0rbO8dptUTtM0vTknfSrFUmbyP8ty1r/fqME4lancjEjuEedBUeNMAC5hx2VtvZz2\nZeVkx5ekI7PUix3cI7ZzzlE8DWfScfCat8iOrnAp3eXxdOPQ58QJpcBKqC+OclglRJXqstxzVmUu\nLjhh6T/xmMpU7gQ567Y+XbtN5TikIHD8VKXI1kvf7n5WZDC8YFguQP8LoPd3r82wl0P/bk6RDPbX\n22np7/9Wsfp3lG4Wq/fZm9XrpPs7Lh7GzemgDO4C5rU9bk4HbfpmeRg2NvL0Oi5Oe20S50iso506\ntjoJdd8w4xtCz+BrdVOcluXBibDeTtjp5pDHTnBdV8dXisAoar7h4kxIoNUhrNS6LLe7WzZqM0o4\n6ARlWGo/H1iY9T3O1QIqniY0Gs8czhnP+46DbbbaCZudhE5X995J/X5eOYJvNBdqAXXfIzQK3xi0\nVljX1T11bHdiVtsDNcH7dO/928YKt6eQWEHKfp1thUM5QaWCiVIuXAhYuBgQ1g1BxWC8TPek2STe\n3qF59RqrX30OsfMYr45SIbjuaZEWIM3yzjs7KBOggxlQPuD10q1BWZAElzZx1qFmzyN+DXS4H/bu\nVERqd4niNXZ3/oO6hNS88wSqjpEA5QCtwRg6yvH9eJXL6Tr3KLhbWuCauCQrPWeCGYyp4+k5at6j\nhJWVG4+6W9ceo/p+5iBtg0qy8Hlrb9wO6HugDeDh9AxSn8vC9ZVGXNdj9xVUNa7mkV7Iys8d3ODJ\nnkmg1f4dBHXfsBOltNPsfoJe6oVR2T0FFU8zrzT2lT2a19rEewlpM0Us2UZBVSNVg1sMqD8xz8pc\nSMXTBEbjG3NHzgV53zGNUuJmQrQTs/PqHpWFgPrFKsFsgF/10Ob2mV97nx3nXNA/Bw3Tvb+f3v9P\nm4fp2m3yOe1hHgXrJPyCca3dyvIwta3T4zTvJP1EnPT19XU+/elPs7Ozg1KKn/3Zn+UXfuEX+Nzn\nPsc//dM/MTc3B8CHPvQh3vnOdwLwhS98gS9+8Ytorfnwhz/MU089daQ+e0T1CMmTUfkAx4U1Kkyi\nDNZp6T5pWGXajBNrUnk4advqtTtJHlpxwvVWwlYnJXWHX10KmAk0Dy/U8E3xhRzj4EFE6FjHRjOm\n6msWKgEmL6faWq43Y9bbCbHNe+32kpEVeaeXnlKcr/ncPRveMqexdVzebrEZpbn9KWA20MwEHlud\nhHZhubN9b3i4To6szvZrFt20KDs88L4ya1iauULz5e/R+NEryNCQc4MJz+F780i0DTK4YdAVXUGF\n80iymznAw/TSPnF1hk13md3Gf2Jdc0grRc2scP/MzyNqhh+k1/hhcoX7/Is8EdxPRWeh7NY2aSWv\nYXSFincPWheEuBcdY4tkjrp0yGq2h6AOP29B4cKA5K13Ye+tQy0vQE5YqnisVAPmKv7Q2/xTJ2y2\nYqw4lmshgRnSnxOaq21eeXGTzpKPLIYMu/rf14q7ZwLO1YI7fi7o7EasP7/Fzg8bpO0htqygdq7C\n/f/lEn61+Mb8SZ5fJ3VOvJ1t6yxjTTk9iDXlYWpbg3Ii4e6e5/Ebv/EbPPDAA3Q6Hf7wD/+Qt7/9\n7Sil+OAHP8gHP/jBA+3feOMNvva1r/EXf/EXbG5u8vGPf5xPfOITpb8UHNxJLZIymGWxyuAN7qrk\niYiMrIdYZvfqKDyMC6uHd1JYZXQfJ9ZROB31rM+ybfX3e6tYZXmIrLDWSnJ/L0AjdqROCLzjty2l\nFFXPjHSYu41ZbcYjSnqrgb8PSyrCdpxyN+GI7kZzGhjNXMVnM8rPuxZgN3bsxlGhXn095/9Gg6kD\nnbSwpnenYXnz+e/Cxo8K+rHYaBVPbDf+O0dcB0lTSHOceEC5hLTxQ7bSbxb0J+zZdV6SbV6OXuKC\nWeRn6++irqsHWhlTZ9Z/K6Prx5Gdoude/qZAeWBmexcTDG+GoG2Ce6AOYdGUrliuBixU8zcNPK04\nPxMW5tEprZi5WEPrtDAvPnHCbpxyYaZSoNOdMRfYjmPj+e2CDRlorXZIWilBrbj2fE+3ceh1lueC\nUYvho2D1dBv1+0m0renarTzWdO12sL9JHK/9f4/SbdTvz6ptHWhfuuUtyMLCAg888AAAlUqFS5cu\nsbm5CQzPEfjmN7/J+9//fjzP4/z581y8eJGXX375SH32hy4UiXNuJPllsXp4t/L7npQJrSiDdRQe\nxoVVBu80OB0X1lE4HdXmNDg9y7YVmuwU2cs5re6d+nq63KR3qzyICO3EcqXRYb0ZYYec7gOkqbC2\nmhBtKyRvj0EEvdnEf+5N9Js7uZefiYXOjnDlzYQozmkjwvZOwquXY3Z2klwuosixuZZiGxluwTcd\n+HuIdASuWFhP8x1PK7CRQr6/jIiQtN+k0fwBHdlDch1whTYB5HDew2rZbVbjF2m6jVwsKwmx7FFR\n9aF3CQiwY5Z5NXw7qyrhfXM/yU9W33rIQQfAWUia3ZCBvOfjcLaBa11HbGfo8xHAVkJad18gXl5A\n8qI5tCZemifZ00iSHcAf7g9sJFx/M2VzK8HlcJY4x/W9DteaEXGe/Ymws5vQ3gDbkaH9QXaSPhf4\n07kAMBXNytsW8ao5C2wFtQtV/JpXiBVbx7W9iNW9iLRAv9OaC06SUxGZ2taYscrg3SmcTtdupzNe\ne39Gye1sW/1y4hfHra6u8uqrr/LYY4/x4osv8g//8A/88z//Mw899BC//uu/Tr1eZ2tra78uO8Dy\n8vK+Uz9K+sns7VgUEdzbQRl1WtbbSSkid1h/vUF1s7kNvXa9UJhxYPU+2/9djoJ1VB6G7S7dLKfj\n5GHcnA5+136svJ3ScdvWMKxB/k+C05u1rVHjtRb43O97XJrNcqM73Zz0Wk5O+nHYlhNhvZWwHSXE\nB3LSY/zdDoFRVH3DDIatdaHVtkQxJIkAGrXjUF52SKr8lPDaOt7qHroZo1oppA70GlLzkXqAXazS\nuf88zvpIopAUYqd4lYQ3rsYEgaJa0SzOGzqRsNuwRJEQJ4KI4uq1hCBQVALF7JyhEii2diztjiOO\nhTRVXb0ki6r2BTUjmEoWdn8jN74Xm93lVBysC2w6iARius63oAKLBKBqCplTqIZASyACibvh/Cqr\nzy6A2JjW2r+S7P0AG22QxttI0gGl8bwKRvl4hNTtMmGwgFYeCp1xJQKezo7pRbC2w6Zcpa22SaRN\nQguXJGxoD9/U8FWVqsxRd/OkpkUqEZYYZzvUqFHz5hAlWLFESpEs/ySvN3cxJuTH73ofS/V7AEdH\nLCqNMa0W3tZVlOtkOx2u70Z4r5tHrgzOamAPJAKXIEkMIojZBBOgtI+YOvGlR7HLC9gwxPk+og0g\n6DRFxzGm1cZs7GCX57G1Ki4IcJ4HewrXvGFbVCTDjzQkIFazJo616x2CQBEGitm6ZnZFsZtaOokl\ndjdy0t9sxAQGQqOZ833a20Jjz9GJhDgWRHRmH56gPNChsHTOsFL3D+Wk3+lzQTgbcOk9Fzj/zmWS\nZkK8k7DzWoPKQkjtQpVg1j+Qk96/4NvqpGy2YyLriG0vAEV4o9HJ7gzwDefrATP+jQ2AO2EuKFq7\n9Z9q3Y62Nfhdj2vtltff7chp3tpt3Dz0Pltm7TYuHoa9d8ftF5QZr9O5YEJz0nvS6XT42Mc+xi/9\n0i/x7ne/m52dnf189M9+9rNsbW3xe7/3e/z1X/81jz76KM888wwAn/nMZ3jnO9/J008/fcs6OFd8\nHX7ZNjDcyE4bq2x/tztWGT7H2d+dgHWWdR8nViNK+f7GHqNCv5M3FS4uxgqvXaf+ypXCNgDb73ob\nzi8u36WU6zpOxaJU5rwXiX/eMuyQ+IC0HXwnGR3WrQVccX+d7e+y/fJfjQCCeypP440oY7bGK6zF\nPxiJtWQuFJZqa6iAN2YfIcHw+IWnOT/3wPB3ShpTf+UbheH0AFb2II0K26RzSzTf878OzT0/KI7R\ngXC9uw2KJbxkR27Xp5tgG8VhlgBP/0SVIChudxpzAYwOoTzpd82oMlkA1gnfvr5blO0AwGOL1cI0\nhqPoNYnv3EnGmq7dxos1XbvdkKltjR9rEjktmgtO7CQ9TVP+/M//nGeeeYZ3v/vdAMzPz+///md+\n5mf4sz/7MwCWlpbY2NjY/93GxgZLS0uHMJ9//nmef/75/f//yq/8ykg9ygz+Mm2g3MMui1VGJhVr\nnDLO5zOu/saJdRq6j6vPk+6vLNbp2MN49Cpbpk1TJsW55POhMGg9668kDb2T8OI2anwlvoweSUTp\nZ6j1UCe9pTwum3ma2ufRmbu4967/GTXKaS4xWSujc++2O9hwdBOtVFGU/9hlrOUEy/Y5prF/1t9b\npVpN54JT6e+sY42zv9v9+dwJuk/qdzzp/k4L63Of+9z+v5988kmefPLJk3HSRYTPfOYzXLp0iQ98\n4AP7P9/a2mJxcRGAb3zjG9x3330AvOtd7+ITn/gEH/zgB9nc3OTatWs88sgjh3B7X2Kwr2Gk9Oc5\n9MIZhslgKMYorKJdksHwiWEymH+R90DLYvXa5uleFqvXpgjrqDyUxYJb56H356R5OMu2VdTfncBp\nat1+DXQ/Z1dTRNAIvs4uxspbQhvIqoMZwdq8/HlBVXx03ce1knxvt2JwuBEn4A5SlzlvWufoJXim\nG7buBJeDpcThOg5jBPHzTvoENIgHOIE8LBySdtM9yMfSfhUTzmPjBnl53CaYwTkwnpd/aq01xgX4\nXp0kbZFHqudVEOvQxkNshhVheN2bY0tXuGQbPGYbzAQzaKOyGuc5nCos4iSrEZ7nOXsGUg1+AEk8\nvE3XflWaIp6f0x8o7XCoLHLC5W0OCDjJbEb1UhWGqSVoBbKf0pCD5YEyDrF5WILfvahxEueCHs5x\nz69HfW+NxsrGtBKX+3wUgnVS6v29/5npXDBdu00oD1PburM4PQrWuOYCOP7xehQeep8fdtB8IuHu\nL7zwAn/8x3/Mfffdt6/Mhz70Ib761a/y6quvopTi3Llz/M7v/A4LCwsAfP7zn+eLX/wixhh+8zd/\nk3e84x2l+uoRPEx6JPVyBoYR20/4rWL1P5RhWD2j68fKexxlsLTWR9J9nFi3wsO4sfqf4a0+n5vh\nIe8Z9utlrc19SUyabQ3qfhK2JXLjFtPjGq8iQioQpZZGbFlvp0TW4WvFcsUwH/qEns5KuXGQUyfC\nbidhvZ3s5/Ia1b0tPfRYqYeERtPuOK6vxuzuWjqx4ByEAdSqhvPnPObnPLCO3R9tsPvSGvFWh7gZ\n4XyDmwlI75olvWcBCX0kAdckqzeeALFDJxbdifHWW5hOAlqRzFdI56tI6EHoEYaaSkWxvOizsuxj\nDDT2LNdWE1pNSycSbMeikxTdjvE3WugohUDj7q7gLoRIzUDFdI/Y+3LUnUDDotYd0hZUx0Fi0WmM\nbrfxdnfQaYIzHnZuHlurIV6AaIOobr67y7DExUSNHxBtfxsbrWI722gT4nsLhOGD1KpP4pkZSNuo\n6Dqku5C0wcXdI33ZzwW3krLHOg21TkKbxLXRyuDhEboKFVtFo3FYIl9xWYVcJ+SiSrkvrBHU78Zf\neAemdhfZKXq2KaEAnEWlESpuY3bW8HbXUa6Xg95tJCrLRfcCnKnh/AUwIbgYFa1CvAW2AzYFLwSv\nigTnIVxEtCGtB6RLdST0cYFBfIX2gNBhZhTKA0nANgUijUuBhKzufOJQeyk66S4kKhqpeYinUJ7C\nDzWVULG04HFuxcf3FZ3UsdaM2EssUeq6eel0N616zwdcC6SdXX6oXJbXXgkVS0uZbfmempj5dbC/\nk55f8/o7KpaIsBenrLVi2ondL98YepoZ33CuntWlV6o4Z/I4OHXO5S6ez9JccDO6T9du48c6adsa\n1L3MeD3utVtZvcpi3Y5rt6PqPtjfpI7XoXqfhJN+WlK0m3UcWGX7K9OuTL7aaeg1if1NMlbR7t9x\n9He721YZPstiXdlpc6WZc6rZJ0+dnyH0ivlKUos3oi67iJCmDj/3dDqT71/ZpgHFIazbCcG/bqBG\nJKs++L/dy9zFemGbtRe2uPKV66gCKAHin16BEeWh/G9dxf/BWmGIrgCtBx5hVLaV2V3DxMWckrRR\nG/9f5uwWyB7XsPHeASwLvK4DLhuf8y7lwXCRmcf/D1RRXXOg+vp/oPd2CtvY+gpSu6v4GYqAtt1w\nhHxJnprHXqoVQ6WCei7OLu8rkIfeM8vyXZVCTvfilO+tj75z4dH5Kov1Yq7O+vt7EueCxFqM1kPr\n3B8VazoXlG9zJ2CdZd3HjTVdu40Xq+x4HRfvZdtNqm315MRvd5/KVKYylUmQce5OGl2uBqgxo1/M\nKjCQFCdeKwWqxP5qmf60otBBh95Z6mjOlMoPmj4qljYVlMqrV7ffYal8XK0MrrfzDVzVPq+agHln\neVfSooagtIfSo2tUq6Ka7EfRSynQXmG9+KNAleG0jJ1qpUrdgeB55RYZUxmvGKVGOuhTmcpUpjKV\nsy+35Un6sLCCYbsbg+3KtBnWblgYRhmsYbkMN4OVFzIxLFzoVrAGZVw8jBMrj9NBMx8XD/2hPUfV\n67h4yNN9UrHK8nDUZ1iE5ZzDCrRTy15sWW8nRIdOpR2gqBpNzTcsV33mKv7+Atk5YXsnZXU9od12\neJ5iYd7j/DmfMDjY51HGa+IkiZIc8wAAIABJREFUKy0XpWy10/3Q4wN6WVCNBL2Tol5roRvpvnMs\nnsJdCHF3VwjOVamEmsVqwFI1wOgb4V7t6w22v3ed5tVdop0EUT7OhGR12LrtfIW9q4JcrOAWgyzM\net/NPsAqCoGORe9GmNUG5kdb6NaAk60BrXBeiAtCkuosrlIf8EIFpbs51daiowTdiQ9sSkiyh+1c\nRuJ1iHbRyqBSk5Vm6091USlOpzjXwSnLFRvzstZUxfGwjZjrOtzK80F7qMoKqn4Rtfi27N89LAWu\nqpGqB0kb02kSvPkm/sYqyvaKYoFdnsM+cS9uaR50gNqKMZfb0LI3no9SuIqPqwQICu0cqhWhk75n\nCKS1ALtcJ50NoGbQFYeuZ6Hu+9K2mCstzGaE7DrEGKwJEN8fyqlfNVRmPBYuBizfU8UPb4QStjvC\n9dWYnUZKM3aoQFB1QQdqH0ocuDa4liJEUw0Vy0s+K0v+Aae97HgdFjo6nQuG63Wz79z+sOxbxcqb\nC46L02FYxzEXTOLabZTu48Q67bXbpNjWsHa329rtNPyCo8wFvVTEPKzbZS4oE+oOt6GT3nuA/V88\nL/9g8IH0COw34FvFKmozDKvohdCvV5n+JomHO53TXrvT5PRWJptRWP1tzqKdpjaru36l0WE7SgFB\nDpW4EgKtME6RrGuSBJL48IVbnicEgeLhB0LmZs0t8dDT64fbbTr7N5EPvNSdQ3UckrjMmaoYxNeH\nnDRPKQIF4VdfQ3Y7pHsxMnhibxQYQ/zQMvbhJaRiEO8w1o3a6Qe+wcH/JRbVSfD/4yre6l7Xix14\nFhrE80mDCvG5u7IJ2g3BUi47wX7tq9C+DkkLSQdiu7VGGQ9x3VxeXFaLHFhXwgs6+65PKI8VpYjT\nRta/c2APHmcrL0CFs8i9PwEPPo1oNeQCNsly7+MO3opD1TLHm4HJWaUOIguXU9SOQ5TmcKk8QSkH\nCMlCiPgGZ8xhHnRWBz28voPf6GRl8JLDnGIU1vOx9ToohnJqAgiqGrsYkCpNHAt2sFSeErQRpGcC\nKbhDl8dll8aFITzxaIWw6/jfyXNBGazbdS7I0+uszAWTzsOk21bZ7zhJnJbR/bh4uNXxWsTDnbB2\nm3TbKjteT70E20nJsJ2QfgKLcgZ6Py9qc1xYgztbR8U6Dt2ttSfOw7iwivgsizVO3XvtTsO2xoV1\nlnUf1c4zGs9oUic5J8UAitiB6whJ88aFWoOSpoo0zULNb1V33zP4nkGklaMToDVS09lN6rm1sxWp\nQJo41OoetHNyuK2ATXEXarjZvHxj1eeg599wL75BfINOHaQ5e8EOVJygTACiydsyFtEIGhWvQ3s7\nB8shLgbP4LrO+TbCi9rRVvC401yUTHsQ0GrfiT/UXxoj6QbMLiK5OYC9iIAAs2yRnLp14mnwNEo5\nHJrhMekKEYPzNbYSkMup00gMZjuGZk6cvAOcgAERldMf2BjasSOpCNkl8UP6FIVLs5vk3aGNhRu6\nJykkKWh96zZ/HGO/SKbz69GxitqUxZrUuWC6djs+vc7i2u0s29adsHa7HcZrmlethtvQSZ/KVKYy\nlanc2dJEeFELW0p41CnucQp9CrW+pzKVqUxlKlOZylRuRm47J70XPtC/czEYejCsTf9n+9sM7sYP\nhjocpb9RWMPyMG4Gq//ft4LV24Eb1mYwfGQSOe3X76Q5vRkeynB6s7Y1Cqu/zUnYVlF/pzleFyoe\nThJiKyRy8JRYdcPd/ZommcvCg+NosN54Fh6MB9vtBOULgemWcTsip84JceKIIgdRN2bZkIWkH/hS\nAhac1dkpsUfWTh3UK+sA0vN1zG6EasUQHeRH1zz8mZDAOWJPDeUB61Cxg7bNcCsGQoOY/udzIyQ+\nvTSLJ4JuxtAa2DE2CvH9rB67cpnOAgxwqnrQs/eCMqh4D4laB7HCkE6tyktpxPVOygN+lbfHKZ70\nnThrjfKrKK+OcW0k6ODSPSRuH4BS1TpqdhbcNlJxSMKQGuGC8gTtSZfe3ljqayOCsoLEgnhkufYM\nCz9PIW2iOnvZ7fLVOQhnkAMX2d2wrXQlxA8E1XbQGQi/88meSUWjZkBiIBYYCGX3q4qgqnEzhgSI\nYumWn++zee1QBkSDVg5JQdKDPCgEv1uKzbnJnV97MilzQf+/J2kuOOl1xs1gTZptndbaLY+H6drt\nzrGt/s9M0totj4f+n08qp6cxXvPktstJhxuk9L54Xtjb4IMbFpIwSLbWwxP9y2ANvoTGhVWke4+H\nXojHuLBuVfeePifFw6CZD2s3eInRKB5galuj+LoZrJPmVORwPpB1wlY7ZquTkDqh6htWqj714ODF\nZK2249r1mM2GJRaHrgm6yg2nksynXqx4LFZ85kIPNYKHTiQ0W47VtZTtHccB09WCqTlMratnB2xT\ngx1wHkOHNwO6KigzPIRfNWO81zYJ1lvUQ4/ZB5aYf/wcXu1GmLsTYbsds9FO2F1rw3aSXVS3e/CS\nM6kb3L1V3IUKUve6XQ3wnljM1V38N3ZgM8EFFZLqPOIHhzcUNDd8XhmClXZQu6/C3mWoOpJzK/ww\njXj9Rz/gnsef5KGn3kUQhHD9GuqlF1FvrKGkgqrciw7PodSN5+3SFmnnR6TJm8i8h7rvQfQjb0PV\nZ/ueDbiOIE2FWIXyupeqhYrD5uWyUmgtgU0LmwKHotmyjQfXvIa0rmOv/wfSXutnAGZWUA/8BNz9\nOGp+AV0/bFskDr3awVzrQCrIgo+9VEPqNy7/QwSaDtYtlVhRrXos3ROyeLGC7tvwiRNhbT1mYzNl\nL7YHarIf4CHKeKiIoVY1XDjnMT/noQfC/U9jXumXYe+RO2UuOOn59XaeC4b1dyt6TdduR9P9Thiv\n/bh3+njtbTAd93gta1snPcYG5bZ00nvSe9AnhVW2vzLtznI9xJPub5Kxei+dk+rvdretMnyOs7+y\n7V7a2GMrKq6l5SnFj52v44/g/jvfa7K9U+a1nJ8P3pPwrhSC4jbLFY+Hl4prqQN8///5IfF2cUm0\n9MlZ7AMzI7H4VjSypjf68OnvoFgv5TXv+7zynX/n/H0P8chPvIfqzOyhdsG/raPWi3V3SwHJe5YG\nNgwOy/BL8wbkzQReG36S2y/J9/8KaW0WtvH+y/+OfuzHRmIV30mQyaOLVRarxbXNW4nle2sN3Ijv\n+JblGrNhccm6s/7+ns4Fp6PXWZ4LzjLWWdZ93FjT8TperLLjdVy8l203qbbVk9su3H0qU5nKnS0i\nQpQ6Kn65i6PGIZ5WI+tUi4M4FvxqQRsRnO5ebFbgJBkDWmUXdhWAQSRZ+HMBD9JOsJ0UU8mfDsQ6\nJEkzzAIsR3Y7uyqYpxTgVzRxXODEiqDiBDHeUDAnjitbL/Ly6jeZPb/Euz/4X5ldXM7FIo5AVDEP\nSiGWgyXOhmBJJBBSiOV7CuspXN6Fed2Ph3OzdEY46UEY0E0syBWtsk2gIkrhcKbEMLGp4CxZykSB\nnMzImspUpjKVqUBxWPRUbk+57U7SB8MJ+qW3wzEszKEn/WERZbDy2gyGPIwLa1ioylGw+tuME6s/\nDGpQjoPTIt37Q2CK+uvpNW5Op7Y1Xtsqwur9LLKOtWZEI7bE1mEdeBpCTzMXeqzUQgKjS/NQ9Foc\nprsAqXPEVmh26643E7cfGiyJghQ0iiBQVCqKlSWf5SUfp4SNVsxOlBClGYZYIAUbKeyeBgtzs4YL\n5wy1miEIsk2BOBbaHcf1tZSdXYeLHaaTYBKHsgIO8EGFIHMaVjwwgrm2i//6NroRo9oxRmv82ZBw\nqcbCW85TuzRPshux9fw1Wtd2SXYi0lYCSiPaINrH6QriGZK5CulCFQk8nO9lTq4Hyr8REl73NSs1\nn7pvCIxCiyLpOKI9y9bViK2rMbaT4LUbeJ0mOo1RqUWMRjwf64cktQWs0bzx/7P35k+SHNmd38fd\n48ir7qruxg0MgAFmgOHN4e5Su+JqjSaZfpDRTCbTX8D/Y/6dFfWDZJKZZGu71BpnuUPOkBwOZzAc\nAINzAPRVd1Uecbg//RAZVVlZEZFR3VHZWdX5zGCN7vT8+stvPI/nx3v+Hv+YT/Z+jpGEuzymrQZ4\nK5t4a3fovPmHdF79LUwC3mf3Mff30Kcj1CACDGJ8xOvi/HXEC0h7LdLNDq7lI55BvCy8O9MddAtU\nJPA4hVMHUfZc8MkW6mNOdahYCw2bLZ+Wpwm0RlIhHjoGRym7X4w43U9p9wzbr7fobniEHYM2luT0\nhNH+Hvu/+iW7//SPiLNsfvd7bL//27Q2NwlW13DaEDthkFgeDxMGics4bft0ck6VIrHCyDr2hwlH\nUYpSis2WYT30Cb3sbgQ9ZcvOCUfHKY8epwyGligSUifnPLRBtyH0FVstj9XQI8zvWSgZF/P2BWXj\nddIXFNVkn9ZrHr5gOnx56QsW178+iS+owlpETsvG6yLb1rzH63Xw0CTWTbMteLbjtcwXXCendXxB\nkdy6RXqV5GSW5U3ARTKriKuDNfnwyrAm+2sS62l1vwrWZD7Kdet1FR5m6bXInDaBdV22VQdrnrb1\n+eGAvWFK1SFiaBTvbfcwej48WOf42S+G9AeOi5egXUDD7wnellTqjhPe3+nR8nWpXs4JX/7ilEef\nDqkCU8bR+uozdJyUH81qhfI1CEhcHsJv2wHH77+LeJfreZ93KLz3nRZrPYMx5Zwef37AV//3P0NS\n3t9jOeQnpz/GSsp2+g1dd3y5V6XZ6XyPu+Fvo6KKMAPPcPj9f4Nrtcp1R/BOYszIFuSUT0C1FO/9\nu02CoDgPDcBah1hBaYXxynlI4xgFmCCoxiI7iTcVdmqdAxReCe+Q2fxP/2nIcOgqQviFV172eflF\nH68i1HLpC+rrvqhY+TPMJ6uz+ls0X7Ccuy05vQ7dl3O3+rrnWEvbuhqnZTizg+dvkeQklJE1+dms\nvII6WHmbyl2S8S5K1UO8CtasNpOfz+KhynAmscp2yq5Dr7o8TP73tFiz2kx+Pi8e6mBN7tA1yUMd\nrKZ4qGNbiZuxyAXc+PbteY1Xo3UWZl26QAdQODVbd7RC62q9tFbYxFYu0AEkAe1cdey0kyy8vWKB\nnoEpMJrKwGdRGEXpAh3G9mBd6QL90J7yXwY/4yf9f2abPq/Fv6JXtEAHEId2pnqBDpDacex39fPR\nrujStylxWbh5pT0YjfbKF+iQfd8Pw8oF+hlWxQI9x9KqeoEO45N0mZVjr/A9VblAz7EW0RfcdP9a\nB6spvfJneFN9QV2sWXo9L7a1iJxO8vq0WLPaTH6+iHO3pm1rOV4Xc7xWnsZX9rCUUmkyAKHpYIam\n8PKX/Tz6yrGqjPlJ8G4iVpM8LKpt1cGq21c9pqpzqSdazW5Tm4MamgnZYr4BrMxmZmFJve5m33k2\nhqsBVqOJKlgv992QHw9/yQ+HP+Oet8V/3/0jNuR0JhMi9ZSvM8bqPWmpY1q1bauOfYmrqVktrDpA\nzY3XOtL0O3ARfUFd/7r0Bc3K88Dp0raeDVbTfS15eD7stHJDQOb5dpyDTIcqTO9Q5LsW06EYOQ35\nDuQ0LU+CVfa9on/Lvze5QzPre0X9Fb2cy3Sf/t518XBVrCq9yr5XxumsNk1z2gQPebtZttXUs67D\nQ5PPsOj35VipcyTWEaWOwyjLvd0a593mebDTWA7F7mROt8tOBg3gG2gZzXo7YLPtX9iVzPSExDmi\n1HKaWA5GltVQsxqc592aJxyvUQz3H8ScnGZ5vnEsWZiyEZRhIu/5fJGXLbNVdvTvQBKFHULoDC/s\n+PS6mjDU+L5GKc7qqPcHjvv3E0Z7MSayWT66JVtsa8ADMQobGEgi2vv7mMEQHSWoKAHFuF65h/Vb\nJEEXz0aYaIBOE1SSgBXEN0jLx4Yho40Nks011NmJtCCS/amTFBPFmJNTeifHbL67SfeldYLVEK8b\noI0540tEwAknn+5z/PFjjneP+NmjX/Hl6AFvBS/xdvtVfOWBCFF8wH76ASP7iDg9IkmPEWfxOhuY\n9hZe70Xa9/4lK3adcO8hZjhARyOIU1Rg8FY6BOtdem/ew3vjFR4fQX9giaKsBBlwVotcBYIKBXOS\nwqFkl/DFZLx6QACECjY1K/d8tnshbU8TjO0mt604dWPbSlkJ9IWcbqM1ic3uUYhSYW8U4xxsdTza\nniEwGk9rxAnJMCU+iek/GHLyZZ/V13p077Xxez5+20Ppy+OuaLxa64hjYRQ5Dg5THjy02bNQuV1n\n/+P7ijCATsdw745Hr6srx+tBlDJKLVutPE++eLwufcHN8gXT3yubNC/SPGOy39s4d5vXHHbe4/Uq\nttX0nGWe64K6zzr/3iTWrO/NY11QNHdbdNualEUcr2UbEbdukT4pztW7Mh9mhy3UxZoVSpHvji0a\n1pKH5rGWnF4N65vjEbujhFFaPMHWCu51Al5cCUuxRIRh6jgeJWy0A8KK8OL9QcTDQcxp7EpPOTu+\n5t3N7sywYWtt5YvWOWH/MOGT3SG0QVVEDttjsKcgSXEoudawtqoxBg4OskvyLokIygo6SnGhhxhV\nHElgLeHDPfRQcK1uBl6EFY8gTIk3N3BheQmvYG+P8MEu3kkfVUSqgvbdFV79n9/HmyrfFUURP/rR\nj/jxj3/Me+9+l9f2N1H75bHmTiwn3OfklXVa934f7ReXkdPDAa8FB2y/c49we7XwGVkrfP14xNcn\n8eVa5BM8MBI4crBuoFX8rI2CtdAjdcJJbMtty9N0A8PhKCUpORn3tGLzcUzy6SmDx6Pi43gFvRfa\nvP6nL2OC6pD0r++PePjI0h+Uu33fh9dfCdje8vG88nH99fGIvWHCqNAAs/H6QjfghV75eIWb/95a\n+oLrwWqivyaxFpXTpW1dHeumrgtmzTOugrWI4/U22FZT4zWX574EW12i6sosh1G0+1IkdQyiLlYd\nveqcPlxFmuLhJmMV7RI+jdxU26qLdTiKGVWUrHIC/dRW6q6UouMbWqb6xkyAQeI4mVGzapA4rMjM\nF+WsF7PWirV1Dz+Cip8IgBup8QK95HMHB4cOqsq0KYV4Cuf7SFVevDEkGxv4qqKGuFJI2Ca5G+J0\n9SLQOx3gH/fLGwgMH5wgqctuRwfSNOXv//7v+eEPf8ibb77Jn//5n7OxscEX/9cHnO7vlUJpZegF\n38K99B2kQi/X7tD77gattfKa3sYo1jd8HriIKk5pK1RbVeZwW4H9UcysbLJB6hiktrw/IHXC/ten\nmEejciCBwaMRzsmsqmkcHFYv0AF8T7Oz7WFm1Gs7HMWMbPV4HcwYr7C47++lL7gaVpN61e1rVn9X\nxZv1+aLa1nLu1qxtLep4XWSsOn3V6e8qeLM+X0ROr2pb5gc/+MEPare+QTIrfGayXZ02s7AmQxfq\nYEH5w3yWWE/LQ/75TeehSax52dZkWYl58jBrF7UOlnMuCxFGshJkBW1anuZuN6BlqneS6+quFfga\nYisUrTU8rdhq+6yHXqWDqcNpPLQ8+mzA8TdxtjXql5xsI+O1nSCponABlzpMPwtrF62z9tNYStBt\nh1mRDMsWYImgUsH00+wyuZLFoihwHY0NvXGTgnYiqMRiRoIojUoSVEGys2hDsrpGpDtoX/Hhxx/w\nF3/xF0RRxJ/92Z/xB3/wB4Rhi8OjlAcHQiIKPYpRBSfNNvCJXtghXemOf3+BXkpQbYdrO0QJLc+g\np7gSEYYj4etvIganLqsPrgseT+rQ94eYL/qZfba97Lj4Ig24WLDHGokF5anCU3lPKbbaHjudACdC\nUrLY7fqaFzY7tFqG+CQprLvutQ2b31lj5aXuTDv1PYVWQhQJRYf3Yah44a5hpWdQqoHx2mluvOZ/\nlrVJxmUYd4cJRkFQ0K+IcBKl3D+NiFJH6GmMLv+NTeg1iXXb5xlN+YI6el1lnnGTOV3O3ZrDusq6\noAqnLtaiz93myeltt60mx+uk3Lpw90kC8t2PKvJyhzK9EznZ9mmxJqUIq0jqYM2jvyZ5mIX1tHpd\nlYd52sPkTtzStjIp4yGxjtg6Boklso6VwDur8exdw/NJrD2rL30SpXQDQ3vcn6/r19+cbnP0MOLx\nFyOiU0s8ctg4bywQqKx2+bqGuwa0QpHfsq3Gqz3AgosV9r7FG1hUev7vGRZgQDyF7RjUPY0JyDYC\n8sV7jpWCjUC+sZiRu5i3DqDkbJ3rtMKt+IivEa2Qs0WwoPI4difofnpek30CS2FRLkXHMQwH0G7j\n/BAxHk40j0++5KOHf4vnefz223/M6996HdvxOBm4ifz9rD9tLTqOMcMR6rSPW13BtUOsH0ycoJ/n\n9YtyeGtgQskW3GbMA4KnFKFRtD2DNzQcH1lG4/6sy+3HZTXCPTDE+A9P0ScpauhgdPYDoaWRtsGu\nesT3VnDWgwTEKvLoBaVdltrgw8oGvLgV0vI0odF440Wkc5m9xzbLXUegFxgCY/CNOrvFPY1S4n5C\ndJTQfzigd7dDsObjd338MIv1qDtek8QRxcJgYOkPHGurhlZLEwYaz3uK8eocK/7Tj9ciKXqPnMYp\nD/sxo/FdFFby6BIhUIrA03R8jRLFILXZnRUTbYxSBFrR8jQv9kLavqnsr4rT5TxjceYZk7npt4nT\nZ2VbTc7din7jTbKt5XhdXNt6UqzreoZXwSrb3Lx1i/RZUjd3ok4YfJNYs3Zfmu7vtmPV4bPJ/p4H\nrJuse9121rnK0la51LGvn/+nPYZHM8qY3VPwenmO95n8YwQVEc8AvGlgZ0ZgvhP4aQwV0e0AyWaA\nC6uxVOoIdkvypC80FPJSdAf9B3z48G+I0xHv3P0j7qy+jlIKG2jSrdYMIFA4ZEYYuVmzeOszoYi/\n0uMIg3LpfLWHdzisbOOMpv/O3cqQe4D3vxOysV4ecp9LLV9gHXrGPQmLOsaaxPrl4xNOk2ZCfd/f\n7tIJqm1+UXlY+oJnh7WcuzWLtZy7ncvStprHWkROrbWYkhKnz31O+lLK5Tnbv1nKUmqWc6sLNt/x\nk50NNtOuxhypNphScDzc56OHf8vxcJe37/whL218G1V4O1sD/dUGq8jpz7EaNYgGZc56PQ++oDho\n/xr7ew44XcqzkaVtLWUpN0eqxuutW6SX7ZJMhiBU7WzkIQh5iPJ1Y02GPORhWrP6m4WV/1kHq0r3\nPAxp3jyUYV2Vh7xtU5zOg4dF57QJ20ptdhkbzuLr4gve5s1pXR6sc9hxMq/RqvDUPQ8nVkaDcdlN\nYoX50g5GCjVKkcBcym8eo2Vh8D6oFKTssnMPJJYstF1R3J8IxBbEjaPgS8KrfACHNg5XlMsOKCUE\nAXiBwiaCFAYMCKP4mI8f/h2PTr7kWzu/y++88qcYPeV2FKDHv/PsHy5jaRHEZSHkZafpCofEQOzK\n8/5FULFFWQNOSk/AlVisyW7RpywgQoNqjfPOlSvl1DNCmsrcfIG1jjQVwOJ5ClNw6i4iJFH2w5QW\n/JKb4ev4AidCklqUVmjrSqshND1eQ6MZpY5UiseYGoe0A1jJUyguoeGprBzjPH3BTfevTc0zZvW3\nqFjLudvFNlVY1zl3WxR7eF5sa1Z/izp3uy5Om+Ch6qT91oW7i5xPhCb/TamLi4HJBzYp022mF/35\nw538t7pYRbpOYhXpXhdruk3TWEVmMm2cTfHQJNYic1qEdV2clj1DEbkQZjN5gUmZXlflQYDUCpG1\nnMSW3WFKZB0K6AWa7XZA29PjS70Wb7ymTojGObePh1ntdshKaG13fLq+IdCaNBFGI8funmXvwGIt\n4AQzSs5ql6vEoZxFpSl6EKGsAwVu3UdebSOrPq7joTw1ca431j0W2E3h2EE0JjYEVjRsexMlwfIF\nr4LEoUcWdZKivhqi92KUA9Ea2w6RwEOMQUINLWB1jBUoxIEbggwUkoIRTSuETttw947H6kq22B6e\nWB5/PqB/mDA6trhRTBKd8MmDf+A3/c/5lv8Sb7deQ/c2sL1VxPdxfgCexvoaGxrEN2d542c578I4\n113QgxQ9clnkvAbXMUhoEC+7aV05h44d6nTMswJ6oO4apK3AI/u8n2Q8PM54cL4h3WiT9lq48SJV\nxxZzOsI/GKKTidV5Pkw8hXQMrudhX2wjmyGiMo6kDy5SkCoCT9EKFZvrHjvbPkGgS+2v7nitstMk\nyWqfn5w4Hj5OGQyz7/d6Kqtz3tEEviaNLNGpZe83EUcPE5wV/JZm8+WAtbsBrZ4haJkzsyvzBVYg\nTi3D1LE7TM7KzQVGsd32WAk8Wp7Bn9h8ug5fkDphfxhzOIwZ2awkYWCyKg87nYDuOIS9H6c8HsQM\nEktsBaOhZTQb7YCNdoA31vO2+9e6vqCsv6fxBVVtmpy7lWE9j/OM5dzt+tcF8OzH63XM3araXJdt\nKXWe131TbetJsYrk1i3SJ2XWDkXTWHX7q9OuKkfhWeq1iP0tMlbRy/w6+1tE2xqmll88OqksWwXw\n7maH1VZ1zm4dPuvqVZfTf7x/RDzjLZk+VtjBjJdtktL79CEqqQaL/2gD2Z6Rny1Ctoqt7tP/0WN0\nRa1xgPTFFvZ31mfGdr+/3aETVD+fz//jr/i7n/yYj5OveNnb4TvB67R1eKnd4R+8ny3UK8Q7HGKG\n1VwJgBJUVZk5wB8co4fVPOQ9zbKu5F9v4Vardb/bNry63m1k7NcZr9YKP/6HPmn1TyQ4HKJmcNpe\nMXz3v1uf2ecHj47pz6gnuNEyvL3Zq1aKZsdrPb7m71+XvqBZrGfhC2471k3WvWms5XhtFqvueG2K\n97rtFtW2crl14e5LWcpSlrKQolStVOLsPHk2Vq0u67RR9fCqnIq1lp/+9Kf8fz/5SzbdCv+283us\n6M6MTmf0N7NF/dTsOtcD1MWqy1VdJzxXubVb8udSh/eFfDZLWcpSlrKUpUzIrTxJLwormN7dmA5R\nKAqtqIs1Hf7ytFhX1b1prKIJZl2sSXNqkofnmdMqOxXJQrEf9yNOY0vqhMAo1ls+W53grARSWX/T\nepWFME3rVRRaVaY7KEaXS3RGAAAgAElEQVSpZWgde4OE43FYLICvFZstw1ro0w3MWf7oddmWdcLh\nKGZ/mBClDq2g7Ru2OwG9wDsLtRqdjkO4D1JOhykSKtjQsGHAG/eZChxYOHAwyHJiraexLR/x1Fn5\nMz2MCY/7mGGCHo2vVZ/KcTahYfVbPdZe6+FvhiQGTmPL7jAhymtoi8CJRe06ZCjZQXpLIdsaVs9z\n2tUgwftyH/PwFH0YgVOI8XGqBeP8a1GQdkPSzQ6u4yMdDxUIqivoUE2tQ7NnGI5LVa23fDY7Ab7O\nSpf84p9+wV/+p7+krTu8t/Y9VtIuyqYwGqJcerbpIKsh6VtbuK02ttdBrCbtgxtq8tvfjYGtTcP2\npiH0FS5ynO4n7H4eMTqdIK0L3DHQVdnqOhJ45OBIzhaiXqjYfDlk/V5AECjSYUL/mwEHHx+TnI6P\nnBV077bZeHeN1np2Oh4dxuz/6oj+w+EZlt/1WP/2KisvdjDrAbGCoyhhf2RJ3Hkm/Wpo2Gp7dH2P\n0OjG31tl41WA4dAxHDke76YcHDryr3tezqlH4IEbOU72Ena/iIj6E5yO0wPoatorhpZv2Gr7rLX8\nC7Xlc73icQrLUZSyN0zPeBhrxjgRgbanaXvZGFsJvZnhi0tfUI71JO/A6bDYsv6e1Bc8qR+bDjV+\nGqzlPCOT5dytWduCJ+f0SdcF1z1erzJ3a2KMXdW28jlYEdaztq2mseps5t+6RXpZuME0iUXkFBn5\nk2I9ifEuGtbkC2bJg6qNNS/bun8asTeIiR1c/jXZZUhtT/PWRgej1UJw6kRIrMW6TEffaPyC8K2r\ncFplp/nn1gkf7Q+IrSORy5dMKSS7xO5ri+xZkpHgLoUOC8pXiJd9XaVkl7VNn8FqwIDpDzBJgkps\n8cVjBjo7LV7647v4HR8vNJd+YzquQf3rHx8xOrZZXrqb6k8JKlDowRHB6QF6mMCooENPI1pz8u5b\nuFaAM+ay7gjKE8ya4PXKLnLLLuM6+OJzfvlXfwUOvtP7HnfCe5f1Qkjf6eLutnFtH6YvFBMBBy2l\n+dZGh8BX+P5lp5umjmRo+WR/yMDZ7FK46Yv2RFCJsOoZXl5pEbQMfnjZttLYkgyyzRLtafy2d6mc\nmbOOdJRik+wyPr/r4xVcrJZYS2KzTQyjwTfmwoIWns17K07yi+PA9xW+V8BpYklGjl/vDxiKyzaf\nLl1emI2L7ZbPi6ut7I6/gvdWYi1xavn4YEji3Di15TJWoBQvrITsdIK58PCssZ70vVUX66bwUIXV\nBA/LudtFrKVtLW3rurCa5LTO3K1J3RcVq2hjJpdbF+5elg+Q/3tVzkBO9Ky8gjpYV+kPqnMU5q17\njmWtnTsPTWFV8XlVrCY5bdK2TuKUUfFdFIAileywV5fcoP5MdFeK0PPmxmneJhXHKHXjtfJluxAU\nsQMOUzgt00ohCeMa41KyECHbMXHgxQlEFXXSLbS3W3Q226VNPKPxjEb6blwnvaA/UUgE3vEAfVRR\nTD11oAXX8nGm7NWvkFShjS29Q+Do8SM+/MlfMzw64r3Od3kxeKV4rEl2luq22rje5bz0rDsFBsJQ\n0+uWuyPP03grGjcYgC2xG6WQQNHteXQrcsa9wOAFptpOjSboBjPfI74x+GYG1jPwBWFg8L3qMeb5\nBs83uD7gytopEge+pwsrGeTiG4OnNSLDijr2iljAN3quvmCWLP3r1bEWzScu524XsW6ybT0Pc7eb\nbFvznrvNwroNnKYVl8ncukX6UpaylKUsgpQUXrux0j864KOf/FcOHn7DW7/7R7zy8ju0frQPMy4r\nqyULGs8lUisFfSlLWcpSlrKUpSylUbl1i/Q8xGBy52Iy7CDPC4DLuyt5CMNkm3lh5W2n20yHVhT1\nN41Vt79ZutfFui5Oy3go668Iq6i/Opw+a3uog7XVDhCJiawjcRdrABvAN9A2zXLalG01wUMyDgWP\nU4cxitBogqlTurPfjbAWGkapI3KS1Wk/42uiZNm2BlxW4mw6tNwjK3nmA0qhYiDiYu1yRUa+p0hU\nG8+PUYlFxfbiQjRU0DIcRSndQUzoZbpP1pe21pGMHFE/qz+tdPZbxOUdjXX3FRJC0l5HdSy6n6CG\nMUzcIq98jbcS4q+10KuaERBHkKRTPIxvWEtPs+hn5QmjqM+v/+FvefD5r3nje7/L9/7bP8XzfUgd\n9m4Lc5pm4fXRxA9UIIFGfA93JNCSjD/DhVWvsg5iGJw49pMRra4haGs8f6K0jHMkVoitRaNQOC5F\nMohk5dpi4eDU0R1qWh2D3zZ43hPYVuKIYiGOHNooWqEmCC7WG0+dI7GOKHUIgq814fgZnp8AjLEi\nxyh2BL6mFWp8/yLWs/QFm+2A4yghtjKVCpKlzARGkVo3E0tEWGt5ZyXO0iksf4yV1MDK8a7yHqni\nYVIWxRdMf2de84zb6AumsfIT2eXcrRprUW2rbO62CLY1T6xJLm7zeG0aa5YveNLxel1jrCpy5Nbl\npOcyOXHQ+nI+3mSbXIpCEiZf+mVtrgurSvf8ARc5o6ti1dF9ut30ILgKVs6D1rqW7lX9XQVrMkSl\nSvd5cTo94Mv6m77oY7qdiHA6rgGcWKHrG3a6IaF3Ga8up03bVs59Wd5NXdtKnXAaW/ZGMUeRxU29\nvfLa5VvtAKPK8mcde4OYx4OYkbXFYesycUlbDKwq2PKyxfWkjGuXy54gokhbHhLkNb9zxQXTHxEc\nDzC+xe2E2BfaMJUvHRrFdtunm2qiw5THn48YHBaFywsYlem0qS9eZjfWXR1H+J/t0RumdLe7bLx/\nj3Czc4HXJBV29xIePko4Oc35n/g8GfHl5z/h66/+iZfefI+3fv/3CTotKApnjizm/gB1P8GJJl7t\nYLutqRxnQYUOrwc6tXBkYVfG6QPnErQ1W6+GrLwcEBvh8TChnxQtuCQr1n0isG9hXy6d6rd6hu3X\nQrZfbWECVWmn1gpHx47dvYT9Q5fVuZ+QTierN95d1Qxcyu4gZWQv6uUpxUbLsOb72BE8fJxydHx+\niVsuee3ynS0frRfDF1gnHA5j9kcJIrDW8tjqhGf1w4uwoHi8ntcuT1AKNlo+G+0AM4X1JP61CV9Q\nxUP+2Tz9a1O+IMd6Fpxexb824QsmZTl3K9d9ul0TPCznbs2P16Y4vQ7bEinPmX6W64KmsBZtvE7K\nrV2kQ3UuwHVg1e2vTrubXA9x3v0tMlY+uOfV3223rYNhzMcHw5n9vb/dpRNUBwp9dTTkm348E4sa\nget16qSjhfAly+XLuabkVxEczlCpo+B9fybWd7c69MLq2uYPHsZ8/Ok5D9amfP2bn/LFZz9h+86b\nvPHmv6TVWiV8Mc0ubKuQ9ADs8WzbCh8Nii/Tm5R3vGwDokoigZ/HM0Pu3/3Xa6zulOTFj+Xo2PJP\nHwyY9azDF1IIqtvYYyE9mB2o9ge/26bdWrya3ktf0DzW0hc0i1WHzyb7ex6wbrLuTWMtx2uzWHXH\na1O81223qLaVy60Ld1/KUpZSLXVfDk1JFDmS1NHtlF/k5EToJ5aOry6dtk2KVhAYRWzL9xa1Aj2j\nMLaIEEeCpKAq3oJGQWgMg7Q4dHYMli0WnapcNKsoQh2MkM1eeaKzE/RghHM+ebm0Qqx4BMcxstYt\nx7JCtB/R2THogqiKTHUhGVqwDqfgwf0P+OyTH7Gyepff+8P/lW5v60wvBg5WdPlvFEH10+zWe69i\nIuHOy6RVSSc0RCo7LK+UUGU3JJaIUqC92TYfxxXP+AxMal000Ao0sa+Ik3K9jJm9XyMiDBJLC4U/\nfTP+UpbylDJvX7CUpSzlyWU5Xp8/uXUn6dPhBLlMhiCUtcklD5GYDG8qalPVX9NYeRhJnf6qsJrk\n4VlzWmW6i8bpZIjfLB6uotfTcjqpe1NY1sHefsLefspw6IhjQQSCQNEKFRsbHttbHok4docJgzgl\ndkLiznNgOxO1y6d1cgKxdUTWsT9MOIxSWp5mp+3T8U2W2z21+tFaE8eOR7sJB4cpo2i8SFeC8rKF\nuuoIpg0rLc12O6A9zhM3Osujjaw7r13ed7CXwrHL8tcjsihwD5zRpKFBPIV/sEv4+D5m2EePRihn\nkW4L12thX9wiff0eWIX/+T5mb4Dqx6hhCsbgPB/nByTtVZwXYAZ7+P09dDLMFukKpBviVjqkr+yQ\nvnIHFYH5eog+SVEDC7HDaxmCnk9rK2Tz22v4KyH7X484fBAT91OioePB4ed8+OBvCfw2b77xx6zu\nvIxKHV6UolOXnXo7snz8kGyxvm0Ah7k/xOzGqKGFYRYp4AKD8z2icdi7SixeZCewssWuItvjQBRh\nNwtN7235hB2D39JYEWLrGKaO3WHMSezIV/hqbHMIEJNtlBxmIfTttmH79RbdDY+wbfBDPZG+PrZT\nC7t7CXv7CaNIiGLBuXHUhJyXn1OBw/TABOO8eg1K5TnxWXtPazZbhvXQJ/R0VkPeZZh57fLDI0ev\nq7m7Y+i0DWGo8LzLdhqljseDiJMoze5ccJJVRdDqQu1yJsLwnma8XuVdU/bOXfqCTOrykIePLpov\nUEo1wumztq2ntYdJrOXc7WbbVpNYizZeJ3VfRF9QVJO9CGuSh3wuWlf3unrVxXpW47VUn9u2SK+S\nnKiyvAm4mGtSRVyOVdVmMpehylBzA61qcxWsuro3yUNTWHV4yGXJaTO6N431Dz8bMBg6yo8cBX/d\nYdaktMwXgEL47Tsr+KY4vyfvz46fdVWJqFFk+cd/GpJUhkUL732nxfqqqfyNx3sRH/710cUL4wqw\nWl/+FDM4rj41bvfAW6k8CUYriHYhTcrbAHb9JaS9VR1G7imSjTXcuOTWfv8bPnzwN1iX8u27f8TO\nyqvZwXzOd6V3sIRHx9W6K4jXVpHCmuznsnrH4+1/sY4pOfGHzP5+/viUyFbZFtxte7y82r5wMVsR\n1t/944AoqkplELwth+lWX/FuFHzvTo+gIgxRRLBW0Lp6/JxGCR/uDWZkAgjvbffo+GYuY/+q728o\nfzc37V9zqeMzlr5g/r5gkTltQvfnxbbqYjUxXm/D3O0mjrGlL7io17xtqwznuQp311pX7lzB7Isn\nprGqJMeq6i/HmrVXUhcrx5v1eR0e8pPfJrCuwmkdvWZhzRpgk3rNk9MmeahrW03ZaY5XB6s6Jlgh\nisoFOpx/PosHrcrrwJ/3qHA19NKqxm9EzVig51g1wrqtMLORqxdiDXpmnrekWVTD8XCPjx7+Daej\nA96++31eXH/7Is9q6mb7AlH5iXhlh6B09WYMgNKqcoEO2XNRNe4HMEZVLtBzrOyVO8MeNJULdBi/\naypbjO1Uzx77KIWd+RubH69N+oLKU4GG/WtdXzBLboN/XVRfsKj+tUrq6n7u754eK9dt1ueLPHer\nkudp7lYli7ouqOsLrsLDIvqCRRyv1trlIh2Y+XCm287abanzEOti1WlTV5rCqmOsi8wp1NtVa7K/\nRcRqitNG7UHI4pwrdZNZ66ML/Tahl9TEUppxKbRyJLFu9tpajf+bpV4N9ZUSZAZWPz3ll1/+A7un\nX/Hmzu/zu6/+D5jC3PccqPr51BFxCszsxfUsJysyGWJe1V9NrBrqOwdmlp2KMHuZft7vzMnZuMhc\nBUrj78lZcpN9wVUjtJ62v+eB07r91ZWbijV5UjaP/pq2rSbfI8u52/yxbrLuV8Fq2hfMwqgrTfHw\nXIW7T+64FO2a1NmVKWozjZU/mOl/q9PfZLvJnaSqvIx5Y022mTTEOlhP2l/ex7x4EMnyAufxrCd3\nDWfprpRqhNNnZVtJAg8fxxweWaJIiBPBOVBGUD6oQNA90L5MnIxmCzCjFIFWtDzNZstnoxPAE/Ke\njvPIR2mW+354kuIGCokUWHCpAgXaCPigWw6/q9jseWy0/LO663lOemwdg8TyaBAzOEhQuw4GktVK\njwWFRaUjiPvow68xB1+jtYc2IdmqXoETpNtCem3s1grpGy9AqvC/PEKfROh+DMMU8Q0S+thWSLSx\nQdoOCHfv4x8doIcD9GgEgLfSIljr0n5pi7X3Xifqw+Gnx0RHWb65GzkwENkRHx7/kt/0v+BbK9/m\njTu/jQnbiNYIGjQQKFQIsqqzW9UHDvYdRIKKslN4pc+X7mIFlaYYm6BTi3IOkqw/GeekJ92QZKWD\nTh0mslkt83F+u99SBB1NZ81j+9UW3Q3/0rvGOjm7f+BglLA/THFMhLuPTUFFFjWyqMME/ZshqysB\nG++s0VoP8Ls+XmhIXfYMo1TYG8UcnFrsKUiURUa4NO+XM5tHKXQry0nXvmR13jUYVZwj/iR2Oj32\n+4lldxCf1RtPRLLHoxWBp1kPfbY6WYnBJsZrE76gyfdW/vccdxbWdN7jovuCum1ugy+oy0O2aXZ1\nTqdl8uRqcrH3LG2rDg+3ZbzeprnbtNTVXSl168frs1gXLOp4bcoXlMmtW6RPSp3wh8kX+dNi1dmx\nvwrWzNDIBrFyJ9kEVtM8zJPTJnlY2lbGwd5RzCd7Q2gpqtR/qRew0w0JZuQS1+Hhs/0BB1FKWvJ6\nEwE3ArSgg3K9QqNpeYqT+HJN9jOxgv4vH+B99ikqPi3PcA5apH/yr7Av70DZ7edxinw0IA26uDAo\nARJ6yRFvverTe3UHVcJXMkj54P/4iF/d/yWf9j/mlc5rvNP7LqFpnUMB6Qsd3Ns96OnyE+NI4Bfx\npZrm03o532FXWrjQK8YSQVnhndd9Nl9oYSpuXf/6eMjuMB3noJfIMMX74Aj9OEaVNDOhJvyTO5wG\nmqTkIYqAPRHsQXXuPEZ4622f7dWg8rb1psardcLRKKYdeLQq7maog1W3zdIXZNK0L1hUTm/qPGPp\nXzNZ2lYmS9tqHutZ2Nbk4v9psRaRh7pYuTxX4e5FMushPyu8ee+dFO0APS3eImLV6aspHhaV03na\nllKKbs9DD2YHR68EXuUCPcerw8NpklTfZ6bAtB3ZEXK5RNYR2fzsuESMwnNH6Pi0WinlcC9uli/Q\nAQKP9M4ablihl1LIxiadV1ulC/Q0TfmHn/89//mz/8y2f5c/2flTul7vMhSgtcOtzKi9GqrMW1Qt\n0pXCdUNcq6Iuu1KIp1i9G1Qu0AH68YwFOoCA2U+oig+3kePoOMZtltdJVwp0oGaWbscqVgKvVjm0\nJsar0Yq10KtVG7cpWdT3VtNYdfpq0hc0KTfRF8DStq5DFpnTecpy7ta8NM3pTR2vz9IXmB/84Ac/\naKTnBZM8vKBqVybf0Zi1a1YXa/LPp8GaDNeadXJSB6uO7kXhJU+KNflnU1jXzYOI0I9TvjmN2Bsm\nKCD0ik+u8pCaeXDqRDiKEr45iTgaJfhald52PgvLOuFgGHO/H3MapWelyp4Eq26bjAOh7RmsuIr6\n5kKUOlLnCD1zqVa6iHASpXxzOuJglGRh8QU8RJHj/oOIvV2Hs2Sl1abWUwpYDQwv9lqsBobYOYrK\noEsC7gTsSQagig6HrcCBxR23wXQhGoCNLyzpBXC9daI33yNtbyFaFWONWysDygiSqixEvqCNOBiM\nHMZAGJzzICL8/Oc/59//+/+Nk8GA93/v3/La9juEI5OFmk8R0b3X5u5vbbK6FpKIFJ40q9Mh/q++\nxP/8N+As4rW4VMNdAesKXjDoDohV44XzhP7jU3SvHxPvJwhC2PHQU8/aOmF/ELM3SrBSfpN721O8\nuBqyud3GJY6kn17aCRJfYV9p4+62x1vSRWMfXCS448kLAQv6NILpOZLAkYojHKdCXMZb+oL8s8k/\nFwXrWfCwiJxexbZmtXtWnNbloeqEa9621STWItvWrDZ5u3na1jznbvlnk38+z76g7nhVqvoSuGc5\nXp+2v7qcTsqtC3fPiZrctZnOB5iUyRyFWW2mCZ6Usv6mH1gR1rSxzQOr7m+c7LMO1jz6a5KHx/2I\ngyglSrN6xHI2OZcsB1QrVkOfF3rBE3M6+XKtw4Nzjm9OY04Te1YnOV80qFwvo7nT8dloB5VY1jm+\nOoku5LfmWBrB14rQ07zYDemFXiXW09qpc47ECVFqORglPBrEY11y3rPvGMVZXrrRiih1RKkjkfPn\no3LdjSawmuhIMRw54khI7fkzVCZb9GpfeO21gJXQIzAK35izxaF1ea6y45vdmMM9h6Rk/4k+w9JG\nwAOlHd5JghrJWT76+fNJz/LSnRriNjZw7R4uaCPaO8fyBAyoUPDWHSiFmuIBJ2BBEkV8oFBWgeTr\n0Al7CBRBCIdHn/Ozn/4V2vN45/t/zPq9l/MHgkodauSgn/JS6NPbahH0fPy2hx6fClvnzurB7376\ngP5PP0WfDFCnEUQTR+hhiPNDbKtL/PvfRq36ECjEV+c7D7nuqcI9tOjDi/noueR56eGaB68YIpdF\nLqQTdjq58t5u+2y2slrk2X0BE7Y1TElOEg73RjwcxUjPQ1oG8c7D+NUYS4D0CBjpiXz0CbsZ/6/y\nHWZtMh/9vM1kXvqrqyHeWJelL2Bu/T0LTifbPO1vnNWmyf6ehW3VwZqWJuZuub9dzt3UhTaTWE3b\n8iKO12m57nVBXU4X1bbqcrr0Bc2Pn7JNiVsX7l70Q6dfUE/aZvIhNI1VtvtyVayqHagnwSoLs1x0\nTqt2sya/+2iQMDw7YZxsr4gdxE5YCaURHpQq3yG8wDuKx8OE84PPCTtBETmInOMFrWdijaywO0wm\nNh8muM6xYsfLK8VlzJq0La01oYbQM+yP0uzCsimdIDucHlphaC1cuGH8Ig/Z83EkjwU3KMJSiFWI\nBQ/FTjfELyjzZbSmrTVtH744TrCFoeYKZxVYULHAnivkVPAQrwdej2QnwHlFr1iVLQpTMIElP+qX\nKR6yenBkl+0dgBScqguKR4++4ZOPf0hiB7zzR/+KO6+9edH2lcouovMNasVn606PoCDk3uhs0dvy\n4eAXX2A+f1SgOxBF6CgCY+GuP66BPiUTupt+CqNiqGQkJCNL3zm4O5mDrwr//143pBNc5lRrTdgN\nCLsBB22N7Re7tkmO3YlCbPGzzn2nvwaqM61P9ncrMLBCLLa0DODSFzxZf01jlcmz5nTePDSFNQ8e\n6mKVtSmbQD8JVpnusJjj1Vp7Y8dr3bnbs7Stsv6axlpE27rpvmARObW2PNHu1i3Sl9Kc3LIgi6VU\nyLyf9Ozp87ORRvWqsUioDcXlZ9Q/3eOTj3/Iyckj3njzX/Ly++/irxY7jWcpSs3fvuYtt/73LX1B\n47LkdClLWcpSllLlC27dIr1s12Iy/CAPP57eTZkOOYbik/lprKI201hlO/vTIRZNYFXpXgcrb5Of\n/JZhLTqnedsqrNDTpM5eCAOfFE9B6gRrHUrNiQfJQtpjJ9hCvQRfKRInM3nQCKHRJFZKLsXKwsad\nzMaapftVnk/Hy07VL6YYXADjTGEl2f1ul7CyEm4q0OjYZSfdBafNShwMU5ITjWp7eAUXm4kIiXV4\nASjjspzqAr2US9FpjHIxaIMUvkKzUmUqcWgFTutiLO2y0G+R8ccFPDhBxRaVarR1OGMYjU747Nf/\nld3Hn/LaG9/nvd/6H/EB3U/Q2uLaIRTudGfPJnaCshZPX87pFxHSQYTXDsHT4ITCa+2NRjlBn0ZI\nJ0T8gv7Gz1A8DZ4ju8mvYAfbB20UGkih5A64zObr2GnHr7atPFWCUONiSAr1EnxP4YnC6CxXv9BO\nEZzI+K4Fi1/Ae5O+wImQpDaLL3EuS9sowEqszd4d1uEZfRaKf1W9bosvyOW6/etVeLgOTuvw0BSn\nTfmCWViLzkP+nUXi4aaP1zpzt7pYN5mH/DuLMF6flIfnldOr8FB2Ig/cvpz0onyUnITp8IkimSRL\nJiaEZW3mgVUU+lEUsjELq0keFoXTIvO9KqfWCYfDmP1Rwih1uPHifW1cj3jyxvHr5HRar8Q69gYx\nh1FCbF12mZ3RbLYDNtrB2aVVdTiNrGO3H3EcpcTWoVWW873V9llvB2cT/Xnalkh2Wd/eMKEfpwxi\nwSWCjVVWvzoeL261oDsOrwPKy/LCz9dLOQfgIkH6CkkUDFLMKMac9Akf7KGHIxTgdXxWv7ND7/VN\n/I02NvQYWcfeKOE4ysqsiYAbTWD1I8xwgHewT/D1V5jRMPt9XojdvIftbeCCDmL8LK/cnS/wBXCh\nRrpZbrSECjWuya472QVyE6wCChU71NCiThLUl0P0YYISiCTmV9FHfHX8a15+8Xu89tL3aFmL9+gh\nwYP76DTJ+ttcIX33ZWRrDbvWRfkGOUsbyPTytGKj5bEReoQA/SHxwSnHv/wNpx99g4vTc7U8PT7K\n12A8UB5Ii+yGO4Vre6RvbODuruBWWojn4RJF2gcZ6WzjRAQVpXiRRaeOwFOEXcPKts/Oax3CTra4\nHaWWx/2I0zi7j8FoRdszbHV8VkP/gp3Osq1h6njcj+gnKYkVPK1o+4adTkAv8FBKkaTC7l7C/n7C\nMMreJe1Qsbnps73l43tZbutpnJ7VLh+mgkOggNPNlmE99Gl5hmCikPnTvAOtCHHqGKaO3WHCSWzP\nel4NDFsdj7aXLdbj1HEUp+wN07NLAFtGs93x6PmGtm8wSj3Ve6uOf52uV9sED1fVqy5WkX+d1V9R\nu7qcilxMn6rjC+rq9aSc5u/8Jji9jba1nLsthm3BcrxW6T5v27qO8arU+f1Nt90XFGFd0um2LdIn\npWzn5bqw6vZXp11VTtGz1GsR+1tkrKKX5nX2d5Nt62e/6HN8Uv06Ui1LcHdmd3T+w4eo/ZJE6LEk\n37tL/N692Vj/+1+hToaVbUavfhfbvVMN5IH6HT87Wa6Q4Cd7qEfx2d9Tl/JJ/yM+6X/Ei62XeXfl\nPVpO8I4+obx4eybD/+lf4LbWKtuYX39N64e/qNYdoHcHCnO4z2XwrZcZ3Z3BA/D9328TBtU2uKjj\n9ecPjyfusSiWex2PV9e7M/uro9cn+332RmllGwCFm7jnoVje3mhfuGzyafRa1HfuomItfUGzWHX4\nbLK/5wHrJuveNAqzmMAAACAASURBVNZyvDaLVXe8NsV73XaLalu53Lpw96UsZSlLuQ3ixPHF4FM+\nPPklW8E2/2b739HzVsYfDp6tcktZylKWspSlLGUpS7k2uZUn6dcdkvyk4T1NhbXMOwytrN2zDh1r\nmtMmw47q6F7nGV53aN+T6jWLB+uEw1HM3iAhsllwcGgU660shcDTOgtJHgkPHsacnFr6A4dzQlZm\n7DyMGCXotsPrgvKLw93HWpB9U8EwQfdj9OM+3if7qNN4HLFtSHsr2F4PF4RI10e1FbKlYc2AVoiz\nxA8+Jfrox6R79+FgH482bbVJjxfxdCfjQBJSBggDHIKEXQjXkbW3oPdCdmu7OPSwjz86yXLZPcH1\nAtIXeqSvbMA4P16dRPhf7GN2B3A44uvRQz4Y/Jq27vLd1d9mI9xClCJdCUk3OzjfgEswowHew/sE\njx6i0zTLOjch0ttCgg7S7iBdH7fmY1/uIL1xgfYowfzmEf6Xj9CHp6j+OOpgomC8ALa1gt16EWl3\nER1mOfnDId7xETrNyrKJNiQrK7juSsZp4OE8TRoaJJwsCC8olQVqh4Gi1VKsr3nc2fEJg8y+otTx\neBBxGqVE1p2FqG+3s/J5uX3NCu0TEUbWnYXOJ9bhT4S7d4OLWEVSNsbyMoKniWV3mDIac+YpxUY7\nSyFojUvEzcIq629SLytCdBbuHnMau4mL6mSidN/kkzvHCoxiu+2xEnh0njLcvazdPEM9i/q7yf71\nacIzi7AWkdOi8TodRlxXr+XcrbhNXay6babb3STbehqsInmS8XpT525l/c1rvF4l3P265/LPYrxO\ny61bpJeFG0wTNG1IUPxA5o1V1GYaq6i/ulg3hYcqrPyFPC8eJh3AIvFwVax52dbH+wMGSdllfIKn\nFDJQuCNNnAjOFYX9ZLWqvbsuqymuKb047uIC5TKWSi0MUtSvEsTpcUhwAVaoOPrq/yQ++gB7eoCk\nySUs47XxVZcN/XLWd0EbtIGwS9B9F+OtoOKEwuu/2wYxGpRCRSnEjofpPr+IPgXg/fBb3A22wGiO\n33kT12nhjCnUXacJ/uMjwr2Tcc54wYvfA0KN3v8EncQwiAqUAjxNvPkaduMuTgdQEEKtcODSTBet\nEUouqvMVyUqAhOZCffcL3XmCCYVgR0iFwovj8sve3tro0PFN5bjYHyZ8fTLKLlYsuTgu0Ip3troE\nRj/VGEtdVlteoTAKPFN8GV9T49U5R+KETw4G9JP04mbWhd/o6Poeb6y38bXGMzf3vVUH62neW3Ww\nrsMXPEu/UsXDbfCvdXW/if71OnRf2tZsrCb1uirW0raax1o0X1CWxnDrwt3LdiXyf6/KGchJnJVX\ncB1YRTuBT4LVpO6z8l8WmdMqPhdd90XFqttflFoSgcLbylGkAulIsFFZm+zfRcgW6KaizVlxsvJn\nLZ6BUGfr1uLNzAwrAnt8n/SwpD44YNNhtmQ1cXnZLWdheIxpCyoqWMTnMrQobcHBgT3h59EnDNyI\n98Jv8bK3k9mvE3AWafk4U/a6VjgvQIsGguINAciuTk9S9GAESYVeqcN1VnC6VdpE0KADUELRjfq5\nXiSAUVMbKVPdpQrruXK9ybZjYkdpPXI4t+Vh6ojcuP8SrMhl7WdhzXqPeDq7OX1evkDr7OZ6J1KZ\nfy5oWp6m7Ze7+OfFF8ySOljXobu19tb7gkXUvWms5dxtOXe7LqxFtK2bjvW0nF6H7mlafufMrVuk\nL2UpS7kBUjd+p0676jX6FRvON7DoxA74YPQZu/aQ7wSv84b/AloVvNBvVbzTUm6aVE2al7KUpSxl\nKUtZypNJ5UHAHPWYi+QhBpM7F9NhB/nfJ8MPpsMcJr9ThpXnPkxjlbWZxJrub3J352mwptuUYZX9\nxiZ5qIM1rftku6flIcdoAmsyv6gOp2U8lPU3+d26PEz/vcq2muK0zLZSm4X9jsb15C+uKlXeSVbz\ne2jxji36VONCH+cZRJ/v+itnMUmMHkboJEath7hugIQ+6HMsLJCCTRTakOWrG87bACpOUcMEdRxB\nPwYTIJ6PYzJsXFA4lHP0Vr6PSSFND0mTI1x6fkO853fxdIeAHkavISpFXIIk5zexYzy010LpFs5Z\njD/uw12M4x6alH8efcZX0UPear/BH7TexxN1IScco85UDB48Jt1cw4Uh1vc4D0EXlBGUD+krXUzo\n0AMLQwvxxDPQ458rChuuY7wh2ASSOOMSwGikGyK9Nmw46CjUSJCI85r1CMpXEIKEgNKoSCACiSc2\nQbRAmLXTbQueghQkVYic8+77ijCAVsfHCxyRc8RWSCdSJfQ4PD3w9Fmd9LOfVWCnmy3DKDWMUkfs\nBDtFQ2CysmR131uT/39d4zW1jsi6s/z2PKfdnwifn/zunU7A/ighGv9GmbBlXykCozDjE7WrvLfK\nOK3z3pput/QF85tnlGE9C1/wJLY1yWkTc7c8CuZpxuuzsK1Fmbs9yTOcbLdInDZtW9P9VenVxHhd\nNNta+oLr8QVlcuty0nMpM6JJmSRpkrwnwSobANeFlRtR0cvnqv01ycN1cJo726Y4rdK9SU5zrHnb\nlkh5fktd2ypbmEyKtZZB6jiOUnaH2UVfl0UgcejdCP3VEL0bo6aaOU+TrrexLY13ekrwcB8TXwzH\nFq2wO12Sb++QrK5i+yBRvvKcECOYniMYnWC+OcL/4ijL957EUgrb7pCuboLWqEGMtvbi1VsipMke\n/eHPSU8/p2Pu0FV3Mepi+SoRi2WAlQjtdzHmDkp3ip+RUYyAj+Lf8NnwC17rvMG3V75DoMMxEQ7l\nIkzUB+UmFsYX2CTtdYleuYN9cRXVA92CS92NLOabAd4nfUoTvcWhklNQJ8hOi+StF3E76zD9vEcC\nj1MYCqxp2DTgT3VoBQ4t7Lvss20NXX1BMRGQBFwf1jyf7Q2PrU0fz7uIlTphfxBzFCWERrPTC2nV\nyPUustPEOvYGMcdxSsc37HRCwoISeM/KFxxHKfujhINRynRVN61gLTS8tNI6+/1FHPTHNdwTJ2y0\nfDbaAUZf7rNssjqNt/QFi+sLrsrpPH3BVWyrqt1tmbvNy7YWebw2jTUv23oe5m6L6guKNtiK+rvN\nvmBSbu0iHTLSqnIGmsaq21+ddje5HuK8+1tkrMmd0Hn0N2/b+nD3hKO4aAV4Luo0Jfjrx1lOdIV4\n8SFEcWWbeH2F0++8XQ0ErP/il+iT6jrprt3FebNrWXuHv4K4Wi/aG0BY+rEVy6+Tb/gw+Q33Wi/y\n7sr7dEynsK2JD1EzeLAbbUZ/+tblBfWUBD96jNqvJt6+1CL9nY3KNpnUSRdwMKNWN8Dv3OkReDez\nTnqT/f3jgyNmDB/eWAvZ6ZbfD3Adei19QfNYt90XzJvTOnw22d/zgHWTdW8aazlem8WqO16b4r1u\nu0W1rVyaWcHeYKkbcjBvqfsAm5KmOVhETuctdThIrONolJC6+fHVpG11fINfcGo3Ke3A0LnTrlzf\niadIdjpIWO6ARIFbDVC+haok7aiPHewiUr44FSD1ApzRlenekg5I41NEyldSIo443sXa/qXPnDg+\nS+7z//b/ll17xH+z9Sf83vr3SxfoYhTpThfXKs9EEiANQ2yUXa5XJp5S9HbamLDiNa+gsxbQLr2c\nr76IgB0qXEKlXgCncYpbsHfEs3hn9QJD1fBRgDdjfDUtS1/QvCwqp/OeZzQtS9taXNu6ybKoHNzk\ndcGirrXmLVfl4dadpE/nCEzmDyiV3eY7GZZQJHmb6XyQSaw8zGI6BGWazqL+irDgPNTjSbHyNtPh\nGXWxiniYNqhprDxkoy6nZbrfdk7P2ivF0ShhdxATpY7ICVaysmSBUbQ9w1bHZzX0Z650rsJD1TPM\nQ6ym63oWPWu4zGlehmqUCnujmH7i2AgNa6FPmNeLFkiHKfFJwuDhkL2Pjhh5IK9mtbulZRBfoxKL\nGibo4xHmswPUcYR7fR17t4d0Q1xed9uBpAo7BHvs0A+/wHv4Mbp/CMMTGA1QfgtlWmjdQZttVGsH\nu7aBa7dwxkeUB0pQIihrUVGMHgyQ4TdI9A1iTyEZImmM9gLQPpoAbTsIjkQfYmWASIRNRigToL02\nWnfxzA67KuSD5AsC0+K91d9iM9wB1GQ6OeLAbfjIq21kxUfaYx5Sixok6NMo42F3SLy9Qbq+igtD\nnO8jSqE9QXmgQsF0YbVr2G77tDxNaLLSW2lkSU4TRocxBx8dkZwmrL+9Svdem6AX4HU8UBBbR5Q6\njqKEvWE6zgufzNwHdXaanuVBu1jh+iBxlnPuUoVSY508UG1Bd0CZy7ac5053fcN2J6Djm9J3bl2b\nz9s0+Q68bl+QjPPRB4lld5jgRNhpB3QDQ2AUvjGX3gVa6ycer0/D6dIX3Gz/mv9/WX+5L5jFw3XY\nVhnWk8zdZvGwtK3leM37a2pdkP+9aR6uc+52Hb6gzB6K5DbbVhVWEQ9lcusW6VWSG1adkIV8sD0t\nVk5vFdZV+pvVrknd543VNA9QbfzPgtNPDwbsDmOqjpW1En7nzmphbeOr6vUsbMuJYGbw8OXBgAf9\nmMpjRBFwAjN4UP/xP8CvP6rc1BC/C9/9X0AHpW1AUJ/8P3D8VWV/TjlS6SOuIGkcOFCGT0yIBGt8\nd/V3uRu+UMpZ+mob+95qddi6CPFXCnHVYW5vvuFz706AruDUOQcOdEFe9qR8uHvKUTyug16mViLE\nDwwU1rk/a0Vwz6HC6lD5tcDw9man1nhdtPdW077g/2fvXWJkOc57z19EPqqq36/z4uOQFHnIEWVe\n6mHKomSLFOlrYGzjWjAGnnstDCBBM9cbb7SwvRXghVeGIQwMeDWLmZ2BgS9m5g5mQYmUREm0JEqU\neUnp8HFEiuTh4Tn97q5XZkbELKqzOzs7MyurO6sqqzr/AHHYXdH/+Oqf35dfRuQXEVC++9Y4uCBb\nq0nPBZOcXwe5PmXToYrX4rnG9exWNh3KrOmk6pCHaxpyQVqbc1XuniXmoG3zckVn3dKQZw1DdKYm\nb9vTfh4ij+1FahrOTOXhyGNXP13HoWnvJtGHC4HJeebWKDXN00YIkes0NCPIHqD3yDLOSI+Sqf71\n1eToL/qWOwtaJw7Q94TkFbvB63adu7XHU2uf53L9rkzNhCX6ritHCESOkmcpyRyg99rInHf9/uvP\nDQLRV3YRefue2Sx3vOZBUfHaLwkPwpU3F+Ttb5pzgRAn30ikceTRtIy5YJLz6zj8YdRcVbzmbzuu\nZ7c8KKNv5Wlb1nFBGbkGyQVljNesN+3napAeLXs4SxvIFnWcXHn48nIJ0b9c5TzoUBSXOXjDLPoO\nwHMMkAbQNM8DVx6ukK8Irp5JffoLjy3L4jIGpA39NlORoseXCQPIvoNmISVEjoxrI3jNqvOK3WBV\nBzzpN7li9MFMRL8uTY4JhnDKJrtdEIBK3GH/CLljTIi+/QkM/XOQwSjd9zsKM9p41Vpj+nCFs+DV\nPbC8uSDPYD68jkXYlce2MmtaxlyQhyv8vHp2q3xrHFzhZ2W8B+bhysM3jHgtor+ic0FRduWxLS/X\nuSp3z1qTPsg6ifDhrCiuqMxxZ4quk+jHNeq1SEXoYExv3UwW16B29VsblKRp3PZwxrZIHeJrg+J9\nCyHY6wastz3avsJTBt8cnW08c7A+d861cwX2qH0rzpX3GhrS1jwbRLjG2QhEYKBroG0wHynoAKui\nd+xXTYALIECBCQRBC/Q+iI2b2B/+Cqu5ebgmXdp1sGpIOYslL4K7iF5cRM3MYmwXLazegNwGbQlU\nzUbbILfex751HdncgvY+eO3eenNpI6kj9SwGzT6bvGH2+NBo7tE+91k2Tn0B4S7D4iPI+fuwlOmd\n+a5Vb5LAGGhYmIaFWnFRd89AQxJOzIiDtd7xf40S6BaYtsAE9P4z4nCQ3LsGkrlZweWLNrOzkpor\ncZyQOztetTm4Pkqz1fHZbAfoXs/H7HBl779Z12at4SCN5PYdn51dRbdr6HoGEQRIr4NsNXE//BB7\nex19aQl17S704ixmpg6ujSMFriWZdy0uzNao29apfCvJT+PxCr29EzylaQWK9ZZPRxmW6zbLNZua\n3TuTPJ4qy5YLBr1vxbmqXHBSh9PkgrRrmCcXxLnK4lvRdnFNk9rEucbtW1GuPNenjPFaNt8aRbwm\ntYHy+lZZ47VfmzjXuDWtcsFxrjRM3SA9iqw6/2Fw5e0vT7tJPmph1P2VmSsrGQEo3TvneNa1E882\nHrS/MurQCRRvbTZpBX1uNTc8WDcknul9ADUvUEt1ehu3p+jld1l45WUs30WIZNsM0L73LjpXLmav\neffaLPzrt7G8o7Jn3yje0Ju8bba4KhZ4RKxiLt2NXrwP4WQc6SY04mELs+SEpQQpMOnf7QCqCcG6\nzGwnJXzysTqzM+k7xQNstDze3+umnHN/hIeW6iw1XGSK7cYY3vnOL9n/2ZtIr5vKY+ou9/4vf8DC\nfCMzNor0019vNdnoBJnFFKt1m48tp5xxP2B/VS4YT39l5uqXC4rub9q58uhZZH/ngWuSbS+aq4rX\nYrnyxmtRuudtV1bfCpH99FahQoWhwpKidwzTCI9ZGvW8nAHaQf+1+HSyB+gAdHtv0DPh1JCNJUSQ\nfk66AIQwfTelw20gnVmE30YZzQ2zza/0OpfELM9a9zMrehvRdRprvc3psmBJmLf7DNDzQeS4c2sN\nKnlvu2NQxvQdoAM0HCt1gA69WeSa7tLKGKADiI7HjNV/rXeR6AS672oHb4THIFaoUAZM8TuaChWm\nDlW8nj9M7Zv0sHwiLDlIaxNFnnZ52oTlGXGEZR1hmUQ/rmi5RBpX+NlZuZJKQrK+41k0Dfvrd33C\nEpE8OuTRNCyZOYsO3UBzp9ml6SvqtuTCbI2GfZJvlL5lTO9t/J2Wh6cM867F2mytd/RZCleapsaY\nXjl+y8M3hkXXZnXGxUnhytJUa8P2TsCHt312OgFixiAbcOLldjPA/qCFuOlhjIVyahhLHhvMGgG6\nJlGzNrgS0xtmH+cxBtkNcLf3cTd2kF4X0W0jks44l6Bcl2Bhju7qMsHC/LG16MZogu13CG6+hPjg\nLXbEEr82hgVR47fkRZZEvdfOcvCXLhIs3w21Br2uYnYJYA64ZPXK9mVCG0A0Pex3N7E2Wui5Gv79\nS5ilmYRBvQFl0F2J2gfdkRxf/947As2a0ywsSxYavXLymnX8Gilt2Gp73G52aQYqWVOgYQsuNFzW\nZlykyPZTb3uf9gebbL1yg/b7GxwbGQtB464Vlj71AIuPXkVY6Rt6FRWvIVfLV+x5Aevt4GDC6AhS\nwELN4uKMy4Jr9+XK09/RV65yQVa7vLlgEB1GlQvi3zHtWk/Dc8aoNZ3kZ7c8OkS/Y1qVzDh9K63d\nJD+7xb/jJPpW2H4aNR00F8D0xmsUUzdID0WIfvmoMPH1CuH/Rx0yXoowTq5B+4tjWnQ4DVceHaJI\n66/tB3yw16WjNL6C6MtJgcGVgpotuW+hTs22RqbDVtvndsvDUxpPm4NBVg8W4FpQtyX3LzYOj0RL\n863bzS5bnYBuoPFNlMtgiYN1yI7FfYuNwzFjmu3vfeCxvXO0RpkIl7B6A0jpedRv7yHbAbQ1+BH/\ntQApMZakfWkJ3XDAAi3kca6DrcXlXof6ZhPpBwgvdoGk6Q3SdYDV2QNM79W+ivQnQddcdM1lW79D\nu/lLdGudoL3Fjna4aa0hMVxlj2Upsa1VFq/+KaY+j7FrmGhBkjBHJl6UsHqwlt4RkcG2OViF37Pd\n+bdbWPseouVBN+KbtsDMuOhZh+6n74b5GmCOD6bNQfVBeEa5BGGbAw0jfga4Elyrt96qdza3OdgX\nIGpX7+cF1+LybO1wrbY16H1LKYJmF2+7ib/Xwplv4C7OYs/VkZEkF33wGDSmTxNjSuvDvRGUMbhW\n7zx5JzKBUdb7aZULxp8LpkmHQblG3d9ZdEh60B/F9Zk0fygjV9l9qwxcZbw/jEOHYcXrOHRIG/xP\nXbl70sxEXLykNvEASJvhGBZX/IKXwXal1Mh1KIorTc/T9LfdUWx7KRvDIOhq6HoaKZLfDA5Lhztt\njz0/tOv4d1VAW/V+LWWyXdHfbbR9modrxqNcAmWgrQx1x2CllIdHue6sB7Q7R38f5TJKYBS4H7WR\nd1LKohWgNMLX6BkbnXjzEpiDt8e1rRbWbgqXFhgsDrbyPj44P2wDsu0h2x5+6yd4rXdpijo37UsE\nlsUVtc6i3kfQ28fOmVtAzV0irjkARnC4KfpFC2ZSbD/4P+vWHvZ7u8m2Bwax28Xa7SKkQCe96Rai\nNyC3QLr6oEzhpF0a6GjoaIPAxxxukRa7Pgc/X5ytsdhIPlM+j59Ky8JdmMFdmEErjezjN0XGa1aM\nWVLSkJKGk49rVHaVPRdMOlcaqvyan2vc13BQrngMnad4nTTfinKN455bVq4y+takc5VR0yAIEnlg\nCgfpFSpUOGdIzucJ7QRHI+hktIzghn0XLVnnSrDOit7NTZ9k1ijLlIQYbX+5cVoBK5QGaW/nK1So\nUKFChQrDwdQN0tNmLaLlB+H6gvhsSlh+YMzR2bhn5Yq2j3PFSxOjpVpJ/WXZlae/Im0fB9egOoT/\nZnFl2RVyzbgW9Y7A1ybxRaykV0qsjRmpb805Nt3AO1HqftAKSwhsAVobBMlcSmt8pQ82BEt+Kx+W\nQXuBoOX5OJbElifX74SlxJYLItAHG7yd5JKWQc27mG4H0dHgJYhqAZZE+BopFFomvCE2Cu3v0jHb\n1EwLW84jjHOSS2qECUCrHq86OWps0eG1ztvc1DUuiw4PqPcR2jvRznbnsIWDCFpg13pv6ZPWoNtg\nOoB7UHoen7k1BhEYdK2ObtSQQQB+wi5vlgBpIfZ8hGVhXOtYGXvIheKgsuBkqfsh9EE7RK8sP8ku\nescB+kpPbLxmtclre5JdVS4oD9egOoQ4i2/5XUXgGRABTs3CcU9WyZwnTcM2eTQdVU4MuZLaDEuH\n8Oey3bfKxDUNuaAaF4xWh7xc0xCvaZUjMIVr0uG4OCGKSOBpXPE2xpzc2CGpv7NwhRd9EK6kNkVy\naX3y/Mthaxq3PWltR1J/cbvy6OApzUary043wFMG52Bn9vimXEk3hLjtRelgjKET6N7mX75CaYNj\nCZZqzokN30KuQPd28275ijttn5Yf7cMc/Be/aRz9bEvBSt1iqebgWpJAa/Z9xXo7oBOEN0zQXYNp\nCozfe8UrbE5uHtdWWDdbWBse7PXq87VlEzg1OLiOBtCuwMzaKKkIurcJ9m+y95vv4q3/EnSvVMix\nV1le+iwzjQeoW6tIY6Czh2xtIXRw9D3sOrgNQNDWTa53fsO7wSZXNXxMC2wDvunQtVv4oovBxrEX\nmLHvZdZ+AEsebBonJcHcPGpuHuXWoeagHImqWRjHOnxzL1yNNQ+Wc1Bu3zWwrmDLHM6LiCDAbu9i\ndZtIz0MIgRYO2qqB6HEZAXrFxVxtoOcdjGujA0HQBBPdPM4yWHMaqw7CMhglUB1Q+/JogkIYRF1j\nz4JVg0ZN0HAsVmccFmrOsV3chxmvebjgdPGa1/ZR54IiuYaZC8J7+aTkgvg1TMoFSefVpvkWQLep\n6ewrNt7vsHPLRx8sCXLqkpV7XBYvucwu2ViOTLQ97eHwtJr206FIrrI+Z5T12S3uW5Mcr+PwrWE+\nu+W1fZTPbkVzlTVeB80FQhydNV6WXDAs30qK1zimcpAeQut8Z9YVxZW3vzztqrNxp4Or3yxZ0f3l\naXdjq8l6O30NTAiBjqxdTkPSgP6U7V7vQsry7BCt7Ve59db/2re3Rxb+BFelH4kWGM11/QFv6X0u\nG8E1Lain2NdYfRKhE97QR7D/yAN4K8vZRmlDbb19fGO7BLjNXUQn+/qoukPzoQvQ5/oIYTAmW/eL\naxaPXGtkG0V5Y2za47XKBePh8juaf3tuHXWyoOYYHvndRRYv1vraVflWsVx59Cyyv/PANcm2F81V\nxWuxXHnjtSjd87Yrq2+FmLpy9woVKmQj77xcnlbGJFRMnxYmx0D+jHOK2hh+bbb5pV5nRdg8qSRz\nffrMOw2RC3m+44iRp+SqwnRgiufkK1SoUKFChanC1L1JTytPiJcxJJUnwMldAJPKJuLlFXm4ktoU\nyZVke1I5Uby84ixcp7U9PiAYtg5pLh5tl1T6ksQ1ib5ljKG747FxfZv2nQ6dPQ8lQc/YqMt19MU6\nOCFfklaG8I2tMaC9gzJ2r7dTu5AgHINoEDsHPZsLrZG3t3Bu3EJu7yH2uhjpot0G/twl9MwSCInw\nu9h7H2G1txHdJkGwg2/22fU+YNt7m8B0EFjMuveyMvsYNXuVGgs9HbUHnRZGe7xv9njN3GHGmuXR\nxd9iqbYKxscETdT+++jm+6B9EBZi5jLW/P1IZw5EAyEMIgig00Lo3qtws1AjuLaKXplBzfbK87Uv\njp1dLoIAd3MLd3sXq9NFBApjOyi3gT+ziLEdEIKZJYsL99eZXXJwagLVCejueGy9scv+zRZGGey6\nxeJD8yzcO4c772Bci063dxb97XWN5xmEgIV5yaULFjMzFo4j8H1Dq6W4dVuxt68j8xzhOilwXUG9\nJlhZsrlwwcV1xKFvjTpek2Is3m6a4/WsXNE2xhj29hUf3fZpthSeB7YNjYZkbcVmZdnBskQurpCv\nqFxQdF5JQvRa580Fh1wG/K6m21Tsbfisv9ul2+zF/uyyxdr9dWYXHepzFtJOPhN6HL5Vxng9C9eo\n4zVeGls9ux21qZ7dJjcXhNzD9C04u6bhM2uR8Rq3a+Bc0Mf2omIs0e5pG6SnlRvEL0qaMFEhk9ZN\nxNukccX7m2SutDaVpslcZdLB2/e58f+9T9AKMH5KqNcl/qeWMCvO8TO4j/eK7kCwITFKQGIJdW9T\nOPuiRromk8t+8wPcX9xAtLqgEm5eUmDcGmiNMAZ8P9F0bSm0rIM7g2XqiAS7PtKbvNq5AdLi0YV/\nx8XalUSbojdOsAAAIABJREFUEAHoAKQE4ybbLgxm1sL/7WVM3Yako8VMb6157cV3sDZbiG5K6bot\nmX1glcvPPIRTtxKPt9NaExwsTZC2xK4lFz/5vkYbgzHgOsnrnLTWdLqaf3utQxBojEn2U9syfOz+\nGhfW7NLG2LTGa5Fc2zsBb93w8AOD1slx6DqCxx6tU6/LKhf04Qp8hQoMGLBrMjFei9QhD9ekxFgV\nr8VzDdu38nKNW4eyaDpu26txQbm5+umQ9vnUlbunfdFQ7H5rBqSUudpA9vqDQfqD7DUKRdo+CFe/\n9S9l1jRLz6JtL7UOvsHf97PXQXc0WKLP+vPeW3MTZLfRSiBEv7XsArm9j9hrpzfRBtHpgC0hSJ6B\nBJDKQtbmQZ8803tL7fFq921ausMn6g9yeeXjiJSBKQgwDthOtlZGYBwLM+Ok1/kLARZYnp8+QAcI\nNO68Q302fb27lBJ31u17rR2nf7xKKam5AgypA3SAQAlsO3tDk/MSr/3sKnMu6Hah60H68gqB5/c+\nnuZc0A95uWzHQlrlyq+D6lAU1yhzYtl9q3p2Ox+5oPKtStNBbB+EKwiC8zNIr1Acsm6UFSYHgnzr\ny/uiyJqbvFx5F8ZHsKdbvNb9Netqm4+79/OAcwUhbdSo14KPukYpZ7zmMasK/fMDkSMuqlxQPCpN\nKwwLlW9VqDA5yJyUmsZydziaxchaewDHZ2rSkMSVNBuThys6m5NmV7TE4jRcUdvSbA8/62d7Hq48\nOsTblV3TQXVIsj/KFbbPwzWIpiFHGpfyFXd+sUXrdhtv38dvBhweh+4KqEv0rI3/wAwsR3coPuhf\nG4SnEG0FWz5qV6IbLtqx0NbRGeECjVAGEWiko5ArElETGIejknAVQKsJe9voGzeovXkLy5pF4iDU\n0SyiqdfQ9TpqZg7l1HBae8h2C9npQHDwmtsCg8YYn0B7yNoynrD5lXeL9/11rjn3cM29F6tWwzgO\nyqqh6nNYRiOU7pXYhzo4RzroRRu5FyCbCtrq6Ax3ATQkpmGhlhzUtblYqXtPB0uAKwV1WzJ3ex/v\njXW8nQ7+XhfTDW0X2PMu7kKd2XuXWP3MPQh5Ot8Kz7nvBpp9P8CxJDO2hWtJHEue4NJa8+GtgK0d\nRbdr8PyjUmgpDbWDtemXLjqsLFuF+GkcZYnXorgG0SHadhg6KKXxfUOnq9ncCrh562iZSG+X/96U\nnW1DzRU06pKr9zo06tYJrioXDCcXDMJVZC5I0z2vDoNqetq4KMK3wr+vfKuK1zJqGm9bjQs4M1de\nHaIok2+lVgqYrKeWCUZUgLQvHxUzqxxhGFxR5xgmVx7bi+Q6T5oac/LsxdNyZdlVlKZGG/ZvtXj/\nl1u0XFB3zUAjxX6tkTc7yPdayC0fEbtLGAHBXA1vdQGhDbKtEUn3uLqAFQ+19wb6tZcxd24lNJI4\nzgrOpU8TXL6Kt3oJ48RKwI3B2t+l/s515O23CbwtjOmdjeRjuCENvxGGe4zFw85F6mufQs0to+pz\nENfCGETgI20fVm3UPTMwk1BU1FFYH7YQewHqcgOzWuuNwk8qy6xjsVy3WZup4SasVfV2Omz98hbB\nnsfSxy8yc9fi4cA8irzx2g0UW22fO22PdnDyFm4JWKxZXF1oYMvk0nVjepuK3b7jY1mCSxddGvX+\na7AmNV5HxTUOHYJAsb6puPWRz95+Wko3LC5YrK5YXFg72hzwNHYVqUN046cyaTrNueA0XGWK1/Pk\nW6PiOk++VdZ4Pe++VcXrSUztIB2y1zEMgytvf3naTfJ5iKPur8xcSbOAw+wvT7tc56QrQ+2F2731\n6hnwl+bQ1sn14FGYzibBG/8Hxu9m9/l7/zNm8Z7MJvL2Ddyf/l89EzG8K3oD9IsHZ503wgqA3/oz\njLOU3d89Eu7JPv/84BuQvq63hweX6qzO9D8ruahr3fQUr63v9bXr0dUZ5mrZ33HSY2za4zVPLlDK\n8OOfNQn6hPWjj9RYXenv81UuKJ5rUn1rHHblaZNHzyL7Ow9ck2x70VxVvBbLlTdei9I9b7uy+laI\nYkawE4ysUojT8p3l82FxnbWvcfJNsqZF8CllWN8M2Nr20fpsfIGn6X7kw14AabYZA/sKJW1MnxuJ\n6PoI38/kEgHI+r0g0rfAENYcdpPeRmtZXLqGmr+H30j4rqXZEobfUZJ/p+XRAN2eQ3gmedf4EBa9\nt/x9rk/DFqw2HOyEt94hbCFwLTlS35IClms2GWZRswRWVoMIqngd/T0wb39hCV0/rtVli6znN8cR\nuP3nkapccAquPH0VxVckV17fyotJ1TTkO8vnw+I6a1/j5JtkTcuoQ9Hx2g/j0DRvn+fFt6buTXq8\n5CBe9y9Eb7e96DoCOLoIxvTOt4vLchqurL+L9hddy5DUZhCuvLbHfzcOHfJyDapD9OfojNWwNU2y\nIapDyBX9fmlc+03Nrds+zWbvbGPP7x1o5hysGZ6fs7hyyaUWe+iOcxlj2NsI2PhNm/auwmtrgq4B\naXpr0mvAgoQFC3YV7Gro0luLrUEIg9AaEShEq4MMFNLiaPMxRW+qz5IYS6JsByVtbOUjg6B3pnhg\neoNh0UWrJqq7ibd9HenO4cw/hOUsIGSD3u7qAuNItGPjzTcIGi6Wb7B8jQk0tzd/zfWP/pWaVeOR\nlY+zbAzm9q+wnEWs2bsRziyIOhgLbAFSoKVF4LiYZRdx2cbMCIQrMPbBNTi8FAZbWqzVLRZrDjW7\nt65bCkGgNZ7StAPFeqv3unKt4VC3JTVLYicM0kcRr55SeMrQ8hUbbZ+6LVmuO9QsiXtg1zTH6zDv\nW4PEa9GanjYX+L6m2zW02orb6wop4eIFm0a9t7O/41hjzwWDfJ+ifAs4M9cwcsE48utZnzOiP0fj\ndZjPGUmxmOVbUXurZ7dsG6pcUOyzWxGaFulb0Z/LGq95vk9R9++z2DBM30p7sz51g/QshE6ap2Qh\nDJAsLiCzTciVpwykKK48thfJVWl61F9ROvi+5qevtPqWrv7Wx2ssL2WXrja3fX753S101rFi0Bu0\nJ56lHGnidXH2mn2I6A3as6vkQWg43MgqHd3VJUCy2bzJ9VsvoXTAw5d+hwvzVw81dPZ2kF6QyWVq\nEu/pC70j3TLwyMoMi/U+5eHGgAHZ5y31qONVaY0s0E/LFmNFcuXVIc93LFrToriU0khZPk2rXDAc\nrlH6Vlnjddp9q0iuKhf0UMVr8VxVvB71d9ZreK6OYEuaMclq2+/z+KzaKOzKy1cE8jhXWTXN01+R\nXEXrQI510Hm6E4O0698sH/LILmSuDvfaG1z/6Mfsd7a4dumz3LV07aR+UvbvVOT9jv1bSCEwBZ6v\nVpifGoMoMF77oeh74CTHa5GaFgUhqlyQp6+i+fLqULSm/VDW54w8XGX2rTJqOg7fqnJBeXNB0XxV\nvB7xFdFf1iD9XK1Jj5aSpCH8LF6yMGyucMZlVP3l4QqDox9XP0cctV3GGJTWqBFeQxVotDJkrRnP\ny2VM741o9oDRYEwOTTEHS8EzuASYcBSb1Z8UKbubR2Dl4aJ350nZXRqgGezz0+2X+PE7/5W1uXv5\nvYf/E3cvP5xwUzRoIXtrzDPNVxBkrHcH0AYdGFSQXXYQKI2a4Hgtyq5AKXQBdoX3vn7JrMz37yK5\n8uaCfpr2synKMam5IC9XGX1r1PGahyu8hqP0rWjbfnaV1bcmNReU8dmtygVHXHl8q4rXyc8FWRNq\nU1funiVaKEQ/YfO0y9MmnBE0xmTOBPXjCi9iPy5jjo6VyGtX1uUvQoeo7UVyxXXQBnzdOy96u+uz\n2ekNtFYj64tdSx6OHfNqmmaXMRB0Nd2WYn/LZ/2dLt2mYuGiw9rVGvV5G7duYTnH19Dk1TQIDBub\nPuubPp2OwfMMCEG9Bo2G5OKaw9KijRAcs90A3sG52TsHOvhdDZsKtjWiYzAevUG0JVC2QNVsjCMR\nvsbqBliBAdUr6cYCYwmUa6HqDkJpnN0mTrOL9AKErzG2wDgWqu7SXZxBuw5Wq4u718LqBghfIYyB\nRu8scnWpjr5YB19jfdDC2vIRrQA6mq7qcH33dd5rvcvHZq7x4NwjWPUZdMMF28IIiZG9Qbm2JUHN\nwrgW0lO4O/vYHR/hBQgvAOOD6kBnC/ZugqVRD9yLfuAqLM5hZhpgJKKjEPsB4t3ecXMzKzVWPr5I\nfbWGO+ciXQvfHGm6ceBbK3WLpeja9YJ8K46i7iOn6S96fzBweCb7jhew0Q7QBpbr1rF18OEqgCJ1\nKFrTaJvw4bEIrjRUueDoIb3ovFL51mDXMHrMURTD1LTyrcmL1yL7q+L1CFUuyI7X+OD+PPlWEqZu\nkB6F1tURbEXbVcb+AF67vUczyJ58ubZcZ7lRzDFZb/9km833PbKiZ/GSw8NPLiWehz1of+12gG1b\nOBlvnwF+eWePPT9DB2MIPgLVtsjcGlz3NowzluzVzaZwSS9AO3Yml0DhrgUwm766Juh2+c3/+yI3\nNq5z78x9PDL3KDWrfqKdN1unc3U1+42+Nsz/5DnE9q3MF/r6rkfAuRuRcM74oe2WgH9/kU7C2edR\nFOlbeX0+66Y/jP76+hZw/0Kdi3Oj1WGSNa1ywfnhKqNvTTJXHj2L7O88cE2y7UVzVfFaLFfeeC1K\n97ztyupbIc7VmvQK0wsv67itA5zx9LLj/XV05gAdQPnFdVirSfptVAY5dBACHKDbhyssbTcZ7YTA\n1Gz61rbbEhrJgwylAt775au8/cpPuFi7xNMX/j2z9lx6l5j+JfdSAF7finvR8mA2+xoZZfB8DX0G\n6UX6VlmRJ8bU9M75VqgwdZjidzQVKkwdqng9f5jKN+nRMoV4uXUU8TKFpBmQIrniJQ9pMy55ufLY\nHr28aRtyxMvfhq1D1K6zcClt2O54bLZ9trsKgyZpm4W6LVlr2KzUXVwrXftB/KGzr2htB6y/22F/\nIzg2YLddwfI9Lqt315lbcUCMTtOmr9j3FOttj3b8DXHHwJ0As20wGlTNRteOvwWXEpYXJRcu2NiW\nYHdfcfu2otM10c6Q3QB3ex/Z8TGOhbcwg5qtJ7xR173vXwNZ18hZgbB79t5861e8+fKPmF1Y4aFH\nvsC8WcZq+djrLaz28UG2tiTBcgN/cQbVcOkVXyfFj0EIg9zdwt7dwH73Day9reNc9Rm8ex5Erd4L\ndgN7u42z20FERtrCEszdPcPytQXkpQZNrVhvB3Ri1Rp1S7I2U6xvhT6QFq/Dum9Fy+LiXMb0jnnb\n9xR3EnzLtQRrDYeVeu9YujS78tgebRcvixuUq6y5IH6tq1xwtlyQt02RXOOO1yyuPNd6GJqWNcaq\nZ7dic0H4/6OM12nOBUnl3afhGvX9YRiaSikP/z2PuSCOqRukhyJEv3z8xpIkZJ42Uf44Bu3vNFxR\njIIrXpIR5Yrf0JOS17B0+KjZZbPt4ymDbwzH3+T2zhO3peCBxcbhemF7SJpqpfEP1qbrwODUJU7D\nwnHlWDVVuneud6sd8Ouf72HaBtOld655RCvs3hvziw81WLmrRq0mcZ3jtgeBxvM0uxsdPvzRnYM1\n3+o4lwDjSoxr07q0iDkYSJv4MWtCsbn5Dm9dfxHLcnjwkd9lafHe2Bt7jVQa6QUYbcCxMLaFltGH\nht5gHMJzcQEjDrbHO+ISRiG9NrT3EQZMvYGuzWCkc4xLaoXwFZeXJRcvu7hzDnbDOVa9EGiNrzRe\n0Jt4cK3h+taw4jVPf3l8qxvoXmGGPDqTfVCucd4DB7WrygXlywWVptOtQ9p37NcmqsVpbZ9WTcep\nQ1k1zWNXXtvPc7xWueB0XMYkT4rBFA7S+2GS1yiM2vayroV8/fYu+xnriAEWXIv/bi29bHqQ/sbh\nD0VxtbZ9XnthC9OnUvnjTy8xv+Jmttl8c5v3XriVTQQ0H7mEck6eNb6zfZO33/w+ntfioWtfYPVC\nwnFqMfQOO8tuQ0oFxQkuoTEmu91jH6+x1OfseajitWiuPHoW2V+Z7ap8q3iuPKg0LW9/Zeaq4rVY\nrrLmgsq3poOrjJoGQYBtJ68+r9akV6hQYaho7m/w9lsvsrdziwce+jyXr3wCS5Jj8D0GlNCkChUq\nVKhQoUKFCucLUzdID9cFRGdK4qUHSSXx0d8bYw7/Pw9XvE2UK6u/OFe8VCvLriyuNNvzckX/fhAd\nsrjy2h7+TZbt8zUbZXy6qvcO9TgMjhRIDIFSyAOeYWmaV4ewXT/f8lWvlFgIsITBsQRWjCsINJ6v\nUYFBSE3NFTiOdaI/z9N0lEbUBMY3EMSXBtA7X9yC3R0fWZfUXIltn7yGfjvAAMKh91Y+6ShxV0DD\nQlga6Wjae3vcePsl1m+/zX0PPMEnHvtDbNvGdQXhpvGeB/4JuwxSa0SgejFhSbRtEX9bLoSh5gqs\ngzLrrmcIAk5wOY7AdcAYiVLg+WEZfkQGaXBdge/n99MqXo/+poh7YPhvGeI1XrZXFFdRvpWXK49v\n5bF90n0rxKjiNcuupDaj9K2iNC2jDtWz23TEaxlzwaC+lcWVV4fw5/MQr6PMBaOM1yy7on+fhqks\nd4+KEyJJ6PCihz9LeXKjgtNwJbUZhCt+SfJw9XOSvFx5dTDm5BqKJB1Oa1ceTbuB5k6ry343QBmD\na0nWZlwW6w4ytu4jXuJSlA55bO/H1Q16g+neBngBKnL5Zx3JhYZDw7LQPuztaT66E9BqHzVyHcHa\nqmRl2ca2BZ2u5vadgO0dzaG5xiC6AXZX9Y4ck6AdSVB3eruvH6BWE1y6YLE4b2H7Ad6Ox9YbOzQ/\nbPfWh0dhATWJmbNRqy7qrhmoW3idNm+/8lM+eOM17r7/Me7/2G+zUJ9ldkZy6YLNwoJ9qEUQGNY3\nfDa2fPY3fUzLR+60cXY6yIPdxA2g6g7B2gxmtkZ9ucbcrOTSBYe5OeuQy/M1d9Z9trYCvKA3gF9b\ncVhdcbBtcaC5YWc34PadgFZbIS3B/JzF5YsujXr/dWZFxP5ZfSuebJK4ks5CzmP7MOM1iSutvzLH\n6yBceWzP4qpyweljLClex+Fbw4zXafetNNvHGa9ZuWBQTUfhW5MQr1n9VblguuK1n11CHJ2Tfh5z\nQRxTOUgPoXW1Xq1ou8rYX5m54jeBJPy3j3ZpqewwVHuGYLN/4YsQJ98Sn2zTf2022rDw1ofgnbz5\nROF/dhl9oXeeeeD7vPvffs6vX/0Zlx+4xkOf/h3qs3PULcknLsyeqAiI483/5x1aH3Yy28zdM8OD\n//3VbNsprz+M2rfKantZucqoaZULpoOr8q1iufLoWWR/54Frkm0vmquK12K58sZrUbrnbVdW3wox\ndeXuFSpMGvIvg04oV4+3yDPlZkzvv6ybhDE5egMTeChl88H113nr5//K8uW7ePI//I/MLi0ftdGK\nwPewavVsrhym5xVLGZNjK7kKFSpUqFChQoUKFcqHqXuTnlR2ECI6w5HWLk+baLuk8otBuKJlH2fh\nipdOJJVynIUrDVEd0lwp2l9SWV+8HKVIHfLaVZQOWe2i1zraRhlzcKSVYaPjsdNV9CrLDWAQiF6p\nuRaYQKC7EOxLCEJ9NAJxMIANh9aR48+MQXgKuxsgA91bTy7AWALlWqi6DZYEpbE6AZanEMogAo3Q\nGhEEiJaHDAIwAV77Pbqd6/j+Frd1h9/QoOY4PPTII6w+/nlkY5buzi12rn+P1q038HfvYKGZW7rI\nypWPce2Tv8/a3Q+hjWBj02d9M6Dd0XTbCjzVK8uPnF1eW3ZZeWSRmQt13HkXu3E0kxzqHmjDZstj\nq+PRVZpAgyMFdVuy0nBYqrtYUkxcvMZLEwf1rTS7zmr7eYjXackFRftpGsqWCyD9mNVBufLqUNZ4\nHZY/lDVe89hV1ng9Sy44bbzmsf08P7tNUy4YpaZn6S+Jq4yaFpkLEj+ftkF62sA07ixpJQlRIdPE\nOw1XWpsoV9bFysM1LNvLyjWtmnYDxWvrTZTJeJetDf6GwLQFJ84iP2JDBBp3swua9FfVFkdj+6QN\n4Q64gt23aL/zf6KCJtvG4Tf2IgBXgx2WTBcAOTvPbfMRvuoQdPcTmWy3zspD/4G1R/4sYaO3o/6k\nUnzq8VlqDYllJ5d4aa15f7fDetsnSNXLUJOST1yYQ4rz7VtVvI5fhzxclQ6Vb42b6yyajtv2suiQ\nl2sSdKg0HQ9XpcP58K20z6euIjRN+OhsX9aagWibIrmy7A37yppNGYft8Rmjs3AVaVe/NqGWWf3l\n5RqW7Vlc9uHsW0ZttxRgBL215Wntem0yB+gACgQmY4De49KqxY7f4XVrhV/bS9yl9njMv304QAfQ\nzT20nz5ABwi8DsKaIwjSJhcO+rNsLDd9gA49LTtK9zauz+ICwFTxWsXrQLb3s2sYmla+VXx+LaNv\nTbKmw+ivrFxpqOL19FxpKHMuGAdXGX2r7FxpKLOmWZUE1Zr0CqnIcuQKQ0auteWj667Z3eZXG9fZ\ncta4J9jlom6mzvCZjBvOYZuctudxwfxeOt3+XMVrhWGh8q3ikVfTSvsKg6LymfGh0r7CoMjymakr\ndw9nJMLZkqw1EXA0w5E1kxFyZbUJuaL9haX30RL8s3IVaVe8DeTT4bSankWHQGm6StMONLvdgPma\nxYxt4VoSx5IDcYVnkbd8xa6nWKrZ1G1JzZLYA3BpY/CVoqsMLU/RCgIWaw51Wx7YZR3qEOoWR6iD\nUhrfN3S7mu09xYfbXUQdhGN65ehS0FuffrTmXHkCvS8wnoAAtBKHn4WX12iNbCls/+DoNUXvzToG\nLAE2aEuibIkV6N6xZ4rDM9U7qslbt3/Kre0bXL38GJftNnL7HXRrE9PexgQeILCcOpasYZs6gTJs\n23fomCa+aeH5TQDcxjyzCxeYX7nMvR//IrW1z7Hb1HQ7JnJ2uUHaBmwQrmHtosXanEvdkjiWOKZp\niG6g+Kjp0fIVXW3wdc92gcGRgpolmXMtLs/VsCJ+H4+LEFW8cqLf09peJFeRmqa1gZOlbNG/SdM0\nbtsocsGwuCrfOv4dyx6vk+RbSVxxvYp4dov2O42+VcXr6HNBHINoOu4YOy1X5VvHv+Mwc0Ha2/ap\nG6SHCIUKxU1Dv/UARXPFJxGK4Mpje5Fco9Rhp+Ox0fbZ6qiDNdrHIQUs1iweWJzBkulcxhi2Oj4b\n7ejGbMdhC8Fqw+aehXrmcWHG9DYpu9P22fNU4ltoRwouzzpcmq311fT2HZ9btwP29jWJ0Wgb7CWN\nNZO+I7vRoNsQbByUuCe9NTYGERhkx8fYEl2zDwb/MWiD2m/ym/d+ynsfvcaVuz/B/Q/8Do7biFBp\n9M57WL/4r7gtRU3MI8XJsnTfdNlpbLH4mYe49pnfZ2HlysnuDs4uf+tmh6CmkfXkr+lKwZU5lwsz\nbqqm2hh2Oj673YDlusN8zU71iaL8dBgxViRXWe9bo9a0ygXl1HQafKtIrrJqOok6jFrTyreK5yqr\nDmXXtPKtyY3XKPK1mkBEZ1OyIKXsK1ZerpAvz+f9uIzJXj+bp69oP0VyjVKHnW7AejtIHKADaMPh\nAD6LSwjBRstjq5M8QAcIjGGzE6D7zFsJIbjd8thNGaAD+Nqw1Tm5G2oS181bHrt7KQN0gEBgOmTW\nfgsJ1ixIC1LLuoXAOBK94KAbTuIAXamA3/zmp/zw5f+dDh0+++T/xLVHnj42QO9RSayl+5hdepSG\nXEocoAM4osZds4/wyaf+Y+IAHUBKwfKSw+yawWqkf01PG7a7Qfb6HiFYbrjcu1Bnoe7kiv88n/fz\nrUG4sjAIVx7fiv57FtvyxmtRXOO4b5VV0yoXFMtVxesRJtm3hBB9+Uat6bh8Ky9XFa9VLoj2U7Z4\nDXWfZN8qIhcca5+75YQhWm6QBa113xKGvFwhXx6ufhCif2lFv88H6TcP1zh0mHdtlupW4gtf6A1H\nF1zrWBlzGpbrDguulboyWQpYqFm5Ami14TDrpIePdcCVNeA3xrDX9QnqGuEoslaGa0+g9ntvzJMb\nGORHe9Te+wjZ7qQv+lYauR8gOv6xNlprbn7wKi/94H9jZ/smTz/zH/n93/8jFhcX06xH2Ab10D2o\nuy5h0mYqHRv/7ivcbvv4Kt0njDGszriZmtpCsOBapYzXPG2Ljtd+bcalQ9k0HSQXlFHTKhcMh6uK\n18n2LWNMlQtyclXxepyjitd8/Y4jXvNqUTbfGoRrENumrtw9KqaUJ3fNE+LkGkPgxO/isiRxxSHl\nyfUI4e+i3HkCLc4V/q3W+tjMVZFcoc3hv0mD1TRN+3HFdUjjSrM9XEfe9BXbXZ8F12HWsagdrFOW\n8qQO8e/Q66+3jtxThn0/YMdTrNRsZpzB17crrfGVoasU+56i6SuW6w6NyPr2qB3GGAJjuN302OsG\ndJXG1waD6JUEaDC+IGiD3hMHb5QFYOjt4m6Qlumt13YMUnapv7eBtdFCND1Ey++tN3ck2nVRNRdv\ncRF/bhE76J19TsDRmnRbYCTc2n+Xtz54ibn5WZ764pd44IGrOI5ESoEfaLyupt3R3NkI2Or6WDMg\nbHO0Vl5rRKeD2Gsib6/D+x9hHrqKWVnCzM5gajUQAkv0StZrlmRtxmGp7qRo2tt/YNcLaPualbpz\nbM+AqG+F/jbKeE2KjTLE6yAxFv0OebhOa/sgXEnxWqSm05ILQq5h+laUa9BckKVpEbmgjPl10JwY\n/q5sOozat7K4zhKv0bbnMRcM89mtygXZXEn9VfE6OZqGfzvqXJAUszCFg/R+0Fr3LUfI0wbSb4aD\ncoWXoAiu0BmK4sqjw6i5lNaZa8Yhv6Z5uIq0/a3NJpudILON0eB9IEFn2z7/qzdxtvYy2yinRufu\n+0gqmtls3uT6rZdQOuD3/+AZHvvkxzP1Wm92ubHdhj6aojX00eGe+Rp3zdezeTgf8VrGGMurQ5gc\ni+CC8mmax2fytqtywXi4yupbkxyvk+5bVbwWy3UeckHlW/nblJWrrL6llMKykpeMVkewnQF5H+D6\nIWmdToToAAAgAElEQVQ26ax8RaCs8zd5v10eHYpRagDk1FRw8IY9q80pr/Nue4M3PnqJ/c4W1y59\nlruWrvHAfcv5+PJoKkXfI91GrjvljdeiMGqbynrfGgfK6lvTngvyoKx+VcXr+FDFa7Eoqw7jwLT7\n1iRjEp/dpm5NetaXDcsQskoW8rQx5mhtxVn7C7ni5Ran5QrbFMEVlmmkcYW29ysDGYemUV3PyhW2\nyeLyVW9DOpXBpbTGlhJBVsnMwTFrsvf/aRBotJBg99k4xxIHA2JDy9vlF+99m5+883+zNncvv/fw\nf+Lu5YcRtkApQ9BHB0sKbJFtl6S3eVv2MN0Q6HzXp4y+NenxGu37LP1NcrzmzQXR75nWX+VbR1xl\njdcy+lY/rcocr2GbMnFVueCIq8oF58e38txHwraj1LSsuaBs8ap19pv2qSt3Vyp9R+1QiOjgMoqw\nXCf8fZqwxpjD0oSsCx4tL8m6SKFdedqktctre5TrrDoMkytN0346xNudRVNIv4ba9M7j7gaana7P\nZkfha8OsI1lr9NbLO5ZEAN7B+e63Wx5NP+TQHL1PNhwf1gqMAd0xmJbA+ALjg/A10lfItoe90cLq\n+AitkLqD0L3/BzC2jbYd/MY8qj5HV3d5+/bL3Nx+k/vWfosHLjyOXa9BDZiXsGZBXVC3LdZmbOYc\ni5ptYcveAD9M+lJKlDZstT022x5dpfE02ILeWeQ1mwszNVxL0PQC1ltHZ5cbA64laNgWqzMOCzUH\nKcRI4jXOVXbfSuOq4rV/f1FNx5ELkrjiduXVIYy7tDZpXNF4zdtf5VvnJ17H4VtJ1zBue5lywSif\n3U7TX1l9q6y5YBQ6VLlg+FzTngsS+5q2QXoU/WYoiubK21+edllrFMZpVxn7GwfXG+v7bHsqs408\neOusTb8yI0O/AnD5zj7263uIzBfUBm95DmPVAAiUx6/Xf8G7G69y19LDPHjx09TsGbhPwqWUM9IP\nIIDHL87h2tk+2A0CXCt7R3xtDIHSfbny6J6WrE7DVVbfysuVR4uy2l5WrjJqWuWC6eCqfKtYrioX\nFM81ybYXzVXFa7FceeO1KN3ztiurb4Wo1qRXqHAKpJ3bHkXaeeyngYDsATr01otbNkor3tt8jbfv\n/Iy1uXv5/EP/AzPuwlE7S2QO0AeB02cWEHrl73ZB/VWoUKFChQoVKlSoMO2YyjfpSeUhSbMb8TKF\nfm3SShOSyjCSuKLlXFlc8bKIYduVV4dhaArJxw8UrUPRmnYDTVtpNtse2111bEBesyRrDZs5tzfj\n2fQV662ATuSccClgsWaxWndxLIGnNOttn92uOraau2EflM8Lgdj12bvZYvuNXfzm0Q7x0pUs3j/H\nwv2zXH//LX740veZcZd4aPWzzNfXjshmgYsWLEqoiYNR/3EdbClYqVss1RzmazYUqGlWm8q3io/X\nOCZV02gZ4Sjsymt7tIww+vsqFwzGFUUVr8VzlVHTNLuqZ7fB7Kp8azCuYWh61lwwDh3K/OwmxNEx\nimXTYRS+FcfUDdJD0aMipq1liAuUdDMbN1e0TTQYztpfkVxptke5ov0NU9OkNnGuonUIz3A3Biwp\ncCPneYdQutcmUBpE76zw8Ez2w/7M0RnuYLClxLXkiSPiAk/hN32CrkLaEmfG4p333+E73/kOjuPw\n7LPPcvXeq/hdTasZcGO7jbIB5+QbdHGwNv7KnMty3Tk4K/74gKjyrfQ2ca4qXgezq+w6FMlVpKaV\nb5U7Xs9qe+VbZ7d93NenygWD2VV2HYrkquJ1/L4V5xq3b6UN2KdukN4PWk/uGoVR234e1r+U0fZB\nuG7evMlzzz1Hs9nk2Wef5ZFHHjn2vVu+4rU7e32Pc/v46gzzNWektk8yVxWvxXKVNV7HYVflW8Vz\n5UGlaXn7KzNXFa/FcpU1F1S+NR1cZdQ0CAJsO3n1ebUmvUKFCcSdO3f49re/zYcffsjTTz/N448/\nXtjDaoUKFSpUqFChQoUKFcaHqXuTrvXZy92HVYpSZAnGpJVznFXTtDZl0MFXmq7qrc3plagL7DOW\njKfZvrOzwwsvvMAbb7zBk08+yRNPPIHjOKk6BNpwY6t1cFyaib1RN9hC4ErB3Qs1Fg/epJdB02kr\nmZq00r4i43WS71tFclW5YHLidZrKRivfKp6rygX5uabFt4rkquJ1cnLBqOI17SXb1A3SIVmgJAHi\nYudpE78Yp+UyZrI2TYprmmR7Xq48OhTJVbQOWmu6ytAOFBud3mZv0Y3jXEuwWrdZqvfOS8/qL+tm\nEG3XarX44Q9/yCuvvMJnPvMZvvCFL1Cv13PrYIw5Ors80FgCluoOKw0XJ75+fkib5KS1GVa8Tqpv\nFa0pjOa+FU8lSVzj8K2iuAaJ1zxcURsnORdU8TqZvlXWeD1vvjXKeE3rLy9Xkb5VxevJNlUu6Nms\ntS5tvA7bt+KYykF6iPBCj4orb3952k3ymqJR9zcOrl/e2WPPT56dCzHnWHx8bTbxRpO3P9/3eeml\nl/jRj37Eo48+ylNPPcX8/PyZbJ9k34omxlH0V2auPFqU1faycpVR00mO10n3h8q3xmNXlQvGwzXJ\nthfNVcVrsVx547Uo3fO2K6tvhajWpFeocArkOff7LEeDK6X4+c9/zve+9z2uXr3K1772NS5cuHB6\nwgoVKlSoUKFChQoTibwDuwrTg6l7kx4vJ4ginOFIKk0Ifx8tixg1V97+si5Z2C5apjao7XC8TOYs\ndhWpwzA1TbuG0fKd4yU04OveWvTdbsBGJ8BThjlHsjbjMGNbvaPYIiP1PJoaY/jVr37Fd77zHRYX\nF3nmmWe46667RqJDkVxF+1aRMZY0izlq3yqaa9TxGi23y+pvULuGFa+n4ZqWXDBpvhW3fdri9bS+\nNez8CqON19P0N+m5YBqf3apckMw1initnt0mOxdA+lKJw8+nbZCeVUYQipklSjS40soWom2yuKIX\nb5K5sso3oo5XRttHxRUoBQiE4MS55klcSf3duHGD5557DoBnnnmGBx98cOJ0qHxr/Fz9NC2z7aPm\nqnJBFa/j5qritRgdqng9yVXFa/n89LzoUPnWYFxpn0/dIL0ftJ7cNQqjtv08rH8pg+03b97k29/+\nNtvb2zzzzDM8+uijmUE7KrvG3V+Zuap4LZarrPE6Drsq3yqeKw8qTcvbX5m5qngtlqusuaDyreng\nKqOmYz8nfX19nX/8x39kZ2cHIQTPPvssf/iHf8j+/j7/8A//wPr6OhcuXOAb3/gGs7OzAPzLv/wL\nzz//PFJKvva1r/H444+PwtTcyHsjyctVJIqyrajvlxdl1aForhAbGxs8//zzvPvuuzz11FN86lOf\nOkysRWlRZk1HiSJ1KKumVbwOh2uUfZVV00n2regbj6L4zrumId+k5oIqXotFWXUomisPpt23Ro3z\nHq8jeZO+vb3N9vY2999/P51Oh7/5m7/hr/7qr3jhhReYn5/nT/7kT/gv/+W/0Gw2+cpXvsL777/P\nt771Lf7u7/6Ozc1N/vZv/5ZvfetbuWctQkgpj/0MR9v7x0sxQhnCN5hxWYriCksj4lxxhH8X/9s8\nXHHHOY3tSf1lccX/rp8OaVxx+8+iQxxpXEk6BFrjKU07UGy2AxxLslyzqdkSx5LYA2oafialZHd3\nl+9///u8/vrrfO5zn+Nzn/vciVm0ojXNo8NpNR22b502XgOte2fYB5qtboCvNCsNm8bhfgGyL1cV\nr+lcSQlqXPEatT0p4Y0iF1TxWqymYfu0XDCMeI3bHuWqfGtyfCvKmce3qme3o5/76ZDEVeWC41xV\nvA43F4wiXkedC5L4YERv0peWllhaWgKgXq9z9913s7m5yU9/+lO++c1vAvD000/zzW9+k6985Sv8\n5Cc/4Qtf+AK2bXPx4kUuX77MW2+9xcMPP9y3r+hAPhQm/uWjZUChoPEJgOjfGGNSSxbiXEKcPCcw\nL1cUw+A6qw5ZXNGfz6ppUn/D5Irq4AWKD/e7bHQCgujh5yjutHwA6pbk2nKDumMNpKnv+/zgBz/g\n5Zdf5pOf/CR/+Zd/SaPROAzSOKLc4WYyZdV0mL51mni9udtmvR3QUcdvmNtdBfR2579/ocZS3Z1a\nTcP+pjle02xP4xpmLpgkTcsWr2X1rbR7cxJX5Vvl8q1wMJHX9n52TbKmVS44yVXFa7ni9TS2T1Mu\nSMPIj2C7ffs277zzDteuXWNnZ+dw8L64uMjOzg4AW1tbXLt27fBvVldX2dzcPFV/abMTIfIIlTRz\ndNr+8nLlcYgi7cozi5eXK+TrxzFqTfNwIQTrLR+V0aSjNJ7WNER2+IQzdEEQ8OMf/5gf/OAHPPzw\nw/zFX/wFi4uLh+3y2J50E0lqM+2+lXQDTGqz0fboZFzEQBtagWKlzzl5ZfXTpBnotP6mOV6L9K1B\nNM2DKl6P+PpxVL5V+dagXHlzwag1DduOiiuPplUuGJyritfxxGteTLNvRTHSQXqn0+Hv//7v+epX\nv0qj0Tj22Wku3muvvcZrr712+POf/dmfHf5/v5KXeLs8bfLc5PrN3OThCj/rx9Wv9GIQ2/M44Kh1\nKJIrb38Cw13zNe60fTrBSU0EMOda1GyrL5dSil/84hd897vf5cqVK3z1q189dta5Noadjs9ON2Cp\nZrNQd5AxPmMMHaVZb3axpWB1poZrJWtxHnwrb7xema9zp+Wz7ymSbod1WzLvOiP1raI17Rc344qx\nPL7V76FxnL5VBFdoW5ULJjcXFKlDWeN1HL5VpA55Y7qM98C8XJMYr3l1CDnKpkOVC45zZWHSx1p5\n+htVLvjnf/7nw///xCc+wSc+8YnRDdKDIODv//7v+eIXv8hnP/tZoPf2fHt7m6WlJba2tg7fLq6s\nrLCxsXH4txsbG6ysrJzgDL9EFKGYQojDGYsspw0vcvwiRNsmcSVhEK6wfCKLK6m/OFcYtINwDaJD\nFOPStF+b02qaZLtjWVyZt7g46+IdrGfe9XxsKZlzeoNzR2brYIzh+vXrPP/888zMzPCnf/qnXL16\nFWMMbc/no6ZH01d4yuAbAwhutzxcKXClYMbprZne9QK8QONpg6bHfXO/165uSy7MuMy7VmG+Fdd0\nkn1rbabGSt3B14ZuoNj3FYE2LLi9fQVcSx4elVemeD2rDv240mxP4ioiXpNsn3TfKksuiH/HStOz\n54Io13nUIe07Vr5V5YIqF5TXt+LfcZI1De/D49Z01LlASnnsRXOIkQzSjTH80z/9E3fffTd/9Ed/\ndPj73/7t3+aFF17gy1/+Mt/97nd54oknDn//rW99iz/+4z9mc3OTW7du8dBDD+XqKz6zEl70EGmz\nL9Hfaa0Tj68okiv+d1k3sEG40mw6re1Fcp1W09P0lzablZfLkpKGlDQcWKjZuXV47733eO655/B9\nnz/4gz/goYceOnbT+GC/xeaxOmxx+K+nwdOG/SAAzLHPQigDbWVoK8XFGXL5VlGaTppvSSmpSajZ\nFgv1Kl4H5ZqkeB2WDsak7xcx7lwwbfE6TE2TUIZ4zaNDWmycRofzmgvKEK9VLpjsXFBm36ridbLj\nVan0tZkjGaRfv36d73//+1y9epW//uu/BuDP//zP+fKXv8w//MM/8Pzzzx8ewQZwzz338OSTT/KN\nb3wDy7L4+te/nhi0FYaLrNmnCsfx0Ucf8dxzz7G+vs6XvvQlHnvssWSfzSmpwGDI9vnq6lSIoorX\nCsNC5VvFI6+maYOWChXSUMVrhQqTg6x4HckRbKNEWkIz5vgW+2kz7dEShPiMyLi4Jtn2cXAllZEM\nq7+trS2ef/55bty4we/+7u/y6U9/Gtd1U7lu7ne50/QOy9xPwmAjMAK0SR+oS+CBpQbLdbtQTcty\nDSeZa5JtHwfXJNte+Va5uUaZC6aNa5JtLwvXJNs+Dq5Jtn3cXJNse5UL0j+fykG61skL8+OlCkno\n1yYsfwz54xcijSs8Qqsf12ltP61deXXIW3J32v6ijl60Dmfxh7hdoabNZpMXX3yRV199lSeeeILP\nf/7z1Gq1TK6wP6UNW22PrU5vc7pAG+yDdearDYelhosA2oHmTrNL0w/oBgYpoGZJ5mo2F2Zq1Gw5\nEh2K1nTcvnUe4jUNkxqvxpjEY0z62TVMTUO/DduV2bcmOV7LoMOo4zXuW2flKqtvRa91kb6Vdn2q\nXFA8V5ULTp8LJi1eq1ww3HhNwtQN0qPQuv8ZeUVy5e0vTzulVOKaiHHbVcb+RsnV7Xb50Y9+xI9/\n/GMee+wxvvjFLzI7O5vKlXYTiyJQCrvPtQ6UworcGE5je4hJ9q08ehbZX5m58mhRVtvLylVGTSc5\nXifdHyrfGo9dVS4YD9ck2140VxWvxXLljdeidM/brqy+FWLk56RXqDCJCIKAl19+mRdffJGPfexj\nfP3rX2d1dbUQ7vixa2lt8gZ1hQoVKlSoUKFChQoVJhdT+SY9qTwpPrsRL3eIlzCEiJcoxEttwt/F\nZUxap5BU7hC3K0+beLu8tidxnVaHUXDFNe2nQ1q702gKHNr96quv8vzzz7O2tsaXvvQlLl++3Nf2\nMmqaVJ6Ux7fiZZfjsH3YvjXKeD1Lf2XWNF4+Nsx4zXsNz2MuOA/xOo5cUAYdxpkLsrjy2F7F68l2\nZfGH85ALxq1D9eyWj0sIcXg9z2MuiGPqBumhCGe5yUaDYdg3hEnlSluHMWmaptlljOHNN9/k29/+\nNo7j8Oyzz3Lfffed2a6y6jCJXJPqW0XbldQmT7yW4RqWlWuSbS8rVxWvw7P9vHNVvpWfa5JtH4dd\nZddhErnKruk4ckHSBAFM4SC9H7Se3DUKo7b9PKx/SeJ6//33ee6552g2mzz77LNcu3ZtYnUokmuS\nbS+aq4rXYrnOEq+naVNmuyrfKp4rDypNy9tfmbmqeC2Wq6y5oPKt6eAqo6ZBEGDbyavPqzXpFSoc\n4M6dO3znO9/h5s2bPP300zz++ONIKRNnxCpUqFChQoUKFSpUqFBhGJi6N+nhgCo6cxEdZEVnUaIl\nCtEShvhMSxpXFNE2aVzxkohBuaIYFtdpdJh0TXd2dvje977HG2+8wRe+8AWeeOIJHMfJxTVNOoQY\nN1elaX6uUcTrWW0vk6aD6pCXK4/tZdKhLL6VxZXH9jJpmtamSE0nQYcy5AIheutap8W3yhKv5zkX\nTOt9q9L0JFcUo8oFaZUvUzdIh5NfXsrkxfnRTUrSRDLm+GL/+AULEb8oSeUNcSdIK4EIubJsz9Nf\nkVxRHYrkymN7P65BNIWja9hqtXjxxRd55ZVX+MxnPsOTTz5JvV5PTPBJXEXrcFbfKkrTsM0odRg0\nXrO4yuBbp+kv2m7a4zWPb4Vtirrnli0XDKJpqENZ4rXMvpXVJs7V7xqed02nKReM8tntrP1F202r\nbw2i6ShzQXygWbZckMU1DfctKWUu2/txTWouiGMqB+khwgs+Kq68/eVpN8lrikbd36Bcvu/z0ksv\n8aMf/YhHH32Up556ivn5+aHYFZ8pPKvt/TDtvpVHzyL7KzNXGX1r0rnKqOkkx+uk+0PlW+Oxq8oF\n4+GaZNuL5qritViuvPFalO5525XVt0JUa9IrTDyUNnQCxYyTfZa4Uoqf/exnfO973+Pee+8t9Kzz\nSULem0OFChUqVJheVLmgQoXJQRWv5w9T9yY9Xk4QRVjOkNUGOCy3yJImnC1JOtcTjpc8xMtZ0rjS\n7Ipz5bErD1ceHbK48rYJ251VBzi6Se11A9ZbHu1A0VUGbcCRULMlizWb1ZkartXb9M0Yw+uvv84L\nL7zA4uIizzzzDFeuXJlYTaOlr0X7VlFcoe5nudaD+tZZriEc3R+qeC02XkepabQ8cdS5YNQxNunx\nOmm+NSjXpMVrmX1rlM9u0f7K7FtVvI4+F/TjmpZntywM27fC7zMI1yTEaxay3r5P3SA9C6FQaWsP\n4PhahizhiubK4olyldX2kG8Udl3faLLnBRjS9VpwLB5eneGdd97hueeeA+DZZ5/lwQcfHLi/cWha\nNFdWm+gtIMsH8/jppPtWUfFadn8YJVeIsvlWXtvDZDtKu/rFa5G5oMgYG3W8hv9W8VrlgrLmgjI/\nu42aK/y3itfRx2ve/s57vI7LH9J4ztUgHSZ7jcKobS/r+pfXb++yH2S7bbC9ztsv/5Dt7W2eeeYZ\nHn300UR9y+oPZeSaZNuL5qritViuPHoW2V+Z7ap8q3iuPKg0LW9/Zeaq4rVYrrLmgsq3poOrjJpW\n56QfYJD5iH4XMu+NJC/XIHxF9JcHYclHEVx57cqlgRBAcr/NnS3e+OkP2b51k2eefopPf/rTmckq\nr/Wj1mEcXKPur5S+lbOvIjH18ZqzL8h+GzANvlXlgvx2jdK3BuU775rm7a+sXFW8lte3yhqvebny\n2J33+pTRt8bBNe3Pbueq3D0sL4DeF4/+nPS7UOCoDHn+LvzbeFlHXM60v0sqUzkrV7RkIovLmN5a\nnTx2neX7xDWNrwGL2x6WhPTTQRlYb3nsdH26gcbThnaryY2f/Ssf/vpNHv3kb/OFJ3+HlbmZE3Zq\nY/CUphtotrs+e55mqW6x4NrULIljSWSCpvEb5qC+FX6PafCts/pIVNN+f3ce4jXuW3niNUmHUcdr\nnnvNIDoU8X0q3xqvpnl9K0vTQXJBUTlxUB3OkgvStMqyofKt8xGvk5oLhhGvlW9V8TppueAs8RqN\nr2P9mrh1U4S8pTXQf9Yub/lDlthFc4UOUlSJUVFco9Sh3W7zvRd/wM9/9jKf/OQn+eLv/R4zMzOJ\nbW/utlnvBHSC9E0cFlyLa8szWNb51RQq3zoN1yh1mGRNy6pDlQuK56ritXiuyreO2pTRt5RSSJl8\nTnKIStMeyqpDlQuK5yprvJY1F4Q4V+XuSeh3kcfFl+ciJs0AnRZFcoV8w+QKgoAf//jH/OAHP+Dh\nhx/mL/7zf2Z5eTmTp+mrzAE6QDvQaAz9V3P1R+Vbw+Eatm8NC0XrUCRGqWmZfauM98BJjteQr4xc\nefqa9nidZN8qay7IY1dZNQ35RsVVVh3Kqul5iNe8Wp2XXDC1b9Kj5QVpTh3OaEC2Aw3KlRVEw+A6\nq+2DcoUlHP1sH4amWmt+8Ytf8MILL3DlyhWeeeYZ1tbWcvW37yl2uj7/f3v3HhxVff5x/HN2N7ub\nhIQQQFTASREURQXKRSsSENTWeqnVEatOvbRVexln7B/UTu1QO3XamZ+jHeu1U20rMx2n1LbOOJ3p\nHyIBh4pJECg3qSBKAbkEAglJNpvdc35/wNluwu7mbHKye87u+zXTKSYnz3n22e+z3/3ufs/usZ6E\n4ubZwz4aDOicqpDGV0UUCLiXO2PLnVjU9OzzlXMd3IxFTYcWq5hzwVBjeXVspW8pZmw5z91LY6tU\n5oJC15Sx5f+aujUX2AviUqyp0zqkK7lF+sBiphfFss6+yD998Zcu/djhxBp4nH1Mrljpd16+sbLl\n7jTWwDqky1SHTEaiDslkUrt27dKaNWtUWVmppUuXavLkyTlj2TEGxupLJtWXtBRLmuruS2hURUiR\n0Onr0UN51DSfOmR7Ja6cx9Zwa5pPLDfr4OWapitmvxa7Dm49fg9Ev7rTr5mOGcl+tWMMN9ZI1oGx\n5d5cEAgEUjGZC8prLsi3X5kLvDMXFKJf7RjDjZWtDk5jDaxDtoV9yS3SB+PWNQpux8rU3CN5Pj/F\n+uyzz/TOO+8oHo/ruuuu05QpUwb9ehEn9SxE7qUUy8+5ux2LfnU3llf7tRh5Mbbcj+WEV3P3Yiw/\n5+52LPrV3VhenQsYW6URy4s1zfWViWV/TTqyK/brN4cPH9bq1at19OhRXXvttbrssssUCJz9qYsA\nit+vKF2MLfdRU4wUxhbgH7n6teTeSU+apoIZXrUYuE0hfWtCPsdIzrYpeDWWaVrqSyYlQwrIUCiY\n+VNIncUamdzb29u1bt067dmzRwsXLtScOXMUCoU8W1N37x//5k4dvB3Lz7kXOpafcy9GLD/n7tVY\nfs59JGP5OXevxPJz7sWO5efcCxHLz7kXM1a2d9tLbpG+7WinxldWqKoiqMrQ/77zOhDovxjN9m5s\neqEsy5Jpmv3+zs1YA49xGsvp+ey7NmlZ6k2Y6kmYOtYTV2fclCUpaBgaEw1qTLRC0VBAkbSvHXOr\nDpbV/8MkstXBMAx1d3dr3bp12rp1q+bNm6errrpKkUgkZx0ybV0ZrKb23wylpiM5HoYTK1Mbj9TY\nynbcwAchP9d0qGMrWywnuWe6DwfWdOD31WaL5Wa/OslrJMeWF8aDn/vVzfvQqzVlLvjf3xW7X4d6\nPq/WlLkgv7xGei4oh34t5+duhvG/a9LLbS7IpOQW6c0HT6b+Pb2+UrXRsCtxTdM71yjkG2tXW6dO\nxnNvEa8MBXTpuOqMuxDyPV++dejt7dX777+v5uZmXX755WpsbFR1dfWQYrmZlxuxMj1YjOT5Cj22\nCl1TJ/V083xejuXFseX3WF6sqZ/71e/jgbFVnLyYC4oTy8+5ux2LfnU3ltN+davuTo/z6tiycU06\niiaRSGjTpk167733NGXKFD300EODftc5AAAAAJSyknsnffPhDo2rDKkmHFJVRVDBM69WDGX7SLbj\nhrJ9ZKjb3TNtm8i2vWLgK2x2rIR5ert7V19SR3vi6kmc+RoCSTXhoMZVVqiyIqhoKCA7oht1yJS7\ndPrVwG3btqmpqUnjxo3Ttddeq/PPP9+VOgw1r+FcjpDpmIGvlGW6HsUvY2s4sYa6lWsoW5OGE8sv\nY8vtcTpQprE1lPvQb2MrvV/dHFuSt+aCwfKiX0d+LhhOrIGGeh8O3Crtt34deL5yGFuF7Fc3z+fl\nmpb6umA4eRWrX+3t7k5j+WVsOY01UMkt0hNJU6Hg2Td6YBEzLZoyDcxMBSx0LKcDwMn5kqapePLM\nBxVIqggGFQhkzj39yYUbdbAsS7t379aaNWsUCoV03XXXqaGhIe9YufLy6n04UjUdbl72MX6uqSzC\ni94AABqfSURBVJux3Lh//Jw7Y8vbsYpVU6+NraHm5efcS3VsjUSsTMcUIy/GlvO8vD62vFZT5gL3\n8ypm7tkuYyi5RfpgTNO/1ygUOnc3r3/Zt2+f3n33XXV1dWnJkiWaPn161knUjdvopJ5unq8cYvk5\nd7djlXq/FrqmXu3XYuTF2HI/lhPU1Lvn83Is+tXdWF6dCxhbpRHLizVNJBIKhTJffc416RhRR48e\n1bvvvquDBw9q8eLFmjlzpmtPqgAAI8/Jk2YAAOCeknsn3d5ikL4QTN92kP4qSvr2g4HbstOflIxE\nrFzHpMfKdj6nsYpVh5MnT6qpqUn/+c9/dPXVV2vOnDkKh8MZY/Ulk4onTcUSp2NGggGFgwFVpH2H\ne751GChbTQfyck2HEss+NlOsoYyt9Fh+qkOuWMPtsVLoV7djDaVfncRKV4g6DFSIucCOkasO9Kvz\nOgxUrnNBrlilNrYM439fvet2XswF5TkX+P25m1/rkCvWSM0Fxahp2W13N00z4wN1uvQipRcvUyxb\ntljpx2SLNXCwZItlf6iLnXu2WPZtdJpXrjq4Faurq0vr16/X5s2b9cUvflHXXHONotFoxlid8YRO\nxPp0PJZUn9l/GAYNaXQkqPNGRRU98333btVhuPeP05q6FctJ7vnG8uLYGqxf86mDG7G83K+lMLZy\nTUxO7x+3xpZX54Jy6dfB8nJ7PNjH56ppMeaCYtTU7bFViH5lLsgvL+aC/8XKZy5wchudHuPVfvXa\nXOBWv/p5LkhXsot0yfk1A27Fcno+J8f57Zqivr4+bdiwQRs2bND06dO1ePFi1dTU5Iz178MnFUvm\nzmlSTVjn11SOaO4jGWvgq20jfb5SHFvpnNTTzfN5OZYXx5bfY3mxpn7uV7+PB8ZWcfJiLihOLD/n\n7nYs+tXdWE771a26Oz3Oq2PLxjXpHuX0Diy2ZDKpTZs2ad26dZo8ebIefPBBRUbVKhQMDjoQqyqC\niptJmTleJgoF/FEHP/HL2EJu+TzQA8BAPH4A/kG/lp+Seyc9/fs/7W0TNntrRPq2hEwCgcBZ2xLS\nY6VvjcgVy97CM/AYJ3kNPMbOa7BYdu7pWz2GkvtgsSzL0o4dO9TU1KTa2tGa9aVrFB4zXvGkqbhp\nyZBUETAUCQVUF6nQ2KqwQoEBt8kwzlyPbqm7L6mjPX1KmjrzPfdBhYNBVQQNDXxYcloH6eytMU5q\nmk8d0mPnqmn6Fh437x/T7P89vE5ijeTYMgzDlZoOZZwOt1/zqYPknbHlNJZbvZ8r1nDHVrb7MFes\nfHO3/7tYc0G2fs2WF/2aOxb9Wry5INd9aI+tgd/JPtJ1KOTYGk6/Zsvdi2NrKDUt1blguDX16rqA\nuSB3rGy5uzW2sim5RXou9mBwsmXBLm6uY6TcxbXP5yTWYMfkE8vNvDLF+uSTT/TOO+9IkpYsWaLO\nUePVl3MMWppaV6UxlRWDns+SFBwkd5uTeo1kHfI9nx2r1MbDSMcqZL/a/Hr/eO18jK38cy/lmrp9\nPpvf6mDHYmx5t6a2cq5pMXL3+3M3p+ejX4vTr05iFaOm2eKU1Xb3TK+Y5Do2FyevtNjncxJrsLyc\nxrLjuRHLfsXPdvDgQa1evVonTpzQkiVLdOmll0qSNh/qGCQjQ4bhXk1zDeiB8QaL5XZNnXBah1zH\n5TO23BqndrxCx3KikGPLy/3qJHc3H7fcGqeDTWL5xLJzcxJrME7yKse5IFcsN87ndr8Ophhjy8/9\nasdzI698YjnBXODdfmVs+X8uyCeWE/Qri/QUp4PGPtbJqyhOzucklpMHXctBLDuek1edBotlD7Dj\nx49rzZo1+uyzz7Ro0SLNnj07NQGYpikZkgYprWlZMi1LgUHqMNg95LQOTl+Ntf/frZo64dZ4KHQs\nO55bNXVyHzrlxX51EsuO58bYcjIhOF082P9fqJra8bzWr/ZxpT62nM4Ffu1Xydk7MfSrv/vVyfmc\n1sHJ/UO/nubVOuQTy4lyeJ7hxZq6+XxYGnwXrpNYdjw36lBW291L5Zp0GYaSpqm+pKVYwtSxWFyn\n4knVhEMaW1lx5rvET19DorRYbl570tXVpbVr12rHjh266qqrNH/+fEUikbPq0GdaOtrVq47eROqa\n9P6DypKhgGrCQY2rrFBlxenvQA8FAv2uSW/r6VMiwzXpliXFk6Z6k6aOx/rU0ZvQqHBQY6NhRUKG\nwmdiWRnqkO0+TD9uuNfMZb0P09jHO7l/8r0GJ/3BxEmsbHVwcj3PYHXIFitT7sOt6cBYxezXkapD\nvuPB72PLK/3qNC8/1NSNuWAkxmm+NS3E2CrG45af+5W5oHyuG843FnNB7li56sBc4H5N7f8u5GNg\nPmMrm5JbpKdzsv3Bvvm5Gt1pLCfHOD1uf0eP2rr7FM/x0efRkKFLx1YrNMi2pnzzisViWr9+vTZu\n3KhZs2bpmmuuUVVVlaNYlmXpQEePDnb15TxXKGAoGjLU3Wfm/HT36orTLwLEk9kPqggYumxctSpC\n7tbBjVjpT5oKcb5Sj+Wknm6erxxi+Tl3N2N5dS7wcyw/5+52LOYCd2PRr+7H8nPubsfyYr/yFWzO\nz+f0OK+OLVtZbXfPxGmhCi2WMHMu0CUpnrTk5kssiURCra2tWr9+vS666CI98sgjGj16dF4xDMNQ\nNBSUlHuRnjAtdcVNWWd9dnt/XX0JSbkHfZ9pafBNRrCV8OtyZcWrj11+lekVdS/wYk4oDX4fWzwG\nAihlJftOejKZTP072ytP9lYFSaktFUONZW81cxrL3lqSLdb+jh4d6Y7LlCFlXMhaCsrS5eNrFAoG\ncsay88qWezKZ1ObNm7Vu3Tqde+65Wrp0qc4555yMx9mvAOWqw4lYXHtP9CiZNXcpcGZZbUmysi7C\nLRlnlvG56hCQpcvG16gikDuvwe6f9PEw2P1jb3HJNbbsrVheG1v2bQwGg1nrYOc+WKzBxpbTWE77\nNZ+aOs3djfFgb9lyo6b5jK3h1rQcxpbTWE7nAiePgaVeU6djyx7Lhe7XXHml517ouYB+ZS4oVk2d\nPG653a9u18Gt+0dyZ2wxF7jfr/bvCjkXeO25W7qSW6THYjHF43H19PQomUwqEAiosrJSkUgkdSeY\npqlEIqHu7m7F43FJUjgcVlVVlUKhkAKBQKqYvb296unpkWmaCgaDqqysVDgcTsVKJpNKJBLq6elR\nPB6XYRiKRCKKRqP9YiUSCfX29ioWi8k0TYVCIVVWVqqioqJfrL6+PvX09Kivr0+mpG4FFVNICRky\nZSh4ZnFeqYQqlVRAUkVFRb9Ydu52rEQioUAgoGg0qkgkolAolDrfRx99pHXr1ikcDmv+/PmaPHmy\nKisrFQqF+sVKr6mTOpiSYgqqR0ElFFBShgKSQjIVUVJVSiogSwkZ6lZIcQWUOLNYD8pShUxVKaGw\nTn+YXE9aHU7HshSSpeiZOgQlhUIhVVVVpeogKVWH7u7urHUwTVPJZFI9PT3q7e2VZVmqqKhIjQc7\nViKRSMVKH1vhcLhfLLsOvb29qbFVW1ubeiBIH1uxWMxxTd0cW4ZhKBqNKhqNKhgMKhAIpOoQi8UU\ni8VSdRjK2LLrEIvFUjUNh8OOxpYdK1sdJCkSiaRi5epXezyEQqHUeLB7366DHcuuQ66a2vdPprFl\nGEa/x5r0mg4cW+k1TR9bTmpq1yGfmo7E2Eqv6cCxNbCmTsaWHcvOfaT6NZ+5IBQKKZlMFn0uyNWv\nucZWIfp1sDpk61enY2uo/VrouSBXv6bPBV7sV7/MBU6fuxmGoa6uroLPBaXQr4Zh9ItViLkgW796\naS4Y+DyD527uzgV2rOrqanV3d7var27OBSP13M2+nQOV3CL94MGDOX9vGM6/dmIwhYxlnfnfYK+7\nOD3foUOH9MEHHyiRSGjevHmaPHnyWa8iuVkHU8rxvvppTm+jk1hOFeo+rKmpUWdnpyfHllfP5+VY\nTng1dy/G8mrudt96LS8vns/LsZzwau5ejOX13AfrWy/eRq/XtFCx/Jy7V2P5KfdMvVsOc8F5552X\n8Xdld026k6I6vaMLGcvponSwOMeOHVNLS4va29s1d+5cXXjhhVm3XLhZh8E3dTi/jU5iOeXX8VCM\nWH7O3e1YhT5fqcfyau5OefE2erWm9Kv/Y/k5d6/G8nPubsbyc+5ejeXn3N2OVejzDTdW2S3Sy1VH\nR4c2btyoAwcOaNasWbr++usdfUokAAAAAKBwWKSXuJ6eHm3atEm7d+/WjBkztGDBAoXD4WKnBQAA\nAADIgEV6iYrH49q6dau2b9+uqVOn6s4771RlZWWx0wIAAAAA5MAivcQkk0nt3LlTmzdv1sSJE3Xb\nbbeptra22GkBAAAAABxgkV4iLMvSnj171Nraqrq6Ot14440aO3ZssdMCAAAAAOSBRbrPWZal//73\nv2ppaVEoFNKiRYuyfpQ/AAAAAMDbWKT72OHDh9Xc3KxYLKa5c+eqoaHhrO86BwAAAAD4B4t0H2pv\nb1dLS4va2to0Z84cTZs2Let3nQMAAAAA/INFuo+cOnVKGzdu1L59+zRz5kwtWbJEoRB3IQAAAACU\nClZ4PhCLxbRlyxbt2rVLl1xyiZYtW6ZIJFLstAAAAAAALmOR7mGJRELbtm3T1q1b1dDQoDvuuEPV\n1dXFTgsAAAAAMEJYpHuQaZratWuXPvzwQ02YMEG33HKL6urqip0WAAAAAGCEsUj3EMuytHfvXrW0\ntGjUqFG64YYbNH78+GKnBQAAAAAoEBbpHnHgwAE1NzdLkhYsWKBJkyYVOSMAAAAAQKGxSC+yo0eP\nqqWlRZ2dnZo7d66mTJnCd50DAAAAQJlikV4kJ0+eVGtrqw4dOqTZs2dr+vTpfNc5AAAAAJQ5FukF\n1t3drQ8//FCffPKJLr/8cjU2NqqioqLYaQEAAAAAPIBFeoHE43Ft2bJFO3fu1EUXXaRly5YpGo0W\nOy0AAAAAgIewSB9hiURCO3bs0JYtW3TBBRfo9ttv16hRo4qdFgAAAADAg1ikjxDTNPXxxx9r48aN\nGjdunG666SbV19cXOy0AAAAAgIexSHeZZVn67LPP1NLSomg0qqVLl2rChAnFTgsAAAAA4AMs0l30\n+eefq7m5WYlEQldeeaUmT57M16kBAAAAABxjke6CY8eOqaWlRe3t7Zo7d64uvPBCvk4NAAAAAJA3\nFunD0NnZqdbWVh04cECzZs3S9ddfr2AwWOy0AAAAAAA+xSJ9CHp6erRp0ybt3r1bM2bM0IIFCxQO\nh4udFgAAAADA51ik5yEej2vr1q3avn27pk6dqjvvvFOVlZXFTgsAAAAAUCJYpDuQTCa1c+dObd68\nWRMnTtRtt92m2traYqcFAAAAACgxLNJzsCxLe/bsUWtrq+rq6nTjjTdq7NixxU4LAAAAAFCiWKRn\nYFmW9u/fr+bmZoVCIS1atEjnnXdesdMCAAAAAJQ4FukDHD58WC0tLerp6dHcuXPV0NDAd50DAAAA\nAAqCRfoZ7e3tamlpUVtbm+bMmaNp06bxXecAAAAAgIIq+0X6qVOntHHjRu3bt08zZ87UkiVLFAqV\nfVkAAAAAAEVQtqvRWCymLVu2aNeuXbrkkku0bNkyRSKRYqcFAAAAAChjZbdITyQS2rZtm7Zu3aqG\nhgbdcccdqq6uLnZaAAAAAACUzyLdNE3t2rVLH374oSZMmKBbbrlFdXV1xU4LAAAAAICUkl+kW5al\nvXv3qqWlRaNGjdINN9yg8ePHFzstAAAAAADOUtKL9AMHDqi5uVmStGDBAk2aNKnIGQEAAAAAkF1J\nLtKPHj2qlpYWdXZ2au7cuZoyZQrfdQ4AAAAA8LySW6SvXr1ahw4d0uzZszV9+nS+6xwAAAAA4Bsl\nt0ivr69XY2OjKioqip0KAAAAAAB5MSzLsoqdBAAAAAAAkNgLDhTAqlWrip0CgDzRt4D/0LeAP9G7\n/bFIBwAAAADAI1ikAwAAAADgESzSgQKYMWNGsVMAkCf6FvAf+hbwJ3q3Pz44DgAAAAAAj+CddAAA\nAAAAPIJFOgAAAAAAHhEqdgKA37W1tenFF1/UyZMnZRiGli5dqq9+9as6deqUfv3rX6utrU3jx4/X\nD3/4Q1VXV0uS/v73v2vNmjUKBAJ68MEHNXPmzCLfCqC8ZOvbVatW6d1331Vtba0k6e6779bs2bMl\n0beAF8TjcT355JPq6+tTIpHQvHnzdM899zDnAh6WrW+Zc7PjmnRgmE6cOKETJ06ooaFBsVhMjz/+\nuJYvX66mpibV1NToa1/7mt566y11dXXp3nvv1f79+/Xcc8/pV7/6lY4fP65f/OIXeu655xQIsLEF\nKJRsffv++++rsrJSN998c7/j6VvAO3p7exWJRJRMJrVixQp985vfVGtrK3Mu4GGZ+nbr1q3MuVmU\nzy0FRkhdXZ0aGhokSdFoVBMnTtTx48fV2tqqRYsWSZIWL16slpYWSVJLS4sWLFigUCikc845R+ee\ne652795drPSBspStbyUp02vX9C3gHZFIRJKUSCRkmqaqq6uZcwGPy9S3EnNuNizSARcdOXJEn376\nqaZNm6aTJ0+qrq5OkjR69GidPHlSktTe3q6xY8em/mbs2LGpxQGAwrP79qKLLpIk/fOf/9Ty5cv1\n8ssvq6urSxJ9C3iJaZpavny5HnroIc2YMUOTJ09mzgU8LlPfSsy52bBIB1wSi8X0zDPP6IEHHlBl\nZWW/3xmGkfNvB/s9gJERi8X07LPP6oEHHlA0GtUNN9ygF154Qf/3f/+nMWPGaOXKlVn/lr4FiiMQ\nCOjpp5/WK6+8op07d2rbtm39fs+cC3jPwL7dvn07c24OLNIBFyQSCT3zzDNqbGzU/PnzJZ1+Jf/E\niROSTr8iOHr0aElSfX29jh07lvrbY8eOqb6+vvBJA2XO7tuFCxf261vDMGQYhpYsWZLaXkffAt5T\nVVWl2bNn65NPPmHOBXzC7ts9e/Yw5+bAIh0YJsuy9Morr2jixIm66aabUj+fO3eumpqaJElr167V\nvHnzUj9fv369EomEjhw5okOHDmnq1KnFSB0oW9n6tr29PfXv5uZmXXDBBZLoW8ArOjo6Ulti4/G4\ntm7dqi984QvMuYCHZetb+4U1iTl3ID7dHRimjz76SD/72c90wQUXpLbi3HPPPZo6dWrWr4P529/+\npjVr1igYDOqBBx7QrFmzinkTgLKTqW/vvvturV+/Xp9++qkMw9D48eP18MMPp65zpW+B4tu3b59e\nfPFFmaYpy7LU2NioW2+9NedXsNG7QHFl69sXXniBOTcLFukAAAAAAHgE290BAAAAAPAIFukAAAAA\nAHgEi3QAAAAAADyCRToAAAAAAB7BIh0AAAAAAI9gkQ4AAAAAgEewSAcAAEXX1NSkFStWFDsNAACK\njkU6AAA+8oMf/ED33HOPOjs7+/38Rz/6ke666y61tbUVKTMAAOAGFukAAPjMhAkTtH79+tR/79u3\nT/F4vIgZ9WdZlizLKnYaAAD4UqjYCQAAgPwsXLhQa9eu1Ve+8hVJp7eKNzY26s9//rMkqa+vT2+8\n8YY2bNigvr4+zZ8/X/fff7/C4bC6urr0/PPPa/fu3Uomk7r44ov18MMPq76+PhXrr3/9qzo6OlRT\nU6NvfOMbuuaaa7Rq1SodPnxYjz76qCTpyJEjevTRR/XGG28oEAjoySef1PTp07V9+3bt3btXzzzz\njBKJhH7/+99r7969qq2t1V133aUvfelLkqTOzk699NJL2rFjhyZOnKgrrriiCJUEAMB7eCcdAACf\nmTZtmnp6enTgwAGZpqn3339fjY2Nkk6/i/2nP/1Jhw4d0tNPP63nn39ex48f15tvvpn6/ZIlS/TS\nSy/p5ZdfVjgc1muvvSZJisVi+sMf/qCf/OQnev311/XUU0+poaFBkmQYxqB5vffee3rkkUe0cuVK\n1dTU6KmnntLChQv16quv6rHHHtOrr76q/fv3S5Jee+01RSIR/e53v9P3vvc9NTU1OToHAACljkU6\nAAA+1NjYqLVr1+rf//63Jk2alHon3LIsrV69Wvfff7+qq6sVjUb19a9/Xf/6178kSaNGjdL8+fMV\nDocVjUZ1++23a8eOHam4gUAgtX2+rq5OkyZNSsXNxTAMLVq0SJMmTVIgENDmzZt1zjnnaPHixQoE\nAmpoaNCVV16pDRs2yDRNffDBB1q2bJnC4bAmT56sRYsWsUUeAACx3R0AAN8xDEONjY1asWKFjhw5\nosbGxtQCt6OjQ/F4XD/+8Y9Tx6dfI97b26vXX39dW7Zs0alTpySdfgfdsixFo1E99thjevvtt/XK\nK6/o4osv1n333afzzz/fUV7jxo1L/fvo0aP6+OOP9eCDD6Z+lkwm1djYqI6ODpmm2e/49H8DAFDO\nWKQDAOBD48aN04QJE7R582Z9//vfT/28trZW4XBYzz77rMaMGXPW37399tv6/PPP9ctf/lKjR4/W\np59+qscff1yWZckwDM2cOVMzZ85MXdf+29/+Vj//+c8VjUbV29ubinPixIlB87v00kv105/+9Kzf\nmaapQCCgtra21AsAfCo9AACnsd0dAACf+u53v6sVK1YoHA6nfmYYhpYuXao//vGP6ujokCQdP35c\nW7ZskXT6XfNwOKyqqiqdOnVKf/nLX1J/e/LkSbW0tCgWiykYDCoajSoQOP1UoaGhQTt37lRbW5u6\nu7v11ltv5cxtzpw5+vzzz7Vu3TolEgklEgnt3r1bBw4cUCAQ0JVXXqlVq1YpHo9r//79Wrt2Ldek\nAwAg3kkHAMC3JkyYcNbPDMPQvffeqzfffFNPPPGEOjo6VF9fry9/+cuaOXOmbrrpJv3mN7/Rt7/9\nbdXX1+vmm29Wa2urpNPb4v/xj3/oxRdflGEYamho0He+8x1J0hVXXKGrr75ay5cvV21trW699VZt\n3Lgxa27RaFRPPPGEVq5cqZUrV8qyLDU0NOi+++6TJH3rW9/SSy+9pIceekiTJk3Stdde2+/aeAAA\nypVh8SktAAAAAAB4AtvdAQAAAADwCBbpAAAAAAB4BIt0AAAAAAA8gkU6AAAAAAAewSIdAAAAAACP\nYJEOAAAAAIBHsEgHAAAAAMAjWKQDAAAAAOARLNIBAAAAAPCI/wf/C8k/LzoH6QAAAABJRU5ErkJg\ngg==\n",
"text": [
"<matplotlib.figure.Figure at 0x14ed8a58>"
]
}
],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"interactive(par_sen.plot, group = par_groups, n = (1,50))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA+kAAAI7CAYAAACQvNrvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3X10U/d9x/GPJCNMkHCxqU09rw2iLXYFpLRgapWDj3Ex\nnDaAT0/BXUPXQ0O7ug4UBoqXdLTA2Uz9wEMLcU4CSWlrwsDF3ZKMZQcfCqMIktSOgWrOssTdQ9OA\nBh5FNqLGkveHD1qEeZCfdC/4/fpLutbvd79X58sfH36/q2vp6enpEQAAAAAAMJzV6AIAAAAAAEAv\nQjoAAAAAACZBSB8gv99vdAkwAfoA9ADoAUj0AegB9KIPMBQ9QEgfIP4BQqIPQA+AHkAv+gD0ACT6\nAIR0AAAAAADuK4R0AAAAAABMwsIj2AAAAAAAMIckowu4l/3+9783ugQYzOl0KhgMGl0GDEQPgB6A\nRB+AHkAv+gCZmZmDnoPt7gAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAAAABMgpAOAAAAAIBJ\nENIBAAAAADAJQjoAAAAAACZBSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAA\nAABMgpAOAAAAAIBJENIBAAAAADAJQjoAAAAAACZBSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCk\nAwAAAABgEoR0AAAAAABMgpAOAAAAAIBJENIBAAAAADCJJKMLuJe9eanL6BJgMNvlywqHw0aXAQPR\nA7HSHaOUOtpidBkAAAD3LEL6IJS/0mZ0CQBgKpULXUodbTe6DAAAgHsW290BAAAAADAJQjoAAAAA\nACZBSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAAAABMgpAOAAAAAIBJENIB\nAAAAADCJJKMLGKiysjJVVlbK4XDEHK+trdUbb7yhcePGaevWrdHjp06dUn19vd59911t2bJFLpdL\nknT27Fm98MIL6u7uVlJSkpYvX66pU6cm9FoAAAAAAJDuw5X0goICPfnkk32Of/jDH9b69ev1iU98\nIub4uHHj9Fd/9VeqqalRWVmZdu3alahSAQAAAACIYaqV9IaGBh0/flwpKSlKS0tTVlaWmpqaVFFR\nIUkKBAKqqqpSTU1NdExXV5dqamr0mc98RvPmzVNOTo4CgUCfuf/kT/7klud88MEHo6+zsrLU1dUV\nXVUHAAAAACCRTLOS3tbWJp/Pp+rqaj3xxBN65513ZLfb1d3dHQ3dPp9PHo8nOiYUCqmyslJz5szR\nvHnzBl3Dq6++KpfLRUAHAAAAABjCNCG9tbVVubm5stvtGjNmjGbOnClJysvLk8/nk9R7X/n7Q3pV\nVZUKCgo0d+7cQZ//v//7v7Vv3z5985vfHPRcAAAAAAAMhGmWjC0WS8z7np4eSZLH49G2bds0e/Zs\nWSwWTZw4MfqZ7OxstbS0aM6cOYM696VLl1RTU6NVq1YpPT39lp/x+/3y+/3R98uWLRvUOQHgfmSz\n2eR0Oo0uI6HsdvuIu2b0RR+AHoBEH6DXwYMHo6/dbrfcbne/xpsmpOfk5Ki2tlbFxcUKh8Nqbm7W\n/PnzlZGRIavVqkOHDsWsoktSSUmJ6uvrtWfPHq1cuXJA5+3s7NQPfvADPfLII/r4xz9+288N5MsF\ngJEmHA4rGAwaXUZCOZ3OEXfN6Is+AD0AiT5Abw8MdkHXNNvdJ02apLy8PHm9Xm3ZskWTJ0+OWU0/\nceJETEi/sfK+YsUKdXV1ad++fZKkHTt2aMOGDXrvvfdUWlqqX/7yl5Kk1157TaWlpXrrrbe0ZcuW\n6I/RvfLKKzp//rx+/vOf6/HHH9fjjz+uK1euJPLSAQAAAACQJFl6biRhk6mvr1dycrIWLVpkdCm3\nNav6qNElAICpVC50KTvNbnQZCcWqCST6APQAetEHyMzMHPQcpllJv5Wb71MHAAAAAOB+Zpp70m+2\ndOlSo0sAAAAAACChTL2SDgAAAADASEJIBwAAAADAJAjpAAAAAACYBCEdAAAAAACTIKQDAAAAAGAS\nhHQAAAAAAEyCkA4AAAAAgEkQ0gEAAAAAMAlCOgAAAAAAJkFIBwAAAADAJJKMLuBeVrnQZXQJMJjN\nZlM4HDa6DBiIHoiV7hhldAkAAAD3NEL6IGSn2Y0uAQZzOp0KBoNGlwED0QMAAAAYSmx3BwAAAADA\nJAjpAAAAAACYBCEdAAAAAACTIKQDAAAAAGAShHQAAAAAAEyCkA4AAAAAgEnwCLZBePNSl9ElwGC2\ny5d5RvYIRw+AHjC/dMcopY62GF0GAABxIaQPQvkrbUaXAAAA7qJyoUupo+1GlwEAQFzY7g4AAAAA\ngEkQ0gEAAAAAMAlCOgAAAAAAJkFIBwAAAADAJAjpAAAAAACYBCEdAAAAAACTIKQDAAAAAGAShHQA\nAAAAAEyCkA4AAAAAgEncsyG9rKxMHR0dfY7X1tbqG9/4htatWxdz/Gc/+5nWrl0rr9ermpoaXb16\nNebvFy9e1Fe/+lW99NJLw1o3AAAAAAC3c8+G9NspKCjQk08+2ef4Qw89pK1bt6q6ulof+tCH9Itf\n/CLm7z/5yU/0qU99KlFlAgAAAADQR5LRBbxfQ0ODjh8/rpSUFKWlpSkrK0tNTU2qqKiQJAUCAVVV\nVammpiY6pqurSzU1NfrMZz6jefPmKScnR4FAoM/c06dPj77+2Mc+ptOnT0ffv/baa8rIyNDo0aOH\n8eoAAAAAALgz06ykt7W1yefzqbq6Wk888YTeeecd2e12dXd3R0O3z+eTx+OJjgmFQqqsrNScOXM0\nb968uM919OjR6Kr5tWvX9OKLL2rp0qVDe0EAAAAAAPSTaUJ6a2urcnNzZbfbNWbMGM2cOVOSlJeX\nJ5/PJ0k6depUTEivqqpSQUGB5s6dG/d5GhoalJSUpDlz5kiSDh48qC984QsaPXq0enp6hvCKAAAA\nAADoH9Nsd7dYLDHvbwRmj8ejbdu2afbs2bJYLJo4cWL0M9nZ2WppaYkG7rs5duyY3njjDW3YsCF6\n7J133tGrr76quro6Xb16VRaLRXa7XQsWLIgZ6/f75ff7o++XLVvW72sEAACJZ7PZ5HQ6h/Ucdrt9\n2M8Bc6MHINEH6HXw4MHoa7fbLbfb3a/xpgnpOTk5qq2tVXFxscLhsJqbmzV//nxlZGTIarXq0KFD\nMavoklRSUqL6+nrt2bNHK1euvOP8LS0tevHFF7Vx40bZ7fbo8U2bNkVf19fXa8yYMX0CujSwLxcA\nABgvHA4rGAwO6zmcTuewnwPmRg9Aog/Q2wODXdA1zXb3SZMmKS8vT16vV1u2bNHkyZNjVtNPnDgR\nE9JvrLyvWLFCXV1d2rdvnyRpx44d2rBhg9577z2Vlpbql7/8pSTp+eef17Vr1/Q3f/M3evzxx7Vn\nz54EXyEAAAAAAHdm6THpjdj19fVKTk7WokWLjC7ltmZVHzW6BAAAcBeVC13KTrPf/YODwOoZ6AFI\n9AGkzMzMQc9hmpX0W7n5PnUAAAAAAO5nprkn/WY8Eg0AAAAAMNKYeiUdAAAAAICRhJAOAAAAAIBJ\nENIBAAAAADAJQjoAAAAAACZBSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAA\nAABMgpAOAAAAAIBJJBldwL2scqHL6BJgMJvNpnA4bHQZMBA9AHrA/NIdo4wuAQCAuBHSByE7zW50\nCTCY0+lUMBg0ugwYiB4APQAAAIYS290BAAAAADAJQjoAAAAAACZBSAcAAAAAwCQI6QAAAAAAmAQh\nHQAAAAAAkyCkAwAAAABgEjyCbRDevNRldAkwmO3yZZ6PPMLRA6AHINEHoAfQa6B9kO4YpdTRlmGo\nCPciQvoglL/SZnQJAAAAAO5xlQtdSh1tN7oMmATb3QEAAAAAMAlCOgAAAAAAJkFIBwAAAADAJAjp\nAAAAAACYBCEdAAAAAACTIKQDAAAAAGAShHQAAAAAAEyCkA4AAAAAgEkQ0gEAAAAAMAlThvSysjJ1\ndHT0OX748GGtXbtWO3fu7Pecr7zyilatWqWSkpI+cz///PNavXq1vF6vfvvb3w64bgAAAAAABsOU\nIf12jhw5og0bNmjVqlX9Hpudna3vfe97mjBhQszx5uZmXbhwQT/60Y/0zW9+U3v27BmqcgEAAAAA\n6JekRJ2ooaFBx48fV0pKitLS0pSVlaWmpiZVVFRIkgKBgKqqqlRTUxMd09XVpa1btyo3N1dtbW26\ncOGCKioqVFBQoClTpmjv3r26fv267Ha7SktLlZmZqUgkorq6Op05c0ZWq1WFhYVauHChHnzwwVvW\n9etf/1r5+fmSpI997GPq7OzU5cuX9YEPfGDYvxMAAAAAAN4vISG9ra1NPp9P1dXVCofDKi8vl8vl\nUnd3twKBgNLT0+Xz+eTxeKJjQqGQtm/frvz8fM2dO1eFhYVqaWnRxo0b5XA4FAqFtHnzZlmtVp09\ne1b79+/XunXr1NjYqIsXL6q6ulpWq/WW2+bfr729XWlpadH3aWlpam9vJ6QDAAAAABIuISG9tbVV\nubm5stvtkqSZM2dKkvLy8uTz+VRcXKxTp05p7dq10TFVVVVasmSJ5syZc8s5Ozs7tWvXLp0/f14W\ni0XhcFiSdO7cORUVFclq7d3J73A47lpfT0/PoK4PAAAAAIChkJCQbrFYYt7fCMUej0fbtm3T7Nmz\nZbFYNHHixOhnsrOz1dLSctuQfuDAAU2bNk1er1eBQECbNm3qM388UlNTdenSpej7S5cuKTU1tc/n\n/H6//H5/9P2yZcviPgcAAAAA3I7NZpPT6TS6DAyRgwcPRl+73W653e5+jU9ISM/JyVFtba2Ki4sV\nDofV3Nys+fPnKyMjQ1arVYcOHYrZ6i5JJSUlqq+v1549e7Ry5co+c4ZCIY0fP16SdOzYsejx6dOn\nq7GxUVOnTo1ud795Nf39IX7mzJn653/+Z332s5/VW2+9pbFjx95yq/tAvlwAAAAAuJtwOKxgMGh0\nGRgCTqdz0Au6Cfl190mTJikvL09er1dbtmzR5MmTY1bTT5w4ERPSb6y8r1ixQl1dXdq3b1+fORcv\nXqwXXnhB5eXlikQi0TGFhYWaMGGC1q9fL6/Xq5MnT0rqfXxbaWmp2tvbtX79ej3zzDOSpE996lNK\nT0/XqlWrtHv3bj366KPD+l0AAAAAAHA7lh4Dbsiur69XcnKyFi1alOhTD6lZ1UeNLgEAAADAPa5y\noUvZaXajy8AQyMzMHPQchj0n/eb71AEAAAAAGOkS9pz091u6dKkRpwUAAAAAwNQMW0kHAAAAAACx\nCOkAAAAAAJgEIR0AAAAAAJMgpAMAAAAAYBKEdAAAAAAATIKQDgAAAACASRDSAQAAAAAwCUI6AAAA\nAAAmQUgHAAAAAMAkCOkAAAAAAJhEktEF3MsqF7qMLgEGs9lsCofDRpcBA9EDoAcg0QegB9BroH2Q\n7hg1DNXgXkVIH4TsNLvRJcBgTqdTwWDQ6DJgIHoA9AAk+gD0AHrRBxgKbHcHAAAAAMAkCOkAAAAA\nAJgEIR0AAAAAAJMgpAMAAAAAYBKEdAAAAAAATIKQDgAAAACASfAItkF481KX0SXAYLbLl3km6ghH\nD4AegEQfgB5Ar+Hog3THKKWOtgzpnDA3QvoglL/SZnQJAAAAAO5jlQtdSh1tN7oMJBDb3QEAAAAA\nMAlCOgAAAAAAJkFIBwAAAADAJAjpAAAAAACYBCEdAAAAAACTIKQDAAAAAGAShHQAAAAAAEyCkA4A\nAAAAgEkQ0gEAAAAAMAnThvSysjJ1dHT0OX748GGtXbtWO3fu7PecgUBATz75pFavXq0dO3aou7tb\nkvTuu+/qu9/9rh555BG99NJLg64dAAAAAICBSDK6gP46cuSINmzYoNTU1H6Praur08MPPyyPx6Pd\nu3fr6NGjKioqktPp1Ne//nW9/vrrw1AxAAAAAADxSWhIb2ho0PHjx5WSkqK0tDRlZWWpqalJFRUV\nknpXuquqqlRTUxMd09XVpa1btyo3N1dtbW26cOGCKioqVFBQoClTpmjv3r26fv267Ha7SktLlZmZ\nqUgkorq6Op05c0ZWq1WFhYVasGCB/H6/1qxZI0nKz89XfX29ioqKNG7cOI0bN07Nzc2J/DoAAAAA\nAIiRsJDe1tYmn8+n6upqhcNhlZeXy+Vyqbu7W4FAQOnp6fL5fPJ4PNExoVBI27dvV35+vubOnavC\nwkK1tLRo48aNcjgcCoVC2rx5s6xWq86ePav9+/dr3bp1amxs1MWLF1VdXS2r1aqOjg4Fg0GNHTtW\nVmvvDv/U1FS1t7cn6vIBAAAAALirhIX01tZW5ebmym63S5JmzpwpScrLy5PP51NxcbFOnTqltWvX\nRsdUVVVpyZIlmjNnzi3n7Ozs1K5du3T+/HlZLBaFw2FJ0rlz51RUVBQN5A6HQ1euXBnOywMAAAAA\nYNASFtItFkvM+56eHkmSx+PRtm3bNHv2bFksFk2cODH6mezsbLW0tNw2pB84cEDTpk2T1+tVIBDQ\npk2b+sx/g9PpVGdnpyKRiKxWq9rb2/t1X7vf75ff74++X7ZsWdxjAQAAAGAgbDabnE6n0WWgHw4e\nPBh97Xa75Xa7+zU+YSE9JydHtbW1Ki4uVjgcVnNzs+bPn6+MjAxZrVYdOnQoZqu7JJWUlKi+vl57\n9uzRypUr+8wZCoU0fvx4SdKxY8eix6dPn67GxkZNnTo1ut3d4XDI7Xbr9OnT8ng8OnbsmGbNmhUz\n383B/v0G8uUCAAAAwGCEw2EFg0Gjy0CcnE7noBd0E/YItkmTJikvL09er1dbtmzR5MmTY1bTT5w4\nERPSb6y8r1ixQl1dXdq3b1+fORcvXqwXXnhB5eXlikQi0TGFhYWaMGGC1q9fL6/Xq5MnT0qSli9f\nrpdfflmrV69WZ2en5s2bJ0m6fPmySktL9Y//+I9qaGhQaWmprl27NqzfBwAAAAAAN7P03Gn5eBjV\n19crOTlZixYtMuL0Q2JW9VGjSwAAAABwH6tc6FJ2mt3oMhCnzMzMQc+RsJX0W7n5PnUAAAAAAEay\nhD4n/f2WLl1q1KkBAAAAADAlQ1fSAQAAAADA/yOkAwAAAABgEoR0AAAAAABMgpAOAAAAAIBJENIB\nAAAAADAJQjoAAAAAACZBSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEklGF3Avq1zo\nMroEGMxmsykcDhtdBgxED4AegEQfgB5Ar+Hog3THqCGdD+ZHSB+E7DS70SXAYE6nU8Fg0OgyYCB6\nAPQAJPoA9AB60QcYCmx3BwAAAADAJAjpAAAAAACYBCEdAAAAAACTIKQDAAAAAGAShHQAAAAAAEyC\nkA4AAAAAgEnwCLZBePNSl9ElwGC2y5d5JuoIRw+AHoBEH4AeQK9E9kG6Y5RSR1sSci4kFiF9EMpf\naTO6BAAAAAAjUOVCl1JH240uA8OA7e4AAAAAAJgEIR0AAAAAAJMgpAMAAAAAYBKEdAAAAAAATIKQ\nDgAAAACASRDSAQAAAAAwCUI6AAAAAAAmQUgHAAAAAMAkCOkAAAAAAJhEktEF3EpZWZkqKyvlcDhi\njh8+fFhHjhyRy+XSqlWr+jVnIBDQjh071NHRIZfLpccee0xJSUl6/fXXdfDgQVksFlksFn31q1/V\n1KlTh/JyAAAAAACIiylD+u0cOXJEGzZsUGpqar/H1tXV6eGHH5bH49Hu3bt19OhRFRUVadq0aZo1\na5Yk6b/+679UXV2tnTt3DnXpAAAAAADcVcJCekNDg44fP66UlBSlpaUpKytLTU1NqqiokNS70l1V\nVaWampromK6uLm3dulW5ublqa2vThQsXVFFRoYKCAk2ZMkV79+7V9evXZbfbVVpaqszMTEUiEdXV\n1enMmTOyWq0qLCzUggUL5Pf7tWbNGklSfn6+6uvrVVRUpOTk5Oj5rl27pnHjxiXqKwEAAAAAIEZC\nQnpbW5t8Pp+qq6sVDodVXl4ul8ul7u5uBQIBpaeny+fzyePxRMeEQiFt375d+fn5mjt3rgoLC9XS\n0qKNGzfK4XAoFApp8+bNslqtOnv2rPbv369169apsbFRFy9eVHV1taxWqzo6OhQMBjV27FhZrb23\n4Kempqq9vT16rtdee0379+/X//7v/+qv//qvE/GVAAAAAADQR0JCemtrq3Jzc2W32yVJM2fOlCTl\n5eXJ5/OpuLhYp06d0tq1a6NjqqqqtGTJEs2ZM+eWc3Z2dmrXrl06f/68LBaLwuGwJOncuXMqKiqK\nBnKHw6ErV67csb7c3Fzl5uaqtbVVO3fu1A9/+MNBXzMAAAAAAP2VkJBusVhi3vf09EiSPB6Ptm3b\nptmzZ8tisWjixInRz2RnZ6ulpeW2If3AgQOaNm2avF6vAoGANm3a1Gf+G5xOpzo7OxWJRGS1WtXe\n3n7L+9pzcnIUiUQUDAbldDpj/ub3++X3+6Pvly1bFufVAwAAAMDQstlsfTILzOHgwYPR1263W263\nu1/jExLSc3JyVFtbq+LiYoXDYTU3N2v+/PnKyMiQ1WrVoUOHYra6S1JJSYnq6+u1Z88erVy5ss+c\noVBI48ePlyQdO3Ysenz69OlqbGzU1KlTo9vdHQ6H3G63Tp8+LY/Ho2PHjkV/LO78+fPKyMiQxWJR\nW1ubJN2y2Qfy5QIAAADAcAiHwwoGg0aXgZs4nc5BL+gmJKRPmjRJeXl58nq9SklJ0eTJk2NW0+vq\n6vTUU09FP39j5X3FihWqra3Vvn379Mgjj8TMuXjxYj311FNqaGjQjBkzomMKCwv13nvvaf369bLZ\nbPrc5z6nBQsWaPny5dqxY4f+7u/+TpMmTdK8efMkSa+++qr+5V/+RTabTcnJyfrOd76TiK8EAAAA\nAIA+LD037w1PgPr6eiUnJ2vRokWJPvWQmlV91OgSAAAAAIxAlQtdyk6zG10GbpKZmTnoOaxDUMeA\n3HyfOgAAAAAAI13CnpP+fkuXLjXitAAAAAAAmJphK+kAAAAAACAWIR0AAAAAAJMgpAMAAAAAYBKE\ndAAAAAAATIKQDgAAAACASRDSAQAAAAAwCUI6AAAAAAAmQUgHAAAAAMAkCOkAAAAAAJgEIR0AAAAA\nAJNIMrqAe1nlQpfRJcBgNptN4XDY6DJgIHoA9AAk+gD0AHolsg/SHaMSch4kHiF9ELLT7EaXAIM5\nnU4Fg0Gjy4CB6AHQA5DoA9AD6EUfYCiw3R0AAAAAAJMgpAMAAAAAYBKEdAAAAAAATIKQDgAAAACA\nSRDSAQAAAAAwCUI6AAAAAAAmwSPYBuHNS11GlwCD2S5f5pmoIxw9AHoAEn0AegC9zNIH6Y5RSh1t\nMboMDBAhfRDKX2kzugQAAAAAiFG50KXU0Xajy8AAsd0dAAAAAACTIKQDAAAAAGAShHQAAAAAAEyC\nkA4AAAAAgEkQ0gEAAAAAMIm7hvRwOKxVq1bp+vXriagHAAAAAIAR664h3WazyWKxqKuLZ4IDAAAA\nADCc4npO+he+8AXt2LFDxcXFSktLk8Viif4tIyNj2IoDAAAAAGAkiSukP//885Kks2fP9vnbgQMH\nhrYiAAAAAABGqLhCOkEcAAAAAIDh169fd7948aLeeuut4aolRllZmTo6OvocP3z4sNauXaudO3f2\ne85XXnlFq1atUklJSczc7777rr773e/qkUce0UsvvTSougEAAAAAGKi4VtIvXryoH/7wh/qP//gP\nSdLPfvYznTp1SmfOnNG3vvWt4ayvjyNHjmjDhg1KTU3t99js7Gx9+tOf1saNG2OOO51Off3rX9fr\nr78+RFUCAAAAANB/cYX0Z555RjNmzNCmTZv06KOPSpIeeugh/fSnP+3XyRoaGnT8+HGlpKQoLS1N\nWVlZampqUkVFhSQpEAioqqpKNTU10TFdXV3aunWrcnNz1dbWpgsXLqiiokIFBQWaMmWK9u7dq+vX\nr8tut6u0tFSZmZmKRCKqq6vTmTNnZLVaVVhYqIULF+rBBx+8ZV3jxo3TuHHj1Nzc3K/rAQAAAABg\nKMUV0t9++2098cQTslr/f3f8Aw88oKtXr8Z9ora2Nvl8PlVXVyscDqu8vFwul0vd3d0KBAJKT0+X\nz+eTx+OJjgmFQtq+fbvy8/M1d+5cFRYWqqWlRRs3bpTD4VAoFNLmzZtltVp19uxZ7d+/X+vWrVNj\nY6MuXryo6upqWa3WW26bBwAAAADAbOIK6R/4wAd0/vx5ZWZmRo/97ne/0wc/+MG4T9Ta2qrc3FzZ\n7XZJ0syZMyVJeXl58vl8Ki4u1qlTp7R27dromKqqKi1ZskRz5sy55ZydnZ3atWuXzp8/L4vFonA4\nLEk6d+6cioqKov+p4HA44q7zdvx+v/x+f/T9smXLBj0nAAAAAAw1m80mp9NpdBkj1sGDB6Ov3W63\n3G53v8bHFdIXLVqkH/zgByouLlY4HNavfvUr/eIXv9CSJUviPtH7n60uST09PZIkj8ejbdu2afbs\n2bJYLJo4cWL0M9nZ2WppabltSD9w4ICmTZsmr9erQCCgTZs29Zl/qAzkywUAAACARAuHwwoGg0aX\nMSI5nc5BL+jG9evu8+bN01e/+lWdPn1aaWlpOn78uEpKSjR37ty4T5STk6PXX39dXV1dCoVCam5u\nlsViUUZGhqxWqw4dOhSz1V2SSkpKNHbsWO3Zs+eWc4ZCIY0fP16SdOzYsejx6dOnq7GxUZFIRJJu\nud39ViF+qIM9AAAAAAD9EddK+r//+79r1qxZmjVrVszxt99+Wx/96EfjOtGkSZOUl5cnr9erlJQU\nTZ48OWY1va6uTk899VT08zdW3lesWKHa2lrt27dPjzzySMycixcv1lNPPaWGhgbNmDEjOqawsFDv\nvfee1q9fL5vNps997nNasGCBDh8+rJdeekmXL1/W+vXr9alPfUp/8Rd/ocuXL+uJJ57Q1atXZbVa\ndfjwYW3fvl3JyclxXRsAAAAAAEPB0hPH8vGf//mf3/KX3FesWKEf//jHAzpxfX29kpOTtWjRogGN\nN4NZ1Uc5VFOQAAAgAElEQVSNLgEAAAAAYlQudCk7zW50GSPS+3/HbaDuuJJ+Y7v4za8l6cKFC7LZ\nbIM6+c33qQMAAAAAMJLdMaT/2Z/92S1fS70B+4tf/OKAT7x06dIBjwUAAAAA4H50x5C+c+dOSdL3\nv/99bd68OXoPucVi0bhx4zR69OjhrxAAAAAAgBHijiE9PT1dkvT0009L6t3y/oc//CH6i+oAAAAA\nAGDoxPXr7h0dHXruued0+vRp2Ww21dXV6de//rXefvttffnLXx7uGgEAAAAAGBHiek767t27NWbM\nGNXW1mrUqFGSpI9//OM6efLksBYHAAAAAMBIEtdK+m9+8xs988wzSkr6/4+PGzdOV65cGbbCAAAA\nAAAYaeJaSX/ggQf6BPKLFy9ybzoAAAAAAEMorpBeWFiobdu26Te/+Y0ikYjeeustPfXUU/rc5z43\n3PUBAAAAADBixLXdfcmSJbLb7XruuecUDodVW1ur+fPn6/Of//xw1wcAAAAAwIgRV0i3WCz6/Oc/\nTygHAAAAAGAYxRXSJel//ud/9J//+Z+6du1azPE5c+YMeVH3isqFLqNLgMFsNpvC4bDRZcBA9ADo\nAUj0AegB9DJLH6Q7RhldAgYhrpD+93//9/r5z3+urKws2e32mL+N5JCenWa/+4dwX3M6nQoGg0aX\nAQPRA6AHINEHoAfQiz7AUIgrpL/44ov6wQ9+oKysrOGuBwAAAACAESuuX3d3Op2aMGHCcNcCAAAA\nAMCIFtdK+te+9jU9++yz+vznP68PfOADMX8jvAMAAAAAMDTiCund3d06c+aMTp482edvBw4cGPKi\nAAAAAAAYieIK6c8995y+8pWvyOPx9PnhOAAAAAAAMDTiCunhcFgFBQWyWuO6hR0AAAAAAAyApaen\np+duH3rxxRd1/fp1ffGLX5TFYklEXfeEo+f+w+gSYDCzPAsTxqEHQA9Aog9AD6DX/dAH6Y5RSh1N\n5huozMzMQc8RV0j/1re+pT/84Q+y2WxyOp0xf3v66acHXcS9alb1UaNLAAAAAIAhU7nQpew0bnEe\nqKEI6XFtd1+1atWgTwQAAAAAAO4srpDudruHuw4AAAAAAEa8uEK6JP32t79Va2urOjo69P4d8iUl\nJcNSGAAAAAAAI01cIb2xsVE/+clPNH36dL3xxhuaMWOGzp49q5kzZw53fQAAAAAAjBhxPVPtH/7h\nH/TEE0/I6/Vq9OjR8nq9+su//EvZbLbhrg8AAAAAgBEjrpB+5coVfeITn5AkWSwWRSIRffKTn1RT\nU9OwFgcAAAAAwEgS13b31NRUBQIBpaen60Mf+pBef/11OZ1OJSXFfUs7AAAAAAC4i7hS9uLFi/W7\n3/1O6enp+tKXvqStW7equ7tbK1asGO76AAAAAAAYMe4a0nt6epSTk6MPfvCDkqQZM2boxz/+sbq7\nuzVmzJhhLxAAAAAAgJEirnvS169fL4vFEn0/atQoAjoAAAAAAEPsrivpFotFkyZN0u9//3tlZWUl\noiaVlZWpsrJSDocj5vjhw4d15MgRuVwurVq1ql9zBgIB7dixQx0dHXK5XHrssceUlJSkjo4OPf30\n0woEAho1apRKS0v1p3/6p0N5OQAAAAAAxCWue9Ldbre2bNmi/Px8TZgwIeZv8+bNG5bCbuXIkSPa\nsGGDUlNT+z22rq5ODz/8sDwej3bv3q2jR4+qqKhIv/jFLzRp0iR5vV79/ve/13PPPacNGzYMQ/UA\nAAAAANxZXCH9zTff1Ac/+EG1trb2+Vu8Ib2hoUHHjx9XSkqK0tLSlJWVpaamJlVUVEjqXemuqqpS\nTU1NdExXV5e2bt2q3NxctbW16cKFC6qoqFBBQYGmTJmivXv36vr167Lb7SotLVVmZqYikYjq6up0\n5swZWa1WFRYWasGCBfL7/VqzZo0kKT8/X/X19SoqKtK7776r4uJiSVJmZqYCgYCuXLmicePGxXVd\nAAAAAAAMlbhC+saNGwd1kra2Nvl8PlVXVyscDqu8vFwul0vd3d3RR7v5fD55PJ7omFAopO3btys/\nP19z585VYWGhWlpatHHjRjkcDoVCIW3evFlWq1Vnz57V/v37tW7dOjU2NurixYuqrq6W1WpVR0eH\ngsGgxo4dK6u19xb81NRUtbe3S5I+8pGP6NVXX1V2drbefvttXbx4UZcuXSKkAwAAAAASrt8POu/p\n6VFPT0/0/Y3geyetra3Kzc2V3W6XJM2cOVOSlJeXJ5/Pp+LiYp06dUpr166NjqmqqtKSJUs0Z86c\nW87Z2dmpXbt26fz587JYLAqHw5Kkc+fOqaioKFqXw+HQlStXbltbcXGxfvzjH+vxxx/Xhz/8YT34\n4IO3vCa/3y+/3x99v2zZsrteNwAAAADcS2w2m5xOp9Fl3NMOHjwYfe12u+V2u/s1Pq6Q3t7eruee\ne07/+q//qqtXr8b87cCBA3cd//5fhpcUDfkej0fbtm3T7NmzZbFYNHHixOhnsrOz1dLSctuQfuDA\nAU2bNk1er1eBQECbNm3qM/8NTqdTnZ2dikQislqtam9vj97XPmbMGH3729+OfrasrEwZGRl9zjeQ\nLxcAAAAA7iXhcFjBYNDoMu5ZTqdz0Au6cT2C7dlnn5XNZtP3v/99JScnq7KyUjNnztQ3vvGNuE6S\nk5Oj119/XV1dXQqFQmpubpbFYlFGRoasVqsOHToUs9VdkkpKSjR27Fjt2bPnlnOGQiGNHz9eknTs\n2LHo8enTp6uxsVGRSESS1NHRIYvFIrfbrdOnT0c/P2vWLEnS1atX1d3dLUlqbGzUJz7xCSUnJ8d1\nXQAAAAAADKW4Qvq//du/6dvf/rYefPBBSdKDDz6o0tJSvfzyy3GdZNKkScrLy5PX69WWLVs0efLk\nmNX0EydOxIT0GyvvK1asUFdXl/bt29dnzsWLF+uFF15QeXm5IpFIdExhYaEmTJig9evXy+v16uTJ\nk5Kk5cuX6+WXX9bq1avV2dkZ/cG73/3ud1q3bp3WrFmjM2fOaMWKFXFdEwAAAAAAQ83Sc/Pe8FtY\nuXKlamtrZbfbVVZWpoqKCj3wwAN69NFH9dOf/rTfJ62vr1dycrIWLVo0oKLNYlb1UaNLAAAAAIAh\nU7nQpew0u9Fl3LMyMzMHPUdc96R/9KMfVUtLi3Jzc/XQQw9px44dstvtmjx58oBPfPN96gAAAAAA\njHR3DOnXrl1TQ0ODpN5fN58xY4a+9rWv6aWXXtK1a9f0hS98YUAnXbp06YDGAQAAAABwP7tjSH/+\n+ef1zjvvaMaMGXrjjTf005/+VI8++qi+9KUvJao+AAAAAABGjDv+cNwbb7yh7373u1q+fLmeeOIJ\nNTc3J6ouAAAAAABGnDuG9D/+8Y/R54lPmDChzzPSAQAAAADA0LnjdvdIJKLf/OY3kqSenh6Fw+Ho\n+xumTp06fNUBAAAAADCC3DGkp6Sk6Omnn46+dzqdMe8l6amnnhqeygAAAAAAGGHuGNIJ4AAAAAAA\nJM4d70kHAAAAAACJQ0gHAAAAAMAkCOkAAAAAAJjEHe9Jx51VLnQZXQIMZrPZFA6HjS4DBqIHQA9A\nog9AD6DX/dAH6Y5RRpcw4hHSByE7zW50CTCY0+lUMBg0ugwYiB4APQCJPgA9gF70AYYC290BAAAA\nADAJQjoAAAAAACZBSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAAAABMguek\nD8Kbl7qMLgEGs12+rHA4bHQZMBA9AHoAEn0AegC97qc+SHeMUupoi9FljEiE9EEof6XN6BIAAAAA\nYMhVLnQpdbTd6DJGJLa7AwAAAABgEoR0AAAAAABMgpAOAAAAAIBJENIBAAAAADAJQjoAAAAAACZB\nSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEklGF3ArZWVlqqyslMPhiDl++PBhHTly\nRC6XS6tWrerXnIFAQDt27FBHR4dcLpcee+wxJSUl6cUXX9SvfvUrSVI4HNa7776r5557TmPHjh2y\n6wEAAAAAIB6mDOm3c+TIEW3YsEGpqan9HltXV6eHH35YHo9Hu3fv1tGjR1VUVKTFixdr8eLFkqSm\npiYdPnyYgA4AAAAAMETCQnpDQ4OOHz+ulJQUpaWlKSsrS01NTaqoqJDUu9JdVVWlmpqa6Jiuri5t\n3bpVubm5amtr04ULF1RRUaGCggJNmTJFe/fu1fXr12W321VaWqrMzExFIhHV1dXpzJkzslqtKiws\n1IIFC+T3+7VmzRpJUn5+vurr61VUVBRT469+9St99rOfTdRXAgAAAABAjISE9La2Nvl8PlVXVysc\nDqu8vFwul0vd3d0KBAJKT0+Xz+eTx+OJjgmFQtq+fbvy8/M1d+5cFRYWqqWlRRs3bpTD4VAoFNLm\nzZtltVp19uxZ7d+/X+vWrVNjY6MuXryo6upqWa1WdXR0KBgMauzYsbJae2/BT01NVXt7e0yNf/zj\nH3XmzBmtXLkyEV8JAAAAAAB9JCSkt7a2Kjc3V3a7XZI0c+ZMSVJeXp58Pp+Ki4t16tQprV27Njqm\nqqpKS5Ys0Zw5c245Z2dnp3bt2qXz58/LYrEoHA5Lks6dO6eioqJoIHc4HLpy5cpda2xqalJ2djZb\n3QEAAAAAhklISLdYLDHve3p6JEkej0fbtm3T7NmzZbFYNHHixOhnsrOz1dLSctuQfuDAAU2bNk1e\nr1eBQECbNm3qM/8NTqdTnZ2dikQislqtam9v73Nf+8mTJ++41d3v98vv90ffL1u27C5XDQAAAAD3\nJpvNJqfTaXQZ96SDBw9GX7vdbrnd7n6NT0hIz8nJUW1trYqLixUOh9Xc3Kz58+crIyNDVqtVhw4d\nitnqLkklJSWqr6/Xnj17brkFPRQKafz48ZKkY8eORY9Pnz5djY2Nmjp1anS7u8PhkNvt1unTp+Xx\neHTs2DHNmjUrOubq1atqbW3Vd77zndtew0C+XAAAAAC4F4XDYQWDQaPLuOc4nc5BL+gm5DnpkyZN\nUl5enrxer7Zs2aLJkyfHrKafOHEiJqTfWHlfsWKFurq6tG/fvj5zLl68WC+88ILKy8sViUSiYwoL\nCzVhwgStX79eXq9XJ0+elCQtX75cL7/8slavXq3Ozk7NmzcvOtdrr72mhx56KLodHwAAAAAAI1h6\nbt4bngD19fVKTk7WokWLEn3qITWr+qjRJQAAAADAkKtc6FJ2GouY/ZWZmTnoORKykn4rN9+nDgAA\nAADASJew56S/39KlS404LQAAAAAApmbYSjoAAAAAAIhFSAcAAAAAwCQI6QAAAAAAmAQhHQAAAAAA\nkyCkAwAAAABgEoR0AAAAAABMgpAOAAAAAIBJENIBAAAAADAJQjoAAAAAACZBSAcAAAAAwCSSjC7g\nXla50GV0CTCYzWZTOBw2ugwYiB4APQCJPgA9gF73Ux+kO0YZXcKIRUgfhOw0u9ElwGBOp1PBYNDo\nMmAgegD0ACT6APQAetEHGApsdwcAAAAAwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAA\nAABMgpAOAAAAAIBJ8Ai2QXjzUpfRJcBgtsuX75tnYWJg6AHQA5DoA9AD6HU/9UG6Y5RSR1uMLmNE\nIqQPQvkrbUaXAAAAAABDrnKhS6mj7UaXMSKx3R0AAAAAAJMgpAMAAAAAYBKEdAAAAAAATIKQDgAA\nAACASRDSAQAAAAAwCUI6AAAAAAAmQUgHAAAAAMAkCOkAAAAAAJgEIR0AAAAAAJMwZUgvKytTR0dH\nn+OHDx/W2rVrtXPnzn7PGQgE9OSTT2r16tXasWOHuru7Y/7+9ttv68tf/rJeffXVAdcNAAAAAMBg\nmDKk386RI0e0YcMGrVq1qt9j6+rq9PDDD+tHP/qRxo4dq6NHj0b/FolEtG/fPn3yk59UT0/PUJYM\nAAAAAEDckhJ1ooaGBh0/flwpKSlKS0tTVlaWmpqaVFFRIal3pbuqqko1NTXRMV1dXdq6datyc3PV\n1tamCxcuqKKiQgUFBZoyZYr27t2r69evy263q7S0VJmZmYpEIqqrq9OZM2dktVpVWFioBQsWyO/3\na82aNZKk/Px81dfXq6ioSJL0T//0T/rMZz6jd955J1FfBwAAAAAAfSQkpLe1tcnn86m6ulrhcFjl\n5eVyuVzq7u5WIBBQenq6fD6fPB5PdEwoFNL27duVn5+vuXPnqrCwUC0tLdq4caMcDodCoZA2b94s\nq9Wqs2fPav/+/Vq3bp0aGxt18eJFVVdXy2q1qqOjQ8FgUGPHjpXV2rtxIDU1Ve3t7ZKk9vZ2/frX\nv9b3vvc9Pf3007JYLIn4SgAAAAAA6CMhIb21tVW5ubmy2+2SpJkzZ0qS8vLy5PP5VFxcrFOnTmnt\n2rXRMVVVVVqyZInmzJlzyzk7Ozu1a9cunT9/XhaLReFwWJJ07tw5FRUVRQO5w+HQlStXblvb3r17\n9ZWvfEUWi0U9PT1sdwcAAAAAGCYhIf3m1ekbQdjj8Wjbtm2aPXu2LBaLJk6cGP1Mdna2WlpabhvS\nDxw4oGnTpsnr9SoQCGjTpk195r/B6XSqs7NTkUhEVqtV7e3tSktLk9S7yr9jxw5JUjAYVEtLi5KS\nkqL/kXCD3++X3++Pvl+2bFl/vwYAAAAAuCfYbDY5nU6jy7gnHTx4MPra7XbL7Xb3a3xCQnpOTo5q\na2tVXFyscDis5uZmzZ8/XxkZGbJarTp06FDMVndJKikpUX19vfbs2aOVK1f2mTMUCmn8+PGSpGPH\njkWPT58+XY2NjZo6dWp0u7vD4ZDb7dbp06fl8Xh07NixaAjftWtXdGxtba0+/elP9wno0sC+XAAA\nAAC4F4XDYQWDQaPLuOc4nc5BL+gm5NfdJ02apLy8PHm9Xm3ZskWTJ0+OWU0/ceJETEi/sfK+YsUK\ndXV1ad++fX3mXLx4sV544QWVl5crEolExxQWFmrChAlav369vF6vTp48KUlavny5Xn75Za1evVqd\nnZ2aN2/ecF82AAAAAAD9Yukx4Cbs+vp6JScna9GiRYk+9ZCaVX307h8CAAAAgHtM5UKXstPsRpdx\nz8nMzBz0HIY9J51fUQcAAAAAIFbCnpP+fkuXLjXitAAAAAAAmJphK+kAAAAAACAWIR0AAAAAAJMg\npAMAAAAAYBKEdAAAAAAATIKQDgAAAACASRDSAQAAAAAwCUI6AAAAAAAmQUgHAAAAAMAkCOkAAAAA\nAJgEIR0AAAAAAJNIMrqAe1nlQpfRJcBgNptN4XDY6DJgIHoA9AAk+gD0AHrdT32Q7hhldAkjFiF9\nELLT7EaXAIM5nU4Fg0Gjy4CB6AHQA5DoA9AD6EUfYCiw3R0AAAAAAJMgpAMAAAAAYBKEdAAAAAAA\nTIKQDgAAAACASRDSAQAAAAAwCUI6AAAAAAAmwSPYBuHNS11GlwCD2S5fvm+ehYmBoQdAD0CiD0AP\noNdI7IN0xyiljrYYXcZ9hZA+COWvtBldAgAAAAAYpnKhS6mj7UaXcV9huzsAAAAAACZBSAcAAAAA\nwCQI6QAAAAAAmAQhHQAAAAAAkyCkAwAAAABgEoR0AAAAAABMgpAOAAAAAIBJENIBAAAAADAJQjoA\nAAAAACaRZHQBt1NWVqbKyko5HI6Y44cPH9aRI0fkcrm0atWqfs0ZCAS0Y8cOdXR0yOVy6bHHHlNS\nUpJOnDihF198UT09PRozZoxWrlypj3zkI0N5OQAAAAAA3JVpQ/rtHDlyRBs2bFBqamq/x9bV1enh\nhx+Wx+PR7t27dfToURUVFSkjI0ObNm3SAw88oJaWFj377LP627/922GoHgAAAACA20toSG9oaNDx\n48eVkpKitLQ0ZWVlqampSRUVFZJ6V7qrqqpUU1MTHdPV1aWtW7cqNzdXbW1tunDhgioqKlRQUKAp\nU6Zo7969un79uux2u0pLS5WZmalIJKK6ujqdOXNGVqtVhYWFWrBggfx+v9asWSNJys/PV319vYqK\nivTxj388er6PfvSjunTpUiK/FgAAAAAAJCUwpLe1tcnn86m6ulrhcFjl5eVyuVzq7u7W/7V391FR\n1vn/x18zQyPqDMhg5iqnEtIgyHRDDOToBmkdU8NKbauttdxaM9o6iWbm5s2mByG11SxLPUISJ9B2\ns3brHM0sDD2Fiha627LebOUNIik3osLM/P7wx3wbxQQHmQt8Pv5iZq7PNe/r8u2lLz6fa6asrEzd\nunVTYWGhEhISPGNqa2u1cOFCDRkyRIMHD1ZycrKKi4s1c+ZM2Ww21dbWavbs2TKbzdq1a5dyc3P1\n/PPPa8OGDSovL1dGRobMZrOqq6tVVVWlzp07y2w+exu+w+FQRUXFeXVu3LhR/fv3b63TAgAAAACA\nR6uF9D179iguLk5Wq1WSFBsbK0mKj49XYWGhUlJStGXLFj333HOeMfPnz9c999yjxMTERvdZU1Oj\nJUuW6PDhwzKZTHI6nZKkb775RsOGDfMEcpvNpsrKyovW+O233+qzzz7TnDlzfDpWAAAAAAAuRauF\ndJPJ5PXY7XZLkhISErRgwQINHDhQJpNJ3bt392wTGRmp4uLiC4b09957TzfffLPS0tJUVlamWbNm\nnbf/Bna7XTU1NXK5XDKbzaqoqPC6r/3AgQNatmyZpk+fft6H1UlSSUmJSkpKPI/Hjh3bjKMHAAAA\ngPbHYrHIbrf7uwxDycvL8/wcHR2t6OjoZo1vtZAeFRWlpUuXKiUlRU6nU9u3b9fQoUN1zTXXyGw2\na+3atV5L3SVp3Lhxys/P1/LlyzVhwoTz9llbW6uQkBBJ0qZNmzzP9+3bVxs2bFBMTIxnubvNZlN0\ndLS2bt2qhIQEbdq0SQMGDJAklZeXKzMzU6mpqV6/JPi5Szm5AAAAANCeOZ1OVVVV+bsMw7Db7T5P\n6Lba96T36tVL8fHxSktL07x58xQREeE1m15QUOAV0htm3sePH68zZ84oJyfnvH2OGjVK7777rqZO\nnSqXy+UZk5ycrK5du2ry5MlKS0vTl19+KUl6+OGH9dFHH+mZZ55RTU2NkpKSJElr1qxRTU2Nli9f\nrilTpmjatGmX9VwAAAAAANAYk/vcdeGtJD8/X4GBgRo5cqQ/3r5FDMjY6O8SAAAAAMBv0u8KV2So\n1d9lGEaPHj183kerzaQ35tz71AEAAAAAuJK16vek/9yYMWP89dYAAAAAABiSX2fSAQAAAADA/yGk\nAwAAAABgEIR0AAAAAAAMgpAOAAAAAIBBENIBAAAAADAIQjoAAAAAAAZBSAcAAAAAwCAI6QAAAAAA\nGAQhHQAAAAAAgyCkAwAAAABgEAH+LqAtS78r3N8lwM8sFoucTqe/y4Af0QOgByDRB6AHcNaV2Afd\nbFf5u4R2h5Dug8hQq79LgJ/Z7XZVVVX5uwz4ET0AegASfQB6AGfRB2gJLHcHAAAAAMAgCOkAAAAA\nABgEIR0AAAAAAIMgpAMAAAAAYBCEdAAAAAAADIKQDgAAAACAQfAVbD7417Ez/i4BfmY5fvyK+y5M\neKMHQA9Aog9AD+CsK7UPutmukqODyd9ltBuEdB9M/WSvv0sAAAAAAL9Kvytcjg5Wf5fRbrDcHQAA\nAAAAgyCkAwAAAABgEIR0AAAAAAAMgpAOAAAAAIBBENIBAAAAADAIQjoAAAAAAAZBSAcAAAAAwCAI\n6QAAAAAAGAQhHQAAAAAAgwjwdwGNmTRpktLT02Wz2bye/+c//6n169crPDxcqampzdpnWVmZFi1a\npOrqaoWHh+vpp59WQMDZwy8pKVFWVpacTqfsdrtmzpzZUocCAAAAAECTGTKkX8j69es1Y8YMORyO\nZo9dvXq1RowYoYSEBL399tvauHGjhg0bppqaGq1YsULTp09XaGioKisrL0PlAAAAAABcXKuF9Pff\nf1+ff/65goODFRoaqrCwMG3btk1z586VdHame/78+crMzPSMOXPmjF599VXFxcVp7969OnLkiObO\nnavbb79dN954o1atWqW6ujpZrVZNnDhRPXr0kMvl0urVq7Vz506ZzWYlJyfrzjvvVElJiZ599llJ\n0pAhQ5Sfn69hw4Zp8+bNGjhwoEJDQyVJQUFBrXVKAAAAAADw0iohfe/evSosLFRGRoacTqemTp2q\n8PBw1dfXq6ysTN26dVNhYaESEhI8Y2pra7Vw4UINGTJEgwcPVnJysoqLizVz5kzZbDbV1tZq9uzZ\nMpvN2rVrl3Jzc/X8889rw4YNKi8vV0ZGhsxms6qrq1VVVaXOnTvLbD57C77D4VBFRYUk6dChQ3I6\nnZo1a5Zqa2s1fPhwDR48uDVOCwAAAAAAXlolpO/Zs0dxcXGyWq2SpNjYWElSfHy8CgsLlZKSoi1b\ntui5557zjJk/f77uueceJSYmNrrPmpoaLVmyRIcPH5bJZJLT6ZQkffPNNxo2bJgnkNtstl9cwu50\nOrVv3z79+c9/1unTp/XSSy+pd+/e+tWvftUixw4AAAAAQFO1Skg3mUxej91utyQpISFBCxYs0MCB\nA2UymdS9e3fPNpGRkSouLr5gSH/vvfd08803Ky0tTWVlZZo1a9Z5+29gt9tVU1Mjl8sls9msiooK\nz33toaGhstvtslqtslqtioqK0oEDB84L6SUlJSopKfE8Hjt27CWcCQAAAABoXywWi+x2u7/LMIy8\nvDzPz9HR0YqOjm7W+FYJ6VFRUVq6dKlSUlLkdDq1fft2DR06VNdcc43MZrPWrl3rtdRdksaNG6f8\n/HwtX75cEyZMOG+ftbW1CgkJkSRt2rTJ83zfvn21YcMGxcTEeJa722w2RUdHa+vWrUpISNCmTZs0\nYMAASdKAAQO0cuVKuVwu1dXV6T//+Y9GjBhx3vtdyskFAAAAgPbO6XSqqqrK32UYgt1u93lCt1W+\nJ71Xr16Kj49XWlqa5s2bp4iICK/Z9IKCAq+Q3jDzPn78eJ05c0Y5OTnn7XPUqFF69913NXXqVLlc\nLnTZQCoAABUuSURBVM+Y5ORkde3aVZMnT1ZaWpq+/PJLSdLDDz+sjz76SM8884xqamqUlJQkSerZ\ns6duueUWTZ48WS+++KKSk5MVFhZ2Wc8HAAAAAACNMbnPXRveCvLz8xUYGKiRI0e29lu3qAEZG/1d\nAgAAAAD4Vfpd4YoMtfq7DEPo0aOHz/tolZn0xpx7nzoAAAAAAFe6Vvue9J8bM2aMP94WAAAAAABD\n89tMOgAAAAAA8EZIBwAAAADAIAjpAAAAAAAYBCEdAAAAAACDIKQDAAAAAGAQhHQAAAAAAAyCkA4A\nAAAAgEEQ0gEAAAAAMAhCOgAAAAAABkFIBwAAAADAIAL8XUBbln5XuL9LgJ9ZLBY5nU5/lwE/ogdA\nD0CiD0AP4KwrtQ+62a7ydwntCiHdB5GhVn+XAD+z2+2qqqrydxnwI3oA9AAk+gD0AM6iD9ASWO4O\nAAAAAIBBENIBAAAAADAIQjoAAAAAAAZBSAcAAAAAwCAI6QAAAAAAGAQhHQAAAAAAg+Ar2Hzwr2Nn\n/F0C/Mxy/PgV+V2Y+D/0AOgBSPQB6AGcRR9cWDfbVXJ0MPm7jDaBkO6DqZ/s9XcJAAAAAGB46XeF\ny9HB6u8y2gSWuwMAAAAAYBCEdAAAAAAADIKQDgAAAACAQRDSAQAAAAAwCEI6AAAAAAAGQUgHAAAA\nAMAgCOkAAAAAABgEIR0AAAAAAIMgpAMAAAAAYBAB/i7gcpg0aZLS09Nls9m8ni8uLtaqVavkcrmU\nlJSklJQUSVJeXp42btyooKAgSdKDDz6ofv36tXrdAAAAAIArW7sM6Y1xuVxasWKFZsyYIYfDoWnT\npik2NlZhYWEymUwaMWKERowY4e8yAQAAAABXsDYT0t9//319/vnnCg4OVmhoqMLCwrRt2zbNnTtX\nklRWVqb58+crMzPTM+bMmTPKzMzUbbfdprCwMHXv3l3dunWTJA0aNEhFRUUKCwuTJLnd7tY/KAAA\nAAAAfqZN3JO+d+9eFRYWKiMjQ9OmTdN///tfWa1W1dfXq6ysTJJUWFiohIQEz5ja2lqlp6crMTFR\nSUlJqqioUGhoqOd1h8OhiooKz+NPPvlEaWlpeuONN1RTU9N6BwcAAAAAwP/XJkL6nj17FBcXJ6vV\nqo4dOyo2NlaSFB8fr8LCQknSli1bvEL6/Pnzdfvtt2vw4MEX3f+wYcO0ZMkSzZ8/XyEhIcrOzr48\nBwIAAAAAwC9oE8vdTSaT1+OGpekJCQlasGCBBg4cKJPJpO7du3u2iYyMVHFxsRITEyWdnTk/duyY\n5/Vjx47J4XBIkoKDgz3PJyUlKT09/bwaSkpKVFJS4nk8duzYFjgyAAAAAGj/LBaL7Ha7v8toFXl5\neZ6fo6OjFR0d3azxbSKkR0VFaenSpUpJSZHT6dT27ds1dOhQXXPNNTKbzVq7dq3XLLokjRs3Tvn5\n+Vq+fLkmTJigiIgIHT58WGVlZXI4HCosLNSf/vQnSdJPP/2kkJAQSdJXX32la6+99rwaLuXkAgAA\nAAAkp9Opqqoqf5dx2dntdp8ndNtESO/Vq5fi4+OVlpam4OBgRUREeM2mr169Wq+//rpn+4aZ9/Hj\nx2vp0qXKycnRQw89pMcee0yvvPKK5yvYGj40LicnR/v375fJZNLVV1+tJ554ovUPEgAAAABwxTO5\n2+DHmufn5yswMFAjR470ax0DMjb69f0BAAAAoC1IvytckaFWf5dx2fXo0cPnfbSJD45rzLn3qQMA\nAAAA0Na1ieXu5xozZoy/SwAAAAAAoMW12Zl0AAAAAADaG0I6AAAAAAAGQUgHAAAAAMAgCOkAAAAA\nABgEIR0AAAAAAIMgpAMAAAAAYBCEdAAAAAAADIKQDgAAAACAQRDSAQAAAAAwCEI6AAAAAAAGEeDv\nAtqy9LvC/V0C/MxiscjpdPq7DPgRPQB6ABJ9AHoAZ9EHF9bNdpW/S2gzCOk+iAy1+rsE+JndbldV\nVZW/y4Af0QOgByDRB6AHcBZ9gJbAcncAAAAAAAyCkA4AAAAAgEEQ0gEAAAAAMAhCOgAAAAAABkFI\nBwAAAADAIAjpAAAAAAAYBCEdAAAAAACDIKQDAAAAAGAQhHQAAAAAAAyCkA4AAAAAgEEQ0gEAAAAA\nMAhCOgAAAAAABkFIBwAAAADAIAjpAAAAAAAYBCEdAAAAAACDIKQDAAAAAGAQhHQAAAAAAAyCkA4A\nAAAAgEEQ0gEAAAAAMAhCOgAAAAAABkFIBwAAAADAIAjpAAAAAAAYhMntdrv9XQQAAAAAAGAm/ZLl\n5eX5uwQYAH0AegD0ACT6APQAzqIP0BI9QEgHAAAAAMAgCOkAAAAAABgEIf0SRUdH+7sEGAB9AHoA\n9AAk+gD0AM6iD9ASPcAHxwEAAAAAYBDMpAMAAAAAYBCEdAAAAAAADCLA3wUYUXFxsVatWiWXy6Wk\npCSlpKSct83KlStVXFysDh066KmnnlKvXr2aPBbG50sPTJo0SR07dpTZbJbFYtG8efNau3y0gIv1\nwI8//qilS5dq//79euCBBzRy5Mgmj0Xb4UsfcC1oHy7WAwUFBVq3bp3cbrc6duyoCRMm6LrrrmvS\nWLQdvvQB14L24WI98PXXXysvL08mk0kmk0m/+93vFBMT06SxaDt86YNmXQvc8OJ0Ot1PP/20+8iR\nI+66ujr35MmT3d9//73XNtu2bXPPnTvX7Xa73d999537xRdfbPJYGJ8vPeB2u91PPfWUu6qqqlVr\nRstqSg+cOHHCXVpa6s7NzXWvW7euWWPRNvjSB24314L2oCk98O9//9tdU1Pjdrvd7h07dvB/gnbI\nlz5wu7kWtAdN6YHa2lrPzwcOHHA//fTTTR6LtsGXPnC7m3ctYLn7OUpLS9W9e3d169ZNAQEBGjRo\nkIqKiry2KSoq0pAhQyRJvXv3Vk1NjY4fP96ksTA+X3qggZvPY2zTmtIDQUFBioiIkMViafZYtA2+\n9EEDrgVtW1N6oE+fPurUqZMk6YYbbtCxY8eaPBZtgy990IBrQdvWlB4IDAz0/Hzq1CkFBQU1eSza\nBl/6oEFTrwUsdz9HRUWFQkNDPY8dDodKS0t/cZvQ0FBVVFQ0aSyMz5ce6NKli0wmk+bMmSOz2aw7\n7rhDd9xxR6vVjpbhy99lrgPth69/llwL2r7m9sDGjRvVv3//SxoL4/KlDySuBe1BU3vgq6++Um5u\nrn766Se99NJLzRoL4/OlD6TmXQsI6ZeI34jiQj0we/ZsORwOVVZWas6cOerZs6eioqJauToA/jZn\nzhyFhIRwLbhCfPvtt/rss880Z84cf5cCP2qsD7gWXDni4uIUFxenPXv2aPHixVq0aJG/S4IfnNsH\nr732mqTmXQtY7n4Oh8PhtUTp2LFjcjgcTdqmKWNhfL70QMNr0tllsHFxcfy2tA3y5e8y14H2w9c/\ny5CQEElcC9qypvbAgQMHtGzZMk2dOlU2m61ZY2F8vvSBxLWgPWju3+eoqCi5XC5VV1dzLWhHLrUP\nqqqqJDXvWkBIP0dERIQOHz6ssrIy1dfXq7CwULGxsV7bxMbG6osvvpAkfffdd+rcubO6dOnSpLEw\nPl964PTp06qtrZV09j6UXbt26dprr231Y4BvmvN3+dwVFVwH2g9f+oBrQfvQlB4oLy9XZmamUlNT\n1b1792aNRdvgSx9wLWgfmtIDhw8f9vxbsHfvXkmS3W7nWtCO+NIHzb0WmNys2z7Pjh07vD5af/To\n0Vq/fr0kaejQoZKkFStWqLi4WIGBgZo4caLCw8MvOBZtz6X2wJEjR5SZmSlJcrlcSkxMpAfaqIv1\nwPHjxzVt2jSdPHlSZrNZgYGBWrhwoQIDA7kOtCOX2gcnTpzgWtBOXKwH3nzzTX311Vfq2rWrJHl9\nrQ7XgvbjUvuA/xe0HxfrgQ8++EBffPGFLBaLAgMD9cgjj+iGG2644Fi0TZfaB829FhDSAQAAAAAw\nCJa7AwAAAABgEIR0AAAAAAAMgpAOAAAAAIBBENIBAAAAADAIQjoAAAAAAAZBSAcAAAAAwCAI6QAA\noE3bs2ePnn322Qu+Xl5erkceeURN+dbZt99+W2vXrm3J8gAAaBa+Jx0AgBYwadIknThxQmazWR06\ndFD//v312GOPKTAw0N+lXVBZWZlSU1OVm5srs7nlfm+/ceNGffjhh6qoqJDValV4eLiee+65VjsX\nkyZN0sSJExUTE+PTfkpKSrRkyRK98cYbLVQZAAAXF+DvAgAAaC9eeOEFxcTEqKKiQq+88oref/99\nPfjgg00e3/B7c5PJdLlKbFFOp1MWi8Xrud27dys3N1fTp0/X9ddfr+rqam3fvr3Va2MOAgDQVhHS\nAQBoYQ6HQ/369dP//vc/1dTUaPHixSotLZXT6dSNN96oJ554Qg6HQ5I0c+ZMRUZGqqSkRPv27VNm\nZqb27NmjdevWqaKiQkFBQbrnnnt0xx13SDo7u7t48WINHz5c69atk8Vi0eOPP66AgABlZWWpqqpK\no0aNUkpKiqSzYfWDDz7Qp59+qpMnTyomJkZ/+MMfZLPZ9PLLL0uSfv/730uSZsyYod69e3tmwo8f\nP64bbrhBTz75pLp27SpJGjdunB577DH94x//kNvt1uLFi72OvbS0VH369NH1118vSbLZbBo8eLDn\n9bq6OuXm5mrr1q2qq6tTXFycHn30UVmtVs+xjRgxQh988IHMZrN++9vf6je/+Y0kafv27Vq9erWO\nHTumjh076u6779bIkSO9ZrwXL16s8vJypaeny2w26/7779dtt93mWTGwdetWffjhh5o3b56npo8+\n+ki7d+/WlClT9Prrrys0NFSjR4/W3LlzVV9fr0ceeUQmk0mLFi1Samqq3nzzTdlsNknS3r17NXfu\nXL311lstuhoBAHDl4l8TAABaSMPsbXl5uYqLixUeHi63262kpCQtXbpUb7zxhqxWq1asWOE1rqCg\nQE8++aSys7N19dVXKzg4WNOmTVNWVpYmTpyorKws7du3z7P9iRMnVFdXp7feektjx47VsmXLtHnz\nZqWnp2v27Nlas2aNjh49Kkn6+OOPVVRUpFmzZmnZsmXq3Lmz5/1nz54tSVq1apWys7PVu3dvff31\n1/r73/+utLQ0rVixQlFRUXrttde86i0qKtK8efO0YMGC885Bnz59tHPnTuXl5elf//qX6urqvF7P\nycnR4cOHlZGRocWLF6uiokJr1qzxOraTJ09q2bJl+uMf/6gVK1bo5MmTkqQ333xTTzzxhLKysrRg\nwYJGl7Onpqaqa9eueuGFF5Sdna1Ro0Z5vX7rrbfq4MGDOnz4sOe5L7/8UomJiZLOrmIwmUzq0KGD\npk+fLofDoezsbGVlZSkkJETR0dEqLCz0jP3iiy80aNAgAjoAoMXwLwoAAC0kIyND48eP18svv6yb\nbrpJo0ePls1mU1xcnKxWqwIDA3Xvvfdq9+7dnjEmk0lDhgxRWFiYzGazLBaLfv3rX6tbt26SpJtu\nukl9+/bVnj17PGMsFovuvfdemc1mJSQkqLq6WsOHD1dgYKDCwsIUFhamAwcOSJLWr1+vBx54QA6H\nQwEBARozZoy2bt0ql8vV6JLw9evXKyUlRT169JDZbFZKSor279+v8vJyzzYpKSnq3LmzrrrqqvPG\nR0ZGavLkydq3b5/S09P1+OOPKzs72/N+n376qR599FF17txZgYGBGj16tFfotVgsuv/++2U2m9W/\nf38FBgbq4MGDkqSAgAD98MMPOnnypDp16qRevXo1+8+oQ4cOio2N1ebNmyVJhw4d0sGDBxUbG+vZ\npuG8NHZ+hgwZooKCAkmSy+VSYWGh10oBAAB8xXJ3AABayJQpU86b3T19+rSysrK0c+dOVVdXS5JO\nnTolt9vtufe8YSl5gx07dmjNmjU6dOiQ3G63Tp8+reuuu87zut1u94y1Wq2SpC5dunhet1qtOnXq\nlCTp6NGjysjI8JrptVgsOnHiRKPHcPToUa1atUrvvPOO1/MVFRWeOkNDQ3/xPPTr10/9+vWTJH37\n7bdasGCBevToobi4OJ05c0YvvPCCZ1u32+0Vhu12u1etPz+W559/XmvXrlVOTo6uu+46Pfjgg+rT\np88v1tKYxMREZWdn6/7779fmzZs1YMAAz3m8mNjYWL399tsqKyvTwYMH1alTJ0VERDS7BgAALoSQ\nDgDAZfThhx/q0KFDmjt3roKDg7V//35NnTrVK6T/XF1dnV599VWlpqZqwIABMpvNysjIuOQPQuva\ntaueeuqpRsNsw5L4c7e/7777PMu/G9OcD7aLiYlRTEyMvv/+eyUnJ8tqtWrBggUKCQlp8j4aRERE\naMqUKXK5XPr444+1cOHCRj95/WL13XzzzaqsrNT+/ftVWFioRx99tNHxje3HarUqPj5eBQUF+vHH\nH5lFBwC0OJa7AwBwGZ06dUpWq1WdOnVSdXW18vPzf3H7+vp61dfXe2bLd+zYoV27dl3y+w8dOlS5\nubme5eqVlZUqKiqSJAUFBclkMunIkSNe2//tb3/TDz/8IEk6efKktmzZ0uT3KyoqUmFhoaqrq+V2\nu1VaWqrdu3erd+/eMplMSk5O1qpVq1RZWSnp7Az9zp07L7rf+vp6FRQU6OTJkzKbzerYseMF7wMP\nDg72uuf8XAEBAYqPj9c777yj6upq9e3b1/Paz2f2g4ODVVVV5bknvsHgwYO1adMmbdu2jZAOAGhx\nzKQDAHAZ3X333frrX/+qxx9/XA6HQyNGjPCE5MZ07NhR48eP18KFC1VfX69bb73V637p5ho+fLjc\nbrf+8pe/6KefflJQUJAGDRqk2NhYdejQQffee69mzJghp9Op6dOnKy4uTqdOndKiRYt09OhRderU\nSbfccovi4+Ob9H6dO3fWxx9/rBUrVqi+vl5dunTRqFGjPDPzDz30kNasWaPp06ersrJSDodDd955\np2655ZaL7rugoEArV66Uy+VSz5499cwzzzS63ejRo7Vy5Url5OTovvvuU1xc3HnbJCYm6uWXX9ad\nd97pFfYbPjhOknr27KlBgwYpNTVVLpdLCxcuVJcuXRQZGSmTyaTw8PDzblUAAMBXJjdfJAoAANAs\nc+bM0aBBg5SUlOTvUgAA7QzL3QEAAJqhtLRUe/fuVUJCgr9LAQC0Qyx3BwAAaKIlS5aoqKhI48eP\nV2BgoL/LAQC0Qyx3BwAAAADAIFjuDgAAAACAQRDSAQAAAAAwCEI6AAAAAAAGQUgHAAAAAMAgCOkA\nAAAAABgEIR0AAAAAAIP4fzhz/EADfXFoAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x14270358>"
]
}
],
"prompt_number": 10
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"interactive(par_sen.plot, group = fixed(None), n = (1,50))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA+kAAAI7CAYAAACQvNrvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8VNX9//HXzCSTjQmQsMQYqawGBlEgYZWCUrFV8SuL\nfGvFpXRBjIhfEiBoUUCRJWyxlDwqYNVq1QRBqbX2QYuRRSKLUMoQUIgKGkmABJIJCUlm5vdHfkyN\nBJLoDZMZ3s9/OnPnnns+985Hyodz5hyTx+PxICIiIiIiIiI+Z/Z1ACIiIiIiIiJSQ0W6iIiIiIiI\nSDOhIr2ZcTgcvg5BAojySYykfBIjKZ/ESMonMZLySYz0ffJJRXozoz8UxEjKJzGS8kmMpHwSIymf\nxEjKJzGSinQRERERERERP6YiXURERERERKSZMGkLNhEREREREZHmIcjXAciF8vPzfR2CBAibzUZp\naamvw5AAoXwSIymfxEjKJzGS8kmMFBsb2+g2mu4uIiIiIiIi0kyoSBcRERERERFpJlSki4iIiIiI\niDQTKtJFREREREREmgkV6SIiIiIiIiLNhIp0ERERERERkWYiILZgmz9/PlOmTCE8PLzOzx0OB3/9\n619JTU01rM/777+fP//5z4Zd79sOFp1rkuvKlaNdhJWoEJOvwxARERERkUby+yLd4/GQmpqKyXR5\nC5Km7O+JjUea7NpyZXju1s5EhYT4OgwREREREWkkvyzSCwsLmTdvHl27duXzzz/nq6++YvXq1WzY\nsIE2bdpw2223AZCZmUlYWBidO3f2tj18+DCrVq1i6tSpzJ07l7S0NO8I/GOPPcazzz5LZGRknX2m\np6dz7tw5EhISvMcdDoe3n+PHj2O32/n1r3+NyWTi3//+N1lZWVRVVdG+fXseeeQRQkNDm/jpiIiI\niIiIiL/y29+kHz9+nJ/+9KcsWbKENm3aYDKZGDx4MNu3b/eek5OTw+DBg/F4PAAcOnSI1atXM336\ndNq3b09iYiI7duwA4LPPPqNdu3Z1FugAf/rTn7jttttYvHgxrVu3rvXZ4cOHmTBhAkuXLqWgoICP\nP/6YkpIS1q1bx1NPPcXChQvp1KkT7777bhM9DREREREREQkEfjmSDtC2bVu6dOlS69i1117LmTNn\nKC4u5syZM0RERBAVFcU333zD119/zQsvvMCsWbNo1aoVAIMGDWLt2rUMGzaMbdu2MWjQoIv29+mn\nnzJt2jQAhgwZwmuvveb9rEuXLrRr1w6AwYMHc/DgQaxWK1999RW/+93vAKiurqZbt24XXNfhcOBw\nOLzvx40b9z2fiMh/BVmCsNlsWK1WbDabr8ORAKF8EiMpn8RIyicxkvJJjJaZmel9bbfbsdvtlzzf\nb4v0kIv83nbgwIHk5ORw+vRpBg8e7D3eunVrqqqqyMvLo0+fPgB07dqV48ePU1JSwq5duxg7duz3\niuXbv0/3eDyYTCY8Hg+9evViypQpl2zbkC9JpLGqXdWUlpZis9koLS31dTgSIJRPYiTlkxhJ+SRG\nUj6JkWw2W6MHYv12uvvFDBo0iG3btpGTk8OAAQO8x8PDw0lNTeX111/nwIEDQE1x3a9fP15++WXi\n4uJo0aLFRa973XXXsW3bNgC2bt1a67PDhw9TWFiI2+1m+/btdO/ena5du3Lo0CGOHz8OQEVFBd98\n843RtysiIiIiIiIBxG+L9G+PXn/7dVxcHBUVFURHR3untZtMJkwmEy1btmTGjBmsWbOGw4cPAzVF\n/datWy851R3goYce4h//+AcpKSkUFRXV6rNz5868+OKLTJ06lfbt29OvXz8iIyN55JFHSE9PZ9q0\nacyaNYv8/HwjH4GIiIiIiIgEGJPn/Kpq8r00xR7sA5b907BryZXpuVs7Ex8VoulaYijlkxhJ+SRG\nUj6JkZRPYqTY2NhGt/Hb36Q3F+dH6Y303K2d6z9J5BLaRVh9HYKIiIiIiHwPKtK/Y926deTk5NQ6\nNnDgQEaNGlXn+T169KBHjx6GxhAfVfeieCIiIiIiIhLYVKR/x+jRoxk9erSvwxAREREREZErkIr0\nZigkrMzXIUiAcHkqCAlz4XGHUHlO/7mLiIiIiDR3Afm39m8v5lZVVcWCBQsoLS1l1KhRDBw48LLG\nkp2dzQ033EDr1q0b3CY4Yk8TRiRXGjNQVdabAP3PXUREREQkoAT839o///xzABYtWuST/j/88EM6\ndOjQqCJdRERERERErkzNqkh/9913+eCDDwAYPnw4t9xyC8uWLaOoqAi3282YMWMuup/53r17efnl\nl7FarcTHxwNQUlLC73//e0pLS5k+fTrJycm0b9/+graHDx/m5ZdfpqKiguDgYJ566inMZjOrV68m\nLy8Pi8XCAw88gN1uJzs7m127dlFZWUlBQQGJiYmMHz8et9tNRkYGeXl5mEwmbr75ZqKjozly5AjP\nP/88ISEhPPPMM1itWnVbRERERERE6tZsivS8vDyys7OZP38+brebJ598ErfbTVRUFDNnzgTg7Nmz\ndbatrKzkj3/8I08//TQxMTEsW7YMk8lEZGQkkyZNYsOGDRfdx7y6upr09HT+7//+j06dOlFRUYHV\nauVvf/sbZrOZxYsXk5+fz7PPPkt6ejoAX375JYsWLSIoKIjHH3+cn/3sZ5w5c4bi4mKWLFnijTU8\nPJx//OMf3H///XTq1KkJnpqIiIiIiIgEkmZTpB88eJB+/fp5R5r79euHxWJh3759vPbaa/Tt29c7\nQv5d+fn5tGvXjpiYGACGDBnCP//5TwA8Hs8l+83Pz6dVq1beIjo0NBSAQ4cO8bOf/Qyo2YC+bdu2\nfPPNNwD07NmTsLAwAOLi4jh58iRxcXEUFBTw4osv0qdPH2644YYG3bfD4cDhcHjfjxs3rkHtRBrD\nYrFgs9l8HYb4OavVqjwSwyifxEjKJzGS8kmMlpmZ6X1tt9ux2+2XPL/ZFOnf5fF4MJlMLFq0iE8+\n+YQ33niDnj17Mnbs2MsaQ12Cg4O9r00mEy6Xi4iICNLS0vj3v//Nxo0b2b59O5MmTaq3j4Z8SSI/\nlMvl4mx5qa/DED9ns9koLVUeiTGUT2Ik5ZMYSfkkRrLZbI0eiDU3USyN1r17d3bu3EllZSUVFRXs\n3LmTTp06ERwczJAhQxg5cqR3Ebjvio2N5cSJExQUFACwdevWBvcbGxvL6dOnOXLkCADl5eW43W7i\n4+O918nPz+fkyZPExsZe9DqlpaW43W769+/P//7v//LFF18ANSPz5eXlDY5HRERERERErlzNZiS9\nY8eODB061Pv78+HDh1NeXs6TTz6JyWQiKCiIX//613W2tVqt/Pa3v2XBggVYrVa6d+/uLdhNJhMm\nk+mi/Z7/XfmLL75IZWUlISEhzJo1i9tuu41Vq1aRkpKCxWIhKSmJoKCLP66ioiJWrlzpHX3/xS9+\nAcCwYcNYtWqVFo4TERERERGRepk89f1oWy67ksrM+k8SaYSqst6cK4/wdRji5zT9T4ykfBIjKZ/E\nSMonMdKlZmNfTLMZSZf/qirr7esQJEBYLBZcLhced4ivQxERERERkQbwuyJ98eLFFBYW1jo2fvx4\nevXq1aRtLyeNeIpRbDabFowTEREREfEjV+R099mzZ/PAAw9csHd5dnY2eXl5TJgwodbxAwcO8PLL\nL3P06FGmTJnCgAEDAPjiiy9YvXo15eXlmM1mRo0axaBBg7ztXn/9dXJycjCbzYwYMcK7pVt9Dr7z\n4Q+8Q5Ea50fS6xMW15bgq1pdhojEn2n6nxhJ+SRGUj6JkZRPYiRNd2+gSy0kV5e2bduSlJTEhg0b\nah0PCQnh0UcfJSYmhuLiYlJTU7nxxhsJDw/ngw8+oKioiPT0dABKSkoa3N/2UXMbFZ/IDzVw/VMq\n0kVEREREmoGAL9LXrVvHhx9+SMuWLYmOjvaOnm/fvp3Vq1dTVlbGpEmTiI+Pr9Xuk08+Yd26daSm\nptK2bVsAzObaO9ZdddVV3tetW7cmMjKSkpISwsPD2bhxI1OmTPF+HhkZ2VS3KCIiIiIiIgEioIv0\nvLw8PvroI9LS0nC5XMyYMcNbpLvdbp577jn27NlDVlYWs2bN8rbbsWMHf/vb33jiiScIDw9vUF+H\nDx+murqamJgYAAoKCti2bRs7d+4kMjKSX/7yl97PREREREREROpirv8U/5Wbm0u/fv2wWq2EhYWR\nkJDg/ax///5Azf7sJ06c8B7fv38/77zzDjNnzmxwgV5cXMyKFStISkryHquqqsJqtTJ//nyGDx9O\nRkaGQXclIiIiIiIigSqgR9Iv9dvzoKCaWzebzbUW1mrfvj2FhYXk5+dfsLBcXdc8e/YsCxYs4N57\n76VLly7e49HR0d5/CEhMTGTlypV1xuFwOHA4HN7348aNa8CdiRjLYrFgs9l8HYY0c1arVXkihlE+\niZGUT2Ik5ZMYLTMz0/vabrdjt9sveX5AF+ndu3dn5cqV3H333bhcLnbv3s1PfvKTS7Zp27Yt999/\nP4sXL2bq1KnExcV5P/N4PHx7Mfzq6moWL17M0KFDvQX5eYmJiezfv5+bb76ZAwcOXHRVv4Z8SSJN\nzeVyaRVTqZdWuxUjKZ/ESMonMZLySYxks9kaPRAb0EV6x44dGThwINOmTaNly5Z07ty5zvO+Ozoe\nGxvLY489xtKlS0lNTaWkpIQlS5bgdDr55JNPyMrKYsmSJXz00Ufk5ubidDrJzs4G4JFHHuHaa6/l\n7rvv5vnnn+dvf/sbYWFhPPzww019uyIiIiIiIuLnrqh90rOysggNDWXkyJG+DuWS/mQe7usQ5Aoz\ncP1TRCZ29XUY0sxpZEGMpHwSIymfxEjKJzHS99knPaAXjqtLY/dIFxEREREREblcAnq6+3fdc889\nvg6hQQauf8rXIUiAsFgstRZGvJiwuLaXIRoREREREanPFVWk+wtNOxajaLqWiIiIiIh/ueKmu4uI\niIiIiIg0V1fkSPrs2bN54IEHLtgHPTs7m7y8PCZMmFDr+IEDB3j55Zc5evQoU6ZMYcCAAQB88cUX\nrF69mvLycsxmM6NGjWLQoEG12r744otkZ2fzyiuvNDi+kp2ffc87E6mtrIHT3aFmynvwVa2aOCIR\nEREREbmUK7JIb+zicW3btiUpKYkNGzbUOh4SEsKjjz5KTEwMxcXFpKamcuONNxIeHg7AkSNHOHv2\nbKP72z5qbqPOFzHCwPVPqUgXEREREfGxgC/S161bx4cffkjLli2Jjo72jp5v376d1atXU1ZWxqRJ\nk4iPj6/V7pNPPmHdunWkpqbStm3Nolpmc+1fB1x11VXe161btyYyMpKSkhLCw8Nxu928+uqrTJky\nhR07djTxXYqIiIiIiEggCOjfpOfl5fHRRx+RlpbGzJkzOXLkiPczt9vNc889x0MPPURWVlatdjt2\n7OCdd97hiSeeoEWLFg3q6/Dhw1RXVxMTEwPA+++/T2JiIq1aaWRSREREREREGiagi/Tc3Fz69euH\n1WolLCyMhIQE72f9+/cHoGPHjpw4ccJ7fP/+/bzzzjvMnDnTO229PsXFxaxYsYKkpCQAioqKyMnJ\n4ac//Skej8fAOxIREREREZFAFtDT3S/1W/CgoJpbN5vNtRbWat++PYWFheTn51+wsFxd1zx79iwL\nFizg3nvvpUuXLkDNgnLHjx9n8uTJAJw7d44pU6aQnp5+wfUcDgcOh8P7fty4cY24QxHjWCwWbDab\nr8OQZsxqtSpHxDDKJzGS8kmMpHwSo2VmZnpf2+127Hb7Jc8P6CK9e/furFy5krvvvhuXy8Xu3bv5\nyU9+csk2bdu25f7772fx4sVMnTqVuLg472cej6fWyHh1dTWLFy9m6NCh3pF5gD59+vDCCy943z/w\nwAN1FujQsC9J5HJwuVzaU10uyWazKUfEMMonMZLySYykfBIj2Wy2Rg/EBnSR3rFjRwYOHMi0adNo\n2bIlnTt3rvO8746Ox8bG8thjj7F06VJSU1MpKSlhyZIlOJ1OPvnkE7KysliyZAkfffQRubm5OJ1O\nsrOzAUhKSuJHP/rRJa8vIiIiIiIiUheT5wr60XRWVhahoaGMHDnS16Fc0p/Mw30dglyBBq5/isjE\nrr4OQ5oxjSyIkZRPYiTlkxhJ+SRGio2NbXSbgF44ri4a1RYREREREZHmKqCnu3/XPffc4+sQGmTg\n+qd8HYIECIvFUmthxEsJi2vbxNGIiIiIiEh9rqgi3V9oyrEYRdO1RERERET8i4r0Zuhg0TlfhyAB\nIuiMi2pXtWHXaxdhJSpEPxkREREREWkqAVOkz58/nylTphAeHl7n5w6Hg7/+9a+kpqYa1uf999/P\nn//8Z8Oud94TG48Yfk0RIzx3a2eiQkJ8HYaIiIiISMAKiCLd4/GQmpp62ReF0yJ0IiIiIiIiYiS/\nLdILCwuZN28eXbt25fPPP+err75i9erVbNiwgTZt2nDbbbcBkJmZSVhYWK090g8fPsyqVauYOnUq\nc+fOJS0tzTsC/9hjj/Hss88SGRlZZ5/p6emcO3eOhIQE7/GKigrS0tJwOp24XC5+/vOfk5CQQEVF\nBcuWLaOoqAi3282YMWMYNGhQEz8ZERERERER8Vd+vQXb8ePH+elPf8qSJUto06YNJpOJwYMHs337\ndu85OTk5DB48mPPbwR86dIjVq1czffp02rdvT2JiIjt27ADgs88+o127dnUW6AB/+tOfuO2221i8\neDGtW7f2HrdaraSkpLBw4UKeeuopXnnlFQD27t1LVFQUaWlpLFmyhBtvvLGpHoWIiIiIiIgEAL8d\nSQdo27YtXbp0qXXs2muv5cyZMxQXF3PmzBkiIiKIiorim2++4euvv+aFF15g1qxZtGrVCoBBgwax\ndu1ahg0bxrZt2y450v3pp58ybdo0AIYMGcJrr70GgNvt5i9/+QsHDx7EZDJ5+/7Rj37En//8Z157\n7TX69u1LfHz8Bdd0OBw4HA7v+3Hjxv3g5yLSVIIsQdhsNl+HIT5itVr1/YthlE9iJOWTGEn5JEbL\nzMz0vrbb7djt9kue79dFeshFFrAaOHAgOTk5nD59msGDB3uPt27dmqqqKvLy8ujTpw8AXbt25fjx\n45SUlLBr1y7Gjh3b6Di2bt1KaWkpCxcuxGw2k5SURFVVFVdddRWLFi3ik08+4Y033qBnz54XXL8h\nX5JIc1HtqtaWblcwbeknRlI+iZGUT2Ik5ZMYyWazNXog1q+nu1/MoEGD2LZtGzk5OQwYMMB7PDw8\nnNTUVF5//XUOHDgA1Cz+1q9fP15++WXi4uJo0aLFRa973XXXsW3bNqCmMD/v7NmzREZGYjab2b9/\nPydPngSguLiY4OBghgwZwsiRI/n888+b4nZFREREREQkQPh1kf7t1dW//TouLo6Kigqio6O909pN\nJhMmk4mWLVsyY8YM1qxZw+HDh4Gaon7r1q31Lur20EMP8Y9//IOUlBSKioq8fQ4ZMoS8vDxSUlLY\nvHkzV199NQBHjx7lySefZPr06bz11luMGTPG0PsXERERERGRwGLynF9RTZqNAcv+6esQROr03K2d\niY/SPulXKk3/EyMpn8RIyicxkvJJjBQbG9voNn79m/RA9dytnes/SaQBgixBVLuqDbteuwirYdcS\nEREREZELqUivw7p168jJyal1bODAgYwaNeqy9K+RSjGK/iVYRERERMS/qEivw+jRoxk9erSvwxAR\nEREREZErTEAU6YWFhSxcuJAlS5YYet358+czZcoUwsPD2bt3Ly+99BJut5tbbrmFu+++GwCn08my\nZcs4efIkbdu25f/+7/+IiIgA4Msvv+SFF16goqICk8nE/PnzCQ4Orrff0IIjht6HXLncJy2EulxN\nc+3IaCrDWjXJtUVERERErlQBUaQ3lZkzZwLgdrtZs2YNs2bNIioqipkzZ5KQkEBcXBxvv/02vXr1\n4n/+5394++23efvtt7nvvvtwuVysWLGCyZMn06FDB5xOJxaLpUH9hq2d35S3JWKI8rEzQUW6iIiI\niIih/HoLtroUFBQwY8YMNmzYQEZGBlCzFVpycjKVlZV1tqmoqGDlypWkpKQwbdo0duzYAUBSUhJO\np5PDhw8TExNDu3btCAoKYvDgwezatQuAXbt2MXToUACGDRvGzp07Afj3v/9Nhw4d6NChAwAtWrTA\nbA64xy0iIiIiIiIGCqiR9Pz8fNLT00lKSuKaa65h9uzZ7Nixg/Xr1zNx4kSs1rpXpl67di0REREs\nXrwYgLKyslqfFxUVER0d7X0fFRXl3WP9zJkz3r3YW7ZsyZkzZwD45ptvMJlMzJs3j5KSEgYPHsxd\nd91l+D2LiIiIiIhI4AiYIr2kpIS0tDRSUlK4+uqrgZqR8OTkZEaMGEG3bt0u2nb//v08/vjj3vfn\nf1PeWCaTyfva5XJx8OBBFixYgNVqZe7cuXTq1ImePXvWauNwOHA4HN7348aN+159i1xuFosFm83m\n6zDkMrJarfrOxTDKJzGS8kmMpHwSo2VmZnpf2+127Hb7Jc8PmCI9PDycNm3akJub6y3S8/PzCQsL\no6io6AddOyoqilOnTnnfnzp1iqioKKBm9Pz06dO0atWK4uJiWrZsCUCbNm3o3r07LVq0AKB3797k\n5eVdUKQ35EsSaY5cLhdl2t7tiqIt/cRIyicxkvJJjKR8EiPZbLZGD8QGzI+kg4KCSElJYfPmzWzd\nupWzZ8/y0ksvMXfuXJxO5wX7nn9br169eP/9973vvzvdvXPnzhw/fpzCwkKqq6v56KOPSEhIACAh\nIYHs7GwAPvzwQxITE73XPHr0KJWVlbhcLg4cOMA111xj8F2LiIiIiIhIIAmYkXSTyURISAipqak8\n88wzvPnmm9xxxx3ExMTw8MMPM2fOHHr06EFkZOQFbUePHs2aNWtITk7GbDZzzz330K9fP+/nFouF\nCRMmMG/ePO8WbHFxcQDcfffdLFu2jA8++MC7BRvULBR35513eleI79OnD717974MT0JERERERET8\nlcnj8Xh8HURz5Ha7+c1vfsOqVasu+6rs5U/efln7E/k+ysfOpKJ9Z1+HIZeRpv+JkZRPYiTlkxhJ\n+SRGio2NbXSbgBlJN1pycjLDhw/3ybZp5WNnXvY+JTBZLBZcLleTXNsdGV3/SSIiIiIi0ihXVJGe\nnZ3Ne++9V+tYfHw8EyZMuODcZcuWXa6wLqDRSTGKzWbT4m4iIiIiIn7kiirShw0bxrBhw3wdhoiI\niIiIiEidrqgi3V+EFhzxdQgSINwnLYQ20XT3C/qKjKYyrNVl6UtEREREJFA1yyK9sLCQhQsXsmTJ\nEl+H4rV3715eeukl7+rud999NwBOp5Nly5Zx8uRJ7+ruERERVFZWsnLlSr766itcLhdDhw71tqlP\n2Nr5TXkrIk2ifOxMUJEuIiIiIvKDBMw+6U3J7XazZs0annjiCZYuXcq2bdv46quvAHj77bfp1asX\n6enp9OzZk7fffhuAjz76CIDFixezcOFCNm7cyMmTJ312DyIiIiIiItL8NcuR9G8rKChg6dKlDB48\nmK+//ppJkyZx9OhR0tPTmT9/Plar9YI2FRUVvPjii+Tl5WEymbz7nt9///3cdttt7Nmzh1atWvG/\n//u/vPbaaxQVFfHggw+SkJDAsWPHyMjIoLq6Go/HQ3JyMiUlJcTExNCuXTsABg8ezK5du4iLi2PX\nrl3Mnj0bqPnN++zZs7nvvvto1aoV586dw+12U1FRQVBQEGFhYZfz0YmIiIiIiIifadZFen5+Punp\n6SQlJXHNNdcwe/ZsduzYwfr165k4cWKdBTrA2rVriYiIYPHixQCUlZUBUFlZSc+ePRk/fjyLFy8m\nMzOTp59+mmPHjvGHP/yBhIQENm7cyO23385NN92Ey+XC5XLxxRdfEB393+2moqKiOHz4MABnzpyh\nVauaKb4tW7bkzJkzANx4441s3ryZ3/72t5w7d46HHnqIiIiIJntWIiIiIiIi4v+abZFeUlJCWloa\nKSkpXH311QAkJSWRnJzMiBEj6Nat20Xb7t+/n8cff9z7/nxxHBQUxI033ghAhw4dCA4Oxmw2c801\n13DixAkAunXrxvr16zl16hT9+/cnJiamwTGbTCbv682bN1NZWckLL7yA0+nkqaee4vrrr/eOxp/n\ncDhwOBze9+PGjWtwfyLNicViwWaz+ToMaUJWq1XfsRhG+SRGUj6JkZRPYrTMzEzva7vdjt1uv+T5\nzbZIDw8Pp02bNuTm5nqL9Pz8fMLCwigqKvpe17RYLN7XJpOJoKCa2zebzbj+/wrYN910E926dWP3\n7t3Mnz+f3/zmN0RFRXHq1Clv21OnThEVFQXUjJ6fPn2aVq1aUVxcTMuWLQH49NNP6devH2azmcjI\nSK677jqOHDlyQZHekC9JxB+4XC7tyR7gbDYbpfqOxSDKJzGS8kmMpHwSI9lstkYPxDbbheOCgoJI\nSUlh8+bNbN26lbNnz/LSSy8xd+5cnE4nOTk5F23bq1cv3n//fe/789PdG6KgoIB27drxs5/9jISE\nBI4ePUqXLl04fvw4hYWFVFdX89FHH5GQkABAQkIC2dnZAHz44YckJiYCEBsby/79+4Ga38h/9tln\n3n9sEBEREREREalLsx1JN5lMhISEkJqayjPPPMObb77JHXfcQUxMDA8//DBz5syhR48eREZGXtB2\n9OjRrFmzhuTkZMxms3fhuG9PRz/fx3dfb9++nS1btmCxWGjdujWjR4/GbDYzYcIE5s2b592CLS4u\nDoC7776bZcuW8cEHH3i3YAO49dZbycjIIDk5GY/Hw80330yHDh2a6nGJiIiIiIhIADB5PB6Pr4OQ\n2sqfvN3XIYg0WvnYmVS07+zrMKQJafqfGEn5JEZSPomRlE9ipNjY2Ea3abYj6Vey8rEzfR2CBAiL\nxeJdb6GpuSOj6z9JREREREQuya+L9OzsbN57771ax+Lj45kwYYKPIjKGRiPFKDabTYu5iYiIiIj4\nEb8u0ocNG8awYcN8HYbhQguO+DoECRDukxZCL9NIep39R0ZTGdbKZ/2LiIiIiPgbvy3SCwsLWbhw\nIUuWLLma8d63AAAgAElEQVRsfWZnZ7N+/XqgZnG6oUOHemNZvnw5TqeTTp068eijjxIUFMTOnTvJ\nzMzEZDJhMpm4//776dmzZ739hK2d36T3IXK5lI+dCSrSRUREREQazG+L9MvN6XTy1ltvsWDBAgBS\nU1NJTEwkPDycV199lTvvvJNBgwaxatUqNm3axIgRI7j++uu9W7IdPXqUtLQ0fv/73/vyNkRERERE\nRKQZC4givaCggKVLlzJ48GC+/vprJk2axNGjR0lPT2f+/PlYrdYL2jidTlauXMmJEyewWq1MnDiR\nDh06kJmZSUFBAQUFBZSWlnLXXXcxfPhw9u7dS69evYiIiADg+uuvZ8+ePQwaNAiHw8Hjjz8OwNCh\nQ8nKymLEiBGEhoZ6+6uoqKhzuzgRERERERGR8/y+SM/Pzyc9PZ2kpCSuueYaZs+ezY4dO1i/fj0T\nJ06ss0AHyMzMpFOnTkyfPp39+/ezYsUKFi1aBMCxY8eYN28eFRUVTJ8+nT59+lBcXEx09H9Xr46O\njqaoqAin00lERARmsxmAqKgoioqKvOft2LGD119/neLiYn73u9814ZMQERERERERf+fXRXpJSQlp\naWmkpKRw9dVXA5CUlERycjIjRoygW7duF2176NAhkpOTAejZsyelpaWUl5djMplISEggODiY4OBg\n7HY7hw8frvMaJpOp3hj79etHv379yM3N5fe//z3p6em1Pnc4HDgcDu/7cePG1XtNEX9hsViw2Wy+\nDkMMYrVa9X2KYZRPYiTlkxhJ+SRGy8zM9L622+3Y7fZLnu/XRXp4eDht2rQhNzfXW6Tn5+cTFhZW\nazT7hzKZTERFRdUqpk+dOkXPnj1p0aIFZWVluN1uzGYzRUVFREVFXXCN7t2743a7KS0trfUffUO+\nJBF/5XK5tAVcALHZbJTq+xSDKJ/ESMonMZLySYxks9kaPRBrbqJYLougoCBSUlLYvHkzW7du5ezZ\ns7z00kvMnTsXp9NJTk7ORdvGx8ezZcsWoGY0OzIykrCwMDweD7t27aKqqorS0lIOHDhAly5duOGG\nG9i3bx9lZWU4nU727dvHDTfcgMlkwm63e/vKzs72LhZ3/PhxPB4PAHl5eQD6VzkRERERERG5KL8e\nSTeZTISEhJCamsozzzzDm2++yR133EFMTAwPP/wwc+bMoUePHnUu2HbPPfeQkZHBtGnTCAkJISkp\nyXvNDh06MGfOHEpLSxk7diytWtVsITVmzBhmzpwJwNixY72LyI0fP57ly5fzxhtv0LFjR2655RYA\nPv74YzZv3ozFYiE0NJQpU6ZcjsciIiIiIiIifsrkOT/UKwBkZWURGhrKyJEjfRZD+ZO3+6xvESOV\nj51JRfvOvg5DDKLpf2Ik5ZMYSfkkRlI+iZFiY2Mb3cavR9KbSkMWhGtK5WNn+rR/CRwWiwWXy+Wz\n/t2R0fWfJCIiIiIiXgFfpGdnZ/Pee+/VOhYfH8+ECRPqPP+ee+65HGFdkkYexSg2m00Lt4mIiIiI\n+JGAL9KHDRvGsGHDfB2GiIiIiIiISL2aXZG+c+dOrrrqKuLi4n7Qdf7whz/Qt29fBgwYQG5uLqtW\nrSI4OJhnnnkGq9VqULT1O3v2LFu3bmXEiBENbhMSVtaEEcmVxOWpICTMd9PdATzuECrPNbs/akRE\nREREmqVm9zfnHTt20Ldv3x9cpJtMJu9vy7ds2cKoUaMYMmSIESE2itPp5B//+EejivTgiD1NGJFc\naXy9z2JVWW+a4R81IiIiIiLNks//5vzhhx/y7rvvAtCyZUvy8vLIzc1l3bp1pKSk4Ha7WbVqFSUl\nJZjNZqZOnUr79u3rvNaaNWv4z3/+Q3R0NEFBQXg8HjZt2kROTg779u1jz549PPbYY3W2ffvtt9m6\ndSsmk4nevXvzi1/8gi+++IJVq1ZRWVlJ+/btmTRpEhEREcyePZuuXbvicDgoKytj0qRJxMfHc+zY\nMTIyMqiursbj8ZCcnMwbb7xBQUEB06dPp1evXowfP77JnqWIiIiIiIj4N58W6ceOHWPdunXMmzeP\nFi1a4HQ6eeWVV+jbty/9+/cH4IknnmDUqFEkJiZSXV2N2+2u81off/wx33zzDcuWLeP06dNMnTqV\nW265hVtuuYWDBw/WuuZ37dmzh927d/Pcc89htVopK6uZbr5ixQp+9atf0b17dzIzM8nKyuKhhx7C\nZDLhdrt57rnn2LNnD1lZWcyaNYuNGzdy++23c9NNN+FyuXC5XNx3330cO3aMRYsWNc1DFBERERER\nkYDh05mw+/fvZ+DAgbRo0QLA+7/nt24vLy+nuLiYxMREAIKCgi76e/Lc3FxuuukmTCYTrVu3xm63\n1/r8UtvB/+c//+Hmm2/2XjsiIoKzZ89y9uxZunfvDsDQoUPJzc31tjlf8Hfs2JETJ04A0K1bN9av\nX88777zDiRMnsFqtl+xXRERERERE5Nt8OpJ+sf3Iv+8+5T+kIK6v7Xc/DwqqeXRms9m7D/VNN91E\nt27d2L17N/Pnz+c3v/kN7dq1u+R1HQ4HDofD+37cuHHfJ3yRZstisWCz2XwdhhjAarXquxTDKJ/E\nSMonMZLySYyWmZnpfW232y8YUP4unxbpPXv2JC0tjTvvvNM73T00NJTy8nIAwsLCiIqKYufOnSQm\nJlJVVYXH46lzNL1Hjx5s3LiRoUOHcubMGRwOR4MXiuvVqxdvvfUWQ4YMwWq14nQ6adGiBRERERw8\neJD4+Hg2b95c78MsKCigffv2/OxnP+PkyZMcPXqUa6+9loqKiou2aciXJOLPXC4XZ8u1V3sgsNls\nlJbquxRjKJ/ESMonMZLySYxks9kaPRDr0yI9Li6O0aNH8/TTT2M2m+nYsSPDhw/nj3/8I3//+9+Z\nOnUqkydP5oUXXiAzMxOLxcLUqVPrHJ3u168f+/fvZ+rUqbRp04brrruu1ueXGp2/8cYb+eKLL0hN\nTSUoKIg+ffrw85//nKSkpFoLxz3yyCN1tj9/7e3bt7NlyxYsFgutW7dm9OjRREREcN1115GcnEzv\n3r21cJyIiIiIiIhclMmjH003OyWVmfWfJOInqsp6c648wtdhiAE0siBGUj6JkZRPYiTlkxgpNja2\n0W18vYWyiIiIiIiIiPx/Pt8nvbGOHj3KihUrah0LDg5m3rx5Tdr2cqoq6+3rECRAWCwW78KGvuJx\nh/i0fxERERERf6Lp7s1Qfn6+r0OQAKHpWmIk5ZMYSfkkRlI+iZGUT2Kk7zPd3e9G0q8Ex6udvg5B\nAsSJ0nJc1b4dSQeIDAolXH/ciIiIiIjUq1n9rXn27Nk88MADdOrUydDrOhwO/vrXv5KamsqBAwcI\nCgqiW7duFz3/3XffZdOmTVgsFiIjI5k0aRJt2rQBYN68eRw+fJjrrruO1NTUS/b7/PPPk5eXh8Vi\noUuXLvz2t7/FYrHUG+/r+bsad4Mizdy9sQmEB7XwdRgiIiIiIs2eTxaO83g81DXL/lLbpBll//79\nHDp06JLndOzYkQULFpCWlkb//v159dVXvZ/9z//8D48++miD+hoyZAjLly9nyZIlVFZW8q9//esH\nxS4iIiIiIiKB7bKNpBcWFjJv3jy6du3K559/zoABA/j4448xmUz07t2bX/ziF0DNXuOrV6+mrKyM\nSZMmER8fT3Z2Njt27KCyspJvvvmGkSNHUllZybZt2wgKCmLmzJm0aNGi1kh8SUkJM2fO5A9/+IM3\nhhMnTvDPf/4Ts9nMli1bmDBhAvHx8RfEarfbva+7du3Kli1bvO979uyJw+Fo0D337v3fBeA6d+5M\nUVFRo5+biIiIiIiIXDku63T348ePM3nyZJxOJ2+99RbPPfccVquVsrIy7zlut5vnnnuOPXv2kJWV\nxaxZswD46quvWLRoEZWVlUyePJn777+fhQsX8vLLL7N582Zuv/32ekfi27Zty6233kpYWBh33nln\ng2LetGlTrWL7+6iurmbLli388pe//EHXERERERERkcB2WYv0tm3b0qVLF1555RVuvvlmrFYrABER\nEd5z+vfvD9RMOT9x4oT3uN1uJzQ0lNDQUCIiIujbty8AHTp04Msvv2xUHA1d0H7z5s18/vnnPPjg\ng426/netXr2aHj161Dlq73A4ao3Mjxs37gf1JdIcWYIs2Gw2X4chP5DVatX3KIZRPomRlE9iJOWT\nGC0zM9P72m6315q5XZfLWqSHhPx3v+SLFcpBQTUhmc3mWvs7BwcHe1+bTCbve5PJhNvt9rY5f92q\nqqofFOu+fftYv349c+bM8cb07f4bKisrC6fTycMPP1zn5w35kkT8navapa1MAoC2pBEjKZ/ESMon\nMZLySYxks9kaPRDrk4XjevXqRXZ2NpWVlQA4ncZsOda2bVuOHDkCQE5OTp3nhIWFUV5efsnrfP75\n56xatYoZM2YQGRl5wecNHYn/17/+xb59+3jssccadL6IiIiIiIhc2S7rSPr5Eegbb7yRL774gtTU\nVIKCgujTpw8///nPL3p+Q4/fddddLFu2jH/961/07t271nnnX/ft25elS5eya9euiy4c9+qrr3Lu\n3DmWLl0KQJs2bZg+fToATz31FPn5+VRUVDBp0iQmTZpEr1696oxn9erVtG3blt/97ndAzVT+MWPG\n1HmuiIiIiIiIiMnT0GFhuWym5fzF1yGIGOre2ARitE+639P0PzGS8kmMpHwSIymfxEixsbGNbnNZ\nR9KlYe6NTfB1CBIgLEEWXNWu+k9sYpFBob4OQURERETEL1zRRfq6desu+O36wIEDGTVqVKOus3jx\nYgoLC2sdGz9+/EWnwddHI45iFP1LsIiIiIiIf9F092YoPz/f1yFIgFCRLkZSPomRlE9iJOWTGEn5\nJEYK6OnuGzduJCQkhB//+Mf1nltYWMjChQtZsmQJAMuXL+frr7/m5ptv5vbbb2/qUGvZuXMnV111\nFXFxcQ1uExJW1oQRyZXE5akgJMz3093P87hDqDznN3/siIiIiIhcdn7zt+Vbb731e7U7ffo0eXl5\nPP/88wZH1DA7duygb9++jSrSgyP2NGFEcqXxyT6LF1FV1hs/+mNHREREROSya7Z/W/7www959913\nAfjRj35E+/btCQ0NZeTIkXWen5eXR0ZGBkCt34I/++yzFBUVMX369ItuuXb8+HFWrVpFSUkJZrOZ\n5ORk2rVrx5///Gf27t2LyWRi9OjRDBo0CIfDQVZWFpGRkRw7doyOHTt690F/7bXX2L17NxaLhV69\netG/f392795Nbm4u69atIzk5mfbt2xv9qERERERERCRANMsi/dixY6xbt4558+bRokULnE4nf//7\n3y/ZZuXKlfz6178mPj6eV1991Xt8xowZLFiwgEWLFl207fPPP8+oUaNITEykuroat9tNTk4OX375\nJYsXL6akpISZM2fSo0cPAL744guWLl1K69atmTVrFgcPHuTqq69m586dLF++HICzZ88SHh5OQkIC\nffv2pX///gY8GREREREREQlkzbJI379/PwMHDqRFi5pVzs//78WUlZVx9uxZ7yj5j3/8Y/bsqZky\nXt+6eOXl5RQXF5OYmAhAUFDNIzl06BA33XQTJpOJli1b0qNHDw4fPkx4eDhdunQhKioKgGuvvZaT\nJ0/SrVs3goODycjIoG/fvvTp08fbx6VicDgcOBwO7/tx48ZdMl4Rf2axWLDZbL4OQ74nq9Wq708M\no3wSIymfxEjKJzFaZmam97Xdbsdut1/y/GZZpJtMph/U3qgF6797nfNxnS/kAcxmM9XV1ZjNZubP\nn89//vMfcnJyeP/993nqqadqtatLQ74kkUDhcrk4W67VUv2VVrsVIymfxEjKJzGS8kmMZLPZGj0Q\n25zWlPLq2bMn27dvx+l0Anj/92IiIiKIiIjg4MGDAGzZsqXBfYWFhREVFcXOnTsBqKqqorKyku7d\nu/PRRx/hdrspKSkhNzeXLl26XPQfACoqKigrK6N37948+OCDfPnllwCEhoZSXl7e4HhERERERETk\nytUsR9Lj4uIYPXo0Tz/9NGazmY4dO9K2bdtLjkhPmjSJjIwMTCYTvXr1qnVufSPzkydP5oUXXiAz\nMxOLxcLUqVPp168fn376KdOmTcNkMjF+/HhatmzJ119/fcH1TCYTFRUVLFq0iKqqKjweDw8++CAA\ngwcP5o9//CN///vfmTp1qhaOExERERERkYsyeYyaG97EXnzxRTp16sSwYcN8HUqTK6nMrP8kET9U\nVdabc+URvg5DvidN/xMjKZ/ESMonMZLySYwUGxvb6DbNciT9u9544w2OHDlyxSyqVrOXtMgPZ7FY\ncLlcvg7Dy+MO8XUIIiIiIiLNmt+MpJ+3Zs0aDh06VOvY7bff3qAR9h/S9nLKz8/3dQgSIPQvwWIk\n5ZMYSfkkRlI+iZGUT2Kk7zOS7ndF+pVARboYRf8nI0ZSPomRlE9iJOWTGEn5JEYK2OnuV5rQgiO+\nDkEChPukhdBmNN39PHdkNJVhrXwdhoiIiIhIs+N3RXphYSELFy5kyZIll73f5cuX43Q66dSpE48+\n+qh3v/QXX3yRvXv3EhISwiOPPELHjh297dxuN6mpqURFRZGamtqgvsLWzm+SexBpLsrHzgQV6SIi\nIiIiF2iW+6Q3R6+++ip33nknzz//PBEREWzatAmATz75hIKCAp5//nl++9vfsnr16lrt3nvvPeLi\n4urdBk5ERERERETEr4v0goICZsyYwYYNG8jIyADg6NGjJCcnU1lZWWebiooKVq5cSUpKCtOmTePj\njz8mJyeHV155BagpqidPnuy9/qxZswBwOBwMGDAAgKFDh7Jz504Adu3axdChQwHo2rUrZWVlnD59\nGoBTp06xZ88ebrnlFvTTfxEREREREamP3013Py8/P5/09HSSkpK45pprmD17Njt27GD9+vVMnDgR\nq9VaZ7u1a9cSERHB4sWLASgrK6Oqqop33nkHgNzcXGw2G0VFReTm5tKjRw9KS0uJiIjAbK75N42o\nqCiKiooAKCoqIjo62nv96OhoioqKaNWqFS+//DLjx4+nvLy8KR+FiIiIiIiIBAi/LNJLSkpIS0sj\nJSWFq6++GoCkpCSSk5MZMWIE3bp1u2jb/fv38/jjj3vfR0READUj7BUVFRQVFXHTTTeRm5vLwYMH\nGTBgQL2j4HV9vnv3biIjI+nYsSMOh+OibR0OR63Pr5S94OXKZrFYsNlsvg5DGslqtep7E8Mon8RI\nyicxkvJJjJaZmel9bbfbsdvtlzzfL4v08PBw2rRpQ25urrdIz8/PJywszDvC3VjXXXcdH3zwAVdd\ndRXx8fFs2rSJzz77jAcffJDQ0FDKyspwu92YzWaKioqIiooCakbVT5065b3OqVOniIqKIicnh927\nd7Nnzx6qqqooLy9nxYoVPProo7X6bciXJBJoXC4XZdraxO9oSxoxkvJJjKR8EiMpn8RINput0QOx\nfvmb9KCgIFJSUti8eTNbt27l7NmzvPTSS8ydOxen00lOTs5F2/bq1Yv333/f+76srAyA+Ph4NmzY\nQI8ePbj22mtxOBwEBwcTFhaGyWTCbrd7r5udnU1iYiIACQkJbN68GYBPP/2UiIgIWrVqxS9+8Qsy\nMjL4wx/+wOOPP47dbr+gQBcRERERERH5Nr8s0k0mEyEhIaSmpvK3v/2NGTNm8NOf/pSYmBgefvhh\n/vKXv1BSUlJn29GjR1NWVkZycjLTpk3zTjWPj4+nqKiIHj16YDabadOmDfHx8d5248eP59133+Wx\nxx6jrKyMW265BYA+ffrQrl07Jk+ezKpVq/jVr3510ZhFRERERERELsXk0bLjzU75k7f7OgSRJlU+\ndiYV7Tv7OgxpJE3/EyMpn8RIyicxkvJJjBQbG9voNn75m/RAVz52pq9DkABhsVhwuVy+DuMC7sjo\n+k8SEREREbkCBWyRnp2dzXvvvVfrWHx8PBMmTPBRRA2nEUYxis1m0wJtIiIiIiJ+JGCL9GHDhjFs\n2DBfh/G9hBYc8XUIEiDcJy2ENsOR9O9yR0ZTGdbK12GIiIiIiPic3xbphYWFLFy4kCVLlly2PrOz\ns1m/fj1QswDd0KFDvbEsX74cp9NJp06dePTRRwkKCsLhcLBo0SLat28PQP/+/RkzZky9/YStnd90\nNyHSDJWPnQkq0kVERERE/LdIv9ycTidvvfUWCxYsACA1NZXExETCw8N59dVXufPOOxk0aBCrVq1i\n06ZNjBgxAoAePXowY8YMX4YuIiIiIiIifiIgivSCggKWLl3K4MGD+frrr5k0aRJHjx4lPT2d+fPn\nY7VaL2jjdDpZuXIlJ06cwGq1MnHiRDp06EBmZiYFBQUUFBRQWlrKXXfdxfDhw9m7dy+9evUiIiIC\ngOuvv549e/YwaNAgHA4Hjz/+OABDhw4lKyvLW6Rr8XwRERERERFpKL/cJ/3b8vPzWbp0KUlJSYwc\nOZLjx4+zY8cOMjIymDhxYp0FOkBmZiadOnUiLS2Ne++9lxUrVng/O3bsGE8//TTPPvssa9eupbi4\nmOLiYqKj/7sidXR0NEVFRTidTiIiIjCbax5lVFQURUVF3vM+/fRTpk2bxvz58/nqq6+a6CmIiIiI\niIhIIPDrkfSSkhLS0tJISUnh6quvBiApKYnk5GRGjBhBt27dLtr20KFDJCcnA9CzZ09KS0spLy/H\nZDKRkJBAcHAwwcHB2O12Dh8+XOc1TCbTJePr1KkTGRkZhISEsGfPHtLS0khPT691jsPhwOFweN+P\nGzeuQfcuEkgsFgs2m83XYUg9rFarvicxjPJJjKR8EiMpn8RomZmZ3td2ux273X7J8/26SA8PD6dN\nmzbk5uZ6i/T8/HzCwsJqjWb/UCaTiaioqFrF9KlTp+jZsyctWrSgrKwMt9uN2WymqKiIqKgoAMLC\nwrzn9+7dm9WrV+N0OmnRooX3eEO+JJFA53K5tFWcH7DZbJTqexKDKJ/ESMonMZLySYxks9kaPRDr\n19Pdg4KCSElJYfPmzWzdupWzZ8/y0ksvMXfuXJxOJzk5ORdtGx8fz5YtW4Ca0ezIyEjCwsLweDzs\n2rWLqqoqSktLOXDgAF26dOGGG25g3759lJWV4XQ62bdvHzfccAMmkwm73e7tKzs7m8TERABOnz7t\n/U36+dH4bxfoIiIiIiIiIt/m1yPpJpOJkJAQUlNTeeaZZ3jzzTe54447iImJ4eGHH2bOnDn06NGD\nyMjIC9rec889ZGRkMG3aNEJCQkhKSvJes0OHDsyZM4fS0lLGjh1Lq1Y1W0ONGTOGmTNnAjB27Fjv\nInLjx49n+fLlvPHGG3Ts2JFbbrkFgJycHDZu3IjZbCYkJIQpU6ZcjsciIiIiIiIifsrk0fLjtWRl\nZREaGsrIkSN9FkP5k7f7rG8RXygfO5OK9p19HYbUQ9P/xEjKJzGS8kmMpHwSI8XGxja6jV+PpDeV\n+haEa2rlY2f6tH8JHBaLBZfL5esw6uWOjK7/JBERERGRK0DAF+nZ2dm89957tY7Fx8czYcKEOs+/\n5557LkdYl6QRRTGKzWbTgmwiIiIiIn4k4Iv0YcOGMWzYMF+HISIiIiIiIlIvvy3SCwsLWbhwIUuW\nLLlsfWZnZ7N+/XoARo8ezdChQ72xLF++HKfTSadOnXj00UcJCgpiy5YtbNiwAY/HQ1hYGL/+9a/5\n0Y9+VG8/oQVHmvQ+5MrhPmkh1A+mu0PNlPfKsFa+DkNERERExKf8tki/3JxOJ2+99RYLFiwAIDU1\nlcTERMLDw3n11Ve58847GTRoEKtWrWLTpk2MGDGC9u3bM2fOHMLDw9m7dy8vvPAC8+bNq7evsLXz\nm/p2RJqd8rEzQUW6iIiIiFzhAqJILygoYOnSpQwePJivv/6aSZMmcfToUdLT05k/fz5Wq/WCNk6n\nk5UrV3LixAmsVisTJ06kQ4cOZGZmUlBQQEFBAaWlpdx1110MHz6cvXv30qtXL++2a9dffz179uxh\n0KBBOBwOHn/8cQCGDh1KVlYWI0aMoFu3bt7+unTpwqlTpy7PAxERERERERG/ZPZ1AD9Ufn4+S5cu\nJSkpiZEjR3L8+HF27NhBRkYGEydOrLNAB8jMzKRTp06kpaVx7733smLFCu9nx44d4+mnn+bZZ59l\n7dq1FBcXU1xcTHT0f1egjo6OpqioCKfTSUREBGZzzaOMioqiqKjogv42bdpE7969Db57ERERERER\nCSR+XaSXlJSQlpbGY489RocOHTCZTCQlJfH73/+eHj161BrJ/q5Dhw7x4x//GICePXtSWlpKeXk5\nJpOJhIQEgoODsdls2O12Dh8+XOc1GrpV2/79+/nggw+47777Gn+TIiIiIiIicsXw6+nu4eHhtGnT\nhtzcXK6++mqgZmQ9LCysztHs78tkMhEVFYXD4fAeO3XqFD179qRFixaUlZXhdrsxm80UFRURFRXl\nPe/LL7/kj3/8I08++SQtWrS44NoOh6PWdceNG2dY3CL+xGKxYLPZfB2GXILVatV3JIZRPomRlE9i\nJOWTGC0zM9P72m63Y7fbL3m+XxfpQUFBpKSkMG/ePEJDQ+nTpw8vvfQSc+fOZc2aNeTk5DBgwIA6\n28bHx7NlyxbGjBmDw+EgMjKSsLAwPB4Pu3btYtSoUVRUVHDgwAHGjx9PUFAQr7/+OmVlZXg8Hvbt\n28d9992HyWTCbreTk5PDoEGDyM7OJjExEYCTJ0+yePFiJk+eTExMTJ1xNORLErkSuFwu7enezNls\nNkr1HYlBlE9iJOWTGEn5JEay2WyNHoj16yLdZDIREhJCamoqzzzzDG+++SZ33HEHMTExPPzww8yZ\nM4cePXoQGRl5Qdt77rmHjIwMpk2bRkhICElJSd5rdujQgTlz5lBaWsrYsWNp1apmxekxY8bw/9i7\n/7gq6zzv469zDiIIB/CgyBA1iWUoSlMhJrqhMlF3ZTKOWju52+rUXUSmLhDaxKa2QoK/KlfvUopa\nfwnc30EAACAASURBVNyCqbdTbvvQbXVMZPyJP844TcY0lS6cQVQEYZFzuP/w9tyhqKAXHIH38/Ho\n0bkuru/3+pyLz/SYD9/v9f3OmjULgPHjx7sXkZs0aRJLlizhf//v/03fvn0ZPXo0AOvXr6empoaV\nK1cCF0cKs7O1cruIiIiIiIg0z9TY2Njo6SBuJYWFhfj4+DBmzBiPxVD7m8c8dm8RT6kdP4u6Pv08\nHYZcg0YWxEjKJzGS8kmMpHwSI4WFhbW6TYdeOK6ttHRBOBEREREREREjdejp7i2xfft2tmzZ0uRc\nZGQkU6ZMafb6CRMmtEdY11Q7fpanQ5BOwmKx4HQ6PR1Gi7gCgq9/kYiIiIhIJ9fpi/SRI0cycuRI\nT4fRKpryK0axWq1ajE1EREREpAPp9EV6R9Tdt8bTIUgn4Wyso7tvxxhJb3R1p/6/9Z8kEREREena\nOuX/I3Y4HMyfP5+FCxcCsGTJEk6cOMGoUaN47LH2XZRt7969/OQnPyE8PLzFbbr5HWzDiKSr6SgL\nT1youY9O+p8kEREREZEW6/T/j/jMmTOUlpbyzjvveOT+e/bs4YEHHmhVkS4iIiIiIiJdU7sV6Tt2\n7ODTTz8F4Kc//Slms5lu3brx7bffUlVVxYsvvsh//ud/8s0333D33Xfz0ksv4XK5WL58OaWlpZhM\nJkaNGsXjjz/ebP+lpaUsX74cgOjoaPf5f/7nf6ayspJXX32VKVOmEBkZeUXbsrIyVqxYQVVVFWaz\nmdTUVEJCQvjXf/1XSkpKMJlMjBs3jri4OOx2O4WFhQQEBPD999/Tt29fXnnlFQBWr17N/v37sVgs\nREdHM3ToUPbv38+xY8fYsGEDqamp9OnTx+hHKyIiIiIiIp1EuxTp33//PRs2bGDevHn4+/tTXV3N\nxx9/zPnz55k3bx779u0jJyeHf/7nfyY8PJxZs2bx7bff4nK5OH36tHva+vnz5696j2XLlvHcc88R\nGRnJqlWr3OczMjJ46623yMnJuWrbd955h1/84hcMGTKEhoYGXC4XxcXF/OUvf2HBggVUVVUxa9Ys\nBg4cCMC3337LokWL6NmzJ5mZmfzxj3/ktttuY+/evSxZssQda48ePYiJieGBBx5g6NChRjxKERER\nERER6cTapUg/evQow4YNw9/fH8D97wceeACA22+/naCgIG6//XYAwsPDqaioYMCAAZSXl/PBBx9w\n//33c++99zbbf01NDefPn3ePkj/00EMcPHjxve7GxsZrxlZbW8vp06cZMmQIAF5eFx/JV199xYgR\nIzCZTAQGBjJw4ECOHz9Ojx49uOuuu7DZbADceeedVFRU0L9/f7p168by5ct54IEHuP/++933uFYM\ndrsdu93uPp44ceI14xXprCwWC1ar1dNhyDV4e3vrdySGUT6JkZRPYiTlkxitoKDA/TkqKoqoqKhr\nXt8uRbrJZGr+5v+vIDaZTO7PAGazmYaGBvz8/MjNzeXQoUNs3bqV3bt3k5ycfN37Xa8wb6nL+7n0\nPZqL1Ww2k52dzZEjRyguLubzzz/nn/7pn5q0a05LfkkiXYHT6eR8rbaLu5VZrVbOaUs/MYjySYyk\nfBIjKZ/ESFartdUDse2y8POgQYPYvXs31dXVAO5/X8+5c+dwuVwMHTqUp556ij//+c/NXufn54ef\nnx9//OMfAdi5c2eLY/P19cVms7F3714ALly4QH19PQMGDKCoqAiXy0VVVRXHjh3jrrvuuuofAOrq\n6qipqeG+++7j2Wef5S9/+QsAPj4+1NbWtjgeERERERER6braZSQ9PDyccePG8cYbb2A2m+nbty/Q\ndIT58tFmk8lEZWUly5YtcxfGv/rVr656j+TkZJYvX47JZCI6OvqafV9u6tSpvP/++xQUFGCxWPjH\nf/xHYmNj+dOf/kR6ejomk4lJkyYRGBjIiRMnmo21rq6OnJwcLly4QGNjI88++ywAw4cP57333uPf\n/u3f+Md//EctHCciIiIiIiJXZWo0am64GKaqvuD6F4l0Mhdq7uO/a/08HYZcg6b/iZGUT2Ik5ZMY\nSfkkRgoLC2t1m06/T3pHdKHmPk+HIJ2ExWLB6XR6OowWaXR193QIIiIiIiIe1+GK9Ly8PL766qsm\n5x577DFGjhzZpm3bk0YTxShWq1WLsYmIiIiIdCCa7n4LOnnypKdDkE5C07XESMonMZLySYykfBIj\nKZ/ESF12urvD4WD+/PksXLjQ0H6zs7OZNm0aPXr0oKSkhPz8fFwuF6NHjyYpKQm4uFL94sWLqaio\noHfv3syYMQM/Pz927tzJb3/7W3dff/nLX8jJyeGnP/3pde/rU/6Nod9Dui5XhQWfDjLd/Ua4AoKp\n9w3ydBgiIiIiIobpFEV6W5k1axYALpeLvLw8MjMzsdlszJo1i5iYGMLDw9m0aRPR0dGMHTuWTZs2\nsWnTJp555hn+5m/+hr/5m78B4LvvvmPBggUtKtABfNdnt9l3EulMasfPAhXpIiIiItKJtMs+6e2p\nvLycjIwMNm/ezPLly4GLRXJqair19fXNtqmrq2PZsmWkpaWRnp7Onj17AEhJSaG6uprjx48TGhpK\nSEgIXl5eDB8+nH379gGwb98+4uPjARg5cqR7v/Uf+/LLL4mLi2uLrysiIiIiIiKdSKcaST958iRv\nv/02KSkp3H777cyePZs9e/awceNGXnjhBby9vZttt379evz8/FiwYAEANTU1TX5eWVlJcHCw+9hm\ns3H8+HEAzp49S1DQxZG8wMBAzp49e0X/u3fvJiMjw5DvKCIiIiIiIp1XpynSq6qqyM3NJS0tjdtu\nuw24OBKemppKYmIi/fv3v2rbo0ePMn36dPexn9+Nra5uMpmuOPf111/TvXt3wsPDm21jt9ux2+3u\n44kTJ97QvUW6IovFgtVq9XQYXYa3t7eetxhG+SRGUj6JkZRPYrSCggL356ioKKKioq55facp0nv0\n6EGvXr04duyYu0g/efIkvr6+VFZW3lTfNpuNU6dOuY9PnTqFzWYDLo6enzlzhqCgIE6fPk1gYGCT\ntrt27WLEiBFX7bslvyQRaZ7T6aRGq6+2G612K0ZSPomRlE9iJOWTGMlqtbZ6ILbTvJPu5eVFWloa\nv/vd7/jyyy85f/48+fn5zJ07l+rqaoqLi6/aNjo6ms8//9x9fPl09379+lFWVobD4aChoYGioiJi\nYmIAiImJYfv27QDs2LGDIUOGuNu5XC6Ki4v1PrqIiIiIiIi0SKcp0k0mE927d2fmzJl89tlnZGRk\n8OijjxIaGsqLL77ImjVrqKqqarbtuHHjqKmpITU1lfT09CbTz+HilNopU6Ywb948ZsyYQVxcnHv6\nelJSEkeOHGHatGkcPXrUvTUbwLFjx+jVqxchISFt98VFRERERESk0zA1NjY2ejqIW5HL5eL5559n\nxYoVmM3t+7eM2t881q73E+moasfPoq5PP0+H0WVo+p8YSfkkRlI+iZGUT2KksLCwVrfpNO+kGy01\nNZWEhIR2L9Dh/+39LGIAi8WC0+n0dBhtxhUQfP2LREREREQ6kC5VpG/fvp0tW7Y0ORcZGcmUKVOu\nuHbx4sXtFdYVNDIoRrFarVpYTURERESkA+lSRfrIkSMZOXKkp8MQERERERERaVaXKtI7Cp/ybzwd\ngnQSrgoLPp14uvvNcgUEU+8b5OkwRERERETcOkWR7nA4mD9/PgsXLjS03+zsbKZNm0aPHj0oKSkh\nPz8fl8vF6NGj3au47969m8LCQk6cOEF2djYREREANDQ08P7771NaWorJZGLy5MkMHDiwRff1XZ9t\n6PcQkebVjp8FKtJFRERE5BbSabZgawuzZs2iR48euFwu8vLyeO2111i0aBG7du3ihx9+AOCOO+4g\nLS3tigJ827ZtmEwmFixYQGZmJh9//DFaSF9ERERERESupdMV6eXl5WRkZLB582aWL18OwHfffUdq\nair19fXNtqmrq2PZsmWkpaWRnp7Onj17AEhJSaG6uprjx48TGhpKSEgIXl5eDB8+nH379gFw2223\nNbus/okTJ4iKigIgICAAPz8/vvlG09hFRERERETk6jrFdPdLTp48ydtvv01KSgq33347s2fPZs+e\nPWzcuJEXXngBb2/vZtutX78ePz8/FixYAEBNTU2Tn1dWVhIc/P+3erLZbBw/fvyasfz0pz9l3759\njBgxgoqKCkpLS6msrLzJbygiIiIiIiKdWacp0quqqsjNzSUtLY3bbrsNuDgSnpqaSmJiIv37979q\n26NHjzJ9+nT3sZ+f303HM3r0aE6cOMHMmTPp1asX/fv3b3bPdbvdjt1udx9PnDjxpu8tIi1jsViw\nWq2eDqPD8Pb21vMSwyifxEjKJzGS8kmMVlBQ4P4cFRXlnnF9NZ2mSO/Rowe9evXi2LFj7iL95MmT\n+Pr63vQIts1m49SpU+7jU6dOYbPZrtnGbDbz7LPPuo8zMzP5yU9+csV1LfkliUjbcDqd2ke+FaxW\nK+f0vMQgyicxkvJJjKR8EiNZrdZWD8R2mnfSvby8SEtL43e/+x1ffvkl58+fJz8/n7lz51JdXU1x\ncfFV20ZHR/P555+7jy+f7t6vXz/KyspwOBw0NDRQVFRETEzMNeOpr6+nrq4OgMOHD2OxWNx/PBAR\nERERERFpTqcZSTeZTHTv3p2ZM2fy5ptvsm7dOh5//HFCQ0N58cUXmTNnDgMHDiQgIOCKtuPGjSMv\nL4/U1FTMZjMTJkwgNjbW/XOLxcKUKVOYN2+eewu28PBwAPbs2cOHH35IVVUV2dnZ9O3bl9dee40z\nZ86QlZWFyWQiODiYl19+ud2ehYiIiIiIiHRMpkbtC9Ysl8vF888/z4oVK5p9l7wt1f7msXa9n0hX\nVTt+FnV9+nk6jA5D0//ESMonMZLySYykfBIjNbcT2PV0mpF0o6WmppKQkNDuBTpcLBxEjGCxWHA6\nnZ4O45blCgi+/kUiIiIiIu2oSxXp27dvZ8uWLU3ORUZGMmXKlCuuXbx4cXuFdQWN7IlRrFarFkYT\nEREREelAulSRXlhYyPz58/H3929yfsuWLWzdupWIiAimTp3aqj4///xzPvvsMxwOB3l5eU36/uCD\nDygpKaF79+689NJL9O3bt0V9mr4ubVUMIldT62XB1KCR9NYy9Q7GFRTo6TBEREREpAvqUkX61Wzd\nupXMzMzrbqvWnMjISB544AFmz57d5PyBAwcoLy/nnXfe4euvv2blypXMmzevRX1WvZnb6jhExDgB\nmemgIl1EREREPKDDF+kbNmxgx44dBAYGEhwcTHh4OPv37ycrKwsAh8NBTk4OCxYscLepr69n4cKF\nxMbGUlpaSnl5OVlZWYwaNYp77rmH/Px8Lly4gLe3N8nJyYSFheFyuVi1ahWHDh3CbDaTkJDAo48+\nyp133tlsXPv27SM+Ph6Au+++m5qaGs6cOUNQUFCbPxMRERERERHpmDp0kV5aWkpRURG5ubk4nU4y\nMjKIiIigoaEBh8NBSEgIRUVFxMXFudvU1tayePFi4uPjeeihh0hISKCkpITZs2fj7+9PbW0tc+fO\nxWw2c/jwYdauXUtqairbtm2joqKC3NxczGYz1dXV14ytsrKS4OD/vyhVcHAwlZWVKtJFRERERETk\nqjp0kX7s2DFiY2Px9vYGICYmBoBhw4ZRVFREUlISu3fvZsaMGe42OTk5jB07lhEjRjTbZ01NDUuX\nLqWsrAyTyeReGfvIkSMkJia6V3u//L325mh3OxEREREREWmNDl2km0ymJseXiuK4uDgWLVrE0KFD\nMZlMhIaGuq+JjIykpKTkqkX6unXrGDx4MOnp6TgcDubMmXNF/y1hs9k4deqU+/jUqVPNvvNut9ux\n2+3u44kTJ7b4HiLSNixeFnytVk+Hccvx9vbGquciBlE+iZGUT2Ik5ZMYraCgwP05KiqKqKioa17f\noYv0AQMGsGzZMpKSknA6nRw4cICHH36YPn36YDab+eSTT5pMdQd46qmnKCwsZOXKlTz33HNX9Flb\nW0vPnj2Bi1u2XRIdHc22bdsYNGiQe7r75aPpPy7iY2Ji+Pd//3eGDx/On/70J/z8/Jqd6t6SX5KI\ntC9ng5Nz2rruClarVc9FDKN8EiMpn8RIyicxktVqbfVArLmNYmkXffv2ZdiwYaSnp5OdnU2/fv2a\njKbv3LmzSZF+aeR98uTJ1NfXs3r16iv6fPLJJ1mzZg0ZGRm4XC53m4SEBHr16kVaWhrp6ens2rUL\nuLh9W3JyMpWVlaSlpfHee+8BcP/99xMSEsLUqVNZsWIFv/71r9v0WYiIiIiIiEjHZ2rsRC9OFxYW\n4uPjw5gxYzwdyk356udjPR2CSJcWkJlO490Rng7jlqORBTGS8kmMpHwSIymfxEhhYWGtbtOhR9Kb\nc/l76iIiIiIiIiIdRYd+J/1yEyZM8HQIhgjITPd0CNJJWLwsOBucng6jwzH1DqbTTDESERERkQ6l\nUxXpnYWm2YpRfDVd64aoQBcRERERT+l0091FREREREREOqrrjqQ7nU6mT5/OokWL6NatW3vEdF0O\nh4P58+ezcOHCdrvn9u3b2bhxIwDjxo0jPj7eHcuSJUuorq4mIiKCl19+GS+v//9Yjx8/zuuvv86M\nGTMYOnRoi+7lU/6N8V9AuiRXhQUfp6a73whXQDD1vldumygiIiIi0pauW6RbLBZMJhP19fW3TJHe\n3qqrq/nkk0946623AJg5cyZDhgyhR48erFq1iieeeIK4uDhWrFjBF198QWJiIgAul4vVq1fzs5/9\njNYsou+7PrtNvoeItFzt+FmgIl1ERERE2lmLprs//vjjLFmyBLvdTllZGeXl5e5/PK28vJyMjAw2\nb97M8uXLAfjuu+9ITU2lvr6+2TbV1dXk5OSQnp7Ob37zG7777jsACgoKePfdd3n99deZNm0a//Ef\n/wFASUkJ0dHR+Pn54efnx+DBgzl48CCNjY3Y7XYefPBBAOLj49m7d6/7Pv/2b//Ggw8+SEBAQFs+\nAhEREREREekkWrRw3AcffADA4cOHr/jZunXrjI2oFU6ePMnbb79NSkoKt99+O7Nnz2bPnj1s3LiR\nF154AW9v72bbFRQUEBERwauvvsrRo0dZunQpOTk5AHz//ffMmzePuro6Xn31Ve6//35Onz5NcHCw\nu31wcDCVlZVUV1fj5+eH2Xzxbx02m43KykoAKisr2bdvH//0T//E8uXLtTWciIiIiIiIXFeLinRP\nFuJXU1VVRW5uLmlpadx2220ApKSkkJqaSmJiIv37979q26+++orU1FQABg0axLlz56itrcVkMhET\nE0O3bt3o1q0bUVFRHD9+vNk+rld05+fn86tf/QqTyURjY2OrpruLiIiIiIhI19SqLdgqKiqorKy8\nZgHcXnr06EGvXr04duyYu0g/efIkvr6+7tFsI5hMJmw2G3a73X3u1KlTDBo0CH9/f2pqanC5XJjN\nZiorK90j7qWlpSxZsgSAc+fOUVJSgpeXFzExMU36t9vtTfqeOHGiYbGLyI2zWCxYrVZPh3FL8fb2\n1jMRwyifxEjKJzGS8kmMVlBQ4P4cFRVFVFTUNa9vUZFeUVHB22+/zbfffgvAv/7rv7J7924OHTrE\niy++eOPR3gQvLy/S0tKYN28ePj4+3H///eTn5zN37lzy8vIoLi52vyt+ucjISHbu3Mkvf/lL7HY7\nAQEB+Pr60tjYyL59+/jFL35BXV0df/jDH5g0aRJeXl6sXbuWmpoaGhsbOXz4MM888wwmk4moqCiK\ni4uJi4tj+/bt7iJ86dKl7vstW7aMBx544IoCHVr2SxKR9ud0OqnRHvNNWK1WzumZiEGUT2Ik5ZMY\nSfkkRrJara0eiG3RwnHvvfce9913Hx999JF7e7F7772XQ4cOtT5Kg5hMJrp3787MmTP57LPPyMjI\n4NFHHyU0NJQXX3yRNWvWUFVV1WzbCRMmUFpaSnp6OmvXriUlJcXd5x133MGcOXN4/fXXGT9+PEFB\nQfj7+/PLX/6SWbNm8dprrzF+/Hj8/PwAmDRpEp9++imvvPIKNTU1jB49ut2egYiIiIiIiHQupsYW\nvCw9efJk8vLyMJvNTJ48mQ8//BCAZ599lo8++qjNg2wvhYWF+Pj4MGbMGI/GUfubxzx6fxG5uAVb\nXZ9+ng7jlqKRBTGS8kmMpHwSIymfxEhhYWGtbtOikfSgoCDKysqanPvhhx/o3bt3q294q9Mq7CIi\nIiIiIuIpLXonfcyYMbz11lskJSXhdDr58ssv2bhxI2PHjm3r+G7K9u3b2bJlS5NzkZGRTJkypdnr\nJ0yY0B5hXVft+FmeDkE6CYvFgtPp9HQYHZIrIPj6F4mIiIiIGKxF090B9u7dy9atW/nrX/9Kr169\nePjhh4mNjW3r+LqkkydPejoE6SQ0XUuMpHwSIymfxEjKJzGS8kmMdCPT3Vs0kv71118zZMgQhgwZ\n0uT88ePHueuuu1p9U09JSUlh/vz5+Pv7Nzm/ZcsWtm7dSkREBFOnTm1Vnw6HgyVLllBdXU1ERAQv\nv/wyXl5enDhxgmXLlvHtt9/y9NNPt+o9d9PXpa2KQeRqar0smBo0kn6jTL2DcQUFejoMEREREelC\nWlSkv/nmm3z88cdXnJ83b557EbmObOvWrWRmZmKz2VrddtWqVTzxxBPExcWxYsUKvvjiCxITE7Fa\nrUyZMoW9e/e2us+qN3Nb3UZEjBeQmQ4q0kVERESkHV2zSHe5XM1+BigvL8disbRNVK2wYcMGduzY\nQWBgIMHBwYSHh7N//36ysrKAiyPdOTk5LFiwwN2mvr6ehQsXEhsbS2lpKeXl5WRlZTFq1Cjuuece\n8vPzuXDhAt7e3iQnJxMWFobL5WLVqlUcOnQIs9lMQkICjzzyCHa7nenTpwMQHx9PYWEhiYmJBAQE\nEBAQwIEDBzzyXERERERERKTjuWaR/rd/+7fNfoaLq6CPGzeubaJqodLSUoqKisjNzcXpdJKRkUFE\nRAQNDQ04HA5CQkIoKioiLi7O3aa2tpbFixcTHx/PQw89REJCAiUlJcyePRt/f39qa2uZO3cuZrOZ\nw4cPs3btWlJTU9m2bRsVFRXk5uZiNpuprq7m3Llz+Pn5YTZfXCTfZrNRWVnpqcchIiIiIiIiHdw1\ni/R3330XgDfeeIO5c+dyaY05k8lEQEAA3bt3b/sIr+HYsWPExsbi7e0NQExMDADDhg2jqKiIpKQk\ndu/ezYwZM9xtcnJyGDt2LCNGjGi2z5qaGpYuXUpZWRkmk8m9MvaRI0dITEx0F+T+/v5UVVW15dcT\nERERERGRLuaaRXpISAgAy5cvBy5OeT979iw9e/Zs+8ha4PI9zS/9ESEuLo5FixYxdOhQTCYToaGh\n7msiIyMpKSm5apG+bt06Bg8eTHp6Og6Hgzlz5lzR/yVWq5WamhpcLhdms5nKyspWv9dut9ux2+3u\n44kTJ7aqvYi0HYuXBV+r1dNh3DK8vb2x6nmIQZRPYiTlkxhJ+SRGKygocH+OiooiKirqmte3aOG4\n6upq8vLyKC4uxmKxsGrVKvbt28fx48d5+umnby7imzBgwACWLVvm3r/9wIEDPPzww/Tp0wez2cwn\nn3zSZKo7wFNPPUVhYSErV67kueeeu6LP2tpa9x8htm/f7j4fHR3Ntm3bGDRokHu6u7+/P1FRURQX\nFxMXF8f27duvWAH/ejvcteSXJCKe4WxwaguWH9GWNGIk5ZMYSfkkRlI+iZGsVmurB2LNLbloxYoV\n+Pr6smzZMrp16wZA//792bVrV+ujNFDfvn0ZNmwY6enpZGdn069fvyaj6Tt37mxSpF8aeZ88eTL1\n9fWsXr36ij6ffPJJ1qxZQ0ZGBi6Xy90mISGBXr16kZaWRnp6uvu7T5o0iU8//ZRXXnmFmpoaRo8e\nDcCZM2dITk7ms88+Y8OGDSQnJ1NXV9emz0NEREREREQ6NlPj9YZ6gV//+te89957eHl5MXnyZPe2\na88++ywfffRRmwfZUoWFhfj4+LRqT/Jb0Vc/H+vpEESEi1uwNd4d4ekwbhkaWRAjKZ/ESMonMZLy\nSYwUFhbW6jYtGknv0aPHFYukVVRU3DLvpv/Y5e+pi4iIiIiIiHQULXonPSEhgUWLFvH000/jcrn4\n05/+xNq1a/n5z3/e1vG1yoQJEzwdgiECMtM9HYJ0EhYvC84Gp6fD6LBMvYO57lQjEREREREDtahI\nHzt2LN7e3uTl5eF0Olm2bBkPP/wwjz32WFvH1yVpeq0YxVfTtW6KCnQRERERaW8teidd2lflwZ2e\nDkE6CYvFgtOpkfSb4QoIpt43yNNh3BL0jp4YSfkkRlI+iZGUT2KkG3knvUUj6QB//etf+ctf/nLF\nCuVX22/8ZjkcDubPn8/ChQvbpP8bUVJSQn5+Pi6Xi9GjR5OUlARc3KJu8eLFVFRU0Lt3b2bMmIGf\nnx+HDx9mzZo1NDQ04OXlxaRJkxg0aNB17+O7Prutv4qItFDt+FmgIl1ERERE2kmLivRNmzaxfv16\nwsPD8fb2bvKztirSbzUul4u8vDwyMzOx2WzMmjWLmJgYwsPD2bRpE9HR0YwdO5ZNmzaxadMmnnnm\nGQICApg5cyZBQUF8//33zJs3j//1v/6Xp7+KiIiIiIiI3KJaVKRv3ryZt956i/Dw8LaOp1nl5eUs\nWrSI4cOHc+LECZKTk/nuu+94++23yc7OvuIPBwB1dXV88MEHlJaWYjKZmDBhArGxsfzd3/0djzzy\nCAcPHiQoKIinnnqK1atXU1lZybPPPktMTAzff/89y5cvp6GhgcbGRlJTU6mqqiI0NJSQkBAAhg8f\nzr59+wgPD2ffvn3Mnj0bgJEjRzJ79myeeeYZ7rzzTnc84eHh1NfXu0fVRURERERERC7XomrRarXS\nq1evto6lWSdPnuTtt98mJSWF22+/ndmzZ7Nnzx42btzICy+80GyBDrB+/Xr8/PxYsGABADU1Tupo\n7QAAIABJREFUNQDU19czaNAgJk2axIIFCygoKOCNN97g+++/51/+5V+IiYlh69atPPbYY4wYMQKn\n04nT6eTbb78lODjY3b/NZuP48eMAnD17lqCgi9NhAwMDOXv27BXx/P73vyciIkIFuoiIiIiIiFxV\niyrGZ599lvfff5/HHnvMXYxe0pbFe1VVFbm5uaSlpXHbbbcBkJKSQmpqKomJifTv3/+qbY8ePcr0\n6dPdx35+fgB4eXnxs5/9DIA77riDbt26YTabuf322/nrX/8KQP/+/dm4cSOnTp1i6NChhIaGtjjm\n5vZp//7771m9ejWZmZlX/Mxut2O3293HEydObPG9RKTtWSwWrFarp8O4JXh7e+tZiGGUT2Ik5ZMY\nSfkkRisoKHB/joqKIioq6prXt6hIb2ho4NChQ+zateuKn61bt66VIbZcjx496NWrF8eOHXMX6SdP\nnsTX15fKysob6tNisbg/m0wm98i22Wx2r4I9YsQI+vfvz/79+8nOzub555/HZrNx6tQpd9tTp05h\ns9mAi6PnZ86cISgoiNOnTxMYGNjkugULFjB16lT3VPkfa8kvSUQ8x+l0UqMVXgGtdivGUj6JkZRP\nYiTlkxjJarW2eiDW3JKL8vLy+NWvfkV+fj5r1qxp8k9b8vLyIi0tjd/97nd8+eWXnD9/nvz8fObO\nnUt1dTXFxcVXbRsdHc3nn3/uPr403b0lysvLCQkJ4X/8j/9BTEwM3333HXfddRdlZWU4HA4aGhoo\nKioiJiYGgJiYGLZv3w7Ajh07GDJkiPueb731Fs8888w1R/1FREREREREoIUj6U6nk1GjRmE2t6im\nN4zJZKJ79+7MnDmTN998k3Xr1vH4448TGhrKiy++yJw5cxg4cCABAQFXtB03bhx5eXmkpqZiNpvd\nC8ddPh39x8eXPu/evZudO3disVjo2bMn48aNw2w2M2XKFObNm+fegu3SQnpJSUksXryY//zP/3Rv\nwQbw+eefU1ZWxvr161m/fj0Ar7/+erPxioiIiIiIiJgaGxsbr3fR5s2buXDhAuPGjWv2nWsxVu1v\nHvN0CCLy/9SOn0Vdn36eDuOWoOl/YiTlkxhJ+SRGUj6JkcLCwlrdpkUj6Vu2bOHs2bNs3LjxikUU\nli9f3uqbyrXVjp/l6RCkk7BYLO61FuTGuAKCr3+RiIiIiIhBWlSkT506ta3juGHbt29ny5YtTc5F\nRkYyZcoUD0V08zRqJ0axWq1a9ExEREREpANpUZF+K68+PnLkSEaOHOnpMERERERERERuWouKdIA/\n//nPHDt2jOrqan78GvtTTz3VJoG1hZSUFObPn4+/v3+T81u2bGHr1q1ERES0etaAw+FgyZIlVFdX\nExERwcsvv4yXlxd79+6loKAAk8mEyWTi7/7u7xg0aFCL+jR9XdqqGESuptbLgqlB091vlql3MK6g\nwOtfKCIiIiJyk1pUpG/bto2PPvqI6OhoDh48yH333cfhw4fdW5B1dFu3biUzM9O973lrrFq1iiee\neIK4uDhWrFjBF198QWJiIoMHD3Zvxfbdd9+Rm5vLu+++26I+q97MbXUcItJ2AjLTQUW6iIiIiLSD\nFhXp/+f//B9mzZrFwIEDmTx5Munp6Rw8eJBdu3a1dXzXtWHDBnbs2EFgYCDBwcGEh4ezf/9+srKy\ngIsj3Tk5OSxYsMDdpr6+noULFxIbG0tpaSnl5eVkZWUxatQo7rnnHvLz87lw4QLe3t4kJycTFhaG\ny+Vi1apVHDp0CLPZTEJCAo888gh2u53p06cDEB8fT2FhIYmJifj4+LjvV1dXp23XRERERERE5Lpa\nVKRXVVUxcOBA4OJe4i6Xi5/97Ge88847bRrc9ZSWllJUVERubi5Op5OMjAwiIiJoaGjA4XAQEhJC\nUVERcXFx7ja1tbUsXryY+Ph4HnroIRISEigpKWH27Nn4+/tTW1vL3LlzMZvNHD58mLVr15Kamsq2\nbduoqKggNzcXs9lMdXU1586dw8/Pz71/vM1mo7Ky0n2vPXv2sHbtWk6fPs3rr7/e7s9HRERERERE\nOpYWFek2m81d9P7kJz9h7969WK1WvLxa/Ep7mzh27BixsbF4e3sDuKffDxs2jKKiIpKSkti9ezcz\nZsxwt8nJyWHs2LGMGDGi2T5rampYunQpZWVlmEwm9/ZVR44cITEx0V2Q+/v7U1VVdc34YmNjiY2N\n5dixY7z77ru8/fbbN/2dRUREREREpPNqUZX95JNP8sMPPxASEsL48eNZuHAhDQ0NTJ48ua3juyaT\nydTk+NKCdnFxcSxatIihQ4diMpkIDQ11XxMZGUlJSclVi/R169YxePBg0tPTcTgczJkz54r+L7Fa\nrdTU1OByuTCbzVRWVjb7XvuAAQNwuVycO3fuin3m7XY7drvdfTxx4sQWfnsRaS8WLwu+l/1vtyvy\n9va+4r9hIjdK+SRGUj6JkZRPYrSCggL356ioqOvunnbdIr2xsZEBAwbQu3dvAO677z4+/PBDGhoa\n8PX1vclwb86AAQNYtmwZSUlJOJ1ODhw4wMMPP0yfPn0wm8188sknTaa6w8XV6AsLC1m5ciXPPffc\nFX3W1tbSs2dP4OIe7JdER0ezbds2Bg0a5J7u7u/vT1RUFMXFxcTFxbF9+3b3YnFlZWX06dMHk8lE\naenF1dqb+x97S35JIuJZzgYn57TfPFarVc9BDKN8EiMpn8RIyicxktVqbfVArLklF6WlpTUZte7W\nrZvHC3SAvn37MmzYMNLT08nOzqZfv35NRtN37tzZpEi/9B0mT55MfX09q1evvqLPJ598kjVr1pCR\nkYHL5XK3SUhIoFevXqSlpZGenu5eNG/SpEl8+umnvPLKK9TU1DB69GgAfv/735OWlsarr75Kfn4+\n06ZNa9NnISIiIiIiIh2fqfHyOdzNyMzM5IUXXiA8PLw9YrphhYWF+Pj4MGbMGE+HclO++vlYT4cg\nIj8SkJlO490Rng7D4zSyIEZSPomRlE9iJOWTGCksLKzVbVr0TnpUVBTZ2dnEx8fTq1evJj+7NHJ8\nq7j8PXURERERERGRjqJFRfof//hHevfuzbFjx6742a1UpE+YMMHTIRgiIDPd0yFIJ2HxsuBscHo6\njA7P1DuY6045EhERERExQIuK9NmzZ7dxGPJjmlYrRvHVdC1DqEAXERERkfbS6o3OGxsbm2xFdmnf\ncDHOHyv/29MhSCfhddZJg7PB02F0CiF+3ti663UaEREREWlbLSrSKysrycvL4w9/+APnz59v8rN1\n69bd0I2zs7OZNm0aPXr0aPbndrud3/72t8ycOfOG+ge4cOECS5cu5c9//jNWq5Xp06e7t5Lbvn07\nGzduBGDcuHHEx8cDcODAAdauXYvJZMLHx4eXXnrJvc/6Bx98QElJCd27d+ell16ib9++AJSUlJCf\nn4/L5WL06NEkJSUBsHv3bgoLCzlx4gTZ2dlERLRshPy1rd/c8HcWkbaR9XA/bN27ezoMEREREenk\nWjQM/v7772OxWHjjjTfw8fFh/vz5xMTE8Pzzz9/QTRsbG5k5c+ZVC3SjfPHFF1itVt555x0ef/xx\n95Zr1dXVfPLJJ2RlZZGVlcX69evdf3zIy8tjxowZ5OTkMGLECDZs2ABcLN7Ly8t55513+J//83+y\ncuVKAFwuF3l5ebz22mssWrSIXbt28cMPPwBwxx13kJaWxsCBA9v0e4qIiIiIiEjn0KIi/auvvuKl\nl17izjvvBODOO+8kOTmZTz/9tMU3cjgcTJs2jaVLl5KWlsbTTz/NuXPnWL16Nf/+7//uvq6goIDf\n/va3TVZpP378OBkZGZSXl5OSktJkNP+VV16hqqqq2Xvu27fPPUI+dOhQjhw5Alwc+Y6OjsbPzw8/\nPz8GDx7MwYMHAQgKCnL3X1NTg81mu6Kvu+++m5qaGs6cOcPx48cJDQ0lJCQELy8vhg8fzr59+wC4\n7bbbbmjJfREREREREemaWlSkWywW97vn/v7+nD17lu7du1NZWdmqm5WVlfHoo4+ycOFCevXqhclk\nYvjw4ezevdt9TXFxMcOHD3e/9/7VV1+xcuVKXn31Vfr06cOQIUPYs2cPAF9//TUhISEEBAQ0e7/K\nykqCg4Pd36FHjx6cO3eO06dPu88DBAcHu7/Lr3/9a7KyskhOTmbnzp3uqes/7uvHbS4/b7PZWv1c\nRERERERERKCF76TfddddlJSUEBsby7333suSJUvw9vamX79+rbpZ7969ueuuu5qcu/POOzl79iyn\nT5/m7Nmz+Pn5YbPZ+K//+i9OnDjB+++/T2ZmJkFBQQDExcWxfv16Ro4cya5du4iLi2tVDFdjMplo\nbGzk3Xff5bXXXuOuu+5i8+bN5Ofn8+KLLwI0WTDPKHa7Hbvd7j6eOHGi4fcQkZvnZfHCarV6OgyP\n8vb27vLPQIyjfBIjKZ/ESMonMVpBQYH7c1RUFFFRUde8/ppFel1dnfudbLvdzn333cezzz7Lb3/7\nW+rq6nj88cdbFVz3qyy6NGzYMIqLizlz5gzDhw93n+/ZsycXLlygtLSU+++/H7g41bysrIyqqir2\n7dvH+PHjr3o/m81GRUUFNpsNp9PJ+fPnsVqt2Gy2JoXxqVOnGDRoEGfPnqWhocH9h4S4uDiysrLc\nfZ06dapJG5vNRkNDQ7PnW6olvyQR8bwGZ0OX387Oqi39xEDKJzGS8kmMpHwSI1mt1lYPxF5zuvsH\nH3zA/v37CQ8P5+jRo3z88cd0796d8ePHM2nSJHr27HlTAV8SFxfHrl27KC4u5sEHH3Sf79GjBzNn\nzmTt2rX84Q9/AC6OeMfGxvLRRx8RHh6Ov7//VfuNiYlhx44dwMVp9IMHDwbg3nvv5fDhw9TU1FBd\nXc3hw4e59957CQgIoL6+nv/6r/8C4PDhw4SHh7v7+t3vfgfAn/70J/z8/AgKCqJfv36UlZXhcDho\naGigqKiImJgYQ56LiIiIiIiIdC3XHEk/ePAg8+fPx2az8eijj/LGG2/w61//+oZv9uPF4H78OTw8\nnLq6OoKDg93T2k0mEyaTicDAQDIyMsjOziY5OZm77rqLuLg4Zs2aRUpKyjXvN3r0aN59911eeeUV\nrFYr06ZNAy6+V//LX/6SWbNmATB+/Hj8/PwASE5OZvHixTQ2NuLv709ycjIA999/PwcPHmTq1Kn4\n+Pi4z1ssFqZMmcK8efPcW7BdKuz37NnDhx9+SFVVFdnZ2fTt25fXXnvthp+fiIiIiIiIdG6mxmu8\naP33f//3fPzxx+7jyZMn8+GHH7ZLYF3Zg4u3eToEEblM1sP9iLR17X3SNf1PjKR8EiMpn8RIyicx\n0o3s9nXNkXSXy8XRo0eBi4umOZ1O9/ElgwYNavVN5dqyHm7dgnwiV+Nl8aLB2eDpMDqFED9vT4cg\nIiIiIl3ANYv0wMBAli9f7j62Wq1NjgH+5V/+pW0ia4UNGzZQXFzc5NywYcP4xS9+4aGIbk5XH60T\n4+gvwSIiIiIiHcs1p7uLZ5w8edLTIUgnoSJdjKR8EiMpn8RIyicxkvJJjGT4dPeOwuFwMH/+fBYu\nXGhov9nZ2UybNo0ePXpQUlJCfn6+e3G4pKQkAKqrq1m8eDEVFRX07t2bGTNmuBehA6ioqGDGjBlM\nnDiRMWPGtOi+PuXfGPo9pOtyVVjwcTo9HUan4AoIpt43yNNhiIiIiEgn1ymK9LZyafV3l8tFXl4e\nmZmZ2Gw2Zs2aRUxMDOHh4WzatIno6GjGjh3Lpk2b2LRpE88884y7j48++si9x3tL+a7PNvR7iMjN\nqx0/C1Ski4iIiEgbu+Y+6R1ReXk5GRkZbN682f3+/HfffUdqair19fXNtqmrq2PZsmWkpaWRnp7O\nnj17AEhJSaG6uprjx48TGhpKSEgIXl5eDB8+nH379gGwb98+4uPjARg5ciR79+5197tnzx769Onj\n3pJNRERERERE5Fo6VZF+8uRJFi1aREpKCmPGjKGsrIw9e/awfPlyXnjhBby9m1+def369fj5+bFg\nwQJyc3OJiopq8vPKykqCg4PdxzabjcrKSgDOnj3r3ts9MDCQs2fPAhcL/82bNzNhwoS2+KoiIiIi\nIiLSCXWaIr2qqorc3FxeeeUV7rjjDkwmEykpKbz77rsMHDiQ/v37X7Xt0aNHeeSRR9zHP36nvDVM\nJpP7c0FBAY8//jjdu3dHa/OJiIiIiIhIS3Sad9J79OhBr169OHbsGLfddhtwcWTd19fXPep9o2w2\nG6dOnXIfnzp1CpvNBlwcPT9z5gxBQUGcPn2awMBAAL755ht+//vfs2rVKs6fP4/JZMLb27vJHwMA\n7HY7drvdfTxx4sSbilVE2obFYsFqtXo6DI/y9vbu8s9AjKN8EiMpn8RIyicxWkFBgftzVFTUFTO3\nL9dpinQvLy/S0tKYN28ePj4+3H///eTn5zN37lzy8vIoLi7mwQcfbLZtdHQ0n3/+Of/wD/8AQE1N\nTZPR9H79+lFWVobD4cBms1FUVMS0adMAiImJYfv27SQlJbFjxw6GDBkCwJw5c9ztCwsL8fX1vaJA\nh5b9kkTE85xOJzVdfDsWbUkjRlI+iZGUT2Ik5ZMYyWq1tnogttNMdzeZTHTv3p2ZM2fy2WefkZGR\nwaOPPkpoaCgvvvgia9asoaqqqtm248aNo6amhtTUVNLT05uMbMPFEbQpU6Ywb948ZsyYQVxcnHsx\nuKSkJI4cOcK0adM4evSoe2s2ERERERERkdYyNeqF6Wa5XC6ef/55VqxYgdncvn/LqP3NY+16PxG5\nvtrxs6jr08/TYXiURhbESMonMZLySYykfBIjhYWFtbpNpxlJN1pqaioJCQntXqCLiIiIiIhI19Wl\nRtK3b9/Oli1bmpyLjIxkypQpHoqoeZUHd3o6BOkkLBYLTqfT02F0Cq6AYOp9gzwdhkdpZEGMpHwS\nIymfxEjKJzHSjYykd5qF41pi5MiRjBw50tNhXFdXn1IrxrFarV1+sTMRERERkY6kSxXpKSkpzJ8/\nH39//ybnt2zZwtatW4mIiGDq1Kmt6vPzzz/ns88+w+FwkJeX5+77xIkTLFu2jG+//Zann36aMWPG\ntLhP09elrYpB5GpqvSyYGjSSbgRT72BcQYGeDkNEREREOrkuVaRfzdatW8nMzHTvfd4akZGRPPDA\nA8yePbvJeavVypQpU9i7d2+r+6x6M7fVbUSkbQVkpoOKdBERERFpYx2+SN+wYQM7duwgMDCQ4OBg\nwsPD2b9/P1lZWQA4HA5ycnJYsGCBu019fT0LFy4kNjaW0tJSysvLycrKYtSoUdxzzz3k5+dz4cIF\nvL29SU5OJiwsDJfLxapVqzh06BBms5mEhAQeffRR7rzzzmbjCggIICAggAMHDrTHYxAREREREZFO\noEMX6aWlpRQVFZGbm4vT6SQjI4OIiAgaGhpwOByEhIRQVFREXFycu01tbS2LFy8mPj6ehx56iISE\nBEpKSpg9ezb+/v7U1tYyd+5czGYzhw8fZu3ataSmprJt2zYqKirIzc3FbDZTXV3twW8uIiIiIiIi\nnVGHLtKPHTtGbGws3t7eAMTExAAwbNgwioqKSEpKYvfu3cyYMcPdJicnh7FjxzJixIhm+6ypqWHp\n0qWUlZVhMpncK2MfOXKExMRE95Zsl7/XLiIiIiIiInKzOnSRbjKZmhxf2k0uLi6ORYsWMXToUEwm\nE6Ghoe5rIiMjKSkpuWqRvm7dOgYPHkx6ejoOh4M5c+Zc0b+R7HY7drvdfTxx4kTD7yEiN8/iZcHX\navV0GB7l7e2NtYs/AzGO8kmMpHwSIymfxGgFBQXuz1FRUURFRV3z+g5dpA8YMIBly5aRlJSE0+nk\nwIEDPPzww/Tp0wez2cwnn3zSZKo7wFNPPUVhYSErV67kueeeu6LP2tpaevbsCVzcV/2S6Ohotm3b\nxqBBg9zT3S8fTW+uiL9eYd+SX5KIeJ6zwdnl90zVvrFiJOWTGEn5JEZSPomRrFZrqwdizW0US7vo\n27cvw4YNIz09nezsbPr169dkNH3nzp1NivRLI++TJ0+mvr6e1atXX9Hnk08+yZo1a8jIyMDlcrnb\nJCQk0KtXL9LS0khPT2fXrl3Axe3bkpOTqaysJC0tjffeew+AM2fOkJyczGeffcaGDRtITk6mrq6u\nTZ+HiIiIiIiIdGymxraYw+0hhYWF+Pj4tGpP8lvRVz8f6+kQROQyAZnpNN4d4ekwPEojC2Ik5ZMY\nSfkkRlI+iZHCwsJa3aZDj6Q35/L31EVEREREREQ6ig79TvrlJkyY4OkQDBGQme7pEKSTsHhZcDY4\nPR1Gp2DqHUynmXYkIiIiIresTlWkdxZdfUqtGMdX07UMowJdRERERNqDivRbkOnrUk+HIJ1ErZcF\nk0bS24ypdzCuoEBPhyEiIiIinUiXKtJTUlKYP3/+FVunbdmyha1btxIREcHUqVNb1afD4WDJkiVU\nV1cTERHByy+/jJeXF9XV1SxfvhyHw0G3bt1ITk7m9ttvb1GfVW/mtioGEfGMgMx0UJEuIiIiIgbq\ndAvH3YitW7eSmZnZ6gIdYNWqVTzxxBO88847+Pn58cUXXwCwceNG+vbtS25uLi+//DL5+fkGRy0i\nIiIiIiKdTYcfSd+wYQM7duwgMDCQ4OBgwsPD2b9/P1lZWcDFke6cnBwWLFjgblNfX8/ChQuJjY2l\ntLSU8vJysrKyGDVqFPfccw/5+flcuHABb29vkpOTCQsLw+VysWrVKg4dOoTZbCYhIYFHHnkEu93O\n9OnTAYiPj6ewsJDExEROnDhBUlIScHHZfYfDQVVVFQEBAe3/kERERERERKRD6NBFemlpKUVFReTm\n5uJ0OsnIyCAiIoKGhgYcDgchISEUFRURFxfnblNbW8vixYuJj4/noYceIiEhgZKSEmbPno2/vz+1\ntbXMnTsXs9nM4cOHWbt2LampqWzbto2Kigpyc3Mxm81UV1dz7tw5/Pz8MJsvTkiw2WxUVlYC8NOf\n/pTf//73REZGcvz4cSoqKjh16pSKdBEREREREbmqDl2kHzt2jNjYWLy9vQGIiYkBYNiwYRQVFZGU\nlMTu3buZMWOGu01OTg5jx45lxIgRzfZZU1PD0qVLKSsrw2Qy4XReXHTryJEjJCYmugtyf39/qqqq\nrhpbUlISH374Ia+++ip33HEHd955p7vtj9ntdux2u/t44sSJrXwKIuIpFi8Lvlarp8NoN97e3li7\n0PeVtqV8EiMpn8RIyicxWkFBgftzVFQUUVFR17y+QxfpJpOpyXFj48VNkuLi4li0aBFDhw7FZDIR\nGhrqviYyMpKSkpKrFunr1q1j8ODBpKen43A4mDNnzhX9X2K1WqmpqcHlcmE2m6msrMRmswHg6+vL\nSy+95L42JSWFPn36XHG/lvySROTW5Gxwdqkt7qza0k8MpHwSIymfxEjKJzGS1Wpt9UBsh144bsCA\nAezdu5f6+npqa2s5cOAAJpOJPn36YDab+eSTT5pMdQd46qmn8PPzY+XKlc32WVtbS8+ePQHYvn27\n+3x0dDTbtm3D5XIBUF1djclkIioqiuLiYvf1Q4YMAeD8+fM0NDQAsG3bNgYOHIiPj4+h319ERERE\nREQ6lw5dpPft25dhw4aRnp5OdnY2/fr1azKavnPnziZF+qWR98mTJ1NfX8/q1auv6PPJJ59kzZo1\nZGRk4HK53G0SEhLo1asXaWlppKens2vXLgAmTZrEp59+yiuvvEJNTQ2jR48G4IcffiA1NZXp06dz\n6NAhJk+e3KbPQkRERERERDo+U+Plc7g7sMLCQnx8fBgzZoynQ7kpX/18rKdDEJEWCMhMp/HuCE+H\n0W40/U+MpHwSIymfxEjKJzFSWFhYq9t06HfSm3P5e+odUUBmuqdDkE7C4mXB2eD0dBidlql3MJ3m\nr5wiIiIickvoVEX6hAkTPB2CIbrSyJy0LV/9JbhNqUAXEREREaN16HfSRURERERERDqTTjWSfj0p\nKSnMnz8ff3//Jue3bNnC1q1biYiIYOrUqa3q0+FwsGTJEqqrq4mIiODll1/Gy8uLzZs38+WXXwLg\ndDo5ceIEeXl5+Pn5XbdP09elrYpB5GpqvSyYNN29zZh6B+MKCvR0GCIiIiLSiXSpIv1qtm7dSmZm\npnuP89ZYtWoVTzzxBHFxcaxYsYIvvviCxMREnnzySZ588kkA9u/fz5YtW1pUoANUvZnb6jhEpP0F\nZKaDinQRERERMVCHL9I3bNjAjh07CAwMJDg4mPDwcPbv309WVhZwcaQ7JyeHBQsWuNvU19ezcOFC\nYmNjKS0tpby8nKysLEaNGsU999xDfn4+Fy5cwNvbm+TkZMLCwnC5XKxatYpDhw5hNptJSEjgkUce\nwW63M336dADi4+MpLCwkMTGxSYxffvklw4cPb7+HIiIiIiIiIh1Shy7SS0tLKSoqIjc3F6fTSUZG\nBhERETQ0NOBwOAgJCaGoqKjJXum1tbUsXryY+Ph4HnroIRISEigpKWH27Nn4+/tTW1vL3LlzMZvN\nHD58mLVr15Kamsq2bduoqKggNzcXs9lMdXU1586dw8/PD7P54qv9NpuNysrKJjH+93//N4cOHeK5\n555r12cjIiIiIiIiHU+HLtKPHTtGbGws3t7eAMTExAAwbNgwioqKSEpKYvfu3cyYMcPdJicnh7Fj\nxzJixIhm+6ypqWHp0qWUlZVhMplwOi++z3vkyBESExPdBbm/vz9VVVXXjXH//v1ERka2eKq7iIiI\niIiIdF0duki/fE/0xsaLGyLFxcWxaNEihg4dislkIjQ01H1NZGQkJSUlVy3S161bx+DBg0lPT8fh\ncDBnzpwr+r/EarVSU1ODy+XCbDZTWVl5xXvtu3btuuZUd7vdjt1udx9PnDjxOt9aRG4VFi8Lvlar\np8NoN97e3li70PeVtqV8EiMpn8RIyicxWkFBgftzVFQUUVFR/5e9+4+Lss73Pv6aGRyoaKv4AAAg\nAElEQVR+DuAgyiK6JzQWHWOrRU10k/SkJ9Mk1x9n03bvfNSWh37oDayyRaGmpKDkZrqntJvOQ+sW\nNd2242kfuoVZ6DEsapu17lVytRAQUBGERWa4//A4G4oKNjAwvJ9/Xddwfa/rc13zeWSf+X6v7/ea\nx3frIn3IkCGsW7eOpKQkHA4Hn3zyCXfffTf9+vXDaDSyffv2FkPdAWbNmsXWrVvZsGFDq0PQ6+vr\n6d27NwAFBQWuz+Pi4tizZw/Dhg1zDXcPCgrCZrNx4MABEhISKCgoYPjw4a4258+f5/Dhwzz11FNX\nvYe2fEki0jU5mhw9ah16i8XSo+5XOpbySdxJ+STupHwSd7JYLO3uiO3W66TfdNNNjBo1irS0NLKy\nshg0aFCL3vR9+/a1KNIv9bw/9NBDNDY2snnz5ivOed999/HGG2+wcOFCnE6nq8348ePp06cPqamp\npKWl8dFHHwEwZ84c3nnnHZ588knq6uoYN26c61wHDx7kxz/+sWs4voiIiIiIiMi1GJovH8PdjW3d\nuhU/Pz+mTJni6VC+l6/+eaqnQxCRNgjOSKP55mhPh9Fp1LMg7qR8EndSPok7KZ/EnSIjI9vdplv3\npLfm8vfURURERERERLqLbv1O+uVmzJjh6RDcIjgjzdMhiJcw+ZhwNDk8HYbXMoSH4TVDkURERESk\nS/CqIt1b9KThs9Kx/DVcq0OpQBcRERERd+tRRXpycjIrVqwgKCioxee7du1i9+7dREdH88QTT7Tr\nnBUVFbz44ovU1tYSHR3N448/jo/PPx7rkSNHeOaZZ1iwYAEjR45s0zkNfy1pVwwiV1PvY8KgnvQO\nYwgPwxka4ukwRERERMSL9Kgi/Wp2795NRkbGFWuct8WmTZuYPHkyCQkJvPrqq7z33ntMmDABAKfT\nyebNm7n11luvWGP9WmqWZrc7DhHpfMEZaaAiXURERETcqNsX6W+99RZ79+4lJCSEsLAwoqKiOHTo\nEMuXLwcu9nSvXLmSnJwcV5vGxkZWrVrFiBEjKCkpoby8nOXLl3PXXXfxox/9iLy8PC5cuIDZbGbe\nvHlERkbidDrZtGkTn332GUajkfHjxzNx4kTsdjvz588HYOzYsWzdutVVpP/Xf/0Xd9xxB0ePHu38\nByMiIiIiIiLdTrcu0ktKSigsLCQ7OxuHw8HChQuJjo6mqamJiooK+vbtS2FhYYu10uvr68nNzWXs\n2LHceeedjB8/nuLiYjIzMwkKCqK+vp4lS5ZgNBr5/PPPefPNN0lJSWHPnj1UVlaSnZ2N0WiktraW\nc+fOERgYiNF4cZJ8q9VKdXU1ANXV1RQVFfHss8+yfv16zTovIiIiIiIi19Wti/TDhw8zYsQIzGYz\nAPHx8QCMGjWKwsJCkpKS2L9/PwsWLHC1WblyJVOnTmXMmDGtnrOuro61a9dSVlaGwWDA4bj4Pu+f\n//xnJkyY4CrIg4KCqKmpuWpseXl5PPDAAxgMBpqbm9s13F1ERERERER6pm5dpF/eO32pEE5ISGD1\n6tWMHDkSg8FARESE65jY2FiKi4uvWqRv2bKFW265hbS0NCoqKli8ePEV57/EYrFQV1eH0+nEaDRS\nXV1NWFgYcLGX/8UXXwTg3LlzFBcX4+Pj4/oh4RK73Y7dbnftz5w5s72PQUQ8xORjwt9i8XQYncZs\nNmPpQfcrHUv5JO6kfBJ3Uj6Ju+Xn57u2bTYbNpvtmsd36yJ9yJAhrFu3jqSkJBwOB5988gl33303\n/fr1w2g0sn379hZD3QFmzZrF1q1b2bBhAw8//PAV56yvr6d3794AFBQUuD6Pi4tjz549DBs2zDXc\nPSgoCJvNxoEDB0hISKCgoMBVhK9du9bVdt26dfzkJz+5okCHtn1JItI1OZocPWqJO4uW9BM3Uj6J\nOymfxJ2UT+JOFoul3R2xxg6KpVPcdNNNjBo1irS0NLKyshg0aFCL3vR9+/a1KNIv9bw/9NBDNDY2\nsnnz5ivOed999/HGG2+wcOFCnE6nq8348ePp06cPqamppKWl8dFHHwEwZ84c3nnnHZ588knq6uoY\nN25cR9+2iIiIiIiIeClDsxe9LL1161b8/PyYMmWKp0P5Xr7656meDkFE2iA4I43mm6M9HUanUc+C\nuJPySdxJ+STupHwSd4qMjGx3m27dk94azaIuIiIiIiIi3VW3fif9cjNmzPB0CG4RnJHm6RDES5h8\nTDiaHJ4Ow2sZwsPwmqFIIiIiItIleFWR7i160vBZ6Vj+Gq7VoVSgi4iIiIi7ed1wdxEREREREZHu\nqkv2pFdUVLBixQpWrVrl6VBciouLycvLw+l0Mm7cOJKSkgCora0lNzeXyspKwsPDWbBgAYGBga52\nlZWVLFiwgJkzZ7Z5Qju/8qMdcg/S8zgrTfg5NNy9MziDw2j0D/V0GCIiIiLSzXXJIr2rcTqdbNy4\nkYyMDKxWK+np6cTHxxMVFcXOnTuJi4tj6tSp7Ny5k507dzJ79mxX29dff53bb7+9Xdfz35bl7lsQ\nkQ5WPz0dVKSLiIiIyPfU5Yv08vJyVq9ezejRo/n222+ZN28ex48fZ82aNWRlZWE2m69o09DQwGuv\nvUZJSQkGg4EZM2YwYsQIHnzwQSZOnMinn35KaGgos2bNYvPmzVRXV/PLX/6S+Ph4Tpw4wfr162lq\naqK5uZmUlBRqamqIiIigb9++AIwePZqioiKioqIoKioiMzMTgMTERDIzM11F+sGDB+nXrx++vr6d\n9rxERERERESk++rSRXppaSlr1qwhOTmZAQMGkJmZycGDB9mxYwePPvpoqwU6wLZt2wgMDCQnJweA\nuro6ABobGxk2bBhz5swhJyeH/Px8nnvuOU6cOMHLL79MfHw8u3fvZtKkSYwZMwaHw4HD4eDYsWOE\nhYW5zm+1Wjly5AgAZ8+eJTT0Yu9ZSEgIZ8+eBS7+UPD222+TkZHB22+/3WHPSERERERERLxHl504\nrqamhuzsbJ588kkGDhyIwWAgOTmZl156iaFDhxITE3PVtl988QUTJ0507V96R9zHx4dbb70VgIED\nB2Kz2TAajQwYMIBTp04BEBMTw44dO/j973/PqVOnrvpDQGu+u0Z7fn4+9957L76+vjQ3aw5oERER\nERERub4u25MeEBBAnz59OHz4MP379wcu9qz7+/tTXV19Q+c0mUyubYPBgI/Pxds3Go04/mdyrTFj\nxhATE8OhQ4fIysrikUcewWq1UlVV5WpbVVWF1WoFLvaenzlzhtDQUE6fPk1ISAgAR48e5b//+7/Z\ntGkT58+fx2AwYDabW/x4AGC327Hb7a79mTNn3tC9iYhnmUwmLBaLp8PoUGaz2evvUTqP8kncSfkk\n7qR8EnfLz893bdtsNmw22zWP77JFuo+PD6mpqSxbtgw/Pz9uv/128vLyWLJkCRs3buTAgQPccccd\nrbaNi4vj3Xff5X/9r/8FXBzu/t0Z16+lvLycfv36cc8991BZWcnx48f5l3/5F8rKyqioqMBqtVJY\nWMhTTz0FQHx8PAUFBSQlJbF3716GDx8OwOLFi13n3Lp1K/7+/lcU6NC2L0lEuj6Hw0Gdl69Jb7FY\nOOfl9yidR/kk7qR8EndSPok7WSyWdnfEdtki3WAw4Ovry6JFi1i6dClbtmzh3nvvJSIigscee4zF\nixczdOhQgoODr2g7bdo0Nm7cSEpKCkaj0TVx3HeHo1+6xuXb+/fvZ9++fZhMJnr37s20adMwGo3M\nnTuXZcuWuZZgi4qKAiApKYnc3Fzef/991xJsIiIiIiIiIjfC0KwXpruc+qcneToEEWmn+unpNPQb\n5OkwOpR6FsSdlE/iTsoncSflk7hTZGRku9t02YnjRERERERERHqaLjvcvS0KCgrYtWtXi89iY2OZ\nO3euhyJyj/rp6Z4OQbyEyWRyTYooHcsZHHb9g0RERERErqNbF+mJiYkkJiZ6Ogy38/Yhs9J5LBaL\n109mJiIiIiLiTbp1kd5eycnJrFixgqCgoBaf79q1i927dxMdHc0TTzzRrnNWVFTw4osvUltbS3R0\nNI8//jg+Pj7s27ePt99+m+bmZvz9/Xn44Yf54Q9/2KZzGv5a0q4YRK6m3seEoUk96Z3BEB6GMzTE\n02GIiIiISDfXo4r0q9m9ezcZGRmutc/bY9OmTUyePJmEhAReffVV3nvvPSZMmEC/fv1YvHgxAQEB\nFBcX88orr7Bs2bI2nbNmaXa74xARzwrOSAMV6SIiIiLyPXX7Iv2tt95i7969hISEEBYWRlRUFIcO\nHWL58uXAxZ7ulStXkpOT42rT2NjIqlWrGDFiBCUlJZSXl7N8+XLuuusufvSjH5GXl8eFCxcwm83M\nmzePyMhInE4nmzZt4rPPPsNoNDJ+/HgmTpyI3W5n/vz5AIwdO5atW7cyYcIEYmJiXNcbPHgwVVVV\nnftgREREREREpNvp1kV6SUkJhYWFZGdn43A4WLhwIdHR0TQ1NVFRUUHfvn0pLCwkISHB1aa+vp7c\n3FzGjh3LnXfeyfjx4ykuLiYzM5OgoCDq6+tZsmQJRqORzz//nDfffJOUlBT27NlDZWUl2dnZGI1G\namtrOXfuHIGBgRiNFyfJt1qtVFdXXxHne++9x2233dZpz0VERERERES6p25dpB8+fJgRI0ZgNpsB\niI+PB2DUqFEUFhaSlJTE/v37WbBggavNypUrmTp1KmPGjGn1nHV1daxdu5aysjIMBoNrZuw///nP\nTJgwwVWQBwUFUVNTc90Yv/jiC95//32WLl36ve5VREREREREvF+3LtINBkOL/ebmZgASEhJYvXo1\nI0eOxGAwEBER4TomNjaW4uLiqxbpW7Zs4ZZbbiEtLY2KigoWL158xfkvsVgs1NXV4XQ6MRqNVFdX\nt3iv/W9/+xv//u//ztNPP33FZHWX2O127Ha7a3/mzJltvHsR6UpMPib8LRZPh9GhzGYzFi+/R+k8\nyidxJ+WTuJPySdwtPz/ftW2z2bDZbNc8vlsX6UOGDGHdunUkJSXhcDj45JNPuPvuu+nXrx9Go5Ht\n27e3GOoOMGvWLLZu3cqGDRt4+OGHrzhnfX09vXv3Bi6uw35JXFwce/bsYdiwYa7h7kFBQdhsNg4c\nOEBCQgIFBQUMHz4cgMrKSnJycnjiiSda/EhwubZ8SSLS9TmaHJzz8uXuLBaL19+jdB7lk7iT8knc\nSfkk7mSxWNrdEWvsoFg6xU033cSoUaNIS0sjKyuLQYMGtehN37dvX4si/VLP+0MPPURjYyObN2++\n4pz33Xcfb7zxBgsXLsTpdLrajB8/nj59+pCamkpaWhofffQRAHPmzOGdd97hySefpK6ujnHjxgGw\nbds26urq2LBhA7/+9a9JT0/v0GchIiIiIiIi3Z+h+fIx3N3Y1q1b8fPzY8qUKZ4O5Xv56p+nejoE\nEWmn4Iw0mm+O9nQYHUo9C+JOyidxJ+WTuJPySdwpMjKy3W26dU96ay5/T11ERERERESku+jW76Rf\nbsaMGZ4OwS2CM9I8HYJ4CZOPCUeTw9Nh9AiG8DC8ZliSiIiIiHiMVxXp3sLbh8xK5/HXcK1OowJd\nRERERNxBRXoXZPhriadDEC9R72PCoJ70TmMID8MZGuLpMERERESkG+tRRXpycjIrVqy4Ys3yXbt2\nsXv3bqKjo3niiSfadc6KigpefPFFamtriY6O5vHHH8fH5+JjtdvtvP766zgcDiwWC5mZmW06Z83S\n7HbFICJdQ3BGGqhIFxEREZHvoUcV6Veze/duMjIysFqt7W67adMmJk+eTEJCAq+++irvvfceEyZM\noK6ujo0bN/L0008TFhZGTU1NB0QuIiIiIiIi3qTbF+lvvfUWe/fuJSQkhLCwMKKiojh06BDLly8H\nLvZ0r1y5kpycHFebxsZGVq1axYgRIygpKaG8vJzly5dz11138aMf/Yi8vDwuXLiA2Wxm3rx5REZG\n4nQ62bRpE5999hlGo5Hx48czceJE7HY78+fPB2Ds2LFs3bqVCRMm8OGHHzJy5EjCwsIACA4O7vyH\nIyIiIiIiIt1Kty7SS0pKKCwsJDs7G4fDwcKFC4mOjqapqYmKigr69u1LYWEhCQkJrjb19fXk5uYy\nduxY7rzzTsaPH09xcTGZmZkEBQVRX1/PkiVLMBqNfP7557z55pukpKSwZ88eKisryc7Oxmg0Ultb\ny7lz5wgMDMRovLiSndVqpbq6GoCTJ0/icDhYvHgx9fX1TJo0iTvvvNMjz0lERERERES6h25dpB8+\nfJgRI0ZgNpsBiI+PB2DUqFEUFhaSlJTE/v37WbBggavNypUrmTp1KmPGjGn1nHV1daxdu5aysjIM\nBgMOx8VJt/785z8zYcIEV0EeFBR0zSHsDoeDr7/+mmeffZa///3vPPPMM9x888384Ac/aHGc3W7H\nbre79mfOnHkDT0JEugKTjwl/i8XTYXQYs9mMxYvvTzqX8kncSfkk7qR8EnfLz893bdtsNmw22zWP\n79ZFusFgaLHf3HxxEaSEhARWr17NyJEjMRgMREREuI6JjY2luLj4qkX6li1buOWWW0hLS6OiooLF\nixdfcf5LLBYLdXV1OJ1OjEYj1dXVrvfaw8LCsFgsmM1mzGYzQ4YM4W9/+9sVRXpbviQR6R4cTQ6v\nXvLOoiX9xI2UT+JOyidxJ+WTuJPFYml3R6yxg2LpFEOGDOHjjz+msbGR+vp6PvnkEwwGA/369cNo\nNLJ9+/YWQ90BZs2aRWBgIBs2bGj1nPX19fTu3RuAgoIC1+dxcXHs2bMHp9MJQG1tLQaDAZvNxoED\nB1zHDx8+HIDhw4fz1Vdf4XQ6+fvf/85f//pXoqKi3P0IRERERERExIt06yL9pptuYtSoUaSlpZGV\nlcWgQYNa9Kbv27evRZF+qef9oYceorGxkc2bN19xzvvuu4833niDhQsX4nQ6XW3Gjx9Pnz59SE1N\nJS0tjY8++giAOXPm8M477/Dkk09SV1fHuHHjAOjfvz8//vGPSU1N5Te/+Q3jx49XkS4iIiIiIiLX\nZGi+fAx3N7Z161b8/PyYMmWKp0P5Xr7656meDkFEbkBwRhrNN0d7OowOo+F/4k7KJ3En5ZO4k/JJ\n3CkyMrLdbbr1O+mtufw99e4oOCPN0yGIlzD5mHA0OTwdRo9hCA/Da371FBERERGP8KoifcaMGZ4O\nwS28uSdOOpe/fgnuVCrQRUREROT76tbvpIuIiIiIiIh4E6/qSe9IycnJrFixgqCgoBafFxcXk5eX\nh9PpZNy4cSQlJQEX18J77733CA4OBuCBBx7g1ltvbdO1DH8tcW/w0mPV+5gwaLh7pzOEh+EMDfF0\nGCIiIiLSDalI/x6cTicbN24kIyMDq9VKeno68fHxREVFYTAYmDx5MpMnT273eWuWZndAtCLSWYIz\n0kBFuoiIiIjcgB5dpL/11lvs3buXkJAQwsLCiIqK4tChQyxfvhyAiooKVq5cSU5OjqtNY2MjOTk5\n3HHHHURFRREREUHfvn0BGD16NEVFRa6l1rxo4nwRERERERHpBD32nfSSkhIKCwvJzs4mPT2do0eP\nYjabaWpqoqKiAoDCwsIW66zX19ezYsUKxowZw7hx46iuriYsLMz1d6vVSnV1tWv/3XffJS0tjfXr\n11NXV9d5NyciIiIiIiLdUo8t0g8fPsyIESMwm834+/sTHx8PwKhRoygsLARg//79LYr0lStXctdd\nd3HnnXde9/wTJkxg7dq1rFy5kt69e/Mf//EfHXMjIiIiIiIi4jV67HD3y9dTvzQ0PSEhgdWrVzNy\n5EgMBgMRERGuY2JjYykuLmbMmDHAxZ7zqqoq19+rqqqwWq0AhIT8433UcePGsWLFilbjsNvt2O12\n1/7MmTO/552JiKeZfEz4WyyeDsPtzGYzFi+8L/EM5ZO4k/JJ3En5JO6Wn5/v2rbZbNhstmse32OL\n9CFDhrBu3TqSkpJwOBx88skn3H333fTr1w+j0cj27dtb9KIDzJo1i61bt7JhwwYefvhhBg0aRFlZ\nGRUVFVitVgoLC3nqqacAOH36NL179wbg4MGDDBw4sNU42vIliUj34mhyeOX69BaLxSvvSzxD+STu\npHwSd1I+iTtZLJZ2d8T22CL9pptuYtSoUaSlpRESEsKgQYNa9KZv2rSJl19+2XX8pZ73hx56iHXr\n1rF582Zmz57N3LlzWbZsmWsJtkuTxm3evJljx45hMBgIDw/nV7/6VeffpIiIiIiIiHQrhmZNQQ7A\n1q1b8fPzY8qUKZ4Oha/+eaqnQxCR7yE4I43mm6M9HYbbqWdB3En5JO6kfBJ3Uj6JO0VGRra7TY+d\nOK41l7+nLiIiIiIiItKZeuxw98vNmDHD0yG4BGekeToE8RImHxOOJoenw+hxDOFhaIiSiIiIiNwI\nFeldkDcOkxXP8NdwLY9QgS4iIiIiN0pFehfkV37U0yGIl3BWmvBzqCe9K3EGh9HoH+rpMERERESk\ni/KKIr2iooIVK1awatUqt543KyuLp556ioCAAIqLi8nLy3PN4p6UlARAbW0tubm5VFZWEh4ezoIF\nCwgMDOTIkSO88sorADidTqZNm3bFkm5X478ty633ISJdR/30dFCRLiIiIiJX4RVFekdJT08HLhbZ\nGzduJCMjA6vVSnp6OvHx8URFRbFz507i4uKYOnUqO3fuZOfOncyePZuBAwfywgsvYDQaOXPmDCkp\nKdxxxx0YjZqrT0RERERERFrndRVjeXk5Cxcu5O2332b9+vUAHD9+nJSUFBobG1tt09DQwLp160hN\nTSUtLY2DBw8CkJycTG1tLUeOHCEiIoK+ffvi4+PD6NGjKSoqAqCoqIixY8cCkJiYyMcffwyA2Wx2\nFeSNjY0EBASoQBcREREREZFr8qqe9NLSUtasWUNycjIDBgwgMzOTgwcPsmPHDh599FHMZnOr7bZt\n20ZgYCA5OTkA1NXVtfh7dXU1YWFhrn2r1cqRI0cAOHv2LKGhF4euhoSEcPbsWddxR44cYd26dVRU\nVPDUU0+59V5FRERERETE+3hNkV5TU0N2djapqan0798fuNgTnpKSwoQJE4iJiblq2y+++IL58+e7\n9gMDA28ohsvXWR88eDCrV6/m22+/Zfny5dhsNgICAlocY7fbsdvtrv2ZM2fe0LVFpHswmUxYLBZP\nh3FDzGZzt41duh7lk7iT8kncSfkk7pafn+/attls2Gy2ax7vNUV6QEAAffr04fDhw64ivbS0FH9/\nf6qrq7/Xua1WK1VVVa79qqoqrFYrcLH3/MyZM4SGhnL69GlCQkKuaN+/f3/69etHWVkZ0dEtl1dr\ny5ckIt7D4XBQ102XxbNoST9xI+WTuJPySdxJ+STuZLFY2t0R6zUvSfv4+JCamsoHH3zAhx9+yPnz\n58nLy2PJkiXU1tZy4MCBq7aNi4vj3Xffde1fPtx90KBBlJWVUVFRQVNTE4WFhcTHxwMQHx9PQUEB\nAHv37mX48OHAxRnnHf+z9NWpU6c4efIkERER7rxlERERERER8TJe05NuMBjw9fVl0aJFLF26lC1b\ntnDvvfcSERHBY489xuLFixk6dCjBwcFXtJ02bRobN24kJSUFo9HIjBkzGDFihOvvJpOJuXPnsmzZ\nMtcSbFFRUQAkJSWRm5vL+++/71qCDeDLL7/k97//PSaTCZPJxKOPPnrFUHcRERERERGR7zI0Nzc3\nezqIrsjpdPLII4/w6quvdvqs7PVPT+rU64lI56mfnk5Dv0GeDuOGaPifuJPySdxJ+STupHwSd4qM\njGx3G6/pSXe3lJQUxo8f75Fl0+qnp3f6NcU7mUwm12sX0jU4g8Ouf5CIiIiI9Fg9qkgvKChg165d\nLT6LjY1l7ty5Vxybm5vbWWFdobv2sknXY7FYuu0kZSIiIiIiPVGPKtITExNJTEz0dBgiIiIiIiIi\nreq2RXpFRQUrVqxg1apVnXbNgoICduzYAVycbG7s2LGuWF588UVqa2uJjo7m8ccfx8fHh2+//ZZ1\n69Zx7Ngx/vVf/5UpU6a06Tp+5Uc77B6kZ3FWmvDTcPcuxRkcRqN/qKfDEBEREZEuqtsW6Z2ttraW\n7du388ILLwCwaNEihg8fTkBAAJs2bWLy5MkkJCTw6quv8t577zFhwgQsFgtz587l448/bte1/Ldl\ndcQtiEgXUD89HVSki4iIiMhVeMU66eXl5SxcuJC3336b9evXA3D8+HFSUlJobGxstU1tbS0rV64k\nLS2Np59+muPHjwOQn5/PSy+9xDPPPMNTTz3Fn/70JwCKi4uJi4sjMDCQwMBAbrnlFj799FOam5ux\n2+3ccccdAIwdO9ZVlAcHBzNo0CBMJlNHPwIRERERERHxAt2+SC8tLWX16tUkJyczZcoUysrKOHjw\nIOvXr+fRRx/FbDa32i4/P5/o6Giys7P5+c9/ztq1a11/O3HiBM899xzPP/8827Zt4/Tp05w+fZqw\nsH/MyhwWFkZ1dTW1tbUEBga6ZoG3Wq1UV1d37E2LiIiIiIiIV+rWRXpNTQ3Z2dk8+eSTDBw4EIPB\nQHJyMi+99BJDhw4lJibmqm2/+uor7rzzTgCGDRvGuXPnqK+vx2AwEB8fT69evbBYLNhsNo4cOdLq\nOQwGQ4fcl4iIiIiIiPRM3fqd9ICAAPr06cPhw4fp378/cLFn3d/f36292QaDAavVit1ud31WVVXF\nsGHDCAoKoq6uDqfTidFopLq6GqvV2uZz2+32FuedOXOm2+IWka7HZDJhsVg8HcYNMZvN3TZ26XqU\nT+JOyidxJ+WTuFt+fr5r22azYbPZrnl8ty7SfXx8SE1NZdmyZfj5+XH77beTl5fHkiVL2LhxIwcO\nHHC9K3652NhY9u3bx89+9jPsdjvBwcH4+/vT3NxMUVER999/Pw0NDfzlL39hzpw5+Pj48Oabb1JX\nV0dzczOff/45s2fPxmAwYLPZOHDgAAkJCRQUFDB8+PAW12pubr7qPbTlSxIR7+hAmkIAACAASURB\nVOFwOLrt2vUWi4Vz3TR26XqUT+JOyidxJ+WTuJPFYml3R2y3LtINBgO+vr4sWrSIpUuXsmXLFu69\n914iIiJ47LHHWLx4MUOHDiU4OPiKtjNmzGD9+vWkpaXh6+tLcnKy65wDBw5k8eLFnDt3junTpxMa\nenEm5p/97Gekp6cDMH36dAIDAwGYM2cOL774Iv/3//5fbrrpJsaNGwfAmTNnSE9P5/z58xiNRnbt\n2kVubi5+fn6d8XhERERERESkmzE0X6ubtwfaunUrfn5+bV7TvCPUPz3JY9cWkY5VPz2dhn6DPB3G\nDVHPgriT8kncSfkk7qR8EneKjIxsd5tuPXFcR9GEcCIiIiIiIuIJ3Xq4e1sUFBSwa9euFp/FxsYy\nd+7cVo+fMWNGZ4R1TfXT0z0dgngJk8mEw+HwdBjyHc7gsOsfJCIiIiI9ltcX6YmJiSQmJno6jHbp\nrkNhpeuxWCzddpIyEREREZGeyOuL9O7Ir/yop0MQL+GsNOGnnnSv5AwOo9E/1NNhiIiIiIibdcki\nvaKighUrVrBq1SpPh+JSXFxMXl4eTqeTcePGkZSUBEBtbS25ublUVlYSHh7OggULCAwM5MiRI7zy\nyisAOJ1Opk2bRkJCQpuu5b8tq8PuQ0S8Q/30dFCRLiIiIuJ1umSR3tU4nU42btxIRkYGVquV9PR0\n4uPjiYqKYufOncTFxTF16lR27tzJzp07mT17NgMHDuSFF17AaDRy5swZUlJSuOOOOzAaNVefiIiI\niIiItK7LF+nl5eWsXr2a0aNH8+233zJv3jyOHz/OmjVryMrKwmw2X9GmoaGB1157jZKSEgwGAzNm\nzGDEiBE8+OCDTJw4kU8//ZTQ0FBmzZrF5s2bqa6u5pe//CXx8fGcOHGC9evX09TURHNzMykpKdTU\n1BAREUHfvn0BGD16NEVFRURFRVFUVERmZiZw8f33zMxMZs+e3SKuxsZGAgICVKCLiIiIiIjINXXp\nIr20tJQ1a9aQnJzMgAEDyMzM5ODBg+zYsYNHH3201QIdYNu2bQQGBpKTkwNAXV0dcLFYHjZsGHPm\nzCEnJ4f8/Hyee+45Tpw4wcsvv0x8fDy7d+9m0qRJjBkzBofDgcPh4NixY4SF/WNGZqvVypEjRwA4\ne/YsoaEXh5yGhIRw9uxZ13FHjhxh3bp1VFRU8NRTT3XIMxIRERERERHv0WWL9JqaGrKzs0lNTaV/\n//4AJCcnk5KSwoQJE4iJiblq2y+++IL58+e79gMDAwHw8fHh1ltvBWDgwIH06tULo9HIgAEDOHXq\nFAAxMTHs2LGDqqoqRo4cSURERJtjvnx99cGDB7N69Wq+/fZbli9fjs1mIyAgoMUxdrsdu93u2p85\nc2abryciPZfJZMJisXTqNc1mc6dfU7yX8kncSfkk7qR8EnfLz893bdtsNmw22zWP77JFekBAAH36\n9OHw4cOuIr20tBR/f3+qq6tv6Jwmk8m1bTAY8PG5ePtGo9G1lvSYMWOIiYnh0KFDZGVl8cgjj2C1\nWqmqqnK1raqqwmq1Ahd7z8+cOUNoaCinT58mJCTkiuv279+ffv36UVZWRnR0dIu/teVLEhG5nMPh\n6PTl9SwWC+e0pJ+4ifJJ3En5JO6kfBJ3slgs7e6I7bIvSfv4+JCamsoHH3zAhx9+yPnz58nLy2PJ\nkiXU1tZy4MCBq7aNi4vj3Xffde1fGu7eFuXl5fTt25d77rmH+Ph4jh8/zuDBgykrK6OiooKmpiYK\nCwuJj48HID4+noKCAgD27t3L8OHDgYsz1F8q/E+dOsXJkyfb1SsvIiIiIiIiPU+X7Uk3GAz4+vqy\naNEili5dypYtW7j33nuJiIjgscceY/HixQwdOpTg4OAr2k6bNo2NGzeSkpKC0Wh0TRx3+XD07+5f\n2t6/fz/79u3DZDLRu3dvpk2bhtFoZO7cuSxbtsy1BFtUVBQASUlJ5Obm8v7777uWYAP48ssv+f3v\nf4/JZMJkMvHoo49eMdRdRERERERE5LsMzc3NzZ4OQlqqf3qSp0MQkS6ufno6Df0Gdeo1NfxP3En5\nJO6kfBJ3Uj6JO0VGRra7TZftSe/J6qenezoE8RImk8n12oV4F2dw2PUPEhEREZFup1sX6QUFBeza\ntavFZ7GxscydO9dDEblHZ/eOifeyWCydPrmYiIiIiIjcuG5dpCcmJpKYmOjpMNzOr/yop0MQL+Gs\nNOGnnnT5DmdwGI3+oZ4OQ0RERESuoksW6RUVFaxYsYJVq1Z5OhSX4uJi8vLyXBPHJSUlAVBbW0tu\nbi6VlZWuieMurcv+t7/9jVdeeYWGhgYMBgNZWVn06tXrutfy35bVofciIj1X/fR0UJEuIiIi0mV1\nySK9q3E6nWzcuJGMjAysVivp6enEx8cTFRXFzp07iYuLY+rUqezcuZOdO3cye/ZsHA4Ha9eu5Ykn\nnmDgwIHU1ta2WKddRERERERE5HJdvkgvLy9n9erVjB49mm+//ZZ58+Zx/Phx1qxZQ1ZWFmaz+Yo2\nDQ0NvPbaa5SUlGAwGFxLsD344INMnDiRTz/9lNDQUGbNmsXmzZuprq7ml7/8JfHx8Zw4cYL169fT\n1NREc3MzKSkp1NTUEBERQd++fQEYPXo0RUVFREVFUVRURGZmJnBx+H1mZiazZ8/ms88+Y+DAgQwc\nOBCAoKCgTntmIiIiIiIi0j116SK9tLSUNWvWkJyczIABA8jMzOTgwYPs2LGDRx99tNUCHWDbtm0E\nBgaSk5MDQF1dHQCNjY0MGzaMOXPmkJOTQ35+Ps899xwnTpzg5ZdfJj4+nt27dzNp0iTGjBmDw+HA\n4XBw7NgxwsL+MZOy1WrlyJEjAJw9e5bQ0ItDR0NCQjh79iwAJ0+exGAwsGzZMmpqahg9ejT33Xdf\nhz0rERERERER6f66bJFeU1NDdnY2qamp9O/fH4Dk5GRSUlKYMGECMTExV237xRdfMH/+fNf+pXfE\nfXx8uPXWWwEYOHAgvXr1wmg0MmDAAE6dOgVATEwMO3bsoKqqipEjRxIREdHmmA0Gg2vb4XDw5Zdf\n8sILL2A2m1myZAnR0dEMGzasRRu73Y7dbnftz5w5s83XExFpL5PJhMViuaG2ZrP5htuKXE75JO6k\nfBJ3Uj6Ju+Xn57u2bTYbNpvtmsd32SI9ICCAPn36cPjwYVeRXlpair+/P9XV1Td0zu++E24wGPDx\nuXj7RqPRtZb0mDFjiImJ4dChQ2RlZfHII49gtVqpqqpyta2qqsJqtQIXe8/PnDlDaGgop0+fJiQk\nBIA+ffowZMgQ1zD32267jZKSkiuK9LZ8SSIi7uJwOG54WT6LxcI5LeknbqJ8EndSPok7KZ/EnSwW\nS7s7Yo0dFMv35uPjQ2pqKh988AEffvgh58+fJy8vjyVLllBbW8uBAweu2jYuLo53333XtX9puHtb\nlJeX07dvX+655x7i4+M5fvw4gwcPpqysjIqKCpqamigsLCQ+Ph6A+Ph4CgoKANi7dy/Dhw93xXD8\n+HEaGxtxOBz85S9/YcCAATfwJERERERERKSn6LI96QaDAV9fXxYtWsTSpUvZsmUL9957LxERETz2\n2GMsXryYoUOHEhwcfEXbadOmsXHjRlJSUjAaja6J4747HP3SNS7f3r9/P/v27cNkMtG7d2+mTZuG\n0Whk7ty5LFu2zLUEW1RUFABJSUnk5uby/vvvu5Zgg4sTxU2ePJn09HQAbr/9dm677bYOeVYiIiIi\nIiLiHQzNzc3Nng5CWqp/epKnQxARL1U/PZ2GfoNuqK2G/4k7KZ/EnZRP4k7KJ3GnyMjIdrfpsj3p\nPVn99HRPhyBewmQyueZbEAFwBodd/yARERER8ZhuXaQXFBSwa9euFp/FxsYyd+5cD0XkHjfayyVy\nOYvFcsOThImIiIiISOfr1kV6YmIiiYmJng5DRERERERExC26dZF+uaysLJ566ikCAgJa/bvdbucP\nf/gDixYt6uTI2ufL6r97OgTxEj5nHTQ5mjwdhniJjsynvoFmrL6G6x8oIiIi4uW8pkhvbm5m0aJF\nV8zg3h39ZvdRT4cgItKplt89CKuvr6fDEBEREfG4bl2kV1RUsGzZMm6++Wa+/vprvvnmGzZs2MDb\nb79Nnz59mDhxIgD5+fn4+/szaNA/3vU+cuQIr776Kv/7f/9vlixZQnZ2tqsH/sknn+T5559vdXm3\n/fv3s23bNoxGIwEBASxevJgTJ06wfv16mpqaaG5uJiUlhYiICD744APeffddmpqaGDx4MA8//DBG\nY5ddml5EREREREQ8rFsX6QBlZWU88cQTDB48mOTkZAwGA6NHjyYvL89VpB84cIBnnnmGkydPAvDV\nV1/xf/7P/+HXv/41YWFhDB8+nIMHD5KYmMhf//pX+vbt22qBDrB9+3aeeeYZevfuzfnz5wHYvXs3\nkyZNYsyYMTgcDhwOB9988w379+/n+eefx2g0smHDBj788EPuvPPOznkwIiIiIiIi0u10+yI9PDyc\nwYMHt/jsn/7pnzh79iynT5/m7NmzBAYGYrVaOXnyJN9++y2vvPIKGRkZhIaGApCQkMC2bdtITEzk\no48+IiEh4arX+9GPfsTLL7/MqFGjGDlyJAAxMTHs2LGDqqoqRo4cSUREBF988QUlJSWu998bGxtd\n1xMRERERERFpTbcv0n2v8g7jqFGjOHDgAGfOnGH06NGuz3v37s2FCxcoKSnh9ttvB+Dmm2+mrKyM\nmpoaioqKmD59+lWv98gjj3DkyBE++eQTFi5cyIoVKxgzZgwxMTEcOnSIrKwsHnnkEQDGjh3LAw88\ncM347XY7drvdtT9z5sw237uIiLfwMflgsVg8HYZ0IrPZrO9c3Eb5JO6kfBJ3y8/Pd23bbDZsNts1\nj+/2RfrVJCQk8Lvf/Y5z586xePFi1+cBAQHMmzeP559/Hj8/P4YOHYrBYGDEiBG8/vrrREVFERQU\ndNXzlpWVMXjwYAYPHsynn35KVVUV58+fJzw8nHvuuYfKykqOHz9OXFwc2dnZTJ48meDgYGpra2lo\naKBPnz4tzteWL0lExNs1OZo4d+6cp8OQTmSxWPSdi9son8SdlE/iThaLpd0dsd2+SP/ubO7f3Y6K\niqKhoYGwsDDXMHODwYDBYCAkJISFCxeSlZXFvHnzGDx4MAkJCaSnp5OcnHzN623atImysjKam5u5\n5ZZb+OEPf8jOnTvZt28fJpOJ3r17M23aNAIDA5k1axbPP/88zc3NmEwmHn744SuKdBEREREREZFL\nDM3Nzc2eDkJauiN3j6dDEBHpVMvvHkSsVUuw9STqqRJ3Uj6JOymfxJ0iIyPb3UbrgYmIiIiIiIh0\nEd1+uHtHeeuttzhw4ECLz0aNGsX999/f4ddefveg6x8k0gY+Jh+aHE2eDkO8REfmU99Ac4ecV0RE\nRKS70XD3Lqi0tNTTIYiX0HAtcSflk7iT8kncSfkk7qR8Ene6keHu6knvgnz96zwdgngJR3MDvv4O\nT4chXsKb8qnZ6Uvj3/VPoIiIiHQ9Xvl/KHa7nT/84Q8sWrSICxcu8MILL3Du3Dnuv/9+Ro0a1amx\nFBQU8OMf/5jevXu3uU2vwE87MCLpaTTxhLiTt+TThbrb8NJ/AkVERKSb8/r/Q/n6668BWLlypUeu\nv3fvXgYOHNiuIl1ERERERER6pi5TpL/zzju8//77AIwfP57hw4ezbNkyoqOj+frrrxkwYACPP/44\nZnPrkwsVFxfz+uuvYzabiY2NBaCmpoaXXnqJc+fO8etf/5qUlBT69et3RdsjR47w+uuv09DQQK9e\nvXj22WcxGo1s2LCBkpISTCYTv/jFL7DZbBQUFFBUVERjYyPl5eUMHz6cOXPm4HQ6Wb9+PSUlJRgM\nBu666y7CwsI4evQov/3tb/H19WXp0qVXjV9ERERERESkSxTpJSUlFBQUkJWVhdPp5Omnn2bo0KGc\nPHmSf/u3fyMmJob169fzxz/+kSlTplzRvrGxkX//93/nueeeIyIigtzcXAwGA8HBwcybN4+3336b\nRYsWtXrtpqYm1qxZw4IFC4iOjqahoQGz2cx//ud/YjQaycnJobS0lOeff541a9YA8Le//Y2VK1fi\n4+PD/Pnzueeeezh79iynT59m1apVAJw/f56AgAD++Mc/8uCDDxIdHd1xD1BERERERES8Qpco0r/8\n8ktGjBjh6mUeMWIEf/nLXwgLCyMmJgaAn/70p/zXf/1Xq0V6aWkpffv2JSIiwnXsnj17ALje5PWl\npaWEhoa6img/Pz8AvvrqK+655x7g4ox84eHhnDx5EoBhw4bh7+8PQFRUFJWVlURFRVFeXs5rr73G\n7bffzo9//OM23bvdbsdut7v2Z86c2aZ2IiJy40wmExaLxdNh9Ghms1nfgbiN8kncSfkk7pafn+/a\nttls2Gy2ax7fJYr01hgMBgwGwxWfdaarFfi9evVybRsMBhwOB4GBgWRnZ/PZZ5+xe/du9u/fz7x5\n8657jbZ8SSIi4l4Oh4Pz9Vpex5O0xJG4k/JJ3En5JO5ksVja3RHbJSbqHTJkCB9//DGNjY00NDRw\n8OBBhgwZQmVlJf/v//0/AD788EPXu+aXi4yM5NSpU5SXl7uObavIyEjOnDnD0aNHAaivr8fpdBIb\nG+s6T2lpKZWVlddc4+7cuXM4nU5GjhzJrFmzOHbsGHCxZ76+vr7N8YiIiIiIiEjP1SV60m+66SbG\njh1Leno6cHHiuMDAQCIjI/njH//I+vXrGTBgABMmTGi1vdls5le/+hUvvPACZrOZIUOGuAr21nrk\nv+vSe+WvvfYajY2N+Pr6kpGRwcSJE3n11VdJTU3FZDKRnJyMj8/VH1d1dTXr1q1z9b4/8MADACQm\nJvLqq69q4jgRERERERG5LkPz9V7a9pCKigpWrFjhmoitJ6lpzL/+QSIicsMu1N3G3+sDPR1Gj6bh\npOJOyidxJ+WTuNO1RmNfTZfoSb+azn4Hvau4UHebp0MQL2EymXA4HJ4OQ7yEN+VTs9PX0yGIiIiI\ntKrL9qRfTU5ODhUVFS0+mzNnDnFxcR3atjOVlpZ6OgTxEvolWNxJ+STupHwSd1I+iTspn8SdbqQn\nvdsV6T2BinRxF/0jI+6kfBJ3Uj6JOymfxJ2UT+JO3X64e2ZmJr/4xS9ca5a7i91u5w9/+AOLFi3i\nL3/5Cz4+Pq7111tTVlbGunXraGhooLm5mQceeIDbbruNY8eOsWHDBurr6zEajdx///0kJCRc9Ty/\n/e1vKSkpwWQyMXjwYH71q19hMpmuG29ZU+0N3afI5U6dq8fR5B3Dk8XzlE/iTsqnGxPs40dA1/rf\nNxERcTOP/Ff+Uue9J9ZB/+KLL/D3979mkb59+3Z++tOfcvfdd/PNN9+QlZXFyy+/jK+vL48//jgR\nERGcPn2aRYsWceuttxIQENDqeX7605/y5JNPArBmzRr+9Kc/XXWG+u96s7Toxm5OREREvNrPI+MJ\n8AnydBgiItKBOq1Ir6ioYNmyZdx88818/fXX3HHHHfz3f/83BoOB2267zbVk2f79+9mwYQN1dXXM\nmzeP2NhYCgoKOHjwII2NjZw8eZIpU6bQ2NjIRx99hI+PD+np6QQFBbXoia+pqSE9PZ2XX37ZFcOp\nU6fYs2cPRqORffv2MXfu3FbXXu/duzfnz58H4Pz581itVgB+8IMftDgmODiYmpqaqxbpt932jwng\nBg0aRHV19fd/kCIiIiIiIuK1OrUnvaysjCeeeILa2lq2b9/O8uXLMZvN1NXVuY5xOp0sX76cTz/9\nlK1bt5KRkQHAN998w8qVK2lsbOSJJ57gwQcfZMWKFbz++ut88MEHTJo06bo98eHh4dx99934+/sz\nefLkqx6XlJTEM888w7vvvktDQwPPPvvsFcccOXIEh8NBRETEde+7qamJffv28dBDD133WBERERER\nEem5jJ15sfDwcAYPHsznn3/OXXfdhdlsBiAw8B9r1Y4cORKAm266iVOnTrk+t9ls+Pn5ERwcTGBg\nID/5yU8AGDhw4BUztl/P9ebK+4//+A/GjRvH+vXrSU9P56WXXmrx99OnT7N27Vr+7d/+rU3X27Bh\nA0OHDm21115ERERERETkkk7tSff1/ce6tFcrlH18LoZkNBpbrMfbq1cv17bBYHDtGwwGnE6nq82l\n8164cOGG4/zqq6+YOXMmADExMVy4cIGamhqCg4M5f/48L7zwAj//+c8ZPHjwdc+1detWamtreeyx\nx1r9u91ux263u/YvXVdERETkciYfExaLxdNhdDlms1nPRdxG+STulp+f79q22WzYbLZrHu+RiePi\n4uJck7OZzWZqa2sJCvr+k6CEh4dz9OhRBg0axIEDB1o9xt/f3/W++dX079+fzz//nMTERL755hsa\nGxsJDg6mqamJnJwcxo4d6+rxv5Y//elPfP75564h+61py5ckIiIiAuBocmhpqFZoySxxJ+WTuJPF\nYml3R2ynFumX3hm/9dZbOXbsGIsWLcLHx4fbb7+df/3Xf73q8W39/L777iM3N5c//elP3HbbbS2O\nu7T9k5/8hNWrV1NUVHTViePmzJnD7373O/7zP/8Tg8FAcnIyAIWFhRw+fJja2loKCgoASE5O5oc/\n/GGr8WzYsIHw8HCeeeYZ4OJQ/p/97GetHisiIiIiIiJiaL7eC9rS6dIOvOHpEERERKQL+nlkPBFa\ngu0K6vkUd1I+iTtFRka2u02nThwnIiIiIiIiIlfnkXfSu4q33nrrinfXR40axf3339+u8+Tk5Fwx\nw/ycOXOIi4u7obh+Hhl/Q+1ELmfyMeFoclz/QJE2UD6JOymfbkywj5+nQxARkQ6m4e5dUGlpqadD\nEC+h4VriTsoncSflk7iT8kncSfkk7nQjw917dE96V+VXftTTIYiXcFaa8HOop0rcQ/kk7qR88l7O\n4DAa/UM9HYaISLfVZYv0iooKVqxYwapVqzwdiktxcTF5eXk4nU7GjRtHUlISALW1teTm5lJZWUl4\neDgLFiwgMDCQ2tpaVq1axdGjR0lMTGTu3Lltuo7/tqyOvA0RERGRDlM/PR1UpIuI3DBNHNdGTqeT\njRs38pvf/IbVq1fz0Ucf8c033wCwc+dO4uLiWLNmDcOGDWPnzp0A9OrVi1mzZvHggw96MnQRERER\nERHpJrpsT/p3lZeXs3r1akaPHs23337LvHnzOH78OGvWrCErKwuz2XxFm4aGBl577TVKSkowGAzM\nmDGDESNG8OCDDzJx4kQ+/fRTQkNDmTVrFps3b6a6uppf/vKXxMfHc+LECdavX09TUxPNzc2kpKRQ\nU1NDREQEffv2BWD06NEUFRURFRVFUVERmZmZACQmJpKZmcns2bPx9fUlNjaWsrKyznxcIiIiIiIi\n0k11+SK9tLSUNWvWkJyczIABA8jMzOTgwYPs2LGDRx99tNUCHWDbtm0EBgaSk5MDQF1dHQCNjY0M\nGzaMOXPmkJOTQ35+Ps899xwnTpzg5ZdfJj4+nt27dzNp0iTGjBmDw+HA4XBw7NgxwsLCXOe3Wq0c\nOXIEgLNnzxIaenFYV0hICGfPnu3IRyIiIiIiIiJeqksX6TU1NWRnZ5Oamkr//v0BSE5OJiUlhQkT\nJhATE3PVtl988QXz58937QcGBgLg4+PDrbfeCsDAgQPp1asXRqORAQMGcOrUKQBiYmLYsWMHVVVV\njBw5koiIiDbHbDAY2nWPdrsdu93u2p85c2a72ouIiIh0JSaTCYvF0qnXNJvNnX5N8V7KJ3G3/Px8\n17bNZsNms13z+C5dpAcEBNCnTx8OHz7sKtJLS0vx9/enurr6hs5pMplc2waDAR+fi4/AaDTi+J9Z\nZseMGUNMTAyHDh0iKyuLRx55BKvVSlVVlattVVUVVqsVuNh7fubMGUJDQzl9+jQhISFtjqctX5KI\niIhId+FwOKjr5OWrtGSWuJPySdzJYrG0uyO2S08c5+PjQ2pqKh988AEffvgh58+fJy8vjyVLllBb\nW8uBAweu2jYuLo53333XtX9puHtblJeX07dvX+655x7i4+M5fvw4gwcPpqysjIqKCpqamigsLCQ+\nPh6A+Ph4CgoKANi7dy/Dhw+/sRsWERERERGRHq1L96QbDAZ8fX1ZtGgRS5cuZcuWLdx7771ERETw\n2GOPsXjxYoYOHUpwcPAVbadNm8bGjRtJSUnBaDS6Jo67fDj6d/cvbe/fv599+/ZhMpno3bs306ZN\nw2g0MnfuXJYtW+Zagi0qKgqApKQkcnNzef/9911LsF2SnJxMfX09TU1NfPzxxzzzzDOuUQEiIiIi\nIiIi32Vobm5u9nQQ0lL905M8HYKIiIjIDamfnk5Dv0Gdek0NTxZ3Uj6JO0VGRra7TZfuSe+p6qen\nezoE8RImk8k114LI96V8EndSPnkvZ3DY9Q8SEZGr6vZFekFBAbt27WrxWWxsLHPnzvVQRN9fZ//6\nLN7LYrF0+uQ94r2UT+JOyicREZHWabh7F/Tl7/d6OgTxEuqpEndSPok7KZ/EnZRP4k7dOZ/8o8Lp\n9YNQT4ch36Hh7m6QmZnJL37xC6Kjo1t8XlBQQElJyRU99BcuXGDt2rV8/fXXWCwW5s+fT3h4OACz\nZs3ihz/8IQB9+vTh17/+dZti2H//EjfciYiIiIiI9CSjdjyrIt0LqEi/zOWzv1/Pe++9h8Vi4be/\n/S2FhYVs3ryZ+fPnA+Dr68vKlSs7IkwRERERERHxQj26SH/rrbfYu3cvISEhhIWFuXrP9+/fz4YN\nG6irq2PevHnExsa2aPfJJ5/w1ltvsXDhQoqKiv5/e/ceFNV5/3H8vbt0WYHlsnhJ0dYL0WogiVZE\nCU7MSNPMmGjBmF7MTNSYxpoUW5toMNSqaYtjSdAWJWIGf0DqOPVSq7bjH07SNFjiRAzYClRLQBsD\nBpAqrqiB3fP7w3EnGzEs6cou+nn9pXues/s5y3eW8+V59hzPzeknT55MIgp2IgAAEWJJREFUUVFR\nnx+HiIiIiIiI3B7MgQ4QKPX19ZSXl5Obm8uKFSv48MMPPdvcbjc5OTnMnz+fnTt3eu33/vvvs3fv\nXl5++WXsdjttbW3Exl67iqnFYiEsLAyn0wlcWwr/0ksvkZ2dzZEjR/ru4ERERERERKRfumNn0mtr\na0lOTsZqtQKQlJTk2TZ58mQARo4cSUtLi+fx48eP8+GHH7Jy5UpsNluPr1FQUEBMTAzNzc2sWbOG\nr3/96wwZMsRrTHV1NdXV1Z7/X5+VFxERERER6Q2LxYLdbg90DPmcHTt2eP6dkJBAQkLCF46/Y5v0\nL/rueUjItbfFbDZ7XdlxyJAhNDc309jY6Fka73A4aG1txeFw4HK56OjoICIiAoCYmBgABg8eTEJC\nAg0NDTc06b78kERERERERHricrm4qNtbBhW73d7ridg7drn7uHHjOHLkCJ9++imXL1/m6NGjPe4z\naNAgXnjhBTZu3MiZM2eAazPwf/vbtVumHT58mHvvvReAS5cu0dnZCUB7ezsnTpzga1/72i06GhER\nEREREbkd3LEz6SNHjiQlJYVly5YRFRVFfHx8t+M+P+MeFxfHkiVLyMvLIysri+nTp5Ofn8+SJUuw\n2+385Cc/AeDjjz9my5YtmEwmDMMgPT2doUOH3vLjEhERERERkf7LZBiGEegQwWDnzp3YbDZmzpwZ\n6Cj8nzkt0BFERERERKSfSdnzCyInjQ50DPmMuLi4Xu9zx86kd6e390i/VVL2/CLQEeQ2YbFYvK6r\nIPK/UD2JP6mexJ9UT+JP/bmeBgwbFOgI4geaSQ9CjY2NgY4gtwm73a6Lh4jfqJ7En1RP4k+qJ/En\n1ZP405eZSb9jLxwnIiIiIiIiEmzUpIuIiIiIiIgECTXpIiIiIiIiIkFCTbqIiIiIiIhIkFCTLiIi\nIiIiIhIk1KSLiIiIiIiIBAndgk1EREREREQkSGgmPcjs2LEj0BHkNqJ6En9SPYk/qZ7En1RP4k+q\nJ/GnL1NPatJFREREREREgoSadBEREREREZEgoSY9yCQkJAQ6gtxGVE/iT6on8SfVk/iT6kn8SfUk\n/vRl6kkXjhMREREREREJEppJFxEREREREQkSatJFREREREREgkRIoAPcqaqqqiguLsbtdjN9+nTS\n09NvGLN161aqqqoIDQ3lueeeY+TIkQFIKv1BT/VUVlbGvn37MAyDAQMG8MwzzzB8+PAApZVg5stn\nE0BdXR0///nPWbp0KZMnT+7jlNJf+FJP1dXVlJSU4HK5sNvtrF69uu+DSr/QUz21t7eTn5/P+fPn\ncbvdzJw5k4ceeigwYSXoFRQUUFlZSWRkJK+99lq3Y3QuLr7qqZ56fS5uSJ9zuVzGj3/8Y+OTTz4x\nOjs7jRdffNH46KOPvMYcPXrUyMnJMQzDME6ePGm8/PLLgYgq/YAv9XTixAnj0qVLhmEYRmVlpepJ\nuuVLLV0ft3r1amPt2rXGe++9F4Ck0h/4Uk9Op9NYunSp0draahiGYVy4cCEQUaUf8KWe/vCHPxjb\ntm0zDONaLS1YsMDo6uoKRFzpB2pqaoz6+nrjZz/7WbfbdS4uvdFTPfX2XFzL3QOgrq6Ou+66i8GD\nBxMSEkJqaioVFRVeYyoqKpg2bRoAo0eP5tKlS5w/fz4QcSXI+VJPY8aMISwsDIC7776bc+fOBSKq\nBDlfagngwIEDTJkyhcjIyACklP7Cl3o6dOgQkydPJjY2FkA1JTflSz3FxMTQ0dEBwOXLl7Hb7Vgs\nlkDElX5g3LhxhIeH33S7zsWlN3qqp96ei6tJD4C2tjbPCQmAw+Ggra3tC8fExsbeMEYEfKunz3r7\n7beZMGFCX0STfsbXz6aKigq+/e1vA2Aymfo0o/QfvtRTU1MTTqeTNWvWkJWVxbvvvtvXMaWf8KWe\n0tLSOHPmDIsWLWLZsmXMnz+/j1PK7UTn4nKr+HIuriY9iBm6O5742fHjx/nrX//Kk08+Gego0k8V\nFxczd+5cTCYThmHoc0r+Jy6Xi4aGBlasWEF2dja7d++mqakp0LGkn9qzZw8jRoygsLCQ3/zmNxQV\nFXH58uVAx5J+TL/jxN98PRfXheMCwOFweC1xOHfuHA6Ho9djRMD3Wjl9+jSFhYVkZ2cTERHRlxGl\nn/Cllurr69mwYQMAFy9epKqqipCQEJKSkvo0qwQ/X+opNjYWu92O1WrFarUybtw4Tp8+zVe/+tW+\njitBzpd6OnnyJBkZGQCepfGNjY3Ex8f3aVa5PehcXPytN+fimkkPgPj4eM6ePUtzczNdXV2Ul5ff\ncIKblJTkWfZ38uRJwsPDiY6ODkRcCXK+1FNrayuvvvoqmZmZ3HXXXQFKKsHOl1rauHEjmzZtYtOm\nTUyZMoVnnnlGDbp0y5d6mjRpEidOnMDtdnP16lX+/e9/M2zYsAAllmDmSz3FxcXxz3/+E4Dz58/T\n2NjIkCFDAhFXbgM6Fxd/6u25uMnQOo6AqKys9LqNSEZGBgcPHgTg4YcfBqCoqIiqqipsNhuLFy9m\n1KhRgYwsQaynetq8eTPvv/8+AwcOBMBisbB27dpARpYg5ctn03UFBQVMnDhRt2CTm/Klnvbt28c7\n77yDyWQiLS2NGTNmBDKyBLGe6qm9vZ2CggLOnTuH2+0mIyODqVOnBji1BKsNGzZQW1tLe3s70dHR\nPPHEE7hcLkDn4tJ7PdVTb8/F1aSLiIiIiIiIBAktdxcREREREREJEmrSRURERERERIKEmnQRERER\nERGRIKEmXURERERERCRIqEkXERERERERCRJq0kVERERERESChJp0ERERuaPU1tby05/+9KbbW1tb\neeqpp/DlLrVvvPEGu3fv9mc8ERG5w+k+6SIiIgHw/PPPc+HCBcxmM6GhoUyYMIGnn34am80W6Gg3\n1dzcTGZmJtu3b8ds9t/f+d9++232799PW1sbVquVUaNGsXTp0j57L55//nkWL15MYmLi//Q81dXV\nbNy4kddff91PyURE5E4UEugAIiIid6qsrCwSExNpa2vj17/+NX/84x+ZO3euz/tf/zu7yWS6VRH9\nyuVyYbFYvB6rqalh+/btZGdnM2LECJxOJx988EGfZ9OchYiIBAs16SIiIgHmcDgYP348//nPf7h0\n6RL5+fnU1dXhcrn4xje+wbPPPovD4QBg9erVjB07lurqahoaGnj11Vepra1l3759tLW1ERkZyXe+\n8x2+9a1vAddmd/Pz85kxYwb79u3DYrGwcOFCQkJCKCkp4eLFi8yaNYv09HTgWrO6d+9e3nrrLTo6\nOkhMTOSHP/whERERrFq1CoD58+cDsHLlSkaPHu2ZCT9//jx33303ixYtYuDAgQB873vf4+mnn+Yv\nf/kLhmGQn5/vdex1dXWMGTOGESNGABAREcGDDz7o2d7Z2cn27ds5fPgwnZ2dJCcnM2/ePKxWq+fY\nHnvsMfbu3YvZbOYHP/gBDz30EAAffPABv//97zl37hwDBgzg0UcfZebMmV4z3vn5+bS2trJu3TrM\nZjNz5sxhypQpnhUDhw8fZv/+/axdu9aT6c9//jM1NTUsX76cTZs2ERsbS0ZGBjk5OXR1dfHUU09h\nMpnYsGEDmZmZbN68mYiICADq6+vJyclhy5Ytfl2NICIitw/9dhAREQmQ67O3ra2tVFVVMWrUKAzD\nYPr06RQUFPD6669jtVopKiry2q+srIxFixZRWlrKoEGDiIqKYsWKFZSUlLB48WJKSkpoaGjwjL9w\n4QKdnZ1s2bKF7373uxQWFnLo0CHWrVvHK6+8wq5du2hpaQHgwIEDVFRUsGbNGgoLCwkPD/e8/iuv\nvAJAcXExpaWljB49miNHjvCnP/2JZcuWUVRUxLhx4/jtb3/rlbeiooK1a9eSl5d3w3swZswYjh07\nxo4dO/jXv/5FZ2en1/Zt27Zx9uxZcnNzyc/Pp62tjV27dnkdW0dHB4WFhfzoRz+iqKiIjo4OADZv\n3syzzz5LSUkJeXl53S5nz8zMZODAgWRlZVFaWsqsWbO8tk+cOJHGxkbOnj3reezvf/87U6dOBa6t\nYjCZTISGhpKdnY3D4aC0tJSSkhJiYmJISEigvLzcs++7775LamqqGnQREbkp/YYQEREJkNzcXBYs\nWMCqVau45557yMjIICIiguTkZKxWKzabjdmzZ1NTU+PZx2QyMW3aNIYNG4bZbMZisfDNb36TwYMH\nA3DPPfdw3333UVtb69nHYrEwe/ZszGYzDzzwAE6nkxkzZmCz2Rg2bBjDhg3j9OnTABw8eJDvf//7\nOBwOQkJCeOKJJzh8+DBut7vbJeEHDx4kPT2duLg4zGYz6enpnDp1itbWVs+Y9PR0wsPD+cpXvnLD\n/mPHjuXFF1+koaGBdevWsXDhQkpLSz2v99ZbbzFv3jzCw8Ox2WxkZGR4Nb0Wi4U5c+ZgNpuZMGEC\nNpuNxsZGAEJCQjhz5gwdHR2EhYUxcuTIXv+MQkNDSUpK4tChQwA0NTXR2NhIUlKSZ8z196W792fa\ntGmUlZUB4Ha7KS8v91opICIi8nla7i4iIhIgy5cvv2F29+rVq5SUlHDs2DGcTicAV65cwTAMz3fP\nry8lv66yspJdu3bR1NSEYRhcvXqV4cOHe7bb7XbPvlarFYDo6GjPdqvVypUrVwBoaWkhNzfXa6bX\nYrFw4cKFbo+hpaWF4uJi3nzzTa/H29raPDljY2O/8H0YP34848ePB+D48ePk5eURFxdHcnIyn376\nKVlZWZ6xhmF4NcN2u90r62eP5YUXXmD37t1s27aN4cOHM3fuXMaMGfOFWbozdepUSktLmTNnDocO\nHWLSpEme97EnSUlJvPHGGzQ3N9PY2EhYWBjx8fG9ziAiIncONekiIiJBZP/+/TQ1NZGTk0NUVBSn\nTp3ipZde8mrSP6uzs5PXXnuNzMxMJk2ahNlsJjc390tfCG3gwIE899xz3Taz15fEf378448/7ln+\n3Z3eXNguMTGRxMREPvroI9LS0rBareTl5RETE+Pzc1wXHx/P8uXLcbvdHDhwgPXr13d75fWe8t17\n7720t7dz6tQpysvLmTdvXrf7d/c8VquVlJQUysrK+PjjjzWLLiIiPdJydxERkSBy5coVrFYrYWFh\nOJ1Odu7c+YXju7q66Orq8syWV1ZW8o9//ONLv/7DDz/M9u3bPcvV29vbqaioACAyMhKTycQnn3zi\nNX7Pnj2cOXMGgI6ODt577z2fX6+iooLy8nKcTieGYVBXV0dNTQ2jR4/GZDKRlpZGcXEx7e3twLUZ\n+mPHjvX4vF1dXZSVldHR0YHZbGbAgAE3/R54VFSU13fOPy8kJISUlBTefPNNnE4n9913n2fbZ2f2\no6KiuHjxouc78dc9+OCDvPPOOxw9elRNuoiI9Egz6SIiIkHk0Ucf5Xe/+x0LFy7E4XDw2GOPeZrk\n7gwYMIAFCxawfv16urq6mDhxotf3pXtrxowZGIbBr371K/773/8SGRlJamoqSUlJhIaGMnv2bFau\nXInL5SI7O5vk5GSuXLnChg0baGlpISwsjPvvv5+UlBSfXi88PJwDBw5QVFREV1cX0dHRzJo1yzMz\n/+STT7Jr1y6ys7Npb2/H4XDwyCOPcP/99/f43GVlZWzduhW3283QoUNZsmRJt+MyMjLYunUr27Zt\n4/HHHyc5OfmGMVOnTmXVqlU88sgjXs3+9QvHAQwdOpTU1FQyMzNxu92sX7+e6Ohoxo4di8lkYtSo\nUTd8VUFEROTzTIZuDCoiIiJyS/3yl78kNTWV6dOnBzqKiIgEOS13FxEREbmF6urqqK+v54EHHgh0\nFBER6Qe03F1ERETkFtm4cSMVFRUsWLAAm80W6DgiItIPaLm7iIiIiIiISJDQcncRERERERGRIKEm\nXURERERERCRIqEkXERERERERCRJq0kVERERERESChJp0ERERERERkSChJl1EREREREQkSPw/Kc3P\nlqT7+H0AAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x150ed048>"
]
}
],
"prompt_number": 11
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"res.plot_objective_contrib()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAxsAAAHMCAYAAAC9erV3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8VPX1//HXvXPvLJlJyELYZF8FAgERKgJxQ1vRurR1\nQa1KLS6ttmoXrdW6tfZntbbVr1upxaqgiLihUjdENhFZBAFBEghZyJ5MZl/v/f0RSImCLMlkMsl5\n+vCRcOfOvWcCmbnv+9kU0zRNhBBCCCGEEKKNqckuQAghhBBCCNE5SdgQQgghhBBCJISEDSGEEEII\nIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISE\nDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQggh\nhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURC\nSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGE\nEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBCJISEDSGEEEIIIURCSNgQQgghhBBC\nJISEDSGEEEIIIURCSNgQQogOori4mOOPP55Zs2YxYsQILr/8ct577z1OPvlkhg8fztq1axk7diwe\njwfTNMnJyeH5558H4Morr+SDDz5I8isQQgghWpKwIYQQHUhRURG//vWv2b59Ozt27GDBggWsXr2a\nhx9+mAceeICpU6eycuVKtm7dypAhQ1i5ciUAa9asYcqUKUmuXgghhGhJwoYQQnQggwYNYvTo0SiK\nwujRo5k+fToAeXl57Nmzh6lTp7J8+XJWrFjBDTfcwObNm9m7dy9ZWVk4HI4kVy+EEEK0JGFDCCE6\nEJvN1vy9qqpYrdbm72OxGAUFBc1h49RTTyU3N5dXXnmFgoKCZJUshBBCHJKEDSGESCF9+/altraW\nwsJCBg0axNSpU3n44YclbAghhOiQJGwIIVLG4sWLefDBB5NdRkIpinLIP+///qSTTmL48OEATJ06\nlb179zJ16tT2K1IIIYQ4QoppmmayixBCCCGEEEJ0PtKyIYRImueee478/HzGjRvHlVdeyeDBgwFw\nu91YLJbmmZYKCgooLCzk2Wef5aabbkpmyUIIIYQ4ClqyCxBCdE1bt27lT3/6E5988gnZ2dk0NDRw\n2WWXsW3bNnbt2sWECRNYvnw5EydOpKysjKFDhzaHDyGEEEKkBmnZEEIkxdKlS7n44ovJzs4GICsr\ni2nTpjXPtPS73/2OlStXsm7dOiZOnJjkaoUQQghxLCRsCCGSQlEUvj5kbP+0rmvXrmXGjBm43W6W\nLVvWPNPS1wdPCyGEEKJjk7AhhEiK008/nYULF1JfXw9AQ0MDkyZNYvXq1VgsFmw2G/n5+Tz99NPN\nYUPmsxBCCCFSi4QNIURSjBo1it///veccsopjBs3jl/96ldYrVb69+/PSSedBDS1dPh8PsaMGQM0\ntWxI64YQQgiROmTqWyGEEEIIIURCSMuGEEIIIYQQIiEkbAghhBBCCCESQsKGEEIIIYQQIiEkbAgh\nhBBCCCESQlYQF0KILmb/vCBf//pt++5nGMZBZwX7tlnCDtxfZhMTQoiuRcKGEEJ0YKZptvg/bsSJ\nxg1ihkHcNIgbBoZpEDfNff8bGPu+N/b/zwHf7/tzzDCImQZRwyBqGhgmmPv/M/edFzAwwWz6agLj\nMjKJKg2Yigko7IsQKND8PewPFQoKCqpiwYKKiqVpi6KgoO77+r8/q83fK6CoqM2PN32vqpamr4ql\nOcCoqnrA+YQQQnQ0EjaEEKKd7G8lMAwDw4gTjkaIGCZRw2gKEWZTiIgaRnMYiBgx/LEY/liUoBEj\nbMSJGiZR02jeP077zWA+ypVOwOLFNI1v37GNSvpfDFH3faeioGBRNHTFiqboaGioioqqWFp8tSgW\nLKoFi0VDUzUJJ0IIkQQSNoQQopX2tzoYhkHciGAaUUwzhkkciMEBXxUlgqoEUdQgoWhfFpbXEDbi\nHObSvcsyMYkTp+ln2OKBwwYaBQULGhYsWNCxqrYjCieaRUezaKiqKqFECCFaScKGEEIcxtfDhGGE\nMc0YEN33fwxVCaKqflQ1gKqFUZQYh7tOtVp6SNBIIBOTGFFiRIEQAcP7rfv/L5xo2FUHVsXeFE4U\nramFRNHQLBq6xSphRAghjpCEDSFEl9cyTIQxjAim2RQi9gcKVQmhql4sliC6HkZR4oc56uHZrPUM\ndaTzVfDbL4JF+zgwnISN4EH3saChoWNXHdj2hRGLomFRNSyKBd2ioVtsWCwWCSNCCIGEDSFEF2Ls\nGxsRj4cwjDAQ4X9hIohq8WGxBPaFicS3N2haA6O79ZawkULixIgT+9YwomPF1hxGtOYwoqkaVs2G\nVbNKEBFCdBkSNoQQncr+VopYPIoRD2GYYZoCRRhFCWGxNKJpPlQ1fNhuTommqnHSdelE1ZnsDyMh\nI/CNxxQUdGw4VCd21dE0wF3V0VUdq25Dt+gSQoQQnY6EDSFEyjIMg3g8Tjwe2BcqIkAYVfVjURvR\nrf4jGjuRTDYtjIZKTEZudHomJhFCRIwQjQf8dSsoWIM2HKoLu+JoDiCaRcem2dE1/aBrmwghRCqQ\nsCE6hUcffZSnnnoKj8fDhRdeyGOPPZbQ8w0cOJANGzaQnZ3NlClTWLVqVULP19XtH08RiwWJGyGg\nKVgoSgCLxY1u9aEo0Q4dKg7Fqtcx0pnDF353sksRSWJiEiZE2Ag1bdg3HEhFRcdGmurCpjrQFR1t\nXwixa3Y0TZMQIoTo8CRsiE7hySef5IMPPuCDDz5g3bp1CT/fgR/uBwsasVgMTZNfr2PRHCziYeLx\nANAULiwWNxatAV0NpWSoOBRdb2RERl8JG+IbDAzCBJvGhxzQEqJiwYqdNIsTm2JHV21YLVbsugNd\n05vXEhFCiI5A3pFEyrv++uvZtWsXZ599Ng0NDc3bi4uLOf3008nPz2f69OmUlpYSj8cZPHgwAG63\nG4vFwsqVKwEoKCigqKjooOeoq6vjrLPOIi8vj9mzZzcvzgbgcrkAWLZsGdOmTeP8889n9OjRiXq5\nnY5hGESiIYLBOgLBvQRDu4nGtmBR12C3r8Hh+ByH40us1gosls4VNAAUxcAl4zbEUTCIE8JPfbya\nilgJJZGdFAW3sdOzjdLG3VQ27qXOW4s34CUajbZ4vxJHp7GxkSeffDIp5545cyb5+fn8/e9/Z9as\nWSxatCgpdQjRWhI2RMp76qmn6NOnD8uWLSMrK6t5+0033cSsWbPYtGkTl19+Ob/4xS+wWCyMGDGC\nbdu2sXLlSiZMmMDy5csJh8OUlZUxZMiQg57j3nvvpaCggC1btnDhhRdSUlLS/NiBrRwbN27k0Ucf\nZceOHYl7wSnMNE2i0QjBUAOBYCWBYDGRyDYUZS02+6c4HBtwOLZhs5Vi0QKdLlgcitUSwi53o0Ur\nNHXFClAbr6Q8upvi8A6KAtvY5dlBeWMJ1Y2VNPjqCYQCxONxCSBHqKGhgSeeeOIb22OxWELPW1lZ\nybp169i0aRM333wzIKvei9Qln26i09g/C9F+a9as4bLLLgPgiiuuaG7BmDZtGsuXL2fFihX87ne/\nY+XKlaxbt46JEyce8tgrVqzgiiuuAGDGjBktQs2BJk2axIABA9rqJaU00zSJxqKEQo0EglUEgnsI\nhXdg8hlW6xocjnU4HFuw2YvRNE+7TDXbUVmttYx0dkt2GaKTiRPDZzZSFSujNFrErtCXFPq2UdxY\nSEVjObWeahr9jUQiEQkfh3D77bdTVFTE+PHjmTRpUnPrdV5eHgAXXHABJ554Inl5ecyZM6f5eS6X\nizvvvJNx48YxefJkqqurAVi4cCFjxoxh3LhxnHLKKYc871lnnUV5eTnjx49v/uzab+DAgdTX1wOw\nbt06TjvtNABuvvlm7r//fgDefffdbz2+EO1JOpWLTu1gH6AFBQU88cQTVFRUcN999/HQQw+xbNky\nCgoKjvpYX+d0Oo+51lTXNN1sjFjMj2kGgCAWSx261Y2qRpJdXoemaR6GufqzUZbbEAkWJYzbCOM2\naoGmmbDswTSclgxsqh2rasWm2bBb02QaXuDBBx9k69atbNy4kY8//phzzjmHrVu3Nt9Umjt3LllZ\nWQSDQSZNmsSPfvQjsrKyCAQCTJ48mT/+8Y/cdtttzJkzh9///vfcf//9vPfee/Tu3RuPx3PI8y5e\nvJhzzz2XjRs3AvDMM880P3aov5M///nPTJw4kalTp/LLX/6SJUuWtOFPQohjJy0botM6+eSTeeml\nlwCYN29ec5iYOHEiq1evxmKxYLPZyM/P5+mnn/7WsFFQUMD8+fMBWLJkSYuxIV1VU8vF/i5R5QRD\nRZjGhn2tFhv2jbOolqBxBBTFxKm3fkVyIY6WiUkQP7XxCsqju9kd3kGh/0uKGwupbNxLvbeOQCiA\nYXTNlscDbzKZpvmN1ut//OMfza0XpaWl7Ny5EwCr1co555wDwIQJEyguLgZgypQpXHXVVfzrX//6\n1q5Yx9LS5HA4mDNnDmeeeSY33XQTgwYNOupjCJEI0rIhOoX90z8eOA3kY489xqxZs3jooYfo0aMH\nc+fOBcBms9G/f39OOukkoClILFiwgDFjxhzy+HfffTczZ87kxRdf5OSTT27xYXPgXabOfBfQNE1i\nsRh+f4hQMIqixsjKLsJmc6MocqHcWroWxKlq+I3E9gUX4nBiRHEbtU2tHzHQwzYyLJk41DSsFjsO\nPQ2b1dap3+8O5cDW62XLlvHhhx+yZs0a7HY7p512GqFQ0/TFuq4376eqanOwePLJJ1m7di1vv/02\nEyZMYP369WRnZx9VDZqmNYe//efbb/PmzeTm5lJeXn5Mr0+IRJCwITqFXbt2AXDVVVdx1VVXAdC/\nf38+/PDDg+6/fPny5u9nzpzJzJkzv/X42dnZvPvuuwd9bH9T+Kmnnsqpp556tKV3WPunoPX7gwSD\nUULBKO76EJ7GMPG4SUamFas1l8ysumSX2ilY9VrGpB/HmsbaZJciRAtRwtTFq5rW/4iCLZRGhiUT\nu+rAptlJs6ah7Vt4sLNJT0/H6z14/0aPx0NWVhZ2u53t27ezZs2awx6vqKiISZMmMWnSJJYsWUJZ\nWdlRh42BAweybt06vve977WYoWrPnj088sgjbNy4kbPPPpsLLriASZMmHdWxhUgECRtCiGaGYRAI\nhAgGwoSCMRobQ7gbwsSi3+xC4XFHqKlyYrP3wOGoTkK1nYumeRnosrKmMdmVCPHtwgSoiQcgDkpU\nIS3owqV1w646sGo20qxOLBZLpwgfOTk5TJkyhTFjxuBwOOjVq1fzY9/73vd46qmnGDVqFCNGjGDy\n5MnNj329xXv/n3/729+yc+dOTNNk+vTpjB079pDnPtTP7+677+aaa64hIyODU089tXm/n/70p/z1\nr3+lV69ePPPMM1x99dWsW7cOq9Xaqp+BEK2lmDIFhRDNnn32Wf7xj3+02DZ16tSEr0ieLKZpEo/H\n8fmCBPwRfN4wtTVBIuEj7xY1ZHgGvft8gUULJ7DSrsHtGcXcko4d3Gbk9iFgKceka/bhF99OxYJL\nyWgacG6xYdcc2K0OLBZLsksTQiSJhA0huhjTNIlEIvi8IQLBCO76EA31IYz4sb0VqBaF4SNd5PZY\njywV0TqBwABeKonSGOu4g+olbIijoaGTrmaSZnFhtzhw2lxomtYpWj2EEEdGulEJ0QUYhkEwGMbv\nCxEIRKmrCeD1tM0FrRE32bMrgK6PITvnizY5ZldltdYwNn0AKxpqkl2KEG0iRpQGo4YGowYlquAM\nd2sa72Fx4LQ50XVrlw4e7777LrfffnuLbYMHD5bVwkWnIi0bQnRSLbpH+cLUVgcIhxI3a1RuTwf9\nB7lxufYk7BydnWlCtXsM88srkl3KIUnLhmgrabjopmVjtzhwWJ3YrfYuHTyE6KykZUOITsI0TaLR\nGF5vkFAwgrshRH1dkHisfe4n1FQFSXN2x2atR7fK6nTHQlHArsnUt6JrCOAjEPNBDGxhB5laDnY1\nDYeehsPmQJV+mUJ0ChI2hEhhpmkSCoXxeYMEAlHqawN4GiMkq72yZLcXm20EPXtvQFXlzvexsGo+\nuus2aqMy4F50HWGCVMXKANAjVrqFckizOHFoaaTZnRI8hEhhEjaESDGmaRIOR/B6g/i9Yaqr/AT8\nHeNuuGnC7iIfmp5Pbo+NyS4nJVmtteRnDOLDuo49K5UQiRIlQm28AuJgiWh0C2fjVNOxaw6cdpfM\nbCVEipGwIUQKaOoiFcXrCeD3RaipbrsB3m0tGjHYWxrDah1Bt8wdyS4n5ahqkF52uYsrBECcGPXx\naurj1ahRlfRwFi5LBg4tDZc9XYKHEClAwoYQHZRpmsRiMbyeIH5/mNqaAB53OGldpI6GuyHctOCf\nrTt2h6yIfTRk3IYQB2dg0GjU0WjUoUZVuoVzcFkySLM6SbNJVyshOioJG0J0MIZh4PX48fnC1NcF\nqa8NpkTA+LryUj92x0B6H+fBYumYrTAdlVX30MvqoDISTHYpQnRIBkbzlLpaVCcrlEuaxYXT5pJZ\nrYToYCRsCNEBmKaJ3x/E5w3R6A5RU+Un1k6zSCVScZEX3TpGFvw7Sla9jnHdhvLfGgkbQhxOjCg1\n8b0QB3vEQaaWS5olDac9HV3TJXgIkWQSNoRIkuaB3p4APm+Yygp/QtfBSIZ43KRkdxBdzyM7Z0uy\ny0kZqiVMd5tcIAlxtEIEqYyVQAxckW5007JJ05247OnSzUqIJJGwIUQ7MwyDxkYfPm+Y6kp/hx3o\n3VYC/hhVFQ5stv44XSXJLidl2LRosksQIqX5zEZ80UYsUQuZ4VxclnSctnTpZiVEO5OwIUQ72N+K\n4WkM4G4IUlXhJx5P/W5SR6q6MkiaMxerrQ5d9ye7nJRg0xvpZ3NSGpaflxCtESdOXbySungl9oiD\nLC0Xh+Yi3Z6OpsllkBCJJr9lQiSQYRj4vAG83hDVlX4a3V13obY9u7xYbSPp2UsW/DsSul5HfrcR\nlFZL2BCirYQIUhErQYkpZESyybBk4rSmk2ZPk9YOIRJEwoYQCRCNRml0+/E0hqjY6yMakYtr04Ti\nQh+6PpbuuZ8nu5wOT1WjZFmTXYUQnZOJ2TyNrh610T3cE6eeTrojQ8Z2CNHGJGwI0Ub2zyjl9QSp\nqwlQl6JT1iZSJGJQXhpH14fRLXNnssvp8GxaBBWQqCpE4kQJUxErQY1ZyI7kkq51w2XPwKpL2hei\nLUjYEKKVYrEYnsamrlIVe72EAp1rRqm25q4PU+NyYbfnYLPXJbucDs2mNzDI4aIo6Et2KUJ0egZx\nauOV1MYryYhk0U3PwWVNx2FzSBcrIVpBwoYQx8A0TUKhMB5PkIb6ANUVAQxDmjGOVHmJH4djEL2P\n86KqnXs2rtbQ9AbyMnpJ2BCinXnMBjyRBmwRBzmhnjitLpk+V4hjJGFDiKNgmiYejx+vp2lGqc4+\nbW0i7S70outj6C4L/h2SqsboZpUQK0SyhAmyN1aMJaaRE+6JS0sn3dFNZrES4ijIb4sQR8AwDBrd\nPtzuIHtLvUSj0ou+teJxk5LiELqeR5Ys+HdINksYDYgluxAhurA4Marj5dTEFbpFc8jQski3ZWCz\n2qSLlRCHIWFDiG8Ri8VodPtoqA9SUe7rUmtjtAe/L0pVZRo2e1/SnGXJLqdDslrrGerMZLu/Mdml\nCNHlmZi4jVrckVrSIi6y9Fycejouh0tChxCHIGFDiIOIRqO4G3zU1QaoqvDLrFIJVFURIC2tJ336\n1aNpgWSX0+HoupvRGX0kbAjRwQTwEYj60KI6OZGepOvdZOpcIQ5CwoYQBwj5fTR6I9RWB6iplgvf\n9lK8y4vVNooesuDfNyhKHJcmPxMhOqoYUapiZdTGKuge7S2hQ4ivkbAhujzTNIkGA0TLS1E3rSOt\nd19c2QOoSXZhXYhpwu5dfjRZ8O+gbFoYKyoRWXFDiA4rTlxChxAHoZimdBARXZNpmkQDfqLlZagb\n1mD5aiv7e9zG+g8mOPk0vqrRCYVk3Yz2kpVjY+DgIBndCpNdSocSjWSyfG93NvvcyS6FGbl9CFjK\nMSX4CPGtLGjkWnqTbu2GyyHT5oquS8KG6HJM0yTq9xHdW4a6bjWWwu0cbFifqeuETptBrasPJZUy\nF1B76TvARd/+u7HZGpJdSodhmirl9aNZWFGR7FIkbAhxlA4MHelpGTKQXHQ50o1KdBmmaRL1+Yju\nLUX9bBX6rq8OGjL2U6JRHO+9Qa8hI+h2YgE7qlQiEbnASrSyPT7sjiH07vM5qiohD0BRDJy6/NsT\nIhXFiVEZL6UmWEFuREKH6HqkZUN0CRG/j2hZCeqnK7AUF35ryDgY02ojNP1cqm09KauKJqRG8T+a\npjBspJPuuRtkwb99/P7BPLfHR8hIbuiQlg0hWqe5pcPWNKZDQofo7ORjvJ0VFxczZsyYNj/uwIED\nqa+vP6J977nnHv76178CcPfdd/Phhx8CsGLFCkaPHs0JJ5xAKBTiN7/5DXl5edx2221tXm97iUWj\n+HcXEn/7VfQFc9GOIWgAKJEwjncW0Wf7CvL6KWia/OokUixmUlocxtM4OtmldBhWay15rsxklyGE\naKX9LR27AtvZ21iKJ9CI3PcVnZl0o+okjubOyIH73nvvvc3fz5s3jzvuuIPLL78cgDlz5tDQ0JCS\nd10MwyBUUY755Wb0NctR2uhusP7lF2TsLmLMmd+nQs2mska6+SSKzxulqiINq7U3ac7kj1VINk3z\nMsQ1kHWeZFcihGgLcWJUxkqpjVXSPdKbdGuGtHSITkluzyZBPB7n2muvJS8vj+9+97uEQiGKioo4\n++yzOfHEEykoKGDHjh0ALF68mJNOOokTTjiBM888k+rqagDq6uo466yzyMvLY/bs2Ye9K/KnP/2J\nESNGMG3aNHbs2NH8Znb11VezaNEinnnmGRYuXMhdd93FFVdcwfnnn4/P5+OEE07g5ZdfTuwPpA2Z\npkmotprgZ5+gzZuDdfWyNgsa+ymhAI7FC+i/ay2j+6tYLG16eHGAyr0B6mr6EIs5kl1K0imKSZom\n4VaIziZGlMpYCbsDO6hq3EswHJCWDtGpSNhIgp07d3LjjTeyZcsWMjMzWbRoEddddx2PPfYY69at\n46GHHuJnP/sZANOmTWPNmjVs2LCBSy65hL/85S9AU4tEQUEBW7Zs4cILL6SkpOSQ51u/fj0LFixg\n06ZNvPPOO3z22WfNjymKgqIoXHPNNZx33nk8/PDDvPDCC7zxxhs4HA42btzIxRdfnNgfSBswTZOw\n10Ng6yaUF+diffd1lFAwYedTAP2L9WQsnsfYHD+52dJImCjFu7zU1owmyUMVOgSrFiDdIv/WhOiM\nYkQpjxVT7Cuk1ltDLCbjA0XnIJ9aSTBo0CDGjh0LwIQJEyguLmb16tVcdNFFzftEIhEASktLufji\ni6msrCQSiTB48GCgaXzFa6+9BsCMGTPIyso65PlWrFjBD37wA+x2O3a7nfPOO++Q+6bi3ZRoOEyk\ntBj1k4+x7t7ZrudW/T4cr89n4ITJdB86lh3lhlwUtzHDgD1FfnQtn5zcTckuJ6mseg1j0vux2l2b\n7FKEEAkSML2URLx447lk6d3plpYpa3SIlCZhIwlsNlvz9xaLhaqqKjIzM9m4ceM39r3pppv49a9/\nzbnnnsvHH3/MPffc0/zYkQYDRVFa7JuKgeJgDMMgVFYCm9ejb/wUJUmvSwGs6z8hc+eXjJ3+ffaE\nXTQ0SHeXthQKxdlbbmK1DSE9oyjZ5SSNRfMzwKmzOvlr+wkhEqwhXkNjvJ4e0T50s2fhtLtkPIdI\nSRKVO4CMjAwGDx7MK6+8AjSFgc2bNwPg8Xjo06cPAM8++2zzcwoKCpg/fz4AS5YsoaHh0AugFRQU\n8PrrrxMKhfB6vbz11lsJeiXtwzRNglWVBFcvQ5s3B33DmqQFjQOpHjdprz7PkLptjOgnOb6t1deG\nqKnuRiTcdWdkUhSwy7gNIboMgziV8VJ2+7+ixlNFOBJKdklCHDUJG0nw9TsTiqLwwgsv8MwzzzBu\n3Djy8vJ48803gaZpai+66CJOPPFEcnNzm5979913s3z5cvLy8njttdcYMGDAIc83fvx4LrnkEvLz\n85kxYwaTJk06oto62h0U0zQJuxsIbFqPOm8O1qVLUKKRZJfVggLY1nxM9vsLye8dISNDRo+3pdJi\nH7U1QzGMrhvmbJqfLM2a7DKEEO0oQojSaBF7vLuo89YSi8lNB5E6ZFE/kRKiwQCRkmIsK97Hsrcs\n2eUcEVNRiEw5g8Y+w9hZJh8MbUXTVIaNTOuyC/7F4w42Vw9kWV1NUs4vi/oJkVwKCjmWXmRas8lI\n69bhbgwK8XVd9/agSAnxeJxQ6R7U9Z+gb/38mBbkSxbFNLGt/ICcHttIO+W7FLpt+P3xZJeV8mIx\ng7I9YazWkWRmfZnsctqdqgbpY5e3biG6KhOT2ngFDcEaekb70s2eicOWJqFDdFjyidWJ1NXVMX36\n9G9s//DDD8nOzk5CRcfONE3CDfXEd2xF/2gJSgo3GVuq9+Jc9BzHF5yJ+7jBFJXLdIat5fVEqa5M\nw2brhSOtMtnltKumcRvyb0iIri5OjL2xYhr8TnIjvcl0ZKPrerLLEuIbpBuV6HBi0SjhPbuxfPRf\nLBWlyS6nTcWO609wypnsrNMJBqWVo7UGD0un93Fb0bSuNWgyGOrLqyUK1ZHErSVzKNKNSoiOKcuS\nS461h3StEh2OhA3RYexf/dvcuhlt5QdtvvJ3R2FqGqHTzqY+ox/FFXKHujVUVWHYyHR69FzXpcZv\nxON2vqwZwvu1Ve1+bgkbQnRcGjq99f5kpeVIK4foMKQblegQouEQ4eLd6B8sRk3SwNf2osRiON5f\nTM+Bw0gRd8XRAAAgAElEQVT/zil8VWMhHJILt2NhGCZ7dvnR9bHkdN+c7HLajaqG6GHrQulKCHFE\nYkQpjRbh93nJsfYgPS1DWjlE0knYEEllmibBygrYvA7rpytSagB4a2nFO0kv38PoM86lJrMXpZXS\nynEsQsE4FeU6NusgXBm7k11Ou5BxG0KIb1Mfr8YTdNM71o8sZw66Jq0cInnk1phImmgoSGD7Fiwv\n/hu9iwWN/ZRoBMd/X6X3lmXk9QPdKr+Sx6KuJkRNTTaRSEayS2k3Vr2RPra0ZJchhOigYkQojRZR\n7t2DJ9CI9JoXySJjNkS7a1oBvAI2rkX7bFWXDBkHY9odBM84lyo9l73Vctf6aCkKDB2RQa8+n6Oq\nqTt72ZEyDCs7a4bxTk37jtuQMRtCpB4dG730fmQ5s6WVQ7Q7uY0q2lU0HCKwYxuWl+aiS9BoQQkF\nSXt7IX13fsLo/iqaJr+eR8M0objIR13NWDrp3AItqGqEbJv8BgkhDi9KmNJoobRyiKSQqxnRLvbP\nNBVZsRT95WdRPe5kl9Rh6Vs3kvHmC4zJbKRHjtyBOhrRqEFZaQRP4/HJLqVdyLgNIcTRqItXsSew\nk1pPNbEUXr9KpBYJGyLhDMMgUFwEr87Huvojac04AmrAj+PNlxhQuo5R/dQuNa1ra3ncEWqqHAQD\nPZJdSsLZ9AYG2F3JLkMIkUIihCnZ18rhDXiklUMknFzCiISKeL0EN65Ff/HfWCrLk11OSlEA6+dr\n6fb2i4zNDZCTJa0cR2pvmZ+6mv7EYvZkl5JQml5PfjcJG0KIo1cbr6RYWjlEO5Cpb0VCmKZJsKIc\n5ZPlWLduTHY5KU31eUh7bR6DJ04ld3AeX5XHu8SYhNbavcuLbh1Nbs/1nbZlSFVjZFr/9+eGyipe\nvOM+fPUNKIrCST86n2mXX9ziOVuWLue/j89BURVUReXcX93IsO+ciK++gbk3307I6+Psm64j7/QC\nAP79i9v40R9+S0b3nPZ8aUKIdhAhREm0kLAvRI4jF4fMcCcSQGajEm0uFokQ2l2I/varqL7GZJfT\nqRiZ2QTPOJfigBN3o9yJOhxHmoUhwzVyun+R7FISxusbzr+L6zEAT20d3to6jjt+OOFAgL9dMotZ\n/3iQnoMHNu8fDgSxpTkAqPiqkLk3384d77zCinkv48zsxpgzTmHOz37Fz/79OFuXraD8y68464Zr\nmp8vs1EJ0TllqNn0sPUhQxYCFG2sk97vE8kSbqgnsmY51peflaCRAKq7nrRXn2do43aG95OGycMJ\nBuJU7VXx+QYku5SEsVnrGepIByCjew7HHT+8aXtaGj0GDaSxuqbl/vuCBjQFD2dWJgAWXSMSDBEN\nR1BVFSMeZ8ULL3PaT65onxcihEgqj1FPSXAndd5aDGk+F21IwoZoE6ZpEigvxVjyGvqyd1GkwSxh\nFNPEtvojsj98lfw+UVzplmSX1KHVVAepre5OJJLepseNx+OcMP6XnPf9+77x2BtvrGFc/k2cMP6X\nnDjhZpYu3dRUS00j06b+lrFjbuSNN9Y073/hBX+ksrLhmOrQtAZGH2TcRn15BXu3f8WAsaO/8dgX\nH37Mg+ddypyf3cqFt98CwAkzvsuWj5bzz+tuZvq1V7PqpUWceN7Z6DbbMdUlhEg9EcKURAqp8lQQ\niUaSXY7oJKQblWi1eDxOcFch+tsLUT3SmtGeTFUlPHU6jb2GUlgm06AeiqLAsOMz6Nl7A6raNnfs\nHnnkdTasL8TrDfLGm3e1eMzvD+F0Ng1O/+KLYn5w4QPsLPwnjz76Jt27Z3DhhZM5Z8a9LP3oARYv\nXsvGjUX84Q8zj7mWusbRPFf6v8X9woEAT8z6OdOvvZoxZ5xyyOftWv85L9/zZ25fvKDF9kCjh+d/\ncxdX//3/8cZf/k7Q4+XUqy5jQH6edKMSoovIsfSku70nTrtLulWJVpGWDdEqEb+P0MbPsL48V4JG\nEiiGgX35e+Qsf4P842KkpUkrx8GYJuwu9FFXm98mxysrq2XJO+u45qdnHXTayP1BA8DnC9G9ewYA\nVquO3x8mFIpisajE43Ee/ceb/Pa3P2xVPTYtjLbv7TwejfHsLXcw4dzvfmvQABg8YRxGLI7f3fJ3\n9/2n5zL92qvZ+M57DJ4wjpl/+gPvPvmvVtUohEgtdfEqSgO7cPsaZHpc0SoSNsQxMU2TYE0VsWXv\nY31nEUo8nuySujStshznq88x0ihl0HEyRe7BRKMG5SUxGt0jWn2sW2/5F395aBaqeui7fa+//gmj\nRt7AjLPv4R+PXgvAZZedwptvrOG7Z93FHb+/mMcff5sfX3k6drv1kMc5Ela9juOdGZimyYK7/0Sv\nwQMp+PGlB923trSs+cKhbNsOAJyZ3Zofr9lTiqemliEnjicaDqPsWxknGgq3qkYhROoJmD72hHdS\n46mS6XHFMZMRpuKomaZJoHQPlnffRKsoTXY5Yh8lHse+9G169BtE+uTT+apWJxSSEHigRneYmion\nNlt37I7aYzrGW2+tJbdHN8aPH8KyZYee5eqCCyZzwQWTWbFiK1f++BG273iKjIw0Fr91NwANDT7+\n358X8uprv2f27MdodPu59VcXcNJJR7/6ua43cnxGX95c8TEb3nqX3sOH8teLrgRgxi9uwF1RCcDk\niy9k8/vLWL94CapmwZaWxhUPtRxzsuSxp5nxy+sBGH/2mcz95W0s/ffzfO/G2UddlxAi9cWJURot\nIuINk5PWA4fNcfgnCXEAGbMhjkosFiNUuAPrmwtQQsFklyMOwdR1QqfNoC79OPZUyFiOrxsyPIPe\nx23GYjn6AZB33PEcLzz/EZqmEgpF8XgC/PCHJ/Of52495HOGDpnNp2v/Sk5ORvO2W2/9FxdccBI7\ndpRjt+v88Icn88Mf/Jkl/733mF5Tg2c0z5ZUHX7HVpIxG0J0XRlqNj1tfUiX6XHFUZBuVOKIRYNB\nwpvWY33lOQkaHZwSjeJ47w16fv4hY/qZWK3yq36g4iIvtTVjjmlxxAceuJKS0rns2v0ML770G04/\nfew3gkZRUUVzV6UNGwoBWgSNnTv3UrG3noKCPILBcPOHdjB47F2VrJYQ9s66eqEQokPwGPXsCRZS\nL9PjiqMg3ajEEQk3uolt+BR9xQfIvYzUoRftQCstJu+Mc6nO6klZlbRyAMTjJiW7g+h6Htk5W1p1\nrP1B4emnlwBw3XVns2jRap5/bim6ruFy2Xnxpd+0eM5ddz7Pnx5o6uY0c+YpXHjBn3jw/73Cffcf\n+5oWVmstI5092Og9til0hRDiSEQIsSdSSMwTJcfVA02TS0nx7aQblfhWpmkSqqmClUvRtmxMdjmi\nFaLHjyGQP5ntFQqxmNyRAujRy0H/gQ04XSXJLqXVTFNhb30eL1dUJPQ80o1KCLFfb20Auc6e6LpM\nTCIOTdrcxSHtX6hPWbxQgkYnoG//gow3XmBMNze9cuVOFEB1ZZCa6lyi0W8uipdqFMXEqcuEAEKI\n9lMR20Olr5xwJJTsUkQHJmFDHJRhGPh3F6K98jyW8tS/6yuaKKEAjsUL6L9rLaP7qVgkc1Cy20tt\n9fEYRuq/HepaEKcqf6lCiPZTHS+nwl9GMBxIdimig0r9T1fR5uLxOIEd27C+/B9UjzvZ5Yg2pgD6\nF+vJeGseY7P95GZ37YtT04TiIh/1dWOTXUqrWfVaxqR3O/yOQgjRhuriVez1l+ALepNdiuiAJGyI\nFmKRCMGtm7AuegElIot4dWaq34fj9fkM3LuRkf1UuvJERpGIQXlpnEb3sGSX0iqa5mWgy5bsMoQQ\nXZDbqKM8UIIn0CgrjosWuvDlhfi6SDDQNLXtGy+hGNL3uytQAOuGNWQuWcDY3BDZme3byhGPx5l9\n/QXccdf133js802fcu75E5h9/QXMvv4Cnp/3BABudz033TyTn8z+PitXf9C8/513/4z6+ppjrsVd\nH6am2kU4lHPMx0g2RQGHRVb5FUIkh890UxYsptHvlsAhmknYEAD4giF2VjZSmdkL/0mnYchUdl2K\n6nGT9trzDK7byoh+lnY776LXnmPAgCGHnE45f+xE5jz1OnOeep0fX/4zAD786C3OP+8ynvy/hSx6\n9T8ArP5kKcOGjiI7O7dV9ZSX+KmpHoRhWFt1nGSyan66aalbf1d37y8e4KxR3+eSgiubt23ZsI0r\nz5rNZafN4sozf8rWjV8e8vnxeJzLTpvFLZf/tnnbo/c9wcxTr+Lun/+xeds7C9/lxadfTsyLEF1a\n0PRRGiqiwVcvgUMAEjYE4A2EWFtUw6Ivapn3pY/XbUPY/MOfUXbp9QTzJ8kEl12EAtg+XU72+6+Q\n3ztCRkZiQ0dNTSWfrv2Yc86+iEN9HB1su67phEJBIpEwqmohHo+z6LXnmHnJ7Dapq7jIS231sS34\n1xFYrTWMlXEbKeu8mefw6Et/bbHt0Xuf4Ibbf8r8j+Zy3W3X8Oi9Txzy+S/+cyGDRwxsauYCfB4f\nO77YyYvL/oNu1Sn8chehYJi3XnqHi3/6w0S+FNGFRQhTEi6kzlsrgUNI2Ojq3L4Aq3ZWs3LX/waC\nl7rDLNnhZt6OAG/ljmfbpb9g78WzCQ8bJcGjC1Dra3G++hzDfYUM65e4Fq7Hn3yA66/9LYpyqLch\nha1bN3LNdedx+x2zKd7TtBL3Gad/n1WrP+Q3t/+EKy67ntffnMdZZ16A1do2YxXicZOS4hCNDXlt\ncrz2ZrEE6JcmLZOpavzkfDIy01ts694zB5/HB4DX46NH74O34FXtrWb1B59wwRXfb5r5AFBUlVg0\n1rRmUjCEpmu88MSLXDL7IiyW9mvFFF1PnBilkSJqPdWy2ngXJ59IXViDN8DKndVsLDv47BGGCYW1\nQQprg2iqwvFDChg6YTrZES85n36IJlPidlqKaWJb+QE5PbaSdsr3KHTb8PvbbhzPJ2s+IjMzh2FD\nR/H5pk8Pus/wYaNYMH8ZdruDT9d+zF13/5znn30Xp9PFn//4NABebyPzX/wn993zfzz8yJ34fB4u\n/tFPGDVqXKvq8/uiVFWkYbX1xekqa9Wx2puigF2TcRudyU133cBPz/0Zf7/ncUzD5N9Lnjrofo/c\n+Si/uPvn+L3+5m1OVxpTpk/m8tN/wndOORGXK42tG7bx019d3U7Vi67MIE5ptIi4N053p6w23lVJ\ny0YX5fZ9e9D4uphhsqUywOvb3cwrMfho/Ll8NfMmas+7nHhO6/rJi47LUl2Bc9F/OD5azJC+bbdC\n7JatG1m9Zikzf3w69z/wKzZ+voYHHvxti33S0lzY7Q4AvjPpFGLxKJ6vTcX83LwnuOLyG/jwo7cY\nO+ZEbv/tgzz7/GNtUmNVZYC6mp5Eo842OV57smo+uusyK1Vncf/Nf+bXD/yStz9/lVvvv4n7fvnn\nb+yz4r1VZHfP4vixwzG/1gHxyhsvY/5Hc/nlPT/nqQef4frbZ/P684v53U//wDOP/Ke9XobookxM\nyqO7qfVVEY/L5DNdkYSNLqjRH2R1Yc0RB42vC8dM1pX5WPRlI/MrdVZNu4SimTfS8L0fYbgy2rha\nkWyKYWBf9l+6r3qLsX3jOByt73ox+5pbeXn+x7z4/FLuuuMRxo87iTtu+0uLfeob/tfX98vtmzFN\nyMjIbH68rKyYurpq8sdOJBwOoezrox4Ot92UzcW7vNTVjEy5Bf+s1lryM2TcRmexdcOXnHbOKQCc\ncd5pbN3wzQHim9duYfm7qzhvwkX8/tp7+WzlBv7w8/tb7LN981cADBjSjw8Xf8Sf/3UfZcXllO5K\nrdY7kZr2xvZQ65MuVV2RtGd1MR5/kDWFNawr8bTJ8fwRg1XFTcfKdGQw/rtX0dNqkFOxC9fqj1Aj\noTY5j0g+rbwE16vPMerUs6nr04/ivdE2O/b+2ajefOslAM4791I+Xv4ub771IhbVgt3u4A93PNLi\nOc88+3d++pNbATjjtHO58+6fMX/BHH5y1S/brC7ThN27fGjaWLr3+LzNjptoqhqkl13643cWfQf1\nZf2qjUyYMp7PVqxnwJB+39jn53dex8/vvA6A9as28sITL3Lf43e12OfpB//F7x+5jWg0SnzfBZ+q\nqoRDsqaSSLymFo5iVK9K94wezTeIROenmDJNQJfhDYRYU1TNJ7sbE36uni6d/N5p9NDiZO/aimPd\nSlRpPu00YgOGEDjpNL6qsRAOdf67VFk5NgYODpLRrTDZpRwxj/d4ntlT2+bHnZHbh4ClHFOmi0iI\nO669mw2rP8dd30hObjbX3XYNQ0cN4cHb/ko0HMXmsHHbg7/i+LHDqams5Y+3PMg/XnyoxTHWr9rI\nC0++xN9eeLB527IlK9i5tZDZv54FwD/ueZxPPlrLsNFDuf+JlqFEiERSsdDPOoSc9O4SOLoICRtd\nhC/YNL3tgbNOtQcF6JdpI6+ngxwi5Gxbh+2LddJ/rxMwdSuhM86hNq0XJZWdf0By3wEu+vbfjc3W\nkOxSjkgo1IfXSixURoJtelwJG0KI1rKg0d86hKz0HAkcXYCEjS7AHwqzrqiGj4uSe5GkKjCku4OR\nOTay40FyNq5AL9x+yAXdRGqIDhtF8IQpbK9SiUY69wXo0OMz6N1nE6radl3IEsWI29hRM5T/1la1\n6XElbAgh2oKGTn/bUDJdWRI4OjkJG51cOBJl/e4aPthRl+xSWtBVhZE90xjSTSc74iF7zYdoe0uT\nXZY4RqbNTvCMc6my5rK3uvO2cmiawrCRTrrnbkBNgea5GnceL5RVtukxJWwIIdqKFTv97IPp5syU\nwNGJSdjoxOLxOFtKannji+pkl/Kt7JrKmN5OBrhUsnx1ZK16H0t9TbLLEscgOiof/9jvsGOvQizW\nOS9GXS6dwcMhK3trsks5LI9vBM8Ut+2NBgkbQoi25FCc9LUPIsMpM+h1VhI2OinTNPmqvJZXNlYS\nT6G/YZfVwrg+Tvo4ILtuL91Wv4/qO7YpekVyGA4noTO/TznZVNd2/O5Gx6JnnzT6D6gmzbk32aV8\nq3C4F4tLbJSG/Yff+QhJ2BBCtDWnksFxjoGkp6UnuxSRABI2OiHTNCmurOfljRWEY6n715vl0Bjf\nx9k0le7eIpyffIQakSkaU4EJxMZNwnf8eLaXGXTGadUHDU2nT98v0bRAsks5JMPQKaodwVvVbdeV\nSsKGECIRMtQs+jj643S4kl2KaGMSNjoZ0zQpr3XzyoYKPOHOM9Vsr3Sd/F5Oci1Rsou24Fi/CrUz\nXsF2MoYrg+D071MazaCuoXON5VBVGDYygx4913Xo8Ru17jyeb8NxGxI2hBCJkqV2p7ezHw5bWrJL\nEW1IwkYnU1nv4c3NFVR6IskuJSEUoH+WjbweDnIIk7P1M6xbNshUuh2YCUQnTsE7eAxflcc7VSuH\n3W5hyAgr3XM3JbuUQ/L6hvPv4vo2iwYSNoQQiZRj6UVvV19sui3ZpYg2ImGjE6n3+HlvayVf1XTc\nbh1tSVVgWPc0js+xkhULkLNhOdZdXyW7LHEIRmY2wdPPoTjowt3YeVo5srvbGTDYT0ZGUbJLOahI\nOJf/ljkpCvra5HgSNoQQidZbG0DP9N5YLJZklyLaQKe5IexyHVsfv+LiYsaMGXPQx0499VTWr1/f\nmrLaTTAcYcOeui4TNAAME3bUBHhju5t5u6O8P2I62y+9ieoLryLWu2+yyxNfo7rrSXvtBYa6tzOi\nn5bsctpMfW2I2upuRMKZyS7loDS9gbwMGXQphEgdlbES6n21yP3wzqHTfOInYn5mRVFSYt5nwzDY\nsbeB1bsbk11K0kTjJpsrfGyuALuuMvbE8+nvUsn21pK56j0sDR1rnZGuSjFNbJ98hLZzG/mnns0u\njwOvL/VbOUqLfdjsQ+nd53NUtWO9HlWN0c0qH9hCiNRhYrI3ugfNbyXLlZXsckQrpUzLxkMPPcRj\njz0GwC233MIZZ5wBwNKlS7n88ssBuPXWW8nLy2P69OnU1tYe8ljr168nPz+fcePG8cQTTzRvDwaD\nXHrppYwaNYof/OAHBIPB5sdcLhd33nkn48aNY/LkyVRXd4y1K0zTZHdVA+9slXUp9gtFDdaWennl\ny0ZerLHzyakz2TXzRtxnXoCR1vlnuRj2t39ywhPPMvHJ5zj5ny984/HtNXVMmzOP9Pv/xt9Wfda8\nvcYf4NRnXmT848/y5vbC5u0/fPF1Kr1tN3UqgKW2CuerzzE8VMjQvp3jnkdxoY/amrEdckyKzRJG\nOiMIIVJJjChV4VL8QZn+PtWlTNgoKChgxYoVAKxbtw6/308sFmPlypWccsop+P1+Jk6cyJYtWzjl\nlFO49957D3msWbNm8fjjj/P555+32P7kk0/icrnYtm0b9957b4suVIFAgMmTJ/P5559TUFDAnDlz\nEvNCj1JlvYe3t1QRM+TO5cF4w3FW7Paw4EsPL/uz+WzGLPbM/Dnead/F0K3JLi8hFOCDqy/hsxuu\nZPW1V3zj8Zw0B3+fcQa3nDyxxfYFX2znuonjWH3t5Tz2SdO//bd2FDG+dw96pTvbvk7DwL78fXKW\nv0l+3xhpaal9ORyLGZTtCeNpHJXsUr7Baq1nmCyYJYRIMX7TS3WoinBUpr1PZSkTNk444QTWr1+P\n1+vFbrczefJk1q1bx4oVK5g2bRqqqnLJJZcAcMUVV7By5cqDHsftdtPY2MjUqVMB+PGPf9z82IoV\nK7jiiqaLszFjxjB27Njmx6xWK+eccw4AEyZMoLi4OBEv86i4vQE+/qoWd7DzTHGbSHWBGEsLG5n/\npZdF9OPzC66n9NIbCJw4BaMjz116DL4teuY605hwXC/0r71mq0UlEIkSisWxqApxw+D/1qzn11Mm\nJbRWrbIc56LnGGmUMOg4PaHnSjSvJ0p1pZVgoFeyS2lB192MTpepJIUQqUNFxUU3LHENd10D8bhc\n66SqlOm/oOs6gwYN4tlnn+Xkk09m7NixLF26lKKiIkaOHNliX9M0j3isxdcHHx1qMJKu/+8iSFVV\nYrHk9ssOR6JsKq3vUgPC21KFN0KFN4ICDMgezeiLJjRNpfvFWqzbNqZOCj8IRVH43n8WYlEVZk/I\n55oTxx7+ScClY0Zy5aK3+df6Tfz5rFN4cu3nXJ4/Grue+LcJJR7HvvQdevQbSPrkM/iqTieUoiG6\nojyAI+04eh/nRtNCyS4HAEWJ49I7YP8uIYTYR0XFgYs0XKhRC3GPSd2mOsp27kK1qIy6RKXHwNyU\nGEsrWkqZsAEwbdo0Hn74YebOnUteXh633HILEyc2dQUxDIOFCxdyySWXMH/+fKZNm3bQY2RmZpKZ\nmcmqVauYMmUK8+bNa36soKCA+fPnc9ppp7FlyxY2b97cLq/raJmmSWFFAx8XNiS7lJRnAsX1IYrr\nQ1gUGN73OwwfO43sWICcdcvQiwsPe4yOZtk1M+md7qLGH+Ds5xYyIjebqQMOPztXht3G65f/AICG\nYIi/rPiUhZeez/VvvIs7FOaWk0/kO/36JLR2rbQYV8VzjDr9bOp692VPRTSh50uU4iIfujWvQy34\nZ9PCWFGJyJS1QogOQEElDSdppDeFC69Jw6YGyr/azdffpgzDoOjdImw/sJLZo2PO/CcOLeXCxgMP\nPMDkyZNxOBw4HI7mUOF0Olm7di1//OMf6dmzJwsWLDjkcebOnctPfvITFEXhrLPOak7JN9xwA7Nm\nzWLUqFGMHDmSE088sfk5BybpZM5SZZomZTVu3pYB4W0ubsKX1QG+rA6gWxRGjzqLwSedTVbIQ/Yn\n76FVVSS7xCPSO71pEHyuM43zjx/GZ2UVRxQ2DvTAx5/wu4KTeGnzdqYO7MsPRg7n4gVv8NaPf5SI\nkltQYlEc771Jr8HDyZhYwI4qC5FIal0gG4bJnl1+dG0sObkd46aFVa/leFd3NvvcyS5FCNEF7Q8X\nDtKxRC3EfSYNXzRQvmM3HEFnkWBNkLK15dhOs+FwOhJfsGgzsqhfinF7A7y1uZxddR2je0ZX4NBV\n8ns76edUyfbWkLniXdTGjtmqFIhEiZsm6TYr/kiEGc+9wp2nnsyZQwd+Y9/7PlpFutXKLVNaDhTf\nWdfAPUtXMu+i7/N/azaQ5bBz4chhfP+FRXz4k0vb6ZU0Ma02QmecS7W9J2VVqdfKkZNrZ8AgL+kZ\nu5NdCqapUl6fx8KKva06jizqJ4Q4EgrKvm5R6VhiFgyfScMWN/VfNmDEjv39Y+g5Q+g3rh9qR2k2\nFoclYSOFRGMxPius4oOv6pNdSpeVYbMwro+TPnbIqiklY/X7qIGOM25md4Obi156A4CYYTBzzChu\nK/gOcz7bBMDsiflUev2c/M8X8ITDqIpCus3Kpp/PwmVrmp3rspcXc//0aQzJzqTGH+BHL75OYzjM\nPadP5YKRw5LyuqIjxhAYdxLbK1RirfiQSob+g1wc168Qq9WT7FJo8Izi2ZLWTdstYUMIcTAKCnbS\ncJKBJaZh+MG9zU3dlvpWhYuvU3WVvJmj6d6/u4zfSBGdOmzceOONrFq1qsW2m2++mauuuipJFR07\n0zQpqqjjpfUVyCy3HUP3NI1xfZz00A1ySr4i7dNlqLHUu/ueKky7g+CZ51Gh5lBZkzo/Z0WBoSMy\n6NUBFvzz+wfz3B4fof/P3p2H113W+f9/fpazn5PlnCTN0rRp0n3faAHZi0CluDHgwiaoozPyG8TR\n0Vm4ZvTrNo6OI46jzowy6iCgIw4gylALgmUt3WhL9zZNs+fs6+ecz/b746SB0gIlzck5Se7HdXld\nknNyzvskTfJ5nft93++zGAYiwoYgCHBquLCzkNibYGh3BKvEra817dXMu3o+/pqxP5ZdGHuTOmxM\nJkPxFL/c2kM4M3EusqaS5ioXyxo91Mk6wQM7cO94AbkSp7tNcDZgLFlJZtFq9vXamJU1rPsNqQ6Z\nufO9hOq3lXXDuK5X8XxfIy8lR786KsKGIExVEh68+AigGA7sHCT2JRnaHcbSxv/3Qcf6dmasnCHa\nqZ4kkogAACAASURBVCYAETYmgHxBZ/P+Pp45mih3KcJbkIBZITeL6t0E7Tyhnc/h2PfyhD5KtxJZ\nPj/a5e+mx6pmMDIxEkdVtZNZsw1qaveVrQbbluiLLeGB3tHv2xBhQxCmjhMrF6rpwM5C8mCS8M4o\nhlb+37uinWriEGGjwtm2zYGeCA9smxgnIQmvUmSYW+9lbq2ToJ4htOUPOLoOl7usScMG9JXnkp6z\njP09FhNhIam5xcf0mT14vGe3b+JsxJMLuecs9m2IsCEIk5cLD36qUU0VOyeROpRmaGcYI1v+cHE6\nNe3VzN8wH1+1aKeqZCJsVLiheIoHXuomWqE/6MKZcSoSixt9zKpSqM3FqX1mI+pQf7nLmhSsqhpy\n6zbQlQ8QjVf+z0n7nABNLXvKNvAvm23j58c0UqPsQRNhQxAmj2K4qEI1ndiaROpQqhguMpX/u/QE\n0U5V+UTYqGCGYfD8wQGeOChOn5pMvA6ZZU1+pvskgokBajY/jpwUsw/Ohg0U1lxIatYi9h+v7Mnj\nsiwxd4Gf+mlby7J/w9B9bB1o5dl4eFSfL8KGIExcTtz4qcZhOkCTSR/JMLhjCD09cfeDnminqp9Z\nX+5ShDcgwkaFsm2bYwMx7n2pB1P8TZ+0qtwKK5r9NLlsgoPHCDyzCVmrnKN0JxorWEf20ndxNOMl\nmazc0OHxKnTMdRCqG/+Bf7YNA/El3NczutZMETYEYeI4ES5Uy4GkyaQ7swxtH6KQLJS7tDFV01HD\n/KvniXaqCiXCRoVKZXI8vLOHw+FcuUsRxkmd38GKRi8NDpPgsf14X3wK2Zg4S9mVwpYkCudfRqJl\nLge7K/frV9fgYeasOP7AsXF/7nhqAfccGxrV54qwIQiVy4mruHJhOYsrF11ZhrYNUUhMrnBxOh3v\n6mDGCjHsrxKp5S5AOJVt2xwZTIqgMcWE0zobDxVPHGupbmfp+xdRJ+uE9m3DteMFcaLVGZJsG9cz\nmwg17MF78VUcSrrIpCrvwjg8mMPrq8PpiuJ0psb1uV1qhlrVScyY/BcggjCZOXDhl6pwmC6kvEy2\nO0fP1kHysXy5Sxt3x544RlVTgGBzsNylCK8jVjYqUG84wc+3dJPVK+8CSRhfsgTtQTcL6t0ELY3Q\njmdxHNgtgscZsmWZ/IVXkJg2i0MVuMohSTBnfhXTmrYhy+P3826aHl4ebOMPkbe/uiFWNgShfBw4\n8UvVI+Ei15NjcFsYLVKeAycqzfR3tNBxUQeqKt5LryTiu1FhCrrBrp64CBoCAJYNhyIahyIaqiwx\nb9YFzFl5GbV6mroXnkDt7ix3iRVNsizcTz2G2jID7zsu52DESS5XOXs5bBuOHkqjOpZR37B93J5X\nlnM0u8Wvf0GodA6c+KQqnKYbqSCT69Xo3xYmNyQ6H06n5/leattraWhrKHcpwmuIlY0Kc6Qvwr1b\nehHfFOHNuNTiUbptAYVgNkbNMxtRwwPlLqui2YpK/tKriNbM4GhvZZ28Ul3jYtZsneqa8Rv4l0gt\n4Mej2LchVjYEoXRUHPil6pFwofXnGdoaJjsoDg45U3WL65h31VzcHne5SxGGibBRQXJankd39vDK\nQKbcpQgTiM85fJSuF4LxAao3P46cEtPm34gxs4Ps2ks4EFbJa5Vzwdw83UfrzG7cntFt3H67ctp0\nHuyCwcLba78QYUMQxo6KA59UhcvyIBVk8v15hrZFyPSL64CzsfADC2ic0ygmi1cIETYqhG3bHOyJ\ncL+YFC6chWq3yopmH40ui+BAJ4FnNyFropf39WyHE23d1YS9jXT1V85ejo65VTS1vIyilH7jtmm6\n2TvUzsbw25smLsKGIIxeMVwEhsOFQn6wwNC2MJleES7Gkr/Zz6JrF+Kv8Ze7FAGxZ6NipLMazx2N\nlbsMYYJLaAZ/OFJc1aj3N7Limo9Tr5qEju7F89IfxVG6wyS9gOexX9M4ewHVqy9gf79MoVD+i+fO\nwykcziXUN5R+4J8sazS4lNI+iSBMcQoqPqkK93C4KIR1wtsipLrFG4ullO5NE+uK4av2idWNCiDC\nRgWwbZvjkTTHYuIdaGHsDKV1Hj9YDB6tNbNZ8v4l1MkFgq9sxfXyFnGiFeA4tBf1+FEWrdvAYG09\nPQPlDWOmadN1NIfDsYRgaFdJn0uSwK1W1t4VQZjoiuEigNvyIhVk9KjB0LYIqS4RLsZb5xPHCDQG\nqGmoKXcpU55oo6oAsWSG+7ccZygj/vALpSVL0B7ysKDORdDKEdr2DI5Dr4jgAegLl5FZupb9vRKG\nUd5VjvppHmbOiuHzd5X0eTStiYeOO+jNn/nmU9FGJQivUlDwSlV4LC+SrqBHDcLbIiSPJctdmgC0\nXd7GrLVtYtBfmYmwUWa2bbOzc4CHd43PplBBOEGVJRZM89JR7SBYSBF6YRNqT2kvbiud5fGhvfMa\negkyEC5v+J/ZHqCldT8OR7pkz2FZTg4OzeG3Q2d+kpkIG8JUJqPgw48HP1JBxohbhLdHSBwRh3JU\nItWtsvSmJdQ21pa7lClNhI0yiyYz3PtCF7Gc6KUXysetyixu9DLTrxDMRql95nGUUQx8mwxswFh2\nDukFq9jXbWKV6Zp6vAb+DcUX89/d/Wd8fxE2hKlERsGLH++JcJGwiOyIED8kwsVE0bG+nZmrZoq9\nG2Uk9myUkW3b9MUyImgIZacZFi91p3kJ8DmdLL/wA7R4IBjro3rzRuT01GkJkADHzi1UH97P0suv\n4bhRRSQ6/j+jtg1HD6dxOJZRV8KBf2LfhiC8SkbGSwAPfmRdxkzYRHZG6D50BJGvJ6buZ7sJzgpS\nFaoqdylTlljZKKNUJscvtx6nO54vdymCcFo1nuGjdJ02wb7D+J99EvltzmWYyGxAX/0OUh1LONBT\nnlWOmloXbR15qmsOlOTxC/kGfnPcyzHtzNq1xMqGMJnIyHiGVy5kXcFM2UR3RokeiIlwMYnMfe8c\npi+eLlY3ykSEjTKxbZsDPREeEHM1hAliWsDBskZv8SjdI3vwbPkjcrl6jMaZVV1Lbt01dGo+4vHx\nX+VomeGjdcZxXO7wmD+2Zakcjczn4YEza6USYUOYyCRkvPjwEkDWFayUTXRXjMj+KJjlrk4oFV+j\njyXXL8ZX7St3KVOSaKMqk3xe5+Ue0fM5GX3741fh8viQZAVFVfnTb/78pNv3vfAkT/z8e0iSjCRL\nXPGRz9C+dC2ZRJT7v3YnWjbFuhv+P+avvRSA+756Bxv+7C4CtXXleDkjBlI6j6cSSEBrzVyWXLeM\nIAXqXtmCc9fWSX2ilZyI4f31z5h97sWkZixg//HxDRw9XRnc7jaapyeR5bEd+CfLBjXOMX1IQagY\nEtLIyoWiO7DSFrE9MXr3dmIb4r3WqSLTnyHRl8Bb5RWrG2UgwkaZ9MbS7Bs48+MmhYnlI1/5Md5A\n9Wlva1+2diRIDHQe4P6v3ckdP3yUXU//jnPWX8+Cc9fx31/6FPPXXsr+F/9AU/uCsgeN17KBrnie\nrngeWYLZjauZv+gdBM0coW1P4zy8v9wlloRk27ie+wOOA6+w7NL1HEl6SaXHL3SUcuCfUykgI7pG\nhIlPQsKNDx8BFEPFykBsd4z+V7qwynyktVBe/dsHCM4I4va6y13KlCPCRhnohsH+/hTiPZVJ7E26\nE51u78j/L2g5vFXFgUOK6qCQz2HoBWRZxjJNnn/kXj5817+WvNzRsmw4MJTjwFAOhyyxYO5ldJxz\nBcF8iuALv0ft7S53iWNOjgzie/BnzL1gHcnpsznYPT6BwzRtjndqOByLCYZ2j+lju5xRZnsCHMil\nxvRxBaHUiuHCi48qFEPFzkL8lQRH9nRhFUS4EF4VOxQj3pegsUOEjfEm9myUQfdQnJ+8cBxT/B6c\nlP7lT9fj8gaQZZlVV/0Jq6/4k1Pus/f5J/j9z75DOhbmpn/4AdPnLkHLpvnVt75AOh7hilvuZODY\nQdy+AMsve3cZXsXZcasyS5p8zPTL1KYj1D6zESU6+Y7SNRpb0C68goMxF9ns+DR8NzR6mNEWxec/\nPmaPaVkKXdEF/Lr/rfdtiD0bQjmdEi5ykNibZGhXWIQL4S01LG9g/pXzcDgd5S5lShFhY5zZts3W\nw/389pWx3+gpVIZUdIhAsJ5MIspP//4TvOvjX2DmolWnve+xPVt56F//gb/4/iMnfTyXTvLLf/oc\nH/zrb/O7//wGWibF+e+9mdZ5y8bjJYwpv0theZOveJRupJeqZx5HzpRuUN14s2WF/MVXEqtr40jP\n+Bwj29YRoHn6PhyOzJg9ZiSxiJ8ef+vhfiJsCONLwoMHL1WohqMYLvYnieyKYmji2Hjh7ZEUiWU3\nLyU0PVTuUqYU0UY1zhKZHC8eExvDJ7NAsB4AX3WQ+edeRvfB3W8YNmYuWoVlmWST8ZF2KoCnHvgh\nF13/cV5++re0LVrFgvMv54Gv3clN//CDcXkNYymdN9ncWZzTUeupYcVVtzLNaRHqPYzvuSeQC2O7\n4Xm8SZaJ+8nfUj+9Df/56zgQcaDlSrvKcexICpdrAQ2NYzfwz6UWUJExRIgQysyFFz9VqGYxXKQO\npji2swdDzKQSzpJt2qQH0wRbgmKj+DgSYWOcmakBNrRDLO+mO6PQn9YZSBUQ+9Ymh0I+h21auLw+\nClqWw9uf45IPfvKk+0T7jlPbWDzvu/fwKwAnBY1I7zFS0SHaFq2m/8h+HM5if6lemPjzWGI5gycO\nF8N2Y6CFZe/5JPWKTvDwbjxbn5nQR+mq3Z34H/wpCy9dT6S5hWO9pbswOjHwT3Uspa5+x5g8ptMR\nZr4vxO5MfEweTxDOlAsPfqpfDReH0xzb0YORFeFCGHsDLw8ybd403D6xd2O8iLAxjkzTxBt+kZqu\n39PsrGK+O4gVaMFomIap+jBlN7rkoiC5SBQUutMKfWmD/lRehJEJIhOPcP/X7gTAMg2WXHw1s1ec\nz5bHfgnAOVddxyvPbWTnk48gKw6cHg/XffYbJz3Gpv/+Vy6/6S8AWHLReu776qfZ/KsfcdmHbx/f\nF1Ni/Smd/lQcCZhZu4BF160gRJ7Q7i0492ybkEfpSoaOZ+PDNLbPpeqci9g/qFDIl+aHt5C36D1u\n4nDOobr64Fk/nsORYF7VdBE2hJJz4R4JF2gyqSNpunb0oqfFNHuh9FLHUySHkiJsjCOxZ2Mc5aLd\nOLZ8HdnIven9bCRsZxWmK4Tla8bwNmKq3uEw4qaAi4Su0JMphpGBZB6xL06YDGQJ5tR5mR9yEjSy\nhLY+hePo2V9Il4PtdKGtu5pBTyPd/aW7iJo+w8/0mZ24XNGzfqxYchH/1fXm+zbEng3h7XK+JlxI\nmkz6aIahHWEKqYndQilMXG2Xt9F+7izRSjVORNgYJ7Ztk+vagnv3D8/+sUbCSBDL14zpacRwFFdG\nDMlNXnKRLCh0Z2X6Uyb9qTwFMRlVmGAcisTCaT7aqxSC+STB53+P2tdT7rLeNn3eYrIrzmdfv4RR\noncFZs+roqllJ7J8dqEmk+ngp8dSaG/SzibChvBWnLiK4cJyFsPFsSxD24coJES4ECqDu9bFshuX\n4a/xl7uUKUGEjXGi6zrWjh/jGHyx5M9lI2E7Apju14YR/0gYKUgnVkZk+tMmfak8BdEaK1Qwt0Nm\naaOPGX6ZYCpM7ebHkeORcpd1xmy3h9zl19Cv1NE3NParHIoqMXe+n7qzHPin69U809vA9lTsDe8j\nwobwek5c+KVqVNOJlJfJdOUY2j5EPjbx95kJk9eiDy6kcU5jucuYEkTYGCe5yHGcL34NySr/L99i\nGPEPt2k1YXqbMB1+jNeEkaQu05tV6E2bDCR1NLFpRKgQAZfC8mYfzW4IhrupemYjcnbsjoAtJX3x\nSjKLV7O/18YY44Dv8zvomAO1oT2jfgzbluiNLuYXfX1veB8RNgQHLvxSFQ7ThZSXyfZkGdoaQYtq\n5S5NEM5Yy3nNzL1sLvLZvEMjnBERNsZJ9vhW3C//W7nLOCMnwojlqsX0NRfDiOrHVIp7RnTJRdJQ\n6c3K9KaKYSQnwohQBiGvyvJmH9McFqHjB/E+/wdko7JbNSyvD+2d76bHqmEwMraJY1qTlxltQ3h9\no283iycXck/X4BveLsLG1OPAiU+qwmm6kfIyuV6NoW1D5MIiXAgTl+pRWXbzMmoaqstdyqQnwsY4\nME0Tfc8vcB7/fblLGRM2DIeRYDGI+Jow1UBxA/vwiVopQ6Enq9CXsuhPFcjp4sJEKK3mKidLG73U\nKTqhgy/j3vZcxR6lawP6inNJz1vO/m6TsSxzVkeA5ta9qGp2VJ+fyc7i3s4cGev0QUiEjcnvpHBR\nkNH6NAa3hskNvfnhJoIw0Sz4k/k0L2gudxmTnggb40CL96O++HVkPVXuUsaFDdiqD8sdxPI2YXib\nMB0BTNmDIbsoSG7ShkJfVqFnOIxkRRgRxogEtAXdLKp3E7LzhHY9j2Pvzoo8StcK1JC7fANd+QDR\n+NiscsgyzJlfNeqBf7oe4KX+Zp5PnH5PjAgbk4+KA59UhcvyIOVltIE84W1hMv2jC6yCMFHMuLiV\njgs6RCtViYmwMQ6yPS/j3vGdcpdRMYphxIvlCmJ5GzF9zRiOquIGdtk9HEZU+nISvSnoT+XJiLN9\nhVFQJJhb72Vu0EnQyBDa8hSOY4fKXdZJbKCw5kLS7YvY1zU2x8a53Aqz57lGNfDPtqE/vpT7e3pP\ne7sIGxPfSeGiIFMYKDC4LUymb2LsfRKEseKd5mX5Dcvw+DzlLmVSE0P9SsyyLKRkV7nLqCgSIBlZ\nZCMLmW4YOvn2E2Gkw1VbbNNqPTmM6JKLtKnSl1XoTdv0J/OkRRgRTsO0Ye9glr2DWZyKxMLFV9B+\n3npqtQTB5zaiDrzxRujxIgGuF/+I4+ArLLtsA0czHpLJswsdec2kr8fC6eygqvrw26tHAo8ijqeb\nTBRU/FIVLstbDBfhAuFtEVLdpw+UgjBVZAezZKIZETZKTISNEtPzGdSBLeUuY0I5EUYwsiiZnjcI\nIx7aXUFMbyPm9CYMZ81wGHGhS24yw2GkJ20zkMqTKtEUZ2HiKJg2O3rS7AA8Dplla99Pq08mmByk\nZvPjyIk3Pu51PMixCL4Hf8rc8y8jMX0uB7vP7oI/Gtbw+apxu2twut7eVHCnmqFadZKo8M32wukp\nqPikAG7Li1RQKET0Yrg4Xv5wLQgVxYZcXIPWchcyuYk2qhLLho/ieuGrSKLlYNzYAIoHy12L6WnE\n9BXDiDWygb0YRgZyMj0p6E/nSWri+zNVVbkVljcNH6U71EXgmd8j58rbq242NJK76CoOpVxkUmf3\nb3P2/Cqamncgy2ceXgzDy46BmfwxNnTKbaKNqvIoqHilAB7Li6Qr6BGD8PYwyWNTY5+gIJyNpjVN\nzH/nPLFvo4RE2CixiXTk7VRiK+7i0b7eaZjeZkxX7WtO03KTNVUGNIXulM1AqkBCEyPYp4K64aN0\nGxwWoa4DeF94EnmsB2KcIVuWyV/4ThLT2jl0FqscqioxZ4GPuvptZzzwz7ZhIL6E+3pOfSdchI3y\nU1CGw4UPSVcwYgbh7RESR5PlLk0QJhxXtYvlN4tp4qUkwkYJ2baNtv+3uA4/WO5ShLdpJIx4phVn\njZwURlzkTAcDmkx3CvrTOomc6HGfbFqqXSyd5qFO1gke2IF7+/PIZfh1abS0or3jnRyIOMnlRhd6\nA1UO2ufY1NS+csafk0gt4MfHxMpGJZBR8OHHjR+5IGMkLCLbw8QPi3AhCGNhyU2LaWhrKHcZk5YI\nGyVU0LKw5duoySPlLkUYY7biOjmMOGsxFc/IBvac5WAgJ9OdhoGUTkyEkQlLAmaFikfpBq08oZef\nxbFv17gepWsrKvlLriJaO4OjvfqoHqOxxUvrzH683v4zun8u18ovj1lEjPxJHxdho/RkFLz48ZwI\nF0mLyPYI8SMJxJddEMbe7A2zmbG8FUmSyl3KpCTCRgnlIl04X/gyki1acKYaW3YN7xlpKLZpuYOv\nOU3LTc5yMKjJdKclBlIFolkRRiYCRYZ59V7m1DoJ6mlCW/6Ao2v83kwwZnaQXXsJB8Mq2ij2GbXP\nCdDU8gqq+tbD2UzTw+7BWTwROXmauAgbY09GxoMfL35kXcVMmkR2RokdjItwIQjjoH5pPYs2LERR\nlHKXMimJsFFC2e4duHd+t9xlCBXIlp3DKyP1WL4WDFcIU3G/ZmXEyZAmczwtMZgqEBFhpOI4FYnF\njT7aAgrBXJzaZzeiDp3ZqsHZsB1OtMveRdjXRFf/2/t3IcsScxYEaJj20lvu37BtGIov4d7X7dsQ\nYePsSch48eElUAwXKYvYzhiRA1ERLgShDNxBNytuWo63ylvuUiYlcfRtidi2DflEucsQKpRkFVBy\nAyi5AYjuPuV2W3Yyw1XDck89VsN0DFew2KYludFlF5rtYCincDwlMZAWYaQcCqbNtp402wCvQ2HZ\n+dcy3SsRTAwfpZt8e8fNnilJL+D5v/+lcfZ8qlddyP4BmcIZzpmxLJtjRzI41GWE6ne++fNI4FJH\n17IlnOzkcKFgpSG6O0rPvqMgfnQFoezy8TxaJi/CRomIsFEitm0jp8XAJGF0imFkECU3CNE9p9xu\nyw5aXTUsdzdg1rdguIdXRqTiJnbNdhDWFLpTEv3pAuGMuKIppaxu8dzwMaPVbh/LL7+JJpdFcKCL\nwLObkLWxP0rXcWgf6vFOFq3bwGBtPT0DZ/Y91nImfT02TtcsAlVH3/S+LkeSRqeH/sJbt10Jr5KQ\nhtuiAiiGipW2iO2O07f3GJYhli4EodLYlo2eEXOFSkW0UZVIQcvCC99ETR8rdynCFGTLKpazFstT\nh+lrwXTVYSgeTMVNQXKTtx1E8jJdKZmBtE4krYvujRKo8ztY0eilwWES7NyHd8vTJTlKV1+wlMzS\nc9nfJ2Gc4cXsjFl+WlqP4HS+8QqMZbrYPzSbx8IDIx8TbVSnkpBw48VHVTFcZCD+SpzI7qgIF4Iw\nQcx9zxxal4rpfqUgVjZKxMzFcWZL378tCKcjWQaKNoSiDeGI7T3ldltSme6qYYmnDjM4HbO5DkP1\nYEqu4ZURJ5G8zPGUzGBaZ0iEkVEJp3U2Hiq2U7bWdLD4/Yupk3VC+7bi2vHimJ1o5dj7MlWdh1hy\n+TX0SkEGwm8daLqOpnG5ZtP4JgP/ZCVPnVuczvJ6rw8XdhYSexMc2d2FdYYtbYIgVJZ8qoBt2+JE\nqhIQKxslkh3Yj/ulb5S7DEEYFVtSsFw1WO764tG+7oZXN7DLbvK2k0h+eM9IRmcoJcLImZIlaA+6\nWVDvJmhqhHY8g+PgnjEJHjZgLDuH9IKV7Ou2sN7im6I6ZObO9xJ6k4F/yfQ8ftQZGfnvqbiy8Wq4\nCKAYDuwcJPYlGdodxhrFqWCCIFSe4NwgS65djKqK9+HHmggbJZLtegn3ru+XuwxBKAlbUrCcNVju\nEKa/ZTiMeEaO9s1LTqJ5heMpGEibDKYKU+jS9MypssS8Bg9zahzFo3RfeBK1u/OsH9fyVZF75waO\nG9VEom++ylEc+GdRU3vqChhAPt/II10ujuczwNQJGydWLlTTgZ2F5MEk4Z1RDE3sfxKEychV7WT5\nzcvFJPESEGGjBGzbJnf4D7j3/3e5SxGEsrAlBdtZjekOFY/29TRgKt6RMFKQnEQ1me6MzEDKYDBT\nYKq3trvU1xylm4lS8+xG1PDgW3/iG7ABffX5pGYv5UC3+aarHE0tXlpn9uHxDpxym2U5OByex28G\ni22hkzVsuPDiPxEucpA6lGZoZxhDnPQmCFODBCtuXU6wJVjuSiYdsVZUArZtI2nRcpchCGUj2SZS\nPoqcj0LiIK7X3W5LMi3OGha6Q1g1LRhNr4YRQ3aRt13ECjLdaZn+jMFgavKHkbxhs7U7zVbA53Sw\n/ILrafFAMN5P9eaNyKm3d5S2BDhfepbag3tZum4DnZqfePz0F859PVk83uk0tSRQVe2k22RZp9Y5\nyhdVwVx4hsOFEzSJ5KEUx3b2YIiT2wRharKhkBUnUpWCCBslYFkWcvbUdwgFQSiSbOsMwkg1C9wh\nrEAzRsM0TNWLOdKm5SKel+nOKPSndQYmWRjJFCye6UwCUO2uYsUVN9PotAj1H8X/3BPImvYWj/Aq\nORHD++v/Zva5F5GasYD9x83T3q/zcBqnczH1pxn451ILyEzseXMu3PioxjEcLtJHMnTt6ENPi1ki\ngiAUiTbJ0hBtVCVQPPb2G6jp4+UuRRAmJRsZ21n1mjatk8NIQXISLygcTysMpHX6J0kYafA7WNbk\npUE1CR19Bc9Lm9/WUbpWqIHspes5mvKSTJ36eW6Pwux5DkJ1L5/08UK+nse6fRzOpSdMG5UTN36q\nUU0nUl4i3ZllaPsQhaR451IQhNObffVsZq6cUe4yJh0RNkpASw6hvvBV5EKy3KUIwpRkIxXDiCuE\n5T8RRnzDYcRFQXKRKCjDKyMG/ck8emVfO5+itcbFkgYPIblA6JWtuF7eckYnWtmyTP4d60g2zeZg\n96mBo67Bw8xZCfyBzpGPWZZKZ2QBDw30VWzYcOLCTzUOy1VcuegaDhdxES4EQTgz7VfOou2cNnH8\n7RgTbVQlYOsaUiFd7jIEYcqSsJEKCeRCAlJHTm3TQqLZWcVcV7C4MlI3DdPhG1kZ0SU38YJMT1am\nP2XSn8pTOH33Udkcj+c5Hs8jS9DRsJIFHzyPoJUjtG0z6qG9bxg8JMvC/ceNqI17WHbhlRyKuchk\nX31x4cEcXl8IpyuC01mcii7LBtXOynpfyoELv1SFw3Qj5SWy3Tl6tw6hxc68xUwQBOG19KxoqywF\nETZKwDY1pAp7108QhFedHEaOnjaMNDkDzHWFsHxNmHVNGCeFERcJXaYno9CfNulL5SmUqdXXsuFg\nOMfBcA5Vllgw5xI6Vr+TYCFJ6IUnUHu6Tvt5an8vvl/9lPkXX0GspY0jPa++gOOdKVzueTQ2zMOP\nLwAAIABJREFUbUOWi7/LnEphzIYQjoYDJ36peiRc5Hpy9G0Lo0VEuBAEYWzkUwUsy0JRlHKXMqmI\nNqoSyPbuxr392+UuQxCEErGRsB0BTFcQy9+E6WnCcPgxZTeG5KYguUjqCj0Zmb60yUBKRxvnTSNu\nVWZJk5cZPoVgJkLtsxtRIkOnva8xvY3c+es4EHGi5Yqhw+GQmbPAQ33DdgAKhRCbumto9/nGpY3K\ngROfVIXTdCMVZHK9GkPbwuSGciV9XkEQpq7q9mqWf2CZGOw3xkTYKIFsz07cO+4udxmCIJRJMYz4\ni2HE14TpbcYcDiPFPSNukoZC73AY6U+WNoz4nArLm33Fo3SjfVQ/sxE5ffKeMlt1oF26nmh1C529\nxcBRVeNk1myDmpp92LZCV2QhmimVJGyoOPG/Jlxo/XmGtoXJDmTH9HkEQRDeiLfBy4qbl+P2uMtd\nyqQiolspWBXW3C0IwriSsJH0FLKegvSxU263gSaHnzmuIKavGTPYhKn6MZVX27RShkpPVqEvZdKf\nLJA7izCSKZgjR+nWeqpZfuUtNDotgn1H8D/7JHJBQzJ0PBsfZtqsOQTWXMz+QYVkvMBQvw+3qwG3\nZ5CAw0Izx6a9QMWBT6rCZXmQCjL5/jxD2yJk+jNj8viCIAhvl6EZGHkDPOWuZHIRKxslkO3agnvX\nD8pdhiAIE5QN2A4/lqsWy9uM4W3CdASKKyPDqyNpQ6E3q9CbsuhPFciO4jitaQEHyxq91KsmocO7\ni0fpWha204W27mqGPI0c79fpmFtFU/MutHwrvRkfabn7ba9sFMNFAJflLYaLwQJD28JkekW4EASh\nMsgOmRW3raCmobrcpUwqYmWjFMTKhiAIZ0ECJD2NrKchfZzXD/C2AVv10e4OYnkaMWY0YTqqMGUP\nhlxs00obKn1Zmd60TV8qT7ZwajgYSOk8nkogATNq57H4uuWEyBPaswXX7x6kad4iqlecz8GuDA7n\nYmprj+CVqziTs/YUVPxS1Ui4KER0wlsjpLr7zv4LJAhvwz/9+p944cDz1Phq+c/b/xOAezbdw3P7\nnkWSJKo8VXzu/X9FQ3XDKZ97wz9/GK/LiywpqIrC9z7xbwD8x+P/zpaDW+ho6uDz7/8CAL/fuZFk\nNsn7z7t2/F6cMKYs3cIyxTXcWBNhoxRs8Q9VEITSkQDJyCCnM8Uw8rp938Uw4qXDVYvpbcJsbcZw\nVBU3sMuvtmn15xR60zb9yTzHYsX/yRLMbjqH+YsvIGhmCe18gYUd84nGVRxqKy4FOM2vOAUVnxTA\nbfmQdBk9ojO0LUKqS4QLobyuWnEl7z33vfzjr/5x5GMfuOAD3LruVgB+/fyv+dmTP+Uv3/vZUz5X\nQuJbt/4zVd6qkY+ltTSH+g7x75/6D7710Lc4OnCU5mAz/7f9cb5+89dL/4KE0poE/T75fJ6bb76Z\nbdu2EQqFeOCBB5g5cya2bXPHHXewadMmbNvmne98J9/5zndKXo8IG6UgwoYgCGVUDCNZMLIomR44\nTRiZpnrocAUxvY2Y05sxnNWvCSMF0qbF8YKDgWWXEVBtfLKNlLGw/MVhVwoKXqkKj+VF0hX0qEF4\nW4Tksf5xf72C8GaWtC2lP3byv0uvyzvy/3OFHFXeN26bsV939SlLMoZpYNs2eT2Pqqj88plf8L5z\n34ciiyNThfL70Y9+RCgU4uDBgzzwwAN8/vOf5/777+epp55i27Zt7N69G9u2ueCCC3jqqae4+OKL\nS1qPCBulILbBCIJQwYphJAdGTzGMsPWk220AxUO7u7YYRrzN6L7p6J4gku2iiRmYSZuB5wc5fliE\nC2Fi+vHvf8TGnb/H7XDx3Y//6+nvJEn81X/9FYosc/XqDVy9+mq8Li9r5q7lk9//JCs7VuJ1ednX\nvY8bL7lpfF+AMCllMhmuv/56enp6ME2Tu+66i/vuu49f//rXAGzcuJHvf//7PPjgg/j9fj796U/z\nm9/8Bo/Hw0MPPURDQwMPP/wwX/ziFwG49tpruf322wFoaGigUCiQz+cxTRNd12lsbCz5ayrnjKbJ\nSxJfVkEQJi4bML2NpFsuINq6hsG6Orpcx9DsNL6EhGyo2LJN45ppzL6mg6a1TbhqXj8aURAq222X\nf5T7/vI+rlh+Jd9/7N9Oe5/vfOw7/PDPf8hXb/oaD7/4ELs6XwaKbVg//PMf8okrP8F/PfFffGTd\nrfx266P8v1/8P+596t7xfBnCJPPYY4/R0tLCjh072LVrF1dddRX79u0jEokAcM899/DRj34UgGw2\ny3nnnceOHTu46KKL+I//+A8Aenp6aG1tBUBVVaqrq4lGoyxcuJArrriCpqYmWlpauOqqq5g3b17J\nX5O4Ki4FSSyjCoIwcViAXjOf2IIb6Vv5CbpW3cKe2R1sdW5mm3YPe3L34aKGYKYRV8LArUvopk7a\nSKO5NVztTto2zGTe9XNpf9cs6pfUoXrFwrkwMVy29DL29+w/7W2hQAiAGl8N71hwAft69p10+8G+\ngwBMD03n6T1/5K7r76I32ktPpKe0RQulI0llffqlS5eyceNGvvCFL7B582aqqqq46aab+NnPfkY8\nHuf5559n/fr1ADidTq6++moAVq1aRWdn55s+9tNPP82TTz5JT08PPT09bNq0ic2bN5f6JYk2qpIQ\nKxuCIFQwCxk9tIRM4wo0lxNN0kiYnUT0xyloiVPu3+a8gun5JbgSxWF/niGdQLOfaDwGgGEYGEbx\nNnzgX+ontCyEpVnoSZ340QSJYwms05yIJQjl0B3pZnpoOgDP7nuW2U2zT7mPVtCwbAuvy0uukGPr\noZe46dKbT7rPTzb9F595z19imAbW8EmUsiSRN/KlfxHCmJNkCanMYWPOnDls376dRx99lL/7u79j\n3bp1fOxjH+Oaa67B7XZz/fXXI8vF60yHwzHyebIsj/webmlpoauri+bmZgzDIJFIEAwGee6551i/\nfj1eb3HP0vr163nuuee44IILSvqaRNgoBVmEDUEQKoclqxTqVpBpWILmVNCkHDHjCDHjYXTtzedc\nNDvOp804D1fMGPmYDHiTJjmvh1w2d8rn6AUdHb24OaQagmtqmXZOA2bOJJ/IEzsQI92bwbbE/jah\n9L7yyy/zcufLJLIJPvTND3LzZbfw4oEXOB7uRpFlmoLN3LHhDgDCyTD//NA/89Wbvko0HeWL9/8D\nAKZlctnSdayevXrkcZ/Z+wzzWuYRDAQB6Giazce/9zE6Gjton9Y+7q9TOHuSIiHJ5Q0bfX191NbW\ncsMNN1BdXc2Pf/xjmpqaaG5u5stf/jKbNm16y8d497vfzU9+8hPOPfdc/ud//od169YBsGDBAr77\n3e/y13/911iWxVNPPcWdd95Z6pckhvqVQvb4S7hf/n65yxAEYYqyZDf5htVkGhagOUAjQ9Q4QMw4\niGlrZ/w4dcpSFkrvwzNkcLo/v4lmJ5FEjLf7Z8TtdqMaKkbWIBfWiO6PkgufGloEQRDGk+pRWf6R\n5VTXVb31nUvk8ccf53Of+xyyLONwOPjBD37AypUruf/++7n77rt59tlnR+5bVVVFMpkE4Fe/+hWP\nPvooP/7xj8nn89x0001s376dUCjE/fffT1tbGwB33nknGzduxLZt1q9fzze/+c2SvyYRNkog270d\n9843ONlCmFDufmgPP3r8ALZt87Er5/EX71l00u3hhMZN33qKgVgOw7T4zPuX8JHL5zCUyHHtVzaR\nyOh86aaVvOfcmQC878u/5/ufOp/GWu/pnk4QRsVS/WiNa8nUdaApFhpJwsY+EvpRLAqjeswquYPl\nyo14Bk8fNAAMB8RCEslkatS1y7KMx+kBXcJI62T6MkQPxigkR1e3IAjCaDn8DlZ8ZDmB2kC5SznF\n7bffzqpVq7j11lvLXcrbJtqoSkF2vPV9hIq3uzPGjx4/wAvfvgaHIrP+7x/n6jWtdDS9+o7H937z\nCivaQ3z1I6sJJzQWfPJX3HBJB/c/dYRPvmsB7ztvJhv+4XHec+5MHnmhi5UdIRE0hLNmOWvJNa8l\nWzMTTTHIkiBc2EOy8Dw2xls/wFvwyY0sc9yAp/+NgwaAqoPbVskoCuYop+5alkXmRCuXB9xz3cxa\nMAs7b2OkdRLHkiSOJDC0s39dgiAIb0b1qDiclXcNt2rVKgKBAN/+9rfLXcqoiLBRCqo4AnIy2Ncd\nZ828etzO4o/JxYsb+fWzx/jstUtG7tMY9LKrMwpAMlcgFHChKhIOVSGjGWi6iSJLmKbFdx/ew8N/\n/86yvBZhYjM808g1nUuuuhFN1snYUcL6HtKFp7AZ203XLrmWFc4/xdtvvmnQOME3oKM3B4jF42Py\n/MXN5unif/ihakWA+pV1mDmLQrJA/HCcVFcKyxCbzQVBGFvuGjeqq/Iujbdu3frWd6pglfcVnQQk\nxYWNhDQZZt5PYYtn1nLXz7YSTeVxOxR+u+U458ytP+k+H79yHpf/ze+YfvN9pHI693/+UiRJ4sOX\ntHPDPz3Ff/7ffr5+6zn826N7ufGy2SPBRRDejOFrJdu8llygDk3Kk7YHGSrsJJv/Pyjh7xUVH6ud\nt+PrN5HO8GlkwJOFrNtFXhv7E3hGNpvLQA00nF9P07mNGFmTfEwjeiBGpj9Tyi+LIAhThCfoGTnp\nSRg74sqnBCTVhe3wIenpcpcinIX5rTV87tqlXHXXY/jcDpZ3hJBfd0rF136xk2XtQZ74+rs43Jfk\nyr97jO3fbaTK6+SR4VWMWDrP13+5kwf/dh1/evdm4pkCn3nfYs6d31COlyVUGAswq+eQbVxNzleN\nJmkkrV4i+nPktPC41SHjZI3n0/j6rTMOGid44gb+Fl9Jwsbr5fLDG8kdIDfKtMxoRjZkjIxBdjBH\ndH8ULXbmm+AFQRBOcFU7y3707WQkwkYJSE4vtqMKRNiY8G67Yi63XTEXgL/9yUu01vtPuv3ZvYP8\nzQeWAdDRVMWsaQH29yRYPadu5D5fvm8Hf/uB5fz8D0e4cHEj157fxrVf3cTvvnTl+L0QoWJYyBjB\nhcUZF25PccaFdZyI/iR5LVamqmTWeD6Df0BCHuVxtL6ITr7KTzo9fr/3LMsiq2WL/+ECR5vKjDmt\nSAUJPW2Q7kkTOxhDz+jjVpMgCBOX6lJF2CgBETZKQHF4MF21KNnecpcinKXBeI6GGg9dg2n+97lj\nPPfP15x0+/zp1Wza0cs7Fk5jIJZjf0+C9sZXT7E42JOgN5rlosWN7DwSweMqTpfXCqPbTCtMPBYq\net0SMo3L0ZwONClH3DxKVH+MgpYsd3kArPF8hkBYRTZH34vk0Gw8tQ6ysoxllWc/hWmaZM3h8OEF\n30IvtYtrsDUbPaUT70yQ7Exi5sXPnyAIp6rE/RqTgTj6tgRM00TfdR/OnifLXYpwli75/KNEUnkc\nisy3Pr6WS5c28cPf7QPgE+vnE05o3PYvf+T4UBrLhs9ft5QPX9Ix8vkf/Mcn+crNq+hoqmIokeP9\nX95EIlPgizeu5H3nt5XpVQmlZMlO8g2ryDYsRHPIaGSJGgeJGQcx7Gy5yzvFKs8d1EYCqPmz/1Ng\nyRCdppBInDqFvBI4nU6cODFzJoVEgejBGOmeNPZZhCxBECaPxTcsZlq7aHEeayJslIBt2+QO/R73\ngfvLXYogCCVmqV7yDWtI188hr9popIkYB4jrhzAp/R6Gs7Hc80nqYvWoubFbicjUOYgYafRC5bcu\nuV1uVEvFyJpokRyR/VFyQzmx2VwQpqjlty4jND1U7jImnbe9XtTZ2ck111zDrl27SlEPH/rQh3jl\nlVe49dZb2blzJxs2bODaa68tyXOViiRJ4Czf9ElBEErHclaTa1xLNjgLTTHIkSSs7yWpv4SlV/4F\n9gmL3R8hlGhAzY1tS5EnrBNo9hMtlGv/yZnT8sMbyR0gN8u0zpyObMjoGYNsf4bogRj5RGUHRkEQ\nxobiVEQbVYlU1Fe1v7+fl156iYMHDwJw6623TtyNOk7/W99HEISKZ7jr0BrPJVvbgibrZIkTLuwh\nVdiMzcTs/Z/nvo6GzAwcmbGvXwZ8SQPN6yWbrby2sTdiWRbZ/HC9bnDNdtE2fybkQU/rJLtSxA/H\nMXJiuKAgTEbOKidOr7PcZUxKozpM2DAMbrzxRhYuXMh1111HLpfjS1/6EmvWrGHJkiV84hOfGLnv\n3XffzaJFi1i2bBkf+tCHAMhkMtx2222sXbuWlStX8vDDDwNwxRVX0NPTw4oVK9i8eTNQbEkC2LRp\nEytXrmTp0qV89KMfpVAosGXLlpFVj4ceegiv14thGGiaRkdHB+UkOfzYZzQSSxCESmJ4m0l2vJ+B\nFZ+ga9WtHFh4PlsDr/BS/qfszt3LkdyjJM3OCRs0ZrneRXNuIc5k6ep3pm28TvfEfbOI4t+5jJYh\nY2co+ApULQvQcW0Hc/9kDm1XtFHTUY3sEOfxC8JkUdNWjdMtwkYpvO09G52dnbS3t/PMM89w3nnn\n8dGPfpSFCxdy2223UVtbC8DNN9/M9ddfz4YNG2hpaaGzsxOHw0EymaSqqoq/+Zu/YdGiRdxwww3E\n43HWrl3Ljh07GBwcZMOGDSMtWrfeeivXXHMN73rXu5g7dy5PPPEEs2fP5pZbbmHlypXcfvvtzJ07\nl8OHD/PZz36WP/7xj3z7299G13X+/d//nXvvvXfsv2JnKJ+OIb/wjyjaUNlqEAThzVmAFZhFpukc\ncv7a4gA9a4CwvpusNcRka95vcVzEHONS3NHSvztvqhCrk0kkK+PErbHmcrlw2k6MrEE+nie6P0a6\nP80YD3QXBGGczL66gxkrZkzoN0kq1ajaqFpbWznvvPMAuPHGG7n77rtpa2vjG9/4Brlcjmg0yuLF\ni9mwYQNLly7lwx/+MO9973t573vfC8Djjz/OI488wje/+U0A8vk8XV1duFyuU57Ltm3279/PrFmz\nmD17NgC33HIL3/ve97jjjjvo6Ohg3759bNmyhc985jM8/fTTmKbJhRdeOKovyFhR3AHMqlkibAhC\nBbEAs2ZeMVx4fOQljYTVQ0TfjKZFyl1eSdWrK5htX4prHIIGgGKA21JIKwqmOTFXgd5MPp8nTx5U\nkBokmqY3ohhKcbhgeHi4YEQMFxSEicLld4mgUSKjChuv/WbYto0kSXzqU59i69attLS08MUvfpFc\nrjjl9dFHH+Xpp5/mkUce4Stf+crIqsWDDz7InDlzTnrczs7Ot3y+E895wkUXXcRvf/tbHA4H69at\n45ZbbsGyrJEgUy6KolCobscx+GJZ6xCEqcxCRg8tLg7Qc7nISxpx6xiRwuMUtMo8nrUUapQ5LJDe\njXvQGNfmTu+gTlVzgFg8Po7POv5syyanDU82d4HaqjCjvRXJkDDSBune4nDBQmriHCAgCFOJJEs4\n/aKFqlRG1XDa1dXF888/D8DPf/5zLrjgAgBCoRDpdJpf/vKXSJKEbdt0dXVxySWX8PWvf51EIkE6\nnebKK6/k7rvvHnm87du3v+FzSZLEvHnz6Ozs5PDhwwD87Gc/45JLLgHgwgsv5F/+5V84//zzqaur\nIxKJcODAARYtWjSalzZmJEkCjzg+TRDGkyWraA3nEFl8Gz0rP87RVR9i13Q/W3mEHdpP2Jt7gL78\n8xTsqRM0fFILS5QP4xnnoAHFPzDeLLjd7nF+5vI6sdk8Y2bIe/J45nuY9Z5ZzL1uDrOuaiM0P4ji\nVspdpiAIw9whN55qT7nLmLTe9srGiYv/733ve9x2220sWrSIP/uzPyMWi7F48WIaGxtZu3YtUBxu\nd9NNN5FIJLBtmzvuuIPq6mruuusuPv3pT7N06VIsy6K9vX1kk/jplrBcLhf33HMP1113HYZhsGbN\nGj75yU8CsGbNGgYHB7nooosAWLZsGQMDA6P+gowpTxAbGUk08QpCSViym3zDajIN89EcEnkyxRkX\nxoMYJ95pnsLccogVzo/i7R//oDFSQ9zA1+xB06ZuS5GhGxgMt68FoHpVNfWr67FyFvlEgdihGKnj\nKTFcUBDKpKatGpfn1FZ+YWyIoX4llM+lkF/4J5RMT7lLEYRJwVL9aI1ryYQ6yKsWOVKEjX0k9CNY\nFMpdXkVx4GeN+078/RZSmX/L6y6JWI1NKpUubyEVyuP2oFgKZsZEi2pE9kfJDmYn2/kEglCxZm/o\nYMZysTm8VCpqzsZk43D5yNctE2FDEEbJctaSa15LtmYmmmKQJUG4sIek/jy2LuYdvBEZN+d47sBX\nAUEDwJG3cUsOMrKMZYmV3tcb2e/hALlJZvrMFmRDxkgbZAazRPdHycfFcEFBKBWxOby0RNgoIVmW\nsQPTy12GIEwYhmcauaZzyVU3osk6GTtKWN9DuvAUtmhHPEMqazx34h+QkK0KSBrD/IM6emOAeHzq\n7JcZDcuyyGqvGS7Y7qRtzkwoFIcLprrTxA/H0DMibAvCWJAUCZdftFCVkggbpeYOYoMY7ycIp2H4\nWsk2ryXnr0OT86TtIcL6TjL5/0P0kIyGzFrPZwgMKsgV1v8vW+DRJLJOJ4WCaHk7U4ZhYBjDwcIH\n/iU+QkuDWJpFIaWTOJIgcSyBVRBhXBBGo3pmFb6gr9xlTGoibJSY7A1iu4JI+Wi5SxGEsrIAs3o2\n2cZzyPmq0SSNlNVHWH+OXD5c7vImhdWevyAQcaIYlRU0TnBHDfzNPqIibIyaXtDR0YvvYFVBcE0t\n09Y0YGZN8ok8sQMx0r0Z7Apa1RKEShaaX4fD6Sh3GZOaCBsl5vTVkm9ci+vY78pdiiCMKwsZI7iw\nOOPC7UWTciSs40T0J8lrsXKXN+ms8Pw5NbEAar5y3+GWAV/cIO/zkclkyl3OpJAvvDpckBBMu3Qa\nLYaKkTXIhTWi+6PkwuJkNkF4I96QR+zXKDERNkpMlmXs6vZylyEIJWehotctITNtOZpLRZM04uZR\novpjFLRkucub1Ja4byOYqEPNVf6kbmfWxlPjIitlEYchjr2RI4adoEyXmdHeCrqEkdbJ9GWIHoxR\nSIqVJUEAcAfd+IL+cpcx6YmwMQ4kXwO24kIyxWkiwuRhyU7y9avITluE5pDQyBI1DhEz/hfjxAZX\noeTmuz9IfboVxwTaMBwYLKDXBUgkRQgtJcuyyGjDK0gecM91M2vBLOy8jZHWSRxLkjiSwNAmzr8d\nQRhLDUvq8fin1tDRchBhYxyogWkYdctwDLxY7lIEYdQs1Uu+YQ3p+jnkVRuNdHGAnv4LTEME6XLo\ncL2bptxcnKmJdbEoG+C2FDKq+urmZ6HkipvNh2ed+KFqRYD6lXVYOYtCskDscJxUVwrLqNxWPEEY\nS75pfmRZLncZk54IG+NAVVVyImwIE4zlrCLXeC7Z4Cw0xSBHkrC+l6T+Epaul7u8Ka/VeSmthRW4\n4hPzYt07qKM3+4nG4+UuZcoa2WwuAzXQcH49Tec2YuZMtJhGdH+MTH9GHAwnTEqKW8Fb6y13GVOC\nCBvjQJIk8NVjIyOJWQFChTLcdWiN55KtbUGTdbLECRf2kCpsxqby9wJMJdPU1bSbF+GKTsygAcXr\nW0/axuPxkMuJDcyVIJcf/j6oIE+TaWltLg4XzBhkB3NED0TRolp5ixSEMRKaFyQQEvs1xoMIG+NE\nDTRi1s5Dje0tdymCAIDhbSbbtJZc1TTycp60HSGs7yad3wQiFFesoLKAedLVuIeMCT+/x5008Ta7\nRdioQCcNF3SBo01lxpxWpIKEnjZI96SJHYyhZ8QqpzAx1bTVihaqcSLCxjhxuLzkmt4hwoZQFhZg\nBWaRaTqHnL+WvJQnZQ0Q1l8imx9C9ElMDH6plUXK9XgGJn7QOMEfNinUBkilUuUuRXgTpmmSNYfD\nhxd8C73ULq7B1mz0lE68M0GyM4mZF6ugQuWTHTLeOq848naciLAxTiRJQgo0Y8tOJEscOyiUlgWY\nNfPINK0m5/GhSXn+//buPEyuss7//vucOqf2qu7qvTskIYQQshJIyCIQFUQIiLLIJiAii8OIbCI4\nv3FmdMbfM/P46CguI46Kjs7gAg6IIjJMhACjUUQYCJgAgQQS0kl6qe6uvU6d8/zRSUsMgWzdp5bP\n67q40l1bf6vpOnU+dd/f+x5xN9NXfoxCod/v8mQ/RMx2FtiXEe2tn6ABYJVcIkaQbMDErWhErVaU\ny7tuLpha1Eznog7cvEtxqMjAC4NkNmfwqmwnexGAjqM6aOpI+l1GwzA8LXQ+YRynjPPMHQRfe8Tv\nUqTOuJiUW+aS7T6aQihE0SiQdjfSX/ojJW/I7/LkAAVJcmz4OuK9LkYdHrFdE9JdFoNqFq8b4XAY\nq2Lh5CoU+vP0rxsgvz2vQVSpCrPPn033EV1+l9EwNLIxgSzLpth+FChsyAFyTYtS29FkO+ZRCAYo\nGHkGnZcYdH5GuaCdmeuJRZhFkWvrNmgAmC6E8xAKhSgWtYxyPRjbXNAGs8dk8qGHYJZNylmHXG+W\ngecHKQ7p/7VMvEhbhGRnwu8yGorCxgQLJHpwQynM4qDfpUgNcc0wxY5FZDuO3LGBXpYB53nSzn/i\nFNRcW69MLI6N3Eh8q4dR5zOMwoMOsZ6owkYd2qXZPAyhw0MceuRUKEI5U2b4lRHS69M4+dpdXU1q\nR8+ibqJJLXk7kTSNaoK5rkvx+fsJrf9Pv0uRKuZacQpdS8i2TqdouaN7XDjrGC6/RAX1/DQGkyXR\nm2jaGsR0GuMwXYoYDCZcMhmNzjWSYDCIbQTxCi6l4TLp9YMMvzKCW67zhC0TzggYHPXB+bQe0up3\nKQ1FIxsTzDRNvNQM7bkhu3CDKfI9S8g2T6EYqJBjiL7SswyXV+OV9WlfIzo2ej2J7Y0TNACCeY9I\nc5CsmcNzG+d5N7pSqUSJ0mizeRO0Lmule2k3Ts6hmC4ysG6QTG9GK3LLAWuf00ZTZ5PfZTQchQ0f\n2KkplLsWE+xd7Xcp4hMn0km+eyn5pi4KZpmsN0Bf+VkypVV4ekdteMdErqGpP4ZVarwUXJVZAAAg\nAElEQVS/hfjWMqXOBENDw36XIj4pFosUKYIFRodB9yFdBJwATtYh35dnYN0A+X5tLij7rnVmK5at\nU9+Jpt+4D+xgmHLXUlDYaBhObDK5niXk460UzBIZbzt95f8lW3wALc8irzc/fAWpoRasQmPuV2C6\nEHEC5GybclkbxjU6z/XI7+xLC0FgcoDJh03GcAycjEPmtdHNBUsj+luRNxdqDpFQY7gvFDZ8Emie\ngpOcjjW83u9S5CBzgUrT4eS6FpGPNe3Y42ILfeXV5Ivb/S5Pqtjs8EW0Z3qws40ZNHaKbC+T6Ikz\nkNZCGrIr13XJFXc0m0cgcmSE5tnNeEWPcsZh+OUh0huGqDRoWJc9m7R0EvHmuN9lNCSFDZ8Eo0ly\nU96FtUZho9a5mDipWWS7j6EQjlIwCgy7r9JXfphiQSdLsndmhM6kMzcde0QnSSYQHamQj0bI57Ta\nmuyZU3Zw2NHXFoemhU20L2rfsblgicEXBxl5dUSbCzY4K2qRmtKsHcN9orDhE8MwCDRP1TK4Ncgl\nQLltPtnOBRRCNgUjT7ryMgPlX1IqaJ657LupwZOZVDyK0JAWA9gpNOISS4Qp5Ato0UTZW2PN5iaQ\ngs4TOuhxu6lkKxQGCvSvGyC3LafZqw1m8nGHkGzXjuF+0dK3PvI8j/z6hwmv+3e/S5E34ZpBiu0L\nyXXMpmCbFIwcA86LDDrP43g5v8uTGtdjL+WIyimE+xU0/pxjw2CrwfDwiN+lSB0wTZNwMIzpmDgZ\nh+y2HAPrBiimtbdLPbPCFvMvmUeqK+V3KQ1LIxs+MgwDo3UGrp3ALOvNtFq4VpRix7Fk24+gYHkU\nyNDvPE+6fCeVit6U5OBpDczlcO8UQgoab8gqQ9izyAYCVCqaXiYHZrfNBQ8LcuiMqVAa3VwwsynD\n4PpBylm9HuvJIcdPoqlDy936SSMbPnNdl8JLjxBe932/S2lYbjBJvmspuZZpFAIOeUboKz/HsLMB\nF61wIuMjYR7KAutSolsdNIt4z1wg3WMxmE77XYrUOTtoEzJCuAWX0kiZoZeGGNo4hNuAS1DXi0A4\nwPyL5tHS0+J3KQ1NYaMK5NNbsB//PGZJb6YTwQm3UehaSi41iYJZJkeavtKzjFRexUOfnsr4i5qd\nLLQ/QrS3oqCxF/LNAfrNAsWCRhZl4oSCIWxsKnmXYrrA4PODZF7LasPJGjL1xKkctmwapmn6XUpD\nU9ioAp7nkX/5McJ//K7fpdQlJ9pDrnsJ+WQnRbNIxuunr7yGTGUL2pJWJlrQaGZx6GPEel0MHX33\nWnqSTf+gFtMQ/4RDYayKhZNzyPcVRjcX7NNqadUqEAow76K5tE5q9buUhqeejSpgGAZm6wwq4TYC\nhT6/y6lpLuAmDiXbvZh8PEXRKDLibqOv/AS54ja0BIn4ySLKseFrFDT2Q6zfoZiMk8lk/C5FGlSh\nuGPX8iAEDjGZcthkKBs4mTLZ3iwDzw9SGi75W6SMmbRsEqluNYVXA41sVAnP88hvXE342W/5XUpN\ncYFK80yy3YvIR+IUjAIj7mb6ys9RcPv9Lk9kjEmQJZGbSPQamBpQ2y/D3Tb9I0O4rn6BUl0syyIU\nCOMVPZxMmaGNwwy9NIRTULO5HwLhAPM+oFGNaqGwUUUKw9sJPPk1AplX/S6larmYlFvmku0+mkIo\nSMEoMuRuZKC0lqKnnhepViZLIjfTtM3CdHTI3V+uCQOdAYaGhvwuReRNjTWb511KwyUG16cZeWUE\n11FQngjTTzuMKUdPUa9GlVDYqCKe55F77RnCT92qptEdXNOi1LqAbOc8CkGLgpFn0HmJQWctZS/r\nd3kie+XYyE0094UJlHS4PVDZNpv+coZyWSvFSe2IhCIE3ACVfIXCYIGBdYNke7Oa2TsOYt0x5pwz\nm0Qq4XcpsoPCRpUpF3JUnvshwS3/43cpvnDNMMWORWQ7jqRgGxTIMuA8T9p5EcdTI57UnoWRa0n1\nN2EV9YnmweACQz02A2k1i0tt2mVzwaxDbnuegXUDFAYKfpdWF2afP4uuGV0Yhj62rRYKG1Uot209\noSc+j+HWf6OZa8UpdC0h2zqdouWO7nHhrGW4/BIV6v/5S307KvIR2gY7sPMKGgdTKW7QH66Qy+X8\nLkXkgAWsAGErvGNzQYfM5gyDLwxSzmr0bl91Ht3JEe+aQTAc9LsUeR2FjSrkui6FFx8k/MKP/S7l\noHODKfI9S8g2T6UYcMgxRF/pOUYqG3FRI53UjznhD9I1cih2Rnu3jIehniD9Q4PoLUzqjW3bBM0g\nXsGjPFImvWGI4Q3DVIo6lryZQDDA3A/MoW1ym9+lyJ9R2KhS+XQv1h9uJZDf5ncpB8SJdFLoXkyu\nqYeCWSbrDe7Y42ITnva4kDp1ROj9HJKfQ3BIAXq8VCwYaDMZHh72uxSRcRUMBQl6Qdy8S3GoyMAL\ng2Q2Z/AqOn17vcNOmcbURVPVFF6FFDaqlOd55DY9Sfjpr9VUs7gTm0yuZwn5eBsFs0jG205feQ3Z\nSi/qhJNGMC14KoeWlhAaVNAYb5lOm77cMJWKPvGVxhEO79xcsEKhP0//ugHy2/MN/RYbaY8w99w5\nJFuTfpcib0Bho4qV8hncP95FcMujfpfyhlyg0nQ4ua5F5GNNFIwiI+4W+srPkne3+12eyITrsY/n\niMpJhPsVNCaCC6R7LAbTWvZaGtNYs3nZpJx1yO3YXLA4VPS7tAk169wj6Z7ZrabwKqWwUeVyfRsJ\n/uGLmOURv0vBxcRJHUm2+xgK4SgFo8Cwu4m+8nMUXa0MI42t3TqK2ZxJeLtTU6ORta7QbNFvFigU\ntJKPiGVZhKwQFKGcKTP8ygjp9WmcfP1+ANJ5dAeHn3Q44UjY71JkDxQ2qpzneeRe+T3hNbdN+AmM\ni0m57SiynQsohGwKRp505WUGyusoeZonLbJTc+Bw5psXEdmmoOGHdI9Nv5bCFdlNMBjENoJ4BZfS\ncJn0+kGGXxnBLddHz2QwGWTueXNIdaf8LkXehMJGDRidTnUnwS2PjevPcc0gxfaF5DrmjO5xYeQY\ncF5k0Hkex9MSkyJvJGb0cIx9BdGtFQUNn5RDBoPNHiMjGb9LEalqoVCIoBfEyTkU00UG1g2S6c1Q\nk+u1GDumTx2h6VPVTmGjRozHdCrXilLsOJZs+xEULI8CGfqd50mXX6RCY833FNkfYbOFRcFriPVW\nMHQk9dVwl01/ZgjXrcWzJpGJZxgG4VCYgBPAyTrk+0Y3F8z318aUxEOOP4TDjpuGHbT9LkXegsJG\njTgY06ncYJJC5xKyrdMoBCqjG+iVn2PY2YCLNg8S2RcWMZaEbyTe6ypoVAHXhMEui7SaxUX2i2ma\nhO0whmPgZBwyr41uLlgaqb7zg1hnjFlnH0lTW5PfpcheUNioIaV8Bnfd3QQ3P7xXt6+EW8l3LSOX\nmkTBLJMjvWMDvVfw0FKRIvvLJMjSyCeI94KpD9KrRq7Vor+So1Qq+V2KSM2zbIuQGcIrepQzDsMb\nhki/PESl4O/5gxEwmHPBbDqmdWj6VI1Q2Kgx+cHNWE9+jUB+627XOdFuct1LySc7KJglsl7/jg30\ntlCbEzJFqpHF0sgnSG4NYGpTrariAkM9NgNqFhc56ILBIEFj5+aCJQZfHGTk1ZEJ31zwsHdPY8qi\nKQQCgQn9ubL/FDZqjOd55Hr/SOjJL+HGJ5PtXkw+nqJoFBlxt9FXXkPO3UZD7+7T4G69+SF+/9BG\nmlojfPWX5wMwki7wuY89yLbNI3QckuCWr76beDK0233v/Jc/8NBPn8c0DKbObOH6z52IHQrw3X/6\nDU888iqHzW7lhs+fBMBD9zzPyGCB9142f0Kfn79MFkc+TtP2EIGyXmPVqBQ1GIi5ZLNZv0sRqWuR\ncISAG6CSrVAYLNC/boDc1ty4nn40T29m5mkziTfHxu+HyEGnPd1rjGEYhNpn0L/4Fp47fAZPBB/j\nD4Xv8mz+B7xSXEnO3YqCRmN71/tn8unvnr7LZXfd9iQLjj+Eb/zqAxz1tkO46+tP7na/rZuGeeBH\nz3Hrvefy1V+ej+t6PPLzF8iNlFj/XB9f+cV5WHaAjev6KRYcVt61ltM/OHeinlZVWBS5lmS/gkY1\nC+Y8InZI0ytExlm+kCdTypC38xhdBoecPIkjL5jJ4WdMp3tJN6Hm3T/QOhCBUICpJ0xR0KhBChs1\nyLJs4vE2HAoU3H6/y5EqM2dxD/GmXQ/yv/3vDZx49kwATjpnJqsffHm3+0XjQSzLpFhwqDguxbxD\na2ccwzSoOC6e51HMOwRsk7u/+RRnfGgegUDjHEKOjlxN82ACq6igUe0S20okEwm/yxBpGK7rkivk\nyDgZCuECocOCHPqeqcw87wgOO20aHfPbsWPWAf2Mw0+fTsukloNUsUykA/s/L76JhZuYljiZofLL\n5N3tfpcjVS7dlyPVHgWguS1Cum/3fVMSzWHOvGIBHz7++wTDAY4+YQoLjj8EgEXvmML1Z9zFUcdN\nIhoP8vz/buOCjy2a0Ofgp7mRy2gZasfKa2GFWmA6EHYDZC0Lx6nfnZNFqpXjOH967cUgPi9Oy/wW\n3IJLaaTM0EtDDG0cwi3tXT/p5LdPpuPwDkyzcT7gqicKGzWsJd7DbOdCnkx/XUvXyl4zDOMNp5hs\n2TjEvd95mm89cjGxRJB/uua/ePie53nHmUdw9lVHc/ZVRwPwlb96mItvXMwDP3qOpx7bxKFHtnL+\nRxdO9NOYMDPD59MxMgU7q5PWWhLdVqbUE2dQS+GK+K5UKlGiBAaQhJbFKToXd1DJuxTTBQafHyTz\nWhbP3X3kuOWIFD3zuwmGghNfuBwUiog1zDAMOpIzmJX4gN+lSJVrbosyuH10NGNgW5am1shut3nx\nme0ceUwnyVSYgGWy7JRp/PEPvbvcZv2zo6NoPdOa+PX9L3HLV95N78ZhXtswNP5PwgeHhd5DT34m\nwREFjVpjAtGMRySy+9+6iPirWCqO9nsEcritLp3v6GTm+Udw+PumM+m4SUTaRl+3oeYQU5dPJd4c\n97liORAKGzUuEAgwqWk+06Nn+F2KVLEl7zqUlT9ZB8DKn6xj6cnTdrvNIdObWffUVooFB8/z+N//\n2cSUw3edH/sfX3yci29cjFN2cXcsd2iYUCrU38n4ZHs5U0oLCaU1dapWhYcrRMNhv8sQkbdQKBZG\n+z2CBQKHmExZMZkjL5jJjDMOJ9WV8rs8OUAKG3UgaEeYklxKV+hYv0uRKvD/XfsgN7//bja/nOay\n477Hf9+5lvf/xdE89dirfOTEO3j6N5t5/9WjU6L6t2b5zIfvA2DarDZOPGsmN7zvLj624scAnHLh\nrLHHXf3gy8yY30GqPUo8GWLa7FY+tuJHlEsuhx7ZOvFPdBy1W8dwmPtOQgP1F6IaTWy7Q0LN4gD8\nn7/+Pxx3/HGc8d4/fTh166238r4z38eZZ53Jhy77EFu2bHnD+z766KOsOG0Fp5xyCt/85jfHLv/8\n5z/P+858H7d88paxy+69916+973vjd8Tkbrmui7ZQpZgc5D2Ke1aWa4OaJ+NOjKY2cLTg99jxNno\ndykiNas5cATzzQuJbHPQW1x9GOkK0pdN41Yae3PT3//+90SjUW755C387N6fAZDJZojHRqeofP/f\nv8+6tev47Gc/u8v9KpUKK05bwe23305nRyfnnncuX/j8F+jo6OC666/j9m/fzt/8zd9wySWXMGXK\nFK6++mq+9a1vadM12W/JpiRtbW3Ytu13KXIQaGSjjjTHupiVPJ+gkfS7FJGaFDcmMy+goFFvYttK\nJBM6Li5atIhk066/h51BAyCXy5FK7T5l5emnn2bKlCkcMukQbNvmtNNOY+WvVmKaJo4zOu0yX8hj\n2Ra33347l1xyiYKG7LdoNEoqlVLQqCMKG3XEMAzak1OZ2/RBTPQiFdkXYbONBaHLiCpo1B3ThUgB\nQlrN5g198Utf5J0nvpN77rmHK6+8crfrt27bSndX99j3XZ1dbN26lVgsxtuXv52zzzmbjo4O4rE4\nTz/zNCeeeOJEli91xLZtUi0pwuq1qisKG3XGMAw6kzOZnbgIdMoksleCJFgYvJpYbwVDE0vrUnjA\nIRbRzsNv5Ibrb+ChXz3EWWedxT/+0z/udv2bzZm//PLLufs/7+bmT9zMV77yFa679jruvPNObrjh\nBm677bbxLFvqjGVZtLa1EovpdVpvFDbqUCAQoKd5PjPj5/pdikjVswizKHId8a2ugkYdM4HYoENc\nJzJ79J7T38OaZ9bsdnlnRydbev/UOL6ldwtdnV273Oa5554D4NBDD+WB/3qAL37xi7zy6its3Kge\nQnlrpmnS2tZKMplUQ3gdUtioU0ErzJSmY5kee6/fpYhULROLYyM3EN8KRmP3DjeEYN4jYgV1MvM6\nGzZsGPt65a9WMmvWrN1uM3fuXDZu3MimzZsolUrcf//9u02V+vJXvsy1115LuVwea8Q3DZNCsTCu\n9UvtMwyDtvY2mpqa9NqsU9pBvI6FgjGmNr0Nx82xMf/ffpcjUmVMjo3eSGJrALOiIY1GEd9aptSZ\nYGho2O9SJtyNH7+Rxx9/nHQ6zTve+Q4+ds3HWPXIKl5++WUCgQCTJ0/m03/3aWC0T+Nv/+Zv+cY3\nvoFlWfzNp/6GK664Atd1Oeecc5g+ffrY465cuZJ5c+fR3t4OwJGzjuS973svR848kplHzPTjqUqN\nMAyDtrY2mpubFTTqmJa+bQCZ/CDPp+/jtcKv/S5FpGocG72Rpu1RrJIOgY0m227TX8pQLpf9LkWk\nobW2tdLS0oJpaqJNPdP/3QYQj6Q4vOkU2oNH+12KSFU4OnINTQMxBY0GFdleJvG6JV9FZOK1tLaQ\nSqUUNBqA/g83iGS0nZlNZ5CyjvC7FBFfzQ9fTstQC1ZeTRqNygSiIy6RaMTvUkQaUnOqmVQqpf1Y\nGoTCRgNpinVyZPO5NFmH+V2KiC+ODF9Ie2YSdrbidynis9BIhVgwrHniIhOsqamJlpYWLEttw41C\nYaOBGIZBS7yHOc0X0mzN8LsckQl1ePB9dOdmYI8oaMio2PYyiYSmU4lMlObmZlpaW7Q7eINR2Ggw\nhmGQivcwp/l8UvaRfpcjMiGmBE/kkPICQkMKGvInVhnCnqWpHCIToDk1GjSCwaDfpcgEU9hoQIZh\nkEr0MLv5XFrt2X6XIzKuuuzFTKucQHjA8bsUqUKxrWWSiYTfZYjUtVQqRWtrq0Y0GpTCRgNLxbuZ\n1fx+2oPz/S5FZFy0BGZxBCsI9yloyBszgUjOIxQO+V2KSF1qaWmhpVU9Go1MYaPBNce7mNl8lpbF\nlbqTMKYyJ3AekW0OagGWNxNJV4iHo36XIVJ3WlpbSLWkFDQanMKG0Bzr5Mjm99EZWuR3KSIHRcTs\n4KjgpUS3KmjI3okNOMTjahYXOVh2btinoCEKGwJAU6yDmc3vY3L4nX6XInJAgkYTC4MfIba1oqAh\ne80ueEQCtjYYEzlAhmGMBQ0tviAAhud52kJXxuQKw7wy/BtezP7U71JE9plFlMWRG0n0ehjas0/2\nkWvCQGeAoaEhv0sRqUk7g4Z2BpfX01+C7CIaTnJY83JmJy7G0J+H1BCTIMdGrie+VUFD9o/pQqRs\nasUckf0QCARo72inpaVFQUN2ob8G2U0wGGFK87HMS15OAK2HLbXA5NjojSS2mZjaSkMOQKSvTCKm\n3g2RfREMBWnvaKe5uRnD0ARW2ZWmUckeua5L79A6nhn6DmUv43c5Int0bPTjNG2PYJV0OJMDV4yb\nDIQdcrmc36WIVL1oNEqqJUUsFlPQkDekkQ3ZI9M06W4+kgXNHyFidvhdjsgbOibyMZr6owoactCE\nMi7RYFgnTiJvIZlM0tbeRjwe1+tF9kgjG/KWPM9jYORV1g3fw0B5rd/liIw5KnIVbeku7JzmTsnB\nVbFgoM1keHjY71JEqlIqlaI51UwwqOnW8uYUNmSvDee2s3H4UTbm/9vvUkSYHb6E7sw07BEFDRkf\nmU6bvtwwlYr+xkR2MgxjdLO+VEpL28peUdiQfVIoZXlt+Cn+OPJDPPQGLP6YETqbQ/LzCA05fpci\ndcwF0j0Wg+m036WIVIVAIEBrW6sawWWfqGdD9kk4GGNqaikLmv+CoJH0uxxpQIcG382kooLGFZ/5\nOJNOXsCC804au+yWL/0D8855B8dccDLn3nQFQyNvPAXoy3d8iwXnncSC807iy3d8a+zyv/ry/+WY\nC07msr+9fuyy//jFT3a5TSMxgWgOwuGw36WI+C4cDmvFKdkvChuyzwKBAD3Ns1mQ+ghN1mF+lyMN\npMd+G4c6ywgPNnbQAPjQe8/j51/5910uO3np2/nfO3/FH374IDOmHMb/+52v7na/NS+u5fZ7fsDq\n79/HEz/4L37x2ErWv7qBoZFhnlr7LH/44YMEbZs1L64lX8jzvZ/dyUfPv2yinlbVCacdYuGI32WI\n+CrZlKS9o52mpiYFDdlnChuyXwzDoD15KPNaLmZS+Hi/y5EG0BaYz+HeyYT6FTQAjj96Calk0y6X\nvWvp8rHNtBbPPZpN27bsdr91G15k8dyjCYfCBAIBlh+zlHseup9AIEDZKeN5HrlCHtuy+efvf4Nr\nLvhww8/LjvU7JBLae0Maz84dwdvb24lGo36XIzVKYUP2m2EYNMe6mNlyBjPj52PQ2CckMn6S5nRm\nB84ist1Bn6ntne/e+yNWHHfibpfPmX4k//PU7xgYGiSXz/OLx1ayaesW4tEYK44/kWMvOpWe9k6S\nsTiPP/sUZ7z93T5UX13sokfYtLUrsjQU27bp6OygtbUVy7L8LkdqmP565IBFQwmmpY4jZnXwx+Ef\nkHf7/C5J6kjU7OYo+yIivQoae+sfv/1lgrbNhSvO2u26I6cdzk2X/iUrPnoRsUiEBTPnjp1Ef/yD\nV/PxD14NwEf+4RN8+upP8O2772Dlbx9l3oxZ/NXl107o86gm8a1lyl1J0moWlwYQj8dpam7SRn1y\nUOhjGjkoLMsa3QCw5SN0h5b4XY7UiZCZ4pjglUS3VhQ09tK/3ftj7v+fX/G9z35lj7e57H0X8Nt/\n/wW/+uZPaE4kOWLq9F2uf3LtGgCOmHIY/7nyPu74p6+zftNGXnz15XGtvZqZLkSKaE8BqWuGYZBq\nSdHe0a6N+uSgUdiQg8YwDFoTk5jVchaz4h/AxPa7JKlhFjEWBa8h1lvB0ALde+WBXz/EP3//Nv7z\nC7cTDu15BaVtA6Ojj69s2cxPH/olF5565i7Xf+a2z/OZqz9BySlRcV0ATMMgXyiMX/E1INzvEI/G\n/C5DZFwEAgHa2ttoa2tTqJaDStOo5KCLhpMcai8jarXzx+EfkXN7/S5JaoxJkMWR64n1ugoae3Dx\n//kojzyxmr70ANNOO5a//cjH+dx3vkqpXObUj14IwNJ5C/nqX/0/vLa9l7/4h5u598vfA+D8mz/C\nwNAglmXxlU/+X5LxxNjj3vvwAyyafRRdbR0AHHXEbI4+/13MP2I282bMmvgnWkVMIJZ2KMZiZLNZ\nv8sROWhisRhNTU3EExrNkINPm/rJuPE8j3R2CxtHVrGp8Kjf5UjNMFkauZnkNgvT0eFJqs9QT5D+\noUH09im1bue0qaZkE8GQRjNkfChsyLjLlzL0Dj/L2syPqHiNPQ1D3triyE009YUJlHRokurkWjDQ\nZjI0/MabJorUgnA4TFNzk/bOkHGnsCETwnVd+kY28tLIL+krP+N3OVKlFkauI9WfwCrqsCTVLdNh\n018YwXG074vUFsMwaGpuIplMEolow0oZfwobMqGy+TS9mTU8n7mLCiW/y5EqsiDyF7QOtmPnXb9L\nEXlLLpDusRjUUrhSQ2zbHp021dSkfWNkwihsyIRzXZftwy/x4sh9DDrr/C5HqsDc8IfoHJmCnan4\nXYrIXiskAwzYJfL5vN+liLylZDJJsilJNBrVtCmZUAob4gvP88gWBtmSeZoXMnfjUva7JPHJzPC5\nTMrOIjisoCG1Jz3Jpn9w0O8yRPYoEAiMjWZoJ3Dxg8KG+KpSqbB9ZD0vjPyUIadxNwxrVNOCKzi0\nuJhQWvPepTaVgwaDKRgZGfG7FJHdxBNxksmkNugTXylsiO88z2Mk30dv5mlezN6rUY4GMck+gRnO\niYQHFDSkto10BenLpHFd9RtJdbBtm+ZUM8lkUqMZ4juFDakalUqFvpGXeTnzX/SV1/hdjoyjduto\nZvNewtsd9Fmb1DrXhMEui7SaxcVnO1eaisfj6s2QqqGwIVUnWxhiW2Ydz2fupOxpl9560xyYwXzz\nA0S2KWhI/ci1WAx4OYpFrbIn/ohEIiSbkiSTSa00JVVFYUOqkud59I+8yqbsb9hUeATQn2k9iBmT\nOMa+guhWBQ2pLy4wNMlmQM3iMsFM0xybMhUKhfwuR2Q3ChtS1UqlPNuzL/HC8D1k3M1+lyMHIGy2\nsij4UWK9FQwddaQOlSIGg3GXTFYjsjIx4ok4iUSCRCKhKVNStRQ2pOp5nsdwro+t2TWsz/5UmwHW\nIJs4i8M3EO91FTSkrg132/QNp9Fbq4wn27Zpbm4m2aQGcKl+ChtSM1zXpW9kI5tzq9lceAxNraoN\nJmGWRj5OvBdMLdYjdc4NwECHydDQsN+lSB0yTIPmpmZi8ZgawKVmKGxIzSmVCvRlX+KlzAOknRf8\nLkfelMXSyCdIbg1gVnSokcaQbbfpL2Uol7WMtxw8iWSCeDyuKVNScxQ2pCaN7kA+RF/uBV7I3EPR\nVVNm9TFZErmJ5LYgAUeHGWkcLjDUYzOQ1nFJDlwkEiGRHO3L0JQpqUUKG1LTPM8jne1lW24N67P3\n4aqfo2osit5Ac18Mq6hDjDSeYiJAf6hEPpf3uxSpUbZt09TcRCKRIBgM+l2OyH5T2JC6MNrPsYHN\n2dVsLv4P6ufw19GRv6R1sBUrryYNaVxDPTb9Q2oWl31jmubYxnyRSERTpqTmaUQzsssAABZxSURB\nVNeXOjY0NMTXv/51v8uYEKZp0tF0GHPazuaY5mtotef4XVLDmhf+MC1DbQoa0vBifQ6JRNzvMqSG\nJJNJurq7aG9vVwO41A2NbNSxDRs2cMYZZ/DMM8/scrnjOHU979PzPPLFDAO5DbyUfYBh5yW/S2oY\nR4YvoCczk+CI43cpIlVhpCtIf3aISqXidylSxWKx2GjzdzJBIBDwuxyRg0pho45dcMEF3Hvvvcyc\nORPbtgmFQrS0tLBu3TrWrl3LmWeeyaZNmygUClx33XVceeWVAMTjca6//np+/vOfE4lE+OlPf0pH\nRwd33nknf//3f08gEKCpqYlVq1b5/Azf3M4m8oHcS6zP/IKs+5rfJdW16aEzmFI4mlBaJ1UiO7lA\nusdiMJ32uxSpQtFodGxjvnr+EFAam8JGHdu4cSPvec97eOaZZ1i1ahWnn346zz77LFOnTgVgcHCQ\nVCpFPp9n8eLFPPLII6RSKUzT5Gc/+xmnn346t9xyC8lkkr/+679m/vz5PPDAA3R3dzM8PEwymfT5\nGe4dz/MYyQ8wkFvPi9mfUXD7/S6p7kwOvpPp5eWEBzSiIfLn8s0B+s0CxULR71KkSoQjYRKJ0aVs\n1fwt9U49G3Xs9TnS8zwWL148FjQAbr31VhYsWMCyZct49dVXeeGF0T0rgsEgp59+OgALFy5kw4YN\nABx33HFceumlfOtb38Jxauek0jAMktFWprYey6K2a5iV+ABBozaCUi3otBZxWGU5IQUNkTcUSVeI\nh6N+lyFVIBQK0dbeRndXNy0tLQoa0hA0ZtdAYrHY2NcPP/wwK1euZPXq1YTDYd75zndSKBSA0eX2\ndjJNcyxYfP3rX+d3v/sd9913HwsXLuSJJ56gpaVlYp/EATAMg+ZYJ03RDlpCh9FXeJ6Xs/dT8kb8\nLq1mtQRmMdM4nfB2B7UxiuxZbMChmIyTyWT8LkV8EAqFxjblCwaDavyWhqKwUccSiQQjI298Ij08\nPEwqlSIcDrN27VpWr179lo+3fv16Fi9ezOLFi7n//vvZtGlTTYWNnQzDIJXooSnWRVvkCAYKL/FS\n9n5tDLiP4sZk5gTOI7JVQUPkrdgFj0jKJmeauK5WamsUO0NGLBYjFAopZEhDUtioY62trRx33HHM\nmzePSCRCV1fX2HWnnnoqt912G7Nnz2bmzJksW7Zs7LrXHwwNwxj7/uabb+aFF17A8zze9a53MX/+\n/Il7MuPANE1S8R6aY920RmYwmH+Zl7L3k3e3+11a1YuY7SywLyPaq6AhsrfiW8uUOhMMDQ35XYqM\ns1A4RCKhkCECahAXGeN5HsP5PgbzG3g584BWr9qDIEmODV9HvNfF0NFDZJ9k22z6yxnK5bLfpcg4\niEajxOKjy9jatq2QIYLChshuPM8jkx9gML+RDbkHGXY2+l1S1bAIszhyE4leD0MzQUT2mcvozuID\naU3brBeGYRCLx0aXsd0RMkTkTxQ2RPZg5z4dg/mNvJb/NdtLa4DGfbmYWCyJ3Exiq4lZadzfg8iB\nKsZNBsIOuVzO71LkAJimSSKRIBKNEIvFtE+GyB4obIi8Bc/zKJbzpHOvsr3wHJvyq6hQ8rusCWay\nJHoTTVuDmI4OGSIHaqgnSP/QIHoLrj2BQIBkMjkWMkxTuwiIvBmFDZF94DgO6dxrpIsv83Luvxpm\nBatjozfStD2KVdLhQuRgqFgw0GYwPKylt2uFbdskkgmi0SjRaFT9GCJ7SWFDZD94nsdwbjvpwqu8\nmnuEtPOC3yWNm2Oi19DSn8IqqElD5GDKdNr05YapVCp+lyJvYucIRjQaJRwOK2SI7CON/YnsB8Mw\naIp1MKXlGI5pv4Jjmj/GpNDxGHW2mvT8yJWk0i0KGiLjILq1TDKR8LsMeQOmadLU1ERnVyfd3d20\ntrYSiURqKmhs2LCBefPmHdTH/PSnP80XvvAFAD70oQ/xk5/85KA+vtSn+jozEplghmEQDSeIhmfR\nnpjOpOxSBoovsjH335S92t4peFb4ItpHurGz+tRVZDyYQDQH+XCYQqHgdznC6CZ88XiccCRMNBpV\nP8afef3eW6//WuTN6FUkcpDYVpCOpsM4ou1dLG67njmJS4kHDvG7rP0yI3QmXbnp2CMKGiLjKZx2\niIUjfpfR0AzDIJ6I09HZQc+kHlrbWonH4zUXNP75n/+ZefPmMW/ePG699VYMw8BxHC6++GJmz57N\nueeeSz6f5/HHH+ecc84B4Kc//SnRaBTHcSgUCkyfPh2A9evXs2LFChYtWsTy5ctZt27d2M95/ex7\nzcSXvaGRDZGD7PU7k7fHjmCosJm+wlpeK/6ailf9n15ODZ7MpOJRhIYcv0sRaQixfodSc5yRkdoe\nDa01lmWRSCYIh8M1GS5e74knnuC73/0uv/vd73BdlyVLlvD2t7+ddevWcfvtt7Ns2TIuv/xy/uVf\n/oXrr7+ep556CoBHH32UefPm8bvf/Y5yuczSpUsBuOqqq/jGN77B4Ycfzm9/+1v+8i//kpUrV/r5\nFKWGKWyIjBPDMIhHUsQjKboqs5icW8ZIaQtbCr+nv7QGj+rrg+ixlzLNeRvhQQUNkYliFz3Cpk3W\nNHHd6jsu1BPDMEYbvqMxItFI3TR8P/bYY5x99tlEIqOjZGeffTaPPPIIkydPZtmyZQBcfPHFfPnL\nX+bjH/8406dPZ+3atTz++OPceOONPPLII1QqFU444QSy2Sy//vWvOffcc8cev1RqtOXe5WBS2BCZ\nAIFAgJbEJFJeD13luQzlX2O4tIlN+UfJVDb7XR4ArYG5HO6dQqhfQUNkosW3lil3JkkPpf0upS4F\ng0Hi8TihcIhoNFp3G/AZhrHblKY/76nwPG/s++XLl/OLX/wC27Y56aSTuPTSS3Fdl89//vNUKhVS\nqRRPPvnkHn+WyL6o3TFDkRpkGAahYJiOpsOY3nYCx3Z8lIXNH2Na9DRsw79VaRLmocwOnENku4Pe\nRkQmnulCpDR6UiwHRyAQoKm5iY7ODiYdMom29jaSyWTdBQ2AE044gXvuuYd8Pk82m+Xuu+/mhBNO\n4JVXXmH16tUA3HHHHZxwwgljt//Sl77E2972Ntra2ujv7+f5559nzpw5JJNJpk2bxl133QWMhpSn\nn3567GepT0P2Vf294kRqhGEYxMLNxMLNdLozmZRbxEipl22F/2Vr8QlcJmaEIWp2ssD+INFeBQ0R\nP4X7HeI9MQY0ZWW/GYZBNBYlGokSjoRrbrna/XX00UfzoQ99iMWLFwNw5ZVXkkqlmDlzJl/72tf4\n8Ic/zJw5c7j66qsBWLx4Mdu2bWP58uUAHHXUUWzdunXs8f7jP/6Dq6++ms9+9rOUy2UuvPBC5s+f\nD+w6stEIv1s5cNrUT6SKeJ6H45RJ519jpLSFzflfM+SsH7efFzSaWRz6GLFeF0NHAhHflaIGAzGX\nbDbrdyk1JRQOEYvFCIfCRGNRAoGA3yWJyA4KGyJVyvM8CsUMQ4UtpEsb2ZRfRcEdOGiPbxFlSeRG\n4r0ehnpSRarGUE+Q/qFBTVd5C5ZtjfZhhEb7MGzb1iftIlVIYUOkBriuS6YwwHBxC32F59hSWE2F\n4n4/nkmQJZGbSPQamAoaIlXFtWCgzWRoeNjvUqrOzoARDAaJRCKEQiEFDJEqp7AhUmMcx2Eo38tI\nqZfthafpKz1NhX2Z422yJHIzTdssTEcvf5FqlOmw6SsMU3G0saZt28TiMQUMkRqlsCFSo0b7OxyG\nC1vJlrczWHyB3uLjlL03n+t9bOQmmvvCBEp66YtUKxdI91gMphtzKVw7aBOLKWCI1AOFDZE6UalU\nGMlvJ1veTrq0kS2F1bv1eCyMXEuqvwmrqLlTItWukAwwYJfI5/N+lzIhFDBE6pPChkgdcl2XbGGQ\nkeI2Rsqb2VL4LdOD76Et3YGdU9AQqRXpSTb9g4N+lzEuDMMgHA4TjoQJBoOEw2EFDJE6pLAhUuc8\nzyNXGKaSqxAoQmC4RCBf0VK3IjWgHDQYTHmMjGT8LuWgCAQCRKNRQuEQtm0TiUSwLEsBQ6SOKWyI\nNBDP83DKDuVcAa/oYGTLWCMOZkWHAZFqNdIVpC+TxnVrc1QyGAwSjUUJBoOEQiHC4TCmafpdlohM\nEIUNkQZWqVQo5wq4xTJesUJgpKxRD5Eq45ow2GWRrpFmcdM0R3fvDkewg6OjF9oDQ6RxKWyICPC6\nUY98Ea9YhkIFa7iMWXLRKYKIv3ItFgNenmJx//fXGS+GYWAHbaKRKHbQHmvw1i7eIgIKGyKyB67r\nUi6WqRSKeMUKRn7HlCvtzSEy4VxgaJLNQJU0i+8MFHbQVu+FiLwphQ0R2SuVSoVyoYRbKOGVKpiZ\nMlbWwajNaeQiNacUNRiMuWSyb76XzniwLItoNEowFMS2bcLhsKZGicheUdgQkX3med6Ofo8iXskZ\nDR/5MoFsBcPxNO1KZJwMd9v0DacZ77duy7KIRCMEg0FsyyYUDmlZWhHZLwobInLAPM8bnXZVKI02\nm5cqGAWHQKaMWVL4EDlY3AAMdJgMDQ0ftMfc2XMRCY82cluWRTA0unKUVo0SkQOlsCEi4+JPPR8l\nvLIDpR2rXRVcrXYlcgCy7Tb9pQzlcnm/7h8IBMZGKmzLxrItwuGwei5EZFwobIjIhNi52pWTL+KV\nHbySi1lwMLMOZlmjHyJ7ywWGemwG0m/dLG4YxmiPRSQ8NmoRCoUIBoOYpqlwISLjTmFDRHyxc+qV\nUypTKZahXMErK4CI7I1iMkB/sEQ+l9/l8p2jFDuDhW3boyMYauYWEZ8obIhI1VAAEdk7njE6ulF0\nygTtIJZlEbACY8FCvRYiUi0UNkSkqu0pgBilCmbewSy6mFp+V+qUB3iWQSVs4kYtsAMYlolhW5hB\nC8u2tHmeiFQ1hQ0RqTme5432gDgObrGM64wGEBwXo7gjhJQUQqR27AwVbsjEjVh4tolhmWCZmEEb\nK2QTCAQ0FUpEao7ChojUjd1CSLmC57wuhOQcAmUXXDQdS3zhGeDaBm4ogBsJgBUYCxWBnaMVWhVK\nROqIwoaI1L2xEFJ2cEujIyFUXDzHg8rOKVmV0Z6QivpC5MCMjVLYBm7YwguOhgnDMjGswOhIRdDS\nalAi0hAUNkSkoe0yGlJ2cMs7g4gLFW80iBQrGCVXDeoC7AgTgdEw4YUDeEETzwpgBAwImBgBE9MK\nYAatsalPChUi0qgUNkRE9mBnEHFdl0ppNIx4FRdcF6/iQWV0ZMQsj07TMhwP0/G0aWEN8wDPHB2Z\n8CwDLxjAtUdHJggYGAETAiamHcDc0ZytEQoRkT1T2BAROQA7w4jrurjlymizeqUCrvenQOK6GDtW\n0DLKHoa7Y7qWekcmzOhoxOiIhGebuEETzx4NDpgGhmmMfW0GTAzLImCPjkooTIiI7D+FDRGRcfb6\nERLXHZ2i5VUqeK6H57rgeqPhZMe/uKMhxajsCCk7A4o7GlDwGjekjIUG08AzDbAMPMvEs0wIgGeO\nBgYMRgPEjv8M83XTm6w/jUYoRIiIjC+FDRGRKvSGAcXd+Z8HnrfjzHtHUBn7nl2vq/wpqOD+6XJj\n7L6jP8/YeV923GaXy3bcFnakHON1X++4+vXn7Dtvs+Myb+dl5mhIIGCO/msaeCY7wsGO24/9y2gQ\nGLtsZ4AYDQ2GOdpw/frQoPAgIlJ9FDZEROrUzsP7nv7d+fVYUNkRNLzXhZXRi73XhY3XBw1jxz+7\nXjaWM4xdQ8nOXa3/PBgoIIiI1C+FDRERERERGRem3wWIiIiIiEh9UtgQEREREZFxobAhIiIiIiLj\nQmFDRERERETGhcKGiIiIiIiMC4UNEREREREZFwobIiIiIiIyLhQ2RERERERkXChsiIiIiIjIuFDY\nEBERERGRcaGwISIiIiIi40JhQ0RERERExoXChojIPigWi5x//vnMmDGDpUuXsnHjRgA8z+Paa69l\nzpw5zJ49m+uuu26vH/Phhx/mjDPOeMPrDj30UAYGBg5K7SIiIhNNYUNEZB98+9vfprW1lRdeeIEb\nbriBW265BYBVq1bxhz/8gTVr1rBmzRoef/xxVq1adcA/zzCMA34MERERvyhsiEjDyGaznH766SxY\nsIB58+bx4x//mLPOOmvs+gcffJCzzz4bgHg8zqc+9SkWLFjAsmXL2LZtGwD33nsvl156KQDnnHMO\nK1euBKCjo4NSqUSxWCSfz1Mul+nq6tpjLb/85S+ZNWsWCxcu5O677x67vL+/n3e/+93MnTuXK6+8\nEs/zANiwYQOzZs3iqquuYu7cuZxyyikUCoWD+wsSERE5yBQ2RKRh/PKXv2TSpEk89dRTPPPMM5x6\n6qmsXbuW/v5+AL7zne9w+eWXA5DL5Vi2bBlPPfUUy5cv55vf/CYAmzdvZvLkyQBYlkVTUxMDAwPM\nnj2bd7/73XR3dzNp0iROPfVUZs6c+YZ1FAoFrrrqKn7+85/zxBNP0NvbOzaC8ZnPfIbly5ezZs0a\nzjrrLF555ZWx+7344otcc801rFmzhubmZn7yk5+M2+9KRETkYFDYEJGGMX/+fB588EE++clP8thj\nj5FMJrnkkkv4/ve/TzqdZvXq1axYsQKAYDDI6aefDsDChQvZsGHDmz72I488wkMPPcTmzZvZvHkz\nK1eu5LHHHnvD265du5Zp06Yxffp0AC6++OKxEYxHH32Uiy++GIDTTjuNVCo1dr9p06Yxf/78va5J\nRETEb5bfBYiITJQZM2bw5JNPct999/GpT32Kk046iSuuuIIzzjiDcDjMeeedh2mOfgZj2/bY/UzT\nxHEcACZNmsQrr7xCT08PjuMwNDRES0sLv/nNb1ixYgXRaBSAFStW8Jvf/Ibjjz9+tzr+vA9jZ9DY\n0/c7hUKhsa8DgQD5fH4/fgsiIiITRyMbItIwtmzZQjgc5qKLLuKmm27iySefpLu7m56eHj772c9y\n2WWXveVjvPe97+Xf/u3fALjrrrs46aSTAJg1axarVq2iUqlQLpdZtWoVs2fPfsPHmDlzJhs2bOCl\nl14C4Ac/+MHYdcuXL+eOO+4A4P7772dwcPCAnrOIiIifNLIhIg3jmWee4ROf+ASmaWLbNrfddhsA\nH/jAB+jr69ulx+L1ow+GYYx9f/nll3PJJZcwY8YMWltb+eEPfwiMhpCHHnqIo446Cs/zWLFixdg0\nrD8XDof513/9V04//XSi0SgnnHAC2WwWgL/7u7/jwgsv5Ac/+AFve9vbmDp16hvW9Ebfi4iIVBvD\n29N4vYhIg7jmmmtYuHDhXo1siIiIyN5T2BCRhrZw4UISiQQPPvjgLn0aIiIicuAUNkRExtHZZ5/N\nyy+/vMtln/vc5zj55JN9qkhERGTiKGyIiIiIiMi40GpUIiIiIiIyLhQ2RERERERkXChsiIiIiIjI\nuFDYEBERERGRcaGwISIiIiIi40JhQ0RERERExoXChoiIiIiIjAuFDRERERERGRcKGyIiIiIiMi4U\nNkREREREZFwobIiIiIiIyLhQ2BARERERkXGhsCEiIiIiIuNCYUNERERERMaFwoaIiIiIiIwLhQ0R\nERERERkXChsiIiIiIjIuFDZERERERGRcKGyIiIiIiMi4UNgQEREREZFxobAhIiIiIiLjQmFDRERE\nRETGhcKGiIiIiIiMC4UNEREREREZFwobIiIiIiIyLhQ2RERERERkXPz/XcOerPOZ84MAAAAASUVO\nRK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x147f40b8>"
]
}
],
"prompt_number": 12
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load differnt res and jco that is better for correlation plotting"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"res2 = pt.Res('cor_testing.res')\n",
"jco_df2, par_names2, obs_names2 = pt.load_jco(r'cor_testing.jco')\n",
"cor = pt.Cor(jco_df2, res2.df)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 14
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Correlation plotting needs some work. "
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"interactive(cor.plot_img_with_dendrograms, use_abs_cor = True)\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA+gAAAI3CAYAAAAIvHGqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xt4VPWB//HPTDITEpMYJhAhMWQ3pYHdAYwBTAkEKKhN\nL3R1F+1WUVvLVoSgSIIiupFIG0phYmxR7C6pj4poXVu0LiD8KEWWIs1SZFnySKmIRRMkkBBCyI1k\n5vcHm5FwDeTy/ULer+fx0XPmzDmfGTOXz3zPxREIBAICAAAAAABGOU0HAAAAAAAAFHQAAAAAAKxA\nQQcAAAAAwAIUdAAAAAAALEBBBwAAAADAAhR0AAAAAAAsEGo6AAAAAACgc1VUVOg3v/mN6urqNHv2\n7OD8AwcO6K233pIk3X777UpMTDQVEefACDoAAAAAXGXi4uI0bdq0s+avXbtWU6dO1dSpU7V27VoD\nyXAhjKADAAAAQA9RV1eniIgISVJDQ4PhNDhTjyvo5eXlpiMAAAAAPV58fPxZ8xwOh4EkV6bdu3er\ntLQ0OO31euX1ei96v4iICNXV1UmSevXq1WX5cHkcgUAgYDpEd6KgAwAAAOadq6CHOnvc+OFla/Y3\nX/D22tparVy5Urt379aECRP02WefKTs7W59++qnefvttSdJtt92m66+/vjviop0o6AAAAAC63bkK\nenhouIEkV6b65nrTEdAF+IkKAAAAgBVCnW7TEQCjKOgAAAAArBDiCDEdATCKgm6I1+tVdXW16RgA\nullMTEybE7oAAIAvhDCCjh6Ogm5IdXW1ysrKTMcA0M0SEhJMRwAAwFpOThKHHo5XAAAAAAArOEMY\nQe8sDQ0NWr58uVwul7xer8aMGSNJ2rp1q3bs2KHQ0FBNmjSJwQPLUNABAAAAWIGC3nlKSkqUkZGh\ntLQ0FRUVBQv6H//4Rz388MM6fvy4XnvtNU2bNs1wUpyOgg4AAADACg52ce80VVVVSkpKkiQ5nc7g\n/EmTJqm4uFgxMTE6ceKEqXg4D14BAAAAAKzgCGUEvb1KS0vbnHjW6/XK6/UGpz0ejyorK5WUlCS/\n3x+cP3DgQA0cOFCff/653n333W7NjItzBAKBgOkQ3am8vNx0BEmnThTFSeKAnofXPgAAp8THx581\nL6H/TQaSXJnKDpZc8PbGxkYVFxfL7XZr8ODB2rlzp7Kzs/XBBx/oT3/6kxoaGnTPPffo2muv7abE\naA8KuiF8SQd6Jl77AACccq6Cfn3iaANJrkyfffoH0xHQBdjFHQAAAIAVAi7qCXo2XgEAAAAA7BAS\nYjoBYBQFHQAAAIAVAqHUE/RsvAIAAAAA2CHUefFlgKsYBR0AAACAFQIudnHvLA0NDVq+fLlcLpe8\nXq/GjBkjSdq5c6c2bdqkQCCgiRMnatiwYYaT4nQUdAAAAABWCLgYQe8sJSUlysjIUFpamoqKioIF\nfffu3br33nvlcDj09ttvU9AtQ0EHAAAAYIVAiMN0hKtGVVWVkpKSJElO5xc/fIwZM0Y+n08Oh0M/\n/OEPTcXDeVDQAQAAANjBTUFvr9LSUpWWlganvV6vvF5vcNrj8aiyslJJSUny+/3B+W+99Zaefvpp\nBQIBPf/883rooYe6NTcujIIOAAAAwAoBDkFvtzML+ZnS09NVXFysHTt2aMSIEVq6dKmys7OVlpam\nZcuWSZJSU1O7Ky7ayREIBAKmQ3Sn8vJy0xEkSQkJCSorKzMdA0A347UPAMAp8fHxZ82Ly/oHA0mu\nTBXvvm06AroAI+gAAAAA7OA2HQAwi9MkAgAAALBDSIB/2vuPQTk5OUa3fzVjBB0AAACAFRwu/8UX\nQrfw+/36j//4D91+++1yu9vu2nDbbbcZSnX1o6ADAAAAsILD8MgwvuB0OrV+/XrdcccdZ92WmZlp\nIFHPQEEHAAAAYAUnI+idpqGhQcuXL5fL5ZLX69WYMWMkSRs3btS+fftUWVmpAQMG6K677jrvOsaO\nHav169crKyuru2L3eBR0AAAAAFZwhraYjnDVKCkpUUZGhtLS0lRUVBQs6BMmTNCECRP00ksv6atf\n/eoF1/HRRx/p3Xff1W9/+1vFxsbK4Th1nXqHw6H8/Pwufww9EQUdAAAAgBWcIYygt1dpaalKS0uD\n02deF72qqkpJSUmSTu2ufrqmpiZVVFSof//+F9zGxIkTNXHixE5MjYuhoAMAAACwQggj6O12ZiE/\nk8fjUWVlpZKSkuT3t/3hY9u2bUpPT7/oNsaPH9/RmLhEFHQAAAAAVghxMoLeWdLT01VcXKwdO3Zo\nxIgRWrp0qbKzsyWdKuiPPPLIRdcRCAT0+9//Xv/1X/+lqqoqeTweZWZm6qtf/Wpwd3d0Lgo6AAAA\nACu4QhhB7yxhYWGaPn16cLr1GHRJevTRR9u1jlWrVum9997TpEmT1KdPHx05ckTvvPOOjh49qn/6\np3/q9MygoAMAAACwBAXdLr/73e80f/589e3bNzjvhhtuUF5eHgW9i1DQAQAAAFghlF3crdLY2Kio\nqKg286KionTy5ElDia5+FHQAAAAAVgijoFslNTVVP//5z3XXXXepb9++qqio0Ouvv64bbrjBdLSr\nFgUdAAAAgBUYQbfL/fffr1/+8peaM2eOWlpaFBISolGjRun+++83He2qRUEHAAAAYIVejoDpCFeN\nhoYGLV++XC6XS16vN3iSuKNHj2rVqlWSpNGjR2vQoEHnXUdERISys7M1ffp01dTUKDo6+qxrqqNz\nUdABAAAAWKEXI+idpqSkRBkZGUpLS1NRUVGwoL/zzjuKiIhQQ0ODYmNjz3nfAwcOaMeOHbrtttsk\nSU6nUzExMZKkt956SyNGjND111/fPQ+kh6GgAwAAALCCy3SAK0hpaalKS0uD016vV16vNzhdVVWl\npKQkSWoz6v3ZZ5/p+9//vqKjo/XKK69o2rRpZ637zTff1E033XTO7fbt21dvvvmmZs2a1VkPBaeh\noAMAAACwQrjDdIIrx5mF/Ewej0eVlZVKSkqS3+9vM/+aa65RWFjYec/G/pe//EXZ2dnnvG3kyJF6\n5ZVXOhYe50VBBwAAAGAFt+kAV5H09HQVFxdrx44dGjFihJYuXars7Gx961vf0ooVKyRJX/va1855\n39ra2vMea+50OnXixIkuy93TUdABAAAAWCHcwRB6ZwkLC9P06dOD063HoF9//fVt5p9LXFyc/vzn\nP59zhH7v3r2Ki4vr3LAIoqADAAAAsEK4OEO4DSZOnKgXXnhBs2bN0pe+9KXg/I8//li/+MUvzjvy\njo6joAMAAACwgpuCboWvf/3r+vzzz/XEE08oNjZWMTExqq6uVmVlpW699VZ94xvfMB3xqkVBBwAA\nAGCF8ECI6QiQ5HA4dP/99+vrX/+6/vd//1e1tbWKjIzU0KFD1b9/f9PxrmoUdAAAAABWcIuC3lka\nGhq0fPlyuVwueb3e4DHob7zxhsrKyhQZGanJkyerd+/e511H//79KeTdjIIOAAAAwArh1JNOU1JS\nooyMDKWlpamoqChY0ENDQ+VyuRQaGqprrrnGcEqciVcAAAAAACuEB7jQWmepqqpSUlKSJLW5ZNrt\nt98uh8Oh7du3a+PGjcrKyjIVEedAQQcAAABgBTf1pN1KS0tVWloanPZ6vW0ui+bxeFRZWamkpCT5\n/f7gfMf/XcouOjpan376afcFRrvwCoBxXq9X1dXVpmMA3SYhIcF0BKBbxMTEtPnyCAAX00thpiNc\nMc4s5GdKT09XcXGxduzYoREjRmjp0qXKzs7WqlWrVFlZqZqaGt1///3dmBjtQUGHcdXV1SorKzMd\nAwDQyfgxCsClcsllOsJVIywsTNOnTw9Otx6Dfvvtt3d43QsXLtTjjz/e4fXgbBR0AAAAAFYIYwT9\nijBo0CDTEa5aFHQAAAAAVnAr3HQEtMM//uM/mo5w1aKgAwAAALCCS5zF3SaffvqpoqKiFBMTo/r6\nev32t7+V0+nUt7/9bYWFsbdDV6CgAwAAALCCy8EIuk2effZZzZ49WzExMXrllVd08OBBuVwu/du/\n/ZtmzpxpOt5ViYIOAAAAwAohjKB3moaGBi1fvlwul0terzd4kjhJOnDggBYsWKClS5decCT88OHD\nio+Pl9/v1x//+Ec988wzcrvdmjFjRnc8hB6Jgg4AAADACqHOCNMRrholJSXKyMhQWlqaioqKggW9\nublZGzdu1I033qhAIHDBdbjdbtXV1amsrEx9+/ZVdHS0mpubdfLkye54CD0SBR0AAACAFULZxb3T\nVFVVKSkpSZLkdDqD8//zP/9TX//61/XrX//6ousYPXq0nn76adXX1ysrK0uStH//fl133XVdExoU\ndAAAAAB2cDo48Vh7lZaWqrS0NDjt9Xrl9XqD0x6PR5WVlUpKSpLf7w/O/+STT1RdXa2PPvpIGzZs\n0Le+9a3zbuN73/uedu7cqdDQUA0ZMkTSqbJ/3333dcEjgiQ5Ahfbr+EqU15ebjqCJCkhIUFlZWWm\nY1iB5wIArk68vwO4kPj4+LPm/W9+sYEkV6ahT/3ggrc3NjaquLhYbrdbgwcP1s6dO5WdnR28/fnn\nn9cPfvCDdp2NvaqqSlVVVfJ4PPJ4PB3OjvNjBB0AAACAFRxORtA7S1hYmKZPnx6cPv0kcZLa3HY+\nR44c0c9+9jPt3btXkZGRqq2tVUpKimbOnKm+fft2emZQ0AEAAABYwhHCMeg2Wbp0qZKTkzVv3jz1\n6tVLDQ0Nev311/Xcc89p/vz5puNdlSjoAAAAAKxAQbfL/v379eSTTyo09FRt7NWrl6ZMmaL777/f\ncLKrFwUdAAAAgBUCTq6DbpMvf/nL+uijjzR48ODgvI8++kgpKSkGU13dKOgAAAAA7BDay3SCHu/1\n11+Xw+FQIBDQddddp4ULFyotLU2xsbE6cuSIPvjgA2VmZpqOedWioAMAAACwQiCEEfTO0tDQoOXL\nl8vlcsnr9QZPEvff//3f2rlzpyorK3XHHXfoS1/6Upv7VVZWyuFwBKdvuukmSVJNTY1cLpduuukm\nNTU1dd8D6WEo6AAAAACsEAjlLO6dpaSkRBkZGUpLS1NRUVGwoI8cOVIjR47UJ598oh07dpxV0GfM\nmHHRdZ9+XXV0Lgo6AHSQ1+tVdXW16RiAlRISEkxHAKwSExOj0tJS0zGs5XdR0DtLVVWVkpKSJElO\np7PNbe+8847+9Kc/adq0aZe0zr/+9a9677339Ic//EG/+MUvOi0rvkBBB4AOqq6uVllZmekYAIAr\nAD9aXVgghHrSXqWlpW1+7PF6vfJ6vcFpj8ejyspKJSUlnTXiPWnSJI0bN04rV668aEk/duyYtmzZ\novfee09//etfNXjwYH3ve9/r1MeCL/AKAAAAAGAFv8tlOsIVw+sd2KaQnyk9PV3FxcXasWOHRowY\noaVLlyo7O1sbN27UJ598otraWk2YMOGc921ubtb27du1adMm/c///I+uv/56jRo1SocPH9Yjjzyi\nmJiYrnpYPR4FHQAAAIAVAqHUk84SFham6dOnB6dbj0E/Xyk/3b/8y7/o2muv1dixY3Xfffepf//+\nkqR33323zQnk0Pl4BQAAAACwgt9FPbFBUlKSPvroI/3lL39R3759FRMTo/DwcNOxegReAQAAAACs\n4HdTT2wwf/58VVRUaPPmzXrjjTf0wgsv6IYbblBDQ4Oam5tNx7uq8QoAAAAAYAV/iPPiC6FbxMXF\nafLkyZo8ebL27NmjTZs2yeFwaM6cOfrqV7+qe+65x3TEqxIFHQAAAIAVAm4Kuo0GDx6swYMH6/77\n71dJSYk2b95sOtJVi4IOAAAAwAqBEE5A1lkaGhq0fPlyuVwueb3e4Eni3nrrLVVUVOj48eP6/ve/\nL4/H0+51ut1ujRkzJrgudD4KOgAAAAAr+N0U9M5SUlKijIwMpaWlqaioKFiqb7vttuDtu3fv1tix\nY03GxBko6AAAAADs4KKgd5aqqiolJSVJkpzOtocONDQ06P3339cDDzxgIhougIIOWMbr9aq6utp0\nDFyihIQE0xFwiWJiYlRaWmo6BoBuYtPnqw2fGba+BwZoJ+1WWlra5v+h1+uV1+sNTns8HlVWViop\nKUl+vz84v66uTsXFxZoyZYp69erVrZlxcbwEAMtUV1errKzMdAzgqmfDF2QA3YfP17asfQ90mQ5w\n5TizkJ8pPT1dxcXF2rFjh0aMGKGlS5cqOztbzz//vPx+v37zm99o1KhRGjJkSDemxsVQ0AEAAABY\nwRFiOsHVIywsTNOnTw9Otx6DnpubayoS2oGCDgAAAMAKDkbQ0cNR0AEAAABYwREaMB0BMIqCDgAA\nAMAKzhAKOno2CjoAAAAAKzgZQUcPR0EHgG5g0+V98AVrz2LcQ9l62ScA3cfJSeI6TUNDg5YvXy6X\nyyWv1xs8SdwHH3ygd999VzfeeKOysrIMp8SZKOgA0A24vA+60tXyA1B1dfVV86MJPzYAlyeEXdw7\nTUlJiTIyMpSWlqaioqJgQb/xxhsVFhamAwcOGE6Ic6GgA7DW1VI6Wl0NxYPSYSd+ALLP1fB6B0wI\nZQS93UpLS9t8Jp95XfSqqiolJSVJkpxOZ7fnw+WhoAOwFqXDPpQOAEBXCqFHttuZhfxMHo9HlZWV\nSkpKkt/vb3NbIMCeCraioAMAAACwgosR9E6Tnp6u4uJi7dixQyNGjNDSpUuVnZ2tvXv3avXq1Tpx\n4oR69+6t9PR001FxGgo6AAC4ath0aIwNe5xwWAquNCEO0wmuHmFhYZo+fXpwuvUY9JSUFD366KOm\nYuEiKOgAAOCqwaExbdnwIwFwKdw0dPRwFHQAuELYMjJowxd+RgUB4OrkclLQ0bNR0AHgCsHI4Bds\n+JEAAND5Qh2cJQ49GwUdAAAAgBVcXA4MPRwFHQAAAIAVGEHvPA0NDVq+fLlcLpe8Xm/wJHEHDhzQ\nW2+9JUm6/fbblZiYaDImzkBBBwAAAGAFt4N60llKSkqUkZGhtLQ0FRUVBQv62rVrNXXqVEnSihUr\n9MMf/tBkTJyhx70C4uPjTUeQJAUCAdMRrMFz0RbPxxd4Ltri+fgCz0VbPB9f4Lloi+fjCzwXbdn6\nfLicPa6eXLbS0tI2J0z1er3yer3B6aqqKiUlJUmSnKcdOlBXV6eIiAhJp0bZYRdeAQAAAABwhTmz\nkJ/J4/GosrJSSUlJ8vv9wfkRERGqq6uTJPXq1avLc+LSOAK2/nwGAAAAALgsjY2NKi4ultvt1uDB\ng7Vz505lZ2fr008/1dtvvy1Juu2223T99dcbTorTUdABAAAAALAAp0kEAAAAAMACPe4Y9HueuMF0\nBElS5o3f1n998FujGdb/Psno9lt95xsT9Ks1G03HUOi+MtMRJEl3fmeS3vjVO0YzNB4/aHT7rf55\nyp16fcUbpmMo7NoE0xEkSXfe+S298cZ/mg1hyeVv7rzzm3rjjdWmY6jpmB3vG/885Q69vuI/TMdQ\ndf0h0xF073336uWXXjYdQ82BZtMRJEn33XefXnrpJdMx1K/335mOoDu/e5veeO0t0zHk6NPfdARJ\n0p23f01vrFpnOobK9/6u7XR5uaEkQPe50InL7fim1QP16W3H2eRtkNj/OtMRrHJ9oh0f3DYYkMR1\nOU/H38YXeC7aShzAa6VV0t/Y8eOzLf7mb/7GdARrJA6w48dWWyRez/cvwEYUdAAAAAAALEBBBwAA\nAADAAhR0AAAAAAAsQEEHAAAAAMACFHQAAAAAACxAQQcAAAAAwAIUdAAAAAAALEBBBwAAAADAAhR0\nAAAAAAAsQEEHAAAAAMACFHQAAAAAACxAQQcAAAAAwAKhF1ugoqJCixYtks/n6/SNr169Wrfccovc\nbrck6bXXXtPmzZt14sQJvfzyy8HlTp48qaVLl2r//v2KiorSrFmz1LdvX33yySdavny56uvr5XQ6\ndfvttysjI6PTcwIAAAAA0NWMjqCvWbNGjY2NwemRI0dq4cKFZy23ceNGRUVF6Wc/+5m++c1v6tVX\nX5UkhYWFKTs7Wz6fT/PmzdNLL72kurq6bssPAAAAAEBnuegI+ukOHTqkwsJCPfDAA0pOTm5z26ZN\nm1RSUqL6+npVVVUpMzNTkydPVkVFhQoKCpScnKz9+/crMTFR2dnZ2rBhg44ePar8/HxFR0crLy9P\nAwcOPOd2t2/frjvvvFOSlJ6eruLiYklS//79g8v07t1b0dHRqqmpUURExCU9CQAAAAAAmNbugl5e\nXq5nn31WM2bM0IABA865zL59++Tz+eR2u/X4448rLS1NkZGROnjwoKZPn66UlBQtW7ZM69at06RJ\nk7R69WrNnz9fkZGRF9x2VVWVYmNjJUkhISGKiIhQbW1tm/t99NFHamlpUb9+/dr7kAAAAAAAsEa7\nCnpNTY0WL16s3NxcJSQknHe5YcOGBUtzenq69uzZo5EjRyo2NlYpKSmSpMzMTK1du1aTJk3qhPin\nHD16VEuXLlV2dvZFl8288dvq0zu+07Z9uf7ub0dIE6YZzTAsOcbo9ltl3DhEuT/4rukYclbVmI4g\nSRqVMVyzc39oNENLU63R7bcanTlKjz6RYzqGQsKiTEeQ9H9/G6ZDOBymE0iSRo1K0+ycqaZjqKXh\nuOkIkk69VjTP+F+HGprNv3eMGzdOesp0Cskf8JuOIEkaP3686QiSpMjwvqYjKGP0SOmxGaZjyBFx\n4YGp7jLqphuUM/Neoxl8P3/57Hk+nwoLC7tkezExMSotLe2SdQOdpV0FPSIiQn369NGHH354wYJ+\nukAgIMf/fZFznPGF7szpi/F4PDpy5Ig8Ho9aWlpUV1cX/CGgrq5OP/nJT/Td7373vLvIn+6/Pvjt\nJW27y0yYplUbXzAaYf3vk4xuv1XuD76rJcWvmY6h0H1lpiNIkmbn/lCFS/7NaIbG4weNbr/Vo0/k\n6Kc/7vwTVF6qsGvb977X1WZLKvT9u9kQDjsu/jE7Z6oKfctNx1DTMTveNzRvthYXdM0X2ktRXX/I\ndATpKWlB/gLTKdQcaDYdISg/P990BPXr/XemI0iPzZBv0XOmU8jRp//FF+oGOTPvPWdBNi0nJ0c5\nOV3z43x7ewxgUru+aYWGhio3N1ebN2/Wli1bzrvcrl27VFtbq6amJm3fvl2DBg1SIBDQkSNHtHfv\nXknSli1bNHjwYElSeHh4u07qNmLECL333nuSpG3btmno0KGSpObmZi1ZskTjxo1Tenp6ex4KAAAA\nAABWatcIusPhUFhYmObOnasFCxYoPDxcw4cPP2u5gQMHyufzBU8Sl5ycrIqKCsXHx2vdunVatmyZ\nEhMTdeutt0qSbr75ZhUUFMjj8SgvL08rVqzQH/7wBzU1NenBBx/UxIkTNXnyZE2YMEE///nP9dBD\nDykqKkoPP/ywJGnr1q368MMPVVtbq02bNkmSZsyYoaQkO0aGAQAAAABor4sW9Li4OC1ZskTSqV3d\nz3UZtFaxsbGaM2fOWfOdTqdmzpx51vysrCxlZWUFp6dMmaIpU6actZzL5dLs2WcfWzd27FiNHTv2\nYg8BAAAAAADrdcvBhJd6zDkAAAAAAD3NJV0HXZJ27typlStXtpkXFxen3Nzcc54p9PQReAAAAAAA\ncG6XXNBTU1OVmpraFVkAAAAAAOix7LheDgAAAAAAPRwFHQAAAAAAC1DQAQAAAACwAAUdAAAAAAAL\nUNABAAAAALAABR0AAAAAAAtQ0AEAAAAAsAAFHQAAAAAAC1DQAQAAAACwQKjpAN0t0pLfJNxyGM/i\nOOk3uv1WjpaAFVkCLSdNRzgl4Deepf5kjdHttzrZ0mhFlpDaXqYjSJL8TfVqrq00HcMK/sY6NR8/\nbDqGTjRWmY4gSTrZUm9FluZAs+kI8gf8VuQIddjxFcvpcFqRxX+ywXQEBVqarcjhrCgzHUGSFDhx\nXAFLsgD4gh1tFQAAAAC6WEJCgrxer+kYwHlR0AEAAAD0CGVlZaqurjYdAzgvCjoAAAAAABagoAMA\nAAAAYAEKOgAAAAAAFqCgAwAAAABgAQo6AAAAAAAWoKADAAAAAGABCjoAAAAAABagoAMAAAAAYAEK\nOgAAAAAAFqCgAwAAAABgAQo6AAAAAAAWoKADAAAAAGCByy7oFRUVysnJ6cwsQatXr1ZTU1NweuvW\nrZozZ45ycnL06quvnrX8tm3b9J3vfEcff/xxl+QBAAAAAKCrWTmCvmbNGjU2NkqSjh8/rhUrVigv\nL08+n0/V1dXavXt3cNn6+nqtXbtWX/7yl03FBQAAAACgw0I7YyWHDh1SYWGhHnjgASUnJ7e5bdOm\nTSopKVF9fb2qqqqUmZmpyZMnq6KiQgUFBUpOTtb+/fuVmJio7OxsbdiwQUePHlV+fr6io6N19913\nq3///oqKipIkDR06VNu2bdOQIUMkSb/61a/0D//wD3rnnXc646EAAAAAAGBEh0fQy8vLVVhYqBkz\nZpxVzlvt27dPOTk5Wrx4sd5///3grugHDx5UVlaWnnnmGYWHh2vdunX6xje+od69e2v+/PnKy8vT\nddddp/Lych0+fFgtLS0qKSlRVVWVJOnjjz9WVVWV0tLSOvowAAAAAAAwqkMj6DU1NVq8eLFyc3OV\nkJBw3uWGDRumyMhISVJ6err27NmjkSNHKjY2VikpKZKkzMxMrV27VpMmTWpz38jISE2dOlVFRUVy\nOBxKSUlRRUWFAoGAXn75Zc2YMeOSMn/lxkmK7R1/iY+086X87QhpgtkMX0qKNhvg/2QMH6pc3WU6\nhhzVx0xHkCSNGj1COY8+aDRDQ8NRo9tvlTkuU/M0z3QMuUOvMR1BkpSRma5cPWw6hhVseS6ammtN\nR5B06rXyRN4TpmPopP+k6QgaP3686QiSJKfDjqMIx40bJz1lOoUU7rrWdARr3jcczhDTESRJGWNu\nkuZmG83g+8nSs+f5fCosLOyS7cXExHTJeoHO1KGCHhERoT59+ujDDz+8YEE/XSAQkMPhkKTgv1ud\nOd1q+PDhGj58uCRpw4YNCgkJUX19vT799FPNnz9fklRdXa1FixbpscceO+9IviRt+8CSXeEnSKs3\n/sJohFW9ZAixAAAgAElEQVTr2/f/rKvl6i4t+feVpmPIuf+A6QiSpJxHH5Tvp8uMZjh2zI4TLs7T\nPBUsKDAdQ5G94kxHkCTl6mEtWfis6RhWsOW5OF7/uekIkqQn8p7Qj5/+sekYqm+pNx1BkpSfn286\ngkIdnXIUYcc9JS3IX2A6hTzXJJqOYM37hjPEbTrCKXOzz1mQTcvJyemyE1EDV4IO/bwbGhqq3Nxc\nbd68WVu2bDnvcrt27VJtba2ampq0fft2DRo0SIFAQEeOHNHevXslSVu2bNHgwYMlSeHh4aqrqwve\n/9ixUyObtbW1Wr9+vSZOnKiIiAgVFxfrueee03PPPaeUlJSLlnMAAAAAAGzVoZ93HQ6HwsLCNHfu\nXC1YsEDh4eHBke7TDRw4UD6fL3iSuOTkZFVUVCg+Pl7r1q3TsmXLlJiYqFtvvVWSdPPNN6ugoEAe\nj0d5eXl68cUXdeDAqdHNyZMnq1+/fh2JDQAAAACAdS67oMfFxWnJkiWSTu3qvnDhwvMuGxsbqzlz\n5pw13+l0aubMmWfNz8rKUlZWVnB61qxZF83z1FMWHGAFAAAAAMBlMnoGk/Mdcw4AAAAAQE/TaWcw\n2blzp1aubHuir7i4OOXm5p7zjKqnj8ADAAAAANDTdVpBT01NVWpqametDgAAAACAHsWOi3QCAAAA\nANDDWXKRTgAAAADoHgkJCcH/jomJUWlpqcE0wBco6AAAAAB6lLKysuB/n17WAdPYxR0AAAAAAAtQ\n0AEAAAAAsAAFHQAAAAAAC1DQAQAAAACwAAUdAAAAAAALUNABAAAAALBAj7vM2rGA33QESVKjAsaz\nOGubjG6/laOpxYosJ45/ZjqCJKmpscZ4lrrmE0a33+qkv8mKLKFN1aYjSJKaWxrUYEkW02x5Lk76\nT5qOIElqCbRYkSUi9BrTEeRyuq3IEe6KNh1BktQr9Bpd26uv6RgKjYw1HUFOd7gVOeqP/tV0BElS\nS3O9GhuqTMcAcAZG0AEAAAAAsAAFHQAAAAAAC1DQAQAAAACwAAUdAAAAAAALUNABAAAAALAABR0A\nAAAAAAtQ0AEAAAAAsAAFHQAAAAAAC1DQAQAAAACwAAUdAAAAAAALUNABAAAAALAABR0AAAAAAAtQ\n0AEAAAAAsAAFHQAAAAAAC4Re7h0rKiq0aNEi+Xy+zswjSVq9erVuueUWud1uSdLWrVu1atUq+f1+\npaWl6e677w4uu3XrVr355ptyOBxKSkrSQw891Ol5AAAAAADoapdd0LvSmjVrNHbsWLndbh0/flwr\nVqzQokWLFBUVpeeee067d+/WkCFDdPDgQb399tv60Y9+pIiICNXU1JiODgAAAADAZemUgn7o0CEV\nFhbqgQceUHJycpvbNm3apJKSEtXX16uqqkqZmZmaPHmyKioqVFBQoOTkZO3fv1+JiYnKzs7Whg0b\ndPToUeXn5ys6Olp33323+vfvr6ioKEnS0KFDtW3bNg0ZMkS/+93v9LWvfU0RERGSpOjo6M54OAAA\nAAAAdLsOF/Ty8nI9++yzmjFjhgYMGHDOZfbt2yefzye3263HH39caWlpioyM1MGDBzV9+nSlpKRo\n2bJlWrdunSZNmqTVq1dr/vz5ioyMVG1trcrLy3X48GF5PB6VlJTI7/dLkg4ePChJ+td//Vf5/X7d\ncccdSk1N7ehDAgAAAACg23WooNfU1Gjx4sXKzc1VQkLCeZcbNmyYIiMjJUnp6enas2ePRo4cqdjY\nWKWkpEiSMjMztXbtWk2aNKnNfSMjIzV16lQVFRXJ4XAoJSVFFRUVkqSWlhZ9/vnnys/P15EjR/TU\nU0/J5/MFR9TPZWzat9W3d3xHHnan+Lu/HaF/mjjNaIbh8ZFGt99q1E3DlKN7TMdQ09GJpiNIksaM\nHa25Tz5mNENjS73R7bcaP3686QiSpLCQcNMRJNnxt2ELW56Lk/5G0xEkSePGjZOeMp1CCnGYP3Iu\nc1ym5mme6RhyhYSZjiBJGp05So8+kWM6hkLCokxH0KiM4ZptOoSk5oZjpiNIkkaPzdBjT84xmmHR\njxafNc/n86mwsLBLtxsTE9Ol6wc6okOfpBEREerTp48+/PDDCxb00wUCATkcDkkK/rvVmdOthg8f\nruHDh0uSNmzYoJCQEElSbGysvvzlL8vpdCouLk7x8fH6/PPPz9rN/nSbd/y2XTm72j9NnKZf/+4F\noxk2rbrO6PZb5ege+Z57xXQMnfh4u+kIkqS5Tz6mn/xokdEMNU1HjW7/dPn5+aYjKNrd23QESXb8\nbdjCluei7uRx0xFOeUpakL/AdAq5LSil8zRPBQsKTMdQuMuOw+4efSJHP/1x55/Q91KFXdu+74ld\nabakQt+/m46h+qN/NR1BkvTYk3POWZBNy8nJUU6O+R+VAFM6dJm10NBQ5ebmavPmzdqyZct5l9u1\na5dqa2vV1NSk7du3a9CgQQoEAjpy5Ij27t0rSdqyZYsGDx4sSQoPD1ddXV3w/seOnfqlsba2VuvX\nr9fEiadGOkeOHKnS0lJJp0bzy8vLFRcX15GHBAAAAACAER0aQXc4HAoLC9PcuXO1YMEChYeHB0e6\nTzdw4ED5fL7gSeKSk5NVUVGh+Ph4rVu3TsuWLVNiYqJuvfVWSdLNN9+sgoICeTwe5eXl6cUXX9SB\nAwckSZMnT1a/fv0kSampqdq1a5dmz54tp9Ope+65J7grPQAAAAAAV5LLLuhxcXFasmSJpFO7ui9c\nuPC8y8bGxmrOnLOPcXE6nZo5c+ZZ87OyspSVlRWcnjVr1nnXfe+99+ree++9lOgAAAAAEOT1eoN7\n5gImdWgX94463zHnAAAAANBdqqurTUcAJHXSddAlaefOnVq5cmWbeXFxccrNzT3nmZhPH4EHAAAA\nAKCn67SCnpqayjXIAQAAAAC4TEZ3cQcAAAAAAKdQ0AEAAAAAsAAFHQAAAAAAC1DQAQAAAACwAAUd\nAAAAAAALUNABAAAAALAABR0AAAAAAAtQ0AEAAAAAsAAFHQAAAAAAC4SaDtDdbgt8yXQESdLggMd4\nlv+X3Gx0+61aeofqZHIv0zF0zZEBpiNIktxh1+qaaLNZ6iqPG91+K6fDqVCH+bepXu4Y0xEkSaEh\nvYxnCQT8RrffKjQkTGGuaNMxVNN01HQESZI/4FdzwPx7uivgMh1BUsCKv1OHw5YxEIcVWZqOHzId\nQS1NJ6zIceLkMdMRJElNLQ3WZAHwBfPv2AAAAAAAgIIOAAAAAIANKOgAAAAAAFiAgg4AAAAAgAUo\n6AAAAAAAWICCDgAAAACABSjoAAAAAABYgIIOAAAAAIAFKOgAAAAAAFiAgg4AAAAAgAUo6AAAAAAA\nWICCDgAAAACABSjoAAAAAABY4IIFvaKiQjk5OV2y4dWrV6upqSk4/dprr+nBBx/Uvffe22a5kydP\n6plnntFDDz2kJ554QocPH25ze11dnaZNm6Zf/vKXXZITAAAAAIDuYGwEfc2aNWpsbAxOjxw5UgsX\nLjxruY0bNyoqKko/+9nP9M1vflOvvvpqm9t/9atf6e///u+7PC8AAAAAAF0ptL0LHjp0SIWFhXrg\ngQeUnJzc5rZNmzappKRE9fX1qqqqUmZmpiZPnqyKigoVFBQoOTlZ+/fvV2JiorKzs7VhwwYdPXpU\n+fn5io6OVl5engYOHHjO7W7fvl133nmnJCk9PV3FxcXB2z7++GMdO3ZMqamp+vjjjy/n8QMAAAAA\nYIV2jaCXl5ersLBQM2bMOKuct9q3b59ycnK0ePFivf/++8HCfPDgQWVlZemZZ55ReHi41q1bp298\n4xvq3bu35s+fr7y8vAtuu6qqSrGxsZKkkJAQRUREqLa2Vn6/X6+88spZu8QDAAAAAHAlumhBr6mp\n0eLFi/XQQw9pwIAB511u2LBhioyMlNvtVnp6uvbs2SOHw6HY2FilpKRIkjIzM7Vnz54Ohw4EAlq/\nfr1uvPFGeTyeDq8PAAAAAADTLrqLe0REhPr06aMPP/xQCQkJ7VppIBCQw+GQpOC/W505fTEej0dH\njhyRx+NRS0uL6urqFBUVpb1792rPnj1at26dGhoa1NzcrF69eumuu+664Pr+Ju2ruqZ33CVl6Ap9\nk73y6jtGM8wZ4je6/Vajhw6R7vqu6RgKGXfMdARJ0qjRI5SjaUYznKivMLr9VuPGjZOeMp1CCndd\nazqCJCkjM125ethwioDh7Z+SkfkVzZk3y3QMnWiqNh1BkjR+/HjTESRJLqfLdARljsvUE3lPmI4h\nV0i46QiSpNGZo6R5s03HkC7x+19XGJ35FWneI6ZjqPFkrekIkqSx48bqybwnjWb40dM/Omuez+dT\nYWFht+aIiYlRdbUd7+fARQt6aGiocnNz9eMf/1i9evXSmDFjzrncrl27VFtbK7fbre3bt+vBBx9U\nIBDQkSNHtHfvXqWkpGjLli0aPHiwJCk8PFx1dXWKjIy84PZHjBih9957TykpKdq2bZuGDh0qSXro\noYeCy2zatEkff/zxRcu5JH2y4/cXXaY7ePUdlf7uV0YzLN7VbHT7QXd9V4tXvmY6hVwlB0xHkCTl\naJp8i18wmuFwZanR7Qc9JS3IX2A6hTzXJJqOIEnK1cNasvBZoxkCATt+2Jszb5YWFxSZjqHDJ/5q\nOkJQfn6+6QgKt6CUPpH3hH789I9Nx9A1YZbs4TdvthYXdG/ZOSeHBVf2nfeIFhc8YzqFauoPmY4g\nSXoy78lzFmTTcnJyuuwqUhfS3oFIoKtd9N3S4XAoLCxMc+fO1erVq/WnP/3pnMsNHDhQPp9Pc+bM\nUXp6evBY9fj4eK1bt06PPPKI6urqdOutt0qSbr75ZhUUFOjpp5+WJK1YsUIPPvigmpqa9OCDD+rN\nN9+UJE2YMEHHjx/XQw89pDVr1rSrhAMAAAAAcKW54Ah6XFyclixZIunUru7nugxaq9jYWM2ZM+es\n+U6nUzNnzjxrflZWlrKysoLTU6ZM0ZQpU85azuVyafbsC++aNX78eGt27wMAAAAA4HJ0+f5Gl3rM\nOQAAAAAAPVG7r4MuSTt37tTKlSvbzIuLi1Nubu45R7BPH4EHAAAAAADnd0kFPTU1VampqV2VBQAA\nAACAHsuCU2oCAAAAAAAKOgAAAAAAFqCgAwAAAABgAQo6AAAAAAAWuKSTxAEAAADA1SghIaFdy8XE\nxKi0tLSL06CnoqADAAAA6PHKysratVx7izxwOdjFHQAAAAAAC1DQAQAAAACwAAUdAAAAAAALUNAB\nAAAAALBAjztJ3H87/2o6giQpxlFtPIvr41ij228VcrRZro8bTMdQ4KT5DJIU8DcbzxLhijK6/VYu\nZ5gVWSpq95uOIEk60XTUmiymnWiq1uET5t/P+16TZDqCJOkad4wVWRwO87/7u0MjFRXez3QMhUb1\nNR1BkhTSK0rua82f0CoQZf69PCQqVq6EFNMxFFsZYzqCJCkivI9iew8yHQPAGcx/kgIAAAAAAAo6\nAAAAAAA2oKADAAAAAGABCjoAAAAAABagoAMAAAAAYAEKOgAAAAAAFqCgAwAAAABgAQo6AAAAAAAW\noKADAAAAAGABCjoAAAAAABagoAMAAAAAYAEKOgAAAAAAFqCgAwAAAABggdDLvWNFRYUWLVokn8/X\nmXkkSatXr9Ytt9wit9stSdq6datWrVolv9+vtLQ03X333ZKkzz//XM8//7waGhoUCAR011136cYb\nb+z0PAAAAAAAdDUrR9DXrFmjxsZGSdLx48e1YsUK5eXlyefzqbq6Wrt375Yk/frXv1ZmZqZ++tOf\n6uGHH9by5ctNxgYAAAAA4LJd9gj66Q4dOqTCwkI98MADSk5ObnPbpk2bVFJSovr6elVVVSkzM1OT\nJ09WRUWFCgoKlJycrP379ysxMVHZ2dnasGGDjh49qvz8fEVHR+vuu+9W//79FRUVJUkaOnSotm3b\npiFDhqh3796qq6uTJNXV1cnj8XTGwwEAAAAAoNt1uKCXl5fr2Wef1YwZMzRgwIBzLrNv3z75fD65\n3W49/vjjSktLU2RkpA4ePKjp06crJSVFy5Yt07p16zRp0iStXr1a8+fPV2RkpGpra1VeXq7Dhw/L\n4/GopKRELS0tkqTbbrtNTz75pN599101NDQoLy+vow8HAAAAAAAjOlTQa2pqtHjxYuXm5iohIeG8\nyw0bNkyRkZGSpPT0dO3Zs0cjR45UbGysUlJSJEmZmZlau3atJk2a1Oa+kZGRmjp1qoqKiuRwOJSS\nkqJDhw5Jkl5++WVNmDBB3/rWt7R37179/Oc/V2Fh4QUzj7hxknr37t+Rh90pvvS3w6UJPzSaoV//\nCKPbbzXqpmHK0T2mYyhQe8x0BElSxpibpLnZRjOcPHnC6PZbjRk7WnOffMx0DDW21JuOIEkaP368\n6QjWsOW5uMYdYzqCJCkj8yuaM2+W6RiSHKYDKCMzXbl62HQMOcMs+YwdlabZOVNNx5DcYaYTaNRN\nNygn+17TMaR6Oz5jR40eoZxHHzSawffTZWfP8/ku+n3+YmJiYlRaWtqhdQCmdKigR0REqE+fPvrw\nww8vWNBPFwgE5HCc+gBv/XerM6dbDR8+XMOHD5ckbdiwQSEhIZKkP//5z7rzzjslSSkpKTp58qRq\namoUHR193u1v/+CdduXschN+qP+38d+MRnj1N7FGt98qR/fI99wrpmMocPCA6QinzM2W7ydLjUao\nq68wuv1Wc598TD/50SLTMVTTdNR0hKD8/HzTEaxhw3PR95ok0xEkSXPmzdLigiLTMeRwmD+1Ta4e\n1pKFz5qOodCovqYjSJJm50xVoc/8OXoC/3eookk52ffKt/Rl0zGkSjs+Y3MeffCcBdm0nJwc5eTk\ndGgd7e0lgI069EkaGhqq3Nxcbd68WVu2bDnvcrt27VJtba2ampq0fft2DRo0SIFAQEeOHNHevXsl\nSVu2bNHgwYMlSeHh4cFjyyXp2LFTI5u1tbVav369Jk6cKOnUi2/Xrl2SpM8++0xNTU0XLOcAAAAA\nANiqQyPoDodDYWFhmjt3rhYsWKDw8PDgSPfpBg4cKJ/PFzxJXHJysioqKhQfH69169Zp2bJlSkxM\n1K233ipJuvnmm1VQUCCPx6O8vDy9+OKLOnDg1Ojm5MmT1a9fP0nSlClT9MILL2j16tVyOByaMWNG\nRx4OAAAAAADGXHZBj4uL05IlSySd2tV94cKF5102NjZWc+bMOWu+0+nUzJkzz5qflZWlrKys4PSs\nWec+rq5fv36aP3/+JSYHAAAAAMA+Rg8WO98x5wAAAAAA9DSdch10Sdq5c6dWrlzZZl5cXJxyc3PP\nebbd00fgAQAAAADo6TqtoKempio1NbWzVgcAAAAAQI9i/nooAAAAAACAgg4AAAAAgA0o6AAAAAAA\nWICCDgAAAACABSjoAAAAAABYgIIOAAAAAIAFKOgAAAAAAFiAgg4AAAAAgAUo6AAAAAAAWICCDgAA\nAACABUJNB+huu/0tpiNIkm4IBIxncRw7ZnT7QY0NVmRpbm4wHUGSFPA3q8WSLAAuzOGw5Xduh0VZ\nIEkK+E0nOCUQsCKLPyLMdAQFXCFW5AipMZ9BkuQMkcNlSZYukJCQcEnLx8TEdFES4NL0uIIOAAAA\n4OpWVlZmOgJwWfi5HQAAAAAAC1DQAQAAAACwAAUdAAAAAAALUNABAAAAALAABR0AAAAALkFCQoK8\nXq/pGLgKUdABAAAA4BKUlZWpurradAxchSjoAAAAAABYgIIOAAAAAIAFKOgAAAAAAFiAgg4AAAAA\ngAUo6AAAAAAAWICCDgAAAACABUIv944VFRVatGiRfD5fZ+aRJK1evVq33HKL3G63JGnr1q1atWqV\n/H6/0tLSdPfdd0uSXnrpJZWWlkqSGhsbVVNToxdffLHT8wAAAAAA0NUuu6B3pTVr1mjs2LFyu906\nfvy4VqxYoUWLFikqKkrPPfecdu/erSFDhui+++4L3ufdd9/VJ598Yi40AAAAAAAd0CkF/dChQyos\nLNQDDzyg5OTkNrdt2rRJJSUlqq+vV1VVlTIzMzV58mRVVFSooKBAycnJ2r9/vxITE5Wdna0NGzbo\n6NGjys/PV3R0tO6++271799fUVFRkqShQ4dq27ZtGjJkSJvtbNmyRd/5znc64+EAAAAAANDtOlzQ\ny8vL9eyzz2rGjBkaMGDAOZfZt2+ffD6f3G63Hn/8caWlpSkyMlIHDx7U9OnTlZKSomXLlmndunWa\nNGmSVq9erfnz5ysyMlK1tbUqLy/X4cOH5fF4VFJSopaWljbrP3z4sA4fPnxWaQcAAAAA4ErRoYJe\nU1OjxYsXKzc3VwkJCeddbtiwYYqMjJQkpaena8+ePRo5cqRiY2OVkpIiScrMzNTatWs1adKkNveN\njIzU1KlTVVRUJIfDoZSUFB06dKjNMn/4wx/0la98RQ6H46KZb077tq7rHX+pD7XTDUseIWma0Qw3\n9wkxuv1Wo0alaXbOVNMx5G88YTqCJCkj8yuaM2+W0QzNLY1Gt99qzNjRmvvkY6ZjqLGl3nQESdL4\n8eNNR7CGLc/FNe7epiNIkjIy05Wrh03HsIItz4XTHW46giRpVMZwzTYdQlIg8hrTEZQxYqhydZfp\nGHLU2vF9w4a/jULfv581z+fzqbCwsEPrjYmJ6dD9AZM6VNAjIiLUp08fffjhhxcs6KcLBALBIn1m\noT5fwR4+fLiGDx8uSdqwYYNCQtoWy/fff18/+MEP2rX9DTt+267lut40vfq7F4wm2PVSmNHtt5qd\nM1WFvuWmY+hkzaGLL9QN5sybpcUFRUYzNJ6sMbr9VnOffEw/+dEi0zFU03TUdISg/Px80xGsYcNz\nERf5t6YjSJJy9bCWLHzWdAwr2PJchEbGmo4gSZqtc5eg7tbSL850BOXqLi35xUrTMRTyeYXpCJLs\n+ds4U05OjnJyckzHAIzp0GXWQkNDlZubq82bN2vLli3nXW7Xrl2qra1VU1OTtm/frkGDBikQCOjI\nkSPau3evpFPHkA8ePFiSFB4errq6uuD9jx07Jkmqra3V+vXrNXHixOBtZWVlqq2tDY7EAwAAAABw\nJerQCLrD4VBYWJjmzp2rBQsWKDw8PDjSfbqBAwfK5/MFTxKXnJysiooKxcfHa926dVq2bJkSExN1\n6623SpJuvvlmFRQUyOPxKC8vTy+++KIOHDggSZo8ebL69esXXPfWrVs1evTojjwMAAAAAACMu+yC\nHhcXpyVLlkg6tav7woULz7tsbGys5syZc9Z8p9OpmTNnnjU/KytLWVlZwelZs85/PO4dd9xxKbEB\nAAAAALBSh3Zx76j2nNQNAAAAAICeoFOugy5JO3fu1MqVbU+8ERcXp9zc3HOebff0EXgAAAAAAHq6\nTivoqampSk1N7azVAQAAAADQoxjdxR0AAAAAAJxCQQcAAAAAwAIUdAAAAAAALEBBBwAAAADAAhR0\nAAAAAAAsQEEHAAAAAMACFHQAAAAAACxAQQcAAAAAwAIUdAAAAAAALEBBB/D/27v/qCjPO+/jnwEE\nQSD8UKIYjVKCJgG0KsUfwRo1lsbj2diw2caYNElzahB/D1ZNskRMg1oYUjUemm5tThM1241tdjcL\nLqnxUYvGsmTrQ+NqfKq2SUQFBSMjKkbm+YNlxgkiGmWum8z7dU6Ozj03XJ+58nXu+c59zzUAAAAA\nLCDIdABf+781t5uOIEma3NjLeBbXhU+Njt/G9UWzWi40mo6hunN/Mx1BknSu+YzxLJHB0UbHt5o+\nve40HUGS1Cs4yniWwKCeRsdvE96zt/reNsR0DNl6WGM+AoJCFNgz0nQMydViOoECgoIVGBJuOobU\nYn4uJEkulyWytAwMNB1BrtsCLJEj4GKM6QitQkPlirZIFgBunEEHAAAAAMACaNABAAAAALAAGnQA\nAAAAACyABh0AAAAAAAugQQcAAAAAwAJo0AEAAAAAsAAadAAAAAAALIAGHQAAAAAAC6BBBwAAAADA\nAmjQAQAAAACwABp0AAAAAAAsIMh0AAAAAADojvr3739TPx8VFaX9+/ffojT4OqBBBwAAAICv4Nix\nYzf18zfb4OPr5ys36LW1tVq9erUcDsetzCNJKi0t1QMPPKDg4GBJ0p49e/TOO++opaVFI0aM0GOP\nPSZJ2rFjh958803FxsZKkjIzMzVx4sRbngcAAAAAgK5myTPoZWVlGj9+vIKDg9XY2KiNGzdq9erV\nioiI0Pr16/XRRx8pOTlZkjRu3Dg9/fTThhMDAAAAAHBzbkmDfvLkSRUXF2vWrFlKSEjwum/Hjh2q\nrKzU+fPnVV9fr4yMDGVlZam2tlYFBQVKSEjQ0aNHNWDAAM2ZM0fbtm1TQ0OD8vPzFRkZqccee0z9\n+vVTRESEJCklJUV79+51N+gAAAAAAHwd3HSDXlNTozVr1ignJ0cDBw686j6HDx+Ww+FQcHCwli1b\nphEjRig8PFzHjx/X7NmzlZSUpJKSEpWXl2vatGkqLS3V8uXLFR4eLqfTqZqaGtXV1SkmJkaVlZVq\naWlx/+4//vGP+p//+R/Fx8frBz/4gftydwAAAAAAupObatDPnj2rwsJC5ebmXnOBg9TUVIWHh0uS\n0tPTdfDgQaWlpSk2NlZJSUmSpIyMDG3dulXTpk3z+tnw8HA988wz+tnPfiabzaakpCSdPHlSkjRq\n1Cjdd999CgoK0rZt27R+/Xrl5eVdM/Mj9z2gAb1vv5mHfUuMGZoq+0MzjWZw3XPW6Phtxo5Lk5bk\nmI4h5/k60xEkSRMmTDAdQSGBoaYjSJLuGz9OS19YYjqGggJDTEeQJI3NGK3Fzy0wmsEWYI1PRo29\n71vS0jmmY1hmPsaMGyW7njUdQ5LLdIDWufhxtukYks0a32Q7ZuxILcr9kekYarkj0nQEjU1O1uLv\nP2o6hgLqvzAdQZI0Ji1V9hyzr0Ud6ze23+ZwqLi42ECa6xcVFWU6Ar7GbuqVRVhYmHr37q0DBw5c\n99cq9XUAACAASURBVAqELpdLNptNktx/tvny7TYjR47UyJEjJUnbtm1TYGCgJLmbfkmaOHGiNm5s\n/4/8y/6l4vfXlbOr2R+aKce/dp63K7ne/dTo+G5LcuRYvd50Cp1oOGA6glt+fr7R8SODo42O32bp\nC0u06ierTcdQSA/zLywlafFzC1RY8DOjGQKDehod323pHDlWvWo6hWw9rDEfdj0rR+HPTceQXC2d\n79PF7D/OluOnJaZjyBbYw3QESdKi3B+puOgXpmPo0mjzK1Uv/v6jKvznt0zHUND/u2g6giTJnjPz\nqg2yaXa7XXa73XQMwJibens3KChIubm52rVrlyoqKjrcr7q6Wk6nU83NzaqqqtKQIUPkcrl06tQp\nHTp0SJJUUVGhoUOHSpJCQ0PV1NTk/vnPP/9ckuR0OvXee+9p0qRJkqQzZ86496mqqtIdd9xxMw8H\nAAAAAABjbuoMus1mU0hIiJYuXaqXXnpJoaGh7jPdV0pMTJTD4XAvEpeQkKDa2lrFx8ervLxcJSUl\nGjBggKZMmSJJmjx5sgoKChQTE6O8vDy9/vrr+uSTTyRJWVlZ6tu3r6TW1d4//PBDBQQEKCIiQrNn\nz76ZhwMAAAAAgDFfuUGPi4tTUVGRpNZL3VeuXNnhvrGxsVq8eHG77QEBAZo7d2677ZmZmcrMzHTf\nXrDg6p+5nDFjhmbMmHGj0QEAAAAAsByjK5h09JlzAAAAAAD8zS1bfnbfvn3avHmz17a4uDjl5uZe\ndVXqK8/AAwAAAADg725Zgz58+HANHz78Vv06AAAAAAD8ijW+pBMAAAAAAD9Hgw4AAAAAgAXQoAMA\nAAAAYAE06AAAAAAAWAANOgAAAAAAFkCDDgAAAACABdCgAwAAAABgATToAAAAAABYAA06AAAAAAAW\nEGQ6gK+9d9cPTUeQJMXF3qvv3BViNMP0GeuMjt8mOCVU4TNiTcdQv+1TTEeQJEX0+Yb63W02y4Uj\nfzI6fpsAW4ACbeafpnpE9DEdQZIUEBxmPIvr0kWj47exBQTKFhRsOoZO1x8wHUGS1HS+zhJZYiIG\nm44gV8tlub5oNh1DirHG84Z69pTrtijTKRT4h7+YjiDb2HpL5DjeYP7fqiQ11o3R8QPvmY4B4Es4\ngw4AAAAAgAXQoAMAAAAAYAE06AAAAAAAWAANOgAAAAAAFkCDDgAAAACABdCgAwAAAABgATToAAAA\nAABYAA06AAAAAAAWQIMOAAAAAIAF0KADAAAAAGABNOgAAAAAAFgADToAAAAAABZAgw4AAAAAgAXQ\noAMAAAAAYAFB17qztrZWq1evlsPhuOUDl5aW6oEHHlBwcLAk6a233tKuXbt07tw5vfHGG+79Ll26\npFdffVVHjx5VRESEFixYoD59+qiurk5FRUVyuVz64osvNHnyZD344IO3PCcAAAAAAL5wzQa9K5WV\nlWn8+PHuBj0tLU3f/e53NW/ePK/9tm/froiICK1du1Z79uzRpk2btGDBAkVHR+vll19WUFCQLly4\nILvdrvT0dMXGxpp4OAAAAABww/r37+/T8aKiorR//36fjonrd90N+smTJ1VcXKxZs2YpISHB674d\nO3aosrJS58+fV319vTIyMpSVlaXa2loVFBQoISFBR48e1YABAzRnzhxt27ZNDQ0Nys/PV2RkpPLy\n8pSYmHjVcauqqvTII49IktLT07Vhw4bW4EGe6M3NzQoMDFRISMgNTwAAAAAAmHLs2DGfjufrNwRw\nY66rQa+pqdGaNWuUk5OjgQMHXnWfw4cPy+FwKDg4WMuWLdOIESMUHh6u48ePa/bs2UpKSlJJSYnK\ny8s1bdo0lZaWavny5QoPD7/m2PX19e6z4oGBgQoLC5PT6VR4eLhOnz6tlStX6sSJE3r88cc7/V0A\nAAAAAFhVpw362bNnVVhYqNzc3Gu+25KamupukNPT03Xw4EGlpaUpNjZWSUlJkqSMjAxt3bpV06ZN\nuyXhY2NjVVRUpIaGBi1fvlzDhg1T3759r/kzUamDFBzV65aMfzN63dlHcePvNZphrvMpo+O3Sb/r\nm5IFlg+4dHcP0xEkSWPSUmXPmWk0wxcNk42O32bc+LFa8sJi0zEU1PM20xEkSWPGjtQi0yFaLptO\nIEkaM26U7D/ONh1DTedPmY4gSRr/7fF6Ie8F0zEUGhJtOoLG3vctaekc0zFk6xVhOoIkacy3hsk+\n9wnTMeRqcpqOoLHj0qQlOaZjyHm+znQESdKECRNMR1B+fn67bQ6HQ8XFxQbS3LioqCjTEfA11GmD\nHhYWpt69e+vAgQPXfTmEy+WSzWaTJPefbb58uzMxMTE6deqUYmJidPnyZTU1NbU7Ux4dHa2hQ4fq\nr3/9a6cN+pnqv97Q+F0lbvy9qt1l9rMf6068bnR8tweldWXms5zbHmY6giTJnjNTjvUbjWa4cORP\nRsdvs+SFxVr9k0LTMRQafafpCJKkRZKKHf9kNIPr0kWj47ex/zhbjp+WmI6h0w0fm44gSXoh7wX9\nZMVPTMdQTMRg0xGkpXPkWPWq6RSyxVnjElL73CfkWPdG5zt2Mdep46YjSEty5Fi93nQKnWg4YDqC\n29UaZNPsdrvsdrvpGIAxnX7NWlBQkHJzc7Vr1y5VVFR0uF91dbWcTqeam5tVVVWlIUOGyOVy6dSp\nUzp06JAkqaKiQkOHDpUkhYaGqqmpqdOAo0aN0s6dOyVJe/fuVUpKiqTWS9+bm5slSU6nUx9//HGH\nl98DAAAAAGB1nZ5Bt9lsCgkJ0dKlS/XSSy8pNDRUI0eObLdfYmKiHA6He5G4hIQE1dbWKj4+XuXl\n5SopKdGAAQM0ZcoUSdLkyZNVUFCgmJgY5eXlaePGjdq9e7eam5uVnZ2tSZMmKSsrSxMnTtS6des0\nb948RUREaP78+ZKkzz77TG+++aY74/Tp0xUfH38r5wYAAAAAAJ+5ZoMeFxenoqIiSa2Xuq9cubLD\nfWNjY7V4cfvPigYEBGju3LnttmdmZiozM9N9e+bMmZo5s/3nbnv06KFFi9p/6jI1NVWFheYvfQUA\nAAAA4Fbo9BL3m3WjnzkHAAAAAMAfXff3oEvSvn37tHnzZq9tcXFxys3NvepKkFeegQcAAAAAAB27\noQZ9+PDhGj58eFdlAQAAAADAb3X5Je4AAAAAAKBzNOgAAAAAAFgADToAAAAAABZAgw4AAAAAgAXQ\noAMAAAAAYAE06AAAAAAAWAANOgAAAAAAFkCDDgAAAACABdCgAwAAAABgAUGmA/jambGZpiNIkiIH\nhOjM2AFGM0x7f7XR8dsMCbmkabc1mY6hjXdFm44gSWqJCdIXd4UYzRDacKfR8dsE9bxNodHms1zu\nG2c6giTJFd7LeJaApotGx3cL7SXFmv//EnnhjOkIkqSQHuGKDL3ddAy1XG42HUGulsuWyBFw6rjp\nCJIkV5NTLgtkOdFwwHQEOc/XWSJH3+i7TUeQJIWH9rFMFgAenEEHAAAAAMACaNABAAAAALAAGnQA\nAAAAACyABh0AAAAAAAugQQcAAAAAwAJo0AEAAAAAsAAadAAAAAAALIAGHQAAAAAAC6BBBwAAAADA\nAmjQAQAAAACwABp0AAAAAAAsgAYdAAAAAAALoEEHAAAAAMACrtmg19bWym63d8nApaWlam5udt9+\n6623lJ2drSeeeMJrv0uXLumVV17RvHnz9Pzzz6uurs5938svv6ynnnpKq1at6pKMAAAAAAD4irEz\n6GVlZbp48aL7dlpamlauXNluv+3btysiIkJr167V1KlTtWnTJvd9f/d3f6c5c+b4JC8AAAAAAF0p\n6Hp3PHnypIqLizVr1iwlJCR43bdjxw5VVlbq/Pnzqq+vV0ZGhrKyslRbW6uCggIlJCTo6NGjGjBg\ngObMmaNt27apoaFB+fn5ioyMVF5enhITE686blVVlR555BFJUnp6ujZs2OC+Lzk5Wfv37/8qjxsA\nAAAAAEu5rga9pqZGa9asUU5OjgYOHHjVfQ4fPiyHw6Hg4GAtW7ZMI0aMUHh4uI4fP67Zs2crKSlJ\nJSUlKi8v17Rp01RaWqrly5crPDz8mmPX19crNjZWkhQYGKiwsDA5nc5Ofw4AAAAA0F7//v1NR/ja\nioqKuqmTyJ026GfPnlVhYaFyc3Ov+T8yNTXV3TSnp6fr4MGDSktLU2xsrJKSkiRJGRkZ2rp1q6ZN\nm/aVAwMAAAAAvrpjx46ZjvC1dbNvfnTaoIeFhal37946cODAdQ/mcrlks9kkyf1nmy/f7kxMTIxO\nnTqlmJgYXb58WU1NTV5nz2/098X17aGeoeYXr78tKlADB4cYzfCdiT8yOn6bbwweaYks/ZIjTUeQ\nJI1NTtbi7z9qNENARqPR8duMGTtSi0yHkOQK72U6giRp7KgU5WqG0Qy2S5eNjt9mzLeGyT7nic53\n7GKXG0+bjiBJGpcxWnpuoekYslngy2HGZqQrV/NNx5At8Lo/Rdilxo5Lk5bkmI4h5/m6znfqYhMm\nTDAdQZIUHtrHdARJ1qgNx+r17bc5HCouLjaQxoyoqCjTEWAxnR49goKClJubq5dfflk9e/bUfffd\nd9X9qqur5XQ6FRwcrKqqKmVnZ8vlcunUqVM6dOiQkpKSVFFRoaFDh0qSQkND2zXbVzNq1Cjt3LlT\nSUlJ2rt3r1JSUrzud7lc1/tYJUm1Jy7d0P5dZeDgEH1y9GLnO3ah8u2/MDp+m+9M/JElsmz8yBqX\n+iz+/qMq/Oe3jGboUXnc6PhtFkkqdvyT6Ri63DfOdARJUq5mqOi1zUYzBDSZfd5qY5/zhByvvmE6\nhi4dO2Q6QqvnFqqw4BXTKRRgM9+U5mq+ilauMR1DAT16mo7QaknOVZsgXzvRcMB0BElSfn6+6Qjq\nG3236QitLFIbX2a327vsW6SA7qDTt7ptNptCQkK0dOlSlZaW6sMPP7zqfomJiXI4HFq8eLHS09Pd\nC8nFx8ervLxcCxcuVFNTk6ZMmSJJmjx5sgoKCrRixQpJ0saNG5Wdna3m5mZlZ2dry5YtkqSJEyeq\nsbFR8+bNU1lZmWbM8Jw9ysvL0yuvvKKPPvpI2dnZqq6uvrnZAAAAAADAkGu+1R0XF6eioiJJrZe6\nX+1r0NrExsZq8eLF7bYHBARo7ty57bZnZmYqMzPTfXvmzJmaOXNmu/169OihRYuufpFrW3MPAAAA\nAEB31+UfFrvRz4gDAAAAAOCPbujDYvv27dPmzd6ff4yLi1Nubu5VF9648gw8AAAAAADo2A016MOH\nD9fw4cO7KgsAAAAAAH7L/PehAAAAAAAAGnQAAAAAAKyABh0AAAAAAAugQQcAAAAAwAJo0AEAAAAA\nsAAadAAAAAAALIAGHQAAAAAAC6BBBwAAAADAAmjQAQAAAACwABp0AAAAAAAsIMh0AF/7+6zRpiNI\nkuxLcuRYvd5ohhMNB4yO3yayx3G9UvDfpmOob/R50xEkSbax9Qr8w1+MZnDdfofR8d16hsoVFW06\nhQJPnjIdQZJkO9dkPIvrttuMju9ms0kBFniP+dvDTSdodWdfS2Sx1baYjiBb7z6yDb3HdAy19LBA\nfUpy9Y5Ry9BE0zG08P5Q0xE0JqOfFj43wnQMvft5mOkIkqTglFCFz4g1HQPAl1jj6AEAAAAAgJ+j\nQQcAAAAAwAJo0AEAAAAAsAAadAAAAAAALIAGHQAAAAAAC6BBBwAAAADAAmjQAQAAAACwABp0AAAA\nAAAsgAYdAAAAAAALoEEHAAAAAMACaNABAAAAALAAGnQAAAAAACyABh0AAAAAAAsI+qo/WFtbq9Wr\nV8vhcNzKPJKk0tJSPfDAAwoODpYk7dmzR++8845aWlo0YsQIPfbYY5Kkuro6lZSUqLGxUeHh4Zo7\nd65iYmJueR4AAAAAALqaJc+gl5WV6eLFi5KkxsZGbdy4UXl5eXI4HDpz5ow++ugjSdKbb76pCRMm\nqLCwUA8//LA2b95sMjYAAAAAAF/ZVz6DfqWTJ0+quLhYs2bNUkJCgtd9O3bsUGVlpc6fP6/6+npl\nZGQoKytLtbW1KigoUEJCgo4ePaoBAwZozpw52rZtmxoaGpSfn6/IyEg99thj6tevnyIiIiRJKSkp\n2rt3r5KTk3Xs2DE9+eSTkqR7771XhYWFt+LhAAAAAADgczd9Br2mpkbFxcXKyclp15y3OXz4sOx2\nuwoLC/XBBx/oyJEjkqTjx48rMzNTr7zyikJDQ1VeXq4HH3xQ0dHRWr58ufLy8nT77berpqZGdXV1\nunz5siorK1VfXy9JuvPOO7V3715JUmVlpS5cuCCn03mzDwkAAAAAAJ+7qTPoZ8+eVWFhoXJzc9W/\nf/8O90tNTVV4eLgkKT09XQcPHlRaWppiY2OVlJQkScrIyNDWrVs1bdo0r58NDw/XM888o5/97Gey\n2WxKSkrSyZMnJUmPP/64NmzYoJ07d+ruu+9WTEyMAgKu/Z7DI48+pAEDO87qK2PHpUlLcoxmcJ6v\nMzp+mwkTJpiOIEkKD+1jOoIka9SGrVek0fHbjPlWqux63HQM6eIF0wkkSWPGjNAi+zNmQ4T0NDv+\n/7JKbVyOviUXot20cSnJ0oxHTcdQwDmX6QgaOzJFuZphOoZcgTbTESRJY7+ZrNwfmq+N1EFnTUfQ\nNwaP1Hcm/sh0DA262MN0BElS+l3flB40m2Fd2evttjkcDhUXFxtI4z+ioqJMR8A13NQri7CwMPXu\n3VsHDhy4ZoN+JZfLJZut9aDV9mebL99uM3LkSI0cOVKStG3bNgUGBkqSoqOjlZubK0m6cOGC/vjH\nPyosLOya4//LW/96XTm73JIcOVavNxrhRMMBo+NfKT8/33QE9Y2+23SEVhaoDdvtdxgdv41dj8ux\n/k3TMWT7/HPTESRJi+zPqNjxS6MZXLfdZnT8NlapjUsJ1njDQjMeVeHmt0ynUGBti+kIytUMFf2T\n+TVpXD2sscxP7g8fVdEG87Xx2P3HTEfQdyb+SOXbf2E6ht79/NqvVX3mwas3yKbZ7XbZ7XbTMQBj\nburoERQUpNzcXO3atUsVFRUd7lddXS2n06nm5mZVVVVpyJAhcrlcOnXqlA4dOiRJqqio0NChQyVJ\noaGhampqcv/85//74tjpdOq9997TpEmTJLUuINfS0vpi4J133tH9999/Mw8HAAAAAABjbuoMus1m\nU0hIiJYuXaqXXnpJoaGh7jPdV0pMTJTD4XAvEpeQkKDa2lrFx8ervLxcJSUlGjBggKZMmSJJmjx5\nsgoKChQTE6O8vDy9/vrr+uSTTyRJWVlZ6tu3ryRp//79euut1neF77nnHv3whz+8mYcDAAAAAIAx\nX7lBj4uLU1FRkaTWS91XrlzZ4b6xsbFavHhxu+0BAQGaO3duu+2ZmZnKzMx0316wYMFVf+/o0aM1\nevToG40OAAAAAIDlGP2AVEefOQcAAAAAwN/csuVn9+3bp82bvRdliYuLU25u7lVX6b7yDDwAAAAA\nAP7uljXow4cP1/Dhw2/VrwMAAAAAwK9Y4ztAAAAAAADwczToAAAAAABYAA06AAAAAAAWQIMOAAAA\nAIAF0KADAAAAAGABNOgAAAAAAFgADToAAAAAABZAgw4AAAAAgAXQoAMAAAAAYAE06AAAAAAAWECQ\n6QC+dqLhgOkIkiTn+TrjWfpG3210/DbhoX0skcU2bYDpCJIkW1Kk8SwT+p8wOn6bQXc7NWH6SdMx\n1OCymY4gSbp92GWl/uCi0QzJAaeNjt8m5e4mPfY981nSWu40HUGSdO/tARqUav6Q/n8CjpqOoKHf\nOKvpU46ZjiGnWkxHkCR9Y9AZTbn/b6Zj6HuT/mA6ggYODlEv26OmY+jpPf9pOoIkKS78Xk3sG246\nBoAv4Qw6AAAAAAAWQIMOAAAAAIAF0KADAAAAAGABNOgAAAAAAFgADToAAAAAABZAgw4AAAAAgAXQ\noAMAAAAAYAE06AAAAAAAWAANOgAAAAAAFkCDDgAAAACABdCgAwAAAABgATToAAAAAABYAA06AAAA\nAAAWcM0Gvba2Vna7vUsGLi0tVXNzs/v2W2+9pezsbD3xxBNe+126dEmvvPKK5s2bp+eff151dXXu\n+3bs2KH58+dr/vz52rlzZ5fkBAAAAADAF4ydQS8rK9PFixfdt9PS0rRy5cp2+23fvl0RERFau3at\npk6dqk2bNkmSnE6nfvvb36qgoEAFBQXasmWLzp0757P8AAAAAADcSkHXu+PJkydVXFysWbNmKSEh\nweu+HTt2qLKyUufPn1d9fb0yMjKUlZWl2tpaFRQUKCEhQUePHtWAAQM0Z84cbdu2TQ0NDcrPz1dk\nZKTy8vKUmJh41XGrqqr0yCOPSJLS09O1YcMGSdK+ffuUmpqqXr16SZJSUlK0b98+jRs37itNBAAA\nAAAAJl1Xg15TU6M1a9YoJydHAwcOvOo+hw8flsPhUHBwsJYtW6YRI0YoPDxcx48f1+zZs5WUlKSS\nkhKVl5dr2rRpKi0t1fLlyxUeHn7Nsevr6xUbGytJCgwMVFhYmBobG9XQ0ODeLkmxsbGqr6+/3scN\nAAAAAICldNqgnz17VoWFhcrNzVX//v073C81NdXdbKenp+vgwYNKS0tTbGyskpKSJEkZGRnaunWr\npk2bdovi37gf/OAHGjRokLHx20yYMMF0BIWH9jEdQZI0dlyatCTHdAzZkiJNR5AkjRmaKvtDM41m\nGBTpNDp+m7sHj9LDk541HUPnXTbTESRJqQmjJJmdjzibNebiG4NHShN/ZDqG+ruiTEeQJPVJuFf3\n6h9Mx1CYrcF0BCUNHiVNNJ1CapbLdARJrc+jmmj+eXTg4BDTEXRbVKAlcvQMutd0BElSrzv7KG68\n2Sy1u/a32+ZwOFRcXGwgDXBrREXd3GuDThv0sLAw9e7dWwcOHLhmg34ll8sl2/++iLN96cXcl293\nJiYmRqdOnVJMTIwuX76spqYmRUREKCYmRvv3e/5Rnz59WsnJyZ3+vl//+tc3NH5Xys/PNzp+3+i7\njY7vtiRHjtXrTaeQbdoA0xEkSfaHZsrxrxuNZpjQ/4TR8ds8POlZ/fb9n5uOoQaLNOjSs9pkeD6S\nAwKNju828Uf6/fZfmE6htJY7TUeQJN2rf9D+939jOob+T8BR0xGkiVLp9tdMp5BTLaYjtJr4rN7Z\nbv55NM72mOkIGjg4RJ8cvdj5jl0sak/7ptSEuPH3XrVBNs1ut3fZItVAd9DpInFBQUHKzc3Vrl27\nVFFR0eF+1dXVcjqdam5uVlVVlYYMGSKXy6VTp07p0KFDkqSKigoNHTpUkhQaGqqmpqZOA44aNcq9\nQvvevXuVkpIiSRo2bJiqq6t17tw5OZ1OVVdXa9iwYZ0/YgAAAAAALKjTM+g2m00hISFaunSpXnrp\nJYWGhmrkyJHt9ktMTJTD4XAvEpeQkKDa2lrFx8ervLxcJSUlGjBggKZMmSJJmjx5sgoKChQTE6O8\nvDxt3LhRu3fvVnNzs7KzszVp0iRlZWVp4sSJWrdunebNm6eIiAjNnz9fkhQeHq6HH35Yy5YtkyRl\nZWW5F4wDAAAAAKC7uWaDHhcXp6KiIkmtl7pf7WvQ2sTGxmrx4sXttgcEBGju3LnttmdmZiozM9N9\ne+bMmZo5s/3nbnv06KFFixZddcz7779f999//7UeAgAAAAAA3UKXfw/6jX7mHAAAAAAAf3Td34Mu\ntX73+ObNm722xcXFKTc396qrkl95Bh4AAAAAAHTshhr04cOHa/jw4V2VBQAAAAAAv9Xll7gDAAAA\nAIDO0aADAAAAAGABNOgAAAAAAFgADToAAAAAABZAgw4AAAAAgAXQoAMAAAAAYAE06AAAAAAAWAAN\nOgAAAAAAFkCDDgAAAACABdCgAwAAAABgATaXy+UyHQIAAAAAAH/HGXQAAAAAACyABh0AAAAAAAug\nQQcAAAAAwAJo0AEAAAAAsAAadAAAAAAALIAGHQAAAAAAC6BBBwAAAADAAmjQAQAAAACwABp0Hzh3\n7px2796td999V++++6727Nmjc+fOmY5lnNPpVFNTk+kYxmzfvt3999OnT2vFihV68skn9cILL6im\npsZgMmtoamrSkSNH5HQ6TUfxuaeeeko///nP9ec//1kul8t0HEs6e/as6QiWsXnzZtMRLOXIkSOm\nIxjT1NSkEydOtNv+t7/9zUAa66qurjYdwedOnz7tPp6eOHFCe/fu5bUGYFE2F6/+utTOnTu1ZcsW\npaSkKDY2VlLrk2R1dbWysrI0YcIEswF9rL6+Xps3b9Z//dd/6cKFC4qJiZEk3X///fre976noKAg\nwwl958c//rF++tOfSpKKi4uVmpqqiRMnqqqqSv/5n/+pvLw8wwl9a+3atXryyScVGRmpffv26bXX\nXlN8fLxqamr0+OOPa+zYsaYj+sz8+fP13e9+VxUVFaqrq9Po0aM1btw4JSUlmY5mxJ/+9Cf98pe/\nVExMjJ5++mmtW7dOly5dUnNzs3JycpSammo6os/86le/ardt586d+va3vy1Jevrpp30dyairNeOr\nV6/WkiVLJEkJCQm+jmTMnj179Otf/1qRkZG6fPmyZs+ercTEREnexxtI2dnZKikpMR3DZ8rKylRa\nWqrAwEBNnTpVZWVlGjp0qD7++GNNnz7d/fwBwBr8pxsy5He/+51WrVqlXr16eW13Op167rnn/K5B\nX7dunR5++GHl5OSosrJSBw4c0Pe//32988472rBhg2bNmmU6ohE1NTVatGiRJOlb3/qW3n77bcOJ\nfO9vf/ubIiMjJUlvv/228vPzFRcXp7Nnz2rFihV+1aCHhIQoMzNTmZmZqqur0+7du7VhwwY5nU6N\nGzdOM2bMMB3RpzZv3qxly5apqalJK1as0LJly5SUlKTPPvtMa9eu9avGo7KyUvfcc4/XmxK7d+/2\nq0b0SsuWLdNdd92lHj16uLc5nU69+eabkqQXX3zRVDSfe+edd7Rq1SpFR0frL3/5i1599VU9Wgi7\nowAADWhJREFU+uijSk9PNx3NiFWrVnV4X2Njow+TmLdt2zY5HA41Nzdr9uzZWrdunaKjo+V0OrVi\nxQoadMBiaNANsdlspiMY4XQ6lZycLElKT0/X7373O/Xs2VOPPvqo5s+fbzidb50+fdp9NqyxsVFf\nfPGF+wqClpYWk9GMcLlcampqUlhYmAICAtS7d29JUmRkpF/OR5s+ffrooYce0kMPPaRjx45pz549\npiP5nM1m0x133CFJ6tmzp/tKgjvuuMPvPgJQXFys3/zmN9q3b5+eeOIJxcTE6O233/a7N3vbLFy4\nUFu3btW0adM0YsQISVJOTo5fNeZtWlpaFB0dLUlKTEzUiy++qFWrVun06dOGk5nx8ccfa86cOerZ\ns6d7m81mk8vl0l/+8heDyXwvKChIPXv2VM+ePdW3b193nYSHh/vdcyjQHdCgd7Hp06dr6dKlSk1N\ndV/ifurUKVVXV+vhhx82nM73IiIitGvXLiUnJ2vv3r3q06ePJP9sSB9//HH33xMSEnThwgWFh4fr\nzJkzGjlypMFkZmRlZSk/P1/f+c53NGTIEBUXF2vUqFHav3+/hg8fbjqeT917771X3d6/f3/9/d//\nvY/TmNezZ0/9/ve/V1NTk0JDQ/Uf//EfGjt2rKqrq9tdnfR1FxYWpqeeekpHjhzRunXr9M1vftOv\nX2CPHj1aw4YN029+8xvt2LHD63nV34SGhurEiRPq27evJCk6OlovvviiioqK9OmnnxpO53uJiYkK\nCQm56vNpfHy8gUTm2Gw290mAZcuWubc3NzcbTAWgI3wG3QecTqf27dunhoYGSVJMTIyGDRum8PBw\nw8l8r66uTm+++aaOHTumO++8U48//riio6PV2Nio/fv3a/To0aYjwqDjx4/r/fff1/Hjx3X58mXF\nxsYqLS3N7xp0eDtx4oR++9vfKjo6Wg899JDeeOMNffzxx+rfv79mzpzpbkj8TUtLi9577z0dOnRI\n8+bNMx3HuCNHjuiNN97Qp59+qg0bNpiO43N//etfFRISon79+nlt/+KLL7Rnzx6NHz/eUDKYVldX\np+jo6Hbr/NTX1+uzzz7zq3U8gO6ABt2H2j7zFBERYTgJrOKjjz7S3r17VV9fL5vNpvj4eE2aNMlv\nGw54tNXG6dOnFRAQQG2gHafTKZfLxTHlCi6XS+fPn1dYWJjpKEa1rdbtjycCrob58GAuAOujQe9i\ndXV12rRpk/785z+7XzA0NTUpJSVFM2bMUFxcnOGEvkdT2mrTpk06c+aMUlJSVFlZqbi4OMXHx+u9\n997TQw895FeLorW5sjYCAgLUr18/aoPakMQbFm04prTH80YrasMb8+HBXADdCw16F3v++ec1depU\npaenKzAwUJJ0+fJl7d27V2VlZXr55ZcNJ/QtGg8Pu90uh8MhqbUmXnzxRf3kJz+R0+lUXl6eiouL\nDSf0LWrDg9rwRm14cEzxRm14UBvemA8P5gLoXgJMB/i6a2xs1NixY91PiJIUGBiocePG+d3XfEjS\nf//3fysnJ0fjx4/XwoULdejQIU2ePFl5eXnasmWL6Xg+FRAQ4K6B+vp690JP/nrZGbXhQW14ozY8\nOKZ4ozY8qA1vzIcHcwF0L6zi3sUGDx6sX/7yl/r2t7/ttYr7zp07NWjQILPhDGhrPCIiIvy+8Zg+\nfbqWLFmifv36qaamRs8884wk6fPPP9fAgQMNp/M9asOD2vBGbXhwTPFGbXhQG96YDw/mAuheuMS9\ni126dEnbt29XVVWV6uvrJbWu4j5q1ChNnDhRPXr0MJzQt/bs2aONGzd6NR4jR47U559/rtdff10L\nFiwwHdGnGhsbVVtbq9tvv90vX1BeidrwRm14UBseHFO8URse1IY35sODuQC6Fxp0+ByNh7cVK1Yo\nLy+v023+gNrwRm14UBvoCLUBAPg64TPoBvnb5+PaREREaNOmTe1eSK1YscJQIjOam5vV2Nios2fP\nyul0uv+rra11v8Ptb6iNVtRGe9RG5zimUBsd8dfa6Ajz4cFcANbDZ9ANev/995WVlWU6hk81Nzfr\n4sWL7sajTVNTk981Hr///e9VVlamhoYGLVmyxL09NDRUmZmZBpOZQW14UBveqI3rwzGF2uiIP9bG\ntTAfHswFYD006F3siSee6PC+5uZmHyaxBhoPj6lTp2rq1KkqKyvTgw8+aDqOcdSGB7Xhjdrw4Jji\njdrwoDa8MR8ezAXQvdCgd7FevXpp5cqVioqKandfdna2gURm0Xi0N3nyZL377rs6ePCgbDabhg4d\nqilTpig4ONh0NJ+iNtqjNlpRGx4cU7xRGx7Uhjfmw4O5ALqXwOXLly83HeLrrLGxUdHR0YqJiWl3\n35kzZ5SammoglXl33nmnysrK9O///u/64IMPVF9fr0GDBnl9R6e/WLNmjc6fP69JkyYpMTFRH330\nkXbv3q0xY8aYjmYEteFBbXijNjimdITaoDa+jPnwYC6A7oVV3GFEcXGxQkNDlZGRIUmqqKhQU1OT\nFi1aZDiZ7y1cuFCvvPJKp9v8BbXhQW14ozbQEWoDAPB1wSruPnK11WT9eYXZTz/9VNnZ2UpOTlZy\ncrKeffZZffrpp6ZjGTF48GAdOnTIffvQoUNKSEgwmMgsasOD2vBGbXhwTPFGbXhQG96YDw/mAuge\n+Ax6F2OF2atrazySkpIk+XfjceTIEf3jP/6jYmNjZbPZdOrUKcXHx8tut8tms6moqMh0RJ+iNjyo\nDW/UBseUjlAb1MaXMR8ezAXQvXCJexcrLS11rzAbHR3t3h4aGqrJkyf73SqzbRYsWKDjx4+3azwC\nAgL8rvGora2VJNlsNknSl/9JxsXF+TyTSdSGB7XhjdrgmNIRaoPa+DLmw4O5ALoXGnQfYYVZbzQe\n3o4cOeJeqXvIkCF+d+bnStSGN2rDg9rw4JjijdrwoDa8MR8ezAXQPdCg+0hzc7PKy8v9/uuSrkTj\n0WrLli364IMPlJ6eLpfLpaqqKqWnpysrK8t0NGOojVbURnvURiuOKe1RG62oDW/MhwdzAXQPNOg+\nwgqz3mg8PObPn6/CwkL3AbK5uVmLFy/WmjVrDCczg9rwoDa8URseHFO8URse1IY35sODuQC6BxaJ\n85FPP/3U66uRkpOTtXDhQoOJzPrDH/7g1XhMnz5dixcv9ssXUzExMWpubvZqwq72XaX+gtrwoDa8\nURseHFO8URse1IY35sODuQC6Bxp0H2GFWW80Hh6hoaGy2+1KTU2VJFVXVysxMVG/+tWvJElPP/20\nyXg+R214UBveqA0PjineqA0PasMb8+HBXADdA5e4+wgrzHr76U9/qsOHD7drPGJjYyX5V+OxY8eO\na94/YcIEn+SwCmrDg9rwRm14cEzxRm14UBvemA8P5gLoHmjQfYQVZr3ReFy/oqIi5ebmmo7hM9TG\n9aM2vPlTbXBM8UZteFAb3pgPD+YC6B64xN1H4uLiWGH2Cp29WPK3xuNa2g6o/oLauH7Uhjd/qg2O\nKd6oDQ9qwxvz4cFcAN1DgOkA/mLLli1av369nE6nzp49q5KSEm3ZssV0LMvyt8YD14/aQEf8qTY4\nptwYasN/a4P58GAugO6BM+g+wgqzAIBbhWMKOkJteGM+PJgLoHvgDLqPtK0w28afV5iFtyNHjrTb\n9uGHHxpIAquhNtARjinoCLXhjfnwYC6A7oEz6D7C1yV5O3LkSLvPPX344YcaOXKkoUTmvPbaa8rJ\nydHAgQMlSRUVFSotLXXPxYwZM0zG8zlqw4Pa8EZteHBM8UZteFAb3pgPD+YC6B4Cly9fvtx0CH9w\n6dIlpaSkKC4uTnFxcUpJSVH//v0VHR2t6OhoDRo0yHREn1q1apWGDBmi2267TVJr4/Fv//Zvmjx5\nsiSpT58+6tu3r8mIPpOamqq1a9fqnnvuUWVlpbZv367nn39ePXr0kCS/mYc21IYHteGN2vDgmOKN\n2vCgNrwxHx7MBdA98DVrFuFPK8xK0smTJ1VcXKx58+bpwIED2rVrl5YuXaqwsDDT0YyoqalRYWGh\nevfurdzcXIWEhJiOZAy14Y3a8KA2rh/HFGqjI/5WG51hPjyYC8AauMTdIvxphVlJuv322zV//nx3\n4/H888/7XeNht9u9bjudTrW0tOi5556TzWZTUVGRoWRmURvURkeojevHMYXa6Ii/1UZnmA8P5gKw\nBhp0+BSNh8eSJUtMR7AUasOD2vBGbaAj1AYA4OuGBh0+RePhERcXZzqCpVAbHtSGN2oDHaE2AABf\nNzToPsIKs61oPNARagMdoTba45jSitpoj9rwxnx4MBdA98D3oPvIa6+9pk8++cR9u6KiQlu2bHHf\n9revSwIAfHUcU9ARasMb8+HBXADdA6u4+wgrzAIAbhWOKegIteGN+fBgLoDugQbdh/i6JADArcIx\nBR2hNrwxHx7MBWB9NOhd7MsrzJ49e1ZhYWEKCgpihVkAwA3hmIKOUBvemA8P5gLoXmjQu1hn3ynJ\nAjcAgOvFMQUdoTa8MR8ezAXQvdCgAwAAAABgAaziDgAAAACABdCgAwAAAABgATToAAAAAABYAA06\nAAAAAAAWQIMOAAAAAIAF/H8sLteJrDWYwgAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x14434908>"
]
}
],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"interactive(cor.plot_dendrogram, method = ('complete','single','average','weighted'), metric = fixed('euclidean'))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA+gAAAI5CAYAAAAythDaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X2QnXV9///Xks3m9izLBpLNDQmQhLtFIRCUEjESDdpS\nKciYsdY6ihTBqUqtdhRrf2aU6kyRYbzBUYnF+4pS0CrVgoAglGqAAFluQggGEkhCEpcsIZCb3d8f\nTM43IZBws2fP52wejxlmsrsXez77zpXrnOc5116nqa+vry8AAABAXe1T7wUAAAAAAh0AAACKINAB\nAACgAAIdAAAACiDQAQAAoAACHQAAAArQXM8bf+yxx+p58y9LpVJJT09PvZcxKJltbZlvbZlv7Zht\nbZlv7ZhtbZlvbZlv7ZhtbTXafCdMmPCCn/cKOgAAABRAoAMAAEABBDoAAAAUQKADAABAAQQ6AAAA\nFECgAwAAQAEEOgAAABRAoAMAAEABBDoAAAAUQKADAABAAQQ6AAAAFECgAwAAQAEEOgAAABRAoAMA\nAEABBDoAAAAUQKADAABAAQQ6AAAAFECgAwAAQAEEOgAAABRAoAMAAEABBDoAAAAUQKADAABAAQQ6\nAAAAFECgAwAAQAGa672ARjF58uh0d1fqvYxBzGxrq/Hm29bWm66uVfVeBgAADBiB/hJ1dzdl5crH\n6r2MQalSqaSnp6feyxi0GnW+EydOqPcSAABgQDnFHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAId\nAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog\n0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACg\nAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAA\nAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAzXva4NJLL82d\nd96Z1tbWfOlLX9rl6zfffHN+/vOfp6+vLyNGjMjZZ5+dKVOm1GSxAAAAMFjt8RX0k08+ORdccMGL\nfn3cuHGZP39+Lrroopx55pn55je/2a8LBAAAgL3BHgP9iCOOyKhRo17064ceemhGjhyZJJk2bVrW\nrVvXf6sDAACAvUS//g769ddfnxkzZvTntwQAAIC9wh5/B/2lWrx4cW644YZ87nOfe8Gvd3V1paur\nq/rxvHnzUqlU+uvmB0SjrbdRtLS0mG0NNfJ8G2HdjTzf0pltbZlv7ZhtbZlvbZlv7ZhtbTXifK+4\n4orqnzs7O9PZ2dk/gb58+fJ84xvfyKc//emMHj36BbfZfoM76unp6Y+bHyCVBltv46hUzLaWGne+\njbHuxp1v+cy2tsy3dsy2tsy3tsy3dsy2thptvpVKJfPmzdvl86/6FPe1a9fmoosuyoc//OF0dHS8\n2m8HAAAAe6U9voJ+ySWX5L777suGDRty3nnn5Z3vfGe2bduWJJk7d25++tOfZuPGjbnsssuSJEOG\nDMkXvvCF2q4aAAAABpk9Bvr555+/26+fe+65Offcc/ttQQAAALA36teruAMAAACvjEAHAACAAgh0\nAAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiA\nQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACA\nAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAA\nACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAH\nAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAII\ndAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAo\ngEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAA\ngAIIdAAAACiAQAcAAIACCHQAAAAoQPOeNrj00ktz5513prW1NV/60pdecJtvf/vbWbRoUYYNG5YP\nfehDOfjgg/t9oQAAADCY7fEV9JNPPjkXXHDBi379jjvuyOrVq/PlL38555xzTi677LJ+XSAAAADs\nDfYY6EcccURGjRr1ol9fuHBhZs+enSSZPn16Nm7cmO7u7v5bIQAAAOwFXvXvoK9fvz5jxoypfjxm\nzJisX7/+1X5bAAAA2Kv0y0Xi+vr6+uPbAAAAwF5rjxeJ25P29vasW7eu+vG6devS3t6+y3ZdXV3p\n6uqqfjxv3rxUKpVXe/MDqtHW2yhaWlrMtoYaeb6NsO5Gnm/pzLa2zLd2zLa2zLe2zLd2zLa2GnG+\nV1xxRfXPnZ2d6ezsfPWBPnPmzPz617/OrFmzsmTJkowaNSptbW27bLf9BnfU09Pzam9+AFUabL2N\no1Ix21pq3Pk2xrobd77lM9vaMt/aMdvaMt/aMt/aMdvaarT5ViqVzJs3b5fP7zHQL7nkktx3333Z\nsGFDzjvvvLzzne/Mtm3bkiRz587NsccemzvvvDMf/vCHM3z48Jx33nn9v3oAAAAY5PYY6Oeff/4e\nv8kHPvCBflkMAAAA7K365SJxAAAAwKsj0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAAC\nHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAK\nINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAA\noAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0A\nAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQ\nAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAA\nAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAA\nCiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEA\nAKAAzXvaYNGiRbn88svT29ubOXPm5PTTT9/p6xs2bMhXvvKVdHd3p7e3N29/+9vzpje9qVbrBQAA\ngEFpt4He29ubBQsW5DOf+Uza29vzqU99KjNnzsykSZOq2/zqV7/KwQcfnHe/+93ZsGFDzj///Jx0\n0kkZMmRIzRcPAAAAg8VuT3FfunRpOjo6Mnbs2DQ3N2fWrFlZuHDhTtvst99+efrpp5MkmzZtSqVS\nEecAAADwMu020NevX58xY8ZUP25vb8/69et32ubNb35zVqxYkQ9+8IP5xCc+kfe97301WSgAAAAM\nZnv8HfQ9ueqqq3LQQQfls5/9bFatWpXPf/7z+bd/+7eMGDFip+26urrS1dVV/XjevHmpVCqv9uYH\nVKOtt1G0tLSYbQ018nwbYd2NPN/SmW1tmW/tmG1tmW9tmW/tmG1tNeJ8r7jiiuqfOzs709nZuftA\nb29vz7p166ofr1u3Lu3t7Ttts2TJkpxxxhlJUj0d/rHHHsvUqVN32m77De6op6fnlf0kdVFpsPU2\njkrFbGupcefbGOtu3PmWz2xry3xrx2xry3xry3xrx2xrq9HmW6lUMm/evF0+v9tT3KdOnZpVq1Zl\nzZo12bp1a2699dbMnDlzp20mTJiQe+65J0nS3d2dxx57LOPGjevHpQMAAMDgt9tX0IcMGZKzzjor\nF154YfVt1iZNmpRrr702STJ37tycccYZufTSS/OJT3wivb29ec973pPRo0cPyOIBAABgsNjj76DP\nmDEjM2bM2Olzc+fOrf65tbU1n/zkJ/t/ZQAAALAX2e0p7gAAAMDAEOgAAABQAIEOAAAABRDoAAAA\nUACBDgAAAAUQ6AAAAFAAgQ4AAAAFEOgAAABQAIEOAAAABRDoAAAAUACBDgAAAAUQ6AAAAFAAgQ4A\nAAAFEOgAAABQAIEOAAAABRDoAAAAUACBDgAAAAUQ6AAAAFAAgQ4AAAAFEOgAAABQAIEOAAAABRDo\nAAAAUACBDgAAAAUQ6AAAAFAAgQ4AAAAFEOgAAABQAIEOAAAABRDoAAAAUACBDgAAAAUQ6AAAAFAA\ngQ4AAAAFEOgAAABQAIEOAAAABRDoAAAAUACBDgAAAAUQ6AAAAFAAgQ4AAAAFEOgAAABQAIEOAAAA\nBWiu9wJg8uTJ6e7urvcyKM7/l4kT59d7ERSora0tXV1d9V4GAEC/E+jUXXd3d1auXFnvZQxalUol\nPT099V7GK3ROvRewR40937K92GwnTpxYh9UAANSeU9wBAACgAAIdAAAACiDQAQAAoAACHQAAAAog\n0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACg\nAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAA\nAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACtC8pw0WLVqUyy+/PL29vZkzZ05OP/30Xbbp6urK\nd77znWzbti2VSiWf/exna7FWAAAAGLR2G+i9vb1ZsGBBPvOZz6S9vT2f+tSnMnPmzEyaNKm6zcaN\nG7NgwYJ8+tOfzpgxY7Jhw4aaLxoAAAAGm92e4r506dJ0dHRk7NixaW5uzqxZs7Jw4cKdtvnd736X\n17/+9RkzZkySpLW1tXarBQAAgEFqt6+gr1+/vhreSdLe3p6lS5futM3jjz+ebdu2Zf78+dm0aVP+\n4i/+Im984xtrs1oAAAAYpPb4O+h7sm3btjz88MP5l3/5lzz77LP553/+50yfPj3jx4/fabuurq50\ndXVVP543b14qlcqrvfkB1WjrbSRmWzstLS3mW0PmWzu7m62Zv3r23dox29oy39oy39ox29pqxPle\nccUV1T93dnams7Nz94He3t6edevWVT9et25d2tvbd9pmzJgxqVQqaWlpSUtLS4444ogsX758l0Df\nfoM76unpecU/zMCrNNh6G4vZ1k6lYt+tJfOtnd3N1sxfPftu7ZhtbZlvbZlv7ZhtbTXafCuVSubN\nm7fL53f7O+hTp07NqlWrsmbNmmzdujW33nprZs6cudM2xx9/fB544IH09vbm2WefzYMPPrjTReQA\nAACAPdvtK+hDhgzJWWedlQsvvLD6NmuTJk3KtddemySZO3duJk6cmKOPPjof//jH09TUlDe/+c0C\nHQAAAF6mPf4O+owZMzJjxoydPjd37tydPj7ttNNy2mmn9e/KAAAAYC+y21PcAQAAgIEh0AEAAKAA\nAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAA\nCiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEA\nAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAId\nAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog\n0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACg\nAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAA\nAArQXO8FAOyos7Mz3d3d9V4GhZs4cWK9l0Ch2tra0tXVVe9lAMArItCBonR3d2flypX1XsZLVqlU\n0tPTU+9lDEpmW1uDdb6evAGgkTnFHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAA\noAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAHsM9EWLFuX888/PRz7ykVx99dUvut3SpUvzrne9\nK//3f//XrwsEAACAvcFuA723tzcLFizIBRdckIsvvji33HJLVqxY8YLb/eAHP8gxxxyTvr6+mi0W\nAAAABqvdBvrSpUvT0dGRsWPHprm5ObNmzcrChQt32e6///u/c8IJJ6S1tbVmCwUAAIDBbLeBvn79\n+owZM6b6cXt7e9avX7/LNgsXLswpp5ySJGlqaqrBMgEAAGBwa3613+Dyyy/Pu9/97jQ1NaWvr+9F\nT3Hv6upKV1dX9eN58+alUqm82psfUI223kZitrXT0tLScPNtpPU24nwbhdnW1mCeb71/rsE82xKY\nb22Zb+2YbW014nyvuOKK6p87OzvT2dm5+0Bvb2/PunXrqh+vW7cu7e3tO22zbNmyXHLJJUmSnp6e\nLFq0KM3NzZk5c+ZO222/wR319PS8sp+kLioNtt7GYra1U6k03r7bSOttxPk2CrOtrcE833r/XIN5\ntiUw39oy39ox29pqtPlWKpXMmzdvl8/vNtCnTp2aVatWZc2aNWlvb8+tt96aj370oztt89WvfrX6\n50svvTTHHXfcLnEOAAAA7N5uA33IkCE566yzcuGFF6a3tzdz5szJpEmTcu211yZJ5s6dOyCLBAAA\ngMFuj7+DPmPGjMyYMWOnz71YmH/oQx/qn1UBAADAXma3V3EHAAAABoZABwAAgAIIdAAAACiAQAcA\nAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0\nAAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiA\nQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACA\nAgh0AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAA\nAChAc70XAAAvZPLkyenu7q73MmhAEydOrPcSaEBtbW3p6uqq9zKAvZxAB6BI3d3dWblyZb2XMWhV\nKpX09PTUexmDktnWVq3m64kdoAROcQcAAIACCHQAAAAogEAHAACAAvgddBjkGvFCW430e4AuKgQA\nQH8R6DDIudBWbTXSkwkAAJTNKe4AAABQAIEOAAAABRDoAAAAUACBDgAAAAUQ6AAAAFAAgQ4AAAAF\nEOgAAABQAIEOAAAABRDoAAAAUACBDgAAAAUQ6AAAAFAAgQ4AAAAFEOgAAABQAIEOAAAABRDoAAAA\nUACBDgAAAAUQ6AAAAFAAgQ4AAAAFEOgAAABQAIEOAAAABRDoAAAAUIDml7LRokWLcvnll6e3tzdz\n5szJ6aefvtPXb7755vz85z9PX19fRowYkbPPPjtTpkypyYIBAABgMNrjK+i9vb1ZsGBBLrjgglx8\n8cW55ZZbsmLFip22GTduXObPn5+LLrooZ555Zr75zW/WbMEAAAAwGO0x0JcuXZqOjo6MHTs2zc3N\nmTVrVhYuXLjTNoceemhGjhyZJJk2bVrWrVtXm9UCAADAILXHQF+/fn3GjBlT/bi9vT3r169/0e2v\nv/76zJgxo39WBwAAAHuJfr1I3OLFi3PDDTfkb/7mb/rz2wIAAMCgt8eLxLW3t+90yvq6devS3t6+\ny3bLly/PN77xjXz605/O6NGjd/l6V1dXurq6qh/PmzcvlUrlla67LhptvY3EbGvLfGvLfGvHbGun\npaVlr5/v5MmT093dXe9lUJCJEyfWewkUoK2tLY888ki/f1/H3dpqxPleccUV1T93dnams7Nzz4E+\nderUrFq1KmvWrEl7e3tuvfXWfPSjH91pm7Vr1+aiiy7Khz/84XR0dLzg99l+gzvq6el5JT9HnVQa\nbL2NxWxry3xry3xrx2xrp1Jxv9bd3Z2VK1f2+/c129oy39oy3+eeqKnFDMy2thptvpVKJfPmzdvl\n83sM9CFDhuSss87KhRdeWH2btUmTJuXaa69NksydOzc//elPs3Hjxlx22WXV/+cLX/hCP/8IAAAA\nMHi9pPdBnzFjxi4Xfps7d271z+eee27OPffc/l0ZAAAA7EX69SJxAAAAwCsj0AEAAKAAAh0AAAAK\nINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAzfVeAAAAUIbJkyenu7u73suou4kTJ9Z7\nCXXX1taWrq6uei9jryPQAQCAJEl3d3dWrlxZ72UMSpVKJT09PfVexkvmSYr6cIo7AAAAFECgAwAA\nQAEEOgAAABRAoAMAAEABBDoAAAAUQKADAABAAbzNGgDshbzX8XO8jZD3OgYoiUAHgL2Q9zquHe91\nDMAr5RR3AAAAKIBABwAAgAIIdAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAII\ndAAAACiAQAcAAIACCHQAAAAogEAHAACAAgh0AAAAKIBABwAAgAIIdAAAAChAc70XAAAAMNhNnjw5\n3d3d9V7GyzJx4sR6L+Ela2trS1dXV72X8aoJdAAAgBrr7u7OypUr672MQauRnkzYHae4AwAAQAEE\nOgAAABRAoAMAAEABBDoAAAAUQKADAABAAQQ6AAAAFECgAwAAQAG8DzoAQD+aPHlyuru7672Ml6WR\n3j+4ra0tXV1d9V4GQE0IdACAftTd3Z2VK1fWexmDViM9mQDwcjnFHQAAAAog0AEAAKAAAh0AAAAK\nINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAA\noAACHQAAAAog0AEAAKAAAh0AAAAKINABAACgAAIdAAAACiDQAQAAoAACHQAAAAog0AEAAKAAAh0A\nAAAKINABAACgAAIdAAAACiDQAQAAoADNe9pg0aJFufzyy9Pb25s5c+bk9NNP32Wbb3/721m0aFGG\nDRuWD33oQzn44INrslgAAAAYrHb7Cnpvb28WLFiQCy64IBdffHFuueWWrFixYqdt7rjjjqxevTpf\n/vKXc8455+Syyy6r6YIBAABgMNptoC9dujQdHR0ZO3ZsmpubM2vWrCxcuHCnbRYuXJjZs2cnSaZP\nn56NGzemu7u7disGAACAQWi3gb5+/fqMGTOm+nF7e3vWr1+/223GjBmzyzYAAADA7u3xd9Bfir6+\nvj1u09XVla6ururH8+bNy4QJE/rj5gfEcz9i46y3kbyU/YdXznxry3xrx2xry3xrx2xry3xry3xr\nx2xrqxHne8UVV1T/3NnZmc7Ozt0Hent7e9atW1f9eN26dWlvb3/Z2+x4gwAAALC3mzdv3i6f2+0p\n7lOnTs2qVauyZs2abN26Nbfeemtmzpy50zYzZ87MTTfdlCRZsmRJRo0alba2tn5cNgAAAAx+TX17\nOBfgzjvv3Olt1s4444xce+21SZK5c+cmSRYsWJBFixZl+PDhOe+883LIIYfUfuUAAAAwiOwx0AEA\nAIDa2+0p7gAAAMDAEOgAAABQAIEOAAAABRDoAAAAUACBTkNbvXp17rnnnnovAyjMmjVr8r//+7+5\n//77672UQWfVqlX53e9+l+uuu67eSxmU1qxZk1tvvTXf//73672UQWf16tX5wx/+kJ6ennovBV62\nZ599Nr/73e+yYcOGei+FGmuu9wL2Fj09PfnNb36T9evXZ/bs2Zk6dWq9l9RwNm/enJaWluqfL7nk\nkjz55JOpVCpZsWJF3vSmN2XEiBF1XuXgs3z58ixevDijR4/O7Nmz09vbm3328dxef1m2bFmWLFmS\nFStW5HWve11e+9rX1ntJDWfHY8Pdd9+db3zjG2ltbc348eNzyimnpK+vL01NTXVeZWPacbZJctdd\nd+VHP/pROjo6cthhh2Xr1q1pbvZQ4pXacb5XX311brvttjQ3N2fo0KFZuXJlTjvttLS2ttZ5lY1p\nx9k+88wzufjii7Nx48bsu+++uemmm3L22Wdn3333rfMqB69NmzblW9/6Vo488si85S1vqfdyGs7z\nj71J8vvf/z5f/epX80//9E857rjj6rSywe3hhx/Offfdl7Vr12b27NmZMmVKXdYx5LOf/exn63LL\ng9iqVauybNmyjBs3LknS19eXq6++OqtWrcqUKVPy4x//OMcdd1xGjhxZ55WW76mnnsrll1+eH/7w\nh3nooYcyZcqUjB49OjfeeGOampryD//wD3nDG96QK6+8MsOGDcuBBx7owfir8Px9d+vWrbn00kuz\nbNmyPPLII3njG9+YIUOG1HmVjev583388cezYMGCNDU1ZfLkybnyyivT2dnpAflL8GLHhlWrVmXj\nxo35yEc+kpNOOin777+/48HL9GKzTZIFCxbkPe95T0499dRMnz7dk3WvwPPnO3ny5FQqley33355\ny1vekre97W1pbW3N6NGjc9hhh2XYsGH1XnLDeLF996abbkqSfOxjH8usWbPyX//1X9lvv/1y4IEH\n1nnFje/592vbLVmypPpY7ZhjjnGseAlebP/t7e1NU1NTfvOb36Svry8HHnhgDjzwQDN9lZ6/7y5d\nujTf+9730tTUlHHjxuUHP/hBjj/++Lr0mkDvZ9/85jfzi1/8IkuXLk1PT08OPPDAtLS05Nvf/nY+\n+MEP5uj+fQY+AAASXUlEQVSjj86qVauyevXqTJw40R3v8yxbtizbtm2r/mP41a9+lc2bN+cf//Ef\n8+STT6arqyvTpk3LPffck61bt1ZfbbzjjjvyyCOP5M/+7M+SxAPyV+CF9t1hw4Zl2rRpOfHEE7Nk\nyZJMmTIlra2tngR5BZ4/38mTJ2e//fbLySefnGOPPTZTp07NjTfemMmTJ2fChAn1Xm5x9nRsuPfe\ne9PR0ZHRo0dn+fLl2bx5c5555pls2LAh++23X51XX7Y9zfa+++7LuHHj8qc//SlPPPFEpk+fnmXL\nlmXlypU54IADPGm3B3ua7wMPPJC2trZMmDAhQ4cOTVNTU2666aasW7cuJ510UvXBObt6KY8ZDjro\noKxfvz6PPvpohg0blgcffDDbtm3LnDlzPAZ7lV7ofm3o0KFJkquuuirTpk1Lb29vJkyYkEqlUufV\nlmdP++/999+ftra27Lvvvlm4cGGam5tz4IEH5uGHH85RRx1VnTUv34777oYNG3LQQQelubk5J554\nYk488cRMnz49t99+e0aOHFmXV9E99fIKLFmyJBdffHE+8IEPZPXq1dXPL1++PM8880zmz5+f+fPn\n54477sjixYvT3d2dI444It3d3UmSo48+Ok8++WTWrFlTrx+h7np7e6v/Jc+dZZA8d3rqbbfdluS5\nU9KefPLJjBo1Ks3NzTn22GPz1FNPZeHChZkxY0aWL1+e3//+93nggQfy7LPP5k9/+lMScb47L3Xf\nvfPOO3PXXXclSSZMmJDhw4dn5MiRWb58eZL/9/fFzl7OfBctWpQk2bZtW+6999588YtfzH777ZdJ\nkybVa/lFeDXHhjvvvDNjxozJM888k+9///v5z//8z1xzzTW55pprdvpee6tXOtuenp50dXUlSZ54\n4olcd911uf7667Nw4cJ8/etfr88PU6BXM9+77747yXPHgyRi5nle6Ww3btyYW2+9NSeeeGKOP/74\nfOUrX8k111yTnp6e/OpXv9rpe/HCXs792p133pkkWblyZSqVSqZOnZq+vr7q/7e3zvrVHBu2P1bo\n7u5Ob29vTjzxxGzYsMGTSy/BS913Fy1alEWLFqW9vT2tra3ZsmVLkmTfffettsVA77sC/SVYtmxZ\n1q5dW/14/fr1mTlzZtra2qp3qkny4IMPpq2trXrKyZFHHpnFixdn69atGTp0aPWiJAcccECampqq\nf+mDXV9f304HpiTZZ599qv8lz134Innuwd+Pf/zjfOITn8jPfvazTJ06NYsXL65+nxUrVuT+++/P\n1KlTc+aZZ+b666/Pz372s5x00kk7/ePjOa903+3s7KzeKSRJS0tLxo4dm0ceeWTgFt8AXs18tz+Q\nGTJkSJ599tlMnTo1kyZNyoIFC7Jp06aB/UHqpD+PDY8++mgefvjhDBkyJO94xzvyjW98I5/61Kfy\n53/+57nyyiuT7F1P3vX3bB966KF0dHSkp6cnW7Zsycc//vG8//3vz+OPP56HH3544H/AOuvv+W4/\ntjY3N2fLli1ZuXJlXvOa11S/796kv2e7/Ynlrq6u/O3f/m3+9V//NWeffXZuuOGG9PT07FXHhZfi\n1dyv3XHHHUmSBx54IO3t7TnuuOOy7777Zs2aNXvNmSD9uf8+8sgjeeyxx9Lb25u77747b3jDG7Js\n2bI8/PDD+dznPpc//vGPA/7zlaw/HpP19fVl6NChWbZsWdatW5fZs2cnGfjHD67ssoPn/2Pafhrv\n3Xffnebm5vzlX/5lNm7cmGOPPTYtLS1Zv3597rnnnsydOzdJqqegDB8+PEly1FFH5Sc/+UlGjhyZ\n4cOH54knnqhu98wzz+w1z341NTXtsmNv2LAht912W9asWZPbb789nZ2decc73lE9wH/uc5/L8OHD\ns3Hjxtxzzz2ZP39+tmzZkhkzZuSRRx7Jli1bcvjhh+eTn/xkkucuwjd16tR0d3enra2tHj9mXfX3\nvtvZ2Zkf/vCH1e/Z3NycsWPH5g9/+EP1NvYmtZjv9jMU+vr6MmPGjMyYMSObNm3KZZddlgceeCDH\nHHPMwP+gA6xWx4Ydfxdy6tSpGTFiRB577LG96lcH+nu2y5cvz5AhQzJlypRMnDgxfX19GTZsWHp7\ne/fKK2LXat8dOnRohg4dmiVLllQfGO5tv1JUi303Se6999688Y1vTJLqdT7Wrl27156t0N/3a0ce\neWTuueeePPvss1m5cmX6+vryne98J3/4wx+yadOmPPvss3n7299el591INVi/926dWsWL16cT3zi\nExk3blyam5szZcqUdHR01OmnrK9aPubd/vj2f/7nfzJjxoy6XUhy73qUvYNX8gzXxz/+8fzyl7+s\nXlXx8MMP3+mVg0MOOSTr1q3L008/nSSZPn16Hn300YwcOTKHHHJI9dmZ0aNHp6ura5cLajSap556\nKslzp+TtOMcd9fX1Zc2aNbnuuuvyta99LbfcckuS5+4UFyxYkAkTJmT+/PnZZ599cvXVV+fEE0/M\n8OHDq2cXjBo1Ku9///vzvve9L5///OfT0dFRfXC4efPmbNq0KY8++mi++93v5oQTTkhbW9ugP4Vq\nIPbdadOm5fHHH69+vbm5OdOnT6/e9tatWwftnAd6vjvekY8YMSLLly+vXpCrUdX72LBly5Y888wz\nWbFiRX7wgx/khBNOSHt7+8D88DVWr9lOmDAhTU1NedOb3pQ//vGP+e1vf5vrr78+48aNy9ixYwfm\nhx8A9dx3t9/e1q1bM2LEiOqZNIPlWFvPfTd57rh788035+67784vf/nLHHnkkXvNVdwH6jHvY489\nlpaWlmzatCmrVq3KiBEjctJJJ2XmzJk59dRTB+rHrYl6Hhv22WefXHTRRbn00kszf/78HHfccWlt\nba0G5mBWj8e8y5Yty5YtW3Laaaclee6K+gNtr30F/aU8w3XkkUfmzDPPrD7D9fnPfz7Dhw+vPlMz\nffr0PPnkk9W3mRkzZkxaW1tz33335bjjjsvQoUNzwAEHZPXq1Xnd616XG2+8MV//+tfzxBNP5LWv\nfW1DP2u7aNGi/Md//Ee++MUv7vYCQb/97W/z61//OtOnT89RRx2Vq6++OiNGjMgRRxyRtra26kXH\n3va2t+X73/9+uru7M3HixDzwwAMZP358kudOr95+gYa77rorhx56aFpaWrJ27dpceeWVue+++zJz\n5szq6YCD/ZWGgdx316xZk7Fjx+bRRx/NNddck9tvvz3vfe97c+aZZ+bUU0/d5S1ABoOBnO/atWsz\nfPjwPPTQQ3nwwQfz8MMP58gjj2zoV3pLODY88MAD+elPf5pNmzbl4IMPzlve8pZB8UCm3rNNnnsg\ns3Xr1lx33XXp7e3NW9/61kHzKk4957vj1dq3HwcOOOCAJIPjjKV6znb69OlJkne961256aabctVV\nV2XcuHE55ZRTBs0Td3syUPdr+++/f9auXZtzzjmnejtLlizJtddem5UrVzbsVfPrfWxobm5Oe3t7\nNVJf//rXV8N1MBwfdmcgH5OtWrUqHR0d+eY3v5mmpqZ8+ctfzkMPPZTTTz89s2fPHtBZD7pAf+qp\npzJ69Ohs27YtTU1NLzjMvr6+PPHEE7n77rurp5LOmjWr+gzXOeeck/nz5+enP/1prr766px11ln5\nyU9+kj/96U8ZP358mpqaqn/Jra2teeSRR3LIIYckSU4++eTceuut2bx5c5YuXZoZM2ZUryB87rnn\nZtGiRdlnn31y7LHHNvTbrE2YMCHbtm2rzuGSSy7JnDlzqldV3/6PYuzYsXnqqacyZ86cHHTQQXn6\n6adz7733ZtKkSTnssMPy+OOPZ+rUqRk2bFhGjhyZJ598MtOmTctDDz2UmTNnZvPmzdmyZUv+/d//\nPStXrsyhhx6aE044IUnS3t6ev/u7vxs0B6cS993try48/PDDGTp0aD72sY/lkEMOacirYpc232OO\nOSZjxoypXiV7y5YtOfnkk3PkkUc6NrzCY8PrX//6JM89O/7JT35y0F1dvITjbvLcqxGHH354vcZQ\nMyXsu8lzr0Ruj8rBop6z3f7uLpVKJaeeemrDv5K7o9Lu13Z8zLv9/5k0aVI+8IEP7BRMjaaUY8P2\nv9/DDjusLnPoT6Xtu8ccc0w6OjqyatWqHHTQQWltbU1nZ2fe+9731uVXZwfV26wtWrQol156ad7y\nlrdkn332edGDwG9/+9t8//vfT3Nzcw4//PD8/Oc/z/7775+DDz44N954Y0499dSMHz8+48aNy223\n3ZbOzs4sXbo0w4YNy0EHHZTk//0jWbJkSR577LGMHDkyW7duzZFHHpm+vr7ccMMNSZ7bAcaMGZMk\nGTZsWKZMmbLT21A0qmHDhuXmm2/O4YcfnrvuuisbN27MnDlzdnpA3NTUlKeffjo9PT0ZM2ZMOjo6\nsnXr1jz66KM5+OCDs3bt2tx+++2ZPXt2Hn300dx///154xvfmAMOOCCLFy/O9773vbS0tOToo4/O\nAQcckHe84x056aSTqq/abn9WbcdTXxrxwJ+Uu+/uv//+SZIpU6ZkxowZmTBhQkaMGFH7gfSzEuc7\nZ86c7Lfffhk+fHiOOuqoHH300dW3WWpk9Tw2bH8FcsiQIdlnn33S29ubvr6+hn1Q+HwlHHe32/7q\nzfbbHAxKm+9g2W+TsmY7WI4LJd6vnXzyydWzErb/P0OHDk1z83OvBzbqvEvaf7dr5Ivulbjvzpkz\nJ21tbRk9enT1rNyOjo66nX03qF5Bf7nPcL35zW/OlClTdnqG69BDD33RZ7iWLVuW448/Pk8//XSG\nDx+eH/3oR1m4cGFGjx6dTZs25a/+6q+SJCeccMJOrzbsaPudQqO/6tvc3Jzx48fnuuuuy7Bhw3LK\nKae84EGkUqmkpaUlixcvzjHHHJNhw4bloYceytixYzNt2rT85je/yaWXXpoHHnggb3rTmzJq1KiM\nHDkyZ5111k7/KI444ogk/+938Xb8x9zos0waY9/d8cF4o90plD7f7bHzYs8iNxLHhtopabZNTU2D\n7gyF0ubbaMfZ3SlptoPluFD6/dpgUtL+u10j78el77slPCYbVIHe3t6elpaW6tu+tLa2vuBpeKNG\njcprXvOa/OlPf8qUKVNy0EEHZfXq1dm6dWvGjx+f66+/Pm94wxuydu3abN68Ofvvv39e//rX56qr\nrsrHP/7xvPWtb81pp52Wk08+OX/913/9gr9Lvv0Z2uf/5Q6mO93DDz883/rWt6pvo7Gj7T9ja2tr\nWltbc9NNN2X48OG55557cswxx1SvQHnAAQfkjDPOqP7uzfb/d/uBavvv12yf5WCZ3fM1wr7byHcG\npc93sMWOY0PtmG1tmW/tmG3/Kv1+bbCx//af0vfdEh6TDapAH+hnuLb/jtgLPdMyWA9QOzrwwAMz\nfvz4HH300bnkkksyb968HHrooTsdUJqbmzNu3LgcfvjhGTlyZHWbJNlvv/2ycePG6tUXt23btss/\niB3/sQxm9t3aMt+B5dhQO2ZbW+ZbO2bbv9yvDSz7b/+x7+7ZoAr0ZGCf4drxa/V+pqUeOjo6sm3b\ntpxyyimZOHFivvvd72b27NnV38vZtm1bmpub09bWls2bN+f444+vXpU2ee5Kle9///urf0974wx3\nZN+tLfMdOI4NtWO2tWW+tWO2/c/92sCx//Yv++7uDaqLxCXJli1bcv/99+cNb3hDrrzyynR0dGTM\nmDG7/P7R+vXr09vbm/333z+zZs3KiSeemCFDhqSlpSW/+MUv8rrXvS5tbW3Ztm3bLs+uDPZntl6q\nYcOGZdmyZRk7dmwOO+ywHHfccens7Kxe8GH73J555pn09vamra1tlyshjh8/viEvOlYL9t3aMt+B\n49hQO2ZbW+ZbO2bb/9yvDRz7b/+y7+7eoHsF3TNcA6epqSl///d/n+S5t9PYfiBavnx5li1bliVL\nlmTlypU5/vjj8/a3v72eS20I9t3aMt+B49hQO2ZbW+ZbO2bb/9yvDRz7b/+y7+5eU9/2SwQOEn19\nffna176WU089NQcffHC6u7tf8P3rHnnkkdx777054ogjMmXKlDqsdPDYfgrJ1q1bc+ONN2bx4sU5\n9thjM23atOy///4v+hYR7My+W1vmO/AcG2rHbGvLfGvHbPuP+7WBZ//tH/bd3Rt0gb6j7ZfvTzzD\nRWOx79aW+QIwmLhfo1HZd3c1aAP9xZ7hmjp1ag444ADPcFEs+25tmS8Ag4n7NRqVffeFDdpABwAA\ngEZS5pu/AQAAwF5GoAMAAEABBDoAAAAUQKADAABAAQQ6AAAAFOD/B7M7NWJUCd2SAAAAAElFTkSu\nQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x14a4b7f0>"
]
}
],
"prompt_number": 17
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 14
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 14
}
],
"metadata": {}
}
]
} | mit |
root-mirror/training | NCPSchool2021/RDataFrame/02-rdataframe-collections.ipynb | 1 | 4299 | {
"cells": [
{
"cell_type": "markdown",
"id": "6c20dcc6",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Working with collections and object selections\n",
"\n",
"RDataFrame reads collections as the special type [ROOT::RVec](https://root.cern/doc/master/classROOT_1_1VecOps_1_1RVec.html) (e.g. a branch containing an array of floating point numbers can be read as a `ROOT::RVec<float>`). C-style arrays (with variable or static size), `std::vectors` and most other collection types can be read this way. When reading ROOT data, column values of type `ROOT::RVec<T>` perform no copy of the underlying array.\n",
"\n",
"`RVec` is a container similar to `std::vector` (and can be used just like a `std::vector`) but it also offers a rich interface to operate on the array elements in a vectorised fashion, similarly to Python's NumPy arrays."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "25b99067",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"import ROOT\n",
"\n",
"treename = \"myDataset\"\n",
"filename = \"https://github.com/root-project/root/raw/master/tutorials/dataframe/df017_vecOpsHEP.root\"\n",
"df = ROOT.RDataFrame(treename, filename)\n",
"\n",
"print(f\"Columns in the dataset: {df.GetColumnNames()}\")"
]
},
{
"cell_type": "markdown",
"id": "0f3633ae",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"To quickly inspect the data we can export it as a dictionary of `numpy` arrays thanks to the `AsNumpy` RDataFrame method. Note that for each row, `E` is an array of values:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "b4664f42",
"metadata": {
"scrolled": true,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"npy_dict = df.AsNumpy([\"E\"])\n",
"\n",
"for row, vec in enumerate(npy_dict[\"E\"]):\n",
" print(f\"\\nRow {row} contains:\\n{vec}\")"
]
},
{
"cell_type": "markdown",
"id": "b896f202",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Define a new column with operations on RVecs"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "4f140a78",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"df1 = df.Define(\"good_pt\", \"sqrt(px*px + py*py)[E>100]\")"
]
},
{
"cell_type": "markdown",
"id": "4ca3b396",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"`sqrt(px*px + py*py)[E>100]`:\n",
"* `px`, `py` and `E` are columns the elements of which are `RVec`s\n",
"* Operations on `RVec`s like sum, product, sqrt preserve the dimensionality of the array\n",
"* `[E>100]` selects the elements of the array that satisfy the condition\n",
"* `E > 100`: boolean expressions on `RVec`s such as `E > 100` return a mask, that is an array with information on which values pass the selection (e.g. `[0, 1, 0, 0]` if only the second element satisfies the condition)"
]
},
{
"cell_type": "markdown",
"id": "e283340e",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Now we can plot the newly defined column values in a histogram"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "9795d4a7",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"c = ROOT.TCanvas()\n",
"h = df1.Histo1D((\"pt\", \"pt\", 16, 0, 4), \"good_pt\")\n",
"h.Draw()\n",
"c.Draw()"
]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.6"
}
},
"nbformat": 4,
"nbformat_minor": 5
}
| gpl-2.0 |
emdodds/matching-pursuit | Notebooks/gammatones.ipynb | 1 | 286117 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import numpy as np\n",
"import tensorflow as tf\n",
"import os\n",
"import matplotlib.pyplot as plt\n",
"from scipy.io import wavfile\n",
"from scipy import signal as scisig\n",
"import pickle\n",
"import sys\n",
"sys.path.append('..')\n",
"import matchingpursuit\n",
"import signalset"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Found 6292 files\n"
]
}
],
"source": [
"sigset = signalset.SignalSet(data='../../Data/speech_corpora/TIMIT/')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"mp = matchingpursuit.MatchingPursuer(sigset, use_gammachirps=True)\n",
"phi = mp.phi"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"phi /= np.linalg.norm(phi,axis=1)[:,None]"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAWYAAAD7CAYAAABZqT4/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXl4FEX6x7+dAwj3fR/hvgVEARFhUEQOFeUSr9X1WMFV\nwRNZlUxY3VVx1XWFRVeFdT0A0Z/iiihqJhwqICL3pVwLhJuQQEhIMu/vj3eamUwmc2amuibv53nm\n6Z7qnp7PVFe/XVVd3WMQEQRBEATrkKBaQBAEQSiJBGZBEASLIYFZEATBYkhgFgRBsBgSmAVBECyG\nBGZBEASLkeRvoWEYMpZOEAQhDIjICPezAWvMRFTqlZaWpkW6+It/eftbzbEi5b0VPf35R4J0ZQiC\nIFgMCcyCIAgWI9Fut5e5MD093Q4ADocDDocDAJCamlpi6o3KdIfDgXnz5l3wzczMBCD+sUqvKP46\nu6v2LCs9Hv3tdnu6zw8EgeGvP8QwDCqP/hJVGIZRLv09qhB/tejsr7M7EDf+0bv4JwiCIMQWCcyC\nIAgWQwKzIAiCxZDALAiCYDEkMAuCIFgMCcyCIAgWQwKzIAiCxfD7ECMA8LwBxWazwWazRVEnMjwH\no5uIf+wQf3Xo7A7Ep38kyA0mFkb81aKzv87uQNz4yw0mgiAI8YIE5jiBCHA6VVuEDhGwejVQVKTa\nJHR++w347DPVFuHx/vtAOba8Y8qMGcC6daotokvYgbmggA8qXxABS5YA//tfuFtXQ2EhcM89wBtv\nqDYJnVtvBZo0Ac6cUW0SGkuXAv36Aa+/rtokdB57DLjhBuD4cdUmoXPbbVzWTfLygLfesv4JkghI\nSwPSXY8HcjqBHj2A+fPVepU3YQXmb78FqlUD/vhH38v//ndg4kSgf3/g1KlI9MqfrCz2+vvfSy97\n6y1g0ybgqaeA3btj7xYIImD6dK7teLJ3L7BsGRfQhQuVqAXFunXAp5+WTFu4EBg7FnjvvZLp2dkc\nrHNyYufnj7y80jXMtWuBzp2BjAx32vz5QO3awJ49MdULyOHDQHExzx85AlSuDBw6BJw/z2nvvw/c\ney+waJE6x7IgclcCjxzhaVYWT7dvBzZuBD74wL1+YWHZlUZt8PX0fY+n8JM3xcVEF11E9N57RI0a\nEW3dWnJ5YSFRw4ZEW7YQ3XMP0Z/+VGoTMcOX/wMPEI0dS1SnDtGxYyWX9etH9OWXRFOnEj38cOnt\n7dtH9OqrRLt3R0nYC2//JUuImjUjqlmT6ORJd/rs2US33060cCHR1VeX3MbevURt2hBddx3R+fMx\nkPbA07+4mKhjRz7E9u93r9OpE9GaNURVqxKdPu1Ov/deonr1uAypwtP/qafYfcUKfn/4MJehP/+Z\n6PHH3Z+54gqibt2IHn205LYOHyYqKoqBtAtP9z172H3mTH6/bBnRwIFEXboQrV/PaffcQ9SjB9HN\nN7u3sXQp0Wuvxc7ZE0//m24iuuwynl+2jL3r1OH38+cT9e7Nscjp5DLeuDHRffcpkPbA5e83vvp7\nhRyYP/6YM8LpJJo2jeixx0ouX7qUqE8fnv/tNz64PA84IqJz54hGjSJKSiIaNozXiwbe/llZvEOz\nsojGjyd64w33sv372bWwkANv/frsaXLiBFGLFvy5hg2JNmwo/X0FBUQHDvA2ouF/xRVEH3xAdMMN\nRO++604fNYro/feJcnOJatQgOnXKvWz8eKKnn+Z8njGj5PZzcvgEm5HB+7O88fT/7DOiiy8muuMO\nolmzOO3kSaLq1Tm/Bgzgg46I39erx0Gjdm0OaiYrVhCNGEH0zjvRcfbln5/PB/7ttxM99BAv++IL\noquuIlq8mOiaazgtL4+oWjV2bNvW7ffll0SGQTR8eMngfPo00dGj0XUn4spRt25E/fvz+5df5grK\nTTcR/ec/nNarF9GCBVy2nU7+LXXr8vvFi3kdp5P349q10XH25Z+TQ5SSwpEqO5srRpMmcTk/eZJP\nmNOn8/F68CDR999z5aVWLfdxMGMGr1Nc7P4d5nyU/cMOzAHHMU+dCjRtCtx3H5CczE3p558HDAMY\nN46boS++yO8BbhLdeivPt2kDDB0KzJkDPPGEWUN3b+vECe4+6NsXePZZ7vMyDOCXX7iPeskSbqbX\nrg106AC0awfUrw8kJAC5ucDZs8C5c/xyOoGkpJIvAHjmGe66GD4cePlldmvcGBg/nvuS//AHXu/r\nr4Grr+bPtW4N9OoFfPIJcMstvHz6dODaa4HZs4EFC3h7mZnsdOYM58Hf/w6kpHD/+1VXAYMGAY0a\nAUePctP2yBH2rlqVu4KqVOFXYiL7O53c3DTnAcBuB+64g5v2e/ZwfufkAF99Bdx+O6+3ciUwaxZQ\nvTowcCDw5ZfAzTdz8/Xrr4E33+TP9OrF+6xTJ+DgQWDECO6XPnCAPaZO5Xzevh1Ys8Z9gaVJEy4D\ntWvzbz17lpvA58/z/jIM3ieeU7M8vPYa7++//pW3X1zMzf377+fvuOQSzvPLLwdWrQKGDOHf06oV\n0LMn+86Zw/2KWVm83554gvflihW8P9avB/72N+5qaNCAy1OvXpw3x49z/mdncz4nJ/MrKYnfm66G\n4W7+EnFTHwD++1/ujuveHXjoIeB3v+P0deuA3r25+2jDBk5bvRro1o1/S0EBsGMH0LEjd40tWMD7\n6LnnuCzNnw888AD36fbuDdx5J/ts3Qps2QLk53N+167NZSo/n8s5wOslJLjz2sTwGpz19NNcRt59\nF/j4Y2DwYN7Gpk3cr3/sGM/n5/M+v+46YNo0YPNmdr/4YuDRR/l3X3MNMHMmbysnB7j7bmDCBO76\n+OQTPi779GHfgwe5rBO5PRMSSnp7p/nir3/lfTV0KMeKn37ivOnZk4+7X3/l/JowgV1//pm7NcaN\n4zL90UdA8+bAvHlAvXrsM3Ysx4DduzlvBg4E9u0Ddu7kstm8OZeNwkL3q6io7Avr/vI/EgIG5nXr\n7Pj0Uy5QffrYUK+eDSNH8rKePVl4wwaez8sDFi/mIGXy5JPAsGG8c6tUAV56iQvDypUcoB55hJff\ndx+vS8TBbMQIvvrauTMfGDt2cGYeP84ZWKMG0KwZF9qUFN7Bmzc7sG2b40KAA4AVK+x4/XUOLAcO\n2LB5sw0Af+fvf8/brlOHA92IEW7vP/yB+zhvuYULwPz57AAAN90EnD7NO3X0aC6Ygwfz72rZkgPi\nsmX8G5cv52CRmsp5VKMG51Nenvtgczq5cO7e7cCePY4SgW3pUjtmzuS8u/VWG5KTbRg2jE84Tic7\n1azJeQHwxajPPuPAPHcuMGYMUKsWv6ZP5wMqLY37E++/n4McEX9m1ix2b9+eD7I//YkLaVYWv7Kz\nOa+aN+fAlZzM3+l08ja2bXNgxw5Hif69116z45ln2L9ePRu6dbNh0iQu7D/+yEEUAK64AnjlFZ7/\n9FPgxht5/uGHAZuNy8nNN3M5mTKFT+J33w3UrQs0bAg8/jjwj39wEP7xRy6Tycmc95deygGjuNh9\noBUW8nuz/5II+PVXB3btcgDg8gQAt91mx9mzfPCfPm3D4cM2HDrEgfnWW4EWLXg/Hj3K+3rgQN53\nN9zA/ec9enD+jBkDDBjALt984y4jXbpw3n/4Ift26cJlrmpVLmPZ2VxGUlI4Dw3DffI2yzgA7Njh\ndjfz/7vv7PjLX9gxL8+Gzp1tWLeOy+m997LzG2/w+/bt+TuuuoqvIa1cyb952DCgbVv+PRs38sk0\nIYH3wwcfcGVlzhx2XbMGOHmSg+aAAbyerwqHd1pxMbBrl9vfZOFCO375hS9UJiXZsG6dDZs3c76b\ngfnXX9m9Vy8OzMuXA5Mn8+dfeIGPs5de4pNlv37Aq69yOR8yhCssn33Gx+bll3NZP3CAfapUKXkS\n9z4Jeuazd/6XC/6q03A1J5xObvJOnEh06FDJKvvjjxM9+STPz59fuo+TiJvejzxC9O9/EzVtWrKP\n0ZMjR8q3aWf6Z2cTPfss0cqVJZdffz035YqKuNl28KB7WUEBN1+3bye65ZbS3QBERD/8QPTSS0Q/\n/1x+zr78169nT8/mV6dORD/9RPTmm9zENjl8mJtx585xc3r1aveyoiKi++8n6tqV6KOPouPs7V9c\nTPTf/5YsN926Ef34I3evfPopp506xd0aBQVErVoRbdrkXv+WW7hJ7d0VQMT7NlpdGgDo1CnuAze5\n8UbeF82bu7vgBg/mro0rr+TfSsSfad6cqEMHbv6bHDhA9OGHRGfPRsfZ052IHbOzOe2BB4ief567\nW06f5mUtWhD9859Ed93F68yfz7+nRg3uviMi2rGDf/e6ddF19uVvXgd6912iceP4+sqxY9w9k5bG\n1yZycrgbZtgwLkPZ2dzX3KABd6uax83Zs+68iJF/7PqYvfnlF6KWLfnHjxjh7rPy5OhR7kPs3p3X\njxWB/OfOJRo9migzky98ePPkkxwAW7fmnR9r/PlPmcInmwkTiP71r5LL+vcn+v3v+TdFux/WH2X5\nT57M7mZ/v0nPnnyBqmPHkt7nznE/rWeffyzw5f/660RDhvBBbzo+9RRfazGDAhEvmzyZg6GKfeDL\n/f33uTy3b8/vi4s5SI8Z4+73P3qUo8INN8RQ1gfe/lu28DWpJk34/dy5RDYbX+gjItq1i73N61tE\nRGfOxL7MmCgPzE4nXzh44gmu1Zw5U54/LzIC+R8/zmfg4cOJXnih9PJz5zjo7d0bJcEA+PP/6iuu\nEdesWTK4EXEttFkzIocjyoIBKMt/8WK+GNa1a8n0mTO5RD7/fAzkgsCX/7ZtpQPX0qWcZl5cswK+\n3HfvZk/PkRd9+nCaZ4Vp48aSo35U4O1fVMSegwbx+5UrS753OrmSEouWYDAoD8xE3KTv2pWbE1Yi\nGP+pU7mm5j1yxAr48y8u5m4jc5SAFSnLPy+Ph2u9917J9IICHvVTUBADuSDw5e90civru+/caUVF\nPARzyZIYygWgLPdJk7gbyeTBB/kkGcuhfMHgy/+f/yRavpzns7M5enkPS7QKkQZmeYiRhRF/tejs\nH6x7QQGPsqlbNwZSIRCM/+LFfEGvYcMYSYVApA8xksBsYcRfLTr76+wOxI2/PF1OEAQhXpDALAiC\nYDHkH0wshPirRWd/nd2B+PSPBOljtjDirxad/XV2B+LGX/qYBUEQ4gUJzIIgCBZDArMgCILFkMAs\nCIJgMSQwC4IgWAwJzIIgCBZDArMgCILFSPQcxO1Nenq6HSg5eDo1NRUOhwOpqaml1led7nA4MG/e\nvAu+mZmZF5aLv/iXh//evXu1ddc973Xzt9vt6aU+ECz+Hj2HMh7bmJaWpkW6+KtNj0d/qzlWpLxX\n6ROmf9iP/ZSuDEEQBIshgVkQBMFiBHxWRgxdBEEQ4gaK5rMyfPV/pKWlaZEu/uJf3v5Wc6xIeW9F\nT3/+kSBdGYIgCBZDArMgCILFCCswl/XAaqull4XVPMXfmulWcpG8V+tTXv7BEvDiX1paWgkJnf5F\nID09HeIfO8RfHTq7A/HpT/Iv2b6Jk39BUK0RNuKvDp3dgbjxl38wEQRBiBckMAuCIFgMCcyCIAgW\nQwKzIAiCxZDALAiCYDEkMAuCIFgMCcyCIAgWIynQCp7/cKLbIG9A/GOJ+KtDZ3cgPv0jQW4wsTDi\nrxZf/rm5QI0aioRCwJe7wwG0bw80a6bGKRS8/d94A8jPByZPVigVAkpuMMnLA86fD/cr1ZKXB5w9\ny/OFhUBBgVqfUCgqAo4d4/lvvwX271frEwpEwG+/8fzIkcDq1Wp9QmXrVsDpBGrWBN57T7VNaBw+\nDOzbBwweDEydCnzzDXDunGqr4CguBj75BJgyhV8dOgC7dqm2ij5hBebBg4Hbb+f548eBP/xBn0A9\ndChw5ZU8f999QLduan1C4ZFHgIYNeX7IED7IdOHHH4F27fhkuGQJkJHBAePHH1WbBUfXrsAXX/D8\nnj3AqFHABx+odQqW/v2BSy7h+bw84OqrgUWL1DoFy+7dwJgxfFIEOChv3gycOqXWK9qEFZjXrAG+\n/57nP/8c+Ne/9DnAfviB/QEgMxP49VeeP3yYa6FWZs+eku/PnOHmXYMG7t9hVQ4e5KnpmZ0NPPoo\ncNll6pyCxWxVHT7M07w8YPFibl4XFLhbYFbl2DGuQAFcAwXY+ZFHuAxZmexsnnpW/ObPB+rWVeMT\nK4IOzBs3cubk5vL77GxunprNip9/5ukTT3AN2kqcOwdkZbGveeb1pKAAeOEFroUWFsbeLxAnTrC7\nGSCysniakwNs384H3bffltwfVsHp5Pw3g9qGDTw9dMjdnC4sBB54ADh6VI2jP4qK3EHN7Io5eZKn\nhYVcZq65Ro1bMBQXlyzzZqDbtg145RXgp5+A06fVuAXC6eSy782BAzzNyADWro2tU6wIKjAfPgz0\n6AG8+SbX2rp0ASpV4jPxnj3A5ZcDW7ZwYHjpJa5B5+fz+0WLfGduLHngAaBNG27+1KwJVKnCNYbD\nh7m2uW8fF1QA2LSJ3w8YYI3mUkEBUL8+8PXX7lrnL7/wNCsL2LuX53ft4hZAhw6c5nRao//82WeB\nTp3cJ5PNm3l65Ig7SKxaBcyaBfz3v3yiWbdOjasvkpOB117jefOkZ5bnwkJufa1aBSxdCkybpsax\nLFavBpKSSgZm8+S3ZQtPN24EatfmY8HcH1Zh8GBgwoTS6WZZuvJKYOxYbr3k58fWLdoEFZgXLOAd\n7HBwIG7dml979nAf0MiRHNj27wcaNQL69uUugy++AMaNA+64g7ezdSvw1FPuC1hHj3IQieaFeyLg\nq694x23eDLRqxVelN28GEhOB7t3ZYedO7otbt44vNqxaBbz/PjvabMD//R9vb8sW9wFaVMTN2mjy\n3Xc8Xb0a+N//uE98/Xp3sNu3D2jShJ1++IHX/fJL4Jln+ASUnc0B+/PPeVl+vrsG6HS6m7bR4osv\nuFyYtZxt27if/MgR9q9Th30Brk1PmcL9obm5wKRJvG8OHHDXVvPyoltefJGZydPdu3lqXnTNzQWq\nVeP5N98Enn+ej5G+fTl4L1rErYKzZ90VFV8ttmixYgVPPYOW6W5WRJYt4+kbb/C+2LIFePVVzuc9\ne9Se4Jcv912bNysjAP+eUaOA2bOB++/nZbt3c54Txb6slBcBh8v16EHYuhV47jlg7lzg3nt5h2Vl\ncaf8Qw/xVV6bDXjnHS6gPXty0Nu+HRg4EHj9deDBB7ng9u7Nwa9fP25+V63KXSRNmnDTPDeXP5uQ\nwDWSoqLAhdnwMSjFMICcHAOtWhGIePuDB3NtMy+PTxizZnEf58UXA489xr/x11+BHTt4WNHGjcBF\nF/Hv3bCB112xgk9SzZtzsCgo4AKdksLz58+7X/4cPd+XNZ+bawAgXHQRkJrK+Xztte5ujW++AW65\nhb9rzRqgY0fOK8Pg961b89CudeuAWrX4hLRlC+dpSgrnd34+t36Sk3m7CQm+8zMccnLYv1YtoHFj\n/h5zX2/fzkFr4EDO3+Jidty+nVsINWpwnrdsyQdZURHn+fbtnN/JyXzQJifzd5X3CaZaNSAri/1T\nUvj7q1Rx/wank8upmX9Vq3KFo149PvElJ3M5adKEuz4KC4HKlflEWb06v09IcJd1wB1EyiOYmHkf\nCPP3GEbp701O5nw4d473X26u+2QezAkmUDnyt9ws++FiGFxOTp3iaUFB9PLaFzk5kQ2XC3iDSadO\ndhDxD/z1Vxt27LChUycupJs28cWD7t05I776CujViwPgQw9x0/vNN7l2N3Qon9UmTeIayM6d3OVR\npw6vd+wYH5g1avCOJ+KCnZTkP1h4ZuyKFQ6sXOm4kPbCC0CLFnY0asRB9OOPbRg0yIazZzlwNW/O\nAe+777gm3bcv+2ZlAZ9+CrRty4Fs3z4+E8+fzzWL2rW5dtqlCx+Ihw5x4a5Uyf1KTi5dCHw5e84v\nX87+ZvoLLwBdu9rRpQvX4uvXt6FZMxs+/5zzuGlT9njiCW7VHD/Ozbr+/YE+fYCFC7mpN28eMGgQ\n/6ZBg4AWLTjPa9fmAy8/nwMPEFmNzsx/kxdeAAYNsmPfPj7ZDRliwzff2DB4MNcsk5K4dvz558CM\nGcD06dwimDYNuPVWDthffMFlqksXbnH17s1lhYjLS2Ehl41AJxSiwIHCl3/fvnasXs1dXseO2dCn\njw1r1rDT+vXcNdauHV9jeeQR4OWXuTX24ovcrbd6NZ/4q1fnCkH9+hzgKlXivDYDnenmPY0k7y+5\nxI6DB82mvw3JyTYUFnKL5ehRPunt38+VpB9/BP78Zy4zn33G5er667mcNG/O61evzsHNDHCB8tsf\n3ss9/c2y37at/UJLCbC5XqUxK3sffcRdMgMHclw5f57LenY2xyszrkSa177wlf8R4euvtz3+gps8\nad+eqGVLosWLiWbPJrrsMqLOnXnZ5ZcT1axJtGgRUV4eNyJuvtn92cJCijme/i+9xE5paUSPPkrU\nsSPRHXcQzZtHVLUq0bXXEuXk8DpXX82f2baNaMuW2HubmP4nT7LXgAFEM2fy/NNPEw0axPM//ECU\nkMDzTifRY48RffutOm8T03/iRHZ78UWepqfztEoVovff5/mlS7n8TJvGvyEnR7E8sf+GDew3fjxP\nb7mFp0OH8rR+faI+fXj+xAmi775Tbc2YeX/ddWaDnl0BPm4BotGjefree7yPVByjZQGAjh93u5f1\nql2b6K23iI4fV21cElf++42v/l4Ba8yeXHopj91s145rhD/8AIwYwcs6deJ+2Z49uZl86BDXyEyS\nQvqm8qdrV562acP9fzt2AOPHc405Lw/o3Jlr688+C1x1Fa/bqZMy3RLUqcPTxERuGgM8bdqU51u0\ncA87Mwxg5szYO/qjeXOedu/O03r13MvatHEvO3iQy45hWOfuurZtedq5M0/Nu+aqV+dpSgrw1ltc\nK61bl1syViIlxT1fowa3qlJT+di94gpuiQ0bxi0Uq2EOiatb1z0SpnJl7paoV4+P4+PH+biIN0IK\nl/37c2Du2NHdTE9N5anNxl0U5oFmBhCr0KMHT/v2dY9qaNmSRzEA7htNnnoq9m7B0K4d3xhgBuPG\njd0nvsaNuRupvPqGy5uePbk8NG7M780Djoj78J94gpdb0b9aNQ7CAwfy+/r1eZqUxF0U3brxScU8\n6ViNwYM5CP/vf+5j1vwN7dpZ++KYYXDffY8ePDQOcHcdLl7MQToegzIQYmCeOBG48Ubewa1acVrv\n3jy97TY+61rx4AL4wD97lnd0Tg6ntWvH6QsW8MgSK7NtGxfCnTv5ffPmPH523TpON0cHWJGRI+HR\n18l9nE2a8Em8atVy6I+LMrm57gBm1uSTkvjaROXK6ryCYeJEfnkel4mJgN3OQ0KtztmzfOI2A3Pj\nxhyYe/bkshOvhBSYExPdNbYqVbhg9u3rXm7VoGxi7siLL+bhZP368fvx49U5BYvZFdSyJXdbdO/O\nF/hGjVLrFSyGwRfQAK5lLltmne6KYDDLdrNmfGF77Fi++KgT5kiitm15bL8ueF6Qbt+ey048B2VA\nni5naeLR3+l0N6mtjrf/iRPcDWP1CghQ2n3HDnerqlEj9zBDq+Lpv28fd8cUFPB1ri5dFMsFQaRP\nl5PAbGHEXy06++vsDsSNf/TGMev+sGrxjx3irw6d3YH49I8EqTFbGPFXi87+OrsDceMf2wflC4Ig\nCNFDArMgCILFkMAsCIJgMSQwC4IgWAwJzIIgCBZDArMgCILFkMAsCIJgMeQGEwsh/mrR2V9ndyA+\n/SPC38Oa4fWgfJOMjAwt0sVfbXo8+lvNsSLlvUqfMP3DflB+WF0ZZZ0ZrJZeFlbzFH9rplvJRfJe\nrU95+QeL9DELgiBYDAnMgiAIFiPgQ4xi6CIIghA3UDQfYuSrYzotLU2LdPEX//L2t5pjRcp7K3r6\n848E6coQBEGwGBKYBUEQLEai5yBub9LT0+1AycHTqampJabeqEx3OByYN2/eBd/MzEwA4h+r9Iri\nr7O7as+y0uPR3263p/v8QBDIP5hYGPFXi87+OrsDceMv/2AiCIIQL0hgFgRBsBgSmAVBECyGBGZB\nEASLIYFZEATBYkhgFgRBsBgSmAUhjtm0CcjOVm0RHqtWAYYBrF2r2iT2yD+YWIiy/ImAwkJg6FA9\n/devB1q1AkaP1s9/1Cg7MjKAsWOB3/3Ouv5l5X266xaHjAzrugO+/SdPtgMAJkwA3n5bP/+I8PUA\nDo8HcZCJ00n00UekFZ7+o0cTLVhAdPy4QqEQMf1ffpkIILrxRsVCIWL6A/zauVOxUIgAoL592b12\nbaLiYtVGweOd91OnKhYKEQB0001u/4IC1UahgQj/wSToO/+OHwcaNABefx1ITQVGjiy/k0O0MO8e\nKi4Gklxtg0qVgIICtV7BYhgG8vIId90FzJ/PaU4nN+90wDAMbNhA6NGD3z/4IPDKK0BiolqvYDEM\nA4D7+JgxA3jmGXU+oWAYBsaMIXz8sTtNpxvpvPM+JweoUUOdT6hEeudfUIF55kzgrbeAnTs5vUMH\nYMeOcL8ydpiB2TuQvf02cNddapxCwTAM3HknYd68kum6HGDeBxcA7N3L3Ro64O0/YACwfLkeJ0Zf\nef/dd8DgwWp8QsWXvy7lHojRLdkLFriDMsDzOhTOsrj7btUGwXPwYOm0Awdi71Fe9OypT4vFm5Ur\ngaVLVVuEz9NPqzaIjHPnVBvEjqACc1lNz59/Bs6cKU+d8qew0Hf6pZcCR47E1iUcfJ0AW7QATp+O\nvUt5kJ0N7Nmj2iJ83nlHr5qbJ99/zy0WXXnsMdUGsSNgYF61Cjhxwvey3r25383KZ7J//9t3+k8/\nAbNnW7/2mZHhO91mA/bti6lKudG5s74nlkWLgG++UW0RPg88oNogfGbP5mssFYEg/vPPf/WgRg0g\nNxfYvp37DqtUKW/F8PHVT+XNgAFAWhowZEhsnEIhkH/DhhwoBgywZtdSIP+ffuKTu1Xx579smTXL\njIk/91mzgIkTgQQL38VQln/XrsDGjdZ2B2Jw8S9QYPOkXz+geXOgf3+gcWPOvHr1gPPngeJifrm3\nXXLqPV9Ioh0yAAAS/klEQVQeXH994MBsUqkScP/9HOQqVwaqVQPy8tg5MdHdfI1lMzZY/0qVgMmT\ngZYtOd+rVsWFsc8m3vkdi0AejH+tWsDtt3MtunZtdk9K4rLjneexzPvERGDkyMD+Dz3EF9SSktjP\nXxmP5ckzmLy/+25gxAgu74WFnOdWOcEH8r/3XmDgQK4YJiVZryZ9/fVRD8xpHik218s/DRtykGjY\nkLs5Klfmgp6YyDve14FWHgfd8eMOnDjhuPB+1650hOrfpQsHi+Rkd5AoLmbvaB9gkfq3bcv5XqkS\nH2TJyb7zO1oBLhL/gQN5OGZhIVBU5HaMZXDz9E9KArZtC86/Vy8u60lJZZfxaJ9Uws37Pn2AOnX4\nGFUZ3MLxHz6c87u4WP1JxZd/VAPzo48S/vY3/xtp2xZo2hSYOhUYNowzyApNjWC6MgBg5kxg1Cig\nSROgevXoewVLMP5DhgBz5gBt2lintmMSyP+yy4B587j8WHFssz//+vWBdev4RGhFAuX9zp1Au3bW\nKzMm/vzXrgUuuSS2PqES9a4Mh4MQ6E7IrCygUSPr7WTDMJCQQH5rAmvXcj+n1dyBwAfX3LnAnXfG\nTCdk/Pk/+yzw1FOx9QmVsvxbtAB++41bJFbFX96fPg3UrBlbn1Apy3/9eh5yaXUiDcwBn5XRoIH/\n5efPW7uAJiSU3UT79lvrn3nLIj3d2kHZH9WqWT8o+2PzZmuXeX8sX279oFwW7dvrEZTLg4AdDq1b\nA7fdVjr9ueeAr7+2fgH9xz98p99zD3DllbF1CYfGjUunVa8OTJ8ee5fyYvdu1Qbh8+qr+gY2ALji\nCtUG4bNhg2qD2BEwMKekAP/5T+n0AQOAq6+OhlL5MnEiB2FP5swB3nxTjU+oZGWVfF+rFlCeD7GK\nNjfcUPL9xRfzhTJdmTxZtUHwPPxwyfc631wCcCyqKATsyvDFL78AF11U3irRIz/fPX/NNcDQodbs\nUw6G666z9tjfQKxbp9ogfGbNUm0QGs2a+X+vE+PHqzaILUEH5uXLub92zRpceFqYLjz8MF+c/Nvf\n9HzWQUoKDzscM0a/4NCmjXte1z5xk/vvV20QGp7X9Z95xv2ERR3RqaVSHgT92E8dMZ8uZ3L+PI/x\n1QVP/zlz3EP6dMEwDBQUEP74R77QqlvfsmEYyMggDB6s15PZAHb//ntC//78fuFCYNw4tU6hYBgG\nmjShC115uoWhqI/KiId/ADHR3X/HDhuaNLHF1CkUfPn/5S92NGvGd/c5HPrlv8Nhx223AZmZgGFY\n19+X+1df2dGvHz8moUEDG4K5OUwVvvzvvdeOGTOAQYP0LDuRUKFqzLoh/mrR2V9nd8Dt/8orwJQp\n+l0TismD8nUlXgqnroi/OnR2B+LGP7oPyhcEQRBihwRmQRAEiyGBWRAEwWJIYBYEQbAYEpgFQRAs\nhgRmQRAEiyE3mFgI8VeLzv46uwPx6R8RRFTmixeXJiMjQ4t08VebHo/+VnOsSHmv0idMf7/x1d8r\nrK6Mss4MVksvC6t5ir81063kInmv1qe8/INF+pgFQRAshgRmQRAEixHwWRkxdBEEQYgbKJrPyvDV\nMZ2WlqZFuviLf3n7W82xIuW9FT39+UeCdGUIgiBYDAnMgiAIFiPRcxC3N+np6Xag5ODp1NTUElNv\nVKY7HA7Mmzfvgm9mZiYA8Y9VekXx19ldtWdZ6fHob7fb031+IAjkQfkWRvzVorO/zu5A3PjLg/IF\nQRDiBQnMghCnZGerNoiMJ59UbaAO6cqwMOKvFp39DcMAQNi1C2jXTrVN6Jj+mma/dGUI1qZvX9UG\nkTF3rmqDyNi7V7WBEA5xX2MuKCBUqqTaJDwMw0C1aoTsbCAp4ANarUc81Hp09Tfda9XSs0vD9D9+\nHKhXT7VN6ES9xvzll4BhAOfPh/sVaqlcGUhJUW0RPmfPAnffrdoiMtavV21QcTlzRrVBZHz4oWoD\nNQQMzCNG8HTjxmirRI/8fODgQdUW4fPuu6oNImPnTtUGkZGfr9ogfIqLVRtExsqVqg3UEEQD2Q4A\nuPRSICNDx38RsAMAZswAbr5ZX3+7Xdd/cbDjvvuAbdv09X/wQaBZM2v7x2vZ2bRJZ//wCeLpcu7l\nuvW1mf1UAPDJJ8CNN6r1CRVPfx372jz9dSs7gNt/9WqgTx/VNqERL3k/bhywcKFqm9CJ6aiM1avD\n/Rr1jB6t2iAyTp9WbVBxeecd1QaRoWNgNvnsM9UGaggpMGdkREsjNpw7p9ogfO65R7VBxeWNN1Qb\nRIauF+4Bvd0jIaTAPG1atDRiw9q1qg3CR/eT4vbtqg0qLs89p9pACJWQ+pgBYMcOoEOHaGuVD579\nbAAwaBAQpf9OjAre/k4nD13UBU//q64CvvlGrU+oePrrnPeAft0Znv7nzgFVqqj1CZWY3/nXsWO4\nX6WezEw9B9ubvPKKaoPw+fZb1QaR8dFHqg0qLl9+qdog9oR1S/b06eWtETvq1NG33+rRR4GsLNUW\n4fP886oNwuemm/SrdXqi83hg3S/ch0NYN/r++c/8GjAAaNTI9zq+mn3BpkWbypW55n/RReocwqVp\nUz65XH21apPQmTaNX6NHc54nJFg37ytXLp2WkMA3XHk2q01/76n3vGquuALo3Bno3l21SXgYBg93\nNYzSr3gk6BtMGJvrxQH5hhuA5s2BxMSSn/BVswg2LRK2bHFg61aHV6rdY94G0//224E2bfhgswrB\n+k+aBHTtar3AFoy/zWbDmDFAcjL321oJT3/33X52jzVsuPlm24Vb/M3y6z31no8FweT9739vQ4sW\n1iozJoH8O3a04dZbbSBCiZdV8O0fPiFf/AOADRvctU0r430BBOC7iNLSlOiEjC9/nS5CefsfPQo0\naKDOJ1R0voDm7V5UVLoCZWV0zntAwcW/KVP0CMploUtQ9sUXX+gTlH2hU1D25sgR1QaRoVNQ9kbn\n+w/CJeTA/PTT0dCIDRMmqDaIjOHDVRuEj84XjAGgYUPVBuFz552qDSJDt6Fy5UFIXRkJCXo9rcq7\nOXTmDFCtmjqfUPH079UL+PlntT6h4um/fbt+Qy11ft6Ep7vDwWP4dULnvAdi3JWh+3hCnYKyNwMG\nqDaIDN2CsicTJ6o2iIyLL1ZtIIRKSIF56NBoaUQf3Z4O5s2oUaoNKi7JyaoNIqNGDdUGQqhYaLBY\ndGnaVLVBZFx1lWqDisu116o2ECoaQQdm3Z5l7I3uTwjTmb/+VbVBZOjcUtSdSZNUG6gh4A0mAwbY\nsXIlj4N0OHT8FwE7AGD2bF3/BcGOJk10/hcHO86d09vfbuc5K/vH6z+YHDums3/4BByVUVREOHgQ\naNmy3L4zZhiGgW7dCN266fmnjuaV6TFjgEWLVNuEjs7/Mg3o7W+6N2kCHDqk2iZ0TP+FC4Fx41Tb\nhE6kozIC1pgTE/UMyiabNqk2iBzd/4xVZ8aOVW0QGY8/rtogMnr1Um2ghrAeYiTEDh1ra57o7t+3\nr2qDyLjsMtUGkdGunWoDNQTsyvC33Oq4mhOqNcJG/NViGAYKCwlJGlZfDMNAdjahVi3VJuGhczcS\noOBZGYJQkdAxKJvoGpRNrrxStYE6pMZsYcRfLTr76+wOxI2/1JgFQRDiBQnMgiAIFiPRbo6e90F6\nerodKDl4OjU1FQ6HA6mpqaXWV53ucDgwb968C76ZmZkXlou/+JeH/969e7V11z3vdfO32+3ppT4Q\nLERU5osXlyYtLU2LdPFXmx6P/lZzrEh5r9InTH+/8dXfS7oyBEEQLIYEZkEQBIsRxD+YCIIgCKFC\n0Rwu56v/Iy0tTYt08Rf/8va3mmNFynsrevrzjwTpyhAEQbAYEpgFQRAsRliBuawHVlstvSys5in+\n1ky3kovkvVqf8vIPloAX/9LS0kpI6PQvAunp6RD/2CH+6tDZHYhPf4rg4l/AwLxkCWH48HA3rxbD\nMDBnDuG++1SbhEecPMhFtUbY6OyvszsQN/7RC8y6PxNVd/84KJyqNcJGZ3+d3YG48ZenywmCIMQL\nEpiFqJKfr9pAEPRDArMQVVwPCRMEIQSCCswad/UIgiBoR1CB2WMUiBBjDh1SbRAZclIXhNAJKjAX\nFUVbQygL3f9+/vRp1QaCoB9B/AewHe++C6xapd8gb8YO809adPTfv19v/3vusWPbNp7X0d/zH36s\n7K+zOxCf/pEQ1DjmKVOAV14pt++MGfEwjll3/+rVCbm5qk3CQ+extDq7A3HjH90bTAA9+wrjIbDp\n7i+BWQ06uwNx4y83mPhj5UrVBhWXM2dUGwiCflSIwPzgg6oNBEEQgqdCdGUAevvr6A7Eh7+uzWmd\n3YG48Y9+V8aJE+F+hRApixerNhAEIZYEXWMGgLNngaQkwAj7PBBbKlVy15g3bAA6dmR3Hf3z8oDE\nRH3cAbf/kiXAkCGqbUKnUiV9a21xUuNUrRE2kdaYgxrHbFKtmg1JSbZwvyvqOJ0OEDm8Uu0AgB49\n4HK3xdQpFPz5V60KJCTYkJBgi6lTKJTlP2KEeULUx79SJU7TZSxtPI4D1t0/EkKqMTudetXYPPuY\nd+8GWrdW6xMq8dJHvnIlcPnlqm1CR+dam87uQNz4R7+P+dQpvYKyN7oFZU9mzlRtEBk6BmVBUImM\nyrAwpv+BA0CzZqptQkdGZahDZ3cgbvzlBhN/fPqpaoPI0DEoC4IQPhUiMLdrp9pAEAQheIIKzJMm\nRVsjuujcN647deuqNhAE/QgqMFetGm2N6FKtmmqDioucFAUhdIIKzElBjHa2Mq1aqTaouKSmqjYQ\nBP0I6gYTpxOw23Ud5K33g+Z197/kEr39dbnJQWd3ID79IyGo4XL5+UDlyuX2nTEjHoZr6e6/dSuh\nc2fVJuGh85Atnd2BuPGP7nA5jfNHEARBO4IKzAkVYlCdIAiCNQgq5JoPdBEEQRCiT9zXhXXsG/ek\nShXVBoIgxJq4D8y6j6PV/QFGHTqoNhAE/QgYmPPyYqERPRYtUm0QGbqfWBITVRsIgn4EDMwpKbHQ\niB4jR6o2iIwmTVQbCIIQawLeYKL7IG/d/X/5xY6NG3leR3/d818Xf53dgfj0jwgiKvPFi0uTkZGh\nRbr4q02PR3+rOVakvFfpE6a/3/jq7xXWxb+yzgxWSy8Lq3mKvzXTreQiea/Wp7z8gyXuR2UIgiDo\nhgRmQRAEixHEQ4wEQRCEUKEIHmLkNzALgiAIsUe6MgRBECyGBGZBEASLIYFZEATLYBjG24ZhnDIM\nI98wjJ2GYUw1DKOrYRgnDMMoMAwj1zCMJ1zrNnKt5zQMo9gwjA9d6XUMw9hlGMZ5V/oaj/RCj/V3\neqT/5kp3Goax3zCMvoZhXOK1/bOGYTzkWv+YR3qmYRiVvL73jGEYN3j8rmmuZdsMwxgaKB8kMAuC\nYCXmAcgFsAdAVwA3A5gG4F0iqgzgRQBTDcPoBOA5ACcBVALwEoBxhmH0ATATQFXX57YB6Gnw3wHN\nBGAAaOiab+CR3hjAva7t1wCwHcBEACdc258JIAXA/wGYBaAOgGqu9Mtcnub3VgXwOoC5BtMFwHgA\nnQEMBzDb9b1lIoFZEAQrUQjgNwCFRFQIYD6AoQCedy3/FzhQNgdwPYC3iagIwBxw0O3iSv8IwDAA\n08Fxro8rPRcAAXgVQLIrfRSAAiJ62yO9k2v9d1zbX+/6XFOXzxkAVQD8w7X9Gl7re27/egDziaiI\niPYC2OVKLxPN//9aEIQ4oxmALAD1XO8PAKhJREdc76uAa6Q/AqgJYLthGOsBtAUHzhxXej9wjbcW\nOGA3c6WfBrAMQDGAyh7p/zMMYy6AHq7vaO1K3+b63qEAnK71qwNYAGA/gDzX9g95rk9Ehw3DSHKt\n3wzADx6/8aArrUykxiwIghYYhlEdwCIAZ4nojCuZiKgXuAZtAGgBjmuniegXV5on6UR0MYARABLB\n3QsAkApglmsZAIz2+N5kcK232GM7vQG0AtegAeCKiH+gBxKYBUGwEgfhDnYAB9wcwzCagoPyp651\nAK4dm4G1KoAiAG3A3SH9DMPYDa7ZJgC4x7W++SDdRNd6DV3puUT0k2EYjQGcdzmY2x8OYJNr+wcB\nFAA4T0QnATRwbae5p49rO+b6B8EnDM/fdBB+kMAsCIKVWAuuvVYyDKMSgAkAFgP4HMBWcBD8zLXu\nVwDudq33GDiefQXgQ3AfcCcA37g+MxLAEo/1HwcH5y9c26tqGEZXAFPAtexVru+9C8Ct4C6LQgBr\nADgAdDcMo4bH+g5zfdf2p3isvxjABNfIjdYA2rnSyyaSR9PJS17ykld5vgB8AB4J4XQFNvMiHgHI\nB9dKN7jSLnelOcHdDO+7tlEXwK/gmm8egDWu9J7g2q65/n881t/vkf4DuG+6LvhCJLkC/Y0e659w\npRcDyABf6PP83gvruz4zzbVsG4ChgfJBbskWBEGwGNKVIQiCYDEkMAuCIFgMCcyCIAgWQwKzIAiC\nxZDALAiCYDEkMAuCIFgMCcyCIAgWQwKzIAiCxfh/fTa0UQMY4kMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x29f23127e48>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sigset.tiled_plot(phi)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(32, 800, 1)"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"phi.shape"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"phi = phi[:,:,0]"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"convs = []\n",
"count=0\n",
"for signal in sigset.data:\n",
" #these = [scisig.fftconvolve(elem,signal,mode='full') for elem in phi]\n",
" #convs.append(np.concatenate(these,axis=0))\n",
" convs.append(scisig.fftconvolve(phi,signal[None,:],mode='full'))\n",
" if count > 500:\n",
" break\n",
" count += 1\n",
"convs = np.concatenate(convs,axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(32, 27945377)"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"convs.shape"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABIwAAAJRCAYAAAAnJixkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmUFeWd//F31b23b28szdYiICgugIqggAsu4JKoaBKT\njCMajfsYTWISo8YxJq0xGaOJvzhmYmIyWdxHjXEXFeUqYjCAKCqLIrLvNL13363q9wfOHDuTmYks\ndtO8X+d4Drc8VfX91h99nvOp53kqiOMYSZIkSZIk6T+FHV2AJEmSJEmSOhcDI0mSJEmSJLVjYCRJ\nkiRJkqR2DIwkSZIkSZLUjoGRJEmSJEmS2jEwkiRJkiRJUjsGRpIkSZIkSWrHwEiSJEmSJEntJHf0\nDYIg+CwwCegG/DaO4+d39D0lSZIkSZK09YI4jj+ZGwVBT+CWOI4v+kRuKEmSJEmSpK3ysZekBUHw\n70EQrAuCYN5fHT8xCIKFQRC8GwTB1X/j1O8C/7a1hUqSJEmSJOmTsTV7GP0O+PRHDwRBEAI///D4\n/sDkIAiGfeT/3wQ8HcfxG9tQqyRJkiRJkj4BHzswiuP4FWDzXx0eB7wXx/GyOI7zwAPAZwGCIPga\ncBzwxSAILt7GeiVJkiRJkrSDba9NrwcAKz7yeyVbQiTiOL4duP1/OzkIgk9mIyVJkiRJkqRdSBzH\nwdact8O/kvb3+qQ235a066ipqaGmpqajy5DUxfi3RdKO4N8WSTtCEGxVVgRs3R5Gf8sqYI+P/B74\n4TFJkiRJkiTtZLY2MAo+/O8/zQL2DoJgcBAEJcAZwOPbWpwkSZIkSZI+eR87MAqC4D7gVWDfIAiW\nB0FwXhzHReBrwHPAO8ADcRwv2L6lStLHM2HChI4uQVIX5N8WSTuCf1skdTZBZ9g7KAiC+Pvf/z4T\nJkzwD6UkSZIkSdI2yGQyZDIZrr/++q3e9LrTBEadoQ5JkiRJkqSuIgiCrQ6Mttem15IkSZIkSeoi\nDIwkSZIkSZLUjoGRJEmSJEmS2jEwkiRJkiRJUjudJjCqqakhk8l0dBmSJEmSJEk7tUwmQ01NzTZd\nw6+kSZIkSZIkdUF+JU2SJEmSJEnbjYGRJEmSJEmS2jEwkiRJkiRJUjsGRpIkSZIkSWqn0wRGfiVN\nkiRJkiRp2/mVNEmSJEmSJP1NfiVNkiRJkiRJ242BkSRJkiRJktoxMJIkSZIkSVI7BkaSJEmSJElq\nx8BIkiRJkiRJ7RgYSZIkSZIkqZ1OExjV1NSQyWQ6ugxJkiRJkqSdWiaToaamZpuuEcRxvH2q2ZYi\ngiDuDHVIkiRJkiR1FUEQEMdxsDXndpoZRpIkSZIkSeocDIwkSZIkSZLUjoGRJEmSJEmS2jEwkiRJ\nkiRJUjsGRpIkSZIkSWrHwEiSJEmSJEntdJrAqKamhkwm09FlSJIkSZIk7dQymQw1NTXbdI0gjuPt\nU822FBEEcWeoQ5IkSZIkqasIgoA4joOtObfTzDCSJEmSJElS52BgJEmSJEmSpHYMjCRJkiRJktSO\ngZEkSZIkSZLaMTCSJEmSJElSOwZGkiRJkiRJasfASJIkSZIkSe0YGEmSJEmSJKkdAyNJkiRJkiS1\n02kCo5qaGjKZTEeXIUmSJEmStFPLZDLU1NRs0zWCOI63TzXbUkQQxJ2hDkmSJEmSpK4iCALiOA62\n5txOM8NIkiRJkiRJnYOBkSRJkiRJktoxMJIkSZIkSVI7BkaSJEmSJElqx8BIkiRJkiRJ7RgYSZIk\nSZIkqR0DI0mSJEmSJLVjYCRJkiRJkqR2DIwkSZIkSZLUjoGRJEmSJEmS2jEwkiRJkiRJUjsGRpIk\nSZIkSWqn0wRGNTU1ZDKZji5DkiRJkiRpp5bJZKipqdmmawRxHG+faraliCCIO0MdkiRJkiRJXUUQ\nBMRxHGzNuZ1mhpEkSZIkSZI6BwMjSZIkSZIktWNgJEmSJEmSpHYMjCRJkiRJktSOgZEkSZIkSZLa\nMTCSJEmSJElSOwZGkiRJkiRJasfASJIkSZIkSe0YGEmSJEmSJKkdAyNJkiRJkiS1Y2AkSZIkSZKk\ndgyMJEmSJEmS1I6BkSRJkiRJktoxMJIkSZIkSVI7BkaSJEmSJElqx8BIkiRJkiRJ7RgYSZIkSZIk\nqR0DI0mSJEmSJLXTaQKjmpoaMplMR5chSZIkSZK0U8tkMtTU1GzTNYI4jrdPNdtSRBDEnaEOSZIk\nSZKkriIIAuI4Drbm3E4zw0iSJEmSJEmdg4GRJEmSJEmS2jEwkiRJkiRJUjsGRpIkSZIkSWrHwEiS\nJEmSJEntGBhJkiRJkiSpHQMjSZIkSZIktWNgJEmSJEmSpHYMjCRJkiRJktSOgZEkSZIkSZLaMTCS\nJEmSJElSOwZGkiRJkiRJasfASJIkSZIkSe0YGEmSJEmSJKkdAyNJkiRJkiS1Y2AkSZIkSZKkdgyM\nJEmSJEmS1I6BkSRJkiRJktoxMJIkSZIkSVI7BkaSJEmSJElqx8BIkiRJkiRJ7RgYSZIkSZIkqR0D\nI0mSJEmSJLVjYCRJkiRJkqR2DIwkSZIkSZLUjoGRJEmSJEmS2tnhgVEQBHsGQfCbIAge3NH3kiRJ\n2pHWro1paIg7ugxJkqQdbocHRnEcfxDH8YU7+j6SJEk72mWX5bnppkJHlyFJkrTDfezAKAiCfw+C\nYF0QBPP+6viJQRAsDILg3SAIrt5+JUqSJHW8fD5m6tSIKVOiji5FkiRph9uaGUa/Az790QNBEITA\nzz88vj8wOQiCYX91XrBVFUqSJHUCf/5zzJAhAR98ELN2rcvSJElS1/axA6M4jl8BNv/V4XHAe3Ec\nL4vjOA88AHwWIAiCXkEQ3AGMcuaRJEnaWU2ZUuSUU0KOOy7k2WedZSRJkrq25Ha6zgBgxUd+r2RL\niEQcx7XAV/6vC9TU1PzXvydMmMCECRO2U2mSJEnbbsqUiGHDIioqAqZMgS9/OdHRJUmSJLWTyWTI\nZDLb5VpBHH/8KdVBEAwGnojjeOSHv78AfDqO44s//P0lYFwcx1//O68Xb00dkiRJn4S1a2OGD88S\nBFkGDw5ZsSLFunVpEglX3EuSpM4rCALiON6qAcv2+kraKmCPj/we+OExSZKknd6zz0YccAAMHRqy\ncmVEnz4we7YvuyRJUte1tYFRQPtNrGcBewdBMDgIghLgDODxbS1OkiSpM5gypUgcR5x5ZorTTktR\nXQ3PPFPs6LIkSZJ2mI8dGAVBcB/wKrBvEATLgyA4L47jIvA14DngHeCBOI4XbN9SJUmSPnnFYsxz\nz0W8/XaeQYPg0END1q4tMGWKG19LkqSua6v2MNruRbiHkSRJ6qReey3iH/8xx4ABeTZvbmPffZPM\nmBHS1pZm6dI0vXu7j5EkSeqcOsMeRtuspqZmu+3kLUmStL1MmRJRWRkzdmxINguZTI6TTkoyaBA8\n/7yzjCRJUueTyWTafY1+azjDSJIk6X9x6KFZ5s/PcvLJEWPGpFiwoEAyGTBlSoKJE1P84Q8lHV2i\nJEnS37QtM4wMjCRJkv4HmzbFDBqUZeTIPAsXtrBoUR/ef7/Il79cz+bNJQRBmnXr0oShy9IkSVLn\n0yWWpEmSJHU2zz8f0bt3zJAhcNxxJVRXJzj88BSpFBx1VAKAN9/0pZckSep6DIwkSZL+B089VWTT\npgILF+a48MJyVqwoUFcXceGF5bS0FICiX0uTJEldUqcJjNz0WpIkdSZRFPPkkxFDh8bU1hY54YQU\nX/zier7xjVrOOaeMmTOzFAoRjzxS7OhSJUmS2nHTa0mSpB3kjTcijj46y+jROSZODDn22BTnnbeR\nzZsj5s3bnSuuaGLVqpBZs0pYvz5Njx7uYyRJkjoX9zCSJEnazp54okg2W2TevDbOO6+cm2+u5+qr\ne/DlL1fys581cOGFZaxdm6OkJOKFF1yWJkmSuhYDI0mSpL/hP/6jSHV1zKGHpmhsLDJnTo5zzqng\nm9/szm9/28QhhyTI5yPiOOL++wsdXa4kSdJ25ZI0SZKkv1JfH9OnTxuDB7dy003lPPlkI/vum+K4\n49L07p3g+uvr2X//FPl8krvvLrJuXZq6ujRB4LI0SZLUeWzLkrTk9i5GkiRpZ/fMM0XiOKK+vsDB\nBye4+OJWFiyoYvToDxgyJMUvf7k7J564jpdf7s/NN9eSzZYwf37M/vsbGEmSpK7BJWmSJEl/5be/\nLdC9e8S555Zyxx2NnHtuJQ8+2MDmzQXeeKON2to8I0emeOmlVo46KkUQFPn9712WJkmSuo5OExjV\n1NSQyWQ6ugxJkrSLi+OYGTNicrkc//APaX772yYuuaSS731vI4lEnjjO8/Wvr+PKK7tzyy31XHhh\nKRUVRf74x2JHly5JkgRAJpOhpqZmm67hHkaSJEkfMWdOkbFjc4wd28LnP5/k7bdzjBwZcu216xgw\nIMeGDUUKhQoefXQA3/1uI9dc04OLLmqhrq6S+vo03bp1mvdxkiRpF7ctexg5opEkSfqI228vkE4X\nueiiMm67rYGvfrUbP/jBRkpK8tx22x5ce201YZjn8svXc+WV3bn11gYuuihNGEb84Q/OMpIkSV2D\ngZEkSdJHPPVUkSjKk8sVOOigEp57ronW1iJDh4acemoVl1/en3Q6x9KlOUpKItauLTJ6dIIgKPK7\n37mPkSRJ6hpckiZJkvSh9esjqquzTJ6cZe7cZn7yk5784z+uJIpaeeqpPQnDmL59U0yb1sCVV26k\nurqMK67ox9SprSxalOK998rI5dKEoe/kJElSx3NJmiRJ0nZw6615giBi7NgEFRUBM2Y00dZW4OCD\nSxgzpoLTT3+Hc85ZwAUX9KNbtwKrVuWpqop59dUsX/5ykmIRnnwy6ug2JEmStpkzjCRJkj60++7N\ntLQUOeCAZi64oJLLLltNHLfy8st786c/rWfVqiyLFrVw6aUDgJBLLllLr15lXHhhH5YuLXDPPaUc\ncUSCl18u7+hWJEmSusYMo5qaGjKZTEeXIUmSdlFNTTFr1gR86lMxa9YUefPNZnK5AhMmlNK3b4Jf\n/Wo1gwYlOeWUKq699gM+97le9O0bsX59nupqeOyxVkaNipk5M8YXYZIkqSNlMhlqamq26RrOMJIk\nSQJ++MM2vvvdiJNOamDixFKuu24t0Mrrr+/HD36wlF69Etx55wekUgGf/vTujBrVjZEju3PWWSvp\n3r2ML36xF7W1cP/95bzySpLx41Md3ZIkSdrFdYkZRpIkSR3pF7/IU1UVMWdOjnffbaVQKPLZz1ZQ\nX5/nlVfqefbZNRQKOVpbc7S0tPKv/7qSsWPLGTIENm7MM2AAPPtsM6lUxDXX5Dq6HUmSpG3iDCNJ\nkrTLa2iI6NGjlZEjc3z60zG33baeIGhlwYLhTJ78DsOHp/n975eRSrWRz0MQlHHWWUNIJAK+9KXd\nOfXUZZSXl3LccT2ZM6eU5ctDcrkKgmCrXuhJkiRtF84wkiRJ2gY339wGhCxd2sSKFa0Ui0XOOacH\nM2fWk8vF3H33CiDPz342jG9+cw/iuMDTT6/k2Wc3U1UVMnJkSH19gSFDAurrmykUQp5/Pt/RbUmS\nJG01ZxhJkqRdXnV1A42NCc44o4V77tlEItHC/PkjmDBhLv37x7z2Wi2HHVbCe+8toVevUurrq1i/\nPskpp/SnoSHgppuGMnHiB5SWljJ6dA9efrkHY8fmmTmze0e3JkmSdmHOMJIkSdpKK1cWWb8+IIpa\n2bAhSxQVuOyy3tx//zr22quU116rI5HIkUjUceWVh3DEEf059tg0kOPJJ9eyYUOeNWuyHHVUCY2N\nRfbeOyCdzjFrFkRR1NHtSZIkbRVnGEmSpF3a+ec38oc/JBg/voU//3kjJSXNzJkzjCOPnEtbWxPN\nzTnOPLOSNWtqmTr1CzQ35xk9+l72228wTz/dzJAhlSQSZfzHfxzAEUcsJpUqo6qqF6tWlXPHHSH/\n9E9lHd2iJEnaRTnDSJIkaSs9/HCBKIIwbAEKXH11NT/96UoGD07Q3Fxk6NAEU6cu5q67Ps2yZfVk\nswXuvfdEZs9eTGVlkaVLW+nRIyST2cykSeW0thYYNapIHIfcdlu2o9uTJEnaKp0mMKqpqSGTyXR0\nGZIkaRcyfXqOxsYEvXrlmTGjhdLSHJ/6VHcee2wjr7++mSDIUSyu5447jqWsLMnRR9/LKac8zOjR\n/fj610cxbFgOKPDmmxu56ablXHNNfxKJHFOn1pNMFlmwIGDz5mJHtylJknYxmUyGmpqabbqGS9Ik\nSdIu6/jj63jxxSSDBzezcuUGbrmlF088sZ7XX99AXV2WceMiRo4s5847j+Mzn3mYffftxbvv1rLf\nfr358Y8nMHHiH9m0qYz58wMGD67klFP609QUcvfdWfbYoz/LlqW44oqAW26p7OhWJUnSLmhblqQZ\nGEmSpF1Sa2tMZWUtcVwOrKCqqplf/3ogl122iLVrG+jVK0+fPnW8/vqZ/PKXr/Pww4v4059OJZeD\no466n5///AQOOqiagw++n/r6agqFEnr27Majjx7Ipz61hCiqoljsR1VVG5s29e7odiVJ0i7IPYwk\nSZI+prvvbiWKkpSUFEgms9x0U3++8533Wbu2ESgQx+u4774Teeut9dx882vcddckRo26kc9//l+5\n775TufDCZ4CYf/u3CfTt2wAUaWlp5uabl/NP/1RFsdhCGAbU1obMnp3r4G4lSZI+HgMjSZK0S/rR\nj1oJQ8hmm+nbt0hTU541a1qAiP792/jOdw5mzz27c8YZj3HnnSdSU/MI69aVM2dOgVmz5nPFFeM4\n44zH+fzn9+ZTn6qmd+8CuVzEK69s5uijK0mns0RRKxDyve+1dHS7kiRJH4tL0iRJ0i7nvfcKDBtW\nTxCkgTX85jfdufzyRTQ0NJNOZzniiCLPP38an//8IwwdWsVnPjOAiRPvAZoBCMNSliy5gq985UUO\nOKAv1103npEj72XZst7EcYp9963ii1/cnX/5F0ilelIs5qiv70VFhe/qJEnSJ8claZIkSR/DjTc2\nEUUhxWLI4MGtzJ5dR2NjK1CkvHwTd9/9aW6/fQ5r1zZz/fXjOfnku4EWIA2kiaIixxzzC+666xQe\neGABL7+8nAceOJGyslogYsmSJqqrQ0pL68nlkhSLIXfd5SwjSZK083CGkSRJ2qXk8zGVlRspFpNE\nUZHf/KbAP/3TAgqFVsrKGrj33jEMGFDOKac8zGuvncMFF9zLtGnLASgrayafT1MohEAJ3/rWGE47\nbQxf+MKfmD37XO66ayE33LCSXK6Miopyrr56KN/7XjfCMKK6usDq1X07tnlJkrRLcYaRJEnS3+ne\ne1vJ5UKKRRg4sIVf/WoZhUKOIMgzeXIvJk4cyBlnPMavfvVpXnrpXaZNWwtEBEGR1ta3KRReBwKg\njVtvnUs6Dd/85lgmT36cK64YzciRBaBAc3Mbq1Y1UlLSSBTFrFkT8NZb+Y5tXpIk6e9kYCRJknYp\nN9zQxJYhUAnnn5/kL39pAgpUVzdy220TOP/8pzn11L0ZO3Y3LrroKaCJLQHRXGBLGBQE7wBJoIHj\nj/8dX/3qIXTrVsL118/gj388kXS6Hoi48841nH12EkgAId/5TkOH9CxJkvRxuSRNkiTtMhYtyjNs\n2GYAystLSSRm09iYJwwbmDXrGF55ZTl33fU2L710Jgce+K988MFKoJREYgnF4joSiQJBEFAoJEil\nhpHP9wSKfOpTI7jnnjMYPfp3/PrXJ1JXl+essxYSx+WMGFHJggUHEcethGGRlpa+pNO+s5MkSTte\nl1iSVlNTQyaT6egyJElSF/atbzUQBCFBEDN4cBONjRGQ49pr9yCKitx446s8+ODnuOqqKXzwwXog\nTRg2UyyuJ5EoUizWUSw2EgQFisWFBEEBCJg69X3++Md3uO++UznvvKc56qjdOf74FJBn/vxW9tor\nBxSJ45Af/rCpQ5+BJEnq+jKZDDU1Ndt0DWcYSZKkXUI2G1FWto44TtO9e0hDw2JgI0OGNDNnzsmM\nHfsHfvzjCZSVhZx22r3k81uWopWXz6WlpY1EIssRR+zOsmVrWLkySRQlSKVS5PNjgRzpdC9mz76E\nxx5bzJQpS3j88S/Sv/8TZLM9SCT6k0rtRltbgh49stTV9e/gpyFJknYFXWKGkSRJ0o70/e83EMch\n0EZjYxKoIwhaefnlE7j44imcdNJejBvXn8mTHyKf3wwkSaffpqUlTxhGlJe38Nprb9DS0gxsIgwj\n8vmYRGIJkCab3cCkSffwta8dQllZkp/85DWefvowIPvhzKRSoEB9fchTT7V04JOQJEn6vxkYSZKk\nLi+OY26/vQUIqa6OiOMGIMdPfjKUxx9/jyVL6vjRj47htNMeoKlpPVBGEKwjn88ShkWiqI7+/XvS\np09PmpubGTNmKFHUQBDkSCRqCYIWoJy1a9dw0UWPc/fdp/CHP7xNPp9n0qQyoJl8Pk/37lkg4Jvf\ndPNrSZLUuRkYSZKkLu/hh5tpaQmABOvWFYBahgwpMmFCP66/fgYPPvg5amoyvP/+KuI4DWTp02cD\nUZQjjps57LC9ef/9Zbz88mPce+8vmDXrDfbbrxdhWCCXy9Gnz2KgQC4X8fzzi3jssUXcc88pnHvu\nU9xxx1hKStqAzbS2tgIJ3nsvYvHiXEc+EkmSpP+VgZEkSeryvva1egBKSuqBXsBapk07htNPf5Sf\n//wE3nprLXfdNZf6+iYgZu+9V7FhQyNBUKRv3yR/+cvr3Hjj1QwduiennTaJU045ntWrVxGGDUCR\njRtbKS+fDyTYvHk9V1/9PD16lHDppQdz9tlP8txzhwIbyOd7kkzmgYCLL97cUY9DkiTp/+Sm15Ik\nqUubPbuVsWM3s+U92QZgAP/yL6uZO3cxvXqVceWV4zj00F+zadMy4riS8vJltLWtI4qyhGEtffum\n6N+/L3Pnvvhf18zn8/TtO4I99xzMG2+sAXpQWlpBW9sgoC/pdJYBA/Zi1qwLOf30xzj88AG89FLE\n9OljgA+APkDEhg270adPogOeiiRJ2hW46bUkSdL/4OyzN334ryRQQlnZJnr2zLNoUS033XQMp5/+\nEKWlTcRxJdBIVVWWKMoSBE0cdNAQ6urqefHFR9pdM5VK8cQTd/Pmm/M58MDdCYIsbW0tDBvWDGTJ\nZtOkUq1cfPGT3HPPqfz2t/O49trBQB1bhl8pIOSKKzYhSZLUGRkYSZKkLuv993MsXAhQAOqB7lx7\nbSXXXfcyDz74Oa699kXiOMfKlW1AnpNOSrNq1UYgz4ABFcydO4/f//42qqp6/rdrH3XUYZx33um8\n++67lJa2AkXefXcd++yzCiiyaNE63nlnLQ8++A53330K5533FGedlQQqgDagyN13Z2lpiT6pxyFJ\nkvR3c0maJEnqsg4/fBUzZ4ZsCYw2kErtxx57PMAPfnA4YRjxne9MZenSpUCKAw9s4p13FhJFbaTT\nDSSTbRx99Diefvr+//H6URQxYMBBVFZ2Y+nSBgqFbpSWdqNY7E0+P4jS0hzdug3gySfP5OmnlzBl\nymbmzDmGQmEFUAmUcMUVKX7yk76fyPOQJEm7FpekSZIk/ZV16wrMnFkEskAZJSURvXpt5thjd+eQ\nQ6r56lefIY43ASUkEpvZsGEtUZSltLSVgQN7kkiEPPLI7/7Xe4RhyPPPP8iSJUvZb7/dCMM22tqa\nOeCAMqCZtrY0Q4eGnH76Q1x22cGUlTVRWRkDTWwJjCJ+9rMWikVfnEmSpM7FwEiSJHVJkyevAxJs\nCYzqGDGiP0GwjJtuOoZ/+IeHmDChmmXLckAbZ501mLVrNwI5evVKs2TJBzzxxF2Ulpb+n/c54IDh\nXHXVpSxcuJCKijxQ4M03lzBpUgmQY+bMdYwbV8355z/OvfeeSi63hLFj+7FlWVozxWLI9dfX7rgH\nIUmStBVckiZJkrqchoYiPXqsYMtG17D33utZsmQQjz+e4NFHX2HTphb+9Kc5QMTZZ+/Gvfc+TRS1\nUFnZQltbHeeeezq//vVP/+77xXHMvvseTlNTK01NAU1NZaTTlfTuvTurV/clmYRDDhnGF74wnLa2\nvbjxxlbCsJG2tm5AKYlEG/n8ngTBVs0YlyRJ+ptckiZJkvQRn/nMKrYMcxqAUnK5xVRVlbJx4wqm\nT1/OK6+8BUDfvq089dTLRFGW3r1DSkuhuro3v/zlzR/rfkEQMHXqQ2zYsIl+/bpRUpIjm22hX78k\nUE+hEFIsbuanP/0zhx5aAKrZZ59lQHegiWIxyY03+sU0SZLUeXSawKimpoZMJtPRZUiSpJ1cc3OB\nl14q8J+zi/r02Uj//sOZODHm299+jrFjq9iwIQ80c9JJA6it3UxJSYEgyLJ582aee+5BEonEx77v\n4MGD+PGP/5mlS98nnc4BeebNW8wll+wDtDF79kbOOWc4F1zwMIceGhBFlZSVtQB5IKSmpm77PQRJ\nkrRLy2Qy1NTUbNM1XJImSZK6lP33X8j8+aVAgUQizcCBb7Lnnsfx3nsvcMEFZdxww3NAlpqasVx/\n/a+J41a6d2+lubmW6677Bt///re3+t5xHHPwwcezZMlKysp6sW4dpNOVjBt3ENOnRwRBiq99bQJT\npvRm3Lj9eeyxV2lsHAKUAkUuvzzkZz/bY/s8CEmStMvbliVpBkaSJKnLWLSonmHDNrJldlEtQbA7\nM2aEHH10GZ///Is89tirZLN5Ro8uYfHiN2hsrGPvvbuzevX77LnnAN56K7PN+witX7+RQYMOpnfv\nfrS0lFBfDyNG7MP77yfJZqsYPLgHffrsz/vvH8vPf17H2WeXE8dr2bI8LUdr616Ulia3w9OQJEm7\nOvcwkiRJu7w4jhkz5l22DG8SlJTkOfLIPA88sJmSkg2sXbucbLZIEDQzZEiCxsZGqqpSrFu3kkIh\nzzPP3LddNp3u168Pv/zlj1m3bg3FYgNQYOHCD7j00tFAK8uWNTJuXEBDQ558PmDgwBzJZBuQAlJM\nnDh3m2uQJEnaVgZGkiSpS7jppnk0NfUCImAzPXrsxuTJJdx552bGj8/x8svLgTZuueU4Hn10OpCn\nWKyjpaUN7jnHAAAgAElEQVSB22+/kUGDBmy3Ws47bzJHHz2OfL6ZoUMriaIc//Zvj3LuuUOBHHfc\nMZNx47Jcfvm7XHRRJT16lAMtQMTMmd155ZXV260WSZKkreGSNEmStNNbvLieffaZD1QDJfTqNY84\nPoLeve+hru5LbNr0O+J4GZMm7cbUqS+QzTYzenQ1b701l/HjRzNt2iPb/ZP2mzfXMXDgaEpKKune\nfTeWL29mjz0G0dxcxaZN5aTTB7P77sdSXf0S8+efRHPzHIrFvQAoLV3Exo3HUVGR2q41SZKkXYtL\n0iRJ0i6rWIw46aTngL5s+eJYK+efP46ePVcyatS+1NYWiOOVpNOtNDSsJJttYciQnsyf/w7pdMhD\nD/16u4dFAFVVPbnnnn+jsXEzmzatJpkssmLFav7hH/YDWshmF7J8eTfKyiJ69mzk6qv3YcveSwXa\n2vbkK195ZbvXJEmS9PcyMJIkSTu1f/mXuSxePBBIAAkmTy7w0EN5wnAxS5ZUEEXvAq1cd93RTJ8+\njzAssnHjcqKojbvv/jl9+/bZYbWddtrJnHLKcWSzTQwb1ps4zvPb3z7Jt789FqinWFzFgAHDqa9/\ni1dfLWHvveuAIlDC3XdneeGFlTusNkmSpP+NS9IkSdJO6+23aznooCeIovFAnjDsxn33hUyeHPDj\nHy/mqqu6AXM488wGHnzwCQqFVg49dACzZs3iC1/4FA8++OsdXmNDQyN77HEIuVzA0KEjePvttfTt\nW02PHkNYvHgCYdiTm27qztVXD+DJJ5NMmtQCtAIRFRUzWbVqMj16pHd4nZIkqetxSZokSdrl5HJF\nJk16hijajy2ziwqceWaar3xlPocf3sY///MzwBAqKt7m9ddnUyhkOfDAAcye/To9e5bzm9/c+onU\n2b17Nx566Nfk8628//5C0mnYsGEjhxzSC3iTKBrKrbc+zZAhOb75zb8walQKaANKaG7enS9/edon\nUqckSdJHGRhJkqSd0jXXvMby5RHQG2ijZ8/erFjxGsnkfixePI1CYQCwlosu2pOFC1dQUhKzePE7\nJBIRDz/8G7p37/aJ1XrCCccwefJnyeWaGTGiN5Dnj3/McOWVg4BS1q6Fbt3ep6lpMP37L6dnz0q2\nLE3bg8cfX8Wjjy75xGqVJEkCAyNJkrQTmjVrPbfdtoAg2DK7qLS0hYqKPLW1DTQ0lLB+/TvAUA46\naCO33fYIkGfkyGpyuVYuuOAMJk4c/4nXfMcdP6ZXr+68/fYCDjtsKIVCG7/85UP06rUY2Iv58zPU\n1lYzb95sCoVSoAFIEcd7cuaZ09i4sfUTr1mSJO26DIwkSdJOpbW1wKRJz1AslhHHPYEco0b1o77+\nTQYPHk02+xZQIAz3Zdmyh4njPOPG7cWcOW+w++69+elPv98hdVdUlPPII/9OEBR4443XqagIaGxs\nYLfdFgJDKRTqyOVW8rnPHUeh8C4TJvT68MzdaW0N+eIXn8M9HyVJ0ifFwEiSJO1ULr30ZTZuLBKG\nW2YXDR/exmuvxdxwwwCeegrgHSBFMtmTurq5lJUFvPHGLEpKAh555N8pKyvrsNqPPPJQLr74LPL5\nVvbZpwoosHDhI5SUDAfyRNE8fve7Ri6+uJxXX40pLa0HkpSW7s306Rv5/e8XdVjtkiRp12JgJEmS\ndhovvriSu+5aQo8eVUTRln1+CoVGhg1r4pZbXiKOuwHvMnbsMeRyrwE59tmnG3Fc4KqrLmHMmFEd\n3AHccsv32H33Psyb9w7jx+9LFG0kn/+A4cNHAm/T0jKQ5cvfp7y8yJgxLUBIW1sfwjDFJZe8wurV\nzR3dgiRJ2gUYGEmSpJ1CY2OOz33uOSBJXd1gIMH++9excuVu9O+/kDVrBgHv0Lt3ljlzyoC/MG7c\nEN56awF77z2Q6677Zsc28KHS0lIeeeTfSaVg1qzX6NYtQRzPZMOG3Ugk1gIrmTIlx/HHtzJ3bpre\nvRuBJHG8F/l8gpNPfsqlaZIkaYczMJIkSTuFM8+cSlMTVFZWARUArFo1n27d0kybNh04AJjFHnsU\niKKDqKiYw5w5fyGdTvDww78mlUp1ZPntjBkzim996yLiOM/gwZXATDZu3Iezzx4OzKWtbR+mTHmM\nOB5APv8XIEGx2JvevSuYN6+Bn/zkjQ7uQJIkdXUGRpIkqdN76KHFPP30Knr1KqOhYQ8gpLz8XQ44\n4Gg2bvwzcdwLqOCEExqZO7ccWEN19WaSyYAf/vBKRozYr4M7+O9qar7NkCH9eeedhRxxRAHozV13\nzWHMmJXAXjQ11ROGS5gwYTylpRuABBs3DiKVSnHNNbNYsqShgzuQJEldmYGRJEnq1Gpr2zj77GmE\nYQmbNpUBZUDI+eeXMWNGgiB4AxhGaembTJ36KnAw/fot4IMPVjJq1H584xsXd2wD/4OSkhIefvg3\npNMhf/nLn0kmXyeKDmLVqjcIgveBfcnlXmXatDTHHbceSAI9KBQShGEJxx//GFHk0jRJkrRjdJrA\nqKamhkwm09FlSJKkTubkk5+kWEyQTofAnkDIgAErmTGjlTh+n2KxGRhBaemzxDGE4Tg2bHiYsrIE\n999/B2HYaYY7/83IkSP47ne/ThjG9O79OjCGNWs2ccAB7wPDyOVW0dycZd99B1BauhFIEEX7UlaW\nYOnSLFdd9WoHdyBJkjqjTCZDTU3NNl0j6AybJgZBEHeGOiRJUudy++1vcfnlM+nWrZSGhj7AEKCE\nG29cxne/WwVMB9aSTF5MoXAuUEYQ3EUqdTQ///m1XHTRlzqw+r9PoVDg4INP4K23mkgkplAsfgbo\nQSLxW4rFHwHjSCYH8qMf9eOqq0qAPEHwNslkC4VCG7Nnf56DD+7bwV1IkqTOKAgC4jgOtubczvvK\nTZIk7dJWrmziW996lUSihJaWABgABEycmOP735/Flo2vF1FaOoJC4WUgT//+xxDHMznyyAO58MKz\nOrT+v1cymeTBB++krKyWYnE5ZWX7A/XAOyQSewHzKBSG8MtfPsvgwcUPz9qLOI5Jp9N8+tNPUihE\nHdeAJEnqkgyMJElSpxPHMRMnPkYymSYIigRBfyBFIpHi7bcfIgz3B94A6slm9wemU1kZs2bNUNLp\nV7nnntsJgq16mdYhhg3bhx/+8CoSiRmkUuNIJIpE0UtUVh4CbAA+YNWqnuy77weEYZI4LicMe1Es\nxtTVFTnnnBc6ugVJktTFGBhJkqRO55//eSZLljR/uCdRN/L5fkBMdfUqNm/eQD6/PzCTqqpS4rgb\nYfg2UVQPjOfWWyfSv391B3fw8V1++UXsvfcHNDSMYvjwPsTxDOrr92LEiCpgFtnsKF577SWqqwFi\ncrmBlJVVEMdJ7r9/Cc89t7yDO5AkSV2JexhJkqROZd68jYwa9TCJRCndu5dSV7cbUVRNOp0im32A\nMNyNKNqP8vLbaWmZCJQycOC/s3p1HyoqbqWhYa+ObmGrLVy4lOHDywmCkykvT9DcfANBMINk8n3y\n+euABykr24MgGE9LS4GysmWUlGwgn4+AHBs3nkdZWbKj25AkSZ2EexhJkqQuoViMOP74JygvLyWV\niikUyomiPgRBRDa7iqqqRqLoAGAGudwKYDzp9DTWrl1DKnUMZ5+9c2/+PGzYEA46qIFk8igqKook\nky8BR9K3byPwF+Bgcrnp5HI5IKK1tZpCoYxstkCxGDJp0pMd24AkSeoyDIwkSVKnce65L1BXV6C1\ntUgq1Z2Ghp5sGa4U6dHjderqyoDeJJNTKBb3BdLE8auEYcBee53F5z5X3rENbAeXXjqEHj0msWFD\nLQMHziOO92f16gKDBs0GRlAs9iSR+DPl5TFQSnNzJUOG9CabDZk2bR2/+938jm5BkiR1AQZGkiSp\nU5g6dQX33PM+UZRk3317k82mgF6EYQ5opbl5JXE8gjD8M1EUEseHkU5nKBZjTj31NFau7M5RR+38\nQ5sTT0wQRUdQWppi2bJ3SCTmAoewYsVcgmApMJRsdj6trQmgCOzGunUwdGglpaUlXHzxdDZsaO3Q\nHiRJ0s5v5x9VSZKknV5ra57TTptCZWUp/fqVsGpVRDbbCwiJoiwlJfMoFLLAQaRSzxJFOYJgPDCF\nqqoKPvOZ6zn66JDS0p3ny2j/kz32CNhttwTf+tZtpNNJSkqmkkgcTSqVIJV6BhgF5IA5hGETkKap\nqYJ16wKCANLpFBMnPtqxTUiSpJ2egZEkSepwkyY9RaEQ0NoaEUXlNDamgCqgmWSynFzubWAQsJp8\nfhWp1CDiOEmxOI9HHrmTadNSnHhi1xnWnHhiSCp1HOPHj6a1dSpRNIJisYRicS5B0AeoIAzfIYp6\nsCU8qqalJcEBB+xGSwssWFDPDTf8pYO7kCRJO7OuM7KSJEk7pd//fj7Tpq0lmw05+uiB1NYWgT5A\nQDrdAswljpuBUQTBSyQSBaLoUIJgKued9wWOPPJQpkwpdqnA6KSTQp59NuLuu2+nsjJPHM8kDMdQ\nLLYQxxmC4ECKxU0EwXuE4VogRRR15803GzjssGoSiRQ1Na+zYEFtR7ciSZJ2Ul1nZCVJknY669Y1\nc/HFL1NamuKAA6qYMaOOfL4c6A7Uks32o1CYxZYhy1DieDpx3EgUHUuvXq9y++0/YN68mIqKgL33\n7jrDmiOPDHn77Zh0uh933nkTyeQLRNFR9OyZIpl8kTgeA2SJ49eIoj2AVqAv+Xw5b7/dQkVFmrKy\nJMcd9xhRFHdwN5IkaWfUdUZWkiRppxLHMcce+xipVBJIUlsLhUIJiUQVW2YXtQJzgXpKSkYCf6as\nrIVUaghxHDJlyjWk02mmTIm61OwigNLSgKOPDnn++YgzzvgcEya0EUUHEkUhYbiCIFhDKrVliV4Q\nrAAWAymCoDvNzTEHHtiXXC7B+vVZLrjghQ7uRpIk7Yy61uhKkiTtFKIo5otffIYFCxrIZkOOP34Q\nq1e3EUVpisXulJZuJJsdBLwK1JLLHUMqNZVcrpa2tmM45JA1jBlzEABTpkScdFLXG9KceGLIlCkR\nQRBw3303k0y+RnPzaMKwlTh+nnx+PGHYQBy/QhAMAxqJoiriuJLp02s57rgBBEGCP/zhPf7f/5vb\n0e1IkqSdTNcbXUmSpE6ttbXAEUc8xOOPryCVChk/vpqnn15HGHZny1I0KBY3Ae8A6ykvHw40UizO\noUePchKJE/nFL44GoLExZvbsiAkTut6Q5qSTQqZMKRLHMX379uHrXx9AFJ1AFDXSu/ccYG+iKAIW\nE8ebCYL3gBTJZCVlZZW8/PIm+vTpRllZyLe//RqXXTaNOHZ5miRJ+vt0vdGVJEnqtDZsaGHEiHuZ\nO3czqVSRiooKFixooqysjGIRoCdBsJx8fj8gQ58+eVpaDieVep7evdPU1+9O//79GDu2BIAXXog4\n7LCQioqgI9vaIYYODamsDJg3b0vIc8MNh5JIjKJQ6EFLy1oSiRmkUicQBOuBV4jjfYB68vkq2tpS\nQILddy8lmaygtLTAr361iJNOepxsttCRbUmSpJ2EgZEkSfpELFy4if32u5fVq9vo3j1Bjx69OOaY\nfmzeHH0YcPQCIAg2AB8QhsuorY2Ag4jjx6mtrWfs2Cv40pcqCIItAVFX3L/oo048MeSZZyIAKioC\nTj21jJKSE4jjNhKJJ8nnjyIMAeYAUFo6H0gSxyUUCpXMndvCZz87kPLy3lRWxjz//BrGjHmA2tq2\nDutJkiTtHLruCEuSJHUaL720gtGjH6KhocA++/SgR4+efOMbe/Poo+tJJispFnNAD5LJ94iig4Cp\nlJUViKLDgRn06hWwxx67sW7dIZx+egrYsmn2lCnFLh8YTZlS/K/fX/pSOfvtdwnFYpE4fpNUqpE4\nHk4iUQdkaGvbiyCoBfqRz8f071/FAw8s5ytfGUoq1ZPhwyuYP7+J4cPvZvHiug7rS5IkdX5dd4Ql\nSZI6hbvums8JJzxJLhdx5JEDCcNS9tor5NprFzFiRBVtbQFBMBCIKBZXARvp338Nzc1NBMGx9Os3\nnU2bNnPrrfeTTAYcdFACgEWLYqIIRozoesvR/tOECSFz5sQ0NGxZlnbSSSmWLu3BCSecQhxDsfgY\nYXgcpaUp4EWgijj+M5AA0qxbF7PXXr358Y8XcMQRFaxdm2TSpEFs2FBg5Mj7mTFjdQd2J0mSOjMD\nI0mStEPEccw117zC+ednCMOAE04YyqZNeVavXsv06Tkuv3x/FizIE4YtxHEF8CZxfAiJxAusW7ee\nysphQMCGDS9y3XWX8eqrfTj99NRfLUdL/NfvrqiiIuDww0NefHHLsrSysoCTT05xwgk3UFFRQllZ\nhkLhAFpbQ0pLI2AaMJwwXAfsRrHYxqpVMHnyfrz4YgvpdAOvvlrPJZccQDYLEyb8ibvumt+RLUqS\npE7KwEiSJG13uVyRz372cW6+eR59+5YxfvxgFizYxLJlGwmCvnzmM3352c8WE8cQx0OBIrAMiEkm\nXwdyNDUdRmXlC+yzz0Cuu+4bPPhgjtNPL/mvezzzTNfev+g/fXQfI4DTT0/x+OMhDz74C7LZjYTh\ndLp3/xSFQhup1IvAEKLoRbYM83rS1BTz6KMbufTSETQ39yafr+W++5by1a+OoqQkxXnnTePb337J\nL6hJkqR2gs4wOAiCIO4MdUiSpG23eXMbhx/+AO++28LBB/chl0vywQeb6NevB6Wl5TQ2bmDF/2fv\nvuOrqu8/jr/OuXvkZi9CSAgBwhJkySZAgAAKCLLcWlygdVWqthWwWvtzgChibVWEKijIRglLgmww\nTNkrISF7J3ffc87vj1RpChKq1gHf5z+ak5ub7/1eHw9P3vfz+Xxzg9Dp9LRqZeXrrxsjSdvRtKYE\nB2dRVbUKk0nF758PjCM7ewUFBdHceaeLo0eDkCQJl0sjOtpLXp6J4OCrt8II4MgRlSFDfGRnm5Ak\nCY9HIza2mqNHg3j00cksWVKEojxNWNjTeL16XK5RaFoIEArEodMtQVU7odOp3H9/HJ98kkOjRj5O\nnHAxYkQCW7bkUlhYS2pqNBkZozAadT/3SxYEQRAE4UciSRKapn2vm6Wr/2M5QRAEQRB+MseOldO0\n6fucPOnmppuacu6cj1OnimnaNBa7XeLYsRJyc0NJSrLywguxfP11BBBA004CYVRVrSM0VAf0QVX3\n8NJL9xIfH8eiRf567WibN6tcf7101YdFAK1a1b3GY8fqPlwzmyWGDdOzdKmfuXNfIyjoJLIsUVMT\ni8/nxGz+AmgHZAAyipJGbOwCNC3AnDl5tGxpo7raSlpaY5YsOUNEhI3rrotk8+ZikpPfp6jI+bO9\nVkEQBEEQfjlEYCQIgiAIwo9iyZITtG37T9xuHaNGNWXNmgKCgyViY2MoKjrJwYMakhTB+PGxREeX\n88wzTsBM3dyd7sjyegwGLxUVRajqUOLjdzNlyiQ0TbuoHS0jQ2XIkGujEkaSJNLTdWRk/HtbmpFF\ni3xYrVaWLv0bmrYcVR1EXJydQKAAWd4HtAZOAyEUFt5O69ZH0ely2bHDS2Wll+zsAEOHtiA/38XZ\ns7V06xZLSYlCYuL7bN2a93O9XEEQBEEQfiFEYCQIgiAIwg/21FOZ3HLLGsxmK506hbJ06XkGDmxE\nURFkZx+nuDgRs9nBhAk2Vq3ax65d8UAUUAucQJKao6rrgQqaNeuD3x/E9u1TANi1S8Ful2jT5sJt\nS93A62vnNuY/5xgNGqTnwAGVggKVfv16MnKkD0XpQXZ2KWFhFgyGDKAbsBLQUNU4jh7tTlCQl+Dg\nw1RXGzlyxMmJExW0aNGI5OQwdu8uJSUlGLPZQp8+nzJjxlc/18sVBEEQBOEXQMwwEgRBEAThe/N6\nA6SlLWb79mKsVhtWq0JVlYkhQ8JYubIMTQug10cRFGQlJuYMxcVhVFREoChRQA0wB50uHUUpJyTk\nY8BDZeVdDB7cnoyMPgA88YQbhwOmTbMAcOaMSo8ePvLzTcjy1d+SBlBdrREX56Ww0ITNVvea77zT\nSZcueh55xITH48HhWInZfAi/fwWq6kBRfoeinAJygYnUDRQvJzj4NFZrLbm5CUiSRkiIE7vdTqdO\nDjZsOIfF4kVVDZSXVzN8eCKffjocvf7aCecEQRAE4WoiZhgJgiAIgvCTO3WqnPj4v5OVVY7JZEFR\nXDidVhITK1m+vAwwEBQUT2SkEVX9isLCJpSVBf8rLCpBkt4EJBSlPUZjBtXV5ZjNFnS6IbzzTk8A\nVFVj8eKL29EGD5avmbAIwOGQ6NRJYvPmC1VG48bVtaUBmM1mXnqpBTU1/dHrJRo1siDLq4BUoABZ\nng2oBALhVFY2wWBIxuE4iixrVFZaKSgoZ926EkaNSkbT7DidTux2G59/fo7k5HfJy6v+OV62IAiC\nIAg/IxEYCYIgCILwX/v446O0aTMfWTbg9+uIiTGi0znw+XI4fjwEqzUEuz0SKCUmpoDa2o5UV0to\nWhyynIckvYMse7DZegG7UNXTtG2bRHFxW/r0sZOQUDefaOdOhZAQidatL8wrqmtHuzbmF/279HRd\nvba0gQP1HD6scv583bXHHmuPzdYIj6cx2dm5REbmIUkVhIa2R1WLgZlIkhdFiSU7W0Wv70hSUj4m\nk0Ig4EBVvXz4YQ6dO0cSHBxJWJgMGKmuVmnRYi6ffXb653nhgiAIgiD8LP7ngZEkSVZJkj6QJOkd\nSZJu/V//PkEQBEEQ/nf8foUHHsjgzjvXERkZRHGxnx49wsjLc+NyuYAmWK0R+P0mJOkMSUk69u6N\nIxAIEAg0Qa8/haa9T2SknnbtYnE6b8BqXUFwsINDh47QrNkjTJoU8u3v+89h116vRmamysCB195n\nXunpcr3B10ajxIgRBj791A+ATifxxBMx6HQjiI0NobQ0D51uFdXVfUhJCcFicaJpM4FqVLUpPp+f\nM2eSGTBAxmiswecLRpICrF1bhM0mUVtrJS2tEZWVKiEhVkaNWs3vfvcFgYD6HSsUBEEQBOFq8lPc\nbY0CFmua9gAw/Cf4fYIgCIIg/A/k5lbTufN85s07gc1moLjYz/XXK3z5ZTF+v4Xo6Bj0+nDcbo3O\nnUvx+Yzs328FJKApkrQfRfmQG25oRE1NBfv3p2E07iMQOINOp5CS0ofKygiGDzcB37Sj+RkzxvDt\nGrZtU2ndWiIi4tppR/tG+/YStbUap079+2lphm/b0gAmTrRjMg2joKAKi8VEbOzXgIf8/H4YjV5S\nUmzALKCE2tqmGI0e1qyx066djaSkKlQ1HE0zkpfnprbWw9at1TzySHtKShRsNj1z5hymZ88PKSio\n/clfvyAIgiAIP63/OjCSJOk9SZKKJEk6+B/X0yVJOiZJ0glJkn7/b99qTN20RQDlB6xVEARBEISf\nyZo1p7nuug84erQGTdNQVT1m82n27zei04WSnBxNaakBRfHRuvVxdu404PUakKRQoDGyvB29/lOu\nvz6SrKzDuN13EhKiR5JeoUWLJlRUVJGW9jJ33mnGaKwLg7ZvV4iIkEhJ+c92tGuvugjqhlamp+tY\nu/ZCYDRggJ5jx1Ryc+uuNWmio2dPCz17PoHb7SQvr4C2bT/C5WqK2z2YmppyrrsuBJ1uDnAOt7s5\nquri8GE7+fkwcqQPSbLi9wcTCDhxuwO8885JHn74Ovx+E6qqcOBAJe3azWXDhuyfZyMEQRAEQfhJ\nfJ87rrnA4H+/IEmSDMz+1/U2wARJklL+9e1c6kIjqPuIURAEQRCEX4lAQOXZZzczfvxqams1goIM\nmEwqLlcBtbUtMZlCCA4O4vRpPw6HE0XZwZEjLTAaa5HllmhaOLCOiIhNmExe9u49DNyNTgeJie8S\nFhbK4cNHmTFjKosXw8SJ1m9/93+2owGsWXNtzi/6Rnq6XG+OkdEoMXKkgU8//fcqIyuyfDNBQRZi\nY0M5fHgnd9yxnUCgIzU1faitrSQ0NEBIyHzgBNACj0chEDDw+ecSvXuXYLfrUdV4VNWFokjMmnWU\n3r1jCAkJweEwUFWlMHr0CqZO3YKiiBY1QRAEQbga/deBkaZpW4GK/7jcFTipaVqOpml+4GNgxL++\ntwy4RZKkt4BVP2SxgiAIgiD8dPLza+jffwHvvHOImhqVmBg9lZXFuN16jMamBAWF4PMZqKyUMRqP\nUlFxDElKw27Pxu/vQCBgB5bTvPkhSksLqK2tQKebQHBwI5KSPiQhIQ5VddGxYxsaN76F5GQdKSl6\nABRF49NP67ej5eVp5OdrdOly7X7+lJYm8+WXKh6P9u21urY0/7df33ijiRMnVObMmUd+fgFJSU1Y\nuHA+KSmzcLt7UF3dDb/fiSTV0qzZamAfkITPF4HXm83OnY3Q6Q6RnKxD0+IBA5qmY926YgwGDbPZ\nRseOMdTUqLz99kHS0hZSWCha1ARBEAThaqP/kZ4njgttZwB51IVIaJrmAu5t6AmmTZv27b+npqaS\nmpr6Iy1NEARBEIT/1oYN2dx66wpcrrpZQg5HFUVFJiQpmrCwMNxumepqHZKkQ9N2ER6eRHFxNK1a\n5XHoUC/AhCwvwGY7yMmTVYCTZs2ewuVKxuf7PbfcMoR58z6msrKWQ4c+4J573PWqi7ZtU4iOlmnR\n4kI10dq1CgMHyuh0125gFB4u0aaNxNatKmlpdXvTv7+e225TyclRSUiQMRol7rzTQlZWEnfeOZJF\ni9bw1FMPMXPmPPT6x6mqmoXRWIHdvhefr5pGjVZTUOBC03oiSRZ8vgz8/l4YDKdITg7h7NkwwI2i\nOCku9gIuAgEbI0a0JCPjJFlZZbRv/x4LF46gf//En3N7BEEQBOGal5mZSWZm5o/yXJKmaQ0/6j9/\nSJISgFWapl33r69HA4M1Tbv/X1/fDnTVNO23V/h82vdZhyAIgiAIPy5FUXn++W28/vpXOJ0a4eF+\nysqqkeUIrNZQDAYb5eV+VNUKBAgLO4TJ1IWyMg8dOrjYvbsdYMBq/QiXayfgpV27MFq1+jOrVrno\n0BpAA8EAACAASURBVGEuslzG7t2HSElpxvLl/8BojOO660rJzY3EZqsrfn74YRdxcTLPPGP+dm1j\nxvi48UYdd9117bakATz/fIDqao1XX71QfXXffS5SUmSefLJuv44fD9C3bznZ2WH07Dmc/fuPcdtt\nI9m//xSVlVby8n6H2fwJSUm55OdX4/dLBAJD8HhSASeNGq0hP/96QkOL8ftL8fk64Pd7kSQnmlaJ\nxSIjy9C7d2NOnSrmzJkqbDaJxx/vzJ/+1BOd7tqcMyUIgiAIvzSSJKFp2vf6tO3H+r/5eaDJv33d\n+F/XBEEQBEH4lSgqctKv3wLeeCMLpxMslhNUVenR66MICYnB7TZQWhpAVS3Ici3DhnmpqemK0egm\nIqKQ3bvbA3r0+rdxubZhs/lZt+6vNG78BEuWOOnSZT57925m//7jzJ79PAcOZJCU1IS5c92MG2f+\nNiy6VDtaIKCxYYPKoEEiiPjPOUYA48bVb0tr2VJPixY6Pv88QFbW58yZ8zyffLKK4uLz9O0bT1jY\nK/j9t3PqVAgGgxejUSEoaAMOx1rARn7+jbRseZKaGitOZxyhoXswmSRkORhNC8Xt1qMoXtavP4Mk\nGRg5MhmPR2LWrK/o128BRUXOn3hXBEEQBEH4sX3fuy6J+gOs9wDJkiQlSJJkBMYDK3/o4gRBEARB\n+GlkZubQqtU/2L07n5oaBZPpAG53GxISIjAYwigpUfD5dEiSncjIavr10/P55xF06+aksLCQ/Pze\n/3qmVwkEDvDoo8PYv/8jHnjgEBs22LDZnmb//m0MHNiHU6c2c//9tyJJEqqq8d57rnrtaF9+GSAu\nTiY5+UIl0c6dGomJErGx12472jc6dZIoLtY4d+5CdXZqqp6zZ1XOnr1wIO3EiVbefdcFwAMP3E5J\nyV5atkzio48+pX17HaGhM9C0R1CUZlRXlxAaqsNg2ITJtBgwcfx4f8zmUyQk6Cgq6oDBsB5Nq8Bo\nDEanC8HjCUNR/BQWVrBmTS733NOaQMDAnj35tGr1dzIzc37qrREEQRAE4Uf0XwdGkiQtALYDLSRJ\nOidJ0j2apinAI8A64DDwsaZpR3/cpQqCIAiC8GNTVY0//GEzQ4YswuPx4vMpRETU4vd3pUePSE6e\nVKit1SPLNsBOWloA8LFtWxidOh1nzx43Xm8fQAH+j8aNy8nLW0pKSgLt2r1NTk4XgoOnYjZ7mDdv\nBqtWvUdMTOS3v3/jRh9hYTKdOl2oJlq0yM/YsYZ668zIUEhPF9VFADqdxKBBMmvXXgiH9HqJUaMM\nLF58ocrollvM7NrlJze37nEORxCbNy9m8eK32LVrHx7Pblq0mEdl5SPceONvOH36FJpWjcGwDbP5\nQ8BAbe1wCgpy6d69CqfzJiTpILJ8AlW1YDI50LRYamtN6PUlvPfecXr0CMNksiPLEkOGLOKZZzJR\nVTF2QBAEQRB+jb7XDKMffRGSpE2dOlUMuxYEQRCEn1BJiYv09I85cKAYk6kGn8+OyaQiSZEEBVVQ\nUBANmJEkC3q9jmHDXKxZ4ycsLBKP5zNqaroTCLQCfMBLvPLKzYwfP5AJE55k794o3O7bCA5+jtGj\nr+PVV58lJMRx0RrGjaukb18jkybVVRgFAhqNGlWzc6edpKQLFUadO3t57TUDffuK0Ajgn/9UWL5c\nYckS47fXvvjCz5QpHr76Kujba5MnVxMdLfPcc/Z6P+90uhg37mHWrNlMXFw6eXn388ADR9i/fxk7\nd54gKioKl6sttbV3Awom01ZiYysoKemOz3cMVT2GoqSj02lomgtNc6HTHUCvb47D4UZR7CQn28nK\nyqdNmwjWrRtPVJTtJ9odQRAEQRC+GX49ffr07z3D6BcTGP0S1iEIgiAI14qMjNOMHr2MQMCNopRj\nMMQRF2cgL0+H11sKJKHTWVBVE1FReuz2rykubkd0tJeCgs9wOocBTQEXCQnvsXv3yyxbto7HH/8r\ngUBnNO0RoqNfYv7839K/f49LrqGwUCElpZTs7EhCQuqCoI0b/Tz9tIc9ey6EHsXFGi1aeCkpMWEw\niJY0gKIijZYt6+9JIKARF1fN9u12mjWrC9v27fMzcmQFp05FXnLvPvvsC2699VFcrrao6tPccMNi\n7rijDU88MRNFCQCd8PsnAyDLWVgsWYSEjKCiohKb7StKSroBBmTZi6o6sVqz8fkchIT4UBQ7nTvH\nsGdPDl6vxqJFI7nxxuSfaosEQRAEQeCXMfRaEARBEIRfAVXVmDjxM4YOXYSinEav1yPLsaSkuDh9\nWsPvdyHLzQErYKVlS3C791JY2BlJ+pqzZz/B6RxDXVhUyXPP5bB9+4sMGnQ3kydPp1GjQQQCDzNh\nwnZOnJj7nWGR16sxdmwlDz9s/TYsgku3o61bp9K/vyzCon8THS3RrJnEjh0XPnDT6yVGj67flnb9\n9QY6dDAweXI1l/pwbtiw/uTmbmfkyFBkeRY7d47mmWeW8O67z9GzZwdkeS8Gw8uAhqp2wunsjde7\nnPBwFb9/EA7HPozGClTVhCzb8HiSkSSFsjIjcXEVfPllNo0ahZOaGseIEZ9y110rRYuaIAiCIPxK\niMBIEARBEK4ROTlVNGnyBu+/vx+H4yCK0hyjEXS63Rw4EEZkpAVNi0dVrRiNNqKjc1HVSrzerrjd\nK6mtPYSiPAhEYTCUc+JEO6CQhIT+FBeXkJIynOzsO3j3XT3z5z+E1Wq55Do0TeP++6uIjJR5/vkL\nrVKBgMbSpfVPRwNYs0bML7qUIUNkMjKUetfGjq1/WhrAhx8Gs2uXnxkzXJd8HocjiMWL57BixR1Y\nrXOpqvo9998/h4SEaGbOnILJdBa9fjoQAFpRWjoEp3MTgcBeFKU/YWElxMSUoqomVNWCosRhs+k4\nciSEkJAs8vJK2bKlhOnTe/LJJ8do0mQ2p0+X/492RRAEQRCEH4u4+xIEQRCEa8Ds2btJSppDQUEO\nzZv7qK7ujE53CJOpGo+nH82ahVFSEgLYMJnMmEx7sFiiOHXKgqYtQNPcqOoDgIP4+ABr14bRr99w\n/vKXfzB0aA9crqacPXsvGRmJ3Htv28uu5aWXnBw+HOCf/wxBli9UDW3aFCApSSYx8cLsIkXRWLdO\nZfBg3aWe6pqWnq4jI0Otd613bz35+SonT14IkoKCZFatCmXGDCcrVni+8/mGDu1Hbu6f6dx5L273\nVBYs2MGf/zyb+fNfoH17KzExMwEP0ITy8jH4fMfQ69dTXd2BJk1CCQ4+gSybUVULtbVRNG3qoLi4\nFz7fLqKiKpk6dQ/33deWyEgLLVv+nRkzdv2PdkYQBEEQhB+DmGEkCIIgCFcxl8tHr17/YN++KqKi\n8nA6o3E6rSQnn6OoqBGBQBhWq4myMis6nRW9PkB8/FHOnWuK319DXFwWeXkmYAKSZKRbNzsREa/z\n2WebaN++JUajjNsdT17eY3z0UTTp6dbLrmfxYg9PPlnNzp3hNGpUPwS67z4XKSkyTz5p/vbanj0q\nd93l58gR0/9ie37VAgGNyEgvR4+aiIm5ELw9/LCLRo1knn3WXO/xe/b4GTq0nHXrwrj+esN/Pl09\nv/nNbj74IIDV+gxebxmTJt2KxWLn73//ksrKJ1BVC1CNXv8h0dEOysp60aZNCLm526is7IDPpwBu\noqLKKSsDqzUPg+EEVVU9SU42MnhwM2bP3k+XLtGsXTuB4GDzZdcjCIIgCML3c1XMMJo2bRqZmZk/\n9zIEQRAE4aqxfPlBQkJeZv/+YuLjKygpicDns9C1q4Hy8qbodJF4vTrKyoLQ6+1IUhmhoZmcPt0W\nvT4fh2MzeXmhwK2YTFZatXKxd+8tbNq0k3Hj0jl37hz9+0+gqOhJ3nsvqsGwaPduH5MnV7NyZehF\nYZHfr7FsmZ9bbjHWu56RoYp2tO+g10sMGCCzdm39KqOxY40sWuS76PFduhh4++1ghg+v4Px55aLv\n/7v33uvK008nIkmvERQUyezZ81mwYCmzZt1FbOwsLBY3YCcQuJvz511Yras5dOgMstydwYMrMRh8\nyLKd4uJIVNVLIBCP09kBo3EzZ8+6effd/Tz0UGvOnKkmNvYNli8/9mNujSAIgiBc8zIzM5k2bdoP\neg5RYSQIgiAIVxmPx096+lts3uzEbq/B6fRisQRhs0USCJSQmNiMEydceDxWFCUYSdJjNB7FYMjH\n6RxESspxjh3bjKZ1BgZis1nQtK9QlFn06NGOkpISGjeOYcqUP3P77fDqq6FMmGC/7JrOnVPo3r2M\nv/3NwU03XVxNsnatn2nTPOzYEVTves+eXqZN0zNwoGhJu5T33guwYYPKwoUXgjZV1YiPr+aLL+y0\nbHnxvr30Ui2LF3vYsiUMm+3yYdyzz5azcGERVVUTMRgClJbW8PDDE8jJ8ZOR0Q+/34Gq+oBFGAx5\nOBy9qalJ4dFHzcyefQqfLxpF8QKl6PW1RERIuFw5uFzBhIYGExkpERUVyZYteYwcmcy8ecOx2YyX\nXZMgCIIgCFfuh1QYicBIEARBEK4iK1bsZuzYVfh8ZozGIiRJR2xsMtXVARISFCCSAwfK0emi8fst\ngIzFkkFERDfy8x3Ex28nO/sYkIYsd0Onk4Ed2Gwf0r9/J7Zu3cWrrz5Lr143kZpayNSpIdx7b9Bl\n11RTo9KzZzl3323hiSdsl3zMb37jom1bmccfvxAmVVRoJCR4KS42YTaLE9IuJS9Po0MHL0VFJnS6\nC3v06KMuIiJk/vSni8M5TdO4995qKitVliypP0fqUo99/PFytm51Ehn5EocO7aeoqIqYmDDuuece\nXnopFlmOwefzAquRpMPExl5PYWFXJkywcvx4PllZDjTNjyRVoWnFREX5cLmqcLuNBAVZMBg0OnVK\nYNOmQux2mWXLbqF374T/xXYJgiAIwjXnqmhJEwRBEATh+8vJKaJnz+mMHJmB3y8jSVWkpbXE4WhO\nYWE1Eycmcf68iWPHqtG0GPx+G6AwfPg5dLo0amvNSNJCsrOPI8ujkeXuaJqKXr+FHj12ExpqwmCQ\nOXQog/79h5OWVsRTTwU3GBYpisaECVV0727g8ccv3bLm82ksX35xO9r69Sq9e8siLLqMxo0lYmMl\n9uyp/8Hbd7WlQd2N4zvvOKioUHn66drLPr8kScycGUbHjlY8nud47rnfERJiRlXhxRdfZdSoTZhM\nRRgMBuAmNK0H+fl7MBg+5ZNPKqiqsvH00w4kSYemhSLL8RQXW3C7ZZo39+F0KpSVBaioKCIyUsVs\nNjJw4MdMnLiS/PyaH2ubBEEQBEH4HkRgJAiCIAi/Ynv3HqVDhydJTJzN9u0SOp2HpCQD06YNZd06\nH+HhGr/9bStmzjyJJJlxu6PQNBvBwW4mTbKwenUiwcFlVFR8RCDgxWq9F1VtiSSB2fwF3bvv5fTp\nU7z++h/5+OM3gVDS0oq4//4gHn7Y0eD6nnyyBq9XY/ZsB5J06eBn48YAKSky8fH1b0vE/KIrk54u\nk5FRfyZR9+46Kio0jhy59Kwio1FiyZJQli/38O67rss+vyRJvP12OHFxepYt68WOHato06Yp8fGR\nLFu2BqNxOlFRFcgy6PWpwI14vUUEAv+koKCKmTNLmTWrEXY7qKoNSYrHaIzn9OkwbLatGAwau3cr\nhIRkAzUkJNhZuPAEzZu/xUMPrebcuaofZZ8EQRAEQfjviLswQRAEQfgV+vDDFURH30mnTh9y4IAN\nvd6IxaLwwgsDadkykWnT9nLrrQlYrbXMmZOL2aynqCgUsDJkSBBJSU7eeUfGZNrK+fMrkWUTOt1E\n3O5YZFlHo0ZbCAlZQfPm8Xz9dQbDhw+kvFxh4MBCxoyx8vvfBze4xrffdrF2rZfFi0MwGL67SmjR\nIj9jx9avLtI0jYwMRQRGV2DIEJmMjPqDr2VZYswYI4sX+7/z58LDZVavDuUPf6jliy+8l/0dOp3E\nBx9EYLVKTJli4LPP5vH00w9gtxswGvUUFz9JeHguqqqi11+PyXQX4Ke2djGKcpRHHy1i3DiZjh0t\naJoVtzuGmJg4amrSCQk5jMNxjq+/TqasLIvERCd6vZuQECsff3yC1q3fZuLEFZw+Xf5jbJcgCIIg\nCFfoFzPDaOrUqaSmppKamvpzL0cQBEEQfpHy8s7z1FMvsnRpIT5fCnq9Hk2zEBoq8fTTPYiNtTF5\n8nq8XitjxkSxcmUWPl8jXC4ZSECWjTzwQBDz5x9BUZrg8SwGirHZQvF47gJCUVWNhIQN6HQZvPfe\nX+nbtxsA1dUqaWmF9O5t5tVXQ7+zWugba9d6ufvuKrZuDaNZM/13Ps7n04iJqebQoSDi4i6EQwcP\nqowa5efUKdOPsHNXN69XIyrKy5kzJsLDL7wvO3YEmDjRxeHDl68Ey8z0Mm5cFZs3h5GS8t3vFdS9\nXyNHFhMaKjN/fgQ5ObncfffvyM0tpqCgAkW5D0nqQiCg4XDUUlX1FhAAkpCkdJo2zWHgwM78/e/F\naJqPpCQfxcWlhIWdo7z8ME5nHwyGAlq3Pk6zZkNYt64STTNjsxlwuz2MGNGCP/yhNy1bRvwIOycI\ngiAIV6/MzEwyMzOZPn26GHotCIIgCFejwsJCFixYxBtvfEhOThzQGpvNjNutp0kTK88+252qKid/\n+9sOKitNGI02LJZCPJ5KCgpikOVoFCUCk8nA4MHlrF0ro2kKPt8KoAazOQRNewSfz4AkyVitHzBp\nUhzTpj2GxVI3MNnpVBkypIg2bYzMmRPWYFh0+LCffv0qWLo0hF69Ln/i1Wef+fnrXz1s2VJ/FtLL\nLwc4d05j9mzDD9m+a8bw4T4mTNAxYcKFU9FUVSMxsZo1a+y0aXP5U+bmznXx4otOdu4MJyLi8lVd\nbrfKsGHFNGum5+9/D0fTNN544wOmTXsDg8FKTc0YAoFuKArYbH50uveori4BooEb0euLefjhlsye\n7SUQ8BEa6kSncxMInCQ5WSMrywZI2GxHCQ7OoUeP4WRmQkUFxMRYcTrdDBqUxB//2Ie2baN+8N4J\ngiAIwtVMnJImCIIgCFeRwsJClixZzkcffUxW1jkCgc5AC0JDgygvV2nZMphHHrmer77KZunSg3To\nkMzhwz4cDoWCgmPAaRRlKD5fGBBMVJQRs/krioo64PUeAbYgSbWkpg5n+/aueL0ysmwgPv5jliy5\ng06d2n27Fo9HZfjwYmJjdcydG3HZE7UAiosVunUr5/nn7dx+u6XB13rXXU46d9bzyCP1K4n69fPx\n5JM6brzx8kGHUGfOnAC7dqnMm1c/oHvySTd2O0yf3vB78fTTNWzf7mP9+jBMpsu/z7W1KoMGFdGl\ni5HXX68LEY8fP80ddzxBQUEFJSVD8fn6oGkSer2Prl13sH37JiTJgSwPQVFMdOx4njNnOlBZ6UOW\nKwkN9dG2rYe8vELAxJkzeqAEvb4Cne5r0tL6ceBAFHl5Xpo0sVNb66ZPnwT++Mc+dOwY+wN2TxAE\nQRCuXiIwEgRBEIRfucLCQpYuXcGiRUvYu3c/DkcShYVJyHJzgoNtlJcrtGgRws03N2X9+iOUlNRy\n001tWLMmn3Pn3ChKPjrdUQYP7sratXH4/eGAjWbNVIqK9uNydUZVM4GvSUjQMXjwU7z/PiiKHtBz\n992neOed0f867aqO368xenQxZrPEggWR6PWXv9fweDT69y9nwAAjf/7z5U9Pg7pWqpiYag4fDqJR\nowtVLTU1GrGxXgoLTdjt4oS0K3HmjEqPHj7y8031Qr1duwLcdZeLo0eDGqwMU1WNMWMqsdslPvgg\nuMHHV1YqDBhQxODBFv7yl1AAAoEAr776D1566R18vpH4/UNRFAXwcsstBaxc+QE+nwFZ7oOmpWAw\nbCQ2djA5ORrgxGqtZMqUZObN+wKTyU5VlZ1AwEV19TF8PhOyfJLWraOoru7MuXNemjSx4nJ56dq1\nMX/8Yx+6dWv8Q7dSEARBEK4qIjASBEEQhF+hb0KixYuXsn//QTp2bE9urp+cnAQkKQGr1YTTCbGx\ndrp2DWXjxsM0bWolPLyK7du91NY2wWgsIz3dyMMPp7F5s5sXXzwLRAEmGjcuwOXyU17eCFgN5PLy\nyxNYty6WjRv1SJIRWbbwwQdB3HZb83prUxSN224rwenUWLIkCqPx8vcZmqZx221VKAosXBjcYCUS\nwLRpbnbvVvj8c3u96ytWKLz5psKGDZdvZxPqa9nSy8KFBjp2vBC+aZpGx461TJxoZPLkhudBuVwa\nffqUMWqUmWeftTf4+NJShdTUQiZMsPGHP4R8e/3QoWPceuvjZGd3wuUagaoGADcdOpxAp/uKrKzz\nyHJbJGkAirKF8PBYysqSAC+SVMxbb3UhMdHI7NmZZGaWoGnhpKaGUlx8kL17a9G0EoKCnJhMvSgv\nl4mJMeL3K7RvH8Of/tSXPn0Svs8WCoIgCMJVRwRGgiAIgvArUVRUxJIly1m8eCn79h1gyJDBREaG\nsWrVPkpK2qCq0UiShMlkRZIkgoKcFBWVExRUQE3NGWy2rpSXxxMRYWT27P707ZvIO+98yWuvHaKm\nJgZNiwD02O1ZBAJN8Hh0wCoSE/UsX/48gwfvoqQkCk0zYLOFsWFDM264wVpvjaqq8ZvflJGXF2DV\nqijM5oZPKps+vZY1a7xs2hSGxdLwPcmyZT4efdTN7t1BxMTUf/6HHvKTnCzx5JOXH8As1Pfoo36i\noyWefbb+vp0+rdCjRy2LFtno27fhPc3PV+jWrYxXXw1i7NiGW9kKCgL07VvIpElBPPbYhdPz/H4/\nL7wwm5dfPovHczt6PQQClVgs+5g82cZrr61E0+LQ6W7GbD6H05kD9AP8QDGNG3v4619voEuXBF5/\n/Uvef/8ksmzl0UdbYzZXM2vWJioqvEAJJlN7NM2C3S4hyzIpKRFMnZrKgAFNG6yUEgRBEISrmQiM\nBEEQBOEXrKio6Nt2s337DjBsWDrp6YM4ffokb765Gr+/L4FAMKqq4HBYqKhQUNVKoJDWrSWaNUvk\n0CGV4mIbOp2dGTP60Ly5ibff3sSqVWfQtGQUJQyPx4wkgcOxh6qqdsB5YCPPPz+G2NgwHnywHE2L\nxmSyYrdH8sUXibRtW7/qRNM0Jk8u59AhHxkZ0dhsDYdFCxe6eeaZGnbtCic6uuGZQ4cPK6Sm1rJm\njY3OnesHGJqmkZTkY/VqA23aNPy7hQvWrFF46aUAX355cSXRhg1+7rjDxc6dQSQkNLyvBw74GTiw\nglWrQrjhhoYrvc6dC9CnTwHPPhvC/ffXb0fMyjrEsGEfUFw8HllWkOUq/P7jjB9fyObNJykoUJGk\nEYSHB1FR8SWKMgAAo9GNqpbjcJznscc6cfvtPZkz5yvefPMIOp2f3/62Df37J/PCC0vYsqUATasF\nmmA26wANq9VCYmIIf/5zf4YMSRbBkSAIgnBNEoGRIAiCIPzCfBMSLV68lL179zNsWDpjxoyiefNm\nzJnzNvPm7UCWB+P1GtE0P5LkxecLQZLcdOqkY+zYDuTm+vnwwz00aZJITo7MhAktSE7WmDt3M263\nSkhIGw4e1OP3WwEdOl0FRuPXuN29gB2EhBxn1ao/8eKLH7Fu3Q2AlaioKAwGBxs3NqF58/pBgKZp\nTJlSQWamh40bY3A4Gg4Wtm/3MXJkJRs3htKuXcMnmpWXq3TtWsvUqWbuuOPiIOL4cZW0NB/nzpnE\nH/j/JbdbIyrKS16eieDgi/duxgwPH37oZ+tWO1Zrw3u7apWHBx+sZvv2cBISGg4CT5/207dvIX/9\nayi3316/nc3j8XLrrR+ybNl1SJKH0FCFioocIiIW0K9fVxYt+gpIw2xuhd2+g8rKZAKBSEBBlmsI\nDS3D7z/FkCEp3HtvHz79NJf5848jSeWMHp3IHXd0ZfPmY7z55pfU1gKEI8uVSJIVi8VM48YhvPRS\nGsOHt7yidklBEARBuFpcFYHR1KlTSU1NJTU19edejiAIgiB8L8XFxfUGVw8dOpixY0czaFAa+/bt\n44UXXiIzsxxF6YPfbwBqcDhM1NQEY7erPP54Z5KTQ5k3bweHDuUzfHgX9u3z4fMppKQEWL8+iwED\nWpOS0obXXivE47ECesCF0fglPl8I0BVYzfDhMdx+e3fuu+9tqqoewGazEBcXg6IY2LixCQkJF4c7\n06ZVsHSpi8zMGMLCGg4Izp4N0LNnOe+9F8yQIQ3PxwkENIYNc9KmjY4ZMy7d6vT66wEOH9b4xz8a\nDp+Ei6Wn+7jvPh2jR1/8/mmaxp13uggEYMEC6xUFcjNnOpk7183WrWFXFCAeOeJjwIAiZs8OY/Ro\n20Xff/PNfTz6qIKmVRMWpuJ2e3C7X2XkyLasXZuN290KSerP0KEu9u8/REFBW1TVSl2bWiWRkYcA\nJ0FBNm67rR+ZmbWcPFmOLBcTE2PgoYf6YrXqmT59JSdOaIAFg6GAQMCKXm8jLMzCa68NZfz4tuh0\nooJNEARBuHplZmaSmZnJ9OnTf/2B0S9hHYIgCILw3/omJFq8eClZWfsYOnQwY8aMIj19EKWlZbz2\n2iwWLPiUsrKmqGpXJMlIVJRESIidEyf8xMRYmDKlM1VVVfzjH9to2jSce+/txd69LubPP0JkpAuX\nq4AHHujLsGFdmDBhD6dOSYAB8AE7ADfQH6hAr9/ArFlj2bp1C8uX5+J2TyQmJpTIyBBUVWb9+ibE\nxl48x+aVV6p4770aNm+OvaK2sqoqlR49ynnwQQuPPHJxMHApTz3lZv9+hTVrbN954trlAg+hYQ0F\nbm63Rp8+tYwZY2DKFHODz6dpGpMmVZOTo7ByZWiDJ+UB7N/vZfDgIubOjWDoUOtF39+0qZKhQ7Px\neIoxGl1YLGG43a8QFFRKkyat2bdPA9KxWPSMG6dj165Cjh6Noe6/eT8WSxk221JqayUUJYIWLZIo\nLAynU6cIoISsrLPcdVc3hgxpwyuvrGH9+ko0TU9oaBk1NRAIBGGx6Jg8uTUvvjgao1HMyhIE7/SS\nSwAAIABJREFUQRCuXldFhdEvYR2CIAiCcCVKSkq+rSTKytrHkCGDGDt2NNdddx27d2exfv0mVq9e\nS2lpFSZTTwKB9miaRIcOEVRVucnJ8RMZaeP++9tw+PBZ1q8/yvjxnXnwwd7s3FnClCnb8Pkq6dLF\nzH33dcNud/H735/g5MnGgBFQgGOYTIV4vd0BPwbDNm64wcy99/ZlypSXqKlpBdxNdHQYoaEWDAYd\nGRnxhIdfHMS89VY1M2ZU8+WXMcTFNfzHc12lUAXNm+uZPdtxRXv20Uc+nnvOw+7ddsLDL13Z8U1L\nVW6uiZAQ0Tb0fRw7pjJw4OVb+nJzVW64oYb337eSnt5wJZffX/d+p6ToeeONK3u/d+3yctNNRXz8\ncST9+19cTbZ/v4f+/c9QXX0OVa3FYokmMXEVJ06s5/rrUzhyxInT2RzohSw7GTNGZt8+OHEiCJAB\nH6mpBtLS8vjoox0cPaqg18chy1GMHx9FRISJf/5zDx07NmHixJ5kZHzNvHlnCQQgJqYCTTNTVGRA\nkhS6dVN58cVh9O3bE1kWVUeCIAjC1UUERoIgCILwP/ZNSLR48VK++movQ4YMon//VPR6E9u372bz\n5m2UlJQSGRlKbu55wsJGU1ISiyxD69ahnD1bjF4fDOgZMiSOPXuOIMsSkyb14dZbu7Bs2SGeeWYn\npaU+brhBpUWLavbu3c2hQzHACMAKaMhyMVbrWWprU5AkMwbDdiZOTKJbt6asWbOR5cs3YjSmo9Pd\njMViJyrKgs2m47PPGuNwXBwWzZ1bw9SplWzeHEPTpg2HB5qm8fDDNZw5E2DVqiurOMnKCpCe7uSL\nL+y0a/fdlUMZGQp/+culhzYLV+ZKh4Zv3Rpg9GgnW7faad684WquykqVHj3KmDzZyuTJV1ZRtnmz\nhzFjilm+PIoePS6uZjp2zMuAAedwOs9TXV2GLIcwblwFS5e+gqLU0KZNM8rKbOTmNgV6AEW0alVM\nWVkyxcV1a5AkLy+80Iwnnkjh9deX8dZbezh/PgzwcN112bRq1YLDhxWqq/3cf38vSkv9zJlzCK/X\nT1hYMbGxjTh61IemaVitx7jjjnhuvXUUPXv2EOGRIAiCcFUQgZEgCIIg/A+UlJSwbNlKFi1awldf\n7aVPn140bZpEVVUtW7fupLKyir59e9KsWQJHjhxky5YswsPvICfHjNWqJy7ORFFRJfHxjTl3zkXr\n1laOHDnB4MGtmTSpD61aRTNzZgZvvnkIlyuEoKBs/P4vCA9vRFFROH7/TUAoAJJUjaYdB5ogSZGE\nh+9nxAgLBQWn2bx5F7Is4fF4ue66P1FW1hK3W0+jRlYiIvQsW9b4kqedffKJk8cfL2fTphhatryy\nmUFvvOHk7393s21bGMHBDf9BXVys0qVLDTNmWBg9+vKnbT32mJ+oqIuPhRf+Ow895KdZM4nf/e7y\n+/jOO17eeMPLzp1BBAU1fB955kzdzKq5c4NJT7+yUG/tWjd33FHCmjXRdOp08c+cOeMjLS0Xna6a\nM2dyUVUDI0cGCA39ik8/3YDdbsLjqcLns+LxDEBRugJnMZvzUJQO+P1BgIrR6GbevLaMH9+Ko0fz\nefDBVWzZUkNQUCUWyw58virCwjpTUGBg8OBWREXF8cEHR/D5nBiNxbRoEc/Jkxo+n0pQUC5m8xbG\njBnGmDGj6dmzOzqdaJEUBEEQfp1EYCQIgiAIPwJVVdm7dx/r1m1k7dr17Nt3kFatWmOz2cnOzqWm\nppa+fXuSmtqT3r17kJubzcyZMzl0qBiLZRS5uRLBwUYMBh9xcXbi4hqRmZlPcLCCplXy0EO9GTq0\nGStXbmHBgq84fVpG0xrhcPhJTDxHTk4+VVVWIB2Io671pgrIR5KC0LTGREcfxm7fQU7OSXQ6sFqN\nDB7ciwEDhrBqVTzZ2Sr5+dC4sY3ERCMff9wIk+niYGflShf331/K+vUxtGvX8LHpAJ995uG++6rZ\nvj2MxMSGQx2fTyMtrZa+ffX8+c+XHnL971q29LJwoYGOHUVlxw+xYoXCm28qbNjQ8Pv64IMuCgtV\nli61XdHpYdu2+bj55kq++CKUtm2vLGRcscLFAw+UsmFDDG3bXrymvDw/aWm52O0Bjh7Nw+WqJjq6\nhP/7vwTsdpnFi9fz2WdbSUiIwu3WOHPmeuqGux8HqpCkFDStLjiyWqt4882m3HVXN86dq+LWW1eR\nlVWKw1FK795mnM5TbNlyDlVNwuGw0bRpMocOeZCkCtzuKhITg6mqclBZ6ScpSUOn20hNTR6jRo1g\n7NhbRHgkCIIg/OqIwEgQBEEQvqfz58+zbt1Gli9fxaZNWzGZzAQFOaiurkWSJPr1603fvj1ITe1F\nq1Yt8fl8fPTRR7z66mt4PI1xu3tRXKwSHGzA73cyenRbbDYH//znMfx+J23bmujRI4iyshOsW3ec\nigoHJlMwQUFNqaw0oNMdwOXKx2iMxO+/AU1rTt3JZ1VANbIMqhqP0bgHv381Ol0tbdo0Y9y4odx8\n8yASExOZNauQV14poF+/EL74wk1cnI127cx88EEsBsPF9wfr1rm5/fYSPv88ms6dr6xS5OBBP2lp\nFaxYEUL37lcWME2a5CIvT2X58obDiDNnVLp391FQYBLHnv9ANTUajRp5KSgwYbdffi99Po0BA2oZ\nMEDPtGkNh3oACxa4efbZGnbtCr+iAekACxfW8rvfVbBpUwwtWlwcNBUXBxg0KBebDU6cKMXpzMLt\nbopev5pevWp44IExeL0KH3+8lh07DpKS0pbjx1tRWdkcOArogFjADihYLHk880wjJk3qz8GDldx7\n71oCATdVVae46abW9OkTy5YtWXz++VkqKszYbKEEAsEEBZVTWuokLMyEJEVRXu6ndetgevSoZdeu\nlRQXlzB69AjGjBlNr149RHgkCIIg/OKJwEgQBEEQrpDL5eLTT5fz6afL2blzD5WV1ciyHoPBQKdO\n7enR4wY6dmxPp04dSExs8u3g4NLSUt5++23eeutvhIX1Jz+/OdXVGlarRFiYxG9/25OiIi9z5hzA\n4/HSpEk5Hs9X+P1+QkLaUVAg06JFBJWVEtnZwUA2ISFlqKoVvb4N5eUtqTsFykldWKQAjYEsgoO/\nIC2tNffeewv9+/fAbDahaRorVlTw5JM5tGxpITTUzPr1tUREWOjd28acOdHodBffG3z5pYfRo+vm\nyvTs2fApWQCFhQo33FDG//1fEOPHX1mo8I9/eJkxw8uuXUE4HA3fo7z9doAdO1Tmz7+yMEq4vP79\nfTzxhI4bb2w40CgqqmsbnDXLws03X9n+T5tWQ0aGj02bwrBYruwe9P33a5g+vW5eVmLixaFRRYXC\n0KG5yLLG8eO1TJhgYvXqHAoKXPh88zAYTtKt23XceedIXK4ACxdmcOxYDUbjcIqLo9C0k4ANCP7X\nP/0YjUeZMCGESZMGsmFDGa+9lkW3bg6OHz9IUJCZSZP6c911MbzyympWr87B77cDMiEh+VRUqOj1\nQQQFRVFRoZKYGMQjj7ShtnYfS5Yso6iomFGjRjBmzCh69+4pwiNBEAThF0kERoIgCIJwCaqqcurU\nGVas+IzPP1/HwYNHKC+vxGg0kJjYhN69uzNs2CC6dOlIXFyjS54qdeLECWbOnMnChSuIjx/LyZMh\n+HwSen2Afv0ak54ez4oV+9myxYeqgt1+gsGDgwkNbca+fdWcOVOKw+EjP78Ev78dJpORpCQXeXlF\nhIa2JDe3BZpmBnxAKXWVElHYbNncc4/ElCkjiY9vVG9Nhw65eOyxbAoLfdx4YwTz51fSvbudI0dU\nhg2z8eqrUZd8Ld+cXLVwYSQDBlxZ8ON2a6SmljNsmInnnrNf0c9s2xbg5pvrBiq3aHFlf0SPGOFj\n/HgdEyaIP7p/DC+/HCAnR+Ott66sbeyrrwIMHepk0yY7bdo0/B5omsZtt1WhqrBgQfAVV4XNnl3N\nzJnffSJfTY3C8OHnkSQNl8tLIKAxdqyDt9/Ox+GoIBD4kOPHdyPLMp06teGWW9JxuwPMnbuL/Pyu\nBAJxBALnABN1879MgAejcS9t2wa4667BrFlTSU5ONffc05Rt2/azZcsJbrutO/fe+//snXd4FHX+\n+F/bS3Y3yaZ3SAGSAAmd0JuAoKBYDvW488Q7T09PxBN74yyoqCiH3dO7UyxgOwtID6FDIIQU0kjv\nySabbC8zvz8COfmC54J3359333k9zzyz8LCzn52ZHebzmneZzIkTzTz++FZqakTUah8+334EIQi/\nPwG93ojLpSYkRM29905k9uxwvvnmKzZs+JTm5hYuvXQ2s2ZNZ+bM6URHRwe0PyQkJCQkJP7d/FcI\no0cffZRp06Yxbdq0/9/DkZCQkJD4D8Tv91NeXkl+fgF79hxg9+69VFZWIwh+NBo1mZlDmDNnJkuW\nLGbQoLR/ui2fz8f27dt55ZVXyMsrJTr6GsrLlQiCHLXax7hxajyeOo4eteHxJKNQ6Jg7N5i7757E\n5s0VvPbaDkTRjd3ejCg6CAubiM0WSUyMje7uWrTaUJqbR9IXCeEDWoAg5PIQhg5V8c474xg5Mvic\ncbW3e3nkkXo+/bSLX/86irw8J93dftLSgti718Xzz0dy3XWm88qiggI3c+a08uc/hzN/vj6gfSoI\nIosXW1Gr4W9/C/7eNu3fpaGhr2X7m2/qmTcvMFnh8YhERLipqtIQHi6lo/0rKCwUuOIKL1VV6oCO\nG8B773l47DEXhw4ZMJt/uI6UyyUyY4aFWbPUrFxpDHhszzxj5d13beTmRhMZea6ccrkEVq7s5M03\nu5k3T8e333azYIGJ6GgZr7zSyq9+FU5KyjH+8pcPyM8vQRBEhg9PY+7cqZw6peGzz4Lw+UIQBAt9\nkXqR9KV59iCT5aLR9DBu3CgqKgzMnJnEsmWZfPbZId56azfp6THcdtsM4uLM3HffVvLyOomIUJKa\n2sSxYydxOpORyw2IYhBqNSxdOoIHHpiG09nBt99uZdu2HezalUd8fByzZk1n1qwZTJkyCaMx8P0j\nISEhISHxr2DXrl3s2rWLxx9//D9fGP0UxiEhISEh8Z+B1+ultLSMo0cLyc8vID+/gGPHTqDVapDJ\nRJxOOyNGDOeKKy5j0aKFpKam/OA2BUFg//79fPDBB3z88SeEhIzE5RpNYyMIggyt1olMdgyjUYPP\nNwCnMxQw8Pvfj2b4cD1PPPEJ5eXt+P1dKJVWxoxJZciQKWzc2I3H04nJ1EJXVy9+/yxEMQoQ6Iso\n0mAwRJCREcrq1alMnhxynu8rsG5dK08+2cg114ShUql4//0uLrsslC1bnCxYYOTppyMIDT1/ZEhp\nqYcZM1pZu9bM1VcH1hId4KGHetm508P27Wa02h++z3C5RKZMsbFokYr77gss3Q1gxw4/99/v4+DB\nwOopSfwwoigSH+9m1y41aWmBFxG/+24nRUV+vv46CKXyh495W5uf8eMtrFxp4Oc/DyxqDeCRR7r4\n+98d7NgRjdl8/vO2uNjNb3/bgsMhkJIiJy+vl3vvjaSgoIctW6z88Y8J/PKX4XzxxVbWrv0bBw4U\n4vV6GTRoAMnJczhwIJmuLh+iaAe89IkjGdAObAe86HRJQAwPPZTN8uUT+eKLo7z66k4qKlq5+eYp\nXH75SB59dDebNzdgNsOSJQns2rWZY8dE+grTa5HLBbKyDNx110QWL85BJoP8/KNs27aTbdt2cPhw\nPiNGZDFr1gxmzZrO2LFjUKkCk6kSEhISEhI/lv+KCKOfwjgkJCQkJH56uN1uiopKOXr0OEePHic/\n/zjFxSeJjo7EbA7G4bBTU1PD4MGpzJs3hzlzZjF+/LiAJmSiKFJYWMj69et5772P8HoTUCiyaGsz\nIYoKRFGOTmdh8mQtSmU4+/a1EhOTQGOjyKWXJtLQUMjBgzX4fF5Uqh4mTx7AsmXXYrMZuPPOXDo6\n3MjlZYiiBUGYAZyJbLKgVMrQaKKJiTHw/POpXH552HkjQb75povly2tJSlJz2WXhrF7dTna2HqtV\njsUi8Prr0eTkfP9EvarKy7RpLTz1VChLlgSWUgbw1786eewxGwcPhhER8cPCQRRFbrzRgdsNH3yg\nDziqBWDFCi86HTz+uDSJ/leydKmX7GwZd9zxwx3tzuDziVx6qZ3sbAXPPReYACop8TFtmoVPPw1h\n0qTAaiCJosgf/tDFnj0utm6NxmQ6/zkmCCLvvmvl/vvbmTlTT1mZDb1ezu9+Z2bt2macToGXXhrA\n5MkmBEFg06Zc1qz5K3l5R/F4PISHT8fhmIfHI+D1WuiLNAoFRGSyehSKXHw+DZCMUily9dXwq19N\nIzw8kT//eS/r1x9k+vQhLF48gb/9rZxvv61FqbTx858PQhTreP/9IzgcaYAOmcyLKHqIjLQwfnwI\ns2YNYcSIYSQnD+DEiSK2bdvBtm07OXWqmilTJvVHIGVkpF/Q70VCQkJCQuJCkISRhISEhMR/BQ6H\ng8LC4tNyqJCjR49z8mQFqakDGTo0Hb1eS3t7GwUFBfj9fubMuYTZs2cyc+Z0wsPDf3D7Xq+Xyspq\nduzI47PPvuTQoQKcTjOCMAhBSEQmUyGKSvR6GTNmRDF7dhp//3sxx483Mn58JocOdSOX27FYynG7\nBZRKJxMnxrJy5S8ZNSqD1au/YNWqo7hc4UA1UIJcPgtByAbkQBc6nYDPF4HJFMTq1aksWRJ93uLU\npaVOli+v4dQpNytWxPLZZ71UVnqYODGYL76wc++9ZpYtM5+3C9oZ6up8TJ3awn33BXPLLYGnxOTl\nebjqqm527TKTkRGYbFizxsW773rYu9dIUNCF3ZMMH+7m9ddV5OQEHgkj8cNs2ODnnXf8fPPNhRUS\n7+wUGDvWxsqVWm64IbD3btni5pe/tLJnj5mUlMDOGVEUue02CyUlHjZtikKv//7j39Hh45572tm2\nzc68eTo+/bSLJUtCGTZMxWOPNTB+vIFnn00iKakvSs3v97N16z5eeukv7NyZj883CkFYgFwOfn8b\n/yiO7UcmKyc4+ChWazCiOAC1uhW5fDvTp2cyffoUnE4zGzcW4vH4WLQoh0OHejl8uBlR7GbcuHCG\nDlXz+ec7qasLRxDCkcsVKJUCcrmHkJBWurvziYqSkZWVSVbWUAYMSKCnx0pRUTHbtu3A4/Ewa9YM\nZs6czqxZ04mLiwto/0lISEhISASCJIwkJCQkJP7j6O3tpaDgRL8YOnr0OFVVNaSnD2LkyCyysoai\n02morj7Fzp25nDhRzMSJOcyePZM5cy4hPX3I9z6V7+21UVZWSWlpRf9SVHSSmpp65HIZfn8oJtMY\nbLZIRFGBICjQaFTMmZPMxIkxFBTUsGlTMenp0QweHMunn1bT0+NEEFqQy11kZ0fw/PO/YNy4dD74\n4FueeuoLqqrkQDLQQ0hICXr9NJqaUgElCkUPCoUbUYxAqdTz8MMDWL48EY3m3AlyV5ePxx5rYP36\nDlasiMXplPHyyx0sWhRKXp6H1FQVf/pTNElJ/zwap6XFx5QpLdx6q5G77jq3HtL3UVnpY9IkC3/7\nWzCXXBJYitj27V5+/nMH+/cbGDDgwopWNzaKDB/upq1Nc15xJnHxdHWJJCW5aW3VBNzJ7AwnTviZ\nMcPG5s1BjBoVmAB69VUHL79sZ//+MEJCApN/giDyq1910NLi5+9/j0Kj+efjzM11cOutLcTHKzGZ\nBA4etPP00zFUVdl5+eVWbrstinvvjcVg+Md56PV62bp1H2vXfsjWrRr8/jn0FZlvAwycqSWm1xcD\nR/H5BuHxmNDp6khJ6aa9vQS9XkN29kQsFiPHj7cxadJwamrk9PR4CApyYLdbmT9/ED5fA5s2naCx\nMQJRNKNSgUYjx2hUMH58MOHhXbS0nKSwsIiODgtDhw5h4MAkQKClpZmCgkKioyP7o4+mTZtCcHDg\nv18JCQkJCYn/iSSMJCQkJCR+0nR1dZ+WQ8fJzy/g6NFC6usbGTYsg5Ejh/e3sTcag9i5M5ctW7ax\nffsuEhLi+wXRpEkT0Gr/URdHFEXa2jr6hdDJk2fkUCUWSxeDBqWQkpKI1+uksrKcmppeIiPn0Npq\nwusFmUwBKMnOjiQrK5SqqkaOHKkjOzsGsxlqa5spLFQiCEFABwMGyHjkkSsZMyaeb7/dzRtvfEt5\nuRswAvEoFCFcfrmesjIZpaUJgAa12oXB4MLhMOH16vnVr6J4/vnBmEznTsB9PpHXX29l5cpGFi0K\nZebMUB58sIWBA9UYjRoOHHDx0ktRXHml4QfTVzo6/Eyb1sJ11wXx4IPn1kT6/uMkkJPTybJlQfz2\nt4EVxj51ys+ECTY+/FDPtGkXnlL25z/72LJF4MMPLywKRiIwJk1y88gjSmbPvvDuc5984mH5cieH\nDxuJjAxMAC1b1kNRkY9Nm0L/afTbd/H5RK6/vh2PR2TDhsgffJ/HI7J6dScvvNDFNdcEkZfXQ2ys\nigcfjOCNN1rJze3l6acTuOGG8HO6t7lcbj77bA8PPlhOdXUKYAc66fsdGwE3Ol0+Mlktbnc6guAB\nqkhP1zJihJmGhkoOHy4hJmYknZ0GTKYoXC4zAweGkJ6uJT+/kpYWK9OnJ6NWd7BjRxXNzWZE0Yha\nLaJWy4mM1LNkyUguuywZp7OFwsJijh8vprCwmKKiUoKDjYSEmHA6HTQ3NzF4cBqXXTaXSy6Zyfjx\nY9FopFpfEhISEhKBIwkjCQkJCYmfBKIoUl/fQEHBCY4dO3F6XUhnZxdZWZmMGpXNyJFZjBw5nPT0\nwbhcLnJz8/j2261s2bIdi6WL2bNnMnv2LC65ZAYxMTH4/X5qauo5efLsiKGTJyuRyWSkp6eSnp7W\nvyQmxlFQkM+HH37Ijh3FhIXNpbMzFJdLQKtVo1RqCApSM3iwkdraBjo6rISECDgcbXR2tgCxQDIy\nmQ6VysovfzmEESOCOXLkMF98sZueHiNebwggYjDEIIqpzJgRwbFjlTQ0pANBqNU+Ro5Ukp/vwecz\nMXWqgfXrhxMTc/5C0Nu2WVm2rIaoKBX33x/H2293sW+fnYULzXz0kY3rrjPxxz+GYzT+8KS/u9vP\njBmtzJ2r46mnQgM+dl6vyNy5XQwfruTFF00BvcdmE5kwoZdf/1rDHXdc3CT22ms9zJsn58YbA6+z\nIxE4Tzzhw2IReeGFi6sP9fDDTnJzfWzbZkCt/uF7Tb9fZOHCbmJj5bz++vk79p0Pj0dk0aI2jEY5\n770XHlC0WVWVh9/9rpWGBi/Tp2v44AMLt90WzowZelasqEMul7FmTRLjx58/HbOmxsrPfrafQ4dU\ngIW+iKNI+tLV7MBuTCYVPT3R6HQduN0NqNVO5s8fxsiRcdTUVPL55/n09Jjx+xNRKMKJjNRy003D\nCAmR8803xRw4UM2YMfFotTYOH26mvT0UmUyJUimiVMqJjzdx442juO66LAYONOP3+zl1qobjx4s4\nfryIgoITHD58FIulG7VaicfjJjU1mRkzJrN48dVMmDAeuVxK5ZSQkJCQ+H4kYSQhISEh8b+Oz+ej\nrKziHDmkVqsZMWIY2dnDGDFiONnZw0hJGYhcLkcQBI4fL+wXRIcP5zNmzChmz57JtGlT0Wr1lJVV\n9Quh0tIKKipOERER1i+Ehgz5hyCKiOirW+TxeNi8eTMffPABX355EJNpFlZrOE6niMmkxWQy0N7u\nJDhYwGLpRBTt+P1dyGRWFAoPZnMCHk8C3d0GVCqBIUNkpKW5qKsr4cSJcvT6WLq7tQiCnqAgmDlz\nLPX1UVgsVjo6qrHbswEzCoWfhQuD2bSpE5fLRGKigo8/zmLs2POLm8pKF3ffXUtRkYNnn02kvt7P\nE0+0ctVVoZSU+HG5RF5/PZqRIwPrOGazCcye3cqYMWrWrDEHPFkXRZFbbumhuVng889DApqsi6LI\ntdc6MBplvP227qKK9vp8IpGRboqLNcTESOlo/w6OHBFYssRLaenFCT1BELniCjsJCXLWrQss6qy3\nV2DSJAu/+IWOu+8OvCufyyVw2WVtJCUpefPNsHOig86HKIps2NDLXXe1MXWqDofDQ2GhkzVr4uju\n9nD//XXMmBHMqlWJxMWdP4qtvNzONdccpbDQg0xmQRSrgCGAGugC8lAqzQiCAZ2uFq/XhlLpJyjI\nyy9/OZ1Jk9LJzy9h06ZiiovB6YwAVISGdpCToyQ8PIrGRpH8/Dbi44PR6wXKyqxYrQYUCgGZTEQu\nVzBgQAhLl47h+uuziY8/Ow3NarVSWFjM/v2H2bp1J4WFxbS3dyKTQUxMFCNHDufSSy9h1qzp/ddb\nCQkJCQkJkISRhISEhMS/mTPFqM9IoWPHTlBcfJK4uJjTUmhovxyKjo7qf58oilRWVpGbm8euXbvZ\nunUHJpOJESNGEBMTD8ipqqqltLSCpqZWkpMTzxJC6elpDBqUgsFw7qTT7/eTm5vLBx98wMcf70St\nnoLdHoXLJRIWpkOnU9Hc7EYQPAiCE+hELu8mKkpBXFwEghBEXZ0fiyUIQTAgl7eh15eRkAAajRar\n1Ut9vQe/PxiZTMm4cUk8++xS/vznU6xffxKPpx5RzARikMtFFi4MobS0l7IyJVqtn7VrB7F06cDz\n7k+r1ccTTzTyzjvt3HNPDDk5Ju68swmTSU56uoGNG208+mgYt90WGnBdn9paHzfc0E56uoo33jh/\nx7Xv4/nn7fz1r0727DFjNAY20XzySRdffuklN9fwg3Vnvo933vGxbp2fI0ekFJt/F4Igkprq4Ykn\nlFx//YWnpQH09IiMG9fL3XdruPnmwI5Vfb2f8eM7eeUVEwsXBiY8Aex2gTlzWklLU7F2rRmDIbDz\n0Wr189BD7WzY0MuSJUY+/7yLzEwNTz0Vw/vvt/Paa20sWxbNH/4Qi053/m1u3drGz39eRHu7gFrd\nicHQSmfnQPoK1rcAx4FoVCoroliJTqdHEGQolXZiYjRcdlkO48cPZejQVD76qIC33ipkGwO8AAAg\nAElEQVSmocGPUmkjJKQVj6cct9tDcHAqDkcwoqjEYNBgsSjweGSo1SI+nwyFQkFKipmlS8ewZMkI\noqLOHyHl9/vJy9vLxx9/xu7d+6ioOIUgiICMgQMTmTBhLGPGjCQrayjDhmVItZAkJCQk/o8iCSMJ\nCQkJiX8Z7e0d/WLoTPRQbW096emDGDFieH/00PDhmRiNZ09kBEGgqKiYL7/cxI4du8nPL0QUZURE\nRKJUqujstOJ2e86SQmdeJycnoVL987QZURQ5fPgw69ev5733vsXvH4PTGYvbDUFBIAgenE4VfZEB\nDlSqDiIi3ERGQne3j+ZmL263EaXSiFIZjt+vJSHBil5fR01NHT6fGoUiGKdTgSiqiYw0sGzZpdx1\n1+WsXLmL554rxOvtQq1OxOtNQCaDnBw9iYk6PvzQikwmctNN4axbl41afe7k3O8Xeeeddh5+uJ55\n80K4++4Y1qzp5KuvrPziF+Fs3GhnxAgta9ZEEhcXWAqRIIi88kovjz3Wzd13m1ixIviCikd/8YWL\n227r4cCBMBISAhMKX33l5be/dXDokJHY2IuLZNixw8/ixV527lSTmSlFQ/w7KSoSmDHDw4YNaqZO\nvbh9XV7uZ/JkG599FsSECYGlDx4+7GXePAtbtpgZMSLwlLieHoFlyyzs2OHktdfCmDs3sMgmgCNH\nnNxySwsGg5zsbCXvv2/hD3+I5MorTTz0UD2HDtl49tlErr32+6Xq88+Xc//91fh8cjIzvXi9dsrK\n9IAI1AD1QBhQgkbThigGAWri44MJChJobKxHp1MwfvxQMjIGUVysYMuWVpRKHy5XK1lZJlJS9Ljd\n3RQXt1JT48XlMqBQqPD7TUAPKpUcn0+NXK4kNTWMm28ew003jcZs/v598Y/r7zd8+eUmCgpOYDSa\nUKs1WCxWoqIiyMoaSlbWUIYP7+vYlpw8AIXi4kSihISEhMR/Bv8VwujRRx9l2rRpTJs27f/3cCQk\nJCT+TyCKItXVtefIIbvdTnb2d1PKhpKePrhf5oiiSHt7J9XVdVRWVnPgwGGOHOnrcNbZ2Y0oglar\nITY2mszMwWRmDmbgwEQGDkwkPT2N2NjoC05fKikpYf369fz5z5vp6krH643G71cAztOLnr5ORy6U\nylb8/jLi4kwEBcXR06Oms9NLTIwOMNDSosXjcWEwNBIa6sRq9WO3i6jVBkRRxpgxyVx77QSuumoc\n4eEG7rtvA2vXVuDxKAgJiaCnJx6ZTEZCgoxf/CKR1asbcTpFhg2Dv/89h6Sk80cD7N7dw5131hAU\npODFFxM5ccLD/fc3c9llJqxWOfn5btati2LePEPA+6WszMvSpR0AvPVWGEOGXFjh6GPHvMyebeGb\nb8yMGRPYhP7kST9Tptj4+9+DGD/+4uoOnREYH32kYvp0abL6v8GOHX6uu65P0GVkXJw0+uYbL7/+\ndZ8ojIsLbBuffOJi2bI+IRkXd2HHeutWJ7fc0smkSRpefNFMWFhg7/f7Rdat62Llyk4WLzZSVWWn\npsbDunXxKBQiy5bVYDAoWLMmiVGjzv97czh83HjjETZutCKTyfjFL8wcOmShpMQH+IEywHH6Xx8G\nulAoTAiCBrlcS3CwjsGDI4iM1NLYWE9xcQ2RkZnYbHH4fHIGDFDQ3NxAcLCGefOGM2ZMEhUVTXzz\nTTHHjlkRRQ1+vxJoPf0ZIchkCiIj1VxxRSorVswiOTn2n+4Hj8fDgQOH2LZtB1u3bqewsJiUlBQi\nIiLx+QTq6hpobW1n0KAUMjIGk5k5hIyMIWRmDiE5eQBKpVRXTEJCQuI/mV27drFr1y4ef/zx/3xh\n9FMYh4SEhMR/K16vl5KSkxQUFPXLob6nz4b+VLIz66SkBLq7rVRX11FTU091df3pdV3/IpfLUKkU\n2O02goMNZGQMZsKEsVx66SzGjh2JTqf70WMuLCzh5ZffYsOGfHp7ByCK4YCKvkmaDdACZmQyiIvz\ncuml0eh0Go4da6GgoAXoSwXp7bWi16dht0eh09nxemsxGER0OiMdHS7S0qK44ooxzJ8/ktGjk/H7\nfXzwQR7vvbebnTt78PtjiYmJoLMzCr8fDAYfy5en8Ze/tHHqlAeDoZe//nUkV16ZdN7vUVPj4p57\n6vojG4YM0XPbbY14vQIzZ4bw1ls93HxzMA8/HI5eH9gk3OsVWb3aygsv9PDYYyHceqsxoHov36Wx\nsS9l6MUXTVx9dWApQ93dAuPG2bj3Xg033XRxaWSNjSITJrh5+mnVRadISVwcf/ubn0ce8bFvn/qi\na0atWuXi00+97N5tQKsNbBurVtn4+GMXeXlmgoIuTFbZ7QIPPdTNhx/aWbPGzLXX6gMWzo2NXpYt\na+PYMRc//7mRd95pZ9IkA888E8Pmzd08/HA9l14awlNPJRAdfX7ZWlraxYIFB6iqUhIUBHffncBb\nb9XS1CQgk/mAUgQBZLJ2QkLqUKl6sVi68fnU9BXP1gIqzGYVw4fHMnx4HMXFFvbvt+N0moiOdpOU\npMRqdVFf38306elcckkmISEGtm2r4PPPy7DZ5MjlXny+OlQqDV6vGVAgl9uIj3cyY4aZrKxB/VGb\nCQlx591HVquV3Nw8tm3bwbZtO2ltbWPcuLGkpqYQEhKCw+GmrKyCkpIymppaSEtL7pdIZ4RSSsrA\nH4wElZCQkJD4afFfEWH0UxiHhISExH8Dvb29HD9edFYh6pMnKxgwILE/nWzw4DSCg4Pp7u7pl0Hf\nlUMAAwcmkpgYh0ajxGbrpbGxgcrKCgYNSmH69MlMmTKJyZMnEh4e/qPH3NZm4euvd/PFF7nk5RVg\nsSiBBCCUPknkRKt1oVDocbl0yGQasrPNjBiho7KymuPHm+nq8iOX24mN1RAXZ8Ju11FVpcHh0BMe\n7iAmRqCzswePx8+8ednMnZvF7NnDCQnRs21bAe+8s528vBKamnpRKOKQyRKJiorEao3E4QC12sMt\ntyRSUuJn+/ZuwMpvfxvDc8+NQa8/90m8zebn6acb+2un3HJLFM8808bf/tbFLbeEs3WrC4VCxuuv\nRzN0aODy5dgxN0uXdhIZKef118NJSrrwKAC7XWDKFAtXX63l/vsDi2jy+0UWLLCTnCxn7drAU4S+\nS2+vyOTJHn72MwX33y9FL/z/4I9/9PH5535yc9UYDBd+7yiKItdd50CrhXfeCUzeiKLI0qU9dHUJ\nfPJJyAXLTYADB1zcfHMnKSlKXnkljLi4wM+fb76xcfvtrYwapSE6Gj78sIuHH47mhhtCWLWqqb+W\n2LJlMWg05wotURR5770qfvObQlwuE2lpGm64IYLnn6/CZpOj1Qoolafo7XUBzUADer2P2NggwsLk\nNDRYaGnx4PdrAQ0goNP5SUgIR61OpKJCicHgxG4vJThYRVCQmbY2L1FRJhYsGMmQIXHs2dPA119X\nYrH40emceDyVGAxh2O1mfD4ZJpOI2WzB6TyK3W5l8OCUs2rBDRmSSmrq2bKnqamJvXv3s2fPPvLy\n9lFeXsGoUSOYPHkio0ePIjTUTH19A8XFJykpKaOkpIyGhiZSUweeJZEyMgaTlpYiiSQJCQmJnyiS\nMJKQkJD4P0pzc8t3Usr6ooeamlpITx9MSsoAIiIi0el0eL0+Ghqa+6WQy+Vi4MBEBgxI+M46gYiI\nMFpbWzh69Ci7d++hoKCQYcMymTq1TxBNnJhz0YVTfT4fNTUNnDhRTm5uPocPl1JW1kBXlwNBADAB\n8YAZUGIwyEhMNNDRYcfhkOPxqAgKEtFq22lvb0IUDajVSuLj9URH6/D73RQX16JSJeDxxCEIciIi\n3LS11TJiRCKXXtoniYYOjefIkQr++tcdbN1aSE1N++kUsygiIjKoqFASExNPU5OKnh4RtdrH5ZeH\nodcH8+GHbfh83QwaBJ99Np0hQ0LO+Z6CIPLeex088EA906aZePrpeA4ccHHXXY1Mm2bAZFKzcaON\np56K4KabggOePLtcAitXWnn77V6ee87MkiVBF9WZTBBErrqqm+BgGe+8ExzwNh54wMn+/X62bAlC\npbrwz/V6RS67zMuAATJee015UWOX+PGIosjNN/toaRH54gsVSuWFHwe7XWTixF5+9SsNd94ZmOz0\neERmz7YwdqyaZ589f9pmINt4+mkrf/pTD08+GcrNNxsC/v04HAJPPNHJm292c+utweTlWenuFnj1\n1XjCwuT84Q91FBU5WL06iSuuCD3v+dnT4+H22w/w/vsdQDAzZ4YyZIiS11+vw+tVoNfDoEFw8mQV\nRmMXvb1lOJ02QESh8JCYaCQjI4ra2h5qanqw2eSAEvABRmSyeLRaOampTkJCejl1ykJbmxeNJhSv\nV052dhyTJmVSVeVkx456ens96HQ2PJ4yjMY4nM4w3G5ITDQyZUo0o0eraGioobS0gtLSChoamhk4\nMOEsiTRgQAJJSfHExkbjcDg4cODQaYG0l8OH80lNTWHy5AlMmtS3mM1mysoqKSk5eZZIqqtrIDl5\nwFkSKSNjMIMGpaJWX1iqrISEhITEvxZJGElISEj8l+Pz+Sgvr+T48SKOHy/i6NFCjh4txOPxERcX\ni8lkQqFQYLc7aW3toLu7h6SkeAYOTPgfUqhvHRHRV/DVYrGwZ88+du/eQ25uHqWlZYwePZIpUyYx\ndepkxo8fS1DQD7fFFkWRri4r9fVN1Nc3U1/fTE1NAydP1lBV1URTUwfd3S7kcjWCIEMul+H3+1Eo\nQvH7o5DJIgAlZrMWgwFaWjpQq7W43Uo8Hjk6XQ86nZ/eXg8xMUFERGiwWjtoamph9OhBDB6cRkmJ\njPx8GzKZE72+l4ULBzFvXjZTp6ZTXd3Mxo37+OqrI5SXNyEIMsLDjUyZksHChZMoLPTz2mvlGI0x\ntLbKkMnkqNU+srJ0DB8ey/vvt+N2d6NQ9PLyy6O5+eZB551Q7t/fy7JlNQC89NIAwsLU3H57A01N\nXq6/PozXXrMydaqe1asjiYwMPEJi714XS5d2MGyYmj/9KYyoqItP5br33l4OHPCwdasZtTqwe4eP\nP/awYoWTw4eNRERceP2bf4WkkPjX8a+QdzU1fnJybLz3np6ZMwOLLOnsFMjJ6WTFiiBuvvniotQA\nios9LF3agVYr4803w0lLCzyypbjYzW9/24LbLXLFFXr+9Kc25s83sWpVLEeP2rjrrloiI1WsWZPE\n8OHnv/YVFHRy1VW7qKmRo1KFcM01kXi9Nj79tA2/X4VMJhAXJ6Orq4m5cyNJTXWzY8d+CgvrcDq9\nqNUyFAo3gtBNenocLpee5mYPVqtAXxpbBBCESlWL33+CmJggDAYzVquKjg4Bv1+HyaQmNTUOt9tI\nRYUDv9+NStWL11tBUFA8Hk8YTqdIQoKJa64ZxvLlUwgL01BefqpfIJWVVVFb20BdXSNtbR3ExESS\nmBhHYmJcv0Tyet00NTVQWlrKgQOHMBoNTJ48sV8gDRkyGLlcjsvlory88iyJVFx8ktraegYMSDxH\nJA0enIZGI3VHlJCQkPjfQBJGEhISEv9FdHdbOXDgMLm5+8nPP05ZWSVNTa1otTrUajVerw+n001M\nTCRpacmnJVD8WVIoOjoSufzciX1rayu7d+85veylurqGnJxxTJkyiSlTJjJ27Jjz3sQ7HE7q65uo\nq/uHEDrz55qaJurr2wEler0BUVTgdvtxuXwoFHLk8r4aSuHhwcTGhtPd7aOuToMoRgFKNBqQyVw4\nnS7kchd6vRmXy4TRKOL1WpHJnISEyLFY2ggP1zBxYgbjx2cQGRnOnj1NbNx4ipYWkbg4GYsXD+KG\nG0bj9brYsuUYn39+kMLCWmQyBUqlgrFj01i8eDJXX52DzQarVh3h3XcbUCjCcDjk6PUyBMHFggVR\nhIeH8tFHHYCDzs42rrgihnffnYzJdO7T8oYGN/feW0dubi9PP53AokVmnn22jXXrOrj11nAKC/2c\nPOnh1VejmDHjhwXcGXp7BR54oItPP3Wwdq2ZRYsCf+/5ePttB888Y2f//jDCwgITP8eP+5k1y8bW\nrUFkZ19cGtmPTYOS+NfT0yMyZYqHxYsV3HffxR3XnTu9XHedg/37DQwcGJjELC/3MWWKhfXrg5kx\n4+KFgd8vsnZtD08+aeWee4JZvtwUsIgUBJF337Vy//3tXHWVEVH08umnVp58MoZf/CKUt95q47HH\nGli0yMwf/5hARMS5QkoQRP70pxJWrDiGIJjQaEK47rpIgoN9vPtuDVarAr8fdDoB6GLyZCOPPjqW\n6Gg5r766ia+/PkJZWTN+v5+QEC2hoQo8HgttbV0YjbHYbEbc7gggBOhEqawjPNyFXi/DZrPS2elD\nrY7C4wnC71egVutQqyNwuVSo1W683l4EoY6goCi83jBcLpHo6CCuvDKTZcsmk5YWcdb38Xg8NDa2\nnBZIfRLpjEw6s9ZqtURHh6NWq3C7nbS1teJ2uxgxYhjTpk1k7txZjBkz+qyIIrfbTUVF1Tkiqbq6\nlsTE+LMkUmbmEAYPTkOrDaymmoSEhIREYEjCSEJCQuI/iL5onG6qq+s5dOgohw8fo6SknNraBiyW\nbjweH3K5DJPJQExMFGlpyWRnZzJoUApJSfH9T34DaYVcX19/OnqoTxK1trYxadIEpk6dxJQpkxgx\nIhuAxsbW/uigPin0DzFUV9eE3e4kKioKkykElUqD0+mnu9tBV5cdv19Ao1Hi9XqRyyEhIZL09IGM\nGZPOgAHRHDpUypYtJVRUgCCEAwpkMh+i6Eat9pOaasRgiKCszI3T6cXns6LR2PD5uhg6NJqZM4cy\nceIwMjIGUlTUyNdfH+Pzzyuw202oVFoWLRrIVVclU1paxZdfHuLIkVMolSo8Hj+DB8exaNF4rroq\nh2HDkpDJZJSWWnjwwYN89VUPfr8BUGAyiWi1Xq68Mom2NgXbt3eTkCBSWlpHRISCTz6ZTk5O1Dn7\n1+Hw89xzzbz8cgu33hrFfffFkpdn5447GsjK0jJ0qIF166zccUco995rRqsNPDrn22+d3HJLBzNm\n6Hj++VBCQ39cgeidO90sXmwlL8/MoEGBCYKODoExY2ysWqXlZz+7uLSSv/zFz2OP+di/X010tCSL\nfko0Nork5LhZteriC5C//LKbt992s2+fkaCgwI7vrl1ufvYzK7m5ZoYM+XG1rKqrvfzmN51YLAJv\nvx1GdnbgEqqjw8c997SzbZudO+8MYePGTmQyGa++Gk9ioprHH29g/foOHnggjt/9Lgq1+tzfr8Xi\nZsmS3Wze3ILZbEYQTGRlGcnJ0bFjRyP5+Y7T3c78qNVOMjNh1aqxzJyZAEBubhFvvbWVnTtP0Nzc\njVIpIzHRTGqqGaXSTUFBE01NoYhiPOBBLm9CEJqQyZxERhqIjzcTFKShttZOU5MXr9dEX9dIE3I5\naDRO3G4X0IFOF4rfH4bHA6GhGhYsGMKSJaOYMGEgGs0/Pw6iKNLR0UldXeNZEqmsrLL/oYbL5QZE\ngoMNJCbGMWxYBuPHjyE9PY3ExDgSEmL7ZZDH46GiouosiVRScpKqqhri42P/h0hKZ/DgVPT6i49K\nk5CQkPi/jCSMJCQkJH5CiKJIa2s7tbUN1NY2UFNTT2VlNcXFZdTU1NPe3okgCIiigFqtIjo6kpSU\nJLKyMpkwYSwTJowhOjrygtNERFGkqupUf3rZ7t17sNkcjBs3hsGD04mNjUcmU9LY2PIdMdRMe7uF\n6OgI4uOjiYyMQKsNQiZT0tPjorGxk6amTiyWHrRaNSDicrkICTGQkhJHdnYaI0YMJjLSjEolp73d\nwrff5rN3by0tLXL8/jBADqhQKATAT0KChjlzhtDQYGffvla6ugDs6HRWRowIY+HCbKZPz2bYsIGU\nljaxefNxNm06ztGjdcTGptLeriY6WseoUVoaGys4eLAMjUaDxyNgMumZP38UV1wxjmnThmIw/KNb\n28GDLdx++yGOHfMjCFp0OhkymZeRI4MYNiyavXvt2Gx+wsJcHDtWh1IJy5dnsnLlyHPqpIiiyEcf\ndbJiRR3jxxt49tlEFAo5d93VSEGBkzvuiOTdd3sxmxW8+mo0gwYFLlssFj/Ll1vIzXXzxhthXHLJ\nj+84V17uY/JkCx9+GMz06YFNqL1ekTlz7Iwdq2DVqosbw7Ztfm64wcuuXWrS0y+ulbvEv5cTJwRm\nzvSwYYOaqVMvLt3wppuc2O0iH30UeAezd95x8OSTdg4cCCM8/MedG6Io8pe/2Fixootf/9rIww8H\nX5Cczc11cOutLSQnq5g0ScOLL7axeHEIK1fG0NTkYfnyGk6dcvPCC0nMmxdy3u+4b18rd9xxgGPH\nujCbQwgPj8Rmg6uvDsNisbJhQwuiqMbrFZHLPcTEuHnuuWyuuSat//rS2+vk44/3sH59LocOVeJw\neNBqFYwalcy4cckUF9vJy+vFbpchiu3I5S0olS68XifgQ6ORkZoaR0REJO3tPiorfbhcevoEUi/Q\nQ9/12ItSqUah6CuYLZOJDB4cxsKFGVx2WSajRyegUl24QHQ6nZSWlvPttzvYu/cgRUWlNDa2oNHo\nUCiUOBwuQkND+usmnUl9++7aaDRQVVX9HZFUSklJGRUVp4iLi+mXSGeKbqenDwoobVpCQkLi/zKS\nMJKQkJD4X8Tn89HU1EJNTX2/FPqHHOp76qrRqDAa+25iHQ47NpuNhIRYhg1LZ9y40UyYMIbhwzMJ\nDT23aHKgCILAwYNH+OqrLezZc4Djx4vx+yE8PBKVSovL5aGtzYLJZCQhIYbExFgSEmKIjo5AqdTi\n9Yp0d9uprGyktLSG2tpWRFHsjxby+Xyno4UGkJ2dRkREKGq1ApfLRX19C1VV9VRW1nHqVCcQhiCE\n4PEEA0rkchWiqEChEDCZlGRnR2A2yykra6GszIXHY0Ch8JOcrOLGG4dz441TiY0Np7Ozl61bT7B5\n83G+/bYQk0nHqFHpVFcLFBR0ExrqwWI5SXCwHJlMTm+viylTMrn88jHMmZNNSkrMWftIFEU+++wU\nv/99EU1NCkBBaKgcj8fJ5ZfHIpcHsWlTF2PGGOjqaufIkUZCQlSsWDGMu+8eilJ57qTzyBEby5bV\n4nD4WbNmADk5Rl56qZ1Vq1q5+eYwurtlfPGFjeeei+SGG0wXJP42brTz+99buOYaPU8+GYrB8OMl\ny5m6MffdF8RNNwX+hP7OOx1UVAh8+WUQCsWF32MUFgrMmuVh40Y1U6ZIsuinzPbtfq6/3svOnWoy\nMi78WLlcIlOn2li4UMUDDwSeTnTffb3s29dXT0uj+fHRZy0tPu64w8KJEx7eeiucSZMCH4vHI7J6\ndScvvNDFbbeF0NjoYPNmG6tXx7J4cQibNnWzfHktAwZoePHFAaSnn1+ilpV1c/vtB9ixowWTSUdG\nRl9nxVmzQoiPF9mwoZbubjkOhwzwYzS6ePDBVJYvH37W9UYURcrLm3jvvV189tkBysqa6Ive0TJ8\neCZOZzgFBVZCQ110d9fi99vx+XqRy70Igo++y44Xo9FAdPRALBYT7e1yZDIFKpUVj6cTUVQDfQ8C\nQAvokMtFZDJISQnikkuSufzy4UyfnoFafXEd0DweD8eOFZCXt/f0sh+NRkdaWhoREVFoNFp6ex39\nkUter/esOkpn1nFx0aejnDrOikwqK6skKirivCLJZDJd1JglJCQk/tuQhJGEhITEvxC3290fcv/d\nKKEzr5ub24iICCMhIZaQEOPpgp9OOjo6qa2tRaNRk509jKysTLKyhpKdPYxBg1IvqOWw3e6gubmN\n5uY2mpr61nV1jZSUlFFVVUtrawc2mxOQERwcREJCzOnQ/cEkJsYSHx+NWq3FZnNTXd1MUdEpCgrK\nqaxswGLpQa/XIJP11SYyGLSkpMSRkTGAmJhw1GolPp+Hjo4uTp1qoKqqjubmduLiokhJSSAiIh6r\nVUF5eTe1tT68XhkKhRJBUAMCer2M8HAZYKOjw4LDIUcmMyOKQSgUGsaPj+Cppy5l8uRk/H6B/PxT\nbNpUwObNhRQXNzBlyhCGDImiutpJbm4HFouAwdCD2eygo8NCcnIU8+ePZs6cEUyYMPi8ExlBEFi5\nspDVq+uw25WoVH1tp0NCRKZOjaeiQqCiwsmCBcEcOVLNsWMdJCToeOqpUdxwQ+p5j0lzs4cHHqhn\n8+ZunngigRtvjGDfPju33tpAbKyS+fNDefbZLubPD2LVqkjM5sCf0Dc3+7j9dgslJV7efjuMCRP+\nNTU8znSmGjdOzTPPBN6Z6p133Dz9tJtDhwyEhFy4QGhoEJkwwc2zz6pYvPjHpdJJ/O/w17/6eeQR\nL/v3a4iJufB7yqYmgbFje3n9dT3z5wd2rRMEkWuu6cZgkPHuu4F37PshPvvMzu23W7jiCj1PPx2K\nyRT4OXzqlIff/a6VhgYft98ezKuvtmE2K1m3Lp6UFDWvvNLKk082ct114Tz2WDxm8/lTudrbnfz+\n9wfYuLEOjUZBTk4ytbUK9Ho506YZKCxs5cCBXnw+FT6fgELh4frrw1m7dux566Q5nW5yc4t5//1c\ntm49TleXDUFQoNcn4PWGk5RkYORIAxUV5Zw4UY/ZrMbn68ViacPvF5HJ5CiVMrxeEypVEl5vMHK5\nj+hoOQaDm85OC11dPvz+IEABaE6vfYAfpdJKZKSP9HQTWVkxJCbGER8fTUJCDPHxMURFhQeUJi2K\nImVl5eTl7WXPnn3s2bOP7m4rEyfmMHnyBEaMyCYsLILm5rb+ekq1tY39dZVaWtoJDzcTH9/3uXFx\n0eh0Ovx+Lzabjba2dmpr6ygvr8JsDukXSN8VSiEhF9fpU0JCQuI/FUkYSUhISFwAfr+fhoYmTp2q\no6qqhqqqGqqr/yGEOju7iIuL7q8XNGBAAqGhwbjdbiwWC7W1dRQVlVBZWU1KygCysob2i6GsrKFE\nRUV+72fbbPbTEqiV5ub20+t/SKEzf+/xeIiKCkOrVSMIPnp6urFYOoiLiyYrK8Ic/wUAACAASURB\nVJOJE8cyf/5sEhMTKS+vp6yslpMnazl+vILi4mrq61tRKORoNCo8Hg9ut5vY2DCSk2OJj49Ar9fi\n83np6emlrq6Zqqo6XC4PycnxpKQkkJKS2L/W60M4ebKbTz45RF5eHQ6HQN81WwPIkcu9iGIver2X\n0FAdXq8ci8VHcHAYMpkBu13kkksGcuONI5k/Pw2LpZctW06waVMBW7YUEhUVTFZWAjqdgurqZvbu\n7UQQYlGpZGi1FmQyC3PnZjNnTjazZ2cTHR36vfu3vd3F0qVH+PrrLgRBidEIougmJyeU6Ggz27f3\nkpqqY+JELZ9+WkJ5eQ+ZmcGsXZvDtGkx592myyXw4ovNPP98MzfdFMFDD8XhcomsWNHE9u027rsv\niq++ctLQ4OO116KYODHwKB5RFHn3XRv33tvFb35j5KGHLiyV5oe2fdNNPVitAhs3hgTcfvzgQR+X\nX24nN9dAevqFy56eHpHJkz3ccIOCFSt+XH0aif9dfmxx8v37fSxcaCcvz8DgwYGdOw6HyNSpnVx5\npZYHHjBc8Gd+H11dfu65p4utW528+moY8+Zd2O9y48Zeli1rY+7cIFJT5bzwQhu//nUYDz4YhcMh\n8Mgj9XzyiYVHH43nlluivrfgtsvl4777jvDGG+X4fCIzZw5ELg/m4MFeFiww4/fb+fTTRkCD3Q6i\n6GPcOB1vvz2GzMzvFxu1tW18881RPvoojwMHKpHJwnC5wlCr1UyaFMz48ZE0N3ezdesJQCQlJRS3\nu4eGhnqam7vw++XI5VGIYiSiGAK4ASdGo5uwMCUej5vOTi9utxFQAWpkMgFR9AECWq0Nvd6JSmXF\n5WrHbu8hJsbcL5L6ZFJsQFKpqampXx7t2bOf8vIKRo0a0d+NLSdnHMHBffvC5/PR0tJGQ0Pz6aXp\nnNdNTa2EhJiIjAwjKEiPQiHD7XbT3W2lqakZozGIoUOHMGxYxlkiKSzMHPA5IiEhIfGfhCSMJCQk\nJP4HDoeD6ur6fiFUVVXLqVO1VFXVUlvbQFhYKCkpSaSkDCAlJYmBAxNJSoonPj6W3t4eiopKKSg4\nwfHjxRw/XoTL5TpHDGVkDO4v4NnbazuP+DlXBPl8PmJjo4iJiTi9jiQ2NpKIiDAcDhuNjXWcPHmS\nI0eO4HS6yMkZx+jRo0hMTEOnM1FX10ZpaS0lJaeoqGigt9dOUJAOmUzEbneg0SiJi4sgLi4MkykI\nQfDR22unubmVmpomjMag0yLobCmUkpJAZGQYMpmMhoYuNmzI58svj3PwYAMOhwAI9KUuKJHJBEJC\nIDpag9Eop67OisfjZ/jwgajVwdTWOujocHHFFUNYtCidjIwQiorq2b+/gs2bj1NV1cqIEYmEhmrp\n7LRw9Gg5kZExuN2RtLSogR4yMlRce+0w5s4dyciRyeft+HYGURTZubOdW289Tnm5B5lMhtksw+dz\nMXduPD09ag4c6OVnP4skOtrDG28U0dzsZOLECF57bQKZmeefJPSls3Xxhz/UMny4ntWrk0hO1vDm\nm508/HAL118fQnCwhnXrurnnHjPLl5tRqQL/v7impq9Yb2fnhRfrDYRVq2xs2OBi924zQUGBSajm\n5r4okXXr9CxYcOEpKF6vyLx5XtLSZKxbd3Ht2iX+/yGKIjff7KOlReSLL1QBdx37Lm+/7ea559wc\nPGgkODiw9zc3+xk3rpPVq41ce+2Pr9n1XbZvd/Kb33SSk6NhzRoz4eGBS1Cr1c/DD3fw8cc9PPBA\nGPv3W9m/38FLL8WzYIGJEycc3HVXLa2tXl58MYlLLvn+FGNBEHjuuRM888wJenp8zJgRz6BB8Xz8\ncSdZWX1SasuWBjo6RGw2OYIgEB0t49lnM7n++sR/mhbq9frYv7+ML788zAcfFNDcrEUUDcjlbQwf\nrmbSpDREUUlxcROHD59i7NgURo9OwunspqmpibKyJmpqfNhsJiCMPnlkA1yAF/CgUMgQBC2iaAK0\nyP4fe+8dHUd57/+/tvddaVe7q131YsmSZWMbbFwozqUluYEUEhISML2ThOYANxcCCQkYTAkJBBJK\nsAMJJZQvCQYCwRDAGHdblizJsrq0Rdt7mZnfHysLG0yQHPjdlH2fM+eZOcfeMprdfeb1vD/vj0yB\nRiMhCCIyWR61OkEq5aesDFwuA0ajGoUC8vk00WgEr9dHKBTB5bJ/BCQVxvJJqJRIJHjvvfcnXUgb\nN26msbGBo45azNKli1mw4AgaGuo/9vtFFEV8vvEPwaQPgFJ//xCjo16USgVarQZJEkgkkqjVSior\n3TQ11XPYYbNYtOgIFiyYh91eVvwuK6qoov6lVQRGRRVV1H+cJEnC7w9MQKACEOrt7Z+EQsFgmNra\nygkgVEt9ffUBcEin0+Hz+Wlv72Tnzg527CiAoc7Obtzu8kk41NTUgMPhRJJkeDwf7wgSRXES/hTG\nD0MhJ263A7PZhEwmw+/3s379Bt599z3Wr9/Apk3bcLtrqatrxmKxk0pJDA8HGBz0EI0mMRi0yOUy\nstkM2WwWq9WM01lCSYkBKMAir9eP3x+ksrL8oFCorq5yMlcJIBiM0tU1xKZNvbz+ejfbt3sZHk6T\nz8soACIVBUCkwG5XUV1tRiZL09ExQn29nUWL6qmuduHz5Vm3bgi/P8lJJ9UxY4aRTCbCtm39bN7c\nRzKZoa6uDLNZQyIRo7NzgLo6J9XV5Xi9sGtXjmxWR1ubjksumcfppy/EYvnkENNEIs+dd+5h1ao+\nYjFQqUQMBoHKSjVz5rjYvDmNUinj/PNdeL1+7r+/g0Qiz5e+5Ob++5fgdh/czSAIEi+8EOKOO0aJ\nxQo5Rccfb2HLliSXXDKMUinjggvKuOOOELW1Kn75Syd1dVMPtRYEifvui/HjH4dZscLC1VdPvR34\nVPXHP6a58soo771nw+2e2g1yJiOxbFmcL35RxQ03TL8kruBoyjM+LvHcc4cGG4r6v1cuJ/GlL+Wo\nr5dx//2HBv0uvzzJwIDICy8Ypuxs2749xwknhHjxxRKOPPLQOvJ9nBIJkRtvDPP443HuvtvKt75l\nmNb72rQpxUUXeTCbFZx1lpHbbvMyY4aGe++toLZWzQsvFMByVZWGFStcfP7zf9/R99hj3fzwh1sY\nHU2zZImdL35xJs8/H8bvz3H88SYGBvy8804YQVCRychQqyXOPdfNTTe14HR+8mfT6w3z+OPv8eCD\n2+npyaFSJdDrA2Qy4yxd2kJVlYtYLMfWrQP4fFHmzavhiCPqOeKIeqqrbfz1rz0899xudu1KABkE\nIYggxCYeXQVkARmFMG0joEEmE1GrC98Der2ChgYjZnOeVMrPwMAQkUichoYKKivtlJWZMBjUyOUS\n2WwKv3+c4WEPQ0OjhELRj0Cl8nI7uVya0dFhenq6aW/fSSKRZMGCww/Y3G73lP+mkiQRCAQnYdLQ\n0Ci7d/fQ2dnDwMAQXu84sVgCURRRKGSYTEaczjJqa6toaWni8MPnMHt2K1VVbkpLDx6EXlRRRRX1\nz6IiMCqqqKL+LZXP5xkcHDmoS2jv3gGUSuUBLqH6+g/29287H4vF2LVr9yQcKmydZDI5ampqcDod\nmM0W1Got+byA3x+cBEKSJE3Cno8DQS6XfRIEHUyCILBrVwevv/4Wr7/+Lps27SIUSmOxOJAkNclk\njkwmj1arQhQFMpksWq0So1GH0ahFqZSRz+eJRmOEw1FKS01UVjqpra3YDwgVoFBVVfkBWUm5XJ69\ne0fp6hqiq2uI3bsH2bVriI6OAOm0GpnMQi4nQy4XEAQ5hRIzDQaDAqdTRyIRIZlMsmhRPUuWNLJo\nUQMajZ5XXunjqafaiUYzNDTokMsT7NnTTyqVweUqlFUlk4UcJpNJS2trDU6nFZlMTne3l507E6jV\nFeh0Wi65ZC7XXLMUo3FqDpsdOyL84Acd/OUvQURRhl4vAFmOOcaJRmPizTdjnHRSKaefXsaf/tTD\nmjV7kSSRM8+sZ9WqhZSUHPyGK5kU+O1v/dx11xh2u4oVK9x8+culxGICN9zg4emnw/zwh062bcvz\nyisJ7rnHwamnfvzf/WDq7Mxy/vkBFAp46KEympoOLUj272nTphxf/GKIV14pZd68qT2+JElccEGK\nUEji6af1U77J31833ZTjz38WWbdOPeX26kX9cyoalTjmmCynn67g2munX1aYy0mccEKco45Scsst\nU3cMvfhimosvjvLuuzZqaj797Kv3389w3nnj1NQo+dWvbFRVTf29FUBviB//OMCFF1rQakXuvdfP\nFVfYWbHCgVwOTz0V5I47RsnlJK65xsW3v12GRvPx7r6XXx7i+9/fQE9PnNZWC5dcMoeNG7O88EKA\n//ovCzpdmhdfHEIQ1CQScmQyicMPN7JyZSuf+9zUXC/hcIqf/nQdjz7aQSqVIpcbweXKkUqlyGQy\ntLXVYLfbkMuVhMNpent9RCIp5s+vZf78OgyGUvr60rz2Wj86nZxZs4yk0z727BlibCxOOi2jAI8U\nFIKz9YCSgjMpD8jQaiVqa3W0ttpoaytDkvL09o7Q3T1Ed/cgKpWSpqYqmpqqqa93Y7OZ0OtVgDDh\nFBpjaGiM4WEPo6NexsdDaLVqjEY9CgVksxkikRAqlYLa2ipaW5uYN28OS5ceSUNDLXa7dVoZgvsk\nSRLhcITt23fx3nub2bFjFz09exkeHiMQCE+4qwrv32q14HaX09hYy4wZDRPAq5CxVFHhwuEo+7tO\n2aKKKqqoz1L/FsDoRz/6EcuWLWPZsmX/1y+nqKKK+v9RsVj8AJfQ/vvDw2OUl9sPCoTq62s+0mEs\nFovz7rsb2bBhCzt2dNDd3cfg4AjxeAqj0YhKpSafF0kkUuj1OlyuAgQqL7dTXm7H7XYcUCbmcjkw\nmYzTAgLhcIytWzt56aU3eeutzfT0DBMOpwAVkiRDoWAi/0dCq1VOdMXJk0ymUanklJeXUV1dTnV1\nOW63g4oK58RYeE3l5WWo1Qeuvhc6x0QmoNDgfnBoiIEBDy6Xg7IyF/m8gZGRDMFgBqVSJJMptLlX\nKLSACrNZTjIZp7rayNFHN7J4cQNLljTS1FTO2rVdPPLIZtatGyKbzSGKUSQphs0mRyYTCIUi6HQK\nZs+uZsYMN0ajAUGQ8PtjdHYO09U1QnW1G4ulju7uPAsXurnqqoWccELdlOBEJiPw6KND3HrrHoaG\ncoCAwZBHoxE59thqhoZgdDTLRRe5OfZYA3fcsY2XXx5Fo4HvfncmN9wwf+IG5KPy+3Pcd5+HX/3K\nx+LFRlascLNkScF99MQTIVasGOVLXzIzd66RH/84wGmnmbnlljLM5qnf0OZyErffHuGee6LcfHMJ\nF19sOiQo80kaGhJYvDjA/febOeWUqbuE7rsvwwMPZFi/3nRI2TWPPprnJz8RWL9ejdNZhEX/DhoZ\nKQSX33abitNPnz688ftFFiyIsWqVjq9/feqOoXvuSfDIIynefts6rbDqqSqblVi5MsK990b58Y9L\nuOii6X0WR0ZyXHGFj61b09x4o5Vnnw3R0ZHhvvsqOeEEE5Ik8frrUe64Y5T29iTf+145F13kpKTk\n4+HUpk0+LrnkXbZsCeF267n22sOIx3U88MAoZWUqZs9W8be/DePx5EkmC90eS0pkXHVVHZdfXkdJ\nySefX1GUWLu2l1WrNrBtm4e6OhljY7uJxaKUl5eg0ShIJtOMjQVwOi1UVBQ6mCUSeYaGgqTTeWbM\nqAXM9PenMBg0fPObbZxyygySyRBr127nnXe66ewcIxqVKJQwawAdBcdqnn0ACTIoFGEsljy1tTrq\n612Ul9swmcxksx/ApL17R7DbSydhUlNTFQ0NFVRU2DGZdIhiHr8/iN8fxOsdp7u7l87Obvr6hvB4\n/MRicWQyJaIIWq2asjIrVVUunE47DocNu906MdoOOLbZSlEqPxkm+v3jdHR0sWXLdjZv3s6uXV3s\n3TtIOp2hpMSCWq1BEEQSiSSpVJrycgcVFfsgUvnkvtv9wbHBMPWsraKKKqqoT9K6detYt24dN998\n878+MPpneB1FFVXUpy9JkvB4fAcFQr29/cTjiUkQtH/ZWENDLTU1lajVaoLBMB6PH4/HP9k5bPfu\nXvbs6WN4eIzx8RCJRApBEFEqFZhMBhwOK1VVFTQ3N9DS0jgJgsrL7TidZeh0h96FKhiM0N09xMaN\nHbz77g62bt3NyIifRCI7CYNAQibbty9gMmlxOEqprt5XLlZJRYVzEgi53Y4DysUOdh79/jB9fWP0\n9Xno6xuju3t40jUkSRIzZ1bT3FxFXZ0bUdSzZ0+M998fob8/hFIpkcnkkMnySJIcMKJQSMjlOWbP\ntvP5z89k6dJGjjyynmw2z/vv7+GJJ7by5pvDeL0FsKRWJ5GkECpVitbWCubNq6Wy0oFcriAaTdHT\nM8bWrX34/VHmzKlh7tw6Zs2qIRbT8Pbbft55Z4TvfGcW3/3u4TQ326Z0rvfujXPjjd0884yXbBYg\ng0aTp7HRREODg/Xrk8yZY+SSS9wYDFluuGEL27YFMRrl3HDDYVx66Sw0moPf7Pb0pLjrrjGefDLA\nN75h46qrXDQ36xBFiRdfjHLrrV4yGYlrr3Xy4INRolGBBx8s54gjppexsmVLhnPPHcflUvLggzaq\nqz+bIOjt23OcfnqY887Tc/XVn1zSt09vvpnntNMSvPuukYaG6YOBV18VOPPMHG++qWbmzOIK+r+T\ndu4UOe64LE8/rebYY6f/t926Nc9JJyV47TUjc+ZM7dqSJIlLL42yc2ee3/3OQm3tZ/N56egouP2U\nykNz+730UpzLL/dy5JFavvAFHTfd5GHGDA3XX+/g2GMLCw3btye4884x/vznMGedVcYVV7iorv54\nJ2V3d5jLLnuXN97wYjKpueaaNpqby3noIQ9btsQ57jgzPl+Ad94ZJ59XIooaFAqJE0+0cdNNM1iw\nYGqhzbt2+bn33s08+WQnS5a4WbCgBJUqys6dA2zZ0svoaJDKShtmsw5ByOP3h/D7o1RUFBZRslkY\nHk6Ry+mRyy2oVEqOPbaSc86Zz8knt5LLCWze3MdTT73NSy9toa8vjSBoKAAkFfs6rxVCtOUoFFnk\n8iC5nB+IoFaDxWLC5bLhctmx2ayYTEYEQWJkZJyRET/Dwz6SyTQVFXYqKx37bR8cu1w2AgEv77+/\niXfe2cDGjVvo6enD5XJTWVmFzVaGTmdAFJkETz5fgFAogsVi2g8oWXE4yj722GotOSDMOxgM0dnZ\nxa5du+no6KKrq4eurj2MjHhwOh3Y7WWYTGZUKhWiWCgpLzibvWg06gOAktvt/Ahkcjim1pGuqKKK\nKmqf/i0cRv8Mr6Ooooo6NCUSSfr7h+jrG5zc9gGhvr5BDAb9h4BQLZWVLkwmI6LIJAzaB4T2H73e\ncdRqFXq9dqLTSZpoNIrBoKW2tpLm5gbmzp3FokULOPLIeej1//jqnCiK9PePsm7dZt5+e9tE1zEf\n4XCcdDq3HxQqhEHLZCJarRKHw0JbWwOLF89n9uxGqqvduN0OyspKp2RFD4fjE0BojP5+zyQYKhx7\n0enU1NW5qKsrp7a2nKamKpqbq6ipcdHTE+K553bw6qtd9PUFJ8JGc6hUedLpHDKZGUlSotdLzJtX\nzimntPL5z8/CZjPw9tu7+ctftrNhw156emJks3okyYBMlsNqzbNwoY3jjmvCbDaQTufp6/OxbVsf\n27b1o9GomDu3lrlz65g3r565c2upr3eycaOX1avbeeqpTg47zMHy5W2cemozJtMnl50JgsQzz4zw\n4x/vYffuFAoFCEIChUJgyRI3kmSgvT3J8uXlnHuuk82bvdx881Y8nhRWq4Kf/vQIzjhjxoR766N6\n990Yq1aN8vbbMS6+2Mnll5fjcKjIZkV+//swK1d6MRjkXH21g1278vzqV2FuuMHGZZeVTiuXJ5US\nufnmMI8+GmfVKitnnDG93JSpKpeTuO22BPfem2DlShPnnKOb8vMMDIgsWhRjzRo9xx8//ZKN7dtF\nTjghy7PPqjnqqCIs+nfU668LfPvbOdatU9PSMv2/8e9/n+WHP0yzcaMRm21q/18QJO68M8EddyS4\n5RYTF1449Wt6Oto/T+yaa8xcfbVlWsH1yaTILbcE+M1vCt8ROp3IqlV+SksVXHedg1NOsSCXyxga\nyvDzn3t49FE/X/hCCddc42Lu3I+HusPDMa66agPPPz+EQqHggguaOP30Zp5+OsBjj3mYN8+AxZJj\n7doBcjk5kqQDZLjdKn7wg3rOPbcavf6TQVskkuaPf+xi9ep22tvHOe20mSxf3sbMmRa2b+9ny5a9\nbN3ax5Ytvezd66W62o7DYUKhkBGNJujrGyObBZPJTiqlJxZTI0lyqqrUfO5z1Xz1q20sXFiPy1XK\n0FCAP/zhr/zxj++xY0eUVEpHITxbQibLI4r7miso0OkkSktFjMYk+XyAcDhENJognxeQy0GjUWEy\n6bFYTJSUmDCZjOj1ejQaDYIgEY0mCQQijI0FCIfjuFy2SYhUXm5FJssRjQYZGxuku7uDsbFh5s6d\nPZmFdPjh87FabYyPh/D5Avj9gYkxeNDjSCRGaanlQ0DpA+eS1VpCSYkJg0FPNBrB7x9ndHSU3t5+\nurp66O7uJZlMMWNGPbW11TgcDsxm88T7EQkEQoyOehkZGWNkxEMoFMHptE/ApPKPdS2ZTJ9e18Gi\niirqX1tFYFRUUUV9pspmswwOjhwAhPr6PgBEsViCmpoKamurcLmcWK1WjEYDarUaSYJQKILHM34A\nCIrHkzidZbhchXIwq7Uwsc5kUoTDYcbGPPT19SGTScyZM4u2thZmz26lra2FtraWyRa701EhjyCK\nxzPO4KCHrVt3s21bz0QWQ4BwOEE6nUcU930fSSgUMlQqOSoViGKadDpMba2Do48+nJNOWsYxxyyd\nctBmMpmeAEEfuIT2B0P5vDAJhPYfa2sLo8lUgGGpVJYNGwZ58sktvP56N3v3BpHLQaGQ0GrzJBJp\ncjkdoEOrhcMOc3DqqYexdGkV773XxVtvdbJz5zAjIyEyGRG5XIdGYyOX0+N0ajnuuGoWLXKSy6XY\nvr2fbdv66OwcprraPgGG6pg7t47DDqs9oMV9X1+Y3/1uF6tXt6NQyFi+vI3vfGcWNTVT+1t5PGlu\nuaWbxx4bJZkErVYgnY5jMChZvLiKnh4Bi0XFZZe5OemkEtas6WHVql1ks3ncbg0rVy7gy18+eImb\nIEj8v/8XYtWqUTyeHFdd5eLss+0YDAoSCYGHHgpy550+mps1XHGFnZ4egVWrgixapOOeexxUVk4P\npvztb2nOP3+cuXPV3HuvDafzs1kNbm/PcdZZEex2Ob/5jYWqqqk/TzIpcdRRcc44Q8VVV03fcTc0\nVChZuvNOFaedVlzt/nfW6tUCP/pRnvXr1ZSXT3++ee21KTZtEnjlFcO0oGtHR56zz45gsch46CHL\nZ5JrBIWOhRddFMDnK3QsnD9/eh0Ld+3KcOmlHnw+geuus6LTSdx+u49kUuTaa52cfnoJarWcSCTP\ngw/6+PnPx2ht1bNihYsTTrB8LAzz+VLccMNGHnusF0mSc8op1Vx33Ry2bMlw330jJBICc+dqePfd\nQbzeLEqlhnxejVIp8tWvOrjxxmZaWkxTPAdhHn+8g9Wr25EkiTPPbOOMM2ZRV1co/U4mM+zY0T8J\nkLZs2Tvxu1BGVZUNg0FDKpVmz54gAwMCklSKJKmQy+PodBkOP9zJ5z7XysKFjRx+eB1qtYzf/vZP\n/O5362lvT5LJmAE1SqUw4YjNI5OBKMqQyTJYLCIzZ1qorjagUEik00ni8TjhcJRgMEQoFCcWS5DP\niyiVckRRmAjg1mE26zEaDRgMRnQ6DXK5knQ6RyyWJBiMEQ7HKCkxotMpEIQ00WiAXC5FY2MV8+a1\nctRRCzjhhKOpq6s96LnL5/MEAqH9gFIQn2988jgYDBMORwmFohNjhHA4ilaroaTETGmpBaNRj0ql\nQBQFcrksiUSCcDiM3z+OTqelpqaChoZaWlpmMHPmDFwuJyqVCr8/OAmSPhgL+0ql8qBAaX/XktNp\nn1L5XVFFFfWvrSIwKqqoov4hCYLA6KjnIyBo3+b1Bigrs2K3l2E2m9HptCgUSkRRJJXKEInE8HrH\nCQTCmM1GHA7bZPnXPiBU2HdgtVqIxaIMDAzS0dHFzp0dtLd3Mj4epLW1eRIK7RvLy52fuLKczWbx\negN4POOMjfnxeMbp6xth165e+vrG8HhCxGIpstl95VgfPJ5SKUenU1NaaqS62onTaUavlwgEhtm8\neTMyGSxduojFi49kyZJFzJ8/D43m4DcT2WyOoSHfAc6g/cFQJJKgpsY5CYA+AEOFfavV/JH3KkkS\n3d0+nn9+J3/5Sxc7d44xPp4ERPR6JXq9SDyeIJlUAoW/S329kYULK9FqM+zePURPj5dAIIEgSJhM\naioqrJSVuUmn9ezeHaW21kRNjRpJCtPV1c/YWIjZs2smnUNz59Yxe3YNBsNHoUIkkubpp7tYs6ad\njo5xvvWtFpYvn80RR5RPyREgSRJ/+YuPG2/sYdOmGEqlHI0mTSyWpKrKRF1dOdu3pzn5ZBuXXuqm\nrAzuuquDxx7bg1wu0dxs4NZbF3L88ZUHfb5USmT1aj933jlGaamCFSvcfPWrVhQKGYFAnl/+cpz7\n7hvnmGMMfPe7dt57L8PddwdZskTH//5vGfPnTw+kRKMi118f4vnnk9x3n5WvfGXqpWHTUT4vsXJl\ngnvuSXDrrSbOO296DgxJkvj2t5MolbB6tX7a7o1IROKoo7KcdZaCa64p3mz8J+gnP8nz/PMCb76p\nnnbOlSBIfOlLCWbOVHD33dMr6cznJe64I8FddyX42c9MnH/+Z+M2kiSJNWsSrFgR5JxzjPzoRyXo\ndFN3VBWyi5L85CfjjIzkue46KxUVCu6800d3d4arr3Zw/vlWDAbFhJsxCe0A8AAAIABJREFUwKpV\no8jlMq65xsW3vmVDpTr484XDGVau3Ma993YiCHIWLizjppvmolbruf/+UdauDbJ0qZHBQS+7doVQ\nqdSAHlGUqK/X8D//08i3vlWJWv3J70eSJN5/f4w1a9p58slOWlpsLF8+m298oxmL5cDvw2w2x65d\nQ2zdupctWwrbjh0DuFwlzJjhQqXSMTiYo7c3QzwuAVE0mhSCkMRgUNPa6uboo2fyuc+1UVVl5MUX\nX+exxzbT05Mnny+U16nVAjqdklQqRz4vIUky9Ho5RqOEQpEgFvORy6WornZQXe3A5bJiNuvRapUI\nQp5IJMr4eHDCxRwgEIiQTmfR6dQolQokSSSTyZLN5tDr9RiNOvR6PQqFgmQyQyKRJpnMkMtJyGQi\nJpMGt7uMpqYa5s5toampdrIMrqLCjlY7NdgoSRLxeOIAgFQYYx86jjI25sXjGScQCBGNxkml0giC\nCEioVAr0ei0Wi5myslJcLifV1W4qK91otRpEUSSbzZBKpYnFYpPnY2zMy8iIh0AghN1umwRK++cp\n7e9g+nuNPYoqqqh/fhWBUVFFFfV3ta8FfV/fIHv3DtDZ2cPu3b309Q1NZgBptVoMBgNqdSGcOZfL\nEY+nyGazOBw2HI4ynM4yHA7bQcYPAiT3dSIRBIG9e/snO5PtG/v7B6mvr510Cu0DQ3V1NQfU5EuS\nRCQSmwRA+8ZCa3sf/f2jDAx4GR+PkskIKJUqQI4oFm5OQEIul6HRqCgpMeJ225gxo5q2tnoOO6yJ\nefOaSKcTbNy4iQ0bNvLee++zY0c7M2c2s2RJAQ4tXryImprqyUlSAawFDloy1tfnwesN4XbbDigb\n2x8MlZdbP7E0LRRK8Mwz23nllU42bx5heDhCPi+g0cgxmZRIUpZ4PEUmU+hoJpMZMBhk2O0KBCGO\n3x8glRJQKOTY7QaamspZtGgGS5a00N4e4bnndrNzZxCTSSSTGUejSXD44R+Aoblza5kxw41S+fEr\n+fm8yKuv9rF6dTtr1+7l+ONrWL68jS98oQG1emoOgHA4y5137uX++weIRCSsVgWpVJR4PMvMmXYU\nChOJhMQll7g5+2wnPT1hVq5s569/HUUmE1mwoJSf/GQBS5e6Dvr44+M57rvPy/33eznySCMrVrg4\n6qjChHd4OMtdd/n57W+DfO1rFi680MbLL6f4xS9CnHCCgf/5HxttbdNzGACsXZvk4osDnHCCjjvu\nKKW09LNxQ+zalePssyOUlsp56CEL1dXTf57bb0/z9NM53nrLiE43vflDNivxxS/maGmRce+9h9Z2\nvah/PUmSxPnn5/F6JZ5/XjUtpxBAKCSycGGcG27Qsnz51EOw96m9vXDd22yF6346brrpyOsV+N73\nAmzdmuWhh8o45pjpu+/eeqsAjrq7s1x7rY05c9Tcc4+Pt95KcNllZVx+eRk2mxJJknjllQh33DFK\nd3eaK64o54ILHJjNB4ew8XiOX/6yndtu20E+L6ey0sCNN87l6KPd/Pa3Hh58cBSXS41KleD998eQ\ny2VYLCWEwxJqtcQZZ7i5/vpGamunBrKzWYG1a3tZvbqd114b4POfr2P58jZOPLEOlerg518QBLq7\nRycBUqGsbS96vQmrtYJAQE4oJOBwyJCkEOPjY+TzIpKkwGDQMGOGkyOPbKSpqYSOji7Wrt3D8LAa\nKEGhyCOKOYzGgns5lcojCDKUSjkul5H6egv19UZsNvD5ggwO+hgc9DI87Mdk0lNVVYBKbnchn0mt\nViKTSWSzaUKhKP39IwwOevB4xolGE5hMevR6LSqVEkkSSSbTxONJ0unsvpsv5HLlBKBTkMuJ6HQa\nHI4S3O4yampcNDRUUlfnpqLCjstlw+22H3RxaLrK5XL4fAHa2wsdYLu6euntHWBoaASPx08qlcFs\nNmMwGFAqVchkMrLZ/OQin0ajpqTETEmJGb1ei0ajRqGQAxL5fJ5MJksymSQajRIMhhFFAbe7nMrK\nciorXZNgaX/A5HI5PnZBraiiivq/VREYFVXUf7jy+Ty9vQNs29ZBR0c3e/b0Mzg4ytiYj0AgRCyW\nAGTI5QoEQUCpVGKxmCgrK6WiopyamgoqKsoPAoPKKCn5+xMbSZIYGRmlvb3zgK2zsxu73XYAFJo9\nu5W6uloikfiHQNCBUGhkxIvHE0IuV6HVapHLlQiCRC4nkM0Kk0BIpVJiNutxOkupqnLS2FjJrFl1\nzJ/fwuzZDej1H6xkRyIR3n+/AIc2bNjI++9vQqGQc+SRCzjyyAUsWnQkRxwxn2Qy97ElY0NDPqxW\n80ecQfvAUFWV4++Clg8rnc6ydm0nL77Yznvv9dPXFyKdzqNUytBq5YhilmQyhUYD+byAKGoAEzKZ\nhFyeQRDiyOU5FAqorCxlzpxqli1rZdmyVuLxNG+/3cOf/9zDjh1hIhEZBkOO1lYzJ51Uz+LFjcyb\nV0d5eemUnUDbt/tYvbqdJ57ooK7OwvLlbZx2Wgs229QdAxs2BPnf/+1i3bowcrmcyko5Q0NBQMaM\nGU48HgWLFpm59NIKjj++hBdeGOSOO9rp7Y2Ry2U5/vhybrzxCObNKzvo4+/Zk+buu8f4/e/HOfXU\nQpB1S0vh9e3eneb223288EKEc86xsny5lSefjPPAAyFOOcXE9dfbaGqa/o1sICBw5ZVB3n47w69/\nbeP446fnoJiq8nmJVasS3Hlngp/+1MQFFxya0+Lll3Oce26SDRtMVFVNL5NGkiTOOitHJALPPqtC\noSjCov8k5XIS//3fORoaZNx///Rh4a5dAsuWxfnznw0sXDh9Z1qh22DBWXfbbSbOPfezcRsBPP98\ngssvD3LyyXpWriw9pI5t69enuOWWcbZty7BihZVly7T84hfjPPdchLPPtnLVVXYqKwvfOZs3x1m1\naoy//CXCeefZ+d73XFRUHPz7KJ3O8/DDu7n55i3kcnLUaiUrVrRx9tmNvPlmjPvuG6GjI0Fjo4zt\n20dIJvNUVpbi98vI5UTmzDFwww0zOPnk8il/hoPBFE89tZvVq9vp7Q1x+umtLF/exrx5n+wCliSJ\nvj7vJEBav76XTZv8ZDJGJElHTY2W2bPNlJbm2bNnjK4uD+PjcSRJgV6voqrKisOhIxpNMDgYJRTS\nAwYMBgGVSkY8nkEmk6FQFLLoBAG0WiX19TYWL67hi19sZcECNx5PkKEh3yRIGhryMzjoZXDQRyAQ\nxe227QeVyiagkgIQyWQyjI8HGRnxMTzsZXDQy/h4CKOx8G8EIUcymSSVSqHRaFEqVYiinGxWQJJk\nqFRqZDI5+byIKEoYjVosFgNlZRacThuVlXZqatzMmFFJc3Mt1dVOSksPHSzFYjG6u3vp7t4zOXZ1\nFfY1GjWNjfVUV1fjdpdjs5VRUmJBq9WRSKQIBsOEQhECgTDBYGHz+4MEg2FisQQ6nQatVjM53xGE\nPOl0hmQyhU6nxmotweksw+12Ul1dQV1dJY2NdVRWuqiocGG326aU61hUUUV9eioCo6KK+jdUIpHE\n5wvg9Y7j840zNDRGd/de+vqGGBnx4vcHCIdjJJOpCWvyviBIAzZb4ce6urqCxsYaWlpmUFdXNekU\nOtQOYePjgQkg1HEAHFKrNTQ3N1FTU43T6cRsLkGl0hAOxw4AQWNjfiKRODZbCQbDvjb3kMnkSaWy\npFJZMpkcgiAil8vQ67WUlhopL7dRU+OiubmaOXMaWbCgldpa98dOpPL5PDt3tk/CoQ0bNjIwMExr\n6xwaG2fidldjNpeRTot4PEHGxgIMD/vp7/eg1ao/tmSsutqJTndoq2eZTI716/fy7LM7eOONHvbu\nDZJMFjIaFAoJQcihVgsolWkyGZF8vlBSADpkMgG5PIskpbHblcyYYWfWrCqOOaaFhgYHgUCU7dsH\n2Latj40b+xkezqPV2kmnVbS1lfKVrzRz/vkLcbtLpv26R0djPPFEIdciGs2wfHkbZ5zRRlPT1Lrx\nQKGbzq9/3c/DD4/g9eZxOFRYLHl27w5iMGhwuRxEIjLOOaeciy5yY7creeihbu6+e9dE7lSKr3yl\niv/5n/m0tJQe9Dneey/GqlVjvPlmlIsucnL55U7Kyws3Wxs3JrntNi9vv53g8svLOPXUEh5+OMKj\nj0b45jfNXHutldra6YMiSZJ4+ukk3/9+kG99y8Att5RgMHw2k+DOzkKWi8kk4+GHDz3LpadHYOnS\nOM8+a+Coo6Z/w37jjTleeUXkjTfU6PVFWPSfqGhU4uijs3z72wquvXb619ALL+S4/PIkGzeaKC8/\ntM/Ljh0Ft5HTWcjuqqz8bNxG4bDAD34QYu3aFPffb+Pkkw+tqcLmzWluuWWc9etTXHWVlVNOMfCb\n3wR49NEgX/mKhR/8wMHMmYXf5f7+NPfc42H1aj+nnFLKNde4aWs7+PPmcgKPP97DjTduJpksuP8u\nuKCJK66YRTQK998/wu9/76OhQcngoBefL0FtrRlR1DM2lkWrhW98w8kll9Ry+OElU4YTPT1Bfve7\nXaxZ045Op5rIq2ulstI85XMiSRKjo0HWrdvNU0+18957Xvx+AYUiyYwZOo49tpq6ulKCwTidnaO0\ntw8zOhomnRaQy2VotSqUSi35vJx0Woko6jAYMjgcavR6DePjGfz+1MSCkwxJAp1OSV1dKcuWzeAr\nX5nN0Uc3otUWXNGZTJaRkfH9gJLvALg0OOhDkqRJoPSBU0mPWq1AkgRSqRQjIz46OnrYu3cIrzdE\nIpEFBDQaBUajnpISEyUlZnQ6PYIgTZS9pSZK39Ikk1lyORGQIZPJUKuV6PUaLBY9VqsZp7MUt9s+\n4V6qoKmpmoaGqk9c3Nv/vHu9vv0A0j6g1Et//yAul5OmpkZaW5tpaWmipaWJ1taZWK2F315BECZy\no8IHAKVAIEwgEGJkxMvoqGcyuykSiZFIpMjlchOQSEIURTQaNUZjIbjcZivF6SyjoqJ8ct46Y0Y9\nNTUVWCymIlwqqqhPQUVgVFRR/wISRZFQKDIBgD4AQfuOR0e9DA+P4fWOEwpFEAQRtbpgI87nc+Ry\nOSwWEw6HlYqKcurqqpk5s4G2tmbmzm3F6XR8aiutsViMnTs72LBhK1u27GTXrm56ewfJZHKUldkx\nGIwoFGpyOYF4PEUgEMFo1ON02rDbS9Hr9UiSnFQqRzyeJhpNEo0micdTk13GVColJpMOm81CRYWd\n+no3ra11zJ3bxBFHtGCxfHJQpyRJBAIRtm7t4K23NrBpUzu7d/cxPOxHrzej01kAJfF4FkGQJlr0\nWikvt07sf3BcWWmntrYcs/kfz5xJp3Ns2TLIE09s4tVXdzM4GCaTKUwAC13VCgCo4BASASWiqEUm\nMyFJGuTyPDabkjlznBx9dB0NDWVotUoymSwDA376+33s3etl584BBEFk5sx6VCorIyMCXm+aL32p\niW98YxYnndSATjf9zleJRJbnn+9h9ep23n9/lFNPbWb58jaOOqrqoIHSB9PwcIpHHhng0UdHGB7O\nolDIaWvTEwyG6e9PYrEYUCgszJih59JLK/jGN+z4/WnuvbeDhx7qwW5X4/HEOOOMBlasmEtd3Udv\nRERR4sUXQ6xaNcbwcJarrnJxzjl2jEYFkiTx2mtxbrvNy549Ga65xsEJJ5j45S/DPPFElLPOsnDN\nNVYqKqZ/fgBGR/NcdlmQrq4cDz9sY/HiQ4OwnyRBkLjrriQrV8a55RYTF1106I6KaFRi0aIY3/++\nhosumj74fPjhPD/7mcD69WocjiIs+k/WyIjE4sUZVq5Ucfrp04c1N9+c5tVXc7zxhhG1+tCupf27\nA95+u4mzz/7s3EZvvJHiggsCLFig4ec/t+JwHBqg2rEjzU9/GuCNN5J873ulnHGGiTVrQvziF+Mc\ndZSB665zsHBh4TcoGMzzwANefvELD3Pn6lmxws3nPndwKCAIIs88s5ebbtpMIJAnmZQ45ZQqrrmm\njcZGC2vWeLnvvhHS6Ty5XITh4TAul466ujJ27EiRzQoYjTJOO62cCy+sYe7cjw/i3l+SJPHOO8Os\nXt3OM890MX++k+XL2/ja15oxGqcP4cPhNE88sY3HH9/O5s0+SkpAFMMkk17mzKlk/vx6Zs6sIJ8X\n8XjCDAz42bPHy/BwiEAgSS6nAjSAFlAjlycxmfJUVhooKythZCTL8HCMdFoEChBCq1VQU1PCsmWN\nnHbaPBYsqMVkOvj3eSQS/whI2udSGhryMzIyTmmpcRIqVVU5qKy0o1LJ8XrHGBoapL9/gMHBIcbG\n/Gg0egwGCwqFmmxWJBpNoNFocDqtWK0WjEYdCoUCQZDIZHKk04VMpX1bMpkhm93XqENCpZKj02kw\nmXRYrSbs9kJpXFWVk/r6Cqqry7HbrZSVlWK3Wz+St5TP5+nvH6Srq4fOzm46Oromxt1otdpJiFQY\nm2ltbZ5SziQUQFMoFCEYDOPx+OntHaCvb4ihoTFGRz2TDqZoNE4ymSabzbHv1lClUqDVajGZ9JSU\nmLHZrLhc9knA5HSWYbVaKCuzYrOVYrOVYDR+Nl1JiyrqX1VFYFRUUf9Hymaz+P3Bj4VA+49+fxCd\nToPZbESr1SCXyxCEPKlUoU18NpujvLxsohNGDY2NtdTWVlFTU0ldXcE2/I+usoiiSDAYmWhXH2Bo\nyEN7+266unrp7x/B6w0QicTJZgVkMjkqlZKSEiPl5QW3ksvlnMgNyBGNpohEEgSDUcLhOJFIgmQy\ngyCIyGQytFo1FosBp9NKdbWTGTOqmD27gSOOaKGlpe6AvKIPK5fL4/WGGBsLTDqAxsb2OYF89PYO\nMzYWIBZLI0kCcrlAaameigo7TU21zJnTTH19xSQUKi+3YrF8+pMHQRDYs2eM557bwtq1HbS3+wmH\ns4iijMJktNAuWKMR0esF5PIUyWSGZLJQWiaXFya1ZWUqmpttNDZacLkKzqz+fj99fV76+30YDFpq\nax3U1Tmoq3NSW2tHqdTT25vmtdcGGBiI8OUvN3PqqS0cd1z9lHOE9pcoSrz55iCrV7fz/PPdLF5c\nwfLlbZxyygz0+qlBleHhFI89Nsgjj4wwOJhBLpcze7YBgyHPxo0+slkZZrOZXE7HN7/p4NJLK5g/\n38TmzePceecuXnppmKoqHUNDEc4/fyZXXz0Hl+ujAC+dFlmzphBkbTIVgqy/9jUrSqUMQZB47rkI\nt93mJZWSuPZaBwsWGLjzziDPPRfjggtKuPJKK07noQU1S5LEI4/Euf76EBdfbOKHPyxBo/lsJqVd\nXQVXkU4n4+GHzdTVHXq4tChKfPWrCVwuOQ88MH2XxMsvC5x9do633lLT1FRc7S0Kdu4UOe64LE8/\nrebYY6d3TYiixKmnJnE4ZDz44KG5dvZp+/aC28jtVvDrX5upqPhs3EbJpMiPfhRm9eo4d91l5dvf\nPvTflN27M/zsZwFeeinBpZeWcMEFFp5/PsKqVT4aGzVcd52T4483IpPJSKdFHn98nFWrRtHrFaxY\n4eLrX7cdNENKkiT+9KcBbrppM0NDKQRBzuzZpaxY0cbnP1/BW29FuO++EV57LYTFkmF4eByFAg47\nzIZOZ2DTpjiiKGIyyTj9dBfnnVfDnDlTc66k03lefHEPq1fv5G9/G+bkkxtZvryN//qvmolsnOkp\nHs/y0ks9/PGPnbz88h4aGszU1WlQqxMTwMGDzxehqqqMhoZyGhvLqaoqQy5X4PdH6e31sWnTEB5P\nlmxWTQEkZYEkanUaq1VJSUkp8biCYDBLKiVSuJeS0GjkVFaaWbKkjq9/fS5LlzZis31yi3pBEPB6\nQx9xKXk8QXy+MD5fCJ8vTDAYpbTUREmJHrVaNlF+HiEQ8CEIWaqqXJPlWw6HHY1GRzAYwesN4vUG\n8PlCeL0B8nkBh6OUsrJSjEY9SqUSUSyEkafTWRKJFLFYagIwZRDFQgc5EMnnc8jlMoxGLSUlRuz2\nkonFMwdutx2brQSr1YLVaqG01EI+n8Xr9TIwMEhnZ9ckUMpmswcApIIrqZmamqp/aM4qSRKxWJyB\ngWG6u/eyZ08//f3DDA2N4fH48PuDhEIREokkKpUKlUqNXC5HFCWy2RyiKGI2myYd905n2QRQKsFm\nK5yzAlz6YL/oZirq31lFYFRUUZ+S9nWt+DDs+TgIFIslsNutOBw2SkstkzXdoiiQyWSIxWIEgyE8\nHh8gTQKgfeP++w5H2SFNPkVRJBAI4/WOT3YK83oDBxx7POOMjvoIBsOo1aqJG+sc6XSKkhIjLpcT\nl8uJ2VyKRmMgmxUYH4/g9YYIBCLEYikymcJqj0JR6CpmsRQmGBUVZdTWumhqqqatrYHDDpuBzXbw\n0qd4PPUhCFQAQftDIY8nSCgUm5y8GI0qRDFDPB7G5xsmEPDS3FzLggVzWLZsEUcfveSAYOpPU/m8\nwMjIOP39Xvr7vWzbNsD69f309oYIhQQEQQ4oKMAhGSoVmM0KjEbI5WIEAnGy2cJjqdUWJMmIKCqw\n29WUlMjI5WJ4vV5Aoq7OOQmE6uocE4DISW2tA5NJRySS5vXX+3jllT288kov+bw4AYlaOeaYmolJ\n4PS1e3eANWvaWbNmF1arluXL2zj99FZcrk+eHAMMDSVZs2aIRx8dYWAgA8iZNUuP0yljwwYPqZSE\nKKrQ6SzYbFq+971KzjqrHItFyZ/+NMRdd+2iqyuKy6Wmvz/C5ZfP4vvfn43N9tEV3kAgx69+5eWX\nv/RyxBEGVqxwc8wxhSDrTEZkzZoQt9/uw2ZTcP31TurrNaxcGWTt2gSXXVbC979vxWo99JvJvXtz\nXHhhgHBY5OGHyzjssOmvoE9FgiBxzz1Jbr01zs03G7nkEv2UnV0fpx/9KMVf/5rn9den7+jYulXk\nxBOzPP+8mqVLi5Ppoj7Qa68JfOc7OdatU9PSMr1rIxaTWLw4xuWXa7j44n8sKDeblfjZz+Lcf3+K\nVatMnHmm9jNzF2zalOG888apqFDywAM2qqsPHeT29ma59dbAJMz+7ndLef31GCtX+tBqZVx3nZOv\nfc2CQiFDFCX+/Ocwq1aNMjCQ4corXZx3ngOj8aPfaYWObSP85Ceb6ewstG/X65Vcc00bZ5xRz/h4\nngcfHOM3vxlFpRJJJArODo1GwYIFdnI5DZs3x5DJJCwWOWec4ebss6uZNWtqnbJ8vgR/+EMna9a0\nMzoa5zvfmcWZZ85i9mzHIZ2nVCrHK6/08sc/dvLSSz24XEZOPLGBY4+tpqpKy9hYgN5ezwFbX58P\nm81EQ0M59fVOrFYzw8Nxdu70MDSUIpFQADkgg1yeRqlMIwh5QItSaUQUleRy+65pEYUCnE4DRx5Z\nw/HHz+S//3s21dXWQ7rOBEEgEIgeAJEKEChEf/8oe/cOMzrqJxCIkUoVHEQqlQyzWYvDUUpNjYum\nphqcThsajRKFQoYkieRyhRyl/eGS1xvE5wsSjSYmAFAhCFurVQMfBGHH4ylisSTRaAqQ0Ok0qNUK\n5HKQJJF8PksqlSabzWI267DZzJSVlWA06pHLIZ/PkUzGCYfD+Hw+kskENTUVNDfX09Y2k/nzZ9PW\n1kJDQ91kc5RPQ4Ig4PcHGBkZY2TEw/DwGCMjYwwOjtDXN8zIyBgezziSJGGx7HvvGuRyBZJUWKBM\nJlPEYgmSyTSlpZaDQKWSyf0Pg6bSUgtKZbFTaFH//CoCo6KK+jsquGr2AZWPh0D79mUy2Ue6gNnt\ntokfV4lMJkMikSAUCjM25mVwcITBwRH0et1HIND+xyUlU7N4A6RSaQKBMOPjIfz+wo99Af74JyYA\ngUko5PeHMJsNOJ1llJeXYTTqkMlEMpk0kUiIsTEPIyM+TKZSSkttKJU68nkZ6XSOeDxDMpkhnxeA\nQq28waDFajXhdFqpqnLS0FBBS0sds2c30txc/RELcyqVOWDCUxjDBwVCgiBOOH5KP1IS5nLZUCgE\nhof76OhoZ+PGTWzZso2KCvdkMPWRRy5gzpzZn8pkQ5IkQqH4hHMpyPBwAQwNDPjYs2eM7m4/4+MZ\nlEo9oqgkny+AIZlMgSTJUKvlGI0KFIo8oVAQrVZEJitkEMhkJhQKK7mcDkkCmayQPdTYWMLs2U7q\n650TYKgAh0pLjR+5NgRBZNOmUV55pZdXXullxw4vS5dWcdJJDZx0UiMtLYcGGAHGx5M8+WQnq1e3\nMzgYnZzMH3aYc0r/f2goyRNPDPPww8P09xcgUUuLnqoqJRs3ekgkBNJpGXq9BaVSw5lnlnPmmU4O\nP9xEKiXw2GN7uPvuDpRKMBhkDA5GuPLKw7j00lmYzR+FMHv3FoKsH398nK9+1crVV7tobS24EmIx\ngQcfDHD33X7mzNFy3XVOzGYFP/tZkLfeSnLFFVYuvbQEi+XQQZEgSPziF1FuuSXCtddauPJK87Q7\nRE1V3d15zjknglIJjzxioaHhH5+IPvtsliuuSLFxowmnc3o39YODEkuWZLjnHhVf//pn49wo6l9b\njz0mcNNNedavV1NePr3PxZ49hUytZ54xcPTR//i1vm1bjrPOilBdreDBB8243Z/NNVsI345wzz1R\nbrqphEsuMf1DUHdgIMfKlQH+8IdCuezVV1vZsiXJrbd6GR/P84MfOFm+vBSNpvD53bChkNm2bl2U\nCy908N3vlk9mtn1Y77wzxi23bGbTpiB2u5FAIMvll7dwySXNlJSo+etfwzz+uJfnnx/HbBYYHw8g\nSTl0OiWLFpUTDMrYti2OXC5RWqrgrLPcnHlmFa2tU8sr6ugYZ82adn73u12UlekmFyXKy6e2KPFh\nCYLIli1jvPpqL6++upctW8ZYuLCCE0+s58QTGzjssPIJB7fAyEjwIyBp3yZJ4HK5EAQ1gUCeSEQG\nZBHFCCqViCDkUanAYNCSz6tIJpmYBygBCSi0tTcaFdTVlbBkSQOnnbaAZcuaP3WXit8f4J13NrFh\nwza2b++kq6uPoSEvOp0Zi8WKWm1EFOUkEjmCwRhGow6HoxSHo2Q+dbLbAAAgAElEQVRiK8VmM6PT\nqVGpCu7nwqJhZmKRNDQ5r/T5Qvj9YfR6LWazEb1eh1qtmmiaIpLJFDroRiIJBEHEYjFgsRgwGrUT\n8KrgYMpkUkQiUaLRKLFYgkwmi0wGkiSg0agxmw2UlZXidjupqamgsbEWp7OM0lLzpLPJai24nD48\n7zwURaMxhodHGRnxTICl0QMA0/DwGKFQdGLOXwgBN5mMaLXaCSAkI58XSKUKHfX+P/beOzyu8szf\nv6f3PiNp1LtkW7KNbUyAYCC0ANlfYpNAMD2QsNlkybIQCAE2BdJoSwkpkMSm2CRAIBAIISG0BIhx\nQ5Zt2epdM5qi6X3m/P44MyPJkm2M7ex3N36u673OO0eyNe2c85z7/Tyfx+ebwuudIhAIYTDo9qNe\nMhf3z/y5zWY+1k3uWPzD4xgwOhb/dJFOp/MgxYfb7SkCn30BkNvtxeudwmDQFSWpBRA0c261mslm\ns8RiMdxuD0NDo8UxODjC2JgLm80yBwLNfKzXz+99k0ql8vBHBECzx/z7MplMsc7cZjNTUmKlrMye\nf942SkqsgEBv7wA7dnTT2dnD4KALvz8MKJDJlORyYlcl0TgR1OrCBdpEebmoCmpsrKStrYH29kbK\ny+35Wvn5V772BUKFeTKZprTUUkxKSkrMOBxmnE7rrJIwp9OK0Tgt4Y9EImzdup1Nm94vGlMnEskZ\nXctWcvzxy7FY5jc53l+Iq03BIgiamJiaMffP2q9SqbBYTKhUWlIpGZFIllAoTToNIEMmkyEI0ryy\nKksul8BslqFSpUmlooTDUVIpsbxMLtchCFo0GjlNTWaOP76CM89s5OMfb/zQnchGR0NFBdFf/jJA\nebmBs8+u55xzGjnllOqP5EdUiGQyw8sv9/HEEzt5441hzj+/gcsvb+OMM2o/lDppZCTGr389xi9/\nOcLAQAKQ0diooaFByY4dHqamkqRSEqRSPaDmM5+xc9VVTk4/3YJMJqG/P8y6dT38/OfdNDcbSCZT\nuFwRbrppKVdf3Tpv2dv770e4555xXn99+qbI6RRvijyeDA8+6OFnP/Ny5pkGbr65hFRKwp13+tiy\nJcGNN1q59trDN6HevTvF1Vf7UCrh0UftNDcfuZXRmZHNCjz4YIzvfS/Cf/2Xnq9+9fBVRQA7d2Y5\n/fQIr7yiY8WKQ7shDwQEPv7xFFdfLeP664+toB6L/cd3v5vhxRezvPmmEr3+0L63f/pTmiuv/Ghd\n++aLVErgzjsj/Pznce6918Allxw9tVFXV4prrvEhlcKjj9pobT081eHYWJq77/bz+ONBLr7YyE03\nWRkaSvHDH7rp6Ehw/fUOrr3WhsEggrC+PhGmb9zoZc0aKzfcUF7sCrlvbN3q4fvf38abb05QV2eh\ntzfC5z9fx5VXNnLCCQ4SiRy//72PJ59085e/+DEaU3i9flQq0OuVrFxZxthYlp07o0ilAg6HnCuu\nKOfSS6toaTm452AuJ/Dmm0M8/vhOXnihp1j2/OlPNx3WtS0cTvLWW0N5gNSH3x/nzDNFeHTWWfVU\nVMwFW4Ig4PeH8/DITV+fi56eCTo7XfT1BQmHJYAWiSQLBJBKI1gsMrRaLdGoaIYumlbLSSQk5HIg\nAiRxSKVZjEYF1dVmVq6s5hOfaGXRoiqcThHcHAmgJJbE9/HBBx188MGO4kgkkrS1tdPQ0Ex5eQ02\nWwlKpQ6fLzxvDhcOx7DbTZSUmCktteZzONE/SaWS5/MDgUwmTTKZJBgM4/MF8XimcLlEwOTzBZHJ\nxPdHpRJLwwSh0NAkQTqdxWo1YLOZsFgMqFQystkkkUiYYDCA3+8nGAyi1WrQ6XQoFGIOm0ymCYdj\nyGSyGRCpUCZnLAKl+YeofjqUYz+ZTDIxMTkHJs2cT0xMYjTqqagQywbLy0ux2awYDAY0GjVKpQqJ\nBGKxJD7fVH4E8Hr9RWNwny+ASqUsVihMj8IitXXWPrvdckRVWcfinzOOAaNj8X8iEonkLPizL/iZ\nuS8YDBfrkmcCIHE4Zu1zOKwIglCEP4UxDYXGcLs9OJ0l8yqDamoqqaoqR61Wk8lk8PuDHwr6FBRC\nsVgCu91chD92uyU/Zs6nh8mkJxKJMzrqpqtrkM7OHjo6uhkcHMfnCxGNJvNt5SUUumioVHJMJh3l\n5Q5qa53U11fQ0lJDe3sjjY2VKJUKPJ7AfqFPQQo9ORlgaiqM2ayfBYD2XamauZ0JgfYX2WyWrq49\ns7qW9fb20d6+aIZ6aCX19XX7/b9SqTQu13zwZ/Y+jyeIxaLPAysrNpsJpVJNLichHM4wNhZmbCzI\n5GSUbBZATGxEebKEXE6CRJJFrRZQKnNkMlFisQhKpUA2G0YiUWAylSOV2ggG5dTUWDjjjEZOPbWe\nU06ppbz8w3eJicfTxUT31Vf7cLsjnHlmPeec08DZZzfMm+geSgiCwKZN4zz++E6efnoP7e0OLr+8\njQsuaMFoPPjq1shIjN/8pgCJkgiClLo6Nc3NKnp6ppiYiCKVyohEFEgkej7+cQP/9m/VnHeeFY1G\nhseT4OmnB9iwoZ+enhAnnuhgbCxIKJTkG984jssua57jt3SwsouhoRT33DPJhg1TXHSRmRtvLGFs\nLMudd3rZuzfFzTfb+MIXTKjVh5eQezxZ7r03yC9/GeGOO8x86UuHpyA4UPT2iqoigHXrTDQ2Hhk4\n4/fnWLkywre+peayyw7tRjaZFPjkJ9MsXizh/vsPvX36sfjnCkEQuPrqDB6PwPPPKw5ZgXfPPQme\neirN3/6mR6M5Mt+1rVtFb6OGBhk/+5mRsrKjozbK5QR+8pMw3/52gKuu0nPjjSZKSw/vb7ndGe69\n188vfhHgggsM3HKLjVAow113TfKnP4X513+1c911dkpKxJtIrzfNT37i5uGH3Zxwgp4bb3Ryyinz\nl4/t3u3nBz/Yzssvj9De7mBkJI5EImHt2jouuaSe1lYzfn+aZ5/18NhjE3R0RFAqo8TjYRQKKVar\nmsWLHQwMpOnujiGVCpSVybnyykrWrq2kqengyqFCY4UnntjJpk3jrFnTwmWXLWLVqurDPs8ODwf5\n859F9dFrr/UXy9fOOqueVatq0OkOfi6MxZL097t4++1e3nijny1bRhkbS5DJ5BCEKBBCpYphs6mx\nWCzIZDr8/ixudwxBkJPNyhDf+hy5XBZRkZRFIskhCGm0Wil2u5raWjNNTSVUVzuKOUthlJSYi23r\nDyVcLhcdHZ2zQNLQ0DCtrS0sXbo4P5awZEk7JpOJVCqN1xtkcjKQL18T80MxZ5ybLwLFHNDhMOW3\nZkwmbVFhJJHkyGQyJJNJpqZCTEx4GRvz4HL58fmCBINRcjkBlUqZX5iDVCpDJpNFrVagVMqQyQQy\nmQSRSAidTk5lZSnV1eVUV5dTUVGKwWAinRZzclHxE2BqKoTfH8x3bguSSKTmhUnTKqb5gZPJZNiv\nz2Yul8Pj8R1UrSQIAhUVTioqyvJ+VGUzIFMZJpMIDr3eKSYnxfubyUlfcTFcHOJ+ny+A0ajfBybZ\nZ8Emcb+9aJFxzIvpWOwbx4DRsfh/MgqGdQcCPzMfJxLJOfBnLgwS99lsllkn83Q6zcjIOIODIwwM\nDO+zHcHr9VNZ6aSurjoPgkQIZLPZ0Ol0yGQKAoFQEfjMrwgSa/wtFuNBoM/sfUZjwbgyycSEl6Gh\ncbq6BuntHWVwcIKxMQ8ezxRTU2EikTjptGg4LR4TouxZpZJjseioqHCwaFEDJ564hNbWBhQKBdFo\nYg702fciL5NJDwp/Ciohm830kZKUmTExMTELDm3Zso3S0pJZpWVLlixGpVIRjSb2owCaDYRCoRgl\nJaY5SZXTacVqNZLJCITDaTyeKHv2TLB9+wgDAz6SySwymYxMRsjDIPKdN2SALJ/ApVAqc5SUKCkt\nlSKVhvH5hhkdHaC0tAWbbQHRqJnR0TRLljg55ZQ6TjmllpNPrsFq/fCGrYIgsHPnZBEQvffeKEuX\nluXLzBpYtsz5kcxB943BwQBPPrmLxx/fiUQi4fLL27j00kXU1JgO+m+Hh2M8/fQY69aN0NeXRCKR\nUlGhYsECDcPDUwwPR9HrlbhcOSQSA62tGr7ylWouuqgEs1lBJJLmhReG2bChn3ffnWTVqlJ0Oinv\nvTeO2azi5puX8rnPNcxRNSUSOZ580su9985v7LpzZ5y77prk5ZdDfPGLNq67zs6uXWnuuMPL+HiG\nW26xcdllpo/ccakQbneWe+4RQdFFF+m49VYTlZVHR12Tywn8+McxvvvdCLfdpue6646MqghEdeF5\n50Vpa5Nx333zKw72F4IgcNllaWIxeOYZBTLZMVh0LA4e6bTA+eenaWyU8PDDhwYZxe9cDIAnnjg0\nVcCBIpkUuOOOCI8+Gue//9vAxRcfPbXR2FiGH/4wyIYNUa68Us/Xv27E6Ty8c4fXm+H++6f46U+n\n+NSn9Hzzmzbkcrjnnkl+85sAa9dauPFGB7W14gJAPJ7j8cfFhgAWi9gQYPVq67zHcF9fkPvv72Tj\nxl7q603YbFo6OgKUl2tZu7aOz3++jooKHcPDCZ56apJ168YZH0+QTk+h02VJp8Hp1NLcbKW7O8Xg\nYBypNEd5uZIrr6zk4osraWg4eNfR8fEwGzfu5vHHdxIMJrnssjYuu2wRLS22w3rv4MOXr32YEASB\nwcEp3nyzj5de2s3bb/cTCiVRKCKkUj6y2RiCIC7g2e0mDAYz8biMYDBDJJIlnZYgkQiIdjcC2WyW\nXE5UJMlkoNHIUKkkSKVpUqkYkUgYu11HefncnMfptBTnZWUWVKoDQ7BoNMrOnbtmKJE66OzcRWlp\nSREgFWBSZWXlAY+RaDRezC09nuAcBfr04qQ412hUs3LOAmQym3WoVAoUCimCIJYAhsNRRkbcjI5O\nMjHhw+cLEghECIdjZDK5onKpkB9LJEJ+wVRLWZmNhoYKli5tZeXKxTQ1VWGzGUkkknmINHME5tk3\nPcLhKEaj/gDqpWkz8H1BlFIpfhahULgIj2ZCpcJ8dHSCYDBMZaWT6uoKamoq52yrqsrRaDRFaw0R\nJnlnAKUCZJr9OByOYrdbipYas1VMtjn7j3WU++eIY8DoWPzDQvR9Ce4DgPavCpLJZAcEPzNVQSbT\n/s0Us9ks4+OuWRBoJhQaH5+kpMSO01mG3W7DZDKh1WrzJ24pqVQany+Yl4OKIGhqKoTRqJ8H+uwf\nApnNc6XEkUiMiQkP/f1j7NkjgqDhYTfj4x48ngCBQIRoNJHvHiaCIJVKgVqtyNeSZ0gm40QiISwW\nI5WVZVRWllNSUopWqyeTkRRXf+aTEBegjwh89oVC4sVZpzu0G8ZDCY/Hw9at29myZRtbtmxly5Zt\nRKNxli9fQUtLG5WVdZjNJUQi6XmBUDqdnTcJ2neYTFqGhvz09LjZu9dFR8cwH3wwzMCAl0gkXVyl\nElVDYqeTggpLKpUjCDJUKillZToWLLCzYIEdqzVFODxKb28nW7a8TzCYoa7uVFSqBiYnVUxOpli5\nsopVq2o55ZQ6Tjih6kOtTs4MrzfGa6/18+qrolxepZIVfYhOP70Wk+nItGMPhZI8++weHn98J7t2\nebnoogVcdlkbK1c6D5oIDA/HeOaZMdatG6WvL4FUKhpzt7VpcLlC9PaGKCvTMDKSJpXSU1am4Jpr\nKrjmmkoqKlSk0zn+9KcxNmzo5w9/GOWEExxUVanZtctHX1+Qiy9u5IorWjjuuLm+SzNbRx93nI6v\nf93JaadNd+V5990oP/yhm82bY3ztaw6uvdbK3/6W4M47fYTDOW691cZFFx2+p9D4eIa77gry+ONR\nLr1Ux003HT1QBNDfL6qKMhlRVdTcfGT/1o03xunoyPLKK7pDfm9uvTXN66/n+MtflGi1x5LIY/Hh\nIxQSOOWUFJdcIuOmmw7tOx2PC3z84xHWrlVwww1H5rxYiC1bRG+jlhYZP/2p8bAVQAeK8fEMd98d\n4rHHIlx6qY6bbzZRUXF4x3cgkOWhh6Z48MEpzjxTy6232rHbpTzwgIdHHvFx3nlGbrqphPZ28Vqf\nzQq8+OIUd989jtud5j//08lVVznQaue+brG72RDr1+/lnXdcnHSSE4lEzrvvejjuOCuXXFLPBRfU\nYDar2LkzwhNPuFm3bpxkMkU87qe8XEEwmKW6WkdVlYWurjgTEykgS3W1iiuvrOSiiyqoqzs4POro\ncPPEE7vYsGEX1dVGLr+8jYsuWoDdfnid9ArxUcrXDhRjY0H++tdB3nprgNdf72Z0NITdniKVGsPn\n68Fs1mAyOZFItESjOTyeFFKpBrlcQzYrJ5kEMaXMkM1mKaSXuRx5s+ksWq0Cu12L06nHalUhlYr+\nQFNTQVyuKdzuAAaDhvJy2wFzKKfTik43fVzNV9K2fXsH6XSaJUva82MxS5a0s3Dhgo/kuSMIAsFg\ndBZUmgmU9oVOBYW7w2Ges7BpsRhQqwtNWzJ4vUH6+4fYu3eI0dFJ/H5RgZ9Oi56cYjMS8SZZqZRj\nMGjylQmiXUJ1dRkNDRU0N1fT0lJDSYmlaF6dzWYJBELzwqSpqf2DJr8/iEajOqB6aSZs0mhURKNR\nQqFQUbU0NDRa9EYdGRnHZDLMC5MKW5ttrvF6KpXKK5fmwqSCcmmmkimbzRZVS3PL5ObuP+a/9L8z\njgGjY3FYkcvl8hcezxwlUGEUfjY56UOrVc+BP/srCdPpPtxFPpfL4XZ7GBgYZu/ePnbv7qWvb4jB\nwTHGx914vQG0Wi16vR6VSoVUKieXE0gmU0Qi8XxnA2Ox7Ksw7HbzPo+ny8Ks1v13NhAEgUAgzMSE\nh76+UfbsGaKvb4yhIRculxevN0gwGCEWS5LLFQ5C0SfIYNBiMukwmw3o9VogRzwez9d9i6AKFKhU\nGgRBTjKZQaEQV6QcDjN2uynffcJUnO8LgiyWf2zrT3F1I0xv7wjvvruVrVt30tXVR3//KPF4Foul\nBI3GAChJJnNMTUVRKGQHSFymkxqzedrwOZfLMTLip6trnL/+dS9btgzQ0zOJ2x0iFssglUoQBEle\nISSl0LpepZKh0ahQqZQIgoxgMIXTaWTZskpOOqmO1lYrgjDJnj0dbN26lS1btjA+7qap6SQslkWk\n0w5GRnKEwxk+/vFaTjmlllWralm2rAKF4tBuLNLpLH//+2jRrLq728epp9YUy8waGz9aV5X5IpPJ\n8ec/D/D44zt55ZV+PvGJGi6/vI3zzmuYU+q1bxQg0WOPjdLTk0Aul2E0ylm6VIfXG6G7O0B9vYHR\n0RRerwKDQcnnPufgP/+zjgULdORyAu+9N8mGDf0888wgTU1GjjvOwsREmNdfH+MTn6jgiiuaOffc\n6nmfy8BAgvvvd/HEEx4+/WnRyLqtTTxfCILAH/8Y5gc/cDM6mubrXy/h8sstvPJKlDvv9AFw2202\n1qw5/DKxkZEMP/pRkI0bj5wq4ECRywn89KcxvvWtCN/8pp6vfU17xBU8Gzak+K//SvD++3pstkM7\nTzzySIa7787y7rtKHI5jsOhYHHqMjQmceGKSu+5S8PnPH9r5c3g4x8c+Fmb9ei1nn31kPTuSSYHv\nfCfCr34V54EHDFx44dFTGwG4XBnuuSfEr34V4eKLRXB0OB3VQDT5/8lPAtx3n5+TT9Zw++126usV\n/PSnXh54wMOKFVq+8Y0STj55uizs3XfD3H33OO+8E+bLXy7lq18tw+GY/70dH4/y5JPdrFu3l1Qq\nywknOJmayvDuux7OOMPJJZfUc/75lSiVMt55J8ivfjXOs896EIQEEkmYmhoVY2Mp6uqMlJUZ6OyM\nMzWVJpfLUlcnwqMLL6ykpubAuWEmk+O11wZ54omdvPxyH6edVs1lly3iU59qRKU6cufn/ZWvnX12\nA6tW1czrrXeg8Hgi/O1vQ7z1Vj9vvTVAd7eHykoZGo2faLSH0dHNeSXMIsrK6tDrS4hE1IyMxBgc\nDODxJIjHAQTk8hwymUAuJ5DJZPN5jyQPlUR1jcWiob7eTnu7k5oaGwaDArkcQqHIvGX7CoUsD5bm\nz8ecTitSaYb+/h527Ohkx46ddHR00tfXT0ND/RyQVFZWdsQ+C5juHrevhcK+kKmwLxpNFBdPbTYj\nFosBi8WARqMgFovg83mZmJjE5fLg9U4RjSZRqVTI5UoEQUomkyOTyZHLiQuMcrkUjUaFwaDFYjFQ\nUmKhvNxehEstLTUsWFCL1Tp/ExuxsiL6oVRMfn+AQCBMIBAmGAwTicQwGHSYTHrMZiNmswGTyYBK\npUAigVwuSyKRyN9PhJiamsLj8ZFKJamsLKOurora2sp9oFIlFRVlRdXT/iIajRXVS/OVxM1WM/nR\natUzGgPNbhJU2IrzA4sBjsU/No4Bo2MxJ8RW61P7BT8zh8fjR6/X7hcAlZU5ZqiC7B+6W4G4shAu\nKnr6+4fp7h6kv3+Y0VERvPh8AcLhCPF4Kq++EUuGtFo1JpMBu91MWZmDqqoySkvt88Ifm82MyfTh\nAEoul8PrDTA+PklvrwiCBgbGGBlxF+WvwWCMeDwJSIrPR2xJq84b8mny7UaVeZPoHOFwHK83wNRU\nBPFCD9lsikwmidmso6zMSnW1k6amGtrammloqMzDIFO+c8U/ltYnkyk8niAeTxCvNzRrK85F0+ix\nsUm83hCxWBqJJIsgpDEYVDgcJqqrS2lqqqW5uYaSEjN2uxGHw4TDIYKumStZMyMcjrFjxwh//ese\nNm3qp6fHjcsVJBRKkU7nZvymBIlEhlQqI5eToFbLKC3VU1YmqqZAxuhokD17JmlosLNsWQXLl1fR\n2molm3XR1bWDLVu2sHXrVkZHx2hpOZ6SkqWAE7dbTnd3gLo6KyecUMUJJ1Rx4onVLFpU8pFAXH//\nVNGs+s03B2losBbNqk86qeqg8OZQIpvN8d57Y/z2t3v59a+7qKkxFVdhbbYDK8mGh2M8++w4jz02\nQk9PHKVSgUolZflyPcFgjM5OP4sXm5mczNDfn0MmU3HGGQZuuaWRj3/cjEQiYdeuKTZs6Gfjxn60\nWjlnneUkkUjx0kuDlJfruOKKFi6+uBGbbf7Pf8uWCPfcM8FrrwW55poSrruujPJyMZnJZASeeSbA\nD3/oBuAb3yhl9WoTzz4b5vvf92EwSLn9djvnn3/48unBwTQ//GGQp5+Occ01em644fB9Rw4WAwMZ\nvvCFEImEwPr1JlpajjyY2ro1wyc/GeX11/W0tx/a6/nDH7JcfXWat99W0tR0zP/gWHz06OzMccYZ\nKZ59VsmqVYf2XfrrXzN89rNR3n1XT0PDkT8m338/xZVXBlm4UM5PfmKkpOToHveTk1nuuy/Io49G\n+Oxntdxyi4na2sODYdFojkceCXD33X6WLVNx++12Fi9W8dhjfu6+e5LycgW33FLKuedO36x1d8e5\n774Jnn7ax4UX2rjhBidNTfNfMwRB4P33J1m/fi9PP91He7uV5mYb3d1hduyY4jOfqWbt2npOP72M\nbBZefdXPww8P88YbISCCw5GhokJNd3eUxkYTdrue7dtjxONZ0ukMTU1qrryyis9+tpyqqgPDo1Ao\nyW9/u5cnntjJjh0eVq9u5oILWvjEJ2qO+LX1SJWvFSIQiPPuu0P8/e8jbNo0wvvvj6DVyqiulqPR\nBIjFehka2kQ8Hmbx4sUsWbKEJUuWoNVWMTYmsG3bODt3uhgYmCKbFdBoIJ1OkkgkyGSySCRi91bx\nHlCESCAgk4HVqqW5uYT29kqWL69lxYo6HA4dgUBkDkiaT/k9nc8ZsVr1SKVZ4vEwoZAXt3uMoaE+\nFApoa2tixYr2oi9Sa2vLQQHFkYpUKl2EST5fiKmpcH5EmJoKEwhEZj32+0P4fCHC4RhyuRS5XEIu\nlyaViiOXS9HptHnjagUyWWFhOk0sliCRSJJMphGEHCBBoRAXKo1GLVaruLBbUeGgpqaMhoZKWltr\nWLCgDoPh4Mo6EGFZKBQpAiQRJoUIBiMEAqE5+wuPCx5O4XAUuVyGUilHJpOQy+VIp1Mkkym0WhUm\nkwGHw0ppqZ3KyjKqq8tpaKihpaWeysoyzGYjarXqoLmVuKAemtNteroD9ex5IpEs/t1pkLTvfNpz\n9pi599GLY8DonyRE8j61X/AzEwp5vVMYjfr9gp99S8MOJC9MJlP5k1SoSMOn56EiEHK5vIyPT+L1\n+gkEwsRiCaRSEbhksxmkUikGQ+HEaqeyspTa2iqammpZuLCRqionNpsZrVZzSDeD6XQ6v+Lgx+Xy\nMjAwTn+/qAYaH/cyOSmqeiKRJMlkJn/ASJBIpPkbZgVKpRKFQp6HEwKpVJpwOI5cLpuh9BEvnBqN\nglQqTiQSxOebZHx8lNHREZxOO0uWtLB0aRuLFy+ivX0h9fW1+zXOO1IhCAKhUGwW7NkXBu07TybT\nRcBjtxsxm3UIQopoNIDf72J0dIhAwENraz0rVrRz0kkr+NjHVtDc3LTf15NIpHC7A/kRZOfOYTZv\nHqS724XLFSIcTpFKiRfaQshk4sVNqVQikciIRjOYTGra2ytob69Ar1eTSglMTITp7Jygp8dDS0sJ\ny5ZVsmxZJQsW2MhmXeza1VGEQ8PDwyxceBzl5cuRy6vx+VR0dQWQSqVFOHTCCVWsWFGB0fjRyh7C\n4SRvvDHIq6/28qc/9RMOJzn7bNGH6KyzGigp+XAJwoeNVCrL668P8fzz3bzwQg+lpVpWr27m4osX\nHtTnoQCJHn9chERqtRJBgJUrDcRicT74wMfxx1uJRAQ6O5Mkk0qWLlVx4411fO5zTuRyKSMjUZ56\nSoREXm+Sz3ymGr1eymuvDTMxEePSS5u54opmFi60zvscEokcv/udn5//fJL+/gT/8R9OrrmmpNjp\nJ5HIsX69eKNTUaHgG98o5Ywz9Dz5ZIgf/MBHRYWc226zc+aZh+9t0teX5gc/CPL88zGuvdbA9dcb\ncTiO7jGaywn8/Odxbr89zM036/nP/zzyqiJBEPjtb9N89Yl61gAAACAASURBVKtxHn5YwwUXHFrC\nvnVrjk9+MsWLLyo58cRjsOhYHH689lqWSy5J8+abShYsOLTv1M9/nuTOOxP8+MdaPv3pI38DkUgI\nfPvbEdavj/PQQ0Y+97kjWwI3X3i9Wf77v0P87GdhVq/W8s1vmqivP7zXlkjk+OUvg/zoRz5aW5Xc\nfrudE0/U8OyzInjP5UTwfuGF5mJp6uRkmh//2MXPfubm5JMNfPGLJZx9tnm/pauJRIYXXhhk3bq9\nvP/+JOeeW43NpuXdd72Mj8f4/OfrWLu2nuXLbUQiWZ59dpKHHhqmszOORBKktVWJ1apk+/YgCxZY\nMBq1bN0aQRAEEok0CxZoufxyER5VVBxs0SPIM8/s4bnnuunq8nHeeQ2sWdPMOefUHXK5+MFivvK1\ns84SS9c+SvkaiIuWvb0+Nm0qAKRRdu1y09BgoaZGgVYbJB7vY3BwKz093dTV1bFkyRIWL15MZWUr\n2ayNwcEY27ePsXXrCOFwgoYGKyUlGjKZFD5fCLc7yNRUgmRSKIIksXtbASZJMBoVVFRYWLDAyYkn\nNrFqVQtLllQX/Suj0cSsXHL+fDLAxIQPjydILJZCoQBBSJFOxzEa1ZSWmqmuLqOlpY729mYaGqqK\nOafDYUKp/J8DA7lcjkgkXoRJPl+Q3t4h9uzpp79/hJERFy6XD78/RDYrQaXS5rsPS0gk0kilUnQ6\nNUqlHKlUhDPZbJZ0Ok0qlSaTyeRVYeIiqFwuQ6sVOxXbbAbKymxUVJRQXV1KXV05LS3VNDdXYzYb\nP3KOIwgC0WhsDljy+QL5ErcJxsbceDyiiXYwGCEajZNMppjdREeJTicu2luthS7NDiwWE2azAbPZ\nUJxbLEbMZiMWizHfcXjuMRiPJ4plcXOB0mzgNLOr9b5AaT4Vk8GgP6ZeOoQ4Boz+F0c2m8Xr9c8L\ngfZ97PMFMJkM+wU/M6GQw2EtEv5EIjkL8MxHqfcHgwKBMJlMNi+N1KNWq/IlOmKLzUQiQSQSJRgM\nIAgC5eUlVFeX09hYTUtLA01NddTWVlFbW4XJ9OEvrrFYPG/i7MPt9uFy+RgedjE4OM7QkKgG8vsj\nRCJiu06pVIZEIiGbFZBIpMjlYkt0iURCLieQTmdRKMROYna7ibIyK6WlljwEEi9g01BIHCqVlL6+\nfjo7d9PZuZsdO3bR2bkbqVRaBEKF7cKFLeh0hw8JBEEgEonj94eLw+cLz1ABzb14e70hVCrFrNWg\n+efiVquV09/fw7ZtH+R9h7YxNDRMe/siVqxYxooVy1mxYhktLc0kEpkiBJqcDOJ2B3C5AoyMeBkc\n9DA6OsXkZIRIJEUmM91prHA4y2QStFqxTM9o1KJWq0mlcoyOBlCrFbS1lbNokZPGRgdyuZxgMMnu\n3W62bRtlYMDPwoWlLF9exbJllSxcaCeddtHZub1YVjY4OMiiRYupqzselaqOUEhPd3eEkZEgxx1X\nPgsQVVXNLyH+MJHLCWzfPlE0q966VVx5LJhVL15cesQvWtFoij/+sZ/nnuvmlVf6WbDAxurVzaxe\n3UxDg+WA/3ZoKMazz46xYcMYe/fG0OlUJJM5Vq40kskk2LrVywkn2JDJ5GzbFsXjkVNTI+Waa8q5\n/voGdDo5fn+SZ58dZOPGfjo7A3zmM1XU1enYutXNG2+Mc9551VxxRQtnnlkxr1G3IAhs2RJl3ToP\nv/mNj+XLdVx9tYM1a6x57y4IBrNzSimWL9fyy18GuesuHy0tSm67zc6qVYfvX9Hdneb73w/w0ktx\nvvIVA1/7mhGr9eiCIoDBwQxXXx0iEhFVRQsWHHlV0chIjq98JUZvb45HH9Vy8smH9jcGB3OcfHKK\nhx5SsGbN0X9PjsU/Tzz2WJZvfzvDe+8pKSs7tHPkm2+mufbaOO3tMh58UEN5+ZEHmX//e4qrrgrS\n3q7g4YeNOBxHH5b6/VkeeCDEww+H+Zd/EcFRU9Ph3TynUgKPPRbkBz/wUV0t5/bb7Zx+uoY//SnC\nD37gZnhYLO296iorGo34GqPRLBs2ePnVrzyMjCS57DIHV13loKVl/9BmdDTCk0/2sG7dHgDOO68G\nQZDx0kujyGQS1q6tZ+3aepqajLjdKX7xi1EeeWSU8fE0Gk2EFSv0KBRS3nvPT1ubFY1GzZYtEZRK\nCdFoivZ2HZddVsUFF5TjdB4Y4o2Ph3nhhR6ee66b99+f4Mwza1izpoXzz2/AbD7yAPBIl68VIpFI\n88EHE0UF0qZNI3i9MZYtK6euToXBECaR6Ke3t4OOjg6AohKprm4hMpkTv19GR8cE27aN4XaHWbKk\nPJ83lZDLZZiY8PPBB6N0dbmYmAgRj2eRSIR8B7eCsjuHRCKab5vNGkpLjdTXO2hvr+Skk5pZvrwO\ni2X+G/R0OpMvJQsyOjrJ9u272bWrh97eEUZHJ/F4gkgkSpRKHYIgJ5HIotGoKC21zJun7pu/Ohwm\n9PpDW0w+UuH1+tizp5s9e3ro6upm9+49dHX14nL5qKioorKyirIyJ2azFYPBhEKhIRpNMDUVwe8P\n4XL5i36moo2FCO3EBiwCuVwub34uAj2pVPRcUquVGI0abDYjTqeN2lqxLK6xsZLq6jIcDit2u/mg\nhucHC0EQ8PunGB4eo7d3kL17++nvH2ZoaIyxMbEaJBKJYTQa0ev1aDSavApIQjabI5lME4nECQTC\nyGTSWRBpX7g0H2gqbAtKLL8/MAsuud2eOaqlwjaTycwLlGbOHQ5bvhrFglZ79Pxc/zfE/wlg9K1v\nfYvTTjuN00477X/66Rx2iGVPcyFQYT5zn88XwGw2zoFAZWXTXkCiTFCNTCYr0uP5wM5cCCTOczmh\neOCaTIY8ITYWSXFhbjDoSKfTRCIRAoEAXq8Pl2uS4WGxHX0wGKampoK6uup9RhV1ddVYLOb9nszF\n8rQIk5P+IgQaHxfVQAMDE4yMTDI5GSAYjBVPqFJpQWorFOuLRQIOSqU8L7HU4XCIHb5EE7vSYit1\nq9WAzWbEZjNhsej3e1LNZDL09s4FQxMTbhYsaJ4FhtrbF1JaWvKhJJvRaAKfLzQL/OwLgqbnIfz+\nCH5/GIVCVnzuVqsBq1VfhFozL57TCiETavX8ry2RSNDRsaMIhjZv3kZf3zANDa3U17fidNZgNjuQ\nSjV4vSEmJgKMjvpwu4P4/RFyOUm+XE5GLid2wRHLxgpm0hKMRjUOh4GyMjMWix6NRoUgSHC5wuza\nNUE2myuCoba2cmpqbKRSOfr7/WzdOsK2baOMjgZpb3eyfHnlLDjU0bG9qBzq7+9n4cJFtLYej07X\nTCxmor8/QUeHi5oaMyecUMXKlSIcamsrPWTvoX1jYiLMn/8smlX/+c99WK2aog/RaafVHvHVTAC/\nP87vf9/Lc8/t5Y03hvnYx8pZs6aFT3+6CafzwK2KC5Bo40YREhkMKiKRHCtXGhCEFFu3eli+3ILT\nqWfz5gi9vQJmc441a2x85zsLqKjQEI9n+P3vR9i4sZ833nBx9tnlfOxjdvr7AzzzTB8tLWauuKKF\nz32uHpNpflWi253iySe9rFvnIZHIceWVDi6/3EF19fTvu1xp7r/fw6OPTpu11ter+PnPA9xzj58V\nK9TcequNE044/It7V1eK730vyKuvxrnuOiP//u8GzOajD0UEQeCRR+LcdluYG27QceONh24+fbDI\nZgV+8pMU3/lOguuuU3HzzSpUqkP7G1NTAiefnOLaa2V87WtHz7vpWPzzxne/m+HFF7O89ZYSne7Q\nvp+JhMD3vpfgZz9Lcccdar70JeUR6yRYiHhc4FvfivDEE3F+/GMjF1xw9NVGIBpZP/hgmIceCvHJ\nT2q49VYTra2Hd11JpwU2bgzx/e/7sNlk3H67jU9+Usd778X40Y/cbNokNg/48pdtmM3Tx/vu3THW\nr/fwxBNe6upUXHWVgwsvtGEy7d/n8e9/d7N+/V6eeaaf4493cMopFUxMJPjtb4eortZzySX1XHRR\nLWVlWnp6Ytx77wC/+c0koVCaioo0J51kJhhM8847PpYssSGTqdi6NYJWKyUcTrJ0qZ5LL63kggvK\nKS098Gfi88V56aXpa+fJJ1eyZk0zn/500xFX/MLRKV+bGV5vlM2bR2cokUbQ6ZSccEIVCxaY0OvD\nJBKDdHXtoKOjg4GBAZqbm1myZAnNze1oNNVEozq6uwNs2zbK4KCfRYvKiursRYvKUKmk9PZ66Owc\n44MPRtixYwyXK4RKJQNy5HJi+WA2K3ZyEyOXz8Fl6HQKbDYdlZVmmppKqa8vobm5nOpqBw6HkZKS\n6dxUEASGh4fp6OjMjx1s376LsTEP1dUNVFXV4XA4MRisqFQ6wuHkHFVTJpOdlffOzYULOfP00OmO\nnk9ZLBajp6ePrq5uuroKQGkvPT39lJTYWbCghdbWJhYsaGbBgmZaW5txOOwkk+li6VwgIOb9U1Nh\nvN4gQ0MuBgddTEx48XpDhEJRYrEkqVSGTKbwGRQ6KItziURUMKnVcnQ6NRaLaBpeWemgvr6C6upS\namvLqKwsweGwYLEYD7nyIZFIMDo6McuQe9+h0aipqiqnrKwUu92O2WxCr9ejVqtRKJRks1mCwQhT\nUyGmpkIEArO3sVgCo1E/AzTNhUoFAFWYq1RK0ukMqVSy2JBpX7Dk9fqLlTBSqQS73VoESKK9yezH\nNpslb3kijv8LHkxvvvkmb775Jt/5znf+9wOj/xeex4Gi0NJwPuiz7z6vdwqTyVBU/JSU2LBaLRgM\nOjQadd5wTQ5IyGQyxQPI7w/Oq/iRSJglBZyGPdPbmSZp+/6sUJMqCELRWLq/f4iBgWEGBkby22HG\nx92UlTnmhUF1ddU4naWz/F1En6QAY2OiMXQB/IyNeXC7/UxOBvD7w0QiCZLJNCBFIpHm/23hfxFP\ndmItcEGuacLptFFebqOqqoS6unKamiqoqirFajWg1X60ZE4QBFwuNzt3ds0CQ3v29FBWVjILCi1e\nvIjGxnqkUinRaGIG1Anj90c+FAgqgJ9p+KPfBwSJMGj2Y8N+4c/+QlSphRkZmWTTpg62bNnF7t39\nDA5O4PNF0GrNKBR6MhkZ0WgalUo09FOrlcV28/F4mkgkRTKZQalUIpeLtduJRAajUY3TaaK21kFt\nrQ2bzYRMJiMcTjI46KO7e5LeXg82m46WllKam0tobi6lra0cp9PE2FiI7dtH2bZtlK1bR5mcjLBk\nSfkMOOQgmZyYBYd6e3tZuHAh7e3LsVgWkUrZGBpKs3nzGMA+pWWVR6TTWDKZ4W9/Gy6aVQ8PBznj\njLpiqVlNjfmw/8Z8MT4e5ne/6+G55/ayebOLM86oYfXqZj71qUYslgO/rgIkeuopERKZzWqmpjIs\nX25AociwbZuHhQuNLF1qZ9u2MJs3J5FKc5x+uo5vf7uFj33MTiaT4/XXJ9i4sZ8XXhhhxQob559f\nSTic4Omn+4hE0lx+eTOXX95MQ4Np3ueRTud4+eUA69Z5ePvtEJ/5jJWrrnJwyimzL7R9fcliO+hL\nLrFwww0OrFY5P/7xFA88MMWqVVpuvdXG0qWH/3nu3JnizjsDvP56guuvN/KVrxgxGv8xpVbDw1mu\nuSbI1FSO9etNLFp05KX3O3Zk+eIXY6hU8MgjWlpbDx2CJZMC55yTYtkyKffdd8w34FgcnRAEgauv\nzuDxCDz/vOIjgdOdO7N86UsxpFLx+75w4ZGHvu++K6qNli1T8NBDRuz2f8z5IhTK8eMfh7j//hBn\nnqnhtttMLFx4eOAomxV45pkwd97pRaORctttNv7lX/R0dSW4665JXnopxDXX2PiP/3DgdE4f+5mM\nwB//KJ7L//KXIJ/6lIWrrnJw+unG/QKQWCzN7343yPr1e9m61cNnP1vPokU2tm6d4sUXRzj+eDuX\nXFLP6tXVGAwK3nsvwPe/38trr4XJZJIsXargYx8z090dZtMmP4sX28nlFGzfHsFslhEIJDj+eCNr\n11ayZk05DseBPR/D4SSvvCKqc//4x36WLClhzRpRnVtdPf817HDjaJSvzQxBEOjr8xXL2DZtGqGz\n00VTk52VKys57rgyLJYYodAAnZ0iRNqxYwdarZYlS5awYMFiTKYG0mkLY2NpPvhgnL17J2lqcnDc\ncRVFkNTa6mB8PMju3RN0d0/S3T3J3r1uurvdyGRS7HaxnDqdThONJohGE8RiqXwXYAFBEH2UCuol\nuRx0OhU2m5aSEiMVFRaqqx1UVdkoLTWj1ysIBj1MTAzT39/Dzp2i0bbJZGTJksUsXtxWNNmurKxi\naiq6X/sFrzeULy+bzs/T6Wwx194XJon5+Nx9VqsBo/Gjl79ns1kGB4fp6tpbVCV1de2lq6sbqVSa\nh0gteYjURGtrM7W11R8K4iQSKfz+UP6+S1xwHxgYZ3jYjcvlx+8PEw7HiMdTpNPZvHJp39chqpjE\n+y4Fer0Gq1X0jBU7LlupqLBTVVVKTU0Z9fXlOByWA/p7CoKAx+NjeHg2UJoJmAKBEJWVTqqrK4qj\nYNBdXV2B01lKJpPNQ6QwU1PB/DY0az4NmsTfKcwVCvm8UMlkMmA06jEYdPn7KyHfUTlDOp0hkUgQ\niyWIRqN5TygRLvl8U/h8AeLxBFaraT9AyVwESzP3Wa3m/TZV+p+M/xMKo/+J5yHK8AL7Vf/M3Dc5\n6c/DDCtmsxGj0YBWq8nDHxkSiZRsNkcqlSaRSObpcbBIUtVqVb6NorE4Cm0Vp+fGGWBo+ov+YU2m\nAYLBUBEAiWBoej44OIJOp6Wurpr6+ppZMKi2tgqbzUY4HGd42J33AHIzOjo5C/4Eg2IZWCKRzq86\nFJQm5P2KxHrpbDaLRCJBr1djNhsoK7NSWWnPAyAnjY2VNDRUUF5u/9CGcIfyuY6MjLJ7997i2LVr\nD7t39yCXq6mrq6eqqoaSEicWix2VSkc0mpwX/vj9YeRy2X4vMDNVQIcLfgqRy+UIBmN4vSF8PvE5\nFcrBxK3YSnV42I3bHSASSSGVCmSzKVQqOXq9Fp1Oh1qtARREIgn8/hggwWzWo9EokUikpFJZQiHx\nsywvN9PQUMKCBeXU1NjRaJRks6JhY3+/N58wTJLJZGlpKc2DIREOtbSUUlNjxeWKsHPnBDt3TrBj\nxwTbto0SCMSLycjy5VUsWuQgHh9n+/ZtxbKynp4eWltbWbZsBWVlbeRyTsbGcmzZMs7QUIClS52z\nAFF19f6VbIcSqVSWzZvHeOutId56a4j33hth0aKSoln1ypUVyOVH54ahp8fP88938/zz3ezd6+dT\nn2pg9epmzjmn/oCy9lxOYMuWAH/4g4vf/95FT08cq1WDx5Nm2TIDanWODz6YpK5Ox+mnO9mzJ87r\nr4eJxbK0tcm48cY6Lr20DoDNm71s3NjPb34zSGWllgsvrMVgkPHiiwO8956b1avruOKKFk45xbnf\nG4XOzhjr1k2yYYOP5mY1X/iCg89+1lb0JgJxxfvll4P84hd+/v73KP/6r3auu86OXC7lgQf8PPxw\ngHPP1XHLLTYWLjx88/cPPkhyxx1B3nknwQ03mPjylw3o9f+YGz9BEPjlL+PcckuY66/XcdNNR15V\nFI8L3HFHgkcfTfH976u5+uqPprjI5QQuuSRNOg1PP6044qqNY3EsZkY6LXD++WkaGyU8/LD8I53D\nRS8wsQPgv/2bkm9+U33IirqDRTwucNttYZ56KsHDDxtZvfofozYCCIdz/OQnYe67L8ipp6q5/XYz\n7e2HB45yOYHf/S7CHXd4yeXg1lttXHCBgdHRNPfdN8njj09x1lkGrrnGyplnzu466fWm2bBBVIsG\nAhmuuMLBlVc6qKvb/3syMhLh8cf3sn79XhQKGWvXNmK363jllTHefNPFOedUsHZtHeeeW4lcLuXZ\nZye4++5+tm9PolKl+MQnDCxfbuSttzx0dARpb7eTTMro7Ixitcrw+xOsWGHkU58q49xzS2hrO7Dn\nSyKR4bXXBnnuub28+GIvdXUm1qxpYc2a5oP6/x1O7Fu+5nBoOfXUGk47rZZTT62lvNxw2H8jmcyw\nY8dEUYW0adMILleE5csr8orrSsrLJbjdvXR0dBTH+Pg4ixYtoq1tCXZ7K+DA55Oxe7eXzs4JqqrM\nHHdcBe3tTtrbnbS1OamuNuP1RovwaBokTTIw4KWszEhlpRmLRYtEIhCNxpmaiuByBfD5ouRyAnK5\nFEHIkU6nAVCpZCgUEiQSgUwmQzyeRKNRYLfrMZvVqNWQycSIRv14PBOEwz7q6spZtKiB5cvbOPHE\nZRx33GLM5v0v5iUSqXxp2NzcfnrM/Xk0msBimR8yHQhAmc26/YIfQRCYnPQUlUhdXd3s3dvLnj3d\nuN0eGhpqaW0tQCQRJLW0NGIwfPTvSiaTyTex8ebv7cbzlR0uxsY8eL1BAoEosVgCQRDyz13sPpzL\nCeRy4vMGETYoFIUucmpMJh1Wq2jn4XTaiobf9fXl1NSUYbfP9qmKx+OMjk7MC5OGh8cYGRlHp9Ps\nA5IqZwGm0lLHvOBqpn/TTKg0NRUiFIrMGuFwbJ/HUUKhKKFQhHQ6g8Ggw2jUYTTqMRr16PVaVCoF\nCoUcmUyatzrJkc1mSKXSJJMpYrE40WiMUGi64kdkBgeCTPuqmyxoNEf3enMMGM0TwWCIbdt2zYE/\nY2NuJiYmcbtF0y+1WlWEP2q1GrlcXlTjpFIZEokk0Wg8r/SRFMGO1WreB/wY54U/VqsIgI5Ux4BE\nIsHQ0OgsddBMtVAymaK6upqyMicOhx2z2YpOZ0AikROLpfNEXuwmEAxGCIcTxONJ0uksAIIgyk1l\nsoIPkKT4fmQyWVKpNFqtcoYKyE5tbRkVFQ7Ky+04nfb81nZUQJBoUiee3L3eEN3dA3R1FUzqRMI+\nNRVGJlOhUmmRSBRkMmKNuEqlxGo1YLFMw5258Ge2CqhQYvVRI5VK4/dHZsGfmcPrnbtvaiqCXq/G\natVjMunQ6dRks5k8/RZPRpFIArlcg1SqJp2WYDKpcTptGI06lEoFuRzE42kCgTguVxCZTEpjYykN\nDQ4aGkqoq7NjMGjJZHL4/TF6ejzFRMDlClFfb58FhApbm03H8HAgD4Zcxa3YOtZEW5uTtray/LaE\naHScbdu2FuHQ3r17aW5uZvnyFdTXL0Emq8LtlrJ16wTbto1TVWWaBYfa28sOu7SsEIlEhk2bRouA\n6P33x2hqsnLqqTWcemotq1bVYLUenfpmQRDo6Jjkuef28vzzPXi9MT7zmWbWrGnmtNOqD/gafb4U\nr77q5pVX3Lz88iRqtRyNRonLlaK9XY/JJNDR4aGsTM1551Xg88GLL/pwuzM4nWm+8IVybr55AXq9\nku7uIBs39rNx4wCCILB2bT0LFhh5441Rnn22n2XL7FxxRQurV9eh080Prvz+DE89Jd5EuN1pLr/c\nzpVXOuZ02+ntTfLLX/pYv95PY6OKa66x8dnPmohGBe69188vfhFg9WoD3/iGjcbGwz8/btmS5I47\nAmzenOLrXzdy7bUGtNp/nHnz6KioKvJ4RFVRe/uRV+y8/rro6XLccTIeeECD0/nRX98tt6R5++0c\nr72mRKM5BouOxdGPUEjglFNSXHKJjJtu+uirr2NjOf793+Ps3p3lkUe0rFp15Fdy33lH7KS2cqWC\nBx80YrP9484l0WiOn/40zL33hjjpJBW3325i6dLDg+mCIPDyy1HuuMNLKJTj1lttfP7zRiKRLE89\nFeAXv/Dh9Wb4whdsXHWVlerq2efkDz4Q/eg2bvTS1qblqqscXHCBFZ1u/zfH77zjYv36vfz2t/2c\neGIpn/tcA7GYwDPPDNLZGeCCC2pYu7aOVavKSCSyPPBAP488MsbgYI7S0iz/3/9no6FBwwsvjLFn\nT5j2dgfhsIQ9e2I4HAqi0RQKhcD555dy7rklnHGGA7N5/9eSTCbH228P89xz4mKN2axmzRrxOrx0\n6ZH3ISxENpujs3OSt94aLOYfNpummHucemoNVVVHRvnk98eKpWyiH9IoKpVsVsl+S4uJgYG9syBS\nZ2cndrud9vYlVFS0oVBUEImoGBtL0tXlIRiMs2iRmNsVIFJ7uxOHQ08mky2qzfcFSn5/lIYGB3V1\nNmw2HVqtIr8oGmVoyMvgoJfJyRAajQKtVolEQlG9lE5nMBpVGAwqVCo5gpAjHo8TjcaJRpOk0xkg\njUKRw2hUU1JipqqqhPr6ShobqyktNWGziXm+3W7EZvvwyqF0OnMQ0DT/z0KhWL65z8EVTRaLHrNZ\nj8mkRaGQMj4+Rnd3L3v29BQ9k7q7+zCbTXMgUmtrE5WVFR+pq+/+IhKJ4XL5cLn8uFw+JiZ8+cc+\nhofdjIyIAoJQKIZcrsh3Y5MiCCKYzmRyZDJZstlc3mxdUvRj0mqV6PUazGbx/qtgI1JZWUJtrZPK\nSgc2mxFByDA15d9v2VswGD6gSqmqqhyt9qN7XqbT6VkASZx/ONi072OFQpbvuqdCqZwfOKXTosgk\nHhf9gGUyKSaTkc2bn6e6uvyIfbaFOAaM5olf//olvvrVO/Kt2oW87CxFNpvFZBJrI+12C1araR74\nMxf8WCzGo07+QJQyjoyMsXNnD7t399PTI7Z9Hx1143L5iEQS6PVGdDo9crkKQZCSSuXybR9TZDLZ\n4kEM4sEr0nwBpVKOQiEvqiYK7SJTqRQWi57SUlsR9pSWWueMkhILDsfhyexmQp/pEZ71WKznnf3Y\n5wsSCsWRySTI5ZDLpUil4qhUovqnrEw88TQ0VNHaWk9lZQkWix6LpXBS1h1WR4ZpT6L5IU/BmHrf\nffF4Kq8+MuQBkB6tVpVv2Sll2jQuQzyeIhCI4XL58XrDRCIpJJIcuVwctZq8T5CdkpISzGYLyaSA\nzxdhdDTA0JAXm01PQ0NJfohgyGbTk82CyxXKy4vd7N3rpq/Pi92unwOEmptFtZBMJsXlCs2CQjt3\nTrB7txuzWTMDCpXR2lqCWh39/9l77yiprjNf+6kc9Z7Y2wAAIABJREFUu6q6ujrnTJODAIECKBOE\nAr4KBmwJCQnPLN8742WPnCWPZc+MZ2wvz9zra8mAACUrgoQIIkgCgZCMJTJ0zrm7cs7n++NUV3fR\nDQLRoLnr413rrLPPOQVdXX3q7L2f/Xt/L21tTZw9e5ba2lpOnz5NXV0dlZWVzJo1i8mTZ6JWl2Cz\nqTh6tI+//rWTaDSeAodmzy7AZBo/YOP3R/j0087kAO2LL3qYODEzOUi78caiK2KMORSxWJxPP+1m\n69YGtmxpQCqVcP/94uD0+uvzz6voiMcFjh51snNnPzt39nH6tJf8fB2BALjdMaZP1yGXx6ittWEw\nKLj//gIUCjVvvNFPQ0MEjcbHvfem88wzk6mqMtHX5+e111p55ZUWOjt9PPxwKbfemsOJE4O89FIj\nEgk8+mg1q1ZVUVg4tk9SLCawb5+LF14YYPduF4sWmXjssUxuu82YUu0rGIyzZYuL9ettnD4d5Nvf\nTufxxzOoqVHT3Bzmf/9vBy++6GLFCgNPPZVBUdHlQ5XPPgvy7LMuTpwI88MfGlmzRp80db0aIQgC\nmzYFeOopD//wDzp++EMdCsX4Tjxstjg/+EGQDz6I8Mc/alm27PI+t+eei/L738c4fFiJxXINFl2L\nqxddXQLz54f4939X8PDDl7cYsHVrmP/1vwIsXqzgN79Rk54+vt97v1/gpz/18MYbQf70JwP33HP1\n1Ebiz4/z5z97+Pd/dzN7tpKnnzYxa9blg6O9e/08+6yVvr4oP/pRBitWGNBopBw75mfDBjt/+YuD\n2bO1rFmTwT33GFAqhz/XUCjO9u0ONm4c5JNPPCxfLqYf33DD+X0+fL4IW7e2snFjPSdO2HjooXIW\nLy7i7Fk3r77ags0W4uGHS1m5soxp08z09oZ45pmzvP22DadTSnW1hJUrc1EoBN58s5OWFh8TJmQA\ncs6c8WMwyFEqBXp7/cyaZWDx4mwWL85m2jTjBfvZI0d62LKlgbffriceFxLwqJp5887fP49HxOMC\nZ84MsH//MEAyGFQjFEjF45YCLwgCra2OpJn2X//aycmTfZSVmZkzpyA5/powwUJ7e1sKQGpoaKC1\ntRWLxUJpaQ3p6RUoFDn4/VoGB+M0NTlRqeRMnpyTApEmTcpBpxPvU683SFPTYFKNNASU6uv7UShk\nVFVlU1mZSU6OAZ1OVLr6/UE6O+00Nw/Q3DyIw+HDbNZhMKhRKmUIQpxgMITL5cPl8mM0qlCrZcTj\nYUIhP36/j3A4hEajQa3WIJcricel+P0RwuFockxusaSNAkqj2xdWDZ0bok+PfxRIGulTOnJzOn2J\n38NHMBjBYNBiNGoxGnUYjToMBi0KBcRiYQIBP16vE7vdyuBgP36/l6KiXCori6iuLmPq1GqmT59I\ndXUlGs2VM3eOx+M4HB76++2JDBTHqHZvrzVZQQ8EtFpNohK1NAGXYkQiokdWJBJFEEYWzRFQKhXo\ndCrS0jSkp6dhsRjJzk4nK8uETqdEKo0TDPrxeNzY7TYGBvrp7BRVSmlpuhSQVFg4DJNEj6Wsq1K9\nOhAIjgBOvjHg02jYNJR+9/7768jJyRz393UNGI0RAwM2Pvnk6Cj4o9Ndflnmiw3R6NmH3e5OPCxE\n87b29h5aWrqS6V42mxu3eyjnVACkCSorlhwXpXAypFJJAnyFCAQCRKMx1GolKpUiefOLss4w8biA\n2SxS3Ly8THJzLYnKYKkAKDvbjNlsuCRKHYlE8XgCuN1+3G5/CvA5F/aMBYSUSnlS6jkS6hgMGmKx\nED6fB5dLfAD09HTS3d1FXp6FyZMrmTSpmokTJzBxomgmp9df2Ah4rIjFYjidvkuGP3K5LNmJDG1G\nowaVSplUpsXjEI3GEp5AQZxOPwMDbgYG3FitHlQqBVlZBrKyDJhMGqTSCKGQG4djgJ6eTgYHbWRl\n5ZCTU0B6ehYymR6fD9rb7QwMeCgqMqcohcrLs8jPTycWE+jocIySCsdi8VFAqKoqi8rKrGSH7nD4\nRymGTp/uRSKRJAYBIhyqqspAqfTQ3d2SBENnz56lqamJ3NxcampqmDhxIpWVE9BqC3E6tRw/3s9f\n/9pJa6uDadNymTu3ILnKVVKSPq7fRa83zCefdCQHYCdO9DF1anYSEN1wQyFpaZef8nShCIdjfPRR\nO1u2NPDuu41kZWmT3glTp57fLN1uD7NnzwC7dvWza9cAKpUco1FFT08Yk0lOcbEStztAfb2D66/P\n4LbbctBoNLz9dj+ffeYHvFx/vZof/7iKRYuK8HojbNnSziuvtPD55zbuvbeQ++8vxm738/LLjRw/\nbuXBB8t55JFq5s49//tqbAywceMgL75oJTdXwerVmXzzmxbS01Oh8alTAdavt/HKKw5mzRInGvfe\nK6YKbNvm4bnnnBw/HmL1aiP/+I/p5OVdPij65JMgv/ylk7q6CD/+sZHVq9PGPT3ly6K7O8aTT7rp\n6YmxebORqVPHV1UkCAJ/+UuE738/wIMPKvjVrzSkpV3e77h9e4wnnohw6JCS8vKrB9auxbUYipMn\n49x+e5i33lJy882Xdw+6XAI/+UmArVsj/OEPGh54QDHuY7yDB0Vvo3nzFPznfxowm6/u9yYQiLNh\ng5ff/MbFtGkiOJoz5/L7sgMH/Pzbv9k4ciTAypVGnnjCyJQpagKBOFu2OFm/3s7Zs0FWrRLB/8SJ\nqcCstzfMSy9Z2bhxgFiMRIEDCwUF539v7e0eXnyxgU2b6tFoZDz6aDWzZ2ezZ4/oo6fRyFi5Uqy0\nVlqaxmefWfnFL+r56CMf8biU+fM1PP54IaFQmPff72Pfvn5ycnSYzTq6u6N4vTHy8pTY7UFisRiL\nF2exaFE2d96Zhdk8tvpIEAROnRpky5Z6tmxpYHDQn1jcqWbBgsJxUzmfL+JxgdrawRSApNUqEmMX\nESKVlIxPKj5AOBzl1Kl+/vrXjqQnUleXi5kzh1PZ5swRK8vG43E6OjpobGykoaEhZd/R0UleXiUW\nywTU6nzCYQN2u5Tubj95ecYUiDRlSi6VlZnJz1JMz/KMGrM2NPTT0iKmuA2NWUtLMzAa1chk4PEE\naW+30tpqpaVlkJaWQQRBIDvbQHq6lrQ0FUqlLOEP68JudyV8fSJEoyCRxNBopKSlqTGZ9JjNoihA\nLpcl0uXE1LjhKmde3G4/JpPuvEBprPMZGWkoFJe2uB6JRHG7/UmA5HKNbJ977Mdmc9Hfb8dud+N2\nBwgEwsRiAhBDJiNRoViTUPSIi+o5ORZMJl1S2TQEpsRNPB7PanSiSMA/JlQabjvo67PS3+9IGF9r\n0WrVyGTyRPVrES6FQmFCoQjBYASQoFDIkUhkyXmXTCZFr1ej06nRalVoNHLkcgkSSZRQKIDX68bh\ncOD1ehKm4FmUluZTWlpIYWFeClQym8d3fvLfJa4Boyscw6XOh8CPqHgZpsap5wcGnAlFjB+FQpbw\nsIgRjUYIh0PI5VJUKiUqlRyZTJZIf4sRDIYIhyNoNOqkIbEgiA93vz+U8NIZhkD5+VnnhUAGgy7l\nZo/H4/h8wSTkcbv9KdBHlNmNfe3cY1EmKpZJT0vTJqDP8DYMgvQpQGhoi0Yj1NU1cvZsHWfP1ifK\nVNbT3t5JaWkxEydWp2xVVRXnpeXhcGRM8DMW8Bk653L5MRi0KQ/2oYe+waBFqRQpuCCI6p9gMIrf\nH8Zu9zIw4GZw0J3cAwkAZCQry5CoDGFIaWdmGgiFvJw4cZbPPz/LyZPNNDf34fHE0euzkEr1BAIS\nQEpxcQbFxRaKijIoLDRTVGRO7DMQBGhpsSVXZ4Y62f5+MYXsXF+hqqosMjOHV/18vhC1tf2jwJDb\nHUxKjSdPzqG83IRC4aa/v5Xa2tokGOro6KC0tDQJhmpqaigrqyIcNlFba+fYsR6OHu3m7NkBCgtN\nzJ07tHpVxNSp45daNhQuV5BDh4YB0ZkzA8ycmZsERPPmFVyRSmbnhs8X5v33W9i6tZEdO5qoqbFw\n//0iJKqoSB/z38TjAsePu9i1q5+dO/s5ccJNaameeFxGW1uAykoNOh20tTmQyWDJklzmzcvEbpfw\nl7/0cvx4AAhQWBjjf/7PYh57rBqVSs6uXV288koLe/b0cMstOTz8cBkmk4zXXmvinXfauPHGHB55\npJply4pRq8cezHg8Md5808YLLwzS2Bhk1SoLq1dnMnmydtTrXn/dybp1Nrq7Izz2mJnHHjNTUqKi\nrS3MunUuXnjBSVWVkrVrTSxfnoZaffkTrQMHRFDU2hrlJz8x8u1v61Eqr27HLggCL74Y5Ac/cPPd\n7+r4yU/GX1XU1hbj7/4uQHd3nHXrtMyde/lpN59/Hmfx4jDbtyuZO/caLLoWX1/s3Rtj1aoI+/cr\nqam5/Hvx8OEoTz7pp7RUyh//qKWoaHzvb58vzo9/7GXLliDPPWfg7ruvrtoIRJP6F17w8K//6mLi\nRAXPPGNi3rzLfx9tbWFeeMHFhg0uiorkPPmkiQcfNKDTSWlqCvHCC2JqcUmJkjVrMnjwQRN6/XB/\nLggCR4542bhxkDfftDN7to7VqzO5917zeZ/58bjAoUO9bNpUz9atrdx4Yy6PPFKFxaLlzTfbefPN\nNioq0li5sowHHyzFYlHx0kut/O53rZw+HUUulzNjhopHHsmnvFzDhx/2s2tXL+3tAUpLTYRCMtrb\ng5SWapBKY7S0eJkyJY3Fi7NZtCib664znVdF1NhoZ8uWBrZsqaepycGyZRUsX17NHXeUoNFc+eIA\ngiBQV2flwIH2JERSKKRJ9dGCBSWUl4/vhNbpDPC3v3UlDbWPHOkkFhOYMSOXmTPzmTkzjxkz8igv\nNycXmMPhMK2trUmANASTGhqa6O8PkZVVg05XjCCYcbkUOJ1RysszmDmzMCW1rago9XeJRmO0t9vH\n9Euy2byUl2cmx7mVlVnk5hpQKGQ4nT7a2sQ0t/Z2G21tIliSySSJcbWZtDQ54bAXl8vG4GA//f19\nDAw4SUszo9OlI5NpiUZleL0imLBY0sjMNJCeriMtTY1Wq0SplCUyBES/1lAoit8fTFQ88ya8UL1o\ntaqU+cVYKqb0dF1ibiTujUbtZalfotEYdrubM2caOXWqntraZpqbO2lr66GnZ4BoFNLTM0hLM6JW\n65DJxKrGoVAMtzuQUDqFSUvTngOUhtsmk25U+9xzGo3qK92foVCYgQHHlwAme8J+xI1Op0kAJrGY\nlCCIf5NgMEwgEMbvDxEIhABJYnFfgUQiJR6PE4nECIdFOxa5XIpMJiAIMSKREBAlLU2D2WwgM9NE\nbq5oAl5WVkBlZTE1NWXk52edt/r2f9e4BowuIfz+4JcCn7HOK5VyzGYDJpM+WXIyEgkTDAYJBHz4\nfH78/gCBQBCpVIpUKiMeF53YRTikQqkUIZBYfUq8kZVKRYL+msnLE2/InJyMJPwxmYb8lVREIrFL\nAjsjX+vzhdBqVSNAjybZHvtYe97rarXyoh4Ebrc7CYNqa4cNqHt7+6msLEsAIVEtVFNTRW5uPm53\n8EvVPiOPQ6Gx5aVDm8mkS6p/YrE4kUgcny+E1ephcFA0kx7aDwy4CYej54AfI5mZaWMAIfG8Tqcm\nHo8zOOiho0PsoI4fb+LEiSaamvro63Pj8cSJxxWo1QIWi4aiogwmTSpm6tRySkqG4VBampquLidN\nTWLVseFtgOZmK5mZ+mQFspGqoaIiM3L5cAcTDkdpaBgcpRrq6XFRXZ2VVAyVlOhRKNzYbG3U1dUl\nVUMDAwNUVVWlgKGJEydiseRz9qyNY8d6EnCoh5YWO9XVFmbOzGfGjFxmzMhj2rRc9PrxV/LY7QEO\nHmxPAqL6eitz5uQnB1Bz5+ZflcHc0HsRS/g28OGH7cydm5cs4Xs+M0unM8zevYPs3Cn6ESmVcnJy\nNFitURyOKBUVasLhIM3NTubMMbN4cS4TJpg5csTDa6/10dYWAdxUV0tZtSqfb36zgsLCND7+uI9X\nXmlhy5YOpkwxsWJFGTNmpLNtWxsvvdSA0ajikUeqWLGikpycsXO743GBgwc9bNw4wLvvOliwwMDq\n1ZksWWJCoRge8IsTAz/r1tl4+20XCxfqWbPGzKJFBgQBduzw8vzzTo4cCbJqlYEnnzSNi5G1IAh8\n+KEIinp6Yvz0p0ZWrtSPO6S5mOjpEVVFnZ2iqmj69PG956JRgf/8zxD/+q8hvv99FT/4gWpcfs/W\n1jg33BDmT39ScO+9V3bF/Fpci4uJTZui/PKXMT79VEl29ngUMhD4938P8Yc/hPj5z9V897vKlJTZ\n8YgDB8I89piLm25S8Ic/GDCZrj54DYcFNm/28i//4qKiQs7TT5u46abLB0fRqMDOnV7WrXPyyScB\nHn5YfIZPn64mGhXYtcvN+vU2Dh708Y1vGFmzJoM5c1JV+4FAnK1b7WzcOMixYz4eeiiD1aszmTVL\nd95xo9cb4e23W9i0qZ7Tp+1885sVrFxZidUa5i9/aWX79k7mz89ixYoy7ruvCKVSyosvtrBhQydf\nfBEkFlNTUSHjoYdyuO++bI4ft7NrVy979vRhNuvQ6TR0dITJylKSmSmnv9+P2x1h0SJRfXTXXVnn\nrbzW2enmnXfEtPKjR/u5665Sli+vYsmScgyGK6tYHgpBEGhstCfh0f79bUgkJP2PFi4sobLSPO6K\niN5eN0ePDo/3jh7txuEIMG1aLjNn5iXGfXnU1GSmjEFBLDnf3NycApNqa5uorx/A61VjNJYhlWbh\n82mIxSRUVKQzfXohs2eXMmVKHlOm5JKRMdoH1ecL0dg4MKZfklQqoazMklDgi/uyMgsWi45QKEJn\npz0JlIagUmurFUEQyMnRo9dLkEj8+P1WBgfb8PlsVFUVUVZWTl5eMSZTNhqNEa83OmruMDjoJhaL\nJ+cGQ5BJp1OhVstRKGRIJCRUTDECgSAulx+Hw5dUMjkcoq9sWpp6xCK77pz9+dq6i0qds1pt1Nc3\nJs22Rb+kRjo6uigqKmDChEqqqiooKiohNzePzMxsJBL5KLXTcCqdH6fTe05bFBacDy4ZjdqEwmlk\nW5t4zXD7y2xEYrFYUmU1NmAS91arE6vVmRA7iAoq0VdIjlQ6ZAsSJhgMJyv/BYMhVColCoUikUYn\n2kxEo3FisXhCySVFIgGlUoZWq8Jk0mE2p5GVNTSfF42/RdHEkG/V8Hbud+ZqxDVgNEacPt3KM89s\nHAGCRAAkCAIZGcaksbFer0GrVaJQyBLmXXF8Ph9OpwuHw4nL5cblEh3zQ6HY0PtFLpehVIo3k0g1\nJUSjcfz+IEqlIlGe0ExmZnrCZV2HWq1CpVImvtBi+pLPF0z5op0LgGQy6UWDnQtBIL1eM67maCPD\nbndw9mxdEg6dOVPHmTON2O1+iopKyMsrxGLJRq9PR6XSEYtJcTh8o+DPuSlfIoHXpxwP0XdBIAl/\nBgdTVT8j9z5fKPnwHgI+I1VA4sN9+DgtbbQU0+MJ0Nlpp6PDTkeHLdG20dFho7m5j95eD3K5gEwW\nIhSyo1bHKS7OoKamiNmza7jlluuYMWMCcrksuXLS2DiQhEFDYKitzUZWVhoVFZlUVGQl9pmUl4v7\noRSyoYjF4rS22kYphpqbbZSUpDN5sphLXlCgQaFw43K109AwDIa8Xm8KEBral5SUYLX6kwOFocFC\nf7+XqVNzkitNM2bkMWlSNirVlSkdabX6+fjj9qRRZEuLg+uvL0gCotmz867Yzx4reno8vPNOI1u3\nNnDkSC+33lrE/fdXcffdFWOaZQuCwMmT7iQgOnbMRWWlAZVKTkNDAL1eisUipbfXg0QSY8mSXO66\nKxe9XsNbb/WzbZsVlysKuJg7V8tjjxVz772laLUKDh3qZ+fObt54o5WMDBUrVpSxZEk+hw/3sXlz\nPU1NblasqOCRR6qZPt1y3t+poyPE5s2DbNo0iFYrZfXqLFatspCVldpR2+1RXn7Zwbp1NgKBOGvW\nZPDoo2ZychR0dUVYv97J+vUuiooUrF1r4sEH08bFR0gQBPbsEUGRzRbjZz8z8fDD41957GLfy8sv\nB/n+9z185zsafvaz8Vc2HT0a5YknAphMEp57TkNl5fgMKOx2gfnzw3z3uzK++93/fqVer8X/f+Of\n/znK9u0x9u9XotONz/epvj7G2rV+/H5Yt07LtGnjOzD3euP86Ede3n03yPPPG1my5OqAg3MjEhF4\n6SUvv/61qAx65hkjCxaoxwUcdHZGeOEFF+vXO8nNFVVHDz9sQK+X0tsbYfNmOxs22FCppKxZY2bV\nKjMWS+qz5dz+5dFHM1m1ykJ29vlX5Vta3Lz4Yj2bNzeQlqZg9epq7ruvjM8+G+SVV1o4dKifO+7I\nY9myQhYvLiAjQ8Xu3V38n//TwoEDHgIBDVlZMpYuNbN2bTGBQJD33+9j585empuD5OWl4XZDNAoT\nJmiJRKKcPeuiulqfUB9lMXeueUzQODjoZ9u2RrZsaeDgwU5uvrmQ5curuOeeSiyWr260e6khCALN\nzY4UgBSNxpMKpIULS6iuzrgiKTV2uz9lXHj0aA+dnU4mT85mxoy85OLhlCk5qNVjT/jdbndKatup\nU42cPt1He7uXWCwdpTKXUEhcnC8tTWPKlDxuuKGaOXPKmDgxB6129P0jCAI2m4/m5sHEZk1pOxx+\nSkoyKC+3jIBKIlhKT9fS1+dKmnC3tYmLvy0t/bS2DhIKRdHpQBC8+HwDaDRxysqymDKlhOuvn8QN\nN8ykpmYCkUh8xEK0O2lHMdx2pRwrlfLEnCQtOTfJyBDtOTSaIVNp8W8Yj8fw+0NJwCRuvpS92x1A\nr1dfEmQaOqfVKmhv70gx3B5qK5XKFMPtiooyKivLKCsruWD2x8g0uiGQNLQfeS4VQA23FQr5CJCk\nGwWUxoZRw22DQZsy7w0GQ9hsLmw2dxIiDbVtNhdWqyu5H7oeDIYxGLTodBrUamXSHkY0YA8mDNgD\n+P1hgCQEEqFSDLlcgUKhQKFQJjyapESjcQKBCFqtKgUijWz/9KerMJku3XLly+IaMBojzpxpYf36\n94jFYoTDIfz+IF6vF7vdRV+fjf5+G263L2ECLUtWAYtEIkgkssQfV4EgSAiH48hkskSZvTR0Oi1K\npSJh/jzsWxMMRvD5Qkmlj1arGkVSv0zedy7wuRyj5q8SgiDg9w//Dh7PcBpbe3sPTU0dtLX10N09\n7L8UiYBGk4ZUqiIalRAMRtHr1WRmjq5QcG4KmNEofqFjMQG3OzBK9XPu3uMJkpGhTwFAF9qbTOdf\n1QIxZ7i725kCgYbg0NC5cDhKQUE6RqMcuTxMMGjHZuuir6+FgoJ0Zs2awOzZ05gxYzozZkwjLc1I\na6t1lEqoqWmQzk4HubnGJAwaCYbKysRy9mP9Tbq7XecohnqprR0gK0vP5Mk5TJqUQ26uEoXChcfT\nSVPTMBiSSCRMnDgxBQpNnDiR/Px8ANrbncl0sqFBQDAYTUKhIUBUVWVJyHCvTPT1eVMAUWenmxtu\nKEwColmzcq+4l8C50dTkSJhW11Nfb2fp0nLuv7+Ku+4qHTPdzeWKsG/fALt2iX5EcrmUkpI0fL44\ndXV+CgqUSCQROjpcXHediSVL8liwIIvu7hgbN3bx4Ydu4vEwcrmHu+4y8vjjZdx6axE9PQF27eri\n/fe7OXCgn0mTTCxalM999xXR0+Nl8+Z63n+/k9tvL+CRR6pYtOj8vgsXuwIcjwscOOBl/Xo7O3a4\nWLrUyJo1ZhYs0CMIsHu3j+eec3LokJ8VKwysXWtiypTxSdMQK/oE+OUvnfh8Aj//uZEHHtCNu1rg\nYqOvL8batW5aW2Ns2mRk5szxfS77fAK/+EWQF18M85vfqHnkkYtTcV5MBIMCd9wRZu5cKb/97dXt\nT67FtfiyEASBxx6LYrUKbN2qGDcYLAgCGzeG+dGPgjz2mJJnnlGPezXAjz4K8dhjbm65Rcnvf5/2\ntaiNQFQGvfqqj1/9yklOjoynnzZx223jA45iMYHdu338+c9ODhzw8+CDoupo1iw1giDw8cc+1q+3\n8d57Lu66y8CaNRncdps+Jd1rSMG6adMg77xj5+abRQXr0qWpCtaREY8LfPxxDxs31vPuu20sWJDH\n6tXVzJmTxe7dPezY0cW+fT3U1JhYurSAu+8uYOrUdI4ft/Jf/9XIjh0O7HYlWq2ChQvTWLu2mMmT\ntezfL6auvf/+AHq9aIhstUaZMkWPwSCjs9PLwECQ22/PSvof5eSM7tdcriA7d7awZUs9e/a0MWtW\nNsuXV3P//VXk53/1MuhfJURjaycHDrSxf784hgoGo9x887CJ9sSJmVfMk8XrDXHiRG8KRGposFJZ\nmZEyhpw+Pe+CPpIi9LHR2NhIfX09X3zRwPHjnTQ3uxkYiCGRWIjHjeh0AoWFWiZNymLOnHJuu206\nU6YUXFCx4feHE55H1lEwqaPDTmZmWlKVdC5UkskktLfbEoqkQU6ebOHMmQ46OmxYrUEikTjgQ6eT\nkJOjp6Iim2nTypk/fzKzZ08kJ8c46rMXhKE5j3vE5rlgGxgFmM6FTRqNEoVCikwmJRyO4HT6LgiZ\nhtputx+tVjWGakmPSiUhEgng9bpwuezYbAP09/fS29uNxWKgsrKY6upSKivLqawsp6KilPLy0ssy\n3hZNo0NjgqSLUTi5XD48HhGgjRRQDIks0tI0KeeG25oR17WoVHKi0Sh+fyCZhTQWaBoCTFarC78/\nRFqaBq1WjVwuClGi0SiRSJhQKEw4LJqvC0IcEKuSK5VKtFo1Wq0GjUbD9u2/o7Ky+Ct/fueLa8Bo\njHjjjT380z/9HyIREeSEQlHC4RjRaByQIUrJJMhkIjCSSmVIJCK4CIejKJXyRAlAXaIEouGigM/Q\nNYPh8vJQLyWGKniJ6qRAAvQERqSojTwOjoBB514T26LRtgy5HAQhSiQSxO/3olBISE9PIysrnfz8\nTIqKcikvL6K8vCDxsBJTwECCw+EbQ/EzGgCd8b6mAAAgAElEQVS5XAFMJu2o9K/hfSoASk/XXbRS\nKhKJ0tvrorvbQVeXg64ue3I/pBYaHPSQk2NM8Qwym1WEQg7s9i46Oho4c+YEnZ2dTJxYw4wZ05gx\nYxoTJ05Gr8+hp8dLY2OqUqinx0VhYToVFZlUVmaNgEOZlJRkoFKNPWmLRmM0N9uoq+untrafurqB\nxNaPRqNg8uRcJk7MJitLhlLpxufroKWlnrNnz1JXV4fRaBylFqqpqSEzMzOZktfQYE2Aod7kKpFG\no0imkw1JjIuLx89g8XzR3e1OpJeJgKi/38dNNxUlAdH06TnJin5XKwRB4MSJAbZuFcvuDgz4ue++\nSpYvr2bhwiKUStmo158+7WbXrgF27uzj889dTJ5sIC1NRVtbkIGBMHl5chwOPxBh6dJcFi/OY/Lk\ndD74wMmLL3Zz7JgfiSRAenqQ5cszeeSRCiZNsvDxx/28/34377/fjdsdZtGifBYvLmDBgmzq651s\n29bGX/7SRGGhnkceqeLhhyswm8cGNpfiMTG0erx+vQ2NRsoTT2SwalU6ZrOc3t4oGzY4WbfOSXa2\nnLVrxVVnnW58/k7xuMC2bX5++UsXsZjAz39uYvly7RWtWHOhEE2ng3zvex6eeELDz3+uH3dj7d27\nI3znOwFuuEHG73+vIStr/O75eFxgxYoI8Ti89pria/scr8W1uFBEIgJLl0aoqJDwxz/Kx7Xv6e+P\n84//GOBvf4vx3HMabr99fKGp1xvnqac8bN8e4s9/NrJo0dejNgIRHL3+uo9f/cqF2Szl6adN3Hnn\n+IAjgJ6eCBs3uli3zonZLOPJJ02sWGHAYJDhdEZ59VUn69fbsNujPPZYBqtXmyksTF1Y8XhivPWW\njY0bB6mvD7JyZQarV2cxZcr5FToeT5i33mph48Z66uocPPBAOffeW8K8edn89a9WduzoYvv2TgKB\nWAIeFXLrrTn09/t4/vlG3nijn85OKVKphhkz1Dz2WCH33ptJc7ObXbt6ee+9HpqaxMVIuz1OQYGa\nqiotPl+YL75wUFqqTaqP5s0zj4JcgUCEPXta2bKlge3bm6iqMifh0fl8DK90tLU5k2Or/fvb8HjC\nKSbakyZlXdH+IBSKcvp0f3Ix8ujRHk6f7icvLy3FE2nGjDwsltGpZ+eGIAj09vZy9mwdn3xyli++\naKO+3kpvbwSvVwXo0Oki5OQoKS83M2NGMTfdNJEFC6ah0114ISsWi9PZ6UiBSCJYEo+lUkmKImko\n1a28PJOCAhM+X4j6+h4++eQEn39eT21tF52dduz2MLGYColEgcEgJy/PQFVVLtOmlVNdnU9xcQb5\n+enk5BjPOy8YGT5fMDmfuhjAFA5Hkx5MY0GmkelzGRki5BXT5EYDpZHtkaogu92TSEGLoVRKkUrj\nxGIhwuEAarUUo1GHxWIkNzeDwsJsSkvzqawsJjvbnJg7azGZdBgMmnGfM8fj8TFtWlLnyGOdG742\n1A4EwomqbWMDp5HntFoVUqn480XRiliN3O8X1Ugulxe7XQROovDCid8fShSwkgAChw+vY8qUqnH9\nPOAaMBozfv3rjfziF6+jVMrQaMTcwsxME4WFWRQUZJGXl0FWlum8Kp8rnVs4UslzLrS58HFw1DWv\nN4hKJR9BRzXnUFL1qGtKpQyn047V2k9vbw8dHe20tjbT1tZKfn5OUn5YUlKWqNiVSSQiSaSPeUeY\nTKcaQTscPgwGzUWpf4Yg01dRrQQCYbq7HaNg0PCxA6vVQ1aWgYKCdAoKzBQUpJOfn05BQXoSEEUi\nLk6dOs2xYycS23Hcbg/Tp09l8uSp5OZWodVmEwqpaG21J8HQwICHkpKMMZVCxcUZF1TCeDxB6usH\nUqBQbW0/ra128vONTJiQRWmpCZMphlTqIhDopr29ntraWhobG1Mqkg3tJ0yYgMk0XIY1FIpy5kx/\nSlrZyZN95OToRymHsrOvzmpYe7szBRA5nUFuvrk4CYimTMm6ogqm80UoFOXw4W527Ghmy5Z6gORg\n7/rr80a9J48nwr59g8mKZlIp1NQYiUYlHD3qQa2WoNEI9PW5mTEjjaVL81m0KAe5XMkbb/Tzl7/0\n0dERBtyUlgqsXJnPQw+VE49Lk4Do8OEBZs7MYPHifBYtyqegQMuePV289147u3d3UlZm4O67i3jo\noQpqas4/IO3rG6piM0gkIrB69dhVbKJRgd273axbZ+PAAR//438M+1MIAuzb5+f55x18+KG4wrx2\nrYmZM8fP9DUeF9iyxc+zzzqRyyX8/OdG7rnn6wVFH38c4dlnvfT2xtm82ch1143vRHNgIM73vhfg\n8OEYf/qThkWLxl/989RTEQ4fjrNvnxK1+hosuhb/fcPtFrjppjCrVsn4p38a/7TJnTsj/P3f+1mw\nQM7vfqfBYhnfvuaDD0I8/riL6dMV/PSnembP/vrUfLGYwFtvic9TnU7C00+bWLJk/CofxeMCe/f6\nWLfOxQcf+PjGN9J44gkTc+aIcOroUT8bNth57TUHc+aIVTOXLTOgVKZ+5k1NQTZtGmTz5kGysxU8\n+mgmK1ZYMJvP//dvanLx1lstbNvWxtmzDu64o4Bly4pZsqQIuz3M9u0iPPr8cxs33pjF0qUFLF1a\ngFYr4+WXm9i0qYva2iiQRnGxgm9+M4cVK3IxmSTs3dvPjh097No1iEqlIh4X4eX115vQaqGx0U1r\nq5/bbstMmmcXFKSqKCKRGPv3d/D22/W8804j2dla7r9f9DyaNSvnaxnjAHR0uJJjrwMH2nE4Atx0\nUzELF4rjr6lTs694fxuNxqivt6ao2Y8f78VoVKeMSWfOzCMvz3DR92ssFqO2ton9+09y5EgTZ8/2\n0dnpxW6XEI1qUChCmM1QVKRn0qRc5s6t5LbbplNRUfylP+PLUt3sdl8i1S1zhEJJBEplZRbcbgdH\njhzn4MFjHD3aRENDNz09blQqMwqFiVhMid8fR69XkZ+fTn6+mbw8E7m5RnJzTeTmmlKOx8pCOF8E\ng+FzQNKFIZPXO5zBcT4Vk8UyZNStSxiBi88VMQXNn1D++LHZPDQ3d9LcPJSVMsjAgCNRsS6IXK5G\nodAgkciJRiEcjqPRKJMpckMgaWg/uq3DZNIy0nT7YqDbV41YLIbXG0yBSGOBpVQBhn/Mcz5fCI1G\nmaJkSkvToFLJk/Y4zz//D2Rnjz9svgaMrlIIgmhWPRbQGQvuXOh1Hs8w5BmCOMOeQ5pz6OW5kjp1\nCs1MS9OcF3BZrTbq6ho4c6ae48frOH26icbGTux2H1lZuWRk5CS8hfRIJArCYbDbfdhsogmbSqVI\npI+NNJbWk5GhT3oMjQRAFsvlG3m53QG6uux0dztTVEEjjz2eYBL+jARBQ2CooMBMdrYh+V5cLhd1\ndfXU1TUkAdHx4yeRyzVUVEwnO7sctTqLSERNf3+ApiYx57mszJKiEBIVQ1kUFqZfsOMXBBEY1NYO\njFIM2e1+qqoyqa7OJDNTjlrtJxYbxOFopaWlgYaGBtxuN1VVVVRVVVFZWZkEQ9XV1Wi1qStxQ3Lg\nkXCorm6QioqMFDg0fXoeRuPVqewiCAItLY7k4OTAgTYCgWhyhWvBghImTsz8WoDAUAndvXtb2bev\nnU8+6aKmJoNFi8q4//4qpk1LLTMvCAK1tZ6kF9GRI06mTTOSmamhry/CiRMeMjPlBAJBBCHC3Xfn\nsHhxLrfcks2ZM35efrmXd9+14vVGiMWczJql4tFHi7nttkJOn3YlIVE8ThIQ3XJLDn19ft57r53t\n29s5dszKLbfkc/fdRSxdWkxe3vlX5MLhONu3O9m4cYBDhzwsX25m9epMbrghbdTgqK0txAsv2Hnh\nBTsFBQrWrMngoYdMpKXJGBiIsnGjiz//2YnBIGXt2uHV5PGKWEzgzTd9PPusC51OwjPPjO/E5lJD\nEATefz/Mr3/tpb8/zo9/rGPVKs24ehUJgsDmzWF++MMg3/qWkn/+Z/W4ebeMjD/+Mcp//VeMw4eV\nZGRcg0XX4r9/dHUJzJ8f4j/+Q8FDD43/op3XK/D000FefTXMb3+rYeVKxbg+awIBgQ0b/PzHf/io\nrpbzk5/oWLBg/NJLLzWGQPwvf+lEoRDB0T33jO/zta8vyqZNoupIr5fy5JMmVq40YDLJ8PvjbNki\nqo5qa0N861vpPP54BjU1qeOQWEzggw9cbNw4yK5dTu6808jq1ZnceafpgmnIAwMBduxo57332vng\ng26mTjWzbFkx99xTQk6Olr17e9mxo5OdO7vJylJz990FLF1ayKRJBnbsaGf9+jY++8wPGElLk3Pv\nvRZWrcpj3rw0jh1zsmtXL1u3iuojvV6L1ytw3XVpVFRocTiCHDpkIzdXzaJFWSxenM2NN2akQLFY\nLM6nn3azdWsDu3e30t3t4ZZbirnjjhJuv72Eioqvr3T3kMJ7yAdpcNDHTTcNK5CmTcu+KnArHo/T\n2uoYYa4tqpEkEkmyQtvQGLas7NKNvd1uLx99dJxDh85y/HgHLS0O+vsj+HwqJJIQen2Y3FwVlZVD\nqqTJzJ07BaPReFH/v98fprXVOiZM6uiwY7Hoz4FJFkpKMgAPnZ2i8XRtbT2nTzfT2NiNRpNOdnYR\nBkM2KpWBeFxNMCh6evb1uVCrFeTlpScAknEEUDKlHOv1lz7Wj0SiiYJAFwJLbpzOIbNuH4FAGKNR\nmwRIJpP2nJQ2bQpgEtVEagIBNwMDfbS0tNLU1EpDQxMNDe20tXVjMJjJyysgMzMHs9mCXm9Eo9Ej\nk6nw+cIJddOwyknc/EilkvPApZEV37TJzWDQjrqmUFx5j8eRVcvPB5YeffSOL1XGfZW4Boy+JEKh\nyGUDnqFrogm15rxqnvNdG636OT/k+bIIh6NJdY/NJlb7amrqoL6+g7a2Pnp6rFitHtzuEPG4DKlU\nRSwmRa2WYTJpyc42kZeXgcUysrKYflTbbNaPK7EVSb13hBLInlQDjQRCsVicwkLzKFXQyGOLRT8q\nNU0QBLq6uhIP4Lrkg/jMmTY8HoHs7AoMhlxkMhOhkIrBwRB+f2RMlVBFRSb5+aYvTX+7UBqZUimn\npiaLggIdBkMMqdRJINBNb28DjY0NdHV1UVhYSFVVFdXV1UlAVFVVRV5e3pg/22bzcexYb3KF5tix\nXjo6nEyalJXSsU6ZknPVKoaBuKp24kQ/hw93cvhwJ4cOdRCPCyxYUJJcwbpSJowXE93dniQg2rev\nDb1ewR13lHL77cXcemsJ6empD2avN8qHHw4my94LgsDMmWZkMhknTnjp7w9hMkmwWr1Mm6Zn2bI8\nFi/Opbw8jT17HGze3M2HH7qQSMIIgovbbjPy6KMl5OebOHBATDX7/HMr8+ZlsWiRCInKy/UcOtSX\nhEShUIy77y5m2bJibrklH43mwh3ZiRM+Nm4c5NVXrUycqGH16iy+8Q1zSvljgFAozrZtopro6FE/\nK1ems2ZNBlOmaBAEgf37/Tz3nJPdu30sX57Gd75jYvbs8UtrAFHR9NproueG2SzjmWfGN3XiUiMe\nF3jnnRC//rWXcBh+8hMdDzygHndz7aamGGvXBnA6Bdat0zBz5pUZnGzbFuM734lw6JCSsrKvZ0X7\nWlyLrxInT8a5/fYwb7+t5Kabrsy9+/nnorl8ZqZoLl9WNr5wKhwWeOWVAP/6rz4yM6X89Kd6Fi/+\nesHRu++Kqb6CIPD00ybuu298FZzxuMBHH/n585/FvuO++/Q8+aSJefNEQNXYGOKFF2xs2mSnrEzF\nmjVmHnjANKp/cjiivP66jY0bB+jqCvPtb2fy6KOZVFdf2A8lGIzy0Uc9vPdeG9u2taPRyLjnnhKW\nLStm/vwcjh2zs317Jzt2dNHe7uOuu/K4++5Cbrklm6NH+9mwoYU9e5zE4wYEQcnChUa+9a08Fi82\nE4nE2LOnj3ff7WH3bitSqYJQSEpBgZobbzShUAgcP+6kvt7LwoWWZPpaSUnqwk5vr5cPPmhj3742\n9u1rRyaTcPvtIjy69dZisrO/PDXrSkVvrye5uLd/fzu9vR7mzi1g/vwC5s8vZO7cgqtaFa6nJ7VC\n27FjPbhcQaZPzx2hRMqnutryleZS8Xickyfb+Oijk/ztb03U1vbT2enH6ZQQi8VQKDxkZEgoLk5L\nqpJuuGEqFRXlqFQX9zmMTHUbTnFLTXUTlUiiIqmkxIzBICESseNwdNHY2JhY6K7H7fZQVVVFWVkV\nubklmEw5aDRm4nEVVquPnh4nvb1Oentd9PQ4kcmk5wAlYxIqDQMmE0bj5QHkaDQ2wifJNwImec85\n9qW8TvRNCiR8k4Zhk8mkQ6kEQQgTCvnw+Vw4nTas1j76+roxGDRUVBRQXV3ChAnlKQbccrkyqXA6\ndz9swO2/4LFSKR8FlsaCTanHqdeutvfwpcQ1YDRGfPJJLffd92+43X4EgQtAHvUIk2n1ecCPeG28\nTagjkShOpz9JR8V8UF9KuldqW6S7wWAEtVqGTBYnFgsSDLpRKiVkZhrIz7dQVpZLdXUJU6dWUlVV\nhMUiev9cyTS7WCxOf7/rnLSw1DSx7m4HGo3ygqqg/Pz0L32AhUIhmpqaqaurp7a2nlOn6jl1qoPW\nVisKhXkEFFLicEQwGNRUVGRTWppBWZmF0lJL0lsoN3e0Gd1YcW4a2dB+KI2svDydjAwpGk2AaHQA\nh6OF9vY6mpqaMBqNKTBoCA6VlpaiVI4tLxUEgbY2BydO9CbMBEXPIYcjMKrDnDAh86qbQdtsfj79\ntCsJiL74opfSUhPz5xcmt/Lyr2/1zOMJsX9/B/v2tbF3bxv9/T5uu00cmN1xRwmlpaaU1wuCQH29\nN6ki+uwzBzNnGikq0uNwxDh0yIFCIUEQIsRiIZYty2bJkjzuvDOHQAC2bh3kpZd6OH7cj0zmR6Px\ncf/9mdxzTxE+H+zZ08Pu3d3odPIkIFq4MAe/P8quXR1s397O3r1dVFebkpBo6tQvB2w2W4RXXxUH\n11ZrlEcfzeSRRzIpLx+9MlFbG2T9ehsvveRg8mQ1TzyRwf33G1GrpVitUTZvdvHnP7tQKiWsXWti\n1SpxlXg8IxIRePllsapPXp4Iim699esDRaLnR5B/+RcfWi387Gd6li1TjbvyLRIR+N3vQvz2tyF+\n/GMV//APqitW6e3IkThLl4bZuVPJ7NnXYNG1+H8v9u6NsWpVhAMHlEyYcGXu4UhE4A9/CPGb34R4\n6ikV3/ueCoVifL+TYmqY+HyRSuEnP9GzfLnqazPvFwSB7dvFYgKhkOgR941vjH/q7+DgUH/iRKmU\n8MQTJr71LSNms4xIRGDXLjfr19s4eNDHAw+YWLPGzOzZ2lH9wJkzfjZtGuSll6yUlalYvTqThx7K\nwGC4MGgXBIHjx21s29bGe++109rqZtGiQu65p4RFiwrxeKLs3NnFjh1dfPRRH9OmpXP33YUsWpSH\nyxXg5Zeb2LJlkEBARzSqZfJkDStW5HLvvRZKS9V8/rmDHTu6eeutPpqbgyiVKmQyKbfdZqa0VENP\nj58PPhjEbFawaFF2Qn1kRquVp7zH+np7Ah61sX9/B8XFhiRAuvnmwjELa1ytGBjw8emnnclx3tGj\nvZSXm5k3r+BrG+NZrb5zKrR109PjYfLk7KSKfurUHCZPzkav/2pwayg74ODBM3zySR0nT3bS3Oxk\nYCBKOAzgQKcLJVRJFmbOLGb+/ElMmjSBgoKCi/ZYHUp1a20V/ZLO3Xp6XOTlGZOpbXl5epTKEOGw\nHZeri7a2RurrG2htbaOgIJ8JE6qZMKEquc/PLyYUktHb60yBScPHYjsajafApLEBUzpm84ULCH2V\nED2GgknANBIunQuYxGteBgdd2GxePJ4gEgnI5QKCECYSCaBQgNGoISPDQE6OmcLCLMrLC6iuLiYv\nz4LZrMNs1p9XDDFkFXMpgGmsY7lcdgmwaezjK5Vedw0YjRGhUAS324/BoL1iH3wsFk8SzKEbfST8\nGbkfuuFHng8GIwnZnCjZMxq1mM16jEY1ghAmGPTgdtuxWvvo7e2kt7eD/PxMJk2qYOLEKmpqqqmp\nqaK6uhKT6eLkk5ca4XCUgQE3vb1O+vrc9PW56OtzJY5dSVPpvj4XZrMuAX1MKRBoCA7l56ePKg1/\noXA4HNTV1XPmTD1Hjpzl1KkOWloGsdnCaLVZSSgUi0koKDBQWZlDdXVuEgyJxD7joqWZ50sjq63t\nx+EIUFGRQV6eGqMxhkTiJBDooq+vjqamesLh8CiVUHV1NZWVlaSlXdgjyOcLc/p0HydO9CUB0alT\nfaSlqZg2LZepU3NSJLkX2yGNV8TjAvX1Vg4f7uSTT0RA1NMjrj7dcENhYvUp/6qlu40V0WicI0d6\n2LtXHHwdPz7AnDm5Sen3jBmp8mpBEGhq8nHggJX9+60cOGAD4IYbzOh0Ks6e9XHsmBujUYrL5WPi\nRC333ZfHkiV5zJhh4vRpP2++2c9rr/XR2Sn6EeXnx3jooVymTLHQ2Ohj9+5uTp92cvPN2SNURGmc\nOePgvffa2L69ndOnHdx2W37SgyE7+8tL83q9MXbscPDGG3Y++MDFkiUmVq/O5NZbjaMmIj5fjDff\ndLJ+vZ3m5hCPPmrm8cczqKhQIQgChw4FeP55J9u3e7nnHj1r15qYP3/8U8Ks1hibNnn5v//XQ2mp\nnKefNrFgwdd3v4RCAi++GODf/s1Hfr6Un/1Mzx13XBkFwF//GuWJJ/zk5Un50580lJZeGbgrVoWK\n8cMfRtmwQcE991xdiHwtrsV4xubNMZ56KsJ//IeCb31LesUmpi0tMb7znQADA3HWrdMye/b4q/7E\nqo8hfv1rHw5HnB/9SMfKlZpxB1SX8n527RLBkdst8Pd/n8a3vqXHaBzfsYUgCBw44GfdOhc7dnhZ\ntkzPE0+YuOkmsY/p6RELLGzYIBZYWLNGLLCQkZH6N4hE4rz/vouNGwf48EM3S5aYeOihDO66yzSq\naMNY0d3tZfv2DrZta+PgwV7mzMli2bJili0rIS9Py/79fWzfLgIkQRBYurSQpUvzMZvlbNvWyquv\n9jAwoAAMWCwKHnwwm/vuy2TePCMOR5g9e3p5/fUuPvjAjiAoiEalTJ+uZ+FCM4IQ5/BhG8ePu5g5\n08TChRZuucXC9deb0WiGn9HRaJy//a03CZC++KKP667LSQKk667LvepFQEZGOBzj+PG+5CLh4cOd\nhMOxlEXCWbNyr6qyHcDtDiYtGU6c6OXkyT5qawfIyzMwdWpOYhPH0aWl6Zc1fna5Apw61c3Bg2f4\n/PMW6uoG6Ory4/GAVOpFEGxYLBKKiw1MnpzH9ddXMnXqRKqqqjCbzZf0syKRGB0d9jFgkqhSiseF\npCrJbFagUAQIh+04nV10dzdQX1+HUqlMgUg1NROYMKGa4uKipMG01xs8L0waUiv19jrx+8Pk5BiT\nMGlIpZS6NybMs6/8fSpWUQsngZLd7qW5uZOGhnZaW3vo7Bygv9+BzebB7Q4il2uQyzWAnFBIQC6X\nYTbrsFgMSYgkbsNQKT1dN+qcXn/hBc6h93VhwDT2Nbc7kGy3tDxHfn7GuH9u14DRV4x4PI7bHbgA\n4BkNeYbBjx+fL4jBMAx8huR0Y+2HcjeHzhkMahwOKw0NzTQ0NFFfL251dQ1YrXaqqsqpqRmGQhMm\nVFJZWY5affmTLEEQcDr9Segjbu5zjkUY5HIFyMpKIyfHmNxyc40pxwUFokmbUnnpA614PE5HRwdH\njpzms8/OcvJkOy0tg/T1+QmHVchkRqJRJQaDnPz8oQoDJVRUZCfUQhlkZ1+8OR6ID+KWFtsoKFRX\nN4BKJaOkxIjFIkWl8hONDuB0ttDefpqBgX5KS0tHgaGqqiqys7Mvyjyvs9OVhEJDW1eXmwkTMpk2\nLZdp08TObdq0HDIyvh55ss8X5siR7sSgoItPP+0kPV2TGBSIq0uTJ389BtVDIQgCDQ129u5tY+/e\nVg4c6KSkxMgdd5Rwxx2l3HhjAVqt4pzXezlwwJYARFYkEpg/30x2thaXK8aBA3as1ghKZYxYLMzi\nxZnce28ed96Zi9Go4MABJ6+91s877wwSCESJRBxMmaLg/vtz0Ou1/O1vdvbs6SYrS5OoaJbPjTeK\nfkj79/ewfbuYaiYIAsuWiVL5BQvyUKm+fGLv8YiQ6M037ezb52LePD0PPJDBN75hxmQa/b07etTP\nunU2Xn/dyfz5Op54IoMlSwwoFBIcjhgvviiu/sZi8J3vmPj2t8XV3/H+Gx08GOL55z3s2OHn3nu1\n/N3fpXH99V8fKPL7BdavFz1GJk2S89Of6rnppiuziuvxCPzsZwFefz3C73+v4ZvfHF+/lJHR1BTn\nySejuN0CGzYomDbtmrLoWvy/H198EefxxyPk5Eh47jk5JSVX5r4WBIFXX43w/e8H+OY3lTz7rBq9\nfvy/q4Ig8NFHYf7lX3w0NUV56ik9q1dr0Gi+PnB04ECQ557zsHt3kG98Q8vatWlcd934w3ObTex3\n1q1zEo/Dk0+a+Pa3DVgscuJxgQMHvGzYYGf7dheLFhlYsyaDW2/Vj1I/DQ5GeOstG2+8Yef4cR9L\nl6bzwAPmi4ZHPl+EvXu7kqnfmZlqli0r4Z57ipk9O5P6enei6loXx4/bWbgwh6VLC5g0ycDhw928\n/HI7DQ0CGo2ZWEzO3XdnsHx5JnfeKaZ/f/GFnS1bunn77V7a2iKAnJwcJbffnsGECTqs1hAHD1o5\ndcrNrFkmbrnFwsKFIkBSq4f7YK83zMGDnUmA1N7uZuHCoiRAqq6+dD+f8Y7OTtcIgNTF2bODTJ6c\nlRwnzp9fSH6+4aq/r2g0RlOTjZMn+5IQ6eTJPux2P5MnZyfH2FOn5jJlSs5lL3YGgxEaGgY5erSN\nTz+t5+TJLlpanNhsMWSyELGYFYXCQ16eiqqqTGbOLGHmzJpkpoFer7/kn+lw+MZUJrW0WOnqcpKd\nnUZBgQGjUYpCESQctuFwdNHdXYfN1mb2EiMAACAASURBVEtlZfkIiCRCpaqqSnS6secdgUCYvr5h\ngJS6Hz7v9YbIzjaMAknnAqaxbEWuVIjzTNGuZGieffZsE/X17bhcAfLzi8jOzsdszkzx9PV4Qtjt\nXux2X2LvJRSKYjaLHk0jQdLYoGn4vMmku6Q5kyAIV+T7fQ0YjRFtbYO8+OLHF4A/ojeRTidWUBsN\nfFKhz1hAKC1N/aU3vNPpor6+kfr6phFgqJGmplbM5nSqqsqprq6gurqSqirxC1xcXPiVyguGQhH6\n+1PBT2+vaxQE6u8XjdNSIZCJnBzDiLZ4PiNDPy5gwOFw8/HHx/nss1pOnWqnqWmAvj4/brcA6JHJ\nJPx/7L13dFv3fff/IgESJEgABLj3XiJl7b23tWzXtmSleZI4sS25cZvRmcTtk+fk/JI0bdw0TZtY\nHnUbN7ZEyVOS43jIkihZogY1THGLFDcBEoPY+/7+uMQlIVKOZJMU/Tx6n3MPCB5bAEkA93tf3/f7\n/dFqQ1AojTlzCpgzp5CCgmRyc3W3DaMEQUCvt9HcPEBTk4Hm5oHhQ4yRpaXFk5ERg0rlIzLSgsPR\njV7fSGdnE8nJyWPiYyUlJeTm5iKX39rzcLl8XL2ql05WoVuFQs6sWWmSc2jWrHRKS6c+UhaSIAh0\ndoaf9BsbB5k9O0066S9Zkk1a2u2f0CZaBoODDz/skLqIBEGQANGN+X9BEGhstEtw6PjxQaKiIlmx\nIpHMTCVWa4DqajMtLS7i4sRxpUVFMezYkc6WLZnMn6/Fbg/y+98b+Z//6ePoUQsymQ+fz8zKlfEs\nXpyI0xnBsWN6WlutrF2bLrmIcnLi6e938s47YtTsww97mDlTx7ZtuWzblktFxa3ZuG22AIcOmTlw\nwMjRo1aWLVOxY4eO++/XjTtFZvRYY7M5wGOP6Xj0UR1ZWdEIgsCZM2727jXz5pt2tmwR3UQrV068\nm8hkCvDb39p57jk7AHv2qPjKV+ImHEjdjqzWIL/5jZNf/MLJkiXiFKOJnno2WocPixOZ1q2L4uc/\njyExcXIWRn6/wDPPBPjnf/bzgx/I+da3ZJMWdburu7oT8vkEfv7zAM884+cf/kHOn/+5bNIiXYOD\nQf76r1189JGfX/9aydatk/cZceaMCI7On/fx3e/G8eSTsahUdw70GgwBXnrJzt69NrTaSPbsUfGn\nfxpHfPzEu45OnXLx3HMW3n7bzubNcezencDq1WIkzWz288orZp5/3sjQUJBvfEPH178unsduVH+/\nl9dfN1FVZeTyZSfbtonwaOPGW4NHwaDA2bMGKbpmMLjYujWH7dvz2LAhC683yB/+0MPhw928+24P\n2dlKtm3LZvHiJLq6zOzbd52aGidqdRI2WzSLFql4+OEUtm9PIjc3BqPRw7vv9vHyy92cPj2EyxWB\nIERSXBzL+vWJFBcr6e52cvy4kbo6KwsWaCUH0qJF2rDNJL3eEdZ/FAwKrF+fKwGk6bBGczi8nD/f\nG1ZXEBcXLW02LlmSzaxZqXdsvWuxuPjkk34JIF250kddnZ7ERKXkQgodxcVJn/vaJxAI0t5upL5e\nz7lz1zh/vo2mpgF6elxAAJlsCK9XT0yMm7S0WAoLdVRUZFFaWkB+fj55eXnk5ubecmdSSH5/gK4u\n8xiQFIq/ud0+0tPj0WgikMvdeL2DmEzd9PU1k5qqpLy8mPLy0mFnkuhOupVNcRDhmQiWzGNcS6Hv\n9fZasFpdw2BJOyYKNxouJSerJhUsWa1WmpuvSdfpjY0tNDW10NLShk6npaysWLpGLysrJj8/j/h4\nLRaLU4JIN0KlkONp9PesVhcqVewwTBoLlMIhUzwLFxZOSjrqLjAaR21tev7rv06EwZ8boY9arZwQ\nGOL1emlruz4GCjU3X8PpdI2BQqHbW6HKgiBgMjnGdf/ceN9ud5Oaqr4BAoWgkFq6n5qqRqmc2PK6\nYDBIb+8Qly61SU6ha9cM9PU5sFoFAgE5UVFetFpZGBRasqSSmTNz0Go/m5vGZnOHwaCmJvG2uXkA\nuTyC9PQYNJogUVF2fD4DFst1enrqkcmEMBgU+rqoqGjMFLJPU6icbzQYuny5n/Z2EyUlSWFgaNas\ndFJS7uxJfTxbsd8flHaDli3LZu7cdBSKyZ8U8Mfkcvmoru4eBkTXaW8fYtWqbDZsyGfDhjxKSkZ2\n2ARBoL7eNgoQGVEqZaxYoSM/P56hoSAnTpioq3MQHS3g8XgoKYll8+YU1q1LYdmyZNTqKDo63Lz9\n9iAvv9zL5ctOoqNdyGRW1q1LICdHTWeni6NH+8nLi5dcREuWpCCXR3D5slHatWxqsrBxYxbbt+ex\neXM2SUmfXtgZktXq5+23zRw8aOKjj6ysWKHi4YdFSKTVjv2biLEyBy+8YOStt4bYtEncmV23TtyZ\nHRoK8LvfWdm714LTGWT37gQefVRDcvLE/n0FQeD0adFN9NZbTrZuFXeqV6xQ3NFdUKMxyL/9m4Nf\n/9rJxo0Kvv/9OCorJ+8isK8vyLe/7eLixQB798aydu3kPVZtbZDHH/eRlCS6L+6WW9/V/81qbg7y\nxBM+PB544YUoKisn7/X+4Yc+9uxxMW+ejF/+Mpa0tMl7rCtXfPz0pw4++MDDn/95HH/xF0p0ujv3\nXg4GBd5/383evTaOHXPzyCNx7NkTz+zZE194bDYH+J//Ebvz3O4gTzwhnp9SUuQIgkBtrYsXXzSy\nb5+FxYuVPP54Itu2qcMmkYXU3+/ltddMHDgwAo927kxk40YNCsWt/T7b260cOtTBoUPXqakxsHx5\nGvfdl8e2bbmkpSk5c2Zg2H3UhV7vZvNmcaKpz+fhyJEO3nvPhFqdjN0eS3a2goceEuHRggUqIiMj\n6Ohw8M47fbz2Wj/nz1ux2UAuj6SiIk5yIDU12fnoowHq620sXKiVHEgLF44AJEEQaGkxS+6jjz7q\nICtLLQGklSuzUammpqD60yQ+TxMff9zF6dPihmR7u5n58zOkNefixVkkJd36mnuiFQwGaWszjYJI\nIkjq67NRXp4ireFDx0Q4/wVBoK/PSkODnqYmA1eudHD1ai9tbSYMBjfR0UGio534/UZcrl40GoGc\nHA1lZWmUlIggKT8/n/z8fLKysm7bYDA05LpJd9IAHR0mVKoo1OoI5HIXHs8gJlMXgmClpCSNmTPF\noumiogIKCwsoKiq87bgdiAaH0LXraJB0I2ASUy7qT43BZWRoSU5WTWjqIeRKampqkSBSCChZLEMU\nFxdIECl0fV9aWnTT6/pQhU04UAqHSqH7ZrODN9/8S5KSJt6ddxcYTYHEfhv9GCjU1NRKV1cPWVkZ\nYS+akpIiSkuLSE9PG3PBJAgCNpsbvX4IvV7sBdLrrdLXo3uC9Hor8fExEvS5EQSNjofpdHGTRmI9\nHh/d3Ra6usx0dBi5erWTq1dFKNTf78BmCwJeIiIcJCSEoFAqs2cXsGzZTBYvriQm5rOdwLxeP+3t\npjFAqLGxn6EhNykp0ahUfiIjrXi9ekymNiyWdrKzk6UP1YKCAum2oKCApKSkz/A78NPQYBgVJxMB\nUWRkxBgwVF6e/JkiehOtgQFH2G5PbW0fRUW6sNx5fn7CHbc2g7hQvXhRz/vvt/P++9epqell9uzU\nYRdRHgsWpEs7U8GgQF2dVeogOnHCiFotZ+XKRMrK1JjNAY4dM3L5sh1BEAgGvZSVKdmyJYVNm1JZ\ntCgRpVKOzxfk9Gkr77xj5MCBfnp7vURE2NDp3CxZoiUmJprLly309DjZsCGdzZuz2Lgxg/R0JS6X\nn6NHe6SomUIhY/t20UW0YkU60dG3dhK3WPzDTiITx45ZWbVKxY4didx3n3bcuBlAR4eX/fvN/Od/\nmoiIgCeeSOQrX9FJIOj8ebGb6OBBG+vXx7FnTwJr1058uenQUJCXXxZ3pT0egd27VTz6aDxJSXe2\nP6e/P8C//IuTF15w8uCDMXzve3EUFU3e+zEYFHjxRS9PP+3m8cej+Yd/iJm0mInTKfDDH/r57W8D\nk97vcld3NZ0UDAo8/3yAv/97P9/8powf/ECOQjE5r32XS+BHP3Lz4otefvrTGL7xjcmdctbS4udn\nP3PwxhtuHntMyV/+pZK0tDv7Odrb6+fFF+08/7yNjAwZe/aoeOSROJTKiXcd1dS4ee45C6+/bmPj\nxjieeCKBdevEc5bTGeS110T3bGOjhz/9Uy2PPJLAokVji7IB+vpGnEdXrjjZvl3Ljh23B4+Ghjz8\n4Q9dvP12B7//fSd5eSq2b8/lvvvymDMnic5OhwSPTp40MG9eIps2ZaDRRHLmTA9vvdVPTIyOYFBN\nMChj27ZE7r1Xx4YNOhITo4Z/v67h+Fo/tbU2bDaIjY3knnvi2LQpieLieC5dsnDs2CCNjXYWLRpx\nIC1YoJXAmd8fpLa2X+pwPHeujzlzUiX30cKF6XfM1XOjLBY3NTXdkqO9pqab9HRVWOVBeXnyhK9V\nblc2m4erV/U3xNr6iI9XhAGke+5Jn9DBM4FAkJ6eIVpaBmhtHaSpSU9dXTfNzQP09tpRKECp9A73\nqPbjdPaQmhozPN05R7rmCR236gwKf3xLGERqaxukubmfa9cGcDp9xMdHEBXlwe8fwm7vRyZzkZ2d\nQElJOpWV+RQXF0pAKT09/XN9bnq9ful6eDynUuj7ZrOTlBTVuE6ltDQNyckq6VCrP5+z3maz0dx8\nTYq4hWJuIVdSaWnRMEgqlr7Ozr71QvTJ1F1gNIFyOBw39AqF4mTXUCiix4VChYX5REVFYbW6JPCj\n1w+FgaAb4ZBMFklqqlpyBKWmam5wB2mk78fETG6JXDAYxGCw0dlppqvLRGenmc5O07Cl0UBHhxGr\n1UNsrEBEhBO324hM5iE7O4Hi4nTmzClk6dJKZs+eQVraWEB2KxIEgZ6eIckp1Nw8wNWrvTQ09NPf\nb0etjiQ+3jf8IdmHydSGWh2gsDCVwsKCMVAoKyvrluNj40mvt4VBocuX+2htNVJYmDgKDIm3aWmq\naXHBFgwKNDQMSCfiU6c60esdLF48Uk69cGHmlI1GvRW1t1ukSWZHj3aQnKyUANGqVTnScw0GBa5c\nGZI6iKqrjWi1UaxencTMmRpMJj9Hjw5SW2vH4wkQEeFnxgwREG3fns68eVoJ4LS1uXjnnUGqqvo5\nd85BVJQft9tMQUEk5eUqrNYg584ZKS/XsHmzGDNbsEC0J/f2OiRAdOxYL3PnJklRs9LSWwdvFouf\nt94S42YnTthYs0bNww/ruO8+LRrN+K/bri4vBw9a2L/fwrVrHv7kTxL42te0LF0qTq+w24O88oqV\nvXvNmEyim+jrX9eQljbxbqJz57zs3Wvj9dedbNwYw549KtasuXPTzkLq7AzwT//k4JVXXHz5y7H8\nzd/EkZMzuQvlxsYAe/Y4cbvh+eeV3HPP5D3ehx8G2L3bz6JFEfzrv0aRknLnP3fu6q6mWj09Ak89\n5aO5WeCFF6JYunQyHUABnnjCSWws7N2rpLR0cj9PuroC/PM/O/if/3HxpS/F8rd/G0du7p292A8E\nxJLsZ5+1cfq0hy9/OY49e1RUVEx8/9vQUGD4PGbBah1xHaWni+ex5mY3v/udmaoq0TW7Y0cCO3cm\njDtlDUR49NprIjyqqxuBRxs23Do88vuDnDrVz6FDHbz99nWcTv9waXYua9dmEggIHD3az5EjXRw+\n3E1MjIzNmzPJzY2hvd3Mm2924nQqUakSGRiQMWOGku3bk7j3Xh0LFqiliKVe7+J3v+vmjTf0XL5s\nx2YTUKvFAu17702moEDJ2bNmjh0bpLnZweLFIw6kBQu0REWJP4/D4eXkyW7JgdTWNsTKlVls2JDP\n+vV5lJf/8QmsU6VAIMjVqwNhrnej0cXixVkSQFq4MHPaOKY6Oy1hTqQrV/rp6LBQUpI0BiSlpsZP\n6O85GAzS3T1Ea+sgra0DtLQM0tysp6Ghj46OIWJiIlCrg8jlDnw+A1ZrJ16vgZwczRiYFHIpabW3\nN+nObnfT0WEaPoxcv26ipaWPlpZ+uruHsNm8xMYKREY68XrN+P1DpKYqyc3VUV6eyaxZhZSVFVNY\nWEBOTvbnuk4bLa/Xj14/NAYk9fZaMBisDAzYMBhsDAzY8Hr9YQApJUVFcrL6hvuhQ/1HJ3eHFAwG\n6erqHnYktY5yJ7ViMpkpLi6grKxkmCMUUVZWQklJ4R8djDSRuguMblOBQICOji4pNja6Y2hw0ERR\nUb4UG8vOziMxMR2lUovLJYzrCgp9Ty6XSRBoBASpJRg0Gg7dzrSwzyubzS0BoM5O06ivxfs9PRZU\nKgWJiTHExgYQBDsOh4GBgQ4CAStlZVnMmVPCPfdUUFExg4qKclJSUj7Tc7FYXMNOIQMNDf1cvtxJ\nU5Oe7m47crlAbKwHMOFw9BAIGMnNVVFSkkpRUTgUysvL+0xFcTfK5wvQ2DhwQxF1Pz5fIAwKzZqV\nzowZKZMO725HNpsnrJz6zJlukpKUYTs1M2Yk39Fy6htlNrv56KMOqazaZvNKo+7Xr88jK0u0YAYC\nApcvD0kRs+pqIykpClatSmLuXA1Go48PPjBy4YINuz2AXB6kvFzJli3JPPxwBrNmJUg/t93u58MP\nzbz6ai8ffjiEzeYnGLSSnBygpCSGqCgZLS12nE6/1EO0YUMGSUkxBIMCtbUDUtSsvd3Gvfdms317\nLps2ZaPT3XpZotns5803TRw8aKK62sbatWp27Ehk+/aEm44J7u31ceCAhaoqC42Nbh54QMMjjySw\nZo1KmrBz6ZKbvXst7N9vZdUqJXv2JLBxY9yE79DZbEFeecXBs8/aGBoKsnt3PF//uorU1Du/c9nS\n4ucf/9HBm2+6efxxcXd+sp+XxyPws595+Ld/8/DDH8bwzW9GT1q3iskk8Fd/5efo0QC//nUUW7fe\n+d/5Xd3VnZQgCLz2WpBvfcvHQw/J+MlP5KhUk/P+CwQEfv1rLz/6kZtvfUvB3/2dgujoyb3gNhgC\n/OIXTp57zsn27Qq+//14SkvvvGu5o8PPCy/YePFFO0VFcvbsUfHQQ8pb6gy6HQmCwPnzbp5/3sKB\nAzbWrFGye3cCGzbEIZNFIAgCdXVuDhwQN1E8niA7d2rZuTOBefPGv8Dr7R2JrYXg0c6dIjwaL+Z2\nMzU1WaTeo8uXjaxdm8H27Xls3ZpDSkosV66YOXy4iyNHurl61cK6delUVGgIBLzU1Q3w0UdmFAot\noMbrjWT9ei3btyexaZOOjIyRa4P+fjcvvdTBW28ZqKtz4HAIaLWRzJunYvPmZDIyYjh7VnQgtbY6\nWLJEJzmQ5s1LkADSwICTo0c7hjfn2vF6g1J8bd26PDIzp+6C9Vak19s5fbpbirFdvDh9nfEATqeX\n+npDGES6fLkPmSxSAkhiCkFMH0zGdUQwKDqTWlsHJXdSyKHU1mYkNlaGVhtBTIwHQTDhdPYyONhK\nZKSVgoLsMSApdNysBPtm8nh8w0kUE9evG2lu7qO+vou2tgH6+mwMDfmRy/2AHb/fglotIyNDRUFB\nEpWVucydW0xlZSn5+XkTMuRpPLlcXgYGbGOOEFi68b7H4ycpKX4UUFLfAJzC7yckjIXXIVfSaIgU\nYhBabcKYrqRVq5ZNys9/FxjdREajaQwUampq5dq1brTaVDIz80hMzEClSiQqKh5BiMbhCISBoKgo\nOWlp4dDnRldQCApNJQQKyecL0NNj+VQg5PMFyMnRkZ2tJSNDhULhx+8fwmbrp7+/jba2OiwWExUV\n5VRUzKCycoZ0m5GRcdsfym63j2vXBmlqMnDhQjtXrnTQ3DxAT48TjydITIyLYHAQt1uPThdBXp6G\n8vI0ysrCoVBycvKEnRBEMm+lsdFAXd1IGXVT0yA5OQlhYGjWrHQyM29v8tpkSxAEOjqGhkfbd/Lx\nx920tBiZMyc9rJw6JeXOTFa7mbzeAKdP90iAqKHByLJlWaxfn8uGDfnMnCn+jf3+IJcujQCikydN\npKfHsGpVIosW6RgY8PL++4OcP2/FYgkQHS1QXh7L5s3J/OmfZlFRoZH+XsGgwKVLNn73u14OHRqk\nvd0HOFGpPBQWRhMXF8n16w4cDj+rV6exenUaq1alMWNGApGRETgcPj74oJvDhzs4cqQTjSaabdvE\n3cSlS9Nua7StySRCogMHjHz8sZ1160RItHXrzSFRf7+PgwdFSFRX5+a++9Q88oiWdevipUWtxRLg\ntddsPP+8hd5eP48/nsBjj2nIzJz4hUhtrdhNVFXlZM2aGJ58UsX69TF33DIOUFfn4yc/cfD++x6e\nekrJt74VNyX9H6dO+XniCSeFhZH8+tdKsrMnb3pTVVWQ73zHx44dMn7848m7KL6ru/oiymQS+Ju/\n8fPBBwF+85sotmyZPJja1RXkm9900tYW5PnnlSxdOvkAx2wO8u//7uRXv3KyenU0P/hBHLNn3/mN\nK59P4NAhJ3v32rh40ctXvxrP7t0qSkom/rnZbAFefdXGc89ZGBjw8+ijGr70JTVlZeKaWxAEPvnE\nTVWVhf37zQQCsHOn6DyaM+fT4VFVlZGrV53cd58Ij9avvz14ZDS6eeedTg4dus5773VTXq7lvvty\n2b49j4oKLYODHt59t4fjx/uprtZjMLhZsiSZ/HwlgYCPTz4xceGCi7g4HU5nLBkZ0fzJnySzdWsS\ny5aFP5fOTicvvNDBkSMD1Nc7cbuDJCbKWLhQxdatqWi10ZIDqa3NydKlOsmBNG9eAnJ5JIIg0NZm\nkeJrR492kJYWJ8XXVq/OmVYudBDXkRcv9g13IXVz6lQXgUCQJUtGNkfnzcsgJubOA9WQxJ4iWxhA\nunKln9ZWIwUFOsmFVFGRQnl5CgUFuknb3BU7Zq1hMCl0e+3aILGxMpKTo4mPD1V7iH2vfX0NqNUx\nYyBSdnY22dnZ5OTkoNFobuu5+P0BenuH6Ogw0tqq5/LldhoauunoMKLXO7Fag0REiJu6MTF+EhMV\nZGUlUFycysyZeSxcWM7s2WW3/bifR263j8HBmwOlkfvircvlJSnpRgfT+IApMTEOm81ES0tbWFdS\nVdVL6HTaCf9Z7gKjcfTqq7/n0Ud/hlqdjEKhAmLweMBq9aJQREmQZ8QFpB73exNdDn07EgSBwUH7\nDTDIHAaGBgbspKWpJSCUk6MjJ0dLWpqKQMCKxdJNe3sz9fWN1NVdpa+vn9LSEioqyqmsnEFlpega\nys3Nua18pd8foLPTzJUrXdTUNPHJJ920thrp63NhtwvI5U78/kEUCiepqdEUFGipqMhk5swCqUco\nKyuLqKiJXVx4PH5aWgZpbBygsXGAhgYDjY0DNDUNotHEUFaWzIwZKZJ7qKIiFaVycsZqfx7p9XZq\na/uore3jwoU+zpzpRhCQomVLl2YzZ07atCinHq1AIMjlywaOH+/k/fevc/JkN2VliZKDaOnSTBQK\nOX5/kAsXLBw/buT48UFOnTKSlRXL6tVJLFmiw2Dw8t57A5w7Z8VoDBATA2Vlsdx7bxJf+1oOpaXh\nMUC93surr/ZQVdXPxYtufD4fCoWL3FwZCQnQ1eXE6w2yalWaBInKyzWhD0/a2qz84Q9dHD7cwcmT\n/SxYkCL1ERUV3d6JaXDQx5tvinGzM2fsbNig4eGHdWzdqkWlGv9ixmDw8dprQ1RVWbh0ycX27Wp2\n7kxgwwaVZJu324O8/baN/fttHDvmZN06JV//uobNm+MnfDKWwxFk3z4He/fa0OsDPPGEim98I56M\njOnxejt3zsePf2znzBkf3/2ukj/7MyVq9eSDoqEhge99z8Vbb/n45S9jefjhqEkDy11dYuzm2jUx\ndrNkyfRxCt7VXU03heKaixeLcc3k5Ml5XwqCwMGDPr79bRcPPBDFT38ai0Yz+RDXbg/y3HMunnnG\nwezZUTz9dBxLl06Ptcu1az6ef97GSy/ZqayMZs8eFQ88oJwUF1ZtrZuXXx5i/34bqakydu1S88gj\nKvLyxN+FIAhcvuyiqkrcdAERHu3YkcDs2ePDo54eL6+9ZqSqykRDg4v77hOnrd0uPPJ6Axw/3svb\nb4vF2ZGREVLv0fLl6SgUMvR6FydP6qmu1lNdbaCpaYjZs3Xk5sbi9fq4cmWI9naB2FgdXq+chQvj\n2bkzjc2bEykoCB+e0dRk44UXunj33QGamlz4/UGSkiJZtEjDli0pKJVyamvFjbjr150sW5YoOZDm\nzNEgl0cSCAS5eFEvxdfOnOll1qwU1q3LZcWKbJYsySQ+fnq8zkISBIGuLmtYjK2hYZDKyhTmz09n\n/vwM5s/PoLw8+bY2+KZCHo+fxsYBCSTV1xuorzfQ32+juDiJ8nLxGqW8XDxKSpImdZ0vDu4JOZNG\nom4hh5JSKScjQ4lGI6BQuAgETLjdfRiN1+jtvU5ERIQEj0aDpNBtVlbWbTllBEHAYLDR2mrg4sUW\nrly5TnNzH11dZgYH3djtEQSDAWQyNypVBCkpSnJytJSVZTJ7dj6LFlUwY0beHe0L8nh8DA7abwEw\nifedTi+JifFhUOk//uMrJCZO/JCku8BoHLW26nnllTNhsbC0NA0pKao7CoFGy2Zz09VlHj5GXEGh\nHqGuLjNKZTQ5OdoxQCg7W7xNTo7j+vXr1NVdpa6unqtX66mrq+f69Q4KCvLD3EIVFTMoLCy45cyo\n0+mludnA2bONXLzYTkNDH52dQwwMeHE4IomIcAJDaDRB0tNjKCxMZObMLObNK6K4uIj8/PwJiY2N\nJ7PZRWOjgYaGgTA41NU1RF6elvLyZMrKkikvT6GsLJnS0mQ0msmxN34eiR/WNi5c6AsDRC6Xj7lz\n05k3L505c9JZvDiL3FzNtHI9Abjdfs6d66O6uosTJ7o4fbqXrCwVK1ZksX59HmvX5qLTxeLzBTl/\n3iKVVJ8+bSI3VzkMiBIwGv28+66Bs2etDAwEUCigtDSWTZuSefzxHEpKwi3TXm+Qw4cN/Pd/d3Hq\nlB2zOYhM5iQjIwKtVsBgcBII/QEkZwAAIABJREFUCJJ7aPXqNMrKRgBRY6OF48d7OXGij+PHewFY\nty6L7dtz2bgxC43m9j4jBgZ8vPGGGDerqbGzcaOGHTsS2bIlgfj48SHR4KCf118XF7XnzzvZulXD\nzp0JbNqkkuz9bneQ3//ewb59Vt5918GyZbF86Utq7r8/HrV64nfSr1wRu4lefdXB8uUKnnxSxaZN\nsZMWtbpdnTjh5cc/tlNf7+dv/zaOxx5TolROzXN7/XUv3/qWiy1bovjZz2LQaidrN1Dg2WcD/PCH\nfv7iL+T83d/JJq3Y967u6v8mhQrhX345wM9/HsWXvzx5hfBmc5Dvfc/NkSM+/u3fYnnwwam5qHa7\nBf77v1387GcOcnNlPP10HOvWTW4h963K4xF4800nzz5ro6HBy9e/rmL37njy8yfedRQICJw86WLf\nPisHD9ooKorikUfU7NypIiNDfDxBELh4cQQeyWRIsbV77hm/c6+72yM5jxob3dx/vwiP1q27PXgk\nup5MHDokRtfq6kwsWJDC6tUZrFqVzuLFqcTEyLHZfJw+bRgGSHrOnzdSUBBPTk4sTqeP+noXFks0\noEKjkbNpk46dO9NYs0ZLXNzIGiAYFLhwYYj//u9u3ntvkLY2NxBAq41k2bIENm1KITpaNuzkNtLV\n5WT5chEgrV6dxJw5CchkEbhcPk6d6uHDD69TXd3NxYt6ZsxIZMWKbFasyGL58mySk+/cVLObyeHw\ncvFiP+fP90pHd7eVWbPSWLAgQ4JIJSWJ08IdfaOcTi9NTYPU1+tpaBigvt5AQ4OB9nYzOTkaZsxI\npbxcvKaZMUO8romPn9xr2dA0t/GcSa2tg8TFRZOXpyUtTYFaHZSAktPZi17fSWdnJz09PWg0mnGB\nUujr9PT0W570JggCZrOTCxeaOXeukbq6Tq5dM9Dba8Vk8uJyyRAEOQqFj4QEGWlp8eTnJ1NRkcO8\neaVUVuaRna2dVvUiXq9/2MEUgklWHnxw/qQ8x7vAaBrK7fbR3T3iBhoBQyOHzxcgO1sbdohASCfd\nD8XcgsEg7e3XJSAUum1ubiErKzMMDFVWVlBSUkx09B9fwBiNdmpr24ZdQp20tg7S2+vAbA7i9UYi\nCFZiYtwkJsrIylJRUpLCzJm5LFxYSllZMSkpKZO2UBELxIbGuIUaGgZwuXyUlYVDofLyZAoKdNNi\nOtl4CsXKRoOh2to+BEFg3rwM5s5NG4ZEGdMSDoHYm3T6dC8nTnRx4kQntbV6ysvFxcTKldksXy6O\nSPV6g5w7Z5YA0ZkzZgoL41i1KpElS3SYTF7eeScEiPxER0dSXBzDpk3JPPZYNuXl4eMkxRG7Fvbu\n7eD99y10dgYBD0lJQbRaAYvFTmRkRJiDqKREjBWKE9VMHD/ey/HjfZw40UtcXBQrV6azapW4eCso\nuP0IosEgQqIDB4ycO+fg3ns1PPywCIlGL+RGy2Ty88YbopOopsbBvfeKTqLNm9XExoqLUZ9P4IMP\nREj09tt25syJYdcuNQ8+GE9S0sS/tl2uIFVVYrSgs9PP44/H89hjKrKzp8f7SBAE3ntPBEW9vUG+\n9704vvrV2EnvEAmpuzvIX/yFi4aGAM89p2Tlysn7vdTXi6PDAZ5/PooZM6bX7uhd3dUXQefPB3ns\nMR8ZGRE8+2wUubmT91lRXe1n924nZWUyfvWrWLKypuY96/cLvPqqm5/+1I5KFckPfhDH9u2KaXMx\n3Njo5bnn7Pz2t3bmz4/mySdVbNumnHA3LIjnzKNHHezbZ+Ott2zcc4+CL31JzUMPqaRzpiAIXLjg\nkjoBo6MjpNhaZeXN4dHBg+I5PgSPdu5MZN06tdQPdKuyWr2cOtXPsWO9HD/eS12diXnzkocBUgZL\nlqQSGyvH4wlQW2uUANKpUwbU6iiysmKx2YJcu+bF748jEIihrEzBQw+lsmNHGjNmhPemuN0BqqtN\nvPJKLx9+aKSvzwsESEiIYOXKBNasSUImk3P1qo1jxwbp7naxYkXIgZTMrFkaCSCJm4LdVFeLm4IZ\nGfHD8CiLFSuyycubnuvVoSE3tbV9wwBJvB0YcDB37ogLaf78DAoLb6/4eSrl9fppbTUOQ6QRmNTc\nPEhyclwYRBJdSckkJk5+NYU4OdwquZFuBEpKZTRFRUkUFSWRlhaDWh0kKspBMGhiYKCbrq4uurq6\n6OzsZHBwkLS0tE+FSomJt17U3tXVz8cff8LFi63U13fT3i72J1ksPgRBiSDEolBEjoq7pVNRkUtu\nbqJ07Z2RkTBtJgtOpO4CoymWzxegt9cyLgQKOYWGhtxkZmrIztaNAUKhr7XascVYgiDQ3d3N1asN\nYa6hhoYmEhN1VFZWhMGhsrJSlMqb0/5gMEhb2wAff3yV2tprw236ZvR6DzZbJIGAQGSkFbVaIDVV\nQV6elhkzMpg7t5AFC8rJy8tFoZhcih2KkYluoREo1NwsxshCbqHRcCgjY3p1DN2oYFCgrc3MhQu9\nw4Con9raPmJi5JJzaO5c8cjMnB5T1sbT4KCTkye7OXGii+rqLhoajMyblyYBoiVLMlCpFHR3uzhz\nxkRNjZkzZ8xcujRESUkcq1YlsWBBAjabj8OHDdTUDDEwEEAuj6SkJIYNG5L4xjeymTlzbOyrr8/F\n3r3tvPXWAPX1Pnw+AbXaR0JCEIfDTnR0BKtXp7NqVSqrV6dRXKwe1Yc0OOwe6qO6uo+kpBhWrUpn\n5UoREOXkfLaSR71eHNd74ICJCxccbN6cwI4dOjZvTkCpHP/kYjb7eestERKdOuVg40YVO3dq2bJF\nJYGlQEDgxAkn+/bZeP11G8XF0ezapWLHDrU0HWaiVV8vuol+9zsHCxcq2LNHxdatsZOyoP8sCgYF\n3n7bw//3/9lxueDpp+PYuTNmyp6fyRRk714vzzzj4amnovnBD2Imzenj8Qj84z8G+NWv/PzoR3Ke\nfFI2bS787uquvojy+QR+/vMAzzzj53//bzlPPSWbNKekxyPw05+6+Y//8PLUU9H82Z8pSE2dGnAU\nDAq8+aaHH//YjtcL3//+1H5O/jG5XEEOHhRdRx0dfh57LJ7HH5+8DQm3O8gf/iBuuPz+9w6WLIll\n1y41DzwQj0Yjnm/FQm0XVVXitDWlMlKCRxUVseP+u11dI86j5uaQ8+izwSMAm83Lxx/rJYB05YqR\nOXOSJIC0dGkqSmUUwaDA1auWUTE2PS5XgIyMGIaGIujtFYiIUKFQyFmyJI6vfCWT7duTSUgIdyeY\nTF4+/NDIgQN9fPSRCZstAPiIj4fVq3UsW5aIXC6jvt7O8eNGentdLFyoZfFiHYsXa1m0SEdiYjSB\nQJArVwwSQKqu7kYuj2TFiizJhVRRkTxtz19Go5Pa2j7OnRtxItls3mF4NAKScnKmJwQLKRAI0tFh\nGeNIqq83EBsbFRZtC92mp0/NtUYIJo3E3MKdSTExcoqLkykqSqK4OJm8vAQ0GgGZzIbFoqezszMM\nKHV1deF2u8nKyvpUqPTHEi3i8+qnoaGZc+euculSK42NPXR2Ghka8qNUpiCXq/H7FTidAjpdLLm5\nieTnJ99g7hCv41NTVXc0+vZZdBcYTaCCwSB6vS0M/tx4GAw2UlJUY9xBo4FQSsqnv5BsNhstLa20\ntIjT2UJf19c3EhenHFM+PWNGOWq1etx/y+32cv58CzU1DVy61EFr6wDd3TZMpgAuVxSC4CEmxoNW\nG0lWVhyFhcncc08OCxeWMmdOGTqdbrJ+nWEym12SS2i0Y6ira4j8fO0YKFRWloxaPf1iZDcqEAjS\n3GwMcw5dvNiPVhsjQaHQkZY2ORG9iVJXl1WCQydOdNHTY2fp0kxWrMhi5cpsFixIx++H8+ct1NSY\nqakxceaMGZ8vyOLFOhYt0lJUFMfQkIcjRwycPj2E0RggMlJGYaEIiB59NIu5c8eejN1uPy+/3MG+\nfX2cP+/EapURG+tHo/HjdjtRKgXWrBkpqS4qEk9+Pl+A8+cHJPfQqVN6srLiWLVKdBCtWJFORsZn\n33Hp7xfLMQ8eNHHxooMtWxLYsSORe+9NkFxBN2poKMDbb4uQ6MQJO+vWqdi5M4Ft29RSRE0QBM6c\ncbNvn5WqKivp6XJ27RIt9aE+homW2x3ktddEN1FLi59vfCOeJ56IJy9v+thz/X6Bqio3P/mJg5gY\nePrpeO6/f+p2zpuaAvzylx5efdXH9u1yvv/9GMrLJ2+n6fTpII8/7qOgIIJf/zqK7Ozpu0i9q7v6\noqmpSXTt+XzwwgtRVFRM3gK/pSXAM8942L/fx4MPRvHd7yqorJyaXeobnZh/93eiE3M6xVk/+WQk\n8rxs2eRHnh2OIIcP29m3z8rRo07WrlWya5eabdviiYsTXweCIHD2rFOKranVMgkelZePv/7s6hKd\nR1VVRlpa3DzwgAiP1q79bPAIwG73cfp0yIHUx6VLg8yalTgKIKURHx817FS3U11tkCBSR4eD5GQl\nNpsMi0UGKMnMlLFxo5bHHsth0SLNmPNne7uTDz4w8vrr/VRXm4mMhGDQR3R0kDVrdCxcqEOhkKPX\nezl3zsLZs2bS0hQSQFq8WMfMmWrk8ghaW80SPKqu7sJkcrNsWSYrVoiu8/nz04mOnr5uDb3ezoUL\nfRJAOneuF78/GAaRFizIJCNjek2TG09izYV1jCOpocGA1xsY40iaMSOF3NyEKQMfgiCg19tGOZLC\ne5MUCjnFxUkSTArdpqXFYrcPjgFJo79WKBTjgqTc3Fxyc3PJzMy8afTN5XLR0tJKU1MzjY3NNDQ0\nU1fXTmtrP1FRCSQmZqNUJhEREY/LJcNs9mG3e8c1how+dLq4aQUepy0wioiIyAeeBtSCIOz8lP9u\nSoCRIAiYTI5xIVAoNtbbO4RGExNGEW+EQenpmluyqrlcLq5daxuGQi20tFyTAJHVaqWoqJCSErHv\np6SkmOLiQsrKSklMTBzzb/X1DXLyZB3nz7dQX99De7uZ/n4XVmsEPp8CmcxFfLyf5ORocnMTKCtL\nY+7cQpYuraC4OO+W86GfV6NjZOFwaCRGJjqGvhgxshvl9wdpaBgI6xy6fFlPampcmHNozpx0kpKm\nX857tARBoLnZFAaIHA4fK1dmSw6iyspkrl1zjnIPmWhpcXDPPWoWLdJSWalGoYCmJisffGCkrs6B\nxxOJIESSl6dg/fokvvKVTBYtShhTPhgIBHn//V5eeqmLEyes9PfLkMsFVCo/Pp8TlSrA+vUjDqKC\nAhEQud1+zp41cPy42D9UU2OgqEgtRcxWrEgnOXn8XcJbVV/fyPjdK1ecbN2q5eGHdWzadHNIZLMF\nOHTISlWVmY8+srN6dTw7dyawfbtG6hsSBIFLlzzs22dl/34rsbGRfOlLYmlnaenkOfmam33s3Wvj\nt7+1M2eOWEp6331KoqKmz4nM6xV4+WUXP/2pg/T0SJ5+Op5Nm6amm0MQBI4e9fOLX3g4ezbA7t3R\nPPWUgvT0yVtE2WwCTz/t58CBAL/8ZRQ7dkxe38pd3dX/ywoGBZ5/PsDf/72fp56S8f3vyycVpAwO\niu7E//gPD5WVMr77XQWbNsmnDHpXV3v5yU/s1NX5+eu/juOJJ6au6+1WNN5Qhccei580Ny2Ik0Xf\nekuER6dPu9i8OY5du9Tce2+cNFgiGBSoqRHh0YEDFrTaEXhUWjo+POrsHImtheDRzp2JrFnz2eER\ngNPp4/RpvQSQamsHmDkzUepAWrYsDZVK3FgaHHRz8qSekycNHD/ezyefWIiPj8PlisLlikYuj6Ky\nMpoHH0zhscdySU8PX2sEgwKXL9t4771BDh0ycP78EGp1JMGgH7vdzezZ8SxdmkhmZhx+PzQ3O6ip\nMdPR4WLuXM0oF5KWjIxY+vrsnDwZciB10dJiZv78tGEH0ogzfboq1C060ofUx7lzPURHy8KibPPn\nZ0y7ycSfpsFBBw0NhjCY1NBgwGh0UlKSNMaRVFSUOKWxrBBMGi/i1tIiwiQRII0FSgkJsZhMpnFB\nUkdHBx0dHQwMDJCZmUleXl7YkZubS15eHpmZmWM6fsXXQi+Njc3DMKmJpqYWGhub0OuNZGeXkp5e\nSEJCOgqFjkAgFocDenutN62euZEvqFRTZ4yYtsBIepCIiKqpBkbXrxt56aWPpRLpri4z3d0WoqJk\nn+oMysq6vTIsn89He/v1caBQCwbDAHl5uRIMEm+LKC4uJCMjI4zout1uPvnkGjU1jVy61E5zs57O\nTitGox+HI2q4xMtDQkIE6elKiooSqazMZsGCEpYurSQhYXz30WTJ5fLR0jJIU9NgWPl0U9MACQmx\nX8gY2Y3yegPU1RnCnEN1dQays9VhnUNz5qSTkPDFcEJduWIYBkTiyTwmRh4GiBIT4zh71iIBorNn\nzSQmRrN4sY65czUkJMgZGvLw8cdGPv7YwuBggOjoaLzeCMrKlGzYkMh996WyaFECMTHhJxqxgHKQ\n//zP67z7ron2dgFBiCIuzkcg4EKjCbBxY6rkIMrPjyciQhxzf/q0XiqovnBhgBkztKxalcHKleks\nX56OVvv5Fx+hSSkHDpioq3OybZtYdrlxY4JUQn2j7PYAR45Y2b/fwocf2lixQoRE99+vkezvAA0N\nIiTat8+Gzyewa5eaXbtUzJypmLT3hNcr8MYbopvo6lUvjz4azxNPqCgqmj5uIgCXS+DFF5380z85\nKCuT8/d/H8/KlVNTIOvxCLzyipd//VcPPh985zsKvvKVaGJjJ/dz6siRAN/8po9162T8/OdydLov\nzufiXd3VF1U9PQLf/KaP1tapmTzo8Qjs3+/jX/7FjccD3/3u1Hy+hHThgo+f/MTOyZM+vv1tJU89\npUSjmV4RitpaD3v32qiqcrJ2bQxPPqli3bqYSYVrAwN+Xn/dxquvWrlyxcP996vYtUvF2rVx0iZK\nMChw+rRDgkfJyXJp2lpJyafDo6oqI9euuXngAR07dug+NzwCcLn8nDkzEmE7f36AigqdBJCWL09H\nrRbPmw6HjzNnBqiu1vPRR/3U1JiRyWLxeqPx+2PQaGDp0ni+9rUsHnwwfcxzc7sDnD5t4dQpC8eO\nGTl92kJcXCSxsQJmswuFQmDpUi2zZ2uJj4/Gag1w8eIQZ86YiYuTsWjRSJRt7twEPB4fH3/cQ3V1\nNydPdlFbq6esLFGKsS1fnjXtwYsgCHR2DkkOpPPne7lwoQ+VKnrYgSQCpHnzMtDpPt+G5VTLZvPQ\n2GgYdiKNOJK6uoYoKNCNcSWVliZN+XRpcXqaPcyNNBoqRUXJRgGkJIqKkiWwpNOJry2Px0NXVxfX\nr18POzo6Orh+/ToGg4GMjIwxICl0ZGVlhQElh8NBS0trGERqamqhqakZjUZNaWkJBQUlpKTkEh+f\nikymwemE7m5LmFFFoZCPMaj8+Z+vRqOZ+NfRpAOjiIiIF4FtgF4QhHtGff9e4F+BSOBFQRB+dpP/\nf8qBUVvbAP/1X2fG9AZ9FpIXCATo6uoeBYVaaWm5RnNzC11d3WRmZkhQaMQtVEROTjZyuZxgMIjB\nYKClpZ2LF1upq+uSYmMDA17s9kj8/jgiIyEuzkdSUhTZ2WpKS9OYPTufZctmUFmZP2UuoZDEPqUh\nmpoGaWoaGD7Er/v77RQU6CgtTQqLkH1RYmQ3yuXy8cknhmEw1EttbT8NDQMUFurCnEOzZqVO652R\n0fJ4/Jw/3y85iD7+uGe4rFCEQwsXZmA2E+YeMhq9LFigZeFCLenp0fj9ARobrZw6ZaS52YVaHUsg\nIMPtFpg3T82WLcmsWZPI3LnqMRNExHH1Q/zud9d58009dXV+/P5YoqP9CIKbhAQ/mzYlsXZtOqtX\np5GXJ9p9Q+WQoSlmV64YmTUrcbigWsz2h3bWPo8EQeDKFSeHDpk5fNhCU5OL7dtFa/nGjRpp1/FG\nOZ1B3nnHyv79Zt57z8bSpXHs3JnAAw9o0GpHTiZtbV7277exb5+VwcEAjzyiYtcuNQsWjF+wOVEa\nPeJ4xgyxbPSBB5TTKpoAYLMF+c1vnPziF04WLYri6afjWbBgamCWwRDkN7/x8pvfeJg1S3QAbNw4\n+Q4Ag0HgO9/xUVMjsHevnPXrp69N/67u6v9GCYLAwYNBvv1tHw8/LOPHP5ajUk3u+14QBI4dEx2M\nZ84E2LNHdDCmpU0NvKmv9/OP/2jnnXc8PPmkku98J46kpOkFjqzWIK+8YufZZ23Y7QK7d6v4+tfj\nSU6e3M/Inh4fBw6I5+m2Nh8PPSSep5cvH4nKBYMCp06J8OjgQQupqXJp2lpR0fjrwY4ODwcPGqmq\nMtLW5mHLlgS2btWycaO48fZ55XL5qanRc/x4H8eO9XLunIHycq0UYVu+PI2EBPG5+XxBLl4Ui7Tf\nfbeHU6eG8PsV+P0KIIr0dNi8Wcuf/Vk+8+ZpxzxWICDwySc2Tp40c/KkmePHTbhcAZKT5fj9Pvr6\nbBQWKlm0SEtBgYrISBnd3W7OnrXQ0GCjokIVFmVLT4/mwoV+aePy4497SE2NG9WDlE1+/vTuEALx\nfX3tmjlsMlttbR/JyXFhcba5c9On5ZTmPya320dz8+AYR1Jrq5HU1PhRA4dGEiNJSVMfwRIEgYEB\n+w0xNxEktbQMIJNFUliYSEFBIoWFSWG32dkJyGTiZ6HX6w0DSiGQFDr0ej3p6eljQNJooBQVFUUw\nGKS7u3sURGqWHEpGo4ni4iLKykooLS2htLSYtLRcYmMTMRo9Uurp6afvJT5+4l8zUwGMlgN24Lch\nYBQREREJNAPrgF7gHLBLEITGiIiIrwBzgH8WBKEvIiLigCAIOz7l37/jHUbi+MA+CQSN7hdqa2sn\nKSkxLDoWgkIFBfm43W46O8URgnV17dTXd9PaOkBPj53BQR8Oh5yIiAQEIQalMkBiopzMzHgKC5OY\nMSOTuXMLmT+/hMTEO9NvY7d7aG4eDANCTU2DNDcPEh8fLY2lLy1Nkm7z8rTI5V/Mix2Hw8ulS/1h\nZdQtLUZKS5PCyqjvuUcsHfyiyG73cvp0jwSIzp/vp7RUN+wgyiInJ4nWVrcEiK5csVJcHMeiRToK\nC5VERgbp7XVy7pyJ2toh1OpY4uIUWK3g8QRZuVLHmjU6Vq3SMWuWatyIWUODiQ8+6OWtt/TU1Lhw\nu2OJjIwkMtKNWu1n0yYdGzeKMbMQIDKZ3Jw82S9NMWtsNLNgQYoUMVu8OGXC/g4uV5CjR4c4fFiE\nRNHREWzfrmXbNi0rVqhuColcriDvvis6id5918rChSIk+pM/0ZCYOLL46+nxUVUlLj7b2308/PDI\n4nMyYYTPJ/D226Kb6OJFL1/9ajy7d6soLZ1+r1+TKcivfuXk3//dwfr1Cn7wgzhmzpya51lXF+AX\nv/Dw+us+Hn44iu98R0FFxeR/jgmCwMsvB/mbv/Hxta/J+D//Rz6tIiJ3dVf/r8lkEvirv/Jz9GiA\nZ5+NYvPmqVnPNDePdKTdd5+c7343hlmzpuax29r8/NM/OaiqcvO1r8Xy138dR2bm9FrHCYJATY2H\nvXvtvPGGg82blTz5pIqVKyfPjRtSe/vIJs/AQICdO8Xz98KFI5s8gUA4PMrIiJKcR4WFN4dHR46Y\nOXLEQnW1jblzlWzZomXr1gRmzIidkJ9rdFT/2LFezp41UFKikQDSihUjTmxBEGhsHOLECT2vv97J\nqVM2XK5ogsEY5HKBwsJIdu5M5bHH8sjNHXtdIrpt3BJAqq42097uJCtLQUxMEKPRicXiYv58LXPn\naklMjMXtFmhosHP6tEnqvFy8WMuSJTrmzNFw/bp5VIytm4gIpBLt5cuzmDkzZdoWaY9WqNN0dJzt\n8uV+srLUYVG2OXPSiIubWpfORCkQCNLebpLqRkIVJA0NBiIjIygrS5FSJiGYlJenlcDMVEoQBAYH\nHbS1Gbl2bXD41khbm3gYDDZycrSjQFI4WIqPH3lPe71euru7x4Ck0NHf309qaupNI2/Z2dl4PB6a\nm1vCIFJjYzMtLa3odFrKykopKyvhRz/635PSLzwlkbSIiIhc4NAoYLQY+KEgCJuH738PEEa7jCIi\nInTAj4H1wAuf4kCasg4jo9EYVjQdipG1tl5DqVSGwaCSkiLy8nKJiVEwODhIZ2cn1651Ul/fTVub\nkd5eO0ajn0AgHplMh98fR3Q0JCVFkZmporAwicrKbObOLaS8PIPMTM0decOA+Abv7LSMgUJNTQOY\nTC6KihLDgJB4m/yFpOIhhcbYX7miDzu6uqxUVCSHOYcqK1NQKL4YPUohGY0uTp7skiJm9fWDzJmT\nysqV2cydm0FUlJJPPrFL7iG5PJLFi7VUVKhQKiMYGvJy+bKFs2eNREXJyMhQA3J6e70Eg7BqlQiH\nVq7UUVkZP+ZkPTjooqamnw8/7OXdd400NweAOIJBOZGRHlQqP2vWJPDAA6KDKCdHXHgYDC5OnOiV\nppi1t1tZvDhVmmK2cGEKCsXELWK7uz0cOWLh8GEzx4+Li7Vt20RIVFp6c7ePOG3FRlWVhSNHhpg3\nT8nOnQk8+GACyckjr5WBAT+vvSba2z/5xMMDD4iLzLVrJ2eE8Gh1dPh5/nkbL75op6hIzpNPqnjo\nIeVNI3R3Utev+/nNb1y88IKT+++P4Xvfi6OkZPLfc8GgwB/+4Odf/sVDXV2Ab35TwZNPRpOcPDW/\no/b2IHv2+BkYEGMw8+ZNv7/NXd3V/6v64IMAe/b4WbIkgl/8Iork5Kmbwvjcc17+/d89lJaKLsct\nW6am56i3N8Azzzh46SUXDz0Uw5NPKpk7Vz7tHB1mc4CXX3bw7LM2BAH27Innq1+NR6ebfMjV0OBh\n/34xRu7xCOzaJZ7X77lHEQaPqqvtVFVZeO21IbKzR+BRfv748MjpDPDRR1aOHLFw5IiZiAjYulWE\nR2vWaG7akXi78ngCnDtn4PjxXo4d6+XMGbHrcdWqDFavFuP8Ot3I+r6ry8FHH/XxX//VwdmzThyO\nKCAamcxLerrAqlUannjkaMAZAAAgAElEQVQilyVL0sYtsDabfZw+bZEgUm2tlbS0aJKSZHi9Htrb\nrcTFRbJoUSKlpWoUCjkmk58LFyxcujREYWFcWBdSVJSfU6e6JRfSwICTpUuzJBfS/PlpX5g1e6j7\ndPRktro6AwUFWmbNSmPmzJThI5Xs7C9WdcdohWJjIyBpZOr1wICDoqLEMSCptDSZ2Ng7t7Hpdvu4\nft00BiZduzZIe7sJlUpxgzNpBCilpYUPt/L5fPT09Nw08tbb20tKSsq4kbecnBwEAdrbr9PU1Mye\nPY8TE/MFdBgNP8iNwOghYJMgCLuH7/8vYKEgCN+67ScxCcBocHCQ99//MKxTqKXlGoIgSFCoqKiQ\n1NQUlMpYIiLAZDLS0dFBc3Mv7e1Gensd2GwyYmJSkcl0+Hyx+P0yEhPFyFhRUTKVldlUVGRTWJhI\nfn44jbwTGhpyj4mPNTUN0tpqRKeLpbQ0efhNOgKFcnI0X7jRgDfKZvNQV2cYBYbEr1WqaO65JzXs\nKC2d2iK3iVJ3t5Xq6pER952dVpYuzWTZsiyys5NwOuVcuDBETY2Z69edzJmTwJw5GnQ6OV6vn6am\nIc6fN2O1+ikv15CQoMRuh5YWF5GREcOASMvKlTrKysJtpX5/kCtXBjlzpo933+3h5Ek7Q0PRRETE\nEQjIkMs95OTIWbkygW3bklm8OJnMTDE33NNjl+DQiRN99PY6WLYsTZpiNndu0oT+PYJBgXPn7Bw+\nLEKizk4vmzcnsG1bAps2JYTFxm6U1xvkvfdESHTokJVZs2LYuVPLQw9pSE0dOalZLAHefNPGvn02\nzpxxsWVLPLt2qdi0Ke6mLqWJkvjYTvbtc3DunJf/9b/i2L1bRUXF9NutcrkE3njDzX/+p4tLl3x8\n+cux/OVfxpGbO/nvP6fz/2fvvKPjOu8z/UwBphcMKgmSAIgOAiDA3ptIkGKnKJGKtLEtxsmuk3ht\nZbM+m40T2Yk38dlNlMRJTryJl7ITS1azRIlNIkiJvYIVAFGIQpAEiD6937l3/7jAACOQKrYIDmm8\n58wBcI5EDAaYe7/v+d73/Un8x3/I/UQaDbz4opZnn00Yt2ieIEj86EcR/uqvBL7zHTUvvqiKq5Lx\nCU1oQrK8XomXXhL4+c8j/O3fJvDcc+NXQB8KSbz1Vpi/+7sgbrfEt7+t4StfScRgePDfv79f5Mc/\n9rF7tx+jUcGuXTqef143bjD980qSJE6eDPLjH7vZv9/H+vV6du40sHat9oEfjkiSxNWrwx2E8qCK\nZ5+VB1UUFY2s9wVB4vhxGR69846T7OzEKDzKyrr3vVmSJOrr/Rw4IMOjy5d9LFtmisbXsrK+vP1E\nKDQ8TVYGSGfO9JCTY2b58klRgJSSMtKZ4nAEOX68l5/97BanT7vp7VUgiglAEKMxRGmphp07J7F5\nczY5OWMhRzAocumSk5MnZYh06pQdnU5JVpaGxETZ9dHS4iQ/38ScOUlMnqwnElHQ0eHn3DkHAwMh\n5s1LGupDSiI7O5GGht4oQGpqGmT27IyoC2nhwkzM5kejLgJGOlKvXeuhtraH2tpeamt78fvDlJaO\nAKTy8nRKS9MeiZ7UT5PXG6KpKXZCdkNDH62tA2RkmEb13o64k1JTH+5UaVEU6e5239Od1Nraj8sV\nJCfHds+4W3Z2Ejpd7PteEIQYoPRJp1JnZyepqalkZWWxZ88eUlNTv/Sf6bEARi+99FL06xUrVrBi\nxYov+s/E6Nq1Wl566QekpiZjMhlRq2XKPTDQT3t7J+3tg/T0+NFo0tDrM1AqkwiFdLjdCkymBKZO\ntZCfn0ZxcSZ5efIfwfTpyUyaZH7ocEUQIrS32+/pFvJ4QhQUpIxxCxUUpDx0mPVlSBQl2trsXLvW\nw9Wr3VEw1N3toaQklfLyNMrL06PUPjk5vieV3U8uV5ArV3q4dKmHixe7OXXqDm53iKVLpzJz5iSM\nRgu9vSLnzzu4eNHB5Mla5syxkpmpQaGQ6OryUlNjp6PDy8yZVnJyLCQkJNDTI3DpkhudThl1EC1f\nbmP69FhbdHe3lzNn7nL06B0OHerlxg0BpdKIIOiQJBVWq8jMmXrWrk3mmWcmkZsrTzATRYnmZgfn\nzvVGS6rt9iBLl06KAqKZM5O/dKedyyVQXe1k3z4HBw7IBZWyi8jKggWmT3X6+HwiR464eecdJ++9\n52TGDC07dlh5+mkrkyaNQCKvV2TvXnnKyscf33tE74OS2y3y/vs+3njDy9GjAVat0rJjh4GtW/Xo\n9fG3uL94UWD3bh9vvBFg7twEdu3SsXmzFq12PE7PRf75n4P867+GWLhQPrlfsWJ8T8+vXhX5+tfD\nmEwK/vVf1eTlxdfvaEITmtBYXbggv28zMxX8y78kkJU1ftcMGYpEePnlICdPCnz964n84R9qyMx8\n8NcOUZQ4fjzE7t1+3n8/yBNPJLJrl461azUP3CX7RdXfH+HNN728+aaXq1fDbNyoY8cOA1VVugd+\nGCDH5QK8/rqLN990k56uisKj7OyRzaEgSBw9KsOjd991MH26hu3bLWzdarlvYTaA3S5w6JCD/fsd\nHDzoID09gQ0bZHi0aNGnr2O+qMLhCBcv9kcB0unTPUybZhwFkCaTlhZbutvW5mb37lu8914fLS1h\nAgEVEEKp9JGZCcuXW3nqqWmsXDllDOCQJImmJm/UgXTypIPBwRAlJQZsNhWBQJDWVif9/UHmzEmi\nrMyK0ZiIxyNSV+fmwgU76emaqAuptNSI2+3mzJlOTp6UKxhyc63Mnp3BnDmTmD07g5kz09BqHw0X\n0rD6+ryjQJIMkerre7HZdJSVpce4kYqKUu7p9nqUNLyfHZmo3Rv9qFIpx3QkFRWlkZVlfWhpndHy\neILRaNsnodKtW3ZSUgz3dSfdq+tJEAS6urro6OhgwYIFJCT8+s6ro0ePcvTo0ejX3//+9x9aJO17\nkiStG/p6TCTtcz+JB+Aw2r+/mu3bv0FSUjY6XQYKhZVgUIvLBeEwTJ1qJj8/nfz8tCgMmj49mexs\n27i3v99PAwPeMUCosbGP9nY7GRnGGCA0bO3LzHx07YyflN3up7a2NyZOVlfXS0qKPuoWmjlT/piX\nZ4uLC8ivIrs9wOXL3VE4dOlSD3fuuCkvT6WsLB2bTe6/am8Pcu6cHY9HYN68JHJz9Wi1Cuz2ILW1\nDurqRk5rMjIMBAJKbtzwc+qUg+TkhKF4mewgysoaWQgEgwJXrvTx8cd3OHSok0uXnHg8GhQKA4Kg\nRalUMW2amsWLzWzfnsHGjWkkJCiHcuweLlzo5cKFPi5c6OXixX5sNg3z5qVFIdGMGbYHYrNvbQ1E\nu4jOnnWzaJEpColycj79NKarK8y+fU727nVx7JiHWbN0bN1q4emnrUyZMvL+DwREPvjAy+uvuzh4\n0MuiRTqefdbM1q3GmCloD0Jer8j+/X7eeMPL4cN+lizRsnOngS1b4m/SDUBfn8irr/rZvduPxyOx\na5eOr3xFx7Rp47OguXRJLpXdt0/g+ecT+Na3NOTnj+9iyu+X+Mu/FPjJTyL88IdqXnhB9dhcjyc0\nod8EhcMS/+f/RPi7vxP48z9X8/u/r4qWH4+XWlvlnqOf/zzM+vVqXnxRw+zZ47PxdTpF3nxTdoV2\ndET4yld0vPCCjsLC+Nt4370r8Mtf+njzTS+1tWE2b5bh0Zo1OhITH+zvTI6j+Xj9dTe//KWbvLwE\nnn3WzDPPmJg8eWSjFw7L8Ojddx28954Li0XJ1q0yPJozR3/ftVEkIjul9++XD8Ha2wOsWWNhw4Yk\nnnzSSmrqlxvjEQSRS5f6OHZMPug7ebIbqzWRuXPTmDMnlblz05g9OwWLZeTg2e0WePvtbn7xiy4u\nXPDgdIIkhQAfen2Q4mINK1dm8NRTOcydmz6m97K7O8ipU/YoRLp+3cuMGQamTdOgVkfo7fVy5Yod\nk0nNvHk2srJMqFRKenpC1NQ4uHnTx6xZVhYsSGL2bAsGQ4Tbtwe5dKmHmpq7NDUNUlBgG4JIGcye\nnUF5+aMHkURRor3dPgSQRkDSzZsOcnOTKC9Pj0KksrI0pk2L/8Lwz9JwvG10R9Lwx/5+H/n5yZ+A\nSWkUFKQ81HjbaEUiInfuOMa4koa/Docj93AmyV9nZdkeWApmvBxG2cjAqGzoaxXQhFx6fRc4D/yW\nJEkNX/hJPABgdO7cTb7znb1Mn54SA4Rycmykp5vi5s3k8QRpbR2kpWWAlpaBGDgUDkfGdAoVFsoj\nA+PlTfFlSBBEbtwYGBMnGxz0U1qaFoVCj4M1s7/fx6VLPVy61B2FQ729Pioq0igvTyM5OQlB0NDZ\nGebSJSdtbV5KSkyUlJiwWFT4/WFu3HBx6ZKdtDQtc+famD3bhsmkobdXHoV6+rSDzExtNF62bFkS\nkyfLr5kkSdy+7ebo0Tvs33+bc+f6uH07hFJpIhLRolbrUCjUzJihZc0aG888k0FlpQmVSkFfnz8G\nDl240IdCAXPnpjF3bmp0YZGa+mBGigqCxOnT7qGpZnbs9ggbNljZuDGJ1astmEz3v8BKksSVK37e\nf9/F3r1O2tpCrF1rYtMmC08+aYqJqYXDEkeOyJDo/fc9zJyp5dlnTWzfbiIl5cEuNORybRkSHTzo\nZ/58DTt3Gti2TT8uvQ1fVIIgcehQiN27fRw+HGLzZg27dulYtixxXLo4IhGJvXvlOEdbm8g3v6nh\nd383kaSk8Qdqx46J/O7vhqmoUPCjHyWQkREf95gJTWhCX1xNTfL7WRDgJz9JoKRk/K8pDofIT34S\n4kc/CpKTo+TFFzVs2pQwbgCroUHglVf8/Pu/+8nNVbFrl44dO7SYTPF3YNHZOQKPrl8Ps2WLnh07\n9DzxxIOHR6PXDO+956Gi4t5rBlGUqKnxsWePkz17nDidIlu2mNm61cKKFcYxk2ZHq6srxMGDcnTt\nyBEXxcW6qPuoslL/pe9pRFGipcUZXevV1PRx5Uo/mZmGURAplcrKlOhQErdb4NgxB2+/3U119SDd\n3RGUyhCC4EOh8JGaKjJzZhJr1mSyffv0MVE2j0fg3DlnFCKdPetg6lQtpaVGrFYFPl+IhgY716+7\nKCoyU1GRREqKlmBQ4sYNHxcvOgCYPdvK7NkWysrM6HThURCpm+ZmGSINA6RHFSKBXHTe0NAX40aq\nre3B6x0daxsBSUlJD2ZtPt4aHtQ0OtrW2CjH2yZNMo0BSfn5yaSlGeNm3w9gt/vu6UyS+5Gd3Lz5\nZ0yaZPnSv+94TEl7DVgBJAM9yGXXrygUiieBvweUwP+TJOmHv9KTiIMpaQ9STmcgCoQ++XA4/OTm\nJpOXl0xurm0oTiaDoYyM+AFbX5b6+31jSqivX+9j8mRTjGOovDydnJykR2Iqwv3U0+MdgkIjcMjh\nCDJrVjrl5WmkpCQRiWi4fTvExYsOmpu9FBcbKSyU3SuhUIQ7d+QTFoVCwbx5NubOtVFRkYRCoebK\nFQ/Hjg1y7pyD6dP10Q6ipUttpKbKLhmfL8yZM93s2dPOiRM9NDe7CQZVSJIenc6AQqFDkpTMn29i\n48ZUVq2yUlZmxOsNc/FiXwwgcjhC0ZOmYUA0ZcqDHaE5OCjwwQdyF9EHHzjIydGycaMMiWbPNnzq\n30cgIPLRRx727nWyb58LrVbBpk0WNm0ys2SJMaZP5vOeFj4IBYMShw7JkGjfPh+zZmnYsUPP9u2G\nBz5S+FfVjRvyRuJnP/Mzdaq8kdi5Uztuzie3W+KVV0L8wz8ESUlR8OKLGrZvT3goHUEOh8R3viNw\n8GCEf/qnBLZsic/f2YQmNKEvJlGU+Nd/jfBnfybwh3+o5k/+RPXA4cO9FA5LvPNOmJdfDjIwIPGt\nb2l44YVEjMbxeS7hsMQHHwTZvdvP0aMhtmzRsGuXnqVLE+JyjXrnjsDbb3t5800fTU1htm7Vs2OH\ngVWrtA/8HnE/V/KmTWPLupuaArz3ngyPGhqCPPmkia1bLaxbZ8Zsvv99JBgUOXHCzf79dg4ccOB2\nR3jySRkerVnz6Ydnv44EQeT6dTs1NfKasKamj/p6O3l55ui6cM6cVMrLk0lMVOFyCZw86aS6epAD\nB/ppbw+i0YQJhbyEQj7U6gDTpumZMyeZTZumsWVLNiaTJub7XbvmHupAcnDihB2ABQssTJumQaWK\ncOeOmwsXBrHbQ1RWWsnPN2MwJOL3i3R0+Ll0yYkoSkMQyUpZmQmdTohCpIsXZYhUWGiLibOVl6c+\nMqXan9TAgG+MG6murherVTsGIhUVpTyyP+cnNRxvGwZJw46kGzcGCAQEpk+3kZtr+8THZLKyrCQm\nxs9rEA5HUKsfTI/euDiMHqQeB2A0MOC9DxQaxO8Pk5eXfM/H5Mmmh96J9CAUCkVoauof6hoagUM+\nX3hMCXVpaRpGY3zEAH8VSZJEV5cnCoeGb0J+v8CsWelUVKSTmirDoY4OGQ5dv+4mP99AQYEBi0Uu\npb5zx8vVqw40GiWzZ9uYNSuJ2bNtFBWZuHUrxIkTdo4dG6SmxkVJiZFly5JYvtzGkiVJJCUlDI1K\ntfPOO20cPtxFXZ2DgYEwkIjBYMBoNBEKaYhEFKxcaWXVqiSWL7eSl6fh2rXBGDh065aHmTOTmTdv\nBA7l5VkeOMCTJImGBn+0sPrKFR8rV5rZuNHK+vVJZGZ++t9Jd3eY/ftlF9HHH3uYOVMXhUSFhbFj\neZ3OCB9+6GX/fg8HDniZMkXNs8+a2bHDRE7Og/17lE8k/bzxho/33vMxY0YCO3caePppPRkZ8XPj\nGi2PR+Stt+SoQnNzhN/+bS0vvKBjxozxczt2dIj84z8GeeWVEKtWyVGNhQsfXuzrnXcifPObYbZs\nUfHXf63GYom/zdOEJjShX0937kj8/u+HaWuTJx0uWPBw1mySJHHmjNxzdPSowK5diXzzmxqmTh2/\n59PTE+HnP5fvA6GQxNe+puOrX9UxZUp8gvJbt4bhkZeWFoFt22R4tHKl9oH3M3k8Ivv2yb2HH33k\no7JSw6ZNRjZtMlJYGNspevdumL17ZXh08qSXJUsMbN1qYfNmCxkZn36PbWkJsH+/nf37HZw542b+\nfGN08lpBwYN1lQSDEa5dG4hCpAsX+mhtdTFjRlKM87y4OAmPJ8LJk04+/tjBkSN2mpp8WK0ioZAX\nl8uNIAQwGpXk5hpZvDiNp57KZsWKzGjdhCRJ3Lzpj0bYTp1ycOuWn3nzrFRWGrFalQSDIRoaXFy+\nbKe7O8CMGWYKCiyYzQmEQtDZGeDyZSeCMAKRSkuN6HQROjsHuXhRPuC9ccNOUVFyTJytrOzRhUii\nKNHR4YiCpGvX5I/t7Q6mT0+KgiQ53pZOVtajH2sbLaczQFvbIG1tg0NOnuHPB7lzx0lGhikGIo2G\nSjbbo9mFey89FsDopZde+lLKrh+UJEmir+9+UGiASESMAUH5+SnRz9PT48sK92VKkiS6uz1j4mTN\nzQNkZ1uHoFBaFA496tlaubfHNeQaGomWyScYGVRWppOaakUUNbS3y3CottZFdrae/HxD1DnU2enl\n2jUHZnMCs2cnReFQRYUVj0fi7FkHZ886OHfOSWOjl4oKUxQQLV6chMmkxm7388477Rw4cIeLFwfo\n7PQTiSjQ6zWkplrQ603Y7SrCYYkVK5JYvtzCkiUWIDjkHurj/PleGhsdFBZaYpxDM2YkjdskuWBQ\n5NgxVxQSCYLEpk1yF9GKFZ8+ZlaSJK5dC7B3r9xH1NwcpKrKxKZNZp580kxycuzNvbk5xL59Hvbt\n81BTE2DJEh0bNxrZsMFIVtaDBR+CIHHsWIA33vDy7rs+cnPV7Nxp4JlnDEyZEp+LEEmSOH06zO7d\nft55J8DSpXIZ6oYNmnF185w5I/cTHTki8LWvJfLNbyaSnf3wNihdXRJ/+Idhrl+XN5BLljx+0H9C\nE5rQiCRJ4q23RL71rTA7dqj4X/9LPW4On3upvT3CP/5jiJ/+NMTatTI8nzdv/O4jkiRx4YJ8b3jz\nzQDz5yfwwgs6tmzRjtskyi+qjo4ReNTWJvDUUzI8Wr78wcMjv1/kyBEfe/fK6w+DQRGFR0uW6GO+\nv9sd4YMP3OzZ4+TAARfFxRq2bJF7jwoLP72SweOJcPiwc6j7yI5erxqaumZl+XLzA5/iCuD1hrl8\nuT8GInV1eamoSImBSMnJek6dcvHxxw6OHnXQ0uIjM1OFJPkYHHQwOOhFkkSSkxMoLrawatUkduzI\no6QkKfq9BgdDnD4tT2I7fdrBpUsucnJ0LFxoZeZMIxaLkv5+H1euOLh82UFzs5u8PCOFhWasVg2C\nAN3dIa5dcxEKiaOcSEa0WmEIIsmHwC0tdoqLk6NRtjlzJlFa+mg7dAIBgcbG/hg3Um1tDy5XMGZa\n2/BHm+3xiLWNliBEuHXLGQOTWltH4JJSqYgBSaNh0tSpFtTq+ITlozVcfj0updcPUvHiMJIkibt3\n3feFQgkJyvs6he7VeP44SZIk7txx0dDQT0ND39DHfq5f70MUpZgoWXl5OiUlqdFc86MqSZJoa3OM\nKqOW3UOJiSpmzUqnsjKd9PQkBCGRtrYgFy86uHrVyZQpOvLy9FHnUGenl9paJ6mpmlHOoSQqK5NQ\nqZScP++MwqFz55xYLGrmz7ewYIGVBQusVFTI0zEOHbrNnj0dnDnTS1ubB59PQqNRkplpIiPDRmKi\ngfZ2Ab9fZPlyK8uXW8jJUWG3u4du3HIGfcoUY/SmPXduKhUVKeh043vD6+4OceCADIiOHHFRWqob\nKqxOorRU96nvpWBQ5OOPPezd62LfPidqtYJNm8xs2mRh6VJDTA9AKCRHzfbt87B/vwevV2LjRiMb\nNxpYtcrwwKebiaI8DviNN7z88peyi0mGRHqys+P3/XH3boR//3e5wFqhgN/5HT2//dtaMjLG78Yo\nCBK//KXcT9TbK8cwdu1KxGR6eNdZUZT4yU8i/OmfCnzjGyr+5/9Uj8vktwlNaELxoYEBiT/+Y4GP\nP47w4x8nsG7dw90suFwS/+//BfmHfwiSmankj/5Iw9at49dzBODzSbz7ruw6uno1zHPPyUXZlZXx\ne49rbw/z9tty51FHRyw8etCvnSRJXLoUZO9eN3v3erh5M8y6dTI8WrfOgNU68jcVCokcO+aN9h6Z\nzSOl2XPn3r80e/j7XL3qY/9+ufuovt7PypVmNmz4fI7tL1MOh3xQObwWvXChF5crxOzZqdGqg7y8\nJNraBI4elQHSzZsBysp0JCQEGBhwcPu2HYdDQK2GSZO0VFbaWLs2kx078khJkUFaKCRy9aqbM2fs\nnDnj4MwZObK3YIGVhQutzJ5twmBQ0Nwsu5CuXHFw7ZqD1FQNRUVmbDYtoqigry9Mfb2LYFAc5UQy\nodUKdHWNdCK1tsoQaTjKNuxEetSnlw0O+qmrG4m1DQ8dMpk0FBenUFSUQnFxCsXFqRQXp5CR8Xga\nIyRJYnDQ9wmINAKTeno8TJ1qGeNKGv56dMQyHvRYOIzG63mIokhnp4uWlgFu3IgFQq2tAxiNmiEI\nZIsBQrm5yY+VLe1+EgSRtjZ7FApdvy5/bGzsx2BIiF4chi8UJSWpTJr06F8oRFHixo3BMXDIZEpk\n9uwMKirSmDzZhiBoaG31U1Pj4PJlJ2lpieTmyrGycFiOlTU0uJg8WRd1DskPG0ajmtpaN+fOOaMO\nort3g8yZI8Oh+fMtzJ9vRa9XcPDgLQ4f7uLSpX7a273Y7fJNMiNDS0GBjUmTkgmFNJw75yEYFFmx\nwkp5uQ6TSb6Z1dTIN2azOTHGOfTJKRfjJUmSuHzZNzTVzM6NGwGqqixs3JjEunWfPfGjtzfMgQMu\n3n/fxZEjbkpLdWzaZGbzZgvFxbFRs95egYMHvezb56G62ktRUSIbNhjZuNFIRYXmgf+tiqLE2bMy\nJHr7bR8pKUp27jSwY4eBvLz4XUCHQhL798s9FSdPhnj6aS27dulYsGB8eyocDpF/+7cQ//iPQbKz\n5aLXzZvHdwN0LzU1ifze74UJBuHf/i2BsrIJV9GEJvSbqurqCP/5PwssWqTg7/8+gZSUh3t9EgSJ\nPXtkwN7VJfGtbyWya5cGs3l8n1d7u8DPfubnlVf82GxKdu3S8dxzOpKT4/d62dYW5q23ZHh0547A\n9u0GduzQs3Tpg4dHAJ2dYfbt87B3r4fjx/3MmaONuo/y8kagjihKXLzoj8Iju12IOo9Wrvz00myA\n/v4wH3wgT1378EMnU6cmRouz5883jvs9trfXT03NSKn2hQu9iKIUdSAVFCQTDCZy+bKfo0cd3L4d\nYPFiCxkZMDho58aNPtrbvfh8IlqtkmnTdMyYkcTSpels2DCN/Hw50dDVFYjCozNnHFy54iY/X8/C\nhTJEmjfPDIhDLiT70MOBUgklJRZSUnSAksHBMI2NHvz+CLNmjcTZtFqBu3eH9w89tLbaKSlJiYmz\nlZY++hBJTlg4aWzsj5oHGhsHaGjoIxSKDEGkkT1iUVEKOTlJY6bjPU4KBgU6OuwxEKmtzR51Kun1\niffsTZo+3fZQKmkmgNE95HQGOH/+9hiXUFvbIElJuntGx3JzbZjNj+4Eri8ivz9MU9NAjFuooaGP\n1lY7kyYZx4Ch4uKUx6ZhPxIRaWwciIFDV670kpysG4qVpTFlSjLhcCI3bvipqbFz8aIDiyWBvLzh\nWJlAZ6ePpiYX2dmGaKRs1izZOWQ2J9DZGYiJll265CI7WxfjHpKkEAcO3OLkyR6uX3dw926AQEAi\nMVFBRoaG4mILRUWpJCcn0dwc5uhRB5GIxMKFJjIzFSgUftraZOtvJCKOmViWnv7wIKfPF+HIEVcU\nEhkMqmjUbMkSEwkJnx41q68PsHev3Ed0/XqA1avlqWbr15tJTVXH/LdXrwajUbPGxhCrVxvYuNHA\nk08aSU9/8O4pSZKoqQnxxhuy3d1olCHRzp16ioriu5+rvl6OFfz85wGKilTs2qXn6ac1D9x99Um1\ntMijpF99dfxHSSCdVgcAACAASURBVH+ahsdsv/yyPGb7D/5g/MdsT2hCE4o/eb0Sf/7nAq++GuHl\nlxP4rd96MEWlX1TnzskR3upqga9+NZH/+l/HP8IrihIffxxi924/+/cHqaqSJ2iuWZMY19fPlpYw\nb70lF2Z3d0fYvl12Hi1erBmX5+31ihw+7I1G15KSVFF4tHChLia61twc4L33XOzZI6+R1q2TS7Of\nfPLTS7NBBoxnz7qH3EcOurpCrFsnR9fWrrVis43/vVdOMnhjSrVravowGNTMnZtGUVEyKpWBu3fh\nzBk3XV0hli61MH++kVDITWNjH3V1g9y+7cPtFlEqwWZLICfHyKxZyaxaNZm1a6eg1SZw5YorOlX4\nzBkHgUAkCpAWLrQyZ44ZhyM8CiDJj8HBEEVFZtLT9ahUKhwOgZYWL15vhFmzLMyebWXGDCM6ncDd\nu/boPqOtzcGMGSmj4mwZzJjx6EOkYQ0M+EZBpP7ovrK720Nenm2MK6mwMPmxmvZ9L0mSRE+P5569\nSW1tg9jtfrKzk6IgaTRMKixMeSBRtwlgdA/V1NzhO985OCY6lpubjMEQ3xu4L1MOR2AUFBqBQ11d\nbqZPTxoDhQoLUx75KNmw5Iihh7q6furq+qir66O+vp/6+n4mTTJG4dDUqTIcamryReGQTqciL8+A\n2ayKxspaWz3k5Rlj4NDMmVaMxgR8vggXLzpj3EPBoBgFQ5WVRpxOD6dO3aWmpp/WVg+Dg2EkCcxm\nFdnZBiork1m2LIPMzGRqawOcOuXk1Ck5clVSosFqjeDzOWlo6GNgIMCsWSN58Hnz0pg27eE6veTS\n7QDV1Q4++MDJyZNu5swxDEXNPrt8cdh6PdxHJElStLB6+XJjTPbe5xM5csTL/v2yk0iegCa7iJYu\n1Y/LJBsZVIV44w35ZFKlIuokKi2Nz+kxw3I6RV5/XY4Q3LkT4Wtf0/G1r+nIzx/fRaIkSRw7Jm9u\nTp+O8Lu/m8gf/IGGzMz4OJE6dUrkG98IM2WKgn/5lwSysuL3dzqhCU3o4ej8eZGvfz3M1KkKfvQj\nNbm58XH9unVLHhKwe7c8JOCP/kjDwoXjDwIcjpH7TVdXhK9+9eHcb76ompuH4ZGXvj6Rp5+W4dGi\nRZpxmeArihI1NQH27pXdR3fuCDz5pIFNm4ysXSsfXg6ruzvM3r0yPDpxwsPixSOl2ZMmffaa/tat\nIAcOyNG1Y8fclJfrWbPGwpo1FubNMz7wjqf7SZIkWltdMX1Ily/3k56uo6wsDZPJgtOppqEhRG9v\niAULzCxaZGHBAhPg58SJLs6e7aOpyUlPT5BQCDQaBRkZWoqKLCxcmMa6dVNJTzdy4YIrGmW7ds1D\nYaGBRYtGIFJOjg67PcSVKw6uXBlxIrW1eZg+3cikSXoSE9W4XBHa2314PELUiTRjhuxE6u62RztQ\n29sdFBTYKCtLpbQ0ldLSFMrKUpk61RzX68cvIp8vTHNzrDmhsbGflpZBMjKMMXvQYaCUnPz4p3kA\nfL4Q7e32Mb1JbW2DHDv2e6SlGb/07/lYAKN4L72OZw0XT9+rX8jtDlJUlEJJSWoMGJo+ffxKjcdD\n/f0+6uuHwVB/FA6p1UpKS1MoLU1lxowUUlMtBINqGhq81NQ4qKmRR9bn5ekxm9WEw2Hu3PFx65aX\noiJztG9o1iwb5eUWdDo1kiRx44ZvTDF1aamR+fMt5OZq6O93UV/fS12dk85OPz6fSEICpKVpKCw0\ns3BhGuvXT6Ww0Ma5cx5OnXJy8qSTmho36elqUlMlwE9PzwC9vW7Ky20x7qHCQuu4LFg++3UPc+SI\nk0OH5IdSCVVVVqqq5IWG1frpC8L+foEDB2QXUXW1m+JibRQSlZZqY26at26F2b9fPnU7cUK2bW/Y\nYGDjRiMFBYnjdoOtr5edRG+84SUUgp079ezcaaCiYvyew68iUZQ4dkw+8d27N8iaNYns2qWnqmr8\nT3xDIYnXXw/z938fxOeT+Pa3NXzlK4no9fHx+l26JPLd7wrU14v89V/Hj3NgQhOaUHwqHJb4m7+J\n8Ld/K/DUUyq++10106bFxzXD7ZZ45ZUQ//APQVJTFbz4oobt2xMeCgSoqwvzyiuyo7WwUMWuXTqe\nflqL0RgfkO1+amwMRWNrg4Mizzwjw6MFC8YHHoG8BhqOrp065Wf+/JHo2ujJrp8szS4q0kR7jz6r\nNBsgEJAHkVRXOzl82MnNm0FWrDCzerW8riso0D7U+6GcEnDEQKTa2kEyM82kpSWhVOrp71fS0RGm\nuFjPokUWFi82s3ixBYNB4oMPbvPRR11cvjzIzZse7HYBUGAyqZk2Tc/MmTYWLUpn0iQrra1Bzp6V\nXUiCIEXh0aJFVubMsaDTqfD7BWprnTFOpLo6J+npOqZM0aPVJuD1inR0+PF4BCorRyCS0Sjicrlj\n9i9eb5gZM1KGQJK8fykrSyUl5fEBKYIg0t5uHxNta2joR6NRDQGk5FFpl1SmTDHHxb7nUdRE6fVv\nmCIRkY4O2WEy3C00/GZLSFCNcQs9jm8wlyvI9ev9Ma6hurp+/H4hemEtLU2hoCAZlUrL7dshrl51\ncvWqi6tXnSQkKMjK0sfEyjo7fZSVWWKcQ6WlFjQaGagNDoY4f37EPTRcTD13rpmUFAUOh4eOjkFa\nW93094eIRMBoVDJtmp7ychsrVkxi8+YsMjL03LwZ4ORJJ8ePOzh61M6dOyFSUkClCjAwYEenCzFr\nVjIzZyZTUSF/LCiwxk0GOBgUOXPGHQVEN24EWL7cHAVEn7WQkCSJhoZg1EVUW+vniSfkqWbr15tJ\nTx85CYtEJM6d87Nvn+wiuntXPl3buNFIVVVsMeSDVlNTOBo3czpFduwwsHOngblz4xsSAdy6FYl2\nShiNCn7nd3Q8/7yOlJTx/5vq7xf5v/83xD//c5AZM1S8+KKGdevUcXONqq8X+fM/FzhzRuRP/1TN\n17+uituJPxOa0ITiT4ODEn/zNwI//nGE55+Xi/EnTYqPa0gkIrF3b5iXXw7S0SHyzW9q+PrXE7Fa\nx/9eMNyZ98orfk6cCPHUU3Jn3qJF8e3OBbh+fQQeuVwizzwjdx7Nn//gOxKH5fGIVFfL0bX9+z2k\npo5E1+bP10UPgUaXZr/3nhOT6fOXZg+rpyfEkSMuDh92Ul3tRKGANWssrF4tPz6rg3I8FApFaGx0\nUFs7wLVrg9TWDnD16iAOh4KUFNsQRFKg06lYssTCypVJLFpkYeZMA0qlgvr6QQ4evMWpUz3U1zvo\n6grg90uoVApSUxPJyzNRVJRMSooZpxNqatzU13soKTHERNmysuShLYIg0tTkHhNp02hUZGUZ0esT\n8PslOjsD2O1hysrMVFRYqKiwMH26FlEM0tIyQF1dP7W18l5Hq1VHXUjyXkc+CDcaH5/UzHAyRI61\nxbqSnM4AhYUpjO5IKi5OJS/P9thE+x60HguHUTw8j3hRMChw48bgmH6h5uYBUlL0Mf1CsnPo8SLP\nIHcsNTQMjHEN9ff7KS5OHgWHUklNNdHXJ3LtmmsIDjlpbfUyebKWlJQEEhIUeL0hurp8+P0CM2ZY\nmD3bFi2lLimxRPt0wmExppj63DknXV0BysuNmEwSHo+X3l4XXV0ePB4RlQpSUhLJzzcxf34q69ZN\nZfnySSQkqBAEkStXPHz44QCHDvVz5YqPcFgkMTGEz+diyhQl8+dbqKxMZubMFGbOTCYjI75+j8Mx\ns0OHHBw65OTECdkFNOwimj//s4sWw2GJEyfkqWbvv+8kFJKiU81WrjSi1Y78/w5HhEOHZEB08KCX\nyZPVQ1PNjMybNz4FlMNqawtHnUQ9PfKJ4s6dBhYuHL8TxV9VgYDEe+/JEYCamjDPPqtj1y4ds2ap\nx30xHgpJfPCBwGuvhfjwQ4Gnnkrg29/WUFYWPzf4lhaR731PoLpa5L//dzW///uquHE7TWhCE3r0\n1Nsr8cMfCvz0pxF+53dUfOc7alJT4+eaUlMjR4EPHBDYsEHNc88lsmaNmoSE8X+Od+9G+I//kA81\nRBFeeEHHV76iY/Lk+LlH3E/19SHefFPuPPL5huHR+B4mRSIS58+PRNd6egTWr5eja1VVBkwm+XW8\nV2n25s0jpdmjY//3kyRJNDUFou6jY8dc5ORoogBp6VIzOl18HHACDA4GqK0dpLZ2kKtX+7lwwUlj\nYxC1Wo9CoScUUpKfr2HxYjMbN6axbFkSFovsjHe7gxw7dpfDhzu5cKGflhb5UFiSFGi1SiZN0jF5\nshWLxYjfr6K+3otSqYgBSLNnm9Fq5ddfkiQ6OrxcvjwSaautddLbG2TqVAMWiwZRVGC3h+nsDJCT\no6ey0kpFhYWZM82kp6vo6nLGHJg3NAyQkWGIupCGD80LC5MfO4jidAbuWbh965aT7GzrmMltRUUp\ncTel7GFrAhg9ghIEkY4OBy0tg7S22mlpGaSlZZCmpgE6OhxkZ1vHFE8XFT1eJBkgHI7Q3Dw4Bgzd\nvu0mLy8pxjVUWJhMIKCirs4dBUNXrjgJBkUmTdKg1ysJhQR6e/34fAIlJWZmzLAMPeTPp07Vx9zE\n71VMnZaWgNksEgj4GRz0YLf7EQQJvV7JlCk6ysqSWLYsnc2bs8nONkf/Lbs9xLvvdnPgQB81NV7u\n3ImgUAgoFH5yctTMn29i2bJkKipSmDHDNu6j7D+v+vvDHD4sO4iqq+WY2dq1VtassfDEE5bPVYY4\nOChw8KCLvXtdfPihm/x8zRAkMjNzpi76O5Akiebm0FBhtZeLFwMsW6Zj40Yj69cbmTZtfE+ubt0S\nePNNGRLduiVPS9m508CSJeNTePnrSJ5EJ7B7t5/XX/dTWZnArl06tm7VotON73MXRYmTJyO8+mqI\nX/4yTEmJkuefT+TppxPialrOrVsSf/mXAu++G+Hb31bzrW+pMJni+/c8oQlN6NFRZ6fEX/2VwOuv\nR/jGN1T8t/+mJikpfq4xvb0ib74Z5rXXQrS0iDzzTALPP5/IwoWqcT9ckCSJs2flIQxvvx1g0aJE\ndu3SsWmTZlx6CX8dSZJEXV14CB55CQYlduyQ4dHs2ePrRL55MxSFR2fOBFi0SBd1H2VljaypPlma\nvXbtSGn26H6kT1M4LHL+vDfqPrp61cv8+cYoQKqsNMTdAZsoSty86ebatQHOnx/g+HE7DQ1BHA4l\noMVkUlBUpGHJEgtbt6azaJEtOs1KkiTa2118+OFtjh27S22tnVu3fHi9IpKkxGxOJDnZiE6nx+9X\n0d0dprzcFAORpk6N7fN0ucJcv+6krs5Jba2TujoH167Jh6sZGXq0WjV+v8jdu0HM5gQqK2UnUmWl\nhbIyM6IY4vr1ESdSXV0/N286yc21jgJJ8l4qJyc+6iy+TA2bLD7pSmpuHiApSUtRkZw6KShIJj/f\nRkFBMtnZ1seqluXzagIYxakCAYH2dvsYKNTSMsidOy4yMozk5dnIy7ORmys3pRcWJpOf//iR4UhE\npL3dGVM+XVfXT0uLnWnTzMyYkRLjGrLZDFy/7omCoUuXnDQ3e0hKSsBsViGKInZ7YAgMmSgttYyC\nQzIY+uRF0eMRuHTJxfnzsnvo9Gk7Ho+AxQKCEMDt9uL1BlEqJWy2BHJzjcydm0JV1RTWrMlEq00Y\n9W+Fqa7uZu/eXs6fd9PeLuDzKdFowmRlqZgzx8CTT6ayeHEa2dmmuLZYB4Mip0+PxMxaWgKsWGFm\nzRoLVVUW8vM/O68uCBIXLvj48EMXhw65qasLsHKlkU2bLGzYYI4pXQyFJI4f97Fvn2yl9vulqIto\n1So9ev34AQX5tCzMvn1+3nnHR3NzmG3bZCfRihXah1b0+EU0MCDy6qt+du/243CIvPCCnq9+VUt2\n9vgXWNfWirz6aohf/CKE1arg+ecTefbZRLKy4gcSAdy9K2/iXnstwn/5L/ImzmaL/9/1hCY0oUdT\nN2+K/OAHEfbsifCtb8lwerxH3n+W2toivPZamFdfDREIwHPPyfCopGT816Ner8gvfxlk924f169H\neO45ObJWXv7w40+fJUmSuHZNLsx+4w0vkQhs26Zn82Y9ixdrxnVd4XLJru29ez0cOCC7tofh0dy5\n2ug6uadnpDT7+HEPCxcaqKoysXq1ibIy7eeGDC6XwNGjLg4fdlFd7aCvT+CJJ0b6j7Kz43cStd8v\ncO3aIPv393D8uIOGhgD9/QokCZKTJQoKElm61Mr69WlUViZjMo0c4Pt8YWpqevjwwzucO9dHY6Nc\nsi0IKlSqRAwGHYmJWnw+JQaDmsWLk1i2zMa8eRYqKkwYDGPXa729AWprHVGQJH/uQqdTk5SkRZIU\n2O0CwaDIzJnyhLbhWFturo72dkcUIA3DpIEBPyUlKTHdSKWlqWRkGOJ6n/KrSBQlbt1y0tQkw6Mb\nNwZpbh6guXmAri43WVnWIZBkG4JJMlTKzIzvPduvowlg9BDl8YRobR0BQaPBUG+vl6wsK7m5STFg\nKC/PRna2FY0mPh0mv47ksZjuMeXTDQ0DpKbqopnbYddQfr6NO3eC0Z6hixftXL7sxOMRsNkSUCol\n3O4Qfr9ASYmRsjJrjGto2rR7n14EgyLXrrm5cMHJ2bN2jh8fpKsriF4vEYkE8fsDRCIhNBqRyZO1\nzJhhZcmSdDZtyqKkxPaJn8fLpUv9HDrUy+nTLlpawni9alQqFZmZSior9VRVJbN9+2TS0j59Elg8\nSO4R8kcdRCdOuCkp0UUB0YIFxk8deT+sjo5QFBB99JGHqVMTWLvWTFWViSVLDDFRs54egYMHZRfR\n4cNeiosTo5CovHz8cv8wDKwC7NvnY98+P8GgxMaNejZv1rF6te6hWPK/qIJBicOHg/zsZwEOHQqy\ncaM8snjFisRxPz26eTPCL34hbzLcbonnnkvkuecS4ypyNqz+fon//b8FfvKTCF/7mor/8T/UpKXF\n/+97QhOa0OOhGzdEvv99Of76x3+s5g/+IP7ir5IkceWKDI9+8YsQKSkj8H/q1PGH/62tAj/9qZ+f\n/tRPWpqSr3xFx7ZtWqZNi797zCc1PE11zx4f77/v59YtgfXrdWzZoqeqSofJNH6vZyQicfasP+o+\nGhiIsGGDDI/WrDFgMMjPxe2OUF3t5sgRD9XVbhyOCE88YWT1ahkgZWV9/qTD7dtBjhxxDkXYXJjN\nquj0tZUrzZ85GOVhS5IkamocvPtuN8eOyRDJ6QQIYDIJFBVpWLzYwoIFKZSV2cjLs0Q7RyVJorPT\nw7FjXXz0USeXLw/S1uYZ+v+1qNUa1OpEwmEVaWlq5s61snp1CgsWJFFebrpnRFAU5VjbsBOprs7J\n5csOWlt9WK2J6HQJBAISDkeYnBwD8+ZZqay0UllpYeZMC0qlGD2wr6vro7ZWfgAxh/ZlZfJezWqN\nX8D36ygQEGhrs0cB0o0bAzQ3y0DJ5QpGnUijXUkFBcmP/AS3CWD0gDU46L8vFHK5guTm2u4JhaZO\ntcRNWfGXLUmS6Ory0Ng40jM0fBHS69VjwFBJSQqgjPYM1dTYuXDBwY0bHnQ6FVqtAr8/TCAgkJ9v\noLLSSmmpNRory86+v601EpFoaPBw7Fg/+/b1cPmyi76+CCpVhEgkhCiGUanC2GwKcnIMzJyZxBNP\nZLJ+/dSYfGsoFOH6dTtXrw5w4UI/J086aG4OIQhaJEmL2aykvFzHE0/Y2L59EkVF+keGQvf1xcbM\n1OqRaWarVn2+mJnHE+HoUQ+HDrn58EM3dnuEqioTVVUm1qwxxbiI5AVncChq5qG5OcSaNQY2bDDy\n5JMG0tLGd5HQ0xPhwAEZEB0+7KekJJGNG3Vs3KinvDz+SzYBXC6RAweC7NkT5IMPgpSWqvlP/0nH\ns89qx720tL9f5K23ZEjU1CTy9NPySfSiRaq4tDs7nRIvvyzwT/8UYccOeYJRZmb8Pc8JTWhCvxmq\nr5d7006eFPmTP1Hze78nr4PiTZGIxPHjAq+9Fuadd8KUlcnx4u3bE7DZxve+E4lIHD4c4vXXA+zd\nGyA7W8VTT2nZtk1LcXF8g4dh3bolsHevj/ff93HmTJDFi7Vs2aJj0yY9mZnj+zO0to5E186fD7B0\n6Uh0bcqUkfVcR0eII0fcHD4sQySzWRmFRytXGj/X+hFk2FFb64vG106f9kQPK1evtrBw4Wd3YsaD\nXC6B06ed7NvXy4kTDpqagiQkiCgUfgIBD/n5icyda6W83EZ5eTJlZTbS00dAQyAgUFs7wJEjdzh7\ndniacphAQA1oUCoTkSQVVquSkhI969als2FDOmVlpvvuKUOhCM3N7qgb6epVB5cvO+jrC2GxaFAo\nlDidAlZrAhUVFhYutEX7kaZO1dLX5x8VaZMP/Ovr+7FaNTHdSKWlqRQU2B67epTRcrmCQwAp1pXU\n1DSAWq2MwqOCAlvUlZSfb8NgiP/X5LEARi+99BIrVqxgxYoV4/79JUmip8d7XygUiUhjYNDw55Mm\nmeJyg/RlyecL09w8SFOT3K/U1DRIY+MAzc129Ho1hYW2GDg0Y0YKNpuOmzd9XL3q5MIFO2fODFJf\n78bhCKPXK4lEIgSDEbKzdUNZ3KSoYyg724BKdf8bhiiKnDnTz5tv3uHYsUHa20O43QokKQKEUSrD\nWK2Ql6dl9mwbS5akU1U1hZSUWOdPf7+fq1cHoo8LF+y0tIQwGi0oFDrcbgX5+VpWrkyiqiqZRYvM\npKTE/8VgWMGgyKlT7iggGo6ZVVXJLqK8vM+OmYmixJUr/iggqqnxMXeunqoqE2vXmpg5Uxfzt9/V\nFebIER9HjniprvZhMCiiLqIlS/Tj2kEgA6sQ+/b52bfPR1NTmKoqGRA9+aSO1NT4P5kE6O6O8P77\nQd59N8CpU2GWLk1k61YNmzdrSE8f35/B65V47z256+LkSYH16xN47rlEqqrUcdsv4fVK/OhHEV5+\nWWDDBiUvvaQmJyf+F6QTmtCEfjN0+bI8mfHqVZHvflfNCy+o4tblGgxKHDgQ5rXXwhw6FGblSrks\ne9OmhHHvyRMEiePHQ7z7rnx/NJkUbNum5amntMyePf7DHX4VuVwiH3zg5/33fRw44Cc3V83mzXJ0\nbbwPshyOCB9+KEfXDh6UHeNVVQZWrzawdKkuWmQtihJ1dQEOH5YB0smTXgoLNVGAtHhxrLv80xQI\nyFN3q6vldWpTU4ClS01RgDRjhu6R+D1GIhK1tR5On3Zx9KidEyecuN0CqakAfvr7B9HpBMrLk6IA\nqbw8mZKSpJguU683zLVrfXz88V1Onuzl2jUPvb0i4XACkAio0OtFpk5NZMECK889N40nnkj91D2T\nxxOmvt411Ivk4MIFO9evewgERPT6BIJBCVBQWGhgwQIbCxfaqKiwUFRkQqVS0NHhjDqRZIjUx40b\ndmw2HUVFco1KYaEt+pg2zfLY7oklSaKvz3dPV1JLyyDJybp7upJycpIees3M0aNHOXr0KN///vcf\nfWD0oJ+HKErcueOKgUItLXZaW2U4pNWq7wmF8vJsJCc/GhetX1XDr40MhUbAUFPTIL29PnJzrUMX\nA/nCUFQkk9WkJC1er0BdnYsLF+wcP97PlStOOjr8KJUKFAqRcDhCZqaWsjIz8+cnRSNlOTmfDobC\n4QhtbU4OHLjDwYO91NX56e8fvnBKKBRhjEaJrKwEFi5MoqpqEitXTiY5WRvzc92+7aGpyUFzs3Po\no4O6OjtOJ2RkJKNWG+jvVyAIChYvtrBsmZUlSyzMnm2MTjZ4FCRJEtevj8TMTp6UY2bDgGj+/M8X\nM7t7N0x1tQyIqqvd2GyqKCBavtyI0TjymjidEY4d83H4sAyJ7t4VWLXKwBNP6Fm92kB+/vgCNq9X\n5MiRAPv3y04ivV7Bpk16Nm7UsWSJNm6hxifV0iKwZ4+8CL5+XWDdOg3btmlYt06D2Ty+sCMclqiu\nliec7dsXZtEieYOwdWsCRmP8vp6BgMSPfxzhhz8UWLFCyfe+p6aoaAIUTWhCE4pPnTsn8md/JtDS\nIvHSS2qef14Z1x16TqfEu++GePXVMDU1ETZvVvP884msWqUe9+ctihI1NWHeeSfIO+8ECAQktm3T\nsm2bhiVLEuP6dRxWOCxx8mSA99/38957PkRRYvNmPVu26Fm2TDuuEFEQ5Oja4cNeDh/2ceVKgPnz\ndaxebWDNGj2VlSMTa0MhkbNnfVGAVFsbYMECfRQgVVToPvfAkMFBgY8+ckYBUiAgRruPVq+2MGnS\no3No29kZ5PRpJ6dOOTl92kVdnZdp0xJITZVQKPz09dm5edNOZqaBoiIrRUVJFBdbo5+P3sv4/QKX\nL/eyf/8djhwZ4MYNORYXiSQAStRqAZtNQXGxnrVrU3n++RymTTN96vPr6wtE3Ujnzw9w8aKDtjYf\nKpUKhUJJKCSRmamlosLCsmXJzJtno7zcjNmcMLS3ctHYOBCzb2xsHMRuD5CXZ43ZLw7DpMd5Ypn8\nmjjHuJKamwe4c8fF1KmWMSCpoCCZKVPM4wrYHguH0Zf9PFpbB/mnfzofhULt7Q6Sk3Xk5trIy0sa\nAkMjgMhieTxzmqPl8YRobh4c8yZvbrZjNifGvLGH3+zZ2RZUKiXhsMiNGx5qauwcOzbAlSsO2tt9\nOJ0CarVcap2WlkhxsZEFC2zMnWtjxgwL06d/Ohhyu0M0Ndm5cKGXjz/u5uJFN11dkSFrZiKgQKOJ\nkJ6uoqLCxLZtk9mwIZPU1JHfl90epKnJEQVCTU1OmpsdtLS4SEpKJCcnCZPJTCSiYWBAQUtLiLS0\nRBYvNrNkiYXFiy0UFo4tyY53jY6ZHTrkICFBwdq1IzGzpKTPtgkHAiInT3qjXUS3b4dZtcoY7SIa\nnVUPBkXOnPFz5IiPw4e91NWFWLBAy+rV8ilURcX4TxLr6BCigOjEiQBz52qiUbOCgvgvx4SR6Wbv\nvhtgz54gfX0iW7Zo2LZNy8qViWg04z+p5swZecLZW2+FycuTIwjPPJNAWlp8Q5dQSOKVVyL84AcC\ns2Yp+Yu//i8zvQAAIABJREFUUDNzZnw/5wlNaEITGtbx4yLf/W6Y3l743vfU7NihjPu1yd27Im+8\nIcOj27dFdu6UI8pz5z6cSWvXrwu8+64Mj27fjrB5swyPVq/WxGXs75OSJIn6+jDvv+/jvfd8NDcL\nrFunY8sWHevW6bBax/cw0+UaORysrvbS0yOwcqUMj1avNjB9+ogbSj5I9EQBUk+PwKpVI/1Hubmf\nHxq0tQWi8Oijj5xMnpwY7T9atswcc4AZ7/J6I1y44OLUKRenTzs5c8ZFUpKakhItGRkKEhNDuFxu\nbtxw0NDgIDFRSVGRleLipCGIJIOkrCxjdE8VDAocOtTFG2/c5vx5J52dEXy+4fWOgE4XITNTzZw5\nZtauncS6dVPJyLh/B48kyf1IdXVOLl60c/r0APX1brq7g6jVagRBwmxWk5Ojp7zcwpIlycyaZaWo\nyIROJ/8uhveZoyHS8D7TYtGMgUiFhclkZZk/dZ/4qCsUitDWZo/G3OSHDJXsdj95ebYxMGnu3MwH\n4kqaAEb3UEeHg7ffvh6FQtOnJ6HXPxobyF9HI63wg9H42PDng4N+8vKSPvGGTaagYASYyRcMH2fP\nDnLsWH+0TG1wMIxSKUfCUlMTyM83MmuWlcWLk5k500purvG+2VpJkuju9tHYOMilS32cPdtLba2D\nW7eEaGZXkhJQKFRYLJCfr2PVqhS2bZvE3LlJKJVKgsEIra3OKAwa7RoKBiMUFFgpLLSQk2MhMVGP\ny6Wio0Pg4kUPAwNh5s41MX++OfpIT390TiqGFQjIMbPqahkQtbUFozGzNWs+X8xMLrwORgHRqVNe\nysp0URfRnDn66GmcKEpcvRrk8GEvR474OH3aT3FxIk88YWD1aj2LFuk+t/X4y1IkInHuXDAaNbt7\nN8L69To2bNBTVaUd94XUrypBkDhxIsSePUH27AmQmCjb6bdu1bBgQcJD2SBcvy5DotdeC6PTwfPP\nJ/Jbv5XA9Onx/5pGIhKvvip3guTlKfjBD9TMm/f4LkAmNKEJPb6SJInDh0W++10Bvx/+4i/UbNmi\nfCSc7s3NEV57TYZHMDJpraDg4dxHbt6UHbvvvBPg2jWBtWs1PPWUhvXrNeNaOP3r6O5dgb175eja\n8eMB5s/XRKNrWVnj393U2SnXD1RXy0NMtFplFB6tWqUnJUU96r8NceTICEDSaJSsXi0DpFWrTKSm\nfr7nH4lIXLrkjQKkmhoPs2YZogBp9mzjI+EkG5YoSjQ0+Dh3zsXZsy7OnXPR0uKnvNzI/PkmCgs1\nWCwiDoeckmhocNDY6KC/P0B+vmUURJJBUmGhJbrHbW/38tprt/jggx4aG/0MDkqIosRwbYfJJJGb\nm8icOTaWLcugqmoKqan3B0myYcDNlSsOTpzo4+pVF62tXvr7w6hUSiIRMJnUZGXpKC01s2iRjUWL\nkmNAkihKdHa6R+1JY5Msw3vTT5oWHtfS7WF5PCFaWmIdSc3NA+zb9xwpKV9+wfYEMPoNlMsVHPOm\na2wcoKVFzpYOv+lGk9xPZkv7+oKcPDnAxx/3cfmyg5YWL319ISQJFAqRlJRE8vL0zJqVxLJlycya\nZSMrS39fEiwIIm1tThobB7l6tZ/z5/u4ft3B7dt+RFGDQqElEklApUpEFJWkp6uZNcvMypUprFuX\nRmGhge5u3yi3kDP6sbPTS1aWcQgMWSkosJCfb0Gl0tDe/v/Ze8/guM47y/t0zo2cCAJEBgGSyDkH\nMShRljZ4xprdqrU22J4Z22NVuXbLu9bq9bhqp2ptz9oznqnxzq69Vd6xZz2WSUq2xAQQqdGIJEiC\nBEEiEzl2vPm+H57u22iRkgGKZHeT91R1QfwCdTe673Of33PO+bMYGHDCbndgfNyDggIjqqqsqK4m\nkCgS3UMAgQqjo250dTlw8SKJmR09apQA0V5jZhsbHC5edOL8efJQqYCTJ604edKCtjZz0JSKqSkG\nFy8SB1FHhwdxcSq88IIR7e0mtLQYERPz9G/6SLaeTDX78EMvDhxQ4ZVXSNSsqurpu5oeVR6PiAsX\nSNTs/fdpZGSo8LnPkZPPwsLQdC7Mzwv4xS8Y/PznDNbXRfzhH2rx5psaFBc//ZPhR5EgiPjVrwS8\n8w6H+Hjgz/9cg+bmyNgEyJIlS9anSRRFfPABiaqpVMB3vqPGqVORAY7IdClyCPHLX7JITVXizTc1\n+PzntThwIDTX6JWVQCdgTw+LpiYtXn9dh9On9UhIiIx1w+0WcP68F2fPkkOz1FSVBI/Ky7UhcnQx\nEjzq6vIiN1cjOc8bGgL9R/4DSz88unLFhawsHY4ft+CFF8xoaDDDaNzb38Ht5tHdHeg/Wlig0dxs\nRUuLFa2tVhw9Gnn3/S4Xh6EhJ+x2pwSReF5EdbUVNTXksLugQI/lZRdu3yYA6datLdy+vY27d3eQ\nlGTA4cMBR5LfnZSQoMfcHAWbbRu/+c199PeTkm2FQoAgkMFASiWLuDgFcnJMKCkJgKTY2E+e/Mzz\nAmZnPbhxYxs9PRsYGdnG5KQby8s0OA4QRQXMZhXS0vQoKLCgujoWLS0JOHbMGlT54XYzmJzcemhX\nrsmkCQJJZE8bh4yMZ3eo1JOUDIyeUfG8gJmZnQfA0MTEJnZ2aOTlxQQVjvm7hT7eXu9wMOju3sDl\ny2vSF3p1lQHHCVAqgfh4DbKyTCgri0JzcwKqq2Nx8ODDL7aiKGJ93YvJyW2fdXITQ0PruH17B8vL\nFDQaLURRC4ZRw2jUQ6XSweMBUlN1qKyMQktLHI4cMUKr5TE15QjqFpqc3IHFokV+flQQGMrPj0Zm\npgVbWzzsdocEhwYHnYiOVqOqKuAeKiszS0Q70kRRAgYHXejqcqKrywGbzYVDh7RobLSivd2655gZ\ny4ro73dLZdUTExSamsw4eZJMNMvNDYyxX13lcPky6SC6eNEDmhalDqL2dmPQpIynJVEUcecOJ429\nHx6m0dSkx8svEydRenpkTEMBgM1NAe+/T1xEly4xKC/X4PXXdXjttdCNBN7cFPCrX5Hy6uvXBbzx\nhgZvvqlBU5M6Ym6wRFHE+++TjZRGA/z5n6tx4kRkbKRkyZIlaz8SBBG//jUB49HR5HrX2ho59zkc\nJ6Kjg8PPf87gzBkO5eUqvPmmBm+8oUVUVGiu2Ts7ZOroe+/R+OgjGqWlal/vUejW5v2K50XYbLQU\nXXO7Rbz6qhGvvWZAa6vhqcfZARILHxjw+gCSB2NjNKqr9b7+o+DqApYVMTgY6D8aHfWistLff2RG\neblxzweCy8sMOjoc6OhwoLPTga0tDs3NBB61tFhRWBh5XbSiKGJhgZbgUX+/A1evupCRoQ+CSEeO\nmACImJlxBkEk/38LgiiBJNKTFIO8vCjwvBqjo07092/h8uV13L3rhUYjAmBA0zR4noFazSIhQYus\nLDNKS+PQ2JiM+vpkHDhg+tT3c32dxs2b2+jqWsfg4DYmJlxYXKTgdvMAlDAalThwQI/8fDMqKqLR\n1paIysqYIJDkn8a9GyL598DLy25kZkY9tErl0yDX8y4ZGEWwaJrD/LwTs7M7mJtz+Cgr+VLcu7eN\nxETjA1+G/PzYhxZl0TSPrq41XLq0hqGhbdy548LqKgOaFqBSETCUmWlCSUkUWlri0dgYj5SUh19E\nNzcpTE5uYXJyG3fubOHGjS2Mj29jbs4FnlfCYNCB4xTwehWIijLCajVCFDVYXeWRmKhBVVU0srP1\niIoSIQgUZmYcUpzM5WIfAEJ5eQQSWa0Ednm9PEZGXD5A5IDd7sTWFouqKqsEiKqqIjNa5pfLxcNm\nc0qAaHjYjYICA5qarGhqsqChwYK4uL0Bm3v3aB8gcqCz04XsbJ0EiOrqTNKoUpdLQHe3R4qZzcyw\naG42SpCooODpn1AB5Cajq4u4iD74wAuvV5S6iNra9Hs+dQoHLSzw+M1vKLz3Ho3BQRZtbVq8/roe\nr7yiQ1xcaF6H1yvi3DkCiTo6OJw8qcEXvqDBiy9qQnJT+agSRRGXLpGohttNTtwjJaohS5YsWZ9F\nPC/iF78g0du0NAW+8x016usjZ20EyFr0/vtk0trlyyyOHydr0UsvaULWL+T1irh4kcavf03j3DkK\nGRkqvPEGgUcFBZFzQDUxEeg9un6dwfHjBrz2mhEvvWRAXFxoIJjDwaOz0yM510mnEYFHL7xgRFZW\n4B7e5eLR1eWWANLCAouWFrMEkHYfdv4+LSzQ6OwMACSXS0BLiwWtrVFoabEiP//3VziEo1hWwNiY\nG3Z7ACItLjKoqLCgutoiQaSUlEBX1Pq69wGQdPv2Nu7fdyMryyqBpNzcaGi1OmxtATduuDEwsI0b\nN1ywWhVQqTjQtBculxccR9xJVqsaKSl65ORYUFQUi+rqBBw+HItDhyzQ6R7+vaFpHuPjO+jsXIfd\nvonxcScWFihsb3MQRQUMBiWSkrTIzTWhrCwazc0JaG6Oh9EY/Pu8XvYBV5IfKun16qB9c25uDDIz\no5CZGQ2r9dkt3t6Lnglg9M4776ClpQUtLS2hfjqPTaIoYnublmBQ4KdD+vfGhhepqRYcOmRFerrV\nl+MkYCg3NwYm04NAhOMEdHev4+LFVQkMrazQ8HoFqFQKxMWpkZFhRHFxFJqb49Henojk5AeJ684O\n7XMKETA0MUHA0NSUCwwDmM16KBRKuN0ClEoFUlIsiIuzQKXSYmdHxPw8DaNRhZwcPeLiFFCrWTid\nLszM7GBuzoWDB00fg0KkZ+jjZFoQRExMeHwXQCcGBhy4dcuDwkKjBIaqqy3Iy4s8i+lubW5y6O0l\ncKiry4GbN70oKzNJgKi21gKLZW+LusPBo6PDJXUReTwCTpyw4MQJK44fD+TCWZac9viLqkdHaZSX\n6yS7cEWFPmS579VVHr/9LXERXbzoxeHDGilqVlwcGnD1KCI2az8kojA1xeOVV3T43Of0OHFCC5Mp\nNDf0HCfi8mVyqnv2LIfKShXefFOL11/XwGqNjPd2t3p7BXzrWywWF4F331Xj858P/zJYWbJkyXrc\n4jgR/+f/8Pj//j8OBQVKfOc7alRURBY4AoCtLQH/9E8sfv5zFteu8Xj9deJ2bW5WhyxqznEiuroY\nvPceia5ZLKRf8I039CgvD010/FG0tsbjgw88OHPGi8uXvSgt1UrRtZyc0PW5Liyw0v3oxYtuGAxK\nvPCCEcePm9DWZgoCW8vLLC5fJv1HFy44oVBAKs9ubzcjKWnvr2N21g+QdtDR4QDLilJ8rbU1CtnZ\ne4dR4abNTVY6WPeDJJNJJcGjmpqHpy+8Xg6Tkzu4fTsYJE1MbCMmRofDh6ORmxsFs9kMhlFhZYXH\nrVse3LnjQUqKFlYrwPMMnE43Njc9cLtZqFQiOI6DxaJCaqoBeXlWlJTEoaAgBtnZ0cjKikJs7IO9\nRKIoYnrajY6OVfT1beL6dQdmZjzY2uLAcSJ0OiUSEkgapqQkCo2N8WhvT0BMjO6B37O87A5yJd27\nt42pqW1MT+/AYFAjKysamZlRvp/R0r/T063QaCLDXbhfdXZ2orOzE++++27kA6NweB77Fc8LWFx0\nfSIMmptzAAAOHSIfxEOHrEH/nZ5uRUqK+RM7gViWh92+iYsXVzEwsIWJCReWl2l4PAQMxcT4wZAV\nDQ3xOHkyCSkpwWDI6WRw9+62FCGbnNzC+PgWJicd8HhEREXpoVZrQNMiHA4Oycl6ZGVFITHRAkCD\n7W0BU1MUFhZoxMWRUmqlkoXb7cbqqgMWiyrIJeQHQ9nZ1k9seF9ZYaSLmt3uwNCQE7GxGl+szIKq\nKitKSyM3WubX0hKD7m4/IHJiZoZGTY0ZTU0WNDVZUVVl3nNpNCn880qAaHTUi9pak1RWffSo3k+O\ncfMm43MQkTx5drZGKqpuaDCGDGCIooirVxl88AHJ3t++zeL4cQNeftmAF180Iikpcv7egiBiYIDF\ne++RuJnHI0p9RI2N2qc6Ane3RFHEwAApHf3lL1mkp5MJZ//yX2qQkhJ5GwoAGB4mjqJbtwS8844a\n/+pfqSKq3FKWLFmynoRoWsTf/z2P736XQ1UVmQp57FhkXucXFvx9eixWVwX8wR+QPr3S0tD16QmC\niKEhVpq45vWKvtiaDg0N2ohZh7xeAZcuUTh71oNz57yIjVXi9GkSXauq0oXs4GX3/eru/iPiPjKh\nvj64/2hyksbFiwQgdXS4kJamkQBSU5Npz1PTCJwIOJA6OhxQKLALIFmRmRm5ZcuiKOLuXW9QlG18\nPHAI74dIubkPT5iQEfH+nqTgeJvLxSIjw4r4eCu0Wj1oWoX1dQEzMzRiYzXIzTUiJkYBhqGxvu7E\n3JwDq6s0tFoFVCoRFMVArRaRlmZEQUEUCgpikJUV5YNJVqSlWR7YE6+v07h4cQU9PRu4dm0H09Me\nrK0xYBgRGo0CsbEaZGQYcfSoBQ0NcXjhhSSkpj742kRRxOqqB9PTBB4RiBSASYuLLqSkmB4ASf5/\nJyYaIxYq+vVMOIzC4Xl8XB4P+xAYtCNBocVFF+LiDEEA6NChqKD/jor6/dTa7WYxMLCJrq4NDA5u\nYWLCicVFAoaUSgKGDh0yoKgoCvX1cTh5MglpaYH2dI+H/RgUIjGy27e34XDwiI01QqfTgucVPtuf\niLw8K44ciUZ8vBksq8T9+wymp2lMT1PwegUYjQJ4ngZFeZGcrEJ+vgl5eVZkZ0chK8uK7GwrMjMt\nsFg+PRLm8fAYGXEGkW+Hg98VKyOAKDExcqNlgH+6HC3Fy7q6nFhfZ9HQYJUAUWmpcU8l1f7fNzFB\no6PDhY4OFy5fdiI5WSPFzBobA+WAc3Os1EF06ZIbJpNS6iBqbTXueQrFk5DHQ25U/FEzvV6BV18l\nLqLGRj202si5+DKMiI4OBr/5DYUzZ2jExCjx+uvESRTqk8eJCQKJ/u//ZaFQkAlnX/iCBrm5kQPh\nPq4bNwR8+9sc7HYB3/qWGm+9pYqo+JwsWbJkPQ15vSL+9m95/MVfcGhpUeK//lc1Dh+OTHAEkImd\n/vVMqw2sZ9nZoVvP/E7iX/+aOInn5nicPk3g0Qsv6EIWp9uvBEHE4CCDs2c9OHvWg7U1Hq+8YsRr\nrxnR3h7a+D/DiLDbvbh40Y0LFzy4fp1GTY1ecsSXlgbgFseJGBnxSABpcNCDkhIDmpvNaGkxo7bW\nCJNp7wDp7l0qCCDpdAofQIpCa6sV6emRHWXyenmMjrqCIJLTyUsH9X6QFBv76a6tnR0a09NOTE05\nMDXlwL17gZ9zcxQsFhNMJhMEQYudHUAUgfx8I/LzjUhKUkMUWSwuOjA+vo2pKRdUKsBsVkGhEOD1\n0nC7aRw8aERurhU5OdE+mESAUmamNaij1+Ph0NGxhq6udQwPk8FNq6skbaNUAtHRaqSlGVBYSAq3\n29oSUFBg/cSybJblMT/vfAAk+f/t8XC+aNuD7qTMzOgH+oPDUTIwegT5y5s/LS7mdDJISwuGQbud\nQgcPfnJO82H/v3v3XOjoWIPdvoWbNx2YnfVgY4MFw4hQKhWIilIjPd3go6TxOHEiEZmZJL5FURzu\n3duR4mP+x8TENjY2aMTFmWE26yCKJEK2scEgKUmPwsIY5OVZEROjxfY2j/v3GUxNUZibY7C1JUIU\neahULOLjVcjM1KGoyIzS0mjk5EQhO9uKgwfNe26i94+JJNZIYo+cmPDgyBGTdEGqqiJUO9KjJATo\nUBIc6upygGFENDcTONTYaNnXlAZS9Eyjs5MAos5OF/R6BVpbLWhpMaO93YyDB8nFaHOTR0eHW7L1\nbm0JQUXVmZmhu2iRhZfDhQtefPCBF11dFCoqdFIfUV5e5Fi6AcDpFPDhhwzee4/C735H4/BhtQSJ\n8vJC222wuCjgl78kJ7L37wdOZMvLI2PC2SdpcpJ0dFy8KOCb31Tjy19WwWiM3NcjS5YsWU9DLpeI\nH/2Ix/e/z+Gll5R45x01srIiFxyJooj+fjJp7R//kUVWFnHM/ot/oUFycmhf18wMh9/8hsTWrl3j\ncPKkDm+8ocNLL+lgsUTOe37vHotz5zw4e5YMGGlt1eP0aSNefjn0ru+dHR5XrpD+owsX3Fhb49HW\nZvQBpOD+I49HQF+fG1eukPvn0VEviosNaGkhAKmubn8AaWKCQkfHDjo7HejsdMJsVgZF2FJTwx8O\n/D4tL9NBE9mGhpxITtZKUbbqaguKisxSB+rvE88LWFhwSzBpasqBmzcduHXLjYUFFjStgkqlA8+r\nEB+vRFaWHrm5BqSm6mA2A/Pzbqkvl6J4JCTofACTh9NJYXXViehorQ8gRfkMDFFS1C05mTiAaJpH\nf/8mOjrWMDi4hclJN5aWKLjdAgARJpMSKSl65OWZUFERg5aWBJSXx8Bi+XRY5nTSQQAp8N87mJ7e\nhtmsfUjcjcCktLRPBlVPUzIweog4TsD8vONT42J6vfohMCjgEEpMNO0bbLhcLHp7N9DdvY6rV3cw\nOenC0hINl4uXCr0SE7XIzDSiqCgKtbWxaG6OR3KyHgzDY3raERQfI26hbayseJGQYEZUlAEqlRoU\nJWJjgwFF8Th8OAo5OVbEx+tgMCjhcvGYnfXi3j0KS0sc3G4lADVMJhEpKRrk5upRXk76jUpKYhEb\n+2jZ3aUlWppY5r/YxMdrJFJdVWVBaak5qPU+UsXzIsbGPBIg6u4mGWG/e6ipyYKcnL2X6BGwwvgA\nkROdnS6o1Qq0tpLFrbXVjIwMcqLh9Qro7fX6bLse3LnDoL7egBdeIAvnsWOhsxQDwP37HC5fpnDp\nkheXL1PgeaC9XY9XXjHixAk9oqMj6++/ukpG7/7mNzS6uhjU1Wnwuc/p8dprOqSkhPaEc2xMwLlz\nLM6eZXH3roDXXiOdD62toet8eFyanRXxne9wOHOGx9e/rsZXv6qCxRLZr0mWLFmynrZ2dkT84Acc\nfvQjHv/8n6vwn/+zGmlpkX0tZVkRFy+STr7332dRUKDC6dMavPaaBgUFoR184L9neO89Gt3dDJqa\ntHj9dR1On9YjISH0m8S9anOTx+9+58XZsx589JEXhw6p0dZmQFubHk1NekRFhfa1+PuPyAS2gJv+\n+HEjWluD+488HgE2WwAgjYx4UVSkR0uLGc3NZtTX7y/CNj7uldxHV644EBurlgBSS4sVKSmRD5B4\nXsT4uFsCSHa7E1NTXpSUmHdBJOK2epTvm9+ddPPmNmy2TYyNOTE1RWN9XQBNK6FWC4iJUSAtTYuc\nHANSU7XQahXY2mIxO+vC+PgO1tYoHDxoQFycFjqdAoLAYWfHi6UlJzweFpmZH4dJ5GdGhhVKpRI3\nbzrQ0bGGgYEtjI87MT/vxc4OSd5otQrfRDjSAdzQEIfa2jgcPPj7o2iiKGJlxf2AK8n/7+VlN1JT\nzZ8Yd4uPfzpT/GRg9BBduTKHP/qjcw9ExHbHxyyWR7MYkpJmBy5fJvRyfNyJuTkvNjdZsKwo9Qsd\nPGjA4cNmH8GMR06OCYuLbszM7GB21onZWQdmZhyYnXViZsaBtTUvkpMtUoSMZRXY3maxvEwhIUGH\njAwzEhL0MBpVAAS4XDSmpryYmaHh8Sih0xnAcWoACqSna3HkiBnV1dFoa0tASUnUninxw+R28xge\ndgaNtXe5+KCR9pWVFiQkRP5FEwAYRsDwsFsCRL29TqSkaHxwiDiI9mNRFUURU1NMkIMIQBAgyszU\n+txkAvr7vejs9KCjw4PhYQrFxXq88IIR7e0m1NQYQhrlIg4nCpcuUbh82Yu1NQGtrXq0tenR3m6I\nOBcRycbzeP990kc0NsbhxAkdXn+dnBaG8iaJpkVcucJJkEitVuD0aQ1On1ajoUEdsq6kx6mlJRHf\n/S6Hf/gHHl/+sgpvv61GTEzkvy5ZsmTJCqU2NkT89//O4e/+jsebb6rwn/6TGikpkX9tZRgRnZ0c\nzp4l66JWq5DgUX19aDvuHA4Bv/0tmbh2/jyNkhK1NCU1OztyJq5xnIjhYQaXL5ODwP5+GgUFGrS1\n6dHWZkB9vS5kfZhAoP/ID4+6u0n/UXOzES0tRjQ2GhETEwBCXq+A/n43OjvJ/ffwsBfHjumlCFt9\nvWnPQ2cEQcSNGx4JIHV1OZCUpJEibC0tViQmhq5Y/HHK4eAwNOTcBZEcEASgosKCykryqKiwIDn5\ns0X2KIpDV9c6OjrWMTy8gzt3vFha4iCKAgAWAI2UFDWysvRITtZBo1GDonhsbjKYm3Njbs6NtDQT\nDh40IiZGA61WBMty2NryYG7Ogfl5FxITDT7HjxVZWVHS49AhKxgG6OraQF/fBq5fd2B62oP1dRY8\nL0KhEBEbSxJAR45YUVMTi8bGeOTlWaDT7e0zwzA85uYcnxh3YxhhF0CKwre/3YCYmMffoyUDoyek\n7W0GXV1r6O3dwNWrO7h3z42VFQZuNw9AAaNRiaQkHbKziVuopMSK9HQtdnYoHwgKAKHZWQccDgap\nqRYkJJhgNOqgUqlA0yK2tzksL3vhcnE4dMiExEQ/FBLhdjNYW/NgdtYNvd6AqCgz1Go9vF4l1td5\nxMdrUFxsQXV1DEpLrSgpseDgwc82LpLnRdy65Q7qHZqc9OLYMZM0say62oqcnKdDRJ+GPB4edrtL\nipcNDLiQm6uX4FBj4/4XgJkZWoJDHR0ucJwoRcxaW83Iztb67JMC7HYKHR0edHZ6MDjoxZEjOrS2\nkoWvvt6w54XsScjlEtDdTflcRBTu3mXR0OAHRHoUF2sjLmK4uSng0iUG58/TuHCBBscBp04RSNTe\nHto+go0NAb/9LbkZvnCBRWGhygeJQn+S+ji1vi7iL/6Cw9//PY9/829U+I//UY2EhGfjtcmSJUtW\nuGhlRcR/+28cfvYzHv/236rwzW+qER//bFxryTANHmfPkjVzdlbASy+pcfq0BidPakLqUvV6RVy8\nSJxHv/sdDbNZgVOndDh1SouWltBNUH0U0bQIu52WANLICIOyMq0EkKqrdSHtGGQYEYOD5KD1yhUP\nbDYeHO5+AAAgAElEQVQKubkatLQY0dxsRFPTgwDJbg8ApKEhL44c0UsRtvp6E6zWvd13+xMIBCDt\noLvbiYMHtZL7qLnZivj4ZwMgiaKI+/dpDA46MTjoxNAQeZhMKgke+X/GxHy21yyKIubmKFy96kB/\n/xb6+7dx44YLTiePmBgFtFoOFOXF1pYTCQlKpKSYYbFooVAo4fUKWF+nsbDgQWysFpmZFiQl6WCx\nqKFWAyzLwuGgsLjoxPS0Ay4Xi8xMqw/akK7erKwoREUZsbrKYXBwG6OjpCdpeZkBTQsABJhMKqSm\n6pGfb0ZlZQyamuJx9GgUYmP3B9B2digp2jY1tY0vf7kMRuPj/8zIwOgziOcF3Lixg46OdQwObuL2\nbRfm573SKD+NRoGYGA3S0gzIyjLg0CE9DhxQg+cZzM8Hu4RYVsChQxakplpgteqh1WrAcQq4XDzW\n12lMT7vgdnNITjb4CKgSgiDA5WKwvu7B1haNtDQzDh60wmw2QRA0cDgUuH+fwdoai8JCM0pKrCgu\ntqCkxIqiIgus1s9+YnH/Pu1zDhEL4vAwybHudg8VF5uh00XO4vb7tLPjH3FP4mXXrnlQVGSU4mV1\ndRZER+/vvZ2bY3YBIicoSgxyEOXmEhsnw5BR935ANDBAoaBAi5YWUlJdX2/Y80L1JOS/Mbh0yYtL\nlyhcvcqgvFyL9nYD2tv1qKzURVRZNUBuJvr7WR8gYnDrFofGRi1OnNDi+HEdCgpC2/tz5w4vnZZe\nu8ajrY24iF5+WYPExGfnewcA29sivv99Dn/91zw+/3kVvvUtNVJTI+vzJEuWLFmRpvv3iZvzl7/k\n8ZWvEDdndPSzde2dnyex7TNnWPT1cWhoIPDo1Vc1OHgwtI6YsTEOH35I48MPGQwNsaip0eDUKR1O\nntTiyJHIcma73QJ6ewMA6dYtFjU1OgkglZeHdoocw4gYGvIDJC9sNjIxeDdAio0N3GdTlAC73YPO\nTheuXHFhYMCDwkJ/hM2EhgYzoqL2dl/OcSJGR91SiXZvrxMZGboggBQTEzlus98n0tHrxdCQUwJJ\no6MuJCVpUFlplQBSWZkZZvNnf92bmwyuXnXi6lUHRkfJz8lJD1JTtUhOVsFoFCAIDLa3SXrH6+WQ\nlGSE1aqHTqcCzwMuF4e1NRoUxSMry4L0dBNiY7UwGBQQRVLAvbnpxeysA9PTO7BadcjKCgCllBQz\nBEGNhQUWd+54cPu2C/fvU3C5eCgUItRqIClJh5wcI0pKotHQEIeSkhgcOmT8xMnoT0MyMNqDNjZo\ndHSsoq9vA2NjDkxNebCyQiaRKRQKmM1KxMdrkZSkQVISiUSoVAyWllwSENJolDh0yIKMDCuSkkww\nGHQSydzaYjEz48LkpBMUxSMuTgeTSQWlUgRN89jepuByMUhLMyIjw4qMDAtSU83QaHTwepVYW+Mx\nNUVhbIxElUpKCBQqKbGguNiC/HzTYynMcjo5X7TMKUEiihKkQmr/WPvf15QfaVpcZNDb60RPDwFE\nd+5QqKoKjLivrjbvuRDPr4UFJshB5HYL0ulEa6sZ+fkBQOQ/+ejs9KC/n0J+fgAQNTQY9rwQPQnx\nvIjRUUaKmPX10Th8WIP2drLwNzToQjo541FESsR5CRBducIgN1eFEyd0OHFCi9pabUhPwzhOhM0W\ngEQul4hXXyUuotZWNQyGyLlx3Kt2dkT8+MekkPXVV1X4L/9FhczMyPpcyZIlS1aka3pawHe+w+Pc\nOR5f/aoaf/zHKsTGPntrjsMh4qOPCDz67W85ZGUppUh3cXFoD4mcTgEdHQw+/JDG737HgGVFn/tI\nhxde0CI6OrLWxu1tHl1dBCB1dFCYneXQ2KiXANKxY5qQOtFZVsTQECU5kPr6vMjKCgZIuzuQKErA\nwEAwQDp8WCd1IDU27h0gsSypuOjocKCz0wGbzYWcHB1aW6PQ0GBBXZ0ZSUnPRp2HXzwv4vZtjw8i\nOTA46MSNG25kZup9LiQCkoqKTI+l59br5XHzpgujow5cverE6KgDY2NOJCZqceSICampWkRFASoV\nC4fDg9lZF6amHJiedkKnUyM+Xg+TSetL/gjY2WGxukohLk6HrCwLkpP1sFrV0GgAluXgdFJYXnZh\neprUyaSnW5CVZUVamhUWixEejwr377NYWKCxsEBha4tMMBZFAbGxGmRkGHD0qBV1dXGoqIhFXp4F\nJtOTh4jPBDB655130NLSgpaWlsfyOy9dWsXbb49hYYHC9jYHniduIatVhehoFaKilDAYeIgihbU1\nF+bnHbBYtL4JaAQKxccboVarwbIkxzk97cKtWzuYnnaCYQRERWmg0ynBcTxcLgYUxeHgQSOysy3I\nzCRQKCODkEudToeVFR43brgwNubE2JgT9+55kJNjRFGRRXqUlJAs6ONYyDhOwM2bwVPLpqa8KCoy\nB00ty8r6bBG2cBOZ1uaVAFFPjxM7Ozzq6y1oaCCPigrTvjudFhdZqaC6o8OFnR0ezc0EDrW2WlBQ\nQP5uuxemjg63ZI31R8waG40hLYIm42FZHyCicOUKhZQUlRQxa27WB1l3I0UbGwIuXaJx/jyDCxdo\nCAIkQNTerkN8fGhvwBwOEefPE0D0299ySEtT4vRpcvpZVhbZk80+TbOzIn74Qw4//SmPU6eU+Pa3\n1cjPj6ybYVmyZMl61nTnjoDvfpfDuXMC3nxTha9/XYXs7Gfz2syyInp7OZw5w+HMGdJN4u89ampS\nh9Q17e9RJO4jGj09LIqK1BJAKitTR1zsf22NR2cnuce8fNmLjQ3Sdenvu8zP14T0nodlRQwPBwBS\nb68XmZm7AZIB8fGBDTxNE4DkL9G22z3Iz9dJHUiNjaY9pxIYRsDgIHEg9fY6YbM5ERenRl2dxfcw\n48gRY8QPMvm4GEbAjRtuKco2OOjAnTteFBQYd3UiWVFYaIRG89mvQzwv4u5dN8bGAvvusTEn1tYY\nHDlixrFjFhw7ZkZamhYmk4CNDS+mpx2YmnL6fjqwuOhBTIwBMTF66PVqiCKpMNnYYOD1csjMtCAj\nw4y4OK3vYF0ERTHY3PRgft6Be/d2oFYrkZkZhaQkKzQaHZxOUimzuspic5MDIEIQBBiNSl/3sQU/\n/nEpUlIMn/k98KuzsxOdnZ149913Ix8YPe7n8Q//MI1vfnMMKhUDivJgY8OBxER9EBBKT7cgJsYA\ngEwWu3vXievXtzA56cD9+x5wnOhznYigKA4cxyE5mQChvLwAEPI/kpKMoCgBN28GfzjHxpzQaBQS\nFCouJj8PH358MS9RFLGwQEtgaGDAgZERF1JTtUHuof2MSIwUUZSAoSGXBIh6e52IjVXvAkRW5Ofr\n973gLi2xUr65o8OFjQ1OAkQtLWYcOUJ+JykHDHQQ+U8u/IDo49npUGhmhpU6iC5fpqDTQYqYtbbq\nkZISefZYhhFhswViZrdvc2hqIjGzEyd0yM8PPYSZmwtMNbPZONTXq/Hqqxq88ooG6enP1vfw4xoc\nFPC973G4cEHAF7+owp/+qRrp6c/WDZAsWbJkRboWF0X81V9x+MlPeDQ1KfGNb6hRV6cI+fr5pESm\nXgk4c4aszRMTAk6eVOO11zR48UV1yN09Xq+I7m7iPvroIwZrawJOnNDi1ClyAJaYGHkHegsLHDo6\nAgCJZeFzH5FHRkZoUw0sK2JkJBggHTpEABK5jw8GSAT6eKQ9Qn+/B7m5Oill0Nho2nPszH/I3dfn\nRF+fC319TqyssKiuNksAqbra/FgqSMJNHg+Pa9dcuyCSE3NzFIqLzUGdSHl5xscGTXd22CDzxtiY\nE9evO2G1qoMMHEVFFmRl6bG8TEDS9LRTciVNTztw754DTieHhAQjLBYt1GolWJYkedbXKURFaZGT\nY0FqqhFWqxpaLcBxHFwuBisr5HcsLLiRkGBGXJwFSqUOHo8KOzsCenqakJtrfSyvd7eeCYfR434e\n9++78OGHM0hPJ31CXq+AiYkdjI5uYHx8B7OzLqysUBAE4jziOAGCICAhQYdDh0zIz4/C4cNRklPo\n0CELEhMN0gdWFEXMznqDyOW1aw7Mz1PIzzcFgaFjx0jZ1uOUw8FhcNAZ5B7iedHXOUTcQ4+jdCwc\ntbHBoq/PhZ4eB3p7XRgddaOw0CABovp6yyONuFxZCQZEq6scmppMUlH1sWMBQORfWDo7ycKSkbF7\nYQm2toZCq6s8Ll/2SoDI5RLQ1mbwxcz0yMqKvM+FKIqYmCAxs/PnGXR3M8jL88fMdKit1YS8W0kQ\nRAwP8xIkun9fxMsvE0h04kRoCzifhnhexLlzBBTNz4v42tfUeOstFazWZ/t1y5IlS1aky+US8dOf\n8vjBD3gkJABvv63G668rQ9pF8zS0tCTg/ffJmn3lCoeqKrUUXcvICD2cmZvj8dFHxH106RKD7GyV\n5D6qqdFE3LRUMjU4GCAZjUq0teklF9KBA6GFIw+7z09P16ClxSDd5yckBAMk0plEImw2mxvZ2Tqp\nA6mpyYzY2L2/prU1FjZbACCNjLiRk6OXAFJ9vQUZGY8njRJucjg4jIw4g4q1NzZYlJVZgiBSRsbj\nS8cIAtnTX78eDJJmZ73Izzfh2DE/RDKjqCiQBHK5WMzMBBxJBCY5ce/eDqamnFCrVYiLM8BgUEOh\nUIKiBGxtMfB4OGRkmJGVZUF8PJk4qFQSd9LWlhf/63+9gOhoeUrag0/iCQCjM2dm8e//fR82NxmQ\n300eMTFapKYakJ1txbFjMSgsjPY5hKxISHj4h8/p5HDjhv8D5MK1aw5cv+6CxaIKAkNFRRbk5Zke\ni5Vut1iW2Ph2u4dmZymUlJiD3EOHDj1b0TKALCzT07QULevtdWJ+nkFNjVkCRNXVZpjN+1/U19a4\nXYDIiaUlDo2NJslBVFRkgEql8HX8+CNmHvT0BBaO1lbTAycPodDOjoArVygJEs3Pc2hu1kuQ6MiR\n0Np/H1Xr68ExMyA4ZhYXF3qXjtcr4tIlDufOsTh3jkVUlEIq2aytVT1ztuKHye0W8bOfkY1GbCzZ\naLzxxrO/0ZAlS5asZ008L+LsWQL+798HvvY1Fd56S/XMH3gAZC27cIHF2bMc3n+fRUqKQppSWl6u\nCnk0jGXJAA9/fG1qikdbm9ZXnq1DenroAdd+5a9JIPCIQmcnhaQkleQ+amnRh/wQlhRZBwOkgwfV\nQQfFiYmBfQCppgh0IPX1uZGVpZUibE1NZsTF7X3fwDACRkfdEkDq7XVCFCEBpLo6C8rKTM/UcKLd\nWl9npIlsfpDEMEJQH1JFhQUHDjxec4bHw2N8/MHUkEKBB9xIhYVmGAyBz6koilhfp4Jibn6X0r17\nDiwseBAVpUNUlA5arQqCoIDLxWFjg8atW68jM9PyWF8LIAOjh2psbAP/83/eRmlpHI4di0VGhgVx\ncZ8OVARBxNSUx+cWCnwwlpcZFBY+6BqKi3v8JWXEuURhYCAw0v7qVRfS0/VB7qGjRx8/mAoHcZyI\na9fcQYAIABobLT5AZEVRkfGRNqL37zPo7XWju9uNjg4XFhYYNDQEImYlJQFAdO0aLXUQdXd7kZqq\nDoqY7V4YQiGvV0BfH41LlyhcuuTF+HhgQkV7uwFlZaGdUPGoYhgRfX0Mzp8nI+/v3OHR3ByImeXl\nhT5mBgArK+RE8tw5FpcvcygrU0mQKDc38m7YHlVLSyTK8Hd/x6OhQYm331ajvv7ZjTLIkiVL1vMk\nu52Ao0uXBLz1lgpf/aoaBw8+H9d3nhfR30+GU5w5w8LpDAynaGtTQ68P/fuwssLj/HkSXzt/nkZC\nglJyHzU1acPiOe5X5B6ckQBSTw+F7GyNBJAaG/WwWkO7/+E4EVevBgBSTw/ZJ/gBUnPzgwBpeDjQ\ngdTb60ZGhhaNjWbU15vQ0GBCevre95Rkr0hLAKmvz4k7dyiUlJgkgFRXZ0FiYuSlCfaqxUU6qA9p\ncNAJvV65y4VEkjZxcY/3PRBFEUtLNK5fdwaljO7ccSMjwyAxAr8j6dAhw0PviTlOwMKCS3Il+V1K\nU1MOnD17CgkJxsf6vAEZGD2StrfZB4jhjRsuxMdrfGDIKv2xc3JMT8QlIIoi5udpjIyQEYQjIy4M\nDDigVCqkaWX+aFlU1LOXXQUAp5OH3U7iZT09TgwMuJGerpWiZQ0Nj2a75DgRY2Ne9Pa60ddHHh6P\ngLo6E+rrScystNQAtVoBQRAxNkZLHURdXR4kJwcAUXOzEUlJoX3/yWkFLUXMBgZoFBVp0d5Oiqpr\nanTQ6yMPIIqiiNu3g2Nmhw+rJUBUUxP6mJn/ed68KeDsWQKJbt3icfIkuXF88UU1YmMj773/LBob\nE/CDH/A4c4bHF76gwte+pkJu7vP1HsiSJUvW86LpaQE//CGPn/2Mx4svksOBsrLn65o/MUHi5mfO\nsBgb4/HCC6Q0+6WX1CEfqgGQQ++REU5yH42NcWho0EgAKTc3PA7c9iv//a8fINntNI4e1aCtzYC2\nNj3q6kI/yZfnRVy9SqOz0y0BpJSUYIC0ex9BOpM86O11o6fHjd5eN7RahQSP6utNUsphr3I6eQwM\nBACSzeZCQoJGAkj19RYUFhpC7pJ7UhJFETMzVFCUbXjYibg4DcrLzSgrs6C83IKyMjMSEh6/4YNh\nBExMuB9gCy4Xj2PHzEFupKNHLSHppJKB0aeI4wRMTnoe+ANubrI4etS8CwyRtvSoqCdDY4l7yYuR\nERdGRpzST7VagfJyC0pLzSgtJbnMtLRnM5cKBI+37+lx4vZtL8rKTNL0stpay75yvn5tb3Ow2TwS\nHBoc9CAtTYu6OiPq602oqzMhN5e8r4Ig4vp1WjoZ6OryICFBLY25b242Ijk59Pnp0VEGnZ1kill3\nN4XMTDXa28kC2dSkh8US+huUR9H6uoCLFwMxM6USUg9RW5s2LGJmAFnQu7o4HyTiIAii5CJqbg7t\nVJVQSBRFnD8v4Hvf43HjhoA/+RM1vvSlZ3McsyxZsmTJelDb2yJ+8hMeP/whh5wcJd5+W4WXXlI+\ns5vQT9LamoAPPiDRtUuXWBQXq/Daa+QQKVxcxltbAi5dYiSApNUqcOoUia+1tmoj9h6SogTYbAGA\ndO0ag4oKLZqbifuopkYHszn0AMmfVOjs9KC7mxxE7wZIu/cZoiji3j0GPT0uCSLdv8+ipsYkQaTq\nauO+6jcEQcT4uFcCSH19LqyusqipCTiQqqvNsFjC4/P6JCQIIiYnvRgZIfDIv/e2WtUoKzP7AJIF\n5eVmJCc/3jibXxsbjM+NFHAk3bzpQlKS9gE30pMyqPglA6OHaHTUgX/3725gfNyFAwf0D3QNZWY+\nOcrKcQImJrxBYOjqVReio9UoKyN00/8zJeXJfEDDQXsZb19evv/MrSiKuHuXkeBQb68bs7MMKiuN\nqKsjcKi21ihNKPB4BAwNUejr88Jm86K314vYWKUPEJnQ3GzAgQOhtW2SSWsMrlwh+e3eXgrp6Wq0\ntJAx983NeiQkROZFnaaDY2Z37wbHzMLp1GtrS8Dvfkcg0UcfccjLU0r9BUePKsPmeT5N0bSIn/+c\nx/e/z0OpJP1Ef/AHSuh0z997IUuWLFmyyIHK//t/JK7mdgN/9mcq/Ot/rYLB8PytCxRFegz9DuTo\n6EDvUXV1ePQYEpc0hw8/JADJbmdRUaGRAFJRkTpi72+cTgE9PRS6umj09FAYGWFQUKBBQ4MOjY16\n1NfrQn4IzPMkybAbICUmqlFfb0BtrQE1NQYUFmqD9qXr65y0x+ntdWN01IvDh3WSA6m+3oTU1P05\nZVZX/WXaBCCNjrqRm6uXAFJ9vRmHDj27pgWA7E2npykfQHJieJjs03U6peRA8kOk1NQn817wvIh7\n94LNLNevBypwPvigHImJj58PyMDoIdraYjEx4cbRo2aYzU/uQkHTAm7edAfFyq5fd+HAAV0QGCot\nffw5ynCTf7y9v3uot9eJmBi1BIcedbw9RQkYHvbsipd5oNcrJDjkt25qNApfzI+T4FBfnxfj4zSO\nHtWhro5cmOvrDUhNDf0Iz+Fh2ucgotHXRyEjQ43mZlLw19SkR3x8ZAIiMrKWw4ULBBD19LAoKAiO\nmYXLVA9RFDE2JuDCBRYffMBheJhDSwuZkPLyyxqkpETmCdzj0MaGiL/5Gx5//dccSkrISXJ7+/MJ\nzWTJkiVL1oMSRRFXrhDn6cCAgC99SYU//mM1EhOfz3VCEEQMDZHeo7NnWaysiHjlFRJdb29XIyYm\nPO4p3G4BnZ2MBJDcbhEnT+pw6pQWx4/rIjpmT/YiDHp6KPT00OjtpREfr0RDgx4NDTo0NOiRlxda\nQMbzJOnQ1+dFfz/Zr6yt8aiq0qOmJgCRYmIC+4Dde6GeHrIfslhUQTG2I0f2t8ei6QfLtBUKBAGk\n0lITtNrI/TzsRaIoYm6ODoJIw8OkQ9cPkfw/n+SAKf+Qraqq6CcCmmVg9JTk8fAYG3MFxcpu3/Yg\nO9vgg0IEEJWUmEOSTXzaWl1lpf4h/3j7ggKDBIgedbz98jIb5B4aG6NQUKCTomV1dSakpZHfSy52\ntASH+vq84DhRgkN1dQaUl+thMIT2YscwJIPtdxDZbDSysoiDqKWF2GhDPQXiUUUifhyuXGHQ1cWg\nq4uFyaTA8eNaKWYWTjcfy8sCLlzgcP48iwsXOFgsCpw4ocapUxq0t6thND6fN7p+3blD+ol+8Qse\nb7yhwje+ocKRI+Hz95MlS5YsWeGn27cF/OVf8vjlL3n8s39G1o7Cwud77Zia4nHuHIePPmLR08Oh\nsFCFEyfUOHGCuI/C5fDs7l0OH31E48MPGVy5wqCgQI2mJg0aG7Worw+fqoBHEYlmsejuJgCpp4eC\n1ysGAaTSUm3I/xZraxzsdgo2GwFIQ0MUUlPVEkCqrdWjsFAngQRRFDExQUsdSD09Lqyv86itNUoO\npKoq0776nUgPUHCZ9uQkhdLSQJl2dbUZycmPvwMo3CSKIu7fpzEy4pLibMPDTtC0IJlB/BApO/vh\nxdbhJhkYPQHt7HC4ejW4b2h6mkJBgTEoVnbsmAlGY2Ru9Pcjr1fAyIgbdrsLAwMu2O0ubG9zqKz8\nbOPteV7EzZuUBIf6+tzY2uJRW2tCXR2JmFVVGWEykd+7vMwFwaFr1yjk5mqDAFFmZuhHyDOMiMFB\n4iDq7KTQ308jN1cjOYgaG3WIjY3Mzw3HiRgZYdHVxaKri0FPD4OEBCWam7VoaiKPcBrt6vWK6Onh\ncP48gURzcyLa29U4fpw8srLC57mGSqIooqtLxPe+x6G/n5wSf+UraiQnh/8CKEuWLFmywkdra8Sd\n+uMfcygrI+7UtjbZnUrTInp7Od+BFYe7d3m0tBB4dOKEGjk54fEe0bQIm41BdzeL7m4G/f0s0tJU\naGwkAKmxMbzu8R5Fc3McensJQOrupjA9zaGyUifF2GpqdCHveOI4ETdv0hJA6u+nsLzMobJSLzmQ\namoMQYfNKyvkwN0Pka5fp3D0qD4oxpaUtL+EhcPBYWDALQGkwUE3TCYlqqvNqKoyo7rajPJyk7RP\ne9a1tERjdDQYIjkcHEpLLUHl2rm54Vcw/kwAo3feeQctLS1oaWl56v//9XVGipP5AdHSEo2iInNQ\nrKyw8Nm35QGExk9MULDbnT5A5MatW14UFhpQXW2WHrm5+4+XOZ08+vsD5dT9/W4kJ2ukaFldnQmH\nD+ugVCp8k84C7iGbzYvtbd5H2gkcqqzUh0VhG02LGBgIOIjsdhp5eRrJQdTQoAuylkaSaFrE4CCB\nQ1euMLDZWGRkqHxwSIOmJi2Sk8PntYmiiOvXBclB1NfHobhYJd2UVVSooFaH10U8VGJZEb/6Femh\ncDoDPRTPu8tKlixZsmR9NlFUoP9OowG+8Q3Sf/e8DYz4JK2tCbh4MXCYpdUSt/Px4+EVX+M4Edeu\ncejuJpNse3pY6HSQ4FFDgwaFheqw2xzvR1tbPGw2WnIgjYwwyM/XSA6khgYdUlJCnxzZ2ODR3x+I\nsQ0OUkhOVqOmRi/tjY4eDbiQPB4Bg4MeyYFks3kQH6/ywSMzGhrInms/oJIUdNNBBoLr1z3IydFL\nAKm62ozCwv1NeYtkra0xEkPwg6T1dRYlJeZdnUgW5OcboFY//e91Z2cnOjs78e6770Y+MHoaz0MU\nRSwtMUGuoZERl0QGSaSM/GHz843PzQd9ZYWB3e6SHkNDbsTFqYO++KWlpn2PbSfWRibIPTQ5yaCs\nzCDBodpaExISyEXYfyH0w6HBQVL87IdDdXUG5OVpw2JRoigBAwOM5CAaHKRx+LBGKqluaNAhOjp8\nIMp+5PGI6O9nfBEzFoODLA4fJoCouVmLhobwsycvL/tvvAgkMpkUPtu3Gq2tGkRFhf4zE07a2QlM\nusnKUuDtt9V4+eXnb9KNLFmyZMl6shJFER9+KOD73+cxPi7gT/9Ujf/wH1SIiZHXG79EUcStW+Sg\n6/x5Lqzja6IoYnKSl+BRdzeDrS0B9fUEHjU2alFeroloMEjTpEbCD5B6e2nExiqDAFJ+fujTDDwv\nYnychs1G+VxIXty/z6GiIgCQamr0iI8n+ywSz6N2xdjccDh4yX1UX29CRYVx3/s9hhFw7ZonCCIt\nLjIoLzdJe8mqKjMOHtSG/D17WtrcZH1mlABEWlwMmFH8E9oKC43QaJ7OnuqZcBg97udBYAWFkREX\nRkcDgIjnEeQaKiuzIDNz/06ZSJXHw0vRMv/D6eRRVWUO+lInJOy/FJphBIyOeneVU7shipDgUH29\nCaWlBmi1St8ENSaonHpxkUNVlV6CQ9XVhrBx5VCUgP7+QEn14CCNwsKAg6i+Xo+oqPCCKHuVwyGg\nt5f19Q8xuHaNQ1GRWoqY1ddrYLWG12ujqOCY2eysiLa2QMwsOzs8PjfhptlZEf/jf3D42c94nDql\nxDe+oUZ5eXj9bWXJkiVL1rOpa9cEfP/7HM6dE/Dmmyp8/esqZGfLa9DHFSnxNb8WF3n09rKSC98M\nTH8AACAASURBVOnuXR4VFRoJINXWakIe8fosInsWVgJI3d0U3G4R9fUEIDU2kh6kcIBkm5s87PaA\nC2lggEJCgkqKsdXWGnDsmE5y2i8uspIDqbfXjVu3aJSUGKQy7bo6kwSc9qOtLQ6DgwGAZLe7oFYr\ngvaalZWm56Lz1y9/3c3ucu25OQpHjpiCJrQVF5ueiBNJBkYPUWfnFv7oj249MMb+SY3IC0f5x9rv\n/rLeuUPhyBFDUPY0N/fRGt9XVljY7YF42ciIFzk5WtTXm6X+oYwMQpMdDh52e2C0fX+/V7qA+fuH\ndtsoQy2vV4DNFoiYDQ8zOHo04CCqr9eHHUTZqzY3BXR3M1LE7PZtHpWVGileVlurDbtIkiiKuHGD\nTDM7f55Dby+HoqJAzKyyUo6ZfZoGBkjs7OJFAV/8ogpf/aoaaWny+yVLlixZsp6+FhdF/NVfcfjJ\nT3g0NSnx9ttq1NVF5j3V01CkxNf82tkRYLMFANLICIf8fFVQjC0pKbIP9ubnAz1IPT0U7t4N9CA1\nNOhRW6sLi30Cz4u4fZuRupBsNi/m5zmUl+t2uZAMSEwk4Mbl4mG3B6ax2e1upKRopB6k2loT8vP3\nv5cWRRGzszQGBgJ9uKOjbqSn63x7UhOqqy04dszw1Bw34SCXi8O1a+4giHT5cjESEh5/sbgMjB4i\nURSfGzDk19ISEwSHhobcSEhQS7GyqiozSkr2Hy0DSA52ZMQDu92DgQEP7HY3dnYEVFUZpcll1dVG\nWK0qiKKIu3fZIPfQ1BSDsrKAe2j3xSkc5PEQQEQcRCS/XFSklUqq6+pCX4D3qFpZ4aWC6itXGMzM\n8Kit1UgRs8pKDXS68PuurKwEx8wMht0xMzWioyPz7/G0xPMizp4lp7nz8yK+/nU1vvhFFazW8Ptb\ny5IlS5as508ul4if/pTHD37AIzGR9By9/rpSPgD6FEVSfM0vEvFipRhbby8ZlkIAkgYNDVpkZ6si\net+2vR3cgzQ8zCA3V4PGxkCM7cCB8Nj3bG8TF5K/TNtu9yI2NtiFVFSkg0ajAM+LuH7dK8XYbDY3\nnE4BNTUm1NYGhhPtd+gRALCsgJs3vUFRtpkZGsXFxiAnUmbm82P2eJKSgdFzKLebx/CwOwgQud2C\nj9CSL1llpRnx8fuPlgmCiNu3adjtbh8c8uD2bQpHjuhRXU3AUFWVEbm5pJyalKpRQeXUBoNCgkO1\ntQYUF+vDwqrpl9stoK8v4CC6epVBcbFWchDV1elgNkcmkJif5yU41NXFYGVFQEOD1hcx06C0VBN2\nNxMAiZn19vpP0DjMzAhobVVLp2hyzGxvcrvJDfhf/iWP2Fjg7bfVeOMN+QZclixZsmSFp/wHHN/7\nHof794Gvf12FL35RBYtFXrd+nz4eX7t3j0dzc/jG1wCyz7hxgwvqQeJ5SO6jxkYtiorUYZM6eBTR\ntIiREVqaxNbbSyMqKrgH6fBhTVhUopB9HyPF2Gw2L2ZmWJSVBbqQamsNSEoiwGtpiYXNRtIlNpsH\nV696kZur9U24Ji6k7OxH6ytyOnkMDQVH2VhWDKpOqaw0IzY2POBbJEkGRs+4eJ5Ey3YT2MlJCkeP\nGlBdbZEAUXb2oxHY5WUSLfMDosFBD+Lj1aiuNkqAqKTEAL1eCY4TcesWjcFBCkNDFAYGKNy6RePY\nMZ0Eh2prDTh4cP+g6klqaYlDfz8Nm41Gby+Na9cYlJYGHES1tTqYTJEHiERRxNQUL8GhK1dYuN2i\nFC9rbtbi6NHwXHRFUcTNm4FpZr29HI4eDZySVVXJMbP9aGlJxI9+RCz+jY1+i78i7G4UZcmSJUuW\nrE+S3U7A0aVLAt56i0SoDx6U17G9anVVwKVLD8bXTpxQo60t/OJrgL93lpfgUXc3g8VFAbW1GinG\nVlmpgcEQuZ8DAmV29yDRcDgE1NbqUFdHHpWV4bMX2dnhMTBASQDJbvciKkqF6mo9qqsNqK7Wo7RU\nD4NBCZomHbY2GwFIfX1uMIyI2lojamsJQKqsNMJofLTXdv8+E7QHHh4mE7YDLiQTSkpM0OnC470L\nV8nA6BnT4mJgatnAAImWJSdrgnqHiouNj/TF8HgEDA8HR8ucThIt8wOiykojEhLUEAQR9+6xGBwk\nE8sGBylcvUohNVWDyko9Kiv1qKjQo7xc/0gxtyclhhExOsr4ABGF/n4aTqeImhodamrIRbm2VvfI\nF65QiliReamg+soVBgCkgurmZi0OHw5fW+/qaiBmdv48B71egZMn5ZjZZ9HYGImdnT1LSkS/9jUV\ncnLk91GWLFmyZEWupqcF/PCHPH72Mx4vvkgOQcrK5LVtP4rE+Jpfa2sCensZyYV08yaH4mK1FGOr\nq9OGJfzajxYXOdhsNPr6yGNsjEFhocYHkEjaIS0tPJw0giBicpKB3U4ibHY7MQwcPqz1ASQCkfzT\nrOfnmSCAdOMGhYICnQSQ6uqMOHTo0VxIfiOFHyANDDy8ozcn5/kZarUXycAogrWzw0nRssFB8tPr\nFYJ6h6qqHs16R4rOKJ97iACiO3doX7QsAIhyckix1vw8h6EhSgJEw8MUrFYlKisNEiAqL9cjKiq8\nokELCwH3kM1G3EO5uWrU1upRU0PgUG6uOmwhyqeJ40Rcv05su34XkcWiRFOTRoJEWVnhC4j8Vml/\nzGxqikdrq0Y67ZJjZo8mQRDx0UcCfvADHjdvCviTPyFjimNjw/NzIEuWLFmyZD2KtrdF/OQnPH74\nQw45OUr82Z+p8PLLyrB0Toe7dt+TXbhA4mstLWocPx6+8TW/3G4B/f2s5EKy21lkZqqkGFtDgxZp\naZF9T+n1ChgeZnwAiUJfHw2dToH6+gBAKi7Whg3k83oFjI5SEkQaGKCwtcWjspK4kKqqyM/ERDW8\nXtKF6wdINpsbAIIAUnm58ZENCG43j9FRd5ATyeHgUVERmMhWWWnGgQOPv0w6UiQDowgRRQm4etWN\nwUG3NGpwYYFBaalJ+iBXVZmRlfVo0bKlJRZ2u1uCQ0NDHl/ptUkCRCUlBuh0SqyuclKszA+IAPjA\nkEFyD4VTMTVA3sOREUYCRP39NChKRG2tToJDlZWR2z+0sSGgv59BXx8Lm43F4CCLtDRSDNjURB7h\nvCAKgojr1wVcvkxiZj09HI4cCY6ZhctCF4na2BDxv/83j7/9Wx5WK/C1r6nxh3+oDKt+MFmyZMmS\nJetxi2VF/OM/CvjRjzgsLYn40pfUeOstFRIT5fXvUfVJ8bXjx9VoalIjMTF876VZVsTVq5wUYevt\nZaHVAnV1WtTWalBbSzo7w3Goy15FhghxQQBpZoZDRUUgxlZbq0NsbPjsC1ZXOQwM+F1IBCLFxDwY\nZdPrFZidZdDX5/E5kdy4dYvG0aN6Xw8SibOlpT064FlZYYL23IODbuh0Ch9AIhCposKMmJjw2us+\nKcnAKAzF8yLGx71BH9Lbt73Iz9dLYKiy0oTCQuMj9bSQ0muvDw4RSERKrwPOoaoqI+Li1Nje5jE8\nTAUBIodDQEUFgUJ+QHTwYHi5cERRxNwcL8XKbDYaN26wOHxYEwSIsrLC63nvVYIgYnyck+CQzUYy\n29XVZKGrq9OiuloT1pZbPyDq7OTQ2cmhq4tDQoLCd2IVvnn5SJIoihgYEPHjH5PY2enTSnzlK2pU\nVcn9RLJkyZIl6/nT8LCAv/kbHv/0TzxeeomsiXJn32eTKIoYHxdw4UKgV/LAASWamtRobiYAKTU1\nfO/n/J2eNhuLvj4GNhuLO3d4lJSofQCJgKQDB8IHrjyKtrd59PcHYmz/f3t3HmRVmeb7/veutXNg\nFEUElElBZMqRzAQphywtFaQcGCzQLkutU13dek73jTj3RpyOuDdC/efEPfeeuHFu921PdXVVa2kX\nSqloqSAOpYkoUyY5MYMMMoMiyJTD3mu994839965ABWBJPfe+f1EZCQJSbI2e+211/qt53neNWva\nNGxYLBUgTZtWoJtuysuY10IYWm3d6lrZ1qxJt7KNH1+QqkBKtrK1tISqq2tJBUgrVpxSQYEXCZDK\nynpd8KwiNyurLdXRU1t7UvX1pzR0aH6kcKO0tLd6987u/eRcCIy6mbVWO3e2pYKh2tqTamg4pWuv\nzY+UwZWW9lGvXj98J3e9mp1by05p27Z2FRUVRgKi0aPzdfq0VWNja2rmUG1ti/bvT6isLD1zqLKy\nl8aMyZyDSZKbr9SeqhxaubJN1tpIa9nkyfkZMxDuhzp2LNTq1S4YWrEirjVr4rrmGi/1RjZtWp4m\nTszMAdVJ3xUQVVe7k4qhQ7Pz+ck0p09bvfxyoOeeC3TsmPTkk76eeMLXwIGZu38AAHC5HD1q9Yc/\nuPfJ3r2lp57y9cgjvvr25X3yYgWBVVNToE8+SWjZskDLlyc0YIDpFCD5GjUqc1vYJOnkyVC1tfHI\njdl+/UwqPLr55nyVlsayuvLdja5oTwVIK1a4YdrpAKlQlZX5GTW39cxWttWrW3XsWLqVLRkiXX21\nr+3b2yMB0rZt7Sot7ZUKkKZN66OhQy98oaXkPKTa2vRomI0bWzR2bLLAw13DT5zYS3l5mfN/eCEI\njC6zgwejJW51dafUq5cXSScnT+6jAQMurMRt//50a9nq1ae1du3pjqHXvVMBUUlJLxlj1NycrBpy\nH59/3q6JEwsiQ6nHjy/IuNWmXMiWiIRDmzbFNXFitHpo5MjsrB6y1mrLlkArV7Z33O2I64svAk2e\nHEuFQ1On5mvQoMw++LilT0N9/HE6ILr6ahcQ/fjHBERdYcuWUL/5TaCXXgo0bZqnp57ydffdHoP7\nAAA4hzC0+stfQj33XKBPPnELQDz5pK/x4zk/uVRcVXzYESC5j/x8RSqQxo7N7ADJWqutW9Pn5itX\nxrVjR6Dy8linEClPgwdnd3XJ/v2JTgFSq9atc9dXnYdpDxuWWW1Y59vKlkhY1dYm5yCd1qpVp9Sv\nn5cKj26+uY9KSnpdVAjY2hqqufl0pEto9+42FRf3jrSzZdtQbQKjLnTmUOra2pM6eTKItJVVVvbV\n0KEX1mP5zTeB6urcUva1tW72kBt63ScVEFVV9dYVV/jatKldtbUtqYBo/fo2jR6dnwqHKisLVVRU\nkJHLCp48GaquLj13aNWqNsViJhIOlZfnX1AFViY4eTLUmjXxVDi0alW7+vf3OlrL3F2M4uLMv4uR\nDIiSFUTLlqUDomQF0bXXZudzlMkSCau33nInu+vXh/rlL339+tfu7h0AADg/e/ZY/fa3Cf3ud4Em\nTHA3Xe6/38v4869sY63Vtm3RAKm9PRogTZyY+Te7vvmm8/m7G6Z91VVeajTEzTfnqagolnE33n8I\n1+oVHabdu7dJhUfJYdqZ9Bg7t7IlQ6TNm9s1fnyBpkwpVFWVC5FuvDFPn3/engqQVq48pZ0721Ve\n3kvTprnxLGVlvTRq1IWtyJZ0/LjLA5JZQG3tSX3zjRuq3blg5LrrMneodk4ERk8//bSqq6tVXV3d\nbdvR2hqqqemU1qzpmqHUrgSvJRUO1dae1v79cZWW9lJlZW9VVrpw6Prr87RjRyLVUlZX16qGhjYN\nHeqroiK9YllZWWFGtme5N5FEZDD11q1xFRfnRwKiYcMyd3Wv7/JdfdLJcOjmm/M0dGjm36E4MyD6\n5JOEBg4kILpc9u+3+t3vAv32twldf73RU0/FNHu2l9VDGgEA6G7t7VaLFoV67rmEtm+3+vWvY/rr\nv/Z17bW8v3aVXbsCffJJoGXL3Pnk119b3XqrnwqQSkv9jB67ILnz4s2bg9T4iJUr27VnT6iKiuQN\nYNchcPXV2XtunBym/dlnralKpC++SKiyMj0HaerUzBqmLZ1/K1t+vtHq1S5Aqqs7rfr6FrW0hCot\n7aXy8l4qK+ul8vLeGju24KL2x8OH46nwKJkd5OWZVAVSVVVfVVRc2Ernl1JNTY1qamr07LPPZn9g\ndLm3o/NQ6uQTfSmHUsfjVuvXR8OhrVvbNGFCYSocqqzsrXHjCrR3b0Jr17aqvr5NtbUtWru2VX37\neh0tZb1Sy9lfeWVmvXCTjh8PtWZNWyQg6tMnWj1UVlaQtRfBp09b1dXFIyWseXnplRimTctTaWl2\nrMQQhlYbNkRbzAiILi9rrWpqXDXRX/4Sat48VzpfXMz/OwAAl9q6dW5I9ssvB/rJT1zVUXV1ZrdP\n5YJ9+0ItX56uQNq/P9S0aekKpIqK7Fg59+jRUKtWpa8D1qyJa/BgL3KTONNnkH6fo0cDrV7dps8+\ncwFSbW2bhg+PRWYhjR2beWNCDh1KpIZpr1njWtmuuspPDdSuqChUcXGBWltd0UZDQ4vq60+roaFF\nBw8mVFxcqLKy3qkgaeLEwosaqv3FF2cO1T6ta66JRbKFsrI+6tPn8l/T50SFUVduR3IodecE8FIO\npXZlc22RcKi5uVWjRuV3rEDmwqGiokLt3+9WLEt+1Ne3qlcvT5MnF6q8vCAVEA0enFm9pUltbVbN\nze2qq2tTbW27amvbtGNHQmVl6eqhqVMLdN11mbn938daqz17wlTl0IoV7dq4MdCkSbFIe1kmL23f\nWTIg6txidtVV0YAok1e9yCXffGP14ouB/uf/DOR5bjjnz3/uq3//zHrzBQAgFx0/bvXSS25ItrXu\nffjRR31dcQXvw5fD4cMuQEq2sW3fHmrKlHSANGWKr8LCzH8ugsBqw4ZEapD2ihVxHToUqqoqLzVM\ne+rUzF7l+Pt0HqbtQqRWnThhVVGRr8rKgtTna6/NrG6RM1vZ6utbtW5dm4YMiam0tEAlJYUqLS1Q\naWmh+vc3ampqTQVI9fUt2rGjTTfdVBipRCopKbzggCcIrDZvTg/Vrq09qfXrW3TjjYWp/KGysq+K\nirp+qDaB0Tns3t2m3/3ucOoJulRDqd1S7/FIOLR27WkNHBiLVA6Vlhbq0KEwFQolP/fv76m83FUM\nuZCoUEOGZGa4Eo9bbdwYV21tm+rq2lRX166NG+O68caYKirSB4vi4nzl52fOweKHaGuzqq+PR9rL\ngkCR3uXJk/PUq1d2PD4CoszT2OjubP7pT4Huucct/3vrrSz/CwBAd7DW6pNPrJ57LqH333eVvk89\nRaXv5Xb0aKhPPw1SAdLGjYHKy9MtbNOmxdSnT3acK331VahVq9pTK7LV1cU1fLiXqkCaNi1f48b5\nGT/T6bscOJBQXV20aCAWM5EQqaKiQNdck1k31YPAatu2djU1tamxsVWNje5zW5tVaWmhSkpcgFRa\nWqBRo/K0ZUur6uvT1UgbNrRq5Mj8VIBUVubCpAttNWtrSw/VTlYj7drlhmpXVvbVM88M65I2NgKj\nc9i+vVUvvPDlRQ+ldv2JyXCoRXV1p2WMIuFQeXkvHT0aRqqGGhradOWVXioUSn6+5prMDIeCwGrL\nlnjkQNDc3K4RI2KqrMxPBUSlpZm1NOMPtW9foFWr0uFQU1NCN93kp8Khm2/O0/XXZ1Za/l0IiDJT\na6vVa6+52Ql797rZCb/6la8hQ7JjvwIAoCc4cMDNEvyXf0lo1Cij//gfmSXYXU6csFqxIl2B1NAQ\nqKgoHSDdckssa6rBEgmr5uZEZJzF11+HmjIlL7VacmVlngYMyN5zdNeVEXQUFrSnigv69zeqqChI\nXT9OnpyfkWNVDh1KREKkpqZW7dwZ19ix+akqpNLSAk2YUKCDB+ORdrbGxhZddZUfCZDKy3tr6NAL\na9s7cSJQfb0Lj/7u74aosPDS7xcERpfI8eOB1q49HakeOnYsUEVFNBw6edKqoaEtFRA1NrZp0CA/\nVTU0eXKhysoKdPXVmRkOWWu1fXsiFQzV1bWpoaFd11zjp9LhysoClZXlq3//7D2QHT8eqq7O9Rqv\nXu0+t7dbTZmSnxpcV1mZp759s+cxJpc17RwQDRgQDYiGDcuex5Nrdu4M9S//Eujf/i1QWZmbkzBz\nppdRK08AAICoM1cr/Q//wdff/E1MI0bw/t1dWlqsVq1KpAZpr1mT0NixyQDJ1623xrJq+PShQ0Eq\nPFq5sl319QkNHeqpsjJPFRXuo7w8llXXJWdKXmN2DpHq69s1ZIgf6U4pK8tXv36Z9zhbWkKtX9+W\nqkJqampTc7MrAkkGSKWlhSouzlcQ2E5zkVrU0HBanmci7WxlZb10ww0Xt0LbpUJgdAFaW0M1NkaH\nUu/ZE1dJSa/U3KGysl6Kx40aGtxA6rVrW9XU1KqhQ2NnVQ5lYnIqpdPfzuFQXV27+vU7O/3NtGn4\nP0Q8brVuXUJr1qQDoi++cCuXVVXlacqUPFVV5WnUqOypHpLSFUTLlhEQZaogsFq61LWdrVoV6rHH\nfP3t3/q68UaeFwAAss3mzaF+85tAL70U6JZb3M2fu+7K/CXic117u1VtbbqFbcWKhEaM8FIVSLff\nHtOQIdlz7hUEVps2JVRXF1ddXUK1tXGtWxfX9dfHVFkZU0WFu7FdUpKXFbOdvk3nLpZkkNTc3K6R\nI9NdLJWV+Sopyb+gWcJdLQytduyIpwKkZEXS8eNhpJ2tuLhAV1xhtGlTW6Qa6fjxoGOFtt4dQVIv\n3XRT4WW/mUxg9D0SCasNG1oj4dDmza0aN66w08yhXjLGqKkpXTm0bl2bhg3L66gaKtDkyYUqLS3U\ngAGZG6wcPJiIBEO1tW3yPHX0lqb7SwcPztzH8H2stdq1K0hVDa1e7VrLRo3yI+HQpEmxrFh9obP2\ndqv6+iA1FPCzz4KzVjEjIMoMX35p9W//Fug3vwk0aJAbnjlvnp81864AAMC3O3XKasGCQP/8z4FO\nnZKefNLX44/7uuoq3uczQSJh1dDgqo8++SSh5csDDR5sdPvtsdRHto1laG+3Wr8+GSLFVVsb15Yt\nCY0blw6QKiqy8xqns3jcasOG9kiItGlTXGPHxiLXrEVFmTsn98iRQE1N6ZlIjY1t+vzzdo0end8x\nYNuFScOHx7R7d3tkuPa+fXEVFRVGKpEmTSrskla0JAKjc9ixo03/+I9fqra2RU1NLRo2LE9VVelw\nyPc9bdjQnhpIvWFDm0aOzIsMpC4tLVD//pkbrBw5EnSaOeRebC0t9qzhY9ddl11VNWf6+uswUjm0\nZk278vNNKhiaMsUNps7G9rlTp6xWrkxo+XL3Rldbm9CYMb5uvdWV2t5yS0xDh2bf48pV1lqtWuUG\nZb7zTqhZs3w9+aSvykqeIwAActG53vufespXRQXv/ZkkCKyam12AtGyZq0S68kqTuuF6++0xjRiR\nfc9ZS4tVU1O8U4iU0K5dgYqKOodIMY0bF5PvZ+/1XmtrqObmeKToYceOhCZOzIt0xYwfn5exox7a\n2kJt3NgemYvU2Nimvn29yCptY8bk6fjxRGSVtm3b2nTjjQV6//3RGjw475JvG4HROeza1aaFC4+p\npKSXCgt9bdnS3jGQuk0bN7bphhvyIiuVlZYWZnTP6DffhKqvj7aVHTkSaPLkgk5zh/I1atSFDdvK\nFK2tVo2N0blDhw6FqqjIi1QPXXdd5gZ53+XIEbcihAuIEtqwIVBpqQuHbr01pmnT/KwegJerTp50\ndxmfe87dZXzqKV+PPcZdRgAAepIvv7T6/e8D/eY3CQ0ebPTUUzH97Gce1cUZ6MyxDp98klCfPka3\n3+7mIFVXxzRqlJeV100nT4aqr0+kqpDq6uI6eDBUWVksMhNpzJjsLho4dSpUY2O6Cqm2tk379gUq\nLc3vVCBRoBtvjGVsy6i1Vl98Ee8IkNLVSF99Fai4OF2JNH58noyxuvnmPl0S/BEYnUNDQ6t++csD\n2rKlXTfemB+pHCouLlCfPpl7UX7qVKiGhmhbWba9OM5HGFpt3Rp0qh5q18aNgW66ybWWJQOibE7M\n9+wJU+1ly5cntHdvqKlTXa/1rbfGVFlJC1Mm27TJzSb64x8D3Xabm2Nw553MMQAAoCcLAqt333VD\nsmtrQz3+uJtfOHp05l5f9HTWWm3aFHZUILmPvDxFWtjGjMnOAElSx4rd8UiIdPy41eTJ6Va2yso8\nDR+evY9Ryp0iimPHAjU3pwOkxsZWbd7cru3bR2vo0Eu/cBaB0TkcOxZoy5Z2FRcXZOQALckduA4d\nCtTcHNe6dW4AWH19e6r8rnNbWSaX352vQ4eic4dqa+O68kov0lpWVpan3r2z83Faa7V5c5iqHlq+\nPKHTp9VRPeSqiEpK/Kx/HnNdPG715psuKNq0KdSvfuXr17+OafhwnjcAABC1fbsbkv3CC4EqKtzN\npXvv9bL2ZmdPYa3V1q3RAMnaaIB0003ZHa4cPhyori5diVRbG1cYKtXGlgyShgzJzs6NpK++CrR2\n7dljWiZPzldpab7KytznsWPzMvp1GY9bxWLqkn2OwCgLnD4dauPGuJqb27Vunfvc3Nwua6Xi4nwV\nFeWpqChf5eX5mjQpcwd8na9Tp0KtXZtIVQ6tWRPXiRM2UjlUWZmna67J3gNUImHV2Bik5g99+qkr\ndU2GQ7femv1vND3J3r1W//qvCf3rvwYaO9aVmT/4oJf1r0UAAND1Wlqs/vSnUM89l9ChQ1Z/+7cx\n/fKXvq65hvOIbGCt1Y4d6QCppiahtjalVmCrro5pwoTsPq+31mrfvjAyVLuuLq5evUykCmny5DwN\nHJiZBRfn68CBhBoa2lMfjY3tOngw0KRJeSorK0gFSZMm5al37+x+rOeDwCiDhKHVzp2JSDC0bl27\n9uwJNHZsrCMcyk+FREOHZndvqeTKcjdsSETmDn3+uRvG1jkgyvY+2pYWqzVrglR72apVbjnPW29N\nt5ixgll2aWuzWrw41AsvBPr001CPPOKGWE+cyPMIAAAuTF2dq1RetCjQXXd5euIJX3ffTdVRttm1\nK9CyZUEqRDp+3KYCpNtvj6moKPvHFFhrtXNn0BEiJVRbG1d9fVxXX+1FhmqXl2fnAkOdffNNqObm\ndIDU0NCuLVviuv76WKQSqawsXwMHZm9Rw7kQGHWTI0cCrVsXDYbWr49r4ECvUzDkKofGQBoD3QAA\nIABJREFUjs3L6uUPkxIJqy1bEqqvT6i+Pt7xkdC113ZuLctXcXFMBQXZ/XiPHQv12WfpAdWNjYGK\nitLVQz/6kZ/16XtPZK3V2rVWL7wQaOHCQJMmeXrsMU9z5/rq2ze791kAAJA5jh61euUV1662d6/V\no4/6evxxX+PGcf6YjfbsibawffWV1W23+akAqaTEz4lQMDlntnMlUlNTQsOGeZo8OS/1UVYWy/oQ\nqb3ddqxslg6SGhvb1b+/FwmQSkszfy7SdyEw6mJtbVabN6fnDCUDopMnQxUVRYOhSZPyNGBAbiSS\nbW2ucigZDDU0JLRunQuHysvdQaK83JUvXnlldh8sJOnAgfT8oU8+SWjHjlBVVen5Q1OnxtSnT3Ye\nJCDt32/17/8e6A9/CNTaKj32mK9f/MLTqFHZv+8CAIDMtmFDqD/8IdBLLwUaNcro8cd9zZ/v64or\nOLfMVvv3h/rkk3SAdOCA1Y9+lF6Frawsd2aXJhJWmzYltHZtXGvXus/NzbkZIoWh1a5diUglUmNj\nu06dsiopiba0jR+fHUUhBEaXiLVWe/YEZwVD27cndP31MRUX50VaykaMyO4Wq85OnQrV3JxIVQzV\n18e1ZUtCo0fHVF4e6wiI8lRamv0HAck9159/HqbmDy1fntDXX1vdcoufajErL/ez4gCAb9fSYvXn\nP7sTtNWrQ82e7euxx3zdcovJmdcuAADIHomE1XvvhXr++UAffhjq3ntdy9odd9Cylu0OHYoGSLt3\nh5o2Ld3CVlGRW9cWZ4ZIdXVxrVuXmyGS5IaIJyuQkiHSF18kNH58XqQSqaQkX/36ZdbjJTC6AMeP\nh1q/PjqAet26dvXq5aWqhZJzhsaPz1NhYWY96Rfj2LFQjY3xSFvZrl2BJkxwwVCyeqioKHtXLDtT\nS4tVQ0Og1asTWrnSBUS+r8j8oQkTsr8PGS4MXLXKtZy99lqgyZM9Pf64rwcf9HJmfwYAANnvyBGr\nBQtcy9qXX1r94heuZW3MmNy57ujJvvoqGiBt3x5q6lQXHk2d6quiwteAAbn1XHcOkerq0pVIw4en\nQ6SKCnetmWmhyoU4dSrUunXRuUgbNsR17bX+WS1tQ4fGum07CYy+QyJhtW1bPDJnqLk5rsOHA02c\nGA2GioryNWhQbrSTJR0+HKihITpv6NChUCUlyXAoprKyPE2YEMuZ1aDC0GrbtlCrV7uAaPXqQBs3\nBho/3teUKb6mTnVtZqNGZfdKB4javdvqpZdcy5nnuZazRx/1NWwYzzEAAMhszc1uEY4//tGt1vrE\nE74eeshXv36cx+SKo0dDLV/uhmjX1ibU0BBoyBBPlZUuPKqsdG1suTZTM5Gw2rjx7Ha2ZIhUUZGu\nRMqFEMnN/I1HKpEaGtqVl6eOACnd0jZmTOyyFCwQGJ1DfX2bfvWrI9q8Oa7rrvMjc4aKi/N1ww2x\nnCr7tNZq795QDQ3xSFvZyZM2FQwlq4duvDE3BrIlffllNByqrQ00YIBRVZULiKZMce1lvXrlzmOG\nc+qU1aJFruWsoSHUz37m7sxVVdFyBgAAsk88brVkiQuPPv441AMPuErp22+nEj7XBIHV5s2hamsT\nqqtz1zDr1we6/npPFRW+Kipiqqz0VVLiq7Awt577M0OkZDvb8OFeKkDKpRDJXasHkQCpoaFNR46E\nKi5OVyLNn99Hffte+sebE4HR008/rerqalVXV1+Sn3nsWKAtWxKaODGvS/7Tu1MYWu3YEaQGUSer\nhzzPRIKh8vKYRo3KnTlLUrS1bM2aQKtXB/r661CVlbFUOFRV5Wvw4Nx6zpEWhlbLl1v94Q+B3ngj\n0LRp7kTqvvu8nHszBQAAPdfhw65l7fnnAx0/Lj32mKfHHvN1/fWc5+aq9nar9esD1dUFqRBpy5ZA\n48Ylq5Dc50mTcmsekuTC0jPb2datS2jEiLNnIuVCiCRJR49G5yL98z8PvKSPraamRjU1NXr22Wez\nPzDKhO3IRJ2XsU9WDzU0JHTFFSYSDJWX52no0Nxqsfq+1rIpU1xINHYsd1x6gh07Qr34YqAXXwzV\np4/0+OO+/uqvfA0ZwnMPAAByl7VWjY1Wzz8f6OWXA02a5G6WzZ3rsYJvD9DSYtXUlAyQXDXSrl2h\nioqSAZIbqD1uXO4NTo/Hz25ny/UQqSvkRIVRJmxHd+u8jH2ycii5jH1ZWV5ktbKrr869FwStZTjT\niRNWr77q5hJt3Gj18MOu5aysjJYzAADQ87S1Wb3zjmtZ+/TTULNm+XriCVaA7WlOnHBdF8kAqa4u\n0MGDocrK3CykZDXS6NG5VVAgnR0i1dXFtX59NESqqHCrexMiOQRGWcZaq/373TL2zc3xjs8Jff55\ndBn78vLcWcb+TK2tVvX1gdasSXSERLSWwQkCq48/dnOJ3n47VHW1u4t2771ezgxmBwAAuFgHDlj9\n8Y+uZa2tzVVf/+IXvkaM4HypJzp6NNTate6me7Ia6cQJdcxDSg/WHj4898LFziFSXZ0LktavT2jI\nEE8lJTGVlOR1fM69kS3ng8Aog50+7aqGOgdDzc1x+b5RSUlMxcUxFRfnqbg4pvHjYzk5g4XWMpyP\nrVtdSPTii4EGDTJ6/HFfDz/sa9Ag9gkAAIBvY61VXZ1rWVu4MFB5uacnnvD14IOeevfmPKonO3Qo\n7DQPKaHa2kCSIgFSRYWvIUNy7ya9Wy09UFNTXE1N7jq8qSmuEyesioujIdKkSXk5/VohMMoA1lrt\n2hVEQqHm5oR27w50002xjnAoryMgimnwYL+7N7nL0FqG83XsmNXChYFeeCHQzp1WP/+5r8ce81VU\nlHtvWgAAAF2ttdXqrbdCPf98oNWrQ82d61rWpk7NvaoS/HDWWu3bZyMrs9XVBerTR6lV2SoqfE2e\n7GvgwNw8H//qq1DNzS5ESoZJW7YkNGKEHwmRiovzNGxYbrT0ERhdZsePh1q3LhoMrVuXUP/+JlIx\nVFwc0003xXJugn1nra3pVctoLcP5SCSsPvjA9d6/916ou+92K37cc4+nWCx3XysAAACX0759Vi+9\n5FrWjHEta48+6uu66zjfQpq1Vjt2hJ0CpITq6wMNGuSlZiFVVsY0ebKvvn1zc9+Jx602b05EQqSm\npoQSCavi4nSIVFKSp4kTYyooyK7/BwKjLhIEVtu3B6lgKFnKdvhwqIkTY6lQqLg4pqKivJxNYZPC\n0GrLlrBjOXu3rP2mTW6ZR1rL8H3Wr3ctZ3/8Y6Dhw13L2bx5vq66in0FAACgq1hrtWqV1QsvBHr1\n1UBTprj5kA884OXkOAxcvCCw2ro1jLSyNTcHuuEGL1UQMGVKTBMn5vYN34MHg7NCpO3b3dzhziFS\nSUlMQ4ZkbgcRgdElcORIqHXrOs8ZSmjDhoQGD/Y6BUOucmj0aD/nliw8lwMHwlQwtGaNS5sHDvRS\nrWVVVTGVldFahm935IjVyy+7lrODB60efdQNYxw/PrfDVQAAgEx0+rTVm2+6lrX6+lDz5rmWtYoK\nWtbw3drbrZqbg0jxwJ49ocrL3XVh8vpwxIjc3pdaW92A7c4hUlNTXHl55qwQady4zOg2IjD6AeJx\nqy1bEmfNGjpxwqqoKBoMTZqUmyuUncuJE1Zr1yY6DgBu9bLTp9Xxwncv/qoqX1df3TP+P3Dh2tut\n3n3XVRN99FGomTNdy9mdd3o9ImgFAADIBrt3W734oruxV1joWtZ+/nNfQ4Zwvobzc+yYq0JKXj+u\nXu2GaievH6dMcS1tAwbk9jWktVZ794ZnhUh79qTnGafnI13+ziQCo3Ow1urQofCsYGjLloRGjvQj\nc4aKi2MaObLnLK+XSFitX598YbsX944doUpK/FR5YVWVrxtuyI0hX+h6iYTVxx+HeuWVUG++GWjC\nBKPHHvP10EO+rriCfQgAACBTWWv16aeuZW3RokBVVZ4eecTXrFme+vfnPA7nz1qrPXtsqgJp9Wo3\nD2nYMC9ynVlS4is/P/f3rVOnQq1fn4iESM3NbvZx5wHbJSV5uvHGrutiIjA6h5qaNs2Zc0wlJXmR\nlrIJE2I5vWTemdzqbWGqrWz16oQaGwONGBF90RYV9YwXLS6dMLRascLqlVdcP/zIkUbz57uQaPhw\n9iUAAIBsc/q01TvvhFqwINDHH7vFSR55xNeMGcw7woVJJKw2bAhTFUhr1iS0fXuooqL0mJMpU3yN\nHt0zihXC0K2u3nk2UnNzQgcPhvr886s1dOiln4VEYHQOYWhljHrETtfZ11+Hqq1NlwWuWRMoFlMq\nGKqq8lVREaPqAxfEWqu1a11ItHBhoCuvdCHRvHmeRo/O7VJTAACAnuToUavXXw+0YEGoxsZQs2b5\neuQRT9XVjBnAxTl50mrt2iASIp06JVVWpkOkqipfgwb1nOuL48dD9evXNfOfCIx6qNZWq8bGdFvZ\n6tWBDh0KNXlyLDKY+rrrcnvwGLre+vWhXnkl0CuvhDJGevhhT/Pm+Zo4seccxAEAAHqqffus/vSn\nQAsWBNq3z2rePF8PP+yrspLrDFwaBw5EV+OurXULLiVn6k6ZwoJLF4rAqAcIQ7e0YecX0YYNgW66\nyY8Mph4/nsQfl8a2baEWLnRB0fHj6RODsjJODAAAAHqqrVtdy9qCBaHCUHrkEde2Nm4cNxJx6YSh\n1ZYtYad5SIE2bQo0frwfKY4YN86T53Ft8l0IjHLQwYNhpK2stjahq67yUm1lyYS1J81jQtfbvdvd\nPXrllUB791o99JCv+fN93Xyz4UAMAACAlOSoggUL3LnjkCFGf/VXvubN8zVsGOeNuPRaWqwaGjq3\nsgX66qtQFRXRDptrryW87IzAKMudOGFVXx/t4Tx5UpGdvrLS1zXXsOPj0jt40Oq119wb/aZNVrNn\n+5o/39Ptt3uKxXizBwAAwHcLAqtly0K9/HKoRYsCFRUZPfKIr7lzfV11FeeT6Dpffulm+HYOkXr3\nliZP9lVamv4YObJnDNU+FwKjLBKPW61bF6RWLVuzJqGdO0MVF/sdQ7561pR4dI+vv7ZatMjNJKqr\nC3XffZ7mz/d1110eq+UBAADggrW1WS1d6trWli4NdfvtrmXtvvs89enDeSa6lrVW27eHqq8P1NgY\nqKnJfT51yqqkJBoiTZjgq6Ag9/dJAqMMZa3V55+nE881a9wOe/31Xmrye1WVr0mTWNIeXe/ECas/\n/9nNJFq+3C2TOn++r3vv9RgeBwAAgEvu+HF3/rlgQaCVK0P99KcuPLrrLk95eZx/4vI5fDhMhUfJ\nz9u3h7rxRi8SIpWU+Bo4MLc6ewiMMsShQ2GqasjNHQrUr59UWZkOhyZPjqlfPw6OuDxaWqwWL3Yh\n0QcfhLrtNhcS3X+/x34IAACAy+bwYatXX3UrrW3d6mZlPvKIr2nTmJWJ7tHSYrVhQzpASoZJV1xh\nIiFSaamv66/P3uHaBEbd4ORJq7Vr0+HQmjUJHT+uVDCUnDs0ZEhupZPIfO3tVu+/70Kid94JVVnp\naf58T7Nm0UMOAACA7rdzZ6hXXgn1xz8GOnHC6uGHXXhUVMRqvOheYWi1c2cYCZEaGwMdO2ZVXBwN\nkSZO9LOiU4PAqIudOXeotjahHTvc3KFkOFRV5WvMGOYOoXskElY1Ne6N9403Ak2YYDR/vhs0OHgw\n+yQAAAAy07p1rmVtwYJA/fq5YdkPP+zp+uu58Y7M8fXX4VmVSFu2hLrhhrNb2jJtsSoCo0soOSSr\nc2sZc4eQicLQasUKq1deCfTaa4GGD3ch0c9+5mv4cPZNAAAAZI8wtFq50mrBgkCvvhpozBgXHj30\nEDdAkZna2qw2bUoGSGEqTOrVS2eFSGPGePL97tmPCYwuQnLuUG1teu5Q375KtZQxdwiZxFqr+nqr\nl18OtHBhoAEDXEg0b56nMWMyK8kGAAAALkQ8bvXhh67y6O23Q02d6oZlP/igp/79uS5D5rLWavdu\ne1ZL2+HDoYqKoi1tkyb5l2XlQAKj83SuuUMnTigVDDF3CJlqwwY3k+iVV0JJ0vz5nubN8zVpEvsq\nAAAActepU1bvvOPCo5oat9LvI4/4mjHDU2Eh4RGywzffWDU3R1vaNm4MNGJEuqXtyScLdMUVl36f\nJjA6h3jcav369NyhNWvc3KGSEhcOJVcuY+4QMtXWraEWLgy1cGGgb76xmj/f1/z5vsrLGQYIAACA\nnufrr61efz3QggWhmppCzZrlKu1//GNPeXmcHyO7xONWW7akW9mefbawSyqOCIzOYfnyhJ588jRz\nh5BVdu5Mh0QHD7rlRufN83XzzSw3CgAAACTt3Zue5bl1q9VPf+pp9mxfd9/tqXdvzpuBJAIjIIvt\n2WP16qtuJtHOnVazZ7s7Jbfd1n2D0QAAAIBssXev1ZtvBnrjjVB1daF+8hMXHs2c6WnAAM6n0bNl\nbGBkjHlA0kxJ/ST9m7X2g2/5PgIj9CgHDli99poLiTZtsnrwQRcS3XGHp1iMNzUAAADgQnz1ldXb\nb7vwqKYm1LRpnmbP9vTAA6y2hp4pYwOj1D9izABJ/7e19q+/5c8JjJDzvvzS9VwvXBiqsTHUffe5\nwdV33eXRKgkAAABcYidOWL37bqhFiwItXRqquNho1ixfs2Z5GjWKxWPQM3R5YGSM+b2kn0o6ZK0t\n7vT70yX9D0mepN9ba//bt/z9/y7p3621jd/y5wRGyElff231xhsuJFq9OtS997qQaPp0VnUAAAAA\nLpfWVqu//CXUokWh3nor0IgRLjyaPdvT+PEsKoPcdTkCo1sknZT0YjIwMsZ4krZKulPSfkm1kuZb\nazcbYx6VVCbpv0v6e0nvW2s/+o6fT2CEnHH8uNWf/+wGVy9f7nqo581zPdRdMfUeAAAAwPlLJKw+\n/dSFR2+8EahPH6PZsz3NmuWrooLwCLnlsrSkGWNGSnq7U2A0VdLT1toZHV//gyTbucrIGPN3kn4h\nFyY1Wmt/+y0/m8AIWe3UKau333Yh0Ucfhbr9dhcS3X+/p379eMMBAAAAMpG1VnV1VosWBVq0KFRL\ni021rd1yC/NFkf0uJjCKXcS/e52kPZ2+3iupqvM3WGv/SdI/nc8Pe+aZZ1K/rq6uVnV19UVsGtD1\nWlqslixxIdF777mBevPmeXr++TxWYwAAAACygDFGlZVGlZWe/ut/tdq0yWrRolD/+T8ntHev1f33\nu7a1O+/0VFDAOT4yX01NjWpqai7Jz7qYCqM5ku6x1v664+ufS6qy1v79D94IKoyQJdrarN57z4VE\nixeHmjzZ0/z5btnOgQN5AwEAAAByxc6dod580w3NXrfOasYMd94/Y4anvn0590d26M6WtGestdM7\nvj6rJe28N4LACBksHncD8hYuDPXnPweaNMlo3jxfc+eyNCcAAADQExw8aPXWW65tbcWKUNXVnmbP\n9nTffdw4Rma7XIHRKLnAqKjja1/SFrmh1wckrZH0sLV20w/eCAIjZJhEwmrZMhcSvfFGoDFjXEj0\n0EO+rruONwQAAACgpzp2zGrxYld59OGHoSoqXHj04INcKyDzXI5V0hZIqpY0UNIhuWHXzxtjZkj6\nH5I8Sb+31v6fF7QRBEbIAGFo9emnVgsXBnr99UDDhrmQ6Gc/8zVyJAd+AAAAAFGnT1u9/74Lj955\nJ9TYsUazZ7u5R2PGeN29ecDlqTDqSsYY+/TTTzPsGpedtVarVrmQ6NVXAw0caDR/vq+f/YwDPAAA\nAIDz195uVVMT6o03Qr35ZqBBg4xmzXJzj4qLjYzhJjQun+Tw62effTb7A6NM2A70DNZa1de7kGjh\nwkC9exvNm+dp3jxf48cTEgEAAAC4OEHgbky/8Yabe2SMUuHR1KlGnkd4hMsjJyqMMmE7kLustVq7\n1ur11wO99looa5UKiYqKSPsBAAAAdA1rrZqaXHj0+uuhjh61mjPHLaLzox8Z+T7XIug6BEbAOYSh\nS/Vff93NJMrPN5ozx9Pcub7KywmJAAAAAFx+mzeHev31UK++GujgQavZs33Nnevptts8xWJco+DS\nIjACOiQSVsuXuwPwG28EuvLKdEg0aRIhEQAAAIDMsW2bu3Z57bVAu3dbzZrlwqPqak95eVy74OIR\nGKFHi8etPvrIHWjffNOtbjZ3rq85czzddBMziQAAAABkvp070+HR559bPfCAC4/uvNNTfj7hES5M\nTgRGrJKGH6K11eqDD0K9/nqgt992y1fOmeOWr7zhBkIiAAAAANlr9+7k/NVAmzZZ3Xefp4ce8nXX\nXZ4KCgiP8P1YJQ09yqlTVkuXusT93XdDlZQkQyJfw4Zx0AQAAACQe/bts1q0yIVHzc1WM2e6kRv3\n3OOpVy+ug/DdcqLCKBO2A5nn+HGrd95xlUQffhiqqsrT3LmeHnzQ1+DBHBwBAAAA9BwHDrjV1l57\nLVR9fajp0114NGOGpz59uD7C2QiMkFO+/trqrbfckpPLloW67TZPc+Z4uv9+XwMHchAEAAAAgMOH\nrd5804VHq1eHuvtuFx7NnOmpb1+um+AQGCHrnXmwu/NOT3Pm+PrpTz1dcQUHOwAAAAD4NkeOpK+n\nPvvMXU/Nnevrvvs89e/P9VRPRmCErJTsxX399UCNjZZySgAAAAC4SEePWr31lpv9umxZqOpqd511\n//2eBgzgOqunyYnAiFXSeoZdu9xSka+/HmjzZjftf84cX3ff7amwkIMXAAAAAFwq33xj9fbbLjz6\n6KNQt9ziZsI+8ADjPnIdq6QhK2zd6kKi114LtGeP1QMP+Jozx9Mdd3jKz+cgBQAAAABd7cQJq8WL\n3XXZBx+EmjLF00MPuQWFBg3iuixX5USFUSZsBy4Na602bLB67TU3uPrIEatZs3zNnevp1ls9xWIc\njAAAAACgu5w6ZbVkiQuPli4NVVHhKo9mzfI1ZAjXa7mEwAjdzlqr+nqr1193IVFrq9WcOb7mzPF1\n881GnsdBBwAAAAAyzenTVu+958KjxYtDlZQYzZ3rruWuvZbruGxHYIRuEQRWq1cnB1eHisWkOXPc\nTKKKCiNjOLgAAAAAQLZobbX64INQr74a6J13Qk2YYDR7tlu9euxYr7s3DxeAwAiXzb59Vu+9F+i9\n90J9+GGoa681mjXLTd0vKiIkAgAAAIBc0NZm9Ze/hHrjjVCLFwfq08fopz/1NHOmp9tuYx5ttiAw\nQpdpbbVavjzUe++5j/37rX7yE0/Tp3u6+25f113HQQIAAAAAcpm1Vg0Nbmj24sWBNm2yuvNOFx7d\ne6+voUO5LsxUBEa4ZKy12rrVaulSFxB9+mmoSZOM7rnH1/TpnioqjHyfgwEAAAAA9FRffmn17rsu\nPHr//VA33GA0c6anmTN9VVYywzaT5ERg9PTTT6u6ulrV1dXdvTk9zjffWH30UdgREgUKAumee3zd\nc4+nn/zE05VX8mIHAAAAAJwtHrdascJq8WI3NPvLL61mzHDh0d13exowgOvJ7lBTU6Oamho9++yz\n2R8YZcJ29BRh6FY0c21mgRoarKZN83TPPa7VbPx4ZhEBAAAAAH64nTtDLVkSavHiUMuXh5o82Wjm\nTF8zZ3Kt2R1yosIoE7Yjlx08aPX++y4gev/9UIMGGd1zjwuJbrvNU+/evGgBAAAAAJfO6dOumyU5\n+8j3k61rnn78Y0+FhVyHdjUCI5ylvd3qs8/Sw6p37XJDyVxI5GvECF6YAAAAAIDLw1qr9evd4Ox3\n3gnU3GxVXZ0enD18ONeoXYHACJKk7dvD1LDqZctC3XST0fTpLiCaMsUoFuMFCAAAAADofkeOuDEp\nixcHWro01LBh6cHZU6ey2NKlQmDUQ508afXxx+mQ6NQpq+nT08Oqr76aFxgAAAAAILMFgdWqVenB\n2fv2Wd1zjwuPpk/3dNVVXNteKAKjHsJaq6am9JL3dXWhqqq8jioiT0VFDBADAAAAAGS3PXuslixx\n4VFNTaji4vTgbK57fxgCoxz25ZdWH3wQaulSN6y6f3+TWs2sutpTnz68UAAAAAAAuam11aqmJjk4\nO1QiYVPh0R13sIDT9yEwyiHxuCvFe+8918f5+eduEFhyRbMbbvC6exMBAAAAALjsrLXavNmmwqO1\na0PdcouXWnlt1Ciul8+UE4HR008/rerqalVXV3f35lx2+/ZZvftuoCVLQn30UajRo01qNbObbzbK\nzycxBQAAAACgs2PHrN5/3w3OfvfdUIMGmY5V1zz96Eee8vJ67rV0TU2Nampq9Oyzz2Z/YJQJ23G5\nJBJWK1e6nswlS0Lt3Wt1991uKcG77/Y0eHDP3akBAAAAAPihwtCqttamwqNt26zuuMONc5kxw9fw\n4T3zOjsnKowyYTu60sGDVkuXuoDogw9C3XCD0YwZLiSqqmLJewAAAAAALpXDh1310bvvunnAgweb\njvDI0y23eCoo6BnX4ARGGSgIrFavTrea7dhhddddbuecPt3X0KE9Y+cEAAAAAKA7BYHV2rVW777r\nAqRNm6xuv91dn8+YkduzjwiMMsSXX7ol75MJ5nXXGd17ryt/u/lm06P7JwEAAAAAyARHjqSrj957\nL9SVV5pUeHTbbZ4KC3Pn2p3AqJuEoVVdnZtF9O67oTZvtrrzTjdga/p0X8OG5c5OBgAAAABArglD\nq4YGV320dGmg5marW29Ndgd5GjMmu6uPCIwuo2QSuWSJSyIHDXJVRMkp7KxoBgAAAABAdjp61OqD\nD0ItXeoCpD59TCo8qq721Lt3dl3zExh1oTC0amy0WrLEhUQbNrhex2Sr2ciR2bWzAAAAAACA72et\nVVNTevRMfb3Vj37kpYZnjx1rZExmZwIERpfYsWMuUVyyxO0UAwYkVzTzdOutudXPCAAAAAAAvt83\n31j95S9hanh2fn565bU77vDUp0/mZQUERhfJWqvmZtezuGRJoMbGdM/ijBmeRo/O7p5FAAAAAABw\n6VhrtWFDcuW1ULW1oaZMSecI48dnRvURgdEFOH7c6sMP08lgQYHRzJnuia2u9tQMie5VAAAI10lE\nQVSrV/c/sQAAAAAAIPOdOGH10UfpjEGSpk/3U9VH/ft3T8aQE4HR008/rerqalVXV3fJv2Gt1caN\ntqPNzKV/06YlZxF5uvHGzEj/AAAAAABA9rLWavPm5MproVauDFVRkV55raio6/OHmpoa1dTU6Nln\nn83+wKgrtuPkSZfwJWcRGSPde6+ve+/19OMfZ2Z/IQAAAAAAyB2nTll9/HHYMTw7VFub1fTpvqZP\n93TXXZ6uuKLrsomcqDC61NuxYkWoe+5pV1WVl1r2ftw4qogAAAAAAED3sNZq2zabCo8++yxUaanR\na6/l65prLn1eQWB0Dm1tVu3tUr9+BEQAAAAAACDztLRYLVsW6u67PXkegdHZG9HNq6QBAAAAAADk\nmosJjFgvHgAAAAAAABEERgAAAAAAAIggMAIAAAAAAEAEgREAAAAAAAAiCIwAAAAAAAAQQWAEAAAA\nAACACAIjAAAAAAAARBAYAQAAAAAAIILACAAAAAAAABEZExg988wzqqmp6e7NAAAAAAAAyGo1NTV6\n5plnLupnGGvtpdmai9kIY2wmbAcAAAAAAECuMMbIWmsu5O9mTIURAAAAAAAAMgOBEQAAAAAAACII\njAAAAAAAABBBYAQAAAAAAIAIAiMAAAAAAABEEBgBAAAAAAAggsAIAAAAAAAAEQRGAAAAAAAAiCAw\nAgAAAAAAQASBEQAAAAAAACIIjAAAAAAAABBBYAQAAAAAAIAIAiMAAAAAAABEEBgBAAAAAAAggsAI\nAAAAAAAAEQRGAAAAAAAAiCAwAgAAAAAAQETGBEbPPPOMampqunszAAAAAAAAslpNTY2eeeaZi/oZ\nxlp7abbmYjbCGJsJ2wEAAAAAAJArjDGy1poL+bsZU2EEAAAAAACAzEBgBAAAAAAAgAgCIwAAAAAA\nAEQQGAEAAAAAACCCwAgAAAAAAAARBEYAAAAAAACIIDACAAAAAABABIERAAAAAAAAIgiMAAAAAAAA\nEEFgBAAAAAAAgAgCIwAAAAAAAEQQGAEAAAAAACCCwAgAAAAAAAARBEYAAAAAAACIIDACAAAAAABA\nBIERAAAAAAAAIgiMAAAAAAAAEEFgBAAAAAAAgAgCIwAAAAAAAEQQGAEAAAAAACCCwAgAAAAAAAAR\nBEYAAAAAAACIIDACAAAAAABABIERAAAAAAAAIgiMAAAAAAAAEEFgBAAAAAAAgAgCIwAAAAAAAETE\nuvKHG2PGSfpfJA2U9JG19jdd+e8BAAAAAADg4nVphZG1drO19klJ8yRN68p/CwDOVFNT092bACAH\ncWwB0BU4tgDINOcVGBljfm+MOWSMaT7j96cbYzYbY7YaY/7Lt/zd+yS9I2nJxW8uAJw/TrwAdAWO\nLQC6AscWAJnmfCuMnpd0T+ffMMZ4kv6/jt+fKOnhjhY0GWMeNcb8P8aYodbat621MyX9/BJuNwAA\nAAAAALrIec0wstZ+aowZecZvV0naZq39QpKMMa9IekDSZmvtS5JeMsbcboz5B0kFkhZfwu0GAAAA\nAABAFzHW2vP7RhcYvW2tLe74eo6ke6y1v+74+ueSqqy1f/+DN8KY89sIAAAAAAAAnDdrrbmQv9el\nq6SdrwvdeAAAAAAAAFx6F7NK2j5JIzp9Pazj9wAAAAAAAJDFfkhgZDo+kmoljTHGjDTG5EuaL+mt\nS7lxAAAAAAAAuPzOKzAyxiyQtELSWGPMbmPME9baQNLfSXpf0gZJr1hrN53nz5trjFlvjAmMMeXf\n8X3TjTGbjTFbjTH/5Xx+NoCeyxhzpTHmfWPMFmPMe8aYK77l+3YZY5qMMQ3GmDWXezsBZIfzOQ8x\nxvyjMWabMabRGFN6ubcRQPb5vmNLx8JBx4wx9R0f/0d3bCeA7GGM+b0x5pAxpvk7vucHn7Oc99Dr\nS8kYc5OkUNK/SPrfrLX15/geT9JWSXdK2i9X0TTfWrv5cm4rgOxhjPlvko5Ya/+vjhOwK621/3CO\n79shabK19uhl30gAWeF8zkOMMTMk/Sdr7UxjzBRJ/6+1dmq3bDCArHCex5bbJf2v1tr7u2crAWQb\nY8wtkk5KejG5UNkZf35B5ywXM8Pogllrt1hrtyna4namKknbrLVfWGvjkl6R9MBl2UAA2eoBSX/o\n+PUfJD34Ld9n1E3HPwBZ43zOQx6Q9KIkWWtXS7rCGDP48m4mgCxzvtc4LAoE4LxZaz+V9F03wy/o\nnCWTL5iuk7Sn09d7O34PAL7NNdbaQ5JkrT0o6Zpv+T4r6QNjTK0x5q8v29YByCbncx5y5vfsO8f3\nAEBn53uNc3NH28hiY8yEy7NpAHLYBZ2zxLpqa4wxH0jqnFgZuYu0/91a+3ZX/bsActt3HFvO1d//\nbT23P7LWHjDGDJILjjZ1pPIAAADdba2kEdba0x1tJG9KGtvN2wSgB+qywMhae9dF/oh9kkZ0+npY\nx+8B6MG+69jSMehtsLX2kDFmiKTD3/IzDnR8/tIY84ZceTiBEYDOzuc8ZJ+k4d/zPQDQ2fceW6y1\nJzv9+l1jzHPGmKustV9fpm0EkHsu6JwlE1rSvq0/t1bSGGPMSGNMvqT5kt66fJsFIAu9Jenxjl8/\nJunPZ36DMaa3MaZvx6/7SLpb0vrLtYEAssb5nIe8JekXkmSMmSrpWLItFgC+xfceWzrPFTHGVMkt\nVERYBOD7GH17vnJB5yxdVmH0XYwxD0r6J0lXS3rHGNNorZ1hjBkq6V+ttT+11gbGmP8k6X25YOv3\n1tpN3bG9ALLGf5P0J2PMLyV9IelnktT52CLXzvaGMcbKHQP/aK19v7s2GEBm+rbzEGPM37g/tr+1\n1i4xxtxrjPlc0ilJT3TnNgPIfOdzbJE01xjzpKS4pBZJ87pviwFkA2PMAknVkgYaY3ZLelpSvi7y\nnMVY+20jPgAAAAAAANATZUJLGgAAAAAAADIIgREAAAAAAAAiCIwAAAAAAAAQQWAEAAAAAACACAIj\nAAAAAAAARBAYAQAAAAAAIILACAAAAAAAABEERgAAAAAAAIj4/wH4KwiwwoCmswAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x29f2337b2e8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(20,10))\n",
"for ii in range(convs.shape[0]):\n",
" histo, edges = np.histogram(convs[ii], bins=25, range=(-1,1), density=True)\n",
" centers = [(edges[kk]+edges[kk+1])/2 for kk in range(len(edges)-1)]\n",
" plt.plot(centers, histo, color=(0,0,ii/32))\n",
" plt.yscale('log')"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def expected_minusabs(A, excess=True):\n",
" \"\"\"Compute expected value of -|A[...,:]| after normalizing, minus \n",
" - sqrt(2/pi)\n",
" which is the value for a standard normal distribution, if excess.\"\"\"\n",
" ans = np.mean(-np.abs(A), axis=-1)\n",
" return ans + np.sqrt(2/np.pi) if excess else ans"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"B=convs\n",
"B -= B.mean(axis=-1)[:,None]\n",
"B /= B.std(axis=-1)[:,None]"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.25951443147481257"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"expected_minusabs(B[0])"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x29f24ee1588>]"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAEACAYAAABfxaZOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XeclPW1x/HPAcRublRiQVFjxYIalYsSZRDLWvGaqEA0\nKldFEyzxxiAxN6wlKnYiNhDrFdCoIMYkgpKRiCJLABWzK0QiomKNIE0pe+4fv1kY1y0zuzPzzDPz\nfb9e+3LKU84+smd+c37lMXdHRETKQ5uoAxARkcJR0hcRKSNK+iIiZURJX0SkjCjpi4iUESV9EZEy\nklHSN7MKM6sxs7lmNqiB93uY2WIzm5n6+U3ae++a2etmNsvMpucyeBERyU675jYwszbAcKAX8CFQ\nZWbPuHtNvU2nuPvJDRyiFki4+xetjlZERFolk5Z+V2Ceuy9w99XAWKB3A9tZI/tbhucREZE8yyQZ\ndwQWpj1/P/VafYea2Wwze87M9k573YFJZlZlZue3IlYREWmlZss7Gfo70MndV5jZccB4YI/Ue93d\nfZGZdSAk/2p3fzlH5xURkSxkkvQ/ADqlPd8h9do67r4s7fGfzexuM9vS3f/t7otSr39qZuMI5aJv\nJX0z0yJAIiJZcvfGSusNyqS8UwXsZmY7mVl7oA8wIX0DM9sm7XFXwNz932a2iZltlnp9U+AYYE4T\nwcfyZ8iQIZHHoPijj0Pxx/MnzvG3RLMtfXdfa2YDgYmED4lR7l5tZgPC2z4C+LGZXQSsBlYCZ6R2\n3wYYl2rFtwMec/eJLYpURERaLaOavrv/Bdiz3mv3pT2+C7irgf3+BRzQyhhFRCRHNJQyBxKJRNQh\ntIrij5bij1bc48+WtbQulGtm5sUSi4hIHJgZnoeOXBGRsvXZZ/DGG1FHkTtK+iIiDVizBu66C/be\nGyaW0PCTXE3OEhEpGX/7GwwcCFttBZMnw777Rh1R7ijpi4ikfPAB/OpXIenfcgucdhpYVhXz4qfy\njoiUvVWr4KabYP/9YeedoboaTj+99BI+qKUvImXuL3+BSy+F3XeHadNgt92ijii/lPRFpCwtXQrn\nnAOvvw7DhsEJJ0QdUWEo6YtI2Vm8GI47DvbZB+bMgY02ijqiwlFNX0TKymefwZFHQteuMHJkeSV8\nUNIXkTLy0UeQSMCxx8Idd5RmR21zlPRFpCwsXAhHHAF9+sD115dnwgfV9EWkDMyfD0cdFSZcXX55\n1NFESy19ESlpNTXQowdccYUSPqilLyIl7I03oKIilHPOOSfqaIqDkr6IlKQZM+DEE8MY/DPOaH77\ncqGkLyIlp6oqTLYaORJ69446muKim6iISMk58kg46yw499yoI8mvvN1ExcwqzKzGzOaa2aAG3u9h\nZovNbGbq5zeZ7isikktz54ZZtv36RR1JcWq2vGNmbYDhQC/gQ6DKzJ5x95p6m05x95NbuK+ISE6M\nHBk6bTfcMOpIilMmNf2uwDx3XwBgZmOB3kD9xN3QV4xM9xURabWvv4aHH4apU6OOpHhlUt7pCCxM\ne/5+6rX6DjWz2Wb2nJntneW+IiKtNm4c7LdfWCZZGpar0Tt/Bzq5+wozOw4YD+yRo2OLiGTkvvvg\noouijqK4ZZL0PwA6pT3fIfXaOu6+LO3xn83sbjPbMpN901VWVq57nEgkSCQSGYQnIgJvvw3/+Aec\nckrUkeRPMpkkmUy26hjNDtk0s7bA24TO2EXAdKCvu1enbbONu3+cetwVeMLdd85k37RjaMimiLTY\nL38JbdvC0KFRR1I4LRmy2WxL393XmtlAYCKhD2CUu1eb2YDwto8AfmxmFwGrgZXAGU3tm9VvJSLS\njK++gkcegVdeiTqS4qfJWSISe6NHw4MPwqRJUUdSWHmbnCUiUsxGjIALLog6inhQS19EYq2mJtwN\n6733oH37qKMpLLX0RaTsjBgR1tgpt4TfUmrpi0hsffUV7LgjTJsGu+4adTSFp5a+iJSVp56CAw8s\nz4TfUkr6IhJb990HAwZEHUW8qLwjIrFUXR3WzX/vPdhgg6ijiYbKOyJSNuo6cMs14beUWvoiEjsr\nV4YO3Koq2GWXqKOJjlr6IlIWnnoKDjqovBN+Synpi0jsqAO35ZT0RSRW3noL3nkHTjop6kjiSUlf\nRGJl5Ejo318duC2ljlwRiY0VK6BTJ5gxA3beOepooqeOXBEpaffeCz16KOG3hlr6IhILy5fDbrvB\n889Dly5RR1Mc1NIXkZJ1773QvbsSfmuppS8iRW/58rCo2qRJsN9+UUdTPNTSF5GSdPfdcPjhSvi5\nkFHSN7MKM6sxs7lmNqiJ7Q4xs9Vmdmraa++a2etmNsvMpuciaBEpH8uXwy23wJAhUUdSGto1t4GZ\ntQGGA72AD4EqM3vG3Wsa2O5G4Pl6h6gFEu7+RW5CFpFyctddYcTOvvtGHUlpaDbpA12Bee6+AMDM\nxgK9gZp6210MPAkcUu91Q2UkEWmBZcvg1lth8uSoIykdmSTjjsDCtOfvp15bx8y2B05x93sIST6d\nA5PMrMrMzm9NsCJSXu66C3r2hH32iTqS0pFJSz8TdwDptf70xN/d3ReZWQdC8q9295cbOkhlZeW6\nx4lEgkQikaPwRCRuli2D226Dv/416kiKRzKZJJlMtuoYzQ7ZNLNuQKW7V6SeXwm4uw9N22Z+3UNg\na2A5cIG7T6h3rCHAUne/rYHzaMimiKxz443w+uswZkzUkRSvlgzZzCTptwXeJnTkLgKmA33dvbqR\n7R8EnnX3p81sE6CNuy8zs02BicDV7j6xgf2U9EUEgKVLw7j8ZBL23jvqaIpXS5J+s+Udd19rZgMJ\nCbsNMMrdq81sQHjbR9TfJe3xNsA4M/PUuR5rKOGLlJoFC+Ddd8OoE8ne8OFw1FFK+PmgGbkiObJ6\nNfzxj+HerVVVsOGG8KtfwaWXRh1ZvHz5ZVhj56WXoHPnqKMpbnlp6YtI0/71L7j/fnjwwVCSuOAC\nePpp+OSTMPIElPizMXw4HH20En6+KOmLtMCqVTBhQmjVz5oFZ50FL7zwzXLETjuFkSc9e4I7XHZZ\ndPHGxZdfwu23w9/+FnUkpUtJXyQLa9eGUSV33gl77RVa9RMmwEYbNbz9TjuFzsi6Fr8Sf9N+/3s4\n9thwbSU/lPRFMrR4MfTrBytXhkSeaWLq1Gl9ix+U+BuzZAkMGwYvNziLR3JFyyOIZKCmBv7zP0MH\n48SJ2bdE6xL/nXfCHXfkJ8Y4c4drroGKCthzz6ijKW1q6Ys047nn4Nxz4YYb4L//u+XHSW/xu8Mv\nfpG7GOPss8/Cjc4//BDGj486mtKnlr5II9xD/f6CC0Iyak3Cr1OX+IcPDx2W5e7FF+GAA8I3p1de\ngR12iDqi0qeWvkgDVqwIrc933oHXXsttMqpf4y/HFv+qVfDb38Kjj8LDD4eJWFIYSvoi9bz3Hpxy\nSljZccoU2Hjj3J8jPfGvWAG//jVYVlNs4uuf/4S+fWGbbWD2bOjQIeqIyovKOyJppkwJHbZnngmP\nPJKfhF+nU6cwHv3JJ2HAAFizJn/nKgbu4Zoeeij89Kfw7LNK+FHQMgwiwNdfw803h9E1jz4KxxxT\nuHMvXQqnnx5a+k88AZttVrhzF8qSJfCzn4WW/Zgx0KVL1BGVBt0YXaQFJk+G/feHGTPCmjmFTPgA\nm28eJnh17BgWaFu0qLDnz7cZM+DAA2GLLcL1VcKPlpK+lK2PPw7LJ/TvDzfdFEbodOoUTSwbbBCW\ndDj11FD++Mc/ookjl9zhvvvguOPCt6h77oFNNok6KlFHrpSd2tqQYH/72zD+/q23YNNNo44qlHeu\nuios3dCzJzz+OMT15nErVsBFF8HMmTB1KuyxR9QRSR0lfSkrs2fDhRdCu3ZhjPh++0Ud0bedeSZs\nvz2ccUYYy9+vX9QRZWfePPjRj0LJbNq04vhAlfVU3pGysHQpXH55WMzr/PPDKJ1iTPh1jjwyfCgN\nHhwmiMVljMP48dC9e2jlP/KIEn4xUtKXklZbC//3f2HJ4y++gDlzwszaNjH4l7/vvvDqq6HMc+GF\nxT2kc80aGDQo3Dfgj38MSb9c5h3EjYZsSsl69dWwoqV7WOTssMOijqhlli4NpZ61a8OQzu98J+qI\nvumjj6BPn3CnsMceg623jjqi8qEhmyKEGbX9+sFpp8HAgaGuHNeED+uHdO6xR/g93n036ojWmzoV\nDj44DDX905+U8OMgo6RvZhVmVmNmc81sUBPbHWJmq83s1Gz3FWmt5cvDiJwDD4Tdd4e33w5DMuNQ\nymlOu3Zh4tiFF4bEP21a1BHB9OlhuYoRI+Dqq6Ft26gjkkw0++dgZm2A4cCxwD5AXzP71mriqe1u\nBJ7Pdl+R1qitDbNo99wzLJA2a1ZIQqXYiXjxxTByJJx8cqj1R+Wdd6B373Bf4OOPjy4OyV4mQza7\nAvPcfQGAmY0FegM19ba7GHgSOKQF+4q0yKxZYd0aM/jDH8LEplJ3wgkwaVJI/PPmhbH9hew0/fTT\nMOGqshJOPLFw55XcyOSLb0dgYdrz91OvrWNm2wOnuPs9gGWzr0hLPfBAWDLhZz8LnbblkPDr1I2B\nf+YZOPvssHZQIaxYET5sTjstfNhK/ORqctYdQKvr9ZWVleseJxIJEnGdjih59dVXcMklYYXKKVOg\nc+eoI4rGdtvBSy+Ffoujj4Zx42CrrfJ3vrVrQwf5brvBddfl7zzSuGQySTKZbNUxmh2yaWbdgEp3\nr0g9vxJwdx+ats38uofA1sBy4ALgk+b2TTuGhmxKsxYsCLM9d9kltPQ33zzqiKJXWxvW43/qqTBG\nPh/3mHUP/Qk1NWGUTvv2uT+HZC9fQzargN3MbCczaw/0ASakb+Du30/97EKo6//M3Sdksq9IpiZO\nDGvd9+sXxqsr4Qdt2oRZu4MHw+GHw9NP5/4ct9wSvlU99ZQSftw1W95x97VmNhCYSPiQGOXu1WY2\nILztI+rv0ty+uQtfykFtbbgp+V13hRErPXpEHVFx6t8/LC1x2mmhj+OGG8JQz9YaMyYMF33lleKb\nGCbZ04xcKWqLF4e7LH3+eWjdd9QwgGZ9/jn85CewcmX4kNx225YfK5kMN3gp1sXpyp1m5EpJeeON\nMNtz553D/WSV8DOz1Vbw3HNhWeaDD4aXX27Zcd56KyT8sWOV8EuJWvpSlKqr4YgjYNiw+C0tXEz+\n9Kdwz4ArrwzrEGUynv/rr0N56Oyz4frrw7cGKU4taekr6UvRWbUKunULSw5ccEHU0cTfu+/Cj38M\nu+4K99//7Q7wtWvDzU4mTw5lnFdfDcNgBwwIK5JK8VLSl5IwaFBYN2fcOC3PmyvpcxueeioMwXzx\nxZDoX3oplM6OPBJ69Qod5f/xH1FHLJlQ0pfY++tfw52jZs+GDh2ijqb0PPgg/PznoXO3Lsn37Nm6\nzl6JjpK+xNoXX4TlBUaMgIqKqKMpXV9/Hda+l/hT0pfYcg834thmG/j976OORiQeWpL0dWN0KQqP\nPhqGCD70UNSRiJQ2tfQlcvPnh+UVXnghlHdEJDOanCWxs2ZN6LgdPFgJX6QQlPQlUtdfH+5wddll\nUUciUh5U05fITJsWFlGbObM07mMrEgf6U5NILF0ayjp33601dUQKSR25Eon+/cNs21Gjoo5EJL40\nZFNiYdy4cEOO2bOjjkSk/KilLwXlDgccAEOHatatSGtpyKYUvWnTYPlyOOaYqCMRKU9K+lJQ99wT\nlkzWaB2RaKi8IwXz+edhTfd//hO23jrqaETiL2/lHTOrMLMaM5trZoMaeP9kM3vdzGaZ2XQz6572\n3rvp72UTnJSWhx6Ck05SwheJUrMtfTNrA8wFegEfAlVAH3evSdtmE3dfkXq8H/CEu3dOPZ8PHOTu\nXzRzHrX0S1htLey5Jzz8MBx2WNTRiJSGfLX0uwLz3H2Bu68GxgK90zeoS/gpmwG16XFleB4pYZMn\nwyabwKGHRh2JSHnLJBl3BBamPX8/9do3mNkpZlYNPAv0T3vLgUlmVmVm57cmWImvug5c3f5QJFo5\nm5zl7uOB8Wb2Q+A64OjUW93dfZGZdSAk/2p3f7mhY1RWVq57nEgkSCQSuQpPIvTBB6Glr7XyRVon\nmUySTCZbdYxMavrdgEp3r0g9vxJwdx/axD7vAIe4+7/rvT4EWOrutzWwj2r6Jeqaa2DRotDaF5Hc\nyVdNvwrYzcx2MrP2QB9gQr0T75r2+AdAe3f/t5ltYmabpV7fFDgGmJNNgBJva9bAyJGhtCMi0Wu2\nvOPua81sIDCR8CExyt2rzWxAeNtHAD8ys58Cq4CVwOmp3bcBxpmZp871mLtPzMcvIsXpj3+EHXfU\nDVJEioUmZ0leVVTAT34CZ50VdSQipacl5R0lfcmbd96Bbt1g4ULYaKOooxEpPVpwTYrKfffB2Wcr\n4YsUE7X0JS++/jrU8qdOhd13jzoakdKklr4UjSefDJ23SvgixUVJX/LinnvgoouijkJE6lPSl5x7\n803417/CipoiUlyU9CXn7r0XzjsPNtgg6khEpD515EpOLVsGnTrBG2/ADjtEHY1IaVNHrkRu9Gjo\n0UMJX6RYKelLzrivX0JZRIqTkr7kzMyZsGQJHH1089uKSDSU9CVnRo8O6+y00b8qkaKljlzJibVr\nQwfuCy9A585RRyNSHtSRK5H529+gQwclfJFip6QvOTF6NPTrF3UUItIclXek1Vatgu23Dx25nTpF\nHY1I+VB5RyLx/POhrKOEL1L8lPSl1VTaEYkPlXekVZYtC7Nv580LHbkiUjh5K++YWYWZ1ZjZXDMb\n1MD7J5vZ62Y2y8ymm1n3TPeVeJswAQ47TAlfJC6abembWRtgLtAL+BCoAvq4e03aNpu4+4rU4/2A\nJ9y9cyb7ph1DLf0YOukkOOMMOPPMqCMRKT/5aul3Bea5+wJ3Xw2MBXqnb1CX8FM2A2oz3Vfi6/PP\nYcoU6K3/oyKxkUnS7wgsTHv+fuq1bzCzU8ysGngW6J/NvhJPTz4JFRWw+eZRRyIimWqXqwO5+3hg\nvJn9ELgOyHrZrcrKynWPE4kEiUQiV+FJHowZA5ddFnUUIuUjmUySTCZbdYxMavrdgEp3r0g9vxJw\ndx/axD7vAIcAe2S6r2r68fL++9ClCyxaBBtuGHU0IuUpXzX9KmA3M9vJzNoDfYAJ9U68a9rjHwDt\n3f3fmewr8fT44/Bf/6WELxI3zZZ33H2tmQ0EJhI+JEa5e7WZDQhv+wjgR2b2U2AVsBI4val98/S7\nSAGNHg033RR1FCKSLU3Okqy9/TYkEqHE07Zt1NGIlC+tvSMFMWZMGJuvhC8SP0r6khV3rbUjEmdK\n+pKVmTOhthYOOSTqSESkJZT0JSujR0PfvmBZVRFFpFioI1cypvvgihQXdeRKXuk+uCLxp6QvGVMH\nrkj8qbwjGdF9cEWKj8o7kje6D65IaVDSl4w89FAYtSMi8abyjjTrtdfg1FPD8gubbRZ1NCJSR+Ud\nyTl3uPxyuO46JXyRUqCkL036wx9gxQr46U+jjkREckHlHWnUV1+FztsHHoCePaOORkTqU3mnBBTT\n596wYbD//kr4IqVESb+IzJ8fxsJffz2sWRNtLJ98AjffrBuliJQalXeKRG0tHHkkdO0Ks2bBl1+G\nYZJRLXlw4YWw8cZw++3RnF9EmteS8k6zt0sspJ49Q6LZeGPYaKP1j+ueH344HH101FHmx/DhsHo1\n3HADtGkD994bft/Bg+Gyywp7w5I5c+Dpp6GmpnDnFJHCKKqW/osvOitXhg7ElSvX/3z1VRhBcu+9\ncM894YbcpWTePDj0UHj1Vdh99/Wvz58P554bVrd88MFvvpdPFRVw/PFwySWFOZ+ItExLWvoZJX0z\nqwDuYP3NzYfWe78fMCj1dCnwM3d/I/Xeu8ASoBZY7e5dGzlHs+WdmTNDQnrkkfDfUrB2LRxxRLj9\nYENJtrYW7rwTrr0WhgyBn/88fBPIlz//OXyzmDMHNtggf+cRkdbLS9I3szbAXKAX8CFQBfRx95q0\nbboB1e6+JPUBUenu3VLvzQcOcvcvmjlPRjX9V1+F3r3hiSfCzbnj7tZb4dlnYfLkppP53Llwzjmh\nzPXAA7DzzrmPZc0a6NIFhg6Fk07K/fFFJLfyNWSzKzDP3Re4+2pgLNA7fQN3n+buS1JPpwEd0+PK\n8DwZOfTQkPBPPz18AMRZdTXceGNI4s213vfYI6xnf9xx4VaFo0fnPp4RI2C77eDEE3N/bBEpDpkk\n447AwrTn7/PNpF7fecCf0547MMnMqszs/OxD/LZEIpR4evcOJZ84WrMmtNyvuQa+//3M9mnbFq64\nInwruOKKcA1yZfFiuPpquO023QpRpJTldPSOmfUEzgV+mPZyd3dfZGYdCMm/2t1fbmj/ysrKdY8T\niQSJJuo3FRWhZXrCCTBpEuy7by5+g8K5+WbYYoswNDJb++0XblnYqxe0a5ebG5tcf30o6ey/f+uP\nJSL5kUwmSSaTrTpGJjX9boQafUXq+ZWAN9CZ2wV4Cqhw93caOdYQYKm739bAey0apz9mDPzyl/DX\nv4YSSBy8+WYYk//3v7duffo5c8IQ1mHDQrmrpebPD/MD5syBbbdt+XFEpLDyNU6/CtjNzHYCFgF9\ngG+srG5mnQgJ/6z0hG9mmwBt3H2ZmW0KHANcnU2AzenbNwzrPOoomDIlPx2cubR6NZx9dqjlt/aG\nJPvuC3/5CxxzTGjxn3pqy44zaBD84hdK+CLloNmk7+5rzWwgMJH1QzarzWxAeNtHAP8LbAncbWbG\n+qGZ2wDjzMxT53rM3Sfm+pfo3z8k/l69QuLv2FSPQ8RuuCEk1/79c3O8/fcPwyyPOy4k/pNPznzf\npUvD6KHp03PbPyAixauoJme1Npabb4ZRo+CVV2DLLXMUWA7NmgXHHhv+m+sPpqqq0L/x0ENhYlVT\nVq4Mk9yGDg3fkK69NvPOZBEpHmW/yuYVV4SlC373u6gj+bZVq0JZ55Zb8vNN5JBDYMKEMCJoYiPf\npVavhvvuWz/884UX4LHHlPBFyklJtfQBFi0Kte6ZM2GnnXIQWI5cc03ouB0/Pr9DIqdOhVNOgbFj\nQ7kLwqzfsWPDjN5ddgkfil0bnBctInGSt2UYCiGXq2z+7//CwoWh1FEMPv4Y9t47JP1CdDS/9BL8\n+MfhrleLF8NvfhOGh/7ud1obX6SUKOmnfPllWJzshRfCmPaoXXxxmFh1xx2FO+fkyWHc/e67h2R/\n/PGadCVSapT009xxB7z4YljXJkrz54d6e00NdOhQ2HMvXhxa+PlcoE1EoqOkn+brr2HPPeHRR0Pn\nblTOPDO0tocMiS4GESlNSvr1PPpoGJo4dWo0pY3XXw9DNOfNg803L/z5RaS0lf2Qzfr69YNly8JQ\nxigMHgxXXaWELyLFo6STftu2YbmDwYMLf6Pxl14KdfwBAwp7XhGRppR00oewPMH3vgcPP1y4c7qH\n9WyuvRbaty/ceUVEmlPySd8stPYrK8PyA4XwzDPhXH37Nr+tiEghlXzSB+jWLcxAvfPO/J9rzRr4\n9a/DwmoaKikixaakR++kq6kJQzfnzoXvfjdvp+GBB0IpKZnUZCgRyS8N2WzGBReEhD90aPPbtsTK\nlWFuwOOPh3v5iojkk5J+Mz74ALp0CePnd9gh98e/9daweuX48bk/tohIfUr6GRg8GD79FO6/P7fH\nXbIkzLxNJsPiaiIi+aakn4HFi8N68i+9BJ075+64V10VlnV+4IHcHVNEpClK+hm65RZ47rkwtHKL\nLVp/vLo1/GfPhh13bP3xREQykbdlGMyswsxqzGyumQ1q4P1+ZvZ66udlM+uS6b5RuOQS2GsvOOig\nUN9vrWuugXPPVcIXkeLXbEvfzNoAc4FewIdAFdDH3WvStukGVLv7EjOrACrdvVsm+6Ydo2At/Tqj\nR8Oll4bJW/37Zz/EcuVKuO02GDYMqqthq63yE6eISEPy1dLvCsxz9wXuvhoYC/RO38Ddp7n7ktTT\naUDHTPeNUr9+YbTN7beHe8suX57Zfu5hWGbnzuEm59OmKeGLSDxkkvQ7AgvTnr/P+qTekPOAP7dw\n34Lbay947bXwuGvX0GJvyowZYZLXjTeGSVhPPqkbi4tIfOR0oQAz6wmcCxRF7T5Tm24a7qf7P/8D\nRxwBjz327W0+/DB8GzjppFC/nzEDevQodKQiIq3TLoNtPgA6pT3fIfXaN6Q6b0cAFe7+RTb71qms\nrFz3OJFIkEgkMggvN8xCXf+gg+C002DKlFCrdw91+9tvh/PPh7ffzs2IHxGRbCWTSZLJZKuOkUlH\nblvgbUJn7CJgOtDX3avTtukEvAic5e7Tstk3bduCd+Q25ssv4bzzQoJfsgQOPhhuukllHBEpLnkb\np58akTOMUA4a5e43mtkAwN19hJmNBE4FFgAGrHb3ro3t28g5iibpw/rO2u22UxlHRIqTJmeJiJQR\n3SNXRESapKQvIlJGlPRFRMqIkr6ISBlR0hcRKSNK+iIiZURJX0SkjCjpi4iUESV9EZEyoqQvIlJG\nlPRFRMqIkr6ISBlR0hcRKSNK+iIiZURJX0SkjCjpi4iUESV9EZEyoqQvIlJGlPRFRMpIRknfzCrM\nrMbM5prZoAbe39PMXjGzr8zs8nrvvWtmr5vZLDObnqvARUQke80mfTNrAwwHjgX2Afqa2V71Nvsc\nuBi4uYFD1AIJdz/Q3bu2Mt6ilEwmow6hVRR/tBR/tOIef7Yyael3Bea5+wJ3Xw2MBXqnb+Dun7n7\n34E1DexvGZ4ntuL+j0bxR0vxRyvu8Wcrk2TcEViY9vz91GuZcmCSmVWZ2fnZBCciIrnVrgDn6O7u\ni8ysAyH5V7v7ywU4r4iI1GPu3vQGZt2ASnevSD2/EnB3H9rAtkOApe5+WyPHavR9M2s6EBER+RZ3\nt2y2z6SlXwXsZmY7AYuAPkDfJrZfF4CZbQK0cfdlZrYpcAxwdUM7ZRu4iIhkr9mk7+5rzWwgMJHQ\nBzDK3avNbEB420eY2TbADGBzoNbMLgX2BjoA41Kt+HbAY+4+MV+/jIiINK3Z8o6IiJSOyIdSNjfx\nq9jFbfLJq5+VAAADKklEQVSZmY0ys4/N7I20175rZhPN7G0ze97MvhNljE1pJP4hZva+mc1M/VRE\nGWNjzGwHM5tsZm+Z2Ztmdknq9Vhc/wbivzj1elyu/4Zm9lrqb/XNVB9jnK5/Y/Fndf0jbemnJn7N\nBXoBHxL6D/q4e01kQWXJzOYDB7n7F1HHkgkz+yGwDHjE3bukXhsKfO7uN6U+eL/r7ldGGWdjGom/\nyQEExcLMtgW2dffZZrYZ8HfCnJdzicH1byL+M4jB9YfQz+juK8ysLTAVuAT4ETG4/tBo/MeRxfWP\nuqXf7MSvGIjV5LPUcNn6H1C9gYdTjx8GTiloUFloJH5IG0BQrNz9I3efnXq8DKgGdiAm17+R+Ovm\n7BT99Qdw9xWphxsS+hmdmFx/aDR+yOL6R52sWjvxqxiUwuSz77n7xxD+sIHvRRxPSww0s9lmdn+x\nfj1PZ2Y7AwcA04Bt4nb90+J/LfVSLK6/mbUxs1nAR8Akd68iRte/kfghi+sfddIvBd3d/QfA8cDP\nU+WHuItb7/7dwPfd/QDCH0NRlxlSpZEngUtTLeb617uor38D8cfm+rt7rbsfSPiG1dXM9iFG17+B\n+Pcmy+sfddL/AOiU9nyH1Gux4e6LUv/9FBhHKFnFzcepYbd1ddtPIo4nK+7+qa/vnBoJHBJlPE0x\ns3aEhPmouz+Tejk217+h+ON0/eu4+5dAEqggRte/Tnr82V7/qJP+uolfZtaeMPFrQsQxZczMNkm1\nekibfDYn2qgyYnyzBjgBOCf1+Gzgmfo7FJlvxJ/6Q61zKsX9/+AB4B/uPizttThd/2/FH5frb2Zb\n15U+zGxj4GhCv0Qsrn8j8ddke/0jH6efGl40jPUTv26MNKAsmNkuhNZ9+uSzoo7fzEYDCWAr4GNg\nCDAe+AOwI7AAON3dF0cVY1Maib8nob5cC7wLDKir0RYTM+sOTAHeJPybceDXwHTgCYr8+jcRfz/i\ncf33I3TUtkn9PO7uvzOzLYnH9W8s/kfI4vpHnvRFRKRwoi7viIhIASnpi4iUESV9EZEyoqQvIlJG\nlPRFRMqIkr6ISBlR0hcRKSNK+iIiZeT/ARAZ4ixRUp6lAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x29f234fc940>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sparsity = [expected_minusabs(b) for b in B]\n",
"plt.plot(sparsity)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The trouble with this analysis is I think it would show that basically anything is sparse if there's a lot of silence, which doesn't really say anything about the structure of the sounds that are present. A better calculation might normalize by the power of the sound for each dot product."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"noise = np.random.randn(800)\n",
"noise /= np.linalg.norm(noise)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"convs = []\n",
"count=0\n",
"for signal in sigset.data:\n",
" convs.append(scisig.fftconvolve(noise,signal,mode='full'))\n",
" if count > 500:\n",
" break\n",
" count += 1\n",
"convs = np.concatenate(convs)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(27945377,)"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"convs.shape"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.26606781330850504"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"expected_minusabs(convs)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABIsAAAJRCAYAAADF+jcdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XuA1nPe//H3t7MixxVyKjonhCLFSDeJ5FATa/e3LGuX\ndVq79zrs4sq61/HelA17L3a5LWZyyirWLsYhSY7pRM4pIkql4zTf3x903dZiNc3M97pmHo+/NLmu\n6/VXTc/5fr7fJE3TAAAAAICIiEZZDwAAAACgcIhFAAAAAOSJRQAAAADkiUUAAAAA5IlFAAAAAOSJ\nRQAAAADkiUUAAAAA5IlFAAAAAOTVeixKkqRdkiQ3JElSXtufBQAAAMD6qfVYlKbpm2manlTbnwMA\nAADA+lvnWJQkyY1JksxPkmTql74+MEmSWUmSvJokyTk1NxEAAACAulKdK4v+FBEHf/ELSZI0iojf\nf/71bhFxbJIknb/0uqRaCwEAAACoM+sci9I0fTIiFn7py70iYnaapm+nabo6Iu6IiCEREUmSbJYk\nyXURsZsrjgAAAAAKW5Maep+2ETHnC79+Nz4LSJGm6ccRcco3vThJkrSGdgAAAADwuTRN1/mkV03F\novWWpnoRULNyuVzkcrmsZwD1jD9bgNrgzxagNiRJ9e4IVFNPQ5sbEdt/4dfbfv41AAAAAIpIdWNR\nEv98w+opEbFzkiQ7JEnSLCKOiYj71nccAAAAAHVrnWNRkiS3RcRTEdExSZJ3kiQ5IU3TNRFxekQ8\nFBHTI+KONE1n1uxUgHVTUlKS9QSgHvJnC1Ab/NkCFJKkEO4VlCRJWgg7AAAAAOqLJEmqdYPrmrpn\nEQAAAAD1gFgEAAAAQJ5YBAAAAECeWAQAAABAnlgEAAAAQJ5YBAAAAECeWAQAAABAXsHEolwuFxUV\nFVnPAAAAAChqFRUVkcvlqv36JE3TmltT3RFJkhbCDgAAAID6IkmSSNM0WdfXFcyVRQAAAABkTywC\nAAAAIE8sAgAAACBPLAIAAAAgTywCAAAAIE8sAgAAACBPLAIAAAAgTywCAAAAIE8sAgAAACBPLAIA\nAAAgTywCAAAAIE8sAgAAACCvYGJRLpeLioqKrGcAAAAAFLWKiorI5XLVfn2SpmnNranuiCRJC2EH\nAAAAQH2RJEmkaZqs6+sK5soiAAAAALInFgEAAACQJxYBAAAAkCcWAQAAAJAnFgEAAACQJxYBAAAA\nkCcWAQAAAJAnFgEAAACQJxYBAAAAkCcWAQAAAJAnFgEAAACQJxYBAAAAkCcWAQAAAJAnFgEAAACQ\nVzCxKJfLRUVFRdYzAAAAAIpaRUVF5HK5ar8+SdO05tZUd0SSpIWwAwAAAKC+SJIk0jRN1vV1BXNl\nEQAAAADZE4sAAAAAyBOLAAAAAMgTiwAAAADIE4sAAAAAyBOLAAAAAMgTiwAAAADIE4sAAAAAyBOL\nAAAAAMgTiwAAAADIE4sAAAAAyBOLAAAAAMgTiwAAAADIE4sAAAAAyBOLAAAAAMgTiwAAAADIE4sA\nAAAAyCuYWJTL5aKioiLrGQAAAABFraKiInK5XLVfn6RpWnNrqjsiSdJC2AEAAABQXyRJEmmaJuv6\nuoK5sggAAACA7IlFAAAAAOSJRQAAAADkiUUAAAAA5IlFAAAAAOSJRQAAAADkiUUAAAAA5IlFAAAA\nAOSJRQAAAADkiUUAAAAA5IlFAAAAAOSJRQAAAADkiUUAAAAA5IlFAAAAAOSJRQAAAADkiUUAAAAA\n5IlFAAAAAOSJRQAAAADkiUUAAAAA5IlFAAAAAOQVTCzK5XJRUVGR9QwAAACAolZRURG5XK7ar0/S\nNK25NdUdkSRpIewAAAAAqC+SJIk0TZN1fV3BXFkEAAAAQPbEIgAAAADyxCIAAAAA8sQiAAAAAPLE\nIgAAAADyxCIAAAAA8sQiAAAAAPLEIgAAAADyxCIAAAAA8sQiAAAAAPLEIgAAAADyxCIAAAAA8sQi\nAAAAAPLEIgAAAADyxCIAAAAA8sQiAAAAAPLEIgAAAADyxCIAAAAA8sQiAAAAAPLEIgAAAADyxCIA\nAAAA8sQiAAAAAPLEIgAAAADyxCIAAAAA8sQiAAAAAPIKJhblcrmoqKjIegYAAABAUauoqIhcLlft\n1ydpmtbcmuqOSJK0EHYAAAAA1BdJkkSapsm6vq5griwCAAAAIHtiEQAAAAB5YhEAAAAAeWIRAAAA\nAHliEQAAAAB5YhEAAAAAeWIRAAAAAHliEQAAAAB5YhEAAAAAeWIRAAAAAHliEQAAAAB5YhEAAAAA\neWIRAAAAAHliEQAAAAB5YhEAAAAAeWIRAAAAAHliEQAAAAB5YhEAAAAAeWIRAAAAAHliEQAAAAB5\nYhEAAAAAeWIRAAAAAHliEQAAAAB5YhEAAAAAeWIRAAAAAHliEQAAAAB5YhEAAAAAeWIRAAAAAHli\nEQAAAAB5YhEAAAAAeWIRAAAAAHliEQAAAAB5YhEAAAAAeQUTi3K5XFRUVGQ9AwAAAKCoVVRURC6X\nq/brkzRNa25NdUckSVoIOwAAvklVVRqNGiVZzwAA+FaSJIk0Tdf5m5eCubIIAKDQHX747TFu3Kys\nZwAA1KomWQ8AACgGc+cujgkTZkfTpo1jyJDOWc8BAKg1riwCAPgWxo6dEYcf3ikeeeTNWLx4ZdZz\nAABqjVgEAPAtlJVNjx//eI/Yb78d4q9/fSXrOQAAtUYsAgD4N956a1HMnv1RDBjQPkpLu0ZZ2fSs\nJwEA1BqxCADg3ygvnx5HHdUlf7+ixx57OxYtWpH1LACAWiEWAQD8G2Vl02P48G4REdG6dfM44IAd\nPRUNAKi3xCIAgG8we/ZHMXfu4igp2TH/tdLSblFePiO7UQAAtUgsAgD4BmVl02Po0K7RuPH/fds0\neHDHePLJd2LhwuUZLgMAqB1iEQDAN/jiEbS1NtqoeQwY0D7uucdRNACg/hGLAAC+xvTpH8TChctj\n3323/5ffGz68W5SXeyoaAFD/iEUAAF+jrGx6lJZ2i0aNkn/5vUMP7RCTJr0bCxYsy2AZAEDtEYsA\nAL5CmqZfeQRtrVatmsXBB+8U99wzs46XAQDULrEIAOArvPTS/Fi1ak306tX2a/+fz46ieSoaAFC/\niEUAAF/hjjumxfDh3SJJ/vUI2lqHHNIhpkyZGx988GkdLgMAqF1iEQDAl/y7I2hrtWzZNAYN6hB3\n3+0oGgBQf4hFAABfMmXKvGjWrHHstttW//b/LS31VDQAoH4RiwAAvuTbHEFba+DAneOFF96P999f\nWgfLAABqn1gEAPAFVVVplJf/+yNoa7Vo0SQOO6xj3HWXG10DAPWDWAQA8AUTJ74Tm266QXTrtuW3\nfk1padcoK3MUDQCoH8QiAIAv+DY3tv6ygw7aKaZN+yDmzl1cS6sAAOqOWAQA8LnKyqq4884Z6xyL\nmjdvEocf3inuustT0QCA4icWAQB87rHH3oq2bVtHhw6br/NrS0u7OYoGANQLYhEAwOeqcwRtrQED\n2sesWQtizpxPangVAEDdEosAACJi9eo1cffdM6O0tHqxqFmzxnHEEZ1i7FhPRQMAiptYBAAQEf/4\nxxvRocPmseOOm1T7PUpLu0V5uaNoAEBxE4sAAGL9jqCt1b9/u3j99YXx1luLamgVAEDdE4sAgAZv\n5crKuO++V2LYsK7r9T5NmzaOI4/sHGPHuroIACheYhEA0OA9+OBrscsubaJt29br/V7Dh3eL8nL3\nLQIAipdYBAA0eDVxBG2t/fffMd5+e1G8/vrHNfJ+AAB1TSwCABq0ZctWx4QJs2Po0PU7grZWkyaN\n4uiju3gqGgBQtMQiAKBBGz/+1dhrr7ax5Zatauw9hw/v7qloAEDREosAgAatJo+grdWv3/bx3ntL\nY/bsj2r0fQEA6oJYBAA0WEuWrIy///2NOOqoLjX6vo0bN4qhQ7u4uggAKEpiEQDQYN133yvRt+/2\nsdlmG9T4e5eWdouyMrEIACg+YhEA0GDVxhG0tfbdd/v46KPlMXPmh7Xy/gAAtUUsAgAapIULl8dj\nj70dQ4Z0qpX3b9QoiWHDunoqGgBQdMQiAKBBuvfeWdG/f7vYeOMWtfYZjqIBAMVILAIAGqSysulx\nzDG1cwRtrb333jaWLFkZ06d/UKufAwBQk8QiAKDBWbBgWUya9G4cdljHWv2ctUfRPBUNACgmYhEA\n0ODcddeMGDhw52jVqlmtf9bao2hpmtb6ZwEA1ASxCABocOriCNpavXq1jRUrKuPllx1FAwCKg1gE\nADQo7723JF544f045JAOdfJ5SZJ8fnXRtDr5PACA9SUWAQANyp13zojDDusYLVo0qbPPHD68W5SX\nz3AUDQAoCmIRANCg1OURtLV69tw6qqrSePHF9+v0cwEAqkMsAgAajDlzPomZMxfEf/zHTnX6uZ8d\nResaZWWeigYAFD6xCABoMMrLp8cRR3SKZs0a1/lnDx/ePcrLPRUNACh8BROLcrlcVFRUZD0DAKjH\nPjuC1j2Tz9511zbRpEmjePbZeZl8PgDQcFRUVEQul6v265NC+OlWkiRpIewAAOqv11//OPbZ58aY\nN+/n0aRJNj8v+/WvH4mVKyvjyisPyuTzAYCGJUmSSNM0WdfXFcyVRQAAtam8fHocfXSXzEJRhKei\nAQDFQSwCABqELI+grdW9+5bRsmXTmDx5bqY7AAC+iVgEANR7s2YtiA8++DT69t0+0x1Jknx+dZGn\nogEAhUssAgDqvbKyaTFsWNdo3Dj7b32GDesa5eXTo6rKUTQAoDBl/x0TAEAtStM07rgj+yNoa3Xr\ntmVsskmLmDRpTtZTAAC+klgEANRrL7/8QSxbtjr23nvbrKfkOYoGABQysQgAqNfKyqbF8OHdIknW\n+amxtaa0tFuMHTsj1qypynoKAMC/EIsAgHorTdMoK5sew4d3y3rKP+nUaYvYcstWMXGio2gAQOER\niwCAeuu5596LiIiePbfOeMm/Ki3tFmVl07KeAQDwL8QiAKDeKiubFscc072gjqCtVVraLe66a6aj\naABAwRGLAIB6qaoqjfLyGQV3BG2tnXfeLNq2bR2PP/521lMAAP6JWAQA1EtPP/1utGrVNLp33zLr\nKV+rtLRrlJV5KhoAUFjEIgCgXirkI2hrlZZ2i7vvnhmVlY6iAQCFQywCAOqdNWuqYuzYwj2Ctla7\ndpvGjjtuEhUVb2U9BQAgTywCAOqdJ554J7bcslV06rRF1lP+LU9FAwAKjVgEANQ7a4+gFYNhw7rG\nPffMitWr12Q9BQAgIsQiAKCeqaysirvumhmlpYV9BG2tHXbYJDp02DwefvjNrKcAAESEWAQA1DOP\nPPJm7LjjJtG+/aZZT/nWSku7Rnm5p6IBAIVBLAIA6pViOoK21rBh3WLcuFdi1SpH0QCA7IlFAEC9\nsWrVmrj33ldi2LCuWU9ZJ9tu2zq6dNki/v7317OeAgAgFgEA9cdDD70eXbpsEdttt3HWU9bZ8OHd\norx8RtYzAADEIgCg/igrm150R9DWOvrornHffa/EihWVWU8BABo4sQgAqBeWL18d99//agwdWlxH\n0NbaZpuNokePNvHQQ46iAQDZEosAgHrhgQdei549t46tttow6ynV9tlRNE9FAwCyJRYBAPVCWdn0\nGD68W9Yz1svRR3eJ8eNnx/Llq7OeAgA0YGIRAFD0li5dFQ8++FocdVSXrKeslzZtNoyePbeOBx98\nLespAEADJhYBAEXv/vtfjT59tosttmiZ9ZT1VlraNcrKHEUDALIjFgEARa8+HEFb66ijusQDD7wW\ny5Y5igYAZEMsAgCK2iefrIiHH34jjjiic9ZTasR3vtMqevduGxMmzM56CgDQQIlFAEBRGzfulTjg\ngHaxySYtsp5SY0pLuzmKBgBkRiwCAIpafTqCttaRR3aOhx56PZYuXZX1FACgARKLAICi9dFHy+LJ\nJ9+JwYM7Zj2lRm2+ecvo02e7GD/+1aynAAANkFgEABSte+6ZFQcdtFNstFHzrKfUOE9FAwCyIhYB\nAEWrPh5BW+uIIzrHww+/GUuWrMx6CgDQwIhFAEBRmj9/aUyZMjcGDeqQ9ZRasemmG0S/ftvHffe9\nkvUUAKCBEYsAgKJ0110z49BDO0bLlk2znlJrhg/vFuXlM7KeAQA0MGIRAFCU6vMRtLUOP7xTVFS8\nFZ98siLrKQBAAyIWAQBFZ+7cxfHyy/Pj4IN3ynpKrdp44xZRUrJjjBvnKBoAUHfEIgCg6IwdOyOG\nDOkczZs3yXpKrfvsKJqnogEAdUcsAgCKTkM4grbW4MEd44kn3omFC5dnPQUAaCDEIgCgqLz11qJ4\n7bWP48AD22U9pU5stFHzOPDAdnHvvbOyngIANBBiEQBQVMrLp8dRR3WOpk0bZz2lzngqGgBQl8Qi\nAKCofHYErXvWM+rUoYd2jKeemhMffbQs6ykAQAMgFgEARWP27I9i3rwlsf/+O2Q9pU5tuGGzOPjg\nneKeexxFAwBqn1gEABSNsrLpMXRol2jcuOF9C1Na2i3KyjwVDQCofQ3vOy0AoGg1xCNoaw0a1CGm\nTJkbH374adZTAIB6TiwCAIrC9OkfxKJFK6JPn+2ynpKJli2bxiGHdIi7756Z9RQAoJ4TiwCAolBW\nNj1KS7tGo0ZJ1lMyU1ra1VE0AKDWiUUAQMFL07RBH0Fb65BDOsQLL7wf77+/NOspAEA9JhYBAAXv\nxRffj9Wr18Ree22T9ZRMtWjRJA49tEPcddeMrKcAAPWYWAQAFLzPrirqFknScI+grVVa2i3Ky8Ui\nAKD2iEUAQEFzBO2fHXzwTvHyy/Nj3rwlWU8BAOopsQgAKGjPPDM3mjdvHLvu2ibrKQWhefMmMXhw\np7jzTlcXAQC1QywCAAqaI2j/avjwblFe7qloAEDtEIsAgIJVVZVGebkjaF82YED7mDlzQbz77uKs\npwAA9ZBYBAAUrIkT34nNNtsgunb9TtZTCkqzZo1jyJBOMXasq4sAgJonFgEABWvtETT+1WdH0dy3\nCACoeWIRAFCQKiurYuzYGY6gfY3+/dvF7NkfxdtvL8p6CgBQz4hFAEBBeuyxt2K77VrHzjtvlvWU\ngtS0aeM48sjOMXasq4sAgJolFgEABckRtH9v+PDunooGANQ4sQgAKDirV6+Ju++eGaWlYtE3KSnZ\nMd56a1G88cbCrKcAAPWIWAQAFJx//OON6Nhx89hhh02ynlLQmjRpFEcf3cVT0QCAGiUWAQAFxxG0\nb6+0tFuUlYlFAEDNEYsAgIKyYkVl3HffKzFsmFj0bey33w4xb96SmD37o6ynAAD1hFgEABSUv/3t\ntejRo01ss81GWU8pCo0bN4qhQ7t6KhoAUGPEIgCgoDiCtu4cRQMAapJYBAAUjGXLVseECbPj6KO7\nZj2lqPTtu30sWLAsZs1akPUUAKAeEIsAgIIxfvyr0atX29hyy1ZZTykqjRolMXRolygvd3URALD+\nxCIAoGA4glZ9paXdxCIAoEaIRQBAQViyZGX8/e9vxJFHdsl6SlHaZ5/t4pNPVsb06R9kPQUAKHJi\nEQBQEO6775Xo12/72GyzDbKeUpQaNUpi2LCuri4CANabWAQAFARH0Nbf8OHdorx8RqRpmvUUAKCI\niUUAQOYWLlwejz32dgwZ0jnrKUWtV6+2sWzZ6pg2zVE0AKD6xCIAIHP33jsrDjywXbRu3TzrKUUt\nSZIoLe0aZWWOogEA1ScWAQCZcwSt5gwf3j3Ky6c7igYAVJtYBABk6sMPP41Jk96Nww7rmPWUemGP\nPbaONWvSePHF97OeAgAUKbEIAMjU3XfPjEMO2TlatWqW9ZR6Ye1RNE9FAwCqq9ZjUZIkLZMk+XOS\nJH9IkuS7tf15AEBxKSubHscc0z3rGfVKaamnogEA1VcXVxYdFRFj0zT9cUQcXgefBwAUiffeWxIv\nvPB+DBy4c9ZT6pXddtsqGjVK4rnn3st6CgBQhNY5FiVJcmOSJPOTJJn6pa8PTJJkVpIkryZJcs4X\nfmvbiJjz+X+vWY+tAEA9c+edM2Lw4I7RokWTrKfUK0mSxPDh3RxFAwCqpTpXFv0pIg7+4heSJGkU\nEb///OvdIuLYJEk6f/7bc+KzYBQRkVRzJwBQD91xhyNoteWzo2ieigYArLt1jkVpmj4ZEQu/9OVe\nETE7TdO30zRdHRF3RMSQz3/vnogYmiTJmIj46/qMBQDqjzlzPolXXlkQAwa0z3pKvbTLLltGixZN\n4pln5mY9BQAoMjV1zXfb+L+jZhER78ZnASnSNF0WET/8d2+Qy+Xy/11SUhIlJSU1NA0AKDTz5y+N\noUPHxo9+1DOaNWuc9Zx66YtH0Xr33vbfvwAAKHoVFRVRUVGx3u+TVOfS5CRJdoiIv6Zp2uPzXx8d\nEQenaXry57/+XkT0StP0jG/5fqlLpAGgYZg1a0EMGvSX+P73e0QuVxJJ4pR6bZk+/YM48MBb4umn\nT4odd9wk6zkAQB1LkiTSNF3nb7Zq6mlocyNi+y/8etvPvwYAkPf442/H/vv/OS68cP8YMeIAoaiW\ndeu2ZfzqV/2iT58bY9KkOf/+BQAAUf1YlMQ/36x6SkTsnCTJDkmSNIuIYyLivvUdBwDUH7fd9nIM\nHVoef/nLUXH88btlPafBOP303nHDDYfHkCF3xO23v5z1HACgCKzzMbQkSW6LiJKI2Dwi5kfERWma\n/ilJkkMi4ur4LEDdmKbpZevwno6hAUA9laZpXHrpk/GHPzwX999/bOyyS5usJzVIL788PwYPvj1O\nOGG3uPDC/V3VBQANQHWPoVXrnkU1TSwCgPpp9eo1ceqp4+O5596L++//bmyzzUZZT2rQ5s9fGkOG\n3BHt228aN900JFq0qKlnnQAAhSjrexYBAPyTxYtXxuDBt8e8eUvj8cdPEIoKQJs2G8ajj/4gqqrS\n6N//5pg/f2nWkwCAAiQWAQA17t13F0e/fn+KHXfcJMaNOyY23LBZ1pP43AYbNI3bbjs6BgxoH3vv\nfWNMm/ZB1pMAgAIjFgEANWrq1PnRp8+Ncdxxu8R11x0aTZr4dqPQNGqUxMUXHxCXXHJA9O9/czz4\n4GtZTwIACoh7FgEANeZvf3stvv/9e+Kaaw6J4cO7Zz2Hb2HixHdi6NCx8atf9YvTTuuV9RwAoAa5\nwTUAkKkbb3w+fvWrR+LOO0ujb9/ts57DOnjjjYUxePDt0b//jjFy5EBXgwFAPSEWAQCZSNM0Lrjg\n0bjjjmkxYcJx0bHj5llPoho++WRFlJbeGY0aJVFWNjRat26e9SQAYD15GhoAUOdWrqyM733vnnj4\n4Tdj0qQThaIitvHGLWL8+O9Gu3abRJ8+N8Zbby3KehIAkJGCiUW5XC4qKiqyngEAfEsff7w8Djro\n1li5sjIeeeT/xXe+0yrrSaynJk0axZgxg+Lkk/eIPn1ujEmT5mQ9CQCohoqKisjlctV+vWNoAMA6\ne/PNhTFo0G0xaNDOceWVB0WjRut8dTMFbvz4V+OEE8bFqFED49hjd8l6DgBQDe5ZBADUiWeemRtH\nHHFHnH++p2fVdy+/PD8GD749Tjhht7jwwv0jSURBACgmYhEAUOvGjZsVJ53017jppsNj8OBOWc+h\nDrz//tI44og7on37TeOmm4ZEixZNsp4EAHxLbnANANSq0aMnxymnjI8HHjhOKGpAttpqw3j00R/E\nmjVp9O9/c3zwwadZTwIAaplYBAB8ozVrquJnP3swrr/+2XjqqRNjzz23yXoSdWyDDZrG7bcfHQce\n2C56974hpk37IOtJAEAtcgwNAPhay5atju997+5YuHBF3H13aWy66QZZTyJjt946Nc4++29xyy1H\nxsCBO2c9BwD4Bo6hAQA16oMPPo3+/W+OVq2axYMPHicUERER3/tej7j77uFxwgnjYsyYZ7KeAwDU\nAlcWAQD/4pVXFsSgQbfFd7/bPS6++ABPweJfvPHGwjjssNviwAPbxciRA6NJEz+DBIBC42loAECN\neOKJt2Po0LFx6aUHxg9/uHvWcyhgixatiNLSsdGkSaO4446h0bp186wnAQBf4BgaALDe7rhjWhx9\ndHnceuuRQhH/1iabtIjx478bO+ywcfTpc2O89dairCcBADXAlUUAQKRpGpdfPjGuvXZKjB//3dhl\nlzZZT6KIpGkao0dPjssvnxh33VUa++yzXdaTAIBwDA0AqKbKyqo49dTx8cwzc2P8+O9G27ats55E\nkRo//tU4/vhxMXr0wDj22F2yngMADZ5YBACssyVLVkZp6Z0REVFePjQ22sg9Z1g/U6fOj8GDb48f\n/nC3uPDC/d0cHQAyVPT3LMrlclFRUZH1DABoMObOXRz9+v0ptt++dfz1r8cKRdSIHj3axOTJJ8WE\nCa/FccfdHStWVGY9CQAanIqKisjlctV+vSuLAKABmjp1fhx22G1x6ql7xTnn7OvqD2rc8uWr4/jj\nx8WcOZ/EvfceE1tu2SrrSQDQ4BT9lUUAQN146KHXY8CAW+KKK/4jzj23r1BErdhgg6Zx++1Hx4EH\ntovevW+IadM+yHoSAPAtubIIABqQm256Ic477+G4885h0a/fDlnPoYH43/99KX7+84filluOjIED\nd856DgA0GG5wDQB8rTRN44ILHo3bb58WEyZ8Nzp12iLrSTQwTz75TgwdWh4XXLBf/PSnvbKeAwAN\nglgEAHyllSsr48QT74vZsz+Ov/71WPeOITOvv/5xHHbY7TFgQLsYOXJgNGnijggAUJvEIgDgXyxc\nuDyOOqo8Nt20Rdx661HRsmXTrCfRwC1atCKGDRsbTZs2ijvuGBqtW3sKHwDUFje4BgD+yZtvLow+\nfW6K3XZrE2PHDhOKKAibbNIiJkz4bmy//cbRp8+N8dZbi7KeBAB8iVgEAPXQlClzY999b4pTTtkz\nRo4cGI0b+yufwtG0aeO47rpD46STekafPjfGpElzsp4EAHyBY2gAUM/cd98rceKJ98UNNwyOIUM6\nZz0HvtH9978aJ5wwLq655pA45pjuWc8BgHrFPYsAgLjmmslx6aVPxr33HhO9erXNeg58K1Onzo/B\ng2+PH/6BUJlTAAAgAElEQVRwt7jwwv0jSdb5e1oA4CuIRQDQgK1cWRnnnvuPeOCB1+KBB46Ldu02\nzXoSrJP33lsSQ4bcER06bB433nh4tGjRJOtJAFD03OAaABqof/zjjejR4/p4881F8dRTJwpFFKWt\nt94oKiqOj9Wr18Ree/0xHnvsrawnAUCD5coiAChS8+YtiZ///KGYNGlOXHPNITF4cKesJ8F6S9M0\n7rprZvz85w/FPvtsG1dddVBsu23rrGcBQFFyZREANBCVlVUxatTT0aPHddG+/SYxY8ZPhSLqjSRJ\nYujQrjFz5k+jY8fNY9ddr49LL30iVq6szHoaADQYriwCgCLy9NPvximnjI/NNtsgxowZFJ07b5H1\nJKhVb7yxMH72s7/FjBkfxtVXHxyHHtox60kAUDSK/gbXF110UZSUlERJSUnWcwCg4Hz00bI477yH\n4/77X42rrjoojj22uydG0aA8+OBrccYZD0THjpvH1VcPjJ133izrSQBQsCoqKqKioiJGjBhR3LGo\nEHYAQKGpqkrjz39+Mc477+EYPrxb/OY3B8TGG7fIehZkYuXKyrj66qfjyiufipNP3iN+9at+0apV\ns6xnAUDBKvoriwphBwAUkqlT58cpp4yPysqquO66Q6Nnz62zngQFYe7cxfHLX/4jnnji7bjyyv+I\n0tJurrQDgK8gFgFAPbFkycq46KKKuPXWqXHJJf3jpJN6RqNG/iEMX/bEE2/H6ac/EJtuukGMHj0w\ndtmlTdaTAKCgeBoaABS5NE1j7Njp0aXLmFi4cEVMn35qnHzyHkIRfI1+/XaIZ589OYYN6xoHHnhL\nnHHGA7Fo0YqsZwFA0XNlEQAUgNmzP4rTTnsg5s1bEtdeOyj69dsh60lQVBYsWBa//vUjce+9s+KS\nS/rHD3+4u9AKQIPnGBoAFKHly1fHZZc9GWPGTInzzusbZ5zRO5o2bZz1LChazz03L04//YGorKyK\n3/9+UPTq1TbrSQCQGbEIAIrMAw/MjtNOeyB69tw6Ro48OLbdtnXWk6BeqKpK49Zbp8a55/4jBg7c\nOS699MBo02bDrGcBQJ0TiwCgSMyZ80mcddbf4qWX3o/f/35QDBy4c9aToF5avHhlXHzxY3HzzS/F\nr3/dL049dS9X7gHQoLjBNQAUuNWr18RVVz0Vu+/+h9hlly1j2rRThSKoRa1bN4+rrjooHn/8+Lj/\n/tmx++5/iEcffTPrWQBQ8FxZBAB14Ikn3o5TThkf227bOq655pDo0GHzrCdBg5Kmadxzz6w4++y/\nRa9ebeOqqw6K7bffOOtZAFCrHEMDgAL0wQefxi9/+fd4+OE3Y+TIg+Poo7tEknhCE2Rl2bLVccUV\nE+P3v38mzjpr7/jFL/pEixZNsp4FALXCMTQAKCBr1lTF9dc/G927XxtbbNEyZsw4NYYO7SoUQcZa\ntmwauVxJPPvsyfH88+9Ft27Xxn33vRJ+cAkA/8eVRQBQw557bl6ccsr4aNascVx33aGxyy5tsp4E\nfI2HHno9zjjjgWjfftO4+uqB0bGjI6IA1B+uLAKAjC1atCJOP31CHHrobXHqqXvF44+fIBRBgTvo\noJ1i6tRTon//dtGnz41x7rn/iKVLV2U9CwAyJRYBwHpK0zT+8pep0bXrmFi1ak1Mn35qHH/8btGo\nkSNnUAyaNWscv/hFn3j55VNi3rwl0bnz7+O22152NA2ABssxNABYDzNnfhinnjohFi1aEdddd2js\nvfe2WU8C1tPEie/Eaac9EK1bN4/RowfGrrtulfUkAKgWx9AAoA59+umqOO+8f8R++/05jjqqc0yZ\n8iOhCOqJfffdPp599kdx7LHd46CDbo3TTpsQH3+8POtZAFBnxCIAWEfjxs2Kbt2ujXfeWRxTp/4k\nTj+9dzRp4q9UqE8aN24UP/nJnjFjxqlRVZVGly5j4n/+57lYs6Yq62kAUOsK5hjaRRddFCUlJVFS\nUpL1HAD4Sm++uTDOPPPBePXVj2LMmEFx4IHts54E1JEXX3w/TjttQqxYURnXXHNI7LPPdllPAoCv\nVVFRERUVFTFixIhqHUMrmFhUCDsA4KusXFkZ//3fk+J3v5sUZ5+9T/z85/tE8+ZNsp4F1LE0TeO2\n216Oc875RwwY0D4uu2xAbLXVhlnPAoCv5Z5FAFALHn74jdh11+tj0qR3Y8qUH8X55/cTiqCBSpIk\njjuuR8yc+dPYcstW0b37tfG7302K1avXZD0NAGqUK4sA4CvMm7ckfvGLh2LixDkxevTAGDKkc9aT\ngALzyisL4swzH4x33vkkfvvbA2PIkE6RJOv8w1sAqDXVvbJILAKAL1iwYFlcccXEuOGG5+Pkk/eI\nCy7YL1q1apb1LKBApWka48fPjgsueDQaNUoil9s/Djuso2gEQEEQiwBgPSxatCJ+97tJMWbMlBg2\nrGv86lf9YrvtNs56FlAkqqrSGDduVuRyj0WzZo0jl9s/Bg3qIBoBkCmxCACqYenSVTF69OQYOfLp\nOOywjnHBBftF+/abZj0LKFJVVWncc8/MyOUei5Ytm0Yut38MHLizaARAJsQiAFgHy5evjuuuezau\nuGJiHHBAu8jl9o9OnbbIehZQT1RVpXHnnTNixIjHonXr5jFiREn8x3+0F40AqFNiEQB8CytXVsaN\nN74Q//VfT0SvXm1jxIiS6NGjTdazgHpqzZqqGDv2s2i02WYbxIgRJXHgge1EIwDqhFgEAN+gsrIq\nbrnlpbj44seia9fvxMUXHxB77rlN1rOABmLNmqooK5seI0Y8Fm3atIoRI0rigAPaZT0LgHpOLAKA\nr7BmTVXccce0yOUei223bR2XXHJA7Lvv9lnPAhqoysqquP32l+Piix+Ptm03ihEjSmL//XfMehYA\n9ZRYBABfsPYmsxdeWBEbb9w8Lrmkf/Tv76f4QGGorKyKv/xlavzmN4/H9ttvHCNGlES/fjtkPQuA\nekYsAoCISNM0JkyYHRdc8GhERFxySf845BBPIgIK0+rVa+LWWz+LRjvttFmMGFESffpsl/UsAOoJ\nsQiABi1N03jkkTfj179+NJYsWRm/+c0BccQRnUUioCisXr0mbr75pbjkksejU6ctYsSIkth7722z\nngVAkROLAGiwnnzynbjggkdj7tzFMWJESZSWdovGjRtlPQtgna1atSb+/OcX47/+64no2vU7MWJE\nSfTq1TbrWQAUKbEIgAbn2WfnxQUXPBozZ34YF120f3z/+7tGkyYiEVD8Vq6sjD/96bNotOuubSKX\nK/EERwDWmVgEQIMxder8uPDCR+PZZ+fFr37VL048sWc0a9Y461kANW7lysq44Ybn49JLn4yePbeO\nXK4kevbcOutZABQJsQiAem/WrAWRy1VERcVbcc45+8ZPfrJnbLBB06xnAdS6FSsq449/fC4uu2xi\n7LXXNpHLlcRuu22V9SwACpxYBEC99cYbC+Piix+L8eNnx9ln7x2nn947NtywWdazAOrc8uWr43/+\n57m4/PKJsc8+28VFF+0fPXq0yXoWAAVKLAKg3pkz55O45JLH4847Z8bpp/eKn/1s79h44xZZzwLI\n3LJlq+P665+NK698Kvr23T4uumj/6N59y6xnAVBgqhuL3AUUgILz/vtL48wzH4hdd70+Nt10g3j1\n1dMilysRigA+17Jl0zj77H3itddOj96928aAAbfE8OF3xowZH2Y9DYB6QCwCoGB89NGyOOecv0e3\nbtdGkiQxY8ZP47LLBsTmm7fMehpAQWrVqln84hd94rXXzoiePbeKAw64Ob773bti1qwFWU8DoIgV\nTCzK5XJRUVGR9QwAMvDJJyvioosejY4dfx+ffLIyXnzxx3H11QNjq602zHoaQFHYcMNmcc45feO1\n106PXXbZMvbb70/xve/dHa+++lHW0wDIQEVFReRyuWq/3j2LAMjM0qWr4pprJsfvfvd0HHZYx7jg\ngv2ifftNs54FUPQWL14Z11wzOa6+enIccsjOccEF+0WHDptnPQuAOuYG1wAUjeXLP7sx6+WXT4wD\nDmgXudz+0anTFlnPAqh3PvlkRYwaNTlGj54cgwd3il//ul/stNNmWc8CoI6IRQAUvFWr1sQNNzwf\n//VfT0SvXm1jxIgSj3wGqAOLFq2Iq69+On7/+2diyJBO8etf7xft2rmSE6C+E4sAKFirV6+J//3f\nqXHxxY9F167fiYsvPiD23HObrGcBNDgLFy6PkSOfjjFjpsSgQR3il7/sE7vsItoD1FdiEQAFZ/ny\n1fGnP70YV175VLRrt0n85jcHxL77bp/1LIAGb9GiFXH99c/GqFGTY889t4lzztk3+vb15zNAfSMW\nAVAwFi9eGddf/2yMHPl07LXXNnHeeX1jn322y3oWAF+yYkVl3Hzzi3HFFU/F1ltvGOee2zcGDeoQ\njRqt878rAChAYhEAmVuwYFmMGvV0XH/9c3HQQTvFuefu63gDQBGorKyKu+6aEZdfPjFWr66KX/6y\nTxxzTPdo2rRx1tMAWA9iEQCZmTPnk/jv/54Ut9zyUgwb1jV++ct9PW0HoAilaRp///sbcdllT8br\nry+MX/xinzjxxJ7RsmXTrKcBUA1iEQB1bvbsj+LyyyfG3XfPjB/+cPc4++x9YpttNsp6FgA1YPLk\nd+PyyyfGxIlz4qc/3StOO61XbLbZBlnPAmAdiEUA1JkXX3w/Lr30yXjkkTfjtNM++wfE5pu3zHoW\nALVg1qwFceWVE+Oee2bF8cfvFmefvU9su23rrGcB8C2IRQDUuieffCd++9sn4qWX5sfZZ+8dJ5+8\nR2y0UfOsZwFQB959d3FcffXTcdNNL8QRR3SO//zPPtGly3eyngXANxCLAKgVaZrG3/72evz2t0/E\n3LlL4pxz9o0f/GDXaN68SdbTAMjAxx8vj2uvnRLXXPNM9OmzXZxzzr6x997bZj0LgK8gFgFQo9as\nqYq7754Zl176ZKxeXRXnn983hg3rFk2aNMp6GgAFYNmy1XHTTS/EVVc9FTvuuEmce27fOPjgnSJJ\n1vnfJADUErEIgBqxatWauPXWqXH55RNjs802iPPP7xuHHtoxGjXyzT8A/2r16jVRXj49LrtsYjRu\nnMS55/aNoUO7+uECQAEQiwBYL59+uipuuOH5+O//nhSdO28R55/fL/bffwc/IQbgW0nTNCZMmB2X\nXTYx5s1bEv/5n33iBz/YNTbYoGnW0wAaLLEIgGpZtGhFjBnzTIwe/Uz07bt9nHde39hzz22yngVA\nEZs48Z24/PKJMWXKvDjjjF5xyil7xSabtMh6FkCDIxYBsE7mz18aI0c+HX/84/MxeHDHOOecfT3V\nBoAaNW3aB3HFFRNj/PjZceKJu8dZZ+0d22yzUdazABqM6sYiB4kBGpi33loUP/3p+OjSZUwsXboq\nnnvu5Pjzn48QigCocd27bxm33HJkPP/8ybFyZWV0735tnHzyX2P27I+yngbAN3BlEUADMWPGh3H5\n5RPj/vtfjZNP7hlnnbV3tGmzYdazAGhAFixYFtdcMzmuvfbZOOCAHeOcc/aNPfZw9BmgtjiGBsBX\nmjJlblx66ZMxceKcOPPM3nHqqe4bAUC2li7954cqnHvuvtG/fzsPVQCoYWIRAHlpmkZFxVvx298+\nGa+8siB+8Ys+cdJJPaNlS0+kAaBwrFq1Jm677eW4/PKJseGGzeLcc/eNI47oHI0bu1sGQE0QiwCI\nqqo07r//1bj00ifj44+Xx7nn7hvHHdcjmjVrnPU0APhaVVVp/PWvr+T//vrlL/eN73+/RzRv3iTr\naQBFTSwCaMAqK6uivHx6XHrpk9G0aaM4//x+ceSRfjILQHFJ0zQef/ztuOyyiTF16vw466ze8eMf\n7xmtWzfPehpAURKLABqgFSsq4+abX4wrrngqtt22dZx/ft846KCd3PMBgKL34ovvxxVXTIyHHno9\nfvzjPeKMM3p7MAPAOhKLABqQJUtWxh/+8Fz87neTYvfdt47zzusbfftun/UsAKhxb7yxMK666qm4\n/fZpccQRneOss3rHrrtulfUsgKIgFgE0AG+9tSiuvXZK3HTTCzFgQPs499y+sdtuvmEGoP776KNl\n8Yc/PBdjxkyJzp23iLPO6h2HHtoxGjVyNS3A1yn6WHTRRRdFSUlJlJSUZD0HoKCsvX/DqFGT47HH\n3o7jj981fvrTXtG+/aZZTwOAOrdq1ZoYO3Z6jBz5dCxevDLOPLN3/OAHu8WGGzbLehpAwaioqIiK\niooYMWJEcceiQtgBUEiWL18dt98+LUaPnhwrVlTGGWf0jv/3/3b1zTAAxGc/THnyyXdi5Min4/HH\n344TT9w9TjutV2y33cZZTwMoGEV/ZVEh7AAoBO++uziuu25K/PGPz8dee7WNM8/sHQMGtHeZPQB8\njTfeWBjXXDM5br75pTjooJ3iZz/bO3r33jbrWQCZE4sAiliapjFp0rsxatTk+PvfX4/vfa9HnH56\nr+jQYfOspwFA0Vi8eGXceOPzMXr0M7HVVhvGz362dxx1VJdo0qRR1tMAMiEWARShlSsro7x8eowa\nNTkWLVoRp5/eK044Yfdo3bp51tMAoGitWVMV48a9EiNHPh3vvPNJnH56rzjppJ6xySYtsp4GUKfE\nIoAi8v77S+O666bEH/7wXPTo0SbOOKN3DBrUwVEzAKhhzz47L66++umYMGF2HHfcLnHmmXvHzjtv\nlvUsgDohFgEUgSlT5saoUZNj/PjZccwx3eL003tH167fyXoWANR7c+cujjFjPrsnYJ8+28VZZ/WO\nkpIdI0n8oAaov8QigAK1evWauOuumTFq1OR4770lcdppveLEE3ePTTfdIOtpANDgLFu2Ov73f1+K\nq6+eHC1aNImzzuodxxzTPZo3b5L1NIAaJxYBFJgPP/w0/ud/novrrns2OnTYPM48s3cMHtwxGjd2\nk00AyFpVVRp/+9trMXLk0/Hyyx/EKafsGaecsmd85zutsp4GUGPEIoAC8eKL78eoUZPj3ntnxdFH\nd4kzzugdPXq0yXoWAPA1pk37IEaNejruvHNmHH10lzjrrL2je/cts54FsN7EIoAMVVZWxbhxs2LU\nqMnx5puL4tRT94wf/WiP2GKLlllPAwC+pQ8//DSuv/7ZuPbaZ2OXXbaMs87aOwYO3NkDKICiJRYB\nZODjj5fHDTc8H2PGTInttmsdZ5zRO448snM0bdo462kAQDWtXFkZZWXTY+TIp2P58tVx1ll7x/e/\n3yNatWqW9TSAdSIWAdShadM+iNGjJ8fYsTPi8MM7xRln9Io99tgm61kAQA1K0zQee+ztGDny6Xjq\nqTlx0km7x2mn9Yq2bVtnPQ3gWxGLAGrZmjVVMX787Bg1anLMnPlh/OQne8aPf7xHtGmzYdbTAIBa\n9tprH8fo0ZPj1lunxiGHdIif/Wzv2HNPPyiC/9/enQZVeeZvHr9uVNz33bjvCzu4JSZtd0ziks5i\nNAoIRA9K5J91ZqpmqmaqUv3yPy/GpJOGEDkxgODehpitTUzbMUm7IEcWcY/7iriDC8s9LzDnn7Zj\nggo8HPh+qlIBfAquKpOH+1znuX83GjbKIgCoI5cu3dCyZR69994Ode3aWq+/Pl6zZ4+Rvz9bzQAA\naGouXbqh1NRcvfvudvXr10FvvjlBzz03ktNOATRIlEUAUMv27j2v997brqysAk2dOlSvvz5e48f3\ndToWAABoACoqqrR+/R4tWbJVp09f06uvjpPLFaqOHVs5HQ0AvCiLAKAWVFVZ/e1vB/XOO9vk8ZzR\nokVhWrx4rPr0ae90NAAA0EBt23ZCS5Zs1caNhxQbG6zXXhuvwYM7Ox0LACiLAOBBXL16U2lpeXr3\n3e1q06aFXn99vObODVCrVs2djgYAAHzEsWOX9Ze/bJfb7dGjjw7Qq6+O0+9/P1DG3PPrNACoFZRF\nAHAfDh++qD//eZvS0/P1hz8M0muvjdOkSf1Z1AEAgPt27dotpafnKSlphyoqqrR4cYTi4kLUqRNb\n1ADUL8oiAKgha622bDmmt9/eqm+/PSqXK1T/8R/j1L9/R6ejAQCARsRaq+++O6akpBx98cUBzZo1\nWomJYxUW1tvpaACaCMoiAPgNt25VatWqQr399jZdu3ZLr78+XrGxwWrXzt/paAAAoJE7e/aa3G6P\nUlJ2qlevdkpMjNCLL45R69YtnI4GoBGjLAKAuyguLlVKyk4lJe3Q6NHd9eabEzRt2jD5+bHVDAAA\n1K/Kyip9/vkBJSXlKCfnlOLigvXyyxEaOrSL09EANEKURQBwh8LCc3rnna1au3aPXnhhlF5/fbwC\nA3s6HQsAAECSdOjQBaWk7NSyZbsUFtZbiYkRmjFjuJo393M6GoBGgrIIACRVVVl9+eVBvf32VhUU\nnFNiYoQSEiLUo0dbp6MBAAD8ohs3KrRmzW4lJeXo5MkrWrQoXPHxYerVq53T0QD4OMoiAE1aaWn1\nqSPvvLNNrVu30JtvTtCcOWPUsmVzp6MBAADUmMdzWsnJOVqzpkhPPjlEiYkReuyxAZzUCuC+UBYB\naJKOH7+sv/xlh1JTc/XoowP0xhvjWVABAACfd+nSDWVk5CkpKUd+fkaLF0coJiZIHTu2cjoaAB9C\nWQSgSdm27YSWLNmqjRsPKTY2WK++Ok5DhjAYEgAANC7WWv3jH0eVlLRDX331o+bMGaPFiyMUHNzL\n6WgAfABlEYBGr6KiSn/96x4tWbJVZ85c02uvjdOCBaG8wwYAAJqE06evKjU1VykpOzVgQCclJkZo\n1qzRbLsHcFeURQAarYsXr2vp0ly99952DRzYSW+8MUHPPjtCzZpxUggAAGh6KiqqtGHDPiUn52jX\nrjNasCBUCQnhGjSos9PRADQwlEUAGp39+0v0zjtblZVVqKefHq433hiv8PA+TscCAABoMA4cKNH7\n7+coLS1P48f3VWJihKZOHcqbagAkURYBaCSstfrmm8NasmSrtm8/qUWLwpWYOFZ9+rR3OhoAAECD\nVVZWrlWrCpWcnKNz50r18ssRWrAgVD16tHU6GgAHURYB8Gk3blQoK6tAb7+9VZWVVm+8MV7z5gWp\ndesWTkcDAADwKTk5p5ScvEPr1u3RjBnDlZgYoYcf7sdpsUATRFkEwCedOXNNyck79P77OxUe3ltv\nvDFBTzwxmMUMAADAA7pw4brS0nYpOTlHrVo1V2LiWEVHB6p9+5ZORwNQTyiLAPiUXbvOaMmSrfrk\nk32aO3eMXnttvEaN6u50LAAAgEanqqp6m39yco7+/vfDiowM0OLFYxUQ0MPpaADqGGURgAavsrJK\nn366X0uWbNXBgxf0yivjtHBhmLp2beN0NAAAgCbh5MkrWro0Vx98sFNDh3ZRYuJYzZw5Sv7+zZyO\nBqAO+HxZ9NZbb2ny5MmaPHmy03EA1LKrV29q2bJd+vOft6lLl9Z6880JmjVrtFq0YFECAADghPLy\nSmVn71Nyco527z4nlytUixaFa8CATk5HA1ALNm/erM2bN+tPf/qTb5dFDSEHgNp1+PBFvfvudqWl\n5enxxwfpjTcmaOLEvswjAgAAaED27j2v99/PUUZGviZO7KuEhHBNmzZMzZv7OR0NwAPy+SeLGkIO\nAA/OWqvvvz+uJUu2avPmI1qwIESvvDKOd6kAAAAauLKycq1aVaiUlJ06efKq4uND5XKFqW/fDk5H\nA3CfKIsAOOratVvKzMxXcnKOSkvL9frr4/XSSyFq187f6WgAAAC4R3l5Z5SSslMrVxbq0UcHKCEh\nXE89NUTNmvG0EeBLKIsAOKKoqFjJyTuUmVmg3/1uoBYvjtCUKYPl58dWMwAAAF937dotrVxZ/bTR\nuXOlWrgwTAsWhKpPn/ZORwNQA5RFAOrNrVuVWr9+j5KTc7RvX4kWLgzTwoVh6tevo9PRAAAAUEdy\nc08rJSVHq1cX6fe/H6iEhHA98cQQ3iQEGjDKIgB17tixy/rgg51yuz0aObKbEhMj9NxzIznVDAAA\noAm5evWmsrIKlJKyU5cu3fA+bdSzZzunowG4A2URgDpRVWX11VeHlJSUoy1bjmrevCC9/HKERo/u\n7nQ0AAAAOMhaq5ycU0pJ2al16/ZoypTBSkgI1x/+MIinjYAGgrIIQK0qKSnTsmW79P77OWrfvqUS\nEyMUGRnIwGoAAAD8m8uXbygzs/ppo7Kyci1cGKb580PUvXtbp6MBTRplEYAHZq3V9u0nlZSUo+zs\nvXrmmRFavDhCEyb0lTG8OwQAAIBfZ63Vtm0nlZKyU+vX79HUqUOVkBCuyZMHsp4EHEBZBOC+lZbe\n0ooVhUpOztHFi9e1eHGE5s8PVbdubZyOBgAAAB916dINZWTkKSVlp8rLq5SQEK64uGB17coaE6gv\nlEUA7tneveeVnLxDy5cX6JFH+ikxcayefJITLQAAAFB7rLX64YfjSknZqU8+2aennx6uhIRwTZrU\nn6eNgDpGWQSgRsrLK5WdvU9JSTtUVFQslytUixaFa8CATk5HAwAAQCN34cJ1padXP21kjJSQEK7Y\n2GB17tza6WhAo0RZBOBXnThxRUuX7lRqqkdDh3bR4sURmjlzlPz9OfYeAAAA9ctaqy1bjiklZac+\n//yAnnlmhBISwjVxIrMygdpEWQTg31RVWX3zzWElJe3Q5s1HFBkZoMWLxyogoIfT0QAAAABJ0vnz\nZfroo1364IOdatmyuRISwjVvXpA6dWrldDTA51EWAfC6ePG6Pvpol95/f6datmymxMSxio4OVPv2\nLZ2OBgAAAPwia63+/vcjSknZqY0bD+n550cqISFc48Y9xNNGwH2iLAKgnJxTSkraofXr92r69GFK\nTIzQww/345crAAAAfMq5c6VatsyjDz7IVfv2/kpICFd0dJA6dODNT+BeUBYBTVRZWblWrSpUUlKO\nzp8vU0JCuBYsCFWPHm2djgYAAAA8kKoqq02bflRKyk5t2nRYs2aNUkJChCIi+jgdDfAJlEVAE7N/\nf/b8WwMAABeBSURBVInefz9H6el5mjChrxYvjtDUqUPVrJmf09EAAACAWnfmzDV9+KFHS5fmqkuX\n1kpICFdkZACjFoBfQVkENAEVFVXasGGfkpJylJ9/VgsWhGjRonANGtTZ6WgAAABAvaiqstq48ZBS\nUnZq8+YjmjlzpOLjwzRhAiepAXeiLAIasVOnrio1NVcffLBTAwd2UmLiWL3wwii1bNnc6WgAAACA\nY86cuaa0tF1yuz1q3txPLleoYmKCGckA3EZZBDQyVVVWX3/9o5YuzdXXX/+ouXPHaPHisQoK6ul0\nNAAAAKBBsdbqu++Oye326OOP92rKlMFyuUL15JNDGNOAJo2yCGgkTpy4omXLPHK7PeratY3i40M5\n+QEAAACoocuXb2jlykK53R6dPn1N8+eHaP78EEY3oEmiLAJ8WEVFlT77bL9SUz36/vtjmjs3QPHx\nYQoL6+10NAAAAMBn5eefldudq8zMAoWE9JLLFarnnx+lVq0Y54CmgbII8EE//nhRbneuli3bpcGD\nOys+PkyzZ49W27b+TkcDAAAAGo0bNyr08cd75XZ75PGcVlRUoOLjwxjxgEaPsgjwETdvVv+iWro0\nV3l5ZxUTE6T4+DCNHt3d6WgAAABAo3fkyCUtW+bRhx/uUq9e7eRyhSoyMkAdO7ZyOhpQ6yiLgAau\nqKhYqam5Wr48X0FBPbVwYZiee24kJ5oBAAAADqisrNJXX/0ot9ujr746pGefHSmXK1SPPtpfxtzz\na2ugQaIsAhqg0tJbWrOmSEuX5urw4YuaPz9ELleYBg9muB4AAADQUBQXlyojI1+pqbmqrLRasCBE\ncXEh6tWrndPRgAdCWQQ0ILm5p7V06U6tWrVbjzzSXwsXhmn69GFq3pxjOwEAAICGylqrrVtPyO32\naN26PXrssQGKjw/VtGms5eGbKIsAh12+fENZWQVKTfWopKRM8fFheumlEPXt28HpaAAAAADu0dWr\nN7V69W653R4dOXJJcXHBWrAgVMOGdXU6GlBjlEWAA6y1+uGH40pN9ejjj/dqypTBWrgwTFOmDJaf\nH/ucAQAAgMagqKhYbneuMjLyNXp0d7lcoXrhhdFq06aF09GAX0VZBNSj8+fLlJ6ep9TUXFVVWcXH\nhyk2Nlg9erR1OhoAAACAOnLrVqU2bNin1FSPtm8/qTlzxsjlClVYWG+GYqNBoiwC6lhVldU33xxW\namquvvzyoJ55ZoQWLgzTpEmclgAAAAA0NcePX9ZHH+3Shx/uUseOLRUfH6bo6EB17tza6WiAF2UR\nUEdOnbqqjz7aJbfbo/bt/bVwYZiiovglAAAAAOC/3lR2uz364osDmjFjuFyuUE2ePJDRFHAcZRFQ\niyoqqvTllwe1dGmutmw5qtmzRys+PkwREX14iggAAADALyopKVNmZoFSU3NVWlquBQtC9NJLIXro\nIQ69gTMoi4BacOTIJbnduVq2bJf69euo+PhQzZkToHbt/J2OBgAAAMBHWGuVk3NKbrdHq1fv1sSJ\n/eRyheqPfxyuFi2aOR0PTQhlEXCfbt2qVHb2Xi1dmqvc3NOKjg5UfHyYAgN7Oh0NAAAAgI8rKyvX\n2rVFSk3N1f79JYqJCZLLFaaRI7s5HQ1NAGURcI/27j2v1NT/Ov5y4cIwzZw5Sq1aNXc6GgAAAIBG\naP/+En34oUdpaXkaPLizXK5QvfjiGHYyoM5QFgE1UFZWrnXrirR0aXWr/9JLIXK5QjVsWFenowEA\nAABoIsrLK/X55wfkdnu0ZcsxzZo1Si5XmMaPf4gZqahVlEXAXVRVWX377VFlZOTpr3/dq4kT+2rh\nwjA9/TT7hQEAAAA46/Tpq0pLy5Pb7ZG/fzO5XKGKiQlS9+5tnY6GRoCyCLjDvn3nlZGRr4yMfHXs\n2FJxccGKigpU797tnY4GAAAAAP/CWqstW47J7fYoO3uvpkwZLJcrVE8+OUTNmvk5HQ8+irIIUPVR\nlStXFio9PV/Hjl1WVFSAYmODFRzcy+loAAAAAFAjly/f0IoVhXK7PTpz5prmzw/R/PkhGjSos9PR\n4GMoi9Bk3bxZoc8+O6CMjHz9/e+HNX36MMXGBmvKlMFq3pwGHgAAAIDvys8/K7c7V5mZBQoJ6SWX\nK1TPP8/BPKgZyiI0KdZabdt2UunpeVq9ercCA3sqNjZIL7wwWh06tHQ6HgAAAADUqhs3KpSdvVep\nqR55PKcVGRmg+PgwdlHgV1EWoUk4fPiili+vnkNkjFFsbJCio4M0cGAnp6MBAAAAQL04cuSSli3z\naNmyXerRo61crlBFRgaqU6dWTkdDA0NZhEbr8uUbWrOmSBkZ+SoqKtacOWMUExOkceM4VhIAAABA\n01VZWaWvv/5RbrdHGzce0h//OELx8aF67LEBvFaCJMoiNDIVFVXauPGQ0tPz9MUXB/X444MUGxus\n6dOHyd+f4+4BAAAA4OeKi0u1fHm+3G6Pbt6s1IIFIYqLC1GfPpwG3ZRRFsHnWWu1a9cZZWTkKyur\nQIMGdVZsbJBefHGMunZt43Q8AAAAAGjwrLXavv2k3G6P1q4t0iOP9JfLFaoZM4apRQveeG9qKIvg\ns06duqrMzHylp+fr6tWbio0N1rx5QRo+vKvT0QAAAADAZ5WW3tKaNUVKTc3VoUMXFRsbpAULQjVi\nRDeno6Ge+HxZ9NZbb2ny5MmaPHmy03FQD0pLb2n9+r1KT89TTs4pzZw5SrGxwZo0qb/8/NhbCwAA\nAAC1ae/e8/rwQ4/S0/M0bFhXuVyhmj17tNq29Xc6GurA5s2btXnzZv3pT3/y7bKoIeRA3aqsrNLm\nzUeUkZGv7Ox9evjhfoqJCdKzz45Q69YtnI4HAAAAAI1eeXmlPvvsgNxuj77//phmzRqt+PgwjR3b\nh6HYjZDPP1nUEHKgbhQVFSsjI0/LlxeoW7c2io0NUmRkoHr1aud0NAAAAABosk6evKK0tDx9+KFH\nrVu3kMsVqnnzgtStGzNjGwvKIjQoxcWlWrGiUOnpeTp16qrmzQtSTEyQAgN7Oh0NAAAAAPAzVVVW\n3357VG63Rxs27NOTTw6RyxWqKVMGq1kzP6fj4QFQFsFxN25U6NNP9ys9PU/ffntUf/zjCMXEBOnx\nxwdxgwEAAAAAH3Dp0g2tWFEgt9uj4uIyvfRSsGJjgzVkSBeno+E+UBbBEdZa/fDDcaWn52nt2j0K\nCeml2NggzZw5Su3bt3Q6HgAAAADgPu3adUbLlnm0YkWhRozopri4YM2ePVodO7ZyOhpqiLII9erg\nwQtavjxfGRn58vdvpri4YEVHB6pfv45ORwMAAAAA1KJbtyr15ZcHlZaWp02bftS0acMUFxesJ55g\nm1pDR1mEOldSUqbVq3crIyNfBw9e0Ny5AYqJCVJEBFPzAQAAAKApKCkp08qVhUpPz9fx45c1b16Q\nYmODFRDQw+lo+AWURagTN29W6LPPDigjI1/ffHNYU6cOVUxMkJ56aohatGjmdDwAAAAAgEP27ClW\nenqeMjLy1bNnO8XFBSsyMkDdu7d1OhpuoyxCrbHW6p//PKGMjDytWVOkgIAeiokJ0qxZ7E0FAAAA\nAPyrysoqffPNYaWl5enTT/dr8uSBiosL1owZw+Xvz0MGTqIswgP7aQ7R8uX5atGimWJighQdHagB\nAzo5HQ0AAAAA4AOuXLmpdeuKlJaWp927izVnzhjFxQUzvsQhlEW4LxcuXNeqVYXeOUSRkQGKiQlW\neHhv/kcGAAAAANy3w4cvKiMjX+nped6DkebNC9JDD3VwOlqTQVmEGmMOEQAAAACgvlhr9f33x5We\nnqe1a4sUEdFHcXHBev75UWrTpoXT8Ro1yiL8KuYQAQAAAACcdv16ubKz9yktLU9bt57QzJkjFRcX\nokmT+svPj90ttY2yCL+IOUQAAAAAgIbo1KmryszMV1pansrKyhUTE6TY2GANGdLF6WiNBmURvJhD\nBAAAAADwFdZaeTxnlJa2SytWFGrEiG6KiwvW7NnshHlQlEVN3M2bFfr88wNKT2cOEQAAAADAN926\nVakvvjigtLQ8bdp0WNOnD1NcXLCeeGKwmjXzczqez6EsaoKYQwQAAAAAaKxKSsq0cmWh0tLydOLE\nFc2bV71NLSCgh9PRfAZlURNy6NAFZWQwhwgAAAAA0DQUFRUrPT1Py5fnq2fPdoqLC1ZkZIC6d2/r\ndLQGjbKokWMOEQAAAACgqausrNI33xxWWlqePv10vyZPHqi4uGDNmDFc/v6MYLkTZVEj9NMcooyM\nfG3axBwiAAAAAAB+cuXKTa1dW6S0tDwVFRVrzpwxiosLVkREHx6quI2yqJFgDhEAAAAAAPfm8OGL\nysjIV3p6npo391NUVKCiogI1dGgXp6M5irLIx+3fX6KsrALmEAEAAAAAcJ+stdq27aQyM/O1enWR\nBg7spOjoQM2ZM0Y9e7ZzOl69oyzyQadOXdWqVYXKyirUiRNX9OKLo5lDBAAAAABALaioqNLXX/+o\nrKwCffLJPo0f31fR0YF67rmR6tChpdPx6gVlkY+4dOmG/vrXPcrMLJDHc1rPPTdSUVGBmjx5oJo3\n93M6HgAAAAAAjU5ZWbk2bNinzMwC/eMfRzV16lBFRQVo6tShatmyudPx6gxlUQN2/Xq5PvvsgLKy\nCrRp02FNmTJYUVEBmj59mFq3buF0PAAAAAAAmoySkjKtW1f9EEdh4Tm98MIoRUUF6rHHBsjPr3Ht\n8qEsamAqKqqP88vKKlB29j6Fh/dWdHSgnn9+lDp1YlA1AAAAAABOO378slasKFRWVoFKSq5r7twx\nio4OUnBwz0YxHoayqAGw1mr79pPKyirQqlW71b9/R0VFVQ/S6t27vdPxAAAAAADAXezefU5ZWQXK\nyipU69bNFR0dqMjIQA0e3NnpaPeNsshBe/YUe/+Dqj6iL0BRUYEaNqyr09EAAAAAAMA9sNbqn/88\noczMfK1ZU6ShQ7soKipQL744Rj16tHU63j2hLKpnJ05c0cqV1Y+qnT1bqrlzxygqKlBhYZxkBgAA\nAABAY1BeXqmvvqo+Ue3TT/dr4sR+io4O1LPPjlD79g3/RDXKonpw4cJ1rVtXpMzMAuXnn9XMmdVD\nsH73uwFq1oyTzAAAAAAAaKxKS2/pk0+qT1T77rtjmjZtmKKiAvTUU0Pl79/M6Xi/iLKojvx0vF5W\nVqE2bz6ip54aoqioQE2b1riP1wMAAAAAAL/s/PkyrVmzW1lZhdqzp1izZo1WdHSgHnmkf4M6UY2y\nqBaVl1dq06bDysws0IYN+zR+fF9FRQXo+edHqUOHhv+YGQAAAAAAqB9Hj17SihWFysws0JUrNxUZ\nWT3HOCiop9PRKIse1E8DrLKyCrR69W4NHtxZ0dHVA6x69mznaDYAAAAAANDwFRScVWZmgVasKFSH\nDi0VFRWgyMhADRzYyZE8lEX3affuc96/yFatfjoaL0BDhnRxJA8AAAAAAPBtVVVWP/xwXJmZ+Vq7\ndo9GjOiq6OhAzZ49Rt26tam3HJRF9+Do0Uu3TzIrVElJmSIjAxQdHaTg4J6cZAYAAAAAAGrNrVuV\n2rjxkLKyCvT55wc0aVJ/RUVVn6jWtq1/nf5syqLfcP58mdaurT7JrKioWLNmVZ9k9uijAxrU8CkA\nAAAAANA4Xbt2S9nZe5WZWaAffjiuGTOGKzo6UE89NaROTlmnLPoFpaW3lJ29T1lZBdqy5ZimTRt6\n+y+h4R5rBwAAAAAAGr/i4lKtWVOkL788qPXr51AW/VuIOiiLsrP3Ki7uYz38cD/v413t23OSGQAA\nAAAAaBooi+5w4cJ1VVRUqUePtrX6fQEAAAAAAHwBZREAAAAAAAC87rcsqv0NcQAAAAAAAPBZlEUA\nAAAAAADwoiwCAAAAAACAF2URAAAAAAAAvCiLAAAAAAAA4EVZBAAAAAAAAC/KIgAAAAAAAHhRFgEA\nAAAAAMCLsggAAAAAAABelEUAAAAAAADwoiwCAAAAAACAF2URAAAAAAAAvCiLAAAAAAAA4EVZBAAA\nAAAAAC/KIgAAAAAAAHhRFgEAAAAAAMCLsggAAAAAAABelEUAAAAAAADwoiwCAAAAAACAF2URAAAA\nAAAAvCiLAAAAAAAA4EVZBAAAAAAAAC/KIgAAAAAAAHhRFgEAAAAAAMCLsggAAAAAAABelEUAAAAA\nAADwoiwCAAAAAACAF2URAAAAAAAAvCiLAAAAAAAA4EVZBAAAAAAAAC/KIgAAAAAAAHhRFgEAAAAA\nAMCLsggAAAAAAABelEUAAAAAAADwoiwCAAAAAACAF2URAAAAAAAAvCiLAAAAAAAA4EVZBAAAAAAA\nAK86LYuMMYOMManGmNV1+XMAAAAAAABQO+q0LLLWHrbWxtflzwCAu9m8ebPTEQA0QtxbANQF7i0A\nGpIalUXGGLcx5qwxJv+Or081xuw1xuw3xvzPuokIAPeHRReAusC9BUBd4N4CoCGp6ZNFyyQ99fMv\nGGP8JL13++tjJEUaY0be/rMYY8z/M8b0/unyWsoLAAAAAACAOlSjssha+52ki3d8eZykA9bao9ba\nckkrJT17+/oMa+1/k3TTGJMsKYQnjwAAAAAAABo+Y62t2YXGDJC0wVobdPvzFyQ9Za1ddPvzeZLG\nWWtfu+cQxtQsBAAAAAAAAGrMWnvPu72a10WQe3U/wQEAAAAAAFD7HuQ0tJOS+v/s8763vwYAAAAA\nAAAfdS9lkdG/DqreIWmoMWaAMcZf0lxJn9RmOAAAAAAAANSvGpVFxpgsST9IGm6MOWaMmW+trZT0\nqqSNknZLWmmt3VPD7zfLGFNojKk0xoT9ynVTjTF7jTH7GZAN4LcYYzobYzYaY/YZY/5mjOl4l+uO\nGGPyjDEeY8z2+s4JoOGryRrEGPNnY8wBY8wuY0xIfWcE4Ht+695ijPmdMeaSMSb39j//x4mcAHyL\nMcZtjDlrjMn/lWvuad1S4wHXtckYM0JSlaQUSf/DWpv7C9f4Sdov6XFJp1T9JNNca+3e+swKwHcY\nY/5TUom19v/eXoB1ttb+r1+47kdJ4dbaO095BIAarUGMMdMkvWKtnWGMGS/pHWvtBEcCA/AJNby3\n/E7Sf7fWPuNMSgC+yBgzSdI1Sek/HUp2x5/f87rlQWYW3Tdr7T5r7QH967a2O42TdMBae9RaWy5p\npaRn6yUgAF/1rKS02x+nSXruLtcZOXT/A+ATarIGeVZSuiRZa7dJ6miM6Vm/MQH4mJq+vuHwHwD3\nxFr7naRfeyP8ntctDfnF0kOSjv/s8xO3vwYAd9PDWntWkqy1ZyT1uMt1VtJXxpgdxpiF9ZYOgK+o\nyRrkzmtO/sI1APBzNX19M/H2NpHPjDGj6ycagEbuntctzesqiTHmK0k/b6qMql+g/W9r7Ya6+rkA\nGrdfubf80p7+u+2zfcRae9oY013VpdGe2208AACAk3ZK6m+tLbu9beRjScMdzgSgCaqzssha+8QD\nfouTkvr/7PO+t78GoAn7tXvL7aFuPa21Z40xvSSdu8v3OH3738XGmPWqfiycsgjAT2qyBjkpqd9v\nXAMAP/eb9xZr7bWfffyFMSbJGNPFWnuhnjICaJzued3SELah3W1P7g5JQ40xA4wx/pLmSvqk/mIB\n8EGfSHrp9sdxkrLvvMAY08YY0+72x20lPSmpsL4CAvAJNVmDfCIpVpKMMRMkXfppGywA3MVv3lt+\nPkPEGDNO1QcSURQBqAmju/cr97xuqbMni36NMeY5Se9K6ibpU2PMLmvtNGNMb0lLrbVPW2srjTGv\nSNqo6lLLba3d40ReAD7jPyWtNsYskHRU0ouS9PN7i6q3sK03xlhV3wMzrbUbnQoMoOG52xrEGJNQ\n/cf2A2vt58aY6caYg5JKJc13MjOAhq8m9xZJs4wxiyWVS7ouaY5ziQH4CmNMlqTJkroaY45JekuS\nvx5g3WKsvdtIDwAAAAAAADQ1DWEbGgAAAAAAABoIyiIAAAAAAAB4URYBAAAAAADAi7IIAAAAAAAA\nXpRFAAAAAAAA8KIsAgAAAAAAgBdlEQAAAAAAALwoiwAAAAAAAOD1/wEO8/ckNbXkVgAAAABJRU5E\nrkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1bb8cf18c18>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(20,10))\n",
"histo, edges = np.histogram(convs, bins=25, range=(-1,1), density=True)\n",
"centers = [(edges[kk]+edges[kk+1])/2 for kk in range(len(edges)-1)]\n",
"plt.plot(centers, histo, color=(0,0,0.5))\n",
"plt.yscale('log')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
jakevdp/nfft | notebooks/NFFTBasicUsage.ipynb | 1 | 8317 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# NFFT Package\n",
"\n",
"The ``nfft`` package is a lightweight implementation of the non-equispaced\n",
"fast Fourier transform (NFFT), based on numpy and scipy and released under\n",
"an MIT license.\n",
"\n",
"The NFFT is described in *Using NFFT 3 – a software library for various nonequispaced\n",
"fast Fourier transforms* ([pdf](https://www-user.tu-chemnitz.de/~potts/paper/nfft3.pdf)), which describes a C library that computes the NFFT and several variants and extensions."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Included Algorithms\n",
"\n",
"The ``nfft`` package currently implements only a few of the algorithms described in the above paper, in particular:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### The one-dimensional forward NDFT and NFFT\n",
"\n",
"The forward transform is given by\n",
"\n",
"$$\n",
"f_j = \\sum_{k=-N/2}^{N/2-1} \\hat{f}_k e^{-2\\pi i k x_j}\n",
"$$\n",
"\n",
"for complex amplitudes $\\{f_k\\}$ specified at the range of integer wavenumbers $k$ in the range $-N/2 \\le k < N$, evaluated at points $\\{x_j\\}$ satisfying $-1/2 \\le x_j < 1/2$.\n",
"\n",
"This can be computed via the ``nfft.ndft()`` and ``nfft.nfft()`` functions, respectively.\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### The one-dimensional adjoint NDFT and NFFT\n",
"\n",
"The adjoint transform is given by\n",
"\n",
"$$\n",
"\\hat{f}_k = \\sum_{j=0}^{M-1} f_j e^{2\\pi i k x_j}\n",
"$$\n",
"\n",
"for complex values $\\{f_j\\}$ at points $\\{x_j\\}$ satisfying $-1/2 \\le x_j < 1/2$,\n",
"and for the range of integer wavenumbers $k$ in the range $-N/2 \\le k < N$.\n",
"\n",
"This can be computed via the ``nfft.ndft_adjoint()`` and ``nfft.nfft_adjoint()`` functions, respectively."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Complexity\n",
"\n",
"The computational complexity of both the forward and adjoint algorithm is approximately\n",
"\n",
"$$\n",
"\\mathcal{O}[N\\log(N) + M\\log(1 / \\epsilon)]\n",
"$$\n",
"\n",
"where $\\epsilon$ is the desired tolerance of the result.\n",
"In the current implementation, the memory requirements are approximately\n",
"\n",
"$$\n",
"\\mathcal{O}[N + M\\log(1 / \\epsilon)]\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Comparison to pynfft\n",
"\n",
"Another option for computing the NFFT in Python is to use the [pynfft](https://github.com/ghisvail/pyNFFT/) package, which wraps the C library referenced in the above paper.\n",
"The advantage of ``pynfft`` is that it provides a more complete set of routines, including multi-dimensional NFFTs and various computing strategies.\n",
"\n",
"The disadvantage is that ``pynfft`` is GPL-licensed, and has a more complicated set of dependencies.\n",
"\n",
"Performance-wise, ``nfft`` and ``pynfft`` are comparable, with the ``nfft`` package discussed here being up to a factor of 2 faster in most cases of interest (see [Benchmarks.ipynb](Benchmarks.ipynb) for some benchmarks)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Installation\n",
"\n",
"The ``nfft`` package can be installded directly from the Python Package Index:\n",
"\n",
"```\n",
"$ pip install nfft\n",
"```\n",
"\n",
"Dependencies are [numpy](http://www.numpy.org), [scipy](http://www.scipy.org), and [pytest](http://www.pytest.org)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Testing\n",
"\n",
"Unit tests can be run using [pytest](http://pytest.org):\n",
"\n",
"```\n",
"$ pytest --pyargs nfft\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Usage"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here are some examples of computing the NFFT and its adjoint, using both a direct method and the fast method:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Forward Transform\n",
"\n",
"$$\n",
"f_j = \\sum_{j=0}^{M-1} \\hat{f}_k e^{-2\\pi i k x_j}, \n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import nfft"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# define evaluation points\n",
"x = -0.5 + np.random.rand(1000)\n",
"\n",
"# define Fourier coefficients\n",
"N = 10000\n",
"k = N // 2 + np.arange(N)\n",
"f_k = np.random.randn(N)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 401 ms, sys: 120 ms, total: 521 ms\n",
"Wall time: 505 ms\n"
]
}
],
"source": [
"# direct Fourier transform\n",
"%time f_x_direct = nfft.ndft(x, f_k)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 10 ms, sys: 2.11 ms, total: 12.1 ms\n",
"Wall time: 7.02 ms\n"
]
}
],
"source": [
"# fast Fourier transform\n",
"%time f_x_fast = nfft.nfft(x, f_k)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Compare the results\n",
"np.allclose(f_x_direct, f_x_fast)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adjoint Transform\n",
"\n",
"$$\n",
"\\hat{f}_k = \\sum_{j=0}^{M-1} f_j e^{2\\pi i k x_j}, \n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# define observations\n",
"\n",
"f = np.random.rand(len(x))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 473 ms, sys: 116 ms, total: 590 ms\n",
"Wall time: 450 ms\n"
]
}
],
"source": [
"# direct adjoint transform\n",
"%time f_k_direct = nfft.ndft_adjoint(x, f, N)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 7.75 ms, sys: 1.56 ms, total: 9.3 ms\n",
"Wall time: 4.94 ms\n"
]
}
],
"source": [
"# fast adjoint transform\n",
"%time f_k_fast = nfft.nfft_adjoint(x, f, N)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Compare the results\n",
"np.allclose(f_k_direct, f_k_fast)"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3.6",
"language": "python",
"name": "python3.6"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
classgrade/classgrade | classgrade/test_files/assignment.ipynb | 1 | 708 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Test assignment..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"test = 2 + 3"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
arsenovic/galgebra | examples/ipython/colored_christoffel_symbols.ipynb | 1 | 16904 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This example is kindly contributed by [FreddyBaudine](https://github.com/FreddyBaudine) for reproducing [pygae/galgebra#26](https://github.com/pygae/galgebra/issues/26) and [pygae/galgebra#30](https://github.com/pygae/galgebra/issues/30) with modifications by [utensil](https://github.com/utensil).\n",
"\n",
"Please note before Python code, there's an invisible markdown cell with the following code to enable `color` and define some colors from http://latexcolor.com/:\n",
"\n",
"```markdown\n",
"$$\n",
"\\require{color}\n",
"\\definecolor{airforceblue}{rgb}{0.36, 0.54, 0.66}\n",
"\\definecolor{applegreen}{rgb}{0.55, 0.71, 0.0}\n",
"\\definecolor{atomictangerine}{rgb}{1.0, 0.6, 0.4}\n",
"$$\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$\n",
"\\require{color}\n",
"\\definecolor{airforceblue}{rgb}{0.36, 0.54, 0.66}\n",
"\\definecolor{applegreen}{rgb}{0.55, 0.71, 0.0}\n",
"\\definecolor{atomictangerine}{rgb}{1.0, 0.6, 0.4}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"from __future__ import print_function\n",
"import sys\n",
"from galgebra.printer import Format, xpdf\n",
"Format()\n",
"from sympy import symbols, sin, pi, latex, Array, permutedims\n",
"from galgebra.ga import Ga"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"from IPython.display import Math"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Base manifold (three dimensional)\n",
"## Metric tensor (cartesian coordinates - norm = False)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"from sympy import cos, sin, symbols\n",
"g3coords = (x,y,z) = symbols('x y z')\n",
"g3 = Ga('ex ey ez', g = [1,1,1], coords = g3coords,norm=False) # Create g3\n",
"(e_x,e_y,e_z) = g3.mv()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle g =\\left[\\begin{matrix}1 & 0 & 0\\\\0 & 1 & 0\\\\0 & 0 & 1\\end{matrix}\\right]$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'g =%s' % latex(g3.g))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Two dimensioanal submanifold - Unit sphere\n",
"\n",
"Basis not normalised"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"sp2coords = (theta, phi) = symbols(r'{\\color{airforceblue}\\theta} {\\color{applegreen}\\phi}', real = True)\n",
"sp2param = [sin(theta)*cos(phi), sin(theta)*sin(phi), cos(theta)]\n",
"\n",
"sp2 = g3.sm(sp2param, sp2coords, norm = False) # submanifold\n",
"\n",
"(etheta, ephi) = sp2.mv() # sp2 basis vectors\n",
"(rtheta, rphi) = sp2.mvr() # sp2 reciprocal basis vectors\n",
"\n",
"sp2grad = sp2.grad\n",
"\n",
"sph_map = [1, theta, phi] # Coordinate map for sphere of r = 1"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle (\\theta,\\phi)\\rightarrow (r,\\theta,\\phi) = \\left[ 1, \\ {\\color{airforceblue}\\theta}, \\ {\\color{applegreen}\\phi}\\right]$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'(\\theta,\\phi)\\rightarrow (r,\\theta,\\phi) = %s' % latex(sph_map))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle e_\\theta \\cdot e_\\theta = 1$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'e_\\theta \\cdot e_\\theta = %s' % (etheta|etheta))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle e_\\phi \\cdot e_\\phi = {\\sin{\\left ({\\color{airforceblue}\\theta} \\right )}}^{2}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'e_\\phi \\cdot e_\\phi = %s' % (ephi|ephi))"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle g = \\left[\\begin{matrix}1 & 0\\\\0 & \\sin^{2}{\\left({\\color{airforceblue}\\theta} \\right)}\\end{matrix}\\right]$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math('g = %s' % latex(sp2.g))"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle g^{-1} = \\left[\\begin{matrix}1 & 0\\\\0 & \\frac{1}{\\sin^{2}{\\left({\\color{airforceblue}\\theta} \\right)}}\\end{matrix}\\right]$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'g^{-1} = %s' % latex(sp2.g_inv))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Christoffel symbols of the first kind: "
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"Cf1 = sp2.Christoffel_symbols(mode=1)\n",
"Cf1 = permutedims(Array(Cf1), (2, 0, 1))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\Gamma_{1, \\alpha, \\beta} = \\left[\\begin{matrix}0 & 0\\\\0 & - \\frac{\\sin{\\left(2 {\\color{airforceblue}\\theta} \\right)}}{2}\\end{matrix}\\right] \\quad \\Gamma_{2, \\alpha, \\beta} = \\left[\\begin{matrix}0 & \\frac{\\sin{\\left(2 {\\color{airforceblue}\\theta} \\right)}}{2}\\\\\\frac{\\sin{\\left(2 {\\color{airforceblue}\\theta} \\right)}}{2} & 0\\end{matrix}\\right] $"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\Gamma_{1, \\alpha, \\beta} = %s \\quad \\Gamma_{2, \\alpha, \\beta} = %s ' % (latex(Cf1[0, :, :]), latex(Cf1[1, :, :])))"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"Cf2 = sp2.Christoffel_symbols(mode=2)\n",
"Cf2 = permutedims(Array(Cf2), (2, 0, 1))"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\Gamma^{1}_{\\phantom{1,}\\alpha, \\beta} = \\left[\\begin{matrix}0 & 0\\\\0 & - \\frac{\\sin{\\left(2 {\\color{airforceblue}\\theta} \\right)}}{2}\\end{matrix}\\right] \\quad \\Gamma^{2}_{\\phantom{2,}\\alpha, \\beta} = \\left[\\begin{matrix}0 & \\frac{1}{\\tan{\\left({\\color{airforceblue}\\theta} \\right)}}\\\\\\frac{1}{\\tan{\\left({\\color{airforceblue}\\theta} \\right)}} & 0\\end{matrix}\\right] $"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\Gamma^{1}_{\\phantom{1,}\\alpha, \\beta} = %s \\quad \\Gamma^{2}_{\\phantom{2,}\\alpha, \\beta} = %s ' % (latex(Cf2[0, :, :]), latex(Cf2[1, :, :])))"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"F = sp2.mv('F','vector',f=True) #scalar function\n",
"f = sp2.mv('f','scalar',f=True) #vector function"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\nabla = \\boldsymbol{e}_{{\\color{airforceblue}\\theta}} \\frac{\\partial}{\\partial {\\color{airforceblue}\\theta}} + \\boldsymbol{e}_{{\\color{applegreen}\\phi}} \\frac{1}{{\\sin{\\left ({\\color{airforceblue}\\theta} \\right )}}^{2}} \\frac{\\partial}{\\partial {\\color{applegreen}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\nabla = %s' % sp2grad)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\nabla f = \\partial_{{\\color{airforceblue}\\theta}} f \\boldsymbol{e}_{{\\color{airforceblue}\\theta}} + \\frac{\\partial_{{\\color{applegreen}\\phi}} f }{{\\sin{\\left ({\\color{airforceblue}\\theta} \\right )}}^{2}} \\boldsymbol{e}_{{\\color{applegreen}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\nabla f = %s' % (sp2.grad * f))"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle F = F^{{\\color{airforceblue}\\theta}} \\boldsymbol{e}_{{\\color{airforceblue}\\theta}} + F^{{\\color{applegreen}\\phi}} \\boldsymbol{e}_{{\\color{applegreen}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'F = %s' % F)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\nabla F = \\left ( \\frac{F^{{\\color{airforceblue}\\theta}} }{\\tan{\\left ({\\color{airforceblue}\\theta} \\right )}} + \\partial_{{\\color{airforceblue}\\theta}} F^{{\\color{airforceblue}\\theta}} + \\partial_{{\\color{applegreen}\\phi}} F^{{\\color{applegreen}\\phi}} \\right ) + \\left ( \\frac{2 F^{{\\color{applegreen}\\phi}} }{\\tan{\\left ({\\color{airforceblue}\\theta} \\right )}} + \\partial_{{\\color{airforceblue}\\theta}} F^{{\\color{applegreen}\\phi}} - \\frac{\\partial_{{\\color{applegreen}\\phi}} F^{{\\color{airforceblue}\\theta}} }{{\\sin{\\left ({\\color{airforceblue}\\theta} \\right )}}^{2}}\\right ) \\boldsymbol{e}_{{\\color{airforceblue}\\theta}}\\wedge \\boldsymbol{e}_{{\\color{applegreen}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\nabla F = %s' % (sp2.grad * F))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# One dimensioanal submanifold\n",
"\n",
"Basis not normalised"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"cir_th = phi = symbols(r'{\\color{atomictangerine}\\phi}',real = True)\n",
"cir_map = [pi/8, phi]"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle (\\phi)\\rightarrow (\\theta,\\phi) = \\left[ \\frac{\\pi}{8}, \\ {\\color{atomictangerine}\\phi}\\right]$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'(\\phi)\\rightarrow (\\theta,\\phi) = %s' % latex(cir_map))"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [],
"source": [
"cir1d = sp2.sm( cir_map , (cir_th,), norm = False) # submanifold\n",
"\n",
"cir1dgrad = cir1d.grad\n",
"\n",
"(ephi) = cir1d.mv()"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle e_\\phi \\cdot e_\\phi = \\frac{1}{2} - \\frac{\\sqrt{2}}{4}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'e_\\phi \\cdot e_\\phi = %s' % latex(ephi[0] | ephi[0]))"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle g = \\left[\\begin{matrix}\\frac{1}{2} - \\frac{\\sqrt{2}}{4}\\end{matrix}\\right]$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math('g = %s' % latex(cir1d.g))"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [],
"source": [
"h = cir1d.mv('h','scalar',f= True)\n",
"\n",
"H = cir1d.mv('H','vector',f= True)"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\nabla = \\boldsymbol{e}_{{\\color{atomictangerine}\\phi}} \\left ( 2 \\sqrt{2} + 4\\right ) \\frac{\\partial}{\\partial {\\color{atomictangerine}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\nabla = %s' % cir1dgrad)"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\nabla h = \\left(2 \\sqrt{2} + 4\\right) \\partial_{{\\color{atomictangerine}\\phi}} h \\boldsymbol{e}_{{\\color{atomictangerine}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\nabla h = %s' %(cir1d.grad * h).simplify())"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle H = H^{{\\color{atomictangerine}\\phi}} \\boldsymbol{e}_{{\\color{atomictangerine}\\phi}}$"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math('H = %s' % H)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"data": {
"text/latex": [
"$\\displaystyle \\nabla H = \\partial_{{\\color{atomictangerine}\\phi}} H^{{\\color{atomictangerine}\\phi}} $"
],
"text/plain": [
"<IPython.core.display.Math object>"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Math(r'\\nabla H = %s' % (cir1d.grad * H).simplify())"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
ivanslapnicar/GIAN-Applied-NLA-Course | src/Module C - Applications/L13 Sparse plus Low-Rank Splitting.ipynb | 1 | 5207833 | null | mit |
pdoehle/fekete | firstdraftprogs/maximumplots.ipynb | 1 | 718 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
kialio/gsfcpyboot | Day_01/01_Pandas/1. Introduction to Pandas.ipynb | 2 | 66381 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Introduction to Pandas\n",
"\n",
"**pandas** is a Python package providing fast, flexible, and expressive data structures designed to work with *relational* or *labeled* data both. It is a fundamental high-level building block for doing practical, real world data analysis in Python. \n",
"\n",
"pandas is well suited for:\n",
"\n",
"- Tabular data with heterogeneously-typed columns, as in an SQL table or Excel spreadsheet\n",
"- Ordered and unordered (not necessarily fixed-frequency) time series data.\n",
"- Arbitrary matrix data (homogeneously typed or heterogeneous) with row and column labels\n",
"- Any other form of observational / statistical data sets. The data actually need not be labeled at all to be placed into a pandas data structure\n",
"\n",
"\n",
"Key features:\n",
" \n",
"- Easy handling of **missing data**\n",
"- **Size mutability**: columns can be inserted and deleted from DataFrame and higher dimensional objects\n",
"- Automatic and explicit **data alignment**: objects can be explicitly aligned to a set of labels, or the data can be aligned automatically\n",
"- Powerful, flexible **group by functionality** to perform split-apply-combine operations on data sets\n",
"- Intelligent label-based **slicing, fancy indexing, and subsetting** of large data sets\n",
"- Intuitive **merging and joining** data sets\n",
"- Flexible **reshaping and pivoting** of data sets\n",
"- **Hierarchical labeling** of axes\n",
"- Robust **IO tools** for loading data from flat files, Excel files, databases, and HDF5\n",
"- **Time series functionality**: date range generation and frequency conversion, moving window statistics, moving window linear regressions, date shifting and lagging, etc."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<iframe src=http://pandas.pydata.org width=800 height=350></iframe>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from IPython.core.display import HTML\n",
"HTML(\"<iframe src=http://pandas.pydata.org width=800 height=350></iframe>\")"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/site-packages/pandas/io/excel.py:626: UserWarning: Installed openpyxl is not supported at this time. Use >=1.6.1 and <2.0.0.\n",
" .format(openpyxl_compat.start_ver, openpyxl_compat.stop_ver))\n"
]
}
],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"\n",
"# Set some Pandas options\n",
"pd.set_option('html', False)\n",
"pd.set_option('max_columns', 30)\n",
"pd.set_option('max_rows', 20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Pandas Data Structures"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Series\n",
"\n",
"A **Series** is a single vector of data (like a NumPy array) with an *index* that labels each element in the vector."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0 632\n",
"1 1638\n",
"2 569\n",
"3 115\n",
"dtype: int64"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"counts = pd.Series([632, 1638, 569, 115])\n",
"counts"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If an index is not specified, a default sequence of integers is assigned as the index. A NumPy array comprises the values of the `Series`, while the index is a pandas `Index` object."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 632, 1638, 569, 115])"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"counts.values"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Int64Index([0, 1, 2, 3], dtype='int64')"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"counts.index"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can assign meaningful labels to the index, if they are available:"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Firmicutes 632\n",
"Proteobacteria 1638\n",
"Actinobacteria 569\n",
"Bacteroidetes 115\n",
"dtype: int64"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"bacteria = pd.Series([632, 1638, 569, 115], \n",
" index=['Firmicutes', 'Proteobacteria', 'Actinobacteria', 'Bacteroidetes'])\n",
"\n",
"bacteria"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These labels can be used to refer to the values in the `Series`."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"569"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"bacteria['Actinobacteria']"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Proteobacteria 1638\n",
"Actinobacteria 569\n",
"dtype: int64"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"bacteria[[name.endswith('bacteria') for name in bacteria.index]]"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[False, True, True, False]"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"[name.endswith('bacteria') for name in bacteria.index]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that the indexing operation preserved the association between the values and the corresponding indices.\n",
"\n",
"We can still use positional indexing if we wish."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"632"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"bacteria[0]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can give both the array of values and the index meaningful labels themselves:"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"phylum\n",
"Firmicutes 632\n",
"Proteobacteria 1638\n",
"Actinobacteria 569\n",
"Bacteroidetes 115\n",
"Name: counts, dtype: int64"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"bacteria.name = 'counts'\n",
"bacteria.index.name = 'phylum'\n",
"bacteria"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"NumPy's math functions and other operations can be applied to Series without losing the data structure."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"phylum\n",
"Firmicutes 6.448889\n",
"Proteobacteria 7.401231\n",
"Actinobacteria 6.343880\n",
"Bacteroidetes 4.744932\n",
"Name: counts, dtype: float64"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.log(bacteria)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also filter according to the values in the `Series`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria[bacteria>1000]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A `Series` can be thought of as an ordered key-value store. In fact, we can create one from a `dict`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria_dict = {'Firmicutes': 632, 'Proteobacteria': 1638, 'Actinobacteria': 569, 'Bacteroidetes': 115}\n",
"pd.Series(bacteria_dict)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that the `Series` is created in key-sorted order.\n",
"\n",
"If we pass a custom index to `Series`, it will select the corresponding values from the dict, and treat indices without corrsponding values as missing. Pandas uses the `NaN` (not a number) type for missing values."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2 = pd.Series(bacteria_dict, index=['Cyanobacteria','Firmicutes','Proteobacteria','Actinobacteria'])\n",
"bacteria2"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.isnull()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Critically, the labels are used to **align data** when used in operations with other Series objects:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria + bacteria2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Contrast this with NumPy arrays, where arrays of the same length will combine values element-wise; adding Series combined values with the same label in the resulting series. Notice also that the missing values were propogated by addition."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### DataFrame\n",
"\n",
"Inevitably, we want to be able to store, view and manipulate data that is *multivariate*, where for every index there are multiple fields or columns of data, often of varying data type.\n",
"\n",
"A `DataFrame` is a tabular data structure, encapsulating multiple series like columns in a spreadsheet. Data are stored internally as a 2-dimensional object, but the `DataFrame` allows us to represent and manipulate higher-dimensional data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data = pd.DataFrame({'value':[632, 1638, 569, 115, 433, 1130, 754, 555],\n",
" 'patient':[1, 1, 1, 1, 2, 2, 2, 2],\n",
" 'phylum':['Firmicutes', 'Proteobacteria', 'Actinobacteria', \n",
" 'Bacteroidetes', 'Firmicutes', 'Proteobacteria', 'Actinobacteria', 'Bacteroidetes']})\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice the `DataFrame` is sorted by column name. We can change the order by indexing them in the order we desire:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"newdata = data[['phylum','value','patient']]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"newdata"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A `DataFrame` has a second index, representing the columns:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.columns"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"newdata.columns"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If we wish to access columns, we can do so either by dict-like indexing or by attribute:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data['value']"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.value"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"type(data.value)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"type(data[['value']])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice this is different than with `Series`, where dict-like indexing retrieved a particular element (row). If we want access to a row in a `DataFrame`, we index its `ix` attribute.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.ix[3]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Alternatively, we can create a `DataFrame` with a dict of dicts:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data = pd.DataFrame({0: {'patient': 1, 'phylum': 'Firmicutes', 'value': 632},\n",
" 1: {'patient': 1, 'phylum': 'Proteobacteria', 'value': 1638},\n",
" 2: {'patient': 1, 'phylum': 'Actinobacteria', 'value': 569},\n",
" 3: {'patient': 1, 'phylum': 'Bacteroidetes', 'value': 115},\n",
" 4: {'patient': 2, 'phylum': 'Firmicutes', 'value': 433},\n",
" 5: {'patient': 2, 'phylum': 'Proteobacteria', 'value': 1130},\n",
" 6: {'patient': 2, 'phylum': 'Actinobacteria', 'value': 754},\n",
" 7: {'patient': 2, 'phylum': 'Bacteroidetes', 'value': 555}})"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We probably want this transposed:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data = data.T\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Its important to note that the Series returned when a DataFrame is indexted is merely a **view** on the DataFrame, and not a copy of the data itself. So you must be cautious when manipulating this data:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"vals = data.value\n",
"vals"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"vals[5] = 0\n",
"vals"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"vals = data.value.copy()\n",
"vals[5] = 1000\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can create or modify columns by assignment:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.value[3] = 14\n",
"data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data['year'] = 2013\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But note, we cannot use the attribute indexing method to add a new column:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.treatment = 1\n",
"data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.treatment"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Specifying a `Series` as a new columns cause its values to be added according to the `DataFrame`'s index:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"treatment = pd.Series([0]*4 + [1]*2)\n",
"treatment"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data['treatment'] = treatment\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Other Python data structures (ones without an index) need to be the same length as the `DataFrame`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"month = ['Jan', 'Feb', 'Mar', 'Apr']\n",
"data['month'] = month"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data['month'] = ['Jan']*len(data)\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can use `del` to remove columns, in the same way `dict` entries can be removed:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"del data['month']\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can extract the underlying data as a simple `ndarray` by accessing the `values` attribute:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.values"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that because of the mix of string and integer (and `NaN`) values, the dtype of the array is `object`. The dtype will automatically be chosen to be as general as needed to accomodate all the columns."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"df = pd.DataFrame({'foo': [1,2,3], 'bar':[0.4, -1.0, 4.5]})\n",
"df.values"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Pandas uses a custom data structure to represent the indices of Series and DataFrames."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.index"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Index objects are immutable:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.index[0] = 15"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is so that Index objects can be shared between data structures without fear that they will be changed."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.index = bacteria.index"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Importing data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A key, but often under-appreciated, step in data analysis is importing the data that we wish to analyze. Though it is easy to load basic data structures into Python using built-in tools or those provided by packages like NumPy, it is non-trivial to import structured data well, and to easily convert this input into a robust data structure:\n",
"\n",
" genes = np.loadtxt(\"genes.csv\", delimiter=\",\", dtype=[('gene', '|S10'), ('value', '<f4')])\n",
"\n",
"Pandas provides a convenient set of functions for importing tabular data in a number of formats directly into a `DataFrame` object. These functions include a slew of options to perform type inference, indexing, parsing, iterating and cleaning automatically as data are imported."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's start with some more bacteria data, stored in csv format."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"!cat data/microbiome.csv"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This table can be read into a DataFrame using `read_csv`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb = pd.read_csv(\"data/microbiome.csv\")\n",
"mb"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that `read_csv` automatically considered the first row in the file to be a header row.\n",
"\n",
"We can override default behavior by customizing some the arguments, like `header`, `names` or `index_col`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.read_csv(\"data/microbiome.csv\", header=None).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`read_csv` is just a convenience function for `read_table`, since csv is such a common format:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb = pd.read_table(\"data/microbiome.csv\", sep=',')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `sep` argument can be customized as needed to accomodate arbitrary separators. For example, we can use a regular expression to define a variable amount of whitespace, which is unfortunately very common in some data formats: \n",
" \n",
" sep='\\s+'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For a more useful index, we can specify the first two columns, which together provide a unique index to the data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb = pd.read_csv(\"data/microbiome.csv\", index_col=['Taxon','Patient'])\n",
"mb.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is called a *hierarchical* index, which we will revisit later in the tutorial."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If we have sections of data that we do not wish to import (for example, known bad data), we can populate the `skiprows` argument:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.read_csv(\"data/microbiome.csv\", skiprows=[3,4,6]).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Conversely, if we only want to import a small number of rows from, say, a very large data file we can use `nrows`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.read_csv(\"data/microbiome.csv\", nrows=4)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Alternately, if we want to process our data in reasonable chunks, the `chunksize` argument will return an iterable object that can be employed in a data processing loop. For example, our microbiome data are organized by bacterial phylum, with 15 patients represented in each:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data_chunks = pd.read_csv(\"data/microbiome.csv\", chunksize=15)\n",
"\n",
"mean_tissue = {chunk.Taxon[0]:chunk.Tissue.mean() for chunk in data_chunks}\n",
" \n",
"mean_tissue"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Most real-world data is incomplete, with values missing due to incomplete observation, data entry or transcription error, or other reasons. Pandas will automatically recognize and parse common missing data indicators, including `NA` and `NULL`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"!cat data/microbiome_missing.csv"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.read_csv(\"data/microbiome_missing.csv\").head(20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Above, Pandas recognized `NA` and an empty field as missing data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.isnull(pd.read_csv(\"data/microbiome_missing.csv\")).head(20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Unfortunately, there will sometimes be inconsistency with the conventions for missing data. In this example, there is a question mark \"?\" and a large negative number where there should have been a positive integer. We can specify additional symbols with the `na_values` argument:\n",
" "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.read_csv(\"data/microbiome_missing.csv\", na_values=['?', -99999]).head(20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These can be specified on a column-wise basis using an appropriate dict as the argument for `na_values`."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Microsoft Excel\n",
"\n",
"Since so much financial and scientific data ends up in Excel spreadsheets (regrettably), Pandas' ability to directly import Excel spreadsheets is valuable. This support is contingent on having one or two dependencies (depending on what version of Excel file is being imported) installed: `xlrd` and `openpyxl` (these may be installed with either `pip` or `easy_install`).\n",
"\n",
"Importing Excel data to Pandas is a two-step process. First, we create an `ExcelFile` object using the path of the file: "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb_file = pd.ExcelFile('data/microbiome/MID1.xls')\n",
"mb_file"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Then, since modern spreadsheets consist of one or more \"sheets\", we parse the sheet with the data of interest:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb1 = mb_file.parse(\"Sheet 1\", header=None)\n",
"mb1.columns = [\"Taxon\", \"Count\"]\n",
"mb1.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There is now a `read_excel` convenience function in Pandas that combines these steps into a single call:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb2 = pd.read_excel('data/microbiome/MID2.xls', sheetname='Sheet 1', header=None)\n",
"mb2.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are several other data formats that can be imported into Python and converted into DataFrames, with the help of buitl-in or third-party libraries. These include JSON, XML, HDF5, relational and non-relational databases, and various web APIs. These are beyond the scope of this tutorial, but are covered in [Python for Data Analysis](http://shop.oreilly.com/product/0636920023784.do)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Pandas Fundamentals"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This section introduces the new user to the key functionality of Pandas that is required to use the software effectively.\n",
"\n",
"For some variety, we will leave our digestive tract bacteria behind and employ some baseball data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball = pd.read_csv(\"data/baseball.csv\", index_col='id')\n",
"baseball.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that we specified the `id` column as the index, since it appears to be a unique identifier. We could try to create a unique index ourselves by combining `player` and `year`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"player_id = baseball.player + baseball.year.astype(str)\n",
"baseball_newind = baseball.copy()\n",
"baseball_newind.index = player_id\n",
"baseball_newind.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This looks okay, but let's check:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.index.is_unique"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So, indices need not be unique. Our choice is not unique because some players change teams within years."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.Series(baseball_newind.index).value_counts()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The most important consequence of a non-unique index is that indexing by label will return multiple values for some labels:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.ix['wickmbo012007']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We will learn more about indexing below."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can create a truly unique index by combining `player`, `team` and `year`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"player_unique = baseball.player + baseball.team + baseball.year.astype(str)\n",
"baseball_newind = baseball.copy()\n",
"baseball_newind.index = player_unique\n",
"baseball_newind.head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.index.is_unique"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can create meaningful indices more easily using a hierarchical index; for now, we will stick with the numeric `id` field as our index."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Manipulating indices\n",
"\n",
"**Reindexing** allows users to manipulate the data labels in a DataFrame. It forces a DataFrame to conform to the new index, and optionally, fill in missing data if requested.\n",
"\n",
"A simple use of `reindex` is to alter the order of the rows:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.reindex(baseball.index[::-1]).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that the `id` index is not sequential. Say we wanted to populate the table with every `id` value. We could specify and index that is a sequence from the first to the last `id` numbers in the database, and Pandas would fill in the missing data with `NaN` values:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"id_range = range(baseball.index.values.min(), baseball.index.values.max())\n",
"baseball.reindex(id_range).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Missing values can be filled as desired, either with selected values, or by rule:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.reindex(id_range, method='ffill', columns=['player','year']).head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.reindex(id_range, fill_value='mr.nobody', columns=['player']).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Keep in mind that `reindex` does not work if we pass a non-unique index series."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can remove rows or columns via the `drop` method:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.drop([89525, 89526])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.drop(['ibb','hbp'], axis=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Indexing and Selection\n",
"\n",
"Indexing works analogously to indexing in NumPy arrays, except we can use the labels in the `Index` object to extract values in addition to arrays of integers."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Sample Series object\n",
"hits = baseball_newind.h\n",
"hits"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Numpy-style indexing\n",
"hits[:3]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Indexing by label\n",
"hits[['womacto01CHN2006','schilcu01BOS2006']]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also slice with data labels, since they have an intrinsic order within the Index:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hits['womacto01CHN2006':'gonzalu01ARI2006']"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hits['womacto01CHN2006':'gonzalu01ARI2006'] = 5\n",
"hits"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In a `DataFrame` we can slice along either or both axes:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind[['h','ab']]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind[baseball_newind.ab>500]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The indexing field `ix` allows us to select subsets of rows and columns in an intuitive way:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.ix['gonzalu01ARI2006', ['h','X2b', 'X3b', 'hr']]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.ix[['gonzalu01ARI2006','finlest01SFN2006'], 5:8]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.ix[:'myersmi01NYA2006', 'hr']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Similarly, the cross-section method `xs` (not a field) extracts a single column or row *by label* and returns it as a `Series`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.xs('myersmi01NYA2006')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Operations\n",
"\n",
"`DataFrame` and `Series` objects allow for several operations to take place either on a single object, or between two or more objects.\n",
"\n",
"For example, we can perform arithmetic on the elements of two objects, such as combining baseball statistics across years:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hr2006 = baseball[baseball.year==2006].xs('hr', axis=1)\n",
"hr2006.index = baseball.player[baseball.year==2006]\n",
"\n",
"hr2007 = baseball[baseball.year==2007].xs('hr', axis=1)\n",
"hr2007.index = baseball.player[baseball.year==2007]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hr2006 = pd.Series(baseball.hr[baseball.year==2006].values, index=baseball.player[baseball.year==2006])\n",
"hr2007 = pd.Series(baseball.hr[baseball.year==2007].values, index=baseball.player[baseball.year==2007])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hr_total = hr2006 + hr2007\n",
"hr_total"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Pandas' data alignment places `NaN` values for labels that do not overlap in the two Series. In fact, there are only 6 players that occur in both years."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hr_total[hr_total.notnull()]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"While we do want the operation to honor the data labels in this way, we probably do not want the missing values to be filled with `NaN`. We can use the `add` method to calculate player home run totals by using the `fill_value` argument to insert a zero for home runs where labels do not overlap:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hr2007.add(hr2006, fill_value=0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Operations can also be **broadcast** between rows or columns.\n",
"\n",
"For example, if we subtract the maximum number of home runs hit from the `hr` column, we get how many fewer than the maximum were hit by each player:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.hr - baseball.hr.max()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Or, looking at things row-wise, we can see how a particular player compares with the rest of the group with respect to important statistics"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.ix[89521][\"player\"]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"stats = baseball[['h','X2b', 'X3b', 'hr']]\n",
"diff = stats - stats.xs(89521)\n",
"diff[:10]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also apply functions to each column or row of a `DataFrame`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"stats.apply(np.median)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"stat_range = lambda x: x.max() - x.min()\n",
"stats.apply(stat_range)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lets use apply to calculate a meaningful baseball statistics, slugging percentage:\n",
"\n",
"$$SLG = \\frac{1B + (2 \\times 2B) + (3 \\times 3B) + (4 \\times HR)}{AB}$$\n",
"\n",
"And just for fun, we will format the resulting estimate."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"slg = lambda x: (x['h']-x['X2b']-x['X3b']-x['hr'] + 2*x['X2b'] + 3*x['X3b'] + 4*x['hr'])/(x['ab']+1e-6)\n",
"baseball.apply(slg, axis=1).apply(lambda x: '%.3f' % x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sorting and Ranking\n",
"\n",
"Pandas objects include methods for re-ordering data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.sort_index().head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.sort_index(ascending=False).head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_newind.sort_index(axis=1).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also use `order` to sort a `Series` by value, rather than by label."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.hr.order(ascending=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For a `DataFrame`, we can sort according to the values of one or more columns using the `by` argument of `sort_index`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball[['player','sb','cs']].sort_index(ascending=[False,True], by=['sb', 'cs']).head(10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Ranking** does not re-arrange data, but instead returns an index that ranks each value relative to others in the Series."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.hr.rank()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ties are assigned the mean value of the tied ranks, which may result in decimal values."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.Series([100,100]).rank()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Alternatively, you can break ties via one of several methods, such as by the order in which they occur in the dataset:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.hr.rank(method='first')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calling the `DataFrame`'s `rank` method results in the ranks of all columns:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.rank(ascending=False).head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball[['r','h','hr']].rank(ascending=False).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Exercise\n",
"\n",
"Calculate **on base percentage** for each player, and return the ordered series of estimates.\n",
"\n",
"$$OBP = \\frac{H + BB + HBP}{AB + BB + HBP + SF}$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Hierarchical indexing\n",
"\n",
"In the baseball example, I was forced to combine 3 fields to obtain a unique index that was not simply an integer value. A more elegant way to have done this would be to create a hierarchical index from the three fields."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_h = baseball.set_index(['year', 'team', 'player'])\n",
"baseball_h.head(10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This index is a `MultiIndex` object that consists of a sequence of tuples, the elements of which is some combination of the three columns used to create the index. Where there are multiple repeated values, Pandas does not print the repeats, making it easy to identify groups of values."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_h.index[:10]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_h.index.is_unique"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball_h.ix[(2007, 'ATL', 'francju01')]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Recall earlier we imported some microbiome data using two index columns. This created a 2-level hierarchical index:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb = pd.read_csv(\"data/microbiome.csv\", index_col=['Taxon','Patient'])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.head(10)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.index"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With a hierachical index, we can select subsets of the data based on a *partial* index:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.ix['Proteobacteria']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Hierarchical indices can be created on either or both axes. Here is a trivial example:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"frame = pd.DataFrame(np.arange(12).reshape(( 4, 3)), \n",
" index =[['a', 'a', 'b', 'b'], [1, 2, 1, 2]], \n",
" columns =[['Ohio', 'Ohio', 'Colorado'], ['Green', 'Red', 'Green']])\n",
"\n",
"frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you want to get fancy, both the row and column indices themselves can be given names:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"frame.index.names = ['key1', 'key2']\n",
"frame.columns.names = ['state', 'color']\n",
"frame"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With this, we can do all sorts of custom indexing:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"frame.ix['a']['Ohio']"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"frame.ix['b', 2]['Colorado']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Additionally, the order of the set of indices in a hierarchical `MultiIndex` can be changed by swapping them pairwise:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.swaplevel('Patient', 'Taxon').head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Data can also be sorted by any index level, using `sortlevel`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.sortlevel('Patient', ascending=False).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Missing data\n",
"\n",
"The occurence of missing data is so prevalent that it pays to use tools like Pandas, which seamlessly integrates missing data handling so that it can be dealt with easily, and in the manner required by the analysis at hand.\n",
"\n",
"Missing data are represented in `Series` and `DataFrame` objects by the `NaN` floating point value. However, `None` is also treated as missing, since it is commonly used as such in other contexts (*e.g.* NumPy)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"foo = pd.Series([NaN, -3, None, 'foobar'])\n",
"foo"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"foo.isnull()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Missing values may be dropped or indexed out:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.dropna()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2[bacteria2.notnull()]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"By default, `dropna` drops entire rows in which one or more values are missing."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.dropna()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This can be overridden by passing the `how='all'` argument, which only drops a row when every field is a missing value."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.dropna(how='all')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This can be customized further by specifying how many values need to be present before a row is dropped via the `thresh` argument."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.ix[7, 'year'] = nan\n",
"data"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.dropna(thresh=4)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is typically used in time series applications, where there are repeated measurements that are incomplete for some subjects."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If we want to drop missing values column-wise instead of row-wise, we use `axis=1`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.dropna(axis=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Rather than omitting missing data from an analysis, in some cases it may be suitable to fill the missing value in, either with a default value (such as zero) or a value that is either imputed or carried forward/backward from similar data points. We can do this programmatically in Pandas with the `fillna` argument."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.fillna(0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data.fillna({'year': 2013, 'treatment':2})"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that `fillna` by default returns a new object with the desired filling behavior, rather than changing the `Series` or `DataFrame` in place (**in general, we like to do this, by the way!**)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can alter values in-place using `inplace=True`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"_ = data.year.fillna(2013, inplace=True)\n",
"data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Missing values can also be interpolated, using any one of a variety of methods:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.fillna(method='bfill')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.fillna(bacteria2.mean())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Data summarization\n",
"\n",
"We often wish to summarize data in `Series` or `DataFrame` objects, so that they can more easily be understood or compared with similar data. The NumPy package contains several functions that are useful here, but several summarization or reduction methods are built into Pandas data structures."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.sum()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Clearly, `sum` is more meaningful for some columns than others. For methods like `mean` for which application to string variables is not just meaningless, but impossible, these columns are automatically exculded:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.mean()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The important difference between NumPy's functions and Pandas' methods is that the latter have built-in support for handling missing data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.mean()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sometimes we may not want to ignore missing values, and allow the `nan` to propagate."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bacteria2.mean(skipna=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Passing `axis=1` will summarize over rows instead of columns, which only makes sense in certain situations."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"extra_bases = baseball[['X2b','X3b','hr']].sum(axis=1)\n",
"extra_bases.order(ascending=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A useful summarization that gives a quick snapshot of multiple statistics for a `Series` or `DataFrame` is `describe`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`describe` can detect non-numeric data and sometimes yield useful information about it."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.player.describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also calculate summary statistics *across* multiple columns, for example, correlation and covariance.\n",
"\n",
"$$cov(x,y) = \\sum_i (x_i - \\bar{x})(y_i - \\bar{y})$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.hr.cov(baseball.X2b)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$corr(x,y) = \\frac{cov(x,y)}{(n-1)s_x s_y} = \\frac{\\sum_i (x_i - \\bar{x})(y_i - \\bar{y})}{\\sqrt{\\sum_i (x_i - \\bar{x})^2 \\sum_i (y_i - \\bar{y})^2}}$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.hr.corr(baseball.X2b)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.ab.corr(baseball.h)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.corr()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If we have a `DataFrame` with a hierarchical index (or indices), summary statistics can be applied with respect to any of the index levels:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.head()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.sum(level='Taxon')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Writing Data to Files\n",
"\n",
"As well as being able to read several data input formats, Pandas can also export data to a variety of storage formats. We will bring your attention to just a couple of these."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mb.to_csv(\"mb.csv\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `to_csv` method writes a `DataFrame` to a comma-separated values (csv) file. You can specify custom delimiters (via `sep` argument), how missing values are written (via `na_rep` argument), whether the index is writen (via `index` argument), whether the header is included (via `header` argument), among other options."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"An efficient way of storing data to disk is in binary format. Pandas supports this using Python’s built-in pickle serialization."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"baseball.to_pickle(\"baseball_pickle\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The complement to `to_pickle` is the `read_pickle` function, which restores the pickle to a `DataFrame` or `Series`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pd.read_pickle(\"baseball_pickle\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As Wes warns in his book, it is recommended that binary storage of data via pickle only be used as a temporary storage format, in situations where speed is relevant. This is because there is no guarantee that the pickle format will not change with future versions of Python."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.8"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
amyschmid/DtxR | ANOVAanalysis-git.ipynb | 1 | 215338 | {
"cells": [
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Using matplotlib backend: MacOSX\n",
"Populating the interactive namespace from numpy and matplotlib\n"
]
}
],
"source": [
"%pylab"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"import pandas as pd\n",
"\n",
"import statsmodels.api as sm\n",
"from statsmodels.formula.api import ols"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>expression</th>\n",
" <th>gene</th>\n",
" <th>strain</th>\n",
" <th>time</th>\n",
" <th>Bio</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.036195</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>0</td>\n",
" <td>A</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>0.010887</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>5</td>\n",
" <td>A</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>0.005983</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>20</td>\n",
" <td>A</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.003750</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>60</td>\n",
" <td>A</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.042606</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>0</td>\n",
" <td>B</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" expression gene strain time Bio\n",
"0 0.036195 idr2 ura3 0 A\n",
"1 0.010887 idr2 ura3 5 A\n",
"2 0.005983 idr2 ura3 20 A\n",
"3 0.003750 idr2 ura3 60 A\n",
"4 0.042606 idr2 ura3 0 B"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data = pd.read_csv(\"~/datamodified.csv\")\n",
"data.head()"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>expression</th>\n",
" <th>gene</th>\n",
" <th>strain</th>\n",
" <th>time</th>\n",
" <th>Bio</th>\n",
" <th>dtror</th>\n",
" <th>didr1</th>\n",
" <th>didr2</th>\n",
" <th>dsirr</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.036195</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>0</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>0.010887</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>5</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>0.005983</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>20</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.003750</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>60</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.042606</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>0</td>\n",
" <td>B</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" expression gene strain time Bio dtror didr1 didr2 dsirr\n",
"0 0.036195 idr2 ura3 0 A False False False False\n",
"1 0.010887 idr2 ura3 5 A False False False False\n",
"2 0.005983 idr2 ura3 20 A False False False False\n",
"3 0.003750 idr2 ura3 60 A False False False False\n",
"4 0.042606 idr2 ura3 0 B False False False False"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data['dtror'] = data.strain == 'tror'\n",
"data['didr1'] = data.strain == 'idr1'\n",
"data['didr2'] = data.strain == 'idr2'\n",
"data['dsirr'] = data.strain == 'sirr'\n",
"\n",
"data.head()"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"36"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sum(data.gene=='tror')"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>expression</th>\n",
" <th>gene</th>\n",
" <th>strain</th>\n",
" <th>time</th>\n",
" <th>Bio</th>\n",
" <th>dtror</th>\n",
" <th>didr1</th>\n",
" <th>didr2</th>\n",
" <th>dsirr</th>\n",
" <th>normexpression</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.036195</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>0</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>0.575864</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>0.010887</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>5</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>0.037007</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>0.005983</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>20</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>-0.231570</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.003750</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>60</td>\n",
" <td>A</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>-0.441094</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.042606</td>\n",
" <td>idr2</td>\n",
" <td>ura3</td>\n",
" <td>0</td>\n",
" <td>B</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>False</td>\n",
" <td>0.649012</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" expression gene strain time Bio dtror didr1 didr2 dsirr \\\n",
"0 0.036195 idr2 ura3 0 A False False False False \n",
"1 0.010887 idr2 ura3 5 A False False False False \n",
"2 0.005983 idr2 ura3 20 A False False False False \n",
"3 0.003750 idr2 ura3 60 A False False False False \n",
"4 0.042606 idr2 ura3 0 B False False False False \n",
"\n",
" normexpression \n",
"0 0.575864 \n",
"1 0.037007 \n",
"2 -0.231570 \n",
"3 -0.441094 \n",
"4 0.649012 "
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data['normexpression'] = np.log2(data.expression)\n",
"data['normexpression'] = (data['normexpression']-data['normexpression'].mean())/data['normexpression'].std()\n",
"\n",
"data.head()"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"g = data.groupby(['gene', 'time'])\n",
"\n",
"def scale(x):\n",
" x.normexpression = (x.normexpression - x.normexpression.mean())/x.normexpression.std()\n",
" return x\n",
"\n",
"data = g.apply(scale)"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"def plotGene(g,time=None):\n",
" temp = data[data.gene==g]\n",
" \n",
" if not time is None:\n",
" temp = temp[temp.time==time]\n",
" \n",
" for i,d in enumerate(['dtror', 'didr1', 'didr2', 'dsirr']):\n",
" if d[1:] == g:\n",
" continue\n",
" \n",
" plt.subplot(1,4,i+1)\n",
" plt.title(d)\n",
" plt.boxplot([temp[temp[d]].normexpression, temp[~temp[d]].normexpression], labels=[d,'dura3'])\n",
" \n",
" \n",
" plt.tight_layout()"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFmFJREFUeJzt3XuQZGd53/HvTxcu4SLtZNe6X3BQOSVSWIEpBRPjEhgo\nScGWweBI5RiLSmpjl4mdip2yKnJJK+JK2Un+oIhky5sUEbdwrQg2lmQFYYxkl2VrpIBAICUbRZRW\nwmhhB12MDEg8+WPOLLOz0zOz22fOvN3z/VRNbffpM+d9t59++jd9+vTpVBWSJLXmmM2egCRJKzGg\nJElNMqAkSU0yoCRJTTKgJElNMqAkSU3aUgGV5IYkv73Z85Am2WIfJXlNkgfWWm/IuelQ66lBkvuS\nXDDQlI7IlgqoRUkuSLJvs+chTbKquqOqfuRofz/Jq5J8OsmBJPuTfDzJKX3OUWurqpdV1Z9s9jxW\nsiUDaj2SHLeR60tbWdcv24DdwNnAWcCTwH/dxGlpmZWe14Z8rpvqgEry95Pck+TJJB8Fnge8ALgF\nODXJU93PqUl2JflEkg8meQK4PMlzk7w7yaPdz7uTPLfb9gVJ9iX5zSR/hY2lKTWijw7bEzFqvaXr\nLu2Xqrqlqj5eVU9U1beBa4F/OPB/b6qsUqvtSf4wybe6V6x3JDmmu+2hJK/vLq/0PHjYsqH+P1Mb\nUEmeA3wS+AAwA3wc+Fngr4GLgEer6oXdz6Pdr10CfAI4EfgQcCXwKuA84EeB84HfWjLMyd22zwJ2\nbvT/SRraKn10NOut1S8/AdzX19y3mjVq8OvAPmAHcBLwb4BR57lb/jw4atmGm9qAYiFYjgfeXVXf\nq6pPAHet8Tt/XlWfrKrvV9XTwM8D76qqx6pqP3AN8AtL1v8+cHVVfadbX5o26+2j9aw3sl+SvBy4\nCvjXvf8Pto7VavA94BTgrO62O2r0iViXPw+OWrbhpjmgTgUeWVaEr67xOw+vsI2lv/PVbtmi/VX1\nN0c/Ral56+2j9ay3Yr8keSkLu91/raruGHfCW9hqNfgPwF7gfyZ5MMkVq2xn+fPgqGUbbpoD6mvA\naUmyZNmZ3b+j/nJYvvxRFnZHLP39R5dc91Twmnar9dGRrndYvyQ5C7gN+LdV9YFxJ7vFjaxBVT1Z\nVb9eVT8M/DTwr5L85IjtrPS8tinPddMcUH8OPAP8apLjk7yFhfeQAL4O/O0kJ6yxjQ8Dv5VkR5Lt\nLOyC+OCGzVhqz2p9dDTrHZTkNOCPgWur6vqe570VjaxBkjcleWkXXo8Dz7Kwy7VpUxtQVfVd4C0s\nHHFyAPjHwH/vbrufhfB5sDuq5dQRm/ltYA64F/gicE+3TNoSVuujo1lvmX8G/DCwa8kRtU/1Nvkt\nZo0anMPCK9WnWAiy36uqz27CNI9I/MJCSVKLpvYVlCRpshlQkqQmGVCSpCYZUJKkJjV9gtPt27fX\n2WefvdnTGMTdd9/9jarasdnz0PTZSn0Ek9lL1mhlTQfU2Wefzdzc3GZPYxBJ1jrLhXRUtlIfwWT2\nkjVambv4JElNMqAkSU0yoCRJTTKgJElNMqAkSU0yoCRJTTKgJElNMqAkSU0yoCRJTWr6TBJH49Bv\nOwa/70qaLEt72P5t01A1mrpXUIt3VlX54JYm0NIeVpuGqtHUBZQkaToYUJKkJhlQkqQmTVVAzczM\nHHzzLglJmJmZ2eRZSZKORi8BleS9SR5L8qURt1+Q5PEkn+9+rupj3OXm5+cPHhyx+DM/P78RQ0m9\na6WPtDrrNJy+DjO/AbgWeP8q69xRVW/qaTxpGt2AfTQJbsA6DaKXV1BVdTtwoI9tSVuVfTQZrNNw\nhnwP6tVJ7k1yS5KXjVopyc4kc0nm9u/fP+D0pIlgH02GNetkjdY21Jkk7gHOrKqnklwMfBI4Z6UV\nq2o3sBtgdnb2iD4FVle/GHadcPgyaToM0kca27rqZI3WNkhAVdUTSy7fnOT3kmyvqm/0OU6ueeKw\nTzYnoXb1OYq0OYbqI43HOvVnkF18SU5Od/x3kvO7cb85xNjStLCPJoN16k8vr6CSfBi4ANieZB9w\nNXA8QFVdD7wV+OUkzwBPA5eWJ9qSDmEfTQbrNJxeAqqqLlvj9mtZOCxT0gj20WSwTsOZqjNJSJKm\nhwElSWqSASVJapIBJUlqkgElSWqSASVJapIBJUlqkgElSWqSASVJapIBJUlqkgElSWqSASVJapIB\nJUlqkgElSWqSASVJapIBJUlqkgElSWqSASVJapIBJUlqkgElSWqSASVJapIBJUlqkgElSWqSASVJ\natJxmz2BviU55Pq2bds2aSaSpHFMVUBVFbAQUouXJUmTqZddfEnem+SxJF8acXuSvCfJ3iT3JnlF\nH+NK08Q+mgzWaTh9vQd1A3DhKrdfBJzT/ewEfr+ncaVpcgP20SS4Aes0iF4CqqpuBw6sssolwPtr\nwZ3AiUlO6WNsaVrYR5PBOg1nqKP4TgMeXnJ9X7fsMEl2JplLMrd///5BJidNCPtoMqyrTtZobc0d\nZl5Vu6tqtqpmd+zYsdnTkSaSfdQ+a7S2oQLqEeCMJddP75ZJWj/7aDJYp54MFVB7gLd3R7e8Cni8\nqr420NjStLCPJoN16kkvn4NK8mHgAmB7kn3A1cDxAFV1PXAzcDGwF/g28I4+xm3J0g8I+xksHY3W\n+sjH9Mpaq9PQZmZmmJ+fBxYeI9u2bePAgdWOGTl6vQRUVV22xu0F/EofY7WqqvyAsMbSWh/5mF5Z\na3Ua2vz8/CGPieVn7+lTcwdJSJIEBpQkqVEGlCSpSQaUJKlJBpQkqUkGlCSpSQaUJKlJBpQkqUkG\nlCSpSQaUJKlJBpQkqUkGlCSpSQaUJKlJBpQkqUkGlCSpSQaUJKlJBpQkqUlTF1CL3+6YZEO/6VFS\n/2ZmZg7p4ZmZmU2ekTZTL1/53hK/nlqaXEN+nbjaN3WvoCRJ08GAkiQ1yYCSJDXJgJIkNcmAkiQ1\nyYCSJDXJgJIkNcmAknQYPzCrFvQSUEkuTPJAkr1Jrljh9guSPJ7k893PVX2MK02bVnpp8QOziz/z\n8/MbMcxEaqVGW8HYZ5JIcixwHfAGYB9wV5I9VfXlZaveUVVvGnc8aVrZS+2zRsPq4xXU+cDeqnqw\nqr4LfAS4pIftSluNvdQ+azSgPgLqNODhJdf3dcuWe3WSe5PckuRlozaWZGeSuSRz+/fv72F60sTo\nrZfsow1jjQY01EES9wBnVtXLgf8EfHLUilW1u6pmq2p2x44dA01Pmhjr6iX7aFNZo570EVCPAGcs\nuX56t+ygqnqiqp7qLt8MHJ9kew9jS9PEXmqfNRpQHwF1F3BOkpckeQ5wKbBn6QpJTk53zGqS87tx\nv9nD2NI0sZfaZ40GNPZRfFX1TJJ3ArcCxwLvrar7kvxSd/v1wFuBX07yDPA0cGn5xU3SIeyl9lmj\nYaXl+212drbm5uY2exrrluSovzAxyd1VNdvzlKSj6qPlj+VxHttDjzuJvTRJz3VD1sgzSUiSmmRA\nSZKaZEBJkppkQEmSmmRASZKaZEBJkppkQEmSmmRASZKaZEBJkppkQEmSmmRASZKaZEBJkppkQEmS\nmmRASZKaZEBJkppkQEmSmmRASZKaNPZXvkuaPnX1i2HXCYdelxj2sWFASTpMrnni8K/13rV581E7\nhnxsuItPktQkX0FJWlGSg5e3bdu2iTPRVmVASTrM4i6cJIfszpGG5C4+SVKTDChJUpMMqB7MzMwc\n3F+fhCTMzMxs8qyk8Sx9TEubwfegejA/P3/YfnqbWpPO95602XwFJUlqUi8BleTCJA8k2ZvkihVu\nT5L3dLffm+QVfYwrTRt7qX3WaDhjB1SSY4HrgIuAc4HLkpy7bLWLgHO6n53A7487rjRt7KX2WaNh\n9fEK6nxgb1U9WFXfBT4CXLJsnUuA99eCO4ETk5zSw9jSNLGX2meNBtRHQJ0GPLzk+r5u2ZGuA0CS\nnUnmkszt37+/h+lJE6O3XrKPNow1GlBzB0lU1e6qmq2q2R07dmz2dKSJZB+1zxqtrY+AegQ4Y8n1\n07tlR7qOtNXZS+2zRgPqI6DuAs5J8pIkzwEuBfYsW2cP8Pbu6JZXAY9X1dd6GFuaJvZS+6zRgMb+\noG5VPZPkncCtwLHAe6vqviS/1N1+PXAzcDGwF/g28I5xx5Wmjb3UPms0rF7OJFFVN7NQlKXLrl9y\nuYBf6WMsaZrZS+2zRsNp7iAJSZLAgJIkNcqAkiQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIkNcmA\nkiQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIk\nNcmAkiQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIkNem4cX45yQzwUeBs4CHg56pqfoX1HgKeBJ4F\nnqmq2XHGlaaNvdQ+azS8cV9BXQF8pqrOAT7TXR/ltVV1nsWSVmQvtc8adZIc/Nm2bduGjTNuQF0C\nvK+7/D7gZ8bcnrRV2Uvts0ZAVVFVBy8fOHBgw8YaN6BOqqqvdZf/CjhpxHoF3Jbk7iQ7V9tgkp1J\n5pLM7d+/f8zpSROj116yjzaENRrYmu9BJbkNOHmFm65ceqWqKkmN2MyPV9UjSX4I+HSS+6vq9pVW\nrKrdwG6A2dnZUduTJs6QvWQfHR1r1JY1A6qqXj/qtiRfT3JKVX0tySnAYyO28Uj372NJbgTOB1YM\nKGla2Uvts0ZtGesoPmAP8IvA73T/fmr5CkleABxTVU92l98IvGvMcZtSV78Ydp1w+DJp/ewlDu+l\nxvrIGg1s3ID6HeBjSf4p8FXg5wCSnAr8l6q6mIX9tDcmWRzvv1XVH405blNyzRMH3zQ8uCyhdm3O\nfDSR7CUO76XG+sgaDWysgKqqbwI/ucLyR4GLu8sPAj86zjjStLOX2meNhueZJCRJTRp3F58kaZN0\nuxIBDnubYRr4CkqSJtTSD8xOIwNKktQkA0qS1CQDSpLUJANKktQkA0qS1CQDSpLUJANKktQkA0qS\n1CQDSpLUJANKktQkA0qS1CQDSpLUJANKkibQzMzMwbOZJyEJMzMzmzyrfvl1G5I0gebn51f8Ju9p\n4isoSVKTDChJUpMMKElSkwwoSVKTDChJUpMMKElSkwwoSVKTDChJUpMMKElSkwwoSVKTxgqoJG9L\ncl+S7yeZXWW9C5M8kGRvkivGGVOaRvZS+6zR8MZ9BfUl4C3A7aNWSHIscB1wEXAucFmSc8ccV5o2\n9lL7rNHAxjpZbFV9BdY8QeH5wN6qerBb9yPAJcCXxxlbmib2Uvus0fCGOJv5acDDS67vA/7BqJWT\n7AR2Apx55pkbO7MeLX/Qbtu2bZNmoim27l6a1D6CQ3tpAvtosBrV1S+GXSccvmyKrBlQSW4DTl7h\npiur6lN9T6iqdgO7AWZnZ2uN1ZuweMr7JIed/l5aNGQvTWIfweb30iTVKNc8seLXbdSuXqbXhDUD\nqqpeP+YYjwBnLLl+erdM2lLspfZZo7YMcZj5XcA5SV6S5DnApcCeAcaVpo291D5r1KNxDzN/c5J9\nwI8BNyW5tVt+apKbAarqGeCdwK3AV4CPVdV9401bmi72Uvus0Q8s/ar5jTTuUXw3AjeusPxR4OIl\n128Gbh5nLGma2Uvts0Y/MNT7g55JQpLUJANKktQkA0qS1CQDSpLUJANKktQkA0qS1CQDSpLUpCFO\nFitJ2gDTfpJqA0qSJtBmn1h3CO7ikyQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIkNcmAkiQ1yYCS\nJDXJgJIkNcmAkiQ1yYDqyeI5sZafG0vSkbGX1m/a7yvPxdeTaT0XljQ0e2n9pv2+8hWUJKlJBpQk\nqUkGlCSpSQaUJKlJBpQkqUkGlCSpSWMFVJK3JbkvyfeTzK6y3kNJvpjk80nmxhlTmkb2Uvus0fDG\n/RzUl4C3AH+wjnVfW1XfGHM8aVrZS+2zRgMbK6Cq6iswvZ9iloZiL7XPGg1vqDNJFHBbkmeBP6iq\n3aNWTLIT2NldfSrJA0cx3nZgM/56GWfcs/qciKbWunqppz4Ce+loWKO1ratGawZUktuAk1e46cqq\n+tQ6J/PjVfVIkh8CPp3k/qq6faUVu2KODLD1SDJXVSP3EW+UzRpXk2HIXuqjj2Dr9ZI1amvcNQOq\nql4/7iBV9Uj372NJbgTOB1YMKGla2Uvts0Zt2fDDzJO8IMmLFi8Db2ThzUZJR8Beap816te4h5m/\nOck+4MeAm5Lc2i0/NcnN3WonAX+a5AvAXwI3VdUfjTPuOoz9snnCxtWEs5eaGXckazT8uJn207VL\nkiaTZ5KQJDXJgJIkNWliAyrJriS/keTyJKcOMVYP23lekr9M8oXulCnX9DE/6Wgt6aN3JTnsCLYk\nFyT5wxG/+4Ykd3en9bk7yevWO14P895yvbTafZfkp5NcsdHjHOF2xq7RNHzl++UsHCXz6PIbkhxb\nVc+utYEkx1XVM31MZo1tfQd4XVU9leR4Ft5MvaWq7uxjbOloVdVVR7J+kuNY+JDmT1XVo0n+HnAr\ncFpfc7KX1q+q9gB7li9ffh/2+Vy3ju2NXaOJegWV5Mok/zvJnwI/0i2eBT7UnZjx+d2JGn83yT3A\n25Kcl+TOJPcmuTHJtm5bf5Lk3d3JHH9tPWN1vzPbXd6e5KHu8uVJ9iT5Y+AzSV6Y5DNJ7un+urwE\noBY81Q1xfPfjUSoa1IjH9g1J3tpdvjDJ/V0PvWXJ7+1K8oEkfwZ8oKr+V1Ut/mF4H/D8JM9d53j2\n0jqMuO9+NcmXu+e0j3TLLk9ybXf5hiTXJ/kL4N8vr9sRjLPpNZqYV1BJXglcCpzHwrzvAe4G5oDf\nqKq5bj2Ab1bVK7rr9wL/oqo+l+RdwNXAv+w2+5yVPgm9ylireQXw8qo60P11+eaqeiLJduDOJHuq\nqpIc223rpcB1VfUXR3mXSEdsrcd2kucB/xl4HbAX+OiyTZzLwpkSnl62/GeBe6rqO0cy3gj2Eqve\nd1cAL6mq7yQ5ccSvnw68uqqeTbKL0XVrukaT9ArqNcCNVfXtqnqCFV7OLvFRgCQnACdW1ee65e8D\nfmL5emOOtejTVXWguxzg33XheBsLuz1OAqiqZ6vqPBYeQOd3u0akoaz12P67wP+rqv9TC59B+eCy\n2/csf5JL8jLgd4F/fhTjrcReWjDqvruXhb1G/wQYtXvt48ve3jisbusYZzWD1GiSAupI/HXP6y16\nhh/cZ89bZVs/D+wAXtkV5+vL16+qbwGfBS48wjlIm+mQnklyOnAj8Paq+r9HsB176ej9I+A6Fl7F\n3NW9gllu+XPbkT7XQQM1mqSAuh34me59phcBP9UtfxJ40Uq/UFWPA/NJXtMt+gXgcyutu86xHgJe\n2V1+6yq/fwLwWFV9L8lr6c7cm2TH4kvyJM8H3gDcv475SH0Z9dhedD9wdpK/012/bNSGusfyTcAV\nVfVnRzjeQ9hLa1npvjsGOKOqPgv8Jgv3zws3YBxooEYT8x5UVd2T5KPAF4DHgLu6m24Ark/yNAun\nIFnuF7vb/xbwIPCOMcb6j8DHsnCa/JtW2cSHgP+R5IssvEe2WJRTgPd1+2WPAT5WVSsewitthFUe\n24u3/83i4zvJt4E7GPEHIPBOFt5buCrJ4lGAb6yqx9Yxnr20hhH3XQEf7N6+CPCeqvpWxviOqpZr\n5KmOJElNmqRdfJKkLcSAkiQ1yYCSJDXJgJIkNcmAkiQ1yYCSJDXJgJIkNen/A0av8soE+0ibAAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x116920850>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plotGene('idr1',0)"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFTdJREFUeJzt3W2MXGd5xvHrihMTCrGzi5ckdkKcFosqVJCGlQUIqgAB\nJSnFkEKbiLfwxaKC0qogYTUUrxGq+vYhok2buhJNIIgEUA0uMaQ4DSSpCHhtEeeFpFiuUWwHvLAm\nTkgg2Ln7Yc+a8XhmdmbP2TP3zP5/0sozZ87M83juuefac+bsGUeEAADI5pR+TwAAgFYIKABASgQU\nACAlAgoAkBIBBQBIiYACAKS0qALK9o22P9nveaC92RrZfq3tR+Zar865AYOmmz6x/aDtS2qaUk8W\nVUDNsn2J7f39ngfai4i7I+Il872/7aW2v2R7n+3I2oBAv0XESyPim/2eRyuLMqC6YfvUhVwfC6eh\nFvdIepekH/VxOsDAavW+Vud73VAHlO3ftb3L9hO2b5V0uqTnSfqapJW2nyx+VtqeKH7jvtn2EUnX\n2H6O7etsHyx+rrP9nOKxL7G93/ZHbf9I0r/37386uNrU6KSt3HbrNa7bWIuIeCYirouIeyQdq/v/\nBfRDh35aYfurtn9me9r23bZPKW7bZ/vS4nKr98GTltX1/xnagLK9VNKXJX1W0qikL0r6Q0k/l3S5\npIMR8fzi52Bxt3WSviTpTEmfk3StpFdKukjSyyWtlfSxhmHOLh77fEnrF/r/NGw61Gg+61ELLGpz\n9MmHJe2XNCbpLEl/Kandee6a3wfbLVtwQxtQmgmW0yRdFxG/iogvSdoxx32+HRFfjohnI+JpSe+U\n9ImIOBQRU5I2SXp3w/rPStoYEb8s1kdvuq1RN+tRCyx2nfrkV5LOkXR+cdvd0f5ErM3vg+2WLbhh\nDqiVkg40FeGHc9zn0RaP0XifHxbLZk1FxC/mP8VFr9sadbMetcBi16lP/l7SHkn/ZXuv7Q0dHqf5\nfbDdsgU3zAH1mKRVtt2w7EXFv+1+c2heflAzu4wa73+w4Tqngi+nU416XY9aYLFr2ycR8UREfDgi\nflPSWyT9he03tHmcVr3Ul/4a5oD6tqSjkj5k+zTbV2rmMyRJ+rGkF9hePsdjfF7Sx2yP2V4h6eOS\nbl6wGS8+nWo0n/VOUBzkMnswxVLbpzc1LzBM2vaJ7TfbfnHx+n9cMwcOPdu/qXZnaAMqIp6RdKVm\njjiZlvTHkv6juO1hzYTP3uKolpVtHuaTkiYl7ZZ0v6RdxTJUoFON5rNeC49IelrSKkm3F5fP73gP\nYEDN0SdrJG2X9KRmguyfI+LOPkyzJ+YLCwEAGQ3tFhQAYLARUACAlAgoAEBKBBQAIKXUJzhdsWJF\nrF69ut/TqMXOnTt/EhFj/Z5HrxZTjaTBrRNyo49aSx1Qq1ev1uTkZL+nUQvbc53lIqXFVCNpcOuE\n3Oij1tjFBwBIiYACAKREQAEAUiKgAAApEVAAgJQIKABASgQUACAlAgoAkBIBBQBIKfWZJAZJ4xe1\n8h1bOTV/mS51wqAb9vcdtqAqMvviGMYXybCICOqEoTLsr2cCCgCQEgEFAEiJgAKAATQ6Onr8Myjb\nsq3R0dE+z6paHCQBAAPo8OHDJ3321Hwg0KBjCwoAkBIBBQBIiV18ADCAYuMyaWL5ycuGCAEFAAPI\nm460/AwqJvozn4VQyS4+25+2fcj2A21ut+1P2d5je7fti6sYF92jRkA16KX6VPUZ1I2SLutw++WS\n1hQ/6yX9S0Xjons3ihoBVbhR9FItKgmoiLhL0nSHVdZJ+kzMuFfSmbbPqWJsdIcaAdWgl+pT11F8\nqyQ92nB9f7HsJLbX2560PTk1NVXL5CCJGgFV6aqX6KO5pTvMPCI2R8R4RIyPjY31ezpogRoB5dFH\nc6vrKL4Dks5ruH5usQx5UCOgGrX1UvOZI0ZGRhZimL6pawtqq6T3FEe3vFLS4xHxWE1jozvUCKhG\nLb3U/PUxEaHp6U4fjQ2eSragbH9e0iWSVtjeL2mjpNMkKSJukLRN0hWS9kh6StL7qhgX3aNGQDXo\npfpUElARcfUct4ekD1QxFuaHGgHVoJfqk+4gCQAAJAIKAJAUAVWBxfDFYYNutkaNdaJGGHSNr+dh\nxMliK7AYvjhs0FEjDKPm1/SwYQsKAJASAQUASImAAgCkxGdQ6IvGz3+GfT86MGzq6l+2oNAXjado\nATBY6upfAgoAkBIBBQBIiYACAKREQAEAUiKgAAApEVAAgJQIKABASgQUACAlAgoAkBIBBQBIiYAC\nAKREQAEAUiKgAAApEVAAgJQIKABASgQUACAlvlG3ArFxmTSx/ORlAIB5I6Aq4E1HTvpmSduKif7M\nBwCGAbv4AAApEVAAgJQIKABASgQUACAlAgoAkFIlAWX7MtuP2N5je0OL2y+x/bjt7xU/H69iXPSG\nOgHl0Uf1KX2Yue0lkq6X9EZJ+yXtsL01Ih5qWvXuiHhz2fEwP9QJKI8+qlcVW1BrJe2JiL0R8Yyk\nWyStq+BxUS3qBJRHH9WoioBaJenRhuv7i2XNXm17t+2v2X5puwezvd72pO3JqampCqaHQmV1okZY\nxOijGtV1kMQuSS+KiJdJ+kdJX263YkRsjojxiBgfGxuraXoodFUnagR0RB9VpIqAOiDpvIbr5xbL\njouIIxHxZHF5m6TTbK+oYGx0L02dRkdHZVvSzCmhRkdHqx4CWChp+mgxqCKgdkhaY/sC20slXSVp\na+MKts928Y5ke20x7k8rGBvdS1Onw4cPKyKO/xw+fLjqIYCFkqaPFoPSR/FFxFHbH5R0u6Qlkj4d\nEQ/afn9x+w2S3i7pT2wflfS0pKui+eyqWFDUCSiPPqqXMz9v4+PjMTk52e9pzMl267OZ9/Dc2t4Z\nEeNVz22hzadGzc9Nr8/VfFRRo+I+A1kn5DYo73WNyvRtt33EmSQAACkRUACAlAgoAEBKBBQAICW+\n8h2LQmxcJk0sP3kZgJ6Mjo4e/9MQ2xoZGdH09PSCjEVAYVHwpiOtj+Kb6M98gEE1+3eMs2b/6H4h\nsIsPAJASAQUASImAAgCkREABAFIioAAAKRFQAICUCCgAQEoEFAAgJQIKAJASAQUASImAAgCkREAB\nAFIioAAAKRFQAICUCCgAQEoEFAAgJQIKAJASAQUASImAAgCkREABAFI6td8TGBa2T7g+MjLSp5nk\nFxuXSRPLT7wOAE0IqApEhKSZkJq9jPa86cgJz5NtxUT/5gMgJ3bxAQBSIqAAACkRUACAlCoJKNuX\n2X7E9h7bG1rcbtufKm7fbfviKsZFb6gTUB59VJ/SAWV7iaTrJV0u6UJJV9u+sGm1yyWtKX7WS/qX\nsuOiN9QJKI8+qlcVW1BrJe2JiL0R8YykWySta1pnnaTPxIx7JZ1p+5wKxkb3qBNQHn1UoyoCapWk\nRxuu7y+W9bqOJMn2etuTtienpqYqmB4KldWJGmERo49qlO4giYjYHBHjETE+NjbW7+mgBWoElEcf\nza2KgDog6byG6+cWy3pdBwuLOgHl0Uc1qiKgdkhaY/sC20slXSVpa9M6WyW9pzi65ZWSHo+IxyoY\nG92jTkB59FGNSp/qKCKO2v6gpNslLZH06Yh40Pb7i9tvkLRN0hWS9kh6StL7yo6L3lAnoDz6qF6V\nnIsvIrZppiiNy25ouBySPlDFWJg/6gSURx/VJ91BEgAASAQUACApAgoAkBIBBQBIiYACAKTEN+oC\nALoWG5dJE8tPvL5ACCgAQNe86YhmjqQvrtuKiYUZi118AICUCCgAQEoEFAAgJQIKAJASAQUASImA\nAgCkREABAFIioAAAKRFQAICUCCgAQEoEFAAgJQIKAJASJ4tFX9g+fnlkZKSPMwGQFQGF2s2eCdn2\nCWdFBoBG7OIDAKREQAEAUiKgAAApEVAAgJQIKABASgQUACAlAgoAkBIBBQBIiYACAKREQAEAUip1\nqiPbo5JulbRa0j5JfxQRh1ust0/SE5KOSToaEeNlxkVvqBNQHn1Uv7JbUBsk3RERayTdUVxv53UR\ncRHF6gvqBJRHH9WsbECtk3RTcfkmSW8t+XhYGNQJKI8+qlnZgDorIh4rLv9I0llt1gtJ223vtL2+\n0wPaXm970vbk1NRUyemhUGmdqBEWKfqoZnN+BmV7u6SzW9x0beOViAjb7b474TURccD2CyV9w/bD\nEXFXqxUjYrOkzZI0Pj7OdzF0qc46USMMK/oolzkDKiIubXeb7R/bPiciHrN9jqRDbR7jQPHvIdtb\nJK2V1DKgMD/UCSiPPsql7C6+rZLeW1x+r6SvNK9g+3m2z5i9LOlNkh4oOS56Q52A8uijmpUNqL+R\n9EbbP5B0aXFdtlfa3lasc5ake2zfJ+m7km6LiK+XHBe9oU5AefRRzUr9HVRE/FTSG1osPyjpiuLy\nXkkvLzMOyqFOQHn0Uf04kwQAICUCCgCQEgEFAEiJgAIApERAAQBSIqAAACkRUACAlAgoAEBKBBQA\nICUCCgCQEgEFAEiJgAIApERAVcT2Cf+iM54vAHMpdTZz/FoEX4jZC54vAHNhCwoAkBIBBQBIiYAC\nAKREQAEAUiKgAAApEVAAgJQIKABASgQUACAlAgoAkBIBBQBIiYACAKREQAEAUiKgAAApEVAAgJQI\nKABASgQUACAlAgoAkBIBBQBIqVRA2X6H7QdtP2t7vMN6l9l+xPYe2xvKjIneUSegPPqofmW3oB6Q\ndKWku9qtYHuJpOslXS7pQklX276w5LjoDXUCyqOPanZqmTtHxPclyXan1dZK2hMRe4t1b5G0TtJD\nZcZG96gTUB59VL86PoNaJenRhuv7i2Ut2V5ve9L25NTU1IJPDsd1XSdqBLRFH1Vozi0o29slnd3i\npmsj4itVTygiNkvaLEnj4+NR9eMPqzrrRI0wrOijXOYMqIi4tOQYBySd13D93GIZKkSdgPLoo1zq\n2MW3Q9Ia2xfYXirpKklbaxgXvaFOQHn0UYXKHmb+Ntv7Jb1K0m22by+Wr7S9TZIi4qikD0q6XdL3\nJX0hIh4sN230gjoB5dFH9St7FN8WSVtaLD8o6YqG69skbSszFuaPOgHl0Uf140wSAICUCCgAQEoE\nFAAgJQIKAJASAQUASImAAgCkREABAFIioAAAKRFQAICUCCgAQEoEFAAgJQIKAJASAQUASImAAgCk\nREABAFIioAAAKRFQAICUCCgAQEoEFAAgJQIKAJASAQUASImAAgCkREABAFI6td8TqJrtE65HRJ9m\ngmyaXxsjIyN9mgkw2Bp7aSH7aKgCanR0tOWy6enpPswGmTT+omKbX1yAeZrtnTr6aKgCavpDxyQt\na1p6rB9TAQCUNFQB5U1HTkp024qJ/swHADB/HCQBAEhpqLagJD4IB4BhMVQBVeeHdwCAhcUuPgBA\nSqUCyvY7bD9o+1nb4x3W22f7ftvfsz1ZZswu5nT83+bdfYtVxjr1Q+NrgtcGekUf/VpdfVR2F98D\nkq6U9K9drPu6iPhJyfHmxK69ltLVqR94baAk+qhQVy+VCqiI+L7Eb6PZUSegPPqofnV9BhWSttve\naXt9pxVtr7c9aXtyamqqpumh0FWdqBHQEX1UkTm3oGxvl3R2i5uujYivdDnOayLigO0XSvqG7Ycj\n4q5WK0bEZkmbJWl8fJx9Ml2qs07UCMOKPsplzoCKiEvLDhIRB4p/D9neImmtpJYBhfmhTkB59FEu\nC76Lz/bzbJ8xe1nSmzTzYSMSoU5AefRRtcoeZv422/slvUrSbbZvL5avtL2tWO0sSffYvk/SdyXd\nFhFfLzMuekOdgPLoo/qVPYpvi6QtLZYflHRFcXmvpJeXGQflUCegPPqofpxJAgCQEgEFAEjJmf+6\n3vaUpB/O464rJPXjr7jLjHt+RIxVOZk6lKiRRJ0ASfRRO6kDar5sT0ZE23NlDdu4g4o6AeUNcx+x\niw8AkBIBBQBIaVgDavMiG3dQUSegvKHto6H8DAoAMPiGdQsKADDgCCgAQEoDG1C2J2x/xPY1tlfW\nMVYFj3O67e/avq/46uhNVcwvo4b6fML2SWeItn2J7a+2ue8LbN9p+0nb/9TLeBXMe9HUCIOl02vc\n9ltsb1jocXp8nNK9VPYr3zO4RjNnCz7YfIPtJRFxbK4HsH1qRBytYjJzPNYvJb0+Ip60fZpmTir5\ntYi4t4qxM4qIj/eyvu1TJf1C0l9J+p3ip1LUCMMmIrZK2tq8vPm1XuV7XRePV7qXBmoLyva1tv/X\n9j2SXlIsHpf0Odvfs/1c2/ts/63tXZLeYfsi2/fa3m17i+2R4rG+afs625OS/qybsYr7jBeXV9je\nV1y+xvZW2/8t6Q7bz7d9h+1dtu+3vU6SYsaTxRCnFT9Dc5RKm+fsRttvLy5fZvvhojZXNtxvwvZn\nbf+PpM9GxM8j4h7NBFWv41EjDI02r/EP2X6oeE+7pVh2zezehqLnbrD9HUl/19xfPYzT914amC0o\n26+QdJWkizQz712SdkqalPSRiJgs1pOkn0bExcX13ZL+NCK+ZfsTkjZK+vPiYZe2+kvoDmN1crGk\nl0XEdLEV8LaIOGJ7haR7bW+NiLC9pHisF0u6PiK+M8+nJJW5njPbp0v6N0mvl7RH0q1ND3GhZr6J\n9OkqxmtjUdcIg6XDa3yDpAsi4pe2z2xz93MlvToijtmeUIf+ytxLg7QF9VpJWyLiqYg4ohabsw1u\nlSTbyyWdGRHfKpbfJOn3mtcrOdasb0TEdHHZkv66CMftklZp5ntiFBHHIuIizbyA1tqufBdWn8z1\nnP22pP+LiB/EzN823Nx0+9Zuw6nL8VpZ7DXCYGn3Gt+tmb1G75LUbvfaF5s+3ujUX2l7aZACqhc/\nr3i9WUf16+fs9A6P9U5JY5JeURTnx83rR8TPJN0p6bIe5zCseq1FO9QIw+73JV2vma2YHcUWTLPm\nfppPf/W9lwYpoO6S9Nbic6YzJP1BsfwJSWe0ukNEPC7psO3XFoveLelbrdbtcqx9kl5RXH57h/sv\nl3QoIn5l+3WSzpck22Ozm+S2nyvpjZIe7mI+g6DdczbrYUmrbf9Wcf3qBRpvn6gRhkOr1/gpks6L\niDslfVQzr+PnL8A4UoJeGpjPoCJil+1bJd0n6ZCkHcVNN0q6wfbTmvkq5mbvLW7/DUl7Jb2vxFj/\nIOkLttdLuq3DQ3xO0n/avl8zn5HNFuUcSTcV+2VPkfSFiGh5qPWg6fCczd7+i9nnzfZTku5Wm18s\nJKn4QHaZpKW23yrpTRHxUBfjUSMMhTav8ZB0c/HxhSV9KiJ+Vnz2XuU4UoJe4lRHAICUBmkXHwBg\nESGgAAApEVAAgJQIKABASgQUACAlAgoAkBIBBQBI6f8B8PQZAnVVDYUAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11607e910>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plotGene('idr2',0)"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUIAAAEYCAYAAAApuP8NAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFWVJREFUeJzt3X+Q3HV9x/Hny5iAVYScOYGEH7E1Y4MZpXiTQRudxAID\njE4UsSVjVRw6Vx1J7R92ysxZCFY6daZ/MAbGNB1oEJ2AOg2mJZghmApxpHJJIRADNU3jkATNSU5C\nBITAu3/cd+PeZfdu9/a7393vfl6PmZ3sfve7+/lkX3ev++53d7+riMDMLGWv6/QEzMw6zUVoZslz\nEZpZ8lyEZpY8F6GZJc9FaGbJS64IJa2T9JVOz8Pqq2Qk6f2SnppqvSLnZr/TSzklV4QVkpZK2t/p\neVh9EfFQRLxjureXNEvSdyXtkxSSluY4PcvkkNOFku6XdFjSiKTvSDozzzlOJdkibISk17dzfWuf\nqiy2AX8O/KKD07E6spxmA2uB+cC5wPPAvxY5j54vQkl/JGmHpOcl3Q2cDLwRuA+YK+lodporaVW2\nBfFNSUeAqyWdJOlmSQez082STsrue6mk/ZL+VtIvKDi8XlEnoxO22uutV71udRYR8XJE3BwR24BX\ni/5/9Zo25nRfRHwnIo5ExAvALcAfF/l/6+kilDQLuAe4E+gDvgN8DPgNcBlwMCLelJ0OZjdbDnwX\nOA34FjAEXAicD7wbWAx8qWqYM7L7PhcYbPf/qddMktF01nMWbVJwTh8AduU190b0dBEyVmAzgZsj\n4pWI+C7wyBS3+XFE3BMRr0XEi8AngC9HxKGIGAFuBD5Ztf5rwA0R8dtsfWtOoxk1sp6zaJ9CcpL0\nLuB64G9y/x9MoteLcC5wIMYfWeLnU9zm6Rr3UX2bn2fLKkYi4qXpTzF5jWbUyHrOon3anpOktzO2\ny+oLEfFQqxNuRq8X4TPAPEmqWnZO9m+9w+5MXH6QsU346tsfrLrsw/e0ZrKMml3PWbRPW3OSdC6w\nBfj7iLiz1ck2q9eL8MfAMeCvJM2UdAVj+/gAfgm8RdKpU9zHeuBLkvolzWFss/2bbZtxeibLaDrr\njZO92FXZWT9L0skTfkmtMW3LSdI84AfALRGxJud5N6SnizAiXgauAK4GDgN/Bvxbdt2TjJXcXkm/\nljS3zt18BRgGdgKPAzuyZZaDyTKazno1PAW8CMwDNmfnz530FnaCNuf0F8DvA6uq3sVxNLfJN0A+\nMKuZpa6ntwjNzBrhIjSz5LkIzSx5LkIzS15XHyRgzpw5MX/+/E5PozDbt2//VUT0d3oezXJO5eCc\n6uvqIpw/fz7Dw8OdnkZhJE31qZeu5JzKwTnV56fGZpY8F6GZJc9FaGbJcxGaWfJchGaWPBehmSXP\nRWhmyXMRmlnyXIRmlryu/mRJ2VQf+NjHeexezqk5KTxe3iLMUeWHpFd/WHqFc2pOCo+Xi9DMkuci\nNLPkuQjNLHkuQjNLnovQzJLnIjSz5LkIzSx5LkIzS56L0MyS5yI0s+TlUoSSbpd0SNITda5fKuk5\nSY9mp+vzGNea45zKwTkVL6+DLqwDbgG+Mck6D0XEh3Iaz6ZnHc6pDNbhnAqVyxZhRDwIHM7jvqx9\nnFM5OKfiFbmP8H2Sdkq6T9I7660kaVDSsKThkZGRAqdnGedUDs4pR0UV4Q7gnIh4F7AauKfeihGx\nNiIGImKgv7+/oOlZxjmVg3PKWSFFGBFHIuJodn4TMFPSnCLGtsY5p3JwTvkrpAglnaHsMLeSFmfj\nPlvE2NY451QORebU19d3/AjVkujr62vHMB2Xy6vGktYDS4E5kvYDNwAzASJiDXAl8DlJx4AXgaui\nlw9326WcUzl0U06jo6Pjjkxdfdj+XpJLEUbEiimuv4WxtwNYBzmncnBOxfMnS8wseS5CM0uei9DM\nkuciNLPkuQjNLHkuQjNLnovQzJLnIjSz5LkIzSx5LkIzS56L0MyS5yI0s+S5CM0seS5CM0uei9DM\nkuciNLPk5fW9xmbWg+KGN8OqU8df7kEuQjOrSzceOeFQ/bGqc/NpFz81NrPkuQjNLHkuQjNLnovQ\nzJLnIjSz5OVShJJul3RI0hN1rpekr0naI2mnpAvyGNea45zKwTkVL68twnXApZNcfxmwIDsNAl/P\naVxrzjqcUxmswzkVKpcijIgHgcOTrLIc+EaMeRg4TdKZeYxtjXNO5eCcilfUPsJ5wNNVl/dny6y7\nOKdycE4567oXSyQNShqWNDwyMtLp6VgdzqkcnFNjiirCA8DZVZfPypadICLWRsRARAz09/cXMjk7\nzjmVQ8/ntH79ehYtWsSMGTNYtGgR69evb+t4RRXhRuBT2atdFwLPRcQzBY1tjXNO5VBoTpKOn2bP\nnt2uYY5bv349Q0NDrF69mpdeeonVq1czNDTU1jLM5aALktYDS4E5kvYDNwAzASJiDbAJuBzYA7wA\nfCaPca05zqkcuimnygEXJI07+EI73XTTTdx2220sW7YMgGXLlnHbbbexcuVKVqxY0ZYxcynCiJh0\ndjH2CH4+j7G6VV9fH6OjowDH/3IePjzZC3/F67acJFWPXdSwXa/bcira7t27WbJkybhlS5YsYffu\n3W0bs+teLCmr0dFRIuL4qVKKVl+l/FyCVm3hwoVs27Zt3LJt27axcOHCto3pIjSzrjI0NMQ111zD\n1q1beeWVV9i6dSvXXHMNQ0NDbRvTB2Y1s65S2Q+4cuVKdu/ezcKFC7npppvatn8QXIRm1oVWrFjR\n1uKbyE+NzSx5LkIzS56L0MyS5yI0s+S5CM0seS5CS0pfX9/xT7RIoq+vr8Mz6n7Vj1ev8ttnLCmV\nTwBV9PIvd15S+OSPtwjNLHkuQjNLnovQzJLnIjSz5LkIzSx5LkIzS56L0MyS5yI0s+S5CM0seS5C\nM0uei9DMkuciNLPk5VKEki6V9JSkPZKuq3H9UknPSXo0O12fx7jWHOdUHs6qWC0ffUbSDOBW4GJg\nP/CIpI0R8dMJqz4UER9qdTybHudUHs6qeHlsES4G9kTE3oh4GbgLWJ7D/Vq+nFN5OKuC5VGE84Cn\nqy7vz5ZN9D5JOyXdJ+mdOYxrzXFO5eGsClbUgVl3AOdExFFJlwP3AAtqrShpEBgEOOeccwqanmWc\nU3k0lJVzakweW4QHgLOrLp+VLTsuIo5ExNHs/CZgpqQ5te4sItZGxEBEDPT39+cwPcs4p/LILSvn\n1Jg8ivARYIGkt0maBVwFbKxeQdIZyo6JLmlxNu6zOYxtjXNO5eGsCtbyU+OIOCbpWmAzMAO4PSJ2\nSfpsdv0a4Ergc5KOAS8CV0UKX4TQRZxTeTir4qmbH7uBgYEYHh7u9DQaIumELwVq9rGVtD0iBvKe\nW7u1ktN0HqdWOKdy/D7loZmc/MkSM0uei9DMkuciNLPkuQjNLHkuQjNLnovQzJLnIjSz5LkIrSP6\n+vrIPhiBJPr6+jo8I0tZUQddMBtndHT0hDc2m3WKtwjNLHkuQjNLnovQzJLXk/sIq/c3dfNBJcys\nviJ/j3tyi7DyoLkEzcqryN/jnixCM7NmuAjNLHkuQjNLnovQzJLnIjSz5LkIzSx5LkIzS56L0MyS\n5yI0s+S5CM0sebkUoaRLJT0laY+k62pcL0lfy67fKemCPMa15jin8nBWxWq5CCXNAG4FLgPOA1ZI\nOm/CapcBC7LTIPD1Vse15jin8nBWxctji3AxsCci9kbEy8BdwPIJ6ywHvhFjHgZOk3RmDmOPUzn8\nuw8BX1PX5GRTclYFy6MI5wFPV13eny1rdh0AJA1KGpY0PDIy0tREKod/rz6Njo42dR89rGtysinl\nlpVzakzXvVgSEWsjYiAiBvr7+zs9HavDOZWDc2pMHkV4ADi76vJZ2bJm17H2ck7l4awKlkcRPgIs\nkPQ2SbOAq4CNE9bZCHwqe6XrQuC5iHgmh7Gtcc6pPJxVwVo+VH9EHJN0LbAZmAHcHhG7JH02u34N\nsAm4HNgDvAB8ptVxrTnOqTycVfFy+c6SiNjEWDDVy9ZUnQ/g83mMZdPnnMrDWRWr614sMTMrmovQ\nzJLnIjSz5LkIzSx5LkIzS56L0MySl8vbZ7pF3PBmWHXqicvMMhN/Rvzz0Z36+vqOHyegchCV2bNn\nc/jw4baM11NFqBuPMPb2qqplErGqM/Ox7jPxZ8Q/H92pcgCVapVCbAc/NTaz5LkIzSx5PfXUGE7c\nfJ49e3aHZmJmZdFTRXjCvp8J+xjMzGrxU2MzS15PFmH1d5aYmU2lp54aV3TiKbHfn9YcP142maLf\nE9yTRdgJfn9ac/x42WSKfk9wTz41NjNrhovQzJLnp8aWnOoX0fw+UwMXoSWmst/J7zO1an5qbGbJ\ncxGaWfJchGaWvJb2EUrqA+4G5gP7gD+NiNEa6+0DngdeBY5FxEAr41pznFN5OKvOaHWL8DrggYhY\nADyQXa5nWUSc78A6wjmVh7PqgFaLcDlwR3b+DuAjLd6ftYdzKg9n1QGtFuHpEfFMdv4XwOl11gtg\ni6TtkgYnu0NJg5KGJQ2PjIy0OD3LOKfyyDUr59SYKfcRStoCnFHjqqHqCxERkuq9MWtJRByQ9Fbg\nfklPRsSDtVaMiLXAWoCBgQG/0atBzqk8iszKOTVmyiKMiIvqXSfpl5LOjIhnJJ0JHKpzHweyfw9J\n2gAsBmr+gtn0OKfycFbdp9WnxhuBT2fnPw18b+IKkt4o6ZTKeeAS4IkWx7XmOKfycFYd0GoR/iNw\nsaSfARdll5E0V9KmbJ3TgW2SHgN+AtwbEd9vcVxrTlfmJOn4yZ/5Pa4rs+p1Lb2PMCKeBf6kxvKD\nwOXZ+b3Au1sZx1rTjTn5M7+1dWNWKfAnS8wseS5CM0uei9DMkuciNLPkuQjNLHkuQjNLnovQzJLn\nIjSz5LkIzSx5LkIzS56L0MyS5yI0s+S5CM0seS0dfcbGk3T8vA8rNbXK4+Uj0Fgt1b9P0N7fKRdh\nTnxYqeb5cbJ6iv598lNjM0uei9DMkuciNLPkuQjNLHkuQjNLnovQzJLnIjSz5LkIzSx5LRWhpI9L\n2iXpNUkDk6x3qaSnJO2RdF0rY1rznFN5OKvOaHWL8AngCuDBeitImgHcClwGnAeskHRei+Nac5xT\neTirDmjpI3YRsRtO/EzgBIuBPRGxN1v3LmA58NNWxrbGOafycFadUcQ+wnnA01WX92fLapI0KGlY\n0vDIyEjbJ2fHOafyaDgr59SYKbcIJW0Bzqhx1VBEfC/vCUXEWmAtwMDAgD+V3yDnVB5FZuWcGjNl\nEUbERS2OcQA4u+ryWdkyy5FzKg9n1X2KeGr8CLBA0tskzQKuAjYWMK41xzmVh7PKWatvn/mopP3A\ne4F7JW3Ols+VtAkgIo4B1wKbgd3AtyNiV2vTtmY4p/JwVp3R6qvGG4ANNZYfBC6vurwJ2NTKWDZ9\nzqk8nFVn+JMlZpY8F6GZJc9FaGbJcxGaWfJchGaWPBehmSXPRWhmyXMRmlnyXIRmljwXoZklz0Vo\nZslzEZpZ8lyEZpY8F6GZJc9FaGbJcxGaWfJchGaWPBehmSXPRWhmyXMRmlnyXIRmljwXoZklz0Vo\nZslr9QvePy5pl6TXJA1Mst4+SY9LelTScCtjWvOcU3k4q85o6QvegSeAK4B/bmDdZRHxqxbHs+lx\nTuXhrDqgpSKMiN0AkvKZjbWFcyoPZ9UZRe0jDGCLpO2SBidbUdKgpGFJwyMjIwVNzzLOqTwayso5\nNWbKLUJJW4Azalw1FBHfa3CcJRFxQNJbgfslPRkRD9ZaMSLWAmsBBgYGosH7T55zKo8is3JOjZmy\nCCPiolYHiYgD2b+HJG0AFgM1f8FsepxTeTir7tP2p8aS3ijplMp54BLGdghbF3FO5eGs8tfq22c+\nKmk/8F7gXkmbs+VzJW3KVjsd2CbpMeAnwL0R8f1Wxu1WlR3c3baj2zmN1605gbOqVmROrb5qvAHY\nUGP5QeDy7Pxe4N2tjFMWEd25C8Y5jdetOYGzqlZkTv5kiZklz0VoZslzEZpZ8lyEZpY8F6GZJc9F\naGbJcxGaWfJchGaWPBehmSVP3fwue0kjwM+nefM5QCcOWtnKuOdGRH+ekymCcyoH51RfVxdhKyQN\nR0TdQ5332rhl5ZzKoddz8lNjM0uei9DMktfLRbg2sXHLyjmVQ0/n1LP7CM3MGtXLW4RmZg1xEZpZ\n8kpbhJJWSfqipKslzS1qvBzu52RJP5H0mKRdkm7MY37dqCqjL0s64QuLJC2V9B91bvsWSVslHZV0\nS7NjtjLv7H6c0++unyyni7OvFH08+/eDzYyZw9xzyamlQ/V3iasZ++KagxOvkDQjIl6d6g4kvT4i\njuU1oSnu77fAByPiqKSZjH33xH0R8XBe43ebiLi+mfUlvR54Cfg7YFF2yp1zGm+aOf0K+HBEHJS0\nCNgMzMtzXkXkVKotQklDkv5H0jbgHdniAeBbkh6V9AZJ+yR9VdIO4OOSzpf0sKSdkjZImp3d139K\nulnSMPCFRsfLbjeQnZ8jaV92/mpJGyX9AHhA0pskPSBpR/bXcjlAjDmaDTEzO/XMK1Z1HrN1kq7M\nzl8q6cksnyuqbrdK0p2SfgTcGRG/iYhtjBXidMZ0TpPIMaf/zr5PBWAX8AZJJzUxZlfkVJotQknv\nAa4Czmds3juA7cAw8MWIGM7WA3g2Ii7ILu8EVkbEDyV9GbgB+OvsbmfVe9f6JONN5gLgXRFxOPtr\n+dGIOCJpDvCwpI0REZJmZPf1duDWiPivaTwkXWeqx0zSycC/AB8E9gB3T7iL8xj74vIX8xqzDufU\nnpw+BuyIiN82O2YdheVUpi3C9wMbIuKFiDgCbJxk3bsBJJ0KnBYRP8yW3wF8YOJ6OYxXcX9EHM7O\nC/iHrIi3MPZ04XSAiHg1Is4HzgIWZ08pesFUj9kfAv8XET+LsfdtfXPC9RubKcEGx6zFOeWck6R3\nAl8F/nKaY9ZSWE5lKsJm/Cbn9aod43eP28mT3N8ngH7gPVlIv5y4fkT8GtgKXDqNefSi6eRRj3Nq\nn3E5STqLsa8g/VRE/G+T99UVOZWpCB8EPpLtBzwF+HC2/HnglFo3iIjngFFJ788WfRL4Ya11mxhv\nH/Ce7PyVk9z+VOBQRLwiaRlwLoCkfkmnZeffAFwMPNngnLpdvces4klgvqQ/yC6vaOOY+3BO9eSW\nU/YY3QtcFxE/msaY++iCnEqzjzAidki6G3gMOAQ8kl21Dlgj6UXgvTVu+uns+t8D9gKfaXG8fwK+\nLWmQsR+Aer4F/Lukxxnbj1kJ50zgjmy/xuuAb0dEzbcmlM0kj1nl+pcqj5ukF4CHqPNHDCDbcf5m\nYJakjwCXRMRPGxzTOdWRc07XMrZv7npJlVedL4mIQw2O2RU5+SN2Zpa8Mj01NjNrCxehmSXPRWhm\nyXMRmlnyXIRmljwXoZklz0VoZsn7f36zUAPbBiyTAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x116668610>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plotGene('sirr',0)"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAVcAAAEYCAYAAADoP7WhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAE/tJREFUeJzt3XuMXOV9xvHn4RZQwmWndowxBJNipYIoTWFlkTSpgAAC\nmsRASAttRIhUuamCUqlphVVUvKRVlV7+iBAkxJUIBFC5qYAbTFxMiMBRCF67wWAujUsdYXPxOl4w\nhKvh1z/2rBnGM3uZc96Zc858P9LKM2fOzvvuPDOPz55zZtYRIQBAsfbp9wQAoI4oVwBIgHIFgAQo\nVwBIgHIFgAQoVwBIYGDL1fZ1tv/B9qdtPzXder2cG2aGDOtlJjnZ3mT75B5NKZeBLddJEfFgRHyk\n2++3fYDt221vsR1VCb5OCsjwJNv32t5pe8z2bbbnFzlHFCMijo+In/R7HjMx8OWah+39sotrJX1J\n0vN9nA66kGU4JGmFpIWSjpb0sqTv93Fa6ELT63HKZb0yMOVq+/dsb7D9su1bJB2YLT/Z9tbp1mte\n1/altp+X9P2IeDMivh0RayW93eufa5AkzPCeiLgtInZFxKuSrpL0+z3+8QbOFHnOsf1D2y9mv008\naHuf7LYttk/LLo9kvzXeaHuXpIvbLevXzzcQ5Wr7AEl3SrpBUkPSbZK+0OV6h2e3HS1pabpZo1mP\nM/wDSZuKmjv2Nk1O35C0VdJcSfMk/a2kTu/TXyLpdkmHSbppimU9NxDlKukkSftL+nZEvBURt0ta\n1+V670haHhFvRMRrSWeNZj3J0PbHJF0u6W8K/wnQbKqc3pI0X9LR2W0PRucPQflZRNwZEe80Zdlu\nWc8NSrkeIWlbS0C/6nK9sYh4vegJYlrJM7R9rKR7JP1lRDyYd8KY0lQ5/YukzZL+y/bTtpdNcT/P\nzHBZzw1KuT4naYFtNy37UJfr8TFi/ZE0Q9tHS1oj6e8j4oa8k8W0OuYUES9HxDci4sOSPi/pr2x/\npsP9tHs9luI1Oijl+jNJuyV93fb+ts+TtDjHeu9h+322Jw+aHGD7wJYnDfJLlqHtBZJ+LOmqiLim\n4HmjvY452f6s7WOz19BLmjhQ/E7/ptqdgSjXiHhT0nmaOHK4U9IfS/qPbtdr4ylJr0laIGl1dvno\n/DPHpMQZ/pmkD0sasf3K5Fdhk8depslpkSZ+i3hFEyX8nYi4vw/TzMV8WDYAFG8gtlwBoNcoVwBI\ngHIFgAQoVwBIoG8fajATc+bMiYULF/Z7GqWwfv36HRExt9/zmC0yfBcZVt9sMix1uS5cuFCjo6P9\nnkYp2G73bqTSI8N3kWH1zSZDdgsAQAKUKwAkQLkCQAKUKwAkQLkCQAKUKwAkQLkCQAKUKwAkQLkC\nQAKlfodWHq1/CIDPrUW3eC5VXz8yrO2W6+SDFxG8GJALz6Xq60eGtS1XAOgnyhUAEqBcASAByhUA\nEqhluTYajT1HB23LthqNRp9nBWCQ1PJUrPHx8b2OCLaeigEAKdVyyxUA+o1yBYAEKFcASIByBYAE\nanlAK5YfIo0cuvcyAOiRWparr9jV9myBGOnPfAAMHnYLAEAClCsAJFBIudq+1vZ22491uN22r7S9\n2fZG2ycUMS6KQ4bVR4blUtSW63WSzpzi9rMkLcq+lkr6bkHjojjXiQyr7jqRYWkUUq4R8YCknVOs\nskTSD2LCQ5IOsz2/iLFRDDKsPjIsl17tc10g6Zmm61uzZXuxvdT2qO3RsbGxnkwOM0KG1UeGPVS6\nA1oRsSIihiNieO7cuf2eDrpAhtVHhvn1qly3STqq6fqR2TJUBxlWHxn2UK/KdaWki7KjlSdJeiki\nnuvR2CgGGVYfGfZQIe/Qsv3vkk6WNMf2VknLJe0vSRFxjaRVks6WtFnSq5K+UsS4KA4ZttdoNDQ+\nPi7p3c8EHhoa0s6dUx036g8yLJdCyjUiLpzm9pD0tSLGQhpk2F6VPnidDMuldAe0AKAOKFcASIBy\nBYAEKFcASIByBYAEKFcAtdZoNPac4WFbttVoNJKPW8u/RAAAk/p1Oh1brgCQAOUKAAlQrgCQAOUK\nAAlQrgCQAOUKAAlQrgCQAOUKAAlQrgCQAOUKAAlQrgCQAOUKAAlQrgCQAOUKAAlQrgCQAOUKAAnU\n9sOyWz8Md2hoqE8zATCIalmuk586bnuvTyAHgF5gtwAAJEC5AkAClCsAJEC5AkAClCsAJEC5AkAC\nhZSr7TNtP2V7s+1lbW4/2fZLtn+RfV1exLgoDhlWHxmWS+7zXG3vK+lqSadL2ippne2VEfF4y6oP\nRsRn845XNc1vZijrObdkWH1lzbD1zTxlfQ2kUMSW62JJmyPi6Yh4U9LNkpYUcL+1MPlkKvmTigyr\nr5QZRkRVXgOFK6JcF0h6pun61mxZq0/a3mj7HtvHd7oz20ttj9oeHRsbK2B6mAEy7CCWHyKNHPqe\nr1h+SL+n1U7pMmw0GrK9Z+vVthqNRlf3VUW9evvrBkkfiohXbJ8t6U5Ji9qtGBErJK2QpOHh4cH6\nr67cBjJDX7Frry0u24qR/swnp55mOD4+3vaxGxRFlOs2SUc1XT8yW7ZHROxqurzK9ndsz4mIHQWM\nj/zIsPpKl+Gerf7WZQOiiHJdJ2mR7WM0EeYFkv6keQXbh0t6ISLC9mJN7I74dQFjoxhkWH2ly7Bm\nW/2zlrtcI2K37UskrZa0r6RrI2KT7a9mt18j6XxJf2F7t6TXJF0Qg7Z3u8TIsPrIsHxc5sd2eHg4\nRkdHu/7+snzkYBHzsL0+IoYLmlLP5M2w39pl122eg5ZhkY9dHv3KkHdoAUAClGtCk6eiSNpzSsog\nnYoCDLJa/iWCshj0U1GAQcaWKwAkQLkCQAKUKwAkQLkCQAIc0AKQTOsB3KGhoT7NpPcoVwBJNJ8p\nU5Y39PQSuwUAIAHKFQASoFwBIAH2uQLTGOSDMuge5QpMYfIgzCAekEE+7BYAgAQoVwBIgHIFgAQo\nVwDJtP5p7UHCAS0AyQzyQcDabrm2/gUAoFs8l9CN2m65DvL/mCgWzyV0o7ZbrgDQT5QrACRAuQJA\nApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAAoWUq+0zbT9le7PtZW1ut+0rs9s3\n2j6hiHFRHDKsPjIsl9zlantfSVdLOkvScZIutH1cy2pnSVqUfS2V9N2846I4ZFh9ZFg+RWy5Lpa0\nOSKejog3Jd0saUnLOksk/SAmPCTpMNvzCxgbxSDD6iPDkimiXBdIeqbp+tZs2WzXkSTZXmp71Pbo\n2NhYAdPDDJBh9ZFhyZTugFZErIiI4YgYnjt3br+ngy6QYfWRYX5FlOs2SUc1XT8yWzbbddA/ZFh9\nZFgyRZTrOkmLbB9j+wBJF0ha2bLOSkkXZUcrT5L0UkQ8V8DYKAYZVh8ZlkzuP/MSEbttXyJptaR9\nJV0bEZtsfzW7/RpJqySdLWmzpFclfSXvuCgOGVYfGZZPIX9DKyJWaSK45mXXNF0OSV8rYiykQYbV\nR4blUroDWgBQB5QrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQr\nACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRAuQJAApQrACRA\nuQJAApQrACRAuQJAApQrACRAuQJAApQrACSwX78nUGex/BBp5NC9lwGovVzlarsh6RZJCyVtkfRH\nETHeZr0tkl6W9Lak3RExnGfcqvAVuxQR711mK0b6M592yLAeyLGzfm3k5N1yXSbpvoj4lu1l2fVL\nO6x7SkTsyDkeikeG9UCOHfRrIyfvPtclkq7PLl8v6Zyc94feI8N6IMeSyVuu8yLiuezy85LmdVgv\nJK2xvd720qnu0PZS26O2R8fGxnJODzNAhvVQaI5kmN+0uwVsr5F0eJubLmu+EhFhO9qsJ0mfioht\ntj8o6V7bT0bEA+1WjIgVklZI0vDwcKf7wyyQYT30MkcyzG/aco2I0zrdZvsF2/Mj4jnb8yVt73Af\n27J/t9u+Q9JiSW1fmCgeGdYDOVZL3t0CKyV9Obv8ZUl3ta5g+/22D568LOkMSY/lHBfFIcN6IMeS\nyVuu35J0uu1fSjotuy7bR9hela0zT9Ja249IeljS3RHxo5zjojhkWA/kWDK5TsWKiF9L+kyb5c9K\nOju7/LSk380zDtIhw3ogx/Lh7a8AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4A\nkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADl\nCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJUK4AkADlCgAJ5CpX21+0vcn2\nO7aHp1jvTNtP2d5se1meMVEsMqwHciyfvFuuj0k6T9IDnVawva+kqyWdJek4SRfaPi7nuCgOGdYD\nOZbMfnm+OSKekCTbU622WNLmiHg6W/dmSUskPZ5nbBSDDOuBHMunF/tcF0h6pun61mxZW7aX2h61\nPTo2NpZ8cpgRMqyHGedIhvlNu+Vqe42kw9vcdFlE3FX0hCJihaQVkjQ8PBxF3/8gIsN66GWOZJjf\ntOUaEaflHGObpKOarh+ZLUOPkGE9kGO19GK3wDpJi2wfY/sASRdIWtmDcVEcMqwHcuyhvKdinWt7\nq6RPSLrb9ups+RG2V0lSROyWdImk1ZKekHRrRGzKN20UhQzrgRzLJ+/ZAndIuqPN8mclnd10fZWk\nVXnGQhpkWA/kWD68QwsAEqBcASAByhUAEqBcASCBXAe0gJRa38oZwbnsqA62XFFaEbGnUClWVA3l\nCgAJUK4AkADlilJqNBqyvWe/q201Go0+zwqYOQ5ooZTGx8f32s86zWeVAqVCuSbWWghDQ0N9mgkw\nuPrxOqRcE5rc8rLN0W6gT/r1OmSfKwAkwJYrSimWHyKNHLr3MqAiKFeUkq/Y1faAVoz0Zz7AbLFb\nAAASoFwBIAHKFQASoFwBIAEOaKG0eAMGqoxyRSk1nynAmzBQRewWAIAEKFcASIByBYAEKFcASIBy\nTaz5w54xO60flg10q/l51KvnEmcLJMZR7u7x2KEo/XguseUKAAlQrgCQAOUKAAlQrgCQQK5ytf1F\n25tsv2N7eIr1tth+1PYvbI/mGRPFIsN6IMfyyXu2wGOSzpP0vRmse0pE7Mg5HopHhvVAjiWTq1wj\n4gmJcxCrjAzrgRzLp1f7XEPSGtvrbS+dakXbS22P2h4dGxvr0fQwA2RYDzPKkQzzm3bL1fYaSYe3\nuemyiLhrhuN8KiK22f6gpHttPxkRD7RbMSJWSFohScPDw5xFXgAyrIde5kiG+U1brhFxWt5BImJb\n9u9223dIWiyp7Quz2fr163fY/lWOoedIKsO+pSLmcXS331jxDKVy5NjXDKX+5UiG7zHjDJO//dX2\n+yXtExEvZ5fPkPTNmXxvRMzNOfZoRHQ8ctorZZlHt/qZYTZ+3x+/Mswhr25zJMPu5D0V61zbWyV9\nQtLdtldny4+wvSpbbZ6ktbYfkfSwpLsj4kd5xkVxyLAeyLF8XOcPxyjD/5ZlmkdVleHxK8McqqwM\nj1+ltlwrYEW/J5ApyzyqqgyPXxnmUGVlePx6Oodab7kCQL/UfcsVAPqCcgWABCpdrrZHbP+17W/a\n3uscQNsn2/5hh+/9Ldv3237F9lV5xu/me1vu50DbD9t+JPvwjSvy3mdV5Mzw9OydRo9m/57a7fjd\nzL3lfgY2w0lTPZa2P297Wa/HneX9FJphLf7MS0RcPpv1be8n6XVJfyfpo9lXUrb3i4jdHW5+Q9Kp\nEfGK7f01cbrMPRHxUOp5lUWXGe6Q9LmIeNb2RyWtlrQgxfwmxyTD7kTESkkrW5e3PqbTPMa59TLD\nym252r7M9v/YXivpI9my62yfn10+0/aTtjdo4lOCJr9vxPYNtn8q6YaI+E1ErNVEyeYd/yfOPubN\n9hzbW7LLF9teafvHku6z/QHb99nekG1tLZGkmPBKNsT+2VdtjzQWmOF/R8Sz2c2bJB1k+31djk+G\nXejwWH7d9uO2N9q+OVt28eRviFnW19j+uaR/bs01x7ilyrBSW662T5R0gaSPa2LuGyStb7r9QEn/\nJulUSZsl3dJyF8dp4r3Vr6UYv4MTJH0sInZmW1vnRsQu23MkPWR7ZUSE7X2z+zpW0tUR8fNu5lh2\nCTP8gqQNEfFGnvE7IMM2pngsl0k6JiLesH1Yh28/UtInI+Jt2yOaxWuzKhlWbcv105LuiIhXI2KX\n9v4143ck/V9E/DImzjG7seX2ld0W6wzHb+feiNiZXbakf7S9UdIaTfwKO0+SIuLtiPi4Jp50i7Nf\nc+uo8AxtHy/pnyT9eQHjt0OG7XV6LDdKusn2lyR1+hX8toh4u+n6bF6blciwauWa128S3e9uvftY\nHjjFmH8qaa6kE7MAX2hdPyJelHS/pDPTTLXy3pOh7SMl3SHpooj43xz3S4bF+UNJV2tia3FdtqXY\nqvW1WMRrs1QZVq1cH5B0ju2DbB8s6XMttz8paaHt386uX9ij8bdIOjG7fP4U33+opO0R8ZbtU5R9\nwo7tuZO/Ptk+SNLpmvhZ6qiwDLPH7G5JyyLipznH3yIynK12j+U+ko6KiPslXaqJx+sDPRhXKlmG\nldrnGhEbbN8i6RFJ2yWta7n9dU98APDdtl+V9KCkgzvdX7bD+xBJB9g+R9IZEfF4F+P/q6RbJ8ee\n4ke4SdJ/2n5U0qjeDW6+pOuz/T37SLo1ItqeflR1BWd4iSb2jV1ue/JsgzMiYnsX45PhLHV4LEPS\njbYP1cSv31dGxIsu8C8kVCVD3v4KAAlUbbcAAFQC5QoACVCuAJAA5QoACVCuAJAA5QoACVCuAJDA\n/wOZIklbflUCFAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1167dd4d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plotGene('tror',0)"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# eq = 'expression ~ C(condition, Sum)*C(dsirr, Sum)' + \\\n",
"# '+ C(condition, Sum)*C(dtror, Sum) + ' + \\\n",
"# '+ C(condition, Sum)*C(didr1, Sum) + ' + \\\n",
"# '+ C(condition, Sum)*C(didr2, Sum) + '\n",
"\n",
"def eq(s):\n",
" e = 'normexpression ~'\n",
" \n",
" for d in ['dtror', 'didr1', 'didr2', 'dsirr']:\n",
" if d[1:] == s:\n",
" continue\n",
" e += 'C(%s, Sum) + '%d\n",
" return e[:-2]\n",
"\n",
"# eq = 'normexpression ~ C(dsirr, Sum)' + \\\n",
"# '+ C(dtror, Sum) + ' + \\\n",
"# '+ C(didr1, Sum) + ' + \\\n",
"# '+ C(didr2, Sum)'\n",
"\n",
"lm_idr1 = ols(eq('idr1'), data=data[(data.gene=='idr1') & (data.time==0)]).fit()\n",
"lm_idr2 = ols(eq('idr2'), data=data[(data.gene=='idr2') & (data.time==0)]).fit()\n",
"lm_sirr = ols(eq('sirr'), data=data[(data.gene=='sirr') & (data.time==0)]).fit()\n",
"lm_tror = ols(eq('tror'), data=data[(data.gene=='tror') & (data.time==0)]).fit()"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>sum_sq</th>\n",
" <th>df</th>\n",
" <th>F</th>\n",
" <th>PR(>F)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>C(dtror, Sum)</th>\n",
" <td>5.671535</td>\n",
" <td>1.0</td>\n",
" <td>30.886299</td>\n",
" <td>0.000536</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(didr2, Sum)</th>\n",
" <td>1.772915</td>\n",
" <td>1.0</td>\n",
" <td>9.655021</td>\n",
" <td>0.014506</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(dsirr, Sum)</th>\n",
" <td>0.130234</td>\n",
" <td>1.0</td>\n",
" <td>0.709236</td>\n",
" <td>0.424157</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Residual</th>\n",
" <td>1.469010</td>\n",
" <td>8.0</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" sum_sq df F PR(>F)\n",
"C(dtror, Sum) 5.671535 1.0 30.886299 0.000536\n",
"C(didr2, Sum) 1.772915 1.0 9.655021 0.014506\n",
"C(dsirr, Sum) 0.130234 1.0 0.709236 0.424157\n",
"Residual 1.469010 8.0 NaN NaN"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sm.stats.anova_lm(lm_idr1, typ=2)"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<table class=\"simpletable\">\n",
"<caption>OLS Regression Results</caption>\n",
"<tr>\n",
" <th>Dep. Variable:</th> <td>normexpression</td> <th> R-squared: </th> <td> 0.866</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Model:</th> <td>OLS</td> <th> Adj. R-squared: </th> <td> 0.816</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Method:</th> <td>Least Squares</td> <th> F-statistic: </th> <td> 17.30</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Date:</th> <td>Mon, 15 May 2017</td> <th> Prob (F-statistic):</th> <td>0.000740</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Time:</th> <td>22:19:10</td> <th> Log-Likelihood: </th> <td> -4.4254</td>\n",
"</tr>\n",
"<tr>\n",
" <th>No. Observations:</th> <td> 12</td> <th> AIC: </th> <td> 16.85</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Df Residuals:</th> <td> 8</td> <th> BIC: </th> <td> 18.79</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Df Model:</th> <td> 3</td> <th> </th> <td> </td> \n",
"</tr>\n",
"<tr>\n",
" <th>Covariance Type:</th> <td>nonrobust</td> <th> </th> <td> </td> \n",
"</tr>\n",
"</table>\n",
"<table class=\"simpletable\">\n",
"<tr>\n",
" <td></td> <th>coef</th> <th>std err</th> <th>t</th> <th>P>|t|</th> <th>[95.0% Conf. Int.]</th> \n",
"</tr>\n",
"<tr>\n",
" <th>Intercept</th> <td> 0.6843</td> <td> 0.247</td> <td> 2.766</td> <td> 0.024</td> <td> 0.114 1.255</td>\n",
"</tr>\n",
"<tr>\n",
" <th>C(dtror, Sum)[S.False]</th> <td> -0.9722</td> <td> 0.175</td> <td> -5.558</td> <td> 0.001</td> <td> -1.376 -0.569</td>\n",
"</tr>\n",
"<tr>\n",
" <th>C(didr2, Sum)[S.False]</th> <td> -0.5436</td> <td> 0.175</td> <td> -3.107</td> <td> 0.015</td> <td> -0.947 -0.140</td>\n",
"</tr>\n",
"<tr>\n",
" <th>C(dsirr, Sum)[S.False]</th> <td> 0.1473</td> <td> 0.175</td> <td> 0.842</td> <td> 0.424</td> <td> -0.256 0.551</td>\n",
"</tr>\n",
"</table>\n",
"<table class=\"simpletable\">\n",
"<tr>\n",
" <th>Omnibus:</th> <td> 2.129</td> <th> Durbin-Watson: </th> <td> 2.631</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Prob(Omnibus):</th> <td> 0.345</td> <th> Jarque-Bera (JB): </th> <td> 0.915</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Skew:</th> <td>-0.100</td> <th> Prob(JB): </th> <td> 0.633</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Kurtosis:</th> <td> 1.663</td> <th> Cond. No. </th> <td> 3.73</td>\n",
"</tr>\n",
"</table>"
],
"text/plain": [
"<class 'statsmodels.iolib.summary.Summary'>\n",
"\"\"\"\n",
" OLS Regression Results \n",
"==============================================================================\n",
"Dep. Variable: normexpression R-squared: 0.866\n",
"Model: OLS Adj. R-squared: 0.816\n",
"Method: Least Squares F-statistic: 17.30\n",
"Date: Mon, 15 May 2017 Prob (F-statistic): 0.000740\n",
"Time: 22:19:10 Log-Likelihood: -4.4254\n",
"No. Observations: 12 AIC: 16.85\n",
"Df Residuals: 8 BIC: 18.79\n",
"Df Model: 3 \n",
"Covariance Type: nonrobust \n",
"==========================================================================================\n",
" coef std err t P>|t| [95.0% Conf. Int.]\n",
"------------------------------------------------------------------------------------------\n",
"Intercept 0.6843 0.247 2.766 0.024 0.114 1.255\n",
"C(dtror, Sum)[S.False] -0.9722 0.175 -5.558 0.001 -1.376 -0.569\n",
"C(didr2, Sum)[S.False] -0.5436 0.175 -3.107 0.015 -0.947 -0.140\n",
"C(dsirr, Sum)[S.False] 0.1473 0.175 0.842 0.424 -0.256 0.551\n",
"==============================================================================\n",
"Omnibus: 2.129 Durbin-Watson: 2.631\n",
"Prob(Omnibus): 0.345 Jarque-Bera (JB): 0.915\n",
"Skew: -0.100 Prob(JB): 0.633\n",
"Kurtosis: 1.663 Cond. No. 3.73\n",
"==============================================================================\n",
"\n",
"Warnings:\n",
"[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.\n",
"\"\"\""
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_idr1.summary()"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>sum_sq</th>\n",
" <th>df</th>\n",
" <th>F</th>\n",
" <th>PR(>F)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>C(dtror, Sum)</th>\n",
" <td>4.258075</td>\n",
" <td>1.0</td>\n",
" <td>21.892869</td>\n",
" <td>0.001584</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(didr1, Sum)</th>\n",
" <td>0.062492</td>\n",
" <td>1.0</td>\n",
" <td>0.321305</td>\n",
" <td>0.586372</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(dsirr, Sum)</th>\n",
" <td>0.875896</td>\n",
" <td>1.0</td>\n",
" <td>4.503413</td>\n",
" <td>0.066605</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Residual</th>\n",
" <td>1.555968</td>\n",
" <td>8.0</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" sum_sq df F PR(>F)\n",
"C(dtror, Sum) 4.258075 1.0 21.892869 0.001584\n",
"C(didr1, Sum) 0.062492 1.0 0.321305 0.586372\n",
"C(dsirr, Sum) 0.875896 1.0 4.503413 0.066605\n",
"Residual 1.555968 8.0 NaN NaN"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sm.stats.anova_lm(lm_idr2, typ=2)"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<table class=\"simpletable\">\n",
"<caption>OLS Regression Results</caption>\n",
"<tr>\n",
" <th>Dep. Variable:</th> <td>normexpression</td> <th> R-squared: </th> <td> 0.859</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Model:</th> <td>OLS</td> <th> Adj. R-squared: </th> <td> 0.806</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Method:</th> <td>Least Squares</td> <th> F-statistic: </th> <td> 16.19</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Date:</th> <td>Mon, 15 May 2017</td> <th> Prob (F-statistic):</th> <td>0.000928</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Time:</th> <td>22:19:17</td> <th> Log-Likelihood: </th> <td> -4.7704</td>\n",
"</tr>\n",
"<tr>\n",
" <th>No. Observations:</th> <td> 12</td> <th> AIC: </th> <td> 17.54</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Df Residuals:</th> <td> 8</td> <th> BIC: </th> <td> 19.48</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Df Model:</th> <td> 3</td> <th> </th> <td> </td> \n",
"</tr>\n",
"<tr>\n",
" <th>Covariance Type:</th> <td>nonrobust</td> <th> </th> <td> </td> \n",
"</tr>\n",
"</table>\n",
"<table class=\"simpletable\">\n",
"<tr>\n",
" <td></td> <th>coef</th> <th>std err</th> <th>t</th> <th>P>|t|</th> <th>[95.0% Conf. Int.]</th> \n",
"</tr>\n",
"<tr>\n",
" <th>Intercept</th> <td> -0.2812</td> <td> 0.255</td> <td> -1.104</td> <td> 0.302</td> <td> -0.868 0.306</td>\n",
"</tr>\n",
"<tr>\n",
" <th>C(dtror, Sum)[S.False]</th> <td> 0.8424</td> <td> 0.180</td> <td> 4.679</td> <td> 0.002</td> <td> 0.427 1.258</td>\n",
"</tr>\n",
"<tr>\n",
" <th>C(didr1, Sum)[S.False]</th> <td> 0.1021</td> <td> 0.180</td> <td> 0.567</td> <td> 0.586</td> <td> -0.313 0.517</td>\n",
"</tr>\n",
"<tr>\n",
" <th>C(dsirr, Sum)[S.False]</th> <td> -0.3821</td> <td> 0.180</td> <td> -2.122</td> <td> 0.067</td> <td> -0.797 0.033</td>\n",
"</tr>\n",
"</table>\n",
"<table class=\"simpletable\">\n",
"<tr>\n",
" <th>Omnibus:</th> <td> 2.559</td> <th> Durbin-Watson: </th> <td> 1.599</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Prob(Omnibus):</th> <td> 0.278</td> <th> Jarque-Bera (JB): </th> <td> 0.440</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Skew:</th> <td>-0.152</td> <th> Prob(JB): </th> <td> 0.803</td>\n",
"</tr>\n",
"<tr>\n",
" <th>Kurtosis:</th> <td> 3.887</td> <th> Cond. No. </th> <td> 3.73</td>\n",
"</tr>\n",
"</table>"
],
"text/plain": [
"<class 'statsmodels.iolib.summary.Summary'>\n",
"\"\"\"\n",
" OLS Regression Results \n",
"==============================================================================\n",
"Dep. Variable: normexpression R-squared: 0.859\n",
"Model: OLS Adj. R-squared: 0.806\n",
"Method: Least Squares F-statistic: 16.19\n",
"Date: Mon, 15 May 2017 Prob (F-statistic): 0.000928\n",
"Time: 22:19:17 Log-Likelihood: -4.7704\n",
"No. Observations: 12 AIC: 17.54\n",
"Df Residuals: 8 BIC: 19.48\n",
"Df Model: 3 \n",
"Covariance Type: nonrobust \n",
"==========================================================================================\n",
" coef std err t P>|t| [95.0% Conf. Int.]\n",
"------------------------------------------------------------------------------------------\n",
"Intercept -0.2812 0.255 -1.104 0.302 -0.868 0.306\n",
"C(dtror, Sum)[S.False] 0.8424 0.180 4.679 0.002 0.427 1.258\n",
"C(didr1, Sum)[S.False] 0.1021 0.180 0.567 0.586 -0.313 0.517\n",
"C(dsirr, Sum)[S.False] -0.3821 0.180 -2.122 0.067 -0.797 0.033\n",
"==============================================================================\n",
"Omnibus: 2.559 Durbin-Watson: 1.599\n",
"Prob(Omnibus): 0.278 Jarque-Bera (JB): 0.440\n",
"Skew: -0.152 Prob(JB): 0.803\n",
"Kurtosis: 3.887 Cond. No. 3.73\n",
"==============================================================================\n",
"\n",
"Warnings:\n",
"[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.\n",
"\"\"\""
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_idr2.summary()"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>sum_sq</th>\n",
" <th>df</th>\n",
" <th>F</th>\n",
" <th>PR(>F)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>C(dtror, Sum)</th>\n",
" <td>1.457169</td>\n",
" <td>1.0</td>\n",
" <td>3.893876</td>\n",
" <td>0.083915</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(didr1, Sum)</th>\n",
" <td>1.532508</td>\n",
" <td>1.0</td>\n",
" <td>4.095201</td>\n",
" <td>0.077617</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(didr2, Sum)</th>\n",
" <td>7.936084</td>\n",
" <td>1.0</td>\n",
" <td>21.206969</td>\n",
" <td>0.001744</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Residual</th>\n",
" <td>2.993765</td>\n",
" <td>8.0</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" sum_sq df F PR(>F)\n",
"C(dtror, Sum) 1.457169 1.0 3.893876 0.083915\n",
"C(didr1, Sum) 1.532508 1.0 4.095201 0.077617\n",
"C(didr2, Sum) 7.936084 1.0 21.206969 0.001744\n",
"Residual 2.993765 8.0 NaN NaN"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sm.stats.anova_lm(lm_sirr, typ=2)"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>sum_sq</th>\n",
" <th>df</th>\n",
" <th>F</th>\n",
" <th>PR(>F)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>C(didr1, Sum)</th>\n",
" <td>2.811780</td>\n",
" <td>1.0</td>\n",
" <td>23.388621</td>\n",
" <td>0.002892</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(didr2, Sum)</th>\n",
" <td>6.224053</td>\n",
" <td>1.0</td>\n",
" <td>51.772194</td>\n",
" <td>0.000365</td>\n",
" </tr>\n",
" <tr>\n",
" <th>C(dsirr, Sum)</th>\n",
" <td>0.669073</td>\n",
" <td>1.0</td>\n",
" <td>5.565407</td>\n",
" <td>0.056352</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Residual</th>\n",
" <td>0.721320</td>\n",
" <td>6.0</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" sum_sq df F PR(>F)\n",
"C(didr1, Sum) 2.811780 1.0 23.388621 0.002892\n",
"C(didr2, Sum) 6.224053 1.0 51.772194 0.000365\n",
"C(dsirr, Sum) 0.669073 1.0 5.565407 0.056352\n",
"Residual 0.721320 6.0 NaN NaN"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sm.stats.anova_lm(lm_tror, typ=2)"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"Intercept 0.684250\n",
"C(dtror, Sum)[S.False] -0.972243\n",
"C(didr2, Sum)[S.False] -0.543586\n",
"C(dsirr, Sum)[S.False] 0.147329\n",
"dtype: float64"
]
},
"execution_count": 46,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_idr1.params"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"Intercept -0.281202\n",
"C(dtror, Sum)[S.False] 0.842425\n",
"C(didr1, Sum)[S.False] 0.102056\n",
"C(dsirr, Sum)[S.False] -0.382077\n",
"dtype: float64"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_idr2.params"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"Intercept 1.074139\n",
"C(dtror, Sum)[S.False] -0.492810\n",
"C(didr1, Sum)[S.False] -0.505389\n",
"C(didr2, Sum)[S.False] -1.150079\n",
"dtype: float64"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_sirr.params"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'd' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-49-59db28077f6e>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mlm_sirr\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mconf_int\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mloc\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m\"C(%s, Sum)[S.False]\"\u001b[0m\u001b[0;34m%\u001b[0m\u001b[0md\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;31mNameError\u001b[0m: name 'd' is not defined"
]
}
],
"source": [
"lm_sirr.conf_int().loc[\"C(%s, Sum)[S.False]\"%d,:]"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"Intercept -2.081668e-17\n",
"C(didr1, Sum)[S.False] -4.192091e-01\n",
"C(didr2, Sum)[S.False] 6.237013e-01\n",
"C(dsirr, Sum)[S.False] -2.044922e-01\n",
"dtype: float64"
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_tror.params"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"Intercept 1.000000\n",
"C(didr1, Sum)[S.False] 0.002892\n",
"C(didr2, Sum)[S.False] 0.000365\n",
"C(dsirr, Sum)[S.False] 0.056352\n",
"dtype: float64"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm_tror.pvalues"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"coeff = []\n",
"sig = []\n",
"conf = []\n",
"\n",
"for t in [0, 5, 20, 60]:\n",
" \n",
" lm_idr1 = ols(eq('idr1'), data=data[(data.gene=='idr1') & (data.time==t)]).fit()\n",
" lm_idr2 = ols(eq('idr2'), data=data[(data.gene=='idr2') & (data.time==t)]).fit()\n",
" lm_sirr = ols(eq('sirr'), data=data[(data.gene=='sirr') & (data.time==t)]).fit()\n",
" lm_tror = ols(eq('tror'), data=data[(data.gene=='tror') & (data.time==t)]).fit()\n",
" \n",
" coeff.append([])\n",
" sig.append([])\n",
" conf.append([])\n",
" for lm in [lm_idr1, lm_idr2, lm_sirr, lm_tror]:\n",
" coeff[-1].append([])\n",
" sig[-1].append([])\n",
" conf[-1].append([])\n",
" \n",
" for d in ['didr1', 'didr2', 'dsirr', 'dtror']:\n",
" try:\n",
" coeff[-1][-1].append(lm.params[\"C(%s, Sum)[S.False]\"%d])\n",
" sig[-1][-1].append(lm.pvalues[\"C(%s, Sum)[S.False]\"%d])\n",
" conf[-1][-1].append(lm.conf_int().loc[\"C(%s, Sum)[S.False]\"%d,:])\n",
" except:\n",
" coeff[-1][-1].append(np.nan)\n",
" sig[-1][-1].append(np.nan)\n",
" conf[-1][-1].append([np.nan]*2)\n",
"\n",
"coeff = np.array(coeff)\n",
"sig = np.array(sig)\n",
"conf = np.array(conf)"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([-0.94700089, -0.2560862 , -1.37565746])"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"conf[0,0,1:,0]"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([-0.94700089, -0.2560862 , -1.37565746])"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"conf[0,0,1:,0]"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x117f93890>"
]
},
"execution_count": 65,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEICAYAAABWJCMKAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl4lOW9//H3Nwlh33cIIcgedghrcMeFRRCqiIIFqoei\ngrZaK9bWen7a1tbaVsQFDhpcUFwqBYG6Vi0ERNl3FCVh3/edkO/vj8w5V4oJAWaSSWY+r+vKlXme\n5565v8Awn3m2+zZ3R0REok9MuAsQEZHwUACIiEQpBYCISJRSAIiIRCkFgIhIlFIAiIhEKQWAlEhm\nttrMrshn2xVmtqWISwoJMxtqZh+Fuw6JDgoAKZHcvZW7f36xzzezMWa2yMxOmtmUC3yumdkfzWxv\n4OePZmYXW0tu7j7V3a8NxWuJFCQu3AWIFCUzi3P3LGAb8ARwHVD2Al9mFHAj0A5w4GNgI/BiCEsV\nKXTaA5ASycwyzKxX4HFZM5tiZvvNbA3QOY+2D5nZCuBoIATec/d/AHsvovvhwNPuvsXdtwJ/Bkbk\nU2eSmbmZjTSzzYEaR5tZZzNbYWYHzGxCrvYjzGxermUPtP820Pa5UO1tiGgPQCLBb4HGgZ/ywD/z\naHMr0BfYE9gDCEYrYHmu5eWBdefSFWgKXAbMBD4AegGlgKVm9o67f5HPc/uRE2qVgMXA+4HniwRF\newASCQYDv3P3fe6+GRifR5vx7r7Z3Y+HoL8KwMFcy4eACgV8M3/c3U+4+0fAUeBNd98V2IOYC3Q4\nx3OfdPcD7r4J+AxoH2T9IoACQCJDPWBzruXMPNpszmPdxTpCzrfx/1UZOOLnHllxZ67Hx/NYrnCO\n5+7I9fhYAW1FzpsCQCLBdqBBruXEPNqEctjb1eScAP5f7QLrREoUBYBEgreBh82sqpklAGMLeoKZ\nxZlZGSAWiDWzMmYWl2u753efAfAqcL+Z1Tez+sADwJRg/xAiRU0BIJHgv8k57LMR+Ah47Tye82ty\nDr2MA4YFHv8awMwaAIeBlfk8dyI5J2JXBn5mBdaJlCimCWFE/pOZDQNaufvD4a5FpDApAEREopQO\nAYmIRCkFgIhIlFIAiIhEqWI9FESNGjU8KSkp3GWIiJQYixcv3uPuNc+nbbEOgKSkJBYtWhTuMkRE\nSgwzy+tO+DzpEJCISJRSAIiIRCkFgIhIlFIAiIhEKQWAiEiUUgCIiEQpBYCISJRSAIiIRCkFgMgF\numXiAm6ZuCDcZYgETQEgIhKlFAAiIlFKASAiEqVCEgBmdr2ZrTezDWY2Lo/tQ81shZmtNLP5ZtYu\nFP2KiMjFCzoAzCwWeA7oDSQDt5pZ8lnNNgKXu3sb4HFgUrD9iohIcEKxB9AF2ODu37v7KWAaMCB3\nA3ef7+77A4tfAgkh6FdERIIQigCoD2zOtbwlsC4/dwD/zG+jmY0ys0Vmtmj37t0hKE9ERPJSpCeB\nzexKcgLgofzauPskd09x95SaNc9rUhsREbkIoZgRbCvQINdyQmDdfzCztsBkoLe77w1BvyIiEoRQ\n7AF8DTQ1s0ZmFg8MAWbmbmBmicB7wO3u/k0I+hQRkSAFvQfg7llmNgb4EIgFXnb31WY2OrD9ReBR\noDrwvJkBZLl7SrB9i4jIxQvJpPDuPgeYc9a6F3M9vhO4MxR9iYhIaOhOYBGRKKUAEBGJUgoAEZEo\npQAQEYlSCgARkSilABARiVIKABGRKKUAEBGJUgoAEZEopQAQEYlSCgARkSilABARiVIKABGRKKUA\nEBGJUgoAEZEoFZIAMLPrzWy9mW0ws3F5bDczGx/YvsLMOoaiXxERuXhBB4CZxQLPAb2BZOBWM0s+\nq1lvoGngZxTwQrD9iohIcEIxI1gXYIO7fw9gZtOAAcCaXG0GAK+6uwNfmlkVM6vr7ttD0P8PBKad\nFAm9mDjKNulM9tH92Oh14a5GIljOx2XhCkUA1Ac251reAnQ9jzb1gR8EgJmNImcvgcTExBCUJxK8\nmLKVqNi+NxU69CGuYnXcszk4fxoH06eBZ4e7PJGLEpI5gUPJ3ScBkwBSUlIuKgKLIjklOqzedpC0\n9AxmLt/GqaxsLmtWkx0Hj7Pv6Cks9TZuGHEvzwzpQLXy8eEuVeSChSIAtgINci0nBNZdaBuRYiHr\nTDafrN3Jy+kZfLVxH2VLxTI4JYERPZJoUqsit0xcQJWypXjg2ub8dsZq+o2fy/PDOtG+QZVwly5y\nQUIRAF8DTc2sETkf6kOA285qMxMYEzg/0BU4WFjH/0Uu1sFjp5n29SZeXZDJ1gPHSahalkf6tGRw\nSgMqlyv1H23NjFu7JNKqXiXuen0Jg19cwKM3JDO0a6LOQUmJEXQAuHuWmY0BPgRigZfdfbWZjQ5s\nfxGYA/QBNgDHgJHB9isSKht2HSYtPYP3lmzl+OkzdLukGr/pl8w1ybWJjTn3h3nbhCrMvrcnP3tr\nGb/+xyqWZO7ndwPbUDY+toiqF7l4ITkH4O5zyPmQz73uxVyPHbgnFH2JhEJ2tvP5N7tIS89g7rd7\niI+L4cb29RjRoxHJ9Spd0GtVKRfPy8M7M+GzDfz1k29Ys/0QLwzrRKMa5QupepHQKHYngUUK05GT\nWby7aDOvLMhk456j1K5Uml9c24xbuyRSvULpi37dmBjj3qub0r5BFe6btpT+z87jqZvbcX3rOiGs\nXiS0FAASFTL3HmXK/AzeWbSFIyez6JBYhfG3dqB36zqUig3diCiXNavJ+2N7cs/UJYx+fTE/vfwS\nHry2OXEh7EMkVBQAErHcnfnf7SUtfSOfrttFrBl929ZlZGqjQr1iJ6FqOd4e3Z3HZ61h4hffs2zT\nAZ69rQO1KpYptD5FLoYCQCLO8VNnmL50K1Pmb+SbnUeoXj6esVc2YWi3htSuVDQfwqXjYnnixjZ0\nTKzKr6avpN/4eTw3tCOdk6oVSf8i50MBIBFj24HjvLogk2lfb+LAsdMk163EUze15YZ29ShTKjxX\n5QzqmEBy4FLRIZO+5OHeLbijZyNdKirFggJASjR3Z1HmftLSN/Lh6p24O9e1qsPI1EZ0TqpaLD5o\nW9SpxIwxqTz4znKemL2WJZv286eb2lGhtP77SXjpHSgl0smsM8xavp20+RtZtfUQlcrEcWfPRtze\nvSEJVcuFu7wfqFSmFC8O68T/zP2eP36wnnU75vHisE40q10x3KVJFFMASImy6/AJXv9yE28szGTP\nkVM0rVWB3w1szcAO9SkXX7zfzmbGqMsa0zahCmPeWMqACek8+aM2DGhfP9ylSZQq3v9jRAJWbDlA\nWnoGs1Zs4/QZ56oWtRiZmkTPJjWKxWGeC9HtkurMubcn97yxhPumLWNJ5n4e6ZtMfJwuFZWipQCQ\nYuv0mWw+WLWDtPSNLNl0gAql4xjatSHDeySV+Ltsa1Uqwxv/1Y0//nMdk+dtZMXWgzw/tCN1K5cN\nd2kSRRQAUuzsO3qKN7/axGsLMtlx6AQNq5fj0X7J3JySQMUypQp+gRKiVGwMv+6XTMeGVXnwneX0\nHT+PZ2/tQGqTGuEuTaJERAbALRMXAPDWT7uHuRK5EOt2HCJtXgb/WLaVk1nZ9GxSg98NbM2VzWsR\nU8CgbCVZnzZ1aV6nIqNfW8ztLy3kgWubc9fljSP6zyzFQ0QGgJQcZ7KdT9buZEp6Bgu+30uZUjEM\n6pjAyNSkqLpCpnHNCvzjnlQefm8lT324niWZ+/nL4PY/GIZaJJQUABIWB4+f5p1Fm3llQQab9x2n\nXuUyjOvdgiGdG1ClXHTOrlW+dBzPDGlPp4ZVeWL2GvpNmMsLQzvRun7lcJcmEUoBIEXqu91HeGV+\nBu8u3sKxU2foklSNh3u35Nrk2howjZxLRYf3SKJ1/crcM3UJP3phPo/f2JrBKQ0KfrLIBQoqAMys\nGvAWkARkAIPdff9ZbRoArwK1AQcmufszwfQrJUt2tvPvb3eTlp7BF9/sJj42hhva1WNkapK+3eaj\nU8OqzL63J/dOW8ov313Bksz9PNa/VdiGtJDIFOwewDjgU3d/0szGBZYfOqtNFvCAuy8xs4rAYjP7\n2N3XBNm3FHNHT2bx3pItpM3P4PvdR6lZsTQ/79WM27omUrPixY+9Hy2qVyjNqz/pyl8//oYJn21g\n1baDvDC0Ew2qFb87naVkCjYABgBXBB6/AnzOWQEQmPt3e+DxYTNbC9QHFAARavO+Y7wyP4O3Fm3m\n8Iks2iVU5m+3tKdPm7q62ekCxcYYv7iuOR0Sq/Dzt5bRd/xc/jakPVe1qB3u0iQCBBsAtXNN7r6D\nnMM8+TKzJKADsPAcbUYBowASExODLE+Kiruz4Pu9pKVn8MnancSY0bt1zqBsHROrlLi7dYubq1vW\nZtbYSxn9+mJ+MmURY69qws96NStwzmKRcykwAMzsEyCvee0eyb3g7m5mfo7XqQD8HfiZux/Kr527\nTwImAaSkpOT7elI8nDh9hhnLtpKWnsG6HYepWq4Ud1/RmGHdGuqu1hBLrF6O9+7uwaMzVvHsvzaw\nbPMBnhnSgWrlo/OqKQlegQHg7r3y22ZmO82srrtvN7O6wK582pUi58N/qru/d9HVSrGx/eBxXluQ\nyZtfbWL/sdO0qFORP/2oLf3bh2/s/WhQplQsf7qpHZ0aVuU3M1bTb/xcnhvakQ6JVcNdmpRAwR4C\nmgkMB54M/J5xdgPL2fd/CVjr7n8Jsj8JI3dnyaYDpKVv5J+rdpDtzjUtazMytRHdLqmmwzxF6JbO\nibSqV5m7pi5m8MQFPNovmWHdGurfQC5IsAHwJPC2md0BZAKDAcysHjDZ3fsAqcDtwEozWxZ43q/c\nfU6QfUsROZWVzeyV25iSnsHyLQepWCaOn6Qm8ePuSboiJYxa16/MrDGX8vO3l/GbGatZnLmf3w9q\nU+yHxZbiI6h3irvvBa7OY/02oE/g8TxAX0tKoN2HT/LGwk28vjCT3YdPcknN8jw+oBWDOiZQXrNZ\nFQuVy5Vi8o9TeP7zDTz98Tes2X6IF4d14pKaFcJdmpQA+l8sP7Bq60HS0jN4f/k2Tp3J5ormNRnR\nI4nLmtbUAGXFUEyMMeaqprRrUIX7pi2j/4R0nrqpLb3b1A13aVLMKQAEgKwz2Xy0Zidp6Rv5OmM/\n5eJjGdKlAcN7JNFY3yb/Q3EdZfbSpjWZNbYnd09dwl1Tl/Bflzbil9e3oJSG2JB8KACi3IFjp3jz\nq828tiCDbQdP0KBaWX7dtyU3pzSgclmNRFnS1KtSlrd/2p0nZq/hf+ZuZPnmg0y4rQO1KpUJd2lS\nDCkAotQ3Ow+Tlp7B9KVbOHE6m+6XVOex/q24umVt3VxUwsXHxfD/BrSmY2JVHn5vJX2fnceEWzvQ\n9ZLq4S5NihkFQBTJznb+tW4XafM3kr5hL6XjYhjYoT7DeyTRsm6lcJcnIXZjh/q0rFuJu15fzG2T\nFzLu+hbceWkjXSoq/0cBEAUOnzjNO4u28MqCDDL3HqNOpTI8eF1zbu2SqLtII1zzOhWZMSaVX767\ngt/NWcvizP08dXPbiJpaUy6eAiCCbdxzlFfmZ/DOos0cPXWGTg2r8otrm3N96zo6MRhFKpYpxfND\nOzJ57kae/GAd/Sek8+KwTjSvEz0zrkneFAARxt2Zt2EPaekZfLZ+F3ExRr+29RjRI4l2DaqEuzwJ\nEzPjvy67hLYJlRnz5lJufC6dPwxqw40d6oe7NAkjBUCEOHYqi/eWbGXK/Aw27DpCjQrx3HtVU4Z2\nTdQVIPJ/ul5SndljezLmjaX87K1lLNm0n0f6tqR0nMZvikYKgBJuy/5j/zco26ETWbSuX4mnb25H\nv3Z19Z9a8lSrUhmm/ldXnvpwPZP+/T0rthzk+aEdqVdFo7dGGwVACeTufLVxH2npGXy0ZgdmxvWt\n6jAiNYmUhlV1lYcUqFRsDL/q05KOiVX4xTsr6Dt+LuNv7cClTWuGuzQpQgqAEuTE6TO8v3wbaekZ\nrNl+iMplSzHqssbc3r0h9fXtTS7C9a3r0qx2Re56fQk/fvkr7u/VjHuubKIhP6KEAqAE2HnoBK9/\nmckbCzex9+gpmtWukHMCr319ysbrMI8E55KaFZh+Tw9+9d5Knv74G5ZuPsBfB7encjldKhrpFADF\n2LLNOWPvz16xnTPuXN2iFiNTG9GjcXUd5pGQKhcfx19vaU+npGr8v/dX0/fZubw4rBOt61cOd2lS\niBQAxczpM9nMWbmdtPQMlm0+QIXScfy4exLDezSkYfXy4S5PIpiZcXu3hrSuV4l7pi5h0AvzeXxA\nK27prLm5I5UCoJjYe+Qkb361ide+zGTnoZM0qlGex25I5qaUBlTQ2PtShDokVmXWvZdy37SlPPT3\nlSzK2M/jN7bWVJ8RKKhPFjOrBrwFJAEZwGB3359P21hgEbDV3fsF028kWbPtEGnpG5mxfBunsrK5\ntGkNnhzUlsubaex9CZ9q5eOZMrILz3zyDeP/tYHV23ImmkmsrhngIkmwXy3HAZ+6+5NmNi6w/FA+\nbe8D1gJRP+rYmWzn4zU7SEvPYOHGfZQtFcvNnRIY0SOJprV1e74UD7Exxv3XNqd9YhV+/tZy+j07\nl78Mbk+v5NrhLk1CJNgAGABcEXj8CvA5eQSAmSUAfYHfAfcH2WeJdfDYad5atIlX5mey9cBx6lcp\ny6/6tOCWlERdcSHF1lUtajNrbE/umrqYO19dxD1XNub+a5pr2PAIEGwA1Hb37YHHO4D8vhr8Dfgl\nUODXWzMbBYwCSEyMjJNPG3YdZsr8DP6+eCvHT5+hS6Nq/KZfS3q1rE2cBmWTEqBBtXK8O7oHj81c\nzXOffceyzQd4ZkgHalQoHe7SJAgFBoCZfQLUyWPTI7kX3N3NzPN4fj9gl7svNrMrCurP3ScBkwBS\nUlJ+8HolRXa288U3u3k5fSNzv91DfFwMA9rVY0RqEq3q6dI6KXnKlIrlyR+1pWNiVX4zYxX9xs/j\n+WEd6ZhYNdylyUUqMADcvVd+28xsp5nVdfftZlYX2JVHs1Sgv5n1AcoAlczsdXcfdtFVF2NHTmbx\n7qLNvLIgk417jlKrYmkeuKYZt3VNpLq+LUkEGNy5Acn1KnH31CXcMnEBv+6bzI+7N9S9KSVQsIeA\nZgLDgScDv2ec3cDdHwYeBgjsAfwiEj/8N+09xpTA2PuHT2bRvkEVnhnSnt6t6xIfp8M8Ella16/M\n+2N68sA7y/jtzNUsztzPHwa1obwuWS5Rgv3XehJ428zuADKBwQBmVg+Y7O59gnz9Ys3dmf/dXtLS\nM/h03U5izejTpi4jU5PooN1iiXCVy5Vi0u0pvPDFdzz90XrWbj/EC8M60aRWhXCXJucpqABw973A\n1Xms3wb84MPf3T8n50qhEu34qTP8Y9lWpqRnsH7nYaqVj2fMlU0Y2rUhdSpr7H2JHjExxj1XNqFd\nQhXunbaUARPm8aeb2tG3bd1wlybnQftrF2DbgeO8uiCTaV9v4sCx07SsW4k/3dSW/u3q6S5JiWo9\nm9Zg9r09uXvqEu55YwlLNjViXO8Wmnq0mFMAFMDdWZy5n7T0DD5YvQN359rkOoxMTaJLo2o68SUS\nULdyWd4a1Z3fz1nLS/M2smLLASbc1pHampGu2FIA5ONk1hlmLd/OlPkZrNx6kEpl4rijZyNu79aQ\nBtV0O7xIXuLjYnisfys6JFZh3N9X0nf8PCbc1oFul1QPd2mSBwXAWXYdPsHULzcxdeEm9hw5SZNa\nFXjixtYM6lifcvH66xI5HwPa16dl3UqMfn0xQycv5JfXNWfUZZdoj7mY0SdawIotB0hLz2DWim2c\nPuNc2bwmI1MbcWnTGnrTilyEZrUrMnNMT3757nL+8M91LM7cz58Ht6NSGQ17UlxEdQCcPpPNh6tz\nBmVbnLmf8vGxDO3akOE9kmhUQ2PviwSrQuk4nrutIy+nZ/CHOWvp/+w8XhjWiZZ1o35MyGIhKgNg\n/9FTvPHVJl7/MpPtB0+QWK0cv+mXzM0pCfp2IhJiZsYdPRvRNqEy90xdwsDn0/n9wDYM6pgQ7tKi\nXlQFwLodh5iSnsH0pVs5mZVNapPqPD6gNVe2qKWRDUUKWeekasy6tydj31jK/W8vZ3Hmfh69IZnS\ncbqEOlwiPgDOZDufrt3JlPkZzP9uL6XjYhjUsT4jejSieR2NvS9SlGpVLMPUO7vy1EfrmfjF96za\nepDnh3WifpWy4S4tKkVsAGRlZzN57ve8uiCTTfuOUa9yGR66vgVDOjegavn4cJcnErXiYmN4uHdL\nOjSoyoPvLKff+Ln8bUgHLm9WM9ylRZ2IC4CjJ7PI2HOU3UdOsjjzAJ2TqvLQ9S24rpXG3hcpTq5v\nXYfmdSpy1+uLGZH2FT+7uhljr2qiqVCLUMQFQNlSsRw6kUW18vGkjehCmwSNvS9SXDWqUZ7pd6fy\nyPSV/PWTb1i6eT9/Hdxee+lFJOK+EsfEGG3qV6JxzQr68BcpAcrGx/L04HY8cWNr5m/YS79n57Fi\ny4FwlxUVIi4AAN24JVLCmBnDujXk7dHdAbjphQW8sXAT7iV2UsASISIDQERKpvYNqvD+2J50vaQa\nv5q+kgffXcHxU2fCXVaRumXiAm6ZuKBI+goqAMysmpl9bGbfBn7nOQuKmVUxs3fNbJ2ZrTWz7sH0\nKyKRq1r5eKaM7MK9Vzfl3cVbGPTCfDL2HA13WREp2D2AccCn7t4U+DSwnJdngA/cvQXQDlgbZL8i\nEsFiY4z7r2lG2ojObDtwnBsmzOOj1TvCXVbECTYABgCvBB6/Atx4dgMzqwxcBrwE4O6n3F1neESk\nQFe2qMWssT1Jql6eUa8t5o8frCPrTHa4y4oYwQZAbXffHni8A6idR5tGwG4gzcyWmtlkM8t3pDUz\nG2Vmi8xs0e7du4MsT0RKugbVyvHO6O7c2iWRFz7/jh+//BV7jpwMd1kRocAAMLNPzGxVHj8Dcrfz\nnNP1eZ2yjwM6Ai+4ewfgKPkfKsLdJ7l7irun1KypOwNFBMqUiuUPg9rw1E1tWZy5n77j57I4c1+4\nyyrxCgwAd+/l7q3z+JkB7DSzugCB37vyeIktwBZ3XxhYfpecQBARuSA3pzRg+t2plCkVyy0TvyQt\nfaMuFQ1CsIeAZgLDA4+HAzPObuDuO4DNZtY8sOpqYE2Q/YpIlEquV4mZY3pyRfNa/Pf7axj75lKO\nnswKd1klUrAB8CRwjZl9C/QKLGNm9cxsTq52Y4GpZrYCaA/8Psh+RSSKVS5bikm3d+Kh61swZ+V2\nBjyXzoZdh8NdVokTVAC4+153v9rdmwYOFe0LrN/m7n1ytVsWOK7f1t1vdPf9wRYuItEtJsa464rG\nvH5nVw4cO0X/CenMWrEt3GWVKLoTWERKtB6NazBr7KW0qFORMW8s5b/fX82pLF0qej4UACJS4tWp\nXIZpo7ozMjWJtPQMbv2fL9lx8ES4yyr2FAAiEhHi42L47Q2tePbWDqzdfoh+z85l/nd7wl1WsaYA\nEJGIckO7eswck0rlsqUYNnkhL3z+nS4VzYcCQEQiTpNaFZkxpie929Tljx+sY9Rrizl4/HS4yyp2\nFAAiEpEqlI5jwq0deLRfMp+t20X/CfNYs+1QuMsqVhQAIhKxzIyf9GzEtFHdOHH6DAOfT+fdxVvC\nXVaxoQAQkYiXklSNWWMvpWNiVX7xznJ+NX0lJ05H10QzeVEAiEhUqFmxNK/d0YXRlzfmjYWbGDxx\nAZv3HQt3WWGlABCRqBEXG8O43i2YeHsnNu4+yg0T5vH5+rzGsIwOCgARiTrXtarD+2N7UqdSGUZO\n+Zq/fvwNZ7Kj71JRBYCIRKWkGuWZfncqAzvU55lPv2XklK/Zf/RUuMsqUgoAEYlaZeNjefrmdvx+\nYBu+/G4v/Z6dx/LN0TNjrQJARKKamXFb10Tevas7ADe/uICpCzOj4u5hBYCICNA2oQqzxvake+Pq\nPDJ9FQ+8s5zjpyL7UtGgAsDMqpnZx2b2beB31Xza/dzMVgfmEn7TzMoE06+ISGGoWj6etBGd+Xmv\nZkxfupWBz6ezcc/RcJdVaILdAxgHfOruTYFPyWOydzOrD9wLpLh7ayAWGBJkvyIihSImxrivV1Om\njOzCjkMn6P/sPD5cvSPcZRWKYANgAPBK4PErwI35tIsDyppZHFAO0LQ9IlKsXd6sJrPG9qRRzfL8\n9LXF/OGfa8k6E1kTzQQbALXdfXvg8Q6g9tkN3H0r8GdgE7AdOOjuH+X3gmY2yswWmdmi3bt3B1me\niMjFS6hajndGd2do10QmfvE9w15ayK7DkTPRTIEBYGafBI7dn/0zIHc7zzll/oPT5oHzAgOARkA9\noLyZDcuvP3efFJg/OKVmzZoX/AcSEQml0nGx/G5gG56+uR3LNh+g3/h5fJ2xL9xlhUSBARCY7L11\nHj8zgJ1mVhcg8Duve6p7ARvdfbe7nwbeA3qE8g8hIlLYftQpgel3p1IuPpYhk75k8tzvS/ylosEe\nApoJDA88Hg7MyKPNJqCbmZUzMwOuBtYG2a+ISJFrWbcSM8f25OoWtXhi9lrGvLGUIyezwl3WRQs2\nAJ4ErjGzb8n5pv8kgJnVM7M5AO6+EHgXWAKsDPQ5Kch+RUTColKZUky8vRPjerfgn6u203/CPL7d\neTjcZV2UoALA3fe6+9Xu3jRwqGhfYP02d++Tq91v3b1F4NDR7e5+MtjCRUTCxcwYfXljpt7ZjUPH\nTzPguXRmLNsa7rIumO4EFhG5SN0bV2f2vZeSXLcS901bxmMzV3Mqq+RcKqoAEBEJQu1KZXhzVDd+\nktqIKfMzGDJpAdsPHg93WedFASAiEqRSsTE8ekMyE27rwPodh+k3fh7pG/aEu6wCKQBEREKkX9t6\nzBiTStXy8dz+0kKe+2wD2cV4ohkFgIhICDWpVZEZ96TSt209nvpwPaNeW8TB46fDXVaeFAAiIiFW\nvnQc44e057Ebkvl8/W5ueHYeq7cdDHdZP6AAEBEpBGbGiNRGvPXT7pzKymbQ8/N5Z9HmcJf1HxQA\nIiKFqFPDqsy6tyedGlblwXdX8PB7KzhxunhMNKMAEBEpZDUqlOa1O7pyz5WNefOrzdz04nw27zsW\n7rIUACIw4EgtAAAHk0lEQVQiRSE2xnjwuhZM/nEKmXuP0e/ZeXy2Lq/xM4uOAkBEpAj1Sq7NrLE9\nqVelLCOnfM1fPlrPmTBdKqoAEBEpYg2rl2f63T24qVMC4/+1gRFpX7Hv6KkiryOuyHssAm/9tHu4\nSxAROacypWJ56qa2pDSsyqMzV9Nv/FyeG9qxSGvQHoCISJiYGUO6JPL30T2IiTEGT1zAzkMnimyi\nGQWAiEiYtUmozKyxPenZpAYZe4/x3e6jRXKpaFABYGY3m9lqM8s2s5RztLvezNab2QYzGxdMnyIi\nkahKuXheGt6ZhCplOX0mm7gYK/Q+g90DWAUMAv6dXwMziwWeA3oDycCtZpYcZL8iIhEnJsaoX7Us\nLepUJC628A/QBHUS2N3XQs5xrHPoAmxw9+8DbacBA4A1wfQtIhKpCvhMDZmiOAdQH8g9AMaWwLo8\nmdkoM1tkZot2795d6MWJiESrAvcAzOwToE4emx5x9xmhLsjdJxGYND4lJaX4DqQtIlLCFRgA7t4r\nyD62Ag1yLScE1omISBgVxSGgr4GmZtbIzOKBIcDMIuhXRETOIdjLQAea2RagOzDbzD4MrK9nZnMA\n3D0LGAN8CKwF3nb31cGVLSIiwQr2KqDpwPQ81m8D+uRangPMCaYvEREJLd0JLCISpRQAIiJRSgEg\nIhKlFAAiIlFKASAiEqUUACIiUUoBICISpRQAIiJRSgEgIhKlFAAiIlFKASAiEqUUACIiUUoBICIS\npRQAIiJRSgEgIhKlgp0Q5mYzW21m2WaWkk+bBmb2mZmtCbS9L5g+RUQkNILdA1gFDAL+fY42WcAD\n7p4MdAPuMbPkIPsVEZEgBTsj2FoAMztXm+3A9sDjw2a2FqgPrAmmbxERCU6RngMwsySgA7CwKPsV\nEZEfKnAPwMw+AerksekRd59xvh2ZWQXg78DP3P3QOdqNAkYBJCYmnu/Li4jIBSowANy9V7CdmFkp\ncj78p7r7ewX0NwmYBJCSkuLB9i0iInkr9ENAlnOC4CVgrbv/pbD7ExGR8xPsZaADzWwL0B2YbWYf\nBtbXM7M5gWapwO3AVWa2LPDTJ6iqRUQkaMFeBTQdmJ7H+m1An8DjeUD+lwmJiEhY6E5gEZEopQAQ\nEYlSCgARkSilABARiVIKABGRKKUAEBGJUgoAEZEopQAQEYlSCgARkSilABARiVIKABGRKKUAEBGJ\nUgoAEZEopQAQEYlSCgARkSilABARiVJBTQhjZjcDjwEtgS7uvugcbWOBRcBWd+8XTL8iIpHqrZ92\nL7K+gt0DWAUMAv59Hm3vA9YG2Z+IiIRIUAHg7mvdfX1B7cwsAegLTA6mPxERCZ2iOgfwN+CXQHZB\nDc1slJktMrNFu3fvLvzKRESiVIEBYGafmNmqPH4GnE8HZtYP2OXui8+nvbtPcvcUd0+pWbPm+TxF\nREQuQoEngd29V5B9pAL9zawPUAaoZGavu/uwIF9XRESCUOiHgNz9YXdPcPckYAjwL334i4iEX1AB\nYGYDzWwL0B2YbWYfBtbXM7M5oShQREQKR1D3Abj7dGB6Huu3AX3yWP858HkwfYqISGjoTmARkShl\n7h7uGvJlZruBzIt8eg1gTwjLEclN7y8pTMG8vxq6+3ldQlmsAyAYZrbI3VPCXYdEJr2/pDAV1ftL\nh4BERKKUAkBEJEpFcgBMCncBEtH0/pLCVCTvr4g9ByAiIucWyXsAIiJyDgoAEZEoVSIDwMzm57N+\nipndlM+2p8xsnZmtMLPpZlalcKuUSGNmk80sOdx1SMlmZlXM7O5w1wElNADcvceFtA9MR/kx0Nrd\n2wLfAA8XRm0Sudz9Tndfc/b6wPsr32WRs1QBfhAAZnZeQ/NYjpB8dpfIADCzI4HfZmYTzGy9mX0C\n1MrVJsPM/mhmS4Cb3f0jd88KbP4SSCj6yqWkMLPyZjbbzJYH5r+4xcw+N7OUwPYjZva0mS0Hup/9\nfgtv9VLMPQk0NrNlZva1mc01s5nAGgAzuz/XvCs/C6xLCnzOvUrOVLwNQlFIUIPBFQMDgeZAMlCb\nnL/Al3Nt3+vuHfN43k+Atwq/PCnBrge2uXtfADOrDNyVa3t5YKG7PxDYDvm/30RyG0fO0Yj2ZnYF\nMDuwvNHMOgEjga6AAQvN7AtgP9AUGO7uX4aqkBK5B5DLZcCb7n4mMALpv87a/oMPeTN7BMgCphZB\nfVJyrQSuCXyrv9TdD561/Qzw97PW6UuFXIyv3H1j4HFPYLq7H3X3I8B7wKWBbZmh/PCHkr8HUJCj\nuRfMbATQD7jadQOEnIO7f2NmHckZ1vwJM/v0rCYn3P3MWeuOInLhzvd9E/L3V0nfA/g3cIuZxZpZ\nXeDK/Bqa2fXkTEzf392PFVWBUjKZWT3gmLu/DjwF6NCOhMphoGI+2+YCN5pZOTMrT85h7rmFVUhJ\n3wOYDlxFzrH/TcCCc7SdAJQGPg4cr/3S3UcXeoVSUrUBnjKzbOA0Ocf//xzekiQSuPteM0s3s1XA\ncWBnrm1LzGwK8FVg1WR3X2pmSYVRi4aCEBGJUiX9EJCIiFwkBYCISJRSAIiIRCkFgIhIlFIAiIhE\nKQWAiEiUUgCIiESp/w/VhWhT/TkDNgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x117b0e190>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"i = 0\n",
"j = 0\n",
"\n",
"ind = range(4)\n",
"ind.remove(i)\n",
"\n",
"plt.errorbar(range(3), coeff[0,0,ind], yerr=coeff[0,0,ind]-conf[0,0,ind,0])\n",
"plt.plot([0,2], [0,0], lw=2, c='k')\n",
"plt.xticks(range(3), [order[z] for z in ind])\n",
"plt.title('%s, %s min' % (order[i], [0,5,20,60][j]))"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"order = ['idr1', 'idr2', 'sirr', 'tror']"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VPXZ9/HPRcK+b4GQTAw7BFmEBEUFRUURF1xYe/tU\n7WJta1trW+vSR21rW61d7lptxVprbfuwqSgWFLcbESuSsMomULYJ+yb7FnI9f2T0TjEhQzKZOZN8\n369XXpzlN3Ouc8iVa85vzvkdc3dERESCpk6iAxARESmLCpSIiASSCpSIiASSCpSIiASSCpSIiASS\nCpSIiASSClQcmNlyM7u4nHUXm1lhnEOKCTP7LzN7I9FxSO2hXKpdVKDiwN17ufvsyr7ezO4wswIz\nO2Zmz53ha83MHjWz3ZGfR83MKhtLae7+D3e/PBbvJRKNBOfSQ2Z2wswOlvrpVNlYSlMulS010QFI\n+cws1d2LgC3Aw8AVQMMzfJvbgOuAvoADbwLrgadiGKpIoMUolwAmu/tNMQ1OyqUzqDgwsw1mdllk\nuqGZPWdme81sBZBXRtsfmtlS4FAksV5y95eB3ZXY/M3Ar9290N03A78CbiknzmwzczO71czCkRhv\nN7M8M1tqZp+Y2ROl2t9iZnNLzXuk/ZpI2ydjdbYmAgnPpTOJU7kUAzqDir8Hgc6Rn8bAa2W0GQ9c\nBeyKfOqril7AklLzSyLLTudcoCswBJgOvA5cBtQFFpnZVHd/t5zXXk3JH4pmwALg1cjrRWIt3rkE\ncI2Z7QG2Ak+4+x8raK9cqgKdQcXfGOBn7r7H3cPA42W0edzdw+5+JAbbawLsKzW/H2hSwaexn7r7\nUXd/AzgETHT3HZEzsPeAc07z2kfc/RN33wT8D9CvivGLlCfeuTQF6Am0Bb4KPGBm4yt4jXKpClSg\n4q8DEC41v7GMNuEyllXWQUo+gX2qOXDQTz9K8PZS00fKmG9ymtduKzV9uIK2IlUR11xy9xXuvsXd\nT7r7v4DfAaMqeJlyqQpUoOJvKxAqNZ9VRptYDjG/nJILJD7VN7JMJNnFO5fKeu9a971QPKlAxd8U\n4F4za2lmmcC3KnqBmaWaWQMgBUgxswZmllpqvZd3bwjwPHCXmWWYWQbwPeC5qu6ESADENZfMbGRk\nW2ZmA4HvAK/EZE+kTCpQ8fdjSroi1gNvAH+L4jU/oqQ74B7gpsj0jwDMLAQcAD4q57UTKPly9aPI\nzz8jy0SSXbxzaRywNtLmeUq+I/prFeKXCpgeWJjczOwmoJe735voWESSmXIpeFSgREQkkNTFJyIi\ngaQCJSIigaQCJSIigRTooY7atGnj2dnZiQ5D5DMLFizY5e5tEx3HmVAeSdBEm0eBLlDZ2dkUFBQk\nOgyRz5hZWaMVBJrySIIm2jxSF5+IiASSCpSIiASSCpSIiASSClQNN3bCB4yd8EGiw5CA0u+HBJkK\nlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlEiSMbNnzWyH\nmS1LdCwi1SkmBcrMhpvZx2a21szuKWO9mdnjkfVLzax/LLYrUks9BwxPdBAi1a3KBcrMUoAngSuB\nHGC8meWc0uxKoGvk5zbgj1Xdrkht5e5zgD2JjkOkusXieVADgbXuvg7AzCYBI4EVpdqMBJ53dwfm\nmVkLM0t3962V2aCZVTXmWsFS69Ow63n48cPY7fmJDidplPyaJjczu42SD4NkZWUlOBqRyolFgcoA\nwqXmC4Fzo2iTAXyuQCmxqq5eejea9BlG454XUad+IwAOffw+e2Y9SfGR/QmOTuLB3Z8GngbIzc1N\n/oortVLgnqgbTWLVhE+4sbbzwDFeXrSZKQVh1uw4SMO6KVzVJ53lm/dx8FgR23MGc9aAofzihj4M\ny2mX6HBFRCoUiwK1GQiVms+MLDvTNnKGik4WM/vjnUwpCPPOqh0UFTsDzmrJozf25qo+HWhSP5Wx\nEz6gWcO6/OnmXO6avISvPl/A6AGZPHBNDk0b1E30LoiIlCsWBSof6GpmHSkpOuOAL5zSZjpwR+T7\nqXOBfZX9/klg7Y6DTF0Q5qWFm9l54BhtmtTnyxd2ZHRuiC5pTcp8TY/2zXj5mxfw+Ntr+MPstfzr\n37t5bHQfzu/cJs7RS1WZ2UTgYqCNmRUCD7r7nxMblUjsVblAuXuRmd0BzAJSgGfdfbmZ3R5Z/xQw\nExgBrAUOA7dWdbu1zcFjRcxYuoUpBYUs2LiXlDrGJT3SGJMb4uLubambUvEFmfVS6/D9K7pzac80\nvjdlCV/404fcekE2PxzegwZ1U+KwFxIL7j4+0TGIxENMvoNy95mUFKHSy54qNe3AN2OxrdrE3cnf\nsJcpBWFmLN3KkRMn6ZLWhPtG9OC6czJIa9qgUu97TlZLZnx7MI++voq/vL+Bd1fv5Ddj+tEv1CLG\neyAiUnmBu0hCYNu+o7y4sJAXFhSyftchmtRP5bpzOjA6N8Q5oRYxucy+Yb0UHrq2F8Ny2vGDqUu4\n8Y//4psXd+aOS7pSL1UDjIhI5Y2d8AEAk782qErvowIVEMeLinl75XamFIR5d/VOih3O7diKO4Z2\n4cre7WlUr3r+qy7o0obXvzuEH09fwePvrOXtVTv4zZh+dG/ftFq2JyISraQsULGqzkGwatt+phYU\nMm3RZvYcOk77Zg34xsVdGDUgk+w2jeMSQ7MGdfn1mL5c3qsd9730Edf8fi7fv6IbX76wEyl1dFO0\niCRGUhaoZLfvyAleXbKFKQVhlhbuo26KcXlOe0bnZjK4a9uEFYUrerVnwFktuX/aR/x85ireWrGD\nX43uS1brRgmJR0RqNxWoOCkuduat282UgjCvLdvGsaJierRvyoPX5DCyXwatGtdLdIgAtGlSn6du\nGsBLCzfz0PTlDP/dHH50VQ7jB4Y0xJSIxJUKVDUr3HuYFxdsZuqCMIV7j9CsQSpjckOMyQ1xdkaz\nQP7RNzNuHJDJoM6tufuFpdw37SPeWLGNR2/sQ7tmlbtyUETkTKlAVYOjJ07yxortTC0IM3ftLtzh\nwi5t+MEV3bmiV/ukueeoQ4uGPP+lgfz9w438fOZKLv/tHH563dlc27dDokMTibua9N13slCBihF3\nZ/mW/UwpCPPyos3sP1pERouGfOfSrtzYP5NQq+T8HqdOHeOLg7K5sEsbvjd1Cd+euIhZy7fx8Miz\naRmQbkkRqZlUoKpo76HjvLx4M1MKClm5dT/1Uutw5dntGZMbYlCn1tRJ8FVwsfq016ltE6Z+bRAT\n5qzjv99azfz1e/jljX0Y2iMtJu8vInIqFahKOFnsvLdmJ1MLCnlzxXaOnyymT2bzku6vPh1o3qhm\nDsKamlKHbw7twtDuadw1ZTG3PpfP+IEh7r8qhyb19askIrGlvypnYOPuQ0wtKOTFhYVs3XeUlo3q\nctN5ZzE6N5Oe6c0SHV7c5HRoxit3XMB/v7WGCe/+m7lrd/GrUX05t1PrRIcmIjWIClQFDh8v4rWP\ntjGlIMyH6/dQx2BIt7Y8cHUOl/RMo35qclzwEGv1U1P44fAeXNYzjbumLGHcn+bx5Qs68v0ruifN\nRSAiEmwqUGVwdxaFP2FqQZhXl2zl4LEizmrdiB9c0Z0b+meQ3rxhokMMjAFntWLmtwfzi9dW8szc\n9Z8NPNs7s3miQxORJKcCVcrOA8eYtqiQKQWFrI08lXZE73TG5GYysGOrQN6zFASN66fy8HW9uTyn\nPXe/sJTr//A+37qkK98Y2jmqx4CIiJSl1heosp5K2z+rBY/c0Jur+qTrqbNnYEi3tsy6cwgPvbqc\n3761mrdXbec3Y/rSJU0Dz4rImau1Bar8p9Jm6g9qFTRvVJffju3H5TntuG/aR1z1+FzuHt6DW8/P\nTvgl9yKSXGpVgYrFU2klOlf2TmdAdkvue+kjfvrPFby5YhuPjeqbtDcsi0j8ValAmVkrYDKQDWwA\nxrj73jLabQAOACeBInfPrcp2z0RZT6Xt3LZxlZ9KKxVLa9qAP30xl6kLCvnJqyu48nfv8cDVOYzO\nzdT3eSJSoaqeQd0DvO3uj5jZPZH5H5bTdqi776ri9qL26VNppxaE2bD7cLU8lVYqZmaMyQ1xfufW\nfH/qEu5+cSmzlm/jFzf21ocDETmtqhaokcDFkem/ArMpv0BVu7KeSjuwYyvuuKQrI6rxqbRSscyW\njfh/XzmP5/61gUdfX8UVv53Dz67vzYje6YkOTUQCqqp/sdu5+9bI9DagXTntHHjLzE4CE9z96Spu\n9z+s2rafKfmFvLy45Km07ZrV5+sXd2bUgBAd4/RUWqlYnTrGly7syJBubfnelMV84x8LGdmvAz+5\n9uwaOzyUiFRehQXKzN4C2pex6v7SM+7uZublvM2F7r7ZzNKAN81slbvPKWd7twG3AWRlZZUbV9HJ\nYv42byNTSz2VdlhOO0bnhhiSwKfSSsW6pDXhxa+fzx9m/5vH317DvHW7+eWovlzUrW2iQ0sKZjYc\n+B2QAjzj7o8kOCSRalFhgXL3y8pbZ2bbzSzd3beaWTqwo5z32Bz5d4eZTQMGAmUWqMjZ1dMAubm5\nZRa8jbsPs/3AURZs+oQe7ZvywNU5XHdOcJ5KKxVLTanDty/tyiU90vju5MXc/Ox8/uvcLO4b0ZPG\nGni2XGaWAjwJDAMKgXwzm+7uKxIbmUjsVfUvwXTgZuCRyL+vnNrAzBoDddz9QGT6cuAnVdlo3RSj\nbZP6/PnmvMA+lVaic3ZGc1791oX85s3V/Om9dcxdu4tfj+5LbnarRIcWVAOBte6+DsDMJlHyXXCl\nCtSbU/9CvbROtH/33RiGWLPpWEXn+I51UMXH/VT1xp9HgGFmtga4LDKPmXUws5mRNu2AuWa2BJgP\nzHD316uy0Q4tGtKxTWN6ZzZXcaoBGtRN4b4RPZn01fModmf0hA/4xWsrOVZ0Mq5xjJ3wwWdPTQ2w\nDCBcar4wsuw/mNltZlZgZgU7d+6MW3AisVSlMyh33w1cWsbyLcCIyPQ6oG9VtiO1w7mdWvPad4bw\nsxkrmfDuOmav2slvxvalVwcNPHumoukqBxg2+lZAjzGPhh75Hr2SY3VRld9HQydIoDSpn8ovbujN\nX27JY+/h41z35Ps88c4aik4WJzq0oNgMhErNZ0aWidQ4KlASSEN7pPHGd4cw/Ox0fvXGakY99QHr\ndh5MdFhBkA90NbOOZlYPGEfJd8EiNY4KlARWi0b1+P34c/j9+HPYsPsQIx5/j+feX09xcbk9VjWe\nuxcBdwCzgJXAFHdfntioRKqHCpQE3jV9O/DGnUMY1Kk1D726gv/z7Ids+eRIosNKGHef6e7d3L2z\nu/8s0fGIVBcVKEkKac0a8Owtefziht4s3vQJV/x2Di8sKMS99p5NidR0KlCSNMyM8QOzeP3OIfRM\nb8b3py7ha39bwK6DxxIdmohUAxUoSTqhVo2YeNt53D+iJ7NX7+SK387h9WXbEh2WiMSYCpQkpZQ6\nxleHdOKf37qQ9BYNuP3vC7hrymL2HTmR6NBEJEZUoCSpdWvXlGnfuIBvX9qVVxZvYfh/z2Humrg9\ndkxEqpEKlCS9uil1uGtYN176+vk0qpfCTX/+kAdfWcaR4/EdKklEYksFSmqMvqEWzPj2YL50QUf+\n+sFGRjz+Hgs37U10WCJSSSpQUqM0qJvCA9fkMPGr53G8qJhRf/wXj81axfEiDZUkkmxUoKRGGtS5\nNa/fOZhRAzJ58n/+zcgn32fl1v2JDktEzoAKlNRYTRvU5Zej+vLMF3PZeeAY1z4xlz/O/jcna/FQ\nSSLJRAVKarzLctrxxneHMCynHY++vooxEz5gw65DiQ5LRCqgAiW1QqvG9XjyC/353bh+rNl+gCt/\n9x5/m7dRQyWJBFhVH/kukjTMjJH9Mji3Y2vufnEp//flZbyxfBu/HNWH9OYNEx2eBJweVBh/OoOS\nWqd98wb89dY8Hr7ubAo27OWK387h5UWbdTYlEjBVKlBmNtrMlptZsZnlnqbdcDP72MzWmtk9Vdkm\nlHyS0acZqQoz46bzzuK17wyma7um3Dl5MWt2HOSEntwrEhhVPYNaBtwAzCmvgZmlAE8CVwI5wHgz\ny6nidkViIrtNY6Z8bRD3XNmDTw6fYNW2AzqTEgmIKhUod1/p7h9X0GwgsNbd17n7cWASMLIq2xWJ\npZQ6xu0XdebsjGac1aoRZpbokESE+HwHlQGES80XRpaVycxuM7MCMyvYuXNntQcn8qlG9VJp1rBu\nosMQkYgKr+Izs7eA9mWsut/dX4l1QO7+NPA0QG5urvpaRESSTKyuEaiwQLn7ZVXcxmYgVGo+M7JM\nRESkXPHo4ssHuppZRzOrB4wDpsdhuyIiksSqepn59WZWCAwCZpjZrMjyDmY2E8Ddi4A7gFnASmCK\nuy+vWtgitVO0t3aI1ARVGknC3acB08pYvgUYUWp+JjCzKtsSEeB/b+2YkOhARKqbhjoSSSLuvhLQ\npfBSK2ioIxERCSSdQYkETCxu7TCz24DbALKysmIYnUj8qECJBEwMbu3Q/YRSI6iLT0REAkkFSiSJ\nlHdrh0hNpC4+kSRS3q0dIjWRzqBERCSQVKBERCSQVKBERCSQVKBERCSQVKBERCSQVKBERCSQVKBE\nRCSQdB+USESsHlOdTGrjPkvy0BmUiIgEkgqUiIgEkgqUiIgEkrkHdyR+M9sJbCxndRtgVxzDSWY6\nVtGr6Fid5e5t4xVMLFSQR6DfjzOhYxW90x2rqPIo0AXqdMyswN1zEx1HMtCxil5tPFa1cZ8rS8cq\nerE4VuriExGRQFKBEhGRQErmAvV0ogNIIjpW0auNx6o27nNl6VhFr8rHKmm/gxIRkZotmc+gRESk\nBlOBEhGRQApkgTKzf5Wz/DkzG1XOusfMbJWZLTWzaWbWonqjDDYze8bMchIdR5CYWQsz+0ai44gn\n5VLVKZc+L165FMgC5e7nn0l7M0sB3gTOdvc+wGrg3uqILVm4+1fcfcWpyyPHqtz5Gq4F8LmkMrOo\nBk22EoHMmfIol6pOuVSmuORSIJPNzA5G/jUze8LMPjazt4C0Um02mNmjZrYQGO3ub7h7UWT1PCAz\n/pEnhpk1NrMZZrbEzJaZ2Vgzm21muZH1B83s12a2BBh06rFLbPRx9QjQ2cwWm1m+mb1nZtOBFQBm\ndlfk+C0zszsjy7Ijv3/PA8uAUOLCP3PKpTOjXIpaXHIp6I/buB7oDuQA7SjZ+WdLrd/t7v3LeN2X\ngMnVH15gDAe2uPtVAGbWHPh6qfWNgQ/d/XuR9VD+savJ7qHkzKCfmV0MzIjMrzezAcCtwLmAAR+a\n2bvAXqArcLO7z0tQ3LGgXIqOcik6ccmlQJ5BlTIEmOjuJ919C/DOKes/lzhmdj9QBPwjDvEFxUfA\nsMgnucHuvu+U9SeBF09ZVpv+6JRnvruvj0xfCExz90PufhB4CRgcWbcxyYsTKJeipVyqnGrJpaCf\nQVXkUOkZM7sFuBq41GvRDV7uvtrM+gMjgIfN7O1Tmhx195OnLDuERHsMasOxUi6hXKqCasmloJ9B\nzQHGmlmKmaUDQ8traGbDgbuBa939cLwCDAIz6wAcdve/A48Bta27IVoHgKblrHsPuM7MGplZY0q6\nxN6LW2TVT7kUBeVS1OKSS0E/g5oGXEJJf/km4IPTtH0CqA+8GekXnufut1d7hMHQG3jMzIqBE5T0\nmf8qsSEFj7vvNrP3zWwZcATYXmrdQjN7DpgfWfSMuy8ys+y4B1o9lEvRUS5FIV65pKGOREQkkILe\nxSciIrWUCpSIiASSCpSIiASSCpSIiASSCpSIiASSCpSIiASSCpSIiASSCpSIiASSCpSIiASSCpSI\niASSCpSIiASSCpSIiASSClQ1MLPlkadMlrXuYjMrjHNIcWFmr5nZzYmOQ2oO5VLtpgJVDdy9l7vP\nruzrzewOMysws2ORYevP5LU/MLNlZnbAzNab2Q9OWZ9tZv9jZofNbJWZXVbZOE/l7le6+19j9X4i\nicylyOv7m9kcMztoZtvN7Dul1imXqpkKVICY2afP59oCPAw8W5m3Ab4ItASGA3eY2bhS6ycCi4DW\nwP3AC2bWttJBiwRQLHLJzNoArwMTKMmXLsAbpZool6qZClQ1MLMNn36aMrOGZvacme01sxVAXhlt\nf2hmS4FDZpbq7i+5+8vA7jPdtrv/0t0XunuRu38MvAJcENlWN0qeEPqgux9x9xeBpcCN5ezHQ2Y2\n1cz+Hjkj+8jMupnZvWa2w8zCZnZ5qfazzewrkelbzGyumf0qsu/rzezKM90fqd0SmUvAXcAsd/+H\nux9z9wPuvjKyLeVSHKhAVb8Hgc6RnyuAsvqVxwNXAS3cvShWG7aSx6EOBpZHFvUC1rn7gVLNlkSW\nl+ca4G+UnJEtAmZR8nuTAfyEkk+X5TkX+BhoA/wS+HMkJpHKiHcunQfsMbN/RYrIq2aWFVmnXIoD\nFajqNwb4mbvvcfcw8HgZbR5397C7H4nxth+i5P/4L5H5JsC+U9rsB5qe5j3ec/dZkWSfCrQFHnH3\nE8AkINvMWpTz2o3u/id3Pwn8FUgH2lVqT0Tin0uZlBTB7wBZwHpKuvVAuRQXqRU3kSrqAIRLzW8s\no024jGVVYmZ3UPJd1GB3PxZZfBBodkrT5sAByre91PQRYFckST6dh5Jk/aSM1277dMLdD0c+8DWJ\nagdEPi/euXQEmObu+QBm9mNgl5k1R7kUFzqDqn5bgVCp+awy2ngsN2hmXwLuAS5199KX4S4HOplZ\n6U95ffnfLkCRIIt3Li095f1KTyuX4kAFqvpNAe41s5Zmlgl8q6IXmFmqmTUAUoAUM2tQ6qokzMxP\nc2/IfwE/B4a5+7rS69x9NbAYeDDynjcAvYEXK7lvIvEU11yipGv8ejPrZ2Z1gf8LzHX3fcql+FCB\nqn4/pqQrYj0ll6j+LYrX/IiSU/57gJsi0z8CMLMQJd0IH5Xz2ocpuew1P3LvxkEze6rU+nFALrAX\n+AUwyt13nulOiSRAXHPJ3d8B7gNmADsoucz8C6WaKJeqmbnHtHdJqpmZ3QT0cvd7Ex2LSDJTLgWf\nCpSIiASSuvhERCSQVKBERCSQVKBERCSQAn2jbps2bTw7OzvRYYh8ZsGCBbvcPakGBFUeSdBEm0eB\nLlDZ2dkUFBQkOgyRz5hZWaMXBJrySIIm2jxSF5+IiASSCpSIiASSClQNN3bCB4yd8EGiwxCRWiRW\nf3dUoEREJJBUoEREJJBUoEREJJBUoEREJJBUoEREJJBUoEREJJBUoERqMd2GIEGmAiUiIoGkAiUi\nIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoEUtwJlZs+a2Q4zWxavbYokGzMbbmYfm9la\nM7unjPUXm9k+M1sc+XkgEXGKxEM8z6CeA4bHcXsiScXMUoAngSuBHGC8meWU0fQ9d+8X+flJXIMU\niaO4FSh3nwPsidf2RJLQQGCtu69z9+PAJGBkgmMSSZjAfQdlZreZWYGZFezcuTPR4YjEUwYQLjVf\nGFl2qvPNbKmZvWZmvcp6I+WR1ASBK1Du/rS757p7btu2bRMdjkjQLASy3L0P8Hvg5bIaKY+kJghc\ngRKpxTYDoVLzmZFln3H3/e5+MDI9E6hrZm3iF6JI/KhAiQRHPtDVzDqaWT1gHDC9dAMza29mFpke\nSEkO7457pCJxEM/LzCcCHwDdzazQzL4cr22LJAN3LwLuAGYBK4Ep7r7czG43s9sjzUYBy8xsCfA4\nMM7dPTERi1Sv1HhtyN3Hx2tbIskq0m0385RlT5WafgJ4It5xiSSCuvhERCSQ4nYGJfFXXOzsP3IC\nB04WOyl1LNEhBdqnT5ad/LVBCY5EREAFqkbavv8oLywoZHJ+mE17DgNw4aPvMDo3xJjcTDJbNkpw\nhCIiFVOBqiGKThYz++OdTMoP8z8f7+BksXNep1bUTTHMjA4tGvL7d9bw+3fWMLhrW8blhbisZzvq\npaqXV0SCKSkLlLpi/ld4z2Em54eZuiDM9v3HaNOkPl8d3ImxeSE6tmn82bF6/ksDKdx7mKkFhUwt\nCPONfyykdeN63Dggk7F5ITq3bZLgPRER+U9JWaBqu2NFJ3lj+XYm54eZu3YXdQwu6taWH1+bxaU9\n06ibUvZZUWbLRnx3WDe+fWlX5qzZyaT5m3h27nqenrOOgdmtGJsXYkTvdBrWS4nzHomIfJ4KVBJZ\ns/0Ak/LDvLSwkL2HT5DRoiHfvawbo3Mz6dCiYdTvk1LHGNo9jaHd09hx4CgvLdzM5Pww35u6hIde\nXc51/TIYmxfi7Izm1bg3IiKnpwIVcIePF/HPpVuZnB9mwca91E0xhuW0Y2xeFhd2aVPlK/PSmjbg\n9os687Uhnfhw/R4mzd/E5IIwf5u3kd4ZzRmbF2Jkvw40bVA3RnskIhIdFagAcneWbd7PxPxNTF+8\nhYPHiujUtjH3jejBDf0zadOkfsy3aWac16k153VqzY8Pn2DaokIm5Yf50cvL+NmMlVzVJ53xA0P0\nz2pJZKQdEZFqpQIVIPuOnOCVxZuZND/Miq37qZ9ah6v6pDMuL4u87PgVhuaN6nLLBR25+fxslhbu\nY1KkUL6woJAuaU0Ylxfihv6ZtGpcLy7xiASBLs6KPxWoBHN38jfsZdL8Tcz4aCvHiorJSW/GT0f2\n4tp+GTRvmLiuNTOjb6gFfUMt+NFVOcxYupWJ+Zt4eMZKHn19FZf3as+4vBAXdG5DHd0ELCIxpgKV\nILsOHuPFyM2063Ydokn9VEYNyGRcXha9M4N3cULj+qmMyQsxJi/Ex9sOMCl/E9MWbWbG0q1ktmzI\n2NwQo3NDtG/eINGhikgNoQIVRyeLnblrdzFp/ibeXLGdomIn96yWfP3izlzVJ51G9ZLjv6N7+6Y8\neE0vfji8B7OWb2Nyfphfv7ma3761mqHd0xg3MIuh3duSWs7l7iIi0UiOv4hJbssnR5hSEGZqQSGb\nPzlCy0Z1ueX8bMbmhejarmmiw6u0BnVTGNkvg5H9Mti4+1DkhuFC3n6+gLSm9RkVuQn4rNaNEx2q\niCQhFagKFAZHAAAME0lEQVRqcuJkMW+v3MGk/E28u3on7nBhlzbcO6IHw3LaUT+1Zt0Me1brxtw9\nvAd3DevGO6t2MDk/zFPv/ps/zP4353duzbiBWVye044GdWvWfotI9VGBirH1u0rOJF5YUMiug8do\n16w+dwztwpjcEKFWNX+Q1tSUOlzeqz2X92rP1n1HeKGgkMkFYb49cREtGtXlhnMyGTcwRLckPnMU\nkfhQgYqBoydO8vqybUycv4kP1+8hpY5xSY80xuWFuKhb7f0uJr15Q751aVe+ObQL7/97F5Pyw/xt\n3gaefX8952S1YHxeFlf1Sadxff0afsrMhgO/A1KAZ9z9kVPWW2T9COAwcIu7L4x7oCJxoL8MVbBy\n634mzS+5mm3/0SKyWjXiB1d0Z9SATNo109Vsn6pTxxjctS2Du7Zl98FjTFu0mYnzN3H3i0v58avL\nubZfB8blZdEns3mtvgnYzFKAJ4FhQCGQb2bT3X1FqWZXAl0jP+cCf4z8K1LjqECdoYPHinh1yRYm\nzd/EksJ91EupwxVnt2d8XojzOrXW/UAVaN2kPl8Z3IkvX9iRBRv3Mik/HClYYXq0b8r4gVlc1y+D\n5o1q5dBKA4G17r4OwMwmASOB0gVqJPC8uzswz8xamFm6u2+tzAbfnPoX6qV1ov2771Y19lpDxyo6\nx3esgyre1KwCFQV3Z1H4EybPD/Pq0i0cPn6Sbu2a8MDVOVx/TgYtNaLCGTMzcrNbkZvdigeuyWH6\n4i1Mzg/z4PTl/HzmSkb0TmdsXohzO7aqTWdVGUC41Hwhnz87KqtNBvAfBcrMbgNuA8jKyop5oCLx\noAJ1GnsPHWfaopKRvj/efoCGdVO4pm864wZmcU6oRW36w1mtmjWoy03nncVN553Fss37mJwf5uVF\nm5m2aHPJM63yQtzYP5O2TWM/BmFN5e5PA08D5Obmenntho2+FdDwPdHQUEfRKzlWF1X5fVSgTlFc\n7Mxbt5tJ+WFeX7aN4yeL6ZvZnJ9f35tr+qZrVO9qdnZGc87OaM59I3oy86OtTMrfxCOvreJXsz7m\n0p4lNwEP6dq2yqO4B9RmIFRqPjOy7EzbiNQIKlARO/YfZeqCQqYUhNm4+zDNGqQyfmCIsXlZ5HRo\nlujwap2G9VK4cUAmNw7IZO2Og0wpCPPigkJmLd9Oh+YNGJ0bYnRuJpkta9Sl+/lAVzPrSEnRGQd8\n4ZQ204E7It9PnQvsq+z3TyJBV6sLVNHJYt5dvZNJ+WHeWbWDk8XOuR1bcedlXbny7HTdVBoQXdKa\ncN+Innz/8u68tXI7E+dv4vF31vD4O2sY0rUt4/JCXNqzHfVSk/tyfncvMrM7gFmUXGb+rLsvN7Pb\nI+ufAmZScon5WkouM781UfGKVLdaWaDCew5/NvTQtv1HadOkHl8Z3JGxuSE6tW2S6PCkHPVS6zCi\ndzojeqcT3nOYqQsKmVoQ5uv/WEibJvW4sX8mY/JCdE7i/0N3n0lJESq97KlS0w58M95xiSRCrSlQ\nx4pO8uaK7UzOD/Peml2YwUXd2vLQtTlc2rMddWvpzbTJKtSqEXcN68Z3Lu3KnNU7mTh/E8/MXc+E\nOesYmN2KcQNDjOits2CRZFbjC9TaHQeYND/MS4s2s+fQcTJaNOTOy7oyOjdERouGiQ5PqiiljjG0\nRxpDe6Sx48BRXlywmcn5m7hryhIenL6c68/JYGxeiF4dgvcIExE5vRpZoA4fL2LG0q1Mzg9TsHEv\nqXWMYTntGJsXYnDNvQKs1ktr2oCvX9yZ2y/qxLx1e5iUv4lJ+WGe/2AjfTKbMzYvxLV9O+hKTJEk\nUaMK1EelHk9+4FgRndo05t4re3BDLb6Hpjbes2FmDOrcmkGdW/Pjw8d5edFmJuWHuX/aMh7+50qu\n7pPOuIEh+me11L1sIgEW1wJV0UCYlbHvyAmmLy75A7R8y37qp9bhqsgoBANr1ygEUoYWjepxywUd\nufn8bJYU7mPS/E1MX7KFqQsK6ZrWhLF5IW7on0krjQYiFaiNH/YSLW4FKsqBMKPi7hw4VsRdUxYz\n86OtHD1RTM/0ZvxkZC9G9sugeUN14ch/MjP6hVrQL9SCH12dw4ylW5g4P8zDM1byy9c/5vJe7dh3\n5ATNGtSoTgWRpBbPbIxmIMyozH5jJo26DWL5hu0cWvEuB5fOYuO2tbwe44Cl5qvb5iya9L2CVw4O\nJaVhU46Gl8Ht5yc6LBEhvgUqmoEwoxrk8tCK2Rxe+yGHV83FTxythlCltjixayN7336avbP/QqNu\ng7CUVOCHiQ5LRAjgRRLRDHJ59XcfA9QnLLH16WCgIhIM8bw7VYNciohI1OJZoD4bCNPM6lEyEOb0\nOG5fRESSSNy6+MobCDNe2xcRkeQS1++gyhoIU0REpCwaIVVERAJJBUpERAJJBUpERAJJBUpERAIp\ncDfqitRGZtYKmAxkAxuAMe6+t4x2G4ADwEmgyN1z4xelSHzpDEokGO4B3nb3rsDbkfnyDHX3fipO\nUtOpQIkEw0jgr5HpvwLXJTAWkUBQgRIJhnbuvjUyvQ1oV047B94yswWRgZXLZGa3mVmBmRXs3Lkz\n1rGKxIW+gxKJEzN7C2hfxqr7S8+4u5tZmQMlAxe6+2YzSwPeNLNV7j7n1EbRDLosEnQqUCJx4u6X\nlbfOzLabWbq7bzWzdGBHOe+xOfLvDjObRslz1j5XoERqAnXxiQTDdODmyPTNwCunNjCzxmbW9NNp\n4HJgWdwiFIkzFSiRYHgEGGZma4DLIvOYWQcz+3T8ynbAXDNbAswHZri7HiQtNZa6+EQCwN13A5eW\nsXwLMCIyvQ7oG+fQRBJGZ1AiIhJIKlAiIhJIKlAiIhJIKlAiIhJIKlAiIhJIuopPpBab/LVBiQ5B\npFw6gxIRkUBSgRIRkUBSgRIRkUBKyu+g1G8uIlLz6QxKREQCKSnPoESqg87MRWIjVrmkMygREQkk\nFSgREQkkFSgREQkkFSgREQkkc/dEx1AuM9sJbCxndRtgVxzDSWY6VtGr6Fid5e5t4xVMLFSQR6Df\njzOhYxW90x2rqPIo0AXqdMyswN1zEx1HMtCxil5tPFa1cZ8rS8cqerE4VuriExGRQFKBEhGRQErm\nAvV0ogNIIjpW0auNx6o27nNl6VhFr8rHKmm/gxIRkZotmc+gRESkBlOBEhGRQApkgTKzf5Wz/Dkz\nG1XOusfMbJWZLTWzaWbWonqjDDYze8bMchIdR5CYWQsz+0ai44gn5VLVKZc+L165FMgC5e7nn0l7\nM0sB3gTOdvc+wGrg3uqILVm4+1fcfcWpyyPHqtz5Gq4F8LmkMrOoRvW3EoHMmfIol6pOuVSmuORS\nIJPNzA5G/jUze8LMPjazt4C0Um02mNmjZrYQGO3ub7h7UWT1PCAz/pEnhpk1NrMZZrbEzJaZ2Vgz\nm21muZH1B83s12a2BBh06rFLbPRx9QjQ2cwWm1m+mb1nZtOBFQBmdlfk+C0zszsjy7Ijv3/PA8uA\nUOLCP3PKpTOjXIpaXHIp6M+Duh7oDuQA7SjZ+WdLrd/t7v3LeN2XgMnVH15gDAe2uPtVAGbWHPh6\nqfWNgQ/d/XuR9VD+savJ7qHkzKCfmV0MzIjMrzezAcCtwLmAAR+a2bvAXqArcLO7z0tQ3LGgXIqO\ncik6ccmlQJ5BlTIEmOjuJ919C/DOKes/lzhmdj9QBPwjDvEFxUfAsMgnucHuvu+U9SeBF09ZVpv+\n6JRnvruvj0xfCExz90PufhB4CRgcWbcxyYsTKJeipVyqnGrJpaCfQVXkUOkZM7sFuBq41GvRDV7u\nvtrM+gMjgIfN7O1Tmhx195OnLDuERHsMasOxUi6hXKqCasmloJ9BzQHGmlmKmaUDQ8traGbDgbuB\na939cLwCDAIz6wAcdve/A48Bta27IVoHgKblrHsPuM7MGplZY0q6xN6LW2TVT7kUBeVS1OKSS0E/\ng5oGXEJJf/km4IPTtH0CqA+8GekXnufut1d7hMHQG3jMzIqBE5T0mf8qsSEFj7vvNrP3zWwZcATY\nXmrdQjN7DpgfWfSMuy8ys+y4B1o9lEvRUS5FIV65pKGOREQkkILexSciIrWUCpSIiASSCpSIiASS\nCpSIiASSCpSIiASSCpSIiASSCpSIiATS/wc6eKxbwvrP9AAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x117e52790>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VfWd//HXh4SwQ8AESIAQQBDCEqqgQxW1VRREYrW1\naJ2Z1qmjnT7sLO2v09o6o11mxk7bmek285MBi60dq7alDeJW28qiqCwlEEBcCGvYkT1Als/8cS9M\niEFCcnLP9ybv5+ORh7n3nHvu5x7z4X3P8j3H3B0REZHQdIi7ABERkcYooEREJEgKKBERCZICSkRE\ngqSAEhGRICmgREQkSAqoiJnZWjO7+izTrjazbSkuKRJmdoeZvRB3HdJ+qJdEARUxdx/t7i8157Vm\n1snM5pjZZjM7bGarzGzaebzezOxbZrYv+fMtM7Pm1NKQu//M3a+LYlkiTRFzLz1oZtVmdqTez9Dm\n1NKQeqnpFFCBMLNMIBPYClwF9ALuB540s8ImLuZu4CNAMTAOmAHcE3WtIiGLqJcAnnD37vV+NkZe\nrLwvBVTEzGyTmV2b/L2Lmc01s3fNbB0wsZF5v2Rmq4GjwAl3f9DdN7l7nbs/DVQAlzTx7T8JfNfd\nt7n7duA7wKfOUmehmbmZ3WlmW5M1fsbMJprZajM7YGY/rDf/p8xsSb3Hnpz/reS8P4pqa00EYu+l\n86lTvdRKMuMuoI17ABiW/OkGPNvIPLcD04G97l5Tf4KZ9QNGAGub+H6jgbJ6j8uSz72fy4DhwJVA\nKfAccC3QEfijmT3l7gvP8tobSfxD0RNYAcxPvl4kaqnuJYAZZrYf2AH80N3/6xzzq5cipi2o1vVx\n4J/cfb+7bwW+38g833f3re5eVf9JM+sI/Ax41N3faOL7dQcO1nt8COh+jm9j33D34+7+Aolvno+7\n++7kFthi4APv89qH3P2Au28B/gCMb2KdIucr1b30JDAKyAX+EvhHM7v9HK9RL0VMAdW68knsBz9l\ncyPzbG34hJl1AH4KnATuPY/3O0LiG9gpvYAj/v5XBN5V7/eqRh53f5/X7qz3+7FzzCvSEintJXdf\n5+6V7l7r7q8A3wM+do6XqZcipoBqXTuAQfUeFzQyzxnhkdzamQP0Az7q7tXn8X5rSZwgcUox57dL\nQyRUqe6lxpat40IppoBqXU8C95lZbzMbCHyuCa/5LxK7FmY03FUBpw+oXn2W1/4E+LyZDTCzAcAX\ngLnNqlwkLCntJTO7KfleZmaXAn8D/Kb55UtzKKBa19dI7IqoAF4gsavhrMxsMInTwscDO+uNv7gj\nOX0QcBhYc5ZFPEzi4Oqa5M/TyedE0l2qe+k24O3kPD8hcYzo0Sg+iDSd6YaF6cPM/hQY7e73xV2L\nSDpTL6UHBZSIiARJu/hERCRICigREQmSAkpERIIUy6WOcnJyvLCwMI63FmmRFStW7HX33LjrOEW9\nJOmoqX0US0AVFhayfPnyON5apEXMrLErGMRGvSTpqKl9pF18IiISJAWUiIgESQElIiJBUkCJJM18\neCkzH14adxkSAP0thEEBJSIiQVJAiYhIkBRQIiISJAWUiIgESQElIiJBUkCJiEiQIgkoM3vEzHab\nWXkUyxNpj9RHImeKagtqLjA1omWJtFdzUR+JnBZJQLn7ImB/FMsSaa/URyJn0jEokTRjZneb2XIz\nW75nz564yxFpNSkLKDWVSDTcfZa7T3D3Cbm5wdyaSiRyKQsoNZWIiJwP7eITEZEgRXWa+ePAUuAi\nM9tmZp+OYrki7Yn6SORMkdzy3d1vj2I5Iu2Z+kjkTNrFJ+2eu7Ni837e2nWYE9W1cZcjIkmRbEGJ\npKOa2jqeW7uT2YsrWLX1ABkdjGMKKJFgKKCk3Tl0vJonl23lxy9vYvuBKgov6Mo3bhrNb1ZVktHB\n4i5PRJIUUG3IqVtUP3HPpJgrCdPW/ceY+8omnli2lSMnarh0SB8emFHENaP6kdHBeHr1jrhLFJF6\nFFDS5q3c8i5zFlfwbPkOOpgxfVwen75iCOMGZsddmoi8DwWUtEk1tXW8sG4XsxdvZOWWA/TonMlf\nXjmUT04qJD+7S9zliUgTKKCkTTl8vJonl2/jxy9XsO3dKgr6dOXBGUXcOmEQ3Trpz10knahjpU3Y\nfqCKuS9X8PPXt3L4RA0TC3tz//QiphT104kPImlKASVpbdXWA8xevJFny3cCMH1s4vhS8SAdXxJJ\ndwooSTu1dc5v1yXGLy3f/C49Omdy1xVD+PMPFjJAx5dE2gwFlKSNIydqeGr5Vh55uYKt+6sY2LsL\n/3hjER+fOIjuOr50Bg05kLZAXS3BqzxQxaOvbOJ/Xt/C4eM1XDK4N1+ZNorrRvfX8SWRNkwBJcFa\nve0AsxdXsGDNDtydacnjSxcX9I67NBFJAQWUBKW2znlx/S7mLK7g9U376d4pkzs/WMgnP1jIoD5d\n4y5PRFJIASVBOHqihl+s2MYjL1ewed8xBmR34f7po5g5cRA9OneMuzwRaaIoj38qoCRWOw5W8egr\nm/mf1zZz6HgNHyjI5u+vH8n1o/uRmaG7wYi0ZwooiUX59oPMXryRp1fvoM6daWPy+IsrhnDJYB1f\nEpEEBZSkTF2d87s3djN78UZeq9hPt6wM/nxSIXderuNLIvJeCihpdcdO1vDLFdt45OVNVOw9Sn6v\nznz1hlHMvHQQPXV8SUTOQgElrWbXoeM8+somfvbaFg5WVVM8sBc/uP0DTBvTP8jjSxrUKhIWBZRE\nrnz7QR5ZUsH81ZXU1DnXF/XnrsmJ40tmGlgrIk2jgJJI1NU5f9iwm9mLK1i6cR9dszK447LB3Hl5\nIYMv6BZ3eSKShhRQ0iJVJ2v55cptPLKkgo17j5LXqzP3TRvJbZcW0KuLji+JSPMFF1C6yGV62H3o\nOD9ZupnHXtvMgWPVjBvYi+/dNp4bxubRMcDjSyKSfoILKAnbuspDzFlSQWnZdmrqnCmj+nHX5KFM\nLNTxpSiY2VTge0AGMNvdH4q5JJHYKKDknOrqnIVv7mH2ko28/PY+unTM4BOXFnDn5UMozNHxpaiY\nWQbwI2AKsA1YZmal7r4u3spE4qGAkrM6Xl3Lr1ZuZ86Sjbyz5yj9enbiS1NH8olLC+jVVceXWsGl\nwNvuvhHAzH4O3AScd0D99qkfk9V3KP0XLoy4xPZF6695Tu7eCLoWn7SG3YeP89jSzTz22hb2Hz3J\nmAE9+Y+ZieNLWZk6vtSKBgBb6z3eBlzWcCYzuxu4G6CgoCA1lYnEQAElp72x8xBzFlfwm1WVVNfV\ncc3Iftw1eQiXDemj40sBcfdZwCyACRMmeGPzTLn1TkAnGzWXTtZqvsS6uyqSZSmg2jn3xPGlOUsq\nWPzWXjp37MDMiYO48/JChuZ2j7u89mY7MKje44HJ50TaJQVUO3W8upZf/3E7c5ZU8NbuI/Tt0Ykv\nXn8Rd1xWQHbXrLjLa6+WAcPNbAiJYLoN+ES8JYnERwHVzuw5fILHXt3MY69uZt/RkxTl9eTfPl7M\njePydXwpZu5eY2b3As+TOM38EXdfG3NZIrFRQLUTb+46zJzFFcxbtZ2TNXVcM7Ivn548hElDL9Dx\npYC4+zPAM3HXIRKCSAJKgwvD5O4sfmsvs5dUsOjNPXTu2IFbLxnIX1wxhGE6viQigWtxQGlwYXiO\nV9dSuqqS2Us28uauI+T26MT/u24En7hsMH266fiSiKSHKLagIhtcCFD6z5/BOnai67cjqKwdyuo3\njOHl08no1puTuys4tGwem9cvYnltDZ+Lu7g04d7omdsikmJRBFSkgwv7TPtrOmb3j6Cs9uvYO8s4\nvOzXHN9cFncpIiLNlrKTJJoyuBDg4tEjqHP4l1vGpqq0NuO+X62hYwfj1w89CDwYczUiIi0TRUBF\nOriwa1aipHEDs1tWVTvUvZNOyhSRtiOKf9E0uFBERIBoLw/V4oDS4EIREWkNkewT0uBCERGJmq5t\nIyIiQVJAiYhIkHTal0gbpPsYSVugLSgREQmSAkpERIKkgBIRkSApoEREJEgKKBERCVJwZ/Hp7CMR\nEQFtQYmISKAUUCIiEiQFlIiIBEkBJSIiQVJAiYhIkBRQIgEws1vNbK2Z1ZnZhLjrEQmBAkokDOXA\nLcCiuAsRCUVw46BE2iN3Xw9gZnGXIhIMbUGJiEiQtAUlkiJm9iLQv5FJX3X335zHcu4G7gYoKCiI\nqDqR8CigRFLE3a+NaDmzgFkAEyZM8CiWKRIi7eITEZEgKaBEAmBmN5vZNmASsMDMno+7JpG4aRef\nSADcfR4wL+46REKiLSgREQmSAkpERIKkgBIRkSApoEREJEgKKBERCZLO4mtDnrhnUtwliLQJ6qUw\naAtKRESCpIASEZEgKaBERCRI5p76a02a2R5g8/vMkgPsTVE5bY3WXcuca/0NdvfcVBVzLufoJf0t\ntIzWX/NF0kexBNS5mNlyd9dtr5tB665l2tL6a0ufJQ5af80X1brTLj4REQmSAkpERIIUakDNiruA\nNKZ11zJtaf21pc8SB62/5otk3QV5DEpERCTULSgREWnnFFAiIhKklAeUmb1ylufnmtnHzjLtVjNb\na2Z1ZqbTPhthZrPNrCjuOkJmZtlm9tm464iKeil66qNzS2UfpTyg3P2D5zO/mWUA5cAtwKJWKaoN\ncPe73H1dw+eT6++sj9uZbOA9jWVmTbposiUEs9dBvRQ99VGTpKyP4tiCOpL8r5nZD81sg5m9CPSt\nN88mM/uWma0EbnX39e6+IdW1hsrMupnZAjMrM7NyM5tpZi+d+kZsZkfM7LtmVgZMarg+460+Vg8B\nw8xslZktM7PFZlYKrAMws88n12e5mf1t8rnC5N/oT0j84z4ovvLPpF5qGfVRs6Wsj+K83cbNwEVA\nEdCPxId7pN70fe5+cRyFpYGpQKW7Twcws17AX9Wb3g14zd2/kJwOWp8AXwbGuPt4M7saWJB8XGFm\nlwB3ApcBBrxmZguBd4HhwCfd/dWY6j4X9VLzqI+aJ2V9FOfuiiuBx9291t0rgd83mP5EDDWlizXA\nlOS3ucnufrDB9Frglw2e0/p8r9fdvSL5+xXAPHc/6u5HgF8Bk5PTNgccTqBeai71UTRarY9CvmHh\n0bgLCJW7v2lmFwM3AN80s981mOW4u9c2eE7r872auk7Sfd2le/2tQn0UmVbrozi3oBYBM80sw8zy\ngA/FWEtaMbN84Ji7PwZ8G2jvuxya6jDQ4yzTFgMfMbOuZtaNxG6zxSmrrGXUS82gPmq2lPVRnFtQ\n84APk9hfvgVYerYZzexm4AdALrDAzFa5+/UpqTJMY4Fvm1kdUE1iv/l34i0pfO6+z8xeNrNyoArY\nVW/aSjObC7yefGq2u//RzApTXuj5Uy81j/qoGVLZR7rUkYiIBCmYMR0iIiL1KaBERCRICigREQmS\nAkpERIKkgBIRkSApoEREJEgKKBERCZICSkREgqSAEhGRICmgREQkSAooEREJkgJKRESCpICKgJmt\nTd5ZsrFpV5vZthSXlBJm9qyZfTLuOqRtUB9JQwqoCLj7aHd/qTmvNbNOZjbHzDab2WEzW2Vm087j\n9V80s/LkayvM7IsNphea2R/M7JiZvWFm1zanzsa4+zR3fzSq5Un7FmcfJZdxsZktMrMjZrbLzP6m\n3jT1UQwUUDEys0wS9+TaClwF9ALuB548j/unGPDnQG9gKnCvmd1Wb/rjwB+BC4CvAr8ws9wo6hcJ\nQRR9ZGY5wHPAwyR65ULghXqzqI/i4O76aeEPsAm4Nvl7F2Au8C6JG8h9EdjWYN4vAauBE0BmI8tb\nDXy0mbV8H/hB8vcRyffoUW/6IuAzZ3ntg8BTwGMk7pq5JrmM+4DdJP4BuK7e/C8BdyV//xSwhMQN\n394FKoBpcf+/0U/6/MTZR8A/Az89yzT1UUw/2oKK3gPAsOTP9UBj+5ZvB6YD2e5eU3+CmfUj8ce8\n9nzf2MwMmFzvtaOBje5+uN5sZcnnz2YG8FMSW2R/BJ4nsaU9APg6iW+YZ3MZsAHIAf4VmJOsSeR8\npbqP/gTYb2avmNluM5tvZgXJaeqjmCigovdx4J/cfb+7byWxRdPQ9919q7tX1X/SzDoCPwMedfc3\nmvHeD5L4f/rj5OPuwMEG8xwCerzPMha7+/PJhn+KxK3BH3L3auDnQKGZZZ/ltZvd/b/dvRZ4FMgD\n+jXjc4ikuo8GkgjBvwEKSGy5PJ6cpj6KSWbcBbRB+SQ24U/Z3Mg8Wxs+YWYdSHzjOgnce75vamb3\nkjgWNdndTySfPgL0bDBrLxK7Hc5mV73fq4C9yUY59RgSDXugkdfuPPWLux9Lfunr3qQPIHKmVPdR\nFTDP3Zcll/M1YK+Z9UJ9FBttQUVvBzCo3uOCRubx+g+Sm+9zSHxL+mjyW1aTmdlfAF8GrnH3+qfi\nrgWGmln9b3rFNGP3oUiKpbqPVjdYXv3f1UcxUUBF70ngPjPrbWYDgc814TX/BYwCZjTcXQFgZv4+\n40PuIHGAd4q7b6w/zd3fBFYBD5hZZzO7BRgL/PJ8PpBIDFLaRyR2i99sZuOTuwj/AVji7gfVR/FR\nQEXvayR2R1SQOE31p+83s5kNBu4BxgM7k2MwjiSDBzMbxP+dCdSYb5I49XVZvdf+/3rTbwMmkDgj\n6F+Aj7n7nmZ/OpHUSGkfufvvga8AC0icaXch8Il6s6iPYmDJUxslUGb2p8Bod78v7lpE0pX6KD0p\noEREJEjaxSciIkFSQImISJAUUCIiEqRYBurm5OR4YWFhHG8t0iIrVqzY6+7BXCRUvSTpqKl9FEtA\nFRYWsnz58jjeWqRFzKyxKxrERr0k6aipfaRdfCIiEqRIAsrMHkleAbg8iuWJiIhEtQU1l8TN8kTS\n1syHlzLz4aVxlxGJtvRZpP2KJKDcfRGwP4plSfPpH6X0pj0R0hZE+e9Qyo5BmdndZrbczJbv2aNL\nWIk0Yi7aEyFyWsoCyt1nufsEd5+QmxvMWboiwdCeCJEz6Sw+kTSjvRHSXiigRNKM9kZIexHVaeaP\nA0uBi8xsm5l9OorliohI+xXJlSTc/fYoliMiInKKdvGJBEJ7IkTOFMu1+ETkvbQnQuRM2oISEZEg\nKaBERCRICigREQmSAkpERIKkgBIRkSApoEREJEgKKBERCZICSkREgqSAEhGRICmgREQkSAooEREJ\nkgJKRESCpIASEZEgKaBERCRICigREQmSAkpERIKkgBIRkSApoEREJEgKKBERCVJwATXz4aXMfHhp\n3GWIiEjMggsoERERUECJBMXMpprZBjN728y+HHc9InFSQIkEwswygB8B04Ai4HYzK4q3KpH4KKBE\nwnEp8La7b3T3k8DPgZuas6A6dw4cO0l1bV2kBYqcS3VtHQerqiNZVmYkSxGRKAwAttZ7vA24rDkL\nWvDdz9P3o//A0L/7Occ2vMLR9Qs5sXUt4FHUKXIGy+pC1xGT6DbqKjoXjsdPVnGippZOmRktWq4C\nSiTNmNndwN0ABQUFjc5TtXEFu3/xdboVXUm30R+ixwemUXN4H8feWMzRdQs5ufOtVJYsbZBlZtFl\n2ES6jrqSrsMmYplZ1BzYyaHXfsXR9QvJ+vePt/g9FFAi4dgODKr3eGDyuTO4+yxgFsCECRMa3ST6\n+H8uAuCJeyZx7GQNL67fTemqShZm59Bz4kcovKArM4rzKSnOZ3i/HpF/EGmbqmvrWPLWXuaXVfLC\nul0cOVFDTvdO3DgujxnF+VxckM1ts4qAezCzFr+fAkokHMuA4WY2hEQw3QZ8oqUL7ZqVSUkyjA4e\nq+a5tTsoLavkR394mx/8/m1G9u9Byfh8ZozLZ1Cfri19O2lj6uqc1zftp7SskmfX7ODdY9X07JzJ\n9LF5lIzP50+GXkBGh5aHUWMUUCKBcPcaM7sXeB7IAB5x97VRvkevrh2ZObGAmRML2H34OM+sToTV\nvz63gX99bgMXF2RTUpzPDePy6Nujc5RvnVZOXSzgiXsmxVxJPNydNdsPUrqqkqdX72DnoeN06ZjB\ntUX9KCnO58oROS0+vtQUCiiRgLj7M8AzqXivvj0686nLh/Cpy4ewdf8x5q+upHRVJQ/OX8fXn17H\npGEXUFKcz9TRefTq2jEVJUnM3t59mNJVlZSWVbJp3zE6ZhhXjcjlvhtGMqWoH12zUhsZkbybmU0F\nvkfiW99sd38oiuWKSGoM6tOVz159IZ+9+kLe2nWY0rLEP1Jf+uUa7v91OVeN6EvJ+HyuHdU35f9I\nSeva9u4x5pcltqTX7ziEGUwaegGfuWoYU8f0J7trVmy1tfgvrd7gwikkTotdZmal7r6upcsWkdQb\n3q8HX7juIj4/ZQSrtx2ktKySp1dX8uL6XXTpmMGU07t5csnK1FDKdLTn8AkWrE58CVm55QAAHyjI\n5oEZRUwfm0ffnmHs3o3iq9DpwYUAZnZqcGGzAuq3T/2YrL5D6b9wYQSltU9ad813cvdGaKfHHRoy\nM4oHZVM8KJuv3DCK1yv2M391Jc+sSXzb7tk5k2ljWv9AuUTjYFU1z5fvpLSsklfe2Uudw8j+Pfji\n9RdRUhzmCTJRBFSTBhc2ZeyGiIQpo4MxadgFTBp2AV8rGc2St/ae3rJ6YvlWcnt0On1W1wcGZUdy\nirG0XNXJWl5cv4vSskoWbtjDydo6CpK7c0vG5zMi8CEGKduZ3JSxGwBTbr0TaL9nz7REez/zqKUS\n6++quMsIXseMDnxoZF8+NLIvVSdr+f0buykt287/vL6Fua9sYlCfLswYl0/J+HxG9u8Zd7ntzsma\nOha/tYfSskp+u24Xx07W0q9nJ/5s0mBKivMZN7BX2nyBiCKgmjS4UETani5ZGUwfl8f0cXkcOp7Y\nhTR/9Q4eXrSR/3zpHUb0605JcT4zivMZfEG3uMtts2rrnNc27kvugt3Jwapqsrt25KbxAygpzufS\nIX3SchdsFAHVKoMLRSS99OzckVsnDOLWCYPYe+QEzyaPVX3nhTf5zgtvUjwoMcbqxnF59AvkIHw6\nc3dWbT1AaVklC1bvYPfhE3TNyuC6on6UjM/nigvT/ySWFgdUKgYXikh6yeneiT+bVMifTSpk+4Eq\nnk6etv6Np9fxzQXruGxIH0qKBzBtTH96d4vvNOZ0tGHnYUrLtjO/bAdb9h8jK6MDV1+US8n4fK4Z\n2Y8uWa0/gDZVIjkGlcrBhSKSXgZkd+Geq4Zxz1XDeGfPEUpXVTK/rJKvzFvDP/6mnCtH5FJSnM+U\non5066QxVo3Zsu//BlJv2HWYDgaXX5jDvR++kOtH96dXl7Y5kFp/DSKSMsNyu/N3U0bwt9cOZ23l\nIUrLEmH1+zd207ljB64ZlRhjdfVFuSm5lE7Idh86ztPJS1Gt2poYqzRhcG++ftNobhibR073TjFX\n2PoUUCKScmbGmAG9GDOgF1+eOpIVW96ldFVijNWC1Tvo0TmTqaP7UzI+n0lDLyAzI72PpTTVgWMn\nebZ8J6WrKnm1Yh/uUJTXky9PG8mN4/IY2Du8sUqtSQElIrHq0MGYWNiHiYV9eGBGES+/s4/SVZU8\nV76Tp1ZsI6d7FjeMzaOkOJ+LC3rTIQ3PRns/R0/UJMYqrapk0Vt7qK51huZ0468/PJwZxflc2Ld7\n3CXGRgElIsHIzOjAVSNyuWpELserx/DSht2UllXyxLKt/GTpZgZkd+HG4kRYFeX1TJvxPA2dqKll\n4YbEWKXfrd9NVXUteb06c+flQygpzmd0fvp+tigpoEQkSJ07ZjB1TB5Tx+Rx+Hg1v12XuCLCnMUV\nPLxwI8Nyu1FSPICS8fkMyQl/jFVtnbP0nX2Ulm3nufKdHDpeQ59uWXz0kgGUFA9gwuC2t3XYUgoo\nEQlej84dueXigdxy8UD2Hz3Js+U7KF1VyX/87k3+/cU3GTugV2KMVXEeeb26xF3uae7OyuTxtQVr\ndrL3yAm6d8rkutGJk0EuvzCHju3k+FpzKKBEJK306ZbFHZcN5o7LBrPjYBULkme6/dMz6/nnZ9cz\nsbBP4qaLY/PoE8MYK3dn/Y7Dp89Q3H6giqzMDlwzsi8lxfl8aGRfOnds32coNpUCSkTSVl6vLtw1\neSh3TR5Kxd6jzE8OCL7/1+U8ULqWKy7MoaQ4n+tG96NH59YdK7Rp79HT99F6e/cRMjoYk4fn8IXr\nRjClqPXfvy1SQIlImzAkpxt/fc1wPvfhC1m/4/Dpga1feKqMTvM68OFW2ILZcbCKp8t2MH91Jau3\nHcQMJhb24ZsfGRPbFlxbElxA6UrcItISZkZRfk+K8nvy99dfxMotB5hfVsnTq3fwbPnOFh8D2n/0\n5Ol7Yi3btB93GDugF1+9YVRwx8DSXXABJSISFTPjksG9uWRwb+6fPopXN+6ntGw7z5bv5Fcrt9On\nWxY3jO1/zrPojpyo4YW1iZv9LXlrLzV1zoV9u/N3145gRnF6nEWYjhRQItIuZGZ04IrhOVwxPIdv\nfGTM6XFIv1ixjcde3UJer87cOC6PkuIBuDvu8Fz5jtNjlU7U1DEgO3HMq6Q4n1F5PTRWqZUpoESk\n3emUmcF1o/tz3ej+Z1zJYe4rm/jvxRV0yuxATa2z7LGV5HTP4raJgygZn7iShUIpdRRQIgEws1uB\nB4FRwKXuvjzeitqPbp0yuWn8AG4aP4ADx07yXPlOHnr2DTp2Nv5t5vh2dS3A0Giti4ShHLgFWBR3\nIe1Zdtcsbru0gIv692BobncmD89VOMVIW1AiAXD39YB2H4nUo68GImnGzO42s+VmtnzPnj1xlyPS\narQFJZIiZvYi0L+RSV919980dTnuPguYBTBhwgSPqDyR4CigRFLE3a+NuwaRdKKAEhGRyER5NSAF\nlEgAzOxm4AdALrDAzFa5+/XNXZ4uGSZtgQJKJADuPg+YF3cdIiHRWXwiIhIkBZSIiARJASUiIkFS\nQImISJAUUCIiEiQFlIiIBEkBJSIiQVJAiYhIkBRQIiISJAWUiIgEqUUBZWa3mtlaM6szswlRFSUi\nItLSLSjdplpERFpFiy4Wq9tUi4hIa0nZMSjdplpERM7HObegdJtqERGJwzkDSrepTh+6SV3LaP3J\nKfpbCIPmVrHaAAADSklEQVROMxcRkSC19DTzm81sGzCJxG2qn4+mLBERae9aehafblMtIiKtQrv4\nREQkSOae+hPqzGwPsPl9ZskB9qaonLZG665lzrX+Brt7bqqKOZdz9JL+FlpG66/5IumjWALqXMxs\nubvr0knNoHXXMm1p/bWlzxIHrb/mi2rdaRefiIgESQElIiJBCjWgZsVdQBrTumuZtrT+2tJniYPW\nX/NFsu6CPAYlIiIS6haUiIi0cwooEREJUsoDysxeOcvzc83sY2eZpjv3noOZzTazorjrCJmZZZvZ\nZ+OuIyrqpeipj84tlX2U8oBy9w+ez/xmloHu3HtO7n6Xu69r+Hxy/Z31cTuTDbynscysSZf8soRg\n9jqol6KnPmqSlPVRHFtQR5L/NTP7oZltSN5zqm+9eTaZ2bfMbCVwq7uvd/cNqa41VGbWzcwWmFmZ\nmZWb2Uwze+nUN2IzO2Jm3zWzMmBSw/UZb/WxeggYZmarzGyZmS02s1JgHYCZfT65PsvN7G+TzxUm\n/0Z/QuIf90HxlX8m9VLLqI+aLWV91KKLxbbQzcBFQBHQj8SHe6Te9H3ufnEchaWBqUClu08HMLNe\nwF/Vm94NeM3dv5CcDlqfAF8Gxrj7eDO7GliQfFxhZpcAdwKXAQa8ZmYLgXeB4cAn3f3VmOo+F/VS\n86iPmidlfRTn7oorgcfdvdbdK4HfN5j+RAw1pYs1wJTkt7nJ7n6wwfRa4JcNntP6fK/X3b0i+fsV\nwDx3P+ruR4BfAZOT0zYHHE6gXmou9VE0Wq2P4tyCOpejcRcQKnd/08wuBm4Avmlmv2swy3F3r23w\nnNbnezV1naT7ukv3+luF+igyrdZHcW5BLQJmmlmGmeUBH4qxlrRiZvnAMXd/DPg20N53OTTVYaDH\nWaYtBj5iZl3NrBuJ3WaLU1ZZy6iXmkF91Gwp66M4t6DmAR8msb98C7D0bDOa2c3AD4BcEnfuXeXu\n16ekyjCNBb5tZnVANYn95t+Jt6Twufs+M3vZzMqBKmBXvWkrzWwu8Hryqdnu/kczK0x5oedPvdQ8\n6qNmSGUf6VJHIiISpGDGdIiIiNSngBIRkSApoEREJEgKKBERCZICSkREgqSAEhGRICmgREQkSP8L\ncBSp8w3+2m8AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x117d76290>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VOW9x/HPLxtLgABZSSAkYQthCwIiEEB2XNhcq9Xr\ngqWtta3V26pVW+u1t7W99XbR1gWR2utaFYOidUHFgCiLhn0RCFsChH3fkjz3jxkwWpaQTGbOJN/3\n68XL5Jwz5/xynN/85jzPc85jzjlERES8JiLUAYiIiJyKCpSIiHiSCpSIiHiSCpSIiHiSCpSIiHiS\nCpSIiHiSClSQmdnPzWxyqOOoKjMbaGarQh2HyDcpl+o+031QdYOZ/QS4C2gMvAJ83zl3NLRRiYQX\nM7sReBo4XGnxpc65j0ISUD2nKygPMbOoqiw7xTajgLuBYUBbIAv4VcADFAkT1c0lv7nOuSaV/n0U\n2OikqlSgaomZ3WVmxWa238xWmdkw//IHzOz//D9nmJkzs4lmthH44FTLqnC4G4CnnXPLnHO7gQeB\nG88QmzOzW83sS398/2Vm7czsEzPbZ2Yvm1mMf9sLzWxzpdeuN7P/NLPFZrbXzF4ys4bVPlEiZxHk\nXDrX2JRLtaiq3yjkHJhZJ+A2oI9zrsTMMoDIM7xkMNAZqACST7HsbLoA+ZV+XwQkm1m8c27naV4z\nCugFtAE+B/oD1wE7gbnANcDfT/Paq4DRwBFgDr5i+HgV4hQ5JyHIJYCeZrYD2AX8A/iNc67sDNsr\nl2qJrqBqRznQAMgxs2jn3Hrn3NozbP+Ac+6gc+7wWZadThNgb6Xf9/n/2/QMr/mdc26fc24ZsBR4\n1zm3zjm3F3gb6HmG1/7ZOVfinNsFvAHkViFGkeoIdi59DHQFkoDL8RWXn57lNcqlWqICVQucc2uA\n24EHgFIze9HMUs/wkk1VXHY6B4BmlX6P8/93/xles63Sz4dP8XuTM7x2a6WfD51lW5FqC3Yu+QtL\nkXOuwjm3BF9z+RVneZlyqZaoQNUS59zzzrk8fIMWHPDwmTav4rLTWQb0qPR7D2DbGZr3RMJGkHPp\nVK+1GrxeakAFqhaYWSczG2pmDfC1LR+m6u3fp9vnev8Q2FN5FphoZjlm1gK4H5hak+OJeEGwc8nM\nLjKzZP/P2fhyKf9U20rtU4GqHQ2A3wI78F3CJwH3VHdn/lFA8cCnp1rvnPsX8DvgQ2ADUAT8srrH\nE/GQoOYSvls1FpvZQeAt4DXgv6t7PKkZ3agbBswsD/iBc+6aUMciEs6US+FFBUpERDxJTXwiIuJJ\nKlAiIuJJKlAiIuJJIXnUUUJCgsvIyAjFoUVqZOHChTucc4mhjuME5ZKEo6rmUUgKVEZGBgsWLAjF\noUVqxMw2hDqGypRLEo6qmkdq4hMREU9SgRIREU8KSIEysylmVmpmSwOxPxERkUBdQU3FN6dJjV39\nxFyufmJuIHYlck703hOpuUDmUUAKlHPuY3yTe4mIiARE0PqgzGySmS0wswXbt28P1mFFRCRMBa1A\nOeeedM71ds71Tkz0zG0kIiLiURrFJ+IRgRxspP40qQtUoES8YyoBGmwkUhcEapj5C8BcoJOZbTaz\niYHYr0h9osFGIl8XkEcdafIvkeAxs0nAJID09PQQRyNSe9TEJxJmNOBI6gsVKBER8SQVKBER8SQV\nKBGP0GAjka8LyXxQIvLvNNhI5Ot0BSUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6k\nAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUiIp6kAiUi\nIp6kAiUiIp4UkAJlZqPNbJWZrTGzuwOxTxERqd9qXKDMLBJ4DLgIyAGuMbOc6u7POVfTkESqRe89\nEW+JCsA+zgfWOOfWAZjZi8A4YHl1djbro4+oOLibBr+8nmPb1gYgPJEzs5jGNOkxkma9xrL99d/A\nd1eHOiQRITAFKg3YVOn3zUDfb25kZpOASQDp6emn3FFZeQXHtxfRpPtIYrtcyJGNS9g3/3UOr50P\nriIAoYp8JbJZEs16j6VJ95FENGjMkY1LwCykMZnZaOBPQCQw2Tn325AGJBJCgShQVeKcexJ4EqB3\n796nbEuJioxgxFU3U1bhuKhrCs/MaURxejcy4htzc14mV/RqTeOYoIUsddTCDbuZMruIt5duIcKM\nS7u3YmJeFg/NaAmDB4csrkrN5SPwfdGbb2bTnXPVao0QCXeB+LQvBtpU+r21f1m1RUUYtwzM4sb+\nGbyzbBtPFazjF/nL+MO7q7m2bzo39MsgJa5hjYKW+qWsvIJ3lm1j8ux1fLFxD80aRjFpUDtu6N+W\nVnGNQh3eCQFrLn/tnitIHHc3cVP+wMEVH1O+f3uAQxX5JqNBWjaxOYOJikuB7/ar8R4DUaDmAx3M\nLBNfYfoWcG0A9ktUZASXdG/FJd1bsXDDbp6evY4nZq3lqY/XMaZHKhPzMumaFheIQ0kdtf/IcV6a\nv4ln5qyneM9h2sY35ldju3BFr9bENvDc1XjAmssjGjbBlR+jxZCbaDHkJo5sWsrBZR9xaNUcKo7s\nr4XQpb6KTmhLbM6FxOYMIioumYrjRzi8Zh7HyiqIiarZOLwaZ6hzrszMbgPewdduPsU5t6ym+/2m\nXm1b0KttLzbtOsQzc9bz0vyNTPuimL6ZLbllYBbDspOIiAht/4F4x+bdh5g6Zz0vzt/EgaNlnJ/R\nkl+MyWF452Qiw/x9UpXm8vG/nArA767ozvTCEl4vjGVtm64kX/xDBndMZGxuKiNyktVkLtWyadch\npi8qYXphCau27ScywhjYIYFxuak89+lGIjuOr3FxggD1QTnn3gLeCsS+zqZNy8b8YkwOt4/owEvz\nNvHMnCK+8+wCMhNiuXlABpern6pe+2LjbibPLuJfS7cCcEm3VkzMy6RHm+YhjqxKAt5c3jY+lh8O\n68BtQ9uzfMs+pheWMH1RCTNXltIoOpKRXZIZl5vKwA6JREfqvn05vZ0HjvLWki3kF5awYMNuAHq3\nbcF/jevCxd1aEd+kAQAvztt0pt2ck7D9JG/WMJrvDMripgEZvL10K5NnF3F//jL+593VfLtvOjf0\nzyC5mfqp6oPyCse7y3zvgYUbdtO0YRS3DMzkhn4ZpDb3TP9SVdRac7mZ0SU1ji6pcdw1Opv563eR\nv6jk5AdOi8bRXNK9FeNy0+iV3kKtEQLAgaNlvLd8K/mFJRR8uYPyCken5Kb8bHQnxnRPpU3LxrV6\n/LAtUCdERUYwpkcql3ZvxecbdzO5oIjHZ63lqYJ1jOmeys3qp6qzDhwt4+X5m3jmkyI27TpMesvG\nPDAmhyt7t/Fi/9JZBau5PCLC6JsVT9+seB4Y04WPV28nf1EJryzczP99upG05o0Y0yOVcbmpdG7V\nLNCHF487VlZx8j3x3vKtHDleQVrzRkwalMW43FSyU4L3ngi/LD4NM6NX25b0atuSjTsP8cwnRbw8\nfxOvfVFMv6x4JuZlMlT9VHVC8Z7D/P2T9bzw2Ub2Hy2jT0YL7r04hxE5daJ/KWjN5QAxUREMz0lm\neE4yB4+W8d7ybeQXFvNUwToen7WWTslNGZubytgetf9tWUKnosIxb/0u8gt9V9V7Dx+nZWwMV/Zq\nw7jcVM4L0VV1nSlQlaXHN+aXY7pw+/COvDR/I1PnrOeWZxeQlRDLTXmZXHFeaxrFRIY6TDlHhZv2\nMLlgHW/7+5cu9vcv5YZH/5LnxTaIYnzPNMb3TPtaf8Pv31nF799ZRa+2LRiXm8rF3VqR4O9vqKuu\nfmIuAC8FYKi0VznnWFay7+Rgh637jtA4JpKROcmMy00jr0NCyPsl62SBOiGuUTSTBrXjpgGZvn6q\ngnXc//pS/vDuKr7dN53/6Kd+Kq8rr3C8t3wrkwuKWLBhN00bRDExL5Mb+meQFl79S2ElvkkDru+X\nwfX9Mti06xBvLPZ9iP0ifxm/emM5ee19I7ZGdkmhSRg2p9ZnG3YeJL+whPzCYtZuP0hUhHFhp0R+\nfklnhndO8tQgM+9EUouiIyMY2yOVMd1bsWDDbiYXrOOvH63lyUr3U3VJVT+Vlxw4WsY/F2xiyhxf\n/1Kblo34pb9/SR+IwdWmZWNuvbA9t17YnpVbfSMB8wtLuOPlRTSMXsKwzsmMz01jcMfEgAwtlsAr\n3X+EGYt9V8SFm/YAcH5mSybmZXFR1xRaxMaEOMJTq1eZbmb0yWhJn4yWbNh5kGfmrOflBZt47fNi\n+reL55aBmVzYUf1UoVTi7196ft5G9h8po3fbFtx7cWdG5KSEff9SXZCd0ozs0c34z5Gd+HzjbvIL\nS5ixZAszFm8hrlE0F3dLYWyPNPpmtlQehdi+I8d5Z+lWpi8qYc6aHVQ4yGnVjHsuymZMj9SwGOFa\nrwpUZW3jY3lgbBd+MqIjL87byNRP1nPz1AVkJcYyMS+Ty3qqnyqYFm3aw9Ozi5ixZAsAF3VNYWJe\nJj3TW4Q4MjmViAijd0ZLevtvgJ69ZsfJK6sX5m0ipVlDxvTwDVvvktoMC/FDeOuLI8fL+WjVdqYv\nKub9FaUcK6sgvWVjfjCkPWN7pNIhuWmoQzwn9bZAnRDXKJrvDm7HzXmZvLVkC5MLirh32lL+551V\nXHdBW67v15akpuqnqg2+/qVtPD17HfPX+/qXbh6QwQ39M2jdQiPGwkV0ZARDOiUxpFMSh46V8f6K\nUqYXFvPMnPU8VVBEu8RYxuWmMbZHKhkJsaEOt84pr3B8um4n+YXFvL10K/uPlJHQJIZrz09nbG4q\nPds0D9svCPW+QJ0QHRlxMonmr/f1Uz364RqemPVVP1VOqu4JCYSDJ/uX1rNx1yFat2jE/ZfmcFXv\n1jRtGB3q8KQGGsdEMbaHb1j67oPHeHvpVvILi3nkvdU88t5qerRpzrgeqVzao5W++NWAc47Fm/eS\nX1jCG4tL2L7/KE0aRDGqSwrjclPp3y6eqDrwZBAVqG8wM87PbMn5mS1Zv+MgUz/x9VO9+vlmBrSP\n55a8LAZ3TFT7ejVs2XuYqf77l/YdKaNX2xbcfVE2I3OS60Qyyde1iI3h2r7pXNs3nZI9h3lzsa8J\n8ME3l/PQjOX0b5fA2NxURndNoZm+mFTJ2u0HTj6uqmjHQWIiIxiSnci43DSGZifRMLpudUuoQJ1B\nRoK/n2p4R17w309109T5tEuMZWJeFpedl1bn3hC1YfFmf//S4i1UOMdF/vuXzlP/Ur2R2rwRkwa1\nY9Kgdqwp3e8f5lzCz15ZzH2vL2VYdhLjclO5sFPd+5Ctqa17j5ws7kuK92IG/bLi+d7gLEZ3bUVc\no7pb3FWgqiCucTTfG9yOif5+qqcK1vHzaUv4n3dXcV3fdK7zSD+Vl24uLK9wzFyxjcmzi5hXtIsm\nDaK4sb+vf0lPJKjf2ic15c6RnbhjREcKN+0hv7CENxeX8PbSrTRtEMXorimMy02jX7v4ejtyc++h\n47y91Dcs/NOinTgH3VvHcd8lnRnTI7Xe3L+pAnUOKvdTzSvaxeTZRfzlwzU8PmsdY3N9/VT1/dll\nh46V8crCzUyZXcT6nYdIa96I+y7pzNV92qh/Sb7GzOiZ3oKe6S2475LOzF23k/xCX6H658LNJDZt\nwKXdWzE+N43urePCtqO/qo4cL2fmilLyC4v5aNV2jpVXkJkQy4+HdWBsj1SyEpuEOsSgU4GqBrOv\nHrZZtOMgz8wp4p8LNvPKws3ktU9g4sBMBneoX/1UW/Ye5u+fbOCFeRvZe/g4PdOb89NR2Yzqov4l\nObuoyAgGdkhkYIdEHhrflQ9W+j6on/t0I8/MWU9GfGPG5qYxLjeVdnXog7qsvII5a30j8N5ZupWD\nx8pJatqA6/u1ZVxuKt3S6n5hPhMVqBrKTIjlwXFduWNER56ft5G/f7Kem56ZT/ukJkzMy2RCz7rd\nT7W0eC+TC9bx5on+pa6tuDkvk15t1b8k1dMwOpKLu7Xi4m6t2HvYd7Np/qJi/vLBl/x55pd0TWvG\nuB5pjOmRSkpc+DV1Oef4fOMephcWM2PJFnYcOEbThlFc2t33BPm+WfW3afObVKACpHnjGG69sD23\n5GWd7Ke657Ul/P7E/VQXtCWxad14wGZFhWPmylImF6zjM3//0g39M7hR/UsSYHGNormqTxuu6tOG\nbfuO8MYi3wi2X7+1gv9+ewUXZMYzLjeVi7q2Iq6xt5uQv9zmHxyyqJhNuw77niTfOYmxPdIYkp1I\ng6i6+0W2ulSgAiwmKoLxPX1NEZ8V7WJyQRF/+eBLHv9oLeN7pjIxL4tOKeF1N/cJh46V8erCzUyZ\ns56iHQdP9i9d1aeNhglLrUtu1pBbBmZxy8As1m0/wPRFvpFtd7+2hPvzl3JhJ99IwGHZyZ55Ckzx\nnsO84Y9zxZZ9RBgMaJ/Aj4d1ZFSXZPXLnoUKVC0xMy7IiueCrHjWbT/AM3PW88+Fm3h5wWYGdkjg\nloFZDOqQEBbty1v3HuHZuet57jNf/1KPNs159NqejO6Sov4lCYmsxCbcPrwjPx7WgaXF+8gvLGb6\nohLeW76N2JhIRnVJYWxuKnntE4L+Ht198BhvLd1C/hclzFu/C4DcNs15YEwOl3RPrTMtKcGgAhUE\nWYlN+K/xXblzZEee+8zXT3XDlHl08PdTjfdoP9XS4r08PbuINxaVUOEco7qkcMtA3/1L4VBYpe4z\nM7q1jqNb6zjuubgzn/lHAr61dAuvfVFMfGwMl3ZvxdjcNM5Lr71H/hw65pvscXphCbNWb6eswtEu\nMZY7R3RkbG4qbeP1iKfqUIEKouaNY/jBkPZ8Z2AWby4uYXJBEXdX7qfq1zbkE8FVVDg+WFnK5Nnr\n+HTdLmJjIrm+X1tu6p9Jerz6l8S7IiOM/u0T6N8+gQfHd/E9NLWwhBfnb+LvczfQukUjxuWmMi43\njY4BeGjq8fIKCr7cTn5hCe8u28bh4+W0imvIxLxMxuamktNKD8mtqRoVKDO7EngA6Ayc75xbEIig\n6rqYqAguO681E3qmMXfdTqbMLuJPM7/kb7PWMiE3jYkDMwOSQOfi8LFyXvl8M8/MLmLdjoOkxjXk\n5xdnc3Wf9Dp9p7rUTQ2ifM18o7qksP/Icd5dto38RSX87aO1PPbhWrJTmvruacxNPaeJLysqHAs3\n7ub1L4p5a8kWdh86TvPG0Uw4L41xPVLpk6FpRgKppldQS4HLgCcCEEu9Y2b0b5dA/3YJrN1+gGfm\nFPHKws28tGATgzomckteJgNruZ9q276v+pf2HDpOj9Zx/OWanozumhLy6Z5FAqFpw2gu79Way3u1\nZvv+o8xYXEL+ohIe/tdKHv7XSs7PaMlY/1T2LU8xcZ9zjpVbfSPw3lhUQvGewzSMjmBETgrjeqQy\nSBM11poaFSjn3ApAl7EB0C6xCQ+N78adIzrxvH9+qv+YMo+OyU24JS+LsbmpAe2nWlbyVf9SWYVj\nVI6vf6lXW/UvhYJaI4IjsWkDbhyQyY0DMtm48xDTFxXzemEJ972+lAemL2NQx0TG5aZSXuE4Xl7B\nYx+uIb+wmNXbDhAZYQzqkMBPR3ViRE4ysZrZudbpDHtMi1hfP9UtAzN5c9EWJs8u4mevLuZ376zk\nugvact0F1e+nqqhwfLS6lMkFRXyydieNYyL5dt+23DQgQ524oafWiCBLj2/MbUM78IMh7VmxZf/J\nkYAfrCzFDJyDRZv30rttC/5rXBcu7taK+BD3Edc3Zy1QZvY+kHKKVfc65/KreiAzmwRMAkhPT69y\ngPVVg6hILu/VmsvO8/VTPV1QxB/f/5K/frSWy3qmMTEvs8qzYx4+Vs5rX2zm6dlFrNt+kFZxDbnn\nomy+db76l7xCrRGhY2bkpDYjJ7UZd43OZv76XfzoxS+Ijozghe9coJvPQ+isBco5NzwQB3LOPQk8\nCdC7d28XiH3WB5X7qdaUftVP9eL8TQzumMgtAzPJa3/qfqrSfUd4du4GnvtsA7sPHad76zj+9K1c\nLu7WSv1LYUxf9mpPRITvOZsZ/hYFFafQ8lwTnxemivCq9klN+PWEbtw5shPPf7aBv8/dwPVPzyM7\npSk352VS4RwRZiwv2cfTs4uYvqiYsgrHyJxkJuZl0SdD/UtnUtvvvUC1RujLntQXNR1mPgH4C5AI\nzDCzQufcqIBEJqfVMjaG24Z24DuDsnhj0RYmF6zjZ68sJjrSaBgVycV/LlD/kgcFqjVCpL6o6Si+\nacC0AMUi56hBVCRX9GrN5eel8cnanfzguc85UlbO3Rdlc02fdM8/PFNqj1oipC7wXBOfnDszY0D7\nhJMPof3e4HYhjkjOlVojRP6dCpSIB6g1QuTfaSiXiIh4kq6gREQkYALZ/6krKBER8SQVKBER8SQV\nKBER8SQVKBER8SQVKBER8SQVKBER8SQVKBER8SQVKBER8SQVKBER8SQVKBER8SQVKBER8SQVKBER\n8SQVKBER8SQ9zbwO0SyqIoGhXPIGXUGJiIgnqUCJiIgnqUCJiIgnmXMu+Ac12w5sOMMmCcCOIIVT\n1+jc1czZzl9b51xisII5m7Pkkt4LNaPzV30ByaOQFKizMbMFzrneoY4jHOnc1UxdOn916W8JBZ2/\n6gvUuVMTn4iIeJIKlIiIeJJXC9SToQ4gjOnc1UxdOn916W8JBZ2/6gvIufNkH5SIiIhXr6BERKSe\nU4ESERFPCnqBMrNPTrN8qpldcZp1V5rZMjOrMLN6O+yzmufu92a20swWm9k0M2teu1F6l5k1N7Nb\nQx1HoCiXqk+5VH3BzKOgFyjnXP9z2d7MIoGlwGXAx7USVJio5rl7D+jqnOsOrAbuqY3YwkRz4N8S\ny8yq9NBk8/FMq4NyqfqUSzUStDwKxRXUAf9/zcweNbNVZvY+kFRpm/Vm9rCZfQ5c6Zxb4ZxbFexY\nvaaa5+5d51yZf/WnQOvgR+4ZvwXamVmhmc03swIzmw4sBzCzO8xsqf/f7f5lGf7z/Cy+D/c2oQv/\n65RL1adcqpGg5VEop9uYAHQCcoBkfH/clErrdzrnzgtFYGGguufuZuCl2g/Ps+7G9w0418wuBGb4\nfy8ys17ATUBfwIDPzGwWsBvoANzgnPs0RHGfjXKp+pRL5y5oeRTK5opBwAvOuXLnXAnwwTfW19f/\n+VVxzufOzO4FyoDnghBfuJjnnCvy/5wHTHPOHXTOHQBeAwb6123wcHEC5VJNKJdqrtbyyMsTFh4M\ndQBh7GvnzsxuBC4Fhjnd+FZZVd9j4f5eDPf4Q0m5dHa1lkehvIL6GLjazCLNrBUwJISxhJsqnzsz\nGw38DBjrnDsUrAA9aj/Q9DTrCoDxZtbYzGLxNf0UBC2ymlEuVZ9y6dwFLY9CeQU1DRiKr813IzD3\ndBua2QTgL0AiMMPMCp1zo4ISpTdV+dwBjwINgPfMDOBT59z3aj1CD3LO7TSzOWa2FDgMbKu07nMz\nmwrM8y+a7Jz7wswygh7ouVMuVZ9y6RwFM4/0qCMREfEkz9zTISIiUpkKlIiIeJIKlIiIeJIKlIiI\neJIKlIiIeJIKlIiIeJIKlIiIeJIKlIiIeJIKlIiIeJIKlIiIeJIKlIiIeJIKlIiIeJIKVBCY2c/N\nbHKo4wgUM3vczO4PdRxSvyiP6h89zTxMmdkNwI/wTaO8D3ge+Llzrsy/viXwNDAS2AHc45x7PkTh\niniWmWUBfwYGA0eBKc65n/nXKY9CSFdQIWZm/zYn16mWnUJj4HYgAegLDAP+s9L6x4BjQDLwbeBv\nZtalxgGLeFB188jMYoD38E31ngK0Bv6v0ibKoxBSgQogM7vLzIrNbL+ZrTKzYf7lD5jZ//l/zjAz\nZ2YTzWwj8MGplp3tWM65vznnCpxzx5xzxcBzwAD/MWKBy4H7nXMHnHOzgXzg+tPEfaN/ArL/NbM9\nZrbOzPr7l28ys1L/FduJ7aea2UP+ny80s81mdqd/uy1mdlNNzqPUb8HMI+BGoMQ594hz7qBz7ohz\nbrH/GMqjEFOBChAz6wTcBvRxzjUFRgHrz/CSwUBn/3ZnWlZVg4Bl/p87AmXOudWV1i8CzvTNry+w\nGIjH11z4ItAHaA9cBzxqZk1O89oUIA5IAyYCj5lZi2r8DVLPhSCPLgDWm9nbZrbDzD4ys27+dcqj\nEFOBCpxyfNNB55hZtHNuvXNu7Rm2f8D/je3wWZadlZndDPQG/se/qAm+fqnK9gFNz7CbIufcM865\ncuAloA3woHPuqHPuXXzNHO1P89rj/m2PO+feAg4Anc7lbxDxC3YetQa+ha8PKhWYAeT7m/6URyGm\nAhUgzrk1+PqEHgBKzexFM0s9w0s2VXHZGZnZeOA3wEXOuR3+xQeAZt/YNA7Yf4Zdbav082EA59w3\nl53um9/OE4Mz/A6dYVuR0wpBHh0GZjvn3nbOHcP3JS8e3xWY8ijEVKACyDn3vHMuD2gLOODhM21e\nxWWnZWajgaeAMc65JZVWrQaizKxDpWU9+KoJUMSzgpxHi8+wvfIoxFSgAsTMOpnZUDNrABzB902p\noob7XG9mN55m3VB8AyMud87Nq7zOOXcQeA140MxizSwPGAv8oybxiNS2YOcRvhF7F5jZcDOLxHf1\ntgNYoTwKPRWowGkA/Bbfm3srkATcU92d+dvA44FPT7PJ/fiaG94yswP+f29XWn8r0AgoxddZ+33n\nnL75idcFNY+cc6vwDV54HNgNjAPG+pv7QHkUUrpR16P839Z+4Jy7JtSxiIQr5VF4U4ESERFPUhOf\niIh4kgqUiIh4kgqUiIh4UlUeShpwCQkJLiMjIxSHFqmRhQsX7nDOJYY6jhOUSxKOqppHISlQGRkZ\nLFiwIBSHFqkRM9sQ6hgqUy5JOKpqHqmJT0REPEkFSkREPEkFqg65+om5XP3E3FCHIdVkZlP8cwEt\nrem+9F6QukAFSsQ7pgKjQx2EiFeoQIl4hHPuY2BXqOMQ8QoVKJEwY2aTzGyBmS3Yvn17qMMRqTUq\nUCJhxjn3pHOut3Oud2KiZ27JEgk4FSgREfEkFSgREfEkFSgRjzCzF4C5QCcz22xmE0Mdk0goheRR\nRyLy7zS2YTYkAAAPg0lEQVSpnsjX6QpKREQ8SQVKREQ8SQVKREQ8KSAFKpDPEBMREYHAXUFNRc8Q\nExGRAApIgdIzxEREJNDUByXipykqRLwlaAVKD7gUCS7nXKhDkHookF/0glag9IBLkeA5erycZSX7\nWLBeLe8SvtTEJ1IHHS93HK9wXPH4XO57fQn7jxwPdUgi5yxQw8z1DDERD2nSMIruaXFMzMvk+c82\nMuKRj3l32dZQhyVyTgI1iu8a51wr51y0c661c+7pQOxXRKovMsK4/9Icpt06gOaNo5n0j4Xc+txC\nSvcfCXVoIlWiJj6ROq5Hm+a88cM8fjqqE++vKGX4H2bx0vyNGkQhnue5AqWhviKBFx0ZwQ+GtOdf\nPx5I51bNuOvVJVz71GcU7TgY6tBETstzBUpEak9WYhNe+M4F/Oaybiwt2cvoP37MXz9aw/HyilCH\nJvJvVKBE6pmICOOa89OZecdghmYn8bt/rWLso3NYvHlPqEMT+RoVKJF6KqlZQ/52XS8ev64XOw8c\nZfxjc/j1jOUcOlYW6tBEABUokXpvdNcU3rtjMN86P52nCooY9cePKfhST3uR0FOBEhHiGkXz3xO6\n8dKkC4iOiOD6p+dxx8uF7D54LNShST2mAiUiJ/XNiuetHw/kh0PbM72whOGPzCK/sFhD0iUkVKBE\n5GsaRkdy58hOvPmjPNq0bMyPXyzk5qnzKd5zONShST2jAiUip5Sd0oxXv9+fX47J4bOiXYx4ZBZT\n5xRRXqGrKQkOFSgROa3ICOOmAZm8+5NBnJ/ZkgfeWM7lf/uEVVv3hzo0qQdUoETkrFq3aMwzN/bh\nT9/KZeOuQ1zy5wIeeXcVR46Xhzo0qcNUoESkSsyMcblpvH/HYMb2SOXPH6zh4j8XMK9Ic05J7VCB\nEpFz0jI2hkeuzuXZm8/nWFkFVz0xl3unLWGf5pySAFOBEpFqGdQxkXd/Mohb8jJ5Yd5GRjwyS3NO\nSUCpQInUQS99tx8vfbdfrR+ncUwU9/nnnGrROOarOaf2ac4pqTkVKBGpsW/OOTXskVm8OE9zTknN\nqECJSEBUnnMqp1Uz7n5tCdc89anmnJJqU4ESkYA6MefUby/rxrKSfYzSnFNSTQEpUGY22sxWmdka\nM7s7EPsUkfAVEWF8yz/n1DDNOSXVVOMCZWaRwGPARUAOcI2Z5dR0vyIS/k7MOfXE9b3YddA359RD\nb2rOKamaqADs43xgjXNuHYCZvQiMA5ZXZ2fv/fMZYpKySJk1KwCh1U86d9V3rHQdBGH02+mY2Wjg\nT0AkMNk599uQBRNAo7qk0K9dPA+/vZLJs4v417Kt/PeEbgzqmBjq0MTDAtHElwZsqvT7Zv+yrzGz\nSWa2wMwWbN+uydBEvqmut0Y0axjNryd04+Xv9iMmKoL/mDKPO14qZJfmnJLTCMQVVJU4554EngTo\n3bv3aceejrjyJoCg3MNR11z9xFxA5666fOdvcChDCFhrhJkFOLQAi4wmrt9VvFp+Jf+cs5xd7z/J\noRW68g9rEVE0bNOFRu36ENk0PiAtEYEoUMVAm0q/t/YvE5Fzc6rWiL7f3MjMJgGTANLT04MTWaCV\nH2fv7Oc4tHI28Rf9kMSxP+VwlyHsfPcxyvephSVcRDRsSqN2vWnUrg+NsnoR0SAWV3aMw+sLOV5e\nQXRkzRrpAlGg5gMdzCwTX2H6FnBtAPYrIqdQldaIcLpBtrzC8ezc9fz+nUjiO/flP0d24ob+GURG\nePwqsB5yzrGm9ADvryjlg5XbWLhhNxUOEps2YGinJIZ1TuLJj9cR2WF0jYsTBKBAOefKzOw24B18\nHbtTnHPLahyZSP1TL1sjTsw5NSInmfteX8qDby4nf1EJD1/ejeyUZqEOr947VlbBvKJdvL9iGx+s\nLGXjrkMAdEltxm1DOzAsO4luaXFE+L9QPD27KGDHDkgflHPuLeCtQOxLpB6r160RJ+acmr6ohF+9\nsZxL/zyb71/Yjh8MaU/D6MhQh1ev7DxwlA9XbeeDldv4ePUODhwto0FUBAPaJ/DdwVkMzU6iVVyj\nWo8jaIMkROTM1Brx1ZxTAzsk8tCM5fzlgzXMWLKF317WnfMzW4Y6vDrLOcfqbQdOXiV9vnE3zkFS\n0waM6dGKYdnJDGifQKOY4H5RUIES8RC1Rvi0jI3hkatyGZ+bxs+nLeGqJ+Zybd907r4om2YNo0Md\nXp1wtKycz9btYuaKbcxcWcrm3YcB6JrWjB8N7cDwzsl0SW12sukuFFSgRMSzTsw59b/vrebp2UXM\nXLGNB8d1ZVSXlFo9bl29ZWPHgaN8uLKUmStKKfhyOwePldMgKoK89gncemF7hmYnkRLXMNRhnqQC\nJSKe1jgminsvyWFMj1TuenUJ3/3HQi7qmsKvxnYhqZl3Pky9yDnHqm37mbmilPdXbKNw0x6cg+Rm\nDRibm8bwzkn0bxf8pruqUoESkbDQvXVzpt82gMkFRfzx/dXMXrODey/uzNV92nj/xuQgOlpWzqcn\nmu5WlFK8x9d01711HLcP68iwzkl0SW0WFudMBUpEwkZ0ZATfv7Ado7umcM9ri7n7tSVM+6KY31zW\njazEJqEOL2S27/c33a3cRsGXOzh0rJyG0RHktU/kh0PbMyQ7ieQwvNpUgRKRsJOZEMsL37mAlxds\n4tczVjD6TwX8eFgHJg3KCsgNol7nnGPFlv0nBzgs2uxrumsV15AJPdMY3jmZfu3iw354vgqUiIQl\nM+PqPukMyU7iV9OX8/t3VvHGohIevrw7Pdo0D3V4AXfkeDlz1+1k5optfLCilJK9RwDo0TqOnwz3\nNd3ltAqPpruqUoESkbCW1LQhj337PMYt28r9+UuZ8Nc53DQgkztHdqRxTHh/xJXuP8KHK0t5f0Up\ns7/cweHj5TSKjiSvQwI/Ht6BIdlJJDUNv6a7qgrv/3siIn4ju6RwQbt4fvevlTw9u4h3lm3l1xO6\nMTiM5pxyzrF8yz5mrihl5optLNq8F4DUuIZc3iuNYZ2T6ZcV/k13VaUCJSJ1RrOG0Tw0vhvjctO4\n+9XF3DBlHpf1TOO+S3NoGRsT6vBO6cjxcuau3XnyKQ5b9h7BDHq0bs6dIzoyrHMynVs1rVNNd1Wl\nAiUidU6fjJbM+NFA/vrhGv42ay0frd7OLy7NYVxuqic+6Ev3HWGm/4bZOWt8TXeNYyIZ2CGBnwzv\nyJDsJBKbNgh1mCGnAiUidVLD6EjuGNmJS7qncteri7n9pUKmfVHMryd0pXWLxkGNxTnHspJ9J6+S\nFvub7tKaN+LK3q0Zmp3EBfWo6a6qVKBEpE7rlNKUV7/fn3/MXc/v3lnFyP/9OChzTh05Xs6cNTtO\nzp20bd9RzCC3TXN+OqoTQ7OTyE6pn013VaUCJSJ1XmSEceOATEZ0SeG+aUtqbc6pbfuOnBzgMGft\nDo4cryA2JpKBHRIZ1jmJIdlJJDRR011VqUCJSL2R1rwRU/xzTj3on3Pqe4PbcdvQ6s05VVHxVdPd\nzJXbWFq87+Rxru7dhmGdk+mb1ZIGUWq6qw7PFai69vRgEfGWE3NODeqQyEMzVvDoh2t4a8kWfnNZ\nN/pmxZ/19YeP+ZruZq70PeuudL+v6e689Bb8dFQnhndOpmNyEzXdBYDnCpSISDC0iI3hD1f1YHzP\nVH4+bQlXP/npyTmnvmnL3sPMXFHKByt9o+6OllXQpEEUgzomMDQ7mSGdEolX013AqUCJSL02sEMi\n79w+iD++/yWTC9bx/vJtxDWKJiYqgkfeXcX7K0pZvsXXdNemZSOuOT+dYZ2T6JsZT0xU3X/uXyjV\nqECZ2ZXAA0Bn4Hzn3IJABCUiEkyNY6L4+cWdGeMfkn6iIK3Yso/z0ltw1+hshnVOokOSmu6CqaZX\nUEuBy4AnAhCLiEhIdWsdR/5tAxj5vx9jwCvf7+/ZJ1DUBzUqUM65FYC+UYhInREdGUGS/ykOKk6h\nFbQGVDObZGYLzGzB9u3bg3VYEREJU2e9gjKz94GUU6y61zmXX9UDOeeeBJ4E6N27t6tyhCJBolsc\nRLzlrAXKOTc8GIGIiIhUpmHmIiISMIFsiahRH5SZTTCzzUA/YIaZvROYsEREpL6r6Si+acC0AMUi\nIiJykm6DFhERT1KBEhERT1KBEhERT1KBEhERT1KBEhERT1KBEhERT1KBEhERT1KBEvEAM7vSzJaZ\nWYWZ9Q51PCJeoAIl4g0n5lb7ONSBiHiFnsVXh+hp3OFLc6t5i3LJG3QFJRJmNLea1Be6ghIJEs2t\nJnJuVKBEgkRzq4mcGzXxiYiIJ5lzwW8hMLPtwIYzbJIA7AhSOHWNzl3NnO38tXXOJQb6oGY2AfgL\nkAjsAQqdc6Oq8Loz5ZLeCzWj81d9AcmjkBSoszGzBc453QtSDTp3NVOXzl9d+ltCQeev+gJ17tTE\nJyIinqQCJSIinuTVAvVkqAMIYzp3NVOXzl9d+ltCQeev+gJy7jzZByUiIuLVKygREannVKBERMST\ngl6gzOyT0yyfamZXnGadpiKg2ufu92a20swWm9k0M2teu1F6l5k1N7NbQx1HoCiXqk+5VH3BzKOg\nFyjnXP9z2d7MItFUBEC1z917QFfnXHdgNXBPbcQWJpoD/5ZYZlalR36Zj2daHZRL1adcqpGg5VEo\nrqAO+P9rZvaoma3yP0QzqdI2683sYTP7HLjSObfCObcq2LF6TTXP3bvOuTL/6k+B1sGP3DN+C7Qz\ns0Izm29mBWY2HVgOYGZ3mNlS/7/b/csy/Of5WXwf7m1CF/7XKZeqT7lUI0HLo1A+LHYC0AnIAZLx\n/XFTKq3f6Zw7LxSBhYHqnrubgZdqPzzPuhvfN+BcM7sQmOH/vcjMegE3AX0BAz4zs1nAbqADcINz\n7tMQxX02yqXqUy6du6DlUSibKwYBLzjnyp1zJcAH31hfX//nV8U5nzszuxcoA54LQnzhYp5zrsj/\ncx4wzTl30Dl3AHgNGOhft8HDxQmUSzWhXKq5WssjL0+3cTDUAYSxr507M7sRuBQY5nTjW2VVfY+F\n+3sx3OMPJeXS2dVaHoXyCupj4GozizSzVsCQEMYSbqp87sxsNPAzYKxz7lCwAvSo/UDT06wrAMab\nWWMzi8XX9FMQtMhqRrlUfcqlcxe0PArlFdQ0YCi+Nt+NwNzTbWhfn4pghplVaSqCOqzK5w54FGgA\nvGdmAJ86575X6xF6kHNup5nNMbOlwGFgW6V1n5vZVGCef9Fk59wXZpYR9EDPnXKp+pRL5yiYeaRH\nHYmIiCd55p4OERGRylSgRETEk1SgRETEk1SgRETEk1SgRETEk1SgRETEk1SgRETEk/4fwtiYfPHr\nNrwAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x116a5e050>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XecVOXZ//HPxdK79M4CixQRFFakKd1g72LFDiqYqDGW\nJ8lPk5gnGqN5HgIiWECsaBLUKFFRelN2jSCgyIJ0pSkIAsLC9ftjBp8J2WVnd6ecnfm+X6957Zxz\n7j3n2pu5uOa0+5i7IyIiEjTlkh2AiIhIQVSgREQkkFSgREQkkFSgREQkkFSgREQkkFSgREQkkFSg\npMTMbI+ZtU52HCJlnXKpYCpQCWJma81sUBK2O9DMPjezvWY208xaxmrd7l7d3dfEan0i0UhGLplZ\nppl5uJAcef06VutXLhVMBSogzKx8rNubWT3g78CvgTpADjClRAGKlBHxyKUItcPFpLq7/66YoUkx\nqUAlgJk9D7QA/hH+5nVPxDeyG81sPTAj3PY8M1tuZjvNbJaZdYhYz1ozu9fMlgLfR5FYFwHL3f01\nd98PPAh0MbP2hcQ5y8weMrMF4Tj/YWZ1zexFM/vOzBabWWZEezezrPD7SWY21szeNrPdZvahmbUp\ncaeJFCCJuVTcOJVLMaAClQDufg2wHjg3/M3rjxGL+wIdgJ+Y2fHAy8AdQH1gGqFErBjR/grgbELf\n5PKL2PQJwJKIOL4H8sLzC3M5cA3QFGgDLAQmEtoD+wx4oIjf/Q1wXHg7vy8iPpFiSWIuHbHOzDaa\n2cTwEYpjUS6VkgpU8j3o7t+7+z5gKPC2u09394PAn4AqQK+I9qPdfUO4fVGqA7uOmvcdUOMYvzPR\n3Ve7+y7gn8Bqd38/nMCvAScf43enuvtH4bYvAidFEaNIrMQzl7YDpwAtgW6EcujFIn5HuVRKMd2t\nlRLZEPG+CbDuyIS7HzazDYS+gRXUvih7gJpHzasF7D7G72yJeL+vgOnqx/jdryPe7y2irUisxS2X\n3H0PoXO4AFvMbBTwlZnVcPfC8km5VErag0qcwoaNj5y/mdA3NADMzIDmwKYo1lOQ5UCXiPVVI3So\nYXkx1iESNMnIpcK2pf9D40idmzhbgKLuc3gVODt8aXgF4OfAD8CCwn4hfEJ1UiGLpwKdzOxiM6tM\n6Jj3Enf/vNjRiwRHwnPJzE41s3ZmVs7M6gKjgVnhw3cSJypQifMH4FfhK4ruLqiBu68Ergb+QuiY\n97mETgYfOMZ6mwPzC1nfNuBiQidYvwW6Ezr5KlKWJTyXCBXEdwgdHl9GqNhdUbLwJVqmBxaWXeEr\nkpYAncMngkWkBJRLwaQCJSIigaRDfCIiEkgqUCIiEkgqUCIiEkiBvlG3Xr16npmZmewwRH6Um5u7\n3d3rJzuO4lAeSdBEm0eBLlCZmZnk5OQU3VAkQcxsXdGtgkV5JEETbR7pEJ+IiASSCpSIiASSCpSI\niASSClSKGzp+IUPHL0x2GCJlnnIp8VSgREQkkFSgREQkkFSgREQkkFSgREQkkFSgREQkkFSgREQk\nkFSgREQkkFSgREQkkFSgREQkkFSgREQkkAL9uA0pvR3fH+DgocPsO3CIKhUzkh2OiEjUtAeVovIP\nHeaht1aQt3UP63bspc8jMxg3azV7fshPdmgiIlHRHlQK2rX3IKNe/pi5q7bTsGYl6lStSP2alXnk\nnc8ZP2c1N/RuxbW9MqlVpUKyQxURKZT2oFJM3tbdXPDEfBat2cEfLjqRzLrVqFmlApNv6M7rI3uT\n3fI4Hp/+BX0emcHj761k594DyQ5ZkkgjdEuQqUClkJmfb+XCsQv4bt9BXrq5B1d0b/Fvy09qXpun\nrz2Ft27vQ+829Rg9I4/eD8/g4X9+zvY9PyQpahGRgsWkQJnZEDNbaWZ5ZnZfAcv7mdkuM/sk/Pp/\nsdiuhLg742at5obnFtO8TlXevL0Pp2TWKbR9p6a1ePKabrx7x+kM6NCQ8XNW0+eRGfzurRVs/W5/\nAiOXo0WRS2Zmo8PLl5pZ12TEKZIIpT4HZWYZwFhgMLARWGxmb7r7iqOaznX3c0q7Pfl3+w8e4t6/\nLeWNTzZzdufGPHpJZ6pWjO6ftV2jGvzlipO5Y1Bbxs7MY9KCtTy/aB2Xn9KcW/q2oUntKnGOXiJF\nmUtnAm3Dr1OBceGfIiknFhdJdAfy3H0NgJm9ApwPHF2gJMa+2rWP4ZNz+XTTLn7xk3bc1q8NZlbs\n9bSpX53HLzuJnw1sy7hZq3npw/W8/NF6LunWjNv6ZdG8TtU4RC8FiCaXzgcmu7sDi8ystpk1dvev\niruxA/mHefO/bwGgyn+XOvaU536YHzav5NVbDiY7lDIj9DEtuVgUqKbAhojpjRT8ja6XmS0FNgF3\nu/vyglZmZsOB4QAtWrQoqIkAueu+ZcTzuew7kM9Tw7IZ3LFhqdfZsm41Hr64M7cPbMuTs1YzZfEG\nXs3ZyIUnN2Vk/yxa1asWg8jlGKLJpYLaNAX+rUBFk0d7fsin4RWqTMWRv3sH3y1+nT2f/BM/qMPh\n8Zaoy8w/Blq4+x4zOwt4ndAhiv/g7hOACQDZ2dmlK78p6tWcDfxq6jIa1arMSzefyvENa8R0/U1r\nV+F3F3RiZP8sxs8J7VH9/eONnNulCaP6Z9E2xtuT2Ismj2pULk+HRqF/ywfPOyFxwZVRv3p9GVsq\nl6f8gBtpfc4tXN+rFdf1yqRWVd2uES+xKFCbgOYR083C837k7t9FvJ9mZk+YWT133x6D7aeN/EOH\n+f20z5g4fy29s+oy5oquHFetYty216hWZR449wRu65fF03PX8Pyidby5ZDNndmrEqP5t6dikZty2\nnaaKzKUo20SlQkY5aobvhTu1dd2SrCKt1KlWkTrVKnLvme15YmYef37/C56au4are7Tkxj6tqF+j\nUrJDTDmxuIpvMdDWzFqZWUXgcuDNyAZm1sjCJ0fMrHt4uztisO20sXPvAa6buJiJ89dyXa9Mnru+\ne1yLU6T6NSpx/1kdmHfvAEb2y2LuF9s5a/Rcbnouh6UbdyYkhjRRZC6Fp4eFr+brAewqyfknKbmu\nLY7j6WtP4Z8/O41+7er/eBXsA28sY9POfckOL6WUeg/K3fPNbBTwLpABPOvuy83slvDyJ4FLgFvN\nLB/YB1zupT17lkZWbdnNTZNz2LxzH3+8uDOXndK86F+KgzrVKnL3T9px82mtmbjgS56d9yXnjdlC\n3+Pr89OBWXRrWfil7VK0KHNpGnAWkAfsBa5PVrzprkPjmoy5sit3bdvDk7NX8+KH63nxw/Vc1LUp\nt/bTOdtYiMk5KHefRihxIuc9GfF+DDAmFttKN++v2MIdUz6hcoUMXhneIxBFoFbVCtwx6Hhu7NOK\nyQvX8cy8L7l43EJ6tanLTwe2pUcZPVx0ZESFKSN6Ji2GKHLJgZGJjksK17p+df54SRd+Nuh4Jsxe\nzSuLN/DX3I2cdWJjRvbPokNjHQovKY3FF1DuzhOzVvOn91bSqUktxl/TrUT3JcXzP9salSswsn8W\n1/fO5MVF6xk/Zw2XT1hE98w63D4wiz5Z9Up02bskTjKLcappWrsKvzm/E6MGtOWZeV/ywqJ1vLX0\nKwZ1aMBt/bPo2uK4ZIeYMLH6sqehjgJo34FD3P7yv3j03ZWc07kJr47oGeibZqtWLM/Np7dm3r39\nefDcjqz/Zi/XPPMRFz6xgBmfbyn1vRAiZUn9GpW478z2zL93AHcNPp6cdd9y0RMLuPKpRSzI2658\nKAYVqIDZvHMfl45fwNuffsU9Q9ox+vKTysxznCpXyOC63q2YfU8/fn9hJ7bt/oEbJuVw7ph5vLPs\naw4fVmJK+qhVtQI/HdiW+fcO4JdndWDV1j1c+fSHXDRuAe+v0Be3aOgQX4DkrP2GW17IZf/Bwzw9\nLJuBHUp/820yVCqfwVWntuSy7OZM/XgTY2flccsLubRvVINRA7I4s1NjMsrp0J+kh2qVQkcYrunZ\nkr/mbuTJ2au5aXIO7RvVYGT/LM46UflQGO1BBcQrH63niqcWUb1SeV4f2avMFqdIFTLKcdkpzfng\nrr78eWgXDh46zKiX/sUZf57N1H9tJP/Q4WSHKJIwlStkcHWPlsy8ux+PXRrKh9tf/heDHp/Nq4s3\ncCBf+XA0FagkO3joMA++uZz7/v4pPVrX5Y2RfchqkFojNZTPKMeFJzfjvTv7MubKk6mQUY47pyxh\nYDgxD6pQSRqpkFGOi7s1Y/qdfRl3VVeqVszgnr8tpd+jM3luwVr2HzyU7BADQwUqib79/gDXPvsR\nkxas5cY+rZh43SkpPWxKRjnjnM5NmPbT0xh/TTdqVC4fTsxZvLBoHT/kKzElfZQrZ5x5YmPeur0P\nE68/hSa1q/DAm8vp88gMxs1aze79GpRW56CSZOXXu7l5cg5f79rPo5d05tLs5Nx8mwzlyhk/OaER\nZ3RsyKyV2xg9YxW/en0ZY2bkcUvf1lzevQWVK5SNC0NESsvM6N+uAf3bNeDDNTsYMzOPR975nHGz\n8riudyuu75WZsFFjgkYFKgneW/41d075hKqVyvPKiB5pdX9EJDOjf/sG9GtXn/l5Oxj9wSoe/McK\nxsxczYjTW3NVjxZRP9tKJBWc2roup7auy9KNOxk7M4/RH6zi6blruOrUFtx8Wmsa1Kyc7BATStmf\nQO7OmBl5PDb9Czo3q8WEa7JpVCu9PnAFMTP6tK1Hn7b1WLRmB3+ZsYrfT/uMcbNXc2OfVgzr2ZIa\nlVP30KfI0To3q834a7L5Ystuxs1azbPz1/LcwnVclt2MEae3SZtntKlAJcjeA/n84rWlvP3pV1xw\nUhMevrizDmMVoEfruvRoXZfcdd/ylxmrePTdlUyYs4bre2dyfa9WKX2OTuRoxzeswZ+HnsSdg45n\n3OzVvLp4Iy9/tIHzT2rCbf2yyGpQPdkhxpUKVAJs/HYvwyfn8tnX33H/me0ZfnprDQFUhG4tj2PS\n9d1ZunEnf5mRx/+8v4pn5n7JsF4tubFPa+qk6TF5SU8t6lblDxedyM8GtuWpuWt46cP1TP3XJoac\n0IiR/bPo1LRWskOMCxWoOPvoy2+49YVcDuQf5tlrT6F/+wbJDqlM6dysNk8Ny2bF5u8YOzOPJ2at\nZuL8tVzdoyU3n9Zaz+CRtNKoVmV+fU5HbuvXhonz1/LcwrX8c9nX9GtXn1H9s8jOTP5g0rGky8zj\n6KUP13PlU4uoVaUCU0f2VnEqhY5NajL2qq68d8fpDO7YkKfnrqHPIzP4zT+W8/UuPXpb0kvd6pW4\n+yftmH/fAH7xk3Z8unEXlzy5kMvGL2TOF9tSZhgl7UHFwcFDh/ntP1bw/KJ19D2+PqOvOJlaVXTu\nJBbaNqzB/15+MncMOp6xM/OYvHAdLy5az2WnNOOWvm1odlx6nDyWxAviyO81w08UuKF3K17+aD0T\n5qxh2LMf0blZLUb2z2Jwh4aUK8PDKKlAxdg33x/gthdzWbTmG4af3pp7h7TXOFtx0KpeNf50aRd+\nNrAtT8xazZTFG3jlow1c3LUZt/VvQ8u6elicpI8qFTO4oU8rrurRgqkfb2Lc7NWMeD6X4xtW57Z+\nWZzTuTHlM8reAbOyF3GAffbVd5w3Zh4fr9/J45d14b/O6qDiFGfN64ROHs/+RX+uPLUFUz/ZxIDH\nZnPXlE9YvW1PssMTSahK5TO4vHsLPrirL/97+UkA3DHlEwY8NpuXPlxf5kZrUYGKkXeWfcXF4xZw\nIP8wr47oyUVdmyU7pLTSpHYVfnt+J+bd05/remUybdlXDHp8NqNe+piVX+9OdngiCVU+oxznn9SU\nd352OhOu6cZxVSvwX1M/pe8fZ/HMvC/ZeyA/2SFGRYf4SunwYWf0jFX8z/ur6NK8NhOu6UbDNLvb\nO0ga1Axd5XRrvzY8PfdLnl+4lreWfsWQExoxakDqXo4rUpBy5YwzTmjE4I4NmZ+3gzEzV/G7t1Yw\ndmYeN/TO5JqemYE+P64CVQrf/5DP3a8t4Z/Lvuairk357wtP1M23AVGveuippiNOb83E+V8yccFa\n3ln+NQPbN+D2gW05qXntZIcokjCRo7XkrvuGMTPy+NN7XzB+9hqG9WrJDb1bUbd68G7ZUIEqoQ3f\n7OXmyTl8sWU3vzq7Azf2aaWbbwPouGoVueuMdtx4WmsmL1jLM/O/5IKx8zmtbT1+OrAtp6TYfSMi\nRenWsg4Tr+/O8s27eGLmap6YtZpn5n3JFd1bMPz01jSuVSXZIf4oJuegzGyIma00szwzu6+A5WZm\no8PLl5pZ11hsN1kWrdnB+WPns2nnPiZe352bTtPIEEFXq0oFbh/Ylnn3DuDeIe1Zsfk7Ln1yIZdP\nWMiC1dtT5r4RkWid0KQWY6/qyvQ7+3L2iU2YvHAdp/9xJvf/fSlrt3+f7PCAGOxBmVkGMBYYDGwE\nFpvZm+6+IqLZmUDb8OtUYFz4Z5nz/KJ1/ObN5bSoW5Wnh2XTun5qj4WVaqpXKs+t/dpwba+WvPRh\n6L6RK5/6kOyWx7F7/8FAH48XiYesBtV57LIu3DGoLRPmrGFKzgamLN7AuV1C4/21a5S8B6jG4hBf\ndyDP3dcAmNkrwPlAZIE6H5jsoa+pi8ystpk1dvevSrLBpOytlCtPnUEjqHHymexdvZhZjz1Km7v3\nJj4Oia2MClTvfAaLelxM+ZoN2LcmFx/RU3vEknaa16nK7y7oxO0Dsnhm3pe8sGgdb3yymcEdGzKq\nfxZdknDeNhYFqimwIWJ6I/+5d1RQm6bAfxQoMxsODAdo0aJFDMIrvXJValL/wv+icvNO7Fr0Gjvn\nPA+ux5SnhEMH2fOvt9mz5F2qnzgQymWoOElaa1CzMvef1YFbw+P9TVqwlvNXhM7b3tYvix6t6yQs\nRwJ3kYS7TwAmAGRnZxd4YiCR5wtWbP6OmyfnsH3PDzxycWcuePhsYFLCti+JM3T8wmSHIBIYtatW\n5M7Bx3Pz6a15cdE6npr7JVc8tYhuLY9jVP8s+rWrH/dCFYsCtQmIfF55s/C84rYJnGmffsXPX11C\nrSoVeO2WnnRupkuTJT7MrA4wBcgE1gKXufu3BbRbC+wGDgH57p6duCglHVWvVJ4Rfdtwba9MXs3Z\nwPjZa7h+0mI6Nq7JyP5ZDOnUKG4j5sTiKr7FQFsza2VmFYHLgTePavMmMCx8NV8PYFdJzz8lwuHD\nzuPvreS2Fz+mfeMavDmqt4qTxNt9wAfu3hb4IDxdmP7ufpKKkyRS5QoZDOuZyaxf9OPRSzqz/+Ah\nRr70MYP/PJu/5m7k4KHYn/YodYFy93xgFPAu8BnwqrsvN7NbzOyWcLNpwBogD3gKuK20242XPT/k\nc8sLuYyekccl3ZrxyvAeNNDIEBJ/5wPPhd8/B1yQxFhEClUhoxyXZjdn+l19GXPlyVQqn8Hdry2h\n36OzeH7hWvYfjN14fzE5B+Xu0wgVoch5T0a8d2BkLLYVT+t3hG6+XbV1N78+pyM39M7UCXNJlIYR\nRxW+BhoW0s6B983sEDA+fM5WJOEyyhnndG7C2Sc2ZubKrYyZkcev31jO6Bl5VKlQjgY1Sv/FPnAX\nSSTLgrzt3PbSx7jDczd057S29ZMdkqQYM3sfaFTAol9GTri7m1lhVwL1cfdNZtYAmG5mn7v7nAK2\nFbirYSU1mRkD2jekf7sGLFyzgydmrmZe3nYyYvDlPu0LlLszeeE6fvvWClrVq8bTw7LJrKdnCUns\nufugwpaZ2ZYj9waaWWNgayHr2BT+udXMphK6D/E/ClQ0V8OKxJKZ0atNPXq1qcfZo+dStWLpxyVN\n68dtHMg/zP1//5QH3lxOv+PrM/W2XipOkixvAteG318LvHF0AzOrZmY1jrwHzgCWJSxCkShVr1Se\nctqDKrnte37g1hdyWbz2W27r14afn9FODxeUZHoYeNXMbgTWAZcBmFkT4Gl3P4vQeamp4fOi5YGX\n3P2dJMUrEndpWaCWbdrF8Mk5fLP3AKOvOJnzujRJdkiS5tx9BzCwgPmbgbPC79cAXRIcmkjSpF2B\n+seSzfzir0s4rmpF/npLLz3ATkQkoMpkgToyJM2UET2j/p3Dh53Hp3/BmJl5dGt5HE9e3Y36NYL3\ngC4REQkpkwWquHbvP8idU5bw/mdbGJrdnN9ecAKVyuvJtyIiQZbyBWrdju+56bkc1mz/ngfP7ci1\nvXTzrYhIWZDSBWrequ2MfOljzGDyDd3pnVUv2SGJiEiUUrJAuTuTFqzlobc/o039ajw1LJuWdXV/\nk4hIWZJyBeqH/EP8+vVlvJqzkcEdG/LnoSdRvVLK/ZkiIikvpf7n3rp7P7e+8DG5677l9gFZ3Dno\neMrp5lsRkTIpZQrUpxt3Mfz5HL7de4CxV3bl7M6Nkx2SiIiUQkoUqDc+2cQ9f11K3Wq6+VZEJFWU\n6QJ16LDzp/dWMm7Wak7JPI5xV3ejXnXdfCsikgrKbIHKP3yYmyfnMOPzrVzRvQW/Oe8EKpZP68HZ\nRURSSpksUPsPHmLllt0cPOT87vwTuLpHS918KyKSYspkgfpy+/fkH3JeuPFUerapm+xwJEUUZ2xH\nEYm/MlmgWtevhjsqTiIiKaxUBcrM6gBTgExgLXCZu39bQLu1wG7gEJDv7tml2a4GehURSX2lvarg\nPuADd28LfBCeLkx/dz+ptMVJRETSQ2kL1PnAc+H3zwEXlHJ9IiIiQOkLVEN3/yr8/mugYSHtHHjf\nzHLNbPixVmhmw80sx8xytm3bVsrwRESkrCryHJSZvQ80KmDRLyMn3N3NzAtZTR9332RmDYDpZva5\nu88pqKG7TwAmAGRnZxe2PhERSXFFFih3H1TYMjPbYmaN3f0rM2sMbC1kHZvCP7ea2VSgO1BggRIR\nEYHSH+J7E7g2/P5a4I2jG5hZNTOrceQ9cAawrJTbFRGRFFfaAvUwMNjMVgGDwtOYWRMzmxZu0xCY\nZ2ZLgI+At939nVJuV0REUlyp7oNy9x3AwALmbwbOCr9fA3QpzXZERCT9aHRVEREJJBUoEREJpDI5\nFp8G9ZRUY2aXAg8CHYDu7p5TSLshwP8CGcDT7v5wwoIUiVKs/o/WHpRIMCwDLuIYt1+YWQYwFjgT\n6AhcYWYdExOeSOKVyT0okVTj7p8BRT3XrDuQF77wCDN7hdBwYyviHqBIEmgPSqTsaApsiJjeGJ4n\nkpICvQeVm5u73czWFbK4HrA9kfGUYeqr6BXVVy1LuuJjDRvm7v9xk3tphMe8PDLu5R4zW3mM5vp8\nRE99Fb1j9VVUeRToAuXu9QtbZmY5enRHdNRX0YtnXx1r2LAobQKaR0w3C88raFs/jmlZFH0+oqe+\nil4s+kqH+ETKjsVAWzNrZWYVgcsJDTcmkpJUoEQCwMwuNLONQE/gbTN7Nzz/x2HD3D0fGAW8C3wG\nvOruy5MVs0i8BfoQXxGiOnwhgPqqOJLSV+4+FZhawPwfhw0LT08Dph3drpT0+Yie+ip6pe4rc9cj\nl0REJHh0iE9ERAJJBUpERAIpkAXKzBYUMn+SmV1SyLJLzWy5mR02s7S5DLSEffWomX1uZkvNbKqZ\n1Y5vlMFmZk+n6pBByqXoKZdKL9a5FMgC5e69itM+PEZZkWOZpaIS9tV0oJO7dwa+AO6PR2xlhbvf\n5O7/MVxQuK8KnS4LlEvRUy6VXqxzKZAFysz2hH+amY0xs5Xhu/AbRLRZa2aPmNnHwKXu/pm7H+tu\n+ZRUwr56L3zJMsAiQjd8pgUzq2Zmb5vZEjNbZmZDzWzWkT0FM9tjZo+FnwDd8+i+S270xadcip5y\nqXgSkUtBv8z8QqAdoZGbGxIaFPPZiOU73L1rMgILoJL21Q3AlPiHFxhDgM3ufjaAmdUCbo1YXg34\n0N1/Hl4OqfE5Uy5FT7kUnbjnUiD3oCKcDrzs7ofC94PMOGp5On0YilLsvjKzXwL5wIsJiC8oPgUG\nh7/Jnebuu45afgj421HzUuFzplyKnnIpOnHPpaDvQRXl+2QHUIb8W1+Z2XXAOcBAT6Ob4dz9CzPr\nSujm14fM7IOjmux390NHzUuHz1k6/I2xolwiMbkU9D2oOcBQM8sws8ZA/2QHFGBR95WFnsp6D3Ce\nu+9NVIBBYGZNgL3u/gLwKJAuh7WUS9FTLkUhEbkU9AI1FVhF6BjwZGBhYQ2tkLHM0kjUfQWMAWoA\n083sEzN7MgHxBcWJwEdm9gnwAPBQkuNJFOVS9JRL0Yl7LmmoIxERCaSg70GJiEiaUoESEZFAUoES\nEZFAUoESEZFAUoESEZFAUoESEZFAUoESEZFAUoESEZFAUoESEZFAUoESEZFAUoESEZFAUoESEZFA\nUoGSmDCzq8zsvWTHIVLWKZf+jwpUnJjZWjMblOBt9jCz6Wb2jZltM7PXws+zObLcwk+/3BF+PWLh\n5zCXlru/6O5nxGJdIpGSkUvh7VY1syfMbLuZ7TKzORHLlEsJoAKVJGZWrKcZR9n+OGACkAm0BHYD\nEyOWDwcuALoAnYFzgRHFiUMkaOKUSxDKpTpAh/DPOyOWKZcSwd31ivELeB44DOwD9hB64mYm4MCN\nwHpgTrjtecByYCcwC+gQsZ61wL3AUuAHoHwx4+gK7I6YXgAMj5i+AVhUyO8eifd6YAPwLXALcEo4\nnp3AmIj21wHzIqY93H5VuO1Yws8f00uvaF/JyiWgPfAdULOQ5cqlRPz7JzuAVH2FE2JQxPSRD+lk\noBpQBTge+B4YDFQIJ18eUDFiHZ8AzYEqJYjhjsikAXYBp0ZMd4ssYEf97pF4nwQqA2cA+4HXgQZA\nU2Ar0DfcvqCkeguoDbQAtgFDkv3volfZeyUjl4BhwKfAn4Ht4fcXRyxXLiXgpUN8ifegu3/v7vuA\nocDb7j7d3Q8CfyKUbL0i2o929w3h9lEzs87A/wN+ETG7OqHEOuI7oHoRx85/5+773f09Qv8BvOzu\nW919EzAXOPkYv/uwu+909/XATOCk4vwNIkWIZy41AzoRypcmwCjgOTPrEF6uXEoAFajE2xDxvgmw\n7siEux8OL29aSPuomFkW8E/gZ+4+N2LRHqBmxHQtYI+Hv6YVYkvE+30FTFc/xu9+HfF+bxFtRYor\nnrm0Dzj2vogMAAAIp0lEQVQIPOTuB9x9NqHCcOTiBeVSAqhAxU9hH9TI+ZsJXcwAhK4MInQIYlMU\n6ymQmbUE3if0be35oxYvJ3RS94gu4XkiQZaMXFpaxPaUSwmgAhU/W4DWRbR5FTjbzAaaWQXg54RO\n4C4o7BfMbJKZTSpkWVNgBqETrk8W0GQycJeZNQ23/TlQ4LpEAiThuQTMIXQBxv1mVt7MegP9gXfD\ny5VLCaACFT9/AH5lZjvN7O6CGrj7SuBq4C+ETsSeC5zr7geOsd7mwPxClt1EKJEfNLM9R14Ry8cD\n/yB0wvdTQidexxfjbxJJhoTnUvg81vnAWYTONT0FDHP3z8NNlEsJYMc+ZCpBYmYVgSVA53ACiUgJ\nKJfKBhUoEREJpIQd4jOzZ81sq5ktS9Q2RUSk7ErkOahJwJAEbk9ERMqwhBUod58DfJOo7YmkKh2N\nkHRRrEEWE8HMhhMaiJFq1ap1a9++fZIjEvk/ubm52929fpLDmASMIXSpc5Hq1avnmZmZ8YxHpFii\nzaPAFSh3n0BoFGGys7M9JycnyRGJ/B8zW1d0q/hy9zlmlhlt+8zMTJRHEiTR5pHugxJJQWY23Mxy\nzCxn27ZtyQ5HpERUoERSkLtPcPdsd8+uXz/ZRyRFSiaRl5m/DCwE2pnZRjO7MVHbFonG0PELGTp+\nYbLDECnzYpVLCTsH5e5XJGpbIiJS9ukQn0gZo6MRki4CdxWfiBybjkZIutAelIiIBJIKlIiIBJIK\nlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiI\nBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIiIBJIKlIhIFIaOX8jQ8QuTHUZaUYESEZFAUoFK\ncfrWJyJllQqUiIgEkgqUiIgEkgqUiIgEkgqUiIgEkgqUiIgEkgqUiIgEkgqUiIgEkgqUiIgEkgqU\nSBrTjdwSZCpQIiISSCpQIiISSCpQIiISSCpQIiISSCpQIiISSCpQIiISSCpQIiISSAktUGY2xMxW\nmlmemd2XyG2LpArlkaSLhBUoM8sAxgJnAh2BK8ysY0nWpZsLJV3FMo9Egq58ArfVHchz9zUAZvYK\ncD6worgrmv7aRCo2aE2j2bNjHGLqUl9F58DWNTCiZ7LDOJaY5REol0pCfRWdWORSIg/xNQU2RExv\nDM/7N2Y23MxyzCxn27ZtCQtOpIxQHknaSOQeVFTcfQIwASA7O9sLajP40usBmBLsb7qBcORQqPqq\naKG+6pvsMGIimjwC5VJxKJeiF6tcSuQe1CagecR0s/A8EYme8kjSRiL3oBYDbc2sFaGEuhy4siQr\n0jcYSWMxyyORoEtYgXL3fDMbBbwLZADPuvvyRG1fJBUojySdJPQclLtPA6YlcpsiqUZ5JOlCI0mI\niEggqUCJiEggqUCJiEggqUCJiEggqUCJiEggqUCJiEggBW6oIxFJHN30LkGmPSgREQkkFSgREQkk\nFSgREQkkFSgREQkkFSgREQkkFSgREQkkFSgREQkkFSgREQkk3aib4nQjpoiUVdqDEhGRQNIelIhI\nFHQ0IvG0ByUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUi\nIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGkAiUiIoGk\nAiUiIoFUPtkBiATFlBE9kx1CkczsUuBBoAPQ3d1zkhuRyH+KVS4lZA/KzC41s+VmdtjMshOxTZEU\ntQy4CJiT7EBE4i1Rh/iUVCIx4O6fufvKZMchkggJOcTn7p8BmFkiNieS9sxsODAcoEWLFkmORqRk\ndA5KJGDM7H2gUQGLfunub0SzDnefAEwAyM7O9hiGJ5IwMStQsUiq8Hp+/OYH7DGzwg5n1AO2Fy/K\ntKW+il5RfdUy3gG4+6BYri83N3e7ma07RhN9PqKnvoresfoqqjyKWYGKVVJFfvM7FjPLcXddcBEF\n9VX0UrGv3L3+sZan4t8cL+qr6MWir3QflEgZYmYXmtlGoCfwtpm9m+yYROIlUZeZK6lEYsDdp7p7\nM3ev5O4N3f0nyY5JJF4SdRXfVGBqjFdb5GFA+ZH6Knrp2Ffp+DeXlPoqeqXuK3PXBT4iIhI8Ogcl\nIiKBpAIlIiKBFMgCZWYLCpk/ycwuKWRZWo73V8K+etTMPjezpWY21cxqxzfKYDOzp82sY7LjiAfl\nUvSUS6UX61wKZIFy917FaW9mGaTpeH8l7KvpQCd37wx8Adwfj9jKCne/yd1XHD0/3FeFTpcFyqXo\nKZdKL9a5FMgCZWZ7wj/NzMaY2crwSBUNItqsNbNHzOxj4NJ0HUSzhH31nrvnhxcvApolPvLkMLNq\nZva2mS0xs2VmNtTMZh3ZUzCzPWb2mJktAXoe3XfJjb74lEvRUy4VTyJyKehj8V0ItAM6Ag2BFcCz\nEct3uHvXZAQWQCXtqxuAKfEPLzCGAJvd/WwAM6sF3BqxvBrwobv/PLwcUuNzplyKnnIpOnHPpUDu\nQUU4HXjZ3Q+5+2ZgxlHL0+nDUJRi95WZ/RLIB15MQHxB8SkwOPxN7jR333XU8kPA346alwqfM+VS\n9JRL0Yl7LgV9D6oo3yc7gDLk3/rKzK4DzgEGehrdDOfuX5hZV+As4CEz++CoJvvd/dBR89Lhc5YO\nf2OsKJdITC4FfQ9qDjDUzDLMrDHQP9kBBVjUfWVmQ4B7gPPcfW+iAgwCM2sC7HX3F4BHgXQ5rKVc\nip5yKQqJyKWgF6ipwCpCx4AnAwsLa2ga7y/qvgLGADWA6Wb2iZk9mYD4guJE4CMz+wR4AHgoyfEk\ninIpesql6MQ9lzTUkYiIBFLQ96BERCRNqUCJiEggqUCJiEggqUCJiEggqUCJiEggqUCJiEggqUCJ\niEgg/X++XxdiBgBD6gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11760ef50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"##Preliminary visualization of node activities.\n",
"for i in range(4):\n",
" plt.figure()\n",
" \n",
" for j in range(4):\n",
" ind = range(4)\n",
" ind.remove(i)\n",
" \n",
" plt.subplot(2,2,j+1)\n",
" \n",
" plt.errorbar(range(3), coeff[j,i,ind], yerr=coeff[j,i,ind]-conf[j,i,ind,0])\n",
" plt.plot([0,2], [0,0], lw=2, c='k')\n",
" plt.xticks(range(3), [order[z] for z in ind])\n",
" plt.title('%s, %s min' % (order[i], [0,5,20,60][j]))\n",
" \n",
" plt.tight_layout()\n",
" plt.savefig('%s.pdf'% (order[i]),bbox_inches='tight')"
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/as305/anaconda/lib/python2.7/site-packages/ipykernel/__main__.py:2: RuntimeWarning: invalid value encountered in greater\n",
" from ipykernel import kernelapp as app\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>idr1</th>\n",
" <th>idr2</th>\n",
" <th>sirr</th>\n",
" <th>tror</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>idr1</th>\n",
" <td>NaN</td>\n",
" <td>-0.543586</td>\n",
" <td>0.0</td>\n",
" <td>-0.972243</td>\n",
" </tr>\n",
" <tr>\n",
" <th>idr2</th>\n",
" <td>0.000000</td>\n",
" <td>NaN</td>\n",
" <td>0.0</td>\n",
" <td>0.842425</td>\n",
" </tr>\n",
" <tr>\n",
" <th>sirr</th>\n",
" <td>0.000000</td>\n",
" <td>-1.150079</td>\n",
" <td>NaN</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tror</th>\n",
" <td>-0.419209</td>\n",
" <td>0.623701</td>\n",
" <td>0.0</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" idr1 idr2 sirr tror\n",
"idr1 NaN -0.543586 0.0 -0.972243\n",
"idr2 0.000000 NaN 0.0 0.842425\n",
"sirr 0.000000 -1.150079 NaN 0.000000\n",
"tror -0.419209 0.623701 0.0 NaN"
]
},
"execution_count": 68,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#final networks used to generate topologies for paper Figure 4. \n",
"net0 = pd.DataFrame(coeff[0,:,:], columns=order, index=order)\n",
"net0.values[sig[0,:,:] > 5e-2] = 0\n",
"net0.to_csv(\"net0.csv\")\n",
"\n",
"net0"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/as305/anaconda/lib/python2.7/site-packages/ipykernel/__main__.py:2: RuntimeWarning: invalid value encountered in greater\n",
" from ipykernel import kernelapp as app\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>idr1</th>\n",
" <th>idr2</th>\n",
" <th>sirr</th>\n",
" <th>tror</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>idr1</th>\n",
" <td>NaN</td>\n",
" <td>0.00000</td>\n",
" <td>0.000000</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>idr2</th>\n",
" <td>0.0</td>\n",
" <td>NaN</td>\n",
" <td>0.000000</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>sirr</th>\n",
" <td>0.0</td>\n",
" <td>-0.96638</td>\n",
" <td>NaN</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tror</th>\n",
" <td>0.0</td>\n",
" <td>0.00000</td>\n",
" <td>-0.512084</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" idr1 idr2 sirr tror\n",
"idr1 NaN 0.00000 0.000000 0.0\n",
"idr2 0.0 NaN 0.000000 0.0\n",
"sirr 0.0 -0.96638 NaN 0.0\n",
"tror 0.0 0.00000 -0.512084 NaN"
]
},
"execution_count": 69,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"net5 = pd.DataFrame(coeff[1,:,:], columns=order, index=order)\n",
"net5.values[sig[1,:,:] > 5e-2] = 0\n",
"net5.to_csv(\"net5.csv\")\n",
"net5"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/as305/anaconda/lib/python2.7/site-packages/ipykernel/__main__.py:2: RuntimeWarning: invalid value encountered in greater\n",
" from ipykernel import kernelapp as app\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>idr1</th>\n",
" <th>idr2</th>\n",
" <th>sirr</th>\n",
" <th>tror</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>idr1</th>\n",
" <td>NaN</td>\n",
" <td>0.0</td>\n",
" <td>0.789413</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>idr2</th>\n",
" <td>0.0</td>\n",
" <td>NaN</td>\n",
" <td>0.000000</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>sirr</th>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>NaN</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tror</th>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.000000</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" idr1 idr2 sirr tror\n",
"idr1 NaN 0.0 0.789413 0.0\n",
"idr2 0.0 NaN 0.000000 0.0\n",
"sirr 0.0 0.0 NaN 0.0\n",
"tror 0.0 0.0 0.000000 NaN"
]
},
"execution_count": 60,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"net20 = pd.DataFrame(coeff[2,:,:], columns=order, index=order)\n",
"net20.values[sig[2,:,:] > 5e-2] = 0\n",
"net20.to_csv(\"net20.csv\")\n",
"net20"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/as305/anaconda/lib/python2.7/site-packages/ipykernel/__main__.py:2: RuntimeWarning: invalid value encountered in greater\n",
" from ipykernel import kernelapp as app\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>idr1</th>\n",
" <th>idr2</th>\n",
" <th>sirr</th>\n",
" <th>tror</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>idr1</th>\n",
" <td>NaN</td>\n",
" <td>0.000000</td>\n",
" <td>0.000000</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>idr2</th>\n",
" <td>0.000000</td>\n",
" <td>NaN</td>\n",
" <td>-0.906313</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>sirr</th>\n",
" <td>0.639498</td>\n",
" <td>-0.562464</td>\n",
" <td>NaN</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tror</th>\n",
" <td>0.000000</td>\n",
" <td>0.000000</td>\n",
" <td>0.000000</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" idr1 idr2 sirr tror\n",
"idr1 NaN 0.000000 0.000000 0.0\n",
"idr2 0.000000 NaN -0.906313 0.0\n",
"sirr 0.639498 -0.562464 NaN 0.0\n",
"tror 0.000000 0.000000 0.000000 NaN"
]
},
"execution_count": 61,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"net60 = pd.DataFrame(coeff[3,:,:], columns=order, index=order)\n",
"net60.values[sig[3,:,:] > 5e-2] = 0\n",
"\n",
"net60.to_csv(\"net60.csv\")\n",
"net60"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"pd.DataFrame(sig[0,:,:], columns=order, index=order).to_csv(\"sig0.csv\")\n",
"pd.DataFrame(sig[1,:,:], columns=order, index=order).to_csv(\"sig5.csv\")\n",
"pd.DataFrame(sig[2,:,:], columns=order, index=order).to_csv(\"sig20.csv\")\n",
"pd.DataFrame(sig[3,:,:], columns=order, index=order).to_csv(\"sig60.csv\")"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"import networkx as nx"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/as305/anaconda/lib/python2.7/site-packages/networkx/drawing/nx_pylab.py:126: MatplotlibDeprecationWarning: pyplot.hold is deprecated.\n",
" Future behavior will be consistent with the long-time default:\n",
" plot commands add elements without first clearing the\n",
" Axes and/or Figure.\n",
" b = plt.ishold()\n",
"/Users/as305/anaconda/lib/python2.7/site-packages/networkx/drawing/nx_pylab.py:138: MatplotlibDeprecationWarning: pyplot.hold is deprecated.\n",
" Future behavior will be consistent with the long-time default:\n",
" plot commands add elements without first clearing the\n",
" Axes and/or Figure.\n",
" plt.hold(b)\n",
"/Users/as305/anaconda/lib/python2.7/site-packages/matplotlib/__init__.py:917: UserWarning: axes.hold is deprecated. Please remove it from your matplotlibrc and/or style files.\n",
" warnings.warn(self.msg_depr_set % key)\n",
"/Users/as305/anaconda/lib/python2.7/site-packages/matplotlib/rcsetup.py:152: UserWarning: axes.hold is deprecated, will be removed in 3.0\n",
" warnings.warn(\"axes.hold is deprecated, will be removed in 3.0\")\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAdgAAAFPCAYAAADuut9iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd8W+Wh//Hv0bJlS962vOI4wyPT2SQhgQYIoyV0UCj7\nR7i/lpYdoKXlcuntuIVyC2G1FDqAMpoSChRoCZAyfgkQkhDiLGI7CRneIx7y0jy/P2Q5to8kW/IZ\nkvV9v155JT6W5Mcp9SfP0XOeI4iiKIKIiIhkpdN6AERERBMRA0tERKQABpaIiEgBDCwREZECGFgi\nIiIFMLBEREQKYGCJosjx48dhsVjg8Xi0HgoRjRMDS6Sx4uJibN68GQBQVFSE7u5u6PV6zcYjiiLu\nuusuZGZmIjMzE3fddRd4uTxR+AxaD4CIostTTz2F1157DZWVlRAEAatXr8aUKVPw/e9/X+uhEcUU\nzmCJNHT11Vfj+PHjWLNmDSwWCx544AEIggC32w0A+MpXvoJ77rkHy5cvh8ViwZo1a9DW1oYrr7wS\nKSkpWLx4MY4ePTr4egcPHsTq1auRkZGBsrIyvPTSS2GP6dlnn8Udd9yBwsJCFBQU4M4778Qzzzwj\n03dMFD8YWCINPffccygqKsIbb7yB7u5uXHrppZLHbNiwAc899xzq6upw+PBhLFu2DGvXrsXJkycx\nY8YM/OxnPwMA9PT0YPXq1bjiiivQ3NyMDRs24IYbbsCBAwcAAPfffz/S0tKC/vLbv38/KioqBj+u\nqKjA/v37Ff6bIJp4GFiiKLd27VpMmzYNqampuOCCCzBt2jScc845MBgMuOSSS/D5558DAN58800U\nFxdj7dq1MBgMmD9/Pi6++GJs3LgRAPDjH/8YHR0dQX/5dXd3IzU1dfDjlJQUdHd3831YojDxPVii\nKGez2Qb/bDabJR93d3cDAI4dO4ZPP/102GzU7Xbj6quvDuvrWSwWdHV1DX7c2dkJi8UCQRAi/RaI\n4hJnsEQakytckyZNwplnnjlsVtrd3Y0nnngCAPCrX/0KFosl6C+/WbNmobKycvDjyspKzJo1S5Yx\nEsUTBpZIYzabDUeOHBn361x44YWorq7Gc889B5fLBZfLhR07duCLL74AANx9993o7u4O+svvmmuu\nwUMPPYS6ujrU1dXhwQcfxLXXXjvu8RHFGwaWSGM/+clP8Mtf/hJpaWl4+eWXI34dq9WKd955Bxs2\nbEB+fj5yc3Nx1113weFwhPU6119/PdasWYM5c+Zgzpw5uPDCC3H99ddHPC6ieCXwhutERETy4wyW\niIhIAQwsERGRAhhYIiIiBTCwRERECmBgiYiIFMDAEhERKYCBJSIiUgADS0REpAAGloiISAEMLBER\nkQIYWCIiIgUwsERERApgYImIiBTAwBIRESmAgSUiIlIAA0tERKQABpaIiEgBDCwREZECGFgiIiIF\nMLBEREQKYGCJiIgUwMASEREpwKD1AKJBn8uDQ6096OhzwenxwqTXIc1sRElWMhKNeq2HR0REMUgQ\nRVHUehBaae1xYG9DF2o7+yEA8Az5m9ALvt8LUhMxJy8FWckJmoyRiIhiU9wG9mCzHTtrO+Hxjv7t\n63UCFhWmojzHqsLIiIhoIoiL92BnzZqFDz74YPBjf1z37fgY6762ZNTne7widtZ24mCzXcFREhHR\nRBIX78Hu379/8M+tPY4xz1xdTgf+8ut7cGD7VvR0dSCncDJ+ff99uOybFyk5XCIimgDiIrBD7W3o\nGlNcPW43vB4PMmx5+PGTLyEztwB7PnoP1119BZbu24fi4mLlB0tERDErLk4RFxcXY/PmzTjZ1Y17\n192AG86ajbsvPQtfHqgc9rg7LlqOfz77O9xz+bm4/oxyGIwmfPN7tyM7fxJ0Oh3mrTwHWXmT8Mmn\nOzT6ToiIKFbE1Qz2h3f/F5prj+GBV7fC0deLh269RvKYbW+/jnXrn4E1LQN6w/C/ns62FjQcP4LD\njZ2wb1wPISERgikRgsns+z3BfOrjhEQg0Of0cfVXTkQUt+Lqp/1br7+Ky+/8BSypabCkpmH1d9bi\nH396ZNhjVl+2Fpm5+ZLnut0uPPlft2DF174NTJ4Hsf11iN0RDEJvDBpmBIj04GNMiYAxAYIgRPjd\nExGRmuIqsK1Njci05Q1+nJlXKHlMxpDP+3m9Xjx1720wGE246ke/wLGWHogiEFHrPC6IvS6IvRGs\nSBaEgRCbpZEeGeSBPw+Lto6bZhARqSUuAiuKwMadJ2DJyEJbUwMKppUBANoa6ySPFSCMeK6IP//i\nh+g62YrbH34WBoMRdqeINo8RWQaXKuMfMhiIjj7A0QcxkiuGDKbB2bAvuqdiHPB09pCQw2Di7JmI\nKAxxEVgIwOuV9cidtwpvPv04ps2eB0dfHza/9MyoT332/rtRf/QQfvTbF2FKTITL7UVTRx8OOczq\nB3a83E6IbifE3q7wnyvohp/KHuV0tj/gg4/VxcV6OiKiQXERWAFAjjUBzikXI2P3c7jz6yuQnp2D\nFWsuxbsb/hz0ea0NtfjglRdgMCXg1vMXDh7PPO9GnH3jNTi7Ih2isw+iow+is9/3Z2c/REf/kI/7\ngMGP+wHRq8J3rADRC7G/B2J/T2TPNyYEnT37I42EIYEeOnvWGzl7JqKYEzdbJX73Lzvx7oEmfGfZ\nZJTnpUCnC/8Httcr4mB9F/627RguX1KE+741J6zni6Lom0UODfKwGPf7Tv9KYj3wOXeMzZjlotMP\nmS0PXQw2csY8NM7+2XYCBIGzZyJSX1zMYAGgzGbFuweasOVgM6bbrDBFEFi3V8SWqmYAQHVT+G+C\nCoLgm8kZI7txgOhxD86ERUcfMCzEfcM+NzLScPYDiNF/S3k9EPu6IfZFsmxb8EU24HvMAU5nJ4x4\nHC+rIqIIxc1PjxKbBQBQ396Ht/fU47y5+TAZxj6zcbq9eHtPPerb+wAA1Y1dEEVR1VOXgt4AwWwB\nzJawnyuKXsDlDHI6u08a7ZEza49bge9IDeLA99QPER3hP11vkKzMFkyJQU5nj7jsymji7JkojsVN\nYEttp+6Es/PISQDAeXPzYdAJIU8Xe70i3F4Rb++pH3weANgdHhxvaMfk/AzlBi0jQdANLjiKhOh2\nSWbIGMvs2emfPccojxtinx1i33guqwoyex66SMyUCIxcKMbZc9T74cZK6AQBqUlGpJqNSEk0IMVs\nRIrZ97HvmO/3cP5BTxND3LwH63B7MPPet4ftQ5yfbsbKshyU5FkBETAO+T+Ay+0FBKCmwY4tVc2D\nM9eh1hx4F//74v8g0ZKsyvcQq0SvF3A5hsyMQ53O7js14/SH3OvR+lvQhsEYcPbsWxA2yi5ivKxK\ncaIoouQ/34J7DHubA0CiUSeJbop5eJiHHzMOhjvZpOf/njEobgILAGc/+AEOt0hXwSaZ9Jg3OR22\nNDPMRh36XL5LcXYfa0evM/gP97L3/o7Vid246V9PM7IKEUXRtznHiFPWoU5nD51Rw+XQ+lvQhqA7\ntSgswHXNobf35KYkY9HrdGPmvW+r8rX0OmFYhP0B9s2WDUHDnWo2wppogFHP2bMW4uocVKnNGjCw\nvU4PPq5pDfv1urPycOitF/D4V9cysgoRBME3GzOYgOSUsJ8vej0QnY7RT2cPXa09dPYcy5dVOXoh\nOnqBSDclCXk6O8jnEuLnsqrOPvVW9Xu8Itp7XWjvjexrJpv0w2bIp0JsGBbmYTPogc+ZjZw9Ryqu\nAltis+KtfY2yvV53lm9bxUNbtjOyUUrQ6SEkJgGJSWE/99RlVYFmyP7LqoZf8ywOvebZ7VTgO1KJ\nf1OSns7wn6vTD4svxjh79i0Mi51NSbr6YmfhX4/Tgx6nBw2d4a+HMOqFwQBbh82gDZLZ8shwWxON\n0EdwxcZEEVeBLRuy0EkO3Zl5EOHbyOLQlu14/IJrcdNbzzCyE8Twy6pSw36+6HFDdDkGg4yRm5AM\nnU0PibN/to1YfffG6xn/piShVmmPvFvV0McajPJ+LyGoOYPVkssjoq3HibaeyP7BaE0YuvDLEHK2\nPPI0d6Ixtt+qiKvAltrCv7wlFE9CIvpTMmDu8q0uPrR1ByNLgwS9wbcSODH8/xYGL6sadjo7wHvM\nks8NHPfE8A9/l8P3D5NInqs3SMKMAFt4SheOhb8pSbwEdrzsDjfsDjfqOqQLRUdjMujw2ysWYPVM\nmwIjU15cBbY4KxlGvQCXR76ZQXdW3mBggSGR/dfTSLTKG3SKH7JeVhXodHbA2bP/PWgHYnZTEo87\n8k1JBMF3inrEFp6BZtMwJaKjOYYvP4tyyQkDC09TzehwurHlSBvSzEaUZCXH1Kw2rgJr1OswNcuC\nqgh2YQqmJ3cSso/sH3bs0NYdp96TZWRJA4LB6DtdmhT+2yKi6AWcjlFnz6f22R6+cCxmL6sSxYHT\n831jutdzS7sNQLHSo4or+elmrCzPQUmuFaLom8H2ur04crIXegGorO9EQWoi5uSlICs5sh3x1BRX\ngQV8OzrJGdi8i78Ow8734HYOf3/i0NYdeOyCa3HzW88wshRTBEHnWyWcYI7o+b7Zc4DT2aPsIhZr\nl1XZPXH341NRi6ZmhNz8x3/i8XhHP+q6HFhUmIryHHnX1cgt7v4L8e3o1CDb67Uarbj9ld/jyW99\nXxLZwx/tZGQp7pyaPUd2WRVcjoDxDXbN89CNSdS8rKrLGzunKqOdP67+3a7eePpxtNQdx3X3PBDw\n8R6viJ21vhXu0RzZuNpoAgA27WvA95/fJdvrJRp1OPCz87H/rfcDRhYApp2+iJElUpjvsqrAs2fp\nzTECzJ7DvKzqnoapeL0rW6HvJn7kp5ux9sxpEW0lqdcJOL8sB1nJJgVGNn5xOoOVT7/LixPtvZjz\ntbNwPWeyRJrxXVZlgmA0AckRXFbl9Qy5+9Tos2d7C68UkMPK8hwYwrhW1uN2Q2/wpcvjFbG3oQsr\ni9NgMERfzuJuBuvxiphx7yY43fKdSvrDNYsGl5Hv/df7ePKb1wecyU5dvhC3bHqWkSWaAC79/SfY\nfvTk6A+koJIT9Chv/QDvbXwG/T3dSMuy4Zq7fomq3dvRfOIYrv/FI2ipP4Effv10rL3nAfzjDw8j\nK78Q3/3v9YPHXv/DwygvmYqtW7Zo/e1IxMaWKTLS6wRMy5Y3cEPvDTvnq6tw/atPwmCSnrI48vFn\nePT8/4N+eyT3NSWiaNLVz+tgx2tqQhfef/kv+Omzb+D3H36BOx57Dln5hQEfW7VrG+7b+B7ufPT5\nYcfuf/k9PPyXl9UacljiLrAAUCbzhhMjb74+lsj2dcm3kpmI1MeNJsYvOyUJbpcT9Udq4Ha7kJ0/\nCTmFxQEf+43vrkOCOQmmxMRhx4yJSegTo+/0MBCngS2R+X3Y6ibpjHTOV1fh+68Fj+xjF1zLyBLF\nsC4Gdtxyi4pxxe0/xWt/WI9bzp2P3919I9pbAu8Xn5GbH/SY0xOdN+WIy8DKvdDpcEv3sPvM+s2+\nYJTIciZLFJNcHi96QtzKksam3+XFsvO/gf/84yt48PVPIAgCXnrsvoCPFSBdCOU/ZorS2/FF56gU\nJvem/063F8faAm9sPhjZhACR/WQXI0sUgzh7lUdN1UHs2bYVLqcDxoQEmBISoQvzbkp6AUhPUu8m\nD+GIy8AWppthlnk/y5Hvww41+4JV+MFrTzGyRBNEV3/s3Koumh043oZXnvg1bl49D7eevxBd7a34\n9o13hf060zOj85KpuLtMx2/NY1uxty6Ce10GcfvqUtxydknIx+zf9AGe+Mb34HYEuIRn2QLcvOlZ\nmFOid1cSIvLpdrjx8aFWdPa50NXv9v0+8Mt3zPe777gbfS6eTg7mO8smozwvJeD2iGNRlGbGqulZ\nMo9KHnEb2Ntf2o1XdtXJ9noXzs3D41csGPVxoSI7Zel83PL2XxhZognG6fYORtcfYX+cQ4XZf2wi\n/5SeyDs5xW1gn/zwMO5766Bsr1dqs+CddWeO6bGjRnbTszCnhr+PKxFNPF6viG6nG529riGRHgjz\nsCC7hs2o/cccMm6qo5SRexGPhV4nRP2G/3Eb2PcPNmPtMztkez2jXsCBn58P4xhXs+1/+0M88fXv\nMrJEpKh+lwdd/f4Au4fPlnuDz5o7+1ywq/he82h30xkqFuIKxHFga9t7seLX78v6mu+uOyOsa2wZ\nWSKKZh6viO7+4dEd7XT20Me4POHlJT/djJVlOSjJswIiYBwyo9UPNLcg1TxwP9joPC08VNwGVhRF\nzP7p27Jey/bbKxbga3PzwnpOyMieNs/3niwjS0QxRhRF9LuCvPfsn00HOMVt73fD6fGiJNeKtSum\nQKcTYNLrkJ5kxPTMZCTKfAWIkuI2sADwjd9+hN0nOmR7vVvOLsHtq0vDfh4jS0Q0nNvjhV4n+O6S\nFKPi8jpYv1KZ9ySuCXEtbCizzjsTN7z+x4DXyX756W48et416OvsGu/wiIhihkGvi+m4AnEfWLn3\nJI58s4iZ556BG17/I4yJCZLPMbJERLGHgZXR0bZeONyRv6c789wz8IN//CFoZB8592pGlogoRjCw\nMvJ4RRxpCbwn8ViFiuzR7ZV45Nyr0dsh3w5URESkjLgOrC0lAdZEee8jOJ7TxH4zzz0DPwhyuvjo\n9ko8et41jCwRUZSL68AKgiD7nXXkCCwAzFy9kpElIophcR1YQJ2br0dq5uqVuOGNP4U4XczIEhFF\nq7gPbLRcqhPMjHNWBI3ssR2MLBFRtGJgZZ7BHjvZi36Zb03FyBIRxR4GVubAiiJwqFm+08R+jCwR\nUWyJ+8BmWUxITzLK+ppyLXQaacY5K3Djm38OHtnVvISHiChaxH1gBUGI6oVOI5WffXrwyO7cg0dW\nX42edkaWiEhrcR9YAFF7qU4wg5E1J0o+d2znHjx6LiNLRKQ1BhbyryRWOrDAQGTf+BMjS0QUpRhY\nyH8tbG17H3ocbllfM5DRZrKPrL6KkSUi0ggDC/lXEgPKrCQOpPys5UEje/yzvYwsEZFGGFgAGckm\nZFmki4bGo0qF08R+jCwRUfRhYAdE+45Oo2FkiYiiCwM7QP6br6tzinio8rOW46Z/hojsOVcyskRE\nKmFgB8gfWHVnsH5lq0JEdtc+X2RPdmgwMiKi+MLADpD7FHFDZz+6+l2yvuZYjRrZ1VcxskRECmNg\nB8h9qQ4A1GhwmtivbNVy3PSvpxlZIiKNMLADUs1G2FLkXUms9kKnkcq+sgw3/etpmJLMks8d37UP\nD/N0MRGRYgRRFEWtBxEtrv7Tp9hS0xrx8wvSzCixWVBqs6Ikx4KlUzMxKSNJxhFGpuqDT/Dbr10H\nZ2+f5HOT5s/CbZtfQHJGmgYjIyKauBjYIX7x5gH8aeuXoz5OrxNgNOhgMuhw1eJCnDMrDyU5FlgT\n5b0rj5wYWSIidfEU8RAjFzplWRKwfFomrl1ejP/55mzkp5gwKTsZk7KTkZtuRoY1ASlGHRYUpUd1\nXIHQp4tPfL6fp4uJiGTGGewQx9t68WF1M0psVpTarMhINg37/MWPfYi2EVsMz80049Frlqg4yvGp\n/nAbHv/qWs5kiYgUxhnsEEWZSbh6WTGWTs2UxBUAJgd4P/VEhzRU0az0zKWhZ7JnX4HutnYNRkZE\nNLEwsGGYlZ8qOdahwl1z5FZ65lLc/NYzgSO7+wAeOedKRpaIaJwY2DAsnZ4tOebR6eD2eDUYzfiU\nnHEaI0tEpCAGNgwzClLhHRFTnU6HXV+2aTSi8fFHNiE5wKlvRpaIaFwY2DDodDoYRels9dPDkV87\nq7WSM07DTf96Omhk+Z4sEVFkGNgwZZqll+McbIjtO9SEimxt5ReMLBFRBBjYMBUFWElc29mvwUjk\nVXLGabgpyOniwci2ntRgZEREsYmBDdPcQuk1ol0OjwYjkV/JyiWhI3vOlYwsEdEYMbBhWlaaIznm\n1evhcMVHZNdzJktENCYMbJim5VjgdQ+PqaATsPNwi0Yjkl/JyiW4edOzASNbt+cgI0tENAYMbJh0\nOh1MgvT4ji8nVnCmr1jMyBIRjQMDG4GsgCuJuzQYibIGI2tJlnyOkSUiCo2BjUBxZoBZXVds7Uk8\nVtNXLPZtRhEssmcxskREgTCwEZgzSbqS2O6Mve0SxypkZPcyskREgTCwETg9wEpi0aBHj8OlwWjU\nEfJ08UBk7S2xuWUkEZESGNgIFGdbpSuJBQHbD8XuloljMf30RSEj+/DZVzKyREQDGNgIJQZYSfxZ\njG76Hw5GlohobBjYCGUlS1cSVzXZNRiJ+qafvgi3vP0Xni4mIgqBgY3Q1CxpXOq7Yn9P4rGatnxh\n0MjW76tiZIko7jGwEZpbmC451u2auCuJA/FHNtFqkXzOH9mu5on9vjQRUTAMbIROL5OuJIZBD3v/\nxF1JHMi05Qtx86Zng0b24bOvZGSJKC4xsBEqyEgOuJL4k5pmjUakHd9MlpElIhqKgR0Hc4C/vc+O\nxOeGC1OXjRJZni4mojjDwI5DdrJJcuxQc3ysJA4kZGT3VzOyRBRXGNhxmJ4tDUmD3aHBSKIHI0tE\n5MPAjkNFkXQlcY87vlYSBzJ12ULc8k6Q1cX7q7F+1eWMLBFNeAzsOATakxgGPdq743sWCwBTly4I\nGtmGAzWMLBFNeAzsOOSkmuF1u4cdi9eVxIEMRjbFKvncYGSbWjQYGRGR8hjYcUrSSTcl3nUsPlcS\nBzJ16QLfe7LBInvWFYwsEU1IDOw42SwJkmOHmrs1GEn0mrp0AW4NNZNlZIloAmJgx2l6jvQ9xqY4\nX0kcyJTT5jOyRBRXGNhxml+cITnW6xU1GEn0Gy2yD/E9WSKaQBjYcTq9JAeiODyogsGAVnv83Fkn\nHKEi2/jFITy06nJ0NnKRGBHFPgZ2nNItCcCIPYkBYGsVIxHMlNPm49Z3nwsa2fVnXcHIElHMY2Bl\nkGyQ/jVWHudK4lCmLJmHW999DuZURpaIJiYGVga5VulK4sNcSTyqKUvm4ZZ3QkSWp4uJKIYxsDII\nuJK4x6nBSGJPyMgePMzIElHMYmBlsGCydCVxH7ckHjPf6eLnQ0e2gZElotjCwMpgeal0JbHOoEdD\ne69GI4o9xYsrQkf2LEaWiGILAyuDlCRTwJXEH1U1aTCa2MXIEtFEwsDKxGIMsJL4RLsGI4lto0X2\noVWXMbJEFBMYWJnkBVhJfKSVp4gjUby4ArdtfiFgZJuqjjCyRBQTGFiZlNlSJMdauJI4YpMXzcVt\nm19AUpr075WRJaJYwMDKZMEU6Urifm5JPC6TF83Fre8+z8gSUUxiYGWytCQ74Eri4609Go1oYhg1\nsl9hZIkoOjGwMklOMEIIsJL442quJB6vyYvm4tZgp4urfZHtqOffMxFFFwZWRlYTVxIrZfLCOSEj\nu37V5YwsEUUVBlZG+SmJkmNftnElsVwYWSKKJQysjEoDrCRu63VpMJKJazCy6amSzzGyRBRNGFgZ\nLZmWKTnm4Epi2U1eOMd3CU+QyPI9WSKKBgysjJZMy4bola4kPtzYpdGIJq6iBbODRra55ktGlog0\nx8DKKMGoh+AJsJK4hpeRKGEskW2va9RgZEREDKzsUkx6ybG9tZ0ajCQ+jBbZ9asuZ2SJSBMMrMwK\n06QriY+d5GYTSmJkiSgaMbAyK8/lSmItFC2Yjdv+zdPFRBQ9GFiZLZ6WJTnmFAR4vV4NRhNfiub7\nIpuckSb5XMuho4wsEamKgZXZwimZkpjq9HpUN3AlsRqK5s/GrZufDx3Z2gYNRkZE8YaBlZnJoIc+\nwGz145oWDUYTn0aN7KrLGVkiUhwDq4DUACuJ99d1aDCS+DXq6WJGlogUxsAqoDDNLDl27CT3JFbb\npHmzRn9PlpElIoUwsAqYlS9dydre79ZgJBQysoePMbJEpBgGVgFLAqwkdgk6riTWyFgie/JEvQYj\nI6KJjIFVQMXkjAAriXXYX8v3YbUyad4srHvvxaCRXb/qckaWiGTFwCrAoNfBEGC2uu1QqwajIb/C\nipm+yGamSz7HyBKR3BhYhaQlGCTHuJJYe4UVM7Hu3y8EjSxPFxORXBhYhRSlS1cSH2/v02AkNFKo\nyLYeOc7IEpEsGFiFzAiwkrjDwZXE0YKRJSKlMbAKWV6SLTnmFnRwe7iSOFqEek92MLLH6zQYGRFN\nBAysQmYVpsHrka4krjx2UqMRUSCFc2eEjuyqyxlZIooIA6sQnU4HoyidrW4/zJXE0cYfWUtWhuRz\nnMkSUaQYWAWlJ0pXEh9o6NRgJDSawrkzcNu/Xwgc2S9PMLJEFDYGVkGTM5Ikx05wJXHUCjmTZWSJ\nKEwMrIJmFUh3Dep0ejQYCY1VwZzyUSPbdqxWg5ERUaxhYBW0tES6J7FHp4PTzchGs9Eiu37V5Yws\nEY2KgVVQeV4qvJ7hMdXpdNj1JVcSRztGlojGi4FVkE6ng0kUJce3H27RYDQUroI55Vj3/l95upiI\nIsLAKizDbJQcO9jYpcFIKBIFs8uw7v2/wpqdKflc29FaRpaIgmJgFVacmSw5VtfRr8FIKFIFs8tw\n23svhoxs69ETGoyMiKIZA6uwOYXSPYm5kjj2jBbZ9asuZ2SJaBgGVmHLS3Ikx0S9Hg4XIxtrGFki\nCgcDq7BpuSnwjrgsR9AJXOgUo8byniwjS0QAA6uKBEF6bMeRNvUHQrLIn1UaNLInj9UxskQEgIFV\nRWaSdCVxFVcSx7TByOZINxNhZIkIYGBVMSVTuidxfRdXEse6/FmlWPfei4wsEQXEwKqgYpL0XqN2\nJ2+8PhFwJktEwTCwKlheapMcEw169DhcGoyG5JY/syR0ZM+8DK1fMrJE8YaBVUFRVrJ0JbEgYFsN\nVxJPFCEje3xgJsvIEsUVBlYliQFWEnPT/4nFH9kU2/gi+9beBvzklb3weqX7WBNR7GBgVZKdbJIc\nq2rmSuKJJn9mCW57L3RkW44cD/r8t/Y24Oa/fo6/bj+Ou/6+h5ElimEMrEqmZklXEjd0OTQYCSnN\nN5PdEDSy61ddHjCym/b54uoeiOrGz2oZWaIYxsCqJNBK4m4XVxJPVHkzpocV2U37GnDTi6fi6sfI\nEsUuBlY69O+2AAAUjElEQVQlp5dJVxLDoEdXr1P9wZAqRous/3Txpn2NAePqx8gSxSYGViV56UkB\nVxJ/XN2s0YhIDaEi236iHuuu+ilufOGzoHH12/hZLX709z3wMLJEMYOBVZE5wN/2rmNcSTzR5c2Y\njts/kEa2qaQCH53+TXjG2MyXB2ayjCxRbGBgVZQTYCXxoeZuDUZCasstHx7ZppIK7P76f0DU68N6\nnZc/q8WPXmZkiWIBA6ui6TkWybFGO1cSxwt/ZO2LV0YUV7+/72JkiWIBA6uiiqIMybEeN1cSx5NK\njwXbzr4s4rj6MbJE0Y+BVdGKshzpQYMe7d2cxcaDd/Y34sYXdo35PdfR/H1XLX74ciUjSxSlGFgV\nZVkTIbrdw44JgoCPariSeKJ7Z38jbnhh16irhcP1yq46RpYoSjGwKkvSSTcl/vwoVxJPZO/sb8SN\nL8ofV79XdtXhhxsZWaJow8CqzGZNkBzjSuKJyx9Xl1znhYN45XNGlijaMLAqm54tXUncxPdgJ6y3\n9zcpHlc/RpYoujCwKltQLF1J3MeFxBPWry+eg4sq8lX7eowsUfRgYFW2rCQHojj8h59g0KO5s0+j\nEZGSDHodHrq0Al+fp25k72RkiTTHwKos3ZIAjNiTGAA+4p7EE5ZBr8ODl6gb2VcZWSLNMbAaSDZI\n/9orj7drMBJSCyNLFH8YWA3kBVpJ3MKVxBOdVpG946XdjCyRBhhYDUzPsUqOtfTwvrDxwPee7DxV\nI/va7npGlkgDDKwGFhanS45xJXH80OsETSJ7OyNLpCoGVgNLA6wk1hn0qDvZo9GISG3+yH5Dxcj+\ng5ElUhUDq4GUJFPglcRVXEkcT/Q6AQ9qFFm3h6dMiJTGwGrEYpT+1e+p5UrieKNVZO/YWMnIEimM\ngdVIfkqi5NiRVp4ijkf+yH5zfoFqX9M3k2VkiZTEwGqkzCZdSdza49JgJBQN9DoBv7mkQtXIvl7J\nyBIpyaD1AOLVwimZeLOmbdix/oG1J6IooqnLgeom+5Bf3Vg904YbV03XYLSkBn9kBfi2O1TD65X1\nAICHLq2AQc9/bxPJiYHVyJLpWfBuOghRBJweL1xuL5xuL9Y8ugXHTvaiq98teU5OgA0qaGLR6wT8\n7yUVANSNrAhgPSNLJCsGViXtPU5UNdlRMzAbrWqyo7a1FyOvmNjb1xX0NWp439i4oEVk3xiYyTKy\nRPJhYBV0pKUb97y2D9VN3WiV4Z6vR9t60O/yINGol2F0FM0GIysAr+xiZIliEf9fpCBLggEfH26T\nJa4AIIrAIc5i44ZeJ+B/v12Bby1Qb+HTG5X1WMeFT0SyYGAVlG1NQKrZKOtr1jTbZX09im5aRfa2\nv3EzCqLxYmAVJAgCSm0WWV+zqpEz2Hjjj+zFCwpV+5pv7mlgZInGiYFVWGmA613Ho6aJM9h4pNcJ\neODbc1WP7K2MLFHEGFiFyR3Yap4ijlv+yH57oXqR/ScjSxQxBlZhJTKfIj5xsg+9Tuk1shQf9DoB\nv76YkSWKBQyswgJtiTheNU18HzaeaRbZDYwsUTgYWIVlWhKQmWyS9TWr+T5s3PNH9hI1I7vXF1kX\nI0s0JgysCuQ+TcwdnQjQLrK3MbJEY8LAqkDuhU5VjZzBko+OkSWKWgysCnipDilJq8jeuuFzRpYo\nBAZWBXIHtr6zH/Z+3juWTtEisv/a28jIEoXAwKpA7t2cAL4PS1KMLFF0YWBVkJZkkv1ertV8H5YC\n8Ef20kXqRvaWvzKyRCMxsCqRfUcnXgtLQeh0Au7/lrqRfWsfI0s0EgOrEvkv1eEMloLzR/Y7iyap\n9jUZWaLhGFiV8FIdUptOJ+C+b81RPbI3v8jIEgEMrGrkDmyz3YHOXq4kptC0iOym/YwsEcDAqkbu\nU8QA76xDY+OP7GWLGVkiNRm0HkC8SEk0Ii81EQ2d/bK9ZnWTHYuLM2R7PZq4dDoBv/rmHADAhh0n\nZHvd5AQ95k1Ohy3VjESjDv0uL5o6+/D50XZs2t+Im17chcevWACjnv+Wp/jDwKqo1GaVN7B8H5bC\nIGdk89PNWFmeg5JcK0QRMBlOBdTlTsWqWbmoabRjy8Fm3LmxEo9cNn9cX48oFjGwKiq1WfBhdYts\nr8dLdWgsRFFEU5cDVU12VDfa4fJ4kZFsxMmeyN7DXzQ1A+fNzYdBJ0CnEySfNw7EtjwvBSU2K3It\n8t5NiihWMLAqKpF7T2K+B0sjtPc4fSFtsqOq8dTvXf3uiF6v/o83IOPc7yOxaC6AU3E9XPkpnrr3\nVqz/5/agz9UNBLjD6cHBZjvKc+S/NzJRNGNgVST3SuLWbifauh3ItMi7SxRFvx6HGzXN3ahutA8G\n9WCjHS12h6xfJ////u7Un9PNOG9u/rDTwaFsfukZbH1zI2oPVWHpeRfh1Q0vIEvmeyMTRTMGVkUl\nOQqsJG7qxjIGdsJyuD040tIzfEbaZMeJk32qj2VleQ4MAU4Jj+Rxu6E3GJCWZcOa627Bvm0fwtnf\nj70NXVg1PUuFkRJFBwZWRckJBhSmm1HbLt8Px5pmO5ZNy5Tt9Sh6PLy5Go+9dwger6jZGGqfuA6Z\nF9yCjKmzseWp/8bjW95FWlYOVqy5dNjj7rhoOc66+Cp8suk1NB47gif/30EsOusCAMDRL/bgZH8D\n6jr70O/yINGo1+JbIVIdA6uyUptV1sBW896wE1ZmsknTuA6l2/13tNQfxwOvboWjrxcP3XqN5DHb\n3n4d69Y/A2taBvSGwD9aDrX1YHZuitLDJYoKvDhNZbJv+t/IlcQTldz/rYxH7Wfv4aLrboYlNQ2Z\nuflY/Z21ksesvmwtMnPzYUpMDPgaHhFo5+5jFEcYWJXJfW/Y6mY7RDE6Zjkkr2gKbE97CzJteYMf\nZ+ZJ79STMeTzwTi5sxPFEQZWZXL/0OzodaGlW96VoxQd0pPlv49wpJLTs9DW1DD4cVtjneQxAkZf\nAGXijk4UR/hfu8qmZVsgjP5zKCw8TTxxleVGxyy2YMFZePPpx9HT1YGTTQ3Y/NIzoz7H43bD6eiH\n1+OB1+uBx9kPq0nm//iJohgDqzKzSY/JGUmyviYXOk1cZVFymlicfzEy8gpx59dX4Dc3X4nlX/3W\nqM95/c+P4nsrSvHPZ3+HT956Ff9xeilefvJhFUZLFB0EkW/gqe67f9mJdw80yfZ6ly+ZhPu+NVe2\n1yPt9Ta34MTWj7Fhxwk8LU7RejgAgO8sm4zyvJSA2yOORVGamdfBUlzhZToaKLVZZA0s9ySOXQ67\nHXUfb0Pd9s/QsOcLNNUcQ8uJZtg7fZdytecWAVf9SONR+mw52IzpNitMEQRWrxMwJ4+X51B8YWA1\nIP+lOr6VxILcb+6SbNwOBxp37kLdth2or9yPpqojaD7WhI42O0KdQ7K2Nao3yFHUt/fh7T31YW2X\nCPjiuqgwldskUtxhYDUgd2DtDjcau/qRl2qW9XUpfF6vFy179qLuk+2o/3wvGg8eRvOX9Whr7oTX\nE/67MQaXE8kdLehJy1ZgtOHbeeQkAIS8m85Q/rhyo3+KRwysBqZmJ0OvE2Tdpae6qZuBVZHX60XX\nl0dx4qNPUP9ZJRoP1KDpSB1aG07C5fTI+rWsrQ1RE1jAF9n69j6sLMtBSZ4VEE/dog4A9APNLUg1\nY05eCmeuFLcYWA0kGPQozkzC4ZYe2V6zutGOM0uj54fwRNLT2IQTWz9G3c7P0bivCk2HT6C1rhV9\nCu5KJAhAWqYF2UW5sNsSET0nin3q2/vwt23HkGTSY97kdNjSzEgzGzElKxnzitIwPTOZew5T3GNg\nNVJqs8obWF6qM26Orq6BBUe70LDnwMCCoxbYu5S9c401xYzsSdmwlUxG3tyZKFiyAAXLlyIhxbco\n6B+767B5w25FxxCOjGQTymxWlOVaUWqzoizXghKbFSmJRq2HRhRVGFiNlNiseGuffPOS6mbtVhL3\nuzw41NwNe787Ju7s4+7vQ8P2z1D76U40VO5HU9WXaD7ehM6T3SEXHI2XOcmI7IIs2KYXIXd2GQoW\nz0Ph8uVIzrWFfJ5Wm00km/QozbWizOYPqe9XFm+PSDQmDKxG5N6TuKbJDq9XjPgaxbFwebw42trj\nu8H34I2+u3G0rQeiCEzLTsa/7/iKYl8/XB63G6179qH2k09Rv3sfGg8eRsvRhogXHI2V0aRHVl4G\nbFMLkDuzBPkLKzDp9GVImVIMnS78vV2mZllg0AlwK3RnHZNeh+k5lmEz0lKbFQVpZq5MJxoHBlYj\ncu/Q0+v0oK6jD5Nk2CXK6xVR19GHqoGI+m/0fbilG64QYTra1qvJ/T69Xi86Dh9B7Ucfo/6zPWj8\n4hCaj9ShtaEdLpe8C46G0ukFZNnSkF2cj9wZ05A/fw4Kl52GrDmzIgppMCaDDlOyklEzzrMUOgEo\nzkoeNiMttVlRnJkEA/cIJpIdA6uR4qxkGPVCyGCFq6bZHlZgRVFEi90xLKJVTd2oabKjN4KVsB6v\niCMtPZiZr9yGAva6etR9/Anqdu5Gw74qNB8+gZa6NvT3Kb3gyIqcyTbYyqYiv2IWCpYuRu6iBTAk\nqHO6tCzXGlZgC9LMkhnptGwLFx4RqYiB1YhR75uVyLkLU3VTN84qD/x+XmevyxfSYad37eiQeSVs\ndZNdlsD2d3Sg7qNPULdjFxr2HhxccNRt75dhlMFZU83IKcqBraQYeXNnoGDJQuQvOw0JVm2v4yyz\nWfEmGiTHsywmlI6YkZbaLLBywRGR5hhYDZXarPIGttGOXqcbh5q7h81IqxvtaOxSNkx+VWGuZnb3\n96H+052oG1hw1Fh9FC3HG9HRJt8K60CSkk3IGrrgaNF8TFqxHEk50Xmp0+zCVCwoShsyK/X9zgVH\nRNGLgdWQb0cn6awkUm/uqceru+sUXQk7murGwIH1uN1oqdyL2o+3DSw4OoKWow042dIFr0KLdwDA\nlGBAVn4GbFMLkTurBPkLKlC4fCnSpkbHBvpjtaosB6vKcrQeBhGFgYHVkNwriZ0Krowdq6omO9oO\nVvtCumsPGr+o8S04amyH2+VV7Ovq9Tpk5qYipzgfuTOm+xYcLT8NmbNmyrrgiIhorBhYDZVEyb0+\n5VTb3oefzr8IRpdDkdcXBCA9KwU5k3NhK5+C/HmzUbh0MWwLF0Bv5PuORBQ9GFgNTc5Igsmgg9Md\nemaXnDCwHV2qGYlGHfpdXjR19uHzo+0RrfZVmj0zFxmNx8b9OilpScielANbaTHyK2Ygf8lCFC5b\nCmNysgyjJCJSFgOrIYNeh2nZFnzR0BXw8/npZqwsz0FJrhWiiGG3CHO5U7FqVi5qGu3YcrAZ9e3K\nbucXjq6s/LACm2RJQHahb8FR3uxy5C+ej8Lly5CUzZtzE1HsYmA1VmoLHNhFUzNC3hLMf/eS8rwU\nTLdZ8fae+sFbiWmtKysv4HFTggHZ+RnImTYJeTNLkL9wHgpPPw2pxcXqDpCISAUMrMYC3RvWH9ex\n3NRapxNg0gk4b24+AERFZO3Z+bAVZiBnysCCowUVKFx+GjLKy7jgiIjiBgOrMX9ga5+4DpkX3IJp\n85eNOa5DmQw6nDc3H/XtfZqfLvbOmosf//UOTcdARKQ1Tic0NvJSnZXlOTCMOCXscbvH9FoGnYCV\nZTkQvdoufGrtdqKtW5lVxEREsYKB1dik9CS0//NBeLpa0PL3n+ORy0/Dpud/j2sXF+HDf2zA7Rcu\nxa9vuAwA8PmH7+DuS8/GD1bNxn3XX4r6L2sGX+eOi5bjreeewAt3XoITD12seWTl3KGKiCgWMbAa\n0+kEnPG9n0Ofko1Vt/4Gj793AIvPuRAAULVrG+7b+B7ufPR5NB47gifuuRlX3PFTPPbu56g4fRUe\nvv06uF3Owdfa9vbruOXBP+Pbj22GoNN2U3feAJ6I4h0DGwVKBk4TpyUnDK4OBoBvfHcdEsxJMCUm\n4tN330DFirMw+7QzYDAYcf5V18Pp6EfNns8GH7/6srWwFRSiICdd9e9hpHD3JCYimmgY2CjgX+hk\nMgx/7zUjN3/wzx2tTcjMLRz8WKfTIcOWj/bmxlOPt/kujzEbtf+fNdiexERE8UL7n8SEb8wrQG5q\nIhYVZQw7LuBUcNOybGhrrB38WBRFnGyqR3pOruTxfQru+TtWVU12iFredYCISGMMbBTITU1EYX4e\nupproZfuKQEAWHLOhajc+h4ObN8Kt9uFTc8/BaPRhJK5C4c9zuX2oqlDm8t0Us1GLJmSgauXTsaP\nzi+HW8G75BARRTteBxslfvKTn+Cmm2/GyZ/fizXX3Sz5fF7xNFz/80fw/G/uRXtzE4pKZ+K2h/4M\ng9E0/IECsPtYu6JjNRv1KM21osxmGbw3aZnNimxrAgQhyL8QiIjijCDyPF5Uef9QC453RHZzdK9X\nxMH6Lvxt2/g32gcAo17AtGzLsBt8l9msKEw3B9y+kYiITuEMNsrMyUtBXZcDnghOr7q9IrZUNYf9\nPEHw3dnHPxMtHfi9OCsZRj3fRSAiigRnsFHoYLMdO2s7w4qs0+0d04b/eamJkhnp9BwLzCZtr5sl\nIppoOIONQuU5vst2xhJZr1eE2ytK4pqeZJTMSEtsVqSaeVNyIiI1cAYbxVp7nNjb0IW6Tt+qYM+Q\n/6Vcbi8gAEea7Kg/2QebJWEwpGW5VmRZTFxwRESkIQY2BvS7PDjU1oP2XhecHi8aO/uRZNRhbn4q\npmQmc8EREVEUYmCJiIgUwCWiRERECmBgiYiIFMDAEhERKYCBJSIiUgADS0REpAAGloiISAEMLBER\nkQIYWCIiIgUwsERERApgYImIiBTAwBIRESmAgSUiIlIAA0tERKQABpaIiEgBDCwREZECGFgiIiIF\nMLBEREQKYGCJiIgUwMASEREpgIElIiJSAANLRESkAAaWiIhIAQwsERGRAhhYIiIiBTCwRERECmBg\niYiIFMDAEhERKYCBJSIiUgADS0REpAAGloiISAEMLBERkQIYWCIiIgUwsERERApgYImIiBTAwBIR\nESmAgSUiIlIAA0tERKQABpaIiEgBDCwREZEC/j+aIcTAVtX7YgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1170fa3d0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAdgAAAFPCAYAAADuut9iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XecXXWd//H3uWV6n8n0TEIKaYSaQKqAEgUlFIHQUyyg\nlGXVdQUerrrqouvuY9WfAiJqSEKJgGIAUYqgppKEFiCFhDDJTKZPptdbzu+PTCZzuZNkyj333PJ6\nPh7zgPnMud/zmUTu23Pu+X6/hmmapgAAQEg57G4AAIBYRMACAGABAhYAAAsQsAAAWICABQDAAgQs\nAAAWIGCBCHLw4EGlpaXJ5/PZ3QqAUSJgAZuNHz9er7zyiiSprKxM7e3tcjqdtvXzve99T263W2lp\naf1f+/fvt60fIFoRsACCXHvttWpvb+//mjBhgt0tAVGHgAVsdPPNN+vgwYNavHix0tLS9JOf/ESG\nYcjr9UqSLrjgAn3729/WvHnzlJaWpsWLF6uxsVE33nijMjIyNHv2bJWXl/ePt3v3bi1atEg5OTma\nMmWKnnzySZt+MwAELGCjNWvWqKysTM8995za29u1ZMmSoGPWrl2rNWvW6NChQ/rwww81d+5crVix\nQocPH9a0adP0n//5n5Kkjo4OLVq0SDfccIPq6uq0du1a3Xbbbdq5c6ck6cc//rGysrKO+zXQc889\np5ycHM2YMUMPPvig9X8QQAwiYIEIt2LFCk2cOFGZmZm65JJLNHHiRF100UVyuVy65ppr9NZbb0mS\nnn/+eY0fP14rVqyQy+XSWWedpauuukpPPfWUJOnuu+9Wc3Pzcb+OWrJkiXbt2qX6+no9/PDD+v73\nv68nnnjClt8diGYELBDhCgoK+v89OTk56Pv29nZJ0oEDB/T6668HXJU+9thjqqmpGdb5pk+fruLi\nYjmdTs2bN0933XWXnn766dD8MkAccdndABDvDMMIyThjx47V+eefr5dffnnQn99333267777jvv6\no0E9WH9sugUMH1ewgM0KCgpCMg3m0ksv1QcffKA1a9bI4/HI4/Fo27Zt2rVrlyTp3nvvDXgy+ONf\nR61bt05NTU0yTVNbt27Vz3/+c11++eWj7g+INwQsYLN77rlHP/zhD5WVlTWqW7Hp6el66aWXtHbt\nWhUXF6uwsFDf+ta31NPTM6xx1q5dq0mTJik9PV1Lly7V3XffrWXLlo24LyBeGWy4DgBA6HEFCwCA\nBQhYAAAsQMACAGABAhYAAAsQsAAAWICABQDAAgQsAAAWIGABALAAAQsAgAUIWAAALEDAAgBgAQIW\nAAALELAAAFiAgAUAwAIELAAAFiBgAQCwAAELAIAFCFgAACxAwAIAYAECFgAACxCwAABYwGV3AwAA\nDNTl8WlfQ4eauzzq9fmV4HQoK9mtyXmpSnI77W5vyAzTNE27mwAAoKGjR+9Wt6qypVuGJN+AdHIa\nR/5ZkpmkmUUZyktNtKXH4SBgAQC2213Xpu2VLfL5Tx5JToehWaWZmpqfHobORo7PYAEAthpOuEqS\nz29qe2WLdte1WdzZ6BCwAICwGzduvF555RU1dPQMK1yPOhqyDR29FnU4egQsACDsGtp79L1n39NL\nu+uCwtXn9Q5pDJ/f1LvVrfIO8fhwI2ABAGG1+Kpr1Xm4Vpse/Ja+sHCqXlj9oJbPLtM/1q3V1y+d\no/++7TpJ0lv/eEn3LvmUvnrhafrRrUtU9dHe/jG+cdk8/XnVA1p2yUKlpqZGZMgSsACAsJp87T1y\nZozRhXf9r3756k7NvuhSSdKeN7foR0+9qn/7f4+q5sB+PfjtO3XDN76rX7z8ls6Yf6F+9vUvyOs5\ndkt4y4vP6hs/e0Qbdx+UyxV5s04JWABA2NS39ej5d6olSVmpiXK7jsXQFV/+mhKTU5SQlKTXX35O\nZyz4pE477xNyudy6+KZb1dvTrb073ug/ftF1K5RVUKwuM/LCVSJgAQBh9NjrB9Tr80uSEo5Obu2T\nU1jc/+/NDbXKLSzt/97hcCinoFhNdTXHji8okqT+8SINAQsACIser0+Pbjl45BvDUK8v8OEmQ8cC\nNyuvQI01lf3fm6apw7VVys4vDDo+wRmZURaZXQEAYs6fd1Srob1HkuRMyVJl+UfyeAe/+jz3okv1\nzoZXtXPrBnm9Hv310V/L7U7Q5NPPCTjOaUjZKW7Lex+JyLxxDQCIKaZpauXG8v7vM+deozf/9JD+\n5Y/367Iv/EvQ8UXjJ+rW7/9cj/7vd9RUV6uyU6frX//vd3K5EwKO85nSpNxUq9sfEZZKBABYbnv5\nYV39q81B9WvnjtPUogw5HMYgrzoxv99UV49Xty2cEIoWQ45bxAAAyw28eh1o/e46eYe5itNRXr+p\nBRNyR9GVtQhYAIClqpq79Nf3awb/WVOXXtxRpd7jfBZ7PL1ev8pr23R6SWYoWrQEAQsAsNTqzQdO\nuNbw9v2H+0PWf5KrWb/fVK/Xrxd3VOni6QWhbjWkeMgJAGCZrl6fnth68KTHbd9/WFVNXVo4JV+T\ni9IlUwGLUHi8fsmQ9la3af2eOqW6nVowKc/K1keNgAUAWOaZtw6ppcszpGOrmrr0+y0HlJLg1Jnj\nslWQlaxkt0NdHr9qm7v09oEmdfb6JEn/deVpMozhPxgVTgQsAMASpmnqkU0fDft1nb0+bdrbcNyf\nZya79fmzSo/780jBZ7AAAEts3NeoD2rbQz7udeeOVXKCM+TjhhoBCwCwxMqNw796PRmnw9DSueND\nPq4VCFgAQMiVN3To1T11IR/3MzMKVJKVHPJxrUDAAgBC7pFN5bJincAV808J/aAWIWABACHV1u3R\n029UnvzAYTqtJEOzxmWHfFyrELAAgJB6anul2nu8IR93xbxTIn5qzkAELAAgZHx+U6s2l4d83Ly0\nRF16RlHIx7USAQsACJnXdtfpQGNnyMe98bwyJboif2rOQAQsACBkVo5gYYmTcTsN3TinLOTjWo2A\nBQCExJ6aNm3c1xjycRefXqz89KSQj2s1AhYAEBIjWRZxKKJpas5ABCwAYNSaOnr1xzcPhXzcWeOy\nNbM0cvd8PRECFgAwak9sO6ieYW6aPhTRevUqEbAAgFHy+Pxas/lAyMctzkzSZ2ZE9qbqJ0LAAgBG\n5cX3a1Td0h3ycW+eO14uZ/TGVPR2DgCICCs3lod8zCS3Q9efOzbk44YTAQsAGLEdlc1640BTyMe9\n8qxSZaUkhHzccCJgAQAjZsXVqyStmD/eknHDiYAFAIxIXWu3nt9RFfJxF0zK06kF6SEfN9wIWADA\niDz6+kF5fKHf9DUWrl4lAhYAMAI9Xp8efz30U3PG56bowin5IR/XDgQsAGDYnnunWg3tvSEfd9m8\n8XI4omfP1xMhYAEAw2KaplZuDP26w2mJLl19TmnIx7ULAQsAGJZt5U16v6o15ONeM6tU6UnukI9r\nFwIWADAsVly9Goa0fN74kI9rJwIWADBklU2devH9mpCP+6mp+RqXmxryce1EwAIAhmzN5gPyh35m\nTlTvmnM8BCwAYEg6e716YuvBkI87pSBd8ybmhnxcuxGwAIAh+eObh9Ta7Q35uMvnj5dhxMbUnIEI\nWADASZmmqUc2lYd83KwUt644syTk40YCAhYAcFLr9zZoX117yMe9/twyJSc4Qz5uJCBgAQAnVdnU\npZQQB6HTYejmOeNCOmYkMUzTtOB5MABArGnt9ujJbRVatblcFYe7Rj3e504v0v03nD36xiIUAQsA\nGBaf39TfdtVq5cZybd7fOOJx/vDVuTpnXE4IO4ssBCwAYMR2VrXoG998SHuKTpXfNfRlDk8vzdS6\n2+fH5NPDR7nsbgAAEL1cO3doxpO/0qTkNO0/fZ4+PGOhutOzTvq6FTE6NWcgrmABACP228u/qF0v\nvNb/vd/hkGfx1aq4cLHermge9DVj0hO18VufVIIrtp+z5QoWADAi9Xs/CghXSXL4/brlxgs088r5\neutgk1ZuLNcL71bLO2B9xZvOGxfz4SoRsACAEdp4/+qgWva4Es24bJEk6ayybJ1Vlq17PztNj245\noMe3HlR7t1c3nFcW7lZtwS1iAMCwdbW06ofj56unvSOgful/36MLvv7lQV/T7fHpnYpmnTch9tYd\nHkzsX6MDAEJu2yNPB4WrOyVZ565YctzXJLmdcROuEgELABgmv8+njQ8E3x6edfPnlZKdaUNHkYmA\nBQAMy64XXlPj/uBt6xbesTz8zUQwAhYAMCzrf7EyqDbl059Q/tSJNnQTuQhYAMCQVb+7W/te2xxU\nX3Dn8vA3E+EIWADAkG345aqg2phTT9GUT3/Chm4iGwELABiSjobDeuPxPwXVF9y+TA4HcfJx/IkA\nAIZky2/XytvdE1BLykzXrKVX2dRRZCNgAQAn5fN4tOnBR4Pq565YosS0VBs6inwELADgpN595kW1\nHKoJqBkOh+bfttSmjiIfAQsAOKn1v3gkqDZj8UXKPWVs+JuJEgQsAOCEDm57Rwe2vBlUZ2rOiRGw\nAIAT2jDI1WvRzKma+Inzwt9MFCFgAQDH1Vpdp3eefiGovvDO5TIMw4aOogcBCwA4rk0PPSafxxNQ\nS83L0VnXX25TR9GDgAUADMrT3aPNv348qD7ny9fLnZRoQ0fRhYAFAAzq7d8/p476xoCaw+XSvK/c\nZFNH0YWABQAEMU1z0Kk5Z1x9iTKLC8LfUBQiYAEAQfZv2Kaqd3YG1RfcscKGbqITAQsACLJhkD1f\ny849U+POO9OGbqITAQsACHC4vFLvrXs5qL6QhSWGhYAFAATY+OAamX5/QC2juECnX3WJTR1FJwIW\nANCvp6NTW3/3+6D6vK/cJKfbbUNH0YuABQD0e2PNH9XV3BpQcyUmaM6XrrOpo+hFwAIAJEl+v18b\n7l8VVD/7+suVNibXho6iGwELAJAk7X1lg+p2fxhUZ9eckSFgAQCSpPWDTM2ZeP4cFZ8+zYZuoh8B\nCwBQ3Z792v3XfwTVmZozcgQsAGDQz15zThmr6Zd+yoZuYgMBCwBxrqu5VdtX/yGoPv+rN8vhdNrQ\nUWwgYAEgzm1d+aR6OzoDagmpKTp3xRKbOooNBCwAxDG/z6cND6wOqs9aepWSszJs6Ch2ELAAEMd2\nPv83NZVXBtUX3L7Mhm5iCwELAHFssD1fp158vvKnTAh/MzGGgAWAOFW1Y5c+/MeWoPrCO9nzNRQI\nWACIUxsGuXrNnzpRpy5aGP5mYhABCwBxqL2+UW8+sS6ovuD2ZTIMw4aOYg8BCwBxaMtv1srb0xtQ\nS87K0Dk3f96mjmIPAQsAccbn8WjTrx4Nqp/7hWuVmJpiQ0exiYAFgDiz4w9/UWtVbUDNcDg0/7al\nNnUUmwhYAIgzg03NOe3yRcoZVxL+ZmIYAQsAceTA62/r4Na3g+oLmJoTcgQsAMSRDb8M3vO1+Izp\nmrBgtg3dxDYCFgDiRMuhGr3z9F+C6gvvXM7UHAsQsAAQJzY99Jj8Xm9ALXVMrs68drFNHcU2AhYA\n4oCnu0dbHn4iqD73lhvkTkq0oaPYR8ACQBx464l16mg4HFBzut2ad+uNNnUU+whYAIhxpmkOOjXn\njKs/q4yi/PA3FCcIWACIcR/+83VVv7s7qL7gzuXhbyaOELAAEOMG2zVn3JyzVTb7jPA3E0cIWACI\nYY0fVej9Z18Oqi/k6tVyBCwAxLCND6yWaZoBtcySQs288jM2dRQ/CFgAiFE97R3auvLJoPq8r94k\np9ttQ0fxhYAFgBi1ffUf1N3SFlBzJSVqzpeut6mj+ELAAkAM8vv92nD/qqD6OTdcodTcbBs6ij8E\nLADEoD0v/VP1H3wUVF9wxzIbuolPBCwAxKDBpuZMunCuimZODX8zcYqABYAYU7f7Q+156Z9B9YXs\n+RpWBCwAxJj1v3wkqJY7oUzTPnth+JuJYwQsAMSQzqYWbV/zx6D6/NuWyuF02tBR/CJgASCGbF35\npDydXQG1xLRUzV5+tU0dxS8CFgBihM/r1cYHVgfVZy+7WsmZGTZ0FN8IWACIETufe0VNBw4F1AzD\n0Pzbl9rUUXwjYAEgRgy25+vUSy7QmMmnhL8ZELAAEAsOvb1T+9dvDaqza459CFgAiAHrf7EyqFYw\nfbImf2qBDd1AImABIOq11TXorbXPBdUX3L5MhmHY0BEkAhYAot6Wh5+Qr7c3oJacnalzbrrSpo4g\nEbAAENW8vb3a9KtHg+rnffFaJaQk29ARjiJgASCK7Xj6BbXV1AfUHE6n5n/1Zps6wlEELABEKdM0\nB52ac9oVn1Z2WUn4G0IAAhYAotSBLW+pYvuOoPrCO5aHvxkEIWABIEptGGTXnJKzTtP4+bPC3wyC\nELAAEIWaK6u14w9/CaovvHM5U3MiBAELAFFo068eld/nC6ilF+TpzCWfs6kjfBwBCwBRxtPVrS2/\nWRtUn3PLDXIlJtrQEQZDwAJAlHnz8XXqbGwKqDndbs295UabOsJgCFgAiCJHpuYErzt85pJLlVE4\nxoaOcDwELABEkX1/36ya9z8IqrNrTuQhYAEgimwYZGGJ8fPOUek5M8PfDE6IgAWAKNHw4QHtfP5v\nQfWFd66woRucDAELAFFi4wOrZZpmQC1rbJFOu+LTNnWEEyFgASAKdLe1a9sjTwXV5331ZjldLhs6\nwskQsAAQBbav+oO6W9sDau7kJM354nU2dYSTIWABIML5/X5teGBVUP2cG69USk6WDR1hKAhYAIhw\nu//6dzXsLQ+qL7hjWfibwZARsAAQ4QabmjP5U/NVOOPU8DeDISNgASCC1ezcqw9e2RBUZ2GJyEfA\nAkAEG2zP17xJ4zT1kgvD3wyGhYAFgAjVebhZbzz6TFB9/m3L5HDw9h3p+BsCgAj1+u9+L09Xd0At\nMT1Ns5ddZVNHGA4CFgAikM/r1cYHVgfVz11+tZIy0m3oCMNFwAJABHpv3UtqrqgOqBmGofm3MzUn\nWhCwABCBBpuaM+1zn1TexHHhbwYjQsACQISpfPM9fbRxe1CdqTnRhYAFgAizfpCr18IZp2rShfPC\n3wxGjIAFgAjSVluvt598Pqi+4I7lMgzDho4wUgQsAESQzb9+XL7e3oBaSk6Wzr7hcps6wkgRsAAQ\nIbw9Pdr80GNB9Tlfuk4JKck2dITRIGABIEK889QLaqttCKg5nE7N+8pNNnWE0SBgASACmKap9b9Y\nGVSf+fmLlTW22IaOMFoELABEgPJNb6jyzfeC6gvvWB7+ZhASBCwARID1g+yaU3rOTI2be3b4m0FI\nELAAYLPmiiq998yLQfWFd65gak4UI2ABwGYbH1wjv88XUEsvHKMzrvmsTR0hFAhYALBRb2eXtvxm\nbVB97q03ypWQYENHCBUCFgBs9OZjf1JXU0tAzZmQoLlfvt6mjhAqBCwA2MQ0Ta2/f1VQ/axrFyu9\nYIwNHSGUCFgAsMneVzeq9v0PgursmhMbCFgAsMlgu+acsmC2Ss6aEf5mEHIELADYoGFfuXa/8FpQ\nnavX2EHAAoANNty/WqZpBtSyyoo147JFNnWEUCNgASDMulvbtG3V00H1+bctldPlsqEjWIGABYAw\n2/bI0+ppaw+ouVOSdd4XrrWpI1iBgAWAMPL7fNrwwOqg+qybrlRKdqYNHcEqBCwAhNGuv/xdjR8e\nCKovYNecmEPAAkAYbRhkz9dTFy1UwbRJNnQDKxGwABAm1e/t0d5XNwXVmZoTmwhYAAiTDb8MXhZx\nzKmnaMpnzrehG1iNgAWAMOhobNIbjz0TVJ9/2zI5HLwVxyL+VgEgDF7/7Vp5u3sCakkZaZq19PM2\ndQSrEbAAYDGfx6ONDz4aVD93xRIlpafZ0BHCgYAFAIu9+6eX1FJZHVAzDEPzb1tqU0cIBwIWACy2\nYZBdc6Yvvki5E8rC3wzChoAFAAtVbN+h8s1vBNWZmhP7CFgACJGmjl5t2d8YUBtsz9eimVM18fw5\nYeoKdmHbBgAYJr/f1IHDndpV3aqdVa1H/lndquqWbqUmOvXbFefK4zfV2dml+ikzlXdjkpr+/Bf5\nmlskSQvuWCbDMGz+LWA1w/z4hoQAgH5dvT7trmnVruo27axu0c6qVu2uaVNnry/guOLsZC2cmq/J\nhelKcDo08I3V390tGYbaNr+utnXP6t9fWiV3clJ4fxGEHQELAJJM01R9W4/er27tvzLdWd2q8oYO\n+U/yLjlrQo4+c3qxXA5DDsfxr0xNn0+Gaeq8CXmamp8e4t8AkYZbxADijtfn1/6Gjv4QPRqojR29\nwx7raLgmuI480vLcyl+q/tBBfeHbPwk61nA6JUnbK4/cKiZkYxtXsABiWmu3R7ur27SzqqUvTNu0\np7ZNvV7/qMcuzk7WivMn9ofrcDgdhi6ekq+81IRR94HIxBUsgJhgmqYqm7oCrkh31bSq4nCXZedc\nODVfrhPcEv44n9crp+vI267Pb+rd6lYtHJ8ll4u34ljEFSyAqNPt8WlfXXv/Ld6jodrW7Q1bD6mJ\nTk1t+LtefeoRdXe0KyuvQEu/9UPteXur6ioO6NYf/Fz1VRX65uXzteLbP9G6h3+mvOJSffl7P+2v\nPfvwzzR18gRtWL8+bH0jfPi/TQAiWmN7T/8TvLuq27SzqlX76tvlO9mTRxabkNiq155ere+uek7Z\nYwpVX1Uh0+/Tnre3Bh27580t+tFTr8owHGo5XN9f+/HTr+rMkqxwt44wIWABRASf31R5Y0fQ3NLa\n1p6Tv9gGYzJS5PX0qmr/XqVn52pM8djjHnvFl7+mxOSUoJo7KUVdJm/DsYq/WQBh19Hj1e6atv4Q\n3VnVqj01bery+E7+4ghRWDZeN3z9u/rTwz/VoXs+0Glzztf1X/uPQY/NKSw+bq3XN/qHrRCZCFgA\nljFNU7WtPQG3d3dWt6q8sUPR/vRHt8evuRdfobkXX6Gu9jY98qN79OQvfqT80nFBxxoKfhDqaC3B\nyYq1sYqABRASHp9fH9b3PXjU9wTvzqpWNXV67G7NEnv37JZR7dO0s2fLnZiohMQk+f3DuwJ3GlJ2\nituiDmE3AhbAiPV6/br3mXe1q7pVe2vb4+p2586DjXpv/UOqKd8np8ulSaefo+X3/lh/f+bxYY0z\nKTfVog5hN6bpABiV2f/1iurbIvNBJKtdO3ecphZlnHB5xBMpy0rWhZPyQtwVIgU3/wGMyvSiDLtb\nsM363XXyjnC6kNNhaGYc/9nFAwIWwKhML47fkKhq6tKLO6qGveyi02FoVmkmyyTGOD6DBTAq0+L8\nKmz7/sOSNKTddKRj4cpC/7GPgAUwKvF8i/io7fsPq6qpSwun5GtyUbpkSu4BGwA4+zK3JDNZM4sy\nuHKNEzzkBGBUfH5TM777V3V74ucJ4hNJSXDqzHHZKshKVrLbocn56Zo9PluTclOV5Hba3R7CiM9g\nAYyKw/Tp1Jwku9uIGJ29Pu2raVNTa7eyElw6qyRTpxVmEK5xiFvEAIbM39Wh3ppKeWoqjn3VV2t8\n9wzt0Cl2txd2ToehSWPSNK0oXdOLMzSt6MhXXlqi3a0hAhCwAIKYfr98zY3y1FSod0CY+loOD3r8\nJEerFON3iNMTXZpWnKHpRX1fxRmalJ/GlSmOi4AF4pzp6ZWn7pA8NZXHwrS2UmZP95DHmGy0WNhh\n+JVmJ2t639Xo9L5QLc1OlmGMbEEJxCcCFogjvvZWeWoOBoSpt6FGo115f6LRGqIOwyvB6dCphWnH\nwrQoQ1OLMpSZzPrAGD0CFohBpt8vb2Ptx8K0Uv52a64009KSNba9VxW9kTv9JCc1of/W7tFAnTAm\nVW52s4FFCFggyvl7uuWprZSnukKe2iOfmXrrqmR6ekN/MsOQK7dA7sKxcheOVULfP53pmZr52Buq\neLcm9Occfos6JS+1/4r0aKDmpydyixdhRcACUcI0TflaDgeFqe9wvSXnMxIS5S4oDQhTV36xHAmD\nPyE7rTBDL4Q5YFMSnJpaeOwJ3ulFGZpSmK6UBN7aYD/+VwhEINPrlae+KihMza5OS87nzMw5FqZF\nY5VQMFbO7DwZjqHfPrV6TeKizKT+ED368NG4nJQR72QDWI2ABWzm62zvmwYzYH5pQ7XkG97m3UPi\ndMo9puhIkBYcCVN3QamcKWmjHjpUaxK7HIYm5af13949Orc0h+UFEWUIWCBMTL9fvqaGgHmlnpoK\n+VqbLDmfkZzS/xlp/1dekQyXNf/ZF2UmKSvFreZOz5Bfk5HkCri9O60oQ5ML0pToYm4poh8BC1jA\n39sjb11VYJjWVsrstWZjcldOvtyFpQFh6szIDutDPYZhaHpRhjZ92Djoz8tyUgJu704rSldJFnNL\nEbsIWGAUTNOUv70lcJGGmgp5G2tHPbd0UC633AWlShgYpgWlciRGxlrA04oy9MaBJk0pTA8I06mF\n6UpPYm4p4gu76QBDZPp88jbWBIWpv6PNkvM50jL7nt49Fqau3IJhPXgUbu09XiW5HHIxtxQgYIHB\n+Ls7+5/g7a3te/io7pDk9Yb+ZA5H/9zSgZ+ZOtPYZxWIZtwiRlzrn1taUyFP9cH+MPU1NVhyPiMx\nqX86TH+Y5hfLcPOELBBrCFjEDdPrkae+ui9MK9Rbe2RqjNlt0dzSrNxjYVp0ZFqMMys3om/xAggd\nAhYxydfRFji3tLZCnvoayW/F3FKX3PnF/Q8cJfTNLXUkp4b+XACiBgGLqGb6/fIergsKU19rsyXn\nc6SkDZgKU3pk+cC8QhlO/lMCEIh3BUQNf2/PkQePBoZp3SFr5pYaRtDc0oTCsXKkZzFvE8CQELCI\nOKZpyt/WrN6ayv7t1jw1FfIerrNkbqnhTuj7rHTA3NL8koiZWwogOhGwsJXp88rbUNMXpgPmlna2\nW3I+R3pW39O7A+aW5uTz4BGAkCNgETb+rs6+XWEGhGldleSzaG5pXlFQmDpT00N/LgAYBAGLkDNN\nU77mBnlqAsPU1zz4GrWjZSQly13QN6+07wle95hiGW6W5gNgHwIWo2J6PEf2La0+KE/t0SUEK2X2\ndFlyPmd2Xt9avGPlLio7stVaVi4PHgGIOAQshszX3hq0Abi3oUby+0N/MpdL7vySAWHaN7c0KSX0\n5wIACxCUXjAAAAAF/UlEQVSwCGL6/fI21h5bi7dvbqm/rcWS8zlS0wdMhSntW9S+UIaTPUEBRC8C\nNs75e7oD5pb21lTIW3dIpqc39CczjP5F7Qcu1OBIy+QWL4CYQ8DGCdM05WttGjAVpm9uaVO9NXNL\nExL71+E9Gqbu/BI5EhJDfi4AiEQEbAwyvV55Gmr6Fmk4Fqb+rg5LzufMyD4WooVlcheWypU9hrml\nAOIaARvl/J0d/bvC9K96VF8l+SxY1N7hlHtM0YAw7ZtbmpIW+nMBQJQjYKOE6ffL19zQPw2mf25p\ny2FLzmckpyihYGxgmI4pkuFibikADAUBG4FMT688dYfUW10x4AGkCmsWtZfkzBlzLEz7psM4M3N4\n8AgARoGAldTl8WlfQ4eauzzq9fmV4HQoK9mtyXmpSnJbO1XE19ZyZE7pgDD1NtRY8uCRXG65C0oC\nwzS/RI6k5NCfCwDinGGaVryTR4eGjh69W92qypZuGZJ8A/4knH0XbyWZSZpZlKG81NE9/Wr6fH1z\nSwPD1N/eOqpxj8eRltG/xdrRh49cOfnMLQWAMInbgN1d16btlS3y+U/+6zsdhmaVZmpq/tAWivd3\nd/UF6JEQ7a2tkKf2kOT1jLbtYIYhV15hYJgWjJUzPTP05wIADFlc3CKeMWOG7r//fl1wwQWSjoXr\ne9s26dffuUs//fPWE77e5ze1vfLIKkYDQ9Y0TflaDgdMhemtqZCvqd6S38NITOqfW5owYG6p4U6w\n5HwAgJGLi4B9//33+/+9oaNnyFeunt4erf7vb2vn1g3qaG1Wfuk4/eCOW3TZpML+K1Ozq9OSnp2Z\nOQOWDzwSps6sPOaWAkCUiIuAHejd6tYhhavP65Xf51NOQZHufuhJ5RaWaMeGv+kr/36HJt9ymcZm\nhWhfUadT7jHFA1Y8GquEglI5UlJDMz4AwBZxEbDjx4/Xb37zG5197hx952u36c1/vKSsvHwtWLwk\n4LhvXDZPn7zqJm3+659Uc2C/Hvrnbl15y9f7f37mJxYpr6RMb9W3jShgHcmpgUsHFpbJnVcowxUX\nfw0AEFfi6p39m/f+h+oqD+gnz2xQT1en/u+upUHHbHnxWX3tp48oPStHzo8FX0tjvWoqPlLWF2+W\nusuPfyLDkCtnjNwfW6jBmZHN3FIAiBNxFbB/efYZXf9vP1BaZpbSMrO06NoVWvfbnwccs+i6Fcot\nLA56rdfr0UP/8S+a/7mrlTv1DOntckmS4U6Qu6DkWJgenVuamBSOXwkAEKHiKmAbamuUW1DU/31u\nUWnQMTkDfn6U3+/Xr7/zr3K5E3TTv/9AptmunGtuObJvaU4+Dx4BAILEVcDm5heosbZaJROnSJIa\naw4FHWMo8BauaZr63Q++qdbDDfr6z1bJ5XIrNadEKRNyw9IzACA6xdWl1yWXXak/r7pfHa3NOlxb\nrVeefOSkr1n143tVVb5P//p/v1NCUpKchpSdwoL3AIATi6uA/Z/7fqC8whL92+UL9L933qh5n/38\nCY9vqK7U3//4mA5+sFN3XXyObv3EVH1p4VRte3FdmDoGAESruFsq8bV99TrY3D3i15dlJevCSXkh\n7AgAEIvi6gpWkmYWZcjpGNlUGafD0MyijBB3BACIRXEXsHmpiZpVmjnskD264H9eKuv+AgBOLu4C\nVjqyYP9wQna4u+kAABB3n8EO1NDRq3erW3WopUvS8faDTe7bD5YrVwDA0MV1wB7V7fFpX2OHmjo9\n6vX5leB0KDvFrUm5qUpys0E5AGD4CFgAACwQl5/BAgBgNQIWAAALELAAAFiAgAUAwAIELAAAFiBg\nAQCwAAELAIAFCFgAACxAwAIAYAECFgAACxCwAABYgIAFAMACBCwAABYgYAEAsAABCwCABQhYAAAs\nQMACAGABAhYAAAsQsAAAWICABQDAAgQsAAAWIGABALAAAQsAgAUIWAAALEDAAgBgAQIWAAALELAA\nAFiAgAUAwAIELAAAFiBgAQCwAAELAIAFCFgAACxAwAIAYAECFgAACxCwAABYgIAFAMACBCwAABYg\nYAEAsMD/B+rVc1uYiq+QAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x117882690>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAdgAAAFPCAYAAADuut9iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAE2FJREFUeJzt3XuQnXWB5vGnL+ncunOBkBshg6AQh1uCUDuwOoJlUGcA\n3Y2iaDG1cXZ2XVx1R7dUGKYkW+gwsiuzOymdcSxGyVimAHUF3GW5uOUiNaIMkMmCgUUmRpIISQhJ\nOuTSl7N/YGJu3enLec/t/XyqupI+ffLm1/1HvvWc0zndVqlUKgEAqqq93gcAgFYksABQAIEFgAII\nLAAUQGABoAACCwAFEFioow0bNqS7uzsDAwP1PgpQZQILNXbqqafmwQcfTJIsXLgwvb296ejoqNt5\nbrnllpx99tnp6enJ6173utxyyy2HfXz9+vW59NJLM2XKlCxatOjg2YHhCSyUXKVSye23357t27fn\nvvvuy8qVK7N69eqDH7/66quzZMmSbNu2LZ///Ofz3ve+N1u2bKnjiaE5CCzU0DXXXJMNGzbkiiuu\nSHd3d774xS+mra0t/f39SZJLLrkkN9xwQy6++OJ0d3fniiuuyLZt2/KhD30o06ZNy4UXXpj169cf\nvN66deuydOnSnHDCCTnzzDNzxx13jPpMn/70p3P++eens7MzZ555Zt797nfnkUceSZI8++yzefzx\nx7NixYpMnjw5y5Yty7nnnptvf/vbVfl6QCsTWKihVatWZeHChbnnnnvS29ubq6666qj7rF69OqtW\nrcrGjRvz85//PBdddFGWL1+el19+OW984xuzYsWKJMnu3buzdOnSfPCDH8xLL72U1atX59prr83T\nTz+dJLn55pszY8aMId+OpVKp5OGHH85ZZ52VJHnqqady2mmnpaen5+B9zjvvvDz11FPV/tJAyxFY\naDDLly/P6aefnunTp+dd73pXTj/99Lz97W9PZ2dn3ve+9+WJJ55Iktx777059dRTs3z58nR2dmbJ\nkiVZtmxZ7rzzziTJZz/72bzyyitDvh3LjTfemMHBwSxfvjxJ0tvbm+nTpx92n2nTpmXXrl0FfgWg\nNXTW+wDA4ebMmXPw95MnTz7q/d7e3iTJL37xizz66KOHrdH+/v5cc801Y/p7V65cmdtvvz0PP/xw\nJk6cmCTp7u7Ozp07D7vfjh07Dlu0wLFZsFBjbW1tVbnOKaeckre+9a2HrdLe3t585StfSZJ84Qtf\nSHd395Bvh7rtttty880356GHHsqCBQsO3n7WWWfl+eefP2yxrlmz5uBDyMDQBBZqbM6cOXn++efH\nfZ3LL788zz77bFatWpW+vr709fXlpz/9aX72s58lSa6//vr09vYO+XbAN7/5zVx//fV54IEHctpp\npx32d5xxxhlZvHhxVqxYkb179+Y73/lO1q5dm2XLlo37/NDqBBZq7LrrrstNN92UGTNm5K677hrz\ndXp6enL//fdn9erVmT9/fubOnZvPfOYz2bdv36iuc8MNN2Tbtm258MILD67bj3zkIwc/vnr16jz2\n2GOZOXNmrrvuutx111056aSTxnxuKIs2P3AdAKrPggWAAggsABRAYAGgAAILAAUQWAAogMACQAEE\nFgAKILAAUACBBYACCCwAFEBgAaAAAgsABRBYACiAwAJAAQQWAAogsABQAIEFgAIILAAUQGABoAAC\nCwAFEFgAKEBnvQ/QCPb0DeS5rbvzyp6+7B8YTFdHe2ZMnpA3zJqaSRM66n08AJpQW6VSqdT7EPWy\ndfe+rN28My/s2Ju2JAOHfCU62l779eTpk3LOvGmZNXViXc4IQHMqbWDXvbQrj72wIwODx//0O9rb\ncsGC6Vk0u6cGJwOgFZTyOdgj43rP367MbTd9esj7DwxW8tgLO7LupV21OiIATa50C3br7n2575kt\nI1quR+pob8s7z5ydWVO7CjgZAK2kdAt27eado4rrQH//b34/WMnazTvTf8htAHAspQrsnr6B/NV/\n/VL+w+9dmI+89Y357LJL8vRPfpTvfvVL+es//USSZMumX+ZfXbgwP/ze6nzy8t/Jn1/7gcNue9+b\nz8sll15a588EgEZXqv+m88CPn8yDd34jn/vGPZl50txs2fTLVAYH8syTPznqvs88/uP82Z0/SFtb\ne3a8vOXgbTff9YMsPnlGrY8OQJMpVWB39w2mb//+bHr+/6Vn5ok5af4pQ973PX/0x5k4ecpRt02Y\nNCV7KqX6sgEwBqV6iHj2Kafmg5/8XP7739yaj1+2JF++/qPZvuVXx7zvCXPnD3nb/oHBQs8JQPMr\nVWC7Otpz0Tvfkz/52nfyX+7++7S1teWOv/yzY963LW1D3tbVUaovGwBjUKpSbN+4PuseeyR9+/dl\nwsSJ6Zo4Ke3to/8SzJjsIWIAhleqwM6d0p47/vLmfGzp4nzinW/Kzu1b896PfmZU1+jrH8zf/I91\n2bpzb0GnBKAVlO6FJv73c1uy4ZWxxXFwsJJnfrE9dz70XGZO7cqNVy/O779pQdrajn44GYByK9WC\nTZJz5k1LR/vYgtg/MJgfrdmcJNm+e38+8bWf5KNf/bE1C8BRSrdgk9G90P8B+/sGcv+jG/L4ui1H\nfcyaBeBIpVuwSbJodk8uWDB9xEu2o70tMyZ05J9+ueOYH7dmAThSKRfsAVt378/azTuzcceeJEP9\nPNjJv/55sF3ZunNvPvetJ3PfExuHvKY1C0BS8sAesLdvIM9t253tr/Zl/8BgujraM3PKhLz+xKmZ\nNKHjsPtWKpV8/x9eyI3fejLbd+8f8prvWDI//+nqJZk1bVLRxwegAQnsGFmzAAxHYMfBmgVgKAJb\nBdYsAEcS2CqxZgE4lMBWmTULQCKwhbBmARDYAlmzAOUlsAWzZgHKSWBrxJoFKBeBrSFrFqA8BLYO\nrFmA1iewdWLNArQ2ga0zaxagNQlsA7BmAVqPwDYQaxagdQhsg7FmAVqDwDYoaxaguQlsA7NmAZqX\nwDYBaxag+Qhsk7BmAZqLwDYZaxagOQhsE7JmARqfwDYxaxagcQlsk7NmARqTwLYIaxagsQhsC7Fm\nARqHwLYgaxag/gS2RVmzAPUlsC3OmgWoD4EtAWsWoPYEtkSsWYDaEdiSsWYBakNgS8qaBSiWwJaY\nNQtQHIHFmgUogMCSxJoFqDaB5TDWLEB1CCxHsWYBxk9gGZI1CzB2AsuwrFmAsRFYRsSaBRgdgWXE\nrFmAkRNYRs2aBTg+gWVMrFmA4Qks42LNAhybwDJu1izA0QSWqrFmAX5DYKkqaxbgNQJLIaxZoOwE\nlsJYs0CZCSyFs2aBMhJYasKaBcpGYKkpaxYoC4Gl5qxZoAwElrqxZoFWJrDUlTULtCqBpSFYs0Cr\nEVgahjULtBKBpeFYs0ArEFgakjULNDuBpaFZs0CzElganjULNCOBpWlYs0AzEViaijULNAuBpSlZ\ns0CjE1ialjULNDKBpelZs0AjElhagjULNBqBpaVYs0CjEFhajjULNAKBpWVZs0A9CSwtzZoF6kVg\nKQVrFqg1gaU0rFmglgSW0rFmgVoQWErJmgWKJrCUmjULFEVgKT1rFiiCwMKvWbNANQksHMKaBapF\nYOEYrFlgvAQWhmDNAuMhsHAc1iwwFgILI2DNAqMlsDAK1iwwUgILo2TNAiMhsDBG1iwwHIGFcbBm\ngaEILFSBNQscSWChSqxZ4FACC1VmzQKJwEIhrFlAYKFA1iyUl8BCwaxZKCeBhRqxZqFcBBZqyJqF\n8hBYqANrFlqfwEKdWLPQ2gQW6syahdYksNAArFloPQILDcSahdYhsNBgrFloDQILDcqaheYmsNDA\nrFloXgILTcCaheYjsNAkrFloLgILTcaaheYgsNCErFlofAILTcyahcYlsNDkrFloTAILLcKahcYi\nsNBCrFloHAILLciahfoTWGhR1izUl8BCi7NmoT4EFkrAmoXaE1goEWsWakdgoWSsWagNgYWSsmah\nWAILJWbNQnEEFrBmoQACCySxZqHaBBY4jDUL1SGwwFGsWRg/gQWGZM3C2AksMCxrFsZGYIERsWZh\ndAQWGDFrFkZOYIFRs2bh+AQWGBNrFoYnsMC4WLNwbAILjJs1C0cTWKBqrFn4DYEFqsqahdcILFAI\na5ayE1igMNYsZSawQOGsWcpIYIGasGYpG4EFasqapSwEFqg5a5YyEFigbqxZWpnAAnVlzdKqBBZo\nCNYsrUZggYZhzdJKBBZoONYsrUBggYZkzdLsBBZoaNYszUpggYZnzdKMBBZoGtYszURggaZizdIs\nBBZoStYsjU5ggaZlzdLIBBZoetYsjUhggZZgzdJoBBZoKdYsjUJggZZjzdIIBBZoWdYs9SSwQEuz\nZqkXgQVKwZql1gQWKI2i1+yBf07FmURggRIqas3evWZT7l2zKTf9i7Mzu8dDzWUnsEApVXvNbtm1\nL5fd+sNsf7UvM6ZMyIorz8qV5823ZktMYIFSq8aarVQq+Xd/93jue+pXh91+2W/PsWZLTGCB0hvv\nmr17zaZ8/FtPHPPPWLPlJbAAvzaWNXvoQ8PDsWbLR2ABDjGaNbviA4vzp3c/fdRDw0OxZstFYAGO\nYSRrdkp3V3Z1to/62tZsOQgswBCGW7OVtmSwZ2LSPrYlas22PoEFOI4j12wlyeCUCUlXx7ivbc22\nLoEFGIFD1+y2/f2pTO2q2rWt2dYksACj8MymHbl85SPpG6z+P53WbGsZ/bPzACVVqVRy60PPFRLX\nJLn/6Rdz2a3/J997cmNsn+ZnwQKM0HAvKFFt1mzzE1iAERjpC0pUk+dmm5vAAhzHUK81XCvWbHPy\nHCzAcdzzj5vrFtfEc7PNyoIFGMbAYCVLv/TDPL91d72PksSabSYCC3AcL+3amz/57v/NA0+/WO+j\nJPHcbLMQWIARqFQq+d6Tm/K5u5/Kjj21+0an4VizjU1gAUbBmmWkBBZglKxZRkJgAcbImmU4Agsw\nDtYsQxFYgCqwZjmSwAJUiTXLoQQWoMqsWRKBBSiENYvAAhTImi0vgQUomDVbTgILUCPWbLkILEAN\nWbPlIbAAdWDNtj6BBagTa7a1CSxAnVmzrUlgARqANdt6BBaggVizrUNgARqMNdsaBBagQVmzzU1g\nARqYNdu8BBagCVizzUdgAZqENdtcBBagyVizzUFgAZqQNdv4BBagiVmzjUtgAZqcNduYBBagRViz\njUVgAVqINds4BBagBVmz9SewAC3Kmq0vgQVocdZsfQgsQAlYs7UnsAAlYs3WjsAClIw1WxsCC1BS\n1myxBBagxKzZ4ggsANZsAQQWgCTWbLUJLACHsWarQ2ABOIo1O34CC8CQ6rFmp07syOLfmpk50ydn\n0oT27O0bzIs79uSJ9dszsbM9P/jUJZk5tatm5xkrgQVgWLVas/NnTs5bFs3OG+b2pFJJujrbD36s\nr38waUv27e/P+89fkFlTJxZ2jmoRWABGpMg1e8FpJ+Qd585PZ3tb2tuHf561o70tFyyYnkWze6p+\njmpqP/5dACCZ3TMpX73mTfmL9y/O9MkTxnydTV+7Nns3/OPB9w/E9edrHs2nrvhnx/3zA4OVPPbC\njqx7adeYz1ALAgvAiLW1teU9S07OA5/83Sz97Tljusb8f/3lTFp47mu/nzk57zh3/mEPBw/nwTu+\nnhv/4Pez/HdOzx/94Yezdff+MZ2hFgQWgFGr1pp9y6LZ6TzOQ8JJMtDfnySZMWtOrvjwx/OWK69K\npZKs3bxzzH930QQWgDEZ65p94Ssfzp71T2Zye38e/uqN+fdvPyfXX/W2/NPTaw6736euvDjf/8aX\nc8PVl+Xf/u6iDPT354K3vStvuuQd6Z4+M0myccee7O0bqOrnVS2d9T4AAM3twJod7Xcatz/57WzZ\ntCFf/O6Psm/Pq/nSJ/7gqPv8+H/dnT++9evpmXFCOjqPnazntu3O2XOnjetzKIIFC8C4jWXNvvAP\nP8iVH/5YuqfPyIlz52fp+5cfdZ+lH1ieE+fOT9ekY7+4xEAl2f5qY7wQxpEEFoCqGc1zs7u3b8mJ\nc+YdfP/EeQuOus8Jh3x8KPsHBkd/0BoQWACqaqRrdurMWdn24uaD72/71cajr5XjfwNUV0djpqwx\nTwVA0zvemj35/Lfl3r9dmd07X8nLL27Og3d8/bjXHOjvz/59ezM4MJDBwYEM7N+bnq7G/AEAAgtA\nYYZbs5Uly3LCvAX5j+9+c/7zxz6Ui3/vXx73enff9t/yb958Rr7/jS/n7//nd/OH//yM3PXXf1HU\n8cfFSyUCUBPHek3j91/0W1k0b9pxXx5xKAtnTM6lr59VzWNWjQULQE0ca80+vO6l9A+Obed1tLfl\nnHmN999zDrBgAai5Q9fsG+b1jOrlEpPmeMF/gQWgbg78hJ4z5vVk3olTMzCCNdsMcU0EFoA6q1Qq\n6R+sZMfe/qzdvDMbd+xJ8tqLSBzQ8eunaE+ePjnnzJuWWX7gOgCMzt6+gTy3bXe2v9qX/QOD6epo\nz8wpE/L6E6dm0oSOeh9vxAQWAArgu4gBoAACCwAFEFgAKIDAAkABBBYACiCwAFAAgQWAAggsABRA\nYAGgAAILAAUQWAAogMACQAEEFgAKILAAUACBBYACCCwAFEBgAaAAAgsABRBYACiAwAJAAQQWAAog\nsABQAIEFgAIILAAUQGABoAACCwAFEFgAKIDAAkABBBYACiCwAFAAgQWAAggsABRAYAGgAAILAAUQ\nWAAogMACQAEEFgAKILAAUID/Dz64byyS3TVHAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x117932e90>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAdgAAAFPCAYAAADuut9iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VPW9//H3ZN83IPtA2EF2SRQRNxRxQ0QkuFewtvfX\ne7toa13qWnfbq/W2tbV1ARGEgKBsboggqCARUAQChBCSsIU9ZM/MOb8/ECoyIZNkzswk83o+Hjxq\nck7mfEwf5OX35Mw5NtM0TQEAAI8K8vUAAAC0RwQWAAALEFgAACxAYAEAsACBBQDAAgQWAAALEFjA\nh0pKShQTEyOn0+nrUQB4GIEFvCwrK0tLliyRJHXu3FmVlZUKDg726Uxr167VhRdeqJiYGKWkpOil\nl146ua24uFiXXHKJoqKi1KdPn5OzAzgzAgsEuAMHDuiKK67Qz3/+cx08eFCFhYW6/PLLT26/6aab\nNGTIEB08eFBPPfWUbrjhBu3fv9+HEwNtA4EFvOi2225TSUmJxowZo5iYGD3//POy2WxyOBySpIsv\nvlgPPfSQhg8frpiYGI0ZM0YHDx7ULbfcori4OOXk5Ki4uPjk6xUUFGjUqFFKSkpS7969lZeX1+yZ\nXnjhBY0ePVq33HKLwsPDFRsbq759+0qStm7dqrVr1+rxxx9XZGSkxo8fr4EDB+qdd97xyPcDaM8I\nLOBF06ZNU+fOnbVgwQJVVlYqNzf3tH1mzpypadOmadeuXdq+fbvOO+88TZo0SYcOHVLfvn31+OOP\nS5Kqqqo0atQo3XzzzSovL9fMmTP1i1/8Qps2bZIkPfvss0pISGj0zwmrVq1SUlKShg8fruTkZI0Z\nM0YlJSWSpI0bN6pbt26KjY09uf+gQYO0ceNGK79NQLtAYAE/M2nSJHXv3l3x8fG68sor1b17d112\n2WUKCQnRhAkTtG7dOknSwoULlZWVpUmTJikkJERDhgzR+PHjNXv2bEnS/fffryNHjjT654SysjJN\nnTpVL730kkpKStS1a1fddNNNkqTKykrFx8efMl9cXJyOHTvmpe8G0HaF+HoAAKdKSUk5+c+RkZGn\nfVxZWSlJ2rlzp1avXn3KatThcOi2225r1vEiIyM1btw45eTkSJIeffRRdezYUUePHlVMTIwqKipO\n2f/o0aOnrGgBuMYKFvAym83mkdex2+266KKLTlmVVlZW6h//+Ick6emnn1ZMTEyjf04YOHDgKTP9\n8J/79eunoqKiU1as33zzjfr16+eRfwegPSOwgJelpKSoqKio1a9zzTXXaOvWrZo2bZoaGhrU0NCg\nNWvWaPPmzZKkBx98UJWVlY3+OWHSpEmaN2+e1q9fr4aGBj3xxBMaMWKE4uPj1atXLw0ePFiPP/64\namtrNXfuXG3YsEHjx49v9fxAe0dgAS974IEH9OSTTyohIUFz5sxp8evExsbqo48+0syZM5Wenq7U\n1FTdd999qqura9brjBw5Uk8//bSuvvpqJScnq7CwUDNmzDi5febMmcrPz1diYqIeeOABzZkzR506\ndWrx3ECgsPHAdQAAPI8VLAAAFiCwAABYgMACAGABAgsAgAUILAAAFiCwAABYgMACAGABAgsAgAUI\nLAAAFiCwAABYgMACAGABAgsAgAUILAAAFiCwAABYgMACAGABAgsAgAUILAAAFiCwAABYgMACAGAB\nAgsAgAUILAAAFiCwAABYIMTXAwAA8EM1DU4VHqjSkZoG1TsNhQUHKSEyVD07RisiNNjX47nNZpqm\n6eshAAA4UFWnDXsqVHa0VjZJzh/UKdh2/H8z4iM0IC1OHaPDfTJjcxBYAIDPFZQfU37ZUTmNppMU\nHGRTdma8+iTHemGyluN3sAAAr+rXr5+WLVt28uMTcf1uzRe6++pzmvx6p2Eqv+yoCsqPWThl6/E7\nWACAV23cuPHkPx+oqnN75SpJS/KmaOXC2Sor3KJho6/VvJnT1TE6zKpRW4UVLADAZzbsqXArrk6H\nQ5KU0DFFYyb/ShdcmyvTPP71/ooVLADAq7KysvTqq6/q7HOG6ZG7f6G1yz9SQsdkjRiTe8p+v712\nuEaOv1VffvCu9u4s0iufFSh75JWSpOLN3+pQ7R7tOlqj2ganX15dTGABAD5x74MPq7xsp56ft1J1\nNdV64de3n7bPqg/n6+4Xpyg2IUnBIa6TVXiwSv1T46wet9k4RQwA8In358/TNZN+qZj4BHVITdeo\niZNO22fUjZPUITVdYRERLl/DaUqHqxusHrVFCCwAwCcO7NurDilpJz/ukJZ52j5JP9jemHqn4dG5\nPIXAAgB8okNyig7u23Py44N7d522j022Jl8nLNg/U+afUwEA2r0rrx2nRVP/rqqKIzq0b4+W5E1p\n8mucDofq62plOJ0yDKec9bWKDWs6wr5AYAEAPvGnp59Qh9QM/W7sCP35l7do+FXXN/k181//P/1s\nRC8tmvqyvnx/nu48v5fmvPIXL0zbfNwqEQDgEysLD2jptv2yd4hWUFDLVqGdEyJ1SY+OHp7MM3ib\nDgDA61Zs269H5m9UQnSY0pOiFOTG71p/LDjIpgFp/vf2nBM4RQwA8KoTcXUYpg4cq9PqwgNqaOaV\nwCdu+O+vt0mUCCwAwIs+27ZfD38f1xMKdldodeEBt+9H3FaepsMpYgCAV3y2db8eWbDRZUgjgoM0\nulcnbT1QpV1HayQ19jzYyO+fB+u/K9cTuMgJAGC55Vv369FG4jrEnqDnrh+oyLDj9xOubXCq8GCV\nDlc3qN5pKCw4SIlRoerRIdov7zncGAILALDUsi3lemzhJpdxPbtzgp4d95+4tiecIgYAWGbZlnI9\ntmCTnC7Wcmd3Pr5ybUur0uYgsAAAS3y6pVyPB2hcJa4iBgBY4ExxHdo5sd3HVWIFCwDwsKUF5frj\nQtdxze6SqGfGDWj3cZUILADAgz4p2KcnFm5uNK7Pjhug8ACIq0RgAQAesmTzPj25yHVcc75fuQZK\nXCUCCwDwgCWb9+mJRZvk6mZMOVmJeua6wIqrRGABAK308aZ9enKx67iek5Wkp6/rH3BxlQgsAKAV\nPtq0V08t3tx4XMf1V3hI4MVVIrAAgBb6cONePf2+67ie2zVJT10XuHGVeB8sAKAFzhTXYcRVEitY\nAEAzfbBxr55evFmubmQ/rFuSnhxLXCUCCwBohg++O75ybSyuT40doLAQTo5KBBYA4Kb3v9ujZ94v\ncBnX87p10JNj+xPXHyCwAIAmLf5uj55tJK7Du3fQE9cS1x8jsACAM1q0YY+e+8B1XM/v3kF/JK4u\n8R0BADSKuLYcK1gAgEtniuuIHh31x2v7KTSYuDaGwAIATrPw29167sMtLrcRV/fw3QEAnGLBGeJ6\nAXF1GytYAMBJ87/ZrT995DquF/bsqMfGEFd3EVgAgKSm4/r4mH4KIa5uI7AAAL23fpf+/PFWl9su\n6tlJj405i7g2E4EFgAD37vpd+t/G4tqrkx67hri2BIEFgAA2b90uvbDEdVwv7tVJjxLXFiOwABCg\nzhTXS3p30iNXE9fWILAAEIDmri3Ti59sc7mNuHoGgQWAAHOmuI7snayHr+mrkCDi2loEFgACyDtr\ny/SXxuLaJ1kPX01cPYXAAkCAmLO2TC81EtdL+yTrIeLqUQQWAALAnK/L9NJS13G9rG+y/nAVcfU0\nAgsA7dzsr0v1f0sLXW4b1TdFD17Vh7hagMACQDuWl1+qv35KXH2BwAJAOzUrv1R/O0Nc/3BVXwUH\n2bw8VeAgsADQDs1cU6K/L9vuctvlZ6XowSuJq9UILAC0M2eK6+izUvQAcfUKAgsA7cjbX5Xo5eWu\n43pFv1Tdf0Uf4uolBBYA2okZX5XoH8TVbxBYAGgHpq/eqX9+VuRy25X9U3XfaOLqbQQWANq4M8X1\nqv6p+j1x9QkCCwBt2Furd+qVM8T1viv6KMhGXH2BwAJAGzVt1U79a4XruF49IE2/H92buPoQgQWA\nNujNVcX694odLrcRV/9AYAGgjXnzy2L9e6XruF4zME33Xk5c/QGBBYA2ZOqXxXq1kbiOGZim3xFX\nv0FgAaCNmPJFsV773HVcrx2Yrt9e3ou4+hECCwBtwBtf7NDrnxe73DZ2ULruGUVc/Q2BBQA/98bn\nO/T6F8UutxFX/0VgAcCPvf75Dr3RSFyvG5yuuy8jrv6KwAKAn2oqrvdc1ks24uq3CCwA+BnTNPX6\n58Wa8mWxy+3jBmfo7st6Elc/R2ABwI+YpqnXPt+hqV/udLn9+iEZ+s2lxLUtCPL1AACA44hr+8IK\nFgD8gGmaenXlDr25ynVcx5+doV+PJK5tCYEFAB8zTVP/XrlD0xqJ6w1nZ+pXI3sQ1zaGwAKAD5mm\nqX+tKNJbq0tcbp8wNFO/vIS4tkUEFgB8xDRNvbKiSNOJa7tEYAHAB0zT1CufFWn6V67jmjs0U/9D\nXNs0AgsAXmaapv75WZFmNBLXidl2/ffF3YlrG0dgAcCLTNPUP5Zv19trSl1uvzHbrl8Q13aBwAKA\nl5imqZeXb9fMxuKaY9cvLiKu7QWBBQAvME1TLy/brpn5ruN6U45d/4+4tisEFgAsZpqm/r5su2Y1\nEtebz+ms/7qwG3FtZwgsAFjINE397dNC5X1d5nL7Led01s+Ja7tEYAHAIqZp6q+fFmp2Y3E9t7N+\nfgFxba8ILABYoKm43npuZ/2MuLZrBBYAPMw0Tf3f0kLNWes6rrcN66K7RnQlru0cgQUADzJNUy8t\n3aZ31u5yuf32YV30U+IaEAgsAHiIaZr6yyfbNHed67j+5LwuuvN84hooeOA6AHgAccWPsYIFgFYy\nTVMvLtmmeetdx/WO87I0+fws4hpgCCwAtIJhmnpxyVa9u363y+2Thmdp8vldvTwV/AGBBYAWMkxT\nL3y8Ve99Q1xxOgILAC3QVFwnD8/SJOIa0AgsADSTYZr634+2av63ruN65/lddcfwLO8OBb9DYAGg\nGQzT1J8/2qIF3+5xuf2nI7rqJ+dleXco+CUCCwBuMkxTf/poixY2Ete7RnTV7cQV3yOwAOCGJuN6\nQVfdPizLu0PBrxFYAGiCYZp6/sMtWrTBdVx/dkE33Tasi5engr8jsABwBk3F9ecXdtOt5xJXnI7A\nAkAjDNPUcx8UaPF3e11u/68Lu+kW4opGEFgAcMFpmHruwwK9T1zRQgQWAH7EaZh69oMCfbDRdVz/\n30XddfM5nb08FdoaAgsAP9BUXH9xUXfdRFzhBgILAN9zGqaeeX+zPty0z+X2/764u27MIa5wD8+D\nBQARV3geK1gAAc9pmHr6/c36qJG4/s8lPTQx2+7lqdDWEVgAAc1pmHpq8WZ9vJm4wrMILICA5TAM\nPb24oNG4/vKSHsolrmghAgsgIDkMQ08t3qwlm8tdbv/VyB6aMJS4ouUILICA4zAMPblosz4pcB3X\nX4/sqRuGZnp5KrQ3BBZAQGkyrpf21A1nE1e0HoEFEDAchqEnFm3W0kbi+ptLe2o8cYWHEFgAAcFh\nGHpi4WYt3eI6rndf2lPXE1d4EIEF0O45nIb+uGiTPt2y3+X2ey7rpXFDMrw8Fdo7AgugXXM4DT2+\ncJOWbSWu8C4CC6DdcjgNPbZwk5Y3Etffjuql6wYTV1iDwAJol5qK6+9G9dJY4goLEVgA7Y7Daeix\nBZu0fJvruN57eW9dOyjdy1Mh0BBYAO1Kg9PQYws26rNtB1xuJ67wFgILoN1ocBp6dP5GrSgkrvA9\nngcLwK99vfOQnIbZ5H4NTkOPnCGuvx9NXOFdBBaA33pv/S5N+OeXunfON2eM7Im4rnQRV5uk+0b3\n1piBxBXexSliAH7p3XW7dE/eehmmNHftLtlk0/M3DFRwkO2U/ZqM6xV9dPWANC9NDfwHgQXgd+at\nK9Nv877RDxet76wtk80mPTf+P5Gtdxh6ZP53+nz7wdNeg7jC1wgsAL/iKq4nzPm6TDYdj6zDMPXw\n/O/0RSNxvf/KPrqqP3GF79hM02z66gEA8IK5a8v029nfqKmfSuPPzlBQkE2rdhw6bZtN0gNX9tGV\nxBU+RmAB+IV3vi7T7+Y0HdcTosODlRgdJpvtP7+TJa7wJ1xFDMDn5jQzrpJUVefU4ap6nVgj2CQ9\neGVf4gq/QWAB+NTs/FLd28y4nnAisjJNPXhVX13RP9XzAwItRGAB+Exefql+/863LYrrCVV1TnVJ\nitblfVM8NxjgAQQWgE/krSnVfa2M6wkrCw/oofe+k+HGHZ8AbyGwALwub02p7pvrmbieMGN1iR4m\nsvAjBBaAV81aU9Lq08KNmb66RI/M/068OQL+gMAC8JqZX5Xovnc2WHqMt1YdX8kSWfgagQXgFW9/\nVaL751ob1xPeWlWivy0t9MqxgMYQWACWm7G6RA94Ka6S1LVjtCZk2712PMAV7kUMwFLTV+/UH+Z9\n57XjdesYrbd/NkwpcRFeOybgCitYAJZ5axVxReBiBQvAEtNW7dTD73oxrp2iNfOuYUomrvATrGAB\neNybXxZ7Na7diSv8ECtYAB715pfFeuS9jV47XvdOx08LJ8cSV/gXAgvAY6Z+UaxH53svrj2SYzTj\nrnOJK/wSgQXgEVM+36HHFmzy2vF6JMfo7buGqVNsuNeOCTQHv4MF0GpveDmuPYkr2gBWsABa5fWV\nO/THhd6N6wziijaAwAJosddW7tATXoxrr5Tjce0YQ1zh/wgsgBZ5dUWRnly02WvH650Sq+l3nUtc\n0WYQWADN5ou4zrjrXHUgrmhDCCyAZvn3Z0V6arH34tonNVbTf0pc0fYQWABu+9dn2/X04gKvHY+4\noi0jsADc8sry7Xrmfe/GdcZdw5QUHea1YwKeRGABNOmfy7frWS/GtW9anKb/9FziijaNwAI4o38s\n267nPvBuXGf89FwlEle0cQQWQKNeXlao5z/Y4rXjnfX9ypW4oj0gsABc+vunhfrTh96La7/0OL11\nJ3FF+0FgAZzGF3Gd/tNzlRBFXNF+EFgAp/jb0m3680dbvXa8/hnHV67EFe0NgQVw0l8/2ab//Zi4\nAp5AYAHIMEzdO+cbvbN2lyQpOjxYg7skKiU+UhGhQaptMLTvaI3WFR9Wdb3TI8cckBGvt+48V/FR\noR55PcDf2EzTNH09BADf2HWkRnPyy/TayiJV1DqUnhipC/okq2dqrExTCgv5zyOjGxyGZJO27T2m\nFQXl2n24psXHHZgZr2mTiSvaNwILBJg6h1Mfb9qnWWtKtbLwgE78BMjulqTRA9MVEmRTUJCt0a83\nDFMOw9SH3+5WftGhZh9/YGa8pt15ruIjiSvaN04RAwGiYG+FZq0p1bvrdulwdcMp207E9cSKdcEb\nf9P+XSWa/NDzp71OUJBNYUE2jR6YLknNiuygzHi9SVwRIFjBAu1YRW2D5q/frdn5pfqm7KjLfdIT\nIzXpou6nnA52V73D0BvLt7t1uniQPUFvTj6HuCJgsIIF2hnTNLV6xyHlrSnV4u/2qLbBOOP+F/RJ\nVsgZTgn/mNPhUHDI8R8dIUE2XdA7WTO/KJItKLjRrxlkT9C0O89RXARxReBgBQu0E/sqajXn6zLN\nzi9V8cFqt74mOjxYfQ4s09LZU1RbVamEjim6/b4ntWX9Vyov3amfP/GS9u8u1b1jz9ekh57Xe//+\nizqmZ+qux1485XM14UlKvulZl8cYbE/Qm8QVAYgVLNCGNTgNfbK5XHn5pVq2pVxGM/9zuVt4hT6d\n86YenbpAiZ1StX93qUzDqS3rvzpt3y1rV+mZ2UtlswXp6KH9Jz/3x7eXaHlBub7aWXna1wzpnKCp\nk4krAhOBBdqgwvJK5eWXau7aMh2orG/x63SKi5KjoV67i7YpNrGDOqXbG933urvuVnhk1Gmfi4mN\nUUZyg/SjwA7pfPx3rrHEFQGKwAJtRFWdQwu/3a28/DJ9vfOwR14ztXOWbr7nUb377xe164Gt6j/s\nIt1098Mu901KTW/0c5Ghp14gdfb3K1fiikBGYAE/Zpqm1pYc1qw1pVr47R6P3UXphNoGQ+ddcZ3O\nu+I61VQe05RnHlDeX59RcmaX0/a16fQLoU58ruYHF1IN7ZKoKZNyiCsCHoEF/ND+Y3Wat65Ms9aU\navv+KsuOs21LgWx7nOp7do5Cw8MVFh4hw2hexBschvYdOf42naFdEjV18jmKCedHC8DfAsBPOJyG\nlm/dr1lrSrW0oFyO5l6x1AKbSg7quxWvaG9xoYJDQtRj4FDd8eCzWjZvhvsvYpPW7zys7C6JmkJc\ngZN4mw7gY8UHqpSXX6p31pZpX0Wd148/8bwu6pMWd8bbIzbGMEwV7K5Q0d4KvTGJuAI/xN8GwAdq\n6p1avGGP8vJLtXpH8+/n60krCsrVIyVWYS0IrMMwdbCihrgCLrCCBbzENE19W3ZUs/JLtWD9bh2r\nc/h6pJN+fC9id9Q7DG0pO6rHx5ylaOIKnIbAAhY7VFWvd9ftUl5+qQr2HvP1OI1y92k6khQcZFOn\niFCN6N6BuAKNILCABZyGqZWFB5S3plQfb9qneueZ7wfsL9ITI3VB72T1TIuVTCn0Bytah9NQeEiQ\nMuIjNSAtTh2jw3w4KeD/CCzgQaWHqjX76zLNyS/V7qO1vh6nxaLCgjW4S6JSEiIVGRqkmgZD5Udr\n9MjVZ6l3SqyvxwPaBAILeEhtg1NDn/hYVR6+GYSvZXWI0oRsu24YmqmUuAhfjwO0GfzyBPCQiNBg\nXdE/Te+sLfP1KK0WERqkqwakaWK2Xed0TZLN1vwrjIFAR2ABD5qYY2/TgR2UGa/cHLvGDErnCThA\nKxFYwINyshLVrWO0ig5Yd3tDT0uICtW4IRmamGNXn9Q4X48DtBsEFvAgm82mCdl2PfdBga9HOSOb\nTbqgZyflZmdq1FkpCg8J9vVIQLvDRU6Ah5VX1Oq8Z5fK6YV7CTdXRkKkcrPtuiE7UxkJkb4eB2jX\nWMECHpYcF6GLe3XSJwXlvh5FkhQWEqTR/VI1Mduu4d07tOiewwCaj8ACHnS0cLuKp72mc/fX6pO4\nS306y1lpcZqYY9fYwelKiOKmEIC3cYoYaCVnXZ2KZkxXxaqligtrUFCQTQ7ZdGPEeB22efc0bGxE\niK4bfPyCpf4Z8V49NoBTsYIFWmj/V1+pbPZ0hVXsVkREsBIiJOn46dcQmbrcsV2zQvt7ZZbzunXQ\nxBy7ruifqohQLlgC/AErWKAZag8fVtGU11W3aY3ios68b6ktTndEjLVsltS4CE3IztSEoXZ17tDE\nMAC8jhUs0ATDMLT7ww+0b/G7inYeVnhosMLd6JndrFDfhnJtDk322CyhwTZd1jdFuTl2Xdizk4K5\nYAnwW6xggUYcKy7WjmlvyNy5STHR7p92ra1xqD6xs+wTb9WnRifdO+fbVs/SKyVGudl2jRuSoQ4x\n4a1+PQDWI7DADzgbGlQ8820d+XyJ4kJqFRTs3gPIDaehCkeEEs6/TFk33qTg0OO3Gayud+icpz5R\nZQserh4THqIxg9KUm23XYHsC9wMG2hhOEQOSDq5fp5KZ0xR6qESRkSFKCJekpuNaVe2U7H3V9fbJ\n6pmVddr2qLDjkXz7q1K3Z8nJSlRutl1XD0xTVBh/RYG2ihUsAlZdRYWKpr6hmm9XKT7K/b8Gjgan\nKoMTlXzltcq44ioFBZ05xGtLDuv6l7844z6dYsM1/uxM5WZnqlunGLdnAeC/+M9jBJxdS5Zo34I5\niqw/qLCwYIW5eQFuRbUUflaOut0xWRGJiW4fb4g9QT2TY7StvPKUzwcH2XRJ72RNzLHr4t6dFOrm\n6WgAbQMrWASE6t27tX3Ka3IWbVBstPshq6t1qi4uXRk33Kzkc89t8fFfXVGkJxdtliR16xit3By7\nrh+SoWQeYA60W6xg0W4ZDod2zpmtQ8s/VGxwtaKCgyQ34moYpirqQxU3bKR63XSTQiJafzemcUMy\ntGXvMeXm2JXdJZELloAAwAoW7c6hjRtVMmOKQvYXKzLS/bfXVFU7Zab3VNatkxTfs6eFEwIIBAQW\n7UJDVaWK3pqmqq9XKC7C6fYK0eEwVKlYdRx1jezXjm3ygiUAcBeBRZu257PPtGfeLEXWlCss3P3V\n6rEqU6F9hqjb7ZMVmey5Oy0BwAkEFm1O9b59Kpr6uhxb1zXvgqU6p2qjUpQ+bqJSL7jAwgkBgMCi\njTAMQyXvztPBJYsUY6tUSIh7YTVNUxW1IYoeOkLdb/uJQqK4KT4A7yCw8GtHtm7VzmlvKGhvoaKi\n3D8FXF3tkDOlu7rc/BMlnnWWhRMCgGsEFn7HUVujoulvqXL1csWFN8jm5hNjnE5Dx4xoJV1ypbqM\nu15BIbwLDYDvEFj4jfJVq1Q2Z7oiju1VeERzLlgyFNJjkLrdPklR6ekWTggA7iOw8Knagwe1fcrr\nqt+cr7ho92++UF/vVE14R6VeO0HpI0daOCEAtAyBhdcZhqGyRYu0/8P3FGNUKCTU/SuBj1bbFDV4\nuLrffodCY2MtnBIAWofAwmsqdhSr+M3XpLICRTfjgqWaGoccHbJkv+l2dRg40MIJAcBzCCws5ayr\n045Zb+vo558oLqxeQW5esHT8AeaRSrjgcmXl5p58gDkAtBUEFpY48PXXKs17S2FHyhTRjAuWKquc\nsnU5S91+cqdiOne2cEIAsBaBhcfUHTmioqlvqPa71Yprxv0cGuqdqg5NVPLV1yt91OXcDxhAu0Bg\n0SqGYWj3ko9VvmiuouoPKTTM/dVqRbUU3v8cdf/JZIUnJFg4JQB4H4FFi1SVlmr71NdkFm9UTLT7\nUa2tdao+PlOZubeoU3a2hRMCgG8RWLjNcDhUnDdLh1d8pNjgGgUHu3cq9/gDzMMUP3ykut54s4LD\nwy2eFAB8j8CiSYe+26CS6VMVcrBYkZHu336wqtopZfRW1m2TFde9m4UTAoD/IbBwqeHYMW2fNlXV\n6z5XXKTh/gPMGwxVBsWp0+ixyrz6ai5YAhCwCGwbVna4WrPzy5SeEKGJOZ55S8vuTz/V3vmzFVm7\nX2HNuWCpylRY36Hq9pPJiuzY0SOzAEBbxuNG2pjaBqc+3rRPefmlWll4QKYpdesYrdxsu9urzB+r\n3rNXRVPLD8fRAAAIxUlEQVRfk6PwG8VGBylektyIa12dU7XRqcq4/kZ1P//8Fh0bANorAttGbNpd\nobz8Ur27fpeOVDecsq3oQJXydx5WTlaS269nOBza+e48HVq6WLG2KkWGBEnRTZ/ONQ1TFXUhijnn\nIvW6+VYeYA4AjSCwfuxoTYPmf7NbeWtKtWHX0TPuO2tNqVuBPbKlQDvfmqKgvdsVFRWshFBJajqs\n1dVOOVO7K+vWO9Sjdx83/w0AIHDxO1g/YximVu04qNn5ZVq8YY/qHIZbXxcZGqyv/nCpYiNOv2ev\no7pa2996U1X5KxQX7nD7AeYOh6FKM0ZJl16lLmOv4wHmANAM/MT0E3uP1mrO16XKyy9TyaHqZn99\nTYNTC7/do5vO+c/FTvs+/1y75s5URNVehYcHKz5SkpqO67EqQyE9B6vbHXcqKiWl2bMAAFjB+lS9\nw9DSgn2ataZUy7ful9HK/ycG2xP09sTeKpryquoL1jXvAeZ1TtVEdlLa2FylXXxx6wYBABBYX9i2\n75hmrSnVvHW7dLCq3qOv/UrVe+oRVOHWvqZpqqImWNFDR6jbbbcrNDrGo7MAQCDjFLGXVNY5tPCb\n3ZqVX6p1JUcsO85H4T3Vo+HrM+5TU+OUo2OWOt98u3r0H2DZLAAQyFjBWsg0TeXvPKy8NaVatGGP\nquudlh8z3qzVrNp3FKpTL45yOg0dc0Yp8cLLlTUhlwuWAMBi/JS1QPmxWs1du0t5+aUq2l/l1WMf\ntUXoi6BMXWSUSDr+APOgrgPU7Y47FZ2R4dVZACCQEVgPcTgNLduyX7PyS7W0oFzO1l6x1ArvB3XX\nYKNCKdeMV9dLL+V+wADgA5wibqWi/ZXKyy/TO2vLtP9Yna/HkSQF2aTP7x+ptOPvywEA+AAr2Bao\nrndo8Ya9yltTqq+KD/l6nNMYpjQnv0y/vLSnr0cBgIDFCtZNpmlqfekR5eWXacE3u1VZ5/D1SGdk\nT4rU8t9doiA379oEAPAsVrBNOFRVr7lry5SXX6qt+yp9PY7bSg/VaFXRQQ3vwaPjAMAXCKwLTsPU\nim37lZdfqo837VODs20u8mfllxJYAPARThH/QOmhauXll2rO12Xac7TW1+O0WlhIkNY8eJnio05/\nAAAAwFoBv4KtbXDqw417NWtNqb7YftDX43hUvcPQh5v2Kjfb7utRACDgBHxgJ72xRl8Wta+wRoYG\n66oBaZqYY1dOVqKvxwGAgBTwgb1qQKq+3XVEg7skKiU+UhGhQaptMLTvaI3WFR/2yu0NPWWQPUET\ns+0aMyjN5XNhAQDeE9C/gz1QVae1ZUdVeqRGhnn8d5YnNDgMySZt23tMKwrKtftwjQ8nbVxSdJjG\nDclQbrZdvVNjfT0OAOB7AXEPvX79+mnZsmWnfK6g/JhenD5fN144SCHBQafEVZJCQ4IUGhykPmlx\nmnRRd2V3S/LixGdms0kX9eqkl285W6seuFQPX3MWcQUAPxMQp4g3btx4yscF5ceUX3ZUziYW7w31\ndXrzuYe06auVqqw4ooikdIUPu0WR3bOtHLdRmYmRys2264ahmUpP4DaIAODPAiKwP3Sgqu54XJu4\nGb/T4ZDhdCopJU33v5KnDqkZWvvZJ3r5D/+jtMl/U0h8ilfmDQsJ0pX9UzUx265h3TpwZyYAaCMC\nIrBZWVl69dVXdf755+vW2yZpxZL3ldAxWSPG5J6y32+vHa6R42/Vlx+8q707i/TKZwUa97N7Tm4/\n+8LL1CEtU3V7Cy0PbL/0OE3MsWvsoAzexwoAbVBABPaEhx95VDt2FOn5eStVV1OtF359+2n7rPpw\nvu5+cYpiE5IU/KOHkh87fECH9+xU56u6yopri+MiQjRuSIYmZNvVPyPegiMAALwloAI7My9PN//u\nCcXEJygmPkGjJk7Se6+9dMo+o26cpA6p6ad9rcPRoFce/pWGXzleGUMH6ottBzw21/k9Oig3267R\n/VIVERrssdcFAPhOQAV2/969SkhOO/lxh7TM0/ZJSkk77XOGYehfj/xGIaFhuv3+J/Xdrtbf9D8t\nPkIThmZqQrZd9qSoVr8eAMC/BFRgk5JTdHDfHmV07y1JOrh312n72HTqRUSmaer1J+5VxaEDuucv\nUxUSEqrI0Ja9uyk02KbLz0pVbo5dI3p0VDAXLAFAuxVQgb3kqrFaNOXv6t5/sOpqarQkb0qTXzP1\n2Qe1u7hQv//7DIVFREiSahqMZh23d0qscnPsGjckQ0nRYS0ZHQDQxgRUYH/z+wd1z6/+W78bO0KJ\nnY5fRfzxzNcb3f/AnjItmztdIWHh+vUVQ09+/uxbfi91OPN7YWPDQzRmcLpys+0alBkvm43VKgAE\nkoC6VWJNg1Nzvt2tJt4Ce0YNTkMvLNrc6D2Kz+mapInZdl01IE2RYVywBACBKqBWsJGhwcqMj1DJ\nkZY969UwTG3bc+y0uCbHhmv80EzlZtvVtWO0J0YFALRxARVYSRqQFqddFXVN3snJFYdhasWWcklS\nSJBNI/ska2KOXRf16qSQ4IC4rTMAwE0BdYr4hJP3Im5GZOsdhj78drcOHavTxGy7rj87U51iwy2c\nEgDQlgVkYCX3I2sYppyGqf1HajSqT7KGdknkgiUAQJMCNrCSdKCqXhv2VGjX0ePPenX+4DsRbJMa\nnKZCbNLFPTrKnsjNIAAA7gvowJ5Q2+BU4cEqHa5uUL3TUFhwkBKjQtWjQzS3LgQAtAiBBQDAAlz6\nCgCABQgsAAAWILAAAFiAwAIAYAECCwCABQgsAAAWILAAAFiAwAIAYAECCwCABQgsAAAWILAAAFiA\nwAIAYAECCwCABQgsAAAWILAAAFiAwAIAYAECCwCABQgsAAAWILAAAFiAwAIAYAECCwCABQgsAAAW\nILAAAFiAwAIAYAECCwCABQgsAAAWILAAAFiAwAIAYAECCwCABQgsAAAWILAAAFiAwAIAYAECCwCA\nBQgsAAAWILAAAFiAwAIAYAECCwCABQgsAAAWILAAAFjg/wMsqF1S0Jt1dgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1179320d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"##Preliminary visulization of resultant network graphs at each time point.\n",
"##Cytoscape used in final paper Figure 5. \n",
"\n",
"for t in range(4):\n",
" G=nx.DiGraph()\n",
"\n",
" colors = []\n",
" for i, g in enumerate(['idr1', 'idr2', 'sirr', 'tror']): \n",
" for j, d in enumerate(['didr1', 'didr2', 'dsirr', 'dtror']):\n",
" if i==j:\n",
" continue\n",
"\n",
" if sig[t,i,j] < 5e-2:\n",
" G.add_edge(d[1:],g,{\"value\":coeff[t,i,j]})\n",
" colors.append(coeff[t,i,j])\n",
"\n",
" pos=nx.spring_layout(G)\n",
" \n",
" plt.figure()\n",
" \n",
" nx.draw(G,pos,node_color='#A0CBE2',edge_color=colors,width=5,\n",
" edge_cmap=plt.cm.RdBu,with_labels=True,arrows=True,\n",
" edge_vmin=-1,edge_vmax=1)\n",
" plt.title('time=%d'%[0,5,20,60][t])\n",
" "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
XInterns/IPL-Sparkers | src/Match Outcome Prediction with IPL Data (Gursahej).ipynb | 1 | 174189 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Predicting the Outcome of Cricket Matches"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Introduction\n",
"\n",
"In this project, we shall build a model which predicts the outcome of cricket matches in the Indian Premier League using data about matches and deliveries.\n",
"\n",
"### Data Mining:\n",
"\n",
" * Season : 2008 - 2015 (8 Seasons)\n",
" * Teams : DD, KKR, MI, RCB, KXIP, RR, CSK (7 Teams)\n",
" * Neglect matches that have inconsistencies such as No Result, Tie, D/L Method, etc.\n",
"\n",
"### Possible Features:\n",
"\n",
" * Average Batsman Rating (top 5) \n",
" * Average Bowler Rating (top 4)\n",
" * Player of the match frequency \n",
" * Previous Encounter - Win by runs, Win by Wickets \n",
" * Recent form (Last 5 Games)\n",
" * Venue - Home, Away, Neutral"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# The %... is an iPython thing, and is not part of the Python language.\n",
"# In this case we're just telling the plotting library to draw things on\n",
"# the notebook, instead of on a separate window.\n",
"%matplotlib inline \n",
"#this line above prepares IPython notebook for working with matplotlib\n",
"\n",
"# See all the \"as ...\" contructs? They're just aliasing the package names.\n",
"# That way we can call methods like plt.plot() instead of matplotlib.pyplot.plot().\n",
"\n",
"import numpy as np # imports a fast numerical programming library\n",
"import scipy as sp #imports stats functions, amongst other things\n",
"import matplotlib as mpl # this actually imports matplotlib\n",
"import matplotlib.cm as cm #allows us easy access to colormaps\n",
"import matplotlib.pyplot as plt #sets up plotting under plt\n",
"import pandas as pd #lets us handle data as dataframes\n",
"#sets up pandas table display\n",
"pd.set_option('display.width', 500)\n",
"pd.set_option('display.max_columns', 100)\n",
"pd.set_option('display.notebook_repr_html', True)\n",
"import seaborn as sns #sets up styles and gives us more plotting options\n",
"from __future__ import division"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Data Mining\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>id</th>\n",
" <th>season</th>\n",
" <th>city</th>\n",
" <th>date</th>\n",
" <th>team1</th>\n",
" <th>team2</th>\n",
" <th>toss_winner</th>\n",
" <th>toss_decision</th>\n",
" <th>result</th>\n",
" <th>dl_applied</th>\n",
" <th>winner</th>\n",
" <th>win_by_runs</th>\n",
" <th>win_by_wickets</th>\n",
" <th>player_of_match</th>\n",
" <th>venue</th>\n",
" <th>umpire1</th>\n",
" <th>umpire2</th>\n",
" <th>umpire3</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>2008</td>\n",
" <td>Bangalore</td>\n",
" <td>2008-04-18</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>140</td>\n",
" <td>0</td>\n",
" <td>BB McCullum</td>\n",
" <td>M Chinnaswamy Stadium</td>\n",
" <td>Asad Rauf</td>\n",
" <td>RE Koertzen</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2</td>\n",
" <td>2008</td>\n",
" <td>Chandigarh</td>\n",
" <td>2008-04-19</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>33</td>\n",
" <td>0</td>\n",
" <td>MEK Hussey</td>\n",
" <td>Punjab Cricket Association Stadium, Mohali</td>\n",
" <td>MR Benson</td>\n",
" <td>SL Shastri</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>3</td>\n",
" <td>2008</td>\n",
" <td>Delhi</td>\n",
" <td>2008-04-19</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>0</td>\n",
" <td>9</td>\n",
" <td>MF Maharoof</td>\n",
" <td>Feroz Shah Kotla</td>\n",
" <td>Aleem Dar</td>\n",
" <td>GA Pratapkumar</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>4</td>\n",
" <td>2008</td>\n",
" <td>Mumbai</td>\n",
" <td>2008-04-20</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>0</td>\n",
" <td>5</td>\n",
" <td>MV Boucher</td>\n",
" <td>Wankhede Stadium</td>\n",
" <td>SJ Davis</td>\n",
" <td>DJ Harper</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>5</td>\n",
" <td>2008</td>\n",
" <td>Kolkata</td>\n",
" <td>2008-04-20</td>\n",
" <td>Deccan Chargers</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>Deccan Chargers</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>0</td>\n",
" <td>5</td>\n",
" <td>DJ Hussey</td>\n",
" <td>Eden Gardens</td>\n",
" <td>BF Bowden</td>\n",
" <td>K Hariharan</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>6</td>\n",
" <td>2008</td>\n",
" <td>Jaipur</td>\n",
" <td>2008-04-21</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>0</td>\n",
" <td>6</td>\n",
" <td>SR Watson</td>\n",
" <td>Sawai Mansingh Stadium</td>\n",
" <td>Aleem Dar</td>\n",
" <td>RB Tiffin</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>7</td>\n",
" <td>2008</td>\n",
" <td>Hyderabad</td>\n",
" <td>2008-04-22</td>\n",
" <td>Deccan Chargers</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>Deccan Chargers</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>0</td>\n",
" <td>9</td>\n",
" <td>V Sehwag</td>\n",
" <td>Rajiv Gandhi International Stadium, Uppal</td>\n",
" <td>IL Howell</td>\n",
" <td>AM Saheba</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>8</td>\n",
" <td>2008</td>\n",
" <td>Chennai</td>\n",
" <td>2008-04-23</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>6</td>\n",
" <td>0</td>\n",
" <td>ML Hayden</td>\n",
" <td>MA Chidambaram Stadium, Chepauk</td>\n",
" <td>DJ Harper</td>\n",
" <td>GA Pratapkumar</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>9</td>\n",
" <td>2008</td>\n",
" <td>Hyderabad</td>\n",
" <td>2008-04-24</td>\n",
" <td>Deccan Chargers</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>0</td>\n",
" <td>3</td>\n",
" <td>YK Pathan</td>\n",
" <td>Rajiv Gandhi International Stadium, Uppal</td>\n",
" <td>Asad Rauf</td>\n",
" <td>MR Benson</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>10</td>\n",
" <td>2008</td>\n",
" <td>Chandigarh</td>\n",
" <td>2008-04-25</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>66</td>\n",
" <td>0</td>\n",
" <td>KC Sangakkara</td>\n",
" <td>Punjab Cricket Association Stadium, Mohali</td>\n",
" <td>Aleem Dar</td>\n",
" <td>AM Saheba</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" id season city date team1 team2 toss_winner toss_decision result dl_applied winner win_by_runs win_by_wickets player_of_match venue umpire1 umpire2 umpire3\n",
"0 1 2008 Bangalore 2008-04-18 Kolkata Knight Riders Royal Challengers Bangalore Royal Challengers Bangalore field normal 0 Kolkata Knight Riders 140 0 BB McCullum M Chinnaswamy Stadium Asad Rauf RE Koertzen NaN\n",
"1 2 2008 Chandigarh 2008-04-19 Chennai Super Kings Kings XI Punjab Chennai Super Kings bat normal 0 Chennai Super Kings 33 0 MEK Hussey Punjab Cricket Association Stadium, Mohali MR Benson SL Shastri NaN\n",
"2 3 2008 Delhi 2008-04-19 Rajasthan Royals Delhi Daredevils Rajasthan Royals bat normal 0 Delhi Daredevils 0 9 MF Maharoof Feroz Shah Kotla Aleem Dar GA Pratapkumar NaN\n",
"3 4 2008 Mumbai 2008-04-20 Mumbai Indians Royal Challengers Bangalore Mumbai Indians bat normal 0 Royal Challengers Bangalore 0 5 MV Boucher Wankhede Stadium SJ Davis DJ Harper NaN\n",
"4 5 2008 Kolkata 2008-04-20 Deccan Chargers Kolkata Knight Riders Deccan Chargers bat normal 0 Kolkata Knight Riders 0 5 DJ Hussey Eden Gardens BF Bowden K Hariharan NaN\n",
"5 6 2008 Jaipur 2008-04-21 Kings XI Punjab Rajasthan Royals Kings XI Punjab bat normal 0 Rajasthan Royals 0 6 SR Watson Sawai Mansingh Stadium Aleem Dar RB Tiffin NaN\n",
"6 7 2008 Hyderabad 2008-04-22 Deccan Chargers Delhi Daredevils Deccan Chargers bat normal 0 Delhi Daredevils 0 9 V Sehwag Rajiv Gandhi International Stadium, Uppal IL Howell AM Saheba NaN\n",
"7 8 2008 Chennai 2008-04-23 Chennai Super Kings Mumbai Indians Mumbai Indians field normal 0 Chennai Super Kings 6 0 ML Hayden MA Chidambaram Stadium, Chepauk DJ Harper GA Pratapkumar NaN\n",
"8 9 2008 Hyderabad 2008-04-24 Deccan Chargers Rajasthan Royals Rajasthan Royals field normal 0 Rajasthan Royals 0 3 YK Pathan Rajiv Gandhi International Stadium, Uppal Asad Rauf MR Benson NaN\n",
"9 10 2008 Chandigarh 2008-04-25 Kings XI Punjab Mumbai Indians Mumbai Indians field normal 0 Kings XI Punjab 66 0 KC Sangakkara Punjab Cricket Association Stadium, Mohali Aleem Dar AM Saheba NaN"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Reading in the data\n",
"allmatches = pd.read_csv(\"../data/matches.csv\")\n",
"alldeliveries = pd.read_csv(\"../data/deliveries.csv\")\n",
"allmatches.head(10)"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Selecting Seasons 2008 - 2015\n",
"matches_seasons = allmatches.loc[allmatches['season'] != 2016]\n",
"deliveries_seasons = alldeliveries.loc[alldeliveries['match_id'] < 518]"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Teams selected:\n",
"\n",
"Kolkata Knight Riders\n",
"Chennai Super Kings\n",
"Rajasthan Royals\n",
"Mumbai Indians\n",
"Kings XI Punjab\n",
"Royal Challengers Bangalore\n",
"Delhi Daredevils\n"
]
}
],
"source": [
"# Selecting teams DD, KKR, MI, RCB, KXIP, RR, CSK\n",
"matches_teams = matches_seasons.loc[(matches_seasons['team1'].isin(['Kolkata Knight Riders', \\\n",
"'Royal Challengers Bangalore', 'Delhi Daredevils', 'Chennai Super Kings', 'Rajasthan Royals', \\\n",
"'Mumbai Indians', 'Kings XI Punjab'])) & (matches_seasons['team2'].isin(['Kolkata Knight Riders', \\\n",
"'Royal Challengers Bangalore', 'Delhi Daredevils', 'Chennai Super Kings', 'Rajasthan Royals', \\\n",
"'Mumbai Indians', 'Kings XI Punjab']))]\n",
"matches_team_matchids = matches_teams.id.unique()\n",
"deliveries_teams = deliveries_seasons.loc[deliveries_seasons['match_id'].isin(matches_team_matchids)]\n",
"print \"Teams selected:\\n\"\n",
"for team in matches_teams.team1.unique():\n",
" print team"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Neglect matches with inconsistencies like 'No Result' or 'D/L Applied'\n",
"matches = matches_teams.loc[(matches_teams['result'] == 'normal') & (matches_teams['dl_applied'] == 0)]\n",
"matches_matchids = matches.id.unique()\n",
"deliveries = deliveries_teams.loc[deliveries_teams['match_id'].isin(matches_matchids)]"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Verifying consistency between datasets\n",
"(matches.id.unique() == deliveries.match_id.unique()).all()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Building Features"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Team Strike rates for first 5 batsmen in the team (Higher the better)\n",
"\n",
"def getMatchDeliveriesDF(match_id):\n",
" return deliveries.loc[deliveries['match_id'] == match_id]\n",
"\n",
"def getInningsOneBatsmen(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 1].batsman.unique()[0:5]\n",
"\n",
"def getInningsTwoBatsmen(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 2].batsman.unique()[0:5]\n",
"\n",
"def getBatsmanStrikeRate(batsman, match_id):\n",
" onstrikedeliveries = deliveries.loc[(deliveries['match_id'] < match_id) & (deliveries['batsman'] == batsman)]\n",
" total_runs = onstrikedeliveries['batsman_runs'].sum()\n",
" total_balls = onstrikedeliveries.shape[0]\n",
" if total_balls != 0: \n",
" return (total_runs/total_balls) * 100\n",
" else:\n",
" return None\n",
"\n",
"\n",
"def getTeamStrikeRate(batsmen, match_id):\n",
" strike_rates = []\n",
" for batsman in batsmen:\n",
" bsr = getBatsmanStrikeRate(batsman, match_id)\n",
" if bsr != None:\n",
" strike_rates.append(bsr)\n",
" return np.mean(strike_rates)\n",
"\n",
"def getAverageStrikeRates(match_id):\n",
" match_deliveries = getMatchDeliveriesDF(match_id)\n",
" innOneBatsmen = getInningsOneBatsmen(match_deliveries)\n",
" innTwoBatsmen = getInningsTwoBatsmen(match_deliveries)\n",
" teamOneSR = getTeamStrikeRate(innOneBatsmen, match_id)\n",
" teamTwoSR = getTeamStrikeRate(innTwoBatsmen, match_id)\n",
" return teamOneSR, teamTwoSR"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(126.98024523159935, 128.55579510411653)"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Testing Functionality\n",
"getAverageStrikeRates(517)\n"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Bowler Rating : Wickets/Run (Higher the Better)\n",
"# Team 1: Batting First; Team 2: Fielding First\n",
"\n",
"def getInningsOneBowlers(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 1].bowler.unique()[0:4]\n",
"\n",
"def getInningsTwoBowlers(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 2].bowler.unique()[0:4]\n",
"\n",
"def getBowlerWPR(bowler, match_id):\n",
" balls = deliveries.loc[(deliveries['match_id'] < match_id) & (deliveries['bowler'] == bowler)]\n",
" total_runs = balls['total_runs'].sum()\n",
" total_wickets = balls.loc[balls['dismissal_kind'].isin(['caught', 'bowled', 'lbw', \\\n",
" 'caught and bowled', 'stumped'])].shape[0]\n",
" if total_runs != 0:\n",
" return (total_wickets/total_runs) * 100\n",
" else:\n",
" return total_wickets\n",
"\n",
"def getTeamWPR(bowlers, match_id):\n",
" totalWPRs = []\n",
" for bowler in bowlers:\n",
" totalWPRs.append(getBowlerWPR(bowler, match_id))\n",
" return np.mean(totalWPRs)\n",
"\n",
"def getAverageWPR(match_id):\n",
" match_deliveries = getMatchDeliveriesDF(match_id)\n",
" innOneBowlers = getInningsOneBowlers(match_deliveries)\n",
" innTwoBowlers = getInningsTwoBowlers(match_deliveries)\n",
" teamOneWPR = getTeamWPR(innTwoBowlers, match_id)\n",
" teamTwoWPR = getTeamWPR(innOneBowlers, match_id)\n",
" return teamOneWPR, teamTwoWPR"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(2.7641806594085776, 4.4721111768026631)"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#Testing Functionality \n",
"getAverageWPR(517)"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Man of the Match Awards for players of both Teams \n",
"\n",
"def getInningsOneAllBatsmen(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 1].batsman.unique()\n",
"\n",
"def getInningsTwoAllBatsmen(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 2].batsman.unique()\n",
"\n",
"def getInningsOneAllBowlers(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 2].bowler.unique()\n",
"\n",
"def getInningsTwoAllBowlers(match_deliveries):\n",
" return match_deliveries.loc[match_deliveries['inning'] == 1].bowler.unique()\n",
"\n",
"def getTeam(batsmen,bowlers):\n",
" p = []\n",
" p = np.append(p, batsmen)\n",
" for i in bowlers:\n",
" if i not in batsmen:\n",
" p = np.append(p, i)\n",
" return p\n",
"\n",
"def getPlayerMVPAwards(player, match_id):\n",
" return matches.loc[(matches[\"player_of_match\"] == player) & (matches['id'] < match_id)].shape[0]\n",
"\n",
"def getTeamMVPAwards(team, match_id):\n",
" mvpAwards = 0\n",
" for player in team:\n",
" mvpAwards = mvpAwards + getPlayerMVPAwards(player,match_id)\n",
" \n",
" return mvpAwards\n",
"\n",
"def bothTeamMVPAwards(match_id):\n",
" matchDeliveries = getMatchDeliveriesDF(match_id)\n",
" innOneBatsmen = getInningsOneAllBatsmen(matchDeliveries)\n",
" innTwoBatsmen = getInningsTwoAllBatsmen(matchDeliveries)\n",
" innOneBowlers = getInningsTwoAllBowlers(matchDeliveries)\n",
" innTwoBowlers = getInningsOneAllBowlers(matchDeliveries)\n",
" team1 = getTeam(innOneBatsmen, innTwoBowlers)\n",
" \n",
" team2 = getTeam(innTwoBatsmen, innOneBowlers)\n",
" team1Awards = getTeamMVPAwards(team1,match_id)\n",
" team2Awards = getTeamMVPAwards(team2,match_id)\n",
" return team1Awards, team2Awards\n",
"\n",
" \n",
"\n",
" \n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"(28, 52)"
]
},
"execution_count": 58,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#Testing Functionality\n",
"bothTeamMVPAwards(517)"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#Function to generate squad rating \n",
"\n",
"def generateSquadRating(match_id):\n",
" gameday_teams = deliveries.loc[(deliveries['match_id'] == match_id)].batting_team.unique()\n",
" teamOne = gameday_teams[0]\n",
" teamTwo = gameday_teams[1]\n",
" teamOneSR, teamTwoSR = getAverageStrikeRates(match_id)\n",
" teamOneWPR, teamTwoWPR = getAverageWPR(match_id)\n",
" teamOneMVPs, teamTwoMVPs = bothTeamMVPAwards(match_id)\n",
" print \"Comparing squads for {} vs {}\".format(teamOne,teamTwo)\n",
" print \"\\nAverage Strike Rate for Batsmen in {} : {}\".format(teamOne,teamOneSR)\n",
" print \"\\nAverage Strike Rate for Batsmen in {} : {}\".format(teamTwo,teamTwoSR)\n",
" print \"\\nBowler Rating (W/R) for {} : {}\".format(teamOne,teamOneWPR)\n",
" print \"\\nBowler Rating (W/R) for {} : {}\".format(teamTwo,teamTwoWPR)\n",
" print \"\\nNumber of MVP Awards in {} : {}\".format(teamOne,teamOneMVPs)\n",
" print \"\\nNumber of MVP Awards in {} : {}\".format(teamTwo,teamTwoMVPs)"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Comparing squads for Mumbai Indians vs Chennai Super Kings\n",
"\n",
"Average Strike Rate for Batsmen in Mumbai Indians : 126.980245232\n",
"\n",
"Average Strike Rate for Batsmen in Chennai Super Kings : 128.555795104\n",
"\n",
"Bowler Rating (W/R) for Mumbai Indians : 2.76418065941\n",
"\n",
"Bowler Rating (W/R) for Chennai Super Kings : 4.4721111768\n",
"\n",
"Number of MVP Awards in Mumbai Indians : 28\n",
"\n",
"Number of MVP Awards in Chennai Super Kings : 52\n"
]
}
],
"source": [
"#Testing Functionality\n",
"generateSquadRating(517)"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"## 2nd Feature : Previous Encounter\n",
"# Won by runs and won by wickets (Higher the better)\n",
"\n",
"def getTeam1(match_id):\n",
" return matches.loc[matches[\"id\"] == match_id].team1.unique()\n",
"\n",
"def getTeam2(match_id):\n",
" return matches.loc[matches[\"id\"] == match_id].team2.unique()\n",
"\n",
"def getPreviousEncDF(match_id):\n",
" team1 = getTeam1(match_id)\n",
" team2 = getTeam2(match_id)\n",
" return matches.loc[(matches[\"id\"] < match_id) & (((matches[\"team1\"].isin(team1)) & (matches[\"team2\"].isin(team2))) | ((matches[\"team1\"].isin(team2)) & (matches[\"team2\"].isin(team1))))]\n",
"def getTeamWBR(match_id, team):\n",
" WBR = 0\n",
" DF = getPreviousEncDF(match_id)\n",
" winnerDF = DF.loc[DF[\"winner\"] == team]\n",
" WBR = winnerDF['win_by_runs'].sum() \n",
" return WBR\n",
"\n",
"\n",
"def getTeamWBW(match_id, team):\n",
" WBW = 0 \n",
" DF = getPreviousEncDF(match_id)\n",
" winnerDF = DF.loc[DF[\"winner\"] == team]\n",
" WBW = winnerDF['win_by_wickets'].sum()\n",
" return WBW \n",
" \n",
"def getTeamWinPerc(match_id):\n",
" dF = getPreviousEncDF(match_id)\n",
" timesPlayed = dF.shape[0]\n",
" team1 = getTeam1(match_id)[0].strip(\"[]\")\n",
" timesWon = dF.loc[dF[\"winner\"] == team1].shape[0]\n",
" if timesPlayed != 0:\n",
" winPerc = (timesWon/timesPlayed) * 100\n",
" else:\n",
" winPerc = 0\n",
" return winPerc\n",
"\n",
"def getBothTeamStats(match_id):\n",
" DF = getPreviousEncDF(match_id)\n",
" team1 = getTeam1(match_id)[0].strip(\"[]\")\n",
" team2 = getTeam2(match_id)[0].strip(\"[]\")\n",
" timesPlayed = DF.shape[0]\n",
" timesWon = DF.loc[DF[\"winner\"] == team1].shape[0]\n",
" WBRTeam1 = getTeamWBR(match_id, team1)\n",
" WBRTeam2 = getTeamWBR(match_id, team2)\n",
" WBWTeam1 = getTeamWBW(match_id, team1)\n",
" WBWTeam2 = getTeamWBW(match_id, team2)\n",
"\n",
" print \"Out of {} times in the past {} have won {} times({}%) from {}\".format(timesPlayed, team1, timesWon, getTeamWinPerc(match_id), team2)\n",
" print \"{} won by {} total runs and {} total wickets.\".format(team1, WBRTeam1, WBWTeam1)\n",
" print \"{} won by {} total runs and {} total wickets.\".format(team2, WBRTeam2, WBWTeam2)\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Out of 21 times in the past Mumbai Indians have won 11 times(52.380952381%) from Chennai Super Kings\n",
"Mumbai Indians won by 144 total runs and 30 total wickets.\n",
"Chennai Super Kings won by 138 total runs and 31 total wickets.\n"
]
}
],
"source": [
"#Testing functionality \n",
"getBothTeamStats(517)\n"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#3rd Feature: Recent Form (Win Percentage of 3 previous matches of a team in the same season)\n",
"#Higher the better\n",
"\n",
"def getMatchYear(match_id):\n",
" return matches.loc[matches[\"id\"] == match_id].season.unique()\n",
"\n",
"def getTeam1DF(match_id, year):\n",
" team1 = getTeam1(match_id)\n",
" return matches.loc[(matches[\"id\"] < match_id) & (matches[\"season\"] == year) & ((matches[\"team1\"].isin(team1)) | (matches[\"team2\"].isin(team1)))].tail(3)\n",
"\n",
"def getTeam2DF(match_id, year):\n",
" team2 = getTeam2(match_id)\n",
" return matches.loc[(matches[\"id\"] < match_id) & (matches[\"season\"] == year) & ((matches[\"team1\"].isin(team2)) | (matches[\"team2\"].isin(team2)))].tail(3)\n",
"\n",
"def getTeamWinPercentage(match_id):\n",
" win = 0\n",
" total = 0\n",
" year = int(getMatchYear(match_id))\n",
" team1 = getTeam1(match_id)[0].strip(\"[]\")\n",
" team2 = getTeam2(match_id)[0].strip(\"[]\")\n",
" team1DF = getTeam1DF(match_id, year)\n",
" team2DF = getTeam2DF(match_id, year)\n",
" team1TotalMatches = team1DF.shape[0]\n",
" team1WinMatches = team1DF.loc[team1DF[\"winner\"] == team1].shape[0]\n",
" team2TotalMatches = team2DF.shape[0]\n",
" team2WinMatches = team2DF.loc[team2DF[\"winner\"] == team2].shape[0]\n",
" if (team1TotalMatches != 0) and (team2TotalMatches !=0):\n",
" winPercTeam1 = ((team1WinMatches / team1TotalMatches) * 100) \n",
" winPercTeam2 = ((team2WinMatches / team2TotalMatches) * 100) \n",
" elif (team1TotalMatches != 0) and (team2TotalMatches ==0):\n",
" winPercTeam1 = ((team1WinMatches / team1TotalMatches) * 100) \n",
" winPercTeam2 = 0\n",
" elif (team1TotalMatches == 0) and (team2TotalMatches !=0):\n",
" winPercTeam1 = 0\n",
" winPercTeam2 = ((team2WinMatches / team2TotalMatches) * 100) \n",
" else:\n",
" winPercTeam1 = 0\n",
" winPercTeam2 = 0\n",
" \n",
" return winPercTeam1, winPercTeam2\n",
" \n",
" \n",
"def displayTeamWin(match_id):\n",
" year = int(getMatchYear(match_id))\n",
" team1 = getTeam1(match_id)[0].strip(\"[]\")\n",
" team2 = getTeam2(match_id)[0].strip(\"[]\")\n",
" P,Q = getTeamWinPercentage(match_id)\n",
" print \"In the season of {}, {} has a win percentage of {}% and {} has a win percentage of {}% \".format(year, team1, P, team2, Q)"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#Function to implement all features\n",
"def getAllFeatures(match_id):\n",
" generateSquadRating(match_id)\n",
" print (\"\\n\")\n",
" getBothTeamStats(match_id)\n",
" print(\"\\n\")\n",
" displayTeamWin(match_id)\n"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Comparing squads for Mumbai Indians vs Chennai Super Kings\n",
"\n",
"Average Strike Rate for Batsmen in Mumbai Indians : 126.980245232\n",
"\n",
"Average Strike Rate for Batsmen in Chennai Super Kings : 128.555795104\n",
"\n",
"Bowler Rating (W/R) for Mumbai Indians : 2.76418065941\n",
"\n",
"Bowler Rating (W/R) for Chennai Super Kings : 4.4721111768\n",
"\n",
"Number of MVP Awards in Mumbai Indians : 28\n",
"\n",
"Number of MVP Awards in Chennai Super Kings : 52\n",
"\n",
"\n",
"Out of 21 times in the past Mumbai Indians have won 11 times(52.380952381%) from Chennai Super Kings\n",
"Mumbai Indians won by 144 total runs and 30 total wickets.\n",
"Chennai Super Kings won by 138 total runs and 31 total wickets.\n",
"\n",
"\n",
"In the season of 2015, Mumbai Indians has a win percentage of 66.6666666667% and Chennai Super Kings has a win percentage of 66.6666666667% \n"
]
}
],
"source": [
"#Testing Functionality\n",
"getAllFeatures(517)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Adding Columns\n"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/gursahej/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:3: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" This is separate from the ipykernel package so we can avoid doing imports until\n"
]
}
],
"source": [
"#Create Column for Team 1 Winning Status (1 = Won, 0 = Lost)\n",
"\n",
"matches['team1Winning'] = np.where(matches['team1'] == matches['winner'], 1, 0)"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/gursahej/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:10: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" # Remove the CWD from sys.path while we load stuff.\n"
]
}
],
"source": [
"#New Column for Difference of Average Strike rates (First Team SR - Second Team SR) [Negative value means Second team is better]\n",
"\n",
"firstTeamSR = []\n",
"secondTeamSR = []\n",
"for i in matches['id'].unique():\n",
" P, Q = getAverageStrikeRates(i)\n",
" firstTeamSR.append(P), secondTeamSR.append(Q)\n",
"firstSRSeries = pd.Series(firstTeamSR)\n",
"secondSRSeries = pd.Series(secondTeamSR)\n",
"matches[\"Avg_SR_Difference\"] = firstSRSeries.values - secondSRSeries.values "
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/gursahej/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:10: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" # Remove the CWD from sys.path while we load stuff.\n"
]
}
],
"source": [
"#New Column for Difference of Wickets Per Run (First Team WPR - Second Team WPR) [Negative value means Second team is better]\n",
"\n",
"firstTeamWPR = []\n",
"secondTeamWPR = []\n",
"for i in matches['id'].unique():\n",
" R, S = getAverageWPR(i)\n",
" firstTeamWPR.append(R), secondTeamWPR.append(S)\n",
"firstWPRSeries = pd.Series(firstTeamWPR)\n",
"secondWPRSeries = pd.Series(secondTeamWPR)\n",
"matches[\"Avg_WPR_Difference\"] = firstWPRSeries.values - secondWPRSeries.values "
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/gursahej/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:10: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" # Remove the CWD from sys.path while we load stuff.\n"
]
}
],
"source": [
"#New column for difference of MVP Awards (Negative value means Second team is better)\n",
"\n",
"firstTeamMVP = []\n",
"secondTeamMVP = []\n",
"for i in matches['id'].unique():\n",
" T, U = bothTeamMVPAwards(i)\n",
" firstTeamMVP.append(T), secondTeamMVP.append(U)\n",
"firstMVPSeries = pd.Series(firstTeamMVP)\n",
"secondMVPSeries = pd.Series(secondTeamMVP)\n",
"matches[\"Total_MVP_Difference\"] = firstMVPSeries.values - secondMVPSeries.values "
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/gursahej/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:8: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" \n"
]
}
],
"source": [
"#New column for win percentage of Team1 in previous encounter \n",
"\n",
"firstTeamWP = []\n",
"for i in matches['id'].unique():\n",
" WP = getTeamWinPerc(i)\n",
" firstTeamWP.append(WP)\n",
"firstWPSeries = pd.Series(firstTeamWP)\n",
"matches[\"Prev_Enc_Team1_WinPerc\"] = firstWPSeries.values\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/gursahej/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:10: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" # Remove the CWD from sys.path while we load stuff.\n"
]
}
],
"source": [
"#New column for Recent form(Win Percentage in the current season) of 1st Team compared to 2nd Team(Negative means 2nd team has higher win percentage)\n",
"\n",
"firstTeamRF = []\n",
"secondTeamRF = []\n",
"for i in matches['id'].unique():\n",
" K, L = getTeamWinPercentage(i)\n",
" firstTeamRF.append(K), secondTeamRF.append(L)\n",
"firstRFSeries = pd.Series(firstTeamRF)\n",
"secondRFSeries = pd.Series(secondTeamRF)\n",
"matches[\"Total_RF_Difference\"] = firstRFSeries.values - secondRFSeries.values "
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>id</th>\n",
" <th>season</th>\n",
" <th>city</th>\n",
" <th>date</th>\n",
" <th>team1</th>\n",
" <th>team2</th>\n",
" <th>toss_winner</th>\n",
" <th>toss_decision</th>\n",
" <th>result</th>\n",
" <th>dl_applied</th>\n",
" <th>winner</th>\n",
" <th>win_by_runs</th>\n",
" <th>win_by_wickets</th>\n",
" <th>player_of_match</th>\n",
" <th>venue</th>\n",
" <th>umpire1</th>\n",
" <th>umpire2</th>\n",
" <th>umpire3</th>\n",
" <th>team1Winning</th>\n",
" <th>Avg_SR_Difference</th>\n",
" <th>Avg_WPR_Difference</th>\n",
" <th>Total_MVP_Difference</th>\n",
" <th>Prev_Enc_Team1_WinPerc</th>\n",
" <th>Total_RF_Difference</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>489</th>\n",
" <td>490</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-01</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>8</td>\n",
" <td>0</td>\n",
" <td>AT Rayudu</td>\n",
" <td>Wankhede Stadium</td>\n",
" <td>HDPK Dharmasena</td>\n",
" <td>CK Nandan</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-13.536521</td>\n",
" <td>0.097342</td>\n",
" <td>5</td>\n",
" <td>60.000000</td>\n",
" <td>-33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>490</th>\n",
" <td>491</td>\n",
" <td>2015</td>\n",
" <td>Bangalore</td>\n",
" <td>2015-05-02</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>0</td>\n",
" <td>7</td>\n",
" <td>Mandeep Singh</td>\n",
" <td>M Chinnaswamy Stadium</td>\n",
" <td>JD Cloete</td>\n",
" <td>PG Pathak</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>4.510188</td>\n",
" <td>-0.570758</td>\n",
" <td>7</td>\n",
" <td>57.142857</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>492</th>\n",
" <td>493</td>\n",
" <td>2015</td>\n",
" <td>Chandigarh</td>\n",
" <td>2015-05-03</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>23</td>\n",
" <td>0</td>\n",
" <td>LMP Simmons</td>\n",
" <td>Punjab Cricket Association Stadium, Mohali</td>\n",
" <td>RK Illingworth</td>\n",
" <td>VA Kulkarni</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-13.615487</td>\n",
" <td>-0.737024</td>\n",
" <td>-1</td>\n",
" <td>46.666667</td>\n",
" <td>66.666667</td>\n",
" </tr>\n",
" <tr>\n",
" <th>493</th>\n",
" <td>494</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-03</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>14</td>\n",
" <td>0</td>\n",
" <td>AM Rahane</td>\n",
" <td>Brabourne Stadium</td>\n",
" <td>HDPK Dharmasena</td>\n",
" <td>CB Gaffaney</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>10.775508</td>\n",
" <td>0.786552</td>\n",
" <td>7</td>\n",
" <td>60.000000</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>494</th>\n",
" <td>495</td>\n",
" <td>2015</td>\n",
" <td>Chennai</td>\n",
" <td>2015-05-04</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>24</td>\n",
" <td>0</td>\n",
" <td>SK Raina</td>\n",
" <td>MA Chidambaram Stadium, Chepauk</td>\n",
" <td>C Shamshuddin</td>\n",
" <td>K Srinath</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>4.569589</td>\n",
" <td>-0.231439</td>\n",
" <td>25</td>\n",
" <td>58.823529</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>496</th>\n",
" <td>497</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-05</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>0</td>\n",
" <td>5</td>\n",
" <td>Harbhajan Singh</td>\n",
" <td>Wankhede Stadium</td>\n",
" <td>HDPK Dharmasena</td>\n",
" <td>CB Gaffaney</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>-18.726971</td>\n",
" <td>-0.755737</td>\n",
" <td>-14</td>\n",
" <td>53.333333</td>\n",
" <td>-33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>497</th>\n",
" <td>498</td>\n",
" <td>2015</td>\n",
" <td>Bangalore</td>\n",
" <td>2015-05-06</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>138</td>\n",
" <td>0</td>\n",
" <td>CH Gayle</td>\n",
" <td>M Chinnaswamy Stadium</td>\n",
" <td>RK Illingworth</td>\n",
" <td>VA Kulkarni</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-5.574733</td>\n",
" <td>0.886535</td>\n",
" <td>5</td>\n",
" <td>35.714286</td>\n",
" <td>66.666667</td>\n",
" </tr>\n",
" <tr>\n",
" <th>499</th>\n",
" <td>500</td>\n",
" <td>2015</td>\n",
" <td>Chennai</td>\n",
" <td>2015-05-08</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>0</td>\n",
" <td>6</td>\n",
" <td>HH Pandya</td>\n",
" <td>MA Chidambaram Stadium, Chepauk</td>\n",
" <td>CB Gaffaney</td>\n",
" <td>CK Nandan</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>5.014283</td>\n",
" <td>1.972348</td>\n",
" <td>17</td>\n",
" <td>52.631579</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>500</th>\n",
" <td>501</td>\n",
" <td>2015</td>\n",
" <td>Kolkata</td>\n",
" <td>2015-05-09</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>AD Russell</td>\n",
" <td>Eden Gardens</td>\n",
" <td>AK Chaudhary</td>\n",
" <td>HDPK Dharmasena</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>6.415078</td>\n",
" <td>0.254813</td>\n",
" <td>-18</td>\n",
" <td>40.000000</td>\n",
" <td>-33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>502</th>\n",
" <td>503</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-10</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>39</td>\n",
" <td>0</td>\n",
" <td>AB de Villiers</td>\n",
" <td>Wankhede Stadium</td>\n",
" <td>JD Cloete</td>\n",
" <td>C Shamshuddin</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-1.343308</td>\n",
" <td>2.062729</td>\n",
" <td>-3</td>\n",
" <td>43.750000</td>\n",
" <td>-33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>503</th>\n",
" <td>504</td>\n",
" <td>2015</td>\n",
" <td>Chennai</td>\n",
" <td>2015-05-10</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>12</td>\n",
" <td>0</td>\n",
" <td>RA Jadeja</td>\n",
" <td>MA Chidambaram Stadium, Chepauk</td>\n",
" <td>M Erasmus</td>\n",
" <td>CK Nandan</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-5.738591</td>\n",
" <td>-0.046456</td>\n",
" <td>16</td>\n",
" <td>62.500000</td>\n",
" <td>33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>505</th>\n",
" <td>506</td>\n",
" <td>2015</td>\n",
" <td>Raipur</td>\n",
" <td>2015-05-12</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Delhi Daredevils</td>\n",
" <td>0</td>\n",
" <td>6</td>\n",
" <td>Z Khan</td>\n",
" <td>Shaheed Veer Narayan Singh International Stadium</td>\n",
" <td>RK Illingworth</td>\n",
" <td>VA Kulkarni</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>6.941454</td>\n",
" <td>1.678318</td>\n",
" <td>28</td>\n",
" <td>73.333333</td>\n",
" <td>33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>506</th>\n",
" <td>507</td>\n",
" <td>2015</td>\n",
" <td>Chandigarh</td>\n",
" <td>2015-05-13</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>22</td>\n",
" <td>0</td>\n",
" <td>AR Patel</td>\n",
" <td>Punjab Cricket Association Stadium, Mohali</td>\n",
" <td>JD Cloete</td>\n",
" <td>C Shamshuddin</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>5.622383</td>\n",
" <td>-1.324729</td>\n",
" <td>-16</td>\n",
" <td>60.000000</td>\n",
" <td>-66.666667</td>\n",
" </tr>\n",
" <tr>\n",
" <th>507</th>\n",
" <td>508</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-14</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>5</td>\n",
" <td>0</td>\n",
" <td>HH Pandya</td>\n",
" <td>Wankhede Stadium</td>\n",
" <td>RK Illingworth</td>\n",
" <td>VA Kulkarni</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-0.677689</td>\n",
" <td>-0.313345</td>\n",
" <td>-11</td>\n",
" <td>66.666667</td>\n",
" <td>33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>509</th>\n",
" <td>510</td>\n",
" <td>2015</td>\n",
" <td>Chandigarh</td>\n",
" <td>2015-05-16</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Kings XI Punjab</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>0</td>\n",
" <td>7</td>\n",
" <td>P Negi</td>\n",
" <td>Punjab Cricket Association Stadium, Mohali</td>\n",
" <td>CK Nandan</td>\n",
" <td>C Shamshuddin</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>-0.716536</td>\n",
" <td>1.824407</td>\n",
" <td>-33</td>\n",
" <td>42.857143</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>510</th>\n",
" <td>511</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-16</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Kolkata Knight Riders</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>9</td>\n",
" <td>0</td>\n",
" <td>SR Watson</td>\n",
" <td>Brabourne Stadium</td>\n",
" <td>RM Deshpande</td>\n",
" <td>RK Illingworth</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-3.303823</td>\n",
" <td>-1.181868</td>\n",
" <td>-16</td>\n",
" <td>50.000000</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>513</th>\n",
" <td>514</td>\n",
" <td>2015</td>\n",
" <td>Mumbai</td>\n",
" <td>2015-05-19</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>25</td>\n",
" <td>0</td>\n",
" <td>KA Pollard</td>\n",
" <td>Wankhede Stadium</td>\n",
" <td>HDPK Dharmasena</td>\n",
" <td>RK Illingworth</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>6.315981</td>\n",
" <td>-0.617777</td>\n",
" <td>-24</td>\n",
" <td>50.000000</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>514</th>\n",
" <td>515</td>\n",
" <td>2015</td>\n",
" <td>Pune</td>\n",
" <td>2015-05-20</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Rajasthan Royals</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>bat</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>71</td>\n",
" <td>0</td>\n",
" <td>AB de Villiers</td>\n",
" <td>Maharashtra Cricket Association Stadium</td>\n",
" <td>AK Chaudhary</td>\n",
" <td>C Shamshuddin</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-2.200375</td>\n",
" <td>0.969143</td>\n",
" <td>5</td>\n",
" <td>50.000000</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>515</th>\n",
" <td>516</td>\n",
" <td>2015</td>\n",
" <td>Ranchi</td>\n",
" <td>2015-05-22</td>\n",
" <td>Royal Challengers Bangalore</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>0</td>\n",
" <td>3</td>\n",
" <td>A Nehra</td>\n",
" <td>JSCA International Stadium Complex</td>\n",
" <td>AK Chaudhary</td>\n",
" <td>CB Gaffaney</td>\n",
" <td>NaN</td>\n",
" <td>0</td>\n",
" <td>-0.521025</td>\n",
" <td>1.039181</td>\n",
" <td>-23</td>\n",
" <td>38.888889</td>\n",
" <td>33.333333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>516</th>\n",
" <td>517</td>\n",
" <td>2015</td>\n",
" <td>Kolkata</td>\n",
" <td>2015-05-24</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>Chennai Super Kings</td>\n",
" <td>field</td>\n",
" <td>normal</td>\n",
" <td>0</td>\n",
" <td>Mumbai Indians</td>\n",
" <td>41</td>\n",
" <td>0</td>\n",
" <td>RG Sharma</td>\n",
" <td>Eden Gardens</td>\n",
" <td>HDPK Dharmasena</td>\n",
" <td>RK Illingworth</td>\n",
" <td>NaN</td>\n",
" <td>1</td>\n",
" <td>-1.575550</td>\n",
" <td>-1.707931</td>\n",
" <td>-24</td>\n",
" <td>52.380952</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" id season city date team1 team2 toss_winner toss_decision result dl_applied winner win_by_runs win_by_wickets player_of_match venue umpire1 umpire2 umpire3 team1Winning Avg_SR_Difference Avg_WPR_Difference Total_MVP_Difference Prev_Enc_Team1_WinPerc Total_RF_Difference\n",
"489 490 2015 Mumbai 2015-05-01 Mumbai Indians Rajasthan Royals Rajasthan Royals field normal 0 Mumbai Indians 8 0 AT Rayudu Wankhede Stadium HDPK Dharmasena CK Nandan NaN 1 -13.536521 0.097342 5 60.000000 -33.333333\n",
"490 491 2015 Bangalore 2015-05-02 Kolkata Knight Riders Royal Challengers Bangalore Royal Challengers Bangalore field normal 0 Royal Challengers Bangalore 0 7 Mandeep Singh M Chinnaswamy Stadium JD Cloete PG Pathak NaN 0 4.510188 -0.570758 7 57.142857 0.000000\n",
"492 493 2015 Chandigarh 2015-05-03 Mumbai Indians Kings XI Punjab Mumbai Indians bat normal 0 Mumbai Indians 23 0 LMP Simmons Punjab Cricket Association Stadium, Mohali RK Illingworth VA Kulkarni NaN 1 -13.615487 -0.737024 -1 46.666667 66.666667\n",
"493 494 2015 Mumbai 2015-05-03 Rajasthan Royals Delhi Daredevils Delhi Daredevils field normal 0 Rajasthan Royals 14 0 AM Rahane Brabourne Stadium HDPK Dharmasena CB Gaffaney NaN 1 10.775508 0.786552 7 60.000000 0.000000\n",
"494 495 2015 Chennai 2015-05-04 Chennai Super Kings Royal Challengers Bangalore Chennai Super Kings bat normal 0 Chennai Super Kings 24 0 SK Raina MA Chidambaram Stadium, Chepauk C Shamshuddin K Srinath NaN 1 4.569589 -0.231439 25 58.823529 0.000000\n",
"496 497 2015 Mumbai 2015-05-05 Delhi Daredevils Mumbai Indians Delhi Daredevils bat normal 0 Mumbai Indians 0 5 Harbhajan Singh Wankhede Stadium HDPK Dharmasena CB Gaffaney NaN 0 -18.726971 -0.755737 -14 53.333333 -33.333333\n",
"497 498 2015 Bangalore 2015-05-06 Royal Challengers Bangalore Kings XI Punjab Kings XI Punjab field normal 0 Royal Challengers Bangalore 138 0 CH Gayle M Chinnaswamy Stadium RK Illingworth VA Kulkarni NaN 1 -5.574733 0.886535 5 35.714286 66.666667\n",
"499 500 2015 Chennai 2015-05-08 Chennai Super Kings Mumbai Indians Chennai Super Kings bat normal 0 Mumbai Indians 0 6 HH Pandya MA Chidambaram Stadium, Chepauk CB Gaffaney CK Nandan NaN 0 5.014283 1.972348 17 52.631579 0.000000\n",
"500 501 2015 Kolkata 2015-05-09 Kings XI Punjab Kolkata Knight Riders Kings XI Punjab bat normal 0 Kolkata Knight Riders 0 1 AD Russell Eden Gardens AK Chaudhary HDPK Dharmasena NaN 0 6.415078 0.254813 -18 40.000000 -33.333333\n",
"502 503 2015 Mumbai 2015-05-10 Royal Challengers Bangalore Mumbai Indians Royal Challengers Bangalore bat normal 0 Royal Challengers Bangalore 39 0 AB de Villiers Wankhede Stadium JD Cloete C Shamshuddin NaN 1 -1.343308 2.062729 -3 43.750000 -33.333333\n",
"503 504 2015 Chennai 2015-05-10 Chennai Super Kings Rajasthan Royals Chennai Super Kings bat normal 0 Chennai Super Kings 12 0 RA Jadeja MA Chidambaram Stadium, Chepauk M Erasmus CK Nandan NaN 1 -5.738591 -0.046456 16 62.500000 33.333333\n",
"505 506 2015 Raipur 2015-05-12 Chennai Super Kings Delhi Daredevils Chennai Super Kings bat normal 0 Delhi Daredevils 0 6 Z Khan Shaheed Veer Narayan Singh International Stadium RK Illingworth VA Kulkarni NaN 0 6.941454 1.678318 28 73.333333 33.333333\n",
"506 507 2015 Chandigarh 2015-05-13 Kings XI Punjab Royal Challengers Bangalore Royal Challengers Bangalore field normal 0 Kings XI Punjab 22 0 AR Patel Punjab Cricket Association Stadium, Mohali JD Cloete C Shamshuddin NaN 1 5.622383 -1.324729 -16 60.000000 -66.666667\n",
"507 508 2015 Mumbai 2015-05-14 Mumbai Indians Kolkata Knight Riders Kolkata Knight Riders field normal 0 Mumbai Indians 5 0 HH Pandya Wankhede Stadium RK Illingworth VA Kulkarni NaN 1 -0.677689 -0.313345 -11 66.666667 33.333333\n",
"509 510 2015 Chandigarh 2015-05-16 Kings XI Punjab Chennai Super Kings Kings XI Punjab bat normal 0 Chennai Super Kings 0 7 P Negi Punjab Cricket Association Stadium, Mohali CK Nandan C Shamshuddin NaN 0 -0.716536 1.824407 -33 42.857143 0.000000\n",
"510 511 2015 Mumbai 2015-05-16 Rajasthan Royals Kolkata Knight Riders Rajasthan Royals bat normal 0 Rajasthan Royals 9 0 SR Watson Brabourne Stadium RM Deshpande RK Illingworth NaN 1 -3.303823 -1.181868 -16 50.000000 0.000000\n",
"513 514 2015 Mumbai 2015-05-19 Mumbai Indians Chennai Super Kings Mumbai Indians bat normal 0 Mumbai Indians 25 0 KA Pollard Wankhede Stadium HDPK Dharmasena RK Illingworth NaN 1 6.315981 -0.617777 -24 50.000000 0.000000\n",
"514 515 2015 Pune 2015-05-20 Royal Challengers Bangalore Rajasthan Royals Royal Challengers Bangalore bat normal 0 Royal Challengers Bangalore 71 0 AB de Villiers Maharashtra Cricket Association Stadium AK Chaudhary C Shamshuddin NaN 1 -2.200375 0.969143 5 50.000000 0.000000\n",
"515 516 2015 Ranchi 2015-05-22 Royal Challengers Bangalore Chennai Super Kings Chennai Super Kings field normal 0 Chennai Super Kings 0 3 A Nehra JSCA International Stadium Complex AK Chaudhary CB Gaffaney NaN 0 -0.521025 1.039181 -23 38.888889 33.333333\n",
"516 517 2015 Kolkata 2015-05-24 Mumbai Indians Chennai Super Kings Chennai Super Kings field normal 0 Mumbai Indians 41 0 RG Sharma Eden Gardens HDPK Dharmasena RK Illingworth NaN 1 -1.575550 -1.707931 -24 52.380952 0.000000"
]
},
"execution_count": 72,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#Testing \n",
"matches.tail(20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Visualisation\n"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x1240fe590>"
]
},
"execution_count": 73,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEbCAYAAADTZlM/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAG6lJREFUeJzt3Xm4HVWZ7/FvBgbBAKE92qIoIvoioOJFBhWZBBFaQNQ2\nioIgqLSgICCNily0HUCR6TpgI5M4gKLggAjILJPIoITh5QKi3aKSlkACYTCQ/mOto5tjcqa9zzlJ\n1vfzPHmyq3bVqrV3KvWrWrVW7UkLFixAktSeyRNdAUnSxDAAJKlRBoAkNcoAkKRGGQCS1CgDQJIa\nNXWiK6DuRcQawF3AzXXWFGAecEBmXjkG21sA9GXm/wyyzL8AG2fmYb3e/niIiJ8AZ2XmqQPmnwrM\nzMyjRlnuhsCembl315Uc/jZfD3w+M9ev0+cB52fmsXX6xUACR2TmR+u8ZwL/DfQB3wEOysxbR7n9\nm4AtMvOBrj+MesoAWHo80v8fHCAi3gacCrxoguqzIbDqBG17cbYu8Nzx2FBEPA34OLAv5WDe7zxg\nK+DYOr0D8GNgR+Cjdd5WwJWZ+SCwfTf16NwvtXgxAJZe/wT8sX8iIt4HfAh4Avgz5aBwJ3AhcH1m\nHhwRW1NCYwPgSGAB8BLKWeAFwIcy86+dG4mITwDvAOYDd9Rynw/sDUyJiAcz8+MD1tm+lv8EcBOw\nNbApsAWwJ7Ai8GBmbrmw8jPzTxFxKfClzDyrlvm36YiYTzm4bVnL+lhm/qAutyfwAUrz519qebdH\nxGrAacBqwO+AZw7y3W4aEW8FVqrfy0HADGCfzHx13c7zgGuANTLz8TpvdeBTwMoRcUpm7hEROwCH\nAstSrtoOysyrI+JZwNeAZwH/XOv0tsy8LyLuAb4N/Avl3/n/Aq+p/25/BXbMzHuBbevnf0/dbr/z\ngMMjYnJmPkkJgI8BZ0TEmpl5N/A64Nxa73uAtwJPBz4D3A2sByxXP/Ml9cpoDvBSYHXgduDtmflQ\n/xUj8EZgZ+BJyonJ48BumTkzItYCTqacNPwRmAR8c+AVmHrLewBLj6dFxE31z++A44DPAUTEVsDB\nwJaZ+XLKweMcygH+XcBuEbETcAqwS2b+uZb5csrBeZ365/2dG4yIPYDtgA0z82XATODUzLwWOAE4\ncyEH/38CTgfeVc8MLwGe07HIupTmgi0XVf4wvospwP2ZuQHwNuDkiOiLiM2BdwOvzcxXAJ8HflDX\n+TJwTWauSwnKtQcp/7mUA+T69Tt6L/A94IURsU5dZi/gtP6DP0Bm/hdwGHBFPfi/CPgssH2tz/uA\nH0TEisDbgasz81XAmpRw2LWjDsvXf8sDgf8EjqvT/wXsXrd3TmZ+GLi/s/KZ+f/rvJdFxHQgKGH1\nU2CnutjfAmCAjYEv1vqeBBze8d4GwBsoJw2rAf+6kPU3Bz6YmesBVwIfqfNPB75T538IeNVC1lWP\nGQBLj0cyc/365/mUs+kzIuIFlP+UZ2bmLIB6VvUcytnpHykHsLOB/8zMyzvKPDUzH8rMx4BvUM4o\nO20HnJKZD9fp44DXRcSyg9RzM+DWzPx1rctplDPHfr/JzP7p0ZTf70u1/N9Q7o1sRjljXgu4qrZL\nfx5YNSJWpQTdqXWdO4GLByn79Mx8uB7cvwlsU19/HXhvREyhHIS/NkQdtwGeDVxU6/MtytnxWpl5\nXK3nAcBXKGfcT+9Y9/v177uAP/V/n3V6OE1v51H2ke2AC+uVwE+A19d7SmTmbQtZ73eZeVN9fcOA\nbf0sMx+rV4k3L6Ie12dmf3PUDZTvfzqwEeX769/uRcP4DOqSTUBLqcy8KiKS8h9rYUE/CVimvl6X\n0iy00YBl5ne8nkxpsmHAvIHTU2vZizJ/Ie8/2fH6oWGWv2BAOQNDYWF1n0I5eP87QERMppypzl5I\neZ3rD9T5PUyiNLtAOeD/EriMcqP4nkHKoNbnosyc0T+jNhPdGxFHUv49TqZcJS0zoH6Pdbx+SrPc\nMJ1HuUp5lHI1CCX0TqSE4cLO/gEe6Xg98Dsb7L3Blun/PjuXH7ivaQx4BbCUqj07XgzcCJwPzIiI\nvvreHpT27zsjYiNgP+CVwCoRsV9HMTMiYrmIWJ7SdPLjAZs5H9ijNllAuXS/vF4xzOfvAdPpSuDF\nEfGyWpe3AKtQDgYDDVb+rFpnIuKFwMsGrLtbfe//UJpzLqO0178jIp5dl9mbv59p/ozSBNPffr/l\nQurT7+0d38vulIMpmfl74GrgGOCri1i383u5mHLGvXbd7vbAb4DlKVdbx2bm6cB9lKuFKYPUaaQu\noTRhbU75nsnMeZSz8n1ZdAD0XL3iuxLYA6Betb6Ohe8T6iGvAJYeT6vNCP0mA+/LzDuAOyLiGODi\netY7i3JDbkVKF78PZuYfImJ34JcR0d8MNA+4ApgOnEW5R9DpJMoNv1/Wcu8E3lnfu4jSnv14Zn6w\nf4XMvD8i3gF8IyKeBH5FOSjOW8hnGqz8TwOn1e6mtwOXD1j3NfXG92RgRmbOBs6vZ9YX1m3PAd6c\nmQsiYh/glIi4jdJj5iYW7bfALyhNMmdTbh73O4XS/PTTRax7NfCZiDg7M3eudTwjIibV72HHzHw4\nIj4FHBURh9X5v6A0X/VEZj4SEXcAy9aePv3OBb4AXNqrbQ3TbsBJEfEB4A+U73hh+4R6aJKPg9bC\ndNvffZByV6L0ejk8M+fVM/RzgdUysyc743DGKYyFGlJfBu7JzCPHc9tLuoj4OPD92iNrZcqV0Haj\nHXug4fEKQOMiIpahdGX8DeWs/7qI+Cul/fptvTj416ad/r7tl0XEQ8BnM/OH9f1LKV1U+894p1C6\nMn46M78xRNmHA/tQzk6hNOPcDRyYmXdExDTKvYTLgIMj4oeU3jDHU+5rfAq4LTMH3khXcQdwZr0y\nm0oZlObBf4x5BaBxUQemvYfSVXCzRfQw6XYb5wI/z8xj6vQ6lLblV2fmbQPHDtRlXlmXeUZmzh2k\n7MPrMvt2zNuV0o1z3Y6eS/33EO4AVszMJyLiYuDkzPxm7z6t1D2vADRePgCcQWnH3x94f0R8G7ih\nv5kpIvamjFWYERGHUAaFzaW0778pM9cYYhvPptwLmZyZT2bmrRGxI+XMfFHWBB7mqb1qhiUzT68h\nsAtwQm16eh7lhvIywPUR8VtKb54X1JvwX6YMgtuccgVyI2WA3Zw64Opayg3tj1F6FH2plrkMcEZm\nfrZ207yIcp9hY0p3y49n5pkRMZXSvfWNlHsHVwEfyMzHazPLWyj3Re6p8+8d6efW0sNeQBpz9Ux8\nE+C7lBumu9YBYSdSehf12wM4MSK2pfSu2ZByxTBtmJs6iNKD5b6I+GFEfAS4OzP/1LHMF+pguXsi\n4s+Ukamv6xywNUK/pox+7fcI5dEJ/eMydqY0eX2kXpkcQjkwb1AHbt0LHNGx/szMfElmnk0ZHHVy\nHdC2EbB1vZKCElznZ+ZGwL9TDvpQgnYDygC19Sjf3YyI2K3Wc6M6AO+n1H73apdXABoP/wacm5n3\nA/fXs+L3U0YqL1+bYeZRHhdwEaUd/3tZHx4WEV+mdAscVGZeXJtfNqEM/NoBOCwitsrM6+piH8ny\nuIg+ykFwVmbe2MVnW8DIequ8kdLtdZuIgDJ+4b6O968AqF1fN6cMlPqP+t7TKV03f0m5d9Lf06hz\nQNbWlLEO/f3tZ9TyvksJkV/V7U4BVhhBvbUUMgA0puqBbDfg0drEAeUZOvtQuhueVN9/DDipdskc\nOFhsyEFBUZ5eeTilS+svKN0mPxsRX6dcZVzXuXxmzoqIGcDMiLgiM783yo+4If/YPXYwU4D9MvO8\nWu+nU/r993uoY7lJlPsX8+qyz6AM3HoG8HgdvQtPHXQ1n47+81GeKTS5lndkZn61zl+O0r1XDbMJ\nSGPtncD/ULp5rlHb8deknM32P7F0R8pzY/oPpOcCb6ndAaHcCxiqt8L9lMFS+9U+9UTECpT28xsW\ntkKWh559BjimY7DZsEV5sNyalKat4Tof2Dcilq3dRk+kPrNpQN3mUJ7Pc0Dd1iqUm9U7DVx2gJ8D\nu9SBapMpA9LeUbe7V+2GC6VX0ukjqLeWQgaAxtq/AUdn5t/O4mvTzvHA/rV9/gbKM4Dure/3P5Lg\n6oj4FbAyQzSzZOZ84PWUh4j9NiJmUm6onp+ZJw+y6lG17E8M47PMqPcPboyIX1NG626RmY8OY91+\n/0G5AXsjcCvlzP3ARSy7C7BJRNxM+SzfycxvDVH+14Dr65+bKU/WPJ7S3v8T4JqIuIVyo3n3EdRb\nSyG7gWqxU+8JvDozj6/TB1B+XGbG4GtKGgkDQIud2kxxEmUg1QLg95Tn9OzC3x8FMdAXhnF2PNg2\nAzhzEW+n4aOlkQEgSY3yHoAkNcoAkKRGGQCS1KgJHQg2a9Zcb0CMkenTV2D2bB+nriWH++zY6Oub\ntshf6PMKYCk1dWovfzxKGnvus+PPAJCkRhkAktQoA0CSGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1\nyp+ElDRuNttsY26//bYRrbP22i/h8suvHaMatc0AkDRuBjuQv+eIizn5kK3GsTYadQBExBTKz/YF\n5Uc79qb8YPWpdXomsE/HD1dLkhYj3dwD2AEgM18DHEr5ce2jgUMz87WU3zod6gesJUkTZNQBkJnn\nUH6mD+D5wAPABsBldd55wNZd1U6SNGa6ugeQmfMj4jRgZ+CtwDaZ2f+I57nAyoOtP336Cj4BcAz1\n9U2b6CpII+I+O766vgmcme+OiH8HrgWe1vHWNMpVwSL57O+x09c3jVmz5k50NaQRcZ/tvcFCddRN\nQBGxa0R8tE7OA54EfhURW9R52wFXjLZ8SdLY6uYK4AfAKRFxObAMsD9wG3BiRCxbX5/VfRUlSWNh\n1AGQmQ8Db1vIW5uPvjqSpPHioyAkqVEGgCQ1ykdBLMF8roqkbhgASzCfqyKpGzYBSVKjDABJapQB\nIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlRBoAkNcoAkKRGGQCS\n1CgDQJIaZQBIUqMMAElqlAEgSY0a1W8CR8QywMnAGsBywKeBW4FTgQXATGCfzHyyJ7WUJPXcaK8A\n3gX8JTNfC7wB+BJwNHBonTcJ2Kk3VZQkjYXRBsD3gE/U15OA+cAGwGV13nnA1t1VTZI0lkbVBJSZ\nDwFExDTgLOBQ4KjMXFAXmQus3JMaSpLGxKgCACAiVgfOBr6Smd+OiM93vD0NeGCoMqZPX4GpU6eM\ntgoaQl/ftImugjQi7rPja7Q3gZ8FXADsm5kX1dk3RsQWmXkpsB1wyVDlzJ49bzSb1zDNmjV3oqsg\njYj7bO8NFqqjvQL4GDAd+ERE9N8L2A84PiKWBW6jNA1JkhZTo70HsB/lgD/Q5t1VR5I0XhwIJkmN\nMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlRBoAkNcoAkKRGGQCS1CgD\nQJIaZQBIUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGmUASFKjDABJatTUblaOiI2B\nIzNzi4hYCzgVWADMBPbJzCe7r6IkaSyM+gogIg4Gvg4sX2cdDRyama8FJgE7dV89SdJY6eYK4C7g\nzcDpdXoD4LL6+jzg9cDZXZQvaQn1wWMv5+FH5494vfcccfGwl11x+an8v/03G/E29HejDoDM/H5E\nrNExa1JmLqiv5wIrD1XG9OkrMHXqlNFWQUPo65s20VVQox5+dD4//uLYNgLscOAP3ce71NU9gAE6\n2/unAQ8MtcLs2fN6uHkNNGvW3Imugho20v2vr2/aiNdxHx/aYCHZy15AN0bEFvX1dsAVPSxbktRj\nvbwCOBA4MSKWBW4Dzuph2ZKkHusqADLzHmCT+voOYPMe1EmSNA4cCCZJjTIAJKlRBoAkNcoAkKRG\n9bIXkMbIeIyqBEdWSq0xAJYADz86n5MP2WpE64xmUM1IA0PSks0mIElqlAEgSY0yACSpUQaAJDXK\nAJCkRhkAktQoA0CSGmUASFKjDABJapQBIEmNMgAkqVE+C0hSz+35+x9xx17fGNE6d4x0G8uuAozs\nGVl6KgNAUs+d9Lwdx/wBhkcccTGvGWnF9BQ2AUlSowwASWqUASBJjTIAJKlRBoAkNaqnvYAiYjLw\nFeDlwGPAXpl5Zy+3IUnqjV5fAbwJWD4zXwUcAnyxx+VLknqk1wGwKfAzgMy8Bnhlj8uXJPVIrweC\nrQQ82DH9RERMzcz5C1t4+vQVmDp1So+rsHTq65u22K4jLcx47H/ur93pdQDMATr/RSYv6uAPMHv2\nvB5vfuk1khGSMPJRlaPdjrQo47HPur8ObbCQ7HUT0JXA9gARsQlwc4/LlyT1SK+vAM4GtomIq4BJ\nwB49Ll+S1CM9DYDMfBLYu5dlanyerAg+XVFqjU8DXQKMx5MVwacrSq1xJLAkNcoAkKRGGQCS1CgD\nQJIaZQBIUqMMAElqlN1AJY2J9xxx8ZiWv+LyHr665TcoqedGOm4FSmCMZj2Nnk1AktQoA0CSGmUA\nSFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlRBoAk\nNaqr3wOIiJ2Bf83MXer0JsBxwHzggsz8ZPdVlCSNhVEHQEQcB2wL3NQx+wTgLcDdwLkR8YrMvLG7\nKgrG/teVwF9YklrTzf/4q4BzgPcDRMRKwHKZeVedPh/YGjAAuuSvK0kaC0MGQETsCXx4wOw9MvPM\niNiiY95KwJyO6bnAmoOVPX36CkydOmWYVdVI9fVNm+gqSCPiPju+hgyAzDwJOGkYZc0BOv/1pgEP\nDLbC7NnzhlGsRmvWrLkTXQVpRNxne2+wUO1ZL6DMnAM8HhEvjIhJlPsDV/SqfElSb/X6rt/ewLeA\nKZReQNf2uHxJUo90FQCZeSlwacf0NcAm3VVJkjQeHAgmSY0yACSpUQaAJDXKAJCkRhkAktQoA0CS\nGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlR\nBoAkNcoAkKRGGQCS1CgDQJIaZQBIUqMMAElq1NTRrBQRKwPfBFYClgUOyMyrI2IT4DhgPnBBZn6y\nZzWVJPXUaK8ADgAuyszNgd2BL9f5JwC7AJsCG0fEK7quoSRpTIzqCgA4Bniso4xHI2IlYLnMvAsg\nIs4HtgZu7LqWkqSeGzIAImJP4MMDZu+RmddFxD9TmoL2pzQHzelYZi6w5mBlT5++AlOnThlZjTVs\nfX3TJroK0oi4z46vIQMgM08CTho4PyJeCpwBHJSZl9UrgM5/vWnAA4OVPXv2vJHVViMya9bcia6C\n9BSbbbYxt99+2yLfn3T0P85be+2XcPnl145hrZZug4XqaG8CrwN8D5iRmb8GyMw5EfF4RLwQuBvY\nFvAmsKS/GexA3tc3zZOWcTbaewCfA5YHjosIgAczcydgb+BbwBRKLyBjW5IWU6MKgHqwX9j8a4BN\nuqqRJGlcOBBMkhplAEhSowwASWqUASBJjTIAJKlRBoAkNcoAkKRGGQCS1CgDQJIaZQBIUqMMAElq\nlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZ\nAJLUqKmjWSkiVgS+DUwHHgfenZl/iIhNgOOA+cAFmfnJntVUktRTo70CeC9wfWZuBnwTOLjOPwHY\nBdgU2DgiXtF9FSVJY2FUAZCZxwKfqZPPAx6IiJWA5TLzrsxcAJwPbN2bakqSem3IJqCI2BP48IDZ\ne2TmdRFxMfBSYBtgJWBOxzJzgTUHK3v69BWYOnXKyGqsv1lvvfW45ZZbFvn+M4/+x3nrrrsuM2fO\nHMNaSaPX1zdtoqvQlEkLFizoqoCIWBs4F3gFcE1mrlPn7wcsk5lHLWrdWbPmdrdxLVJf3zRmzZo7\n0dWQhs19dmz09U2btKj3RtUEFBEfjYhd6+RDwBOZOQd4PCJeGBGTgG2BK0ZTviRp7I2qFxBwMnBa\nbR6aAuxR5+8NfKvOuyAzr+2+ipKksdB1E1A3bAIaO15Oa0njPjs2et4EJEla8hkAktQoA0CSGmUA\nSFKjDABJatSE9gKSJE0crwAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSo0b7NFAthiJiMvAV4OXA\nY8BemXnnxNZKGlpEbAwcmZlbTHRdWuIVwNLlTcDymfkq4BDgixNcH2lIEXEw8HVg+YmuS2sMgKXL\npsDPADLzGuCVE1sdaVjuAt480ZVokQGwdFkJeLBj+omIsJlPi7XM/D7w14muR4sMgKXLHKDzV7Un\nZ+b8iaqMpMWbAbB0uRLYHiAiNgFuntjqSFqc2TywdDkb2CYirgIm8fffapakf+DTQCWpUTYBSVKj\nDABJapQBIEmNMgAkqVEGgCQ1ygDQYi8iVo6Ic8ZhO9tExEX19TIRMTciVu14/7qIuLBjOiLinohY\nLSJ+Ospt7hgRn+q+9tLIOQ5AS4LpwPpjVXh9iuqHgY9RB89l5l8j4krgVcC5EdFHOWGKiFghM+cB\nrwUuzMx7qQPwRiozfwT8qAcfQxoxA0BLguOB1SLibMpgt/0pB+PrgX0y89GI2BfYFVgReBKYkZm3\nRcQ9wJnAG4H5lIP8gcCLgAMz87vAS+qf9wIf6tjuxcBrgHOBbYCLgNWBzYHzKAFwbkSsAVyamWtE\nxKmU5zFtADwX+GRmnhIRhwPPqdt9PvD1zPxMROwObJGZu9e6ng5sWz/Hbpl5fUSsB5xK+f96BbBd\nZq7V7Zcq2QSkJcGHgHuBQykH6Vdn5vrAfcBBEbES5VHYW2TmesA5wAc61r83M9cFbqA8Jvv1wLuA\njwJk5i2ZuRdw/4DtXkQJACgH5fOBC+pr6ns/X0h9V6eEww7AUR3zX1a3vTFwSESsspB1/5KZGwEn\nUMIK4DTgsPqZ78YTN/WIAaAlyZaUM+hrIuImYCdg7cycA+wCvD0iPkc58D69Y73z6t+/Ay6rD8j7\nHaVpaTA3AmtFxLKUR23/ArgQ2CIingvcn5kDQwPggsxcAMwEVu2Yf0lmPp6Z91HCZuWFrPuz+vdM\nYNV6D2KNzOy/x3DyEHWWhs0A0JJkCvDdzFy/ng1vBOwbEasDVwOrUA72p1KehdTv8Y7Xw346amY+\nCVxLaVq6IzMfy8z/pvy/eQMlDBbm0br+wOesPNrxesGAOg5cpv/9JxaxnNQ1A0BLgvmUZo9LgZ0j\n4pkRMQn4KuV+wIbAnZl5DOWAvR0lLHrhYuAAStNPv0uA/Vh0APRMZj4I3BkR29VZu1DCQeqaAaAl\nwZ+B3wPHAp+kHJRvoey/R1AOzpMj4lbgGuAe4AU92vZFwDo8NQAuqOVf1aNtDOXdwGERcQPl/sEj\n47RdLeV8Gqi0mIuIw4ATM/OPEfFm4J2Z+ZaJrpeWfPYmkBZ/vwcujIi/ArOBPSe4PlpKeAUgSY3y\nHoAkNcoAkKRGGQCS1CgDQJIaZQBIUqMMAElq1P8C53RXGpdv3jgAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x124056e10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Graph for Strike Rate \n",
"matches.boxplot(column = 'Avg_SR_Difference', by='team1Winning', showfliers= False)"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x11d0824d0>"
]
},
"execution_count": 74,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAEbCAYAAADUCE9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGppJREFUeJzt3Xm4XlV59/FvyAExGPBgj1YURUVvFETeIiAOIaAoWMGx\nRkGQAAoiyKAvggOvtbWC1QrWGQNBrAUnqDUGxACiTFoQEIGbog2oWEklQiRMgfSPtY48nveMz9ln\n2vl+risX5xn23vd5eM5vr732WnvPWrt2LZKk9lpvqguQJE0sg16SWs6gl6SWM+glqeUMeklqOYNe\nklquZ6oL0OhFxBbAL4Cf1admA6uBYzLz0gnY3lqgLzP/Z5j3/DWwU2ae0PT2J0NEfAf4RmYuHvD8\nYuD6zPx4l+vdATgoMw8dd5Gj3+bLgY9l5nb18VLg/Mw8uT5+FpDAiZl5fH3u8cCvgT7gX4H3ZOYN\nXW7/GmB+Zv5h3L+MGmXQzzz39v8hA0TEG4HFwDOnqJ4dgE2naNvT2dbAkydjQxHxaOD9wOGU0O63\nFNgNOLk+3gv4d2Bv4Pj63G7ApZl5F/DK8dTR+b3U9GLQz3yPA37b/yAi3g68C3gI+B3lj/8W4ALg\nqsw8NiJeRtk5bA+cBKwFnk1p1X0PeFdmPti5kYj4IPBmYA1wc13vU4FDgdkRcVdmvn/AMq+s638I\nuAZ4GfBiYD5wELARcFdm7jrY+jPzvyPiYuDTmfmNus4/PY6INZQQ27Wu632Z+a36voOAwyjdk7+v\n67spIjYDzgA2A24FHj/MZ/viiHgDsHH9XN4DLADemZkvrNt5CnAFsEVmPlCf2xz4MLBJRJyemQsj\nYi/gA8AGlKOw92Tm5RHxBOALwBOAv6w1vTEz74iI5cBXgb+m/H/+f8CL6v+3B4G9M/N24BX19z+w\nbrffUuBDEbFeZj5MCfr3AWdFxNMz85fAS4Elte7lwBuAxwAfAX4JbAM8qv7OF9UjnbuB5wKbAzcB\nb8rMP/YfAQKvAl4LPExpgDwA7J+Z10fElsBplMbBb4FZwFcGHlGpWfbRzzyPjohr6r9bgVOAjwJE\nxG7AscCumfk8SkicSwnytwD7R8SrgdOBfTLzd3Wdz6OE8HPqv0M6NxgRC4E9gR0yc1vgemBxZl4J\nfB44e5CQfxxwJvCW2tK7CHhSx1u2phzm7zrU+kfxWcwG7szM7YE3AqdFRF9E7AK8FXhJZv4f4GPA\nt+oynwGuyMytKTvErYZZ/5MpQbhd/YzeBnwdeEZEPKe+52DgjP6QB8jMXwEnAD+sIf9M4B+AV9Z6\n3g58KyI2At4EXJ6ZOwNPp+wE9uuoYcP6//LdwBeBU+rjXwEH1O2dm5lHA3d2Fp+Z/1mf2zYieoGg\n7JS+C7y6vu1PQT/ATsAnar2LgA91vLY9sAelcbAZ8DeDLL8LcERmbgNcCvzf+vyZwL/W598F7DzI\nsmqYQT/z3JuZ29V/T6W0js+KiKdR/vjOzswVALWV9CRKa/O3lKA6B/hiZl7Ssc7FmfnHzLwf+DKl\nhdhpT+D0zLynPj4FeGlEbDBMnfOAGzLz2lrLGZSWYL/rMrP/cTfr7/fpuv7rKOcu5lFawFsCl9V+\n448Bm0bEppQd2uK6zC3AhcOs+8zMvKeG+FeA3evPXwLeFhGzKWH7hRFq3B14IrCs1vMvlNbulpl5\nSq3zGOCzlBb0YzqW/Wb97y+A/+7/POvj0XSZLaV8R/YELqgt++8AL6/nfMjMGwdZ7tbMvKb+fPWA\nbZ2XmffXo76fDVHHVZnZ3410NeXz7wV2pHx+/dtdNorfQeNk180Ml5mXRURS/oAG23HPAtavP29N\n6c7ZccB71nT8vB6lq4UBzw183FPXPZQ1g7z+cMfPfxzl+tcOWM/A8B+s9tmUkH4vQESsR2l5rhxk\nfZ3LD9T5OcyidJdACfYfAz+gnLBdPsw6qPUsy8wF/U/U7p3bI+Ikyv+P0yhHPesPqO/+jp//rDtt\nlJZSjjruoxzdQdm5nUrZ6Q3Wmge4t+PngZ/ZcK8N957+z7Pz/QO/a5oAtuhnuDqS4lnAT4HzgQUR\n0VdfW0jpn74lInYEjgSeDzw2Io7sWM2CiHhURGxI6fL49wGbOR9YWLsaoBxyX1KPANbwyI6k06XA\nsyJi21rL64HHUv7oBxpu/StqzUTEM4BtByy7f33tryjdMD+g9Ke/OSKeWN9zKI+0HM+jdJ3096/v\nOkg9/d7U8bkcQAlNMvM24HLgk8Dnhli283O5kNKC3qpu95XAdcCGlKOnkzPzTOAOSut/9jA1jdVF\nlK6nXSifM5m5mtLKPpyhg75x9QjuUmAhQD0KfSmDfyfUIFv0M8+j6+F/v/WAt2fmzcDNEfFJ4MLa\nil1BOTG2EWXo3BGZ+ZuIOAD4cUT0d9+sBn4I9ALfoPThd1pEOfH247reW4B962vLKP3ND2TmEf0L\nZOadEfFm4MsR8TDwH5TwWz3I7zTc+v8eOKMO47wJuGTAsi+qJ6DXAxZk5krg/NpSvqBu+27gdZm5\nNiLeCZweETdSRqhcw9D+C/gRpSvlHMpJ3H6nU7qNvjvEspcDH4mIczLztbXGsyJiVv0c9s7MeyLi\nw8DHI+KE+vyPKN1OjcjMeyPiZmCDOrKm3xLgH4GLm9rWKO0PLIqIw4DfUD7jwb4TatAsL1O8bhvv\nePFh1rsxZZTJhzJzdW1xLwE2y8xGvnSjGec/EerO6DPA8sw8aTK3PdNFxPuBb9YRUJtQjmz27Hbs\nvkbHFr26FhHrU4YDXpeZe3S+lpl3R8QDwE8i4kFK//IbxxLyEfFeYOfMfE19PIvSCr+tjlLpf9/P\nKaM6dgTeSWkprqV0gdwBHJaZN0fEhzpeh9JXvDGltf7u4WqLiPmUrpv/pIxMuhe4ISKuy8yl9T1f\nAs7KzO/XQDuEcsRzCuWk6l2UI4vlo/0MWuhm4Ox6pNVDmbxlyE8wW/TqWp2sdSBluN28IUZvjGf9\n21K6Fv4iMx+OiO2Bf6Z0bWxTx5o/kdLV8xfAe+t7D+9YxxHAWzPz+TXoB77eS2lVHpyZ5w9Ty3zK\n+P1tOp57HqXf+9V1qGnn+39JGTv+o9ot85TMPHgcH4fUNVv0Go/DgLMoQXsUcEhEfBW4ur8rKCIO\npYzrXxARx1EmSq2i9LW/JjO3GGrlmXldRKymnIC9hjLh5zuU8dt7Ufr2dwMuqn3Rg61mGXWewRCe\nAMyhjMgZk8y8NiI+BRxNOXF7MaXf/m8oY/AXRcQ/UD6n2RHx6MzcN4aezLWYMlTxGfX3/CBlwtku\nlKOTn1Ims91dJzctppzMfAplWO2xABFxIGXc/UPA/1B2dL8aatLWWH9vzTyOulFX6oShFwBfo5yk\n3K9OkjqVMnKn30Lg1Ih4BWXkyg6UI4C5o9zUeZRx4PBI0C+hTOOHoSf8EBE9lB3LRR1PL6iTzW6O\niN9TjhAOycwfj7Kega6lzBL9kzqM8nZg3zp/oH9S2b4jTOYCmJOZW9ehocdRTtBuXydJ3Q6c2PHe\nx2TmS4AXAkdExNPqUcZJwB518tm3gfePMGlLLWeLXt16B7AkM+8E7oyI/6L0SX8U2DAink9pNfZR\nWtUnA1/PesGriPgMJaRHspSyE/k68Ljayr8N+FydsLQbfz5rc0FEvLj+vAFwFWWiWL+zM/PwOhnr\n05QJSkvH/uv/yVrGNmqkczJX/3P9k7mgjLrp9yrKkNTd63s3oJxz6PdvAHUk1R2Uo4FdKBcy+1V9\nrf+CZofxyKSt/uUfrrVci1rNoNeY1Vbg/sB9tQsByknNd1KG7C2qr98PLKrDGgdOoBrtRJnvU0a4\nvIo6lDEz/xAR1wGvA1bVce39zu7sgx9KZj4QEYdTdgQfq7V3YwceuZroaAw3mQv+fCLZbODIjpO9\nj6GMve832KSkNXSMS49ywbOnMsykrTHUrhnKrht1Y19K3+9mmblF7Wd/OmW8ef/VNPem9FX3j8lf\nAry+DqmD0qUy4kiAOvY7KX3a3+l46TuUKzZ2PeGnXs7gHZRzC3811uXrJLR3UEbVjNZwk7kGOh84\nPCI2qDuEUxn+fAOUbqqXdaz/EMqObLhJW2o5g17deAfwT5n5p1Z57ZL5FHBUZv43ZebldVmurkhm\n9k+7vzwi/gPYhNF3eSyldDF0XpdmCeVCY+Oa2ZmZP6Jce+bTdfjmcJ4Rj1xQ7mpKX/g+HdefGc32\nzq/LXVCPSvahTuYa5O1/ByynnIS9gdJif/cI6/8ZZajpeRFxLeX6R4dm5s8p/fJn1ef/jjppa7S1\na+ZyeKUmRe2zf2Fmfqo+PoZyw5IFwy8pabwMek2KOlN2EWVo5FrgNkoLcx8eudzBQP+Ymf8yORVC\nRPyQoUcDvSQzV01WLVKTDHpJajn76CWp5Qx6SWo5g16SWm7SJkytWLHKkwEToLd3DitXejlvzRx+\nZydGX9/cIYcH26Kf4Xp6mrwZkTTx/M5OPoNeklrOoJekljPoJanlDHpJajmDXpJazqCXpJYz6CWp\n5Qx6SWq5cc2MjYjHU27Ftntm3tRMSRrMvHk7cdNNN45pma22ejaXXHLlBFUkaaboOugjYn3gC/z5\nfSs1QYYK7ANPvJDTjtttkquRNJOMp+vm48Dn8ebCkjStddWij4gDgBWZeX5EHD+aZXp753iNiwnS\n1zfUTZGk6cnv7OTqtuvmQGBtRLwM2A74ckTsXW8KPSivVjdxVqzwDneaOfr65vqdnQDD7Ty7CvrM\nnNf/c0RcTLnL/JAhL0maOg6vlKSWG/eNRzJzfgN1SJImiC16SWo5g16SWs6gl6SWM+glqeXGfTJW\nkgby2kzTi0EvqXHDBbbXZ5p8dt1IUssZ9JLUcga9JLWcQS9JLWfQS1LLGfSS1HIGvSS1nEEvSS1n\n0EtSyxn0ktRyBr0ktVzX17qJiNnAqUAAayn3jb2+qcIkSc0YT4t+L4DMfBHwAeAjjVQkSWpU10Gf\nmecCb68Pnwr8oZGKJEmNGtdlijNzTUScAbwWeMNw7+3tnUNPz+zxbE5D6OubO9UlSGPid3Zyjft6\n9Jn51oh4L3BlRDwnM+8Z7H0rV64e76Y0hBUrVk11CdKY+J1t3nA7z667biJiv4g4vj5cDTxc/0mS\nppHxtOi/BZweEZcA6wNHZea9zZQlSWpK10Ffu2je2GAtkqQJ4IQpSWo5g16SWs6gl6SWM+glqeUM\neklqOYNeklrOoJekljPoJanlDHpJajmDXpJazqCXpJYz6CWp5Qx6SWo5g16SWs6gl6SWM+glqeW6\nuvFIRKwPnAZsATwK+PvM/HaDdUmSGtJti/4twO8z8yXAHsCnmytJktSkbm8l+HXgG/XnWcCaZsqR\nJDWtq6DPzD8CRMRcSuB/YKRlenvn0NMzu5vNaQR9fXOnugRpTPzOTq6ubw4eEZsD5wCfzcyvjvT+\nlStXd7spjWDFilVTXYI0Jn5nmzfczrPbk7FPAL4HHJ6Zy7qsS5I0Cbpt0b8P6AU+GBEfrM/tmZn3\nNlOWJKkp3fbRHwkc2XAtkqQJ4IQpSWo5g16SWs6gl6SWM+glqeUMeklqOYNeklrOoJekljPoJanl\nDHpJajmDXpJazqCXpJYz6CWp5Qx6SWo5g16SWs6gl6SW6/pWgmreESdfwj33jf0+6weeeOGY3r/R\nhj3881HzxrwdSTPTuII+InYCTsrM+c2Us2675741nHbcbmNapq9v7pjvvznWHYOkmW08Nwc/FtgP\nuKe5ciTNJB6FzgzjadH/AngdcGZDtUiaYTwKnRm6DvrM/GZEbDHa9/f2zqGnZ3a3m1tn9PXNnbbL\nSIPxOzv9TdrJ2JUrV0/Wpma0sbZ0umkddbMdaSh+Z6eH4XaEDq+UpJYz6CWp5cbVdZOZy4EXNFOK\nJGki2KKXpJYz6CWp5Qx6SWo5g16SWs6gl6SWM+glqeUMeklqOYNeklrOoJekljPoJanlDHpJajmD\nXpJazqCXpJabtBuPSGqfg277Njcf/OUxLXNzN9vZ4LHA2G5ZqEcY9JK6tugpe0/KPWNPPPFCXjSm\nJdTJrhtJarmuWvQRsR7wWeB5wP3AwZl5S5OFSZKa0W2L/jXAhpm5M3Ac8InmSpIkNanboH8xcB5A\nZl4BPL+xiiRJjer2ZOzGwF0djx+KiJ7MXDPUAr29c+jpmd3l5tYdfX1zp+0y0mD8zk5/3Qb93UDn\np77ecCEPsHLl6i43tW4Z62iEbkYwdLMdaSh+Z6eH4XaE3Qb9pcBewNci4gXAz7pcjzo4JlnSROg2\n6M8Bdo+Iy4BZwMLmSlp3OSZZ0kToKugz82Hg0IZrkSRNACdMSVLLGfSS1HIGvSS1nEEvSS1n0EtS\nyxn0ktRyBr0ktZxBL0ktZ9BLUssZ9JLUcga9JLWcQS9JLWfQS1LLGfSS1HLdXo9ekgA48MQLJ3wb\nG21oVI2Hn56kro31RjlQdgzdLKfujavrJiJeGxFfbaoYSVLzum7RR8QpwCuAa5orRx4GS2raeP7i\nLwPOBQ5pqJZ1nofBkibCiEEfEQcBRw94emFmnh0R80e7od7eOfT0zB5jeRqNvr65U12CNCZ+ZyfX\niEGfmYuARePd0MqVq8e7Cg1hxYpVU12CNCZ+Z5s33M7TcfSS1HIGvSS13LiGX2TmxcDFjVQiSZoQ\ntuglqeUMeklqOYNeklrOoJekljPoJanlDHpJajmDXpJazqCXpJYz6CWp5Qx6SWo5g16SWs6gl6SW\nM+glqeUMeklqOYNeklrOoJekljPoJanlurrDVERsAnwF2BjYADgmMy9vsjBJUjO6bdEfAyzLzF2A\nA4DPNFaRJKlR3d4z9pPA/R3ruK+ZciRJTRsx6CPiIODoAU8vzMyfRMRfUrpwjhppPb29c+jpmd1d\nlRpWX9/cqS5BGhO/s5NrxKDPzEXAooHPR8RzgbOA92TmD0Zaz8qVq7sqUCNbsWLVVJcgjYnf2eYN\nt/Ps9mTsc4CvAwsy89ou65IkTYJu++g/CmwInBIRAHdl5qsbq0qS1Jiugt5Ql6SZwwlTktRyBr0k\ntZxBL0ktZ9BLUssZ9JLUcga9JLWcQS9JLWfQS1LLGfSS1HIGvSS1nEEvSS1n0EtSyxn0ktRyBr0k\ntZxBL0ktZ9BLUst1eyvBjYCvAr3AA8BbM/M3TRYmSWpGty36twFXZeY84CvAsc2VJElqUre3Ejw5\nImbXh08B/tBcSZKkJo0Y9BFxEHD0gKcXZuZPIuJC4LnA7iOtp7d3Dj09s0d6m7rQ1zd3qkuQxsTv\n7OQaMegzcxGwaIjXdouIrYAlwDOGW8/Klau7KlAjW7Fi1VSXII2J39nmDbfz7KqPPiKOj4j96sM/\nAg91sx5J0sTrqo8eOA04o3brzAYWNleSJKlJ3Z6M/R2wR8O1SJImgBOmJKnlDHpJajmDXpJazqCX\npJYz6CWp5Qx6SWo5g16SWq7bCVOSNKR583bipptuHPL1x//T///cVls9m0suuXICq1p3GfSSGjdc\nYPf1zfVaN5PMrhtJajmDXpJazqCXpJYz6CWp5Qx6SWo5g16SWs6gl6SWG9c4+nq/2CuBJ2Tmfc2U\nJElqUtct+ojYGPgEcH9z5UiSmtZViz4iZgFfBN4H/FujFWlQw00pH2w6OTilXFIxYtDXG4AfPeDp\nW4GzMvPaiBjVhnp759DTM3vsFQqAG2+8YapLkBrT1zd3qktYp8xau3btmBeKiFuAX9eHLwB+nJnz\nhltmxYpVY9+QRuR1QzTT+J2dGH19c2cN9VpXXTeZuWX/zxGxHHh5N+uRJE08h1dKUsuN+zLFmblF\nA3VIkiaILXpJajmDXpJazqCXpJYz6CWp5boaRy9Jmjls0UtSyxn0ktRyBr0ktZxBL0ktZ9BLUssZ\n9JLUcuO+1o2mRkSsB3wWeB7lLl8HZ+YtU1uVNLyI2Ak4KTPnT3Ut6xJb9DPXa4ANM3Nn4DjKbR2l\naSsijgW+BGw41bWsawz6mevFwHkAmXkF8PypLUca0S+A1011Eesig37m2hi4q+PxQxFhV5ymrcz8\nJvDgVNexLjLoZ667gc4bb66XmWumqhhJ05dBP3NdCrwSICJeAPxsasuRNF15qD9znQPsHhGXAbOA\nhVNcj6RpyqtXSlLL2XUjSS1n0EtSyxn0ktRyBr0ktZxBL0ktZ9Br2oiITSLi3EnYzu4Rsaz+vH5E\nrIqITTte/0lEXNDxOCJieURsFhHf7XKbe0fEh8dfvTR2jqPXdNILbDdRK69X/DwaeB91gllmPhgR\nlwI7A0sioo/SAIqImJOZq4GXABdk5u3USWpjlZnfBr7dwK8hjZlBr+nkU8BmEXEOZULYUZTQvQp4\nZ2beFxGHA/sBGwEPAwsy88aIWA6cDbwKWEMJ83cDzwTenZlfA55d/70NeFfHdi8EXgQsAXYHlgGb\nA7sASylBvyQitgAuzswtImIx5VpD2wNPBv42M0+PiA8BT6rbfSrwpcz8SEQcAMzPzANqrWcCr6i/\nx/6ZeVVEbAMspvxd/hDYMzO3HO+HKtl1o+nkXcDtwAcoYfzCzNwOuAN4T0RsTLk88/zM3AY4Fzis\nY/nbM3Nr4GrKpZtfDrwFOB4gM3+emQcDdw7Y7jJK0EMJ3/OB79Wfqa99f5B6N6fsBPYCPt7x/LZ1\n2zsBx0XEYwdZ9veZuSPwecpOCeAM4IT6O/8SG2JqiEGv6WhXSov4ioi4Bng1sFVm3g3sA7wpIj5K\nCdjHdCy3tP73VuAH9SJvt1K6hIbzU2DLiNiAcvnnHwEXAPMj4snAnZk5cOcA8L3MXAtcD2za8fxF\nmflAZt5B2alsMsiy59X/Xg9sWs8RbJGZ/ecAThuhZmnUDHpNR7OBr2XmdrV1uyNweERsDlwOPJYS\n6osp1/np90DHz6O+kmdmPgxcSekSujkz78/MX1P+PvaghP5g7qvLD7yOyH0dP68dUOPA9/S//tAQ\n75PGzaDXdLKG0l1xMfDaiHh8RMwCPkfpr98BuCUzP0kJ5j0pO4UmXAgcQ+my6XcRcCRDB31jMvMu\n4JaI2LM+tQ9lJyCNm0Gv6eR3wG3AycDfUsL355Tv6YmUEF4vIm4ArgCWA09raNvLgOfw50H/vbr+\nyxraxkjeCpwQEVdT+vfvnaTtquW8eqU0TUTECcCpmfnbiHgdsG9mvn6q69LM51l9afq4DbggIh4E\nVgIHTXE9aglb9JLUcvbRS1LLGfSS1HIGvSS1nEEvSS1n0EtSyxn0ktRy/wvhGTZsjievEwAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11e74a390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Graph for WPR Difference\n",
"matches.boxplot(column = 'Avg_WPR_Difference', by='team1Winning', showfliers= False)"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x11d0ad590>"
]
},
"execution_count": 75,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEbCAYAAADTZlM/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGtpJREFUeJzt3XmYH1Wd7/F3Jw3GQIDg084VcWQU/YI4gBPZhsWAogIK\nggsKLgTQQREVdRhcLi5XhuXKCK6oBALqKI4sV2UJSNhk8xpEQOEbAwIqLj0aSCBsgcwfp1p+tN2d\n7nR1Ounzfj1PnvyqflWnTlcq9ak6dU511/Lly5Ek1WfSeFdAkjQ+DABJqpQBIEmVMgAkqVIGgCRV\nygCQpEp1j3cFNHoRsQlwB3BLM2sysBT4YGZeMwbbWw70ZOZ/D7HMXsB2mXlM29tfFSLih8D3MnNO\nv/lzgFsz87MrWe42wCGZedioKzn8bb4SODEzt26mLwLmZubJzfQLgQSOz8yPNPOeCfwW6AG+DXw4\nM3+5ktu/CZiZmfeN+odRqwyAieOhvv/gABHxJmAO8IJxqs82wIbjtO3V2RbAxqtiQxHxdOBjwHsp\nJ/M+FwG7ASc3068FfgDsDXykmbcbcE1m3g/sOZp6dB6XWr0YABPXM4Df901ExLuA9wGPA3+knBQW\nApcC8zPzqIh4BSU0ZgAnAMuBzSlXgZcA78vMxzo3EhH/G3gLsAxY0JT7XOAwYHJE3J+ZH+u3zp5N\n+Y8DNwGvAHYCZgKHAOsA92fmrgOVn5l/iIgrgC9m5veaMv86HRHLKCe3XZuyPpqZ5zbLHQK8h9L8\n+eemvNsjYiPgTGAj4G7gmUPs250i4g3Aes1++TCwP3B4Zv5zs52/B64HNsnMR5t5zwE+DawfEWdk\n5qyIeC3wcWBtyl3bhzPzuoj4O+CrwN8B/6up05sy808RcRfwn8BelH/nTwA7Nv9ujwF7Z+a9wKua\nn//gZrt9LgI+GRGTMvMJSgB8FPhORDwvM+8EXg5c0NT7LuANwLrAscCdwIuBpzU/8+XNndFi4B+B\n5wC3A2/OzAf67hiB1wD7Ak9QLkweBd6embdGxKbA6ZSLht8DXcA3+9+BqV0+A5g4nh4RNzV/7gZO\nAY4DiIjdgKOAXTNzK8rJ43zKCf6twNsjYh/gDOCAzPxjU+ZWlJPzi5o//9K5wYiYBewBbJOZWwK3\nAnMy8wbgVODsAU7+zwC+Aby1uTK8HHh2xyJbUJoLdh2s/GHsi8nAXzJzBvAm4PSI6ImIlwHvAHbO\nzJcAJwLnNut8Cbg+M7egBOVmQ5S/MeUEuXWzj94J/Bfw/Ih4UbPMocCZfSd/gMz8DXAMcHVz8n8B\n8O/Ank193gWcGxHrAG8GrsvMHYDnUcLhbR11mNL8W34I+BpwSjP9G+CgZnvnZ+aRwF86K5+Zv2rm\nbRkR04GghNWFwD7NYn8NgH62A05q6jsb+GTHdzOAV1MuGjYC3jjA+i8DjsjMFwPXAP/azP8G8O1m\n/vuAHQZYVy0zACaOhzJz6+bPcylX09+JiH+g/Kc8OzN7AZqrqmdTrk5/TzmBnQd8LTOv6ihzTmY+\nkJmPAGdRrig77QGckZkPNtOnAC+PiLWHqOcuwC8z8+dNXc6kXDn2uTkz+6ZXpvw+X2zKv5nybGQX\nyhXzpsC1Tbv0icCGEbEhJejmNOssBOYNUfY3MvPB5uT+TWD35vNpwDsjYjLlJPzVFdRxd+BZwGVN\nfb5FuTreNDNPaer5QeDLlCvudTvWPaf5+w7gD337s5keTtPbRZRjZA/g0uZO4IfAK5tnSmTmbQOs\nd3dm3tR8vrHfti7OzEeau8RbBqnH/Mzsa466kbL/pwPbUvZf33YvG8bPoFGyCWiCysxrIyIp/7EG\nCvouYK3m8xaUZqFt+y2zrOPzJEqTDf3m9Z/ubsoezLIBvn+i4/MDwyx/eb9y+ofCQHWfTDl5/xtA\nREyiXKkuGqC8zvX769wPXZRmFygn/J8AV1IeFN81RBk09bksM/fvm9E0E90bESdQ/j1Op9wlrdWv\nfo90fH5Ks9wwXUS5S3mYcjcIJfS+TgnDga7+AR7q+Nx/nw313VDL9O3PzuX7H2saA94BTFBNz44X\nAj8D5gL7R0RP890sSvv3wojYFng/8FJgg4h4f0cx+0fE0yJiCqXp5Af9NjMXmNU0WUC5db+quWNY\nxpMB0+ka4IURsWVTl9cDG1BOBv0NVX5vU2ci4vnAlv3WfXvz3T9RmnOupLTXvyUintUscxhPXmle\nTGmC6Wu/33WA+vR5c8d+OYhyMiUz7wGuAz4HfGWQdTv3yzzKFfdmzXb3BG4GplDutk7OzG8Af6Lc\nLUweok4jdTmlCetllP1MZi6lXJW/l8EDoHXNHd81wCyA5q715Qx8TKhF3gFMHE9vmhH6TALelZkL\ngAUR8TlgXnPV20t5ILcOpYvfEZn5u4g4CPhJRPQ1Ay0FrgamA9+jPCPoNJvywO8nTbkLgQOb7y6j\ntGc/mplH9K2QmX+JiLcAZ0XEE8BPKSfFpQP8TEOV/xngzKa76e3AVf3W3bF58D0J2D8zFwFzmyvr\nS5ttLwb2y8zlEXE4cEZE3EbpMXMTg/s18GNKk8x5lIfHfc6gND9dOMi61wHHRsR5mblvU8fvRERX\nsx/2zswHI+LTwGcj4phm/o8pzVetyMyHImIBsHbT06fPBcD/Ba5oa1vD9HZgdkS8B/gdZR8PdEyo\nRV2+DloDGW1/9yHKXY/S6+WTmbm0uUK/ANgoM1s5GIczTmEsNCH1JeCuzDxhVW57TRcRHwPOaXpk\nrU+5E9pjZcceaHi8A9CoRMTnKQ9YofQU+jVPtvPukJmdbb5k5uLmRPmniFhIab9+00An/4g4FHhN\nZr5uiO13N2XcmZnP7/fd/6GEzUsovWUWZ+bh/ZbZH/g3Snv7Y5SeRo9Tmh/WAs7KzBNXsA8+Q2lO\n2oBy1frbiNiRMhBvYfNQeD6wc7Nvzqd0gzyZ0hXyE8AtmbnXUNuZ4BYAZzd3Zt2UQWme/MeYdwBq\nTV9/8cz86QqW2xT4aWZusILlRhIA9wBvycxrm/ldwG2UPvQzKe3qF1LuNB7uWP8ySu+bs5pypveN\nWI2IDYCfA/+SmRcPUYfPAOtm5gc65s0CPgW8KDMf6Jj/PEoPmWmZ+UTT3PblzPzOUPtCGgveAWjM\nNP3uT6ScfB8FPpaZl1DayadFxE2ZuXVEvJPSI2VtStfBYzPzayPc3DcpYxqubaZnUtrxdwLIzOub\ngNqX8tyjL4i2ojwP+RuZeV9EzKc8RB40AAZZ94yIeBvlgfEcmnChdLWcAtwYEfcA/wQcF+XVC1+l\n7K+dKQ985wPvz8wlEfFbynOArShjOm6iPGvYmHKn8q3MPKH5mS4EfkQZjb0B8JFmgNxalPb9PSnP\nFa6mPPBdRrlT2pfyzORO4D2Z+YeR/Mxa89gLSGOi6XH0XcpI0a0oo1H/s+lhMwtY0pz812um92gG\nFx1IGSU8Ut8CXt+c5KD0WprTb5kvUUYa93knZZzBQwwgIjanBEj/B8zD9XPKyNhOe9P87Jm5N+VE\nfmRmfp7y2oaHgBnNPvtvysjbv5aXmZtn5g8oP++pzWC37YA9I2K/ZrkXAN/PzG0oJ/a+/XkEpbfU\nlpRxBc+gDNaaRQm5bZvBeT+iDC7TBOcdgMbKDsDtfc1BmXlLRNxA6XZ4Xd9CzTOBfYDXNiNjX8JT\nBzwN172Uk+meEfEjYHueerKHcuV/YjPQ6XeUnic79lvm6ojoGzPwAOXkfONK1AfKc4SR9GR5DeVn\nf3VEQLkjurezbvDXB+k7Uu4cjmu+W5fSrfNmyhiBuc38zsFar6A80+hrAntDU965lDuRnzbbnczf\njqvQBGQAaKwMdHc5iX5jAyLiuZSmjVMpJ7hz+dsRx8N1FqUZaH3g/Mx8vDmhAaWfe0ScSbnivYUy\nKvXOfmXsnO29tXIbBh8PMJDJlDumSwEiYhpPPRE/0LEclLetPtIs20MJm2cBD3c8VO8ckLWMjr71\nUd43NKkp79jM/Hozfwql6UgTnE1AGivXAVtERN9grX+kXLVeQTkRdTcParehvPzr3zNzLuXFZCt7\nXJ5HucN4N4O/M+grlJfLvYPSJNS6iOhq+vdvzJOvbBiOucAREbFW03PodMp4h6doxjTMB45stjed\nsr8HfJbR4UfAgRGxdtMT62uUJqC5lFdYTGuWO5a/HfOhCcgA0JjI8kK5/YGvRMQtlJd9va254v4d\n5Qr8l5S3kfYCGRE/o/TaWdSM7h3pNpdSxhR0ZebtgyzzK0pX1WCED3ZX4MAoL+L7GaUpajfKS+0e\nWcF6nT7Jk4PQfkF5cPyvgyz7ZmCXiLiZ8iK3MzPz7BWU/2VKE9GNlP1/NyUET6WMkr4+In5BeR5w\n8AjqrTWU3UAlqVI+A9Bqr99gs/6OyMyrx3j7L6K8Qnsgv8jMAwf5TlqteQcgSZXyGYAkVcoAkKRK\nGQCSVKlxfQjc27vEBxBjZPr0qSxa5OvUtebwmB0bPT3TBv0Nfd4BTFDd3W3+8ihp7HnMrnoGgCRV\nygCQpEoZAJJUKQNAkiplAEhSpQwASaqUASBJlTIAJKlSvg56DbbLLttx++23jWidzTbbnKuuumGM\naiQNzWN29TKur4P2VRBj5+Dj53H60buNdzWkYfOYHRu+CkKS9DdG1QQUEdsBJ2TmzIh4CfBD4FfN\n118Zxu8olSSNk5UOgIg4Cngb8GAzawbwH5l5UhsVkySNrdE0Ad0B7NcxPQPYKyKuiojZETFtdFWT\nJI2llb4DyMxzImKTjlk/AU7LzPkR8THgE8CHhypj+vSpvgJ2DPX0mMFas3jMrlptdgM9LzPv6/sM\nfGFFK/jLH8ZWb++S8a6CNCIes+0bKlTb7AU0NyK2bT6/HJjfYtmSpJa1eQfwbuALEfEY8AfgXS2W\nLUlq2agCIDPvArZvPt8I7NhCnSRJq4ADwSSpUgaAJFXKAJCkShkAklQpA0CSKmUASFKlDABJqpQB\nIEmVMgAkqVIGgCRVygCQpEoZAJJUKQNAkiplAEhSpQwASaqUASBJlTIAJKlSBoAkVcoAkKRKGQCS\nVCkDQJIqZQBIUqW6R7NyRGwHnJCZMyNiU2AOsBy4FTg8M58YfRUlSWNhpe8AIuIo4DRgSjPrP4CP\nZ+bOQBewz+irJ0kaK6NpAroD2K9jegZwZfP5IuAVoyhbkjTGVroJKDPPiYhNOmZ1Zeby5vMSYP0V\nlTF9+lS6uyevbBW0Aj0908a7CtKIeMyuWqN6BtBPZ3v/NOC+Fa2waNHSFjev/np7l4x3FaQR8Zht\n31Ch2mYvoJ9FxMzm8x7A1S2WLUlqWZt3AB8Cvh4RawO3Ad9rsWxJUstGFQCZeRewffN5AfCyFuok\nSVoFHAgmSZUyACSpUgaAJFXKAJCkShkAklQpA0CSKmUASFKlDABJqpQBIEmVMgAkqVIGgCRVygCQ\npEoZAJJUKQNAkiplAEhSpQwASaqUASBJlTIAJKlSBoAkVcoAkKRKGQCSVCkDQJIqZQBIUqW62y4w\nIm4EFjeTv87MWW1vQ5I0eq0GQERMAboyc2ab5UqS2tf2HcBWwNSIuKQp+6OZeX3L25AktaDtAFgK\nfBY4DXgBcFFERGYuG2jh6dOn0t09ueUqqE9Pz7TxroIq9ZaPX8gDDz024vUOPn7esJdd9+lr8e3P\n7DnibehJbQfAAmBhZi4HFkTEn4FnAb8ZaOFFi5a2vHl16u1dMt5VUKUeeOgxTj96txGt09MzbUTH\n7MHHz/MYH4ahLgTb7gV0MHASQERsBKwH/L7lbUiSWtD2HcBsYE5E/BhYDhw8WPOPJGl8tRoAmfko\ncECbZUqSxoYDwSSpUq0PBFP7jjj5Kh58eOQtaSPpUQGwzpRuvvCBXUa8HUlrJgNgDfDgw8vGvEcF\njDwwJK3ZbAKSpEoZAJJUKQNAkiplAEhSpQwASaqUASBJlTIAJKlSBoAkVcoAkKRKGQCSVCkDQJIq\nZQBIUqUMAEmqlAEgSZUyACSpUgaAJFXKAJCkShkAklQpA0CSKmUASFKlWv2l8BExCfgysBXwCHBo\nZi5scxuSpHa0fQfwOmBKZu4AHA2c1HL5kqSWtB0AOwEXA2Tm9cBLWy5fktSSVpuAgPWA+zumH4+I\n7sxcNtDC06dPpbt7cstVmHgOuef7LDj0rBGts2BltrP2BvT07LMSa0pPtSqOWY/X0Ws7ABYD0zqm\nJw128gdYtGhpy5ufmGb//d6cfvRuI1qnp2cavb1LRrTO8cfPY8cRriMNZFUcsx6vw9PTM23Q79pu\nAroG2BMgIrYHbmm5fElSS9q+AzgP2D0irgW6gFktly9JakmrAZCZTwCHtVmmJGlsOBBMkiplAEhS\npQwASaqUASBJlTIAJKlSBoAkVcoAkKRKGQCSVCkDQJIqZQBIUqUMAEmqlAEgSZUyACSpUgaAJFXK\nAJCkShkAklQpA0CSKmUASFKlDABJqlTbvxReY+Tg4+eN+TbWmeLhoPaM9THr8Tp6XcuXLx+3jff2\nLhm/jU9wBx8/j9OP3m28qyENm8fs2OjpmdY12Hc2AUlSpVq7h4qILuC3wK+aWddl5kfaKl+S1K42\nG9GeD9yYma9tsUxJ0hhpMwBmAM+OiMuBh4AjMzNbLF+S1KKVCoCIOAQ4st/sw4HjMvO/ImIn4JvA\nNkOVM336VLq7J69MFTQMPT3TxrsK0oh4zK5aKxUAmTkbmN05LyKmAsua738cERtFRFdmDtrTZ9Gi\npSuzeQ1Tb++S8a6CNCIes+0bKlTb7AX0CeADABGxFfCboU7+kqTx1eYzgOOBb0bEXpQ7gYNaLFuS\n1LLWAiAzFwF7tVWeJGlsORBMkiplAEhSpQwASaqUASBJlTIAJKlSBoAkVcoAkKRKGQCSVCkDQJIq\nZQBIUqUMAEmqlAEgSZUyACSpUgaAJFXKAJCkShkAklQpA0CSKmUASFKlDABJqpQBIEmVMgAkqVIG\ngCRVygCQpEp1j2bliNgXeGNmHtBMbw+cAiwDLsnMT42+ipKksbDSdwARcQpwXL8yTgUOAHYCtouI\nl4yuepKksTKaJqBrgXf3TUTEesDTMvOOzFwOzAVeMcr6SZLGyAqbgCLiEODIfrNnZebZETGzY956\nwOKO6SXA84Yqe/r0qXR3Tx5mVTVSPT3TxrsK0oh4zK5aKwyAzJwNzB5GWYuBzn+9acB9Q62waNHS\nYRSrldXbu2S8qyCNiMds+4YK1dZ6AWXmYuDRiHh+RHQBrwKubqt8SVK7RtULaACHAd8CJlN6Ad3Q\ncvmSpJaMKgAy8wrgio7p64HtR1clSdKq4EAwSaqUASBJlTIAJKlSBoAkVcoAkKRKGQCSVCkDQJIq\nZQBIUqUMAEmqlAEgSZUyACSpUgaAJFXKAJCkShkAklQpA0CSKmUASFKlDABJqpQBIEmVMgAkqVIG\ngCRVygCQpEoZAJJUKQNAkirVPZqVI2Jf4I2ZeUDH9GeB3zSLfCIzrxxdFSVJY2GlAyAiTgFeBdzU\nMXsGcFRmnjPaikmSxtZomoCuBd7db94M4OCIuDoiToqIUd1hSJLGzgpP0BFxCHBkv9mzMvPsiJjZ\nb/6lwPnAr4FTgcOALw5W9vTpU+nunjyiCmv4enqmjXcVpBHxmF21VhgAmTkbmD3M8k7PzPsAIuL/\nAa8fauFFi5YOs1itjN7eJeNdBWlEPGbbN1SottYLKCK6gJsjYuNm1suB+W2VL0lqV2sBkJnLgUOB\ncyPiSmAq8PW2ypcktWtUD2kz8wrgio7pS4BLRlclSdKq4EAwSapU1/Lly8dt4729S8Zv4xPALrts\nx+233zaidTbbbHOuuuqGMaqRNDSP2VWvp2da12DfGQATVE/PNHtUaI3iMTs2hgoAm4AkqVIGgCRV\nygCQpEoZAJJUKQNAkiplAEhSpQwASaqUASBJlRrXgWCSpPHjHYAkVcoAkKRKGQCSVCkDQJIqZQBI\nUqUMAEmq1Kh+JaRWLxExCfgysBXwCHBoZi4c31pJKxYR2wEnZObM8a5LTbwDmFheB0zJzB2Ao4GT\nxrk+0gpFxFHAacCU8a5LbQyAiWUn4GKAzLweeOn4VkcaljuA/ca7EjUyACaW9YD7O6Yfjwib+bRa\ny8xzgMfGux41MgAmlsXAtI7pSZm5bLwqI2n1ZgBMLNcAewJExPbALeNbHUmrM5sHJpbzgN0j4lqg\nC5g1zvWRtBrzbaCSVCmbgCSpUgaAJFXKAJCkShkAklQpA0CSKmUAaLUXEetHxPmrYDu7R8Rlzee1\nImJJRGzY8f3/j4hLO6YjIu6KiI0i4sKV3ObeEfHp0ddeGjnHAWhNMB3YeqwKb96ieiTwUZrBc5n5\nWERcA+wAXBARPZQLpoiIqZm5FNgZuDQz76UZgDdSmfl94Pst/BjSiBkAWhN8HtgoIs6jDHb7AOVk\nPB84PDMfjoj3Am8D1gGeAPbPzNsi4i7gbOA1wDLKSf5DwAuAD2Xmd4HNmz/vBN7Xsd15wI7ABcDu\nwGXAc4CXARdRAuCCiNgEuCIzN4mIOZT3Mc0ANgY+lZlnRMQngWc3230ucFpmHhsRBwEzM/Ogpq7f\nAF7V/Bxvz8z5EfFiYA7l/+vVwB6Zuelod6pkE5DWBO8D7gU+TjlJ/3Nmbg38CfhwRKxHeRX2zMx8\nMXA+8J6O9e/NzC2AGymvyX4l8FbgIwCZ+YvMPBT4S7/tXkYJACgn5bnAJc1nmu9+NEB9n0MJh9cC\nn+2Yv2Wz7e2AoyNigwHW/XNmbgucSgkrgDOBY5qf+U68cFNLDACtSXalXEFfHxE3AfsAm2XmYuAA\n4M0RcRzlxLtux3oXNX/fDVzZvCDvbkrT0lB+BmwaEWtTXrX9Y+BSYGZEbAz8JTP7hwbAJZm5HLgV\n2LBj/uWZ+Whm/okSNusPsO7Fzd+3Ahs2zyA2ycy+Zwynr6DO0rAZAFqTTAa+m5lbN1fD2wLvjYjn\nANcBG1BO9nMo70Lq82jH52G/HTUznwBuoDQtLcjMRzLzt5T/N6+mhMFAHm7W7/+elYc7Pi/vV8f+\ny/R9//ggy0mjZgBoTbCM0uxxBbBvRDwzIrqAr1CeB2wDLMzMz1FO2HtQwqIN84APUpp++lwOvJ/B\nA6A1mXk/sDAi9mhmHUAJB2nUDACtCf4I3AOcDHyKclL+BeX4PZ5ycp4UEb8ErgfuAv6hpW1fBryI\npwbAJU3517a0jRV5B3BMRNxIeX7w0CrariY43wYqreYi4hjg65n5+4jYDzgwM18/3vXSms/eBNLq\n7x7g0oh4DFgEHDLO9dEE4R2AJFXKZwCSVCkDQJIqZQBIUqUMAEmqlAEgSZUyACSpUv8DU6sC76Sz\n6HoAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11d418e50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Graph for MVP Difference\n",
"matches.boxplot(column = 'Total_MVP_Difference', by='team1Winning', showfliers= False)"
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x11d418850>"
]
},
"execution_count": 76,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAEbCAYAAADUCE9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHLxJREFUeJzt3XuUXFWZ9/FvpzshBJqk0UKNBuIYfUAYyEwEBkKSBgMS\nBsiL8oKAYAiXYRkF5KIQI6MsmYmCAWfEQSOhEYfRMRJEsAmQO3eB8EoweSIioILaQCc0CQGa9PvH\n3iWVsruqui592fl91spK1Tl1znm6+vSv9tlnn1N1XV1diIhIuob0dwEiIlJbCnoRkcQp6EVEEqeg\nFxFJnIJeRCRxCnoRkcQ19HcBUjozGwv8FngiTqoHNgMXuPt9NdheF5Bx9xcLvOafgQPd/bJqb78v\nmNntwEJ3b8mb3gKscferylzv/sAZ7n5OxUWWvs0jgG+4+/j4vBVY7O7XxOcfAhyY6+6Xxmm7AX8A\nMsD/ABe5+6/L3P7jQLO7b6j4h5GqUtAPPq9l/5ABzOwEoAX4YD/Vsz+waz9teyDbG3hfX2zIzHYE\nvgR8lhDaWa3AYcA18fkxwM+BY4FL47TDgPvcfSNwVCV15O6XMrAo6Ae/dwAvZJ+Y2dnAucBbwJ8J\nf/xPAXcDj7r7F8xsKuHDYQLwdaAL2IvQqrsLONfd38zdiJl9GTgJ6ATWx/XuAZwD1JvZRnf/Ut4y\nR8X1vwU8DkwFDgGagTOAnYCN7n5od+t39z+Z2XLg2+6+MK7zr8/NrJMQYofGdc1291vi684APkPo\nnnwprm+dmY0GbgRGA88CuxV4bw8xs+OBXeL7chFwIjDL3Q+O29kdeBAY6+5vxGljgMuBkWZ2g7uf\nbmbHAHOAYYSjsIvc/QEzexfwXeBdwLtjTSe4+1/M7BngZuCfCb/nfwUmxt/bm8Cx7v488LH488+M\n281qBb5iZkPcfSsh6GcDPzKzv3P3p4GPAnfEup8Bjgd2Bq4Angb2AXaIP/OyeKTzCvD3wBhgHfBJ\nd381ewQIHA0cB2wlNEDeAE5z9zVmNg5YQGgcvADUAT/MP6KS6lIf/eCzo5k9Hv89C3wL+HcAMzsM\n+AJwqLvvRwiJWwlB/ingNDObDtwAnOzuf47r3I8Qwh+O//4ld4NmdjowDdjf3fcF1gAt7v4QcB3w\n425C/h3ATcCnYktvGfDenJfsTTjMP7Sn9ZfwXtQDL7v7BOAEYIGZZcxsCvBpYJK7/wPwDeCWuMy1\nwIPuvjfhA3HPAut/HyEIx8f36CzgJ8AHzOzD8TVnAjdmQx7A3X8PXAasiiH/QeDfgKNiPWcDt5jZ\nTsAngQfc/SDg7wgfAqfm1DA8/i4vBL4HfCs+/z0wI27vVnf/PPBybvHu/ps4bV8zawKM8KH0C2B6\nfNlfgz7PgcA3Y73XA1/JmTcBOJLQOBgN/N9ulp8CfM7d9wHuAy6O028C/idOPxc4qJtlpcoU9IPP\na+4+Pv7bg9A6/pGZvZ/wx/djd28DiK2k9xJamy8QgmoR8D13X5mzzhZ3f9XdXwd+QGgh5poG3ODu\nm+LzbwEfNbNhBeqcDPza3f9frOVGQksw61funn1ezvqzvh3X/yvCuYvJhBbwOOD+2G/8DWBXM9uV\n8IHWEpd5ClhaYN03ufumGOI/BA6Pj78PnGVm9YSw/W6RGg8H3gMsifX8N6G1O87dvxXrvAD4DqEF\nvXPOsj+N//8W+FP2/YzPS+kyayXsI9OAu2PL/nbgiHjOB3df281yz7r74/HxY3nbutPdX49HfU/0\nUMej7p7tRnqM8P43AQcQ3r/sdpeU8DNIhdR1M8i5+/1m5oQ/oO4+uOuAofHx3oTunAPyXtOZ83gI\noauFvGn5zxviunvS2c38rTmPXy1x/V1568kP/+5qryeE9BcBzGwIoeXZ3s36cpfPl/s+1BG6SyAE\n+8PACsIJ22cKrINYzxJ3PzE7IXbvPG9mXyf8PhYQjnqG5tX3es7jbbrTStRKOOrYQji6g/DhNp/w\nodddax7gtZzH+e9ZoXmFXpN9P3Nfn7+vSQ2oRT/IxZEUHwJWA4uBE80sE+edTuiffsrMDgDOAz4C\njDKz83JWc6KZ7WBmwwldHj/P28xi4PTY1QDhkHtlPALo5O0Pklz3AR8ys31jLZ8ARhH+6PMVWn9b\nrBkz+wCwb96yp8V5/0johllB6E8/yczeE19zDm+3HO8kdJ1k+9cP7aaerE/mvC8zCKGJuz8HPABc\nDfxXD8vmvi9LCS3oPeN2jwJ+BQwnHD1d4+43AX8htP7rC9TUW8sIXU9TCO8z7r6Z0Mr+LD0HfdXF\nI7j7gNMB4lHoR+l+n5AqUot+8NkxHv5nDQHOdvf1wHozuxpYGluxbYQTYzsRhs59zt3/aGYzgIfN\nLNt9sxlYBTQBCwl9+LmuJ5x4eziu9ynglDhvCaG/+Q13/1x2AXd/2cxOAn5gZluBRwjht7mbn6nQ\n+r8G3BiHca4DVuYtOzGegB4CnOju7cDi2FK+O277FeDj7t5lZrOAG8xsLWGEyuP07HfAvYSulEWE\nk7hZNxC6jX7Rw7IPAFeY2SJ3Py7W+CMzq4vvw7HuvsnMLgeuMrPL4vR7Cd1OVeHur5nZemBYHFmT\ndQdwJbC8Wtsq0WnA9Wb2GeCPhPe4u31CqqhOtynevlU6XrzAenchjDL5irtvji3uO4DR7l6Vna6U\ncf61ED+MrgWecfev9+W2Bzsz+xLw0zgCaiThyGZauWP3pTRq0W+H8i682h043MxOJYzoWFCNbbj7\nK2b2BvBLM3uT0L98ArDMzPYANuYt8rXsEMpqiKNibo5PdwVGElqPEEbJXF3mehuB5wh99BeV8Pp/\nA0a4+/lFXncK8Hl3/0jOtIeBd7v77jnTFhNO0A6N672ywDrHES6QeiJv1jX9OJxxPfDjeKTVQLh4\nSyFfY2rRb4di0K9x951zpr2XMKxxShzBUqttLydnXHxfiF1Vx7v70X24zd0JY/yPJIxyKhb07wSe\nJxyhbDSzdxP6szcTxqCvjqOQ2gHLGdFSaJ3jgEfcfVTOtDGE4J/o7k+W+ePJIKMWvQAQ++5/Qzhp\neC3bXsz0NxcfES52+T3wIXf/E4CZPQh81d1by63DzLYAcwknJUcTjjKyl/BfSjhZ3An8BpiR1+/c\nm+3UEbqWjos/19PAZ+JFWhMJ1yYMJwyLbHX3s2NwthLOZxxI+Pu5mHCy14CHgFNi19SZhJOwDuxY\nrB53f9HMVgOTCMMfjyacPN1IuJJ1NWHM+W/c/Q9m9jVgZ3c/38z+wNujaHYHbvZ4i4NutvN7M3ua\ncCHTk/Hcwb/E96CNcGHZejP7IeFCsQ8AP4vvx7XAPxFGyix09y8X+7lkYNCoGwHAzA4inATckW0v\nZur24qMYsIsIF2JhZnsRQnFxCZu7Mueir+y/d8R5OwAvuvtEwlWac81suJkdSxj5clC82OZ3hA+c\ncp1OGKVzQLyg6x7CBUkQRifNdvcDCBeQHW9m+8V54wghtzfhxPA8QpfUPoQRJPsDuPtl7v5tejd8\nMDvmHcJVrLcTzmscG6f1dHETwI7uPolw5fEFseX+N8zsEGAs4cT3YYSrkQ+Jv9trCCfjs4a5+97u\nPptwpewQwns2HjjUzCb14meTfqQW/fYrd/ROA/AiYaTLu9j2Yqbci4+yy2YvPppPGF54FSE4b4gX\n5BRzcZGum5/F/x8jBP9OhNbqT+KoGtz9ghK2U8jRwD8Cj8Sfq563x+ifChwVTxzuSWjZ7wxsAra4\ne3akzW8JYfgqgJm9QGX3/WkFro3DOQ8m3G7hTWCP2LWTvfK5Oz+Dv7bYX4x1bAIa837PbcBJ7v68\nmV1EOBJ5IOd3m4knSSGMAMqaSjji2UoY239IBT+n9DEF/fZrm5ujZcX+7NyLmXq8+Mjd7zWzhjhG\n/2RCOFWlNoA4HBLCBTad5Iy3NrNRwKgSLlbqST1whbvPj+sbTri+oI7QN/4I4ejkR4SfK3uRz+t5\n6ynnIqae/JIwzHQ64bYIW2Jti4EjCN0oD/awbE8XMXV093uO6gkfzl+K26kH3hPPEcC2+0H++787\nsMndXyr9x5P+oq4bKabQxUcQLmf/T8JRwHM1rOMe4ONx2CaEe69U0qpfTLiNQWN8fgVhbPw7CF0T\nX3T3RYQbt72f6l7E1K3YWr6HcOOx23Nm3U5oyS8p8YipVIuBUyzcWA1gFuH33Z17gE+bWZ2Z7UC4\nd9DEKtYiNaQWvRTk7j1efBRfciPhhl0n9WK1V5rZnLxpt7j75d2+OtTxizhk8r7Y2nyScO+ecl1H\nODJ5MK7vGWBmPCl6JfC4mb1MuGXE/YTuqz9WsL1StRKOjnL74u8k3AysqmP243s6j3APni7CiJ5P\n9PDyfyXcg+hXhA+9m939tmrWI7Wj4ZUiIolTi16qyswu5u3bF+S70t3/u4rbOpRwv5nuLPNw694B\nw8xOo+fuprIv4hIpRi16EZHE6WSsiEjiFPQiIolT0IuIJK5PTsa2tXXoRECNNDWNoL1dt/OWwUP7\nbG1kMo09fuObWvSDXENDza/jEakq7bN9T0EvIpI4Bb2ISOIU9CIiiVPQi4gkTkEvIpI4Bb2ISOIU\n9CIiiVPQi4gkTrcpHgQmTz6QdevW9mqZPffci5UrH6pRRSIymCjoB4FCgT1z7lIWXHJYH1YjIoON\num5ERBKnoBcRSZy6bkSk6nReaWBR0ItI1em80sBSNOjNbChwIzAWeAs4C+gEWoAuYA0wy9231qxK\nEREpWyl99EcBDe5+MHA5cAUwD5jj7pOAOmB67UoUEZFKlBL064EGMxsC7AK8CUwAVsT5rcDU2pQn\nIiKVKqWP/lVCt8064J3A0cBkd89+PWAHMLLQCpqaRuhbZWook2ns7xJEekX7bN8qJeg/Dyx290vN\nbAywFBiWM78R2FBoBfp+yNpqa+vo7xJEekX7bPUV+vAspeumHdgYH78MDAVWm1lznDYNWFVBfSIi\nUkOltOivBhaY2SpCS3428Agw38yGAWuBhbUrUUREKlE06N39VeCEbmZNqX45IiJSbboFgohI4hT0\nIiKJU9CLiCROQS8ikjgFvYhI4hT0IiKJU9CLiCROQS8ikjgFvYhI4hT0IiKJU9CLiCROQS8ikjgF\nvYhI4hT0IiKJU9CLiCROQS8ikjgFvYhI4hT0IiKJU9CLiCSu6HfGmtkMYEZ8OhwYDxwCXAN0AWuA\nWe6+tTYliohIJYq26N29xd2b3b0ZeBQ4F7gMmOPuk4A6YHpNqxQRkbKV3HVjZh8B9nb37wETgBVx\nViswtQa1iYhIFRTtuskxG/hqfFzn7l3xcQcwstCCTU0jaGioL6M8KUUm09jfJYj0ivbZvlVS0JvZ\nKMDcfVmclNsf3whsKLR8e/vm8qqTkrS1dfR3CSK9on22+gp9eJbadTMZWJLzfLWZNcfH04BVZVUm\nIiI1V2rXjQFP5zy/EJhvZsOAtcDCahcmIiLVUVLQu/uVec/XA1NqUpGIiFSVLpgSEUmcgl5EJHEK\nehGRxCnoRUQSp6AXEUmcgl5EJHEKehGRxCnoRUQSp6AXEUmcgl5EJHEKehGRxCnoRUQSp6AXEUmc\ngl5EJHEKehGRxCnoRUQSp6AXEUmcgl5EJHEKehGRxJX0nbFmdilwLDAM+A6wAmgBuoA1wCx331qj\nGkVEpAJFW/Rm1gwcDEwkfCH4GGAeMMfdJwF1wPQa1igiIhUopUX/MeAJYBGwC3AxcBahVQ/QChwR\n50sFPnfNSjZt6ez1cjPnLu3V63ca3sB/nj+519sRkcGplKB/J7AHcDTwfuA2YIi7d8X5HcDIQito\nahpBQ0N9JXVuFzZt6eTn36z9wdExF/6MTKax5tsR6Yn2v75VStC/BKxz9zcAN7MthO6brEZgQ6EV\ntLdvLr/C7UxbW0evXp/JNPZ6mXK2I1JN2v+qr9CHZymjbu4FjjSzOjMbDewELIl99wDTgFWVFiki\nIrVRtEXv7reb2WTgYcIHwyzgd8B8MxsGrAUW1rRKEREpW0nDK939C91MnlLlWkREpAZKCnoRke5o\npNjgoKAXkbJt2tLJgksO69Uy5Qwg6O0Hg2xLt0AQEUmcgl5EJHEKehGRxCnoRUQSp6AXEUmcgl5E\nJHEKehGRxCnoRUQSp6AXEUmcgl5EJHEKehGRxCnoRUQSp6AXEUmcgl5EJHEKehGRxCnoRUQSp6AX\nEUlcSd8wZWaPAa/Ep78DrgBagC5gDTDL3bfWokAREalM0aA3s+FAnbs350y7DZjj7svN7DpgOrCo\nZlWKiEjZSmnR7weMMLO74utnAxOAFXF+K3AECnoRkQGplKDfDFwFfB/4ICHY69y9K87vAEYWWkFT\n0wgaGuorqXO7cMZzt7H+zB/0apn15Wxn2CgymellLCmyLe2zg0MpQb8eeCoG+3oze4nQos9qBDYU\nWkF7++byK9yOXL/7sSy45LBeLZPJNNLW1tGrZebOXcrEXi4j0h3tswNHJtPY47xSRt3MBL4JYGaj\ngV2Au8ysOc6fBqyqrEQREamVUlr01wMtZnYvYZTNTOBFYL6ZDQPWAgtrV6KIiFSiaNC7+xvAyd3M\nmlL9ckREpNp0wZSISOIU9CIiiVPQi4gkTkEvIpI4Bb2ISOIU9CIiiVPQi4gkTkEvIpI4Bb2ISOIU\n9CIiiVPQi4gkTkEvIpI4Bb2ISOIU9CIiiVPQi4gkTkEvIpI4Bb2ISOIU9CIiiVPQi4gkrpQvB8fM\ndgMeBQ4HOoEWwheFrwFmufvWWhUoIiKVKdqiN7OhwHeB1+KkecAcd58E1AHTa1eeiIhUqpSum6uA\n64Dn4/MJwIr4uBWYWoO6RESkSgp23ZjZDKDN3Reb2aVxcp27d8XHHcDIYhtpahpBQ0N9RYVuL2bO\nXVrzbey841Aymcaab0e2D+XsS321jATF+uhnAl1mNhUYD/wA2C1nfiOwodhG2ts3l13g9mTBJYf1\nepmZc5eWtVxbW0evlxHpTm/3pUymsaz9T/tsYYU+CAsGvbtPzj42s+XAOcCVZtbs7suBacCyqlQp\nIoNSXxyF7jS8pHEj0oNy3r0LgflmNgxYCyysbkkiMlj05VGolK/koHf35pynU6pfioiI1IIumBIR\nSZyCXkQkcQp6EZHEKehFRBKnoBcRSZyCXkQkcQp6EZHEKehFRBKnoBcRSZyCXkQkcQp6EZHEKehF\nRBKnoBcRSZyCXkQkcQp6EZHEKehFRBKnoBcRSZyCXkQkcQp6EZHEKehFRBJX9MvBzawemA8Y0AWc\nA2wBWuLzNcAsd99auzJFRKRcpbTojwFw94nAHOAKYB4wx90nAXXA9JpVKCIiFSka9O5+K3B2fLoH\nsAGYAKyI01qBqTWpTkREKla06wbA3TvN7EbgOOB44HB374qzO4CRhZZvahpBQ0N9RYVKzzKZxv4u\nQaRXtM/2rZKCHsDdP21mXwQeAnbMmdVIaOX3qL19c3nVSUna2jr6uwSRXtE+W32FPjyLdt2Y2alm\ndml8uhnYCjxiZs1x2jRgVYU1iohIjZTSor8FuMHMVgJDgfOBtcB8MxsWHy+sXYkiIlKJokHv7puA\nE7qZNaX65YiISLXpgikRkcQp6EVEEqegFxFJnIJeRCRxCnoRkcQp6EVEEqegFxFJnIJeRCRxCnoR\nkcQp6EVEEqegFxFJnIJeRCRxCnoRkcQp6EVEEqegFxFJnIJeRCRxCnoRkcQp6EVEEqegFxFJXMHv\njDWzocACYCywA/A14NdAC9AFrAFmufvWmlYpIiJlK9ai/xTwkrtPAo4Evg3MA+bEaXXA9NqWKCIi\nlSgW9D8Bvhwf1wGdwARgRZzWCkytTWkiIlINBbtu3P1VADNrBBYCc4Cr3L0rvqQDGFlsI01NI2ho\nqK+wVOlJJtPY3yWI9Ir22b5VMOgBzGwMsAj4jrvfbGbfyJndCGwoto729s3lVyhFtbV19HcJIr2i\nfbb6Cn14Fuy6MbN3AXcBX3T3BXHyajNrjo+nAauqUKOIiNRIsRb9bKAJ+LKZZfvqzwP+w8yGAWsJ\nXToiIjJAFeujP48Q7Pmm1KYcERGpNl0wJSKSOAW9iEjiFPQiIolT0IuIJE5BLyKSOAW9iEjiFPQi\nIolT0IuIJE5BLyKSOAW9iEjiit69Uvrf5MkHsm7d2h7n7zbvb6ftuederFz5UA2rEpHBQkE/CBQK\n7EymUbd8FZGC1HUjIpI4Bb2ISOIU9CIiiVPQi4gkTkEvIpI4Bb2ISOIU9CIiiStpHL2ZHQh83d2b\nzWwc0AJ0AWuAWe6+tXYlishgo4v8BpaiQW9mXwBOBTbFSfOAOe6+3MyuA6YDi2pXoogMNrrIb2Ap\npevmt8DHc55PAFbEx63A1GoXJSIi1VO0Re/uPzWzsTmT6ty9Kz7uAEYWW0dT0wgaGurLq1CKymQa\n+7sEkV7RPtu3yrnXTW5/fCOwodgC7e2by9iMlEKHwTLYaJ+tjUIfnuWMulltZs3x8TRgVRnrEBGR\nPlJOi/5CYL6ZDQPWAgurW5KIiFRTXVdXV/FXVaitraP2G9lO6TBYBhvts7WRyTTW9TRPF0yJiCRO\nQS8ikrg+6boREZH+oxa9iEjiFPQiIolT0IuIJE5BLyKSOAW9iEjiFPQiIokr5xYI0s/MbAjwHWA/\n4HXgTHd/qn+rEiku90uM+ruW7Yla9IPT/wGGu/tBwCXAN/u5HpGi4pcYfR8Y3t+1bG8U9IPTIcCd\nAO7+IPCR/i1HpCT5X2IkfURBPzjtAmzMef6WmakbTgY0d/8p8GZ/17E9UtAPTq8QvvQla4i7d/ZX\nMSIysCnoB6f7gKMAzOyfgCf6txwRGch0uD84LQION7P7gTrg9H6uR0QGMN29UkQkceq6ERFJnIJe\nRCRxCnoRkcQp6EVEEqegFxFJnIJeBgwzG2lmt/bBdg43syXx8VAz6zCzXXPm/9LM7s55bmb2jJmN\nNrNflLnNY83s8sqrF+k9jaOXgaQJGF+rlce7fn4emE28yMzd3zSz+4CDgDvMLENoAJmZjXD3zcAk\n4G53f554oVpvufttwG1V+DFEek1BLwPJfwCjzWwR4aKw8wmh+ygwy923mNlngVOBnYCtwInuvtbM\nngF+DBwNdBLC/ELgg8CF7v6/wF7x31nAuTnbXQpMBO4ADgeWAGOAKUArIejvMLOxwHJ3H2tmLYT7\nDU0A3gd81d1vMLOvAO+N290D+L67X2FmM4Bmd58Ra70J+Fj8OU5z90fNbB+ghfB3uQqY5u7jKn1T\nRdR1IwPJucDzwBxCGB/s7uOBvwAXmdkuhFs0N7v7PsCtwGdyln/e3fcGHiPcvvkI4FPApQDu/qS7\nnwm8nLfdJYSghxC+i4G74mPivHu6qXcM4UPgGOCqnOn7xm0fCFxiZqO6WfYldz8AuI7woQRwI3BZ\n/JmfRg0xqRIFvQxEhxJaxA+a2ePAdGBPd38FOBn4pJn9OyFgd85ZrjX+/yywIt7o7VlCl1Ahq4Fx\nZjaMcAvoe4G7gWYzex/wsrvnfzgA3OXuXcAaYNec6cvc/Q13/wvhQ2VkN8veGf9fA+wazxGMdffs\nOYAFRWoWKZmCXgaieuB/3X18bN0eAHzWzMYADwCjCKHeQrjXT9YbOY9Lvpunu28FHiJ0Ca1399fd\n/Q+Ev48jCaHfnS1x+fz7iGzJedyVV2P+a7Lz3+rhdSIVU9DLQNJJ6K5YDhxnZruZWR3wX4T++v2B\np9z9akIwTyN8KFTDUuACQpdN1jLgPHoO+qpx943AU2Y2LU46mfAhIFIxBb0MJH8GngOuAb5KCN8n\nCfvpXEIIDzGzXwMPAs8A76/StpcAH2bboL8rrv/+Km2jmE8Dl5nZY4T+/df6aLuSON29UmSAMLPL\ngPnu/oKZfRw4xd0/0d91yeCns/oiA8dzwN1m9ibQDpzRz/VIItSiFxFJnProRUQSp6AXEUmcgl5E\nJHEKehGRxCnoRUQSp6AXEUnc/wcTSa1A6IIIigAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11d59e390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Graph for Previous encounters Win Percentage of Team #1\n",
"matches.boxplot(column = 'Prev_Enc_Team1_WinPerc', by='team1Winning', showfliers= False)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Graph for Recent form(Win Percentage in the same season)\n",
"matches.boxplot(column = 'Total_RF_Difference', by='team1Winning', showfliers= False)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# Predictions for the data"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from sklearn.linear_model import LogisticRegression\n",
"from sklearn.neighbors import KNeighborsClassifier\n",
"from sklearn import svm\n",
"from sklearn.ensemble import RandomForestClassifier\n",
"from sklearn.naive_bayes import GaussianNB\n",
"from sklearn.cross_validation import train_test_split\n",
"from sklearn import metrics\n",
"from patsy import dmatrices"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"y, X = dmatrices('team1Winning ~ 0 + Avg_SR_Difference + Avg_WPR_Difference + Total_MVP_Difference + Prev_Enc_Team1_WinPerc + \\\n",
" Total_RF_Difference', matches, return_type=\"dataframe\")\n",
"y_arr = np.ravel(y)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Training and testing on Entire Data"
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 58.1039755352 %\n"
]
}
],
"source": [
"# instantiate a logistic regression model, and fit with X and y\n",
"model = LogisticRegression()\n",
"model = model.fit(X, y_arr)\n",
"# check the accuracy on the training set\n",
"print \"Accuracy is\", model.score(X, y_arr)*100, \"%\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Splitting train and test using train_test_split"
]
},
{
"cell_type": "code",
"execution_count": 80,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# evaluate the model by splitting into train and test sets\n",
"X_train, X_test, y_train, y_test = train_test_split(X, y_arr, random_state = 0)"
]
},
{
"cell_type": "code",
"execution_count": 81,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 58.5365853659 %\n"
]
}
],
"source": [
"# Logistic Regression on train_test_split\n",
"model2 = LogisticRegression()\n",
"model2.fit(X_train, y_train)\n",
"# predict class labels for the test set\n",
"predicted = model2.predict(X_test)\n",
"# generate evaluation metrics\n",
"print \"Accuracy is \", metrics.accuracy_score(y_test, predicted)*100, \"%\""
]
},
{
"cell_type": "code",
"execution_count": 82,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x11d87f990>]"
]
},
"execution_count": 82,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAD3CAYAAADxJYRbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXmQHNd95/nJuq+uPqu7QaABkAT4SIIyRYKkCIi0aMlc\nW7JlybOxM7Na22vKHFkeOULDlXdsydI6HOsJx+xa9CGLtnWt1rQ11koeztiURdMSaVokSFEkdRAg\n+ECAFxpAn+iu6rqv3D8yszqruu6q7qrqep8IBLorr/e6Mr/5e7/3e7+fpus6CoVCoRgOHL1ugEKh\nUCh2DiX6CoVCMUQo0VcoFIohQom+QqFQDBFK9BUKhWKIcPW6AfVYXt5oOrRofDzA2lpyO5uzY+ym\nvsDu6s9u6gvsrv7spr5AZ/2JREa0Wtt2jaXvcjl73YSusZv6ArurP7upL7C7+rOb+gLb159dI/oK\nhUKhaIwSfYVCoRgilOgrFArFEKFEX6FQKIYIJfoKhUIxRCjRVygUiiFCib5CoVAMEUr0FQrFwLOR\nzPJX3zxNNlfodVP6HiX6CoVi4DlxcoGvfusMPzq32uum9D1K9BUKxcATS2YBSGXzPW5J/6NEX6FQ\nDDyJlCH2maxy7zRCib5CoRh4EqkcABnl02+IEn2FQjHwxJXoN40SfYVCMfAk0obop5V7pyFK9BUK\nxcBjWfoqZLMxDYuoCCEcwAPAjUAGuFdKeda2/VbgfkADFoBfkFKmhRAvADFzt9eklPcIIQ4BXwZ0\n4CTwESllsYv9USgUQ4au68TNiVxl6TemGUv//YBPSnkM+C3g09YGIYQGfB64R0p5B/AIcEAI4QM0\nKeVd5r97zEPuBz4ppbwT4yXxvi72RaFQDCHZfJF8wbAdVfROY5oRfUvMkVI+A9xi23YNsArcJ4R4\nApiQUkqMUUFACPGoEOIxIcTt5v5HgSfMn78J/GQX+qBQKIYYK3IH1ERuMzRTIzcMRG2/F4QQLill\nHpgCjgO/DpwFHhZCPAcsA38AfAE4DHxTCCEwrH+r7u0GMFrvwuPjgZZKhkUiI03v2+/spr7A7urP\nbuoLDH5/NrKbHuKCPvj9sbMdfWlG9GOA/coOU/DBsPLPSilPAwghHsEYCfyx+bkOnBFCrAJ7ALv/\nfgRYr3fhVooCRyIjLC9vNL1/P7Ob+gK7qz+7qS+wO/pz/uKmjMST2YHvj0Un3029l0Uz7p2ngPcA\nmG6aF23bXgVC5gQtwJ3AKeCDmL5/IcQVGKOFS8D3hRB3mfu+G/hOs51QKBSKaiTSm6kXVPROY5oR\n/YeAtBDiBPCHGP77DwghPiSlzAK/AnxFCPE94LyU8hvAF4ExIcSTwFeBD5qjg48BvyuEeBrwAF/f\nhj4pFIohIm7z6avoncY0dO+YIZUfrvj4Zdv2x4DbKo7JAh+ocq4zwDvaaqlCoVBUIa4mcltCLc5S\nKBQDjRW94/e6yBf0UvimojpK9BUKxUBjif70uB9Qfv1GKNFXKBQDjeXeiYwHAOXXb4QSfYVCMdAk\n0nkcmsZE2Acov34jlOgrFIqBJp7KEfS78HuNuBQl+vVRoq9QKAaaeCpHyO/G5zVW76v8O/VRoq9Q\nKAaWoq6TSOcI+t34PIalr3z69VGir1AoBpZ0Jo+uQ8jnxu8xLX3l3qmLEn2FQjGwWJE7Qb8Ln+XT\nV5Z+XZToKxSKgcUqnhKyu3eUpV8XJfoKhWJgsWrjBn2bE7lqcVZ9lOgrFIqBxXLvhNREbtMo0Vco\nBoBYIsu5i9HGOw4Z5aKvQjabQYm+QjEA/O0T5/j9B19gbSPT66b0FVbenaBPLc5qFiX6CsUAsLaR\noajrvLG4O6pCdYuEOZEb9Ls3o3eU6NdFib5CMQAkM4a4nV+K97gl/UU8vdW9o3z69VGir1AMAEmz\nJOC8Ev0yNuP03XjNiVwVvVMfJfoKxQCQUpZ+VRKpHG6XA6/bidOh4XE5lKXfACX6CsUAYLl3FteS\nymdtw0q2ZuH1ONXfpwFK9BWKPieXL5LLGyUAdR0uLCd63KL+IZHOEfTZRN/tVJZ+A5ToKxR9juXa\n0czfzy+pCB6AfKFIKlMg5HeVPvN6nMqn3wBXox2EEA7gAeBGIAPcK6U8a9t+K3A/xj25APwCUAC+\nBBwEvMDvSSn/TghxE/Aw8Ip5+J9JKb/atd4oFLsQS/T3TYc4vxRnfklZ+rA5uR20uXd8ytJvSDOW\n/vsBn5TyGPBbwKetDUIIDfg8cI+U8g7gEeAAhvCvSinvBH4a+FPzkKPA/VLKu8x/SvAVigZY/vxD\ne0fRNGXpW9hX41p43E4KRZ18odirZvU9zYi+JeZIKZ8BbrFtuwZYBe4TQjwBTEgpJfA14FPmPhqQ\nN38+CvyMEOJfhBBfFEKMdKEPCsWuxrJoR0MeZsYDnF9OoOt6j1vVe+zJ1ix8Kqd+Qxq6d4AwYE/6\nURBCuKSUeWAKOA78OnAWeFgI8ZyU8jEAU9S/DnzSPPZZ4AtSyueFEL8N/A7wG7UuPD4ewOVyNt2Z\nSGT3vEN2U19gd/Vnp/vivmhY9tOTIQ7NZXjyhxfRXS6mJwJdOf+gfjevLhrhqzNToVIfRkeM4ujB\nkJ/IuL9nbesW2/HdNCP6McB+ZYcp+GBY+WellKcBhBCPYIwEHhNCzAEPAQ9IKb9i7v+QlHLd+hn4\nTL0Lr60lm+sFxh9neXl3DHt3U19gd/WnF31ZMK9XzOeZHjVE7YcvL3DT4UjH5x7k7+bCYsz4oVhg\neXnDEMii4da5uBCFfL7O0f1PJ99NvZdFM+6dp4D3AAghbgdetG17FQgJIQ6Zv98JnBJCzACPAr8p\npfySbf9/FELcZv78LuD5pnqwS1mPZ0p+SYWiFpZ7x+91MTcdAtQiLdjMuxPylfv0Qbl36tGMpf8Q\ncLcQ4gSGf/4eIcQHgJCU8nNCiF8BvmJO6p6QUn5DCPHHwDjwKSGE5dt/N/BrwGeEEDmMSJ8PdbtD\ng8Tv/9XzBLxu/o9fvgVN0xofoBhKrIncgNdFZMxwWSjRt/n0/VV8+iqCpyYNRV9KWQQ+XPHxy7bt\njwG3VRzzUeCjVU73AvD21pu5+8jlCyyvp4E0by7GOTA7mH5VxfaTsln64yNegj6XEn2qR+94raRr\nytKviVqc1SNiiU23zomTCz1siaLfKVn6PheapjE3HWJ5LUU6O9g+606xJ1uz8LpVycRGKNHvEbFk\ntvTzd19aUHHFipqkbO4dMBZp6ah0DPYCKhaW6KsFWrVRot8jonFD9D1uB7FkjlOvXe5xixT9SjKT\nR4NSkRA1mWsQT+Xxe524nJsypnz6jVGi3yMsS//Ot1wBwNOnlItHUZ1kOo/P68JhTvbvnzbmf4Zd\n9CuTrcGmpa+id2qjRL9HRONGrdMbD00yOxHghTMrpdA8hcJOKpMn4N1cpHjFVACHpinRT+XK/Pmw\nOZGrRL82SvR7hDWRGw56OH7DLPlCkefkUo9bpehHkpk8fu+muLldTmYnA5xfjlMc0nQM2VyBbL5Y\nFrkDyqffDEr0e0TUdO+MBj3cfmQGUFE8iq0UdZ10haUPhl8/ky2wEk33qGW9pVq4JtgsfSX6NVGi\n3yNi8QwaEAq4mRr1c+3+Mc6cX2dlPdXrpin6iHSmgA4EKnzXpcncxeF08cSrRO6AkVoZlHunHkr0\ne0Q0mWMk4MbpML6CY0dmATWhqygnmTHEze8tF7d9ESuCZzDz5nRKwpz/qmnpK9GviRL9HhFLZAkH\nPaXfb7l2GrfLwYlTiyptrqJEKmOIV6BC9Ic9bDNRZWEWbObeUT792ijR7wG5fIFUJs+oTfT9Xhc3\nHZ5i8XKSM2+u9bB1in4iaeaX8Ve4McZCHkJ+N/PLwyn6JZ9+hdvLoWl43A5l6ddBiX4PiCaMSVy7\npQ9w/IY9ADz+/HzDc+i63vXJqnyhSC6vHpZ+IlmxGteilI5hPV1asTtIZHMFCsX2V6FXS7Zm4XM7\n6z4bmVyBYnF4R9NK9HtALdE/cuU44aCH7/zgQsNzPCeX+fd/+ERXLb0//a8v8p/+cqizXfcdKVve\nnUosF8+FlcFKx5DNFfiPf/40X3v8XNvnqBW9A4Zfv5aln0zn+Y3PPsV/f/K1tq896CjR7wGxhBWu\n6S373OlwsH8mRCyRbZhM67VLMXQd3lzs3kTeuQtR3lyKl+UFUvQWey79SiZGjPvHSukxKKxtZIgl\nsrx+Kdb2OTZFf+vfxVvH0l9eT5FI5zl7IVp1+zCgRL8HxEqW/lYrZTTgKdun0Tns2To7IZXJlyIi\n5od0crAfqUy2ZsdybViujkHBGulGk+232yqgUs29Y1n61QIiLINmdUjXN4AS/Z5Qy70DEA55yvZp\ndI5oItOVNtkfgmGNCOlHknXcOyXRH7Dqa5sGS/v3bjydQ9Oqj4B8bieFok6+sFX0rVHR5Y300K5m\nVqLfA2q5d6AdS787Q/uVmBL9fsSy9KuJm+XPHrSSm5bBksoU2g4cSKSMZGuOKhXn6pVMtCz9fEEf\nOLdYt1Ci3wPqWvrB3oi+svT7E8unX9W9Y1r/g+besd+zjUa0tYhXSbZmUS+9sv3aq7HhdPEo0e8B\nsUQWTYORKjetFbtf72EoFvWSxdLuQ1OJ9QC4nA4uriRUUZc+IdmUpT9YIZvRDkVf13USqXzVSVwA\nr8f4vFrJRPv1htWvr0S/B8QSWUYCHhyOrUPTZiz9eCqH5Y7smnvHfACuPzhOoaizsJrsynkVnZHK\n5HG7HLhdWx/VoM+NxuC5d+z3bDv3bypToKjrWxZmWfjqlEy0X28lOpx5rpTo94BoIks4sNW1AzAa\n8pb2qXe8xUYy19EiF4vVaBqnQ+PIlROAcvH0C8l0vqprB8Dh0Aj4XAM3kduppR+vszALjGp0UD0V\nQ5mlH+tOEMSgUf1usiGEcAAPADcCGeBeKeVZ2/ZbgfsBDVgAfgHIVjtGCHEI+DKgAyeBj0gph8qP\nkM0VSGcLjIaqi37A58Lp0OpaQPZtOhBP5kovi3ZZjaWZCHs5MLNZlelYR2dUdINUJr8lw6adoM9d\nEsFBoVNLP1FnYRaAz3Tv1PLpj4U8rMezyr1Th/cDPinlMeC3gE9bG4QQGvB54B4p5R3AI8CBOsfc\nD3xSSnknxkvifd3qyKBQitGvYek7NI3RkLeuBWSdw2MO+Tv16+fyBWKJLFOjfvZFgsDwZm/sJ3Rd\nJ5nJVw3XtAj63SRSuYFJ0qfrxnyUde92Ivq1LH0r02Y6Vz7XkS8UiadyzE4ECHhdaiK3DpaYI6V8\nBrjFtu0aYBW4TwjxBDAhpZR1jjkKPGH+/E3gJzvtwKBhCfRolcgdi/Gwl1giW/NBts6x1xToTv36\n1jB3Muwj4HMzGfZxfnmwlvbvRnL5IvmCXnUS1yLkd5Mv6AOTYMwI0yyW7t223DulZGs1JnJN9042\nV+5E2EhuVqubGvWxGk0PzMuymzR07wBhwL5muSCEcEkp88AUcBz4deAs8LAQ4rlaxwCalNL6K28A\no/UuPD4ewOVy1tuljEhkpOl9e8U5s+jFFTMjNds7FvJyLh8lFPZXHdrnzL/g4f0TvHZpA93p6Kjv\n5y8bE1r794SJREY4NDfGd08t4PK5GR/xtX1eO4Pw3TTLTvVlzbREx8O+mtecHPMD4A14iYwH2rrO\nTn43F8xcUVftG+ONhQ1S2ULL19dcywDsmQlvOTYSGWF6yhilujyusu1RM031zFQIzeHgzaU4vqCv\nauh0v7Ad300zoh8D7Fd2mIIPhpV/Vkp5GkAI8QiGVV/1GCGE/dU7AqzXu/DaWvMRJJHICMvL/e+S\nOH/ReBc6db1mey2hffXNy8xUeZAXzOMiYcOPP38p1lHfX33zMgA+l4Pl5Q2mR43r/+D0AjdcOdn2\neS0G5btphp3sy6VVY7TlgJrXdJkBYG/Or6O1sdBpp7+b18y04T6Xg1DAw8p6quH1K6NwLpj5poq5\nfNmxVl8y5khg9XKibPsb84bceBwwYo4S5KvLHJwNd9ir7aGT76bey6IZ0X8KeC/w/wkhbgdetG17\nFQgJIQ6Zk7t3Al8EztU45vtCiLuklP8MvBt4vMW+DDybeXdqWxdjtkRa1UTfOse+DobIdizf5qQp\n9vYCHd0QfUV71EvBYFGK1R+QydyYzcUyGvSw3KA86F//0xm+XSPVeK2JXG9pRW65e8dKWRIOeHA5\nDRfQajTdt6K/XTQj+g8BdwshTmBMvt4jhPgAEJJSfk4I8SvAV8xJ3RNSym+YET9lx5jn+hjweSGE\nBzgNfL3bHep37AXRa2GJfi1ffTSRw+91MjVqDO07zYppRTFMVYi+SrzWW1J1VuNaDFr+nZhtTisc\n9HB+KU4mVygJdSUvvX4Zl9PBtQfGyj6fGPGW5gUqqVUcvXTtkKc0TzKMETwNRd8Mqfxwxccv27Y/\nBtzWxDFIKc8A72irpbuEWLyxpT9uiX4NMY8lMoQDnlKWzk5ziKxG02ja5nUj4368bqeK1e8x9Vbj\nWgTNVamDIvqWtT0a9JQi2GKJLBFzbsKOruusRtNcMRXgf/vXb236GrWid+zpT6z525UhjOBRi7N2\nmGgyi0PTag5Nody9U0mxqLORyjEa9OB2OQl4XZ1b+rE0YyFvacjr0DT2RYJcWk2Syw/VMoq+oiX3\nzoCIvt29aa1VqTWi3UjlyOaLTIZbCybw1XDv2MOlrVHtMFr6SvR3mFg8y0jAXTUFg8VYqLalv5HM\nouubI4Vw0NNRyGa+UOTyRqbkz7eYmw5RKOqlyUTFzpOqU0DFYtDy71j1H+yWfq05KUuQK+/NRpR8\n+jXcO+GgUV/Y43Yo0VdsP9FktmGI2Lhp2VSz9CszdIaDHuIdpGJY38ig6zBVYU3ts03mKnpDrfq4\ndoK+wSqkEk1kcDk1/F5XaV6rltFSmmtq0dJ3ux1oQCa71b0T9LlwOR1omsZk2DeUC7SU6O8gmWyB\nTLZQdxIXDOvN6dCqWvqxiong0aAHnc2FJ61SGbljMadEv+fsVvfOaNCDpmmlgkG1RH+lTUvfoWl4\nPM6q7h27wTU56iORzg9kYflOUKK/g1iRO40sfU3TarptovGtlr7981ap9WDtiyjR7zX1SiVa+DxO\nnA5tICZydV03kg1aBksj907MiirbOsnbCK/bWZZaOV8okkjnywwuawQxbNa+Ev0dpJkYfYtw0EO0\nSiqGTUvfa/7vKfu8VUoPVsUQ2u91ERnzcX4pPpRL1fuBekXRLTRNI+h3E0/3v7WayuTJF/SSL7+R\npd+uTx+MyVy7e6faszc5pJO5SvR3kFgTeXcsRoMecvnilvSwtSz9didz6w2h90VCxFO5rhVqUbRG\nMpNH0zYrQdUiOCDplaO2OHkwXFMOTatr6XvdzlKFsFbwVrh3Ko0lsIm+svQV20W9MomV1BLzWMlF\n5C7br11htqyciSqTZcqv31tSGSOXvlalDqydkN9NIp3r+0Lflda2Q9MYCbjrWvqTo76G/a+G1+0k\nky2URqmbxtJmqPRU2HAbrShLX7FdtGrpw1YxrzxHowiIRqzG0owE3FVXRM5Nb+bWV+w8yXS+rmvH\nIuR3o+v0/YTkZobZTWt7NOgpzXXZSabzJDP5lmP0LbweJ0VdL5X9VO6dTZTo7yAtWfqB6mIeTWTx\ne124zeyjzdTUrUVR17kcS5cWqlQyN6Ms/V5iWfqNsMI2+z2Cp9r9Hw56SlFtdmpFlTWLtUDLco9W\nc++Mhjw4HZpy7yi2j1Ymci2/ZzVL3z5SGKnxcmi2PfmCXtOamhr14fU4VQ6eHlAs6qSzhbrhmhaD\nEra5uSJ208VSMloqrP3KfFCtUsq/Y0bwWO4d+7Pj0DQmwt6hs/RbnyFRtE0s0TgFg0W11YqFYpF4\nMseeyc1EU26Xg6DP1ZboN4qDdmgac5EQZy9E+eiffKdsW9Dn5jf+7VurzgUomkPXdR74byfZFwnx\nvjuuLNuWyjaO3LEYlPw7mwnPNq3t0txVPMu0Lf9OydJv171TsSo3ViNcejLs4+U318nlC6XRs8Xf\nPnGOy7EM/+6917fVhn5FWfo7SDSRYSRoRCw0olpeko1kDp2tN64V3tkqpZC4Og/WT9y0l71TQUJ+\nd+mfx+Vk4XKSJ390qeVrKjY5dyHG83KZf/nhxS3bkk1k2LQIlTJtDoZP314qtFYgQifhmmBPulZu\n6Y8Eyg0uaw3A5Yoi6RvJLI98902ePrVAro06Bf2MsvR3kFgix8x4cwtNqkXv1JoIHg16uLSaJF8o\nlpKmNUMzftNjN8xy7IbZss9SmTz3feZJTpxc4L1vP9hWdIUCTpw0XpprGxniqVzZCLCZGH2LQfHp\nxxJZXE4Hfu+mRV1rnclKh5a+5dPP2iz9kN+95fmw7v2VaJqZic3aFc+eXqJQNCJ/VmMZZifaq0rW\njyhLf4dIZ/NkcoXSgpRGBLwuXM7yGOZaE8HW762mYtj0m7a24tHvdXGziLC0nuLcxVhLxyoMcvki\nz55eKv1+frG8QlKqiRQMFoPi04/aUjBYbK4oL7e0V6NpXE6tNOJtFY+73NKvnAuzmKyxKvfpUwtl\nbdlNKNHfIUpWeqC5m7haKoZaln67C7Q68ZseP2JY/ydOLjTYU1GNH55dIZnJExkz/vaVEVLNJFuz\nKLl3+jjpmq7rbFRJNrhp6Ze3fTWaYiLsa8oVWg2frZBKLm+kYKgWQGG39C0urSZ49WIMp5kJd7dF\n9yjR3yGslLKtFGEOB8pTMdSK/mk3bHM1msbvdTVlTVZy3cFxRkMevnd6UeXcbwPLkvwf33E1sFX0\nU00UULEIDoClnzRTMNQyWOyWfjZXIJbMte3agfLonY06Oa+qxepb383b37IHgJVo/ZKOg4YS/R3C\nXjGoWUaDHvKFIqmMORlVy9IvRfqUD5Hroes6K9F02w+W0+Hg2PWzJNJ5fnRupa1zDCsbySw/OrfK\n3HSIoyKC2+Xg/HKFpZ9uxb3T/9E7lelDLIJmKga7T7/TGH0oj96p9dyAUXZRs12zqOs8fXIRr8fJ\n3bfsM9qj3DuKdmglRt9iM7IhU3aOLRO5DRJXVSORNuYY2o2DBkoTvMrF0xrWJOHxG2ZxOhzsnQpy\ncSVRWj0KzZVKtHC7nHjcjr5Oulbr/ndoGuFgeSqGWkkAW8EevVNvUaTL6WBsxMuqac2/cn6d1Via\nW0SEmYkAmqZEX9Em9ayNWlT66q1zjARq+fSbt/Q6DYkDIzfP3HSIH51bLQ2hFY05cXIBTYO3XT8D\nGAVr8gWdhcvJ0j6tTOSCEcHTz5Z+ZR0IO5Uhx924NzdLJhbKyiRWY3LUx9pGlkKxWDJgjh+ZNV4I\nIa/y6Svaox1Lv3KSK2ZW/nG7HBX7mTV1W3DvrDQRo98Mx47MUijqZZEoitpcWk3w2qUYR66cKJXF\nrJbYrpWQTTAmc/vZp19tRazFaNBLNlckbS5I63RhFtRw79SIBJoK+yjqOktrKZ6TS0yEvYgD40Yb\nbC+E3ULDO0oI4QAeAG4EMsC9Usqztu33AfcCy+ZHvwocA37Z/N0HvBWYBa4EHgZeMbf9mZTyqx33\nYgBoJe+OReUkl70AhR1rwUkr7p3NAhWdif7tR2b42j+f5elTC7zr6L6OzjUMWJOEVvQTwH5T9OeX\n4nDE+KyZAip2Qn4355fiLa/V2ClqrYg1PjPu32gii8/jKhkkndybXlv0TjOWPsC3np8nlSnwzpv3\nlaKGpsI+zs5HWdvItFXMpR9p5o56P+CTUh4TQtwOfBp4n237UeCXpJTP2z6TwJcBhBCfBb4kpVwX\nQhwF7pdSfrorrR8gYoksTodWirRoBvvClXyhSDyVY+9UcMt+LqeRiqGV6B0rIqGTITQYRdyPHJzg\n5GuXubSaKEsRoSjHPkl40zWR0ufV6hG34tOHzQieyupQ/UI9S9/uxpwZD7AaTaNpMDbi3bJvs9ij\nd7JmdFktS98aUXznh8ZiuWO2F7I9ume3iH4zJsEdwCMAUspngFsqth8FPi6EeFII8XH7BiHELcAR\nKeXnbPv+jBDiX4QQXxRCjHTW/MEhmsgyEmguBYOF/WGwFl7VunFHQ97WLP0uuXcAjpsTuk+fWuz4\nXLsZ+yShPZV10OdmIuzdIvoet6Npqz1k+v771cVTz9K33JPW/bsaSzM+4u1oxOJzl0/kamxNwWBh\nCXu+UOTg7AhX2AyranH8g04zZkQYiNp+LwghXFJKK1Tgb4DPAjHgISHEz0opHza3fQL4XduxzwJf\nkFI+L4T4beB3gN+odeHx8QAuV/2qQXYikf58h+i6zkYqx95IqOk2RiIj+EPGDZfKFXF4jK9qZqr6\nOabG/FxcSTA2Htzi869GNJnD43Zy1YGJjtMo3H3cz4OPSp49vci/+/kfw+HYer5+/W7aod2+/JfH\nDK/oe+64ass5rt43xvdeWsTt8zA2Yvi4Q35P8/eLOcJye90tt28nvptkJo/H5WBu79iW+23fbBiA\nguZgfCLI+kaGaw9OtNUu6xhd19E0KOrG6Gck6GF2ZrTqMYdt7vq7bz9Qdt2r5yYASBf0ntzD23HN\nZkQ/Btiv7LAEXwihAX8kpYyav38DuAl4WAgxBggp5eO2Yx+SUq5bPwOfqXfhtbVkvc1lRCIjLC9v\n1Nyu6zp/9U9nOLx3lNuPzNbcD+CpFy/xxuIG//O7DrcsiPFUjr/4u1PlFpdu+BaDXlfdNlpYfdF1\nHZfTwcpakjfmjT+bx0HVc/jN4eyrb6yWZb7M5gr8xd+d4vJG+STv/FKc6XE/KyvdSZt88zURnnpx\ngRPfP4/YP161P7uBZvoSS2T53N+fIlERQnlhOcFE2MtM2LvlHDPmytwfvLzAkYMTbCSNkWGzfzeH\nuYDvwqUo0yPNu3ea6c/3Xl7izPl1PvCT9Z+HlWiK//KtV/i37zpMZKzcFbIaTRMOeqreb5o5SXpx\nMcYrr65Q1I30y63eM5V98bqdxBNZLsfSTFT5m5euXzDWwTgdGkfmxsr2c2G07c2L0ZrHzy/F+e9P\nvcYH33Nd0+64Rjzy3Tdxup3cffPeto6v97JoZvz0FPAeANOn/6JtWxg4KYQImS+AdwKWb//HgW9X\nnOsfhRBqw2zEAAAgAElEQVS3mT+/y7bvthNL5nj8hQt89fGzFIu1y8rlC0W++thZvvXc/JaHthnk\nm+uceu0yF5bjLKwmjX+Xk/g8Tn7s6smWzqVpGqNBN9FEtuFkVKnoSkXo5PNnlvn+Kyvl7VlN4nI6\nuNnmV+6Utx4yzvXqJZWL56U3LvPS62tV/uYaP33b/qouvlKVskWjEH0qk29ppfR2Jl371nPn+fbz\n86zH67sPX5DGvfbos+fLPi/qOrEaQQhQnmmzWwEGYPj14+kcqUy+5nMDxsvhqIjwrqP7trRxokZu\nHjtP/OAiz8tl5JvrNfdpBV3X+fsTr/Nkleyr3aCZu+oh4G4hxAlAA+4RQnwACEkpPyeE+ATwOEZk\nz7ellP9gHieAVyvO9WvAZ4QQOWAB+FA3OtEMpQiYeJaX3rjMDVdWF+AXz62WHpyVaKqp3Pd2rEUe\nH3rvEW65drqDFhuEgx7OL8VL4Zi1HxwzAqLiwbTijv/PX3lbWRbBbmPlkNlNvs92seZL/v3Pv4W3\nHppq6hh72GY2V6RQ1Al4m7/3SknXtiH/jvWdrkRTjNeZXLX2++7pRf7Nuw6VfPLJdJ5CcWsKBgt7\nyc9uhRKDIebLa8bz2Chx20d+/i01zxEOuOsu0Dq/ZIwAulWucjWWJpXJc2B2e9xJDUVfSlkEPlzx\n8cu27Q8CD1Y57v+u8tkLwNtbb2bn2C3gEycXaor+iYrsegdNf2OzrHRhCbmd0aCX1wobpYU7NSdy\nKybDwEjZ+9Lrl7n6ivC2Cj4Mb73RapSyl7YgXNNjfjwuB+eX4rbInebns7Yrp36+UGTdNJhWo2kO\n14nKtazheCrHi6+uctNhY/TXKFw54HPhdGjEEtmuLMyy8LmdWGP6epZ+IyZHfZxfilPU9S2jNF3X\nOb+cADYjrjplfsk435VXVJ+D6JT+C+jdJuwW8AtyuepbOZHO8cOzK1hfazsC1s2oGNi04K3Ijpru\nnSp5yb/70iK6zpZ8+NtBwOvC53HuutWL7dDOi9/h0NgbCXFpNVFa3RzwNW/pW9Wzuu3eWdvIYE4X\nNPxuV6Pp0rNjT83RyDXpMDPKRhPZjvPo27HCNqG1lfCVTIZ95At61eg4yyqH7om+NXK48orWDM5m\nGRrRt8Tw4OwI2XyRF84sb9nne6eXyBf0kltmpQ0BW42l8bgcNcPDWiVsWvAXVxLm7/WHyPaX24mT\nCzgdGrddN9OVttRD0zSmRn2sRtOlrKDDymo0TdDnanlSb246RKGol2oUtGLpl+L0uyz6dsOnkRG0\nGkszOxlgbyTID8+ulFI9l5IN1nGxhAOecku/S+6d0vk7Ef06o1h7mG233DvWOQ/uUZZ+R1hv6Z9+\n236gepKwEycX0ICfOXYAaN/Snxz1da2alCXm+YJO0OeqGbtcaem/ubjB/HKcGw9NtTwv0S6TYR/p\nbKFrFs8gous6q7H2spdafv0z540JwWZX4wIEtylO327d1zOCUpk8iXSeyVEfx4/Mki/ofM9MzVFK\nK17HxTIa8pDNF7mwkiAc9JSKoHRCNy19qD7SqZY6o1POL8UJ+lxMjW1P/emhEX3Lr3j1FaMc3jfK\ny2+scdn2JS6uJTl7Icr1B8eZmw7hcTladlWks+aN38Vi4XYLpZ61UpmKwVruf6xBeGo3UX59Q3Sz\nuWJbPulORN/pcBDwurpeSKVZS98+j3H7kVk0NufHmsk7VYo+S2S79vz4dsDSn6+yiroTMtkCS2sp\n5qZD21aGdGhEf/PGc3P8hll0ykuiPW1a/sdumEXTNCZNV0UrdHMSysJuodSzVlxOByG/Ed5ZKBZ5\n5tQiQZ+r5TDRTlCi31mysH0RQ/TXzDUV/haL2wT9rq5b+pZ17/M467ru7PMY4yNerjs4ztn5KEtr\nyabcO/Zt3Xp+umXpW+kXqo10zi/FS1W6uuHemV+Jo7OZmmM7GBrRjyay+L0u3C4nt147jcvp4OlT\ni+i6jq7rnDi5gMe9Gbs+Oeojkc639EV2M9zMollLH4wbO5bIcvr1NaKJLLddN9PU6txuYfV7mMM2\nV9bbf/EHfK6y+PRWQjbByrSZ7+qcivUCP7RvlGy+yEaNl0qlwWONMJ8+tdiUe8e+rZM8+nYsn74G\nhDqYYyu5dyrua8sqPzg7gsvp6Ip7x3IXzUWU6HeMvTBywOfmrYenuLiS4I3FDV6Zj7ISTXP0mml8\nZrqDqSYWZVTSjYo/ldgfhkaiHw56SKTzPGEu6ji+A1E7diyLaJgjeDpdXDRns/Bace+AMZmbLxRL\nCca6wWo0TTjgZtYM+a01itssfGLcA0dFBI/bwYmTl4jGM3jcjpJFXA37vd1tS38k4MbpaF/qAuak\nfGXf55c3rfKA19kVS78k+jNK9DuiUCwST+bKbix7Ye9SulubSLbjqij5Nbso+n6vs2StNxqiWttf\nOLPMzLifq7Yp5KsWyr3TuYvPLvqtundCXY7gKeo6lzeMwISpGtauRWW/fR4XR6+JsLye5vxynHDA\nU9dHbb+3u+3T78SfbzEZ9rESK3dv2a1yv8/dFZ/+/FIch6ZVzabbLYZC9DeSOXTKb6wbrpog5Hfz\n3ZcWefb0EmMhD9cd2MwZU2/GvhbdKP5QiaZpJWu/GUsfKMXmb9dEUM3rB9y4XY62Ql13C53eAx1Z\n+l1OxRCNZ8kXdCbDvs0Xeo3vdiWaxunQynzzx28wCovremODxX5vd8to8ni6J/pToz4y2UJZahar\nrvHcjGHpd+re0XWd+eU4s5MB3C0kmmyVoRD9atEDLqeDt10/w0bSyM1x+5HZsuyQ7aRUXTVvfKsi\nUrewHiRr1W3N/Wz928moHQtN05gItz4BvptYjabxuB1th8nu60D0u23pb7qq/JuuuzrunYmwt2zF\n6nUHxhkLNWewbMdErmXpd6O+QLVR7HmbVR7wusgXiuTyhbavsRJNk8oU2BfZ3poUQyH6tZaB2905\nlf7vRjd5NVbMPODVUgt3gmXpN2stXbNvdEuWw51iKuwlnsqRybZ28z9zaoFnXhr8AutWjH67o6zI\nmB+vx4nToeFxt/Z4bubfac7ifPTZN3lB1i5zaXfZ1DOCcnmjOlVlkRGHQytltG107wa8LlxOjYC3\n9UVttfB20dKvHPkXdZ35pU2r3GpzMtO+6JfcRdsYuQNDIvqWpV954x2cHeHQvlGuOzBeCpezGA15\ncDq0pt07uXyBaDzbVX++hdg/xviIl+nx+kJ+5Z4wHpeDu2+d63obmqUkDi24eHRd58FHJV97/Nx2\nNWtHsBYodVJhyaFp3HRoiqv3jrb84mhlgVY0keVvHjvLX/7DSzX3KVVXC/sI+lx43dXTbKzGMqX9\nKvnxG68g4HVxaF/91aWapiH2j3P9lRMN294s+yIh/F4n1+wb6/hcUxUvvZVomnR20yq3MqJ2Mpk7\nXxL97c3b351Xap9Ta3GIpml8/H+5ueoxDk1jIuxt2tK/XOfG75Sfum0/P3Xb/ob7XTEV5IGPvaOl\n6lzdZtI2Qmp2Msoa1hbqpLweBLq1TuNDP3ekreNKln4Tom/ld3lzYYNCsVg1uqUk5uYK81prV+r1\ne3YiwJ/8hzubuic/9m/e2nCfVoiM+fnsfe/oyrkq3TvzFVa5FV7biV9fWfpdJFrD0gdD+GtZVJNh\nH9FEtik/Xbeza7ZLLwUf2gt1tW72bK5IvtC9cMOdZjNZWHfndJqllfw71t88ly+ysFq9WFFlHpzJ\nsI9kZuvaFfuIoBq9vie7QaV753yFVW7lSUpm2p9POb8UJ+R3l+ZBtouhEP1a7p1GbEYsZBrsuT2r\ncQeRdsI2tyNpVS/o9T3QykSuPX2A/e9vZzWWJuB1lVwXUzW+2+1Yn9JvjATcRmqWaKXom5a+GTmV\natOnn8rkWVrf3vQLFkMh+palP9JiTu1aK/Gq0U4O9d1IO6Gu3c5f0isqFyjtNK2EbNqF3go9tKPr\neil5oEWt+Zpev+x2gpJ7q2Tpb5RZ5SVLv83cRxfMnPzb7dqBIRH9WCJL0OdqOSVBKytMh8HaaYax\nEQ8OTVOWfg/we42on0ZlPnP5IpdWk6XCOtUs/UQ6TyZXKHPZ1DKCVqNpNA0m6lTV2g1Mhn3EUzmi\n8QzL6+kyq9zy6bdr6Zdi/ndA9IdiIjdapz5nPVqJ1V8xC0hMDLml73Q4mAh7S37eRljDWotupaft\nBdUWKO0kmqYR9DVOunZpNUGhqHPt/jEKRb2q6Jf89FUs/WrunbGQt2ba792C1f8fnlsFKhbS+ayQ\nzfYsfes7qIwi3A5297eEUe4tnsq1VS6tFf/0ajTNaMiz62/8ZpgM+8zVnI0nZa1hrTUKG2hL34zR\n7+XEZdDvbij6dn/0lVeEicazZRXXoHoFuFJCPdvIN18ocnkjMxQjXKv/P3hlBahImWHF6bdptJxf\n2sDp0LhiG9MvWOx6hdpIGg9AO9bXxIgXjcbunUKxyNpGpqP47N3E5KgPHcrqFdTCGtZebeYJGlRL\n31qg1GvxC/rdJNI5inUybdpF/+Ae4+8+X2HtV8sjZRg15a67dbOc4jDMZVnf7anXLwPVU2a0Y7QY\nC70S5kKv7ZfkXS/6jepz1sPldDA24mW1gatifSNLUdd7/sD3C61MgFsCdM2csYBmUC39eguUdpKQ\nz42uQ7rO39HuSrCKb1e6eKqFIDusNBu2l/kwzWVZL8BcvojTobFnctMq78TSX1lPkckVtjWdsp2G\nPn0hhAN4ALgRyAD3SinP2rbfB9wLWEVnf1VKKYUQLwAx87PXpJT3CCEOAV8GdOAk8BEp5bYGZpdi\n9Nv0s06O+nj1QqzmAhbYnkRrg0wrq3KtYe2hvYb4DGr0Tq8ncS3sBdKrFVbXdcOHPzXqw+91lYpv\nV4p+rf5Mhn2cfmONbK6Ax+3crCExBKJvf74rrXKf14lGe0bLTi3KsmhmIvf9gE9KeUwIcTvwaeB9\ntu1HgV+SUj5vfSCE8AGalPKuinPdD3xSSvnPQog/N8/zUCcdaEQnlj4Yw9az89G67pt+eeD7hVrx\n3JXYh7VWOO2gunc6zaPfLTZX5eaZHt+6PZrIEk/lOGymRdgzZZQG3SL6sTQel4ORisRx9mybeyaD\ntjDV3X/vj4W8OB0ahaK+RaAdmobf62rLaNlp0W/GvXMH8AiAlPIZ4JaK7UeBjwshnhRCfNz87EYg\nIIR4VAjxmPmysPZ9wvz5m8BPdtT6JrBKtbWbdKmZydxGKxKHjWYnwO3D2m7kLukl/XIPlBZo1YgX\nrxQYp0NjbyTExZVE2cS7FaNfuVCocsX1MFn6DofGuBmWWk2gB0X0m7H0w0DU9ntBCOGSUlq9+xvg\nsxiunIeEED8LvAH8AfAF4DDwTSGEwLD+rRmmDaBuFqbx8QCuFvJKRyJbExXlzKsd3DdedXsjDuwd\nA94gq2s1j09kjYfl8MGJtq5RjW6dpxeMjRvx37FUvtSPav155ZKR/+XaKyfZv9fw6ef1/u97tfbF\nzfjsw1dOEpnc/giMWsyabXO4nFXbeflFI5PpDYcjpe2H94/z2qUYGV1jT2SEZDpHIp1HHNh6Px80\nk5dli8bfwSqfeM1VU6Wqc71ku++dPVMhVqJpbjg0veVa4ZCHxcvJlttwcTXJaMjD1Qcnt7xkt6M/\nzXxLMcB+ZYcl+EIIDfgjKWXU/P0bwE3APwFnTYE/I4RYBfYAdv/9CLBe78Jra9VzglQjEhlheXlj\ny+eLK0ZIYCGbq7q9EV5zLPTa/BrLB6pn67uwaExdOArFtq5RSa2+DBKjIQ+XVuIsL2/U7M+ps8Y0\n0ETQTWLDsBijG+m+7nutvlxc3EDTQM/le9p+t2ZYOafOrXBk/9b79eXXjBjzsNdZ+m4iZq6gH728\nSNClMW9GVI34XVv64jE16fUL6ywvb3BpJcFIwM1GNEWvv7WdeG72RQKcnXcyHtj6t3GbdXIXF2NN\np1dfWk+xeDnJW66aZGWl3MXWSX/qvSyace88BbwHwHTTvGjbFgZOCiFC5gvgncDzwAcxfP8IIa4w\n97sEfF8IcZd57LuB77TSkXaIxjt07zQRibISyxDyu0v5uxWGG2BtI0OxTuZM+7DW4dDweTqvPtQr\n+mWB0nUHxgl4XTxzaqHq335+KY7X42TKVm/BcitY30e9sp/2+ZqirnPZXJswLPz8nVfxf/3a8apF\ncqywzXS2+Xv4mZPGyOu266a708AmaOYOfQhICyFOAH8I3CeE+IAQ4kOmhf8J4HEMAT8lpfwH4IvA\nmBDiSeCrwAfN0cHHgN8VQjwNeICvd79L5cSSOYI+V9sPY6Mycbp14w+BT7MVJkd9FIo66/HayerO\nL8UZCbhLL+R2faK9xlinsT21FFrF7XJy63XTrMeznH5zrWxbLl/g0mqSuUiobAGZtQrUSrdcLxpt\nbMSLphmiH0sY5RT7od87hcvpKOU4qqS0KrdJw0XXdU6cWsDjcnDzNZGutbERDd07Zkjlhys+ftm2\n/UHgwYpjssAHqpzrDNCdBNdNEo1nOqqc43U7GQm4a1r6sWSOXL44FNELrdDoZZlM51mJprn+4Phm\n/hKfi/WNxhlN+421jUxfrdM4fsMsT/zgIideXODIwc2iJBdXkhT1rZEnAZ+LybCP8+bq6HrRaC6n\ng/ERLyuxtIpaq2CzelZzon/uYoyltRS3H5npWrWwZtjVi7PyhSKJdL7jGpmTYR+rsUzVVY7VcpQo\nNqM8auUtmq+SYMqy9PU6q0n7kWopC3rJob2jRMZ8vHBmuczV8KZpyVeLEpmbDhFLZIkmspsROTX6\nM2m67pbW+iNiqV9odVXuCdO1c3yH61nvatG3UjB0WiNzctRHvlBkI5Hdsq3fHvh+oVHYZrUwtYDX\nZawmbbG+bq/pt7BFTdM4dmSWTK7AC2eWS5/PLxmW/L4aog+Gi2c1ZiSOGwtVz5o5OepD1+HshWjp\nd0Vrq3Jz+SLfO73IaMjDdQerLKjYRna16Hcao28xWcdqHaZl6K3QKK9+ZeUh6E6d0V7QjwuUjt1g\nWI+WNQmGoGtQqutqxz6ZuxpNMz7irRmBYn23Z86vl/0+7Gxm2mx8//7o3AqJdJ7br5+pudJ/u9jV\not9uxaxK6vmn60U6DDONLP355biZvyRQ+qxVn2i/0I++7ZnxAIf2jnL69TXWNjKl9AuRcX/VeHpL\n9F+7GCOaqD8pbW27YIZDq3vfINDC/Vty7dywZ1vbVI1dLfrRePWC6K1SL61APz7w/YDP4yLkd1d9\nURaLOvPLcfZMBsuiqgIdpqftFf2ae+n4DbPowDOnFljbyJBI52uu+oyM+/G6naUMkvXuZ/s2v9dV\nNcfPMOK3RqoN7t+NZJYfnVtlXyS0Y6tw7exq0bdyhI8GO6voUy2PuMVqLI3P4ywJlmKTybCP1Wh6\ny8Ts0nqKbK64NYpkgC39cMCNx91f6zRuvW4al1PjxMmFhkv9HZrGvkiwVPmp3gusWo59RfP377On\nlygUdY7fsLMTuBa7WvSjXXLv1LL0dV03CmdUyVGiMCzCbL5YcrNZ1BIg/wD69Iu2e6DfCPrc3Hho\nigsrCZ4y3Qn10vfav4+6lr5N6JVrZ5NmRf/pUwtoGtx+ZGYnmrWFXS36pQybHYp+wOfG73VuEf1k\nJk8qU1DWTg2sv8vi5fJ0GrVEfxDdO9YCpX69B6xwwOdeXgLqJ/WyR/XUm5T2uJ2EA4ZLp1/73Qua\nMVourSZ49WKMIwcnakZHbTdDIfojgc59jpNhHyuxcleF8ufXx/q7LK+VF6GZbyD6g2Tp9/s98Jar\nJ0spA/xeV912Nmvp27f3a797QTNGy9OnFgF65tqBXV4YPZrIEvK7u5IPZWrUz/xygm9+983S+S6t\nquiFelh/lye+P8/rFzYF5dWLUUaDni0jMH8LIW/9wmYe/f4slelyOrjtumkee+ECc5FgXTeklY5B\nAyYaWPCTo35eu7Sh7n0bLqcDj8tR8/4t6jpPn1zA63Fy0w6mXahkV4t+LJHt2hBqz1SAH5yFr//z\nua3bephKt5+xwjGffvEST1dsu+nw1Jb9B9G988aisco1Mtafog9wx4/t4fEXLnD1vrqZzPF7XeyL\nhCgUiw0NpblIkOdfZkcKeQ8Sfp+r5kj10kqC1Via24/M4O3hpP+uFf1c3kjBsH+mO/mof+74lRze\nN7Ylc6Hf40Qc2NkVdYPCnskgn/jFo+B0Eottung04FAVARo0905R13nm1CJ+r5Nrq6Qx7hcOzob5\n3Q/e1tSL6b5/fWNT5/yp2/Zz0+GIEv0KAl5XKRNAJcumK3DfDtXCrcWuFf2NZHcmcS28HidvPbTV\nOlXU59De0abzgg/a4iz5hrHw6cdv3NN34ZqVVEu9UA2rMlQjPG5n0+ccJgJeF0trKXRd3+JK65eU\nLbt2Irdb4ZqKncPtcuByagNj6Z84ZYRBHtvhhFmK/sXvc1Eo6mTzxS3b+mXSf9eKfrfCNRU7h6Zp\nBLyugfDpZ3IFnpPLTI36ODzXv64dxc5Sb15qpU9Wbu9a0VeW/mDi99aeCOsnvn9mmUy2wO1HZssK\nkiiGm3rzUqvRNC6nxmiot5q0a0VfWfqDScA3GNWzNhNmKdeOYpN681KrsTQTYV/PjYRdK/qWpR8O\nKNEfJPxeF7l8kVwVn2i/sB7PcOr1y1x1RZjZiUDjAxRDQ6304NlcgVgi23PXDuxi0S+lVe7xUErR\nGoMQtvnMqUV0XVn5iq3U8un3U92NXS36Gt1JwaDYOVopRNErTpxcwOnQuO263iTMUvQvtdw7/VRo\nZ9eKfjSRJeh373hVGkVn+Pvc0n/tYpT55Tg/Zstpo1BY1HLv9Eu4JjSxOEsI4QAeAG4EMsC9Usqz\ntu33AfcCVjHOXwVeBb4EHAS8wO9JKf9OCHET8DDwirnvn0kpv9qdrpQTS2QZD/cmi52iffo9FcNj\nz50HlGtHUZ1adXL7qdBOMyty3w/4pJTHhBC3A58G3mfbfhT4JSnl89YHQoh7gFUp5S8KISaAHwB/\nZ+57v5Ty013rQRVy+QLJTJ4Dge6kYFDsHP28KrdQLPLEC/MEfS5+7Gq1OluxlVpzUv1UVrUZ38cd\nwCMAUspngFsqth8FPi6EeFII8XHzs68BnzJ/1oC8bd+fEUL8ixDii0KIbVHlWMLIfaEmcQePRsXR\nM7lCKTXzTmPVm731uhncLuU2VGzFKh1ZabSsRNNoGow1meZiO2nG0g8DUdvvBSGES0pp9epvgM8C\nMeAhIcTPSikfBjBF/evAJ819nwW+IKV8Xgjx28DvAL9R68Lj4wFcruZzmkQixjskY+ZEm5sNlz4b\nNAa13bVotj+zEUPQNaez6jF//cjLfPVbks/+7+9krkvJ9JrlhUfPAPCet1+1q74f1ZfuEQobSe0K\nenlb1uJZJkf97Jmtn+m0ku3oTzOiHwPsV3ZYgi+E0IA/klJGzd+/AdwEPCyEmAMeAh6QUn7FPPYh\nKeW69TPwmXoXXltL1ttchj2plwedX/9Xb+GaubGmEn31G80mKBsUWulPLmOM0pYvJ6oeI19fRdfh\neycv4nNc0dV21iOVyXPiRxfZMxVkMujaNd/PbrrX+qEvuq7j0DTWY+lSW/KFIqvRFIf2jrbUvk76\nU+9l0cwY9SngPQCmT/9F27YwcFIIETJfAO8EnhdCzACPAr8ppfySbf9/FELcZv78LuB5tgFN07j5\nmoiKrhhArOFxqsZErjUhdn6HXTwvnFkmmy/yE0fnVD1kRU00TcPvdZa5d9Y3Muh6f0TuQHOW/kPA\n3UKIExj++XuEEB8AQlLKzwkhPgE8jhHZ820p5T8IIf4YGAc+JYSwfPvvBn4N+IwQIgcsAB/qcn8U\nA47fa7jzak3kWhNiO+3Xt9Iu/MTRfVDs39XCit4TqCik0k+RO9CE6Espi8CHKz5+2bb9QeDBimM+\nCny0yuleAN7eejMVw0LAa1r6VUQ/nc2TMEcA55fiVXOWbweXY2lefmONw/tGmZ0M9tyFoOhvAl43\nC5c3XdMrfRS5A7t4cZZiMPF5nWhAMr21+pBl5QMk0nnWNjI70qanTy2go2LzFc3h9zrJ5AoUzBFh\nPy3MAiX6ij7DoWn4vC6SmcKWbdYw2XIB7YRfX9d1TpxcwOV0cOu109t+PcXgU5qXMu/hfsmjb6FE\nX9F3BLwuUpmtlr41TH7LVZPAzoj+G4sbXFpN8tbDU6WHWaGoR2leyhyt9kuZRAsl+oq+w1/L0jcf\nnhvNWsU7IfonXjTz5quSiIom2ZyXMu7h1ViacMDdN3WUlegr+o6Az0U6k6eo62WfW+4dMTeG3+ti\nfnl7RT9fKPLd04uE/G5uuGpiW6+l2D3YLf2irnM5lu4bfz4o0Vf0IQGvCx1IV8lf4nRojIW8zEWC\nLFxOks1tHRF0i5OvXWYjmeNt18/gcqpHRdEcm6kYCkTjWfIFnclRf49btYm6kxV9R62kayuxNOMj\nXhwOjbnpEXQdLqwktq0dT6uSiIo2KGWKzeT6Ko++hRJ9Rd9RLb1yLm9YTVas89xMCNg+v34yneP7\nr6ywZzLAwdndk5tGsf2UakKk830XrgnNrchVKHYUf5VMm5djRky+FQGxL7K9ov+9l5fIF4ocv2FW\npV1QtIS9+lu+aMxL9UvkDijRV/QhgSrunZWKGqN7I0E0bftE33Lt3H69cu0oWsN+/24kjbBNZekr\nFHWollO/cpjsdTuZGQ9sSzqG5fUUZ+ajXLt/rK8eVsVgYB+plkS/jyx95dNX9B3VfPqlykO2h2du\nOkQqky9NlnWLp09ZE7h7unpexXBgv39XomkCXlfJkOkHlOgr+o5q0Tursa0TYvumDb/+/FL3Inis\ntAsel4OjItK18yqGBytOP5UxJnL7bbSoRF/Rd1Rz76xE02jARIWlD3B+qXtZL1+9GGNpLcXN10RK\nLx+FohWcDgdej5Pl9RSZXKGvXDugRF/Rh9Ry74yGPGWLpPZPdz+Cx8qbf0zF5is6IOB1sWpFnClL\nX/JKcekAAAf4SURBVKGoTynO2bT0C8UiaxsZpipWNY6PeAn6XF0T/Vy+yLOnFxkNerj+4HhXzqkY\nTgK2UaKy9BWKBlT69Nc3shR1fYvFpGkac9MhltZSZLKdp2P40blVEuk8tx+ZwelQj4aiffy2idt+\nKZ5ioe5sRd/hdjlwuxwl9069cnP7IiF0YH6lc2vfito5pjJqKjqkzNJXoq9QNMbIqW+I/ko0BVR/\neOa65NePp3L88OwK+yIh9s+otAuKzlCir1C0iJFT37T06xSh6FYOnmdPL1Io6iq5mqIrWC5Kj8vB\niL+/iu8o0Vf0JQGfYenrur6ZqbCKxbR3qjvpGJ4+uYCmwduun+noPAoFbIYdT476+i53U8NAZCGE\nA3gAuBHIAPdKKc/att8H3Assmx/9KvBKtWOEEIeALwM6cBL4iJSy2LXeKHYNAa+LfEEnly/WtfTd\nLiezEwHmO0jHsHA5ybmLMY5cOcH4iLfjtisUlnun3yJ3oDlL//2AT0p5DPgt4NMV248CvySlvMv8\nJ+sccz/wSSnlnYAGvK8bnVDsPuxhmyuxDCG/G6+nerm5uekQ6WyBNxfjbCSzLf/7zg8vAipvvqJ7\nWPdvv/nzobmEa3cAjwBIKZ8RQtxSsf0o8HEhxCzwDSnl79c55ijwhPnzN4H/AXiosy4odiPW8DiR\nznM5luaKqWDNfeemQzx7eonf/fL32r6e1+3k5sMq7YKiO1j3b7+Fa0Jzoh8GorbfC0IIl5TSWi75\nN8BngRjwkBDiZ2sdA2hSSqvw6QYwWu/C4+MBXK7miwlHIrsn6mI39QVa78/kWACAlOniuSISqnmO\n977jEJfjWTIdlE5825FZ9u0da2rfYf9u+pl+6cu7wn4uraV5308cYnykfeHfjv40I/oxwH5lhyX4\nQggN+CMpZdT8/RvATbWOEULY/fcjwHq9C6+tJZtonkEkMsLycvdysPSS3dQXaLM/ReNWOfWKMVU0\n4nPVPccv3n1N2+2zaKaN6rvpX/qtL+87foB8OsdyOtfW8Z30p97Lohmf/lPAewCEELcDL9q2hYGT\nQoiQ+QJ4J/B8nWO+L4S4y/z53cB3mu6FYqiwhsfnl42onH70jSoUg0gzlv5DwN1CiBMYk6/3CCE+\nAISklJ8TQnwCeBwjSufbUsp/MCN+yo4xz/Ux4PNCCA9wGvh6l/uj2CVYE2FWKGY/FZZWKAaZhqJv\nhlR+uOLjl23bHwQebOIYpJRngHe01VLFUGGFvC2v1V6Nq1AoWkctzlL0JZalb836K9FXKLqDEn1F\nX2IvL+fzOMtymSgUivZRoq/oS+wiP9WHS9kVikFFib6iL/H3cREKhWKQUaKv6Et8HieWca/8+QpF\n91Cir+hLNE3bTFqlRF+h6BpK9BV9i7+PMxUqFIOKEn1F32JZ+pUF0RUKRfso0Vf0LfZCFAqFojuo\n4GdF3/ITN+9j/8wI4UB/lZtTKAYZJfqKvuXWa6e59drpXjdDodhVKPeOQqFQDBFK9BUKhWKIUKKv\nUCgUQ4QSfYVCoRgilOgrFArFEKFEX6FQKIYIJfoKhUIxRCjRVygUiiFC03W98V4KhUKh2BUoS1+h\nUCiGCCX6CoVCMUQo0VcoFIohQom+QqFQDBFK9BUKhWKIUKKvUCgUQ4QSfYVCoRgiBrqIihDCATwA\n3AhkgHullGd726r2EEK8DfjPUsq7hBCHgC8DOnAS+IiUstjL9jWDEMINfAk4CHiB3wNeYgD7AiCE\ncAKfBwRG+z8MpBnQ/gAIIaaB54G7gTyD3ZcXgJj562vAf2Kw+/Nx4OcAD4auPcE29GfQLf33Az4p\n5THgt4BP97g9bSGE+I/AFwCrGOz9wCellHcCGvC+XrWtRX4BWDXb/dPAnzK4fQF4L4CU8u3AJzFE\nZWD7Y76U/wJImR8Ncl98gCalvMv8dw+D3Z+7gOPA24F3AHNsU38GXfTvAB4BkFI+A9zS2+a0zTng\nX9l+P4rxlgf4JvCTO96i9vga8CnzZw3DkhzUviCl/G/Ah8xfDwDrDHB/gD8A/hy4aP4+yH25EQgI\nIR4VQjwmhLidwe7PTwEvAg8Bfw88zDb1Z9BFPwxEbb8XhBAD57KSUv4tkLN9pEkprfwYG8Dozreq\ndaSUcSnlhhBiBPg6hnU8kH2xkFLmhRD/L/AZ4K8Z0P4IIX4ZWJZS/qPt44Hsi0kS4yX2Uxhut4H9\nbkymMIzW/4nN/ji2oz+DLvoxYMT2u0NKme9VY7qI3W83gmFhDgRCiDngceBBKeVXGOC+WEgp/1fg\nGgz/vt+2aZD680HgbiHEPwNvBf4SsFedH6S+AJwB/kpKqUspzwCrwIxt+6D1ZxX4RyllVkopMeaO\n7CLftf4Muug/BbwHwBzevdjb5nSN75s+PoB3A9/pYVuaRggxAzwK/KaU8kvmxwPZFwAhxC+ak2tg\nWJZF4LlB7I+U8sellO+QUt4F/AD4JeCbg9gXkw9izuEJIa7AGPU/OsD9eRL4aSGEZvYnCHx7O/oz\ncK6QCh7CsF5OYPiQ7+lxe7rFx4DPCyE8wGkMV8kg8AlgHPiUEMLy7X8U+JMB7AvAfwX+HyHEvwBu\n4D9g9GEQv5tqDOp9BvBF4MtCiCcxols+CKwwoP2RUj4shPhx4FkMY/wjGBFJXe+PSq2sUCgUQ8Sg\nu3cUCoVC0QJK9BUKhWKIUKKvUCgUQ4QSfYVCoRgilOgrFArFEKFEX6FQKIYIJfoKhUIxRPz/A2J8\n+uDIM1UAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11d734450>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# KNN Classification on train_test_split\n",
"k_range = list(range(1, 61))\n",
"k_score = []\n",
"for k in k_range:\n",
" knn = KNeighborsClassifier(n_neighbors = k)\n",
" knn.fit(X_train, y_train)\n",
" y_pred = knn.predict(X_test)\n",
" k_score.append(metrics.accuracy_score(y_test, y_pred))\n",
"plt.plot(k_range, k_score)"
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 65.8536585366 %\n"
]
}
],
"source": [
"# Best values of k in train_test_split\n",
"knn = KNeighborsClassifier(n_neighbors = 50)\n",
"knn.fit(X_train, y_train)\n",
"y_pred = knn.predict(X_test)\n",
"print \"Accuracy is \", metrics.accuracy_score(y_test, y_pred)*100, \"%\" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Splitting Training Set (2008-2013) and Test Set (2013-2015) based on Seasons\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#Splitting\n",
"X_timetrain = X.loc[X.index < 398]\n",
"Y_timetrain = y.loc[y.index < 398]\n",
"Y_timetrain_arr = np.ravel(Y_timetrain)\n",
"X_timetest = X.loc[X.index >= 398]\n",
"Y_timetest = y.loc[y.index >= 398]\n",
"Y_timetest_arr = np.ravel(Y_timetest)"
]
},
{
"cell_type": "code",
"execution_count": 85,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 51.724137931 %\n"
]
}
],
"source": [
"# Logistic Regression on time-based split sets\n",
"model3 = LogisticRegression()\n",
"model3.fit(X_timetrain, Y_timetrain_arr)\n",
"timepredicted = model3.predict(X_timetest)\n",
"print \"Accuracy is \", metrics.accuracy_score(Y_timetest_arr, timepredicted)*100, \"%\""
]
},
{
"cell_type": "code",
"execution_count": 86,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x11d9d5d90>]"
]
},
"execution_count": 86,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAD3CAYAAADxJYRbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXl0I9d95/spAARAkACXJpts9qZepCtZu7pblmxtsTZv\niZVkkvPG45exHI3tHE/G4+O8F9uxX47P89tmYjuJYyfxNsp44rETJ8oiW7J2ydqsXiS71VLfVi9S\nr2SzuYEkiB3vj6oCiyAAFklsBH6fc/o0idruBYFv/ep3f4uRy+UQBEEQWgNPvQcgCIIg1A4RfUEQ\nhBZCRF8QBKGFENEXBEFoIUT0BUEQWghfvQdQjtHRadehRT09ISYmYtUcTs1oprlAc82nmeYCzTWf\nZpoLrG4+/f1ho9S2prH0fT5vvYdQMZppLtBc82mmuUBzzaeZ5gLVm0/TiL4gCIKwNCL6giAILYSI\nviAIQgshoi8IgtBCiOgLgiC0ECL6giAILYSIviAIQgvR0MlZgtBInByZ5m8ff4NYLLXg9WDAy2/e\nsp1QsK1OIxME94joC4JLHtt/mmd/ea7otnB7G/fcvL3GIxKE5SOiLwguiSfSAPzxh/fQ2W5a9els\nli/9zT6efPkM77txK21NlhUqNB/i0xcEl8STGQA2rAuxrivIuq4gAz0hbrlmiOlYihcOjdR5hIKw\nNCL6guCSeCqDx4A238Kvze3XbcLrMXh07ymk/ajQ6IjoC4JL4okM7QEfhrGwgGFvJMiey9Zz5sIs\nh94cr9PoBMEdS/r0lVIe4BvA1UACuE9rfdSxfQ/wFcAAhoEPARngu8BFQAD4ktb6X5RS1wIPAm9Y\nh/+l1vqHFZuNIFSReDJNe6D4V+auPZt58dAIj7x0iiu2ravxyATBPW4s/XuAoNb6RuAzwJftDUop\nA/gWcK/W+ibgYWArpvCPaa1vBt4N/IV1yC7gK1rr26x/IvjCmiGRyhAsIfoXDUa4ZHM3r54Y58zo\nTI1HJgjucSP6tpijtX4R2O3YdgkwBnxKKfU00Ku11sDfA1+w9jGAtPXzLuB9SqlnlFLfUUqFKzAH\nQagJ8WSmpKUPcPeezQA8uu9UrYYkCMvGTchmBJhy/J5RSvm01mmgD3gH8B+Bo8CDSql9WusnACxR\n/xHweevYl4Bva633K6X+CPhj4A9KXbinJ7SsRgL9/c1zD2mmucDan08mkyWVztIe8JWcy+3rOvnR\n08d54dAIH/2Nq+nqDNR4lCtjrf9tnDTTXKA683Ej+lHAeWWPJfhgWvlHtdavAyilHsZ8EnhCKbUZ\neAD4htb6+9b+D2itJ+2fga+Vu/ByWoX194cZHZ12vX8j00xzgeaYTyxuZuG2B3xl5/Ku6zbyt48e\n4UePan7tpm21Gt6KaYa/jU0zzQVWN59yNws37p3ngPcCKKVuAA46th0HOpVSO63fbwYOKaUGgEeA\nP9Raf9ex/0+VUtdbP98O7Hc1A0GoM3aMfjn3DsA7rxwkFPDxxIHTpNKZWgxNEJaFG0v/AeBOpdTz\nmP75e5VSHwQ6tdbfVEr9LvB9a1H3ea31j5VSfwb0AF9QStm+/fcAvwd8TSmVwoz0+WilJyQI1cAW\n/VILuTZBv49brxnioZ+fZO/h87zjig21GJ4guGZJ0ddaZ4GPF7x82LH9CeD6gmM+CXyyyOkOAO9c\n/jAFob64tfQBbrxikId+fpLX35oQ0RcaDknOEgQXxJPmMpYb0R/q66A94OXYmWi1hyUIy0ZEXxBc\nkMhb+ktHk3kMg+0bIgyPx5iZSy25vyDUEhF9QXDBctw7ADs2dgFw/OzUEnsKQm0R0RcEF9junaDf\nnehvHzJF/6i4eIQGQ0RfEFwQT1mWftCtpR8BxNIXGg8RfUFwQTyxPPdOR7CNDetCHD8bJZuVcstC\n4yCiLwguSNiWvkv3DsCOoS7iyQxnL8xWa1iCsGxE9AXBBfmQTZfuHYDtlovnqLh4hAZCRF8QXLDc\n6B2AndZi7rEzIvpC4yCiLwguyJdh8Luv+jrU10HQ7+X4WYngERoHEX1BcMG86Lu39D0eg+1DEc6N\nSZKW0DiI6AuCC+LJNIE2Lx6PsfTODux4fbH2hUZBRF8QXJBIZpbl2rHZaS3mil9faBRE9AXBBfEV\nir5t6R+TCB6hQRDRFwQXxFMZAisQ/c72NgZ7JUlLaBxE9AVhCbK5nOXecb+I62THUMRM0hqTJC2h\n/ojoC8ISJFYQrunErrgpfn2hEVjSdFFKeYBvAFcDCeA+rfVRx/Y9wFcwWykOAx8CksWOsXrp3g/k\ngFeBT1iduQShYbFLMKxe9KPces3Gio1LEFaCG0v/HiCotb4R+AzwZXuD1Rf3W8C9WuubgIeBrWWO\n+Qrwea31zZg3iQ9UaiKCUC1WkpjlZGNfBwG/VxZzhYbAjejbYo7W+kVgt2PbJcAY8Cml1NNAr9Za\nlzlmF/C09fNDwB2rnYAgVBu77k6gbWU+fY/H7KR1bizGbFyStIT64uZTHAGcJkpGKeXTWqeBPuAd\nwH8EjgIPKqX2lToGMLTWdgjDNNBV7sI9PSF8PvfWVX9/2PW+jU4zzQXW9nyGowkAenvagZXN5cqL\n+3n9rQnGZlNctLm3ouNbLWv5b1NIM80FqjMfN6IfBZxX9liCD6aVf1Rr/TqAUuphTKu+6DFKKaf/\nPgxMlrvwxETMxfBM+vvDjI5Ou96/kWmmucDan8/weXPs2bTp5lnJXDZ0BwE48NowW9aFKje4VbLW\n/zZOmmkusLr5lLtZuHHvPAe8F0ApdQNw0LHtONBpLdAC3AwcKnPMy0qp26yf3wP8zNUMBKGO5KN3\n2lbm0weJ4BEaBzeW/gPAnUqp5zEXX+9VSn0Q6NRaf1Mp9bvA961F3ee11j+2In4WHGOd69PAt5RS\nfuB14EeVnpAgVJrl9sctRmd7GwM97Rw/FyWby+ExllfDRxAqxZKfYiuk8uMFLx92bH8CuN7FMWit\njwC3rmikglAnVhu9Y7NjYxfPvzrMuQuzbOzvrMTQBGHZSHKWICyB7d5ZSRkGJ3kXj1TcFOqIiL4g\nLMFKaukXY8eQ1T5R/PpCHRHRF4QlyMfpr9LS39TfSaDNK4u5Ql0R0ReEJYhbZRjaVyn6Ho/Btg1h\nzo3FiEmSllAnRPQFYQniicos5MK8X186aQn1QkRfEJbALri2WvcOzIu++PWFeiGiLwhLEE+mafN5\n8HpW/3WxF3MlgkeoFyL6grAEK22VWIxwyG8maZ01k7QEodaI6AvCEsSTGQKrKMFQyPahLuYSac6N\nua8tJQiVQkRfEJYgvopWicXYudFy8YhfX6gDIvqCUIZcLkc8mSYYqJylL8XXhHoioi8IZUils+Ry\nq6uwWcjG/g4zSUsWc4U6IKIvCGWoVLE1J16Ph20bwpy9MCtJWkLNEdEXhDLEKxij7ySfpHVOrH2h\ntojoC0IZ4onV19Ivxo4h268voi/UFhF9QShDNdw7ANslgkeoEyL6glAGuwRDpUU/EvKzXpK0hDqw\n5DOr1frwG8DVQAK4T2t91LH9U8B9wKj10seAG4EPW78HgWuAQWAb8CDwhrXtL7XWP1z1LAShSlSq\nln4xdgx18cKhYYbHYgz1dVT8/IJQDDef5HuAoNb6RqvJ+ZeBDzi27wJ+R2u93/GaBu4HUEp9Hfiu\n1npSKbUL+IrW+ssVGb0gVJl5n35lLX0wk7ReODTMsTNTIvpCzXDj3rkJeBhAa/0isLtg+y7gs0qp\nZ5VSn3VuUErtBi7XWn/Tse/7lFLPKKW+o5QKr274glBd8tE7FYzTt9luL+aeFb++UDvcWPoRwPmp\nzCilfFrrtPX7D4CvA1HgAaXU+7XWD1rbPgd80XHsS8C3tdb7lVJ/BPwx8AelLtzTE8Lnc/9l6+9v\nnntIM80F1u58vJbYD6wP5+dQqbn09nbQ5vNwbnyuru/PWv3bFKOZ5gLVmY8b0Y8Czit7bMFXShnA\nn2qtp6zffwxcCzyolOoGlNb6ScexD2itJ+2fga+Vu/DEhPuCVP39YUZHp13v38g001xgbc9nfGIO\ngEQsyejodMXnEgm1MTY1V7f3Zy3/bQppprnA6uZT7mbhxr3zHPBeAMunf9CxLQK8qpTqtG4A7wJs\n3/4twOMF5/qpUup66+fbHfsKQkNi98ethk8fINLhJzqbJCcRPEKNcGPpPwDcqZR6HjCAe5VSHwQ6\ntdbfVEp9DngSM7Lnca31T6zjFHC84Fy/B3xNKZUChoGPVmISglAtqhWnbxMJ+UlncswlMoSClY8Q\nEoRClvyUaa2zwMcLXj7s2P494HtFjvuvRV47ALxz+cMUhPqQSFanDINNpMMPQDSWFNEXaoIkZwlC\nGebdO9UR5Lzozyarcn5BKEREXxDKEE9m8HoM2nzV+apEQiL6Qm0R0ReEMsRTleuPWwyne0cQaoGI\nviCUIZ6osuiH2gCx9IXaIaIvCGVIpDIEquTPB/HpC7VHRF8QyhBPpmvk3pEOWkJtaPkYsX94+hiG\nYfAbt2wvu98rb1zg8f2n+Pg9V9ARbKvR6GrLP/3sOC8cGl70+kBviE/+m6vweprTRvi7J44SCvp4\n/zsuWvB6OpMlnclVVfQ72tvwGIZY+kLNaM5v8TJ44sBpHv75SdKZbNn9nnrlDIfenODJA2dqNLLa\n89zBc4xNJUhncvl/0ViKV4+PMzw+V+/hVY0nXj7NY/tOLXrdTsyqRrE1G49hEA61iegLNaOlLf1U\nOsNcwvxinxyZYftQpOh+uVyO42fNtnaPHzjNu9++BZ+3ue6XuZwp8FsGOvk/Prwn//pDP3+Lv3/y\nGCPjMTY2YfnfdCZLMmX+i8VThBxPcdWO0beJdPgZnWzem6rQWDSXci2T6Oy8H7Vc27qRiTlm5lIY\nBkzNJHnp9ZFaDK+mxJMZUuls3sdsM9ATAmBk3H3xu7VELJ7O/zwysVB48yUYAtWz9MEU/XgyQ9Iq\n4ywI1aS1Rd8RG12uprl9Q7hrz2YMAx7Ze6rpCmTZ7gU7WchmoNcS/WVUPF1LxBIO0S+4sdklGIJV\ndO+AhG0KtaWlRX/K8SUrZ+nb266/bIBdaj0nR2bQJydL7r8Wsd+LQkt/fXc7BjStT99p6Q8XiH61\ni63Z2O/5lCRoCTWgpUV/2hI6w4CxaIKJ6UTR/Y6djdLm87B5fSd37dkMmNZ+MzEdKy76bT4P67qC\nzeveScy7+Eq5d6oZpw/z7/n0rIRtCtWnpUXfdu/s3Gi2rTtexMUzl0hzenSGiwbD+Lwedm7sYsdQ\nhF8cvbDIMlzL5N07HYvDUQd7Q0zNJplzuEKahfKWfnVr6dvk6++IpS/UgJYWfdulce3F/QAcOxNd\ntM+b56LkcrDDujEA3LlnMzng0SJhfmuVqRI+fWhuv/6Chdzx2IK1mpq7d8SnL9SAlhb9aSsL8uqd\n6zAMOFrE0j9qhWruGJoX/V2qn3WRAM8dPMfMXHM8ktvvRaF7B0xLHxZbws2AvZDrb/MQT2YWLKYm\nUjUS/ZDt3hHRF6pPS4u+/QXv725nU38nb56bXpSkZS/i7tg4H8Pv9Xi4fddmkqksT7/SHMla0RIL\nuQADPe0AjDThYq5t6V80YPYUdd7YahmnD+LeEWpDy4t+R9CHz+thx8Yu0pksp87P5LfbSVnrIkG6\nOwMLjr3l6iECfi+P7z+9ZDZvvZmcSZBKlx/jVCyJYUBnkRITze3eMZ9wtlmJec7F3HiiNpZ+WEI2\nhRqypAmjlPIA3wCuxuyDe5/W+qhj+6eA+4BR66WPaa21UuoAYDvJT2it71VK7QTuB3LAq8AnrHaM\ndSEaSxK2Hq13DEV46uUzHD0zxbYNpgCct5Ky3nZRz6JjQ0EfN1+1gcf2nebVE+Ncs7OvpmN3SzSW\n5A//6gXuvn5L2fpC0VnzvfB4jEXb1kWC+LxGU0bw2O6d7UNdwKkFc4ynqtsq0cbn9dAR9IlPX6gJ\nbiz9e4Cg1vpG4DPAlwu27wJ+R2t9m/VPK6WCgOF47V5r368An9da34zZZP0DFZrHsslks8zEUvlH\nazuCxxmvfzTv2ulafALgkk3dgHlzaFTGpuKk0llOjkyX3W86liy6iAvg8Ris7wkxPD7XdElptntn\n24Zi7h3b0q9+tZJIhz+/riII1cTNp/km4GEArfWLSqndBdt3AZ9VSg0CP9Za/z+YTwUhpdQj1jU+\np7V+0dr3aeu4h4C7gAdKXbinJ4TP597K6u8Pu953IhonB/T3hujvD9PX10k45OfN4en8ec6OHwdg\n9+Ubip57u/Uljaezy7q2Gyp1vjPWDSkaS5U8ZzJl1iDq62kvuc+WwTBnL8zibw/QHQ4U3acclX5/\nKkUqk8Pn9XDpjn46gj4uRBP5sdq3t00buggG5r8q1ZhLX3eIc2MX6OntqHldp0b926yEZpoLVGc+\nbkQ/AjjDWjJKKZ/W2o51+wHwdUxXzgNKqfcDbwF/AnwbuBh4SCmlMK1/+7s0DRQ3oS0mluFD7u8P\nMzpa3pp1Ylu+Aa+RP27bhjC/PDbGGycu0N0Z4NCxC7T5PIT9nqLnNixf/pmR6WVdeymWO5dynLPm\nOToRK3nOC1PmjSHYVnyeAD3WE9GhN85zyebuZY2hkvOpNFMzCUIBLxcuzNDf3c7p0RlGRqJ4PAbR\nmQSGAdGpGNOG6faq1lyCbabQH39rnJ4V3FRXSiP/bZZLM80FVjefcjcLNyZFFHCewWMLvlLKAP5U\na31Ba50EfgxcCxwB/ofWOqe1PgKMARsAp/8+DNStlkGxEMUdeRdPlHgyzanRGbZaSVnF6Orw4zGM\nkpm8jYDts56Np/O1ZArJvxcl3DvgWMxtMr9+LJ6i3Vq8HuwNkc7kGIvGAdO9E/R7MYzF6xyVJp+V\nKxE8QpVxI/rPAe8FUErdABx0bIsAryqlOq0bwLuA/cBHsHz/Sqkha79zwMtKqdusY98D/KwCc1gR\nxUIUd1oRHMfOTnHi3DS5HOwcKv0w4vEYdIf9TEzHqzvYVeBMPpqYKX5zshcQu4qEa9rYYZvDTRTB\nk8vliCXSdATNB97CKKVEMlPVWvpOpG2iUCvciP4DQFwp9TzwVeBTSqkPKqU+qrWeAj4HPIkp4Ie0\n1j8BvgN0K6WeBX4IfMR6Ovg08EWl1AuAH/hR5afkjmIZqNuGIhiGuZhbLD6/GD3hABPTSbLZxlzg\nnI3PLw6OR4vfnGyhCZex9O0ErfNNFKufSpudsUIBW/QX5iOYrRJr03LCrrQpETxCtVnyE22FVH68\n4OXDju3fA75XcEwS+GCRcx0Bbl3RSCtMsQJjQb/PTNIans5beNvLWPoAveEgx3JRpmaTNfXFusVZ\nOriUG6pUsTUnkQ4/Qb+3qSx9+70JWZZ+YeZxPJmhNxKsyVgkQUuoFS2bnFUqA3XHUIRUOsuhE+Os\niwSWFHJ7+3iDunjmHO6dUpa+G/eOYRgM9IYYGZ8j2yRhm7brK2/pOxrGZLM5kuls1ROzbKTSplAr\nWlb07drlXQUuDXsxN0fp+HwnvZboT0QbczHXjaU/794p3/DdXOjMlrx5rDXyom8t5LYHfHR1+Bke\nj9U0Rh/m3Yzi3hGqTcuKfnQ2ib/Nsyjb0in0O5Zw7QD5x/9GjeBZ4NNfQvTLuXeg+Wrw2LX0bfcO\nmHMci8aZsd63Wlv64t4Rqk3LNkafjqWKlxHuaaezvY2ZuZQrS7/R3TuxeJrO9jZSmSzjJZ5GpmOp\nfA2icgw4fN6Xb+ut6Dh/cfQCAFcvUc7i/ESMA0cucPf1m1cdSlno3gFzjkdOT3FqxKzBVO0SDDaB\nNi8Bv7fulTb3HT7PweNjrvbtDLVxz03bafO1rO24JmlJ0c/lckRnk1w0uDiBwTAMrt65jtfenGDL\nQOeS52p0Sz+WSBMK+vB6jJKhpVOzySWtfJhf6KxGrP5//6nGMJYW/cf2n+axfae5eFOXq5tyOQoX\ncmF+jm+NmGWjamXpg+lqrHfLxL997AhTM+7HsL67nVuv2VjFEQmVpiVFfzaeJpPNlQxR/PB7LiWb\nzblKh7cTtEpZ0fVmLp6mNxwgFPBxbixGIrUw9jyTzTI7l2Kor2PJc+XdOxWuNZTN5ZiaSeLzLW25\n2/0LxqLx1Yt+CUsf4K1hy9KvUZw+QLijjQtn42RzOTw1SAgrZC6RZmomidrczYffe2nZfWPxNP/3\n9/bzyN5T3HL1UE0S2ITK0JKiv1SIotfjwW35E4/HoKuzMRO0UuksyXSWUMBHj+OJxLZmAWZiKXIs\n7c8Hc8EzEmqruKU/O5cim8uRTOVIZ7Jlb7a2UFfiyapwIRecom9b+rX7ikRCfrK5HLNzqbI5E9XC\nTkrbtL4zH8lUjusvG+CFQ8O8emKcK7evq/bwhArRks44twuXbumNBJicabwELdt90R5sc0QZLbw5\n5cM1XYrMQG+I0am5ivYQcGahxpbow2tvr4joF1nIXd/djoFZoA4gGKiheye/mFufsE07P8FpFJTj\nrj2bAXhkb/O0DW0FWlL03cSlL4eecJBMNtdw4XZ2g5BQwOdYcF4olna0SLhIQ/RiDPSGyOVgdLJy\nLh6n6DvzCophb69E2Ggx906bz8O6rvmErGAt3Tuh+pZisKOy7Mzkpdg6GObSLd0cOjHO6dGZpQ8Q\nGoKWFH23celuyVvRDbaY61yotBecF4n+Mp96qtEv12nZ1tbSX7yQC/MuHqixe6fO9Xdst92gC9eO\nzZ1i7a85WlP0LZGplKU/L/qN5de3LdmO4LylXyiWUSsD1LV7pwqx+k6Rc+YVFMPeXirnYDnMxtP4\n2zyL1hCcolfT6J06x+oPj8fweY1llZ64emcf63vaefHQSMM96QrFaU3Rr7BP314kbbQIHqf7ojds\nj3HhjSnqou6Ok4GqWPoOn34Z9046kyWZMtcSJmcSZLKrW1eYi6cXuHZsnO6NWsXpQ30t/Vwux8jE\nHOt7QkVbZpbCYxjcuXsz6UyWJw+cruIIhUrR0qJfqQiJRnfvtAd9tAfM5J/Flr7t03f3XtgLnecr\nWHhtyuVCrnNbLsey4slLnS9UpBH8YG99LP16NkifjqWYS6TzT3LL4aYrN9AR9PHky2dIpYv3bBAa\nh5YU/elYEq/HyNdRXy2NmpU7v5DbhmEY9IYDJS19t+4df5uX3kiwopb+tMuF3MJtq3Hx5HI5YiUt\n/fr49LvyjVRqH72z3MgdJwG/l1uuGWI6luKFQyOVHppQYVpS9O0M1EollHR3BswErQa19O2bW284\nYHbQSs1bY9HZZL4EgFsGe9uZnEkST5ZfdHWL070zW0b07W122v9qnqwSqQzZXG7RIi7AukgQn9f8\nbNTS0m8P+PB5jbr4xu1F3IEViD7A7ddtwusxeHTvKXJNUoW1WWlJ0Y/GkhWL3AFHglYNffqH35rg\nM3/1AmNTpZ8u5pOPTGHrsfz6kw6xjM4u/72wheHshfLW/ng0zh9960WeXsLX6zZO346rH1rXkT9/\nKSZnEnz2my/ma/osOle8eOQOmH/P9dZibi0zcg3DIBzyr8q9c+JclE9//Tlee3N8WcfZfRJWYumD\nWY5kz6XrOXNhlv/wX57iP/yXJ/P/Pv4nT/HS6/IE0Ci0nOgnkhmSqWzFFnFtesMBJmcSNUvQ+uXx\nMc5PznH0zFTJfQrj0HsjlhvKEstsLsd0LLXsKKbLtvYA8OzBc2X3e3TfKc6Nxdh/uPQXPpfLEY2l\n6O70W2Mu7dqw57Op3xT9cpb+kVOTjIzH+GWJ4mHFYvSdvP/GrXzgpm3LWtSsBJEOP9FYcsXW8oPP\nv8nEdIJ/evbEso6bj9FfmegD/NpN27hsaw/bhyJs22D+u2gwTDKd5aXXz6/4vEJlWdJhqZTyAN8A\nrgYSwH1a66OO7Z8C7gNGrZc+BhwHvgtcBASAL2mt/0UpdS3wIPCGte9faq1/WJmpuKNUHf3V0hMJ\ncuxslGgsSXdn9Tto2YJXziosjEMvTNCKWTWIlnsDvPbifvq6gjx/8By/cct2OtsXPynMJdI884uz\nAGWfRuLJDKl0lsHeEJMzSVcLuRv7OxfMoxi2j7rU01epGH2bGy4fLHnuatLV4eet4WniyQztJW5I\npRiZiPHKG+aTzdHTUxw/G2X7UPl2n/ljx2O0B7z5to0rYbA3xP/2b69d9Pqnv/4cx85MkcvlpEZP\nA+DG0r8HCGqtbwQ+g9Xw3MEu4He01rdZ/zTwIWBMa30z8G7gLxz7fsWxb00FHyofrmljR/DUKmzT\nLqdQLqY7Fk/j83po85kuCtu9M15ww1jue+HxGNyxezPJdJanXj5TdJ9nf3mOuYS5dnChTPauPYa+\nrna8HsPVQu5gb8isGlrGvWP7qEstrs9b+pVz81UCu9z3SmL1H9t7mhxwy9VDADyy96Sr47KOcM1q\niPL2oQhTs8myN3+hdrgR/ZuAhwG01i8Cuwu27wI+q5R6Vin1Weu1vwe+YP1sAGnHvu9TSj2jlPqO\nUmpxbeMqU+lwTZtaJ2jZwl1u0S8WTy2IULLdO4VPCSt5L26+agPtAS+P7z9NKr0wXj6bzfHovlO0\n+Tz0dwe5MDlX0l0x5bjxhII+Vwu5ne1tdHcGlrD0zRtNKRdQsbo7jYBdDmO5fv3ZeIqfHTzLukiA\nD911CZv6O9h3eNSV0I5H46Qz2RX785fCbkZ09GxpV6RQO9x84iOA86+VUUr5tNb2t/MHwNeBKPCA\nUur9WusHASxR/xHweWvfl4Bva633K6X+CPhj4A9KXbinJ4TP534hrb9/6XtI7qjp4920IeJqf7ds\n3dQNQDLnbhxLUe4c2WyOyRlTzBLpbMl946kM4Q5/fnt7p2npzybS9PeHOXzGrCS5cSC8ojHffcNF\n/NPTxzh8Zop37d6Sf/35X57lwlScu2/YyuR0gp8fGibYESz6RPHGuWkAhgbCRDr8zMbTJceSs6zQ\njRsirO8Nod8ap7e3A29BRm0ul+O89XQxHUvR1R3CX7Aga/hMH/Pg+uXPvZKfm0KG1pvuGMPnXdZ1\nnnniDZKpLB949042DHbxm++6mD/74Su88Pp57v3Vy8seG7eCubZv6q7K3HZfvoG/e/Io5ybiVX3v\noLp/m3oCd0f7AAAgAElEQVRQjfm4Ef0o4LyyxxZ8pZQB/KnWesr6/cfAtcCDSqnNwAPAN7TW37eO\nfUBrPWn/DHyt3IUnlpEA1N8fZnR0esn9zljNMYxM1tX+bvFaluyps9FVn3epuUzNJEhnzOtdmIgV\n3TeXyzETS9EXCea353I5Am1ehi/MMjo6zelz5r3ck8utaMzveNt6/vmZY/zD429wxZbuvGvg7x8/\nAsDNVwzyhBW588aJC2wZWPwBzo8hm8Xv8zISmys5lrFJ8/MQjyUJt/vI5uDom2OLygZEY0lm5+YX\nhN84cSEfjWMzemEWgHQitay5u/2crRRvznxqOnUuys4iTX6Kkc5k+ednjhHwe7luxzpGR6d52+Zu\nIh1+HnrhTW6/dqjk+kB/fxh9wjSEwgFvVebWFfTg9Ri8enS0qu9dtf82tWY18yl3s3Dj3nkOeC+A\nUuoG4KBjWwR4VSnVad0A3gXsV0oNAI8Af6i1/q5j/58qpa63fr4d2O96FhWi0sXWbHprmKA1XhBy\nWYxkOksmm6Pd4b4wDIPeSGDevWOXYFjhe9HX1c5utZ6T52c4fNK8lx8/G+Xo6Smu2rGOob6OkoXe\nbArdO+lMtmRWpzPvwC4rUcx9c95y7dje6WL7LLWQWy/CKyjFsE+fZ2I6wc1XbcjPp83n4V3XbWQu\nkV4yymq1MfpL0ebzsnUwzMmRGZIpyditN25E/wEgrpR6Hvgq8Cml1AeVUh+1LPzPAU8CPwMOaa1/\nYr3WA3xBKfWU9a8d+D3gq0qpp4B3Al+q/JTKU+liazZdnX4MozKFwJbCKWLRWKqov3y+2NpCQe8J\nB5iZS5FIZSqyqG3XVH/UqrJoLx7a1RdLFXqzsbNPIx3+fPhkKb++uTBt0ObzlCwVDfORO1ssS7nY\n4vpSIZv1omuZ5ZVzuRyPvHQKA7hj9+YF2267diM+r4fH9p0qG0psx+i7aZyyUrYPRchkc7w53DyW\n+FplyU+81joLfLzg5cOO7d8DvldwzCeBTxY53QFMsa8b0dkkBmZT50ri9Xjo7gzUJEHLjrM3MLtj\nFQvvc9bSd9LrSNCyK2yuRvR3bOxix8YIrxy9wGtvjrPv8Cib+jt4mxXLPx/VVPwJKFpg6ZtjTxcN\ne7XLJthPLLC4KQzMd4C6bGsPbw1PF336sqt1Fqu9U08iy6y0+cbpKd4cnmbXJf2s715YNycS8vOO\nKwZ55hdnefmNC+xS/UXPMTIeW/D+V4OdG7t4bN9pjp2d4pLN3VW7jrA0LZecFZ1N0tHehtdT+ann\nE7SqnIZuW83243gxq7CU+8JpIUetGkSrtXbv2mMu4n79gYNkcznu3LM579/vWaJx/FQsiWFAZ7Bt\nXvRLxOrHEmnaLZEuDD91Ylv6dhJZsWvP2cXoatgZyw2d7W0YhntL365jf9f1m4tuvzP/JFY8fDOV\nznJhKs7gCgqtLQc7gue4FTwg1I+WFP1Ku3ZsesIBMtlc0S/siXPRfFPv1WKL2EUbTPdFMauwlPui\nx5GVG61QDaLrLuljXSTIXCJDpMPPDW+bT2zq6Vza0g+H/HgcN59S5ZVj8fR8HaFIaffOyHiMgN/L\ntg0R69rF3TtBv7cqN//V4PEYhNvbXIn++YkYLx8ZZduGMDtLNInf2NfBFdt7OXJ6ihPnFgvu8Ngs\nuRysr5I/36Y3EqC708/Rs1NSm6fONNYnvsqkM1liiXTFE7NsektYtadHZ/jS3+zjm/9yqCLXGY/G\nMQzYvN7MTC1q6cfnyyovGKNjATQaS+aTgVaD1+PJW5Tvum5jviAamAuK3Z2BMj79+THYrhY7ht5J\nKp0hncnmbwyRkN9M0Cpw3diJRoM9ITqCPvw+T8mF3EZbxLXpDgcYiybKlqQAeGyfmYzlfLIqRrle\ntmetNofVitG3MQyDHUNdTM0kGatAq0th5bSU6FcrG9emp0RW7iN7T5EDXq1QL9Hx6QRdHf68FV3O\nvVO4kGv72M+NxSpag+iOXZv4/d+8kvfesHXRtnXdQSamE4ssvFQ6Yz0dmGMsZ+nPFhRI83gMujv9\ni97riWiCVDrLQG87hmHQEwkW9emXKqvcCLz9sgHSmSzP/KJ01E0snuJnvzxHTzjAbrW+7Pkuv6iX\njX0d7Dt8ftET15lRM3S1mou4Njusp5Fj4uKpK60l+rHqhGvazIcnzn+xpmaTvHhoGH+b+Vavtpdo\nNpdjYjpBT3g+2alYVm7JhVzLLfLWiBlFsZpaK048HoNrL+5f1HoQzNDOZDq7KCpnquAm3BEsLfrF\n3FU9kSBTM8kFHbRGCiJResMBpmOpBWGg2VyOuRINVBqBW64ZItDm5bH9p0p2B3v6F2dJpDLcsXtT\n0ffciWEY3LlnM5lsjsf3L6x4evaCbelX16cPsGOj6W47VqZIoFB9Wkv0Z6sTrmlTLDzxyQOnSWdy\n/NZtOyvSS3Q6liKTzdEbCeTFsljTjVILue0BH4E2L+es5KRqPfU46bOiSgqtzHy4puXeaS+zkOvs\nAmbTGw6QzeUWdNAaKWgGUuxvEk+kydF44Zo2HcE2brpyA+PRBPv16KLt6UyWx/efJtDm5Varzs5S\n3Hj5AJFQG0+/cnZBH4QzozMYwPoqL+QCXDQYxusxOHZWLP160mKibycjVcmnXxCemExlePLlM3QE\nfdx05YaK9BK1fdg94UDZnqqlFnINw6AnHMB2tNRC9Nd1FV/rsG9+9k24nHunWN5BsQSt4YISwYX1\nhpznalSfPsAdezZhAD99aXFTkv16lPFogpuu2uD6aaXN5+VXrttELJHmuYPD+dfPjs6wriuYL8pX\nTdp8XrYMhDk5Mi1tFetIa4m+7d6pktDZCVq2wLz42gjTsRS3XrORgN9bkV6itg+7NxykM2iG902V\ni94pImy2EEL1boBO+m1Lv1R/3sKF3CILmMXcVcWs+Lx7x3JXFAvtzD8FNailD6Z76pqL+zhxLrrA\nB57L5Xhk70kM4M7dm5Z1zl+xkrUetZK15hJpxqOJqmXiFmOHJGnVndYS/QLLstLkE7SsRctH9p7C\n6zG4fZf55axEL1Fb4HojATO8L+Rf0GPWJu8OKSJstlhCjSx9S/QLI20KF9bzln4Z906oSNVQp9to\neDxGONSWfyIolhy2Fix9mI+6+akjxv7omSlOnJvmmov7FtUTWopIh58bLx/g/MQcvzh6gfMT5lPR\nYA0WcW1kMbf+tJbox6rr3gFTZCamExw8Ps7ZC7PsuWz9ApFdbS9RW7zsc0ZC/pJx+oE2b9FFPtst\nAjXy6XfZPv0CSz+28Cbc5vPg93ncL+QWWPHpTJYLk/EFkSjFngbmI4EacyHX5pLN3WwdCHPgyCij\nVtXQR16ykrH2FE/GWgpn+Kb9VLS+Bou4NrKYW39aS/TzlmX1vux2gtY/Pn0MWPzldPYSPbTMPqbg\nsPQtwYt0tDGXyCxyF8USqZKWbE+kxpZ+CZ9+seJ37UHfEpb+/L6F9XcuTMXJ5nJ51w44IqqiTvdO\n8cimRsMwDO66fjO5nBmTf35yjgNvjLJ1MLziUgYb+zu5fFsv+tQkP3/NfNqsdoy+k3WRIF2SpFVX\nWk702wPeqi5a2dbnyfMzXLK5m4sGF7ersxOZbKttOYxPJzAw1w+AkmGb5eLQbZeHAXS2V1/4/G1e\nwqG2kj59540nFPCVt/QdN7KujoUJWsPji5t7F0vQmlsj7h2APZeup7vTzzO/PMu/PneCXM40JFaT\nRX239fl72WqtWEufvmEY7LSStGrVZU5YSGuJfixV9YVL5yLp3SUewbdtiHDJ5m5ePTHOmWUma41H\n43R1+vNuG3s+zrDNbC5XNuPUfkroDFWnBlGpa05E4wusu+mY2dnL6YIKBU3RL7QCiy3k2glatqDn\nSwQ73Dt2tJJzPWEtLOTa+Lwebt+1iUQyw3MHh+kJB9hzaflkrKW4fFsvQ30d1vkN+gr6EVSb7baL\nRzpp1YWmFP1UOsu3/vU1vvyDlxf8m7ZqzVQT2+Wwvrudq3f2ldwvX5J4n3trP5szO2b1FPHJOy39\nRDJDLlda1Gz3Ti1cO/lrhgOLErSmivw9OoJtZHM5EqlCd1WJAnKRIJPTSbLZ3KIYfZveSJBoLJVv\n67hWFnJtbr1mYz65713XbVwyGWspDMPIf/429HXg8dS2WXm+faL49etCU4p+PJnm4PExDr05seBf\nDlBbqlvWdcdQF+FQG/fcsq3sl+manX10d/p55Y0Lrn2bM7EU6Uwu754BRyNth+gvJWqhgA+1uZsr\ntvW6um4l6CmItMlks8zOpRb15y0Vqx+Lp/G3eRYJXj5BazaZd+8UJhrlF3OtFpOFJR0anc72Nu7e\ns4X+7iC3XrOxIue88fIBNq/v5HpHcbxasXUwjAGcPr/6kiTC8lkbn/plEg75+dPfv6loiePVWklL\nsa4ryJ/9p5uX3M/jMdi5qZt9h88zOhVfVAu9GHZ5h2ILsdOOCJ58rfhA8QVrwzD4w3933ZLXqyS9\njiiaLQNhZmIpcix+2nBm5TpvSbFE8TWKHkdI5sjEHOsigUX9cPOiHzXf57m8e6exo3ec/Pot2/n1\nW7ZX7HxtPi9f/Mj1dWkxGGjz0hsJ5m/SQm1pSksfTFH1eT2L/jUSO4eWF742EV0YuQPz4Y5O985c\nA7YCLMyezWfjLsPSLxZiaZ93eDzGxHSiaOx6YcvGWDyFAQQbrJZ+KzHQ287kTHJBSQihNiypCkop\nD/AN4GogAdyntT7q2P4p4D7ALhLyMeCNYscopXYC94NZdBL4hNWZqyWZT1SZ4sbLl37MHnckZtnY\n4Y7Lce/Ug/n69+bTynx29EIhDxUpupbL5YjF00VDC20r/vDJCaB4+GFPQYKWvcjtWWUfAWHlDPSG\neO3NCc5PzLFlwF0DeKEyuDF97wGCWusbgc8AXy7Yvgv4Ha31bdY/XeaYrwCf11rfjBkx+IFKTGKt\nsmUgjM/rvgDV+PTCxCygaP2dRoxOmXexWE3ZS5S57ihSUz+RypDN5UqUlDCt+NffMkW/WPhhb0GC\n1mw8XTRTWagddhawuHhqjxvRvwl4GEBr/SKwu2D7LuCzSqlnlVKfXeKYXcDT1s8PAXesfOhrnzaf\nh60DYU6fn1kUrVIMW7Scou/zeugI+haEbDbiQmVhIlW+4qkL9065J5fCHgbFSgQXNrdp5AYqrYJ9\ncx4R0a85bj75EcDpdM4opXxaa/tb+QPg60AUeEAp9f5SxwCG1tpeXZ0Givd4s+jpCeFbRiJVf//a\ne0y8Ymc/x85GmZxLc8XQfGRRsblMz6UxDLh4W9+C9YnucJDpWDJ/jGFtGxqMNMx7MrShm65Os2RE\nf3+YtPUp2LKxe8EYN1j1YAyfN/96zNp5XXdo0Xx613Xi9RhksuY+l+3sp7+vc8E+fbkcfp+H6FyK\n3t4OEskM3eHgit+bRnlPK0U95vM2w/yMTsZSFb2+/G2Wxo3oRwHnlT224CulDOBPtdZT1u8/Bq4t\ndYxSyum/DwOT5S48MeHeCqhHFEIlGLIs0/2vDTNg+b1LzeX8+CyRDj8T47MLXu8I+jg7OsPwyBRe\nj4dRa3tyLtUQ74k9n64OP8PjMc6fjzJsNe/IpNILxpi0Io9Gx2bzr58+Z9oPRi5bdD7dnX7Gogm8\nHgNPJlN0n55wgNHxGCfPmB85n8dY0XuzVj9npajXfIxsFq/H4K1z0YpdX/42C48thRv3znPAewGU\nUjcABx3bIsCrSqlO6wbwLmB/mWNeVkrdZv38HuBnrmfRpOxwGcGTszpmOWP0bSIdfnKYcfzQuGUG\nesNBkikzQStfbC1U6NMv494pEWJpJ6v1d7eXzDDuCQeIxlL5qKFGe29aDa/HQ393u7h36oCbT/4D\nwJ1KqecxF1/vVUp9EOjUWn9TKfU54EnMKJ3HtdY/sSJ+FhxjnevTwLeUUn7gdeBHFZ7PmqM3EqQn\nHODY2Si5XK5kTZXpfGLW4pR5WzinZpN0dQZKZq/Wmx5HQ5PobJJAm5eAf6H7br45ukP07QJppcpK\nRAJwBgbKdH+y/fp22YtGWuRuVQZ7QwyPx5iZS9HZvnZyJtY6S37yrZDKjxe8fNix/XvA91wcg9b6\nCHDrikbaxOwYirBPj3JhKp5vOFJIsUVcGzvs0bae7YXcdn9jCdt8FE2c6GyyaK/idit23tlIpVQX\nMBv7PSlXOMzex24E3mg3xFbEroY6PB5j58ayy3srZi6RXhQkYRgGkVDbqorWrWXkk98A7NjYxT49\nyrEzUyVF344x7y1SHKswbDNmhSTWuqbKUthPKWPRBNOxFBcNLvY7ej0eAn6v6+gdmH9PypUItm84\np8XSbxicETzVEP3T52f44v1784v8Tu7cvZl/e8fFFb/mWkA++Q2As5vQDSWStMbLWPpd+fo7lk8/\nkWpIUetxCG8mmytZ8C0U8BW4d8qL/o2XDzIxneDtbxsofW3bvWM1hO9o8AYqrUC1Y/UPnhgjk81x\n6ZbuBZ+1w29N8NQrZ3j/O7Yuqv3UCjSeMrQgW/NJWqUXc8u7dyzRt9w7sUQ6362qkbB9+m9Z/VFL\nfeE6gr6FTU+WcO90trfx27+ys+y1bUt/1AoJbRf3Tt2pdqy+3ZLxd9/3tnwjH4BH957ifz7+Bk+9\nfIZffee2qly7kWmsYjQtip2kder8DMkSSVp2Nq6zBION071jNrzONKSlbwvvyRHTxVLO0p9LpPMF\n84p1zVr2tS1L337Qb8T3p9Xo7vQTaPMyPD5X8XPncjmOnZmiu9O/6Dtz01UbaA94eeLAmXy57VZC\nRL9B2D7URSab483h4nG5E1GzY1Z3Zxn3TizZsJE7YFZ27GxvI50xv2ilGtSHgm3kgHjCvAHai7rt\nqyiQ1hH00eZb2KxFqC+GYTDQ0875yVjRirirYSwaZ2o2yY6NXYsWbNsDPm65eoip2SQvvT5S0euu\nBUT0G4SlGkaPT8eJODpmOQn4vQTavERnG1v0YeGTSilLvz1fiiFl/Z8m6PeuqsuX3UHLRiz9xmCg\nN0QylWVyurKtE23Xjt2wpZDbd23CMMwG8a3Wq1dEv0GwoxeKFV8rl5hlEw61EZ1NzidmNWiteGee\nQaRIyCY4ErSsG1ilauU43z9ZyG0MquXXt40n25gqpK+rnd1qPafOz3DYKtbXKojoNwj5JK0zU4ss\nj+k5MzGrp0hilk1Xh5/pWIqZePlEpnpTrEJoIYXllc0m76sXafv983qMfPtBob7YBfKGJyrr1z92\nNorXYxQNC7a563qzZeQje923LG0G5JPfQOwYijA1m+R8wRdgvnlKaUs/0uEnk81xYdI8tlHdF27c\nO/lKm9Zi7lylLH3r2u0BX8sm5jQa1bD0U+kMJ0em2TIQpq1MwcYdQ13s2BjhF8fGODc2W3K/ZkNE\nv4HYbvkfD785vuD1Ym0SC7HDH+2Y50a39L0eo+SNyQ6nnI2niCfS5KjMTcy+aTbqe9OKDFQhVv/N\n4Wky2VxJ146Tu/dsAeCxfacrdv1GR0S/gbD9+vrkQh+jHaNfrO6OjW01D481tujbc4h0+Eta27Yr\nZy6ermgXMNu909Gg700r0tneRmd7W0Ut/aUWcZ1ce0kf6yJBnjt4jpm51JL7NwPy6W8gtg6ateH3\nvjaM33E7fu1N8yZQLDHLxg5/zFv6DeresZ9WImUyIZ0LuZXsAma7dxr1vWlVBnrbefPcNOlM1lUf\n64npBG+cnmTPpeuLGg5LLeI68Xo83Ll7Ez944ihPv3KG99140bLHv9aQT38D0ebzcvGmLg6fnOQf\nnj6+YJvHimkuhW3pj06arqDVJDJVk95wgI6gj6G+0nVynAu5lbT0+7raCfi9RZunC/VjsCfEsTNR\nxqbiZYvm2fy3h17n1ePjBP0+rtqxbsG2XC7H0bNTdHX6WVekTlUxbr56iH969gSP7T/N3ddvcXXj\nWcuI6DcYv3fPFUzMpZmaWriY2xMO0FUkMcvGDn+0k1wa1YXR5vPyxY9cT7BMBVDnQm4lsnHz5w36\n+D9/93op49tg2EI/PB5bUvTPjM7w6nFzzevRvScXif54NMHUTJJdl/S7Xqy3k7Ue2XuKva+f58Yr\nite/ahYaUxlamHDIz/at65bdMacwEqaRG38XqxTqxGnpz9ohqBWaTyPWJGp1BpcRwfPoPjO8srO9\njUNvTnD6/Ayb1s+3x7TrV2134dpxcseuTTy67xQ/3XuSGy4faOroruZ+jmkhnKJvGBD0r7xkQb0J\nBnwYmBm5jdoFTKgceUt/iVj9aCzJ86+OsL67nQ+/51JgcYz9Uduf72IR10lfdzu7Lunn5MgM+mTZ\nLq5rHhH9JiEU8OG16ueH1ngcuscwaLfKK9vunUZ1VwmrZ721VrWUpf/UgTOkM1nu2L2Jay7uY6Cn\nnRdfG863wAQ47iIpqxR3XW+GbzZ7spaIfpNgGEbe2m8GqzgUtETf7gLWwO4qYXUE2rz0hANlY/VT\n6QxPHDhNe8DHTVdtwGMY3LlnM+lMjicPmDH2yVSGt4an2TLQib9t+U+6Ozd2sX0owi+OXmjq3r1L\nfpOsfrffAK7G7IN7n9b6aJH9vgmMa60/o5T6MPBha1MQuAYYBLYBDwJvWNv+Umv9w1XOQbCIhPxM\nTCcaNnJnOYQCPkYm5/KtH5vhRiaUZrA3xOtvTZBIZQgUEewXXxshGkvxnrdvyQcBvPOKDTzwzHGe\nOHCG996wlWOnp8hkc/kkx5Vw157N/NU/H+LRfaf40F1qxedpZNxY+vcAQa31jcBngC8X7qCU+hhw\npf271vp+rfVtWuvbgP3Af9JaTwK7gK/Y20TwK4vdK7cZ4tBDQR+JZCafMNOoBeSEymD79QtLkIAZ\nhvno3lN4DIPbd23Kvx7we7n1mo3MzKV48bURDr9lRvW4ic8vxS7Vz7pIgGebOFnLjTrcBDwMoLV+\nUSm127lRKfUO4O3AXwOXFmzbDVyutf6E9dIu82X1AUxr/z9rrUuGqfT0hPCVqZ1RSH//8v14jcpK\n5rK+twOOj9PTFWy492K54+npagcmmZxN4jFg88buhun522jv7WpphPns2NzDUy+fYS6dWzSeV46c\n5/ToLLdcuxG1o3/Btt++S/HTl07y+IHTbFpvHnf9lRvpdxHvX4oP3LqT7/7rIfa9cYHfuv2SFZ+n\nElTjb+NG9COAs8h7Rinl01qnlVIbgD8Gfh347SLHfg74ouP3l4Bva633K6X+yDr2D0pdeGLCvV+t\nvz+87DDHRmWlcwl4TVH0QkO9FyuZj32rHxmfpT3gY2xspvIDWwHN9DmDxplPp5WCfuTNMS4ZWih0\nf/foEQBuvWpD0bHuuWw9Lx4a4ezoLF0dfox0elVzum7HOv7W7+VfnjnGTZcP1C1ZazV/m3I3Czez\niQLOM3i01nbX6t8C+oCfYLp+Pmj581FKdQNKa/2k49gHtNb77Z+Ba91MQHCHvZDbDLXibR9+MpWV\nRdwWoFSs/tkLsxw8PsbFm7rYtqG42+auPWaJZNOfH1l15Foo6OPmqzYwOZNk7+HzqzpXI+Lm2/Qc\n8KvA3ymlbgAO2hu01n8O/DmAJfaXaq3vtzbfAjxecK6fKqV+X2v9EnA7pr9fqBB2PZtmaPrtXJeQ\nRdzmZ11XEI9hsFefX9BIyO6edpdVDbMYFw1GUJu70acm80ULV8sduzfz+P7TPLr3FDde3lwZum4s\n/QeAuFLqeeCrwKeUUh9USn10ieMUcLzgtd8DvqqUegp4J/ClZY5XKMOlW3vYtiHCldt76z2UVeO8\ncTXDwrRQHp/XwzuuGCTon8/PiCXSYBhcvq2Xay/uK3v8b9y6ne1DXexS/WX3c8v67nYu2dTNm8PT\nJFKZipyzUVjy26S1zgIfL3j5cJH97i/4/b8W2ecAptgLVaAnHOAL/3730juuAZzJWM3grhKW5iPv\nu2zFx168qZs/+/RtFV2f2NDXgT41yfmJOTY7Sj2sdSQ5S2hInCGazeCuEtYegy4zhdcaIvpCQxIS\n945QZ9b3Vr6rVyMgoi80JLKQK9Sb5VT/XEuI6AsNSUh8+kKd6bMiikaWqP651hDRFxoSce8I9cbn\n9dDfHRT3jiDUgkCbF4+VZCMLuUK9GOgNMTOXaqo6PCL6QkNiGEbe2hdLX6gXeb/+MkrCNDoi+kLD\nYou9LOQK9WKgCRdz5dskNCy22MtCrlAvBqxY/eHx5S/mnhmdIb6KbN72zvK9pFeKiL7QsEQ6/Hgc\nbh5BqDUrDds8cGSUv/jHg0vvWIadm7v53L+7blXnKIZ8m4SG5d/ctoNbrxkq2klJEGpBdziA3+dZ\ntk//oZ+/BZgVQL0r7ANx/ZVDKzpuKUT0hYZlU38nm/qbp+aJsPbwGAbre0KMjM+Ry+VclW0+emaK\nY2eiXLOzj//l9otXfO1q9TqQhVxBEIQyDPa2k0hlmJxJutr/kb2ngPk6/42GiL4gCEIZlhPBc2Fy\njv36PFvWd6K2dFd7aCtCRF8QBKEM9mLusAu//mP7T5PLwV3Xb151B69qIaIvCIJQhoEed5b+XCLN\nz355lq5OP9dfNlCLoa0IEX1BEIQyDPTadfXLx+r/7JfnmEtkuP26TXVrpu6GJaN3lFIe4BvA1UAC\nuE9rfbTIft8ExrXWn7F+P4DZVB3ghNb6XqXUTuB+IAe8CnzC6swlCILQkHS2t9ER9JUtvJbN5nhs\n3yn8Pg+3XbuxhqNbPm5uR/cAQa31jcBngC8X7qCU+hhwpeP3IGBorW+z/t1rbfoK8Hmt9c2AAXxg\ntRMQBEGoJoZhMNAbYnRyjky2uI164MgoF6bivOPKDXS2N3YGuRvRvwl4GEBr/SKwoAmrUuodwNuB\nv3a8fDUQUko9opR6Qil1g/X6LuBp6+eHgDtWMXZBEISaMNATIpPNMTYVL7rdDtO8c/emWg5rRbhJ\nzooAU47fM0opn9Y6rZTaAPwx8OvAbzv2iQF/AnwbuBh4SCmlMK3/nLXPNNBV7sI9PSF8PvfZmP39\nYas3caoAAAXsSURBVNf7NjrNNBdorvk001ygueZTrbns2NzNC4eGmcssvsaRkxMcPTPF7ssGuOrS\nwYpetxrzcSP6UcB5ZY/WOm39/FtAH/ATYBDTuj8M/E/gqCXwR5RSY8AGwPlsFAYmy114Yhmpz9XK\nXqsHzTQXaK75NNNcoLnmU825dAZM4/PIiTG29oUWbPvhI4cBuO3qDRW9/mrmU+5m4ca98xzwXgDL\nTZOvIqS1/nOt9S6t9W3A/wt8X2t9P/ARLN+/UmoI82nhHPCyUuo26/D3AD9b3lQEQRBqjx22WRir\nPzYVZ9/hUTb1d3LZ1p56DG3ZuBH9B4C4Uup54KvAp5RSH1RKfbTMMd8BupVSzwI/BD5iPR18Gvii\nUuoFwA/8aHXDFwRBqD7zYZsLRf/x/afJ5nLc3cDJWIUs6d6xQio/XvDy4SL73e/4OQl8sMg+R4Bb\nlz1KQRCEOhL0++ju9C8Q/blEmqd/cYaujsZOxiqkcTMIBEEQGojB3hBj0QRJqzHKswfNZKx3XbeR\nNt/akdK1M1JBEIQ6YhdeOz85Rzab49G9p2hbA8lYhUg9fUEQBBc4a/CMjM9xYSrOrdcMEQ756zyy\n5SGiLwiC4AJ7MXd4PMYvj40BcOfuxqyZXw4RfUEQBBfYJZZfev08p87PcOX2dQz1ddR5VMtHfPqC\nIAgu6O9uxzDg1PkZwKyZvxYR0RcEQXCBz+uhv8t08Wzq7+BtayQZqxARfUEQBJfYETx37lk7yViF\niE9fEATBJb9y3UYioTZueFtlC6vVEhF9QRAEl1yzs49rdvbVexirQtw7giAILYSIviAIQgshoi8I\ngtBCiOgLgiC0ECL6giAILYSIviAIQgshoi8IgtBCiOgLgiC0EEYul6v3GARBEIQaIZa+IAhCCyGi\nLwiC0EKI6AuCILQQIvqCIAgthIi+IAhCCyGiLwiC0EKI6AuCILQQa7qJilLKA3wDuBpIAPdprY/W\nd1QrQyn1duD/01rfppTaCdwP5IBXgU9orbP1HJ8blFJtwHeBi4AA8CXgNdbgXACUUl7gW4DCHP/H\ngThrdD4ASqn1wH7gTiDN2p7LASBq/XoC+L9Y2/P5LPBrgB9T156mCvNZ65b+PUBQa30j8Bngy3Ue\nz4pQSv3vwLeBoPXSV4DPa61vBgzgA/Ua2zL5EDBmjfvdwF+wducC8KsAWut3Ap/HFJU1Ox/rpvzX\nwJz10lqeSxAwtNa3Wf/uZW3P5zbgHcA7gVuBzVRpPmtd9G8CHgbQWr8I7K7vcFbMMeA3HL/vwrzL\nAzwE3FHzEa2Mvwe+YP1sYFqSa3UuaK3/Cfio9etWYJI1PB/gT4C/As5av6/luVwNhJRSjyilnlBK\n3cDans/dwEHgAeBfgQep0nzWuuhHgCnH7xml1JpzWWmt/wFIOV4ytNZ2fYxpoKv2o1o+WusZrfW0\nUioM/AjTOl6Tc7HRWqeVUn8DfA34W9bofJRSHwZGtdY/dby8JudiEcO8id2N6XZbs38biz5Mo/W3\nmJ+PpxrzWeuiHwXCjt89Wut0vQZTQZx+uzCmhbkmUEptBp4Evqe1/j5reC42Wut/D1yC6d9vd2xa\nS/P5CHCnUuop4BrgvwPrHdvX0lwAjgD/Q2ud01ofAcaAAcf2tTafMeCnWuuk1lpjrh05Rb5i81nr\nov8c8F4A6/HuYH2HUzFetnx8AO8BflbHsbhGKTUAPAL8odb6u9bLa3IuAEqp/9VaXAPTsswC+9bi\nfLTWt2itb9Va3wa8AvwO8NBanIvFR7DW8JRSQ5hP/Y+s4fk8C7xbKWVY8+kAHq/GfNacK6SABzCt\nl+cxfcj31nk8leLTwLeUUn7gdUxXyVrgc0AP8AWllO3b/yTw52twLgD/CPw3pdQzQBvwnzHnsBb/\nNsVYq58zgO8A9yulnsWMbvkIcIE1Oh+t9YNKqVuAlzCN8U9gRiRVfD5SWlkQBKGFWOvuHUEQBGEZ\niOgLgiC0ECL6giAILYSIviAIQgshoi8IgtBCiOgLgiC0ECL6giAILcT/D95D0gfYtUVOAAAAAElF\nTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11e8e5bd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# KNN Classification on time-based split sets\n",
"k_range = list(range(1, 61))\n",
"k_score = []\n",
"for k in k_range:\n",
" knn = KNeighborsClassifier(n_neighbors = k)\n",
" knn.fit(X_timetrain, Y_timetrain_arr)\n",
" y_pred = knn.predict(X_timetest)\n",
" k_score.append(metrics.accuracy_score(Y_timetest_arr, y_pred))\n",
"plt.plot(k_range, k_score) "
]
},
{
"cell_type": "code",
"execution_count": 87,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 63.2183908046 %\n"
]
}
],
"source": [
"# Best values of k in time-based split data\n",
"knn1 = KNeighborsClassifier(n_neighbors = 31)\n",
"knn1.fit(X_timetrain, Y_timetrain_arr)\n",
"y_pred = knn1.predict(X_timetest)\n",
"print \"Accuracy is \", metrics.accuracy_score(Y_timetest_arr, y_pred)*100, \"%\""
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Support Vector Machines"
]
},
{
"cell_type": "code",
"execution_count": 88,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 48.275862069 %\n"
]
}
],
"source": [
"clf = svm.SVC(gamma=0.001, C=10)\n",
"clf.fit(X_timetrain, Y_timetrain_arr)\n",
"clf_pred = clf.predict(X_timetest)\n",
"print \"Accuracy is \", metrics.accuracy_score(Y_timetest_arr, clf_pred)*100, \"%\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Random Forests"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 47.1264367816 %\n"
]
}
],
"source": [
"rfc = RandomForestClassifier(n_jobs = -1, random_state = 1)\n",
"rfc.fit(X_timetrain, Y_timetrain_arr)\n",
"rfc_pred = rfc.predict(X_timetest)\n",
"print \"Accuracy is \", metrics.accuracy_score(Y_timetest_arr, rfc_pred)*100, \"%\""
]
},
{
"cell_type": "code",
"execution_count": 90,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Feature Importance according to Random Forests Model\n",
"\n",
"Avg_SR_Difference : 0.303135787959\n",
"Avg_WPR_Difference : 0.280738074933\n",
"Total_MVP_Difference : 0.172786216394\n",
"Prev_Enc_Team1_WinPerc : 0.13956540915\n",
"Total_RF_Difference : 0.103774511565\n"
]
}
],
"source": [
"fi = zip(X.columns, rfc.feature_importances_)\n",
"print \"Feature Importance according to Random Forests Model\\n\"\n",
"for i in fi:\n",
" print i[0], \":\", i[1]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Naive Bayes Classifier"
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy is 50.5747126437 %\n"
]
}
],
"source": [
"gclf = GaussianNB()\n",
"gclf.fit(X_timetrain, Y_timetrain_arr)\n",
"gclf_pred = gclf.predict(X_timetest)\n",
"print \"Accuracy is \", metrics.accuracy_score(Y_timetest_arr, gclf_pred) *100, \"%\""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
DistrictDataLabs/yellowbrick | examples/walkthrough.ipynb | 1 | 3586 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Walkthrough\n",
"\n",
"This notebook contains the code for the [walkthrough in the quickstart guide](http://www.scikit-yb.org/en/latest/quickstart.html#walkthrough). We've purposefully omitted the text of the guide so that you can follow along in code using this notebook as a template! The scikit-yb developers also use this notebook to verify that the quickstart code is correct, so if this code doesn't match what's on the guide, please leave us a note on our [GitHub Issues](https://github.com/DistrictDataLabs/yellowbrick/issues)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib notebook"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd\n",
"from yellowbrick.datasets import load_bikeshare\n",
"\n",
"X, y = load_bikeshare()\n",
"print(X.head())"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from yellowbrick.features import Rank2D\n",
"\n",
"visualizer = Rank2D(algorithm=\"pearson\")\n",
"visualizer.fit_transform(X)\n",
"visualizer.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from yellowbrick.features import JointPlotVisualizer\n",
"\n",
"visualizer = JointPlotVisualizer(feature='temp', target='feelslike')\n",
"visualizer.fit_transform(X['temp'], X['feelslike'])\n",
"visualizer.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from yellowbrick.regressor import ResidualsPlot\n",
"from sklearn.linear_model import LinearRegression\n",
"from sklearn.model_selection import train_test_split\n",
"\n",
"# Create training and test sets\n",
"X_train, X_test, y_train, y_test = train_test_split(\n",
" X, y, test_size=0.1\n",
")\n",
"\n",
"visualizer = ResidualsPlot(LinearRegression())\n",
"visualizer.fit(X_train, y_train)\n",
"visualizer.score(X_test, y_test)\n",
"visualizer.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"\n",
"from sklearn.linear_model import RidgeCV\n",
"from yellowbrick.regressor import AlphaSelection\n",
"\n",
"alphas = np.logspace(-10, 1, 200)\n",
"visualizer = AlphaSelection(RidgeCV(alphas=alphas))\n",
"visualizer.fit(X, y)\n",
"visualizer.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.linear_model import Ridge\n",
"from yellowbrick.regressor import PredictionError\n",
"\n",
"visualizer = PredictionError(Ridge(alpha=3.181))\n",
"visualizer.fit(X_train, y_train)\n",
"visualizer.score(X_test, y_test)\n",
"visualizer.show()"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
TEAMDSS/KBO_Player_Salary | hitter/hitter_final.ipynb | 1 | 64005 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"doosan_hb_df = pd.read_csv(\"basic/doosan_hb_15.csv\")\n",
"hanhwa_hb_df = pd.read_csv(\"basic/hanhwa_hb_15.csv\")\n",
"KIA_hb_df = pd.read_csv(\"basic/KIA_hb_15.csv\")\n",
"KT_hb_df = pd.read_csv(\"basic/KT_hb_15.csv\")\n",
"LG_hb_df = pd.read_csv(\"basic/LG_hb_15.csv\")\n",
"lotte_hb_df = pd.read_csv(\"basic/lotte_hb_15.csv\")\n",
"NC_hb_df = pd.read_csv(\"basic/NC_hb_15.csv\")\n",
"nexen_hb_df = pd.read_csv(\"basic/nexen_hb_15.csv\")\n",
"samsung_hb_df = pd.read_csv(\"basic/samsung_hb_15.csv\")\n",
"SK_hb_df = pd.read_csv(\"basic/SK_hb_15.csv\")"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"doosan_hd_df = pd.read_csv(\"detail/doosan_hd_15.csv\")\n",
"hanhwa_hd_df = pd.read_csv(\"detail/hanhwa_hd_15.csv\")\n",
"KIA_hd_df = pd.read_csv(\"detail/KIA_hd_15.csv\")\n",
"KT_hd_df = pd.read_csv(\"detail/KT_hd_15.csv\")\n",
"LG_hd_df = pd.read_csv(\"detail/LG_hd_15.csv\")\n",
"lotte_hd_df = pd.read_csv(\"detail/lotte_hd_15.csv\")\n",
"NC_hd_df = pd.read_csv(\"detail/NC_hd_15.csv\")\n",
"nexen_hd_df = pd.read_csv(\"detail/nexen_hd_15.csv\")\n",
"samsung_hd_df = pd.read_csv(\"detail/samsung_hd_15.csv\")\n",
"SK_hd_df = pd.read_csv(\"detail/SK_hd_15.csv\")"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"doosan_df = doosan_hb_df.merge(doosan_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"hanhwa_df = hanhwa_hb_df.merge(hanhwa_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"KIA_df = KIA_hb_df.merge(KIA_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"KT_df = KT_hb_df.merge(KT_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"LG_df = LG_hb_df.merge(LG_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"lotte_df = lotte_hb_df.merge(lotte_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"NC_df = NC_hb_df.merge(NC_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"nexen_df = nexen_hb_df.merge(nexen_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"samsung_df = samsung_hb_df.merge(samsung_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]\n",
"SK_df = SK_hb_df.merge(SK_hd_df, left_on=\"name\",right_on=\"name\")[[\"name\", \"team_x\", \"AVG_x\", \"G\", \"PA\", \"AB\", \"R\", \"H\", \"2B\", \"3B\", \"HR\", \"TB\", \"RBI\", \"SAC\", \"SF\", \"XBH\", \"GO\", \"AO\", \"GO/AO\", \"GW_RBI\", \"BB/K\", \"P/PA\", \"ISOP\", \"XR\", \"GPA\"]]"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"doosan_df = doosan_df.rename(columns={\"team_x\":\"team\"})\n",
"hanhwa_df = hanhwa_df.rename(columns={\"team_x\":\"team\"})\n",
"KIA_df = KIA_df.rename(columns={\"team_x\":\"team\"})\n",
"KT_df = KT_df.rename(columns={\"team_x\":\"team\"})\n",
"LG_df = LG_df.rename(columns={\"team_x\":\"team\"})\n",
"lotte_df = lotte_df.rename(columns={\"team_x\":\"team\"})\n",
"NC_df = NC_df.rename(columns={\"team_x\":\"team\"})\n",
"nexen_df = nexen_df.rename(columns={\"team_x\":\"team\"})\n",
"samsung_df = samsung_df.rename(columns={\"team_x\":\"team\"})\n",
"SK_df = SK_df.rename(columns={\"team_x\":\"team\"})"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"doosan_df = doosan_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"hanhwa_df = hanhwa_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"KIA_df = KIA_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"KT_df = KT_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"LG_df = LG_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"lotte_df = lotte_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"NC_df = NC_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"nexen_df = nexen_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"samsung_df = samsung_df.rename(columns={\"AVG_x\":\"AVG\"})\n",
"SK_df = SK_df.rename(columns={\"AVG_x\":\"AVG\"})"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"doosan_df.to_csv(\"doosan_hitter.csv\",encoding='utf-8')\n",
"hanhwa_df.to_csv(\"hanhwa_hitter.csv\",encoding='utf-8')\n",
"KIA_df.to_csv(\"KIA_hitter.csv\",encoding='utf-8')\n",
"KT_df.to_csv(\"KT_hitter.csv\",encoding='utf-8')\n",
"LG_df.to_csv(\"LG_hitter.csv\",encoding='utf-8')\n",
"lotte_df.to_csv(\"lotte_hitter.csv\",encoding='utf-8')\n",
"NC_df.to_csv(\"NC_hitter.csv\",encoding='utf-8')\n",
"nexen_df.to_csv(\"nexen_hitter.csv\",encoding='utf-8')\n",
"samsung_df.to_csv(\"samsung_hitter.csv\",encoding='utf-8')\n",
"SK_df.to_csv(\"SK_hitter.csv\",encoding='utf-8')"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"hitter_df = pd.concat([doosan_df, hanhwa_df, KIA_df, KT_df, LG_df, lotte_df, NC_df, nexen_df, samsung_df, SK_df]).reset_index(drop=True)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"hitter_df.to_csv(\"hitter_final.csv\",encoding='utf-8')"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>name</th>\n",
" <th>team</th>\n",
" <th>AVG</th>\n",
" <th>G</th>\n",
" <th>PA</th>\n",
" <th>AB</th>\n",
" <th>R</th>\n",
" <th>H</th>\n",
" <th>2B</th>\n",
" <th>3B</th>\n",
" <th>...</th>\n",
" <th>XBH</th>\n",
" <th>GO</th>\n",
" <th>AO</th>\n",
" <th>GO/AO</th>\n",
" <th>GW_RBI</th>\n",
" <th>BB/K</th>\n",
" <th>P/PA</th>\n",
" <th>ISOP</th>\n",
" <th>XR</th>\n",
" <th>GPA</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>박건우</td>\n",
" <td>두산</td>\n",
" <td>0.342</td>\n",
" <td>70</td>\n",
" <td>175</td>\n",
" <td>158</td>\n",
" <td>31</td>\n",
" <td>54</td>\n",
" <td>12</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>17</td>\n",
" <td>35</td>\n",
" <td>40</td>\n",
" <td>0.88</td>\n",
" <td>4</td>\n",
" <td>0.41</td>\n",
" <td>3.59</td>\n",
" <td>0.171</td>\n",
" <td>29.2</td>\n",
" <td>0.308</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>김응민</td>\n",
" <td>두산</td>\n",
" <td>0.333</td>\n",
" <td>4</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>1.00</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>3.67</td>\n",
" <td>1.000</td>\n",
" <td>0.9</td>\n",
" <td>0.483</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>고영민</td>\n",
" <td>두산</td>\n",
" <td>0.328</td>\n",
" <td>41</td>\n",
" <td>77</td>\n",
" <td>67</td>\n",
" <td>13</td>\n",
" <td>22</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>4</td>\n",
" <td>8</td>\n",
" <td>16</td>\n",
" <td>0.50</td>\n",
" <td>1</td>\n",
" <td>0.27</td>\n",
" <td>3.75</td>\n",
" <td>0.149</td>\n",
" <td>11.8</td>\n",
" <td>0.301</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>김현수</td>\n",
" <td>두산</td>\n",
" <td>0.326</td>\n",
" <td>141</td>\n",
" <td>630</td>\n",
" <td>512</td>\n",
" <td>103</td>\n",
" <td>167</td>\n",
" <td>26</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>54</td>\n",
" <td>146</td>\n",
" <td>145</td>\n",
" <td>1.01</td>\n",
" <td>13</td>\n",
" <td>1.60</td>\n",
" <td>3.72</td>\n",
" <td>0.215</td>\n",
" <td>118.9</td>\n",
" <td>0.332</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>양의지</td>\n",
" <td>두산</td>\n",
" <td>0.326</td>\n",
" <td>132</td>\n",
" <td>513</td>\n",
" <td>442</td>\n",
" <td>70</td>\n",
" <td>144</td>\n",
" <td>27</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>47</td>\n",
" <td>81</td>\n",
" <td>159</td>\n",
" <td>0.51</td>\n",
" <td>12</td>\n",
" <td>0.61</td>\n",
" <td>3.78</td>\n",
" <td>0.197</td>\n",
" <td>89.9</td>\n",
" <td>0.313</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>허경민</td>\n",
" <td>두산</td>\n",
" <td>0.317</td>\n",
" <td>117</td>\n",
" <td>453</td>\n",
" <td>404</td>\n",
" <td>64</td>\n",
" <td>128</td>\n",
" <td>20</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>23</td>\n",
" <td>136</td>\n",
" <td>101</td>\n",
" <td>1.35</td>\n",
" <td>1</td>\n",
" <td>0.74</td>\n",
" <td>3.66</td>\n",
" <td>0.067</td>\n",
" <td>56.0</td>\n",
" <td>0.264</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>김재호</td>\n",
" <td>두산</td>\n",
" <td>0.307</td>\n",
" <td>133</td>\n",
" <td>488</td>\n",
" <td>410</td>\n",
" <td>63</td>\n",
" <td>126</td>\n",
" <td>24</td>\n",
" <td>3</td>\n",
" <td>...</td>\n",
" <td>30</td>\n",
" <td>101</td>\n",
" <td>148</td>\n",
" <td>0.68</td>\n",
" <td>6</td>\n",
" <td>1.29</td>\n",
" <td>3.85</td>\n",
" <td>0.095</td>\n",
" <td>63.3</td>\n",
" <td>0.274</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>민병헌</td>\n",
" <td>두산</td>\n",
" <td>0.303</td>\n",
" <td>129</td>\n",
" <td>561</td>\n",
" <td>491</td>\n",
" <td>80</td>\n",
" <td>149</td>\n",
" <td>20</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>34</td>\n",
" <td>131</td>\n",
" <td>143</td>\n",
" <td>0.92</td>\n",
" <td>6</td>\n",
" <td>0.68</td>\n",
" <td>3.78</td>\n",
" <td>0.122</td>\n",
" <td>76.8</td>\n",
" <td>0.274</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>정수빈</td>\n",
" <td>두산</td>\n",
" <td>0.295</td>\n",
" <td>128</td>\n",
" <td>570</td>\n",
" <td>491</td>\n",
" <td>79</td>\n",
" <td>145</td>\n",
" <td>27</td>\n",
" <td>7</td>\n",
" <td>...</td>\n",
" <td>36</td>\n",
" <td>172</td>\n",
" <td>110</td>\n",
" <td>1.56</td>\n",
" <td>5</td>\n",
" <td>0.61</td>\n",
" <td>3.78</td>\n",
" <td>0.096</td>\n",
" <td>70.1</td>\n",
" <td>0.260</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>오재일</td>\n",
" <td>두산</td>\n",
" <td>0.289</td>\n",
" <td>66</td>\n",
" <td>213</td>\n",
" <td>180</td>\n",
" <td>33</td>\n",
" <td>52</td>\n",
" <td>11</td>\n",
" <td>1</td>\n",
" <td>...</td>\n",
" <td>26</td>\n",
" <td>29</td>\n",
" <td>52</td>\n",
" <td>0.56</td>\n",
" <td>4</td>\n",
" <td>0.57</td>\n",
" <td>3.79</td>\n",
" <td>0.306</td>\n",
" <td>39.2</td>\n",
" <td>0.323</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>최주환</td>\n",
" <td>두산</td>\n",
" <td>0.282</td>\n",
" <td>100</td>\n",
" <td>270</td>\n",
" <td>238</td>\n",
" <td>34</td>\n",
" <td>67</td>\n",
" <td>16</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>23</td>\n",
" <td>70</td>\n",
" <td>68</td>\n",
" <td>1.03</td>\n",
" <td>2</td>\n",
" <td>0.74</td>\n",
" <td>4.04</td>\n",
" <td>0.147</td>\n",
" <td>33.8</td>\n",
" <td>0.267</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>오재원</td>\n",
" <td>두산</td>\n",
" <td>0.280</td>\n",
" <td>120</td>\n",
" <td>474</td>\n",
" <td>411</td>\n",
" <td>60</td>\n",
" <td>115</td>\n",
" <td>20</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>33</td>\n",
" <td>108</td>\n",
" <td>98</td>\n",
" <td>1.10</td>\n",
" <td>6</td>\n",
" <td>0.50</td>\n",
" <td>4.15</td>\n",
" <td>0.139</td>\n",
" <td>64.6</td>\n",
" <td>0.265</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>유민상</td>\n",
" <td>두산</td>\n",
" <td>0.263</td>\n",
" <td>15</td>\n",
" <td>45</td>\n",
" <td>38</td>\n",
" <td>5</td>\n",
" <td>10</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>2</td>\n",
" <td>8</td>\n",
" <td>12</td>\n",
" <td>0.67</td>\n",
" <td>2</td>\n",
" <td>0.56</td>\n",
" <td>4.29</td>\n",
" <td>0.105</td>\n",
" <td>5.8</td>\n",
" <td>0.252</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>홍성흔</td>\n",
" <td>두산</td>\n",
" <td>0.262</td>\n",
" <td>93</td>\n",
" <td>352</td>\n",
" <td>301</td>\n",
" <td>39</td>\n",
" <td>79</td>\n",
" <td>12</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>19</td>\n",
" <td>84</td>\n",
" <td>79</td>\n",
" <td>1.06</td>\n",
" <td>4</td>\n",
" <td>0.71</td>\n",
" <td>4.09</td>\n",
" <td>0.110</td>\n",
" <td>40.6</td>\n",
" <td>0.256</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>로메로</td>\n",
" <td>두산</td>\n",
" <td>0.253</td>\n",
" <td>76</td>\n",
" <td>305</td>\n",
" <td>265</td>\n",
" <td>30</td>\n",
" <td>67</td>\n",
" <td>16</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>28</td>\n",
" <td>64</td>\n",
" <td>92</td>\n",
" <td>0.70</td>\n",
" <td>4</td>\n",
" <td>0.60</td>\n",
" <td>3.86</td>\n",
" <td>0.196</td>\n",
" <td>40.8</td>\n",
" <td>0.260</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>김재환</td>\n",
" <td>두산</td>\n",
" <td>0.235</td>\n",
" <td>48</td>\n",
" <td>180</td>\n",
" <td>153</td>\n",
" <td>24</td>\n",
" <td>36</td>\n",
" <td>8</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>15</td>\n",
" <td>44</td>\n",
" <td>36</td>\n",
" <td>1.22</td>\n",
" <td>2</td>\n",
" <td>0.56</td>\n",
" <td>3.86</td>\n",
" <td>0.190</td>\n",
" <td>22.5</td>\n",
" <td>0.257</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>정진호</td>\n",
" <td>두산</td>\n",
" <td>0.234</td>\n",
" <td>77</td>\n",
" <td>172</td>\n",
" <td>154</td>\n",
" <td>37</td>\n",
" <td>36</td>\n",
" <td>5</td>\n",
" <td>3</td>\n",
" <td>...</td>\n",
" <td>12</td>\n",
" <td>55</td>\n",
" <td>39</td>\n",
" <td>1.41</td>\n",
" <td>3</td>\n",
" <td>0.58</td>\n",
" <td>3.49</td>\n",
" <td>0.149</td>\n",
" <td>19.0</td>\n",
" <td>0.232</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>국해성</td>\n",
" <td>두산</td>\n",
" <td>0.200</td>\n",
" <td>11</td>\n",
" <td>26</td>\n",
" <td>20</td>\n",
" <td>6</td>\n",
" <td>4</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>2</td>\n",
" <td>7</td>\n",
" <td>6</td>\n",
" <td>1.17</td>\n",
" <td>0</td>\n",
" <td>0.40</td>\n",
" <td>3.46</td>\n",
" <td>0.200</td>\n",
" <td>2.7</td>\n",
" <td>0.226</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>류지혁</td>\n",
" <td>두산</td>\n",
" <td>0.200</td>\n",
" <td>14</td>\n",
" <td>5</td>\n",
" <td>5</td>\n",
" <td>3</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>4.20</td>\n",
" <td>0.000</td>\n",
" <td>0.1</td>\n",
" <td>0.140</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>장민석</td>\n",
" <td>두산</td>\n",
" <td>0.189</td>\n",
" <td>53</td>\n",
" <td>63</td>\n",
" <td>53</td>\n",
" <td>15</td>\n",
" <td>10</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>2</td>\n",
" <td>14</td>\n",
" <td>17</td>\n",
" <td>0.82</td>\n",
" <td>0</td>\n",
" <td>0.54</td>\n",
" <td>3.59</td>\n",
" <td>0.038</td>\n",
" <td>4.3</td>\n",
" <td>0.187</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>김진형</td>\n",
" <td>두산</td>\n",
" <td>0.167</td>\n",
" <td>14</td>\n",
" <td>21</td>\n",
" <td>18</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>3</td>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>1.00</td>\n",
" <td>0</td>\n",
" <td>0.43</td>\n",
" <td>3.90</td>\n",
" <td>0.278</td>\n",
" <td>2.1</td>\n",
" <td>0.240</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>최재훈</td>\n",
" <td>두산</td>\n",
" <td>0.152</td>\n",
" <td>71</td>\n",
" <td>114</td>\n",
" <td>99</td>\n",
" <td>6</td>\n",
" <td>15</td>\n",
" <td>3</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>3</td>\n",
" <td>35</td>\n",
" <td>31</td>\n",
" <td>1.13</td>\n",
" <td>0</td>\n",
" <td>0.16</td>\n",
" <td>3.64</td>\n",
" <td>0.030</td>\n",
" <td>2.5</td>\n",
" <td>0.151</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>양종민</td>\n",
" <td>두산</td>\n",
" <td>0.125</td>\n",
" <td>32</td>\n",
" <td>18</td>\n",
" <td>16</td>\n",
" <td>6</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>8</td>\n",
" <td>0.13</td>\n",
" <td>0</td>\n",
" <td>0.40</td>\n",
" <td>3.78</td>\n",
" <td>0.188</td>\n",
" <td>1.0</td>\n",
" <td>0.178</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>루츠</td>\n",
" <td>두산</td>\n",
" <td>0.111</td>\n",
" <td>8</td>\n",
" <td>30</td>\n",
" <td>27</td>\n",
" <td>2</td>\n",
" <td>3</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>10</td>\n",
" <td>9</td>\n",
" <td>1.11</td>\n",
" <td>0</td>\n",
" <td>0.33</td>\n",
" <td>3.83</td>\n",
" <td>0.111</td>\n",
" <td>0.9</td>\n",
" <td>0.131</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>노경은</td>\n",
" <td>두산</td>\n",
" <td>-</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>니퍼트</td>\n",
" <td>두산</td>\n",
" <td>-</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>양현</td>\n",
" <td>두산</td>\n",
" <td>-</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>이원재</td>\n",
" <td>두산</td>\n",
" <td>-</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>이현승</td>\n",
" <td>두산</td>\n",
" <td>-</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>진야곱</td>\n",
" <td>두산</td>\n",
" <td>-</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>245</th>\n",
" <td>이진석</td>\n",
" <td>SK</td>\n",
" <td>0.500</td>\n",
" <td>6</td>\n",
" <td>2</td>\n",
" <td>2</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>6.50</td>\n",
" <td>0.000</td>\n",
" <td>0.1</td>\n",
" <td>0.350</td>\n",
" </tr>\n",
" <tr>\n",
" <th>246</th>\n",
" <td>김기현</td>\n",
" <td>SK</td>\n",
" <td>0.429</td>\n",
" <td>9</td>\n",
" <td>9</td>\n",
" <td>7</td>\n",
" <td>0</td>\n",
" <td>3</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0.00</td>\n",
" <td>0</td>\n",
" <td>0.67</td>\n",
" <td>4.22</td>\n",
" <td>0.000</td>\n",
" <td>1.8</td>\n",
" <td>0.357</td>\n",
" </tr>\n",
" <tr>\n",
" <th>247</th>\n",
" <td>이현석</td>\n",
" <td>SK</td>\n",
" <td>0.333</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>3.33</td>\n",
" <td>1.000</td>\n",
" <td>1.3</td>\n",
" <td>0.483</td>\n",
" </tr>\n",
" <tr>\n",
" <th>248</th>\n",
" <td>홍명찬</td>\n",
" <td>SK</td>\n",
" <td>0.333</td>\n",
" <td>5</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>3.33</td>\n",
" <td>0.000</td>\n",
" <td>0.3</td>\n",
" <td>0.233</td>\n",
" </tr>\n",
" <tr>\n",
" <th>249</th>\n",
" <td>정의윤</td>\n",
" <td>SK</td>\n",
" <td>0.320</td>\n",
" <td>91</td>\n",
" <td>297</td>\n",
" <td>259</td>\n",
" <td>38</td>\n",
" <td>83</td>\n",
" <td>14</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>28</td>\n",
" <td>56</td>\n",
" <td>77</td>\n",
" <td>0.73</td>\n",
" <td>5</td>\n",
" <td>0.57</td>\n",
" <td>3.71</td>\n",
" <td>0.216</td>\n",
" <td>53.2</td>\n",
" <td>0.313</td>\n",
" </tr>\n",
" <tr>\n",
" <th>250</th>\n",
" <td>이명기</td>\n",
" <td>SK</td>\n",
" <td>0.315</td>\n",
" <td>137</td>\n",
" <td>582</td>\n",
" <td>521</td>\n",
" <td>88</td>\n",
" <td>164</td>\n",
" <td>30</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>35</td>\n",
" <td>177</td>\n",
" <td>98</td>\n",
" <td>1.81</td>\n",
" <td>1</td>\n",
" <td>0.41</td>\n",
" <td>3.87</td>\n",
" <td>0.083</td>\n",
" <td>75.4</td>\n",
" <td>0.265</td>\n",
" </tr>\n",
" <tr>\n",
" <th>251</th>\n",
" <td>최정민</td>\n",
" <td>SK</td>\n",
" <td>0.308</td>\n",
" <td>8</td>\n",
" <td>15</td>\n",
" <td>13</td>\n",
" <td>1</td>\n",
" <td>4</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>5</td>\n",
" <td>1</td>\n",
" <td>5.00</td>\n",
" <td>0</td>\n",
" <td>0.33</td>\n",
" <td>3.60</td>\n",
" <td>0.000</td>\n",
" <td>1.5</td>\n",
" <td>0.238</td>\n",
" </tr>\n",
" <tr>\n",
" <th>252</th>\n",
" <td>김성현</td>\n",
" <td>SK</td>\n",
" <td>0.297</td>\n",
" <td>129</td>\n",
" <td>449</td>\n",
" <td>397</td>\n",
" <td>49</td>\n",
" <td>118</td>\n",
" <td>20</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>28</td>\n",
" <td>121</td>\n",
" <td>118</td>\n",
" <td>1.03</td>\n",
" <td>5</td>\n",
" <td>0.74</td>\n",
" <td>3.49</td>\n",
" <td>0.111</td>\n",
" <td>53.3</td>\n",
" <td>0.263</td>\n",
" </tr>\n",
" <tr>\n",
" <th>253</th>\n",
" <td>최정</td>\n",
" <td>SK</td>\n",
" <td>0.295</td>\n",
" <td>81</td>\n",
" <td>330</td>\n",
" <td>275</td>\n",
" <td>43</td>\n",
" <td>81</td>\n",
" <td>17</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>34</td>\n",
" <td>45</td>\n",
" <td>74</td>\n",
" <td>0.61</td>\n",
" <td>10</td>\n",
" <td>0.59</td>\n",
" <td>4.20</td>\n",
" <td>0.247</td>\n",
" <td>58.5</td>\n",
" <td>0.316</td>\n",
" </tr>\n",
" <tr>\n",
" <th>254</th>\n",
" <td>허웅</td>\n",
" <td>SK</td>\n",
" <td>0.294</td>\n",
" <td>18</td>\n",
" <td>19</td>\n",
" <td>17</td>\n",
" <td>2</td>\n",
" <td>5</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>8</td>\n",
" <td>0.13</td>\n",
" <td>0</td>\n",
" <td>0.67</td>\n",
" <td>3.89</td>\n",
" <td>0.059</td>\n",
" <td>2.3</td>\n",
" <td>0.254</td>\n",
" </tr>\n",
" <tr>\n",
" <th>255</th>\n",
" <td>이재원</td>\n",
" <td>SK</td>\n",
" <td>0.282</td>\n",
" <td>140</td>\n",
" <td>559</td>\n",
" <td>489</td>\n",
" <td>58</td>\n",
" <td>138</td>\n",
" <td>18</td>\n",
" <td>1</td>\n",
" <td>...</td>\n",
" <td>36</td>\n",
" <td>115</td>\n",
" <td>156</td>\n",
" <td>0.74</td>\n",
" <td>11</td>\n",
" <td>0.64</td>\n",
" <td>3.66</td>\n",
" <td>0.145</td>\n",
" <td>71.8</td>\n",
" <td>0.270</td>\n",
" </tr>\n",
" <tr>\n",
" <th>256</th>\n",
" <td>박정권</td>\n",
" <td>SK</td>\n",
" <td>0.281</td>\n",
" <td>124</td>\n",
" <td>494</td>\n",
" <td>438</td>\n",
" <td>66</td>\n",
" <td>123</td>\n",
" <td>23</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>44</td>\n",
" <td>96</td>\n",
" <td>102</td>\n",
" <td>0.94</td>\n",
" <td>5</td>\n",
" <td>0.39</td>\n",
" <td>4.02</td>\n",
" <td>0.196</td>\n",
" <td>71.1</td>\n",
" <td>0.278</td>\n",
" </tr>\n",
" <tr>\n",
" <th>257</th>\n",
" <td>나주환</td>\n",
" <td>SK</td>\n",
" <td>0.268</td>\n",
" <td>96</td>\n",
" <td>273</td>\n",
" <td>246</td>\n",
" <td>31</td>\n",
" <td>66</td>\n",
" <td>15</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>20</td>\n",
" <td>70</td>\n",
" <td>64</td>\n",
" <td>1.09</td>\n",
" <td>3</td>\n",
" <td>0.26</td>\n",
" <td>3.94</td>\n",
" <td>0.122</td>\n",
" <td>25.6</td>\n",
" <td>0.236</td>\n",
" </tr>\n",
" <tr>\n",
" <th>258</th>\n",
" <td>김연훈</td>\n",
" <td>SK</td>\n",
" <td>0.267</td>\n",
" <td>49</td>\n",
" <td>73</td>\n",
" <td>60</td>\n",
" <td>4</td>\n",
" <td>16</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>2</td>\n",
" <td>11</td>\n",
" <td>16</td>\n",
" <td>0.69</td>\n",
" <td>0</td>\n",
" <td>0.33</td>\n",
" <td>3.99</td>\n",
" <td>0.067</td>\n",
" <td>7.7</td>\n",
" <td>0.235</td>\n",
" </tr>\n",
" <tr>\n",
" <th>259</th>\n",
" <td>이대수</td>\n",
" <td>SK</td>\n",
" <td>0.264</td>\n",
" <td>36</td>\n",
" <td>86</td>\n",
" <td>72</td>\n",
" <td>9</td>\n",
" <td>19</td>\n",
" <td>3</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>5</td>\n",
" <td>18</td>\n",
" <td>13</td>\n",
" <td>1.38</td>\n",
" <td>1</td>\n",
" <td>0.26</td>\n",
" <td>3.95</td>\n",
" <td>0.125</td>\n",
" <td>7.5</td>\n",
" <td>0.244</td>\n",
" </tr>\n",
" <tr>\n",
" <th>260</th>\n",
" <td>조동화</td>\n",
" <td>SK</td>\n",
" <td>0.261</td>\n",
" <td>119</td>\n",
" <td>304</td>\n",
" <td>245</td>\n",
" <td>38</td>\n",
" <td>64</td>\n",
" <td>6</td>\n",
" <td>1</td>\n",
" <td>...</td>\n",
" <td>9</td>\n",
" <td>78</td>\n",
" <td>55</td>\n",
" <td>1.42</td>\n",
" <td>1</td>\n",
" <td>0.60</td>\n",
" <td>4.13</td>\n",
" <td>0.057</td>\n",
" <td>34.1</td>\n",
" <td>0.237</td>\n",
" </tr>\n",
" <tr>\n",
" <th>261</th>\n",
" <td>브라운</td>\n",
" <td>SK</td>\n",
" <td>0.261</td>\n",
" <td>137</td>\n",
" <td>539</td>\n",
" <td>464</td>\n",
" <td>82</td>\n",
" <td>121</td>\n",
" <td>21</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>51</td>\n",
" <td>116</td>\n",
" <td>102</td>\n",
" <td>1.14</td>\n",
" <td>9</td>\n",
" <td>0.52</td>\n",
" <td>3.98</td>\n",
" <td>0.235</td>\n",
" <td>81.7</td>\n",
" <td>0.286</td>\n",
" </tr>\n",
" <tr>\n",
" <th>262</th>\n",
" <td>정상호</td>\n",
" <td>SK</td>\n",
" <td>0.254</td>\n",
" <td>113</td>\n",
" <td>324</td>\n",
" <td>279</td>\n",
" <td>34</td>\n",
" <td>71</td>\n",
" <td>11</td>\n",
" <td>1</td>\n",
" <td>...</td>\n",
" <td>24</td>\n",
" <td>62</td>\n",
" <td>66</td>\n",
" <td>0.94</td>\n",
" <td>5</td>\n",
" <td>0.28</td>\n",
" <td>3.96</td>\n",
" <td>0.176</td>\n",
" <td>42.1</td>\n",
" <td>0.261</td>\n",
" </tr>\n",
" <tr>\n",
" <th>263</th>\n",
" <td>박진만</td>\n",
" <td>SK</td>\n",
" <td>0.248</td>\n",
" <td>78</td>\n",
" <td>162</td>\n",
" <td>133</td>\n",
" <td>12</td>\n",
" <td>33</td>\n",
" <td>5</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>7</td>\n",
" <td>31</td>\n",
" <td>48</td>\n",
" <td>0.65</td>\n",
" <td>1</td>\n",
" <td>1.10</td>\n",
" <td>4.12</td>\n",
" <td>0.083</td>\n",
" <td>17.7</td>\n",
" <td>0.252</td>\n",
" </tr>\n",
" <tr>\n",
" <th>264</th>\n",
" <td>박재상</td>\n",
" <td>SK</td>\n",
" <td>0.248</td>\n",
" <td>108</td>\n",
" <td>292</td>\n",
" <td>250</td>\n",
" <td>34</td>\n",
" <td>62</td>\n",
" <td>12</td>\n",
" <td>2</td>\n",
" <td>...</td>\n",
" <td>21</td>\n",
" <td>70</td>\n",
" <td>66</td>\n",
" <td>1.06</td>\n",
" <td>5</td>\n",
" <td>0.60</td>\n",
" <td>4.24</td>\n",
" <td>0.148</td>\n",
" <td>34.1</td>\n",
" <td>0.252</td>\n",
" </tr>\n",
" <tr>\n",
" <th>265</th>\n",
" <td>김강민</td>\n",
" <td>SK</td>\n",
" <td>0.246</td>\n",
" <td>96</td>\n",
" <td>328</td>\n",
" <td>293</td>\n",
" <td>43</td>\n",
" <td>72</td>\n",
" <td>17</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>21</td>\n",
" <td>74</td>\n",
" <td>65</td>\n",
" <td>1.14</td>\n",
" <td>5</td>\n",
" <td>0.28</td>\n",
" <td>3.88</td>\n",
" <td>0.099</td>\n",
" <td>31.4</td>\n",
" <td>0.228</td>\n",
" </tr>\n",
" <tr>\n",
" <th>266</th>\n",
" <td>윤중환</td>\n",
" <td>SK</td>\n",
" <td>0.240</td>\n",
" <td>15</td>\n",
" <td>28</td>\n",
" <td>25</td>\n",
" <td>1</td>\n",
" <td>6</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>8</td>\n",
" <td>5</td>\n",
" <td>1.60</td>\n",
" <td>0</td>\n",
" <td>0.50</td>\n",
" <td>4.43</td>\n",
" <td>0.120</td>\n",
" <td>2.9</td>\n",
" <td>0.234</td>\n",
" </tr>\n",
" <tr>\n",
" <th>267</th>\n",
" <td>박계현</td>\n",
" <td>SK</td>\n",
" <td>0.231</td>\n",
" <td>97</td>\n",
" <td>302</td>\n",
" <td>264</td>\n",
" <td>27</td>\n",
" <td>61</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>2</td>\n",
" <td>103</td>\n",
" <td>56</td>\n",
" <td>1.84</td>\n",
" <td>0</td>\n",
" <td>0.44</td>\n",
" <td>3.76</td>\n",
" <td>0.008</td>\n",
" <td>20.2</td>\n",
" <td>0.192</td>\n",
" </tr>\n",
" <tr>\n",
" <th>268</th>\n",
" <td>김민식</td>\n",
" <td>SK</td>\n",
" <td>0.167</td>\n",
" <td>23</td>\n",
" <td>26</td>\n",
" <td>24</td>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>11</td>\n",
" <td>7</td>\n",
" <td>1.57</td>\n",
" <td>0</td>\n",
" <td>1.00</td>\n",
" <td>3.73</td>\n",
" <td>0.000</td>\n",
" <td>0.1</td>\n",
" <td>0.146</td>\n",
" </tr>\n",
" <tr>\n",
" <th>269</th>\n",
" <td>박윤</td>\n",
" <td>SK</td>\n",
" <td>0.111</td>\n",
" <td>17</td>\n",
" <td>29</td>\n",
" <td>27</td>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>2.67</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>3.66</td>\n",
" <td>0.000</td>\n",
" <td>-0.8</td>\n",
" <td>0.092</td>\n",
" </tr>\n",
" <tr>\n",
" <th>270</th>\n",
" <td>김재현</td>\n",
" <td>SK</td>\n",
" <td>0.105</td>\n",
" <td>46</td>\n",
" <td>20</td>\n",
" <td>19</td>\n",
" <td>13</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>8</td>\n",
" <td>3</td>\n",
" <td>2.67</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>4.10</td>\n",
" <td>0.105</td>\n",
" <td>1.2</td>\n",
" <td>0.120</td>\n",
" </tr>\n",
" <tr>\n",
" <th>271</th>\n",
" <td>안정광</td>\n",
" <td>SK</td>\n",
" <td>0.105</td>\n",
" <td>10</td>\n",
" <td>19</td>\n",
" <td>19</td>\n",
" <td>0</td>\n",
" <td>2</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>6</td>\n",
" <td>4</td>\n",
" <td>1.50</td>\n",
" <td>0</td>\n",
" <td>0.00</td>\n",
" <td>3.47</td>\n",
" <td>0.000</td>\n",
" <td>-0.6</td>\n",
" <td>0.074</td>\n",
" </tr>\n",
" <tr>\n",
" <th>272</th>\n",
" <td>유서준</td>\n",
" <td>SK</td>\n",
" <td>0.083</td>\n",
" <td>17</td>\n",
" <td>13</td>\n",
" <td>12</td>\n",
" <td>5</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>4</td>\n",
" <td>4</td>\n",
" <td>1.00</td>\n",
" <td>0</td>\n",
" <td>0.33</td>\n",
" <td>4.15</td>\n",
" <td>0.000</td>\n",
" <td>-0.3</td>\n",
" <td>0.090</td>\n",
" </tr>\n",
" <tr>\n",
" <th>273</th>\n",
" <td>고효준</td>\n",
" <td>SK</td>\n",
" <td>-</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>274</th>\n",
" <td>박정배</td>\n",
" <td>SK</td>\n",
" <td>-</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>...</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>0</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>-</td>\n",
" <td>0.0</td>\n",
" <td>0.000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>275 rows × 25 columns</p>\n",
"</div>"
],
"text/plain": [
" name team AVG G PA AB R H 2B 3B ... XBH GO AO \\\n",
"0 박건우 두산 0.342 70 175 158 31 54 12 0 ... 17 35 40 \n",
"1 김응민 두산 0.333 4 3 3 1 1 0 0 ... 1 1 1 \n",
"2 고영민 두산 0.328 41 77 67 13 22 1 0 ... 4 8 16 \n",
"3 김현수 두산 0.326 141 630 512 103 167 26 0 ... 54 146 145 \n",
"4 양의지 두산 0.326 132 513 442 70 144 27 0 ... 47 81 159 \n",
"5 허경민 두산 0.317 117 453 404 64 128 20 2 ... 23 136 101 \n",
"6 김재호 두산 0.307 133 488 410 63 126 24 3 ... 30 101 148 \n",
"7 민병헌 두산 0.303 129 561 491 80 149 20 2 ... 34 131 143 \n",
"8 정수빈 두산 0.295 128 570 491 79 145 27 7 ... 36 172 110 \n",
"9 오재일 두산 0.289 66 213 180 33 52 11 1 ... 26 29 52 \n",
"10 최주환 두산 0.282 100 270 238 34 67 16 2 ... 23 70 68 \n",
"11 오재원 두산 0.280 120 474 411 60 115 20 2 ... 33 108 98 \n",
"12 유민상 두산 0.263 15 45 38 5 10 1 0 ... 2 8 12 \n",
"13 홍성흔 두산 0.262 93 352 301 39 79 12 0 ... 19 84 79 \n",
"14 로메로 두산 0.253 76 305 265 30 67 16 0 ... 28 64 92 \n",
"15 김재환 두산 0.235 48 180 153 24 36 8 0 ... 15 44 36 \n",
"16 정진호 두산 0.234 77 172 154 37 36 5 3 ... 12 55 39 \n",
"17 국해성 두산 0.200 11 26 20 6 4 1 0 ... 2 7 6 \n",
"18 류지혁 두산 0.200 14 5 5 3 1 0 0 ... 0 1 0 \n",
"19 장민석 두산 0.189 53 63 53 15 10 2 0 ... 2 14 17 \n",
"20 김진형 두산 0.167 14 21 18 3 3 2 0 ... 3 4 4 \n",
"21 최재훈 두산 0.152 71 114 99 6 15 3 0 ... 3 35 31 \n",
"22 양종민 두산 0.125 32 18 16 6 2 0 0 ... 1 1 8 \n",
"23 루츠 두산 0.111 8 30 27 2 3 0 0 ... 1 10 9 \n",
"24 노경은 두산 - 1 0 0 0 0 0 0 ... 0 0 0 \n",
"25 니퍼트 두산 - 1 0 0 0 0 0 0 ... 0 0 0 \n",
"26 양현 두산 - 1 0 0 0 0 0 0 ... 0 0 0 \n",
"27 이원재 두산 - 1 0 0 0 0 0 0 ... 0 0 0 \n",
"28 이현승 두산 - 2 0 0 0 0 0 0 ... 0 0 0 \n",
"29 진야곱 두산 - 2 0 0 0 0 0 0 ... 0 0 0 \n",
".. ... ... ... ... ... ... ... ... .. .. ... ... ... ... \n",
"245 이진석 SK 0.500 6 2 2 1 1 0 0 ... 0 0 0 \n",
"246 김기현 SK 0.429 9 9 7 0 3 0 0 ... 0 0 1 \n",
"247 이현석 SK 0.333 3 3 3 1 1 0 0 ... 1 1 0 \n",
"248 홍명찬 SK 0.333 5 3 3 0 1 0 0 ... 0 0 0 \n",
"249 정의윤 SK 0.320 91 297 259 38 83 14 0 ... 28 56 77 \n",
"250 이명기 SK 0.315 137 582 521 88 164 30 2 ... 35 177 98 \n",
"251 최정민 SK 0.308 8 15 13 1 4 0 0 ... 0 5 1 \n",
"252 김성현 SK 0.297 129 449 397 49 118 20 0 ... 28 121 118 \n",
"253 최정 SK 0.295 81 330 275 43 81 17 0 ... 34 45 74 \n",
"254 허웅 SK 0.294 18 19 17 2 5 1 0 ... 1 1 8 \n",
"255 이재원 SK 0.282 140 559 489 58 138 18 1 ... 36 115 156 \n",
"256 박정권 SK 0.281 124 494 438 66 123 23 0 ... 44 96 102 \n",
"257 나주환 SK 0.268 96 273 246 31 66 15 0 ... 20 70 64 \n",
"258 김연훈 SK 0.267 49 73 60 4 16 1 0 ... 2 11 16 \n",
"259 이대수 SK 0.264 36 86 72 9 19 3 0 ... 5 18 13 \n",
"260 조동화 SK 0.261 119 304 245 38 64 6 1 ... 9 78 55 \n",
"261 브라운 SK 0.261 137 539 464 82 121 21 2 ... 51 116 102 \n",
"262 정상호 SK 0.254 113 324 279 34 71 11 1 ... 24 62 66 \n",
"263 박진만 SK 0.248 78 162 133 12 33 5 0 ... 7 31 48 \n",
"264 박재상 SK 0.248 108 292 250 34 62 12 2 ... 21 70 66 \n",
"265 김강민 SK 0.246 96 328 293 43 72 17 0 ... 21 74 65 \n",
"266 윤중환 SK 0.240 15 28 25 1 6 0 0 ... 1 8 5 \n",
"267 박계현 SK 0.231 97 302 264 27 61 2 0 ... 2 103 56 \n",
"268 김민식 SK 0.167 23 26 24 4 4 0 0 ... 0 11 7 \n",
"269 박윤 SK 0.111 17 29 27 1 3 0 0 ... 0 8 3 \n",
"270 김재현 SK 0.105 46 20 19 13 2 0 1 ... 1 8 3 \n",
"271 안정광 SK 0.105 10 19 19 0 2 0 0 ... 0 6 4 \n",
"272 유서준 SK 0.083 17 13 12 5 1 0 0 ... 0 4 4 \n",
"273 고효준 SK - 1 0 0 0 0 0 0 ... 0 0 0 \n",
"274 박정배 SK - 1 0 0 0 0 0 0 ... 0 0 0 \n",
"\n",
" GO/AO GW_RBI BB/K P/PA ISOP XR GPA \n",
"0 0.88 4 0.41 3.59 0.171 29.2 0.308 \n",
"1 1.00 0 - 3.67 1.000 0.9 0.483 \n",
"2 0.50 1 0.27 3.75 0.149 11.8 0.301 \n",
"3 1.01 13 1.60 3.72 0.215 118.9 0.332 \n",
"4 0.51 12 0.61 3.78 0.197 89.9 0.313 \n",
"5 1.35 1 0.74 3.66 0.067 56.0 0.264 \n",
"6 0.68 6 1.29 3.85 0.095 63.3 0.274 \n",
"7 0.92 6 0.68 3.78 0.122 76.8 0.274 \n",
"8 1.56 5 0.61 3.78 0.096 70.1 0.260 \n",
"9 0.56 4 0.57 3.79 0.306 39.2 0.323 \n",
"10 1.03 2 0.74 4.04 0.147 33.8 0.267 \n",
"11 1.10 6 0.50 4.15 0.139 64.6 0.265 \n",
"12 0.67 2 0.56 4.29 0.105 5.8 0.252 \n",
"13 1.06 4 0.71 4.09 0.110 40.6 0.256 \n",
"14 0.70 4 0.60 3.86 0.196 40.8 0.260 \n",
"15 1.22 2 0.56 3.86 0.190 22.5 0.257 \n",
"16 1.41 3 0.58 3.49 0.149 19.0 0.232 \n",
"17 1.17 0 0.40 3.46 0.200 2.7 0.226 \n",
"18 - 0 0.00 4.20 0.000 0.1 0.140 \n",
"19 0.82 0 0.54 3.59 0.038 4.3 0.187 \n",
"20 1.00 0 0.43 3.90 0.278 2.1 0.240 \n",
"21 1.13 0 0.16 3.64 0.030 2.5 0.151 \n",
"22 0.13 0 0.40 3.78 0.188 1.0 0.178 \n",
"23 1.11 0 0.33 3.83 0.111 0.9 0.131 \n",
"24 - 0 - - - 0.0 0.000 \n",
"25 - 0 - - - 0.0 0.000 \n",
"26 - 0 - - - 0.0 0.000 \n",
"27 - 0 - - - 0.0 0.000 \n",
"28 - 0 - - - 0.0 0.000 \n",
"29 - 0 - - - 0.0 0.000 \n",
".. ... ... ... ... ... ... ... \n",
"245 - 0 0.00 6.50 0.000 0.1 0.350 \n",
"246 0.00 0 0.67 4.22 0.000 1.8 0.357 \n",
"247 - 0 0.00 3.33 1.000 1.3 0.483 \n",
"248 - 0 0.00 3.33 0.000 0.3 0.233 \n",
"249 0.73 5 0.57 3.71 0.216 53.2 0.313 \n",
"250 1.81 1 0.41 3.87 0.083 75.4 0.265 \n",
"251 5.00 0 0.33 3.60 0.000 1.5 0.238 \n",
"252 1.03 5 0.74 3.49 0.111 53.3 0.263 \n",
"253 0.61 10 0.59 4.20 0.247 58.5 0.316 \n",
"254 0.13 0 0.67 3.89 0.059 2.3 0.254 \n",
"255 0.74 11 0.64 3.66 0.145 71.8 0.270 \n",
"256 0.94 5 0.39 4.02 0.196 71.1 0.278 \n",
"257 1.09 3 0.26 3.94 0.122 25.6 0.236 \n",
"258 0.69 0 0.33 3.99 0.067 7.7 0.235 \n",
"259 1.38 1 0.26 3.95 0.125 7.5 0.244 \n",
"260 1.42 1 0.60 4.13 0.057 34.1 0.237 \n",
"261 1.14 9 0.52 3.98 0.235 81.7 0.286 \n",
"262 0.94 5 0.28 3.96 0.176 42.1 0.261 \n",
"263 0.65 1 1.10 4.12 0.083 17.7 0.252 \n",
"264 1.06 5 0.60 4.24 0.148 34.1 0.252 \n",
"265 1.14 5 0.28 3.88 0.099 31.4 0.228 \n",
"266 1.60 0 0.50 4.43 0.120 2.9 0.234 \n",
"267 1.84 0 0.44 3.76 0.008 20.2 0.192 \n",
"268 1.57 0 1.00 3.73 0.000 0.1 0.146 \n",
"269 2.67 0 0.00 3.66 0.000 -0.8 0.092 \n",
"270 2.67 0 0.00 4.10 0.105 1.2 0.120 \n",
"271 1.50 0 0.00 3.47 0.000 -0.6 0.074 \n",
"272 1.00 0 0.33 4.15 0.000 -0.3 0.090 \n",
"273 - 0 - - - 0.0 0.000 \n",
"274 - 0 - - - 0.0 0.000 \n",
"\n",
"[275 rows x 25 columns]"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"hitter_df"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
quoniammm/mine-tensorflow-examples | fastAI/deeplearning1/nbs/char-rnn.ipynb | 17 | 20147 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using gpu device 2: GeForce GTX TITAN X (CNMeM is enabled with initial size: 90.0% of memory, cuDNN 4007)\n"
]
}
],
"source": [
"from theano.sandbox import cuda\n",
"cuda.use('gpu2')"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using Theano backend.\n"
]
}
],
"source": [
"%matplotlib inline\n",
"import utils; reload(utils)\n",
"from utils import *\n",
"from __future__ import division, print_function"
]
},
{
"cell_type": "code",
"execution_count": 144,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from keras.layers import TimeDistributed, Activation\n",
"from numpy.random import choice"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Setup"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We haven't really looked into the detail of how this works yet - so this is provided for self-study for those who are interested. We'll look at it closely next week."
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"corpus length: 600901\n"
]
}
],
"source": [
"path = get_file('nietzsche.txt', origin=\"https://s3.amazonaws.com/text-datasets/nietzsche.txt\")\n",
"text = open(path).read().lower()\n",
"print('corpus length:', len(text))"
]
},
{
"cell_type": "code",
"execution_count": 272,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"are thinkers who believe in the saints.\r\n",
"\r\n",
"\r\n",
"144\r\n",
"\r\n",
"It stands to reason that this sketch of the saint, made upon the model\r\n",
"of the whole species, can be confronted with many opposing sketches that\r\n",
"would create a more agreeable impression. There are certain exceptions\r\n",
"among the species who distinguish themselves either by especial\r\n",
"gentleness or especial humanity, and perhaps by the strength of their\r\n",
"own personality. Others are in the highest degree fascinating because\r\n",
"certain of their delusions shed a particular glow over their whole\r\n",
"being, as is the case with the founder of christianity who took himself\r\n",
"for the only begotten son of God and hence felt himself sinless; so that\r\n",
"through his imagination--that should not be too harshly judged since the\r\n",
"whole of antiquity swarmed with sons of god--he attained the same goal,\r\n",
"the sense of complete sinlessness, complete irresponsibility, that can\r\n",
"now be attained by every individual through science.--In the same manner\r\n",
"I have viewed the saints of India who occupy an intermediate station\r\n",
"between the christian saints and the Greek philosophers and hence are\r\n",
"not to be regarded as a pure type. Knowledge and science--as far as they\r\n",
"existed--and superiority to the rest of mankind by logical discipline\r\n",
"and training of the intellectual powers were insisted upon by the\r\n",
"Buddhists as essential to sanctity, just as they were denounced by the\r\n",
"christian world as the indications of sinfulness."
]
}
],
"source": [
"!tail {path} -n25"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"corpus length: 137587200\n"
]
}
],
"source": [
"#path = 'data/wiki/'\n",
"#text = open(path+'small.txt').read().lower()\n",
"#print('corpus length:', len(text))\n",
"\n",
"#text = text[0:1000000]"
]
},
{
"cell_type": "code",
"execution_count": 124,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"total chars: 60\n"
]
}
],
"source": [
"chars = sorted(list(set(text)))\n",
"vocab_size = len(chars)+1\n",
"print('total chars:', vocab_size)"
]
},
{
"cell_type": "code",
"execution_count": 134,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"chars.insert(0, \"\\0\")"
]
},
{
"cell_type": "code",
"execution_count": 270,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'\\n !\"\\'(),-.0123456789:;=?[]_abcdefghijklmnopqrstuvwxyz'"
]
},
"execution_count": 270,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"''.join(chars[1:-6])"
]
},
{
"cell_type": "code",
"execution_count": 135,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"char_indices = dict((c, i) for i, c in enumerate(chars))\n",
"indices_char = dict((i, c) for i, c in enumerate(chars))"
]
},
{
"cell_type": "code",
"execution_count": 136,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"idx = [char_indices[c] for c in text]"
]
},
{
"cell_type": "code",
"execution_count": 276,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[43, 45, 32, 33, 28, 30, 32, 1, 1, 1]"
]
},
"execution_count": 276,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"idx[:10]"
]
},
{
"cell_type": "code",
"execution_count": 274,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'preface\\n\\n\\nsupposing that truth is a woman--what then? is there not gro'"
]
},
"execution_count": 274,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"''.join(indices_char[i] for i in idx[:70])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Preprocess and create model"
]
},
{
"cell_type": "code",
"execution_count": 139,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0\n",
"nb sequences: 600862\n"
]
}
],
"source": [
"maxlen = 40\n",
"sentences = []\n",
"next_chars = []\n",
"for i in range(0, len(idx) - maxlen+1):\n",
" sentences.append(idx[i: i + maxlen])\n",
" next_chars.append(idx[i+1: i+maxlen+1])\n",
"print('nb sequences:', len(sentences))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"sentences = np.concatenate([[np.array(o)] for o in sentences[:-2]])\n",
"next_chars = np.concatenate([[np.array(o)] for o in next_chars[:-2]])"
]
},
{
"cell_type": "code",
"execution_count": 277,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"((600860, 40), (600860, 40))"
]
},
"execution_count": 277,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sentences.shape, next_chars.shape"
]
},
{
"cell_type": "code",
"execution_count": 213,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"n_fac = 24"
]
},
{
"cell_type": "code",
"execution_count": 232,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model=Sequential([\n",
" Embedding(vocab_size, n_fac, input_length=maxlen),\n",
" LSTM(512, input_dim=n_fac,return_sequences=True, dropout_U=0.2, dropout_W=0.2,\n",
" consume_less='gpu'),\n",
" Dropout(0.2),\n",
" LSTM(512, return_sequences=True, dropout_U=0.2, dropout_W=0.2,\n",
" consume_less='gpu'),\n",
" Dropout(0.2),\n",
" TimeDistributed(Dense(vocab_size)),\n",
" Activation('softmax')\n",
" ]) "
]
},
{
"cell_type": "code",
"execution_count": 233,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.compile(loss='sparse_categorical_crossentropy', optimizer=Adam())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Train"
]
},
{
"cell_type": "code",
"execution_count": 219,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def print_example():\n",
" seed_string=\"ethics is a basic foundation of all that\"\n",
" for i in range(320):\n",
" x=np.array([char_indices[c] for c in seed_string[-40:]])[np.newaxis,:]\n",
" preds = model.predict(x, verbose=0)[0][-1]\n",
" preds = preds/np.sum(preds)\n",
" next_char = choice(chars, p=preds)\n",
" seed_string = seed_string + next_char\n",
" print(seed_string)"
]
},
{
"cell_type": "code",
"execution_count": 236,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/1\n",
"600860/600860 [==============================] - 640s - loss: 1.5152 \n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f8cf2398810>"
]
},
"execution_count": 236,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.fit(sentences, np.expand_dims(next_chars,-1), batch_size=64, nb_epoch=1)"
]
},
{
"cell_type": "code",
"execution_count": 220,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all thatscrriets sdi ,s lrrbmh\n",
"fceelsora tec\n",
" n yiefma\n",
"cnostencnrut - o\n",
"pen.htt\" oaiosovo stialpts es rb b\n",
"ea ie\n",
"ohatnmauyielueysiutlmo,es etfrne oh\n",
"ohnio iis e.eosme o rdorfdbteirnse ohdnotafi enicron e eietnyn sytt e ptsrdrede httmi ah\n",
"oo, tdye es r,igyct toehitu abrh ei isiem-r natra lnspamlltefae a\n",
"cni vuui\n",
"twgt fatieh\n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 236,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/1\n",
"600860/600860 [==============================] - 640s - loss: 1.5152 \n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f8cf2398810>"
]
},
"execution_count": 236,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.fit(sentences, np.expand_dims(next_chars,-1), batch_size=64, nb_epoch=1)"
]
},
{
"cell_type": "code",
"execution_count": 222,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all that he maluces indofely and is; pticrast', and re onerog je ivesantamale as whered\n",
"and ror and kytinf? on chaninn nurdeln--ans prory. heke the pepadinar; anf bom,\n",
"puntely\"\" ones to bucf, alcherstol the qisleves: the the wite dadong the gur is prang not galcaula rewinl\n",
"more by than sic appads not pepow o mee, a more\n",
"bins c\n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 235,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.optimizer.lr=0.001"
]
},
{
"cell_type": "code",
"execution_count": 236,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/1\n",
"600860/600860 [==============================] - 640s - loss: 1.5152 \n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f8cf2398810>"
]
},
"execution_count": 236,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.fit(sentences, np.expand_dims(next_chars,-1), batch_size=64, nb_epoch=1)"
]
},
{
"cell_type": "code",
"execution_count": 237,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all that schools pedhaps a new prisons of the ashamed in which\n",
"a coverbine estimates of the assumption that one avoid; he will curse about pain:\n",
" people, he-equally present to\n",
"the lalier,\n",
"nature. that he has\n",
"rendered and henceforth distrain and impulses to perceive that each other\n",
"former and dangerous, and cannot at\n",
"the pu\n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 250,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.optimizer.lr=0.0001"
]
},
{
"cell_type": "code",
"execution_count": 239,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/1\n",
"600860/600860 [==============================] - 639s - loss: 1.2892 \n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f8cf167b410>"
]
},
"execution_count": 239,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.fit(sentences, np.expand_dims(next_chars,-1), batch_size=64, nb_epoch=1)"
]
},
{
"cell_type": "code",
"execution_count": 240,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all that account has its granitify them.\n",
"\n",
"131. the new \"dilence,\" out of the\n",
"same light,\n",
"interpretation thereof: under the \"thinking\"\n",
"there, to counter-arguments in the monality, so many language:\n",
"though\n",
"all nobilitys of higher impulses, man and hence to everything of seldom man.\n",
"\n",
"\n",
"\n",
"chapter i. woman decides according the injur\n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 242,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.save_weights('data/char_rnn.h5')"
]
},
{
"cell_type": "code",
"execution_count": 257,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.optimizer.lr=0.00001"
]
},
{
"cell_type": "code",
"execution_count": 243,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/1\n",
"600860/600860 [==============================] - 640s - loss: 1.2544 \n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f8cf2398f50>"
]
},
"execution_count": 243,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.fit(sentences, np.expand_dims(next_chars,-1), batch_size=64, nb_epoch=1)"
]
},
{
"cell_type": "code",
"execution_count": 249,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all that is military\n",
"contemplation of distance itself is in physician!\n",
"\n",
"249.. in every\n",
"to strick in the man of disguise and in the\n",
"will to wind at any progress, the\n",
"religious estimates of vehapance has a powerful and religious nature of manner, who had the problem of\n",
"decided expression of his equality, which, sometimes power? \n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 258,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/1\n",
"600860/600860 [==============================] - 640s - loss: 1.2218 \n"
]
},
{
"data": {
"text/plain": [
"<keras.callbacks.History at 0x7f8cf2a21590>"
]
},
"execution_count": 258,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model.fit(sentences, np.expand_dims(next_chars,-1), batch_size=64, nb_epoch=1)"
]
},
{
"cell_type": "code",
"execution_count": 264,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all that\n",
"the belief in the importance. the employs concerning\n",
"seriousness and\n",
"materialism, it is circles which alone is already attained, that he sees\n",
"also the day after thinking\n",
"of mankind, brightness, resistance--and after the value of \"nature\" in order to nevertheless\n",
"have taken a system of liberal fatalists are willing him\n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 283,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ethics is a basic foundation of all that were beought by the temptation of truth--for the rest of a sublime medely and take part of life, which lacks himself the\n",
"credibility about this, in short, and raise such a\n",
"gods; and on the\n",
"other hand, the explanation of\n",
"the case, as the most ingredient, and insight, and approach as to the\n",
"peculiarly prolonged \"distrus\n"
]
}
],
"source": [
"print_example()"
]
},
{
"cell_type": "code",
"execution_count": 282,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model.save_weights('data/char_rnn.h5')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
},
"nav_menu": {},
"toc": {
"navigate_menu": true,
"number_sections": true,
"sideBar": true,
"threshold": 6,
"toc_cell": true,
"toc_section_display": "block",
"toc_window_display": false
},
"widgets": {
"state": {},
"version": "1.1.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
anshbansal/anshbansal.github.io | udacity_data_science_notes/intro_machine_learning/lesson_05/lesson_05.ipynb | 1 | 2350 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Lesson 5 - Datasets and Questions\n",
"\n",
"## What is a person of interest?\n",
"- people who were sentenced\n",
"- people who settled without admitting guilt\n",
"- testified in exchange for immunity"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Accuracy vs Training Set Size\n",
"- size of training set is important as it has a big affect on the accuracy that we are able to achieve\n",
"\n",
"example\n",
"- physics problem\n",
"- was using naive bayes to classify particles\n",
"- 1000 events\n",
"- Was this much events enough to capture all trends in the data?\n",
"- divided training data into batches of 200. Trained it with 200, 400, 600 and 800. Then test it with remaining 200 events\n",
"\n",
"\n",
"\n",
"- we have around 30 people in our Enron data set. Is that enough? We don't really know. There is no good way except to try it out\n",
"- we need to find how the accuracy changes with the number of training data. Can we get more data? If we can then asking this series of questions can be really helpful\n",
"- Having more data almost always helps the performance of your algorithm "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Enron Data\n",
"- Katie downloaded the data set and cross checked the mails with the persons of interest list\n",
"- Found that the data set only had 4 or 5 people whose inbox was there in the data set. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Types of Data\n",
"- Numerical \n",
"- Categorical - limited number of discrete values (category)\n",
"- time series - temporal values (date, timestamp)\n",
"- text - words"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
stefanv/selective-inference | doc/notebooks/quadratic_decisions.ipynb | 4 | 14505 | {
"metadata": {
"name": "",
"signature": "sha256:3432ba9d07003772ad32db08c6a860b389a9c29e7cff16fbb7ff9bde535c7ae7"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We are interested in inference after a selection procedure, say, $S$, for\n",
"which the selection event is the intersection of a list of quadratic inequalities:\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
"\\{S(y)=s\\} = \\cap_{i \\in I(s)} \\{y: y^TQ_iy + a_i^Ty\\leq b_i \\}.\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"The quadratic forms are not assumed non-negative definite, but we can, without loss of generality\n",
"assume they are symmetric.\n",
"\n",
"## Example: first step of forward stepwise\n",
"\n",
"If we consider forward stepwise with groups the selection procedure is just\n",
"choosing the first group, $g^*$ and we have\n",
"$$\n",
"\\{g^*(y)=g\\} = \\cap_{h \\neq g} \\{y: y^T(X_hX_h^T/w_h^2 - X_gX_g^T/w_g^2)y \\leq 0\\}.\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We want to slice through the selection event along a ray with direction $\\eta$ that passes through $y$. \n",
"That is, we need to find\n",
"$$\n",
"\\begin{aligned}\n",
"\\left\\{t: S(y+t\\eta)=s \\right\\} &= \\cap_{i \\in I(s)} \\left\\{t: (y+t\\eta)^T Q_i (y+t\\eta) + a_i^T(y+t\\eta) \\leq b_i\\right\\}. \\\\\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"For any given $i \\in I(s)$ we see that\n",
"$$\n",
"\\begin{aligned}\n",
"\\left\\{t: (y+t\\eta)^T Q_i (y+t\\eta) + a_i^T(y+t\\eta) \\leq b_i\\right\\} &= \\left\\{t: t^2 \\cdot \\eta^TQ_i\\eta + t \\cdot(2 y^TQ_i\\eta + a_i^T\\eta) + y^TQ_iy + a_i^Ty - b_i \\leq 0 \\right\\} \\\\\n",
"&= \\text{Intervals}(Q_i,a_i,b_i,y,\\eta)\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"Each value of $\\text{Intervals}(Q_i,a_i,b_i,y,\\eta)$ above is one of:\n",
"- $\\emptyset$, in which case the selection event is also the $\\emptyset$ (so this never occurs);\n",
"- $(-\\infty, L(Q_i,a_i,b_i,y,\\eta)] \\cap [U(Q_i,a_i,b_i,y,\\eta), \\infty)$ if $\\eta^TQ_i\\eta < 0$;\n",
"- $[L(Q_i,a_i,b_i,y,\\eta), U(Q_i,a_i,b_i,y,\\eta)]$ if $\\eta^TQ_i\\eta > 0$;\n",
"- $(-\\infty, L(Q_i,a_i,b_i,y,\\eta)]$ if $\\eta^TQ_i\\eta=0$ and $2 y^TQ_i\\eta + a_i^T\\eta > 0$;\n",
"- $[U(Q_i,a_i,b_i,y,\\eta), \\infty)$ if $\\eta^TQ_i\\eta=0$ and $2 y^TQ_i\\eta + a_i^T\\eta < 0$;\n",
"- $(-\\infty,\\infty)$ if $\\eta^TQ_i\\eta=0, 2 y^TQ_i\\eta + a_i^T\\eta = 0$ and $y^TQ_iy + a_i^Ty - b_i \\leq 0$."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import numpy as np\n",
"%load_ext rmagic\n",
"\n",
"DEBUG = False"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"The rmagic extension is already loaded. To reload it, use:\n",
" %reload_ext rmagic\n"
]
}
],
"prompt_number": 15
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def Intervals(Q, a, b, y, eta, tol=1.e-8):\n",
" quad_term = (eta * np.dot(Q, eta)).sum()\n",
" linear_term = 2 * (y * np.dot(Q, eta)).sum() + (a * eta).sum()\n",
" constant_term = (y * np.dot(Q, y)).sum() + (a * y).sum() - b\n",
"\n",
" if DEBUG: print quad_term, linear_term, constant_term\n",
"\n",
" discr = linear_term**2 - 4 * quad_term * constant_term \n",
" if discr < 0:\n",
" if DEBUG: print 'case5'\n",
" return []\n",
" elif np.fabs(quad_term / constant_term) > tol:\n",
" L, U = sorted(((- linear_term - np.sqrt(discr)) / (2 * quad_term),\n",
" (- linear_term + np.sqrt(discr)) / (2 * quad_term)))\n",
" if quad_term < 0:\n",
" if DEBUG: print 'case1'\n",
" return [(-np.inf,L), (U, np.inf)]\n",
" else:\n",
" if DEBUG: print 'case2', discr\n",
" return [(L, U)]\n",
" elif np.fabs(linear_term / constant_term) > tol:\n",
" if linear_term > 0:\n",
" if DEBUG: print 'case3'\n",
" return [(-np.inf, -constant_term / linear_term)]\n",
" else:\n",
" if DEBUG: print 'case4'\n",
" return [(-constant_term, np.inf)]\n",
" elif constant_term < 0:\n",
" if DEBUG: print 'case5'\n",
" return [(-np.inf,np.inf)]\n",
" else:\n",
" if DEBUG: print 'case6'\n",
" return []\n"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"Q1, Q2, Q3, Q4 = np.identity(4)\n",
"y1, eta1, a1 = np.random.standard_normal((3,4))\n",
"b1 = 0\n",
"Intervals(Q1, a1, b1, y1, eta1)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 17,
"text": [
"[(-inf, -2.0706897009098504), (0.77985629493237207, inf)]"
]
}
],
"prompt_number": 17
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"Q2 = -np.identity(4)\n",
"y2, eta2, a2 = np.random.standard_normal((3,4))\n",
"b2 = 0\n",
"Intervals(Q2, a2, b2, y2, eta2)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 18,
"text": [
"[]"
]
}
],
"prompt_number": 18
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"Q = np.zeros((4,4))\n",
"y, eta, a = np.random.standard_normal((3,4))\n",
"b = 0\n",
"Intervals(Q, a, b, y, eta)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 19,
"text": [
"[(0.30949914672354295, inf)]"
]
}
],
"prompt_number": 19
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"Q = np.diag([-1,-1,1,1])\n",
"y, eta, a = np.random.standard_normal((3,4))\n",
"b = 0\n",
"Intervals(Q, a, b, y, eta)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 20,
"text": [
"[]"
]
}
],
"prompt_number": 20
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To find the intersection of a set of intervals, one\n",
"only needs to track the upper and lower bounds. In our case,\n",
"there will be some intervals and some complements of intervals.\n",
"\n",
"This can be handled by handling the union of the complements and then taking the complement."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def find_intersection(y, eta, *quadratic_list):\n",
" '''\n",
" Find the intersection of \n",
" \n",
" [Interval(Q, a, b, y, eta) for Q, a, b in quadratic_list]\n",
" '''\n",
" \n",
" upper_int, lower_int = (np.inf, -np.inf)\n",
" upper_union, lower_union = (-np.inf, np.inf)\n",
"\n",
" for Q, a, b in quadratic_list:\n",
" intervals = Intervals(Q, a, b, y, eta)\n",
" if DEBUG: print intervals\n",
" if len(intervals) == 1: # a single interval\n",
" upper_int = min(upper_int, intervals[0][1])\n",
" lower_int = max(upper_int, intervals[0][0])\n",
" elif len(intervals) == 2: # complement of an interval\n",
" L, U = intervals[0][1], intervals[1][0] # by construction our intervals always have this form\n",
" # could also use sorted(intervals[np.isfinite(intervals)])\n",
" upper_union = max(upper_union, U)\n",
" lower_union = min(lower_union, L)\n",
" complement = [(-np.inf,lower_union),(upper_union, np.inf)]\n",
" \n",
" if upper_int < upper_union and lower_int > lower_union:\n",
" return [] # the intersection of the intervals is in the complement\n",
" elif upper_int >= upper_union:\n",
" if lower_int >= lower_union:\n",
" if DEBUG: print 'case1'\n",
" return [(max(lower_int, lower_union), upper_int)]\n",
" else:\n",
" if DEBUG: print 'case2'\n",
" return [(lower_int, lower_union), (upper_union, upper_int)]\n",
" else: # lower_int <= lower_union\n",
" if upper_int <= upper_union:\n",
" if DEBUG: print 'case3'\n",
" return [(lower_int, min(upper_int, upper_union))]\n",
" else:\n",
" if DEBUG: print 'case4'\n",
" return [(lower_int, lower_union), (upper_int, upper_union)]\n",
" "
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 21
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R -o X,Y,groups,weights,sigma\n",
"source('http://statweb.stanford.edu/~jtaylo/notebooks/group_lasso.R')\n",
"set.seed(0)\n",
"n = 20\n",
"p = 10\n",
"sigma = 1.3\n",
"X = matrix(rnorm(n*p),n,p)\n",
"Y = rnorm(n)*sigma\n",
"groups = c(1,1,2,2,2,3,3,4,4,5)\n",
"weights = c(2,2.5,2,2,1.4)\n",
"results = group_lasso_knot(X, Y, groups, weights)\n",
"Z = results$L / (sqrt(results$var)*sigma)\n",
"Zlower = results$lower_bound / (sqrt(results$var)*sigma)\n",
"print(data.frame(Z,Zlower))\n",
"print(pvalue(results$L, results$lower_bound, results$upper_bound, sqrt(results$var), results$k, sigma=sigma))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
" Z Zlower\n",
"1 2.650602 1.296633\n",
"[1] 0.06909894\n"
]
}
],
"prompt_number": 28
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"print(results)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"$L\n",
"[1] 8.502982\n",
"\n",
"$lower_bound\n",
"[1] 4.159526\n",
"\n",
"$upper_bound\n",
"[1] Inf\n",
"\n",
"$var\n",
"[1] 6.089294\n",
"\n",
"$k\n",
"[1] 2\n",
"\n",
"$chi_max\n",
"[1] 3.445782\n",
"\n",
"$gmax\n",
"[1] 4\n",
"\n"
]
}
],
"prompt_number": 29
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"Qs = []\n",
"Xs = []\n",
"norms = []\n",
"for g, w in zip(np.unique(groups), weights):\n",
" Xg = X[:,groups==g] / w\n",
" Qs.append(np.dot(Xg, Xg.T))\n",
" Xs.append(Xg)\n",
" norms.append(np.linalg.norm(np.dot(Xg.T,Y)))\n",
"max(norms)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 30,
"text": [
"8.5029821317815024"
]
}
],
"prompt_number": 30
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"imax = np.argmax(norms)\n",
"P = np.dot(Xs[imax], np.linalg.pinv(Xs[imax]))\n",
"eta = np.dot(P, Y)\n",
"eta /= np.linalg.norm(eta)\n",
"W = (eta*Y).sum() \n",
"final_Qs = []\n",
"for i in range(len(Qs)):\n",
" if i != imax:\n",
" final_Qs.append((Qs[i] - Qs[imax]).copy())\n",
"I1, I2 = find_intersection(Y, eta, *[(Q, 0, 0) for Q in final_Qs])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 31
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the group LASSO first step, what we called `Zlower` can be recoverd from `W` and `I2[0]`.\n",
"I'm not quite sure what can be done with `I1`, if anything. It can probably be used to get a little more power,\n",
"but I'm not 100% sure."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"V1, V2 = W / sigma, (W+I2[0]) / sigma\n",
"%R -i V1,V2\n",
"V1, V2\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 26,
"text": [
"(array([ 2.65060154]), array([ 1.29663281]))"
]
}
],
"prompt_number": 26
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"print((1 - pchisq(V1^2, results$k)) / (1 - pchisq(V2^2, results$k)))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"[1] 0.06909894\n"
]
}
],
"prompt_number": 27
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is the same $p$-value as above."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 27
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 27
}
],
"metadata": {}
}
]
} | bsd-3-clause |
schlegelp/pymaid | docs/source/tiles.ipynb | 1 | 3280137 | null | gpl-3.0 |
JaeGyu/PythonEx_1 | 머신러닝 딥러닝 실전개발 입문 책 연습/텐서플로우5-4장.ipynb | 1 | 3676 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.2.0\n"
]
}
],
"source": [
"import tensorflow as tf\n",
"print(tf.__version__)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"a = tf.constant(120, name=\"a\")\n",
"b = tf.constant(130, name=\"b\")\n",
"c = tf.constant(140, name=\"c\")"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Tensor(\"a_2:0\", shape=(), dtype=int32)\n"
]
}
],
"source": [
"print(a)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"v = tf.Variable(0, name=\"v\")"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"calc_op = a + b + c"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"assign_op = tf.assign(v, calc_op) #변수에 할당할떄에는 assign함수를 사용한다."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"390\n"
]
}
],
"source": [
"\n",
"with tf.Session() as sess:\n",
"# sess.run(tf.global_variables_initializer())\n",
" sess.run(assign_op) #이렇게 할경우 변수 초기화를 안해줘도 된다. #이부분이 실행되야 할당이 되는 것이다. \n",
" print(sess.run(v))"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"a = tf.placeholder(shape=[3], dtype=tf.int32) #shape가 [3]은 [1,2,3] 이런것을 뜻함"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"b = tf.constant(2)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"x2_op = a * b"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[2 4 6]\n",
"[20 40 60]\n"
]
}
],
"source": [
"with tf.Session() as sess:\n",
" x2_op_val = sess.run(x2_op, feed_dict={a:[1,2,3]})\n",
" print(x2_op_val)\n",
" x2_op_val = sess.run(x2_op, feed_dict={a:[10,20,30]})\n",
" print(x2_op_val)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [Root]",
"language": "python",
"name": "Python [Root]"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
thewtex/ieee-nss-mic-scipy-2014 | 1_Docker.ipynb | 1 | 7304 | {
"metadata": {
"kernelspec": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"display_name": "IPython (Python 2)",
"language": "python",
"name": "python2"
},
"name": "",
"signature": "sha256:6fd45713bed841308d7d20f942fe36abe295acaad6ed6b0442f20d4888c4afcd"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 1,
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Docker"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"The Problem"
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Even though computers are often considered deterministic, **computational software is a rapidly evolving and changing landscape**. Libraries are constantly adding new features and fixing issues. Even libraries with the strictest backwards-compatibility policies can change in significant ways. As **computer hardware evolves**, software is forced to adapt accordingly."
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "slide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"A replicatable computational environment is **sufficiently consistent for the computational task at hand**. For example, this can consist of a similar CPU instruction set, libraries and executables available with a specific version and configuration options, a specific operating system version, etc."
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Close But Not Good Enough"
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Source code\n",
"\n",
"Does not include:\n",
"\n",
"- Compiler\n",
"- Hardware it was built on\n",
"- How it is configured"
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Package managers and distributions\n",
"\n",
"- Packages become unsupported over time\n",
"- What to do if a required library is not packaged?"
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "slide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Virtual Machines (VMs)\n",
"\n",
"- Inefficient utilization of computational resources"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Docker Improvements"
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"<img src=\"images/docker-filesystems-multilayer.png\" width=500>\n",
"\n",
"Docker is an open-source engine that automates the deployment of any application as a lightweight, portable, self-sufficient container that will run virtually anywhere."
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "slide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"<img src=\"images/docker_vm.jpg\" width=\"600\">\n",
"\n",
"Docker works with images that **consume minimal disk space**, **versioned**, **archiveable**, and **shareable**. Executing applications in these images does not require dedicated resources and is **high performance**."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"In the `docker/src/itkka` directory is an example Docker image, also [available](https://registry.hub.docker.com/u/thewtex/itkka/) on [DockerHub](https://hub.docker.com/) for reproducing [an article on PET image series kinetic analysis]( http://hdl.handle.net/10380/3469).\n",
"\n",
"The requirements for reproducing this computational analysis, the Ubuntu 14.04 operating system, the GCC 4.8.2-19ubuntu1 compiler, and particular versions of the dependencies the Insight Toolkit (ITK), libxml, sundials, and Boost, are now runnable on any x86_64 operating system, archiveable, and shareable.\n",
"\n",
"<img src=\"images/itkka.jpg\">"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "subslide_end",
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Learn more!"
]
},
{
"cell_type": "markdown",
"metadata": {
"internals": {
"slide_helper": "subslide_end",
"slide_type": "subslide"
},
"slide_helper": "slide_end",
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"* [Interactive Brower-Based Docker Tutorial](https://www.docker.com/tryit/)\n",
"* [Docker Documentation](https://docs.docker.com/userguide/)\n",
"* [Reproducible Research: Walking the Walk Tutorial](https://reproducible-research.github.io/scipy-tutorial-2014/)\n",
"* [IPython DockerHub Repositories](https://registry.hub.docker.com/repos/ipython/)"
]
}
],
"metadata": {}
}
]
} | apache-2.0 |
5x5x5x5/Machine_Learning_Life_Science | Model2D6.ipynb | 1 | 22154 | {
"cells": [
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"import warnings\n",
"warnings.filterwarnings('ignore')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Train/Test split already done"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#from sklearn.cross_validation import train_test_split\n",
"\n",
"# create 80%-20% train-test split\n",
"#X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5555)"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"twoD6_test = pd.read_csv(\"data/test2d6.csv\", index_col='SID')\n",
"twoD6_train = pd.read_csv(\"data/training2d6.csv\", index_col='SID')"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>ActivityScore</th>\n",
" <th>apol</th>\n",
" <th>a_acc</th>\n",
" <th>a_acid</th>\n",
" <th>a_aro</th>\n",
" <th>a_base</th>\n",
" <th>a_count</th>\n",
" <th>a_don</th>\n",
" <th>a_heavy</th>\n",
" <th>a_hyd</th>\n",
" <th>...</th>\n",
" <th>vsa_acid</th>\n",
" <th>vsa_base</th>\n",
" <th>vsa_don</th>\n",
" <th>vsa_hyd</th>\n",
" <th>vsa_other</th>\n",
" <th>vsa_pol</th>\n",
" <th>Weight</th>\n",
" <th>weinerPath</th>\n",
" <th>weinerPol</th>\n",
" <th>zagreb</th>\n",
" </tr>\n",
" <tr>\n",
" <th>SID</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>11114095</th>\n",
" <td> 85</td>\n",
" <td> 25.967930</td>\n",
" <td> 0</td>\n",
" <td> 5</td>\n",
" <td> 0</td>\n",
" <td> 1</td>\n",
" <td> 23</td>\n",
" <td> 0</td>\n",
" <td> 13</td>\n",
" <td> 5</td>\n",
" <td>...</td>\n",
" <td> 74.321251</td>\n",
" <td> 17.742489</td>\n",
" <td> 17.742489</td>\n",
" <td> 71.454041</td>\n",
" <td> 28.375498</td>\n",
" <td> 92.063744</td>\n",
" <td> 207.12199</td>\n",
" <td> 272</td>\n",
" <td> 13</td>\n",
" <td> 58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11111502</th>\n",
" <td> 41</td>\n",
" <td> 52.303032</td>\n",
" <td> 0</td>\n",
" <td> 0</td>\n",
" <td> 12</td>\n",
" <td> 1</td>\n",
" <td> 45</td>\n",
" <td> 0</td>\n",
" <td> 21</td>\n",
" <td> 20</td>\n",
" <td>...</td>\n",
" <td> 0.000000</td>\n",
" <td> 5.682576</td>\n",
" <td> 5.682576</td>\n",
" <td> 254.943600</td>\n",
" <td> 0.000000</td>\n",
" <td> 5.682576</td>\n",
" <td> 278.41901</td>\n",
" <td> 810</td>\n",
" <td> 40</td>\n",
" <td> 118</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11111413</th>\n",
" <td> 0</td>\n",
" <td> 35.143032</td>\n",
" <td> 0</td>\n",
" <td> 0</td>\n",
" <td> 0</td>\n",
" <td> 3</td>\n",
" <td> 36</td>\n",
" <td> 0</td>\n",
" <td> 12</td>\n",
" <td> 9</td>\n",
" <td>...</td>\n",
" <td> 0.000000</td>\n",
" <td> 41.167557</td>\n",
" <td> 41.167557</td>\n",
" <td> 133.040590</td>\n",
" <td> 0.000000</td>\n",
" <td> 41.167557</td>\n",
" <td> 174.31200</td>\n",
" <td> 215</td>\n",
" <td> 13</td>\n",
" <td> 52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11112630</th>\n",
" <td> 20</td>\n",
" <td> 32.461517</td>\n",
" <td> 1</td>\n",
" <td> 0</td>\n",
" <td> 6</td>\n",
" <td> 0</td>\n",
" <td> 26</td>\n",
" <td> 0</td>\n",
" <td> 14</td>\n",
" <td> 11</td>\n",
" <td>...</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000000</td>\n",
" <td> 166.094760</td>\n",
" <td> 13.166624</td>\n",
" <td> 5.682576</td>\n",
" <td> 204.29700</td>\n",
" <td> 298</td>\n",
" <td> 17</td>\n",
" <td> 76</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11110827</th>\n",
" <td> 0</td>\n",
" <td> 64.246994</td>\n",
" <td> 5</td>\n",
" <td> 0</td>\n",
" <td> 0</td>\n",
" <td> 0</td>\n",
" <td> 57</td>\n",
" <td> 3</td>\n",
" <td> 28</td>\n",
" <td> 21</td>\n",
" <td>...</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000000</td>\n",
" <td> 0.000000</td>\n",
" <td> 267.817900</td>\n",
" <td> 16.917038</td>\n",
" <td> 67.834602</td>\n",
" <td> 408.92200</td>\n",
" <td> 1670</td>\n",
" <td> 70</td>\n",
" <td> 168</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>5 rows × 187 columns</p>\n",
"</div>"
],
"text/plain": [
" ActivityScore apol a_acc a_acid a_aro a_base a_count \\\n",
"SID \n",
"11114095 85 25.967930 0 5 0 1 23 \n",
"11111502 41 52.303032 0 0 12 1 45 \n",
"11111413 0 35.143032 0 0 0 3 36 \n",
"11112630 20 32.461517 1 0 6 0 26 \n",
"11110827 0 64.246994 5 0 0 0 57 \n",
"\n",
" a_don a_heavy a_hyd ... vsa_acid vsa_base vsa_don \\\n",
"SID ... \n",
"11114095 0 13 5 ... 74.321251 17.742489 17.742489 \n",
"11111502 0 21 20 ... 0.000000 5.682576 5.682576 \n",
"11111413 0 12 9 ... 0.000000 41.167557 41.167557 \n",
"11112630 0 14 11 ... 0.000000 0.000000 0.000000 \n",
"11110827 3 28 21 ... 0.000000 0.000000 0.000000 \n",
"\n",
" vsa_hyd vsa_other vsa_pol Weight weinerPath weinerPol \\\n",
"SID \n",
"11114095 71.454041 28.375498 92.063744 207.12199 272 13 \n",
"11111502 254.943600 0.000000 5.682576 278.41901 810 40 \n",
"11111413 133.040590 0.000000 41.167557 174.31200 215 13 \n",
"11112630 166.094760 13.166624 5.682576 204.29700 298 17 \n",
"11110827 267.817900 16.917038 67.834602 408.92200 1670 70 \n",
"\n",
" zagreb \n",
"SID \n",
"11114095 58 \n",
"11111502 118 \n",
"11111413 52 \n",
"11112630 76 \n",
"11110827 168 \n",
"\n",
"[5 rows x 187 columns]"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"twoD6_train.head()"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Column names:\n",
"['ActivityScore', 'apol', 'a_acc', 'a_acid', 'a_aro', 'a_base', 'a_count', 'a_don', 'a_heavy', 'a_hyd', 'a_IC', 'a_ICM', 'a_nB', 'a_nBr', 'a_nC', 'a_nCl', 'a_nF', 'a_nH', 'a_nI', 'a_nN', 'a_nO', 'a_nP', 'a_nS', 'balabanJ', 'BCUT_PEOE_0', 'BCUT_PEOE_1', 'BCUT_PEOE_2', 'BCUT_PEOE_3', 'BCUT_SLOGP_0', 'BCUT_SLOGP_1', 'BCUT_SLOGP_2', 'BCUT_SLOGP_3', 'BCUT_SMR_0', 'BCUT_SMR_1', 'BCUT_SMR_2', 'BCUT_SMR_3', 'bpol', 'b_1rotN', 'b_1rotR', 'b_ar', 'b_count', 'b_double', 'b_heavy', 'b_rotN', 'b_rotR', 'b_single', 'b_triple', 'chi0', 'chi0v', 'chi0v_C', 'chi0_C', 'chi1', 'chi1v', 'chi1v_C', 'chi1_C', 'chiral', 'chiral_u', 'density', 'diameter', 'FCharge', 'GCUT_PEOE_0', 'GCUT_PEOE_1', 'GCUT_PEOE_2', 'GCUT_PEOE_3', 'GCUT_SLOGP_0', 'GCUT_SLOGP_1', 'GCUT_SLOGP_2', 'GCUT_SLOGP_3', 'GCUT_SMR_0', 'GCUT_SMR_1', 'GCUT_SMR_2', 'GCUT_SMR_3', 'Kier1', 'Kier2', 'Kier3', 'KierA1', 'KierA2', 'KierA3', 'KierFlex', 'lip_acc', 'lip_don', 'lip_druglike', 'lip_violation', 'logP(o/w)', 'logS', 'mr', 'mutagenic', 'nmol', 'opr_brigid', 'opr_leadlike', 'opr_nring', 'opr_nrot', 'opr_violation', 'PC+', 'PC-', 'PEOE_PC+', 'PEOE_PC-', 'PEOE_RPC+', 'PEOE_RPC-', 'PEOE_VSA+0', 'PEOE_VSA+1', 'PEOE_VSA+2', 'PEOE_VSA+3', 'PEOE_VSA+4', 'PEOE_VSA+5', 'PEOE_VSA+6', 'PEOE_VSA-0', 'PEOE_VSA-1', 'PEOE_VSA-2', 'PEOE_VSA-3', 'PEOE_VSA-4', 'PEOE_VSA-5', 'PEOE_VSA-6', 'PEOE_VSA_FHYD', 'PEOE_VSA_FNEG', 'PEOE_VSA_FPNEG', 'PEOE_VSA_FPOL', 'PEOE_VSA_FPOS', 'PEOE_VSA_FPPOS', 'PEOE_VSA_HYD', 'PEOE_VSA_NEG', 'PEOE_VSA_PNEG', 'PEOE_VSA_POL', 'PEOE_VSA_POS', 'PEOE_VSA_PPOS', 'petitjean', 'petitjeanSC', 'Q_PC+', 'Q_PC-', 'Q_RPC+', 'Q_RPC-', 'Q_VSA_FHYD', 'Q_VSA_FNEG', 'Q_VSA_FPNEG', 'Q_VSA_FPOL', 'Q_VSA_FPOS', 'Q_VSA_FPPOS', 'Q_VSA_HYD', 'Q_VSA_NEG', 'Q_VSA_PNEG', 'Q_VSA_POL', 'Q_VSA_POS', 'Q_VSA_PPOS', 'radius', 'reactive', 'rings', 'RPC+', 'RPC-', 'rsynth', 'SlogP', 'SlogP_VSA0', 'SlogP_VSA1', 'SlogP_VSA2', 'SlogP_VSA3', 'SlogP_VSA4', 'SlogP_VSA5', 'SlogP_VSA6', 'SlogP_VSA7', 'SlogP_VSA8', 'SlogP_VSA9', 'SMR', 'SMR_VSA0', 'SMR_VSA1', 'SMR_VSA2', 'SMR_VSA3', 'SMR_VSA4', 'SMR_VSA5', 'SMR_VSA6', 'SMR_VSA7', 'TPSA', 'VAdjEq', 'VAdjMa', 'VDistEq', 'VDistMa', 'vdw_area', 'vdw_vol', 'vsa_acc', 'vsa_acid', 'vsa_base', 'vsa_don', 'vsa_hyd', 'vsa_other', 'vsa_pol', 'Weight', 'weinerPath', 'weinerPol', 'zagreb']\n"
]
}
],
"source": [
"col_names2D6 = twoD6_train.columns.tolist()\n",
"\n",
"print('Column names:')\n",
"print(col_names2D6)"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Isolate response variable\n",
"ActivityScore = twoD6_train['ActivityScore']\n",
"y_train = np.where(ActivityScore >= 40,1,0)\n",
"\n",
"ActivityScore2 = twoD6_test['ActivityScore']\n",
"y_test = np.where(ActivityScore2 >= 40,1,0)"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"((4433,), (1109,))"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# looks right sized\n",
"y_train.shape, y_test.shape"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([1, 1, 1, ..., 1, 0, 1])"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_test"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# We don't need this column anymore\n",
"to_drop = ['ActivityScore']\n",
"inhib_feat_space = twoD6_train.drop(to_drop,axis=1)\n",
"inhib_feat_space_test = twoD6_test.drop(to_drop,axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Pull out features for future use\n",
"features = inhib_feat_space.columns\n",
"features_test = inhib_feat_space_test.columns"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X_train = inhib_feat_space.as_matrix().astype(np.float)\n",
"X_test = inhib_feat_space_test.as_matrix().astype(np.float)"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"((4433, 186), (1109, 186))"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X_train.shape, X_test.shape"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"552"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"n_pos1 = y_test.sum()\n",
"n_pos1"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"2219"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"n_pos2 = y_train.sum()\n",
"n_pos2"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Feature space holds 4433 observations and 186 features\n",
"Unique target labels: array([0, 1])\n",
"Feature space holds 1109 observations and 186 features\n",
"Unique target labels: array([0, 1])\n"
]
}
],
"source": [
"print('Feature space holds '+repr(X_train.shape[0])+' observations and '+repr(X_test.shape[1])+' features')\n",
"print('Unique target labels: '+repr(np.unique(y_train)))\n",
"\n",
"print('Feature space holds '+repr(X_test.shape[0])+' observations and '+repr(X_test.shape[1])+' features')\n",
"print('Unique target labels: '+repr(np.unique(y_test)))"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"186"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X_test.shape[1]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Scale the features before training model"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# This is important\n",
"from sklearn.preprocessing import StandardScaler\n",
"scaler = StandardScaler()\n",
"X_train = scaler.fit_transform(X_train)\n",
"X_test = scaler.fit_transform(X_test)"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn.cross_validation import KFold\n",
"\n",
"def run_cv(X,y,clf_class,**kwargs):\n",
" # Construct a kfolds object\n",
" kf = KFold(len(y),n_folds=5,shuffle=True)\n",
" y_pred = y.copy()\n",
" \n",
" # Iterate through folds\n",
" for train_index, test_index in kf:\n",
" X_train, X_test = X[train_index], X[test_index]\n",
" y_train = y[train_index]\n",
" # Initialize a classifier with key word arguments\n",
" clf = clf_class(**kwargs)\n",
" clf.fit(X_train,y_train)\n",
" y_pred[test_index] = clf.predict(X_test)\n",
" return y_pred"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"K-nearest-neighbors (training set):\n",
"0.717\n",
"K-nearest-neighbors (test set):\n",
"0.678\n",
"Support vector machines (training set):\n",
"0.755\n",
"Support vector machines (test set):\n",
"0.725\n",
"Random forest (training set):\n",
"0.729\n",
"Random forest (test set):\n",
"0.707\n"
]
}
],
"source": [
"from sklearn.svm import SVC\n",
"from sklearn.ensemble import RandomForestClassifier as RF\n",
"from sklearn.neighbors import KNeighborsClassifier as KNN\n",
"\n",
"def accuracy(y_true,y_pred):\n",
" # NumPy interpretes True and False as 1. and 0.\n",
" return np.mean(y_true == y_pred)\n",
"\n",
"print(\"K-nearest-neighbors (training set):\")\n",
"print(\"%.3f\" % accuracy(y_train, run_cv(X_train,y_train,KNN)))\n",
"print(\"K-nearest-neighbors (test set):\")\n",
"print(\"%.3f\" % accuracy(y_test, run_cv(X_test,y_test,KNN)))\n",
"print('Support vector machines (training set):')\n",
"print(\"%.3f\" % accuracy(y_train, run_cv(X_train,y_train,SVC)))\n",
"print('Support vector machines (test set):')\n",
"print(\"%.3f\" % accuracy(y_test, run_cv(X_test,y_test,SVC)))\n",
"print(\"Random forest (training set):\")\n",
"print(\"%.3f\" % accuracy(y_train, run_cv(X_train,y_train,RF)))\n",
"print(\"Random forest (test set):\")\n",
"print(\"%.3f\" % accuracy(y_test, run_cv(X_test,y_test,RF)))\n"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"([('K-Nearest-Neighbors training', array([[1537, 677],\n",
" [ 553, 1666]])),\n",
" ('Support Vector Machines training', array([[1687, 527],\n",
" [ 543, 1676]])),\n",
" ('Random Forest taining', array([[1732, 482],\n",
" [ 760, 1459]]))],\n",
" [('K-Nearest-Neighbors test', array([[366, 191],\n",
" [171, 381]])), ('Support Vector Machines test', array([[440, 117],\n",
" [184, 368]])), ('Random Forest test', array([[423, 134],\n",
" [218, 334]]))])"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from sklearn.metrics import confusion_matrix\n",
"\n",
"y_train = np.array(y_train)\n",
"class_names = np.unique(y_train)\n",
"\n",
"confusion_matrices_training = [\n",
" ( \"K-Nearest-Neighbors training\", confusion_matrix(y_train,run_cv(X_train,y_train,KNN)) ),\n",
" ( \"Support Vector Machines training\", confusion_matrix(y_train,run_cv(X_train,y_train,SVC)) ),\n",
" ( \"Random Forest taining\", confusion_matrix(y_train,run_cv(X_train,y_train,RF)) ),\n",
"]\n",
"\n",
"y_test = np.array(y_test)\n",
"class_names = np.unique(y_test)\n",
"\n",
"confusion_matrices_test = [\n",
" ( \"K-Nearest-Neighbors test\", confusion_matrix(y_test,run_cv(X_test,y_test,KNN)) ),\n",
" ( \"Support Vector Machines test\", confusion_matrix(y_test,run_cv(X_test,y_test,SVC)) ),\n",
" ( \"Random Forest test\", confusion_matrix(y_test,run_cv(X_test,y_test,RF)) ),\n",
"]\n",
"\n",
"#draw_confusion_matrices(confusion_matrices,class_names)\n",
"confusion_matrices_training, confusion_matrices_test"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.79710213956578524"
]
},
"execution_count": 46,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(is_churn, pred_churn)"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
vivekec/datascience | tutorials/cpp/Ipy notebooks/Linear search.ipynb | 1 | 1226 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"#include <iostream>\n",
"#include <iterator> // for size\n",
"using namespace std;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Linear search"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"double vec[5] = {11,5,8,7,4};"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number 8 detected!!"
]
}
],
"source": [
"for(auto i = 0; i <= std::size(vec); i++){\n",
" if (vec[i] == 8){\n",
" std::cout << \"Number 8 detected!!\";\n",
" break;\n",
" }\n",
"}"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "C++17",
"language": "C++17",
"name": "xeus-cling-cpp17"
},
"language_info": {
"codemirror_mode": "text/x-c++src",
"file_extension": ".cpp",
"mimetype": "text/x-c++src",
"name": "c++",
"version": "17"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
tuanavu/coursera-university-of-washington | machine_learning/2_regression/assignment/week4/week-4-ridge-regression-assignment-1-exercise.ipynb | 2 | 264537 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Regression Week 4: Ridge Regression (interpretation)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this notebook, we will run ridge regression multiple times with different L2 penalties to see which one produces the best fit. We will revisit the example of polynomial regression as a means to see the effect of L2 regularization. In particular, we will:\n",
"* Use a pre-built implementation of regression (GraphLab Create) to run polynomial regression\n",
"* Use matplotlib to visualize polynomial regressions\n",
"* Use a pre-built implementation of regression (GraphLab Create) to run polynomial regression, this time with L2 penalty\n",
"* Use matplotlib to visualize polynomial regressions under L2 regularization\n",
"* Choose best L2 penalty using cross-validation.\n",
"* Assess the final fit using test data.\n",
"\n",
"We will continue to use the House data from previous notebooks. (In the next programming assignment for this module, you will implement your own ridge regression learning algorithm using gradient descent.)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Fire up graphlab create"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import sys\n",
"sys.path.append('C:\\Anaconda2\\envs\\dato-env\\Lib\\site-packages')\n",
"import graphlab"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Polynomial regression, revisited"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We build on the material from Week 3, where we wrote the function to produce an SFrame with columns containing the powers of a given input. Copy and paste the function `polynomial_sframe` from Week 3:"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def polynomial_sframe(feature, degree):\n",
" # assume that degree >= 1\n",
" # initialize the SFrame:\n",
" poly_sframe = graphlab.SFrame()\n",
" # and set poly_sframe['power_1'] equal to the passed feature\n",
" poly_sframe['power_1'] = feature\n",
" # first check if degree > 1\n",
" if degree > 1:\n",
" # then loop over the remaining degrees:\n",
" # range usually starts at 0 and stops at the endpoint-1. We want it to start at 2 and stop at degree\n",
" for power in range(2, degree+1): \n",
" # first we'll give the column a name:\n",
" name = 'power_' + str(power)\n",
" # then assign poly_sframe[name] to the appropriate power of feature\n",
" poly_sframe[name] = feature ** power\n",
" return poly_sframe"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's use matplotlib to visualize what a polynomial regression looks like on the house data."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"sales = graphlab.SFrame('kc_house_data.gl/')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As in Week 3, we will use the sqft_living variable. For plotting purposes (connecting the dots), you'll need to sort by the values of sqft_living. For houses with identical square footage, we break the tie by their prices."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"sales = sales.sort(['sqft_living','price'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us revisit the 15th-order polynomial model using the 'sqft_living' input. Generate polynomial features up to degree 15 using `polynomial_sframe()` and fit a model with these features. When fitting the model, use an L2 penalty of `1e-5`:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"l2_small_penalty = 1e-5"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note: When we have so many features and so few data points, the solution can become highly numerically unstable, which can sometimes lead to strange unpredictable results. Thus, rather than using no regularization, we will introduce a tiny amount of regularization (`l2_penalty=1e-5`) to make the solution numerically stable. (In lecture, we discussed the fact that regularization can also help with numerical stability, and here we are seeing a practical example.)\n",
"\n",
"With the L2 penalty specified above, fit the model and print out the learned weights.\n",
"\n",
"Hint: make sure to add 'price' column to the new SFrame before calling `graphlab.linear_regression.create()`. Also, make sure GraphLab Create doesn't create its own validation set by using the option `validation_set=None` in this call."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\"><table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">name</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">index</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">value</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">(intercept)</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">167924.854552</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">103.090960935</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_2</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0.134604539736</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_3</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-0.000129071357153</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_4</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5.18928934082e-08</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-7.77169258564e-12</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_6</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1.71144799293e-16</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_7</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4.51177980576e-20</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_8</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-4.78839847247e-25</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">power_9</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">None</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-2.33343497452e-28</td>\n",
" </tr>\n",
"</table>\n",
"[16 rows x 3 columns]<br/>Note: Only the head of the SFrame is printed.<br/>You can use print_rows(num_rows=m, num_columns=n) to print more rows and columns.\n",
"</div>"
],
"text/plain": [
"Columns:\n",
"\tname\tstr\n",
"\tindex\tstr\n",
"\tvalue\tfloat\n",
"\n",
"Rows: 16\n",
"\n",
"Data:\n",
"+-------------+-------+--------------------+\n",
"| name | index | value |\n",
"+-------------+-------+--------------------+\n",
"| (intercept) | None | 167924.854552 |\n",
"| power_1 | None | 103.090960935 |\n",
"| power_2 | None | 0.134604539736 |\n",
"| power_3 | None | -0.000129071357153 |\n",
"| power_4 | None | 5.18928934082e-08 |\n",
"| power_5 | None | -7.77169258564e-12 |\n",
"| power_6 | None | 1.71144799293e-16 |\n",
"| power_7 | None | 4.51177980576e-20 |\n",
"| power_8 | None | -4.78839847247e-25 |\n",
"| power_9 | None | -2.33343497452e-28 |\n",
"+-------------+-------+--------------------+\n",
"[16 rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed.\n",
"You can use print_rows(num_rows=m, num_columns=n) to print more rows and columns."
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"poly15_data = polynomial_sframe(sales['sqft_living'], 15) # use equivalent of `polynomial_sframe`\n",
"poly15_features = poly15_data.column_names() # get the name of the features\n",
"poly15_data['price'] = sales['price'] # add price to the data since it's the target\n",
"\n",
"model1 = graphlab.linear_regression.create(poly15_data, target = 'price', \n",
" features = poly15_features, l2_penalty=l2_small_penalty,\n",
" validation_set=None,verbose=False)\n",
"model1.get(\"coefficients\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"***QUIZ QUESTION: What's the learned value for the coefficient of feature `power_1`?***"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Observe overfitting"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Recall from Week 3 that the polynomial fit of degree 15 changed wildly whenever the data changed. In particular, when we split the sales data into four subsets and fit the model of degree 15, the result came out to be very different for each subset. The model had a *high variance*. We will see in a moment that ridge regression reduces such variance. But first, we must reproduce the experiment we did in Week 3."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, split the data into split the sales data into four subsets of roughly equal size and call them `set_1`, `set_2`, `set_3`, and `set_4`. Use `.random_split` function and make sure you set `seed=0`. "
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"(semi_split1, semi_split2) = sales.random_split(.5,seed=0)\n",
"(set_1, set_2) = semi_split1.random_split(0.5, seed=0)\n",
"(set_3, set_4) = semi_split2.random_split(0.5, seed=0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, fit a 15th degree polynomial on `set_1`, `set_2`, `set_3`, and `set_4`, using 'sqft_living' to predict prices. Print the weights and make a plot of the resulting model.\n",
"\n",
"Hint: When calling `graphlab.linear_regression.create()`, use the same L2 penalty as before (i.e. `l2_small_penalty`). Also, make sure GraphLab Create doesn't create its own validation set by using the option `validation_set = None` in this call."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def get_poly_model(set_data, l2_penalty):\n",
" poly15_data = polynomial_sframe(set_data['sqft_living'], 15)\n",
" poly15_features = poly15_data.column_names() # get the name of the features\n",
" poly15_data['price'] = set_data['price'] # add price to the data since it's the target\n",
" model15 = graphlab.linear_regression.create(poly15_data, target = 'price', features = poly15_features, \n",
" l2_penalty=l2_penalty,\n",
" validation_set=None,verbose=False)\n",
" return poly15_data, model15\n",
" \n",
"\n",
"def get_coef(set_data, l2_penalty):\n",
" poly15_data, model15 = get_poly_model(set_data, l2_penalty)\n",
" return model15.get(\"coefficients\")\n",
"\n",
"def plot_fitted_line(set_data, l2_penalty):\n",
" poly15_data, model15 = get_poly_model(set_data, l2_penalty)\n",
" return plt.plot(poly15_data['power_1'],poly15_data['price'],'.',\n",
" poly15_data['power_1'], model15.predict(poly15_data),'-')"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 585.865818914 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x23b4fe10>,\n",
" <matplotlib.lines.Line2D at 0x235454e0>]"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEACAYAAABlOdt4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXl4VdXV/z+LJIQ5IQxhSBhUHHAoCBIUkFhFAQeoFgUH\nkKK00ret2iraQbGt7+tQ69D+xNIqUgWRigpWQUCNRRRwQKUiAipIgswEkBmyfn+cc7gnl5vkJrk3\n595kfZ7nPHffffbeZ50LOd+z9l57b1FVDMMwDCOe1AvaAMMwDKP2Y2JjGIZhxB0TG8MwDCPumNgY\nhmEYccfExjAMw4g7JjaGYRhG3KlQbETkFhH5r4gsF5FpIpIuIlkiMl9EVonIPBHJ9JW/U0RWi8hK\nEbnQl9/DbWO1iDzqy08Xkefd/MUi0tF3bpR7jVUiMtKX31lElrh1potIWmx+DsMwDCMelCs2ItIe\n+BnQQ1VPB1KA4cAdwHxVPRF4w/2OiHQFrgK6AgOBx0VE3OYmAmNUtQvQRUQGuvljgG1u/sPA/W5b\nWcBdQC/3uFtEMtw69wMPuXV2uG0YhmEYCUo03WipQCMRSQUaARuAy4Ap7vkpwFA3PQR4TlUPqepa\nYA2QJyJtgaaqutQt909fHX9bM4Hz3fRFwDxVLVbVYmA+MMgVr/OAFyJc3zAMw0hAyhUbVS0CHgK+\nwRGZYlWdD2Sr6ia32CYg2023Awp9TRQC7SPkF7n5uJ/r3esdBnaKSIty2spy7SiJ0JZhGIaRgFTU\njdYcx/PohPPwbyIi1/rLqLPeTU2teWNr6xiGYSQhqRWcvwD4WlW3AYjIi8DZwEYRaaOqG90uss1u\n+SIg11c/B8cjKXLT4flenQ7ABrerLkNVt4lIEZDvq5MLvAlsBzJFpJ7r3eS4bRyDiJg4GYZhVBJV\nlYpLVY6KxmzWAb1FpKE7VnIBsAJ4BRjllhkFvOymZwPDRaS+iHQGugBLVXUjsEtE8tx2rgNm+ep4\nbf0QJ+AAYB5woYhkuh7WAOB115N6CxgW4frHoKpJedx9992B22D2B2+H2Z+cRzLbHy/K9WxUdamI\nvAB8BBx2PycBTYEZIjIGWAtc6ZZfISIzcATpMDBOQ9aPA54GGgKvqepcN/9J4BkRWQ1sw4l2Q1W3\ni8gfgPfdcveoEygAMB6YLiJ/dG16ssq/gGEYhhF3KupGQ1UnABPCsrfjeDmRyv8v8L8R8j8ETo+Q\nfwBXrCKcmwxMjpD/NZBXvuWGYRhGomArCCQo+fn5QZtQLcz+YDH7gyXZ7Y8HEs8+uqAREa3N92cY\nhhFrRAQNIEDAMAzDMKqNiY1hGEaMGfI/79L3gmIGD4bi4orL1wVMbAzDMGLIZ5s/499Z57No97PM\nmQNjxwZtUWJgYzaGYRgxYv/h/fT6ey82rG7DtvXN6bn2eebPh8zMiusmCjZmYxiGkeCMnz+ek1ue\nzPyfT6TBSe8wb54mldDEkwrn2RiGYRgV89rq13j5i5f5+Mcfk9kgk+bNlWLW0pzOQZuWEJhnYxiG\nUU02fbeJG2bfwDM/eIbmDZsjIvTt0JeF3ywM2rSEwcTGMAyjGpRoCdfPup4x3cdwbsdzj+b369CP\nd755J0DLEgsTG8MwjGrwlyV/oXh/MXf1v6tUvnk2pbExG8MwjCryycZP+OPCP7LkhiWkpaSVOndG\n9hls2L2BLXu20Kpxq4AsTBzMszEMw6gCew/tZcTMETx80cMc1/y4Y86n1Evh7JyzeXf9uwFYl3iY\n2BiGYVSBX837Fd3bdufaM64ts4x1pYUwsTEMw6gks1bOYu6auTw++PFyy/Xt0NeCBFxMbAzDMCrB\nht0b+PG/f8zUy6eS0SCj3LK92vdi+ebl7D20t4asS1xMbAzDMKKkREsY+dJIxp01jrNzz66wfKO0\nRpyRfQZLCpfUgHWJjYmNYRhGlDz07kMcOHKAX/f7ddR1+uZaVxqY2BiGYUTFhxs+5MF3H+TZHzxL\nar3oZ43069iPd9ab2FQoNiJykogs8x07ReTnIpIlIvNFZJWIzBORTF+dO0VktYisFJELffk9RGS5\ne+5RX366iDzv5i8WkY6+c6Pca6wSkZG+/M4issStM11ESge5G4ZhxIjvDn7HiJkj+Mugv9Axs2PF\nFXz0ye3D4sLFHC45HCfrkoMKxUZVv1DV7qraHegB7AVeAu4A5qvqicAb7ndEpCtwFdAVGAg8LiLe\nctUTgTGq2gXoIiID3fwxwDY3/2HgfretLOAuoJd73C0i3ojc/cBDbp0dbhuGYRgx5+a5N9OnQx+u\nOu2qStdt0agFOc1y+HTTp3GwLHmobDfaBcAaVV0PXAZMcfOnAEPd9BDgOVU9pKprgTVAnoi0BZqq\n6lK33D99dfxtzQTOd9MXAfNUtVhVi4H5wCBXvM4DXohwfcMwjJjxwooXeHvd2zw28LEqt2HjNpUX\nm+HAc246W1U3uelNQLabbgcU+uoUAu0j5Be5+bif6wFU9TCwU0RalNNWFlCsqiUR2jIMw4gJ63eu\n56ev/ZSpl0+laXrTKrdjkzsrITYiUh+4FPhX+Dl3O8ya2hLTtt40DCPuHCk5wnUvXcctvW+hV/te\n1WqrX0dnBei6vHNwZRbiHAR8qKpb3O+bRKSNqm50u8g2u/lFQK6vXg6OR1LkpsPzvTodgA0ikgpk\nqOo2ESkC8n11coE3ge1ApojUc72bHLeNY5gwYcLRdH5+Pvn5+ZGKGYZhlOL+RfcjItx2zm3Vbqtj\nRkdSJIUvd3zJCVknxMC62FFQUEBBQUHcryPRKq2ITAfmqOoU9/sDOIP694vIHUCmqt7hBghMwxnQ\nbw8sAE5QVRWRJcDPgaXAq8BjqjpXRMYBp6vqTSIyHBiqqsPdAIEPgDMBAT4EzlTVYhGZAcxU1edF\n5AngY1V9IsxmrctvEoZhVI0lhUu4bPplfDj2Q3Ka5VRcIQqGvzCcgScM5Ppu18ekvXghIqiqVFyy\nckTVjSYijXGCA170Zd8HDBCRVcD33e+o6gpgBrACmAOM8z3xxwH/AFbjBBrMdfOfBFqIyGrgZtzI\nNlXdDvwBeB9HoO5xAwUAxgO3unWau20YhmFUi90HdnPNi9cw8eKJMRMasM3UovZskhHzbAzDqCyj\nXh5Feko6ky6dFNN2P9n4CVe+cCVf/M8XMW031sTLs7HN0wzDMFyeW/4cSwqX8OHYD2Pe9mmtT2PT\nd5vYvGczrRu3jnn7iY4tV2MYhgGsLV7LL+b+gueueI7G9RvHvP2Ueimck3sOi75ZFPO2kwETG8Mw\n6jyHSw5zzYvXML7PeLq37R6369Tl+TYmNoZh1Hnu/c+9NE5rzC1n3xLX69TlIAEbszEMo06z6JtF\nTPxgIst+vIx6Et/377Pan8VnWz5jz8E9cemqS2TMszEMo85SvL+Ya1+6lr9f+nfaNm0b9+s1SG1A\ntzbdWFy4OO7XSjRMbAzDqJOoKje9ehMXd7mYS0+6tMauW1e70kxsDMOokzzz6TMs37ScBwc8WKPX\nratBAiY2hmHUOdZsX8Mv5/2SaVdMo2Fawxq99jm557CkaAmHjhyq0esGjYmNYRh1ikNHDnHNi9fw\nu3N/xxnZZ9T49bMaZtEpsxOfbPqkxq8dJCY2hmHUKSYUTKBFwxb8rNfPArOhb25fFq6rW11pJjaG\nYdQZ3l77NpM/nszTQ58mtFt9zdO3Q1/eWV+3ggRMbAzDqBNs37ed6166jqeGPBX42mR1cTM1ExvD\nMGo9qsrYV8ZyxSlXMPCEgUGbQ4eMDqSnpLN6++qgTakxTGwMw6j1PLXsKdZsX8N9F9wXtClH6duh\nb52ab2NiYxhGreaLrV9wxxt3MO2KaaSnpgdtzlHq2uROExvDMGotB48c5OoXr+YP5/2Brq26Bm1O\nKera5E4TG8Mwai2/ffO35DbL5cc9fhy0KcdwautT2bZ3Gxu/2xi0KTWCiY1hGLWSBV8tYNryafzj\nsn8EGuZcFvWkXp3aTC0qsRGRTBF5QUQ+F5EVIpInIlkiMl9EVonIPBHJ9JW/U0RWi8hKEbnQl99D\nRJa75x715aeLyPNu/mIR6eg7N8q9xioRGenL7ywiS9w600Ukrfo/h2EYtYGte7dy/cvXM2XoFFo2\nahm0OWVSl7rSovVsHgVeU9VTgDOAlcAdwHxVPRF4w/2OiHQFrgK6AgOBxyX0WjERGKOqXYAuIuLF\nII4Btrn5DwP3u21lAXcBvdzjbhHJcOvcDzzk1tnhtmEYRh1HVRkzewxXn3415x93ftDmlEtdChKo\nUGzch3s/VX0KQFUPq+pO4DJgiltsCjDUTQ8BnlPVQ6q6FlgD5IlIW6Cpqi51y/3TV8ff1kzA+x9y\nETBPVYtVtRiYDwxyxes84IUI1zcMow7zxAdPULirkD9+/49Bm1IhPdv1ZOXWlew+sDtoU+JONJ5N\nZ2CLiEwWkY9E5O8i0hjIVtVNbplNQLabbgcU+uoXAu0j5Be5+bif68ERM2CniLQop60soFhVSyK0\nZRhGHWXFlhXcVXAXz13xHPVT6gdtToWkp6bTvW33OrGZWjTbQqcCZwL/o6rvi8gjuF1mHqqqIlJT\n6y5U6joTJkw4ms7Pzyc/Pz/G5hiGkQjsP7yfETNHcN/593FiixODNidqvK60AccPCOT6BQUFFBQU\nxP060YhNIVCoqu+7318A7gQ2ikgbVd3odpFtds8XAbm++jluG0VuOjzfq9MB2CAiqUCGqm4TkSIg\n31cnF3gT2A5kikg917vJcds4Br/YGIZRe7ljwR2c2OJEftT9R0GbUin6dujLn979U2DXD38Jv+ee\ne+JynQq70VR1I7BeRLxXhQuAz4BXgFFu3ijgZTc9GxguIvVFpDPQBVjqtrPLjWQT4Dpglq+O19YP\ncQIOAOYBF7rRcM2BAcDr6qxe9xYwLML1DcOoY8xZPYeXVr7EpEsmJWSYc3mck3sO7294v9ZvphaN\nZwPwM2CqiNQHvgRGAynADBEZA6wFrgRQ1RUiMgNYARwGxmloadNxwNNAQ5zotrlu/pPAMyKyGtgG\nDHfb2i4ifwA8r+oeN1AAYDwwXUT+CHzktmEYRh1j03ebGDN7DM9d8RzNGzYP2pxKk9kgk+OaH8ey\njcvo1b5X0ObEDanNS1yLiNbm+zOMuo6qcvG0izmz7ZlJEX1WFj999acc1/w4fnnOL4M2BRFBVWPu\nHtoKAoZhJC1/WfoXtu/bzt397w7alGrRr2O/Wr+ZmomNYRhJyaebPuUP//kDUy+fSlpKci8g4m03\nUJt7YkxsDMNIOvYd2seImSP484V/5vis44M2p9rkNMuhcVpjvtj2RdCmxA0TG8Mwko5fzfsV38v+\nHteecW3QpsQMb6vo2oqJjWEYScXsL2bz2prXmHjxxKQLcy6Pvrm1e1FOExvDMJKGDbs3MPaVsUy9\nfCoZDTIqrpBE1PZtok1sDMNICkq0hFEvj+KmnjdxTu45QZsTc05pdQrF+4vZsHtD0KbEBRMbwzCS\ngj+/92f2HdrHb879TdCmxIV6Uo8+uX1qrXdjYmMYRsLz0bcf8cCiB3j28mdJrRftwifJR23uSjOx\nMQwjodlzcA8jZo7gsUGP0SmzU9DmxJXavJmaiY1hGAnNLa/fwtk5ZzP8tOFBmxJ3erTrwaptq9h1\nYFfQpsQcExvDMBKWmStm8ubXb/KXQX8J2pQaoX5KfXq268l7698L2pSYY2JjGEZCsn7nesa9No5p\nV0yjaXrToM2pMWrruI2JjWHUMsaOhfx8GDwYiosrLJ6QHCk5wsiXR3Jz3s21etn9SPTtUDsnd5rY\nGEYtY9UqePttmDPHEZ5k5IFFD6Cq3N7n9qBNqXHOyT2HDzZ8wMEjB4M2JaaY2BhGLaNRI+ezZ0+Y\nNClYW6rC0qKlPLLkEZ75wTOk1EsJ2pwap1l6M7q06MJH334UtCkxxcTGMGoZ06bBsGEwfz5kZgZt\nTeXYfWA3V8+8mscHP05uRm7Q5gRG39y+LFxXu7rSTGwMo5aRmQkzZiSf0AD8bM7POK/TeVzR9Yqg\nTQmU2riZmomNYRgJwfT/Tue9wvd4ZOAjQZsSON6yNSVaErQpMSMqsRGRtSLyqYgsE5Glbl6WiMwX\nkVUiMk9EMn3l7xSR1SKyUkQu9OX3EJHl7rlHffnpIvK8m79YRDr6zo1yr7FKREb68juLyBK3znQR\nSe6t+gwjRiRjNNra4rX8fM7Pee6K52hcv3HQ5gRO+2btyUjPYOXWlUGbEjOi9WwUyFfV7qrqxSHe\nAcxX1ROBN9zviEhX4CqgKzAQeFxCm05MBMaoahegi4gMdPPHANvc/IeB+922soC7gF7ucbeIeOuK\n3w885NbZ4bZhGHWeZItGO1xymGtfvJbb+9zOmW3PDNqchKG2baZWmW608F2KLgOmuOkpwFA3PQR4\nTlUPqepaYA2QJyJtgaaqutQt909fHX9bM4Hz3fRFwDxVLVbVYmA+MMgVr/OAFyJc3zDqNMkWjfa/\nC/+XhmkNufXsW4M2JaGobZupVcazWSAiH4jIjW5etqpuctObgGw33Q4o9NUtBNpHyC9y83E/1wOo\n6mFgp4i0KKetLKBY9WiHpr8tw6jTJFM02qJvFvH4+48zZegU6okNIfupbZ5NtGt191HVb0WkFTBf\nREp1JKqqiojG3ryIVOo6EyZMOJrOz88nPz8/xuYYRmLhRaMlOjv37+Tal65l0qWTaNe0XdDmJBwn\ntTiJ3Qd2U7irkJxmOXG7TkFBAQUFBXFr3yMqsVHVb93PLSLyEs74ySYRaaOqG90uss1u8SLAHyCf\ng+ORFLnp8HyvTgdgg4ikAhmquk1EioB8X51c4E1gO5ApIvVc7ybHbeMY/GJjGEZioKrc9OpNDDph\nEJeddFnQ5iQkInJ0nbR4rngd/hJ+zz33xOU6FfqtItJIRJq66cbAhcByYDYwyi02CnjZTc8GhotI\nfRHpDHQBlqrqRmCXiOS5Yy7XAbN8dby2fogTcAAwD7hQRDJFpDkwAHhdVRV4CxgW4fqGYSQ4z376\nLJ9s+oQ/XfinoE1JaGrT/jbReDbZwEtuQFkqMFVV54nIB8AMERkDrAWuBFDVFSIyA1gBHAbGueIA\nMA54GmgIvKaqc938J4FnRGQ1sA0Y7ra1XUT+ALzvlrvHDRQAGA9MF5E/Ah+5bRiGkeB8uf1Lfjnv\nlywYuYBGaY2CNieh6duhL898+kzQZsQECelA7UNEtDbfn2EkG4eOHKLf5H6MOG0Ev+j9i6DNSXgO\nHjlIiwdasP6W9WQ2qJloDxFBVcOjj6uNhX8YhlFj3PP2PWQ1zOLneT8P2pSkoH5Kfc5qd1at2EzN\nxMYwjBrh7bVv89Syp5g8ZDKhed5GRdSWzdRMbAzDiDs79u1g5MsjefKyJ8lukl1xBeMotWUzNRMb\nwzDiiqoy9t9j+cHJP2BQl0FBm5N0nJ1zNh99+xEHDh8I2pRqYWJjGEZcmfzxZFZtW8V9F9wXtClJ\nSdP0ppzU8iQ+2PBB0KZUCxMbwzDixqptqxi/YDzTLp9Gg9QGQZuTtPTNTf5xGxMbwzDiwsEjB7l6\n5tX8Pv/3nNr61KDNSWpqw2ZqJjaGYcSF3735O9o3a89Pev4kaFOSnr4d+rLom0VJvZmaiY1hxJBk\n3LgsHrzx1RtMXT6VJy970sKcY0CbJm1o0agFK7asCNqUKmNiYxgxJNk2LosHW/du5fpZ1/P00Kdp\n2ahl0ObUGpJ9vo2JjWHEkGTbuCzWqCo3zL6B4acO54LjLgjanFpFsm+mZmJjGDEkmTYuiwd/+/Bv\nrN+1nnvPvzdoU2odyb6Zmi3EaRhGTFixZQX9n+7PO6Pf4aSWJwVtTq1DVcn+UzYfjP2ADhkd4nYd\nW4jTMIyE5cDhA1w982r+7/z/M6GJE/7N1JIRExvDMKrNnW/cyQlZJzCm+5igTanVJPNmaiY2hmFU\ni7lr5vLCiheYdOkkC3OOM8m8KKeJjWEYVWbzns38aNaP+OcP/klWw6ygzan1dGvTjbXFa9mxb0fQ\nplQaExvDMKqEqjJ61mhGdxtNfqf8oM2pE6SlpJHXPo93178btCmVxsTGMIwq8delf2Xr3q1MyJ8Q\ntCl1imTtSotKbEQkRUSWicgr7vcsEZkvIqtEZJ6IZPrK3ikiq0VkpYhc6MvvISLL3XOP+vLTReR5\nN3+xiHT0nRvlXmOViIz05XcWkSVunekiklbdH8IwjOhZvmk5v//P75l6+VTSUuzPryZJ1iCBaD2b\nXwArAG/Syh3AfFU9EXjD/Y6IdAWuAroCA4HHJTRiOBEYo6pdgC4iMtDNHwNsc/MfBu5328oC7gJ6\nucfdIpLh1rkfeMits8NtwzCMGmDfoX2MmDmChy58iBOyTgjanDpHXk4eyzYuY//h/UGbUikqFBsR\nyQEGA/8APOG4DJjipqcAQ930EOA5VT2kqmuBNUCeiLQFmqrqUrfcP311/G3NBM530xcB81S1WFWL\ngfnAIFe8zgNeiHB9wzDizG3zb+P07NO57ozrgjalTtKkfhO6turK+0XvB21KpYjGs3kYuA3wr22d\nraqb3PQmwNtUvB1Q6CtXCLSPkF/k5uN+rgdQ1cPAThFpUU5bWUCx6tG1tv1tGYYRR/696t+8uvpV\nJl480cKcAyQZu9JSyzspIpcAm1V1mYjkRyqjqioiNbUmTKWvM2HChKPp/Px88vPzY2iOYdQdvt39\nLTfMvoGZV84ks0EdXPgtgejboS9PLnsyJm0VFBRQUFAQk7bKo1yxAc4BLhORwUADoJmIPANsEpE2\nqrrR7SLb7JYvAnJ99XNwPJIiNx2e79XpAGwQkVQgQ1W3iUgRkO+rkwu8CWwHMkWknuvd5LhtRMQv\nNoZhVI0SLWHUy6P4Sc+f0KdDn6DNqfP0ye3DmNljOFJyhJR6KdVqK/wl/J577qmmdZEptxtNVX+t\nqrmq2hkYDrypqtcBs4FRbrFRwMtuejYwXETqi0hnoAuwVFU3ArtEJM8dc7kOmOWr47X1Q5yAA4B5\nwIUikikizYEBwOvuyppvAcMiXN8wjDjwyOJH2HNoD78997dBm2IA2U2yad24NZ9t+SxoU6KmsvNs\nvG6s+4ABIrIK+L77HVVdAczAiVybA4zzLbs8DifIYDWwRlXnuvlPAi1EZDVwM25km6puB/4AvA8s\nBe5xAwUAxgO3unWau20YhhEHln27jPveuY+pl08ltV5FnSFGTdE3N7kW5bQtBgzDKJM9B/fQY1IP\n7u5/NyNOHxG0OYaPycsmM++reTx3xXMxbde2GDCMWsTYsZCfD4MHQ3FxhcUD49bXbyUvJ8+EJgHp\n17EfC9ctJFleqE1sDCMAVq2Ct9+GOXMc4UlEXvz8RRZ8vYC/Dvpr0KYYETi++fEcLjnMup3rgjYl\nKkxsjDpBonkSjRo5nz17wqRJwdoSicJdhdz06k1Mu3waTdObBm2OEQERSaqtok1sjDpBonkS06bB\nsGEwfz5kJtiUlSMlRxj50kh+3uvn5OXkBW2OUQ7JFCRgYmPUCRLNk8jMhBkzEk9oDpcc5tbXb+WI\nHuGOvncEbY5RAcm0ArSJjVEnSGRPIlHYsHsD5//zfFZuW8nMK2dWe7KgEX++1+Z7rN+5nm17twVt\nSoWY2Bh1gkT1JBKFBV8toOekngw4bgBzrplDy0YtgzbJiILUeqn0zumdFJupmdgYRh3mSMkRfv/2\n7xn50kievfxZfnvub6kn9lhIJpKlK82mAxtGHWXzns1c++K1HDxykA/Hfkjbpm2DNsmoAv069OM3\nb/4maDMqxF5hDKMOsnDdQnpM6sFZ7c5iwcgFJjRJTK/2vfhk0yfsO7QvaFPKxcTGMOoQJVrCA4se\nYNi/hvG3S/7Gveffa+udJTmN6zfmtNansbRoacWFA8T+lxm1hrFjnfk0jRo50WcWDFCa7fu2M+rl\nUWzdu5WlNy6lQ0aHoE0yYoS3mVr/Tv2DNqVMzLMxag2JNnEzkVhatJQz/3YmXbK68Pb1b5vQ1DL6\ndujLO+sTe3KniY1Ra0i0iZuJgKry2JLHuGTaJTx80cP8+aI/Uz+lftBmGTGmT24f3lv/HkdKjgRt\nSplYN5pRa5g2zfFoJk2KfRdaonXRRWPPzv07ueGVG/hy+5e8N+Y9js86vuYNNWqEVo1b0bZpW5Zv\nXk63Nt2CNici5tkYtYZ4TtxMtC66iuz5eOPH9Px7T1o2bMm7Y941oakD9M3ty8J1iTvfxsTGMKIg\n0broyrPn2U+fZcAzA7gn/x4mXjKRBqkNat5Ao8bp17FfQo/bmNgYCUOibQPgp1UraNkyNl6Td5+5\nudC3b9XuN9Jab6rKhIIJ/O6t3/HWqLe4+vSrq2+skTT07eCsAJ2om6mZ2BgJQ6J1VflZtw62boUF\nC6pvm3efhYWwaFHV7je8y/DA4QNc99J1zFkzh8VjFnNa69OqZ6SRdHTO7Iyq8nXx10GbEpFyxUZE\nGojIEhH5WET+KyIT3PwsEZkvIqtEZJ6IZPrq3Ckiq0VkpYhc6MvvISLL3XOP+vLTReR5N3+xiHT0\nnRvlXmOViIz05Xd27VotItNFJC1Gv4cRIInWVeUnlrZ5bTVrFps2t+7dygXPXMD+w/t5a9RbZDfJ\nrp6BRlKS8JupqWq5B9DI/UwFFgN5wAPA7W7+eOA+N90V+BhIAzoBawBxzy0Fernp14CBbnoc8Lib\nvgqY7qazgC+BTPf4Eshwz80ArnTTE4GflGG7GsnDjh2qw4Y5n4lGLG3z2lq7tvptfr7lcz3u0eP0\nzgV36pGSI9U3zkhqHlv8mN44+8ZqteE+NyvUhsoe0ReERsCHQC9gJZDt5rcBVrrpO4Hxvjpzgd5A\nW+BzX/5w4AlfmTwNCdoWNz0CmOir84RbT4AtQD03vzcwtwybq/WjG0Yis+DLBdrqgVb61EdPBW2K\nkSB8tOEjPfmvJ1erjXiJTYVjNiJST0Q+BjYB81R1qSs0m9wimwDPb28HFPqqFwLtI+QXufm4n+td\nZTgM7BSRFuW0lQUUq2pJhLaMWkoiBw8Ewd8//DtXv3g1/xr2L0Z3Hx20OUaCcEb2GWzYvYEte7YE\nbcoxVDi42/5vAAAgAElEQVSp032odxORDOAlETkt7LyKSE2FP1T6OhMmTDiazs/PJz8/P4bmGLEg\nmgmK3qC6V37GjJq10btu0BM7j5Qc4Y4FdzDri1ksHL2QE1ucWPNGGAlLSr0Uzs45m3fXv8uQk4dE\nVaegoICCgoL4GkYlVhBQ1Z0i8hZwEbBJRNqo6kYRaQtsdosVAbm+ajk4HkmRmw7P9+p0ADaISCrO\nuMw2ESkC8n11coE3ge1ApojUc4Uwx20jIn6xMRKTaIQkEYIHgha8PQf3cM2L11C8v5jFNywmq2FW\nzRpgJAXeZmrRik34S/g999wTF7sqikZr6UWaiUhDYADwOTAbGOUWGwW87KZnA8NFpL6IdAa6AEtV\ndSOwS0TyRESA64BZvjpeWz8E3nDT84ALRSRTRJq7137d7VN8CxgW4fpGDRKrrq1ohCR8Xkn4tWui\nmy1IwSvaVUS/yf3IapjFvOvmxVVorMsyufFWgE44yhvQAU4HPgI+AZYDv9VQpNgCYBWOKGT66vwa\nJwptJXCRL7+H28Ya4DFffjpOdNlqnGi3Tr5zo9381cAoX35nYImb/zyQVob91RooM8qnf38nxASc\nqKqqUpVIrzZtQtceOjR2tsTazljw4YYPNefPOfp/C/9PS0pK4n69mvgtjfix9+BebXRvI/3uwHdV\nqk+cAgS8sORaiYhobb6/oBk82JmQ2LNn6ZnsNUFWFuzY4aSHDIGDB4OzJZ7MWjmLG165gScufoIr\nul5RI9cM8t/ViA3nPHkO937/Xs7rfF6l64oIqiqxtslWEDCqTKQlU2qKHj2cz27d4Omng7UlHqgq\n971zHz997ae8dvVrNSY0UPt+y7qIt3RNImGejZGUeOM08dhOIGh2H9jN6FmjWb9rPTOvnElOs5yK\nKxmGj9lfzOavS//KvOvmVbqueTZG0lATA8zx3E4gSL7Y+gV5/8gjq2EW/7n+P1EJjQ3oG+H0ye3D\n4sLFHC45HLQpRzGxMWJOeQtq2oOxbGatnEW/yf24pfctTLp0Eump6VHVS+QFTI1gaNGoBbkZuXy6\n6dOgTTmK7dRpxJzyQoSDnquSiBwpOcKEgglM+WQKr4x4hbycvErVT4Q5SEbi4W2mdmbbM4M2BTDP\nxiiHqnoh5Q0w24OxNDv27eDS5y7lP9/8h/dvfL/SQgM2oG9EJtE2U7MAAaNM8vNDXsiwYbHxQiIN\n7CfCMjBBsLRoKcNfGM6Qk4bwwIAHSEuxnTKM2LG2eC1nP3k2G27dgDOXPjriFSBg3WhGmcTSCylP\nUOpa11qJlvDwew9z/6L7eeKSJ7j8lMuDNsmohXTM6EiKpPDlji85IeuEoM0xsTHKZto05+HfsCEM\nHVo9z8MvKF26wFlnhdqKd9daInlORbuKGPXyKPYf3s+SG5bQuXnn4IwxajX+zdQSQWxszMYoEy+8\neN266kc7eYLSpImzvbK/rViPOYSPNQUZreW35ZkPXuTMSWfSv2N/Cq4vMKEx4k7f3MSZ3GmejVEh\nsfA8PC9pxw5YsKB0W56oxYrwbrkggxJWrYK33/sOBt7Mf14sYMG4WfTO6R3z6ySS92YkDv069uOx\npY8FbQZgnk2dpLJRZtX1PMaOdbrhvvsO/vGP+EdOhYtLNPbHa/7P/uyF8OMzadGyhM9vXhYXoQGb\na2NE5tRWp7Lpu01s3rO54sLxJh6reybKga36HJGyVvW98Ubn3KBBsV3ZuKZXEY60OnNF9xZrG3fu\n36nj/j1O2z7YTs/50UtxXyl60CDH9p49a35VaiOxGfTsIJ25YmbU5QlqW2ij9lFWt1K83o7j0Y1V\nnicSaSmbiu4tlja+tvo1Tp94OgeOHOCzn/6XRU8OjXu3ls21McoiYfa3iYeCJcqBeTYRKWtflli9\nHXteRE6Oana2akaGauvWqsOHx85zKs8TieTFVHRvsdirZsueLXrti9dq50c66/wv51e9IcOIIZf8\n9D/a9Nazov67I06eTeCCEM/DxKZyhD9wq9qt5hcC/9GyZdkCEYnyrh8uHv6yffoce514bnx2pOSI\nPr3saW3zpzZ685ybq7xplWHEg37n7VOuGK5QEtXfnYmNiU2NE8l7CBeA8ryIZs1C9bt3V73gAo3K\nc/LabN68bHEKFw+/rd4untF6aNUZq1pauFTz/p6nvf7eS5cULqlcZcOoASrbY2FiY2JT40T6Txou\nQJEEyROCtWtVhwxxtm3esUN15EjVVq0c0SnvP324Z9S0qdNWtLauXVs5L6YqwQEbd2/U0S+P1jZ/\naqOTl03WIyVHoqtoGDVMZb16ExsTm5hT0Ru995905MhQuXDvpDJvTdE+1HNySotNNCJQnW6yytzD\nwcMH9aF3H9IW97fQX77+Sy3eV1z5CxpGAhOY2AC5wFvAZ8B/gZ+7+VnAfGAVMA/I9NW5E1gNrAQu\n9OX3AJa75x715acDz7v5i4GOvnOj3GusAkb68jsDS9w604G0CLbH49+i1hDtw99fLivL6abyPI3K\nPOSjfaj7x1y8LrjKiIg/QKFPn4q7x6K5h5KSEn1t1Wt68l9P1oueuUg/3/J59AYZRhIRpNi0Abq5\n6SbAF8ApwAPA7W7+eOA+N90V+BhIAzoBawitLr0U6OWmXwMGuulxwONu+ipguoYE7Usg0z2+BDLc\nczOAK930ROAnEWyPz79GLSHah79XrkmT6D2NSEQrTN71MjJUBw+uvLcSKUChOnNnFn2zSM+dfK6e\n/NeTddbKWVpSUlL1xgwjwUmYbjTgZeAC12vJ1pAgrdSQVzPeV34u0BtoC3zuyx8OPOErk+emU4Et\nbnoEMNFX5wm3ngBbgHpufm9gbgRbY/3vUKuI9uHvlWvXTo8O/PvHUGI9GbS6kWPhAQpVDeX++NuP\n9eKpF2uHhzvoUx89pYeOHKqaQYaRRMRLbCo1qVNEOgHdcbqvslV1k3tqE5DtptsBhb5qhUD7CPlF\nbj7u53pXHQ4DO0WkRTltZQHFqloSoS0jSiJNfiyvXGd33chdu+C220LnX3klNGFy9Ojy24pmWZho\n7Sqr7UOHnOVxPv20ahMd12xfw9Uzr+aiZy9iwHEDWPU/qxjdfTSp9WwpQcOoKlH/9YhIE2Am8AtV\n3e3fjEdVVUQ0DvZFolLXmTBhwtF0fn4++fn5MTan9lHWoo7Nmjmf4bPsDxwIpbWCf5147l3jb3vY\nMOjYsXLtF+0q4vdv/56Zn8/k5t43M+nSSTSp3yR2BlYSW1zTqAkKCgooKCiI/4WicX9wxl9eB272\n5a0E2rjptoS60e4A7vCVmwvk4XS1+bvRjnaRuWV667HdaEe72tzvf8MZ0wnvRjsb60aLGWUFDpTV\nveVFqHXrFv14TDzW8Kpq2xt2bdBb596qWfdn6e3zbtete7bG1rAqUtNryhmGaoBjNu6D/Z/Aw2H5\nD+COzbgCEx4gUB8nYuxLQgECS1zhEY4NEPCEZzilAwS+wgkOaO6l3XMzgKs0NJZjAQIu0Uy8LK+u\nN5ky2iiw8sZYwq8dy5n81W17XfE6/emrP9X0u5pr+xt+puddVlglu+K1gKktrmkEQZBi0xcocQVk\nmXsMdIVgAZFDn3+NE4W2ErjIl++FPq8BHvPlp7vi4YU+d/KdG+3mrwZG+fL9oc/PY6HPR4lm4mU0\ndYcMqfhaNb2acnXa9mw9d+gqvXbGjzTr/iwdP3+8nn3BxmrZGK97jOcSO4ZRFoGJTTIfdVVswt+I\nK/OG7A9zrmimv2rFD9pE6jbrOXi5csUI5baW2nXc3bpt77aY2GgeiFGbiJfYeN1btRIR0dp8f+F4\nA8ppac72y5MnO4PKxcXOuUmTyh9kHjsWVqyApUudiC5wBtozMyMPVI8dCy+84Oy+2b07nH46zJvn\nBAz06AH/+leonP/aJ58MX33lSFSfPs5A/rp1lR8Ij+a+xo6FFxd/wK7v3cvhtu+h795C9yM38eac\nZkfrRPv7VMcOw0gWRARVlYpLVpJ4KFiiHNQxz6aq3UpeF1j4ZMiMDGc+jT+/ZcvI5Tt2dMr767dp\nE/lNP7xcNKtBV2VcZOG6hdr8Zxcpt+QoeY8qaXs0J6dym6oZRl2DOHk2NnGgFuFtANakieNtFBeX\n/6YdHobs1W/cGPbsgZ07nfk0/na3bg1tQObfcOybb5zyfjZuhC5doEEDx3tp1gxatXLa9jjjDKdN\ngIwMePDBim3t0gXOOutYL2vVKmjYSBn7fwt4ZNkfWb9zPe133smOqbPgSDrdu8Obb0beVM1rI5ah\n2IZh+IiHgiXKQR3zbHbsqNyeMeFjDd6AtBfK3LKls7bYBRc4KzeHL8LpH8D2bwdQv77zWa9eaQ8G\nVFNTS5dbu7b0Wmh+z0k15HmkpzvnU1Iie07n9i9RTpql3HiWNr3jFH3mk2f00JFDumNH6ZWnK/oN\nEh3zxIx4gwUImNhEQ2UeniNHOg/xtDTVzMxQQIAnIuGbkJUXHeUJUePGzsOwRYtjBSaS+AwbFnnt\nNU9IytqIzTt+OOywTl8+XZvedoby4256/CUv6Lbtxy73X9ZDOtkivmzujRFvTGxMbKKiooenf0Vk\n/+ZmkTwLv3CNHOkIQPPmjrD4tx3wBMrzPkC1QYOQ0CxcWNrj8g5vHk+4R+UXHC/Ps7VbN2eLaeod\n1E5DJ+sJj5yovf/RW6d/9G/94bCSMu+7uuNZsS5fVZLNEzOSDxMbE5uoqGh5/fI8hcaNSz+Q/cIV\nXs/fHeY9vL3uM3A8pUjei78bLHwez44doV02/WW8jdiGDVPduGW/PvT2RG30647a7x/n6RtfvaEl\nJSUVTmSt7EM6fOfPWO3VU12SzRMzkg8TGxObiFQUUeZ/+J10UkgkvC6rjAzVAQMij8n48R7W4aKU\nkhLqfvMLTOvWpdsK9168/EirAHiC440ZDRrkiMz/W/r/NOfPOTro2UG66JtFpeyraCJrWQ/pssTZ\nf7/g/D7lYR6HUVswsTGxiYjfExg6NLTLpScq/oefP+S4TRvVzp1Vs7OdrrF27VTz8kpvjObHG2jv\n2DEkKuGD9d4DPjU1dPTvH3mMxOuW87cRvq10nz6qpO5TzvqrNvxNjg6eOliXFC6J+DtUdSJrWeK8\nY4czllWWFxbOyJGOOEYzEdYwEhkTGxObiOMC/iiwIUNKD+qHzynxxk0aNTp2/kwkTygS/jr+hzGo\n5uaW7l4Lb89vv+f5eEfz5qVt3Xdon3a9/i/Kre0146aL9Y3Pl5b724R7LpXdqC3S3jeVWWDUBu6N\n2oKJTR0Qm/IGmW+8sbRnMmxY6bzTTy//jf7GGx3PJT1d9ZNPnLzwriKvW23t2rJtiRQ5Fmkcx5/n\neUplCZW/zN6De/XRxY9qu4fa6UVTLtHzr3u/VBh0w4aON9SiRWQPrLJ4ouSNCVU1Us260YzagolN\nHRCb8t6O/ec8L8Cf16KF88CL9NAMr+9FnK1dG1kgvFBo73vDhk53W/36jgfQunWoPZFj64cfLVo4\n9jRqFBKXvLzS4rb34F595L1HtN1D7fTSaZdqx94faEaGY6snfuErD+TkOPdWlUiwG28sHV1XXYGw\ngXujthAvsbG10RKIwYOd2fktW8JJJ4Vm3M+b58yyP3zYmf0+cCB8+y0sXuysQ5aSAkeOOG0MG1Z6\nFrw3s/6zz5w2mjSB775zzrVs6Ty2t22rvK0DBji2zJ0Lu3eH8v22+GnYEPbtC31v0wb69YNHH9/H\n82v+xgOLHqBX+17c1f8unrj7TJ56KtROTg4cf3xopj84qxesWOGsTJCfHzrXsmVoxYJ160IrF4Sv\nueavE+l3M4y6SrzWRrPlahKIadMccdiwARYtcvJatgwt5wLQv78jNP4HpfdQDt9BE0ovxyICBw86\n6Xr1Qu2KOKJTGT77DC6+OCQgDRvCeec57S9YcGx5v9AAfK/nXs6+5W/0mPIgeTl5vHr1q3Rv2/2o\nzd49paTAO+/ATTc535s1c4Rm8WJHSODY5XQACgtLf4YvRePVAWcR0fDfzTCM2FIvaAOMEJmZzgPR\n2365SZPSIuCtWZaW5nyv5/vXa9cO5s8vvVZYfr4jCh6qIbEpKQm1EY3Q+HYBp2FDOPdcx9bDh528\nli1Da54NHQoLFzptp6aG2Zq2l3p9/szrJx/PrY8u5Ns/vcbbN71E1sHuR9v3hCAtDT76CO69F3bt\ncryhTz91xNYTGnBEetgw6N3b+e79fv5trBs2dH6PwYOdNeOmTYMhQxxbw9dLMwwjDsSjby5RDpJk\nzCbSXBP/jPv69UtPmMzNVW3VqvwdNRs2DJX3LxMTaWC/skdubunxE28sJ3y8qdSYUpvvlLP/pHJb\nG23+k8uV7I9LtdmoUeg3CB93Ch/LqmjpGa++vx2LFjOM6MACBGqv2ER6EHrzZcoacPcPkocvWjlo\nUOn5K+EhylU5/PN2/OHVUFpo/JFlgwapkvadNhrwoKbdma3p112hcz76JOK9+UO4w0OlPeH1Ir2i\nFQ7/71HehFXDMEKY2NRisYkUNhv+QPeOjIzID84bb4wsKvXqld1WZY9GjZyotEgRbOFiOODi7/TO\nfz+g6b/J1hY3/VDJ/uSoGPmFEJyw7fCVpsPXbvOLalUmbHrL3pjQGEb5BCY2wFPAJmC5Ly8LmA+s\nAuYBmb5zdwKrgZXAhb78HsBy99yjvvx04Hk3fzHQ0XdulHuNVcBIX35nYIlbZzqQVobtsf+XiAOR\nwma9B2r4g90LBfaXjxQW7D+yskp3w1Xm8LrdInk0EY/6u5U+9yu/ytacW4bppxs/jTifxxOv1q2d\n+4m00rTf66nK/JdEm/sSbYi2bSNgBEmQYtMP6B4mNg8At7vp8cB9bror8DGQBnQC1sDR8OqlQC83\n/Row0E2PAx5301cB0zUkaF8Cme7xJZDhnpsBXOmmJwI/KcP2ePxbVJnKPET84w/hs+29pVO89vxd\nUH6PJpJYRXP4PY/69R2PqX9/Z0mbSGUckdml9LlP+VVr5YdXakrb5Ue708LHoMIP/0KX4TP6mzev\n+uTNRJv7Em33n40vGUESaDeaKxx+sVkJZLvpNsBKN30nMN5Xbi7QG2gLfO7LHw484SuT56ZTgS1u\negQw0VfnCbeeAFuAem5+b2BuGXbH+t+hWoSvYxYtI0eWfjh7Ezhj1T0WfnjiFr7/TFZWKH1UxNJ3\nKv3uVW5rpVwxXGm9/GiZtLTQhMxIghhJcMqb0Z/sROtpJZpHZtQt4iU2VZ1nk62qm9z0JiDbTbfD\n6QrzKATaA4fctEeRm4/7ud5VhsMislNEWrhtFUZoKwsoVtWSCG0lHN6kykaNYP/+UL6jhdGxbl0o\nnZLiTMKcM8cJBQbo1s0JcT50qGo2Nm7sTITctg3S00NzYrzwaCi9fXNKCjRqUcyukx+DXn+BLy+C\nyW/D1lNKtXvoEPTt64RH79jh5GVlwd69pX8LcLaQPvNM6NDB+a3uugs2b4arrw5NyPT/lq1aOb9L\no0bHTthMVLx5VJMmlW9vtOUMI5mo9qROVVURqcSjs3qXq6HrxAz/pMrWrZ3Pbt0gI8OZ9xH+4Ax/\niN5+O7z3nlNPxBGGXbucT4AWLZxrpKdXXWz27AnNkTlwwDnC+eILt/2G2zmS9yi7ev0/WHUJPLUI\ntp1YZtsbNpQWre3bI5dLS3PmCnm/VWpqaA6PNyHT/1v6J7uGT9hMVLx5VLEqZxjJRFXFZpOItFHV\njSLSFtjs5hcBub5yOTgeSZGbDs/36nQANohIKs64zDYRKQLyfXVygTeB7UCmiNRzvZsct42ITJgw\n4Wg6Pz+f/Pz8sorGBW+CYs+e8MILcNttzhvrKac4b/PgCIX3gG/RIrR8zNixztu9NxFT1REaKC0Q\nNcGBlK3Q52Ho+QSs/AH1nlpCw33HH2NDs2aOUHii4heaskhJgUsvhbfecr57k1cBmjcPze73/5aZ\nmc5KBZFWTfDj94aSxQMyjJqkoKCAgoKC+F8omr42jh2zeQB3bAa4g2MDBOrjRIx9SShAYAmQhzPm\nEh4gMFFDYzn+AIGvcIIDmntp99wM4CoNjeUkbIBAWYPU/jEM/2KWrVqF+utHjow81nHM4Hw8j2bf\nKBfdrIxvrlwyVsn8KibteiHZ7dodu92BN2aUklJ6Pxz/bxnt4H+kwfZYL8JpGLUJggoQAJ4DNgAH\nccZWRrtCsIDIoc+/xolCWwlc5Mv3Qp/XAI/58tNd8fBCnzv5zo1281cDo3z5/tDn50mC0OfwB5wX\nLNC0aen5JLm5zjYA0aymHNej1X+VoSMdkbnwl0qz9TFrWyS0zYH3u3gBB927O+Ljj16rTkRWpMH2\n8H18goz4sjBnI9EITGyS+UgksQl/wPkju/zCUqNeS6Sjw0JlxCXKr7KdKLMG2+NyHS/6zB+hB6Gw\nbv++OZ73cdJJWmrbgWgobw6TJ25BPuQtzNlINOIlNrbFQDUoazwgUr63fQA44zJHjjgLQiYE9Q7B\nKS9C70eh8WZ491fw8Sg43DCulx02zBl38SLVUlOdBTP37nWCIZo0Cf1Gbdo4+d6YVU4OrF9ftesW\nF8P11zvXmDw52HEc7/9Fz56lF1I1jKCI1xYDJjbVINI+Ktu2lV5Ov2NHZ/B/0ybn/TWhaLQFekyC\nsybC9hNgyc9g5VDQlJhepl69YwMFRBxxKSmJvP+NV8b/m9Wv7wRL+PeyKYtkCQwoLrYwZyOxiJfY\n2BYD1cCLjvL2hiksPHbflqIiJ+osoYSm7YcwZDT87ERo/jVMfRWeLoDPr4i50LRuDd//vpNu3tzx\n6sD5PQ4dOlZo/FsZNG3qhIKD8+b//vuOR1OR0EAoTHrOHOdhnqh4Yc4mNEZtxzZPqyInn+zsqwLl\nh/d6c0UCp8EOOH0anPkkNNwO798Ej62BfS3idslu3ULhzN7b+3HHHVvO2z20e3d47DFnB09wusza\ntXO627w3/2i7zvxh0rYxmmEEj3WjVYGTT3YmOSY+Cp3ehu5PwkmvwJqL4KMb4OvzQWPv1Pq7y9q1\nc1Y1CH9jHzDAGadp1gzy8kKrF7zxBnzve/Cvf0GXLo6nGE13WVlY95RhVA0bs6kC8RKbzEzYudN/\nnUTqJlNo8wmc9hycNh0ONnUE5tNrYW/LuFzx1FMdgdixw+m68jya228/dtwkkgj4x76GDYMHH3SW\nuXnnnYqFJlnGZgwjWTCxqQLxEpsGDSIv6RIcCi1XwqkzHIFJ3Q//He4cm87AmUcbXy6/3AmC+PJL\nRzy+/dbZwtmLNBs2rOwlWCJFZEUrIuFCZcu8GEb1MLGpAtUVm/AHXu/eCdR9Vu8QdHjH6R47aTak\nHICVP4DlI6CwNzUhMGXhX7fM+37SSU7Xmbfem/93BWcRznbtnHXhOnZ0us+qKlSGYVQdE5sqUF2x\n8b81B486kWOd34TOb8AJr8P242HVpfDFpbCxG0EKjEdaGvTv74zLZGU5XYy7doUWCR0yBJYsCa0L\n16IF9OrllFm06Nj2KhIRG5sxjNhiYlMFqiM2Y8fClCmhRTBrHldcct91BeZNx3v5+vvOsWYQ7G4X\nlHGAExCg6iyk6UXdZWY6Av3HPzorPocLyNChznnPa/Hw5tA0a+YIT7du0KlT8JMuDaOuYWJTBaoj\nNjXu1TQohvZLof0SyFnipEtSYf3ZIYHZejKJ4L14pKVF3tagfn1nfs133zmehz+0+c03QysHhE/2\nzMlxggK8lbFNZAyj5jGxqQJVFZuxY53tAMLfvmNC+k5o9Tm0+gxarXCO1p85c1++PRMK86Aoz/nc\nlUMiiUs4nhfi3xIgEoMHO2U8ASkuDoU3e9iYi2EkBvESG5vUGYFVq2IgNA12hMTELyoNdjg7Wm4+\nFbZ0hbX5zmdxp5jP3o81mZmOuHjeiLdOWSSx8YSoZ0+YOrW0iGRmwllnOQP71l1mGHUD82x8eNFn\nn31W+q27XNJ3OiLS+r+Ot9La9Vjq7y4tKlu6wpZTYWeHuEyojCcpKU6kWIcOx47BeJvC9e7tDPp7\n4vHII+V3h9nAvmEkJtaNVgUqIzZjx8LTT5e3tbJC1hpnLKXNJ464tP6v0/21pasjKptPC4nKrpyk\nExU/KSml1y0LD2cGOO88ePHFsidrGoaRfJjYVIHKiE3btqFwXMCJ/Mp9FzoVOAP27d6Hg02gqJcz\ntrL5NEdUijsltaiUh7ddtX8b5oYNQ4uN2iRKw6h92JhNHBk71n1rz/waTnkJjp8HuYscL+Xr78P7\n4xyR+a5N0KbGhcxM+Phj+MUv4L33YPPmUPeY1xUGzu+0Y4cjOrbApWEYlaHOezZri9dy+ogZfJf7\nL8hc5+znsmYgfH0e7G9eQ5bWDF4Isp/mzWHZstAaZBV1h1l3mWHUbqwbrQpEIzb3v3M/dz3yFQc/\nuhLW9XfmtiQhPXs6c1sOHYLly53xli1bnAH7du2cuS+PPHLsQL5FgRmG4cfEJgIiMhB4BEgB/qGq\n94edj2rMpn17Z7Z7pB0lEw1v4F4Enn8ebr018urIZXkg5pkYhlEetlNnGCKSAvwVGAh0BUaIyClV\naatzZ+czUYSmaVOAAsDxRNauddYUGzrUWVV52DDYvt35XL8+8jL8Ze0AWVM7QxYUFMT3AnHG7A8W\ns7/2kbRiA/QC1qjqWlU9BEwHhlS2kbFjnRWG40VKhHmaPXs62xT06OF8b9rU2VRs6FBnAH75cmja\ntIC1a50B+44d4eWX4aWXnHQybCOc7H9sZn+wmP21j+QcoHBoD/g3CS4E8irbSKTVAiINpJdFaqrT\n/XbWWc72Azt3OuJRvz4sXgwZGXDNNfDBB065xYsrHozPzHS6x6qyQ6VhGEYiksxiE5PBJm+v+vCB\n9F/8whkXeeQRRyy8mfNpaTBrliMS0ewkCfDqq5HzvS4twzCM2k7SBgiISG9ggqoOdL/fCZT4gwRE\nJDlvzjAMI0AsGs2HiKQCXwDnAxuApcAIVf08UMMMwzCMY0jabjRVPSwi/wO8jhP6/KQJjWEYRmKS\ntAalqHIAAASNSURBVJ6NYRiGkTwkc+hzmYjIQBFZKSKrRWR80PYAiEiuiLwlIp+JyH9F5OdufpaI\nzBeRVSIyT0QyfXXudO9hpYhc6MvvISLL3XOP1vB9pIjIMhF5JdnsF5FMEXlBRD4XkRUikpdk9t/i\n/t9ZLiLTRCQ9ke0XkadEZJOILPflxcxe9/6fd/MXi0hM4zfLsP9B9//PJyLyoohkJKL9kWz3nful\niJSISFaN2q6qterA6VJbA3QC0oCPgVMSwK42QDc33QRnvOkU4AHgdjd/PHCfm+7q2p7m3ssaQp7o\nUqCXm34NGFiD93ErMBWY7X5PGvuBKcCP3HQqkJEs9uOE+n8FpLvfnwdGJbL9QD+gO7Dclxcze4Fx\nwONu+ipgeg3YPwCo56bvS1T7I9nu5ucCc4GvgayatD3uf+A1fQBnA3N93+8A7gjargh2vgxcAKwE\nst28NsBKN30nMN5Xfi7QG2gLfO7LHw48UUM25wALgPOAV9y8pLAfR1i+ipCfLPa3B74BmuMI5Svu\ngy+h7XcfXv6HdczsdcvkuelUYEu87Q879wPg2US1P5LtwL+AMygtNjVie23sRos02bN9QLZEREQ6\n4bx1LMH5w9vkntoEZLvpdji2e3j3EZ5fRM3d38PAbYB/YZ9ksb8zsEVEJovIRyLydxFpTJLYr6pF\nwEM4grMBKFbV+SSJ/T5iae/Rv3VVPQzs9HcN1QA/wnnbhySwX0SGAIWq+mnYqRqxvTaKTUJHPIhI\nE2Am8AtV3e0/p85rQkLaLyKXAJtVdRkQMQY/ke3Hefs6E8f1PxPYg+P1HiWR7ReR5sBlOG+r7YAm\nInKtv0wi2x+JZLPXj4j8BjioqtOCtiUaRKQR8Gvgbn92TdpQG8WmCKdf0iOX0uocGCKShiM0z6jq\ny272JhFp455vC2x288PvIwfnPorctD+/KJ52u5wDXCYiXwPPAd8XkWdIHvsLcd7q3ne/v4AjPhuT\nxP4LgK9VdZv7JvkiTpdxstjvEYv/L4W+Oh3ctlKBDFXdHj/THUTkemAwcI0vO9HtPx7nReUT9284\nB/hQRLJryvbaKDYfAF1EpJOI1McZvJodsE2IiABPAitU9RHfqdk4A724ny/78oeLSH0R6Qx0AZaq\n6kZglziRVAJc56sTN1T116qaq6qdcfpu31TV65LI/o3AehE50c26APgMZ+wj4e0H1gG9RaShe90L\ngBVJZL9HLP6/zIrQ1g+BN+JtvDjbmtwGDFHV/b5TCW2/qi5X1WxV7ez+DRcCZ7pdmjVje6wH1BLh\nAAbhRHutAe4M2h7Xpr44Yx0fA8vcYyCQhTPovgqYB2T66vzavYeVwEW+/B7AcvfcYwHcS39C0WhJ\nYz/wPeB94BMczyAjyeyfAHzuXnsKTvRQwtqP4wFvAA7i9O+PjqW9QDowA1gNLAY6xdn+H7nXWuf7\nG348Ee332X7A++3Dzn+FGyBQU7bbpE7DMAwj7tTGbjTDMAwjwTCxMQzDMOKOiY1hGIYRd0xsDMMw\njLhjYmMYhmHEHRMbwzAMI+6Y2BiGYRhxx8TGMAzDiDv/HwWYVwMLwVFjAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x23a57c18>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_1_coef = get_coef(set_1, l2_small_penalty)\n",
"print set_1_coef[set_1_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_1, l2_small_penalty)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 783.493809363 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x23c00668>,\n",
" <matplotlib.lines.Line2D at 0x23c00860>]"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEACAYAAABlOdt4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXuYFdWZ7/95+0Jz7xuXBhsaNKCAIEgLJhptIyKiI2RG\nBE3EMY6cxHNOkskZr5lJ8CQzifFnjJmJetREgYiIeImON1DBS4wCkZsiNiAQaW4KNCj3pt/fH6uK\nXb17d+/d3Xt37d39fp6nnr32qqpVb9XuXt9613rXWqKqGIZhGEYqyQrbAMMwDKPtY2JjGIZhpBwT\nG8MwDCPlmNgYhmEYKcfExjAMw0g5JjaGYRhGyklIbESkQEQWiMhHIrJWRMaKSJGILBKRShFZKCIF\ngeNvE5H1IrJORMYH8keLyBpv372B/DwRecLLf1dEygL7rvWuUSki0wP5A0XkPe+ceSKS2/LHYRiG\nYaSCRD2be4EXVXUIMAJYB9wKLFLVwcBr3ndEZCgwFRgKTADuExHxyrkfuF5VBwGDRGSCl389sNvL\nvwe40yurCPgJMMbbfioi+d45dwJ3e+fs9cowDMMw0pC4YuNV7l9X1T8AqGqNqu4DLgdmeYfNAiZ7\n6UnA46p6TFU3AxuAsSLSB+imqku942YHzgmW9RRwoZe+GFioqtWqWg0sAi7xxOsCYEGM6xuGYRhp\nRiKezUDgMxF5RETeF5GHRKQL0FtVd3rH7AR6e+m+wNbA+VuBk2LkV3n5eJ+fghMzYJ+IFDdSVhFQ\nraq1McoyDMMw0oxExCYHOBO4T1XPBA7gNZn5qJvzprXmvbH5dQzDMDKMnASO2QpsVdVl3vcFwG3A\nDhEpUdUdXhPZLm9/FdAvcH6pV0aVl47O98/pD2wTkRwgX1V3i0gVUBE4px/wOrAHKBCRLM+7KfXK\nqIOImDAZhmE0EVWV+Ec1jbiejaruAD4VkcFe1jjgQ+B54Fov71rgWS/9HDBNRDqIyEBgELDUK2e/\nF8kmwDXAnwLn+GVdgQs4AFgIjPei4QqBi4BXPE9qMTAlxvWj7bdNlZ/+9Keh25Aumz0Lexb2HBre\nUkUing3A/wYeE5EOwEbgOiAbmC8i1wObgSsBVHWtiMwH1gI1wI0auYMbgUeBTrjotpe9/N8Dc0Rk\nPbAbmOaVtUdEfgb4XtUd6gIFAG4B5onIz4H3vTIMwzCMNCQhsVHVVcBZMXaNa+D4/wD+I0b+X4Hh\nMfKP4IlVjH2PAI/EyN8EjG3UcMMwDCMtsBkE2gkVFRVhm5A22LOIYM/CYc8h9Ugq2+jCRkS0Ld+f\nYRhGshERNIwAAcMwDMNoKSY2hmEYRsoxsTEMwzBSjomNYRiGkXJMbAzDMIyUY2JjGIZhpBwTG8Mw\nDCPlmNgYhmEYKcfExjAMw0g5JjaGYRhpjKrS9/YLGDvhEyZOhOrq+OekI4nO+mwYhmGEwIodK9hb\nu4XtCweAwowZMH9+2FY1HfNsDMMw0phZK2dRuns6aBbl5fDgg2Fb1DzMszEMw0hTjh0/xuMfPM4r\nP/4Lv9jnhKagIGyrmoeJjWEYRpry0oaXOLXHqYwacEpGNp0FsWY0wzCMNGXWqllMHzE9bDOSgomN\nYRhGGrLn0B5e++Q1rhwWcxHjjMPExjAMIw2Z98E8Lhl0Cfkd88M2JSmY2BiGYaQhs1fNbjNNaGBi\nYxiGkXZ8/PnH/G3f37jolIvCNiVpmNgYhmGkGbNWzeJbw79FTlbbCRg2sTEMw0gjarWWOavnMP2M\nttOEBiY2hmEYacXiTYvp2bknw3sPD9uUpGJiYxiGkUbMWjWLa8+4Nmwzko6JjWEYRprw5dEvee7j\n57hq+FVhm5J0TGwMwzDShKfWPsV5ZefRq0uvsE1JOiY2hmEYacKsVbPaXGCAT0JiIyKbRWS1iKwQ\nkaVeXpGILBKRShFZKCIFgeNvE5H1IrJORMYH8keLyBpv372B/DwRecLLf1dEygL7rvWuUSki0wP5\nA0XkPe+ceSKS29KHYRiGERZbqreweudq/m7w34VtSkpI1LNRoEJVR6nqGC/vVmCRqg4GXvO+IyJD\nganAUGACcJ+IiHfO/cD1qjoIGCQiE7z864HdXv49wJ1eWUXAT4Ax3vZTEfHnbrgTuNs7Z69XhmEY\nRkbyx9V/5MphV5KXkxe2KSmhKc1oEvX9cmCWl54FTPbSk4DHVfWYqm4GNgBjRaQP0E1Vl3rHzQ6c\nEyzrKeBCL30xsFBVq1W1GlgEXOKJ1wXAghjXNwzDyChUldmrZ7fZJjRommfzqogsF5EbvLzeqrrT\nS+8EenvpvsDWwLlbgZNi5Fd5+XifnwKoag2wT0SKGymrCKhW1doYZRmGYWQU71W9B8DYk8aGbEnq\nSHQuhHNUdbuI9AQWici64E5VVRHR5JsXk9a6jmEYRqswa6UbWxPpcWh7JCQ2qrrd+/xMRJ7B9Z/s\nFJESVd3hNZHt8g6vAvoFTi/FeSRVXjo63z+nP7BNRHKAfFXdLSJVQEXgnH7A68AeoEBEsjzvptQr\nox4zZ848ka6oqKCioiLWYYZhGKFwpOYI89fOZ8X/WBHK9ZcsWcKSJUtSfh1RbdxREJHOQLaqfiEi\nXYCFwB3AOFyn/p0icitQoKq3egECc3GCdBLwKvAVz/t5D/g+sBR4Afitqr4sIjcCw1X1eyIyDZis\nqtO8AIHlwJm4PqO/AmeqarWIzAeeUtUnROQBYKWqPhBlu8a7P8MwjDBZsHYB9y+/n9emvxa2KQCI\nCKqadBcrEc+mN/CM597lAI+p6kIRWQ7MF5Hrgc3AlQCqutYTgrVADXBjoMa/EXgU6AS8qKove/m/\nB+aIyHpgNzDNK2uPiPwMWOYdd4cXKABwCzBPRH4OvO+VYRiGkVG01elpoonr2WQy5tkYhpHO7Dqw\ni8H/OZitP9pK1w5dwzYHSJ1nYzMIGIZhhMTcNXOZdNqktBGaVGJiYxiGERKzVs1qU0s/N4aJjWEY\nRgis3rma3Qd3c8HAC8I2pVUwsTEMwwiB2atmc82Ia8iS9lENt50Frg3DMDKEmtoaHlvzGEuuXRK2\nKa1G+5BUwzCMNGLRxkWU5Zdxao9Twzal1TCxMQzDaGXay9iaICY2hmEYrUj14Wpe3vAyU0+fGrYp\nrYqJjWEYRivy5IdPMu7kcRR1KgrblFbFxMYwDKMVaY9NaGBiYxiG0Wps3LOR9XvWM+ErE+If3MYw\nsTEMw2glZq+azVWnX0Vudm7YprQ6JjaGYRitQK3WtvmlnxvDxMYwDKMVePtvb9O1Q1dGlYwK25RQ\nMLExDMNoBdrD0s+NYdPVGIZhpJiDxw7y9LqnWfuNtWGbEhrm2RiGYaSYZ9c9y9mlZ9OnW5+wTQkN\nExvDMIwU017H1gQxsTEMw0ghVfurWFa1jEmnTgrblFAxsTEMw0ghj615jH8Y8g90yu0UtimhYmJj\nGIaRIlTVNaGNbN9NaGBiYxiGkTLe3/4+h2sOc06/c8I2JXRMbAzDMFLErFWzmD5iersdWxPExtkY\nhmGkgKPHj/L4B4/z3j+9F7YpaYF5NoZhZCQzZkBFBUycCNXVYVtTn5fWv8SQHkM4ufDksE1JC0xs\nDMPISCor4Y034KWXnPCkGza2pi4mNoZhZCSdO7vP8nJ48MFwbYlm98HdvL7pda4YekXYpqQNJjaG\nYWQkc+fClCmwaBEUFIRtTV3mfTCPiYMmkt8xP2xT0gYTG8MwMpKCApg/P/2EBqwJLRYJiY2IZIvI\nChF53vteJCKLRKRSRBaKSEHg2NtEZL2IrBOR8YH80SKyxtt3byA/T0Se8PLfFZGywL5rvWtUisj0\nQP5AEXnPO2eeiLS/Ze8Mw0hLPvrsI7bu38q4k8eFbUpakahn8wNgLaDe91uBRao6GHjN+46IDAWm\nAkOBCcB9Egkwvx+4XlUHAYNExF+E+3pgt5d/D3CnV1YR8BNgjLf9VER8n/RO4G7vnL1eGYZhGKEz\ne9Vsvj3i22RnZYdtSloRV2xEpBSYCDwM+MJxOTDLS88CJnvpScDjqnpMVTcDG4CxItIH6KaqS73j\nZgfOCZb1FHChl74YWKiq1apaDSwCLvHE6wJgQYzrG4ZhhMbx2uPMWT2n3S793BiJeDb3ADcBtYG8\n3qq600vvBHp76b7A1sBxW4GTYuRXefl4n58CqGoNsE9EihspqwioVtXaGGUZhmGExuLNi+ndtTen\n9zo9bFPSjkZnEBCRy4BdqrpCRCpiHaOqKiIaa18KaPJ1Zs6ceSJdUVFBRUVFEs0xDMOIkImBAUuW\nLGHJkiUpv0686Wq+BlwuIhOBjkB3EZkD7BSRElXd4TWR7fKOrwL6Bc4vxXkkVV46Ot8/pz+wTURy\ngHxV3S0iVUBF4Jx+wOvAHqBARLI876bUKyMmQbExDMNIFV8c+YLnP36eX4//ddimNInol/A77rgj\nJddptBlNVW9X1X6qOhCYBryuqtcAzwG+fF8LPOulnwOmiUgHERkIDAKWquoOYL+IjPX6XK4B/hQ4\nxy/rClzAAcBCYLyIFIhIIXAR8IqqKrAYmBLj+oZhGKHw1EdPcf6A8+nZpWfYpqQlTZ2I02/G+iUw\nX0SuBzYDVwKo6loRmY+LXKsBbvTEAeBG4FGgE/Ciqr7s5f8emCMi64HdOFFDVfeIyM+AZd5xd3iB\nAgC3APNE5OfA+14ZhmEYoTFr1Sz+95j/HbYZaYtEtKDtISLalu/PMIz0YHP1ZsofLKfqR1Xk5eSF\nbU6LEBFUNelrItgMAoZhGC3kj6v/yNRhUzNeaFKJiY1hGEYLUFVmr5ptSz/HwcTGMAyjBby79V2y\nJIuz+p4VtilpjYmNYRhGC/DH1tjSz41jy0IbhmE0k8M1h3ly7ZOs/B8rwzYl7THPxjAMo5k8//Hz\njCoZRb/8fvEPbueY2BiGYTSTTJyeJixMbAzDMJrBzi938udP/8w3h3wzbFMyAhMbwzCMZjB3zVwm\nnTqJrh26hm1KRmBiYxghMGMGVFTAxIlQXR33cCMNsSa0pmFiYxghUFkJb7wBL73khMfILFbtWMXe\nw3s5f8D5YZuSMZjYGEYIdO7sPsvL4cEHw7XFaDqzV83mmhHXkCVWhSaKTcRpGCFQXe08mgcfhIKC\nsK0xmkJNbQ2lvy7lzeveZHDx4LDNSTqpmojTBnUaRggUFMD8+WFbYTSHhRsXMrBwYJsUmlRiPqBh\nGEYTsMCA5mFiYxiGkSB7D+3llQ2vMHXY1LBNyThMbAzDMBLkybVPctEpF1HYqTBsUzIOExvDMIwE\nsSa05mNiYxhpjg0ATQ/W717Phj0buPiUi8M2JSMxsTGMNMcGgKYHc1bP4erTryY3OzdsUzISExvD\nSHNsAGj41GqtLf3cQkxsDCPNmTsXpkyBRYtsAGhYvLnlTbrndeeM3meEbUrGYoM6DSPNsQGg4TN7\n1Wxb+rmFmGdjGIbRCAeOHuCZdc/wrRHfCtuUjMbExjAMoxGeXfcsXy39KiVdS8I2JaMxsTEMw2gE\nG1uTHExsDMMwGmDr/q0s37acy0+9PGxTMh4TG8NoAjbAsn3x2OrHuGLoFXTK7RS2KRlPo2IjIh1F\n5D0RWSkiH4jITC+/SEQWiUiliCwUkYLAObeJyHoRWSci4wP5o0Vkjbfv3kB+nog84eW/KyJlgX3X\neteoFJHpgfyBnl3rRWSeiNgoK6NVsAGW7QdVtSa0JNKo2KjqYeACVR0JjAQmiMhY4FZgkaoOBl7z\nviMiQ4GpwFBgAnCfRGIF7weuV9VBwCARmeDlXw/s9vLvAe70yioCfgKM8bafiki+d86dwN3eOXu9\nMgyjWTTFW7EBlu2H5duWc/T4Ub7W72thm9ImiNuMpqoHvWQHIBdQ4HJglpc/C5jspScBj6vqMVXd\nDGwAxopIH6Cbqi71jpsdOCdY1lPAhV76YmChqlarajWwCLjEE68LgAUxrm8YTaYp3ooNsGw/zF41\nm+lnTLexNUkirtiISJaIrAR24ir/pUBvVd3pHbIT6O2l+wJbA6dvBU6KkV/l5eN9fgqgqjXAPhEp\nbqSsIqBaVWtjlGUYTaYp3oo/wLI1hcb6iVqfo8ePMu/DeVwz4pqwTWkzxJ1BwKvUR3pNWM+IyOlR\n+1VENFUGRpvT1BNmzpx5Il1RUUFFRUUSzTHaAnPnugr9wQfT01vxPS9wdtpsAqnnhcoXGNpzKAML\nB4ZtSspZsmQJS5YsSfl1Ep6uRlX3ichiXPPWThEpUdUdXhPZLu+wKqBf4LRSnEdS5aWj8/1z+gPb\nRCQHyFfV3SJSBVQEzukHvA7sAQpEJMsTwlKvjJgExcZof8yY4Srrzp2dqMQSk1ROB5PI9eNh/USt\nz+zVs9tNYED0S/gdd9yRkuvEi0br4UeaiUgn4CLgI+A5wP8lrgWe9dLPAdNEpIOIDAQGAUtVdQew\nX0TGen0u1wB/Cpzjl3UFLuAAYCEwXkQKRKTQu/YrqqrAYmBKjOsbRh3Cjh5LxvWtn6h1+fzg5yze\ntJgrhl4Rtiltinh9Nn2A10VkFbAU12fzIvBL4CIRqQS+4X1HVdcC84G1wEvAjZ44ANwIPAysBzao\n6ste/u+BYhFZD/wQL7JNVfcAPwOWede+wwsUALgF+JF3TqFXhmHUI2yvIBnXv/lm2LULrr7a+mxa\ng3kfzOPSwZfSPa972Ka0KSSiBW0PEdG2fH9GfKqrw+2PScb1KyoifTZTpiTW5JeM5rv2ylkPncW/\nf+PfGX/K+PgHt0FEBFVNegieLTFgtGnCnp4/GddvjndkQQXNY+1na9n2xTYuHHhh/IONJmHT1RhG\nmtOcPpuwmw8zldmrZvPt4d8mOys7bFPaHNaMZhhtkLCbDzOR47XHKftNGa98+xWG9RoWtjmhYc1o\nhmEkTNjNh5nIa5teo6RrSbsWmlRizWiGkQA2ir/t4y/9bKQGa0YzDI/GIrj69IEdO1x68mR45plw\n7TGSy/4j++l/T382fH8DPTr3CNucUElVM5p5Nobh0dgAzCNHIunWen8Je0Bqe2LB2gVUDKho90KT\nSkxsDMOjsQiu0aPd58iR8Oij4dtjJBdrQks91oxmGB6NRXCFEd0V75rWzJYcNu3dxJiHx1D1oyo6\nZHcI25zQsWg0w0gxjUVwtXZ0V1BIGsIGbiaHP67+I1OHTTWhSTHWjGYYKaCl0WuJ9Nds3Og+8/Ph\nrruabWq7RlXb1QzPYWJiYxgpoKWd+4n015SVuc99++Cmm5pnZ3vnnU/fITcrl/K+5WGb0uYxsTGM\nFNDSzv1Epqjp3r1l1zBs6efWxAIEjLQjuuP75pszryO8NQIKbEqalnHo2CFO+vVJrP7eakq7l8Y/\noZ2QqgABExsj7YieUn/XrqZPsW+khrYUAffEB0/w8IqHWXTNorBNSStsUKfRbohugmrN8SYt7dhP\n9PxMnf6mLQ00tcCAVkZV2+zmbs/INPbuVZ0yxX3G+p5Kzj9f1c0R4K6ZqvNbep2wuOQSZ3N5eev8\nHqli+xfbteCXBfrlkS/DNiXt8OrNpNfHNs7GSDuCY1oSGW+STFrqRcU6P1bTU6bNDuDfQ26umxvu\nkUcyuwntsdWPMfm0yXTp0CVsU9oPqVCwdNkwzybjaW0PoKVeVKzzY91Da3prySDdPLHa2lo9WnO0\n2eePuH+ELt60OHkGtSEwz8Zoj7S2B9DQTAGJdozHOj/WPbTGjATJ7MwPyxPbf2Q//7LwX3hx/Ysc\nOX6EIzVHOHL8CEePHyVLshh38jjuuuguRvQekXCZK3esZN/hfZxXdl4KLTfqkQoFS5cN82wynnTx\nAFryZh/WPSTTGwnjHt7Y/IYO+M0AveG5G/STPZ/ozi93avWhaj107JAerz2uh48d1nvfvVfL7inT\n/Yf3J1zuP7/8z/qvr/1rCi3PbEiRZ2Ohz0a7ozlv/BMnugis8vLGB1qmE5loM8DhmsP82+v/xmNr\nHuPBv3uQywZf1ujx1//pevJy8rjv0vviln3s+DH63dOPt657i0HFg5JlcpvCQp+NNkWYob/NCd9N\nZER/upGJNq/csZKzHjqLT6o/YdV3V8UVGoC7L76b5yufZ/GmxXGPfWXjK5xSdIoJTQiY2BihEOZ4\njeb0P/h9LJlSaUNm2Xy89ji/eOsXjJ8znpu/djMLpiygZ5eeQPwXk4KOBTxw6QP80/P/xIGjBxq9\nzuxVs5k+YnoK7sCIh4mNEQqJVvixKpqWekWZ+MbfEtJ9AOmGPRs479HzWPTJIpbPWM41Z1xTZ66y\nRF5MLh18Kef0O4fbX7u9wevsPbSXhRsXcuWwK5N9C0YipKIjKF02LEAgbUm0wzlWJ3e6heGmO+n6\nvGpra/WBZQ9o8Z3Fes9f7tHjtcdjHpfoQNLdB3dr37v76ltb3oq5//5l9+uU+Wn0ANIULPTZaEsk\nGvobywPKtAGRDdFa84yl4/Pa/sV2rn/uenYd2MWb173J0J5DGzx27tzEJhwt6lTE7yb+ju/86Tus\n/O5KOufWHQk8e9Vsfvz1HyfrFoymkgoFS5cN82wynlgeULqEQ7eU1vI40u15zf9gvva6q5f+2+v/\n1qKBmQ0xbcE0/dHLP6qT9/HnH2vvu3rrsePHkn69tgYp8mwSqbD7AYuBD4EPgO97+UXAIqASWAgU\nBM65DVgPrAPGB/JHA2u8ffcG8vOAJ7z8d4GywL5rvWtUAtMD+QOB97xz5gG5MWxPxW9hGEmhrcwz\nlih7D+3Vbz31LR38n4P13U/fTdl1PjvwmZb8fyX6zt/eOZH349d+rP/88j+n7JptiTDFpgQY6aW7\nAh8DQ4BfATd7+bcAv/TSQ4GVQC4wANhAZCmDpcAYL/0iMMFL3wjc56WnAvM0ImgbgQJv2wjke/vm\nA1d66fuB78awPTW/hmEkgXTzOFLJoo2LtN+v++n/fOF/6oGjB1J+vfkfzNfT/uu0EwNA+9/TX1du\nX5ny67YFUiU2caPRVHWHqq700l8CHwEnAZcDs7zDZgGTvfQk4HFVPaaqmz2xGSsifYBuqrrUO252\n4JxgWU8BF3rpi4GFqlqtqtU4T+oScaEqFwALYlzfMFpEc6O3mnpeJoUmN5eDxw7y/Ze+z3V/uo6H\nL3+Y/5r4X/X6UlLBlGFTGNZzGDOXzOSNzW9Q2LGQM0rOSPl1jYZpUuiziAwARuGar3qr6k5v106g\nt5fuC2wNnLYVJ07R+VVePt7npwCqWgPsE5HiRsoqAqpVtTZGWYZxghkzoE8fKCqCiy5KTASaOwYo\nzLFD6RjevKxqGWf+vzP5/ODnrP7uasafMr5Vr/+7ib/jkZWPcPvrtzP9DBtbEzYJR6OJSFec1/ED\nVf0iGAevqioirTUvTJOuM3PmzBPpiooKKioqkmyOEYt0WdGxshJ27HDpV191dsWLgmtu9FaYUV++\n0EFi95hKjh0/xr+/9e/cv/x+fjvht0w9fWoodvTu2pt7Lr6H6c9M55mpz4RiQyawZMkSlixZkvLr\nJCQ2IpKLE5o5qvqsl71TREpUdYfXRLbLy6/CBRX4lOI8kiovHZ3vn9Mf2CYiObh+md0iUgVUBM7p\nB7wO7AEKRCTL825KvTLqERQbo/VIZuXXEuEKroPTpQvs3eve/G++ueEyY4XaJmJDz55uC0NY0yW8\ned3n67jmmWso7lTM+zPe56Tu4TY4XHX6VZxdejYlXUtCtSOdiX4Jv+OOO1JzoXidOoDg+lfuicr/\nFXCLl76V+gECHXARYxuJBAi8B4z1yowOELjfS0+jboDAJ7jggEI/rZEAgale+gEsQCCtSGakVUtn\nXJ40STUvL1LGpEmxy7zhBpdfWqp6zjnuHnzbE7EhzMGTYQcbHK89rve+e68W31ms9y29T2tra8Mx\nJAr/Nw3+lkbjEGI02rlArScgK7xtgicErxI79Pl2XGDAOuDiQL4f+rwB+G0gP88TDz/0eUBg33Ve\n/nrg2kB+MPT5CSz0Oa2IVfk19x8/GcJVWBgRgsmTY5cZFIvgsYna0N5CmX1Wbl+p42aP07EPjdXK\nzyvDNqcO6Tp7QjoTmthk8mZiEz5BgTnnnOb947f0rf2GG1QLCtx1R4xw5USXecMNEUHKyorYOWmS\n23fOOaolJaqbNzcsmmF7F61JbW2tLt60WC+ec7H2vbuv/vqdX6flgMn2+gLQEkxsTGzSnuhK+IYb\nVPPzIxV3SUk4//jBt9tJk+ruO/VU1dxcrePN9OjhPkeOdHZGvx2357fl47XH9em1T+uYh8bo4P8c\nrA/99SE9fOxw2GY1SHt6AUgWqRIbmxvNSBrRQQG7dsG+fe57YSG8+y7cdFP8Oa5aQqyO/GDn+aOP\n1j1+xw44dizyvbAQli+va2fw/E6dYPVq933UqPSZayyVqCqVuyuZ/+F85qyeQ0HHAm455xYmnzaZ\n7KzssM1rlNZYfttIDFup00ga/frB1q2Qnw+rVsH3vufGnBQWwooVUFaWWDktiT6rqIgI3pQprqKp\nrm54IseePeHzz13atzvaTv/8Tp3gT3+KCOikSfDss7Q5tn+xnWXblrGsahnLti1j+bbldMrtRP62\nb5L78VWU1JzN43OlTQ9Gbc+kaqVOExsjaZx7Lvz5zy49ZYqr3BOZrTeaWIKRKE1dCnnLFvja12Dk\nSHjsscaPD9pVWAiffJLYfaXLmKNoDh07xPYvt7Nxz0YnLp7AHKo5xFl9z+KsvmdR3recs046i77d\n+rbodzEyh1SJjTWjGUmje3f36Y/1aG4TRkvGjMQbI9OzpxMYv+IvK4OqmCO0GrbL99QSFY1UDrhU\nVfYd2cfug7vZc2gPuw/tPpGuPlx9Ynv9L+6ztkM1xX33sefw5xyuOUxJ1xIGFAygvG8504ZN4+7x\ndzOwYGCdxct80mUsj5GZmGdjJI3Gmqt8EnnLT6ScppQbfCPv0SPSbNbUt/Pm2AVN97aiOXTsEGs/\nW8vaz9ayqXoTm6s3n9i27t9Kx5yOFHcuprhT8YnPok5FFHYspKBjAQUdC/j1LwpY+34+HC7gkgsK\n+ONDbn8sUUn2/RuZhTWjNQMTm/QjuimmoCCxJqZoMYmeAWDy5Ei5eXkuVqxzZ1fBg5uqprzcle+n\n41X8LW0csVv6AAAgAElEQVT+8s/PzYX166G01Hl/DZU1YwZ8XKlo0cdc8aO3+d1zf+ZT/sKRTlsY\n0mswI0qGcXLhyQwoGHBi69e9H3k5eXFtaangGe2HVIlN6OHJqdyw0Oe0I3rcgx8OHSss2Sc6hLpH\nj7qDNHv0iIQrd+1aN4wZVPv3V+3ZU3XcODdOJl4orB/CHbxGc0KcgyHSvn2xyvrswGc6e+Vs7fm9\nK5Wbeig/LNP+P/yWDrrqfqX3SiX7SItDrC0E2EgULPTZaAv4fSqdOjlvxG/SAmioRaeyMhIBlp1d\n95yuXSPfS0vhtNOc5+IzapTzTP78Z5d/003xm86CfSzQvD6KGTPqhkgXF0c8qgcfhB1f7uCJD55g\n/tr5fLDrAy4ceCG9D1zGZ4/dTfngUhYtgquvhvU7k9NHYiHARuikQsHSZcM8m7Qk2lMB1W7dnNcR\nC98bys6OeBsjR7qpZMaNq+spTZ+uWlTkPImJE11eU0aR33CDaocOES/JL6OpRA8k3btX9e+vPKQP\n/GWOjp8zXvN/ka/XPH2Nvlj54olBkdHeh3kjRhhgno3RVgh6KllZUFsLX3wR2+uYMQP273dez/Hj\nbtbmvn1h8WL3th7dab1wIezZ487t0MHlRXtTjfXBVFbC0aMu/eWXbqbo5oQ3ByO37rh3E79Y9gBv\nlT/ClxtG8Z2R3+GZqc/UW0Qs2vtoijfSWP9SuoZeG+2MVChYumyYZ9MoYc2I63sahYURD6AhryPW\n5JgN9e2o1u1niT4ukWlmfNtAddSoxJ9LdNl79tTq+de+rhc9OlGL7yzW//PK/9H1u9cnVpg2/bdp\n7N7a8/Q6RtPB5kYzsUk2qaqE4lWUweaheE1FfuXfrZvWma+sIfxmtVjHJdKc5i9JMHly/WNuuMEF\nNBQWuusE9/tljy4/ro8tf1bHPjT2xNxhB44eaNjgBmjqb9PYvQX3TZ9uU+4bjWNiY2KTdFI1I24y\nRcwXo82bVQcOVO3d2/WpFBS4Cj+68mxMvPbudWVEr1XTnPuKvrfPd9fo2H96TE/7z2E66oFR+uSH\nT2rN8ZomlR8U6ei+qHjHNxZlF3wm5uUY8TCxMbFJOs3pgG7Ma/H3+WG+zRGxxsqP1aTWWEhxLFpS\n2cZqYqutrdVnP3pWh/1umH714a/qy+tfbnDhsMYWZ4u2rVev2N5VS+/Fptw34pEqsbEAgXZErI7i\npobDBsOC/SWQly93074E9+XlwYIFTe9c378/Mr9a9NQunev2p9cJKc7Lg1decTb59sTCL6NHD3jz\nTSgqgtGj4cknG+5U96e4yc11gyM7dIBHHoEVexcz7a7bOXD0IKdV/ZIXfncphYUNj4ULPp+t3oLo\n110HzzxT//527XLXa+z5NWf6mFjT+RhGq5AKBUuXDfNs6pCMJhT/zTi4wFhpad19/jZwYGL9A0G7\n/LDjWG/efn/KxImRt37fO+vevb49sfCPDy7kFq9TPdp7WrF9hV40+yI95d5T9LQpjylyPKFnGgzh\njhXEEBzkmojnYaHRRirAmtFMbFpKMppQ/AouLy8iOqtWRfYFK8tghd6jR8OiEy1SpaUNLyfdUAe3\nLwjZ2apjxzZ8Lb+TPycncr0uXep2+AdX7SwujqzyefrZO3T6k/+kve/qrb9b+js9WnNUS0vdvvz8\nhscJRT87X8hiBTGYgBhhY2JjYtNiklmRjR0bqaxLSmIPRPRFJDiFjP/2H925HRSpaEFpyMsICtjm\nzU6kgnbF8jSi+31EIunJk90xwSl0CgtVyTmknPNL7fCvLoR576HIA2zqUtfRS0yHQVgh70ZmYGJj\nYpMy4nVcxyLaG4nlufjC07ev1nv7j27SayhiKi8vIgg5OZGZB7p0iV3Jx/Peojv5fa8l2KQVGatT\nq93PXqD8YKAWfHeSLv+kssHyEvUW0yEaLB1sMNIXExsTmzo09e20qVFeOTlOQBp6+w42mQU9F9/L\nCV4vlrfhV9I9ekQEzvdoGptUMxitFauSj/beooW0b1/XLyTihMsXsmBz4LhxqpS8r13+13l62r3D\n9bx/fLXB5rumeovpEA2WbBvMU2pbmNiY2NShqW+njR3vVz5+J3uw879Dh/iDM/0xIf7WtWvdTvDo\nTv9gU1JQiIJNZKWl9csNbmPHNt4UFWvm5nhbaanqri936bULZmjej3vrr9984MRYmXjPO9EKN4w+\nmWjbkm2DeUptCxMbE5s6RL+dxqvsGnqbDVb8q1a5yqK4WOv1ZzRWiUQHBgQjw4KC43fCx4o+y8pS\nzc2ta6MffdaxY92yRo6MbVdwhH/Q9kS2Tl2O6cyXfqs9ftVDf/DSD3TPwT0nymxs7JB/zaC4pluF\nm2oxSAdvzUgeJjYmNnWIfjuNV6E09DYb6zy/sz3evGUNjWAPeijR28CBEYFpaPObs3yCnfDZ2REx\njLYrVnNgtGhGbxUVqj3GvKqDfzNML5x1oX6w84MGn09eXn1PKvqahYXxn1WqK+TopsOWDLJNBIug\na1uY2LRzsWmu5xKPxubN8iuRhvorGhK4zZsjodF+s5p/jejxLdnZEY/G3zp3rnu96GAE/5hzznGf\n3bu7CjWW2HTqVD/fD3vOL9ukxd/7B+106wCds+zpOiP/oz2a6Ps89VTX5xO0vaCg4Wa9RLyLRGZn\nSESsYj2H6HByw2gIE5t2LjbN9Vzi0VAUWHBAZrRA5OS4fX6UWffuqtOm1Rcqf0LLoNcTSziiRSS6\nH2fcuEhAALgosmibwNnjN7l16eKat6ZNi3Fs7gHtdvlPNOf2YuW8/6vkHKwXTRd8Fr5nFBTy4Ho8\neXnxp5ZJ5GUgWTM3R/fBWfOW0RRMbNq52DTHc2lq001wgGKwwu/UKbYw+M1ZvigEj28ohHrvXre4\nWbCcYNRZz54REQsGKkyaVHc25mjRys52whLsLwoOoHRbrTJ0vube3F+/OXeqVkzaUu/6fjRddPki\nriz/fvz77dw5sfEyibwMJDpzc6IzCwRF3iLGjEQxsWnnYtNUzyV6NcxEOoaDHkCwwz8oPP42YkTd\nmYkbihyLNYgz6BH161d3rEu0iPmeTCzR8m0UUR09um7kWYcOdfsrTj1vpRb9qEK73zJCx89Youef\n72wOrvYZtHn69PrNe+COv+EG90zy8ur3L0Xfa1Mq9sZ+45b2i1jEmJEooYkN8AdgJ7AmkFcELAIq\ngYVAQWDfbcB6YB0wPpA/Gljj7bs3kJ8HPOHlvwuUBfZd612jEpgeyB8IvOedMw/IbcD25P8SGUKw\ncmmo01o19rT2OTlOCDp2dJWqX2Hn5LiK3W9GC745Byt/f8vKingDwX3ByK3oPpFYwQX+YMvoaWvO\nOcd5Uf5aN8H7PSGQ3bZq56v/UXv9qrfet/Q+PXb8WL2KNygsvrA1FGwwaVL8ijvRir01vQ2LGDMS\nJUyx+TowKkpsfgXc7KVvAX7ppYcCK4FcYACwARBv31JgjJd+EZjgpW8E7vPSU4F5GhG0jUCBt20E\n8r1984ErvfT9wHcbsD0Vv0XaE5zbq7FOa9W6FWNRUey3eYhENkV7ANERabHEoqFoMH8RMv/aeXl1\nhcjfYs06EOs6+fmRZraLLv1CqfiJyi3FWnrtbTrusuoTzUn+sxk1SnXQoNgTY/qV88iRkWv5c5kl\nOktBcH8sYWlp0EBTsIgxI1FCbUbzhCMoNuuA3l66BFjnpW8Dbgkc9zJwNtAH+CiQPw14IHDMWC+d\nA3zmpa8C7g+c84B3ngCfAVle/tnAyw3YnezfISMIVmKNLaEcrHiD/SPRW48ebtGy4OSVsTyAkpLG\nB2IGhScnxzVBfeUrLh1LZKIr4mCfkn9dv4+mQwfnzUy4pEbvfeshLbmrj3a55luaU7ylQa8keoaC\n3NxI5J3fxBb0oHr2jCxl7e+LJQTTp0cCGxoTlnii1ZymUMNoKakSmyyaR29V3emldwK9vXRfYGvg\nuK3ASTHyq7x8vM9PPWWoAfaJSHEjZRUB1apaG6OsNsWMGVBR4dZQqa5O/LzgOiePPtrwcZWVsHev\nS9d6TzM/363fAlBY6NaL2bcPdu6EmhqX37cvfPklDBgA77wTKW/HDujSBSZNcjbn5ta/5rBh7rOm\nBn7+c/jsM5c+fjxyTFbgr3LUqMhaLUePus99+9x1Bg6EIUOgpARGjlLeq/4TLw8Yyc+em8PzVz9H\n+d/+SM3u/ifKEqn7bLKi/vqXL3fr1rzxhlsjJzfXff/zn+HQIWfr3r1uv7/vjTfgpZfcb+WzZQt8\n/rkrw8+PtfbM3LkwZQosWhR7bZnKSnev/m+R6Jo1hpGOtHjxNFVVEdFkGJPI5VrpOmlBcLGtIUNg\n/HhXkfmLn918sztm2TLIyXGLei1fXn+BrNNOc0KQmwvjxsGSJW5xLl9gfHJy3IJi/fvDmWfC7t0R\nMfIpKHAV/fr1kTwR9+6dkwMvvuj2l5c7odqxo+75H3wQSS9Y4M7zKS6GsWNdBesvoLZnj7v3PXsi\nYgPw2mtuwbRNmxROfpXdZ/4r6GG6LfsPBuddxk8+kDpiN2KEW/AM3LPp1AlWrozsf+std8zGje57\nVpZ7Rv595uRExNYXwKuvdt/Ly115FRXut/GvGy0s0YuWxVu8zheowkJYsaLhxc5iLYpnGOlGc8Vm\np4iUqOoOEekD7PLyq4B+geNKcR5JlZeOzvfP6Q9sE5EcXL/MbhGpAioC5/QDXgf2AAUikuV5N6Ve\nGTGZOXPmiXRFRQUVFRUNHRoaDVUWwZUbd+xwFfnnn0fOeeut+pX5uefCp5/WrcQ++QSOHXPpp56K\npKOpqYHLLnPXOHQo9jHf+AY8/XTdvJUr4cILI7ZVV7u3+qKixu9bo14ddu+G9993q3X6bNkS+9wj\nR+BI77fh739MVv4Ozjr4f6l8dgr7qrN4x7u/7GxX8VdUuOcRXcn74pGTA3fc4VbrLCtzq2jW1jqh\n9+/BP7ZnTzj1VJg82ZU9ebITscmTIy8GkyY5j6UpwhKLRFfVDL6URK9uahjxWLJkCUuWLEn9hRJp\na6N+n82v8PpmgFupHyDQARcxtpFIgMB7wFhcn0t0gMD9GunLCQYIfIILDij0096++cBUjfTlZHSA\nQEMdxdFzjvn9IV27unR0yHDnzvUHV95wQ91jevZsvE+loQABf4sOS87Pd30p0bbk5MQvq9lb/zeV\nb1+s/LBMGfUH7dHrWKN9Pv7KnfEm58zKqttHMmpUJEw7ug+rqf0vDdGSAIB487al+vpG24SwAgSA\nx4FtwFFc38p1nhC8SuzQ59txUWjrgIsD+X7o8wbgt4H8PE88/NDnAYF913n564FrA/nB0OcnyLDQ\n5+h/cL+iyslxlXbfvpFBkdOmOYHo3Ll+iK8/qn7IEHfO5s31hSs6hHf06Lrf/an2/XS8ectaIiC5\nuXUr86ZttcqgF5TvnKN8/xTlzIeU7MMJTbiZn++eT6wJQhva+vZ1v01w5gJfgILji2ItGtcUWjL+\nJXhuc6ejsfE3RjShiU0mb+koNtERRn7UUrTHEOstOriVl6uefLITqOJiJzTRyxlHR5A1tEV7Jf7W\nkLcQPQtzolsittTbpEYZ9oTy3TOU7w1XTn9cyTrWbMFLZCssjESaBW32ZxdIZhhxS8a/JGPsjI2/\nMaJJldj4TVxtEhHRdLu/iopI+3p2diQKq6Qk0v+Sm+v6VURcR3UwUis7G7p3h9GjYenSSP+G3zHt\nRy8FO7Sbi19G0M5Wo2M1jPoDjPkv+LIE3rodKi/FtcLWtzEe/jPNyXHSEX0/fpBDdrbr96qpiQQp\nAIwcCYsXR4IyktUZX12dWL9Mss9NZhlG20JEUFWJf2QTy023yjiZpJPY+EEAH37oOtKzs9129KgL\nN37zTfjJT1xne1VVwxVoYWEkQqxDB3d+584wfDi8917r3U/KKP4Yxv4nDJ8LGybAuz+AqrEtKjIn\nxz0jX5ijxXPUKHjmGRc95gc5+OI0fDiccooLAigoqPuyMGWKdcYbbY9UiU1zx9kYTcSPGPr8cycS\nx4/XHTdy4YXue2lpw0KTnR0ZG1Je7kKe24TQZB+FIU/BtyfAd74OhwvgvjXw1NwWCw245+kLTU5O\nfa+mf38XhXbWWe57166RiL2TT3ZCFB0h6Ic1N3cslJEc7PlnDubZpJBgSPOxYy4cuLzcVVyvvuqa\nw/bvd5Xbl1+6c4LNaUGi38b9Zp+MpvhjOPP3cMYs+Pw0WHE9fDgFajql7JLRz61rVzj7bBf2DO43\n27s38ltFD7iMbnZKladjY2cSwzzN5JMqzybpnUDptBFygED0tDF+p/L06S7CrKTEdeQHV56cNi1+\nRFhGbx33KKMeVq77uvIvvZVxNyvFH4diSzCSLTitT1MCAFLVwW5RYolhAQ7JhxQFCCS9wHTawhKb\nhsY/+PmxxMQPXW1otuF4W2PjTELfcg8ow+Yp0yYpt3ZXrvx75bSnlayjKbtm166qEyfWj/Lr0sV9\njhxZNwqvV6/mVVaJCFNzxrJYJZoYNsFo8kmV2FgzWgoIuvalpbBmjYtimj8/Ei0WJCvLNeccOQId\nO9Y9Ji/P5WccuQfh5Fdh2HwY/N9QNQbWXA0ffROO5LeKCQMHQq9eblaCrCw3jc7w4S7I4pFHXLPL\nq69Gjm+oGSbYpNWzp5vVYONG18/TvXv8Zq7mNPUEm+uSHQFnGI1hzWjN2AjJs/HfSnv0iAzOjLWM\ncXRTTqytc+fUvPmnZOv8mTLyEWXqZOW2bsq1FcqY3ypddqTsmsOHx36GhYV1n3msUf9790ZWIc3N\ndbNGx/I+4i1tkOgyzc31UqxJzWhNSJFn0+KJOI26zJjhOv1LStybb3CsBtQfF6JxHK+DB5NvY/JQ\n6LkWvvIKnPoclKyATRfCum/Ccw/DoeKUW1BZWf8ZirgosuXL3ffu3d1s02+8UTeK7PnnI17jsWOR\niL7o+cWCEWjRwR3ByTYbItE5zhoi1ozRhpFpWDNakvArr2AkmT9WIysrMsNyTo77HpzBOKPotNs1\nj33lFThlIdTmwIaLofLv4JMLkxpJlpXlhCMZA0onTYLVq514Hz3qBCoYKuu/BPTo4Sba3LIl0kx2\n//1wwQVuaYVOnVyT529+Azfd1DqDIa1JzWhNbFBnM2hNsQm2ywfp3NnNoJyxjzn3IJS+CwMWO4Hp\nsQ42nw8bx8PGi2H3IKJH9SeDDh3cDNSvvuo8iNxcJwaqdcW7Wzf44ou65/qh5L73kZfntoMHY49h\nKihwv93Pfw7bttX3RqdMccsNpEOIrYX6GqkmVWJjzWhJwl8HJZr0bgaLQd5+6PcOlL0BZW9CySrY\nOcIJzKI74dOvwfG8lJtx9Cg891xEHILLImRlOQ+kvNwJyoIFkeM6dHBiMXmyCw7YsgUOHKi7bIFP\nSYkTodJSuPRS58l8/LHbF91MFly7JsymLGtSMzIV82ySxLnn1n8jzgi6bYOT3oP+b8OAN5znsq3c\nicuW82Dr2XCsS6ublcicZ2VlrokpOsIv2hPxp/UJUlAAmzbVXYfGp7QU3n67bjNZuswhli52GG0X\na0ZrBqkWGz8kduNG12yT9tNl5ByCPu+7ZrHS99xn7gE3JcynX3MCUzWmVTyXxsjNdc1l8cQmOE+c\nT/furm/me99zyzWXl8Pvf+88l1NOccLir3xZVuamOXnppbqeTEPLNBtGe8DEphmkWmwa6qdJC7Jq\noMdH0GcFnLTUCUvPtbBrmBOXrWfD1rGw5yukos+lNejVy3kwhYWuaW33bpfvj6k5cMBNstmrl+tM\nh/pege8p3HVX63X4G0Y6Y2LTDFIpNqed5jyampq6HdahkHMIeq9xocd9VjjvpeeHsL8Udoxy3srW\nsbD9zJTOO5ZquneHw4ddk1i3bq6p6+c/dwJx8sn1vZwgJSXw0UexhSQYBj16tJsnzQTHaK9YgEAa\nEBxJvn17pJmn9YRGoftW6PWh81JKVjqBKdoIuwc7Mdk+ClZ/G3acAUe7tZZhzaZDByccvlfSED17\numd/2WWub+yLL5zQzJ/vfpdYv0HwJWDHDvjHf4Rnn61/XGVlJGT91VddeQUFJkCGkUxMbBLEH+gX\na7qZ5KOQ/6nzTnqujYhLz7VwtAt8Ngw+G+o68N/9oWsaC7mfpbkMHer6WBpj2DDnxRQUOO8G6kZj\nVVbW/V2GDHHf/T4bP5JNGnhX8yO8wDW7PfigCxyIFiALMzaM5mNikyDRFVpyUMj/W0BM/M+P4GhX\nJyi7hrkmsBXfcd8PFSXbiFahoSURVq6Mf+6GDa6ZbPRoePjh+n0rvlgUFbnrnHQSvPOO23/++U4s\nRo1y86HFYu5c5/WIRBZJiyVAhmE0H+uziUP0CpvNIygqAW+lx0euqWvXsIi3smsYfD4kY0UlGQSF\nKbo/LNZARr+TPzgg0z+uuaHC1dX1Bcgw2gMWINAMmio20QtWxZqpufHxHwrdtkOvD5yo9PrQS691\nnoovKrs8YflsKBwubNE9ZgKxxrnEo29f118S7MsZNQpef73hit8PY7bwZcNoPiY2zaCpYhMMZe7Q\nwVVuDS+37HXW9/0r9F0OfbxPgF2ne6JyekRg2rGn0lRGjHC/w/DhsHWrW6X0G99wwt+YgNiAR8No\nORaN1goE2+mPHo3uT/BmOB7wRmQqF6l1o+23j4bl33XpL/qSqeNWWpOxYyNCnpfnJtv0PcaBA51Y\nlJU5sTl+3H2PJyAFBdaJbxjpiolNgJ49I+msLHjhlUNccetCqns/C4NfgCPdYMv5sH4ivHonVJdh\nwpLYOKPSUujdG/76V/e9pMQ1e61c6TrzgyP+H33UHRMr8swwjMzEmtECVFTAG3/5Ak57FoY8Q87g\n1/hq2WjefeSbHPvw76B6QMpsTVfizVGWm+vWjfmXf3H9JLHO9ftQrr664T6VWE1g1ixmGK2P9dk0\ng6aKzYDv/pAtBbPgb1+n/4F/YPEDl3Fyn+LMnWSzheTkuLDjMWPctDBdurhZrAsLYc+eunOMgZth\n+dxz4YUX3IDL6ClgTDwMI/0xsWkGTRWbZ1Yt4v/9bASdjveuE+7qRzn58221B7KynJCMGFFfJEw0\nDKPtYmLTDJI1N1p1NRQXhzz/WQJ07w5nnunCt7dtq7tv6FDnjQwfHmn62rUL8vOd55Kb6yLw7rjD\nzZD89tsRj8UwjPaDiU0MRGQC8BsgG3hYVe+M2p+0iThzcpKzPHFLyMtzgnfsmFue+PDhyODHCy6A\np5+OeBpvv+1Gz//3f7tBidFeiHknhmHEIlVik5XsAlsLEckG/guYAAwFrhKRIam6XiorZBG46CIn\nDuCEDZynUlICb73lork+/hjWr3fpjz5ykVwdO8KqVfUHO557rhPHSy5x4cArVy6pdz/xxq20VZYs\nWRK2CWmDPQuHPYfUk7FiA4wBNqjqZlU9BswDJqXqYn/9q/MsgvTq5ZqewAnDxIlwzjnue1bgyWZn\n1z0vNzdyTkmJWzFy4UI3I/GUKa5TfsoU1+G+fbsTjk8/dc1aZWWR9IgRcOiQ+4yH/TNFsGcRwZ6F\nw55D6slksTkJ+DTwfauXlxLKytwswCUl7nt5ufM0du6MCMMLL7hmqylT4JNPYNIkN3vw+++780pK\nYPNm11cSFBO/b8T3NsrK2q/XYRhG2ySTB3W2emdTQYFrvoru6wiOWg+OYg+unbJ9e92ybKS7YRjt\niYwNEBCRs4GZqjrB+34bUBsMEhCRzLw5wzCMELFotAAikgN8DFwIbAOWAlep6kehGmYYhmHUI2Ob\n0VS1RkT+F/AKLvT59yY0hmEY6UnGejaGYRhG5pDJ0WgNIiITRGSdiKwXkVvCticViEg/EVksIh+K\nyAci8n0vv0hEFolIpYgsFJGCwDm3ec9knYiMD+SPFpE13r57w7ifliIi2SKyQkSe9763y+cAICIF\nIrJARD4SkbUiMrY9Pg8R+Wfvf2ONiMwVkbz28hxE5A8islNE1gTyknbv3rN8wst/V0Tizzeiqm1q\nwzWpbQAGALnASmBI2Hal4D5LgJFeuiuu/2oI8CvgZi//FuCXXnqo9yxyvWezgYhnuxQY46VfBCaE\nfX/NeB4/Ah4DnvO+t8vn4Nk+C/iOl84B8tvb88ANg/gEyPO+PwFc216eA/B1YBSwJpCXtHsHbgTu\n89JTgXnxbGqLnk2rDvYMC1XdoaorvfSXwEe4f7DLcZUN3udkLz0JeFxVj6nqZtwf1FgR6QN0U9Wl\n3nGzA+dkBCJSCkwEHiaywFC7ew4AIpIPfF1V/wCub1NV99E+n0cO0NkLJuqMCyRqF89BVd8C9kZl\nJ/Peg2U9hQvUapS2KDatOtgzHRCRAbi3mPeA3qq609u1E+jtpfvinoWP/1yi86vIvOd1D3ATEJwq\ntT0+B4CBwGci8oiIvC8iD4lIF9rZ81DVKuBu4G84kalW1UW0s+cQRTLv/UQ9q6o1wD4RKWrs4m1R\nbNpVxIOIdMW9WfxAVb8I7lPn47bp5yEilwG7VHUFDSyb2h6eQ4Ac4ExcE8eZwAHg1uAB7eF5iEgh\n7u17AK7S7Coi3w4e0x6eQ0OEce9tUWyqgH6B7/2oq85tBhHJxQnNHFX15yvYKSIl3v4+wC4vP/q5\nlOKeS5WXDuZXpdLuJPM14HIR2QQ8DnxDRObQ/p6Dz1Zgq6ou874vwInPjnb2PMYBm1R1t/fm/TTw\nVdrfcwiSjP+JrYFz+ntl5QD5qrqnsYu3RbFZDgwSkQEi0gHXefVcyDYlHRER4PfAWlX9TWDXc7iO\nULzPZwP500Skg4gMBAYBS1V1B7Dfi1gS4JrAOWmPqt6uqv1UdSAwDXhdVa+hnT0HH+8+PhWRwV7W\nOOBD4Hna1/PYApwtIp08+8cBa2l/zyFIMv4n/hSjrCuA1+JePeyoiVRswCW46KwNwG1h25OiezwX\n10exEljhbROAIuBVoBJYCBQEzrndeybrgIsD+aOBNd6+34Z9by14JucTiUZrz8/hDGAZsAr3Rp/f\nHrS2X1AAAABySURBVJ8HMBMXOLMG15md216eA87L3wYcxfWtXJfMewfygPnAeuBdYEA8m2xQp2EY\nhpFy2mIzmmEYhpFmmNgYhmEYKcfExjAMw0g5JjaGYRhGyjGxMQzDMFKOiY1hGIaRckxsDMMwjJRj\nYmMYhmGknP8f1OBNqnCKhoEAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x23b5dba8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_2_coef = get_coef(set_2, l2_small_penalty)\n",
"print set_2_coef[set_2_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_2, l2_small_penalty)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+----------------+\n",
"| name | index | value |\n",
"+---------+-------+----------------+\n",
"| power_1 | None | -759.251878505 |\n",
"+---------+-------+----------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x24286d68>,\n",
" <matplotlib.lines.Line2D at 0x24286f60>]"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEACAYAAABlOdt4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXmcVMW5978PDAw7MwPIsIMGUeKGGHCNQ0QENEJiUOIC\n1xCJEmPymrjmJsIb770u8fWaRY3GBRdE3JcIMiDjlgBGQFHAARSVQbYZBldkmef9o+o4Z3q6p3tm\nuqenm+f7+ZxP16lTVaeqB+rX9dRTVaKqGIZhGEYqaZHuChiGYRjZj4mNYRiGkXJMbAzDMIyUY2Jj\nGIZhpBwTG8MwDCPlmNgYhmEYKSeu2IjI/xGRd0RkpYjMEpFcESkQkWIRKRWR+SKSF0p/jYisFZE1\nIjIqFD/Ul7FWRG4LxeeKyKM+frGI9As9m+zfUSoik0LxA0Rkic8zW0RaJefrMAzDMFJBnWIjIr2A\nXwBDVfVwoCUwEbgaKFbVg4GF/h4RGQycAwwGRgO3i4j44u4ApqjqQGCgiIz28VOAch9/K3CjL6sA\n+D0wzF/XiUhnn+dG4BafZ4cvwzAMw2imJGJGywHaiUgO0A7YBJwJzPTPZwLjfXgc8Iiq7lHVDcA6\nYLiI9AA6qupSn+6BUJ5wWU8Ap/jwacB8Va1U1UqgGBjjxWsE8HiU9xuGYRjNkDrFRlXLgFuAj3Ai\nU6mqxUB3Vd3ik20BuvtwT2BjqIiNQK8o8WU+Hv/5sX/fXmCniHSpo6wCX4+qKGUZhmEYzZB4ZrR8\n3MijP67z7yAi54fTqNvvpqn2vLG9dQzDMDKQnDjPRwIfqGo5gIg8CRwHbBaRQlXd7E1kW336MqBP\nKH9v3IikzIcj44M8fYFN3lTXWVXLRaQMKArl6QO8BFQAeSLSwo9uevsyaiEiJk6GYRj1RFUlfqr6\nEW/O5kPgWBFp6+dKRgKrgOeAyT7NZOBpH34WmCgirUVkADAQWKqqm4FPRWS4L+cC4JlQnqCsH+Ec\nDgDmA6NEJM+PsE4FXvQjqUXAhCjvr4WqZuV13XXXpb0O1j5rn7Uv+65UUefIRlWXisjjwDJgr/+8\nC+gIzBGRKcAG4GyffpWIzMEJ0l5gmlbXfhpwP9AWeEFV5/n4e4AHRWQtUI7zdkNVK0TkD8AbPt0M\ndY4CAFcBs0Xkel+nexr8DRiGYRgpJ54ZDVWdDkyPiK7AjXKipf9v4L+jxL8JHB4l/mu8WEV5dh9w\nX5T4D4DhddfcMAzDaC7YDgIZSlFRUbqrkFKsfZmNtc+IRFJpo0s3IqLZ3D7DMIxkIyJoGhwEDMMw\nDKPRmNgYhmEYKcfExjAMw0g5JjaGYRhGyjGxMQzDMFKOiY1hGIaRckxsDMMwjJRjYmMYhmGkHBMb\nwzAMI+WY2BiGYRgpx8TGMAzDSDkmNoZhGEbKMbExDMMwUo6JjWEYRj1ZvHExFV9VpLsaGYWJjWEY\nRj352fM/Y33F+nRXI6MwsTEMw6gHu/buorS8lMO71zp42KgDExvDMIx68M7Wd/hWwbdok9Mm3VXJ\nKOKKjYgMEpHloWuniFwmIgUiUiwipSIyX0TyQnmuEZG1IrJGREaF4oeKyEr/7LZQfK6IPOrjF4tI\nv9Czyf4dpSIyKRQ/QESW+DyzRaRVcr4SwzCM2Cz/ZDlH9zg63dXIOOKKjaq+p6pDVHUIMBT4EngK\nuBooVtWDgYX+HhEZDJwDDAZGA7eLSHDE6B3AFFUdCAwUkdE+fgpQ7uNvBW70ZRUAvweG+es6Eens\n89wI3OLz7PBlGIZhpJTlm5czpHBIuquRcdTXjDYSWKeqHwNnAjN9/ExgvA+PAx5R1T2qugFYBwwX\nkR5AR1Vd6tM9EMoTLusJ4BQfPg2Yr6qVqloJFANjvHiNAB6P8n7DMIyUsXzzchY+NISiIhg7Fior\n012jzKC+YjMReMSHu6vqFh/eAnT34Z7AxlCejUCvKPFlPh7/+TGAqu4FdopIlzrKKgAqVbUqSlmG\nYRgpYV/VPt7e8jY7Vh/Fyy/D3LkwdWq6a5UZJCw2ItIa+D7wWOQzVVVAk1ivumiq9xiGYdTgvfL3\n6NGhB51ynTX/mGPgrrvSXKkMIaceaccAb6rqNn+/RUQKVXWzN5Ft9fFlQJ9Qvt64EUmZD0fGB3n6\nAptEJAforKrlIlIGFIXy9AFeAiqAPBFp4Uc3vX0ZtZg+ffo34aKiIoqKiqIlMwzDiMvyT5YzpMcQ\n7p7lRjR33QV5efHzNWdKSkooKSlJ+XvEDUoSSCgyG5irqjP9/U24Sf0bReRqIE9Vr/YOArNwE/q9\ngAXAt1RVRWQJcBmwFPgH8CdVnSci04DDVfUSEZkIjFfVid5B4N/A0YAAbwJHq2qliMwBnlDVR0Xk\nTmCFqt4ZUWdNtH2GYRjx+PWLv6ZLuy5ce9K16a5KyhARVFXip6wfCZnRRKQ9zjngyVD0DcCpIlIK\nfM/fo6qrgDnAKmAuMC3U408D/g6sxTkazPPx9wBdRGQt8Cu8Z5uqVgB/AN7ACdQM7ygAcBVwuc+T\n78swDMNIOlOnQlER3P/icg7uaG7PDSHhkU0mYiMbwzCSQVERvPyywlVd+P6Hq3n2ke5x82QqaR3Z\nGIZh7M+0awfkfUgracMDd2Sv0KSS+jgIGIZh7JfMmgVjf72MDocMyXiHgHRhYmMYhhGHvDw45bzl\nOF8loyGYGc0wDCMBlm92bs9GwzCxMQzDSIBlnyyzPdEagYmNYRhGHLZ8voWv9n5F/7z+6a5KxmJi\nYxiGEYdgp+fqDeyN+mJiYxiGEYfln9ixAo3FxMYwDCMOyzYvM+eARmJiYxiGEQc7nbPxmNgYhmHU\nwZd7vmTjpxs5uMvB6a5KRmNiYxiGUQel5aUcVHAQOS1sDXxjMLExDMOogzXb13Bo10PTXY2Mx8TG\nMAyjDtZsX8MhXQ9JdzUyHhMbwzCMOli9fbWJTRIwsTEMw6gDM6MlBxMbwzCMGOyr2sfa8rUM6joo\n3VXJeExsDMMwYvDhzg/p0q4LHVp3SHdVMh4TG8MwjBiYCS15JCQ2IpInIo+LyGoRWSUiw0WkQESK\nRaRUROaLSF4o/TUislZE1ojIqFD8UBFZ6Z/dForPFZFHffxiEekXejbZv6NURCaF4geIyBKfZ7aI\ntGr812EYhlGNeaIlj0RHNrcBL6jqocARwBrgaqBYVQ8GFvp7RGQwcA4wGBgN3C7VW6XeAUxR1YHA\nQBEZ7eOnAOU+/lbgRl9WAfB7YJi/rhORzj7PjcAtPs8OX4ZhGEbSWL3NPNGSRVyx8Z37Sap6L4Cq\n7lXVncCZwEyfbCYw3ofHAY+o6h5V3QCsA4aLSA+go6ou9ekeCOUJl/UEcIoPnwbMV9VKVa0EioEx\nXrxGAI9Heb9hGEZSWFNuZrRkkcjIZgCwTUTuE5FlInK3iLQHuqvqFp9mC9Ddh3sCG0P5NwK9osSX\n+Xj858fgxAzYKSJd6iirAKhU1aooZRmGYSQFM6Mlj0Q2+8kBjgYuVdU3ROR/8SazAFVVEdFUVDAK\n9XrP9OnTvwkXFRVRVFSU5OoYhpGNbP9yO7v37aawQ2G6q5JSSkpKKCkpSfl7EhGbjcBGVX3D3z8O\nXANsFpFCVd3sTWRb/fMyoE8of29fRpkPR8YHefoCm0QkB+isquUiUgYUhfL0AV4CKoA8EWnhRze9\nfRm1CIuNYRhGogSeaNl+Omfkj/AZM2ak5D1xzWiquhn4WESC/bVHAu8CzwGTfdxk4GkffhaYKCKt\nRWQAMBBY6sv51HuyCXAB8EwoT1DWj3AOBwDzgVHeGy4fOBV4UVUVWARMiPJ+wzCMRmMmtOSS6J7Z\nvwAeFpHWwHrgQqAlMEdEpgAbgLMBVHWViMwBVgF7gWleHACmAfcDbXHebfN8/D3AgyKyFigHJvqy\nKkTkD0AwqprhHQUArgJmi8j1wDJfhmEYRlIwsUkuUq0D2YeIaDa3zzCM1HH6rNOZevRUxh0yLt1V\naVJEBFVNuu3QdhAwDMOIgo1skouJjWEYRgS79u6i7NMyDsw/MN1VyRpMbAzDMCIoLS/lwPwDadXS\ndsFKFiY2hmEYEZgJLfmY2BiGYURgYpN8TGwMwzAiWL19te2JlmRMbAzDMCKwkU3yMbExDMMIUaVV\nlJaX2lHQScbExjAMI8RHOz8iv00+nXI7pbsqWYWJjWEYRggzoaUGExvDMIwQJjapwcTGMAwjxOpt\n5omWCkxsDMMwQqwpt5FNKjCxMQzDCGFmtNRgYmMYhuGp+KqCr/Z8Rc+OPdNdlazDxMYwDMMTjGqy\n/SjodGBiYxiG4TETWuowsTEMw/CYJ1rqMLExDMPwmCda6khIbERkg4i8LSLLRWSpjysQkWIRKRWR\n+SKSF0p/jYisFZE1IjIqFD9URFb6Z7eF4nNF5FEfv1hE+oWeTfbvKBWRSaH4ASKyxOeZLSJ2ypFh\nGI1izfY1HNrNRjapINGRjQJFqjpEVYf5uKuBYlU9GFjo7xGRwcA5wGBgNHC7VM+23QFMUdWBwEAR\nGe3jpwDlPv5W4EZfVgHwe2CYv64Tkc4+z43ALT7PDl+GYRhGg9i1dxcf7/yYg/IPSndVspL6mNEi\n3TPOBGb68ExgvA+PAx5R1T2qugFYBwwXkR5AR1Vd6tM9EMoTLusJ4BQfPg2Yr6qVqloJFANjvHiN\nAB6P8n7DMIx6s65iHf3z+ttR0CmiPiObBSLybxG5yMd1V9UtPrwF6O7DPYGNobwbgV5R4st8PP7z\nYwBV3QvsFJEudZRVAFSqalWUsgzDMOqNmdBSS06C6U5Q1U9EpBtQLCJrwg9VVUVEk1+9qNTrPdOn\nT/8mXFRURFFRUZKrYxhGNrBm+xoO6bL/OQeUlJRQUlKS8vckJDaq+on/3CYiT+HmT7aISKGqbvYm\nsq0+eRnQJ5S9N25EUubDkfFBnr7AJhHJATqrarmIlAFFoTx9gJeACiBPRFr40U1vX0YtwmJjGIYR\ni9XbVzPqwFHxE2YZkT/CZ8yYkZL3xDWjiUg7Eenow+2BUcBK4Flgsk82GXjah58FJopIaxEZAAwE\nlqrqZuBTERnu51wuAJ4J5QnK+hHO4QBgPjBKRPJEJB84FXhRVRVYBEyI8n7DMIx6Y2a01JLIyKY7\n8JR3KMsBHlbV+SLyb2COiEwBNgBnA6jqKhGZA6wC9gLTvDgATAPuB9oCL6jqPB9/D/CgiKwFyoGJ\nvqwKEfkD8IZPN8M7CgBcBcwWkeuBZb4MwzCMenPrv25l+5fb+Xa3b6e7KlmLVOtA9iEims3tMwyj\ncagqv1v0Ox5b9RjFFxTTt3PfdFcp7YgIqpr0zeESdRAwDMPIKvZV7ePSFy5l6aalvHbha3Rr3y3d\nVcpqTGwMw9jv2L1vN5OemsSWL7awaPIiOuV2SneVsh4TG8Mw9iu+2P0FZ805i9ycXOaeN5c2OW3S\nXaX9AtuI0zCM/YaKryo49cFTKexQyBNnP2FC04SY2BiGsV/wyWefcPL9J3Ns72O5d9y95LSoadiZ\nOhWKimDsWKisjF6G0XBMbAzDyHrWV6znxPtOZOK3J3LLqFtoIbW7vtJSePllmDvXCY+RXGzOxjCM\nrObtLW8z5uEx/O67v+PiYy6Oma5dO/d5zDFw111NVLn9CFtnYxhG1vL6R6/zwzk/5E+j/8Q5h51T\nZ9rKSjeiuesuyMurM2lWk6p1NiY2hmFkJXPXzmXS05N48AcPMvpbo+NnMABb1GkY+y1Tp7r5hHbt\nYNas/ftXd6I8svIRfvXir3hm4jMc3+f4dFfHwMTGMJo9wcQ1OOGZMye99Wnu3PHGHfzXq//FggsW\ncHj3w9NdHcNjYmMYzRybuE4MVeW/Xv0v7ltxH69c+AoH5h+Y7ioZIWzOxjCaOTZxHZ8qreLXL/6a\nhR8s5MXzX6RHxx7prlLGYg4CDcDExjCynz379vDT537Kuop1PP/j58lvm5/uKmU05iBgGIYRwVd7\nvuKcx89hT9Ue5p8/n/at26e7SkYMbAcBwzAykp27djLm4TG0b92eZyY+Y0LTzDGxMQwj49j6xVZG\nzBzB4G6DeegHD9G6Zet0V8mIg4mNYRgZxYeVH3LSfSdxxsFn8Nexf6Vli5bprpKRADZnYxhGxrB6\n22pOe+g0Lj/ucn517K/SXR2jHiQ0shGRliKyXESe8/cFIlIsIqUiMl9E8kJprxGRtSKyRkRGheKH\nishK/+y2UHyuiDzq4xeLSL/Qs8n+HaUiMikUP0BElvg8s0WkVWO/CMMwmjdvlL3BiJkjuP5715vQ\nZCCJmtF+CawCAj/iq4FiVT0YWOjvEZHBwDnAYGA0cLuIBC50dwBTVHUgMFBEgs2KpgDlPv5W4EZf\nVgHwe2CYv64Tkc4+z43ALT7PDl+GYRhZysL3F3L6rNO56/t3MenISfEzGM2OuGIjIr2BscDfgUA4\nzgRm+vBMYLwPjwMeUdU9qroBWAcMF5EeQEdVXerTPRDKEy7rCeAUHz4NmK+qlapaCRQDY7x4jQAe\nj/J+wzCyjCdXP8mPn/gxj014jDMHnZnu6hgNJJGRza3AFUBVKK67qm7x4S1Adx/uCWwMpdsI9IoS\nX+bj8Z8fA6jqXmCniHSpo6wCoFJVq6KUZRhGFnHv8nv5+Qs/Z9758zi5/8npro7RCOp0EBCRM4Ct\nqrpcRIqipVFVFZGmWqZf7/dMnz79m3BRURFFRUVJrI5hGKnij//8I39Z+hde/o+XObjLwemuTtZS\nUlJCSUlJyt8TzxvteOBMERkLtAE6iciDwBYRKVTVzd5EttWnLwP6hPL3xo1Iynw4Mj7I0xfYJCI5\nQGdVLReRMqAolKcP8BJQAeSJSAs/uunty4hKWGwMw2j+qCrXLryWp997mlcvfJU+nfvEz2Q0mMgf\n4TNmzEjJe+o0o6nqtaraR1UHABOBl1T1AuBZYLJPNhl42oefBSaKSGsRGQAMBJaq6mbgUxEZ7udc\nLgCeCeUJyvoRzuEAYD4wSkTyRCQfOBV40W92tgiYEOX9hmFkMPuq9vGz53/Gwg8WmtBkGfVdZxOY\nsW4A5ojIFGADcDaAqq4SkTk4z7W9wLTQTpjTgPuBtsALqjrPx98DPCgia4FynKihqhUi8gfgDZ9u\nhncUALgKmC0i1wPLfBmG0aywQ8/qx9d7v+b8p86n4qsKFk5aSMfcjumukpFEbNdnw0gRRUXVh55N\nmGCHntXF57s/54eP/pAOrTsw66xZtMlpk+4q7bekatdn267GMFKEHXqWGOVfljPygZH07dyXORPm\nmNBkKSY2hpEiZs1yI5riYjOhxaLs0zK+e/93+W6/73L39+8mp4XtoJWtmBnNMIy0sLZ8LaMeGsXF\nQy/mqhOvSnd1DI8dnmYYRtawYvMKxj48lhlFM7ho6EXpro7RBJjYGPsVyfQQM2+zhvHqh69y1pyz\nuP302/nR4B+luzpGE2FzNsZ+RWmp8xCbO9eJRXMpa3/hH6X/4Kw5Z/HwDx82odnPsJGNsV+RTA8x\n8zarHw+//TCXz7+c5378HMN7D093dYwmxhwEjP2Kyko3CrnrrsabvZJZVrbz5yV/5qZ/3sS88+bx\n7QO+ne7qGHWQKgcBExvDMFKGqvJ/X/6/PLTyIYovKKZ/Xv90V8mIg3mjGYaRUVRpFb+a9yte/ehV\nXrvwNbp36B4/k5G1mNgYRgMwT7S62bNvDxc+cyEf7vyQRZMXkdfGvqD9HRMbI6NoLp184IkW1Mn2\nPavmyz1fcvZjZwPw4vkv0q5VuzTXyGgOmOuzkVE0F3dj80SLTuWuSk576DTy2uTx1DlPmdAY32Bi\nY2QUzaWTt33ParPl8y0U3V/EkMIhPPCDB2jVslW6q2Q0I8wbzcgYpk6FVatg/XpYvBj69Ut3jZof\n6TIzbqjcwKkPnsr5h5/P70/+Pe6MRCMTsSMGjP2e0lJ4/XXYvBmuuCLdtWmepMPM+O7WdznpvpO4\nbNhlXFd0nQmNERVzEDAyhuZiQmvONPV3tGTjEsbNHscto27hvCPOS/0LjYzFzGhGxhBesX/llc3D\nK6250ZS7GhSvL+bcJ8/l/nH3c/rBp6f2ZUaTYTsINAATm+zFjlxOL4+vepxp/5jGE2c/wUn9Tkp3\ndYwkkpY5GxFpIyJLRGSFiLwjItN9fIGIFItIqYjMF5G8UJ5rRGStiKwRkVGh+KEistI/uy0Unysi\nj/r4xSLSL/Rssn9HqYhMCsUP8PVaKyKzRcTcXvYzUmUumjrVCdnYsW6UkOmkoj13v3k3l829jPkX\nzDehMRJHVeu8gHb+MwdYDAwHbgKu9PFXATf48GBgBdAK6A+so3r0tBQY5sMvAKN9eBpwuw+fA8z2\n4QJgPZDnr/VAZ/9sDnC2D98BXByj7mpkJzt2qE6Y4D6Tycknq4K7JkxIbtnpINntueHVG7T///bX\n0u2ljS/MaJb4fjOuNtT3iuuNpqpf+mBrLyIKnAnM9PEzgfE+PA54RFX3qOoGLzbDRaQH0FFVl/p0\nD4TyhMt6AjjFh08D5qtqpapWAsXAGHGuLiOAx6O839hPyMtzprNkz0tkmxNCstqjqlxZfCUPvv0g\nr134GgO7DExOBY39hrhiIyItRGQFsAXX+S8FuqvqFp9kCxDssNcT2BjKvhHoFSW+zMfjPz8GUNW9\nwE4R6VJHWQVApapWRSnLMICGm48ybbFmvHYmoz17q/by02d/yisfvsIrF75Cr072382oP3Fdn32n\nfpSIdAaeEpHDIp6riDTVLHy93zN9+vRvwkVFRRQVFSWxOkZzpaF7lwUjpkwhXjvr257IRaFtOuzi\n3CfO5fPdn7Ng0gI6tO6QvMobzYKSkhJKSkpS/p6E19mo6k4RWYQzb20RkUJV3exNZFt9sjKgTyhb\nb9yIpMyHI+ODPH2BTSKSg5uXKReRMqAolKcP8BJQAeSJSAsvhL19GVEJi42RXcRaLT91Krz9tgsP\nGZId5rBYJNvsFxavCy/+jE/HjqdL2y489+PnyM3JbfwLjGZH5I/wGTNmpOQ98bzRugaeZiLSFjgV\nWA08C0z2ySYDT/vws8BEEWktIgOAgcBSVd0MfCoiw/2cywXAM6E8QVk/Ahb68HxglIjkiUi+f/eL\nfgJrETAhyvuN/YhYq+Wfew527HDhHj0ywxzWUJJt9gvE68jjtvNR0SkclH8Qj5z1iAmN0WjijWx6\nADNFpCVOmB5V1RdEZDEwR0SmABuAswFUdZWIzAFWAXuBaV4cwHmd3Q+0BV5Q1Xk+/h7gQRFZC5QD\nE31ZFSLyB+ANn26GdxQA5wE3W0SuB5b5Moz9jFi/6r/+ujrcunXT1qmpSbbZb9YsOH/aRtYdN4of\nfGsc/33Kf9v2M0ZSsEWdRsYSa7X8qafCggXOhPbSS9k9skk2b256k7PmnMWlwy7lN8f/Jt3VMdKA\n7SDQAExs9k+acsuWbGHllpVcV3Idizcu5o+j/si5h5+b7ioZacLEpgGY2BiZSFMeE/De9veY/vJ0\nFn2wiCuOv4JLvnOJHXi2n5MqsbFdnw2jmRH2CDv6aOjbN/nCs3PXTq5deC1zVs3h8mMv5+7v321u\nzUZKMbExjGZG2PEhN7dh64Xq4uk1T/OLub9gzLfGUHppKflt8xtfqGHEwcxoRtaTrtMrG0p4zunc\nc51r9zHHNN69edNnm/jF3F/wztZ3uOuMuzi5/8nJq7SRNdhJnYbRQNJxemVjCO/7lox1NFVaxd/+\n/TeOvPNIBncdzFsXv2VCYzQ5ZkYzGk1zHzlk8uaajV1Hs65iHT955ifsqdrDosmLOOyAw+JnMowU\nYCMbo9E0ZOSQjHNWEi0jkdFBvLIy7ZwbVeXEX93J4FuOY/srZ/H8D14zoTHSSyrOLWguF3aeTZMw\nZow7L+WYYxI/XyYZ56wk86yWeGXFe37RRS7NmDHJP2Onvmz6dJOOeWiMdrh8qNJ1VdaczWM0DaTr\nPBvDiEdD5hWSYdpav959du4MN98cPU2iI5J49Yn3vCnmhRJpy5x353DU347iOz2/wwlr/gXbD81I\n86GRhaRCwZrLhY1smi3JOGnzhBPij2wSHf3Eq0+85w0Z3dWXutpS8WWFnvvEuXrwnw/WJRuXJFRn\nw4gGNrIxMp3wL3No/EmbnTq5z7p+uSc6gop38me8501x6Fqstix4fwFH3nkkBW0KWP6z5QzrNSyh\nOhtGU2LrbIyUEvZU+/RTeP11Fz9hQuMXKFZWuhX2PXs64YnmCZfIPmnN3ZsuILItX+z+gmsWXsNT\na57injPvYdRBo9JdRSMLsL3RGoCJTfopKqpeAV9YCJs3J2eBYrTyBwxo2NYu4TKSIYJNwcsbXuYn\nz/6E4/scz22jb6OgbUG6q2RkCbao08hIwqafxYvrZ2pKxB05fCJnz54Nm6TPpHU4X+z+gsvmXsa5\nT57LrafdyoM/eNCExsgITGyMlBKey+jXL/E5hGAfsLrEo7S0+kTOvn0Tm8OJV8fmakIDeOmDlzji\nziPY+fVOVl6ykjMHnZnuKhlGwpgZzUgJwTzI+vVOZGLNqcQibNrKz4f336+dd+zYmvuGBe+NnJ9p\nbnMy9a3P5s8385v5v+HVj17lr2P/yhkHn9E0FTX2S+yIAaPZE8sZYOPG6ueJzocEpq38fFi+PHqH\nPGtWbXGJVn54y/761CFVIpVoffZV7eOOf9/BjJdnMGXIFFZNW0X71u2TUwnDaGJMbIykEe5ECwvd\nZ6dOTnjqMm1F69SjCUkkV14JW7e6nZHrEoP6zMnEEsxkbe+faH3eKHuDi/9xMR1ad6BkcgnfPuDb\nyXm5YaSLeAtxgD7AIuBd4B3gMh9fABQDpcB8IC+U5xpgLbAGGBWKHwqs9M9uC8XnAo/6+MVAv9Cz\nyf4dpcCkUPwAYInPMxtoFaXuyVrnZEQhcouW8MLGDRvcgsLgs66FhQ3ddiZZCzZjlVlYmJqFmnXV\n5+OdH+vkpyZr95u768wVM7Wqqip5LzaMBCBFizoTEZtC4Cgf7gC8BxwK3ARc6eOvAm7w4cHACqAV\n0B9YR/Xc0FJgmA+/AIz24WnA7T58DjBbqwVtPZDnr/VAZ/9sDnC2D98BXByl7qn5axiqWruzb+iK\n9fqsvg/VZXjYAAAdfUlEQVQL3MiRyReDaILZFCvwd+7aqdcuuFYLbizQaxdcqzt37Uz9Sw0jCmkT\nm1oZ4GlgpB+1dNdqQVqj1aOaq0Lp5wHHAj2A1aH4icCdoTTDfTgH2ObDPwbuCOW50+cTYBvQwscf\nC8yLUtdk/x2MEMnaoqUukYocPYUFbty45ItBU2/x8sXuL/SPr/9Ru9/cXSc/NVk/qvyoaV5sGDFI\nldjUa85GRPoDQ3Dmq+6qusU/2gJ09+GeOFNYwEagF7DHhwPKfDz+82OvDntFZKeIdPFlbYxSVgFQ\nqapVUcoyEiDe5Hcik+Px5lUSnWCv68yWyMn08HzH/fc37r31rUsy+Xz35/x92d+56fWbOL7P8RRf\nUMzh3Q9P/YsNI00kLDYi0gF4Avilqn4mUu0Zp6oqIk3lY1yv90yfPv2bcFFREUVFRUmuTmYRdMRv\nv129RiXa5HciHlPxOuaGeoGFCcSlQwdX37//Ha64oqbARbpZr1pV3baBA+E736kWnXS7QW/+fDN/\nWfoX/vbm3zi538m8cN4LHFV4VNNWwjBClJSUUFJSkvoXJTL8wc2/vAj8KhS3Bij04R5Um9GuBq4O\npZsHDMeZ2sJmtG9MZD7NsVrbjPaNqc3f/w03pxNpRjsOM6MlRNgMVZcJrC4TWaJnt4TLmDSpYee9\n7Nih2rVrzbmheG0Krg4daucLJv0DM1xTsXrbav3pMz/VvBvy9JLnL9G15Wub7uUxaE5n8BjNB9Lo\nICDAA8CtEfE34edmvMBEOgi0xnmMrafaQWCJFx6htoNAIDwTqekg8D7OOSA/CPtnc4BztHouxxwE\nEiAQgKOOUh0/vn5b6gedU+vW1R32+PGx3xUuIywIAwbUr5Pr3dvla9VKdfhwd3/CCbW94Fq2dJ+H\nH+7qFc2BID8/sbong7379upz7z2npz98uh5w8wE6fdF03fr51tS+tB4k8/A5I3tIp9icCFR5AVnu\nr9FeCBYQ3fX5WpwX2hrgtFB84Pq8DvhTKD7Xi0fg+tw/9OxCH78WmByKD7s+P4q5PidEYybAo40g\n6hodxPIcS+QcmjDh9JFX0Jbc3Oq4sWNjtzWox5Ahqfs1v3HnRp1RMkP7/L8+Ovzu4XrPsnv0i91f\npOZljaApzuAxMo+0iU0mXyY2jSPWOpqOHfWb0VGi62fCnmP17eSC9J06aY0RTFgwwiOWAw5o+CFo\nDWXXnl36xKondNwj4zT/hny9+LmLdfkny2OmT4YJq7Fl2OFqRjRMbExsmpSLLlLt3FlrjSASXaip\nGltUYnVysTrP8HvD8zfjxlXnKSjQWiOeZBGrXvuq9ukrG17Ri569SAtuLNAR94/Qe5bdo599/Vnc\nMpNhwjIzmJEKTGxMbOpNY375hjuynBzX0df33SecoNq2rZtnqasOQT3Do5NYnWekgIXrGZjSkm0W\niuzUV21dpdcuuFb73dpPD7v9ML3xtRvrvT4maEeHDs6015D6mhnMSAUmNiY29Sayk4wmPrEEKejI\n6ur86xKzsNdXPAGJnAuqqwOOHBUF9eza1YlaYaETxmR6Wo0Zo0qHT7T3hP+nR95+tPa8paf+5sXf\n6IpPViS0nUy0uiTiZRcPM4MZqcDExsSm3tQ1Cgg6t1immB07qgWja9ea3l8BdXmYhUcpwXxLrNFR\nUM+CAjeKiieQYYION+xEUFgY2wmhPiL06a5PdeaKmfq9e0dpq9/l6Y8fnawL1i/Qvfv2xvvqa7wr\n1ojNRiZGc8TExsSm3sQaBYQ7t7rMOUH+Aw6o7izD7sLh8iLTBF5f7dpF72ij1bN79+q0rVo5wUjE\ntBauS1hwogllvHmO3Xt36/PvPa8TH5+onf+ns54x6wydvXJ2g7zJ4q1pspGJ0RwxsTGxqTeRv+Kj\ndW6JmHPCHX7g6hzMyQRmq3CaLl2c2MRa6xKtjmFRgtojo7DnWSyzVHiX5sCJIXKEE01wq6qq9J8f\n/VOnPT9Nu93UTY+/53i9fentuu2LbQl/t9GIt6bJFlUazRETGxObehOeN6lrAWMsc06kp1fg6hzN\nUy0Qlfbta8aHBW7QIJcvN1e1WzcnKK1a1RSVYFQTlBcWuWhmqa5d6xbTyLaF06yvWK+/e+l3euBt\nB+ohfzlE//DyH3R9xfqEvttEPMHijVzMm8xojpjYmNjUm2gjkmjE6hQjPb2COZdwfH6+24omGOUE\nz4LOPfzrPZqwRF4tW6q+9VbtkUqkCSww/dW3w/9y95f68NsP64j7R2ib33XVXlN+qcef9W+tqHAT\n/Q3ZiqehoxKbszGaIyY2Jjb1JhgdFBREn+CPR7BNTGSHHnSS+flOgKIt3pw0yYlFsAAz1tWihfs8\n9FDVnj1rOhHEmnMKzFJB+yLnZaIJxrJNy/Tn//i5drmxi456cJQ++s6jelLRrlptS8WBbKkswzCS\njYmNiU29ieapFTY7xSOcLxjBFBY6U9gBB1QLQ7Rf6JGuz/n51eXl5dUUod6949fnoovcO1u1coIQ\nNonF9ERruUuH/fRBHX73cO17a1+dvmi6bthRrWZ1OUzYaMPYXzGxMbFJiGi/6sMeZ5G/2i+6yHXQ\n+fm1vdHqGsGEy4j2Cz1swgsWhUYTh/z86PNEdblZR446Ij3Ruh30kfK936pc0V1bTzlV2x/9jJ4y\ncm8t8YjlMGGjDWN/JlViU6/D04zmT7QzZLp1c9enn7p4EZg3z8UddBBs3uziFyyoee7M66+7z88+\ng507q8+WAWjf3p0ZU1kZ/Vybtm3dcxE48kg48UR31syHH8LWrS5NTg6UlNQ8UyZc/6OPhr593Xtb\ntapO06ULbNoEffq4Mtu2hW4HKNvavUzL4//MjgGLOLDyAjqveJnlxYPYDSyk9pk60erdVIenGcb+\nRrD1f1YiIprN7Yt2ENjYsTB3rjvJsrjYxRUVVXfgkeTmwtdfu/CQIfDSS9Wdf+h8PETglFOgdWtY\nsgTKy138hAnRO+cTT6wWq7qIzB+uf25udRnjxlXXY9u2UNmyDwY/QefTb+TzXV+y75+XwdvnM2Fc\nRz7/3JUFTtiGDoWyMidQnTrV//C0aN93ug9jM4xkIyKoqsRPWU9SMVxqLhdZbkYLz4v06+dMTSNH\nunC0814ir3btVH/4Q+dAEJ6DCUxZ0fKE16rE2llAtaYLdKwr2jb/YTNWrPmTMWNUyflK25zwN+UX\n39L2lx2nD7/5jI4es6+Wm3OXLrHfH+kAEM8TLdEdGOqzfsbW2hjNDWzOxsQmksh5kbATQDg8cmTN\nFf6BF9jw4dFX6EcKTSAcubmqIi7cqlXN9wTb+nfuXJ0mfIXjcnNrL3KMtVAzcv6k8qtKva74Bm3z\n2x76vb+frkWTX9GKiqpai0wDIo8nCD6jrSmKXDsUSaIOBfVZPxNOWx/nDcNIFSY2+4nY1OeXbrSF\nlMFEf6RDwLhxNdetRB5I1rJltZdXpIvxhg1u77PATTnWNX58dFfnnJxqMWzXLvoeafE66PN+9on2\nufBqbfXbAp3wyHn61ua3Eso/aZJbQHryydVtibemqGVL54YdOWpL1KGgPh5tdTlvxMNGRUYqMLHJ\ncrGpzzb7AUFHF4hLIBhBhxq5VUzQ8Y4c6TrTYIQTKRjhdNF+rce6xo6NPqoJj6aCnQMiPd+CNT3h\nDTsvukh12Oi12ueSn2nOb/OVMZcqeR9EPVY6soOv7/cZebR0Xea2eNTHoy3yb1gfl2vbgcBIBSY2\nWS428TZtjEVgPgqvzg/MMZG/4sPviDxsLLj69atpThJx62KCuY+WLWub5IKrTZvYczVHHFF7NBUW\njeHDq+MLC1VL3ntT25x/tnJFV2XEf2rXflu+GQHk5dVMG22rmvp+n5GdfixzW6oI3j9pUuKjFVsT\nZKSCtIkNcC+wBVgZiisAioFSYD6QF3p2DbAWWAOMCsUPBVb6Z7eF4nOBR338YqBf6Nlk/45SYFIo\nfgCwxOeZDbSKUffk/yVSRNBxtG9fc7I+HrHmV6L92g13TkGnetRR1XMvRx1VWxDCV+/e1Z1hvFFO\nNBGL3KwzPApyYlmlDFionD9KW17RS+X4W5TWn34jcrFGTeGjCHr3dm0IRmwtWqieemrinXHQ6UcK\ndbCvW9eu9T9ILiC8pimamS7y75noyNaExkgm6RSbk4AhEWJzE3ClD18F3ODDg4EVQCugP7COavfq\npcAwH34BGO3D04DbffgcYLZWC9p6IM9f64HO/tkc4GwfvgO4OEbdU/G3SAmJ7L4cyUUX1d4dOeiQ\nc3Jqn5C5Y4cbTZxwQk2vtSDcvXtNR4NIERs5MroYBe8MT8KH90mLHI20bl3zHtmnHPqEytTvKJcO\n0v7j79VuhV8nJGLBotC6BLB378b/fcKjvYaWV5eHX4CNVox0k1YzmheOsNisAbr7cCGwxoevAa4K\npZsHHAv0AFaH4icCd4bSDPfhHGCbD/8YuCOU506fT4BtQAsffywwL0a9k/13SCl1dTTRJoPr2pgy\nVmcW6f0ULRy+WrWqOa/TrVtNgQHVI4904vLWWzV/aU+aVFu8aswRtdylDPm7cukg5afDtOOwJ3Xc\n+H26Y0dtEY0lNJFb5kTOubRoUXMkkugIJfL7Dr6fWA4O9fn7gmrHjtH/1jZaMdJNcxObHaGwBPfA\nn4HzQs/+DpzlTWjFofiTgOd8eCXQM/RsHdAF+DXw21D8f/q4LsDaUHyfcN0i6p3cv0IjSfTUyUTX\neAST6sHEe6xfziKugx05submlcHoIp6XWfjKyXHCcuSRtZ+FjwHo3bt6pFPryq1UTrhRubyncv5p\nSv9FClUK1XMwkUcMtGxZ00TYpk3tTjqaYBYV1fzuI/dki0Xk971hg0vfUKEJ6jhuXN1ecYaRblIl\nNo3erkZVVUS0seUk+romek9KiLaVTJhgq5TwqvRu3dwWL+++69IccwzcdZcLb9/uPquq3Kr61q3d\nti579tQsV9VtN7NggVuVn5vrtpLZt686f6Ls3eu2twm2uAmzbJnbEmfnzhiZO5bBsbfBkHtg7Vh4\n+AXYcmSNJJs3u/Y/9hgUFLi6g6vrF1+4sAgMH16z6Lw8+M533I4BLVpUt6lzZ/cZ/u7BfbevvRa7\nncHWPMH3nZcHH38cO30i5OXB009X39u2OMb+REPFZouIFKrqZhHpAfjdrijDjTQCegMbfXzvKPFB\nnr7AJhHJwc3LlItIGVAUytMHeAmoAPJEpIWqVvmyymJVdPr06d+Ei4qKKCoqipU05UR2YNEIRCha\nhy3i9iQL0u3aVfP5ggXQsmXddQi2pkkFMTvjbqvg+D/CIU/Disnwt2Wws1/UpDk5cPPNcOWV1UIT\niaoTjkMPhdWrXdrSUie048c7IX35ZTjqKLj/fpcn+O4POwwqKuCf/3Tb1kD0LWdmzXLxgdAkwtSp\n8Nxz7jseOtQJpm1fYzR3SkpKKCkpSf2LEhn+UNuMdhN+bga4mtoOAq1xHmPrqXYQWAIMx5ndIh0E\n7vDhidR0EHgf5xyQH4T9sznAOT58J83YQSB8OuXQobVXuEeSiKdX27Z1mKia+Ip9Xk2VcuB85dzT\nld90V066XmlbnlCZrVpFP2itXbvouz+3bVt9P3Zs/XdzbuyWM7H+drb2xchESNecDfAIsAnYDXwM\nXOiFYAHRXZ+vxc27rAFOC8UHrs/rgD+F4nO9eASuz/1Dzy708WuByaH4sOvzozQj1+fILfujeXcF\nnVBYiALPsWCxZX2u4JyXdAsPqHNV/s5flJ8folxyuHL0XUrOl0kpu2tX1YkTq9vapUtt77jWrRNz\nrgjT2C1nIsuB6Pu+GUYmkCqxsV2fk0zkDssirvsJ6NoVBg1yuw4XF7s5kMbQqhWsXQv9+zeunEZT\nsBaG/RWOeBA2jIAlv4APv4sbyCaPnJzq76xLl+rdp8MUFjrzWmDCCv9Nou1SXVlZ22QWbffsgFg7\nPVdWwn/8h/ub33efmdCMzCRVuz6b2CSRqVPh8cfdnAG4znD3bncezKBBbo6hxvb4mU7OV3Dok3D0\nPXDAO7BsCvz7EtjZN6mviRRscB35Mce4eapoDBhQfRbOnj0uXaRw1HU8QDQBCognXoaRyaRKbOzw\ntCRSWlotNEEn99ln7n77djdx3Latuw97TGUWCj3fhCH3wrcfhbJh8MY0eO/7sC836W/Ly3OHr8U6\nj+eAA9xhbOHvMz8fevaszjNunBOFSOGoyzuwrkPUEnH0MAyjJi3SXYFsIuiEunZ15p7wyZjl5c4s\n869/ufuME5qCtfDd62Ha4TDhbPisJ9y5Ah6eC6t+1GihkRi/o2bNcu7ChYU14ysr3WjluOOckATP\ng9M/O3Vy98cc49yft26Fc891+QIaKhqzZrl3RprXDMOIjZnRGklgilm/Hnr1cmti+vVzp1kGtGxZ\nvaYlo8jbAIMfg8NmQ6cyeHcCvDMRNh4H2jS/U9q0ga++ciIxaJATjY4d3YgxbBYLnwwajGICM9j4\n8dHNXnWZygxjf8XmbBpAU4hNu3auM8wKZB/0WgoHPw+DnoMOn8CaHziB2XAyaJxFPPV9XWguJpZZ\n8bDDoE8fN5oAJw433wxXXJH4hH5dzwzDqImJTQNoCrHJycnQUUtAxzIYsAgOXAADX4DPu0PpGVD6\nfdg4POkCE6ZlS+jQoXoBazRHgIBgwn/9ejdy7NSptidYrFGKjWAMI3FMbBpAqsVm6lTn4tpY9+Um\npf1W6PcyDHjJiUy7bbChCD74nttCpnJAk1YnEJiwS3MknTo5T76waRKqTWINXblflzeaYeyvmNg0\ngFSJTdC5RdsfrFnR8msoXAG9l0DvxdBrCbQrh49OdOLywfdgyxFNNv8SjWBkGO3P1LZttYmysNB9\n3506OceLsEkscm1Tou7I5sJsGLUx1+dmRLMUmlZfuLUuhW9B97eg57/dfcVA2HgsrD8VXvlP2H5I\nWsUlkmijmU6d3IT/7t3V62Mef9zN00Sbrwm8ygCGDEnMs2zqVHj77frlMQyj4ZjYNID0Co1C54+q\nRaX72y7caaMTki1HwOYj4d2z4ZOhsLtDOitbbwoK4Oij4eGH4Ze/dG7keXnOfTkYeUSOQGbNir9y\nP9JkFl4T1bevmdAMI9WY2NSTQw5pwpe1rYBu70L3lW6UcsA7Tlx2t3eisuVI5y1WMh3KD4aqVk1Y\nueSSk+MWY27b5kYzF17oxGD7dncfLLqMFI0rr6w5XxOLyAWc4TU2wc7QNodjGKnDxCYK4bUz5eVN\n4Nrc6gvothoOCInKAe9A7mew9duw9XDYehisOsuJzJfdUlyh1BKskwnO3hFxHfu2bdVpVKMvuowU\nja1bq0eaYVGKJFpZkR5q8c4bMgyj4ZjYRCHyoK2k0WIPdCn1I5SQsHQsg/JBTlC2HA5LLnPhnX1J\n9kaW6aR9ezj5ZLj9dhgxwo1a9uxxwhIcBAfOZHb//c6M1q1bzRFGpGice271s7rmXqKdTxMpJrYN\njWGkDvNGiyC8mWaD9y+TKrf6/ptRiheWgnVOQLYe5i8/Yqn4FlRll+7HWrAZeH1FepAF5OXBihVu\nLU00b7HINTPJ3GnZ1uMYhrk+N4iGiE24g+vWraZppyYKbXdA/vvQ5T3o+h50XePCXdbCl12qxSS4\nth0Ke9s2pknNnhYt3KR+cTGceSZ8/rmLLy+v6a4crOoP1td07gwnnOAcAxLZFcAwjNRgYtMAEhGb\nKq2i3//2o0eHHgzIH8CTM3ux97POCC256KctueuuKsj91M2f5O6EDpud51enjW5CvrI/bB/kzGDb\nBzmPsPKDYXfHpmlkMyK8B9yECW4+JRDu3r1h5craK/6juTIH2EjDMJoeE5sGkIjYqCoXXLKZdzdt\nQDt/wMoPPqGq9U63T1iLfW5Nyted/NURPi+ET3u7az8TlAMOcPuUvflmzfjDD4eDDnKjmPC5Meee\nayMTw8g0TGwaQKJmtFjzB4ajUye3ALJfPzfaOO88N68ydy5cf33N+ZPI+RQbmRhGZmFi0wASFZtg\nbqBrV7dqPTiHZn+gbVu3jX+wwHHIEOeV9frrbj+yQYPsiGPD2J9Ildg0n31LGoCIjBaRNSKyVkSu\namg5wWFYLVpkh9C0bOkWSIKbgH/rLdiwwc2bnHyyiz/sMHea5erV8P777jTL8ePhpZfg+efd9/HP\nf8JTT5nQGIaRBFQ1Iy+gJbAO6A+0AlYAh0ak0fqQn6/qHHab39Wiherw4aoi7r59+0X61luq48ap\nnnqqas+eqm+9pTphguqOHe4KwmFixTc3Fi1alO4qpBRrX2aTze3z/WbS++xMHtkMA9ap6gZV3QPM\nBsY1psBgu5MWKf5WYh2BfOyxbrSxYYOTmB07qkcc5eWweDFUVLhRx6WXlnDEEe7I5PnzoawMjjjC\nrUXJy3NXEA4TK765UVJSku4qpBRrX2aT7e1LBZksNr2Aj0P3G31cg3nsMdeRByYoaLzwjBjhzFg9\ne7q5oR07nGCMHeu2zQ/iVOFf/3Ki0a+fy5uX58QkbMoKxKJNm8bVyzAMoynJ5GXrSfdsCDryDz+E\n44+Ho46C//kfGDPGbfRYXu7StWnjHAmefx5uvRVefdUd7HXEEbFXtJeV1XzXP/6R7NobhmE0XzLW\nG01EjgWmq+pof38NUKWqN4bSZGbjDMMw0oia63M1IpIDvAecAmwClgI/VtXVaa2YYRiGUYuMNaOp\n6l4RuRR4EeeZdo8JjWEYRvMkY0c2hmEYRuaQyd5oMUnWYs+mRET6iMgiEXlXRN4Rkct8fIGIFItI\nqYjMF5G8UJ5rfBvXiMioUPxQEVnpn92WjvbEQkRaishyEXnO32dN+0QkT0QeF5HVIrJKRIZnWfv+\nj/+3uVJEZolIbia3T0TuFZEtIrIyFJe09vjv51Efv1hE+qW5bTf7f5tviciTItK5SduWisU76bxI\nYLFnc7yAQuAoH+6Am486FLgJuNLHXwXc4MODfdta+bauo3qkuhQY5sMvAKPT3b5QOy8HHgae9fdZ\n0z5gJvATH84BOmdL+3DLCt4Hcv39o8DkTG4fcBIwBFgZiktae4BpwO0+fA4wO81tOxVo4cM3NHXb\n0v4fNAVf8nHAvND91cDV6a5XA9rxNDASWAN093GFwBofvga4KpR+HnAs0ANYHYqfCNyZ7vb4uvQG\nFgAjgOd8XFa0Dycs70eJz5b29QI+AvJxQvqc77wyun2+cw13yElrj08z3IdzgG3pbFvEsx8ADzVl\n27LRjJb0xZ5NjYj0x/0qWYL7h7/FP9oCdPfhnri2BQTtjIwvo/m0/1bgCiB8/mm2tG8AsE1E7hOR\nZSJyt4i0J0vap6plwC04wdkEVKpqMVnSvhDJbM83fZGq7gV2ikhBiupdX36CG6lAE7UtG8Umoz0e\nRKQD8ATwS1X9LPxM3c+IjGyfiJwBbFXV5UBUH/5Mbh/u193RONPC0cAXuFH1N2Ry+0QkHzgT92u5\nJ9BBRM4Pp8nk9kUj29oTICK/BXar6qymfG82ik0Z0Cd034ea6txsEZFWOKF5UFWf9tFbRKTQP+8B\nbPXxke3sjWtnmQ+H4yP2L0gLxwNnisgHwCPA90TkQbKnfRuBjar6hr9/HCc+m7OkfSOBD1S13P+S\nfRJnss6W9gUk49/jxlCevr6sHKCzqlakrurxEZH/AMYC54Wim6Rt2Sg2/wYGikh/EWmNm7x6Ns11\niouICHAPsEpV/zf06FncRCz+8+lQ/EQRaS0iA4CBwFJV3Qx86j2hBLgglCdtqOq1qtpHVQfgbL8v\nqeoFZE/7NgMfi8jBPmok8C5ubiPj2wd8CBwrIm19vUYCq8ie9gUk49/jM1HK+hGwsCkaEAsRGY0z\nY49T1V2hR03TtqaekGuiibExOG+udcA16a5PgnU+ETeXsQJY7q/RQAFuUr0UmA/khfJc69u4Bjgt\nFD8UWOmf/SndbYvS1pOp9kbLmvYBRwJvAG/hfvl3zrL2TQdW+7rNxHkvZWz7cCPsTcBu3PzDhcls\nD5ALzAHWAouB/mls2098PT4M9S+3N2XbbFGnYRiGkXKy0YxmGIZhNDNMbAzDMIyUY2JjGIZhpBwT\nG8MwDCPlmNgYhmEYKcfExjAMw0g5JjaGYRhGyjGxMQzDMFLO/wdgF1XPVq7VCQAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x23d4aa58>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_3_coef = get_coef(set_3, l2_small_penalty)\n",
"print set_3_coef[set_3_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_3, l2_small_penalty)"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 1247.59034404 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x2450b898>,\n",
" <matplotlib.lines.Line2D at 0x2450ba90>]"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAEACAYAAACODmB7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXt8VNXV978rJEFCIFcghnBJFVQEC3L1gsSCijyt0FZa\n1BaqPPA82lb7PL5eoH0V39qLtrbV1kvtRa1VkWK12ioCCmq1gjcUFeQioRDknqCgQiDr/WOf45xM\nZpKZZCYzSdb38zmf2bPPOfusOYH9O3utvdcRVcUwDMMwEk1Gqg0wDMMw2icmMIZhGEZSMIExDMMw\nkoIJjGEYhpEUTGAMwzCMpGACYxiGYSSFmARGRPJFZKGIrBGRd0VktIgUisgSEVknIotFJD9w/BwR\nWS8ia0Xk7ED9cBFZ7e27NVDfWUQe9upfFpF+gX0zvGusE5HpgfpyEVnhnTNfRLJafjsMwzCMRBHr\nCOZW4ElVPQE4CVgLXAssUdWBwDPed0RkEPB1YBAwEbhDRMRr505gpqoOAAaIyESvfiawx6v/JXCT\n11YhcB0wytuuF5E875ybgFu8c6q9NgzDMIw0oUmB8Tr0sar6RwBVPayq+4DzgPu8w+4DpnjlycBD\nqlqrqpXABmC0iBwNdFPVld5xfwqcE2zrEWC8Vz4HWKyqNapaAywBzvUE60xgYYTrG4ZhGGlALCOY\ncmCXiNwjIq+LyO9EpCvQS1V3eMfsAHp55VJga+D8rUDvCPVVXj3e5xZwAgbsE5GiRtoqBGpUtS5C\nW4ZhGEYaEIvAZAInA3eo6snAATx3mI+6fDOtlXPGctsYhmG0ATJjOGYrsFVVX/G+LwTmANtFpERV\nt3vur53e/iqgT+D8Mq+NKq8cXu+f0xfYJiKZQJ6q7hGRKqAicE4f4FlgL5AvIhneKKbMa6MeImJi\nZBiGESeqKk0f1TRNjmBUdTuwRUQGelUTgHeAJ4AZXt0M4DGv/DgwTUSyRaQcGACs9Nr50JuBJsA3\ngb8FzvHbOh83aQBgMXC2N4utADgLeNobMS0Dpka4frj9abVdf/31KbfBbGo/NqWrXWZT27UpkcQy\nggH4LvCAiGQDG4GLgU7AAhGZCVQCX/M69HdFZAHwLnAYuExDVl8G3At0wc1KW+TV/wG4X0TWA3uA\naV5be0Xkh4A/erpBXbAf4BpgvojcCLzutWEYhmGkCTEJjKq+CYyMsGtClON/DPw4Qv1rwJAI9Qfx\nBCrCvnuAeyLUbwJGN2q4YRiGkTJsJX8rU1FRkWoTGmA2xUY62gTpaZfZFBvpaFMikUT73NIJEdH2\n/PsMwzASjYigrRXkNwzDMIzmYAJjGIZhJAUTGMMwDCMpmMAYhmEYScEExjAMw0gKJjCGYRhGUjCB\nMQzDMJKCCYxhGIaRFExgDMMwjKRgAmMYhmEkBRMYwzAMIymYwBiGYRhJwQTGMAzDSAomMIZhGEZS\nMIExDMMwkoIJjGEYhpEUTGAMwzCMpGACYxiGYSQFExjDMAwjKZjAGIZhNMLs2VBRAZMmQU1Nqq1p\nW5jAGIZhNMK6dfDcc/DUU05sjNgxgTEMw2iEnBz3OWIE3H13am1pa4iqptqGpCEi2p5/n2EYyaem\nxo1c7r4b8vNTbU3yERFUVRLSVnvugE1gDMMw4iORAmMuMsMwDCMpmMAYhmEYSSEmgRGRShF5S0Te\nEJGVXl2hiCwRkXUislhE8gPHzxGR9SKyVkTODtQPF5HV3r5bA/WdReRhr/5lEekX2DfDu8Y6EZke\nqC8XkRXeOfNFJKulN8MwDMNIHLGOYBSoUNVhqjrKq7sWWKKqA4FnvO+IyCDg68AgYCJwh4j4/rw7\ngZmqOgAYICITvfqZwB6v/pfATV5bhcB1wChvu15E8rxzbgJu8c6p9towDMMw0oR4XGThQZ/zgPu8\n8n3AFK88GXhIVWtVtRLYAIwWkaOBbqq60jvuT4Fzgm09Aoz3yucAi1W1RlVrgCXAuZ5gnQksjHB9\nwzAMIw2IZwSzVEReFZFZXl0vVd3hlXcAvbxyKbA1cO5WoHeE+iqvHu9zC4CqHgb2iUhRI20VAjWq\nWhehLcMwDCMNyIzxuNNU9QMR6QEsEZG1wZ2qqiLSWvOBbd6xYRhGGyAmgVHVD7zPXSLyKC4eskNE\nSlR1u+f+2ukdXgX0CZxehht5VHnl8Hr/nL7ANhHJBPJUdY+IVAEVgXP6AM8Ce4F8EcnwRjFlXhsN\nmDdv3mfliooKKioqIh1mGIbRIVm+fDnLly9PSttNLrQUkRygk6p+JCJdgcXADcAEXGD+JhG5FshX\n1Wu9IP+DOBHqDSwFjvVGOSuAy4GVwD+A21R1kYhcBgxR1UtFZBowRVWneUH+V4GTcTGg14CTVbVG\nRBYAj6jqwyJyF7BKVe8Ks90WWhqGYcRBq67kF5Fy4FHvaybwgKr+xOv8F+BGHpXA17xAPCIyF7gE\nOAxcoapPe/XDgXuBLsCTqnq5V98ZuB8YBuwBpnkTBBCRi4G53vVvVNX7AnbNx8VjXge+oaq1Ybab\nwBiGYcSBpYqJERMYwzCM+LBUMYZhGEbaYwJjGIZhJAUTGMMwDCMpmMAYhmEYScEExjAMw0gKJjCG\nYRhGUjCBMQzDMJKCCYxhGIaRFExgDMMwjKRgAmMYhmEkBRMYwzAMIymYwBiGYRhJwQTGMAzDSAom\nMIZhGEZSMIExDMMwkoIJjGEYhpEUTGAMwzCMpGACYxiGYSQFExjDMAwjKZjAGIZhGEnBBMYwDMNI\nCiYwhmEYRlIwgTEMwzCSggmMYRiGkRRMYAzDMIykYAJjGIZhJAUTGMMwDCMpmMAYhmEYScEExjAM\nw0gKMQmMiHQSkTdE5Anve6GILBGRdSKyWETyA8fOEZH1IrJWRM4O1A8XkdXevlsD9Z1F5GGv/mUR\n6RfYN8O7xjoRmR6oLxeRFd4580Ukq6U3wjAMw0gssY5grgDeBdT7fi2wRFUHAs943xGRQcDXgUHA\nROAOERHvnDuBmao6ABggIhO9+pnAHq/+l8BNXluFwHXAKG+7XkTyvHNuAm7xzqn22jAMwzDSiCYF\nRkTKgEnA7wFfLM4D7vPK9wFTvPJk4CFVrVXVSmADMFpEjga6qepK77g/Bc4JtvUIMN4rnwMsVtUa\nVa0BlgDneoJ1JrAwwvUNwzCMNCGWEcwvgauAukBdL1Xd4ZV3AL28cimwNXDcVqB3hPoqrx7vcwuA\nqh4G9olIUSNtFQI1qloXoS3DMIxGmT0bKipg0iSoqUm1Ne2bzMZ2isgXgZ2q+oaIVEQ6RlVVRDTS\nviQQ93XmzZv3WbmiooKKiooEmmMYRltj3Tp47jlXnj0bFixIrT2pZvny5SxfvjwpbTcqMMCpwHki\nMgk4CuguIvcDO0SkRFW3e+6vnd7xVUCfwPlluJFHlVcOr/fP6QtsE5FMIE9V94hIFVAROKcP8Cyw\nF8gXkQxvFFPmtRGRoMAYhmHk5LjPESPg7rtTa0s6EP7gfcMNNySs7UZdZKo6V1X7qGo5MA14VlW/\nCTwOzPAOmwE85pUfB6aJSLaIlAMDgJWquh34UERGezGUbwJ/C5zjt3U+btIAwGLgbBHJF5EC4Czg\naVVVYBkwNcL1DcMwGuXBB2HqVFiyBPLzmz7eaD7i+usYDhQZB1ypqud5M7wW4EYelcDXvEA8IjIX\nuAQ4DFyhqk979cOBe4EuwJOqerlX3xm4HxgG7AGmeRMEEJGLgbmeCTeq6n1efTkwHxePeR34hqrW\nRrBZY/19hmEYBogIqipNHxlDW+25AzaBMQzDiI9ECoyt5DcMwzCSggmMYRiATd81Eo8JjGEYQGj6\n7lNPObExjJZiAmMYBmDTd43EY0F+wzAA5xabPduJi03f7bjYLLIYMYExDMOID5tFZhiGYaQ9JjCG\n0YaxmV9GOmMCYxhtmETN/DKhis6RuiOpNqHNYgJjGG2YRM38sinKkdl/aD89ftaDi/56Ee/tfi/V\n5rQ5TGAMow0QbYSRqMSNNkU5Mk+tf4qTep3E4B6DGXvPWKY/Op0Nezek2qw2gwmMYbQBoo0w8vPd\n+0xaOq3YMgxHZuGahVw05CLmjJ3Dhss3MKBwAKf84RQu+dslvF/9fqrNS3tMYAyjDZDsEUaihKo9\n8UntJyzasIgpx7s3snfv3J3/O+7/sv676+mb15dRvxvFrMdnsblmc4otTV9MYAyjDWAjjNbn6Y1P\nM6J0BD269qhXn39UPvMq5rHuu+volduLk+8+mUv/filb9m1JkaXpiwmMYbQBbITR+ix8dyHnn3B+\n1P2FXQq58Qs38t533iP/qHyG/nYo33nyO1R9GPUFux0OExjDMIwwDh4+yD/W/4Mvn/DlJo8tzinm\nJxN+wppvr6FLZheG3DmE7y36Htv3b28FS9MbExjDMIwwlry/hCE9h1CSWxLzOT279uRnZ/+Md7/9\nLhmSwYl3nMiVT1/Jjv07kmhpemMCYxhpiC18TC0L313I+YOiu8caoyS3hF+c8wtWX7qa2rpaBt0x\niGuWXMPuj3cn2Mr0xwTGMNIQW/iYOg4dOcQT657gKyd8pUXtlHYr5bZzb+PN/36T/Yf2c9xvjmPu\nM3PZ8/GeBFma/pjAGEYaYgsfU8eyTcsYWDSQsu5lCWmvrHsZt//H7bzxX2+w5+M9HPeb47hu2XVU\nf1KdkPbTGUvXbxhpiL2bJXXMenwWxxcfz5WnXpmU9jdVb+JHL/yIx9Y+Rr8d36XLqu/RvXMeDz6Y\nHn9rex9MjJjAGIYRD4frDnP0LUfzyqxX6J/fP6nX2rh3I6fN/SE73hgBK7/D1KluKnqqSaTAZCai\nEcMwjPbAc5XP0T+/f9LFBeCYwmM4+d/38tTK9usKtRiMYRiGxyNrHml0cWWiae8ZGsxFZhhpzuzZ\nblZZTg5p46dvjxypO0LvX/Tmn5f8k2MLj021OSnDXplsGB0Im7LcOry45UVKcks6tLgkGhMYw0hz\nbMpy69CSxZVGZExgDCMK6bKavr376dOBOq1z8RcTmITSqMCIyFEiskJEVonI2yIyz6svFJElIrJO\nRBaLSH7gnDkisl5E1orI2YH64SKy2tt3a6C+s4g87NW/LCL9AvtmeNdYJyLTA/Xlnl3rRWS+iGQl\n6H4Yxmck2zUVq4BZJuXks2LrCvKPyuf44uNTbUq7olGBUdVPgTNVdSgwFJgoIqOBa4ElqjoQeMb7\njogMAr4ODAImAneIiB8suhOYqaoDgAEiMtGrnwns8ep/CdzktVUIXAeM8rbrRSTPO+cm4BbvnGqv\nDcNIKL5rKjcXqqsTP4qx2Er60FRqfqN5NOkiU9WPvWI2kAUocB5wn1d/HzDFK08GHlLVWlWtBDYA\no0XkaKCbqq70jvtT4JxgW48A473yOcBiVa1R1RpgCXCuJ1hnAgsjXN8wEsaDD0JxMezfD0uXJl4E\nLLaSHqgqC9dY/CUZNCkwIpIhIquAHbgOfyXQS1X9HNQ7gF5euRTYGjh9K9A7Qn2VV4/3uQVAVQ8D\n+0SkqJG2CoEaVa2L0JZhJIz8fBg50pVbKgKR3GGJjq2kS8yorfHqtlc5KvMoBvccnGpT2h1NruT3\nOvKhnnvqUREZHLZfRaS1FpvEfZ158+Z9Vq6oqKCioiKB5hjtnQcfTExOMN8dBq49P6aSyNQgka5h\nNI3vHgt58zsWy5cvZ/ny5UlpO+ZUMaq6T0SW4VxXO0SkRFW3e+6vnd5hVUCfwGlluJFHlVcOr/fP\n6QtsE5FMIE9V94hIFVAROKcP8CywF8gXkQxP/Mq8NiISFBjDiJdEiUBruMPM5RY/qsojax5hwdSO\nq8bhD9433HBDwtpuahZZsT9DTES6AGcBa4DHgRneYTOAx7zy48A0EckWkXJgALBSVbcDH4rIaC+G\n8k3gb4Fz/LbOx00aAFgMnC0i+SJS4F37aW9p/jJgaoTrG0Za0hpTjW06c/y8ueNN6rSOYSXDUm1K\nu6TRVDEiMgQXRO+EE6OHVfVGb4bXAtzIoxL4mheIR0TmApcAh4ErVPVpr344cC/QBXhSVS/36jsD\n9wPDgD3ANG+CACJyMTDXM+dGVb3Pqy8H5uPiMa8D31DV2gj2W6oYw0gw7Sl1zQ+e/QGHjhzi5rNu\nTrUpaYOl648RExjDSDwVFaFYT7qkmG8Oqsrxtx/P/V++n1G9R6XanLTBcpEZhpEy2kus551d7/BJ\n7SeMLB2ZalPaLSYwhmHERXuJ9Tzy7iN89YSvdtjZY62BucgMI4W0p3hGW2PInUO46z/u4rS+p6Xa\nlLTCXGSG0U6wdDGpYe3utez5eA+n9Dkl1aa0a0xgDKOZJGLlfHuJZ7Q1fPdYhlgXmEzs7hpGgHhE\nIxGjj/YSz2hrLFyzkK8O+mqqzWj3xLyS3zA6AvGkW0nE6CPR6WKMptm4dyPbPtrG2L5jU21Ku8dG\nMIYRIB7RsNFH22TBOwv48vFfplNGp1Sb0u6xWWSGEaCmJjHJLZuDzShLPkfqjnDsr49lwfkLGNnb\n1r9EIpGzyMxFZhgBUumysmzIyWfRhkUU5xSbuLQS5iIzjDTBZpQln9tfuZ3LRlyWajM6DCYwRocm\nnV7S1doxnXT67a3Bxr0bWVm1kmmDp6XalA6DxWCMDk17SdzYHDrab79q8VUoys/P/nmqTUlrLAZj\nGAkiFrdUew2+dySX3Ce1n3Dvm/fy8syXU21Kh8JcZEaHJha3VHtN59KRplkveGcBI0pHcEzhMak2\npUNhLjLDaIJJk5y4jBjR/M64vY6C2gqjfjeK68ZdxxcHfjHVpqQ9luzSMFqRRDzpNzYK6mjB9tbm\nlapX2HlgJ+cee26qTelwWAzG6HBEG01Eq4+0NibeEUlj8Y5Ur39p76OrO169g0tHXGor91OBqrbb\nzf08w6jPuHGq4LapU5uuj6eNaFRXu+OqqxvuO/dc186IEZH3J5t4f0tbYveB3Zr/03zduX9nqk1p\nM3j9ZkL6YHORGR2OaKOJeGZVxTsDyx8FRRodpDrY3p5nk9276l6+NPBL9OjaI9WmdEgsyG+0aYLu\nnR49YPPmpl090fKNxZOHLJU5yxJNe/otQeq0joG/Hsifv/JnxpSNSbU5bYZEBvlNYIw2TXCxYHEx\n7N7tyh1h4aDROIs2LGLuM3N5bfZriCSkv+wQ2Cwyw/AIuneGDnXl4mLYtq1ls7KSMbOrJW3Gc67N\nSnPc/srtfHvkt01cUkmigjnpuGFB/nZPMHjul087Lf6g9axZLth97rmunXgD3+HnR6IlwfRkTkBo\nj2yq3qRFNxXpgUMHUm1Km4MEBvltmrLRpgmfQrxggXtyh/iC1uFTheMNfAfPHzAARo5sGAdqSTA9\nmRMQ2iO/ffW3TP/8dHKyclJtSscmUUqVjhs2gumQNDYlOBrhU4XjbcM/Pzc3+uihOXY159yWXKc9\nsLlms/a4uYe+t/u9VJvSJiGBIxgL8hsG9WdSXX11/AsP/fOrq2Hp0pallWkp7X3hZGN8XPsxp//x\ndC4achFXnnplqs1pk9gsshgxgWm/JLMTbUka+3SY8tvR0vD7qCoX/vVCMjMy+dOUP1lwv5m06iwy\nEekjIstE5B0ReVtELvfqC0VkiYisE5HFIpIfOGeOiKwXkbUicnagfriIrPb23Rqo7ywiD3v1L4tI\nv8C+Gd411onI9EB9uYis8M6ZLyJZibghRtsgmRmOWxLDaGxBZWvRUWMwN714Exv2buDuL95t4pIu\nNOVDA0qAoV45F3gPOAG4Gbjaq78G+KlXHgSsArKA/sAGQiOllcAor/wkMNErXwbc4ZW/Dsz3yoXA\nRiDf2zYCed6+BcDXvPKdwH9HsD3R7kkjTUhmepVExTBimVmWDDpiDObv7/1dS28p1a37tqbalDYP\nCYzBNCdw/hgwAVgL9NKQCK31ynOAawLHLwLGAEcDawL104C7AseM9sqZwC6vfAFwZ+Ccu7zzBNgF\nZHj1Y4BFEWxNwu030oG20InadOHWYc2uNdrj5h760r9fSrUp7YJECkxc05RFpD8wDFjhicsOb9cO\noJdXLgWCr43bCvQGar2yT5VXj/e5xVOEwyKyT0SKvLa2RmirEKhR1boIbRnthMbiLJEyHKcbHdVV\nlShiibPVfFrD5PmT+emEn3JKn1Na30ijUWIWGBHJBR4BrlDVj4I+TlVVEWmtaHpc15k3b95n5YqK\nCioqKhJsjpEsUp3GvqU8+CCcfDJ07gwXXui+N2eGWkelqb//kbojXPDIBUw8ZiKXDLuk9Q1sJyxf\nvpzly5cnpe2YBMYLoD8C3K+qj3nVO0SkRFW3i8jRwE6vvgroEzi9DDfyqPLK4fX+OX2BbSKSiYuz\n7BGRKqAicE4f4FlgL5AvIhneKKbMa6MBQYEx2hbBEUCXLm52VCo75nhnruXnwyefwIsvuu/f+pab\nZdaWRbOlxHMPmxoBznlmDoeOHOLnZ/88OcZ2EMIfvG+44YbENd6UDw0X7/gT8Muw+pvxYi3AtTQM\n8mcD5bjAvB/kXwGM9toMD/LfqaHYTDDI/z4uwF/glzUU5P+6hmIzFuRvZ1RXq5aXu9QvBQWpj2c0\nJ6YStHvKlNS/+yXVxHMPG4uz/fnNP2v5r8p194HdSbGzI0NrBvmB04E6TzTe8LaJXue/FFgHLPY7\nfu+cubjZY2uBcwL1w4HV3r7bAvWdPcFYj4vf9A/su9irXw/MCNSXe4K1HngYyIpge7L+BkaS8Wdg\nBTtof6X8hAmJ6ZzjneVVVuZsyMtTrayM7RoTJrhzhg1rXoaA5pKqGWxNkQiBfaXqFS2+uVjf2v5W\nYo0zVLWVBaYtbyYwqaUlnVzwSRdUhw5VLSqq//Tb0k403hFJc5JoBkdhrdnZp+sMtpYK7AcffaB9\nftFH//ruXxNrmPEZiRQYS9dvJI2WLIb0/e9Dh8KUKbBsGYwa5ep8n3xLF1tu3Og+8/LgZz9z5cZS\n3XfvXv/6sZCfD337ujhMMhaFRiNS/Cod0ve3ZCHqwcMH+crDX2HmsJl8+YQvJ944I/EkSqnSccNG\nMCmlJe6QSE+64XUtdbdEGpEEn/yLi+uPOpr79J2ouEs8I7agrek6mgmnsd9XV1enM/82U788/8t6\npO5ISuzrKGDJLmPDcpGllmTn5Wpp+5MmuVFFMDGlX5ebC/v3u+PC83nFO5ssUfehuTnGJk46zNNv\nvE3n3uvoM3gTY8+rZNfBrXxc+zGfHv6UTw9/SifpRE5WDr1ye1GaW0ppt1L65/dnZO+R9Mvr1yqp\nVxr7fb9Z+Rt++9pv+dfMf5GbnZt0WzoyluwyRkxgjMaI1PHHkhU5VckkIwliJD49/CnPb36eFza/\nwEtbX+KVqlf4eHsZR7afADXlDCvvz/Xf60PX7K50yexC58zOHKk7woHaA+zYv4NtH21j20fb2Fi9\nkZVVKzmiRxjdezRjysYwuvdoRvYeSffO3Vvt9z276VkufORCXpr5Ep8r+FzCr2vUxwQmRkxg2jap\nTDvvC02XLrB5c30bYunom2N7U+dEEkT/nKO61nLxjYv52/sP8I/1/+CkXicxrt84TutzGmPKxnDR\nVwtiEqdwVJWtH27l5a0vs6JqBS9vfZlV21fRL78fp/c5nYnHTmT858YnRHAi/b5N1Zs45Q+n8MBX\nHmD858a3+BpG0yRSYFIeJ0nmhsVg2hQtfW1xMohkQyyxmFhtD/7m5sxSGz7pTeU/LlWuKtaiq0/V\n21ferjv372xwXCKnRx86fEhf2/aa3vLSLXr2/Wdr7o9z9Yx7ztAfP/9jfX3b6wmLkXx08CMdcscQ\nvfXlWxPSnhEbWAwmNmwE07rE89Qe6dhw19P+/bG5hJI50unTB7ZudTPI3noL+vVr+hyI3Z0V/M0l\nJbB9e9PnHKk7wuPvPc5tK2/jX+vWcfDF/2JI3Td5/vHyhPz2eO/nx7Uf81zlcyzasIhFGxdR82mN\nc6WVjmRU71GMKB1BUU5RzNffsHcDv3vtd9z75r2cf8L5/GbSbyz9fitiLrIYMYFpXWKJTcyeDU88\nAbt2wZEjoWPz82HhQhf7GDYMnn02dHxTwfFkxkROPz2U6iWetmMN7AeFaOFCuOqq6OccrjvM/Lfn\n88Pnf0jBUQV8b8z3GH/0V/n2pVkJnUjR0vu5Zd8WVlatZGXVSl7Z9gqvffAaxTnFnwnOwKKBfFL7\nCfsP7f9s++jQR+w/tJ9V21exdvdaZnx+Bv958n9yXPFxiflRRsyYwMSICUzrEstTe7DzAigogPff\nd2td/PrJk+Gxxxqe25LrNpdg24MGNYzHBGnsyT/avliEKCgsvbr2Yl7FPM7sf2bSnuoTfT/rtI51\ne9Y5wal6hY3VG+ma3ZXc7Fxys3Ldp7cNKBrA+PLxdM7snJgfY8SNxWAsBpOWxOLn99eEgGpWlmqP\nHi4djL9Kv7g4/lXv0a4bbV1FPPXxrCcJ7i8vD7U1fbpLLxNvfKWurk4fXfOoDvz1QB37x7H6zPvP\naF1dXaPnJCJFTFt4146RPLBUMSYwbZXqatXJk13ix2BQG1Q7d1YdPbp+R5yodDPBTj3eep+mFkwG\n9wd/W3FxqFxQEJvYvVr1qo67Z5wOvmOwLlq/qElhifU3xEq65jIzko8JjAlMm6Gx0UJ4IktQ7dJF\n6yWUjKfDDL9WNEGIt96nqSf74P5gW37Cy4KChkkyw3/fln1bdPqj07Xk5yV696t3a+2R2sZ/dBiJ\nyhqQDjP4jNRgAmMC0yaYNSu6ayg8maXfAYePYOLpMMM7xUiCMGuWG12UlDTs7BPhGjruOPebCwtV\nJ01qOoOy//tOHnlIb1h6sxbdVKRzl87VDz/9sFnXT5R7q7lCZSOfto8JjAlMi2itTiDY4Ye7hvwO\nrHt3rfd0H96xNdVhBn+LP1JorFNsLNdYpDbjvT9BQS0ra7q96mrVihnP6fG/PlEn/nmibtizIa7r\nJetv2VyhSpeRjwld8zGBMYFpEa3VCfhiEck15HdglZX1OzK/fvr02DqI4G+ZPDn2SQa5uZHvQfio\nK5IINdZ5+fGWnJzQb452v3fs36EDrpqhna8t02EXLtS9e+vHWWLpJNOlQ/dJlxeqpdt9aUuYwJjA\ntIjW6gRWSQ44AAAeEElEQVTCn4JnzXKuqYKC0EvDonWisXYQkX5LUyOGqVOjj3aC1+3UKVQuKQkd\n15htlZVu5BIU1PAXlR2pO6J3vXKX9ri5h5ZdcqWS/WHEtmK5B+nSofukywy0dLsvbQkTGBOYFpGq\nTiA87jJ1avRONNYOItKIp7GUK774TJjgZrKFtx0cdUWyNx7bfIL2TPjmazrqd6P01D+cqm9uf7PR\ntmK5Trp06OmG3ZfmYwJjApNQkumvjhQjAdWuXd33aCOJ6dPdGpnSUtdBl5U1vj4mKAYlJdE75qZG\nBf4bKHv1ciOOrKyGbcXSeTX43Z33ac8Zl2uPm3rqH17/w2f5uhpryzpJIxWYwJjAxE1jIpIsf3V4\nPKOwULVnz/rTk6PFTSLNMmvMxuDTfnhcJ9px0Vx04dcuK2tJsLtOR874i3b5fm/9xoJLdPeB3fE1\nZBitTCIFJjMh6QCMtMd/vTC41CT5+aHUJVlZrj6eVwHHes19+1y5UyfYu9eV/esNGwb33hs5FYn/\nyt/u3eHDD0OfxcWwbZtLZxJMufLgg/VTrkR7QVheHvToETov/L4sWBC6tm/js8/Gny4lJwfI30T3\nC7/NR8dv5unzHmJsv7HxNWIYbRzLRdZBCM8vFZ77Kzs71DmH5826+urQ9x496ufjCu4Lz7/lXzM7\n271XZd8+6NoVDhwIXTc855h/7aws91bJX/3KJYD82c/c57Zt8SefDOY/Ky6G3btduaQEBg9u+GKx\nmhr41rdABO65p2lxCd6vHj1g078P8UH/X/Dvsp9z7Rn/h+9/4X856cRs3n/fjWlOO8397nizTXcE\nOurvTicsF5m5yOImnvfZh7vMwteOxBKkV3VxlOJi1fz80DF+TMOPwTR27fApwsHV/127huIz0day\n+DPW/DxnwVX1/pad7WwaNy72qdF++5EmFeQNeUG57ETlonN10oXvf3Z80FUYiyuyo06z7ai/O53A\nYjAmMC0lltXlvvj402y7dw91AP6+WIUqfO2Jv/XrV79T79q14TF+R+MH76PFZaJ1+uDynFVWumv4\nIhe+ZWY2TwCys1XJ2aXFl8zUznN6K4P+osNH1NW7H0FhPumkpgUslhlk7XExoU0vTj0mMCYwSSVc\nfIKddXhQvrGFkX5n0amT67wj5R7zRxd+px7s5MOD8eH7/O/+MY1NDAiKRvgoJnyLpXP7LCt0Rq0y\n6teacU0P/e/HrtDN2/dFFO7KSjfi8tPHRKOpadRBEvG0n24iZTPnUo8JjAlMs2lOhxJt5lVw6nCk\ntSfV1fWf3EFVJFTu1Ck0KvEXIQZFJNrixmgzvIKvAgjfgqlqoo1ihgxxI6qg2y3S4lC/jYKTn1Uu\nHaxZM7+gw85++7PU/LG+CqCpGWxNiUb4As7mYC4pIxwTGBOYBjSnAwu+sySWxYyNdfa+UOTm1u+I\nG+v0wwVn0qRQ20E3UrTMy+H5zaqrI7vR8vMbdsD+KKZ7d9WzzgqNFhqLP4E7rrK6Us9fcL72uaWf\nnnLJI3rqaXWf7Q+PUflE6sgj1cXjImpsQWmsmEvKCMcExgSmAZE6q2BnO2WKq4v2zhL/nKZGOMHO\nPiPDfQ4bpjptWuQYRnW1GxX4I4aCgpCodOtWPx1LaWlogWVQpCIJmojLvBxuZ3W1W2vji0c0l1Q0\nV0x4h1tPILM/1OP+6zotvKlQb1h+g3586GM97rjQ7z7ppJBwRRPaYEceqS58gWlj4p8IcTCXlBGO\nCYwJTAMidTbhCxpV63cokc6J562NkUYe4Drc4IghKHSRRiLg3gMT7f0vvisouEUSs1jiF00JaHiH\nW12t2qPkoDLq15p5bS/92vxvaGV16McFZ4eVljZ0C/puvkixqkgLQiONwKKNTkwcjGTQqgID/BHY\nAawO1BUCS4B1wGIgP7BvDrAeWAucHagfDqz29t0aqO8MPOzVvwz0C+yb4V1jHTA9UF8OrPDOmQ9k\nRbE9KX+AdCRSZ+M/TQ8dGvtTfKxvbQyOPCZPbugKC3b6QTE46qhQOSenvvAE08kEX50cHscJbiNG\nuE67pCR6cspos8v8Y6K5F88Yd0SHXjRf+91yjJZcOVGfX/dGg/vRubN+Npp7883I7jxf3FUbCmj4\ntcPPTZXrKt2C/6mgo96D1haYscCwMIG5GbjaK18D/NQrDwJWAVlAf2ADocWcK4FRXvlJYKJXvgy4\nwyt/HZivIRHbCOR720Ygz9u3APiaV74T+O8otifpT5BeRPuPEG/OrOrqyC6qIP5+vyP0xWv69JAb\nbNiw0JN6sMPMy3Pn+t/9clCAJk1y7iXf/Qb1A/LBmE1Wlhs1+O+UifbkHylPmb+Vlzd8KVpdXZ0W\njHxSmTVCmT1cT/vGM1HvcfgL0iKNQHz3pGpDAQ8XHF9ghwypPwpr7c7Ogv8d9x60uovME4ugwKwF\nennlEmCtV54DXBM4bhEwBjgaWBOonwbcFThmtFfOBHZ55QuAOwPn3OWdJ8AuIMOrHwMsimJ3Em5/\n+tGS1wqHnxvsIP0n7+A5vXqF9vsuoXAbJk9u6Erz3wmTnR2q693biUz4CCcoLiKhUcfQoSH7gscE\nN1+AREJlv/3cXGeXH6MJj0PlF9TpQ689oSPvHqkZ3zlRGbRAkSMNfk9wdOQLhj/iCp9K3a1bfXdh\nUwteoz0UtHZnZ8H/jnsP0kFgqgNl8b8DvwYuCuz7PfBVzz22JFA/FnjCK68GSgP7NgBFwJXA9wP1\nP/DqioD1gfo+QdvC7E74zU9Hgp1cr14Np9QGCe+owv8TBUccRUVuv98hh482Gnsy9+MmIk5EKiud\nUAXdWME1MI1twbU34Qsog1tWVvTRTHDkU1gYemWys7tOM0/8m3b9n+Ha7eoheu/Kv+j4CUc+E7UG\nwX7qT2IoL2943aD7rzFBiDWO0tqdncV3Ou49SKTAtDjZpaqqiGhL24n1cq10nTbB7NnwxBPwySfQ\nsyeUl8OKFW7f0qWh5I1BNm50n3l5Lr9XXl79JJFdukB1NWRkwJ49LpeYBLIS+eWuXWH/fnf+gQOu\n/qyz4OijXZ6z/fvdcaqwaxdcdpk77siR0PWHDXN2Dh0Kb78Nhw83/I1+7rJ773V5z95919UPGQI7\ndsDOnSG7amvdBi65pn+tLl1g1CiXjywzM5R084wvfEr28AfIvPwXcCSbA09dB+9N5rF1GfQuhc6d\nobISTjwR+vRxOdUOHXI50qqrYcYMl5etpsYl4vR/15lnut/v5zhrLIFoeGLOaIQn80w2sdrVnrF7\n0HKaKzA7RKREVbeLyNGA99+cKtyIwqcM2OrVl0Wo98/pC2wTkUxcnGWPiFQBFYFz+gDPAnuBfBHJ\nUNU6r62qaIbOmzfvs3JFRQUVFRXRDm1zrFsH27eHvmdkhMrDhkXu2Pr1g61bXeLJq65y/4H8/0Sz\nZ4eEoa7OfWZluY5aPWmvrXWd+YEDrgMN8vzzMGZMKLFkkJUr4aijQt/373dZigFWrQplWA7Hv87Q\noa4j97Mzr14dOkYkZJ+PLy7ghKGoKJDoMmc3jLiTf4+8A7YPgydug01fwA3GQ/YfPOi2mhqXZNO/\nli8eWVkhQQPXIU2cCB98AOvXu2vGkijziSfcdYYPh7/8JXrC0Z074cILW5YE0pJJGuEsX76c5cuX\nJ6fxWIY5NHSR3YwXawGupWGQPxs302sjoSD/CmA07n9xeJD/Tq88jfpB/vdxAf4Cv+ztWwB83Svf\nRQcN8gfdNkVFzhUl4txY48ZFniEVzCsWvviwqVQr4VvQDQRuwaJvUzDWkjbb0a8qX5qlXJOvnDdT\n6fF2QtuPFHtqykUW7a2ZjS34bEkMpqMGro3YIYEusljE5SFgG3AI2AJc7HX+S4k8TXkuLo6yFjgn\nUO9PU94A3Bao7+wJhj9NuX9g38Ve/XpgRqA+OE35YdrRNOV4ZgtVV7tObcqUyLGJSB1TY4srG5sO\n3NTmC1unTiGhS7mgoEr2R8rJv1NmD1e+108Ze6OS+4FCw4B8LNuJJ4ZiUkOH1p8wEIzV+DGZ8AWX\n4QQfEoKz7/y/RSxJReP5NxXtDaKG4dOqAtOWt7YoMOHp6v18X029Mjg8CD1sWP2Oye/oInUwwWsG\n13WkXByavdUpvVco/3Gpck2BMm2ycuyTihxuVnvBAP7kyfWDv8HyrFnub1RS4tbEREsbE+zwKytV\n+/Z1I9AJE+o/AATzrLUk4Bw+w6+8vOksAUbHxQQm1h/XBgUmKAjROrxo75KfPNmtIwmunwhfWd63\nb8N1Lv41MzNdZ9rY6KNLl0SJQBK2go3KGf9P+c5A5bvHKuNuULpviXp8vKOsSEkloy3inDo1ejLK\nxtxf/jTsRI4wmlp7YxhBTGBi/XFtQGCOO851QMXFrhPyFzL6U3j9p2f/M7zjCXZw/or2goL6uayC\nsZLg07i/kjw4DbmpLW1cX/6W+4Ey4g7lktOUq3oo535H6f2yQl2T5w4eHP/1unQJ3dfp0+sv0gwX\nh2juSH8qePgoc8SIyOljwol30WVTa28MI4gJTKw/Lo0Fxu8kgutCysrqP12WlbkOJzfXLdjLznau\nF1UnTOEp5+OJKWRluVXo0XKDpfWWt1kZ80vl4rEuYP/VC5SBTygZh1rVjuDIMDPT/W2a6sjD3VWq\n8bu/WjoCCb9eR02JYkTGBCbWH5fGAhM+eygnJ7jwr36nFHxKLitruGAx0tacAHZab0XvKaf/xKVv\nubpImXyxMuDvSuYnSbtmVlb0+9i9e8O0MOGdfXNyvfk01uknegTSHMEyUWq/mMDE+uPSSGDC/0P6\nncTgwc6d5fvoI2Xd9d1lvgjFMp24KQFK+y3zE+WYRcrEy1085X9LXdC+fGlSRypBF2BTmQaCo7/w\nd9NE+9tXVjYMssf74rFErzCPR7B8W4O/3eI47QsTmFh/XBoJTHiHEUlIqqtDMZnwBJC+u0y1flDe\nn/XVLra8zcqIO5ULvqTM6ebiKmN/pJS8obHEVBIhLsF31fh/s27doh/vi0ukN0pG6oxLShrGZlr6\n4rGWEo9ghT/cWByn/ZFIgWlxqhgjOsFV0/5KdT91iL8y+623XNoRgBNOcCvNgylTRoxwK9APH4aB\nA93KcaedMHq0a3/Xrtb9XQkj6wD0ewE+txSOeRpyt8OGibD6AnjsHvikqFXN8e8rwEcfuWwBJSXw\n9NMwcqRLExPMGqDqshO8/37kFfHr1jXMahDMvOD/W7jwwvrfoXVTw8STEiUnx30OHQr9+8M991g2\nAKMREqVU6biR4hFMtPUHZWXRkzIGt549G04rbdNbRq1S9pKbSvytM5S5Xd3nGf9PKftXs9epNGek\n0lSMKrgOaOpUN0IpK3OBfD9Lge+yDBJpUWP4gszwmWJtKaliW7LVaB4kcATjp3Fpl4iIpvL3TZrk\nkkXm5rocXW+9FUrOGAtFRS5JY21tw7xfbQOF4rVuhPK5pdD/OajpD+9PcNvmsVDbtdWs6dnTjRb9\n/GFHHeVGgeGjjPAcY0VFLonlnj1u36OPwgUXwD//CT/6UWiU2qMH/O1voXxpkye7PGj+qCTaiMTy\ngxnphIigqtL0kTG0ZQKTPGpqYMAAL8Fih0ChYBP0ew7Kl0H5M1CXCe+f5QRl0xfgQM+UWRcUjqIi\nOP54l2k5KPwZGaFEn9EoK4MtW1y5oiIkUJ8l0wQKCqK7zsIJtjF1qmXwNVJLIgXGYjBJJD/f+e79\nUYyfqbj9oFC4wY1M+j0H/ZdDxmHYPA4qK+C562DvMfhZilNJRkb9Ucm+ffDii648ebL7FIHHH498\nbl6eG/3k5LiRi48fkxgxwv29ly514nLOOe61BbGMSoJtNJba3zDaGjaCSSLHH+/ev3L4cP33k7Rd\nFIrf88TEExTNgEpPUDaPgz0DSAdBiZVhw9xrA66+2qXNDwbhfYqKYNw4+PvfobAQjjkGund3wnHF\nFe4B4vOfh9//3r0C4e67nbjEOiqpqWk6oG9uNKO1MBdZjKRKYI4/3rlHgk/MbZKMWih5E/q8BH3/\nCf2eh8OdvRGKJyrVnyNdBKVLF/fytXAyM53IZ2aGYik+WVnu3S0zZtSPxRQUhGb3BdsIMnWqc61F\nEhI//jZiBCxZ0nJBSKYbzcTLCGIusjQh0n/M2bPhvfdSbVkz6bIH+vzLCUqfl6D0VReU33IqrJ8E\nS25239OUTz+NXH/mme5vc/fdbsRx//2hqca1tXD66e4NmT7DhrlA/pgxbkQTdG/6QuO/1TJ8+rlP\noqcZJ9ONFpxOHektqIbRXGwE0wKOPjrkUpk8GR57rP6TZlrT6SD0Wu1EpPdKJyjdtsHW0U5QtpwK\nVaPh07b9OJuTA6eeGnpTZKS/z5tvQt++8K1vubdrlpU5F9iddzqXV3V1KLayfDmMHx8K5gdnisUi\nJM0dLcTiRmsuiR5tGW2bRI5gEjLXOV03krwOJrhCO7gKPO22Tp8qpa8ow+9SvvSfyn8NU77fRbl0\niDL5W8rI25Veq1ptHUqytsbeYeOvkPdT6Efapxp5VX2s2Yhjyc+VjqnybW2LEYQEroMxF1kLGD48\ntD5F02EgKHWQvwl6vu1t77jPwg2w91jYNhw+GA5vzIQdJ0FtTqotTijBv0FwUkV+vovPVFS4FfpB\nunZ1I5SaGndcJFdU+Er3aO6vWFxN6ThjLJ6V/IYRD+Yii4GgW2PDBqisdJ1ZYWF8CycTQsZh6L4F\n8ivdmpP8SicqPdZA8Rr4uBh2DnbbrhO9zxPgcJdWNrR1CKZuiVY/aRIcOFDfNZaV5da7+CLkB85b\n4oqKxdWUTFeXYSQCm0UWI4kSmKDfPtJsooQiR6DbB040wkWkYBPkfgAHekF1uQu413ifu4+HXYPg\nYPckGtc2yMlxgfoXX3Q5s5Ytc/m+nnoqlENr167QOpjsbLdeyZ963NyO38TDaA+YwMRIogQm+GS6\naVP9aa7xo9B1pyccEUQkbwt8UuCEI1xEqsvhwz5wJLvFv6mtEG2EEolu3dyIZMgQV87NdaKxebMb\nseTmhpIz+n/TggKXRHTFCteGraQ3OjomMDGSKIHxn0y7dHFTkP3OqFG67nTxj6J1ULARCjeGPg8f\n5YlHQDj8ck2/duvOSiZZWdCnjxMT3+1VXg5794ZygwXFIzja8Ec3NovKMExgYibR05TDp7h+9nTd\nfQv0fdFN9+25Gnq9BZ1qYccQ2HOcW4y49xioPsZ9HsxLmE3thXhGKn6+sG7dXNA+O9u5xF59NSQu\nWVkuUajvBmssN5i5tgwjhC20TBKzZ7t0IQcPuhli/toJH38GEDm7YMBT6LGLoO8LkHnQrRvZOgb+\n9b9uhtZHpaTLCve2QDzPAePHu7/Lz37m1qls2xYSEnAzyF59Fa691n0vKIA33oguHjaLyjCSg41g\nAoSPUKZMcSu6AXYe2MnvVzzAvIUPU5u3BjaNd6vbK8e5KcAmJjFTVBSKY/mjkREj3JTh555z6Vye\nfx6uuw7+9S83U88frfhB+6BY+PGUwYOdS+yll6BfPxuZGEZzsIWWMW7EudDSX0Dnb1+afEgfW/OY\nTn5osub9JE+nPzpd/7pqsfYoOZjyRYXptnXtGn3faaeFXrg1dKh74dakSaqlpe4FXv4iv0gL/vy6\n8Jd0BbGFgoaROEjgQksbwQSoqYHjjoOdew5S9qV7yTjjp5TllXLJ0Et44bdfo/K9buTkhFKI/OUv\nSTS+DdC5s5OQceOci6lnz1CCz+7d4cMP3WugX3rJ1dlowjDSHwvyx0i8AlN7pJZf/fNurl/yE047\n9iS6vPp9Pnz7NHJyXGfp+/lzc52f35+d1BHIyHBrRVascKKxb1/IFeXz1lvuDZErVrjcXiYohtH2\nMIGJkVgExl+lf7Dni3x4xqWU5vXip+N/yvDS4fViMiUlLrFlcbHz8zf11sN0xl8sOmAA/PvfblLD\n0KFOCF5+2U3Vve22UJJHf/oumGgYRnvHBMZDRCYCvwI6Ab9X1ZvC9jcpMKeP/5AXc/8Hjn2aMft+\nwUu/m4qIu7fBBZbHHusC/gcPBttPXQ6ybt1cenrfJfXCC+7zjDPc6MrPNtCtm0s7D/DOO27UkZcX\nEgqILhoWJDeMjocF+V2v3gnYAPQHsoBVwAlhxzQZ0Dp70qfKGT/UYWP2NQgSB4PHwSy4/nbWWS5I\nHUsW5R49/PIyzcuLPXh+4onuGtnZ7vvgwapTpjibKitdduDKyvp2V1a6APqkSbEFvpctW9b0Qa2M\n2RQ76WiX2RQb6WgTCQzyZyREpVLDKGCDqlaqai0wH5gcbyMPP9CZqb1+wLNPdW/wlO6vjwhm2fUZ\nMsTtO+kkmDix6euMHOlWkl9zzXJqalzCzLIyFyAHN8W2tDT0HdyLsv75T3eNHTvc+S+84EZS+fku\n/rFlS/04CLjvVVXwj3/ENvJYvnx50we1MmZT7KSjXWZTbKSjTYmkLS+07A1sCXzfCoyOt5FYF9k9\n+KB7IVVtrVs57ue0irTvhRfcOg/fhTZ0KDzwgDt+3jx3ji8O4W6oaG4pWwxoGEZboy0LTKtGP/Lz\n3RsrY9m3ebN7De8//gE33th4DCNcOExIDMNoL7TZIL+IjAHmqepE7/scoE4DgX4RaZs/zjAMI4Vo\nR59FJiKZwHvAeGAbsBK4QFXXpNQwwzAMA2jDLjJVPSwi3wGexs0o+4OJi2EYRvrQZkcwhmEYRnrT\nlqcpR0VEJorIWhFZLyLXJPlafxSRHSKyOlBXKCJLRGSdiCwWkfzAvjmeXWtF5OxA/XARWe3tu7WF\nNvURkWUi8o6IvC0il6faLhE5SkRWiMgqz6Z5qbYp0F4nEXlDRJ5II5sqReQtz66V6WCXiOSLyEIR\nWSMi74rI6BT/mzrOuz/+tk9ELk+D+/Q/3r/x1SLyoIh0TgObrvDaeltErvDqkm9TohbUpMtGDAsw\nE3y9scAwYHWg7mbgaq98DfBTrzzIsyfLs28DoVHkSmCUV34SmNgCm0qAoV45FxerOiEN7MrxPjOB\nl3HTylNqk9fG/wIPAI+nw9/Pa2MTUBhWl+q/333AJYG/YV6qbQrYlgF8APRJpU245RPvA5297w8D\nM1Js02BgNXAUrn9cAhzTGja16I+ajhtwCrAo8P1a4NokX7M/9QVmLdDLK5cAa73yHOCawHGLgDHA\n0cCaQP004K4E2vcYMCFd7AJygNdwi2VTahNQBiwFzgSeSJe/H05gisLqUmYXTkzej1Cf8nvltXM2\n8EKqbcIJzL+BApwIPwGclWKbzsel0vK//wC4ujVsao8uskgLMHu3sg29VHWHV94B9PLKpZ49Pr5t\n4fVVJMhmEemPG2GtSLVdIpIhIqu8ay9W1ZWptgn4JXAVEExfmmqbwK3zWioir4rIrDSwqxzYJSL3\niMjrIvI7EemaYpuCTAMe8sops0lVq4BbcCKzDahR1SWptAl4GxjrucRygEm4B6uk29QeBSatZi2o\nk/qU2CQiucAjwBWq+lGq7VLVOlUdivvHPVpEBqfSJhH5IrBTVd8gyitJU/j3O01VhwHnAt8WkbEp\ntisTOBm4Q1VPBg7gvAOptAkAEckGvgQ0eENTCv5NFQDn4bwapUCuiHwjlTap6lrgJmAx8BTO/XWk\nNWxqjwJThfPD+vShvuq2BjtEpARARI4GdkaxrcyzrcorB+urWmKAiGThxOV+VfXzDKTcLgBV3Qcs\nA85JsU2nAueJyCbc0+8XROT+FNsEgKp+4H3uAh7FuRNTaddWYKuqvuJ9X4gTnO2pvlc4EX7Nu1eQ\n2vs0AdikqntU9TDwV5zbPqX3SVX/qKojVHUcUA2soxXuU3sUmFeBASLS33uy+TrweCvb8DgusIf3\n+VigfpqIZItIOTAAWKmq24EPvVk5AnwzcE7ceG38AXhXVX+VDnaJSLE/S0VEuuD80mtSaZOqzlXV\nPqpajnOxPKuq30ylTQAikiMi3bxyV1x8YXUq7fLa2iIiA72qCcA7uBhDyu6VxwWE3GP+tVNl02Zg\njIh08dqaALxLiu+TiPT0PvsCXwEepDXuU3OCRum+4Z5o3sPNfpiT5Gs9hPO1HsLFfi4GCnGB43W4\nYWl+4Pi5nl1rgXMC9cNxncgG4LYW2nQ6LqawCnjD2yam0i5gCPA68KbX3g+8+pTeq0Cb4wjNIkv1\n36/c+9utwvnP56SJXZ8HXvH+hn/FBf5TbVNXYDfQLVCXapvm4R6eVuNm3mWlgU3P4x4IVgFnttZ9\nsoWWhmEYRlJojy4ywzAMIw0wgTEMwzCSggmMYRiGkRRMYAzDMIykYAJjGIZhJAUTGMMwDCMpmMAY\nhmEYScEExjAMw0gK/x+ZE59PkAtf6wAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2424e358>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_4_coef = get_coef(set_4, l2_small_penalty)\n",
"print set_4_coef[set_4_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_4, l2_small_penalty)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The four curves should differ from one another a lot, as should the coefficients you learned.\n",
"\n",
"***QUIZ QUESTION: For the models learned in each of these training sets, what are the smallest and largest values you learned for the coefficient of feature `power_1`?*** (For the purpose of answering this question, negative numbers are considered \"smaller\" than positive numbers. So -5 is smaller than -3, and -3 is smaller than 5 and so forth.)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Ridge regression comes to rescue"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Generally, whenever we see weights change so much in response to change in data, we believe the variance of our estimate to be large. Ridge regression aims to address this issue by penalizing \"large\" weights. (Weights of `model15` looked quite small, but they are not that small because 'sqft_living' input is in the order of thousands.)\n",
"\n",
"With the argument `l2_penalty=1e5`, fit a 15th-order polynomial model on `set_1`, `set_2`, `set_3`, and `set_4`. Other than the change in the `l2_penalty` parameter, the code should be the same as the experiment above. Also, make sure GraphLab Create doesn't create its own validation set by using the option `validation_set = None` in this call."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"l2_new_penalty = 1e5"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 2.58738875673 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x249290b8>,\n",
" <matplotlib.lines.Line2D at 0x249292b0>]"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEACAYAAABlOdt4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXt4VdWZ/z9vroRbQghykYjRxgsztiAodmrHOBVFbIWZ\nEcWphSojv9anv9rfzNN6md9TccZfq3Ys6nTUMrUWnSLgDfVBEFDTaW0BrahUpQEs1ASJGAjXAIG8\nvz/W2pydw0lyEs7OOSd5P8+zn73O2mut/Z5D2N/9rvWutURVMQzDMIwoyUm3AYZhGEbPx8TGMAzD\niBwTG8MwDCNyTGwMwzCMyDGxMQzDMCLHxMYwDMOInA7FRkT+j4j8QUTWi8gCESkUkVIRWSkiNSKy\nQkRKQuVvE5GNIrJBRC4N5Y/zbWwUkQdC+YUissjnrxaRUaFrM/09akRkRii/QkTW+DoLRSQ/NT+H\nYRiGEQXtio2InAz8b2Ccqp4D5ALTgVuBlap6BvCK/4yIjAauAUYDk4CHRER8cw8Ds1S1EqgUkUk+\nfxbQ4PPnAvf4tkqB7wPn++MOESn2de4B7vN1dvk2DMMwjAwlmW60PKCviOQBfYFtwJXAfH99PjDV\np6cAT6pqs6puATYBE0RkODBAVdf6co+H6oTbegb4kk9fBqxQ1UZVbQRWApd78boYeDrB/Q3DMIwM\npF2xUdU64D7gzziRaVTVlcBQVa33xeqBoT49AqgNNVELnJwgv87n488f+fsdAXaLyOB22ir1drQk\naMswDMPIQDrqRhuE8zxOxT38+4vIdeEy6ta76a41b2xtHcMwjCwkr4PrlwB/UtUGABF5Fvg8sF1E\nhqnqdt9F9okvXweUh+qPxHkkdT4dnx/UOQXY5rvqilW1QUTqgKpQnXLgVWAnUCIiOd67GenbOA4R\nMXEyDMPoJKoqHZfqHB2N2WwFLhCRIj9WcgnwPvAiMNOXmQks8ekXgOkiUiAiFUAlsFZVtwN7RGSC\nb+drwPOhOkFbV+ECDgBWAJeKSIn3sCYCL3tP6jVgWoL7H4eqZuVxxx13pN0Gsz/9dpj92Xlks/1R\n0a5no6prReRp4C3giD/PAwYAi0VkFrAFuNqXf19EFuME6Qhwk8asvwn4BVAEvKSqy33+o8ATIrIR\naMBFu6GqO0Xk34A3fLk71QUKANwCLBSRu7xNj3b5FzAMwzAip6NuNFR1DjAnLnsnzstJVP4HwA8S\n5P8eOCdB/iG8WCW49hjwWIL8PwET2rfcMAzDyBRsBYEMpaqqKt0mnBBmf3ox+9NLttsfBRJlH126\nERHtyd/PMAwj1YgImoYAAcMwDMM4YUxsDMMwUszs2VBVBZMnQ2Njh8V7BSY2hmEYKaamBn71K1i2\nzAmPYWJjGIaRcvr2defx42HevPTakilYgIBhGEaKaWx0Hs28eVBS0nH5TCKqAAETG8MwDOMYFo1m\nGIZhZC0mNoZhGEbkmNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZhRI6J\njWEYhhE5JjaGYRhG5JjYGIZhGJHTodiIyJkisi507BaRb4tIqYisFJEaEVkhIiWhOreJyEYR2SAi\nl4byx4nIen/tgVB+oYgs8vmrRWRU6NpMf48aEZkRyq8QkTW+zkIRyU/NT2IYhmGkmg7FRlX/qKpj\nVXUsMA44ADwH3AqsVNUzgFf8Z0RkNHANMBqYBDwkIsGibg8Ds1S1EqgUkUk+fxbQ4PPnAvf4tkqB\n7wPn++MOESn2de4B7vN1dvk2DMMwjAyks91olwCbVPUj4Epgvs+fD0z16SnAk6rarKpbgE3ABBEZ\nDgxQ1bW+3OOhOuG2ngG+5NOXAStUtVFVG4GVwOVevC4Gnk5wf8MwDCPD6KzYTAee9Omhqlrv0/XA\nUJ8eAdSG6tQCJyfIr/P5+PNHAKp6BNgtIoPbaasUaFTVlgRtGYZhGBlG0mIjIgXAV4Cn4q/5TWO6\na+MY26DGMAwjy8jrRNnLgd+r6g7/uV5Ehqnqdt9F9onPrwPKQ/VG4jySOp+Ozw/qnAJsE5E8oFhV\nG0SkDqgK1SkHXgV2AiUikuO9m5G+jeOYM2fOsXRVVRVVVVWJihmGYfRKqqurqa6ujvw+Se/UKSIL\ngWWqOt9/vhc3qH+PiNwKlKjqrT5AYAFuQP9kYBXwGVVVEVkDfBtYCywFHlTV5SJyE3COqn5TRKYD\nU1V1ug8QeBM4FxDg98C5qtooIouBZ1R1kYg8Arytqo/E2Ww7dRqGYXSCtG4LLSL9gK1Aharu9Xml\nwGKcR7IFuNoP4iMitwM3AEeAm1X1ZZ8/DvgFUAS8pKrf9vmFwBPAWKABmO6DCxCR64HbvSl3hcSu\nAliIG795C7hOVZvj7DaxMQzD6ARpFZtsxcTGMAyjc0QlNraCgGEYhhE5JjaGYRhG5JjYGIZhGJFj\nYmMYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiR\nY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFjYmMYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEY\nkZOU2IhIiYg8LSIfiMj7IjJBREpFZKWI1IjIChEpCZW/TUQ2isgGEbk0lD9ORNb7aw+E8gtFZJHP\nXy0io0LXZvp71IjIjFB+hYis8XUWikj+if8chmEYRhQk69k8ALykqmcDnwU2ALcCK1X1DOAV/xkR\nGQ1cA4wGJgEPiYj4dh4GZqlqJVApIpN8/iygwefPBe7xbZUC3wfO98cdIlLs69wD3Ofr7PJtGIZh\nGBlIh2LjH+5fVNWfA6jqEVXdDVwJzPfF5gNTfXoK8KSqNqvqFmATMEFEhgMDVHWtL/d4qE64rWeA\nL/n0ZcAKVW1U1UZgJXC5F6+LgacT3N8wDMPIMJLxbCqAHSLymIi8JSL/JSL9gKGqWu/L1ANDfXoE\nUBuqXwucnCC/zufjzx+BEzNgt4gMbqetUqBRVVsStGUYhmFkGHlJljkX+JaqviEi9+O7zAJUVUVE\nozAwAZ26z5w5c46lq6qqqKqqSrE5hmEY2Ut1dTXV1dWR3ycZsakFalX1Df/5aeA2YLuIDFPV7b6L\n7BN/vQ4oD9Uf6duo8+n4/KDOKcA2EckDilW1QUTqgKpQnXLgVWAnUCIiOd67GenbOI6w2BiGYRit\niX8Jv/POOyO5T4fdaKq6HfhIRM7wWZcA7wEvAjN93kxgiU+/AEwXkQIRqQAqgbW+nT0+kk2ArwHP\nh+oEbV2FCzgAWAFc6qPhBgETgZdVVYHXgGkJ7m8YhmFkGOKe2x0UEvkc8DOgANgMXA/kAotxHskW\n4Go/iI+I3A7cABwBblbVl33+OOAXQBEuuu3bPr8QeAIYCzQA031wASJyPXC7N+UuVZ3v8yuAhbjx\nm7eA61S1Oc5uTeb7GYZhGA4RQVWl45KdbLcnP4xNbAzDMDpHVGJjKwgYhmEYkWNiYxiGYUSOiY1h\nGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFjYmMYhmFEjomN\nYRiGETkmNoZhGEbkmNgYhmEYkWNiYxg9jNmzoaoKJk+GxsZ0W2MYDhMbw+hh1NTAr34Fy5Y54TGM\nTMDExjB6GH37uvP48TBvXnptMYwA2zzNMHoYjY3Oo5k3D0pK0m2NkW3YTp1dwMTGMAyjc9hOnYZh\nGEbWkpTYiMgWEXlXRNaJyFqfVyoiK0WkRkRWiEhJqPxtIrJRRDaIyKWh/HEist5feyCUXygii3z+\nahEZFbo209+jRkRmhPIrRGSNr7NQRPJP9McwjJ6ARaMZmUiyno0CVao6VlXP93m3AitV9QzgFf8Z\nERkNXAOMBiYBD4lI4JI9DMxS1UqgUkQm+fxZQIPPnwvc49sqBb4PnO+PO0Sk2Ne5B7jP19nl2zCM\nXo9FoxmZSGe60eL78K4E5vv0fGCqT08BnlTVZlXdAmwCJojIcGCAqq715R4P1Qm39QzwJZ++DFih\nqo2q2gisBC734nUx8HSC+xtGr8ai0YxMpDOezSoReVNEbvR5Q1W13qfrgaE+PQKoDdWtBU5OkF/n\n8/HnjwBU9QiwW0QGt9NWKdCoqi0J2jKMXs2CBTBtGqxcadFoRuaQl2S5L6jqxyIyBFgpIhvCF1VV\nRaS7wr46dZ85c+YcS1dVVVFVVZVicwwjsygpgcWL022FkS1UV1dTXV0d+X2SEhtV/difd4jIc7jx\nk3oRGaaq230X2Se+eB1QHqo+EueR1Pl0fH5Q5xRgm4jkAcWq2iAidUBVqE458CqwEygRkRzv3Yz0\nbRxHWGwMwzCM1sS/hN95552R3KfDbjQR6SsiA3y6H3ApsB54AZjpi80Elvj0C8B0ESkQkQqgElir\nqtuBPSIywY+5fA14PlQnaOsqXMABwArgUhEpEZFBwETgZT955jVgWoL7G4ZhGBlGh5M6vWA85z/m\nAb9U1R/6SLHFOI9kC3C1H8RHRG4HbgCOADer6ss+fxzwC6AIeElVv+3zC4EngLFAAzDdBxcgItcD\nt/v736Wq80N2LcSN37wFXKeqzXG226ROwzCMTmArCHQBExvDMIzOYSsIGIZhGFmLiY1hGIYROSY2\nhmEYRuSY2BiGYRiRY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFjYmMYKcQ2LjOMxJjYGEYK\nsY3LDCMxJjaGkUJs4zLDSIytjWYYKaSx0Xk08+bZxmVGdmILcXYBExvDMIzOYQtxGoZhGFmLiY1h\nGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZhRI6JjWEYhhE5SYmNiOSKyDoRedF/LhWRlSJSIyIrRKQk\nVPY2EdkoIhtE5NJQ/jgRWe+vPRDKLxSRRT5/tYiMCl2b6e9RIyIzQvkVIrLG11koIvkn+kMYhmEY\n0ZGsZ3Mz8D4QTFq5FVipqmcAr/jPiMho4BpgNDAJeEhEgnjth4FZqloJVIrIJJ8/C2jw+XOBe3xb\npcD3gfP9cYeIFPs69wD3+Tq7fBuGYRhGhtKh2IjISGAy8DMgEI4rgfk+PR+Y6tNTgCdVtVlVtwCb\ngAkiMhwYoKprfbnHQ3XCbT0DfMmnLwNWqGqjqjYCK4HLvXhdDDyd4P6GYRhGBpKMZzMX+C7QEsob\nqqr1Pl0PDPXpEUBtqFwtcHKC/Dqfjz9/BKCqR4DdIjK4nbZKgUZVbUnQlmEYhpGB5LV3UUS+DHyi\nqutEpCpRGVVVEemuNWE6fZ85c+YcS1dVVVFVVZVCcwzDMLKb6upqqqurI79Pu2ID/BVwpYhMBvoA\nA0XkCaBeRIap6nbfRfaJL18HlIfqj8R5JHU+HZ8f1DkF2CYieUCxqjaISB1QFapTDrwK7ARKRCTH\nezcjfRsJCYuNYRiG0Zr4l/A777wzkvu0242mqrerarmqVgDTgVdV9WvAC8BMX2wmsMSnXwCmi0iB\niFQAlcBaVd0O7BGRCX7M5WvA86E6QVtX4QIOAFYAl4pIiYgMAiYCL/uVNV8DpiW4v2EYhpGBdOTZ\nxBN0Y90NLBaRWcAW4GoAVX1fRBbjIteOADeFll2+CfgFUAS8pKrLff6jwBMishFowIkaqrpTRP4N\neMOXu9MHCgDcAiwUkbuAt3wbhmEYRoZiWwwYhmEYx7AtBgyjBzF7NlRVweTJbsM1w+jpmNgYRhqo\nqYFf/QqWLXPCYxg9HRMbo1eQaZ5E377uPH6820LaMHo6JjZGryDTPIkFC2DaNFi5EkpKOi5vGNlO\nZ6PRDCMryTRPoqQEFi9OtxWG0X1YNJrRK2hsdB7NvHnmSRhGe0QVjWZiYxiGYRzDQp8NwzCMrMXE\nxjAMw4gcExvDMAwjckxsDMMwjMgxsTF6DJk2cdMwjBgmNkaPIdMmbhqGEcPExugxZNrETcMwYtg8\nG6PHEOXEzdmznefUt69baibdE0MzzR6j52CTOruAiY2RKqqqXBcduDXN0r3UTKbZY/QcbFKnYaSR\nTOuiyzR7DKMjTGyMjCGTo8mGDIGystR0VwXfs7wcLrywa9/XVo02sg3rRjMyhkzuGkqlbeG2AjLt\n+xq9l7R0o4lIHxFZIyJvi8gfRGSOzy8VkZUiUiMiK0SkJFTnNhHZKCIbROTSUP44EVnvrz0Qyi8U\nkUU+f7WIjApdm+nvUSMiM0L5Fd6ujSKyUETyU/R7GGkkk7uGUmlb0NbAgalr0zAyHlVt9wD6+nMe\nsBqYANwLfM/n3wLc7dOjgbeBfOBUYBMx72ktcL5PvwRM8umbgId8+hpgoU+XApuBEn9sBor9tcXA\n1T79MPCNNmxXI3vYtUt12jR3zjRSaVvQ1pYtmft9jd6Lf252qA2dPZLuRhORvsCvgW8CjwMXqWq9\niAwDqlX1LBG5DWhR1Xt8neXAHGAr8Kqqnu3zpwNVqvoNX+YOVV0jInnAx6o6RESuBf5aVb/p6zwC\nVAOLgE+AoaraIiIXAHNUdVICmzXZ72cYhmGkMRpNRHJE5G2gHlihqmtxD/p6X6QeGOrTI4DaUPVa\n4OQE+XU+H3/+CEBVjwC7RWRwO22VAo2q2pKgLaOHksnBA4ZhdEyH20L7h/oYESkGnhORv4y7riLS\nXe5Dp+8zZ86cY+mqqiqqqqpSaI6RCpKZoBgsRROUT8dguk2kNHoi1dXVVFdXR36fDsUmQFV3i8hr\nwGVAvYgMU9XtIjIc160FzssoD1UbifNI6nw6Pj+ocwqwzXejFatqg4jUAVWhOuXAq8BOoEREcrwQ\njvRtJCQsNkZmkoyQZELwQCYInmGkmviX8DvvvDOS+3QUjVYWRJqJSBEwEfgAeAGY6YvNBJb49AvA\ndBEpEJEKoBJYq6rbgT0iMkFEBPga8HyoTtDWVcArPr0CuFRESkRkkL/3y34Q5jVgWoL7G91Iqrq2\nkhGS+Hkl8ffujm62TBC87sC6LI1IaC96ADgHeAt4B1gP/F+NRYqtAmpwolASqnM7LgptA3BZKH+c\nb2MT8GAovxAXXbYRF+12auja9T5/IzAzlF8BrPH5i4D8NuzvWjiGkRQXXaQK7pg2revtdCXSa9iw\n2L2nTk2dLam2Mxvpjt/SyFxIdzRaNmLRaNEyebJbzn/8+O6fyV5aCrt2ufSUKXD4cPps6Wmk89/V\nSD+2EGcXMLGJlihXWe6IiRNh1SoYMwZee83lpcuWnkY6/12N9GNi0wVMbHou9kA0jGgwsekCJjbp\nwUKEuxf7vY1UYlsMGFlDe9szW6RT6rHtsI322Nm0k7t/czfpfvE2sTFSTnshwvZgTD29JSTb6Dxr\natdw7k/PpX5fPUf1aFptMbEx2qSrXkh7e63YgzH12N42RjyqytzfzeUrT36FuZfNZe6kueTlJD2H\nPxJszMZokyj2l0k0sG9jDoaROnY17eL656+nbm8di69aTMWgik7Vj2rMJr1SZ2Q0qfRC2hMUWwbG\nMFLD2rq1XPP0NVx5xpUsumoRhXmF6TbpGCY2RpssWOAe/kVFMHXqiXkeYUGprITzzou1FXXXmnlO\nRk9HVXlwzYP8v1//Px758iP83dl/l26TjsO60YwOSUV3WjArvX9/2LevdVupnjMTLy5Tp6Zvu2kT\nOiNqGg82MuuFWWxt3MriaYs5bdBpJ9SehT4baSMVnkcwiH3BBce3VVLiBCBVD+L4iLd0BiV0V/Sd\nhZT3Tt7c9ibj5o1jRP8RvH7D6ycsNJESxYJrmXJgC3Em5MYb3WKLl1+e3KKSJ7oAZfh+3bEV8uWX\nu0Ukx49390nG/s7+Jl21JSps8czeRUtLiz64+kEdcu8Qfeq9p1LaNhEtxJl2QYjyMLFJTFsPpqge\nuN39IEwkLh19t6hs7K6VortL1Iz009jUqH+/6O917CNjdWPDxpS3H5XYWDdaL6StbqWounyi6MZq\nr9soUbdcR98tqq62VHcRtoXNtekdvPXxW5w771yG9hvKb2f9ls+UfibdJiVPFAqWKQfm2SSkrbft\nVL0dB17EyJGqQ4eqFhernnSS6vTpqfOc2vNEEnkxHX233rJXjZGdtLS06H+u/U8tu7dMF65f2Km6\nne2xwLrRTGyiJv6B29VutbAQhI+ysrYFIhHt3T9ePMJlv/CF4+9jYmJkK7sP7tarn7paxzwyRms+\nrel0/c52EZvYmNh0O4n+SOMFoD0vYuDAWP2xY1UvuUST8pyCNgcNavs/Sbx4hG0NdvFM1kOLaqzK\nME6Ut7a9pZ958DP6jRe/oU3NTV1qo7M9FiY2JjbdTqI/0ngBSiRIgRBs2aI6ZYrbtnnXLtUZM1SH\nDHGi094ffbxnNGCAaytZWzsb8WaRXEam0dLSog+/8bCW3VumT65/8oTa6qxXH5XY2KTOXkxHEw6D\nyZZFRbB1qyvX3Ox2yAy2DP6Hf0h+C+FkJ4eWl0Ntbeu8jiZjnsjEUNsG2cgk9hzaw+wXZ/PBpx/w\n1LSnOGPwGd16/6gmdSbjHZQDrwHvAX8Avu3zS4GVQA2wAigJ1bkN2AhsAC4N5Y8D1vtrD4TyC4FF\nPn81MCp0baa/Rw0wI5RfAazxdRYC+Qls78wLQK8j2Tf6cLnSUtdNFXganXlrStadD4+5BF1wnene\nCgcofOELHXeP2XiOkSm8/fHbWvlgpc5+YbYeOHwgLTaQrm40YBgwxqf7A38EzgbuBb7n828B7vbp\n0cDbQD5wKrCJ2LI4a4HzffolYJJP3wQ85NPXAAs1JmibgRJ/bAaK/bXFwNU+/TDwjQS2R/Ov0UNI\n9uEflOvf/8S6m5J9qAf3Ky5WnTy58yKQKEDBuseMTKalpUV/+uZPtezeMv3lu79Mqy1pE5vjKsAS\n4BLvtQzVmCBt0JhXc0uo/HLgAmA48EEofzrwSKjMBJ/OA3b49LXAw6E6j/h6AuwAcnz+BcDyBLam\n+t+hR5Hswz8oN2KEHhv4D4+hpHqA/UQ9jfgABZvoaGQyew7u0WufvlbPeegc3bBjQ7rNyYxJnSJy\nKjAW1301VFXr/aV6YKhPjwDCPe61wMkJ8ut8Pv78kVeHI8BuERncTlulQKOqtiRoy0iSZCccBuUq\n/LYYe/bAd78bu/7ii7EJk9df335byazh1dWJkEHbzc1u8c1337WJjkZm8279u5z3X+fRL78fa/5x\nDWeWnZlukyIj6S0GRKQ/8Axws6ruFYmNH6mqikh3jcR36j5z5sw5lq6qqqKqqirF5vQ82gocGDjQ\nneNn2R86FEtrB/86Ue5dE2572jQYNSq798axFaN7LqrKo+se5bZXbmPuZXO57rPXpc2W6upqqqur\no79RMu4PbvzlZeA7obwNwDCfHk6sG+1W4NZQueXABFxXW7gb7VgXmS9zgR7fjXasq81//iluTCe+\nG+3zWDdaymgrcKCt7q1g/syYMcmPx0TRtdXT1gezkOyeyd5De/W6Z6/Tv3zoL/WDHR+k25zjII0B\nAgI8DsyNy78XPzbjBSY+QKAAFzG2mViAwBovPMLxAQKB8EyndYDAh7jggEFB2l9bDFyjsbEcCxDw\nJDPxsr26wWTKZKPA2htjib93KiO/UtX2iY45ZfuK0Ub3sb5+vZ71k7P0hiU36P7D+9NtTkLSKTYX\nAi1eQNb5Y5IXglUkDn2+HReFtgG4LJQfhD5vAh4M5Rd68QhCn08NXbve528EZobyw6HPi7DQ52Mk\nM/EymbpTpnR8r3StptyVttuy9URtzPYVo43oaWlp0UffelTL7i3T+W/PT7c57ZI2scnmo7eKTfwb\ncWfekMNhzh3N9Fft+EGbSd1mbdl6ojaaB2K0x75D+3TGczN09H+O1vc+eS/d5nSIiY2JTYcEb+6X\nXBJbIkY1+TfkG290kyDz81s/lNvyCOK73GbMcBM+Bw2KCVWie595prtHXp5rd8aMrnVDJbspWmDT\n4MGJReFEPQjzQIy2+EP9H/Tsn5ytX1/ydd13aF+6zUkKExsTmw450W6l+MmQxcVuPk04v6wscflR\no1z5cP1hwxI/gOPLJbMadKpWoB45snObqhlGV3ls3WNadm+ZPrbusXSb0imiEpukQ5+NzCfYAKx/\nf9i1y81jaS9cNj4MOajfrx/s3w+7d7v5NOF2P/00tgFZeMOxP//ZlQ+zfTtUVkKfPi4MeeBAGDLE\ntR3w2c+6NgGKi+FHP+rY1spKOO+81uHAbYUJBzYCjB0Lr76aeFO1oI1sDpU20s+O/TtYvmk5T73/\nFJt2bqJ6ZjV/cdJfpNuszCAKBcuUg17m2eza1bk9Y+LHGoLuoCCUuazMdasF3XLxWwSEu4/C2wEU\nFLhzTk5rrwJc11m43JYtrddCC3tOqjHPo7DQXc/NTew5tReuHV55uqPfINMxTyyzaGlp0d9v+73+\na/W/6oT/mqADfzhQ/3bh3+rPfv+zrOk2iwfrRjOxSYbOPDxnzHAP8fx81ZKS48dZ4jcha29sIhCi\nfv3cwzAYHwkLTCLxmTYt8dprgZC0tRFbvLB09L3bekhn23iLzb1JP3sO7tFn339WZz0/S4f/+3A9\n4z/O0O8s+46u3LxSDzYfTLd5J4yJjYlNUnT08AyviBze3CyRZxF+gMcP/scP6u/aFfM+QLVPn5jQ\n/PrXrT2u4Ajm8cR7VGHBCfICW8eMcVtMxwtLR987VWHSqSrfVbLNE+sp/PHTP+qPf/tj/dL8L2n/\nH/TXiY9P1Pt/d79ubNiYbtNSjomNiU1SdLS8fnueQr9+rR/I4Qd4fL1wd1jw8A66z8B5Som8l3A3\nWPw8nl27YrtshssEG7EFtiQSlo4msp5ImHRbgQ5tlY/S48g2TyxbOdh8UFdsWqE3L7tZP/PgZ3TE\nfSP0xhdu1Oc+eE73HtqbbvMixcTGxCYhHUWUhR9+Z54ZE4mgy6q4WHXixMRjMmGCh3W8KOXmxrrf\nwgIT733Eey9BfqJVAALBCcaMkvEWOprI2tZDui1xDn9fcL9Pe5jHkf3U7q7VeW/O0ylPTtGBPxyo\nn//Z5/WuX92l6z5epy0tLek2r9swsTGxSUjYE5g61T00w55H+OEXDjkeNky1okJ16FDXNTZihOqE\nCa03RgvMbTnaAAAYAElEQVQTDLSPGhUTlfjB+uABn5cXOy66KPEYSdAtF24jflvp+DGj9ujqRNa2\nxHnXrtbzjTpaTWHGDCeOyUyENTKDI0eP6Ot/fl3/5ZV/0TGPjNHSe0r12qev1SfeeUJ37N+RbvPS\nhomNiU3CcYFwFNiUKa0f0PFzSoJxk759j58/k8gTSkS4TvhhDKrl5a271+LbC9sfeD7BMWhQ295U\nMt5CvOeSbHdTe3vfdGaBURu4zw4aDjTogncX6Fef+aoOvmewnvPQOXrrylv111t/rc1Hm9NtXkZg\nYtMLxKa9QeYbb2ztmQQz+4O8c85p/43+xhud51JYqPrOOy4vvqso6FbbsqVtWxJFjiUaxwnnBZ5S\nW0IVLhMmXjBuvFG1qMh5Q4MHJ67TWYJ7hMeE2rp/e1g3WmbS0tKi72x/R3/46x/qhT+/UAf8YIB+\nZcFX9JE3HtGtjVvTbV5GYmLTC8Smvbfj8LXACwjnDR7sHniJHprx9YOIsy1bEgtEEAodfC4qct1t\nBQXOAzjppFh7IsfXjz8GD3b29O0bE5cJE1qLWzxnnumulZXFxC9+5YGRI13ZrkSChZexSUXXlw3c\nZw77Du3TFza8oP/rxf+l5T8u14r7K/RbS7+lyzYu06bmpnSbl/FEJTbB0v89EhHRbPp+kye72fll\nZXDmmbEZ9ytWuFn2R4642e+TJsHHH8Pq1W7jstxcOHrUtTFtWutZ8MHM+vfec2307w/79rlrZWXu\nsd3Q0HlbJ050tixfDnv3xvLDtoQpKoKmptjnYcPgi190m7DFr3Iwezb8/OexdkaOhNNPj830B7cy\nwPvvu5UJqqpi18rKYisWbN0aW7kgfvOxcB04/nczsosPd33ISxtfYunGpbz+59cZP2I8V1ReweTK\nyZxVdhbhzR6N9hERVDXlP5gtV5NBLFjgHrTbtsHrr7u8srLYci4AF13khCb8oAweyvE7aELr5VhE\n4PBhl87JibUr4kSnM7z3HlxxRUxAiorg4otd+6tWHV8+LDQA557b9sO9pib2nXJz4Te/gW9+030e\nONAJzerVTkjg+OV0AGprW5/jl6KJX8Ym/nczMpvmo8385s+/YenGpSzduJRdTbu4vPJyZo2dxcK/\nX0hxn+J0m2jEYZ5NBhJ4OP37Q2FhzPPo1w8+/3mXXrXKCUZLi/s8YoQTgPi1wgKPpi3CbbRHWJCK\nimDKFGdjsB5aeTmcdhrk5zu7//mfnTDm5DiPLHyf/HzIy4sJ0KBBsG5dTDyC75+fD2++CT/5ifNi\nNm9uLTIBjY3u++7a5X6XgQNhz57Yefx4GD3aeTrB2mkAX/+6+16PPWZbLmcD9fvqWbZpGUs3LmXV\nh6uoLK085r2MGzGOHMlJt4k9gqg8m7SPq0R5kCVjNonmmoRn3BcUtJ4wWV6uOmRI+ztqFhXFyoeX\niUk0sN/Zo7y89fhJMJYTP94UP04UjNEE4zXho2/f2G8QP+4UP5bV0dIzQf1wOxYtln0cbTmqa2vX\n6h2v3aHj543XkrtL9KrFV+lj6x7T7Xu3p9u8Hgs2ZtN5ssWzCY8fBGMH5eWxLqB4Bg+OeTsjR8L6\n9e7NPLzy8YoVsa6o/Hxobj4xG/PynIcyfrzztoJuPoh5EEG5TZuc9xEegzr9dOdZrF4NF154/Hcb\nNMh5JuHfIN47Gz8eVq6EqVOP/70SEf49mpud1xO0YZ5MZrL74G5WfriSpRuXsmzjMkqLSrmi8gqu\nOOMKvlD+BfJz89NtYo/HPJse7NkkCpsNz5eJD01ONNP/xhuPn/cSeDVttdXZo29fF5WWKIItPvos\n7KGE75+X13oiJ7iw7fiVpuPXbgvPGerKhM1g2RuLFsssWlpa9P1P3tcfvf4jrfpFlQ74wQCd9N+T\n9D/W/Id+uPPDdJvXKyFdoc/Az4F6YH0orxRYCdQAK4CS0LXbgI3ABuDSUP44YL2/9kAovxBY5PNX\nA6NC12b6e9QAM0L5FcAaX2chkN+G7an/l4iARGGzwQM1/sEehALHzz+JDwsOH6WlrbvhOnME3W7j\nx3detOJXZE4kXied5L5PolUDgiN+wmdnJ2xmytyXZEO0e/o2Ak3NTfpSzUv6raXf0or7K7T8x+X6\njRe/oS/+8UXdf3h/us3r9aRTbL4IjI0Tm3uB7/n0LcDdPj0aeBvIB04FNhELQlgLnO/TLwGTfPom\n4CGfvgZYqDFB2wyU+GMzUOyvLQau9umHgW+0YXsU/xZdpjMPkfD4Q/xs+2DplKC98CoCYY8mkVgl\nc4Q9j4IC5zFddJFb0iZRmURHeKJm/BhU/BFe6DJ+Rv+gQV2fvJlpc1+SHTfqieNLWxu36sNvPKxf\nXvBlHfCDAXrhzy/UH/76h/ru9nd71bpj2UDaxMbdm1PjxGYDMNSnhwEbfPo24JZQueXABcBw4INQ\n/nTgkVCZCT6dB+zw6WuBh0N1HvH1BNgB5Pj8C4Dlbdid6n+HEyJ+HbNkmTGj9cM56KZKVfdY/BGI\nW/z+M6WlrcWko3by82MTMhMJYiLBaW9Gf7aTrKeVaR5ZV2g+2qz/s+V/9JaVt+g5D52jZfeW6XXP\nXqdPrn9Sdx7YmW7zjHaISmy6Os9mqKrW+3Q9MNSnR+C6wgJqgZOBZp8OqPP5+PNHXhmOiMhuERns\n26pN0FYp0KiqLQnayjjCg9QHD8bynRYmx9atsXRurgsOWLbMTYwEGDPGDaJ3NQigXz83EbKhwQ3+\nByHJ4ZDo8PbNubkuvLmxsf12m5tdMMCRI7HB/9JSOHCg9W8Bbgvpc8+FU05xv9X3vw+ffAL/8A+x\nCZnh33LIkNahzNkw4B/Mo0o0kbUr5TKNTw98yvJNy1m6cSkrNq/glOJTuKLyCn765Z9y/snnk5uT\nm24TjTRywpM6VVVFpBOPzhO7XTfdJ2WEJ1WedJI7jxkDxcUuCi3+wRn/EP3e9+B3v3P1RJww7Nnj\nzuAi02pqnEh0VWz273cHuBUJDh06vswf/xhr/+jRjoUmYNu21qK1c2ficvn5bq5Q8FsF0W8Qm5AZ\n/i3Dk13jJ2xmKiUlydmZbLl0o6q8vf1tlm5cyksbX+K9He/xNxV/wxWVV/DvE/+dkwdm7DugkQa6\nKjb1IjJMVbeLyHDgE59fB5SHyo3EeSR1Ph2fH9Q5BdgmInm4cZkGEakDqkJ1yoFXgZ1AiYjkeO9m\npG8jIXPmzDmWrqqqoqqqqq2ikRDMVB8/Hp5+Gr77XffGevbZ7m0enFAED/hwWPPs2e7tPpj1rxoL\nMQ4LRHcQL0C5uc4birdh4EAnFIGoJDNhNDcXvvIVeO0197lfv1i7gwbFZveHf8uSklgoc3uz/8Pe\nULZ4QJnMvsP7WPXhKpbWLOWlTS/RN78vV1RewZ1Vd/LXo/6awrzCdJtodJLq6mqqq6ujv1EyfW0c\nP2ZzL35sBriV4wMECnARY5uJBQisASbgxlziAwQe1thYTjhA4ENccMCgIO2vLQau0dhYTsYGCLQ1\nSB0ewwgvZjlkSKy/fsaMxGMdHQ3OZ8MRhGSPGHH8dgfBmFFubuv9cMK/ZbKD/4kG21O9CGdPp+bT\nGp37u7k68fGJOuAHA/SSxy/Rub+bqzWf1qTbNCMCSFeAAPAksA04jBtbud4LwSoShz7fjotC2wBc\nFsoPQp83AQ+G8gu9eAShz6eGrl3v8zcCM0P54dDnRWRB6HP8Ay4IFhgwoPV8kvJytw1AMqspZ+sh\nEtvmIPhdgoCDsWOd+ISj104kIivRYHv8Pj7pjPjKxDDn/Yf368rNK/U7y76jlQ9W6oj7Rug/Pv+P\n+uz7z+qeg3vSbZ4RMVGJja0g0E3ErzJcWhrragqvO9bWqsk9jWHD4IMPWncngltzbcmS1uvDXXAB\nPPWUO2/fHlszLX6NtEQE66aFB9uDtsEtwvnqq+nrXku0ekTUqCrb923nw10fHjs279p8LL2zaSdj\nh491M/crr2DMsDG2anIvIqoVBExsToC2xgMS5YcfcIMHd26QvacybZobdwki1fLy3CKfBw44AQ5H\nvA0b5vKDMauRI+Gjj7p238bGzFmEM/i7SPUyOgeaD7ClcYsTkp1eSBqdmPxp158YUDiA0wad5o6S\n0zi99PRjn0cMGGGLWvZiTGy6QNRik2gflYaG1svpjxrlBtfr62PeS28j0crSIk5cWlra9uTitz4o\nKHDBEuG9bNoiWwIDEnleHbH30F5q99RSt7eO2j21Lr2njtq9sfSeQ3s4teTUYwJy+qCYmFQMqqB/\nQf9ov5iRtZjYdIGoxSZ4K21vmf5wCG9v5KST3BydVatcZFlOTvubtYUFZuBAF6m3Y4d783/0UbeH\nzm9+03EXWjq6p04EVWXv4b3U76unfn/9sfPHez9uLSp76zjScoSRA0cycuBITh5wcsL0kH5DzDsx\nuoRtnpZhnHWW28QM2g/v7c1CM2ZMLJw5eHs/7bTjywW7h44dCw8+6HbwBNdlNmKEE4vgzT/ZrrNw\nmHQ6NkZTVQ40H6ChqYGdTTtpONBAQ1PDcWISTudKLkP7D2Vov6HHzsP6D+Ovyv+qlaCU9CmxMRQj\n6zDPpgucdZab5Gi0pr3N3AImToxtcDZhQmz1gldegc99zgUCVFa6CZvJdJe1RVe6pxKhquw7vI/d\nh3az++Budh3cdUw4gvPOpp3Hfz7QgIgwuGgwg/sOPnY+qe9JxwlKcO5X0K/rhhpGirButC4QldiU\nlMR2qHT36b3jMQB/8RdOIHbtcl1XgUfzve8dP26SSATiu7x+9CO3zE0y3WVtjc20aAv7D+9nf/N+\n9h3ed+zYc2gPuw/uPiYerc4J8vYc2kOfvD4UFxZT3KeYQX0GxcQjJCSlRaWtRGVw0WCK8osi+80N\nIypMbLpAVGLTp0/iJV16M3/3dy4IYvNmJx4ffwzvvnv8hmgAR1uOcvDIQZqONNHU3MR11zfxP79t\n4qxzmrj3x03k9mli7n80UVvfRF4fd528JpqONLH/sBOPQESqf7uPXfv3QcE++g3aT79BTlSampvo\nm9+X/gX96VfQz53z+zGwcCDFfYqdeHgBae88sHCgbdhl9CpMbLrAiYpN/FvzBRdkaPeZtEDOEXfI\n0Vi6w+Mo5DRD7mHIO+TOx464z62ut3ftMHl9DnGkxX/ObyKnsIncwiY0twkpaKL56BFyWvqQ21LE\nkEFF9Mkt4qM/FVGYW8ThA0X0zS9if2MRzQeK4EgfTh9VxN9+uYii/CL6F/Q/dvTL78fd/9afN1/v\nz+jP9Oe/f96f4WVOWPrm97UBcsPoAiY2XSAZsVmyYQmv//l1WrSFFm1B0WPp55a0sO3jFvcw7+yB\ndq1eWDhaiUI7oiEKR/OhJRda8jo+NK7ckUI4WuCPcLqgE9fc9VwK+Nw5Bby1ppCB/fORo044jjQV\nwZEivjypD2+sLqR+u/tbHjwYzj/fBQOEt5oO6Gj+SarGZgzDcFg0WkT0y+/HSf1OIkdyEBFyJIcc\nyWHRwhzq1+fAkRzQzh7ShTr+QLxwtCEMCcUjPW/wOTlurCo3NxZ1N6AEHvs+3HWXW/E5XkDygMOh\nLshgu4SCAvd54EAnPGPGwKmndjzpMltWSDaM3k6v92zaIn55GeN48vMTb2tQUODm1+zb5zyPcGjz\nq6/GVg6In580cqQLCghWxjZPxTC6H+tG6wJdFZvZs912AMHgtpGYwAsJbwmQiMmTXZlAQBobY+HN\nAalersUwjK4RldjYCGoCampMaBJRUuK8kYBgnbJ+CaaHDBzozuPHwy9/6bq6AiEpKYHzznPpMWNg\n6lQTGsPo6ZjYhJg923Wfvfdeui3JLHJzobzczaeJXy1h/HhYu7b1FtVTp7qw52nT2haRBQvc9dde\ng+eeM6ExjJ6OdaN5Zs+GX/yi61sr9zTitzoIb8MccPHF8OyzbU/WNAwj+7ButIh58UUTmjBHj7pF\nMMF5L2PGuHRRaFJ8WVnrrrFwV5lhGEYYExvcG3n8W3tvoqQEtmxxG5eddJLLGz/eTWANusKeesql\nv/CF2PV0LHBpGEZ2Yt1owPDhrXeL7KkEIchhBg2Cdetia5B11B1m3WWG0bOx0OcukKzYlJZmf/TZ\n+PHOK2luhvXrXTfYjh2u+2vECDf35f77Y1srJztp0jCM3oWtIJAAEZkE3A/kAj9T1Xu60k5RkROb\n9jZByxSCgXsRWLQI/umfEq+O3JYH8sEH5pkYhtH9ZO2YjYjkAj8BJgGjgWtF5OyutFVR4c6ZIjQD\nBgBUA84TCcZTpk51qypPmwY7d7rzRx8lXoa/rQH77hrIr66ujvYGEWP2pxezv+eRtWIDnA9sUtUt\nqtoMLASmdLaR2bPdBl1RkZt7fN748W6bgnHj3OcBA9ymYlOnOg9r/XoYMKCaLVvgd79zYrJkiZuP\nMmpUdkR9Zft/NrM/vZj9PY9s7kY7GQhvElwLTOhsI4lWC0g0kN4WeXmu++2881z01u7dTjwKCmD1\naiguhq9+Fd5805VbvbrjwfiSEtc91pUdKg3DMDKRbBablEQ2BHvVxw+k33yzGxe5/34nFsHqxfn5\n8PzzTiSS2UkSYOnSxPm2YrFhGL2FrI1GE5ELgDmqOsl/vg1oCQcJiEh2fjnDMIw0YqHPIUQkD/gj\n8CVgG7AWuFZVP0irYYZhGMZxZG03mqoeEZFvAS/jQp8fNaExDMPITLLWszEMwzCyh2wOfW4TEZkk\nIhtEZKOI3JJuewBEpFxEXhOR90TkDyLybZ9fKiIrRaRGRFaISEmozm3+O2wQkUtD+eNEZL2/9kA3\nf49cEVknIi9mm/0iUiIiT4vIByLyvohMyDL7/4//21kvIgtEpDCT7ReRn4tIvYisD+WlzF7//Rf5\n/NUiktL4zTbs/5H/+3lHRJ4VkeJMtD+R7aFr/ywiLSJS2q22q2qPOnBdapuAU4F84G3g7Aywaxgw\nxqf748abzgbuBb7n828B7vbp0d72fP9dNhHzRNcC5/v0S8Ckbvwe/wT8EnjBf84a+4H5wA0+nQcU\nZ4v9uFD/D4FC/3kRMDOT7Qe+CIwF1ofyUmYvcBPwkE9fAyzsBvsnAjk+fXem2p/Idp9fDiwH/gSU\ndqftkf8H7+4D+DywPPT5VuDWdNuVwM4lwCXABmCozxsGbPDp24BbQuWXAxcAw4EPQvnTgUe6yeaR\nwCrgYuBFn5cV9uOE5cME+dli/8nAn4FBOKF80T/4Mtp+//AKP6xTZq8vM8Gn84AdUdsfd+1vgf/O\nVPsT2Q48BXyW1mLTLbb3xG60RJM9T06TLQkRkVNxbx1rcP/x6v2lemCoT4/A2R4QfI/4/Dq67/vN\nBb4LhBf2yRb7K4AdIvKYiLwlIv8lIv3IEvtVtQ64Dyc424BGVV1JltgfIpX2Hvu/rqpHgN3hrqFu\n4Abc2z5kgf0iMgWoVdV34y51i+09UWwyOuJBRPoDzwA3q+re8DV1rwkZab+IfBn4RFXXAQlj8DPZ\nftzb17k41/9cYD/O6z1GJtsvIoOAK3FvqyOA/iJyXbhMJtufiGyzN4yI/AtwWFUXpNuWZBCRvsDt\nwB3h7O60oSeKTR2uXzKgnNbqnDZEJB8nNE+o6hKfXS8iw/z14cAnPj/+e4zEfY86nw7n10Vpt+ev\ngCtF5E/Ak8DfiMgTZI/9tbi3ujf856dx4rM9S+y/BPiTqjb4N8lncV3G2WJ/QCr+XmpDdU7xbeUB\nxaq6MzrTHSLydWAy8NVQdqbbfzruReUd/394JPB7ERnaXbb3RLF5E6gUkVNFpAA3ePVCmm1CRAR4\nFHhfVe8PXXoBN9CLPy8J5U8XkQIRqQAqgbWquh3YIy6SSoCvhepEhqrerqrlqlqB67t9VVW/lkX2\nbwc+EpEzfNYlwHu4sY+Mtx/YClwgIkX+vpcA72eR/QGp+Ht5PkFbVwGvRG28uG1NvgtMUdWDoUsZ\nbb+qrlfVoapa4f8P1wLn+i7N7rE91QNqmXAAl+OivTYBt6XbHm/ThbixjreBdf6YBJTiBt1rgBVA\nSajO7f47bAAuC+WPA9b7aw+m4btcRCwaLWvsBz4HvAG8g/MMirPM/jnAB/7e83HRQxlrP84D3gYc\nxvXvX59Ke4FCYDGwEVgNnBqx/Tf4e20N/R9+KBPtD9l+KPjt465/iA8Q6C7bbVKnYRiGETk9sRvN\nMAzDyDBMbAzDMIzIMbExDMMwIsfExjAMw4gcExvDMAwjckxsDMMwjMgxsTEMwzAix8TGMAzDiJz/\nDxqRPKLgrFuOAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x247fe438>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_1_coef = get_coef(set_1, l2_new_penalty)\n",
"print set_1_coef[set_1_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_1, l2_new_penalty)"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 2.04470474182 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x24bbc0b8>,\n",
" <matplotlib.lines.Line2D at 0x24bbc2b0>]"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEACAYAAABlOdt4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXuYFdWV9/9ZfYXm0hfuTXPTECMJBAIBI2bSTlCRmbFJ\nJkQmE2UML52JmcSZN4/X3/NEfWOcqK9j9Dc/zZh4jzdiFE3UCIpgJCqioBjFxksrNHIRurkj3Zz1\n+2NXeaqrT/c53X2qzznd6/M89ZyqXVW7du2G/a2119p7i6piGIZhGFGSl+kCGIZhGL0fExvDMAwj\nckxsDMMwjMgxsTEMwzAix8TGMAzDiBwTG8MwDCNyUhIbESkTkYdE5C0ReVNEZolIhYisEJE6EVku\nImWB6y8Vkc0isklETg+kTxeRjd65GwPpxSLyoJf+ooiMC5xb5D2jTkTODaRPEJGXvHseEJHC7leH\nYRiGEQWpWjY3Ak+o6onAFGATcAmwQlU/CzzjHSMik4CzgUnAXOBmEREvn1uAxao6EZgoInO99MXA\nbi/9BuAaL68K4KfATG+7XERKvXuuAa737mn08jAMwzCykKRi4zXuX1XV2wFUtUVV9wJnAXd5l90F\nzPf2a4D7VbVZVeuBd4BZIjIKGKSqa73r7g7cE8zr98DXvf0zgOWq2qSqTcAK4ExPvE4FHkrwfMMw\nDCPLSMWymQDsEpE7RORVEfm1iAwARqjqDu+aHcAIb78S2Bq4fyswOkF6g5eO97sFnJgBe0VkSAd5\nVQBNqhpLkJdhGIaRZaQiNgXAl4CbVfVLwEG8LjMfdXPe9NS8Nza/jmEYRo5RkMI1W4Gtqvqyd/wQ\ncCmwXURGqup2r4tsp3e+ARgTuL/Ky6PB2w+n+/eMBbaJSAFQqqq7RaQBqA7cMwZYCewBykQkz7Nu\nqrw8WiEiJkyGYRidRFUl+VWdI6llo6rbgS0i8lkvaQ7wV+APwCIvbRGwzNt/DFgoIkUiMgGYCKz1\n8tnnRbIJcA7waOAeP69v4QIOAJYDp3vRcOXAacBTniX1LLAgwfPD5bdNlcsvvzzjZciWzerC6sLq\nof0tKlKxbAB+BNwrIkXAu8B5QD6wVEQWA/XAtwFU9U0RWQq8CbQA52v8Dc4H7gT646Lb/uSl3wbc\nIyKbgd3AQi+vPSLyM8C3qq5UFygAcDHwgIhcBbzq5WEYhmFkISmJjaq+Bnw5wak57Vx/NXB1gvRX\ngMkJ0j/BE6sE5+4A7kiQ/j4wq8OCG4ZhGFmBzSDQR6iurs50EbIGq4s4VhcOq4fokSj76DKNiGhv\nfj/DMIx0IyJoJgIEDMMwDKO7mNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiRY2Jj\nGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhZDm1tVBdDfPmQVNT0suzEhMbwzCMLKeuDlavhiefdMKT\ni5jYGIZhZDklJe53xgy49dbMlqWr2ESchmEYWU5Tk7Nobr0VysqifVZUE3Ga2BiGYRifYrM+G4Zh\nGDmLiY1hGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFjYmMY\nhmFEjomNYRiGETkmNoZhGEbkmNgYhmEYkZOS2IhIvYi8LiLrRWStl1YhIitEpE5ElotIWeD6S0Vk\ns4hsEpHTA+nTRWSjd+7GQHqxiDzopb8oIuMC5xZ5z6gTkXMD6RNE5CXvngdEpLC7lWEYhmFEQ6qW\njQLVqjpNVWd6aZcAK1T1s8Az3jEiMgk4G5gEzAVuFhF/BtFbgMWqOhGYKCJzvfTFwG4v/QbgGi+v\nCuCnwExvu1xESr17rgGu9+5p9PIwDMMwspDOdKOFp5w+C7jL278LmO/t1wD3q2qzqtYD7wCzRGQU\nMEhV13rX3R24J5jX74Gve/tnAMtVtUlVm4AVwJmeeJ0KPJTg+YZhGEaW0RnL5mkRWSciS7y0Eaq6\nw9vfAYzw9iuBrYF7twKjE6Q3eOl4v1sAVLUF2CsiQzrIqwJoUtVYgrwMwzCMLKMgxetmq+pHIjIM\nWCEim4InVVVFpKdWKbPV0AzDMHKMlMRGVT/yfneJyCM4/8kOERmpqtu9LrKd3uUNwJjA7VU4i6TB\n2w+n+/eMBbaJSAFQqqq7RaQBqA7cMwZYCewBykQkz7Nuqrw82nDFFVd8ul9dXU11dXWiywzDMPok\nq1atYtWqVZE/J+my0CJSAuSr6n4RGQAsB64E5uCc+teIyCVAmape4gUI3IcTpNHA08BnPOvnJeDH\nwFrgceAmVf2TiJwPTFbVH4jIQmC+qi70AgTWAV/C+YxeAb6kqk0ishT4vao+KCK/Ajao6q9CZbdl\noQ3DMDpBVMtCpyI2E4BHvMMC4F5V/U9PCJbiLJJ64NueEx8RuQz4HtACXKCqT3np04E7gf7AE6r6\nYy+9GLgHmAbsBhZ6wQWIyHnAZd7zr1LVuwLlegDnv3kV+K6qNofKbmJjGIbRCTImNrmMiY1hGEbn\niEpsbAYBwzAMI3JMbAzDMIzIMbExDMMwIsfExjAMw4gcExvDMAwjckxsDMMwjMgxsTEMwzAix8TG\nMAzDiBwTG8MwDCNyTGwMwzCMyDGxMQzDMCLHxMYwDMOIHBMbwzAMI3JMbAzDMIzIMbExDMMwIsfE\nxjAMw4gcExvDMAwjckxsDMMwjMgxsTEMwzAix8TGMAzDiBwTG8MwDCNyTGwMwzCMyDGxMQzDMCLH\nxMYwDMOIHBMbwzByktpaqK6GefOgqSnTpTGSYWJjGEZOUlcHq1fDk0864TGyGxMbwzBykpIS9ztj\nBtx6a2bLYiRHVDXTZYgMEdHe/H6G0ZdpanIWza23QllZpkvTexARVFXSnm9vboxNbAzDMDpHVGKT\nUjeaiOSLyHoR+YN3XCEiK0SkTkSWi0hZ4NpLRWSziGwSkdMD6dNFZKN37sZAerGIPOilvygi4wLn\nFnnPqBORcwPpE0TkJe+eB0SksLsVYRiGYURHqj6bC4A3Ad9MuARYoaqfBZ7xjhGRScDZwCRgLnCz\niPgKeQuwWFUnAhNFZK6XvhjY7aXfAFzj5VUB/BSY6W2Xi0ipd881wPXePY1eHoZhGEaWklRsRKQK\nmAf8BvCF4yzgLm//LmC+t18D3K+qzapaD7wDzBKRUcAgVV3rXXd34J5gXr8Hvu7tnwEsV9UmVW0C\nVgBneuJ1KvBQgucbhmEYWUgqls0NwIVALJA2QlV3ePs7gBHefiWwNXDdVmB0gvQGLx3vdwuAqrYA\ne0VkSAd5VQBNqhpLkJdhGIaRhRR0dFJE/h7YqarrRaQ60TWqqiLSU174Tj/niiuu+HS/urqa6urq\nNBbHMAwjt1m1ahWrVq2K/Dkdig1wMnCWiMwD+gGDReQeYIeIjFTV7V4X2U7v+gZgTOD+KpxF0uDt\nh9P9e8YC20SkAChV1d0i0gBUB+4ZA6wE9gBlIpLnWTdVXh4JCYqNYRiG0ZrwR/iVV14ZyXM67EZT\n1ctUdYyqTgAWAitV9RzgMWCRd9kiYJm3/xiwUESKRGQCMBFYq6rbgX0iMsvzuZwDPBq4x8/rW7iA\nA4DlwOkiUiYi5cBpwFNeLPOzwIIEzzcMwzCykGSWTRi/G+sXwFIRWQzUA98GUNU3RWQpLnKtBTg/\nMNDlfOBOoD/whKr+yUu/DbhHRDYDu3GihqruEZGfAS97113pBQoAXAw8ICJXAa96eRiGYRhZig3q\nNAzDMD4lo4M6DcMwDKM7mNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZh\nRI6JjWEYhhE5JjaGYRhG5JjYGEYGqK2F6mqYNw+ampJebhg5j4mNYWSAujpYvRqefNIJj2H0dkxs\nDCMDlJS43xkz4NZbM1sWw+gJbCJOw8gATU3Oorn1Vigry3RpDCNOVBNxmtgYhmEYn2KzPhuGYRg5\ni4mNYRiGETkmNoZhGEbkmNgYhmEYkWNiYxhZjg0ANXoDJjaGkeXYAFCjN2BiYxhZjg0ANXoDNs7G\nMLIcGwBqHGk5Qr+Cfj3yLBtnYxh9lLIyWLrUhKav0nSkiS/c/AXea3wv00XpFiY2hmEYWcz5j5/P\nGcefwXHlx2W6KN2iINMFMAzDMBJz7+v3sn77el6pfSXTRek2JjaGYRhZyAdNH/DvT/07y7+7nJLC\nkkwXp9tYN5phGEaWcSx2jHMeOYcLT76QaaOmZbo4acHExjA6gQ2wNHqCa9dcS35ePj/5yk8yXZS0\n0aHYiEg/EXlJRDaIyBsicoWXXiEiK0SkTkSWi0hZ4J5LRWSziGwSkdMD6dNFZKN37sZAerGIPOil\nvygi4wLnFnnPqBORcwPpE7xybRaRB0SkME31YRgdYgMsjahZt20dN7x4A3fPv5v8vPxMFydtdCg2\nqnoEOFVVpwJTgbkiMgu4BFihqp8FnvGOEZFJwNnAJGAucLOI+PHatwCLVXUiMFFE5nrpi4HdXvoN\nwDVeXhXAT4GZ3na5iJR691wDXO/d0+jlYRhdojPWig2wNKLk4NGD/PPD/8xNZ97EmNIxmS5OWkna\njaaqh7zdIqAQUOAs4C4v/S5gvrdfA9yvqs2qWg+8A8wSkVHAIFVd6113d+CeYF6/B77u7Z8BLFfV\nJlVtAlYAZ3ridSrwUILnG0an6Yy1ct99sGABrFhh416M9POT5T9h5uiZLPzCwkwXJe0kjUYTkTzg\nVeB44L9Vda2IjFDVHd4lO4AR3n4l8GLg9q3AaKDZ2/dp8NLxfrcAqGqLiOwVkSFeXlsT5FUBNKlq\nLEFehtFpOmOt+AMse5LaWieIJSVO7EzkeiePvf0YT737FBu+vyHTRYmEpGLjNepTvS6sR0TkC6Hz\nKiI9NSdMp59zxRVXfLpfXV1NdXV1Gotj9Abuuy+7p4PxLS9w5expsTOiZ/uB7Xz/j9/ndwt+R2m/\n0uQ3pJFVq1axatWqyJ+T8jgbVd0rIs/iurd2iMhIVd3udZHt9C5rAIIdjVU4i6TB2w+n+/eMBbaJ\nSAFQqqq7RaQBqA7cMwZYCewBykQkzxPCKi+PhATFxuh7pGIVRGmtpMMqMT9R70ZVWfzYYhZPW8wp\nY0/p8eeHP8KvvPLKSJ6TLBptqB9pJiL9gdOAt4DHgEXeZYuAZd7+Y8BCESkSkQnARGCtqm4H9onI\nLM/ncg7waOAeP69v4QIOAJYDp4tImYiUe89+yptZ81lgQYLnG0YrMh09lo7nm5+od3Pzyzez6+Au\nLv/a5ZkuSqQks2xGAXeJSD5OmB5U1SdE5EVgqYgsBuqBbwOo6psishR4E2gBzg9Mu3w+cCfQH3hC\nVf/kpd8G3CMim4HdwEIvrz0i8jPgZe+6K71AAYCLgQdE5CqcP+m2rlaA0bvJtFWQjudfdBHs3Anf\n+Y75bHobb+56kytWX8Ga762hML93j+CwJQaMXk2mp+dPx/Orq+M+mwULUuvys6CC7OeTlk846baT\nOH/G+SyZviTTxfmUqJYYMLExjCxn3jzXDTdjRupdaV0RKKNnuWjFRdTtruORsx8hPhwx89h6NobR\nR+mKzybT3YdGxzz7/rPcu/Fefv0Pv84qoYkSs2wMoxeS6e5Do30aDzfyxV99kVv/4VbmfmZu8ht6\nGOtG6wImNoZhZBOqysLfL2TEgBHcdOZNmS5OQqISG1vPxjBSwBzuRjr47eu/5a87/8qdS+7MdFF6\nHLNsDMOjI0EZNQq2b3f78+fDI49ktjxG7vF+4/vM/M1Mnj7nab448ouZLk67WICAYURMRwMwP/kk\nvt9T3y+ZHpBqpI+WWAvnPHIOl8y+JKuFJkpMbAzDo6MIrunT3e/UqXDnnZkvj5Fb/OL5X1BcUMx/\nfOU/Ml2UjGHdaIbh0VEEVyaiu5I907rZcoO1DWv5h/v/gVdqX6FqcFXyGzKMRaN1ARMbI1dJRUhs\n4Gb2c+DoAab9zzSu/turWfD5BclvyAJMbLqAiY2RKbprdaQiJGPGwNatUFoKr70G48a1vcbILEse\nW0JzrJk759+Z6aKkjAUIGEYO0V3nfir+Gl9c9u6FCy/sWjmN6Fi2aRkr61dm7XiansbExjAioLvO\n/VSmqBk8uHvPMKLjo/0f8a9//Ffu+cY9DC4enOniZAXWjWZkHeEuqIsuyj1HeE8EFNiUNNlJTGPM\nu3ces0bP4spTo1mILErMZ9MFTGxyk7C/YudOc4RnCxYBl5ybXrqJ+zbex5/P+3NOrlFjPhujzxDu\ngurJ8Sa1tU7s5s1zlkNU93f3OZnCBpp2zBs73+Bnz/2M337ztzkpNJGiqr12c69n5BqNjaoLFrjf\nRMdR8rWvqbo5Atwzo7q/u8/JFGee6co8Y0bP/D1yiSPNR3TKLVP0N6/8JtNF6RZeu5n29tgm4jSy\njrKyeFdZsNumJ+iuFZXo/kRdT7k2O4D/DoWFbm64O+6wLrQwlz1zGceXH8/3pn0v00XJTqJQsGzZ\nMMsm5+lpC6C7VlSi+xO9Q09aa+kgVy2xnmLFuyt09PWj9eODH2e6KN0Gs2yMvkhPWwBBqypIqo7x\nRPcneof2npNO0unMzzVLrCfZc3gP5z16HnfU3MGQkiGZLk7WYtFoRlaTLeG93ZkaJlPvkM7pbLLl\n75BtqCrffujbVA2q4oa5N2S6OGnBFk8z+iRRWABd+eLvzpd9T1gxiUinNZKpd8h27nrtLt7++G3u\n+cY9mS5K1mOWjZERMjleoytf/Ln4ZZ+LZc4l3t3zLifddhIrz13J5BGTM12ctGGDOruAiU32kskZ\ni+fNc+NEZszoeDoYIzvIxoGkLbEW/uaOv2HBpAW9bo0aG9Rp9CpS7eJJNPixuwMiU5l3rDeRqwNI\nfbJxIOnPn/s5A4oGcMFJF2S6KLlDFCFu2bJhoc9ZS6qhv4lCbi0Mt3Pken1l20DSF7a8oMOvG64N\n+xoyXZRIIKLQZ7NsjIzgO5yTWRaJLKDeEobbUxZHrtdXNlmi+z/Zz3cf/i63/N0tVA6qzGxhcgzz\n2RhZTSInd29xfPeU36q31Fc2sPjRxQDcVnNbhksSHRnz2YjIGBF5VkT+KiJviMiPvfQKEVkhInUi\nslxEygL3XCoim0Vkk4icHkifLiIbvXM3BtKLReRBL/1FERkXOLfIe0adiJwbSJ8gIi959zwgIjbr\nXS8kkQWUqlWU7fSUxdFb6ivTPPzWw6z+YDU3nnlj8ouNNqTSjdYM/Ieqfh44CfihiJwIXAKsUNXP\nAs94x4jIJOBsYBIwF7hZRHyVvAVYrKoTgYkiMtdLXwzs9tJvAK7x8qoAfgrM9LbLRaTUu+ca4Hrv\nnkYvD8PIGbKpe8jomIZ9Dfzg8R9w7zfvZWDRwEwXJydJKjaqul1VN3j7B4C3gNHAWcBd3mV3AfO9\n/RrgflVtVtV64B1gloiMAgap6lrvursD9wTz+j3wdW//DGC5qjapahOwAjjTE69TgYcSPN8wukVX\nfSmdvc8sjtwgpjH+5dF/4Ydf/iGzqmZlujg5S6cCBERkPDANeAkYoao7vFM7gBHefiWwNXDbVpw4\nhdMbvHS83y0AqtoC7BWRIR3kVQE0qWosQV6G8Sm1tTBqFFRUwGmnpSYCXQ21zWSIbq6HN2czN754\nIwePHuSyr16W6aLkNClPVyMiA3FWxwWquj/eM+bi5ESkpzzxnXrOFVdc8el+dXU11dXVaS6OkYhs\nGYhXVwfbt7v9p5925UrmiO+qLyWTUV++0EFq72ikxus7Xufq56/mpf/1EgV5vXN2r1WrVrFq1arI\nn5NS7XnO998D96jqMi95h4iMVNXtXhfZTi+9ARgTuL0KZ5E0ePvhdP+escA2ESkASlV1t4g0ANWB\ne8YAK4E9QJmI5HnWTZWXRxuCYmP0HOls/LojXMF1cAYMgMZG9+V/0UXt53nffW2jt1Ipw7BhbsuE\nsOZ6eHM2cqTlCP/88D9z3WnXcVz5cZkuTmSEP8KvvPLKaB6UbCAOIDj/yg2h9GuBi739S4BfePuT\ngA1AETABeJd4iPVLwCwvzyeAuV76+cAt3v5C4AFvvwJ4DygDyv1979xS4Gxv/1fAvyYoe9dHNhnd\nIp0D8bozKLGxUbWmRrW4OJ5HTU3iPJcscelVVaqzZ7t38MueShkyOXgy19bH6Sn8v2nwb5kqFzx5\ngX5r6bc0FotFUrZshYgGdaYiNqcAMU9A1nvbXE8IngbqgOW+CHj3XIYLDNgEnBFInw5s9M7dFEgv\n9sRjM/AiMD5w7jwvfTOwKJA+wROvzcCDQGGCskfyxzCSk6jx6+p//HQIV3l5XAjmz0+cZ1Asgtem\nWoZsG+ludP0D4Kl3ntKq/6rS3Yd2R1a2bCVjYpPLm4lN5gkKzOzZXfuP392v9iVLVMvK3HOnTHH5\nhPNcsiQuSHl58XLW1Lhzs2erjhypWl/fvmiadZF9dOUDYNfBXTr6+tH69LtPR1u4LMXExsQm6wk3\nwkuWqJaWxhvukSM7/x8/HQS/bmtqWp874QTVwkJtZc0MHep+p0515Qx/Hef6XGN9ic5+AMRiMf3G\nA9/Qnzz1k2gLlsVEJTY2N5qRNsKhv3V1sHevO1deDi++GP0gxkQhwEHn+Z13tr5++3Zobo4fl5fD\nunWunM8+68oZvL9/f3j9dXc8bZo547Odzo5lun397bzb+C4//9ufR1uwvkgUCpYtG2bZ9ChVVe5r\nv7TUdTf5XRjl5e44Vbrj1E1kdXT0detbMcFyh/HvP/fc1pZa2Erq7XTn75IL1H1cp0OvHapv7Hgj\n00XJKFg3molNthP2yXTVh9GdbqrO9tHX16tWVqrOm9e55Q7Ky1N/r97SSPfm7sOjLUd15q9n6o0v\n3pjpomScqMSmd45SMjLC4MHu1x/r0dV167szZiTZGJlhw+CDD+LjZcaNg4aEI7TaL1d5Oaxfn3rX\nTDYMuEzHINvePJbnZ8/9jPJ+5fxo5o8yXZTeSxQKli0bZtn0KKlYMql85XfFIuoo3+AXebDbrCtj\ndrpiqWVDSHQ6rJLeGm33/AfP64jrRui2fdsyXZSsgIgsG1vPxuhRwmu4lJWl9sUd/jIPzwAwf348\n3+Ji16yWlLivcHBT1cyY4fL395MFKnTXGvDvLyyEzZuhqspZf+3llewduxNUMW+eC9xI5b37Evs+\n2cfUX03lhjNuoOZzNZkuTlYQ1Xo2Gbc+otwwyybrCH/l++HQHTncwyHUQ4e2HqQ5dGjcYhk4MJ7u\nb2PHqg4bpjpnjvPRpGp9BZ/RFWugsxZVlCHWvdUq6S6LHlmkSx5bkuliZBVYgICJTW8gGNn1ta+p\nFhTEG1R/tH6YYKObn99aSILiUlXlBCV4ftq0zg8mDc8k0JXur+Ag0WnT4uXqzAwE2dD91ptZ+sZS\nnXjTRD3wyYFMFyWriEpsbJyN0aOUlbnt0Uddt1dLi0sfNAh++cvE9/iO6fz8eBDC1Kmu6+ykk9zx\njBmwcSNUVrrlBIYOdV1HK1e2DVzoiNpaeOEFtz9woMujK91OdXVu0k+AsWPhd79LPsYovJiaLa4W\nHVv3beWHT/yQ337ztwwoGpDp4vQJLBrN6HGCgz3z8iAWg/374cIL20Zq1dbCvn0gAseOuQa8sjI+\n4LKpqXX02fLlsGePu7eoKN5o19a6AZnz53fsA6mrg6NH3f6BA26m6FQa+rC/JTyQNJXIvPA1nYnm\n68i/lC3LPWQLMY2xaNkifjzrx8wcPTPTxek7RGEuZcuGdaN1SKbGfwQHe/pdVu11FSWaHLOjwZRB\nP0v4ulR8IH7Z/O6vVOslnHc65nPrzN+mo3frzeNjusJ1a67T2bfN1pZjLZkuSlaC+WxMbNJNVI1Q\nsoYy2BAna5T9xn/QIG01X1l7+L6RRNel4gPxlySYP7/tNUuWuICG8nL3nOD5dPtXOvu36ej5wXO+\nryzXB5h2lfUfrdeh1w7V9/a8l+miZC0mNiY2aScqB3QUUVT19aoTJqiOGKFaVORmcZ4zp23j2ZF4\nNTa6PMJr1XTlvcLvlo5or6BIpxJQELy+oyi7YNn6spVz6OghPfG/T9S7N9yd6aJkNSY2JjZpJ92D\nJ/1zfphvV6O4Uhmc2dVBmumYCqezXWw+HS3OFi7b8OGJravuvktfjnD70RM/0rN/d3afWwyts0Ql\nNhYg0IdI5Cju7NQpwalX/CWQ161z074EzxUXw0MPdd65vm8frFkTTw+WL7jEM7hZl4cMcYM0i4vh\nqadcmfzyJMLPY+hQeO45F7k2fbqLFmvPqe5PcVNY6KLTiorgjjvc9Z1xvgfrZ6u3IPp558Ejj7R9\nv5073fM6yq8r08ckms6nL/Cnd/7Eo28/yobvb0Ak/eMVjRSIQsGyZcMsm1akowvF/zIOLjBWVdX6\nnL9NmJCafyBYrqKi9r+8fX/KvHnxr37fOhs8uG15EuFfHxx7k8yp3pH11Jk69esnOFYoGMQQHOSa\niuVhAzVTY+eBnVp5faWufG9lpouSE2DdaCY23SUdXSh+A1dcHBed116Lnws2lsEGfejQ9kUnLFJV\nVe0vJ92eg9sXhPx81Vmz2n+W7+QPDiYdMKC1wz84IHPIkPgqn4m6zsLLKqRSd75AJQpiMAFJL83H\nmvWs+8/SC5dfmOmi5AwmNiY23SadDdmsWfHGeuTIeJ7BZ/giEhzl73/9h53bQZEKC0p7VkZQwOrr\nXcMfLFciSyPs9xGJ7/szGASn0OkolFq187MThJeYzgS9ZcmDZKz/aL1O/5/pevo9p+uR5iOZLk7O\nYGJjYhMZyRzXiQhbI4ksF194Kiu1zdd/R+NSgueKi+OCUFAQnyNtwIDEjXwy6y3s5PetlqCYBAVm\n+PDU8kvVWsyGaLBsKEOUHDp6SC9ecbEOu3aY3v7q7RYQ0ElMbExsWtHZr9PORnkVFDgBae/rO9hl\nFrRcfCsn+LxE1obfSA8dGhc436LpaFLNZCIQtt7CQlpZ6fxCIk64fCELdgcGx+r4IcXtdd911lrM\nhmiwdJchmyylZ957Rj9z02f07N+drdv3b89sYXIUExsTm1Z09uu0o+v9xsd3sged/0VFyQdnhie/\nHDiwtRNIA651AAAbHUlEQVQ87PQPdiUFhSjYRZZoUs3gNmtWx11RiWZuTrb5gQWJBCRZfafa4GbC\nJxMuW7rLkA2W0u5Du/V7y76nY/5rjD626bHMFKKXYGJjYtOK8Ndpssauva/ZYMP/2muusRgyRNv4\nMzpqRMKBAcHIsKDg+E74RNFneXmqhYWty+hHn/Xr1zqvqVMTlys4wj9Y9lS2kpLEwpVs7JD/zKC4\nZlvXVNRikElrLRaL6YNvPKij/u8o/bfH/033HtnbswXohZjYmNi0Ivx1mqxBae9rNtF9vrM92bxl\n7Y1gD1oo4W3ChLjAtLf53Vk+QSd8fn5cDMPlStQdGBbN8FZd7d61PQsp7D8KXxd+Znl58rqKukEO\ndx12Z5BtKmQqgm5dwzqdc/ccnfT/TdI1H67p2Yf3Ykxs+rjYdNVySUZH82b5jUh7/or2BK6+Ph4a\n7Xer+c8Ij2/Jz49bNEErI/i8cDCCf83s2e538GDXoCYSm/7926b7Yc8VFe0HRIQtmvB7nnCC8/kE\ny15WlppotWddpDI7QypilagewuHkuczbH7+tC5Yu0FH/d5Te8vIterTlaKaL1KswsenjYtNVyyUZ\n7UWBBQdkhgWioMCd86PMBg9WXbiwrVD5E1oGrZ5EwhEWkbAfZ86ceEAAtF0Qzd8qK+NdbgMGuO6t\nhQsTX+t/9QefE2zIg3XhW0ZBIQ+uHFpcnHxqmVQ+BtI1c3PYB9dbpqbZuner1j5Wq0OuGaJXP3e1\nLXoWESY2fVxsumK5dLbrJjhAMdjg9++fWBj87iy/sQ5e357F0NjoLIpgPsGos2HD4iIWDFSoqWk9\nG3NYtPLznbAE/UXhpZWDYtXeOCA/mi6cv4jLy38f/33b8/WESeVjINWZm1OdWSAo8tkUMdZZdh3c\npRctv0jLf1GuFy6/UHcf2p3pIvVqTGz6uNh01nJZsqT113cqjuHgl37Q4R8UHn+bMqX1zMTtRY4l\nGsQZtIjGjGk91iUsYkFxCNeHX0YR1enTW0eeFRW19ldMnRqf5sbvFpwzxx2Hy+53HYa798Bdv2SJ\nq5Pi4rb+pfC7dqZh7+hv3F2/SDZEjHWG5mPN+njd4/qPD/6jlv5nqS55bIlu2bsl08XqE2RMbIDb\ngR3AxkBaBbACqAOWA2WBc5cCm4FNwOmB9OnARu/cjYH0YuBBL/1FYFzg3CLvGXXAuYH0CcBL3j0P\nAIXtlD39f4kcIdi4tOe0Vk08rX1BgROCfv1co+o32AUFrmH3u9GCX87Bxt/f8vLi1kDwXDByK+wT\nSRRc4A+2DE9bM3u2s6L8tW6C7xsUyLC/ItzwBoXFF7b2gg1qapI33Kk27D1pbWTD+J5UePvjt/WS\nFZdo5fWVOvPXM/WWl2/RxsNZXOBeSCbF5qvAtJDYXAtc5O1fDPzC258EbAAKgfHAO4B459YCM739\nJ4C53v75wM3e/tnAAxoXtHeBMm97Fyj1zi0Fvu3t3wL8aztlj+JvkfUE5/bqyGmt2rphrKhI/DXv\nN9iJJq8MR6QlEov2osH8Rcj8ZxcXtxYif0s060Ci55SWtu1mCw4a9buT/LqZNk114sTEE2P690+d\n2to6CubdmVkFEglLd4MGOkM2z7m278g+/c0rv9HZt83WEdeN0J889RN9Y8cbmS5WnyWj3WiecATF\nZhMwwtsfCWzy9i8FLg5c9yfgJGAU8FYgfSHwq8A1s7z9AmCXt/9PwC2Be37l3SfALiDPSz8J+FM7\n5U733yEnCDZiHS2hHGx4g/6R8DZ0qFu0LDh5ZSILYOTIjgdiBoWnoMB1QX3mM24/kciEG+KgT8l/\nru+jKSpqPQFnY6MLcgiKZ9gqCc9QUFjYtostaEENGxZfyjrYHRcWgnPPjQc2dCQsyUSrK12huUIs\nFtNV76/SRY8s0tL/LNWa+2t02VvLLLIsC4hKbPLoGiNUdYe3vwMY4e1XAlsD120FRidIb/DS8X63\neMrQAuwVkSEd5FUBNKlqLEFevYraWqiudmuoNDWlfl9wnZM772z/uro6aGx0+zGvNktL3fotAOXl\nbr2YvXthxw5oaXHplZVw4ACMHw9/+Us8v+3bYcAAqKlxZS4sbPvMz3/e/ba0wFVXwa5dbv/Ysfg1\neYF/ldOmxddqOXrU/e7d654zYQKceCKMHOmue+klePJJV29lZTB2LDQ3x/MSaV03eaF//evWuXVr\nVq92a+QUFrrjNWvg8GFX1sZGd94/t3p1/Jk+H3wAH3/s8vDTE609c999sGABrFiReG2Zujr3rv7f\nItU1a7KZLXu3cNVzVzHx/53I+U+cz+Thk3n7395m2cJl1HyuhsL8BP9ojF5BtxdPU1UVEU1HYVJ5\nXA89JysILrZ14olw+umuIfMX6rroInfNyy9DQYFb1GvdurYLZH3uc04ICgthzhxYtcotzuULjE9B\ngVtQbOxY+NKXYPfuuBj5lJW5hn7z5niaiPv2LiiAJ55w52fMcEK1fXvr+994I77/0EPuPp8hQ2DW\nLNfA+guo7dnj3n3PnrjYADzzjFsw7f33W+c/dChs29ZW7KZMcQuegaub/v1hw4b4+T//2V3z7rvu\nOC/P1ZH/ngUFcbH1BfA733HHM2a4/Kqr3d/Gf25YWMKLliVbvM4XqPJyWL++/cXOOrOAWyY40nKE\nZZuWcceGO3i54WXO/vzZ3PeP9/Hlyi/bQmZ9iVTMHxJ3o4309kcR70a7BLgkcN2fgFm4rrZgN9qn\nXWTeNSdp2260T7vavOP/wfl0wt1oX6GDbrTLL7/80+3ZZ59Nn62ZRtrrl080s3KwSyXskPd9K2GC\nXUnt+WT8bcyY9kOdQfWb32yb9tpriX0o4RDnVLaRI104cWfuKS93Yc/DhrV+P3/A6GmntZ1iJtg9\nVVAQ7/IK+6XC7zBsWHxMkd/VFu5OrKlJj38kVT9LNkaaxWIxXdewTs//4/k65JohOufuOXrv6/fq\noaOHMl00I8Szzz7bqp0ky3w21+L5ZjyBCQcIFOEixt4lHiDwkic8QtsAAV94FtI6QOA9XHBAub/v\nnVsKnO3t/4ocDxBor7EIzznm+0MGDnT74ZDhkpK2gyuXLGnbWHbUcCcTo3BYcmmpE7hwWQoKkueV\njk3EvVNHPh9fgJNNzpmX11qEpk2Lh2kHt0Qrd3Y12qs7AQDJ5m2L+vmJ2Hlgp97wwg06+ebJOv6X\n4/XKVVdqfWN99zM2eoyMiQ1wP7ANOIrzrZznCcHTJA59vgwXhbYJOCOQ7oc+vwPcFEgv9sTDD30e\nHzh3npe+GVgUSA+GPj9IjoU+h/+D+w1VQYFrtCsr4xFU/hd7SUnbEF9/VP2JJ7p76uvbClc4hHf6\n9LaNtd/AiiSft6w7AlJY2LoxT5fYJLumtNTVT6IJQtvbKivd3yY4c4EvQMHxRX4D3dVor+5YJcF7\nuzodTTqsosPNh/UPb/9Bv/ngN7X0P0v1uw9/V1e+t1KPxY51LUMjo2TUssnVLRvFJtyF40cthS2G\nRF/RwW3GDNXjjnMCNWSIE5rwcsbhCLL2trBV4m/tWQvhWZhT3VIpSzZs5eXxSLNgmf3ZBdIZRtyd\n8S/pGDvTlTxisZhu3LFRr//L9XrGPWfowKsH6im3n6K3rrtVmw43da0gRtYQldj4XVy9EhHRbHu/\n6uq40z8/Px6FNXJk3JleWOiiqEScozoYqZWfD4MHw/TpsHYt7Nvn0n3HtB+9FHRodxU/j2A5s41U\n39Ov04ICJx3h9/GDHPLz4ZRTXJ5+kALA1Knw7LPxoIx0OeObmtoGDvTEvZ3JI6YxNn28iTUfruH5\nLc+z4t0V9CvoxxnHn8Hpx5/OqRNOpaxflkUlGF1GRFDVtEdumNj0EH7E0F//6sJi8/PddvSoCzd+\n7jn46U9dhFRDQ/sNaHl5PEKsqMjdX1ICkye70F+jLQUFro58YQ6L57Rp8MgjLnrs449dmi9OkyfD\n8ce7SLaystYfCwsWdBxNlqscPHqQl7e9zJoP1/CXrX/hhS0vUNG/gpPHnMzsMbOZc9wcjq84PtPF\nNCIiKrHpduizkRrBMGZfJPwGb+9e+PrX4ctfhqoqF96ciPz8+NiQGTPgttvgK18xoUlGS0tcaBJZ\nQmPHwrhxrv6ffBIGDnTjiACOO84JkU94vEy2hx2nQsO+BtZsWcNftvyFNVvW8OauN5kyYgqzx8xm\n8bTF3HbWbYwcODLTxUxIb6j/voJZNhES/I/Q3OwG+c2Y4f5DPP206w7bt6914xbsTgsS/hr3u32M\nzhGut4ED4aST4He/c8e1tc5y9P9W4QGX4W6nqCydKBrRmMZ4r/E9Nu7YyIbtG3h1+6u8+tGrHD12\nlJPHnMzJVScze+xsZlTOoF9Bv+4/sAfoC5ZmT2PdaF0g02IT/I9QU+MsmltvhQsucF/Q+fnxEe67\nd7vG7TOfgYcfbj2A0YiGoPDU1MCyZW6/M76QefPc3zKRMHWH7jaiuw7uYuPOjWzcsZGNOzfy+o7X\neXPXmwwpGcLk4ZOZMmIK00dNZ3rldMaVjsvZwZVR1X9fxsSmC2RKbML+Gf8/gu9cfuGFtmJSVQUb\nN8L8+fFGpjNksxM/EwwcCH/zN657cffuePqAAXDwoHP419fHpwEaPhzefjsaJ31XrJRUGtFDzYfY\nvHszdbvr3Lan7tP9Y7FjTB4xmcnDJ38qLl8Y/gVK+5V27gWznHQESRitMbHpApkSm+BXqS8iF13k\nvk79aLEgeXmucfzkE+jXr/U1xcUu3eg8EyY4EXn1VVfHAwY4/1Z5uXP4L1jgust82rMggmIxbJjz\nqb37rvPzDB6cXEC6YqU0NcGS2hj/57+2c8kv6qnbWU9scD1fOfMDth58l7rddew6tIvjyo/jhCEn\n8Nkhn221DSsZlrPWipFZLEAgh/CdyEOHugbpO99xvplEQiPi5ijzHdhhYcnPj7asuc7kyW6+tfA3\nRXm5mzDUD18eOtRZmatXuwa/rMz5aSor3SSbhYXw4YfOogiLRzC4w88HYKs3TWxtbWpznAXnSlNV\ndh/ezbb922jY18C2/dvYtn8bW/Ztob6pnvqmej6c8iF/fqCMQ0Xj2a/j4IPxDFw+lZ9f+A1OGHIC\nY0vHkp9n/0CM3MAsmzRTWwtvvhn/8g1HiaVj/IsRJ5HlJ+ImEn3jDXdu8GAX3rx6desuzT/8IfGE\npGHrI9ilFQ7uCHZzqSoHjh5g16Fd7Dq4i12HdrHz4E4+3L2L+x77iEmzGtj1iROVj/Z/xICiAVQO\nqqRyUCWjB42mclAlVYOrGF82nvFl4xlbOpaSwhLzSxg9inWjdYGeFJvaWtd4BSPJ/LEaeXnxBq2g\nwB1bAEBy8vKccKTDF1VTA6+/DocOubpXbb1sg/8RMHQonHAC1H/YzOjj99KvrJH//f808v1/b6J0\nRCN5JW47+bSPWbFmF5/54k4aj8bFJU/yGFYyjOEDhjNswDCGlbjNF5XKQZWMHjyaUQNH0b+wf0pl\nD/ol0j2o1DDCmNh0gZ4Um2C/fJCSEtdN04urORKKiuDv/95ZEfv2OeFuaXH1GBTvQYNg/37/LoWC\nI5RU7OdQ8wEGlO/nYMt+CgccoKBkP59wgFjBfig6AEX7oXg/FO2nYFATX5zZxDsNjRymkaPSBIWH\n4UgZHCmjvH85HC6n8aMyOFzOCePL+F//5AmJJyi+uJQUlkRaLxbqa0SN+WyyHH8dlDCHDvVsObID\nhbwWyD/a/lbwCRQcdo16gt+jhYd5ZP9h9GR33Bw4r4WHKeh/mJJBh9GCw/DJQSceRQcgVkBxySCO\n7h5ITAdReGgQsSMDOXxoEHwyCI4OhKOD4JPBDJJKij4ZxDDK+PCuciYMKeODt8s5uq2cQf0Gsn+f\nfNp19Z3vBLqy7smcRZHI/2MYuYBZNgEOHj1IS6wFRYlpjJjGUHX7fpp/HE779sIYr74aA1GQGOD9\n+sfdSSNwTmKQd8w15uL9tnecyjWp5BEUibzmjkUk/ygUHIVjBXCsqOOtpT8090/4K8f6o0fbP09z\nf0YO68+Bxv4c2DMgLiSxQhYscL6Y8IwNQcrK3MJriULNq6rg+efhwgvjIbXZEmKbLeUwei/WjdYF\nOis2p9x+Cq/veJ08ySNP8hAR94u0OvbTGvfk0dIsNDfnocfyiMUENA/U+8U/TjUtcK6jtFgBxPLd\nr+Z3fJzKNcmOk4lGeIsVeuXtGoWFrrssWSBFcJ44n8GDnW/mBz+IWyK33QZ/93dujrPVq+MrX44b\nF3f+J3L4G0ZfxMSmC0Tts2nPT2P0DMOHOwumvNz5cfzBm/6YmoMHXRTa8OHOmQ5trQLfUrjuutaW\njGH0VaISm65/fvZxPve5+BiOPKvFHmHwYNclBi4wYMUK5yR/773W4cuxmAsaiMXglVec5XLiie7c\n0qWtxaSszG0nneSCERYsaB2lZhhGerBmshPU1jprZt48+OijeDdPeJyGkTpFRTBkSPLr/JH7X/6y\nO96/H666yonHRRcl/hsEPwK2b4d/+ZfEedfVufP+BJy1tW4bNQoqKuC000yADKO7mNikiD9KfPVq\n96Xsj/g3usekSW39LmE+/3knCGVlzrqB1tFYdXWtZ2c48UQ3M8D69c7/49Pe7C0lgWjladNcvokE\nyDCMrmNikyLhBs3oHO019Bs2JLcM33nHrStz2mlwyy2uqyvoxPfFoqLCWUmjR7tJUKdMga99zZ2b\nNs3Nh5aI++5zgz7nz4eVK12+iQTIMIyuYwECSQjP4GxET3Dq/+AATkg8kNF38m/bFvej+dd1NVS4\nqcl1u4nEV+k0jL6ARaN1gc6KTXgq+EQzNdvcZp0n0TiXZFRWunnNgssDTJsWtzwSYXOIGUb3sWi0\nHsCf3ffJJ2HECDdeI9x1ZkLTeTorNFOmOEuyvzd1WH6+60LrSGjAfSCEu9gMw8gOTGwCBPvpjx51\n/gQjGmbNiu8XFzuL0WfCBCcW48a542PH4iHKHVFW1ja02TCM7MDEJsCwYfH9vDwXhTRyZObKkyuk\nMs6oqgqmT48fjxzpur0qK90Kmaed5tJnzIA773T7iSLPDMPITUxsAnzwQXw/FoObboK33op35/RF\nCpJM1VpY6EKMfbFIdO+MGW610uHD48d33gmPPw4NDc6CSdQFZt1ihtF7MLEJkCjctazMLcTVFyko\ncGHHvkgMGOCisyoq3HF5OWze7Hwsy5dDfb2zYF57zYnEO++0FouOxCNRF5h1ixlG78Gi0QK0F+7q\nRzn58231BfLynMUyZUrb8GGbedgwei8W+twF0jURZ1OTGyyY7dPSDB7srLC6OjfmJMikSbBnD0ye\n7Lq+1q1zk1iWlsLMmS6tqAiuvNLNkPz883EHvWEYfQcTmwSIyFzgl0A+8BtVvSZ0Pm2zPhcUpGd5\n4u5QXOwEr7nZ+ZGOHIkPfjz1VHj44bil8fzzbvT8H//orLSwFWLWiWEYibBxNiFEJB/4b2AuMAn4\nJxE5MarnRdkgizgHuz+1iu9YHzzYRW39+c/OF/L2285HUlXlAhc2bIB+/ZyPJDwG5ZRTnDieeabz\ne2zYsKrN+/RVf8iqVasyXYSswerCYfUQPTkrNsBM4B1VrVfVZuABoCaqh73yirMsggwfHp/yfvBg\n59uZPdsdB8OB8/Nb3+dPDumLyfvvOwf7smWtHesffOBmlz7lFNiyxXVrjRsX358yBQ4fdr/JsP9M\ncawu4lhdOKweoieXxWY0sCVwvNVLi4Rx49wswP64mxkznKWxY0dcGB5/3HVb+Wus+JM7vvqqu2/k\nSBextXNnazHxfSO+tTFuXN+1OgzD6J0kGUWR1fS4s6mszHVfhX0dwYkhfcEAZ6n4fPRR67zCk0ka\nhmH0ZnI2QEBETgKuUNW53vGlQCwYJCAiuflyhmEYGcSi0QKISAHwNvB1YBuwFvgnVX0rowUzDMMw\n2pCz3Wiq2iIi/wY8hQt9vs2ExjAMIzvJWcvGMAzDyB1yORqtXURkrohsEpHNInJxpssTBSIyRkSe\nFZG/isgbIvJjL71CRFaISJ2ILBeRssA9l3p1sklETg+kTxeRjd65GzPxPt1FRPJFZL2I/ME77pP1\nACAiZSLykIi8JSJvisisvlgfIvIf3v+NjSJyn4gU95V6EJHbRWSHiGwMpKXt3b26fNBLf1FEks83\noqq9asN1qb0DjAcKgQ3AiZkuVwTvORKY6u0PxPmvTgSuBS7y0i8GfuHtT/LqotCrm3eIW7ZrgZne\n/hPA3Ey/Xxfq438D9wKPecd9sh68st8FfM/bLwBK+1p94IZBvAcUe8cPAov6Sj0AXwWmARsDaWl7\nd+B84GZv/2zggWRl6o2WTY8O9swUqrpdVTd4+weAt3D/wc7CNTZ4v/O9/RrgflVtVtV63D+oWSIy\nChikqmu96+4O3JMTiEgVMA/4DeBH0fS5egAQkVLgq6p6OzjfpqrupW/WRwFQ4gUTleACifpEPajq\nn4HGUHI63z2Y1+9xgVod0hvFpkcHe2YDIjIe9xXzEjBCVXd4p3YAI7z9Slxd+Pj1Ek5vIPfq6wbg\nQiA4VWpfrAeACcAuEblDRF4VkV+LyAD6WH2oagNwPfAhTmSaVHUFfaweQqTz3T9tZ1W1BdgrIhUd\nPbw3ik2fingQkYG4L4sLVHV/8Jw6G7dX14eI/D2wU1XXE7dqWtEX6iFAAfAlXBfHl4CDwCXBC/pC\nfYhIOe7rezyu0RwoIt8NXtMX6qE9MvHuvVFsGoAxgeMxtFbnXoOIFOKE5h5V9ecr2CEiI73zo4Cd\nXnq4Xqpw9dLg7QfTG6Isd5o5GThLRN4H7gf+VkTuoe/Vg89WYKuqvuwdP4QTn+19rD7mAO+r6m7v\ny/th4Cv0vXoIko7/E1sD94z18ioASlV1T0cP741isw6YKCLjRaQI57x6LMNlSjsiIsBtwJuq+svA\nqcdwjlC832WB9IUiUiQiE4CJwFpV3Q7s8yKWBDgncE/Wo6qXqeoYVZ0ALARWquo59LF68PHeY4uI\nfNZLmgP8FfgDfas+PgBOEpH+XvnnAG/S9+ohSDr+TzyaIK9vAc8kfXqmoyai2IAzcdFZ7wCXZro8\nEb3jKTgfxQZgvbfNBSqAp4E6YDlQFrjnMq9ONgFnBNKnAxu9czdl+t26USdfIx6N1pfr4YvAy8Br\nuC/60r5YH8AVuMCZjThndmFfqQeclb8NOIrzrZyXzncHioGlwGbgRWB8sjLZoE7DMAwjcnpjN5ph\nGIaRZZjYGIZhGJFjYmMYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEYkWNiYxiGYUSOiY1hGIYROf8/\nq/0FGyqRqCsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x2452a9e8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_2_coef = get_coef(set_2, l2_new_penalty)\n",
"print set_2_coef[set_2_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_2, l2_new_penalty)"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 2.26890421877 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x24da68d0>,\n",
" <matplotlib.lines.Line2D at 0x24da6ac8>]"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEACAYAAABlOdt4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXmcVcW57/19egCasbuZmpmOIajXCUFwiEmbACL3HiEm\nCCeJ4vDKTbx5k3PzXseTT8QTT07UawyeRD1GT0RfERAj0cQBHNqcaw5DHBAVZBIjjQxCN6Ao0vRz\n/6ha9Orde/feu9mr99DP9/NZn12rVlWtqt1Qv/1UPVUlqophGIZhRElRtitgGIZhFD4mNoZhGEbk\nmNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuQkFRsR+Z8i8paIrBWRBSLSVUQqRWS5iGwQkWUi\nUh5Kf4OIbBSR9SIyORQ/1pexUUTmheK7isgiH79CREaEns3279ggIpeG4qtFZKXPs1BESjPzdRiG\nYRhR0KbYiMgQ4P8FxqrqyUAxMAu4Hliuql8CXvD3iMiJwEzgRGAKcLeIiC/uHuBKVR0FjBKRKT7+\nSmCPj78TuNWXVQn8FBjvr5tEpI/Pcytwh89T78swDMMwcpRUhtFKgO4iUgJ0B7YDFwLz/fP5wHQf\nngY8qqqHVXUrsAmYICKDgF6qusqneyiUJ1zW48DXffh8YJmqNqhqA7AcuMCL13nAkjjvNwzDMHKQ\nNsVGVeuAO4C/4USmQVWXAwNVdadPthMY6MODgW2hIrYBQ+LE1/l4/OcH/n2NwD4R6dtGWZW+Hk1x\nyjIMwzBykGTDaBU4y2MkrvPvKSLfDadRt99NR+15Y3vrGIZh5CElSZ5PBN5T1T0AIvJ74Cxgh4hU\nqeoOP0S2y6evA4aF8g/FWSR1PhwbH+QZDmz3Q3V9VHWPiNQBNaE8w4AXgb1AuYgUeetmqC+jFSJi\n4mQYhpEmqirJU6VHsjmb94EzRaTMz5VMBN4BngJm+zSzgaU+/CQwS0S6iEg1MApYpao7gP0iMsGX\ncwnwh1CeoKxv4RwOAJYBk0Wk3FtYk4DnvCX1EjAjzvtboaoFed10001Zr4O1z9pn7Su8KyratGxU\ndZWILAFeAxr9531AL2CxiFwJbAUu9unfEZHFOEFqBK7W5tpfDTwIlAFPq+qzPv4B4GER2QjswXm7\noap7ReRnwGqf7mZ1jgIA1wELReQWX6cH2v0NGIZhGJGTbBgNVZ0LzI2J3ouzcuKl/znw8zjxrwIn\nx4k/hBerOM9+B/wuTvx7wIS2a24YhmHkCraDQJ5SU1OT7SpEirUvv7H2GbFIlGN02UZEtJDbZxiG\nkWlEBM2Cg4BhGIZhHDMmNoZhGEbkmNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiR\nY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFjYmMYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEY\nkWNiYxiGYUSOiY1hGIYROUnFRkRGi8jroWufiPxQRCpFZLmIbBCRZSJSHspzg4hsFJH1IjI5FD9W\nRNb6Z/NC8V1FZJGPXyEiI0LPZvt3bBCRS0Px1SKy0udZKCKlmflKDMMwjEyTVGxU9V1VHaOqY4Cx\nwEHgCeB6YLmqfgl4wd8jIicCM4ETgSnA3SISHDF6D3Clqo4CRonIFB9/JbDHx98J3OrLqgR+Coz3\n100i0sfnuRW4w+ep92UYhmEYOUi6w2gTgU2q+gFwITDfx88HpvvwNOBRVT2sqluBTcAEERkE9FLV\nVT7dQ6E84bIeB77uw+cDy1S1QVUbgOXABV68zgOWxHm/YRhGpMyZAzU1MHUqNDRkuzb5QbpiMwt4\n1IcHqupOH94JDPThwcC2UJ5twJA48XU+Hv/5AYCqNgL7RKRvG2VVAg2q2hSnLMMwjEjZsAFefhme\necYJj5GclMVGRLoAfwc8FvtMVRXQDNarLTrqPYZhGHHp3t19jhsH992X3brkCyVppL0AeFVVd/v7\nnSJSpao7/BDZLh9fBwwL5RuKs0jqfDg2PsgzHNguIiVAH1XdIyJ1QE0ozzDgRWAvUC4iRd66GerL\naMXcuXOPhmtqaqipqYmXzDAMI2UWLHAWzX33QXl58vS5TG1tLbW1tZG/R5xRkkJCkYXAM6o639/f\nhpvUv1VErgfKVfV67yCwADehPwR4HviiqqqIrAR+CKwC/gTcparPisjVwMmq+n0RmQVMV9VZ3kHg\nr8DpgACvAqeraoOILAYeV9VFInIv8Iaq3htTZ021fYZhGAaICKoqyVOmWW4qnbGI9ADeB6pV9YCP\nqwQW4yySrcDFfhIfEbkRuAJoBH6kqs/5+LHAg0AZ8LSq/tDHdwUeBsYAe4BZ3rkAEbkcuNFX5ZaQ\n2FUDC3HzN68B31XVwzH1NrExDOOYmTPHzdN07+6smny3Ztoiq2KTr5jYGIaRCWpqnEMAwIwZsHhx\nVqsTKVGJje0gYBiGkQRzCDh2zLIxDMNIQkND4TgEJMOG0dqBiY1hGEZ62DCaYRiGkbeY2BiGYRiR\nY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFjYmMYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEY\nkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZhRI6JjWEYhhE5KYmNiJSLyBIRWSci\n74jIBBGpFJHlIrJBRJaJSHko/Q0islFE1ovI5FD8WBFZ65/NC8V3FZFFPn6FiIwIPZvt37FBRC4N\nxVeLyEqfZ6GIlB7712EYhmFEQaqWzTzgaVU9ATgFWA9cDyxX1S8BL/h7ROREYCZwIjAFuFtEglPf\n7gGuVNVRwCgRmeLjrwT2+Pg7gVt9WZXAT4Hx/rpJRPr4PLcCd/g89b4MwzAMIwdJKja+cz9XVf8d\nQFUbVXUfcCEw3yebD0z34WnAo6p6WFW3ApuACSIyCOilqqt8uodCecJlPQ583YfPB5apaoOqNgDL\ngQu8eJ0HLInzfsMwDCPHSMWyqQZ2i8jvROQ1EfmtiPQABqrqTp9mJzDQhwcD20L5twFD4sTX+Xj8\n5wfgxAzYJyJ92yirEmhQ1aY4ZRmGYRg5RkmKaU4HfqCqq0XkV/ghswBVVRHRKCoYh7TeM3fu3KPh\nmpoaampqMlwdwzCM/KW2tpba2trI35OK2GwDtqnqan+/BLgB2CEiVaq6ww+R7fLP64BhofxDfRl1\nPhwbH+QZDmwXkRKgj6ruEZE6oCaUZxjwIrAXKBeRIm/dDPVltCIsNoZhGEZLYn+E33zzzZG8J+kw\nmqruAD4QkS/5qInA28BTwGwfNxtY6sNPArNEpIuIVAOjgFW+nP3ek02AS4A/hPIEZX0L53AAsAyY\n7L3hKoBJwHOqqsBLwIw47zcMwzByDHH9dpJEIqcC9wNdgM3A5UAxsBhnkWwFLvaT+IjIjcAVQCPw\nI1V9zsePBR4EynDebT/08V2Bh4ExwB5glncuQEQuB270VblFVef7+GpgIW7+5jXgu6p6OKbemkr7\nDMMwDIeIoKqSPGWa5RZyZ2xiYxiGkR5RiY3tIGAYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEYkWNi\nYxiGYUSOiY1hGIYROSY2hmEYRuSY2BiGYRiRY2JjGIZhRI6JjWEYhhE5JjaGYRhG5JjYGIZhGJFj\nYmMYhmFEjomNYRiGETkmNoZhGEbkmNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSkJDYislVE\n3hSR10VklY+rFJHlIrJBRJaJSHko/Q0islFE1ovI5FD8WBFZ65/NC8V3FZFFPn6FiIwIPZvt37FB\nRC4NxVeLyEqfZ6GIlB7rl2EYhmFEQ6qWjQI1qjpGVcf7uOuB5ar6JeAFf4+InAjMBE4EpgB3i4j4\nPPcAV6rqKGCUiEzx8VcCe3z8ncCtvqxK4KfAeH/dJCJ9fJ5bgTt8nnpfhmEYhpGDpDOMJjH3FwLz\nfXg+MN2HpwGPquphVd0KbAImiMggoJeqrvLpHgrlCZf1OPB1Hz4fWKaqDaraACwHLvDidR6wJM77\nDcMwjBwjHcvmeRH5q4hc5eMGqupOH94JDPThwcC2UN5twJA48XU+Hv/5AYCqNgL7RKRvG2VVAg2q\n2hSnLMMwDCPHKEkx3Tmq+qGI9AeWi8j68ENVVRHRzFcvLmm9Z+7cuUfDNTU11NTUZLg6hmEY+Utt\nbS21tbWRvyclsVHVD/3nbhF5Ajd/slNEqlR1hx8i2+WT1wHDQtmH4iySOh+OjQ/yDAe2i0gJ0EdV\n94hIHVATyjMMeBHYC5SLSJG3bob6MloRFhvDMAyjJbE/wm+++eZI3pN0GE1EuotILx/uAUwG1gJP\nArN9stnAUh9+EpglIl1EpBoYBaxS1R3AfhGZ4OdcLgH+EMoTlPUtnMMBwDJgsoiUi0gFMAl4TlUV\neAmYEef9hmEYRo4hrt9uI4ETjCf8bQnwiKr+i/cUW4yzSLYCF/tJfETkRuAKoBH4kao+5+PHAg8C\nZcDTqvpDH98VeBgYA+wBZnnnAkTkcuBG//5bVHV+qF4LcfM3rwHfVdXDMXXXZO0zDMMwmhERVDXW\nIezYyy3kztjExjAMIz2iEhvbQcAwDMOIHBMbwzAMI3JMbAzDMIzIMbExDMMwIsfExjAMA5gzB2pq\nYOpUaGjIdm0KDxMbwzAMYMMGePlleOYZJzxGZjGxMQzDALp3d5/jxsF992W3LoWIrbMxDMPADZ3N\nmeOEprw8efpCxRZ1tgMTG8MwjPSwRZ2G0UmxiWujEDCxMYwcxyaujULAxMYwchybuDYKAZuzMYwc\nxyaujY7EHATagYmNYRhGepiDgGEYhpG3mNgYhmEYkWNiYxiGYUSOiY1hGIYROSY2hmEYRuSkJDYi\nUiwir4vIU/6+UkSWi8gGEVkmIuWhtDeIyEYRWS8ik0PxY0VkrX82LxTfVUQW+fgVIjIi9Gy2f8cG\nEbk0FF8tIit9noUiUnqsX4RhGIYRHalaNj8C3gECP+LrgeWq+iXgBX+PiJwIzAROBKYAd4tI4EJ3\nD3Clqo4CRonIFB9/JbDHx98J3OrLqgR+Coz3100i0sfnuRW4w+ep92UYhmEYOUpSsRGRocBU4H4g\nEI4Lgfk+PB+Y7sPTgEdV9bCqbgU2ARNEZBDQS1VX+XQPhfKEy3oc+LoPnw8sU9UGVW0AlgMXePE6\nD1gS5/2GYRhGDpKKZXMncA3QFIobqKo7fXgnMNCHBwPbQum2AUPixNf5ePznBwCq2gjsE5G+bZRV\nCTSoalOcsgzDMIwcpKSthyLy34Bdqvq6iNTES6OqKiIdtUw/7ffMnTv3aLimpoaampoMVscwDCO/\nqa2tpba2NvL3tCk2wNnAhSIyFegG9BaRh4GdIlKlqjv8ENkun74OGBbKPxRnkdT5cGx8kGc4sF1E\nSoA+qrpHROqAmlCeYcCLwF6gXESKvHUz1JcRl7DYGIZhGC2J/RF+8803R/KeNofRVPVGVR2mqtXA\nLOBFVb0EeBKY7ZPNBpb68JPALBHpIiLVwChglaruAPaLyAQ/53IJ8IdQnqCsb+EcDgCWAZNFpFxE\nKoBJwHN+s7OXgBlx3m8YhmHkIMksm1iCYaxfAItF5EpgK3AxgKq+IyKLcZ5rjcDVoZ0wrwYeBMqA\np1X1WR//APCwiGwE9uBEDVXdKyI/A1b7dDd7RwGA64CFInIL8JovwzByijlz3Fk03bvDggW2Y7PR\nubFdnw0jImpq3KFnADNmwOLFWa2OYaSE7fpsGHmGHXpmGM2YZWMYEWGHnhn5iB2e1g5MbAzDMNLD\nhtEMwzByhIsfu5jVdauTJzSOYmJjdCrmzHET91OnumGuXCnLyB827NnAy++/zMkDT852VfIKExuj\nU7Fhg/MQe+YZJxa5UpaRP9z713u54rQr6FbSLdtVySvSXWdjGHlNJj3EzNus83Hw8EEeWvMQf53z\n12xXJe8wy8boVCxY4Na8LF9+7B5imSzLyA8eXfsoZw87m5HlI7NdlbzDvNEMwzBSQFUZe99Yfv71\nnzPli1OSZ8hTzBvNMAwji6ysW8n+Q/uZfNzk5ImNVpjYGEY7ME+0zsdvVv+G74/7PkVi3WZ7sG/N\nyCtypZM3T7TOxe5PdvPHDX/k8jGXZ7sqeYuJjZFX5Eonb55onYsHXn+Abxz/DSrLKrNdlbzFxMbI\nK3KlkzdPtM7D4SOHueev93D1GVdnuyp5ja2zMfKGOXNg/36oqoIlS7LbyZeX5+aRAXaGTuZ5+M2H\n+WLlFxk3eFy2q5LXmGVj5A0bNsArr8COHXDNNdmuTW6SK8OMhcLhI4f55//4Z2766k3ZrkreY2Jj\n5A25MoSWy9h3lFkeWfsIw/sM5ysjvpLtquQ9tqjTyBvC58Nce60NF8XDztDJHI1NjRz/6+O5/8L7\nqRlZk+3qdBh2nk07MLEpXOzIZSNqHlrzEA+8/gAvX/ZytqvSoWRlBwER6SYiK0XkDRF5S0Tm+vhK\nEVkuIhtEZJmIlIfy3CAiG0VkvYhMDsWPFZG1/tm8UHxXEVnk41eIyIjQs9n+HRtE5NJQfLWv10YR\nWSgipRn6Pow8IarholxZx5MpCq09HUVjUyO3/PkW5n51brarUjioapsX0N1/lgArgAnAbcC1Pv46\n4Bc+fCLwBlAKjAQ20Ww9rQLG+/DTwBQfvhq424dnAgt9uBLYDJT7azPQxz9bDFzsw/cA30tQdzUK\nk/p61Rkz3Gcm+epXVcFdM2ZktuxsUGjt6SgeXvOwnvvv52pTU1O2q9Lh+H4zqTakeyV1EFDVgz7Y\nxYuIAhcC8338fGC6D08DHlXVw6q61YvNBBEZBPRS1VU+3UOhPOGyHge+7sPnA8tUtUFVG4DlwAUi\nIsB5wJI47zc6CYHrcabnJQptgr3Q2tMRHGk6ws/+/DNu+upNuO7GyARJxUZEikTkDWAnrvNfBQxU\n1Z0+yU5goA8PBraFsm8DhsSJr/Px+M8PAFS1EdgnIn3bKKsSaFDVpjhlGQbQ/uGjfFusmayd+dae\nXGDhWwvp370/X6v+WrarUlAkXdTpO/XTRKQP8ISInBTzXEWko2bh037P3Llzj4ZramqoqanJYHWM\nXCVYbwKuQ07VgSBXF2smIlk7021PZ18UGlg1/3rBv3Yaq6a2tpba2trI35PyDgKquk9EXsINb+0U\nkSpV3eGHyHb5ZHXAsFC2oTiLpM6HY+ODPMOB7SJSgpuX2SMidUBNKM8w4EVgL1AuIkVeCIf6MuIS\nFhujsEjUMc6ZA2++6cJjxhT28FGmh8naK9KFwuK3F1NZVsnEL0zMdlU6jNgf4TfffHMk70nmjdYv\n8DQTkTJgErAOeBKY7ZPNBpb68JPALBHpIiLVwChglaruAPaLyAQ/53IJ8IdQnqCsbwEv+PAyYLKI\nlItIhX/3c34C6yVgRpz3G52IRKvln3oK6utdeNCgwv51nulhss48xxNYNXNr5nYaq6YjSWbZDALm\ni0gxTpgWqerTIrICWCwiVwJbgYsBVPUdEVkMvAM0Ald7cQDndfYgUAY8rarP+vgHgIdFZCOwB5jl\ny9orIj8DVvt0N3tHAXAecAtF5BbgNV+G0clI1DEeOtQc7tKlY+vU0WR62G/Bgs67KHTJO0vo060P\nk74wKdtVKUhsUaeRtyRaLT9pEjz/vBtCe/HFztdpGumz/cB2ah6s4a4L7iroI59TwXYQaAcmNp0T\n27LFSIeV21byzcXf5Pvjvs+N597Y6YfQTGzagYmNkY90do+wjmT+G/O5Zvk1PHDhA/zd6L/LdnVy\ngqjExs6zMYwcI+wRdvrpMHy4CU+maWxq5Jpl1/CnjX/i5cte5oT+J2S7SgWPiY1h5Bhhx4euXTu3\nK3IU7Dm4h5lLZlJSVMLK/2clFWUV2a5Sp8DOszEKnnzbjDLszty7t4vrjK7IUfDWrrcYf/94Th90\nOn/69p9MaDoQm7MxCp58Po7AnB0yxxPrnmDOH+dw5/l38t1Tvpvt6uQsNmdj5Cy5PqGdzwsV8237\nnFykSZu45c+38NvXfssz33mGcYPHZbtKnRKzbIxjpj2WQyYEKtUyUrEOkpWV64Iaj3ysc6b5+POP\nmb10Nh8e+JDfz/w9VT2rsl2lnCcqyybjZxbk0oWdZ9MhXHCBOy9l3LjUz5fJxDkrmTyrJVlZyZ5f\ndZVLc8EFmT9jp7109rNsNu/drCfdfZJe+Ycr9bPDn2W7OnkD2TrPxjCS0Z79uTIxtLV5s/vs0wdu\nvz1+mlSdA5LVJ9nzRPu0ZZJ0HR3yefjwWHlhywuc/cDZ/Pex/53f/t1v6VrSNdtVMqJQsFy5MMsm\nZ8nESZvnnJP8l3uqv+6T1SfZ8/ZYd+mSrqUS1WmmuUxTU5POWzFPB94+UF/c8mK2q5OXEJFlY3M2\nRoeR6TmEqVOdJTFuXGKrKpU0maAjvMY6qi35yqHGQ3z/T9/n1Q9fZenMpVRXVGe7SnmJbVfTDkxs\nsk9YYPbvh1decfGZcEFuaHAr7AcPdutR4glYJpwDcgVzg07Mhwc+5KLFFzGk1xAenP4gPbv0zHaV\n8hYTm3ZgYpN9wp5qVVWwY0dmf5mHy6+ubt/WLvm8DseAVXWruGjRRXxv3Pf4x3P/sdNvpHmsRCU2\n5iBgREp4knrFivQcCZJNiMeeyDl4cPsm6TvzRHq+89Cah/ivC/4rv5n6G37ylZ+Y0OQwZtkYkdLe\noZ9gH7B9+9x9PIsjbJFMmwaff96+OQ0bnso/GpsauXb5tTy14SmWzlzKfxnwX7JdpYLBhtHagYlN\n9gjmQTZvhhEjEs+pJCIsJBUVsGVL67yxE+bBe2NFI9fmZHKtPvnG3k/3MnPJTARh4bcWUllWme0q\nFRQmNu3AxKZjSeQMEJDOfEggJBUV8PrrTrBiSdUiae+cTFSiYHNE7eftXW8zbeE0ph8/nV9M/AUl\nRbbjVqaxvdGMnCd8DkuV3xWkd28nPG3Nh8Tr1BcsSC4k114Lu3bBt7/dthikMyeTSDAzub2/zRG1\nj6Xrl3LVU1fxy8m/5JJTL8l2dYx0SbYQBxgGvAS8DbwF/NDHVwLLgQ3AMqA8lOcGYCOwHpgcih8L\nrPXP5oXiuwKLfPwKYETo2Wz/jg3ApaH4amClz7MQKI1T92NZ22QkIXaLlvDCxq1b3YLC4LOthYXt\n3VYlUws2E5VZVRXNQs3OuNjyWDjSdERvrr1Zh/5yqK7atirb1Sl4iGhRZypiUwWc5sM9gXeBE4Db\ngGt9/HXAL3z4ROANoBQYCWyiebhuFTDeh58Gpvjw1cDdPjwTWKjNgrYZKPfXZqCPf7YYuNiH7wG+\nF6fu0fw1DFVt3dm3txNNZ/V9WOAmTsy8GMQTTBOF7HHg0AG9aNFFetb9Z+n2/duzXZ1OQdbEplUG\nWApM9FbLQG0WpPXabNVcF0r/LHAmMAhYF4qfBdwbSjPBh0uA3T7898A9oTz3+nwC7AaKfPyZwLNx\n6prpv4MRIlNbtLQlUrHWU1jgpk3LvBiY1ZE7bN67WU+++2S9YukVtpFmBxKV2KQ1ZyMiI4ExuOGr\ngaq60z/aCQz04cG4obCAbcAQ4LAPB9T5ePznB14dGkVkn4j09WVti1NWJdCgqk1xyjJSIBNb6ieb\nV0l1gr2tM1vC80Bz5rSc73jwwWN7b7p1MTqOF997kW8//m1+8pWf8D/O+B+2fqYASFlsRKQn8Djw\nI1U9EP7jq6qKSEe5faX1nrlz5x4N19TUUFNTk+Hq5BdBR/zmm1Bf3xwX28HGdvLxOuBkHXMqZSQj\nEJeePV19778frrmmpcDFulm/805z20aNgjPOaBYdczvObVSVX6/6Nf/8H//Mgm8u4GvVX8t2lQqe\n2tpaamtro39RKuYPbv7lOeAfQnHrgSofHkTzMNr1wPWhdM8CE3BDbeFhtKNDZD7Nmdp6GO3oUJu/\n/zfcnE7sMNpZ2DBaSoSHodoaAmtriCzVs1vCZVx6afvOe6mvV+3Xr+XcULI2BVfPnq3zBZP+wTBc\nZybXzuD57PBnesXSK/Tku0/WLXu3ZLs6nRay6CAgwEPAnTHxt+HnZrzAxDoIdMF5jG2m2UFgpRce\nobWDQCA8s2jpILAF5xxQEYT9s8XATG2eyzEHgRQIBOC001SnT09vS/2gc+rSpbnDnj498bvCZYQF\nobo6vU5u6FCXr7RUdcIEd3/OOa294IqL3efJJ7t6xXMgqKhIre6dgVw6XG37/u165v1n6jcXfVMP\nHDqQ3cp0crIpNl8GmryAvO6vKV4Inie+6/ONOC+09cD5ofjA9XkTcFcovqsXj8D1eWTo2eU+fiMw\nOxQfdn1ehLk+p8SxTIDHsyDasg4SeY6lcg5NmHD62CtoS9euzXFTpyZua1CPMWNy49d8NumIM3hS\nYeW2lTr0l0P1n2r/SY80HcleRQxVzaLY5PNlYnNsJFpH06uXHrWOUl0/E/YcS7eTC9L37q0tLJiw\nYIQtlgED2n8IWkeRiSGsYy0jF76L+W/M13639dOl65ZmrxJGC0xsTGw6lKuuUu3TR1tZEKku1FRN\nLCqJOrlEnWf4veH5m2nTmvNUVmoriydTRDG3kYkhrFwaBkuXw0cO64+f/bEeN+84fWvnW9mujhHC\nxMbEJm2OpZMMd2QlJa6jT/fd55yjWlbm5lnaqkNQz7B1kqjzjBWwcD2DobRMDwtF0akH7ejZ0w3t\ntae+uTIMli57Du7RSQ9N0kkPTdI9B/dkuzpGDCY2JjZpE9tJxhOfRIIUdGRtdbJtiVnY6ytZRx07\nF9RWBxxrFQX17NfPiVpVlRPGTFojx9qpx6tLKl52yciFYbB0eWvnW3rcvOP0x8/+WA8fOZzt6hhx\nMLExsUmbtqyAoHNL9Ku9vr5ZMPr1a+n9FdCWh1nYSgnmWxJZR0E9KyudFZVMIMMEHW7YiaCqKrET\nQntEqL2dejKLLV8tk/aydN1S7XdbP53/xvxsV8VoAxMbE5u0SWQFhDu3toZzgvwDBjR3lmF34XB5\nsWkCr6/u3eN3tPHqOXBgc9rSUicYqQythesSFpx4QtmR8xzJ1jTlo2XSHo40HdF/qv0nHXLHEF3x\nwYpsV8dhG4jbAAAY00lEQVRIgomNiU3axP6Kj9e5pTKcE+7wA1fnYE4mGLYKp+nb14lNorUu8eoY\nFiVobRmFPc8SDUuFd2kOnBhiLZxMWROpWEjJ1jTl2qLKKDhw6IB+c9E3dcJvJ2jd/rpsV8dIARMb\nE5u0Cc+btLWAMVEHHOvpFbg6x/NUC0SlR4+W8WGBGz3a5evaVbV/fycopaUtRSWwaoLywiIXb1iq\nX7+2xTS2bZmyJlKxkJK9K5+9yVJhy94tevLdJ+tlSy/TTw9/mu3qGCliYmNikzbxLJJ4JOoUYz29\ngjmXcHxFhduKJrBygmdB5x7+9R5PWGKv4mLVNWtaWyqxQ2DB0N+xdPjpOEzEkgkLqZDnbF7Y8oIO\nvH2gzlsxT5uamrJdHSMNTGxMbNImsA4qK+NP8Ccj2CYmtkMPOsmKCidA8RZvXnqpE4tgAWaiq6jI\nfZ5wgurgwS2dCBLNOQXDUkH7YudlUhWMdBwmYsmEhVSIczZNTU1614q7dMDtA/T5zc9nuzpGOzCx\nMbFJm3ieWuFhp2SE8wUWTFWVGwobMKBZGOL9Qo91fa6oaC6vvLylCA0dmrw+V13l3lla6gQhPCSW\nqidaLG05TBSitRE1wUaaJ919km7euznb1THaiYmNiU1KxPtVH/Y4i+2Er7rKddAVFa290dqyYMJl\nxPuFHh7CCxaFxhOHior480RtuVnHikhbnmgDB8ZvW6J6F6K10RFs379dz7r/LP3Gwm/YRpp5TlRi\nk9bhaUbuE+8Mmf793bV/v4sXgWefdXHHHQc7drj4559vee7MK6+4zwMHYN++5rNlAHr0cGfGNDTE\nP9emrMw9F4FTT4Uvf9mdNfP++7Brl0tTUgK1tS3PlAnX//TTYfhw997S0uY0ffvC9u0wbJgrs6wM\nBgxw5fbsCaNHw5lnwu7dzW2IbRvEr7cdnpY+q+tWc9Hii7jq9Kv4yVd+QpEUZbtKRi4ShYLlykWB\nWzZtWTHhYaBE570EE/9BOHYn5HA6EWcdTJ3qXJuTDVO1tVNzIgsltv7hMqZNc9f06fHLnjattQt3\n2OIpKYl/PMGxft+dwX25LR5e87D2u62fPrHuiWxXxcgQ2DCaiU0s4XmRESNcpzdxogvHO+8l9ure\nXfWii5wDQXgOJuhAE4lDeIuYRB132AU60RVvm//wMFai+ZPYXaCD5/HcnMPCmEzokglHqg4F6QhQ\nvopV45FG/V/P/S/9wrwv6Nqda7NdHSODmNiY2LQidl4k7AQQDk+c2HKFPzgvsAkT4q/QjxWaQDi6\ndnUWDriJ+vB7gm39+/RpThNrGYWtqdhFjokWasabPwnvAh08j11kGhArTLECFX5/7NqhWFJ1KEhn\n/Uw4bTrOG9lk78G9OvnhyTrxoYm2kWYBYmLTScQmnV+68RZSBpPh0NIhYNq0lutWYoeiioubvbxi\nXYy3bnV7nwVuyomu6dPjuzqXlDSLYffu8fdIS9ZBt8fqUHUedP37u+dBW5KtKSoudm7YsVZbqg4F\n6Xi0teW8kYxsWEVv73pbv3jXF/UfnvkH20izQDGxKXCxSWeb/YCgowvEJRCMoEON3Som6HgnTnSd\naWDhxApGOF0q8z7BNXVqfKsmbE0FOwfEeocFa3rCG3aGO9OwOMY7Vjq2g0/3+4w9Wrqt4bZkpOPR\nFvs3TMfluqN3IHhy/ZPa/7b++rvXfxf9y4ysYWJT4GKTbNPGRATDR+HV+cFwTOyv+PA7Yg8bC64R\nI1oOJ4m4dTHB3EdxceshueDq1i3xXM0pp7S2psKiMWFCc3xVVcsdBIJhusACKC9vnTa2g0/3+4zt\n9BMNt0VF8P5LL03dWumoNUFNTU16y8u32EaanYSsiQ3w78BOYG0orhJYDmwAlgHloWc3ABuB9cDk\nUPxYYK1/Ni8U3xVY5ONXACNCz2b7d2wALg3FVwMrfZ6FQGmCumf+LxERQcfRo0fLyfpkJJpfifdr\nN9w5BZ3qaac1z72cdlrbXmRDhzZ3hsmsnHgiFrtZZ9gKit3Kprq6pZVRXJzYagofRRB4mwUWW1GR\n6qRJqXfG8eaDVJv3devXL/2D5ALCa5riDdPF/j1TtWyjFJqPD32sMxbPsI00OxHZFJtzgTExYnMb\ncK0PXwf8wodPBN4ASoGRwCZA/LNVwHgffhqY4sNXA3f78ExgoTYL2mag3F+bgT7+2WLgYh++B/he\ngrpH8beIhPr69A/Tuuqq1rsjBx1y4OobO+dQXe06ubDXWhAeOLClo0GsiE2cGF+MgneGJ+HD+6TF\nWiNdurS8D67wSZuJrKfYK1gU2pYADh167H+fsLXX3vLa8vALyKUdDN6rf09PuecUnf3EbNtIsxOR\n1WE0LxxhsVkPDPThKmC9D98AXBdK9yxwJjAIWBeKnwXcG0ozwYdLgN0+/PfAPaE89/p8AuwGinz8\nmcCzCeqd6b9DpLTV0cSbDG5rY8pEnVms91O8cPgqLW05r9O/f0uBAdVTT3XismZNy1/al17aWrza\ncjLo16/ZSy1WRBMJTeyWObFzLkVFLS2RVC2U2O87+H4SOTik8/cF1V694v+tc2UHg5fee0kH3j5Q\nf/Wfv7KNNDsZuSY29aGwBPfAvwLfCT27H/imH0JbHoo/F3jKh9cCg0PPNgF9gf8P+MdQ/E98XF9g\nYyh+WLhuMfXO7F/hGEn11MlUva2CSfVg4j3RL2cR18FOnNhy88rAukjmZRa+SkqcsJx6autn4WMA\nhg5ttnTSuYI5mNgjBoqLWw4RduvWupOOJ5g1NS2/+9g92RIR+31v3erSt1dogjoGC1MTecVlm6am\nJv31yl/rgNsH6PLNy7NdHSMLRCU2x7xdjaqqiOixlpPq6zroPZEQbyuZMMFWKXPmuLTdu7stZd5/\nH95+26UZNw7uu8+FP/rIfTY1ua1ZunRx27ocPtyyXFW33czzz0PXru6qr4cjR5rzp0pjo9veJtji\nJsxrr7ktcfbtS728WHbscO1/7DGorHR1B1fXTz5xYRGYMKFlvvJyOOMMeOYZKCpqblOfPu4z/N2D\n+27/z/9JXI9ga57g+y4vhw8+aH+7gjouXdp8nyvb4hxpOsLq7at5euPTPL3xaT5r/Iy/XPEXjqs8\nLttVMwqI9orNThGpUtUdIjII8LtdUYezNAKGAtt8/NA48UGe4cB2ESnBzcvsEZE6oCaUZxjwIrAX\nKBeRIlVt8mXVJaro3Llzj4ZramqoqalJlDRyYjuweAQiFK/DFnF7kgXpPvus5fPnn4fi4rbrcOhQ\nenVOh2PtjMHtl3b77XDttc1CE4uqE44TToB161zaDRuc0E6f7oT05ZfhtNPgwQddnuC7P+kk2LsX\n/vIXt68atBT3BQucKCxY4OIDoUmFOXPgqafcdzx2rBPMVPN2NO83vE/t1lqWbVnGss3LqOpZxdQv\nTuV/T/7fnDPsHEqLS5MXYhQEtbW11NbWRv+iVMwfWg+j3YafmwGup7WDQBecx9hmmh0EVgITcMNu\nsQ4C9/jwLFo6CGzBOQdUBGH/bDEw04fvJYcdBMKnU44d23qFeyypeHqVlbVviCqKK9l5Ne25Skvj\nH7TWvXv83Z/Lyprvp05NfzfnY91yJtHfLpdO39xav1UffP1BvWzpZTryVyN1wO0D9OLHLtZ/++u/\n6d8a/pbt6hk5BBENo6UiNI8C24HPgQ+Ay70QPE981+cbcfMu64HzQ/GB6/Mm4K5QfFcvHoHr88jQ\ns8t9/EZgdig+7Pq8iBxyfY7dsj+ed1fQCYWFKPAcCxZbpnMF57xkW3hir0Sebe29+vVTnTWrua19\n+7b2juvSJTXnijDHuuVMbDkQf9+3juLjQx/rn7f+We/4yx0687GZOuLOETrw9oE687GZes/qe3Td\n7nU26W8kJCqxCayOgkREtKPbV1PTcm5AxHU/Af36uS3we/eG5cvdHMixUFoKGzfCyJHHVk6+UFLS\n/J317Qt79rROU1XlhteCIazw32TGjNZzJQ0NrYfMpk518z/jxrm/U3g4LN6wW1DOZZe5v/nvftcx\nQ2iHjxzmrV1vsXr7albVrWL19tVs2ruJkwacxPjB4zljyBmMHzKe0X1HIyLRV8jIe0QEVc34PxYT\nmwwyZw4sWeLmDMB1hp9/7s6DGT3azTGEz1gxUiNWsMF15OPGuXmqeFRXN5+Fc/iwSxcrHIlEA+IL\nUEAy8YoCVeXDjz/k7V1v8+bON3lz15u8ufNN3v3oXaorqhk/ZPxRcTll4Cl0Ke4SfaWMgiQqsbHD\n0zLIhg3NQhN0cgcOuPuPPnITx2Vl7j7sMWUkprzcHb4WthbDBIemhb/PigoYPLg5z7RpThRihaMt\n78C2DlFLxdGjvXx6+FM27t3I+o/W8+5H7/LuHn999C5lpWWc0O8ETh14Kl8Z/hV+cMYPOLH/ifTo\n0iOzlTCMCDDLJoMEQy/9+jmLJnwyZlCNHj3g4MHWv9Q7O/GsF4Cnn4azznJWYTx362nTnMv3K6+4\n0ztLSuDVV+H665uHwU480bmPx1owbQ2VtUVbVk8yVJXdB3fzXv17bG3YevTa0rCFdz96l52f7OQL\nFV/g+H7HM7rvaHf1c58VZRXpvcww2oENo7WDjhCbYChm82YYMsR1aiNGwMqVzWmKi5vXtBjp0a0b\nfPqp6+BHj3ZWTK9ezmIMi8SXv9w8PBlYMYEgTJ8ef9jrWEQjHqrKvkP7qNtfR92Buhaff9v/N96r\nf4/3971PWUkZ1RXVjCwfycg+I4+GR/cdzYjyEZQU2YCDkT1MbNpBR4hN9+6uMzTSJ2zNJBpWPOkk\nGDbMWSTgxOH22+Gaa1Kf0G+vBQNOQA58foBdn+xi9ye72fXJrhbX7oO72X5gO3UH6th+YDslRSUM\n6TWEIb2HMLjXYBfuNYThfYZTXVHNiD4j6NW1V/u+MMPoAExs2kFHiE1JiVkt7aW4GHr2bF7Ammgo\nDZon/DdvdpZj796tPcESWSkNDXDVHGXebz6lqete6j+tp/6zeuo/rWfvp3uPhus/c/d7P93L7oO7\nj4pLaXEpA3oMaL66D6B/j/4M6DGA/t37M6jXoKMC07NLz+i+MMPoAExs2kHUYjNnjnNxPVb35c5M\nIDBhl2aHQskhKD1Iz4pPOW70Qda8cxC67oeuB6DLAcaefYBvX76fR5YcYP2WAzQWH6Ciaj+nnnGA\nz/QABw4d4MDnB9h/aD8NnzVQJEVUllVS0a2CirIK/vZuBYcaKimjgr//RgWDyl18ZVnlUWHp370/\nZaVl2fp6DKPDMW+0HCLYliTehHVBIE1QfAiKP3cdfvHn/kolLvQsHFf6KZR8CqUHXbj0IJR8inY5\nCCUHaQzFHU1zpBQOd+fjxjLeauoOx3enuLEXRw72pqJHL06Y2IsP9vXmo729OLhrIHz+RXZu6M0n\nB3txy0970btrb3p16UWvrr0o71ZOt5JuLZoZdmHetBd+niN7lRlGIWJiAzyx7gmatAnFr3ZF3b26\nz+AK4hdtbGL/kCYY2gSo65yPXrH3mUpzBIqOQFFj60sSxMdLn1LaI9DY1V1HuvjLh9uMCz2Ljfu4\nNzSWweHu/vLho3HNz3qVlfHlCWUc/rz46PqYJUvcPM3R+ZpfNw+XvXsX/O0vLjxmDPzxl8nnZebM\ngTffbM6TaRdmwzBaYmIDPLL2EZq0CRFBEESEIilqcQnNcft7F0GvIlABLWq+iLnXNtI0lSRP0+J5\nscvT6ooTn07aVul9mOysNq+shNPHwIJH4Ec/cm7k5eVu9+bAiyx2/cuCBclX7scu4AyviRo+PHc3\nzDSMQsHmbNLk+OPh3XczWqSBm7OpqHA7LEDL3Zuh2WU5VjSuvTa1nZZjV/1//HFrD7W2dhQwjM6C\nzdl0IOG1M3v2mGtzpgnWyQRn74i4jj0QGnBOA/FW6seu+t+1q3nu7Pnn458TBPHLivVeS3bekGEY\n7aco2xXIRYJOZ9s2E5pM0qOHW/Oydq1zZe7m5+tVmw+CAzdk9uCD7uC4/v1bWhixohHcQ9tzLwsW\nOIsmsGKC7WjaKtswjMxhYhNDeOK4yL6ddhPeYDj4Hj/5xAnOiBFuniTYNy5MeTmsWeM+33/fWTuB\nxQKtRWPBArdlzfTp8OKLiYe+4olLLLFlG4aROWwYLYbwxHHfvi2HdozkFBW5Sf3ly+HCC93cCLjh\nyLDFEFgRwfqaPn3gnHPgkUeaO/p4lkbsBpmxRy0fC21tvmkYxrFhDgIx9OzpfoEXF0NtLZx7bjR1\nK0TCe8DNmOHmU4I5kKFD3fBZ7Ir/eFvPBGR67zLDMJJjOwi0g1TFJuyFFD7QrK3tUzojAwa4fcpe\nfbVl/Mknw3HHOSsmfG7Mt7/d/j3JDMPIDiY27SBVsYk9XdNoSe/ebh5rxAhnbXznO/DGG05Ibrml\n2fKItUTMMjGM/MPEph2kKjaJzqHpDJSVOa+wYJ5qzBhn4b3yijtDZvTojjvi2DCM7BOV2OS1v5WI\nTBGR9SKyUUSua285gRdSUVFhCE1xsVsgCW4Cfs0a2LrVzZt89asu/qST3GmW69bBli0tPbr++Ef3\nffzlL/DEEyY0hmFkAFXNywsoBjYBI4FS4A3ghJg0mg4VFapulib3rqIi1QkTVEXcfY8eL+maNarT\npqlOmqQ6eLDqmjWqM2ao1te7KwiHSRSfa7z00kvZrkKkWPvym0Jun+83M95n57NlMx7YpKpbVfUw\nsBCYdiwFjh3rPqNeXyMJDNQzz3TWxtatTmLq65stjj17YMUK2LvXWR0/+EEtp5zi3H6XLYO6Ojjl\nlOa1JInWlaSy3iQXqK2tzXYVIsXal98UevuiIJ/FZgjwQeh+m49rN4895jryitBR78cqPOed54ax\nBg92c0P19U4wpk6FqqrmOFX4z/90ojFihMsbrCEJD2UFYtGtW+J3GoZh5Br5vKgz454NQUf+/vtw\n9tlw2mnwL/8CF1zgNnrcs8el69bNORL88Y9w553wH/8BK1c6y6KhIf4OxHV1Ld/1pz9luvaGYRi5\nS956o4nImcBcVZ3i728AmlT11lCa/GycYRhGFlFzfW5GREqAd4GvA9uBVcDfq+q6rFbMMAzDaEXe\nDqOpaqOI/AB4DueZ9oAJjWEYRm6St5aNYRiGkT/kszdaQjK12LMjEZFhIvKSiLwtIm+JyA99fKWI\nLBeRDSKyTETKQ3lu8G1cLyKTQ/FjRWStfzYvG+1JhIgUi8jrIvKUvy+Y9olIuYgsEZF1IvKOiEwo\nsPb9T/9vc62ILBCRrvncPhH5dxHZKSJrQ3EZa4//fhb5+BUiMiLLbbvd/9tcIyK/F5E+Hdq2KBbv\nZPMihcWeuXgBVcBpPtwTNx91AnAbcK2Pvw74hQ+f6NtW6tu6iWZLdRUw3oefBqZku32hdv4YeAR4\n0t8XTPuA+cAVPlwC9CmU9uGWFWwBuvr7RcDsfG4fcC4wBlgbistYe4Crgbt9eCawMMttmwQU+fAv\nOrptWf8PGsGXfBbwbOj+euD6bNerHe1YCkwE1gMDfVwVsN6HbwCuC6V/FjgTGASsC8XPAu7Ndnt8\nXYYCzwPnAU/5uIJoH05YtsSJL5T2DQH+BlTghPQp33nldft85xrukDPWHp9mgg+XALuz2baYZ98A\n/v+ObFshDqNlfLFnRyMiI3G/Slbi/uHv9I92AgN9eDCubQFBO2Pj68id9t8JXAM0heIKpX3VwG4R\n+Z2IvCYivxWRHhRI+1S1DrgDJzjbgQZVXU6BtC9EJttztC9S1UZgn4hURlTvdLkCZ6lAB7WtEMUm\nrz0eRKQn8DjwI1VtcXCyup8Redk+EflvwC5VfR2I68Ofz+3D/bo7HTe0cDrwCc6qPko+t09EKoAL\ncb+WBwM9ReS74TT53L54FFp7AkTkH4HPVXVBR763EMWmDhgWuh9GS3XOWUSkFCc0D6tqcNjxThGp\n8s8HAbt8fGw7h+LaWefD4fiY/QuywtnAhSLyHvAo8DUReZjCad82YJuqrvb3S3Dis6NA2jcReE9V\n9/hfsr/HDVkXSvsCMvHvcVsoz3BfVgnQR1X3Rlf15IjIZcBU4Duh6A5pWyGKzV+BUSIyUkS64Cav\nnsxynZIiIgI8ALyjqr8KPXoSNxGL/1waip8lIl1EpBoYBaxS1R3Afu8JJcAloTxZQ1VvVNVhqlqN\nG/t9UVUvoXDatwP4QES+5KMmAm/j5jbyvn3A+8CZIlLm6zUReIfCaV9AJv49/iFOWd8CXuiIBiRC\nRKbghrGnqepnoUcd07aOnpDroImxC3DeXJuAG7JdnxTr/GXcXMYbwOv+mgJU4ibVNwDLgPJQnht9\nG9cD54fixwJr/bO7st22OG39Ks3eaAXTPuBUYDWwBvfLv0+BtW8usM7XbT7Oeylv24ezsLcDn+Pm\nHy7PZHuArsBiYCOwAhiZxbZd4evxfqh/ubsj22aLOg3DMIzIKcRhNMMwDCPHMLExDMMwIsfExjAM\nw4gcExvDMAwjckxsDMMwjMgxsTEMwzAix8TGMAzDiBwTG8MwDCNy/i/J5vA7zTDJtAAAAABJRU5E\nrkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x24beb9e8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_3_coef = get_coef(set_3, l2_new_penalty)\n",
"print set_3_coef[set_3_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_3, l2_new_penalty)"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------+-------+---------------+\n",
"| name | index | value |\n",
"+---------+-------+---------------+\n",
"| power_1 | None | 1.91040938244 |\n",
"+---------+-------+---------------+\n",
"[? rows x 3 columns]\n",
"Note: Only the head of the SFrame is printed. This SFrame is lazily evaluated.\n",
"You can use len(sf) to force materialization.\n"
]
},
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x250229e8>,\n",
" <matplotlib.lines.Line2D at 0x25022be0>]"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAEACAYAAACODmB7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXucVNWV77+r6W5eDd00IA02IHfEtw4IgpOYsb0+gmQi\n3rlBiWM0xpEZzU385M7E1+RGvJPJ9XG9jk6ijiY+4gQVNb4SH7TRdnyMML4hiiDaRN6I3SBvml73\nj72Ptbuoqq7qrqpT3b2+n8/51K59ztln1WnYv7P22nsdUVUMwzAMI9+UxW2AYRiG0TsxgTEMwzAK\nggmMYRiGURBMYAzDMIyCYAJjGIZhFAQTGMMwDKMgZCUwIlIjIg+LyPsi8p6ITBeRWhFpFJHlIrJQ\nRGqC468UkRUiskxETgvqp4jIEr/v5qC+v4g86OtfE5Hxwb7z/TWWi8h5Qf0EEVnkz3lARCq6fzsM\nwzCMfJGtB3Mz8JSqHg4cAywDrgAaVfUQ4Pf+OyJyBHA2cAQwA7hVRMS3cxtwoapOBCaKyAxffyGw\n2dffBFzn26oFfgxM89vVIlLtz7kOuNGf0+LbMAzDMEqETgXGd+hfUdW7AFS1TVW3AGcA9/rD7gXO\n9OVZwP2quldVm4EPgekiMhoYoqqL/XG/Cs4J23oEONmXvwosVNVWVW0FGoHTvWCdBDyc4vqGYRhG\nCZCNBzMB2CQid4vImyJyp4gMBkap6gZ/zAZglC+PAVYH568GDkxRv8bX4z8/ASdgwBYRGZ6hrVqg\nVVXbU7RlGIZhlADZCEw5cCxwq6oeC2zHD4dFqMs3U6ycM5bbxjAMowdQnsUxq4HVqvqf/vvDwJXA\nehGpU9X1fvhro9+/BhgbnF/v21jjy8n10TnjgLUiUg5Uq+pmEVkDNATnjAWeBz4DakSkzHsx9b6N\nDoiIiZFhGEaOqKp0flTndOrBqOp64BMROcRXnQL8AXgSON/XnQ885stPAHNEpFJEJgATgcW+na1+\nBpoA3wIeD86J2voGbtIAwELgND+LbRhwKvCs95heAGanuH6y/SW1XX311bHbYDb1HptK1S6zqefa\nlE+y8WAAvgf8WkQqgZXABUA/YIGIXAg0A2f5Dv09EVkAvAe0AZdowupLgHuAgbhZac/4+l8C94nI\nCmAzMMe39ZmI/CMQeU/XqAv2A1wOPCAiPwHe9G0YhmEYJUJWAqOq7wDHpdh1Sprjfwr8NEX9G8DR\nKep34wUqxb67gbtT1H8MTM9ouGEYhhEbtpK/yDQ0NMRtwn6YTdlRijZBadplNmVHKdqUTyTfY26l\nhIhob/59hmEY+UZE0GIF+Q3DMAyjK5jAGIZhGAXBBMYwDMMoCCYwhmEYRkEwgTEMwzAKggmMYRiG\nURBMYAzDMIyCYAJjGIZhFAQTGMMwDKMgmMAYhmEYBcEExjAMwygIJjCGYRhGQTCBMQzDMAqCCYxh\nGIZREExgDMMwjIJgAmMYhmEUBBMYwzAMoyCYwBiGYRgFwQTGMAzDKAgmMIZhGBmYOxcaGmDmTGht\njduanoUJjGEYRgaWL4cXX4Snn3ZiY2SPCYxhGEYGBg1yn1Onwh13xGtLT0NUNW4bCoaIaG/+fYZh\nFJ7WVue53HEH1NTEbU3hERFUVfLSVm/ugE1gDMMwciOfAmNDZIZhGEZBMIExDMMwCkJWAiMizSLy\nroi8JSKLfV2tiDSKyHIRWSgiNcHxV4rIChFZJiKnBfVTRGSJ33dzUN9fRB709a+JyPhg3/n+GstF\n5LygfoKILPLnPCAiFd29GYZhGEb+yNaDUaBBVSer6jRfdwXQqKqHAL/33xGRI4CzgSOAGcCtIhKN\n590GXKiqE4GJIjLD118IbPb1NwHX+bZqgR8D0/x2tYhU+3OuA27057T4NgzDMIwSIZchsuSgzxnA\nvb58L3CmL88C7lfVvaraDHwITBeR0cAQVV3sj/tVcE7Y1iPAyb78VWChqraqaivQCJzuBesk4OEU\n1zcMwzBKgFw8mOdE5HURucjXjVLVDb68ARjly2OA1cG5q4EDU9Sv8fX4z08AVLUN2CIiwzO0VQu0\nqmp7irYMwzCMEqA8y+O+rKrrRGQk0Cgiy8KdqqoiUqz5wDbv2DAMoweQlcCo6jr/uUlEHsXFQzaI\nSJ2qrvfDXxv94WuAscHp9TjPY40vJ9dH54wD1opIOVCtqptFZA3QEJwzFnge+AyoEZEy78XU+zb2\nY968eV+UGxoaaGhoSHWYYRhGn6SpqYmmpqaCtN3pQksRGQT0U9XPRWQwsBC4BjgFF5i/TkSuAGpU\n9Qof5J+PE6EDgeeAg72Xswj4PrAY+B1wi6o+IyKXAEer6sUiMgc4U1Xn+CD/68CxuBjQG8Cxqtoq\nIguAR1T1QRG5HXhbVW9Pst0WWhqGYeRAUVfyi8gE4FH/tRz4tar+H9/5L8B5Hs3AWT4Qj4hcBXwH\naAMuVdVnff0U4B5gIPCUqn7f1/cH7gMmA5uBOX6CACJyAXCVv/5PVPXewK4HcPGYN4FzVXVvku0m\nMIZhGDlgqWKyxATGMAwjNyxVjGEYhlHymMAYhmEYBcEExjAMwygIJjCGYRhGQTCBMQzDMAqCCYxh\nGIZREExgDMMwjIJgAmMYhmEUBBMYwzAMoyCYwBiGYRgFwQTGMAzDKAgmMIZhGEZBMIExDMMwCoIJ\njGEYhlEQTGAMwzCMgmACYxiGYRQEExjDMAyjIJjAGIZhGAXBBMYwDMMoCCYwhmEYRkEwgTEMwzAK\nggmMYRiGURBMYAzDMIyCYAJjGIZhFAQTGMMwDKMgmMAYhmEYBcEExjAMwygIJjCGYRhGQTCBMQzD\nMApCVgIjIv1E5C0RedJ/rxWRRhFZLiILRaQmOPZKEVkhIstE5LSgfoqILPH7bg7q+4vIg77+NREZ\nH+w7319juYicF9RPEJFF/pwHRKSiuzfCMAzDyC/ZejCXAu8B6r9fATSq6iHA7/13ROQI4GzgCGAG\ncKuIiD/nNuBCVZ0ITBSRGb7+QmCzr78JuM63VQv8GJjmt6tFpNqfcx1woz+nxbdhGIZhlBCdCoyI\n1AMzgV8AkVicAdzry/cCZ/ryLOB+Vd2rqs3Ah8B0ERkNDFHVxf64XwXnhG09Apzsy18FFqpqq6q2\nAo3A6V6wTgIeTnF9wzAMo0TIxoO5Cfgh0B7UjVLVDb68ARjly2OA1cFxq4EDU9Sv8fX4z08AVLUN\n2CIiwzO0VQu0qmp7irYMwzAyMncuNDTAzJnQ2hq3Nb2b8kw7ReQvgI2q+paINKQ6RlVVRDTVvgKQ\n83XmzZv3RbmhoYGGhoY8mmMYRk9j+XJ48UVXnjsXFiyI1564aWpqoqmpqSBtZxQY4EvAGSIyExgA\nDBWR+4ANIlKnquv98NdGf/waYGxwfj3O81jjy8n10TnjgLUiUg5Uq+pmEVkDNATnjAWeBz4DakSk\nzHsx9b6NlIQCYxiGMWiQ+5w6Fe64I15bSoHkB+9rrrkmb21nHCJT1atUdayqTgDmAM+r6reAJ4Dz\n/WHnA4/58hPAHBGpFJEJwERgsaquB7aKyHQfQ/kW8HhwTtTWN3CTBgAWAqeJSI2IDANOBZ5VVQVe\nAGanuL5hGEZG5s+H2bOhsRFqajo/3ug64vrrLA4UORH4O1U9w8/wWoDzPJqBs3wgHhG5CvgO0AZc\nqqrP+vopwD3AQOApVf2+r+8P3AdMBjYDc/wEAUTkAuAqb8JPVPVeXz8BeAAXj3kTOFdV96awWbP9\nfYZhGAaICKoqnR+ZRVu9uQM2gTEMw8iNfAqMreQ3DMMwCoIJjGEYgE3fNfKPCYxhGEBi+u7TTzux\nMYzuYgJjGAZg03eN/GNBfsMwADcsNneuExebvtt3sVlkWWICYxiGkRs2i8wwDMMoeUxgDKMHYzO/\njFLGBMYwejD5mvllQmUUAhMYw+jB5Gvml01RNgqBCYxh9ADSeRj5StxoU5SNQmCzyAyjB9DQkHiH\nyezZ+X+HiU1RNiLyOYuss/fBGIZRAhTaw6ipsRdvGfnHPBjD6AGYh2EUC1tomSUmMIZhGLlhCy0N\nwzCMkscExjAMwygIJjCGUYLYwkejN2ACYxgliC18NHoDJjCGUYLYwkejN2CzyAyjBLFpyX2DuXOd\ntzpokMvKUAp/a5umnCUmMIZhlDKFztDQFWyasmEYRi+gtw+FmgdjGIYRE6U4FGpDZFliAmP0Bkpx\nnN7ovdgQmWH0IWzKstFTMYExjBKnt4/TG70XGyIzjDSUytBUKY7TG72Xog2RicgAEVkkIm+LyFIR\nmefra0WkUUSWi8hCEakJzrlSRFaIyDIROS2onyIiS/y+m4P6/iLyoK9/TUTGB/vO99dYLiLnBfUT\nvF0rROQBEanIx80wjJBCD01lmw4meleLiYvR08goMKq6CzhJVScBk4AZIjIduAJoVNVDgN/774jI\nEcDZwBHADOBWEYmU8DbgQlWdCEwUkRm+/kJgs6+/CbjOt1UL/BiY5rerRaTan3MdcKM/p8W3YRh5\nJRqaqqqClpb85wSz2IrR2+k0BqOqO3yxEqgAFDgDuNfX3wuc6cuzgPtVda+qNgMfAtNFZDQwRFUX\n++N+FZwTtvUIcLIvfxVYqKqtqtoKNAKne8E6CXg4xfUNI2/Mnw8jRsC2bfDcc/kXAYutGL2dTgVG\nRMpE5G1gA67DXwyMUtUN/pANwChfHgOsDk5fDRyYon6Nr8d/fgKgqm3AFhEZnqGtWqBVVdtTtGUY\neaOmBo47zpW7KwKphsPmz3ertxsb8zP8ZRmYjVKjvLMDfEc+yQ9PPSoiRyXtVxEpViQ95+vMmzfv\ni3JDQwMNDQ15NMfo7cyfn58AezQcBq69KKaSz9Qgqa5hGJ3R1NREU1NTQdruVGAiVHWLiLyAG7ra\nICJ1qrreD39t9IetAcYGp9XjPI81vpxcH50zDlgrIuVAtapuFpE1QENwzljgeeAzoEZEyrz41fs2\nUhIKjGHkSr5EoBjDYTbkZnSF5Afva665Jm9tdzaLbEQ0Q0xEBgKnAu8DTwDn+8POBx7z5SeAOSJS\nKSITgInAYlVdD2wVkek+hvIt4PHgnKitb+AmDQAsBE4TkRoRGeav/ayfd/wCMDvF9Q2jJMn3cFhc\n1zCMXMi4DkZEjsYF0fvhxOhBVf2Jn+G1AOd5NANn+UA8InIV8B2gDbhUVZ/19VOAe4CBwFOq+n1f\n3x+4D5gMbAbm+AkCiMgFwFXenJ+o6r2+fgLwAC4e8yZwrqruTWG/rYMxjDxTKuuDjMJguciyxATG\nMPJPKaaYN/KH5SIzDCM2LNZjZIt5MIZh5ISlrund2BBZlpjAGKWOxTOMUsOGyAyjl2DpYozejAmM\nYXSRfKyct3iG0ZsxgTGMgFxEIx/eh61dMXozWa/kN4y+QC7pVvLhfeQ7XYxhlBLmwRhGQC6iYd6H\n0V2e/OBJFq5cGLcZBcMExjACchGNfL8IzLIh9y0+3fEpc387l6rKqrhNKRg2TdkwSgRbId+3OPc3\n5zJy0EhumnFT3KZ0IJ/TlC0GYxglgs0o6zs8+cGT/Mfq/+Ddv303blMKig2RGX2aUhqWKnZMp5R+\ne1+idVcrF//uYn7x9V8wuHJw3OYUFBsiM/o0fXlYqi//9jj56yf+moqyCm77i9viNiUlNkRmGHki\nm2Gp3prOxYbkik/jykYaP2pk6cVL4zalKNgQmdGnyWZYqremc7Fp1sXl892fc9GTF3HHX9zBkP5D\n4janKNgQmWF0wsyZTlymTu16Z9xbvSAje777u++ys20nd826K25TMmLJLg2jiOTjST+TF2TB9t7P\ni80v8vgHj3PjaTfGbUpRsRiM0edI502kq0+VziVXjyRTvCOX9DSFwLyrwrJj7w4ufOJCbv3arQwb\nOCxuc4qKeTBGnyOdN5FLrCXXuEwmLyjuYHtvjTGVCv/r+f/FtAOnccahZ8RtStExD8boc6Tr0HPp\n6HMVhUxJLefPj/cNkXELXG/mtdWvMX/pfJZcvCRuU2LBgvxGjyYc3hk5Elat6nyoJ90rf3N5FXBv\nem1wb/otpcSutl0c+6/HMq9hHmcdeVbc5mSNvTI5S0xgej/hYsERI+DTT13ZFg4acfMPv/8Hlm1e\nxsOzH0YkL/11UbBZZIbhCYd3Jk1y5REjYO3a7s3KKsTMru60mcu5Nistft5c9ya/eOsX/Hzmz3uU\nuOQdVe21m/t5Rm+mpUV19mz3GZW//GVVcNvs2dm1c9FFqieeqHr66a6dE0/MrY3k81ORa5tdPbc7\n1zG6z+623XrMbcfor97+VdymdAnfb+alD7Ygv9GjSQ6eL1jgntwht6B18lThXAPf4fkTJ8Jxx+0f\nB+pOML2QExCM/HLty9dSP7Sec485N25T4idfSlWKG+bB9ElCryZbTj/dPfFPndrRG8q2jej8qqr0\n3kNX7OrKud25jtE93l3/ro64foR+suWTuE3pMuTRg7Egv2HQcSbVZZflvvAwOr+lBZ57rntpZbqL\nLZyMh7b2Nv7sl3/G3GPnctGUi+I2p8vYLLIsMYHpvRSyE+1OGvtSmPJrafjj4fpXrmfhyoU0fqux\nRwf2izqLTETGisgLIvIHEVkqIt/39bUi0igiy0VkoYjUBOdcKSIrRGSZiJwW1E8RkSV+381BfX8R\nedDXvyYi44N95/trLBeR84L6CSKyyJ/zgIhU5OOGGD2DQq4+704MI4oJxek1WAym+Hzw6Qdc/8r1\n3Pn1O3u0uOSdzsbQgDpgki9XAR8AhwPXA5f5+suBa335COBtoAI4CPiQhKe0GJjmy08BM3z5EuBW\nXz4beMCXa4GVQI3fVgLVft8C4Cxfvg342xS253180igNkmMm+SRfMYxsZpYVAovBFJe2fW36pV9+\nSW957Za4TckL5DEG05XA+WPAKcAyYJQmRGiZL18JXB4c/wxwPDAaeD+onwPcHhwz3ZfLgU2+/E3g\ntuCc2/15AmwCynz98cAzKWwtwO03SoGe0InadOG+wc2v3awn3HWC7mvfF7cpeSGfApPTNGUROQiY\nDCzy4rLB79oAjPLlMcBrwWmrgQOBvb4cscbX4z8/8YrQJiJbRGS4b2t1irZqgVZVbU/RltFLyBRn\nyZTbq1Swoaru0RMmK3zU8hH/+8X/zasXvkqZ2Lr1ZLIWGBGpAh4BLlXVz8NxRlVVESlWND2n68yb\nN++LckNDAw0NDXk2xygUcaex7y7z58Oxx0L//nDOOe57V2ao9VVK/e+vqvz1E3/NFSdcwSHDD4nb\nnC7T1NREU1NTQdrOSmB8AP0R4D5VfcxXbxCROlVdLyKjgY2+fg0wNji9Hud5rPHl5PronHHAWhEp\nx8VZNovIGqAhOGcs8DzwGVAjImXei6n3bexHKDBGzyL0AAYOdLOj4uyYc32irqmBnTvhlVfc929/\n280yK+VOs9Dkcg9L3QO844072L53Oz84/gdxm9Itkh+8r7nmmvw13tkYGi7e8SvgpqT66/GxFuAK\n9g/yVwITcIH5KMi/CJju20wO8t+midhMGOT/CBfgHxaVNRHkP1sTsRkL8vcyWlpUJ0xwqV+GDYs/\nntGVmEpo95lnFnZyQk8gl3tYynG2Va2rdMT1I3TphqVxm5J3KGaQHzgBaPei8ZbfZvjO/zlgObAw\n6vj9OVfhZo8tA74a1E8Blvh9twT1/b1grMDFbw4K9l3g61cA5wf1E7xgrQAeBCpS2F6ov4FRYKIZ\nWGEHHa2UP+WU/HQ6uc7yqq93NlRXqzY3Z3eNU05x50ye3LUMAV0lrhlsndEbBLa9vV1n/NsM/ccX\n/zFuUwpCUQWmJ28mMPHSnU4ufNIF1UmTVIcP7/j0291ONFePpCtJNEMvrJidfanOYCtlryRb7nnr\nHp10+yTd07YnblMKQj4FxqY9GAWjO4sho/H3SZPgzDPhhRdg2jRXF43Jd3ex5cqV7rO6Gm64wZUz\npbofOrTj9bOhpgbGjXNxmGK+kjhV/KoU0veXwkLU7rDu83X8sPGH3HXGXVT0s7XdnZIvpSrFDfNg\nYqU7wyGpnnST67o73JLKIwmf/EeM6Oh1dPXpO1/DQrl4bKGtperNJFOqw3oR7e3tOuv+Wfqj3/8o\nblMKCjZEZgLTEyj0cEh320/V8WeTFTnXjjBf96GrQhH+pnzFrwpBqQvhA0se0CN+foTu2rsrblMK\nigmMCYyRBzJ5SVFwPpXXEVdH2FVPqKXFeWOl3HmrlvYEgI3bNuqoG0bpa5+8FrcpBSefAmPZlI2S\nJc6V3FFW5IEDYdWqjjbMnOniKZlS8nfF9s7OSZWpOdvrZGNz3JRCJup0zHl4DmOHjuWG026I25SC\nk89syrF7GYXcMA+mR9Hd1xYXglQ2ZDPkla3t4W/uyiy1bK/TG2ZvxcVv3vuNTrxlou7YsyNuU4oC\n9spkoxTJ5ak91bFdfW1xIT2daKbZ0KGJmWbZ5EHL1vbwN9fVZXdOV66TS+62npADrFh83PIx333q\nuzz4jQcZWDEwbnN6HvlSqlLcMA+mqGTzNH3RRap1dar9+nU89qKLEosqc12UWEhPpytehWr2todx\nh+bm3L2MQngmpeA5lgJrtq7R/3Lzf9GfL/553KYUFWwdjFGKZPM0vXw5rF8P+/a578OGJda0tLS4\nunHj3FNztmsmCpmzKlz70tl6knANDXS0Pd36mvnz3VsnGxth/Pjc14gUYl1JqecAKwYrNq/ghLtO\n4OKpF3PJcZfEbU7PJV9KVYob5sEUlWyepqMndlCtqFAdOdJ5LtEq/REjcl/1nu666aYT51Kfy3qS\ncP+ECYm2zjvPpZcphleQj7UkfT1e8/qa13X0/x2td75xZ9ymxAI2TdkEpqfS0qI6a5ZL/BgOP4Fq\n//6q06frfkNn+Ug3E3bqudZHdDaNNtwf/rZwivCwYdmJXVfJ1/BWqS96LBTPrXxOR14/Uh99/9G4\nTYkNExgTmB5DJm8hOZElqA4cqB0SSubSYSZfK50g5Fof0dmTfbg/bCtaUzNs2P5JMvMd78jXWpK+\nGId5cOmDesANB+iLzS/GbUqsmMCYwPQILroo/dBQcjLLqANO9mBy6TCTO8VUgnDRRc67qKvbv7PP\nx9DQoYe631xbqzpzZueTFfK9uDBfw1tdtaunej4/W/QzPfDGA/Wd9e/EbUrsmMCYwHSLYnUCYYef\nPDQUdWBDh2qHp/vkjq2zDjP8LZlW36eyKTnXWKo2c70/oaDW13feXncFoVB/y67aVSqeT7b3pb29\nXX/8/I914i0T9aPPPiqafaWMCYwJTLcoVicQiUWqoaGoA0uemhvVn3dedh1E+Ftmzcp+kkG6XGPJ\nXlcqEcrUeUXxlkGDEr850/3O1FY2nWSpdOgRpZLuJZv70ravTf/myb/RKf86RTds21BU+0oZExgT\nmG5RrE4g+Sk4WgMzbFgi6WK6TjTbjjPVb8nGY0jn7YTXDdfq1NUljstkW3Oz81xCQc30orJMbWVz\nD0qlQ48olRlond2XnXt36l8++Jd68r0n69ZdW4tvYAljAmMC0y3i6gSS4y6zZ6fvRLPtOFN5PJkW\nR0bic8opbiZbctuh15XK3lxsi8hkT6a2srlOqXTopUam+9K6s1Ub7mnQsx46q9dnRu4KJjAmMHml\nkDGZVDESUB082H1P50mcd55bIzNmjOug6+szr48JxaCuLn3H3JlX0NLi1rCMGuU8joqK/dvKplPP\nNjaUqS0Tj/yzePViPfiWg/V7T31P2/a1xW1OSWICYwKTM5lEpFDj+MnxjNpa1QMO6Dg9OV3cJNUs\ns0w2ZptyJdkrSHVfkq9dX9+9YHc2sSGjsOxr36fXvXydjrx+pC5YuiBuc0qafAqMJbvsIyQnkoyS\nSw4aBBX+za/5Tg2yfDls2eLK/frBZ5+5cnS9yZPhnntSpzmJ0pUMHQpbtyY+R4yAtWtdypUwEeP8\n+R1TvYeJHcPkjdXVMHJk4rzk+7JgQeLakY3PP597KpYw3Uq632gUh7Wfr+W8R89j977dvD73dcZV\nj4vbpL5DvpSqFDfMg/mC5Cf3TE/YyU/14ffk2V2ZPKPompWVCU9m8OCO100mOUYSeSPRZ3dT2oer\n6uvqUg9fhdkGsvE6Ut2f5BjPoYe64bbycre/s3Z76nqS7pLv3/34ssd11A2j9Jqma3Tvvr3db7AP\ngA2RmcDkSvJ4fqYAcvKQWboOOlOQXtV1tiNGqNbUJI6JYhpRDCbTtZOnCIer/wcPTsRn0k3xjWas\nRXnOwlX10VZZ6Ww68cTsp0ZH7aeaVJDuzZHhUGE24lhq04+LRb5+9449O/SS316i428ary+vejlv\n9vUFTGBMYLpNLqvLo2m2Q4cmOoBoX7ZCBR3XnkTb+PEdO/XQw0nuaKLgfbq4TLpOH1yes+Zmd41I\n5JK38vKuCUBl5f4Clnw/QuE55pjOBSybGWS90cvp7rTr9vZ2fWbFM3rEz4/Qsx46S1t29pIbU0RM\nYExgCkqy+ISddfJwWqaFkVFn0a+f67xT5R6LvIuoUw87+eRgfPK+6HuqYb9MkwOSvZjkLZvOLcwK\nDYmJAOmEu7nZeVxR+ph0dDaNOiQfT/ulJlLdmTn35to39ZRfnaKH/Msh+pv3fqPt7e35N7APYAJj\nAtNlutKhpJt5FU4dThUbaWnp+OQOqiKJcr9+Ca8kWoQYiki6xY2pOvbQzlRbmKomnRdz9NHOowqH\n3VItDo3aiGwPXzGQbpgt1X3vbAZbZ6KRaQFntvSGobjmlmb9q0f+Suv+b53euvhW3dO2J26TejQm\nMCYw+9GVDix8Z0k2ixkzdfZRZ1tV1bEjztTpJwvOzJmJtsNhpHSZl5Pzm4WdfrjV1OzfAUdezNCh\nqqeemvAWMsWfwB2XfF+yicGk6shT1eUyRNTVt22GlFomgFzYvGOz/t2zf6e119Xq1S9cbSvy84QJ\njAnMfqTqrMLONuoY072zJDqnMw8n7OzLytzn5Mmqc+akjmG0tDivIPIYhg1LiMqQIR3TsYwZk1hg\nGYpUKkETcZmXk+1saXFrbSLxSDcklW4oJrnDTRbI5Jlvhx6a+N3HHJMQrnRCG3bkqeqSF5hmEv98\niENPXMzuHMxgAAAaEElEQVS5c+9OveGVG3TE9SP0b578G127dW3cJvUqTGBMYPYjVWeTvKBRtWOH\nkuqcXN7amMrzANfhhh5DKHSpPBFw74FJ9/6XaCgo3FKJWTbxi84ENLnDDQVr0qT9zwlnh40Zs/+w\nYDTMlypWlWpBaCoPLJ130hPFoTvsa9+n971zn46/abzOun+WvrfxvbhN6pUUVWCAu4ANwJKgrhZo\nBJYDC4GaYN+VwApgGXBaUD8FWOL33RzU9wce9PWvAeODfef7aywHzgvqJwCL/DkPABVpbC/IH6AU\nSdXZRE/TqTrGdOdk+9bG0POYNWv/J/2w0w/FYMCARHnQoI7CE6ZVCeMayXGccJs61XXadXXpk1Om\nm10WHdPZ8GKmzAD9++sX3tw776Qezgu9nmQBTb528rlxDV2VWvC/cWWjTrp9kh7/i+P1pVUvFeWa\npXYPikWxBeYrwOQkgbkeuMyXLweu9eUjgLeBCuAg4ENA/L7FwDRffgqY4cuXALf68tnAA5oQsZVA\njd9WAtV+3wLgLF++DfjbNLYX6E9QWqT7j5DNE27yuamGqEKi/VFHGInXeeclhsEmT048qYcdZnW1\nOzf6HpVDAZo50w0vRcNv0DEgH8ZsKiqc1xC9Uybdk3+qPGXRNmFC6peiJQ8vprvHyS9IS+WBhHGb\nTAtewyzPRx/d0QsrdmdXKsH/t9e9rafdd5oefMvB+vAfHi7qzLBSuQfFpuhDZF4sQoFZBozy5Tpg\nmS9fCVweHPcMcDwwGng/qJ8D3B4cM92Xy4FNvvxN4LbgnNv9eQJsAsp8/fHAM2nsLsDtLz2681rh\n5HPDDjJ68g7PGTUqsT8aEkq2Ydas/YfSonfCRGtGQPXAA53IJHs4obiIJLyOSZMS9oXHhFskQCKJ\nctR+VZWzKxrySo5DhZMGkocXk0UqOY4SeVzJU6mHDOk4XNjZgtd0DwXF7uziDP63t7frS6te0m8s\n+IaOumGU/mzRz2KZGdaTJ0B0h1IQmJagLNF34F+Avwr2/QL47354rDGo/wrwpC8vAcYE+z4EhgN/\nB/xDUP8jXzccWBHUjw1tS7I77ze/FAk7uVGj9p9SG5LcUSX/Jwo71uHD3f6oQ072NjI9mUdxExEn\nIs3NTqjCYaxwDUymLVx7k7yAMtwqKtJ7M6HnU1ubeGVymM4mnDSQPLyYbgiwpcV5QcnXDYf/MglC\ntnGUYnd2ccR3tu/Zrve8dY9O+dcpevAtB+str90S68ywvhbjisinwHQ72aWqqohod9vJ9nJFuk6P\nYO5cePJJ2LkTDjgAJkyARYvcvueeSyRvDFm50n1WV8MNN7jPMEnkwIHQ0gJlZbB5Mzz9NIgkzo/K\ngwfDtm3u/O3bXf2pp8Lo0XDmmW4fuC520ya45BJ33L59ietPnuzsnDQJli6Ftrb9f+Pgwe68e+6B\nyy6D995z9UcfDRs2wMaNCbv27nUbuOSa0bUGDoRp01xSy/LyRNLNE0+E+nqoq3PHRvfuggtgzBjo\n3x+am+HII2HsWKishD17oKrK3aPzz4dVq6C11SXijH7XSSe53//cc50nEE1OzJmO5GSehSZbu7qL\nqrJozSLufutuHnrvIY6vP555DfOYOXEmZVJWeAMyUKx70JvpqsBsEJE6VV0vIqMB/9+cNTiPIqIe\nWO3r61PUR+eMA9aKSDkuzrJZRNYADcE5Y4Hngc+AGhEpU9V239aadIbOmzfvi3JDQwMNDQ3pDu1x\nLF8O69cnvpcF/x8nT07dsY0fD6tXuyzHP/yh+w8U/SeaOzchDO3t7rOiwnW+6qV9717XmW/f7jrQ\nkH//dzj++ER24pDFi2HAgMT3bdtclmKAt99OZFhOJrrOpEmuI4+yMy9ZkjhGJGFfRCQu4IRh+HCX\nifnTTxP1a9Y4gUgmsn/3bre1troMztG1IvGoqEgIGrgOacYMWLcOVqxw1+xMDKKHhN27YcoUeOgh\nd06YAXr+fCeuGzfCOed0zCKdK8ntxpXlecO2Ddz37n3c9dZd7G3fy3cmfYclFy/hwKEHxmNQH6ap\nqYmmpqbCNJ6Nm8P+Q2TX42MtwBXsH+SvxM30WkkiyL8ImI4bUksO8t/my3PoGOT/CBfgHxaV/b4F\nwNm+fDt9NMgfDtsMH+6GokQ6ZuxNjrmEecUyvb43my0cBgK3YDEccsqlrd6wpYo9dTZElu6tmZkW\nfHYnBhNn4HrLri06/935esb9Z2jNtTV6wWMX6EurXrKULiUGeRwiy0Zc7gfWAnuAT4ALfOf/HKmn\nKV+Fi6MsA74a1EfTlD8Ebgnq+3vBiKYpHxTsu8DXrwDOD+rDacoP0oumKecyW6ilJZFWPlVsIlXH\nlGlxZabpwJ1tkbD165cQurg7/M625IB8NtuRR3ZcFxNOGAhjNVFMJnnBZTLhQ0I4+y76W2STVDSX\nf1OZ3q5ZCDZs26B3vnGnnv5vp+uQnw7Rr/36a3rXm3fZqvsSpqgC05O3nigwyenqo3xfnb0yODkI\nPXlyx44p6uhSdTDhNcN1HXELQKlsYQB/1qyOwd+wfNFF7m9UV+fWxKRLG5O8xmbcOOeBnnJKxweA\nMM9adwLOyTP8JkzoPEtAd2huadab/uMm/fO7/1yr/0+1nvXQWfrAkgd0y64t+b+YkXdMYLL9cT1Q\nYEJBSNfhpXuX/KxZbh1JuH4ieWX5uHH7r3OJrlle7jrTTN7HwIHxdfT53nL1slIllUy3iHP27PTJ\nKDMNf0XTsPPpYXS29qa7bN21VZ9Y9oR+76nv6WE/O0xHXj9Sv/PYd/S3H/xWd+7d2f0LGEXFBCbb\nH9cDBObQQ10HNGKE64SihYzRFN7o6Tn6TO54kt+mGGX+DXNZhbGS8Gk8WkkeTkPOd6dcyttRR+V+\nzsCBHTMnh4s0k8Uh3XBkNBU82cucOjVz1oBUf/NsRKiztTe5sn3Pdn2x+UW9pukaPeGuE7Tqp1V6\n8r0n67UvXatvrH1D97Xvy71Ro2Qwgcn2x5WwwESdRLgupL6+49Nlfb3rcKqq3IK9yko39KKaeAVv\n2PnlElOoqHDrPtLlBrOt8y30DMvL3d+ms448ebhKNffhr+56IMnX60yw1m5dqw//4WH9wTM/0Gl3\nTtNB/zRIp905Tf/+2b/XZz98Vrfv2Z67EUbJYgKT7Y8rYYFJnj00aFDHhX9hpxQ+JdfX779gMdXW\nlQC2bR23ior093Ho0P3TwiR39l3J9RaRqdPP96LL8N/ifztrm7686mW9+bWb9dzfnKsT/nmCDrt2\nmH7t11/Tn/77T/XF5hd1x54dfTZPV18gnwITTSHulYiIlsrvS15/cM45bhHjUUe5hX+vvurWqLS2\numMHDnRrNAYNcmtINm925ffecwv8Uq01CQkXGhrZE66pGT7c3fd0DBvmFlxG5Y8+Sr2uJPzb33ab\nW4g5ZgwMHZpY45K8NqWhIfE3nj2744K/6N9IdxZdqiqrt65mycYl/M9rl/JByxIGTHiLstqPOeKA\nI5gyegpTx0zly2O/zKEjDv1i0WP0W959N/Hbk+0zejYigqpK50dm0VapdMCFoJQEJrnDuOOO/YVk\n/ny3UHH9erfAMFrZPnOm+w/98stOhGbOdOJUXu6EZPfu2H5WryLKUqAKQ4bAsce6v9mQIfD556mP\nV3Xi8tZb7m8TkqozrquDP/kTeOUV9332bLeAMllMor/x1KnQ2Ng9IVm3bR0rNq9g6calLN24lCUb\nl7B041IGVgzk6AOOZmL1USz+7VHc+PeTOf5PjqSyX2Xa9sJ/x9B9+4zSI58C0+1UMUZ6wifXaKV6\nlDokWpkddj6HH+5WmocpU6ZOdSvQ29rgkEPcyvFIM6dPd+1v2lTc39VbCZ9FPv/cZQuoq4Nnn4Xj\njnNpYkIPR9VlJ0jnuSxfvr+nGWZeiP4tnHNOx++QW2oYVWX9tvV8+NmHrPhsBSs2r3Cfn61g5Wcr\nGVw5mINrD+bIkUdy9AFHc/ZRZ3PUAUcxYtCIRCNnZHePBg1yn5MmwUEHwd13m7gY6TEPpoCET3uz\nZjkxGTPGeSxbtybyV6XjgAPggw9cbq/OhsSM7BFxnl+q3GcRZWWJdDmzZ7u8bSecAL/7XUJsoiHL\n0HMJHyr27k2kuVm71j1QTJ0KDz/s0vRE4tHZkFe7trPu83Ws2rKKVa2r+OOWP7qy/75qyyoGlA9g\nYu1EJg6fyMHDDmbi8IlMrJ3IwbUHUz2gOm/3Lh/Dc0ZpY0NkWRK3wETDHFVVbujr3XcTyRmzYfhw\nl6Qx6qiM7nHAAc5bjPKHDRjgvMBk8U7OMTZ8uEtiuXmz2/foo/DNb7ohy3/6p4SgjBwJjz+eyJc2\na5bLgxZ5Jckd8772fWzeuZmLf7iO5evXwpC1zPqrdXy2dy3rtq1j7edrWfv5WjZu30jtwFrGV49n\nXPU4xlePZ3xNx3LNAOvtjfxgApMlcQtMaytMnNgxwaIRH6FwDB8Ohx3mYmCh8IeeSzrq6+GTT1w5\n4aUqw+t2sHlHCwzaRNWoTfy/2z9lB5vYtGMTm7Zv4tOdn7Jpu/v+6Y5PadnZQs2AGnZtGsP29aPh\n8zEcVj+G7543mjFDxjBmyBhGV42mrqqO/uX9C3RXDKMjJjBZErfAQEcvJspUbBSfZOEoL08MkX19\nVhv7yrazr3wbC5u2oeXboXIb9N8KA1qRga30r25lF630q2rltK+3sqesldZdrbz/cSs72luRAVsQ\nraR9ew39do9kxKARtG8bySAdyTlnjmBs7UhGDnb1Iwe5cu3AWsrLyvMW0DeMfGACkyVxC8xhh7n3\nr7S12bTh3FEoa4OKnVC+y2++/EVd8vfkup1Q6cUi1VaxHRmwDSnfQ799g9m3s4r2XVWwpwr2DIbd\nQ2FXDf2p4aBRNXy4tIbB5TWMrqlhaGUN186r4V9uqOGlxhr+9LBq7rqz8ovYShg362wabzZxjVJJ\ns2/0fkxgsiQugTnsMDezKBzHz4yCaOJT2jsv47+X7QPZl+GzLYtjunBsv73Qbw+U+c9U3zPtS/t9\nb0IotAzaBkLbALftjcqp6gbQTweyb3fHOvYMoaytivZdgynbV0VVZRVbN0UiUkW5VrHivQF8+9vS\nIRYTrnGBjh5PRLopxpC/acYRmdbFdBcTLyPEpinnkZadLXzpri+5laco7dr+RVnVf09T3rpVadvn\nOvqqIa7T375D2fPf2juKQKZy+DJQFdepqgCZyv47Au39QPul/mwvT78v5Wd59sfuq4R9Fe6zbSDs\nrk58b6/ouD+X7+0VCXFoz+2fZ7u4W5vMyae6TvOOO+DSS+G++xJTjduAr3zFvSEzYvJkF8iP1iSF\nw5uR0ERvtUyefh6R7zdQRtODO3tDZlcIp1OneguqYXSVPu/BtLW3sXzzcgShTMoQEQRBxH/PUP7T\nPxU2bXQd/4wZwr/dJ5xxRhmvvpIkApnK4aeRdwYNgi99KfGmyOSFggDvvAPjxsG3v+3erllf71bZ\n33abm07c0uJm8Q0bBk1NcPLJiYkb4UyxbISkq95CIacHWwzICMmnB5OXfDOlurmfVzjCRJEivSvT\ncE/cMr3DJsoTFqXQT7VPNXUiyWyzEWeTnyvON0qmozvvmjF6H77f7HK/G25lneiPkYEpUxLlqNsw\n4iO8//36Jco1NW46ckPD/ilfBg92Hkprq/ueaiiqpsYNG0VP9vPnuzhI8tN+NNT09NPO20hFIYe6\nukry7zOMfNHnh8iyIRzW+PBDaG52nVltbW4LJ438E6ZuSVc/c6bL7RYOjVVUuGnL0cy+KHDenaGo\nbIaabCW8UerYLLIsyZfAhOP2qWYTGaXFoEEuUP/KKy5NywsvJLJXRzm0Nm1KJJysrHTpX6Lsxl3t\n+E08jN6ACUyW5EtgwifTjz/OnMLdyC/pPJRUDBniPJKjj3blqionGqtWOY+lqiqRnDH6mw4b5pKI\nLlrk2rDU80Zfx6YpF5loyunAgW5s3wSmeGQrLhUVLhfYqlUJsZgwwb1rJ8oNNnt2xzhK5G2kymZs\nGEb3MQ8mB5KnuObydG1kJpd7GaV9id7TUlnphsRefz0RU6mocIlCo2GwTC8Es6Etw0iQTw/GZpEF\nzJ0Lo0e74P2ppyZmFkVEM4AiTFzyRy738uSTnTeyZIn7PO4457VE4tKvnxOboUPd9+iFYOnEw2ZR\nGUZhMIEJWL7crdyOFtZdcEHH/fPnuxdQGd1j+PBEucz/C5w6FU480ZWrq93ix1mzXIp9cN4KuCD9\nggVuGz/efUZCctRR7n07K1fCMcckphN/9NH+b5s0DKPwmMAEdOah1NTA++8nOj0jweDB6fd9+cuJ\nezZpErzxhguyjxnjPItoTcljj7lyc7MTiMcecy9cC72VF17Y39OIhOSll2DNmoSYmGdiGPFiMZiA\n1lY49FC3tiWa3hp1TuFamCiFyEMPFcjwHkL//k6ETzzRdeQHHJBI8Dl0qHtj5+GHw6uvujqLcxhG\n6WPTlLOkK0H+MOB72WUJUdm6NREwrqpy4/zR7KS+QFlZItZx+OHut7/6asehp3ffdW+IXLTI5fYy\nQTGMnocJTJZkIzCZkg+Gs8bq6lx8ZsQIN/W1s7celjLRYtGJE+GPf4Tdu53HVlMDr73mhqtuuSUR\ni4pWpoOJhmH0dkxgPCIyA/hnoB/wC1W9Lml/pwKT6T0b4QLLgw92Kdx37w7bj28m2ZAhsGtXYkjq\npZfc55//ufOuomwDQ4a4tPMAf/iD8zqqqxNCAelFw6bvGkbfw7Ipu169H/AhcBBQAbwNHJ50TMas\noarpM+OqdswyG2bBjbZTT1V9553ssiiPHBmVX9Dq6s6Pj7Yjj3TXqKx03486SvXMM51Nzc0uO3Bz\nc0e7m5tVx4xRnTkzuwy5L7zwQucHFRmzKXtK0S6zKTtK0SYsmzIA04APVbVZVfcCDwCzcm0kXWZc\n6DgLKXmG2dFHu33HHAMzZnR+neOOc9e5/PImWlvdTKn6+sTU3GiKbfQd4KST4OWX3TU2bEjMlHr0\nUWfT+PHwySf7T8EdP97Npvrd77LzPJqamjo/qMiYTdlTinaZTdlRijblk56cKuZA4JPg+2pgeq6N\nRCLSGfPnuxdS7d3rVo5HOa1S7XvpJZdOJhpCmzQJfv1rd/y8ee6cSBySh6HSDUtla6dhGEap0JMF\npqjRj5oaty4jm32rVsEJJzgP4ic/yRzDSBYOExLDMHoLPTbILyLHA/NUdYb/fiXQrkGgX0R65o8z\nDMOIEe3rs8hEpBz4ADgZWAssBr6pqu/HaphhGIYB9OAhMlVtE5H/ATyLm1H2SxMXwzCM0qHHejCG\nYRhGadOTpymnRURmiMgyEVkhIpcX+Fp3icgGEVkS1NWKSKOILBeRhSJSE+y70tu1TEROC+qniMgS\nv+/mbto0VkReEJE/iMhSEfl+3HaJyAARWSQib3ub5sVtU9BePxF5S0SeLCGbmkXkXW/X4lKwS0Rq\nRORhEXlfRN4Tkekx/5s61N+faNsiIt8vgfv0A/9vfImIzBeR/iVg06W+raUicqmvK7xN+VpQUyob\nWSzAzPP1vgJMBpYEddcDl/ny5cC1vnyEt6fC2/chCS9yMTDNl58CZnTDpjpgki9X4WJVh5eAXYP8\nZznwGm5aeaw2+Tb+J/Br4IlS+Pv5Nj4GapPq4v773Qt8J/gbVsdtU2BbGbAOGBunTbjlEx8B/f33\nB4HzY7bpKGAJMADXPzYCf1IMm7r1Ry3FDfgz4Jng+xXAFQW+5kF0FJhlwChfrgOW+fKVwOXBcc8A\nxwOjgfeD+jnA7Xm07zHglFKxCxgEvIFbLBurTUA98BxwEvBkqfz9cAIzPKkuNrtwYvJRivrY75Vv\n5zTgpbhtwgnMH4FhOBF+Ejg1Zpu+gUulFX3/EXBZMWzqjUNkqRZgHlhkG0ap6gZf3gCM8uUx3p6I\nyLbk+jXkyWYROQjnYS2K2y4RKRORt/21F6rq4rhtAm4CfgiE6UvjtgncOq/nROR1EbmoBOyaAGwS\nkbtF5E0RuVNEBsdsU8gc4H5fjs0mVV0D3IgTmbVAq6o2xmkTsBT4ih8SGwTMxD1YFdym3igwJTVr\nQZ3Ux2KTiFQBjwCXqurncdulqu2qOgn3j3u6iBwVp00i8hfARlV9C0g57z/Gv9+XVXUycDrwXRH5\nSsx2lQPHAreq6rHAdtzoQJw2ASAilcDXgf3e0BTDv6lhwBm4UY0xQJWInBunTaq6DLgOWAg8jRv+\n2lcMm3qjwKzBjcNGjKWj6haDDSJSByAio4GNaWyr97at8eWwfk13DBCRCpy43KeqUZ6B2O0CUNUt\nwAvAV2O26UvAGSLyMe7p97+KyH0x2wSAqq7zn5uAR3HDiXHatRpYrar/6b8/jBOc9XHfK5wIv+Hv\nFcR7n04BPlbVzaraBvwGN2wf631S1btUdaqqngi0AMspwn3qjQLzOjBRRA7yTzZnA08U2YYncIE9\n/OdjQf0cEakUkQnARGCxqq4HtvpZOQJ8KzgnZ3wbvwTeU9V/LgW7RGRENEtFRAbixqXfj9MmVb1K\nVceq6gTcEMvzqvqtOG0CEJFBIjLElwfj4gtL4rTLt/WJiBziq04B/oCLMcR2rzzfJDE8Fl07LptW\nAceLyEDf1inAe8R8n0TkAP85DvhLYD7FuE9dCRqV+oZ7ovkAN/vhygJf637cWOseXOznAqAWFzhe\njnNLa4Ljr/J2LQO+GtRPwXUiHwK3dNOmE3AxhbeBt/w2I067gKOBN4F3fHs/8vWx3qugzRNJzCKL\n++83wf/t3saNn19ZInb9KfCf/m/4G1zgP26bBgOfAkOCurhtmod7eFqCm3lXUQI2/TvugeBt4KRi\n3SdbaGkYhmEUhN44RGYYhmGUACYwhmEYRkEwgTEMwzAKggmMYRiGURBMYAzDMIyCYAJjGIZhFAQT\nGMMwDKMgmMAYhmEYBeH/A25YnqeH2p1FAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x24c7dba8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"set_4_coef = get_coef(set_4, l2_new_penalty)\n",
"print set_4_coef[set_4_coef['name'] == 'power_1']\n",
"plot_fitted_line(set_4, l2_new_penalty)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These curves should vary a lot less, now that you applied a high degree of regularization.\n",
"\n",
"***QUIZ QUESTION: For the models learned with the high level of regularization in each of these training sets, what are the smallest and largest values you learned for the coefficient of feature `power_1`?*** (For the purpose of answering this question, negative numbers are considered \"smaller\" than positive numbers. So -5 is smaller than -3, and -3 is smaller than 5 and so forth.)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Selecting an L2 penalty via cross-validation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Just like the polynomial degree, the L2 penalty is a \"magic\" parameter we need to select. We could use the validation set approach as we did in the last module, but that approach has a major disadvantage: it leaves fewer observations available for training. **Cross-validation** seeks to overcome this issue by using all of the training set in a smart way.\n",
"\n",
"We will implement a kind of cross-validation called **k-fold cross-validation**. The method gets its name because it involves dividing the training set into k segments of roughtly equal size. Similar to the validation set method, we measure the validation error with one of the segments designated as the validation set. The major difference is that we repeat the process k times as follows:\n",
"\n",
"Set aside segment 0 as the validation set, and fit a model on rest of data, and evalutate it on this validation set<br>\n",
"Set aside segment 1 as the validation set, and fit a model on rest of data, and evalutate it on this validation set<br>\n",
"...<br>\n",
"Set aside segment k-1 as the validation set, and fit a model on rest of data, and evalutate it on this validation set\n",
"\n",
"After this process, we compute the average of the k validation errors, and use it as an estimate of the generalization error. Notice that all observations are used for both training and validation, as we iterate over segments of data. \n",
"\n",
"To estimate the generalization error well, it is crucial to shuffle the training data before dividing them into segments. GraphLab Create has a utility function for shuffling a given SFrame. We reserve 10% of the data as the test set and shuffle the remainder. (Make sure to use `seed=1` to get consistent answer.)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"(train_valid, test) = sales.random_split(.9, seed=1)\n",
"train_valid_shuffled = graphlab.toolkits.cross_validation.shuffle(train_valid, random_seed=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once the data is shuffled, we divide it into equal segments. Each segment should receive `n/k` elements, where `n` is the number of observations in the training set and `k` is the number of segments. Since the segment 0 starts at index 0 and contains `n/k` elements, it ends at index `(n/k)-1`. The segment 1 starts where the segment 0 left off, at index `(n/k)`. With `n/k` elements, the segment 1 ends at index `(n*2/k)-1`. Continuing in this fashion, we deduce that the segment `i` starts at index `(n*i/k)` and ends at `(n*(i+1)/k)-1`."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With this pattern in mind, we write a short loop that prints the starting and ending indices of each segment, just to make sure you are getting the splits right."
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0 (0, 1938)\n",
"1 (1939, 3878)\n",
"2 (3879, 5817)\n",
"3 (5818, 7757)\n",
"4 (7758, 9697)\n",
"5 (9698, 11636)\n",
"6 (11637, 13576)\n",
"7 (13577, 15515)\n",
"8 (15516, 17455)\n",
"9 (17456, 19395)\n"
]
}
],
"source": [
"n = len(train_valid_shuffled)\n",
"k = 10 # 10-fold cross-validation\n",
"\n",
"for i in xrange(k):\n",
" start = (n*i)/k\n",
" end = (n*(i+1))/k-1 \n",
" print i, (start, end)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"Let us familiarize ourselves with array slicing with SFrame. To extract a continuous slice from an SFrame, use colon in square brackets. For instance, the following cell extracts rows 0 to 9 of `train_valid_shuffled`. Notice that the first index (0) is included in the slice but the last index (10) is omitted."
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\"><table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">id</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">date</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">price</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">bedrooms</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">bathrooms</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sqft_living</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sqft_lot</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">floors</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">waterfront</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2780400035</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2014-05-05 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">665000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2.5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2800.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5900</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1703050500</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2015-03-21 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">645000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2.5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2490.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5978</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5700002325</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2014-06-05 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">640000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1.75</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2340.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4206</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0475000510</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2014-11-18 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">594000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1320.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5000</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0844001052</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2015-01-28 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">365000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2.5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1904.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8200</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2781280290</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2015-04-27 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">305000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2.5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1610.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3516</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2214800630</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2014-11-05 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">239950.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2.25</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1560.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8280</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2114700540</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2014-10-21 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">366000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2.5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1320.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4320</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2596400050</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2014-07-30 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">375000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1960.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">7955</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4140900050</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2015-01-26 00:00:00+00:00</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">440000.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1.75</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2180.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">10200</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" </tr>\n",
"</table>\n",
"<table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">view</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">condition</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">grade</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sqft_above</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sqft_basement</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">yr_built</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">yr_renovated</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">zipcode</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">lat</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1660</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1140</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1963</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98115</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.68093246</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">9</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2490</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2003</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98074</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.62984888</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">7</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1170</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1170</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1917</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98144</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.57587004</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">7</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1090</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">230</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1920</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98107</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.66737217</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">7</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1904</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1999</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98010</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.31068733</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1610</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2006</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98055</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.44911017</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">7</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1560</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1979</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98001</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.33933392</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">6</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">660</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">660</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1918</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98106</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.53271982</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">7</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1260</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">700</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1963</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98177</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.76407345</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2000</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">180</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1966</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">98028</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">47.76382378</td>\n",
" </tr>\n",
"</table>\n",
"<table frame=\"box\" rules=\"cols\">\n",
" <tr>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">long</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sqft_living15</th>\n",
" <th style=\"padding-left: 1em; padding-right: 1em; text-align: center\">sqft_lot15</th>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.28583258</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2580.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5900.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.02177564</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2710.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">6629.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.28796</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1360.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4725.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.36472902</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1700.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">5000.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.0012452</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1560.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">12426.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.1878086</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1610.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">3056.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.25864364</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1920.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8120.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.34716948</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1190.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">4200.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.36361517</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">1850.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">8219.0</td>\n",
" </tr>\n",
" <tr>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">-122.27022456</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">2590.0</td>\n",
" <td style=\"padding-left: 1em; padding-right: 1em; text-align: center; vertical-align: top\">10445.0</td>\n",
" </tr>\n",
"</table>\n",
"[10 rows x 21 columns]<br/>\n",
"</div>"
],
"text/plain": [
"Columns:\n",
"\tid\tstr\n",
"\tdate\tdatetime\n",
"\tprice\tfloat\n",
"\tbedrooms\tfloat\n",
"\tbathrooms\tfloat\n",
"\tsqft_living\tfloat\n",
"\tsqft_lot\tint\n",
"\tfloors\tstr\n",
"\twaterfront\tint\n",
"\tview\tint\n",
"\tcondition\tint\n",
"\tgrade\tint\n",
"\tsqft_above\tint\n",
"\tsqft_basement\tint\n",
"\tyr_built\tint\n",
"\tyr_renovated\tint\n",
"\tzipcode\tstr\n",
"\tlat\tfloat\n",
"\tlong\tfloat\n",
"\tsqft_living15\tfloat\n",
"\tsqft_lot15\tfloat\n",
"\n",
"Rows: 10\n",
"\n",
"Data:\n",
"+------------+---------------------------+----------+----------+-----------+\n",
"| id | date | price | bedrooms | bathrooms |\n",
"+------------+---------------------------+----------+----------+-----------+\n",
"| 2780400035 | 2014-05-05 00:00:00+00:00 | 665000.0 | 4.0 | 2.5 |\n",
"| 1703050500 | 2015-03-21 00:00:00+00:00 | 645000.0 | 3.0 | 2.5 |\n",
"| 5700002325 | 2014-06-05 00:00:00+00:00 | 640000.0 | 3.0 | 1.75 |\n",
"| 0475000510 | 2014-11-18 00:00:00+00:00 | 594000.0 | 3.0 | 1.0 |\n",
"| 0844001052 | 2015-01-28 00:00:00+00:00 | 365000.0 | 4.0 | 2.5 |\n",
"| 2781280290 | 2015-04-27 00:00:00+00:00 | 305000.0 | 3.0 | 2.5 |\n",
"| 2214800630 | 2014-11-05 00:00:00+00:00 | 239950.0 | 3.0 | 2.25 |\n",
"| 2114700540 | 2014-10-21 00:00:00+00:00 | 366000.0 | 3.0 | 2.5 |\n",
"| 2596400050 | 2014-07-30 00:00:00+00:00 | 375000.0 | 3.0 | 1.0 |\n",
"| 4140900050 | 2015-01-26 00:00:00+00:00 | 440000.0 | 4.0 | 1.75 |\n",
"+------------+---------------------------+----------+----------+-----------+\n",
"+-------------+----------+--------+------------+------+-----------+-------+------------+\n",
"| sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above |\n",
"+-------------+----------+--------+------------+------+-----------+-------+------------+\n",
"| 2800.0 | 5900 | 1 | 0 | 0 | 3 | 8 | 1660 |\n",
"| 2490.0 | 5978 | 2 | 0 | 0 | 3 | 9 | 2490 |\n",
"| 2340.0 | 4206 | 1 | 0 | 0 | 5 | 7 | 1170 |\n",
"| 1320.0 | 5000 | 1 | 0 | 0 | 4 | 7 | 1090 |\n",
"| 1904.0 | 8200 | 2 | 0 | 0 | 5 | 7 | 1904 |\n",
"| 1610.0 | 3516 | 2 | 0 | 0 | 3 | 8 | 1610 |\n",
"| 1560.0 | 8280 | 2 | 0 | 0 | 4 | 7 | 1560 |\n",
"| 1320.0 | 4320 | 1 | 0 | 0 | 3 | 6 | 660 |\n",
"| 1960.0 | 7955 | 1 | 0 | 0 | 4 | 7 | 1260 |\n",
"| 2180.0 | 10200 | 1 | 0 | 2 | 3 | 8 | 2000 |\n",
"+-------------+----------+--------+------------+------+-----------+-------+------------+\n",
"+---------------+----------+--------------+---------+-------------+\n",
"| sqft_basement | yr_built | yr_renovated | zipcode | lat |\n",
"+---------------+----------+--------------+---------+-------------+\n",
"| 1140 | 1963 | 0 | 98115 | 47.68093246 |\n",
"| 0 | 2003 | 0 | 98074 | 47.62984888 |\n",
"| 1170 | 1917 | 0 | 98144 | 47.57587004 |\n",
"| 230 | 1920 | 0 | 98107 | 47.66737217 |\n",
"| 0 | 1999 | 0 | 98010 | 47.31068733 |\n",
"| 0 | 2006 | 0 | 98055 | 47.44911017 |\n",
"| 0 | 1979 | 0 | 98001 | 47.33933392 |\n",
"| 660 | 1918 | 0 | 98106 | 47.53271982 |\n",
"| 700 | 1963 | 0 | 98177 | 47.76407345 |\n",
"| 180 | 1966 | 0 | 98028 | 47.76382378 |\n",
"+---------------+----------+--------------+---------+-------------+\n",
"+---------------+---------------+-----+\n",
"| long | sqft_living15 | ... |\n",
"+---------------+---------------+-----+\n",
"| -122.28583258 | 2580.0 | ... |\n",
"| -122.02177564 | 2710.0 | ... |\n",
"| -122.28796 | 1360.0 | ... |\n",
"| -122.36472902 | 1700.0 | ... |\n",
"| -122.0012452 | 1560.0 | ... |\n",
"| -122.1878086 | 1610.0 | ... |\n",
"| -122.25864364 | 1920.0 | ... |\n",
"| -122.34716948 | 1190.0 | ... |\n",
"| -122.36361517 | 1850.0 | ... |\n",
"| -122.27022456 | 2590.0 | ... |\n",
"+---------------+---------------+-----+\n",
"[10 rows x 21 columns]"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"train_valid_shuffled[0:10] # rows 0 to 9"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let us extract individual segments with array slicing. Consider the scenario where we group the houses in the `train_valid_shuffled` dataframe into k=10 segments of roughly equal size, with starting and ending indices computed as above.\n",
"Extract the fourth segment (segment 3) and assign it to a variable called `validation4`."
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"19396\n"
]
}
],
"source": [
"print len(train_valid_shuffled)"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# start = (n*i)/k\n",
"# end = (n*(i+1))/k-1\n",
"# validation4 = train_valid_shuffled[(n*3)/k : (n*(3+1))/k-1] #5818, 7757\n",
"validation4 = train_valid_shuffled[5818 : 7757]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To verify that we have the right elements extracted, run the following cell, which computes the average price of the fourth segment. When rounded to nearest whole number, the average should be $536,234."
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"536353\n"
]
}
],
"source": [
"print int(round(validation4['price'].mean(), 0))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"After designating one of the k segments as the validation set, we train a model using the rest of the data. To choose the remainder, we slice (0:start) and (end+1:n) of the data and paste them together. SFrame has `append()` method that pastes together two disjoint sets of rows originating from a common dataset. For instance, the following cell pastes together the first and last two rows of the `train_valid_shuffled` dataframe."
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+------------+---------------------------+-----------+----------+-----------+\n",
"| id | date | price | bedrooms | bathrooms |\n",
"+------------+---------------------------+-----------+----------+-----------+\n",
"| 2780400035 | 2014-05-05 00:00:00+00:00 | 665000.0 | 4.0 | 2.5 |\n",
"| 1703050500 | 2015-03-21 00:00:00+00:00 | 645000.0 | 3.0 | 2.5 |\n",
"| 4139480190 | 2014-09-16 00:00:00+00:00 | 1153000.0 | 3.0 | 3.25 |\n",
"| 7237300290 | 2015-03-26 00:00:00+00:00 | 338000.0 | 5.0 | 2.5 |\n",
"+------------+---------------------------+-----------+----------+-----------+\n",
"+-------------+----------+--------+------------+------+-----------+-------+------------+\n",
"| sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above |\n",
"+-------------+----------+--------+------------+------+-----------+-------+------------+\n",
"| 2800.0 | 5900 | 1 | 0 | 0 | 3 | 8 | 1660 |\n",
"| 2490.0 | 5978 | 2 | 0 | 0 | 3 | 9 | 2490 |\n",
"| 3780.0 | 10623 | 1 | 0 | 1 | 3 | 11 | 2650 |\n",
"| 2400.0 | 4496 | 2 | 0 | 0 | 3 | 7 | 2400 |\n",
"+-------------+----------+--------+------------+------+-----------+-------+------------+\n",
"+---------------+----------+--------------+---------+-------------+\n",
"| sqft_basement | yr_built | yr_renovated | zipcode | lat |\n",
"+---------------+----------+--------------+---------+-------------+\n",
"| 1140 | 1963 | 0 | 98115 | 47.68093246 |\n",
"| 0 | 2003 | 0 | 98074 | 47.62984888 |\n",
"| 1130 | 1999 | 0 | 98006 | 47.55061236 |\n",
"| 0 | 2004 | 0 | 98042 | 47.36923712 |\n",
"+---------------+----------+--------------+---------+-------------+\n",
"+---------------+---------------+-----+\n",
"| long | sqft_living15 | ... |\n",
"+---------------+---------------+-----+\n",
"| -122.28583258 | 2580.0 | ... |\n",
"| -122.02177564 | 2710.0 | ... |\n",
"| -122.10144844 | 3850.0 | ... |\n",
"| -122.12606473 | 1880.0 | ... |\n",
"+---------------+---------------+-----+\n",
"[4 rows x 21 columns]\n",
"\n"
]
}
],
"source": [
"n = len(train_valid_shuffled)\n",
"first_two = train_valid_shuffled[0:2]\n",
"last_two = train_valid_shuffled[n-2:n]\n",
"print first_two.append(last_two)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Extract the remainder of the data after *excluding* fourth segment (segment 3) and assign the subset to `train4`."
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"17455\n"
]
}
],
"source": [
"first_part = train_valid_shuffled[0:5817]\n",
"last_part = train_valid_shuffled[7758:]\n",
"train4 = first_part.append(last_part)\n",
"print len(train4)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To verify that we have the right elements extracted, run the following cell, which computes the average price of the data with fourth segment excluded. When rounded to nearest whole number, the average should be $539,450."
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"539458\n"
]
}
],
"source": [
"print int(round(train4['price'].mean(), 0))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we are ready to implement k-fold cross-validation. Write a function that computes k validation errors by designating each of the k segments as the validation set. It accepts as parameters (i) `k`, (ii) `l2_penalty`, (iii) dataframe, (iv) name of output column (e.g. `price`) and (v) list of feature names. The function returns the average validation error using k segments as validation sets.\n",
"\n",
"* For each i in [0, 1, ..., k-1]:\n",
" * Compute starting and ending indices of segment i and call 'start' and 'end'\n",
" * Form validation set by taking a slice (start:end+1) from the data.\n",
" * Form training set by appending slice (end+1:n) to the end of slice (0:start).\n",
" * Train a linear model using training set just formed, with a given l2_penalty\n",
" * Compute validation error using validation set just formed"
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"def k_fold_cross_validation(k, l2_penalty, data, output_name, features_list): \n",
" rss_sum = 0\n",
" n = len(data)\n",
" for i in xrange(k):\n",
" start = (n*i)/k\n",
" end = (n*(i+1))/k-1\n",
" validation_set = data[start:end+1]\n",
" training_set = data[0:start].append(data[end+1:n]) \n",
" model = graphlab.linear_regression.create(training_set, target = output_name, features = features_list, \n",
" l2_penalty=l2_penalty,\n",
" validation_set=None,verbose=False)\n",
" predictions = model.predict(validation_set)\n",
" residuals = validation_set['price'] - predictions\n",
" rss = sum(residuals * residuals)\n",
" rss_sum += rss\n",
" validation_error = rss_sum / k # average = sum / size or you can use np.mean(list_of_validation_error)\n",
" return validation_error "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once we have a function to compute the average validation error for a model, we can write a loop to find the model that minimizes the average validation error. Write a loop that does the following:\n",
"* We will again be aiming to fit a 15th-order polynomial model using the `sqft_living` input\n",
"* For `l2_penalty` in [10^1, 10^1.5, 10^2, 10^2.5, ..., 10^7] (to get this in Python, you can use this Numpy function: `np.logspace(1, 7, num=13)`.)\n",
" * Run 10-fold cross-validation with `l2_penalty`\n",
"* Report which L2 penalty produced the lowest average validation error.\n",
"\n",
"Note: since the degree of the polynomial is now fixed to 15, to make things faster, you should generate polynomial features in advance and re-use them throughout the loop. Make sure to use `train_valid_shuffled` when generating polynomial features!"
]
},
{
"cell_type": "code",
"execution_count": 102,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['power_1', 'power_2', 'power_3', 'power_4', 'power_5', 'power_6', 'power_7', 'power_8', 'power_9', 'power_10', 'power_11', 'power_12', 'power_13', 'power_14', 'power_15']\n"
]
}
],
"source": [
"poly_data = polynomial_sframe(train_valid_shuffled['sqft_living'], 15)\n",
"my_features = poly_data.column_names()\n",
"poly_data['price'] = train_valid_shuffled['price']\n",
"\n",
"val_err_dict = {}\n",
"for l2_penalty in np.logspace(1, 7, num=13):\n",
" val_err = k_fold_cross_validation(10, l2_penalty, poly_data, 'price', my_features) \n",
" print l2_penalty#, val_err\n",
" val_err_dict[l2_penalty] = val_err\n",
"print val_err_dict"
]
},
{
"cell_type": "code",
"execution_count": 99,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{10.0: 491826427769017.6,\n",
" 31.622776601683793: 287504229919132.1,\n",
" 100.0: 160908965822179.8,\n",
" 316.2277660168379: 122090967326083.66,\n",
" 1000.0: 121192264451214.84,\n",
" 3162.2776601683795: 123950009289897.55,\n",
" 10000.0: 136837175247518.97,\n",
" 31622.776601683792: 171728094842297.34,\n",
" 100000.0: 229361431260422.75,\n",
" 316227.76601683791: 252940568728599.8,\n",
" 1000000.0: 258682548441132.5,\n",
" 3162277.6601683791: 262819399742234.16,\n",
" 10000000.0: 264889015377543.8}\n"
]
}
],
"source": [
"import pprint \n",
"pprint.pprint(val_err_dict)"
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(1000.0, 121192264451214.84)\n"
]
}
],
"source": [
"print min(val_err_dict.items(), key=lambda x: x[1]) "
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.21192264451e+14\n"
]
}
],
"source": [
"min_val = min(val_err_dict.itervalues())\n",
"print min_val"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1000.0\n"
]
}
],
"source": [
"print min(val_err_dict, key=val_err_dict.get)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"***QUIZ QUESTIONS: What is the best value for the L2 penalty according to 10-fold validation?***"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You may find it useful to plot the k-fold cross-validation errors you have obtained to better understand the behavior of the method. "
]
},
{
"cell_type": "code",
"execution_count": 126,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"+---------------+-------------------+\n",
"| l2_penalty | validation_error |\n",
"+---------------+-------------------+\n",
"| 100000.0 | 2.2936143126e+14 |\n",
"| 316227.766017 | 2.52940568729e+14 |\n",
"| 100.0 | 1.60908965822e+14 |\n",
"| 3162.27766017 | 1.2395000929e+14 |\n",
"| 31.6227766017 | 2.87504229919e+14 |\n",
"| 1000.0 | 1.21192264451e+14 |\n",
"| 10.0 | 4.91826427769e+14 |\n",
"| 31622.7766017 | 1.71728094842e+14 |\n",
"| 10000.0 | 1.36837175248e+14 |\n",
"| 3162277.66017 | 2.62819399742e+14 |\n",
"+---------------+-------------------+\n",
"[13 rows x 2 columns]\n",
"Note: Only the head of the SFrame is printed.\n",
"You can use print_rows(num_rows=m, num_columns=n) to print more rows and columns.\n"
]
}
],
"source": [
"l2_penalty = graphlab.SArray(val_err_dict.keys())\n",
"validation_error = graphlab.SArray(val_err_dict.values())\n",
"\n",
"sf = graphlab.SFrame({'l2_penalty':l2_penalty,'validation_error':validation_error})\n",
"print sf"
]
},
{
"cell_type": "code",
"execution_count": 127,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAELCAYAAAA86fb3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAE5RJREFUeJzt3X+s3fdd3/Hnq3GyYkq5Qh0GYndBSwoUscWql2YpnQ9i\nZcmFGrQlohooKPtxQxBQwdqxVUG5035oSEPtUtTUXldIpbmJi5Qs7WzRIPWYwCSvENtN2mROpICc\nQt2KxF0bj40q7/1xj72r43vuPefc8+Pej58P6SjfH5/z/b4/Ove8/M33x+ekqpAktek18y5AkjQ9\nhrwkNcyQl6SGGfKS1DBDXpIaZshLUsNmFvJJPprkXJKnhmj7d5I8meQvk/yDNda/PsmLST44nWol\nqQ2zPJL/TeDWIdv+CfAzwOEB6/81cHwSRUlSy2YW8lX1BPDy6mVJ/nqSY0n+MMnvJfmeXts/qaqn\ngFf7t5PkLcC3A5+eRd2StJ3N+5z8IeAXqmof8F7gQ+s1TvIa4D8A/2wGtUnStrdjXjtO8jrgbwOf\nSHJx8TUbvO3ngKNV9adZ9SZJ0trmFvKs/F/E+arau0G71YPr3Ay8PcnPAa8Drknytap637SKlKTt\nbKjTNUn+OMnnkpxM8j8GtLk/yXNJTifZKLipqv8FvJDk9t77k+Rv9G+297r4np+uqr9WVd8NvAf4\nmAEvSYMNe06+gE5V7a2qm/pXJlkErq+qG4Al4IE12nwc+O/A9yQ5m+Qu4KeAf5zkFPA0cKDX9m8l\nOQvcDhxc57ZLh9CUpHVkmKGGk7wA7KuqPx+w/sPAZ6rq4d78s8D+qjo3yWIlSaMZ5Uj+d3u3Ov7T\nNdZfC5xdNf8isHuzxUmSNmfYC69vq6o/S/JXgceTPNu77321/rtdPJUiSXM2VMhX1Z/1/vuVJI8A\nNwGrQ/6LwJ5V87t7yy5JYuhL0hiqauxbxjc8XZNkZ5Jv6U1/M/AjQP+F0MeAO3ttbmbl1sjLzsdX\n1aZe991336bbrbWuf9l688NMT7N/o/Ztq/RvWp/dJPo3q89unP6N+vfaWv8G9XUe371J9G+c795m\nDXMkvwt4pPfs0Q7gv1TVp5Pc3Qvug1V1NMlikueBV4C7Nl3ZGjqdzqbbrbWuf9l684OmJ2GY7Y3a\nt7WWz6N/0/rs1lreUv9G/XttrX+D+jqP795G7bZstmz2X8BhX0Dddttt9fLLL1eL7rvvvnmXMFUt\n96/lvlXZv+1uJabHz96Zjl1z7NgxlpaWZrnLmZn0kcVW03L/Wu4b2L8r3VD3yU9kR0nt27ePxx9/\nnIWFhZnsU5K2uyTUJi68zjTkX375ZQNekkawrUJ+VvuSpFZsNuTnPZ68JGmKDHlJapghL0kNM+Ql\nqWGGvCQ1zJCXpIYZ8pLUMENekhpmyEtSwwx5SWqYIS9JDTPkJalhhrwkNcyQl6SGGfKS1LChQj7J\nVUlOJvnkGus6Sb7aW38yyb2TL1OSNI4dQ7Z7N/AF4FsGrD9eVQcmU5IkaVI2PJJPshtYBD4CDPp1\nkrF/tUSSND3DnK55P/Be4NUB6wu4JcnpJEeTvHli1UmSNmXdkE/yY8CXq+okg4/WnwT2VNXfBD4I\nPDrZEiVJ49ronPwtwIEki8Brgdcn+VhV3XmxQVV9bdX0sSQfSvJtVfVS/8aWl5cvTXc6HTqdzibL\nl6S2dLtdut3uxLaXqhquYbIfeE9VvbNv+S5WjvYryU3Akaq6bo3317D7kiStSEJVjX3dc9i7ay6q\n3k7vBqiqg8DtwD1JvgFcAN41bjGSpMka+kh+0zvySF6SRrbZI3mfeJWkhhnyktQwQ16SGmbIS1LD\nDHlJapghL0kNM+QlqWGGvCQ1zJCXpIYZ8pLUMENekhpmyEtSwwx5SWqYIS9JDTPkJalhhrwkNcyQ\nl6SGGfKS1DBDXpIaNlTIJ7kqyckknxyw/v4kzyU5nWTvZEuUJI1r2CP5dwNfAC77Je4ki8D1VXUD\nsAQ8MLnyJEmbsWHIJ9kNLAIfAdb6xfADwIMAVXUCWEiya5JFSpLGM8yR/PuB9wKvDlh/LXB21fyL\nwO5N1iVJmoB1Qz7JjwFfrqqTrH0Uf6lp3/xlp3UkSbO3Y4P1twAHeufdXwu8PsnHqurOVW2+COxZ\nNb+7t+wyy8vLl6Y7nQ6dTmeMkiWpXd1ul263O7HtpWq4g+4k+4H3VNU7+5YvAj9fVYtJbgY+UFU3\nr/H+GnZfkqQVSaiq9c6krGujI/l+1dvp3QBVdbCqjiZZTPI88Apw17jFSJIma+gj+U3vyCN5SRrZ\nZo/kfeJVkhpmyEtSwwx5SWqYIS9JDTPkJalhhrwkNcyQl6SGGfKS1DBDXpIaZshLUsMMeUlqmCEv\nSQ0z5CWpYYa8JDXMkJekhhnyktQwQ16SGmbIS1LDDHlJatiGIZ/ktUlOJDmV5Okky2u06ST5apKT\nvde9U6lWkjSSHRs1qKq/SPJDVXUhyQ7g95Mcq6oTfU2PV9WB6ZQpSRrHUKdrqupCb/Ia4Grg1TWa\njf1r4pKk6Rgq5JO8Jskp4Bzw6ar6bF+TAm5JcjrJ0SRvnnShkqTRbXi6BqCqXgVuTPKtwCNJvr+q\nPr+qyZPAnt4pnduAR4E39W9neXn50nSn06HT6WyidElqT7fbpdvtTmx7qarR3pD8KnChqn59nTYv\nAG+pqpdWLatR9yVJV7okVNXYp8OHubvmDUkWetPfBLwDeKavza4k6U3fxMo/Hi9dtjFJ0kwNc7rm\nO4EHk1zFyj8KD1fV0SR3A1TVQeB24J4k3wAuAO+aVsGSpOGNfLpm7B15ukaSRjb10zWSpO3LkJek\nhhnyktQwQ16SGmbIS1LDDHlJapghL0kNM+QlqWGGvCQ1zJCXpIYZ8pLUMENekhpmyEtSwwx5SWqY\nIS9JDTPkJalhhrwkNcyQl6SGGfKS1LB1Qz7Ja5OcSHIqydNJlge0uz/Jc0lOJ9k7lUolSSNbN+Sr\n6i+AH6qqG4EbgVuTvHV1mySLwPVVdQOwBDwwrWIlSaPZ8HRNVV3oTV4DXA282tfkAPBgr+0JYCHJ\nrkkWKUkaz4Yhn+Q1SU4B54BPV9Vn+5pcC5xdNf8isHtyJUqSxrVjowZV9SpwY5JvBR5J8v1V9fm+\nZul/21rbWl5evjTd6XTodDojFStJret2u3S73YltL1Vr5vHajZNfBS5U1a+vWvZhoFtVD/XmnwX2\nV9W5vvfWKPuSJEESqqr/QHpoG91d84YkC73pbwLeATzT1+wx4M5em5uB8/0BL0maj41O13wn8GCS\nq1j5B+Hhqjqa5G6AqjrYm19M8jzwCnDXdEuWJA1rpNM1m9qRp2skaWRTPV0jSdremgz5paUlOp0O\ni4uLnD9/ft7lSNLcNBnyZ86c4fjx4xw7doylpaV5lyNJc9NkyO/cuROAffv2cejQoTlXI0nz0+SF\n1/Pnz7O0tMShQ4dYWFiYyT4laRo2e+G1yZCXpFZ4d40kaSBDXpIaZshLUsMMeUlqmCEvSQ0z5CWp\nYYa8JDXMkJekhhnykrRFTWLsLUNekoY06xFuz5w5s+ltGPKSNKRZj3B7cbDFzTDkJW1bsz6ynvUI\nt4cPH970NhygTNK21el0OH78OAB33HEHR44cmer+5jHC7dQHKEuyJ8lnknw+ydNJfnGNNp0kX01y\nsve6d9yCJGlYsz6yXlhY4MiRI9tqCPMNj+STfAfwHVV1KsnrgD8CfqKqnlnVpgP8clUdWGc7HslL\nmqgr4bcjNnskv2OjBlX1JeBLvemvJ3kG+C7gmb6mYxchqQ1LS0ucOXOGnTt3cvjw4akH78Ujaw02\n0oXXJNcBe4ETfasKuCXJ6SRHk7x5MuVJ2k78feWtZ8Mj+Yt6p2p+G3h3VX29b/WTwJ6qupDkNuBR\n4E3921heXr403el06HQ6Y5Qsaavy95U3r9vt0u12J7a9oe6uSXI18CngWFV9YIj2LwBvqaqXVi3z\nnLzUuCvhHPmsTf03XpMEeBD486r6pQFtdgFfrqpKchNwpKqu62tjyEvSiKZ+4RV4G/DTwOeSnOwt\nex/wRoCqOgjcDtyT5BvABeBd4xYkSZocH4aSpC1s6g9DSZK2L0NekhpmyEtSwwx5SWqYIS9JDTPk\nJalhhrzUsFn/qIa2HkNeapgDhsmQlxrmgGHyiVepYQ4Ytv1NfYCySTHkJWl0DmsgSRrIkJekhhny\nktQwQ16SGmbIS1LDDHlJapghL0kNM+QlqWEbhnySPUk+k+TzSZ5O8osD2t2f5Lkkp5PsnXypkqRR\n7RiizV8Cv1RVp5K8DvijJI9X1TMXGyRZBK6vqhuSvBV4ALh5OiVLkoa14ZF8VX2pqk71pr8OPAN8\nV1+zA8CDvTYngIUkuyZcqyRpRCOdk09yHbAXONG36lrg7Kr5F4HdmylMkrR5w5yuAaB3qua3gXf3\njugva9I3f9loZMvLy5emO50OnU5n2N1L0hWh2+3S7XYntr2hRqFMcjXwKeBYVX1gjfUfBrpV9VBv\n/llgf1WdW9XGUSglaURTH4UySYD/DHxhrYDveQy4s9f+ZuD86oCXJM3HhkfySX4Q+D3gc/z/UzDv\nA94IUFUHe+1+A7gVeAW4q6qe7NuOR/KSNCJ/NESSGuaPhkiSBjLkJalhhrwkNcyQl6SGGfKS1DBD\nXpIaZshLUsMMeUlqmCEvSQ0z5CWpYYa8NENLS0t0Oh0WFxc5f/78vMvRFcCQl2bozJkzHD9+nGPH\njrG0tDTvcnQFMOSlGdq5cycA+/bt49ChQ3OuRlcCR6GUZuj8+fMsLS1x6NAhFhYW5l2OtgGHGpak\nhjnUsCRpIEN+ArxjQtJWZchPgHdMSNqqhvkh748mOZfkqQHrO0m+muRk73Xv5Mvc2rxjQtJWNcwP\neb8d+Drwsar6gTXWd4BfrqoDG2yn2Quv3jEhaVo2e+F1x0YNquqJJNdtVMe4BbRgYWGBI0eOzLsM\nSbrMJM7JF3BLktNJjiZ58wS2KUmagA2P5IfwJLCnqi4kuQ14FHjTBLYrSdqkTYd8VX1t1fSxJB9K\n8m1V9VJ/2+Xl5UvTnU6HTqez2d1LUlO63S7dbndi2xvqidfeOflPDrjwugv4clVVkpuAI1V13Rrt\nmr3wKknTMvULr0k+DuwH3pDkLHAfcDVAVR0EbgfuSfIN4ALwrnGLkSRNlmPXSNIW5tg1kqSBDHlJ\napghryuag8updYa8rmgOLqfWGfK6ojm4nFrn3TW6ojm4nLY6f/5PkhrmLZSSpIEMeUlqmCEvSQ0z\n5LXleO+6NDmG/DY06xCc9f68d12aHEN+G5p1CM56f967Lk2OIb8NzToEZ72/w4cPc8cdd/D44497\n77q0Sd4nvw3N+gEeHxiS5seHoSSpYT4MJUkayJCXpIYZ8pLUsA1DPslHk5xL8tQ6be5P8lyS00n2\nTrZESdK4hjmS/03g1kErkywC11fVDcAS8MCEattWut3uvEuYqpb713LfwP5d6TYM+ap6Anh5nSYH\ngAd7bU8AC0l2Taa87aP1P7SW+9dy38D+XekmcU7+WuDsqvkXgd0T2O5lhv0w12u31rr+ZevND5qe\nhGG2N2rf1lo+j/5N67Nba3lL/Rv177W1/g3q6zy+exu126rZMqkLr/33cE7lhviWP4hht2cIbry8\npf4Z8t011xnywxvqYagk1wGfrKofWGPdh4FuVT3Um38W2F9V5/ra+SSUJI1hMw9D7ZjA/h8Dfh54\nKMnNwPn+gIfNFSlJGs+GIZ/k48B+4A1JzgL3AVcDVNXBqjqaZDHJ88ArwF3TLFiSNLyZjV0jSZo9\nn3iVpIYZ8pLUsLmFfJLvTvKRJJ+YVw3TlOTHkxxK8lCSd8y7nklK8r1JHkjyiSQ/O+96piHJNyf5\nbJIfnXctk5akk+SJ3me4f971TFpW/NvecCt3zrueSUvyg73P7j8l+YON2s8t5Kvqhar6J/Pa/7RV\n1X+tqiXgZ4GfnHc9k1RVz1bVPaz0623zrmdK/jnw8LyLmJJXga8Bf4WVhxdb8xOsPKT5f2mwf1X1\n+73v36eA39qo/URDftBgZkluTfJsbxCzX5nkPmdpzP7dC/zG7Kocz6h9S/JOVv7Ijs661nGM0r/e\n/3l9AfjKPGodx4if3xNVtQj8C+BfzbzYMYzYvzcBf1BV7wHumXmxYxgzW/4hcHjDjVfVxF7A24G9\nwFOrll0FPA9cx8qtl6eA71u1/hOTrGGar1H6x8pTwL8G/PC8657WZ9dr86l51z6Fz+7fAO8Hfgd4\nlN5daFv5NeZ375rt8v0b8fP7KeCOXpuH5137ND4/4I3AoWG2PYmHoS6pqid6T8eudhPwfFX9MUCS\nh4AfT3IO+HfAjUl+pap+bZK1TMMo/QP+LvDDwOuTXF9VB2dY6shG/Oy+Hfj7rPzv/n+bYZljG6V/\nVXVvb/5ngK9U71u1lY34+X0v8PeABeCDMyxzbCN+9/4j8MEkbwe6s6tyfCP27xngHwEfHWbbEw35\nAdYawOytVfUSK+ert7tB/fsFtskXaB2D+nYcOD6fkiZqzf5dnKmqB2de0WQN+vz+PfDIfEqaqEH9\n+99AC9f7Bv59VtXysBuZxYXXLX8UtEkt96/lvoH92+7s3xBmEfJfBPasmt9DW1e8W+5fy30D+7fd\n2b8hzCLk/xC4Icl1Sa5h5ba7x2aw31lpuX8t9w3s33Zn/4Yx4SvEHwf+FPg/rJxLuqu3/Dbgf7Jy\npfhfzvtKtv27svpm/+zfVn9Ns38OUCZJDXPsGklqmCEvSQ0z5CWpYYa8JDXMkJekhhnyktQwQ16S\nGmbIS1LDDHlJatj/A6O/Pbf9MmFzAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x24c93320>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the l2_penalty values in the x axis and the cross-validation error in the y axis.\n",
"# Using plt.xscale('log') will make your plot more intuitive.\n",
"\n",
"plt.plot(sf['l2_penalty'],sf['validation_error'],'k.')\n",
"plt.xscale('log')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once you found the best value for the L2 penalty using cross-validation, it is important to retrain a final model on all of the training data using this value of `l2_penalty`. This way, your final model will be trained on the entire dataset."
]
},
{
"cell_type": "code",
"execution_count": 95,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"PROGRESS: Linear regression:\n",
"PROGRESS: --------------------------------------------------------\n",
"PROGRESS: Number of examples : 19396\n",
"PROGRESS: Number of features : 15\n",
"PROGRESS: Number of unpacked features : 15\n",
"PROGRESS: Number of coefficients : 16\n",
"PROGRESS: Starting Newton Method\n",
"PROGRESS: --------------------------------------------------------\n",
"PROGRESS: +-----------+----------+--------------+--------------------+---------------+\n",
"PROGRESS: | Iteration | Passes | Elapsed Time | Training-max_error | Training-rmse |\n",
"PROGRESS: +-----------+----------+--------------+--------------------+---------------+\n",
"PROGRESS: | 1 | 2 | 0.028003 | 2461778.986191 | 248914.007014 |\n",
"PROGRESS: +-----------+----------+--------------+--------------------+---------------+\n",
"PROGRESS: SUCCESS: Optimal solution found.\n",
"PROGRESS:\n"
]
}
],
"source": [
"poly_data = polynomial_sframe(train_valid_shuffled['sqft_living'], 15)\n",
"features_list = poly_data.column_names()\n",
"poly_data['price'] = train_valid_shuffled['price']\n",
"l2_penalty_best = 1000.0\n",
"\n",
"model = graphlab.linear_regression.create(poly_data, target='price',\n",
" features=features_list,\n",
" l2_penalty=l2_penalty_best,\n",
" validation_set=None)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"***QUIZ QUESTION: Using the best L2 penalty found above, train a model using all training data. What is the RSS on the TEST data of the model you learn with this L2 penalty? ***"
]
},
{
"cell_type": "code",
"execution_count": 96,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.28780855058e+14\n"
]
}
],
"source": [
"poly_test = polynomial_sframe(test['sqft_living'], 15)\n",
"predictions = model.predict(poly_test)\n",
"errors = predictions-test['price']\n",
"rss = (errors*errors).sum()\n",
"print rss"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
qwertzuhr/2015_Data_Analyst_Project_3 | .ipynb_checkpoints/Data Analysis Project 3 - Data Wrangle OpenStreetMaps Data-checkpoint.ipynb | 3 | 44523 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Data Analyst Project 3\n",
"Data Wrangle (Retrieve, Analyze and Clean) OpenStreetMaps Data from the City of Dresden\n",
"\n",
"_by Benjamin Söllner, [email protected]_\n",
"\n",
"_based on the Udacity.com Data Wrangling With MongoDB_\n",
"\n",
"\n",
"<img src=\"city_dresden_json.png\" alt=\"The city of Dresden as a JSON object illustration\" width=\"400\" height=\"312\" style=\"display: inline; margin: 6pt;\" />"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Abstract\n",
"This paper describes describes the process of downloading, analyzing and cleaning of an OpenStreet Map data set of my former home town as a student: [Dresden](https://en.wikipedia.org/wiki/Dresden), a state capital in eastern Germany, [a baroque town beautifully located on the board of the river Elbe](https://www.google.de/search?q=dresden&newwindow=1&es_sm=122&source=lnms&tbm=isch&sa=X&ved=0CAkQ_AUoA2oVChMIrc3d_cT3xwIVh2fbCh3Y6QYu&biw=1920&bih=969) and town home to a high-tech conglomerate from the micro-electronics sector called [Silicon Saxony](https://en.wikipedia.org/wiki/Silicon_Saxony).\n",
"\n",
"In this paper, first, the pipeline (and python script) to perform retrieval, analysis and cleaning of the data is introduced (chapters [Approach](#Approach)) and results of the analysis stage are presented (chapter [Overview of the Data](#Overview-of-the-Data)). During the analysis, interesting facts of Dresden are uncovered, like the most popular religion, sport, beer, cuisine or leisure activity.\n",
"\n",
"For the cleaning stage (chapter [Problems Encountered in the Map](#Problems-Encountered-in-the-Map-/-Data-Quality)), canonicalizing phone numbers present in the data set and unifying cuisine classifications where the challenge of choice. Some other cleaning techniques like cleaning street names and post codes where tried, but proved not fruitful. The paper is finally concluded with some further ideas for data set cleaning (chapter [Other Ideas about the Data Set](#Other-Ideas-about-the-Data-Set))."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##The Approach\n",
"I implemented retrieving / storing / analysing and cleaning in a python script. The script can be used like this:\n",
"```\n",
"# python project.py\n",
"Usage:\n",
" python project.py -d Download & unpack bz2 file to OSM file (experimental)\n",
" python project.py -p Process OSM file and write JSON file\n",
" python project.py -w Write JSON file to MongoDB\n",
" python project.py -z Download and install the zipcode helpers\"\n",
" python project.py -f Audit format / structure of data\n",
" python project.py -s Audit statistics of data\n",
" python project.py -q Audit quality of data\n",
" python project.py -Z Audit quality of data: Zipcodes - (see -z option)\n",
" python project.py -c Clean data in MongoDB\n",
" python project.py -C Clean data debug mode - don't actually write to DB\n",
"```\n",
"\n",
"Different options can be combined, so ``` python project.py -dpwfsqc ``` will do the whole round trip. During the process, I re-used most of the code and data format developed during the \"Data Wrangling With MongoDB\" Udacity course. For example, the data format used for storing the data (```-p``` and ```-w``` option) is completely based on [Lesson 6](https://www.udacity.com/course/viewer#!/c-ud032/l-768058569) - with some fine-tuning.\n",
"\n",
"Some output of the script is shown on the terminal, some is written to local files. If a file is written, this is indicated in the terminal output. A sample of the script's terminal output is included in the ```output_*.txt``` files included in the submission."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Data Format\n",
"**Try it out:** Use ```python project.py -f``` to obtain the data for this chapter. This is a long-running process which might take a few hours to complete! There is an output file written to [```Project/data/audit_format_map.csv```](Project/data/audit_format_map.csv) which can be beautified into an [Excel spreadsheet](Project/data/audit_format_map.xlsx).\n",
"\n",
"\n",
"\n",
"First, the data format was audited, which consisted of going through all the documents and aggregating the occurence of any attributes and the prevalence of their types (```str```ing, ```int```eger, ```float``` and ```other```). For this, batches of 1000 documents each are retrieved from the collection and each combed through by the python code while a Python Dataframe keeps track of the counters. Since there are 1,360,000 elements, this process takes many hours; an alternative would be to run the query natively in JavaScript code on the MongoDB shell or to issue the command as a BSON command.\n",
"\n",
"The overview of the format showed no obvious big problems with the data at first glance but provided some valuable insights:\n",
"\n",
"* One area of improvement could be the phone number, which is scattered across multiple data fields (```address:phone```, ```phone``` and ```phone_mobile```) and was identified as a potential candidate for cleaning (see [Auditing Phone Numbers](#Auditing-Phone-Numbers) and [Cleaning Phone Numbers](#Cleaning-Phone-Numbers)).\n",
"* Some values are present in the dataset as sometimes ```str```ing, othertimes numeric: The XML parsing process takes care that each value is, whenever parsable, stored as integer or float. For attributes like street numbers, mixed occurences may be in the data set.\n",
"* This automatic parsing of ```int``` or ```float``` turned out to be not always useful: a problem are leading zeros which in certain cases hold semantics. For german phone numbers, a leading zero signifies the start of an area code (```0```) or the start of a country code (```00```). For german postcodes, a leading zero in a postcode represents the german state of Saxony. As an outcome of this insight, I changed the parsing routine of the XML data to only parse values as numeric, if they do not contain a leading zero (```not s.startswith(\"0\")```)\n",
"* I checked some of the lesser-common values for sanity. E.g., there is a parameter ```dogshit``` which appears three times. As it turns out, this is not a prank of some map editors, who document dog feces they find in the area, but an indication about whether a public trash can contains a dispenser of plastic bags for relevant situations."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Overview of the Data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Try it out:** Use ```python project.py -s``` to obtain the data for this chapter. See Sample Output in file [```Project/output_project.py_-s.txt```](Project/output_project.py_-s.txt).\n",
"\n",
"A couple of basic MongoDB queries were run to explore the data set based on the knowledge of its format from the previous chapter. The queries produce mostly rankings of values for certain data fields. Some of them are subsequently also visualized in a ggplot graph (png file) relying on the skill set gained in [Udacity's Intro to Data Science course, Lesson 4: Data Visualization](https://www.udacity.com/course/viewer#!/c-ud359/l-692548568) while not too much effort was put in making the graphs look particularily beautiful. The graphs are located in ```Project/data/stats_*.png```."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Filesize, Number of Nodes and Ways\n",
"The total file size of the OSM export is 281.778.428 Bytes, there are 208813 nodes and 1146807 ways in the dataset."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'way', u'count': 209356}, {u'_id': u'node', u'count': 1148321}]\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function Project.audit_stats_map.stats_general\n",
"pipeline = [\n",
" {\"$group\": {\"_id\": \"$type\", \"count\": {\"$sum\": 1}}},\n",
" {\"$match\": {\"_id\": {\"$in\": [\"node\", \"way\"]}}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Users Involved\n",
"There were about 1634 users involved in creating the data set, the top 10 of all users accounts for 40% of the created data. There is no direct evidence from the user name that any of them are bot-like users. This could be determined by further research. Many users (over 60%) have made less than 10 entries."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1634 users were involved:\n",
"[{u'_id': u'Wolle DD', u'count': 145807},\n",
" {u'_id': u'NESDD', u'count': 79159},\n",
" {u'_id': u'Thomas8122', u'count': 75621},\n",
" {u'_id': u'stw1701', u'count': 57403},\n",
" '...',\n",
" {u'_id': u'chkr', u'count': 1},\n",
" {u'_id': u'The King', u'count': 1},\n",
" {u'_id': u'mowsw', u'count': 1},\n",
" {u'_id': u'kicherschleife', u'count': 1},\n",
" {u'_id': u'choess', u'count': 1}]\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_users(...):\n",
"pipeline = [\n",
" {\"$match\": {\"created.user\": {\"$exists\": True}}},\n",
" {\"$group\": {\"_id\": \"$created.user\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"print str(len(l)) + \" users were involved:\"\n",
"pprint.pprint(l[1:5]+[\"...\"]+l[-5:])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Types of Amenities\n",
"The attribute ```amenity``` inspired me to do further research in which kind of buildings / objects / facilities are stored in the Open Street Map data in larger quantities in order to do more detailed research on those objects. Especially [Restaurants](#Cuisines-in-Restaurants), [Pubs](#Beers-in-Pubs) and [Churches / Places of Worship](#Religions-in-Places-of-Worship) were investigated further (as can be seen below)."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'parking', u'count': 2689},\n",
" {u'_id': u'bicycle_parking', u'count': 959},\n",
" {u'_id': u'recycling', u'count': 892},\n",
" {u'_id': u'post_box', u'count': 793},\n",
" {u'_id': u'restaurant', u'count': 684},\n",
" {u'_id': u'vending_machine', u'count': 616},\n",
" {u'_id': u'waste_basket', u'count': 536},\n",
" {u'_id': u'fast_food', u'count': 330},\n",
" {u'_id': u'telephone', u'count': 329},\n",
" '...']\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_amenities(...):\n",
"pipeline = [\n",
" {\"$match\": {\"amenity\": {\"$exists\": True}}},\n",
" {\"$group\": {\"_id\": \"$amenity\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l[1:10]+['...'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Popular Leisure Activities\n",
"The attribute ```leisure``` shows the types of leisure activities one can do in Dresden and inspired me to invesigate more on [popular sports in the city](#Popular-Sports) (```leisure```=```sports_center``` or ```leisure```=```stadium```)."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'pitch', u'count': 575},\n",
" {u'_id': u'park', u'count': 431},\n",
" {u'_id': u'sports_centre', u'count': 193},\n",
" {u'_id': u'garden', u'count': 190},\n",
" {u'_id': u'swimming_pool', u'count': 108},\n",
" {u'_id': u'track', u'count': 48},\n",
" {u'_id': u'dance', u'count': 23},\n",
" {u'_id': u'water_park', u'count': 22},\n",
" {u'_id': u'stadium', u'count': 19},\n",
" '...']\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_amenities(...):\n",
"pipeline = [\n",
" {\"$match\": {\"leisure\": {\"$exists\": True}}},\n",
" {\"$group\": {\"_id\": \"$leisure\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l[1:10]+['...'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Religions in Places of Worship\n",
"Grouping and sorting by the occurences of the ```religion``` attribute for all ```amenities``` classified as ```place_of_worship``` or ```community_center``` gives us an indication, how prevalent religions are in our city: obviously, ```christian``` is the most prevalent here."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'christian', u'count': 140},\n",
" {u'_id': u'muslim', u'count': 3},\n",
" {u'_id': u'buddhist', u'count': 2},\n",
" {u'_id': None, u'count': 2},\n",
" {u'_id': u'jewish', u'count': 2},\n",
" {u'_id': u'multifaith', u'count': 1}]\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_religions(...):\n",
"pipeline = [\n",
" {\"$match\": {\"amenity\":{\"$in\": [\"place_of_worship\",\"community_center\"]}}},\n",
" {\"$group\": {\"_id\": \"$religion\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Cuisines in Restaurants\n",
"We can list the types of ```cuisines``` in restaurants (elements with attribute ```amenity``` matching ```restaurant```) and sort them in decending order. We can notice certain inconsistencies or overlaps in the classifications of this data: e.g., a ```kebab``` cuisine may very well be also classified as an ```arab``` cuisine or may, in fact a sub- or super-classification of this cuisine. One could, e.g., eliminate or cluster together especially occurences of cuisines which are less common, but Without having a formal taxonomy of all cuisines, I decided that is probably best to leave the data as-is in order to not sacrifice preciseness for consistency."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'german', u'count': 66},\n",
" {u'_id': u'regional', u'count': 56},\n",
" {u'_id': u'italian', u'count': 52},\n",
" {u'_id': u'greek', u'count': 28},\n",
" {u'_id': u'asian', u'count': 28},\n",
" {u'_id': u'pizza', u'count': 17},\n",
" {u'_id': u'chinese', u'count': 12},\n",
" {u'_id': u'international', u'count': 11},\n",
" {u'_id': u'indian', u'count': 11},\n",
" '...']\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_cuisines(...):\n",
"pipeline = [\n",
" {\"$match\": {\"amenity\": \"restaurant\"}},\n",
" {\"$group\": {\"_id\": \"$cuisine\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l[1:10]+['...'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Beers in Pubs\n",
"Germans do love their beers and the dataset shows that certain ```pub```s, ```restaurant```s or ```bar```s are sponsored by certain beer brands (often advertised on the pubs entrance). We can analyze the prevalence of beer brands by grouping and sorting by occurence of the attribute ```brewery``` for all the ```amenities``` classified as respective establishment. Most popular are [```Radeberger```](https://en.wikipedia.org/wiki/Radeberger_Brewery), a [very popular](https://www.youtube.com/watch?v=QJ9-euumMzQ) local beer, [```Feldschlösschen```](https://en.wikipedia.org/wiki/Feldschl%C3%B6sschen), a swiss beer and ```Dresdner Felsenkeller```, a very local and niche-sort-of beer."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': None, u'count': 867},\n",
" {u'_id': u'Radeberger', u'count': 10},\n",
" {u'_id': u'Feldschl\\xf6\\xdfchen', u'count': 3},\n",
" {u'_id': u'Dresdner Felsenkeller', u'count': 3},\n",
" {u'_id': u'Warsteiner', u'count': 2},\n",
" {u'_id': u'Rechenberger', u'count': 2},\n",
" {u'_id': u'Feldschl\\xf6\\xdfchen;Schwarzer Steiger', u'count': 2},\n",
" {u'_id': u'Einsiedler', u'count': 1},\n",
" {u'_id': u'Eibauer', u'count': 1},\n",
" {u'_id': u'Freiberger', u'count': 1},\n",
" {u'_id': u'Freiberger;Jever;Astra;Lech;Tyskie;B\\xf6hmisch Brauhaus',\n",
" u'count': 1},\n",
" {u'_id': u'Kulmbacher', u'count': 1},\n",
" {u'_id': u\"Neustadt Helles;Lenin's Hanf\", u'count': 1},\n",
" {u'_id': u'Feldschl\\xf6\\xdfchen;Paulaner;Schwarzer Steiger', u'count': 1},\n",
" {u'_id': u'Radeberger;Eibauer', u'count': 1}]\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_beers(...):\n",
"pipeline = [\n",
" {\"$match\": {\"amenity\": {\"$in\":[\"pub\",\"bar\",\"restaurant\"]}}},\n",
" {\"$group\": {\"_id\": \"$brewery\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Popular Sports\n",
"To investigate, which sports are popular, we can group and sort by the (occurence of the) ```sport``` attribute for all elements classified as ```sports_centre``` or ```stadium``` in their ```leisure``` attribute. Unsurprisingly for a german city, we notice that ```9pin``` (bowling) and ```soccer``` are the most popular sports, followed by ```climbing```, an activity very much enjoyed by people in Dresden, presumably because of the close-by sand-stone mountains of the national park [Sächsische Schweiz](http://www.saechsische-schweiz.de/en/saxon-switzerland.html)."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'multi', u'count': 55},\n",
" {u'_id': u'9pin', u'count': 5},\n",
" {u'_id': u'soccer', u'count': 5},\n",
" {u'_id': u'climbing', u'count': 4},\n",
" '...']\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_sports(...):\n",
"pipeline = [\n",
" {\"$match\": {\"leisure\": {\"$in\": [\"sports_centre\",\"stadium\"]}}},\n",
" {\"$group\": {\"_id\": \"$sport\", \"count\": {\"$sum\": 1}}},\n",
" {\"$sort\": {\"count\": -1}}\n",
" ]\n",
"l = list(project_coll.aggregate(pipeline))\n",
"pprint.pprint(l[1:5]+['...'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Where to Dance in Dresden\n",
"I am a passionate social dancer, so a list of dance schools in Dresden should not be abscent from this investigation. We can quickly grab all elements which have the ```leisure``` attribute set to ```dancing```."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[u'Tanzschule Graf',\n",
" u'Tanzschule Weise',\n",
" u'tres tangos',\n",
" u'Tango im Salon',\n",
" u'Studio24',\n",
" u'La Academia Tango',\n",
" u'Tanzschule Herrmann-Nebl',\n",
" u'Tanzstudio Sandana',\n",
" u'TSC Casino Dresden e.V.',\n",
" '...']\n"
]
}
],
"source": [
"from Project.notebook_stub import project_coll\n",
"import pprint\n",
"\n",
"# Query used - see function: Project.audit_stats_map.stats_dances(...):\n",
"l = list(project_coll.distinct(\"name\", {\"leisure\": \"dance\"}))\n",
"pprint.pprint(l[1:10]+['...'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Problems Encountered in the Map / Data Quality\n",
"**Try it out**: Use ```python project.py -q``` to obtain the data from this chapter. See Sample Output in file [```Project/output_project.py_-q.txt```](Project/data/audit_buildings.csv). The script also writes a CSV file to [```Project/data/audit_buildings.csv```](Project/data/audit_buildings.csv), which is also beautified into a [Excel File](Project/data/audit_buildings.xlsx)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Leading Zeros\n",
"As already discussed, during the parsing stage, we are using an optimistic approach of parsing any numerical value as integer or float, if it is parsable as such. However, we noticed that we should _not_ do this, if leading zeros are present as those hold semantics for phone numbers and zip codes. Otherwise, this cleaning approach gives us a much smaller representation of the data in MongoDB and in-memory."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Normalizing / Cleaning Cuisines\n",
"As hinted in section [Cuisines in Restaurant](#Cuisines-in-Restaurants), classification of cuisines is inconsistent. There are two problems with this value:\n",
"\n",
"* There are multiple values separated by ';' which makes the parameter hard to parse. We overcome this by creating a parameter ```cuisineTag``` which stores the cuisine classifications as an array:\n",
"\n",
" ```python\n",
" db.eval('''db.osmnodes.find({\n",
" \"cuisine\": {\"$exists\": true},\n",
" \"amenity\": \"restaurant\"\n",
" }).snapshot().forEach(function(val, idx) {\n",
" val.cuisineTags = val.cuisine.split(';');\n",
" db.osmnodes.save(val)\n",
" })\n",
" ''')\n",
" ```\n",
" \n",
"* Some values are inconsistently used; therefore, we unify them with a mapping table and a subsequent MongoDB update:\n",
"\n",
" ```python\n",
" cuisines_synonyms = {\n",
" 'german': ['regional', 'schnitzel', 'buschenschank'],\n",
" 'portuguese': ['Portugiesisches_Restaurant_&_Weinbar'],\n",
" 'italian': ['pizza', 'pasta'],\n",
" 'mediterranean': ['fish', 'seafood'],\n",
" 'japanese': ['sushi'],\n",
" 'turkish': ['kebab'],\n",
" 'american': ['steak_house']\n",
" }\n",
" # not mapped:\n",
" # greek, asian, chinese, indian, international, vietnamese, thai, spanish, arabic\n",
" # sudanese, russian, korean, hungarian, syrian, vegan, soup, croatian, african\n",
" # balkan, mexican, french, cuban, lebanese\n",
" \n",
" for target in cuisines_synonyms:\n",
" db.osmnodes.update( {\n",
" \"cuisine\": {\"$exists\": True},\n",
" \"amenity\": \"restaurant\",\n",
" \"cuisineTags\": {\"$in\": cuisines_synonyms[target]}\n",
" }, {\n",
" \"$pullAll\": { \"cusineTags\": cuisines_synonyms[target] },\n",
" \"$addToSet\": { \"cuisineTags\": [ target ] }\n",
" }, multi=False )\n",
" ```\n",
" \n",
"This allows us to convert a restaurant with the MongoDB representation\n",
"\n",
"```{..., \"cuisine\": \"pizza;kebab\", ...}``` \n",
"\n",
"to the alternative representation\n",
"\n",
"```{..., \"cuisine\": \"pizza;kebab\", \"cuisineTag\": [\"italian\", \"turkish\"], ...}```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Auditing Phone Numbers\n",
"Phone re scattered over different attributes (```address.phone```, ```phone``` and ```mobile_phone```) and come in different styles of formating (like ```+49 351 123 45``` vs. ```0049-351-12345```). First, we retrieve a list of all phone numbers. With the goal in mind to later store the normalized phone number back into the attribute ```phone```, this value has to be read first, and only if it is empty, ```mobile_phone``` or ```address.phone``` should be used."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from Project.notebook_stub import project_coll\n",
"\n",
"# Query used - see function: Project.audit_quality_map.audit_phone_numbers(...):\n",
"pipeline = [\n",
" {\"$match\": {\"$or\": [\n",
" {\"phone\": {\"$exists\": True}},\n",
" {\"mobile_phone\": {\"$exists\": True}},\n",
" {\"address.phone\": {\"$exists\": True}}\n",
" ]}},\n",
" {\"$project\": {\n",
" \"_id\": 1,\n",
" \"phone\": {\"$ifNull\": [\"$phone\", {\"$ifNull\": [\"$mobile_phone\", \"$address.phone\"]}]}\n",
" }}\n",
" ]\n",
"l = project_coll.aggregate(pipeline)\n",
"\n",
"# Output too long... See the file Project/output_project.py_-q.txt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Cleaning Phone Numbers\n",
"**Try it out:** Use ```python project.py -C``` to clean in debug mode. See Sample Output in file ```Project/output_project.py_-C.txt```. The script also writes a CSV file to [```Project/data/clean_phones.csv```](Project/data/clean_phones.csv), which is also beautified into a [Excel File](Project/data/clean_phones.xlsx).\n",
"\n",
"Cleaning the phone numbers involves:\n",
"* unifying the different phone attributes (```phone```, ```address.phone``` and ```mobile_phone```) - this is already taken care by extracting the phone numbers during the audit stage\n",
"* if possible, canonicalizing the phone number notations by parsing them using a regular expression:\n",
"\n",
"```python\n",
"phone_regex = re.compile(ur'^(\\(?([\\+|\\*]|00) *(?P<country>[1-9][0-9]*)\\)?)?' + # country code\n",
" ur'[ \\/\\-\\.]*\\(?0?\\)?[ \\/\\-\\.]*' + # separator\n",
" ur'(\\(0?(?P<area1>[1-9][0-9 ]*)\\)|0?(?P<area2>[1-9][0-9]*))?' + # area code\n",
" ur'[ \\/\\-\\.]*' + # separator\n",
" ur'(?P<number>([0-9]+ *[\\/\\-.]? *)*)$', # number\n",
" re.UNICODE)\n",
"```\n",
"\n",
"The regular expression is resilient to various separators (\"```/```\", \"```-```\", \" \", \"```(0)```\") and bracket notation of phone numbers. It is not resilient for some unicode characters or written lists of phone numbers which are designed to be interpreted by humans (using separators like \"```,```\", \"```/-```\" or \"```oder```\" lit. or). During the cleaning stage, an output is written which phone numbers could not be parsed. This contains only a tiny fraction of phone numbers (9 or 0.5%) which would be easily cleanable by hand.\n",
"\n",
"```\n",
"The following objects couldn't be parsed:\n",
" normalized\n",
"55f57294b1c8a72c34523897 +49 35207 81429 or 81469\n",
"55f57299b1c8a72c345272cd +49 351 8386837, +49 176 67032256\n",
"55f572c2b1c8a72c34546689 0351 4810426\n",
"55f572c3b1c8a72c34546829 +49 351 8902284 or 2525375\n",
"55f572fdb1c8a72c34574963 +49 351 4706625, +49 351 0350602\n",
"55f573bdb1c8a72c3460bdb3 +49 351 87?44?44?00\n",
"55f573bdb1c8a72c3460c066 0162 2648953, 0162 2439168\n",
"55f573edb1c8a72c346304b1 03512038973, 03512015831\n",
"55f5740eb1c8a72c34649008 0351 4455193 / -118\n",
"```\n",
"\n",
"If the phone number was parsable, the country code, area code and rest of the phone number are separated and subsequently strung together to a canonical form. The data to be transformed is stored into a Pandas Dataframe. By using the option ```-C``` instead of ```-c``` the execution of the transformation can be surpressed and the Dataframe instead be written to a [CSV file](Project/data/clean_phones.csv) which might be further beautified into an [Excel File](Project/data/clean_phones.xlsx) in order to test or debug the transformation before writing it to the database with the ```-c``` option.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Auditing Street Names (Spoiler Alert: No Cleaning Necessary)\n",
"Auditing the map's street names analogous to how it was done in the Data Wrangling course was done as follows: Check, whether 'weird' street names occur, which do not end on a suffix like ```street``` (in German ```-straße``` or ```Straße```, depending on whether it is a compound word or not). It is assumed that then, they would most likely end in an abbreviation like ```str.```. For this we use a regular expression querying all streets <u>not</u> ending with a particular suffix like ```[Ss]traße``` (street), ```[Ww]eg``` (way) etc. This is accomplished by a chain of [\"negative lookbehind\"](http://www.regular-expressions.info/lookaround.html) expressions (```(?<!...)```) which must all in sequence evaluate to \"true\" in order to flag a street name as non-conforming."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from Project.notebook_stub import project_coll\n",
"\n",
"# Query used - see function: Project.audit_quality_map.audit_streets(...):\n",
"expectedStreetPattern = \\\n",
" u\"^.*(?<![Ss]tra\\u00dfe)(?<![Ww]eg)(?<![Aa]llee)(?<![Rr]ing)(?<![Bb]erg)\" + \\\n",
" u\"(?<![Pp]ark)(?<![Hh]\\u00f6he)(?<![Pp]latz)(?<![Bb]r\\u00fccke)(?<![Gg]rund)$\"\n",
"l = list(project_coll.distinct(\"name\", {\n",
" \"type\": \"way\",\n",
" \"name\": {\"$regex\": expectedStreetPattern}\n",
" }))\n",
"# Output too long... See the file Project/output_project.py_-q.txt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Skimming through the list, it was noticable that the nature of the german language (and how in Germany streetnames work) results in the fact, that there are many small places without a suffix like \"street\" but \"their own thing\" (like ```Am Hang``` lit. 'At The Slope', ```Beerenhut``` lit. 'Berry Hat', ```Im Grunde``` lit. 'In The Ground'). The street names can therefore not be processed just by looking at the suffixes - I tried something different..."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Cross Auditing Street Names with Street Addresses (Spoiler Alert: No Cleaning Necessary)\n",
"I did not want to trust the street names of the data set fully yet. Next, I tried figuring out if street names of buildings were consistent with street names of objects in close proximity. Therefore, a JavaScript query is run directly on the database server returning all ```buildings``` with the objects nearby having an ```address.street``` parameter. This should allow us to cross-audit if objects in close proximity do have the same street names."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from Project.notebook_stub import project_db\n",
"\n",
"# Query used - see function: Project.audit_quality_map.audit_buildings(...):\n",
"buildings_with_streets = project_db.eval('''\n",
" db.osmnodes.ensureIndex({pos:\"2dsphere\"});\n",
" result = [];\n",
" db.osmnodes.find(\n",
" {\"building\": {\"$exists\": true}, \"address.street\": {\"$exists\": true}, \"pos\": {\"$exists\": true}},\n",
" {\"address.street\": \"\", \"pos\": \"\"}\n",
" ).forEach(function(val, idx) {\n",
" val.nearby = db.osmnodes.distinct(\"address.street\",\n",
" {\"_id\": {\"$ne\": val._id}, \"pos\": {\"$near\": {\"$geometry\": {\"type\": \"Point\", \"coordinates\": val.pos}, \"$maxDistance\": 50, \"$minDistance\": 0}}}\n",
" );\n",
" result.push(val);\n",
" })\n",
" return result;\n",
" ''')\n",
"\n",
"# Output too long... See the file Project/output_project.py_-q.txt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The resulting objects are then iterated through and the best and worst fitting nearby street name are identified each using the [Levenshtein distance](http://stackoverflow.com/questions/18134437/where-can-the-documentation-for-python-levenshtein-be-found-online). For each object, a row is created in a DataFrame which is subsequently exported to a csv file [Project/data/audit_buildings.csv](Project/data/audit_buildings.csv) that was manually beautified into an [Excel File](Project/data/audit_buildings.xlsx). \n",
"\n",
"\n",
"\n",
"As can be seen, street names of nearby objects mostly match those of the building itself (Levenshtein distance is zero). If they deviate greatly, they are totally different street names in the same area and not just \"typos\" or non-conforming abbreviations."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"###Auditing Zip Codes (Spoiler Alert: No Cleaning Necessary)\n",
"**Try it out:** Use ```python project.py -Z``` which runs the auditing script for zipcodes. See Sample Output in file ```Project/output_project.py_-Z.txt```. To be able to run this script correctly, the [zipcode data from Geonames.org](http://download.geonames.org/export/zip/) needs to be downloaded and installed first using the ```-z``` option (see output in ```Project/output_project.py_-Z.txt``).\n",
"\n",
"This part of the auditing process makes use of an additional at [Geonames.org](http://download.geonames.org/export/zip/) to resolve and audit the zip codes in the data set. During the \"installation process\" (option ```-z```) the zipcode data (provided as a tab-separated file) is downloaded and, line-by-line, stored to a (separate) MongoDB collection. However, we are only interested \"zipcode\" (2) and \"place\" (3)\n",
"\n",
"During the auditing stage (option ```-Z```) we first get a list of all used zipcode using the following query:\n",
"\n",
"```python\n",
"pipeline = [\n",
" { \"$match\": {\"address.postcode\": {\"$exists\": 1}} },\n",
" { \"$group\": {\"_id\": \"$address.postcode\", \"count\": {\"$sum\": 1}} },\n",
" { \"$sort\": {\"count\": 1} }\n",
" ]\n",
"```\n",
"\n",
"The zipcodes are then all looked up in the zipcode collection using the ```$in```-operator. The data obtained is joined back into the original result.\n",
"\n",
"```python\n",
"zipcodeObjects = zipcodeColl.find( {\"zipcode\": {\"$in\": [z[\"_id\"] for z in zipcodeList]}} )\n",
"```\n",
"\n",
"The following output shows that there the lesser used zipcodes are from the Dresden metropolitan area, not Dresden itself:"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[{u'_id': u'01847', u'count': 2, 'place': u'Lohmen'},\n",
" {u'_id': u'01896', u'count': 17, 'place': u'Pulsnitz'},\n",
" {u'_id': u'01665', u'count': 18, 'place': u'Diera-Zehren'},\n",
" {u'_id': u'01689', u'count': 63, 'place': u'Weinb\\xf6hla'},\n",
" {u'_id': u'01833', u'count': 93, 'place': u'Stolpen'},\n",
" {u'_id': u'01477', u'count': 134, 'place': u'Arnsdorf'},\n",
" {u'_id': u'01737', u'count': 165, 'place': u'Tharandt'},\n",
" {u'_id': u'01471', u'count': 325, 'place': u'Radeburg'},\n",
" {u'_id': u'01796', u'count': 516, 'place': u'Pirna'},\n",
" '...']\n"
]
}
],
"source": [
"from Project.audit_zipcode_map import audit_zipcode_map\n",
"from Project.notebook_stub import project_server, project_port\n",
"import pprint\n",
"\n",
"zipcodeJoined = audit_zipcode_map(project_server, project_port, quiet=True)\n",
"pprint.pprint(zipcodeJoined[1:10]+['...'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Other Ideas about the Data Set\n",
"\n",
"### Auditing City Names for Correctness and Completeness\n",
"The Geonames.org data could help us to validate the entered city names or add them, where missing. One could compare the ```address.city``` attribute of any OSM element with all of the 4 hierarchically names of the Geonames.org document which belongs to the zipcode referred by ```address.postcode```.\n",
"\n",
"* If no ```address.city``` is present in the OSM element at all, the lowestmost value in the Geonames.org hieararchy could be added and the data therefore enhanced.\n",
"* If the value of the OSM element does not match any name of the Geonames.org data, the element could be flagged for manual processing.\n",
"\n",
"**Cost**: Relatively easily implementable, however, out of scope for this project. We should, however, strive for implementing the related query in native BSON code in order to not hit the database with every zipcode-to-Geonames-element mapping request for each OSM element.\n",
"\n",
"**Benefit**: Potentially high, depending on how many cities are not entered at all (quick win) or entered correctly (some additional manual work required).\n",
"\n",
"### Cuisine Taxonomy\n",
"\n",
"The taxonomy of cuisines could be further formalized to contain super- and subsets of cuisines (e.g. each \"italian\" cuisine is also an \"international\" cuisine). With domain knowledge, coarsly classified restaurants could potentially also be sub-classified.\n",
"\n",
"**Cost**: High, The creation of a proper cuisine-taxonomy would require substantial knowledge of the subject matter of cuisines and the subtle differences in culinary art. Also, rather than a tree-based classification, some \"fusion\" kitchens might overlap: any simplification or unification we carry out here comes at the cost of sacrificing detail.\n",
"\n",
"**Benefit**: Medium-high in certain use cases, higher number of restaurants with a certain classification lets us better find the restaurant of our taste and compare various restaurants with each other. \n",
"\n",
"### Other Open Questions\n",
"Overall, the data set of Dresden is pretty neat and tidy. Compared to other, huger cities (e.g., in India) I might have had an easier job. Further open questions or ideas (out of scope for this report) include:\n",
"\n",
"* The users might be analyzed further: Why are so many nodes (many thousands) created by so few users? Are bots at work? Why are so many users only contributing with very few edits? (Maybe gamification - leaderboards for who has the most edits during the recent week - would provide help.)\n",
"* One could audit for completeness by parsing several sample websites for addresses and trying to retrieve those addresses in the Open Street Map data.\n",
"* One could feed the normalized phone data back into Open Street Map by either using a Web Service or using the XML format."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"##References\n",
"- [Project Rubric](https://docs.google.com/document/d/1TpfNxDzUjhibq9Qb8cOQHtlvZUelft-W0fb7pCTTyYE/pub)\n",
"- [Sample Project](https://docs.google.com/document/d/1F0Vs14oNEs2idFJR3C_OPxwS6L0HPliOii-QpbmrMo4/pub)\n",
"- [Lesson & Problem Set 6 of Udacities Data Wrangling with OpenDB Class](https://www.udacity.com/course/viewer#!/c-ud032/l-768058569)\n",
"- [Project Evaluation & Submission](https://www.udacity.com/course/viewer#!/c-nd002/l-3168208620/m-3189488621)\n",
"- [Python CSV Reader Documentation](https://docs.python.org/2/library/csv.html)\n",
"- [Python ElementTree Documentation](https://docs.python.org/2/library/xml.etree.elementtree.html)\n",
"- [MongoDB Aggregation Framework Operators](http://docs.mongodb.org/manual/reference/operator/aggregation/project/#pipe._S_project)\n",
"- [MongoDB: Indexes](http://docs.mongodb.org/manual/indexes/)\n",
"- [Regex Lookarounds](http://www.regular-expressions.info/lookaround.html)\n",
"- [MongoDB University](https://university.mongodb.com/)\n",
"- [BZip2 Module](https://docs.python.org/2/library/bz2.html)\n",
"- [MapZen Metro Extracts](https://mapzen.com/data/metro-extracts)\n",
"- [MongoDB Extended JSON](http://docs.mongodb.org/master/reference/mongodb-extended-json/)\n",
"- [Retrieving URLs](http://stackoverflow.com/questions/22676/how-do-i-download-a-file-over-http-using-python)\n",
"- [Using the Levenshtein distance](http://stackoverflow.com/questions/18134437/where-can-the-documentation-for-python-levenshtein-be-found-online)\n",
"- [Zipcode Helper from Geonames.org](http://download.geonames.org/export/zip/) ([cc-by](http://www.geonames.org/export/))\n",
"\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| agpl-3.0 |
widdowquinn/SI_Holmes_etal_2017 | index.ipynb | 1 | 12440 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<img src=\"notebooks/images/JHI_STRAP_Web.png\" style=\"width: 150px; float: right;\">\n",
"\n",
"# `SI_Holmes_etal_2017` - index"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This repository contains files detailing the process of fitting the model of the enrichment array experiment described in [Holmes *et al.* (2017)](). These files are intended to enable independent reproduction, exploration and extension of the analysis reported in the paper.\n",
"\n",
"To encourage exploration and reproduction, we have tried to make these notebooks compatible, so far as is possible, with [MyBinder](http://mybinder.org/), to enable you to run them in the cloud without having to install software on your own machine. To use these notebooks, click on [this link](http://mybinder.org:/repo/widdowquinn/si_holmes_etal_2017), or the button below.\n",
"\n",
"[](http://mybinder.org:/repo/widdowquinn/si_holmes_etal_2017)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Table of Contents\n",
"\n",
"1. [Files and Directories](#files)\n",
" 1. [How to get help](#help)\n",
"2. [Quick Start](#quickstart)\n",
" 1. [Use the notebooks](#use)\n",
"3. [Replicating the manuscript model](#replicate)\n",
" 1. [Data QA](#qa)\n",
" 2. [Fitting the model](#fitting)\n",
" 3. [Crossvalidation](#xval)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Quick links to notebooks\n",
"\n",
"* [`01-data_qa.ipynb`](notebooks/01-data_qa.ipynb) - Data QA and cleanup\n",
"* [`02-full_model_fit.ipynb`](notebooks/02-full_model_fit.ipynb) - Model fitting\n",
"* [`03-crossvalidation.ipynb`](notebooks/03-crossvalidation.ipynb) - Model crossvalidation\n",
"* [`04-etpD.ipynb`](notebooks/04-etpD.ipynb) - etpD complementation results"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"files\"></a>\n",
"## Files and Directories\n",
"\n",
"\n",
"* `data/`: directory containing the raw microarray data, and the genomic data used in the analysis\n",
"* `models/`: directory containing Stan models in plan text format\n",
"* `multiplexing/`: directory containing scripts used to generate multiplexed data for *k*-fold cross-validation, and to fit the cross-validation models\n",
"* `notebooks/`: directory containing Jupyter notebooks describing and enabling reproduction of the data QA, model fitting and model validation\n",
"* `requirements.txt`: file describing the Python dependencies of the notebooks and scripts, which can be used to create a virtual environment for replication of the analysis from the paper.\n",
"* `LICENCE`: a copy of the MIT licence that governs the code contained in this repository\n",
"* `README.md`: this file"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"help\"></a>\n",
"### How to get help for the code/analyses in this repository\n",
"\n",
"Please raise any issues at the GitHub issues page for this repository:\n",
"\n",
"* [GitHub issues page](https://github.com/widdowquinn/SI_Holmes_etal_2017/issues)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"quickstart\"></a>\n",
"## Quick Start\n",
"\n",
"### Set up the environment\n",
"\n",
"We would like our analysis to be reproducible, and for this we recommend using a Python virtual environment to ensure compatibility of dependencies and to replicate the environment used for the analysis. The virtual environment separates installation of Python packages from your system Python installation, enabling the running of these analyses without interfering with the system Python.\n",
"\n",
"Using `pip` to install the required dependencies listed in `requirements.txt` should ensure that the code in this repository runs as expected.\n",
"\n",
"#### Create and start the virtual environment\n",
"\n",
"**NOTE:** You will need to have installed `virtualenv`[[*](http://docs.python-guide.org/en/latest/dev/virtualenvs/)] for your system.\n",
"\n",
"```bash\n",
"virtualenv venv-SI_Holmes_2016 -p python3.6\n",
"source venv-SI_Holmes_2016/bin/activate\n",
"pip install -r requirements.txt\n",
"```\n",
"\n",
"**Read more**\n",
"\n",
"* `virtualenv`: [The Hitchhiker's Guide to Python](http://docs.python-guide.org/en/latest/dev/virtualenvs/)\n",
"* `pip`: [Installing Python Modules](https://docs.python.org/3/installing/)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"use\"></a>\n",
"### Use the notebooks\n",
"\n",
"We have used the [Jupyter notebook](http://jupyter.org/) environment to facilitate [literate programming](https://en.wikipedia.org/wiki/Literate_programming), and to encourage exploration of and experimentation with the code and model. These notebooks have sections of explanatory text that are punctuated by code snippets. In the Jupyter notebook environment, all of these code snippets are editable and runnable.\n",
"\n",
"#### Start the notebook environment\n",
"\n",
"From the top level directory of this repository, start the Jupyter notebook server by issuing the command:\n",
"\n",
"```bash\n",
"jupyter notebook\n",
"```\n",
"\n",
"A new browser window or tab should open, containing the Jupyter homepage, which will show a listing of files and directories in the top level of the repository.\n",
"\n",
"**Read more**\n",
"\n",
"* `jupyter notebook`: [Quick-start guide](https://jupyter-notebook-beginner-guide.readthedocs.io/en/latest/)\n",
"* `jupyter notebook`: [Tutorial](https://www.datacamp.com/community/tutorials/tutorial-jupyter-notebook)\n",
"\n",
"#### Opening the notebooks\n",
"\n",
"From the Jupyter homepage in your browser window, click on the link to the `notebooks/` subdirectory. Then click on the link for the notebook you wish to use. The selected notebook should then open in a new browser tab.\n",
"\n",
"When they were committed to the repository, the notebooks contained output from the original runs, so they can be read and understood without needing to rerun the models. If you would like to rerun/reproduce/modify these outputs, we recommend restarting the kernel and clearing all output before beginning. This can be done by clicking on `Kernel -> Restart & Clear Output`, in the notebook window.\n",
"\n",
"<a id=\"replicate\"></a>\n",
"## Replicating the manuscript model\n",
"\n",
"To replicate the manuscript model from scratch: start the virtual environment, then run the notebooks and scripts as described below (remembering to use `Kernel -> Restart & Clear Output` in each notebook to remove the original/existing outputs):"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"qa\"></a>\n",
"### Data processing, QA and normalisation\n",
"\n",
"* `01-data_qa.ipynb`: this will take the input data from the `notebooks/data/` directory, and process it into the output files:\n",
" * `notebooks/datasets/normalised_array_data.tab`: used for the full model fit, and to produce the multiplexed output datasets.\n",
" * `reduced_probe_data.tab`: a subset of `notebooks/datasets/normalised_array_data.tab`, used for testing code\n",
" * `reduced_locus_data.tab`: a subset of `notebooks/datasets/normalised_array_data.tab`, used for testing code"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"fitting\"></a>\n",
"### Fitting the model on the full dataset\n",
"\n",
"* `02-full_model_fit.ipynb`: this will fit the Stan model described in the notebook to the `notebooks/datasets/normalised_array_data.tab` processed data file, and conduct analyses to produce the final set of genes for which the estimated effect on enrichment due to passage (treatment) was positive, and render the figures used in the paper.\n",
"\n",
"**NOTE:** the complete fit takes between 5 and 9 hours on my laptop (2013 MacBook Pro, 2.8GHz i7 16GB RAM)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id=\"xval\"></a>\n",
"### 10-fold crossvalidation\n",
"\n",
"The crossvalidation dataset construction and model fit were conducted in the `multiplexing` directory, using Python scripts rather than Jupyter notebooks. To reproduce the dataset construction and fits, first change directory to `multiplexing`:\n",
"\n",
"```bash\n",
"cd multiplexing\n",
"```\n",
"\n",
"then build the input datasets with the `multiplex_data.py` script:\n",
"\n",
"```bash\n",
"./multiplex_data.py -v -d ../notebooks/datasets/normalised_array_data.tab \\\n",
" -k 10 -o 10-fold_CV --seed 123456789 \\\n",
" -l 10-fold_CV_multiplex.log\n",
"```\n",
"\n",
"This will create a new directory called `10-fold_CV`, containing one new subdirectory for each training/test split of the input dataset.\n",
"\n",
"Next, use the `run_multiplex_models.py` script to fit the Stan model to each of the multiplexed training/test sets.\n",
"\n",
"```bash\n",
"./run_multiplex_models.py -v -i 10-fold_CV --script ./run_model.py \\\n",
" --seed 123456789 \\\n",
" -l 10-fold_CV_run_models.log\n",
"```\n",
"\n",
"**NOTE:** the `run_multiplex_models.py` has a dependency on the [`pysge` module](https://github.com/widdowquinn/pysge) for submission of jobs to our local cluster. This is not included in the `requirements.txt` file, so the script will fail at this point. The command-lines that this script produces in the log file can, however, be copied for execution on any system available to you. If you happen to be running on a cluster with SGE scheduling, then installation of `pysge` in the virtual environment will enable use of the cluster to fit the multiplexed models.\n",
"\n",
"Finally, use the `join_multiplexed_data.py` script to combine prediction output from each of the 10 test sets into a single `.tab` file. This will contain predictions for each of the probes from the input dataset, using the model fit to the remaining training data.\n",
"\n",
"```bash\n",
"./join_multiplexed_data.py -v -i 10-fold_CV -o 10-fold_CV.tab \\\n",
" -l 10-fold_CV_join_data.log\n",
"```\n",
"\n",
"The combined data produced in this way can then be used as input for the notebook `03-model_validation.ipynb`.\n",
"\n",
"* `03-model_validation.ipynb`: this will conduct analyses on the combined output from 10-fold crossvalidation on the input dataset in `normalised_array_data.tab`. These analyses estimate the ability of the model to predict unseen 'output' array intensities by training it on 90% of the data at any one time, and testing it on the remaining 10% of the dataset."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### NOTE: PRNG seeds\n",
"\n",
"All random processes in the model building and fitting can take a seed value for the pseudorandom number generator. For replication of the values in the paper, this seed should be set to `123456789` for all processes:\n",
"\n",
"* the seed used for the main Stan fit (in notebook `02-full_model_fit`)\n",
"* the seed for splitting the input data into multiplexed sets (`multiplex_data.py`)\n",
"* the seed used for the multiplexing Stan fits (`run_multiplex_models.py`)\n",
"* the seed used for fitting *etpD* complementation results (`04-etpD.ipynb`)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.10"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
davidzchen/tensorflow | tensorflow/lite/g3doc/performance/post_training_integer_quant_16x8.ipynb | 3 | 18857 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "c8Cx-rUMVX25"
},
"source": [
"##### Copyright 2020 The TensorFlow Authors."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"cellView": "form",
"id": "I9sUhVL_VZNO"
},
"outputs": [],
"source": [
"#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"#\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"#\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "6Y8E0lw5eYWm"
},
"source": [
"# Post-training integer quantization with int16 activations"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "CGuqeuPSVNo-"
},
"source": [
"\u003ctable class=\"tfo-notebook-buttons\" align=\"left\"\u003e\n",
" \u003ctd\u003e\n",
" \u003ca target=\"_blank\" href=\"https://www.tensorflow.org/lite/performance/post_training_quant_16x8\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/tf_logo_32px.png\" /\u003eView on TensorFlow.org\u003c/a\u003e\n",
" \u003c/td\u003e\n",
" \u003ctd\u003e\n",
" \u003ca target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/g3doc/performance/post_training_quant_16x8.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/colab_logo_32px.png\" /\u003eRun in Google Colab\u003c/a\u003e\n",
" \u003c/td\u003e\n",
" \u003ctd\u003e\n",
" \u003ca target=\"_blank\" href=\"https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/g3doc/performance/post_training_quant_16x8.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/GitHub-Mark-32px.png\" /\u003eView source on GitHub\u003c/a\u003e\n",
" \u003c/td\u003e\n",
" \u003ctd\u003e\n",
" \u003ca href=\"https://storage.googleapis.com/tensorflow_docs/tensorflow/lite/g3doc/performance/post_training_quant_16x8.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/download_logo_32px.png\" /\u003eDownload notebook\u003c/a\u003e\n",
" \u003c/td\u003e\n",
"\u003c/table\u003e"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "BTC1rDAuei_1"
},
"source": [
"## Overview\n",
"\n",
"[TensorFlow Lite](https://www.tensorflow.org/lite/) now supports\n",
"converting activations to 16-bit integer values and weights to 8-bit integer values during model conversion from TensorFlow to TensorFlow Lite's flat buffer format. We refer to this mode as the \"16x8 quantization mode\". This mode can improve accuracy of the quantized model significantly, when activations are sensitive to the quantization, while still achieving almost 3-4x reduction in model size. Moreover, this fully quantized model can be consumed by integer-only hardware accelerators. \n",
"\n",
"Some examples of models that benefit from this mode of the post-training quantization include: \n",
"* super-resolution, \n",
"* audio signal processing such\n",
"as noise cancelling and beamforming, \n",
"* image de-noising, \n",
"* HDR reconstruction\n",
"from a single image\n",
"\n",
"In this tutorial, you train an MNIST model from scratch, check its accuracy in TensorFlow, and then convert the model into a Tensorflow Lite flatbuffer using this mode. At the end you check the accuracy of the converted model and compare it to the original float32 model. Note that this example demonstrates the usage of this mode and doesn't show benefits over other available quantization techniques in TensorFlow Lite."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "2XsEP17Zelz9"
},
"source": [
"## Build an MNIST model"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "dDqqUIZjZjac"
},
"source": [
"### Setup"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "gyqAw1M9lyab"
},
"outputs": [],
"source": [
"import logging\n",
"logging.getLogger(\"tensorflow\").setLevel(logging.DEBUG)\n",
"\n",
"import tensorflow as tf\n",
"from tensorflow import keras\n",
"import numpy as np\n",
"import pathlib"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "srTSFKjn1tMp"
},
"source": [
"Check that the 16x8 quantization mode is available "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "c6nb7OPlXs_3"
},
"outputs": [],
"source": [
"tf.lite.OpsSet.EXPERIMENTAL_TFLITE_BUILTINS_ACTIVATIONS_INT16_WEIGHTS_INT8"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "eQ6Q0qqKZogR"
},
"source": [
"### Train and export the model"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "hWSAjQWagIHl"
},
"outputs": [],
"source": [
"# Load MNIST dataset\n",
"mnist = keras.datasets.mnist\n",
"(train_images, train_labels), (test_images, test_labels) = mnist.load_data()\n",
"\n",
"# Normalize the input image so that each pixel value is between 0 to 1.\n",
"train_images = train_images / 255.0\n",
"test_images = test_images / 255.0\n",
"\n",
"# Define the model architecture\n",
"model = keras.Sequential([\n",
" keras.layers.InputLayer(input_shape=(28, 28)),\n",
" keras.layers.Reshape(target_shape=(28, 28, 1)),\n",
" keras.layers.Conv2D(filters=12, kernel_size=(3, 3), activation=tf.nn.relu),\n",
" keras.layers.MaxPooling2D(pool_size=(2, 2)),\n",
" keras.layers.Flatten(),\n",
" keras.layers.Dense(10)\n",
"])\n",
"\n",
"# Train the digit classification model\n",
"model.compile(optimizer='adam',\n",
" loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),\n",
" metrics=['accuracy'])\n",
"model.fit(\n",
" train_images,\n",
" train_labels,\n",
" epochs=1,\n",
" validation_data=(test_images, test_labels)\n",
")"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "5NMaNZQCkW9X"
},
"source": [
"For the example, you trained the model for just a single epoch, so it only trains to ~96% accuracy."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "xl8_fzVAZwOh"
},
"source": [
"### Convert to a TensorFlow Lite model\n",
"\n",
"Using the Python [TFLiteConverter](https://www.tensorflow.org/lite/convert/python_api), you can now convert the trained model into a TensorFlow Lite model.\n",
"\n",
"Now, convert the model using `TFliteConverter` into default float32 format:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "_i8B2nDZmAgQ"
},
"outputs": [],
"source": [
"converter = tf.lite.TFLiteConverter.from_keras_model(model)\n",
"tflite_model = converter.convert()"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "F2o2ZfF0aiCx"
},
"source": [
"Write it out to a `.tflite` file:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "vptWZq2xnclo"
},
"outputs": [],
"source": [
"tflite_models_dir = pathlib.Path(\"/tmp/mnist_tflite_models/\")\n",
"tflite_models_dir.mkdir(exist_ok=True, parents=True)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Ie9pQaQrn5ue"
},
"outputs": [],
"source": [
"tflite_model_file = tflite_models_dir/\"mnist_model.tflite\"\n",
"tflite_model_file.write_bytes(tflite_model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "7BONhYtYocQY"
},
"source": [
"To instead quantize the model to 16x8 quantization mode, first set the `optimizations` flag to use default optimizations. Then specify that 16x8 quantization mode is the required supported operation in the target specification:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "HEZ6ET1AHAS3"
},
"outputs": [],
"source": [
"converter.optimizations = [tf.lite.Optimize.DEFAULT]\n",
"converter.target_spec.supported_ops = [tf.lite.OpsSet.EXPERIMENTAL_TFLITE_BUILTINS_ACTIVATIONS_INT16_WEIGHTS_INT8]"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "zLxQwZq9CpN7"
},
"source": [
"As in the case of int8 post-training quantization, it is possible to produce a fully integer quantized model by setting converter options `inference_input(output)_type` to tf.int16."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "yZekFJC5-fOG"
},
"source": [
"Set the calibration data:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Y3a6XFqvHbYM"
},
"outputs": [],
"source": [
"mnist_train, _ = tf.keras.datasets.mnist.load_data()\n",
"images = tf.cast(mnist_train[0], tf.float32) / 255.0\n",
"mnist_ds = tf.data.Dataset.from_tensor_slices((images)).batch(1)\n",
"def representative_data_gen():\n",
" for input_value in mnist_ds.take(100):\n",
" # Model has only one input so each data point has one element.\n",
" yield [input_value]\n",
"converter.representative_dataset = representative_data_gen"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "xW84iMYjHd9t"
},
"source": [
"Finally, convert the model as usual. Note, by default the converted model will still use float input and outputs for invocation convenience."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "yuNfl3CoHNK3"
},
"outputs": [],
"source": [
"tflite_16x8_model = converter.convert()\n",
"tflite_model_16x8_file = tflite_models_dir/\"mnist_model_quant_16x8.tflite\"\n",
"tflite_model_16x8_file.write_bytes(tflite_16x8_model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "PhMmUTl4sbkz"
},
"source": [
"Note how the resulting file is approximately `1/3` the size."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "JExfcfLDscu4"
},
"outputs": [],
"source": [
"!ls -lh {tflite_models_dir}"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "L8lQHMp_asCq"
},
"source": [
"## Run the TensorFlow Lite models"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-5l6-ciItvX6"
},
"source": [
"Run the TensorFlow Lite model using the Python TensorFlow Lite Interpreter."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Ap_jE7QRvhPf"
},
"source": [
"### Load the model into the interpreters"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Jn16Rc23zTss"
},
"outputs": [],
"source": [
"interpreter = tf.lite.Interpreter(model_path=str(tflite_model_file))\n",
"interpreter.allocate_tensors()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "J8Pztk1mvNVL"
},
"outputs": [],
"source": [
"interpreter_16x8 = tf.lite.Interpreter(model_path=str(tflite_model_16x8_file))\n",
"interpreter_16x8.allocate_tensors()"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "2opUt_JTdyEu"
},
"source": [
"### Test the models on one image"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "AKslvo2kwWac"
},
"outputs": [],
"source": [
"test_image = np.expand_dims(test_images[0], axis=0).astype(np.float32)\n",
"\n",
"input_index = interpreter.get_input_details()[0][\"index\"]\n",
"output_index = interpreter.get_output_details()[0][\"index\"]\n",
"\n",
"interpreter.set_tensor(input_index, test_image)\n",
"interpreter.invoke()\n",
"predictions = interpreter.get_tensor(output_index)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "XZClM2vo3_bm"
},
"outputs": [],
"source": [
"import matplotlib.pylab as plt\n",
"\n",
"plt.imshow(test_images[0])\n",
"template = \"True:{true}, predicted:{predict}\"\n",
"_ = plt.title(template.format(true= str(test_labels[0]),\n",
" predict=str(np.argmax(predictions[0]))))\n",
"plt.grid(False)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "3gwhv4lKbYZ4"
},
"outputs": [],
"source": [
"test_image = np.expand_dims(test_images[0], axis=0).astype(np.float32)\n",
"\n",
"input_index = interpreter_16x8.get_input_details()[0][\"index\"]\n",
"output_index = interpreter_16x8.get_output_details()[0][\"index\"]\n",
"\n",
"interpreter_16x8.set_tensor(input_index, test_image)\n",
"interpreter_16x8.invoke()\n",
"predictions = interpreter_16x8.get_tensor(output_index)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "CIH7G_MwbY2x"
},
"outputs": [],
"source": [
"plt.imshow(test_images[0])\n",
"template = \"True:{true}, predicted:{predict}\"\n",
"_ = plt.title(template.format(true= str(test_labels[0]),\n",
" predict=str(np.argmax(predictions[0]))))\n",
"plt.grid(False)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "LwN7uIdCd8Gw"
},
"source": [
"### Evaluate the models"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "05aeAuWjvjPx"
},
"outputs": [],
"source": [
"# A helper function to evaluate the TF Lite model using \"test\" dataset.\n",
"def evaluate_model(interpreter):\n",
" input_index = interpreter.get_input_details()[0][\"index\"]\n",
" output_index = interpreter.get_output_details()[0][\"index\"]\n",
"\n",
" # Run predictions on every image in the \"test\" dataset.\n",
" prediction_digits = []\n",
" for test_image in test_images:\n",
" # Pre-processing: add batch dimension and convert to float32 to match with\n",
" # the model's input data format.\n",
" test_image = np.expand_dims(test_image, axis=0).astype(np.float32)\n",
" interpreter.set_tensor(input_index, test_image)\n",
"\n",
" # Run inference.\n",
" interpreter.invoke()\n",
"\n",
" # Post-processing: remove batch dimension and find the digit with highest\n",
" # probability.\n",
" output = interpreter.tensor(output_index)\n",
" digit = np.argmax(output()[0])\n",
" prediction_digits.append(digit)\n",
"\n",
" # Compare prediction results with ground truth labels to calculate accuracy.\n",
" accurate_count = 0\n",
" for index in range(len(prediction_digits)):\n",
" if prediction_digits[index] == test_labels[index]:\n",
" accurate_count += 1\n",
" accuracy = accurate_count * 1.0 / len(prediction_digits)\n",
"\n",
" return accuracy"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "T5mWkSbMcU5z"
},
"outputs": [],
"source": [
"print(evaluate_model(interpreter))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Km3cY9ry8ZlG"
},
"source": [
"Repeat the evaluation on the 16x8 quantized model:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "-9cnwiPp6EGm"
},
"outputs": [],
"source": [
"# NOTE: This quantization mode is an experimental post-training mode,\n",
"# it does not have any optimized kernels implementations or\n",
"# specialized machine learning hardware accelerators. Therefore,\n",
"# it could be slower than the float interpreter.\n",
"print(evaluate_model(interpreter_16x8))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "L7lfxkor8pgv"
},
"source": [
"In this example, you have quantized a model to 16x8 with no difference in the accuracy, but with the 3x reduced size.\n"
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "post_training_integer_quant_16x8.ipynb",
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
fraserw/PyMOP | tutorial/trippytutorial.ipynb | 2 | 602846 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"TRIPPy examples\n",
"========\n",
"\n",
"Introduction: SExtractor and emcee\n",
"--------------------------------\n",
"\n",
"To perform photometry and source subtraction, in addition to having a good PSF (which trippy will generate) one needs three very important parameters: x, y, and m, or source position and amplitude. \n",
"\n",
"When one has the PSF and TSF already generated, one can run a fitting routine to solve for these. For this purpose, we use [emcee.](https://github.com/dfm/emcee) *emcee* is an MCMC routine which allows for good estimates of (x,y,m) and their uncertainties. We use a likelihood definition as the natural log likelihood of the exponential flux, basically exactly what you'd expect. If you are uncertain of what this means, or care for more detail, please go read the *emcee* documentation.\n",
"\n",
"If the PSF or TSF is not yet known, to get a centroid (x,y), we need to use some other software. We haven't included this inside trippy because there is no point in reinventing a wheel that has already been nearly perfected. For this purpose, we use the venerable [SExtractor.](http://www.astromatic.net/software/sextractor) All jokes on its name aside, *sextractor* does exactly what we need, as well as we would ever need it to be done. \n",
"\n",
"Trippy includes a module *trippy.scamp* with functions defined in *scamp.py* and *makeParFiles.py* that mearly provide convenient wrappers to call *sextractor*. This has been done in a couple other packages, but not in a way that satisfies me. Hence my own implementation. A couple details to note: makeParFiles creates all the parameter files in the working directory (eg. *makeParFiles.writeConv()*), and scamp is responsible for *sextractor* execution and catalog reading (*scamp.runSex()* and *scamp.getCatalog*). Catalogs are stored in FITS_LDAC format. This choice was done to facilitate execution of the *sextractor* sister program *scamp*, though we won't need to know what that means for full use of trippy. If you are unfamiliar with *sextractor* and its use, don't adopt trippy as a blackbox. [RTFM!](http://www.starlink.rl.ac.uk/docs/sun226.htx/mud165.pdf)\n",
"\n",
"With that out of the way, on to actual business.\n",
"\n",
"\n",
"The *trippy* tutorial\n",
"------------------\n",
"\n",
"The first thing to do is import all the necessary packages. Note that this notebook assumes you have the optional packages installed, as well as SExtractor available on your command line.\n",
"\n",
"**NOTE: proper use of psfStarChooser requires plot interaction. So for this tutorial you'd best comment out the first line, %matplotlib inline. But for my web presentation, I leave inline.**"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"#%matplotlib inline\n",
"import numpy as num, astropy.io.fits as pyf,pylab as pyl\n",
"from trippy import psf, pill, psfStarChooser\n",
"from trippy import scamp,MCMCfit\n",
"import scipy as sci\n",
"from os import path\n",
"import os\n",
"from astropy.visualization import interval, ZScaleInterval"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The function trim catalog is a convenience function to simply return only those sources that are well enough isolated for PSF generation. It rejects any sources within 30 pixels of another source, any sources with peak pixel above 70,000, and any sources that sextractor has flagged **for what ever reason**. We may fold this into psfStarChooser in the future.\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"def trimCatalog(cat):\n",
" good=[]\n",
" for i in range(len(cat['XWIN_IMAGE'])):\n",
" try:\n",
" a = int(cat['XWIN_IMAGE'][i])\n",
" b = int(cat['YWIN_IMAGE'][i])\n",
" m = num.max(data[b-4:b+5,a-4:a+5])\n",
" except: pass\n",
" dist = num.sort(((cat['XWIN_IMAGE']-cat['XWIN_IMAGE'][i])**2+(cat['YWIN_IMAGE']-cat['YWIN_IMAGE'][i])**2)**0.5)\n",
" d = dist[1]\n",
" if cat['FLAGS'][i]==0 and d>30 and m<70000:\n",
" good.append(i)\n",
" good=num.array(good)\n",
" outcat = {}\n",
" for i in cat:\n",
" outcat[i] = cat[i][good]\n",
" return outcat"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Get the image this tutorial assumes you have. If wget fails then you are likely on a mac, and should just download it manually"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"We already have the file.\n"
]
}
],
"source": [
"inputFile='Polonskaya.fits'\n",
"if not path.isfile(inputFile):\n",
" os.system('wget -O Polonskaya.fits http://www.canfar.phys.uvic.ca/vospace/nodes/fraserw/Polonskaya.fits?view=data')\n",
"else:\n",
" print(\"We already have the file.\")\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First load the fits image and get out the header, data, and exposure time."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"with pyf.open(inputFile) as han:\n",
" data = han[0].data\n",
" header = han[0].header\n",
" EXPTIME = header['EXPTIME']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next run sextractor on the images, and use trimCatalog to create a trimmed down list of isolated sources. \n",
"\n",
"makeParFiles handles the creation of all the sextractor files, including the .sex file which we call example.sex, the default.conv, the param file which is saved as def.param.\n",
"\n",
".runSex creates example.cat which is read by .getCatalog. getCatalog takes as input the catalog name and the parameter file \"def.param\".\n",
"\n",
"The parameters that are actually used by psfStarChooser and psf.genLookupTable are XWIN_IMAGE, YWIN_IMAGE, FLUX_AUTO, and FLUXERR_AUTO, which are the x,y coordinates, the flux, and the flux uncertainty estimate respectively. The latter two are used in the SNR cut that psfStarChooser makes."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"scamp.makeParFiles.writeSex('example.sex',\n",
" minArea=3.,\n",
" threshold=5.,\n",
" zpt=27.8,\n",
" aperture=20.,\n",
" min_radius=2.0,\n",
" catalogType='FITS_LDAC',\n",
" saturate=55000)\n",
"scamp.makeParFiles.writeConv()\n",
"scamp.makeParFiles.writeParam(numAps=1) #numAps is thenumber of apertures that you want to use. Here we use 1\n",
"\n",
"scamp.runSex('example.sex', inputFile ,options={'CATALOG_NAME':'example.cat'},verbose=False)\n",
"catalog = trimCatalog(scamp.getCatalog('example.cat',paramFile='def.param'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, find the source closest to 811, 4005 which is the bright asteroid, 2006 Polonskaya. Also, set the rate and angle of motion. These were found from JPL horizons. The 1 degree increase is to account for the slight rotation of the image.\n",
"\n",
"Note: in this image, the asteroid is near (4005,811) and we apply a distance sort to the catalog to find correct catalog entry, and the source centroid, which we store in (xt,yt).\n",
"\n",
"Setting the important asteroid parameters. xt,yt contain the location of the asteroid itself (near 811,4005), rate and angle are the rate and angle of traililng, in \"/hr and degrees. We find the actual centroid as the location closest to that point."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"dist = ((catalog['XWIN_IMAGE']-811)**2+(catalog['YWIN_IMAGE']-4005)**2)**0.5\n",
"args = num.argsort(dist)\n",
"xt = catalog['XWIN_IMAGE'][args][0]\n",
"yt = catalog['YWIN_IMAGE'][args][0]\n",
"\n",
"rate = 18.4588 # \"/hr\n",
"angle = 31.11+1.1 # degrees counter clockwise from horizontal, right"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now use psfStarChooser to select the PSF stars. The first and second parameters to starChooser are the fitting box width in pixels, and the SNR minimum required for a star to be considered as a potential PSF star. \n",
"\n",
"Optional but important inputs are autoTrim and noVisualSelection. The former, when True, uses bgFinder.fraserMode to attempt to determine what FWHM corresponds to actual stars, and rejects all sources with FWHM outside +-0.5 pixels of the modal value. noVisualSelection determines if manual input is required. When set to false, all stars are considered. **Until you know the software, I suggest you use noVisualSelection=True for manual selection, and autoTrim=False to see all sources in the plot window.**\n",
"\n",
"For each star provided to psfStarChooser, it will print a line to screen of x,y and best fit alpha, beta, and FWHM of the moffat profile fit.\n",
"\n",
"Then psfStarChooser will pop-up a multipanel window. **Top left:** histogram of fit chi values. **Top right:** chi vs. FWHM for each fitted source. **Middle right:** histogram of FWHM. **Bottom right:** image display of the currently selected source. **Bottom left:** Radial profiles of all sources displayed in the top right scatter plot.\n",
"\n",
"The point of this window is to select only good stars for PSF generation, done by zooming to the good sources, and rejecting those that are bad.\n",
"\n",
"Use the zoom tool to select the region containing the stars. In this image, that's a cluser at FWHM~3.5 pixels.\n",
"\n",
"Left and right clicks will select a source, now surrounded by a diamond, displaying the radial profile bottom left, and the actual image bottom right.\n",
"\n",
"Right click will oscillate between accepted source and rejected source (blue and red respectively). \n",
"\n",
"**Keyboard funcitonality is now also implemented. Use the left/right arrow keys (or a/d) to cycle through each source, and the up/down keys (or w/d) to mark a source as rejected (red) or accepted (blue).** This is probably the fastest way to cycle through sources. *Note that for some mac python installs, key presses won't be recognized inside a pylab window. To solve this, invoke your trippy script with pythonw instead of python.*\n",
"\n",
"When the window is closed, only those sources shown as blue points, and within the zoom of the top right plot will be used to generate the PSF.\n",
"\n",
"The array goodFits is returned for convenience and contains the moffat fit details of each accepted source. Each entry is [FWHM, chi, alpha, beta, x, y, local background value].\n",
"\n",
"The array goodMeds is just the median of goodFits, and provides the median moffat alpha and beta of the selected stars.\n",
"\n",
"Note on a couple starChooser options: \n",
"\n",
"--bgRadius is the radius outside of which the image background level is sampled. The fitting is relatively insensitive to this value, however, if you happen to know what the FWHM is approximately, then the best fitting results can be had with bgRadius>~3xFWHM in pixels.\n",
"\n",
"--ftol is the least squares fitting tolerance parameter passed to the scipy least sqaures fitter. Increasing this number can result in dramatic performance improvements. Default is 1.4e-8 to provide an extremely accurate fit. Good enough fits can be had with 1.e-7 or even 1.e-6 if one has a need for speed.\n",
"\n",
"--repFact defaults to 5. If you want to run faster but still preserve most accuracy in the fitting procedure, use repFact = 3\n",
"\n",
"--quickFit = True will provide the fastest moffat fitting. The speed improvement over quickFit = False is dramatic, but results in slightly less accurate moffat fit parameters. For the majority of use cases, where the number of good psf stars are more than a few, the degredation in PSF accuracy will not be appreciable because of the fact that a lookup table is used. But the user should confirm this be comparing PSFs generated in both circumstances.\n",
"\n",
"--printStarInfo = True will display an inset in the starchooser plot that shows the parameters of the selected source, such as alpha, beta, and FWHM, among others. "
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Fitting stars with moffat profiles...\n",
" X Y chi a b FWHM\n",
" 1657.51 157.63 73.05 15.16 2.45 17.36 \n",
" 1009.42 363.71 0.22 2.84 2.56 3.17 \n",
" 251.90 684.70 0.24 2.86 2.59 3.17 \n",
" 1211.61 936.20 0.22 3.23 1.59 4.78 \n",
" 1587.22 945.88 0.12 2.68 2.36 3.13 \n",
" 1081.55 914.77 0.21 2.77 2.49 3.15 \n",
" 1315.03 1023.28 0.17 2.84 2.58 3.16 \n",
" 1652.57 1014.63 0.17 2.78 2.53 3.12 \n",
" 383.82 1238.34 0.20 2.90 2.63 3.19 \n",
" 1241.75 1286.83 0.53 3.58 2.27 4.27 \n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/fraserw/anaconda3/envs/tomtom/lib/python3.7/site-packages/scipy/optimize/minpack.py:449: RuntimeWarning: Number of calls to function has reached maxfev = 250.\n",
" warnings.warn(errors[info][0], RuntimeWarning)\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
" 510.65 1902.63 67.89 15.30 2.04 19.50 \n",
" 1106.80 2196.58 0.19 2.88 2.59 3.20 \n",
" 855.31 2362.30 0.18 3.00 2.70 3.24 \n",
" 1606.23 2700.56 0.25 2.77 2.53 3.12 \n",
" 433.79 2761.05 0.17 2.94 2.63 3.23 \n",
" 1458.17 3023.19 10.96 7.85 2.68 8.53 \n",
" 1071.70 3291.51 0.25 2.91 2.65 3.19 \n",
" 1633.35 3827.17 0.18 2.96 2.69 3.22 \n",
" 357.50 3746.18 0.16 2.90 2.63 3.19 \n",
" 1269.99 4429.10 0.26 2.86 2.55 3.20 \n",
" 1483.94 4477.91 0.29 2.96 2.68 3.22 \n",
" 820.38 4243.44 0.17 2.84 2.56 3.18 \n",
" 1919.63 4017.65 0.25 2.93 2.68 3.19 \n",
" 294.44 4080.45 0.19 2.66 2.32 3.14 \n",
" 812.20 4004.29 7.49 5.60 2.51 6.33 \n",
" 1635.10 3908.77 0.23 3.41 1.44 5.38 \n",
"\n",
"Doing auto star selection.\n",
"[ 84.70768692 41.6144249 35.56198657 94.58783846 233.17555986\n",
" 39.62598656 155.84688636 62.84335534 48.10485395 39.05423745\n",
" 60.86310199 66.99832771 207.35720041 36.89843163 99.45595997\n",
" 66.79367114 40.65964094 196.24253632 167.55192925 38.25481959\n",
" 205.88964577 69.79585181 40.96002558 36.23118415 697.32827074\n",
" 49.50273039]\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbIAAAE1CAYAAACCxmV8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOydeXhV1bXAfyshIcyzAcIQRgVkENCK0BZxqFO1rXVEBaul9llbX7UVtU99rSgd1T6llKrFAQdqreJUa63gUEWgMiiggkBIIAhhEAhDSNb7Y+8bTsKdkpubm5us3/ed756zp7P2PueedfY+e68lqophGIZhpCsZqRbAMAzDMBLBFJlhGIaR1pgiMwzDMNIaU2SGYRhGWmOKzDAMw0hrTJEZhmEYaY0pMqPJISIqIv1TLYfhEJE9ItI3Svx6ETm1PmUy0gtTZEZaIiLjROTfIrJLRLaLyDsicnw9nn++iFwdJT7fK8w9flsvIlMD8eeJyFIR+UJEtonIv0Skj4+7Q0TKAnn3iMhP66NeqUBVW6vqZwAiMltE7ky1TEZ60SzVAhhGTRGRtsCLwPeBuUA28GXgQCrlikB7VT0kImOA10VkKbAGeBT4FvAvoDVwOlAeyPe0ql5WkxOJSDNVPVRHchtG2mA9MiMdGQigqk+qarmq7lPVf6jq8lACEfmOiKwSkR0i8qqI9A5XkIg0F5HfiEiBiGwRkZki0iIQH+w5rRWRM0RkGk5x3u97S/fHElhV3wU+Ao4FRgDrVPV1dexW1b+qakFNG8L39G4SkeXAXhFpJiJTvay7RWSliHwzkH6yiLzt67xDRNaJyJmB+D4i8qbP+08ReUBEHg/En+h7wjtFZJmIjI8g15Ui8kLg+FMR+UvgeKOIjPD7KiL9RWQKMBH4qW/XFwJFjhCR5b4H/rSI5EQ477JqPVkNySgi54rIR172+SIyKJBvkA/b6dOcG4ibLSIzROQVX+Y7ItJVRO71bbhaRI6LfbWMpKGqttmWVhvQFigBHgHOBDpUiz8P1+sZhBt1+Bnw70C8Av39/j3APKAj0AZ4Abjbx50A7AJOw7305QHH+Lj5wNVRZMz352kGCDAWKAVOAfoC+/25TwZaV8t7B/B4nG2xHlgK9ARa+LALgO5e5ouAvUA3HzcZKAO+C2TierWbAPHx7wK/wfVyxwFfhGTx9S8BzvJln+aPu4SRqy+w06frDmwACgNxO4CMMNdjNnBnmDq+78vpCKwCromjbaYAq/39MtC3w2lAFvBTf49k++M1wC3+eAKwGzg6INM2YBSQg+tFrwOu8G14J/BGqv8XTXlLuQC22VabDaekZgOFwCGcMsr1ca8AVwXSZngl0tsfK9DfK5i9QL9A2jG43hLAH4F7Ipx/PvEpsp3+ob0K+GEg/kTcsOhWnFKbjVdoOEV20OcNbd0jnGc98J0YbbUUOM/vTwbWBOJaejm7Ar18W7YMxD/OYUV2E/BYtbJfBSZFOO9GYCRwMTDLK6NjgCuBeYF08SiyywLHvwJmxqjzOOBzYKA//h9gbrV7oggYj+tdF+MVq49/ErgjINOfAnHXAasCx0OBnan+TzTlzYYWjbREVVep6mRV7YEbrusO3OujewP3+WGincB2nNLKq1ZMF9yDfEkg7d99OLheztoERe2sqh1UdZCq/j4g/3uqeqGqdsE9SL8C3BrIN1dV2we2TVHOsTF4ICJX+OHQUJ2OBToHkhQH5Cj1u61xbbg9EFa97N7ABaFyfdnjgG4R5FqAUxRf8fvzga/6bUGU+oSjOLBf6uUNi4j0xL0kTFLVT3xwqFcIgKpW4OqW5+M2+rAQG6h6v2wJ7O8LcxxRHiP52GQPI+1R1dUiMhv4ng/aCExT1Tkxsm7DPYSGqGpRmPiNQL9Ip62NrGELUl0kIs/iFE6tigjt+G+Bf8INYb6rquV+gonEUc5moKOItAwos56B+I24Htl345RrAfB1oA9wF65nORHX6430XTGhdvXfN58D7lXVVwJRm3A9p1A6wdWtCDfJpqeIZASUWS/gE4y0wHpkRtohIseIyA0i0sMf9wQuAd7zSWYCN4vIEB/fTkQuqF6Of2j9CbhHRI7yafNE5Gs+yUPAlSJyiohk+LhjfNwW3Lee2sg/TkS+GzjnMcC5AfkToRVOGWz1ZV9JnApSVTcAi4E7RCRb3EzLrweSPA58XUS+JiKZIpIjIuND1yEMC3DfAFuoaiHwFnAG0An4IEKeWrer52Fgtar+qlr4XOBsfy2zgBtws1z/DSzE9fJ+KiJZfnLI14GnaiOAnxwyu5byG7XAFJmRjuwGvgQsFJG9OAXwIe7hhKr+Dfgl8JSIfOHjzoxQ1k24D/3v+bT/BI725byP+55zD27SxwLc8BrAfcC3/ay13x9RanR24hTXChHZgxvO/Bvu209CqOpK4Le4SRtbcL2Qd2pQRKjHVIKbxPA0flmDqm7ETaS5BacoNwI/IcJzxA/r7cEpMFT1C+Az4B1VLQ+XB/fyMNgPXT5XA7lDXAx8s9rMxS+r6sfAZcD/4XriXwe+rqoHVfWgPz7Tx80ArlDV1bU4P7ieXk3a3EiQ0EwlwzCMIxCRp3E9nNtTLUs6ICLZwDJgmKqWpVqepoIpMsMwKhFnHWU7bnr56bjvTWNUNdJQoGGkHJvsYRhGkK7As7jvWIXA902JGQ0d65EZhmEYaY1N9jAMwzDSGlNk9YS33zY+1XKkOyIyWEQW+3VATR5Jcxcn4mxb/k+q5WiMiPOi8HjslKlDRHLlsG3P34rjz3428PvxlmPfyOoJVR2SahkiISIKDFDVNfWZt5b8AviNNoIxcRG5A2eaqUZW7hsTqnpNqmWoT0RkPs7k14OpliWZ+DWIv1XVk2IknYJb8tBWVVVEvoyzh9lDVffGez7rkRkpw799xX0Pikg33ALb2qwvMpKAiNjLsBGOs4GX40jXG1gZeDHtDayviRIDzGhwfW04w6en+v07cJYGHsUt7v0IGB1IexPOdM5u4GPglEC+Z3CLVHcD/wGGB/J1B/6KW6y6jqpGajNxC1nX+rxLcAs338RZgtiLW7x6URjZ++MWA+/CvT097cOPyAt0wPkK24ozlvsi7u0qVNZ8YBpuweg+X/Zk3ELZ3V7uiRHa8Argn9XCpgbqtBL4ZhKu3WzgAeAlf56FVDU0fAzwGm7a+sfAhT48G2ew97rANXgHuA1n4eIgzhL9HmBZnLJcjrMDWIKzzVh5X9VhfecDd+OM/H4BPA909HH5/ppfBRQAb/rwE3FWMnbi1lGN9+EXAYurlf/feKPBVDMSjLPKv8a35Ty8seTAeZtVk/PqaPdoHHXdAIzy+xP9OYb446uA5+qwXafhzGHt99f8fh9+ErDIy74IOCmQpw/uf7Ybt1j/AQKeEfx/InQ//A9HPmeCacNeowiyDvLtuxP3fDo33v+DT/MfYGS0+vlyynD/gz04E3P7fRvtAf437rat6z+9bRFvjOo32H6cO4xM3EPjPR93NM5iQvAP3C+Qrwz4Ns71xI24B38Wrne9BPeQzMaZ+fkM+JrP+xNghS9fgOFAJx9XaX08guxP4h6aGTg3FuMCcVXy4qZtn48zxtsG+AuBh4H/cxQAQ3BD2+1wD8uQy4xu+AdJGDl+DTxQLSyiy5Iw+S+lqkX56luvCPlm4x4UJ3iZ5wBP+bhW/npd6eOOwz1IB/v4Y3EKfZBvw/eAzMD1jMtdi08/2P/BvwI0B36Hs1YfVpHhlHzE+kY5z3zci9Sxvn5/5bAF/Hx/zR/1cS2I4t7F3we7ccPPofIXARcH2vZOvz/Bt91IX7//47CiDJ03kiKLeI/GaNNHgRv8/izcS9H3A3H/nYS2vTpw3NHfH5f7++cSfxz6b0ZzqxO6H8b5+N/gng9HKLJo1yiMjPG4tQn7fwj8h4twz5lY9au8/v54MvB2jZ+vNc1gW+02jlRk/wzEDQb2+f3+OPcTpwJZ1cq4A6/w/HEGztDrl3Emmwqqpb8Z+LPf/xjvyiOMbLEU2aP+T96jFnlHADsCx/OBnweOW/k///l4f1pRyvoTMD1GmqWR6pnAtZsNPBg4Pgtn7QKc8nyrWvo/ArcHjm/w7b+Dqg/0ygdNnHLcVu2B0Qr3NpuMHtn0wPFgf55MDiuUvoH4qO5dcDYab/P7A3APxZaBtg0psoeAXwXKaI17MOcTW5FFvEdj1PUqDvcOVwFXc/glZQO+V1HHbRtUZJcD71dL8y7ugR7Lrc5twJOBuJbB+4GqiixuFzzE59Ym7P8h0KYPxapf9evvjydTC0Vm38hSR3W3FDniXNWvAa7H3YSfi8hTItI9kLbSrYY6o7eFuB5Jb6B7NRcbtwC5PnkiLkl+inu7et/PvvxOpIQi0lJE/igiG7ztwjeB9iKSGaEOe3HK4Bpgs4i8FDDMW50duF5e8HyxXJbUFZHciPQGvlSt3SfiFhaHeMSne1lVP01Ahu4c2XYlCZQXjaD7lg24t/TOEeJ7E929yxO4N3FwveLntKqrmBDVXa3swdWvuvudcMR9j1ZjAfBl//01EzfkP1ZE8nGjBUvjLKe2VKmzJ+RCJpZbner3QymR74dY16i6TLHc2kRzq3MWh7+PRatfnWGKrAGiqk+o6jjczac4A7ghKt1q+IkSPXAuKjbiHEIGfVi1UdWzfPJoLkliyVOsqt9V1e64cewZItI/QvIbcMOXX1LVtrhhMKjqRkSrlf+qqp6G+1OtxvW8wrEc5+nXFXjYZckPcEMV7XEGgsNOzReRidWMyVbfekVuhYhsBBZUa/fWqvr9QJoZuG+FXxORccGq1/Bcm6l6/VvihnLDIiK3RKtvjHMF3bf0wvWMtkWQPeTeJdgGrVR1uo9/DegiIiNwCu2JCOfcxGGjzIhIK1+/ItyQMbheR4jKl4Ua3qME8q3BPYivww1jfoF7SE/B9QwqwuVLoG2rX/Mqdfb0wtW50q1OIC54XTbj/v8hmVoQ+X6IdY2qy9Sz2kSskExR8Z4Fvoq75qGyItWvzjBF1sAQkaNFZIKINMd9R9sHBP9Mo0TkW3622PU4y+Tv4T7M7xaRm0SkhTg3G8d623kADwK/EJEBfrbgMBEJ3fRRXWeIyAVy2FXHDtyfMSRT9bxtvMw7RaQjcHuM+uaKyHn+oXUAN+Yf9uGB+3OMFJEcf1wjlyWqOscrmUhbQTRZI/AiMFBELhfnAiRLRI4XkUFepsuBUbghkx8Cj4hI6O11C5AffGCIW/szP8K5ngHOEecGJhv4OVH+w6p6V7T6xqjXZeLW7LX053lGI1usj+reRZ3x3L/gvnF25PBDrjpP4tzmjPD3/13AQlVdr6pbcQ+/y/w5vkPgxSzaPSoi88UtdYjEAtzLUMjZ5/xqx0eQQNtW/7+8jLt/LhWRZiJyEW4o90WN7VbnGVy7n+TvhzuI7HeuJi54EnFrMw5Y7l8IotYvjrIAt8RHYqzBNUXW8GgOTMe9/RYDR+G+dYV4HjcUF/qA+i1VLfMPmXNw36TW+fwP4oZHwE0MmAv8A/fB+CHch3pwf4BH/JDDhWFkOh7nMmUPbibZj1T1swh57/XlbsMp2L/HqG8G8GPcm9t23Nvc98MlVNUtwL9wrkTQxF2WJIyq7sYZ170YV4diXA+6ue/h3YtzCbJHVZ/APZju8dn/4n9LROQ/fj+iCxBV/Qi4Ftej2Yy7BwrrvFKOx3DfL4pxkyd+GCmhxufe5Qncd9+/qOqhCOX8Ezfz7q+4+vXDtWuI7/pyS3CThf4diIt2j8Zyq7IA9wL2ZoTjuqSK+x9VLcH9b2/A1eunwDmqGur9RnOr8xGuJ/kUrr324L6vH6h+0jivUShtIm5tqky7j6N+URHna3A3bqJa5HT+A5uRBogtoEVEBuO+OZ2gjfDmFefN+RT/AEiVDPNpJIt2fY9jrsZemJsWSBS3Or6nvxM3oWhdvQvnZFgJfNu/ZNZFeZfhZjHfHC2dLWY00gr/Bzk+ZsI0RVVHpFqGxoQ6z9Rpq8TkSLc65+FGbELxXwdexw0p/gbXc1lf74JS6Yvt0bpSYgCqGpeJLVNkhmEYDZdYbnXOww0DC27Y+uJUjVT4Iclwk0eSjg0tGoZhGGmNTfYwDMMw0hpTZEba4qdVXx1n2rEi8qlf5/ONBM65R0QiLlWollbjWctUCxnGi0hh4DguF0HJkqcmSJq7nYlFvPXzy05W+WUGRoKYIjOaCj/HGWltrarPRVKCIjJGRP4dJj8APv9nkeLjRUQmi8jbiZbjZRqiqvProiwAEcn3Si9tv6GLyCUi8kRDrYtfSvIGbuG1kSCmyIy0QKqauKoNvXFWvGMR1v1EQ3sQGjGJ141IKpmDs0JiJIgpMiNliMgg3zPa6YfHzg3EzRaRP4jIyyKyF+eHLFZ53/HDNTtE5FVxJqwQkbU4awov+KHBu3GGUe/3x/cHiqm0E+ff5K8VkU+BTwNh/f1+JxF5QUS+EJFFInJnmF7WqX5Ic6eIPCCOQcBMYIw//84I9ekozlvuJl+nsH7YgsNZ3mrDLSKyVpzX3SV+UWn1PONEZGOEIcnQQuCdXr4xIpIhIj8TZ0PzcxF5VETahcmLiHQWkRd9nbeLyFtS1dzRCBFZLiK7RORpOWypBRH5rois8fnmibczKiL/KyL/5/ezRGSviPzaH7cQkf3iLMmETLedhluMX+O6iLPfuUFESkTkf6q1bwsRecRfj1Ui8lMJDPNWa4cMEZnqr0WJiMwNyehZCPQN3adGAmgNrQzbZltdbMTnKmIXMBbvmiNMGfM5bP38PF/eINyykp8B/w6kXU/ASjzVrJD7sEr3E/5YceaUOuIt8xOw9o+zqPAUzv7fYJy1hLcD5SnOFE97nH25rcAZPm4yMax84/w9PY3z8ZYFfNWHjwcKw9WNONz14HyhbcQtKg933nyOtDT/Hd++fXEGYp+lmjX1QNq7cYo6y29fDrTpepw5te6+XVcB1/i4aG5cJgAr/P5JOAPYCwNxywLnPxF4tzZ1IbZrlOk4yx8dcHYOl0e5Fj/CWbfp4evzRwLW6n2a5QR8fdlWu816ZEaqOBH3EJmuqgdV9V+4h/4lgTTPq+o7qlqhqvtjlHcNcLeqrlJnAuku3Jt/Td52zwL+rv4J47lbVber6r5gQj/UeT7OXUupukWgj4Qpc7qq7lRnx/ENnAmxmIizxn4m7iG/Q50Zsoi2/wJcDfxMVT9WxzKtaiXkAtwD9UxVfT8eWTwTgd+p6mfqrNLfDFwcYci1DPdS0NvL/Va1Nv29qm5S1e3ACxxuk4nAw6r6H1U94M8xRpwl+neBAeLsg34FZ2ItT5w1i69S1S5irGHFaHX5NvCCqr6tbl3UbVQ19HshcJe/JoXA76Oc5xrgVlUt9PW5A2eeKthmu3EvOkYCmCIzUkU8riI2Ej+9gfvksIuK7bgeSU3cRQTdT8SSoQuu57cxRtpo7i6i0RPnwmNHnOmD+aK567keZ7LpwxqWW90dxwZc/XPDpP01rsfzDxH5TESmVouP1CYR3bj4F4nFOKX1FZzi+jeux15dkYW7jvHWJZZrlCrxRL9HewN/C9yTq3Dej4Nt1gZnVspIAFNkRqqIx1VETVbrbwS+p1XdVLRQ1UgzEKuULUe6n4glw1ac08Og9fAjvkVFIVbdNuJceNT0bT2Wu54LgG+IyI9qKFt1dxwhp49bjsisultVb1DVvsC5wI9F5JSYkkd34wJOWU3AeeFe5I+/hvNU/KbP0xXXGwwZYa5pXWK5RqkST/RrvhHX8w3ekzmqWuTLboYb6l0WpQwjDkyRGakiEVcR4ZgJ3CwiQwBEpJ2IXBAlfXV3GtXdT0RFnbeBZ3EuNlqKcwZ6RQ3k3QL0EGefLlz5m4FXcH61Ovg2+kq4tNWI5q4H3EP8FOBHIhLWywBOSVdQtX2eBP5bRPr44by7gKc1jCV7ETlHRPqLiOC+c5YT2TVPkIhuXHz8Alwbr/TDfvNxQ6nr1Ll5ATccGxwermldYrlGmYu7zzqISB7O3UskZgLT5PCkoy4icl4g/gRgvTp3LaH1gWZqqRaYIjNSgibmKiJceX/DuU95Spxn6g992ZGo4k6D2k3X/gHOTU4xzt7dk4RxoRGBf+GWAxSLSCSXFpfjvjetxrnnuD6OcqO56wHAf687BZgqYdbS+eG0acA7fljsROBhXB3fxBmw3Y9zIRKOAcA/cZMm3gVmqOobsQTX2G5c/u3rEpqJuNLLEXS3Ut2NSI3qorFdo/wcZ/Nwna/jM0S+5vfhXMr8Q0R24yZ+fCkQPxGn7EL0pKprGiNOzNaiYVA37idE5JdAV1WdVHeSGfHih+qKgb7x9qzjKDOqaxTfq71YVb9aw3KPwvUwjwtNZBKRB3H+2l5NXPKmhfXIjCaP1NL9hIgc44fuREROAK4C/pYUIY146Aj8T6JKTES+7oeLW1HNNYqIdBNn7ixDRI7GOYys8TVX1c9VdVBwNq6qXm1KrHZYj8wwaok4X1FP4maybQFm4abb258qjfE9o29z2DXKf6nqxz6uN259Xx9cT+0p4GY/VG6kCFNkhmEYRlpjQ4uGYRhGWmOKzGhUSAOwdt7UZBBnF/POZJ+n2jlv8UOAtclbxQ2Okf6YIjPSGmnk/q3iJV3aQerIJ5qq3qWqcfmiMxo/psgMwzCMtMYUmZG2iMhjOPNCIfcsPw1ETxSRAhHZJiK3BvJEdK0RGI6bFC5vmPO3EJHfinP5sUtE3vYmjaqn6y7OJcl2cS5KvhuIO0FEFotzBbNFRH4XiDtRRP7tF/IukwheoOu6HcKUP15ECv1w3jbf+5sYpV0iuWIJLVxe5uW8KEzeDSIyyu9P9NcjZK3lKvGubETkDhF53O9HvW7+Os0Wt/h9JXB8tXOGdSckzvLHTvFm1ETkTyLyebDdRSSeRepGsqlLU/q22VbfG0e6Z8nH2df7E84KxHCc5YVBPj6ia41YecOc+wGcmaQ8IBPnXqQ51VyH4CxIzABycJbetwITfNy7wOV+vzVwot/PwxmrPQv3wnmaP+6S7HYIU/Z4nC3C3/m0XwX2UtXlzp1+P6IrFh9f6QYnwrkeBW7w+7NwBpC/H4j7b79/B/B4nHWdDryFW2fWE2f1pdDHxXInVACM8vsfA58Fyi3ALWhO+f+gqW8pF8A22xLZojzAewTC3sdZXwBngfyUQFw3nBmoZrHyVjtvBrAPGB4mLlROM//gLAfaBOLvBmb7/TeB/wU6VyvjJqr5+wJeBSYlux3ClD0ep8haBcLm4hYfQ1VF9hDwq0C61r7cfH8cS5FdBcwLyHg18JQ/3gCM9Pt3cKQii1TXz/B+4PzxFA4rsi/jrIFkBOKfBO7w+48BPwa64hTZr3DuWULryDIi1cW2+ttsaNForERyFRKPa414XK90xvWworlMAbdYeruq7g6EBd3VXAUMBFaL8zJ9TkDOC0JyelnH4RROTUikHYLsUNW91erQPUy6iK5Y4pR3AfBlcf7YMnEKc6w4n2TtgKVR8kZzDxN0txJ04RLLndACnCL/Cu6lYz6uR/pV4K1q+YwUYYrMSHdquqI/qmuNGrANZ2w2mssUcNbmO4pIm0BYpbsaVf1UVS8BjsIZPX5GnGmkjbgeWVDOVqo6PcJ5kt0OHbxcwTpsCpMuliuWqKjqGpwSug43JPkFTkFNwXnUro3i2ExVdyu9qskbzZ3QAlyvbbzff5vwPtCMFGKKzEh3qrtjiUUs1xpx4R+oDwO/85M5MkVkjDj3I8F0G3EWze8WkRwRGYbrhYUmKlwmIl18eSEHixU+/usi8jVfdo6fdBH0hRWkPtrhf0UkW0S+DJwD/CVMmliuWOKRcwHOs0BIUcyvdlxTgq5XelDVan9Ud0Kq+iluCPkyYIFXrFtw3sFNkTUQTJEZ6c7dwM/8ENmNcaSP5VqjJtyIMyi7COeR+peE/09dgvuOswlnYPZ2dS5LAM4APhKRPV62i1V1n1eA5+EmIWzF9aB+EqF8SH47FAM7fB3mANdoGJc7GtsVyx3AI17OCyOcawHOc/KbEY5ryv/ihgvX4dzbPBaQNx53QguAEn9NQsfCYeediMiDInJ/LeUzEsRsLRqGERXfS3lcVSP1Bg0jpViPzDAMw0hrTJEZhmEYaY0NLRqGYRhpjfXIDMMwjLQmZW4m6oLOnTtrfn5+qsVo0CxZsmSbqnapaT5rW8NovNT2udBQSWtFlp+fz+LFi1MtRoNGRDbETnUk1raG0Xip7XOhoWJDi0bTYs4cyM+HjAz3O2dOqiUyDCNB0rpHZhg1Ys4cmDIFSkvd8YYN7hhgYkSvJIZhNHCsR2Y0HW699bASC1Fa6sINw0hb0rpHtqJoF/lTXzoifP30s1MgjZFMysrKKCwsZP/+/bUu45iCAiRMuBYUsHrVqtoLZxgNlJycHHr06EFWVlaqRUkqaa3IjKZDYWEhbdq0IT8/H5Fw6igOevVyw4nVkF69GDRoUIISGkbDQlUpKSmhsLCQPn36pFqcpGJDi0ZasH//fjp16lR7JQYwbRq0bFk1rGVLF24YjQwRoVOnTgmNYqQLad0jG5rXjsU2jNhkSEiJweEJHbfeCgUFroc2bZpN9DAaLQn/Z9KEtFZkhlFjJk40xWUYjQwbWjQMwzDSGlNkhmEYRlpjiswwakB+fj5Dhw5lxIgRjBgxgnnz5jF79mx+8IMfVKY555xzmD9/Pp06deLgwYOV4RUVFXTq1InJkyfTu3dvAMrLy+nSpUuV/A2dkpISRo8ezfDhwxkxYgTPPfdczDw33ngjubm5HHvssZVhRUVFjBs3jiFDhjBy5Ehee+21ZIpdb0Rrn4ULFzJs2DAGDRrEhRdGcpB9mFtvvZVjjz2WkSNHViln7ty5DBgwgIEDB/LCCy8kpR7phH0jM4wa8sYbb9C5c+fK49mzZ4dN17dvXzZt2kTI+HJxcTE9e/YEoHXr1ixbtoxdu3aRm5ubbJHrlLZt2zJ//nxat27Ntm3bGDp0KOeeey4ZGZHfi7/1rW9x8cUXM3ny5MqwZs2a8cADDzB8+HA2bNjASSedRFFRUT3UILlEah+Ayy+/nIcffphx48axdevWqOUsXryYf/zjHyxdupSdO3dy3HHHccopp9C8ee6G40cAACAASURBVHNuuukm3nvvPQ4cOMDJJ5/M2WefHbX9GztNt+aGkWT69etHYWEhV199NVdffTWFhYX069cPgHPPPZd58+Yxb968yodcupCVlUXr1q0B2LVrFwcOHODQoUNR85x00klVlD9Abm4uw4cPB6B3794cPHiQAwcO1FievXv3kpeXxy233ALAokWLGDFiRMqmnUdqnyVLltClSxfGjRsHQJcu0Y3Pr127lhEjRtCsWTM6d+5MXl4eixYtYuHChQwZMoTc3Fx69epFz549Wb58edLr1ZAxRWYYNeTkk0+uHFrcuXMnAE8//XRl2FtvvQU4RVZUVMTGjRvZsmULhYWF9O3bF4BRo0bxwQcf8MknnzBw4MBayfHrX/+68pyhbVo9rYnbvXs3Q4cOZdiwYcyYMYPs7OyEynv11VcZOXIkzZs3r3HeVq1asXz5cp588klKS0v5zne+w+zZs8nJyQmbvj7aLVz7FBQU0K5dO8444wyOO+44ZsyYEbWMwYMHs3DhQkpLSykoKGDVqlUUFxdTXFxMt27dmDlzJnPnzqVr165s3ry5TuVPN5I6tCgi7YEHgWMBBb4DfAw8DeQD64ELVXWHuAUP9wFnAaXAZFX9TzLlaypY29Yt1YcWAS666CLuv/9+wH0jA6fINmzYQE5ODtnZ2axfv55+/fpVDil17dq18s29NvzkJz/hJz/5Sa3zJ0KbNm1YsWIFq1atYsqUKZx//vm1NoNUXFzMDTfcwPPPP19reTp16kTLli256qqruPzyyxkxYkTEtPXRbuHaZ//+/bzzzjusWLGC9u3bM3r0aM4444zKl5vqDB06lMmTJ3PSSSeRl5fHySefTE5ODuXl5QBcc801ADz77LNJrUs6kOwe2X3A31X1GGA4sAqYCryuqgOA1/0xwJnAAL9NAf6QZNmaEta2KaBfv37885//ZMiQIQwZMoTXXnutykPrrrvu4mc/+1mty09ljyzEoEGDyMrKYtmyZbXKv3//fr797W/zm9/8pnLYtbYMGzaM4uJibrzxxqjp6rPdgu2Tm5vL4MGD6dWrF23btmXUqFGsXr06av4f//jHLF26lJdeeoni4mJ69epFt27dqvTAQj20pkzSemQi0g74CjAZQFUPAgdF5DxgvE/2CDAfuAk4D3hUVRV4T0Tai0g3VW3afea6wdo2BfTr148FCxZwzTXXkJWVxfTp0yt7bQDt27dPqPxU9ciKiorIycmhU6dOFBcXs3LlSvLy8irjb775ZgDuvvvuqOWoKldeeSWXXnopZ5xxxhHxd9xxB/Pnz2f+/PkxZdq6dStvvPEGP/vZz2JOekh2u0VqnwEDBlBQUMD27dtp3bo1K1asqPJiE67dSkpK6NSpEwsWLGDHjh2MGjWKsrIyPvroIz7//HMOHDhAYWEhw4YNS1p90oFkDi32AbYCfxaR4cAS4EdAbuABWgyEpmzlARsD+Qt9WJWHrYhMwfUq6NWrV9KEb2RY26aAvLw8MjIyGD16NM2aNePQoUOV0+7TmYKCAqZ4P27l5eX88pe/rNIjCPe95tprr+XZZ59l27Zt9OjRgxkzZtCxY0eeeeYZVq1axaxZswB4+eWX6d69OwAbN25k7Nixccl01VVXMWHChFr3DOuSaO1z7733MmHCBMrKyrj00ks55phjKvOFa7crr7ySNWvWkJWVxWOPPYaIkJ2dzfTp0yvb5p577mnSMxYB91aUjA0YDRwCvuSP7wN+Aeyslm6H/30RGBcIfx0YHe0co0aNUiM6wOLG0LYrV65MtQhGPTN8+HDdtm1bzHQzZ87UCy+8UAsKCnTIkCH1IFl6Ee6/AyzWJD37U7ElU40XAoWqutAfPwOMBLaISDcA//u5jy8Cegby9/BhRuJY2xppx9KlS+nUqVPUNJ9++in33HMPM2fOpGfPnnTr1o3TTz+9niQ0GgpJU2SqWgxsFJGjfdApwEpgHjDJh00CQlOV5gFXiONEYJfaN5y6wtrWaJQMGDCA1atX06FDBwBee+01/vGPf6RYKqO+SbZlj+uAOSKSDXwGXIlTnnNF5CpgAxCy0/Iybnr4GtwU8SuTLFtTwtrWMIxGS1IVmaouxX0rq84pYdIqcG0y5WmqWNsahtGYaeJTXYzGTvn+8lSLYBhGkjFFZjRa9izfwzsd32HPij2pFsUwjCRiisxolKgqqyevpmJ/Basnrw4tOzAMoxFiisxolGx5fAuln5SCQunHpWyZsyXVIjUaaupH7NVXX61iDio7O5ulS5dGDK8tt912G0OHDmXgwIGVC6wbGrXxwZaZmVnZRj/84Q+B2vmEa9SkeiFbIltDW7TbEKGWCx8bWtvWZEF02c4yfbP9m/oGb1Rub7V/S8t2lSVRwqZDcXGxLl26VFVV169fr927d48776ZNm7R///5xh8fL3//+dz3nnHP00KFDunz5cj3zzDNrXVYyqU3btWrV6oiwgwcP6u7du1VVdevWrdq1a1ctLy8Pm98WRBtGGrL25rVU7K+oEla+v5zPbv4s4bI/+ugjTj31VAYOHMgvfvELrrvuOhYtWpRwuelEIn7EnnrqKb797W/HHR4v8+bNY/LkyZSVlXH//fdz/vnn17qsZFJXPthq4xOuMWOKzGhU7Fmxhy2zt6D7q34T0/1K8Z+LE5r4sX//fi644ALuu+8+li1bxoMPPkhRURHHH398omLXioZg/b6mfsTmzJnDxRdfHHd4vCxZsoTdu3fTqVMn3n77bS655JKo6dOp7fbv38/IkSMZO3Ysb775ZmV4XfuES2tS3SVMZGtow18NEZrY0OLq763WNzLeqDKsWLllvKGrr1ldaxleeOEFvfTSSyuPu3btqm+//Xaty0t3Nm/erEOGDNE1a9bElX716tU6aNCguMPjpby8XPPy8lRVtbS0VC+//HL9xS9+Uevy6oOatN3mzZtVVfX999/XvLw8LS0trRK/cuVKHTdunB48eDBsfhtaNIw0I+/aPDKah7+tM5pnkHdtXti4eFi6dCnHHXccAJs2baJ169ZxW2dPBqnsVdTGj9gTTzzBRRddFHd4vHz88ccMGDAAgBYtWjB27NhK55ORSKe269q1KwDHH3883bt3Z/369VXiE/UJ1xhItokqw6hXWg9tTe7kXIr/XFxleFFyhK5XdqX1sbX3yJydnU1RkbO1fPPNN3Pw4MGE5U2EVPkjU43uRyySP7InnniCF1988Yj0kcLj9Uf2wQcfcODAAcrLyzl06BBPPPEEv//976PmSZe22759Oy1atKBFixasX7+eoqIievXqFdMnXFPDemRGo6Pf3f3IyKl6a2fmZNL37vAu5ePl0ksv5c033+Too49m+PDhjBkzhuuvvz6hMtORd955h2eeeYZZs2ZV9mY2bdpUGb958+YjfGstXLiQ1q1bc/TRR8cVDvH7I1u6dCn79u2jX79+jB07lkmTJlVOqGho1LTtVq9ezYgRIxg2bBjf/OY3efDBB2nVqhUFBQWMHz+eoUOHMmHChCN8wjU1xA2XpiejR4/WxYsXp1qMBo2ILFHVcPYuo9LQ2nbVqlUMGjQo7vTFjxXzyfc/oWJvBRmtMhg4cyBdL+uaRAmNumbEiBG8/vrrMV25nHbaadxzzz0ce+yx9SRZehHuv1Pb50JDxXpkRqMk97JcWg5sCQItj2lJ7sTc2JmMBkU8/sjA9VqCnpaNpocpMqNRIiIcM/sYMnIyOObPxyAiqRbJSBIbN26kWTP73N+UsatvNFpaD2vN2O1jyczJTLUohmEkEeuRGY0aU2KG0fgxRWYYhmGkNabIDKOJcOONN5Kbm3vE7L6FCxcybNgwBg0axIUXXlgZPnfuXAYMGMDAgQN54YUXYqYPRyRr7+livT2S/NEs90dqt0jhkQhn9R5q1v5NhlSbFklka2hmlBoiNDETVUZk3nnnHV20aJEOGTKkMqy8vFwHDBigb731lqqqfv7556qqeuDAAc3Pz9fi4mLdsGGD9u3bV8vLyyOmj0Qka+81sd6eSuKxVh+03B+p3SKFRyOc1fuatr+qmag6AhHJEpHjROSoGuTJFJEPRORFf9xHRBaKyBoReVpEsn14c3+8xsfn10Q2IzLWtomzZs0aRowYQWlpaaUR108++STVYtWIk046ic6dO1cJW7JkCV26dGHcuHEAdOnSBXBv/UOGDCE3N5devXrRs2dPli9fHjF9JCJZe68r6+0vvPACEydOrDy+/fbbueeee2pcTiTisVYftNwfqd0ihdeUmrZ/UyGqIhORmSIyxO+3A5YBjwIfiEh089KH+RGwKnD8S+AeVe0P7ACu8uFXATt8+D0+nVE3WNsmSP/+/bn66qu55ZZbuO2225g0aRIDBw5MmTx1ZSuwoKCAdu3accYZZ3DccccxY8YMAIqLi+nWrRszZ85k7ty5dO3alc2bN0dMHw/Vrb3XhfX2M888k3fffZe9e/cCbvju0ksvjZg+kXaLZK0+aLk/UrtFCo9GOKv3ibR/oyZadw34KLB/PfCc3+8KfBCruwf0AF4HJgAvAgJsA5r5+DHAq37/VWCM32/m00m08hva8FdDBFjcGNq2IQwtVlRU6IQJE3T8+PFaUVGRanFqxbp166oMLT7++OPatm1b3bBhg+7atUsHDBiga9eu1blz5+rVV19dme6iiy7Sl19+OWL6WESz9h7Lenssrr/+en388cd14cKFetZZZ9WqjFhEkr+65f5I7RYpPNY5Vatava9N+9vQIgStop4GPOeVX3GcevJe4KdAyMthJ2CnqobGEAqBkKXLPGCjL/8QsMunNxLH2rYO2Lt3LyUlJezYsYM9e2rv16wuqKseWW5uLoMHD6ZXr160bduWUaNGsXr1arp161alxxDqUURKH41Y1t4Ttd4+adIk5syZw5w5c7jiiiuipq1Nu0WTv7rl/kjtFik8GuGs3tem/ZsE0bQc8AZwDnAcsBPoqoff6lfHyHsOMMPvj8f1yDoDawJpegIf+v0PgR6BuLVA5zDlTsH1Mhb36tUr6puIUdkjS/u2bQg9silTpugf/vAHffDBB/XKK69MtTi1onqPbOfOndq9e3ctKSnRAwcO6JAhQ3TVqlWVkxO2bNmiBQUF2q9fPy0vL4+YPsTUqVN16tSplccVFRV68cUX6wMPPFBFjsLCQt22bZuqup5Hbm6ubtq0qTL+9ttv169+9atx12vkyJHap0+fI3x1JUok+UP0799fV68+7OMuUrtFCg9Rvd1KSkoq67Ju3Trt3r277tmzJ2b7h6Mp9MhiWfb4HvB73FDi9Xq4J3YK8FKMvGOBc0XkLCAHaAvcB7QXkWbqegY9gCKfvsgrtkIRaQa0A0qqF6qqs4BZ4AzbxpDBcFjbJsgrr7zCZ599xsyZMxER/vKXv/D8889z3nnnpVq0uLn22mt59tln2bZtGz169GDGjBmce+653HvvvUyYMIGysjIuvfTSSruF06dPr7Q+f88995CRkUG7du0ipgeO+O4Tsva+atUqZs2aBcDLL79MQUEBU6ZMAaC8vPwI6+3xWr4P8a1vfYuPP/6YFi1a1K5xIhBJ/u7du4e13J+dnR223SKFh6jebqtXr+bKK6+kefPmZGZmVlq9B6K2f5OlPrQlvkfm9/8CXOz3ZwL/5fevBWb6/YuBubHKbWjfcRoiuB5W2rdtQ+iRGfXH8OHDK3ts8XDmmWfqa6+9lkSJ0pcm3yMTkaje6VT1h9HiI3AT8JSI3Al8ADzkwx8CHhORNcB2/8A16gZrWyOtCC0ujkVJSQljxoxhzJgxnHLKKUmWymioxBpavAb3fWUusAk367DGqOp8YL7f/ww4IUya/cAFtSnfiI61rdFY6dSpU9qt5zPqnliKrBvuAXgRcAh4GnhGVXcmWzDDqI6qmjsWw6gBbhSx8RN1+r2qlqjqTFU9GbgSaA+sFJHL60U6w/Dk5ORQUlLSZP6YhpEoqkpJSQk5OTmpFiXpxOWPTERGApfg1pK9AixJplCGUZ0ePXpQWFjI1q1bUy2KYaQNOTk59OjRI9ViJJ1Ykz1+DpyNMzH1FHCzHl7MbBj1RlZWFn369Em1GIZhNEBi9ch+BqwDhvvtLv+NQgBV1WHJFc8wDMMwohNLkdkrsGEYhtGgiarIVHVDuHARycB9MwsbbxiGYRj1RSw3Lm1F5GYRuV9EThfHdcBngLkmNQzDMFJOrKHFx3A+w94FrgZuwX0f+4aqxrf03jAMwzCSSCxF1ldVhwKIyIPAZqCXtxRhGIZhGCknlj+ystCOqpYDhabEDMMwjIZErB7ZcBH5wu8L0MIfh6bft02qdIZhGIYRg1izFjPrSxDDMAzDqA2xhhYNwzAMo0FjiswwDMNIa0yRGYkxZw7k50NGhvudMyfVEhmG0cSIy/q9YYRlzhyYMgVKS93xhg3uGGDixNTJZRhGk8J6ZEbtufXWw0osRGmpCzcMw6gn0rpHtqJoF/lTXzoifP30s1MgTROkoKBm4YZhGEnAemRG7enVK2xwSavw4YZhGMkgaYpMRHqKyBsislJEPhKRH/nwjiLymoh86n87+HARkd+LyBoRWe69Uht1QNLadto0DjRrWSVoLy25bs80/uu/6uQMhmEYMUnm0OIh4AZV/Y+ItAGWiMhrwGTgdVWdLiJTganATcCZwAC/fQn4g/+tMeGGG2PRyIcj66xtqzBxIlddDndyK70ooIBe3MI0nmQimbNgxoyEz2AYhhGTpCkyVd2MMzKMqu4WkVVAHnAeMN4newSYj1Nk5wGPqqoC74lIexHp5ssxEiNpbTtHJzKHI2colpcnWrJhGEZ81Ms3MhHJB44DFgK5gQdoMZDr9/OAjYFshT6sellTRGSxiCwuL92VNJkbGTVu261bt9abcIZhGImQdEUmIq2BvwLXq+oXwTjfQ9CalKeqs1R1tKqOzmzZrg4lNYJt26VLl1SLYxiGERdJnX4vIlk4JTZHVZ/1wVtCw1oi0g343IcXAT0D2Xv4sIgMzWvH4sb9bauuqHHbxkvv3m4ddLhwwzCM+iCZsxYFeAhYpaq/C0TNAyb5/UnA84HwK/wMuxOBXfZ9rM5IWtv27x8+/Kyz6qJ0wzCM2CSzRzYWuBxYISJLfdgtwHRgrohcBWwALvRxLwNnAWuAUuDKJMrW1EhK286ZA//6V4QTvlwXZzAMw4iNuM9U6UnzbgO026R7a5SnkU+zPwIRWaKqo2uab/To0bp48eKoafLzww8ruvNCRUVNz2oYRn1Q2+dCQ8Usexi1JpolqghGPwzDMOocU2RGrYmkrERg2rT6lcUwjKZLWhsNtlmLqWXatKpeXMApsWuuMS8uhmHUH9YjM2rNxIkwa5abai/ifh97zExTGYZRv6R1j8xIPRMnWu/LMIzUYj0yI2HmzHEzGDMy3O+cOamWyDCMpoQpMiMh5sxx38k2bABV9ztlSh0oM9OOhmHEiSkyIyFuvbXqZA9wx7femkChSdOOhmE0RprcguhINNaF0slcEA2uwxTuFkpoQXSklda9e8P69bUs1DCSyJw57u2toMCtS5k2rUF/PLYF0YYRINJasoQWREdaaR1tBbZhpAobQUg5psiMhJg2DTIzq4ZlZia4IDop2jHF2De/xktSxteNmmDT7z35U1+qcZ7GOhxZE/78ZygvV0Aqw8rL4Z13EhhZCbfSumXL9DUXEnpjD9Un9MYODXr4yYiTVI0gpNlwZjKxHplRa+bMgddfr6rEQsyalUDB4VZaz5qVvn9Se2Nv3KRiBMGGM6tgisyoNe45fKQSA9crS4iJE93EjooK9xtOiaXLcJ1982vcTJvmRgyCJHsEwV6OqmBDiwlQm+HIZFOfw50FBeF7Y+B0S0wSGRpJp+G6Xr3Cz8JM529+xmFC91t9DvPZy1EVrEdm1JqczAouYQ7ryKecDNaRzyW4XlHMqfeJDo2k0xtpKt7YjfolnhGEuqQxTohKAFNkRq3Ys2IP3zz0FH9iCvlsIAMlnw38iSlemcVYn5ioIkqnN9LG9s3PSD32clQFU2RGrSh6oIhp3EIrqiqjVpRyF3Eoo0QVUbq9kdb3G7vRuLGXoyqk9Tcy80eWOvKuzaPlHzeGjetFHMoo0e9GjW2KvmHUFHM9UYn1yIxa0Xpoa0qa5YWNK6AXmZnhJ4FUkujQiL2RGobhMUVm1JqOf7iLfbSoEraXltzCNB55JEbmulBENlxnGAZpPrRopJbMqy/nwJLd7J95J+0opoCe/KbVnZz9x4nx6RQbGjEMow5Ia+v3IrIb+DjVcqSIzsC2ONL1VtUuNS1cRLYCoY9YUc+VT/6gbLJbHuRg6XrWr6rpuWpAvHWuDxqKLCZHVUyOqkSSo1bPhYZKuiuyxY3JFUFNqM+6N5R2bihyQMORxeQwOdJBjmRj38gMwzCMtMYUmWEYhpHWpLsiS8TGerpTn3VvKO3cUOSAhiOLyVEVk6MqDUWOpJLW38gMwzAMI917ZIZhGEYTxxSZYRiGkdakrSITkTNE5GMRWSMiU1MtTzIRkYdF5HMR+TAQ1lFEXhORT/1vhwTP0VNE3hCRlSLykYj8KEya8SKyS0SW+u22RM4ZRZb1IrLCn2NxmHgRkd/7a79cREYmQYajA/VcKiJfiMj11dIkrT0SueYiMsmn+VREJiVBjl+LyGrf9n8TkfYR8ka9jnUgxx0iUhRo/7Mi5K2zZ0UEOZ4OyLBeRJZGyFsn7RHpv5qK+6PBoKp1tgEPA58DH0aIF+D3wBpgOTAyEDcJ+NRvk2KcJxNYC/QFsoFlwOC6rEtD2oCvACOD7Qr8Cpjq96cCv0zwHN1C1wNoA3xSvU2B8cCL9VDf9UDnKPFnAa/4++lEYGGS5ckEinGLSOulPWp7zYGOwGf+t4Pf71DHcpwONPP7v4x078W6jnUgxx3AjXFcuzp7VoSTo1r8b4Hbktkekf6rqbg/GspWp5M9ROQrwB7gUVU9Nkz8WcB1uAfRl4D7VPVLItIRWAyMxjmyWgKMUtUdEc4zBrijffv2p/fr16/O5G+MLFmyZJvWYgV/586dNT8/PwkSGYaRakLPBRH5IzBfVZ9MtUyJUKe2FlX1TRHJj5LkPJySU+A9EWkvIt1wb7avqep2ABF5DTgDiNS4ecDGNpJJ93Nv5uaJX2VMv851VY1GhYiE8ZUSM0/+qFGjWLw4odEgwzAaKIHnQiHueZrW1LfR4Dwg6MQq1IiRwo9ARKYANwFt9xwoZdzaJVw6K5vvje/P1DMHJUnspoOItAb+WtN8+VNfihi33nzGGYaRRNJusoeqzgIuA/7TqnlzmpXvYMi+tcxc8Bn3vPZJqsVLa0QkC6fE5qRaFsMw6oUeQFGqhUiU+lZkRUDPwHGoESOFR2IRMCCzAvRQCd9quZdmGcJ9r3/Kgk8+r3OhmwIiIsBDwCpV/V2q5TEMI6lk+lmNpwOvplqYRKlvRTYPuMJPnz4R2KWqm3ENebqIdIincVX1EPCDzIpDoKV8sWkfd5/VB4Br53zArtKy5Nek8TEWuByYEGn6sGEYjYZBuA7Bz0NzE9KZOlVkIvIk8C5wtIgUishVInKNiFzjk7yMm+65BvgT8F8AviF/gWvYuBpXVV8Wyv1RMwaXb+KE/A7sOXCI2+d9GC2rEQZVfVtVRVWHqeqIVMtjGEZS+VBV+6vqn1MtSF1Q17MWL4kRr8C1EeIexq1Dix8JLR2oYOPKFdx1/tWc9rsFPLd0E1eN68vQHu1qVJxhGIaRfqTdZI8g5bRh+64elB0qp+DD1fQ/qjXnjugOwC9eWpli6QzDMIz6oL6n39cpBbs/ZtZb+yktb8OEQf/goq1buf7UgTy/dBPvr9vOu2tLGNOvU6rFNAzDMJJIWvfIurcfxb1fvoIfnnorS9aPYcZ9u+jTuRUTjjkKAe573abjG4ZhNHbSWpFlNNtG63176dxqLd86YT4PP9YRgO9+uS8KvPfZdpYX7kytkIZhGEZSSWtFpiK0OuCm2vfIPcCWbc0BOLFvR/p0akmGwKw3P0uliIZhGEaSSetvZLv3fZ8bPryQL9Y2p2Pb5vTs8AmqIxARLhuTzy9eXMnLKzazedc+urVrkWpxDcMwjCSQ1j2yvfsmcXbbF+jadgPL1vdh7/7mfLFtGwDfGNGdTIEKhTnvFaRYUsMwDCNZpLUia958E38puZQDh1ryozMf5sChNsz7awkAnVo359TBuWRlCk8tKqCsvCLF0hqGYRjJIK0V2cCjf8pzfc/lshN/S88Oaxmc9xFvLzhUGf/N43pQVq5s23OQ11ZuSaGkhmEYRrJIa0UmIuxrDpkcQit2s2N/b7L1sDeYk4/pQpvmmbTIyuSpRRujlGQYhmGkK2mtyEpKzqQ0S8g4dJAlnx3L2i35DOnyz8r45s0yOWtodw6VV/DWp1sp2rkvhdIahmEYySCtFdmWLZdx/vJ/cfsrT/CvVWfyk0sWsa9kLRXl5ZVpvj68O2UViio8u6QwhdIahmEYySCtp98PGjSR72d3YXtOazK67OOoo65l65pD7CjeRKc8597sxL4d6dQqGwSe+U8hP5jQH+d6q+kgIh2Bp4F8YD1woaruSKVMhmEYdUVa98gqKlrxyf5BFJUMYF9ZKw7sOQDA9sLD38OaZWbwtWO7sntfGRtKSlm8oUk+v6cCr6vqAOB1f2wYhtEoSGtFtmLF87y++TwWFp3O3S89xNvLOwIZlBRWXTd29tBuHCxXsjMzePY/TXJ48TzgEb//CPCNFMpiGIZRp6S1Ihsw4Dpu+Mp/M73vD7l2wk945t0TONh8BNs3VVVWX+rTkfYts8ht25wXl29mf1l5hBIbLbneEzdAMZAbLpGITBGRxSKyeOvWrfUnnWEYRgLUtYfoM0TkYxFZIyJHDF+JyD0istRvn4jIzkBceSBuXjzna9VqFWXZzWi/r5yu7TZyXP4qlm865QhF1iwzg9MG5bJtzwF21PBKIgAAIABJREFU7z/EG6s/T7iu6Yp3bqoR4map6mhVHd2lS5d6lswwDKN21JkiE5FM4AHgTGAwcImIDA6mUdX/VtURqjoC+D/g2UD0vlCcqp4b73kPZWeRfagCFaF5s71UZHRke1Eh7nl9mDOO7cq+sgratcjibx8U1baa6coWEekG4H+briY3DKPRUZc9shOANar6maoeBJ7CfZuJxCXAk4mc8NChdhzKykaAvRWt+c+6IZw4fA9lB/azZ3tJlbRj+3emZXYm3drlMP/jrewqLUvk1OnGPGCS358EPJ9CWQzDMOqUulRkeUDQfEahDzsCEekN9AH+FQjO8d9n3hORiJMRgt9xPvxwNi8vu4KHSq7i//7+W4b1/ICB+a4ntr2o6vBiTlYm44/uQvEX+zlYXsErH24OV3xjpDMwHThNRD4FTvXHhmEYjYJUTfa4GHhGVYOzLnqr6mjgUuBeEekXLmPwO07//rez+2BHNh/qyvlj7+cbI//MoYNZAGzfdKRJqtMHd2VnaRnd2uXw/NJNdV+rhsk2VS1R1VNUdYCqnqqq21MtlGEYRl1Rlwuii4CegeMePiwcFwPXBgNUtcj/fiYi84HjgLXRTnjgQHc+LjmOt3d1pcv7BRwc9Fe6DVayclqwY/ORiurko4+iWYaQ174F760rYcsX+8ltmxN3BQ3DMIyGR132yBYBA0Skj4hk45TVEbMPReQYoAPwbiCsg4g09/udgbHAylgn3Lz5e0w+8ykW9j+Bs0c9zN/+8x3efL85HbvnHTFzEaBdyyy+1LcjW77Yjyq8sKzJ9MoMwzAaLXWmyFT1EPAD4FVgFTBXVT8SkZ+LSHAW4sXAU1p1WuEgYLGILAPeAKarakxFlp9/O6ecWEZOxgEG573L+aMe4KX3etIutwc7NofvDJ42KJeNO/bR/6jWpsgMwzAaAXX6jUxVX1bVgaraT1Wn+bDbVHVeIM0dqjq1Wr5/q+pQVR3ufx+K53ytWi1nwPGnA9CsvIy+XT6ieEcbWnfoxRfbtlJ28MAReU4d7NYC9+rYgmWFu1i/bW+t62sYhmGknrS27FFaOoSuw4ZTIZBdfpANJYPIbbeD5q2PAlV2Fh85M7FHh5YM6taWbXsOAja8aBiGke6ktSJbt+5/WbQkm9IsYU3RCJ5ZfC2nDn2PzKwOAOwI850M4LTBuXxYtIvjerZn3rJNRyyeNgzDMNKHtFZkXbs+yuTJ8KUVH/Kn9+5kSN67DMpbgdISIOzMRYDTB+dSoZDfuRWffr6H1cW761FqwzAMoy5Ja0XWqdMLTJgAHZptY9RRb1K8pw/T/vYDPvywGa07dgo7cxFgSPe2dGuXw469B2mWIU1pTZlhGEajI60V2Y4dp7N4MTw05ix+dPRtXHz27zhv1HP8/Pfd6NAtjx2bws9cFBFOHZTLwnXbOalfJ15YtomKChteNAzDSEfSWpFt3/41brwRMlvuJ/ugsrtVW0b1foODZbCjfBjbNx9pPDjEaYNz2VdWzoDcNhTt3Md/Cpqkw03DMIy0py4te9Q7qlksXQrPLnySzbt70XLdTr7R93EypZwW7buxZ/Ve9u3+gpZt2x2R98S+nWjTvBk79h4kJyuD55YWMTq/YwpqYRiGYSRCWvfIsrI+57774BuDHuQvQ84g/6tLefzd6/hiTzOOP8FN+Ij0nSy7WQbjjzmKBZ9s5ZRjcnl5RTFl5RX1Kb5hGIZRB6S1ItuzZzhDh8Izq7/HK8XfZuuaXhyqyKRVzgFatj0KONIKfpDTB+dSsvcgx+a1Zfveg7z1qXlFNgzDSDfSWpEdONCTf/8bzh3xMLvKOtKx3RauP/XH7NjbEpWWZGZlRTRVBTD+6C5kZ2awdfcBOrTM4rkPbPaiYRhGupHWiiw7ewvLlsGxfd/npqN+xZfHzGPXvs50brOTvTsO0j63W8ShRYA2OVmc1L8T/1z1OWcP68Y/Vhaz58CheqyBYRiGkShprchyc92C6A27jkEVthd0469LruWUoe+xZ8cBOnbvEXEKfoivDelKwfZSRvbqwP6yCl5Z0XgdborIGSLysYisEZGpsXMYhmE0fNJ61mKXLs9w5ZVTue3mO/nV3na0/Hwnpw96khOP3s2e7X3pmNeDNYvfo/xQGZnNssKWcdrgXG752wrWb9tLfqeW/O2DIi4Y3TNs2nRGRDKBB4DTcN67F4nIvHi8DCSL/Kkv1XmZ66efXavzRctXG+rzXEZqiXStk3Gd7b4KT1orMhH4wQ8ga+13Of6lAl45L4+somwyMgaye8d+uo3uiVZUsLO4mE49/p+98w6Pquga+G92N7vpvfeEhEAgdAi9Sa8igoA0BZFmBcVe3k99bWDBl94EFUSQDtKR3gkEQkJCCqmkkN53d74/dtGIlIBBCe7vee6z986dcu7svffcmTlz5ubKydlaQ0s/R3ZEXWVQU2++3H2J1LxSvOwt/uarue+0AuKklPEAQohVwECqse6bCRMmTDzI1GpFdh0LjRUWijLUlWWUq22RugIKrxm6FgGupSbfUpEB9Grozn82R/FOv1CkhHWnU5jaNfjvEv/vwgtIrnKcAoRXjSCEmABMMB4WCSFijPvOQPa9Fiw+udeUf+KOctxrWfeQ7p7rpAbr4y/JUcOY5PgjzuKTv1eOW9xXt6oPv/sqzN/MQ6HInO3dATCrKCfXwgr7kgKKcstw8PACbj2X7DrXFdmZ5DzCAxxZezqVKV2CEELcd9kfJKSUC4AFN4YLIU5KKVv8AyI9kHLAgyOLSQ6THLVBjvtNrTb2ANiyBd5e8Qbt4g4xZ91XXMhqSUV5AbpKPdpKJdZOzuSkJt82D097C5r42LPtfDpDWviQkF3MyaSHzmVVKlC1WeptDDNhwoSJWk2NK7I7WcYJIcYKIbKEEBHGbXyVc2OEELHGbcydysrN7cLEiTB9hoYN/gPoUvdHdu4YzoXUZiBLKMwpw8nLh2t3UGQAfcM8OJ9aQENPW6zUSlafuHOaWsYJIFgIESCEUAPDgI13SGPChAkTDzw1qsiqWMb1BkKB4UKI0JtE/VFK2cS4LTKmdQTexTBu0wp4VwjhcLvy0tMnsGQJdOttw+qiQaRl1cG700V2Rg1H6osovFaGk7cvOanJSP3t3U/1DjN0T+6OzqR/Y082n0unsKzyLmvgwUVKqQWmAtuBi8BqKeWFaib/U3fjP8SDIgc8OLKY5PgjJjn+yIMix32lpltkv1nGSSkrgOuWcdWhJ7BTSnlNSpkL7AR63S5BaWkwERHg4QHzMp/jl5ixXN7dlORrwWi1RYYWmbcP2vJyCrIzb1u4t4MlTX3t2XwunSda+lBaqWPT2YdrTpmUcquUsq6Uso6U8sO7SPdAPAwPihzw4MhikuOPmOT4Iw+KHPebmlZkN7OM87pJvMFCiHNCiDVCiOvjNtVKK4SYIIQ4KYQ4qVCk89pr8O67sL1NYxZ27YymfiECyekEXwpyynDy8gUgJ+XOXYX9G3lyMb0Aa42Keu42rDx+pVoXbcKECRMm/jn+CWOPTYC/lLIRhlbXt3eTWEq5QErZQkrZQqMpQAhDi+z9uFl8eHQ+pXG2KBVaTsTVpTCnFCdvgyLLTk66Y979GnkgBGw6l87wVr5EpuYTmZJ/D5f48GDyBmLChIkHnZpWZHe0jJNS5kgpy42Hi4Dm1U17I0KUo1bDxIlwJLsrWeWeqHzKkFJBaaWSwpwyzK2tsXZwJKcaiszV1pw2gU5sjEjl0SaeWJgp+f7YndM9DAghfIQQe4UQUUKIC0KIF24y5jleCFFYxVDnnfskS6IQItJYxsmbnBdCiK+NyvWcEKLZfZAhpMp1RgghCoQQL94Qp7MQIv9+1IcQYokQIlMIcb5KmKMQYqfRGGrnrcaQ79Zo6h7k+EwIEW2s+3VCCPtbpL3t/1gDcrwnhEitUv99bpG2xj7GbiHHj1VkSBRCRNwibY3Ux82eVWP4335/PDBIKWtswzAvLR4IANTAWaDBDXE8quwPAo4a9x2BBMDBuCUAjrcrz9V1uQQpv/5aymW928i9LetL55UREnQy1PucnDt1r9Tr9XLNh2/Lb199TlaHH49fkX4zNsszV3LljDVnZchbW2VeSUW10j6IACdl9f47D6CZcd8GuAQMB7ZXibMAuFid/P7KBiQCzrc53wfYBgigNXDsPsujBDIAvxvCOwOb71OZHYFmwPkqYZ8Crxn3XwM+uUk6R+Mz6Gh8juIBhxqWowegMu5/cjM5qvM/1oAc7wHTq/HfXQYCq7yTQmtSjhvOzwTeuZ/1cYtnNfSfuD8elK1GJ0RLKbVCiOuWcUpgiZTyghDiPxheqBuB54UQAwAtcA0Ya0x7TQjxfxjMxAH+I6W8drvybGxOkpMzitdegzrWn+NSVkDOqIbYW+VQXqFEV6mnJL8CZ19/kn/ZhF6nQ6FU3vYaeoW58/aG86w7ncLI1n6sOpHMTyeTGd8h8K9UzQOPlDIdSDfuFwohLgL1+eO4ZRZgXjWdqOINRGWhaq60d8fRoZCcYmsUKj16nQKFUo++XImQ0MApk3StBbnXbJBWOihT4ueQRdoVZzSeZVgpy7E1d6fMQ5HlVN8ZbbwKvbkKRaUeq4AScoqssXT0xscrk1ytlb6oUoMqVWDu6SMbumQRmeeMr20OGVec0LvqIFeFp0c2VwqcUJtrsVGVUaTVUFmgRq+WqM21uKvzib+sQFdSfKsZ8I8Al6WUf1vzXEq5Xwjhf0PwQAzKEwxd8vuAGTfE+c1oCkAIcd1oamVNySGl3FHl8Cjw+L3k/VflqCY16prtdnIIIQQwFOh6L3nfhQw3e1a9+AfujweFGvfsIaXcCmy9IeydKvuvA6/fIu0SYEl1y7KwSMDeHnr2hI1rQ8nUlVGn2ynqFUVzJTEQKSvIzyrF2ccPXWUluRlpOHnd3iGwrbkZ3ULd2Hg2jTf7htLcz4EVR5N4ql0ASsW/w9OH8UFtCqwBPG847S6EOAukYfga/s0biMbPW3Zyeproidb45ClR5wqEDopCKrFwKOWjxuuZdmwSKV2XErBxAvaRKr54eR4vfvVfXFuXMK3JTr7+YSB9B56iXK9i/65GqHMFUgltHjtLeqktF6J9QA/tml/gwPZGNO+YyFTvPUzaO5ojfeazMN+H2SumEb6/hISBFnTudI6Tyxvj0aoMM3Mtdd4qYuuvP9N53DOkjqrE+pAlWguw3vjx7apkGLd+0NvcUB/VndJwL7gZX2JgaCG63SROdQ2uaoqngR9vcU4CO4QQEpgv748F3VQhxGjgJDBNGiyeq3JH12w1SAfgqpQy9hbna7w+qjyrx3gw74+/hVrt2UOjSaNZM/Dygs9GPMreOl1o02gnv57rR+vAX5D6fIMi8/UHICspoVr5Pt7Mm9ySSvZEZ/JUO3+SckrYG3178/2HBSGENbAWeBGI44/jlpXAx1LKxsBsYH3VtDaWZSQOtEdhXcl/Bq3CIksilTCx9T4qkqz5KvERLnddStisyahsK3j3xeVMXTARsx7Z2O214PNt/Zk1djH/576XIz83Rm8GWisYP3orL7vtZLrPdtb1nI3KvoInnY/gGp4BwKT9o5jYeh8DWvRhZkR3wvpFUxBgzorHv6FQqyFs5HnmtPsemWBF0TeSN642wv2tywS/kIqqdzazJ83DTOhuVR9qYADw001On8bQ3XjT+rifSEM/kfy7yrsZQog3MfSsfH+LKO2llM0wjLFOEUJ0rGER5gJ1gCYYWigzazj/u2U4t2/Z1Gh9VH1WpZQFVc89CPfH30mtVmQA338Px47Biyu20Tr2KCtnvUJg+HnqukeALKAg22C5qFAqq63IOgQ742qjYc2pZHo1cMfTzpzFB6uXtjYjhDDD8GB8L6X8mT97AxmEoZV2veVtJoRwvp7eX12ECCuga/Al3jzxKGWOAqcLWpau64aiUqDunsS8PC/GPbUVhVLPu3NG03PoUZY3XIbLkVxsYwXLrrZjQV5jioMqiR05lzK/CvzV2fQ7OIXJSycSUe6DNk/NjoKGOFsUUdk5HaHUk1lhw5ZTvxDdaQlL/H6hfEgeiZXOrArYQ2SmJ1M3PIXWSs/ehms59HZrjkUGkTjXjWt5VkxZNJFKecsu597AaSnl1RtPSCkLpJRFt6qP+8BVIYQHgPH3Zl9Xf4srMiHEWKAf8KTxpfknpJSpxt9MYB2Gbr4aQ0p5VUqpk1LqgYW3yP/vqg8V8Bi3bp3WaH3c5FmFB+j++Lup9YosIwNiYsDHJQ4rUYhSUUHkvrZcTG+GWlNEflYpKjMznLx8yEqMr1aeKqWCx5p5szcmi2vFFYxp68+R+BzOpz68pvjG/v3FGIw5ZsFNvYFsxTi2IIRoheH+ybmex8VSB6zMKziUHEDX4Et478pj/dwvWTbyG+wa5rA9LYJ9uSHMXd8bq71WVNjCmdebMebdacQ8a0fdUTEcPx2Mnzqb4S2OMSyhK2qrCv43fgiuTgU8P2ID5qKSbs0vsG59ewAuzWmF8x4NqWX2BGx5hqCtz9L4hxdQbXDgjaODKNFXoNUrmN57E4cGzqTNG1NI7aLAMklFWboVjvbFVNpJ5KVbenG55Ve2EMLdWG83rY/7wEbgupXZGGDDTeJsB3oIIRyMVms9jGE1hhCiF/AqMEBKWXKLOFZCCJvr+0Y5zt8s7l+Qw6PK4aBb5P93uWbrBkRLKW/qobwm6+Nmz6qRB+L++Ceo9YpsxgwICoLk7CAqMMfTJQF1QAnfHnqL3GJBfqbhOXPxDySzmi0ygKEtvNHpJT+dSmF4uC/WGhXzfr18vy7jQaAdMAroeoM5sy8wS0pZB8OX23njmNDXwLCqX+P1LXJx7HeJyngbxrnsRz+zgI4nx/Nq7OPkFVjyTHI7vMzzIKiYUjeBdbIkqY+K/LoQP3g+xyKDOD9oNudKfPjI7RwnEvyw22qFx8eXMVPomWifylubn+BJ5yPo1ZKfg3bSoWk0OU0lSQUOaNJVOHvkYxZYyIkP5tIn9ALt/vsi8qg969Kb0nHVK3R4/hi2sYKwftEAZF+xp9JeR92wP7+PjS+c7sDPVcImCiEmGg8fv119/BWEECuBI0CIECJFCDEO+BjoLoSIxfDi/NgYt4UQYhEYjKaA60ZTJ6iG0dQ9yPENBmu5ncb7ZJ4xrqcQ4vr4uBtw0Fg3x4EtUspfaliOT43m7OeALsBLN8pxk4+xu3HNVl054CbjqPexPm71rP7t98eDgqih5+4foXnzFvLs2ZPodDC252qGXVrEMv8u/Hh6OuQr6dLoAMMfEYyb2YHTWzewb/kiJs5fgZX9bV04/sawBUdIzSvl1+ld+OSXaBYeiGfv9M74OVnd5yurOYQQp+TftIxDi8bmssOygWgUWgq0Fpx/pxFSKZAqKPRSUdSuBM1ZSywzJC+/sYphNrl0H/4UWY0tiHhtDqOTOhL5XUNUvbPp7hVNVoUNuy7Up0P9S5zJ8GZh4xW8mzCQ7fU3o5N6lELB6KSOfOX9C49FDycp2p34wfPpGDmIlEuutGoWy6kkX0Y2OM6WWZ0o9hQoWuWh0ykoK1bj5FREbowjvTqeYfFj+yhPSvl3WPOYMPGQUatbZEKAlODtDS8/U4mvOpmOAeuxGp2BEJLEDE/KS7SUFlbiGlAHgMyE6reqRoT7kXytlP2xWYxrH4BKoXjYW2V/iZgye2Z6nGbN9nb0c4hg3+KF/LpgAdYxueTX06GrVFC3byzH/zuXeS8+TuDOp+k7Zy8tnzzLJznBdHWIJr+eDqv/2bFleXvK9Up8vHJY7ref/v7nee6DqXxZZzU9PZswOy+QNmcHs9xvP83Xv0Tptx64HhOsKnRghM9xVMUK/uu9kTDvVL6NaM3g6bu48NwcevhG47DaGj/PHGxn2eByEmxVpYYZaSZMmKiV1OqFNaUU6PWGcbJP1w7meGJzlPl5lNk5opcCW006UmrJu1qCq38dEIKM+FgCmlavgdKzgRvO1mq+O5rEojEtGdrSmx9PJPNc12A87S3u89XVPvR6Qf35k7FNk0zaP4r/tlvLwkmPkTZUwzvd1/D+vkdJW1CHMPdgHv94H8sjw9mfE0w9m6ss2tYNhwvgWaQnvb0KdS5Ez2tAXn1ovWIimjw92mdyGXB4Mh6Pqvl6j8D8qpK6Zyeh9C1l3Uff0PnIZIbZ5NL0RE/cm2Yw0a89+SPrYOOiYFl8d9yG57PjSj30dRRcaLCBqZ+E08ImgU/P9yDMbss/XX0mTJi4R2p5i0zi7g56PfzwozllUk1cZmO0lw1Kpl3QZqQ+l7yrJWgsLXH08OJqfFy189eolAxv5cvu6Eyu5JQwsZOhVTdnX/Xz+DfhrCnCKk1S0rMQTYoZHywZTuLTei4+O4ePVw/GwrmECmvBwsmz2Z0Rgr5CyZk4P37e1A6plNSbeIHwN07gu6OMHsOPUuIu8GqeRvHgAq70gWGBp/BwykdVoqfuS6d4dPBBKm11xHZexjPxQ1gfPg+Awjh7CrZ4EPddUz5+fwFFfnpOPfMlX81+nB6+0fR6/ChBKydyaFlzPj3fA+tNNiRWWP/DtWfChIl7pVYrMjAYejg4gEYDyRV+SKkArUAIiad9PEIaFBmAW2AQGZdjuZtxwSfD/VAKwbdHEvF2sGRoCx9+PJFM8rWbGmv9q8nMsWf69FUAnH76K7x6XMH8ggWhh0cC0MLrCg3HXODVlydxbY8HfcMiURSokCHFWAQWUMcym6gxdYl7woxt61rzzYR5lGlVaCPsqf9FNslljnxbbwVZk0rI3+THR27nsI1V0eXCQKIifem/9mUei+vOqG77cfv6MP9r/QMAmmwFg3uNptwB1p1vQlaFNTbxCoraGf7Dp2dspExXqzsnTJj4V1PrFVl5OSiVoFCAnVkeGmUpViMyUCp17I0ZjNq8gGsZxQC4B4VQnHuNwpzsaufvbmdOnzAPfjyRTEFZJVO7BiGE4Kvdt5q8/+9Fr5HMSeyM40orwtY8j691LtomRcxp+gOaXMHZ1Q2JzPQktbOCISP2cXhxM9qFR6FPsqIo3ZofoltQPLMcC9cSljw9m2dPjuTaaVdUTfKIfcaN7AorFl5rizxqT36xBX0eGUJBaCVJaU5YpijRWeg5E+PPL2n1Ybc3U46O4JUPn8Wu3VVE6lV+GPcFP3ecy/GdDdjz2udsbDuH8hRrDufXobLSpMhMmKit1HpFZm8PZWVw4AC4WKaCVFC63hWtTkV0WjgKRR7X0gyKzDM4BID02Ji7KuOZDoEUlWtZdfwKHnYWjG7tx8+nU4jOKLhz4n8RrtYF7A9bR7G7kqCwFK4UOeBmX8hz54bx7fNfoO+YR36eJYHrylkeGY7LkGTa2l3GLLAQC9cSlEo9tpoyotp+R2tzJS6rLXA5rUe1y56fhnxJU9tkNn3fnm8mzMPNrpDcJk4k9F2IKl1DZbMiXI4p6dYoiiX1V7C9/mbqe2dgm1iBk0UJtpsFL8UN5alzY7C/JMnQwbTeYwh68SgVehVCefsVxP9uhBA68Ufv+/5CiDNCiCbG8yohRJEQYmSVNKeEEM2EEGOFEN/ckN8+IUQL436iEOLADecjRBWP7jec8xBCbK6GzIfvcD5MCLHsTvmYMHG31HpFNmIEFBcb/C22D9zMz/V74tkmBwu3EjIKfCgpzqMwp4yKMi0u/gGozNSkx0bfVRlh3na0rePE4oMJlGt1TO0ahLVGxX+33l0+Dzt5lZa8nxXKmTfn0NzxCq/7b+Vqng0OlqVk6Gx5M3QbskJJxovl/K/1D6QV2LIuvSmlBea8E7aF0kxLdL1yKdFXEHp4JOmDKuj/3h7GTN7KiFPjmOEUS9PB53n3hfHsCl2HVELf5r3o8chp7LZaMfn1tew61YCrOmvqz5/MhVhv8uuoyZvty8U19fgiaDUFhRbk9i9hwOHJZH0muDSvFZcXh0DJ7Z1J/wOUSimbVNkSgUNAW+P5xhi8nreF3+a81cHg3b062AjjorZCiPp3iPsyBs8Zt0VK2fYO5yMBbyGEbzVlNGGiWtR6RTZmDFhbQ24ubLo0lkEXdqHMKkblV46reQbHooKQUktueglKlRmugUGkxVy863Imdw7iakE5a0+lYm+p5rmuwfx6KYt9Mf8OH4zVQZdrxpoVnWn96kQ+cjtHZws9MR2Ws7fhWhakdSSpwpnTvb4iMvwHPp08Ck/bArbX34woVvLummF0aBrN2rj9NP7hBdr5JHCy0/8YansGc1HJR40Nbgxd1EXoNAKlUFB3ShRipeBQWgAVdoKxtpk4++bR2ULPyrFfENdnPk3Hn2PTl1/w+sSVTHrjBVoGJLE+fB5uazVU7nDGc4+COuNiUFpr/+HaqxaH+V2RtQXmYfAzCAZ3R6eklDd3GvlnVgNPGPfv5CNwMPALGFxTCSE2GFt4sUKId69HEkIUGX8HCSF2CwMeQohLQgh3Y7RNGCYPmzBRY9R6RSYEDBpkGCPLLXXGSlFEygVvis7a09DyFLlFTkhdDjlpRQB41wvlakIclWVld1VOuyAnmvjYM2dfHJU6PWPa+uPvZMl/NkdRoX2wuqX+KZxc86FdHi1eOEPIgdGELJ3E+1mhBG2fwIV0D4banmFE//G0OTsY8+R8clb50NOzCd51M/nqiSWc2tiQ1UXefDZoBbvONMBBacnQyKf5+oeBxJR5kFBZhK2qjIOz5xO482mOHGjAeK8DnGm5iojX5tBpwgRONFvNvlIFGqEj7MhodkeH8G1BKJ0sksnoqqNCp6TfwSnYXC6koHkZJS4KAi2z8dA8cO7HLKp0K64zhlVtkbUF9gPlRtdHbTEouus8UbVrErhxzslaDL4BAfpjUDB/QggRAOTK3xfDBYPSHAw0AoZc77K8jpRyHQYnvlMwtOTelVJmGE+fxOAl3oSJGqPWKzKAJk1Ap4OOYZvpZbudxwZ8g+WoDPbm9MbbIRYhssnC8K4LAAAgAElEQVRJMSqy+g3R63Skx93dOJkQghceCSYlt5SfTqagVil4t38D4rOKWXSwej4cH3aySm0oTrFhS0QjYjosx791MnaqEqxi1IgYK0a+Mp1L0zU0d05h6+6faD3hNMlvtWWy/z6eX/M0Pp8d59PzPXjUqojh4UcBONFsNVGT5zDDKZYAM2uyKmx4PyuU+O5LUFTCggG9+SQnmGb/mUSJq5L68yfT2ULP8FnTKStWE999CS86JDLgvVcID71MPZurkK0hcaA9H7Vex4znV7Lp+/Yk5zn9w7X3J6p2LQ4CMK6Hpja2buoBMRjcDIVjUGSHqqT/sWrXJAYFUpUcIFcIMQyD66ZbmeF6YFiHrio7pWGl91IM7rva3yTdcxiWayqXUlZt7WXy56WBTJj4SzwUiuzSJYN3j8IyF/rZbMLNPJHKaCsUComFRotak0tWciEAniH1EUJBctTd++vsHOJCU197Zu+JpaxSR5d6rvRs4MbXu2O5kmMyx7fVlBE/eD7dGkXR9MPJFFRo+OpwdxoOiMYm0RDnw5brufRifboPf4rsCit6DzrK+z8M59LouSyN38erDXeQUFnE/7nedLV4vvE6xrsuUdRdPonwrhfYuvsntqQ1xH9EHHXGxaANKaHzuGdwP1zArLarCVg/gcC1zzJu+kay3g5g5clwnuh0mPqPxDIztjsLJz1GubMkzPHGd/UDy2FgCJBu9Ot4FIPvvVYYfADeDT8C/+P23Yql3LCYKn9eHuRm81m8AT3gJoSo+p4xN+ZpwkSNUaOKTAjRSwgRI4SIE0K8dpPzLwshooQQ54x96H5VzlW10ror79Q5OfDWW+Dvns8bGf9lzS8vYBZYiq9HIkrphF6bQXZyEVIv0Vha4RZYhyvnqzsm/gf5ebVnPdLzy/j2cCIA7w1ogEqh4PV15+5qftrDSEGBJcsKXNl7MIyCYD1HGq+lW6Mozu6oR06nckKnRfL558OIHaUmYYCGQMtsXNWF6EOLuFhRwjvpPRlrm0mvo5PZVGLLM8ntWFbgetOyAlomc+hYKHVWTyQlw4GEXCcurKtH0LOXWTrvCy6/rCKj0o6VveYyq9f3xJa6kRGuQZQpWLO9HaM9jmA7y4YdKxaiCioksuB+rr5SoxzGsFbcdaV1BBgNZEgp77Z/dB3wKbf3fn4J8L8hrLsQwlEIYQE8yh9bgteXNFmCYeztIgZjkevUpYa94JswUWOKTAihxPB11xsIBYYLIUJviHYGaCGlbIRhXatPq5yr2pUy4G7K7twZ1q2Dt6cp+NhjBpM7v4Jd/2tcyQmgmc1FSvLTqCgrJz/L8CHoG9aEjLgYKkrvvhXVpo4TXUJc+GZvHNeKK/Cws+C13vU4FJfD98eu3HV+DxNmBZKxtplYpCvw26qlb7uBHP2pMapiiO22iFNLG5FXT4Ie9GrJ/g/a8MOS7ljttWLgqmks9DlE0MqJ7Gszh5f2DWehzyHG2t7cmGZ7/c04nRFcHjqPPqEX+KHxEiJfnsOVqWE8lzCEIfVPM/9/Axm1ZirmopIDX4fzypg1SCsd0rcUc1HJKwu+I2jTRIiwRVFaa5wtHgICMSoy44rASv44PlYtpJSFUspPpJQVt4lTDFwWQgRVCT6OYYztHLBWSnljt+UbwAEp5UEMSmx8FcvILoDJH5iJGqUmW2StgDgpZbzxwVgFDKwaQUq5t8r6RUcxdD/8ZUaPNqxJ1mpIb55L+5qPNy0lfUR9Arql4H3tElKvReoyyUwyzPvyC2uCXqe7p+5FgDf61KekQsfMHYZxtifDfWkf5MxHWy+SkF1cE5dUKzHzKufLXH8qbSXaaTl03BiFQ/d0djz/Kd2fmoDnsER6dTxDwqMLcArIJWtoKXa90ikMhEuj59LlwkAsAgvwUFlj7Xznejz+37kA9HOIYHqX4bQ5O5hyZz1JuQ7s+rIdZ96cg3VILr0syzEfkcHnSx9HodbRJiCe1y8MorE6h/pvJ1DqrSXQ9U/rZv6jSClv6jNLSnlCSimklLuqhPlLKZ+tcrxMSjn1hnSdryscY/zsG84nSikb3kKcb4CxVY5TpJRdpJTBUsr3b5RZSvkfKeXLxv1CKWU9KeVFIYQGg9HJtjvXgAkT1acmFZkXkFzlOMUYdivG8ccb2lwIcVIIcVQI8eitEgkhJhjjnczKMoxrJCRAfj48+6zAxTyNEPsIAnoXceW8B7bZecaUGWTEGxSZZ0goZhpzEs7c+CFZPYLdbBjV2o8fjl8hMiUfIQSfDWmEmVLBC6vO/GutGLV6Be6qfJaN/IZGjml8GxOOraaMdnufJ629GWqFli2RYYQsnQRA4H+1vBy4E52Fob6S0pzQH7dnWnozIsN/qHa54ZpcNh5cR0a6A3HD5zGu7mFyG0BPzyZ80XA1Ab+MJ+OMOyXeOiY0PsiB8yGUn3BkSuIgUkcG06FxNLk6y/tSJw8DRivExBrIyhd4zbhGmAkTNcY/Yuxh9EbQAvisSrCfcd2sEcCXQog6N0srpVwgpWwhpWzh4uICwOLFMHiwwbtHdHEjIrLbk7jFhpJMM04VhGNrY4dKlc7VBMMQgsrMDN+wJsSfOXHP41ov96iLk5WGN9ZFotXp8bCz4JPBYZxLyeejrXc/T+1hoK55PktD/HguajhbjzZhd6t5vOW7GSenIqLHzyXcIRHbSDU2iWCtKUf5ZS4/ZzcjfvB89pUqMLeqQNEqj5kep9lXWv1bs+PJ8fxU5MQXHVYxLb0Zz9nHYx6cT2WPFtgrSknotYgNw2bSp3UEM5xiURYoiZo8hysrgjj7yhxS3wxGmtZxuS1SyusLM/6ptXcXecRKKffVqGAmTFCziiwV8Kly7G0M+wNCiG7AmxiWSf9tboqUMtX4Gw/sA5pWu+BU+O47iIiASr0akCiVEopVvJH5EY5Ka8qLrpB1pYDKCsN80cBmLSnMziLrLlaNroqtuRnvDQglMjWfJYcMefRq6MFT7fxZdjiRDRF/uvSHnsg8Z7anRVB81Bk733w+vPoIEWW+ZKfYE7BxAjOcYrHrlc7UaWvZ22ADqfl2HEkIZGpqOJ0t9ES1/Y6RQSfQST2dLarfqp0S8isDrK6y5VpjZnqcpk/0AIqyrciaVMKMgHBK9BXYK/Rs39uMXF0JIV+m0DFyEAV1IHjfWFIeUXOt1NQiM2GitlKTiuwEECyECBBCqDHM3v+D9aEQoikwH4MSy6wS7mDsP0cI4YzBnDiqugVrtQY3VUKAg2UKna32oTYzDMVdq3Qi6nwQuspSdJVXyYg3tMrqNG8FQhB7/G4tln+nb5gHPULdmLnjEnGZBvP+N/rUp5W/IzPWnuNcSt4dcnjIUEp6B7bG9VQlwwJPEfVmGJszG5EwYAFmeUrqLp9ES+ckBlol0vizyYS5pmG/y4LDi5vR71JvVhU6MMMploGxfatd5KpCBxZ/PoDlBQFcKXJgWYEry4JXkdB3IQ1cM9ieFsFVXQVTEgcxpe82hl0ayjcHV5F12IM3Hl2L63pzKhx0+Fjl3seKMWHCxP2kxhSZsd97KgZT3ovAainlBSHEf4QQ160QPwOsgZ9uMLOvD5wUQpwF9gIfSymrrcgyjSpRCCgsd+NYSWuKiwxf2HqpIDLaF4RAahNIjTa8sKzsHfCu34DYY4dule0dEULwwaCGWGlUPL8ygnKtDjOlgjkjm+FsrWHctyf/Vcu92JmXsTZuP/sWL2R9SiOu1VPzuPspwo6NoH/3Y5jlC9adb8LAqCex65XOZLe95DaQfP/aTC4d9ef1/Y/zWFx34ncFcLGievU2zCYXt9GJTLRPJdg2i6uVdryT3pNlBa5kfGDone524Dkq9CrG2EYxyXcffZa8iiYXvn+2L6HTIsFMkpL7wE2INmHCRDWp0bUrpJRbga03hL1TZb/bLdIdBsLutVy12vCr0wEo0FJ19WaBIzm4uXuRm59ESszvX951W7dnz5J5ZCUl4OIXcE9lu9qY8+ngRoxffpL/bo3mvQENcLbWsGRsSx6fe5gxS4/z07NtcLLW3Ovl1RpslaUsLwjDXFGJh1UB6b3hs28fR2ch2bW/NeoK8FwieXL+IYZapzAyvi+bBs9i0qQXCNh2hEmxcYSYZTK8YDr11Xfu6mv82WT0HfOojLSjY/kgQuwzydda8JXXXh6JHI7fW5fRST36IjPe8t3MpCv9AOgz4Ci2qjK+296JomvurOv2De3/NOvRhAkTtYWHwrNH3z/0RClRoUWI38dYnJXZeKg0VJSkcTU+lbLiSgBC2nRAoVQSdWDvXyq/W6gb49oH/GFsrK6bDYvHtiQtr5RRi4+TV3LLqToPDckFjmzObMSn53vwc9BO2rom4LstD+tkqLSCgjalJPU256vZj9PrwhNEZ7rx6LGJrFvwFbRuxKNWRdRXWyKV8GWuPwDDEroC8Fhc998MQKalN6PFu5M4+8ocigvMiR4/lw2h3zPFdQ9bl7an2ZIXeML3FFdLbOjj1YwXOuzgyY1TuJDpTmeHGGIK3didEcKbA9YyI2g7MwLC8XKv/hp1JkyYeLB4KBTZ00//8ViLyrBStJGFRZNxuWyYrKwtj+HKhRwALG3tCGjakqj9e9BpK/+SDK/1rkcrf0deXXOOiGTD2FhLf0fmj2pBXGYRIxYeI6eo/A651HL0gm4uFyHClk9ygjk/pSH6mQV0mngMmhTQNfgSWis9+fV0KL50Zk5Tg4n9Y9HDqfi/fAJ3Ps1jcd1x7JPKj1eaA9DZIYb1xda847OZKYsm0vOx0cz0OM3J9+cSOmcyp7oalt1qvv4lnvjhRVa+/Dk2ibDwuz4kRbsT/2kbBlqf59KQOUwJ+ZWZEd2JPuXHtT0eXK2048P/jqL5GT1XCkxdiyZM1FYeCkVmbw9mZtePBAIQgNLYcZpd7oDZxWhcffyR2hgSz/3+9d24Wy9K8vOIO3H0L8lgplQwd2QzXGw0jP/2xG++FzvVdWHhmBZczipi6PwjpOQ+vGNmYY5ZnC7wpVHvaMr0ZvRevJ9LSe5s2RLOo3XO0dwmEUWF4J3u60jppmTy0olU5JqTvd2LtOOeCKUkucABOcuVojIN72eF8snR3kzbMpJZGd358OnlDFqym4D1EwjeNxa7y3rezuhCyNJJ+G7V073Had5P7UdZ/3zKGpSCbSXje++ix6GpRFZUsiM7FG2BGr1zBeVOkgM5QWS3r2T95UYIrcn83oSJ2spDocgAbGwMv02aQEvvnTS3PIK83rsoDC+pADsndJVXuXw66jczfL/GTbFzdeP0tpuuYnFXOFlrWPZUK7R6ycjFx8jINywV06muCyvGhZNVWM6gOYc5m/xwWjOWSD11LLO5kOnOaPvjzFvbG+eDZjidl8SXODPQOoYWrS9xKD8YgLLgMiycS2g95Cw2iSCuanAZlcW+xQspKdbQ0yYSd49cHIOuoVHoeNSqiPPF3li4Gj4GXnjvR/ZsaI5UQko3JYfSAriQ6Y7H52q8XPLY3flrFm/phrhiwYyAcHo4R9GhcTTBY04TO3IuLR2SsIpRozxqi7O9abVvEyZqKw+NIrOyMvxGRMDJ1K6cLGmDXm+Y7GzmoENTty6u52NQmqkpLzxNUqShe1GhUNKsz0DSYqJIu/TXJzIHuVqz7KlWXCuuYMTCo78ps1YBjqyZ1Ba1UsHQ+UdYeyrlL5f1oJGY4UaIeTqfha3lsYjx+Owug8dyyBhQzqqAPQx/9iWif6zH/sQ6jOq2H48tanweP08D61TMHsskbvg8Zp7ZQtMPJzMz/CeeOTuKa6ddyYtyYqHPIQLXPsu2Q02x3mSD/S4LhtnkEjV5DpqQfHQOWnr7RmH3nQ2Tl60hxD6Trlte5tLoufR45DSx3zZjon0q51Y2pGBbHcKOjWC0/XGkAqwy9GSV3tQjlAkTJmoBD40iMzMDjdEwUC9V8FsHI5TnKNjk9iK6s2ep16wVuoqLnN/3+3pkYV16YG5jy5G1q2pEliY+9ix7qiWZheU8Pu/wb/4X67rZsHFqO5r62jPtp7O8uuYsxeUPj7ceqYSelql8NH0Mh5ov5/LTgu5e0SjSDKuAZI4rJT9UyyfNfmbFro6kddXDbm++T2jF1Uw7AB49NhGbAel8lfgIkeE/oA7Nxy4W5uV5ET94Po5B1xjx6jZOfDCX0UkdCd43lqJ0a/qGReKqLkBdqCPELJOjaX7YRasIPTySb7yOETxXS5tpE1FUSB71PkdJki1PX3qS0SN2oh51FVHx0DwKJkz863hont7wcIObqpsiFbyyvBOoVAQVloGQJJ7dQUG2wRu+mbk5Lfs/RmLEKZKjImtEnuZ+jgyzb8/Z+U1o2ETL+OdLyMszdD9+Ny6cqV2C+OlUCn2+PsDxhGs1UuY/jV4j6fHuNNLbKlld5I3dcXPO5XuhdTYY0pgdsqVpaAKvrBuFRbqCBvWSSc61p5/PecytKghYP4HKTAtSL7qhftuOkAOjGVf3MCNf3MaO7FDqz5/M435n2PFoM6alN+PA2XpYW5WhLFVQrlcxf3UfkkbrGLhqGpHhP1DaroiA57JZVehAka8leXUVzHplPt/FtaR+kyT2NtjApve6kp5jR0OnWrMemQkTJm7goVFkb74Jq1dXDTEMkCmVhqPKCsG5ehPRbd5KSKsO6MrPcnzTmd9iN+3VDxsnF/Z+uxC9XveX5XnpJVj/vRUz37ckZGA8P+69RliLcoqKJCqlguk9Q1j1TGv0UjJ0/hFe//kcucW120Q/yDaTJ6dtY/ZjS1hZz5NKa0jcFkC3BhcJnTOZgmAt0ZluxI6cS1GQlvhsJ6LafseJXD80ZlomdthLaNgVAteVkxNmhddiNS86JLLmnZ78HLSTU898SVyJK+k93Pn5RAtCFpVwpuUqGrW8DIDjRT115koWDJlPRHk5ep2C/rsjGWaTS8Xoa/jsKiHErIAGrhlEn/Ljk5xgdnw1m5ENjv/DNWfChIm/wkOjyBo0ANVv07uvdytK4yRpA9/mjEJfWEgYChRKM87v+Z6SQoNJvJnGnE6jxpGVGM/pLRv+kiyJibBiBezeDRNGmbP384YMnZZBDnn0mppElrHM8EAnfnmhI+PbB7D6ZAqdP9/HogPxlFX+dUX6T5CU4sYTNud57uenSZ3RlnInieuZCvYn1sH9eAWH+82id0AUHSMH4f6r4db7MtefmOP+KDcb3FPFXnXh62//h83QNNLam9FjyFiymikIXPssI+P7olFoGTZxJ147BbEvmpFQWcT5w0F85bUX5birOH56hQk/PUuGzpaewRdZl96UpieG4fiBOSkvaZmSOIgTJ+riEHKNZWu60+S7F1h2qD3yposcmzBhojbw0Cgy+H2MzMDvY2TXyVCYY93tEcq++4EWPQahq0hi6ze/LxdSt3U76rQI5+CPK+7ZmTDA8eOGxT7tDMM+2FmYsWhMc54YouDcaRXdv/iVn04mo9dLrDQq3uoXytbnO9DI244Ptlyky+f7WHEk8W9TaEKIRCFEpNFt2EljmKMQYqcQItb463CnfCrtJJ2PTObNAWvx6nGFNwespefMX3GzL2TPskW8lDyAdeebkH7WnawWMKvJT3y9pychrRJxOZLLM8ntcFtpzqPHJrKk7ve4Hdfx9JINOJ+VfNRjNT8H7eQbr2NcKPIg/I0TPNHgFAFm1mwf/hlJWi22mjIidoegqAB3ZQFbIsO4FO9ByXkHrvS05lD4AkonO3FpyBxWhy3B6byOS6Pnsq73bOOkDRMmTNRGxL0uY/Ig0KJFC3ny5O9rinXsaFjKxcBNrkulpywulYT+/bHs0J7tCksKMmPoNeVtGnRsCUBJfh7LX30OtYUFIz6Yhbn13VuzHTgAkyfDuXO/Wf4DMGMG5JWUkx16ilNJuTT1teetvvVp7uf4W5xDcdnM2nmJU0m5OFmpGdnajxHhvrjZmt+1HABCiFPG5XFuFycRw8rd2VXCPgWuSSk/FkK8BjhIKWfcLh+rYA/ZoM10rnbS4e+fieoDRy4/rmZL/y9YlNOe6S77KZPQd6HB16Hr/w7z+uVzhJgZFtPUST3lUkvH919A6MB6eBpJ0e4ErSon9kk1QT9WIrSS5G6WXHx2DqFzJlPmpkNRIfig34+8/8NwzJtdI/+KHUqncgaEnEOj0LJtUXsKA/XonSuQpSpUthXocjRYJSmJfHkOIUsnYbfqDU6eLTNpMxMmaiEPVYvslsYe19EqaD/GA5cXXqB49x56NG6AQmXP9nmfkHbpEgCWdvb0f+l18jMzWf/Z/1FZXnbXcrRrBwoFfPQRVFaClLBnDyxZAtOf1/DTs2349PFGpOaWMnjuEcYuPc7JRIPBR7sgZ9ZMbMPKZ1rT2Meer3bH0vbjPUxYfpIdFzIo1/5t3Y4DgW+N+98Ct1zs9Do6vQLn8Uk4HVeRlOZEyOdR2EUrGbB6Gls3tmbIS9P4tTSQCgc9xT6Sip1+dDDX0ueTVwlYP4GJKR34LKcJNkPTKKgDS+p+z0c9VlP2Tj6Y69m5cimxT6rRqw0fKVGT56DOVWARWMDst5/AumU2tgttiR88Hw+nfI591BJXdQGq3tm4nIRXW24nPCwOsyhL4gfPR2sFDWZPJuapuVTK2tmda8KEiYesRZaUBP7+VWPc/NoOHNTjt3wKRQcPUvzCB/y6dzUKRTkDp79OYFND4yX68H62fP0ZPvUbMvCVt9BYWt2VbMnJMGYMREb+Pll7zhzo1ev3OCUVWpYdTmTh/nhySypp7GPPqNZ+9A3zwEJtsFJJzC5m5fErrD2dSnZRObbmKrqHutOzgRvtg52xVN/e73M1W2QJQC6GCpsvpVwghMiTUtobzwsg9/rxDWknABMAzFxsm7+/tx0LdzyCzkJPvQVFAERPsMZ3K5S4Kg1eN0rVrGi9mMVZHdl7MIy44fOYmhrOqWxvbHtfpqxfKzLaKOnY7Rx7joRRd1Ee0S/YYBVnRs+hR3FVFzLDKZaALc+gsNDS2DeF6Ew31PttiXhtDhHl5Yz/6EWmT1/F0hA/Xr98jqe3PoP5VSW7J3zKgHNPY60pp3C1Jy4rztD6WAFznzhIZlSOqUVmwkQt5KFSZGDwhF/5m9vEm1+bQq2nOKOU9GeeoiwmhuRh73D+wmakLocW/QfRdsgIzDTmXDy4j1/mfIG9mwf9X34dZx+/askVFwdLl0JWFjRsCJ06QViYoZV2M0oqtKw5lcKyQ4nEZxdjo1HRq6E7/Rp70ibQCbVKgVan50BcNpvOprEr6ioFZVrUKgWt/B1pF+RMmzpONPC0xUz5x0Kqqci8pJSpQghXYCfwHLCxquISQuRKKW87TmYR5Cn9n3iFD59eztzgILanRVBv0SSCOiYSe8if4HaJbK67jWeS29HAOpXMClu2LWrPmTfn0HXseDKbqilvXIKHUz59Pc+zeEs3nBpnkpHghH/w1d/KUSt0xJ/yoU2HCzzmfJq5VzozL2gVH2X05PLb9dmzbBG/lGh4/cIgbMzLSc+xw2a/BcoKKOufT3//86ze05ZR3fazYW4n3pm2gjF90imMyTApMhMmaiEPnSJ79FHY8Aejw1tfX3BgJcPtvic/MRt1q+bklieCLoGGwdngP5FK84ZYq5LZvXofJ2LDcfWy56VXnenTz4zkZLCwAHd3OHECrK2heXPYvNngxHjMGCgpgR07wNwcjhz5vWV2Ha3WsJkbh7/0esmvUddYsSuTI1dTKa6oRF1oR7tGVvRs7kCwrTPZVyyQSMw8cjmWcpX9sVlcumpo+ViYKanv5Eg9F3v8be04sM6B75Zq7qjIqiKEeA8oAp4BOksp04UQHsA+KWXI7dKae/rIBn1ewnp4GnsbbGBVoQPfpbfmcfdTrKznScrrbXG6qCWrsYoKBz1rB37FoF1TUWeqcGuRQXKCCyrbCjRnLSnx1qEqViB0YNs4B8cPzNm6dhkNF0ylcY9oTh6ti85Kz8R2exltd4bORyYT02E5CZVFjHvmRRIeU+C5R0HrGQbT+t3ftkZrAV6/FpHZ3Jq502bzxsRn2bNsEQEbJ6Cc/R7xkcUmRWbCRC3koVNke/dC165VQ+7n9d3P915Nya24rSITQlgBCilloXF/J/Af4BEgp4qxh6OU8tXbldSssUae3O7LvlIF8zI642Weh4/5NZbP7o2yXw5Tgvbxn52DUFQIrFIUnH1lDk1PDKMoxoHOnc6x92AYOgctTYOSiEjwQWmmR1yxQPqWoqtUYGdfgt08G3p/uo8BNme5qrPmpfND+aLhasZtmoBvg3TkLFdem72cKZufomXLSxSOtGHLoQ1MTQ0nrdSW4koNl5LcSei1iDZnB5OZY4tlhAVxq2ZRfiXZpMhMmKiFPFTGHgBdutyoyO63srm+1TSCm00huA+4AQeNq3MfB7ZIKX8BPga6CyFigW7G49uSobXgmeR2PPXr03iZ57H+YmNedEhkwvMbuZZnRSeLeOIHz6dXxzNU2BrcTlktt6Nnl9Oc+L4x03tvIq7nAi6vC0bkqgn4H1Ta6vis5Rr8PHNwHRhNck8la77oxvbiUDpb6FFtcGDCT8+iV+tJyXIgaaDgpRXjCApL4cK6elx82Z2OkYNILHakbJwN7wdsIKHXIkLnTKZwnxvWpyzwPFgEKv2dLs+ECRMPKDWuyIQQvYQQMUKIOOOX/I3nNUKIH43njwkh/Kuce90YHiOE6HmvMuzefa8p/wryFltNIG6y1QxSyngpZWPj1kBK+aExPEdK+YiUMlhK2U1KeUc/WmqhZdepBphlmnH6mg+KNHNanh7KulAX7A6a89TElwjYOIGIj5sgwgqYuXkA1htO0c8hArMe2Xy6ux9XtCV0G3mUy0PnEfukGswNCiZrlxcJH7fh8tB5ZLfR8tWvPZiX58Wv//mKyf234eybh88yFWqHMup0SSDzZ1+KQiqx883n2h4PQmyusvXXnxlz4inaTJsIQLGfFo8DBQjVFoQAAAUfSURBVGz/eTleVg/nigQmTPwbqFFFJoRQAv8DegOhwHAhROgN0cZhsIALAr4APjGmDQWGAQ2AXsAcY373xI4df5CMv6FlcwtupeD+6vbgkZ7vQN+WZ9k+/DNST3my44nPeDLgOOW9W9JwzAX2LV6IokzBwplf4P92OYpK8Dmk4Z3/M1gROp9UMCJqDBd7OdFrwEgsXEvw8cph9rNPoM6XqIIKmZfnxfAWx3ih0w7slSXk6yvoaRVF8VFn6vzfRd5vsokL0T64RJTgu0GQl2ONXYKezb+EE3ZsBCLGCu2T12jUO5ovuv+A5ayr1F0+iXytxT9dfSZMmLhHarpF1gqIM37lVwCrMMxHqkrV+UlrgEeM5t0DgVVSynIpZQIQZ8zvnujeHYKCbgytrjKrDUMlt5NRVCPOfUBAfB9bHtk4De89lTyycRpH8wJJH1vO+55b6fPIEPy2ahm0fBo91pzAJhF2XahP6aP5XM23oaAOmKu0DD1wltiR1pgdssVWU0ZSXzPy2pTjOyyaz073IKXMnq+OdeNciQ/L85vy2NLpRE2ew0KfQ3z++TASBizgkXmHKPRW4uOVw6j3NlHhqqWkWIMmVzAlaB9nUrx5P6of507U4dcRn1F6zaTITJiordSosYcQ4nGgl5RyvPF4FBAupZxaJc55Y5wU4/FlIBx4DzgqpfzOGL4Y2CalXHNDGb/NWwIaAudr7AL+GZyB7DvGunf8pJQu9zH/3xBCZAHF3N/ruVfuVM9/Wz2ZMGGiZrn9bNoHECnlAmABgBDi5N2Ylj+IPAzXcB0ppcuDej0PqlwmTJj469R012Iq4FPl2NsYdtM4QggVYAfkVDOtCRMmTJgw8QdqWpGdAIKFEAFCCDUG442NN8TZCPx/e3fsGkUQxXH8+0OsooUKigQFBf8AwTKtFtYiWsVeQTvBUkhjIdZCBBEtAiqm04AWVkIShJCLqEXEhGiQFNoGn8WMuHfiJZLgzay/T7N7s1fMvikeOzO8Gc33Z4DnkeY3J4FzeVfjEeAYaTu4mZnZH23r1GJErEu6BDwFdgB3ImJe0nVgOiImgXHgnqT3wBop2ZH/NwF0gHXgYsSGlVxvb2f/B6QN79BU6vuU2i8z26KqK3uYmZm1rrKHmZn9X5zIzMysatUmso1KYZVG0iFJLyR1JM1Lupzb90qakvQuX/selVKq0sZD0qKkOUmvJU3ntlbE2sy6VblGlktXvQVOAkuk3ZLnI6Iz0I71kY9CORgRs5J2AzOkU5cvAGuNKvN7IuLqALv610ocD0mLwImI+NJou0HlsTaz39X6RbaZUlhFiYiViJjN99+ABWCY7pJdd0nJrTa1jEcbYm1mPWpNZMPAx8bvpdxWhVzx/zjwCjgQESv50SfSsSq1KXE8AngmaSaXNYN2xNrMelRXoqp2knYBD4ErEfE11UtOIiIk1TfXW6aRiFiWtB+YkvSm+dCxNmuPWr/IqixnJWknKYndj4hHuflzXj/7uY62Oqj+bUFx4xERy/m6CjwmTX+2IdZm1qPWRLaZUlhFyUfVjAMLEXGz8ahZsmsUePKv+7YNihoPSUN5Qw2ShoBTpFMS2hBrM+tR5a5FAEmngVv8KoU1NuAu9SVpBHgJzAHfc/M10jrZBHAY+ACc3cxpzKUpaTwkHSV9hUGaPn8QEWOS9tGCWJtZt2oTmZmZGdQ7tWhmZgY4kZmZWeWcyMzMrGpOZGZmVjUnMjMzq5oTmZmZVc2JzMzMqvYDyD9f96Et7BAAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 5 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[3.17000000e+00 4.16144249e+01 2.84227249e+00 2.56096454e+00\n",
" 1.00941845e+03 3.63707502e+02 1.21819794e+03]\n",
" [3.17000000e+00 3.55619866e+01 2.85898474e+00 2.59391865e+00\n",
" 2.51904915e+02 6.84704324e+02 1.20387501e+03]\n",
" [3.15000000e+00 3.96259866e+01 2.77353665e+00 2.48730270e+00\n",
" 1.08155135e+03 9.14770754e+02 1.22451532e+03]\n",
" [3.16000000e+00 1.55846886e+02 2.84205057e+00 2.57704736e+00\n",
" 1.31503491e+03 1.02328459e+03 1.22901780e+03]\n",
" [3.12000000e+00 6.28433553e+01 2.77870790e+00 2.53265039e+00\n",
" 1.65257487e+03 1.01462975e+03 1.22730834e+03]\n",
" [3.19000000e+00 4.81048539e+01 2.89508158e+00 2.62900216e+00\n",
" 3.83816005e+02 1.23834251e+03 1.21315248e+03]\n",
" [3.20000000e+00 6.69983277e+01 2.88419385e+00 2.59493770e+00\n",
" 1.10680319e+03 2.19658165e+03 1.23222269e+03]\n",
" [3.24000000e+00 2.07357200e+02 2.99534186e+00 2.70155817e+00\n",
" 8.55306404e+02 2.36229528e+03 1.23123005e+03]\n",
" [3.12000000e+00 3.68984316e+01 2.77325258e+00 2.52678610e+00\n",
" 1.60622802e+03 2.70056419e+03 1.23215373e+03]\n",
" [3.23000000e+00 9.94559600e+01 2.93663622e+00 2.62525047e+00\n",
" 4.33790608e+02 2.76105321e+03 1.22674322e+03]\n",
" [3.19000000e+00 4.06596409e+01 2.91413345e+00 2.64812787e+00\n",
" 1.07169935e+03 3.29150670e+03 1.22771019e+03]\n",
" [3.22000000e+00 1.96242536e+02 2.96213513e+00 2.68553007e+00\n",
" 1.63334565e+03 3.82717334e+03 1.23892120e+03]\n",
" [3.19000000e+00 1.67551929e+02 2.90098393e+00 2.62599605e+00\n",
" 3.57495177e+02 3.74617700e+03 1.22220076e+03]\n",
" [3.20000000e+00 3.82548196e+01 2.86162324e+00 2.55233803e+00\n",
" 1.26998994e+03 4.42910156e+03 1.23268336e+03]\n",
" [3.22000000e+00 2.05889646e+02 2.95934251e+00 2.68396876e+00\n",
" 1.48393614e+03 4.47791465e+03 1.23992188e+03]\n",
" [3.18000000e+00 6.97958518e+01 2.84447044e+00 2.55785399e+00\n",
" 8.20382356e+02 4.24344218e+03 1.22683711e+03]\n",
" [3.19000000e+00 4.09600256e+01 2.92936446e+00 2.67560381e+00\n",
" 1.91962918e+03 4.01765066e+03 1.23542356e+03]]\n",
"[ 3.165 40.62020573 2.84216153 2.56900595 1045.48490021\n",
" 799.73753887 1221.35662935]\n"
]
}
],
"source": [
"starChooser=psfStarChooser.starChooser(data,\n",
" catalog['XWIN_IMAGE'],catalog['YWIN_IMAGE'],\n",
" catalog['FLUX_AUTO'],catalog['FLUXERR_AUTO'])\n",
"(goodFits,goodMeds,goodSTDs) = starChooser(30,200,noVisualSelection=False,autoTrim=True, \n",
" bgRadius=15, quickFit = False,\n",
" printStarInfo = True,\n",
" repFact = 5, ftol=1.49012e-08)\n",
"print(goodFits)\n",
"print(goodMeds)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Generate the PSF. We want a 61 pixel wide PSF, adopt a repFactor of 10, and use the mean star fits chosen above.\n",
"\n",
"**always use odd values for the dimensions. Even values (eg. 60 instead of 61) result in off centered lookup tables.**\n",
"\n",
"Repfactors of 5 and 10 have been tested thoroughly. Larger is pointless, smaller is inaccurate. 5 is faster than 10, 10 is more accurate than 5.\n",
"\n",
"The PSF has to be wide/tall enough to handle the trailing length and the seeing disk. For Polonskaya, the larger is trailing, at ~19\"/hr*480s/3600/0.185\"/pix = 14 pixels. Choose something a few times larger. Also, stick with odd width PSFs, as the even ones have some funny centroid stuff that I haven't fully sorted out.\n",
"\n",
"The full PSF is created with instantiation, and running both genLookupTable and genPSF."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Full width at half maximum 3.170 (in pix).\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQcAAAD8CAYAAAB6iWHJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy9yY9tWZbm9Vt779PczrrX+XMPD4/IjIgMICkEKlWNGCIBQioxQRQjRjVighiQcyZMkZCQGJQQI/gHSmLAHCmLLovMUnSZ7uHNa62/zTlnN4vB2vfYc8+ozPRShspDelsymdk1u/ecs5u11/q+b60tqsr79r69b+/bN5v7V30D79v79r59N9t74/C+vW/v229s743D+/a+vW+/sb03Du/b+/a+/cb23ji8b+/b+/Yb23vj8L69b+/bb2y/FeMgIv++iPxMRH4pIn/027jG+/a+vW+/3SZ/2zoHEfHAz4F/D/gC+GPgH6rqn/2tXuh9e9/et99q+214Dn8P+KWq/rmqTsD/AvyD38J13rf37X37LbbwW/jMj4DP3/n9C+Dv/1Vv8CcrDefnSBbcBCjgoDSgQaEIUkAdUEAA9SCpvnZ8vQAC6hWJgkv2fyXY6wi4CUoLoEgwr0mTQ1J9b/0/vOIGoTT1Jt3DfUiG0qndZxHwClkQfbgP9aDBroPUzxAIIaMIpQgiiqqgCkRn93905Fx9tneapPqMPPSR+nqJbNdTqf1RP0dy/bvW1+ozam8f1LeJMQY0Ca4p6OBBH/pV4jfuxVnfHj8L7G/uOBby8Ag2UNaXqFgf1nsLIZMmD2pjPj+HHsfn+IxqX9khoaDR4aL9uQT7u2vsWXTv5+dz2e5HnfWZlPrcrY3ju31iz1pfl3f6rICL9d4EclOfxSsioFnmvjjOPbSOg1fcJDYu/p3+q3+nPIyTqM1L6rxWefhZukxwhZQ9mmS+R8TmlXhF88N4SBS7lldIdW4WwXWZ4Vcv3qrqE/6G7bdhHP5GTUT+EfCPAPz5GR/+V/8l/WtHd21TK7fC4ZkSnyRk73EJm1R7QZIw/v5gE6XLuC971NvfSqfwgx3l8xXtjRmI/fczukyIU9zrjvDJFueUVT9xe78gve0JW5t0koXprKAOukvH+DSjdVL7ncNNQnMnHD7KuEHwo5A7xdef/QC5heGDjHs00jSZ4XJBd3GgaTKP1zsud0uGQ0toMuvFyBgDd6/WhNtAe20zo3QwfG9CGpvV4gu87ehfu9lQaoC0UMLBJsT4NKNtMUMVBW0USYIbxSZqgbgpuEnY/PiGVBwni4GXb07RIujo6b9sQCFulHyW6L5qUGfXSAu1/lczVKWpiznYvYznBV2lhwnszYDKziNJ0E6RSdBWWX14z/6zE0pXOPtngXgCzR1IUXYf2wKJzyJ+kfj4yTUvb04Ydy3+dUvYC+qU8XHm5MN72pA5TA36x6e2oAqsvlTGMyFuoNnC8EjrooX8dEJHh0wOXWXIgl9F8j4gu0BzZ2PZ3EN/rYynggY4PFHSpsBpRPcBv3XzhhbPCs2tww9C7pW4UZYvbD5Pp0LuHoy7OggDpAWklc335Vc27n7SeYPafh/iRxObsz0pO/Y3C9tERocuMjSFxWYkRU/cNVCE9lUgL5R8mgmXgbwp+J1j+ZMb/r9/8N989m3W6G8jrPgS+Pid379XX/taU9X/UVX/rqr+Xb9em+XTBysvfwUUIgou2M7vvH7t9d/UNBRcY1+IWX0RRUQpxQZY0jteQ7XMGuzrOMmPnoNd7N0b4mtex7v3oXX3c04JruBE7a31+qpiO63KvGPMrYgtWgVV24VcrjvbO/+rctwl673K170VfeeLb1yjqF2D2+bB2zjev3795+NsOXon6r5x7aNn4HQeT/NqBMkC9d7VW1+ot/ccd8vjDn30QI73c/SuXJsprZJbJewEKUJRIRfBu4J6GJ7lB0/xN80FweZBo2Y8631L7Svr49rX6RtvPo6v1GetAyYK/Wv/MHePXuTxi3e+Y4a0NPXrG9vzQ3/Wr/qMpbgHj6fY3PhaO/b70cubf1bUKeUvTa6/vv02PIc/Bn4sIj/EjMJ/Cvxnf+U7FJp7IS2VXW+WOC+UeJ5xW09ZFHPp2sLiVYsf4HDfIFFIjacB0iqD2EIvyVMuIofHitw1+HXChzx3dP7FmvGkMEzC+Z8JYVD8pOQWXv+9YrttFuJaOflZ4O4PEuHOvJf21u7v7J854kZIC7t3qRPpOOhuEspVx5SFZi9MtxsO68yNnOB3jv6NY/9hho+2nCwH9NmWrV8x5cDpL2A6FaYTz+IHe37y+DW9T7z6cMOnLx7ZJH3bUdpCc+vRoIzPEuE2kAT6F8EWUafmVj8bOTnZMUwNT1cHbg89d786o3/juFoq/SS2g+0dCMS14mxDJW4K3aV5Vf4gxI0Sn08wejY/D/gJwl65/wE0t46yN88mrQp4CBcDvG2IZ9lWUfQQCjdfnkBQ/L0nLR/CgJt/zayv3zvcXSBn4ddXz5CzidBkktpumzYFNpHtqzXdxYFShObfvmXtC/d+Q1p6umsbi7ufJj745JLd2HL/doUkQbYeyYJOwuKVB1o4Ufq3tsu399DeKfvnQnelHJ6Yh6jLzGo9st01uAjLF4JLyngO2kLuAFHcKOw/zux+qCwe7zlcLWzH7wpu63FRCHtbsLmF7SeKPwiigj/YfadVRvae/OdnEGA5PmyebnK4FIjrjvKkELKQnk5MH0TcbcBfB9Jpon0bKA3sbhffeiH/rRsHVU0i8l8A/xvggX+sqn/6172vhGNcprgouCTQFPyNRy8S4s3K574GpF1G1oXTzYHd9TnNjS1eyUIOGedsZ47RkQdPzgGyEDJ0N0LYe3Kn7L4n9K+FxVXh7hNHeLLDh4IqeF/YxxPCyUTOHTnJjHW4SchLJfcWW4ad4CJMp2oDGMU8lGKLShql9Gb5VSCuFCnCODbcFMdw09O+CviD4LJ9Rlln2pBYNyNFHY3LLNcjALsiOFEiNlH8JpKyWL+kQLsXhkeQzxM/+uAtv/r8qRnH4mwXjkJa272rgB9soroJ6OugOKX0yuGDTPfWUzq7L2qMqw5KxXTUM+Mz6sE9tpDqexc3/PK2s/6IDn8QSgiEg1A8NFuZ3++CYQLNtbdwrQBPE/KyIx8C2Sllle0iAnLfIAo5ebo+zp6YqJCeTahvKYvC6umOV68tdPLXDX6C3Cl5XXAHRzwxTyevCvu2eg3RMW2E6UyRLMQTpZxHZBc4dB1ucMQnib0EJGEb2WBzQIp5Hckp7uAYh8Y8pLrYtVHSOiMayItC/8ZbWLyz+ZMu7F7CowEfCkNZmpcTxcKgIsjoWH3qbc1oxcL2ATIWAq5souUWtFHDkr5l+61gDqr6T4B/8m3eM7vrtY3nhf50ZBw8TZ9I0eNEOXyYcIPDd5mmyez2HfEs09x6pLr96fUCDYqo0Nw7Sqixd7JYOvXC+DTjt454mkkLR1o6+/u+IXlFFdpltEHOgtSYXaoBKo3aV1eQ7Mi9AWnqIG3qBHZYjB0UbWyQKPY9q6OsMpIcxReIwvQo27ONjunM/NBUHENumHJgSA05O9zRba9urt8Lcdvgd56SBT+BH7AFNjp+9c8/xI1C3mSGbQujp03mQvdv65gdAWAHfrJnTKGg4mh2ntJULyRTfd9qDAQSwvQogSj+LswgsnWBmnGNjjJ6Eh5dZHLx6KOJMnSIsz7KPbhVJI1uDjXKtsF5QJQ8BJrLYNfcFFw1aHny5CbXMFEsXJkcfgT1QtdEpjaQs6O9EfToziuUrtDc2TJIp4rfOygwPFa6K9uNB22J54mmT8QitF1kuBC6PjJNSwOhJ8PCSmtzbQ7DqpdHV+AYpoaCtIV4juEe74aAzsIugHTVk08n3OgoUtB1plub0d2+WJt3t7CxTmuFVUKTkLLgBiFsDVyO3bvx4d+8/SsDJL/Waqc0W2H//UR8rHzygzd4V9iv96TsGWJgHBrai4E4BMq2IacWBM4+vONGT8itezAyDuRgYJxkWLwUXFSGR44wAG89YQeDOHKvjI9h9bmw+dOW7e9n84AF2h9vebI+sFuPlCJMvzxBnJrbfpaQwUMRumshrsB5JbwJ6E8N9IxTIJ5DOVhXNzfBdunKTOQNTPtAuPesfy34QXFZcVlQH7hvlvzT20/Q7JCDZ/WZ7RZLhd1PR+gzuXcQlLzKSHTsnxfzvBRWH98TXOHmaoXsAkSHeiUtFckwnVRvKFfjcPQAGkWjA/ewECWbay2jo7lxxI2BfC7a4sBbrK0KZfIM9w2/tsekW0Zym4m04Cuesw9Mj82wU9F+96InnSXSSpHBE+487bWQ9g3qzQsLA6w/dcS1sP29RLuIDPedhQpFWLxxHH5glEY5j1x9eYY/mWagNZ1m6Aq+T+RDIG4KGhQ3OtJZorkKhK2BkM3LlrQu+HXig4s7vnj9jMO4JGw94xPh2Q8vidlxfblBLxuaO0c8qZOwepCrL4W4cUi2TXA6UdvZ1wnNSl4qaV1IW0deF5prR3dl/ZunjtIVtC08eXbLj87eMhXPPy/CfntC2ArxokAG97YxwPxecBmae9tExr0nrb89vPidMA5SIC+ry1onyd3QcX25pllE+j4yTcGor9sGvLn1AKUv3N0vkGXm5KM7Yvbs73qYnO3iKxuo0gphX929haH8pcEsvULYCc1OKY3QXjrGx5mz8x1NyLx6eQajQ5Kwfm305niGxXaVrciN0OzA3ZibPNZF0naRFD0sE2UXQM3SS4Fm6zg8M1fUj0JawXhuaDdqBoiDGYNw6w3I20FcV1D2ujF69CBMvUNUZsalfytMp8r+0xPr5EWxBQyEyRG2dp2wh+nM7qc0Sjwxo7H+3IE28+KPpwWJUJYZ1PognSVoFNl5tCtQhHSS6R8d+PD8lpg9l9slbassuomYPf1iYrft8a8tZkeF6XHG3zvS02j0WxL8aSKrkNeJ0Ru+VPrKZC2geKHZgj84pl1L86oh9zrTyHJwlAaWv+jwIwxPzACldcGfTvR95Gx54H7ouD9YH/m9UCrmNV4UCwmHSh++6Ph895gwCCU7cl/wVw13m56UHGwD+nRkOPNIU9DkYHLzfFOBMEJc2VzXTYLJIdEZC3fvZkwjRZkp+NIVmouB8vmKm/sF/+f2Y7QITZtIZwl1Hncwwy0FfMWPmq2gzvCTvFDi2Tdc879B+04YB6jAr2IuVF9QFU7OjcLJ2RFfWQ9rn/H3fo6zymnh46fXND7z4vYEVQh9JEmAg/2fH22AJAtp+YD2Gx34gPAeY1/raGGYGsYYYDKrq0ErGMSMbqdVQftC3luse+TIc/T4PjEODev1wG7XQ1vICyVNtoidq4s8GRWZG4uF9Wj81O7NrSKJujur3b8fayzplTJ6cyFLBfaOfTkJ/V4Yz5X2fCD2DeIL8b5BojdqL1BDJAPTtCvIYK6uKDbxFKMig0IwF7U0jnAdSE+jAXvVa21OR3IWXtycoCoMdx3teiJlT87OMI/kKI1hLsVbqJUXNRQ4mcj7Oi2rK5xPEySHG2z39XszDKWF0iuuyag0qFdbEL3CWaT7srcwaXxgQLSpugBgN7YcDi3u4Ah7o6Hj00JuzdhpAT/az8UL7enIVCpN7BXZO1JylOwhC2XXEG4Nm6GGskf2ASobU+eRazIlWyfnhb2my0y/GRkUXGxscxDwXimVZdMixF1DGgMyOttUFkaLaHiY02FvBtxFcKMxRd+2fWeMg4E4ghSbNHf3C0p0kGrPLgo4JSwSCcxAiHXum/sVqkLOBrbl5NHk8BHKoiDFgSp+Evq3NuemaMi7TWzbLXNvvHhcm5WNFeeQZDGcS0J7YwM2ndoEU2eId3tr3L6Ltsj8lz1Tr5S2kJcTpQpY/F7oruz/0hIkGo4xfJBZfeqJJza47a2QlhZ+aJ2QbhJK+3CNmXalxqlitGhplMNzA7CkAE6Zti1y8Og6GTefheKU1MP0zKgWOZi10kov+r3M6DgnoL0iTbGw6gQTHU2OsjRWSRTKdgEfDnifTOjllemuY/3BgAKHbYfufV2MwvC0wEk0OnX0hJApjcOHTBla0yAkM07pNCO3ASnQ3Sq5gebaEVNnXVEesBBxyvBYK7uk+AED6NbyIDzDaFLccYFiz9MZVekGb8a+AJtIfLmkv3a4yYDDMAjj0KBJCKOQpRr9SUBsvrixahkUDicGEmpXaLtEBHRoTUgFaBTzsPpA7o2FoissuomxX1JeLtGV6X50ne15ywPojdgaKgEOH2X8zs3ej3yT+vwbtO+McWjuHP1b8IMZg90nDc2tp39bxTsrGJ5n8t7iSsR2WUbP4YsNzb0tdpyNentngqUymqhEG5g2SvpAZ4Q8rQvttfHTca2MF0rpy6x4dJ8ukAxdFFZf2efGtTCdmkIy3Bviv/zKMZ5DOFQefYJ4lpFlwofCTx6/5v+++gQmRzzPxIv6zDeeeJFwW486ZfdJtgEehN0PkvHvk4kJ1CulhemUmer1+4ofnGUkCeHRgcViwoly+/kp9IqMJj5icpDFdk2vhK1NpLgyUMwNtrDc3hiTw1PrJyqI6wehrBRuG0pjk717vidOgTx6tFO6F56wh3y1hGlJWUJYKC7C/svHDB9FFr9u7P77I8ah+JedXTvBGDoWf9EynRfolPPfu2I/dAakDhZa7T/JaAgmNPpSKgVooWFcmWbBtYlxk4nqKY3Rg6KQ9o5Cw34fGPaGqbhk86kEaK49pVXczlPWmakX+peB0nhUYHycbdECLnk2/08HQDgoN39gXsvREwy7BxywtFQRVsGvIuOVCePGLlCKcPqDG25enHB7t6TsA2FwtL9/x2Hbcffzc0LFEtS1+AgUT+7g8ElEBkc+zTRvDD8pAbTPJK8m1GowA/ct23fCOEiG7ga6m8J0YrEibaG0jtyaxTt8z9BwGWwxlxoLF8y1Ks0Dkt7cmTtnghkboMUr0yKkve2+tAoepjOLLbVRtCm4g6dsbCeNF5U92Jtis7QwncB0XkxBtzOsYPG2MJ25ijTXhwplFjFNxWhUSULYOsJP7vG+sO0WtMtInBb40zjvZjkaG6NF0E5qCGVu/XRuCse0zoStKQ8B2ERONwcWjQFx+ycHQsjEKZhX9bYj7IUknrB3hD2IKmlRDU9jO29cZdzkzYPwMF5Yv0g2KtJNMs+z4dK4+zAYSq8BY1kqm+ESlMLs4nanA3EdTG5dJdDaGCuw/7CgCZo3DWlj96ONGtC394R7c9dzB7JIpJUtYvUGHHZvbWyOCs7Drp0FQ0dpeRHIq4zbRDR62DtTQw7C+Kgg0SjpqcqyTbYtxE0h7IRwEPxoFLio7ch+sJ+bnaKtbUQlVWxrjQGGp4Xu0qOD9fUUWmgLXZuIi4QePDF7Y7ZuDLAF2F8vTOiXbIN0GXINP4/zrHkbCDthfCJVrm/PfJRUqze6+V9G7vidMA6AgUULIS9sh6TITIepxxabUNV/5mIfJdVghqAsCv7eBCaSTIIcTyzYiiuPr/r1GW9wxgqIYkCYOtwolM7AR/9oJIWASqA0FdxZ2nUQR1rYjmO6BmY0es73wO7veljgDh43CvFR4u88e0nrMp8tznnx6gx3cOTWDAhB8SsDYQ+7Fs2249NZWFUcgKO99DS7Csp2juI8+7FBRDlMDXEI5MaRR89Hz6/5Kp0RQzBjN0gNG8zb8TtHXhXcTma85ahj0KOasOYBlMqbhxtP3hS6K2eS8a4Cq5OQekhL8zzMpbX3jlcLXGOLqTS2UJorj4uweOUYnprhK52FeQosTwZ2ZUEuhjcd50V8NtEsIodxRTpL5C7Mc6W5s/+R9JDbkJs6Uarq8Eg15tbmgYVaEPYWKpYGove40REOVIAP+kvYfQ/ihyPpqkWym3EobbMt7OhsAYsjri0sDTubd8ULaeXw15546mm6xLgILLuJXatz7kZOQrgyHKW9Nno6tw/z6qjAlKot03cUm+YBesK94CcT8+nx+b9F++4Yh/rQ+UcHmtYAqCiQ96btd50t8hIdWhRxgp8MoILaSVEofcFdegMNFdxgrrfFgmbRp1AXdJI5N+BIr+VVQRYZTUK/mMhtYmhahqcduTNREAVKWwwTEIjLCtrVRSAZiIYWaxHT/TdKKUBb+Oz2gjYk3tys6X7VmxY+id1ro+h9z65vzSBkm+jhxpKKSms7VGkF3duzm5xZidEz+ECM3vJIRCn1+0MilsWpLuksD54BswralcrHa5Z3DDL1jwJF63WVuFZKgOl7E+1XLWU0A68eopihPyLmzdlAbM2Vc9fNvPuFveFM/mDe2GFZgeKm0IbEocmUYFRu2Dni0wiipCnQTBYWHY3Au3JldzExNQ2She6VXSz1GW4b/OhotkJ7C7uPC6VXyiiEzjQsR12KFiVcOsKufv6RUauAb+5sTsW14HYW9pimRsirKhGv4rlZGl01OKUY/kER+pAgFFyXKbsGNzjcCIgB6n5UVL6OG2gNiSSbfHs6fZCiI0qzM3xERUB+R6nMEowazJ3gf7kgO8BDA/Pildcd+SSz+DJw+DARtiZWaXdmGdtLE73EE2hvlOGJWfoj0n54ntFFYfkXVcZXjD7C2WJobp3p9TNM59apu7YntInvP7/i13JBaBP6YsnitU20/fcTza1n+31ob6F/a0IeM1TO3PHJc/fzc9qdo7uGw9hyeXdhxqjP5ItC6Uyp113ZTuMSlOhJ3sIolyA9ShYHL2x30oOgwTyksBcSgeiV9HZRGRilBKVbj9wcevzLjvamGrEMhyf28/BBpn2yn/NNUnJMfYt4JQHupqF5HeiujfJUp4wfKOlxpFlFom/JG2F1OrA7eBNi9QV/cHRXYthCgOmDyOlq4F6FeNuZAGyRiW1g2AUzJheJdGKTuHvlcS8895cX+AJ0xsyErVCa6iW4CqYWYfooIqHQ/6wn90r7oiGeBPyTgbxrcNHGrP9FRzjA4akaQ3InLL8ydmY6Vw7PM/1rDwOo8zS3NifSCpYvleJh9YUwDD3DRxH9yMLdw66hexFw0dHcWQgQ157DU8v52H+c53kn2cKX+OdrKLD51294dbPBLzLlbYerYW5zaUYv7JXhkYU++TRbuBMddNmM7IV5NnmTkUlw0ZDq8dy8tLQqNDe/o8YBpwakNLbruGiYgen5q3FIgrSZ0phgyE91YewAZE719YMNDFXC6pqKQnu7zvC4zPHinAKuD7tnac1YoAJ3DXHhuF+16ODRUPCDEA72f5Kkxp3Q3ir9bSYNDpcVv3O0P9oSoycNDVNvN5E2hc0vPYdnSp6Oi9Xi2aY+i3rLaZDoHpJ/qirS7fxMVR3vN3fmirpg9Jsky8hkcEyhmWXcxbCzGoNXOW4oNE1G1ZKXprEx4BI4pkwb1SmkvoJ9i2QbkSjSG4i67kd2bWWYNgkd2qojMU1Js4qk7EnR46vYR6PlwuTemCQqKyP5IURzIwYaRkHrmEp+mB/aOEP71xHvC4ePEn5nhiA8PdD1kX0RkMYA40pt+slyYlSMNSqNMl1k6DNxsFCptIo2Qqnx/pHqTmsLm2R0ZG2gsU1HxcK0ZqfEtTxkrS7zjEGhIPfBsIljyQAV4hDQ5HDVKzm26cS8KhetD7JiadoRZB/meRD2QjwR/OBmnMVNlXJtH/I4vk37bhiHSsmlle2mJQvtlenrwwFKENKywLapiU01SSUbStzsmcOIY3bfnMPvvtbXaKuEazdzwsc8fzB6SoOST5OBgnsH55lNN3GlkJNj80rm3Hs32c+SbEI099mwjvZhILTmMkj9Wnzl8YOy/ErIiwrEBXMHpw3kXuf6COWdugyMhocIULIlfElvtKNLtnByZyh3eT7gvFKSY7keGQ4tzWi0Wntnzz2em3GVyTFNAS3CD59ectdN3C96vCvcvdzgKpd+zAhFoSTH+uzA6WJgN7aIKNf3S6Qt0E42yWtWY4nAAsssVEF3oWIezhbd+UTMHVNnHlFpkoG3bx3TqRLPMuHOU4Ky+sJVGtfCHRXQYC58HDwaHP7gyI8i/a9bhp3JzVfrgeQWlUEwEPPdjEp9+JV+PTEcPOodfm9YgR9tjP2kFG9jvngjpKUnt4o2nv3HyZimvWMYTaOSNgU5m/CuhsOClRi4bPB1sacT0/RoxVLCVmjvq+6lo4qXLCHOH4S892ZUi80/P9qN517RtpAVdJnpvmxngN4wk2+/LL8bxqHIDJKlJVAgnhRSEig20cJBKNODqMQmuJK7qkxsoL8pRjdtHM3O0OvSVm45FKuNsDfAkmSW20W7du4sri6Poqkhs9C/dpTrBZ/tgo2PU+7+zYnmdcPmU6v3sHilhFFp7wvbD1tyB8Njob0B/ukpfXyg7XwdpNLIQ0puFQEdsROoz5ogLwtFTRjW3Hkk2mTRoKaYDDpz3WWpEIUSlHLfQFeQnWeXHL5PDJ9Ywtb0pn0A4JL1ffl0hTr4sksWVrxagrPMyLzK5A3EjSOfJ7ovWkRgHBqmNvLD80ucKD8vT+i6yP2btSH8F4ncW4ghy8T3H99wtV/MuozV547cOdK1J19kmtMRHwrPTu/57LMnpHUFNKdAbpXu2sLG6cTwC4WvF76JDrmr4qqdZ3yUkaZYNq4am+KvhGYP3W3i5t8p5LeN1e24tvCHKnf3O2NCJML4SPF766vtD4S8KOg64UJh+ScL1p/b2MZ14PDMwp7lS+Xmp+bpydEw7D3dW09709LeWciXO6EEx/6LNWFv89xPlpAGNlfc5Nn/MFr26krnvAu/s/8/FilyKrRvjLlw2dNdG3OSFkLphLj+9svyu2EcMEqwHGsnhIIMBljFE+uMdJLNnWzM3U7LWnikeghpCXknhFGRbDLjtBDyRcK1mUUfObxZ0uzMcKgYPgFU8ZJQqPRVa8VeDs+F/pUpARFICgQlPosM9625uAr9dSb1jrQ0t9JNPOz+NZmpNGrFa9bC8pXgRlvYYWvPot48npmBEaAtuF2Y1Xt+wjQSxwQejCqTYjkaNEpxxVz9+0DYOZKHrOAXybIynw/oVUcz2jNL0bk6VkrOQpCaThz2wn4F4c6THkWIzhShB0+6D7wdA2/fnLA8GYjR4/0RQAUZ/ez16OD56vJ0DilM5ls9t8DfVwEAACAASURBVErFhsYyaV/ebPB3nrS0Nx/rHaTlsaAO6K5S1Z3OzApt4Uc/+YpFiPzq6hG72wXirV5HKWK6CfXc/GGmvfTIUClvD4efDoQms1lMxBhgJ6QMYRCm0yq/TzYHAXxrWbtHANpcfuiuzDsD6K4cw5NCaBJJvGX0ioWT47n1/eK1GiV+55jOakGYmrruMgxPlLQq+FVCF4mya9j8IhDX0NzXfllAf2XK0Li2eZKWkHqZCwIV/44h/RbtO2EcJNvDjufAYO58XpcqxXUWxw5GBWZXs986i5vT2pSN6sxY5P74u7llzauGtPakJzawaVOIQ3UHA7M4RtR27CxqHHiuLt6dhQnDs8Tm6ZZNP5KL4+r1E6uwNAq7DxuaHcSlTfrDB4X22sHIQ1hQd8zcW/ggxYRYzb0t7uULmxzjGVANBaOj2TrC1ig2P6pp8NuqfTjy+DXBR0WMqouuTj5huxDcviGvHe7gKMsyKw6ButMIRCXFYDhCzW+xmLneuLNOshCjZmne2/TZSwdqWZwyGnhzBD5lEnSTiUNABMqTifyq4/DE3HU3gTs4hl1LaK10XLOvoqSWuU7GUaTk6u2UxjQsZWH1N94t7rK763Fvq/w4C/tFi2DYjGSh2YlpaBY15j94Yq7KyRc9qxsIbcUHorP7qEAiQB5NGTo8UkqwcegudS4QMzyy0KN/7TiEpRlyqTL5Rs0LrUalvVHCYPMCmAvVFAfhXnCjZ1ybUlj6DAQTVxUzDKVT0tKM5XheU/1bRb2NQ2mVtID27ncVc1CbBO2NMD0+6gSsfoOofVd5h3Js1NgkMY/jSLWph4I8VBU6VsUB4nVvk6jqG47fRYXcPqASPhRKYzqGEmzQcqfIKnGxPLBuR1JxvK3cf1paooufHjq/f+M4PCssXpkwanyWjc7qLUXbvaq1Jwpz8lFzb9bfxVqmrlPo3zH3FZcp/kiFAelBQ2AyWqE63LhJiEsoi4w0bk5nP/a3H2q3eaG9t1Bne2YhB+tCaYyxaa6tA911Y96Vt4WJM5oYILfmB+vB097XhVognhfTSURn4/YOo5bWhemRsvjKKFpxStw1dCcjadHS3toKKg2zJ3VMET9SjaWzEmi223p20Wp9LDcju8nTf9EgGcYL0ItI8h5ZZqYTY1JctM+L567m1hTTBdTScuO5GaBmJ1+jMEkyy5bTsi700TasY13To7xdmyNoq6SFJy+U1ZeO4m0jKQEkK83uYcNIK5vbIhZek6WCxI7+7dHQKNNauH2qX5NGG5hb9UK+6n+WhXiMVb5F+24YB7H8efWw+CJYlmPxtL9c095YDT6XYPehIgerF7D+zBE30F/W+gwXRrUdPkpIbzoFaQty2Vqc1hYWTw+MY8O49KzPDqTkGS4XuMGx/Mqx/enET55e8v31Nf/HV5+w259w/6OqxjkEXt1u+DKekQ4BV+WxR928ilFdGqDZWv3C/fNCd+1oLx3dpbB+YZPh/mNIjdURlAKLt8rwuO5UlUkpBcqmkFslfmATqr2Dk19BaT1jzaTMne0e2inaZUtQOtR6mApn/29ju5LA9vcsaU2yXdsyOGtm5qmw+NITT5T1v3EFwPXLE3KRyrnLnLlZThKyCyYiHMFPgelxojkb0XMlXvcsvgronaPZ+ppqDfuPTMiWe0tWIyhxbV6OfN7jHbhPWxpPLTRc62ZUgVtaU2s2VkWmVws3o+D3jpd/+tTYpJ3gzx928uVLy9xMG7V6B5tC2Hnz4s4K/t4hONLCQHA/UoVZNU/huQHgushzuCTJPLPSmIp0OhPc37nFOSVHT0qekhxy06DF078Klob+aGTc90gyOlkDDBeQ12YEmq1U423fV587XGrnMPjmD7Rm09ZiPYN5za7mZ0xPjOpc/LqhSRXMH4R0+jualSmlgnDvJONpqOKZXmapdHtnqHkJMtfhmzYyU5ii5saG00QODu8LcVFwe4fbeqY3DWVhnsi2LCE6/K4WBe3AV6HV5bjkcGirK41lIgLDXWe79eDnmHyuiNTAdGbhzOGxkJcZbZXcP6j0Um87b1rWh6y0ZW5lFoGFPTVsElLuaLY1l6OxBaxiSrl4Umhv3Iy2yySoc/PiCXtT1YVBbQuqWMKxSvSxalOYwGUT2DQ7KJ1w/eqE/mwwrYZ7KHh6XKjU2o/2GbW4ilecL4yXizkEOCpRSwAX3q025cxDVJOuy2QeoKSan+JtPI8FdCSbyzFXIs8W27vk5gI0uVf0YoLXnWEoi0IeHKV58JgsOY25+E7uLZemnBbaF5ZCLomH4rnZ6N/SqIU3xzqYyZuEfWFjGU8KbBJdcaRkKd3H5odjsSG7vvdHpS+zh+UiuFtXS8cZLZ47QA2AXbyx8CXXSlwuWh+oLyYf/4Zq8l0cxI82Run026/L74RxUFfrFh7z2BuL1/pLZXFZmFbVta3W8eheznHm17hKmV/T+rN2OtOCVoXZ+OKjFv74Ni0w5kBSkx33bwwhThcJ6bJlI+KtsEpf43Yx19P0CPZhm18raeNw11LrIMisFAyH6gbKO+pMarp2X9OYO5058NJYTsVwAX5lu0RpjuGUTeD2piLS6aF0/rFf53wPtckZP4hQhFEbW4wLId9XDEdMkyCdVcyW+kjaGPMhzq6Zo5tj51L/x/WZrk10z+8pKoxXp/MuHDcWvlm2omVIukEovWN6bjUPj4sxL47GoRrOzu5ba7IXNQ+kLIy2Q7DiM/eCjp0Vg9nB8IOEe93N9R2O4Yk2Cl0mdzVHIpq77g9m6HOvc22Eo4YknydK5w2oVqMp5WC1L3NXy785pWkSKXmW/cTd3YK2j+TSUZaFfBDysrDoI9snNgYaghUhSg9jKanqN5yy+569lha2GVrGpal906qgi0xxoF5s46ygZ3srVvOiVlQ0yvp3FXPoC+En94yHhnLfsPwiVHGKcFDLYWjvlGanDBfWUeOFRdfdpfG40wmzbDRnR0nOUrEnYfHS02zNQxkeV0px58mtLdbc19z3P1vw67uWcO84/9QAwP6mcPPjht333Ky4RKC5d4Zkqxkf3Tv6SwOY/GiZmocnpkOQY9jkLPYfH2fDBDbGXU9nMD2tJd2P3l8wkc1YvRk6JZ0X/CbStolh1+L+vGf5UmfQzk8wngm77ynD01LTeGVW2YWtszoX2XAW54To1FiWmqfR3giHvrU06uP4JEc6LYaZHAwj8Fv3NSBQQub+yxMLbYoQAowbq1KlQZnOKtuwF7obBZyV339qMXFpy3zOwsmjHXeXKxgdy88DiNUs8JMVIbbd0cBVqvArngibP7dQwY8QXrVW8asKp0y5aju/ZiGtCuvPPP4A/XUxI9DBcFGPM3he0NYyX/21UYRcteS+shYOxucRnHL2aEvXJK5uV4hTbrcr/MuW8SSzuhH8GKqoy0DPs8dbRJTh00cVlDYjOJ+TIVUtPMDheaK5D5RgXuXh6cMGIqNn8YWfi/zuP7Bw6/C8oLUoT/s6GF0//o4aB42Ow+UCGTztnTEE08bQ/+ERtaxZLdqyMkuYe4s5Dx/Y9tXUdF0XhfOzHde3K0p0hL2ju7JpLtVzmM6qu193ew0mgGpvhFBl1OO57TjTmWc6UTizswpQ8FtPXFn9SIDurWd8nMldYLx494yCas3roSbH4rOWZ2GAWF7YZPe3wRK6soCriU6bhA4eWSZQaNpM2yW6JpKSlSMbJmcVkSalvS4cnloiU2lMNeemWvmqr7UyTifL9tw2pL5YcZ3TRDxYVuDyS8u81OvGmIBVRU7bzOb0wH7f8YcfveBP/uJ7dKuJnBz+ZyuyCt1rz/CRKQHTSYa2kIqgbaF96+dzPY5HD8zU9fF8iz4T2sTpYiCfO4ahYRhMAGS7fv1eQdnu4sA0NFaRa7BFndU2gHSWmaKFf0dRnB8E2QvTI6OCm3slHODkL/ZMpy13nzS0d9Bf1bqg3UPdBqv9YZ/R3HiaOyGdgTSFu7sFvsmk1wtbhItCGMyVn06sDBwKrBL7L9doXwhXAbdU2jvbJErN97F5InMeR3vlWX1l88wqdFv5uFLFX2AbZerN4JWl/a9fJjOCC48LRrN+2/adMA6EwuLRgeGrFS464spens4tIUaDIsmjwXYOSdiOUNOgj660qFUNuljsyUWI2bONjsO+mePO8cLSj503Y+Ankwa7mmHpB8vOkwKHC3MT8kIJX3Q2uSrGMDxLc2qtOhMq+XpQyRE9zp0Zq7wuFrsnZ8xIYyh+jm5G/CVZOfPy2MpMNU0m3nbIJDTniTjYUJVaQTruW5pa9HZ8BCpCCZ7x3BKhtLXcgaOLbNcQyn1D/yrUUnQGqEo928BPBmS6XNWZmP4gJ2fyalGcK/z69gwdHbq00E2dkl8uYGHu9hGrUVfxlgq0HtOO08Li9XLMMkzONB1eaZrMIlgl6XwIyFHTIaDe0V3a4vAHZ+noyUExlsdNiizeYWWw3TaueZATO1h9agVjTj6b2D9tODzrGU88wyMb6/HCmeR7e9TRiG0cB2OLcs06XXxm+RsAxSubLx1pAUOwNG+3iaTqDfqDI00OPzg0V0xotLGbTi2/BoFxcDNb19xahap2Z6B47sxgHet/uqliNKFSv52FTKjYyWpeiK3CJBV7+HbtXyLL+2+/HZN+/lJ79yAOYQbGgL9cTFe+/u9f+9NRC5DhePjHnFb9zueUqi84llyfNf75wX0+XgtHBebeie2PXxWIOwJy796fZDH3uR70IukYa75zgXfwkn/hQ+k3fv7GQTbvvvWIO6hX2ktD2/u3D0lYerwX/cZ7K8UoVR3ahEwIhTZYPoUl+5VKHeucHfrXzSrrYzNIs8ikfjmn+Hr4z1/X9J1KSHM79oGv9SVO+cYY6YPK1tsxAC7pfBzAsRbFDO79C5ofa7n6WoXcpZr/UI8tkCxmuI6VqI8Zu4WvzeNjSb+jnmSuvPXO0YsuKi7+5Zs5ZmQe81DmMgcFSnYGjOavG8tv074TnoMqlD855fk/L+yeGVOx/0DJ5xF3Hwj3jsVrYdpg/PlpQTcmYR0v3FzlaP1poL9q+Yu3H3NMnV5tK910rvP5hW4ycDMuLd1avYUp46OC39vOJAXKQtk/zUYxvQ2UzqS0frIqTs1tmIt5llYZnpraUPZiJcy25umUyqL40X539eyCI2WlriLnq4xvCn0f2d0skGxpzOnFEs4n0usF7IWxV7o781SmMzMK6flI+lFhsxpIxeFEuXu5IS8di5duxjKO4pv7H1uJ/3KSkENNhuqV/Qd1BwJoC9N1D03BtZm3v3yErqz8G1nIyWpC5ie2s6VlnGXmx/Mrc52s3aVhDYurTFy5OWvWdZnuZ4sq6lGGZsHPvtdR7htLxa7io7Iwb6t0toNLEfJ9Mx9jaJoVYzmae6V/05CqZDi31W13VuU5L8zT+OrfDdWAmjxevYVE6k3spQ7SSUFubTc3nMi8wRIq/aigy4x/3XD3+2UuRKSrhIjiHo/k0eOvPbmmlrvJktiKr2Hlk9GOIjwdLXls15oQ78byIz77jyslFSLuujHh2mQbVlo9iMXCwYr54GD1ZMvu0M6bqOE83659J4yDOHOB49Li/7C3487a25bm3qzi6lXm6qd+flgRKJM3gQ3QPhoYtqsZqW+qIizsYfvJMTwpczVnPxp96Ct1BoKKZUHOKO8kuCEQtgY2HrUFolW9Vi32Uf5cFLp7O0iku9ZqdIQDlv11PBnLTzIzCH6sk7dVO8PiTc/+1CM7f8y3IdwL0TdzSrmrtSHjqc670unZniZklrUS1Ou7Ne35wHTdk5ZSKxlXRsgpbh0prg6/Vql3jefLwia9azMlWR1IE95Y8lnJRpnG2w4ZHe2x7N6ZbbmahOXZwPZmaR7JZJW1NQjqPd1dPVeyEcampdnWuptV0JYmq/ykzox5rjU0wp2fjTtS8wtqzcbcK9OJ1MpfMpf+A3umUHUDYV8ZqKXla+ROWbyu6tRzM9bjRxG2BiJ2b+rJWYG5SM2xwI8uE6HLiCukpa/VsgRXbNzlrjWvItbM3StPeweph8PHCb+zepW6a0wl6jBV7LVHN8WAyt6YIBEITWIcPTqYQtUerjIYamAvGHV6c7VC9oHuxlXa93dU58DBhDnbjx54f9u9HsCkcWMDOT3K+BMrLZ6zI0arbnG6PvDm1Pg4Nxg1JYV6MK/j7seGope+gFOmYxn3ZJ5F7o+dzRxnqle6tyY+ijVjMve2SPxB5pOvumtYfVlpqGwCKD8eaUpLxnHJDFVaM1deRqt8u9ik6y5tp5z2rekiNtlCEY4UrOEsmrSi6+YN+b3jftdzcbrDu8KmGblrO6YUSHs70UmDZe1x53EquFrv4Wvq0t5oV7oMo59LjbmmkPcB521BxqaBRbbUYaeUiofgqAf/2j1LKBSv+NG8MVSYToTFpc5GVr3Op51115YtyliLlHgz4Ehd8BXvOZ5SfexHze+EjuUvh3S5puEbIF03A68U/05xFMx454WaVDmbh0oRpnMDQMP9ER+ye/ddpl9Mdi7IpkFHi0n7t44pB5qdaRPipm4enc7lBqFet7r9bhL04FEx7waqwK0x3CeEY1UjC9viqtb9SHZvVlld5z4Kb0w4tXipFcj8HQUktVGm5xGy0H/ZzHXvVm+sA9o7O+k4nthkFmB3vcDdBjtz8scTh6mBRkGVEgrDQipg2FpHjlZctZykWXiiHsbHxdR2XcHtvJ2StbWdvr0Rzn8ZaW4jb/+tJSrC/pNavXnvOB5HnztqFuNDfHdM285VkyFqHH48tV3zCKCOj2qK9h9sObxezpJoDYYPNPcmjEkrE1DF02oUask0M2LgRHnz6pTmwysalwm+kEuhnCUYjuiiUp5O5MnR/WJJO5ih232ciefZKjUdGtZnB8YxgAr6oqPsPCwKfm8pxmShObGTl3J2jNpbeb57b6XSVHh+csdVk7hre9L9mnSSiE8MsBwvbDcGWHwZ7MRpLLYujakdj259XlTjJTrvlrmru/hpQq7CLFkeLnRWCMqhnqWBsSCrP+vmWg65g92JUaPxPHP/E/Ok9LZFxmPpeebw4giKx/Ns495TPTarPt1vDjx5emcHL40N+75HoptPP5eLkVHtbNNj+St3sGd0FSw0mtyRPhxxoZi68oXV8syfL4n1/FXvdKad07LQf7LF+8Lw81POfmb3NV7YiWlWkcq8y+nkd9Q44JR2ZRRb6m2H6m7shCoU7j+23a+5E3L06F2AVbadrlg8ffjzE9jYxPA3D5WCjtRXXptSEgXZhVohCvx9PVkI5sGSiAl8Grj+ScPqhWd4BOvPldLYe5s7o5yOtOEsmlkYCzJe2ERubx5Ao2NZNFMW6gPdOMIUjUr0tVjr8fi5Y1p66SxGVYH+ba1fydHrAP1siWuVr6bHSJ/xbSZfmwgobE0FOp0XwzpqSbzSWPzuD46sSrzpQWF7vbS09SL4OqfcOloKvYDbeqJrYT2hxc01JsNOYG+L8Fftk3p+JeRH0TAPb97L+KwwXZjB0qCEQ2B8bJRh7nTOjZlOCnoRCV1CLy03ZvnCFKOGPbkZHyltPWN1FQ25r8CoOCV0ifGifQBZa0lBF6lHDjhSFMKTg51m/ao39qAxUPMovsIppZ5mJXsP1y2xLby9tSo6mw/u7fT2ZUYPpgSVIsRDQJxaERqxRY2DUmy+yI15Su2NkDYN/vEBsEpjdihyqZXGTV/TbI2d8nvPISyhKyxvqiEA1l8Uwq+Uw7kjrYTuWombb78s/1rjICL/GPiPgNeq+of1tQvgfwV+AHwK/Ceqei0iAvx3wH8I7IH/XFX/r7/2LlTIyVve+3kVA+HrobK26EprLuERBPInkXLTGji1C/WAVm+D+A5qr87oHj6aYGepb26SOYY8CpuOGZa+5hyYzNbmdBgKLroZzJNiyTylU9ibK2ry2JqUpBYXl8YW8xGbsNLkJkFOa5t86RyIwqJNHBYFbWVeSMfnKI253nlxdDdtUYSauoxaTF0iZHW4a4/7/S3pyKbI8XmqKCs+UMDTCXN+gvQZdgEd3XyWAoIVyAmF2Fbpb7JJHmuFZ6LDV8C1tNVQNNnOdFAxwFgx5FkFWSa0LXbwK+Y9UWA8rbUa+szY2msaHTG2hJ2j2ZkYTsXmxfBM5kxJO3jGzQe/uPuA1s+I0dHwALS6ybIjc281M9zFwKaPdE3i8mrNMXfimH7uR2eK2q5SDbVf/daRGhPa4eBieeBSl+Q2o2+t8lTusdL/Y813yVjWbSjkIHV8LaNWCmhb6LrI7r6HwnwKlo6uHtpj6+XIvEmROSw65tpIFm4+Mu+huX+QpH/b9jfxHP4n4L8H/ud3Xvsj4H9X1f9WRP6o/v5fA/8B8OP69feB/6F+/6ubYEDWwdNeeSgWw4PFS24SmttaditaHKyvrNbe6uWxTLwynpp1jStm6vCY/iowS6glm5FpbmzASgKHEE/MCFBz6nML4mFaOfx0pJRsYuaOmUbLneIrPtLcW5bj/QV1d9Z5IZajxqGIKSD3HrkYKc6z6CbCB5nh0Fop+ehw0cq4+6karXryVnsnjOHhIJPoFX8A544ItqLJ22K/CzOn7veO9P9T9yaxmm3Znddv7eY0X3Pb6F6XmfZz2sguMCBECcQAiREjz0piRJWQagIzBtSMaU1rhORZeUIzgwEThFRiVICqkKiicJNpv5fvRXvjtl9zut0wWPucGy9tpzNMufR8pFCEbnz33u87zd5r/de/OQ3kOhNrPVerV0KqLOOTiLGKEWA0SBiBeKIuz+PRYzpbrNCEFNxSmc38gVnvkk3RoZSoN2zWBd8oNdu6ROi9KjbLTo5oy5R9ApcxmxFjkkYgAqmyj+O9pKC136nn5uy2bCYheIffjkxNAq+YgY6Ny3VfKcHJ9EbxkIMlrB29QJxvlPKnfW3LdALAkJ8MuvCbRBib70y37cFwnDzj6Kibic42j+PTNiIHU3gnUL23jOfKjck+L6NISWig8ugUbJfvjjVdV9Lcgzp6xVrbk2i0/TaTKnvtlJfF2g7KmnXHX+JJ/7njL1wccs7/m4j86Oe+/DvAf1j+/Q+Bf4QuDr8D/F7OOQP/WETOROSTnPPrX/hLIsT7StHnX9/T7yvC1pPPR+zrGjtqS6Eei5awUZAvW9h/qgwx25uSK6EhslKIfc17ZaCFo6O5NfS1Yf1KmDZq7dW+c5ggNO8zx09Uz5GsFJ8I7TO7LxOMhuMLy/pbJdWYAP15JK5U0en2UN8nuicGM2bWr/QOe/g3BmTv8A+62/t3vszdFXycDh67N9yEU8xKDVnkugKrrLbdrySyg/XPhLDREJrjZ0lNYj9XyXKqMu1PdDGzBblP7xrNWeg15at7rg+G3U5KLXeWZIT+aQHeCk377JMH7m7WECwyCc3TgXUzcvuzNanKi/8ESdh+DdUuc3wqRYCU2fxM06gkOcWJNo+uVxrKk0gvBrWUOzh16Iq688ZajWnTOhB3njhrOs5H0iYyZPAHg+sydlSKerVTfAqB69/OEIX1auAhGA0vjqI+Fh7SkxH/uia0perykFaJPFrCbcW4Cdg7RzzXgORpq/hO+0Zdl/ZZRWWK+STa16plmBe499dbcm+ZmkheR6aNobmB8corEW6lGoyxcqx/ZmnfZ+qHzHAi3H+ZCduM21vy7QbnoH2ni5odfBkVK+A4bqF/rlka7ZVgvtVR7Pt/SwinQUfAQRfe/qkGBC+xDB9x/GUxh+cfPPBvgOfl358B33zwum/L1/7U4iAifxf4uwD28kxt2E9HnIvYWo1kc+e0jTjqDr/IjIs1lsyjN6/KuLSO2FUgPPjSUwqp0gRsyZ7mGrJ1rN4mxqMQa/e4Ypc+dzbOmKXQmhFZiCVt4vCFliR+LzSv3SMfvqguY6tlXH+hF3J92nPILSHq9GOedMy7QqwNqc3YTdBo91dr/E5LyFldN09BQlPwiFoNTppXJZcxCcfnsgQDx9OIf++W752NcWauw48/e8cfpeeaK3qotaLwOjp8vt0xRUvnK9Jg6d6t6MyKatCdy+8VGBUPx+cwrYX+yWOA7XAmujjETGgNsaLQ1fMyhm7aERE0Yi9DfygNsclINOSjw+7VEzIbbRMo7cN4qrqDWAnNbcJ12n71Z8omjNkwRUsaLVKpa1VaJWRndaM56u7b/eqgiL5LGqeuQy09n6XiyWXRwbCwPO1R4Cj6Pi2a2O0S7tpjriqdflUaV9e/CGAc4TIgnUFswrisVnPW6njZqjlMXCVWP3zg+NUJzTtDbB6B+LlCwxTsqtZ7aNroNbWVYjWzMbIZHq3wzaQckdR+/EP+/xuQzDln+TPpjX/h9/0u8LsA9Q8/z3KwJJdY1yOVC+xtoqknHm7WRMpYK5mldE2VThlibdSks0q49UTTjhyv6uIKLYuJrL/Xm6u+g/b9hB0ddlRDF5KoWjIorRfQfvf5oKlR9zWSpZjfOvJ2wnV+ER65o5KfwlpvsvFMUXAJwvhyw5zJYI/FFOWDs17dK/losp4+CrbTEBXKrH7OQCBreTuPwczlQLex+LcVcZWYkpatqpZ8ZPvNfWisS95FMHx9fU7ulSk5B57IJBA8rx5OOO5rcm8xR/vYOrX5OyrPsNXU7uz0s66/Voei9dvEsBVMpVXOQqgCuBzgqmYaFfBJSQGR+e5JPhNTXtLOZsp1imZ5H/N72P1KYjgv54oyss7Qvja0vzZxdDXGZagi6bpWi71tIjwPGJ+4OD1w3NSE65bqxmKCMIpbKtLYFnOa0mLO6e8qR8/YwmiVoKpOybqIKQCsCecyquTd3Tr8ThiS5pOyio90/jM10o0nkXF0VLeG5kaTyPyhgNFFXh8ez2TJL0lkZ8mzHaGbwWYFWvPM8rXolO4jj7/s4vB2bhdE5BPgXfn6S+CLD173efnaLz5shpOJ9bbn6mbLaj0Qg2UsblBzXNs8Xlq49m0ilIfW1JGzkyObeuCr7Yq0EsKgFA1O9wAAIABJREFUbsT+XmiuM/W9ClZCa6keAocX1TJz98eEPxi1aQMQqGpluU0l3ETBOWULhpWO0ATdPX3OCu6tdTX3t0ZtwWyZ75+pJX6aBKl0HMuMQwD4pDqGqiDLWd+E3xXOhJ/VjEJsDNF5pNfP5u+t3kAGUtC4uvFSQUYzlEDXIKQg5MkwHFukeEqaW7XEm6XjfVdhXCI6Q6qS4hwzcFuwgfn8LE5bBd8JK5haddWOGcImL1OEvFagOa8jn5zveOjrhacybbSl8SejjlLPjxz6LTnpmNuvRoLxGvx1Y4q1vDJVu+cFpG0MkjLDZaZKhbr83hHXCXdQrwQzKZaTsvDD01tumxWvkpBv1rgDJKfS5+OLpJOwolmYjyzaFmWXSbVhvMia0N0poJ2KdF8CjKPBnI2MsSJXmerWKehrlEgWG5aJ08w3EcmkOnN8Lotn5rhlWQCzUewpW5a4BvXL0HuovrGEVoWDdiy29hEwAncf/6j/ZReH/wn4T4G/X/7+Hz/4+n8hIv8dCkTe/4V4A8BkqL6u2T9R59+j12DVwes2qeazpXUoLtHZJ6SO0BvclQc8t68b3l9Oio6bR6p093lgPNMSvLoTjnuNuFu9zbz9d8sEoQF/vmfaV9j7kitwX+NWAdsEYvDYW6dsvF5HVO4oxcNPL9zxBwFpA64OpGQYj47qjVewKLDMy3MTF12H2Tmdp986phJ7N55FZO+YzqF5bRfJMVkvenVvyDtDc1W0A+hON51EZFJQrXpvyxRFq5nYKoknF7rx9IOAbyfiD5L25pNmYfrfXyMu094rDtA9S0pVXs0W8RAuJ9qznpyFsXfQOcZz3bljo+VuejoiNyXpq1JiUX06EKvIfdcw/j+nZFfCjJ92VFVgGBz1ZuCwazDnA/Fe07FCrwEQ9mA4fhHwtxpAHLYlAPiTnu7MYWolZk3Rqi2fKFB48ifQPdWwZvQ08n/99AfIzlHdGWZzGjPqeLO5MmRn6D4JrL5Vr4lc61THbCcEiLcVJCkMXmH9ukyUamG4BHdnCVXSqIBYfCLL2Ph4Fug+DfDbRw0Ser3BNJHhuqUZ5wpXOHyhC/J4WgxlBbpn89gW0rOJ6tMBZxPH3z/D7aG6VfyHrPR9MxUSWP3xD/kvM8r8b1Hw8YmIfAv81+ii8D+IyH8GfA38rfLy/xkdY/4EHWX+nV/qXeTCJiwtgClhqNPmEVfAZpUaFyKMjAZZKwXVFd9CO0CfNT4vNRptl8VovF15oMl600iG4bSsxA7SSn0X/GZkCnoTmTrSrgZCsAwrIR+sjiNdJjQJsMRW/Ra/6xojijaPSnSp7tQRSAkqmXSq6FDO2v9mqy0QUkZrLhWfRm2bZuFXcmqcYpRnpAYvhf/hd2r8GjbqcxEKdZiclzHtMk71IDcV+XkiDVo5yGQWd2dtZQp/Y0b653EkKF4iauOek2BWYVEfIlZ1EL3V5CYpI0CXFnHdVNKn5h9nbRFaZdHXZIgPlU4bAFtF5RzVOu1JtdH7gYQcHCkKBJ0+GEmE8AHtEUhWz58Zy2RFUNPi04kRr2BxKctTCebVe2ROYy87sMtYF3WxKtMXeJyE2FlXIbqhhaVy1HM5T7rMTqvO8VRfPC/gEoT+8wl/5cid4gj+QaBgH5J0MZ1ZvbmzDM7T3da097K0nWoLWPCHMtn4KyFB5Zz/kz/nv/6jP+O1GfjPP/pdgF68ziyjGo0y//CHlweoCA5SlbBFXdkWJqXrMyYYHv7GhG0ixkYmU3NydmSHOoHKXcNsyto9z0wXEWxmfXkkJb05pxLam3pH7ypiNHBVU7835b1Zhou0UHzVowEVKPlEGJwqHYMwnCeS0++btrpgOR+XzzRt1J9Q/SEysgq065EO7WFT5UhFuanGqllpIKInrbqXRUMQVuopKN3sVcESBy8mU19r5UGG4wsY1x6zChrElCAHow7W5ecP5xp7x2QwhbUoGWJv6XaNjjtHteCTwu+I61TIIQn/4IhjVizGGXqT2Zx2WMnsmrzQoHPWhK0wOOJbv6Ryu04NeeJaF5NZ6ShRqF75x0CXqVExnjEkoH9QHGG28QsrFj+G+lp78ebaE2tP98XE+CIuJrh+75dWqf3WqmGMaAU6nQspKq282osaAgetHoazct5yoWjPxriFrjIrfpNFE7CicLIayMCus2w2A/vJIkdNRZNklhTx4TIROqG+Ex1rZgUkc7CavbxX45xUFvRU57LwFrftXQb5K1gc/pUcRgGztImEoZTrpcxbUGT7aPACIOugu0mTGM9Um9F50bg7l8hva6ZVwt1bHtjozkfhpI/aH4a1OgPX65FUqLC8q/H94wMSekNuEr7sqv2zgjbXicnonDpNwvQ8YO49eed0ATkLavYSi+HKRgEuuzOwWxPWSuZyByVR2UFNZcnC8aHRMV9Z/IbLSK51DFlXgTBZ7VvftUxbDbP1D0L1oO5UZpDF5XnWLNhBHY8k5iLVNpjo6V+oMCpX8+9KxG1kKMKvzYWWvsdjzXBu9TNWCXql9spkiCtdTO3OIJ0uWNlaXTSDVg7Ve4t523A8Vd1IOonKZ6gi/W3DMBnNcyzl8HCRGZ5FrR5CATXKZwonUXkKNYTzgGkD203Pw5st9sZjj8LJn5QIgLIJxDo/Gv3UykcZzxL2wREvJ2SlQGX3XKtBt7eEZ5HNHzvqm2IyNKkS1N9amncag9A/1RyV7KB9V4DplS52ZCGeB8376LWyEiMKVDaRrnBabKuEMQZD/d4SWp3u5GcDfV3pAmo+MMqJj89E862nuVHz5f6TgLSR1WbgcNti7xyp1lZnzrn4mOP7sTjkIl32usOq0w+L/NUfBPEZszPLnDkNNf5He7Zf3nBVn2GOWs5W15a094rw9wb7K3ti78lJaF65ZRwaMuStOiz1dw1mr9/vSv5lbGZsIy9IuT9kwlHUPak2VHdaovbPEmIK+27QEr+vNe2JNsO9ms34ve7oYVMWuTI6M4PQlHi1IUnZ4RR4659mGHV0J4Axmemh0jwFr78vX0bCVoN7Ta+vm0vZXCdM0CCfUGtZO62Uf2AG9EZ/X8xXfGGH3pnF16LrKpwrwp8sWrrv7CJpJyuZxwxC+1YR9tVVkXC3omDt3hU3aZBk6J9HpNdWLFWG5o1blJbyAcGsem9J3uI6obnS99dfZuKXHbFy5M7itwPToeIgDe03KqvXDMzM/lc0PyTZIlzLWkmFdSLVxRkqQr5zpG0kjpbVe4OZDGEN1a3iDe37rDGCotwHdxRNwupkuU+JFDPbsnlFVZHGWjEeEkt8gb8zjM+TGuRQQPag9zhJFzypI0070d9XahAz55WeariT3SmL1Q5qbzA9m6i2o2ZuZrQlXSfMZJk2KmX/2OP7sTiA7lJfaRmpYx5Zch39LjOcy6MNvIP0fGDVDDxb7+FzuHtYsWlHHuoVdEXc0gt1FRhfr7VX9Zk8CqEpAM0kmJVmc/JkUBPUa1vo01KwELNQT0OrOvw5mWo81QXE9kIYSrhvKhLuNmL2btEJ+J16AVSdUL0Shl4ZhuNl1IxcW6LfBaoHne9Xd3NkmiYoOx+pXODgNRZ+vuDrrwqAWoMZoPsk4h9Mka8XZeBKMMW+bjgvRiXucVQ3W6+Nq3I5QnnPbxvyp0c+vbinD4638ZTUWap3bkHyZXpkLmaB41N9IEIjBax9nGpU9xA2RtueDOMlC2U9tBRqccksnVu2AsRV9/ozBGhPerrQUlWRMCaeXjzw7rIubZRiAWZkQfdtpya642mCpwPjTrkw7Wud9Lh3KtEOq0JGOhR8yqrEenF5ns9V+TwzcKImyQWQ3eZlI7AfYB9Ziy38TghrW+7tUvGdZKqHov3pFK/qOkf7Wlub5HU0TJXIg9FqexOZek0Hc9eevJ7Ik3psMKr0O3md4Ky/NR/9SH5vFocssP9BwnVafsWV9lsaLCNL/J0SeTL5qqJ5Fli5kZWfOFSBfvC4OpJvvO726LWTCHmdSJUl5ExVOA+4TN1OhG8b3L7SeX6RZC8hu7Mewmkr4nrdPVdvlHmZRaPbKSNXkqhDUm+1GoJFdTePoFwBsIBlnBkL7ZgipTYiS9gv5Y8xiWFyCnQWO31gCfCp7sH2mWmrVc1ceppJJeea41Bu3gdZKoVlRGwh1Yn2tX20Nt8I07uW9tl7Xt2cst727I8bVTR+MeouFVSgsnpTLVJsO+rPG5qiKi38EeOUBzCnTUnUEa2Zis+F6HvUgJe89PCSNQ8kG2F/XxG8wxwsB99Qvaq4sieFuak/c/My4XfC6ipy92t2ceiaD1kF8mSIraG6l++ka5kgJWGsEOy2ZZHYZKYnE6HXnNLQF71DAdND8TCNK60K3U6Yijfp8QdhMbi1XbGCE8UC5hCcWPPB18v7zIWrUO5H+qLTGMCKXUy0AMJ1g9sb+sng762O2ssmZ/4VMiT/5R4+EU4ibmcXY49UK+Kdqsw0k0+89otmgrhOvHp5wavpCXanLDh1gk6YZwNiM2ITv/n0Lf/7zVrL3KcT+VZFWtnA5g8qxlNPqgqvXxTDGJ5mTK/EltSk0vPpjdK+VQfs5jbx8Gv6PiUK9Sv9OTOOUN3OFQjsfmvUcehgmZ4I8pNKEfCgJXncxsVRyg6W7rOAWU8k1+hCEcHeW7pug1yM2JORcF+qowlO/lirGjtkumeKovfPdDG1XZGFiwrAkoVwEZjOBJqEvdFSnKIBIMPxV5U16O+tWqCvIrd9i3ORH19e8YdZOA5b8lETpHICs4rc/2ag/caVm1XoPo0FjYPmkwPTT7eL8EzORy7OD9zvG8bTYtlUplYLSSzPpK+slV55ut29xQ6O6gEO4hnPdYQrVinS1R/WvP2bIDEznWhlEGvFWlKbYOehSvj3yi6aF6rQKgt0uIxMvz4SB4t/47Gj2t1P5wokZpdxD/rwrd5oRiqjAp/JZZq3eu+4I3Q/CFS3WqU0b/SaTaUymZ5GppNAvPbLxGJ2Jnd3yss4+Spx92PNUw0XQd22gxC2IE8HhqNDBkO9Mzr1GiGORgsaO1fhcP/bH786fC8WBxFUkCRWkVxAmoi8txh0RDOdqKnosqqWv2UWQsmjgUrqnVqKOeG2XymivlaHpFTbR1/HRMnC0L4fYMIQzwI5q/hoUScazaeYDUhMyZsUY4r1uxCLCYjrimhLNz7cO094gpqlov9nRv3+2OhWG4p5hxlFpx5WTUJsr+zKaZseQ11MfsymKIzRGRmn/JVcJjRAEqbLwtaKgru3mCIdTvYxpVtXVhYDF7JhehJwN47gM/u+xtrEu+MWkSKQmnc5m/F1YJjso2mOQYHLDO7O0R8r/AQ5KqYz1o5dXTMdK6R8zpkRmUs1lX2paJy2XMcfxuUDBptJtSOtI1KpvV6ora5FFapknGQRmM1ZJ7IK8ODV26PQjeewmNRm4lo3GBHdXCQrEC6TIG3Q7JLRalxg8ZucPSdng6FZjan3mN6fuUlMW/N460a9/3JSvwjTswTZUEbuEqE/V5fx2CYlCw5WR5kngVloaQbB7Vk4LnZgOZdzBWLbuVT95Y/vyeKgN9gSXAIYl1RdWGXsjSGvIqkrEehWipxWjUEkgD0oSBaT4J4faZqJxgde77YwjyZHi2wnYsl/tKM+GDPvQQJldg3z3Dlt9cFK2VJ3KqoykzCuFQegjpgb3YHmix5rvUFDmU3HNmNXQW+MOpN8eb2UMrK4NMXakm3GtYHNuufu4InG6A1b1JLGJaxNjBcRf2fJwOEzdZSyg9J2w2lEVoF0XWnC9r1e5vpGCv9B5+8SPqAli87f06qYyETBnI3kUqHsb1eI1VCXcXTL5EBNVA2XJwfejI5s/dK22c4znpaR9Jv6Aw9GdOf2kclHYqOr22wvX++gfyJM7SPpTaJ+zxLxNZglhSpHg2nC4zSjzUhn4CQQ1rrDp+K2zb2nvrZMaw3C6V8UF/FisptdBpepauVAxFqnONYLeVD9CUHt/PPeEtba85vxsVWa9Sdz6lf/REfl04llvKtxd456J4zP0PuvSiSMMkidsnFTxRKNR4k4EB9Jo1m4Pjnr55dQWLRFQb+Y7pZbOfmMr/7V0af/pR45i7Ik7wyUcda0cbTXQvu2XJze0z3XEWK0WhKbO1dABUA0PzM2gvnphvvfHjm2gTRaTB1JO48pN5QkvZD9E71hmmtZQM9Y/BMp96BtIl88u+Grb54ybYu4p4a73wB/OuCrwDEKR29ZvbSLECug1c5imb9TyXNqI3ZVkpZsxrzosSZx9qLj6u0pTIJ91XC3rqDWTEkpBCpcxnzVagLzjOwXbEadknTK4k5GQueoPz8wdB4ePP5WJxauV5/F4RJIWUlXg3IYyJC9gbVmHsQHj7S6cBsf8XVg/36tQqUq6QI9GmQ0vPr2AqkS4dORsPZglJHpOq2GxstA2KjsPNQZc+fZg3o6OM0RmXvw7oUu5vEsYKqI8VFNZQar7aJJpAThhxP2ba3RgQ8r5GzCzMCzy7i31eK56Xbl4ZkXwgD9j0bak57+5aYImnRhUA8IHRdTJj6hiLPmhTYFQS5GjqaIXU4mDWGOwlEaBXeLc3nYRMLbtZ4zr56VZPDXjvDZoDZ8QeMX/YPFfrlneL0i1lICaUCycjjcnSWcaWZnKopT94GQL6yVACilEpvFeNamj34uvx+LQ7Edy6/9MtqrbxQUau4Tw9YsgSJhm/EnqqufJJNKmZWN8t1dpw9k+1XFeOZorw3DZWJ1rdtKaHPBLvJiFJsNHL6A8TzoKrxXvCA2mXjv+Vm+gFFJKd0LpahmC+FlS1dMW9NJoH8mxI3uvNWNJaxUgrwAXYOQrVls4LOF7abj7nbNzjbI0WopXpBU306E941WSL3BPNjvmHaMl1GNYqNoJdpbZTq6SL5pGe8deaM9rO2FaaMKyWwyfm+obvWHzWxK2wuSDKOxqpIVNVhN1jA+FcaH6lHM1un5kElZq83pQOX1g+5Mi68D04nTNuW6Xl4nBZCr7oVhrHQs+GWP2Ey4qst1N/RPM3EwqhWpCpo4GmgDqbf6cGShPhhkr23U5ByxTtAkZBWJQYimnPcyXfAPsuRwknVjynXSXbiJ+HZi2lfEYMmj0RF16Q/tg6O+Ka7U2wyXialVHIJgMN/UGAoIPBvFlPMVPh+omonxWDGcZaqdPvh5Muq0vZ1IyRPXifBqXTw4hPEkqX9mgDRZ8iZhT0ZOt0eOfc0wrRjOFRSbTtRIWUpFPEcDxsHQhY+3gvpeLA5EYeo85rQIXgZDfWOQHXpRpsz6dSGX3Dim0WjvWDCGXCfsKjCeOEwjtO9nsE8YLsoJSzCcKfAW1xrtZm48sc0010IcRMG1wRBcXgRHHwpvUvPoKK1O0EIaMtNpYnN55OAb6nbCuUS/P1EVZMpLDHtcmbJAFGNTC7fXGxgsw96r3n+vUw6SZarVF9PffLCzF5ENQPAJ6yJTpy7QtJEcM2FyS+mJKAgX1roghSfTQioyRfq75EiuC7NuFrzVkf7TDD7RbEb6+xrzoAzGWHJGZ1wlZwglQNZVgd/65DXfPJxTucBuUysr8tAQxZMmg0RD2EbCFqxV0VHOSjLLQNxqjy3BKA6ZRIHnIiKzneh1KAa940k5KTZj1xoZ2JX0sJQc9U2hbIv6hsbTwPbyQN+pzJoE2RqmUKsX5tGqJ6mwtLzJ6Ugx+UysMs/O9lzLWs+lTSRR1mZa6f/PMvb6yuD+oCGuaqTNhB/1jEeHtBH3Wq38eKhVMnCaFM+KStjLPpMnAavYVVxp6ROiVfp6nTA7y3heqObnA6F3pC2Yl9XidjbrSj7m+Pjv+Ks64i+md0rKiyu0FLxhNlj9mEOlD98FNfUXaAWz9HdlDv8h0Pf4ZubRZF7GgMt/CYv2X3/h4/doRfD43ik9IwnySo1vl1CV9N3fNzxT5H8Zx80/p7w+G8UkEC2dtVfVP/JB+MmfAnQ//Iwf/M5cwElsRn4uHTr/Gac8lRzInIWcDN/uzohJ1F3pT10ECoj3OK/7c1X/H76/n7tef+71ge+GAs2nqXzubNBF5MPfubx+PicfnleW0fZ8D6aV6kFE5vf/wS//ufe2jBvLdZ3Pq7Fl/P0LzuvM+cjFPVuSKGC7AGUzsMBCRSeBvXOPo92ZVfmRx/eicjABmm8qzATHL3THmANWDp+XdmCTMH3i4p8LoTGEda2WcJvMeAkRR/rVnpyE/qmHZ72Ka4LBX2sQaS7pRM3TjhiFdOOo3xsefmtCqkizmog/3WAG7d3NpDkHsTOIzzRv7ZJtmR1F0ASxMvRdhfVJ06kn4fRrgewUmGx1PDir/jAgE7jOME4ev9PXZqMknPFCVZtm54rvoxK6+hcBqqTOylWiOetV1Vcl3MlEfL2CpwNp71n/cMfhaoUMRv0V69IGmKyjx1EXjNWbzLQWbK8aiOZ9ZvdDjx01TPbT33jHFC0rP9H/yVa9MYstfmoTZjNhjDI3nYvsvz3BdIbrtw1pHTGrQFUHukk9QrEZf2eoHgR/sPRPEva2kCBWmeksYjqDjIJMlrQpQKMkotFwYbdTin3bCcdP9AGLF6V3GwxxrIg2I4WHIJNWGN2zpCh/G9mue9K8mLUROap/RarVnr/eiTIS11nX7POJnISuMVByJF599YTqyhLXmShw8lJUtv9cvTzs054YDEOs1Ug4CKs/Eab3K20T/ON42Q6qvmxfWpobxY9IsPvSEE+D3gumtAp/2BJsSz2orqh/Ihw/i1ot7h3SW+JZwO/0mcpJ8PuPfy6/F4tDcpqLaT7QNNih7KhFcDSX+CZo9JiOFfX73GWHtZlVM5CzcDueaElUAm+m80DylniiIqv+qgUD7a2huof42pGtY2wrViUmLhT9RWxzqSYUYARAcqEuF7/Gy5GmHdXOXdTNqHuuWMS0zrhOkKNd3LLd4dEsNBvVVQxnSvu1I+SDlsD+oDP37LJiGb483MVncZqsWr51lmhVUxFnx6TBYTeBfNQyWaIuMKFzypMoUW39hTIt7ai7Y71L9AdNn/Yb4f39BmMyN9P6g0g5vRb+vMe5hDGabH7YN3r9TCZfjJpHWgfG3i0BRBKE6SxhoiVZpfjWN7qIStSdMFeZLGqZZlaBGIxWFi6pu3Wh13cvVBgmVv0xcm8xvdHvhw/A6qKGPZ9otwPj6FTTYBLGqj9HmpR1iE9kp5RrkmIUsbbEILCKUCeVuk8Wf1XRvBfioaSqnRW9zjrAXcV0r9YDzYNZ2p9ql0mVumeFVqcc1b0sFVHYZMb4KJyrbg29Kz6gR9205jHonBxvRpZ7NBfWq33vlSE66vNlPn5Y8f1YHEBL8+rBgFhN0555+5NGktmDKbhBoT9X6uyTfSaMjuQSg/Ua1eYzzkemymipnUT73CqSj07nwaU6SbVOH7JVw9JqV9h6rTCc6eouqC8AlCo16YKlo0tZSmpAd8YHtaYzA1Doy7kqnyHI0qdTvt+MOjFRI1NZFg61GcskY7DbiYvTA/3k6HvPdKjUPi2j1YQp1WwSmjeOYRRcMTVNte6s9tZh94bUWPWUCPo+Nc9BbejUPASkMPaaoiCNUZjWUePWCvbhzONIbRodaVCT12xRLkGGvvL6GWdF5zopZ6TRB9AezaK7sFYAdWWan+tYlJgZNC+jOHypdiQjLmF9IhYjWrJeq+SKycyom4nthXhwdL0Fl+myaFBPE0iTXUakpo6kyi4uX6CVUq5y8QmBSTzGJw1yztBc5yUcWBKstgOHzqkv56TeoQF97bjRjW3aPnpnZrW6ZHgx4a+VCm+SOowhovhb0MlUchDIxdxHbRCndYnCW+UlczVuknJ2Bg1dqu7/nLbtFxzfm8VBJn1IZiPZ2GjLYKJQ3WiC1XSauf91VShKKKXnKJhDRXLQXYpadZlM/uma/EKNOU7PD9wfTvVi+4QtTExJgjtkTv+o9HKS6Z7LooqLlxPNdmDoPPlN/Z0eMjaJuNKHpNmMbNueN1cX2L1lPM0Mn6vpTHPZMd40GiizDnBbLdFsoGzKmVp9eKpfNFO5L03mix++x9tIbQPOJP74+lK58ybzq5+85/1+zRStKjl9xlaJ/kVg83xP11WaRjVp5RJbJS7VqxHnEiEYbv/GCjOKpjSdZJK3jOcl8zPB2aojJMP6ZOQbzuD9GjsK/acTT04O3B7aBWdxV15bl1wowj/s8EVFOj1UCpq6hKkj0zMlGSEgr5ridiSsXynHYTzJhE3UtvCt8kKyUBS1eXHzbv6o0QeleFSGdVJJe+ZRUp918uSKZiVVGbMdWD/taauJqz98ovkVE5j3LXG2tsvKfWmuDaEx9J9Pet0mQz44zAD3vxkwnWH9rSofV2/gtjrBJUiNummNF6oiVVxBR8qrl1arh00knIDdqQrWHdWHNDaQKj0PqVKbw1z+f3gScU96uocK01nsUQldeR05e7JnmBxtPXL71TkuG2L9KAj7mON7szik84mxq5hOEtNBWW12LLTXn/N1cPeOsIm4ThV0ZtKejZct0UP/ImqI7cGS15HTtmd8YZU8NDp4pUKGbDLHF0L/mbInETAHS74YsT7x9PTAvqvJg9XMjLKgZNS8JZwrndXaxN1+hTlY3Rldoj3pmUZHU030vtYJwcHrDbxS/URsFAfpP026o7czO1Hfi9SRu67BSqYfPZUPdMeKs9MD1Xnk5e0p/b7W6cKtx+8MPLS0BzgeT3S3fFpOXkbRd6MZFAAn656rdU0SFbwBHD8rpfpRq4sX6wfG5Pj69pzppmFVwoGxmTFaun1N7hz+zrJ6KTz8WIlScRM4W/ccjjXTfa10cONoTgfONkfuDy3j6DCiTlrqVwHZCP5BN4lp45i2Fv+gOpNpmxk+mbAb7f/z9JgKBepryTrAjV8A3bBV3orfKeGrvtE+4+Bbxhel8vGZVNiyM3D7nfFuKKzDIt+fKeGpVuVlOAtMa8Nw9khZNxN0T6dF8n746pRsVIY+9Qqkx61euiywAAAgAElEQVSS1cRk4mwKUxXWqrBY90mCOX/E/Zt3fHl+i5PE79tnjMMKv1N+T1wbnm32/OT1U53+1InJZ8ByiH9NhVeSWGih2WcNWYkCpkS99aqom7kOqVKEd2aQzeyw+aHKtYqschHuvLo5IQwO65Wk4grybEq+oN1O5HfN0jLYOlBVGkrbT4ojmCBEMrFJS8lpysx9mizj0eNHAWNIDYSgfANn0wdpXpZ879VQZT7KTZwtynFIIMHgbw1TEA4m06xGpsnSVBPWRbxNeJNo65Fx8OpOlKvl/ZtJreRcB+7g6X88KKOwjrgqMA5O/SqTqPdFJSRvtGytEraOxEkQl9mNDUN09INX/UIRNpGEbT3Qnzr62hNCy7S12F5fE6ziBM5HJlMmHuuJVTNwWqvF3OAdxiTuT1v8gyleocUYtUQLaACQLhzhQu3p1s3IGCz7vXKUJagv55Iknh7FW7PXZbLgpg/csGwmRmFEWy13lEXgpQpMbVmzmGUiZgajA6I5Zq9ofGYDlupeqHbano1nYKpI44OOc9uI9BZSmXCZjD/raZuJtpp49/6EPLdfSSuHbIsn6ZOBaVAjmE0z6HspjlezjyRSDJKzjuCd1fZNyvX4cCT/yx7fi8VhPsIqq/FpNPhXfpkTqwMU2HITVPeG5Azrl5nxVAVHsQTHxIpC/9VWwdw5gs3k3hKi0m9tceYNbSZuE9vVwPBppK4Cw+h4cbZj5TUgtQ8O//yBh/eXi6yZLJinPZ9e3rMfKkQyd5PV0s5nqBKXpweMqCYhTPZxp9sGYlXArzK6lDaQcMwpVzk/jkhNGSOm0XK0FaH3vD2e8e/9xk/5yd0TkMzUO6qdBv5KhPFce1qdyetNGp1VCm0Wpt4Ro1FQzidCKlyHpO1ArCzSa4DN692WVTVR1xNjnYi1umXbVeC8PnKcPAI8rD3TxhA2sagOM9ZkzFwJZSFn2B0axuDwNnJ/t6LdDNheNC9zpSBwsmBMiYqLj5b70ls1RQHdGeOjVDwt5ystKVjz+DCvomoxOkVTs82Y7cTZtmPlJ74+bVUrMWrc3ty+yLHwNrr8ODIvf/l7g51QwlGxhnMdhRGa9bP0jm70fLJ94M3xWbECFMJKfTmNyRyONYdjjdyootX13x1jS9Ix8TznHIPV6IDgiQ8V67cGd4ThQshVYu1HrI84Gxc173gRSf7jI6++F4tDrhPtkyN9WLM+6fE2cjue4m/tMv4bTxTVN0OxRRN4+BJipWrGbAuAJ1Cd93RWS3kzGqo/qnX38HmR3iafyc8H/oMvf8o/e/cpw6FifLMiryOvomriY2ep3qpizkWlRLc/1CTrw6Hh5b94Xjj1SkGOJ0GTrPaWN99cYPaP9mZprQatcZ1wnSnfoztbxKlv485ryEobmS41Hcp83XKsGgzgftTzW7/6mjE5LqojPzi55er1KUv2pRNshPpGd7nxXMd823XP0Sb4yZrqXlh12j5E0D43Ka1aSiq07T3Tme6IJ83Ai/UDlYn838kQLw3x6Fm1I28OJ9Q2ss+iJKkzu5S/uMz716caDDwancAYCD4TB+HsxzeIzXS7hvOfsbh0hxb6T0o8fRE82aMQtklHnG9qxtzorig6nnRzgHGlaWLxk4F8dEySkTppbuhYKVeg0OfzXcWdb7m6P1PQt0mkbWa3MlrFFBOX6raMeRtYvdYwpGmrlOXhLNO+1WwOiWXqttXPEFY6Xem7iq9uz0mNGq/EJlFfq9vT+G6luFnW8z+eR/b/+sTp/1njA2y/jRyfGsLPGsZzraYejpcc+yeMX3Ygmf5Z+sBbQvhn/+IHSBRubhrVisxepOu/pvRpYDEWPewaVcQVFpxyDbQXjbWyFFNdXG46U4RNRRG31v46Z+3Xc1K6sSS18MqFvPTw40w8Czw5O/Cz3QUPDy2yd+rFdzkyHbwmMo3FRYi8ZBk82Ry4Obaaj1FVSjiyarwhtY7FYhJN7I7FFeqzCbMOxHWgWY901y1knXIgGbsvQrDCoQ+mJCSvwmMYsIHu9YbfL7P5277lXzt7x6ef33B1uyU2XhWdsKRLzQBkSFriZ1jwm4Xk5RRLSRFslGW6IScjl+cHXn57wfDCYY0CmCkacufofeIO8FbtzmKvYixZBTXcLVMiNbfIuKPaw4dWR7b3z9fkm0oBRi/0T9CFstKEprhJilMMljR6te6/tuoxWkxsDl8oOD1Zi33aQ+fIUcNjFPzM0Fukq5C2hPheJvxOmaqhLxF/ZxOnzw/sDg2shOnE6D107QmrAg7WsxdlIp4HeuuUCDWp5F2msug4/QypBpLaynWiFvapkJlsr7Zz1bX6McRCwZcguDpw+Kwq960lNtA9zWWMD3OwjXndqDo3CGmjil1ZBfJRTXhmEZmsNF5B1h//TH5vFodcPALPz/cYgeubGnfUE+K6zHgiC4qc6ow/HZgqjQmTa4/EwjhLcLrpiUmYtpa9X5HFE8rJ8bsCZWe43zfcTGvsy0bRYAvdriSIDMoNEPRixEornMZN1K7i+roli4qe7L6YgQYheos5GlavzULrlVpNZZMx9HtV5UlWEtV4XqykC9/BBMjFxCMMFimJzKwD1Wpk6D2/9skV39ye8Qc84+31KbGz+KEYlBQ37ZhYyvvDz04wo9CWnhhK6hbqGZmapG2GlAWljaw3A883O+ynibOmow/+cVwrmTQZUiUEMaTJqDjqqGNObUmyOmt1QtwkNU05LS2HBWOS+oJuEsOFjlztsegNBkX1ZYtWRYXRmCpIQbkv44kyF7EZ87SnXQ1qypuFdjWwj6ZoMSJyVKVoaK1yMAqxjBJnPznHXX+iC5rXTcHdO/i8I7xrGE8UbJxHqARlSM7hQRkwRZodKsgewjZim0gUzalwJV6hvlIb/+pWFpwsP3YNxGBIZ8rHGXY6R48b3fXdO3V2IqmPJl7Fb3YdiAf3yLot0yINYFZXqeT+mlYOYjJtPRIuLCkZ9n21qBmX1yTKjqGKuJQVT5CspZ/rv5sI9LBb6U1779Rb8kFLfK1C0JXYZC4ud7zdezIKYEqrrUkOenOlAe0pS3T9u/2G/aGBncd2JYi3yHpV7pvI9WN2QFiraU1wSenZlIudwDgV/USnN3qYVOpbPSgBLDmnLZOBMHjkq5ov/v1XdMHT3bZ8+uI1x9FzcDVTZ6ke1KsizSYfCYQyxhJ1UVok8eVcSlRTF3tUzUB1axkrXSyG6Nj3NVKmJQBtOyopycDQeRVWdQ4G84iZlAsnJyPRO+xmIohGjqeoM/r4tqW5Ngsiv1znqAu4CTDWasoy05mzsEwTZjqwawNhsBypiUclDOzvvYqVJiHlkntiyzkoe4PrhLHXHA5ZjIwfJdvJZbyLGlI7UUJxHt+n3U7Eg1scwaOg3BarVa7dW+xFrwC4jzr1KFXD6jUcvsgLzhO3Cddb/INhdB7qhNgiDkxC/c6qGe5QjG5nLl7xnszziN0pgWv+jM07Q1dlZFCn7I89vheLQx4tNy81amr3siVuEs29YdqAO0B/oa7BoTAcZTQ6v280kWnaZsYziINFOst1Fth5chvJTWL17EB3UpNHQ6w91Z0hDJ7xaLn54w1SyjJ3FMK7mngSsHvFB+ImUr10dJcBOVpuX57qjgHkT3qmToFE8+BY/9Rp0tC2MD4LIaV6b0l3lnAalQhVDE/MBL2H6pMDq2bktt5Qf1PpKG+fyd4oQ9JmZBOYXiS+/urpIkL6J//HjxVLaSNUif6J0FyZxQTVH7SMl8Kj6J4nuucooWet4Tux88TREFai/o1Voj4ZGHrPT795hn1XcXxeIybza59e4W3k63zO5frIm7st3kcOoyX7hG2DMg2B2dp/+2yPlcz9ZMjFXm281HFgaNWIpj7vaarA7vUW06l03wyixLOTkfbXDxz2DWllmbLGF6RKJeGpa+BC07vWFx05Q7evkdtKqwIxJVFKJxihVWOd7DN2Z6nuNDQ5jVo52ludXKxeZ8afbUnPM/t/p4MM0/tazX/fOIYXIFXSdPLNhLws7FBRtWxuIqt6YrpqiWOF+Mz4NDDazDEY7MmohjPBsDnr6LoTJAjrFwcA+t4TftRjXWLaVxDVuKa6Vyp0dWWZzgV7MRA7dYM6+/TAzrZYlxg3Du5amtcWOypg+bHH92JxIJfVW1hyAWexiDtqmRx6SJUhreNS2kmhmZoAU6ueA2k0zJHrjMpIHAev/VkdibUnuTmOTpY+EJEi6sqYg+6kca3vbbicRUeFgSYKjMZeA2GUMq3veVoXvnxVIvx8AjHYo97sswpyHsfmJtLWkwqUhrLz18oMDCtNc5bRwG1FOhuVL4GOK92DKbRu+Y6JrR0eTVWUTlveY3G1kk6Ioyc9V6+ENAm5QsvqIAy7eqGeh4uJz57f8e5ugzVamlYusPIjJ+seI5mjqwGDtQnnIsNkEJdZn3asKv1sUkBTjTbR6y0RyMJwUIm06Q1plZgKczQ1GSeZ2kWOJsPpSKgc2ahvxnQZcLcOd+UJ50KHRhjmpA7ci7xdWIJlMQpGUyWi0UUx+UcsxnYanei7vFynutGSoTc1swkQUciD0UnTYHEBrQZH9Dxny/FYl2tVANOo30eVMCYx9RWMhv3rDVVXgpwmS86Qi4nNFEzBr5T3M2sy5pF9VQW6ncdMws2rU84/eeD+fqU+JgFCqU6+wxX6JY/vx+IgLGGuthOdFDRZ+e15DgQVZKLEtmmAq0R9oM2kVOUwWmQwSKcuP7FCy/WjUxNUQJ6O5MksfALKA5MFxjO9+VOdCPLB6u6dApyzclQgmoxtI2nK6gHQ25LMrYCUnI86Knxbs/lGufTzkb3KkxFF8vtRqcZ4dYOa7cJsr1p8M+hntV/XuuAIhZJbFsbLgAzqGGX3hrBKmiwdSo7oXgNik9OFSyJMTUJGi6nKyAudiXM64apAnEpS9d7x8uUFtokcJ2VK9aOnC559py1HOur5MYVOLT7hm8BJ27PxI7d9W9SLOknKSZQ1ySO+E7LAaWB91tEdKuKkvfJ0V3MTDfm+gu1UVIa6qNs7R3WnVaU5WhIwJMG49KhITTqyzqV1y2slHbkqEiqL+9YRZM5iVd1DrIToC7HuA2p8LgY3qcrFNh9ia7ETxQi56BgmIZwG1quBh94RM3q/zoB5NJxuenYmM1y3eg9HbW3Gdy2cTOTRKsGujsRawe1pmxcaenWngUedNLhbp2PfOtFWE4cqMmUpEvMMRgr56+OO78fiUObO6eCIpxPce3WerpU+HU3JqqgTslYRFbao5ZwQzhJ2M3GyGniIG+gNwydRH3yB6k0ZzWWoL0f663YxCJ1Tk5Iv2YKjlFk4jKYhb1TfkPcO92AXZ+rsIFQJgmF6cJjLkWOjJiQkVMPRxqWa8PtiuHKieQd2KBkWa+ivW/W4nEyxvE/YuohsgiwKSr9TGzgMhE0k+ULQCQrmZp8Ip0rqaqrA9LM10Wh1oeE2wnCeF89OU0WMZMyVW5LKqzpwvj3SjZ6YDMdug/iEsZE+OE7rnh8/ec+YLOebI/fHlvpMPfJjMORvVtQHYTpJvLptWD09YG1ite7ppGbVqNHp/e0aSUL7tcV1MJ6hFeFZx+npEWeTOmONBvNto+YwlwWzaRJYSFWEGwWlm7eaJTKeavVVPxj1Qygirhm8dLVG6023NfZoqO5gkXVbBb1jI/SX+jU7ZvprVY3KpOE/45NI9V4nYfWtQYrH6fGzqMzZ4mD1cLV5tJ+zqLFtqUBDNAz7mvalw/zb9xxParjzmpv6TlmvyVniRrAnaugzVto25zYinV2wGBNAnh9xLvH6zTnGJ9b/vGE41zyLsHPI0+GjH8tfJivzC+D3gOfl8v1uzvkfiMgF8N8DPwK+Av5WzvlWRAT4B2hm5hH42znnf/oLf8kkmFcN1VEAr2k/Rll+ycLpnySmtXD/pSFUjvWzAyKZ/fu14mtOiUK1D5y/eODQ1fz4+RXvDhuuvjln8w30B6tuyID5gGcwPZ+otwNhcoy1p35nF6fpXCW++PyaXV+zrkfe3W6JL/VGcUchoDdM89YyHRs4i7jLjpwM8aopqVAUe/NiW15l6r0uApKgurEqIAsVrkTO2V5bitTqmFOCsjljDdN5IvtEe9EpISiDeV+r96PL+HYkRqMP6rNB9SNXals2XGYNTOlUyh53ntRE8tNAfdpjTKb2quE4bXtiFg6rFl8FcjLc3K8Z15YxKIkqJWHdDohYXLHNj4PuuEMBcKfRkX1kHDxx75iaie5YwcPjrTfvcMlDHC1Pt3ulVT/ZcXe7Jh8M47nmiM6gJzYje6c6lMSS7QkK2I1nSUvxg1lcxQnFcHY0SEmjGs6rR1Nc0es0XkYdSxrFt+zJSNNMiGSMZFIWhjOHyUJ/9DAZ3MnIZjXQ9x6bDCloTGDaqKrWDAJPRpzXCutifeRwrOlfWOpomN2+UuHtpArEQ7RW+ShJVDGaBGnUuzQNFvGJaZt5su0I0dBcaBvXnTVML0ZslYiT0YXpI49fpnIIwH+Zc/6nIrIF/omI/C/A3wb+15zz3xeRvwf8PeC/Av5j4Mflz98E/pvy9597zONCUBl0dV9KrDOVpX6IwMtgVI7s0rIqYxPjoeLoI95GLk4OPG32PAxKlglNCR71JeZ8FTEHS3Vr4K4irL0G6c5KvkJH9beWN7dbpmPF2RdX+CrQlUi+7VcOd6ywRYo7FSeiOFnSwVPtPoi1f6HkqPn9tleFjJPnfrSwDmfJOiii/qDgmES9afMK2EwYk+nuG+qtStTHs0mDfGxWNuagjkmSBKKmk+diYisllFZ8sUYrO5m1iW07MAaLt3oxfrC+5+3NCZvVwN3dGpIwVI6hrzjZHrEmc9Z2GDIv70+ZRqdVwzaDBVyiaUcVipXduztU8F5JaWaUEvr6iAmkVyu+LizInKHdDnTFVZlRHyKMqjFdV6ZUgy6c/adq6e//uNXsTNEJUjoN+nlLG/rhyC+ssxoNl/XB7yA22oLGVXlQu5bDU8eT5w+LKc3+rmV7ftQRsEv4KjAMXnNSB4tpw6MpcGcWB6+cYfxmzZ90HnlfkdeRygfNZmk0xV2CPpm2h+SKteAqwL2G/sZGeSASVWhoJ9jWA+92G5xJTEErXCale8sqULcfjFp+yeOXCdJ9Dbwu/96JyP8LfAb8Dpq+DfAPgX+ELg6/A/xeCdX9xyJyJiKflJ/zZ/8OKQAdOvufL1x1X0p4KaGlk/o5xKAMRhmlJA4rMOitahkaF3h9POH22GL2VoksbfE7zILdBCIgV4bpVC293LOOaVdhJltGQVoKDscK4yPv92u6XfOd9/3oDFTu/aOBvkakqC0LrTY7zZOUoPhIf6mlIKn4DHjd2ZLXxcGMCsZln/XGSGp2k13G+aQGq8EQJqfju9KHz05W7XlHt6tV0h2L/Hk0jwsPqClIOc/uycDJque86QAW96bWqqpVilNTNv8fdW8Wq2uW3nf91vRO37Cns88+51SdquqqHuPGdmwTOzFEwRFB3CPCBQahSAEJLhCXXMANkYCLcEeiSNwERbIiAiQX5AZLYFlYEJzEsU27q6uraz5nnz1/0zutgYtnvd8+1e5u92nSUvFKW6dqj9/3Dms9z//5D0jFEBS7rsDaiDWBTVeSktB8965DXmGKSOW8VBRrJ7iAV1BH3GGHv6whSWsUiowLGHltkCuAUsxUk0r72L1kIA4atxL5figTJinctREjWOR8TjJ7vCIhQPVkOTfdeHs/BMgLhGJ4kh+kUTE8HnHPHfbKcTerskeDorgwbNaW6smWEDRVMXJzudiHzkSThAmbad3Ky2Qi6kwJ31ncTuGVaETixlHeSKugAyQ/vY8g3paVZ+iMjCotwv/IJ2mKWrA6Yk3Ex0gwUJzbLO2GfvbTqRz2h1LqLeBPA/8ncPbSA/8caTtAFo6PX/qxT/LnfujiAOzzKf0MxgO5YH6WCMvAemdkUcjBuLwohYbcaQnDubHYrWJzd4RfBq6XI3HtBFewQjGNCy/BotlmSzee3dtw+E8c/YnCfjJj/MYoydJHHr0z4oY9aNwnjs0D4TXEnAK3O0u4rcrScu53npXsTuMyB7ceyy5cXJn9rNx2MDZk5alIfUOtGU4iajkQNcS1E+v5zIhDSa7lqJyg10VCldJHqjJiry0oTXWhSLqk+KWNVElRMa4ENVe93ntApJnfG6OG65LnO8t5cSBYSVAw8/zaL36b/6N8i8qJ54EykbLwNNXAvBz4+ZNP0CoxRMt3Vqc8U0s2bzn0YsR9UOFDyfVzMZcthwlEkwzQ9VuNMGA99KfCNjNHPfG8kkWxErl2UXjaymYqvKK6UrRneRT6cxusDYznM2KhsRtN9ULcpfRsZPlkx+CttKDn8z2jNmmITaA67Oi7hlgIX8VuJFxX38pjYQYRYx1+W2IJh2dzin/5Tkx2VjOKW024W+AXidVDjb4V1mSshafgHw645wXFneLg/cjmScmk6Fx9A8bDSJp53McVRaco7mSj2T1OeWqVxOh31IyXtSzU2RvVtJbxKFB/5KiuEx+Nr0lrlsOd1GHE3kn7ioLU/hQBSaXUHPh7wH+cUlqpl5SFKaWkfqgJ4A/9fX8V+KsA5uiI+4CZPHZJ4pybtNnz7nUrb1Zn9heAuzXC9tPSd6pRw2VJsblnoMUyK+e8QimJwDMm0hnJkBDNRX5otPwOnR18yeKvKSMRLbLq5GD79oiqxEDG3gmirDLqbDqZRycjC8oUKy9GMXx+F1e5wtBJ6K/kqUO2hY+DiGrGB3Gvo9Ctxm8dqtWkPPZEJ4ZenLNTgsdHa8aoee4NUWedh4tCMc5+k2xzpmYUt2WsOE2VzcBjd8OsGiiMAGDmyNOUA/Ni4KBo6aOlDQ4fDXddRTeJoiY2Yy2lr04Qs24iFlIu65faqqn8rpse/9TTrirJyPCCa0wZJW4jEQLDMhvUTHbr+dokk2AQc5Runt9vrnrM5t6kV1pMTb8tsBu9d7caDhLVC72PtTO95JW6NmGGRCg1bXb7Ikl1aFvYVAi/o0hMpjGpM8KjuFOU1wm3DXtjne5ECVnOIQBppub77GkSXcr3EjKOn3nxy7ize9UtIGCmF9JVMsJ0BcAm7JWRQGGbMZ3FT4khqZRyyMLwd1JK/2P+9PnULiilHgMv8uc/BZ6+9OOv58997kgp/S3gbwFUT56m8lbRngqSXtyJuErGVEIfDvMIRWS0sgPbLLOVMlwuuI7ZjdjLhfMkxsMkFFqdiJUhdA5tZc4co2L7utyY/cPAfd4lwlyr5Gf9kMegWe8PeXpwaYmlIRyP0qfqRBjvDUWiU9L72oRCVJvmUhOnmzlLx/fGonncN5W9qYyiisKgOk1xbRiOAnYnzkiql0VMb/V+6lLcCFZjbWTVlZzOtrx2essnz4/2RjjKhOwlKZiE8CAyOSq/Fq0Tf+fTX+HmbkZbO+xxRwia1a7C6UhnHG1wdMExBMu2KyjLkV0lMuxQChU5oTHZ6ESkw5kKvxANSroTSjOA94YQpPyf7sxJ1anGqa2UFqpYKbqdjFbtnZFdFkgOIT2B+EoEzTCIzZrywoD0iyAMShPF70EBAexO4+di31afZxMeqwhOxpvRKcbbUs5XHbGtYZxBmEkcgfZ5xF571HWxt8A3febs9DKej04JoKpkwlN0yOaXq8pJYDgcyfWQhLGEP/TCAk6g6sC4cjQfG3aPMl6F3uedxpzK3T0dqT9we4eoVzl+nGmFAv474Fsppb/+0pf+AfDvAv9l/vfvv/T5/0gp9RsIEHn3o/CG6RjnclKSncw/ZKetzg3DcSRUQfImR0U0Gncnvde0MMQiSXJ0jv2yO7ffTcxlse+FU1cSy8RYRkH3vYywJAFEEatI9cJK+GsDPCvwy8jBH1qxkPOwfioy2dW/MKAyvffgXb2XGw+HoitQQcHCS3pX40lesysM5bXZA7ChSnKDLkbo5UGpPnPYDQxHimhk4qGSlJnFjTwIySbMNldSvVQpw4G85v4kwPmMbua5uVygdEJfFLi3NvjRsFzsWK0bWRAe9uJD2RkR7rQyLutMybuXTyiOOobB4kfDYimYxKYvGKPme1fHNOVIiIrdqmJ5tOOrbz7nX3/0B/xvj7/G7333qQDCMxlDJ2MYlzJVUZ0Q1EynSBuhMfetI+ZxX/IWszG0qt5XcsNhIinZAEhQvl9RXsP8s0B3oOlO1X1Ke4L1dw4Fu9EJVSJhyhZwmYwVNMy9vPdZYHSG5mNLcZf9GA20DxO+1nt+CXnBTkGxeidb1mnQd26vgGTjSIVsTLpX3HxDcfkLhvJa5OLDcUCt3B6kDZmA5ueJ+rlULqpAWq3FSGgNeC2LYJGnXqPmza895wP3kOKwx/yzeZa483nJelB0jwPu7qdj9vKrwK8Dv6+U+qf5c/8psij8XaXUXwE+BP7N/LX/BRljvoeMMv+9P/EvqBw6+lBW/JDDaZUXroOUfhZ15SgGKU19I8atbk12oVbEMtA82FE6z41dSHlfB9EuqCRxb4di34ZNqFaizFIh1nEoCMsgseXZP7K4U/ilPHjbp2RQUaYH7sIJSPe4Z/2lSDi8z9LAJGbHLSbB7ramPuhoLxupenayqOkRSIruoaFX8pAnm7DbvOCZLLBR4rU4Ke1Mp1Aut2FJEPn2TIxH3I0m1THjCUref2/gtVbMYYylHx3LxY7NrmJYlTx4fMe2K6iKkU1R4s8bUZcGxbzpqJznajWjsIHeG46allVXEYKmGy27bYmrPKvrGfOq53+9+IY4Vh+09L0jJIVqPKOG6qRF68juuiHpxKjt52IQVROEpBak3SguZNdPuW2MlsxNkHtmdh7pl5r+OHM4ovA5+FSqitFElFL4k1GuTVAySfCaZtmxW1UCbO8cxkvfP84F90omMbw24K8lCNcMyOsa7H0Vmdj7cdhbg38QhCxlo1QGTgxZ7FrjNsLALO4Mmzeyp0Om0YdG1C9NrN0AACAASURBVLDb12MWG8LQyOjUNp5wVaI9hLnoKViMlMbTPNgx5njCvVv90UAYDL22zN+Tca9vfown/fuOH2da8dt8vkN++fiLP+D7E/AfvuoL6Y8ETFHZ4wCV8AspvYmiFYj2vhyfeALjnPuY8kGmGAd1x2ZWCssO6bPRCfWwx6hEupWHepI4R3Vvxkp21klKUGM9gu7U3q5u+rt2lxcBBclOwShKRpZKMi13G7GYM3eG4XaODQq/CLSn9zfE8t0ptCWfiNz/xiILhnp9bxraRFKn9hmMvo7CxssLiKo9Y3TiNp2ApIm9gTIQ1o6+lDFoSgr3ffFoSiV2XbHvcVIUs9XaeWZuoDr2lMbTB7llDuuWZdVx21bMjgdevH+CW2k+U0cMpxYfNN1OPCyLo47lrGM3c7IA7Sqhv0ehk3uXx6wg0XCZ2BXngegtITuQ+7nEIfq5RY1iyhtzONC02Jpe4VZ5JK1ARWlpuoOEroKY7uSP7UWDbjxmJ6zSFKXkj1nGnmzClEEYskrajilnxG40fhZhEJrzpPZUrfhW4GSENXu4ZXvZEGqFr/MiN7LPZo1FtgPI0yzBtAQvSy7iOyst4JSNshgJzmCflbyrzlBXcu+VN6AHSffufUV63O/5OipBeftKkOB0K35BjuxbMI3XIIN0Ju2/9rmAEO6/7weFmrx8KCOp1drIzVHc6n2boUOuBrwAgvtwEf19vzbjAWnCBX7Q5/KiphQojZTh+vMvTr087ov5fav00s9zb97xx97I/b/p+79XpXuQ8QedW82e3jwd6Qect5TUvYNSUPio8UkToiYmUcMCGBWxKqJzT/xyGExMIslWWRatVMJo2UlN/v+9evOlf0UpG+V9TH4QL1/z6bpM/04fGc/YK1FTdobKX5+cqOQNvvzx0smaFkU9XRP5lDHxPlQml+x7sDCJhuNzv++l+3fCCyTEiPvr/n3fP1XJE/bzebB6OgH5f1++V9L9+97fD/klMF3H/Pr+/6vKfOkiqiAnPMwi7lYRlcoOwFkbMMC4gO4sEGqF3ag9GKdH6J81fNg6ZouONmrCxrF8uGGzqairkRAD26fCuIkz0LXHvV9DgvqFJtzJWGsq0cZl2nMwkpXXGKsgluoT9bqJUurpBK3BXRlCk1i7Au0lgMXPJsBs4jOIJ8DukSwWs4+kyokGGb3OAnY+Uny7kfL2SBh+YiYS0L2GBz1h6wQXuCspKo972rH+bIHZGqludon+kbQZKRvM9K1j+3wmwbw7I0G+s5aYFPNi4NPigBDEIOatg2sAntY3/N9Xb3C9bXjz6IY/evaQP/X4nPWuJAaNPh5QZ55KsWdQhq3l7PUbnszv+Nb5I/7c0+/xyfYQrRJ3GYwbdQkRihcWlasSU4I/8tjFQHE6srurM0gsQJ4/CJnfotm+AaREMpHld2TkLa7TokI9+PKNVETXNTFXdCloTO0J2aPCreQjOhE3dacJfzKibGTedNx0lnreM55a3ji542rbsHFzsJGx1Oi1xewUzXPh3Ky/PnJ0vKEuhCeyHRaYIWMlUe7fVORqwCDhvk3W7uhE8WlB8zyxsgbTW/RXN3gXKR4NfOngjjEavtc+JrViY68U7J4k6udScZQ3il6JKtVtJHZAfb5Q/LGOL8TioD1UF4r24ZSCzT5hOKm0zw7UUxmfvRMmM85p5yhuBBTsi8QuK+iIin6wxFEL1z2yX3VRiFrQJCHe+UzG0bKCm+6ekktSwuVXiN5/otwmZJw55BsOSywMxbUgxypNbtNIyrIR1aSKoAaFn4vWYnpdKuURYCEGMb4Ry/XkxFpdKg6xKRty26R1QhUR5zyV86zzvNtcG0BhVoKndG0hir+kUKMmKdkV28Fx1LT0wWBUzDkcsJwJj6I2I3PTM3MDbeF4o7nhD4Yn/D/PztBa6MRaR2LQuXLSeC/p27vBsfMFdTlw3i246ysKE2RHTsgIu9d7n1ABAgWw9MayXOxIS5k6+MEQNw7dCUBpW4XPlyGW0B9Ju5dMvk+M+HqE1ux38+iFZRlui3sbtSQLf3Ry7UOVsp5EfqiaDYyD5eHRmpgUdTHSLkbCzu6jBicjGJXJbYO3DN7SlIOEG52OkMQXdTjOOFKbiWlRyX2Y20sVEBPiJFyfufMYE8WodihxOovq5oE0qJx9Ko5oe+q/EVA8GXmWtq+9elvxhVgc9hkDTsZroX6pd1BSTfTHCFU5yEVXjScoS9JaAKhp0dASWltW0l8PNnKy3KKWW4Zg6EdxUrY20LUFReEZ7X3JNzkWJyXgV5qUhtPKq5BS+UCMTCZarxq0pDr1ORF8FDDc7oQCq10SDGA57stitFQhSZm9v0PSyPhSJ8YPZyy/J39zZcy+gollJHojij2gu5Ek7mGwGJU4e+2G80+OGJdy87mNFnuzjaU+afFeMxZWOA1V4Hi243Gz4nurYzrv8F6i63bOsbA9pfas/D071OqQ4+YN1sruGILwLZRO1FmHML6UR6lUorEDVtc8bNaEpOhGyzB3RGfweXGoXyi6s0RqJL365mqR08MVHIxyfV66zyequ+6El6BH6I4lkFad9BwfbrjoD/YbxdTmKa+EjdlrkdgDWiuGBcR5oG4G6nLg6fKO1juGKMauIItrGLRMXEbZxIbjSCwFU3A3li0NRMW2qOHIMz/asUmNUOg7s+d4jIcytqrnvRDWBiuKZKeoL2SE2j2WHWp70aDKKByQB4N0Giozei17/EXUpWIWIwnr/EQAwhdicUhGSi0ShEc9RS0PdncoiLNfyZzWFFnzvoh7SWtsoMtpyIvvGqJThEvHkJWEwWvawVE6v0+BHtYF49ZiW0V7ZFGZIBKd5uA97tuKCCpoGU1GWaTKbNU1Lgxq6aViyC5Talfs06qGpVQLSclOVJ9npWcosVtBxYeNwYyG7lhKYf1nbtEq8dbBHeebOdfbQ/rjTHwJ4rYcnvQSMacq2ObL55VQdqNi2xZoHdG1J1TZ0CBCrBK6NVkwpZk/2lBYz+AtH50fc/TGjsEbdn3BO2eXtN7xZH63v0bfXp/xrY8foTS8Wz/k555+wrcvH1I5T2ci27sa+7wgGlhtHehE85Fld3nEu09naBf5w8HRriueF0u+dHYl50wlZg+27KqSlBSr03wXayieSUzeBOLZxwNdglgIDbu4sxRB7a3+kwa3E9n1uBRiUj9a8ZQcLHR6T9EuboxY6mlB8pOSysGNIqMfBmFWXrYzrjeNtElBs5y3rDc1am0lL6KQaqG8kIXY9MiG5u3eV8O9vWZz1eyl8fW5vnfUjgpmnuHDuVQQyKIxHLEXhEWf76/OSLYn8v9mLelwe3JdIQtDstlFvE6Myyj//XDgVY8vxOIwKRff+OYzXpvd8aDc8Pd/7+dRm5w94SJJS7CqilBdiANwdSESZj1KtZFyK6C8wm8twRoOTyRB9KDsuI4NRouteogKtbLYW5udmwWcFN/K+2pBjzlhKVOYiTD7GIZDA5+ZfX+rR+lVU8y+ExnUGpeRcOzZuTxuOhzhWYEeFeUdmDYxLKB9EvhzZ59x3TccFi3N4cD1p4cMB2ki3YmTlI0cLXZcBi2mriqB0kQXiJsC03h8MBgX8E64EHaX3Y7mfq8sVCrR9gXDIDmW371+QD9YFk3PUbXDjSXHxY4X3ZxCi7Tb2Iixkeu2YWcLHsy31HZk1Ve02dhkf1gxWa0uFdGJ8/OucTRnW4becVJtebE+Q5tE5TybbsZX337Gdiz49IMHqCBtQ/nZVOrD+rKRxKy12bNp+5MoD0QRJTC5zOHGi4CrR1YXc6HN10IrdreSz2F6YSVGK1OjpEA/6NlthF9h36sZyppPT2voRP8x+8iwXdYU24n9Kh/9kXAU/CxiOk15JcbC9UVid6bYXdcUL6xobTSUNxKmNC4yXb61+xZZZb8IEpidvMcxKyqLjcK8kEe2feoJhx51bYUgGKDIArWkxcNSz0dpTQe7Z96+yvHFWBzyKHIq2z7YnKBvLcVKEwoZYWEgLD2qDviNRc09HSVJp/1oL1QQYO8DSFCEpAjecLWbsWklQyKsijy3Ft+BaQzl0eL/N8jiMM607CrHg7QMSjIeQ53VhNwD3p+LOc/97j5PcxpzRWHl3fsgCjW3WGvGA+iClTyCqGm92/ez6Ok9SbqW0dPYL8jrQkQ2fi6itPVg9gDp3r26iqitJTQe3wpguC/Pg+AyfrSEOGBVpNAeqwLv35xgdKL3hrF1eBsxiy2VHQlJc9PVdIMj3haiRC0TsVLYg5FxbtG93j9EU2lrXcDn6YdSiauruWAxWmLtSbIDmpzhMMUFTqh9PBA7umTzL4wKiigPlc4XJSmcC4w2Zqcv4YqYXpGcnJOYU75imd22lEi0pRTPPT+gXp5qZFxIRQH6ostELguxUPl1CzA4ztXeHDcZ9lMKk2XtajKSSeJpObXMe/Zsxqv2lGyTQ27UvYelP5CeSLxCs+NUylaKfc5LaX+yx/wLsTgkKzvA9W8/4tnXD4iDwQ05iDblNKZFjnOvPMN1QczuRsmIMeqkgITcT2beweauJo2avi5I5yXJJeoXJnskvPwi5Bq0Z4pxJg/c/HnAbQ2jTYQBlJWLHC2UVxOrUwxbvAFfT0BQxisKaVeMiwJ0xoQxspiJh4E4DoUsJ/90c8C6rXAmcHu+4PjNG+7WDVpH0mcNqjUMxnHnauazjtsXCzG0MWJAQgIKyWnwwWZcIzEciUUeVZDA2UELrWKCdQbNOEgKltEJpwOfrE95VK/pR4vWic1Ng9qKKvB2W3NQdkDcVyHJRZIzgpZfGHpVUV9p6kthvCYrW1rfFUSvuGznKCXp3GkQVe1NV7PrC8xOKOjdw4TP+gAJidX3NnNVkAi5bBxrykDzrER52HxJADvvM7Nwo/bxBWYAdaco1vm6zWUjSUks7vQLg91Cscr+EpWjeS4P8LAUBWjSAkAmPS0KAo7vtUGJ+w0gIp4LZyPmxhIt7M407VlEn3bEjUN5vfel8C89kaFIIiU4kWs1PpxiGxN6mt5kRa7ZSVp6UqBGxfhGTzPrsSayGuY/0XP5hVgcdC+OOpPnn761kpIcFMvvyAM2LAw3P6PwOwl4iZkmOxyJaUt1KYSYUIs/5Oy7jlBDeW0Z5/dTB7eG6jrRHSt2T2JGhuUExzLSnSjMTECcizMRfZn3RTU3HEX0AN0DYWeaVmLgQyOjQj2onMasSAu/f3DD2gniVUTCqqAYp2AdxeqrEeaeZtHtHZ6dDcwe7NAKwm0BhwPu9S3OBZ4sxVNgjIazd9akpHj3ozPxfMyVSUpq7xgUjqJY6wH1t6rchoHKJ1vFHBxMwWASN0Hzu/51UlL8k8vX6D5cYDolg5Zepjmtn/NH64rF4Y7drqRperBJaNvLkXFn0fMRPq2xbUIHTfdkEANaL4vBZ7/7WBbQOmKOe06P1iyLnvPzQ4xXzD6TvntKUzedsAzHByOqiBTViB8t8aqQ6sQlxplQzGMRsybG4BY9YSU4URwkDbt7Y6DdSnRfXHr0ykKC/rLG1bLz98eycCcT6X5lS0oSeXB9M2NcO+zGUqzI04U8IYmZxj9XdKeR5Xc1yw8jOlT4Wu5VVCLUQpOu/1ktG+ORonsQxaPBZyFaEQVjcAJ82octp4cb1l3JOFr680b8SPJ0wvSK9mHM1xRYO/SiY/Rm7zv6qscXYnFIGnwloF9VD8Snnu66Ymfki3Ynq/zx74szFICfWUIB5bXGtNwr8xR5FZfvs7tMLS6niDnZNab+TsVMTtTcl/H5EBabVCZC8c67g057RmN5rRh7zXAaJGinDNJDukCx8HvviRQhrYpsviK7nS6Ea09nGEuLMeIBOCuGfZSe2WniTDNG4Shct41kcgTDo+Uao2Rhmp9uiVFR2MBrB3d8UB/zYC6OWR+dH8skIVdH47G8aeWlOksmCWMRCHcFsRrxXpNKoWsno7LTkqhRy0tDZxNrXUNUdEYcqZJL0ItRbBqLDOyqfUUXLypSE1BFwDeiI0lNQOtINziMEhOXpGUs55ucpl1FkpXFV28ssYr0o87VnlzDMqspQ5mgEsl0bC0pKWyvJAynn15IHmF27Bd1GW2L6U77SCqByQR4WAkXoy0CrvT0vehbhgMBm4fHo9i2jfckKOUV/RGi5DyLuJXOBC1pQ7qHkVBpylupOGMlUzbtZKrkmhFvEqwL7FYz7gpWZcU4muyuFRlO5L2aa8u4vM/3SFlbolXCFSNtEVE7w6seX4jFYaIjhyrtiTrFYc9YW4ZdSbSC+qpwTx3e96NJlGyhADJVVNygFRSSv+hrMVwFiK1hWMoNZTollNxJjZhnxWaiVZucqj3NjqfxZsYUugeiHJ3MQSc1pd4aYlR0o6FedsQY6a9rsJHixuYbUchb7VLK2qIU89EQFUMwDF5yIU2rCLsMmhrDSsl7Hm8qPg0anQFWZwJeaUrn2Qwl2xcz2l2BUgiFOueHupUiKRnfiZjp3iVqeoq1jqRk9m7TMpNX4sINuFEx+8Cye12+f0hgbsUHwm4U3RMvFnELw7hhP5bWp2IuC+RFJ+GagcWso3ae3eAkTDbKBMCtswBKiVAtlimfO8GTzHwkrS0qSFuqfAaPd0ZMcgZJrvIzAZSNBTSYOwE0Q5Ww15PsGdn5s8w8NBJxmGxuyRIMgyEGaYH8LGG0AM70WrQvgnkyHCTC0UhvLaFQ1M801VViOJTNLRZyv9vdSw9BRMb4vUGNWhyl/LRogTKRzU0jVWBnhDOD4FmA2ATmNnJqN7bbCmNzuE589erhC7E4CJgowpNxkNV+sueeQkD9PFBdZV4BQpzaAzdBFgO3A595ClOMGbBPJzIr0bhPveDeHWqZE3Q0qFuLrxImW9XbVmzibQtJizJQNB5CzhoX+efySMqVnsEWmLVBB0PXiuEsZXzptas87iKPISSVW2vBUO4us7X4ypLqJEa1NmJsYLipIMH8fQuPokwfpoc4H5UdxbQ3U5Wj0ZgrtyeSaS9TGD3kViGBJNeS5eUyYpwA4ukQjwMl5TSC/KPAB4e7k11Xj+zNV2MpJim+iWJZZvXeS8Js5MEbTUlrIzFmF+5R4w8Cw5jxi2u1v2bBQ/8wyPlQSQhNJpPWotoHzKAEkzB3hqAEYAyzQDoOqBuHedTCh6JKfRlI3nNZMktXCGfi2kSC0WvR6cR709jixjAu414dvKc+a6l44mgINffUbiW/N5QJnXkRE39lOsxO442RrFiPuJFPxL28gNuVIcwjtvT42gpAuSqYwpl1p8UJ32kYtWg+XvH4QiwOguwj6PDOorayGxSt2u8G1AFfW3z29dNjoj0VE1DfgF9E1KgIRyPu0uHzym86CYCpL8RSTCVYf1kINvpBL2Ygo8acl+gRjv8gMTZw+/VEWHrCnaV+rmheROlXf7YTpLzXApCpRHO2xRoxZb3eNoyHA+miZJyJW3YKEhdni0BoPMPKodsJaQe7ssTrOf1RwOTRlpwY4HEvpfXWEoOjvLBZhRlZ6Mhh06LniZtdzfp6xsZGVt95iPpKh99ZbONplh1D6dk8MnBTYB+2dKsCd2UFKHVJFoY8QlvfNqTWcO2NJFQXCT+H5Xcs1WVi/tnAcGBpzsHXmu5Y07yIdIea+joyzBTjQrF7kti8FYkHXtoOr7FXjlBF/LFndrJD68j6pqHtG3HuKhOpDsx+9ppdV9CnOW4llePsM4WfadSqlOrtdMg5pbLwpjKgikjaWs7Obnlxe0p5bUQ0tzGoO1HhqvcbzE7s2seZhNAQoXi046DuWa0b1Ec1plMcvBfxpSHUiv4AUs64GBdCNIpvdKTbgpRJWG4jsvFQGcFzjjzuzrF9IhtM+1DaW/fmlu62glFhWlHc6itHPB0kktBFwtMR+26NHqC8rogO2tfEDd0/HFEmMd6VMm6/LKke73DOMwyWflWidkZEeKPCH4Yf9vj90OOLsTjAvvRUbeYca7UX0SQtK+40858WkmSTtCJK+l3dK2Er5vgyMb0wxFryIGIhDkUsRup5L5FvmxI6QXqrS4mOm0ZVUyxaLERRF4pc0SQojzqGFw3YRLstqWc9nbfSq0eF2ynYGuJGSuLxSDMmhbouZOyWH5jZccu2qlGtQc9H2Q2zHj9WkXnTM46GIWiUjYS1EXXmLMjCoBJWRR4tBJwcvGGYZ+q4F7/HvnP4Ti61jnKuVR3wc51bKtFYpNLLyCxkIHVnsVdO8kUTzD6L1Bcj5fM12s8w25FkNf1xSXndc7gb8Ec18zFy8/WGUClCqYhbwSSGh9I66VERrGK3LimbUUa9pWhlpjI6RE3Ktuu2Q+6H3M8nLdMpZSKqk13cL6Ssti4wGiMxfpOzks2YUyNTFcGEhMEa6iQ5ETtL8IbaecamZzOXdrZfCiV/D3Y6MJNI66XxpOzs9/iK7nObkT1ApwmWjLmz+MxG0FnMtv89aT/yTVFlD9KJ5CRAZSrEQcp39/RtlWPxvDf4cZpU3T87qv/p+Dn81A8FeytwYlaTRen9VQBtwA/ZDy8J4SiUKqcZpz/2+5JjX2LqMQOUg4BjoUkU9cisGri6meeQHEmAri/l5nc7QzKGq6Xe+wiGUnaZ2Av6O6gCs9X4h575smX7wQH+8Y5hWzA/2rFdCkgxCXp0p0l9sadoT733blWh7yypSMSNgCa60/vFz3tD8LJgWie7eHKJ2WFLbUdea+74g+tHAGx3pQCgy4CxiZD1AU3T0+bWYwQeH244rFq+pR7JjaPkQVEmkbLTFTqJ5fpO4bYZ01FQXO3g4obiboP/9DMAmqMjKBxp12LfC6iypDr7KtFpfKUYjuTmNysrYUMlgCZoi3eR1Iv2QXZQwV22s1J4CpW4h0+CuylU1t0axo2j3GgxwTnuKMtRxpeLgWXdsW0W+D7vyh6ihqM371gva7rWQVAUzy1+FFl88JpVV9LuBAhWHsyYQElI7liw12LEMhOnFHt2pR6k9XRbaWlFZakFLFTsQd1JITupaNM+5FaLkazXmCqQLkqqa+hOoLxO3PxckBAiZBFMQPCKiKZ8YehW4upNJ1OMabwajeA9r3p8IRYH08HhH8kD2B0LT30C0FQQBpvqtKz+ZSJpSXhefCAqOC9REuzeGsVZejGStg7VePxcuOfdaSRWifn7Bi4W9HGBfSBx8HYL9WWkvAskDWMjN/XsAyvgUplHlrPI7ChrE3qLPx1RW8vWVcSlZznrWCEuwOZBj984wjh5SwrWILsJpEZusjSKBj8VMQto5EE6+eoV17dzuusKPZOIt7G3pAOPq0deO7jjum3og+Xqdk76sCE8GkAlzt68ph8tzOGg7vj08hBXeKwNPDzc8Ktn72MQotOjes376xNC0vzs4af84+unfPjsBPNZSXmrWH4vUmwCvtYc/M7H+GfnED9fooabm/truVyCtbi1p9YWX0srMBwmwjwwRhkPh1kUy/RqJFyK9ZrdTkQVGFcFATCPeroTjXkuLEs1CFXcrRTRSsWnkiICTTEy6MjttuDyTmb7/q0OLsp83hPORLSJqLWVUe/bktM5VpaD5ZbCBmLUbOfik7B9zeBWUq3aVjEU99UqJhFa8TAVKrS4mcdSBHXERPNMPESHw8T4+sDZ2S2DN/hgpIpk4kXICHPYFlRLEbx1pSMazfyjhO2S2AS6CBq6rUP1muZc76MPGTS4TLZbDqSuRHW5qMl5K69yfCEWBxJ0D6RXGw6jOEvfCTVZB6ifywnevSVuPv5swI+a2cd276akR+h2RuboVcDdGEKrRQFnErrxcFOw/rKnvLBZ+ZkYjoLs6loWhGShP1QUd8JDsBNxxovp69DLKYu9EQIOwGWJaxVX7RG6VdzVtQjAstWdySw/27OfuJgrJ6B7JYG7MXtX2ltLdam4OFxiykDxwjIuBZ1OlWAl8dOa5/WC1bOFvAad4MHIo7NbbjcNh1XLR7sjlEr4qFE6cnawZlH0nJYbMYVNhq8sLviLiz/kO7NHnJgNV2HO7aLhYj2nMyVJw/LdNebZJWnX4lerP/FShvw91T+NlK+fofqRYn3E1Z+y6NEwPJR8SxUU5lnJdmFFo6IS3YFGF4F0XUh2KhBaSRHb98wmEZeezooVW/t6IKnEz5xd0HrHGCq4cwytFa4Acu4n89XzD4+FCv2Jpv+FFj8a+hcNeMXm/Uo2Iq/Eq8XLONVXyN/XCXct17+4FW5CcV7sKweZPggtOpkERyPdUO4NXUwReHG5JF1LopXJpCkZsyfxDA0ivlK5gtSjPANmEGv+2XFLuytwHxeoBM3zxFZJtVJeWPyUZ9FWhHlgWEaUjfuF6FWOL8TioGLCrRLd2xAfDjSznvF2Kb1mvkiqkBGhSgiwdOQxIyQP/XHWyJ8MVI3Ia/0sO/IUEX1nJQp9K0i4Htn3aaoJxCIyLgtR1alMUU3ZFiyyH3uGRhh9SifJUrBRXKKWgXgQmR10Mu46b9BJCRnHJNJkOutkCqDD/e+Nhcop0Akc+ENPawxKQdP0rB856qOWblPi6lHGmL7iqGnZLius8yyanptVQ2U9TdXzoNqiT0RK/Vpzx11b8WcefMiZW/F2+YJVqHhk73hq7/hG0fCv1B/glAFuCAcf8l/U3+R3Dr/Ee88ecvvhgoPf+6M/Vi38SUe4vIJLEVfNzNfpl0d0x4po7UvYAeASbC3lw91elnzrNaYIGBuwNu5HiDEo0sYKM7GWc0sETBJ9x+johjw5qfMDeWnzNY3gNdWznIkRwV9XEnSce/9Q632ojB6lvR0eCE6iGo8+L3F3ao+DlVcyEk4K3FacsYlKov00aCugZXktfqe9LcUWLijsTu+T3fQIKIhaYhNCn3G3eWD1FZh/oFk/NYyLRHdTC+v1rS5jEmVWMSuGL3XMFh0xe3q6epSR6E5Ehq96fEEWB/ZyW1NlPCD3mm6b9uObYqX3mIPtnASkKumHY5FIraFXjtjZLGe9/9CdxnaSmzAJVMohJwAAIABJREFUYPaGoJnPHg17d+OJ0z8cJpJT+EqYkGkwsjiMilRKz2jWgmarw7QfVakIxVai7lROVkYpGXtOi0N+SOI8SLLTRSPxepea3WlifTVDdZqhd9icYXl1O0cFxW50uMJTOM+sGOhqyxBEVtwFy9z1xKRY+5J3jq9og2NnCjQRoxKP7JrTXPnIwiCHUZp/+/D/4szd8T+lP811+RQ9a0htS/I/QVQzEOcFOgjjddKKqCFb5QUFi5F+59A20SuHdjK2NSYyr3p6YxmDYRgMfg6u9PjRYExkvJGQmc5bYmLvZCXS+7RXK5o7Ae9IkqIWytzrGwnkVdmUx/SiqJ2IRGSJdNUMdJUj2ZyCrYXxGA/knNTfLXAbudcmB7OUpo1F/p4aJARaRSH96RGZtiwS7lbk36JNuR9NK69Y/XwPvaE46gg3FVM8AqOAncWtbGraJKyOBKXQLpJizimJwlN51eMLsTgMB4qrXxR/QPPRjOs0Z/6JwrZiY+5n4vew/K7kB/hKsXss+ETS0L02ogaNW+botVHB4SjZAddZWlsniaVTCe404zLSfKrZpYJkoXsiLYvuhMk2HIogp3m4pd2UpFGjyyBRZ2UkVBFzK4yoSei1ORdDS5sDfKd0cNMp/FLYeypC884dNrMC60xi+QtP3+N/N+8QgmbrGtyzEr+ImJMelcHE2o383NNPuHww50G94a6quW1rnAk8XGx43Ky4cHN2vuDbn55R1QPWRBZVzy8dfciR3TImyy+UH/ON4oc7jr7j5rxz+Cn/weGnfPUv/Tuo+E0e/MPvEs5f/NCf+aFHTitrno9o77Bbxe3XMgdglnDLgSfZXalynttVQzovGSnpj0aacnzJZk4WMWsDMeeBupWMKi+eH2Aq4auEU2krixup2HwdSScDrvJ0VxV+LS1r8cIynIbsmKTYviZhwiixuyeB2hr0ieA1utO0r4/orfA43EoxHiVMERgOHWaUbA63UsTCCFjYRPoTAaabz6Q9LlY5uMaxNy4q1jkpfqYkV7QRcl6YBZplR/tctCh6PpKiwhYef1HTf6mHlQDarB2rCLNFJ7L+TmgBYk786pfuC7E4AOx9EIPKRqH3UwgJsJGVz4w5DcjlcZJGDDBaw9hZAWW0MMfStIMgi4saBJqfTFXiy22YTaKJOBxJu/uWpClHrIkMo9izx6iIQcnON8giEJXYzcXOCoEmwexDRXcKEtYDdm0obgSD6DrHvBHQqbCy87TBSZJSuJfdknfCMMhlGoOhsQNGRwodaEdH7w0xKY7KHQ/KDb+w/Ig/3DzhO/ohi7qnMIFvHj/jX5q9S0Dxtr3jS+7HF+K8++f/Nm9f/fs8+EdH8JMsDi8ZVaqY0F5ITcmIHN9Xhj6Iz4TXmrIa2VYFatQoBbNioDSeIRqej0uUTvKgDAr1sJf09SZAr4XMFQSwnNq4WIgr1uHhjrZ3oLN5rM5VjIskZQgOaVNMQm/FOWsKl5kmS7GJ6MbL6FEn9JWQtqKJmEA2Lc6VZ0okK6S24k7tw2iSFilAqJPwGfIR8ngeMoBoc3U6C5TOs8s5F7ETtmtQU8Seknu3lKdfGSGxWRsIVjMWkTiq/XPwKscXZ3FASj/Ts5e8Kk+278omGpB5COrepWkCuEcFvRA+1KiIxqJbs1e7kbKJZ75IU4hrmMU9sKhnoyQX50h7Xrp442AFHBskUIas0ExWxqll5emDFpWoyTvLOr+X7D0JclOUpWcMhrocWG9qUlJ8NDvC2kjUiVEnuTFHufipN5iZF4Z20lgV+Wh9xPWmoW8dx43kSTgVcCqwcB1109OPdm8IW6mRRo8c6lefd//Sz73H86+8Q/2Hr/yj8rref46rK0x3yO5JhRkMZoCAgpuC1byiXVWUJxuG3u4Nf+PWsh0KtsgqrnXk5GjDxeZIWsGbYr+I0xrcfBBsIsv6kzGk7Glx+2KBmd2HyU64jy4CyTjZxW1uM3O7N6ksfW9Yjw3upOV4uWPdlOzOZ/iZ0K+jM/hZRHkZm7oNUoW6iWMhreQkDKwus9ZjMHtTIbeR17TO8Qym1YQDj7KRwgoYGoISgV0C+2GF9ooxik0+mU8TLawWBaqWPA57Z/duZq96fGEWh6QSetSQFOVNylJscKu8Enu4+7LC9GKj1T8eJTF61NKD1jb7MkB5ZRjzyHASSMU8BmU54Fe1UJ/nMWMOidOzOy4+PWSKeE9aFqHLzw4oDztJcTIafTQIQ1IrQiXcC3en6WYFrvKMd6WM7OZyapPNgGoQElcsxdwkREU3OOElbB0fqmMByBqPWwyM2qHLgDGJkBTWedZdSTezDNFwu6vF28EF5kXPzx98wpgMje65GyVX8WsPXlBoz184+Bb/YqmIuM/hCz/u8Xff/k1+66//Jn/tf/75n+za7lo4WLB7UrE9y76Xg/iDpqTYXTUyhUgKbWRUFw49i5Mts2KgD+KA1PdiCFscdfjBMF90+KCxJlI+9LSDo22l4qAJhDpAJ6NkoojK7FqSx6IVQlPaOGaXiuEAUAk3Hzh9/Zpn753ek5tGzeLRmnG0LMqeR7M17yZF15SYF8Ue1xJSlICD40LGtSSIg8ZuxZDI17B5I+75GmYt52P1NS+L4smAdZ5+JbmaDx+saAeHGjXjbUX1zO5zU1KuMBU536SUaZabjYybArccGJ3wKVr3Uw7S/WkdKmYjjp1kPq6+nKguZMetrhL9kez2/cOwT9bGCJmp96UQh457wqpAL0b6HHtGFRgWCnvlJCxmrfFR1ILTrhCOEwya23WNWRmqt9fEA0V72WCrkbGrhEUZlHD1j7wAQb2muJXFwdcCDumZJDuHZaC4k7YlFrB9GkhlNo0tPTFBNzi6bQF3Ti7uYGTyoQ16Nsi0xEbGVuTe/W3F8rVbdr6gNCK06gaHMTKu/Lg74uPtEd+rTvhofcw3Ts/5lcP3eWTv+LX6M1ZRMdflj74QP+L48xX8tZ/wZ8NqhX7jCWOt6R4ASs5ZaKIY585HymrE6Cw3PxyYzzveOrrh3fNTYfwBYe3oao22CZvJQFMOxvqTpaRXBcXiZCumXUnYoTEp4k3JZN5qJko+CGV/Ju3H4l1HdI7L2QwORIiW6sD8dMv6cgZB8eLllmxr9+Yuxbne79y+yRkjcy9MxiOFv5CH3W4UySnYCnlLT65hlTiYGxvo1yU6J41f1XP8nSgz3UomaKEUN/ZQgB414zy/l6hQLuJHg+o1cZal+zrtxYSvcnwhFgeQ6iDkiYDNAIo/SIydEi7+LOEOenEg9hplxBUJnWRc0xv0ThOtgTq7+xZZrJQFOnHQEqiaRTLNc0UyDtMrhk48/rYvZvKCouRNxo0mnnpo88o7SOk4qT8nspbeGHpXUOwUYSnjVe2llLRrTRzk81SJbnD40ZAGQ/Pahhg1p8sN22PH9fmSsvAMZcC6QEz3ISy7vuBayQ57e76gPm7FSQj4eHvE5W7GGA1fObjgG7Nn/Kuzb3FqIg/M7J/LNbr99T/L4X//O692Xa0l/vI3efEzNf2Rov9Sj3aRqh6YVz0HZcdqKDmpd9x0NUYnNm2JM4EX2zn9uoRetkeVhW3WBrpdQZuzP4dNIaNmKzJwkw1odFL0SP89zLzgA5k7MIUi605n42JFscrkpqSIpSbpRFikffaEesnBfHa6I1WBkAl50cpYM+SoQhSUs4Gi8GxWNRTyeTHLBaUUKjs7pSJSLXpCUAyrkvIz2czGZcT3RtLBPTTn2c5wFJ3Q3mFLgV0OxKgwJhKTEnasjoQiYmYjqat+9IX6AccXY3FI3Hs0qklrkd+8zb0gMAW3mNoTg5wIpRPaJkJIxLkQniZtwv7IISnJTB8y5WgfTqVZ2s+qx0JARqJQXOMD4f5HlTJJnftx1Uuj0s8d+7CW+/cRLWAjZekprEcpZIHIEvWYFEYLtXa3K/dS3PuRbNpje5O12F69mhRj0vig6b2lNgON7mlUoFH//C7x+KprjDaouhZeQub5oxPWeUonvhVDFLbgmD8K67HWUtjA4CepuZx3bcWtyZpIPRsYBnMfkJPPLwqsEbVqym2KH60kiOcow5fDXibdA5myzzTmzhZ7ykSsfolTkZDFIyrxnvCTFb7keO5Dhhbj/nb5Y6FLL91D3x96hI3ZIj/f9/Heh0Ps8u5Tvvb3nSKniav9rycoxptKgFUvzMlXPb4Qi4OKMP9QRpp+Af7Ys200GOjR6JMe5wL8/oJ6zT77b/2lrG5MUK20+O0h/ZdqZGxpTKR85vDzSKhjziMMIv5ZyGKSqgBXhYxM+8xgbBXbK7EStweeNPeow4jK5an29689GQEe1bUT89IbR/tE/C7VjSPOJMLeXhS0145dtg8Xo5PErz79LufdgiEYiieBi7s5wVucDTw+XBGixpnAL598wD/44JvEqHHXlnAzxz8aiCeKtxeX/KWzF/zmi69z2c+p5iOfhYYPveWbxZoDXf1EeMPLxz/+z/4G/9rf/PFwB/v4EcM7jxgrw/ZxsZdD209LeGfk9m7GritxzjMrZQLTj5b1ruLNk2vO1wvuPjmguhAlpZ8Hvvr4BYeFgK8+ab51cUb73gFGJenho+LBkzsK6/ns2RFqa9GtJhyNNCeSKTlSikipErq6ajXrnxmkL39iKa6zV+g84m4N/rbgdiNu2sklcBFTBoZetDN6a4hHI+XZlhA0pY0ivnt3Tndi6XOSVcxW+9ElyrVmyJmn/kjAxu6yxh32lLOB8WmUtum2xJ073EbRnkV2jzX9W724fd0VJJ0k+HdQDKnBbXP1fRApriXbxLYwNnbvsvYqx5+4OCilKuC3gDJ///+QUvrPlVJfAn4DOAF+F/j1lNKglCqBvw38InAF/OWU0gc/6m+IPbg4STefGEJl0L0AeHanGJ5X9C7hcuBMNFkIZLLWYlpVNcIzWBlCVAQb6RtFOoxwOKA2TlyAyijhui5XHjqidhnZycQXtFiUq4OB06M1g7fMioHP9FLyGjJo5NfibLz8I0u02eXZJsKBzL9DYVGd3pNQdFDENzqI0MwG+s5x3i3ovcUnTWk9MWiSlwi6MRg2vaD171WnnC02jMHw4dEMvdOkQXPXVbx5es2bxSW/dPwRZ27FV4rnHOqeMY0Y1P/nhWE67ONH+GfPf+jXt//GL7N9ZFi/KepWd6f2LML2azJyOlvsuN0Iz6LvJScDYF71XLQFu7HAmkiykf5EdCdm7il04LBo6YMloniyXPHuoZQz9VHLOFgeL1ZoEuujknW/IByPLE62nMx23LUVN63LYTqCW/mHA0SFLT1jUIyTD+SgGA9kk1F5KqJ7TRw0oRSQMzVeApm1bELjYGkHKw7k8/uphwpQXMgDarcyiZvSv3ERfeOwO8U41KSlBD0HI56ZsUj4GaQ64DtFGjQJsSLQg8Zt5W8kqxhnwshMZUB7mZgpn1O8Hvx0Koce+LWU0kYp5YDfVkr9Q+A/Af6blNJvKKX+JvBXgL+R/71JKX1ZKfVvAf8V8Jd/5F9Q9zPpUIjOICylAkjGEJcedyHSYbdOuXJQsvIPeTw5gHagUk7KMorQiLuvHiEMRuy/H3XMmp5+sAwvJGpu9Bo1k5JU9yKAiTbhrjWjLzlXB2gT2DknAGFShJVDDWJeOh57fCPmoZBbCC98CGHhKWJM+xtFm8C4rmA28NbZFW80N3xndUrvLb90+hEfvjiGoGjKAWdkzr3pSna+oB0ltXp/6EQ/Wnax4NrPuR5nxKT42J7wZv0x65gIf1KY6Cscaf6DyVP27bf43n895/f+7H/L39s84CrM+U57xm99+g4A3zx9xu3Q8PvfeoO7bU2/LUhBUS17rA2kpLjZ1oyrgtu6YhxFG5GCzPG1jlR2pNYDVgVe9AtxqppGj/novSwcXVugenGCGgZLW4ir99SuTdwFV4//L3VvFmt7lt93fdbwn/Z45jtU3Rq723Y7dow8KGZIIqIICSIRJBAREiBegnhA4p0XkBA88AoPxIpwQEJOFAFJcIgUHAeMZVtpEw/ttt1dXVW3bt176557hj3/hzXx8Ft7n1t2d7vLdkvVf6m6+t7aZ+99/v+1fus3fAdiMDTNILV6yMCVQjgJpoj4Wj4n1NJULiqPv2zkZ28KcRtvS8HZRIXaWKqXmlDLWvS5Ybh3wwpNQp33xHWBXhRywu9kOuenGVPhNapXQtbzclCFSUTVGc20MgchWxTZbV4RIsTmrkmpvKA+7e570JDMrtmb/Mci/5OAfxX49/Lf/y3gv0CCw7+Z/z/A3wX+O6WUSulb2bbmzygTuzcC5rgn+EYESAzSRLzXo69KSAJD7U5ls/dnET11pJFGlQHnG/y5y/TnKFE9KorKEx4kWBYSNJ7VrI6tPPidaDiGKlJctIzqgeVyxHTW0u4q/GUtgedJLR6WRaLYZWOdmXSjY19gyyCKULmOLDYKf5GVnzSQEnEcKGc9w66gtBHfeELQnNZbvvLyESFqzscbzooN/9YP/ia/9Mm7vLyeykw/16YfwKFHYaaO2cMdm13FyXjHh7tT/t/Ld1n3JY9mS1wybGPFo+KaHyrdt7v1n/26Xf6hv4r/8o/x83/nZ/OfDH9tegvcwtET3P1f41d6w0+UA39385DXRwt++enbzC6WvLyZ8sWLl1y3I/7c+Yc87+b8Bq/xzvENH9yeEEcKZxLJi077rz9+g6/whpzMCs5PVnzhrRf4qJmWPVtXHkx/D2a8OtHfNLxYVaIe3hlUHbj32i3bnJFtnzSsbyVNL0873MsGPQ1oE4hPRyJAY6A532FtoDCBm12Bv2qwg7hf+U3N+KlgDcp1Eu3Sc4Ufge6hXAnt3HaJVis6p1EjT1QGr8zBo0KtZf2yLijW4uTtZkG0Mp1CPxetDtsJonKYSVNTDyIUHMuMj6mjoH3zFZrvUc9BCW7114EvAP898E1gkVLag+0/Bl7L//814AlASskrpZZI6XH1B97zrwN/HcAeHYtvZG/kCylIE0/zYUkoLdqLGnR3Lsq9xVKUluO6wGzNIW21VwVhLOnoXo1Z68T56ZLtpGS9acQFa1cexkp+hOgzLCsZJ74s2V2WYuSbH1gY5U5zFSGKdR0aRkctu6B4eLzm2aaUxRiERn5oXgVFcdQRnDlQur2XsqFb1HxleJMU4Z2HV7w2WjI3LSFp/sKD9/hl/Q6fmJkIvw7mgKZ0weC95stnL3jRTjmvNzRGRoFvH93wpYkgGQvliWi+7ra8bf/kPQeA4UfexPzi9eHPX/+Zn+SDf+Nnvu3rC2X48zVAyV8efchYD7Sh4JvLM2wRuGlHlCZQaY9Pmi+cX7Ec6jvJ+1Y0G8ujwNCLfJvblKASL5lxW3hcb6kax2zU5cZulMxAISzKBO4EEhHVa9RO88Idi1fF2OfucsLsNG4iVO7j+VZ6F7tSpiU60V6NJKMoIrPTLdttjTMFe3n40GSwU5v9K4bMq6gVxUYy3lggEgG/X9Hdi9hOZd0IUAspS91ccBn9QycmPotCmqNe8DoqgDMQHsgBqFtN1SsmTxSxkJ6ZimRFqvwg3tx922f07a7vKjiklALwY0qpI+B/A37wM3/SH37PvwH8DYD69UdJeSUmNE3KUGaNbxLuvqN4Ial8MlKrhV5utLnNgJosFiqeAqLim6KC1ogdnrO5m5uwNpJq0RHo94pJIAEpCmU7VRE1ZBetk0Eyg3UpvYM+m5gYTbcrD3qD49PdwV5uV9YU2auzHwx17QiFpINaJ8G8FwKQ0Vq66e8/O6N4PfCjk48ZmZ7fWT/A74kzORVu+1IaYSoResPT7ZyUFBtfoVWi95ZbRjwv5rho6KPltNgyNIaQrljGius45r5Z8ePVZ6fw/msPfwzD/3f48zf/lx/jg7/47QPDH7we2Ak/Uj3nH/KjvD5Z8GIxpSkcr48X7GLJcbnjw/Upy7am7QuGtpC1YBJN6XB7slV+XkolmsoRo6JdV+KBkcebSot/ZtoPmPos8b6VjeeVoCdTAqYeIkRlpIwBlpsas1fldgq7ExRkQqOqgDWiY0nmYkQFymtsC8UmYVwi9jLKVlERrUCqYylkQu0UfiwQ/P5eIFSiqRmbSDHvcZsSXQskXzth7qqoUEMmGVYC5U75dw5lOgSGfXDY9+BipV4Z0Xz312eaVqSUFkqpXwR+GjhSStmcPbwOPM0vewo8Aj5WSllgjjQmv/37agjjgOpFUDOi0FHqteKyQDthwKUioWYDPpWHXoO8gRiAxFFAVYGj4y0+atqqwq1L1vllfitMRr8o8bWldPKzyun8PfJMG+SB11JfVpXHD+IeJHh7Abk0o4E2Ki4XE/xg6a0gHpPTeGVlkRaRcTWw3DZMqp7FaiSKT0n6I/F4f8opfvfDB/TBSnMy6oMbNSoRtxXVscjPKwUpKH7q7DExKX578RBvdYZXKzSJl+2Ee9WKiOKf795iV1f8wuLLfGF0Cc0TRJcdLsOWiz8CB/GT//l/wtnf/k3g06fPe3/xZ7/jz32r621bUxnPN1dnGBO52TXMyxZN4t3RS9aupg8SzGPQ6MaRkuLBdMW7x1eU2vN7zT1ePj0iRsXRqGXxbEZ50jEZdcSoWa0awbk4OZVFc1Q+X2DzudF9LLBrdWAuakK0qKhwUeGLiFkZTJa2dxcBXQTqRnwntREJfFTCrAtsK1YIclor+mNpnttOYP/EzPx9pcrbK3/vORK607jKolrN0f0tm12NGzRqyBYJCFXA7BRhDvPjLZuyxnwyQg/cjWczMxikIdytPzsA7ruZVpwDLgeGBvjLSJPxF4F/G5lY/IfA38s/8vfzn38l//d/8p36DfIhCXM0EG8qqrfW7JYN5mVBtcj8hAFCoVi/o2BRZ5kxGQfGmcc+LcVQ9DiSgtScu/fmJAv1rWY4Muh7nYwlbcDMHelS3iQWoFtFzCjH+qF4OYatpZxLdz3uu9mdkcZpIWXGbtHAoHFOiyBJETFLQc3F3DBNReTFN85Io8CHlyPUKMgJMB8wNojUeac5en3NetNQ6MCL3ZQYFfNxS/AaYyP2pBN2oonsrkd86d3n1NpxUaz4v9sv8M70Gj/WfGlySaED//rJb/HMHfPxcEwfLT/79F/kp08/oNKOdWj4z57/GX5n8YD3vvEA3WmhCSc4+Q3D2f/waaDTCb+yR6F/6vrftxP+6njzLf7Lt78KZfgPTn+Znwl/AaMjnyynPN3M+TgdAXDdjdkOUgJW9d0u2rqSB82SN+sbJnbg16JiuR7x4ZNzVFSM6oHNrsaYyGsXC55fzwmPOuLO4t8W+zyigkEzeiJiP9W1pb2fZPRdB+JxRL0UVzThTCR42DG0lth4xrVju6zZrWra9QR9OpAGjZ044sOO9aygvDISgJqEacW8aHfisCOPXxeULy3FRgyRTJv9MXtNsZFgVa40oSuJVeL2diL0gHXOeJK8n5sFaMXubvnh0SHgdedZDjGT9rTP/QjP98y34gHwt3LfQQN/J6X0fyilvgb8nFLqvwL+OfA38+v/JvA/K6XeA26Av/bdfJHz4zVXwGzUMfQFpivZPUhMBkmJQiG/+F6oxc2ES//otWue6FP0MjMygcFZwixgxp7elhQLjbupKFaadTFG2YjOEnTW5Rotk61aRnKK7DSDqgRdlhC5t2xbBhCVQu8splXYraW9L3oN9ZWiP0F0/JAOst1oQtYyCHvjkexxmbyGWgRijU48uT0SrkEU6G89Gpg2os3wcLLi/dsTmpOWL85e8qBYMDUd43LgvBRb+4npMSry0k9Zh5o2FNwvV/zDyy9TG8/IDrw1uuYf/D8/QXWtmS9h8iwIESlB8/e+ewTkf/m1v8Jf/cmf+65f/+oVEeBXSuqAjrQ6YHRk18tUKEZNUXqKwouRr0q4Vwb203HHKjZEr6hLx6gaOK5FdPcTPYUgIKoUFbYKFKUoMw9LIX4ZpcQEx8pkQuskI24yF8cm6srRDgal452PRxC2ZMgGt34vCa8zUTDdkfL0gIwmS0HpDqcBu7PYTkB1KsLOJjFryobOqUjEuWc2a9lua2Jh5UBM4ObZ1lCBGXlia3IjXDKLuN+lCVKGiSetvmfTit8C/oVv8ffvAz/1Lf6+A/6dz/QtkqJ3ltGop85Nt717tQqZpeakThMtRvFbiJ3mejOiaBzOKfRYkIf7cVR0+iCuoZyiWiiqRXnQnOweOrEcq7IakNdZsVhhWkW67ylLjzGR7XVzR+LKhq174ktoknD1C9FKLJdZDSiC7sQrY8/liHWCqcOWAo92mY697GtOR1vWuxM54ZLQcwdd0JqID5plWVPZwDBYfv4rf5Z/fPIDlKXn/mzNLpQsXYOrDJtQMTEdm1Cx9RX/6PrLxI9H/Gb7OjjNb37wQzz8vYBtHeU/+mef6VG9el38NyX8r3+8n9UkGutolzXPyhmbXcX1eMwn66kgX01kPtsSoxCrjIq8vz7lspiwHBp2XUVK3An+esN60+Bmhh88ecFrp0u2Q8mNnqC16EYWVsbC6zdgcJq0tYJ89JroBD1LUofxYGoCo8rhBktZBrbbGrWRBmeaBAFTZV1LNKhOav80krXqpjKJ29OlR8ctu8sx7WuiyZmKRPNCYbaaYq2ItaFaiGJ3Zy2rQWQAy1aQl6ZXUEXKkWPoDaGzmKycHvJnqiSlyx5VG4s8tPns+rKfD4QkWvgGKSmuNmP8pmC0AZTCze6AHHuzW5AeAzZhTaTz4iERswaAUgnVeGkk1obgDHES2L6eKG/NHYW1SODuegwoEeCI5LrOBtpljTKi1FOslGQIGeFYLATcJL6XfApG7Y+kkyzvbSg2eVTlJGjt7QtFr0Gz6So6Z4XkJcQNMIm6GZjWPUMwnNZbtEqEqOjrEu/kFN25gpthzLPNnMY46VtEy4t+xst2wroTHUNTRkLur9RXA2Yz/MkQEL/6W/xCa/hLzWdTEtmmkuftjKvdGNUaVusRYWt5Op+z3jT4nQWv2XXFSQdSAAAgAElEQVQV9+ZrChM4q7cAfLA6kXu1lmayLoPIonXioN47y8ZVdN6y60tCZ4hWcXG+PdgMgkx8Wp3QJhFuKpIRk14zqIM8gFOW9bTCbQXLEDsjALkEpvYEr1CdPuh6hOyqhkkEqyiW5qCuF1VBG5V4c6R8uCXJLPSgqJYQS011nVi/JcCvA9aiFR0K5TkArtBJ6ObWikkx4EfZazOTyqJXpLEnlK84kn+G63MRHJRXmF+d4abQTiImKraPRHjVJ6huFe1Ror8vG6487kiX0nRaP55z70svuWSGuqqIU0+8raFMeAqOfsfQn0DzScH6hwf6MlF/IuY49qoQya5xpPqkPKRlyYA/9rx2tGFZ1Wyuxlk/QmDSZimQ7VAl/Fgyhe5UMBn1aKDdlaLEs6wO4JVkpXNe3WjCrjgsKH8asFvNatBULyxFAf61HmOFdBOCZjcULFcjChM4b7b8+Tff4+f6H8d9OCEGuB7G/OLJOakOuKjRKvHVl/fpugK1j0/HA9VXG2aPIxAxv/o7JDf8iZ/df/vln+C//vl7/MKX//4f+drbsOMf7h7xf17/yEGpSpSXZCLxyfNjlI1Us55RPZCS4mYn9PPGOmrjuFpOZMLQSTkWexl17oPFetnwG4/fJY1EnNda8GeON2a3nFVbPtoeo3Vkez3h+GwtCNSxQS/EejBZef7h9Y7xpOd41HJjI31XkFrR+oh1JOwseuRRY4hOYz8pBdXYGtLYUxwP+Imhahz9szHllYFrMYvee3qKH6dkou25oljDcCR6EGawtA89dIb+h1q4EiOf07M1y3VDMR0wNjIgbM9oIU2FXGYmji89uOTrzy+oi4B3Bl989q3+uQgOkMlJRZK025NtwPJkoBR6KkFSsKEsBSASpZa6XY9IyxIzKOKgiROZWiidcLOG4TjiR4rJyY5hsKgnE4qlOiAztRFpOCIHXUgUMlLb5e6nynbtSqYa/VlAD9LIS8aISpBJFDbQ6yxEm8uapCVj0FlPcF8eAbixsPmU0zLyKiLTWYvRkY2uaKqBti+JO8u6q3gwXjE1HZOm57oaSRqcu+0oWG6bPLZFxr8J3LYQK/odFNsoRCj/pwOMSn1P9Z9W8Avf+XX/tNVchgd80J9zrxKFamOi1NleDHsA0s4yJIhB4xYV5UlHWXp8FK5Nioqi9DibsqN4PhFz2cZOEIchZWBRLRv2o9Uxt9WIm13D7c0Ec2O5DbPDKNtklKIfifR83BbsEEj3MAhBjvjKhCwqEQaykZSd1Xybm5GzhLFCPx86S6oDfiwoxWjvULh78xrtJCCUq+zilvsVewJgXBXonDWHTNIrCjEgTjbhs3K1tpHYGUJvuO0awqYg1prUGSi+VUv5O1+fj+CQ0Y9VULjTiEITioQe9GGj+lNPMRlwZcHkeMduMRPfgWSydZE6OGenWjaqUunQuVUJNi8mVCetWIoBzTN78MZQAdJIGlEoUFVg+/FUMA+tEXBVJxgHEZ9RWcRFxmQxlwvOG4yVnR9MIo0i5ZUV6HbKY6y9OhViFmt6SErjppEwipmmrXFbGcP6TsQ+QtAM0dLFggfTFTfHY2FmdtnMJJdU3gtbMQQps/RKpOCrZcLXGttF+CMGSJ/lCr/7Df6jj/4V/sc3funbvmabSnax4taNWLgR6nlN/0bA1F4WeRR3rpRZlkqLDNqwqBjKgqcqcTxqMxcmcXx/xWZXEa0h6AR9blRGhX/Qi8/HUBJq2UBHdctR1fL+8zP0VUl1rXFe4U79p+DXoZGRuB554rbgthrh1qLnUbTyzCGD8KpIshrdafrjSJo5wqChM3SpkoAVFOW1lJXFVrQYfAPDsXimhFJ6BNFCLBRunjJ8n8P3UhNPrDXls0JKsHUhvhSYOwPkjM9QUZq8RWaSapMImdH6Wa/PRXDQXkxlNq9r9M7QfCIagP1Jys08GL1f4CeWyiu2rRFcUDYCiR+PGL+UmTJo3MQTb6WD3Fwm3ERGPaoRBecXXQGL4jDvtjsJLHajKBeGUILrpCk5PMjMTSVd373PhT4dSJeV2LhVmskHGjet8JNSPCo2ClUkjr4B3YnC7hK2g36uaO+JYhWAn0SqKyOItpEAatpdJXiLQdOcOtqkcF4xfGPGYrLj0k150Cz5mrmP0YFQlqSxZ3Ik+g4PT5YHJqdWiee//Yj+WPoi42/2mM5jXntIuLom9f2fyjP8tX/wI/y5f+kev/Rn/zYuBUZaQFYhRX59CHyte5evbR7y4fqEVVdRvbNiNurohoLeWR4cLfhkOWWXHcHdJ6OMSBUw26qfsirGIsu+LVE2Mpr0bG9KEdrpRX8hFcKHUORn4DWxgN9/fJ+icdjHAhk0g7Sbpr9XsHsYaV4oip0Y0wwzBVNHLCLBG+qPi8OULNQc7Bj1oMRhW7R5UOsSPYiCNNHgp+mgth1LGIzoV/YXQujqjbzetvK+YYDQRJpnhvZ+xM4HcStrS/xasDHTX2loz8G1mupaMxxJcIh1JG4z5NorPn7vYm9Gjho0MXyfKkHFApbvaoEpZ3aldhCmgWQ16VRq47SzAiddZdRYyHjzgBiPjBN+GhjPO7axAafZ3RNHq/5RB0lxsxqLzbsXostwJOCUciXpv90hIyMF5VLhJ5ZyIcEKJOLHOsKqoForgivu/AyD9CT6k8DsPS0O07WMtdp7itFz8epMFvz9gdGs43zUor4Az37/QhpQrSFsRNXaLg2rcoy5KTAq4Y8Ct7uGX3r2Di4YtEpy4lYRpaBrS7SJdN6KFgIFN8/mzHfCBkwqsXtQYfqCcT87+Er8aVzjZ4n2H1/wpWf/MUSFmTh+6s3HTIuOp7sjJkXPk/URMSl8MNSlY9uXIv0WFR8+P2U+37HT0Ew7dlEdbN1UVGL0mzSUEdPIBClmiLTyWZo9r5PxqGd1O8Iq6eKbTlG+X5FUxfybkWGm6I/FsKa9h+AI2kRzHTGdZv2GwucMxi9LmrXwJQDaM4XRckr35w5za2X6lUl7kDVCSohllHLRgPWyrouVItQGFubAj9BBpnMARZYeUBHCVcVa35W1bh6JV5Ih7bVQ7U7RvFB0p4b+PGB26uCt4RsY8lj+W9lG/lHX5yI47L0onM0+A4VEdt3lWm5dkIp4YNk1l2IBpryMCKtreVjJiILPdin+k6ZX+Kmw9sbTjvX1GLdqMK2MkcIkYjZaKpe9Pf2QMEbed/tWoHmwoQ9TVBTV5P2lRh7fGAkUGkKZbedNoroy0iAy0NxETK9Zv60OYqOhFgJQXxYMpRO/hSrmMZo6QHjLpSLW9uC9oDtN31vpzl8JFkIN8v3nxytG1UBpAvOy4ze/8Qh7U1A62LwZSQbJbgYATSoM+mj+x5Ob/xbXxf/1hHg8YfzsiP5I4euCX1l8EXs0UNWO0np2XYm1UfxBy0AcDMkrKXsSLG5LmMo4GpWoz1u6m/ow2j2ICQPDbS2eE0tBMA5nnjJDqTebmvJpid2C3WUrvhyko80s3qzruXerCpXCjbIYsJYpEkpITCpkDZFaNvhwEihWuZTNyMbqWk4Pu4Pto3ggDiYVCVrh0ESbMK062OclnejupexpCdorph8CEdxUH8B+KkF3krkafcL0iv4i4kcCngq13JQ0Drisil7dZMi0ERFl/f0sE5cygER3Kt+ELLxSpkNHO009ugxs30RGOTsZC+2j7nAaUPOBk6Mty+uTA748adhtZSS5F2qJGTiStGzoUMki8GOR4PKNWMHvbhtsyIszQ2yTTQRtP6UglDR090NmxAXKpSUWsH7dUK4kvdQZ0rqvad+6d82D0ZLLdspyOkbriFMFJo8G/Y34MJo+U3GLRPDihkV2wiaDdurS8fbshrGVMkEVUZy0oqS5qZDFVN8IlNcd1VQf/+k9P//xU8z0i6IOHoTQZtcGnyHlxfxu3GlKASQ5IGDu9A0TBJctB3uDK+/coklAkTB1oKodPvcYtLeEElQlmUR8xaTYj2GYS/BO2bxomJnDpgNp/A3TiHaWZKTHNfokcfNFDYPGdJr2QcKPZBMWWygWGu0zAvagVsahhNgbJqm9ie8gJW8sJMhEJVoXB+b9K4d6P5celG8gVq8EsFoUzLpzRX+SqepZnn7fv1I2ZkAfB/mApBIKybA/6/W5CA4pTwLSyUCIit3DzMbbg1J6jV1p3HEgZg3HBHmEIw+uvs648xcVN+sCA0KweW3g9Qc3LNqa9YuJ6FPGfXdaBGUwSaCrC42bSnPU7hReZ4BUDsLJQHWjCI2oSMVSvl8qIt29IEEsasobIyKjeTGt34JyCcNMHvzkfMus6Xj/2RmL44bluuF4vmXblfjCCPLORsJ9B1lvYnq+Efm4pCRAJFmc+4D18mvnfHJyxP37Cyk3WksaRZnfNwFlI7t3YDi26F5z9PUSP3qL0T/ZErfbP/EztG8+YvUDx2zvG4aZZDpJg72x+FMobOC1+VJk9ZdH3L6YoWtR69JDfh6two01bm6pN4rhRKNOBuxkYDwSlOjqZsygJXiYtZGMwCZ0EcVoOImU//DQoXaGVAdUGTk+3nB7PWWYG6qFZAHaK/ypo/mgJBbQ3hNLgFglyd6ipP1uLrLz0UrZWC5FOl95EXBRScqa7mEgjQJ4RX3ciZZEVxBus7S+B/+wp3q/Fuf2TKOOr3fEl5U0iaOmvR8PiN3yVhHrrDTmoP+BltgZTu6tWIzGDDeVNLkf9Dw4XbKeVawvJ5SLIk/F5Pc4YDA+yzP9E6+KP4VL5f9RKvFDbz2n9QVXmzHrJzJqMjuxgncPAmpVyMlvM4qwEe/J9kJhTnp8azGNR20atJdR3uVywtAWmJVl8pFi+3oSVQqX0/msK+nH8p7KZ5JLEi8Nu8u9A5tIThYCUSYXulfEKiPjTBKXovoujU1WUrxyIUFMRVhdjdmkMeVLy3VUzI92DN4wDPbuOEkiYZbKBFWgsgFfelGsVhmktVeXcmC3mt6VXBYzWdh7Tw+b0JWctoMt8F6hGsUwNaikGX3xTcy2I3zzMZ/VD/PVK7Ud/Vzfpbha0mDtFGFnWG4aTpodHs3xqGVRjdF7TU+d/UlRFDvZtHYHaE03VyQr47vdrkLZKMjSIhKrvPhD9vfoxFfE9ArzaIczFlNEmmbg3mRDNxS4SYkKivom4SeKMBL4sQp7uXwwQRGUTJhCk2DmcdqSxp5kBaOiXW4kmtyMTFDeaMJO3OD1aeT+fM3LzZi111I6eUXKEPyDJqSWQF5meLMZQF9rYs5u+rOYe1qCgDQf1WgLi3pM3Flsn5G3EZa7RoZQSTKZYZ41RfYmvZ/x+lwEh6QE0xB7w2ao2LkC583B21B7QEH9QZXlvKXpJ6kDtPciplWHmjMsS+qNzI7ddUEfFWorMObmJrJ5UzapGURJKmVuhT/2uUSwmT+fTwgHzUpl2HaiO71L0ZJJ0gCawFBraf7UGQ9hEs7ug47GN1AtuRPAjaALEUM1KhGWZVbukVLAnPVUtaMwgavLmYz9LquDOzcqU5KzkUqoFN3WSqmxLzuSgHScFjNhM5OVufyhivFjw+hyhHY1pdYQAvHx0z8WOCrdO6E7UYdeUCykjILcXPbSQB3ZgS4U8jtnP8xuXB82Z8yNu2TkvuM1qYyEmDvCuWSYnm5ZM5bNYGSUWdzISe5PHPfmGzZVRWkDi9WI27oRg+WJkCBUVHSPBlHsKvRhh8cyp/z5IFABlBGzIW2ll5BEe0ZS/0L6ZMNppuRPHPbjmnZbcWODlLNZwFhFMLcyPu+PpeelvPSYdC9rsj8S/EOopTkaJqKkrspIVIm4KgQjkac6B0j/YHClOKbJhCZLxhlx507192lDsmgcr335BdebER994x46N20mNwo3kihoOtHBUyFH2zJRvNRopylXspi2H00xreLkPejOct9iUHBrhXWpYf1Ii1VZrg0PjDegO1fEmSdMA8W8J3zSCHtvKY1K7bnbAI3HO0nZ0r4uzkYp5cUO92wsdW6C0TPN5q1AKhP9eQZGNYFkDfGmYpHp4GoQH4wwDWIfryOjasB5QzPr0DqxnWe696CJjyR17XYWN7GYDpTX4OUe6a1I47Ep90kEfhZJKmE6jR/B5kHB5LmjezRHh0S1bb+jRuS3uvR4jHKBo/c93dxgXBQ/0/sSUPvTRFoX/N5H9zFFZDbdEbcFQ9A0X6+YLcU7UpyxFW4eSTphN/qQFYSg0SYStBbRFRvRa0t1JajDYgOTZ5HuSNEvSl4sL7CPtoSo8a3lxXCEMlHuPWIKw6CxK0O5FJYkSnoI7ihSn7YMnaVsHO2iRvcas6wpVjIJMG1+5knhxlC/sHQPHXEwqCKhrkoWO4tqPKNZx7YzRCeakMM84efhgOHRbW6w576SekU9XY8FkxM7IUxor8TqoJLAER70VCOHX9Sk98fYVjG5kf6GHyshkkXAf7/CpxW8Nbumsp7HX5dSYvRCbnqohe9AklTfRDmVsJHmUk6KcpVT9iCLv70wdOeCgS/W4oGhvKJ76DBjT90MOGfwH45pXiiqRWKYKuqkaY8TmECMMtGwG30IJDFb81W3ilhKHbkXDQ1NwiwtZBCSXStBqzVJ1KYAs5Xpi+k0yhvKFbQXhr6K2Buh8iadgVhVpMzGLd1QCEFLSZPLrmXE55qc00YZ5zaXCpMbde2b7kAKS1Vk/IGVDRGgXJoDfaPcRrpjS33tCJXBvXUPc+8E1TvC734DPR4Tt1sJAG88hBBRPpDWW0gRTo9JdUF/NqKfmcO9CiW4idTv9rzF3dSkncUXkZv1XFLdXrN72zF6sKR0lt2mIppEXJQ0Fzu6TUU1GrA2MvRWIOmbMrMoE7GKhJGk+NrB7Q+Irb2fBKqXBpfGhKCwMmGU77ITU9tYwOQDWf4qgJ/k0d896VW4DyfYDtqHRkyMLnrc1pK0lQyyFeyKdnJwxVLR3VMHa8VyoVG3mu5Msw0Ct1d7TdGclZptRsdmncdYShupuhE1MTeVTEFnqDhAOnYEVVDeanSvcBeJflegWlnnZpB1Gkr5Dr6XTLS336eZQ6kDR0XLpZoeKNEpQ5v32HMi2Zp8jznlDv2YnYb2Wv96uIMomw7SKBeFeUR2NGrpveW6aUhaRpC2TbiZohwNxKCxRaCjPBiygkK7RLGR72S63POwWW9ir7uaYctmyIy9lCcfVSQaLb+XzYK4Wf5uLymX9rVvqwmFZlJLE25U9ww2CJQ7p9woME0g5GCwH8eFSjIkVQbsRMoDt5bfo7qREifUIoAiDV1FKBR+YuinhvCaxfbiwXA0rdk+bLCbwO5eQbmN6D5hhkixGDOcNgwz+XxfKfojCeh6bzM/DaRxYDbqWXSFwHj3D1dHQbZmKrTVEWNjNqkl+05IOSK6mQLqUlY0O9AJ00rWt/dDVXtpvqju1ofKvaNOQRYfdlMx9I1iyn2AKe/HpckmUkgHQhNJ4qAadA4GCjOIA3xzmeiPFd1Fzu/1/kG+Mo0gI2m9wOT33zEvFcJY+id+FGHm6VQp4L65R+1E6VqmEgpz0uEmiq5RFLfZcjEqdBBBGtNK6esbOUzdmccP+lMTke/2+lwEBxc1V73YjInfIPSn4MZJUuwqkHSBGnuiyQts0Acnbu0FvUjWSvCNbMg9KOkQGLTg+C9vpwR/B83eP0Tlob+VubqzMk/e248lJTiK7iRhW3VnaKMlRQ0lxCqPzVojQUllZGYirwI+rdZ1GGWpO3+SDOU+MDr3f68SIetHmE44AFU9MChhs7I0eVQq6t3yQ+nwOW6eCANUVxrTi5RZf6zELrCVDaSiSI2FuAf51HRzQ1EoQqlQK3mNiolYWfxI4xoJ1qHcYzjkI4utNE2TU4xKx7oM+AR6Wci4txQ24/QDy+L+uSz+H95I+psyzqA3RBtJSVLyT123JWYnjUs9fPo57gP33kC52AoQLloZDx4k4zO+xrQJbaWkUK3YEuq90ti32lRK+D7RSiM8WagvNe1rMuUwPXfjxSjjRLsWWjYRyYRVIqGygS+CdcnyiNpDCgq1sBQrzeh5or0wDMcxY0BEGzNaUJljYu63cDk+mPQUW1kL6dLijuIfWk/fzfW5CA7DpuTX/+kPEo34GAIQoXhrw7zuRRFn7FGbQjbOzGOflwxHskk3b4A7dwIIajV+LKg4u1O0r3majy3DcaB6WuDHiYhIiOlh31RSEgB0YvS4wO7k1Nm+HhlmUgsfEHAaokzgsFuZOQ/HsoJSkXEUa4ub3PU8lEMAXHUgRSOehz2yCfLpJvqX+VANYFeGF0+PRa+wCPirmnKliQb6B457r99ideTs7IpvXJ0xPEysLzRV4yhNxK9qwvOR3K9xxE9FkVvfyohr+3bELjXDEczfUyRtuP0yVNdiKttcJvq5EVGSV67+KC8ZBbtzjfbSoI15SiNBFNEyOB04OtpxVOescFmgPIRJQPeacORZ/bSH6wrdQXjRkAppoM1GHZzJCHS7q0hOs3g2E+zEqRPdgkoCUiykH3X2o5f0zrJtK4ZnI6obKQnLldznci19PB0V/budNAqDRl8XhCagnMaedoTnjYijJBi9X8r0aWUOGdswj4KHGUeYOdJg0LWn+VqDSiZPpmD3WhSdhqxyPRwlSRpK6fnsD6ykk6zHhRx89bVimIHqpMxcvQukzDW5rbFLI6VslYTLUYIbDO4NLwGhDhQjJ3J2fcGkcqxfTvis1+ciOKgo0d6dRWx7lya6KOnkPg0rMwrNRfGwCLUo+aoIqhXWXrkQzX7TK+prRAk6R+W9xFt1ZUTF14s0l/KSXSQNzUvF5GkQyzyj2T2IxCOPXoq7N1qwFWESCZWcfjELeqSs8ZfM/t8cspP9KZ60eGKokLUgjaSa5eLOw3EP1fbHwLLAjTR2pw+NumI6cNLssDpyr1kxuj/w25cPcM4wdJa4s5RHPUMvBCEUVBc7lEq0XqOWBsYeHy3mtOe2qoVNeDEQbZHFSaT5NfswyClZwPWXRZGoWsj3ixbcROFmIrVmttIcZMj2d0FMeRZdI27iuW4+f3TLy6dHFNMet6gxThFrUX/2R4F0PDCtpKRarBuxc/MKsxPPSHtdYLcixe4yAtZPA6udTAlSZ1BanvUeFenH+++bpKRaFuJC5aTUMzsBNrmlSNiHfebZSkrvzzx2I6xLdxQJRUBvZDqwL0eG4yTfK4+si7XOsm3pIPZDkomxb+48Ne1aC6KRDJTL6E1UVjybhLvRtE5SCu8TKS/Zx16FWkWIweCc5v7JitYGem9ojtvPvC8/F8EhWuhPhb67p1H7UcJmwdcUFXoj0VJFgRW398RkxDeShmmnSCHTYU8jMYGvX6HYIjedvV5Dk1BVIh45OU5UQrfmcJrvx2mHejQ3tZKCOJGut8iM5wZjFMwFSoHJ8FwP9UtZmPvGYSqFX6HySeAnYscXmgzuytR1+cJkhGA69F1Ukpn/45vjg3zc3k06BM398yXPnpze/Tzy/Z0zFEWgOW4ZlhNxdN4jE8/6gzDuHjth2/wcGikpQv2KDyTilxAqEVMNx1kjUcskZZjJ9//pH/gm192YZ6sZcVugBsXRWwt+4uIJXwEeTlZ8UJ+w6eZSIrTZiMhqdq6gMIEU7zZfsRR152gFNBeaJH2DPLa1Rti4IUoTTg9yuvbHcv+ikRGxT4hCUxlFoyOf2CqA3glOYvbNfECNoFpGtLeix+ikXLInAy6VFKNBxIQyVsFuOaxhPeQm4yRJmanJz5ADiza9suZByjIRMM7P+17PbNxhdGS5ksZWLDPmYRCexoFjEsmMYbAXQvtXKnE+2dL771c9h0QetwgiTWUi1KYakx4CuZF1iJZ/oHxS+wUS82w9Ctw01HsWXZb1joJrKDaQtPw51vZg1JsUuAns7klk7s4EP6EugrhMZRi1ZBrIZGKUiCMZD5Kp3HqQB6QzJp8IthVKdyxkAoNShHGAsRej3kIaYNEm6kvF5s2IGjTjh2smdc8nw4ksgE5qD6UgRH0IDntzXeAw+xbpcrlZYVMQK7mByuZfNr8+DoZ62uOcwc0kUO6nHtHcyZ2HRgIaZAh6oURV2WuCF+l3gBTlfn/lozc4mW/p2jsZ/JTVsUNU+Gz+K2zH/AyaiNpaFttGzIa3BTglPJteuAvSfJbnLYFWsByrmzFqYyg2WXatQDK9vUrXq//kvgODYAIOBK4q4YskILEoatJ72Ht5m5ulTsnvWwcenqx4enUEtSfU9o7DkDioQe+5DknnDexh826UDNPIGjIZzJQUFB0ol4FhEdaLkWhXLEpSkZh8rBk/i4KLOFGH/RNGUTJYmzidtoSoRWksaobwvRGY/Z5fpofJYxnPbR8mGev0ssHi+xOaLC2+HyX6ScLPPWZjGD1XTJ5FVm9ohnmSUyuBPhpoawO9pr60FB/L+M7NpZeQph7Viv6g3WlpFBlws0R/mvIDlZMqXTf4kWQz7sJJ42vQYiZyq2i+riW9nkgGFE4c3UUkdqI3aNaGMMoOW7VgGIJCwDWt5bU3rrn/9oqNq7hpR1y9d4p2UFwZtuOGti05ur+m7QvCBxPS8wr1omHw8FF1JipUFz3jWYcLhsnFlovsqdl5y8unRzRPxKzMTeUU09dyynvfwIV4QoTeiA+DSbSPImZjuPqSKA4dz7cM25r+5YhqIc5OfpQIpzJeSp1wJEZfWFKYwBdPrtj5UmTyr0ULkSMRbam046fvP+Ybq3O6J1PMIONFN0vo2qPHjnE9sNw0Ehh6LeSji0j7AMYfZbZmuiNQjR8b+lOR8uvOIu4kSN9qJcEuVknEXyLYtcLsLNrJWHKfEUUL1Y0hZjOYPfYgKQU6US7E0FYFhf5YOq+PdxcUxx2xL1BZl2GPZhw/iWwfagHJeagXCdsl+rmifi5j7mhEMm6Yy2aP5wP+ssR0ijiKVO839Oceu5IGbGgSm3c97X2N2Sn82R5uqVCtETTxVnElLj6ooFi8Ii70Wa7PRXAQTT0BwACHqGt3dzNsORPoTOoAACAASURBVKle6eZn1SjfQD/Lr3EKlzURtI6Uc8cwWNxOUyRpAMVaHu6+K62yKOf+c/fYehTETsQ47A60BYv4GZBFZZS/s5b3dfbOKLMijzPojURr6Z5ripXONXDCjgeMERWf16cLSi0Kyzft6MDQK7YwrC1hpFjezkk2SuUV5XuZnswiTOKV4Q27pBh6S99YWmcZvBU79knKtG25j8nIwoxVwlSi+xAzkm8/jkuGQ5c7JUVZevoqsH0oGga81sKmEFGRrcHuBOLcNANWRZ6uZvL51xW2U/gjRWsq/tnVm0zKnsvNBLsRqTQ/yk3ZrF4ln4loNg6voCN1YpiLDkZSUN3qw8K3a3Vgw1JG6KXmj0ZRP9d09wKm1VLKmYxP8AKDTlrWVSzlOfbH0hcaP1MUq8Qwz9liVIfReZgG9MQxn3RcLeoDInTfWE5KftZqafIO08zMLdXhNQKjvhO3TZ2wTE2vxChZp8P0fv/eqtcon8uw2gsXJyrU3ue1vCtXqudGUJLfz6xMlWQxqPyPTAwE3GO6HDyylHcyChfyaDCK3VhoJO0NjXgEhuyvaG3Aq1dKEiMMRRLEZCi36qAO7EdJbPCOO/xgCUMFSoKHbSE6aXyqrAK0H5L7WhErWViUkTgIcEYPkvKZ9g+k/FGUnqKKhJc1vz++wJrIo9mtWLlpCSgH5KVOMHH8yFvP+OrjhwBoVxFbcSZXQWFvCoa1Jc48o6OWi9GatatpXcGmblBLI3oZJhGRBZ6yQU/0iuALWfxFFOHSJCPRybylKR2jwuFDnXkocj/DspQmpIb6pabYwOqoYqsqfls9YPVyIo5RJwO+NZRHPTFoPn7vQpyzFxZDbuBqBef9p4KR7wqhReey0U9FeMcHEUVR2dJeKZn+yO8nJ7FvMjYgKMLY0x6LCW4aSuHcqBzg9/2kV8bZccLBe6K9J32XYSabNEwD0Sma54YhGTywtLV8TpkoVor+XARbZLQrbxwraUSGKI30kH0ty1tRjwaNDorQKeqXMl4uF5pik+jWluo24SbSc9oHQxUF43Cgjuf2TNIy7dq/RgX1h0rx7+b6XAQHP4L1m6CipG4kASVVCzj+6oru4QjlEx//peJwso1Pd7SPpxIldzLSUu9sUZ2FWWI+23E+3qJU4v2oCI/H0rhci94jQBp7emPQrRZ7srnHTB2uLTA3xUF0pr0Qxua+EaQHYcpVN5rmZWJPEXUTEa2FfTaUF0YhD6m/CNi1xvQWrizKwWinWMUj7FbxG7NjSEpO2SYRKiivDKES4tnXLt+mfntNjIr+zODf8Af7t+g1069WRFvSXVi+6gyTUc/peIdSUHxxxW5Vg9OYtcFuNHql6E8jtgwEk4itzUjNklAmhoeOzcsx7djzcshHXR5Bxnyah+xOvnszsveMRIEPmmrecTRpqa3n8dNTUlT4RZmnRXLiu7loDYQSEdW9qYlecXOZs40s1iJ6FBaXzblUVISxTJrcLNI9iOhJhi9vLPbWEkaRYR7RvUZvzMGr0o9EV8HNInYj0OX9M/PTvDbKiBl50pOa9mEQEtZINEX2QL3xE0WylvZ8TOmhPwt05xJ0+7MISnQ7VZTm7TBLxGlA9Zr6uaE/lxK6P5WgoiJMP4Td/dxTQTAQvoZ4pg6yAEwcyWlUKmi+2jB6Lv219lwdUJLdacrIYERVavv9mjnYuxrRbu1BjGOYKvy8ojs2eSKxT9mUmNGWKXeQZSQ5KsW52pjItq1ISaGUaA4O4yg6j43U1Afy0wEsA3prqM52OJVwjRC/XNDERvw591lAqBO61Uwfx0OzyjefvvnF+i7C96d5/l9EwVTkxpFyKqe3AmyKZW6OvYL+NP0dS3E4SYzrAR80HCOQ6n0aHgSdmLK4R1hVrKK4f1XjgdIGXO2pjhwbNZb6O+U0PCNCXVCYrsB0ErBVJylp2FnB9ZYxTw6yJ2lUd+rRCkyTU1wFu5eyi1/cNJTHYpqgjdz74SQctA/N1KGe1GgPrrfib2kyynIvyJIzlZhl1lSSzSaTBQiDTDhSI6NbEcfJqXqU3D0UCV9EmicFsZD7GWpRfPbDXbc/ofGzIJOpJEDOpDPITiGTpUqJqEo2RJLPUndIxvxvGbPm6U/um+mbQg6RDuIyMzT9/oTPJXMGZ4Gsq30ATa9OzlTGxGR/l2jutCVQ8p32AjSQUcafdVt+5p/4XlxJ6niz01QLiXj9XEaA3WkhVOAKhnsDGDFJ9dcNzScGu5VAUqwU7a4idIazBwvaoWBUDcyrjve7UyklEDFQ5eUzg42CuowFOluTxYN9u7xGRSDkE2fuJYWbeNLO4iZyGpWbJOaprcBY3TSy+4KDICNY00lpEjLqsthYorkz6UFJGTUcp4M8OkiAKdby2baVnsHVM+ElKCPIOJYFxUoxnIU7LcOgwCtmk5bT8Y42jwWVSty+nKI6afCpINnTaDSgVGI+aVk8rwh5Y6YqHAg7utWYhShcxaQkOMwGysqTksJ1Fq3jQZ6dqA7NvqEqUDvLoBN65GEEZeVxgyVsLZNrqfvXTSF4l6OILyNVa7FbycCSlXsUmkwD31PkTWaAdgrfa3QrNXvIzFj58vl+3lqKrQSZYpvwXsBvbpYOEyvgYN4bW4sq5M8ppGyam7KYsRxY++mVzm5mqUiyXspMErQCaXYzEY0dTgOT903e1IJS9dM7TVE3VZnun41shrtA6fffc2dRdTgokyWdTZ+GfWDlQCkfjmD0XOPG36/BISjs2uQmJOggp0Nzlbj5QUN3XxpJovmAINvI0vWZHhxqGWfhxCDGOaEIK+SE1SNPdIbkFNOvS6d+PVNgFWkUUDs5dboMny5uzQGUdIDmKqnlQlLYrSYWClI6NMFSAVEn4tmAWku9vJcjLxcKP7YH6HPKo1Dt94rGMiIzgyI5Oa20h/ZCiGemzfW106jRIG7T2wJlEmaQPogb535AHSAqZnXPsqvpnWVa90J7ziM8gYSL0e+oEg7GqHBcNeLCpL3CryzpdEDbRAiKVClGTwx+Z+gvPLE3B0X41FrseMDb/UZLkHkEtgr4zqAzkEcpaConupdOi5JTHj8TFWo2oBQMUVG/yM8hQLVM9HsIR8p4h/0ouQ6onbBQdS+laSr2DlB5BLvPEH3m3GTemj/xB8IUKkHGu5BybykKRoWgKGcDIWhCY3ETRXVLdl6HaAVz40eSDYZG1oY7E6HkYR7RrWB09vc4VEIgq1/cbcV9432vyq7yZtfDXRmXnCY0CTcVqv5eSW04itSXIoxULqx4q4z4FN7nu70+F8HBdDD/OriZzM2TUrTnGS+QoHppSH9mjYqKunZsFiMZCxrBkJsuMfswsfhShZsmdnVN8ophVbHsNcVCizKQlgi9u58otpIm6uuCMAv4aUC3mvLSsgfdqKDoL2TnhlIkzIuNAi318uKHvTQLTULZRD3p8V7z8GjD9WhMt6rwyVJfSmCbfKTpzjPM+HggrAup/XtpUu1HWpz1pFVJKsQ5u1yqA0gGIG4t1WlLbGQ02kVpDA6nAktWO8PZOzfEpJhWPV86fslNL6Y41gRubyb40tI8tej3a15uLbrT3Nzr0YNi8yjKVGfi+dE3n9L6gvas4ONPjnETYZaqoNCzQEpQlJ4eAWGlbFmf6kiYB+w458d1QJuELQJF4SlsYHE1wV4V9OeRPgmKMwTxZJg2PS/6I9o3oqBfk6K9j5Q0k8DkeIdzhn5SQa8pnxeHQKsyx0QFLT0pk4N5KQ3GaGH1o078VXM5uU/XVRQg3V6RXHtRC4sG/DRxMtuy2tWkNz1DnMoo+4UcaHsU5t4gt7oW9SgUtO8MksnUnuA065NcAuXsrH1NalCzvWNXyt6Q8i2WCfPGltePV+xcQecsaz0WgduJgPG6kyg9sgcBNSh2DyPlgy3WRpz7HuIcspHuV4CnKaW/opR6G3HYPgV+Hfj3U0qDUqoC/ifgx4Fr4N9NKX34nd47GYHhDnPpEictJ0KzVviJ1FU+KarKY1SCtZVNNQjhp7qVtKrY5Jk05UH737YSwdXGwNwd5uOxSGL0ITpfQB7dISIwB0bdfs6ZSV2hEsCSCRlUNXUUpYiiVoVHayMMQ3NHdhF8RlabamQck1rJIuxaZYv2XPNaxeB11q2Qky00mdj1QBS0VYKmGvBeY0yi12VG4GV6eSPThkVbY3Wk0IH1UAmS0hXyHvkkklNKkJtaCeo0GUmhq8YxK+9gt6YQjUJqYZmmBHFd0Je5M66SMEX/f+reJNayLc3v+n2r2Xuf9nbRx3v5XmaWqyrL1SEKLBkh0YywLZjQWDAACammILAAzxjAgBEgIRlZ8gAxMYIJMEBYGNUIJEQVQthlV1W2772IeBFxu9PubjUMvnX2jSzsqnyFsvTySE8ZEXnvPffsvfZa3/f//o2AFBObqh45vl3oBMk70rlWPaBfE+dJ8YeSgG7MA8GLUDwuTnTsuoC/QXRjOFRIZ6nfa9V5umaSYVyVPr20iGGRyD6Ty6EiNin+VMal9sYrNrFMJFd0D1nJeKRSsdqEN0nDnoOlXUZi7XR9+tIiFiarO5Q8Ekexq3dkk4kJ/GLUCVpbrtvBFvo2xWNEfUxdC5NFIYqBqHu3mgrPzjra3BCzEPZqaZijyggAiJmxd4QRYvvTJUH9W8DfA9bl7/8J8J/mnP+miPyXwL8J/LXyv3c5558Tkb9cvu5f+aN+cPJw+EjL6Nio6CRb6C+hv1LwalWrI5K3epOHi4gZhOa9oT8XwGB6CM9yOQUEyZnqTqm/qcqM4mEe9QEQg7lTXfyQNZcgzj4o88sim5yPC4PTFUxgPIuY9cjZ+sixq9SBKqvB6c1hTtdWSGtIq0DovP7OVxF7sMRV0pFnJXTPI7PXWsYuXmf6TohVRbVVUVc2OmrMf0iPn5LBmIwpyc9mEIwv8E0wmoyUDBH4/O6cvvesFh1/7sWP+IPFY66XC9q4xB71Z7udRa5KS2C0EprVA+e+5ZvzG/7W618kHB2mKmVVGaNJMXSVqN6WKQriE3lQzcJgPbZQklMQcl9zbCoOdcLd6EThNIo77mtd3JIZaqtGJ3OUnGX0IQIgQ387U2+LQmxKrtAzTp1TATF1U9E2C6dUdSRzdn7kUFeMt+rUdAJVTaeVnO10Y7fdA9gnn9dcLxbEaDhbtsovKXR8KK1AUn7OySQ5lX+rb3TjDkfDiMrt2VtYBuXHBB3nZikjccBsT58hqwGNS8TCeMygbZrRC3J6b4lCTvkBmA2Gaj4i858S5iAiHwF/EfiPgX9HRAT4Z4B/tXzJfwX8h+jm8C+UPwP8d8B/ISKS8x8RsWS077KDmcg9Uo7u+toSZobD8Yxcesf150ZJKkE4fBowy5HtpmL9+6p4nL/NHF7qgpu9y+y/8TArz4Oy6+LlyOWTLdtnc+K2ovmBw70R+is4/nyvoqjOqrHIwU1jyXGZVY1XJeRtzd1goTOYwRCSTha6pz2PHu04ziouF0c+50oj3m1Wq/vecbk+crebY0ymTSczCMtwlonLyJisouE+Ez/qsD5yuT7y7t0ZOUNIhv52pr/fesT+yJJNGf2tB6zJVC7gbKLtZqTBcr9d8/58yaZt6DuP6YTVj0C+Z+kvhGM106DWR2onb03mf/nhL7Ced1zfrZDOkmaJNEN9CcKJpJORs4Gw99hdeVKSkJ931M3I8YlRSXIZuxqfNLUpn/QSWhm0cwtROH+24/7VWoG+qwE7D3qQ3+j3hEWElJHliLmf0dyo1qN9lsiLoDvkKNpzJ8C4iWyVBeLVqMndNhOSaGtZyHPzJweO7xeYoJ9jOBe6J0EfwirB7QxcZlvo8vtfHGAw+FurLlsuk52he5ZZ/MhOFofjSo1mMCBHq1F6FqxJXHx0z83NkhAM/p0vrEwga96JbRWsb+8bxkHT6AHO5m3ZUIun5Xt1A+se6+aWHZj3FePCQXGU+iqvn7Ry+M+Afw9Ylb9fAfc559M7fgG8LH9+CXwOkHMOIrIpX3/94Q8Ukd8EfhPAXp6rMWsFpi5aiKDldqwfxjzNO1tGnAr4tM9VCRhFc8b78wcgxx0pIzkFi8a1au5TpaSTcWnY3F4py63V3jRG6B/rKWPuHHGRmH+vYlzrlGFclfFbawheH2Ixil7XN4bmvY689qnmxuhE4d40mG0x5bCZ/WAxW8f70aq5CYpwr/++02CVazg+cWRXfpcMORjOzzUler7u6L6/Qi6OVDeWbC1yciPyMP9S2FcN19tKNzCbtIXZG+I68nc/e07aeWQZCJeB/l7B2XFVXJx7Hf+mpL4O7a6mbz1iwF72WBeZ1SMhGfZvl1y+vGe7m9PMBjqTCacE8yg4k+nainx0Ssop7Zx53hKTMJ7FgvRbFcK1luwzY7SaWXE9w31PCUbjUjehZMC9101ivNSWcfttVVq6gyBbjx2UtNRfRfxGp1PVRlSeXym4enu/0I2qf6g+47xkaixH4s5Ofg86/YGcDLIIGJepqsCQBPFKipLMRAhLlbZd/UWpmE55LE79Rk1vdELiM74KXH9+rs5fy4GhN4wXqPv4rFS0jdBcC33yuF3F8WwGCQ5VJp+HaRx/mnh9aIo0e2vojBCrP+SH8RO8/tjNQUT+EvAu5/zbIvJPfeV3+Ie8cs5/HfjrAM2Lj/P8R06VmWX+5A+UkSOQVbhS3xeuwULLvPkrq2OipdFxUJkspIoJwBtXZTxYdmLTq64+zDQPw7RaRkpQA5RcJdwsEHqDOxsYV8qBP5WZ4UL3Q3+rJrRhHXUB+IfxU30v+O+0HNqK/VYFRPW19rFtsTdj7zVXojhFd48y40XCdEK8HJGDVTs4ICTPvVtgBLrOE1eR/f2cutfrEOaZ7rF6E7qDTjxSMV1h63FXPcF4pDekpDyE+rsNw3maCEBhkWnequBsfK7tUT8WN2wB5wPOJbyNLOqBd3cr3L1ls54T7ysurjZsJNO7yNB66D2xeGPqDadMELKOMSuv0wwgFNHV7I1aox3cDIKOnYEfk8Bnm8lBH7jqrGdIyr8wdxVaXiu/IM3SJNOvbwzrH0bCzDAsVckYSyizGYVqo4pNSQbzTG3pjnVFfWvLKPlBexMHDacJ9ajAaxLWv+txbZ7wjttfS1TrniEIsfg2pFoJW8nplKF5uWdWDxy7Gnc2EG9rRuto3ik2YVvH8ZOAPRgFG1DdyMn57DSqFafYTvKe48uolclcMacsmf5KD67uTzB6+Em+5Z8A/nkR+QtAg2IO/zlwLiKuVA8fAa/K178CPga+EBEHnKHA5D/0lW1xKlorjpCLB55YHVHGOlPttI87nT7Zlb73NEb8QwSwiVRSQj9OwSPZKF4gs4itItF5sjWE0Wg82c4SouC2lmA9Tfl9zFBQ7H1hQE6uTqreW7wCM5bgXhE2X5ypUrNQi12R7PqNndyukleMI5s8TUFsJ7TLkjWx0cWbraoTrw/nVBcdsjmNqIpfwTwRRAlJaVCAVYK6MMmoD7pUScv6Jk4P7AlrjY2eNt1jXXAnQPWUPCVGU7uNSayannb0LBcdhzhnDJomHrOwanqlf2dhaB2yL4S2IqySrMzJ46rBNpFkMznr9QvrRAiGsFRmYgqGZKyK10Q3lVNbaeKE9eLPO6oq0q881V3psx1kMfhP93SuJlutNNTFSiuB6sYyPA6sf8dpDkmjdOZFPWpU32xO9ywT5laFU+mDsbYV+s+WOq6k0gnYc6G5BlKmurGMeVZAkLIWCznKREgJ+taTkjB0Hve6ZnEt7L+VcXuUGdqADOV7hpKlolwyUqUbdrKQ9k4nWkchzhWfEHR92aOleV9CcvY/BYZkzvmvAn8VoFQOfyXn/K+JyH8L/IvoxOJfB/778i3/Q/n7/17+///1j8Qb0A9e3wix0j57bDQm/hRDlp32lKFR5Z7tCilkkWludNNINfidVgXjSugv8kR/Rh5MRSUBVcLPRqoqsC8Pu9/r/NmMgr3XMvcUmkKi+Flm0qctsXPYGzWcmb9WZmKy2u40t1oFVI+PhNFpsMmlwX+h7Ux9B/e/AGmRlDHpVPh0uFKOBiZj7x28GDChYvYuM7tWBL27MGz+7Ix8OSI+wWPdDMy1Aqv2S41+M0FJL7FW85zh4JDOqnTivSU20H06qLPz4wj3XhWmt1qCH23D2CTFH64rJaXNEzw/8vp4ppqKo0E8ml/qE6/fXCA2k48OczRIlZl/oa2E30Fzl4iVMK6ENtTYX94QvSFUlpBqnZ6MQnVrMV/OVYy1UEDWHQV3Mt+tcinVhfHNHK56os3EJwNjrKZwnNhkxtHy9MU9b805X/45rx6aRV8yzjIyGA4v4ex7Wfk1o7DtL9h+0k28h+adtrfVRkV+7eOSZZH0fVKVObxMNO8LD6cwOuu3Vo2F7rTiTV5/Z4DjC+Ve1FUhkK081Z1l+QNHc5MZznWdy8VA3FRwsuXPhfdiIb3sShK5wbytibWa5cQmIbd+MiE6fJIm3sdXff3/4Tn8+8DfFJH/CPi/gL9R/v1vAP+1iHwXuAX+8h/3g06xcicOeq61/w1eGWXVrS2uzGXBWDP5Bvpdpn1cTFKq4lZd+s+T8u6EGahjEzAaxlJnSa0nqZSJRL0Rji9jEeWIcu2LqEWCEG/rMufXUZPff0CtLZLybGDY1tPDzjIqP6AHtT8v48JysuT3NdSqAUhnI/Ey4IBhnahvDKExeurlPAm3AJaLjs57us4SO2UXhWXG9JCfdTDaac4+5a+VDTPZRM5Km46h0mtfZYwV8BlTRYzJhHVQFeDlQH/05N7ii01Z+81BRVpR1YTuVk95U9osSbppjmvIVlmZQ0kUO75fYBYjOWn5m1eRMTrcQRhXFJ5BUUAWtmEqcfWQp/SpsK3ogtGNrjg/SYS4DiyakcvZkc1qxlhHOl9Pbl2mFfwnB8Z2+YBrJd0g8qaCmdL5w0LvK0nH6v4IJhadw+NEvlT+wjDUClpnIVW6KY8XieyMnvSFfAW6eYSd1xbsUGHOBo4v6hLWpEG6JogyNBOkOpMqUU5ZodXnJMwXmsCNyUUBKvit1azZDoYziAW/s3+CMPWvtDnknH8L+K3y5+8D//g/4Gs64F/6qr/ICdU9jYWmVsHn4qYTFCE/HwmdpXnl1fkpZOqNkl7UxEVPPyNA0Ac4zhS/EK+2W249IMUlR2xGFiPj0jI+Ckh0UytS3YuWzVkFQiQUDb9IhN7S4TkFy6hJa5mw3Alxpgu9fxYw88C4cvhd0T8UjoX4RB61l0yVlq/jsTyotf8xZ6wpy6DM+bM19KMjjCocU5lvYebVmbyppqzQSbUnPDhcFfOacNPQ3JWx47lyDlaP99Qustk3SK1tAlHIg1XcouAcrtHwWoDjMJ8kyONZmpy0s9Oq0ISCbSzLHrUY+YWP3vL3P382jUMflJJlEz8JX9HfV0LGxkINLj6fyQsJp+NKyvdEJTa184ofpkvGwdHMBg5Liy/COHsU4veWSOGSnCjWElAsodJN8hRJ0D0puo5RN6nqXpmY4fjQ9sS68FqqTPsi0Dxq6dMc2ytofGLa1jd6kgxBPT7TEuyoa3hc6z0PVcZuLe5givtZ8eUsSWxSXNLIZf0Nmt2h5rdM2FforVZLXx2P/HowJMMMtr80YmaB2WKg6zyDqXBnA2wqFcIA7umRFC3RZdxBJxnHpwpAhVUiv9VRoKv0lO+fROzeEM4isy8+YD5Kia5HzVaqLx3z12B6T5xn/E5Bo+Fc1XKICmAkQYQHVgrQX+poM7+2045/si+XKNidJc8D9c9tyT+fkCyYtsK5iPdR/SaWSohKtZ4S+UmPrwNX6wNvrs55+nhDiJa2rbGjLae93u3VsuXu4GlnSfGE1uK2Fil8DNMD6BQgXw662blE1YwE78jHegoitr36YRx+cEb3rFXD1yZNoDBRyIuoZqzzwHzeT0lU0hvC41HFWo1OWVLrNXS40SpgXMLweMQcLa6KXB8XzBY9g0ucr49s1w3deaUq0zJeNL2Zouzd4UGvkY0eKPPXRoOPF1rWx7rc5Mc98q6meyy4KrBseriEQxSkN4wlI5UkDOeOcZGxg6gB8TxOWEtYJF78yls+f33Jr3zrFb/7xXPi0RFWgmSl/QPFlUlVlnIx4KvI+fLI23VF2hlyzRQbYI8FuH5nlVQ3ylQp9Y+U12MOlrRQsHtYJ9zREiu1FJBRWaTtsSYXkDcsdFM4+Z6cDonmVgB5sB78Cq+vxeZwOh1yFoZBg2Trd44habqPCWXq8PeWej+fRg2yWZxs5YrHoUMBH0fZVR922myV1jpcZWI0pMGqycneYqKw+2YmPBqQo/bJ1Z0tPhLQPitS26OF1hIp7L7CupNRqHZ6io0rkKLJSJUa0uSSHC3mx2/QMOjlN0UVmEUNctu5p995WKvk/JP1Hd+/v6K7b0AywapfRBgN3UKtsKuLnmFXcVLsVVvtr8M8s/75O9ZNTxccQ7D0o6Nyke3gdNMwTFhOPBrqO8M4zFm8FcKf32Nt0vK10g1NJLOed+zaerpvMgrzFy1d55nNBg6b2dSqxEb5/WGlngopKRvybrMgvW1IZ4GtbQijgqnVfKBPgp8PpFdz3ewKuWi4SMSFtn2mTJCyhTSLVO8dfqfYTjrOlCPSWUISbpmTosW0GjiUi13fSS6ePeSTW1IJn81ZQcrPX13x7PkdjR2pm4E2Cu6m1hbW5OnBdkErKnlXM6wi707TmlTWpUetAbFqatvrJlfdFw1KC7EyjJc6baFUU/V7PfROk6VcJ4bbZsJp0kKvaZ5FzbYo1YYtWIP6kfwUAMk/jVc2IJUGpOo/lECYochcoxJBJnRftIQLDcRzvcjuILg9ehJcFOqs07GXGbQ1CEu9uNZF0mjUXKaIcaSU6zIqXlFtNM8QEc0tnAfyXkk6eTR6twXwCbvx04jpxHBLFmwsJepJtuvipGDsezudxk5gyjx06GiujlRW9Qgpi5qF1lEBwJSVQ7ggsQAAIABJREFU7Wcjvg4EOS1CUYp3k0jWTmYm1mS81WubsuDsQOMCQ7Acd2XmKzom1L6bB1+A0XK2aPn4/J7P7i6oXEAk07jAu4OSZeXkrF0qjBgNxqfSH+upqJiREEeDzALreccWaF2t1zRpyCxJmZaAkpScXkegWMKVBT9+cBoWglJygNOHqL4xiJWHn50MaSwUZVcmNPOI7TQJzEQdqWaLuk9JxlaJaCx+NrKuepwkZSUWjOwEjJ+cpWOj2JYkiIsf9/WchFOTURBkaxVbm5Vi1Dy4kskop6k+GG2HyTptMj6RgsC9UilPz0myxdksPQjLbOEK/cy2FRgVLbXv52AybmNproX9J3k6UVVJVyYYfYm4S9DcwOZXVcodVmo3bstJI1FUQBRkEsSEuSH0TgNTRqOOwUetPjKKC/gj1LeqADy5McXeUu9Ee9xBSIPBbQ2xWMUlp6dPsvnBWarwI1JlCEbj4UNvkZ3DlBOl/saefrfEiKhNW8EImtnAr1y85ufW1/zc/B1/58vn5L1TwZnR8aVbDzSzgVgZKhfZlU0o9fVUQWSBmR9ZuIFgDV1wHAfdEMbRQhPpnurKsV0JYC1BK/0ZzGYDN/dLvmwvIApHn5SXsejJxd1p2NbQJJpqLOlUaqbrA0VhWsa4O1N8LQxfHq+wB8PsmzsALhYt19sFKRolVEmenMGmEJoTDpF0/Hvylsw2k8/T5FlgBimeGLp+GAxBrLqMw+TzSLHKk1we7LK+YlBwNw6Fo5AMQ7LcdAvatlJSWXsCqXUTDfOHWMRqI8RaqeSmnO7TKwNNws8HhtzgN/8AzYPooSThJN/WzSVVuWx0wMYXG0WtWMMylfxVA2II5XAc1lpx/cy2FWToP1vSbHXxhHmmfZyxT1vYKbXYDMLwS0dyFObLno1bUV9bFq8zy9+riukGjBEWXyjjcfG5nXQbwyM9frLX3d+d9Yx7ZT+GZWb2pcE63RiywO6bwvBknExO/HxguFLzE1sCXu1QJNm+TC2sxs11jxLuSctq2bL7O1fY1iA7Cx+3U2txQuEB0oWmg5tNQfvngb6r+B9/59eR1vJbpSSs++L008NwJsS24UCD6YVBwB9V2OWjOgbZgyGuImMyvJhv+Fu//x3yW20F9pejpir5VJK6Mv3FwNn5kZe/tuEwVnTBsTnMuDw7cJx5+t6ToiHsPcd2jgRDeD2HVWDx9MgQXDHXAbb6AGnAENT3me6RMOtMCXnVh7H7fEV2maOfayjRKOztTD0qzhLLzwzHF2qOM5QTPpYKJc0S/l4zPcKx0QnBKk8bHD9/wEZDVQW6twuIEM90HZgmkMs0IBv1nwSdjvl1z7jT6+SWI85HrvcL9ndz5t+tqG8zs9ukAUPnysDtL04MTFR5u4xQJ7IXuiox/1wp+O6Vo3saGQe13BvXakdQ3evGbFtRT4qjaDbLTMeh7gi7T4QYBL/zxFq5IaxGcm9xi5F4U5PrhHt+JD2DphnZXS+IxyI6/Iqvr8fmYCAtoqZWFzYZGOJdjfOFvOIgtupI1BrIy0Cf4XiwtE8T7qi9Y5xplkVsmNyqJ+fdCMwyHz+9Y9dXXD655bvfe0ZOQqx1hDR7X0rEAdyNBvXGy6T5CYkp98K2infYXola/YUwXBTm5SqwmPes6oH7WuPzJCiekkeDP6pwRgT6zquUfFTNh3mieoSUhC4oKUvzMTN2UwRARUocT1hNwTekYCtEmL2yhfSlvhbbsSF2Fj9ognk3s1q6niVkrnoEVweMSSy9ltBXTeTLL8+pfWB3s9BA2ajfn62Cvup5YRkWjtWyZd30zNzI7/eesG9I88hwppjM5HKUQaoTSU3FThgzyaWTL3Z8vWFcQXo8YN7UDE+CqjQvBuJgkKObDIhdVnMTEFIl9FeRJ6sjYzR4m+jCUl28RN8vnoF0ZgpQMuOpPxdC75BB77d8NoNW2D8vI92k1gImqC28ukdrC2o7HX2bk2dolPIeJxKVVpW2M0STND2+Vbwhi1bGyek1sEOJYpxpdgZZiDNN0NJKJBPOMqt1SwiW9bzj3W2tbfVdw/nzLbv9DDuLpN6S+5+uKvOn9wqCu3caS55BFkFLwkMB7IKWbOOZ9mg5wWzV0yYNgK3u1A3ZVCDJlpg09W7IgoKCTnW3crR88f6CZjZwe3zgOcTGEleR/szpPL5w35MDU0X+7Ms3/F2e43xk6B35y3riN1QbHakmrzeuu1C15LLqWX/7nu1WhU8k0ZQn0ZLWVokURZWIxUjVukjtR8ZoydEUZt2pFC6YBCcbOt3I+stCqBp0KhF8Yc9VmdmnO4bgOAYPgyFW+YNxXcb5pKLTwTLuavYC22VDTIY2zKG13L9ZI/MwcRKSV7cl5XqoRVvoHV3lsUYdpFMUbOFkxEanPWFRzFmchsQyFhflvSDDqf3IZUPXnqJ/pGSs8SpgZoFkdCxZr0d2+xl9bggHw+ydMLtOHJ7pJm+Phnfv11SzkfWi0zYTBahTTorZlFHxNN6lYBmjMlXNqAIm2z/09Sc85vhU/Tez1/dyxcOBDHGZkFlAbCbh9AHv1LPStsrRCatczG+Vwp8thDpT3yi4aQLsfrlnspz/YTGyKZthLMpNQSMDZ35UtzOfaVY9m81cA362HpqIdD+jm4MU/XuqSsCJKL/c3bkH01wBuzc6GsNrrNvRqsCqJAvvPlUH4lQXd6YyW05NWRkGCBD3juNdxfCo1ZzDg1XdvlhdLOX9PnyZYqVjrbYlyZbQESMTb6DaQRjB3HuqZ5HGjngXcVVkOGifHysFNSnuzrm4V5ley8pxcDx/ck0fHSFYQlHpnfpt7R31l6y2ZfPzQnJWR77FG6G688SkWoyhd1y/OcNv7NR75kq5FtZpWRWykCTz7SfXLH1PSIYvdytoVLxVNSMDwNZPoT3TNcoKRnZtRbtrlEBli/z9RBl2Kjw6gZ5ii/WaFFCv0MhzuV+SjEYEFMLPJBEfdPIDqLlMechV1yIaEHxZWrYs9Lua2/DgECW9PvihaB2gcCtKdem3Qt8YTb4ehYyhuVazGFvUo36nxLcwCPlZR5g74tEye62+DKnK5OBJs4gMZtKGTK8//FdTDrNSlbpWKyo6q2XWImB7qxmaZ6X1CIK7t+yakoJVwG0EulttWWSuiuUc/wRoJCB/DLP5T+U1e/Zx/tV/9t9m/9Jw/PWWxVJJ5LvbBe69p7kRBQjPheFcf9+T8MQM8hAqWgwy+kcRf694g9qJKesSlBlnXrbqMF1HcgL7RcmKPIlZCjXb73VRIooW+21hrxWA6eTQ1F9F6ttCFd7rZzq81JASedEhprQloGKk1kKdEJfgrtLch/6E6Kdi5Ko323RG/81m3K3TTMmnLeHdjFwrB8EsR9LRFaJQeWJXo14fm4mtxd47Zu8M3VUmXASkiSzXLR+dbfjB9RVhtMTbGhk089M96uBHczWnMXliZSphSyuG4SxNfIM4T9Tv3BRX119qxqP0+nBUN5bhaaA+70jfXZIdxWuDD3CUzHip36MPAJBPcXLCeBGRJiIu4atA/P5SqfMOFl8Ih29kmvdKnQf9dxOKtuOgl3Q4U9u9MD9NDLLaA5T7fDqA0iyT54H5uiP87noCBJVmr0YxbmsJS7XLl9Ew/9wyLtW3Q0ajff7BYYuALjXF9HYVJn2L8ZF8X2kgbzBIq8bGUiYzT3/tLbuu5uPze373s+e4LwoWctTPdAp7GlfQPY5Ud7boWdSfZLjUw8KM8IN/96/8ds75N37S5/JrUTnozqlmn2k0tMda2YsukXwmzGUSIJ288Gx5mJRLD/2jcuqMgttr+lIqYh0EHVNm7ZNTeVBzgjSWPrwDKKhvETFJ1Bt1KjmTK1WIKQ+s2KmPhIeSE6DaahXUrj3zqyMpaYZGR0Xo7ESD1nwKeQhEsaKisglPKP6H5ffPJjPe18qQmwVlLRqwe6VK57meVsZl4sERrbozybVnXOhD7O4d8am+4X6oGXqHMXka42YrjE1FcxTGokI9Rf1hHkZsJyfvOLkuaxVnHHSlMsmCMv2OwhCEECxSqojYFCfvYqKaHTRXLUPnCHuvLcfOaCsQYQo1yeB9JGUm3YCk/MCODCqvn1ilUu6L0UmHKTkRWXRqERcJGgVl0+gV37noiYPF2cToIGc92Ydz5SDILJAPZmJWnti9p2pJzYp1tHx6f7fXKcjgT5ZjKiDM/kEsNbU6HsiZJ/MdfXDM3YCxJdy3sGHr24wdMsenJbB3EemXEXvnqG4VH5Lh9Nz8jPIcMOrNP7vOpLpSYPFlRw4GW3bRWGTYsfB8bKdlufLRT61DJkarJXMyOu7bKfjHiZPuM8ZGkhOsV7DmtObqW5CkD3WIVrn9ZYzmjmXcdzi5DqvzVLZC/EZH13iq94W7ILpzSwIZDN1nK/LVwOgs6bamujOMF1LYg4VEE7QlkjKX1+uSCw9ce17baxK5+MRs1SEC83rg/bs1NintmKMyFOPRqQu0zcTRMNvrBhgWDyX6aZM8vdJZIODINuNXPcO5xa0U5Y53dQEgtfzvLxJ2NWpVsh6Je09sDLHXa2Z6IXrFUkxZzKYz1PVIO6v1s4/qU3AK3pUELy42bLuGjW8YDxWpM4qnRG3/UlRiUO80i2H+pU5BxpUQFolxWVSuW6P29eEBCzg5bkssHaShZEkyEZ9ODs4xGFwdaNtqcrOOdZFlzwN5UKl/cqqf0YxUfR+/VZBxdHbKuzCD/ny/09ZGF1MmF+l4TErbz7P00HUk+NHmgvvNQlm9HxT51TZjR/2v2uo1ODllZVvMZcqUK88i8TzyVV9fi80hV4n7P9/raO2gNGf7uqFqFXUO6xMhSquBJ/+H8P4f1USg5kYrC+l1HCQZFl9kjs8E1ykm0Z8X78d5VCDqzVxpwLcVrhdCidXzVtuT00U1PbQfRYjao/v7QlopSPvwKCqwt/fgEsOTzGB0ynGqBOr3WmraL2riLOOPwvBUwTW2uvDqGxX12DvdWNpPA6aKWJc0un60EFSmXb3TCUrnkrptn8Hs+7U6AD1Sd2Lp9KSu7rVs716MtB+FQiEXhV82nkMSDjdzpDOEUhqfWoHzVcuNmVPVI32nnpx2NHqtHo1cPt3y7YsbjqGiDZ4fjI8IZwbzgZGp9IZcJyTD7jsjdmPpjhWrj7fsf3hGfDoQDjX1vU6aFt+5w5vIX/r47/A/vfolhnnP9v4Cc7CYoFMSudeJQTeL5FWmTWrfny1wPhCeBiUq/e6K2Xth961I9pn2pW5O1b2huoex6BjqaylEqFQcviGuIhwdo9cyv2i9sJ1Q3wntUIMoezKvAnTaihw+ydiDwR/UCXyaRFSR6AWZBboLddCq37rJy9R2woBuqGOVS5CRupXdvjrHn3fsjg2fPrvhc3dOu6vpHlvqOz2gdBwfyfOoo/fOfpDdAesne9rO81VfX4vNgSTkvdOSr9WSXT7YJWXQHV2BMMF1aSLshLnOlyUWG+8E/qigXS4koOwoYidtVao7PeHcQegen+h3INH8WLiIJLA7vfF2axjPEvWNaigkQZoziajMximoZpUE0z3Rfry+kR+rAPS9CihYPmS11fJSiq05RYiUsmjLUEcl5LSW2dsSpPLzA4d3C8bR4k7goFAyFShou7ZsEoyyShs1mol1wm7dZB3PeqRqAmFUWXfuK27ulgCE8PCwa4smiMscu5o/uHlMzMIwOOS2Ii0KCSeX6Uqjeo/YWPyqJwwz6kYzQR88KIvXomdKC790BxoX2B4b3eyiEEtLmQVNrC5jxeQp2Z+Qe8vYKajMs1JSSsFktv5hPUhpT8s16y8jucpq0FspviJR2z0ZRa3hi0ArnmT/hTnr5wPBKLiVB0ssnynOdY2GqyKv33iYPSyBWOeHzeGoVcVE8oqCGbXiA2WKOhe5O86YNaN6dSa1MKh6mT7H4qJlGCyhcYxeP7vMA8/XW753fPyVH8uvx+YQRJlimYlym1zGD6eblImrqPJTk3n7GxVxqSpJM1i6T1UTkYu2qr3SxG1MxvZaXuZFoFkO+jB12oO59oH6mhyMl1Fn4DPtQ8PMkB8N5Cj45QDv5oyrRDwLGntXbiRjCa5JAAqaShCVPo9lbl08KGNFKScN1a0+eMcXGtIiUani7saRKkvz6Y6uraibgWNnGc9hO9cRJNdz3MYy2JrxIw1KsR1TW9NfJsVxZhmChu2oIMdgtmrMOo5WP7NPzJuBIxWX6wPvWKsMu1aAx/lAXkBEcYCcteze9jMdb46G6iCEbHF7bSHcUfUusXYPTk4+0b+Z0zUJPwj19yu6Z5FstCI7fLlit5nxP9tf4sv7Ff2+nvJDJGkVmV0mrLRdM6N6ekooPIpBPS2rq45hUz9sAO9qXMFT7KC8lLDIjGeRMC+5JYVqfwIms9Fw4B97FbZsNgqA9peWvmowrYFHPW7VE7wniNMJijAFEGULroqM0RRNhP7IeJ5ol8p2HVptBSf5eKt4S7erWZy3iGTmtSaedblMmBrFTliPWJMwRqnrnI2qgVkdOY4V8br+yo/l12NzKLNmSRBXiVyr6tC8UyVeNoJ7b+l+Tg0ustVWxG514VCYdbFRsCo2ZTRV/ABM0MUcgwquYlV27qjEkpPtvGkCOVT6C5XT3bytkQhdr/2jOwjJKc06Wzu1D7YXqnv91lTB8cXJbJQChDGRqBh1EZtRgbOYmXIShvOSayj68M7m/SQtz1mJM6YpXgs+cX55oO09/f2yZEqW67Msmouy8FNryfZkGqLydtWwWNJCGKMlRcOxr0gFDLStIZ8LGflDdm9qFJv2bpKD+10Rvo2FGFYrF0P7cKGbzfBbU1iTpWIp/9kehjkaFSDwo7sLxt4pL6OkP5GyKkSLtsJc9fSVBgeF0WJHxTayCGPvtKUpvAmREkGYzVTBhbmO+nJRqRqXicXhW8bTiFMBbM2QEOI8q4nOKjIundoHHgz2KAxzR/NoIEWLPOoJe/U1PblopcnhWt/DHcthUXwnY2Op3nglmfV66GQHKUGsNP6x9nC3mzMcK/JRfTVSlXXDylp5pZP8vXyuEC2vrxf8f6zSfoLX12JzkARhFZX8NGhZaA+G9mmaQBzbgXujjjdInphn4ypPvWRzo2YiYQHhLOIvOg5PildhEMZdhTla+kt9ACVD885Bgu7jYjwyi5hGR1H5KmJrZQ/+Iy9f893bRxz/4JzcREwwD5x1A90nA/3jIle2GXvrSYvEsFaVoBnAB60qfGFeugOY0egpP9NyuXmn4avHl6oe3b9bYJeBZtnTHSuqwp7kBws4j+z+4FzNYRyI01FjnME4GvKiUIV9gkrFZuzVg+L4QsvZWCtSHqPRLEtQ8xCfiT4hn831IZ6pXT2rgJjMsKvwN04JWhYOn4RJHWtKbx4bqO51o7j4vw3dVTHl8Yr4h7XAauRYTjnvIyla9m+X2IOh2ZpJTp4qSPsC8C3V8s6fqUv4GGf4vaW6V0OdIxX1rVYWT/43S72LvP4nDbO3WhkcvpHgWc/PP39HzIbv/ugp2SpHxN6que8pv3RYJ/bfLtdxMZIOnuXTPd32jOpOmH8JdsiEHzr6yzOa07UYVESWD444i8yfHFg0A/cAX1YqIksw+9JokO7v1dNY+ER48xuhe6KOZONxwe2swZ/15N5g1iOxrPs4z4StZ1+8JbBKsss7z3bvoY5UPw2buD+NlyQFi5JxUEw7cumjhKxmLfnBXUiSUN8a3EG/JpYHPVmdeLSPFLsY6wo6g99YlWtfFNCpVgOZ1OtI7XRBTYmfr+rA6CzDXUPIAjvH79dPOO5rXAT7TllvYZGmjEMG80BuyaLRbsVy3wQzsfCy0yi/5HR8e3KQYkRPxFLWJpexJk15v+22wc8HxsGRBosr48vZe2E/LyesASig6tYqkg4klxSZb52O/k4WDS6DyxpMs1XQMSwt0plJuDQh/RFSnbFew2zsPJDFa7urbHcymTxXpy65sR98ZnQ61Ovf7SCK19R6rcNQvCKBdNDT0x0UaIzFKHeiVEcIxSfR+0i7r7EH3VCzLVOt80DovU4ZKgjNAw5yEuTFKLw/LFQ5GQRp1K4vrnX8mK0l1jKNLcnCyyf3bNoGI8oVqW+LjXxRU5oADGojb49lsuMNySh2s9nPCIODZULK4XLCC1JV+DjF0Sp5SGWKY0YhJaAuitVYFKyFAOY3oiZHSdfk2fOtslpHBViU1frVn8uvzebgd4YQZdILpEaNUXJZnONCkXi7U+KJJPsgaxUUNIoqhFm+ypjRMBw8w6PIeBGJjYJN/p2hL6DScK6ajCxAUu1GriKDWB2dLTXNqk/yYLF+UOCwv0qKe/ikG0Npd7BaRmoEn+YdnDQeJz1CNiAxKx4g5bN6IRs78SSa94b+qS6EFLSUDr0jjwa70RM7LhKhsZj1SGod0QtgP0hu1p1lPDpVth4VXA1LlZvHoiwN68L+3BuidbjWFDVqyVrIMJ5HZBaom4GchW5f40uGYzY6mZDIZAQbGyWqxV7l9q5TAO74TC3p3XpQ6Xx6kDYvVx0HAykI8q6ZBFqgClddK6Ib0W3FsXEaVDzA4WVhSlYZSk9vBnVYCnWR71v9txPHJCVD26srd/RKb8dpQHF2prgwGWIBs169O8c6pXNPStGM2vcVItUJNM0eElqBSdRWB9AslGUgBD8dLKYvJjMus/6eMJwVD9Q6k+tI9orJkCD1FtMbWI2kJhFrM23eJ1r85m7B+fMt/ahK4HFwhNMp8xVeX4vNIZsSX1b8FE6cBInqi5etMhRNp7uj3ygAaKJqIMarQPXekZziDovX6vfgjkI8KBXW7VVuHRvdRE4yYtvqQgrLYnzSWkZfdvarlvWi42Zw5Pc11V5o3ivI6I6GsCiMyeIgFM6DyoJngeTAv6mKYlPBz/23A+7e4loV3LijpnqZhUqd2xe6eZz9nuIs6abCHw2pPACnYB4zlJOmNXSfDDy+2LPxM2I0yG5WCEUPdvrjOROGcrJko1Ify/HxiNk60lkgZasqzdIqpTpR/dDQPUIrK6e6iZwFufeadl1YpXkR9GceHdhM91Q9GGMtLL4wHJ8p/hOWqrDkixmj0xBcfNK2ryRm2Te1LvRSDZrTnwt5SuaBbC2MwuxtIbTZTB7L4RKVABRrOLzQzby6k8krMi61+hmjpd/WuKMh9xoXFldR2ax1IlaGtIo8fnGvcvtoSFkYRgcm0z7VIKZxoWBvqvMUejueRQXEVyNxW+ELs9F2Qvdy1LV2wjZSiTxwicPLivH5gNl4sk/Ur/2UvD7FKhoIvcUuR51iUQJ8l6UKlszmbqHv75KK1H5WSVA6nirko2U5tURPqzEb7LOWJ2cH3r45J9VG+7myeZz8FsZ1YniqgNX9L9iJhOT3hvRoZLyUwkDTasPttRR3rX5dfaNS4v7loN6OMRN6x32ek3qLKxuAerTrw3kyH4nzcsKKBuGw8YQng55Eg8EENV5xmzIqLK1E96hQbQvA5zaFYj3ThXyydH/wfdTrdQpZVcNG9ZJUQ1uBs4gpoGuWTHMtgNqgmai2/Hilbj95ds/bLy50M46C2xpS73EHUdqtzWy+E5RpV2tKVXdbwSrgjno9Yq2th52VdrBTurRmceom1T7Nk79tXEWkjkS8pnw3EbYOdzC0dobda1xgOM9U75WvYXuYvRXaZ5n4zZZZPTI4rwj8h+PJ0/h5b9Twp1jvSUCvgyjZjgz0lsPNHHersm3JyqNAdGNJnaHaGNJBuPZrchJMFfFVICWhXvf0Al3rC3FKNwaM4l0U3wteN5x9Zphdq/v25ud0pM4JPBboXgQun6kV4O4Da3l375i/0Vbp+LyEDgXBdUK+d8RgEIFwHnRcXa47QI4CrSXUCXqDDD+rm0Od6X+xxbxqqO+KYeYRslj8TmhnNdfJqLLsNH0o2X/hTM1dSDI5eA+f9ipRLaWUb0YCJ1agshiTV578h5Rsd4R46yfHKV50GJsQm1XU5BP9eYWJTHgHgHuv0l0zqiFtdhBqNQqRQScuroWT+7N+6PK9Ww1YcRsdoVaf7Am/vaZ/lFj9oGAGlolFaooOwQwg2RD3hl0zR/rC2KtOCeL6GewAXaP+AimUPI415NGwOcz4+JNrXr0/Zz4bOJoZ0lniKOQmKq4QRROyNh476oYVxDE+GTF1xBUQMe4duKyZC4810j60Vk1yrZbh4hL0FvumVqZghvFXOwIQrFNOhAGpIs4n0v1MQ5IHvQaxzlirpjK1D9ztPO0TmaTSbq9kBDMKMeVpkoTAuNQNeVzoQ2b3egiZgcnM+LQO/E4VpNlo1ReL81LaenpfSHqLMN1/iWALzd61KulmnjAukSoNP0pWCs4EDKZsetqKpINw69aQhMtnGwDu7YL0riZLWUcJkimVg+h9kK2OWmOtQDpoOzP7bqPvNcvEJKrW/BO8vhabA1k1FW4AvwUMuENmOPsg47JgD5T+NNtMWGel7uK1XHZ6Eao6MAyl/JCsdmM7N9m/Z5enUJpsdOGE5UMyVjZKJXaSp2AX0B83nOUHECqUm50egLPT+MwsNHk7ilKW/V7boJzKGC0XAk+jTDrbCsOlGs6mZwmcxgOuP4sa5GpgnAvHZ0L/UWb2Rg1AyJBbq2PH0u9nKWPEoASrfi+MlwqEnujgdm/pqpo7F0tgTWkPbCacR2bnnXoEXK81QWnM6pCE0plNrRZ1VRWIMXIc9BTTBGttxk1XfqdKp045Q/XOMXtbwpKlWMF9uBYSNIuB2gfuzyrGzhHLAxwXCaJROfupXDh9poI9YU7uWwpGIqp9qW8oEn7FZbJV2XgavGI/NgOGuEzEYs6KQLfMxKOObN3e6lStOF0R9FCQDz1D0NjGtk6wqXGj3gN11JYJEB0v1L9k8sIshLRu8FibHqQDSdtWW9LNTq5VfmPIKTNcqqmMXwyM9x9EB54elRIQnKvMV319PTYH0IzDTrCDIqv9hZbr3eORetVhMJwyAAAgAElEQVQTRs17BD1F8nJUmuirhvXrgksslL0YVyNuHtQZx0P/do6/N4SlTDmGQdTC3rZC+yKSF0FzHncaMOvvPN1HGa5n5HW5AfOB2S8e2G1mmLHB75lswmKtG0yqM5f/j9C9m2Fb2H+SGK8C4PSm7lTVmKoCRs4iMjp1vd5axtpx+a1bUjJslnPaJ7Wu+1Et321nCKtIWCkKXd1YqhvL8nNVSnYXTjGUhXIODs91oZuDRZ52hKSWbikJ5t7BhW7MXVs93AyXaDcN7bu55jf0Vk1LR12kyx8Z2qeO9O0jVjLYhHtXMX+jm1gX9Ge5g9C+DNhFIL+vSWeR8eRj0BQ7td9bstjqphwbS/dipG89sZDEhrXyUOZfGPy9Ra5n7F4WtpvJ5MuRcO+RswH3ZoYdFJPpr7K6PkXRXt6VacjFiHuv4Te52OXZVneW7HVsODwN2HmY2Jayc/itqAr33hHmmTE6qDLxeU/oVPfhjjoFSU7FZqAV7vU/lpQPUXxQ7UFl3SdbuizQvFaQOdyuGSww18Cj9oniWuFSKxV356jfm4KbFZ6KM+T3nnoofhl11jW8F/zOqdHxz+q0AigU40L4KDbbMqI99V2DKxFw2eXiKK3gpe3Adko/jrWW3cNRP5Y7qIlGqhMmChIVzPF3dgo/AbTkPTglVhWXoVTraVFthbgQzK0n7B3becRu7GQBrpJgPbpSpfP7cel0bFbpaSWjmRymJQhpqZJfSlxe9oWdB9g7x51dkTO4t9XUf5rwoHyUmYJd7B2p1kqluzSqTr3UCugkvAkzlUErdVQ9KFPWcZsEOB40pTkVg1p/0ZGTUcv7m6XiJkY5EblI4E/V3Phuxv1cN4K6E/oLQDLjZcAcC425YBXVQRidUxm85OnnmCBU90qDP009krUMB89ip7iGedLRjjPiKjL/zBFvi5/DReDs4sDGqLHJaewKWmU8fXlHPzru366K36Iw4Kf2AXhIRcsgxYnaLkaaZmQwjrHV/JDshf6qKH/rDOuAbDwZp+twKJuCnEbAyvLNXg+BuIr6IDcJszm1A8ruTLM0hf6EmVZdeRnJg2EsWI2Zq2YkJJDglELuS7bKqhxyL7WdkyoRjhY7WKp7Vdn2Vz+rlUPUGLThTKcEw1kRPwng0oQRSCgsOJ81P6KUlcN5mWcv8vSgY3SqUN0K49JQ3YEZDMdvD6SgD299pzuwFKWfX/dUVSR4Q59V5WYGnSxI0H4uAwj0F7rCmuuSaGSAJDRvnP4u87JhrALiEmOvi8D07sE0FaFad4ztTO3DjirX7is1oI2rpNZ2uSRSLwJmNvJo0WEkc+sXjL6i+tLhjqopCTNFzscnI+NgVIpcgEspNGYpp6sZZbLZdz4ydHZqo3IW6O3k9jw8jtid1fYDodpCqoXR632KszxRgqtrp3P+AMk74uWoI7dlIIxesZE6E2fq8l3tMq7TqDnTG+xOHaL6i0y+UPTVf7onvZsznGXieUB6i2001LebebW1Py2nBqgT503L0VZshjPV5hTAMKNUebu301RHgq4x1wld62hLolTOQgg66QIePDdSaRPLeshQgm0+wDAyqqSso7ZVp+tfNrFswH+yp7+eaTsKJSdFiKX9TU5xj2HvseedBu0U/4ZU63gzLBP1rdXPYzO50hbv9F7y1fcF4GuyOdge1t/P3H9HlXLx2UBoVTJttm6y+x5fDsitJ12M2oYUkkt9qz9n8Vrtu/xOCCudILgj9BcqaArzzIcZFrZTkG9KERJYNj2NC1y7xLFdMpyXHv54OvmtyoF/aU/oPK1zyCvL8rOSzDWDw4sM32hx855PF0fGaHkt51ycH7iTMx3Jloi9MFo4H5l/cqT/Py9L2K6OnlKVCS978mAQl9VR6v2c61Z9J+XEhLOKm8SyMfSPSq1apQfRVtFAaLUkDI8V4X7+aMOX12cMhwo5OGIBIYegnhPL72mV1J/rYowNbL6ji912MqVCu6O6FFUb3WjDMtOdJaonR2qb6FzCuUR6Ggl7j7tzCgYKdFcaTHP4ZiS7hLlzVHea2HSwleZeFC8DvxeS1zWRDw03VaDb1ohLtM9VgYnNEIQ32zX94MjzSFgoMGzbEnHYRHIZjZtRW68TScreO5Jz7FuHv3Y0vRKyxqUa+0gUlVr3QrV1SNA2sT9PkIrHR7GAI6ulYfd2gXvUUdWBAwv8vVVF6PdWjN9KpMe6CSbJD36PNiMHS1gAWQ1j6zoQ10aDeA9eQ5NcJjTKl6nuDMmr0teMRcjHVFB9pddPtDmIyA+BHXqOhZzzb4jIJfDfAJ8CPwT+5ZzznYgImsL9F4Aj8G/knH/nj3yDsotmwPVCvPW4IlaSkYlqGmalJCzATv6oJQXD9kwVnbHShdy+iEUUZYizQoU9nZQzp+5RZUQWZgW0qTJ1PTIEq2pIyWSfiLMHH8HhPCtgtUh8crnli+tzolNJdvtUH4rkij6kdbSS+WzfqJHKdcX91jN/pTJyKcSu4dCw+EK4/2XL5dtckPXygM0FXtUlC0Pt8ZobQ/uxhqmYucqF/b4Ex1YQ1pGPv/2eV+/ONervsxmySjRPDzgX2ckC6a0G60ad9YsAgyEvArG3GJ9odw1+q6G7KcH8Sw14bR9ndS1KwvpbO25fnQMwRMHfmwkMI2kLFb+/ZJhlzOOOlGXymdCFqxmP3WOVPxMErBruJC+Fg1K8MkVbhfaljlYjOn5uN7VqV0wmLVSybI4WCbA/nGFGYbZ7SNFOVcZcDKSgAracHkhqyWflk4yC2IxdjOQb3fy6x8o+9E9aYrDEjWc8i4yibZ6pIt4k4sJibIYvZsU8x9B6DSNKyXDcNirr3ujBZfsyfixgeg5lTB8MFD5NNpAaOB5r4kF7O7N1uFEITwbOLw/cmzVUicGU9qgR6o2GSoNyO77qy/zxXzK9/umc869/YDP1HwB/O+f8Z4C/Xf4O8M8Bf6b895vAX/vjfrDGo8NJDaf/SGH5MTksmRO78KhGqsaUD5whu6TlnKHQaR9OCvhxlqJayqmHQ6qzWrZVEW8jMRnGYIlR6alQANBCA6bWfn9Mhtg6zGAwUUdS2ZTWQ3Shh8GSequCr3VAzgcFP+1DuacVTNZR5InZGCjhK3qapVoXfrYfXLSk3AhsMcEtiLY9ajaFdYl48Pr5gHZXM69G1Y0MAucDkqEfHbGzmox9cMjBkY7/L3VvEmPbluZ3/Vazm9PEiYgbt31N5nuZlVWuxhgEwhOELCEhMfIEeYoBqSYgMbTFkJGnHiFKSMgeIGBi4QGyQEiMkCVkVOUqU1mV5ax83e2jPd1uVsPgv/Y+Ny03+ZASvTzS1b0vXjQn9t5rre/7f//Gkw9SWH6YGZEK/dtVCVcntvtW83w05YiNbP7DqsQC9iXQZh04W3UsFgO2icJpCg/CFmejD3MpKPRp94EcORt0NJVbPpfLxV9yfmUzmwqnRdK9roWZTIYrcbDkzmGPMlrBlClPrcposnMLR48bJqdxg99ZxtdL8rsGv3OylysjIFtq9zQ44uBmp20ALNQ3jtg5cjF6MUmtwbgpBsKjJXVOVeIo8JeoUasdChYzOEwj7Q5Fh8EoYpbGGMLhbG/onkV2n8LxkyAs4uz/X2v6vwr8lfLvv4MCdv9G+fjfzTKn/IfGmAtjzIuc86t/0TdKlWi17XW5EEGAWmxOfo1uKDPeAvLYgyWObrZ0J5pCSjqF3/gyLZg+H5tPTs5OduKp1RjI+8Sxr3m62WFM5tXthmqhvt2MBu4k+km9aNuv351TvauoHswJga/VWlCpF8RA9a5ifDJCsJg3ntzkk7elg+YO2rvM2U+lsEtO0wwMM7uyf5IwzUTTRr9Hb3/OfHcC1WxtuPnxFX5nqUrqtL+3jCvLO3+G84mxSVR1JDSZRT2yq0XRdYcC4Gb9zuO6cCaClK4iY2Wsk8T704s7fvzqqfwFRitD1qJViZ1whdFn4T82YQu7cnJQJktybWejV0QIywKkqwdpMiarv7iW07OcuYp6sS86kCrNG0V9V0xeC4/B/MaO/puVHJpArt8GBRMVq/5sgGwIZxOBCRhPlm+msGo5Lxkj76qfO8gwmRSdQo7TaQQ/gd7jpXQ7ybjT15SNd/HOsD1XG52bqO9r0egzGHBgYsa+llWBicXgt3x9Bn1+HUmjgSTOi+tkE2eCIZlvv9R/0a/IwP9qlHv23+Scfw949sGCfw08K//+GPjqg6/9unzsX745/FaHe9OQqkxzY0WGcjJsFVtQLMrsZM6R2gQHr4WIbsRwkai2luZG+ZZxKI7GPlF9diAlo8jzOwXXWpuJ2ZK/WDGiB+7l4kzVRwfU4MoCG1elJO0sy5eW9FIgkitZnWGZZ8l0/UaBLrmqcMfyCwLjk0D7dcXxhcJQmxulbvdnivaTjZv+noxX6wfonmXW50eO7zcMm0xV0PpAgy2pSN0nQSrJEare4nfMdPH2LaSPgS9bhqcBqsx4qGAVePPlIwXwrgPs6/lamiSQEUpLs9DkYPHK0cUld23LqhkUnHJdn4xjpgdrb2YxmPWJm/dnrM473MsGXzbvVEP7O3c8PdthyfzpTz7C9Jbmvajli/eZLhj6Rzq9pSPQBMkftMm3b5wqletGHJQM1VauWMvXhuPTzHCzwPeG8TxJk3JfYTtVlqnRtR4vEn5vab70HH40sHm0ZwyOrnPzYROuSshREB/CDKo6qq8axvOK6tZS96ZoQjSRGhbg38uXkk6+EvH5wH5jZwPh6sFw8U8EZB8+NuRnPc4lxvtGU7i2kM8uA24tLvnl5kCIls/WO0K2bG+X8FDh91Y+oc+O9GY5b9bU376t+EU3h38n5/yNMeYp8L8ZY3784f/MOWdjvh0maoz5XdR24K4u5NNgM2kdGXszS1fJhZBSSjg7CLAbngeqd56wEU128VYThWqnpOOH3w7Y0ZMXorGer47EZNmazLB3hFY01Q85/AAklbn+CAFZkKcmaSLBKZNzPGMORHHdCfiZCDn9lURd1pXSGOZsimwzeM2pYyO8QhuCJN3LV/pd2/f6e/mVZ79ucelU5meD5OXLwHiQ94EdmIVSecq5mAx6e4PvINZeYa5NnjkAuXOYNhIeiZPQNCPH6wVnz3Z66IChlmlptROpKw2Ow1DNOaC206K2QdfSDRTzXAj7Cnu0HLaetgjXqj3szzPDoeHy8Vu8KerHvp5bzFTGzdVD0RZUYqZOrdcwmQq3eVZG5lJxYU/tILZgGo97eN3ohK7kE5F8xmcjd7Ba79vee/ZNK1xiHUjF35FkqG78PImYv38SHR9TQG9b2lWvak+Wbcygdx4ti8sjQ1+RFgb3psWWmaXfG/qHimTB3wnPSmsBwP5sJL1uyT5zEw2+jty4pdynDn62qDPJMrLAReXEksHe/JIqh5zzN+Xvt8aYvwf828CbqV0wxrwA3pZP/wb49IMv/6R87J/9nr8H/B5A84NPsnGnnEg3BZxU4i+kilnrDsIeSJxyDXx5kCxixjUaS4ato36rseUbc6FSf7BUe5Vd8gGELI8Rqq3s5ieUV56CGqFO+QjVg8WkPMutp8DZ7GA8Vyu0+lq8hlRlOVJN/fQ8wlR5PjxSvqM/OLlHFXZbf2FmGzFbzE3zzhM2EX/v5uxQu/PkB081ZYiWcr17rPYpO7HpbCg279PhYTW+zMFKj5EoAIjYgMdOszgDM89hCptJlTZt18PDbkEKFrN3pFpKxpyQ01ax2pNitvh/GgnlbCzV1irD+4YvLy71vnYVzbV8QRfXie7CMmx0n7MtG/PRzGPboQTJhDy1VaeNOJeRa/Ly3fQHQ75eEM4yHE0ZdQv87D7R2MTdOxbvINaWo6tPk49ccLHx5C8RFnpWuieZyaxoSnkPTWb58Y5127PrGg5RfJGZyVls34bBa7eYWgwDza1huDKSv1cSptkyQXr26IFX0WAtxM4xZk1zAMz5QHAVdVHs5kUiFzNgv7dze/NtXv/KzcEYswJsznlb/v3vA/8V8PeB/wj4W+Xv/7l8yd8H/nNjzP8A/GXg/l+GNwAQIQVLPov42+KyZFVKjWcCltLBUd+Xz89gOuUJzjiEU/+aykk93rUs7kocu4e4KKPR4edDRWOTqe/lzFTtZUxrR+EVx+dpDlnREDrRP/pAh18W+7iC4cWIOTpyExk21XxqT3F8djTyTqglTwf5S3ZPc2G1iUzlD9ogUqsF7imnTknezls38yRWX1q1Ib3+u3tSItmmFqdssGHBHJgislkmH7you0d5T+Socec0BiTBw9u1/m3E9bCjWrxUZ2wZ5+UoC7rJg2Jy3zLFAdlc9SwWA/3PzlRaZ4hOWILfa+TsbNLlLL22QnrMbA4z8QYoGILrlb/pema8xSRDe6PPa28yJluGy0y6HBlrT3PripRa7WS2pTpcGRJFb9OKJ2IS5LVWkzm6Oc4w+VPKmI1K854s3UzSRhzKszIMjofU0ncV1b2dE97JYFxSIE/S9TNJ1yM5OD5VXob1iZgrqJOqDYOS0q8bksv4o3AVlpLQp8FhO1s8M4yo3U2Gs5GxKvF+3/L1i1QOz4C/pwklHvjvc87/wBjzfwH/kzHmPwW+AP5a+fz/BY0x/wyNMv/jf+VPSAYeZKuVqsz+kwwXA74JxLuW6tbRXhfih6d4+FnCEtY/cxyfy6JeJCL9/8vfdzT3E5IO45nKu+yEXbTvlZsQWsPiXWZcq+LoH8vrQPZqicWqB2AcPPH1gmprxCloM35nOH4aqM57XLKkrccdNVYNrXrO6qJT7xgs1XtRb9OTAUzmyb95B13D9vUZQAFNRakmGlGXn4thePFkx+EPLzXaKxXUZKjb3J2qjf0nooebg7wIFz9zXPw00l4PbD9pcJ3l+EIn6jTJMUG0X9cr/7PeCgtZ/Os33H95LnLPJhI3yLuxLJblP16I8HWW5cHw6ztxDjqBtu5Jx8XmwP12QfPezuG5w2WaT9Hm2nH7+jnjeabdyb4utHD/A8vh85HmvGM8VuSDxxXp+nBuGC70LHRPo3CQJ4mwlOP27W/Kafzs+ZbcVQQjn85UZzY/cSRfWIW9qsP6XgrdcZM5PJMidfMHNdsfKuQ2GwjnaQ4GDusSWmMVRhQWFCr3oAjHMsHpdg3riwPbKy1ytwiEfcWTx1tyNvRdLSertUa604Ho36hq8dGQD5a4Mdi942f9Uy5+YnGdnvdsDfvrDWGVaQ8ilIVlaY2OVqPdwoo9++kvYXPIOf8U+Ev/nI9fA//eP+fjGfjPvvU7yRTv/+L3Z0+ip6kHtSOzNFcTh9I31lroqTDQXKdTYRoZZiN6KxkSJ7ILWSWw7wqzrSDMqZWk2VcRN1mn1YHxPDCOAhfnXIoPTTSK34HJzOYcxqgcNUMJfUko7CXpJHiy3tNdVIz7GowchFKjvEQOnkjAHi3dUJWpiE7X9o0thrEZ32VCT8lX0IxvCmxJlWFcGtzRE5aykMvopNU1FYhabbU5qLXSQ39/u5IOoJ2MVJLGtHmKeDv97h8qIEnMjlfXN2vsu1oO040+f86lnJiC02g3gj+oTB/K6Tf2XsE9afIF1aaYnVS0qSq2goM4MVML53aW7fsVpnPYoy2LqbSB5d92hPbGMJxPv0RpH4Ks30ypmuJSm032Yi2qzSpxevnkV5oLcS8nQxwd7D3D0ivq0Gb5aBRozpjMctXR9xWxreYWNTYQF0kWf6PFP0i34Q4GE92pRUXM4GGjwyZ0Dl9Gr5ONfm4suU4kDw+/9ssDJH+5L5vJq0j1phJN2RnSbc3QykK9ejD4w4l/jz2NlrKFxaviQuTKw2dV9tkA40KjQTOWUXCrsvjhc1i8hWqfqQ6JVMm0I7syevNptkoHlAH54Gefzik30R5lIR+Pbs4wDIsMZyoNQZteWxD44zM1sMYarMk0LuB9IngFn9hA0VAIRIwlZKZ/uWL58tQ7hhVKgUICrNgYYiuLdbdTKTxJiBViawkLuTJV3syuSDaWn5dE8spWxILxDNzrmsVbU743xIVAX783JZGJk8qzl1kLo50VgN5HHj964OX2CfVD5vgMVt+IoDMZ3PaPk3r/hTYTV5ylxrNcQm1l6mJGeUeGlXYWvxe20j+O2F6ThynAJrW5YEpoca8kV89torsqGoZlxr41uGNmeVAr0x+dRuhnke3nnos/USux/xiy+YC7YE/jVe0m4nOk2hW2pYG9o94aerugvbGM5xCzwa5HYjFeScky9l6BRNPBVCdynZU3el1R34q67Y8wXIAb9VxXxwTonna+Yv35PYftxQeHntG0rqS3fatpQXl9JzYHMxqWP6lpbjP9pW6yHSHVDr/XbtpfSKCTKkO1z+w+MYyf9jTnRyoXCdHRVIF3b86xVeT4op6zLZRFgNoXk2luHPUD2KBLdvdrnuMTcdZtb2BwND/TSR36JfEv7OC+UsRYVinbPZPNe/ZIG/KqYtyIPON6g3st3wd3MDTHgt4fxVgbgRgNL2/PWS96hr7C3CrKKzu1NOwVWlJ96ah2mbCE4zPhGOi5oF/I4ej4xOKPmcs/svSPzFxhxYUeuu7KENpy6iDgTMY6uZzyp0pMWaTqZ+v7MtJsBdb6Q5k+LDPjpwOhjsRrORzV945uX+H2JWbOgfknZ9wOZzz5JvPwmcHkzMMPlQg+npcFVmWqb6pZ61FtM3d/QWCsP1jM/Ylk1n0UOHwaqC47Drta9zODedYx3NdU946wEAmuejCs/3HF/iMdDsNFwuzEJZmiFB9+e5AOB2YMIz7vWZ31xEeWm6uG9staIOjRzHoae7ASUPVqY+MmEC6AbMiVvDCyywxXGWszY+GPmGAwbxpuOkd73rNoBnpfUW1VAVTb4iURrcxwVglz7YQddKqq734jFbKbmy3pTITGRw4fdZgvlfu6+jqzfGnoL2U6e/jo2yOS343NoZzosl+DFPTvbqXNYPaJzIXpWMZ0ZDOHrux3LWnVw2BJxdnHBLDZEF3WgiuldPdc3yh7gw35FG9fTExNmIAvjS37twsWbyyxgXGZZ/pwKJmHVRUZrqJEMQmyszQ3bjZoTUUNnZySkMKuwnSWrncMvRiJrkwaxotEu+mprwLH/YVO5LX62nGtUtbYMsqsxD+Ysj6mUR7o94lNqSjKGC0uytfZTL03M4JuxxIw6wTW2mLFnmrdA5ngmnnsa0tk32LZs33QL5cqJX3VRX59/DQQVgZbi+C2fK33cvgIsp3UgtA9j2JWLjN2zHI0aiKmU4xhriHH0lrWCVtF1suebbI0rVh/IVgZsviifkXTnNgiHkOdSZsAoxWvxVEqRFQlFsXsZGo8jk6CqaiW1e8LNpP4+RM4G8iZyWfEHixuMMQSbpRXEbxs8ewI8azE9F3Asu3nqvQEFJvZJUw5o4ZUOZLTNC75TFwm0sIQ62KZuFOVGaLF+UhY6HkeV1O2Ksz2Y9/y9Z3YHLLRzn18KsBH5CLDeJEYLhXTprFi8eqr9aBOWQrdsca5hLeJKbgUpxI5PhuUau2EpNdv5czT3ElIc3xsGM/lJozJotX2Zv4Zptx41+mB659GGBwff3rNsRh43j8sMStZtudoMctA2rbEGoaLSFVUhq7T6ZsaBfQmCwmP3TuqvUhc2eUZ5xgvo/pMU3CUQ7FvSxNWUK7doF5dm6euiYvCWqp9pr8CrEr3uEgz3pDq0r9bU9SEGZ72HOtaZry3qjbCWcJ1jvqgn2edUPzd/WLOmsilX5/m/tP4k6Tpy/FpnoNebGkdsxU/oL47gay+Q6rRkrk5vUw02HtPWhv6pSclw/FQY2wm9g63iKROyeq5SYyPM+mriu5poHpwuJuqcBukYsxVpj3r6X2FeaUAHBvKBCZDTlZ2drXXppwgnQdcU1qUwcHUuliozjri2jFuK6pbUatHIDeGtEw0b2XnlV2m/aLm9ngpEtSgVi82qo7iWZ7Zj/5sRP0bs0BscvmOZxF/p/tjR7h7ewY+UR0UZGSyUrNMNgxned40v83rO7E5YFQxCN/SQ+MGiFsROKbR47gus3ZfbN7eVsRX1VxVmL/YMXHM3d7Kz+AooxI2o6rQkpswJTybVLgMdcS4TEqGhKoEAHcL6y/taWa/0BTj6XLLq/2GnI127OTJD7X4/9Hgdzo141js26rSz1tIF6JTu9XIYjGwP54JTC3agr6rMFabwHQSj5sybx9M8UIw5Gcdg69JlY6HiZ8R28k7knncOmySzFxLeGvunPwGFoYqTuBuqQx6S8p5dkOqnh7pzILkpT41ydAfLNXblnGT5tPJ9eYE1DaRuDT4/clsJJeNJDkzW7/lyaatZG64Y54xkEmcZaJRynVV8BpD2Ygl5GK05PtK1WE0iidsIscXBrOMmFtHWossNwGIORj6Q6VFnk/XiWAZb1oBoAUDWrzRKb2zXga2o525G6G8pzSDhWbeJO1gSKaA0UUnNHNmqgTOkIozVWwLUFmwFdtGmnZkbHPRoqg6a6+Ouq0ZetcSF8pKsW2Q0/Rl1M8w8kaZuSmLX1FAMlt4+IuDyCHv6iJEUTnoizLP7wrnodYisVFeDfvvR2kHzhOH33/E5lqIfHudGZfTCNMQDh53J8OYtIrkt5bhKtG+lP+kfV8T19L4V1vLuNbo6v43E9W9LRWL3Kmzs/zRNx9JCRgt6W0LLtNcq82o72DxToaihxeaANz/5kkwM/EJYu84xAbOR+JV5vnVPS+/uiJ0nuarmtpnYgX1ljJrV9U0rkoU/E5GJBJX6ePte+Ea1TaLTZj1tanJmEVQstPBMz4KZYav9+v3VkKg3OAGGfNOyVX+1Ro/4xIq18XolF1ZtdPHQ3lfJoF73VDfiZ6cHXA5yLPijfQBU5VrkuH4PML5yPjc0N1VpFUkLQ11yb4gy0A4LyPm4Ih/cI4tTlImlHbJgXutcd3xeSLvHTYZKMlXtlOLwPkAO2EjlDSzSf2bmkz1XhJs1xncqBDmsEYj3juLe10XTwFNnvwAACAASURBVIdM/zxQnQ2kZIkHj7/2+M6wfJnprorbefE6dQOq3pYaIbffVPNkpL9Uvkm6iNh7sUn99QL7sKCqBM72V5nx44HWZF5cPPCz11eznigfHRwci7eW5jaXiIaJjp+Jq/ir6z5tg/jnqRG5Rc7JpZQaNJNvbqF7JmTbAMPjgO0r8jIQR93s5tbQ3GWGbKh2WdMHK8BIP0gnoS1gDvE0Fpr6dgC/A5CtV/a2lPHSGkzGMOOxwt16bSxJve1EyU6Vmem8UOi8hSBEBHO0iHeTSVYbSl6NDMFj20AaS8wZlPSlwsikXJPCPvQlDs3vrNqKAuQq3ETOV9MJbEejSMBS2chFqzArJz/No7CF6mEigmW6R0XlWCs+oBst/SMZ1uIzoY7w07b0w3l2yZ5yQ2dxEkh4VGskGls3L7K8jjifSdP9+LCdyLpv2WcWm46+qugWmoqY4LDFci75TPICs1NbxoxFKTu5kIdlJsVa5Xk+Uc1TlcWurabrq2mK79QO1dP16AQqS7Ni6J+YOSUswuwfUh0kbx83yuMkA8kJCDUnpu+4zrM3JP/M2nUdajdquUNlr1FoCJab/ZK096pYitMUm5F83UogNxTpQaMWym5G/r+MK74Tm8MErulhNdhYAkjCpN4z1LtcVG5lrlx2TYLYjSfrmxOwNFFux0q8d9uLLmuioX90YlbmQt32D472rXTwJp/ITrNcfGJWuoy7FcNwCjKZ4tOggJljJpVTe5LckqF6Jj8Aa4vm+KcrMBB6y30VlfwUCqZSFhqcJis5m3mDsKMhBcBklZA1HF4UI9JwKnEnrwJbRyVKDUUZGSjp5YW6vjCc/TmYmHFjxvWZ7lEZHR40SpvAMxMNLAOu5FxM4cMUGbnd+nn68uHL9oZs3Zy/MGENOUPdjgxVVVStmeRK5VDuqzGZzebI3fVagJ13DFMK9zKBsaRQWq+S4WlMZriMuIMESe1bP/8+arc0pcoftAKTZF6bfJ5H5qGlgITacN3eMoSlNv3NOOeE7p9buquSinXR0T80hJUmW3GZ4MHNlVP3LGCWkXoxsmwH7o4bjJFhiywOxeHIgyFejORkNRI9yuQlN4X7v/dz+2FDZrjUAWIf9aTB8XMAzi/4+m5sDq700BMZJshFp76TL+LheWb7vbJgCvXVJI1/ADgfCbVn7yRNxsAxWRm5VughXURZrs8elBaaxHhWyr6jYfnKyCk4q9SLn3ekvcfffnCZSm9qh4JkH21xKCriqywm56vfEtOSJHNRO+h3Gva1AmJBN+zpqD45GcJQaK5J71s5BWolkqP4AMpzIJxpvj+xKbNzNDdiez58DuNVwB7dfEJWD5bhGfNc3pbKIVvYf2zmCur4RInVaYDdxyIPuZIS5bdye4rnQW5JsSY6TT6yB/PgBOwOlnQWOBpfpkTg3mmqsXxj5KbtmUee7sYT15a+dloIDx7bCVjLSyH+VRuI0bJaHdm1QYdx7ZUV2WbYa7GYDw6GSbHr9kogN8HJ0WklbYTrhfdV94buWSLVZeIxGtZf6/2tv5S+YzzLjBdxfgbqa0dcJ5o3yr0YrlJJ51IrRZYZbHhYYT2kTSCeZ3w7cnCtniOfqc97Voue2+s1ORn81s3XfFyrtY51Jl0EHj/a8f7tht3glKnRlCpmpQ1ChkhgvQH0fieau7v79g6z34nNwSRkLIJOkqpXedvciKm2MFq0ooba2e4tPB2xVcRVkXhdF0tyldeHj/NcSfmtZVxE8tVAVUXRcaPBHB3ttSmqRWhvpa1QEhYMD1Uxjpk0/WWsVOfiNDydMCr7p1wENfqZxXlH/OOzWSa9ebRn2Qy8/eMnYvQVAtLJGUr+ksNGCd2gEaPthbeo/CzBJlsnNmRSFkV9Jx4I6D25s5HUJPJgiVEELd411AfZ6MVWped4lkgTHTjr/Ywbw/pLLbBqrxNo/6keNre3LC46jrTa1LLeW1iUceNoCuhWWrRbj9+dRqbK99Bh6+fsTMvQGcLaUj1MpsCZvIisH+857BvCu5ZcZb65nzIAgE0Um3YlYRLRSFvmshKjDLRvywZXsOrV68Sw0j3vrrT42Oj584XzYAMcH8OUdzFcibfQPj7y0eU9+6Hm+uEJ1Y3j4ieJsDCM67ZI9lEbWnCLVOlAGisHZyOh99ijmJbuwTEkoxb1pmK8NDS92g0SUucWdm+3MvTBydMjGqo9xLGwO5OqxO6RMDkTldxFlUhHXyZ3335dfic2h2wKAaXV3/6Y6S8m8EtjttiKPSZ9hIC9yUfRFKTcHeQsNJ5pt51yGNo3jrApxjC3DRUT1bhwHMpp010ZYjWh5xl7pkyM+tbSfRRFHbaATwxJbUVYJnlDFHnx5NFIhu7Nis1bw/BRxrWBRT0SU2HzlfYoLDN9U0CxLLyje5aoboUn5HWgjx77vCMFC9sKjhA3EbcecS4xuIZx8LOdWjaZ+FDrvxdx7mdFz9WDF5dF7rxMuFUgTUKqZPC7iv1H0NwW7McUp+Q2El2m8pGud0LcrdytF18XNaC1isKLH4wiTemOcinnLaTy/0Krjy1fGQ4vptFxGZkuAqumZHMaMF+1s99nqpAHBQbrMvm6nt25w2UoPh6ZXFn8gxa5yXD3a3amUYfVybF6MpzJHmKZvoSlcBRzMWCA7rblp9cLVbkXEdNb9h9ZbA/LV8zYgSYLGlHKC8SQnWV0ildIC5HlUpA/SEKVaBzLpr1MxGyJrTlNUZKh66TRyMGw+0H52vNRpkTbhuBlApTOgn6nbfG3XORTS/wtXt+JzWEiClU7WLzLVMdEWDiaO53k/aMyBiz99lzaVwnn9Ge0J6DORKSkLCSX7jnkYq+Vap1OE9FnUhqCTspUc8IiklyxZ/DSGFiP5L0XeHooXpRHuTHvPksC6pLB7P2ccWiOjmiY/Q9iCylOBKmT29W0SdmzkbCIuDpiX7fUD5ZuWWMGQ24SqRLfnvXJ+mtqn6CMIzuN26IpJJ4JHC126GY0GAP1a89wEAvxdP3KuDRrsaSCCekD5fKbArBS7oeB/rGs+uzjXsSwr1Y61aI2ANfJadrGzO4jy7g6Laipr59k5nEhbYu3CWcT1irHYXLDNpNWYXqVysRExIvpLOHRWAhW8rIgiy5PkhAruyLH/+xI/74htwlzdCzK1CMuVbXVC21Qg81UVaR/vZRCdES/X9nMYsvMA8kW6rtcnilDt1DGZ6yKG1UxHJIDlZi81KmkvucychfmIEWqwpliFcnWkoOZ1wTo/0/8kgl4T4tC/GsjZvfLc4L6pb5ynel+raNejOzeLRVe8+mB8U+Xms9vAn2l+Hg7GNrD1PtCGBzDsaE9GB79OJCcYfuJY/x8xPlEuFZ/5+6VkG0HIdHVNnN4YWZvgmEjW/Ls8qnFiQ221+ZUPagX7SdL8jrLGSgb3IMj1VY5kK3Q6ZyViD1sVO6avWN32EgxWSoCe+8L6JgJSwFr2ZqZh9CeHzk8NXSXlsurHbevN7M5qwkGvl4wXASZqg5GbVcnKXjywhqOK0ScKlXU5Uf3xGTZ/fl5CVT5AOAcCn28lKDTOMz10Lx39EjRuj+cs3yj8t91WnDtbaLfKCH6OC4ICfIyEZaJcKHJClkeCPX2pIqUIa20A8vXei8PP8yYy4HQe179P08LHlVo8CbTvhXZyTxU8Ntb6irwcOGwb6uZzt6+MxytJ3zUM156aCLufS3CVVJ1OcXRDXf1jFXU92Y2i7Gl9eu+PKP6eE9+09ItkmTUg3r+/rEyMv3BzNF6bphatpLs5UVCyte1ks+CmUfyksPrZ/omYg81ZucL/V0q4ea9Y/FVRXznYZWhyqw+2rF3Le16oLtrcQ9ulujPPIxe7YWxmfWnD996XX4nNgcAisjJlPI6DI74JGI2BSdwmfZPGzkW2+LLYFEsWTJFS2+FCVTgKqUlz4SQRSKbk0DLBlPGhICBaq8qov84ka1WR1gnFoW9aIdyOtusScnREmuV1ZOrsVsFPn/+npAsX/6TFxJiDRR/imJ40ug95gev8WKVcL1AVBO1MHMQKHk8NKSHCttb7txKJ2aEydTERDTZmCznE7PidHw2MvYWWlm9k1UVdUOF91HVSlE4xsbM79UNAlazUZVhZ9IVReWJsAwnIZk8O8F3if68uFUvUtFNFA+KaOGuaAEsHJ7l2cAntZnjRaS6caqyEqw+v+eT83uOoeLL2xckryowL4pS8SAbuMUb2B4rYsGPpnR2nBKw49XI5eWe47Kmu23naijVENuEO8obo3nviqmOpX9SDHUqTV/cVu+7v1nAWdCF8Qm7K9T5kgJvI+x+NFKtB469x7+sae6EJ2VrCE8TaRkZncXvLGGTVAm6QvVeJthXmE8GjW6jwV1X+K0VX6UY5IyXurbWSlgxdAKx7VDGpIdCl7fK96jWA4tW7ey3fX0nNgdXJR4/eWB7aJnsvZqfNqRaPgvhejF7MfgSljKuoWkHjrHBrkdCbxlWWjTDeebJxY4xOq7fttR3luGqlPFNIvVWxh2TlqMYutb3mWzdXIKbguL4HbP2ItcJrCVHbRIgwNN1hvHgud4vOfZFb1BDMMUUJDKfyDZCopiKVPk0aszauMxBZq/mUUe0lU6EnXT51dbO4FJcZGV/2tNCrh40aaG3uKOmInY0s0DH2owzojbHq0B7XVM/6PeILbOwatqIhstEauSTUF9rIuKOZUxZvDNiA8PKMq41QTKjPnd4FEnBYg/ioMwO414irFSLnJTdB05WAbqu4r5teTi2VA+yPUtVZpwYhkYYhR1kWjNGg7sYCJUHn3HXFfWdobcV936pjXSQojR5tS1qz+xpkzWnP+EqYKoER1fk4YbkrQhVywhBN8AUvoQJcHyWtGm4RLvu6duKWJdNPPz89/dHg99rKnH4OEpN7LPcuYphrun0M6b2ItcFpC2b7u6rjfQ7/pQVkh0zcW04Z24zH65XCjH+lq/vxOaQM+RsqKpA9dk9j5ZH3m1X9K/WLP+4xe9h+3lSCTqRSBKMP9lgWj2M7Y3h+Ewb+3AVeH+/5nx9ZPKdXHzjZhHOZNgS1hoLLt9MD6c+dxJKuaMedmnkNVo7+5MKO8qxJ/6gI+79DEK1X1Xcjue4g1XM24NO43GTaN/p54eFxpNmWqyrUe5Ok9nKKJmw6yH9dIUrZKhkNL7tH6nJzXVm+YXEY8OFGIdhJV8KE4E6EauMXQRGKGlhluOXZxxcxgVD9a4iLJgnCRqbUhakHrb6VvGENjA7dJkog5fjx0LEzc7T3E5qTD3A/Uc6Ras6cHi/pH9UeCCln7a9rPWzBywMH43YrcdvDemrFa9fLhXSYgHUu6++Uul8/rNIaMRgHH/qiZVn+K2jqrqMmK7vPO17S2caUiPz2EkHEVYJfC4ZprD+pzICjr1heAztRcc4OmIwxIV0PdWDQOSuGLnoPkms5gp7svMVsYkkk+Fpz5CVOdJcy1+ze6LpyfqbzP6FrnFzrRCcMTuyt5jzEeuy7A4H2Rwen+ln5lbgst16pW4ZHQjLV5nusaYV3ROxLf3OYXae+OCp98LGvu3rO7I5GB72LWF0rNcdb+7PGEdH89ax+fOESZmwkttPdnLlISsLwO/KgqqZ2YGLpwcAnq+3vL/cwE0jR+CFyv/9sxG/CMTBYa8rRcgVw1dbkrPb60I6cqVlWSbyWeAYpbGPy0zcatTZvp9KOfA7BaqastCaGzk2x1bJXM21kV2+hfAk8Ohiz+6LlvqtZf11YjiD7rEVh8NymmEXpR8uw9nIo0c79m+vCAtYvLbarM4Dpk4a0x7kxpSSyF0mF6JWbzi8kC3buIlkUxSSEzrfZvoXGm26bQlsNeLpuyNM9nipVnk9cUjGAOsvLO17kX22nxlC40jJKufxvWdKJ/f7gm9sdd3Mb2xZ1CPvwgX54Ln4cbnujad/pA3HJLU7doT9cyehmGGOn0vRyP6/pFaPa1Um7TtLbOw8ORnXScBjJexHUwn5iFRbhdx2VcP60YEjCAR9LWcmsyuU7rJq4jJhbiwT8c5ECEU6XvU6TKrPd/RPPeZNM0vgp4T37rFal/aNo7kuk5Y7q9bBCluIbZ5blxTkF2FGSJ3+3T2L9DfuJJMPBtaZ+HTAv1RVODm4f9vXd2NziIbhroFo6KpIihZbThgh2IUGvSylUdm9Yyu8Yb7zRn10iirJLFnpTZ+MuJ2bw0oYLdGpZ0wlRyLVkPvTBmMj9OemnMaZvDoFxacKqeLWIyHXxNpq7hwE8CkMlWIwC+svJVlO1TSS1ZjNtQE3IcvlTkwtgwH5EbYClMiGhCc3CTeF7VSUk7hsHD7zF77/ip+8ekq+U8Brrq0yNxP4gzYpfyxZDbjZLWpmMxo0F096j0y5DUmtHECulPhNGSNP92Zc2dk1PC8ji+VAUwXub1fzFGmypDepDDsMDIOXorZUhW4Ak5S92V9p4xe9vczwm4JXeOaRtfOJUCUyluzE5ZjMbFRml8nBZFJj8lx2xybjvdqb6sGQvOfQNMooKRkWP8cTyBR2qS3RBGC9qgl/cCV8Sc9aXQWsTXRGrtc2wvJdIDYeMLiXuidzeFM2pEpszlzJS9QOU/ti8FvdDzcU46CzkeHCnUb3xanKN4Hs61nu7fe/oqPM6YE0nZOQKRk2Zx13n1RsD/WcD2E7JUfZJpJGlbHGZpmuTKOlDEMJVd2HWg9BsbUnAYtEtRhp2pHjsSY2ltgUQ42kXTZ7iJW48WGjCYTZCdRT0I56wuBKanXh5E9/qgc5HFVbPcipqA6zg+XbxOGF1YPtK86e9tyU8J7jYzuDdhmZyYTakU3xOfBZxqGjbOPc0cyAoBsMabD8yTfPcC4RFgnrrDaTe9mXTZ6TZjTFIdpw/GwkOz8vlFyV3hdVB8116a8zM4uSqHiAMUkRa6N4F1PMu8lANIRRwbs5iihlhxIUO83uy62p68CyGbhvI7HxCsJN5bR0efagCMsJ5ygj6FZ/ANL7Bn+QpR0UCvsgrGc4O20ogJ6z8tyZOs0nPwbWX2X8wdIfW0zxztTI8gQuTslmk/7BJC3g/pFsAsei7XBHw7IZ2HU/f2zLY8PM5sMfjnKHTSacR8wyYLZFhDVpQGrFLthY2JMrxQqEVSGhlRG+bSJPL7d8s6/I1hOXhvr+V7StYDRs/qim2maGiyUmwfFigblIHD6SGq/9uhLl901Fqj1cjUrizoXMEqB7EcFm6ioy3DV88e6SsK1mBpnfGgIwJhjvG+zBUvWG9Ot7xvuGsLBgLclldp+B+d6es3ZkGDx9J+n3NE71B0uw2s2Hy0T3UWL5pccf9cCEYtBiPzmw2zTEl14U6/Kc2ACpiXzx9hGpzXTLwHChDWBKEzdlbu3XIy+u7tkPFdt9Sxg8x6/PqEsFMZ4haq/NpIeKFz94zzfHilRl2q8ruV6NeqCS14O9K85Ai4uOY17M4KppI7/z/Ze82m54/3rDcKmeOy60SFfflFO/NthgGc4T8VJJ4vE3B7pb/YKPPr7j9meXjB/wI0xSPNvySy/qcpHmdz8+5609pxr03m7+tXJaTxVhqWCqy46qiqRkGUaHryLpUJGTYfXjBtfB4jrTn1uqvYR3sYbD5yNmKGAiQEZt5W2jsd/ne/aPa0yd8C8bqvtihTf5kzbS/VR7OP/zEdclYqt25d1fKtZwi+IYfjDYTw6EwVMtB67v1oy7GlMMbWILt78uHUT7rmSKTJJsp/QrrCN2tkQlGs5+lmm2Eb+L3P5Gw3BeckbrRP3W435jy5P1gW3ZhEJw/PajV2TgZXhMqizN9a/o5jA5PLnZ3ky7ZG4K+LMIJO+xPScb9L1mwUpdLg//xsg5KBlM5wjDgvpOrseTtVr2uTgzmzL5MPSDk5AnK7zWHww56ViL0dLfLKhuHU//UeLwRCh5fylewXSiuq2jfV/8/faZ8cwybrJYnMtAWMngpaph8Uanz6Gq9UANBpw2uryQliBEK4T54Amd52a/JEZLKIarvjdyyvZ5NrDNHqp7xzdfP6JajYydLy7TWoT9hZnFXPZYJjtfrFncynYeA8PG8Ud8DDsvrGShxW3iSXiWvBbd6htlIgz7mmwz4/f6OUTl7m41C+VSm+Y2y+3tXN7Pf5exabgKwlSOTr+Th/q9mx26etuQ1gr7JYOvCiCCHLirXTHbbTPJQXfFLPzKTeLiagfA/f2SuhmJ1wuGi0QsbmLGinLfTzTkBO5gi6hO38d1SSa/CcZl2RSqiaFriW3ictVxcGWhvmsx2VDfiXhng5SWsUHPV8OckRoXuh5hWdyjgpSg2amS3f+wntPiJ7vA5GF8ueLlYoFdBNbrjpwN1/2K75/dcv1oxdBVDHftt16X34nNYTpVhjNDKGITvzNkIxekONl4WYhOFyY3CRsEfvVPohKdnh4Vz/ZmTXtj53bEl/I7rLKi142DqJsxbALNYlTeY20IPhMXltwmbLSkvprn0cnJsBNb8JBKegPTW43mvAJvjo8t/VUingfWdWDsPFOgTP2QaW8Sxyur6LKgNgXEyJNZCRhXgMXBkLPlYnnkoWuItSVajVxtZzHPOz1kB93KbKB5WWHHmnqUEWuq5bUwtQ6pzsRHcq5yb+viaYACZGrhNNHLqj3Vot7WNzLAmUx+YzNpB8r3W2SqNjAstLCty8RGD7lpo6z7kpF/ZDCwFwhc7ZBfwiAjVF9Fgs3kYLEPvpjHFLOU0ZKCKYazlm5cKE5uaxg2+rN8LYXqZNGeDao8RhkB94OuU4y2tJsK1iWXDI6gUBpc2cgcJ9VvhvHM0b4bOH6v4fDUEDYBqkTcejlNVYm7uxWppGHjyxi7CN6m1iasy4ZbNkg36B6Epa53zplxrfdlzw3JKYPFles+bpSfKgl82cBtpvaREC1fby+oXaTfNpidp9p++2X5ndgcTAF4TCwltT2BghqdmXmuDgVU8kkuQUGnQjKW1Hu6XEhBAYw9IcNQHjKj0emsyoqG/qE5za4HI35AhpQ9dhlmmbgbyxeVSlkcg/yBTj8Xrb4+z+w9XIFxSp6W/2Jm/8LNpyVGeAGUEWoyMwkKK2DPVInHiz1D1Ak3jp44iNQTv1kQL0fszhWh1ElybAd5EiQ/tRUCS20hT00qWL1ZTgDdtsLt5KTVF0KTfDYzYXWabLQ3zEnTdpAuQ7+Yqjf/UNyRtjXjZdDCKJMH+XvqZ9pegGroHeNo8YtAspm0sPLI9GBGVVVmW0nLMhrCJpEvB1LfiBF6PN0Dk2X3ZgB772m/t+Ws7XElmT0lQ1qWhVsA2Cl1bRrHTg5XUxRfbHVrh4uK/lwsTzMaMoVDsUhQJZxP5EWQkjQ44tExnAVpe6LB7exse0/BlyaOie6JmQ/MaR2sXweGM0fswLVGeNTCzhIBEcAMMYlM2I+ej9b3vF5uGJPEdN/29Z3YHLKR1DSdKZglLjPjOnP+E+3kh+fawcMild05424qCUp8xB6c0PgvG3KlCdscqVcufn9VgKeDY/V8z8XyyOPFnj/88iNS7/Cbgc3ZgZQslY+8f3+G2VViYDaJtMxc/1ZFf1XCWM/DbNoS1hE7WA7P7ezqnJ02rd3bFVQZe9XTfL/jdX3B1R+q7L34Mdz/qISaeD2Myy+8+AOFIGV7OR3/wR9/H3sUYBlXCbMuv0+T5J94dOqp301huNpsdo/kYREvgk7i0WCKv4RSnPI85fFHWH9lCEvPcCaE/8NcDlNEbemFStfbC4+/05g0f9xhgObRkXHw8K45eVlEcD/syBmGriIuM4s3RoQ3L95BduAeHHEdCfc1bjPi70SkckeLzUYnYOEb2EGTH/OuJlwGwpmhenDsPymIPZnFaxn21LeWoz3jeN5KvTla7GokXY34NnB5vsfZRDdU3D13mEOZZLWZ5pMd1maG3tOPjsOLuixsaVaad+7kUFaL8zGOFlxmuGmhSRifYS/wOm6CdDnBcPiB3M/aLxq6jQDbyQzYHuU3GReZ3aew+0QuU7GZkFwwB6c2tJgINa2y+iofub9f8vt3S87Oj2qNP/kVnVZkJ3uxia3mykWYZLapysQa0jpSXSv70g3l5AXS+YjZe1Ip/ynhsbkg3a4vYFswmFVg6D17V/NvPfmSP+QjiHJJCtHhXZxdgc9+4hjXju5plPtTieYz0WDqSJ4i2q0pp6qqg7BKJ3FTsCUQxfDibMufuXPGlWH3qbCH4TJILm2yNprldB0Kf6NkdZI4ZTEUpiEAwRA7+SBEb2dwy3VqmyZxl1sE8r0yMNzR4mv10sMmkSoYN5rEVFu1DJOfRPZ6EDEnrUG8kSFrXsZ5OmBMxvnEsu052kxPo/eZdX+9FxgYRk88CxyfV7MF3ORgNd07RrBOn2/SB0a6/YnMM7lbUSYj02k7tXv1tZ2dnFOl8n6SdQPkbCT395F9Vwvk7D0UTUKqdL1DsDRNmMv2bGXem4pALFuNtbEZ/7bWMxccaTV5OVpyJV7JtIHQa5PHqVrpr9QW56poIUp7k1CVVj0oYLm5hu5xCWyyMGYIpkyxfCYly27farx91EULazvzXr7t6zuxOQCQob6ToCpV2rVTPY1wVFpRek9rxNwz0ZJqO5eCdkTW8HYSwUzfLysyPRrYVuRDw/Zjyz988xnuq5bmYAgrzxawXjeS+ylLQYsiNkkn9jKo7O8dtj+d5NRJz13U7+J6Qwp6mEcgZcNttyDXmd33tPkdPkbloM+zHNwkg3+wkkiPhqoo95pbM4+99k2JOisp2VhZlptlICw86UKK0bjIhHWC85HHFzuOy57tF+ezLJpCjEol18MfDPVWlVFojXwlraLr5IStTYrNSN5WZf5fOBi7ilQ7YjS07UhX67qbLN/E8FAAsQc5PcVGG48dNfIjlzEnIiSFYDGNsKXsBDhNjtQmTWW+9AW2K1OeUobnVaB3jsXXOkja94bsLXE0pLX4KhPPob9vtdFHq0TsYqFngXAeeX6+Z10PHMaK292S47IiILLXZV/rSAAAEwRJREFUFKxkcBKYnUXZ5z94zNHN1zYPpjhMKc7A75QLYvYe96hXyE1pz+r3DjvIcGdc6bCsH6C5Mzz8SD4f8WBZvDGkozafcH6idM+JWp0qur6vWG06Du5XtHLAZsbnI/5Ys3wlMOnwkZm9920vsMb86EhvWtyDZ7gUDTpQNAVbw8NvBgXkfLxjf7MQY26hxVyvB4Z9rRDTM/Aucr9fkD87ctxXmCbCQ0VaqzesdnYG8ZprS761hVDjGM41aksLkYsmTX5uJQxyWyca9irPferia8/25ROqoqWYVJJAITUw+xE0N+Jb2CCQVgg2M1uOLJ5Fdlm/Y6+PXf6fsiBavE9c/05hzS0jHDxv355jbiuoJUpyhcHnOn3tVDX0G8v+U1VtU3ZH2CTseiT1Dnfnqf+0xSQ4fJbIi4RphAXYrSOlmt0i4R9syZUsv+NdjUmwfCXh1P2PlOwUfSY1Br+z2sw2EXtQdkWujERFh1POqTsyVxnh3ooSv0pUd3be8HI0+M2A+Tf2HI81aVdRv//g5MzILq+3VAfDeGlk824gPBJY5TpDPMu8+cljdp9u6Y418V3L4r0mO8lLT2FH+VNma0kvOozLRMAcHcuXIkkdn1u6p0EVUmc5+wIefmi4/P4Nx74mbEbc1zVTaHD/g57BJYwFTKZ73crgZ6c0rfZ9qbSsqhF/7whnUTmlU3u5DuRgMO9adouK1T/9JTlBGWMugP8W+J3yKP8nwJ8A/yPwGfAz4K/lnG+NEnf/NgrTPQB/Pef8f/9Lv380uFtPcysDz+xF8919Xxx4e9nT9w5zrPB36junTMDpgpoEtmgaumOtU7WYweTO4FzCOGVw2pctYVkxuoy/UJ+WRzsz22wbSI0j1uIaVPtSxq21oF1RwKVlxq4DabQYl4XQZ4hrqPaeyV9yYtjFVlqC9KIjR0t+8GJ7jj9f8iWPHIQKY3AKJxkuigK0KezEVnb6OckrcftZWzYPVR5YgaE5ZvIw/X76GaFgFskbFm8EPra3ieNjEbRMpci+5kYV2phq3FVP7C3juZmnL6a35CwdSiwjuNxGQkahLtNJVoRj7gjrl5GwcOx+mARoRlWE4zprE0oVto3kZLBbib2ma+CGKbKPYs6qCmsOphkhjpaQPTHYEsCrqZbtDPmRpkDupqLaaqManyVSXURYdaS+qxguM/7WK9j5mzMJnB4mq8ICjk+IannlbEi9KhA7fCA0szIOysmQgqW/qLFj5u5+JfZrL6PchKqZfHRk3PytF9c6mFwP288jxyfadIZHEf/gqLYGkx2x0QaZvW6y2zrqe7le+eMvstJ//vWLVg5/G/gHOef/0BhTA0vgvwT+95zz3zLG/E3gbwJ/A/gPgB+VP38Z+K/L3//iVwaSYfe9THOjMtQfDLGczAD1UuPGuNQIc7hUfkI4D7iteNZpHUnJ8GizZ+tamXHeNPi95ehbMeN8wsWCMvtMnCYDSeVk3lYkm2m3llDUlLkIoSY0OSO3IVPLaKb6aUv/OBKnyQri5GefMZ1+jj8gHX8F3a4S52FrGbPRbN9mOAuMJfbMJFG3U3Hibm7NzNnwD67QvoWyL/6sobmH9TeRWJesxtLP58xsbjtZ26WmBM64zPJVxfobaVWa+0hoT7kYM7/Bltaq1/h0EpMx9fDFdMWkstB76TpykaBPfhOuN/SX4Dsr5ajN2J0lXgbCVcQYWK06dhkuzvfc3qyJi6TkrPEULBSrif1o5mi7CV9KXu/dn49UdeAImE3C/mSptux1gx3UwmJhOJOr9TG3Woydw/XQvtPiPj4tj2CC9lohQWIyGuygCrHayW16f1WmEecjuWs0/sbQXMNwpUwTGwz9ZWHeRsNy1bMfHLGVBaEe9oRxmXbdY23mMK4xo2H9lTxFTBIuZLKc2E0SfnV8WtYSlnw1EBOE6CSkO7H/f+HXv3JzMMacA/8u8NcBcs4DMBhj/irwV8qn/R3g/0Cbw18F/m5J2/6HxpgLY8yLnPOrf/EPoXD8Mz2WuEr4rRKCzaBdMEarsNrCHJuESKa3J5dqUMmYLHF0OlFLMIkeZMCoBTERYnQKKSnl/ZyMXcZxdlDGYqrs3B6QIK6ldpxSk4cL7WBub+f35fc6yfzBUO1c4QyIw2GKz6IdhY1gIGW5+0x5lBMxLNaqAGJt6J9Gll8JHWc0NH9eyyfxOtPcixmYKhFmbF/alt7NQObkSTF5A7AOxEZjOYBsHeOZIgCzKwSbdUmIahLLTUd/U83CoOqiJwZLVUfGhSfvfTnhS1BwG2T5Hgz11xXVg36vxXXi4YdC9ONSieapqFt3qSUdPIe2IfeO9o2nuQE7agQ7bCba8SnHJC0yMWjzNEn3MAZLDDX54Ak+0W6FW03RdGGJWsOmXIukShPDROjUo1kwjilKcVxqUwkLAZ0+m7nKmzCL6B0+KEdkEq6ZErM4gY22tyTv6HsPe18UnuWeDRqRD7XHuUQura54D3oOJ9xoihaYq9SysVeLkfC+LmI7WS9+29cvUjl8DrwD/jtjzF8C/hHwXwDPPljwr4Fn5d8fA1998PVfl4/93OZgjPld4HcB3OWlLLMGQ3zek4NlbCMMlrM/c8SvlwyXInvIrEUgjVK1PyiXiyXW/d2SfPTzxjFcCU12nebRYaXy3mSob1V61feacFTbzPGJFkt0hryMRCA8irhlIF038nSIFv+qJqxF8TOlGqm2hu6FOBjjJpGcLaWdHmIzCujT7q/pR15GzN5Bk+ifZep3nljB+DiodXhfY0e4+kd2ZgsOm+JF4aG/VJs1nOv97z8pKsZVpjrvid2CtIikvWH10tBfGmL3/7Z3djGSVFUc/526VdU93TPMx+6qi7uAEIIhUWGzMRAJMRoNIcYnHjAmGqIvfiQaHwzExMQ39cGo0YhETXxQAfEDQmIQgefFRRZYWFcWdskCWZZddmZnevqrqo4P51RPZ5mVHbZnuhPrn3S6urq66999q86999xz/kfJspSsoSxPmxHrztnvSJcwg5WYpF28GpFnwqo2CYVQf92UvXuFGdFsvgfLCcmK/b9lPEq/bTL7djMpWdNK6529SvwmFludECjjI+JjdfqzBXpomiQ2g9afttGbLe9a0BuF3Uii1gGkZ0x4WINSOxXoNIIV7Vnokp1NaX2og7ZjkrcCjRNWaKj9PneaFsLMjhVWFhtoP2LlsmLN+enygBory1flg0pXUkDzuJWcs+LOEC+77mc3Ipu2YLuo7+pXi97J1dR7+giViP5MTOSJfBblaisPKFanogjgI7FsSpl+JaKzwzQcon6gO2eGThITyS0S07PsLs1Qy6E/az65lcs3HucQvfMhxMAe4Beqej3QwqYQA/goYUOmSVXvUdW9qro3TDcHqayR5wvg1nagxe+9Xz5la78a1pY9Q8dCr6PVCFmN0dXYtr0XIykIixZ+HTpeqt2TtMpQ1qwhZHUTmY3btuZfeBISs33qs11qtb79Y0HNMjc97qKeE3v5vaQFyaIN/6Ku3bQDwY5g/oJS2EQyP3YptsI0pxLKlGiN3enYigk9y+bLUwb1DMpiMVKs+SQKz6oc1Kpo5DQbXYrZPrX5Dr1tBa1dOlgutYawz5Ql69YC0nCxXP+Pe6Z+Fbf9v86wFZbh78H+y7xmxVyknpsSVTsaVOyyK8qXZ/s2DQlxgUxZpGG8KjSPB2aOuqCLnws1jcqsrmgjs4CohqlCD037B/Jr0gmm1nW6Zn6RYq3mSZ7aCpjlmZg2YxBFQuHRr2t1PQdTlnJU6UapjKFJVpWk5aHbQ5oJ0SU2lI3b1nODtVnhDum4ZddyUfNrohxN9iLiMzFSs6zW+lTPG3RNTqBITZg3dHy62rM2KX9/KV40KNgkNs3dKC5k5PAq8Kqq7vPXD2DG4Y1yuiAiO4GT/v5rwO6hz+/yfeeFFGs6etnplLhjMeqhExG6tlRW71vQi0YMbuzyUcY9lBdJsmRS7KUTkNy0/ZMVE4Y1oRG/wMsCMPk6vBTK2P1dC4sAHO0m1Gp9OqupDQ2lQJO1m6n8HjN24lWNbF9oWYp5aNvNHkW2fq2pUtiqHNFUZvUPMytRp8F7hGDJTkVsc+58SlkZyvsvksQy+hpidTeHECUFaZrRjQv6c/ZeMteBfiDPfW4cC0yZMzgvL67cDGTpZxlMhfqmmtV+PySnI/pqgVehbUrQeSqEbiDLXC+xkZN57ErqWZ6hLWTdYL8nq1lH8J6u3TCZmMaG13kEN66pFQoKaUHeDmgupG8G09ZomDaCTuVWQMZvaJkzcdiF+RVa7Rr58rRlaMYeJ6MWLZkVZkBCMyMPgTyNbJrYH7I8Zeq2QlEv6OyIKBJzdk4fN8NWJEI/saVd5vtoK7UpiCuma4CoJYSuS/ClEHzkG/V9VOvTmyTkdPvx4BosRyzmB4NsykZ2eU1Rz1HJmwWSB5IWg84Q2BxpelU9ISLHReQaVT0MfBJ4wR9fBL7vzw/6Rx4Cvi4i92KOyKX/6W/Abs7ZlwtqSzlnrk4svr0e6G5TTu+1YJL0rWgQR57PKFE/ZvpVu5j7Tevp62/acDddgs6C0tueQ90iyMLZQOFhzMFHIKZp4MPvFaH5utJdkIEwRm8+Jz6RorGy8t7UNC7BxEjfLGtKWmJQYeUBrDbCa7C6076ziMXLy5fh0oq2wlo8RFugsFRjjZVGs8dqLR1oWZTLYSZjz0AROl2KaM/2vVdU2pdmLBwIRD0LcV78iHUlS2eaaDvQwnpT5nuIKP0zdaSRkayYg3GwrCkMzl00TFlKd3aIIiVvx2R5Mggqax41H0O6FOjs8LiB3T2rrRB7VbDMvrBILMw8dMwgRj0fHYFJvwtcun2RN+IZuks1enOBxgnLUUEteUuD2hC/9AEMzb0zl1+PGxl5x5LcaqciC8ZKlFa9RpYFQgbJqjkRJY9o7TZrXhQW/p2vBhuxNa2aNsDMyxHZlAWVdbcVtoQdF4jX8tQIWjsjsjrmvcwhrAYkN52F3pzatCKDEFmAWtZYkwQYlCHQcqQs5O3Aai3lkmaHzlSKEpNNCfVTkLfsuPSs0rrM/Ft5oqRnIpKzgfppJV32HJOmHdurbXzkIDYjeIeDRK7DljJT4GXgDmyAfT9wGfAKtpT5li9l/gy4BVvKvENV97/D9y9jS6OTgu3AqXGTGMIk8ZkkLjBZfCaJC7ydz+WquuNCP3xBxmGzISL7VXXvuHmUqPicH5PEBSaLzyRxgYvn8y5mIhUqVPh/QGUcKlSosC4mxTjcM24C56Dic35MEheYLD6TxAUuks9E+BwqVKgweZiUkUOFChUmDGM3DiJyi4gcFpEjnsC1Fef8jYicFJGDQ/sWRORREXnRn+d9v4jIT53fsyKyZ8RcdovIEyLygog8LyLfGDOfuog8KSLPOJ/v+f4PiMg+P+99noCHiNT89RF//4pR8vFzBBF5WkQengAux0TkORE5ICL7fd+42mpORB4QkX+LyCERuXGkXFR1bA8gAC8BV2IxFM8A127BeW/GQsIPDu37IXCnb98J/MC3bwX+hsXr3ADsGzGXncAe354B/gNcO0Y+Akz7dgLs8/PcD9zu++8GvuLbXwXu9u3bgfs2ob2+BfweeNhfj5PLMWD7OfvG1Va/Bb7s2ykwN0oum3oTXsCPuxF4ZOj1XcBdW3TuK84xDoeBnb69Ezjs278EPrfecZvE60HgU5PAB0vN/xcW6XoKiM9tN+AR4Ebfjv04GSGHXcBjwCeAh/3iHgsX/971jMOWtxUwCxw99/eNksu4pxXny+AcBzaaZTpy+DD4eqy3HhsfH8YfwPJlHsVGd4uqWqZODZ9zwMffXwK2jZDOj4FvM1D2YNsYuYClmfxdRJ7yzGIYT1sNZ0s/LSK/EpHmKLmM2zhMJNRM65Yu44jINPAn4JuqenacfFQ1V9XrsF77o8AHt+rcwxCRzwAnVfWpcZz/PLhJVfdgokZfE5Gbh9/cwrbalGzpYYzbOGw4g3MT8YZYdilykVmmG4WIJJhh+J2q/nncfEqo6iLwBDZ0nxORMlFv+JwDPv7+LHB6RBQ+BnxWRI4B92JTi5+MiQsAqvqaP58E/oIZz3G01XrZ0ntGyWXcxuGfwNXufU4xJ9JDY+LyEJZdCm/PMv2Ce3tv4AKyTDcCERHg18AhVf3RBPDZIaYZiohMYf6PQ5iRuO08fEqetwGPe4910VDVu1R1l6pegV0bj6vq58fBBUBEmiIyU24DnwYOMoa2UtUTwHERucZ3ldnSo+MySmfNu3Ss3Ip56F8CvrNF5/wDpkzVxyzwl7C56WPAi8A/gAU/VoCfO7/ngL0j5nITNvR7Fjjgj1vHyOfDwNPO5yDwXd9/JfAkcAT4I1Dz/XV/fcTfv3KT2uzjrK1WjIWLn/cZfzxfXq9jbKvrgP3eVn8F5kfJpYqQrFChwroY97SiQoUKE4rKOFSoUGFdVMahQoUK66IyDhUqVFgXlXGoUKHCuqiMQ4UKFdZFZRwqVKiwLirjUKFChXXxX/EneRGgCE2iAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"goodPSF = psf.modelPSF(num.arange(61),num.arange(61), alpha=goodMeds[2],beta=goodMeds[3],repFact=10)\n",
"goodPSF.genLookupTable(data,goodFits[:,4],goodFits[:,5],verbose=False)\n",
"fwhm = goodPSF.FWHM() ###this is the FWHM with lookuptable included\n",
"fwhm = goodPSF.FWHM(fromMoffatProfile=True) ###this is the pure moffat FWHM.\n",
"\n",
"print(\"Full width at half maximum {:5.3f} (in pix).\".format(fwhm))\n",
"\n",
"zscale = ZScaleInterval()\n",
"(z1, z2) = zscale.get_limits(goodPSF.lookupTable)\n",
"normer = interval.ManualInterval(z1,z2)\n",
"pyl.imshow(normer(goodPSF.lookupTable))\n",
"pyl.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now generate the TSF, which we call the line/long PSF interchangeably through the code...\n",
"\n",
"Rate is in units of length/time and pixScale is in units of length/pixel, time and length are in units of your choice. Sanity suggests arcseconds and hours. Then rate in \"/hr and pixScale in \"/pix. Angle is in degrees counter clockwise from horizontal between +-90 degrees.\n",
"\n",
"**This can be rerun to create a TSF with different rate/angle of motion, though keep in mind that the psf class only contains one longPSF (one rate/angle) at any given time.**"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Using the lookup table when generating the line PSF.\n"
]
}
],
"source": [
"goodPSF.line(rate,angle,EXPTIME/3600.,pixScale=0.185,useLookupTable=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now calculate aperture corrections for the PSF and TSF. Store for values of r=1.4*FWHM.\n",
"\n",
"Note that the precision of the aperture correction depends lightly on the sampling from the compute functions. 10 is generally enough to preserve 1% precision in the .roundAperCorr() and lineAperCorr() functions which use linear interpolation to get the value one actually desires.\n",
"\n",
"**NOTE: Set useLookupTable=False if one wants to calculate from the moffat profile alone. Generally, not accuarate for small apertures however.**"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" Radius Flux Magnitude\n",
" 0.32 10270.345 -10.029\n",
" 0.48 15150.563 -10.451\n",
" 0.72 22154.787 -10.864\n",
" 1.08 31351.858 -11.241\n",
" 1.63 41925.572 -11.556\n",
" 2.46 52717.400 -11.805\n",
" 3.71 60598.976 -11.956\n",
" 5.59 65057.701 -12.033\n",
" 8.42 67398.991 -12.072\n",
" 12.68 68592.485 -12.091\n",
"0.10455723641238102 0.17889568495959374\n"
]
}
],
"source": [
"goodPSF.computeRoundAperCorrFromPSF(psf.extent(0.8*fwhm,4*fwhm,10),display=False,\n",
" displayAperture=False,\n",
" useLookupTable=True)\n",
"roundAperCorr = goodPSF.roundAperCorr(1.4*fwhm)\n",
"\n",
"goodPSF.computeLineAperCorrFromTSF(psf.extent(0.1*fwhm,4*fwhm,10),\n",
" l=(EXPTIME/3600.)*rate/0.185,a=angle,display=False,displayAperture=False)\n",
"lineAperCorr = goodPSF.lineAperCorr(1.4*fwhm)\n",
"print(lineAperCorr,roundAperCorr)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Store the PSF. In TRIPPy v1.0 we introduced a new psf save format which decreases the storage requirements by roughly half, at the cost of increase CPU time when restoring the stored PSF. The difference is that the moffat component of the PSF was originally saved in the fits file's first extension. This is no longer saved, as it's pretty quick to calculate. \n",
"\n",
"Default behaviour is the old PSF format, but the new format can be flagged with psfV2=True as shown below."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"goodPSF.psfStore('psf.fits', psfV2=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If we've already done the above once, we could doing it again by restoring the previously constructed PSF by the following commented out code."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"#goodPSF = psf.modelPSF(restore='psf.fits')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And we could generate a new line psf by recalling .line with a new rate and angle"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"#goodPSF.line(new_rate,new_angle,EXPTIME/3600.,pixScale=0.185,useLookupTable=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let's do some pill aperture photometry. Instantiate the class, then call the object you created to get photometry of Polonskaya. Again assume repFact=10.\n",
"\n",
"pillPhot takes as input the same coordinates as outputted by sextractor.\n",
"\n",
"First example is of a round star which I have manually taken the coordinates from above. Second example is for the asteroid itself.\n",
"\n",
"**New feature!** The input radii can either be singletons like in the example below, or a numpy array of radii. If photometry of the same source using multiple radii are needed, the numpy array is much much faster than passing individual singletons.\n",
"\n",
"enableBGselection=True will cause a popup display of the source, in which one can zoom to a section with no background source.\n",
"\n",
"The detault background selection technique is \"smart\". See bgFinder documentation for what that means. If you want to change this away from 'fraserMode', take a look at the options in bgFinder.\n",
"\n",
"display=True to see the image subsection\n",
"\n",
"r is the radius of the pill, l is the length, a is the angle. Sky radius is the radius of a larger pill aperture. The pixels in this larger aperture, but outside the smaller aperture are ignored. Anything outside the larger pill, but inside +-width is used for background estimation.\n",
"\n",
"Trimbghighpix is mostly made not important if mode=smart. But if you want to use a mean or median for some reason, then this value is used to reject pixels with values trimBGhighPix standard deviations above the mean of the cutout."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Current background value: 1217.866\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAaoAAAEICAYAAAAOW7ATAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO2deZgcVdX/P9/JHgjZiBCyEJSwRFSWsAiICIgRFBDZ4gIqCCio7w9cUBQQUcEFlFdeEQEJsoSAKEGi7AFBWQIEhLAFCCSQkJA9ELLN+f1xbyfV1T1d3TM9M9095/M89UxV3Vv3nrrVU6fuPfeeIzPDcRzHcWqVps4WwHEcx3FK4YrKcRzHqWlcUTmO4zg1jSsqx3Ecp6ZxReU4juPUNK6oHMdxnJrGFZXjODWBpKskndfZclSKpH0lzelsORoZV1SO41SEpFmSVkpaIWmxpNskjehsuWoVST+R9F9JayWdk0o7WNIDkpZImifpckn9EulHSfq3pHckTU1d+5H4DJKbSfpsC3IMknSDpIWS3pJ0raRNUnm+JekVSW9LelbSNom0IZKuk7Q0Pvdrq9E+5eCKynGc1vBpM9sYGAq8CfxvJ8uzHkndO1uGFDOB7wK3FUnrD5wHbAFsDwwDfplIXwT8Bjg/faGZ/cvMNs5twKeAFcA/W5DjPGAgsBXwPmAz4JxcoqQTgOOBg4FceW8lrr8ZmAeMBN4D/KrEPVcVV1SO47QaM3sXuAkYkzsXewlPSFomaXaRXsTesZewJKZ/KV2upH6S7pV0sQKDJd0ay3xU0nmSHkjkN0mnSHoReDGe2zPmXRr/7pnIP0vSAYnjcyRdE/dHxfKOk/Ra7H2cmcjbJw5TLpY0A9g1o40mmNk/gOVF0q4zs3+a2Ttmthj4I7BXIv0uM5sEvFGqjshxwE1m9nYL6VsBfzOzZWa2FPgr8P54T03A2cD/M7MZFnjJzBbF9AOBEcB3zGypma0xsyfKkKkquKJyHKfVSOoLHA08lDj9NnAsMIDwdf41SYfF/FsC/yD0wIYAOwLTU2UOBu4GHjSzb1rw83ZJLHdzwgv5uCLiHAbsDoyRNIjQg7kYGAxcCNwWyy6XvYFtgf2BsyRtH8+fTeiRvA/4RAuytJZ9gGcqvUjSRsARwIQS2S4BPiVpoKSBwGcJzwJgeNx2iB8Pr0j6cVRgAHsAzwMT4tDho5I+WqmcrcUVleM4reFvkpYAS4GPkxiuMrOpZvZfM2s2s6eA64HcS+1zwF1mdn38Kl9oZklFtQVwH3Cjmf0QQFI3wkv17NjzmEHxF/LPzWyRma0kKMgXzezPZrbWzK4HngM+XcE9/tjMVprZk8CTwIfi+aOAn8a6ZhOUYZuR9HGC0jurFZcfThimu69EnseBnsDCuK0D/i+mDY9/DwQ+AHwMGE8YCsylHwjcS/hY+DVwi6RNWyFrxbiichynNRxmZgOA3sCpwH2SNgeQtHsctlsgaSlwMpB7oY0AXipR7sFAH+DSxLkhQHdgduJccr/YuS2AV1PprxJsQOUyL7H/DsFukys7WVe6noqRtAdwHXCEmb3QiiKOA6620l7GJwEvAP2ATQjP4ZqYtjL+/YWZLTGzWcAfgIMS6bPM7Ir4gTGR0AbrhynbE1dUjuO0GjNbZ2Y3E77O946nrwMmAyPMrD9B6SimzSYMmbXEHwmTAabE4SyABcBaNnz1Q1B4BeIk9t8AtkyljwRej/tvA30TaZuXkCnN3FT9Iyu4tgBJOxHa6ytmdncrrh8B7AtcnZF1R+APZva2ma0gPJecInoeWE1+Gyb3n0odp9PbFVdUjuO0mjjR4VDCbLJn4+l+wCIze1fSboThvhzXAgfEadfd4ySJHVPFnkp4cd4qqY+ZrSPMODtHUl9J2xFsYKWYAmwj6XOxnqMJEz7+HtOnA8dI6iFpLMG+Uy6TgO9HW89w4BulMsc6ehPet90l9Y7DmUjagaCYv2Fmtxa5tlu8tjvQFK/tkcr2ReDfZlaqpwrwKHBCnAzSBziRoIAws3eAG4Dvxoksw2N6rr3+CgyME0y6STqC8OHwYEad1cHMfPPNN9/K3oBZhKGgFYSZbE8Dn0+kH0EYDlseX3S/A65JpH8EeBhYRuhhHRfPXwWcF/ebCD2EOwjDi0MIkyOWEV64FwB3J8o0YOuUnHsDjxHsaI8BeyfS3htlWMGGSRfXxLRRsbzuifxTgRPift8o2xJgBvAdYE6J9roqlpfcvhTT/gQ0Rzly2zOJa79U5NqrUuU/BxxfpN7Pp8raCriVYJ9aRFCQoxPpmwAT43ObTbCVKfXc/htlnAZ8pKN+c4oCOI7j1A2SLgA2N7NqzrhzahQf+nMcp+aRtJ2kD8ahxt0Is9H+2tlyOR2DKyrHqTMkXSlpvqSnW0hXXCg7U9JTknbuaBnbgX4EO9XbBFvKr4FbOlUip8PwoT/HqTMk7UOwE1xtZjsUST+IYOA/iLAA9rdmtnvHSuk41cN7VI5TZ5jZ/QRjeEscSlxTY2YPAQMkDe0Y6Ryn+tSa80bHcdrOMPIXpM6J5+amM0o6kTANmcGDB+8yatSojpDP6YI89thjZmat6hy5onKcLoyZXQZcBjB27FibNm1aJ0vkNCqSVmbnKo4P/TlO4/E6+Z4ThrPBI4Pj1B0dpqgkHS+pYOV1PRNXiVtcxV3Nck+WdFc1y+wI2qs9nIqZDBwbZ//tASw1s4JhP8epF0oO/UlakTjsC6wi+PQCOMnMyo7waGZXAFdULKHjOEQ3OisJPaVfEny7baoQAv1soAeAmV1KcB90ECFg3zvAlztBZMepGiUVlYWokUAINEZwIVLzX/qSulnwD9alycWSMbPmzpalHpHU3czWdrYcacxsfEa6Aad0kDiO0+60aegvOje8RNJcSXMk/bKIw8Rc3vXDWYkhopMlvaQQtfOHkraV9IhCRM5rFUNKSxoXFy/+WNKiGNTryETZE+MCxzskvQ18WNIgSdfFUAOvSPpuHArpK2mFpK0T1w+TtFIhmBiSPhMXSi6R9C9JYyjNYQoRQxdI+qkkxXK2kzQ1yrxA0gRJ/RL1jpJ0i0IE0bck/bpIu0nS/yqETein4GDzYoXgZS9J+qaktYn8D0k6V9LDhK/pLSSNlDQlyvGCpOMS+SdK+mHieJykmYnjeZL+n6SnE8+lZyL9TElvxi/7L5RqpCjbOfEZr5B0s4JT0knxN/BQcthQ0g6S7lGIpPqsYvC9xDN6Ml73mqQfJNI2ive1KD7DhxPPdp6kvRN5z5d0eeJ5rZX0VUmzCT0TJH0klrFE0uOS9kpcX817mijpN5Jul7Rc0oMKgQYB7o9/n4/1rL+uhbZ+b8yX21ZKejemdVP4X3otPrsrk79Lx6k5KnREeUDq3C+AfxFizWxGcBZ5ZgvXn0wImAbByaQBNxJivOwErAFuJ7jmH0QIJ310zD+O4Ob/54TAXwcQXsJbxfSJhHUluxOUby+Ch+Nc+VsDrxAdZxLCEPwoIdvphBDNECJZzgV2AboRpu6+QMJBZeK63H3cTohmuhXwMvCFmL4dsF+UeXNCFNTzY1oPgrfp8wnDqn2APZNtRejxXk1wJNk7pv0PIYjbUELk0vuBtQmZHooybBvr6E5wvnlRbJexsa32SrTdDxPXjwNmJo7nETwkb0ZwDDqTDQ41DyMY6beL7fyX2B7DW/gNPBTveVTiGT9HCKrXneBx4PcJB5lzCY41uxHCfS8iOh4lRF19f3zeO8e0cTHtW4Tw6H1iubsCGyXuJ+mc9Hzg8sTzMuDyxDMZRXDieUCs6yBC2ImB7XBPE4H58X56xHu4KvVbK9q2Gf+7is/mT/H461HmLaNMfwf+uMsuu5jjtBfA29ZKp7RtnUzxeULUzbfM7E3gPILL+XI538xWmNkTBGUwxcxeNbNFBK/JOyXyriVE3FxtYfjxLvJd899kZg/bhmGuzwLfi+XPBH6TkO06QvTKHJ+L5wBOAn5nZo9ZiLVzGeEFv0uJ+/i5hWBjrxA8RY8HMLPnzOyeKPO8KEMu0unehJfEDyxELV1pZv9OlNmLoGh7AJ8xs3fj+aOAC81srpktJHwspLnczJ43szUE5fmhWM8qM5tGiI5ayXO6yMzeNLMFhF5GLizDUcAf432uAH5cRlmXm9msxDN+1szuszDEdhMbnvlngKfN7Nr4HB4lKOzPApjZ3Wb2jIUoso8TPkxybbuGoFTfZyG666Nm9nYF93tW7pkQAtLdbGZ3xbqmEDxmH1jte4pMMrPH47O7jg1t3RbOIgT7Ozkefx74ZfxfWwacGc85Tk3S6nVUcXhrc/KjW1YaQfPNxP7KIscbJ44XJF7Wubq2SBwnFzhuTvj6fa0F2W4HJkj6EPAuMJrwwoDwlXmUpO8kru1J6ftKR/vcAkDSFsBvgT0Jvsqa2LDocgTwirVsP9oe2AjY2fLtJOnoouVEOl0QX7pJGfcvcT9p0pFOc9FatwCSgd7KiXRa7jPfEthHIdx5ju7AYoA4/PYzQoyhngTF/ueY7wrCb+AmSRsTeqU/svLsls1m9kbieEtgvBJDzYSPh+Rvryr3FGkpqmyriEOEJwC7mdmqeDod/fZVQu/RcWqSVveoYlduHvlRNJMRNKvNpgozn5J1JV8oSaeF8wgxXkam8r8OEL9WbyL0fD4H/DXxIp9N+KIekNj6Wohi2hLpaJ85uX5JcKK5g5ltQnhhJCOdjlKc8FCE6cDXgNslvTdxfi6VRzodohAoLSljzUU6TTEbuCP1HDY2s/+J6ZMIw2q5KLJXEds29hzPMrPtgH2AI4Fj4nVZ95t2fjmb0GNKyrGRmV3UDvdUioqdcioE5fsj8FnLn56ejn47kg2hyJ22IIXNqSptHfq7Hjg7Go/fQxhCuKbtYhWlB/AjST0l7Qd8nDDuXkD8cvwr8LNoWH8fwW6RlO06wstrPBuG/SCs0v+GpLEKbCzpEEnJl1ua70nqL2kUITrpDfF8P4Lz0GWSRgKnJa55gBCg7CcKEzz6SNozdR9XEYZT70kY1ScB/0/S5pIGA98uIRcEm9J/gfMk9VLwpH1coi2mA5+SNEDSMDKilaaYRIgYuk3suZxVwbVZ/A3YSdLRChFSe0raI9YlQk9joYUosnsSlBEAkg6QNCZ+BCwjDBvneq7TCT2k7gprjA7NkGMCcKSk/eMkhD5xvxKFnnlPWRfG3/RSQsC/3H3mJiXtkc4vaRDBu/hpZvZIKvl64NsKk2z6EX5j16XLcJxaoa2K6izCeP0zhBfAgxS3mVSDWYQXzjzgSuDLZvZyifwnxb+vAvcQDOTJdV/3Ewza/Qn2LgDM7EHgm8AfCBE8XyD0ukp90d5GmOAwjWBXyimBswi2qKUExblescZe3UEE+9EcwjDlZ9IFRxvZrwnKajjBBvZvQrs/QjCEr0pfl7jeCC/xMYS2uwH4jpk9ELNcSVBmr8Wyri9xn+my/0pQ7P8iTCC4vdxryyh7MfAJwhqguYRewHlAj3hPJwO/krQc+C6h3XMMI7ykc9Fnp7Dh4+EHwAcIz/b7hAkMpeR4mWBD+jHwFuH39C1a8b9T6p7KLOIs4MY4+/AQQm92MeG3kGY3glL7fWLm31sx7feEkBn/Bl4iTOg4rUgZjlMT1EWYD0njCBMcts7M3MWQ9BnCpJRtO1sWp2ORdAIwzMzKmcSSifv6qwK5Yb86eK92NJLeMbONWnOtO6WtM+JQzYcJkxiGAT/EI512Sczs8s6WwXE6AndKW380Edb+LCUM/T1OGD5yHMdpSOqiR2Vm/yQs2u3ymNlSwoJQx3GcLoH3qBzHcZyaxhVVmSj45TNF/4NF0mdJOqDKde6r4EOv7miP9ihR16WSftQRdRWp25TwG9lVZXCc9qQuhv4cpxRmdnJ2rrYjaSpwjU9icJyOxXtUXQRJ3TpbhpaoZdkcx+l8alJRSTpDIYTFckkz4lqhlvL2UQifkQub8N3kcJmk7RVCbSyR9ExcKJlL6y/paoUQHK8qhBppimndJP1KIfzGy8DBZYi+a5R3saQ/5Vw+SRoo6e+xnsVxPxn6YVDM/0ZM/1sL9/rNWP7wePxdhRArb0g6ITkEJOkqSb9XCO/xNvCxjPs9R9I1ibryhjpjG/5EIfTEcoWQKpsm8n8xlrlQ0pmlGqkF2XrF9s6FnrhUCbdPZdzreYm8X1UIC7NI0mQFn4u5tFx4mRfjb+ISKdvnjaSfAh8BfqewePZ3ieQDWipP0lfi73KxQviOLRNpZcsSf48/0Ib/i8ckFbjPynjGW0u6TyFcy1uSbkhct11WGziBUWfc1tkidD2slW7X23MjeFLYgqBIjyb4ZxvaQt7zgfuAgQQfeE8Bc2xDKI2ZBG8EPQkhN5YD28b0qwkeDPoRwjS8ABxvG0JtPEdY/T8IuJfgnaIg3EfMP4vgBSGX/0HgvJg2mODdoG+s60ZiWJGYfhvBc8LAKPNH4/l9E/dyFmEq+hDbEI5jHiHURV+CNwxjQ8iIqwhT2PeK7dg7437PIQxr5WQalbxfYCrBi8E2BAemU9kQsmQMwVXUPgTnsBcSvIgc0EJbFZPtIkII9UFRvlsJXunLvddcW+9H8CCxc5Tlf4H7E3UbwQPHAIKPuwXE8CBl/C6nEoKHUk55BPdMMwkOhrsT1rz9uzWyAN8huMLaluDT8EPA4EQ52wBPELyc3ALsEI9XE5Yx9CR4HTkz0eZ7x+s3AmZ7mI/y2PJ7f285MSz17Thh6gjaEOaj05VSWUIG90yHtpD2MvCJxPEJbHi5fyS+4JoS6dcTXsrd4j/xmETaScDUuH8PcHIi7UCyFVUy/0HASy3k3RFYHPeHEvzQDSySb1+C89gLCb4B+yfSriS+yOPx1kVe3lcn0rPu9xyyFVUybtXXgX/G/bOAiYm0jWJdpRRVUjYRPkbelzj3YYJ3+XLvNaeorgB+kci7MSHsxyjb8FJPxqOaBJxR5u9wKsUVVdHygH8QPwTicRPBI/qWlcoCPE/L/wMG/JTw224mfDhMIviyPIngqulrhA+Vy0jFtCJ8DP7LFVV5uKJqHXRiPKp2QdKxkqbH4ZAlhK/DTVvIXirsxRbAbMsPpZEL97EpoffSUpiSdLnlhLBoKdxHX0l/iEMxywh+Bgco2GZGAIss+IErxgBC8MafW1hDlXdvLdRd7FzW/ZZDSyEo8mSxEPtpYUZZSdmGEHpKjyWe+T/j+YLyKX6vOfJCWFiIk7WQ/PusaiiNEuVtCfw2cU+LCEq5NbKMIPRoW+JjhIgAItz/fvH4VWAdIcjld2P6IwrD4F9JyLl7qRt0nM6k5hRVHMP/I8EL+WAzG0AYUmvJjlAq7MUbwAjlh9LIhbh4i/Cl3VKYktaEsGgp3MfphCGb3S2E+9gnnhfhpTtI0oAWylwMfAr4kxIh0Kk83EfW/VYt3IeCp/nBGdekZVsJvN82hL/ob2a5l3Y595ojL4SFpI2iLNUIP1OpA7fZwEmWH9ajj+UHyKykrPeVSL+A8FsxwrDgEgtxzEYShgOHmdk8M/uqmW1B6Gn9X7QnngysXLBgQSvEcpz2p+YUFWHYyAjj9Uj6MqFH1RKTgO8rTFgYRlBwOR4mfKV+VyGswr7ApwnDVOvitT+V1C8qyNPY4Pl8EvBNScMlDQTOKEP2U2L+QQRbQDLcx0pgSUw7O3eBhThB/yC8NAZGOfdJFmpmUwkRWG+WtFtCvi8rTBbpC5RcR1TG/U4nBPUbKak/wbN4udxECBWyt6SewLlU8NuKPd4/AhcphItB0jBJn4hZKrnX62PeHSX1IgRXfNjMZmXJoQ0TSEa1kOVNEmE2yuBSwm/z/bH8/soPwFgJlxNCwoxW4IMK4XU+FdOfIQz7vUH47SnxjG+O9R+pDZN4ckrteqJiGzJkCI5Ti9ScojKzGYSwFv8hvBg+QJiY0BLnEr4YXyGE67iJGPbCzFYTFNMnCV/t/wcca2bPxWu/QehJvEywAV1HsIdAeHHeTgjf8Tjxnz2D6wihyF8mDNPkZqL9hjAB4S3gIcKwVpIvEno7zwHzgYJAemZ2J/AV4FZJO5vZP4CLCZM8ZsZyoUTIj1L3G8u/gTAZ5TGCkb8szOwZ4JRY3lzCS7DShcrfI95HHB69i9ALpZJ7NbO7CIrsL1GW97EhaGIWIwhDZS31vn4LHBFn8F2cVZiFMCgXABPjPT1N+C22hgsJCvsOQoytKwi/qVwveyohZMkggo1qKzY84wcJ97Qr8LCkFYSJK98ys5fNbDnBBus4NUldhPmoBElfA44xs492tiwdiaTtCS/CXpYfur7haK97lfRDYIGZ/aFaZXYkccTg22b2KUk3An8xs4mSLgWeMrP/K3W9h/koj1Fn3Mas81tYreJhPlpEbQjzUXM9qkqRNFTSXpKaJG1LsAd1ibAXkj6jsP5oIOHL/dZGVVIdca9mdl69KqkifA84TdJMgo3uik6Wx3FaTd0rKsL6kD8Q1kfdQ1hDUvLLsYE4iTBU+BJhZtfXOlecdqUr3WurMLOpZvapuP+yme1mZlub2ZEWQtk7Tl1S977+zOxVSk+2aFjMbFxny9BRdKV7dRwnn0boUTmO4zgNTN33qDqanuplvZWwB6ZtpgWrvYos/0obWrOuKcif5ZrOSh4WLyPrRipNzxYrU4as/Jnt2OLJUpW0oo5KKX3fy23xW2bmc8UdJ+KKqkJ6ayP26P6J9cfWnP+SUVPqJaTCTqutXZOfpVvKeXjqGlu3rnT+ggqa8w9T1wOoe4+S1xTInU5Py1CkjgKx0veRIUNB2/bI/7na6tX56cXapUj7l6ozs+3Tz7c1ZLTtnWsmluMFxXG6DD705ziO49Q03qOqFCv80i+ZvYyeRuFF+V/Y6a/4dI8s/YWezq+ePQvrSN9DVg+qChT0oNK9k1RTFfRe0j2srF5hMdrYg8rsQbeGdE9wTfFsjtNV8R6V4ziOU9O4onIcx3FqGldUjuM4Tk3jNqpKUYZdIm0vKjZBr6kVs9dK1ZEx09DWZHsayrS1pG1YGXa6YnY8NaXsQxnmu8JZf6VtVi0UUlF6Vjs09cy3i9na/LYtet+p51lgB7OqzHl3nIbFe1SOU4dIGifpeUkzJRWEoInhWu6V9ISkpyQd1BlyOk41cEXlOHVGjAx9CSFkyBhgvKQxqWw/BCaZ2U6EMCddxf+l04C4onKc+mM3YGZ0PLuaEIfq0FQeAzaJ+/3ZEG3aceoOt1G1ldZ4MkjbZjK8J6TtIOqRWheV9uiQ9nyRXm9UrI4qe2CoxvqiAk8UKVtbQR3FbHup+6pkDVyxOtLPIit/WWVWvtZuGCE0fY45wO6pPOcAd0j6BiFq9gFFZZFOBE4E2GWXXSqVw3E6BO9ROU5jMh64ysyGAwcBf5YKv4jM7DIzG2tmYztcwgZi1Bm3dbYIDY0rKsepP14HRiSOh8dzSY4nhK7HzP4D9AY27RDpHKfKuKJynPrjUWC0pK0k9SRMlpicyvMasD+ApO0JimpBh0rpOFXCFZXj1BlmthY4FbgdeJYwu+8ZSedKOiRmOx34qqQngeuBL5mlY5Y4Tn3gkynaSoULRsMllTk2VffUpIKMiQ+tctaaQYEj3DRZi5DJvu+C9NSsk6zJFazLXzhdVK6sxdRpmVKLsSsuD7LbPysUSbEizaYAU1LnzkrszwD2qrhgp13I2bBmnX9wJ0tSn3iPynEcx6lpXFE5juM4NY0rKsdxHKemcRtVxSh/YWnKrlLO4s1KQ8kX2n9Kh5pPO8It7iBWJY8L8lfoKLcgKGIRuQoCIablTi9czrSDFcpY8DzSDmDTC7azHARXGtqeyhcZO46Tj/eoHMdxnJrGFZXjOI5T07iichzHcWoat1FVilne+p20DaPAplHMZlGhA9is/E29euXnTzuxLWetT5q0TFl2lvR9luNnNW3vaet6ryL2oyx7Xdrel2mTSjsALmNNXHr9V9pRboEz3Yp91DpOY9NQPSpJvSU9IulJSc9I+nE8v5Wkh2OQuRui2xkk9YrHM2P6qM6UvxGxtWsLNsdxnEpoKEUFrAL2M7MPATsC4yTtAVwAXGRmWwOLCQ47iX8Xx/MXxXxOhdia1UUVUktKaX36mtX5mysxp4Fwj+rVo6EUlQVWxMMecTNgP+CmeH4CcFjcPzQeE9P3l9T2QEoNTlrBVLXspJJz13SO49CANqoYpvsxYGtCuO6XgCXRkSeEIHPD4v76AHRmtlbSUmAw8FaJCvLtGGnfcOngfkXtQ6WD+RWscUrbOFL5m1etys9fjq+/LPtQQsRO7ekklJWtWQ1NG9qzHHtgod0qo+2zyixot7QPxCJrudI+CdM0e0/ScUrRUD0qADNbZ2Y7EmL07AZs19YyJZ0oaZqkaWvs3TbLWC/UpE2peV3YHMfpMjScosphZkuAe4EPAwMk5bolySBz6wPQxfT+wMIiZa2PgtpDvdtd9s6kbiY9NK9rl6FHx3Fqj4ZSVJKGSBoQ9/sAHyfE67kXOCJmOw64Je5PjsfE9Hu6csyemldOLeAKy3Eam0azUQ0FJkQ7VRMhoNzfJc0AJko6D3gCuCLmvwL4s6SZwCJCpNQMLM9uYavTfvay1ywVrLVJ+5tLv3TT627SPu969iydvwSN9ILPKVol15VlrVkrWMNUuu0K1rSVYQ+s2O7lI5uOk0dDKSozewrYqcj5lwn2qvT5d4EjO0C0mqSRlFQSW7UqX1k5jlPXNNTQn1M+jaqkclhqJqTjOPVLQ/WonGzq1Q7VGnLKSt39Z+449Yz/B7eVrPhERciKH5UetipYm5VaV1WQ3oLvwK6kpJLY2rUb2jRtg0rHE2uH2FHpuFpZ8cWc+se9UlQXH/rrAtTFdPN2xlatasjhwEr9WzpOPeKKqsHp6gqqC1Cpf0vHqTtcUTUwrqQKabQ2aYV/S8epO1xRVYyCjSG3pbBmy9uw5sIteb2awlqe5NZs+VuadevyNjUpb0NNDfdCriZ5Q6GpZ6Nu3fK3VNumN1u3Lm8rRlaZbUVSN0nTgfnAnZT2b5m+dr17sAULFrRZFqc6uI0rH1dUDUijTz138mmLf8uke7AhQ4a0m4yO0xZcUTUY3pMqn0abZFKmf0vHqTtcUTUQjfTSdcqjFf4tHafu8HVUFWR0A2kAAB+YSURBVJPv6y/tx63ATlF0nVUqT5YvvzLWTbmSaj22dm0izlVljvbSNqbWrMNqo52qUv+WjlN3uKJyHAgxrpqyHQrXGpX6t3ScesSH/hoA701VCQ/I6Dg1iSuqesdfrtXF29Nxag5XVI7jOE5N4zaqilH+ZIdUELwCw3iRQHqZpK8pmGsR6vAhv3aihL2qGpMn0s/X1nbZoNKOUxbeo6pTXEk5jtNVcEXlOMWocVuVpHGSno/e0c9oIc9RkmZEr+rXdbSMjlMtfOivDvHeVAdRo1PW45qpSwiLe+cAj0qabGYzEnlGA98H9jKzxZLe0znSOk7bcUVVKWYtOh+F8mwY6UXCBXauVERaV0ydR9aC7nIW66Z/A+reI50h/zgVZ7EIuwEz41opJE0EDgVmJPJ8FbjEzBYDmNn8zFIdp0bxob86w5VWx1KjDn6HAbMTx8W8o28DbCPpQUkPSRpXrKCk9/R2ktVx2owrKsdpTLoDo4F9gfHAH3M+AZMkvad3sHyOUzauqOoI7011DjXYq3odGJE4LuYdfQ4w2czWmNkrwAsExeU4dYfbqCpFKrQxlaSIPStjbZWtS6UXdWzrdAYFNsjUx4N69Cy8Juvnkv49ZduoHgVGS9qKoKCOAT6XyvM3Qk/qT5I2JQwFvpxZsuPUIP4GdJw6I0buPRW4nRDSY5KZPSPpXEmHxGy3AwujF/V7ge+Y2cLOkdhx2ob3qOqEGhx+6lLYmtVFe0udhZlNAaakzp2V2DfgtLg5Tl3jispxHKcMRp1xW1nnWlPurPMPbrHsYmldDVdUlZJeR5W2N5VhTypYV5OxFsd7UzWCNRdZE5X9L5R+furVKz9DiXV5juO4onLagf6bbsIen96F7ffYhlHvH8GW2w+j7yZ9eev1Rbz+4lxmTn+F/97/LNNun86a1fUzkzE/ErDjOB2FKyqnamy769Z87geHs/vBO9Ote+EL/T0jN+U9Izdlp/0/wJGnH8LbS9/h9qvuZdIvbmHh3MWdILHjOPWAKyqnzWwyuB+n/PYr7Pe5vQFYu2Ydj9z3HNP//SIzZ7zBimXvgAE9ezBks/5ss8Mwdv/odmw9ZgsO/9bBfOrkA7n67Bu48de30pyemu84TpfHFVWlpNZRWQuxohInCoqwtemFMqX9ydUy24x9H+fe8j0GDx3IypWr+evN0/jLTY/wRq/EPfQJf9b0WQ3vLOC2RxbAI9PZod8gjjv6w3xsr2054fwvsNtBO3PO4b9k+aIVnXMz5dC8Lt8uVc4aN6V+E62JYeU0DD5JonJ8HVWtU8PhJnba/wP86t5zGDx0IE89+RpfPf5yrrh8KkuWvFPW9S/NWsBZF0zm9LNvZMHC5XxwnzH85oHzGLR5gacfx3G6MA2lqCSNkHRvIgbPt+L5QZLulPRi/Dswnpeki2NMn6ck7dy5d1A/vPeDW3L2X75Nn416c+ffHuPbp1/H3LlLWlXWI0/M4qRvX8PLL8xj5HbDOO/v36f3Rr2rLLHjOPVKQykqYC1wupmNAfYATpE0BjgDuNvMRgN3x2OATxL8n40GTgR+3/Ei1x+9+vTkrBtPZ6NN+jJ1ypNc+MObWddG29KChSs44+QJvDF7IaN3fi9f/+2XqySt4zj1TkPZqMxsLjA37i+X9Cwh/MGhBC/SABOAqcD34vmr4yr+hyQNkDQ0llMWWfGn1FTkBZ6yaxRck7SB1eDQ33HnHs2w0UN5+ZX5/OySO1i9RT/e3DV/bVDzzssLruvRI38q+pIZ+UN8esD43s/+xuW/PY5PfmU/pk58kMfveqr6N9COFLMvZsUfc2qXlhbjOh1Lo/Wo1iNpFLAT8DCwWUL5zAM2i/vlxPXJi9mzxt5tN5nrgcFDB3LoKSG00QW/msLqNdVVpK/OXsiE6/8NwJd+ckxVy3Ycpz5pSEUlaWPgL8D/mNmyZFrsPVU07SoZs6eHOs52UoseKQ79xifp2bsn9/3rOZ5/cV671HHT5MdYvORttt99NB/cZ0y71OE4Tv3QcIpKUg+CkrrWzG6Op9+UNDSmDwVyYbnLievjJPjYMXsBcNNf2y8g7Lur1nDr7WHI72Pj92q3ehzHqQ8aykYlScAVwLNmdmEiaTJwHHB+/HtL4vypkiYCuwNLK7FPhUrTuj57KCxzrVWN2jBGvX8Em496DwvnL+PhxfOxLTZ4E++5x6K8vE/sOrHg+vnr3s473vvdr+Udr/pv3/X7d0x/kWOP/jC7H7wL8McqSF89kjbFtA0yy2+j4ziV01CKCtgL+CLwX0nT47kfEBTUJEnHA68CR8W0KcBBwEzgHcCnmpVgm7HvA+CZJ1/D2nnN6szZC3h7xbsMGT6YAe/pz5L5S9u3wkpoXuc+/xqAUgtvq+EV3akeDaWozOwBoKVP2v2L5DfglHYVqoEYNnooALNmzs/I2XbM4NWX5jPmQyMZvs3Q2lJUjuN0KA1no3Laj40HbgTAsiVvZ+SsDsuXrASg38CNO6Q+x3FqE1dUTtk0dQs/l/S6r/aiubk5r17HcbomDTX01yGY5U0bT4cnL8uYnl7wm1okWqsG+RWLQ0+qX/++WEp3rF6bb7N5bFXh1Pq7VuyYd9w8p2/ecY+V+RMT+vULSwGWL65dJ7UFzy69uBcyJ8vUkxNix+kM/FPVKZt5r7wJwPBRm3ZIfcPfOyTW2/42McfpCHySRutwReWUzYuPvwLAmA+OyMjZdoZtPoABgzZm6VvLmP/aW+1eX0X4jD/H6VBcUTllM/OJV1g8fylbjBzMNiOGtGtdH/vwNgA8dkd9+fpzHKf6uI2qUiTUK+GANWtiQbHAiVl2jRpd8Nu8rpl//eUhDvnaJxi/6w5c+O/b16e9+2D/vLzHvPStgut7LM+3vQ2ZmX+ffWcHG1hTtyYO+dgHAJg66cGqyN5ulBM4Me24eE3KCXH3Hvn5a89zluN0Kt6jqmHyIsnWCH+7eArNzc2M+8QHGbp5/+wLWsGBB3+ILYYPYs4Lb/DwbY+3Sx2O49QPrqicipj9/Bvcc+0D9OjRjW+fdlBBlPW2MmjwxpzwzQMB+PO5N9LcxjhXjpPFqDNu80kONY4rKqdiLj19AovnL2Xnnbbk+C/vU7Vye/bqzo9+cTSb9O/DI1Me557rHqha2Y1KpVGtHaceqb2xpVrHDFuzIQBgpoPZIhQEW1y7Jj+92FqcGmLpW8v4xbH/y3l//z6fH78nq+ev4NobH8nLs7Zv4U+r27v5trnuy1et3+/dpyc//Nlnef8HRzD/tbf49Qn1EWy5nGeV/L1A1dfJ5aJaPy6pH/CYpDuBLxGiWp8v6QxCVOvvVbNix+kovEfltIppdzzJRSdeSnNzM1/+1oF8+/ufpm/fntkXFmHEqE351eVfYdd9t2fZwuWcefDPWDRvSZUlbkzMbK6ZPR73lwPJqNYTYrYJwGGdI6HjtB3vUdU46t4dW7s2O2MncPtVU3l72Uq+f803GXfwh9h57Ciuuvw+7r7jacqRuF//Phz++T054tg96dmrB2+8NI8fHPQzXn+xskgrHUoNr6EqM6q149QdrqicNvHAzQ/z9bHf4zt/OoVtd92a7555CF85cV+m/ut5pj0+ixdmzmPJkndobja6d29i880HsM12Q9lzr9F8eM/R9O4TemH//NM9XHraBN5e+k4n31F9ko5qrcQsFzMzSUXXUUg6ETgRYOTIkR0hquNUjCuqKlNgb0qvkSlG2vdfBzl9rRavzpjDN/c8k/3G7834HxzOyO2GccThu3LE4buuz2NmqMgUwUf/OZ1rfnIjM/7zQkeK3GoK7IvpNXE9Cv+l1JQ6l3q+bfX1VyqqtZnNTUW1zq/b7DLgMoCxY8fW1w/P6TK4onKqQvO6Zu665n7uuuZ+tttta/Y+fHe22200W31wSzYZtDGSaF7XzMK5i5n5+Cv894Fnuf/G//Dmqws6W/TyqfZc/CrQiqjWjlN3uKKqA2rZTlWM5x6ZyXOPzFx/3G/gxvTeuDdLFyxj9bvudqHKVBrV2nHqDldUTruzfPGKmg7VUc9UGtXaqV9GnXEbs84/uLPF6BRcUbWGhC8+a863L7XGb1+BXaPObFRdhWJrpgrWRJVhbyqwa6XtmB6eynHy8HVUdUI6QKPTsdSa30VJ4yQ9L2lmXNDbUr7PSjJJYztSPsepJq6oHKfOkNQNuAT4JDAGGC9pTJF8/YBvEdZVOU7d4orKcTKotd4UsBsw08xeNrPVwESCJ4o0PwEuAN7tSOEcp9rU3H9gzSPl2RSy1sAUXROVtlul8hSs1cmlN3WDZjdgdCrpNW9r8mcxlqPUCmxdlfv+GwbMThzPAXbPq0PaGRhhZrdJ+k6LsiQW/O6yyy6VytFlcW/rHYv3qOqNGnbh04jUYG8qE0lNwIXA6Vl5zewyMxtrZm7DcmoWV1SOU3+8DoxIHA+P53L0A3YApkqaBewBTPYJFU694orKcVqidnuvjwKjJW0lqSdwDMETBQBmttTMNjWzUWY2CngIOMTMpnWOuI7TNupvXKPTsTwbU9reULBGppj9QaX9/6X9BabtIvXmqaJeKfrs0vbFViiztN2yBX+xLV9vtlbSqcDtQDfgSjN7RtK5wDQzm1y6BMepL1xR1SmurNqXWrdNmdkUYErq3Fkt5N23I2SqZXKTHxrNs0NX8VbhQ391TK2/TB3HcaqBKyrHSeEfAI5TW7iicpwErqQcp/bw/8oqU9QAn0XKQF/M+WmL9XXvDmoqWHjqdAwFz1vZ336q2cmEjlObNFyPStKVkuZLejpxbpCkOyW9GP8OjOcl6eLo2POpuJrf6aJ4b6pr01ZvE225ftQZt7m3ixI0nKICrgLGpc6dAdxtZqOBu+MxBKeeo+N2IvD7DpKx6rh39bbhSspxapeGU1Rmdj+wKHX6UGBC3J8AHJY4f7UFHgIGSBraMZJWH1dWrcOVlOPUNl3lP3QzM5sb9+cBm8X9Ys49hwFzE+fyHHf2pm+eHSLLKW0xm5W6pRybrs0Irph2hFpQZ+LYHddWhpTfnpZafJuxoLfAgXB6sTZFFoVnOCF2HCefhutRZWFmBlTkCiDpuLOHereTZNXDewjl4e3kOPVBV1FUb+aG9OLf+fF8lnPPusVfwqXx9nGc+qGrKKrJwHFx/zjglsT5Y+Psvz2ApYkhwrrHX8bF8XZxnPqi4f5jJV0P7AtsKmkOcDZwPjBJ0vHAq8BRMfsU4CBgJvAO8OXMCszybBqtsS80ry60YyQpKDNjnVWBzSph01KPnr7GKklTtzwbkXrmT0CxNaX9JxascUs/m55FJrQU2KQybJKO4+TRcIrKzMa3kLR/kbwGnNK+EnU+7sB2w4zIrMkvjuPUHl1l6K/Lo+7dfcjL6VIUW0TrC2vrE39zOQ2Nry1znPrHFVWlqLRdKr1GpmgRGXatzHU26eB96etLBG/M9aq6wlCgevUqsA8VkJGeZZNKk2XjchynclxRdVEaWWGpV6/OFsFxnCriiqqL00gKyxWU4zQmrqicQD27Xspwc+Q4nYVP3KgOrqjamWL2qCwbVIH/uHbwDVd07VXyhV8HSqtgFmMxe1N6nVOP0tdk2QOzbJBFY4lllFFQZ+03veN0KK6onKLU8pCgT7N3nK6F/8c7JakVhaUePTNn3DmO05i4onLKolgvpl2VV1O34sNojuN0OVxRVYrl2xgy7UUqdP6R6estdU1W/gIZ0r4Ay1jbk+U/sKlnj7zj5tVr8mxaORlao7zWL8pN23KKxHYqWU4xvZaO5bU63++huuffV6Vk+l2s0jVO41GtiRa5cmadf3BVyqtFXFE5VWV9z6uIgi4YuiuWx3EcJ4W/KRzHcZyaxhWV4ziOU9P40F+lpH39ZdmTis1USw95pfO0dXZbOf4G07aZ9Hqj9FouS5VZMIyXX14xu0tBmWkbVLotM2TMbMciVDxBI52/Od8GV+BXsUj5boNynLbhispxnLqn0gkFlUxk6EjvEu7Jojg+9Oc4juPUNK6oHKeOkXSlpPmSnk6cGyTpTkkvxr8DO1NGx2krrqjaiK1bl781W/aWviZrS12PmvK3AqGa87diNCl/y2LduvwtAzWpYCvI071H3lZGoflb+j7T6WoqaMs0Benp69eszdvSdTb17JG3ldMWZT2f8rkKGJc6dwZwt5mNBu6Ox45Tt7iicpw6xszuBxalTh8KTIj7E4DDOlQox6kyPpnCcRqPzcxsbtyfB2zWUkZJJwInAowcObIDRKttanEyQ6UyjTrjtpKTSurRk4X3qBynDpE0TtLzkmYCXyuSfpqkGcCTwEaStixWjpldZmZjzWzskCFD2llqx2kdrqgcp86Q1A24BPgkMAb4NJAMb/wm8CowFvgEsBD4RQeL6ThVw4f+KkZ5i0CVjnKXdoJabOFrKnhf2mlswcSDLJ94GXUWdZxbLHBiJWW0YrFtmoI6MoIaZgcgrFyGggW66YXPBempRcvrUjKtyXd6C0U8z2ctEs+eq7IbMNPMXgaQdCtwXCJ9MjDazP4i6ZvAP4HRmaU6To3iPSrHqT+GAbMBJF0PnAQMkTRH0vHA+cDHJb0IHACsAf5RrCBJJ0qaJmlax4juOJXjPSrHqWPMbLykLwK7m9mpiaT9ASR9ATg1bsWuvwy4DGDs2LHZvrfqgFqcEOG0DVdUjlN/vA6MSBwPj+fykHQAcCbwUTNb1UGyOU7VcUVVMVbWgtccRZ2gZl2fthelnLdmOVZtTWTcAltagc0pv8wCB7MF9qLsRcQFeTKc6ZbjADazjowyC65PV1HgpDZ130UiIRdQcN8Vj8A/CoyWtBVBQR0DfC5PDmkn4A/AODObX2kFjlNLuI3KceoMM1tLGMq7HXgWmGRmz0g6V9IhMdsvgY2BGyVNlzS5k8R1nDbjPSrHqUPMbAowJXXurMT+AR0ulNPu1ONi3WrgPSrHcRynpvEeVTtT1AbSnDrXVJnNKdMelBVgsCW5SlyTVWfFa79CoSWP03VmlVmQnzLWSaXXbqVJt1NrYiCm5c5Yw+Y4Tj7+H0K+OxpJ7mnacRynhujyiqqIO5rxksZ0rlSO4zhODh/6K3RHM5EQJmFGp0rlOE4mvri3NI0y+cIVVcIdTWQOsHsyQzIUArDizjUTFwJvVU2CtN2jUjtI8fybUk0Zy6uzUtomYzkyZOVZk5He3u1YnKKezh2nq+KKqgySbmYAJE0zs7GdKFImLmN1qAcZHafR6fI2Ksp0R+M4juN0Dq6oEu5oJPUkuKPxVfyO4zg1Qpcf+jOztZJy7mi6AVea2TMZl12WkV4LuIzVoR5k7FI0ygSBWqUW27fLKyoo7o4mI3/Nv7xcxupQDzI6TqPjQ3+O4zhOTeOKynEcx6lpXFFVQK24WpJ0paT5kp5OnBsk6U5JL8a/A+N5Sbo4yvyUpJ07SMYRku6VNEPSM5K+VWtySuot6RFJT0YZfxzPbyXp4SjLDXGSDZJ6xeOZMX1Ue8voOI4rqrKpMVdLVwHjUufOAO42s9HA3fEYgryj43Yi8PsOknEtcLqZjQH2AE6J7VVLcq4C9jOzDwE7AuMk7QFcAFxkZlsDi4HjY/7jgcXx/EUxn+PUBKPOuK1hPXW4oiqf9a6WzGw1kHO11OGY2f3AotTpQ4EJcX8CcFji/NUWeAgYIGloB8g418wej/vLCQH+htWSnLGuFfGwR9wM2A+4qQUZc7LfBOwvKTuUseM4bcIVVfkUc7U0rJNkKcZmZjY37s8DNov7nS53HCLbCXiYGpNTUjdJ04H5wJ3AS8CSGEU3Lcd6GWP6UmBwe8voOF0dV1QNiJkZoWfQ6UjaGPgL8D9mtiyZVgtymtk6M9uR4JFkN2C7zpTHcZxCXFGVT627WnozN1QW/86P5ztNbkk9CErqWjO7uVblBDCzJcC9wIcJw465NYZJOdbLGNP7Aws7SkbH6ar4gt/yWe9qifDCOgb4XOeKlMdk4Djg/Pj3lsT5U2P4kt2BpYmht3Yj2m6uAJ41swtrUU5JQ4A1ZrZEUh/g44QJEvcCRxDskGkZjwP+E9Pvib1Cp8qkJwXUkpeEWiBr0kSx9PS55HGtt68rqjJppauldkHS9cC+wKaS5gBnE178kyQdD7wKHBWzTwEOAmYC7wBf7iAx9wK+CPw32oAAflBjcg4FJsQZnU3AJDP7u6QZwERJ5wFPEBQu8e+fJc0kTGY5pgNkdJwujyuqCqjU1VI7yjG+haT9i+Q14JT2lagQM3sAaGlGXE3IaWZPESZ5pM+/TLBXpc+/CxzZAaI5jpPAbVSO4zhOTeM9KsdxOpW0t+6W7C+lbCyVnnPyyfKY3tke1b1H5TiO49Q0rqgcx3GcmsYVleM4jlPTuKJyHMdxahqfTOE4TodR7sSJlq5zWkd7tl9HLBz2HpXjOI5T07iichzHcWoaV1SO4zhOTeOKynEcx6lpfDKF4ziZVMNzgU+IqE9qwduH96gcx3GcmsYVlePUIZLGSXpe0kxJZxRJ7yXpPkmrJb0r6YLOkNNxqoErKsepM2L8rEuATwJjgPGSxqSynQDsCGwHHA+cVCSP49QFrqgcp/7YDZhpZi+b2WpCJOJDU3m+SIiu/DJwA9CjSB7HqQvkkbQdp76QdAQwzsxOiMdfBHY3s1MTeV4DHjCzz8XjN4Fbc9ck8v0ZODwe9iVEV+4ougNrE387g1J1t6dc1Si7tWV0VHun6+ljZq3qHPmsP8fpwpjZFwm9LyRNM7OxHVV3rr6OrreYDJWmtWe97V1GR7V3uh5J01pblg/9OU798TowInE8PJ5L8gbwXgBJ3YGNgZc6RDrHqTKuqByn/ngUGC1pK0k9gWOAyak81wJjJG0FHA2sKZLHceoCH/pznDrDzNZKOhW4HegGXGlmz0g6F5hmZpOBPwJHAc8DzcDvzOyZjKIva0+5S9TX0fUWk6HStPast73L6Kj2TtfT6np9MoXjOI5T0/jQn+M4jlPTuKJyHMdxahpXVI7TxSjT/dINMf1hSaPKLPdKSfMlPZ04d6SkZyQ1S/pGot4LJK2UND1ul0o6TdIMSS9KWiFplqSLJalK97xU0lpJ8xLnfynpOUlPSfqrpC9KMkljJX0/yvq8pE+kymqx/YrUWzKvpKPifS+O7q6S7ZeWb0A8PyrdfolrdpH0SnSftaSFZzxS0r2SnohlH1RmOxZ7xj+JZUyX9LqktyQ9rcDF8d6fkrRz4tybklZJek3ScZkVm5lvvvnWRTbC5IuXCFPXewJPAmNSeb4OXBr3jwFuKLPsfYCdgacT57YHtgWmAnMS9c4AXkxd/zHCouNHgF8QPGr8A/hkle75aIJXj5W5ewYOBLrH/YuA2cBDwJGxbXoBW8Xru5XTfhW29WjgCWBgbL/9U+2XlO8C4IK4PyqZL1XmI4m2/ifwcpF6LwO+FvfHALPa8Iw3Sez/FrgJeBo4KD4/AXsAD8dzd0WZDgSmxf2Bper1HpXjdC3Kcb90KDAh7t8E7F9Or8bM7gcWpc49a2bPA5sAsxP13gr0S+W9F+gf815PWB92NXBYZbdYQO6ebwDmA0uJ92xmd5hZznvC1sBM4F3go8BEM1tlZq/E87tRXvul6y2V96vAJWa2OLZf3lq3lHwPEdqkRSQNBd4DPGPBfdYEYEGReo3QzhDa/I1S5SbkKfaMlyUO5xHaj1jn1RZ4CBgAjAeeBe40szsIv4EHgXGl6nVF5Thdi2GEXkOOOfFc0TzxJbkUGNzGensBbyaO5wGD49DTfZI+kqh7DsGR7j9akK9S0ve8Jl2mpJ2BscAV8dQQirdTOe3XUr3F8m4DbCPpQUkPERRkS3yF0CY5tmqh/ZYl6p1D6M2l6z0H+IKkOcAU4Bsl6s1E0k8lzQY+D1yYkCV9/6MIPaykfCuKyJeHKyrHcTqDJcAEM9sJOA24TlLuC39zgtL4ZUcIIqmJ0HN8irBQuiPpThj+25fQ2/g5Rd7Lks4k+M3LyTcXGNlC+5XDeOAqMxtOGI77c2yHVmFmZ5rZiCjfsa0tpyV8wa/jdC3Kcb+UyzNHwf1Sf2BhG+tdBWyWON6cOMxlZo9JeonQu3gv4cU9wsxWSSomX6Wk77lHqsyTYno34JUo22rCkNk1MU9Sjqz2a6neYnnnAA+b2RrgFUm5+tcj6UvAp4D9LRqCzGwVoU3T7fc6YUgvV+/weC/peo8nDreZ2X8k9QY2JQyNtoVrgTsJvdZi9/8IYdgxKd8bReTLw3tUjtO1KMf90mQgNxPrCOCe3AuyDSwHRiTq/TzwdwBJOeW0EaFH8Rzw3mgXOxa4pY11r79ngpLqT7xnSeMIw15bmNmWZjaKYAs6AfiIwgzIraJ8j1Be+xXUWyLv3wi9KSRtSpi4sTqXGOX7LnCImb2TOD9EIS5Zsv1eNrO5BGWzQ5T7OMIwZrre1wgTN5C0PdCboJgrRtLoxOGhbLCzTQaOjTP99iAMIU8kTLA5UNLHCcN+exO8rLRMW2bT+Oabb/W3EYZ6XogvlDPjuXMJL0PiS+tGwgSCR4D3llnu9YQhqTVssDN9Ju6vAhYDb8d6rwOeIdiqXgI+TZgN9ibB7dPKmPd3RA86VbjnZYThs3VRpsmEr/nZwPS4XUqYoTgWODPK9jyJmYfF2q8NbS2CTWcGYTh0car9Zqbli9d9NrbfdOBx4NOJOscCswgKb2kL9Y4hTGJ4MpZxYBue8V8Is/yeIvSM3kyk30NQgK9HuUQI+jk//iZmA1/OqtddKDmO4zg1jQ/9OY7jODWNKyrHcRynpnFF5TiO49Q0rqgcx3GcmsYVleM4jlPTuKJyHMdxahpXVI7jOE5N8/8BxSGxxvfgOPgAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 3 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"#initiate the pillPhot object\n",
"phot = pill.pillPhot(data,repFact=10)\n",
"#get photometry, assume ZPT=26.0\n",
"#enableBGselection=True allows you to zoom in on a good background region in the aperture display window\n",
"#trimBGhighPix is a sigma cut to get rid of the cosmic rays. They get marked as blue in the display window\n",
"#background is selected inside the box and outside the skyRadius value\n",
"#mode is th background mode selection. Options are median, mean, histMode (JJ's jjkmode technique), fraserMode (ask me about it), gaussFit, and \"smart\". Smart does a gaussian fit first, and if the gaussian fit value is discrepant compared to the expectation from the background std, it resorts to the fraserMode. \"smart\" seems quite robust to nearby bright sources\n",
"\n",
"#examples of round sources\n",
"phot(goodFits[0][4], goodFits[0][5],radius=3.09*1.1,l=0.0,a=0.0,\n",
" skyRadius=4*3.09,width=6*3.09,\n",
" zpt=26.0,exptime=EXPTIME,enableBGSelection=True,display=True,\n",
" backupMode=\"fraserMode\",trimBGHighPix=3.)\n"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Current background value: 1237.619\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAaoAAAEICAYAAAAOW7ATAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO2dd5gcxdGH35+kUxZKyCgjshBgkkyGD4PAAmyCyWCQCRbRYIONZTAZG3AAkwyInKMBgwkiimRyRkRJBAmUs1DW1fdH96LZ1d7t7d3ebbh6n2eem5nu6a7p2Zua7uqukpnhOI7jOKVKi2IL4DiO4zi14YrKcRzHKWlcUTmO4zgljSsqx3Ecp6RxReU4juOUNK6oHMdxnJLGFZXjOCWDpJslXVBsOfJF0o6SJhZbjkrFFZXjOHkj6UtJCyXNlzRL0qOS+hVbrlJF0vmSPpC0TNI5GWl7SHpJ0mxJkyVdL6lTIv2vkiZImivpK0mnJ9K2j88guZmkfWuRZYiktyV9J2mipAMSaSMlfSqpWtIvM65rI+lSSd/GZ/4vSVWFaJ9cuKJyHKe+/MzMOgK9gCnAFUWW53sktSq2DBmMBU4DHs2S1hm4AOgNrA/0Af6WSL8BGGhmqwDbAIdK+jmAmb1oZh1TG/BTYD7wRDYhJA0C7gTOiPVuDLyVyPIecDzwdpbLRwCDgQ2BdYHNgD/lvPMC4IrKcZwGYWaLgPuBQalzsZfwTuwFTMjSi9hO0v9iL2JC5td7zNNJ0nOSLlegu6RHYplvSLpA0kuJ/CbpBEmfA5/Hc9vEvHPi320S+b+UNCRxfI6k2+P+gFjeMElfS5ou6YxE3nZxmHKWpI+AH+Voo1vM7HFgXpa0O83sCTNbYGazgOuAbRPpn5rZd4lLqoG1a6hqGHB/Rv4kfwKuNbPHzWyZmc0ws3GJuq4ys2eARVmu/RlwuZnNNLNpwOXAkTXfdeFwReU4ToOQ1B44EHg1cfo74HCgC7AHcJykvWP+1YHHCT2wHsAmwLsZZXYHngFeNrOTLPh6uyqW25PwQh6WRZy9gS2BQZK6EXowlwPdgUuAR2PZdWU7YD1gZ+AsSevH82cDa8XtJzXIUl92AMYkT0gaIWk+MBHoQOgVkZGnA7AfcEstZW8V834gaZKk22M71RVl7PeV1DmP6+uFKyrHcerLQ5JmA3OAXUgMV5nZaDP7wMyqzex94C7g/2LyIcDTZnaXmS2NX/VJRdUbeB64z8z+BCCpJbAvcHbseXxE9hfyhfGLfyFBQX5uZrfF3sNdwCeEnkFdOdfMFprZe4RhsY3j+QOAP8e6JhCUYYORtAtB6Z2VPG9mFwGdCMNttxHaPJOfA9MJbVcTfYHDCG25DtCOug/ZPgGcLKmHpJ7ASfF8+zpeX29cUTmOU1/2NrMuQFvgROD5+AJD0pZx2G6apDnAscCq8bp+wLisJQb2ILxAr0mc6wG0AiYkziX3s53rDXyVkf4VwQZUVyYn9hcAHRNlJ+vKrCdvJG1F6CntZ2afZaZb4B1gIXBuliKGAbda7Z7GFwI3mdlnZjYf+Auwex1F/DPwDqH3+z/gIWApwT7ZqLiichynQZjZcjN7AFhOGCqD8MJ9GOhnZp0JSic1bDSBMGRWE9cRvt4fi8NZANOAZYQeQYpsswyTL+lvgdUz0vsD38T970jvDfSsRaZMJmXU3z+Pa1dC0qaE9joy2ohqoxUZ7RdnXO4I3Jrj2vdJb6M6h8+IPcsTzayPma0JzADeMrPqupZRX1xROY7TIOJEh72ArsDH8XQnYKaZLZK0BWG4L8UdwBBJB0hqFSdJbJJR7InAp8AjktqZ2XLgAeAcSe0lDSTYwGrjMWBdSYfEeg4kTPj4b0x/FzhIUpWkwQT7Tl25F/ijpK6S+gK/ri1zrKMt4Z3bSlLbOJyJpA0JivnXZvZIxnUtJB0T61FsyxMI9rskhwH/S06MqIGbgCMkrRltiyNY0R5Iah3lFFAV5WwR0/pI6h3l2Ao4k2Cra3zMzDfffPMtrw34kjCMNJ8wk+1D4NBE+n6E4bB58UV4JXB7In174DVgLqGHNSyevxm4IO63IPQQniQML/YgTI6YC7wBXAw8kyjTgLUz5NyOMP16Tvy7XSJtzSjDfFZMurg9pg2I5bVK5B8NHB3320fZZgMfAb8HJtbSXjfH8pLbL2PaTYSZfPMT25hEGzwBzIznPwNOB5RR/ifAUVnqPTRVVuLcuYQe6jSCvatrxj1myrljTNshPvcFhI+IQ2u630JvigI4juOUFZIuBnqaWSFn3DkliA/9OY5TFkgaKOmHiSGwo4AHiy2X0/i4onKcMkPSjZKmSvqwhnTFRbJjJb0vabOmlrGR6ESwU30H3AP8A/hPUSVymgQf+nOcMkPSDgR7xa1mtmGW9N0Jxv3dCYtfLzOzLZtWSscpHN6jcpwyw8xeIBjXa2Iv4noaM3sV6CKpV9NI5ziFp9QcNzqO03D6kL4YdWI8Nykzo6ThwHCA7t27bz5gwICmkM9phrz11ltmZvXqHLmicpxmjJmNBEYCDB482N58880iS+RUKpIW1vdaH/pznMrjG9K9JvRlhTcGxyk7mkxRSTpK0iO5c5YPcdW2xZXphSz3WElPF7LMpqCx2sPJm4eBwxMeBOaY2UrDfo5TLtQ69BfdyqdoDywm+PMCOMbM7qhrRWZ2AyEAmOM4eRLd2iwk9JT+RvDrtqpC+POzgSoAM7uG4Dpod0KwvgXAEUUQ2XEKRq2KykLESCAEGSO4Dyn5L31JLS34BmvWpHx0WRM4jaxEJLUys2XFliMTMzs4R7oR/ME5TkXQoKG/GOXyqhiAa6Kkv0mqqiHv98NZiSGiYyWNU4jY+SdJ60l6XSEa5x2K4aQlDY2LF8+VNFPSF5L2T5R9d1zg+KSk74CtJXWTdKdCmIEvJJ0Wh0LaS5ovae3E9X0kLZTUNR7vExdKzpb0okL45trYWyFa6DRJf5akWM5ASaOjzNMk3SKpU6LeAZL+oxA9dLqkf2RpN0m6QiFkQicF55qXS5oR2+4kScsS+V+VdJ6k1whf070l9Zf0WJTjM0nDEvnvlvSnxPFQSWMTx5Ml/VbSh4nn0jqRfoakKfHL/he1NVKU7Zz4jOdLekDBIem98TfwanLYUNKGkp5ViKL6sWLgvcQzei9e97Wk0xNpHeJ9zYzP8LXEs50sabtE3oskXZ94Xssk/UrSBELPBEnbxzJmS3pb0raJ6wt5T3dL+qekUZLmSXpZIcggwAvx76exnu+vq6Gt14z5UttCSYtiWkuF/6Wv47O7Mfm7dJySI08nlEMyzv0VeJEQZ2Y1gqPIM2q4/lhCsDQIDiYNuI8Q32VTQlyTUQS3/N0IoaQPjPmHElz8Xwi0BoYQXsJrxPS7CetKtiQo3zYE78ap8tcGviA6USSEIDgzIdupwENxfyvCNN7NgZaEqbufkXBOmbgudR+jCJFM1wDGA7+I6QOBnaLMPQkRUC+KaVUET9MXEYZV2wHbJNuK0OO9FXgEaBvTfkMI4NaLELX0BWBZQqZXowzrxTpaERxvXhrbZXBsq20TbfenxPVDgbGJ48nAy/H59iAMJ6Wcae5NMNIPjO3879gefWv4Dbwa73lA4hl/Qgio14rgbeDqmHeV+BwOjc/hR1HutWP6zsAG8XlvFtOGxrSTCaHR28VyfwR0SNxP0jHpRcD1iedlwPWJZzKAEM5gSKxrd4Izz66NcE93A1Pj/VTFe7g547eWtW1z/O8qPpub4vHxUebVo0z/Ba7bfPPNzXEaC+A7q6dT2oZOpjiUEHFzuplNAS4guJuvKxeZ2XwLwcA+Ax4zs6/MbCbBY/KmibzLCNE2l1gYfnyadLf895vZa7ZimGtf4A+x/LHAPxOy3Qkkh08OYUVo52OAK83sLQtxdkYSXvCb13IfF5rZbDP7guAl+mAAM/vEzJ6NMk+OMqSinG5HeEmcbiFi6UIz+1+izDYERVsF7GNmi+L5A4BLzGySmc0gfCxkcr2ZfWpmSwnKc+NYz2Ize5MQGTWf53SpmU0xs2mEXkYqJMMBwHXxPueTPZhbNtm+TDzjj83seQtDbPez4pnvA3xoZnfE5/AGQWHvC2Bmz5jZGAsRZN8mfJik2nYpQamuZSGy6xtm9l0e93tW6pkQgtE9YGZPx7oeI3jL3rXQ9xS518zejs/uTla0dUM4ixDo79h4fCjwt/i/Nhc4I55znJKk3uuo4vBWT9IjW+YbPTMZGXJhluOOieNpiZd1qq7eiePkAseehK/fr2uQbRRwi6SNgUWEkMypGYmrAwdI+n3i2tbUfl+ZkT57A0jqDVwGbEPwU9aCFYsu+wFfWM32o/WBDsBmlm4nyYwsWpcop9PiSzcp48613E8mmVFOU5Fae5MeF6cuUU7r+sxXB3ZQCHWeohUwCyAOv/2FEF+oNUGx3xbz3UD4DdwvqSOhV3qm1c1uWW1m3yaOVwcOVmKomfDxkPztFeSeIjVFlK0XcYjwaGALM1scT2dGvv2K0Ht0nJKk3j2q2JWbTHoEzWT0zEKzqsLMp2RdyRdK0mnhZEJ8l/4Z+b8BiF+r9xN6PocADyZe5BMIX9RdElt7CxFMayIz0mdKrr8RHGhuaGarEF4YySinAxQnPGThXeA4YJSkNRPnJ5F/lNMekpIvopKMcprBBODJjOfQ0cx+E9PvJQyrpSLI3kxs29hzPMvMBhJi6OwPHBSvy3W/mc4vJxB6TEk5OpjZpY1wT7WRt1NOhYB81wH7Wvr09MzIt/0JCtXJBylsTqPT0KG/u4Czo/H4B4QhhNsbLlZWqoAzFSJQ7gTsQhh3X4n45fgg8JdoWF+LYLdIynYn4eV1MCuG/SCs0v+1pMEKdJS0p0I0zJr4g6TOkgYQIpPeE893IjgPnSupP3BK4pqXCEHlzleY4NFO0jYZ93EzYTj12YRR/V7gt5J6SuoO/K4WuSDYlD4ALpDURsGT9rBEW7wL/FRSF0l9yBGpNIN7gaMlrRt7LmflcW0uHgI2lXSgQnTU1pK2inWJ0NOYYSGC7DYEZQSApCGSBsWPgLmEYeNUz/VdQg+plcIao71yyHELsL+kneMkhHZxPx+FnvOecl0Yf9NzCMH+UveZmpS0VWZ+Sd0InsVPMbPXM5LvAn6nMMmmE+E3dmdmGY5TKjRUUZ1FGK8fQ3gBvEx2m0kh+JLwwpkM3AgcYWbja8l/TPz7FfAswUCeXPf1AsGg3Zlg7wLAzF4GTgKuJUTv/IzQ66rti/ZRwgSHNwl2pZQSOItgi5pDUJzfK9bYq9udYD+aSBim3Cez4Ggj+wdBWfUl2MD+R2j31wmG8MWZ1yWuN8JLfBCh7e4Bfm9mL8UsNxKU2dexrLtquc/Msh8kKPYXCRMIRtX12jqUPQv4CWEN0CRCL+ACoCre07HA3yXNA04jtHuKPoSXdCry7GOs+Hg4HdiI8Gz/SJjAUJsc4wk2pHOB6YTf08nU43+ntnuqYxFnAffF2Yd7Enqzswi/hUy2ICi1qxMz/6bHtKsJ4TL+B4wjTOg4JUsZjlMSlEWYD0lDCRMc1s6ZuZkhaR/CpJT1ii2L07RIOhroY2Z1mcSSE/f1lyepYb8yeIeWApIWmFmH+lzrTmnLjDhUszVhEkMf4E94lNNmiZldX2wZHKcpcKe05UcLwtqfOYShv7cJw0eO4zgVSVn0qMzsCcKi3WaPmc0hLAh1HMdpFniPynEcxylpXFHVEQW/fKbofzBL+peShhS4zh0VfOiVHY3RHrXUdY2kM5uirix1mxJ+I5urDI7TmJTF0J/j1IaZHZs7V8ORNBq43ScxOE7T4j2qZoKklsWWoSZKWTbHcYpPSSoqSSMUQljMk/RRXCtUU952CuEzUmETTksOl0laXyHUxmxJY+JCyVRaZ0m3KoTg+Eoh1EiLmNZS0t8Vwm+MB/aog+g/ivLOknRTyuWTpK6S/hvrmRX3k6EfusX838b0h2q415Ni+X3j8WkKIVa+lXR0cghI0s2SrlYI7/Ed8OMc93uOpNsTdaUNdcY2PF8h9MQ8hZAqqybyHxbLnCHpjNoaqQbZ2sT2ToWeuEYJt091uNcLEnl/pRAWZqakhxV8LqbSUuFlPo+/iauk3H5wJP0Z2B64UmHx7JWJ5CE1lSfpyPi7nKUQvmP1RFqdZYm/x9O14v/iLUkruc/K8YzXlvS8QriW6ZLuSVw3MFcbOCsYMOLRYovQvLB6ul1vzI3gSaE3QZEeSPDP1quGvBcBzwNdCT7w3gcm2opQGmMJ3ghaE0JuzAPWi+m3EjwYdCKEafgMOMpWhNr4hLD6vxvwHME7xUrhPmL+LwleEFL5XwYuiGndCd4N2se67iOGFYnpjxI8J3SNMv9fPL9j4l7OIkxF72ErwnFMJoS6aE/whmGsCBlxM2EK+7axHdvmuN9zCMNaKZkGJO8XGE3wYrAuwYHpaFaELBlEcBW1A8E57CUELyJDamirbLJdSgih3i3K9wjBK31d7zXV1jsRPEhsFmW5AnghUbcRPHB0Ifi4m0YMD1KH3+VoQvBQ6lIewT3TWIKD4VaENW//q48swO8JrrDWI/g03Bjonign1Ra1PeO7CG7OUm2+XTzfAZjgYT7qzup/+K9ZWOpbbFHKBhoQ5qPoSqlOQgb3THvVkDYe+Eni+GhWvNy3jy+4Fon0uwgv5ZbAEmBQIu0YYHTcfxY4NpG2K7kVVTL/7sC4GvJuAsyK+70Ifui6Zsm3I8F57CUE34CdE2k3El/k8XhtVn5535pIz3W/55BbUSXjVh0PPBH3zwLuTqR1iHXVpqiSsonwMbJW4tzWBO/ydb3XlKK6AfhrIm9HQtiPAbbipZ6MR3UvMKKOv8PRZFdUWcsDHicqiXjcguARffV8ZQE+peb/AYttkusZ30pwedU34/oDgRddUdUdV1T5QxHjUTUKkg6X9G4cDpkNbMiK0BKZ1Bb2ojcwwdJDaaTCfaxK6L3UFKYks9y6hLCoKdxHe0nXxqGYuQQ/g10UbDP9gJkW/MBlowsheOOFFtZQpd1bDXVnO5frfutCTSEo0mSxEPtpRo6ykrL1IPSU3ko88yfi+ZXKJ/u9pkgLYWEhTtYM0u+zoKE0ailvdeCyxD3NJCjl+sjSj9CjrY1cz/i0WP/rCsPgRybk3DJH2Y5TNEpOUcUx/OsIXsi7m1kXwpBaTXaE2sJefAv0U3oojVSIi+mEL+2awpTUJ4RFTeE+TiUM2WxpIdzHDvG8CC/dbpK61FDmLOCnwE1KhEAn/3Afue63YOE+FDzNd89xTaZsC4ENbEX4i85mlnpp1+VeU6SFsJDUIcpSiPAz+Tp1mwAcY+lhPdpZeoDMfMpaK0eeWp+xmU02s1+ZWW9CT+tf0c43gTB87jglSckpKsKwkRHG65F0BKFHVRP3An9UmLDQh6DgUrxG+Eo9TSGswo7AzwjDVMvjtX+W1CkqyFNY4fn8XuAkSX0ldQVG1EH2E2L+bgRbQDLcx0Jgdkw7O3WBhThBjxNeGl2jnDskCzWz0YQIrA9I2iIh3xEKk0XaA7WuI6rD/b5LCOrXX1JngmfxunI/IVTIdpJaA+eRx28r9nivAy5VCBeDpD6SfhKz5HOvd8W8m0hqQwiu+JqZfZlLDq2YQDKghixTSITZqAPXEH6bG8TyOys9AGM+XE8ICbOOAj9UCPPyPbmesaT9tWISzyzC/1k1wU6WM9SI4xSLklNUZvYRIazFK4QXw0aEiQk1cR4hTMYXhHAd9xPDXpjZEoJi2o3wtfkv4HAz+yRe+2tCT2I8wQZ0J8EeAuHFOYoQvuNtQliEXNxJCEU+njBMk5qJ9k/CBITpwKuEYa0khxG+hD8BpgIrBdIzs6eAI4FHJG1mZo8DlxMmeYyN5UItIT9qu99Y/j2EyShvEV5edcLMxgAnxPImEV6C+S5U/gPxPuLw6NOEXij53KuZPU1QZP+OsqzFiqCJuehHGCqrqfd1GbBfnMF3ea7CLIRBuRi4O97Th4TfYn24hKCEniTE2LqB7FF5a/tN/wh4TdJ8wsSVk81svJnNI9hgHackKYswH/kg6TjgIDP7v2LL0pRIWp/wImxj6aHrK47GuldJfwKmmdm1hSqznPAwH3VnwIhH+fLin4aDCnuHNhZqQJiPkutR5YukXpK2ldRC0noEe1CzCHshaR+F9UddCV/uj1SqkmqKezWzC5qrknKcUqbsFRVhfdS1hPVRzxLWkPyrqBI1HccQhgrHAcuB44orTqPSnO7VcZwEZe/rz8y+ovbJFhWLmQ0ttgxNRXO6V8dx0qmEHpXjOI5TwZR9j6qpaa021pZ62QMdp07MY9Z0M+uRO6fjNA9cUeVJWzqwpXZecSLTh6gyOqnVyzPSM/LXNmMol6/UzGtzlZ3b92pG/ox7SXPwkWf9+dadWXaLDAfruWTJRUPkyffa2srKUt7T1ffVxQuK4zQbfOjPcSqA6F39HUn/jcdrSHpNwYv8PXEhtuOUJa6oCo1Vp29S+pZJbekr3F5m7zHkKnsl2XKUl+/1+dxbQ8ls11yy5Noyr8+11XYvua5tGk4GPk4cXwxcamZrExZgH9VUgjhOoXFF5ThlTnSLtAfBzRIxptVOBC8tALcAexdHOsdpOK6oHKf8+SfBM3rKcNcdmJ1YED2R/LzkO05J4YrKccoYST8FpprZW/W8frikNyW9OW3atAJL5ziFwWf91YeknSLfmXUNsVk01N6Rr60o14zFXLMCayPXrD5ylFUIu1dt5WXKV9usv8Z85rnZFthT0u6EqL2rEJzndpHUKvaq+lKDo10zG0kIpsjgwYPdaZ1TkniPynHKEElDJX0K7A9caWYDCF7inzWzQwke5t+T9A7BE/7YognrOA3EFZXjlBkxMvRVhJAhg4CDJQ3KyDaPENutE/AGYbKF45Qlrqgcp/zYAhgbY0ktAe4G9jKz0WYWY08wF7g6Tk8/lxXRph2n7HAbVaHJZbNqiIeFQttlcpHT9pKHTSqTlWxS2covgMmkrm2Wj62x0B5BMm19uelDCB+fYiKwZUaec4AnJf2a0LMakrVqaTgwHGDzzTfPVw7HaRK8R+WUBtXL07dCTUAo3gLcYnMwcLOZ9QV2B26TVtaIZjbSzAab2eAml9Bx6ogrKqe4pBRTU1L+yuoboF/iONusvqMIoesxs1cIMwJXbRLpHKfAuKJympZUr6YYCqpyeANYJ/rza02Y7fdwRp6vgZ0BJK1PUFS+UMopS9xG1dTksus0pR0q33VQuWwptV1f/r2YFeRcT5ahgHPde2b+HJjZMkknAqOAlsCNZjZG0nnAm2b2MHAqcJ2k3wIG/NKskh6C05xwReU0LuX6bkw5oi1RzOwx4LGMc2cl9j8iLAZ2nLLHFZXTOJSrgkqSuocSVliO0xxwG5VTeCpBSSWptPtxnDLDe1QNpdBf27X5lGtoxN5MMiczZK5tykzPtKXkE6243Kmtd9WQ9WTZyqzgZnSc+uA9KqfhNKf1Sc3lPh2nhPAelVN/mutL221XjtOkeI/KcepLc1XUjtPEeI+qPjTkBdXYdqeGyJJJNn98vkg3nfpMY/eemOPkhfeonLrjSio73rNynEbFe1ROblxB5abEFwg7Tjnjiqo+NOSFVMhhw1xl5z19PGOatVq4ksqHlLLK6WKpgdPZHaeZ4UN/TnZSjmOd/PBhQMcpOK6onHSa05qoxsLbz3EKiisqZwX+gnUcpwRxG1WhyWUnysfOVOhpzzWlu4IqPGltmsMm5e3vOLXiParmjr8kHccpcSpKUUlqK+l1Se9JGiPp3Hh+DUmvSRor6Z4YFRVJbeLx2Jg+oJjyNylui3Icp0yoKEUFLAZ2MrONgU2AoZK2Ai4GLjWztYFZwFEx/1HArHj+0piv8nEF1bR4eztOg6goRWWB+fGwKm4G7ATcH8/fAuwd9/eKx8T0naVGXrWZ6snU1KNJrcMphBhqkb55L6p4JJ/DSmkq7HN3nAqjohQVgKSWkt4FpgJPAeOA2Wa2LGaZCPSJ+32ACQAxfQ7QPUuZwyW9KenNpSxu7FsoPNXLfU1UsfH2d5x6U3GKysyWm9kmQF9gC2BgAcocaWaDzWxwFW0aLGOT4i9Ix3HKnIpTVCnMbDbwHLA10EVSaip+X+CbuP8N0A8gpncGZjSxqI2De5YoPfx5OE69qChFJamHpC5xvx2wC/AxQWHtF7MNA/4T9x+Ox8T0Z83yNOJk2pxy2RtypWeWV5s9qzaZnNLE/fw5Tt5U2oLfXsAtkloSlPC9ZvZfSR8Bd0u6AHgHuCHmvwG4TdJYYCZwUDGELhiuoEof97LuOHlTUYrKzN4HNs1yfjzBXpV5fhGwfxOI1vi4knIcp0KpqKG/ZolPOS8//Hk5Tl5UVI+qKOQ7jJPPSyrf+FMVTstWLem/fh969FuVbj27IMHSxcuYNWU2X3/yLdMmTC+2iHWnIT4dHaeZ4YqqHGlGCmqV7p3Y+dDt2fpng1l/q3Vp26Hm5QFzZ87nrVHv8sojb/LSg6+zdPHSJpTUcZzGwhVVOdGMFFTvtXpy6J/25ccHb0dV6xU/02/GTmbSF1OZOXkO1dXVtG5Txap9utF/vV50+UFnfnzwdvz44O2YNWU2D189igcufZQF8xYW8U4cx2korqjKgWakoDqvugp/fvSPrLv5WqiFWL68mtdGvcczd7zEu89/xJxpc7NeZ2b0Xms1ttxtE4Ycsj3rbDqAYeccyB6/2oWrT7mZF+57pYnvxHGcQuGKqtAUMh5VtuMKZvCuG3PytcfQc/UeALzz4if887e3MeXrGd+3gzq0D5mrM9pl2TImTZjFQyOf46GRz7HxtutwxDn7s/4Wa3PmPafw+E+e5Yrjr2PpkmWUHM3oGTtOfXBFVco0kxdYlx905rhLfslOh2wHwDfjpnDHPx7j2ftfq3eZ773wCb/d+QJ2P3JHhl94MLsduRP91+vN6XtcyIK5CwokefGR1BZ4AWhD+H++38zOlrQGcDfBd+VbwGFmtqR4kjpO/fHp6U7RkMRuR+3EjR9fxk6HbMeiBYu5/uz7Gb71WQ1SUinMjEdveI5Td/kzUydMZ4NtB/Lnx06nbfsy89dYO/mGtnGcssMVlVMU+k/9m3wAACAASURBVK3Xm78/ew6nXHccnbp24M1nPuSYbc7m/iueYPmywvrEG/veV5w65AKmTZzBhtusxx9u/XVByy8m9Qht4zhlhw/9FZp818Qk4xM1A6elVa1bcdAf9+HgET+nqk0rZk2bx8jzHmT0Y+8DoK5dALCqjJ9mq5bpx8vTfea1WLAo7dgWpA/vTf12NiP2/BuXPXsW2/18S3567K7895onC3BHDURq8BBvdBn2FrA2cBW1h7bJvHY4MBygf//+DZLDcRoL71GVCs1ASW20/fpc8+7fOfzsA6hq04on7nqF4Tv9hdEPvdUk9U/8fDKXn3wzAMf8/XC69+7WJPXWSj2VlKShkj6Nfip/ny20jaQDop/Lp2NalupXhLDp0aNHvWRxnMbGFVWxaQZBDTt17chvRx7DJc+fR/+BfZjw+WRO2/9yLjvtbubPbtqJDc8/8DovPvQGbdu3Ydi5BzRp3YUi9qCuAnYDBgEHSxqUEdqmG/BHYFvglwRnzI5TlriichqVHx+0LTd8dCm7Hz2EJYuXcvtfH+H4Hc/ng1fHFU2mG8+5n2VLl7HrL3/MD/qvWjQ5GsAWwNjobLkz8BCwV0Zom6nA62Y2ixDK5r5iCes4DcVtVMWkgqef9xzwA07616/40dBNAPjgjS+4/OwHmDB+GnTqRHWHtmn5l3ZLP17cJf2nubR9+jdV6/npNqp2k9NtVFVTMn7a1XO+3500YRYvPvgGPz5ga3YdtiO3n38/RSXTrpn7Z9EHmBD3exEUUUfgUFaEtjkJ2FPS4cAC4NHsVa+wUW2++eb1Et9xGhvvURWLClVSLVu1ZP/f7cl1H17Kj4ZuwrzZC/jn7+7ktMNHBiVVIoy69QUAdjl8x+IK0kBiaJszgbvNbEMzOy8mLQFeBVYBBgP/SgUVzbj+extVkwntOHniPapiUKFKat3Ba3HKyGNZa5MBAIx+6C2uPfvfzJ4+D+vUobjCZfDeCx8zf/Z39F5rNXr07c60iTOKLVI+fAP0Sxz3jeeSTAReM7OlwBeSPgPWAd5oGhEdp3B4j6qpqUAl1a5jW46/7AiuePUvrLXJACZ/NZ0zDryci0+4mdnT5xVbvKxUVxtjXv0cgA23X7/I0uTNG8A6ktaQ1JoQmfrhjDwPATsCSFoVWBcY35RCOk6h8B5VU1KBSmrrPQdz4hVH8YN+q7J82XLuu/457rj8KRYvXEL1aiumfy/p1i7tuu96V6Udz109/ZtpYb90n3xqtzjtuM0X6Tatbq3SjzvPTbdZMXflb7LxH3zNlkM3oe+6vbLcWeliZssknQiMAloCN5rZGEnnAW+a2cMxbdc4PX05YQp7WXUbHSeFKyqnXnTv3Y0TLz+S7X6+JQCfvvMll5/5AOM//rbIktWd6d/OAiiN9VR5YmaPAY9lnDsrsW/AKXFznLLGFVVTUSG9qRYtWvDTY3fhyL8cQodV2rNg/iJuufgR/nvTC1S3KS8fevNmfQdAx87tiyyJ4zi14YqqKagQJbXGRv357bXHsP5W6wLwyqj3+dcZ9zL929lFlqx+VEU3TSUZ+sNxnO9xRdVQlGH7sOrs+cqYNu1ac+iZ+7H/qT+jVVUrpk+ezdVnP8DLL8dFu906A7C0e/rMvu/6rOhhzeuf3k7z10kPE7/umhPTjjfpln789sx+acdffZvuEahFpq6pw8dBu07BrrV4YZGjX1TIh4zjNBauqBqbMn8JbTbkh5x89a/ovVZPqqurefiWF7nlr4+yYP5i6FTeQ2Z91u4JwKRxk4ssieM4teGKyslK51VX4dhLhjHkFzsA8MVHE7n89Pv55J2viixZ4Vhjg9Ar+/rjzCVIjuOUEq6oGpMy7U395Jc7Mvzvw1ilW0cWL1zCHX9/lH9f/RTVVeU1WaI22nZow6Ct1qG6upqPXvms2OI4jlMLrqgaSk02qTJUUn3W6cVvbzyRjbcNkyXefvFTrjzrASZ9PQPatWd5905p+Rf2TB/6m71O+s9p7norDEfrrTshLW2HVcemHa/ZZmra8Utz1007Hju+Z9px94ylq+2mpK+bUmZ8qmXpRqzBu29M6zZVjPnfp8yZPpeikr+vP8dpVriicmhV1YoD/7AXh56xL1VtqpgzYx7Xnv0Azz3+QbFFazT2OnYXAJ6/939FlsRxnFy4omoMyqg3tcG2A/ntdcey+sAQAPbJu1/h+vMfCmuM2rXNcXV5sv6P1uSH2w3kuzkLGHXTc8UWx3GcHLiiaqZ07NKBoy/+BXv8aggQo9+OuIcPXvm8yJI1Li1aiOMvPhSA/1z1BAvmLSyyRI7j5MIVVX1Irp0qw3VT/3fANhz/zyPo1rMLS5cs475/Pc3dl49iSbt20HWV7/Nlroua3y+9hzVzULptpfdW6bPnzh/w1Pf7A1unh/h4Y1H/tOObJm6bdvz5x33Sjru/l74Oq/O49LVPraalO7+179IVkC0NNqp9T9mDdTZZnSlfTeOuvzxA0ZFWXovnOE4aFaWoJPUDbgVWI5ikR5rZZZK6AfcAA4AvgQPMbJYkAZcBuxOCy/3SzN5ukBAlPOy32uo9+PWVR7PlHpsBMOb1cVx+2t18/XlcR9SulosrgMG7bMQRZ+8LwOXHX8eiBYtzXOE4TilQUYoKWAacamZvS+oEvCXpKeCXwDNmdpGkEcAI4A/AboQYPesAWwJXx78VRVWbKob/9RcMPXJn2nZow/w5C7jhnH8z6r43sBJWrIVk4x3W50+3nkCLFi245Zx7eP3xd4otkuM4daSiFJWZTQImxf15kj4mhO3eixibB7gFGE1QVHsBt0ZP069K6iKpVyynIui/fl+uev1C2sbQ788/+AbXnH4Ps6bORW0rZ11Ubey4z2BO+edhtG5bxZO3jOaO8/9dbJEcx8mDilJUSSQNADYFXgNWSyifyYShQQhKLLnAZ2I8l6aoJA0HhgO0pX26XSppX6heXjD5C8HWew7mD7eeRNsObVm+bDnXn/cgD10/GgC1aY0l7FEAi3qnr5Oas2brtOPZA9N7Xxttnr6Y6a8D0m0+61atsHH9c9YGaWkjP94u7dg+SJelx/j0ulb5It3mVDUlfe2T5i9IL2/pErqttgoXPnjq9zMaH756FFeeeEPp9SLL0M7pOE1JRSoqSR2BfwO/MbO5SiyoNDOTlNebysxGAiMBVlG3EnvLZWfIL3bgdzceT8tWLXn5v29z1e/vYNac5mOT2Xr3Tfj9NUfTvmNbqpdXc/kJ1/HoyKeLLVY6mQt9HcfJSsUpKklVBCV1h5mlPvGnpIb0JPUCUm4QvgGSbrn7xnNlzbZ7b8Hvbw72mNsvfpjbL/wPAGpf4bMlgFV7deG48/djm902BmD+rO/4+9H/4uUHXy+yZI7j1JeKUlRxFt8NwMdmdkki6WFgGHBR/PufxPkTJd1NmEQxp072qeTQkZXWcN+ADfrxh1t/HSYNXPgf7rr0cWgdwr7bKh3T8mYO9c3YKN1mNW/TdDdE+2zwbtrx/l3fSDt+deHqaccjvtr0+/13PlwjLa3Lh+k/vc5fpYf9aPtt+lBei3npx8yZn3ao5UvZ48gd+eWZP6dDp3YsmLeQG8+4k0f+9STV1SU4tOa9KcepMxWlqIBtgcOADySl3qqnExTUvZKOAr4CDohpjxGmpo8lTE8/omnFLSwtWrZgxO0n0a5jW565+39BSTUD1hjUh5P/fjADN18TgJcefJ2rTrqB6d/MLLJkjuMUgopSVGb2ElDTp+rOWfIbcEKjCtWE7HPS7qy18QAmfTGVy066GajshaRt2lVxyKm7s99xQ2jZqiXTJs7gqpNu5OWHfJjPcSqJilJUzZm2HdryizP3A+Cq393O4oVLUIX66gPY7P/W58S/HkTvAT2orq7moSsf56Yz7ioPl0g+7Oc4eeGKqj5ke9EUecrzT47YkY5dOjDmlc9585kxqGVLVFWVlmd55/SwHPP6p08/T4blABiy3qdpx5t1TA+aePuMbdKOnxq/Xtpxy/dX2MR6jk+3E3WcmDHdfMZ3acfKsEnZojBjsfOqHTnm3P3Yab8tABj33pf885hr+eT19LAhjuNUDq6oKoQ9fhXCVjxw9VM5cpYvux68Nb86++d06tqBxQuXcNu593L/Jf9l+bLSmtBSK96bcpy8cUVVCIrcm+o54AessVF/vpuzgNcefzf3BWVGnzV7cNIF+/HDGNDxzVHvctnx1zH5i6k5rnQcpxJwRVUBDB66CQBvP/cRy5aWUe8iB1WtW7L/sTtz0Im7UNWmFbOmzuGaU27m2TtfKrZo9cN7U45TL1xR1YcSc5u0xkYhZMZHb4yDFomXYcuWafmWt8k8rr3c1yalh+J4btw6acctvkxfQLzKF+nXd5qwYm1Umym1r4tSRliOQZv15+R//IL+6/YC4PEbn+W6025j3sz09VNlSWYP3BWY49SKK6oKoN96wZfd1599W2RJGk7Hzu048oy92e3QMFHj60++4bLjRvL+8x8VWbIG4sqoJBkw4tHv97+8aI9GKbvQ5TZHXFFVAF16BIeuMyfNKbIkDeP/9tyMY87bl649VmHpkmXcc/FD3PmXB1i6eGnuix3HqVhcUVUAVW3CY1y6pDxf6Kv17cqJZwzjRzsHD+vvv/ARlx07kq8/KXu3iwHvTTlOg3BFVR+Sdimp6LP+qpeHNUotW7aE6oQsy9PtZ63mpXtP7zgpfR0VZNiwPu2adtx1Tvp9dpiSvu6q9cyM8PAzV6yN0qL0um3BIlq0bME+w3fisNN+Stv2rZk3az7X/eF2nrjh2dILxVFfsikpV1yOkxeuqCqAGZNm03/9vnRbrTNffVwevZB1N1mdk/5+CGtvFJzXP3f3y1z925uZNWV2kSUrIK6QHKcguKKqAKZNmA5ArzV68M7o4sqSi3Yd2nD4qbvxs8O3o2XLFkz+ciqXH38dbzxRYeu/XEk5TsGobK+lzYTP3hwHwAZbrZMjZ3HZcsgGXPvkaex9xA5gxr1/f5hfbXhK5SmpJkRSP0nPSfpI0hhJJ8fz3SQ9Jenz+LdrrrIcp1TxHlUhKLKd6oMXPwZg4+0HourlVKfsVBl2oRaz09cgdfgy/au/7ZR034CZtFyYPllDC9LL18IMO9SSYLPqtlpnjv/rL9juZ5sB8OkbY7l0+LWMe+/LWusra/L5PTSs97UMONXM3pbUCXhL0lPAL4FnzOwiSSOAEcAfGlKR4xQLV1QVwBcffM234ybTe62ebLLjBrz97IfFFgkASexx+HYcccZe3wczvPnMu/nPlU+UZjDDMiQG+pwU9+dJ+hjoA+wF7Biz3QKMxhWVU6a4oqoAzIxRNz/HEecfzM9+tVNJKKoB6/XipL/sx/qDQzDD//3nDa486cbv7WlOw5A0FLiMMFXz+thzGgBsCrwGrGZmkyTtC9wPZHXpIWk4MBygf//+2bI4DSS5qDiFLwLOD7dRVQhP3PAsixYsZpufbc7AH61VNDlat6li2O9354pHT2X9wWsy49uZnLvf3zl7n7+6kioQkloCVwG7AYOAgyUNBv4N/MbM5sZ8nYCTCYor61ikmY00s8FmNrhHjx5NIr/j5Iv3qOpDCc7omjl5Ng/881EOOf3nHPe3Q/ntj8+jekn6uibmpn9Ut1icnt6iVY6fQ8a6LMsIr7HJNmvx638cRu81f0B1dTUPXz2KG/54Jwvmpvv1q3hy/T4abs/cAhhrZuNDdboXuBO4xsweiHmmAP8ALgbOAGY2tFLHKRbeoyoUJaC87rn4IaZ+PZ2Bg9di2Fn7Nlm9nbt35HdXDOPCB0+l95o/4IsPvuY3253JFSdc3/yUVNPQB5gAIEmEntUCM7skkedVYGszexToCTyfrSBJwyW9KenNRpbZceqNK6oKYsG8hfzl0MtYvryag36/J0MO2bbR69zlwK247qWzGHLAlixeuIQbz7iT4zY/jY9f/azR63YA2DZufSW9G7c9gLWAuZI+B7oSJlSsRHLor+lEdpz88KG/CmPMy59w7e9u4fhLj+CUfx3F8mXVPHfvKwWvp/caPfj1RQeyyXYh/PzbT7/PZcddx7fjJhe8LmclvgH6AZjZS5JOj/sXAkjqDAxkxQSKdsDtkvY0M+85OWWHK6oK5MHLHqNjlw4cfvYBjLjhGAas14ubz74XW8nGlO6rj4wp48qIZ2VmtG7Tiv1O2o2Df/dTWretYva0uVz7u1t4+rYXGuVeSoqahndz2ZwKH3/qDWAdSWsQlNZBwCErqrM5wKorqtNo4HeupJxyxRVVhXLbufcxb+Z8jv3HMA46bU82H7IRl598E5+99UXui2vg58fvyhFn70vrtmFh8JM3j+ba39/K3BnzCiV26VICNsgUZrZM0onAKML09BvNbIyk84A3zezh4kroOIXFFVUhKQFP6kkeuuJxvvjga067+UTW2WwNrnjxPF559G0evHIU77/wcfb5yhm0qmrJlkM3Zs/hO7Px9gMBWLJoCWfscSHvPlf89VpNQgkpqRRm9hjwWMa5s2rIu2NTyOQ4jYUrqgrnvdFjOGrQb/jFWfuxz0m7s/Uem7H1Hpsxc8ps3njyAz5790smfDqJ2dPnsXTRElq3qaJ7ry70WbsnG227HhvvMJDO3TsBMHfmfN5+6j0uPWZk85nNV4JKyike2RbvOo2PK6r6kOw1Zb7ISqxXBbBowWKuH3EH9//jEX567K4MPXInVlu9Bz85bHt+ctj2Oa//4oOveeKmZ3ny5tHMn/1dzvwVQeZzre2Z5lJmLdJtfWnxzOpyveM0c1xRNSNmT5vL7effz+3n38+ADfqx+a4bM2DDfvRbrw8dOrenqk0Vy5cuY/o3M5k6YTofvfIZH774MRM+/bbYojcdrjQcp+RwRdVM+XLMBL4cM6HYYpQOrqAcp2TxBb+Ngb/0yovMoTnHcUoK71HVh6QiUoauNw9fUTaknqNV517rVNvHR65rM38T/iHTKGROdMjXQ3nq+vpc11R1NVY5pU7F9agk3ShpqqQPE+eyRjtV4HJJYyW9L2mzAgpSsKKcAiP583GcMqLiFBVwMzA049wIQrTTdYBn4jEEZ57rxG04cHUTyegUC1dQjlN2VJyiMrMXWDmkwV6scMp5C7B34vytFngV6CKpV8GE8Zdi6eC9KMcpW5qLjWq1GLIbYDKwWtz/PlxCZGI8NylxLi0KalvaZ9gk3CZV8tRFQa1kk6rF9pivb79863YKTj4LdTPtPnW5NpmnPvYijwJcOxXXo8qFmRk1RDut5ZrvQyFU0Sa/Cn1GWfHwXpTjVATNRVFNSQ3pxb9T4/nvwyVE+sZzTrnjCspxKobmoqgeBobF/WHAfxLnD4+z/7YC5iSGCAuH96qaDu9FOU7FUXE2Kkl3ATsCq0qaCJwNXATcK+ko4CvggJj9MWB3YCywADiiTpUkFU8uv22Z6U7jkI+NKRuZdiXL47nl4xewPvkdp5lTcYrKzA6uIWnnLHkNOKFxJXIanRYtfaF1M6G5LHB10qk4ReU0I3xI1XGaBc3FRlU6+Mu1MHg7Ok6zwXtU9SE5zJTL3uA2q8KSas+c7djAocCGTMjIFX8qp2/A+lftOJWIKyqnfPDZfE4eFCsar0cBLjyuqJzSxxWU4zRr3EZVbPwlXDvePo7T7PEeVX3IZ91Lof3CNTdS7ZNLYeWr0HLaiXKk11p2nvGnMtd8OY6Thv+HOI7jOCWN96gcx3Gy4JMiSgdXVIUm1xBSrqnLzZWGuhXKd6iuIen5Dhvmws1wjlMrPvTnOI7jlDSuqBzHcZySxof+nKYlNfTpQ56OUyu12ciam1NeV1T1oUH2izynLtdWdjmRus/U/Rd6unlD11vlY+MqdJgO9/zuOLXiisppXHzBruM4DcQVVTnzfS+lBHtarqAcxykQrqgqgVJSWK6gHKfO+FqtuuGKqj4kFUKhX8y1lZ25BiuXvaupFVdD2iLftUn5rkdraNs1xGblyttxGoRPT69kpOxbscpxCo6kGyVNlfRh4lw3SU9J+jz+7VpMGR2nobiiao7UpHhcIZUNkoZK+hTYFbg7I3kEsBhYCmwIvCNp9SYW0XEKhisqxykzJLUErgJ2A9YEhgBtEln2Am4CBgObAW2BvzaxmI5TMNxGVWhy9UBy2S+StpRMO0qprbfJJ3xFpg0p89p811XlKi+znVdqywb4Eswlay57WG1l140tgLFmNj6Io0eAYYn01czs3zFtIdAB6JutIEnDgeEA/fv3z1eOopGahNDcFr42V7xH5TjlRx9gQuJ4MlCVLaOZWUx7PFehPXr0KIhwjlNoXFE5TuUxRVIvAEknAgb8LVtGMxtpZoPNbHBTCug4+eBDf45TfnwD9Esc9yRMnEjxMDBM0pvAWcANZra4CeVznILiiqqhNDSk+Ur2iVrsGQ2tKzPkeS47TyaZ1+e0vSTSG7rWKNc6qnztdw2513z9OWaS8/raLwfeANaRtAZwEfDzUIwmAmfHc48B58W8Z+Us0SkrMhcKV7rNzof+HKfMMLNlwInAKMLMvnPMrAq4EZhmZjOAecAswkSKZyU9XCx5HaeheI/KccoQM3uM0GtKnjsrsT+kyYVynEbCe1SO4zhOSeM9qvpQSJ92+aTnu35nJf93ecbCysd+li1/Pv7x8qWh67LytTOVgsNfx2mmeI+KFe5oJI2VNKLY8jiO4zSUASMerRjv7M1eUWW4oxkEHCxpUHGlchzHcVI0e0VFwh2NmS0hOPjcq8gyOY7jOBG3Ua3sjmYisGUyQ9IfGjD/6er7ZgDTm0a8BHUzk6xKTbI11MyS7/Ur569ZtobS8Hurv2yFb1f3dO44CVxR1QEzGwmMTB1LerNUXc64bPWjlGWrdOqyWLUmW0ul2GCKTakvGPahv5Xd0fSN5xzHcZwSwBVVwh2NpNbAQQRfaY7jOE4J0OyH/sxsWfQwPQpoCdxoZmNyXDYyR3oxcdnqRynL5jjNmmavqCC7O5oc+Uv2peay1Y9Sls1xmjuuqBzHKSlK3bBfriQnntTUtnXJUwzcRuU4juOUNK6o8qDYrpYk3ShpqqQPE+e6SXpK0ufxb9d4XpIuj7K+L2mzRpatn6TnJH0kaYykk0tFPkltJb0u6b0o27nx/BqSXosy3BMn0yCpTTweG9MHNJZsjuPkxhVVHSkRV0s3A0Mzzo0AnjGzdYBn4jEEOdeJ23Dg6kaWbRlwqpkNArYCTojtUwryLQZ2MrONgU2AoZK2Ai4GLjWztQmxm46K+Y8CZsXzl8Z8juMUCbdR1Z3vXS0BSEq5WvqoqQQwsxeyfN3vBewY928BRgN/iOdvNTMDXpXURVIvM5vUSLJNAibF/XmSPiZ4/Si6fLGO+fGwKm4G7AQckpDtHILC3CvuA9wPXClJsRynifDFvPmTrc0qoR29R1V3srla6lMkWZKslni5TwZWi/tFkzcq002B10pFPkktJb0LTAWeAsYBs2O03Mz6v5ctps8BujeWbI7j1I4rqgoifvEX9atfUkfg38BvzGxuMq2Y8pnZcjPbhOB5ZAtgYDHkcBwnf1xR1Z1SdbU0RVIvgPh3ajzf5PJKqiIoqTvM7IFSkw/AzGYDzwFbA10kpYa/k/V/L1tM7wzMaGzZHMfJjiuqulOqrpYeBobF/WHAfxLnD4+z67YC5jSWfQrCLD7gBuBjM7uklOST1ENSl7jfDtgF+JigsParQbaUzPsBz7p9ynGKh0+mqCP1dLVUUCTdRZiYsKqkicDZwEXAvZKOAr4CDojZHwN2B8YCC4AjGlm8bYHDgA+iLQjg9BKRrxdwS5y52QK418z+K+kj4G5JFwDvEBQt8e9tksYCMwkfJU4BqVSjf7nQkEXV2RYFN/YibVdUeZCvq6VGqP/gGpJ2zpLXgBMaV6K0+l4CVENyUeUzs/cJkzsyz48n2Ksyzy8C9m8C0RzHqQM+9Oc4juOUNK6oHMdxnJLGh/4cx8lJoWwQbocqH0rJObD3qBzHcZySxhWV4ziOU9K4onIcx3FKGldUjuM4Tknjkykcx2kQmUb3bEZ4n0ThNATvUTmO4zgljSsqx3Ecp6RxReU4juOUNG6jchynzuSzCNTtUqVPQ59RUz1j71E5juM4JY0rKscpQyQNlfSppLGSRmRJbyPpeUlLJC2SdHEx5HScQuCKynHKjBhX6ypgN2AQcLCkQRnZjgY2AQYCRwHHZMnjOGWBKyrHKT+2AMaa2XgzWwLcDeyVkecwQrTl8cA9QFWWPI5TFsgjbDtOeSFpP2ComR0djw8DtjSzExN5vgZeMrND4vEU4JHUNYl8twE/j4ftCdGWm5pWwLImvK7QZdSnrqastzY5Cpk3F+3MrF6dI5/15zjNGDM7jND7QtKbZja4qWWob72FkLcp7zlZV7HaOt+6CymnpDfre60P/TlO+fEN0C9x3DeeS/ItsCaApFZAR2Bck0jnOAXGFZXjlB9vAOtIWkNSa+Ag4OGMPHcAgyStARwILM2Sx3HKAh/6c5wyw8yWSToRGAW0BG40szGSzgPeNLOHgeuAA4BPgWrgSjMbk6PokY0pdyPUWwh5m/KeR9aw39TkU3ch5ax3WT6ZwnEcxylpfOjPcRzHKWlcUTmO4zgljSsqx2lm1NH90j0x/TVJA5qo3tckLYsun56RtLqkv0n6RNL7kh6U1CWR/4+xrE8l/aS2enLVnbh2X0kmqa7Tt2+UNFXSh4lzSZlflvR5rPdiSQslvRu3a2L+AySNj/c9T9LlklS3Vq1RrhrvN8o8XdJ8Se9EOe+Kf9+V9KSk3jGvojxjY/pmiXKGxXv7XNKwmtojo+4ay6sVM/PNN9+ayUaYfDGOMHW9NfAeMCgjz/HANXH/IOCeJqr3ZGAb4EPgOIJHjV2BVjH9YuDiuD8oltEGWCOW3bKGejbMVXcssxPwAvAqMLiO97UDsBnwYeLcroSJai2BWcA1sd6PgM8zrl8HeAd4C9gK+AHwx8m1lQAAA4lJREFUOLBbY7V1lPnfwLeJtvwqkX5S4vnvHuVRlO+1eL4bMD7+7Rr3u2ZrjwzZspaXa/MeleM0L+rifmkv4Ja4fz+wc0O/8OtSr5ldRlj/BUFZ9DWzJ81sWfJcQsa7zWyxmX0BjI11ZKvnhDrcM8D5BGW4qK43ZWYvADMzzqVk3gL4EugU632EoAyT/Aq4HehgZq+a2VTgVmDvusqQhVrbOsq8iBUjap1JX4fXAUjNstsLuNUCrwJdJPUCfgI8ZWYzzWwW8BTBW8pK7ZFBTeXViisqx2le9AEmJI4nxnNZ88QX7hygexPUm+Qowpd3kiMT52oqL9v5AbnqjkNQ/cyskAGW+hB6HCmZJwPd43Db85K2B9YFfgj0lPSqpKHZ5KtHvbna+p8EJTEReAz4taQ/S5oAHAqclaOsfJ9nPrKthCsqx3FKjc7AYOBvqROSziD4nLuj0JVJagFcApxa4KJ/TuiZpGSeDdxiZpsCpwB3Am2B/oShv4MJ6986FliObOwJzDKzvoThuNuAM82sX5T3xNoubmpcUTlO86Iu7pe+zxPdL3UGZjRBvQDbAj2APc1scZThl8BPgUMtGjpqKS/b+S9z1N2JYMcaLelLgu3k4bpOqMhGlHkjgk0qJXNPohsrM3sr7n8H/AfoE4cwPyPYeLK1TV2pS1sfSOgpY2avEBTmqjHtDmDfHGXV9XnWR7aVaaiR1DfffCufjWDkH0+YgJAytG+QkecE0idT3NtE9W4KfAV8ljg3lDAJoUdG3g1In0wxnjCJIFs9P8xVd0bZo6njZIqYfwDpkylSMvfMqPdDYKOYZ834gt6PYA98nWD3mQA8DezeyG09GpgY99cHprDCAcSvgfvj/h6kT354PZ7vBnxBmEDRNe53y9YeGfVmLS/nPRX7H8c333xr2o0w1PMZ4Yv+jHjuPEIvBsLX9X2ECQqvA2s2Ub2TgeWE4bIlwLtRhglx/12iAo35z4hlfUpillwN9dRad4acdVZUwF3AJIIvxYkE21pS5nGEIb9xhKG+MfE+xwE/iy/sS6JiWRQVxpUppdEYbR1lnkZwrbUE+Bp4kaBI3ydM+ugTrxEhSOc44INkuxBshmPjdkQt7XEscGyu8mrb3IWS4ziOU9K4jcpxHMcpaVxROY7jOCWNKyrHcRynpHFF5TiO45Q0rqgcx3GcksYVleM4jlPSuKJyHMdxSpr/B83g/wmvLQgSAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 3 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"#example of a trailed source\n",
"phot(xt,yt,radius=fwhm*1.4,l=(EXPTIME/3600.)*rate/0.185,a=angle,\n",
" skyRadius=4*fwhm,width=6*fwhm,\n",
" zpt=26.0,exptime=EXPTIME,enableBGSelection=True,display=True,\n",
" backupMode=\"smart\",trimBGHighPix=3.)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The SNR function calculates the SNR of the aperture,as well as provide an estiamte of the magnitude/flux uncertainties. Select useBGstd=True if you wish to use the background noise level instead of sqrt of the background level in your uncertainty estimate. **Note: currently, this uncertainty estimate is approximate, good to a few percent. Future improvements will be made to get this a bit more accurate.**\n",
"\n",
"If the photometry radius was an array, then so are the products created using the SNR function.\n",
"\n",
"verbose=True puts some nice terminal output in your face. These values can be accessed with their internal names."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" SNR: 985.58472371526\n",
" Flux: 767173.3189246762\n",
" Background: 1237.3789471250184\n",
" Background STD: 29.765017423853983\n",
" Num Pixels : 181.74\n",
"\n",
"17.991052570092045\n",
"0.0011016163082006166\n",
"767173.3189246762\n",
"985.58472371526\n",
"1237.3789471250184\n"
]
}
],
"source": [
"phot.SNR(verbose=True)\n",
"\n",
"#get those values\n",
"print(phot.magnitude)\n",
"print(phot.dmagnitude)\n",
"print(phot.sourceFlux)\n",
"print(phot.snr)\n",
"print(phot.bg)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's get aperture corrections measured directly from a star."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAD4CAYAAADlwTGnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO3de3xcdZ3/8dcnk1uTtknTJG2TaZtSaimUXtJQgQIKuoiKFC2iiCIsK7qsyu6ioKjs47e6u7qCFVF3FxEKK+ClUEG5iKhsEVogTZumFAqFpm3SS9Km6S1tc/v8/phpSUPSJJPLmcm8n4/HPGbmnO+Z+Zw+IO855/s952vujoiIJJ+UoAsQEZFgKABERJKUAkBEJEkpAEREkpQCQEQkSaUGXUBf5Ofne0lJSdBliIgklFWrVu1y94LOyxMqAEpKSigvLw+6DBGRhGJmm7tarlNAIiJJSgEgIpKkFAAiIklKASAikqQUACIiSUoBICKSpBQAIiJJKikC4Pdrt/HAi10OgxURSVpJEQBPVu3g9qdfp7m1PehSRETiRlIEwKJ5xTQcbObZDXVBlyIiEjeSIgDOm1ZA/sgMHq6oCboUEZG4kRQBkBpK4dI5Rfz5tToaDjYHXY6ISFxIigAAWDQvTEub89ia2qBLERGJC0kTADMmjOa0otE8XKEAEBGBJAoAgEWlYapq9/L6zv1BlyIiErikCoCFc4pITTEeXqXOYBGRpAqAsSMzeO/0QpatrqW1TdcEiEhyS6oAALhsXjF1+4/w3MZdQZciIhKopAuA808pJDcrTaeBRCTpJV0AZKSGWDi7iKfX72TvoZagyxERCUzSBQBErglobm3n8bXbgy5FRCQwPQaAmd1jZnVmtq6LdTeamZtZfjfbTjKzp83sVTNbb2Yl0eVTzOxFM9toZr8ys/T+7khfnF6cw7TCkbo1hIgktd4cASwBLuq80MwmAhcCW06w7f3A9919BjAfOHo3tu8Bi939ZGAPcG0fau43M2PRvDCrNu9h066DQ/nVIiJxo8cAcPflQEMXqxYDNwHe1XZmdiqQ6u5/jH7OAXdvMjMDLgCWRpveB1waQ+398tG5xaQY6gwWkaQVUx+AmS0Eat298gTN3gU0mtkjZrbazL5vZiFgLNDo7q3RdjVA8Qm+6zozKzez8vr6+ljK7dK40ZmcM62AZatraW/vMsNERIa1PgeAmWUBtwC39tA0FTgX+ApwBnAScHVfv8/d73L3MncvKygo6OvmJ3TZvDC1jYdY+dbuAf1cEZFEEMsRwFRgClBpZtVAGKgws/Gd2tUAa9z9reiv/d8CpcBuINfMUqPtwkAgd2i78NRxjMpMZak6g0UkCfU5ANy9yt0L3b3E3UuI/KEvdfcdnZq+TOQP/dGf7RcA693dgb8Al0WXfxZ4NKbq+ykzLcTFsybw1LodHDzS2vMGIiLDSG+GgT4ErACmm1mNmXU7YsfMyszsbgB3byNy+udPZlYFGPCzaNObgX82s41E+gR+3r/diN2i0jBNzW08UaVrAkQkuVjkB3liKCsr8/Ly8gH9THfn/NueZXxOJr+87qwB/WwRkXhgZqvcvazz8qS8ErgjM2NRaZiVbzWwtaEp6HJERIZM0gcAwEdLI6NQl63WbGEikjwUAEB4TBZnnTSWRypqSKRTYiIi/aEAiFo0L0z17iZWbd4TdCkiIkNCARD1wZnjyUoPsVS3hhCRJKEAiMrOSOWimeN5fO12Dre0BV2OiMigUwB0cNm8MPuPtPKHVzpf0yYiMvwoADo4c8pYinNH8HCFRgOJyPCnAOggJcX4WGkxf32jnh17DwddjojIoFIAdPKx0jDtrmsCRGT4UwB0MiU/m3mTx/CwrgkQkWFOAdCFRaVhNtYdYG3N3qBLEREZNAqALnx41gQyUlM0abyIDGsKgC7kjEjjwtPG81jlNo606poAERmeFADdWFRaTGNTC395rS7oUkREBoUCoBvnTiugcFSGbg0hIsOWAqAboRTjo3OLeXZDPbsOHAm6HBGRAacAOIFF88K0tjuPrtkWdCkiIgOuN3MC32NmdWa2rot1N5qZm1l+N9u2mdma6OOxDsuXmNmmDuvm9G83Bse7xo1iVjiHh3UaSESGod4cASwBLuq80MwmAhcCW06w7SF3nxN9XNJp3Vc7rFvT64qH2KLSMOu372P9tn1BlyIiMqB6DAB3Xw40dLFqMXATMKwvl71kdhFpIdM1ASIy7MTUB2BmC4Fad6/soWmmmZWb2Uozu7TTun8zs7VmttjMMk7wXddFP6O8vr4+lnL7ZUx2OhecUsija2ppaWsf8u8XERksfQ4AM8sCbgFu7UXzye5eBnwK+KGZTY0u/zpwCnAGkAfc3N0HuPtd7l7m7mUFBQV9LXdALCoNs+tAM8tfH/oAEhEZLLEcAUwFpgCVZlYNhIEKMxvfuaG710af3wKeBeZG32/3iCPAvcD8mKofIuefUsjY7HSdBhKRYaXPAeDuVe5e6O4l7l4C1ACl7n7cNFpmNuboqZ3oKKEFwPro+wnRZwMuBd4xwiiepIVSuGROEc+sr6OxqTnockREBkRvhoE+BKwApptZjZlde4K2ZWZ2d/TtDKDczCqBvwDfdff10XUPmFkVUAXkA9/pz04MhUWlYZrb2vnd2u1BlyIiMiAske55X1ZW5uXl5YF8t7vzwTueIyMtxKP/sCCQGkREYmFmq6L9scfRlcC9ZGYsKg1TubWRjXUHgi5HRKTfFAB9sHBuEaEUXRMgIsODAqAPCkdl8p53FbCsopa29sQ5dSYi0hUFQB8tKg2zY99hXnhzV9CliIj0iwKgj943o5DRmam6QZyIJDwFQB9lpoX4yOwinnplB/sPtwRdjohIzBQAMVg0L8zhlnaeqNI1ASKSuBQAMZg7MZeTCrJ5eFVt0KWIiMRMARCDo9cEvFTdwJbdTUGXIyISEwVAjD5WWowZuiZARBKWAiBGE3JGsGBqPg9X1NCuawJEJAEpAPph0bxiavYc4qXqriZMExGJbwqAfvjAaePJTg/pmgARSUgKgH7ISk/lw7Mm8ETVdpqaW4MuR0SkTxQA/bSoNMzB5jb+8MqOnhuLiMQRBUA/nVGSx8S8EbomQEQSjgKgn1JSjI/NDfP8m7vY1ngo6HJERHqtN1NC3mNmdWb2jnl7zexGM/PonL9dbdtmZmuij8c6LJ9iZi+a2UYz+5WZpfdvN4K1qDSMOyxbraMAEUkcvTkCWAJc1HmhmU0ELgS2nGDbQ+4+J/q4pMPy7wGL3f1kYA/Q7TzDiWDS2Czml+Tx8KoaEmmKTRFJbj0GgLsvB7oa6L4YuAno0188MzPgAmBpdNF9wKV9+Yx4dNm8MG/tOsjqrY1BlyIi0isx9QGY2UKg1t0re2iaaWblZrbSzI7+kR8LNLr70XGTNUBxLHXEkw+ePp7MtBRdEyAiCaPPAWBmWcAtwK29aD45OhP9p4AfmtnUGL7vumiIlNfX1/d18yEzKjONi04bz+8qt3G4pS3ockREehTLEcBUYApQaWbVQBioMLPxnRu6e230+S3gWWAusBvINbPUaLMw0G3vqbvf5e5l7l5WUFAQQ7lDZ9G8MPsOt/LMqzuDLkVEpEd9DgB3r3L3QncvcfcSIqdwSt39uCuhzGyMmWVEX+cDC4D1Hukl/QtwWbTpZ4FH+7EPcePsqfmMH52p00AikhB6Mwz0IWAFMN3Masys2xE7ZlZmZndH384Ays2sksgf/O+6+/roupuBfzazjUT6BH7en52IF6EU42OlxSx/Yxd1+w8HXY6IyAlZIg1bLCsr8/Ly8qDLOKE36w/wvtv/j298aAafO++koMsREcHMVkX7Y4+jK4EH2NSCkcyZmMtSXRMgInFOATAIFs0Ls2Hnfl7Zti/oUkREuqUAGAQfmTWB9FAKS9UZLCJxTAEwCHKz0nn/qYU8VrmN5tb2oMsREemSAmCQXDYvTMPBZp7dUBd0KSIiXVIADJLzphWQPzKDhyt0GkhE4pMCYJCkhlK4dE4Rf36tjoaDzUGXIyLyDgqAQbRoXpiWNuexNZonQETijwJgEM2YMJpTJ4zm4QoFgIjEHwXAIFs0L0xV7V5e37k/6FJERI6jABhkC+cUkZpiukGciMQdBcAgyx+ZwXunF7JsdS2tbbomQETihwJgCFw2r5i6/Ud4buOuoEsRETlGATAEzj+lkNysNJ0GEpG4ogAYAhmpIS6ZXcTT63ey91BL0OWIiAAKgCFz2bwwza3t/K5yW9CliIgACoAhc3pxDrPCOfzgj6+zfe+hoMsREVEADBUzY/En5nCkpY0vPriaFo0IEpGA9WZO4HvMrM7M1nWx7kYz8+ik791tPzo6l/CPOyx71sw2mNma6KMw9l1IHFMLRvIfi2axavMe/vOp14IuR0SSXG+OAJYAF3VeaGYTgQuBLT1s/21geRfLr3T3OdFH0twz+ZLZRXzmzMn87LlNPP3KjqDLEZEk1mMAuPtyoKGLVYuBm4BuJ741s3nAOODpWAscjr558QxOL87hxt9UsmV3U9DliEiSiqkPwMwWArXuXnmCNinA7cBXumlyb/T0z7fMzE7wOdeZWbmZldfX18dSbtzJSA3x0ytLMeD6B1dxuKUt6JJEJAn1OQDMLAu4Bbi1h6bXA0+4e1dXP13p7qcD50Yfn+nuQ9z9Lncvc/eygoKCvpYbtybmZXH75XNYV7uP7zy+PuhyRCQJxXIEMBWYAlSaWTUQBirMbHyndmcBX4y2uQ24ysy+C+DutdHn/cCDwPyYqk9wf3PqOD5/3kn8YuUWHtWcASIyxFL7uoG7VwHHRu1E/8CXufuuTu2u7NDm6mibr5lZKpDr7rvMLA24GHgmtvIT31c+MJ2KLXv4+iNVnFaUw8mFI4MuSUSSRG+GgT4ErACmR4dzXnuCtmVmdncPH5kB/MHM1gJrgFrgZ32oeVhJC6Vw5xWlZKaFuP6BVTQ1twZdkogkCXPvdhBP3CkrK/Py8vKgyxgUz71Rz1X3vMRH5xZz+8dnc4J+cRGRPjGzVe5e1nm5rgSOE+dOK+DLF0zjkYpafl2+NehyRCQJKADiyJffN41zTs7n1kdfYf22fUGXIyLDnAIgjoRSjB9+cg65WWlc/8Aq9h/WraNFZPAoAOJM/sgM7ryilK17DnHzw2tJpD4aEUksCoA4NH9KHl/9wHSeqNrBkheqgy5HRIYpBUCcuu7ck3j/jEL+/YlXWb1lT9DliMgwpACIUykpxu0fn8O40Zl88cHV7DnYHHRJIjLMKADiWE5WGj/5VCn1+4/wz79eQ3u7+gNEZOAoAOLc7Im5fPPiGfxlQz3/vfzNoMsRkWFEAZAAPnPmZD48awK3/WEDK9/aHXQ5IjJMKAASgJnxvUWzKBmbzZceWk39/iNBlyQiw4ACIEGMzEjlp58uZd+hFm745Wra1B8gIv2kAEggp4wfzbcvnckLb+7mh8+8HnQ5IpLgFAAJ5vKyiXx8Xpg7/7yRZzfUBV2OiCQwBUAC+teFMzll/Cj+6Vdr2NZ4KOhyRCRBKQAS0Ij0ED+5spTm1na++GAFLW3tQZckIglIAZCgphaM5LuLZlGxpZHvPfla0OWISAJSACSwj8wu4qqzJnP3Xzfx1LodQZcjIgmmVwFgZveYWZ2Zreti3Y1m5maWf4LtR0fnE/5xh2XzzKzKzDaa2Y9McyDG5BsfnsGscA5fXVrJ5t0Hgy5HRBJIb48AlgAXdV5oZhOBC4EtPWz/bWB5p2X/BXwOmBZ9vOPzpWcZqSF+8qlSDLj+gQoOt7QFXZKIJIheBYC7Lwcauli1GLgJ6PaqJDObB4wDnu6wbAIw2t1XemTGk/uBS/tQt3QwMS+LH1w+h1e27eNff78+6HJEJEHE3AdgZguBWnevPEGbFOB24CudVhUDNR3e10SXdfUZ15lZuZmV19fXx1rusPf+U8fx+fecxIMvbuG3q2uDLkdEEkBMAWBmWcAtwK09NL0eeMLda3po1y13v8vdy9y9rKCgINaPSQpfuXA6Z5SM4ZZlVWys2x90OSIS52I9ApgKTAEqzawaCAMVZja+U7uzgC9G29wGXGVm3wVqo9scFY4uk35IC6Vw5xWljEgL8fe/qKCpuTXokkQkjsUUAO5e5e6F7l7i7iVETuGUuvuOTu2udPdJ0TZfAe5396+5+3Zgn5mdGR39cxXwaL/2RAAYn5PJHZ+cy8b6A3xz2TpNKi8i3ertMNCHgBXA9OhwzmtP0LbMzO7uxcdeD9wNbATeBJ7sTS3Ss3Om5XPD+6bxyOpafvny1qDLEZE4ZYn0C7GsrMzLy8uDLiMhtLU7V9/7Ei9uamDZ9WdzWlFO0CWJSEDMbJW7l3VeriuBh6lQirH4E3MYk5XG9Q9UsO9wS9AliUicUQAMY/kjM/jxp0qp2XOIm5euVX+AiBxHATDMnVGSx80XTefJdTu49/nqoMsRkTiiAEgCnzv3JN4/Yxz//sSrVGzZE3Q5IhInFABJwMy4/eOzGZ+TyRcfqGDPweagSxKROKAASBI5WWn89MpSdh1o5p9+vYZ2TSovkvQUAElkVjiXb108g2c31POPv1rDfo0MEklqqUEXIEPr02dOprGphcXPvM6arY3c8ck5zJ00JuiyRCQAOgJIMmbGl943jV9//iza2p2P//cKfvrsRp0SEklCCoAkVVaSxxM3nMsHZo7nP5/awKd//iI79x0OuiwRGUIKgCSWMyKNH18xl/9cNIvVWxq56IfLeWb9zqDLEpEhogBIcmbG5WdM5PdfPocJOSP4u/vLufXRdZpaUiQJKAAEgKkFI1n2D2dz7TlTuH/FZhb++Hle36lJZUSGMwWAHJORGuJbF5/Kvdecwa4DR/jInX/lFys36x5CIsOUAkDe4fzphTz5j+cyf0oe3/ztOr7wi1U0NunqYZHhRgEgXSoclcl918znGx+awZ9fq+ODdzzHyrd2B12WiAwgBYB0KyXF+Nx5J/HI3y8gMy3EFT9bye1Pb6C1rT3o0kRkAPQYAGZ2j5nVmdm6LtbdaGZuZvldrJtsZhVmtsbMXjGzL3RY96yZbYiuW2Nmhf3fFRksp4dz+P2XzuGy0jB3/nkjl//PCrY2NAVdloj0U2+OAJYAF3VeaGYTgQuBLd1stx04y93nAO8GvmZmRR3WX+nuc6KPur6VLUMtOyOV7398Nj+6Yi5v7DzAh+54jscqtwVdloj0Q48B4O7LgYYuVi0GbgK6HCLi7s3ufiT6NqM33yXx75LZRTxxw7lMGzeSLz+0mq/8ppKDR1qDLktEYhDTH2UzWwjUuntlD+0mmtlaYCvwPXfv+JPx3ujpn2+ZmcVShwRjYl4Wv/78WXzpgpN5uKKGi+/8K+tq9wZdloj0UZ8DwMyygFuAW3tq6+5b3X0WcDLwWTMbF111pbufDpwbfXzmBN93nZmVm1l5fX19X8uVQZIaSuHGC6fz4N+dyaHmNj760+e5+7m3dFM5kQQSyxHAVGAKUGlm1UAYqDCz8d1tEP3lv47IH3vcvTb6vB94EJh/gm3vcvcydy8rKCiIoVwZTGdNHcuTN5zL+dML+c7jr3L1kpep33+k5w1FJHB9DgB3r3L3QncvcfcSoAYodfcdHduZWdjMRkRfjwHOATaYWerRUUNmlgZcTCQcJEGNyU7nfz4zj+9cOpMX39rNB+9YzrMb1K8vEu96Mwz0IWAFMN3Maszs2hO0LTOzu6NvZwAvmlkl8H/Abe5eRaRD+A/RvoE1QC3ws37uhwTMzPj0mZP53ZfOIX9kBlff+zLf/v16jrTqpnIi8coS6T4vZWVlXl5eHnQZ0oPDLW38xxOvct+KzZxWNJofXTGXqQUjgy5LJGmZ2Sp3L+u8XEMzZcBlpoX4fwtn8rOrytjWeIiLf/RXfvXyFt1UTiTOKABk0PzNqeN48obzmDspl5sfruKLD61m7yFNRC8SLxQAMqjG52Tyv9e+m5sums4f1u3gQ3c8x6rNXV1XKCJDTQEggy6UYlz/3pNZ+vdnE0oxLv+flfzoT2/QpmsGRAKlAJAhM2diLo9/+RwumV3ED/74OlfctZJVmxvUNyASEAWADKlRmWks/sQcfnD5bF7bsY9F/7WChT95nmWra2hu1W2mRYaShoFKYA4eaeWR1bUseX4Tb9YfpGBUBle+exJXvnsyBaMygi5PZNjobhioAkAC197uPLdxF/c+v4lnN9STHkrh4tkT+NsFU5hZnBN0eSIJr7sASA2iGJGOUlKM97yrgPe8q4A36w9w3wvVLF1VwyMVtZxRMoZrFkzhwlPHkRrSGUuRgaQjAIlLew+18Jvyrdy3opqtDYcoysnkM2eVcMX8ieRmpQddnkhC0SkgSUht7c6fXt3Jvc9Xs+Kt3WSmpfDRuWGuWVDCu8aNCro8kYSgAJCE9+r2fdz3QjXLVtdypLWdc07O55oFJZw/vZCUFM0pJNIdBYAMGw0Hm3nopS3874rN7Nh3mMljs/jsWSV8vCzMqMy0oMsTiTsKABl2WtraeWrdDu59fhMVWxoZmZHKZfPCXH12CSX52UGXJxI3FAAyrFVubeTe5zfxeNV2WtudC6YXcs2CKSw4eSyaclqSnQJAkkLdvsP84sUtPPjiZnYdaGZa4UiuXlDCx+aGGZEeCro8kUAoACSpHGlt43eV27n3+U28sm0fOSPS+OT8iVx1VgnFuSOCLk9kSCkAJCm5Oy9X72HJC5t4at0OzIwPnDaOaxZMoWzyGJ0ekqTQryuBzeweIpO317n7zE7rbgRuAwrcfVendZOBZURuOpcG3Onu/x1dNw9YAowAngBu8ERKI0kIZsb8KXnMn5JHbeMh7l9RzS9f2soTVTuYWTyaq8+ewkdmTyAjVaeHJPn06gjAzM4DDgD3dwwAM5sI3A2cAszrIgDSo99xxMxGAuuAs919m5m9BHwZeJFIAPzI3Z88UR06ApCB0NTcyrLVtSx5vpo36g6QMyItEhIleZSVjGFmcQ5puu2EDCP9OgJw9+VmVtLFqsXATcCj3WzX3OFtBtHbT5vZBGC0u6+Mvr8fuBQ4YQCIDISs9FSufPdkPjV/Es9v3M1v19TycnUDf1y/E4ARaSHmTsrljJLIkcPcSblkpeu2WTL8xPxftZktBGrdvfJE51GjRwmPAycDX43++i8Dajo0qwGKu9n+OuA6gEmTJsVarsg7mBnnTMvnnGn5QGQE0UvVDby8qYGXq/fwoz+/gTukphinFecwv2QMZ5TkcUZJHmOydT8iSXwxBYCZZQG3ABf21NbdtwKzzKwI+K2ZLe3Ld7n7XcBdEDkFFEO5Ir1SODqTi2cVcfGsIgD2HW5h1eY90UBo4L4XNvOz5zYBMK1wJGUlecyfEgmF8JisIEsXiUmsRwBTgSnA0V//YaDCzOa7+46uNoj+8l8HnAs8H93mqDBQG2MtIoNidGYa508v5PzphQAcbmljbc1eXq6OBMLvK7fx0EtbACjKyeSMKXnHThudXDBS9yeSuBdTALh7FVB49L2ZVQNlXXQCh4Hd7n7IzMYA5wCL3X27me0zszOJdAJfBdwZ4z6IDInMtNCxEUUQuVPpazv2HTtl9MKbu3l0zTYAcrPSKJv89hGCOpYlHvV2GOhDwHuBfDOrAf7F3X/eTdsy4Avu/nfADOB2M3PAgNui4QFwPW8PA30SdQBLggmlGKcV5XBaUQ5XL5iCu7N5d1OHfoQGnnk10rGcmZbC3IljOCM62mjupFyyM9SxLMHShWAig6hu/2HKq/fwUjQQXt2+j3aPhMfMotGRTuXoqaM8dSzLINGVwCJxYP/RjuXqBl7etIc1NY00t7YDcFJ+NrPCOcwK5zIrHDmy0P2LZCBoTmCRODAqM433Ti/kvdGO5SOtbVTV7OWl6gZWb2lkxVu7+W20HyHF4F3jRnF6cQ6zJuYyqziHUyaM0lXLMmAUACIBykgNUVaSR1lJ3rFlO/cdZm3NXqpqGllbu5c/vVbHb1ZFLptJCxmnjB/N6eEcZhVHjhamjRupDmaJiU4BicQ5d6e28RBVNXuprNlLVW0ja2v2sv9wKwAZqSmcVjSaWeFcTi/OYfbEHKbkjySkYagSpT4AkWGkvd3Z3NDE2prG6NHCXtZt20tTcxsA2ekhTivOYXY4h9PDucwO5zApL0t3P01S6gMQGUZSUowp+dlMyc9m4ZzIXVTa2p036w+wtmbvsWC4b8VmmlsjVy+Pzkw91sE8KxoMRTmZCoUkpiMAkWGspa2dDTv2U1W791gwbNixn9b2yP/3+SPTOb347aOE08M5FI7KDLhqGWg6AhBJQmmhFGYW5zCzOIcr5keWHW5p49Xt+44Lhf97vZ5oJpCXnc7ksVlMzsti8tjsyOvo89jsdB0xDCMKAJEkk5kWYu6kMcydNObYsoNHWlm/fR+VWxt5s/4Am3c38XL1Hh6t3EbHkwQjM1KZlJd1XCgcfT1hdKbuf5RgFAAiQnZG6rFbXXd0pLWNrQ2H2NJwkOpdTWxpaKJ690E27NjPM6/upKXt7XRIT01h4pgRlIzNZtLYrOOei3NHkJ6qoarxRgEgIt3KSA1xcuFITi4c+Y51be3OtsZDx0Jhy+7I8+bdTbzw5m4OtbQda5tiUDxmBJPzjj9qmDw2i0l5WZpwJyD6VxeRmIRSjIl5WUzMy2LByfnHrXN36g8cYfPupugjEgybG5p4vGo7jU0tx7UvHJXxdijkZTFpbBbjRmeSl53OmKx0crPSdLHbIFAAiMiAMzMKR2VSOCrzHaeVAPY2tbC54eDx4bC7iefeqGfpviNdfubozFTystPJzUo/Fgx52WmMyU4nL+vt5XnZadHQSNfFcD1QAIjIkMvJSmNWVi6zwrnvWHeouY0tDU3sOnCEPU3N7DnYTMPBFvY0NdNwsJk9Tc3s3HeYDTv203Cw+bhTTR2ZQc6ISBiMyUrrEBrpjMmOLOv4Pi8rnZwRaUnVka0AEJG4MiI9xPTxo5jOqF61P9Tcdlw4NBxsprGp5bj3e5qaqW08zCvb9rH7YPOxO7B2lnI0NDocVWSmpZAeSiE9NYW0UOSRnppCesiOvX57WQppqUZ6KERayEhLTSEjlELa0XWhFNKPrk+146R+UUsAAAT+SURBVLcLpQz5EYsCQEQS2oj0ECPSR1CUO6JX7d2dQy1tkWA42EJD9Cjj2NFGU3T5wWZq9jTR3NpOc1s7LW3tNLe209Lmx5YNtFCKkRay4wLn6PPPP1vG5LHZA/p9CgARSSpmRlZ6KlnpqYTH9Ny+O+5Oa7tHQyESCEcD4mhYNLe109IpQJrbvItl7bS0+nGfc3Tbo8sy0wb+NuAKABGRGJhFfq0n8uikHis3s3vMrM7M1nWx7kYzczPL72LdHDNbYWavmNlaM/tEh3VLzGyTma2JPub0f1dERKQvehNdS4CLOi80s4nAhcCWbrZrAq5y99Oi2//QzDp2+X/V3edEH2v6VraIiPRXjwHg7suBhi5WLQZuArq8nai7v+7ub0RfbwPqgILYSxURkYEU08krM1sI1Lp7ZS/bzwfSgTc7LP636KmhxWaWcYJtrzOzcjMrr6+vj6VcERHpQp8DwMyygFuAW3vZfgLwv8A17n503NTXgVOAM4A84Obutnf3u9y9zN3LCgp0ACEiMlBiOQKYCkwBKs2sGggDFWY2vnNDMxsNPA58w91XHl3u7ts94ghwLzA/luJFRCR2fR4G6u5VQOHR99EQKHP3XR3bmVk6sAy4392Xdlo3wd23W2RmiUuBd4wwEhGRwdWbYaAPASuA6WZWY2bXnqBtmZndHX17OXAecHUXwz0fMLMqoArIB77Tr70QEZE+S6g5gc2sHtgcdB29kA/s6rHV8KX91/5r/+PLZHd/RydqQgVAojCz8q4mYE4W2n/tv/Y/MfY/ca9hFhGRflEAiIgkKQXA4Lgr6AICpv1Pbtr/BKE+ABGRJKUjABGRJKUAEBFJUgqAAWZmITNbbWa/D7qWoWZmuWa21MxeM7NXzeysoGsaSmb2T9H5L9aZ2UNmlhl0TYOpq7lCzCzPzP5oZm9En/sx51Z862b/vx/973+tmS3rdAv8uKMAGHg3AK8GXURA7gCecvdTgNkk0b+DmRUDXyZyW5SZQAj4ZLBVDbolvHOukK8Bf3L3acCfou+HqyW8c///CMx091nA60RufBm3FAADyMzCwIeBu3tqO9yYWQ6RW3/8HMDdm929MdiqhlwqMMLMUoEsYFvA9QyqbuYKWQjcF319H5F7fQ1LXe2/uz/t7q3RtyuJ3CwzbikABtYPiUyS095Tw2FoClAP3Bs9BXa3mWUHXdRQcfda4DYiM+RtB/a6+9PBVhWIce6+Pfp6BzAuyGIC9rfAk0EXcSIKgAFiZhcDde6+KuhaApIKlAL/5e5zgYMM78P/40TPdS8kEoRFQLaZfTrYqoLlkTHmSTnO3My+AbQCDwRdy4koAAbOAuCS6O2xfwlcYGa/CLakIVUD1Lj7i9H3S4kEQrJ4P7DJ3evdvQV4BDg74JqCsDM6CdTRyaDqAq5nyJnZ1cDFwJUe5xdaKQAGiLt/3d3D7l5CpPPvz+6eNL8A3X0HsNXMpkcXvQ9YH2BJQ20LcKaZZUXnuXgfSdQJ3sFjwGejrz8LPBpgLUPOzC4ichr4EndvCrqenvR5QhiRE/gSkbke0oG3gGsCrmfIuPuLZrYUqCBy6L+aBLolQCyic4W8F8g3sxrgX4DvAr+Ozhuymci8IMNSN/v/dSAD+GPkdwAr3f0LgRXZA90KQkQkSekUkIhIklIAiIgkKQWAiEiSUgCIiCQpBYCISJJSAIiIJCkFgIhIkvr/OqT+c2ddh2gAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Round aperture correction for a 4xFWHM aperture is 0.184.\n"
]
}
],
"source": [
"phot.computeRoundAperCorrFromSource(goodFits[0,4],goodFits[0,5],num.linspace(1*fwhm,4*fwhm,10),\n",
" skyRadius=5*fwhm, width=6*fwhm,displayAperture=False,display=True)\n",
"print('Round aperture correction for a 4xFWHM aperture is {:.3f}.'.format(phot.roundAperCorr(1.4*fwhm)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, let's do some PSF source subtraction. This is only possible with emcee and sextractor installed.\n",
"\n",
"First get the cutout. This makes everything faster later. Also, remove the background, just because.\n",
"\n",
"This also provides an example of how to use zscale **now built into trippy** and astropy.visualization to display an astronomy image using the zscale scaling."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQEAAAD8CAYAAAB3lxGOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy8d7Bl2XXe99v7pHtufvfdl0O/zml6Yk+OHGSCEAiSpkhaTLJMU5ItmabKJcpll81ScNllV7Fss1QULcEMJgkzAQIIYIYABoPJqWd6ejrnl8PN+YS9/cd6aMgSRpYswZwq9Pqn+7137jnnnrP3Wt/61reWstZy227bbfv+Nf0XfQO37bbdtr9Yu+0Ebttt+z63207gtt2273O77QRu2237PrfbTuC23bbvc7vtBG7bbfs+t++ZE1BKfVwpdUEpdVkp9Xe/V9e5bbfttv27mfpe6ASUUg5wEfgIsAK8Dvyktfbsv/eL3bbbdtv+nex7hQQeAC5ba69aayPg94FPf4+uddtu2237dzD3e3TeOWD5X/h5BXjw/Q52sjkb5CoAGA+UBQy4I0tUArensEqOTbOgI3BGkITg9SxJKH/UESR5cPpgHVAGjCv/99sWqyEuKvymxbgKBSQBWBfQlqBmSTIa4wEKsBBsDRlNZuSerFzXePJ/FOhk92fznc+YAJyh/N648nuvC0kG/LbB+HIN44DfMVitsI4iDUDHYBVYDcaX81hXzm98uU+nr7COnNc6oNLdzzhyfWXkdwDWA+tYnIE8o2+fV0e7x+1+L+vI/Tjx7nPevXaSBTyL01OkHvgdS5JV3zm/I+fU8e597P7sDixJRuEk8oydETij73x3kM8YF9y+IclqjCvP0ypwh5bUV6RZix4q0HKssnJ+ZwBpRq6pjDwjq3afnyPfT6eyRlSYQtcBwOtborzCBhYseC05d1yyeA2I84pMLSUqOrJ+fDmvM5JrOSNDVNR4PUuakedgtTxDnUIafOd44+2u5933oWNIcnLvzsgSF9St92u1HJOG8tydkSD0JJD7swpsYJnMdWgnGUZdX/aEAr8l9/Ltdfnte/32e05CuYfh5sqOtXbiX95/3ysn8P9qSqlfAH4BwMuPMfmrf5vSew69RYvXVgQNS3cR/JYiu2HpzSp0BLkNQ+opGsdg4i1Lpp7QnfVIQoXx5Ytndiy5zYQ4qxlUNbkNQ3fGwbryUhb+eJWz//UEe/5Q0Zl3SQNF+/4huXczBE1LVFRg5Vo7dyrGzkPQNvSmNN1FmHrNMBzTeH3LoCL/dvYo/CYMJy35mxAVFflVQ2u/pvpuQuOQe2vjdA4mlN91ad4dUzjn4XUtw6qici5l8wFNbkVRWElYfVIT1PStzQ5QvGbZejhl+nnNcFyThNDdnzD5okPjGMw9FxO+cZXrv3iEpGAJako+r2AwYyhdUKS+YvrVLt3FLFFeFk+SUQyrFmUU1XdTNk9qMjWFM2LXEcsCxkJu1ZJpGnrTmkzDMhjXRCUYjVkyOwqdQOFmSm/GobNk8JvyHaKyoXxO0d4H2XVFnJdNPfXaiMbhgOrpAStPh+RvWvrTisJNw+ZjBpUosisOOoagaYnziuE4jKYSSu+5FG8mJKGmP6mJCpCp21sbr363Yeab0Dzo0N8XUT7lExV3HdUQKudj1h51cSLFxNsJSUaz8ZglXHNwe/LMrSPPwLqWoK7Ibhr5zmNQeS8lzmmcyNLaq1EGBvMp889a6oddlIHquzH1Ix7hjsHrW5r7xcFMvjVkVPawGmo/0Sf7bJ7WYUu4qfGbFh3DqKIoXU1Z+ZilcMmlN2cYTxVBXRE0Lc4QBpPy/+y2Yetezdh5i1WK7oJiMJey5wspnXmPU7/5yze+6178HnECDwP/rbX2Y7s//wqAtfYffbfjS9lZu/8//DtUzvVZfzSHSiHcls3YPJGQWXdx+5CpWdIAWoct1TcVlXcaNE6U8QaW9qIjUdiH7KZl5x6LjhXVU5bmYcl6wk2LTkAlsvhGJYXfsVgHerOK4ayE4YlXHImEEVTOdBhMZ+lNObAb8QZVhXURRzUPE28bgkbC5v0BQdPiDqA3o4hKlnBLMZi0FG5AbiOlcdClfDWlvegQF2ShDicMQU0z/coIgNodAbkNQ6aesPaojzuA8uWUwbgmDQQV+W1L+wDMvCQbIA417b2KoCHPNGhaenMSaYKmJc6JY/HbCWngsPGQx3AxovyWj3EhKsP0yxFJ1mHtSUWwo3EiyC8b3KGlfsQh3LI0j0C4JUikdCWledAhv2xJM5BpGFr7HKyC0tWUzoKD8WUTtBddrFa0jqVU3tZk6oaNH4nwLoSkWUv+BsQFxfi7MTq1XP+UQ27ZYfzdmHC9R/3OEjt3W1SqUBbmvpGw9rhL0FBEJ7v4r+fJ1C3uwNLeK2hj8s2EJFREBU1+LSHJavxmQrDSZOvxSZSVyJ8G0D0U49ZcSlcgKihy6wa/YxiOOejEMqhq0gz0ZwzFy5r8urzDmedbXPrZAn5DM6oYbD5h8jmP7JZAqo0HfUpXDFFxF+35kF8zjEqK4bi8y8KyJfUF1W7dD06kqJyxDCuaOPcdpJCEFnegUAn4HWjdGbHwRU3qKdY+ZJl6QbP5iKF4wUUngiZ684rq6ZS1xxTXf+nvvGmtPfkv77/vFSfwOnBQKbVXKeUDPwF84f0OHo479OYVW/flyG5YStdTCisjnJGleN5l7IIh3LaMyoqoJAu0eQSu/WiF7GZMHCqUkY0x/XKf3oyieEljHUv9uDzoqGTwO5awZhi7OKA3o8huGaKCwmpIM5bp5xyK51y2n4jJbaZsPxGz+WCR3rRDb0HRWZJFM5y0lK6kGE+x8PURvRmH/rSH25dN3Z1TxAVL9bSlenrE/NcjhuOKzZMOk2+N8LqpRIWOwLTKacX813ts3xtw7acUYxdj2ksat5egj7cJ6pb+hKZ52KJjiRBBx5C/AVt3e2yd1Hh9Q+mKAWDsYkTjGORXDJ39Ke29iuadMeuPOqw9kmH5Qy5eB+a+JPBCJ5D6lt6Mx+b9GrejcCKY/0qdzqIm3BxSvmJIM4r8TXFq068OaS855NYs42/s0J9WOENL+VKK8SANFJm6ZVg1pL5mMKEIawY9VNTuTdm6XxO+HbLwtT6FaxLNMtuWmz+oGZVdwjUHDIzGHJJCQH9a4Q4UQUORXVX0p1xKl2Di1IjCMznyq4bOHoXxBEE4Q9h4yGHrPo1VUD/isfLJlJ0TAct/aYqwYchtJpSuJowqlsI5j6SU0p2XtVQ/ptg54bL1aErjiCYNIbduOPybdQprCa29Dl7fUru7iHUlkI6dVYTXfbrzivaSx84Jn9G4we8Z4oJi8o0u4bYl9RT9KUVUtERlWdfF6xHbJ2HiLZh9PqG1X5NkJaDFBXsrzZl+JUKn0DoRU33Ro3HIpT/hUD7tEmcVe75oyTQsztAStAyTbyQs/PJFxs6q992s3xMnYK1NgP8U+CpwDvictfa99zveb1kyNW7luc7IUDueofZIjPEhyimyWwm9RUNu1RJuWSZOGeKCoT/tMRzXBA3LqKJYfSpLfzGldC3GZCzlC5AGlrnnDLm1mO27HG5+NEtuXTytTmEwocgtK2p3yQIIr/msfERReM8HC/m1hIVn++hIETQN4aaifsxh6uUWylhGJdi+R1BF0DKMXUoJGorGEU1rv8/OnQFeF7yuwhkmRAWH7rwmDaB6OqZ8acDKh3L0FlNyF3y27/IINy0bD2UJny1gfIHwysBwXNKe7oxDnFckOUtcSmntdehPabLbhps/naISaO/RuB2Nd2eT8ddcgppEcBMaCsuGjYcVzeOJ5IwWMs2U/DLMvJIQFSyDuQJuH3rzITt3KdoHDKMKeD3F9p0ZUl8c3qWfrTKcSqkfcWntdXBGsHOPIC1npNi+26F82dBe0lRPQbjqUroA4+/FLH8kS24jJb9smXhpG7ej6U1rcuuWwbR85upnAmaf7xIvjIjzlkzd0llU9GcU/WmP9kFZN+E2hNsJSUYRF+1uaijIwetYxl/xBK7PGIZljflbO7QXXSpnLHEBMpsuk28lTJ4a3EqF8ldcypcMU68PGVY0/aUSnZ9vk+QEMfSnFcGWw9QbMaVrMX4T3IGsqf68YfGZlNpRl1HZsvlAnrCWsPVkTKYG+WVFpqZw+5bNBwJyNzWjomZUllRER4JQSxfAb8LsCylrj3tEJcvcVzV+1+B2d3mwyNJ4dERrn0f9DglWmw9otk66rP3DA/Tm/n92AgDW2j+z1h6y1u631v6Df92xSVbhdS1eT3Jrt5+SqRn8NY+xCwlh3dCdcVn4airkkAQ8Dv/qORpHFK2jCcWbQ+Z/5zLRmCF3zaG118NraGp3WYrXoLnfZVRxKV80hJtQv8NSWEkIGoYkZ/G7luyqoru4G2m3HCpnYzqP9Vl/2CUNHPI3BRbm1iTSWM9h5amQ2ReHzL6Y0l1Q9CckLUkDyC1bvK4gm+6iIS5abnwyizLy98V/voPXjtl8IAtA9Q1NdtMy8XZM4xhkNw3GUfgtS+ceSRVGFUNUhM5eQ5wXziR/zcW6QtptPGYZ//MMU2+mJAWLc7DLf3Xsyyz93CWyT2wLkRgpNn94iL/UJbPukoSQvwn1wy759ZTGQY/suuLGj1laxxPMLpdSuqgYTiXMf2OATmDqjYjhbIrXU4y/JdEy3LHoCMJ1yZlVosivWEoXOgKnpwSqj8YUnQUXLKz8SMKwqmifGKd62hLnhcwqXlGMXUwZP63oLoTs/yeWPQ+uCN+yYhmNG8KdlMy2Is4qdGTZvscjzivyNyHcUIzGLYNJxagijrR1PCHNp+gE+p+bJreVsn1SuJbCdUvjkEtnIRDSsGdxRhDnFPUjAbn1lOZ+j+jVCuVLhtGYpfpugrLQ2uOx+oRHkpWUtHomoXhR0zjo4Xcgt6ZwRpaVDzkUzvk4Q0vpWszYRVk3xWsGr2dpHTZsPGGY//MmMy910QnUTqZEJWgccjE+7P2TLqsfshhPkeTB7ULtoZjSaxla9w8ZOyv8TdBQuD248Rl7i4/6bvaBUAzqFPJrMbV7U+aeG6AjQ/Fan+JVSAONdaB5RKBh5VyPOKfoTTlc+rvHwILbcdg5EXLpl/aTv6HJrxnyGynZdUX+hkYl8mKSQKJp97E+hWua7XtcNp9OCDcU7sDQOppQviD3ZDxL/ZiH3cigjOLqT2pK10dYBzY+kjDxTszWyTxJaNGxoTPvomPoz1m279WEW5bRmKJ0qcvWvULw6Uig7OpTitlvjVj5eJW46BFuW2GUI0sSQpzXjJ3bZdtdaByD8qs+bk8z+4IlGpO8VFkYu5SSXzbyki0sfUHe9sZDDuOnLT9+6C0+nF3h1I0FWt0QE1icSOFcDRl0AnKrlr1/uIPVEJUsO3e4lK4lJHkoveMz/4xiUNWULkH5SszUS5qbH84QNA25X1nFOpbFL7bozSgW/6zFsKJuVWOcAeTWxBFuPFIizgmRdfIjZ/FbwvkEdah8KyC7bmktOXTnBNV190BvHqwW4jLcidm6L2TjywuMyrvVDBcahzwq52IGkwrjKiZOxbRPRKS+YjghSLD6bow7gGEVdD4ms+7RnVMMq4qtk/JuejOK2l1yr905TW/e0t4rFYjKewNSX7H5kNpFbwl+KyUNLdt3C1LoLlrmnoswrvAhm/c5zHxtC79tGVZAx8IVuV3Zcr05WYuNQw6F65bOoqY/rbDFmPJpl+37Sqw9nifcsix8Fak8KZh7LqG7lKPytkN3VpNkoHQjxtvySANw1wMA8suWqGgxD7WY/5LDaNy87/77nhCD/7aWG1+w9zzxtxiMOxgX2gcAA2PnIbeR0N7jSqkjJ5G6dAF6C4q9v7fFzc9MomOovjNi7fGA8kVDklG0DsP4O5bNJ1KyNzx0DN0DMWNvu6S+Ii5C0ABnKGmE1QK/0oyQko3jFpWAnu8TvpJn8o0+Kx/OEm5arFYMqxAXDU5foVMlUeQYLH1hQHcxw/Z9Eg3dgZA6XteS20ho7fdwhlKujMqKJAvFq1YcQEbhd4RkVNYyHPdoHnConE8wriLKa3RsaR3U+M3dMp/dLTUNoD9jGT9j6c5ruocjspd9BtOGvcfX2GwXCL5apH5/zOwzLtHP1NnZLOKve/gtxejeHrkXcozGYPGrHdYeL1A5F7P2syMm/iikO7dbYutYwrpBGUu/6hC0DUlG4w6NVDZWFe3DCaWzLtYRpr5+TJj18gWF/Us1Jn41YPOBAlERCjcNaaCIigqzS7YOphTTr4wYVdzdkpelN+2QhIqpVzssf6TAYC4hu+IKItPQ3ZdQfs8lDb5TGvY7lsp7A1afzJLdsHT2QXC8SfTOGPnlXZLYQJRXtA8anIFi7vlEHHoiqVcaSGWks89QOSPp4M5dmjS0jJ2R+86vpTSOOEy+GbPytEPxisLrSpk1ySlGFciuSSm7fSKicNaneiZi+WlZl0nBMv62ovpajZVPVKVcaGQd/otl8Kig6O4xVE4LMV2/P2b8FY8kK+sot2aJc0KwFq+ltPc6hE9uk/Mjbr43w/W//d2JwQ+EE8jMLthDP/5fMHFqwLVPBxSuatDQWTKMn1Z4fYNOLKtPaYJtTZq1OEMFBioXUupHHVQqC2pUFBbX6woMdEYQ5+UBGVeR25RIaVyFE1niUDEqa3IbKe0lh2jXOfTmDeGGJlMTJzGcsMw+nxDnHepHNJk6dPZYwm1F92BMpjxk6p9l2LrPo3zJ4A4Ng4pDpmFY/UzMzD/3aO0XIk3Hlu6CIJTS9ZQop4kKAheVlcrC3v9zlc2nZ+kufsfBjJ+GsfNdtk7m8brs8hGa1rEUt63J7Mji6B6OIFG4LZfcsmI0Ls85yVom79xk/coEwbZD+aKUQL2eIrtmSQOFTi3F6zHDcZex17fYfmyK7qIiDS1xOaV01qVydkRmucXqxycxgUD3yTcTtu9xmXwrZlRy2HzEsv/3RwymAuKcBgtRSZHdTCVH7xqwljjvsP64QsUKtKX6luSzjTsNe76Q4g5TLv+Mw54/Vuyc8OjPSCXFeBa/pYjKluIVmHhhk5s/Oo3fsgwrUhatnE+pHXdwB6KBGE4IgjKelPxGEylzXxcOajDuMna2zebDJdr7DFOvQXdW44ygsJJQP+reKpMOpgyTr4H+2S2GfzyF8ZW803mY/0bE1r0B2S2LTiyjkiIJFf05g9fWBA0o3pDANvuVTc7/vTLV53wpSyP6Cq8nRLAT7aYjeUmX82uJlDOHism3YoyvWH/YISmlZG9KqjCcSVDZBL0ZYDKGH3r4Le7KLfMflTZwZi5/VyfwF6YT+H/YrhiisyegdEkRlWD83ZjRmEdnEfyWg3Vg3x8NGFU8+hMOhZWYNKMYVBycgdR8hxWBkmkMWJh5SdCB8cUBpBkYjmlKVyLqxyTvG40JO95xHZIQyhcNW49Yjv6jFbp3z9He4zJ2IUGds6w94VK8IpUErLolRslf8BhVhfzxWzAcUzROGsbecOjOOfjXHNY+lODvWNyBIdyJaR3IULma0pl3JN++mjIsa5Kswh3C1Z+Zw+tCtHdIuhFQuK7YucfQXSgw+WbE5gM+g7mUR+88z4XfPEpuI2FUdqR2f9PHbyIR6pBDGoj2onwDNp1Jlr4cs323RPY9Xxnh1fu0jpWJlKQgm/f7OPc16c5OU7qW0spo5r8e05nz6M3CytM+zmgSZwjTrw7pLAZEBdnoGw94KAuFy9DeF6JSy6Cq6N83YOKLATt3amZeSvDaETc+kSW3BuNvw/YTMQtzNXoXpsnUDcXzDl53hPrVHbJ/vkh32tKfMVTeleg8mFRkt0QkU1gesf6xacItS/1OS/mspAvbd2sm30rZucMht2qJi4rOPkNmR5PkLdMvKpIQmgc9pl/qo0YpztDi9hVeNyUJNeUrCamvmH2+R2t/ltbxlCO/3ubGpyuUPzuJGVf0ZyyFq7D450NWngxx+xDWhAB2RoI2daJx+4I+UDCYtGw9PsniHyTU7lC4AxiVhSvxOkL+dg4ZnI4m3ILuvMLrO7h9xXDSEK73GE1mmXlFSOJRGYI6xIdiPn7oLI89eJGfKDT+TbffX7w5A8l9e7NahCwvD2gvuQQ1mDwV0z6SUr6ccP1TGVJfcsTVp1xUIunC2OUEq+QhhnVhh4fjio2HAlAw8Zaw2s4Qcuspa48FuD1L0DQEDSml5dclr05CRfG8Q/fuOVZ/QNM+aDC+ojvrEuwovJ4l3FT0FiwTbxqMa0UgdAM2njAMJiWijr8sUK91OCUuGu47fpU0tPQnHbqzPrkVy6goQqb+tKV2h8OoosjUDW7fMpxOpFrS9hiVRbxUviClx/6kx/zXehQuuVz4J0cJ2gbjKVp7NZ0DCUEdxs9FJBlN4aZEyqBpKV8esvjlmNY+n/FzMZlawtpjGVRiqN2hyK8ljMaEpHK+XoZHm7T2OyQzEStPeQwnFPPf6LHny0OKVy3DqqU756OMoEmvK05k+uWIzsF0V2shLH3+lZD2Xs34e5at+zzWH83htxStQ5bmIdj/W4b+/zUtm/deTVQG6ypufmuRaGxXE/GibP7mHQn7P7sKFgZ7YuKCy6gsETNc17hDyG4brAPDspZN2TAUrsPYe7viqGIq4qK8KEiTvEf3YInGccvSF3sMKw7R8T5RQdObcdh8IEd7r0L3NSsfraAj6E9q/LYFIynsqOyRX7YELUvtqIeOpVqkrKRqfldEb8ZVVN4TzYWODePvxYyfGRLUhYtKM0Icz3xT3dKZzH9zQHtJk1+1+E3NxmNl+pMuGw+Ko+nvSXjwp0/x6SPv8L/Ovfpv7ADgA+IEkoJlNCay3XDH0Nqfwe9YSjdiUl9TPO/Qn3AwnqU/5dCfViTTEeuPOvQnXfpVB79jMYFl8z5PpJkjyG5YgjqsPyUqN7dvqR8T8KOsbHgsxFnFqKSYejMit5Ey/XIbgPJ5hSkmbN2nqd2fMJg26FgWvzNUrH8yoXwJxs7uSpl7Gp0ovI6lP6OIc4rcsoOaHPHOywdx5vv0pyW/i/OKxlGBnPllRemyIclKfdpqYfxLV1OmXlIkWcuwKjnq5BuGrScStk7mKCwbWgdh7SloLbnCcfSFSK0d9ck0UvozQkB5Xbj+qQwbDwaoFHqTLlHRIb9iGSyWKFyH5n6P7KahfoeiemZIb7XA3Dc6lF4LMB4UrxuWP5pj4+GQ5mFgdojVivaSpnFECxRfiPG6CfPPWLI7IiZKQoG55Usp9aOawf6RMOtnYtTkiNJl2L4rQ39GVKHflv1uPBgy9WrMzF0bVM5Ydk7I38ffcLj0C7NkGin5Cx5xThFuWZIsor1ILXFWkIlxETSz5DAcVzQ+MsDrQP6qS7htaDwSSTntPo/GYYc9X06o3ZETB3YlJMmIbqN4M8WJoHhZE5Usw0nD1Gtdth8wzH8jIpmJaC+67DyYEjQN/VlDVNBsPCJlRPb2dsuTUs5tHtRMnLL0pzzSQNNeCmgdT8muKWZeFofQOCgKxNyqYvuukDSA9l7Fvt9aJcnK+o0nYvpTCq/p8AOl8/xPM2/9K/trK+2x9yt/7X333wfCCeiRIrumaH5oQPFan/odFr9r6E261I86pJndCH1F44ws4RbM/6mDM9jV2yfQOAKTbxrmvjXEGUDxRspgQhEVYPIlReVMF+sIsTX5VoKOhTPoz1jyaylWQ2vJwxmmrD5VpHHYpTej2POHivIFmP6mw9Rr0F5ycIaSQ098zcdqqLzbpj+jyF/X7Pl8C4C9v71Cb8HIYrqWQS32iPoe2U0hk5xIJKjGh6gAvRl5FZWzFr9jcfvQmXdo79Fk1xWZGpQvicgms+yRX0sZjimqpy0Tr2m6SxL5Jt6Eqdd66AS6sw65VUMSCuxNqjF6V99vPEh9WaCb93lMfW0NZcHvGirvWZY/HFB9Q7P691LKVyKyG4qtexVeB8YuJuhEMfs5j86iItwWmW4SKiZedImKHlFes/aYxviSYikDQSuleM1S/ZZPGloahzzcyyFWSeT2mxDWDUFNiLXSlRR3kLL+zjRhLaVyTq6TaRqMZ1l/VKLgcEwzmJS14HcsufWYqKgYP2OJyoo4p0WdaWDqTwKKN1Im3o6oH1dMPSPVmcVnOpQvp/SmPcpXRnQXFGPnxZkD7JxwKF4XR12+CFOvWGp35MjdcBhMehz6tSHdRRG3dRYcxs4puvOKhWdTvC4s/S+a1j5N4bJDf8aQqYmOo36HYlARMVX2pkNvwbL8dEC4Y0izlqBpyW2kjMqQXbeULxou/vVZKcPWDIf/8RC3D5U7t9nnb33X/fUzl36cT5549/3337/n/fz/ySRXsuRfzrL2RJ7sukghuwuKyvlUYPXRlCQLlbMDmidHOENL8ZrU9OsnLEtfHJDZjlh7JMPs1+p4vZRMzZJbE+Z962SB1FfoGBqHXTp7NBOnYrLriuUfS+lPSS5+7ScV3X2JMLtZy9a9Aut6MxqsJbduKF4XDXhUFDVi80iBwk2J1hf/8wDrwLWfnr8lfoqqKfcurOBt+vRn7K1aelSyZDcs1oOpNwdMnEpo7dNsPZJSfWdA+2iMdWRjjJ8dika9r/B60FpysBp27lY0D0Owo2kfMOgUtk7m6CxJbTi/FuF3LNW3uxTOiEQ4DRSZhqQQQcPiDuHKz81RfbtPuD7AiaBwXcQwo3Mlmgd9/LYltyaS1dWnNLkVS3fWYeEfvITxFEt/VEenIuLZvN9jMKGZ/0Z6ixWP84o47zCYULhDy8wLltGYNDdNvNkiziry6ymF8/VbjH/jsEN7KWD/5zpERYdBVWM1jIoar6NJ8ob8WkphJRXeowu59Yjlj/joyJIEorFIPai+m1K+JP0MxoWNB3yiqd2qS1HRW8gS/Xyd9pLi+l+TdbP5REpuxbLylEvpiqF2XNbGYFLd0qqMxi3tJc2FvxmirBCOysD4uz0yNUvtmEdnr+Hyj2dIMyLPNqWE3rwlLlrmvxbhxFKByOxIr8fC10a09muiSoo7tGw+qHD70DwmhHJuWUjk+mGH9ceKxEXoDgMeCLzvur+aw5Bnn7n3ffffB8IJpBnFYErKdOGWxetY/I5h6s2Y+hFh/sfOaOafaVI7HpK9FHD9h2vUpgkAACAASURBVBU6kV4CPVK0DoSsPhEydjGldnKM1pJH6WpEdjsl3I5pHUuZerVF47gwriDs+tTrHSaf9fDbELRTlj4HxQsufhuq71gq51J6M5rspmHzISWqw5MSuYs3EnYeTBmNicY7f9OSfydD+XLE3HMDKu9KFHE6Dq+e3Y/bUUTTMf1pWXheT6FSS+Ws4cYnMvRmHEZVw9QLms6egOI5DyeC5gGNcRTdOUWmLmgmyQmJVLoAi18eMHkqRqUCIavvDtn7hSHF5Vg+9+k2Nz9eQMcw+8KQsGbozgk8jvOKUcWy73M1Vp7OElUytPZqBlXF9MttcquK1pGUUVnRWRJuxW9qGndII8/W33gELKx+rCI6/FCi9dilmK175P79rkS0QUXEUI3DmlFJ76pDFed/MU/9LkNvyuH8rxQId4xwAlq6LC/+XI61pw3FGwnFm+ZW5+OeLxk2HlE4I0PQFAe/8VDA5BsGv2upnTRktw3tg8IN6NTSXTR0Zx32fKFO9ppH4wiUrscYB9TvVylfMox/NQPA1PMO46fbpDnhi7IbCq/lEDQs9WMOTgS5ZUWmZtEdF6sgzlsmTw1o78tSvJkQF8FvaEqXNPkbopNwtz0yO4qJtwzXf9glzkFhNSHJKfJrhmHVw3hQuOwSFRTlcwq/bfEbmu5SgtWQ2zQ4EXT3GHIP7vDrd//uv7KvXhwaDvzeL5L/H4q3unC/m30gnIBFIOq3IZvflQi88gMOE6dilIHslsF6DpWzAwZThpnnRC/v9aBwQwgjdwjdOYd4t9W1edBn5WnNjY8HBNsOcSlDZlszKsOwauhPefQWsrQOiE67P+7QPOijE2gdS0kDRWdBug8HVY0zUARvXGL2ecvYpYTGYZfZr0suPJhQZGspQdPS2uuz9lhIez9MvRYB4LQdijcM5bd8xi4muENBAXFOCbG2m79mtjWtA1pKnispbldy8Z27AkpXDUkG+rPCIcQF6ba7+fGQJKspXtWMXTK0lgK27guJcw7tJZ/0TInMjrQFd+d8shsxfmtXoDSEsXOWaCJH+ZJh4yHpagualtqdBXRiWfySwR3A1GsQbolCLahpshuW/oyQglFRzlW+AKWrhuUPOxRuWlr7JUdPfVHeBa0U64iQavqVmOrphPxVF5tPiAugt3yG45rBXILXkc07/qbGrzls3+WSWxlQu1PQS2fOZeJNWTP5VYNxpemrtd/BiSyVU5pBRVN929I6KO+3eEWR5GD5ExWS0JKpKZr7PHrT0igUFSS4lK7FlC/2uPaZIuGaw849isq5Ec5QSOfkWA93YOgtWMqXRhSuacJNhXUszf0ZnMhy86MOXlvI7f6UxR0KWrGLAxHAHXCYf1ac5vrDDmMXIkGC92qSrHBYo7L0cRhfUrHMhks0Blv3abpLKfvuXOXn9r3ME+K3+Pmbj/OVfsDeL/3H/NXf/Zuk+ZTm/oDKe+8vBfhgOAEH9EhaTVMPNp4WRV7poqI759LeL4Rc81COrfuyhBuazoJm4yeHWM2tNmMdCdwajUH1nQ7lSxFeR+P1FKUrhp0TAXFBNl/5gghz+hOa8TPprTbk7rxl5tlNpl6UHLN9NBby8LE2E6cMV3/5DowLnXmXws2UoJmIom3bEuxEDCuKzl6Ye75Pdl1RP+JLKe0ly9bDIhJyhhJFjQvFmwnN/Q7J7IjeLPQXErJr0gnX2ufQOpoydqZN4WZKa5+meiZm+pVYWmwNTLwd4zeFcbYKRgV165n2JyXa7v+N63Qe65PZsdRPKHbuDChdG+E/ucOoDL3pXWLqgKZ8weC3Idwx6Fj+rZ3wyNQMmw99W45qya5Jvhw0pOxmtaWz19CfVtSPCT8yHFPMvJSgU6m1G0+EP6XLUhJtHPJo73FJsjD+gk9/QbiZqADlmTa9Bwb0Z0T4ZRyonEtZ/nCO2RdEyJVpGvLLI1aeculNayoXYvqz4ig3H5A8W9Sl4lRrj0pACRoWryOy2t6cYViVKoayCOkcKDbv87n58QKTb8pzyGwrmgd9UCI6y76cY1TUBDXFjR8MyG4ZBjMGkzXU7jEMKhp3oOgcFd3Ety1TN5h6QFSUtbD+lyM6eyBTVzT3+wynUvY8uELlPVFoFpalya1ydnRrnRlPSpJ6fMRqo8SRYA2Az7YnefWLJ/jPXvtJMsseXk/h1VzSULHz/tnAB8MJ6AQmTseMnVW0D8Kh3xjRm3KJymqXrbe0F122HrFktwxJ1lI9HRG8kWf7wRQdQfX0CCeyuF3werB1f4HejHT2+S1h3f22RUeKTFM6Clv7pK+7s+DgdsE6iuy6YrB3jCRQDCuKqecdgqYlfKZAVNAEddi+R+8ytQ7XflgT5xTNOwzNQyEA2RMNrn8qpHk8IdOwmP0DejMOwaZDfk0GVkRFMJ6ieUDknt7NgIWvj6icckiywnaPypbMhkP9RImgkeAOYetej86Ci9tyyK1A7biHOwR3IBAapFTm9i31e1I6e+Dy/1zFuRZiXVh4JpIodDAg89sVrAtuX/J/vwXFa1LBcAcSrd2hYVQRKa0zlHJa8wjk1xMGU4apNwcUroqjrb4NlXMJ/i40z24Zmgc84lDIx+ympX7YIyoqVj8kUlrjsYtqFP6Og61GpHd2Sa0imxPSa+4bMeNnLM2DUu9f+ZQ4lOLZOjt3heRvShCoH/YoXtKE25bSJShdM7gDKbn5LUV4xScqSQpkfBFqVc4opl5PRCiVCGncXZQ+/HDLsnWfMPTd/QmZuiHNWGa+4eAOLNXTXboHEtyeqPnCTU2w6ZJbdsg0pYSs+g47dyvGLlg2H5HIvvAVy8zL0nOQeyWL21fkVg2t4ymFKw71P5hn+7GY+mGf1FeUr0R0533CLVFTBjVF4weGKOC/vOMZ/scbH+e+N3+cv/+lH6Hy2AbqRkiSt+z5/RVyK2oX8f0FNBD921gayAvMbqXMPp+w9lQBnUBUkF7/b7+g2a/vTpwJLc39PvPP1PFrDk4M2/cEFG/IRvE6Fr9taR3Q6ESIR2Vg535hajcf0Ozcqai+M2JQlZJempHJP9EY7Nzl0zgueawTi/f+du/32KWYcFMIp3DLMv+swMTieQedQG9viv9HY0y8achfdVGpJfdKlsk3uphAFtXWSXVrMlJ/Rr6PM1SsPpEhaFvGLgm7PfNSymBfxPaDhsGkaOSND2MXh+RXZHhHkoXhOCSh1MP7s4r+7G7u2XZE6be965y2DBsPBQwmLJmGDEnJ7AAKCqsprWMJ/ZkQv6WoH3VvlRJnXkjJbZjdeQ2K2RdSNu/38JuaUdkj05DuTqvlc+GOJbtjaB7STL/SwYkhty6NQZULMVERVKyIC4q5rzUZlUQXULpsmfjzgMzLeexLY6SvjaFjES9tPWzJrlvSUFF+PaB0NaW/VKa7aImLQsjpRARS1lH0ZqTs2z4gQSEqW4KmpCw62p0YpGFYUSRZTeV8xKCi2XjYQSUw+bJiVFaMnbMUllMmXnFoHnRIM8JpxDnFxkMFctddZr81kilUdbvLHUj6I9WZ3XRkn6Z0zsHr7RKzmwPGzybEeZFp79ytmHxJkdsQ5DH/Zw79WUt2K0Gllu37DbV7DSqBzrEImyr2T2/zD099ggvXZ6ivlsEo1i5PYJVwFWu/lqV5V0waQOnS+++/D4QTCBqG3ryhs+Cw+oRLdl1y7L1/2qY3JaxwYUXq9VZDblkzmIL6XWPSIPJORJyHUdkhyYijyDRSCjekiaV2MpXxWmFKdsMy942E4jVRvs0932c09p06s9+Ahc9vUb4g5TO/ndI4LKWoqCjM98TpIcpAf0pROFsjvFrD+NA8BEd+bYfBhPS1j5+JGY5rCssp1z+VI6grlr7YJ7csss/BtMEZKqrvyAKVsWkWPTKkuznegc+mHPi9EcOyZvkjDnt/d4PubEB/2tJZlH5zvwUbD8sCD2oCXXUK2TVFmk8J1xwWvzKUtCuG/Ioiuz4irEknYlSClU+mVF9z2LnTIb9q6O5NGJVlY4WrPbBQvCJQfeeES7glBGvjkMugKpyKcSEqWmp3WhoHNc4QunuypJ68E+NKc1G4bdn3pyNmXuxz9UdLt0Zr9WaVDNHQ0J82DCelsy7ctix+0TAaU5QvSbVjVNSsPO2Kus6D8XMJrWMJAL1Zy+KvvkThZsLCMxFREby2TCMynjhDZyCIrrsvoTujqR/x8fqW/b+1TVKQErXXg8YxRf5Gn0FVnG6wrVn6k7oIekIYu5jSXvJJQsndlZWhM8aVeQrVdyKahzRxQcjcJIT1xxX1Owosf0I4gvS/b5JdV/RmNOtPGoKOoXZUulFXn3BpHBJOS6XSOp696hNeyLD65T2Y1ZDMDZ/cdZmvMPWSOOkkBzxbIVyW9uk49wFHAuzClfYBS/EqbD9oyNQsNz9RorsHZr7ZYv1Rl6k3DOFWRPFmSrgJ2w8Z+jOKrXt9xt9L8TupzJ0zsPxRh/6UaMiDTZfiDcOBf/rt43cfzHhC7Y6QoCVIIXv/Dv0Ziw19RmOK/LKluV96+3PrhtL1hHDLUjueYfx0B+PB1uMTXPjrMxRupuz/PzZZ+/gUMy92CRopW/d5TL4hXY/5G7L4m4eyREVYe9RFJYIu1p80OEOLE8GopFl90ifJWQZVh6ufCejPSNlx9nmLSg1xTiop1dMSnd2BpXpKCEZ3IOipfkzIvcyqh07g8k95ZHZk2k1nyTCYCtCJOIXFL9apvuCRaQrcHY5pxt4VYq95BDYeKzGY0EQlkbcGdem9mH6pT35FHImMJ1Pkl8EUBHEFTUtnzsEdWjYeF6beayfU7065+pmAq5/J4HdEJi4aeUtvTsZuuXN9Clc17b0wKisahz2KN1K27/alPfxGRPEqlK4YciuWzfsdKqcc6kcdnINdBl/dS2fRZfUpn+yGOKzRPsmrWwc0E6cHhBsKPRIHFuely3TzyQmS0BIVNMMqTJ3c4Pqn8xRvpEy9PmTqjYjm8bJ0prryHPyOEa6klTL+XkpckFmGjWOw8ZBPZhvmn0vIrRuikuLgb8vayV/xGJWh+TvzmN35jVMvaupHHYImBHXF3DdjsjuG/Ipl8lWY/1pE5uEdmVkZQpo1nPtPfp3hhKG7AEEzZVhxmHwrIipIkMhuGgaT77/9PhBOIAk1lbOWmReFMBt/SyJ+krOEG4qr/0ERHSvaCw7d+YDBuMaJZQCl24c9n9+hMyczBCrnhNWf/abA+bgAS3/aQqVw7YeFkEkzluKNmGDDoz+laDw5xB1YOu+Nk9lRXPorRfp3Dkiy4kQ6H+2xfVLY6CRUkjaUA4IG1O5NWfyqSHTXPzJNd8HSPJgjyQp/oGPDqKTJ7hgGVakvOxGiXX/VYAJL9XWHiVcb9BYMpStDwi1F9e1dgU1NNBOtYwnrjyqSySJjF4ZU3rO09zqkgdTuCzcj4pxi5wnJ+XNrMocxvyxTkJb+1NDcH9BbSuVZLjqknqCH5vEytXsNq09DuKluTQYalRVJKM8wzch8AynbiYDFuhrjSYTxursVgIKifErmJmYaQra19jkc/qcD1p8w7NwZ4o0NsQrGTyuCuqVwQ2r5TiRDSLrzPjOfDWgdjyldEeju9i3rj4uuIbOjufGDHs2HpZ7eOgx2X5+gJahh6p9lWDk/hTuQ77P3r16kdC3BDhzivJCa6w+HWAcO/2aD/qKU3UYVRevJIfv/eERvRmNcS+a/KzLzQsL6D8Vc+5RP7Q6f2glFXIDBbEqSUdSPOsQ5aSuuH3YI6rD2sUTmOyKk6NqjLu09st06+/KknqJ8WZBp9fUGuTWRFCeBYu/vrDL+3hCA+lGfxiFpM96+D0YVj8I/LjF4tCuffUNIx9yypngNGgelTbo3JbJ1Zyhakurp9x8o8IFwAjqVjTEqarr7U5xIyld+U1onva4iu27pHEoJ2inZnZT8WoLXlqaM9R+o0jkkg0iigqY7JyosgP58SlIK0Kl47nR3Tlt70aN4clvGin3ep35CUT4P1Xcjlr4Usfg7LqWrCZ29hpnPBjhDRfNkxHBCtOHtPT759ZSxdx2SnEPQkQrDvj/pM6wo0kBRfXfA5b+cQyeWYUn6BGonYOKdiOIlTRIoipeleeryXxkj2NZc/2SG/HpKd9Zh/EsXGM6kNA9pctddDv3GNsNqhsahDL1ZTe/4UGAfsPZ4wNilhMyNgN6hiFFFonz58pDtezXB1oDOXshdc5j9VkL7RMTmh2NG49A8qDn0S2/i9KXcOfV675aAK7Mj5ao0A50FTflqQu0ugfZuL5ZpyY5oPXTy7YnFFr9nWftQKhN0A9D9iOobIu+e+oOQyddE5YmCzh5F5UJKEgqKSUJFGmryl6VeHm5aMk1LuCFOp3I+Yd/nR4y9EGA1FC/Dgb8vlaL6XYbunMuh3+5SuDli5ht1lv+3gyx/DGa+qUkzlt6CzF5sH0pY/sFx8ldcxi4KqlLLGdYeCRlMGSpnLSs/kKNxyGPyWZ/cqqZzJCa3upsa7DgMxxSjA0OcSDGqmFsioj1/pJh8a0R2w9Lc74oStC2drjs/NiDTkMpUmlFc/Ykx+jMKvy3t5bVHZjCuYvxcTG/OkmQtg9mUg7/Tpr2k6f+NJtlv5Sksi/MCQQWDCUV3yTCcEKVqd18icwtS0MkHvESohynRbs5SeVvklVNfucFgStp5J9+KZczSWQevndAfd1j+kEPpsmjn2/sNE69qRmVF6wBMvRkTdCzDcUXlHU0aaJxIWlC9tgz07OyF4H+vkN2QoRlzzyV05xVrj3tc/yGf9h6XtcccsmuaQdWlfB7CKz6VM+KgmkelxGM8RXuPS2/KIdwxNA5nQUHjsGbjwZDcyu58vbqUv8bOiUbfHch4s/YBmY2Q5g1xyTLzckr9sIPXs6z87BEW/0wgely0NO6bYDjmMKwqhuOW0msZvLbcizOC5U9IqTV/zmfuOYkkjUMZlj7fZTidJRoX1WVn3iW87lN5WboN06xl9ZceYOpVYek3Hs6JsvLehDgvMwrKF4WnGJYdqqdkozeO5BmMa6Zejwlrhqgk99GfFidcmOqShFC4YWmeEJIvU09Zf1QxKkldPfUEbeWvdZl421K+YKg/GrH2mJCnXk/mQvamtUz/VXL/Nz+aoTeniPOitbjy3wT0JzTBtkP1jTaXfipPZyFg+Ycqohl42yHJKIK63p3Qa5l4zaF7KEZZaC9JM9DctxIyNUt2TZrZxi6mZOr2lvTa33SZfL3DYN+I/A3L5Jt9nI2AwWwiA2wMt/icG/83c+8ZZOeZnuld7xdOzqlzALqJRBAgwQSC5JDD4Ywmz0gTlFZhg7S1q7K3Vuty7R97xyXbtV6HtWyvaiWPyytrZGlXmtHE1WiYRuQQJAESmciNRuc+fXI+50uvfzyH0JbLlGqtUDx/iEA00Od8b3ie576v+1M2g5KUO4kth8Gkxhxpki/EqT0g4FfliXnuPShMbzagN2Ow/XQYNybE53BDEa4Ia7F4wcH8Wh4vCvUjIogDufZHaprcJYU10yfaCLAyDoOJgEh1TLx6v/X3l1m8Sqm7SqnLSqkLSqm3x7+WU0q9oJS6Nf5v9i/6Ok7WlFnyuiNOvy3N+k8vYs30idQ1u4/ZBLY0VlZ+MkSkFRBuGCS2Hay+IjmeSXtRRailqB6zaS4ZJNdlW1a+JtT0iG9rcteEfZ9chVDTI9TWpO+4uAm5vptD8bZ3Z4UBF61Ik7I3oyhdkK59cssjfVNRecggsS3Q0OSmR2fOoHkQ+pNyDfZikF71SN8JaC5blJ8KxBLalWtz64hH6W1pUmUvG8y8MhYgnR7Sm1F0lj12nrAwHLmloETlOP9vbhPdkytpb14TqRikV3ySN8VTHliw9WyEUEs0C8NSlEHRYt/XfXLXRIZtjmAwIaPE2Jb48pvL0owyB5L5kLlgk1qBUUrRmTMYTbvUj2oMH0ZJg+oJ8bj3ixatfTJC9GLgHu6LX/9yhkhdkzvfILbrMCgqyo9ahOsGiV2f0oUBQUgYkMOJGM0loSlHbocpnZUmXnfaQJvSMOzNaQZF+f5iW4r4tmbqDdmczMsJnIxgwtY/nSZ/SVE7JrTk2lGT5hG5bs/8sIcbFyeo6WjsqjXGtAnNaO0ziu68aAn8EIQbnizgwviknnHo7I8z8ZJNf1KUqqnbojIdlDSDh/rkr7qUH7PJXBdcvgpg7RNhDEd0C+1lmHzLZ+sZi1g1IHNdSNraArsttCC7KwK1UUbK2sIln5UvhnFSJr2fbOHFRCB158tjWKwrNOv4rkfkjQRuVJF+RQ4hgFjlr7cc+LDW+sH/AFbwT4GXtNb3AS+Nf/7nvgxHOu8bHwvRn5Q5fn86IPudGPEdDzcVMPuyQ2IzYOnfOgwzBk46YPfxCHMvdGkd8gjC0uX24jA4PpDGWt4gWpOxmDYUrQPQnTJY/7hJ/aEAPyzyWGvo49uKqVcqhBsQqSmcok/zYfnwvagsjMCSebSTNAksMRb1SiaDvMHms5bISLcUqTsw+9KAUBsqD0n3PLkREN2U/6ezoOg+PiBUl268NYDmQU35cZv4VoCTFkfg1KvCkC+d9wR7nTeoPAxbP7UsN4miXGGl7jMYPtojviXsPXMA8S25Rax/RtPer6gdDVM/bAqxuSF8PDcpG0F8E6Y+tiGb1l2X+I5DZsUVtWRROt35M6LQ68waFM63SK4adGYtwh1flJ5NmSaEL8UINzXFiwG9GcX2R3Ksfj7EKCffS2xXs3fCYOO5KNFqIGXflDD6G0dEOj7Myby/e9DF8MRvMflmQPGCjzXQKC2c/cYBk0hNkGvhunTmI1VZ8Ll3Rd4d2OMgj7imvS9KuCn+BTcuLML0ivQ6tCkQ1Ox1IUu1l2FQtOlN27gpTXLTx2jY9CZlROjFNf2JMbJuMcAaKkLXhBdpdcXnkrk9YuKMCwFMnHXxbUXxnYB+0SR3GcqPyhSqcUQYGn5YfAuBDZGGFsvzpKJ6zCR3WdHab9LvRShe9GjtM8helE2gfj+EWi47T4lL1kkpak+4ZG57hJtitnrf9ff/e+m//+tzwG+Pf/zbwOf/oj9gdwUguvhtUbU1DppE9wzcmKSvzH/fZe/hMNGqx96JqHSpewbRsqY3E2XmZcVgIiC2q8leD4iejzLzqkv7sIc5CkjfCageC1M8Jyd06rZQeFv7bPqzAdtPRkmuDbj5dwqSKuTAzAuK5d/2GTzSB0TSPMyajLKKYVbIwoPi2AWYEhLsYELfuwo274uQv+qQP7krqsYJ416jZua1AdbtKKGmYuKMK138isz5UTBKmsx8a0MszlkDcxDQLwlJ2HQUvTlJLYpUxgKetsbJ+ZjX4nTnFPFNce+19xnM/DBg8k9NrD5050X+G63I5tHcbxE802RYVKTvuNx9ZxbDFYFP7f4I9YMyRTFH0FkENNSOKaJVzdqnMkTqctNqLlm4KTFqZW/60hcYQb9oMPcnHSINzeyLAYkN2H1MrOB2V5G+renMjR1+Gua/W5MbWlcTqQcypqtYNPebdBaFALT1PMTLPqG2pjtlMnFmxDCvKJyTa/goq2k86hJuaNKrQwZT8r0WzkmTM9QLCLVE7djeLw1Qc6SZfLlC/qKoSTtzUjbmL2nCLZ/2PoPl36lJX2fToLPsMyjJIRAfj7MnT0PyrigRA0sx86cdbv1ciDufD7H1cy7xbdEj1D48QptStg5zirkXXdykJnsVOnPWmKspeLVw0ye+LpkbqTuaxI5HuK7JvBKhXzSZenPIYELK6PiWYlAKUTwnAikvpoiuhjA8TeuAUJff7/WX3QQ08AOl1DvjRCGACa31zvjHu8DEX/RFnKRJbC8ApehNyxU8uSbsuWHGpD9hU7zgsP1kiHBLap/Epjx0nTmTaMWh+LYo/pykgD82nreZfknRL8pJPCxoUre7eDEEG74jp0Hmqpwct/6uTeYmxMo+qXVfvOCPR5n5XRsnFzD7imwGw4KIYqJ14dUHFsy+0sMPSZOveNGhsygE5eoDIfbOTYCG7rymdN5h6kdtVv62QeZWQO6axzBnEm77ImhJavYe13QWFbf+gbgQ+5OavYfFfdgvSRmTuaZwUuOO/a6ccpnpNm46YDTp4iZgOCGn89azBuGGD1p8CYOSnIC9GdnIpv87i2hZ05mzSd8UFd8oA5lbDoltKR1QULgQ0J1TmANF8cV1zJFAQJ209CcYW4l3HxP+nulo7B7c+rmYyLo9aagWLmkSGzIfT2w5FC57Y1Cn4sbfywpZaaCpH1UEpnAmE1sBkT1Fa59NbN2kdkRcoL05zc6pMG5Cj0tDsfkWfmSTuz5i6+kodssg3JSRaqRi0Nxv0TykMUYSb5deldShnedL9EsShRZqjR9upQhCoiG59o/SVE96Y3m4SeJkRUZ0YUHclR8XwM1gQtO4z2L76STRQp/SWci8GJWmow8z37RpLxqU3pEmYnvBpvS2GJSGeSlFJt5s0ZkP0Zu00IZIrFWg2TkpP2/vl022diRCYk0+/+78GGeWMqg/5JNcl3FlZ8YivqnI3vDed/39ZTeBp7TWJ4BPAL+ilPrQf/ibWgCG/59tSaXULyul3lZKve0PengRRe3+KOEm5P/3N6gfVUy91iTcGmf1GYr4lpBaIk2ZDkSrHlOvtagejbL7oYDerKZwro0XVcy84pG82x8LTyS5pnkoQfG8Ix+uDa0DIrH1YorQto0fkgewuWQS2/MYFjSxO02mXw1Y+VKEUVoiydpLYsON7UhSzcbzcQJL6u/6wRDRPSVI8CSkb8Pstzbxkz6DvEXzUILZb5qUnwpY/ySMsgb9okliS7IK0jdkxJS+CbE9n2hZSD+hlmLydaH5jvKKhW/XKFz0CUxF7ZGAeNghd6iGmXQZ7HeIbksSUGLdYOeUXLVTdwOyV6E7J9ZaP6zozUYZFhThttSuew+HpfZNiTQ2VvZQvhhWlv7NFpE6rPzSApGaJnO9S6gt7EF3YUTngEe4q4kJQQAAIABJREFUoTA82WBTa0OSt01mXu7QmZVwDCepiFY9Unc9dp4I0zggTrnUiia5KvVwd9pk6rRHd8akvV+x97jkOxqulptSPiBzO2DhuwMKlz32fatDZy5MuBWw95wzTn+yiG9r/Jhm+tUOo7QitSZqvIm3BPPlh8dEpIGYjwZTGm0qRlkoXvJEJWrIBnL4f6hhDAQFl7saEPtXGcJtoUj1CwbLX+tQOW5Tekd6FMkNn8LXYngRRfVJ2ZjbCyadGVEkNpeFPynvu3ARkxsB8S0oP5EmVpHO/+LvbxPb6oslfcplMKHw0pJgFFgwLMoJX7igMRz5vuKrEkiy95DBKCcj5Phq+30X8V8ZaFQp9RWgC/wS8KzWekcpNQX8UGt98M/7s/HCnJ77B7+K3YPElk/1QYP8ZdnZvLAsUjcu2XXvxWwFlii/hnmDzmJA9qpowr0o9PZ5RDctEpv6HtO9+hCYfVn8dleRvhPcuzUkNh22fsVltB1n8XseW08Ld3/yR3V2P5S7F+jYXfSJbZkkNgNx+o3DSOPbGietSGwEDHOGKMNisPiNOv35FJ05KSOcjDSkRhlNYkM4Ab2SSWbFYe2zJqU3JGSFQFN5MEx8J2BQMLCG+p6qsbOgmHzLxXACdk6FGU346IjPP3vy2/xiao/f72T5dvVBrlQmcc9liW9pYTgajEsBj+1nxhTfoXzN1JqH3fPwbYPN50Jkbgri3epIrNkoC4P9DrGVEKE2pFdcWvtsmiccQjs22eua1ud7OBtxrL40Z0MtTeO4TG2iNY/mfpvuQoC2IHdR4cUV5kBTerNO84EsTkKuyMk1Kceazw1JvxphUFQUrniEmh4rv6DIvRGieUiTvCu5g5NnHQg0g3/ShP+riOFDqOXRL9l0FmUU2D3gkr5kk393xDBv4cbFUDTMKey+TJHmv1Pj9s/myF6THojdlXURaQQElsIeBGw/JeVX9pqmdlyu8nsnQpL0NGdIktGaIOIqJyAoOmRfDzOYUAz2ORBA5kKIzr4A5Y4zG1dlmhLbE1+B4UJq3ae5JL2O9j6ZHhiOZET2Jk06CyKqazzgk5lpM3Rswq8lSW74JG612H4+J2sjKyWkAFM1F3/jn/zVxpAppeJKqeR7PwY+BlxB4sZ+Yfy//QLwrb/oa/nhP0vUDXUC/LCmN2HQXjDFajvODQi1IHtjhN0TmIibkBM3uWoQaQbEd3z6sz6RXZEeNw/JtTiwFPF1oRR7GZ+ZH/YlsDKQxtEoZ+OtJEjdNmgv2Ey+5TMswdpnc0Rqcm2zOxq7aVA65xDfdsncCCi94+ImRc8NMCgaZG85TJwZkr/is/nxHPUjlgRGNoT115/U5N/VNI4F1I6YNI/LiCpcMdl7QrP7WIjWUoj8uy7dWdlQnJQiWta0l6B03mP9kwaDks1wyuNnnjzNs/ff4IuJdQC23Sxn7i4CMJz0iLQC6kc1jaMB8V2X6jGbSEVReidgVPTJrLis/YSmuT9C5cEwybsyc7Y6SvT+SQi1YfJF2VS1gt2TNuZIE9qxKV4MaN1ncHhilyAm9XekNj6R7pp05pWEhc5o0jeVOEAXhfhkutA4nqV5n0FnHxQvaHrT8utTfxhCBTD3Ypf2vEXjYJjwehi7J6KyxJZPak3SjPuTNv3vT2D4sPOMZuPnfQxfC/hkyWP6BwbWQLPzRJjujJjGetOKcEuT2PQwXNh6Ps/kGZ+9J2WMmtzwhDL98w3St3v0CybRsuDjtCmz996kjZPSuDFB0yXWRQHamTPwMx5T35Wg3GHJJ3YrROlPbdr7A4pvw9QbPsk12QBQ0F4S1uXU6x0GeYPCJYfWMhQvBhTPa0ZzjrhNY6KpAZlI9Ich3LsJctcdnITB3qmshNXMSXLy8OfqtA95tA789egEJoAfKaUuAmeA72mtvw/8c+CjSqlbwPPjn/+5LwnNHEstD9gkV4WTl7/ikLnt4EUVo6x0Z+uHw1hDjZeA+rGA+LpBvCykXv9v15j/fgCBjL/MoSKxahIre3hxiG0bRDcs9h6OUTkht4BIVbP3kMHS17tYfen27j1iMZx1cI/0aS0ZxHYDOvth+kcug4LF9ofCuAlF/bBNakX+fietidQCutM2taMRulPygb338qJqjMLW7D2ssBsGcy/1Ce/aNO4LkVrRhMsm068PMVyoPWDfi/u2BtD6mPQkAlOh4x7hlk/ptMnvvnWSs9vz/FbzCL/byfO93aN8ePkmzsUsZt/ASRgc/p93SN8wMUc+dgcyKx69SZPcBYPyIyEW/2Ac9z2CcFvMV9mbktLjpjTtAz67H5IOeu6Gg+GJNsHw5CpqOHDh0n7yb5vEykKEei+W3Y9qqg+YlM7KVdyPQOGSYMeVLxMP5UlSkRuTbMfurKJ2xCTc0mw9m6A/OQ5yWdHYfU10z2GQN2gcUoRaHnsnNaOcdNqzFw0yr0So36+oH9MoV7H3qASSukkJF+ksKGJlKS0rD9oktgLy1xyav9ghc8kSDsI+GzeuUd/Kc+fHEyJgCsP0qyP2nnHJXhPDmR+Tm0Tt8HvUqDF74RWL7rTJsKSJr0sZobQmsSZp0k7CYJiTyUJyTWN1FYOigR+zxI4+J6VFa9GkuWQw+YIlzdD7XIrnAkJtzWBKNAfpW1B+RLDl9Sccsjf62B35TFP/W4pQ1cTqvX9j8AOROxCdmtOHP/uPUb5EgA/yBk5KIplHKRlHDWbiNJdEa231IXvbo3pUGiWpu5rurMxxw42AxiFF4bIm3PS4+zOa9JkwwyLMvDq8FzHVmxbJ8XsEm0hVmG07zwbMvKBkDJmRvIH4uiJ916V+2BbHYVicenZbUbjs0Zkz76Xbzr7coz8VofyoQXxbItKmX1YMs7Lftp8dkHwtSmpdUnUDW4QpgS2zajepmHxrwPapKLGyJr7jMcybmCPpVHsxg1HSFIVZS9N+ZoDXsclctGnd72NkR4Suxu4FcIQb4i3ozSoKF31J3KkrJt7qc/ezUZb+XYfuQpzY7oiVL0RI3THoT2oyNxFnXFuSlNOrPjtPKYpvS2bhzikLw1UMZ1wiG7Z01feNOX5nfTF+lcbjulnIXB87HnOK0jmH5lKI7rxm6k3pa+x+YUTkYgw3Ic+jtuTvz72rGRQNUuuCT7d6ohconQ0kXGNPk7vYpnkkSXJzxN6DUbK3XWkoTxrkrzjU7g9JGG01ILbVZ1SI0Dgg2K/kHXEw5q4FtPbLTa+9YGP1BRsWbkDzqEfugozYAlsxLMLEWy7dWYv8xS63fypO6rZB5o7Lxs+7hK/EJOQ2LO9j8wBoW4C0w6yiN6uZOKsZpaTMNTzI3nLYeUJ8BqM8xDc1xR+V2XtWGsuSECXlbmpVUzuuiW9INLyTUIRbciOLVCG96tKdthjmpQTNXIfOvOLmf/Wrf6OpxP9RL3MoSa0qEIZ6qCPKs+60LK7BdJy9B21mvrtNpApz39ql/IiQckvnZIYe29E4Kdj7qIsf1QzyCj9kkDwfZpSF6ddGbD8lxJfunMJ5UKSxxfMew2mXUQ5qRxXpqxa7pxShnnAA3YwvuoWSQERQ8jAXzwXEdzRbH5YPwovCcHmENhTN+0xyV0VwkrkyTjxKiJTYr0SIlwPcuElsW7H4HUe63zUZNRGIys/wIL06wosbVB8CJ2kQ2erQnrPECbcrD3Uh2yG+KvJao2+QeCPGYGmE1ZP5d6Qust7MDTEeRXflRGgcjAoQ41MpvIhi89kY+UuS1Jxcg71TY3XhnIU1gPohk9JZ6CwY7Dwh6ULmEAqnLVDS2RayjowBE1s+g3kXuyduRielmHi5zCgfsPZZaYqVzmnMQcD2szD7NZvkhmDBp970yF2RJmBrySC56bP5CWne2V1N/pKmeswQkIyn2TuZor1osPKlEHZP050Sj4fyxBben5bsyNr9JuXHk6x9SfIcU7clqKZ40aMza2C3hdLcm1bUjyqu/spv0F4OCDVM4ns+3QWZLBUuyiZo9zT1owniWwbhllCZ7BsxyYvIBvhRERxZfYmf6yzI1T9zE3Y+5dCbUUy93kYFmtWfhFHBJ7UuKsJQT7P1qcmx5VwRqwZYvfHodUqRWlFEGoJrbx71aO+XVKrurCZ2+jbxHQmlDdfl2cvefP8YMvMrX/nK38hC//Nev/Yv/+VXFvKPUT+imHuhzcYnwoRaCiOAUQ7QBm5KMZpIYA2h/lCShW81GExH2XtMMSgqwi3wowq7YjGa9MAX77bhya/7tom2ZOfNXfMwd8M4GYXSwqo3HRkxjvKa+JZBatWhs2iBVky93gPDxO4H1L4wJLwSAqUId4Rf51vjkImOhT0wCLegOyOCkkhdgiP7s9Cf80nfMnFS8tC4CQMnKfFaiR0fbShiFel39KcUnXmLQVEyB4cF8KNRFNI/6c4rAtugv5cQGMiGR+STVXK/r3CiUQYlzbAopF1rCIMJYxzFbhCpixAmsyIbT7gh2v/CpQHbT9toQ5G8qxhlpRmb2Bb3mzmSW5gfVTjZgMieQXcRDE/hR8QIZPXkPa0/AMUzJvWjkLktUNb6gwmKFwOyVwM685a4PJFr8TArII4grKicMHDHSVLWSMq6ydc9BkWLiTMdDE8xmJDsx+48pNalqx/fUveAsSgR24wy4mw0xsat5jGf/BkJCdWW8BX9sEliRxZJctMnf7GHHwnxO994GGNkUnrHYVCwIVAEYUVv2iC2B3YfWvsNolUNSuzjU6eHdBYsctcEhKu0lKbBY21+8uk3eGswy2DBJ/FuGC+hCUJh7L6mcF7jhS0CU8aS8R0Z8baXDJIfLpP6Qx8nE6Y7D7M/HNKftCmca5PcAjcWYjDtE4QU4aaCXJ6dL42wd2zyV1y8mEGoq9m49sLOV77yld/6f6+/D8RNwO5JQyl3VVN9KEXhvAhgIvXgXq8ge90nWpfTYJjXbH4iR7Tqk1pRRCvy4ffmPaJPV9m/VBbAx5RB4xD07h8S3/UkTSY8TijOCsBBBRIKkb7jkloLSN+G7pws3Pi2dGH3Hkmw+REDbSjMSwnCTT3WAZhMviZNotRdn8GUR/2ISfWYIr3q40fB8DW5az1CLUWkLKM6wYXLWz+YkFn7KGMQqQd05qUUcjIBhgeROiQ2QHlyIjQPCrjCTQj00/Ag3AqoHbYYfmeC3ZNx4tsBqVWwO4qZVwfYXTGudKdN4mVxM86+7DAoCCdw70Meia2ArWdjLPzJECcjJc97E4X6EUX/wIjaQwHNw/JZ5M8bpO969+bfuXclVDN3YyiswWsK3xZz1O4pUXOm1gLaiyZezKD32IDYrhaO/jcHaAuSa0M6C+L8U76cenYbOouK3pRYojc+mmLj+RBeVIC0uauixw9MaD47HBuRFM1DmvJJeb76k4p+SW5iufMyokNDe39ArCwjwfphY8yLsFj9fILMbYfdk4ruoqZ+JMwwKzLt9rJ4JIZ5RfW4InM7IL7rU3nSQwVQfjTCMCeTrdrP9mgeFDfiYr7OPyteZfVzv8XZj/063ftHTL8m5OLM9Q6DnEVvJiBW8bEGcvNTgXhBaq04jftTGL4ErA6Kkmp85z+zKD8SIbPiS+9rR0rS7s+0iFyMYQ2h/Ji8b63Fv1nF4H/0y4sLfbazIOMwaxDQOgCVEzD1apNhXghBrf0miW0PLx2QveWx/hk5YdyEXI/NgcFCus7npy7iJjWjnGCmln/Tp3rcJtTyyN3wsLviu+/MiyqxcdCgM28TWIrqoz6ZmzDMWzQPyAOU2BY3XP2gTXo1oLMowZSpVemWvxcYOvWqQeGyh91VbD2nxVseV6x+Nj7WoUtt54dErPMex08bMMhLNn10T0I0D3y1SWBD4UJfPP8/GNJeDph6Xeb5B399k8DS5K94YrLZE+S5pBqL98HuwZ2fCNM8KDp0q6/pThuMsprqA2H8sHgYCqdlVu9HNLd/2sbqyQza6kH+qsvciyPS58NEyibpG4p+SW4vzWWLSEV6MdXjinBTU34kSuaOS6wiwSeZmxBEZPMuf1wAH+15k/iZKIYnGvmdJ6WHUX4kRuaGNBrtjozFYpUAw4Hy0wHmSOMlNNnrcmDUnnSFY5ARNWb+TyJEK45AWu8a976PcB2ytzy6CwGNBwJ6szIaLJ6D3NUR6RXxlLgpmDzjMv0jT07aCzD5ZkC0KhOi9ErAga82JfPRlJKwvSA6j/ybFuGGJn/VJXNDHLGpP0qQuypBpyP/zxL/Cmac/I9CdGYt+rM+9QdS7D3pk75hUD9s4aSEedBcNshf8yh+PUr5WZ9o1bunEPRDCutqnMwdn51TimFBnunkuiby9QyxsmaUFgl2b0p+//1eH4jGYLwwpyf/6T8mf1Ee8GFOAJnKF3WbNqW+DmyFOZRYKz8kv+7FoHjBo7lkydRg7PayBjLWay9Lg6ZwQYQqIHXdMG8w+UaHtU8khfqblF00sSkEX1FwaeyuGod/Qn9CE6kqJs722HomTn+/S+lVi8rJgOKbBvEdh9WfhdjNMPmrHs1lubJmb7pUj9rMf32LG78yRWLdoDsfkLmhKL1aYeVvFYnURKj03sna2Q9O3ie+KpJcNx0w+4Kmdr98zWFROsqZ2wFuVObuXnTMrm8HuHGD/oSicMWl/KhNpCLvVeGSw9YzNuZIaubCFY/N5wymXxt38c95RKoOrf1RUqsDmgeijDKK3DWXtc8qZl5UuDEDpcVOnF4Zsvq5MH7aJ3fWor0ss+/unHD9CldcWgu2dOIfgdxlUYVmbge09hmEm+IB0Ar2HjWwxu/35Ft9unMRBgXhOQ6LmtwVCevce9jAWxwSuxgl1NJC4u2O5+xjdJg50nTnJT8hveqy8ZxNYlPCZuy21ObDYoDdMnAyAYXzikFJwKOpOwaxsk/1mMH06x7NJZvenIiiMlcsChf6+BGTrQ+HcLI+uYsmobb8/f1JxWjG4fD/1KbxYA67F1B+zMSZcPnDj/wGv777PG+uLcJqnMAWjwBZB3stfO9ItjuiF1Ce0IsiVT3ObZAp2tQX7lL/P+Yl6LQk0vpoWZBx3WkT6/kqwzcKIsE/FlB42yAw4fxX/4p1An/Vr2hZ0VoWG7FINzUTrzWI1DWjvMydY3s+9kBGWCCsNT+qWf+09A5iFVFrvbcB9GYVXiKgdFbcd6GOJrPikjtboXXYo3EoQWJD8NWGIwkve0/4OEnNxFt9zJFYVb2YNC8jNUV6zcNJhzAdpCO/LPl0XhQqJ8LkXw/hpmWBZG94FC4NsXrCy68/McXEGVmMQURktNs/VgIFblyaa7GK2KMXv9Oj+OYYU34DdNSnelQkvvHtAKurmHhH8gS9mEwrhscG9GYU3WmTUFf4/JXjtvDwk6Kr3zsRIr4tiyV7K6C5ZJG9qu6NIndPmuycimEPAtY+FRV011WX3pTF4jcD3JhB/p0avWmD9MqQ0J0yhqsw4xKUAtCble7+3PfqdKcshgWoHVdkr0hzzElLIzjUEmHOIG/QOGjiJX0KV3xGWc320zF8W5FedfFi42yJJYOtzwsdKXwtSvaWzL/1ONA2sKRRaHflGfHDeswRtIjUZBEZroS3JDYDEmsGkZo0CPdO+bgnO2SuSzRd/bBJahXKj9pC/b0DxlA2pMpDMcqPhln6WhXDMQh1RNLtpAQ5nrgeYufDBcqnNK1FySMIlW2+/M3/lNffPILbDZG8Kwh3w1FYW2Fy1zTJu+PFoKF/YiAj7IrGDymSGz6Z24EAbv/VHG5MbjmxsnyfSgtqfeJsj87lvODopxQzL0F3RmEPPuA8AW1I13fmT4dMnx4Sq0i098ancrT3QeltiQzzIgbdWYNQL2DqdIf8m7Z8EEOJkO7MSEJxEEJmxD7kzxsktqVrrwJN9ZjN3Z+c4Mh/s0VyY8Toc03ai6IZqB/TlN4wCbUUlRMxMrck1KI/J1OB9jGHjY8jBN2kXNVz1wKie4r+tIzs7L4egyVNhlmT9Y9LBsB7UIfutBiFkrdMdk9C/spITsx3PQxH4q7iW4rNDyeoPObjJBVOQqH6JtOnh5IwdEoIOuVHbKLrLVEtbir2/WsY7htJ3Fo3IL4VMCxIbyFaltiz+I7G6mnSqwHNZUNy+palHEHDwveHpO76jJIGsW1pDm4+ZxFuB9SOhrBGmu59GdCw/vEIrSfmQEP6h1Ga9wdMvhHgTAqMVWlNuC0+j+WvNejsh0hNQjz6E4rmAx6Z2wGNJxy5MV0yaRwQybDEpMH6J+T9GpU8Yjua4kthlK/IrAiG3l7oCYUqpsje8uhPK0Y5yUdM3xIp9yglC9s53pPn4/kG1QcFIBvqaBI7Pvu+7jP/348t3od8AltupeG6lIGBJSEgkZpMobQJK3+rwOTrmsoJcRGaQyhcDOjt84nv+qRumAyLUr6kViBIeUy/qomshzBc2H4uIFxXmMvdsZw6wMn6WH0JcPWiinA7EOVsROGHFH4Idk5JOWMNACVajHAzILqnaS3HSN2B2I4if8WnM2fix8TL8X6vD0Q5EJ2c00s/96sAdA645M9YZG8O2T0ZJbYrJh0vqjB8TfGdDs2DCTn9JgTuqJXw7JoHNbkrwnwbFKTr7GQDgqgmsSKZhrMvdth9InkP/mCOxF0XasmIyBrKlbx4ts3qF1KkVpCs+6sSTT1KG3TnNRNvB+w9bJC5IYo+c6hJrXtiKR6JsKX5qR7mlQTDko9OeMRuCuEo/67L2mcUUz802HsUEmvSufciiviux8bzJpnrYql2owZ+SDTi2Rs+1QdM0isBybUhvdkImXMVbvzDIplr47SjkZQTjcPgzw8J3Y4ynPQonTbpLIxxYXmP1DWbzG2PUcYgseVgdV3WfyxJ7poIr6yRmHimfuSz/mmYftnA7vq09tsMivK5pW+LXLo/MW7QOZr2okl3Xjrt2auK1n1SeweWovqQJrZlyARmQz5PFUDtIR+V8Jj/PZPdkzbG/W2S307i29A6CHZLxseZlYDtDwcYI0NyDYqaibM+9UMWfkSaaKYDnSUPFSistkFyTVx5gfXerF1TuKzZeRKKb8uiGkyI739QVEz/qE/9cJT6h0akzkZEb2FzLylYPdBGX5FEn+IFCRf1wxJZl9iA+kM+k68aJDZHdOfCGK7GixrEtx1aSyHqJzwmXjXxQ+oeVcmLB8S2jfHtRazdkZY0y924Inl3yNYzMUoXXOLXKgSpGHe+mCZ3VcJS4mXRckRq0iQdZY17JXF/YvzvOuGz/vf/8w9uOWA6chOI7QYkVmz6U4phIYSTEt949UmXaD2gswi1B5LEKh7hZoCb0GIZveNTP+4TpD2idZ9+0UQrgWICHP7nW2hr7FMvRYVZN9RkbvtMvtHBHElTLNTWdBZFNbf2uTTRsqL2cMCgqFj/eILqCZh6pUJiXRh9+UvSlR7moXCpR3faEgNJWJPcGJH+4ziRqsbsGWTPhMje9CGA6EaHxIpF4ws9omWD9B2PUNvHHGmay9KQ6s4ptj7u094nu35gyhV1OOlReUTm/JUHFXsfKpG6KVfRxhHpZ7znjzDXI5hDSF2z8Md8//iWQg3H0tkJk96UwZ0v2rjJEMP7hgzyBr0ZhVaK1ApUjltkLgkfr/yoTfqOS7gOk2+6ksQTlelFuO2z+4Q4CnNXRB48KAmL/70NObEmY7+JMzLZAMjcHpG4Y2FthqkftsncDEh8NynI8Lwi1FQSCrLs0JkzSEx2ie7IY7vvG20qxyziWxq7DYXLIgHOvGsR2TFJrUDqriuBH7bYlXNXNeXHYf8fOfQnhMo8mJH3Xpuw/bQIfVQ1hJsUUMd7TVLlg7OaJLA1E2c9UPLcDkuCIhuUFGbaIXO5ydYzUWoPKCI1j2jNY/N58TwU3rJo7zfoTYuxaP//cp30TTnMwm3ZSPNXulSOm+ydkDFz42CUcAM2Pmpy85encDMRYruK7oxB86Bm8yfEYuzFFN1ZicQzHGiecEjehc4+OPw/Vt93/X0gNgEvIjveoGhIus2Opr1gMv26R/ZSE6Nr4duK5d+pUXs4oPxIiMCS7PbAkvl+5l0L1bVoLVq0D4wz81qayTc0zZMzhOua/FffwI8I3HKUVViDgK1nksR2ZBYdaUon972O8sT/eprMuwZOViLO517w2fhUEcPXpFeF1NKflDitxqE4oY405KIVRe2wCJMm/90NJs4G91KCMys+O89Kvn305QSJTWnm1A/blE/Kv7k3ZRAtg12x5fpcdgm3xo2stiDP2vdBqK1oHNUMS2NOwQ9lWlF9zCe+rYnuiYFmWBBef79k0JvR93oAhYsdctc84qsmrX0hln9TxCoooe8W32qQWgtkNGtLx752v5RCrSUbLyY4rNS6R/2gfQ9wmtj0yF0XnFr/+AA/BJG6WMBHObGIK18ezsaBMPHdgPimWMhD3QAvCpNvSfBIfFv+jNm0GOU0o+tp/DD0HuszKkRJrsttpLvks/5JmfMPShCtakZ5xdpnTPoTBoXLLoYr5OJo2cCLmmBArOyBJ5uBk9IkNgJaBzXmdB+7K83KUU7TWQqEITgzwF8c0lyyJLb81oho2SBzrU20oolcirHx6RxeXBPfVGw9I1Hw8XVFkJDNxhzAqBgQWwmx9+MHcROKzG2X3VOyHsqPJclf8dn3rQ6BrfCjQkHKXVKkV6B2NIKTguSGIPMSFyIUzrWJ1AMytwWHpk1Inw/hJhV2W1F//P1xwx+ITQDGeXLbAa0PD+gsykOz/aTFnS9nCdUFC904niN7WZRRIPw5gEjdk9pu3WDydEfYAgZgyLw1tusQ2FD95SdwYwaJHY/AFDJr+q4s5vy7Pt0pk1hZRocA6//lKdJ3XKK70nhDi5BHwkFNAlsAG5sfMRll1D3y7iirSW57RGoerY8coDdhEqv4jPKw/YxiMCETDmsA5celnPBicn32otA9MqI7r+8BIlZ/3CK94lJ8G0IH2vzxf/Iv8GeHxHYkUUkdbaM01I5KbuK+bwRkr/fI3nCJ1CXYxOqL1txelEtSAAAgAElEQVTNiky3sz+gfjQpuQETspBaSzF2H7OJ7mmiNc3aZ3K0FyTyLbUakFnxmPvmLsOiINIB8hcUtSM2k2/2yFxTWD3N7kmb+mGTSAXUToTEtoAv4zsOM68KL9B0IHULimfaJDdGDEvS1GstWlifrmJX+0TqAbUHNcpTFI9U0Es9gpAmcytg6g/C7JwK0Z0VYc3iH3mohEdzv4k2NMl1j0EpYOK0TEHqhyTpqT8pG2PlIZv0HRHYzL4c0FwyiFSV1N45F303juFq/JAmcqTJfcc2+MTT5/F6Nn7bpjf/HlAljN2G3SczdBZh/js10AL58MNiemsvWIyyENqzqB1XjAqyoN8zMg2LmmHW5OBv1Wnvl+mVkzC48fdiJDc8hnlxMw4L0hcwB8JkCCzhadpdzdZH0+w+FVA/YtI8JBmRg5JmmJeSqzf5/kv9A7EJmK6cgMOMInYmJgq0EIQ6SqylnmTi2f0AP6TwEn8mnIntBTSWQzSOCGetfDLJKGUwecYlWpX5dP1wBGsAxfNdohUZ+cTKmu68NPD8MGx+2sdJiyIuWtb0pzX7v7ZN7f7QPYpud9omXg5g3MgE+W/hPMR3AxoHZRRj9RWVBy22nrVJrvYYFuXq7SYDcpcUybtytezOKeb/xCfckD5E87CmP60wGjbRPYXdEyahOTCo3W9jujBcSfHflp8n9WaU3rQiUlH415JYPX0PMOKHDDafS9A4YGP3AmJlTfvHeky/5jH3fXnPjZE8pKk1n+J5yTxI3xFhkRuXtGRrIKWa/FvFftt4tETuyp8lSId6mswdj2EpTP0hHzepmHtxIJTgupzw3WmD9n5Y+7TNKGlSemdAfzqg9pSDlwmz80SU2ZekdrP7mvq1PHd/Ikdz2SDUlEy/qXibLx68QO5QjepDip0nFdrSY1GVZvbXbpF5I8z0qx2ZEA19MjcUqds9YSmsybW+cEnk0NGKxo3KKLq9YDH33LpEiT/qE70TJr0it4Yg7vPw5CZ9N8S11gSLi3uSetVXtBcM7L6m+YBH6WyHzA24/g8zhJvybE2+2SPUFjvw5FmHxJqMqyOVMdUoJL2ESEWJJf6ghOkEtsis01ctGgctDEc2+NSqL/L0gqK9X8rE1j6J60ut+iRXhEJUfAcS64r8uxo3F9Bb9Ai3PuDTAT8EjaN6rJQTM09rWRZkYttjMO1TedBg50nJ8DPGeuogFpBY75O54xLMD4jtBbhxwVM17rNx42oMCpFFXDuaYPN5k9SGR+OwdKm9KBTPj6Rj6wnjDgXKhfrjkxQvjGgd8slfkuZQd9qgdV9AtOrTWVCkVgdE6vKAZa8LrXeU1RQvCHe+Ox8jvinjmok3NZmVIe390mxyk9LhV4GcGJmrivxln9iOQfquT2fOwo9qQg1F5o4QmQ0f/vjSUdznWgwPypXZKfiEuoHU3Rua3SdM5n7Qlii2JVPEMecSrP24/J4fkZNK4KgmgakwXE31WJTUmk932aN21CS54ROtaAqXRkye7tObMmkclEyIaC0ABdvPBtQPWvRKJrM/UPgR2PxIlMwtmT4EIRkX5i9rJk+DNZTsgXDVIHklzPaTEZLrAY1DEdr7DOrHAuyOQfamgEMCW2M92KQxinG7V6Q3DKFnBC9udwSlFtvqc/7rRwEoP54kWlZUjkVwY4rdU0ny744wR9IDqh01sbuCS6s9qO+RlGq/Nyfg1abJ4m9cl95QU1gM5UGSRGjE6naBu3dKRPcUobaiv+xQOQGxDYudp5I4KcX0yxIZH9ialS9HiVXEMjxKm7hJRfqmiLW8xaGMp/tSBsXKPrX7TQITqo/IqDtSC0jdDejPeQwnPHaegWFJ0zs0IrBE19E4Jn0mgFFOM5jQ9CYNUuselROKwlmDwplxI/J9Xh+ITQBA+fIAjfYLS1/bmtYhH3MQEK6YLH91k9i2Irkh8/5hEcyewZ0vJOjMWBz4tR7lxyDUEU1Ab0bTnTWI1gUeklkZ0V6Cqdc1o5RJYl3R3ecz8+qQ3rRNbFsUhtmrknY7+4qDk1KMshb5c9LkCnWkHDjwO10qD1kQgJMJ0Z0WNdjuMwGJLbHJ+rZw40dpIejOvjTAixj0psJ4Mfk68U1ZtF5Mar6JP61QPSa2082PaVr3aSbf8hkVJDewsygGoMT1ENnfSTD/b0WkYqZcdk8psrd8Wksw/arLjV+SBzBzS9SO4aYmdTlEdFdRvDAis+JSP2iTvyrm9MAWsUx70SR13SJ/xWf3lJxIw4JN43CU5gERU8UqAVY/ILHtkVyxGBYDYtWA6s/08cMQmNLgMmSkzygjYZy9SVFFomVj0EpO5N6k3DKCkFCXnaw4Sb2Iwuwruo0YM/EW9yeFWqc1mCPR/dtdTfV4EqsPky+WiZcDusseTkZuhkEI2oshakct6odFMhzbC3BKHnbLoHLcJtyA/JUe89+pMfeiw8bfOcT0ax5+SGF0TVZ/uEj59xfQPYvMJdFdBDbYezbmQBgCg5Km9YBL/bCJ3QFzqo85UGw9K5//KCXUpOb9HqVzAeZmhPayhMMoranfL1Of/pTiwP/ZZerNAX5YjTMMLRa+q9HhgNi2YnqqgTsGqyZWLVJrPnYvYOHfD8hf0iQ3A1r7LGlsH9M0D8PEmc77rr0PxCZgeAJC9MOa2FXpaJsDBb6ifiRMqAl3fnGOcFNGImgYzjv3UNzpVYfeUpbsNYFVjNIiI43UNNXjUm+39oeZf2HIIGtQeGUDNwF2QwI1y8/4dPbB9KviLdh5UrF3Iozhwt4j8jB2lj3cuCKz4nLj70eF1x8R/oG2kGnAuxamo5n5oYeTNGgt2DSOyDVs58ko9fvFcLL4PU/UfR/fw3Q109/bJDAVN/6LJJNvuvTnPKZfUsy+5FM7IshxgOyNgO6CbPvdaelJNI7A7P9tsfx7PfYeFnBKZ94mdtemtd+iPW8yLPn0J+T6OMrC9lNhakekrg1MRfZ6l2FOouHTq/69WPOlP5TMxVDbR4/db/2SonGfSfWYTW/CovTOELtjsPkZj6nflBh2J+/TnhcyTuquT+GipvCOQfuAT/2YjLHiW1KCDIqK1LpPYAuoM9QVXmFgQf5Sh/iOJhR3uPjNI7xaWeZfHP867IVJ34LcFdmwhwUxYN398iTRikP6qsXCt1toC4Y5mZjYT9QJtQSQogLN3HdFlaeV3PB2Tya4+xN5tj4cYup0Hz8yjrCrCYreTYjvoHUgoDcXMJjymXrdZ+IdiVybe9ll4Rsw+eaI9n0BsdcTxDcUsR2D9gMOXlymHJFd4QykbolAzovJbXXhOy28iGLibZftZ9PUD0bozgsBy4tB44BNZNNmMKGpn55k+hWxwce3AxqHTJSv2XwuRuWE6CIMF5LrPlOnxUq8cyr5/uvvr3+J/8UvP6LpT4roJlITW66X0Ey/pmmfHOCmJKfOSSkJophW5E/b2G1RoDUOhuiXxhSiAAqXBsTGJpTYthiFYns+u49F6eyH1mMz6IfbGL4iUneY+b547LszFpFmcA9q4ibEmVZ4d0BsXVJ6O3MWk6+YjHJg96SuVj6sfjoifoQ5i9Z+KUUSOz7zP/DwI5C94bP0B21mX+6y+3iIybMOnddKaKXY+sws0XpA7qUIrSWb1HULux/QOGCTueUThN5LPTKYe8Efx4RBuOqQWoHtpy28RIjsNc3y73XpLELxoovdkcReHRHicmLLI7Gpmf9+h0FJCMB+1KD8aJJQCybfkEVRuDjC8GD3ZIz4rkBKDU8CWOf/fYvBpKTc9CcVq58L4SY0pZdD7JwKE1iQuGPhh+Wz7c6Y1I7JaRnZNUmsGwJijQptabDoYA0CrD60lqSBNXVaICG3fypBbM8n+YM4weMtdpop/tGZn2LyTRHrNA+IfLw/71M9LunUXkzKmJWflll+bFfk5aMzOYz3kng0lB+RJvDUGyMJZc1A6ok9Fr/VpfJgjN3HTUn1mfVoHXPRhjwPiXWDoOSQvmEShBTdKZP8uyPaCzb1wzYY0quwxrqR3FWP3Fs2vWk9TgKSkXLtpMfEma6wHmYU1RMpIq2A6lGb/nRA7pqEx7T2G2RW/HsYu+iuCL62PiERZmhBqd/9ksBJtK2pnXKZON0iWpGrmDah8/DwfdffB2ITsHqKIBIQrYlktn94xPSrQp2xV6IYLuTelR07sTFkOO0zLMiGYfWhccy/hwBLbAbsnIrSOuxTfVqIuW5cEb/TxO5qpl/ziNRczDMprB7snIxSe8AUrcFDAe15k/6pLvEdjZOEqZer4AujvzetGOYFoll6x8NJCWJaHmixKcd3fMnliwicc+tDtsyXkwbNQ0n2TiRQHmw/GWKUl4UUbmpiuw75KwLuHBY0ew/auAkx/kgTziVa1dQP2aTvBJgj2P6QkHzRSKbAEcXuqRTZa5q1L4kJa1gIyL9pMcwaGE6Ak1K0l+PEdsSyGtseMMrB1I9aVE4oOnMmrf2he2k4w7Q8IqOsQFhWvyguz+Rd+fWJt6QR6kXFsOSm5DMZ5eXv6s0Fkrp0UDbCUFPGV+FmQGtZEbsTon5QeID7/utzDEvCldSmxnAVuydN3M80MV9PM9pMELoWY+8RRXrFYf6FIa19Bku/7+DGRS/ihwzKjwqV2Rpq0qviz89d98V3vyQ3s+LFgP6EYuOjgjFDQ+utEitfSmAONaGWoj/nYfYMFv5INl3/yRZWXzPxfaEIlR8zsAZQPRZmlFZk7nh0ZmwO/usW/UkxWDkpaYpOvhUw/41dIlWNkw6Ir9i0lmJUH/GJbwkbYvN5Cb5d/K7D7V80cdIymu1NSCiMVpIDqXxY+l0pc72IwuopIusyKQFQfZPOcoLtpyNUHpIsy+lv2++7/j4Qm4CXErnuMGdgjCB5IczewwatZYiWZQY+KCqsnpxOqesmuese7WWxpyZvCcevPzlufiiI7JgwMnFjIimmXKX15JDtpyxa+8Mk10WHrQ2pYWtHTeJrJqGWJvVSnM6cCIgqj+dZ/7Eow5w5FjXJVby1X24GTkbGN+/l6NUPm1QfDohvS4ZiuK7I3XDxbSh/yKc3pwl1RNkXRDVWT4Ijwms1bn85Qe5cAwzpJo/ywRhlbjAs2ETqAcOS6O4HJZnbD+cd8pclpSbUGot3Nh1it8IULsooykkrihcGrH3SZur1Lt0ZKZdUoLn76bh4Bk6lmXhrrFJLKPJXegQpbzzK9HET8m+O7EnuQnt/gN0RC27mVoCbUJgDGfVmb47I3BDnWu6yYNUm3pbvxRpqSucE1Arj2rormDf3yaN40yNqD8hV3G4rYtuK4HRW+hpVUXXaLcX2U2Fu/7RNEJKg2aAo7kEnITDQWCWgOw/lx0xCbdlM0dxbVJGqyygnC2qUC4hUofSOx75vDXDSitTdgNkXFeGqQXvBEsT6hbQ0/UzF0m/vkboF1YcFnupkNdtPG8R3PbY/kiNSFb/LMGOgLU3zPpNbf3eC1JpL8Zw0wzsLBsbQoPTKNsOsIXW/qbj7ybDEjW8apO4I1q27LPRjw5Xnbe+hCPFdAcY4aQHchP4f5t40WM7rvPP7nXfpt/f1bn33i30HSADcSZGUREmWNZK8VSw7M0mccmJXMhMnNZlMVZLRFyeTpFIz5aRij1Pl8ozHiyRbsiVqp0SKFEmQIEFiIRYCuMDd7+2+va/vevLhaWBcjmm7bH9gV7EINi/6dr/9nnOe5//8lybkroltnN2NSG6Kse1wXExhPujxodgEzJ4ie3dIvBaR3JKZttVVMDMQq+UsTL/Spb1PRn5OU+MnDRa/McRLK+nJVyMyqxIuoR5u4jRh5gWF5Yq7y+YvHGL82w7JbQG7dh6S0qx0NcD0FAvfbDOYiOgsyUVWGrxZjzAup1sQh+K1gPRGiJ+CqVdbpDbFxrtxUJFZhf7pAYX3IzK3pV+/Z7h597MiHV76SkRiR9xoS1cDtCFlo9NUrP70DPu+3KV5Ik/2FlQeiDH5Jgym5OTaPSGOReZAkV0dUrwmXvXpUp/qabHt6h306M+FbDwdRxuQWh+S2RCd+/qzCQxP0TiUIn8rxAg09YMCHvVmIsauDHFzIzTfhJ2H0phN2Vw781LbJyshnX0h7YMB+etSwdyz7Z75Xp3miUC88iZkwzJdadfcgiy83O0+YUyx+YyMF0vvRTgNCeEclhStPTHMTYdEVeFNe2TvSj9seKIizKxo4nVB7FUIC3+middGJ+SKQ+2ISWrLYzgd0Jk1mXg7YulPu2RXAomPu2kx/92Q0rUhO2fiLH7TJf8+pNYNvBz4aYOVTyeI1zVeSqzE+4u+5ExUpfTu7/FI1ANWPz/J+BsNClcM4ruawlVNmA/ECGZKsilCB1oHI8JCQGY1onBdxExayeupCKbOQefkJMOi2JvHuoL55G9FJKqa2nFFf0ZTuCiAsZdR2J0A04PqaQF093x1IMzFMeiXRTjXK1v4aVGmpjY15gd3A3/9JqCU+h2lVEUpdeXPPfeX5g0qefyGUuqWUuqSUurBv8kmEJnQXoqT2vLE3bYr9mL5Hybk5tuRG23fH/YYjgnbrzNnsPqJuKDRlvSGtROj9/dKHrcgCH3uxdsjS2eRD7s5UfHFWgblVwdUT1nYbVj9VJbkpkHxPU3jgEl/v8vED2OEMcX892T+vfG0Qa8slNvOnjSGL4YoxWsi45z9AwvDl4qgOyvR3iqE6RcNxi6H+BmL8istWnsMDFdTumDSm5aZ+9y3duksJumPy+w6uaNpLRlkl+XEnrggCUt2F3aPJ4hM6CxphjdzQtIZaIpv2OSuC7V47ErA6qcSrH3UEtLQrpSkbk7ROGhiDWXj7CyJyrJ6Mo6bF9pvrC2js71f6YtByPUu6TVNZ95k7G1Bq1v7uW+VpQ1F41Se1F2LWEfK8NCRqixR0cz9cEB6K6Q3kyC1HUDap3E8xOpH9MtSBRSvS9u28F0XN69Z+IpB7YSiPx0xmBJtQpCAsVe3iDXFP6J6ysZpag78bpP0+ujanHTIXxZTzshS3Pz5lGgHbCFxxSsDKg+KEUeQMqmd0JSu+IxdCnAaAUE2onlAevbWAc3SV2RRho4AzZMvWlRP2oxd8mkez0s7elgCTae/a1F/yCe7LNfG6muSWwbFN2ycZkjpQoNYR16vdHmAORAMpLHPIr8cUj9iUT8kArbmfoPEbsDUmxK8YgQjl6w4RDGhBserBkag2XwyRXtJjGv3/EnrvvgpTIgy9R635m+9CQC/C3zyLzz3QXmDnwL2j/75ZeA3/wavLxdsEKFCjZcXu+R7yTfTz69RPxmy/I8NOntShCWfyXMdUpuaPX/cYuqPrtPf79KZUyw9P8RwRWFn9cTi6+5/sZ/0uqa5X7zXvUJE9o6cQMs/7VC8FomFuSeGnNnbPdLrmgO/6TH+S3fJroU090pff8/qOrMWUT1t4KcVO2dMvLRcaDXKCzSHAtIYPkyc71A/YrA74oIPJyW1uL0oRpD5WxHTrw7Y+PgYdi9i7LKLNRjZWJ93IYLmETG1GIxLleQW5AQQw1DBFfplxeRLVYhkdNqZtph4Syqr1Z+Ur7m1x0RpOVnz7/cYFgwydw12HpGxmd2R2HbThURNM5iK058NWf6ptPg6KCE4GYHG7okvQP24VEn5610ROhWhP2awe0IRa8oGsX02QfTLVRIVj8qDNsmrcXLXLIKkQWpNNovse3USuxGDMZvpVwOqp4SGXHhPUbqoqTwEjcddNj85TRSTqcD4JR9rEFE/VRBvwYWI/HNbJGoRnQU5yYuXJcfPCARA23g2S/GqT3te8iQzywaxts+waLL9SAy7aZC9A/F1m9kfhjQOODSPimlMake+h+L1kJWfFeci72caxHcVsy/2qB8ymHzRonB9SGo7xM2rEe1ZEVmKyiMF2vMWYy+usnsySW9OjFIkeNXEaWgW/kwYh9apJrVjNs29JtocMWA1TJ3rSRLTjpaNqaGZf75G8VpI42CClc/kmX4loD+lGLvoM/1KXwJ7Plg68DdTESqlFoHntdbHRv99g78kYEQp9W9Gf/7Dv/hzf9Xrx6fn9JHP/BrDkmL8HY/KgzESFUm87U1ZBElxUw0c6fuVhuiBDurdDIldobyGjoBRiS2D/tEh818yGRQtUlserT3CoZ79VpXrv1qUIIcLsnt7ec3er3TZeSRDb1qT3FZMnetKOTzUDCYVfkbGLM1DjPIEBSUPsuJcvPF0nOFEwL4v+YSOycZTNn4uYvy8GHtoE8Yu++wet5k6N2Tz8Th+Rnp4MS4V8xLDl8ipjc/5pC7HCdIi+nHzBsWrLstfUGSuxsQduaapH9dEiYiJ10ySVUkH7s6OTFjO1jG+VaB1QFO4ouh9ukPi+xnCmGL80oDG/jhuUZHajO7LrDtzhgRd+DCYiNj3Rz1WfyJDkBTvwHgNrJ4ms+HTnbbx04p4TbQAmVWP+hGHwnWX5v4Y2lQEcQmIje+C92yLuf9Vsf1oFiOQTXcwIbRrpykBnYNJSaQW+zSpbqKYIrMWsHPGpHhNUz0NYS4gvi7gJRoyD1cZ/GgctyDqRNMXc5l+Wai18Zpi6o0hzX0O7b2jv3MXpr63yfI/mmHsUkisGbB7wiGxK9e7dTgksW4SJDXeVED+XaEdO02ZUsVasrjdonyPTk2yAu22j+mGbD+awcvK/W26o8rl4YjEpjgm2z1NZwGmXxXl6b3QFS+vmHxrgJ+2RMJsi6lI7REJt5j+ngFK+AMgqkhJwgpp7jMlQk1Bb0ZTfk2kxPcmMRd+5+/XVOSD8gZngLU/93Pro+f+f48/H0OmWz1CR1H+cZ/6oZigzGnFsGjKFKAeUT+iyK75YsO9qYm/mKF4XebfhisXKtaUnrbwqoP5azuj9sKicVKwhM2PjXPot5osfd2VPPoOzP4wYPln0nQXIkpXBNVf+2ga0xVvgOGkMLJSOwHa1GSWZbOpH8/SnYnRXnTI3tYkNi2WP+uQuLXL3A9czJ6BlxGxUuFGiNUXQc3O2TjZu3Ki3BPVjF0ULbifgp2HDOK34kQxsZ1uLxo4zYjBhM2h3+iiQsjfDhl7p8X0K5qJ14T23Ngv6sv5b9SZetMj/JGIlMyBOCdbr4mrcG9Gs/pcnERNQlNMVxJ8pfzUcLJNei1i4i3ozyYJHQGX8jcjWgdDrKEmvt5m97ScYkpLn9rcF6M3rdn5lSF2D8yBtHQqGsWpfSdLfyYp+YaenOQoaC/B9uNClkpUoHSlL6+Zg8x6gAqFV5C/Cd1Zg9wNRfZKjOGsR/79iMjRtN8aJ9YUHYVbEKDRy4qGf+4HAX5as/1wnM48xJqK3E2ItTU7H5uWKcikweaTgnvEaxKouvD1kHhNRFjlH5gEKSnFDV/+bpAQN6PMHSFDYQgrcPVTCbYfzZBdDQiSmqlzLun1iOpD4mKEltO7dibEz0dsPm6hbRkBx3qazv6AnTMJIkvCbmdfaOHlFPl3bXKX7ZEfp0zBJt90Kb4njMftR4Vsp03ZeINpDy8jKsTsiowYP+jxdwYG/6q8wb/m7/221vqM1vqMkU2hQk2QssitBCSqYvbg5gzmv7JOZCnChCYyxTDCTykK77sM8waxNvQeGojV1a2I7HJE7o6P+T8XuPtZi9BROFWhioYObD5bYud0giCl6U1rgqSB3VHk3hcjiqlzQ3LLEj3VnzBIrpuMv6tp7JOrGDqKzG0DNy9hGYndEPXzVfysxqkZbH+8TO1IHLsrN2SsJxhDkDBxSxFTbw7EswBGCD30x03qJ6SnRcP8v3yLICknxdIfbOI0ZRNrHs1jBFIa+vk4jQMmpTcq1B6VFCOrD5XHCrSWbIrXfZy2LLTOrASRtk94RDFNegUyr93BHEIQN8jeje63Rf6tDI0jkhcYWdJy9KcE4MzdMOlPGKx/aoyZF6EzD15KcI8godCLA4xzOWonBRNI7UR4+Qg3Z1B7zGP9WYPutIkRSvuXvRNhDaQdaD47IFGLqB1L4mXkNbUhhqGVB21i3YjSez6dPbJxTb5k0Zk3GH8nIndbZLz594Vm250Tr8YgoagfsjE8Sa3OLsPEW8Icbe43CBKK+e92R9ZyGi8vhjF2VzMsWWRXfIZjsP0opNcivPyI2p5R+FmJzAuSUs3dy1lUgYxs/aRBvKaonnJIVH3yV2Vs6RY11YciSm+b2G2DsUsRpXcVqS2P7oyB1TSJLNg9btEvR/TnUmgLOotS1bQWbQZjBrsnFf1Jm52nA8rnPBafF5VkkITuUsCefystsIpg8xkZLX7Q42+7CeyM2gBG/66Mnt8A5v7cz82OnvurH5GMATeetkmu9RgWxZI7sxlQeXYGFWmmXofkSgtvFIG99YRDvCnocfLtBOnNkNBWMl6KNOsfTVG6YLDzMJgDuThWX8gi9zTwU2/IIvEz8uU6DaieEl+7IAndvaGQlDKK7FrI9CsiHsrf8kcOM4r2vMXORoHSJS1uxbc9xi72SW5rnCa0FwzKrw3YPWETpkMqDySonjIovxYSxNVI0qwx+1Jiqgg2fu0MKCSmupDCzY905YfEkdjuhjT3OTgNjV/OMvWCReF9DxVq6g/7NA9rWntsEhWP1Lr0++k1Rer9GBPnRzdEPkuyGtJZlGu2/ah4O+75ahe7o7jzOYPOrJxc2WXolsVaywggfyugdsQkswJBSja7mRdqmDeTJLclZccaaHKXa4RFn96sInXdYfwtRWYjpDsjissgLrRpp2pgLieI7/r4aQHBTA9aSxbFS/c8HjWtRZvyj6XXLlxp4zQ15lDTHCVdprZ8ErsBfgqsIffp0qX3hEfSXVCsfyxG+dWA1JYo7VQgQF32tuhF/IxInPvjBm7BInI0h367QXfWYOr1SCYNefGfDBJShk+9ETL1f72BNRSjldbRgO6MYEOJ3ZFbcVEA4JkfhWRummhDMgGqPzXEyygaBxyCuNDlvZwYhhavyDhShVC4Jp/H7mu6c4wyLYVVe+fnNZUHHVBSpacGPPwAACAASURBVOz9UkDtaJzsXcHHShcM6kf//rUDH5Q3+HXgH46mBI8Arb8ODwBB2LUpfVr1TJbyCxWa+0y8tJhl9Cflba5/ckxuvMSIr10SznmyEtHcJ6BXelXROCSlXZBS5PfVBV/YiFBa+k27J24ymx9ReGmDyTcj+jPRKIpLCCbDcU1yzaRwXeN/usnuCZN+yRSSyMM2mTUXqw/J3Yj8RdmdtVLsnnConEli96TSSFQ1nXmH4jVx8xHEWIn2QIkYyi0qSpc142+3iLUlkjtICN3VHU+iDUVnQfrlYcGgV5ZeMbMe0Jl1CBKKu5+2GEwq8hdiZG4bEgh6ME4YUwzGDNp7JbrKy8oCvP2L42LoqsGb9nDq4m5UPZ0mdzskfdcSD4R9wqGPHORns9BatJj/Ths/da/8hmv/XWaUXwCDSQl4ufbfZym8KVRiPyvJu92yidMAw9PYA3k/w+mQWEtRO+aIV8FhsdiyBnJNpl5p0Zm2aB4PqJyWMJStJ/PYPc3mFzyCxEguO22z/WgMbWhS2z6tg0K2ae4bOTVVJJR25yGbYVFRuqSpPpghSEL9wYjUpmbu2y2Sm4rxi0OGBUXmDuw8XmQwFVE7Zo4qR1j4tsfuSUP8BjImd379ITrzElxq9gwx+UjI/SSW9BJPtvW4SXdJXKTsjib14xTNYwGdBVkLqjwUXUReshI3n5V2I7fs4haheLHN7Es+6Y2IqZfrxCoWB//vIU5Dj6ZVsPyzom8I4tDaJ+BtrPV32ASUUn8IvA4cVEqtK6V+iQ/OG/wWsAzcAv5f4Ff/utcHCOMSjlC6MmAwplj/yQlJ1AlEotsvi7OOn4XSxS7RyL25dKVPZjXC7mvJlmtHpHZC2vsiUhuasYsDrC+XaO8Vskj7iaEIivIQa0L5x5r0ps+gaJBalZCPqR9UqB2zKF6W6iTWiRhczTP+rgRU5m5C7qaAaf2yeAw0T/pCQpkRr8LyKy0StUD06Z9tSEn2pEFnr9hwT77eIrklo7juUoRbHOkLnsyTvxmKJ8DXPYYTkpU3GJdIdD+jRiNUSROqHbEJHZmx524aODUxXHULkKz4mB5MXBiQ3IlIbht0F7g/kjQCUVfmbkfs/Xcad++Q9rxMPDJ3euSWQ1pHAqZ/KAlL/amI1LYsqu7ZAb25FOlN8cjXFmSuxDBdYb459REY+kpMQN26WL/HG5rW4ZDuvMbLmXSnhQ1Jxmfy/BAvC5PnfRIbJslKSOHmkJv/1KF6NisEsG2L4ZxHkJTPuPNERLQdJ39DQFU/pShcj4jvKjYfj1F6V9Erq1GrJBRqtyT3hjmE2nFB7TN3Nft/byC+DjlHbM/0KDRmUtFdkByFwg2Rixev+fhZ4WzEd2U0HWsp2ejyBhPnJRwmvRHRXjTE2/KUgNpWXxGrSwCM3dekN0MWvqnxxwMSu5r5iTrxqsz764cMzI6B3VXUjsaJteHWL2ZYe9amvWhw/b/MM3ZZs/FMjolXKoJhVAPshkHn4QFjl3rEazDzo+j+mvlL1/iHwWMwOS6W4+PvyGisdjbAGJgk1w1mftDizs9kKb4nZov9KUXxmohcvLRB8b0uQcpm50ycWEcsqcORHjvWkdNn6lyf+hEBW5yW+A/aXQG1TE+PkpAN2guyg8dbEdWTMq9f+lqbO5/PEq8quksRh/7VBpWPzlI/pskuG5TeG7L1SBy3JOSY7G2pVNCIqUlW5tPpNdn5TV9Q+PwtyVnUJqQqIWufhNJ5k3grorVkyg20IOEgRijv03T1feZbd04xeT6gdswitanJrLp4OYvEzpD2niS9ssGwJG676VWFlxPuQf7mkK3HEsR3Nflll8hU7Jx1mH6lz9rHk6RXNfpzNXi+JGrBXoiXlSprWBA7K8ousWsJElVB+QvvD1j5VILssgBTfkpaGyOE/udbBBfzlF/zqJ6IyebuCzqu1YjmOqrQYh0ZuxUvq/tjMbcwyjOckcWaXx6yfTaB09BoSxKInJFde2Qp3KLEivXHTKyhAKvpdc3umYjS2wa9WdkEs8saFWm6c/KdN45qUuvync99s0bzeIHGARlVF25KVHh2JSLWDvHTJnY3ZPMJQfVjbc3OE5rZ72m2HzGx22IX1tkfSEhrNaQ/IfH0fkrMVvtlIcTF2lLmN48HJDZlpSa3NcWrA+pHEmgDcrc9ds46ZO9GVE/D0jdcgrhJGDfYfMrAHEgEXJCSljeyIbkj908Y1xihsF9v/7MPseV4ZMuFqB0XpVvpLYu578uJ6E4mpVQ8rqg9ICh6fNejMyP03P50gsppQdMbxyP8kSw3vRWNUnGhtS+B0xbr8M6CwaAsaG68GZFZc9n4iEH1AeHGB0lF5laH9Brkb0CQccisyHuc+27I8j+awy2IX15/UtPc56ANiDUN4lVhyFkDTW9ORl8LX6uS2hAkOYqBVorh0QH1IyZeXoJNtFIULpqEjhoBSprKT7jYPXk/9WMwKBoMCwaJWkR7L2hTs/4f+fSPDHHaEr++8RGD2vGU2F7dCBi7JCcwwPglX8DMrDXyMlBYHY/NJx20BbunkuJa247I/GZOqKpTJluPiZVb7YhEreXeV+iqRGj56ZF/wNNJ/JyItNp7IHcnwMspdk9pBrezlC6H1A7HyN0N6e/xcVqa5sMeraMhvXnZAJSGxiEDLE1yNySxG5G/6TEoh/hpRWIHMhs+W48mmH65w9i7bQbjivJrAd09IZGtaB0NKF4N2TljEiQVrc/2ZKTrauI7JoNJxWBGUpP6ZcXO41IVRJZYcJlD0Z/c+ZmSlOtd6M8F5F5dIXcnws0qds7aBI5UYUqLsWjnZzsYfYP+hMmeh1eJj1qBsTdN6k94VH9xIAzOjYipN32SFTFbMYIR7Xw0KZl5eYCf0lh9zconE6hAQkg7c2Jjv3tSkdrXwsvYdOZtds6a2C2hSccbAlx250fpz7YwaZ2mIjrcZeHs+geuvw9FJZCYmtN7/uF/i4rkJDE8KL/cono2S/GanFz3tOkiItI0DzHSxg9Y/WQcp6ZI7sjFdPMGhieyVKcV0pu0aBzV5G6IZj65rSld6bFzVmhUpieiF7svfn9+RoglWkHulqjnpl8bEDomjf0xcnd9akdt4rvSizYPQemS/NnwNemVHpFj4eVsujMW7b3i5JO/GdErG6S2JG5sUA4pXpKqRBsSm2b35KbML/topWgtWTite7RluRaZ1Wg0QhVkOrWphc9/3GPhqwqn7rLxkTTTP+7Tn3LI3GgxWMiw8jnIv2OLFXhLNP6ZmyaDSY3TkMzFzSdTpDYl9TZ3U1F/xMNyQpJvJKWs7skG2p8QgxPDE/AtsiTPMLUdUX1Q3We5qQj6U1oW64xFZ0G8/zMro2t3EMqvBfdTjonk83SW5PnIUjT2W4xdlnRhkJSlZEUzGJOWxmlqqk/4lM7ZQvwKZLLkZeWeqJ4Vboc2YOFbLmu/EmBcTZNdlsAQq69pHNPM/iDCy96rtISVl70jlaKbNaif1IxdUPfdrzMbAWvPQf6KhdOKiGxF84DwErJ3Q6xBROUBm2RF+vXBuKI3H5JaFR+I9l4IcgFWwyJRUQymZNM2XUZBOAFhwqB+yKR4PaR2WEhP4nkp+obmXqkqd08YTL4VUn3AInl6F/fVMfqHh1hOgN+NQahY/eV/9uGtBKyBFsFIT9+XdfYW04Rxxeon48R3BcktvB+Mbir5QnszmjBh3k+myd3u4ydHNtITSmin45L/V7wsC2bxazX6ZUVkSSyXEWhSOyH1o5C+25XgipY44cy94AmwE0FnzsFPmfgj+mXxakBvRtE8BESjeDFb+P0bT2fZOZOkflg49PPfcVn4dpfAEVJTaAt3fOaH8lqxTnTfAgvE4bZ60qa9YGEEwh9I1CLai2KTZgSyiBMVzdxvvEsoa4PEnRh2L2DjaclLtN7foPqAQeNUnt1jNvENm3gjYjApDMfMTZMgKZOSuT/dxs/YmEOhYWfuGBSvDpl53mLPvw5Jb0X4abBcTf6mi9OUxdibFVA3soSQIiw9+T7KL9XvjzeNQNM4rIk1FeXXPapP+gRxSK0LxyHW+A/5g52P90Tv8bgl8fOPtdDWyIi0pRm7EtBekgmCl5NNuvyCRX9KkVkZ4LRCGkek8qs8qpk5vEPuhnhWDMZtxv4kybAs31+iJtd+7B1hQvbHDbpzBnPfqJK7JVmJm58RsdrEG2I51tonv3f3mIXVNmme8RiMG3TmFcWrGhWIhLo3aWF60ubUTggz0BwY9E8OSG0LX6J4wSK5Ja3r7A+kSurMKdIbgcTQZw3UmRYbHxlNSbTEvI9d8qkfkVFo44AA2NWTFnYH3FfHuPKP/x+WP/47fO2Rf4Od9lDeh9xjMLIUMy+2USFMXAjEXSghqSuGK6f35JsR1VMW/Tkh3fi5EG1pth6N0dpjkNoOqR1LCX10T4jhywgmu+LSOCQndGcB+gtZkpuatY8nJeorp/BSBoXr4I4nCRICvu2elF45jCkyqxHJbZ/WkgkKiea25Ibd/1sbxGsSTmkPItJrMs+ORnr65n6T3eNxNp9MS0aCIUCaOYTGQRPDh+1HTQkHrXj4aUXjgEkUAzcvvAS7B72yye5pARPrh01aSwZeTjF86ih+WtE+JoGqG09IGZnYjdj6uf1YfUn46S0FWD3h9Q9nPTqL8jnnvt8mSCoqT00SJgSjqJ2WYI/KaelJKw9l2Hw2YuKCL5qN55xRLmDE4vM+vRnpxZMVn9yKP8pmgMFMhmHBINaW6UWiIorO1ecs4isxejMC6E2/1CR3J8QcwsKX1il9LcmB363j1BVuKaLw79NsPSbTFG1BY79F7iYktwXRn//GLtUHZZO4+R87WF2fKBExnArJXTdpP18WbKGqqT5gUHlQUXrbJLMSsf1xnyAlVVXlAZt+WVO67NPfk6d2SjNxIUAPTeyOGo2RNUE2IrGjibVlY5l4STQMToP7NODetKZ2SuPUNXY3QttiDmq4UHohztpPirdgZI/a142A5t4Yjf0GU+c9Wks2w6JB4WoX+4c5Clfl59yCpnEIzGGI4UJ7v9yH7SVxZPKy0lq/PBIMnRssEY/7GMMP+SYQJKE3n8JPKTqzFnooc9SNZ0eW02MRjYOiqR47b+DlNPkrFiqQEju9oamekrLbLRgULhlMvOORqGiqJ+M4DUVvxiC5rQjjBpMvrJO7Laqwue80CR1FshKw+bg18sV38XMh4xf9UXuhCNLC4TZ8iY7aOW0y+eaQq/9inDAmXvqDkkHnpzrUj9gSqtkVfvdgQqLDxl7ZwGkIS04860dl34osWj9tMX7RE6nxUDjq/al7466Q4iVRmaU2NKX3xJ0ILY6y6Rs2+fc6ZO+K3Dj7X60xfLpDf8kntRORXLVwmprdkyYEBvGqgEiDqSRBXDabzqxFdjXEKLr0pxQz39ohtemSv+WTed9iWJBNyy9K75+/qth8yqFwPaJ4LWTlMyY7p4Xzn16BjWdEbp2oaDCkT86uBuRvjFR0Wjal9oEs3WmTMAbX/8k0zf0GtdNFwjg4dYOtxxTJLaE29yelott9WHgW2oCtp8cwPChdGZC9bhHFTKZeNii+Y9Av65FgTGO5oo0oXoVkNWRYNLB3YgRxAfeMABKHmjQO2jT22aRWRaAz923IrIhqs19WFC4JCac7L3L0wbgAzqED24+pUUCsQsci2WDPWKTvmmTvDChe1dQ/PmTiZQsvD/mbHqYLlQdsyl+5ycS7PhtP2gzH5F5rHUhhuprG8YjWfhn15W7BxlNxqTIagsuECc30yxo/I5XNf3buP+FPullKVpfenRyFax+8/j4Um4Ak/opUMkhA8W2LwFHYbUkpnn0hvC8oCmPiL2cNpY+tftodES+k/7yXtFs9ESOMcb/ELL/ap703Yve4ye5HZjE9QZe3nsrjZRTJO03KrwcUb/iYwwC7JWk4QVJOAC8lBpETF4aMXQlRkcIt2qTfc5h828NLGzKT7zlC04xJCR8mNImqMPBWf25WQLBQPkdkyc2nQlmEq8+ZbD8sJheZVdlU7J7i7hc04+eFQNXca97nkc9/u8nmEzYzrwh56cYvp2Ta0VS0fnOe6EYau2oxKBmUXx9id2U0llyx7oOxrSWZuystrZiKYOybcZI7mt6BEp2FOJuPy+bQn5BKYd/v+6LqSynSKzK1aC+Y5K6ahAnZ+NyiIvc+DCaFDTj9kuAHjf2Cz/hpRWRJkm5kynuZesOVJKUIGj/Rk5PVgwO/XSVejwhtxewP+8x+t47ZkU25cSy6fy/c+oIkPG09FqezYFB/MCIyZTrTPCSYS+G6OPY29lsESfEs0JZs9IOpiExcXJU6+0My6yEbH7HYPSHsRG1KhmF/WlH7iMfsD0PCpCbWlKlN+bUe2ZvCRNSmjDQjG9xFl9RWxM7DSQFThyaDcUWQ0vQnbRL1EHc84vZ/s4+1j5r4BQnWkVm/ovawT3LdRDvSatRPyUGQ3hgBij8aYHiK9oJJat0gfKyFfSPJ/3jxs/yL9z5DrGncNxz5yx4fik3g3sMIYO6bVSJb+O73yMi7J2wxBtHS62fvyM0zdsnHWI3jZcX7z3AViYrk1t8DEruLEZm1kOrJpDCwYprmAelRIxNaxyVIs/LEGN1pi7WPmUQxKf9SGxLvrE3I3ewx/WpAdyZGY7+J3RMd++z36tQOx4h1IzLrIcn3hM5r9WDzI8JVz6yFmF5EZjViOAbejE/tbIA2pYyz+5rOoqJ0UbH45Ypo8T1NGJexWO68I/LcmCLW1ix8TbTvUUzak8qDMQaTiiP/covOL7TJ3o1Ibg7Z8+UG6TUJUx2Mx9h+KmLq3JDpV/oMxwWHcVqa2e/siqNRSdNaFFqvn1bUjlqkNj2sgSJwZEQa39XUj8RxR45DTieiud9k8vxAsAFbXjd/Syi1C9/sYN9IYrqjL9OA6ZfF4yG9BqmNgbAEQ33/HjBdyH03RRiXcd2NXxnHyyiGY1IN3PnpovAOmpryyzK5mXh7yJ6v+PQnRUHqFjXjbxik1xXZO9IaJrcjgoSB4cHMCy1APAeDhPDtY02DnDOkeSwgvWxihJrSRQE9lZaNojtrEB3uAqIVAHHKdnOKypkUvTnBrlJbERNvB/TmIoqvxPDSivF3XNyCYulLMHbFI39tlDkRN7A6MsazOwbGwCC1IWYwrX1gNmziVU3uvZFT9F1TNtKEGlGFzRGYKv6HyeezmC64vRjRqwViLfCK0QeuO/OLX/zi3+9K/ls8fv3/+FdfPOQ/SK9s0TqUIkiKfNb0FOlNibkuXZOTKExqBhPg5QzcvMnC821MLPpjlphDomjv1yz+7++w8w/KOA0DP2XgZaF9MCRzW5DW9rxF/raGQJJtnKbQRSfOa/ysRRhTlK66oESFNRh3cAsmyVpIvKEJ4gaDcYMgHZc0pFpEd8bE8KTXHn/HJbVlMPZuj/aSg9IGnQWT4o0Qu2aRuWtg9+UmKP/pHaJ8jsGkQbqiae1xqD4qmXtKj9DouOL8r/8m/1vtNMOcRetQxLAUZ/JCQGiL+Gfzkzns98SDYecRG8tz0IYiWQ+pHzLJ3lZsP2nSK8eweopYV+bvQSaBNhXJHUH4w5hC23LqNQ7b5O5EoxRi8LOK3J0AP22QWwloHLRwCxprKCezNZATs3lQdAebz9hgwLBgklkVXkF60yO37FE/FqOzIISiyFa09lsMylLpYUgoR+tAksSO/E5tGsTrAfWTJvlbElEexgxaR0Naeyy0YQmNeXyUP7nKyCRFkb8doM17gR8GQdqhPw0zL/XQlo3Vg/4U+K/lKV4Vrkp61WTnUen7h+MaayjVQuqi2InZbYP+YY99v+cxmIjRnxGcxByYtD7RJ3Erdp84FTmKzpwl4Gpfsf24SWZN01kQ6bY1VCSqsimltuV7sPp6ZIyqyGxEDMYNhif7OGs2w3LIsKjI35IJWHfOItZRjF+MsFxJsYpvWqSf3aERJLG6ivoPv7f1xS9+8bf/4vr7UFQCpie20CoS9x40zH9LIsH8pASQVB6wxFwkktFgdllTuuZz93M5ds4KkJZdiWg+4JPYMlj+nx5gz1dao8htzeyLPRa+oQlSkLm4TW9O2FzxXU2YkDDK4nty2vbHDboL0qOHjqj2cis+kQW9CZP6QZNkJcId0zQOS8k7LJq092q6i+K2Uz/iMMwb7DycoXlQbKb6U0KGyt9y8VPgpYX4dPc/3SNR3U3NxtNpvJyYdWoTSu8NsYaazEbA4d/6VWmJ4pqJc6JVrx+0mXy1zmDcYPplX6S7zYixi5rN5yK684ph3sRpQXcBnKpB4YbMkqe+s45bjBiWZHE0Dsu4bfpry2RXxDo9SEBzn3G/ssquygbgZxR+ysTqwvSPA5xmSJAQxVr+dkjxPen3x95RpO9KDHn1jB55KTisP5OECGZe7uNnBUzz9w6IVwXAG5bke7YeaJKsRti9gPFzNbaeSJK/KqdnmIkoXg8onTfF1XcP7PnSLktfd4nvmNgDsV3rzWj64ya7p2QCoEIxKTWHit5MgtoJESClNhW9WUBrstds+hMGVk+IX0HJJ70eYbcN0psh8W2pAuI3HWrHknQXIsKYJnPbFFOcq2ma+ww6C7KpGr4mTMDsS0N602Kj1zgkVYnpQu62T3de2igvqyjc9MVy/IAIy7YeNUhuRyTeSdKf1sy8oMguG2hDcefzlpjKpmFQMO5X0NqA4CsTxJoGpvchbwciS5hhIEKR4nUJ3khUNcbPVenNCmWzswipTRFRDEsCZFkDAepUBK0lA0JFsqIZu6ipPJQTzUAAa8+lsHsSb115ZobMHYOpcy71E5p41WDyLY/2gkGQVLQPhMSrBtsPC8tr94RJ9aRNshJJ/kBLpgdBQrPv9+tMvBOQXRkS2TD2rgRKhHFoHJHxXv6GlM1jFyVr7/YvGrT3SUvTLYvCUTTgCrsjIFSiIrbcldNx2kvCjkxtSbpy4ZqcZqav6Rz02Xq6NMJCTKbOuQwL4sqTuCvKRy8jbUSsqZg67xFZkjW4/YlZ8tfEUyC0heuQrAY0n1gYmVwE9xOIvKwo/zrTFkHcoHAjkLwArakdtbE7AZNv9dl4WlE7ahJviFNQZtVDj+ztsrdlohHriIJw6rxHa08Cuy2U2+SlhPgYtiLsnlB9hzdzOM2Q0DHxJmU+25sRbn1yzWT3hIVbEqKP6UKYjUOoCVKa5l6T+jGh6oYxAREzy10Gk5rU5kipaCqsgWI4GZGsRGRvy7UevygBJ3MveHT3Bhz+P9sSiLoqfpSGL1yBwVxAdx5SawbJTYP0ZiTiIVfalERlBEx2NG4hYvthccOaecXHHMqGXnnKZzBuYfXEu8JPw6Bk4WVh/7/r0DwSMPOjkPqxES9kXfp/bchBklw3aR0UvclwTA6x5I6MkLVC3KprH7z+PhSbgN0JKF73RwCZwaAoWXVeRtH/wQTxKjBKlIWRu29TQJL+bEh6TSqE7EpE4aJJe1HRmzQYjkkv62cU7lhI7UicwbiMHOONiO5sjPxVuTm8rCkuuXlF8V1Bf52GiHnuod/2IGIwHaC0ZumP26RXDbb+F4XVDemVHaZfFvlmcktCJ8cviGeAEcDmZ3ycpvRl0uPJgsCAibf7RJYQU4KU4ASdRZFMJyqaIBfej6y2BhpreC8Hz6D0piVhLQZ0Zk3aizHcgmLu+x7DciiVgwO9sqJ70GP1OYvdUyJGStSEMwBSNndnDcyBUGPb+0O60zZzv/EudkdUeaEjNlXVh6IRG01OqVhTs/NQAi9rU34VkluaxM6QRC0iSIodm9XXFN73mX65g580yN4Z0B+3qD4sCz5zB7r7ffrT4s409Vqf9FZAekWx8bTF6nMWYcwgsSO+guUf1SV8c1ewo9ABrxhy9zMpdk8ksdsKL69xauLehJKcgq0nc+TfByJB392Mum/Iag1E2NOdV+ycjo+SjDWH/3Wd9pECfvZe6rOM/rQJyVULu6vo7BPN/uaz4g3YP+zKoiyJhmD7yQjDE4JPYkcIYWjIrMDUTIPqwxFBSvIn0+tyn8c64u6c2JCRdKylGIyPMC9PphPWYER0a8sEpfyaZHnm7vgUr/VI1OXwaR/4YEzgQ7EJaNukfkgstrUhJ4GXUQzKEoJpuqI2q5yF3gzMfH0dN68Yf7vF/LciYXSVFNsfC2gcDwmPdCXi+WqANRSDCadqMvXV22LEuN+jflTR2qtonJAFXjtqktkIyd4NaTwzlJOzI/Lg/oRBf9ygdtiidEHK/vrJLGOXPcxvFHCLNjsPi9Nw7lZEb07RXRRwz81LT58/57D6+YjWokW8Js9NvDOgN6PZejRJZiOgOycONSoSB+TIkQqpdMGUz5iXEyZZ8Ri/6KG0gJaZ1YjIuTcJkVlyr2wz/RJ42YjMekR2JaJ0ziYs+cy8JIzD3pQ40XTnxB/BaQpaXT8UI3fdJL3ps/VLp3DaEbGmbHCRBYlNE2fXG8Why2IqXvUZjFn0xw3yt102n0jTmTew+pL9FyQV3WmL1U9k6CwoBpNx4s2QxIakAvkpRelNi7F3NaXLfbpzcbYet3CLMrFIVAw68zZOW+jJd3+qSG/CJPuzmzh1IU+NvWWSuwndefEtnHg7Yu5rG+yeEB5DalvyA2qnQ4I0jL/rok0YlBS7Z+7RjWU8G8WgdMWjtejQfGBMfPqyspDsjqI7B05Dfk9kwd4vexghlF8yxEZ+2SEY98UsJq1IbFpYQ1G/9qcVG09Z+GlN85Bm8O1J4tuiORgWDIYFsW4zhxo/rcndiTBc+T2mK+/NLXE/wt5Py6bem4vYfjhB7iZ0Zm12T6SoHzLZ/GhI+ccf8ixCP6XoHPAp3pA+NPf2tjjNbBl0Zi3xaLMVYxcU5VcDVn92VhyAPpkX3XzVJzIhvhpj3x94lP+9uO0OCibptSF2VxKA7/zKPkwPPnXyCmFcAjy1HYk3e1xTO2Kye8og+3qCxlkfAj6WGAAAIABJREFUt6CoHxUbbz8tohC3IJ77zYPi85fcDbG7IXv+ZMhwPGLnyYggKVbbjf2mWGmnFJOvNpj5tnk/zTZR1djVHmpErfVTJku/v4kRStSXNRDB0dTrHayBlKCdPRG1pzwqDyTwsoIIx7paDFni0us2DomYpHFY4dQDrL7CzSk68wbxRsTYKzHilQGDSU17r/gKJrckfHTitTrDomgrnGaEUxlg9TU7TweieFsXW+tYC/ysLYDljHAKdk/YdOcU3QVNa8mBUWCpimRkiILC9b6Id+5GbD9qsHvcxi1F5FZ8rIHo801Ps/GRFMOCQXJTMf/tNpk7MBjXo3AXk+6MiTsW4hbhxaN/RuOYxvjcLrWnXToLSjIDphTbjxhc/R8m8Cd9vHxE/VCM3mzEwjc0bl4TxQxaB2RsWrpgCkawGDJ2xaf0XsDgnzSZ+P4qgzEDpxUy8wLM/KhPb79HrCXAaqyjmTzvUT8SJ38rZOupiP4hl+Gcj9Gy6M6L6WwY02Rva+pHpA0BGLssbljxesRwr0jThyUZWZZfHxDZivKroqnpzlrMvtin/Lo4XoeHuvTKBqWrkhfZm1bs+1KP5I5mOK4Yu9DCHXkYJNYlJfqDHh8K7UCqNKeP/OSvkdgNUFpGgrPfqrP5saKozQzpqVp7DCbPe9z9vMGeL4d05mP0J0X4ow3BCkxXQkWLlzX9SYPMWkh7ySR3OxQm25zCz0SkV6XkH7/Qo3ZMbK9UpBkWTXplUe8NxiVQon7QIr4rwpbWkoXdk5EQBoxfcFn/WIzMMvdVivkbXW5+Ic3cD0I2n7SIVwUw04ZiUFKMXRowHIvR2C/kpNSmFgBvImD8TfN+kAfIDVR4P6RxwMTPiBeBn5ITgVGWX/VjLkYlRrwquIE11MTaIZUHZLSa2NXkr3fF964Ai39cZ/UfFBm/6ONlTPyEaM5TGyKT3XzSYvrHAb1JS5iXbYlDy65E1I+KLiCxG1E/rph5KaA7beGnRDjVnRMCl5s36M1oSpe09LIaJt8K2R2pHiNbNmYVanaeDpn9loHT9Ln9BZPMNZtYS9PaLwKYwVTE5DnYfkLj7JpMnvdZfc7E6ksuQXY1oPKgRaw9Ys/ti4g1DErvhdhdsfBCQXJLMSyBOx6y7w+H3P65hMSMNUR7b3qIOU1MTmSrLyV/vCHJx7WjFuPv+kS2mMn0pzXlV0PsbsDm43HUaCnFmhCkxUU71oLUjgTq+oUIFSisjgSaTr0pXo+RLaBtal0AxCCuRq2I4Aq52yF+Sqq1RDWiecAgUYHOnojEjoCLRiC6Dj8t7V1qO0SbUnFqQ3CY1776Tz+82gHRt2sSWz2GBZPSez5bzxTF5eVjPfI3PRHXdGHtYzbxLYv2YozBhMLL6fvWSbUzAZXHJDarvWQwdsWjP2ky/3vLbD+mSNSFdJSoyAZgDjR+xmYwqfCyBp05C2ugcRqa/M0eyZ2IjaeMkX2zonHAIndXiDozP2hJnNVZh4VvC83ZLUjf7I4lKF1SNPbfc8KRLza0ob1PMxyLsfOQCQbkliXww6lDfEfIJeK6KxqI/K2I/rgxUvAhrjkDJNjjqs+wKOkyi897wmYMNG5G0ZkR0DSzHhHEoXEkzdhn1ok1IMyK8rFbtuhNCsCYqIhgpjtjETqanbM2TivCLYiAp3Q1oPqAwnAl2MNPKSbeilh/2hrhFGL4ml6XftdPQfGKuDIltxST50PWnxGuu+HLZ1ShpvKoZv/v+tidgMZ+h/T79sjoVJFekw3eqYnL0dSP1QhviUgvtJh90Rdv/0WL1IaAYIndCKdmEFlCr777WUWiqlj6047Itjc0VsdAmwYTbzJKltL0ZyLMoWbrCQER0UI6qz/p0jho4uZMElW5LqEj06NYSxKbdk/EcccE7EyvCwktf1OOe21JrmOiqjAGErVuDpWIyGYd0lsBka1QPrg5kUYrPfJm3Imw27JGujOK0lUPt2Awdknwh/x1Rf5WyGBScJH0lrS/6S1RlbpZ2cwMX8xoPujxodgEjAicZsjqT+TpTRsMCyamp8ndjoi9nabyoCNlayVi8ZsSy6xN6B522fdvq9g9MRZZ/Kom877F1LmQ4vWQ1qLNxJsdln95D+NvQepWWwJHLvu090jk2covRAzKAdUHRyW/q8ms+fhpGzdvMPaOqOtiLc3UuQGN/RZ+UrHx0RzjFz28gmbjyQRTr3eY+34Ha6gJEmLFZbqiZjM9CZbozcgNUDsq/SCRjC+HpRH3flu8+XIv3hLbs5Ri56xYkJmu5NIHaS2jxmLI1mMWE+8MMALN3U879Gcitj8i0lunI4m9/TGDzpKUme3fn8H0NCufTgIywtPPNHDzUvmk18V/QUVC+unMmmRXJKR17TMRsbYoA8VhSNHca5J/H4YlOTXNIRTeH0rrsCFef50luQ67xy101mdYEjfgxgHRS5TeNlj5ZILaMUfyIbY15d+9LO9lXBSIw6lQMh8jqbbufsZmcD3Pnc9JhPs9YlX3qMvuSSHQpDbBboMxkJHZyqez9MtaJNR9xdZjCdDQmbHwiyHZmwb9afGP1EqUpX4a9FAAYy8rZfzkeZ/+hMH4BSEkaUM2//nvBBghNPdD/9Ee3WkTfbqNW5QqNozdyw3QDBZFg2G5mm7ZGvEBJGNQG/KZB2f6pDbFrKZyWgxv4ncb/0Estiug4DBvULwird3OWVsAz0Dwm+JVyXvI3umT2gk+cP19KNqB5MSc3vsLIiV2Whq7F5Fe7rL5TI7cXQHtBntczN0Y+RsyB79nLXZPlFN/boBzOSmndvyeNbhc+OxqQLdsktqRSG0vY9CdEUPH1JaQMHJ3AuqHpfwdljT596UUy94Rx2JtQvUBg5kXPbYfdijcjGgtGaQ2NXY/YlgQe/EgLYSR4rsybgTupyhFNoy/K8Sde6VjkJCS0QhEQ5HYkZl1ekOQ6ngjorXXxE8xOmWhdVAmI6k1g+yatApTbwyJTMX2ow5BSrPwzSHNfXGRTu9oqg+HxHZNxi/K63oZRXuvOPRmb0uys1uw6E2ZdB4bkHg3MbLAlt6+uyAbg+Eqxi5pdh4SZWZ/SsZWIBZiRJCoiFoyuSMlfeau8OvTa5rc8oB+2WHjo5r0bYv+zKh0vxqy8amQhT+WNqs9b5FZC6kdlVGxOSLAWH35XdZQqozpF+vUTxaILKid0sy+GI3kx9IDh3G5bn5KNnhrIAu6fWbIzJ/aDPMGiVqI6Wphi9pQuCrWXkYgBjW9skGiKq3O+EWf7rQ1YvrB0h9scOcXZ7D6kLsT0p4zyayH9MommbWA6imL9KqmdUDaEaeh6ZeVBM2OmIjNfSbDMSnt70Wj6X09oo0kdstg4kJAd8akOyeOUPGqqBgjW2T1piuHR+lyl9s/nZa8hmuw+1BIetkSZq0X8dIP/vmHtx0AyK0EhAmZeyZ2XJZ/LkusrbHbAbEWJG865G5Bbtlj+6dcsisBzcOa4gWx79LbcRIVsRmbe6FPkNDk7oS0DgWEMeH1t+dMvIxB7ZhkDpZf6xHrRQwmJQMu1tL4GZg8H+HmxZqqtTdG/ZBJGFOMvRux+glJFPaTit5+j9CR0VxrH6M8OMXinwm2kahFdPZGtA4HxGua9KomXnUZTkY4Dc30yz1ytzTZFTHRiO/KzuAWBCRLbwQYgdBgU5uCQ1gDiNUNFr7lE+sI+Qig8mCcxkGH4jWxSN98MoHSMHbFJ9aJMAaGnNp5g/aSMcoaUOz7vV0SjYiV/1wENdmVgNA18bLSZuVui/PzwvMDFr7pi7/ChNw2/SnxHjRdaVuKlzXZZdEI2J0Rnfct4Xek1zXFdxpEtpSnsV2T0jVfJN5I3zr3DYPqKZuds7b4NR638DNidOLmDKzhCPfxNLVRBuCNX8rfP2XtrqI/ZlI7auIVJPNRRRJ+OizJRjAYl1K/8GNHQlIeCmnulVShWENahPELXWrH1GhjN8Q3cUL667WPS/r11Os95r7f4fp/XWbxyxWydwVTsrsjgHMwcktqQW9WEWuq0ZREWjmlNa09JnYnZPwdj/w1mc5kb0lAr3U5TeaOgZ8Tb0wvJ4BvvCrWatk7EUt/VMFpizeFNdRUzqRZ+sbgPpZQuChkrvpBm/7k3yGQ9ANiyL6olNpQSr07+ucn/tz/++ejGLIbSqlP/E02ACOAxj6L0mWfeDNi+afjjL8jLrJ3P2MzflF46aGjqB92MO8k2HzCIntLsfzzBbxRZHR2xWNYUmw9lhSrr3e3mf2+wu6EDMqawk2f9pKUd047onI6hZc2yN2E3eMmbl4xdjGkckasuUwPWvtlYQ7zhqjOOgo3Z2L3Ioy2RWo7FC34SwGxTkR/7v9j7r2DLT3v+77P89bT6+11d+92YFF2sVgsOkGwAJRIiRIlqkaUEke2YymyndCTjDMZJzP2OJPRSI4oy5Y0apFZ1EhRrCBANKID27D97t5+7znnnt7f9uSP39lVJhYkRbZncGY4CwK7d895z/s+z+/5/b7fzzekctylOy0aBYDZ74gOvL0H7CubzH8rpD8hY7LetIzqgpiU2plVj71/3sdpa9oLFlY/YliA2t0h+WuBmKXqULnHJXtzKIvTOdFYNI/Iey+eFyaCSFsDEtsD2bWnFantgLnvdOnNCDN/8yPjbH48IPlagkRF5NT7/kATpDXN/TDMGPgJRflEgq1H3VFasaZ4Ts7/Vhdmv12jX1SUHpFk6cRuRGfPqKHbDG6XqOsfK7BzKoaXMlCRjAwNX6q5QU5R3y/Bn/GSpr1PztdTr4Zsfb8viK4peU+1Y5rJlxUz322SWjMwfWEKjJ2V3drLR5JspCXSvj8mcnO3oZl5scOwAIOPtHjrf/11jIExirP3wZDFqHosRWodUlsCnI2XNe3DvnAr35KHuT8Zo3kgyezzERsfm6Cx32T7AZPq/YEcmQyBikpjT+4LtBxnYhWJtCu+G1C632HlBwyhTG0G0uzdFQpVej0gjAv6LrMSkb0Z0FmUnoPTjth8aoJBXo4K/TGDwuUhw7xDMO5RO+kz8WqLxp3C4Cjf/9c8f3+LZ/R3+I9jyAB+WWt9z+h/XxstAEeBTwN3jP7M55RS7z2bGL1CF7ycZvthC7cZMvOipnyfIswFGD7UDsWIlyQYRBuQ2FQsfHsgKjAlpVFnMaJyz6h3UNJ4R/oM9xRF6jtt4U/41I6IxTeyZEHxUxI24aUVe/60JkaLtMHk6yFuQ5FejXAaBn5WSq5bsVJuU8q9WEU4+kFCsX3axv+ZGsW3ZZaef2SH9h5FfMdgkBWgZv6ypvwD+9l+UOAPrUWTxI6M0ZoH5BzanbbpT7js3qOo3Rew/aDD9MtDnLpJa9HCHnWsTQ86M44k3xakBM29K+dDbUoZ7Kdg87E4608mJTsQ4eH3ZmJSok/KGHLmqxbpzZDdOyw6ezTueh2rLRDN1HbI2JmOVCpl4QlaHUXuWh8VaYYFTftgltY+KL5l0i8aOK2Q2e8GeGnF1iMuuWsQ3w0YP+PRPehReiIgf1mOJbfETO09ULgs/YfQVcy8GBGvBQyzBul3ZOGIlxTxsiK5Lgj2zt4UaMj93it0DvkMM6PO+JoxokNBal1heIJF600rmvsTZG5qpn4txp2/8g8w+4rWoYDqnTaJbU3mZl+uU1Kaq05THs79v+vTPADlx3wiB6pHTVp7DXpjJoUrcnZPrSnmvmHQWJLgmSATMfvdNp1ZA+3KaFhFoj0pnBVqVPFCiFu2MPvirzCHkmEw/YqPnzAonJFruvOgMCXstpImcllCSHtTCj85gtbOOrQWLeLXXcZetqnemyG5Jo3b4tn/BNmw1voFoPY3/b7R6xPA57XWQ631TYQ6/NesQYwuDCR2RLu/9lGDftFg9rsB4y9bTL4mTZ/avSGpDQnQtAaa+oGYvL/R3Dm5IU2izFqA1Y/IfyfGytMuw4xBcjsgftPBaWhaR3zCuCa1PmQ4FrF7t43b1JQfyNO8I6S9qKgdlh2qtde4HcdtDTW56yGDorDgzaFIU5WG5qGQeAVi/z6P6Umq0PCPJ0mviIe+tQSLf1SiuWRQPeULcbYlYRfdaeEMZpZh59GIYd5g6xHpFsdXbCbf8PGyFvPPDIls2P5giN3VeGnZtby0ug1XDV0JQxnkDdJrIbNPrJNe1WRvSMhHdjlkmJOfj4bihRAvq+hOSAmd2hSFXfX0JOZAxqPDrMGNT6bozsitsvpUnMjWlO5LUHoiwBwo2rMmYSrET0i1Uz5us3vMxvQgdAV9Vj3q4O72cbZtklcd+uOGEHeOSW6jW5Ppy7Cg6c5FbD5uEMQNSk/69Kakqsgty8M293+9jdPW9AvSgL35r06TvG4Ta4jnP3KkJzT7bIvWwZBhUdGZE2Rcb8KgPyYPRO/IELOv2PNnQj+qPuSx8vE41ceGTL7Vp7MgJqrycZuVj8cJigF22Wb8HWmyWX0xnZXukwVkWBCjV3JLFuLkqsnGB9O4dU3xdYvxs77QgUIBzjaPBgxyxsgBKPTh3ROa9v6QzcctSk95tPYJiSq9LPdiGJMHfvlTKdIbAcULIeZQjirlB/Rt09HuyRAvoyTyrKdvbwJ/1es/pSfw342Sh3/7Vioxf8cYsmAgOKnehMH0izJvdr/+JpXTAU4rlN5A3RTSyrsKtxVRPSEgUrujRo09ufk7MxatPeZtPmCiGlK635ZEn70w9qo8UOUTcfIXFAtf2aVxSOa0mcsm+csh6bVIxnST0ShdRyTM7TkTqy/nQhVBrKJoLcHB3+7QPCI76S2IZfW0T3dGrLSxXcXNT09KvLVvyBm/FDCY9+SztQVF7pYsYrWIKBOQv6JJlDWVu22qR01ufNImVtUUX7VofKBPfFcTq4d0Z2UUVjuqyKyFrD4lzMDMX5xn9bW50UIpxN4gJoasidcBDdsPKYrveiRLIbFdaO9RZG+EVI/BYFpm+n5CkdqQXkRqO8TwJQ3Ky8GeL0rOoOlp3LKF09Yyt78Z3VYv+uMytupPaK78fAJvPGAwLrvioKhI31TU7kC6/I/VmHs2oHhOHHqVewwKrzhMvxoSJJXg1jzY+dnjxHZ9IkuOUG5VnHql+wxS6xq7BVOv9ulPJcheFo19YluNvhtN4YooB5MXXawB1A479GdCCCQg1dp0Kd8j9OTKcRnzpdYUU8/KNGSYNZl5eSDgl4vi8UhUQwYHB1SPKVr7oXPQpzsf0puWazEoKPpFk960CHh6EwZjrwuJWEUw8Zam/lMd5r8ZYnUNpl4JSZ6PMftCwLCA3BcmTL4uG1VyQ9B5nWmTWFXT/UiHqZdEbCVCO5k6pLZCSqdg/tvD/+yLwK8DS8A9wDbwf/7//QH/7xgy20nKjr4WMswKDqv/iZNMvmBSP+jQ3C8a68iUqmGQN0isW2RvhLg1abZsPyTKuMZB6OyTxlzjiGCtYxWYe84ntSZlcnfaIbUZ0ptSBLk4429HxCqSAx+6isYhg+SWx+LXQ4wA+nt8vKwQg1UomfJjb7bEkx8JDzF9zWQ4HqG0aOcLr9qk1zRBymHinYFYoCcVUy9KyMfa0waxdYdhTuKk4mXN9Pc8hlnFxPM2tTskiFMbQiAyBjK6Sm8GGKuC/TI9ocgsfK1Bal0cZDMvyC5087P3kLsq8JLGAagfC2ntFTfgMGvQOKrZ+xWP8gmH7pRJ/spQZvC+9De0IUk4gwkoXBwSxLmtVzD74uL0shLF3ptSox1JbsDOnPy+3qRi/+/JrmkOFLFNG5wItybEn+R2RPOOkMSOYvtBRfBiAYD2omLuuQHaguZBTXtWXHKNoxHDPLSXIrrTDq0DEd0FkSXHdjXZZWjtk8bZjU+6rH1CKiYJD4XssSphOqQzbdFadBiMabyM8Cu1rTm4b5vYU2Ue++A53KamtVcYA5Nv+LQXNYOisB8S5YD1J106izKKqx3T9MZMaNrMPeuhFVhVi8lXFE5Dzuz5ayHtRYPiBR8vZdCf0hTPtymfsAhi8vAObqRZ/7AwMzszojYNEgbpVU39iBplRkjac6wuoJTerMbugvF2msiC0qOiT8jcjGjtkyTqWNmgfsh9z2fx77QIaK1LWutQax0hISO3Sv6/cwyZlxXjyDAvHeedB2Tnn/nidRa+ORCeugNGKLvywldqtBZNGncLVWf2ObHHjp3VxEqW8PZvSlPL7kmOYeQoEmXxAmw/LI2tndNJtp4Q3bXTkGgsFSABlnPCgZ/+jvDoTE9gqP2i4sp/m2T8TES8pCgflz7A2FuS9nNrnt2bliy6+gEXu6nILAsIor1gMP91TawsZWv5fvm52w86TLzaInOzT2xXoYKI4VhErKaJYhHJcsDmYxbTL4sYpHrEwWkpLv9inCChiDUjQkeRWoMgGdGZlZl/ehWWvhjIsakc0t6ryVxX7N4ZwxxKo8/LWfQmFU4jQIXSzEytK1Jr0qfIXQ8ZFkS9uPQHFUlPCjSJSsTUaz6dGQGcoGD+a1VSWyG56xFeVvowe/6khp+OmP6mLf6QimLn4QirMCC9LuEoQUL6G0Tg5SzSN2H2uxHZFZ/elCJWNgkTAt6o3qNxmgYqlAWpPy4EnnhFWAjxHYPCGxYzL/WJV8XC3H5rjKnnDXLXh5i+jDz9hSF///u+yZnv+xX+j6U/orSVY7ufoblfqMGhq2ks2eQvwfg7PdrzBu1ZizCu2fvlPokdySvojysy10xu/rhi6fN1ChflHsguazpzCnMYMfmmR2O/LTgwV9ObTZC5oUlvyPeZWZYqrXZU0Tygae2H7YcVzf1yVE5tiny8dTigflRcg0TSZzACiO+GZC5KIE1ixye1LhMHu/uXLt3/bIvArRzC0esHgVuTg68An1ZKuUqpvcAB4PW/+QdCdhlCR8QiVk/GJF4Gtj+1HxA0dRAfufyu+Gx8tEB/QpO9YOM2InbvElyUn1CYfXCbwtqr3i0ij7WPmgzz0vizu7Kjt/fIf7MbJktf6JK7Jjl32RtSrg7zIkl1WnK+MkI547tNzb4vynz+1vuP70rjsnVA+HvtfRGzz7XxsgKI0AbU75BRk5/WbD1s4mfkXJnYkpGdn43oLSRZ/1ACp6XZeUCcie09isW/iKgdstnz1T6dGZPGXT5GKE3OsRcc/JQET9YPy1c6/bJmOB6R3AnwU4rNR2O0Fwz8uIA//ZR0ubWC5KY8/ONnAzYfjVE6aYtMOSUGlSAuuQOZlYjWvMm1nxvH7kXUD5qYXsTGB005d+43qB4PaR/Msf2IorVo0Fq06Mwr1j5eEOXfvEGQ0oyfGZLYsEi9kBB6cl3DsTbpn92keEmyGJoHxCuglSxmfloz/lbE2NmQeMmACA78fhsvI74Ou2wzdn7A5BuSXh0kFMufdqjcI8rD7LKmuWRQOhmjdhRiZYPkuRhfXDtO1ogzZYYoO+LyW4vSyL3qM/OydNe9jKK9GJNxsgVWx6A74+JlpLl5KzYttuZw40fzdGYVlZMRlZNSrVXvkGgwreRoECsbrH8ETF+z8WGN1YtoHpJK1GkprK4ic11uryDxl6Pg/kxA4R2T+LZcExXd+lXk9pEtxqbN/8ans6hHQjMZR7/X6+8aQ/avlVLnlVLngA8AvwSgtX4X+CJwEfgG8A+11uHf9HeELsQaIUFSLvYtF1hiR9RxpZNxVKhGufXQmbFIlDV2W9HeG+EnRThUvBgQxhSD8YjmPnGU7f/DJu09CrcuAJFhTnoOmWWDwqWQ7nxEkIpoLSVJbA8IktCdMpj7lgBJvJTMrtuLUD4pUtL+mMHNTwie22lpihdEsuonFdMvwNSrIeNvw+5dKeJlyKwGzL7UJ39RsFtOSzH7goBCe1NiC7W7EU7NIF4aCMW2HhG6euTrFyx3eiMismVefvRflRkUZUa/+7BPZiUitSxsAqel2b3LZOxtRXfaor0/xO6IIjF/uUPhoghVIkucdL1pzc4pl+YeGdFJ/JpMbPyUNOXCuKZ2xMDLyxl8kBUJcPlem8lXR14KDSoQ/sLM85rxMz6mJ7vU+BmfIC4WXOXD9oOuSF+XfSp3m0JY+g2H+ufnKH1qwIu/9htc//F/C8jCHatqChckwdnwheunQti9NyOf46xHYlux+UiMnfttuadqmj1fDvHzIXZbjx7sCLemmX4lpLcYYA7hI7OX+MzaI5z65i+SfSNGmIxIr0jvZ+VTEnranxR3Z2pVyMS3BDzxitynXhaq94Zkr0fYbbEMT74ivQ0vI8ixQcFi4kyf7M2I3HJErCTsQpWQI9P0i3IdB2MRsaoIsaKsjzZl4YksKL5pkt4ISFQiimcVQWKUzDUjoNPcDekZzP6WI/iyrCazGtCbib33M/5+UAy6e+b0wU/+E3ozmtwlsZ2anqZ6b8jEK+bIiabozCsWvt4mTNpsPSipQ0EyIrluCNDisQSpDeG2WwORdcZ3/jKOrDsfMf4W9H64SW85S6xijBgCIsa5tUsXLoj5yGlKVFdr0cXwJUCzN2bQm1YM5j3mvmZSP2gKTVf/pXgmsyyuLrchvxqBlG6Tb0qIhdMW8UtueUBrIUasLgk6jf0mbk2EIU5Lk6iE2O2Q5j5HtP7zMH42ornHZPY7TRp3pOnMGlz4xc9x5N/9A8JDXaa+4LL9oIyS4mXR8bf3RoTJiMS6RW+fh1m3R7p8+cx2R0Jd64fETNOf0MR2BZM2dj5g/WOa2LotunhDei0TbwjPIH8tonRSRndeRkuAiCF9ETTUHx4SuxbDaYySiTIGvQmDwekOM7/tsPmYTawqo8rClQGl+0bJO3m49Pc+x/ddfYorr+/Brcr1BLkO2dEumdwJ8JMGzX0m6XVpniktXXq7p6kfNggdTXJD/r8aZUR0ZxSZR0q0n5/EPl2jeylPYkuOi40DUmXALY6CJBElVyXDYjCmiZUVkQOLX66y9cEizaMB81+HnU8PyTyboHCxj1XrsvqD40QOJLZkV87ejG7zLTszJuNnB5RPxBjmRb0pikYn/ZrgAAAgAElEQVSNN+eRuObiNMXUlLrWpH5Pju6UgdWH5uGQsbdkOmJ3NPXDiv2/tcnyZ+YwB3INwhjs/UKFzsE8rQWL87/6j/9KxeD7YhFIFuf12L/8BRa/oll72iBzRcrsyBYNQHZZhEPz3x6y9mEXty5Nus4iRJbGrRoUroSkrjdpHs1RvVPspCKXjbAbBk5Tjgl+SvoKbk1TvS/kwO97bJ9OMH5mSGyrTeTarD+VJbLFbNKblLy43A2f9qxFkFD0pjSFi6JuDOOICMSW5s+tuK5E6VaWvXzG3n6P7FkHLwtuFSbebLP9SJrelCZeknIVQ244w5fdvD8u1Y8ozGDyjZD6QYvZZ1sMJuKsP2ky8aZUIFoJeHOQl/J9MC4jTKdhYHUkcttpysK4/zc3KX9glv6kTA2sgaZ8Ut7n+FtCcu5NGKQ2QzYfl9LUbYjktfVEj+RLSVHHdaH8SIDZFMpt+/iAxMWYmF4MGBTl2pie/GwVyOw+SGom3tS0FoXgnL0mFWB/WjP/LY/qnS4qErRa9WhspOcQxV98N6J+WEhEhfOK2r0Rky/JccsaanaPCSOheFGmB71xE2soi1dix6c979A4BONnNJXjinBqiL3uyrFoQ9G4zyN51UEFMhUYO++LmrAh7z1R0lQ/2iccmhz61QGV+zO094q5q/mhHunvJrA7GrcZsf4hQ0azd1bRXy6OBGGyMKe2Q7Yel8opVjaIbJh6zWf9SZN4SXpMmVWhFKkIOncPGHvWpfv9LfyrGYJ0xMJfRLT2yMSk+kCA2bBIbsriFJlyzfoTo6SiAwbX/pe/ehF4X8iGI0cw2JW7BYTRWdBMvCWmnYl3pGyeeTGgveAS25WZaOexLvEdxdIXu5geJG92WPlkgSCm2Pf5OoOiZvcekaf62UhgHSGkNjWxiqZ2d0ThHZMbPxjDy2nil3fY+uAYGx/OktjW7PnTmkRyO7IQ1Q9IxJU2YfEbQ7yMorsgXnmrr/EzMrc2AvEjVO/WJEohsZomvRYx8bxNvBLdDt6snEgxGNNECUn7bR2IMLyR917L8SC2K2Xg4tcHxHeU5BgWNPUjacrHbXJXFF5KDEb9SXGNqUiSmfxsRHzbQPlS1tttkSOPnY3YenqO1hLkr4aEMWmGxkuihjQCES81jvlsPgGxisHsC8HtHIX9//tAEOOP9PHSCqtqYfbl3DnxTQfjgTpuMyJ7wyeyNLlrtxKifSHhbmvCZET9gOxi6VVBr6Hkxl35Ppv8VZ/WUsTNjzsEcembdOcUrSMBpSd98pc1sV2RyhbfNAhiit2PDYhXPLyi0JRWfljjNDyp3iYMrL6mueSIdXtTFk2nrjC3ZAFQoTzk8WVHOAkp2ZG7ExaZmxFBQsrx7owi7FkYdsRgKkH78R6hq0mUQ7iZIDIV1bsVqYtlcpdFLjz2zwxCV65RaiuUNOduxPhrBukbBuYAhhMh8bUm8bKgwfLXQvpFA7cuxqzC8y61O8B6MYs5UEy+LL2IWw5Xp2SRWpOKqnPII7cckV4XPFz5pFCX3uv1vlgErL442OwObD0uwqHlH47jdGU81DgizrxBQVhyhg9qOYnb0HiFmIyajqQJXTmbr328gNuQHSy2C9nLJoMxRXdeDDi1Y5rcRYPJZ0tEcdG7X//5BQZjMo6LHKicypO74QsIciBNovTakNRmROXuGOmNgOwV4QHmrnnkL8qqm7suY8XUikHp1EiltmSQ2vCoHpM0o+pdEkw69x2PxJpJ+QEBciYqEbnrERNvdQldUeV1jw5ZfSpG/qpHv2Aw+UbE7gnNYDy6HaA6/XIPsy9Nx9BVuPtaxKc7dPcG9BfEbhukYOLtiO3HBIxqtxXNPSZeRnbh8bM+RqBo7THYeUAR27aJb8sMul+UfMbujMG1nyqQqISwJay8/GXx/GdWAqyhJnpVBFPl4zZBetSY1Rq77ZO/qKjdE7L0H4YMpkIm3xT/w+bTwvhXWkaJO6dskuvi4IxVNbnrPokt0YrEl12cTiRgk6ToNIKEYuF3LDozLskVOVJNftfi5g/EZNw8pUlsD4jVIgqXh/SnJEVYGxCvKJKbiulXArI3BNARutJ1d2tSYbT2yrExXpb+DYEBFZfIVSReSZLcMNg9ZhFkRcg2+XrE5X80hRHIbnzjR0VGE1kiF9aGdPQrTw6xuiJnthsG3kQKw5OFZvMjkcBGiorsio/d09gdEYblrka4jZCdUzbtvdIwn//OELchwrrcWw69cYO1p2WBSWwZ5C+8z63EkSXcP++xFpPfE5LPvj8ZsP2o7CjTL2rcuqjF2ksyqvOK0tzaeMKiuU9kpE5DsftAgNMAP6mZeDu6ra4LYwL8NIeaxJbBoKjwZ7KklgXdNfVqSJCQDn9/fMQgnLFus/nLJ2y6s67IQRMSXuG25eBYO+LSXpRVu7nPpLXHoD8hoyy3Buk1TeOAgzXaMdMrYh22Wx69GTH3mJ4WN1lOUT2WoLXHoHZHnLk/M4kcze4xB23Jym91FOZQUblPeHODMUdw311oHogYrqSZzzeY31tB+eJln3uuT3vOZOJVgaokt0efdUbiv4ZZMZu4dY1bk3N0ZI+iwevC8hsWRr2ChCEhF7Fb9l6oHbFpLUjewqAgKVFuxcBpqNtqQ22A2TWx311l/+eH+EmDWDUAz7hNErL6ElZafNcjXg2oPzmgco9N5CgBoZY0zT2W0HUcheErmodDVj5uUnpQtA1KQ3veYOoVKcvnnvFY+X6xT9/4pI0KFG7FxGlLCrE2Yfsh8WkkyyHeWIhXkJFz9YGAeGWk7pwTUVLhbZP5b4dsPKlo75Por2ExYvxVg9Ze8Vvs/w9dag95hI5i6rVwJI2HqVegcsJg95hD7HoMIxTiUvqG3EfakGZe7qwNCorvBmw+YtFcGqVGjQhM2w8LRKV4TpNZCfGyFl5Wkb8ylKdaQ/aKSf6qUJIGhfc5bVibkL0R4ryQoXpMMRyLMIdS1pXul7lne96VB/mikHzdkiXNnWUIUpr2Hjm/JVZsBhOQKClaCyaDgmL8nE/uasT4d9bJXW6TuxEy9eqQ7dNxhnlN5biBlzHQltCBjQCae02BaoyJKcZPanYe1nSnpUcQulC5R4Qgflpcc0YgvYbscsjYeXENtg6FJMoS1e3WZMFrne6TvxJSeiCNEYi2oV8c8fqPainjBvKAlU6YZK8pOgd8yTaYMVn8eh+rq1j4lqjNulMmg/GImedqWD3FDz3xKvcV1njh2J9y4Qf+DZ1DHjun4ngZSG6JUSa+GxAvCamnOycCn8LlQMjHGqy+NKnQ0Nxry4guJZLVICa9CqsnC+ZgQsr5W6nQtXtD3JqieCkkvRqRXQ658cMxnJY06GofO8S1n7bZfFKz+bhN8S1T4CNlgXCGDqz8COwes1HrMYKEprVfvAa1R4b4acl4jNUkizC5bpJcMymcNYhVRRUZJDS1wya1OxSVe138fEjtiEly3cTLCQLO8IXO21mIyF/SlO632Tllkly1cGoGXg6y520GRWnujp0L6U/K7ly6z2byZUXhrDRWJ94chZikpCIsnUoTu+4K5HVSIvTiZemD+PkAayA9Em3A9b9n0ZuWBrYQgoQwZPc0jSULhUjj3ZZoXJoH4cpnfl2I0R8SFnz1qEVyW8xrKtTkr3u0liI609ZtT8J7vd4Xi0BoQ6zm3e7+OnWDxsEk+XOyC/bHhMw7PNSnNyOW38jRDCfkIXDqQq9pz1skdjSLf96kO6eJ1aQbXDtk05026B6b5sanMmw/pKgcd/Fymvxlsf/WjihUoIjc0XtoCVTDastiklpTHP7fbmIEotrTJqTWoL1gkLkpyUL1I+IbH2YNhmlhxc1+B0onbXozQhDqTRrkn48RukqShgaSatObkb83sWmw9ahFakv6B3ZXbo70VZv2rIk51JSPJxhMBiRevkr9jlGHv22w83CB/EU4kbzJnCN2j2f6OaZm6oK3vqvD9mmXKBNQvtcWrUBMdne3rqkdkYU1SGkm3/BlQfQF1xU6isJ5RfOQFj27K9dIK5h6RaLTd++VnTV13WI4FhG4it6kQXPJJH9BMcwbRM5I4960sBsmsV1F9UTIsKiJ7wYMiopBURFbdShcCph/xqPwriZ/XlG9RzP+jIvdGTV2j0mj0OpBciuieipg+qUWiUpI8V09okcpOksBVssks6IpXvDJXjOYezagflcoYR/7m1TvUuz9tWvkL0rz1PQgfyUSklMXjKFUPNqE8XM+Vk/O2s6PlgRisjkkXovIXRZsfHJHgnODuPwZLzsiaHlQfMOi9UBfglEMcFdcZp/vk73ewxzIsXjsnQ61Q5I4tPSHdVKbHs19BsOixm4p9v/ffx8vG5F7U0JzAZpLpuDjXcXazwSkVg2Gn2gwKMox4r1e74tFABPqB2Lkz7fEoXZVOGrtvaKsGjs/IH/VI/lOnPzlEHMondzCGVEY5q6Lhl6FEt7QOJwme0UERqmtiPadHt35iM3HLTLXYPJVmVcHyeg2hw0Dxt/RTL8UULwgASitoz6pDWgdDDBCzfan9mN3IIgZLH61yWBMOq9BTJG/HJG7oshdgvxlidbqTsvYb/J1n8SGQRiX3b1+VHBPgSvgVG2MSuWBdIQ1sHuXcObGzvkYAUy+2b8dhaVC2P+HHuVPHZW02r7AJTp7JHTzs8/9CL/5yx/n3jc+zf/whf+K3bMTFC57pL6TZPaFPnbJRlsyhlv6Uktm2EVx2w3zMv4S4Yk8SCoQk5M2JbLcaY2EKxMC39BKRmkoJAHoRJeZF6QqQEvDT5siYc4th1gt0ehHtuz6mJrEpsJLSzpUGJMRl90Oqd7hEsQlli59U/pCrYMBtXtlA9j8oDQse5MGM98yWPtIBrsXsf2oHNWmvzdk4numeAL6Ec19I0BqwuDA7w/pzmj0i3kK5+HSv9hLb1oxdkbsw+X7oD8lPyezLpw/bcDO/cJutNsGgz+dxOppdo/Fae4zaR7Qoyak6DvCuGbqa2vAaIRsQ+FSn9hFkX5HtigXw7hJ9ViS7qwivRGy/qH0KCMSrvzTBI39Luk1GS3OPduRVOYtg2Hh1uILvamI0kMR3bmIsGfRn9AkvpSldZeQod/r9f5YBEYPb/1YBpTQVZ2mnHdylxTVIzG2H3AoXvDozJgyex9FjfcnRyXyNwY0Dmt607JrZVY90isQL/vYOzZj7wiUwQilfFYRkA4IbVj4RlMAnnHF9kMWtSOSpjv/dXEMpm5Y1O+McFoj4cWEwdZjWXqLPqm1Pv1JRWfeIH9lSPV4xMrH40y91pEU25mI0il7FA4CraWIzHWD3HWfxlHNxP90Y7RDSK+hdsQAA2I1xcQrdYK4QWqlS2fWxUtLf8JtRVTuTdBcgvyVPv3piLE360SOZuujAbmzNv0xRXMtK5mKW4rVj1okdiNWPxZj4i3p0keWZvOJLM29FuZAdqtbdKdhQbP/D6riyouJ+MpL30JmC4glfzWkdk9E9U4Tq6eZekWENcmXk2w8YVC7Q6637IiK+K4EguQvi0x64k05UhCJ/2PzqZDKPSapDU16RfDnpidai8YB8T1oE3IXLMyOePUT6ya7JyKcpia90ruNlTN7Br35gPaC8LictqZ+aARxHTEpS/cnsTuKwiWf8uM++XMmXlaORl5GkbusSGxL76N00iBRCoiVDQqXZGGI7SLMhbwSkdliyKHP7VC9Wzr6YVwMRms/tsjEOwFTrwmObuvhBLnrEfGymLuK5zX1A45ck7cDakdMgqQASooXfI788wpuQzDxQT5A+SHJknAs0qua1Jq8x1jFYO+fRsR2DZLXHOyONIrtuP/+Pw4YAaTWI4K4/HP+knToAcbOdchf92Q+e6fDxNt9MX1MKTI3RIbZndW0FmKSYTc9pHkINj7gMP56na1HXIK5IbWjkFmRBk1mPSB/pY+7IqaKm5/MkFkJmHx2i+nvCQWoN61o7pFgj+K7PqmbJtZAs3NaUF+JUgSm4LHjZZETD8ZsMY3UFbt3Jxl7N2DidQhimn0fuonVldU7UYnYekT8DeefOQQKYlUpsa17Grd1A1c/k8NPGDQOS6SVnx6p5O5WdGfFMGN2PfLvKm78SJ78eUV82cFtRrgNzdwzgtOy25r8uwrD01htxSAnVVaQ0Mz/2Q6ZdeE2jJ8LcFoiypp8LaL0SBEvD4kNk8KlALehidUjEpsG6RVZENLXTCJXkyxF+HE5tvlJ0e6j5eFe+FqTmWdrtPYpxs55ZG4OqN4b4bRDJt/oMvGyKEAnn7PY89W2+EcsOWolyhLmEVnS3A0S0DwUkbsKxfMi8jr4Ox3644rth9K3SUK5S4rEhkX2hoxzvYxi4Ztt7I70j/y4kHtz1yPCmIFVsUlthZJbcNCjfc+Q0JVpjlvThDFNd9piOC5YOas3ihV7LqC3INFryRUTbz5P8Yz0rYY5Tem0fGf9vMnOaYfsNVkUy8elAV68OKC5V46Dndm/bKDOvBxQPR4yKJhc/9d5UU3WImaeMejNJdn4kNjIG4cguR2S2NEMJiKae2zsllynyAano8l+W2To7/n8/Rd+vv9WL8EhCeU1MgVxbXVl9yidSlO5y8FLC7Z78/E4GJLWUzummXs2Ihjz6U+Mdvq1GMWzmpmXA/pzabLLEZk3Y4yfGRF/R7lwVq1LrALV0z6JbUV/zOTmT8yy+kPyc7PLEZk1CSMpn7CJ1TSNJYP4tjTMTB+cbZsgKc3Cfb+9xiBnUL5fUFrjr7dQgQBUp18JKf3eHlIbEWFMytzCu5rZ52WG7talSZRa09jfykqibBbmnwkpPyQgTasv2LPutGLm5ZDcVcGRbz6Rw/Q0S79bwk8ruLeFNdTEq5qND0lac+1uCR5t7rNwm1A9KXr44jnF9Z+dpLVgMcxB5S6L3PVw1O03R8EpGv9453YFVj6tGT/niQnGkaPJ2BnNzgMjJWVRM/X6gP5MiDfriTJuX4qdhwukVjX9MYvVj8VIbJhs/aRHfzKG04lEm3DQYPWpNM5IaWkOIPvmFnZXSEntwz5z3+mSvSaGne60TJVKp7PACL7ZC2kuGYSjxN7elIPTGkFhijF6UzJZGeYNYrWQxNaAflGqDC9l4KcU6YsO8asuw7ywDGONiMw1EfSMvS1CpWFe4aU1qz+sUUPF5mOywNX3x27z/k1PYTeEel19zMNPappLgom/xbAMEiaxmr59VNp4Uu6vrYctJr8nU5NwLYmXlt5R+QeHJDZ75M8ZZNYiclfkGbL7EZEbUb8rIr0VEKQk0Sh05D655T34q17vi0XAHAhcojs/skX6mtyyD5EENcZqQq8dpg32/FGFeEnm73bbYOtRk/iqQ3c24vt+9kVUAP1xg+Zei9phmyAuZfb24xHVjw0YP9fHGEa0jxQEc77qMChAe0FktvN/brDwzZDSA9LJL58w0JbMpJWG/rTIYbcejxg/G4nDcQA3PrMgduhrEkyy+WQW04sY5kza8wIp6cwaqADWnjYkmHPBkjDQUHZYI5Rmm+Fp9vzpLtU7bFLLYtdNrwtwtHA5ZPMxKVcjV49MVQbV05PSxHolQ+2wSeW4IrZt4icMnJrg2lObIW4jIr5uk7sCuyciJt6KCD/QYPqVoRwnHoN4GSZfH+JlRcqaeD5F7WTA5Js+yRWT1Y8KGr0zK4DW9oJ8LhVCvKSoHo1hDAzm/0xAJfWDJl4W4vWQ+lFxaTotTbAboz1n0tgnyc/CRJRg0+S2CGtufGZeJNxtzZ4/hq1HkwQxmb/PvNjF8MCtR3hZTWrTI77SwG2Al5YmXP2ghILWHxpSudsmcjVj5wMa93g0DthsPZoYsQCFS5HaCsndkLFgGBe8+fYPegzzUH9wSOVkRGxXRoUTb0ckrzo4TYPCOUV8vSXld1vTmwtw6jD/7JD2rE38iotbU3hjAoUxAql6d4+JL+XQr6zh1n0Mb4RFKwTs3i3AVgwZ55oDsJ2A0j8PaO2D1oJBa5+icsJg6wOQuWJhdcQkZrfkO4lXhNF5Kw/yr3q9LxYBP61Y+KbHxBtCeLk1n88tDymfEPdVf9wgWQq49pkxtAmTbwzILmucumLmxQFWV/Fnn38E43AHreSc1p2L6E1IMyZ9zSLoW3SnXWpHXHYeMEivBbdpLZNv+vRmFJGlaOy3mXlBU7lXpg4gMIrsckhyTRYVp2ZidyJae2MMxrXEbgdysadfDrD64JZ72L0IPyX2ZxAJ7fjrBs39ozwDR3aw7OU2nVm5EVGw/BNFYhU5E3ZmTWK7PsZQRpfJDYNEKWL6pVAAH5mRFn5Fzur9RZ/5b3k4bcFVOy2Z/3dmTFQoJXTlhHjou1MmY7+RJIwbsqtEIlpa/ZkIvxAyWPRoHAtwShaNJWmqOfNd7DZ0jnqsfZ9kITgtdRuYqk2YPFZi83HhMsx/u4XTBHfXwxwo0iuQveGTvSz24+685BiEroz1Zr+9CyNu3jAfMcyLeKe1YDH3TAsvJ72ZndNJxs/0cTqRYMRPxwjGUlhdTX9KNCJBSlO8EDLzFVv6G7bgz+2yWHp7e6WKjNXkDA7QmZb+R+Y69McszLUYQVIz/VWb5LpJYidiMB6x/aDB9Ct9BlMBg3HF9uNj9CcRKOiWReSIJd309G2x0cxzBqmNIa19ImuPVUW01LlnlpWnXZJrUnFMvmhSPC/TmXjJYOalHun1kMV/ERC+UEBpyW60WxDfVsQ3TCJXLNqV48LQOPDr6wQJ6Z0kd95bMfi+8A6k8vN67hf+MYOpELNrEKtImVm47ItF8k6b7qIYJiJLVtDIEmiFisTxltoUslBrH+z7Yp2r/2Oc+IU4TlP6B0rDcN8A6g6JbXGlxXcjEps9qnen8BMybupOGyR3IkJb5LhhTEi6nWlRnqXWbuUTyG5WvUuCO2K7IuIoXPGo73ew+prkTsDa0wYTr4lIyO5KQ6l61KY3G5FZNggdCQjZvUuNXH2StDT3TJsbn0wx+WZEY8nEbsNgXLrAflrCSpSGmb/YpL80RuUel84RD7tiE7oaq6OwOyIt1epWwIv0WryMJpocknvFFYPRvoiJN8THnl4V3l+8JGPD3XtFonsruMP9kRLNZ6cYFuScnFoRKKvhC1ZrmJcyvnDFo7nHJoyJJVyForvvj8sIDQWdeTFVbT+kcOoG6TVNf0zRPTbA2naJb8t4dJiT95LaDlj5hGLhL2DnlMnYeU1zr1z73rRi4m2f1Y8rFr8sScmhO5q2KNlR/aR4TlI7AY19NkFS5u+7dykyN6FxSJNeMWgeiLA7snkEqRCzK6NqtyYGK7sz2slHaUFBQiqDmW+UuPazE2SvQfX+AKdikVqTyUlnTt7fyg/B2Pcsmgek+oiXJX0qsmVU7eU0c88K1r4/E+LumqTWNI0jMP1yyOYHhK5ld0dJRRYky+IpSeyIx0Yb4OdD3JJF/rJoCzqLESu/9E/fv94BgOz1iORNU7BJM6LVDl2DnfttUlsRuYsG9Q/3idWj23HX+Wsj4IYJ1TtMdh8WbFT5dJ6pLzt0Dw1l7DUpVs3cKy5uXSSgKoR+0cCqtJj4s+sYocA9sjclAtrpSHNtWIhAC4rcbqlRF13GlqEr6TipjYjWErQOhuyccsSAM6XY/Cmf4tsGtTsVXsqgdJ/N6g9C99hA/AEdzfRLbZr7jJH1VWKl7Q5U70oRryhK9xnEalr6IDfES6BCcZZ1ZzRbT82y+rTN2HmP1GUxvix8M0RFisGY8AXzV0OMULrV2eWIzA1wbsao3+czLEAUF6PKvi/WxWizpUjuSAz77AsRw4IEtFQf9ej8xRS96YinP/QGp05ewU+CtiFWE/aAcPU1K99v0jiq6cyL1dYIILc8YJjXNO+QcePMSyFbH/cFrZ0WUk7/3j6GJcxBI4DdU9K/QI3s1NctKvdYZJdvuRhDgoRiMBnS3Gez+BXN5gcsEiUh9vpJRfsTbWp3i6+/cUTjNHwm3urSmwvpzMg0JlEJmXxdTE9j7ygWvjVg4RseVsskuamYfE0qKC8jAqnK/dFtZ2vh0lAamXeOEbmSBRjfsBk7K79n98MDAHrjFmbTpD+pmHg7Yvb5Du09ivlvd0lsKTr7JTuydtiVrMqG4NL8lASmlI9bjL2tbo+UB0VF/uqQ+n4xEfUmFFOvhISuJn/WxK3Jwp4sCWPyvV7vi0VAm9A4KM2Z5HaI3RL4YvWoSf5qROVesZFG5Ri1Iybl+1zsjuyYhg9+RjDcubccxs5JHmF7wWTpdzWT31hl6nmD4VjIvh+/xvy3e3JWqoa0F2G4WOTK/7xErBax9KWBBHm8GmL64q6L7xh4KQFh2B1GyjHN+hMi8dQ27D49ILI1hXOS5JO7NpDP8mqC5kFI35AScfHPm8x9zcDecCmcV+Su9ujOJxg/42N31G0sWpCA9qIsSLGadOGH2ZFYRYHbgM0PaVLr0v2d/07I+pM2Vg/Gz0RU77DxCiFTr0bUDxoMs4ImC10hLHVnZFfPve1QuBSx8FUoXAq49tk4w5yieUo61p1jQ9Y/pkmtGvzyh/6QvXMVWicHMD6k6ce5tDuJ25AbsnkgYvxMiNvSTH8vJHfRIHPdILkh1Uj88QrLP6sIJj0K7xhYXc3aJzTJczEyqwHJTUV8R+FeiGNfiROZ0DjukVixcRua+pFRxFpBtAuGLwtLv2BQuOKRXDNpHpBOv9mXnT9ekkWg8Pkkk98Tc1SYDbn+aZfa0QSH/l0Tuyvo9dJJ6aPYbag85rH2ZIzmXkcs2bsRnTmD7owaRdPLaLI3KTv4jR81JPn5TEnMPa8PMfuIBsUBKi6pDU2QgOw1xfTLfRpLJtsPpkhtaEr3J+nNaMZel/ForCGJWrFdRe1OgYf6SWkgd6cVzf3SNDd8QeWZHsw8UyN3I2TtY6Jf8JOSjG0Eip3TImx7r9f74jgQn5RA0siBideaXPlMhnjJILEtsVGdU33m/lDOpMPCqLTcHiX1rEuQQ+AKhIxRf04AACAASURBVMFtQmuf4KqSm9EoBkwEHL0pKWszKxF2NyR0ZQ3s5w2qp32ckk16Rd7TrTy8WEXegznK2vMymrHzmsZ+g/7hAbErMaH0tiJK9xsE6Qgj55F8Iy5fwkBKbGMkEZWYKfkCh0VBmic35YsvHzewOwp1X5PeehpMzdRLivJ9QpCZfjmkdtiiuzcgedOiPykzYcOT86HyDBKbJuk1KQGHebFhu80QL23cDlotnw6xmybpm/JZtSk3lVuXzwrQf6iDV49hdg3CeMT4Yp3PHvgmn/3zH+e+B65yZ3qLz//hE4x/cJO1C9PYLQM/HeHMd4k9l5ama1V2X0l/EgahWxuy/VBSACRa+gnDyZD4hnAZWvshe03Gpd05WPjWgPqBGJ15OdIVLka0FmQuHq+IjDm9NqB2OE71tE/qsoM1EK5g4yAU3xWpbmozovxhj8TFmBCK3o6oHTHJXwkpnzBIbsnnVoGAU1Gy42tTqMy9idEEIa0YTGj2nl7jyvIMC19WuHWP6z/uMvOcoMjDuCxUbk2q2rF3kLyGWUOyA/OG2NlbERsfC9n7BRgUZGTc3Cv/LbmlKb5ZpXlHXpB6SWlwmgMByfRmNdMvhVTutVABjJ/1ae61yd70ac9bDHNSSSV2Rs/AUPPOb/6T9+9xwAjEnNGfUFz+h0nmnovwcprunKTIZl6KYYwQzbGygC4ABhMRnTlF5YT8HD+tSW2Gtxtu/XGDICmjmPphRe9ETxaWhGi/rW7IIGdQPRmy50tyDm4uCaIsMqE7K3mFhi9pPLnrEgQZOjD+jo+15TL7Ul8aekWJNy++ZWCsxvCycOK+a+w5uYEKZQVv7RWwhuHJlxzfMfDyEdX7QrYeG4VX7vV5dH6Z3//+z6HdCGsQjei7Ug6On/Vxdk1SmxGzz0sTLrMaEtu02fcnPlYXMjd6tO7yiBxN+YGQQd6UYJOVkMr9EclVS+jLe2ShM3x56IpnWkS2QEW4nsQYGBw/dY0vPPVrvH7vl/ihVIvrP/Zv+fzeZ/lA6iIXfuFz/OTca8QX22hDE+UCgpspsjd96g8N6U6ZDLMC5xzkDOoHLeqHEgzGNd29IU5Tk7mpmXlWFsf2PlmQhjkZ5Y6fKOGnxBijDQk66RcV2Sd3yF8Jqd3vj1KshbFoV+zbd3T9iHTvDV/TmxPU+tizLoYnMvPaUSmX6wdNZl8MiFUjifZyRNFZv0PT2+8x92xPshTa0s/oTwp0Zuurizhli96ESXMpjl2TZKtbhqrUmiwo6WUZ8xkhpNcECGN6ck9W7zBJXXGoHXYon4TIVLf/fOjAxkfHqB0xaS2YFN+u4Ta4LZgqXNC09khewbCg2XpE0rIbSzb1O2Xx7U0JYg1DEHfv9bL+Cz/ff6uXtsDsi4osuWFROikmivwV2bGDmEFjyWbyJY2f0PTzEvjhVqQjHrkGSmviFVFITb4Og7ymeKGPCiNaexN0FhT7fg2GeTmPNpdMdu9ycJqSibdzSjr3kSNNrlgjIrVqYviSRNPca0lTaUOor8OcQawM/XGHIKXxBgqtJB4rd0HkpW+/dgCnYdC/3wPPYOlLAYYXoSIba6DJrGq6ByUTYc8HV5hNNDm7O8P+eJmHYnI3Rz+/S+PNSeIluT6bj1m4NUVrUTH2bkRqXdObMJl4O6B0Xwwvq9l5IMWB3+qx/iEHZ82iMydjPy9jkNiUm8zqKYIZD/ddOdaMnQ+4+t+7pM7KYnjnj13kWHqTH868w5Kd+o++s1vv7+eyO6Tv/Cr/0nwKbzdFrKLozFrErtojdJgtvIYdRX9KY3qKzHVNsqRp7FeMnR1i+hGJnRixRkTzJ9voco4gAZW3Jlms9+gsmOQvigY5tRlS/9YU7Y96TD4nt293RrILQCpEtx0y9VKH5R/JktxQLH2hR3sxxjArMFOQ8SHA+NmAnftFIp3chM6iJrEtCPvuhEN7wWJYkMh5cyj3av5MFT85RnYlonK35EpOvCMZk7nrEd0pg+7MKGm6EbHzSER405JxXwTVu+QaJ7akAvTSBtG4R+i6FC8GbD1iMPfcgGs/4TDxqknowJWfy2O3IXctYvdu8VcEqYip72kGEwZuXdEfE2UkWZ/ktkKFkjSdXQnExPQer78NY3BeKfWcUuqiUupdpdQvjv59QSn1baXUtdGv+dG/V0qpXx1FkZ1TSh3/m/6OyBKpamY1IEgKLTc62qF22BiZf0wyawGJHV/OQqEgwayBeL1DR44GTlOPYqA91CiEVZsiAElsK6p3xvHS8pFzV2Vs1to/kq4qCSJNbBkMxsT51VmUBmV3yiRyRFIrGQSa/FWP/NWA0ieHIjlOQua6wd4/DujMyyoc5gNCV7P0BxH58yalkzH6Ey6Fy5L7150ySFx36C8N+emZV/j38y/z4NRNbBXyb+qLJIs9ul+ZEsT3usRbWT0ZUWZvRtQOW9TuEJ2F0prBuMbqqZFZReHlIvy0jKHqd2g6+wJyj+9geqD2dYlfcYksSFQidk6bFF5w5b+F8Mb6Ap8tXvsrF4D/7+tHUk0OFCuogUn/3h7V0z6DA0NqhyT/zmkoBg92BAhjQu0Bn9aCRawqoI+Nx+KYPvhJg8GVLJED//Wnv4Fe6tLaG8fqKcbOdunMw+5nukQOxG86VO6T5u6+L9VlWtNQJLc9WgsWGx/OEcakSRkmLIZ5g9ZBMWX5GYlHj2xo7Jco9vwlKFwaMnZGNBmbT4d0FzStPdL4tbsR3fmI4lnN1pPj8nMSCm/PALsFG0+HwgKYMph+tkbkaAYTmkHB4MAfePSmI+Llv+wr9WYi4jUp1dsLiuxrYiorHxdIy8r3x4lP9OiPyZQitWpQvBCS2vQEDDuCkfbHDOaf8YlMSJQlpDX3ikv9sMi0u/MRvVHewXs+439TT2BEFp7WWr+tlEoDbwE/APwMUNNa/yul1D8D8lrrz45yCf8R8DRwCvgVrfWpv+7viM3M6zs/+kt05hT5KyGV4wZuVTH1ao/thxLklkO2PgAT35My0enKaEibI1fWRZ/k5Qo3fnoGFQiJZvydIZFjsPm47JydQx7ZMw7x3YjmksHYBVkdvexofj+A3oxYXdPrAfWDFpmVkPa8OaILyXjQ6kNmZcjaR11Sq9LAS25KGWcO9W3yqwA+hA6bvi5BEKErUtXe1GghWg7wEwa1I4pHP3yO7y4fIKy5ECpiuwaDpSFG1Wb6ZU0/Lyq4/4e5Nw+yMzvP+37n2+++9t7oRmNfB5jBLJiVM8OdlEhREm1JiSKXnFixZMWyHMdxVSphVeLEKieWLFcU2VWWtS+USImkSHEZkjNDzgLMihnsQGPpve/tu+/fdvLHewFRFkeLZVfNrUINBo3uRt/v+8457/s+z+/xajGZ2wM2H0vJ/FzB1NmY7rSJ247pzQp0NfRE/6Bt4TD+z+/7An8vt3H3Pf/l5hw/9+KHSd5wGB0d4F5I4Gc1YTnArtqcfPwqv7X0Vey/PEXu7usXGrv5N288RSo9pL+cw2kI1GI4qYlnh1i3vPE1E6FTUA6Y+7JJ5T6D7DK098mce1jWOIfaDG5liBMx3qaFtyO7nNuJaO+yGJXAaTDOitDkrkoPRBj9sPfTLdbfm8d8oo77+3mq94tD08+LQSp3K2T7AROnJQ9Z/nrMznGFe7yJ+bWCpEi78j3CpCDpIhcyt4RX2X1ggHM1IWGsyxFBwqCzWxEm9N1xYuFqNM5dhPZuRaKq6c3JKbd0MWRQNOnNSVhLa79ct8FMSO6yRfojW1QaGZSh8ZsuKjAwiiMy306K+SuHgE+a4kdxGwbFixFGpNl6yCS5IaPf4tuK1HZIa8nmrX/zn4gX01pvaq1fH/++A1xCUoU+Dvza+K/9GrIwMP7zX9fyehnI/0eI8j//UnIaQMubnbklzY/2ngTFKyG1o3Ijbj8eY/oaPyUNkkRF0z3i052z2Hr/DEu/tYXbELzX2lMOfsYgd1VsoFPfFPFGohpQuiBJtPWTsnont0R5l7sqPoTMW9t3c+ClwSNpsV5DmIOr73NJrYmOwO6INLd1ICa5ExGkhNE3LIoTLbFhMcrfQUnLgmv4wjqs3GvRnTXILcPZ3z6BupXAKI7IXxb2wO7fhKWTEtvQmxe/QPOAQeNQksiROXP2OrR2m3jNGLcZM5jQJLdjrKGw/IyRglzwZxYAgP8+v86BpS2xvaaGDA6McNoKZ8vGbSjOb83wH9q7+Ou8JqwOpUKXTjVNXPYZlWNiG+yWIpkayWkqlJ8/taKY/oZF+OM1URk+GuBVFZ3DAWEmRr2Yk7DRnC8aj4Kgulc/JO+dtyMj1tJbmsKeOoVrPk4LvEbE5Osx60/nBQZypigN0XWD7mGf8psxyTHmLb0ChashYUozyor1O3izQH9GM/dcj8jRuC1NYkfjZ2RcvHNKM3FuSPLNhCQO7wtoL5p375egEJG5KdOY/oQ8XomdkOmzIkoyhzLp2njcIExJmtNgwpDFJqGZ+4YisxrReH6auV9zCCoJSmctjJHCWEkQpmSzcWvgF2OCDIJa68vpNbKFlDQqghGMgb1HbFr3/2dKIFJK7QbuBc4AU1rrzfGHtoCp8e//SlFk3xlDFnd6kgaU0XfDO/uz0t3tzFnkr8XkLpgUXzdJbQaU32jRPu7Tn1akrkiKT/OwZvMD02Rvh7jNiNTGGLZREofXnbn8ygcdmntNzAEc/oU6/WnRqU++4ZPaklHV6vfPSWNl0sTuaeoPiCKssyDz7OwN7vq+3YYoHLPLhoSVjC/+zMvRWO2lJZCzGlN6q4PbkjzF2NLEthwZmwcgtR2T2lDkv56gfK4vnLyPW2x/aRf1gyIYkSOrjI+0JTbj9j4RD8Wmws8a7P7SiORWQJCW+b/S8J4D177r9fRjE/uDO6ivF9B9E061MEdKUn0Ck+Av0pp+l9fjidsUvAFTcw10YODWDPq7JcBzcCOL3VZMviH/plQlonoKEr9YIHyixcTzNk5Lk1q2mR7z8zr7ItzzSQqXI0qXIvwCLH5OTj+9OU3/wx1GOYPs/5tj60GH7GpI7ZhF/ZBJbz6mcUiO3ru+uIPVB++2w849BlvvDdl81KRxVLP5qAA/IkeRuyo7f/YGrL4vhdWXhyiyFf5sQPqWJDzVD7sUroX05zTT3xAHZW9O4R/uk3/bIlGTRVjFYqNee69J9YRN/qqwD/LXfBLbhiRaH2mRrMQUrgVYA0Vrj8nOCZlaaAVkQvy8YubbYn1365rGEY3T1ez7zQ69vcH4JBPi52DrYdERTJ+RpGqvEdFdCqH3zu2/v/IioJRKA58BfkZr3f7Oj2mpKf5as8bvjCEzUymyt2KCbER3UVG8PGLqlRinJWaf7qx48cOkorXXobM3g+pZOC0kuORGRHLNoLuoaRy0GOVNcaI5MkaKbejNGEy+0BBhzL6QN/6XX+KnvvjH2D3FYDpm8xGHMGEQm9KkTK+Lnt/PKMovWvQO+Fg9SFTUODpMjW23Mc1DmtRWTOhBaismtRWxddokUY9o3BNTfSgmthUrH8qy+ZiJ0zYI8jGFS9KpztxGdiIl3enbH03SemBI7rJJ98SQwXRMkFE0PiKZjZGtyNwSjl/pnL6bI5i5PWT7lEd70aFwJQZLfA5rvfx3vQb/dOnLNM+XsPqaxLoFr+YY7h2hDU0YmPzSpSf4mc0/d3p8x9eCleYPD36WjDuCSHH/R85TPmPhlyNSK6K2axwwcRtiKTYCxa2/pYnfzrFzSqYkx773MtvfM6J72EeFMrmonJKNYepsQOU+iWyz24rsH6bxGjFbp21Sp3foTZpC6zHFvJNdFgforU+UsQYi3TUiReaC4Ngmz0rYrOErhmUJjjV9EXo5bbl3GgfFO2LVxGVYOyphKBtPGCS2ZDJljiB3I6b8JY/hhNjBzZEoL+uP+6jgTtdf0d0bMZiwGRUFJ9fdTOOnFZX7JNS0eDEkSGmMSLP6AZP8GYf89ZDNH/TJXjMZFRVe1aD2wSHr782BFZO/JvdX9nZMek+L9oGI/qSFW1Osvt8kf97CyPvveN3+SouAUspGFoDf0lp/dvzH23eO+eP/VsZ//teOIlOhcNnMnlzE2lGPyimD7K2I+r0RiR1h6cUO5JZ9tk4bJDcMZp+pMveNDtZQvP5Wf+x3nzToL4R0jo0YlpRk7I1g9XuKWG2D5z7yrwD4RusIi5+rE6dD0ivCB/Rz8mDbvZjaPYrcTUkUKr1oU7o4xO7KouIXxfpc+YBPVAqwu6LNdlohzf0m7o4ic26b/AUDu2FQP6aZfC2g/Kam/FbE/DPydbQp8+iJ1zuMStB6dMjSH7RZ+D2Tma9tM/0lRzrjGszLaaqnuJsclNwUDcAoL7Xqre9NSP25HyofG5K+IjfW7WqB/2710T/3vv/ki/8VaneP3i6RQccuGDVh2x1Z2ES/nuNLX32AX25+10zZP/d6yx9Sj31ubZcozra48ktHaS/B5EsSAy+ed7Ed569H5K5C8rpD/mpMcs3k4MF1fnfpG/z6I/+e33ny35LYNJh7pkWU0HTmTLYeEnjpnbFmb9agdo9IzKMvlog/2iB25HRmDhRmAOZArMhOJ6a7JxyjxSB3RbIJwtQ4PagPRijTpdhBTDxpWQwmzg3Em/AElC5E9GelzDKHUDonk4PwzghOQfltCdHd95t1Jr9m4zYV+eUItxORWDdp7TVIbsq/26nJaat4KaJwbcjq+w2mz8T0pkwmXoXGiYjWkkXmxQRhEvpzMdNnfYxVjzAFuTdctt4TEbriMgzPFpg4Ky5Lt6GZezZmMAXu+cQ7Xre/ynRAAf8euKS1/lff8aHPAz82/v2PAZ/7jj//b8ZTgtNA6zvKhu/6MgONEWryl+UCDsuw9Nk2jUMm3rY41pQWgEh7t0P+smjoN94/wfZDGQZFIRJbY1IwGtLLFvlXXOyOiHymX2pjd6F0XvOeL/0sJ37uJ/mj5x7k1ieK7PqCQZiUldSrSRqS0wopndPUjpoUL8m8tb3oYg01ySequDvSyJn/rEXxZYcgZZBfjhiULQazkpgcZxJoQySfiW2DIGOyc4/CbQTYnYj8tSGFKxGJiqZ2PCMPw7kE9RNZRnmT1okyjYMGiR25cadeCZj9lngeGsc09ZMxg5JFkJPpQHYZipcCIldz4P/oE6YlbTleS/Lqb5zgwTc+ydlRwP9WPcqeP/wJLDtCr6Twc7KIhkmBuCTWLNZ/f4kgJ9Sgf33haVbC7l92q/CZ1im+1DvAZLFN+EyZRC0kUVE4nViCYjxINGKGeQkg8ZoC89w5KYtQtZfij3pp/sHbP8IPf+MnJHb8B7Jklw16C7Hszpuit/dqmvRaTGpVJMP55YDSLyTxdjTdxZjhok9iJ6Q3a+O2NRsfiMlesSi9qfAL4thEiVx9VNb052O0gplvt8ncEhGSnx1nJSQsiEGbYnCyOwrTV6S2Je3Hqwn9qXJaU7wg2pPKewLW31+iN2eIgnAkXfpEVaTcsS1MzNiFYVl0C60lj/Rtg9hSZNZC/KwiddMiSAnSzmlJjsTN75del9WD7mJM7rzNqGDc5VJ2FoVVUH6ry8Zjws78m0JFHgV+FHhaKfXm+NdHgH8BvF8pdQ143/j/Ab4E3ACuI2GlP/mXfYMgKWGho5LUM4ltTexaOE1xfYWeeMdzVxS1U4KtcjoSd22ONK19ou02hLnIcFKL/2AMDc2sxoRpB3Ogqd2jMIYGiVrM5KuQWtNsP2Bi+Bq3GUpq8ZRF/YjL9iPCFSi8UiG7EtI4hAA5+h5/64eepbsU0fnxNn5GUT9ssvXJEfmLHUqvG/R3RWw9XsQcCc127ufPsnNC4e0ourMON3/Aoj/j4rYiBpOCzt65RzEqSVU1yin8jKjw3EZIalPTWrLZOm2QvdzE7hhkr0o6k9NUbD8q/oXVD46DQA4WiG1ZGLyqQZCGIDT5sV/9h/z2hQekeLuZJCwFOE2DwrURbk0RpNQ4wzDC6koX319N8d7f/iecOPvD/ODy+/7c9atEPVrxgMPeBv/izIfZuFWmuyQ4t8GUpnKfRW5Zk9rQd9N/OovyXo5KmonX5aSX//kM//u//FH4SpHETUcUb5uK8ltDVKSIHOnr9OZFHdqbFTVo9orJ6tM2Ww95hAnF7i/4TH7TpnLKpj8lJd78lwzcpqa1DwoX1F1BUm9OPp69bpC5pVn5cJZBWchUQU4WqfpBmyipyV61MB9sMJyMRaU5K+pAq+tjBJr0TZP2ojgj7YrNYEo2prX3OlRO2qS3BCDbOCjqw+1TNrs/P0Aboh7VxlgyvsugO20R24rZb/VIbQhh2QgkyShz1SJZibD6MPst+bzenGRWzD3bJUxqZl4csfloBiOQUWJvV/yOz9+7QjacnNilZ/7pP2LxT0Zs3++RXo/Jv9Xkxg8VsHpCs81ekwvem1fMvOiLpz0XMvmsuMWcrmbziRinbqIt6UhPnAtYf8Ji8rWY/oRJf0aTuSXqKacjxqOdhyLMjonVV+M5vIzuIkf0BhuPeBSuxdSOirHHHEFnKaZwXpRYRgDJ7RAjiFn5sI05VJTfjBkWDGJbFI92V1KEoqTGqRskH9ihfaFE6W2ZQ6c2NG4npnbEJLUpHen2gkAjGgcMBnMhiYk++T9Is31a3rPS/hrDr0/cNVCpWAwl1kCw1LX3jLA2XayeuhuTVj8ZkbluMSxLfuIdDkB3T4jhG8SZkF1fMNg6bbLvN+rc+r6S0Iy0zOB7SyGYmqP71/ivZ17mK41jfPvGXmwnxHglS/56JFFqDVn4gowkHLUOQOECAkjpGSQ2DYIMFC7H1I8pCpc09SOyAeSW5efQSsaxVl/ApukVEXB15+WhnXlpyOr7Xey2dNsHZcVgPsTbtHAbYrBqL8pR28/JRCJ3U04hbjsWHUVGdtz2goWfl4QmFYNXjwmSskhgwLAompQgJSEepdcFoDLxZsDtT8Dclw3qR8Tp2V0Q1qTXkOzG/NWY1j6DiTekaTn5uk9/0qK53yByNU5bRpTDRZ+9vx6z9pSH3ZGciOSGPJuDKSlpg5SiP6cJCyG7PyMhp8mtmM6CgX+8j1qRCLfMTXnve3OazE2ZFCQqmjf/7XeXDb8rFoFMbl4Xf/EfUP6WI7bMMYDRq+m7kMrCtRHbD3hEjnwsyMVSMx0WnFfpYkDtiJhoggz0lkJyFy1iS+CZIFHT2dtyo85/rcnqB/OU3wrwcyatJSHhunXhwycqWjLg9xo4LUlFmv226AYaJyLspklyXWrdwXzE7s9FdGdtGkdg1zMBm6cdIk+yD7ydgK3THoUr8vlGIBLU1LqAQd1mTGK9x86pLOnNEK0UQdqgccig9HZEd9YktR0zHOvBzZF8XmvJFJPRTsDOPR5WX0aYsSPmmSghclynrckt+2w+5jKcDkndshjd08e4kSC5JbVsmBBGXmJdYrzu0HGlySbvR/N9A5LJEYOhza5yk+12Bv1qDqcJzRMBxsAkudimu5Midd2mtxRiNU20LSYkPyNfL7ktMuzmAQOrJ72C3PUYP6vGwRyyADSOQGJLkdyWGK0oKRbp/PUYFWk2nwS7abDw1SFbDySIEqKNcFryddBjavSSPBjhB5voFwqoCNymaDq68zIaHE1EJFdNMWuVY9K3DKbOdKidSDMsSmMvcuXfltyS+8nPiJ/Bz8oCErlyb6pYZOFhUk4ukSs9jOYBWHhmyPrjCQZzIbPfNGgckIyG8ptjtmFOFga7K3L1zm75OSRMRxqXblN6VvVD9l3UuzWQE3PjY33s19NkVmPqRxRTr0bsHBOZ+PI/exd7B9Cw648kI8DwZddKbscULnZlVLQHqic8BpPS5LF7kL+k6OySDi1A44BNd19ImILilZDsZYvEjsSTJ7clmzB/PaR60qQ/G1M/nmPmhT6dBQu3EdLf61N+K6KzV8Y48m8YUbwSkajHpNYV/UmT/rSi+IY0MJPVmOS2Jn3DpLXbpnlQdpzN0w6LX2yRXZYZfvWER/6amHjiMaUouSU7rIqFfOuXPHpziv6ERXOfRXvRECeaIfFYg5IiUY8xf7CK04vZ+FjAxDmf3qRJ5AmKPL0eMvlmgF+MCDLc9fHXHwqIHbnUky+a4lt4NUmQi8neErKy29B4m+ZYwx9TfjvEq0ucmZ8fsxL+JMHw7TzhyGK7ncF6Nsfo6IBEPab4msXsc5r+zSxOxcKra0qvyU58J1tvsCskta5RIVRPgVeRh2TqrE/1PkX9PqmD6/eHFC60iS3Rb6CEf6gCOYlFtmLrEUXmqoh9tk8lUFqapYavmPtGm1FeM/XKiGFZ3IlhUmF+rcBgSu4h0xeL7sSbId4OzDwLk6/7EvxxSZFZj9h4MiPGswWRmptD6UUNiyLbnf/8OvnlgMnXg7H1XXIHnLaMMcOEorVfgmer7xuRqCqWf9AhTGnKr5hsPCneD7ujiG1Fb09A8aKMnrvzWpriW4rpsxGZFfE2ePWY/qR5F0svJyaN2wjJX+2R/nqK6TNDWnsM0qvQL5u4TXAOtb/7s8e7ZRFQ0Dhg4bRlh2gdDak8AIOZBL1Zxe7P90mvR0y/pAXN5MuFMCLZRcpv+3g1jbttkdqIMcZ1eP2wzH4NX5O9HVE7KpCF9G2DwuUuvXkPP6toHHAovWzT3Gey/zc6Y8eXYlSw8SojgoTARWL7DotepM07JxS1+ySBZjAlR1iQPkT1VFakmga0D4dUHjBofLjP9Jk+QUZ2VyOAYcGgcdCgdszFbUD1dMTEm0NSG9L8yj1zVYRROzHZC3X0706w8ahJ4pLHrR/RdPbGNA5IQEtzv01ryUabmok3faEbNTXFMzbVEwKgjC2oH5EdObFp0l60yC8H1B4KMQNIbWoSe9uECUXjRETsCA68eTSk8nCEPxFhbbgMb2bQTzfY/3MDmvsNGvdIh9waKIoXxLUZpBSl85IKNPm6MBSCjNTz2hScnNPWbD3skNhWpK+LbXj/f/CpnspiDmV8X1hN0QAAIABJREFU6zYimnssZl+Qns1gUjF9uCI9oBg6x0doBcOlEbnrMVuPZEluKVY+4BCkNE5L09kfkqxELH4poHparmF/WlM9YYm60lG0F6WTPywpUqt9EhWRoe89tEFmJZaSzpV7bvK1Ea1T09z+HkV7UXwB+mSHwsVxUOt7AryalhDcpMX8Z2VOn79okNhWdOcVi18UKvHCV7uSt/l1k50TshGaI2nQ5m6HNPda9Cck51LF0DoQ41UkQzK7EtNeNFl9n8Nw0qP4t9eonPKw+gLdMUfiqOxvvLP8+11RDri75/XMP/kZ7KaB25Sj3ORrI1p7HcKEkGnCpBav9muiOx9MKmZe8iUdJ4Ti5QGbjyaZfHXEygccvJoQe3vz0gew+pL/5mdl1e3sjtn1TMT2/TZGIA+lCiF3O8TqRlROuXh16Y5nVkNqx21mXpD48yCtKV6U46Tdj4lNYdr7WZMg8aekGYFxwmCPz75fi1j5gEfmpuQhpNYVpfMjGgddJt7o0TyQpHFEjq2Z1Yj6ESHFtHcrRqWYxHyH4WqG1KrIpfPXI9p3JM1ZETD1Ptoh/wdpGofG0uGEAC3DBLT3aYgVdk9WKrcmZcWoqBiWY+y2gbcjC5225Bg9ykk8eXpF09oP9r4Og6ZH6rpDbyHErcqN7dal9Jj/eofYManem8TqSckSuora/TGl1wwyKz6xbdCds+jNiRe/cElTP6Zw6zLS6s0p0ity8ogd6aWEKY3dNshd1yItvxpJAlFNSEa9uZjCBUX9VEj6mpSEo5KUBl5VkV6Xv28O5WdzG5rIEQ8GWshOka3YuU+TvWYwnJR7YeLNkMr9Fm5dYCPFSzG9KYNhWUJr6sfGjd6liMx1EZaFCYmCz12VxSS3HFM7oUitSh+qPymlRWozZlCWEjRyJBy2dswkcuXeqh8RNaFXNbA7MJjWpNagvUd8L3ZXfALpjYjWHgtzpIlt8c/Uj4qeZTCpcZsiXx/OhKz8xP/07i0HVKCYeR6iPUMGUxIM0trjSNx2LWbXVzvkrolUtDtjMXxvB23Aygcs3JYes9ySpNZjKve5JKryRgNMn4lo75X6rTdn4LQ1wxJMvww799gUro5tl/cN6C3EeFWpnTMrEj+WWQ3xqgOSW7IglC6E5K9CZnWENdA09lvUjpp0ZyyMUAxJ2kRCN8YireLLNq0lT5RprgIl2XatPQ7NewI2H0kxKCsWvuxjBLDxhElkg9OVmK2JVxW7/k/Y++kBgwnpk7iNgOJl+fvZG3ISMV7JUjsqYSTTZ3zMkYyKBhOK5IZBoqIYToZyzE4yRp1rps5opl4L8Boxc1+tEttADOl1eW/q98V4NUXh91Ls/gOFf6KHU5feQfktAWcWL4fc/L40QdoifG+T+gnN9qOawZRCBdKEq97nsvG4xbCscJqQuy6U6TApLMXGEU2QFjWknLoCkhuKxNafLlCDQ0MpD97wCRPiIp19XpOqRKRuCBW6PyN+gqmzMq932nKcD5OSVNQ4LCfK1GaM854d2X0jzcKXQzp7YrzKOAo9LXJef4xzq94n/QOvpth+b0jkaXI3I4yhon3MZ1iUJmViW0Cw2oL2bgOrK6K3xhHph5gjKYfyN6SMyN6K2TotbEmnJURnb0fh1oy7ZQBalIaZW0qCef0xD3FWGt6jwnh6MohZ/MqI4OEO2ZvQWwzvkobe6fXuWATGppvc8x4zL4xr8K2I6T9ZxatH7Nybxs8q+jOSHcebWSbOjQlEa0NKF4eoSL5G6VJwd77rtmJWPwTFt8Hua9yGJlkNhYWXkcSd6kkRfUx+wcWrGqhI8vD8rPD5W3tt1p/KEnpQuT9JbCtGOcWNj7u0F00WPrNBclvj5xXdWZPcNeH8Ox2p7bQBU59bZudUjDkYQ0qb0pX3swpv3SbIwNSrQ4YliyClmHwlxm3K6NQaaJxezOZjOZY/mSB3fWxQKtvc/oiF29SYgWaU1/gFzey3A3I3InpTNtZA6tL55wZMvTqgtxiRPy8eipkXByR2RBEZucJX2Ho8BkMyCc0AWnsN5p4bUvoOtmN7wSKsedgdGTtVT0rsdu/vNtF7+kQ/WyM+m2fqZVj4krgYjaGYWbp7RRobpLXM6YHqEwELX46o3G+T2JYswe68+Cx6Mxa5mwEzL/SZfL1Pey+4NyRpOExKhuIoq+jMm8SmuqsqtbvisnNropJb+zFR4UkKkiJOxlQfDiX0dTtLckORf6uJWxmQuWlgREI67k0JvCR2xDeSXZa+w8S5Ibs/rShckAlC/ooie94hURHxVn9XhN2F6ZelJEAJSMbqKDoL4jUpvaXYfFiAIKGn2PfpLuZA3IXpG+Z4UhIzyhu4TekbVO+TnAy7B9m3qmhTej5uQ+A3kQedeZOd4x7+egoVgTEUupPTeZfnDliDO+kwCqcd0txn0ps2ufHjC4wKJqW3+3I0t5AGW07TL0u3uHkgQf2gQDwGEwbbD9jMvCgXP7kVsPQHEfYgJrUZyEPVC+nslvJBYp6hcD0gSMgO2jiUQpsyaqvdF9Of1uz64g6N41IT2t2YICsPslfTXP7paSHQjMGZQUoxnBAE1OjxDuYIKh/by8y3FJlVzcQ5aT6ZQxkDuQ35NSra1I6ZJGoxvRk5WgYpoQ/bXdnRGDcSczci3FbE3s+OiFxIr/ly7E/HrL/HZlgQ7Hl3KSTIwNZDCYKkhVs1CZMw/VJMc78neQ8ONA6OF8KXTW5+soSflriv2IbBhE1qS+jJax8RyErpNYMgq3FaBuk1mST4z5VxzqXof3qawrWI5n6D1pJN4aImSsekVg1Kr1jMf6NP5ta4o96JWfyMonbUlvJkKKGnu77Wp7UfuguKzUcsbn7Cw8/b5C9LrFfrgJCT85dE6hs83h5rDiKIudsr2Ho4SbISYdxMsPT5PsVLMoEwBgZ2zSJR0Sx9GvqPdln53iLdPWm0CZ0lUX5aQ8mzjF1N9aGY5kFhPd74O1A9IbHgg7JxV+6duzli43GDhS/GmEPN9v02rf0wWAjGUJcYbctoz/Q1iYpi19fa8j13JzGH4NYNpl/uy0M7hsT2pzS5GxHTZwbklwMKV32Wf2yKYVHh52UBULGMov2clAr5S8K9SGwbtI5Gd2nX3+31rlgEIlcCHRI7MWYvoHQxwBqIvNZtRtz6WJLBhDiwOrtMChchUYvJXYX6PeINT22IDNetwdbDDvOfuc3moy7Vky7bDxpsPC75e2tPJQkKEWtPJe+GUli9CKcr9UPp1QbT324KQNPU+HM+yz9SonBewA2dOYvipQg/H9M4LFDKXc90sQYCzuzPapKbWnbscxniMRjUHMViLS5bxAlR0MWWprs7JrkdM8oa7PrGAMZd7siVMVlnb0RjnwhnUmsGXiOmcsqgP2lROZkQcU/RxmvEuDuiZqvfG+E0Fft/0ye1Id34YcnE2wGUPMxBWqFiLVmHkdh3+1Nyo4xyEq3uFyPaSyZBSkCoiRUbb0fMPUYgI04/q+6mFZtD6a1snZZ+zJ1x354/CNAWTH7mMvVDCXpzakzIEc38naar09aU39IMpl3BZK8KMnz2WzGdeQs/qyhcgCglxKD2Xkl0Tn4lQ2c3ZJZNervucBWgPxOz9j6D7HVYf0+K6n3yfeeejZk+Gwm2e9am9Pkkg0NDth6WMnLvbzbYuceTjv2sZBN6W6bEe23EOLek8Wb2FaXzQ4YfbJPaiNm+32P6ZY3dC5l4pcFgMSBOxCRu2RSuRNSOK7yKeFOSWz7mULP1SJbaIwE7Jw0GD3exO9Dak6C1X7BoYVLUs5nrXSr3Jth+wGZYtAh2jdj96S2mX+4TZJR4CuoxQVr6Eu29Uj6bA/C2TFJb7ywWelcsAsQw+UpM9X5o7U+RWO3gNSIGZYMgZVA8L0z45KamfUgSgduLJrEF++9Zpfn+wXh+Dpm1iNz1mMv/eBdRQlN+2x+n+0idV7wUsfgFCZYwQknC9fMWrb0miZ2Yyz+dYeUjefl6fYODvySZhq0DUkeHScX6hyLchoHTUtSPwPInk9g9jZ82SN8WGXR3TuHVNMNpSadNX21QersnpqMdU+bjriT6Vu8XiObakwnqRyWi2+6KL37+GU3p0pDBpKJ7ciiy1a5Cq7HDzYOd4ybDvMFwJiC5rYVfMISt00n60wIZGZQMhiXZbVPXbfozsjhsPmzhVaRR6TY0XlVGknZXkbtkYnckFVpF4OdjiW3f96cpvYmqeDbqDwVkViW9KLssX8sayChu5YMudhs2f/gwmTWxcuduRGw/BN6Oxi/EpDckaam1x6C1W6jTYUqUoGvvV3R2Q/66T2e3wtuSvkLpvMSLt54aULw4HicCk69JjLcuBmSvGVhDOUW6NSnHOvMW5lAWLa8ZkV4Zkjsrkl1zpLn9fUXyywLqMHxIbY5wa+A0xYjm1mVhz6xounMOo1sZth+Rh6w7a7L+eILrP1Kg8LqF2TXEHJcymHs+ZFQQtWvtiEf9gVBgNMUeuWuQeDnNYFLT3aWY/6Z4Znp7AkaTCSqns+MNS8AldGwqT0yx+XASqy/X0qtF5C+PJcZNEVcZEQzmQjrz7/KeAMCwKEqy6gOw8tEi1RM2mdWQ+hGT7SdDWgc19dMBc8/IiCnyBLd186UFrj35q/hZgYH2Jw1aew1SawZ7f7dF9V6H2W+FOB1N+WyN3pRJa9HGn/Xpzpl0dtlU7rWYfb4n9WTdonBVUnCcpkHl/jSZ1YDkhkFqTRaOwmsSZJGoatKrCq9ikNoKGeUNmocFeFK8Egkt6ZpJej1k68kym4+maRwwiE2BcC58xSf7rZukb4uW3hyJR6K9ZIi5JTNWtuUsBhOahd81ZQfyZYQJwlmceiWgflxTOisPR345xG2KqzG5KTt67Ir3IEjLkTu5obD6EeZIFpPSRR8/p2g9MMKti8TXDDSN+0KGRcWorCm/Lp310nnN5OvSCOvOSSmRuiqGemuo6c1C64DUusOC6NwBULD6YyHrT2vqh03Stwx6T/ZwmgbNfWKs0QqKl8O77IXetEFyxaT0tqY3Y+PtaIaTIVOv+nTmDWrHTazLSar3KfoLoWDC1mRsOfUVm0QtpnHIYDAf4DakGWiEmp17bDq7Fe0Fi63TSYZlIQsRS4zcKCtoObsH1RMJUpWI4SRMvzygcDWgPyeL9KhgiHpUyQTKHGrcOkyfjTGHMPdcSHuPQXdOMSzIzL56WsQ93pqNn9O0NzJCrMqO05i74FWGctq9YFM/7AjefBEm3xiSqMZoQ/pjpYuBNJuByv1SotQPWXeNdIYvMmNz9C7vCcSOyEONAHZ9TTTRiapm5UMm2Rua+S+aGL4i+5ZDZ04in0sXQyJXJKcHf+Xv321cgeC0MysRlYdyxCa0d1t05w023lvGDDSZ9ZD8a+7dZmJuWbP6/hT9SYU5EENI5IlKLsgoVt8vUttUJaQ3O47bqgiyq3VAzCC3f0QitQGGU5KMnF4f0T4QEWRMDJ+7AR52V1F8ZYede1xu/v198nlK+ADTL0Vkbsf05hW5yya1oyarHwJvR9HaLSVNmJSxoNfQOA0J/owTMdZQ+gbrTxr4GRmx9acUu78gQazNfTZOW75WdiXE3e4K2LOouP0Ri1FB495ymTjbuCtDTl23sYaSEB16AlLx6hGjggiCJs6FWH3Gke2KYVGIyakV6ZQnq5EEYphyk2e+nUQFgnDv7I2Z/g2PxV94m9Sm1LWRB5uPiGXWacsJ0O6KzyBIKQpXfLxti1sfN+ntjgjSMkHRtmbhi1JWrL4/TWpDJNndWfEEODsWtQdCWnuMu1oTtHw/p63JXxVz2rCsxkx/wcwlqjGtwyGxpchfjenNuZijmPSK0IS1gtpJTelVE6U1sSVNOHEoKkkwGonKcJQzyF/38TZMjAiKF6U76lUsGiciym9HhJmY1vGAnZNpQk/R3h/h1aVULp7X+FmLMKGY/pZBbymkO2MRZGT0OSpJpkSYEHZi4UpA7Ajx2Bq88/P3rlgERDUnkt4gOZ7DXhlSPCc7fnvRxBwoCtcC0fzbsPoh8QvUj4kf3xpovKYQaKe+toaKRZk3WAjGb3BAaisie9Nn57iFn5FZcuOo7O5WH+af7WN3ob3oMv3SABVB9mZEYktKktrhOw+hwulq8hcVc8+NHW1vevhZmH4J0jflwQxSFslVk+6sQflch/mvNhkVpYbGNKT30YfixZDkVszaUxYbjwm4curVALcpcMv8eYvUpoSZZm9F7P5/3sbqSVCJEcDKRw3mvi7w00RVU35NGpu5ZY3bhMp9DqOCGK9KF4eMitA4aNE8XpDdrqOxW1L3l9+KqD5QoHSmejdoZeZbHbYfFShm+dyIzrzIsTuLkH5znfLbA8kEyMnt5DY1M9+sSjKupQgnA3q7NKNyjNeIIRfgVRS7vhax8YTJ6k8dJ1kJURHkrguMNEzKqWLi1RbmSHo3Xj1m57hL6XxEcsVk6gVF5pYhUulsyMZjJoULAvfoLozlzjuykGsTZp8x8IvxeKGSWG+vquWUeVSR3gzp7ZMAG/k5pLRLrlpsPaqpPCi7a/2Qi9PR9O4Z0j4YsfDliM5umfZ09spJY1gQaEjjKHdTsAAqpxwSVX13XGyEkF3WLH5BHIrlVw3KL4lZqD9hsPjHEc0Dwowc5Q2GBWmgWyP5HK8ZEzky+px+kbE7MWL1Q4pR3qR5NKT0lqQXv9PL/NSnPvVf9gn/K7z+5f/6f39K/52HMHwLpys7ZX/aorsg0dDNQ4rZb4dU7rPJrsY4HRFUtPZYhAnI3hYnIRhYLYvW8RxeU9ObNjAWB0R9Cz9p47agO2eRqAJKZsyRY9B4MMCum/hZi/SW6LI7iw7l19oEBUccbAlRX5m+YuqVPpFnjhNoDOaeqZNeD9j5qCZzycQeQPb3ztB8egEjVBSu+uycTBLkXHI3Q3qzJu7AZvshm8ztmOYBE2sAXgNSW9KYS1Yj1j4Ahm8QeqBQFMcr+82/Vyb2pDm365kOxC47JxVeHbK3fNp7pInWn0MIurtFTpvakNPA7j/awdQO6ds9vKbCDIXMlNgysIZQfTzE6aYYlgyyt6G532X2+YDK/TbaMok8qTe9Oozmc6w/ZWN3FZkNAaiGSUV/VwrDH3v2XZOFr/qAnMi8NRFQtJdM0qsCyBwWTUYlaXBNvRqSX/aJXIPVDyfwdsZj5HF6dewoTJ/x94LMmsboWYQZeViy5ywyKzFB2qB5UAQzYUKO7m5dMXFO+JNhQpGqRBi+wcQbPu3dNqU3wQwlzSe5HeM2I2LLYOLNiP60SXpdGp7WEGb/uI+KPRqHTXI3xoangQiATB9CV9FbjBlOawzfIFGTrq/b1mRvj1h/n4U2ZdduHHDGSUGawoU27T0JZr9Zo7uUIjYNnK4W5+WEgFGCpEFm1WdYsrAG3NXA7Dyg8SoGU2cCEbBlHFr3+8x8U7F66Wubn/rUp/7df/z8vStOAmFSuAFOW+PVZDTjtgW/ZURC39l82CazokmtdAmSBnYroD8Xs+sZH3MUU7yoSW9GuE1N6AmkJPI0fsNjancdry6LQvOQpn58PEZ5YUXMLJtS47st4ePvHLeEHBRFrL9PmkqdJ/sk6hIuGqYsTD8mUY/wdjRbTxTpLaTJPefRmzLp7DK4+c9PE1uKqRdbDIsWxSsyttSmqLdUKE24+jHZpcKUonFY09qrSFYiwoQBlia1Ksdkp63ZPiXy4AO/PiR7zSDIaXZOyFgruaUYTCi2TrtyrG/qu1FV2WUoXIKdp0d094Tc+Ntltk6b9OeT1I46VE4ZuDUJrqx+aIS35mD3YiZfG9GflHq3cr/LcCYksqX3Ujll0F4yqH2iT2pNZt+jnEHposiVM6sho6KivV+asnZjSJBWTJ/1yawJvyBIa7oLkF4bieswGzP/zSG9GZPWbpdBWWbcdl/ShkJX9AaRp8gt+3QXxQdQfVqav05DmrGtg7DxkRAjgMwtCficfD1m6TfWZOTnSA8mchSJbTknx45Be0l23+6swfTZId15g50TDkFaZvrJDRHqdBcgtT5i9cM5WnsFNFJ9QPiXVk/TfHhEb17R2i/hs4k1kyArPoFRQTiaa08nRI26bLD6tM0oLwudnzHo7slQujTk2o8WaR4YZx6UDPLXIHsT0ELbHkw49KYNsrd8/ON9tj8YkL1iUj0l6sGb32/iNGHiGw6NA+/cGHxXyIYz2Xl95Hv/EalNn/X3eKRX5AZOb4RsnZY6dljSLHxtJDFaMw7DoqJwNaBx0KazN2LhyzErHzDJXTPoLGqiTIRKhCSueBghDItSN868IF38yJHkYpQIi/pzMVNnxOtt9QUu6nZiQldRfLNB83iBYIw7rx+RFN4gq/8M6bd2TLwCiS2ZsbsNzbCkcDqQvx5w6+OK5Io1FvEI5yBIydFdRfpuWlLzkGb+mzLz7k9JU8eIIHe+TuNEET8jdWftHpGjdvbE5C+JXNlriLV0/pkO9WNpaqdispdN/LyMi6KEzNHvmKRQCCthvyVW4P0mw6Imc1sWkOF0RPaKyagknXK7Kzdg6UJE5ZMDuJEifxUSOxGJrT7bp7N33//JF0xqJzW5K+Mm5gfbON/M0Twe4K3b5G5IUlLuZkT9sMlgNsLsyr7k1RWhJxMJbcu12/VliBwRLo1ycjKz+5rY+tPU5/60IlGVgNpRzqD6aIizZeG0FcVLYhvuLWgWvjxi+0FPJk57ZNxp9zS14/J1Etti240tTWpNQmz8XCzlx7Qmsa3u9rIyq5GYvo4G2DVLEOsTMXHZR/ctVKhIrcpEqLdL4DlGoOnN3cnF1LT2a5a+4FM/5DLK3/naMPNCj9sfSWJ3FX5Ok7sqsnNroBgtjci+5lK6MKKz4OC2YlpLJp2DAbnzNq3DQi4GkYi/+cvvYhehNhVePWTrIY/pl32GZUXtMZ/etIU2RQ2nDdh60MPPW/SnBRm9ddomSIudNEga5K4adBc0cSLm8ME13BseJz56CXMAiarIMGtHTBpH7ghCRILb2R+ip0ZkbnQZzEsHfefBiEFRwkRrp4oAtPYLtcWIwGkLnXjtI3fCTAzsniJKxYJ1eq7LqChW08xayPqTFru+Mg44saRurh+RRtugrPCzsiDlr4/wdiSItXbcpvzCNu3dBo39BtuPlQhScpwMEwq1p8fUmRZxQtOfVbT3xRTfEMRW7URaZM6vGeSXA/ycwC/dmoxKW4dDrIHAPIZ5k/RaTPWk3Kj5K3JdgqzGrZg4HY3TkMWjdUQUl+ZI476eJszFDEuK1Q8rqvdlxE1XCshctXDbEft+p0tnSY7y7jNZEjsxqRs25fMRjYMSfDrMG5QuhqRumYSFkLnnQyIb0quayVdg9lmYeNmksd8SvkJZdsf2HnEU1o9KbR2kFNrUBCmonjSpH9dkL9ik10Suu/GYybAMQT5i+36PyBZJ9agsoaYoKfeMQNSpqVVZ1DNrAu6IXY050Oz9rR2UFl/D9NcrrHyfjAfT12zCaZ/Ylh2+9KyLt2Vx4Fe6DKaEBm23BSsWpETnn1kLxWviaG5+r8NgSjEqapymNBN78wlUpFChBOLWnhI34vyzA7KvuWgTbn6/xc6TPqOcvC/ulo2KIXPdIns7pP9Il8Yj/5low/+lXnLENrG7jIGf4KV9dh4PyC6DebiDYgzmcBS5GxGdOVkgUuui4mocMKVeGkHqtsmlK/MMZwMu/P5h/KwAIfr7fPLXY2afD7E7CmsI/YWQiTMmyTcTrD+ZpXRWiEYqVESexH81DslOY/qK1Jom2j0ktRmRXg9I3HRIVoU0Ex7tsvBFaeCtPZUmfy2itzegeo9F5iasvVe6yb3FiNzNkPSqiJzsnozVYhvqh128qpYASw8q75kiuS0/o3AVhgQJRWYtIFxPcvP7sky8bDD5aoDVU2w+VSL05H3qT4topH7IpnRO8hTMQB6epT+MGZYVgyk54g7KMqLsLo7JuTmFtSQiqPpRKF0Y4bQ0c88I73BYNBnlNcoXpaVbMWk8NpJY8jOiQ+jOmrT2p8nekFNX42RId1YMUFY/xggUteMKe6AJkgZuS2O1LNaesrj4U7+ENqB+VLH5qIh23IaUZn4WkpUQ81CHYVEx+VosC2lBekVBRkac7o447+5kQGRvCoeifMbEq2vMQKYDiQ2xYg+LBsYIvJpsGp29sTAJWiFBNmbiFQGShMWUcBpaiss/XcbZtElWYrqHfLKvu4wODkTv/wM1hjMhtz+eAw2tfZJB4HZkBA1QPSHTA9IhuWvyXmp7TJfKK7YfEv2L3ZMw1rk/sunNxRiDUO67EEqvG0x8wxG8e1czfSbAHGo6hwO27zcp/1ESd9l7x+fvXbEIuM2YrQcNAXx2ZAWMrqXxbjn0ZxTRlQzJDcXkayI+qR82MQNxiCktumpzBKGniV3JZstettj7OxHtQyGJHU1qU3Pgl8cR0rss3IamsyDCk96sKNzCNNRPxsRPNsleNWkfiBhOyQiwfjImvaJxujHpMwmGRQOrFxIlZBRlBJB9JkV3xhK3mikc+NR1G68u0Mq5b8q/7cCvdulNW6S2Y9mJCoqgGNO9X0RPRiTH2ighfEQjFBBlshKz8WiC7qKivWCz/EO/jDmSeOzmPpvkliJ/zad4UR4U8cArevcNJNbrpIXT0aTWFWtP23K870gH3Qhl6mK3JZk3tiH5jNhPTR+CjIWKoXrSoDenqJ3QnH7qgiQAe4CG3b+uyN2QcVrpLTlt7dyrSFYjvKroGLqLMYufqbBz3CZR/VM9/h3QSu6qaOGP/H8/SelCj9x1mHs+xmlC7aEQYyTH5J1jDnP/2iazFqEimeejZbHOLksDMcjISS9IaWr3RgRpUZ3WTsWECRkFejXN4NBQAK17YwbTsogbARTeFq3IqGCRWjFwujGdXSbXftQZn6LAm+lRvCTTAO+2gxFo4q7N//Xjv8ovH/1Nbn7s3zH72BqZGwbqeJvcDYGI+gU67I20AAAgAElEQVToLsCeX12ledLHXnNo3BMRJeSaaVOuQemcqBxbBzRTr2jMYUzummJU9mgvSlnbnZfEZWsgUuPaEZv2XnC2LQqnqqKUDN/5+fubxJB9Sim1/h9xB+98zj8bx5BdUUp98C/7HrGlKJ/TdHYZZG9HJGriWguTmlFBoqODNNjdGD9tMPdsn1Fe5sipzUCAFTMx2ZuQ3FDEi/IwucsV0jcsvIbcYMYwoHFY0TgustnUuqTF9BdCogQs/nEbDAjP5WkdDnnt4z/P4ZO3sXd3Kb4u2OutRxWj/Nh/vpRg+uXorqY/uROJkGdeyDC5WzICHJZgMCW9CBRsPJlDxbD24RivJmMqt2pS+KYnOnQLhlMRhUt3EoPl2Fs7ZjIqaFQgiLRjv/iTDKci3IaoGYM07Bx36OxSLH62Iv2OCA7+w9vj5NqQ5n6D9EZEmI5FeFKThSizGpG/JsalMCkPjteQetsYKWpHZXZvBIogFxOlYs797jHyV6G3EBO7mlsft1h/ymCUF5SY3Vbs+WyPIGnQOAK1B0OmXob6/WWyt+Ox1l3R2mfcRYLX743HKC3NrY+mKL9YYfV7Y1oHY5I3bRZ/5TpuUzP7rQ6bjyRoLZn4Gfn88rkYb3xaCD25Jv05zcxLEaXXRfwTpjR2QxiTiW0Z1eXOeOSvjyi/ocguG+SWIwpXA0YldRdiYgTQL8toEQ3EiHz6lSzDokHzWEjxYkR3F3zuQ7/Ix1J9TrkioPrZ3V+ls6QZraSpf7KHn5F7r3BRs/2+edKXHZy2In9BbMuFi0LD6p4YUnkkYlTQzH5LgnSb+2wyqxHVkzbJbX3XBu+nBbJTPSVTCrsj9uztlSJ2R+7H/+RFAAiBf6y1PgKcBn5KKXVk/LGf11qfHP/60ngBOAL8EHAU+BDwS0r9xVlWKpIdo3QpJEwYVO8Tqo4CJt4QPNTMS0Oae4U8HGRtRiUJDakdcwiT4pUP0kou0rrk21/96V3jeb9m5sUhW0/IGzL7LJTO+7Q+0MefCph80USb0DiSIXfRxM/F/N3HnqdgJvnjA3/CcCdBNOYEmH3xwfenNW5b8gXugBtqhy1qJzSl8xI8Ujtm43TEOuo0FO09Cq8qNZ/pa/LnbIK0mEBGe0QaXH6rJ+O6DZPQk687yksfInc9ZvrleMzM7zB9ZkjxnHS5I1cWDK8uxKLKYxPMPTcksxKz8t8ews8r/JTBcFrwasVzBtV7vDHrTmTLQUrhNqX+zV2Hyn2K/HXxSeSWY+E2XIqJJ3wy1+RadOcU3rYhIquKSemcsP7yb1nkbsR0dicJUoo9f9hn9hlBpjWOKDaeFi9FaiOmcDli62FhI8w8p2gdkGDYzApUnpgkd86hcEEx91yf5f9hL0YA609lyKzEjIqa+hGBl5q+qDUnXmkRZGRDmHhds/0jQ4ZlKScyNwwSVUV70aA3Oy57hppB2ZYewRheWztqM5jQDCbju2KnxiM+KoYjP7dFe7/APUFUgqlbFtufGBHO+tzj/Nmj90eTQ/7Hj36e2W9r0n+SJns7wulotp8SM1vpQkB6NSY2BW8+KCvBv+84mB15dCJHILBBCnbuscRyrWSi1Ts4wvTHUfd12awm3goYTmrshslgPsDq/w0Ug39BDNk7vT4O/K7WeqS1volQhx/8i76HX4J4dsgoY5La8HFaitnP3SKxKbbd9G2o3OsxcW7IKK/YOS4jvcGCWDXvWEfvJM0mthV2TzP7fERrr4dXD2jtcRmW5Ci59QmfxkEH42qKxc8q7F7M/8/cewdbdl1nfr994s355dSv3+vc6G50A0QkAJJgBilCgaIsjdJIVR5bli1p7JLLrrGnNGON7ZpxeVyyNMEqDy2NqJFEgqRIkSKRA9ENdEDn+FK//N7N8dwTtv9YF82ZKYJSSXYVblVXdXrpnnP23mut7/t9Ey80JHikJzlyz28d4PVexM8uP4HZFk15/XgfvxjQL4VMf7dHbd5iz9da2C2N05YOfmrZoDVuUrrcZeI7dXpFAX3abZlCRLbMmbsFEZPYLU13RBO7FRPl4SdT5K4qnLo0Ip2m7PJuxWf7YU17xKQ367HyiTTtMUdItQUpoeJbGrszaCqVQ7ShaOwx5OZfCUlu+OQvGgyd81AD5HZ6WTT0mw/bNGaFltSd64OSurhXMLCbA8jrdERtziB+LYafFKJTd0qCUuPbErtWPQRjL0tgR3w3oFsU38H6E0l2fqzLxMse7pEaySWLeCWiNWGwc8ogSMhNvXO/InK0fE1PfAr1gwHtCcXqUwlK78jiG5kQqwRkFiF/Xfz+QVxgsAs/lpUI8pbAVLklttogIXyK+hGf4fN9ySfoiZbBTwo8NLMA7TETp6EJU+IRSa0IdzJ93qV6VHP9vxpn/OWA4bMRuTviDYntahJnEygr+oFE5k7ksvHjHpWjmuaUiVMPGXnRIrGp2HrQxk/KacNPWKRXIxm7XlUD4VhE+ktv8m4gVGJTMjP7WUVjjyJ/xqF6GExPnKrdEc3OcRvly4lA9Uy53u/x+tvEkAH8yiB5+PffTSXmrxlD9h98Ez2FtRxj56GIzYddrDYs/N09or1fCqgdlAfhzs/KrtXPapyqonDOonxMM/PVMvEtLXl1xXctsNJ4ac4oOiMSVRYrw8SXl3GvxKkfDtCGrPhKw93/VphzzVm5Me5eGOc3f+PvsfJbBwjTIbWDmtHnLSa/bWBXTar75aG9/VNJUuviTRcRibAEvLzNxpNZ8jcCsoue4MGWZHJgN4XYE8RkBl58Z9AIGgrJX5dSJRTrOLX9QiPefsAlsWbS3BuRuuIS2RqnIcabxKakJVXuD/HjitqDHnc/rVl/whXJ6k5E5YjJzv0usaqmfNSlM6po7ZHZtp+BwpWQ1F0YPqvJnXOwOnKC8VOKfilk43FF/rJi4uU2sYq4+5Z/SrPvix69okA98jc8kmuKfkp0A1un5PO4dVG16aWkJEiVk5hd2HzYoD0Tkrkti2dqNcJqS+MxsygEYbupSK5In6U7FVA9YNAZkpNbc9rGTyjcRoTdltNVenUAfVmR91SmDHJEzi762B2NXbHoDEtknN3SdMblFDR8zhfG4XExcA2/Yd4Dw5QuBZIOvGhgtRX1vTa795mEjqJyIiRywMtpYlfjnH97ng+c/wkAznp9VoIWX149QdizKJ1XtPaGbDxm0dgj0mSrK43T3rBI3LtFCa4FCVGp7jNZ+R8elTyNNU17TBGkoHjZw2kIMyJ7S8q26uCMriIhEFkdyN4UyMl7Pn8/9Kn/914/IIbsd4E54ASwAfzTv+7nGny+e1mEQbfNxIt9DG9gQTXFO2B6mq0P2Ex/OyC+rcm/ZdOdkLzA7pgAMZyawfJni/LDBNLoUlrw0u0xk6ELwT1fQawSUX5qisxSxNS3IH9D05mIaEyZDP1+gsROROGKkI3cimLtw0IfSt0S4AVA+T9pM3ompHClI7SXawovK6grtyL21uphaA9yDGvzFisfd9l6SBxoxcsdVCQ4qeaU4LM7owa9kZDkitzchet9/BRkb4HyIbPkM3xOKEJO3WDogkfxiqZy2GL7pEX1AZ/aPpPcFYsgqYgtuxJi2RcMWeWQyZ7nauTuBGw/ICjqzGJEfNMg/9pdrBbsHpOQk9o+mYOjBHbZOtZj/AWxMWsD7vx4nORWSHJVYW1IzTv+Wkh7xGTpGQcvJwtHe9gisSXNxo3H1T3Vn5dXWHHpbAOkb8sorzOqacwaeMUIFYgxKb4jLkyjD8VrAXZVcgNrBzXxHRmT9nMSU1Y9BNs/2aU5adErCrwjvhvgVqXvEJlQ3ecQxERb0R4TvUGQUAMJr1xrnqpitSTOfucBTZCSmLnNh0yZJo1JOK3V1fhzXVqTBsllS3IM5rp0pgNSywaVqyV+pzbFL138WZ7+g/+azcvD2Js2248IstxpKCZe6RLENcl1WSTDmPxMQUIRWfLQ2k153yaf7zB8to2Xlfo+tqNZ+aRNfDeidVxOyCoUe3PkgN2QJqmXlxF1+N4BRH/zGDKt9ZbWOtRaR0jIyLtH/r9WDNm/n0Vo20maUw5hMiK1HuHlBqTWeYPMgtS4dkdOBbENi94QZG8qUmsRbhU6c1IHmD1IrwfEdjW7J+RNsZshkSVd691j8ubWZw0Sd9u0Rw0mXpRm0toHLZEZhxCrR3I8TYQ4g1TazJKIcLy7KTolE6MfYjfFzRe6Cqsju2FqGea/WJbswMMDxkFFkdgw6IxHbD6SJLEp9tzIll6ICmH0NUXneJf2uMHS5wzG3uzTGZc59e5xh51jDrGyRoXQGbGlHixr+rmI9FUHpyYXe+z5HRIbYi11q6LsGznj0ZxP45Z9UkuKiZdDGrMSrrryUzMEg4iw+K5PbyTE6Ct2ToqdOH4jRmtcjseGD7Nf67N1ysTsCf67ciRBe0zcjbnrggNPr4aU3qrSHVJ0xhWRGzH6Ro1YWWra7Itxth7RhMmI9FpI5o5B5IiCcOhtCFMRdlsaojK+g61TJpk70BuSnkh7XHBaRh+Sq9LND+8mMHvyHnmliJ3jNl5ehF/Fa308kXvQzwrjz+5oWYwMebi7oxE9zxYB1tNtsjcN4lsGiQ2D2I5ME8ZfCzFCAc6w41K85JNZFur0yHMxCudN2lMRYdHnD37r03hnCjgNdY8ClL1uycnIhds/Y7Hnz7vYHRkBW01F/mZAb0imNUFCdBSRBasfSbD42QTtCVFPlk9GjL8q5KHUxRidiYg9X97B2+vdE6uZfRk1N6YtIRz9TReB94oh+4/ixp8FLg9+/zXgC0opVyk1C+wDzvzQr6Gl/o2tW/fm1XZbRjDlE5qtUyKPbE1a0tE/1KI1DfW9AtmY+JaJ09Kk1iOq+yxJIG7InLw1KbLP5Ou3yN2UciG7GFE9kqF91GPzYRMVCuXFrWlCR+Sp9pEGzrpNEJcR3M4JWYGjeES8ErF7Ik1vCCZf6uEnFbFqSKckWodrv5EhvqPJX1UkNyLaE1IGDJ0Vs47ha5IbIaOn+2I1PRBIrX0pLk25qxbV/Q6pFU3oaAxPBCutSQnz8LLGQDQU4dQMElsy1lp/3GD1U0PEqtKfCF2pcSuHXdqjJoufc0luCZhy4qU2w2cjJl5soBWMnIlYfyxG6W1DcvGuyKiwNxRRutTDT8g83yvY5K8LD99pyq7cGRZGXxBX1OYNKodMNj5coDMVSmLOHYvVp3NSp9eFv2/0DJKLJrv3Ces/SkSMno7wsobkND5ZozssNXFnVGN15UHC0BTfEZVlrKzpjssiHztcI39VdtHOuAA6R97y6E4EdEYVvYLF+Gs96vMyzlUhZJZ9vIyicFkzelpKkcTLKUrvdNCLSWLViF5B0xmLaB4QY1F91qJ6CLLXTayWonyfTbcoZWpr3KA1BUSK2IqD5Wn6h7uEMTkxxncU7XHNzv0G3dk+mWs2fsZGRTIN6e7xWXvSZPgt2XDeTSOKVTS9qT6xskLbwk3I3DSpz1i0JzXt+7vENw1Wf9tCVW3pZ8TkRNaYHaRWv3co8d8qhux/UUpdUkpdBD4E/BqA1voK8O+Aq8C3gP9ca/1D2hIMuPeK0qWQsRfLpFci8jc8MishYUJskF5Jc/AXrhF+tkrmW0mcuhLZ6YiBNgaBnZ5cMK+g6Mz1Mfri7PJysPQrh3BacmQPHcX2h/pY6w6JjUFwpQfZRXmgdx6E7JfS9Ish2cUQP63JX4fmI13iqxaxbY/Mik9yTdMZcQiSMpcOY7JgJO7IMbk7pNg9rkgvGGSWZDzZGRdlWnvMZPmnI2pzNrFNYRhENhQvB3TGNImtkCCmiG8rGsf6eBkplfxP1fDyIoDp/WyVWFlYhLGKlhDOHpSPGMTLAYmtiOyiR2dU05qWRahyyKQ7rNk9nsBqh9z9WIZ+McTLGDgNKFxqCMNwkLpcOq9Y+ZiL1ZXdqTZnYnc1468FFC97uLtykybX+wyf62B6EiNndTRjr8iDG98W7Hh3VDN0wWPo6DZhwaczGZG7GTHxF1uMPy/UqPaUTFm6Cxm0BeOvdohvy5zbbmnm/6gnIR+W2GeTyyZeAaLv5ekOyXSocEV2y91jLolVi/SyZuekYutXe3LNJiQhau1Jm/yNHuX7FDsnDOEuOBCkbLQhD3VyTdyOI6+a93o+pXfk/UyuQ/toj+yiT2sKGvf1iW8pctfFMl45aOJejhPZmsqJkPa4pAfZLTnqZxfFClybs0iuKTKXbWa/2qU1YdKZkvvBCAWvn77q4DQ0aqxHaz5AGwLQMbuKqT+0GLrgE7ydJ74pOo7MsuRXmn1F7lZ4j8/wg14/ZH0YPJ9av4ZM6/7j1zd/yMf8Y+Af/1Wf+95LfR/BbPYy9PIGdtdi4zFF6YyB5UVEjkHc9Jkr7HInXqAzHkEkKrOdZ7uUvhqnWzCY+WafXsnG8B3iO8LCH7nlU99rk7laI8jFQCmae+JkFjStCUAL5MNPWLQmYfwVYRhmblooHZC7BukVj/4bcfoZ8EoOO8ctSpdkbUuuR+wct3AaMHzOpzZvk73doZ9OMvndFpWjKWpzDuklDVoWofz1Hk7TpZ/SJDdl57absjjYLQnx7JYM0ish8bJFbV7R29On+PUcwaiwFtf3peGoJArFKhpti64fYP0xi/HXAiJTkVxXdEYEUS3efxGXVA452E1g3SRzt8/qUzbt6RStcZOhd3y2Ttnk7gQ4bxlUDpp4eTEZRSasfSHEXYgx+r0+tTmH7VMxmnMBiVU52VWPaGa+4aNCi9q8yfzvr7HyYxOsP+5S+pclCsMG1fsimtMm/cwwkSVS3bHXQ5xaX7DlHU2vJIpMPy68xV4hiTYF/OEnpFxyaqLD2PcvVln8mSlyd0Rq7lYET96YFjn01H/TY+knc6QXFUqL/r8xG2Pqu33qsw6NOQ8jsCQmfE0Uqm5VmAChIxuFP0jIKl7UpJd6NOZiLH82QgURuXMOsUqE5cn9YzeFKNzLm3RGLJyapr7PIv74LqXfzVLdZ5FeDbF6Mt7cOWVQPRinV4T4mjAH3LKUw35KTFPJTYfmpIXd1jQnTdLLWvwlfT2gPA28Bb0Is2fQz2h2jxkktt67Mfi+MBAlRqb07M//umi3u2Jo6eVNavsFp115whOBRs2BrE/imkvxSsDGT3vouwmCTEh6tEnvam4gnVSULspO2pocJO+c9WjMODitCLsTUT5s0xmPyNwxKF7psXMsJjdbUuaxKpLAD7stAiW7q+nmDTrjkgvXGVWkVzTNKZmLJ5ctCtcDtu+3SK3KEdlpSP1p9sSgNPvVPuUjMVQkiOjOPo+R520iSwIyk5sRnSGD+hGJUOsOCbrLaUp+QnxDkdySjv7qJyMm/8KgmzdIrwWsfNyUcqOtKR82Sa2Jeak9GTH2mpQQoQvFS13ufjQhwSQVGSm2JuXfvOGQ5KLJyNke3ZKNn5QGWf6m5OdtPRaRWrSwOuISXP2w1MvtWZ/cRVsUa1rq1ZlvRGx+QNSS9X0RyTUZVQaxQfQ30rNoTYot2OhDZkUajM3ZCMY8kmfiBEl5+LojQkPyk+DWxXQTq4pa009J7oLhi9IytqvpDSnpmWRF0Vi8KklLrXETPy0npvrxPqXXbXGt1kN277OZ/uoO3liGnRMuzX0BmRti923OBxTfNilc77LwbAwVKApXRSeRvxUS3+mzcywOSvwV6ZuWaEceCEkuWwy/7bHxmEt8W669NmTRn/zyCtXHJvETiuRmwN2nTdyK6DmmvyHBMrGKZvspn9Q1B8MXbYCKILHlUz7iDLgJEYmtPr2iTWgr6nOSUpzY1pSPCafx9efex7kDViskd0cowulVsdFWD4s2u3pYoyoOaGmgWesO3bGI6i818asu4YiH1TDp3MphtRXmdFty7dIG6ZUeqbWI5IZQY7QhdbLdCihe8Zn+dkhqPWTh5yF/yxdoZ17Gd90hTW3eoFuUFdnLGLQnlXSbM4rubB+zr/GGIvIXTdIrEZ2SyehpX3bcrkwj0JBZDklsiFqwOywKyaELPqmrLkFcQiqchvD1eiVI3bYIEjLamnyxRXIzJLYt7MHqQQOnFlB4y6KfNKgdFAx4FI+oHlCUD8uE4V2DitmVxOReQdErKZafieNN9Jn8boN+VpFa65O/GZJa0cz9kSe7+H6Xfspg94GIwlVPgBZZg/RtC3sQ5Fo9YDHypjx48bu2mKLqEcnNgMwtk9pecX/20+J4cyua/M0eVlfTHdIMn+1JsyyCfk5w4P2UQf1QKA5KYPLr67gD1eLw2wJvMT0p+6rHQ3ZOSpxb6aKccmr7ZWExfU1sV9MdVgyf6+HUIIgZNCdFPZpajUhsR8SXHPykJPk0Jyx6Rc3qJ4dYf9wltS5TChVJyGjhgomfUuwOHnS7KTP64rWAneMG3ZJD42BIrBLJ9YuD3dWkb1m4j+2yc9Jl8qUufur7epb0WsiNX52iOWmQv9GlPWoR3zLoTvlkr0rUWPFaH21C6TUbr6RFVjxAhVUPOBSv9ElsCY/Ty9lsPWDQHjPI3hFfQejA0DmRZb/X632xCIRxU+Kh70B9r0l7xCDISuRU6bzCnWyxf3qT+x+8jT8UEMUiJrN1YlsWsxO7ROM9YmXZYaLFpOQPnK1QPhqnfJ+iOS1GEqctJpHy4Ri9vMn2/Ta7x0ySl2OUj9gSgT4VMvlChyCpyd+M6A4r/IQcn3t7PBJbIcPne8z8qSJ7vYHRk4mDNqQHUD4iiUZOU5NZ7LLnuTLtMROzC0vPOPjpSIRORdHi1+e4F9E1/bUK3qhPZzyieDmg8rDP7Z9M0C2IlTVWDYltQ22fQ+SIfj93QxaVzDWL6e/2SGwNhEmR7BbpZShcD7G6IjJJrCtS1x12TqYpXexz9yMuG49JA84rORSu+1ROhBgBzH3Jo/3361T32bSnBPXVmJOOej+tBw+QLATNfSGbjyq2Twk9eOzlMo0DAUqD1ZL0360H4iQ3Q8K4ZvGzjjRwW5C7LvdBYicge82kMW0x+hWHykOj2G3ZMasHjIEqEJrTEF+zyF2H3ful0Wp1NXN/sEMYU7RHxeiTWYpoTrl0xqQnULzao5eX6VAQU9IoPBLg5YTfl70N4682sTrQ/MkGw3Nl9IerxLYNKveHdB9u08/KWLp/uEvuVoTVCklsiNho/AUhD4kbEfy48B79l0qELphtAcHmbwc4DbnXRfSjWfjRGLsPhvRzGivt4324QeGKpj1ii2OzGTHzDemHNPYIaCZ0xXDXmJXmdmQrUncVo6c7Mj5vaMnHDCCx/N5ZhO+LciA2OaUPfebXiFWkDtaG4KW6IxFGXxHGND/14dfZ6af4J2PP88G3fpn2TgIr7RP6BvaKS/6GIJq9YsTs1/t4eRsvY9CaEv23qPYiykcFvW11xS1nN+X3TlOz9bg4zNyG+Ny1KRFokSMxaJMvBPgpg8a0ec/ggRbLbfaW1MHJFaHbhq5k3eUHN3j2Tpf63riImJR8XJAUKbDZl+N6kBDZbnvUkK74qQ7upYTMy0uiKEtsRrTHRYXXnoxIrRj0szDz53W2P5ChV1QUrod0iyIQ8fIaPx+SWrDkBmuJBDm2IypHuxWy+ZCNNxIw8R01wI3LKSKIDxKB9xvEtyGzHFDdbxEOAKatGbk2wmWEoXNtVj+UpHQlYPUjCqspvMFeKWLvVzy8os3qhwxiu8Y9jmRnWJG7E7L5iEFkaaJERGzTGoRqyE5mt6WMiFUkiKW216R0qc/Gow6JTckhiNwIbM3cH4Ysf8K913xz6tKAC10lwI5JKd8SKxLzZvZFj9IeM6kfDiicM6l8wMdoWnzt2f+NI06cvd/9RWK3YoSOoM+6s33wFfFiF85nyCzLqK49qclfhdo+EeoYgWDLTE9KFK2E94CC7K02S8+kJY9yNCS5ZBLGBizGvMh/lZYma2YlkE0qIbDY1Q9bg5BVufeSq4rGXMTwGWhNyr2RWwjZPSrhs5UTEfE1k+v/06+/j8uBtuQIVPebVB/wZdwyG2BMdhg9tclDD93g2exZ/snY8+TNBIeHN/nMqQu8/cTv8q2n/g/c+2psPwhhQqOLfbYejLF9Uurc7G0Zz7UmxIDTL4T0M4Owxt4gp+/xHlZPUzhnSk03a9KY13hPNXAacsPnroPd9KnuNwkfqxMkpc4sXg2I7Uj3Or5p0JoVLqCflLiq4ukdGp9psfzJOLX94gWIb8vCqw1ojxtUD0jDLb4b0ZgxcGua1FoE6zE5DZ1toALhCzb2GPSGJOAzvWjQK2ryNyI2H80KKWdbk7m4S32/8PfHXw1wdmWOP3Q+op/XtCciOqNywpEdRJO6bdGaMGmPibnFT0qjLrPUA8SV2E8bTLxQI7MY0fhEG+XD0DnBYOdu9Vn5eJLC9ZDt+y2G31Skl5DJT8WgM+qwdcpk9qs+2oTWfR52J5J6dqsnTbxrCjvXI7GuGf2eTDXSqxGVD/gUrwluvLbXJLUWsfwpi/i2qO2iVEjhgkliwaZyyCW1MoCENGHkdFMEVQdE/Wf2AFPTGxKxUnPawO5END/Qxa6ZVB72yZ13+O1P/xFHHFHYLDz9+xQe2xRM/f115r4YYVcs9OUM3N+gPWYw8nodt6IGGHaF1YtQWohGTk3KHm2KPbi232DtyTSZRTE7WU2D1t4AryDTktSSQexURQxVJ6VXkV6RE+rSsxBkQopX+hSuh8S3xJ6eXjDw8hJtnlmRhnhyQ1Ofh+lvRETuez9/74+TwMSUHvlHv4LRsIjtiEy2th/8Qsgj990C4N/OvvgDP/ZKv8szL/wXjP+FSWNWusAqkqaYEYhySnDQ0ixKr4j+PYzreyt0+m5IP2PQGTLwMwKz6BWE6decFOVdfR8E433iN13yN0M6QwaRpQY7iaQALT1rUThnEMaE/OPWZYbt/UIV54sFennZza2eoM6ah3yUE6LbFqkFi86JLuZqjPFXA1Hc7QiIM3Q1e5/rs3UqRuF6gN0O2CqNfWgAACAASURBVDku+v2J17pS3hQUky+2WXsySXZR5sxowZLJ5MMgf6XByieyxCpyrB85LTugW9WoSJps2gK0OA7vfkqTu2iTXfLZOWbT2eNTPCNyW7eh2XhSk71m3rMBa1O8CP2MojUlOPbWdIQ72yR6J4tbkx5Bd1oaifWDIaklk15RuvCjZ7pU52N0xuTape5G1OcN9n5xjbXPTGB6mvxNj+2TMZrzAaOvCCcwtR6wc0LGeu823vo5jdUWDwZAYltyDaoHLFp7AkrTNdqnS/SzEWE+IHPRIVYR70OQiRjeW+bNE3/6H9xrT1x6ls1zo9hNxfQ3a9z9eI70SiShImURjHWHRB3p5QcO0IQmsSlxcq0p7uUfWB2o3ReQWhAeouGLL6TxaJfYlTipNX2PIOUnhZ1o9qXsUSHUDhhYLfkaky806ZVibDxmMfZ6QHvMIlaLZHRcDrn7MZMoHbDyd3/zB54E3heg0d/65//sf5xxH8fsS+3bnJXoKhUqEoUuPzf+Bged/g/82GHTppXrcGZ0mAMnV1gyMwSuIRitQLrpnTGBUzoNTawe0c8YgNwgzce6dJIOoSuYq/o+0SzYbbENZxZFvZha07ibFnYHcjfadIcdIluR2InojBmgDGlGrorkVhBR0szs1JIoH8qnQpRvSk2dMRh7JcSLuWTuSNMusBWl8watCelgV44owpLP/Jd8GntidMagM2qy85hm+IyoDoO45Bd2xyKChIvpy4gotSJzZD9pYHc0ya0+vSFhm8d3I1pTCqMvIJYwLmSjxJamNwR7v7TL3U+kcKriWPHTJpN/vkWsmQQD+hmD4qUWxbc9eiMuQUJKjOFzfVJ3u/RzDqVLATsPKEZPQ2XEJkhH2HUDpw1WSxJxgofa5F8V9FdyM2LtCVuszHGF05K6Gq3YfSQzqKV7rD0VlwdrzSRIDlBglRC0Qf2QHKNbe8RzryKFV4TWgT6BbRPEDLyiHMvN80nMPoQJyF4zSW5rekWD4rUQL22RmWnw29/+EJeLNn9S3cuzuWXG0ou8wh7avkvlSAzDV7SnoHBFdtzuWESsbJDaiGhPQORK/kBj1qA7AlZPUbgmaU1yEv0+5i67ELD5pEb7JoYnG0nzQEB7PqA3FuHHFPEtRfWwYuStHrWDFr0hSXVef9KVRd+EykMBdsUCxPzlp2U8GJomlRf+8v0LGiVS9zDP3qgQcsxsH3ekw5HsBp9LvrcZ+kvNPL9//lG87QTnr86CFjPF1Hd9rDZ4OYPZP1hl6IJHrBKx+rTUye8SfZJnEsR2Bd9U32uSu65ozkBzjyJ3TVHbZ+A2NNuPyoWzWxqjLaimwvW+oK4amq3HIsKYNOPKT3lEzrsuwIjJb1bwU4rcJWtwo0haT2dEPOGRI7uHXRf7cGpdGAFuRZRnu/fFcVoRI2dFR194y6IxY0lCzYTsmhMvRdiD0EmrI39XOWThNjS1fSbbJ2OsfkySfHoFg+I7QtqNHM3Y97oSCz6uKF6SDnlsV05JsbKmuSdi7ZMjuFWf5pRBYy5i8bMpeqMJ+hnZ5dyqZusBh37epTUpDdKx1+W0gBuSXBr87JWI2K4087q7CWpzJkag2XrQYO5LVeKViNydiPbjLXpFqaFjO1C5T9OacBl5y6dwTdOaFchK/YCmOSE24OwVk/ztPqklg5HvrGEEQtmZfk58D8nNCCKBlAQfrBPfiShc0oy+XMb0xDS09aBJGNdsnhvFz4R858wxbv/vhzl19vP8vVf+DvVqkvwlCT1NbMhpo1c0yN6GPV8X1FxrzMBpKpy6Yve4Kb6Vsvx/FUEvb5BZjuhN9zECMfmsfthm5HUDZ9dk6IJkbyQXLYZedpj+ikHpPNQ+2hVL84E4fkrGxzuf9Iime8w+1wIN438hVKfmjML0NI3He/Qz34+k/0Gv90U5kCxN6cOf/jUBfwTQOBCi4yET4xVOlu7yz8ff+oEf99Frn2F5u4DtCDbFeDNLZyxi6rvS7Bq6EFL/uQb6jTxWW8YkkaOIlaUedBshK58yUJ4iNtMkvJylXxJIiF03MDsy6x99o87isxnSi1B+MMRsGwydhfJRRfa2rOSJzYj4bsDO/Q5+Ug+ahQaJZzZpf3MUsyfHQSOQksAIoD0RYXqK/b+zSvmDE9TnDWLb0qjUhkwzNh/TJJdNWa4fqZH804yMFUuK+Jam/GSf5BWX5HpEc0bwVbFdOZa6NcGWGaFi9Ht97KbPzskkvYJ05Q1fWIdKS+OtsRfcmujXy4csUmsC4Rx908foC/O/O6ZJrCkKN/r0MybrzwRM/4lB6BqsflQz8rpBtygqwn5a4rlbU2L3Tq6JUAqgfiQkfdMkSIqEN7Igsxyxe0LIOoYv71NmKSKyFG4jZOPzfWIXEiTXI8rHFIYHiS2R4iotU4bGrKI3HjD8uknlCAQlH7QidcMGJQ7UzB2IV0N6OZlKgdCe3yUk2S1N7XCE1ZT3M74t/RGrLbQnp67ujS5jVRmZ9ooGuVs+rQmL5GaI4Ucsf9ZEuyHDr9hUD8HMt3qsfCxG7oZAQMK45CWaXUXpkqYzZNxzj3p58ROgZVQcxKTc6g2LXqQzJovAvo8scOXsHrF+b0lT8MBnb7LzP+/9/th13qBwLeLNP/7779/GIEijLrEtKK/h2TJG3aL85iijzvdHG893TZ7v/od8kmOTa/g3MrjfzWC1wS0btEdFKtoaM+HVPMm1iOyCT/Fyh9S6zJe7QwadIYvYpsnwoR2enbuIebRO4ZwBobAFhy/4ZBcDlj+TJb0Ezb2QWrAYf0WmB5lFWQDcqhzNWxM2qbsRZl8x9LbYgesvjlK/X04O2Tsw880mKhQ12sHfKzP/B1XqD4zLuC0htl4R6Mg4a/8XO7g1TXckwruepbbfoDkju0drWlF4zRGbrikz7eSa7Oh2Wx70zAKMnPHZeNThzufjuLWIPV+rSa9gN2LnAxE7J8UIVbgi8t4gZkgY6rSk7gRxg9o+h8zdEA2gYO2DNqmlNsnLgySnUOOUTSqHFW5ds/1oSO6OmHZKFzRjr3u0J+T00R2BoTcN2g+JE1MbkNwQ0ZJTNzB8RW+6LzttVxPawuKLtmN0R0TyG6RlNNfPCE9g9k8b97rre54TD4jVU1i7NhPfktOakJaEV1ibs6jvg+xinzAm5YjVkZgxP60oXDSIbytG3goFIFOVUd7ImZDOmDTe+hnF7jGhUcd3IrYetDECWPuQQfWAw9hLkL7m0Ngr2LTWhEtsW/IrJZBWrMJ2W1iC2pCHPLcQ4NYUqRVZAConRM+SXo2YfMGnOyJTJ7sN1743S5QOmf1qn9TdiOJVnwtn5tl41GT7pEXoiJaiNv/ej/r7YhHQSoAPVlfiobZWCuhin9Sy5l+dfoK93/lFPr/wEWLKZyfI8Fw7RSvqUe/FOHt5L8l1dQ8rNXrao3xc31tRI1viozcetdh4NEltzhTPexa6JVldY1bAPxq+xJVH/pDaIaHPxHY15cM226csht8OyKz4jL0ekL0TYnXFBVZ9sidQk46mNSOutO1HNW5ZFofMckh7NiB1TR6U2kEIY5Z0jd/W7DxcYveBPE4zJL4b4VRl4Shd7tGcdmlPwu3PpwbsP4PR0+Egq06Ru+2TWdSEMUWYEOVirxTh5RT5mxGdcU1qrU8Yk8ARbWniGwJHufOFLPnrXZozBplbJkYgU4XmtEFsWzBVqTXRCmw/wGA8J9Ob5Lpi6J0ublXRnkoOFIo2G4+Y5G7IohNZMPKaIVmHXRFXubtd8jcido4LQCSz1CP7cpzh8z7ZxQinJU5NbYhCcOprMqqsz5p0R2QHzl0V0Ebutk/+opCD7RYUT++w9LkstQOa7G3JZwiSisyCJrMI9TlzcFqT+yuMaZl25EPKR11SGyFeWtHYG7F7PI7Vlp85vhNROWgRZCLyNwNK72hWP6ZILxo0ZyO6YxHFy5qlZ4tsf9qjcD2ieKFOfMMguRnR2GOSXRC3aawuatTxl2uSHcC7lnm5bmZncBKJwE8YjL3aJLJkwZr6luQo1GcN7j5tywKxKj2y5JrC2bKozbuk1vtsPCybVGRD/kZEkFD0Pta4ByT5Qa/3xSIQuZD6wC5rnw4pXPNQvsK9ExMQgqmx77q8fWeGf7DwOb6QrvK5ZIvf3HgSEDdaY07slv0MbD7sYvgi3IkcmPk3C0RP1ShdjMgtiDU4VhGKjdKyo/7KjEwe/vvt+wgTEdqCkW8uklkKUQHU5iwaMzb1WZv2qEmvIJaLzJtxWpOK7VOK1IpBa8IgtWCSW/BJboTYzZDcZYv2TEh61cfdVXSHHZT0sUQ+qmDpZyJ2Tsil2POVCs1Jlzf/199j/APrZBbEzGN1oTNkMvvHO/JwnrQpH9MSOLkkXefRNzX1oz6NGYPMHbj7tCOyWUfGg0MX+qx/SIAsm48myN0OMXsy/mxNC0Zdm4CS6LfUaoTTEHu13YpIbMr7ducnHBLbkeglDEWQlByG9F2P8mN9QkfhtCJWPxS/p17ceCLH5id83KoIWtoTLqGjaI1beBlFaEPlkCHjyrsSRe5WZTHPLkRkB6Ko8gMhpheRu9UfCIk0i18YZvSMT/KuQXw3IBigtwRAoxh9oyOGovs16bua1KoIkGLbFq0pTXW/id3RjH5PwDSdcaHztKYM2jMBRtdg9XOhiHZ2THHx3TbQlsathWQWI/b+K9j6EY/aoQyt+YCdE7LoRJZMaJxaQPhMlTufzw6asBJPb/ia5F2DcE76MoUrAi3dfiBNei0gdDWha+CsOtgtSK3IiWTzEZf2pGxG/mSf2kFJSA4TmspBi+wtqM0bdMY1zgtZiaF7j9f7oieQ2Deuh37j1zDbJpMvBHh5ye/r5yRCPBrqExuEiLT39YllPcLbKcKpHqm34igNie0ILyONpPaYkIIzN0xyd3zaIxbdEQFL9IbFL2A3JakGxBDjzDbxVlO4AyELQPeBDsnvJYhVIir3ScjmuyIjpwHDZztsn0yIvr0rCKpYWQg2oWNgNwNWfjHEupVAW1pw128b9IqDMI6ivsfzyyz1Wfm4Q/EiFM+WWfqxEqEjFufSpR5rT8Tw9nqkLro0D/gMvy75C+0pCV7ZeMTCbon4CaB+MGTojIHTjti9zxwEh0asPWkTupr8FUWsLvV2Ystj61Sc0TfbLH86gd2Q5mlqRaAdRiBGljCmqN0XYDZF6dYd0wydFaGMCmUi4tY0TjOiMWsKDWhY4095pM/HsDqa2iGBZpaPmCQ2xJKcXgQMyTbUA+Wo6UkOoEA0NNXD0icY/V6f5pRNd1gRJDVOTUQz2TsiokrdlX6B3ZSfIXcTiu+0aE8nKB8WNoHVkUW481CHxOkE3TFN4ZKUC92iwfiLFe5+qoCf1oy9FlCbtwld0SQ4Dc3uSQmCzSxJA86tAhG0piXyzGpDrBoR3w2pzds0Z2RcqpWcdrvDMjUSGrREmtUPhOQvG/SziuydkPWnZGrRGddMvtCnOe1In6cqzUXDl3IttSZ/bk0qxr7XY+d4jM6oZuStiMphk9RdTXIzYPuXO1z/0X/4/u0JRF2TxEib0dMRK58yiFVE5pq7KdipUrGJnxaBR+6Cw+i/lrO+ey1Oei3EK4iUsrlXLL25Wz7JJVNSbl1RXpk9mP5WnfimkHOCpEBDJ1700WM9nJczmB0JCw3iUrOnX41TPxKwe7/wCfwM1A9I+o42oDEbw+pq+hnN2Cv1AedusEsfMdl8yGXo65KoBHJRewOC7dSX1zB8oSwndkPqcw7jr4U0ZxR3nynJkfrtkO6opnw0RpDSDH/XpnWiR+lNi9oB+ZmMnsHqh03i2zLhcOsCZSmeN4hXAtafkKyE+h6L9cccxl4PmP2qh5dXVA6Y9JOKrVNxMishjb1xnJo0rCZfCkhuhZQuSupw6CqasxG5ixaxXXnw3F1R4dUOaCrHRP+vFVSOSAqznwIUTP2Jhd2SxujY61q+bkYeBpB+hNPUZE6UQctiUDki90btgKgEh85FDF0IKB91KD8gIFezN0h6qsDWkyFmT8RX2VtSkuRuQOV4xNJnU4P06Yjx1zoDYAfo9RiNY33MruQueFkZLdeO5u7lCmw+bAPCLngX6T3+iqZ4NaSfVoSupn4oxOrJgh26UD/pUT2gWPmYid0SNalbFcCMn1L08xHmQ1WGz4uM2E9B4R2D9IqErgRxRWrJJH/Tw60q6rMOfkLRHZGSojuk6KcVpcsB3SHFzkMRnamAOz8tmQ6jZyKakyZ+8vtBqP6NzHs+f++LRcDswci/iAvauS9Y5d6Q0GPQ0H5tiJlveahAkdgK2T7lkL0p9Jhe1iAapBS5ZUXlkKI+Z1O4HtCe0lhdSYnVBtz8hRSGD9Pf8dAGBAc7dEZsSn8Zo3FQ6m2nIQ228dcCUush2asWuetiSQ0d2PunTfopA6uj2T0uK3r2Fqx9NCv58iHS7DJhz1d2pUa/0aV4STz2reM9avf5LH1hArslR+VeziS1FlI9YJFZjChe8SWpOW6QXAUigZRaXU3pBRerJx6AICELZXrBIHfbxytptp4U8k1jL7SHLWIDLJrV0USupjZns/ZknN6wvjeWTa9GdIvGPedZZkHTHrXoDBv4KQPD13gFiG8bxCtyBI3vaLJLg+Qe5IF0a3qgAJTRIhr6431ZKA4K6CKIyTh46vlgUP8rvPketX0G7dMlxt4Iyd/QxHalWVa4LNmHXsagus/C6mhGXn33+xRseGtPhLNtkVqT8i1/o4tbE/R7bMMkSMmRP74bYHgBtUc8Rk97lM7DyIsWmQU5/rcfb+OnNbFKSO5WiHeyRe5WRO62T3tykEM4KbJvL21gBOJezF6VgrszIRj1sW/bZO9AYl1k642nuiS2fVrzAWZfsgTM7+QpH7FJ7Mj7UN8vdOrubF9i5W1oTjm0ZkOCpMJ/uk72plCIYxVNei2gUzIpXAsYewlmviZsSBXKRCBIyHubWo1Ye8LC6vx/wBj8//MV2eBlTXp5g+wNRe1knyAms+fOmNysK59wsTqKzUek1iqfjIiyAV5eSMPxbWHSJTYV499cJ3QV6QXolkzKx8RUMf9Hnth1Rxxi5Yj0q6LlV5Fmz1cCUsvy/eTuiNW4OSU6edMTDUFiU7P8qYwgwANILynKJyQemkgAEO2pSPwLv3ODG79cILURUjkcJ7nm0ZiH4osuxbekOWi1hXFXeqsisWKBaL/XP2jRz0ZUDhlopWhNa5yGoj1qkr0j4JP6wVCYfTlF7WhAZ1hSjpJ3hMRcuCJBKZEL1fs0/Zxi5ExE/aTHyNs+hcsC3vAKivh2f4DfFhBFY1aszbWDmuDvlEluyi7r1DSVQwYjZ31aU4rAVWTv+Ngtg+JFDRGUj0l/YfekRJGbjkSB56/ICchpRThNaMxYdCfE3jv5Zfm94UPlsCUsxqtC8jEC6OVN+lm5vn5asHPJTfn53UbEyJuasTcCuX+WAtoTMYHM9ECdrJO5aRDb0XRGbJafyXDgn/VY/qTDzilozBjY3Qj3UJ3x/8chtq1ozFj00wal5xJ0Swa7x20Zu97fRStYe1J6HoYvu3bujnyvI6dl7Gv8/Pa90WNkQfrVOGtP2qhQQSTwUxXJ6XDnhM34q12yN6C9J6RwxqZ2NLpHBspeNckuBOwtlqk+7uGWNZ2PN1l70qAxB9snLTaegCBhUD8syVZeVjH0jo/Zg+2HRTpuPVB9z+fvfdETiI1P6ZF/8KuU3hIVWGdEM/vVJovPpvFzEbN/FmB6Ibd/yqV4zqBXkuaI4Sv8fV1iF+P4ac38/7VO9aExvIy694CoSI6lqVXRw6dXhbuf3IjuSTGDmPy/xl6F1ZK6rzUFe77eYuODacwuDL3TYe2JhIRC3pKHp5+V3S6+re7ZYuO70uFu7DGIb4sJJ3KkBs0sC8jz3YZRe0IaevENxeSfLROMF2jNJPCTBumVPgs/YZJasO7BVw1fHgIvpxk9HWL0NcufUeQuW9gdTe2g5BsoDUMX+qx8zCJyNflLBn76+4k78rUVU9/pEKRsVn4mIPNmnOwAgNF4toV/O03xkkR1xbf7hDGT5oRFZlnk0UNvGjTm5CTkloVRKAo/KUm0EmvvyNmQzpDkGW6fUrjVgcpvW7z+hWs+VickcgxWn7JRc23G/m+X5c8qZr4ms/Je3sTqaexmyPrjNrPPNVh9OktqNaI9Jq69d7E3maWI9oiBnx7wBzdEeuzv76LWYlhtxeTzHSpH4rSmBcw58nafux+1mHx+UMPPiXHNqcnC5VaE9xckRYPRT3//vvIKskBnFiJy15uEKYfGtJCzC+eFP2H4g3LAEmlxfd/37/1gwpMmeD4ic9vArUWEjqQkjb2i2DmpMOdacDkNQGQLrbq918dsmRh9RWxXGo2dEYGnmh70hgSI2twjHpnMUsSZf/s+1gkoDU7VpLlH4adg9HTIzV9xSS9CYsWUpsiwC6Fk8Dk16aIWL4eEXfHy90shKz8+wdYzHpZ4XkR1V9UMvSNiotLlHr28QXxHjvK9vKJ8RLrn24+GeEPCNQhdRZDWbD+QpvSOR3cEykfFRz56JroXcjL/r9cYe0NIrlZH09wrjrtYJWTi1S7puwF+WlZ4swdOM2T4nEwOMisBTk2RXJXj5dqPzuDnBONV2w/bp1yy18TppiJR2AVxGeUF2UjcfHGDqW9D7agQlYN0RGotoleS7rg2IXNLqMd68KB0h2XSENmaxt44jRmL4W+4JDdCGjOyCye+nZYO/phB5bDB0jMO/YxJfR8s/axm7CX53E4NkqsiNupnoXaiT3OP2LXb48LUu/sJKWX8uGLsjYjC9XBQWkn9vPwZxcLPK3bvc8jdBPd0it3jNokVi7sfM2mPWDSnDOxmyPKnLJy6YvkzWfyUJlYdxHZ5gvtWoZQbhWui2EytR+zeL2nCY3/mkLwruof6vBiDEuvSWOuWLCZeiqjN2wRJsNqSnPRuGrYxKPGslpzc2lOCOM/diURi3pRwkNrBNJWDMXY+EGG2DLyiqC6d+gBDn4Pdx33Sy2J2szqK6S+ZpFc0ueuK1ow0+WL1COWLfX3yBR/3lTQjZ3ycGjg1KRXsikX2hqQMeXk51WkFpUu+mNe21SDMRpBpW4/+7UCjMaXUGaXUO4MYsn84+PtZpdTpQdzYHyulnMHfu4M/3x78+56/8muE0oTJ3hY5b+WgReF1h+YspFckmcVPKLI3DNojNoWrXXp5g+aEyZ4/VTRmDbJXpPnk3IyLvLctzb/aIRktRRa0x5x7eQT5q9CajYhvy//NXbbIXxS1m93WZG7KW7Nz0iV7R3b89EpEaqFJ7o4sKt39w/QKJvmbEsBRuKgovRMSJAz8lEVtXsAahQsyZrPaolC8+1GDbsHCCCC74NPcF1I/1scpd1l70oTZDq2DfSa+skJiR1Jr/bTMkd/tOdgtTS9rsP6EwZ6viYkpvmay/Yhmzzd6bDzqkL8su3/oyOmgdcjDbslRNH8NyvdJT6J8TFHbZ1K81BUWwzstGa/lNallTekCVA5K06n4ooufNKjPQ+G6T3OPYvjtFmFcM/5tmRo0DoTYbaEqpe5Y5BZ6NOZBaWkKbp8U+7NXiDB6BsWXnXt6+slvl7GbwvlPbBhoJTyEpR8xmP7L8J4pLEhrKodsvHxE/XDA+OsBzX1yFF56VnIKAEZOayZeiWiNm4QubH9AjtmRKZMegOwvrnL3x0N6JRlH2g2F8kPqh0KGz8rJLrfgk9iNaMyLfdtPKar7ReE39nqTxrwg5dvjisxNk8witOZ8/JRi6GyLxh6DqedbZN9xJIPwKx7JNU2QFElzcxZmn+uQvdnE7EXSN+hGqEDTK8HGoxZ+CiZebmK3pNzrDktpXLiqaU6KwGv3mM3sH67ip2UTrO43Sa5q0rffWyjwV5YDA9pwUmvdGqDHXwP+S+DXgS9rrb+klPo94B2t9e8qpf4z4JjW+j9VSn0BeFZr/ZM/7GukClN69ud+neGzHbySQ2NQi0vkmGb0TUnTAdg+aZBZgNSaz/ZJh+SGuNZMT+K6sgshu8cNRt6W5OLIEi2+1dVU9wubLbklktHKR3vkXorRmlQUr0TYrZDIVgMCMYy9EbD2hEV6WbBcK5+QuXdyVR5IPwnD5wJx4tX1PRVZYiukts+813grXJMZs9mPWPq0xfRfhhBBfdZm9LUK6x8q4GdkzJhdDOnlpeYNEgZuLaBbsth8OmDiGyZWJ6I1aQlfDwjjMvPujGoSG3JjR4501Yffkh27ts8gcjXJFUX9SEhqokG7FSP/UkyCU2aE1e9W5Vhv9GH8391m6ZfmSWxphl/dYenzw/RzEYz1MFbimF35/xNfWyUYzdEdjbH+mEmYDimck9zC9IqUP8XLIe0xE6Mv2HKvIJiw+I5wF7QppwWUkHFDV/pAs8+12Ho4TXxHRFDvlkLxAS/P6moSuxF2I8Ar2NjNkPpem+yCj9UVOlFn1GHrIUHUR7Zi7KUK3nCS+l6H7rAisxjRKxr4KeiVxHjUHVKSCh2XkXP1gEFqVe4ztHyPk893aM7E2L1fGnD9YohdNYntyijQbmvq+zSZhcG1dOXeaOyVqYWKxPhU22sJ2q0UkV6UHAq7NUizWvep7nPEkbki91zkSE5k6ZJGhZr6nIlTk/dh96hJb8qneFpchPW9cko2Ak18p88LL/13f7NyQMvrXQePPfilgQ8D73ot/w3wucHvf2TwZwb//pHBQvKeryAuUVrrTySoHLSIVQUJppWM5naPWDQnROcd35bMQT8t2K93F4B+RtGeCWiPmsS3FGtPyY7emo3oDJtUDn1/TLVzzKIzotj7f0qfYOyNPvGdPn7KpHpAGmx2U9EeEfqPW9N4RYd+KaR4UdOelOO1Uwcva5DYCTECzfYTPkEcqgdN/LQmvSy/UPL/1p60yV+VaUB7zAIDdh7Mk7/p41YguxSSuVymO6zYud+ifETq5OoBA/pyqexWyLzERgAAIABJREFUQPkRn+xSQPFan+S6Hiwwg5PCj+8S3xV8ttMUHYB1X13ENjYQKJJ/nGX4m64Yo07ZFK55pFdkepHciFARrH1hHiOUHWr5R4dxyxC5mtE/c7GaCj8tnIalf5pm86EUbtmncEWw8bnbfbqjEa1Jg96kT2Qr3KqEeGhT6tXIlocsdGHovCegk7Imfz2kXwopXNGsPp0elEdiGY5MKFyV0sNpaBrzUJszsboh8e0+vYKJW49k0Xw4RvlojMiUZJ4grqgfDlj+TIHqAZdeUey8u5/u4Sdh5l/eoHRBkb/Rp3QppDWlcOsCfCldCmnukYdz4rsVkmua6iFJpp79ukythl83iaZ7OHW53n5SMXJGtAPr/y9zbx5k6XWe9/3Ot9x9v7f3fXr2BcBgXwkCBCHC3CSTElWSK7ITle0oTpVJO3ZSTqVSTpTISSouqxzHS2RLthRJFCVRIkWJK3ZiGQwwwOxrz/R6u+++f/vJH+9FU5UiJFmyqnCrUDOY7unuud/3nfOe932e3/NRSZJyytJDiWzZxNysiZeXoJziBalW+0sRoym5dnees8jf8snfgM6RCNORRuPKV7uYXsRg2sTqi37BKRiECc3cNw26B6A3ZzJYCGkdNSRMtmB/4PP3Zw0fMZVS54A94NvATaCttX4/8PiPR43tx5CNP94Byn/S14/vuVhDeagGSwHDSQM3Z4w5AMK3D+OQqnpktkPChIxoJIpaPmc0FTH9ijSEYj3NzMua+tMuuuQJt34oq3NyV7H8+22MAHYfSNG7x8XPmuydTtBZMcitSbKwNZTMg9mXAyJbMSqZJKoWnQMG8Yb41fN3AvI3hwwrJsMJg8RGjMKNkFgbDE/YgXuPhmgF6R2fA7/eonTJYTBr0FuSJKAwqRhOWbgF6C6adO4qk70TUbocktmQEVR6S5Pcssi9cJ3YjR0yl2L0Fiz27o3RPgL9Bbm5RvcP6b0xwe4DBplNSO6OyN1xmfwXCYbTion3HErvKaofCxjMCGIrfzOifldCQjBj0DyuKF73mP1uk8p5f5x1qAnSMsvuzZvk1yJMRx7g+f/dHFOgZGdNb2usvsfR/2ODwo2QxKbN7oPQWxKiUPuYJkjKFCe7KaV2FDNEhXfboXncJFYzyd8cYvdF2p3a0TgPDPDzY3rUVMhgXpEf76jVh1Pc+jHhBaLBHkb7uZL9BQO7JzJxTEk0Ml25H1QIxe8kKV4LafyVwzSPw84jcbaelq8bxCWNefsz/piyrOgdzgu7zxb5cvNIgsVvDrCcCOuG9BrS2+JDaB4zyF+FqVdF9owWn0Prfp/eouQNJHeh+xM9tAWp3YiFb4uBbeu5kAO/49I6bI/7OEJIXv6dOpsfz1M/ZZFsRJi+xnI1k99ax+7L9MzuKzI7EVPfV7hFSXlunPhgsPifaREYJw3dg6QJPQgc/bP8vT/p9cdjyEapgIl3fQYLmsJ5i+yG7KzZdRFo+Gm5KPVTSdycwdz3umQ3PBZ+f4/UrqZzUJG9beCURO3Xn1dYo4hj/2iPiW8LasrwJWswXQ0JMpKRl2hocm/HGZUkDahywZcwyp6k3Kz+lsPO49Z+Uy53U8q06TMjcjehecSidTTNaFIRxhRTZ3yCpIRfTLwrYaNH/vUAbSq2PxKneyzP5seSws2Pafy8yHb78+K2SzQ1zWOSb2cEokxUEaR3Q6bO+Oz85FG2f+wAXl5jjuEShivgysymJv5uCiOA3JpQd6sPZ4n9D1U6qzGGSwGNYwkwIP9uTBJ3JySMtXTFI9bTNO8PmH49ZONpm9Y9BZyiyaH/ax1r+IMEHS8vfgIjUMT6mut/TR4iPykLqDXS7D6cZe1nlmgeEZRbdk0Yj0YAh//lHpV3hPfn5hVuJaJ1yBbU2HSMwvWIzCZ0VlPkbwW4ZeFBxN9Ok6iNjwEdAz8ts/LUbiTn36ZQl3tLBp0DJnMvjTBdaZY5MyH5G5rsZZvieQkeHSyIdbhw3WEwbcokCdlVU5smzlRIZidAhZA9myB3A9p3+/RnTXpLikQ7YudxqVpv/E3p7xieHHUSTekvpLc0jQcD9h6CYMLb1++rkUnjvpDdpwKCDDi3soS2AE+3nrSYOuNSfkP0HJajiXXEaOQWFDtPV5g45xPrwM7HQkJb0Tpk0Hp8gYVvim/B7guWbThlULiiyN/28Qr/iUCjWus28DzwCFBQSr2/vPzxqLH9GLLxx/NA44d8rf0YMpVL0161MR1F/o7P9o9IdHN/Xs5xhZsRqd0IyxEF1Npns/TnY2x9YnJMDx6Pa4pSLoUJze4DNsFMkcGsCCaGH+9juiLAqd+VkpJrENFdjUjvhiT3JMm19+CI2r0G/aWI3YdSJKviODRdTeMukWtWH0ySqoXjJttYTTbUNI+Ki8zqK6yhmGI6x7ICwuyL9j+1I2qz0gVN+W1hFQbpcYPqpkP5kqjPqg9L7l5kQ2/OIkgZlC855G/7+EV5L7IbgjIrXo/oHhBoyuxLQ9yCTBy0ATtfWWZUUcRqJp0jcuPHeprZV4RZEMaUdP5XYea7JlFMEeRDkrWA1hHF3scX8ZYdEnXpXKtI6LX561IqW32D1mETpTW7D8lD2l+MiLcFMtI7IJgtbYiNt/bEFIav6c/GGE4rcjcUo0lxPnYOmNTuk1J696MhTtHEdGUh9PKaVFX09tnbiPPufkmIsobyADaO2Uy96dI/6NM+mKC3JPNybWh6y2K/9QqK0UxA8aJi8us3MZ1AlI4G6MURvcOiV8heN2kcl+sZxaG3DIX3JN3HK0b0FgymXwvZe8Bg6dcFXWcPhN3olM39kNH0mk32psHk92KECYGPxGsmlTdMDv1bn8EJh/SmQaYaClzkOtz5pI01lIg5FQmrMFXVpB+vkbsdcPvHJDZt8iULPyfX380r7nwqj5+FynmH8stbki35iEvrkET8/bkXAaXUhFKqMP59Evg4Ek/+PPD58af9DPB749///vj/GX/8e/pP6T6+f06aeEfyBlK3YhTOtwXbtSUx1LG+PFQT7/rMvezjpxS9w6Gct8vj7L2mdESLl/U4aSYlmXYJRfk3U+TXHIFA3vJx5j0GUwZzL+j9KiHWhoVfF/NFFBdcuIrAGsg5L9YRZ2CqqqmdtnAqEqmVqkV4BUV/dfyz9mD78R807yQY1SXWl8bY1pNyY/eW5OYLUlKeenlJuo1sRWpbPscpyVl/+wnF+sfjrD9nEK+bdA8Y7Hw0ws9p+rMGQUIWSLccw3Sg8l6In4WZ5+tEMVFCTr8GnYMGqd2A7qL0RZSGxgmTqbciOisG9VMmq18O2H7CJrWrcEuKie/EyW4GxHoRfkbT+CsOTtlg81kRCKV2NfXnXKLE+H1qGZiOZv05axyzrhms+vsI+ciWPAg/q8fmKCnj87dC7K70csqvW1iuKCNjbfn57ZH0EoYz8mepqlRL/VVfehAnXHqLMfIXbdySInc7onHSpnTOpHwxJHdLPBBLX5NF4frfW6VzKI2Xl1I880oKu20ymtbMvtgGBTOvDPGyMk3xszCYUSSrstvuPG6S2FO0DsekqRqH7qo0Yr2cpnLBp3Q5oL+o2XtE+hzxlgBk+osKPxcjfTFBkJIJljOhyewE5K4bDGYN5r8XkmhFTL3cwC0q2u9VGE6aHPr3PuXzmtZxmHjHo7MingNrKCawxrEEa39tgdYxuf+CtCQ1/bkXAWAGeH4cN3YG+LbW+uvAPwS+pJS6gZz5f2n8+b8ElMd//iXgv/3TvoHpyrhpVDaxRprypYDqz8Psi136syaFy106KxZ2P2RUsqifikna6nWTwaxm4m2RpBq+pnVKM5wysEbixoq3x42WdsD2Y0m8iZBRxeTgLwcM5iHR9AiSBsVrnlCGJ8SYk9qQ8AhtiAV4MA7JGJXE4jp1xid7R+NnJW0m3tKU3zKo3TcOgthW1B8I6ayI7BZD0VmVB9scKZyiYJ+S9YjkrsFwJqK7ZJGoQ+ntlvDyajL6c0ua1JZBkNbYXaHyJvc0yQ2L1LZ8jYO/2qJ4JWLjE9BfFtuvV4i49YUKmU1N7nZIetMhuafZu9eWfINNzfaTjAk5InmdesuncTxBZkMYAUFCrlHtbpvtz/rYfcXk78YpXPcpnzXRFjgVReUbcYrnDToHJEuyvyhobutzNbysRGyltyJmX4kYzIgMWwUiUQZRaQ5mhBHZWxbkWeeAQbwTMZzRzL7Qo3XYxJ8IsAaSE9F4xKd8IcTsmUy8pTCbNq0TWqAxGpI1CacFgccaPjQe8ems2rgLHnZ3fB12ZBMI0jI6njwTsf5cgam3HIYzcewTXQZz0vWPbCm1Czc8pl8LJb8yCVOvS3xb9rZMa8KkuP9ahywMH8pnJb5t4h2X/Jqo+eqnbKzhuNqbN/CLIaOyRawn7sndB20ax02u/FwRLyck48JNhzvPJUlVhcB1+ydEwLT4mxuiTlwPCdKgbcjeAu2aDI675J6ufuDz9+FQDM4v6KWf/RKmJ2KHO59U5K5KZz6zHVK7x9hXnjklxdyLfdafzZBoSvc1yMmNECUilr8WQqSpPhTHHkhnP96N2P6I4si/abH3cAkUpGohyZ0R1UezmO773DeD0mWf4XgqkN1wsdouw8U0W08azLyqyV7v4E5n6C7Y2ENN9cmI2e8Z9BZEhJTZ9GgfklmwN+1jNm1ibTF77N0r82vTE0mrUxGgZ+Z6h81PlMmuyygt1pWdKndLjkSxLhjeWC1Y0qQ3BSjRWVUEmYjV3xpy/aeTqEB2KW2CnxHDSqIuTcPBcsjy74e0V+39rPrIAu/4CPNWQgi5ox9YrFUoqkIvJ6PHhd/ZpHvvDHunpekYJOSh0aaM9KyBYuZ1h85KHD+j6BwLOPwrDsOZJE7RoH5/SGJP1I/pbQkeVZHeD+PIbMtY1XRkR411oHs4IrFnCDxWSyBMvDVWd570qHzfpnG35tg/q7L7sRmcssK5a0hUSzDxliJVC7j9GYXdNonimtwNmRL0lyTINUhHhBkxRaHAfapL9veyhAkRf3UOiuqzdW9ArGrJLt7UjCqiLUk2BHjSOi6uxeExh+TVBKXLoeQJzmjMoaJ0VZp9258OMPdilC6ImjW7KZVj67AcC01X+kLiSFRkb0ulZPdkGmIEmt6SwXA+ZPI1hVuQ5nmQlCrKy4p+wc2DW46IN+SenHq5Tv9w8cOdQGT3NEFKFqPkRo/CRWm0qBCqn3OZOBcRb/hkNwIZS306zdRZHz8jyrfl35W0lck3FJt/w2fzZ33ciujgE60Qux+y9I2A5ukihZsSadabt+gdSJOsRfsPhelB+5CYOtDQPBpHXV1jMGUy95LMXev3F9k7HcMZA0nSkwPaqyLX7C0pGifjaAMmz0bEdmySu1KWWqMIdzLYv8Gm3uyRu6Wp3WNx7a+XyGyJ/ba/oEnVAsyR8AlVBN3ViO5BQU5ZA0XrrpDWcWm0xZoGtdNp0usmi98Myd2JiHVh6Rsjcrfk/Y11NYt/EDGctCTs42bI4IDP3ItD0meSJGuimvTTsmBMfuWKNEJvRRSuSTzYzb8xz95pg8p5kc36OdFw2D2IDowYzYb4aUsWgOMSy7b+IxmGEzKyKlyysAbQXw4IEko4ih2NW9JYjmb3YVnscushURzKlx0MRzH5tk/+TsBgVlN5T861qb2I0hmb+kMBlXcUl/7BJKGtJMLu5ST5awbtI9BeFW7fyldlwq0iGfNpOyJ7R2MuDJn9nsFwTjPzQoPFfyIQDzevqN0nx43+ImBo9KEBybqm/pRL6UqAVgovLcE2qW0R7ahmTKYVD0k4yMQ78vNuPwU7Tyjia3HpF42kuunPmlQfkWDdzIbGLWs6q9A8HTH9uk/3gDQX07sh3VVRcGoD7JZBrC9u0ciSkWvjlEn7iMB5MluaVNUg3hH359azE7QOf/B04ENRCSRnFvThz31Jdq6WJnfHobsoIp7RbEhyRyK/tYLRI33y30rTuC8iviuSS8vR+3p9r6BJ7CmSdU3xyoDtj2Sw+jDzfI3tj0+Q2osIbUkPdstSivePeMSqtqCkyrIq20ORYlpORKzzA8Q3SOjo3r029kAsxxPviNCodjqGl9fMveBjOSH1k0kim/EYDIpXQxJND2MUsPNEFhVIg0cheggVQWYzwhqJCMRPQ+F6RKrqA1C/O06sq/fFLOltj8YJcRVmN+Wc7xZEWuxnxHEWb4zDJ3ZEMVe4Jjem5er9rMZEXcJNEnWZODgT4lAsXxBfuzEyCAsBR/9Zj5s/VcTw5abvLclCVLwiWoXhhARovJ8fqA2p7BonbPmZUjJRCGMQJmTu7xVh8q2AzNl1mk8tA5I2lN4WbHzlvYD2QYvyJY+tJ2yy6xBvC8MgVQvZfMpg4i1F/bQmtW2QuxOyd5/B9JsSUpJbj+jPiEU4MqWC6p7ysGs22VsCg03WFOmtiOYJRfGKiMCCpCK7EdL76S7pL+dpnFKktxSGJ7vzaC5g5gVRmIaJ98eomoP/74Dtj2bFb5CUaVTjpFirTV98CN1VmHwrwk8LbTiypWLNbLt0/kEf748mGE1KfyU3/hmnzsg4dTBlktoT5WTjhEwxsjdNuodlWl96VxrKYUIxmpKwmciWBe3cv/p7H17k+D/5x//n/5h85lFKVwKqT4JybRSyIKCF5BJZUhIWzliMJgwKV6Fzj4+fMOmcCsC3yGxETJ112X1UEM9axbCG4Ewp/FwKPyvThsGswjnkCLX3oKb4rikahTkTr6iYeNejt2QTmVC/x6DxkEaHhqTdlhT9BZPMppzX/ZxChQr1n9cJLmewB4reksnesyH5iwajaZmnT77jU33URBsWia4kIKMUU2c8QluOCfG2xqkY9OcNildDQltyALysyfYzssqPjnrEd6yxmk0T2SLhHcxLYlJmSxNkFMmGLHYSxy6S0v5xHx1ZBClF7rbP5qcEYqpN4QKmGiGZHQ+nZO/r5CfPhnhZ0QIM59Kk72sQeytJFFNEcYXlKNCKzkFF/vY4eWk+onhJk2hrdj7vkz9n0f9MD9ePEW9LDyG9G9E5KACR/ryJN1cQOMaCnNFHkwq/oPGy5ngxhlQNUnsBzWM2/Ycc7O0YM6+5gou/pUm2IqqPGSQakmLVe8jBj2LEuxojUMS7osvwM5C9YdB9wiFEYQ4NIlORaImhyx5A55jGT5qwkaS3JADW3l0u+csGlfcc/GeHNBcMFv7Ao33QpnIhYjhtYA+k2grSAoMtv+fQX7KZe3mEm7dItAU80jlo4JYU2hZYijOh2LvfhMsZeocDwqQmd0PQ49ZA8OFeRsCnXs6g/qBm+vWI0LLoL0UsflNyC/ysKBgNX5O/JWpIFcm1rL/8zR+KHP9QVALx+QW9+F9+kYl3I5pHZLyiIpj7Zo3OyRKtI+Y+McfLiwy3ecwk0ZSzsgplldUGJNohYczAKcoDH+uIAcfNGyRa0Ri/LGDQwZycMWdfEjfd3r02M685VB9MiPNvHB6RuwH5Wx47j8aJdeVnK1z3iTcc+stpnKJiOK3IbEhDp3tAlI1BGkoXQ4KEQesY+BMB2Ss22hSX33DSorsi0Wn5qyIumn9+yObTKQkpGciuCogIZgCDWRE8eUVp6Hk5RXonGiO9NN1FQ7QAN0NaR2QkWbjhMJyOkfnbW/DfFdl9KItbguDIkMS5FGgYzsr5O0zA7Msu/XkBWXQedpj+Rgw/qUjvSRmcvtbgyn81IRl32wa9Yx7l120yOwG799ksfqtPdyWFPYrozVoM56Sv4GfG8mAkZdgIQflQvKr36cGTb0fs/oTDzK/F2f6Iid0TebJTkj5BZiciUffZuz9O6VJA87gFWo44o5JAWLPrIgyLTFnw7Z5oLRJNn/WPx1EaKuckbTpISi/ECIXU45YjDFdRugj9H+2iz+UxXQgf7LJYanFrt4Lfj4GhwZWQVrekKV/QuDmFPRSmQndJ7NDdRYv+gkyW3KIE3qgQMCC1rYn15d+uAkjUFDP/8iyNn7qXwbwoCO2+VBl+KWD+jwzaq6ZElY+1M9ZIxtajSbmXB3NC245iivpJC9OTEJf+vMGl/+1DHEOWaAQkGora3WKyiHWF/LL+8zH6s+a4Cy/x3NoUb782oXjNI7IVXkEudhiDwaRJ67BBoiXa6t6ywi1KA6W/IMGSnYNCF4p1BPLYX0gwKpvE2nDrr0qgaHJXi4ZdQbIZUX0kPlY1auJtTZAy2Hg2S/UROXelNwWrlVsPiJIiqSWC7ac1vUVxe2Wu2lTedVEB1E/G6C0ajGYDdMmjc0RAm9WHUyTqkpyb2Q7x7h7IiG05IF0VPXyQkvfNHgjVyBrJzVR9WG4KFULtXoPiR6p0D8Dmx5L050xunJ+nczhNmJSUpfRrKfoHpNuuAkWiIfPo7lKM+v0RziTM/p6Nn1KYvlCIVaRpPDzJ5JuQXjfwcmDXbFrHNU7BpHwp5Obn0gRJRfUhc78MTzQi4k1NvKNZ+OWr5G5B7obYtYOkIrGniJ9q0zxmcvB/dmgetcisK7J3NO3THs5MgOnJJGY4JWlDtdMWsy/1GcxH9KdNwoTCmwz2TVFGKKNXPwu7DxjUTyZkTNgUw9RgVhKog6R4GYKMbCiV9+SaAUy/4YGGUS3FdjeHdSFN9opN5kqM1S8HBCmpZmKdkOYjHvXTMJyQx6p51MbwYOqtiOx6hD1QFK9EwkU4PERpiUE78JUeE+/I9b7+v56muyrXN7Mh1aaKIHfJpjcvG6SXk8XBGiFehowg6go3A+ZeksmI4b4P3pWsgg89aNTPSAa8ESp2H8jgVBSF6yEz/zRG8ZpPohVSvhiOfdmiBUjuQm/eJkjKmxDGoHNYOuipHTFMRLaifEEeHGdCHp7kpsXUGZ+Z10JGKx52T6KcE00R6dx/+oaMLK86kvNmaoK43IwqkmpDRRLoMfN9l1jLYOKdEa1Tmu2PaXrzFot/EO0r5FIbFkFWU7we4FY0o0mbws2A7GZE8VpIYtdi8TdMSu/JCFJyDGV0FSQUy/9cTCdz31Fk1vpyTrwTSdRVzqBwTX7tzxpMnpEdL7KFK+B8ZYrcGjgL3j4c0/QEajH5/DaZnZDSO1Lqx7rSOY+3Ne3jmvwVUfs5BVFTaqVoHhUBTbwTMpiRyDZ32ie1LTmCyYbsxrGOov5gyOK3XEqXfDLriuZJMQAlmhHNTxwi1pX3cziforMqxiXrmwWydyI6xwuSDLwSYQ8iCu/EWPqaePrdsoBX/LRmtOSxd1+G0nlpVLaPBxTetXEqY3jqvMjIh7MRsa7CqYiDcO7bTbyCJt6WcV73cETrrpD573hMv6ZpHTFwpkOG3YQcE+oa5Rm4FwuESRmbzr7YE1Pb2BXTPG5TfjXGkX++g+nItKlyXojAzaMCzAnSUrm17vNhK4mbVyz9+gZBJobdD8ne6JO9bZC9DUtfazOYk0yF9wElyYaEt4RJjflkE9OFqbPykCfacp+7WZPaPTabH5NNrXZ3kuGkQeFG+IHP34diEdDjxmV6QzOcldl7ZCnqp5J0ly0aJyxGZTkfi6QYsttCFXLLY6FNQSyew9mI5umI9oE4owk5BuRv+aS3NLmbmolzAbGWR3vVIn8uRnpbmAOdFZvOYXj3hcN0VyOqD4q815h2aJ5QtI7LDqs09OcMJs75OBWbuZclGiu9YWBkfFnFDai8ustoRlSF5Xc1piMW1e6yQXJnxGDKYOu5kMwdCUSJrLHUc0YejjAJyXpAdyWBPZCAy+qjeQpXofBeGz8jR4X6vRrT16T2hIU/KglsM9EcpyGdjii/buNMRBSvuBi+ZukXzxOlkwymTVQg8VlhTFO85oOCytviStRKyD2RrUg2ApyZkNGUpn6XRboaMTrgkl6zyW0EpGoh/RkLtySpvaW3TRrHE3SXLSbf6rH88AYqhMZJeSB6SwaDOUXjpwYYvuxs79u8dz4q1VdYDGicEC3IYEqSikuXQhJ1TXobkrdjqEjgJMP5kFjTpHsoIkhLo9Ipyb2kyi6JhsZd8BhNa27/aAltyDExTELumkGsYbLxbIz2IdltK2cNFn7PpLNiS2RbIF5+wxMfwM0fz7B3f1zs0KFUG6laSPORGekbLQrtZ99NeSqg/K5MViZftCW12IfByWmcss3u/THcqZTciwfhxk/lKV8MsfuK1d/uS0r1pMHeg1C4DP5rJSITth9NUrwSUj9p0Vm2iPdCUZFeEuZFkJRxdGflLyYW+kt/WUNN75hH+5jGrwRk16C7IiV8dkMkvYN5RbwhiK3m0w6tQxaVd11iHaG7TpyF4jWfZNVg9nkBgpYuSYe5syzyUqUlkNKZjIsaryI33nBaDCbpDUVqR7r0KMhsRVS+lmDqrQiNZPt1V2Tktv2YxWDKoL0aZ/nLe6Ch8q0Ecy+K6nH7E9OU3zEYzogLrnUkJgGhbbj215MM5jQz37ZI7wX74xttKOa/64lxqg93Pm0yqhgkajCYEhekPdRc+Ts5susRpcsBR39xhyCpaB0xsFxN894Qt2DgZYXsM3HGILUXkl0z8PIW9VMmN/7RSVp3F8huBAwWFJnbkmlQv9umP2cQjZtVw1mJ7u4vispv6vuK7B05v1qOJnkrjuHB1kcM7G5I/XFf/o1Vm8GconjVxXTh1l/N0P7lBby8BJa6JRG4WEMYNZKkqhIiUr4U0l0xOPrfX6N11CB5K0asA0t/6DCcVuRvB/TnBNYaWXK27jzmkN6JBNS5BlEyIkpG5K/1CLMRiboidi1JdxWMjjUu3eHgr/XwM7LoeHm5V9IbCj8rPTIVSeDJ+8Gi+aui6HNWXCJLHuD+ckCUC2gdlQdNhEFyRFOBYlgxSe3KmT+5Keaz0ekR7aPib4l3NHunbUGeD2D3fptYPyK1I8Kk5hGTWBd2H8gS2aIHKF4UlefsSwO8PDgTMlrWhixE249L+pM1kntleNyh/YC7X7H8sNeHYhEI4wrlmqQ3DRa+Pg7xXAgwfE1belemAAAgAElEQVRvwWQ4o8jc0QznJVl27ivCfLvzKZtEQzNYHM+af3bE6J4R3WWT9IaU1PGn6mSqoVQFBSkP907LA2UE7KOX/LzGdDTxTkSU1JiO2H+1AdUHDTKbiuZxgUXkbgeUL8r3HM4oWvdVKNwMJJDkoE1qL6C3EpG/5ZLaUfvVht2XI8nk69LwyqyP2DttU7oUEMUkmaZ+V5zhbET7tM/8dwSA2VuRhqaXFz5/7opF7taQ2j0Wo0MTBAnxT/QWDQrvCUt/5vs9MutiRHKKJl4B+rMm8TaEGRHrbHxG2IgAO4+aQutpyO5RvhAS6yg6yxZByad51CJ3Y0DvkRHakPGUCmSRztwx2HgmhhEXmEiQ0vsN1MbpiIXvePQX5Gg2mFUESU2iFdFfDrFaFolmtC9fTjQ03acPY7hCBy5d9bn96YTM37/gCtq8JOOzVFWjduPkr/WlJ1FRmD2TZGXI9pN58hdlLGoPBAY790JEqhYS62raJ7JkN6L9ZKLOAdELvH92Hk0o8jciMlsabWnaRzUz3w9JX4lj9+QYkF63wDMoXRyPVicF4pFbEwGVW1A07tLMvhTiZ7XQhc8mSe7KgwxSXdqDsWsxpdn6MR8/K43leEemYplqiDXUxHoiNe/PK7orSRJNyF9XlM/7+0/y+8ATexjRPKbI5kckb8WJN/8TGYj+0l4aymcNDE9W3yClOPzvRky83SN3OyC7HlE+12X+u6KgG06YmL7GcBR+SlG4AoNpE/vlHOHIZLAQMXysT281Iv7vijh5A78Ukb/pk6hDoi60HcOD8mUfp2Sw8C2PIC0Ayew1k3hbk66GtD4zJHsHhlOa0aJPrCfusVHZYOI3LjD30giA5lFrP7C0+lCM3A2D6kMJKucdEd6sO9gDzWBJzmZRDNY+k2LuxRFOycQpS7LQYD4itW1QfsOifcCieFky5gZzGqei8X+yKd3gqYTIiocBkS19gvzNED8HwZTHzmNZCrd8Oisyi175D5tMnh0IM+C2iZ8DfAOvGEmjqadI1BStZ0aMpgQlHm9ppl/rkbkSI9HQNE9kKH4ngTsRoQKYfWXEqGIwmhHLs2lGwjYYewGqD8fJXzXpLseItUVzEaQ188/7tA+Z2G0J8uwtyoRk6i2feEeLHXYA1Scitp60WP3NLm5ZE3s3PYaeCjEpSCvsrsGtz2XRZQ/ThelTu7z00L8i+2yVwi0fuy9zeC8nC1rrsEX3ANTuE1l0bs1jNBMSb8nsPtZSZDYiRlOa7B1HJk8jReGqkH4kNUhTuqBJ1DW5q5IKHSYgWRV0W+PeiPS2IrceMfWGZv1TkNpR7DwqR5rMdkjupojCknuy+VgjzeK3XRZ/wyRZEw6kVGDQnzZJ1uU6WSPF/PfEmdo9KFOh/pzF0te7jGYCEs2IwbwkJZUuaea/JMlP2c3gAx+/D8WIMDm1oOe++EViHcXkWZf2oRh+RjGajsjckTmnU2b/7Ng5HmAMDZK7slNntjROSdE9EpCojOBClkRDRCVeVua1mQ29r/1WISRb8gaOyoIPT1cD9u63CRNygSNLzsFBysDNGsQGEhiZuxPQXrWIYnImjzekW1u6ElI7bcgUYFu219Zhg5nvy7/HCKTicYsw+ZZP+5CNn5FGY/Ga0GviTX5ANz4WYnUNShc0raOKA7/VonVXgdYxWfR6yxJIKhJhufnKFxysgY9biqMNhVsUL0Z/RhyE6S1ZaHPrIZvPanLTPXrtFDpUVF61cQsKZ1KTuSPvtelJcGZ6NyTeCqjfFSe1G9E8KWfjeEvUnvGuEIVbJzSZNdlRJ9+SkVlmK6B9SJJyZeHwccoWTtHAqUijFw2FGz610zZBSkZdhifXKRyfadES7lK8FtJdNMddc+l7NO8PKL1liVR7MsAYmEycgeYpRemCFkNPJSR9W4Q0Xl4zdTZk9z6T0uVxGOuKNEf9jNxjsY5m4myX1vEcowlRhw4WJejF8DV3nrNY/YrD5lMpgrSMkVUEE6/XcRbyuHmT9JZDd0XCcZrHFNnb0LxLYu4sR5Nf82kejaEC6YtFlnhohpNCespuRFKhzIckdk3ChDQJjQAMX5GoQX9Zk10DPyvK1FFZUT4/wq3EqD5ocuB3enQPZtAGvPlrH2LQqOnD0kObpHY1blGEM9ZAvPIqFKlnoiad3P6CpnzWZOZVcRROvOfj5hXdowGVMybxl4XK6meES9i6z8crRPQXpGOtTeHSm24k7ru0wDcbJ+wxx15hhILO3nnUIr0+JLLBdCP8DGx83KB80cW9d4CfFlvuaCFg7/MO2TUZ07g5RX9OQk86q7IApGoCs1CBSJOLVz3ytyLS28KHm3nVJdYTdkK6GlI6Z+AXJAshsuHKz+XkrD8Z0DwhtF6novalsNZQ0z4Y59rPpHDKwjc0Aslh9Aow86rYbb0cqL+1x+T3TfTLRTLn45hJYST273EoXoTWPQHlCwPq92i8gkRpbzwbw8tDZ9XggacuU74gIZndg7D1zJiJoAS7Hs06+wTnrackD6B0UeNVQpyyRRAXyrM1gNx6QKIVSR9kIEKX3qGA0fT4TDsjSjm3LOWyYN/6coQYT2sWvq7oLwi2a+oFk8k3RRyTrEquYqyDsLDGr3B1RHfRkqPajkfrhKZ4RTM44VK+KLmDXl5x88dzeDkJRvEKmsnXFc0jNvWTMTGBTcTQpnzfZCtiOK249l+UaR2OsfNRqfRGEwaDaQNty+Qme0vMba2TEXZXAluz24FMuBJw58cjGndJjkbzuCgnS+cM0puaibclxRoNk2elGWu40Lo3oHzRZ+cxWTj37ktheALjvf53bfqzBm7+Qx5NHj8wpw9/9u8zmpYAkfxaKGOVaZFEFm4EdA5YY086+zdM5byIMcK4IrsV0puTs685ElSXNYgI0qK0qrxRp3OqTP5Ck9Y9JTqrYmXNX5cdejA/tsVWFUFyzLsva6beimiNeYHaFMkwABrufF5jti3hIFyXefhwVhFvyjincVKRHDsF411xQA6npeS3+zIb9/KSaDSYMsluBYxKooFINiVYBSU7/fucvc5hzeSb0jiNLLnopis30GguwHCkOpp9STOcNAhSwhlw81KyrvyHDS7//VnsriEy6QkBagRJmZOXLkBvQc68+ZsRxW9f5+YXD5PeZN+uqpV47IvXAuonpcR1KxKxbfgK94DD4pdNiMDLS3NzOK0xHUXhRkR71cCdiCi9KzSjyB6DYMdHod4Rn9xlm6kzQ9Y+m6R0XmTOXlqauKUrwmF8/30ZToos2BoIVaq3ONbyR+wjvVK7YsApXO5y5e+kSN2MkazJWT+9adA96ZHYiBHZsrPm7nj4OYvIUlQ/4zL7OzHSG0MIIjZ/JE92jI+PdUSvEcYVqVpE67DB7CsOhi+aD23I4hvvaGqPBUy+ZFG81OXOp/LEOlLdZNYFsqpNaY6ipR/VuEuT2pHrvPTVGrWHK3QPyNGivyzy+HhbjhKidZCfoT8n1bPEkWmqj8LCt0Je/oN/+OGtBKyOsT8am359SLwloZKldw3m/u0FandbJOuStFq4JmKI0uVASLRXnX0RDWoczX3SpXbaYPcBG2fc3Nv9SIXQhp2nKhTfbWE6MP26QDZSuyG565DcVcz+YZXMVsRgQZpVQVxCLxJNjXPQpT9r0Vuw6M9aFM7GWPmqS/GyeLvDuDi/TEdT/+wIIxhPHaqeNOCUlNmHf3XAzKsiNPFKcizxn+kwmDLpHpSHvna3SfHaiOG0whpoSi9vMPVyi9mXpNucaIgstHIhoHQloHwpZOZFyQRMbxm0D0mab+FmINbchOyau8/Ok7ltSjBLyaTyTo94U5Nb0yRqMlHIr0XEW0LP3fnCEWZfDihe9RguCC1p4j2HeHMc/a5kAbB7BpX3hIKTfTtBZ0XCW2IdyUeYOCfXb1QyiPVg5atC2pl6qU68HTH9eh8VKforIclNW+LYJ+PkbkDnoCwSrWcc4m1N9qXr+Gk1Tk7W9A6FLHyjydQbPexBhH9kRLwrOYepXc30GyOSjYDmccWdTxZI3ontA1IO/8J1yaW4FiOzLmrM2EDjFSxUpLEHIdO/H6c/Y7L2oxkGKxmyd6IfGIyWIsKEovOAy85jApi5/ck4tz+ZJNEQsU9qL9rPn0zWA6qP5YX+kxAAzmhC4UxEzL08YvNZTfOoSWRB8bJUU0YIu09UxsEtokqceyHAmdQkGxHpHR9tSsXYPiiqz+G0JkpFeBmRHY/KH3IDUWJ2QS/9rS+x+M0+w5kkiabH5keTTL0pRp14B0YToqCyHE3hco/egQxOSXLwEjURtPhZYdcl92QG3DwhvLWJcz6dFZtYT9M4JW9qMOui6jEq5+TGz65BvKeJdUO8nIlTVIRxgZiOJsVroH2D6e9YDKcMshtju+i0Jt5UVM579Ods4p0IpyCIcRVKM0xpcZKl1k1ydyJ68waGL91kuyfhFL1jHunrMfysJrMu+vrcmuQYePmI0gXJnxvMCz8hveNRfThBclcMLdNvONTuEvN/ai8SWfQjIgvWCryC5sBXurgTKdoHbFL1iJ0nNVppUpsWmU2pFroPOKQvCKAzvxaNM/rkOoV39TnwP3nsPFUi3pH7pn0ISpc1XkbhFhXD4w6ll+IM5kT8VL4gPRSQXc/wZRoTxgSX5UwIey9ccZj8WpzUrsfNnzQpnLeZeqNHb0Vk2f1F9inDo0lRe4YxQYT7KalcnLJi7vkenUNpmifHZOBSSOVNc/+oMpqQ0Jj8jXEGQx8mzg3Yuz9NuioPjelqGp90iJ1PUboS0ps394NH0KIVya+5qEBTvztJ51BEvDkOm0lJEEj+2oCbP54h1lUsfLtP9aEMRiDHVLkv5D3Nr/n0Zywa94ZMvWrQOWRABO5UyOqX5TkoXwxx8gb2UOOUDcGe3zZI1sVIFaTkZ+svyCRKG8JmHK14JNdilC+HtA6ZXP6FD7Fs2PDljLPxjDQwdh5OktnQdA7Y43KYfVT13rMe20/msfvR+CFVFK/LaApg8m2H4pU+flqRaMhNs/24tc+1z2xIFJSxG6d0QdGfE0mv0uJCBIh1Q7Lr0k3107K7L/6myfzXTVpHZcEZlQ3ytwLJe9uKCNLm2MloYo3x590VWUiqD8nXVRqqj2syH9vF7mv8XERmc0xV3rMJk4ASB1h6WzOYlePAzKtCRbZGcnxpnlCMJmym33AYzEk3e+90guINHy8PzZPiIMu9mAQN6W3N1JsRdz6d584nDbLbAbV7FaW3RfseSr6ruBHPJkhvReRuR2Q2HGJdTWpXozRkvpum+qREq7UPQ7wbYrpKXI5qjFnbipOpBhRuSJRW54AlGPS4aCRUJBSd2uP+/lgsuaeIX0zSWTHYfjxB4bwoQbc/kkWF4roLlx1MV5O/FYiuoKDRNuw+Jrr/MC676d4DWcqvbGH1FX4hZOoVOYP7WcVgZpwcVIxonpBjjT3UWO3RfqVkOdIoZFN28vZBST/K3wwl/u1jI7KbPjuPJAhS0micfVkchFOvtkjWNL0FA7PnEOsqpt70qJ1Oo00hUM18f0RuXTr9fhrWfzwiSArzYFQRdkLxWsTMC9A6nCB3S1M/JclctftFTDb3fMTMK138tFRIqaqm/piPs+DReMgnshQYMPWCheVINRsm/4Tn7y/jof6PfinJoMutRfgpY39u6pZk1Uw0NOWLIYu/dhs6krXnZ8VdmF2TcZ+fEYDG3r0J2kfSggvriGKsdEnvWzb9NMy96FN+T/z6U2c9Ek3BVFkD8aC3D9rYPZ/MdkjvcEBvWTDh/RmTzLokyvRWoHXEonRJEGftgybdZwYSRmooeqshhesS9JncU8y8KItP5S0D85cqDOYVy18LGX6+sw8eVb48FH4aao/7WENNvAGZ232GsxprhEAm+orBjMnNL1iULodYrmDL6idtEnXwKgGVdyOckmLqLYcwAd0lUxSTb8olz12XpJt0NSK5K1Li/rwanyXFWNM8liTZCOiuwmgmJNaXsamTNzA8CfDI34xI3NwjsgVFFsU01Qdt2gcN0hua7EZI+/h4d5qRBpuXUaz+WsRgVgw1/YXxdboi75k5ErpxoqHZ+oRMWorfTeDlFbW7LeItwZwVrkbkL5v7VKBY26BzOKJ3ega7D5k1MRc5RWFEekVN+aJP4YJBrCty4N6Son1XaeziDGkdkYZuvCEV2vTrI/yUovkTkldvXU3hZU2GKz69BZvhtGZUNihegtpDRboHhGu489QEhg8bH7fI3ZHS3c0phjNxtp+WhnB6W5M/EyezE5K9PZ4MOdBelZ+htyy6Em3K+2gOJcW6edRisJCWSUdO4vPWnvt/SKzHKLwTGwe9SkKzOYLG3YrYB0cRfkgWAQ1EsioPpxTxtnTz05taaD1bAfW7TG7/Z8sc/pUBKoJRWbLavbyiPysptbGuzNKbJyTJJkwo0huiWw9SctHdU0M6B2xax6E/Z+IWhAWoFfSW9X6oyM0vxKndY5DYkVLWHkoSTHbTp3jdJYppCjcDavcZdJcEIqFupslsSwNPZwIx3niClGofFCVX7bGAzoopLPs5m5lfkCTa9IawEMzpkUAhbkkqj1eA2v05crckwcdPi9IujEH5jMlwUpKYko1IrMgTkNiy6S2I8KZ5NI7pQvdowHBanIobn4qI9zSNE4JKN11NOBYcFW7J4uMWFcUrI5yCiTVUFC+IZLV2j0F/URHZGsuRUnzj8wu0Twakqpp4wyCzoZl6S6qD1mGTyTdgcMQl1lIc+O0+nSMRjRMJ4oe7lM4LNsvqKxI1V0AdKyIhdwuKwjmbzLoEguTWRIa9+4Qk9HhZaWj2lgWrnb8Vkb9qENqKwUNDBovSK+ock/Tk9KZiVDbHJqEAryA+k/bn+wxnNFtPWsSb78NHZN4fpExRCtaSMr3JysKe2LQZTiumzoYYntCd3bzk/q0/JxMZr6ApXFVsfcRi7nmf7kHozxgktyz0mAg0mNMMJk06R6R/EKShciGg+rA0la0RZO/IpKt8UdM+aOBnNNVHDAGZ7miytzWP/d2/TXpHegT9RZlCaQWjKQgykdjyP+D1F4kh+2Wl1JpS6tz4v3vGf66UUr84jiF7Tyl175+6CBhS7jeOm/QP+eSvDShfDDF9ecjvfFoy5BINjVtOkNsIBBEdinAjXZUxkgph+nXprl7+Ypb+omjI0xsSjeVUFKVvycV8fxad+/p7OE/1mDrrs/AdH9OVG8BuGyTqiuk3fKzxUSNZ0/RnbdoH48w9H1E/aY07/Br3gIufi/DSis7dHsU3Y+TXPNyCYjATI1EXNWLpjMXUGYfWISnxWkfTGF2LyIbZV0Imfje5j9fKrY0wPGjeG9B8wt0/4nh5qWqymz7aUAwWI0qv7YwzEuXvJuuidTA8OQevfEV4eMmaeAny79YJ4yJGGU0q3II0W4cTIqapvOvSPpSkcKlHesxOKJ+TGzGzqfGmA9Z/IiRMiANPBfLrxDmf8oUBzaM26aqQjup3K4pvCgB1/dksdk+COdNfzRHvRAw+2SNMaXYeT9E+pslsQKIdMZrUdFcj3CIUr4dsPyOEY7tl0jwllt1YVzP5FoIRnxbtgZcxiBpx4nWTwrUBk6/LsTC9E+LmDXrL0DxmMZyRQJTUN7MsfcNh+o1QGtQhFG765C+bbH7MlsTrbYv+gsLuGfQOSEMv3ob2AYvBnPQfCrdCkfaeF6FV6YIm3hZvQZgwxoEwUvXUHwoZTYmgp3jNJcyFOBVRqjaOW5TfFeFZbs3BKSlGFbHHz3+nx+Q7EXMviEgs3hFpvN2TDM3IlN7J9OsDrBHk1jTa0PtAnB/2+uCW4Q9eLvD0H48hU0r94fhj/43W+iv/v89/Djg0/u8h4P8e//qBL3HmyWKQv2hz+9OW2C6vhqS3I8laW5TyrHEyJufdG4KPHsxFVM4JlryzYpBsKEoXNXtpiyAbMpq0CFKaiTcMkk0fN28ymDGovOdTP2XT+cxdcNGgdpfALlWo0UrScw0fGids4i1N47hJsi7nz1FRUTk3onI+SWQrVGjihDGmzoTsPAzJtRi9JY3pxHAmItI70jRLf26PVrVIek/O4ZnNCG0qyY43YFgxGU0KNSjRDFn7TAptRVgti4Xf1gymJGxlNBeQvyjhI2FCyuDmwzOkquOG4EJEvKOEwz9nkbsdcvuzFtqWnbHwnkXveJncmiQjqxAWvt2nfnea4jUXw49RuydOkIbhTJ7RTEhyWyYBK8/eZvi/zOEWY1h9Gy8/Fl9tmwynIYzb2H3Bw9VOWyz/iysMJ44yeabL2mezlC6LXLt1xBBL9b0GUSdBqi+7aJiJ6C+aNB8MWfiaZlg2aZ2K2L3fYPJVg2Q9QCubVC2it2hg92WhV6E0RIOeIr0b0B6J3iSyDVrHFV4pIH/rfcaDVJzFi4r8bZfOcpztJ5Ik97QQfExF7W6b0tUA9+khpe8kYCxM2rs/Lg9zV9M9oEk0FJPv+JijMbFpJAnMICrF1hHxo4QxhXdsSGYjSXYNnIpFck/TWzRQoc3C1yNUGLLxI1J1RZZwCNc+GydZFfZg+zDEumlStYDOso3pwbBiULgRsPOoRaoKhWsD9h5NYf3KNtx3iOGUYvI1k/7CB+sE/iIxZB/0+izw78d/73Ukn2DmT/oe1lDjliF/QySPxSsiydz6qMIeRSK3DAT3HG9Jk0uF7De03o8Xnzjn0VswCVKKqdfB6ggxyO7LBGBUthhV5Obb+ohF/lZI9TmPRB1h5KXkYnUPRpQu+6T2QpI16fhKtoGit6Qo3AroraTZeI79Wb7hKtoHLOJtuZkTdUV2wyPWMRhOSQOn84czZN9OkLnUYPLtgN3HI/pziuyaaBtGk6L6ah8VGXQU09g9seZuPxZjOCXI8+SGheVIs84aCmodRBiUqkXMviw3ZO1uCyPQ+CmDylmDxa8DVoQ91GQv1ileHmG4sqvd+EKKVC1i55EEzVNCBypck7HexBnjB5CTL5ZoHIvhlPQY0CoS6Pdt3tZQMgSmX+uR2tGs/ddHmf1eg7Ufy1K+qIm3QvozYtUtXZFFyeha5G7Lz1x+S5ptlVdsavdYTH1jjdJ70v2v36vZeMakczykdq+ElXpZRe0ek9xtsYIPJxVRTLHyeyM5Vy8lKVyF5a9KIzl3O6SzKo7UIKWo3S0AmbkXBiKYmjXZeVKEaMMJk9Kvp9l4xmb9EzbDaZsgAYOlkNGEOAuTtTG9uWzRn4tRuhxQ/UhEohmQ3QiI9RTpnRCnZJB8O0X9KZcwriheCUm0NHMvDgmSCqdosvO4SXrDJLsR0LhPovhmXn0fVCNJ2e3DBr05Gz8rSDQUdJYt0tvQfWRE+0ia5KbJ5X+8Iv20pmbvsXD/Wflhrz9XDJnW+o3xh35+XPL/U6XU+99mP4Zs/PrjEWU/9OVn5fzfOiqRUdlNl+G0YuZVYaplNqF1QhpjibZ004OUPGypqpRJKtSECYPUXkTl7S5hXAQ8w1nN4KBPoqFIb3tMvD0k1hPSTeuISf7NBOZIk7ktJGO7r0nuGvhZE7svxwwiEf8ECRELDSdMtj8akb9k7Y+EwoQmvxYy970eRiDpsdWH48RbUL4oSToT5xzydwJ2np1CaU32hlBuMWD2u3WiOOSv90nUpGycPAPuiouf1cSb0iRqHTZxZiXaLFUdvydNEYj0lyLi7ZDOssVgVrHw3SFeXmH81B6Wo2mctKh836Y/p9h7YpLhbEKYiM97JKsGuw8YzH+vT/6alP7pHQ8/F+073ronfbaeyUsuwAVJfX4/GCNIyRHFHkq4yvWfTuOWFM50QJS0KV6W5mD1YYG2EMjkJHfdIFEzqH5cIKz2UAJVG/dHVN4Lqf3ICn5asfRHDrroEaUisjdMDv5qk0RDk92MKF+QMd7O4+I5aB+wsO/U0Eq6/cVLPdafs9j5aESQFCGN1ReRjxxlwCvEpJS/5pG/aLL9hEXjvhDjb+4Rbwg+vX3IINGAqe9L5Va6KKV4akfMafmbQxonLMpnTdo/16ezIpj1IKlwSjKBSlxPYHiCrUtv/n/svXeQXWl63vf7Trw5dk5ooBEGwAAYAIPBYmZnZvNyE3fJpUhaMmmTEm2TDpRklUv8h7W2VXZZRZtF2QqULbpkSZREUstNJHdnd3bCTgQmIefQOd8cTv78x3und4vi0BIlarDjOVUoXNxudN9z7zlfeN/n+T19Fj+aYetUjN0VM5dWgnc3fEGQ9YYN+rPhznWYW9BkNyJ6Y5rupIFXhd6k1E/MpRRbD8HU021KlywyW2KYyt6zsI82/t0GgT8eQ6aUehD4FSSO7BRQQXII/o2PH4whi3pdOtOK6W/3KNxNuPeZFHYH3EZEYioK8xG6EuKNaDaPmdQfkHZcb1JMM6Yvg0J9v6gK5z9TJLMZYfc009/xseqWJNQ86OINu1QudQgKIr31S5BbEeGREcL2qVhqDwVFmDNo7AcGM87w+Yj1UzbtWXnn3PrASTgiQpnOpMnamTxOU7N+Kk9Q1AQFWPhijLtt0J5x6Q2ZWF3N0odlxtv1lS3cpubaf5cnymhu/VReglMnFZanqT7nkF0RnJhbF4n1yEtSPNs+Koz9VD3Gr2oqlxQLnzYozkcU7iV4wzIzpX6jwuYJAbV0JxWTz/VIHPCLiuyKYvUxQW5pE278FUkGUjHc/hkDp2Yw8aKYpHZ9BYKCZvSbC2wflQEToH5SeA2pbU1nyiCz6jP9VEyUgn3/JGDliQKNfRITl1vSZDZjpr6bkF32ae8WU075nARmNucMCrche1fen96o8BLnP5mi8j2XM0duCl3qcJn+iGLjlHSH+mOavf+iR2c2wQyg9sQ0bkNaqwufKjD+Pc3efxrgF9WOItMvKkxflJB+yUQlsPJB0XpMPR0w/Uew9b1xRt4MGH4rInalrrP2ZIK7LUEuYf77HISFT2Yp3JPCsPpmmYmvLVA/NHCzNmSgtPrQPGziQ8EAACAASURBVO3x9f/41+j9ahu7C2bHpHiphtWVdjMKzJ5McsNvdqicsxh5M6J0XVG+4dGasXBrit6EfG96bSAeuwGF24p7n88RFOTzbe6y5LP5evGd78V/W7GQUupXgZ7W+td+4LkPAX9Da/1ZpdRvAs9qrf/54GvXgQ9prVff6Wdmh6f1rl/467g1iVhWsaY3YtIbVTuc/qAgS6+gKJV80xf/9Nvx37Er+8LR12NqByz8ssbuKOKUCEsSa2A0KksPffK5kLXTDuOvBGwfdCgsxKw/YjD97YD2jEMyWC6iobAY0Z6QFOFwwNov3B3EZWdli9KbkBag5clg0nrYI301ReJK28duQ6ou4I8oLW0xty4mkcZeg/KNhO0jiupFLWCQNZFBxy5MPN/mxs+nqZ4zSdcSGnOyP7f6glxLbDESOQ2DypWE7LLH5vEMUVr261EaRl8Lduyra6cdRs8GxGmDtdMmia1JbxgU78SoGFYfNXb4/uXrMalNn/nPiOagcllurM4uyC7JuXV2KbLLeqc15VXUIENSLs7mfglodWvCCNw6psguiSV742Ebv5IwclZaWW5N0dkTUbooibwbD8vg0N/jk7np4jRg/OkNVj86QpQV92Rsi7rRr2iiYoJdMyTVCAlYaRwQfX9+wefe5xzGX9BsnBRUeKoxkP82hHxs9gfndKrP+O87xI6iOSeJv05DUb0c0poVqrPTEp+HNhWNORGIpTY1dl/ahn4ZyTS8K85Wt2YQpTXheIDqWqTWhZ1pd/UOe7E7qaheFiHa0MU+q2fSJCaERSlwF+9KfkXlqki+rU9v4T03ROwg2oBzIe1JSwRuIwnaEkqUNuHib/wZxULvEEN27e19/iB2/AvApcF/+Rrws4MuwQeA5p82AIDcyLnFhPphTe2AyfYhS/Twrpb+akVcVrGjJOttJMFuS+x38XaCNxqRXVbs/lqH2BGybnZFEWVk2ZpflHSdIC9prZlVRfe/aZLaBmezz9jLbVq75I3qTDoEBcmlN31Nd1pQ2vnlSNKMxhJ605EIPLqy5/KGBozBllxAURqUMdCu7/Kx27JX9ioiYXabCbu/1kMbMvONvh7SHZULJMgJ904leieP/u6P5zj4G3XMADYeltBVI5TK+OjZhPSqwZ7f9ync1mwdU7RmUzgtjVvT2B15v7aOOGwfcqjvd/CrCY29DlFKboTSVUVvPGHlQ7B+WpyQ2oDM45t4JYPaoTSFOxCOhfhlg+x6jN1WlG6H9MYUsSPaeSOUYpaEkkjIqhnK4ByUxJ7r5xXBULTjcixfTyjcNNg8oSjckuVwakUERpsPyQChIiidc3HrmsJCxMbjwzv5gUFO0dptMPXNGkqDPdTHiGWGNyLJgph8LkQlmrUPpBh7WeTORiDKwMbeAbRlSuONRhTvSILPzD8x8QsGjf0GTkv0KJ25CK9q0htT9KYjko/X8QsGTjOS66soGv5+xaCzSyhW2pS2dWrTGGwJNc6yg3Zlq1m+HtLaDcMvbhDmpfa0cdLACDRrp9IMnQ+JchrDl0xCM5B6mFuP8CvQOl8lsy7t0fSGpr7PRlty7nv/2iuyzR2SVes7Hf8uMWT/TCl1EbgIDAF/a/D9fwjcAW4B/yfwS/9fvyCxRGAz/JramU06U4rdX25RuSS5etbAF56uxWQXxBiz9ZCmdkiqn40jEYsfz7P6uOzzCvMRu74l2szVDw/iqPtyk8Up6D8zTG9Ms/zRIvc+nxNO2yCEo3ItoDtq0twrr09FELsGfsnA3TbILFr4ZcE6W/2BCOVCi1RdMgPGP7GIey0t8dddC29YSEedGU3hXsDGxwPWH8mK3mEyIrXSk6yDtkScxS7U91sERU1+ISF/F27+3BCZjZDxFyIax0JyKwmxKxmFsQsLn0hhhuLlDwqKjSdDmgegcUhTPS8z8vB5j8x6zOSz4ohc/4BgzutH5P+N7NkmdgYKwQSM367SnVKUbgVkV2PK52z6w7D4SRi6EHL3iyLRLl8bJCRlJW7dbrMTjPH26qFySTH5fITd1zibFkMX+hihrMyy6zH5+QFt+TtNaUde7FC6LTOZtsAbkQG29QutAR1ZDyi7gvtqHC0RTgYMFzvYLQnkyC4n+JWEMGdid7VQdyckOi27PEipXpaBPr2umHxa0RsxSW9oagedgbZA2qq1EwmjLxrUDinCOdke9a6VBgVGE9PXjJ4Tl6oRSVuuO25SumzhNIV47G4b9IYM7I7CXbGJXc3yhy2MUNE5VKW9JyG/FJNZEx5jlIOVJyVqzq0r2rtg64jDzDebrDzuUr0S425LPSxKD4JTKlA/JJ8fjxxh9LU+KoLccvCO99/94R2YmtYPPfFXhey7HdGesvGG5OIu3RTLr1uXD60zI4m6mw9ZDJ+P6I4KbkqbspRz6xpvWO24t0p3YrYPSUhJe0biwPy8SZAXGq0EQQpoJLOR0B0TA0Z6Q+8Epdo9Cf2MU7KsN30RZWyeEL9/f0hcbH5JY/XkAw9Kcm6VK7Jsa+1LKF2V5J3EVtQOmoRHupjXs+TmZZ+cuddi7YkKpdsBnQlb8vyaQu+p7zfJrmo2nwipviTcu2DWw14U0s2u315g60PTWL6mM27Q3h+TnTcZPefhrLSIyxnWH8kRDyr5qZqsNJy2bD+6M+KijPIJu/4gobHHxuqLZNfsiw69eN7B7gpVOcgZ8hpKCZk1YzCQy1YpuyQZBiuPG9htgYKOvyw3YOOhgNFnLdrTBvnHN6hdGMatSX+7tytCxYrUmok3EmN4Bu6eFupskfFX+qw/LFuSKC1CHJRkM469GrB11KF7xKNa6dB5bYjsolwvrYMRIy+aqETTHzaw26IvcNsxvSGT2JV2n+DQYpY+rjE8AxUrZv/AZ/twSqTXG1J8TCzoPuhTeN2lsBAR5A3ZMuyHyWcjGntscmsxyx8WTqFXUXT2xIy+JGKi2JUU5tS2hIKoCDr7QgpXJPE4zEnwC0rQYfm7BuVrPn7Zoj0jvz/MSWG7edpDbTuUr8rAn9iicUlvydayfEVTuNtn9TGZcC7/2n3sHUDD6ici+sMGrWmb+kGpfNsDRFXlqqit4jRMPROx9MWI4q1k50Ms3klERZeWVNihCyFRRpPZ0Kw+Kl/vjcgF25izKNzt47YSRv/VDay+LNvcRkJ6I6B1QCrv/WHFxmMxXkXRGzGEDnxdXHRhTsg7Zk/IRtm1WCTKI6EQal7vkVsUnNjKRzT5lYjMskHtVMT2z3ex+okwEy5nsbqQXw7ZPmyx9KkKvUmNV7UIioqwkDD+Ypvtw+ZOqlD1RRHhJI5m6BlpyNhdCGaHac0p+lUBg5hdg+xKguHH3P3pEdZO5+jsEjNT4ggvIbsa7zAVKpcGyK4lk62jNo2TAWFOetzeSMLQSzZRRjIIW7tMth6NMH3ILhk7A0t+YcB96GsMXzP0prg+TU+oxWEOJr4ly+zefp/e0yPMfMuncDeW0NRrFsUrJiNvhGSWTJymIrxRIL2hWXk0PaAJQZzRO1uWxJYAlrFX+mQvpdieL5NdkpkwsUGlYmnP7jMYfssjtxbReAAac8LkNyJpadodse9OPyUdp/y8YvVMitZcgtKatdPGwL+iqbwgHIHaQQunLdX/0jWoHZCBM8woKm8ZbD4RirbEUzR3GyLeCgUPrg25YQHMtklvUtPaK2wIlHyteF2RWY9p7nGkhrGeUPzwGpl1UaLmLqRwa3ILe1VNd19A47AUud3aQCmbs4myUht6p+O+GARMTwQ2sQP1BzXVi4PRvoxQeT9skXmwzszvrbD+sM3E12zWPxxheZogL8t9pyHkoNINMIKE4i0p4lUvyAgcZcFpGmTWEu78eIrOlMHGF/aTW4nYOmJhdzX1/S7lCwblmzG98YShsyYzv7dE9ZJPd8wgVQtpHBTqjNNOCEqa1j5o7TZp74biBYfcSszSRzKkazF+WTN0ziTMSNHK6JgkbxTpjVhULwektmXfXntAREWdPRFBVXrK5esh+dsGN/4rgYN4Q4rWXEL5llSHqxcFX51ZkULp3S+4g2W4cAoMX4wjix/PMnQhpj+uGX9RfA+9iYT8vCLKGLSP+Ew+0yJKqZ2BoHg7RlkJQVGKmZlVg+IdH7chNGgMKFyyyayLpj27orn41/4elQtN/LKgvlc/aFG80UUrmHomGBRERf/Q2pcw+Q2Rzq6fSuGXDIxY4w1LN2X7kM3YWU9uhpbC8jUTL/XpTSYEB3tYXcWur20LyefUOtsPWmwdTWN6klTdG5WZWWnIXnFpHhA9xfKTKWoHbIJKTGdPTHYlIMyKWSuzHhMUFPk3Vxm6EJKY8n9GzkFrTmZepy0+lKAgSkzpIpm09yQ094HVF+bkxgc0o08vU31JjFDGZJ/sirQ+0fJZTn63SeN4QHYtwW4ZFG/IwNCakwEVDbUTElyT2OIX2TitaTw3RmuPWJNjR/b+bytJrW2b3B1rB6BauA2bRx3sh+q0H/Lf8f67LwaBKKfJLUqoR2bVoDX79klomgcjVAStdpraB8ZwmjIb5a84pLZjeWNtmSUtD4q3+nhDNvkF2QMZkaZ+MqRyJWbkjZDOtKT2qggaDwg1OChJ1b49K0EUnXGT9LpBf1jRfmiM7Qddxr7XJDFlJHdbCduHTZyWaOj9ilR3i3ci1k8bxAe7mJ7YmmsPatbPyPLPCGUP3ZmUTPugIOizzq6EuBJRuGahQkXv8Q7bh23iFEx+1Wb6j5o7nH57o0N3SrP1kLxHYR5yqzHTT0WyVCxo0lsJRqiIU4rUlqCqra5i+7CJX1ZoS+MXoXbIoPCWy62fzhFmB/6KbdkeTn7FJn16i/UzmtLNmDs/YRNmFYXbULoZE5ShuRe2jhpk1yOO/G+/xPqZIqXbCUFB8hnnP5PHqxo09jp4I287QaWL0ZkwBxhv2duHGUVQjgmKMhisPZJi+M1IYthyit6oy+grMP67LsPnQzbOVIirIfXnx/CP9vBLsm3qTQiQc/zFmMx6QvVSSPkKDL/hU7qZkFtJhEC1YbLyuCskng+FtGZNgjxsPTnF/F+UjIveuKY5Z5C/awj8xAKnI+EhcUral4W7Uh+wWwL0iLKa0mWDOz87hRFB7XRIFEg3J7sisufYgY1HCow9bRHkv99ZCYdDwpKIptLbCXv/acDGEwKt1RbMfjUS5N6C5AiUbouUXmTmenDOmsrlHp09sfhwmprgfJnUrXdWC90XNYGiPaJ3/dKvCLDilS2u/2dVStcUlSsezbkUjQekF2p3NEPnO6yfypPZlBnTCKToVj0v5Jj+kEHsCnEmVYupHZIUmN6E4Ja2HoL8Xcki2Dxu05+McTdNSeGJob0/In9TdAWxC1EOgmJC+Yq0C/NLEfc+r6i+LrUIaVEJ8Sa7KnFPQVEAHbErUIswKy7H4t2E9UcEj26GYPUSNk5axK5m9+lFTCNhf2GDr108xu7/B/yKRW9YQCGjL9a4+l8XmfyO3MwA4y8HqEgTFC2ae0zyCzGJJS3I2tHvm3nSWzGrj5niuExJYbQ3Lqgqtya0Wq9qSsjnhvAO7bbUDbIrAfUHXKKBFdWtaeqHJScvux5j9RLsXsTWkTRRWr4ugAuZ+RMbhi+EdCYs3IbUUQq3wC8rhi6FtKcs0rXBoNqA/tj337vwRAf7zZzkMDgw8npI4ir8gokRvv2+SpU/u57QnjKpXvLRBtT3uxiR1HX6IxJQm95KMP2E7cM2uSWRHRvRgPwz6OO7TU1n0sCrarJLinRNTFKdKekG2W2hEZWvyHYkTinstliVvSr4oxGj35PCtdXXbH/ao/BceiflqHo1prFXHLC5RdEdbB+RSPahi/J++GVF+YbElq+fVuz/h5vMf3GU3JJc43YvoTdi0pmSRCMjFkOdX5aos+ItSExFUJK2ulbQ+WiXWz/5q/dvTSAsuXSnZbm09qEhdv1BSH9EUX8gRXorxuzLAJBbiUgcE6ejyd/qUPtAQHMfmHMdeiMG3XFTbJmLIiFdf8TGacoFMvZqTJRS4s3PQ+2gTW5JM/c7AfGBroRULsY429Kb16ZcEEFJsuxjR4gu7rZH9p6AIIcuhZiBHsA+5KIq3Ywp3oChCz5+VZaJ3pAALd6mvPTGDLySyFuDYkLhNgynO+Rsnz+8cZjSqw7tGYcwLR9PlFZsnq4w/qzB2o8F0vvPalbPONz5i4r1UwaFezHdMfFFqETShiaf7dP5bJvaAxamLxmMfglRppVDsktys7VnLGqHZGXhlQVmohLZTrV2O2TXYuH/eYJPmzmyKoXQgigrVx5L0zgRDGAZmtYeMEKx7WpT/BexK5To4g3phasE1h6x2T4Rs3nMJLMi7czCrUHMVhtSL+dIbcnNqQ1hPm4dtkhMyC359MYV+SUZ+LILXbwqNHeL76E7Jd6SxgMMQl0VW0dNWrssxl7uCfJsSqr5KBnwi3dDGnsFPKsSEfUEOVkhlW4lZNalPTf9dExzr4iMWgfECBSlYepZDxKoH1JsPyLcRnUvTf1MIACQakJmpU9mTVgSAGuPKkbPiSJw44SNV1F0ZyLakya1gyb5uwbzPzGK6cPGYzGNfQZbRy1yKyIs6I1Ii9IIpH6Wn5fZP06JUrU7IUi6zPdy73j/3ReDgNJQviLL8/ojAc05R1DMPiw/KUWx9m5Y/zmP+v406c2Im/9JnumvmlQvajLfztHeLw4wuxXTmjVpzZqMv+jjtqRQ0xsyyS1H+EVjwHoXQvHm0TTuG1nSmwIEcWvfV9Rtnw7J35G3yPSlk7D48TxTTzXp7o7wCyZLn43BgNI1RW8mYvWDAio1/YTJZxPGXxQBTuyIzqF0A9oP+sQpxfYhselqC978+iGub43AvQypuhhczFBApq0jsqfuTBqk30wz+WyP3Lx4+UtvOUx/J5DkHE/26FoJnXnrWJrpvy0XhTcuA5bdkRl+5nfkvKqXY4p3Q6k2n/LoTMse02nJ+9/eBe0pk9643qEjr70wKX71KUVm3Se7oqm+aDPyhkdzr3gd+p9os3HCpnw9Zuh8QGYjoTOrcTrJIPhFC2nYTTB9yK1FEomeHuQ0NBMyG8mA0qxJ1WDkzYTCfILbTvCrtugTHGlL3v2xPLt/vyE3dFqKh/mFhPLVQZG5owd/Q3cqxcQ31yjcMOlOJvTGxB8y/2kpFpZuBlQvaYpnU+SWJU+ifL5Ob0Tsu405m5HX5TwK1038kqZyPaI/7JBak1rHgb/XI7FkJTT5VYvNk+C0DJafzEmaVSgrCbtpsH7SFg9IXWbuwg2L5rEAfzimNZfgNKRgOPWUYuq7Pfp7fFozFk5rEHV3fQMMmP7DGuUbAdqAyvWQxpyFSqQW9na+xJ903B+DQAKNAwLHLJ1zCT/VIEqLyq98RdxYo+diRv5xmv6oojNlMfoKrJ022T4q/WWraVC9qOlMOUQpEdI05xxqhwxyK6F8yH9BeG6j5zwSSz6E5nHh1ae3EnLLEiS6+LEMUQYm/8gkzA1inPaKdqFyLaZ+pMCur4v4J31bfl+qrildsIRCW1asPpZm46QlJpSrMXFKlnJxCgrnXbyqnPvYKzGdaak6xy+XifKiYCvfiGnMGdQPKqqv2OSXhUirEqgflEp5mFUMv9GlN2rTH00G7TOD5gGYfN4js5Gw8kSeMKMw+qaAP8oC0qjvs7G6mrVHDFYec3AbGnPVJX9XzsUvSdspfw+60wnpTYU3KgIXuw2NYyGxo/EqDtnVkPYeWH84NegSJEz+7+Jy2zxu0J6yWf+8z+zX+jT2mmSXNYkjNub0PYegINiuiec75NZiKld6VF9apbnbwO7KzZZbjulXDfpVGcS3HrSIM4PPYHOAYd+blxlyoMHfPiIcAhKpR8SOdHw6kwaLXxijdDtk5lsifCrfEIBsdiVh87hLbMsqyauaTDzbZPtEhfSm5EY0H5DWoN2WQqnbUMS22sHGOU3F/OeKO69t/ZTB1NMS9aZNCMsRlif1oLFXJWzVaWq6kyK6ah0JOPi/NjH7BkNvSvs7SitML6GxL03mhkt6S1YmURoap8bpTCm2Hi6z/ISEtc5/VqA6sSt/LO+dt/33RU0gMzytjz/xy6w/YuA0FKXbMcufTMjckajw9VMpxl7pE2VMlj9sU7whVKDMqs/66Qz5hZjmnEl+XpbkYU7OyYilSm71oT0XM3zOIL/gs/5wiu5sjLtlMvxmRHP3IBRiNSbMGGx+zMe9kyI3r3HbsgTsD0m0lzaAAbugcjXEL5msn9HYDYPsitxAax/UjLysaO4zKNzWbB/TpNdE61C+5dEdl/2q3Y5Z/k9DnLeyIlA5otGuvPb0ssnw+ZB+1cKrKEq3JIbb8AdipnEp1PkDPYI2hU40/JZAL9q7RDVZvB2y8rhFblFUfL1xjdkT67URabyizG5xapABMFhFpDfE8tuak3rM5Lc2Wfj88ICIE7D0V0Lc13L0R6VdZ3elkDb2aszWEfFwuDX5eSqC9lxCnE3IzEuUd/GmLKeLd0UePfJGnzBvsX1IFG/l6zGtXSb9UREyKQ12C6pXA8KsSWNOAmLyiyHLT9pYXRENDV0QnURuReLri7cHWvxAuiVBUWoIb9OoyjdjtCEtzKG32nR2ZTF9zcoHTcbOJnRHDcK8onwjYvuQhd2B7FrCxglFdnmgRwklJSjIGahYahXekDhCtYL2LlEdekMDDsGWonJNNC7dKSkW109ElN60ya3GtKdNWgdijJ4Qi7yquCiDooia+iOawl2ZlEZfC2nMDXIdBrfy25kQ/VHJkMgvRSx+wuTeL9/HuQPaQBx9N+VitvoJzrrF1DMdFj7h0psUU1FQMJl4TqKnm3tMbv+UK2abCXOHAZdZ15iBIrckLZ70pqY7LQIYr6LYfCglMs41E7MPSz8uVXXLE54cGuwFl9kv1wgKisacuNNqxxJpUZVkj4oWFFnsKHJ3TcrXZEnZHTMYeUWRWQ9xtyG7GhBnRTKb2Y6p70/RG5Gc+a1jDupOBqVlJZS/a+Cum2hL1m5eyZQOwrBm64hFlIbxF5poU9Efkvy+kbeE1ZfagtwC2G2xuZq+KMlWfjYgtSXYc63kdQ9dinCaMauPyt48u5YMYrOgcUJWRk5bgBhiVNEsf2IYuwO9EcXyhx2S5QyF+Zj8XRlA0PL7Nx+yBoGhWqrrhyJQ0mpLL1r0dkU4TUXtRMz4i128osHQRZ/WbIqtIzZjr/YxPdmCFO9GqBimvtujekmgG0HBpD1lUrkW4bbEOTr3L+q4dZmBjVDTH9esP2IwfD6S969ssH3YoDcmqwK3kaASqcgvf1RqG40D0B/LsPzpmMZei3jcZ+ljmsxmQnCyQ69qkthS61j5cELxtrRPzUBmWa0E1R7mRHIe5qQrFDvCQ+xMaZyGYMsSR8JKOzOCtMtsJow/beJXYOVJoSiPvCxtwc4uRfWq1AychiK7npBfkIEhVYPOpEisU1uiK0ltKvyKWMDRUoDdfMi+/7cD2hJxhBGJZFhY+or5T+UoX5PU2LFXhay6ddSmdUCy3XL3BOCQuGB3E9q7xDllBFC4F9LZHdGZVoy+CgufNHdUcjNPBbJXvRCSu5AiuyqOMqcpRT6noZj/XIXEgV2/u0J63aB80SB3z6B6SVO6IQEVvXFNqhHT2SWvLbGld7x5EtZPuZTuhGycdCldtsguSYhm6aa/k4MYFDX5e/K31Vc0D0ekapC7bZMcb1O82SVVkzTjMC8+iY1HCix91CS3kmCEsHHcJlXTGPFAxXjcYewVn9S2hFJkv5clcWD1g1KtdlqKMGNg+gnpDYPcajSAc8hsvvu39cADYOCVDaqXQ0bOSQW6OykpviOvJYy9pOmOmRTvheSWpF7gVRRBQXrY7VkJ+Tz0P69Svhmw9fk+2VXNyEsSsmk3THrjKaKsYunDDrErtYr1U2nyS1LYre+3qFzRdKZTtKdNhi4k2G2RgG8+ZLH6hGb7sMXGmTLVKx6T32my+qjsf/P3FK0Za6dK74/Kdupt5Fl/VNGfEgXN1mMh+XtSuJz6hkiMTTvh4N8VDHzqpRyNQ3IT+2WBgrZ3wfZRhVbCFeiOyXk1DmjWvxBQvagZeVXR2gvT3wkp3hIr+PD5AKcB66chvckOhr0/JCYyd9tg46TIkzOrspT3SpITaXcFYtodl5VB6VZIlJLtcGYjofKWQeWqFGg7R3ysnhjUVAJDb/07QEX+QxwqEU5c+WoHu6NZ/KjF2Ms+/nBEMJAKbx8ycZsS7Gn0pfhUuh2JjXQkYf6ziqGLeoCDTmjP2BSuWfgzPqtPSmAHCO5644SL007YPG6LYaUR05mLKN6N8Ibl+6yBm6x7cJjsSkLxdkBQGEAgE7EHD10Qc1H1rcHS8kaM5QkIQiUw/0UprrmNhKAkbIR7n3XILwQU5mPCaR80DL+RYPWF+BNlRP7MxTwrH8qzfUQCP7JLSiKpxhSZFeH9OS3N2Cs++SVJzNGmwm7B5nEXt5Ew8ZRB40hEmNdMfVeUbVEa6g8YWL1w4D2wcBpQvBOLTHjWwQjAq0g60PZBG79o4D3ZJspoytditg+bbJwUjl5jTir8pg/ZVU1mzSBOazIrwgC88V9OsfykTeE7GZx2wsaHZO+99//eZPtBmf2G3xIEeWuPpAttnDQEBVaR6DdtCHG6tdtk/kdNCgMStLMtrTW/LPTl+pEC2tQkria3KoXi7mQiHhDr+yAavyre/eFXDQxPkbvqMPpKk8ZB4Tg2HtDEdZf1x4SsjIKxl2VwHH/Jw/QU2WXZfoV5kbpHaVEzZlYM3EtpvJ9uUD8gSdpLPxdSe8KnfD2mvtdBW1C5qGg8GBGUJfG5vVvIWGFek5+H6iVNZ1quDbkeFfVjMd6wTCCJBfe+KBi0oKRJ1aVLEacMxl/UjH3TJniwx/pp8Um8rb35k477YhAwAvFBL30kLxFcl6E/YqP0QOnXEu365gnp2+7+hkdQ1PQrpoyKwN5/Hu44rOxOTNP89QAAGvlJREFUjF9UFOcjDv0PW6SXTNq7DBJT8gEv/vW/x9aDNqVbCYV5aTE5NRO7HTL13T69iYTq5YDW3oSNEzbNOYOgZEl1uStFp6HvOXhlMW1Ynijt1h82cOsR7SmTqe80Kb7l0N4Xs/5BucmjDFTPK+593iJMG0x81Raz1MSAjzAuFW23ofHGI6qXQnIL0juvXvEwAyHPJhYYnnj+6/tdOuMW7rZkLUz8/h0SW0izsSvmKsMfhLgGmqELMUEpYeETOSpXxcs/8lpbQBs92T82HwrIrmp6IxZRToqi6e/m0BmJPfeGE6y+2LSHLoqyb+RNj9qDmu6M7LHR8rlWz2uqF6XgVTtsMvKsSGsXPzfC6NmQ/D2x3bb2J0SFhOUnc8QpSVKOMppUXdPcZ9Df7+NVNIVrJlHGoHo5ZuoZj87uGG9o0EWwRfI7/oIMHtPfCTB96dbM/q50CTIbCQf+UZ2gkuB0RK1n9WDxE0XcbYU2FOVLiuFXDWrHpVdvtzUbDxv4FQiKFvl5TfOAJrNiELsSGy8+l1hqDzlN5p8WyS3KoGNdzpJ/I4VXEgqV29BsHdeYbZPJ5yLGn9li6A0YuhQy8bxcj40f65IM9D3tGYP+ZExqzcJpKCae71G9HJG7YdOesjACRZAXitbqY3IttacNRr8snIigoIhy93kqsUo0uRXJDth60BIYwh6DzIJJ8W5MlNZUzsm+xs8bNPak2PVHfQFObEmM1NJH0rSmLVp7E7yKLOncesjmkxP09oSirf5MW2KekK1Hb8igvt8kyMtsU3sgTZQx2fNlj96ozdyXRXiiIig8d0d6/UWoHZIl4ND5HplVveMjT28onKb0hFcfL4q46ZxB9p5FZzbCaWm2Tmpm/jChP6LY/Mk+tcMyOPSmYpyWwi9IVRo3Ye20TWEhwuwpvKqg1nOLMPxWIGm+e4QOXLrt052U7cadX9hD6WaMW5MCVexA5dG1wevtsnXEpHxFkV8QGIp7oMmNX3TwiwZOJyHIGxQuOtSOSSbe7Jdr2B1F/URE7qaNX1Tk5g1Gz4Xk70Jr1mXkJZOVD6bI3zXI3ZW2Z/FuSJiT4uj6acnbG3slpD+kdgI410/btGdEv1C+qFChvK9WT9H5Qgsjgu0jULyZkLrpYnmKzqyIgrQBGydT2A0Ds69Y/hhktmKyy8lObHrtkMvo2YTRczGbDznUHorpjRgsfrpKat2gscfErYsCNFXTTD3dojVtUn9Q2sfV182da1Qb0qpc+mJEa7fCGu/R2RfiNqDzqQ6Zdc3q47IsL1/VuM2Y9qx0fdwGdB7u09on13qQV+TvGoyeTVj6iMndnxjCqxhsHbHZPCbQ2fwf5Bh6S7P+AQHZDr8qRiyrC7d+3sIvmGRXpeiZuILXM0KN3VS0p03i1GBS2jIIChDl39k8YH7pS1/6873D/w2Ov/Xrv/4l63OPDbzvUg9QWpY82bWE2DEp3oko3o5IUgbNvQb9YZvEARUrWociJr8bA4rCvGjXjVixedKivTcmvWAz/V2fjX0OsWnxa6vHUbHB8PmAzpTJ0HmP/JLGSBROM6IznaI7YdCZshl5PSBKmwS7KvTGFMW7CVZXBCRmbLD5sMKpSwFn/BWP7lSa9U+GpFYsulNikVYaKpeh/gkP945DlJFqeM/KUrwLvQmY/k5M4Y5PlB0YWzoWY2d9OpM2I+c9WrM2iSOJx70xi9ZeGLoghbHWL7QJaimCvEFmU9M4oPCH5HdjKPw7OboT4Jdd/CFNd3dEYprklhLsqy65OyaVi202H04TpQycjqZ/IGD4BRNl2bT2GIw/LxRfbb/diRABlTekAGESZlckWGTihS6rj6VQGvxKwtirUDtoYoQG9Ycjxr8Xsv5BmH4qIsxJwrA3pChdfztWS2PdSVG8o0lvCttR6UHuXtdg6vcXWPx8ifS6mKesvsLqiEGnOy2zbXdasg/DnEFzj0GU0eTmTapXA7lm9mpAyXuhTNoPhjT2pRi+IAPFxPc8DK1Y/4CJ5Snchpyn0bYICwmfOXGef3j0XxAf8jh7fS/9mYTRFwy2j4rtt181yS8Ja8IIFWbNljAcJXbf8k3JnzQDab1anjAQZn7zEna6TG/UJLcckllXZDbls+zuTkivKWLTJMwrhi759MZsht+K2DwhHoPR10NacybeRER2wdzRTQA0nnpq9Utf+tI//OP3332xEtCG7K+itBIGfV/29cW7Cb1hcVjV99vUDrkU7vQYezXEGxbxR1CA7D2LzNnbpLdjjFB6uX4RMisymvdnQlYeTbH3H4cYAeRvWjh1WP2AI4W842l6IxbN3SaNfSnSm+FOEERzj40ZyFLKG5IcwNac7JdXz5joQb/bbsOdvyAJsKPfshl5vUfpBgIhOdanXzUoPJfGG5Ze+/qpNOWbYlpJbSrmP2Ow/khmJ1iycjVg6SMOzX0w/6kUTluTW0qwegluI6F0TQCr9f0G1lfKjL84SEzKKSa+F2H2xQdgRJBdTTAixfjzDUpXwV2zqVxNSGwBq3pVg/VHi9I2bQg3TwcG+XmPe19QTD4f4hcN+uOazp5Iknp6mqGLfaz+wNvvKXqDrdnamSzagt6UyK13OIRpGH7Rwi/bmB0Dv2hieprCPQ+VCB1o87iBV5JW28qHwKsY8nOV6CIAFn9yRhgPg6JYe7dkSrZnB2G0txNGziE5iWXZQhXuSmt17bRD/dD3qUPVc2LRHn3Gonhdsf0zXdyaYvlDaXojJrkFkYv3Hu/QfcAntSk1rK9eOMaMlSNvepw6chsjLYa26iVNfiGgdjokvRWRXZKZXCViVW/tEUjK1hGJjXeamuFzEKVk27f4nz9Ie8oiVU/ojdiEGYPS+W1auxXFqyZOSzMx+KzXH05hepruqEU4HGLEsPAjJkEhwV23SG+Jr6V8TVSv73TcF4OAGUD1ohTRJCsO/LyisU9G9f1/dwmnrTFCjdnyaMzZlK7Jkr4wn5Bd1jQ+vp8wZ5BZ7TP8qkHxrrRJqhe75G7baBtu/WVzcENAZ3dC+UaCVoL68ioGqW0RE60+5lK6mez0gGNHluipbXHaFW5Dc7fF/v9jgT2/F9IfbEtIoL07oTNtsHk8g1dR7P6qz+xvSR6929S4NZGlBkW5EIq3Q6IMFG4K0rw/pChf8+hM2gy/mTB2NmbymZDmHnkv/JLJ1lFZums18DvMvo3Ijhm6GLB92MYbjeiPqB2lo9WHa78o8Pnp7/bZOCF+B8uXQcwMpG36dqJv4ZLD1tEM1ddMjCChPSue/8lvS8KO20ww+yFhFuy2IhoOd5BvY6/0qFxJSG2Ihn7juMH2GaEQnf2f/j6dMZPqeUVrVtyXm8fTOx56I1D0RxTtXQbutolbF2JOlB5g5ooyAOXnobVP9uCz3wix+rIs1iY090gc+NS3G9K6XITasYR7P2YMYt40e77s7bj2uhNKAmQyCuPVIm5DM3RBsi2yqzFhHjLP5yi+6WKGshqhb3Lk1b/Ihc4Ubz2/n8z5NFvHTJo/3hED2xWHrSMOqUZC5aqAVlafSDA9RaomTsytD0TkVmL6wxJBnl2QluH2mZDaYdnKdb7Q4vZfGgKgeEe6Af2qxehrIfnFRFyQGxHZm5LrYHqKJJ0w860u7RkJ3xFmxjv3CO+LQYAEVj+U0J2UGXf8ZY/euMIbjehMKTY+MkV+KcT0oD9TxG0Kg709o6gdUmydEONQ/kaTxY/lRFxzoYFb00QZW7z7HbBXHcrnGxTmI9KrxiA5WAQYnRkBdrp1TfFWgtOOmXxqC5VAcT6k8YAmzGn8gkF3WvzcG5+YoXbQZfRsIBz7S4ZQelcSwqwEZzb2puhMOVLBHjIYeSOksBhSupEQ7OvTHZeCoxFqNp4MB0TeNFpBd9zEK5lsnHQGfEPpedsdxcZg+Tf7lW3K1xLsLjR3m6x+wCHMwsQzcuML5VZjBLDvHwf4ZUWYsdjzlS6pLc32j/aIUuzQi6OcKArzSyInbs9CZ8qRYJdX5X1p7rZZ/BHF1rE8hfkEv6LJXXWYeLaN6cHtX5SZNrUlhbihi5rMbQdvTGawzoykF3lVTeEOVC/5YqtuSOHSiJEe97BoP7SpmH6qSWdKk10VU1B2LcZuGlgd2ftrJcYsbcDEix4qhvnPlCTsdRdMPg3T34TMqtCkVx/LELuK4TeFPhRl5fd35kK0gtaMRXpTU98vHEC3mRDkJWlo7NUQu2GSnC1x/u8fJXFkxvXLCfpCgX5VwCBRWj6zxo91aTzsU75oYvXF6AMw9U2D9DffEP+DLVoVvwyl1x2srvgeMt8oUL2kmX66h/vfrtIfkQ7P6qMWhVsdOrMJ6ydtyjdjwiwUb4BdN0kck8LdhDgN9cNCNXqn474YBMKCxmqZxDPeoEUWERY0M38Ik8/5bD+c0Jmw8YZF+FC+0iZ/TzQFbk1MQSSwfaIsfddRze2/VKYzo2jOOaKwmxbXXHdvgSAv6r3MS1nyS3Jh5u8YhFkDu6slkvtRi/nPD+GXFMtPWkx9R7BPdm+wNago6h/1KN0OWX3UIShqWrvFsbZ5UqSzb+fL1R+QyjFAa5dFmBOjzwO/Wqd8rUftiKa9C6ovC1QzzMnPyS8JIGL8ZQ9vTNqh7VkR4iQ2rD2mWf1QlcRW9M50sTt6R2+x+kG50Eq3YjED5aGxP4M3omnss9k6mqU/onDezO3wCmJXYbcU6niT5m6T+n6bzKrMJFYXesMGqTfuEqfEt2+G0NgnmHjTh9XH85KFcDdF7ZBBe7fUdVq7xL5dfcNkz1N/mT1f6eJVDIbfkvdy5XGX7FpC7ahYup2GnF/xiqwUOjOaGz+XI84lg5aweAyC0QirPyAiZRUbj0DiwvahFIWFCCOGyed7jJ2Ncesh3VGJIPNLmvINGfDrB0wmn0uYejakOyHvmd3TDF3y6EyKEMqvQG4poHQ7Ib2umf+ilgCSJmw/JPCU9LqSZOJNGUxiV9KEjBByf5TDaMpkZARSaHZrIgVu/9hJogGfsTUn4rYoC73dIbkFWa1tnFQsfjzDvZenGXkjIL2doGLFxqk8e77iU70S4xcM3CaUbvQZPZew8niK+gOyFbE6iqGL71wYvC8GAacpCKvsm2nsFix+LEdmRbF1xGLzuEv1dUO2An2xwAaVFI1D0rft7I3ojkgBpHDPx5+WyrmKhGrTnhEuW2rLILOqiVJyyioW1sDGcRvLg4mvLwj+yZEPpHBLoryirDxuztn4ZdkPmn3ILyaY91KsnXaYfM6nckVUW2NnPcZfkAhpqy+Fq+yKYulzMbnlGLepSQbOtdVPjnPvcxlK1yUtOU6JnDfKCLS0Nyw8vMacy8Ffr9Gd1GSXBSM19WxEZtnEGxaBVP7ZjJiHBim17raB09Q058RYVL4uIp6RcwlGqKmdFCz52FkPqzdw7dXEnx7cLqASGHmjT2tOcgf8qqazC27+jf04LRFo9YcV/ozP0MWI5jGBpGTWE+K0JkqJii5VkwAXIxD/ffE1l+3DWZr7pEq+fTImzEuce/GayfqjmlRDCMpxCvL3ZLuhQoXdlDZd9UpMZiPA3rTwhhTNQzFWT1p23mhEqpaw+phJ7wGfhU9kWD9lsvlQCtOHxkH5nLaOmLhtuTHWzpisnnFIr2smnjbZOCUDibZE0IMWIElmPZBAkRW5ZrQl25f2jEFvQt7j4dc7tGZlYHTamvasIrMR425JbaN4J8Zpi1qxOy7cysxmRHdKFH+1EzFhDnLXbVoPSyt8/KVElIWripWfD9h8SEJ7MxsJa6fTRCnF9kPiv1g/naF20KQ/KcEn4bSPWxel4zsd98UgALKfM32oXvbJz2vaxz160xHVyyHbxxO0ocgvxxRuGSw/YWO1Fdm1hMJVi+K9UNj0n3Zxlm38sqJyVbYIbkPtcO/qxxIaP9GhMyVAT6el6c+EOC3N2qem5efNBzLyr0YYIQxdFNlrlJaVR2OftOhqhxXDbyQkFtQecMXg4cPGiRS5hR5GKAKO9ozCrSdMf1X2o9tHpYXjV6QHXrgjvfnWXEJ+SUJMZ74d4jYkJ69xQIp7qx8dYebbvtzYewEN/RGph/hlscqm1/s7LMY4rbF7spe2OzG5e11ULI7Nzi6YeNocBKmatE76NI+GtGcMMlsJI6/JTNyaTTH+krj97Ja09tyGkq3P9QinobE2HRY/m0BgEOYU3XED05Pgl33/aJ2tIwMeYlmTqol8FgVGJAPAxNOK9JpBUJD6hd0w6P2lBnZHiEkqkdkztWlgt2T29YoGCx9LkVuEwkfX0IbQfuy2xm6YNPYLMTl3wSWxNSOvJ/THZNDJLkowrOlDvyJLZrOvKNwRVHh9n0HpmuhTQERso6+FuDVo7XLxyybhjI9WousYOZcMCsMSjDv/mfxAXixx6aOvCqJ89jdvYkSwdka2A60jMmhmV2Na0zajr4akNkyMnhikOocCchdSZNZkC1i5GlG+GRAvZbA7sjJrzZrCZhw1sAb055E3PHKLsrIO8prKc65Exf0pHqH7YhBILFmG+UXojdrS237eZfisydojNumJDk4nEZVaUSK+2N+lO26QXU9Y+KmY4rUWu7/SY/brHbKrCb1hA7/KQO0X0zggy8sgsEhtarmYKgZ7fzsitxTsvIY4JaCS3rBFqiGQUKclsWjjL3TRFsx/zmT4jYTeiMHMUz3yKxGpusgzU9ua5r4sVg82TkrcenuXQXPWojNhsve3NkTDsC3swvpBjd2KKF9WrHzQoHZU09plow2Fu22QXZQYs96k5vbPyMeVXZbiUGbVwPtUi9HXQ4r3YmqHcwy91sKvyPesPZHgj8RsnHBYezSPSmD5w2II6o0IOLUzYTHxDYvxp8Xd15406UxIkbR4u4fTkCV3UNTMnFkSxd2QhLFanhRJrS0bwxfTztgrfcJiQvVylxv/xQhBUZNdFiOL3YHht0RPP/u1HoZnYIaaKAetA5EUiC9r2jfKjJ31UBq2T8bklhLyC1KojR1JocqsKroTUHtlDMMzaO+L8T/WIiwLf1FFg3xLYOOEQXZJSdsw0GyejjE9GTjrP9qTJGKt8cqGkJGKAgBJbUq7eukjJnEaag+KLX3u/9ISEgJkNgLKN2T11p1JsNswdjYkyoqaL7XZx/Q0139ljigluDurB86aTWY9YuUJk/phTXfMonBHqEHVyzH5S5J9Ub3kk9hCn64dcBh7SVKpTV8z9c1tkgH7YvS1mHtfUNz+GZngrJ44QL0hkdFnbtbe8f67L3QC/+Pf+fUv5R49Q34Byle6KMukN2pieUKoUSspOpMS3T313YAwb8KWS2ZDs3Ea8ldt6gdT9MYdakdcgoKieC/GCBWbj8Z4FZPcojjohr8nYZn9UcXo631aMykUMmpvnYD6g8IGKF/vUjuUEl34hEF3EsK8Q+GuZvRsKLCNjYTGnEvtiGL86Qabj6RJHJkxnZ6muU9j+galOzGWJ1i02vGctAHzmjitGDubUN/vUH8oJrtkUr6qMUPojRmSjlOCkTdDgryJ8kw6s2JgKt0R9V7xBZulH4+IcET59qMWRl/Rm07I3bMIyolEhKUkL7FyFWpHE9y6QW5F2oSZjYj2lEV3SlpxhUXpcNSO2lg9WbIqFJvdPPG0x565dRp5k9akwisa2F2D4i3YOKNJLAeVGNh9k86UQVSKsTomlWsB9YMWjYMaTIXbNgR2sWpQuBvTnjGoXozpjZgU5jVLnzRQoUH1vISSFOY1lqfIL4pLMbOpaR2OSO1pU/62S/qJGs3NHHbB58Sxu9zzyvgjCW7NxPRlldabifFmYspvWjSPReTuGXQLFoVbis1TDFJ+RTU48UKX1h6HoYsxZt9AJYrsqhTvupM2pZseaJtULaI3ahOUhA3Qn47xixJx3pwzSTUMgryB0xKKUXO/nIfZV7R3m1Qua0A6E1FO1I3tWXEdoiB2pC5iBor2oZBEDYJWHUV/PI2KFUMXfGoHHYbe0kx9tcnakyncmmLid25hpovUjoEycqyc/5N1AveFlVgp1Qauv9uv48/pGAK23u0X8edwvFfPC96757ZLaz38x5/8N4km/w9xXP+TfM7vhUMp9dp78dzeq+cF7+1z+5OO+6Im8P7x/vH+8e4d7w8C7x/vH/8/P+6XQeBfK1a8h4736rm9V88L3tvn9q8d90Vh8P3j/eP949077peVwPvH+8f7x7t0vOuDgFLqR5RS15VSt5RSf/Pdfj3/todS6reUUhtKqUs/8FxFKfVtpdTNwd/lwfNKKfV3Bud6QSl14t175X/6oZSaVko9o5S6opS6rJT65cHzP9TnppRKKaXOKqXOD87rvx88v1sp9erg9f9LpZQzeN4d/PvW4Ouz7+br/3M5tNbv2h/ABG4DewAHOA8cejdf05/hHJ4ATgCXfuC5vw38zcHjvwn8L4PHnwb+CFDAB4BX3+3X/6ec1zhwYvA4D9wADv2wn9vg9eUGj23g1cHr/R3gpwfP/wPgFwePfwn4B4PHPw38y3f7HP69vyfv8gdyBvjWD/z7V4BfebfflD/Decz+sUHgOjA+eDyO6CAAfhP4j/6k77vf/wBfBT7+Xjo3IAO8AZxGxEHW4Pmd6xL4FnBm8NgafJ96t1/7v88/7/Z2YBJY/IF/Lw2e+2E/RrXWq4PHa8Do4PEP5fkOlsDHkVnzh/7clFKmUuotYAP4NrIabWito8G3/OBr3zmvwdebQPU/7Cv+8z3e7UHgPX9omUJ+aFswSqkc8K+Av6q1bv3g135Yz01rHWutHwKmgEeAB97ll/SuHu/2ILAMTP/Av6cGz/2wH+tKqXGAwd8bg+d/qM5XKWUjA8A/01p/efD0e+LcALTWDeAZZPn//7ZrxzoJBEEYx//TIFYQE1+AxJbKgoInsKaWwscg4RHsLK0p6KiFB4ACoyYkSm9lQU1xFDNnLhYWBF1xv1+yyd3uFTPNZGdyTTMrf6Ovxv6ZV5w3gI9fDvVHpS4CC+AiJrM1fPAySRzTIUyAfjz38X663L+OSXoH2FSu1n+KmRlwD6yKoritHB11bmZ2bmbNeD7F5xwrvBj04rOveZX59oBZ3ID+j9RDCXyq/Ir3ZYPU8ewR/wh4B7Z4L3mD94xT4A14AM7iWwPuItdn4DJ1/N/k1cWv+k/AY6yrY88NaAPLyOsFGMZ+C5gDa2AMnMR+Pd7Xcd5KncOhl/4YFMlc6nZARBJTERDJnIqASOZUBEQypyIgkjkVAZHMqQiIZE5FQCRzO2cmPRFXQAvGAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Data = data[int(yt)-200:int(yt)+200,int(xt)-200:int(xt)+200]-phot.bg\n",
"\n",
"zscale = ZScaleInterval()\n",
"(z1, z2) = zscale.get_limits(Data)\n",
"normer = interval.ManualInterval(z1,z2)\n",
"\n",
"pyl.imshow(normer(Data))\n",
"pyl.show()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now instantiate the MCMCfitter class, and then perform the fit. Verbose=False will not put anything to terminal. Setting to true will dump the result of each step. Only good idea if you insist on seeing what's happening. Do you trust black boxes?\n",
"\n",
"Set useLinePSF to True if you are fitting a trailed source, False if a point source. \n",
"\n",
"Set useErrorMap to True if you care to use an estimate of the poisson noise in each pixel during your fit. This produces honest confidence ranges.\n",
"\n",
"I personally like nWalkers=nBurn=nStep=40. To get a reasonable fit however, that's overkill. But to get the best... your mileage will vary.\n",
"\n",
"**This will take a while on a computer. ~1 minute on a modern i5 processor, much longer if you computer is a few years old. You can reduce the number of walkers, nBurn and nStep to ~10 each if you are impatient. This will drop the run time by ~4x**"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Initializing sampler\n",
"Executing xy burn-in... this may take a while.\n",
"Executing xy production run... this will also take a while.\n",
"Best point: [ 1.99158194e+02 1.99250979e+02 -1.21151240e+08]\n",
"Executing amplitude burn-in... this may take a while.\n",
"Executing amplitude production run... this will also take a while.\n",
"Best point: [ 1.23285034e+03 -5.85968100e+06]\n",
"Executing xy-amp burn-in... this may take a while.\n",
"Executing xy-amp production run... this will also take a while.\n"
]
}
],
"source": [
"fitter = MCMCfit.MCMCfitter(goodPSF,Data)\n",
"fitter.fitWithModelPSF(200+xt-int(xt)-1,200+yt-int(yt)-1, m_in=1000.,\n",
" fitWidth=10, \n",
" nWalkers=20, nBurn=20, nStep=20, \n",
" bg=phot.bg, useLinePSF=True, verbose=False,useErrorMap=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now get the fits results, including best fit and confidence region using the input value. 0.67 for 1-sigma is shown"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Best point: [ 1.99189126e+02 1.99269755e+02 1.23285499e+03 -5.85967900e+06]\n",
"[ 1.99189126e+02 1.99269755e+02 1.23285499e+03 -5.85967900e+06]\n",
"[[199.14670495929735, 199.19197884103002], [199.22953765902565, 199.27727480832817], [1227.4222981766077, 1232.8547814123483]]\n"
]
}
],
"source": [
"(fitPars, fitRange) = fitter.fitResults(0.67)\n",
"print(fitPars)\n",
"print(fitRange)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, lets produce the model best fit image, and perform a subtraction. Plant will plant a fake source with the given input x,y,amplitude into the input data. If returnModel=True, then no source is planted, but the model image that would have been planted is returned.\n",
"\n",
"remove will do the opposite of plant given input data (it actually just calls plant). "
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQEAAAD8CAYAAAB3lxGOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAXUUlEQVR4nO3de4xc53nf8e8zZ2Z29r7kcnkRSUmUw0SVnYRWGEpu3cJ24FQWitIBHENOUAmGECWtDNhAUFRKgjZBYyApmrgQUDsXWIkcuJFUJ4GJVoorS0riAJFky5Jl3ShRF5qkdpfL5d64l9mdc57+cd5dDilSXO7scIZ8fx9gsGfec2bmfUnuj+fyznnM3RGReBVa3QERaS2FgEjkFAIikVMIiEROISASOYWASOSaFgJmdouZHTSzQ2Z2T7M+R0QaY82YJ2BmCfAa8HHgKPBd4DPu/vK6f5iINKRZewL7gEPu/qa7LwIPAvub9Fki0oBik953O3Ck7vlR4KbzbVy2Dq/Q3aSuiAjADBMn3H3o7PZmhcAFmdldwF0AFbq4yX6uVV0RicK3/RuHz9XerMOBY8DOuuc7QtsKd/8Td9/r7ntLdDSpGyJyIc0Kge8Cu81sl5mVgduAA036LBFpQFMOB9y9ZmafA74FJMD97v5SMz5LRBrTtHMC7v4I8Eiz3l9E1odmDIpETiEgEjmFgEjkFAIikVMIiEROISASOYWASOQUAiKRUwiIRE4hIBI5hYBI5BQCIpFTCIhETiEgEjmFgEjkFAIikVMIiEROISASuYZuL2ZmbwMzQArU3H2vmW0EHgKuBd4GPu3uE411U0SaZT32BD7q7nvcfW94fg/wuLvvBh4Pz0WkTTXjcGA/8EBYfgD4ZBM+Q0TWSaMh4MD/M7NnQ0UhgC3uPhyWR4AtDX6GiDRRo7cc/7C7HzOzzcBjZvZq/Up3dzM7Z9njs8uQiUhrNLQn4O7Hws/jwN+QVyMeNbNtAOHn8fO8VmXIRNrAmkPAzLrNrHd5Gfh54EXycmN3hM3uAL7ZaCdFpHkaORzYAvyNmS2/z/9y9781s+8CD5vZncBh4NONd1NEmmXNIeDubwI/fY72cUB1xkUuE5oxKBI5hYBI5BQCIpFTCIhETiEgEjmFgEjkFAIikVMIiEROISASOYWASOQUAiKRUwiIRE4hIBI5hYBI5BQCIpFTCIhETiEgEjmFgEjkFAIikbtgCJjZ/WZ23MxerGvbaGaPmdnr4eeG0G5mdp+ZHTKzF8zsxmZ2XkQat5o9gT8Hbjmr7Xz1Bj8B7A6Pu4CvrE83RaRZLhgC7v4PwMmzms9Xb3A/8DXPPQUMLBciEZH2tNZzAuerN7gdOFK33dHQ9i5mdpeZfc/MvrdEdY3dEJFGNXxi0N2dvDDpxb5OZchE2sBaQ+B89QaPATvrttsR2kSkTa01BM5Xb/AAcHu4SnAzMFV32CAibeiCZcjM7C+BjwCbzOwo8F+A3+Pc9QYfAW4FDgFzwGeb0GcRWUcXDAF3/8x5Vr2r3mA4P3B3o50SkUtHMwZFIqcQEImcQkAkcgoBkcgpBEQipxAQiZxCQCRyCgGRyCkERCKnEBCJnEJAJHIKAZHIKQREIqcQEImcQkAkcgoBkcgpBEQipxAQidxay5D9tpkdM7Pnw+PWunX3hjJkB83sXzer4yKyPtZahgzgS+6+JzweATCzG4DbgPeH13zZzJL16qyIrL+1liE7n/3Ag+5edfe3yO86vK+B/olIkzVyTuBzofLw/ctViVEZMpHLzlpD4CvA+4A9wDDwBxf7BipDJtIe1hQC7j7q7qm7Z8CfcnqXX2XIRC4zawqBs8qN/wKwfOXgAHCbmXWY2S5gN/BMY10UkWZaaxmyj5jZHvJqxG8Dvwrg7i+Z2cPAy0ANuNvd0+Z0XUTWg+WVw1qrzzb6TfauqmYiso6+7d941t33nt2uGYMikVMIiEROISASOYWASOQUAjEqJFjHuydoWamMdXRQ6O3FSmWSLZspdHXl64rFM15jxSJJX1/eXirnP4vFlfcHKFQqZ7xm+b2kvSgEYpSlkKanf2nNAPClRbxaxRcXwTNIUwobBijuyGd+W7mcB0h4XXpqFuvsJNm+Fa/VwAp5AGT5VeFsYQGvnp4Sns3NXcJBympdcJ6AXJm8VssXCglJfx/pxMTpdeEXNz0xnm/S1UVhcCNWKmHlEj47B0mCzy9gSYHa2z+i0NtLNjOTv4EZVi6fEQDSvrQnELssPSMAzlBISDZsyP8Hr1bJpqbxbZspDPSTzS9gBcM6O/O3WQ6AQgLuCoDLiEJAzi8ERKG3l3RyCl9cJHv5dTzNSK5/H8mOq6iNjgGQbNiQH1ZkmiB6uVEIRGjlXMAqZTMzFHddk//vnqWkY2Okr75B1tdFcXv+NZJ0YiI/Z3D2Z9WfGOzubqzj0hQKgQh5rUbyY7su6jW1tw5T3LqFwp4bKFQqFDorZC+8ii8uUvjA9WC2cghQfxXAq9X8SsPQENns7LqOQ9aHTgzGanwSKxYp7Lqa9PU3KXR1rZy9L1QqWE83fmoW6+/DzKiNjOJLS9iREZb2Xk9xeoHk7XdIx8bh+Fh+BaGY4JPTpJOTFCoVsoUFIL/qkI6N5XsFmeNLi60cuZxFIRCpbG4uv0IwNk6y+zoA7EfHSLZuJjs5mQfAzquw+SrUarDvJ2FqHtwpvzOJl4os/dR1lA7mt4vIxk/ii4skmwZJNg+RHh8j6euDcmnlKoNXqytzFHTisH0oBCJUqFSwzk7cjHRyimTLEDY1Q7JhgNrhIxS3bsl370tFvFyi1l+hurGDpevyY/qeH82TdhYp1DKWfmI7yUKN5MQ0Pr9AOj5Boa+H4tU78KlpSBIK3d1YTzfp2Hh+GKH5Am1FIRChbGGBpNKB9XRTSBI4Pk5WrVLYMkQy0I/XalipRNZZIisXOXlDF3PbjLTikMHYni4qJ4yu407neI3S2Cmyni4KC1UK12yHiSl8+hTW30ft8BGSLZtXPtvKZaxaPT1PQVpOJwYjlc0vQJJP7/X5eaxcIhsexXp7sVIJyiU8KVDrLZF2GLX3n2Lbzw5T27WAXTvL3J55qv3G3KYitcFurLoIxSK2VIPBDaQTE/j0KYrbtpJNTmGFAsXNm/LzBZo+3Fa0JxApr1ZJR49jpTKFzgokCdbbC0tL+IY+5q/uZ2GwyKkdBd6//1Ue3PXEGa9PPePX/9k+Djz1MxSrnXR2Fqm8fAyfncMqHfkko1Oz+MQExWt2Qprhs3MUd11D9s5Ii0Yt56IQiJAVi2Guv+Vn7pcWKW7dEnbRC2TdHSz2Fxm9ZZG/+8h9XF3sedd7JFbgf2z7Hr906z/xSwN3Mfi3FdLyTjrGF7DnDuJLi/nVh64uaoeP5JcJN23EJ6byGYcjC5d+4HJOqylDttPMnjSzl83sJTP7fGjfaGaPmdnr4eeG0G5mdl8oRfaCmd3Y7EHIxak/Hi/09ua/qCOj+Nw8PjhAWilS7TW+/M+/fs4AqLevo8Shj/4Zk/9mlupAQtpVItt3A8WdO/BaDU/zGYS+tEhteATSFJ+bb+r45OKs5pxADfh1d78BuBm4O5Qbuwd43N13A4+H5wCfIL/L8G7gLvIaBdJGlmfxWbFEoaebbH6eZGiIwtAgLC6x1Fdi7irjhvL4qt/z4L/8GiMfTRndW8GLBgUjGRpamUW4fB4gnZ7WScE2s5oyZMPu/v2wPAO8Ql5VaD/wQNjsAeCTYXk/8DXPPQUMnHWLcmkxX1yk0NWF15bIpmcobt2CJQXSd0ahmFCcTynOwX8dvrh6snfe/B3mrsqY2dHB4s7B/GTjzAwUErL5eQrd3fm3DXWJsK1c1NUBM7sW+CDwNLDF3YfDqhFgS1heVSkylSFrHUsSsoUqSX9fPpXXHe/rodDdiU3PUqimdI1kPD+2nePp6qf6frr/Wco7Z6mcTKn1lPC+bqxUzu9NAOCenyfQdwjayqpDwMx6gL8CvuDu0/XrPL9v+UXdu1xlyFrHazXwDF9cAvL7BqSvvYFVKpCmlA6PUaw6tUc3cdOjX1j1+/54qZvaUsLs1iJdr41hkzMkWzeTDG7MA2duLv+iUaJC1e1kVSFgZiXyAPi6u/91aB5d3s0PP4+HdpUia3PJQD/JwADZ3ByFSmXlGD0dn8hPEHZ30vedt+g8kdExXGLX//2VVb3vbx3/SXy4wsChBUhTasMj1I4cxecXyGbnV+5glE5PX+Cd5FJazdUBA74KvOLuf1i36gBwR1i+A/hmXfvt4SrBzcBU3WGDtIF0cop0YoJkaCifH9DRgZXK+NIihUol7BV00H9wmmsePUXPwRIfeOqX+erU1vd834e+9WE2PQfFiXn8VH4YUejuJpudzb80ZIWVIJD2sZp5Av8C+HfAD83s+dD2G8DvAQ+b2Z3AYeDTYd0jwK3AIWAO+Oy69ljWTTo2lh+jD/STTc1Q6OrCyqX8dmMjx0mSBE+62fZPc5yc6ON3R/8tX94xyed3P8HtfSfOeK+f+M7tbP+HGslCho2dhKV87yKbnSXp68NrtfyEoEKg7agMmaxIdl+HHxvBrtqCVZcgKeBTM9Suv5pad5HF/iJTuxKyEvmjw6l1OUPPQlJ1KuM1ShML2Ctv5F8YOjG+sicA+d2HznsrM2k6lSGTC0pffxPr7cm/AFQp4x1l2LqJ0ugUluW/6IMvLVE6BV0jTvdR2PwMFJag/4VxyifCIcDQJrLJKQq9vXi1mn8rkfzuQ8mmwVYOUc5B04ZjV3eLcCC/l8DSIkkhwYoJdFbwYkLlrRPMv28ThdTZ9vczeClhYUsX5aklSsOTsLgEo6dgcQnv7s7rEJRL+Pw8tZHR/G5EA/35ct0NTKT1tCcQuyzNr+WHegKW5P8k0rGx/Caic/NYLcXLJSo/PEL56CRpTwe2lNL93BGSqQWyngrUaqSTU2Tz81Ct5vcrmM+/H1C8ZieUStRGRkkGN2Jdna0csZxFewKycrsvJ6FQLkO4LRhZSm1kFCC/J2G1CsV+ku8fpDDQDx1lshdfzWcfdlbyOw4Xi6RjY/l3EjZvIhufoHY4nztWvO5aam++fdE3OpXm0t+GAGFuf5KQTk+TbBpcuSXYsvTQWwAkgPV0Q6lE+s4oydAQ6fhJmJvLTwKGW5STptTe/hHFbVspDPTjU9MrAVAY3Eg6evwcvZBWUAgIcLpEWNLXB7XaeY/b08mp/KvIJyfzmX9LixQqHZBlK1cBVgqRANn0DLhT6O+j2N9H7chRBUCb0TkBOUM2N4cv1fDFxXMWLYUw7ThL83sRTE3jS7WVSkTver/5BbK5OWrDI/jC6SsF0j4UAhFaPiYvVCr5ScE6XqvlE3y2bcXK5QvfCszzW4hnc3MUd+6geO3VZ37OWRWJsumZ84aLtIZCIEJeq5EMbiRbyAuKJoMb85N6dWpHjpLNzmHlEoVKZaW90Nt77vesVvNd/WMjJIMbVz6nfvt0bAyyjEKPvkXYThQCkUrHTwL5L2p6ciK/CcimwTO/5pulpJNTwOkSYsvH++cMg0ICnpGOn8znBdRVKl4OmWxhYeWzpT3oxGDkTn+D8Py/mMuVhM5oqzv5d7oxXbl1QLawcPpSI2i6cBvTnoBI5BQCIpFTCIhETiEgEjmFgEjkFAIikVMIiESukTJkv21mx8zs+fC4te4194YyZAfN7OIqWIjIJbWayULLZci+b2a9wLNm9lhY9yV3/+/1G4cSZbcB7weuAr5tZj/u7mdOIheRttBIGbLz2Q886O5Vd3+L/K7D+9ajsyKy/hopQwbwuVB5+P7lqsSssgyZiLSHRsqQfQV4H7AHGAb+4GI+WLUIRdrDmsuQufuou6fungF/yuld/lWVIVMtQpH2sOYyZGeVG/8F4MWwfAC4zcw6zGwXsBt4Zv26LCLrqZEyZJ8xsz3k1YjfBn4VwN1fMrOHgZfJryzcrSsDIu3rgiHg7v8InKuA3CPv8ZovAl9soF8icoloxqBI5BQCIpFTCIhETiEgEjmFgEjkFAIikVMIiEROISASOYWASOQUAiKRUwiIRE4hIBI5hYBI5BQCIpFTCIhETiEgEjmFgEjkFAIikVvNjUYrZvaMmf0glCH7ndC+y8yeDuXGHjKzcmjvCM8PhfXXNncIItKI1ewJVIGPuftPk9cYuMXMbgZ+n7wM2Y8BE8CdYfs7gYnQ/qWwnYi0qdWUIXN3PxWelsLDgY8B3wjtDwCfDMv7w3PC+p8Lty0XkTa02uIjSbjd+HHgMeANYNLda2GT+lJjK2XIwvopYHA9Oy0i62dVIRAqDe0hrya0D7i+0Q9WGTKR9nBRVwfcfRJ4EvgQMGBmy3UL6kuNrZQhC+v7gfFzvJfKkIm0gdVcHRgys4Gw3Al8nLw8+ZPAp8JmdwDfDMsHwnPC+ifc3dez0yKyflZThmwb8ICZJeSh8bC7/x8zexl40Mx+F3iOvF4h4edfmNkh4CRwWxP6LSLrZDVlyF4APniO9jc5XYm4vn0B+MV16Z2INJ1mDIpETiEgEjmFgEjkFAIikVMIiEROISASOYWASOQUAiKRUwiIRE4hIBI5hYBI5BQCIpFTCIhETiEgEjmFgEjkFAIikVMIiEROISASuUbKkP25mb1lZs+Hx57QbmZ2XyhD9oKZ3djsQYjI2q3mRqPLZchOmVkJ+EczezSs+4/u/o2ztv8EsDs8bgK+En6KSBtqpAzZ+ewHvhZe9xR5fYJtjXdVRJphTWXI3P3psOqLYZf/S2a2XEFkpQxZUF+iTETazJrKkJnZB4B7ycuR/SywEfhPF/PBKkMm0h7WWobsFncfDrv8VeDPOF2DYKUMWVBfoqz+vVSGTKQNrLUM2avLx/mh7PgngRfDSw4At4erBDcDU+4+3JTei0jDGilD9oSZDQEGPA/8Wtj+EeBW4BAwB3x2/bstIuulkTJkHzvP9g7c3XjXRORS0IxBkcgpBEQipxAQiZxCQCRyCgGRyCkERCKnEBCJnEJAJHIKAZHIKQREIqcQEImcQkAkcgoBkcgpBEQipxAQiZxCQCRyCgGRyCkERCKnEBCJnEJAJHIKAZHIKQREImf5HcJb3AmzGeBgq/vRJJuAE63uRBNcqeOCK3ds17j70NmNqyk+cikcdPe9re5EM5jZ967EsV2p44Ire2znosMBkcgpBEQi1y4h8Cet7kATXalju1LHBVf22N6lLU4MikjrtMuegIi0SMtDwMxuMbODZnbIzO5pdX8ulpndb2bHzezFuraNZvaYmb0efm4I7WZm94WxvmBmN7au5+/NzHaa2ZNm9rKZvWRmnw/tl/XYzKxiZs+Y2Q/CuH4ntO8ys6dD/x8ys3Jo7wjPD4X117ay/03h7i17AAnwBnAdUAZ+ANzQyj6tYQz/CrgReLGu7b8B94Tle4DfD8u3Ao8CBtwMPN3q/r/HuLYBN4blXuA14IbLfWyhfz1huQQ8Hfr7MHBbaP8j4N+H5f8A/FFYvg14qNVjWPc/kxb/hXwI+Fbd83uBe1v9h7KGcVx7VggcBLaF5W3k8yAA/hj4zLm2a/cH8E3g41fS2IAu4PvATeSTg4qhfeXfJfAt4ENhuRi2s1b3fT0frT4c2A4cqXt+NLRd7ra4+3BYHgG2hOXLcrxhF/iD5P9rXvZjM7PEzJ4HjgOPke+NTrp7LWxS3/eVcYX1U8Dgpe1xc7U6BK54nv8XctlegjGzHuCvgC+4+3T9ust1bO6euvseYAewD7i+xV1qqVaHwDFgZ93zHaHtcjdqZtsAws/jof2yGq+ZlcgD4Ovu/teh+YoYG4C7TwJPku/+D5jZ8jT6+r6vjCus7wfGL3FXm6rVIfBdYHc4M1smP/FyoMV9Wg8HgDvC8h3kx9PL7beHM+k3A1N1u9ZtxcwM+Crwirv/Yd2qy3psZjZkZgNhuZP8PMcr5GHwqbDZ2eNaHu+ngCfCHtCVo9UnJcjPKr9Gflz2m63uzxr6/5fAMLBEfix5J/kx4+PA68C3gY1hWwP+ZxjrD4G9re7/e4zrw+S7+i8Az4fHrZf72ICfAp4L43oR+M+h/TrgGeAQ8L+BjtBeCc8PhfXXtXoM6/3QjEGRyLX6cEBEWkwhIBI5hYBI5BQCIpFTCIhETiEgEjmFgEjkFAIikfv/29XpQtQqES0AAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"modelImage = goodPSF.plant(fitPars[0],fitPars[1],fitPars[2],Data,addNoise=False,useLinePSF=True,returnModel=True)\n",
"pyl.imshow(normer(modelImage))\n",
"pyl.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now show the image and the image with model removed for comparison. "
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQEAAAD8CAYAAAB3lxGOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy8d7Bl2XXe99v7pHtufvfdl0O/zml6Yk+OHGSCEAiSpkhaTLJMU5ItmabKJcpll81ScNllV7Fss1QULcEMJgkzAQIIYIYABoPJqWd6ejrnl8PN+YS9/cd6aMgSRpYswZwq9Pqn+7137jnnnrP3Wt/61reWstZy227bbfv+Nf0XfQO37bbdtr9Yu+0Ebttt+z63207gtt2273O77QRu2237PrfbTuC23bbvc7vtBG7bbfs+t++ZE1BKfVwpdUEpdVkp9Xe/V9e5bbfttv27mfpe6ASUUg5wEfgIsAK8Dvyktfbsv/eL3bbbdtv+nex7hQQeAC5ba69aayPg94FPf4+uddtu2237dzD3e3TeOWD5X/h5BXjw/Q52sjkb5CoAGA+UBQy4I0tUArensEqOTbOgI3BGkITg9SxJKH/UESR5cPpgHVAGjCv/99sWqyEuKvymxbgKBSQBWBfQlqBmSTIa4wEKsBBsDRlNZuSerFzXePJ/FOhk92fznc+YAJyh/N648nuvC0kG/LbB+HIN44DfMVitsI4iDUDHYBVYDcaX81hXzm98uU+nr7COnNc6oNLdzzhyfWXkdwDWA+tYnIE8o2+fV0e7x+1+L+vI/Tjx7nPevXaSBTyL01OkHvgdS5JV3zm/I+fU8e597P7sDixJRuEk8oydETij73x3kM8YF9y+IclqjCvP0ypwh5bUV6RZix4q0HKssnJ+ZwBpRq6pjDwjq3afnyPfT6eyRlSYQtcBwOtborzCBhYseC05d1yyeA2I84pMLSUqOrJ+fDmvM5JrOSNDVNR4PUuakedgtTxDnUIafOd44+2u5933oWNIcnLvzsgSF9St92u1HJOG8tydkSD0JJD7swpsYJnMdWgnGUZdX/aEAr8l9/Ltdfnte/32e05CuYfh5sqOtXbiX95/3ysn8P9qSqlfAH4BwMuPMfmrf5vSew69RYvXVgQNS3cR/JYiu2HpzSp0BLkNQ+opGsdg4i1Lpp7QnfVIQoXx5Ytndiy5zYQ4qxlUNbkNQ3fGwbryUhb+eJWz//UEe/5Q0Zl3SQNF+/4huXczBE1LVFRg5Vo7dyrGzkPQNvSmNN1FmHrNMBzTeH3LoCL/dvYo/CYMJy35mxAVFflVQ2u/pvpuQuOQe2vjdA4mlN91ad4dUzjn4XUtw6qici5l8wFNbkVRWElYfVIT1PStzQ5QvGbZejhl+nnNcFyThNDdnzD5okPjGMw9FxO+cZXrv3iEpGAJako+r2AwYyhdUKS+YvrVLt3FLFFeFk+SUQyrFmUU1XdTNk9qMjWFM2LXEcsCxkJu1ZJpGnrTmkzDMhjXRCUYjVkyOwqdQOFmSm/GobNk8JvyHaKyoXxO0d4H2XVFnJdNPfXaiMbhgOrpAStPh+RvWvrTisJNw+ZjBpUosisOOoagaYnziuE4jKYSSu+5FG8mJKGmP6mJCpCp21sbr363Yeab0Dzo0N8XUT7lExV3HdUQKudj1h51cSLFxNsJSUaz8ZglXHNwe/LMrSPPwLqWoK7Ibhr5zmNQeS8lzmmcyNLaq1EGBvMp889a6oddlIHquzH1Ix7hjsHrW5r7xcFMvjVkVPawGmo/0Sf7bJ7WYUu4qfGbFh3DqKIoXU1Z+ZilcMmlN2cYTxVBXRE0Lc4QBpPy/+y2Yetezdh5i1WK7oJiMJey5wspnXmPU7/5yze+6178HnECDwP/rbX2Y7s//wqAtfYffbfjS9lZu/8//DtUzvVZfzSHSiHcls3YPJGQWXdx+5CpWdIAWoct1TcVlXcaNE6U8QaW9qIjUdiH7KZl5x6LjhXVU5bmYcl6wk2LTkAlsvhGJYXfsVgHerOK4ayE4YlXHImEEVTOdBhMZ+lNObAb8QZVhXURRzUPE28bgkbC5v0BQdPiDqA3o4hKlnBLMZi0FG5AbiOlcdClfDWlvegQF2ShDicMQU0z/coIgNodAbkNQ6aesPaojzuA8uWUwbgmDQQV+W1L+wDMvCQbIA417b2KoCHPNGhaenMSaYKmJc6JY/HbCWngsPGQx3AxovyWj3EhKsP0yxFJ1mHtSUWwo3EiyC8b3KGlfsQh3LI0j0C4JUikdCWledAhv2xJM5BpGFr7HKyC0tWUzoKD8WUTtBddrFa0jqVU3tZk6oaNH4nwLoSkWUv+BsQFxfi7MTq1XP+UQ27ZYfzdmHC9R/3OEjt3W1SqUBbmvpGw9rhL0FBEJ7v4r+fJ1C3uwNLeK2hj8s2EJFREBU1+LSHJavxmQrDSZOvxSZSVyJ8G0D0U49ZcSlcgKihy6wa/YxiOOejEMqhq0gz0ZwzFy5r8urzDmedbXPrZAn5DM6oYbD5h8jmP7JZAqo0HfUpXDFFxF+35kF8zjEqK4bi8y8KyJfUF1W7dD06kqJyxDCuaOPcdpJCEFnegUAn4HWjdGbHwRU3qKdY+ZJl6QbP5iKF4wUUngiZ684rq6ZS1xxTXf+nvvGmtPfkv77/vFSfwOnBQKbVXKeUDPwF84f0OHo479OYVW/flyG5YStdTCisjnJGleN5l7IIh3LaMyoqoJAu0eQSu/WiF7GZMHCqUkY0x/XKf3oyieEljHUv9uDzoqGTwO5awZhi7OKA3o8huGaKCwmpIM5bp5xyK51y2n4jJbaZsPxGz+WCR3rRDb0HRWZJFM5y0lK6kGE+x8PURvRmH/rSH25dN3Z1TxAVL9bSlenrE/NcjhuOKzZMOk2+N8LqpRIWOwLTKacX813ts3xtw7acUYxdj2ksat5egj7cJ6pb+hKZ52KJjiRBBx5C/AVt3e2yd1Hh9Q+mKAWDsYkTjGORXDJ39Ke29iuadMeuPOqw9kmH5Qy5eB+a+JPBCJ5D6lt6Mx+b9GrejcCKY/0qdzqIm3BxSvmJIM4r8TXFq068OaS855NYs42/s0J9WOENL+VKK8SANFJm6ZVg1pL5mMKEIawY9VNTuTdm6XxO+HbLwtT6FaxLNMtuWmz+oGZVdwjUHDIzGHJJCQH9a4Q4UQUORXVX0p1xKl2Di1IjCMznyq4bOHoXxBEE4Q9h4yGHrPo1VUD/isfLJlJ0TAct/aYqwYchtJpSuJowqlsI5j6SU0p2XtVQ/ptg54bL1aErjiCYNIbduOPybdQprCa29Dl7fUru7iHUlkI6dVYTXfbrzivaSx84Jn9G4we8Z4oJi8o0u4bYl9RT9KUVUtERlWdfF6xHbJ2HiLZh9PqG1X5NkJaDFBXsrzZl+JUKn0DoRU33Ro3HIpT/hUD7tEmcVe75oyTQsztAStAyTbyQs/PJFxs6q992s3xMnYK1NgP8U+CpwDvictfa99zveb1kyNW7luc7IUDueofZIjPEhyimyWwm9RUNu1RJuWSZOGeKCoT/tMRzXBA3LqKJYfSpLfzGldC3GZCzlC5AGlrnnDLm1mO27HG5+NEtuXTytTmEwocgtK2p3yQIIr/msfERReM8HC/m1hIVn++hIETQN4aaifsxh6uUWylhGJdi+R1BF0DKMXUoJGorGEU1rv8/OnQFeF7yuwhkmRAWH7rwmDaB6OqZ8acDKh3L0FlNyF3y27/IINy0bD2UJny1gfIHwysBwXNKe7oxDnFckOUtcSmntdehPabLbhps/naISaO/RuB2Nd2eT8ddcgppEcBMaCsuGjYcVzeOJ5IwWMs2U/DLMvJIQFSyDuQJuH3rzITt3KdoHDKMKeD3F9p0ZUl8c3qWfrTKcSqkfcWntdXBGsHOPIC1npNi+26F82dBe0lRPQbjqUroA4+/FLH8kS24jJb9smXhpG7ej6U1rcuuWwbR85upnAmaf7xIvjIjzlkzd0llU9GcU/WmP9kFZN+E2hNsJSUYRF+1uaijIwetYxl/xBK7PGIZljflbO7QXXSpnLHEBMpsuk28lTJ4a3EqF8ldcypcMU68PGVY0/aUSnZ9vk+QEMfSnFcGWw9QbMaVrMX4T3IGsqf68YfGZlNpRl1HZsvlAnrCWsPVkTKYG+WVFpqZw+5bNBwJyNzWjomZUllRER4JQSxfAb8LsCylrj3tEJcvcVzV+1+B2d3mwyNJ4dERrn0f9DglWmw9otk66rP3DA/Tm/n92AgDW2j+z1h6y1u631v6Df92xSVbhdS1eT3Jrt5+SqRn8NY+xCwlh3dCdcVn4airkkAQ8Dv/qORpHFK2jCcWbQ+Z/5zLRmCF3zaG118NraGp3WYrXoLnfZVRxKV80hJtQv8NSWEkIGoYkZ/G7luyqoru4G2m3HCpnYzqP9Vl/2CUNHPI3BRbm1iTSWM9h5amQ2ReHzL6Y0l1Q9CckLUkDyC1bvK4gm+6iIS5abnwyizLy98V/voPXjtl8IAtA9Q1NdtMy8XZM4xhkNw3GUfgtS+ceSRVGFUNUhM5eQ5wXziR/zcW6QtptPGYZ//MMU2+mJAWLc7DLf3Xsyyz93CWyT2wLkRgpNn94iL/UJbPukoSQvwn1wy759ZTGQY/suuLGj1laxxPMLpdSuqgYTiXMf2OATmDqjYjhbIrXU4y/JdEy3LHoCMJ1yZlVosivWEoXOgKnpwSqj8YUnQUXLKz8SMKwqmifGKd62hLnhcwqXlGMXUwZP63oLoTs/yeWPQ+uCN+yYhmNG8KdlMy2Is4qdGTZvscjzivyNyHcUIzGLYNJxagijrR1PCHNp+gE+p+bJreVsn1SuJbCdUvjkEtnIRDSsGdxRhDnFPUjAbn1lOZ+j+jVCuVLhtGYpfpugrLQ2uOx+oRHkpWUtHomoXhR0zjo4Xcgt6ZwRpaVDzkUzvk4Q0vpWszYRVk3xWsGr2dpHTZsPGGY//MmMy910QnUTqZEJWgccjE+7P2TLqsfshhPkeTB7ULtoZjSaxla9w8ZOyv8TdBQuD248Rl7i4/6bvaBUAzqFPJrMbV7U+aeG6AjQ/Fan+JVSAONdaB5RKBh5VyPOKfoTTlc+rvHwILbcdg5EXLpl/aTv6HJrxnyGynZdUX+hkYl8mKSQKJp97E+hWua7XtcNp9OCDcU7sDQOppQviD3ZDxL/ZiH3cigjOLqT2pK10dYBzY+kjDxTszWyTxJaNGxoTPvomPoz1m279WEW5bRmKJ0qcvWvULw6Uig7OpTitlvjVj5eJW46BFuW2GUI0sSQpzXjJ3bZdtdaByD8qs+bk8z+4IlGpO8VFkYu5SSXzbyki0sfUHe9sZDDuOnLT9+6C0+nF3h1I0FWt0QE1icSOFcDRl0AnKrlr1/uIPVEJUsO3e4lK4lJHkoveMz/4xiUNWULkH5SszUS5qbH84QNA25X1nFOpbFL7bozSgW/6zFsKJuVWOcAeTWxBFuPFIizgmRdfIjZ/FbwvkEdah8KyC7bmktOXTnBNV190BvHqwW4jLcidm6L2TjywuMyrvVDBcahzwq52IGkwrjKiZOxbRPRKS+YjghSLD6bow7gGEVdD4ms+7RnVMMq4qtk/JuejOK2l1yr905TW/e0t4rFYjKewNSX7H5kNpFbwl+KyUNLdt3C1LoLlrmnoswrvAhm/c5zHxtC79tGVZAx8IVuV3Zcr05WYuNQw6F65bOoqY/rbDFmPJpl+37Sqw9nifcsix8Fak8KZh7LqG7lKPytkN3VpNkoHQjxtvySANw1wMA8suWqGgxD7WY/5LDaNy87/77nhCD/7aWG1+w9zzxtxiMOxgX2gcAA2PnIbeR0N7jSqkjJ5G6dAF6C4q9v7fFzc9MomOovjNi7fGA8kVDklG0DsP4O5bNJ1KyNzx0DN0DMWNvu6S+Ii5C0ABnKGmE1QK/0oyQko3jFpWAnu8TvpJn8o0+Kx/OEm5arFYMqxAXDU5foVMlUeQYLH1hQHcxw/Z9Eg3dgZA6XteS20ho7fdwhlKujMqKJAvFq1YcQEbhd4RkVNYyHPdoHnConE8wriLKa3RsaR3U+M3dMp/dLTUNoD9jGT9j6c5ruocjspd9BtOGvcfX2GwXCL5apH5/zOwzLtHP1NnZLOKve/gtxejeHrkXcozGYPGrHdYeL1A5F7P2syMm/iikO7dbYutYwrpBGUu/6hC0DUlG4w6NVDZWFe3DCaWzLtYRpr5+TJj18gWF/Us1Jn41YPOBAlERCjcNaaCIigqzS7YOphTTr4wYVdzdkpelN+2QhIqpVzssf6TAYC4hu+IKItPQ3ZdQfs8lDb5TGvY7lsp7A1afzJLdsHT2QXC8SfTOGPnlXZLYQJRXtA8anIFi7vlEHHoiqVcaSGWks89QOSPp4M5dmjS0jJ2R+86vpTSOOEy+GbPytEPxisLrSpk1ySlGFciuSSm7fSKicNaneiZi+WlZl0nBMv62ovpajZVPVKVcaGQd/otl8Kig6O4xVE4LMV2/P2b8FY8kK+sot2aJc0KwFq+ltPc6hE9uk/Mjbr43w/W//d2JwQ+EE8jMLthDP/5fMHFqwLVPBxSuatDQWTKMn1Z4fYNOLKtPaYJtTZq1OEMFBioXUupHHVQqC2pUFBbX6woMdEYQ5+UBGVeR25RIaVyFE1niUDEqa3IbKe0lh2jXOfTmDeGGJlMTJzGcsMw+nxDnHepHNJk6dPZYwm1F92BMpjxk6p9l2LrPo3zJ4A4Ng4pDpmFY/UzMzD/3aO0XIk3Hlu6CIJTS9ZQop4kKAheVlcrC3v9zlc2nZ+kufsfBjJ+GsfNdtk7m8brs8hGa1rEUt63J7Mji6B6OIFG4LZfcsmI0Ls85yVom79xk/coEwbZD+aKUQL2eIrtmSQOFTi3F6zHDcZex17fYfmyK7qIiDS1xOaV01qVydkRmucXqxycxgUD3yTcTtu9xmXwrZlRy2HzEsv/3RwymAuKcBgtRSZHdTCVH7xqwljjvsP64QsUKtKX6luSzjTsNe76Q4g5TLv+Mw54/Vuyc8OjPSCXFeBa/pYjKluIVmHhhk5s/Oo3fsgwrUhatnE+pHXdwB6KBGE4IgjKelPxGEylzXxcOajDuMna2zebDJdr7DFOvQXdW44ygsJJQP+reKpMOpgyTr4H+2S2GfzyF8ZW803mY/0bE1r0B2S2LTiyjkiIJFf05g9fWBA0o3pDANvuVTc7/vTLV53wpSyP6Cq8nRLAT7aYjeUmX82uJlDOHism3YoyvWH/YISmlZG9KqjCcSVDZBL0ZYDKGH3r4Le7KLfMflTZwZi5/VyfwF6YT+H/YrhiisyegdEkRlWD83ZjRmEdnEfyWg3Vg3x8NGFU8+hMOhZWYNKMYVBycgdR8hxWBkmkMWJh5SdCB8cUBpBkYjmlKVyLqxyTvG40JO95xHZIQyhcNW49Yjv6jFbp3z9He4zJ2IUGds6w94VK8IpUErLolRslf8BhVhfzxWzAcUzROGsbecOjOOfjXHNY+lODvWNyBIdyJaR3IULma0pl3JN++mjIsa5Kswh3C1Z+Zw+tCtHdIuhFQuK7YucfQXSgw+WbE5gM+g7mUR+88z4XfPEpuI2FUdqR2f9PHbyIR6pBDGoj2onwDNp1Jlr4cs323RPY9Xxnh1fu0jpWJlKQgm/f7OPc16c5OU7qW0spo5r8e05nz6M3CytM+zmgSZwjTrw7pLAZEBdnoGw94KAuFy9DeF6JSy6Cq6N83YOKLATt3amZeSvDaETc+kSW3BuNvw/YTMQtzNXoXpsnUDcXzDl53hPrVHbJ/vkh32tKfMVTeleg8mFRkt0QkU1gesf6xacItS/1OS/mspAvbd2sm30rZucMht2qJi4rOPkNmR5PkLdMvKpIQmgc9pl/qo0YpztDi9hVeNyUJNeUrCamvmH2+R2t/ltbxlCO/3ubGpyuUPzuJGVf0ZyyFq7D450NWngxx+xDWhAB2RoI2daJx+4I+UDCYtGw9PsniHyTU7lC4AxiVhSvxOkL+dg4ZnI4m3ILuvMLrO7h9xXDSEK73GE1mmXlFSOJRGYI6xIdiPn7oLI89eJGfKDT+TbffX7w5A8l9e7NahCwvD2gvuQQ1mDwV0z6SUr6ccP1TGVJfcsTVp1xUIunC2OUEq+QhhnVhh4fjio2HAlAw8Zaw2s4Qcuspa48FuD1L0DQEDSml5dclr05CRfG8Q/fuOVZ/QNM+aDC+ojvrEuwovJ4l3FT0FiwTbxqMa0UgdAM2njAMJiWijr8sUK91OCUuGu47fpU0tPQnHbqzPrkVy6goQqb+tKV2h8OoosjUDW7fMpxOpFrS9hiVRbxUviClx/6kx/zXehQuuVz4J0cJ2gbjKVp7NZ0DCUEdxs9FJBlN4aZEyqBpKV8esvjlmNY+n/FzMZlawtpjGVRiqN2hyK8ljMaEpHK+XoZHm7T2OyQzEStPeQwnFPPf6LHny0OKVy3DqqU756OMoEmvK05k+uWIzsF0V2shLH3+lZD2Xs34e5at+zzWH83htxStQ5bmIdj/W4b+/zUtm/deTVQG6ypufmuRaGxXE/GibP7mHQn7P7sKFgZ7YuKCy6gsETNc17hDyG4brAPDspZN2TAUrsPYe7viqGIq4qK8KEiTvEf3YInGccvSF3sMKw7R8T5RQdObcdh8IEd7r0L3NSsfraAj6E9q/LYFIynsqOyRX7YELUvtqIeOpVqkrKRqfldEb8ZVVN4TzYWODePvxYyfGRLUhYtKM0Icz3xT3dKZzH9zQHtJk1+1+E3NxmNl+pMuGw+Ko+nvSXjwp0/x6SPv8L/Ovfpv7ADgA+IEkoJlNCay3XDH0Nqfwe9YSjdiUl9TPO/Qn3AwnqU/5dCfViTTEeuPOvQnXfpVB79jMYFl8z5PpJkjyG5YgjqsPyUqN7dvqR8T8KOsbHgsxFnFqKSYejMit5Ey/XIbgPJ5hSkmbN2nqd2fMJg26FgWvzNUrH8yoXwJxs7uSpl7Gp0ovI6lP6OIc4rcsoOaHPHOywdx5vv0pyW/i/OKxlGBnPllRemyIclKfdpqYfxLV1OmXlIkWcuwKjnq5BuGrScStk7mKCwbWgdh7SloLbnCcfSFSK0d9ck0UvozQkB5Xbj+qQwbDwaoFHqTLlHRIb9iGSyWKFyH5n6P7KahfoeiemZIb7XA3Dc6lF4LMB4UrxuWP5pj4+GQ5mFgdojVivaSpnFECxRfiPG6CfPPWLI7IiZKQoG55Usp9aOawf6RMOtnYtTkiNJl2L4rQ39GVKHflv1uPBgy9WrMzF0bVM5Ydk7I38ffcLj0C7NkGin5Cx5xThFuWZIsor1ILXFWkIlxETSz5DAcVzQ+MsDrQP6qS7htaDwSSTntPo/GYYc9X06o3ZETB3YlJMmIbqN4M8WJoHhZE5Usw0nD1Gtdth8wzH8jIpmJaC+67DyYEjQN/VlDVNBsPCJlRPb2dsuTUs5tHtRMnLL0pzzSQNNeCmgdT8muKWZeFofQOCgKxNyqYvuukDSA9l7Fvt9aJcnK+o0nYvpTCq/p8AOl8/xPM2/9K/trK+2x9yt/7X333wfCCeiRIrumaH5oQPFan/odFr9r6E261I86pJndCH1F44ws4RbM/6mDM9jV2yfQOAKTbxrmvjXEGUDxRspgQhEVYPIlReVMF+sIsTX5VoKOhTPoz1jyaylWQ2vJwxmmrD5VpHHYpTej2POHivIFmP6mw9Rr0F5ycIaSQ098zcdqqLzbpj+jyF/X7Pl8C4C9v71Cb8HIYrqWQS32iPoe2U0hk5xIJKjGh6gAvRl5FZWzFr9jcfvQmXdo79Fk1xWZGpQvicgms+yRX0sZjimqpy0Tr2m6SxL5Jt6Eqdd66AS6sw65VUMSCuxNqjF6V99vPEh9WaCb93lMfW0NZcHvGirvWZY/HFB9Q7P691LKVyKyG4qtexVeB8YuJuhEMfs5j86iItwWmW4SKiZedImKHlFes/aYxviSYikDQSuleM1S/ZZPGloahzzcyyFWSeT2mxDWDUFNiLXSlRR3kLL+zjRhLaVyTq6TaRqMZ1l/VKLgcEwzmJS14HcsufWYqKgYP2OJyoo4p0WdaWDqTwKKN1Im3o6oH1dMPSPVmcVnOpQvp/SmPcpXRnQXFGPnxZkD7JxwKF4XR12+CFOvWGp35MjdcBhMehz6tSHdRRG3dRYcxs4puvOKhWdTvC4s/S+a1j5N4bJDf8aQqYmOo36HYlARMVX2pkNvwbL8dEC4Y0izlqBpyW2kjMqQXbeULxou/vVZKcPWDIf/8RC3D5U7t9nnb33X/fUzl36cT5549/3337/n/fz/ySRXsuRfzrL2RJ7sukghuwuKyvlUYPXRlCQLlbMDmidHOENL8ZrU9OsnLEtfHJDZjlh7JMPs1+p4vZRMzZJbE+Z962SB1FfoGBqHXTp7NBOnYrLriuUfS+lPSS5+7ScV3X2JMLtZy9a9Aut6MxqsJbduKF4XDXhUFDVi80iBwk2J1hf/8wDrwLWfnr8lfoqqKfcurOBt+vRn7K1aelSyZDcs1oOpNwdMnEpo7dNsPZJSfWdA+2iMdWRjjJ8dika9r/B60FpysBp27lY0D0Owo2kfMOgUtk7m6CxJbTi/FuF3LNW3uxTOiEQ4DRSZhqQQQcPiDuHKz81RfbtPuD7AiaBwXcQwo3Mlmgd9/LYltyaS1dWnNLkVS3fWYeEfvITxFEt/VEenIuLZvN9jMKGZ/0Z6ixWP84o47zCYULhDy8wLltGYNDdNvNkiziry6ymF8/VbjH/jsEN7KWD/5zpERYdBVWM1jIoar6NJ8ob8WkphJRXeowu59Yjlj/joyJIEorFIPai+m1K+JP0MxoWNB3yiqd2qS1HRW8gS/Xyd9pLi+l+TdbP5REpuxbLylEvpiqF2XNbGYFLd0qqMxi3tJc2FvxmirBCOysD4uz0yNUvtmEdnr+Hyj2dIMyLPNqWE3rwlLlrmvxbhxFKByOxIr8fC10a09muiSoo7tGw+qHD70DwmhHJuWUjk+mGH9ceKxEXoDgMeCLzvur+aw5Bnn7n3ffffB8IJpBnFYErKdOGWxetY/I5h6s2Y+hFh/sfOaOafaVI7HpK9FHD9h2vUpgkAACAASURBVBU6kV4CPVK0DoSsPhEydjGldnKM1pJH6WpEdjsl3I5pHUuZerVF47gwriDs+tTrHSaf9fDbELRTlj4HxQsufhuq71gq51J6M5rspmHzISWqw5MSuYs3EnYeTBmNicY7f9OSfydD+XLE3HMDKu9KFHE6Dq+e3Y/bUUTTMf1pWXheT6FSS+Ws4cYnMvRmHEZVw9QLms6egOI5DyeC5gGNcRTdOUWmLmgmyQmJVLoAi18eMHkqRqUCIavvDtn7hSHF5Vg+9+k2Nz9eQMcw+8KQsGbozgk8jvOKUcWy73M1Vp7OElUytPZqBlXF9MttcquK1pGUUVnRWRJuxW9qGndII8/W33gELKx+rCI6/FCi9dilmK175P79rkS0QUXEUI3DmlFJ76pDFed/MU/9LkNvyuH8rxQId4xwAlq6LC/+XI61pw3FGwnFm+ZW5+OeLxk2HlE4I0PQFAe/8VDA5BsGv2upnTRktw3tg8IN6NTSXTR0Zx32fKFO9ppH4wiUrscYB9TvVylfMox/NQPA1PMO46fbpDnhi7IbCq/lEDQs9WMOTgS5ZUWmZtEdF6sgzlsmTw1o78tSvJkQF8FvaEqXNPkbopNwtz0yO4qJtwzXf9glzkFhNSHJKfJrhmHVw3hQuOwSFRTlcwq/bfEbmu5SgtWQ2zQ4EXT3GHIP7vDrd//uv7KvXhwaDvzeL5L/H4q3unC/m30gnIBFIOq3IZvflQi88gMOE6dilIHslsF6DpWzAwZThpnnRC/v9aBwQwgjdwjdOYd4t9W1edBn5WnNjY8HBNsOcSlDZlszKsOwauhPefQWsrQOiE67P+7QPOijE2gdS0kDRWdBug8HVY0zUARvXGL2ecvYpYTGYZfZr0suPJhQZGspQdPS2uuz9lhIez9MvRYB4LQdijcM5bd8xi4muENBAXFOCbG2m79mtjWtA1pKnispbldy8Z27AkpXDUkG+rPCIcQF6ba7+fGQJKspXtWMXTK0lgK27guJcw7tJZ/0TInMjrQFd+d8shsxfmtXoDSEsXOWaCJH+ZJh4yHpagualtqdBXRiWfySwR3A1GsQbolCLahpshuW/oyQglFRzlW+AKWrhuUPOxRuWlr7JUdPfVHeBa0U64iQavqVmOrphPxVF5tPiAugt3yG45rBXILXkc07/qbGrzls3+WSWxlQu1PQS2fOZeJNWTP5VYNxpemrtd/BiSyVU5pBRVN929I6KO+3eEWR5GD5ExWS0JKpKZr7PHrT0igUFSS4lK7FlC/2uPaZIuGaw849isq5Ec5QSOfkWA93YOgtWMqXRhSuacJNhXUszf0ZnMhy86MOXlvI7f6UxR0KWrGLAxHAHXCYf1ac5vrDDmMXIkGC92qSrHBYo7L0cRhfUrHMhks0Blv3abpLKfvuXOXn9r3ME+K3+Pmbj/OVfsDeL/3H/NXf/Zuk+ZTm/oDKe+8vBfhgOAEH9EhaTVMPNp4WRV7poqI759LeL4Rc81COrfuyhBuazoJm4yeHWM2tNmMdCdwajUH1nQ7lSxFeR+P1FKUrhp0TAXFBNl/5gghz+hOa8TPprTbk7rxl5tlNpl6UHLN9NBby8LE2E6cMV3/5DowLnXmXws2UoJmIom3bEuxEDCuKzl6Ye75Pdl1RP+JLKe0ly9bDIhJyhhJFjQvFmwnN/Q7J7IjeLPQXErJr0gnX2ufQOpoydqZN4WZKa5+meiZm+pVYWmwNTLwd4zeFcbYKRgV165n2JyXa7v+N63Qe65PZsdRPKHbuDChdG+E/ucOoDL3pXWLqgKZ8weC3Idwx6Fj+rZ3wyNQMmw99W45qya5Jvhw0pOxmtaWz19CfVtSPCT8yHFPMvJSgU6m1G0+EP6XLUhJtHPJo73FJsjD+gk9/QbiZqADlmTa9Bwb0Z0T4ZRyonEtZ/nCO2RdEyJVpGvLLI1aeculNayoXYvqz4ig3H5A8W9Sl4lRrj0pACRoWryOy2t6cYViVKoayCOkcKDbv87n58QKTb8pzyGwrmgd9UCI6y76cY1TUBDXFjR8MyG4ZBjMGkzXU7jEMKhp3oOgcFd3Ety1TN5h6QFSUtbD+lyM6eyBTVzT3+wynUvY8uELlPVFoFpalya1ydnRrnRlPSpJ6fMRqo8SRYA2Az7YnefWLJ/jPXvtJMsseXk/h1VzSULHz/tnAB8MJ6AQmTseMnVW0D8Kh3xjRm3KJymqXrbe0F122HrFktwxJ1lI9HRG8kWf7wRQdQfX0CCeyuF3werB1f4HejHT2+S1h3f22RUeKTFM6Clv7pK+7s+DgdsE6iuy6YrB3jCRQDCuKqecdgqYlfKZAVNAEddi+R+8ytQ7XflgT5xTNOwzNQyEA2RMNrn8qpHk8IdOwmP0DejMOwaZDfk0GVkRFMJ6ieUDknt7NgIWvj6icckiywnaPypbMhkP9RImgkeAOYetej86Ci9tyyK1A7biHOwR3IBAapFTm9i31e1I6e+Dy/1zFuRZiXVh4JpIodDAg89sVrAtuX/J/vwXFa1LBcAcSrd2hYVQRKa0zlHJa8wjk1xMGU4apNwcUroqjrb4NlXMJ/i40z24Zmgc84lDIx+ympX7YIyoqVj8kUlrjsYtqFP6Og61GpHd2Sa0imxPSa+4bMeNnLM2DUu9f+ZQ4lOLZOjt3heRvShCoH/YoXtKE25bSJShdM7gDKbn5LUV4xScqSQpkfBFqVc4opl5PRCiVCGncXZQ+/HDLsnWfMPTd/QmZuiHNWGa+4eAOLNXTXboHEtyeqPnCTU2w6ZJbdsg0pYSs+g47dyvGLlg2H5HIvvAVy8zL0nOQeyWL21fkVg2t4ymFKw71P5hn+7GY+mGf1FeUr0R0533CLVFTBjVF4weGKOC/vOMZ/scbH+e+N3+cv/+lH6Hy2AbqRkiSt+z5/RVyK2oX8f0FNBD921gayAvMbqXMPp+w9lQBnUBUkF7/b7+g2a/vTpwJLc39PvPP1PFrDk4M2/cEFG/IRvE6Fr9taR3Q6ESIR2Vg535hajcf0Ozcqai+M2JQlZJempHJP9EY7Nzl0zgueawTi/f+du/32KWYcFMIp3DLMv+swMTieQedQG9viv9HY0y8achfdVGpJfdKlsk3uphAFtXWSXVrMlJ/Rr6PM1SsPpEhaFvGLgm7PfNSymBfxPaDhsGkaOSND2MXh+RXZHhHkoXhOCSh1MP7s4r+7G7u2XZE6be965y2DBsPBQwmLJmGDEnJ7AAKCqsprWMJ/ZkQv6WoH3VvlRJnXkjJbZjdeQ2K2RdSNu/38JuaUdkj05DuTqvlc+GOJbtjaB7STL/SwYkhty6NQZULMVERVKyIC4q5rzUZlUQXULpsmfjzgMzLeexLY6SvjaFjES9tPWzJrlvSUFF+PaB0NaW/VKa7aImLQsjpRARS1lH0ZqTs2z4gQSEqW4KmpCw62p0YpGFYUSRZTeV8xKCi2XjYQSUw+bJiVFaMnbMUllMmXnFoHnRIM8JpxDnFxkMFctddZr81kilUdbvLHUj6I9WZ3XRkn6Z0zsHr7RKzmwPGzybEeZFp79ytmHxJkdsQ5DH/Zw79WUt2K0Gllu37DbV7DSqBzrEImyr2T2/zD099ggvXZ6ivlsEo1i5PYJVwFWu/lqV5V0waQOnS+++/D4QTCBqG3ryhs+Cw+oRLdl1y7L1/2qY3JaxwYUXq9VZDblkzmIL6XWPSIPJORJyHUdkhyYijyDRSCjekiaV2MpXxWmFKdsMy942E4jVRvs0932c09p06s9+Ahc9vUb4g5TO/ndI4LKWoqCjM98TpIcpAf0pROFsjvFrD+NA8BEd+bYfBhPS1j5+JGY5rCssp1z+VI6grlr7YJ7csss/BtMEZKqrvyAKVsWkWPTKkuznegc+mHPi9EcOyZvkjDnt/d4PubEB/2tJZlH5zvwUbD8sCD2oCXXUK2TVFmk8J1xwWvzKUtCuG/Ioiuz4irEknYlSClU+mVF9z2LnTIb9q6O5NGJVlY4WrPbBQvCJQfeeES7glBGvjkMugKpyKcSEqWmp3WhoHNc4QunuypJ68E+NKc1G4bdn3pyNmXuxz9UdLt0Zr9WaVDNHQ0J82DCelsy7ctix+0TAaU5QvSbVjVNSsPO2Kus6D8XMJrWMJAL1Zy+KvvkThZsLCMxFREby2TCMynjhDZyCIrrsvoTujqR/x8fqW/b+1TVKQErXXg8YxRf5Gn0FVnG6wrVn6k7oIekIYu5jSXvJJQsndlZWhM8aVeQrVdyKahzRxQcjcJIT1xxX1Owosf0I4gvS/b5JdV/RmNOtPGoKOoXZUulFXn3BpHBJOS6XSOp696hNeyLD65T2Y1ZDMDZ/cdZmvMPWSOOkkBzxbIVyW9uk49wFHAuzClfYBS/EqbD9oyNQsNz9RorsHZr7ZYv1Rl6k3DOFWRPFmSrgJ2w8Z+jOKrXt9xt9L8TupzJ0zsPxRh/6UaMiDTZfiDcOBf/rt43cfzHhC7Y6QoCVIIXv/Dv0Ziw19RmOK/LKluV96+3PrhtL1hHDLUjueYfx0B+PB1uMTXPjrMxRupuz/PzZZ+/gUMy92CRopW/d5TL4hXY/5G7L4m4eyREVYe9RFJYIu1p80OEOLE8GopFl90ifJWQZVh6ufCejPSNlx9nmLSg1xTiop1dMSnd2BpXpKCEZ3IOipfkzIvcyqh07g8k95ZHZk2k1nyTCYCtCJOIXFL9apvuCRaQrcHY5pxt4VYq95BDYeKzGY0EQlkbcGdem9mH6pT35FHImMJ1Pkl8EUBHEFTUtnzsEdWjYeF6beayfU7065+pmAq5/J4HdEJi4aeUtvTsZuuXN9Clc17b0wKisahz2KN1K27/alPfxGRPEqlK4YciuWzfsdKqcc6kcdnINdBl/dS2fRZfUpn+yGOKzRPsmrWwc0E6cHhBsKPRIHFuely3TzyQmS0BIVNMMqTJ3c4Pqn8xRvpEy9PmTqjYjm8bJ0prryHPyOEa6klTL+XkpckFmGjWOw8ZBPZhvmn0vIrRuikuLgb8vayV/xGJWh+TvzmN35jVMvaupHHYImBHXF3DdjsjuG/Ipl8lWY/1pE5uEdmVkZQpo1nPtPfp3hhKG7AEEzZVhxmHwrIipIkMhuGgaT77/9PhBOIAk1lbOWmReFMBt/SyJ+krOEG4qr/0ERHSvaCw7d+YDBuMaJZQCl24c9n9+hMyczBCrnhNWf/abA+bgAS3/aQqVw7YeFkEkzluKNmGDDoz+laDw5xB1YOu+Nk9lRXPorRfp3Dkiy4kQ6H+2xfVLY6CRUkjaUA4IG1O5NWfyqSHTXPzJNd8HSPJgjyQp/oGPDqKTJ7hgGVakvOxGiXX/VYAJL9XWHiVcb9BYMpStDwi1F9e1dgU1NNBOtYwnrjyqSySJjF4ZU3rO09zqkgdTuCzcj4pxi5wnJ+XNrMocxvyxTkJb+1NDcH9BbSuVZLjqknqCH5vEytXsNq09DuKluTQYalRVJKM8wzch8AynbiYDFuhrjSYTxursVgIKifErmJmYaQra19jkc/qcD1p8w7NwZ4o0NsQrGTyuCuqVwQ2r5TiRDSLrzPjOfDWgdjyldEeju9i3rj4uuIbOjufGDHs2HpZ7eOgx2X5+gJahh6p9lWDk/hTuQ77P3r16kdC3BDhzivJCa6w+HWAcO/2aD/qKU3UYVRevJIfv/eERvRmNcS+a/KzLzQsL6D8Vc+5RP7Q6f2glFXIDBbEqSUdSPOsQ5aSuuH3YI6rD2sUTmOyKk6NqjLu09st06+/KknqJ8WZBp9fUGuTWRFCeBYu/vrDL+3hCA+lGfxiFpM96+D0YVj8I/LjF4tCuffUNIx9yypngNGgelTbo3JbJ1Zyhakurp9x8o8IFwAjqVjTEqarr7U5xIyld+U1onva4iu27pHEoJ2inZnZT8WoLXlqaM9R+o0jkkg0iigqY7JyosgP58SlIK0Kl47nR3Tlt70aN4clvGin3ep35CUT4P1Xcjlr4Usfg7LqWrCZ29hpnPBjhDRfNkxHBCtOHtPT759ZSxdx2SnEPQkQrDvj/pM6wo0kBRfXfA5b+cQyeWYUn6BGonYOKdiOIlTRIoipeleeryXxkj2NZc/2SG/HpKd9Zh/EsXGM6kNA9pctddDv3GNsNqhsahDL1ZTe/4UGAfsPZ4wNilhMyNgN6hiFFFonz58pDtezXB1oDOXshdc5j9VkL7RMTmh2NG49A8qDn0S2/i9KXcOfV675aAK7Mj5ao0A50FTflqQu0ugfZuL5ZpyY5oPXTy7YnFFr9nWftQKhN0A9D9iOobIu+e+oOQyddE5YmCzh5F5UJKEgqKSUJFGmryl6VeHm5aMk1LuCFOp3I+Yd/nR4y9EGA1FC/Dgb8vlaL6XYbunMuh3+5SuDli5ht1lv+3gyx/DGa+qUkzlt6CzF5sH0pY/sFx8ldcxi4KqlLLGdYeCRlMGSpnLSs/kKNxyGPyWZ/cqqZzJCa3upsa7DgMxxSjA0OcSDGqmFsioj1/pJh8a0R2w9Lc74oStC2drjs/NiDTkMpUmlFc/Ykx+jMKvy3t5bVHZjCuYvxcTG/OkmQtg9mUg7/Tpr2k6f+NJtlv5Sksi/MCQQWDCUV3yTCcEKVqd18icwtS0MkHvESohynRbs5SeVvklVNfucFgStp5J9+KZczSWQevndAfd1j+kEPpsmjn2/sNE69qRmVF6wBMvRkTdCzDcUXlHU0aaJxIWlC9tgz07OyF4H+vkN2QoRlzzyV05xVrj3tc/yGf9h6XtcccsmuaQdWlfB7CKz6VM+KgmkelxGM8RXuPS2/KIdwxNA5nQUHjsGbjwZDcyu58vbqUv8bOiUbfHch4s/YBmY2Q5g1xyTLzckr9sIPXs6z87BEW/0wgely0NO6bYDjmMKwqhuOW0msZvLbcizOC5U9IqTV/zmfuOYkkjUMZlj7fZTidJRoX1WVn3iW87lN5WboN06xl9ZceYOpVYek3Hs6JsvLehDgvMwrKF4WnGJYdqqdkozeO5BmMa6Zejwlrhqgk99GfFidcmOqShFC4YWmeEJIvU09Zf1QxKkldPfUEbeWvdZl421K+YKg/GrH2mJCnXk/mQvamtUz/VXL/Nz+aoTeniPOitbjy3wT0JzTBtkP1jTaXfipPZyFg+Ycqohl42yHJKIK63p3Qa5l4zaF7KEZZaC9JM9DctxIyNUt2TZrZxi6mZOr2lvTa33SZfL3DYN+I/A3L5Jt9nI2AwWwiA2wMt/icG/83c+8ZZOeZnuld7xdOzqlzALqJRBAgwQSC5JDD4Ywmz0gTlFZhg7S1q7K3Vuty7R97xyXbtV6HtWyvaiWPyytrZGlXmtHE1WiYRuQQJAESmciNRuc+fXI+50uvfzyH0JbLlGqtUDx/iEA00Od8b3ie576v+1M2g5KUO4kth8Gkxhxpki/EqT0g4FfliXnuPShMbzagN2Ow/XQYNybE53BDEa4Ia7F4wcH8Wh4vCvUjIogDufZHaprcJYU10yfaCLAyDoOJgEh1TLx6v/X3l1m8Sqm7SqnLSqkLSqm3x7+WU0q9oJS6Nf5v9i/6Ok7WlFnyuiNOvy3N+k8vYs30idQ1u4/ZBLY0VlZ+MkSkFRBuGCS2Hay+IjmeSXtRRailqB6zaS4ZJNdlW1a+JtT0iG9rcteEfZ9chVDTI9TWpO+4uAm5vptD8bZ3Z4UBF61Ik7I3oyhdkK59cssjfVNRecggsS3Q0OSmR2fOoHkQ+pNyDfZikF71SN8JaC5blJ8KxBLalWtz64hH6W1pUmUvG8y8MhYgnR7Sm1F0lj12nrAwHLmloETlOP9vbhPdkytpb14TqRikV3ySN8VTHliw9WyEUEs0C8NSlEHRYt/XfXLXRIZtjmAwIaPE2Jb48pvL0owyB5L5kLlgk1qBUUrRmTMYTbvUj2oMH0ZJg+oJ8bj3ixatfTJC9GLgHu6LX/9yhkhdkzvfILbrMCgqyo9ahOsGiV2f0oUBQUgYkMOJGM0loSlHbocpnZUmXnfaQJvSMOzNaQZF+f5iW4r4tmbqDdmczMsJnIxgwtY/nSZ/SVE7JrTk2lGT5hG5bs/8sIcbFyeo6WjsqjXGtAnNaO0ziu68aAn8EIQbnizgwviknnHo7I8z8ZJNf1KUqqnbojIdlDSDh/rkr7qUH7PJXBdcvgpg7RNhDEd0C+1lmHzLZ+sZi1g1IHNdSNraArsttCC7KwK1UUbK2sIln5UvhnFSJr2fbOHFRCB158tjWKwrNOv4rkfkjQRuVJF+RQ4hgFjlr7cc+LDW+sH/AFbwT4GXtNb3AS+Nf/7nvgxHOu8bHwvRn5Q5fn86IPudGPEdDzcVMPuyQ2IzYOnfOgwzBk46YPfxCHMvdGkd8gjC0uX24jA4PpDGWt4gWpOxmDYUrQPQnTJY/7hJ/aEAPyzyWGvo49uKqVcqhBsQqSmcok/zYfnwvagsjMCSebSTNAksMRb1SiaDvMHms5bISLcUqTsw+9KAUBsqD0n3PLkREN2U/6ezoOg+PiBUl268NYDmQU35cZv4VoCTFkfg1KvCkC+d9wR7nTeoPAxbP7UsN4miXGGl7jMYPtojviXsPXMA8S25Rax/RtPer6gdDVM/bAqxuSF8PDcpG0F8E6Y+tiGb1l2X+I5DZsUVtWRROt35M6LQ68waFM63SK4adGYtwh1flJ5NmSaEL8UINzXFiwG9GcX2R3Ksfj7EKCffS2xXs3fCYOO5KNFqIGXflDD6G0dEOj7Myby/e9DF8MRvMflmQPGCjzXQKC2c/cYBk0hNkGvhunTmI1VZ8Ll3Rd4d2OMgj7imvS9KuCn+BTcuLML0ivQ6tCkQ1Ox1IUu1l2FQtOlN27gpTXLTx2jY9CZlROjFNf2JMbJuMcAaKkLXhBdpdcXnkrk9YuKMCwFMnHXxbUXxnYB+0SR3GcqPyhSqcUQYGn5YfAuBDZGGFsvzpKJ6zCR3WdHab9LvRShe9GjtM8helE2gfj+EWi47T4lL1kkpak+4ZG57hJtitnrf9ff/e+m//+tzwG+Pf/zbwOf/oj9gdwUguvhtUbU1DppE9wzcmKSvzH/fZe/hMNGqx96JqHSpewbRsqY3E2XmZcVgIiC2q8leD4iejzLzqkv7sIc5CkjfCageC1M8Jyd06rZQeFv7bPqzAdtPRkmuDbj5dwqSKuTAzAuK5d/2GTzSB0TSPMyajLKKYVbIwoPi2AWYEhLsYELfuwo274uQv+qQP7krqsYJ416jZua1AdbtKKGmYuKMK138isz5UTBKmsx8a0MszlkDcxDQLwlJ2HQUvTlJLYpUxgKetsbJ+ZjX4nTnFPFNce+19xnM/DBg8k9NrD5050X+G63I5tHcbxE802RYVKTvuNx9ZxbDFYFP7f4I9YMyRTFH0FkENNSOKaJVzdqnMkTqctNqLlm4KTFqZW/60hcYQb9oMPcnHSINzeyLAYkN2H1MrOB2V5G+renMjR1+Gua/W5MbWlcTqQcypqtYNPebdBaFALT1PMTLPqG2pjtlMnFmxDCvKJyTa/goq2k86hJuaNKrQwZT8r0WzkmTM9QLCLVE7djeLw1Qc6SZfLlC/qKoSTtzUjbmL2nCLZ/2PoPl36lJX2fToLPsMyjJIRAfj7MnT0PyrigRA0sx86cdbv1ciDufD7H1cy7xbdEj1D48QptStg5zirkXXdykJnsVOnPWmKspeLVw0ye+LpkbqTuaxI5HuK7JvBKhXzSZenPIYELK6PiWYlAKUTwnAikvpoiuhjA8TeuAUJff7/WX3QQ08AOl1DvjRCGACa31zvjHu8DEX/RFnKRJbC8ApehNyxU8uSbsuWHGpD9hU7zgsP1kiHBLap/Epjx0nTmTaMWh+LYo/pykgD82nreZfknRL8pJPCxoUre7eDEEG74jp0Hmqpwct/6uTeYmxMo+qXVfvOCPR5n5XRsnFzD7imwGw4KIYqJ14dUHFsy+0sMPSZOveNGhsygE5eoDIfbOTYCG7rymdN5h6kdtVv62QeZWQO6axzBnEm77ImhJavYe13QWFbf+gbgQ+5OavYfFfdgvSRmTuaZwUuOO/a6ccpnpNm46YDTp4iZgOCGn89azBuGGD1p8CYOSnIC9GdnIpv87i2hZ05mzSd8UFd8oA5lbDoltKR1QULgQ0J1TmANF8cV1zJFAQJ209CcYW4l3HxP+nulo7B7c+rmYyLo9aagWLmkSGzIfT2w5FC57Y1Cn4sbfywpZaaCpH1UEpnAmE1sBkT1Fa59NbN2kdkRcoL05zc6pMG5Cj0tDsfkWfmSTuz5i6+kodssg3JSRaqRi0Nxv0TykMUYSb5deldShnedL9EsShRZqjR9upQhCoiG59o/SVE96Y3m4SeJkRUZ0YUHclR8XwM1gQtO4z2L76STRQp/SWci8GJWmow8z37RpLxqU3pEmYnvBpvS2GJSGeSlFJt5s0ZkP0Zu00IZIrFWg2TkpP2/vl022diRCYk0+/+78GGeWMqg/5JNcl3FlZ8YivqnI3vDed/39ZTeBp7TWJ4BPAL+ilPrQf/ibWgCG/59tSaXULyul3lZKve0PengRRe3+KOEm5P/3N6gfVUy91iTcGmf1GYr4lpBaIk2ZDkSrHlOvtagejbL7oYDerKZwro0XVcy84pG82x8LTyS5pnkoQfG8Ix+uDa0DIrH1YorQto0fkgewuWQS2/MYFjSxO02mXw1Y+VKEUVoiydpLYsON7UhSzcbzcQJL6u/6wRDRPSVI8CSkb8Pstzbxkz6DvEXzUILZb5qUnwpY/ySMsgb9okliS7IK0jdkxJS+CbE9n2hZSD+hlmLydaH5jvKKhW/XKFz0CUxF7ZGAeNghd6iGmXQZ7HeIbksSUGLdYOeUXLVTdwOyV6E7J9ZaP6zozUYZFhThttSuew+HpfZNiTQ2VvZQvhhWlv7NFpE6rPzSApGaJnO9S6gt7EF3YUTngEe4q4kJQQAAIABJREFUoTA82WBTa0OSt01mXu7QmZVwDCepiFY9Unc9dp4I0zggTrnUiia5KvVwd9pk6rRHd8akvV+x97jkOxqulptSPiBzO2DhuwMKlz32fatDZy5MuBWw95wzTn+yiG9r/Jhm+tUOo7QitSZqvIm3BPPlh8dEpIGYjwZTGm0qRlkoXvJEJWrIBnL4f6hhDAQFl7saEPtXGcJtoUj1CwbLX+tQOW5Tekd6FMkNn8LXYngRRfVJ2ZjbCyadGVEkNpeFPynvu3ARkxsB8S0oP5EmVpHO/+LvbxPb6oslfcplMKHw0pJgFFgwLMoJX7igMRz5vuKrEkiy95DBKCcj5Phq+30X8V8ZaFQp9RWgC/wS8KzWekcpNQX8UGt98M/7s/HCnJ77B7+K3YPElk/1QYP8ZdnZvLAsUjcu2XXvxWwFlii/hnmDzmJA9qpowr0o9PZ5RDctEpv6HtO9+hCYfVn8dleRvhPcuzUkNh22fsVltB1n8XseW08Ld3/yR3V2P5S7F+jYXfSJbZkkNgNx+o3DSOPbGietSGwEDHOGKMNisPiNOv35FJ05KSOcjDSkRhlNYkM4Ab2SSWbFYe2zJqU3JGSFQFN5MEx8J2BQMLCG+p6qsbOgmHzLxXACdk6FGU346IjPP3vy2/xiao/f72T5dvVBrlQmcc9liW9pYTgajEsBj+1nxhTfoXzN1JqH3fPwbYPN50Jkbgri3epIrNkoC4P9DrGVEKE2pFdcWvtsmiccQjs22eua1ud7OBtxrL40Z0MtTeO4TG2iNY/mfpvuQoC2IHdR4cUV5kBTerNO84EsTkKuyMk1Kceazw1JvxphUFQUrniEmh4rv6DIvRGieUiTvCu5g5NnHQg0g3/ShP+riOFDqOXRL9l0FmUU2D3gkr5kk393xDBv4cbFUDTMKey+TJHmv1Pj9s/myF6THojdlXURaQQElsIeBGw/JeVX9pqmdlyu8nsnQpL0NGdIktGaIOIqJyAoOmRfDzOYUAz2ORBA5kKIzr4A5Y4zG1dlmhLbE1+B4UJq3ae5JL2O9j6ZHhiOZET2Jk06CyKqazzgk5lpM3Rswq8lSW74JG612H4+J2sjKyWkAFM1F3/jn/zVxpAppeJKqeR7PwY+BlxB4sZ+Yfy//QLwrb/oa/nhP0vUDXUC/LCmN2HQXjDFajvODQi1IHtjhN0TmIibkBM3uWoQaQbEd3z6sz6RXZEeNw/JtTiwFPF1oRR7GZ+ZH/YlsDKQxtEoZ+OtJEjdNmgv2Ey+5TMswdpnc0Rqcm2zOxq7aVA65xDfdsncCCi94+ImRc8NMCgaZG85TJwZkr/is/nxHPUjlgRGNoT115/U5N/VNI4F1I6YNI/LiCpcMdl7QrP7WIjWUoj8uy7dWdlQnJQiWta0l6B03mP9kwaDks1wyuNnnjzNs/ff4IuJdQC23Sxn7i4CMJz0iLQC6kc1jaMB8V2X6jGbSEVReidgVPTJrLis/YSmuT9C5cEwybsyc7Y6SvT+SQi1YfJF2VS1gt2TNuZIE9qxKV4MaN1ncHhilyAm9XekNj6R7pp05pWEhc5o0jeVOEAXhfhkutA4nqV5n0FnHxQvaHrT8utTfxhCBTD3Ypf2vEXjYJjwehi7J6KyxJZPak3SjPuTNv3vT2D4sPOMZuPnfQxfC/hkyWP6BwbWQLPzRJjujJjGetOKcEuT2PQwXNh6Ps/kGZ+9J2WMmtzwhDL98w3St3v0CybRsuDjtCmz996kjZPSuDFB0yXWRQHamTPwMx5T35Wg3GHJJ3YrROlPbdr7A4pvw9QbPsk12QBQ0F4S1uXU6x0GeYPCJYfWMhQvBhTPa0ZzjrhNY6KpAZlI9Ich3LsJctcdnITB3qmshNXMSXLy8OfqtA95tA789egEJoAfKaUuAmeA72mtvw/8c+CjSqlbwPPjn/+5LwnNHEstD9gkV4WTl7/ikLnt4EUVo6x0Z+uHw1hDjZeA+rGA+LpBvCykXv9v15j/fgCBjL/MoSKxahIre3hxiG0bRDcs9h6OUTkht4BIVbP3kMHS17tYfen27j1iMZx1cI/0aS0ZxHYDOvth+kcug4LF9ofCuAlF/bBNakX+fietidQCutM2taMRulPygb338qJqjMLW7D2ssBsGcy/1Ce/aNO4LkVrRhMsm068PMVyoPWDfi/u2BtD6mPQkAlOh4x7hlk/ptMnvvnWSs9vz/FbzCL/byfO93aN8ePkmzsUsZt/ASRgc/p93SN8wMUc+dgcyKx69SZPcBYPyIyEW/2Ac9z2CcFvMV9mbktLjpjTtAz67H5IOeu6Gg+GJNsHw5CpqOHDh0n7yb5vEykKEei+W3Y9qqg+YlM7KVdyPQOGSYMeVLxMP5UlSkRuTbMfurKJ2xCTc0mw9m6A/OQ5yWdHYfU10z2GQN2gcUoRaHnsnNaOcdNqzFw0yr0So36+oH9MoV7H3qASSukkJF+ksKGJlKS0rD9oktgLy1xyav9ghc8kSDsI+GzeuUd/Kc+fHEyJgCsP0qyP2nnHJXhPDmR+Tm0Tt8HvUqDF74RWL7rTJsKSJr0sZobQmsSZp0k7CYJiTyUJyTWN1FYOigR+zxI4+J6VFa9GkuWQw+YIlzdD7XIrnAkJtzWBKNAfpW1B+RLDl9Sccsjf62B35TFP/W4pQ1cTqvX9j8AOROxCdmtOHP/uPUb5EgA/yBk5KIplHKRlHDWbiNJdEa231IXvbo3pUGiWpu5rurMxxw42AxiFF4bIm3PS4+zOa9JkwwyLMvDq8FzHVmxbJ8XsEm0hVmG07zwbMvKBkDJmRvIH4uiJ916V+2BbHYVicenZbUbjs0Zkz76Xbzr7coz8VofyoQXxbItKmX1YMs7Lftp8dkHwtSmpdUnUDW4QpgS2zajepmHxrwPapKLGyJr7jMcybmCPpVHsxg1HSFIVZS9N+ZoDXsclctGnd72NkR4Suxu4FcIQb4i3ozSoKF31J3KkrJt7qc/ezUZb+XYfuQpzY7oiVL0RI3THoT2oyNxFnXFuSlNOrPjtPKYpvS2bhzikLw1UMZ1wiG7Z01feNOX5nfTF+lcbjulnIXB87HnOK0jmH5lKI7rxm6k3pa+x+YUTkYgw3Ic+jtuTvz72rGRQNUuuCT7d6ohconQ0kXGNPk7vYpnkkSXJzxN6DUbK3XWkoTxrkrzjU7g9JGG01ILbVZ1SI0Dgg2K/kHXEw5q4FtPbLTa+9YGP1BRsWbkDzqEfugozYAlsxLMLEWy7dWYv8xS63fypO6rZB5o7Lxs+7hK/EJOQ2LO9j8wBoW4C0w6yiN6uZOKsZpaTMNTzI3nLYeUJ8BqM8xDc1xR+V2XtWGsuSECXlbmpVUzuuiW9INLyTUIRbciOLVCG96tKdthjmpQTNXIfOvOLmf/Wrf6OpxP9RL3MoSa0qEIZ6qCPKs+60LK7BdJy9B21mvrtNpApz39ql/IiQckvnZIYe29E4Kdj7qIsf1QzyCj9kkDwfZpSF6ddGbD8lxJfunMJ5UKSxxfMew2mXUQ5qRxXpqxa7pxShnnAA3YwvuoWSQERQ8jAXzwXEdzRbH5YPwovCcHmENhTN+0xyV0VwkrkyTjxKiJTYr0SIlwPcuElsW7H4HUe63zUZNRGIys/wIL06wosbVB8CJ2kQ2erQnrPECbcrD3Uh2yG+KvJao2+QeCPGYGmE1ZP5d6Qust7MDTEeRXflRGgcjAoQ41MpvIhi89kY+UuS1Jxcg71TY3XhnIU1gPohk9JZ6CwY7Dwh6ULmEAqnLVDS2RayjowBE1s+g3kXuyduRielmHi5zCgfsPZZaYqVzmnMQcD2szD7NZvkhmDBp970yF2RJmBrySC56bP5CWne2V1N/pKmeswQkIyn2TuZor1osPKlEHZP050Sj4fyxBben5bsyNr9JuXHk6x9SfIcU7clqKZ40aMza2C3hdLcm1bUjyqu/spv0F4OCDVM4ns+3QWZLBUuyiZo9zT1owniWwbhllCZ7BsxyYvIBvhRERxZfYmf6yzI1T9zE3Y+5dCbUUy93kYFmtWfhFHBJ7UuKsJQT7P1qcmx5VwRqwZYvfHodUqRWlFEGoJrbx71aO+XVKrurCZ2+jbxHQmlDdfl2cvefP8YMvMrX/nK38hC//Nev/Yv/+VXFvKPUT+imHuhzcYnwoRaCiOAUQ7QBm5KMZpIYA2h/lCShW81GExH2XtMMSgqwi3wowq7YjGa9MAX77bhya/7tom2ZOfNXfMwd8M4GYXSwqo3HRkxjvKa+JZBatWhs2iBVky93gPDxO4H1L4wJLwSAqUId4Rf51vjkImOhT0wCLegOyOCkkhdgiP7s9Cf80nfMnFS8tC4CQMnKfFaiR0fbShiFel39KcUnXmLQVEyB4cF8KNRFNI/6c4rAtugv5cQGMiGR+STVXK/r3CiUQYlzbAopF1rCIMJYxzFbhCpixAmsyIbT7gh2v/CpQHbT9toQ5G8qxhlpRmb2Bb3mzmSW5gfVTjZgMieQXcRDE/hR8QIZPXkPa0/AMUzJvWjkLktUNb6gwmKFwOyVwM685a4PJFr8TArII4grKicMHDHSVLWSMq6ydc9BkWLiTMdDE8xmJDsx+48pNalqx/fUveAsSgR24wy4mw0xsat5jGf/BkJCdWW8BX9sEliRxZJctMnf7GHHwnxO994GGNkUnrHYVCwIVAEYUVv2iC2B3YfWvsNolUNSuzjU6eHdBYsctcEhKu0lKbBY21+8uk3eGswy2DBJ/FuGC+hCUJh7L6mcF7jhS0CU8aS8R0Z8baXDJIfLpP6Qx8nE6Y7D7M/HNKftCmca5PcAjcWYjDtE4QU4aaCXJ6dL42wd2zyV1y8mEGoq9m49sLOV77yld/6f6+/D8RNwO5JQyl3VVN9KEXhvAhgIvXgXq8ge90nWpfTYJjXbH4iR7Tqk1pRRCvy4ffmPaJPV9m/VBbAx5RB4xD07h8S3/UkTSY8TijOCsBBBRIKkb7jkloLSN+G7pws3Pi2dGH3Hkmw+REDbSjMSwnCTT3WAZhMviZNotRdn8GUR/2ISfWYIr3q40fB8DW5az1CLUWkLKM6wYXLWz+YkFn7KGMQqQd05qUUcjIBhgeROiQ2QHlyIjQPCrjCTQj00/Ag3AqoHbYYfmeC3ZNx4tsBqVWwO4qZVwfYXTGudKdN4mVxM86+7DAoCCdw70Meia2ArWdjLPzJECcjJc97E4X6EUX/wIjaQwHNw/JZ5M8bpO969+bfuXclVDN3YyiswWsK3xZz1O4pUXOm1gLaiyZezKD32IDYrhaO/jcHaAuSa0M6C+L8U76cenYbOouK3pRYojc+mmLj+RBeVIC0uauixw9MaD47HBuRFM1DmvJJeb76k4p+SW5iufMyokNDe39ArCwjwfphY8yLsFj9fILMbYfdk4ruoqZ+JMwwKzLt9rJ4JIZ5RfW4InM7IL7rU3nSQwVQfjTCMCeTrdrP9mgeFDfiYr7OPyteZfVzv8XZj/063ftHTL8m5OLM9Q6DnEVvJiBW8bEGcvNTgXhBaq04jftTGL4ErA6Kkmp85z+zKD8SIbPiS+9rR0rS7s+0iFyMYQ2h/Ji8b63Fv1nF4H/0y4sLfbazIOMwaxDQOgCVEzD1apNhXghBrf0miW0PLx2QveWx/hk5YdyEXI/NgcFCus7npy7iJjWjnGCmln/Tp3rcJtTyyN3wsLviu+/MiyqxcdCgM28TWIrqoz6ZmzDMWzQPyAOU2BY3XP2gTXo1oLMowZSpVemWvxcYOvWqQeGyh91VbD2nxVseV6x+Nj7WoUtt54dErPMex08bMMhLNn10T0I0D3y1SWBD4UJfPP8/GNJeDph6Xeb5B399k8DS5K94YrLZE+S5pBqL98HuwZ2fCNM8KDp0q6/pThuMsprqA2H8sHgYCqdlVu9HNLd/2sbqyQza6kH+qsvciyPS58NEyibpG4p+SW4vzWWLSEV6MdXjinBTU34kSuaOS6wiwSeZmxBEZPMuf1wAH+15k/iZKIYnGvmdJ6WHUX4kRuaGNBrtjozFYpUAw4Hy0wHmSOMlNNnrcmDUnnSFY5ARNWb+TyJEK45AWu8a976PcB2ytzy6CwGNBwJ6szIaLJ6D3NUR6RXxlLgpmDzjMv0jT07aCzD5ZkC0KhOi9ErAga82JfPRlJKwvSA6j/ybFuGGJn/VJXNDHLGpP0qQuypBpyP/zxL/Cmac/I9CdGYt+rM+9QdS7D3pk75hUD9s4aSEedBcNshf8yh+PUr5WZ9o1bunEPRDCutqnMwdn51TimFBnunkuiby9QyxsmaUFgl2b0p+//1eH4jGYLwwpyf/6T8mf1Ee8GFOAJnKF3WbNqW+DmyFOZRYKz8kv+7FoHjBo7lkydRg7PayBjLWay9Lg6ZwQYQqIHXdMG8w+UaHtU8khfqblF00sSkEX1FwaeyuGod/Qn9CE6kqJs722HomTn+/S+lVi8rJgOKbBvEdh9WfhdjNMPmrHs1lubJmb7pUj9rMf32LG78yRWLdoDsfkLmhKL1aYeVvFYnURKj03sna2Q9O3ie+KpJcNx0w+4Kmdr98zWFROsqZ2wFuVObuXnTMrm8HuHGD/oSicMWl/KhNpCLvVeGSw9YzNuZIaubCFY/N5wymXxt38c95RKoOrf1RUqsDmgeijDKK3DWXtc8qZl5UuDEDpcVOnF4Zsvq5MH7aJ3fWor0ss+/unHD9CldcWgu2dOIfgdxlUYVmbge09hmEm+IB0Ar2HjWwxu/35Ft9unMRBgXhOQ6LmtwVCevce9jAWxwSuxgl1NJC4u2O5+xjdJg50nTnJT8hveqy8ZxNYlPCZuy21ObDYoDdMnAyAYXzikFJwKOpOwaxsk/1mMH06x7NJZvenIiiMlcsChf6+BGTrQ+HcLI+uYsmobb8/f1JxWjG4fD/1KbxYA67F1B+zMSZcPnDj/wGv777PG+uLcJqnMAWjwBZB3stfO9ItjuiF1Ce0IsiVT3ObZAp2tQX7lL/P+Yl6LQk0vpoWZBx3WkT6/kqwzcKIsE/FlB42yAw4fxX/4p1An/Vr2hZ0VoWG7FINzUTrzWI1DWjvMydY3s+9kBGWCCsNT+qWf+09A5iFVFrvbcB9GYVXiKgdFbcd6GOJrPikjtboXXYo3EoQWJD8NWGIwkve0/4OEnNxFt9zJFYVb2YNC8jNUV6zcNJhzAdpCO/LPl0XhQqJ8LkXw/hpmWBZG94FC4NsXrCy68/McXEGVmMQURktNs/VgIFblyaa7GK2KMXv9Oj+OYYU34DdNSnelQkvvHtAKurmHhH8gS9mEwrhscG9GYU3WmTUFf4/JXjtvDwk6Kr3zsRIr4tiyV7K6C5ZJG9qu6NIndPmuycimEPAtY+FRV011WX3pTF4jcD3JhB/p0avWmD9MqQ0J0yhqsw4xKUAtCble7+3PfqdKcshgWoHVdkr0hzzElLIzjUEmHOIG/QOGjiJX0KV3xGWc320zF8W5FedfFi42yJJYOtzwsdKXwtSvaWzL/1ONA2sKRRaHflGfHDeswRtIjUZBEZroS3JDYDEmsGkZo0CPdO+bgnO2SuSzRd/bBJahXKj9pC/b0DxlA2pMpDMcqPhln6WhXDMQh1RNLtpAQ5nrgeYufDBcqnNK1FySMIlW2+/M3/lNffPILbDZG8Kwh3w1FYW2Fy1zTJu+PFoKF/YiAj7IrGDymSGz6Z24EAbv/VHG5MbjmxsnyfSgtqfeJsj87lvODopxQzL0F3RmEPPuA8AW1I13fmT4dMnx4Sq0i098ancrT3QeltiQzzIgbdWYNQL2DqdIf8m7Z8EEOJkO7MSEJxEEJmxD7kzxsktqVrrwJN9ZjN3Z+c4Mh/s0VyY8Toc03ai6IZqB/TlN4wCbUUlRMxMrck1KI/J1OB9jGHjY8jBN2kXNVz1wKie4r+tIzs7L4egyVNhlmT9Y9LBsB7UIfutBiFkrdMdk9C/spITsx3PQxH4q7iW4rNDyeoPObjJBVOQqH6JtOnh5IwdEoIOuVHbKLrLVEtbir2/WsY7htJ3Fo3IL4VMCxIbyFaltiz+I7G6mnSqwHNZUNy+palHEHDwveHpO76jJIGsW1pDm4+ZxFuB9SOhrBGmu59GdCw/vEIrSfmQEP6h1Ga9wdMvhHgTAqMVWlNuC0+j+WvNejsh0hNQjz6E4rmAx6Z2wGNJxy5MV0yaRwQybDEpMH6J+T9GpU8Yjua4kthlK/IrAiG3l7oCYUqpsje8uhPK0Y5yUdM3xIp9yglC9s53pPn4/kG1QcFIBvqaBI7Pvu+7jP/348t3od8AltupeG6lIGBJSEgkZpMobQJK3+rwOTrmsoJcRGaQyhcDOjt84nv+qRumAyLUr6kViBIeUy/qomshzBc2H4uIFxXmMvdsZw6wMn6WH0JcPWiinA7EOVsROGHFH4Idk5JOWMNACVajHAzILqnaS3HSN2B2I4if8WnM2fix8TL8X6vD0Q5EJ2c00s/96sAdA645M9YZG8O2T0ZJbYrJh0vqjB8TfGdDs2DCTn9JgTuqJXw7JoHNbkrwnwbFKTr7GQDgqgmsSKZhrMvdth9InkP/mCOxF0XasmIyBrKlbx4ts3qF1KkVpCs+6sSTT1KG3TnNRNvB+w9bJC5IYo+c6hJrXtiKR6JsKX5qR7mlQTDko9OeMRuCuEo/67L2mcUUz802HsUEmvSufciiviux8bzJpnrYql2owZ+SDTi2Rs+1QdM0isBybUhvdkImXMVbvzDIplr47SjkZQTjcPgzw8J3Y4ynPQonTbpLIxxYXmP1DWbzG2PUcYgseVgdV3WfyxJ7poIr6yRmHimfuSz/mmYftnA7vq09tsMivK5pW+LXLo/MW7QOZr2okl3Xjrt2auK1n1SeweWovqQJrZlyARmQz5PFUDtIR+V8Jj/PZPdkzbG/W2S307i29A6CHZLxseZlYDtDwcYI0NyDYqaibM+9UMWfkSaaKYDnSUPFSistkFyTVx5gfXerF1TuKzZeRKKb8uiGkyI739QVEz/qE/9cJT6h0akzkZEb2FzLylYPdBGX5FEn+IFCRf1wxJZl9iA+kM+k68aJDZHdOfCGK7GixrEtx1aSyHqJzwmXjXxQ+oeVcmLB8S2jfHtRazdkZY0y924Inl3yNYzMUoXXOLXKgSpGHe+mCZ3VcJS4mXRckRq0iQdZY17JXF/YvzvOuGz/vf/8w9uOWA6chOI7QYkVmz6U4phIYSTEt949UmXaD2gswi1B5LEKh7hZoCb0GIZveNTP+4TpD2idZ9+0UQrgWICHP7nW2hr7FMvRYVZN9RkbvtMvtHBHElTLNTWdBZFNbf2uTTRsqL2cMCgqFj/eILqCZh6pUJiXRh9+UvSlR7moXCpR3faEgNJWJPcGJH+4ziRqsbsGWTPhMje9CGA6EaHxIpF4ws9omWD9B2PUNvHHGmay9KQ6s4ptj7u094nu35gyhV1OOlReUTm/JUHFXsfKpG6KVfRxhHpZ7znjzDXI5hDSF2z8Md8//iWQg3H0tkJk96UwZ0v2rjJEMP7hgzyBr0ZhVaK1ApUjltkLgkfr/yoTfqOS7gOk2+6ksQTlelFuO2z+4Q4CnNXRB48KAmL/70NObEmY7+JMzLZAMjcHpG4Y2FthqkftsncDEh8NynI8Lwi1FQSCrLs0JkzSEx2ie7IY7vvG20qxyziWxq7DYXLIgHOvGsR2TFJrUDqriuBH7bYlXNXNeXHYf8fOfQnhMo8mJH3Xpuw/bQIfVQ1hJsUUMd7TVLlg7OaJLA1E2c9UPLcDkuCIhuUFGbaIXO5ydYzUWoPKCI1j2jNY/N58TwU3rJo7zfoTYuxaP//cp30TTnMwm3ZSPNXulSOm+ydkDFz42CUcAM2Pmpy85encDMRYruK7oxB86Bm8yfEYuzFFN1ZicQzHGiecEjehc4+OPw/Vt93/X0gNgEvIjveoGhIus2Opr1gMv26R/ZSE6Nr4duK5d+pUXs4oPxIiMCS7PbAkvl+5l0L1bVoLVq0D4wz81qayTc0zZMzhOua/FffwI8I3HKUVViDgK1nksR2ZBYdaUon972O8sT/eprMuwZOViLO517w2fhUEcPXpFeF1NKflDitxqE4oY405KIVRe2wCJMm/90NJs4G91KCMys+O89Kvn305QSJTWnm1A/blE/Kv7k3ZRAtg12x5fpcdgm3xo2stiDP2vdBqK1oHNUMS2NOwQ9lWlF9zCe+rYnuiYFmWBBef79k0JvR93oAhYsdctc84qsmrX0hln9TxCoooe8W32qQWgtkNGtLx752v5RCrSUbLyY4rNS6R/2gfQ9wmtj0yF0XnFr/+AA/BJG6WMBHObGIK18ezsaBMPHdgPimWMhD3QAvCpNvSfBIfFv+jNm0GOU0o+tp/DD0HuszKkRJrsttpLvks/5JmfMPShCtakZ5xdpnTPoTBoXLLoYr5OJo2cCLmmBArOyBJ5uBk9IkNgJaBzXmdB+7K83KUU7TWQqEITgzwF8c0lyyJLb81oho2SBzrU20oolcirHx6RxeXBPfVGw9I1Hw8XVFkJDNxhzAqBgQWwmx9+MHcROKzG2X3VOyHsqPJclf8dn3rQ6BrfCjQkHKXVKkV6B2NIKTguSGIPMSFyIUzrWJ1AMytwWHpk1Inw/hJhV2W1F//P1xwx+ITQDGeXLbAa0PD+gsykOz/aTFnS9nCdUFC904niN7WZRRIPw5gEjdk9pu3WDydEfYAgZgyLw1tusQ2FD95SdwYwaJHY/AFDJr+q4s5vy7Pt0pk1hZRocA6//lKdJ3XKK70nhDi5BHwkFNAlsAG5sfMRll1D3y7iirSW57RGoerY8coDdhEqv4jPKw/YxiMCETDmsA5celnPBicn32otA9MqI7r+8BIlZ/3CK94lJ8G0IH2vzxf/Iv8GeHxHYkUUkdbaM01I5KbuK+bwRkr/fI3nCJ1CXYxOqL1txelEtSAAAgAElEQVTNiky3sz+gfjQpuQETspBaSzF2H7OJ7mmiNc3aZ3K0FyTyLbUakFnxmPvmLsOiINIB8hcUtSM2k2/2yFxTWD3N7kmb+mGTSAXUToTEtoAv4zsOM68KL9B0IHULimfaJDdGDEvS1GstWlifrmJX+0TqAbUHNcpTFI9U0Es9gpAmcytg6g/C7JwK0Z0VYc3iH3mohEdzv4k2NMl1j0EpYOK0TEHqhyTpqT8pG2PlIZv0HRHYzL4c0FwyiFSV1N45F303juFq/JAmcqTJfcc2+MTT5/F6Nn7bpjf/HlAljN2G3SczdBZh/js10AL58MNiemsvWIyyENqzqB1XjAqyoN8zMg2LmmHW5OBv1Wnvl+mVkzC48fdiJDc8hnlxMw4L0hcwB8JkCCzhadpdzdZH0+w+FVA/YtI8JBmRg5JmmJeSqzf5/kv9A7EJmK6cgMOMInYmJgq0EIQ6SqylnmTi2f0AP6TwEn8mnIntBTSWQzSOCGetfDLJKGUwecYlWpX5dP1wBGsAxfNdohUZ+cTKmu68NPD8MGx+2sdJiyIuWtb0pzX7v7ZN7f7QPYpud9omXg5g3MgE+W/hPMR3AxoHZRRj9RWVBy22nrVJrvYYFuXq7SYDcpcUybtytezOKeb/xCfckD5E87CmP60wGjbRPYXdEyahOTCo3W9jujBcSfHflp8n9WaU3rQiUlH415JYPX0PMOKHDDafS9A4YGP3AmJlTfvHeky/5jH3fXnPjZE8pKk1n+J5yTxI3xFhkRuXtGRrIKWa/FvFftt4tETuyp8lSId6mswdj2EpTP0hHzepmHtxIJTgupzw3WmD9n5Y+7TNKGlSemdAfzqg9pSDlwmz80SU2ZekdrP7mvq1PHd/Ikdz2SDUlEy/qXibLx68QO5QjepDip0nFdrSY1GVZvbXbpF5I8z0qx2ZEA19MjcUqds9YSmsybW+cEnk0NGKxo3KKLq9YDH33LpEiT/qE70TJr0it4Yg7vPw5CZ9N8S11gSLi3uSetVXtBcM7L6m+YBH6WyHzA24/g8zhJvybE2+2SPUFjvw5FmHxJqMqyOVMdUoJL2ESEWJJf6ghOkEtsis01ctGgctDEc2+NSqL/L0gqK9X8rE1j6J60ut+iRXhEJUfAcS64r8uxo3F9Bb9Ai3PuDTAT8EjaN6rJQTM09rWRZkYttjMO1TedBg50nJ8DPGeuogFpBY75O54xLMD4jtBbhxwVM17rNx42oMCpFFXDuaYPN5k9SGR+OwdKm9KBTPj6Rj6wnjDgXKhfrjkxQvjGgd8slfkuZQd9qgdV9AtOrTWVCkVgdE6vKAZa8LrXeU1RQvCHe+Ox8jvinjmok3NZmVIe390mxyk9LhV4GcGJmrivxln9iOQfquT2fOwo9qQg1F5o4QmQ0f/vjSUdznWgwPypXZKfiEuoHU3Rua3SdM5n7Qlii2JVPEMecSrP24/J4fkZNK4KgmgakwXE31WJTUmk932aN21CS54ROtaAqXRkye7tObMmkclEyIaC0ABdvPBtQPWvRKJrM/UPgR2PxIlMwtmT4EIRkX5i9rJk+DNZTsgXDVIHklzPaTEZLrAY1DEdr7DOrHAuyOQfamgEMCW2M92KQxinG7V6Q3DKFnBC9udwSlFtvqc/7rRwEoP54kWlZUjkVwY4rdU0ny744wR9IDqh01sbuCS6s9qO+RlGq/Nyfg1abJ4m9cl95QU1gM5UGSRGjE6naBu3dKRPcUobaiv+xQOQGxDYudp5I4KcX0yxIZH9ialS9HiVXEMjxKm7hJRfqmiLW8xaGMp/tSBsXKPrX7TQITqo/IqDtSC0jdDejPeQwnPHaegWFJ0zs0IrBE19E4Jn0mgFFOM5jQ9CYNUuselROKwlmDwplxI/J9Xh+ITQBA+fIAjfYLS1/bmtYhH3MQEK6YLH91k9i2Irkh8/5hEcyewZ0vJOjMWBz4tR7lxyDUEU1Ab0bTnTWI1gUeklkZ0V6Cqdc1o5RJYl3R3ecz8+qQ3rRNbFsUhtmrknY7+4qDk1KMshb5c9LkCnWkHDjwO10qD1kQgJMJ0Z0WNdjuMwGJLbHJ+rZw40dpIejOvjTAixj0psJ4Mfk68U1ZtF5Mar6JP61QPSa2082PaVr3aSbf8hkVJDewsygGoMT1ENnfSTD/b0WkYqZcdk8psrd8Wksw/arLjV+SBzBzS9SO4aYmdTlEdFdRvDAis+JSP2iTvyrm9MAWsUx70SR13SJ/xWf3lJxIw4JN43CU5gERU8UqAVY/ILHtkVyxGBYDYtWA6s/08cMQmNLgMmSkzygjYZy9SVFFomVj0EpO5N6k3DKCkFCXnaw4Sb2Iwuwruo0YM/EW9yeFWqc1mCPR/dtdTfV4EqsPky+WiZcDusseTkZuhkEI2oshakct6odFMhzbC3BKHnbLoHLcJtyA/JUe89+pMfeiw8bfOcT0ax5+SGF0TVZ/uEj59xfQPYvMJdFdBDbYezbmQBgCg5Km9YBL/bCJ3QFzqo85UGw9K5//KCXUpOb9HqVzAeZmhPayhMMoranfL1Of/pTiwP/ZZerNAX5YjTMMLRa+q9HhgNi2YnqqgTsGqyZWLVJrPnYvYOHfD8hf0iQ3A1r7LGlsH9M0D8PEmc77rr0PxCZgeAJC9MOa2FXpaJsDBb6ifiRMqAl3fnGOcFNGImgYzjv3UNzpVYfeUpbsNYFVjNIiI43UNNXjUm+39oeZf2HIIGtQeGUDNwF2QwI1y8/4dPbB9KviLdh5UrF3Iozhwt4j8jB2lj3cuCKz4nLj70eF1x8R/oG2kGnAuxamo5n5oYeTNGgt2DSOyDVs58ko9fvFcLL4PU/UfR/fw3Q109/bJDAVN/6LJJNvuvTnPKZfUsy+5FM7IshxgOyNgO6CbPvdaelJNI7A7P9tsfx7PfYeFnBKZ94mdtemtd+iPW8yLPn0J+T6OMrC9lNhakekrg1MRfZ6l2FOouHTq/69WPOlP5TMxVDbR4/db/2SonGfSfWYTW/CovTOELtjsPkZj6nflBh2J+/TnhcyTuquT+GipvCOQfuAT/2YjLHiW1KCDIqK1LpPYAuoM9QVXmFgQf5Sh/iOJhR3uPjNI7xaWeZfHP867IVJ34LcFdmwhwUxYN398iTRikP6qsXCt1toC4Y5mZjYT9QJtQSQogLN3HdFlaeV3PB2Tya4+xN5tj4cYup0Hz8yjrCrCYreTYjvoHUgoDcXMJjymXrdZ+IdiVybe9ll4Rsw+eaI9n0BsdcTxDcUsR2D9gMOXlymHJFd4QykbolAzovJbXXhOy28iGLibZftZ9PUD0bozgsBy4tB44BNZNNmMKGpn55k+hWxwce3AxqHTJSv2XwuRuWE6CIMF5LrPlOnxUq8cyr5/uvvr3+J/8UvP6LpT4roJlITW66X0Ey/pmmfHOCmJKfOSSkJophW5E/b2G1RoDUOhuiXxhSiAAqXBsTGJpTYthiFYns+u49F6eyH1mMz6IfbGL4iUneY+b547LszFpFmcA9q4ibEmVZ4d0BsXVJ6O3MWk6+YjHJg96SuVj6sfjoifoQ5i9Z+KUUSOz7zP/DwI5C94bP0B21mX+6y+3iIybMOnddKaKXY+sws0XpA7qUIrSWb1HULux/QOGCTueUThN5LPTKYe8Efx4RBuOqQWoHtpy28RIjsNc3y73XpLELxoovdkcReHRHicmLLI7Gpmf9+h0FJCMB+1KD8aJJQCybfkEVRuDjC8GD3ZIz4rkBKDU8CWOf/fYvBpKTc9CcVq58L4SY0pZdD7JwKE1iQuGPhh+Wz7c6Y1I7JaRnZNUmsGwJijQptabDoYA0CrD60lqSBNXVaICG3fypBbM8n+YM4weMtdpop/tGZn2LyTRHrNA+IfLw/71M9LunUXkzKmJWflll+bFfk5aMzOYz3kng0lB+RJvDUGyMJZc1A6ok9Fr/VpfJgjN3HTUn1mfVoHXPRhjwPiXWDoOSQvmEShBTdKZP8uyPaCzb1wzYY0quwxrqR3FWP3Fs2vWk9TgKSkXLtpMfEma6wHmYU1RMpIq2A6lGb/nRA7pqEx7T2G2RW/HsYu+iuCL62PiERZmhBqd/9ksBJtK2pnXKZON0iWpGrmDah8/DwfdffB2ITsHqKIBIQrYlktn94xPSrQp2xV6IYLuTelR07sTFkOO0zLMiGYfWhccy/hwBLbAbsnIrSOuxTfVqIuW5cEb/TxO5qpl/ziNRczDMprB7snIxSe8AUrcFDAe15k/6pLvEdjZOEqZer4AujvzetGOYFoll6x8NJCWJaHmixKcd3fMnliwicc+tDtsyXkwbNQ0n2TiRQHmw/GWKUl4UUbmpiuw75KwLuHBY0ew/auAkx/kgTziVa1dQP2aTvBJgj2P6QkHzRSKbAEcXuqRTZa5q1L4kJa1gIyL9pMcwaGE6Ak1K0l+PEdsSyGtseMMrB1I9aVE4oOnMmrf2he2k4w7Q8IqOsQFhWvyguz+Rd+fWJt6QR6kXFsOSm5DMZ5eXv6s0Fkrp0UDbCUFPGV+FmQGtZEbsTon5QeID7/utzDEvCldSmxnAVuydN3M80MV9PM9pMELoWY+8RRXrFYf6FIa19Bku/7+DGRS/ihwzKjwqV2Rpq0qviz89d98V3vyQ3s+LFgP6EYuOjgjFDQ+utEitfSmAONaGWoj/nYfYMFv5INl3/yRZWXzPxfaEIlR8zsAZQPRZmlFZk7nh0ZmwO/usW/UkxWDkpaYpOvhUw/41dIlWNkw6Ir9i0lmJUH/GJbwkbYvN5Cb5d/K7D7V80cdIymu1NSCiMVpIDqXxY+l0pc72IwuopIusyKQFQfZPOcoLtpyNUHpIsy+lv2++7/j4Qm4CXErnuMGdgjCB5IczewwatZYiWZQY+KCqsnpxOqesmuese7WWxpyZvCcevPzlufiiI7JgwMnFjIimmXKX15JDtpyxa+8Mk10WHrQ2pYWtHTeJrJqGWJvVSnM6cCIgqj+dZ/7Eow5w5FjXJVby1X24GTkbGN+/l6NUPm1QfDohvS4ZiuK7I3XDxbSh/yKc3pwl1RNkXRDVWT4Ijwms1bn85Qe5cAwzpJo/ywRhlbjAs2ETqAcOS6O4HJZnbD+cd8pclpSbUGot3Nh1it8IULsooykkrihcGrH3SZur1Lt0ZKZdUoLn76bh4Bk6lmXhrrFJLKPJXegQpbzzK9HET8m+O7EnuQnt/gN0RC27mVoCbUJgDGfVmb47I3BDnWu6yYNUm3pbvxRpqSucE1Arj2rormDf3yaN40yNqD8hV3G4rYtuK4HRW+hpVUXXaLcX2U2Fu/7RNEJKg2aAo7kEnITDQWCWgOw/lx0xCbdlM0dxbVJGqyygnC2qUC4hUofSOx75vDXDSitTdgNkXFeGqQXvBEsT6hbQ0/UzF0m/vkboF1YcFnupkNdtPG8R3PbY/kiNSFb/LMGOgLU3zPpNbf3eC1JpL8Zw0wzsLBsbQoPTKNsOsIXW/qbj7ybDEjW8apO4I1q27LPRjw5Xnbe+hCPFdAcY4aQHchP4f5t40WM7rvPP7nXfpt/f1bn33i30HSADcSZGUREmWNZK8VSw7M0mccmJXMhMnNZlMVZLRFyeTpFIz5aRij1Pl8ozHiyRbsiVqp0SKFEmQIEFiIRYCuMDd7+2+va/vevLhaWBcjmm7bH9gV7EINi/6dr/9nnOe5//8lybkroltnN2NSG6Kse1wXExhPujxodgEzJ4ie3dIvBaR3JKZttVVMDMQq+UsTL/Spb1PRn5OU+MnDRa/McRLK+nJVyMyqxIuoR5u4jRh5gWF5Yq7y+YvHGL82w7JbQG7dh6S0qx0NcD0FAvfbDOYiOgsyUVWGrxZjzAup1sQh+K1gPRGiJ+CqVdbpDbFxrtxUJFZhf7pAYX3IzK3pV+/Z7h597MiHV76SkRiR9xoS1cDtCFlo9NUrP70DPu+3KV5Ik/2FlQeiDH5Jgym5OTaPSGOReZAkV0dUrwmXvXpUp/qabHt6h306M+FbDwdRxuQWh+S2RCd+/qzCQxP0TiUIn8rxAg09YMCHvVmIsauDHFzIzTfhJ2H0phN2Vw781LbJyshnX0h7YMB+etSwdyz7Z75Xp3miUC88iZkwzJdadfcgiy83O0+YUyx+YyMF0vvRTgNCeEclhStPTHMTYdEVeFNe2TvSj9seKIizKxo4nVB7FUIC3+middGJ+SKQ+2ISWrLYzgd0Jk1mXg7YulPu2RXAomPu2kx/92Q0rUhO2fiLH7TJf8+pNYNvBz4aYOVTyeI1zVeSqzE+4u+5ExUpfTu7/FI1ANWPz/J+BsNClcM4ruawlVNmA/ECGZKsilCB1oHI8JCQGY1onBdxExayeupCKbOQefkJMOi2JvHuoL55G9FJKqa2nFFf0ZTuCiAsZdR2J0A04PqaQF093x1IMzFMeiXRTjXK1v4aVGmpjY15gd3A3/9JqCU+h2lVEUpdeXPPfeX5g0qefyGUuqWUuqSUurBv8kmEJnQXoqT2vLE3bYr9mL5Hybk5tuRG23fH/YYjgnbrzNnsPqJuKDRlvSGtROj9/dKHrcgCH3uxdsjS2eRD7s5UfHFWgblVwdUT1nYbVj9VJbkpkHxPU3jgEl/v8vED2OEMcX892T+vfG0Qa8slNvOnjSGL4YoxWsi45z9AwvDl4qgOyvR3iqE6RcNxi6H+BmL8istWnsMDFdTumDSm5aZ+9y3duksJumPy+w6uaNpLRlkl+XEnrggCUt2F3aPJ4hM6CxphjdzQtIZaIpv2OSuC7V47ErA6qcSrH3UEtLQrpSkbk7ROGhiDWXj7CyJyrJ6Mo6bF9pvrC2js71f6YtByPUu6TVNZ95k7G1Bq1v7uW+VpQ1F41Se1F2LWEfK8NCRqixR0cz9cEB6K6Q3kyC1HUDap3E8xOpH9MtSBRSvS9u28F0XN69Z+IpB7YSiPx0xmBJtQpCAsVe3iDXFP6J6ysZpag78bpP0+ujanHTIXxZTzshS3Pz5lGgHbCFxxSsDKg+KEUeQMqmd0JSu+IxdCnAaAUE2onlAevbWAc3SV2RRho4AzZMvWlRP2oxd8mkez0s7elgCTae/a1F/yCe7LNfG6muSWwbFN2ycZkjpQoNYR16vdHmAORAMpLHPIr8cUj9iUT8kArbmfoPEbsDUmxK8YgQjl6w4RDGhBserBkag2XwyRXtJjGv3/EnrvvgpTIgy9R635m+9CQC/C3zyLzz3QXmDnwL2j/75ZeA3/wavLxdsEKFCjZcXu+R7yTfTz69RPxmy/I8NOntShCWfyXMdUpuaPX/cYuqPrtPf79KZUyw9P8RwRWFn9cTi6+5/sZ/0uqa5X7zXvUJE9o6cQMs/7VC8FomFuSeGnNnbPdLrmgO/6TH+S3fJroU090pff8/qOrMWUT1t4KcVO2dMvLRcaDXKCzSHAtIYPkyc71A/YrA74oIPJyW1uL0oRpD5WxHTrw7Y+PgYdi9i7LKLNRjZWJ93IYLmETG1GIxLleQW5AQQw1DBFfplxeRLVYhkdNqZtph4Syqr1Z+Ur7m1x0RpOVnz7/cYFgwydw12HpGxmd2R2HbThURNM5iK058NWf6ptPg6KCE4GYHG7okvQP24VEn5610ROhWhP2awe0IRa8oGsX02QfTLVRIVj8qDNsmrcXLXLIKkQWpNNovse3USuxGDMZvpVwOqp4SGXHhPUbqoqTwEjcddNj85TRSTqcD4JR9rEFE/VRBvwYWI/HNbJGoRnQU5yYuXJcfPCARA23g2S/GqT3te8iQzywaxts+waLL9SAy7aZC9A/F1m9kfhjQOODSPimlMake+h+L1kJWfFeci72caxHcVsy/2qB8ymHzRonB9SGo7xM2rEe1ZEVmKyiMF2vMWYy+usnsySW9OjFIkeNXEaWgW/kwYh9apJrVjNs29JtocMWA1TJ3rSRLTjpaNqaGZf75G8VpI42CClc/kmX4loD+lGLvoM/1KXwJ7Plg68DdTESqlFoHntdbHRv99g78kYEQp9W9Gf/7Dv/hzf9Xrx6fn9JHP/BrDkmL8HY/KgzESFUm87U1ZBElxUw0c6fuVhuiBDurdDIldobyGjoBRiS2D/tEh818yGRQtUlserT3CoZ79VpXrv1qUIIcLsnt7ec3er3TZeSRDb1qT3FZMnetKOTzUDCYVfkbGLM1DjPIEBSUPsuJcvPF0nOFEwL4v+YSOycZTNn4uYvy8GHtoE8Yu++wet5k6N2Tz8Th+Rnp4MS4V8xLDl8ipjc/5pC7HCdIi+nHzBsWrLstfUGSuxsQduaapH9dEiYiJ10ySVUkH7s6OTFjO1jG+VaB1QFO4ouh9ukPi+xnCmGL80oDG/jhuUZHajO7LrDtzhgRd+DCYiNj3Rz1WfyJDkBTvwHgNrJ4ms+HTnbbx04p4TbQAmVWP+hGHwnWX5v4Y2lQEcQmIje+C92yLuf9Vsf1oFiOQTXcwIbRrpykBnYNJSaQW+zSpbqKYIrMWsHPGpHhNUz0NYS4gvi7gJRoyD1cZ/GgctyDqRNMXc5l+Wai18Zpi6o0hzX0O7b2jv3MXpr63yfI/mmHsUkisGbB7wiGxK9e7dTgksW4SJDXeVED+XaEdO02ZUsVasrjdonyPTk2yAu22j+mGbD+awcvK/W26o8rl4YjEpjgm2z1NZwGmXxXl6b3QFS+vmHxrgJ+2RMJsi6lI7REJt5j+ngFK+AMgqkhJwgpp7jMlQk1Bb0ZTfk2kxPcmMRd+5+/XVOSD8gZngLU/93Pro+f+f48/H0OmWz1CR1H+cZ/6oZigzGnFsGjKFKAeUT+iyK75YsO9qYm/mKF4XebfhisXKtaUnrbwqoP5azuj9sKicVKwhM2PjXPot5osfd2VPPoOzP4wYPln0nQXIkpXBNVf+2ga0xVvgOGkMLJSOwHa1GSWZbOpH8/SnYnRXnTI3tYkNi2WP+uQuLXL3A9czJ6BlxGxUuFGiNUXQc3O2TjZu3Ki3BPVjF0ULbifgp2HDOK34kQxsZ1uLxo4zYjBhM2h3+iiQsjfDhl7p8X0K5qJ14T23Ngv6sv5b9SZetMj/JGIlMyBOCdbr4mrcG9Gs/pcnERNQlNMVxJ8pfzUcLJNei1i4i3ozyYJHQGX8jcjWgdDrKEmvt5m97ScYkpLn9rcF6M3rdn5lSF2D8yBtHQqGsWpfSdLfyYp+YaenOQoaC/B9uNClkpUoHSlL6+Zg8x6gAqFV5C/Cd1Zg9wNRfZKjOGsR/79iMjRtN8aJ9YUHYVbEKDRy4qGf+4HAX5as/1wnM48xJqK3E2ItTU7H5uWKcikweaTgnvEaxKouvD1kHhNRFjlH5gEKSnFDV/+bpAQN6PMHSFDYQgrcPVTCbYfzZBdDQiSmqlzLun1iOpD4mKEltO7dibEz0dsPm6hbRkBx3qazv6AnTMJIkvCbmdfaOHlFPl3bXKX7ZEfp0zBJt90Kb4njMftR4Vsp03ZeINpDy8jKsTsiowYP+jxdwYG/6q8wb/m7/221vqM1vqMkU2hQk2QssitBCSqYvbg5gzmv7JOZCnChCYyxTDCTykK77sM8waxNvQeGojV1a2I7HJE7o6P+T8XuPtZi9BROFWhioYObD5bYud0giCl6U1rgqSB3VHk3hcjiqlzQ3LLEj3VnzBIrpuMv6tp7JOrGDqKzG0DNy9hGYndEPXzVfysxqkZbH+8TO1IHLsrN2SsJxhDkDBxSxFTbw7EswBGCD30x03qJ6SnRcP8v3yLICknxdIfbOI0ZRNrHs1jBFIa+vk4jQMmpTcq1B6VFCOrD5XHCrSWbIrXfZy2LLTOrASRtk94RDFNegUyr93BHEIQN8jeje63Rf6tDI0jkhcYWdJy9KcE4MzdMOlPGKx/aoyZF6EzD15KcI8godCLA4xzOWonBRNI7UR4+Qg3Z1B7zGP9WYPutIkRSvuXvRNhDaQdaD47IFGLqB1L4mXkNbUhhqGVB21i3YjSez6dPbJxTb5k0Zk3GH8nIndbZLz594Vm250Tr8YgoagfsjE8Sa3OLsPEW8Icbe43CBKK+e92R9ZyGi8vhjF2VzMsWWRXfIZjsP0opNcivPyI2p5R+FmJzAuSUs3dy1lUgYxs/aRBvKaonnJIVH3yV2Vs6RY11YciSm+b2G2DsUsRpXcVqS2P7oyB1TSJLNg9btEvR/TnUmgLOotS1bQWbQZjBrsnFf1Jm52nA8rnPBafF5VkkITuUsCefystsIpg8xkZLX7Q42+7CeyM2gBG/66Mnt8A5v7cz82OnvurH5GMATeetkmu9RgWxZI7sxlQeXYGFWmmXofkSgtvFIG99YRDvCnocfLtBOnNkNBWMl6KNOsfTVG6YLDzMJgDuThWX8gi9zTwU2/IIvEz8uU6DaieEl+7IAndvaGQlDKK7FrI9CsiHsrf8kcOM4r2vMXORoHSJS1uxbc9xi72SW5rnCa0FwzKrw3YPWETpkMqDySonjIovxYSxNVI0qwx+1Jiqgg2fu0MKCSmupDCzY905YfEkdjuhjT3OTgNjV/OMvWCReF9DxVq6g/7NA9rWntsEhWP1Lr0++k1Rer9GBPnRzdEPkuyGtJZlGu2/ah4O+75ahe7o7jzOYPOrJxc2WXolsVaywggfyugdsQkswJBSja7mRdqmDeTJLclZccaaHKXa4RFn96sInXdYfwtRWYjpDsjissgLrRpp2pgLieI7/r4aQHBTA9aSxbFS/c8HjWtRZvyj6XXLlxp4zQ15lDTHCVdprZ8ErsBfgqsIffp0qX3hEfSXVCsfyxG+dWA1JYo7VQgQF32tuhF/IxInPvjBm7BInI0h367QXfWYOr1SCYNefGfDBJShk+9ETL1f72BNRSjldbRgO6MYEOJ3ZFbcVEA4JkfhWRummhDMgGqPzXEyygaBxyCuNDlvZwYhhavyDhShVC4Jp/H7mu6c4wyLYVVe+fnNZUHHVBSpacGPPwAACAASURBVOz9UkDtaJzsXcHHShcM6kf//rUDH5Q3+HXgH46mBI8Arb8ODwBB2LUpfVr1TJbyCxWa+0y8tJhl9Cflba5/ckxuvMSIr10SznmyEtHcJ6BXelXROCSlXZBS5PfVBV/YiFBa+k27J24ymx9ReGmDyTcj+jPRKIpLCCbDcU1yzaRwXeN/usnuCZN+yRSSyMM2mTUXqw/J3Yj8RdmdtVLsnnConEli96TSSFQ1nXmH4jVx8xHEWIn2QIkYyi0qSpc142+3iLUlkjtICN3VHU+iDUVnQfrlYcGgV5ZeMbMe0Jl1CBKKu5+2GEwq8hdiZG4bEgh6ME4YUwzGDNp7JbrKy8oCvP2L42LoqsGb9nDq4m5UPZ0mdzskfdcSD4R9wqGPHORns9BatJj/Ths/da/8hmv/XWaUXwCDSQl4ufbfZym8KVRiPyvJu92yidMAw9PYA3k/w+mQWEtRO+aIV8FhsdiyBnJNpl5p0Zm2aB4PqJyWMJStJ/PYPc3mFzyCxEguO22z/WgMbWhS2z6tg0K2ae4bOTVVJJR25yGbYVFRuqSpPpghSEL9wYjUpmbu2y2Sm4rxi0OGBUXmDuw8XmQwFVE7Zo4qR1j4tsfuSUP8BjImd379ITrzElxq9gwx+UjI/SSW9BJPtvW4SXdJXKTsjib14xTNYwGdBVkLqjwUXUReshI3n5V2I7fs4haheLHN7Es+6Y2IqZfrxCoWB//vIU5Dj6ZVsPyzom8I4tDaJ+BtrPV32ASUUn8IvA4cVEqtK6V+iQ/OG/wWsAzcAv5f4Ff/utcHCOMSjlC6MmAwplj/yQlJ1AlEotsvi7OOn4XSxS7RyL25dKVPZjXC7mvJlmtHpHZC2vsiUhuasYsDrC+XaO8Vskj7iaEIivIQa0L5x5r0ps+gaJBalZCPqR9UqB2zKF6W6iTWiRhczTP+rgRU5m5C7qaAaf2yeAw0T/pCQpkRr8LyKy0StUD06Z9tSEn2pEFnr9hwT77eIrklo7juUoRbHOkLnsyTvxmKJ8DXPYYTkpU3GJdIdD+jRiNUSROqHbEJHZmx524aODUxXHULkKz4mB5MXBiQ3IlIbht0F7g/kjQCUVfmbkfs/Xcad++Q9rxMPDJ3euSWQ1pHAqZ/KAlL/amI1LYsqu7ZAb25FOlN8cjXFmSuxDBdYb459REY+kpMQN26WL/HG5rW4ZDuvMbLmXSnhQ1Jxmfy/BAvC5PnfRIbJslKSOHmkJv/1KF6NisEsG2L4ZxHkJTPuPNERLQdJ39DQFU/pShcj4jvKjYfj1F6V9Erq1GrJBRqtyT3hjmE2nFB7TN3Nft/byC+DjlHbM/0KDRmUtFdkByFwg2Rixev+fhZ4WzEd2U0HWsp2ejyBhPnJRwmvRHRXjTE2/KUgNpWXxGrSwCM3dekN0MWvqnxxwMSu5r5iTrxqsz764cMzI6B3VXUjsaJteHWL2ZYe9amvWhw/b/MM3ZZs/FMjolXKoJhVAPshkHn4QFjl3rEazDzo+j+mvlL1/iHwWMwOS6W4+PvyGisdjbAGJgk1w1mftDizs9kKb4nZov9KUXxmohcvLRB8b0uQcpm50ycWEcsqcORHjvWkdNn6lyf+hEBW5yW+A/aXQG1TE+PkpAN2guyg8dbEdWTMq9f+lqbO5/PEq8quksRh/7VBpWPzlI/pskuG5TeG7L1SBy3JOSY7G2pVNCIqUlW5tPpNdn5TV9Q+PwtyVnUJqQqIWufhNJ5k3grorVkyg20IOEgRijv03T1feZbd04xeT6gdswitanJrLp4OYvEzpD2niS9ssGwJG676VWFlxPuQf7mkK3HEsR3Nflll8hU7Jx1mH6lz9rHk6RXNfpzNXi+JGrBXoiXlSprWBA7K8ousWsJElVB+QvvD1j5VILssgBTfkpaGyOE/udbBBfzlF/zqJ6IyebuCzqu1YjmOqrQYh0ZuxUvq/tjMbcwyjOckcWaXx6yfTaB09BoSxKInJFde2Qp3KLEivXHTKyhAKvpdc3umYjS2wa9WdkEs8saFWm6c/KdN45qUuvync99s0bzeIHGARlVF25KVHh2JSLWDvHTJnY3ZPMJQfVjbc3OE5rZ72m2HzGx22IX1tkfSEhrNaQ/IfH0fkrMVvtlIcTF2lLmN48HJDZlpSa3NcWrA+pHEmgDcrc9ds46ZO9GVE/D0jdcgrhJGDfYfMrAHEgEXJCSljeyIbkj908Y1xihsF9v/7MPseV4ZMuFqB0XpVvpLYu578uJ6E4mpVQ8rqg9ICh6fNejMyP03P50gsppQdMbxyP8kSw3vRWNUnGhtS+B0xbr8M6CwaAsaG68GZFZc9n4iEH1AeHGB0lF5laH9Brkb0CQccisyHuc+27I8j+awy2IX15/UtPc56ANiDUN4lVhyFkDTW9ORl8LX6uS2hAkOYqBVorh0QH1IyZeXoJNtFIULpqEjhoBSprKT7jYPXk/9WMwKBoMCwaJWkR7L2hTs/4f+fSPDHHaEr++8RGD2vGU2F7dCBi7JCcwwPglX8DMrDXyMlBYHY/NJx20BbunkuJa247I/GZOqKpTJluPiZVb7YhEreXeV+iqRGj56ZF/wNNJ/JyItNp7IHcnwMspdk9pBrezlC6H1A7HyN0N6e/xcVqa5sMeraMhvXnZAJSGxiEDLE1yNySxG5G/6TEoh/hpRWIHMhs+W48mmH65w9i7bQbjivJrAd09IZGtaB0NKF4N2TljEiQVrc/2ZKTrauI7JoNJxWBGUpP6ZcXO41IVRJZYcJlD0Z/c+ZmSlOtd6M8F5F5dIXcnws0qds7aBI5UYUqLsWjnZzsYfYP+hMmeh1eJj1qBsTdN6k94VH9xIAzOjYipN32SFTFbMYIR7Xw0KZl5eYCf0lh9zconE6hAQkg7c2Jjv3tSkdrXwsvYdOZtds6a2C2hSccbAlx250fpz7YwaZ2mIjrcZeHs+geuvw9FJZCYmtN7/uF/i4rkJDE8KL/cono2S/GanFz3tOkiItI0DzHSxg9Y/WQcp6ZI7sjFdPMGhieyVKcV0pu0aBzV5G6IZj65rSld6bFzVmhUpieiF7svfn9+RoglWkHulqjnpl8bEDomjf0xcnd9akdt4rvSizYPQemS/NnwNemVHpFj4eVsujMW7b3i5JO/GdErG6S2JG5sUA4pXpKqRBsSm2b35KbML/topWgtWTite7RluRaZ1Wg0QhVkOrWphc9/3GPhqwqn7rLxkTTTP+7Tn3LI3GgxWMiw8jnIv2OLFXhLNP6ZmyaDSY3TkMzFzSdTpDYl9TZ3U1F/xMNyQpJvJKWs7skG2p8QgxPDE/AtsiTPMLUdUX1Q3We5qQj6U1oW64xFZ0G8/zMro2t3EMqvBfdTjonk83SW5PnIUjT2W4xdlnRhkJSlZEUzGJOWxmlqqk/4lM7ZQvwKZLLkZeWeqJ4Vboc2YOFbLmu/EmBcTZNdlsAQq69pHNPM/iDCy96rtISVl70jlaKbNaif1IxdUPfdrzMbAWvPQf6KhdOKiGxF84DwErJ3Q6xBROUBm2RF+vXBuKI3H5JaFR+I9l4IcgFWwyJRUQymZNM2XUZBOAFhwqB+yKR4PaR2WEhP4nkp+obmXqkqd08YTL4VUn3AInl6F/fVMfqHh1hOgN+NQahY/eV/9uGtBKyBFsFIT9+XdfYW04Rxxeon48R3BcktvB+Mbir5QnszmjBh3k+myd3u4ydHNtITSmin45L/V7wsC2bxazX6ZUVkSSyXEWhSOyH1o5C+25XgipY44cy94AmwE0FnzsFPmfgj+mXxakBvRtE8BESjeDFb+P0bT2fZOZOkflg49PPfcVn4dpfAEVJTaAt3fOaH8lqxTnTfAgvE4bZ60qa9YGEEwh9I1CLai2KTZgSyiBMVzdxvvEsoa4PEnRh2L2DjaclLtN7foPqAQeNUnt1jNvENm3gjYjApDMfMTZMgKZOSuT/dxs/YmEOhYWfuGBSvDpl53mLPvw5Jb0X4abBcTf6mi9OUxdibFVA3soSQIiw9+T7KL9XvjzeNQNM4rIk1FeXXPapP+gRxSK0LxyHW+A/5g52P90Tv8bgl8fOPtdDWyIi0pRm7EtBekgmCl5NNuvyCRX9KkVkZ4LRCGkek8qs8qpk5vEPuhnhWDMZtxv4kybAs31+iJtd+7B1hQvbHDbpzBnPfqJK7JVmJm58RsdrEG2I51tonv3f3mIXVNmme8RiMG3TmFcWrGhWIhLo3aWF60ubUTggz0BwY9E8OSG0LX6J4wSK5Ja3r7A+kSurMKdIbgcTQZw3UmRYbHxlNSbTEvI9d8qkfkVFo44AA2NWTFnYH3FfHuPKP/x+WP/47fO2Rf4Od9lDeh9xjMLIUMy+2USFMXAjEXSghqSuGK6f35JsR1VMW/Tkh3fi5EG1pth6N0dpjkNoOqR1LCX10T4jhywgmu+LSOCQndGcB+gtZkpuatY8nJeorp/BSBoXr4I4nCRICvu2elF45jCkyqxHJbZ/WkgkKiea25Ibd/1sbxGsSTmkPItJrMs+ORnr65n6T3eNxNp9MS0aCIUCaOYTGQRPDh+1HTQkHrXj4aUXjgEkUAzcvvAS7B72yye5pARPrh01aSwZeTjF86ih+WtE+JoGqG09IGZnYjdj6uf1YfUn46S0FWD3h9Q9nPTqL8jnnvt8mSCoqT00SJgSjqJ2WYI/KaelJKw9l2Hw2YuKCL5qN55xRLmDE4vM+vRnpxZMVn9yKP8pmgMFMhmHBINaW6UWiIorO1ecs4isxejMC6E2/1CR3J8QcwsKX1il9LcmB363j1BVuKaLw79NsPSbTFG1BY79F7iYktwXRn//GLtUHZZO4+R87WF2fKBExnArJXTdpP18WbKGqqT5gUHlQUXrbJLMSsf1xnyAlVVXlAZt+WVO67NPfk6d2SjNxIUAPTeyOGo2RNUE2IrGjibVlY5l4STQMToP7NODetKZ2SuPUNXY3QttiDmq4UHohztpPirdgZI/a142A5t4Yjf0GU+c9Wks2w6JB4WoX+4c5Clfl59yCpnEIzGGI4UJ7v9yH7SVxZPKy0lq/PBIMnRssEY/7GMMP+SYQJKE3n8JPKTqzFnooc9SNZ0eW02MRjYOiqR47b+DlNPkrFiqQEju9oamekrLbLRgULhlMvOORqGiqJ+M4DUVvxiC5rQjjBpMvrJO7Laqwue80CR1FshKw+bg18sV38XMh4xf9UXuhCNLC4TZ8iY7aOW0y+eaQq/9inDAmXvqDkkHnpzrUj9gSqtkVfvdgQqLDxl7ZwGkIS04860dl34osWj9tMX7RE6nxUDjq/al7466Q4iVRmaU2NKX3xJ0ILY6y6Rs2+fc6ZO+K3Dj7X60xfLpDf8kntRORXLVwmprdkyYEBvGqgEiDqSRBXDabzqxFdjXEKLr0pxQz39ohtemSv+WTed9iWJBNyy9K75+/qth8yqFwPaJ4LWTlMyY7p4Xzn16BjWdEbp2oaDCkT86uBuRvjFR0Wjal9oEs3WmTMAbX/8k0zf0GtdNFwjg4dYOtxxTJLaE29yelott9WHgW2oCtp8cwPChdGZC9bhHFTKZeNii+Y9Av65FgTGO5oo0oXoVkNWRYNLB3YgRxAfeMABKHmjQO2jT22aRWRaAz923IrIhqs19WFC4JCac7L3L0wbgAzqED24+pUUCsQsci2WDPWKTvmmTvDChe1dQ/PmTiZQsvD/mbHqYLlQdsyl+5ycS7PhtP2gzH5F5rHUhhuprG8YjWfhn15W7BxlNxqTIagsuECc30yxo/I5XNf3buP+FPullKVpfenRyFax+8/j4Um4Ak/opUMkhA8W2LwFHYbUkpnn0hvC8oCmPiL2cNpY+tftodES+k/7yXtFs9ESOMcb/ELL/ap703Yve4ye5HZjE9QZe3nsrjZRTJO03KrwcUb/iYwwC7JWk4QVJOAC8lBpETF4aMXQlRkcIt2qTfc5h828NLGzKT7zlC04xJCR8mNImqMPBWf25WQLBQPkdkyc2nQlmEq8+ZbD8sJheZVdlU7J7i7hc04+eFQNXca97nkc9/u8nmEzYzrwh56cYvp2Ta0VS0fnOe6EYau2oxKBmUXx9id2U0llyx7oOxrSWZuystrZiKYOybcZI7mt6BEp2FOJuPy+bQn5BKYd/v+6LqSynSKzK1aC+Y5K6ahAnZ+NyiIvc+DCaFDTj9kuAHjf2Cz/hpRWRJkm5kynuZesOVJKUIGj/Rk5PVgwO/XSVejwhtxewP+8x+t47ZkU25cSy6fy/c+oIkPG09FqezYFB/MCIyZTrTPCSYS+G6OPY29lsESfEs0JZs9IOpiExcXJU6+0My6yEbH7HYPSHsRG1KhmF/WlH7iMfsD0PCpCbWlKlN+bUe2ZvCRNSmjDQjG9xFl9RWxM7DSQFThyaDcUWQ0vQnbRL1EHc84vZ/s4+1j5r4BQnWkVm/ovawT3LdRDvSatRPyUGQ3hgBij8aYHiK9oJJat0gfKyFfSPJ/3jxs/yL9z5DrGncNxz5yx4fik3g3sMIYO6bVSJb+O73yMi7J2wxBtHS62fvyM0zdsnHWI3jZcX7z3AViYrk1t8DEruLEZm1kOrJpDCwYprmAelRIxNaxyVIs/LEGN1pi7WPmUQxKf9SGxLvrE3I3ewx/WpAdyZGY7+J3RMd++z36tQOx4h1IzLrIcn3hM5r9WDzI8JVz6yFmF5EZjViOAbejE/tbIA2pYyz+5rOoqJ0UbH45Ypo8T1NGJexWO68I/LcmCLW1ix8TbTvUUzak8qDMQaTiiP/covOL7TJ3o1Ibg7Z8+UG6TUJUx2Mx9h+KmLq3JDpV/oMxwWHcVqa2e/siqNRSdNaFFqvn1bUjlqkNj2sgSJwZEQa39XUj8RxR45DTieiud9k8vxAsAFbXjd/Syi1C9/sYN9IYrqjL9OA6ZfF4yG9BqmNgbAEQ33/HjBdyH03RRiXcd2NXxnHyyiGY1IN3PnpovAOmpryyzK5mXh7yJ6v+PQnRUHqFjXjbxik1xXZO9IaJrcjgoSB4cHMCy1APAeDhPDtY02DnDOkeSwgvWxihJrSRQE9lZaNojtrEB3uAqIVAHHKdnOKypkUvTnBrlJbERNvB/TmIoqvxPDSivF3XNyCYulLMHbFI39tlDkRN7A6MsazOwbGwCC1IWYwrX1gNmziVU3uvZFT9F1TNtKEGlGFzRGYKv6HyeezmC64vRjRqwViLfCK0QeuO/OLX/zi3+9K/ls8fv3/+FdfPOQ/SK9s0TqUIkiKfNb0FOlNibkuXZOTKExqBhPg5QzcvMnC821MLPpjlphDomjv1yz+7++w8w/KOA0DP2XgZaF9MCRzW5DW9rxF/raGQJJtnKbQRSfOa/ysRRhTlK66oESFNRh3cAsmyVpIvKEJ4gaDcYMgHZc0pFpEd8bE8KTXHn/HJbVlMPZuj/aSg9IGnQWT4o0Qu2aRuWtg9+UmKP/pHaJ8jsGkQbqiae1xqD4qmXtKj9DouOL8r/8m/1vtNMOcRetQxLAUZ/JCQGiL+Gfzkzns98SDYecRG8tz0IYiWQ+pHzLJ3lZsP2nSK8eweopYV+bvQSaBNhXJHUH4w5hC23LqNQ7b5O5EoxRi8LOK3J0AP22QWwloHLRwCxprKCezNZATs3lQdAebz9hgwLBgklkVXkF60yO37FE/FqOzIISiyFa09lsMylLpYUgoR+tAksSO/E5tGsTrAfWTJvlbElEexgxaR0Naeyy0YQmNeXyUP7nKyCRFkb8doM17gR8GQdqhPw0zL/XQlo3Vg/4U+K/lKV4Vrkp61WTnUen7h+MaayjVQuqi2InZbYP+YY99v+cxmIjRnxGcxByYtD7RJ3Erdp84FTmKzpwl4Gpfsf24SWZN01kQ6bY1VCSqsimltuV7sPp6ZIyqyGxEDMYNhif7OGs2w3LIsKjI35IJWHfOItZRjF+MsFxJsYpvWqSf3aERJLG6ivoPv7f1xS9+8bf/4vr7UFQCpie20CoS9x40zH9LIsH8pASQVB6wxFwkktFgdllTuuZz93M5ds4KkJZdiWg+4JPYMlj+nx5gz1dao8htzeyLPRa+oQlSkLm4TW9O2FzxXU2YkDDK4nty2vbHDboL0qOHjqj2cis+kQW9CZP6QZNkJcId0zQOS8k7LJq092q6i+K2Uz/iMMwb7DycoXlQbKb6U0KGyt9y8VPgpYX4dPc/3SNR3U3NxtNpvJyYdWoTSu8NsYaazEbA4d/6VWmJ4pqJc6JVrx+0mXy1zmDcYPplX6S7zYixi5rN5yK684ph3sRpQXcBnKpB4YbMkqe+s45bjBiWZHE0Dsu4bfpry2RXxDo9SEBzn3G/ssquygbgZxR+ysTqwvSPA5xmSJAQxVr+dkjxPen3x95RpO9KDHn1jB55KTisP5OECGZe7uNnBUzz9w6IVwXAG5bke7YeaJKsRti9gPFzNbaeSJK/KqdnmIkoXg8onTfF1XcP7PnSLktfd4nvmNgDsV3rzWj64ya7p2QCoEIxKTWHit5MgtoJESClNhW9WUBrstds+hMGVk+IX0HJJ70eYbcN0psh8W2pAuI3HWrHknQXIsKYJnPbFFOcq2ma+ww6C7KpGr4mTMDsS0N602Kj1zgkVYnpQu62T3de2igvqyjc9MVy/IAIy7YeNUhuRyTeSdKf1sy8oMguG2hDcefzlpjKpmFQMO5X0NqA4CsTxJoGpvchbwciS5hhIEKR4nUJ3khUNcbPVenNCmWzswipTRFRDEsCZFkDAepUBK0lA0JFsqIZu6ipPJQTzUAAa8+lsHsSb115ZobMHYOpcy71E5p41WDyLY/2gkGQVLQPhMSrBtsPC8tr94RJ9aRNshJJ/kBLpgdBQrPv9+tMvBOQXRkS2TD2rgRKhHFoHJHxXv6GlM1jFyVr7/YvGrT3SUvTLYvCUTTgCrsjIFSiIrbcldNx2kvCjkxtSbpy4ZqcZqav6Rz02Xq6NMJCTKbOuQwL4sqTuCvKRy8jbUSsqZg67xFZkjW4/YlZ8tfEUyC0heuQrAY0n1gYmVwE9xOIvKwo/zrTFkHcoHAjkLwArakdtbE7AZNv9dl4WlE7ahJviFNQZtVDj+ztsrdlohHriIJw6rxHa08Cuy2U2+SlhPgYtiLsnlB9hzdzOM2Q0DHxJmU+25sRbn1yzWT3hIVbEqKP6UKYjUOoCVKa5l6T+jGh6oYxAREzy10Gk5rU5kipaCqsgWI4GZGsRGRvy7UevygBJ3MveHT3Bhz+P9sSiLoqfpSGL1yBwVxAdx5SawbJTYP0ZiTiIVfalERlBEx2NG4hYvthccOaecXHHMqGXnnKZzBuYfXEu8JPw6Bk4WVh/7/r0DwSMPOjkPqxES9kXfp/bchBklw3aR0UvclwTA6x5I6MkLVC3KprH7z+PhSbgN0JKF73RwCZwaAoWXVeRtH/wQTxKjBKlIWRu29TQJL+bEh6TSqE7EpE4aJJe1HRmzQYjkkv62cU7lhI7UicwbiMHOONiO5sjPxVuTm8rCkuuXlF8V1Bf52GiHnuod/2IGIwHaC0ZumP26RXDbb+F4XVDemVHaZfFvlmcktCJ8cviGeAEcDmZ3ycpvRl0uPJgsCAibf7RJYQU4KU4ASdRZFMJyqaIBfej6y2BhpreC8Hz6D0piVhLQZ0Zk3aizHcgmLu+x7DciiVgwO9sqJ70GP1OYvdUyJGStSEMwBSNndnDcyBUGPb+0O60zZzv/EudkdUeaEjNlXVh6IRG01OqVhTs/NQAi9rU34VkluaxM6QRC0iSIodm9XXFN73mX65g580yN4Z0B+3qD4sCz5zB7r7ffrT4s409Vqf9FZAekWx8bTF6nMWYcwgsSO+guUf1SV8c1ewo9ABrxhy9zMpdk8ksdsKL69xauLehJKcgq0nc+TfByJB392Mum/Iag1E2NOdV+ycjo+SjDWH/3Wd9pECfvZe6rOM/rQJyVULu6vo7BPN/uaz4g3YP+zKoiyJhmD7yQjDE4JPYkcIYWjIrMDUTIPqwxFBSvIn0+tyn8c64u6c2JCRdKylGIyPMC9PphPWYER0a8sEpfyaZHnm7vgUr/VI1OXwaR/4YEzgQ7EJaNukfkgstrUhJ4GXUQzKEoJpuqI2q5yF3gzMfH0dN68Yf7vF/LciYXSVFNsfC2gcDwmPdCXi+WqANRSDCadqMvXV22LEuN+jflTR2qtonJAFXjtqktkIyd4NaTwzlJOzI/Lg/oRBf9ygdtiidEHK/vrJLGOXPcxvFHCLNjsPi9Nw7lZEb07RXRRwz81LT58/57D6+YjWokW8Js9NvDOgN6PZejRJZiOgOycONSoSB+TIkQqpdMGUz5iXEyZZ8Ri/6KG0gJaZ1YjIuTcJkVlyr2wz/RJ42YjMekR2JaJ0ziYs+cy8JIzD3pQ40XTnxB/BaQpaXT8UI3fdJL3ps/VLp3DaEbGmbHCRBYlNE2fXG8Why2IqXvUZjFn0xw3yt102n0jTmTew+pL9FyQV3WmL1U9k6CwoBpNx4s2QxIakAvkpRelNi7F3NaXLfbpzcbYet3CLMrFIVAw68zZOW+jJd3+qSG/CJPuzmzh1IU+NvWWSuwndefEtnHg7Yu5rG+yeEB5DalvyA2qnQ4I0jL/rok0YlBS7Z+7RjWU8G8WgdMWjtejQfGBMfPqyspDsjqI7B05Dfk9kwd4vexghlF8yxEZ+2SEY98UsJq1IbFpYQ1G/9qcVG09Z+GlN85Bm8O1J4tuiORgWDIYFsW4zhxo/rcndiTBc+T2mK+/NLXE/wt5Py6bem4vYfjhB7iZ0Zm12T6SoHzLZ/GhI+ccf8ixCP6XoHPAp3pA+NPf2tjjNbBl0Zi3xaLMVYxcU5VcDVn92VhyAPpkX3XzVJzIhvhpj3x94lP+9uO0OCibptSF2VxKA7/zKPkwPPnXyCmFcAjy1HYk3e1xTO2Kye8og+3qCxlkfAj6WGAAAIABJREFUt6CoHxUbbz8tohC3IJ77zYPi85fcDbG7IXv+ZMhwPGLnyYggKVbbjf2mWGmnFJOvNpj5tnk/zTZR1djVHmpErfVTJku/v4kRStSXNRDB0dTrHayBlKCdPRG1pzwqDyTwsoIIx7paDFni0us2DomYpHFY4dQDrL7CzSk68wbxRsTYKzHilQGDSU17r/gKJrckfHTitTrDomgrnGaEUxlg9TU7TweieFsXW+tYC/ysLYDljHAKdk/YdOcU3QVNa8mBUWCpimRkiILC9b6Id+5GbD9qsHvcxi1F5FZ8rIHo801Ps/GRFMOCQXJTMf/tNpk7MBjXo3AXk+6MiTsW4hbhxaN/RuOYxvjcLrWnXToLSjIDphTbjxhc/R8m8Cd9vHxE/VCM3mzEwjc0bl4TxQxaB2RsWrpgCkawGDJ2xaf0XsDgnzSZ+P4qgzEDpxUy8wLM/KhPb79HrCXAaqyjmTzvUT8SJ38rZOupiP4hl+Gcj9Gy6M6L6WwY02Rva+pHpA0BGLssbljxesRwr0jThyUZWZZfHxDZivKroqnpzlrMvtin/Lo4XoeHuvTKBqWrkhfZm1bs+1KP5I5mOK4Yu9DCHXkYJNYlJfqDHh8K7UCqNKeP/OSvkdgNUFpGgrPfqrP5saKozQzpqVp7DCbPe9z9vMGeL4d05mP0J0X4ow3BCkxXQkWLlzX9SYPMWkh7ySR3OxQm25zCz0SkV6XkH7/Qo3ZMbK9UpBkWTXplUe8NxiVQon7QIr4rwpbWkoXdk5EQBoxfcFn/WIzMMvdVivkbXW5+Ic3cD0I2n7SIVwUw04ZiUFKMXRowHIvR2C/kpNSmFgBvImD8TfN+kAfIDVR4P6RxwMTPiBeBn5ITgVGWX/VjLkYlRrwquIE11MTaIZUHZLSa2NXkr3fF964Ai39cZ/UfFBm/6ONlTPyEaM5TGyKT3XzSYvrHAb1JS5iXbYlDy65E1I+KLiCxG1E/rph5KaA7beGnRDjVnRMCl5s36M1oSpe09LIaJt8K2R2pHiNbNmYVanaeDpn9loHT9Ln9BZPMNZtYS9PaLwKYwVTE5DnYfkLj7JpMnvdZfc7E6ksuQXY1oPKgRaw9Ys/ti4g1DErvhdhdsfBCQXJLMSyBOx6y7w+H3P65hMSMNUR7b3qIOU1MTmSrLyV/vCHJx7WjFuPv+kS2mMn0pzXlV0PsbsDm43HUaCnFmhCkxUU71oLUjgTq+oUIFSisjgSaTr0pXo+RLaBtal0AxCCuRq2I4Aq52yF+Sqq1RDWiecAgUYHOnojEjoCLRiC6Dj8t7V1qO0SbUnFqQ3CY1776Tz+82gHRt2sSWz2GBZPSez5bzxTF5eVjPfI3PRHXdGHtYzbxLYv2YozBhMLL6fvWSbUzAZXHJDarvWQwdsWjP2ky/3vLbD+mSNSFdJSoyAZgDjR+xmYwqfCyBp05C2ugcRqa/M0eyZ2IjaeMkX2zonHAIndXiDozP2hJnNVZh4VvC83ZLUjf7I4lKF1SNPbfc8KRLza0ob1PMxyLsfOQCQbkliXww6lDfEfIJeK6KxqI/K2I/rgxUvAhrjkDJNjjqs+wKOkyi897wmYMNG5G0ZkR0DSzHhHEoXEkzdhn1ok1IMyK8rFbtuhNCsCYqIhgpjtjETqanbM2TivCLYiAp3Q1oPqAwnAl2MNPKSbeilh/2hrhFGL4ml6XftdPQfGKuDIltxST50PWnxGuu+HLZ1ShpvKoZv/v+tidgMZ+h/T79sjoVJFekw3eqYnL0dSP1QhviUgvtJh90Rdv/0WL1IaAYIndCKdmEFlCr777WUWiqlj6047Itjc0VsdAmwYTbzJKltL0ZyLMoWbrCQER0UI6qz/p0jho4uZMElW5LqEj06NYSxKbdk/EcccE7EyvCwktf1OOe21JrmOiqjAGErVuDpWIyGYd0lsBka1QPrg5kUYrPfJm3Imw27JGujOK0lUPt2Awdknwh/x1Rf5WyGBScJH0lrS/6S1RlbpZ2cwMX8xoPujxodgEjAicZsjqT+TpTRsMCyamp8ndjoi9nabyoCNlayVi8ZsSy6xN6B522fdvq9g9MRZZ/Kom877F1LmQ4vWQ1qLNxJsdln95D+NvQepWWwJHLvu090jk2covRAzKAdUHRyW/q8ms+fhpGzdvMPaOqOtiLc3UuQGN/RZ+UrHx0RzjFz28gmbjyQRTr3eY+34Ha6gJEmLFZbqiZjM9CZbozcgNUDsq/SCRjC+HpRH3flu8+XIv3hLbs5Ri56xYkJmu5NIHaS2jxmLI1mMWE+8MMALN3U879Gcitj8i0lunI4m9/TGDzpKUme3fn8H0NCufTgIywtPPNHDzUvmk18V/QUVC+unMmmRXJKR17TMRsbYoA8VhSNHca5J/H4YlOTXNIRTeH0rrsCFef50luQ67xy101mdYEjfgxgHRS5TeNlj5ZILaMUfyIbY15d+9LO9lXBSIw6lQMh8jqbbufsZmcD3Pnc9JhPs9YlX3qMvuSSHQpDbBboMxkJHZyqez9MtaJNR9xdZjCdDQmbHwiyHZmwb9afGP1EqUpX4a9FAAYy8rZfzkeZ/+hMH4BSEkaUM2//nvBBghNPdD/9Ee3WkTfbqNW5QqNozdyw3QDBZFg2G5mm7ZGvEBJGNQG/KZB2f6pDbFrKZyWgxv4ncb/0Estiug4DBvULwird3OWVsAz0Dwm+JVyXvI3umT2gk+cP19KNqB5MSc3vsLIiV2Whq7F5Fe7rL5TI7cXQHtBntczN0Y+RsyB79nLXZPlFN/boBzOSmndvyeNbhc+OxqQLdsktqRSG0vY9CdEUPH1JaQMHJ3AuqHpfwdljT596UUy94Rx2JtQvUBg5kXPbYfdijcjGgtGaQ2NXY/YlgQe/EgLYSR4rsybgTupyhFNoy/K8Sde6VjkJCS0QhEQ5HYkZl1ekOQ6ngjorXXxE8xOmWhdVAmI6k1g+yatApTbwyJTMX2ow5BSrPwzSHNfXGRTu9oqg+HxHZNxi/K63oZRXuvOPRmb0uys1uw6E2ZdB4bkHg3MbLAlt6+uyAbg+Eqxi5pdh4SZWZ/SsZWIBZiRJCoiFoyuSMlfeau8OvTa5rc8oB+2WHjo5r0bYv+zKh0vxqy8amQhT+WNqs9b5FZC6kdlVGxOSLAWH35XdZQqozpF+vUTxaILKid0sy+GI3kx9IDh3G5bn5KNnhrIAu6fWbIzJ/aDPMGiVqI6Wphi9pQuCrWXkYgBjW9skGiKq3O+EWf7rQ1YvrB0h9scOcXZ7D6kLsT0p4zyayH9MommbWA6imL9KqmdUDaEaeh6ZeVBM2OmIjNfSbDMSnt70Wj6X09oo0kdstg4kJAd8akOyeOUPGqqBgjW2T1piuHR+lyl9s/nZa8hmuw+1BIetkSZq0X8dIP/vmHtx0AyK0EhAmZeyZ2XJZ/LkusrbHbAbEWJG865G5Bbtlj+6dcsisBzcOa4gWx79LbcRIVsRmbe6FPkNDk7oS0DgWEMeH1t+dMvIxB7ZhkDpZf6xHrRQwmJQMu1tL4GZg8H+HmxZqqtTdG/ZBJGFOMvRux+glJFPaTit5+j9CR0VxrH6M8OMXinwm2kahFdPZGtA4HxGua9KomXnUZTkY4Dc30yz1ytzTZFTHRiO/KzuAWBCRLbwQYgdBgU5uCQ1gDiNUNFr7lE+sI+Qig8mCcxkGH4jWxSN98MoHSMHbFJ9aJMAaGnNp5g/aSMcoaUOz7vV0SjYiV/1wENdmVgNA18bLSZuVui/PzwvMDFr7pi7/ChNw2/SnxHjRdaVuKlzXZZdEI2J0Rnfct4Xek1zXFdxpEtpSnsV2T0jVfJN5I3zr3DYPqKZuds7b4NR638DNidOLmDKzhCPfxNLVRBuCNX8rfP2XtrqI/ZlI7auIVJPNRRRJ+OizJRjAYl1K/8GNHQlIeCmnulVShWENahPELXWrH1GhjN8Q3cUL667WPS/r11Os95r7f4fp/XWbxyxWydwVTsrsjgHMwcktqQW9WEWuq0ZREWjmlNa09JnYnZPwdj/w1mc5kb0lAr3U5TeaOgZ8Tb0wvJ4BvvCrWatk7EUt/VMFpizeFNdRUzqRZ+sbgPpZQuChkrvpBm/7k3yGQ9ANiyL6olNpQSr07+ucn/tz/++ejGLIbSqlP/E02ACOAxj6L0mWfeDNi+afjjL8jLrJ3P2MzflF46aGjqB92MO8k2HzCIntLsfzzBbxRZHR2xWNYUmw9lhSrr3e3mf2+wu6EDMqawk2f9pKUd047onI6hZc2yN2E3eMmbl4xdjGkckasuUwPWvtlYQ7zhqjOOgo3Z2L3Ioy2RWo7FC34SwGxTkR/7v9j7r2D7LzS887f+eLNqW/niG5kECQIECTBPBxO4oxmpLFkzcorlUcO67C2SrZ37dotb23tbpVd2trakm0l29IqrTwaydbMKExiGKZhBEkAJIjUQOfue2/fnL909o/3AtqqFSWtZFfxVrFAEkD37e9+3znved/n+T0hldMu3WnRKADMPis68PYS2Fe3mf9OSH9CxmS9aRnVBTEptTPrHgd+v4/T1rQXLKx+xLAAtXtC8tcDMUvVoXLKJXtrKIvTRdFYNI/Jex+7JEwEkbYGJHYHsmtPK1K7AXPPdunNCDN/+1PjbH8+IPl6gkRF5NTLv6kJ0prmQRhmDPyEonwmwc5j7iitWDN2Uc7/Vhdmv1ujP6YoPSrJ0on9iM7SqKHbDO6UqJufLbD3QAwvZaAiGRkavlRzg5yiflCCP+MlTXtZztdTr4Xs/IAviK4peU+1k5rJVxQz32uS2jAwfWEKFC/Ibu3lI0k20hJp3y+K3NxtaGZe6jAswOBTLc7/z7+AMTBGcfY+GLIYVU+mSG1CakeAs/Gypn3UF27leXmY+5MxmoeSzL4QsfXZCRoHTXYfNKneH8iRyRCoqDT25L5Ay3EmVpFIu7H3A0r3O6z9oCGUqe1Amr37QqFKbwaEcUHfZdYisrcCOovSc3DaEdufmWCQl6NCv2hQuDJkmHcIxj1qZ30mXmvRuEsYHOX7/5Tn78/xjP4q/98YMoD/U2t9avTPH40WgOPAl4ATo7/z80qpD59NjF6hC15Os/uIhdsMmXlJU75PEeYCDB9qR2LESxIMog1IbCsWvjsQFZiS0qizGFE5NeodlDTesT7DpTGR+k5b+BM+tWNi8Y0sWVD8lIRNeGnF0u/VxGiRNph8I8RtKNLrEU7DwM9KyXU7VsptSrkXqwhHP0gods/Z+H+9xtjbMkvPP7pHe0kR3zMYZAWomb+iKf/gQXYfEvhDa9EksSdjtOYhOYd2p236Ey77pxS1+wJ2H3KYfmWIUzdpLVrYo4616UFnxpHk24KUoLn35XyoTSmD/RRsPx5n86mkZAciPPzeTExK9EkZQ878gUV6O2T/hEVnSeNu1rHaAtFM7YYU3+1IpVIWnqDVUeSu91GRZljQtA9naS3D2HmT/piB0wqZ/V6Al1bsPOqSuw7x/YDxdz26hz1KTwbkr8ix5LaYqb0EhSvSfwhdxcxLEfFawDBrkH5HFo54SREvK5KbgmDvHEiBhtyvv0rniM8wM+qMbxgjOhSkNhWGJ1i03rSieTBB5pZm6udi3PWzfw+zr2gdCajeZZPY1WRu9eU6JaW56jTl4Tz4az7NQ1B+3CdyoHrcpHXAoFc0KVyVs3tqQzH3LYPGigTPBJmI2e+16cwaaFdGwyoS7UnhglCjxt4LccsWZl/8FeZQMgymX/XxEwaFd+Wa7j0kTAm7raSJXJYQ0t6Uwk+OoLWzDq1Fi/gNl+IrNtV7MyQ3pHE7duEvIRvWWr8I1P6sPzd6fQH4itZ6qLW+hVCH/5Q1iNGFgcSeaPc3Pm3QHzOY/V7A+CsWk69L06d2b0hqSwI0rYGmfigm7280d05uSZMosxFg9SPyz8ZYe9plmDFI7gbEbzk4DU3rmE8Y16Q2hwyLEfv32LhNTfnBPM0TIe1FRe2o7FCtA8adOG5rqMndCBmMCQveHIo0VWloHgmJVyD27/KYnqQKDf/jJOk18dC3VmDxd0s0VwyqD/hCnG1J2EV3WjiDmVXYeyximDfYeVS6xfE1m8k3fbysxfwzQyIbdj8eYnc1Xlp2LS+t7sBVQ1fCUAZ5g/RGyOyTm6TXNdmbEvKRXQ0Z5uTro2HsvRAvq+hOSAmd2haFXfXcJOZAxqPDrMHNL6bozsitsv6ZOJGtKd2XoPRkgDlQtGdNwlSIn5Bqp3zaZv+kjelB6Ar6rHrcwd3v4+zaJK859McNIe6clNxGtybTl2FB052L2H7CIIgblJ7y6U1JVZFblYdt7t+8jdPW9AvSgL31L8+RvGETa4jnP3KkJzT7XIvW4ZDhmKIzJ8i43oRBvygPRO/YELOvWPqa0I+qD3usfT5O9fEhk+f7dBbERFU+bbP2+TjBWIBdthl/R5psVl9MZ6X7ZAEZFsToldyRhTi5brL18TRuXTP2hsX4BV/oQKEAZ5vHAwY5Y+QAFPrw/hlN+2DI9hMWpc94tJaFRJVelXsxjMkDv/ojKdJbAWPvhZhDOaqUH9R3TEf7Z0O8jJLIs56+swn8Sa+/TE/gvx0lD//K7VRi/oIxZMFAcFK9CYPpl2Te7H7zLSrnApxWKL2BuimklfcVbiuiekZApHZHjRp7cvN3ZixaS+YdPmCiGlK635ZEnwNQfE0eqPKZOPn3FAvf2KdxROa0mSsm+Ssh6Y1IxnST0ShdRyTM7TkTqy/nQhVBrKJorcDhX+nQPCY76W2IZfWcT3dGrLSxfcWtL01KvLVvyBm/FDCY9+RnawuK3C1ZxGoRUSYgf1WTKGsq99hUj5vc/KJNrKoZe82i8bE+8X1NrB7SnZVRWO24IrMRsv4ZYQZm/vAS66/PjRZKIfYGMTFkTbwBaNh9WDH2vkeyFBLbh/aSInszpHoSBtMy0/cTitSW9CJSuyGGL2lQXg6Wvio5g6anccsWTlvL3P5WdEe96I/L2Ko/obn6dxJ44wGDcdkVB2OK9C1F7QTS5X+8xtxzAWMXxaFXOWVQeNVh+rWQIKkEt+bB3k+eJrbvE1lyhHKr4tQr3WeQ2tTYLZh6rU9/KkH2imjsE7tq9NloCldFOZi87GINoHbUoT8TQiABqda2S/mU0JMrp2XMl9pQTD0n05Bh1mTmlYGAXy6LxyNRDRkcHlA9qWgdhM5hn+58SG9arsWgoOiPmfSmRcDTmzAoviEkYhXBxHlN/cc7zH87xOoaTL0akrwUY/bFgGEBuS9MmHxDNqrklqDzOtMmsaqm+6kOUy+L2EqEdjJ1SO2ElB6A+e8O/7MvAr8ArACngF3g//j/+wX+3zFktpOUHX0jZJgVHFb/C2eZfNGkftiheVA01pEpVcMgb5DYtMjeDHFr0mzZfViUcY3D0FmWxlzjmGCtYxWYe94ntSFlcnfaIbUd0ptSBLk4429HxCqSAx+6isYRg+SOx+I3Q4wA+ks+XlaIwSqUTPniWy3x5EfCQ0xfNxmORygt2vnCazbpDU2Qcph4ZyAW6EnF1EsS8rHxtEFs02GYkzipeFkz/X2PYVYx8YJN7YQEcWpDCETGQEZX6e0AY12wX6YnFJmFP2qQ2hQH2cyLsgvd+qenyF0TeEnjENRPhrQOiBtwmDVoHNcc+IZH+YxDd8okf3UoM3hf+hvakCScwQQULg8J4tzRK5h9cXF6WYli702p0Y4kN2BnTv5cb1Jx8Ndl1zQHiti2DU6EWxPiT3I3onkiJLGn2H1IEbxUAKC9qJh7foC2oHlY054Vl1zjeMQwD+2ViO60Q+tQRHdBZMmxfU12FVrL0ji7+UWXjS9IxSThoZA9WSVMh3SmLVqLDoOixssIv1LbmsPLu8Q+U+bxj1/EbWpaB4QxMPmmT3tRMxgT9kOiHLD5lEtnUUZxtZOaXtGEps3ccx5agVW1mHxV4TTkzJ6/HtJeNBh7z8dLGfSnNGOX2pTPWAQxeXgHN9NsflKYmZ0ZUZsGCYP0uqZ+TI0yIyTtOVYXUEpvVmN3wXg7TWRB6THRJ2RuRbSWJYk6VjaoH3E/9Fn8Cy0CWuuS1jrUWkdIyMjtkv8vHEPmZcU4MsxLx3nvQdn5Z756g4VvD4Sn7oARyq688I0arUWTxj1C1Zl9XuyxxQuaWMkS3v4taWrZPckxjBxFoixegN1HpLG1dy7JzpOiu3YaEo2lAiTAck448NPPCo/O9ASG2h9TXP1vkoy/GxEvKcqnpQ9QPC9pP7fn2b1pyaKrH3Kxm4rMqoAg2gsG89/UxMpStpbvl6+7+5DDxGstMrf6xPYVKogYFiNiNU0Ui0iWA7Yft5h+RcQg1WMOTktx5afiBAlFrBkROorUBgTJiM6szPzT67Dy1UCOTeWQ9gFN5oZi/64Y5lAafV7OojepcBoBKpRmZmpTkdqQPkXuRsiwIOrFld+sSHpSoElUIqZe9+nMCOAEBfN/VCW1E5K7EeFlpQ+z9J9q+OmI6W/b4g+pKPYeibAKA9KbEo4SJKS/QQReziJ9C2a/F5Fd8+lNKWJlkzAh4I3qKY3TNFChLEj9cSHwxCvCQojvGRTetJh5uU+8Khbm9vkiUy8Y5G4MMX0ZefoLQ/7u577Nu5/7Wf73ld+ltJNjt5+heVCowaGraazY5D+A8Xd6tOcN2rMWYVxz4Ot9EnuSV9AfV2Sum9z6McXKV+oULss9kF3VdOYU5jBi8i2PxkFbcGCupjebIHNTk96SzzOzKlVa7biieUjTOgi7jyiaB+WonNoW+XjraED9uLgGiaTPYAQQ3w/JXJZAmsSeT2pTJg52949duv/ZFoHbOYSj1w8BtycH3wC+pJRylVIHgEPAG3/2F4TsKoSOiEWsnoxJvAzs/shBQNDUQXzk8rvqs/XpAv0JTfY9G7cRsX+34KL8hMLsg9sU1l71HhF5bHzaZJiXxp/dlR29vSS/ZzdMVn67S+665Nxlb0q5OsyLJNVpyfnKCOWM7zY1y1+V+fzt9x/fl8Zl65Dw99rLEbPPt/GyAojQBtRPyKjJT2t2HjHxM3KuTOzIyM7PRvQWkmx+IoHT0uw9KM7E9pJi8Q8jakdslv6gT2fGpHG3jxFKk7P4ooOfkuDJ+lH5SKdf0QzHI5J7AX5Ksf1YjPaCgR8X8Kefki63VpDclod//ELA9mMxSmdtkSmnxKASxCV3ILMW0Zo3uf43xrF7EfXDJqYXsfVxU86dBw2qp0Pah3PsPqpoLRq0Fi0684qNzxdE+TdvEKQ04+8OSWxZpF5MCD25ruFkm/RPbjP2gWQxNA+JV0ArWcz8tGb8fETxQki8ZEAEh36jjZcRX4ddtileGjD5pqRXBwnF6pccKqdEeZhd1TRXDEpnY9SOQ6xskLwY46sbp8kacabMEGVHXDm/KI3caz4zr0h33cso2osxGSdbYHUMujMuXkaam7dj02IbDjd/NE9nVlE5G1E5K9Va9YREg2klR4NY2WDzU2D6mq1PaqxeRPOIVKJOS2F1FZkbcnsFiT8eBfdnAgrvmMR35Zqo6PavIrePbDE2bf8tn86iHgnNZBz9Ya+/aAzZzyilLimlLgIfA34aQGv9PvBV4DLwLeDva63DP+t7hC7EGiFBUi72bRdYYk/UcaWzcVSoRrn10JmxSJQ1dlvRPhDhJ0U4NHY5IIwpBuMRzWVxlB38rSbtJYVbF4DIMCc9h8yqQeGDkO58RJCKaK0kSewOCJLQnTKY+44ASbyUzK7bi1A+K1LSftHg1hcEz+20NGPviWTVTyqmX4Sp10LG34b9u1PEy5BZD5h9uU/+smC3nJZi9kUBhfamxBZqdyOcmkG8NBCKbT0idPXI1y9Y7vRWRGTLvPz4vywzGJMZ/f4jPpm1iNSqsAmclmb/bpPi24rutEX7YIjdEUVi/kqHwmURqkSWOOl605q9B1yaSzKik/g1mdj4KWnKhXFN7ZiBl5cz+CArEuDyvTaTr428FBpUIPyFmRc04+/6mJ7sUuPv+gRxseAqH3YfckX6uupTuccUwtIvOdS/MkfpRwa89HO/xI0f+0VAFu5YVVN4TxKcDV+4fiqE/Xsz8nNc8EjsKrYfjbF3vy33VE2z9PUQPx9it/XowY5wa5rpV0N6iwHmED41+wFf3niUB779U2TfjBEmI9Jr0vtZ+xEJPe1PirsztS5k4tsCnnhF7lMvC9V7Q7I3Iuy2WIYnX5XehpcR5NigYDHxbp/srYjcakSsJOxClZAj0/RLch0HxYhYVYRYUdZHm7LwRBaMvWWS3gpIVCLGLiiCxCiZa0ZAp7mb0jOY/WVH8GVZTWY9oDcT+/Bn/KOgGHSX5vThL/5jejOa3AdiOzU9TfXekIlXzZETTdGZVyx8s02YtNl5SFKHgmREctMQoMXjCVJbwm23BiLrjO/9cRxZdz5i/Dz0frhJbzVLrGKMGAIixrm9SxfeE/OR05Sortaii+FLgGavaNCbVgzmPeb+yKR+2BSarv5j8UxmVVxdbkN+NQIp3SbfkhALpy3il9zqgNZCjFhdEnQaB03cmghDnJYmUQmx2yHNZUe0/vMwfiGiuWQy+2yTxok0nVmD937q5zn2b/8e4ZEuU7/tsvuQjJLiZdHxtw9EhMmIxKZFb9nDrNsjXb78zHZHQl3rR8RM05/QxPYFk1a8FLD5WU1s0xZdvCG9lok3hWeQvx5ROiujOy+jJUDEkL4IGuqPDIldj+E0RslEGYPehMHgXIeZX3HYftwmVpVRZeHqgNJ9o+SdPHzwt3+ez137DFffWMKtyvUEuQ7Z0S6Z3AvwkwbNZZP0pjTPlJYuvd3T1I8ahI4muSX/rUYZEd0ZRebREu0XJrHP1eh+kCexI8fFxiGpMuA2R0GSiJLrkmExKGpiZUXkwOLXq+x8fIzm8YD5b8Lel4ZknktQuNzHqnVZ/6FxIgcSO7IrZ29Fd/iWnRmT8QsDymdiDPOi3hQeGBhaAAAgAElEQVRFo8ab80hcd3GaYmpKXW9SP5WjO2Vg9aF5NKR4XqYjdkdTP6o4+MvbrH55DnMg1yCMwYHfrtA5nKe1YHHpX/2jP1Ex+JFYBJJj87r4L/4hi9/QbDxtkLkqZXZkiwYguyrCofnvDtn4pItblyZdZxEiS+NWDQpXQ1I3mjSP56jeJXZSkctG2A0DpynHBD8lfQW3pqneF3LoNzx2zyUYf3dIbKdN5NpsfiZLZIvZpDcpeXG5mz7tWYsgoehNaQqXRd0YxhERiC3Nn9txXYnS7Sx7+Rl7Bz2yFxy8LLhVmHirze6jaXpTmnhJylUMueEMX3bz/rhUP6Iwg8k3Q+qHLWafazGYiLP5lMnEW1KBaCXgzUFeyvfBuIwwnYaB1ZHIbacpC+PBf79N+WOz9CdlamANNOWz8j7HzwvJuTdhkNoO2X5CSlO3IZLX1pM9ki8nRR3XhfKjAWZTKLft0wMSl2NiejFgMCbXxvTka6tAZvdBUjPxlqa1KATn7HWpAPvTmvnveFTvclGRoNWqx2MjPYco/uL7EfWjQiIqXFLU7o2YfFmOW9ZQs39SGAljl2V60Bs3sYayeCX2fNrzDo0jMP6upnJaEU4NsTddORZtKRr3eSSvOahApgLFS76oCRvy3hMlTfXTfcKhyZF/NaByf4b2ATF3NT/RI/29BHZH4zYjNj9hyGj2rir662MjQZgszKndkJ0npHKKlQ0iG6Ze99l8yiRekh5TZl0oRSqCzj0Dis+5dH+ghX8tQ5COWPjDiNaSTEyqDwaYDYvktixOkSnXrD8xSio6ZHD9f/qTF4GPhGw4cgSDXblHQBidBc3EeTHtTLwjZfPMSwHtBZfYvsxEO493ie8pVr7axfQgeavD2hcLBDHF8lfqDMY0+6dEnupnI4F1hJDa1sQqmto9EYV3TG7+UAwvp4lf2WPn40W2PpklsatZ+r2aRHI7shDVD0nElTZh8VtDvIyiuyBeeauv8TMytzYC8SNU79EkSiGxmia9ETHxgk28Et0J3qycSTEoaqKEpP22DkUY3sh7r+V4ENuXMnDxmwPie0pyDAua+rE05dM2uasKLyUGo/6kuMZUJMlMfjYivmugfCnr7bbIkYsXInaenqO1AvlrIWFMmqHxkqghjUDES42TPttPQqxiMPticCdH4eD/NhDE+KN9vLTCqlqYfTl3TnzbwXiwjtuMyN70iSxN7vrthGhfSLi7mjAZUT8ku1h6XdBrKLlx1z5nk7/m01qJuPV5hyAufZPunKJ1LKD0lE/+iia2L1LZsbcMgphi/7MD4hUPb0xoSms/rHEanlRvEwZWX9NcccS6vS2LplNXmDuyAKhQHvL4qiOchJTsyN0Ji8ytiCAh5Xh3RhH2LAw7YjCVoP1Ej9DVJMoh3EoQmYrqPYrU5TK5KyIXLv4zg9CVa5TaCSXNuRsx/rpB+qaBOYDhREh8o0m8LGiw/PWQ/piBWxdjVuEFl9oJsF7KYg4Uk69IL+K2w9UpWaQ2pKLqHPHIrUakNwUPVz4r1KUPe30kFgGrLw42uwM7T4hwaPWH4zhdGQ81jokzb1AQlpzhg1pN4jY0XiEmo6ZjaUJXzuYbny/gNmQHi+1D9orJoKjozosBp3ZSk7tsMPlciSguevcbf2eBQVHGcZEDlQfy5G76AoIcSJMovTEktR1RuSdGeisge1V4gLnrHvnLsurmbshYMbVmUHpgpFJbMUhteVRPSppR9W4JJp171iOxYVJ+UICciUpE7kbExPkuoSuqvO7xIeufiZG/5tEvGEy+GbF/RjMYj+4EqE6/0sPsS9MxdBXucov4dIfugYD+gthtgxRMvB2x+7iAUe22orlk4mVkFx6/4GMEitaSwd6DitiuTXxXZtD9Mcln7M4YXP/xAolKCDvCystfEc9/Zi3AGmqi10QwVT5tE6RHjVmtsds++cuK2qmQlf8wZDAVMvmW+B+2nxbGv9IyStx7wCa5KQ7OWFWTu+GT2BGtSHzVxelEAjZJik4jSCgWftWiM+OSXJMj1eT3LG79YEzGzVOaxO6AWC2icGVIf0pShLUB8Yoiua2YfjUge1MAHaErXXe3JhVG64AcG+Nl6d8QGFBxiVxF4tUkyS2D/ZMWQVaEbJNvRFz5B1MYgezGN39UZDSRJXJhbUhHv/LUEKsrcma7YeBNpDA8WWi2PxUJbGRMkV3zsXsauyPCsNy1CLcRsveATfuANMznnx3iNkRYlzvv0Bs32HhaFpjEjkH+vY+4lTiyhPvnPd5i8vtC8ln+TwN2H5MdZfoljVsXtVh7RUZ13pg0t7aetGgui4zUaSj2HwxwGuAnNRNvR3fUdWFMgJ/mUJPYMRiMKfyZLKlVQXdNvRYSJKTD3x8fMQhnrDts/vIZm+6sK3LQhIRXuG05ONaOubQXZdVuLpu0lgz6EzLKcmuQ3tA0DjlYox0zvSbWYbvl0ZsRc4/paXGT5RTVkwlaSwa1E3HmvmYSOZr9kw7akpXf6ijMoaJyn/DmBkVHcN9daB6KGK6lmc83mD9QQfniZZ97vk97zmTiNYGqJHdHP+uMxH8Ns2I2cesatybn6MgeRYPXheU3LIx6BQlDQi5it+29UDtm01qQvIVBQVKi3IqB01B31IbaALNrYr+/zsGvDPGTBrFqAJ5xhyRk9SWsdOx9j3g1oP7UgMopm8hRAkItaZpLltB1HIXhK5pHQ9Y+b1J6SLQNSkN73mDqVSnL557xWPsBsU/f/KKNChRuxcRpSwqxNmH3YfFpJMshXjHEK8jIufpgQLwyUnfOiSip8LbJ/HdDtp5StJcl+ms4FjH+mkHrgPgtDv6HLrWHPUJHMfV6OJLGw9SrUDljsH/SIXYjhhEKcSl9U+4jbUgzL3fBBgVj7wdsP2rRXBmlRo0ITLuPCERl7KImsxbiZS28rCJ/dShPtYbsVZP8NaEkDQofcdqwNiF7M8R5MUP1pGJYjDCHUtaV7pe5Z3velQf5spB83ZIlzZ1VCFKa9pKc3xJrNoMJSJQUrQWTQUExftEndy1i/NlNclfa5G6GTL02ZPdcnGFeUzlt4GUMtCV0YCOA5gFToBpFMcX4Sc3eI5rutPQIQhcqp0QI4qfFNWcE0mvIroYUL4lrsHUkJFGWqG63Jgte61yf/NWQ0oNpjEC0Df2xEa//uJYybiAPWOmMSfa6onPIl2yDGZPFb/axuoqF74jarDtlMhiPmHm+htVT/JUnX+O+wgYvnvw93vvBf03niMfeA3G8DCR3JFotUfKJl4TU050Tgc/Y+z5uQ+hMdkeqKMOD5gH7TnPTaUk32vBlwRiMKYZj0nBL7kpZXzsV4tYU4xcDsqsh2dWQmz8cI16VBl3ts0e4/hM2209ptp+wGTtvCnykLBDO0IG1vwr7J23UZowgoWkdFK9B7dEhfloyHmM1ySJMbpokN0wKFwxiVVFFBglN7ahJ7YSicq+Lnw+pHTNJbpp4OUHAGb7QeTsLEfkPNKX7bfYeMEmuWzg1Ay8H2Us2gzFp7hYvhvQnZXcu3Wcz+YqicEEaqxNvjUJMUlIRlh5IE7vhCuR1UiL04mXpg/j5AGsgPRJtwI2/bdGblga2EIKEMGT3NI0VC4VI492WaFyah+Hql39BiNGfEBZ89bhFclfMayrU5G94tFYiOtPWHU/Ch70+EotAaEOs5t3p/jp1g8bhJPmLsgv2i0LmHR7p05sRy2/kaIYT8hA4daHXtOctEnuaxd9v0p3TxGpyc9aO2HSnDbonp7n5Ixl2H1ZUTrt4OU3+ith/a8cUKlBE7ug9tASqYbVlMUltKI7+r7cwAlHtaRNSG9BeMMjckmSh+jHxjQ+zBsO0sOJmn4XSWZvejBCEepMG+RdihK6SpKGBpNr0ZuT7JrYNdh6zSO1I/8Duys2RvmbTnjUxh5ry6QSDyYDEK9eonxh1+NsGe48UyF+GM8lbzDli93imn2Nqpi5467s77J5zibIB5dMS+hHEJCbNrWuqd9m0FySoZfKNIV5G+he9KT2yUiuah6CzKL0SwYPBwrc9/CTsn5LPJrVqMSxGeCnhNjRXTPLvKXoTBpEz0rg3LeyGSWxfUT0TMhzTxPcDBmOKwZgitu5Q+CBg/hmPwvua/CVF9ZRm/BkXuzNq7J6URqHVg+RORPWBgOmXWyQqIWPv6xE9StFZCbBaJpk1zdh7PtnrBnPPBdTvDiXs42CT6t2KAz93nfxlaZ6aHuSvRkJy6oIxlIpHmzB+0cfqyVnb+dGSQEy2h8RrEbkrgo1P7klwbhCXv+NlRwQtD8betGg92JdgFAPcNZfZF/pkb/QwB3IsLr7ToXZEEodWfqtOatujuWwwHNPYLcXB//vv4mUjcm9JaC5Ac8UUfLyr2PjrAal1g+EXGgzG5BjxYa+PxHTAXZzXJz710xTPt9h4Okv2ZiSjnbhGG5qlP/SIbCmh0hvCW7sNiRgWxBhTvs8QZnxW4qZCR86LY+9pdj8ZYDQtDF+Rvcodf3rtnojxNw3a84owoSm8r3HrwmbrzJjUzgQU3rao3RNSuGAS2XJGTJQjMtfbbH5K3qsfVyOqsTjWctf7lM8k8LIyYhq75FM9YaO09DPaByLSN4XGk9oNqJyy8dMyJUjtRJRPy4eauSV2Uj9lkigNqdwTJ3REmFK82KN+LH5Hlx6riYx04i3NzsdDxt6yCD9Xp3dJgBvzz/k0l2wKHwxYfzqGORhFtX+tgTcWp3TWxeyLtj6xK6POYU7K/0FRM/uCz2DMwo8r/BFlJ4gLQ8HqR/QmTfm5bhl0Huox+5s2w5xJb1yUgLGadPezayGl+wwSu4rOoqDAess+uXdskiVZ1CunTIwApl8Zsn/SxWnLrtidkj2rdVgst3bdJMhEFN+S4116QwRcE+/6rH9Wkdi0mHxzSHfGYZhVJPdCepMCk8lshMT3Bqx9LkGsKuPU8kMhqVsWqS2pOurH5UiUuWGQ3g4ZZgz27x3BQfdhUJTR8m2LcJCC/kRE/rIcb60u9Cc1B39xg9W/tShBOD2YflXG2aEr2o3uHMy+4NNatOnMKYqXQmpHJOoucqB714DCSy6GD/WjsPy1Lvt3J/EyMp3yshGpdYP2gYgoHmF2DcKcmJ0K72tKHw9IfeBw+Wc+wtMBQkleqZ/MgBK6qtOU807uA0X1WIzdBx3G3vPozJgyex9FjfcnRyXytwY0jmp607IAZNY90msQL/vYezbFdwTKYIRSPqsISAeENix8qykAz7hi92GL2jFJ053/pjgGUzct6ndFOK2R8GLCYOfxLL1Fn9RGn/6kojNvkL86pHo6Yu3zcaZe70iK7UxE6QF7FA4CrZWIzA2D3A2fxnHNxP9wc7RDSK+hdswAA2I1xcSrdYK4QWqtS2fWxUtLf8JtRVTuTdBcgfzVPv3piOJbdSJHs/PpgNwFm35R0dzISqbijmL90xaJ/Yj1z8aYOC9d+sjSbH0iR/W4izmQ3eo23WlY0CN0myZIR9SPOPSLBk5HMyhKqk/hakDtBFTvMlGhZupVcbGlvp9g41NSihvhKAknrojvSyBI/orIpCfekoeCSPwf258JqZwySW1p0muCPzc90Vo0DonvQZuQe8/C7IhXP7Fpsn8mwmlq0mu9O1g5s2fQmw9oLwiPy2lr6kdGENcRk7J0fxK7oyh84FN+wid/0cTLytHIyyhyVxSJXel9lM4aJEoBsbJB4QPpBcX2EeZCXonIbDHkyM/vUb1HOvphXAxGG//VIhPvBEy9Lji6nUcS5G5ExMti7hq7pKkfcuSavB1QO2YSJAVQMvaez7F/XsFtCCY+yAcoPyRZEo5Fel2T2pD3GKsYHPi9iNi+QfK6g92RRrEd9z/6xwEjgNRmRBCXf89/ICsgQPFih/wNT+azdzlMvN0X08eUInNTZJjdWU1rISYZdtNDmkdg62MO42/U2XnUJZgbUjsOmTVp0GQ2A/JX+7hrYqq49cUMmbWAyed2mP6+UIB604rmkgR7jL3vk7plYg00e+cE9ZUoRWAKHjteFjnxoGiLaaSu2L8nSfH9gIk3IIhplj9xC6srndpEJWLnUfE3XHrmCCiIVaXPYJ1q3NENXPtyDj9h0DgqkVZ+eqSSu0fRnRXDjNn1yL+vuPlX8+QvKeKrDm4zwm1o5p4RnJbd1uTfVxiexmorBjlh/wUJzfzX9shsCrdh/GKA0xJR1uTrEaUnxulNK9I3TbI3A+y2TFcS24qJ8xq7FZLYkSNU9lZAEJNxpZ8U7T5aHu6FP2oy81yN1rKieNEjc2tA9d4Ipx0y+WaXiVdEATr5vMXSH7TFP2LJUStRljCPyJLmbpCA5pGI3DUYuyQ78eFf7dAfV+w+nL5DEsp9oEhsWWRvyjjXyygWvt3G7kj/yI8LuTd3IyKMGVgVm9ROKLkFhz3ap4aErkxz3JomjGm60xbDccHKWb1RrNjzAb0FiV5Lrpl483nG3pW+1TCnKZ2Tz6yfN9k755C9Loti+bQ0wMcuD2gekONgZ/aPG6gzrwRUT4cMCiY3fiYvqslaxMwzBr25JFufEBt54wgkd0MSe5rBRERzycZuyXWKbHA6mux3RYb+oc/ff+Hn+8/1EhySUF4jUxDXVld2j9IDaSp3O3hpwXZvPxEHQ9J6aic1c89FBEWf/sRop9+IMXZBM/NKQH8uTXY1IvNWjPF3R8TfUS6cVesSq0D1nE9iV9Evmtz6a7Os/xX5utnViMyGhJGUz9hSbq8YxHdF1WX64OzaBElpFi7/ygaDnEH5fkFpjb/RQgUCUJ1+NaT060uktiLCGNjtkML7mtkXZIbu1qVJlNrQ2N/JSqJsFuafCSk/LCBNqy/Ys+60YuaVkNw1wZFvP5nD9DQrv1bCTyu4t4U11MSrmq1PSFpz7R4JHm0uW7hNqN4nZffYRcWNn5yktWAxzEHlbovcjXDU7TdHwSmawYMdgoTg2ssPafLXhiMRi4y3iu9qtp60RAk4ppl6Y0B/JsSbFZVQZznF3iMFstcj+kWL9c/GSGyZ7PzXHv3JGE4nEm3CYYP1z6RxRkpLcwDZt3awu0JKah/1mXu2S/a6GHa601J2l85lgRF8sxfSXDEIR4m9vSkHpzWCwozF6E3JZGWYN4jVQhI7A/pjUmV4KQM/pUhfdohfcxnmhWUYa0Rkrougp/i2CJWGeYWX1qz/sEYNFduPywJXPxi7w/s3PYXdEOp19XEPP6lprggm/jbDMkiYxGrSDM2tysTB6sPOIxaT35epSbiRxEtL76j8Q0MS2z3yFw0yGxG5q/IM2f2IyI2o3x2R3gkIUpJoFDpyn9z2HvxJr4/EImAOBC7RnR/ZIn1NbtWHSIIaYzWh1w7TBku/WyFekvm73TbYecwkvu7QnY343E++hAqgP27QPGBRO2oTxKXM3n0iovrZAeMX+xjDiPaxgmDO1x0GBWgvyLlw/vcNFr4dUnpQznnlMwbakpm00tCfljPgzhMR4xcicTgO4OaXF8QOfV2CSbafymJ6EcOcSXteICWdWQMVwMbThgRzLlgSBhpqYduH0pA0PM3S7+1TPWGTWhW7bnpTgKOFKyHbj0u5Grl6ZKoyqJ6blCbWqxlqR00qpxWxXRM/YeDUBNee2g5xGxHxLYupV0P2z0RMnI8IP9Zg+tWhHCceh3h51BjMipQ18UKKnU+EzD3XY/w1g81Pioy5fCZGZn14Z1qAQoJPDrkYA4P5rwk5qXFQSnenG1E/Li5Np6UJ9mO050way5L8LExECTZN7oqw5uaX50XC3dYs/UfYeSxJEJP5+8xLXQwP3HqEl9Wktj3iaw3cBnhpacLVD0soaP3hIZV7bCJXU7wU0Djl0Thks/NYYsQCFC5Faickd1PGgmFc8Oa7P+QxzEP9oSGVsxGxfRkVTrwdkbzm4DQNChcV8c2WlN9tTW8uwKnD/HND2rM28asubk3hFQUKYwRS9e6fFF/KkZ/dwK37GN4Ii1YI2L9HgK0YMs41B2A7AaV/HtBahtaCQWtZUTljsPMxyFy1sDpiErNbcq/FK8LovJ0H+Se9PhKLgJ9WLHzbY+JNIbzcns/nVoeUz4j7qj9ukCwFXP9yEW3C5JsDsqsap66YeWmA1VV87SuPYhztoJWc07pzEb0JCXJIX7cI+hbdaZfaMZe9Bw3SG8EdWsvkWz69GUVkKRoHbWZe1FTulakDSMMsuxqS3JBFxamZ2J2I1oEYg3EtsduBXOzpVwKsPrjlHnYvwk+J/RlEQjv+hkHz4CjPwJEdLHulTWdWbkQUrP61MWIVORN2Zk1i+z7GUEaXyS2DRCli+uVQAB+ZkRZ+TaCp/UWf+e94OG3BVTstGed1ZkxUKCX0zqMm2hx1/X8pibaU7CqRSFpv/VWDIBMxHA9pL0c4JYv60biQlSyBo7YPBax+yaK9pEhsK8bfGZLektzE/LEq208Il2Hu2ZZkDezJ55Reg+xNn+wVsR935yXHIHRlrDf73X0YcfOG+YhhXsQ7rQWLuWdaeDnpzeydSzL+bh+nEwlG/FyMoJjC6mr6U6IRCVKasfdCZr5hC3XIFvy5XRZLb++AVJGxmpzBATrTMrLM3IB+0cLciBEkNdN/YJPcNEnsRQzGI3YfMph+tc9gKmAwrth9okh/UprT8R2LyBFLuunpO2KjmecNUltDWssia49VRbTUOTXL2tMuyQ2pOCZfMhm7JI3keMlg5uUe6c2Qxf8lIHyxgNKS3Wi3IL6riG+ZRK5YtCunhaFx6Bc2CRKyACf3Plwx+JGYDqTy83ruH/4jBlMhZtcgVpHuc+GKLxbJu2y6i2KYiCxZQSNLoBUqEsdbalvIQq1lWP5qnWv/fZz4e3GcpvQPlIbh8gDqDoldcaXF9yMS2z2q96TwEzJu6k4bJPciQlvOt2FMSLqdaVGepTZu5xPIbla9W4I7Yvsi4ihc9agfdLD6muRewMbTBhOvyyTD7kpDqXrcpjcbkVk1CB0JCNm/W41cfZK0NPdMm5tfTDH5VkRjxcRuw2Bc9Ah+WsJKlIaZP9ymv1Kkcsqlc8zDrtiErsbqKOyOTAC0uh3wIr0WL6MJix751x1plE4rpl732DvnULgcUTsmwpTsms/egxZuVbwayXLI7o+JQWaYVxDJNRiMyQKXKMmRyxpo0hsenVmHyBl9TqH8/qAoEeyRrejMi6lq92GFUzdIb2j6RUX35ABr1yW+K+PRYU5GmKndgLUvKBb+EPYeMCle0jQPyLXvTSsm3vZZ/7xi8euSlBy6or/XSnZUPyk/R2ovoLFsEyRl/r5/tyJzCxpHNOk1g+ahCLsjm0eQCjG7Mqp2a2KwsjujnXyUFhQkpDKY+VaJ6z85QfY6VO8PcCoWqQ2ZEHXm5P2t/RUoft+ieUiqj3hZ0qciW0bVXk4z95xg7fszIe6+SWpD0zgG06+EbH9M6Fp2d5RUZEGyLJ6SxJ54bLQBfj7ELVnkr4i2oLMYsfbT/+QjPB0AsjcikrdMwSbNiFY7dA327rdJ7UTkLhvUP9knVo/uxF3nr4+AGyZUT5jsPyLYqPK5PFNfd+geGWJ4MJwUq2buVRe3LhJQFUJ/zMCqtJj42g2MUOAe2VsSAe10pLk2LESgBUVut9Soi64pXhoQupKOk9qKaK1A63DI3gOOGHCmFNs/7jP2tkHtLoWXMijdZ7P+Q9A9ORB/QEcz/XKb5rIxsr5KrLTdgerdKeIVRek+g1hNSx/kpngJVCjOsu6MZuczs6w/bVO85JG6IsaXhW+HqEhGe9mbEflrIUYo3ersqpwjE9dc6vcGooWPa5rLNsu/usUgL4q97C0JGF38g44EoaQVtSMWS/9GCE7WwzX8+9tYfenwp7ZEr2D1pf+w/TGH+nG5+dMbcqbPXZOmbv3uSB6al0N2Pu8LWjstI87+vX0MS5iDRgD7D4ifHzWyU9+wqJyyyK7edjGGBAnFYDKkuWyz+A3N9scsEiUh9vpJRfsLbWr3iK+/cUzjNHwmznfpzYV0ZmQak6iETL4hpqfiO4qF7wxY+JaH1TJJbismX5cKysuIorRyf3TH2Vr4YCiNzLuKRK5kAca3bIoX5M/sf3IAQG/cwmya9CcVE29HzL7Qob2kmP9ul8SOonNQsiNrR13JqmwILs1PSWBK+bRF8W3pN2hD8Gz5a0PqB8VE1JtQTL0aErqa/AUTtyaAkmRJGJMf9vpILALahMZhac4kd0PslsAXq8dN8tciKveKjTQqx6gdMynf52J3ZMc0fPAzguHOnXcoXhTFW3vBZOXXNJPfWmfqBYNhMWT5x64z/92enJWqIe1FGC6OcfV/XCFWi1j5nYEEebwWYvrirovvGXgpAWHYHUbKMc3mkyLx1DbsPz0gsjWFi5Lkk7s+kJ/ltQTNw5C+KSXi4u83mfsjA3vLpXBJkbvWozufYPxdH7uj7mDRggS0F2VBitXE7DLMjsQqCtwGbH9Ck9qU7u/8syGbT9lYPRh/N6J6wsYrhEy9FlE/bDDMCposdIWw1F6UG7r4mkXxYsj8Mx7ZWwEf/HfTBDFF5VxAc9mmdhw2nk4z/UKT7v2S+tFeiJHejGit5uBKitS2RxgXJNjkm0MyGx7T3x+SvS5R4G5NCESDj7VZ/ZsmXjFk7G0Dq6vZ+IImeTFGZj0gua2I7ync9+LYV+NEJjROeyTWbNyGpn5sFLFWEBGQ4ctu3C8YFK56JDdMmoek02/2ZeePl2QRKHwlyeT3xRwVZkNufMmldjzBkX/bxO4Ker10Vvoodhsqj3tsPBWjecARS/Z+RGfOoDujRtH0MprsTcoOfvNHDUl+frck5p43hph9JAvQASouqS1NkIDsdcX0K30aKya7D6VIbWlK9yfpzWiKb8h4NNaQRK3YvqJ2l4xd/aQ0kLvTiuZBaZobvqDyTA9mnqmRuxmy8Vmw2yMa81KEESj2zomw7cNeH4njQHxSAkkjByZeb3L1yxniJYPErq4sKgEAACAASURBVMRGdR7oM/dbFo0VW6KqQ/GrS16dBDkErkAY3Ca0lgVXldyORjFgkmjbmxJpbmYtwu6GhK6sgf28QfWcj1OySa/Je7qdhxeryHswR1l7XkZTvKRpHDToHx0QuxoTSm8ronS/QZCOMHIeyTfj8iEMFOl1WTxur+C9KfkAh2OCNE9uywdfPm1gdxTqvia9zTSYmqmXFeX7hCAz/UpI7ahF90BA8pZFf1JmwoYn50PlGSS2TdIbUgIO82LDdpshXtq4E7RaPhfi1EzyH0hPQFtCtHVbkt6jDdh/yCe24RCrSslv9yJqR02WvrpH6clJ+uOKuWe73PxiQqYygbD9hnMe09+xGGYV6a0AcxDROOiQXZMUHGMYUj6bJHTkOOMnYTgZEt8SLkPrIGSvy7i0OwcL3xlQPxSjMy9HusLliNaCzMXjFZExpzcG1I7GqZ7zSV1xsAbCFWwchrH3Raqb2o4of9IjcTkmhKK3I2rHTPJXQ8pnDJI7slOqQMCpKNnxtSlU5t7EaIKQVgwmNAfObXB1dYaFryvcuseNH3OZeV5Q5GFcFiq3JlVt8R0kr2HWkOzAvCF29lbE1mdDDvw2DAoyMm4ekN9L7mjG3qrSPJEXpF5SGpzmQEAyvVnN9MshlXstVADjF3yaB2yyt3za8xbDnHwmib3RMzDUvPPv//FH9zhgBGLO6E8orvz9JHPPR3g5TXdOUmQzL8cwRojmWFlAFwCDiYjOnKJyRr6On9aktsM7Dbf+uEGQlFFM/aiid6YnC0tCtN9WN2SQM6ieDVn6HelsN1cEURaZ0J2VvELDlzSe3A0JggwdGH/Hx9pxmX25Lw29MYk3HztvYKzH8LJw5r7rLJ3dQo3O3a0DAtYwPPmQ43sGXj6iel/IzuOj8MoDPo/Nr/IbP/DzaDfCGkQj+q6Ug+MXfJx9k9R2xOwLUlZn1kNi2zbL/8nH6kLmZo/W3R6Royk/GDLIiwIvsxZSuT8iuS7JPrUTsnCaA4hcKLxWEqNLVlF8RSAi3XlN64CiO2ni5TRX/96EgEXfD9n8RxHaFhu109R4hRB32ya1NaB2JqC1YNFecEhUIoZZk+rxGINJl96UpnsgxGlqMrc0M8/J4thelqpwmJNR7viZEn5KjDHakKCT/pgi+9Qe+ashtfv9UYq1MBbtin3njq4fk+694Wt6c4JaLz7nYngiM68dl3K5fthk9qWAWDWSaC8H6sc19ROa3kGPued6kqXQFr5Df1KgMzt/sIhTtuhNmDRX4tg1Sba6bahKbciCkl6VMZ8RQnpDgDCmJ/dk9YRJ6qpD7ahD+SxEprrz90MHtj5dpHbMpLVgMvZ2DbfBHcFU4T1Na0nyCoYFzc6jkpbdWLGp3yVHn96UINYwBHH3oc/ff+kH/M/z0haYfSHGFr9vUTprYnUV+asRU2/4QntZsZl82cAINP28BH64FUlmcZpi5IlXRCE1+YbsEpNv9ph5qYPbkLP08s8hjrh6SGRp9u8W73hq1WLvAUcEFo6k5sYaIsVM7EouQG9S8hBSW+KKa67YxMqK/rhDkBLJsFZQPROR2hQ12duvH2L7e/PU7vcZTAUsfnuI3ZZmpzWQEIooHRDfsjh61yZPPH6R8ZkGB+NlHo7JRxP9nX0ahwUIkl7XbD8ugRitRZkipDY1vQmTibcDSvcJA2/vwRSHfjnAHCqSGxadOWENtBZNEtuC4LZ6Cn/aGxmDYPydAR/8k3HQkN4I2X/Mo7MgMuvI0TTODpk6WcLqSM/AHERM/5KD3ZLSu7UM8R2T/BVN/XCc+IZN7obHoKAo3W+IyamIhHW8r5n7jlRWyV2P+L5HYk9259ihpjS20lA5P4lT9+gsRKS2pCJJb4a0vjPFzqdDJp8XEGx3Rtx1IBVieitg5atNSmcNupMmK789xK1HI2PRKKtyBDoZvxCwd7/Qnd0a9GY0iV2D6Zc1ubcc2gsy9zd8OWZqC/LvVnFamonzEe1FRWtZMfFOhOEJviy1KWRgkPuoeTygvWDQOGQQxKF6t6RDJXZk4uS0NNG4RNqNXQ7wchGFD/q0DwZk1mRqcfVv5OmPS7Rdd1ZTP6JEfbouFmy3rugXhchF1ie5G41i7KUiM4K/hFhIKTWvlHpeKXVZKfW+UuqnRv+/oJT6rlLq+ujX/Oj/K6XUvxpFkV1USp3+s75HZIlUNbMeECSFlhsd71A7aozMPyaZjYDEni9noVCQYNZAvN6hI0cDp6lHMdAeahTCqk0RgCR2FdW74nhp+ZFz12Rs1jo4kq4qCSJN7BgMiuL86ixKg7I7ZRI5IqmVDAJN/ppH/lpA6YvD0cUWjfmB/xjQmZdVOMwHhK5m5Tcj8pdMSmdj9CdcClck9687ZZC44dBfGfITM6/y7+Zf4aGpW9gq5F/XF0mO9eh+Y0oQ35sSb2X15EbO3oqoHbWonRCdhdKawbjG6qmRWUXh5SL8tIyh6ic0neWA3BN7GAGo5S6Ja0LwSW8LQnvi+yaxhngBklfcEckWDv7iBoe/fJ7Ml6oc/L92idVD1n9Es/Wkw9Lvd3DrivSG+AOqJxXtJcVgKqR6QvomTkPRf6SDNZDPuvRoRGvBIlYV0MfW43FMH/ykweBqlsiBv/mlb6FXurQOxLF6iuKFLp152P9yl8iB+C2Hyn3S3F3+nbpMaxqyqLQWLLY+mSOMCU48TFgM8watw2LK8jOy0Ec2NA5KFHv+Ayh8MKT4rmgytp8O6S5oWkvS+LW7Ed35iLELmp2nxuXrJBTe0gC7BVtPh8ICmDKYfq5G5GgGE5pBweDQb3r0piPi5T/uK/VmIuI1KdXbC4rs62IqK58WSMvaD8SJT/ToF2VKkVo3GHsvJLXtCRh2BCPtFw3mn/GJTEiUJaQ196pL/ajItLvzEb1R3sGHPuN/Vk9gRBae1lq/rZRKA+eBHwT+OlDTWv9LpdQ/A/Ja6386yiX8B8DTwAPAz2qtH/jTvkdsZl7f9emfpjOnyF8NqZw2cKuKqdd67D6cILcasvMxmPi+lIlOV0ZD2hy5si77JK9UuPkTM6hA3G3j7wyJHIPtJyzcmqJzxCP7rkN8P6K5YlB8L5ASNzua3w9kF0huCe+/ftgisxbSnjdHdCEZD1p9yKwN2fi0S2pdGnjJbSnjzKG+Q34VwIfQYdM3JAgidEWq2hsZYXKrAX7CoHZM8dgnL/K91UOENRdCRWzfYLAyxKjaTL+i6edFBRf7f5h772A7z/y+7/O8/fR2e0WvRCHB3rmVy20qu7aiGVuOE1m2FCWOPJlxMplknXHi0diRHSdRZM9YVlnH8lq7WmmLdkVuIblLEiBIAgTRcVFuv6f38rYnf/wOoI29tOU2wzODAeYC95yL932f5/n9ft9Wi8ncGbD1ZErwcwXTZ2K6MyZuO6Y3J6aroSf8B22LD+Pf/MjX+Cu5zXvX/Dea8/zqqy+Qu2jTeXhA+myCICUuRIXLEgvmVRXt/RHEismzivzvvs61f/QQB37hTQCsmWnKn9hD7QFJYW7vg+xNqB+LcWtiemoEYmkeTvo4G2Pfg74iTGmCiYD5b5mUHxDxV3uf4NzDCY1zqM3gdoY4EeNtWXhV4f+7nYj2osWoBE6DcVaEJndNZiDi0Q97v9Ri48N5zKfruP8yT+VBUWj6efEHzN0O2XnIxGnJIsvfiKkeU7jHmpgvFiRF2pXPCJNiSRe5kLktfpXdhwY41xISxroSESQMOrsUYULfgxML16Jx7iK0dykSFU1vXqTCpUshg6JJb17CWlr75b4NZkNyVyzSL2xTbmRQhsZvuqjAwCiOyPwgibZE50EsQ+L23hi3YVC8FGFEmu1HTJKb4nVQvKBI7YS0dtu8+3/+ewqItNZbWuu3x3/uAJeRVKHPAr89/me/Pd4YGH/9d7S83gDy/4pF+b/+UnJCoOViZ27L8KO9J0HxakjtqNCddp6KMX2Nn5I+NlHWdI/4dOcttj86y+5/to3bEF37+nMOfsYgd01koNPfE/JGohJQuihJtPWTsnsnt4V5l7smOoTMuzv3cuBlwCNpsV5DPAfXPuKSWhcegd0Ram7rQEyyGhGkBCcfFiXIMrFpMcrftZKWDdfwxeuwfL9Fd84gtwJn/t8TqNsJjOKI/BUpTXd9EXaflNiG3oLoBZoHDBqHkkSO4MzZG9DaZeI1Y9xmzGBSk9yJsYbi5WeMFOSC/98GAPBX8xvs27ctG5ehaR+QSiO1oXA6MW5NSuDsdZkndBdkszzwC2/y7c1z/JVrNwm3dyj+09dJ3zLRFmRXBL3IXRNcfVQUfwanoUjlhmLN3RN+QWpVMfNdi/Av10jsKGpPBHgVRedwQJiJUa/lJGw05wvHoyBqybXn5dp5VYFYS+9qCnvqFK77OC1p96bejtn4UF7MQE4XZSC6YdA97DNxLiY5tnlLr0LhWkiY0oyyMiANzhXoz2rmX+4RORq3pUlUNX5G4OLqKc3k+SHJcwlJHN4X0F427z0vQSEic0vQmP6kLK9ENWTmjJCSzKEgXZtPGYQpgWcHk4ZsNgnN/HcVmbWIxiszzP+2Q1BOUDpjYYwUxmqCMCWHjVsDvxgTZBCrtb5Ur5EtTkmjIhjB2LD3iE3rwf9ICURKqV3A/cBpYFprvTX+q21gevznP1MU2Y/GkMWdnqQBZfS98M7+nEx3O/MW+esxuYsmxbdNUlsBE++0aB/z6c8oUlclxad5WLP1sRmyd0LcZkRqc2y2URKF111cfvXjDs29JuYADv+Dugyp5hRT7/iktgWqWvupeRmsTJnYPU39IWGEdZYEz87e5J7u220IwzG7YkhYyfjmz74RjdleWgI5KzGldzu4LclTjC1NbEvJ2DwAqZ2Y1KYi/50EE+f74pP3WYudby5SPyiEESlZBT7SliTptvdJ/xybCj9rsOubI5LbAUEa4oQkIj1z4PqPvZ/NQQLj0zUKLyVw6ibDE/K5rb0mYVIGhP1ZTZSISYxj01f/5TEAfjrdvvc+s7/2Gqkd0c/bPU3rYITVFRZhfykk8mB4M4PdUUy9FYgnZDmicgoS/7BA+HSLyVdsnJYmtWIzM/bP6+yLcN9LUrgSUboc4Rdg+Q+l+unNa/qf6DDKGWT/7xzbDztk10Jq91nUD5n0FmIah6T0XvxGFasP3h2H6nGD7Q+HbD1h0jiq2XpCDD8iR5G7Jid/9iasfSSF1ZdFFNkKfy4gfVsSnuqHXQrXQ/rzmpnvmlh94Ub4h/vkL1gkarIJq1h8E9c/bFI5YZO/Jt4H+es+iR1DEq2PtEiWYwrXA6yBorXHpHpCUAutgEyIn1fM/kATpkTM1DiicbqafV/s0NsbjCuZED8H248JujNzWpKqvUZEd3cIPet91/WfeRNQSqWBLwN/XWvd/tG/09JT/DthjT8aQ2amUmRvxwTZiO6yonhlxPSbMU5LTqPunEGUEC+51l6Hzt4MqmfhtJDgkpsRyXWD7rKmcdBilDdFiebIgDC2oTdrMPXDBnEiprsv5J3/8df5pW98HbunGMzEbD3uECYMYlOGlOkN4fP7GcXEaxa9Az5WDxJlNY4OU2PZbUzzkCa1HRN6kNqOSW1HbD9qkqhHNI7HVB6JiW3F6vNZtp40cdoGQT6mcFlOycwd5CRSMp2+88kkrYeG5K6YdE8MGczEBBlF4wXJbIxsRea2+PiVzut7OYKZO0N2Tnm0lx0KV2OwROew3sv/2HvwNw98i+Z7JXEEHijSbyRp7w+lzUCgWKurmDwtm6Fx8gjTv+lx/9/+RT4+dxKAb2+e49ub59j+mSHtvVD5xAhjpPALmqmfXmX+JXH5yd4QDL56wsYbS4qNQHH7z2niCzmqpwQlue/TV9j51IjuYR8VCpRaPiUHw/SZgPIDEtlmtxXZP0jjNWK2H7VJPVqlN2WKW48p4p3siihAb//kBNZAqLtGpMhclLZk6oyEzRq+YjghwbGmL0Qvpy3PTuOgaEesmqgMa0clDGXzaYPEtiBT5ghyN2MmvukxnBQ5uDmSlqr+lI8K7k79Fd29EYNJm1FRNBXdrTR+WlF+QEJNi5dCgpTGiDRrHzPJn3bI3wjZ+pxP9rrJqKjwKga1jw/Z+HAOrJj8dXm+sndi0ntatA9E9KeE6bn2UZP8exZG3n/ftfhn2gSUUjayAfwzrfVXxl/euVvmj38vj7/+7xxFpkLxZTN7chNrRz3KpwyytyPq90ckquKlFzuQW/HZftQguWkw91KF+e92sIai9bf6spD6Uwb9pZDOfSOGJSUZeyNY+1QRq23w8gu/BsB3W0dY/sM6cTokvSr+gH5OFrbdi6kdV+RuSaJQ6TWb0qUhdlc2Fb8o0ufyx3yiUoDdFW620wpp7jdxq4rM+R3yFw3shkH9Ps3UWwET5zQT70YsvCTvo03Boyff7jAqQeuJIbt/v83SvzCZfXGHmW86FC6JqMS8kqZyinvJQckt4QCM8tKr3v50QvrP/VD+zJD0VXmw7lQK/PzaE//adf/v3vgcenFId1lo0H4OzIE4Juef2aZ4OWThez0aR6B2n+L2Z/PsPGQz/Y/PsPL3HgXgwCt/EYCfv++HYs6R9FGRQi8MaP7WIpWTBlNnRXUXueBVNF4rJn8jIncNkjcc8tdikusmBw9u8Hu7v8vvPP5P+OfP/iMSWwbzL7WIEprOvMn2I2JeOpgaE2XmDGrHhZIcfaNE/MkGsSPVmTlQmAGYA5EiO52Y7p5wbC0GuauSTRCmxulBfTBCQZdiBxHxpGUzmDw/EG3C01C6GNGfkzbLHELpvMJtjWPWARRMXJCJ/74v1pl60cZtKvIrEW4nIrFh0torqJOKwKlJq1u8HFG4PmTtowYzp2N60yaTZ6FxIqK12yLzWoIwCf35mJkzPsaaR5iC3Dsu289EhK6oDMMzBSbPiMrSbWjmvx8zmAb3vcT7rr8/CzqggH8CXNZa/9qP/NUfAT83/vPPAX/4I1//i2OU4FGg9SNtw499mYHGCDX5K3IDhxOw+yttGodMvB2L2BZiyWA6pr3LIX9FOPSbH51k55EMg6I4Eltjp2C0wH75N13sjkBRM6+3sbviNPTMN3+FE7/6i3z15Ye5/ZNFFr9mECZlJ/VqkobktEJK5zW1oybFy4K3tpddrKEm+XQFtyqDnIWvWBTfcAhSBvmViMGExWBOEpPjTAJtCOUzsWMQZEyqxxVuI8DuROSvDylcjUiUNbVjGVkM5xPUT2QZ5U1aJyZoHDRIVOXBnX4zYO5V0Tw07tPUT8YMShZBTtCB7AoULwdErubA3+4TpiVtOV5PcvZ3T/DwO5/nzCjgf64cZc8f/AI6NDBve2M2mpbglQsKs6+IvjhF46BF+cEUqXVFUBQ66mgiYvCJB0ityaOz+2fe5YVnfopXa/sZTGocKySeH5J7OUGiFpLaAGsYj/P3IFGPGeYlgMRripln9aRsQpVeiq/20vxXF36W/+y7vyCx4z+dJbti0FuK5XTeEr69V9Ok12NSa0IZzq8ElP5BEq+q6S7HDJd9EtWQ3pyN29Zsfiwme9WidE7hF0SxiRK6+mhC01+I0Qpmf9Amc1tISH52nJWQsCAGbYrAye4oTF+R2pG0H68WYIRim1a8KNyT8jMBGx8t0Zs3hEE4kil9oiJU7tgWT8zYheGE8BZauz3SdwxiS2A9P6tI3bIIUoLgOC1xNbr1UzLrsnrQXY7JvWczKhj3fCk7y+JVMPFul80nxTvz32Qq8mdBB54EXgUucC+Xhf8BmQt8CVgC7gB/TmtdH28a/xfwPNAH/nOt9dl/02d4c4v64Od+hTAppbgRaibO9ymfSjGYkRShUUEGeI0TMcV3pNxqHpThTm9eUbwc05s27oVbhEmB+7yaWFMlt32ae13a+2VqPnlWLliQUHR2y/vkbgdUjzmyINIyGZ9+TVE4W6Z7dIKtR8VrcPhch5858Ba//cpT5JZahK8WCZMQHuqz9+8G1O7PUjsVk7sknoD9WcXS3znDrb/1EG5NkdyJKT+umX1Z4TZDth92iDwxzlBA/opAkeZIiCvL3wzoLjj3Itr2/3adW58v4dYksrqzLC46dssk8jSpNYPczT+1XBtMSo9tP1Zn+HaR8GCfqO5itQ2CiZDUis3sawN2Hkpg98SxaeZ0RHtZ8h0NX+y4QldScZuHZIpvDsXiOlGNKX8k4NDyFrde3oWfiyWJaGynZg4keSd0hZVYP2wSpEVT3zoAE+dk2Ju75dPc5xBbcr+VFn5E6eKQOy+4OA3ZAHqLCmMkisy7xqe9eY3blICZyfNDOosunV1izpLcljnKKGfQGiMYd63gwjQMJjWZOwqrJwQ1cwBTb4+4/Rmb7DVR9Q1m5TnUzzbor+RwawZ2BwYzmt1/0KF5MC2M1LE7dXuPPNupNUm7NvuKqXMBg6JFa5/Cq4ncef7lPhvPJhlNxBTfFX6BOZJhdJhSTJ3t0TiYvJeKrQ2pUArXhIyV2QxpLVsMZkRvMfdql1ufTbH4ok/1uMtgWuL6hpMxt//6jxcQvf+0YPzSWv8AeTZ/3OvDP+bfa+CX/m3v+6MvI5DAkeU/HrHzoEdiQ2O2Rwymk1hdgTqy1wVqcSsm2VWfO89bxLkQ66pNek02svbBEKduok0JmyxdDNh42mLqLU3tiEd/VpO9DpFnoA1NZEPtoQizI1DNYNoRyWc9wukaTFwI2Hzcw4imqB018GpCFvHXU3ztW89QNMB4q0BuJ8AIYlZzHrc+l2DiXEzhvDw8vTlxo735vzxElJQyMniujnmxRGRrth9yxFikE1M7YpLakk1rMGGQqAmt+ObnTRKTHfK/n6a9D67+fIHS/grD70wS24rEjia5JUNQayAino2fCLC2XHrz6l5MWn0jS6YD0e0E0+9pOksKt27T3RNyc9ZFhTEL340YFWwyZ1bpLO4hTECiK/fp7s9kBJI2ZN9xmXg3onHIZOlfGLCaIfOgRptS6g6mFanNmPp9MrisndQYoSKxJSYy1iBGRaKEa++F1n6H3IpoQVQscKwRaO4875K+rfCawuE3RjD7+pC1j7rE1jh5t6PoLYd4WxbVY9444ENK7eYBoVbnbsUkNw1MP8arCwW4cDXEHFiMCsKtcBuysbb2OGSvCdvOzwkFeFQAfy1L6T1Ff1ZyFFvHobucor1HNoXeUozTUUy+I9mNXiNmVDKYPB9SPWYz9baP0hbN/QaRq9l8Ook2Ic6G5G7GdJY9zCH0FoVMVLsvyWBaWtogJRtKWAgoXRJBmJ8SD0e9PGCkEtz+VIrsDagedwXpuiVIQf7yB5wxaPqCI7d2u1gDedg2Pl4kd0NgwPxlRenykFFRDCk2n3DAENiveUhopk47In3TIrkp9l795ZDmPptEWVE9btCf1dKz1qW0Lr7bYjAlstOpt8QT7q4bbPWYxbAgbEAVQ39CbljxcogRaOJETHu/9JS9WcXqpwwwFMULgjm7rYj+jJxOpUsRU28PcdqKuZc1bhP0N0uClXvSgiQrEemVLqlNTXozxOrHZNZj6kckNDV3yaLwpTSjrKL4rmLyTXD+aRFtgtONya+MCDKyGEZ5KQdzp73xaS3XOHfTxytbdA6IhVj1U0OCtMYaQv6SRXLDIPY0jf02iR3N9md2o0JNooz8vuMzKkL1fpmgW5vuOAwjZvHFLpvPWNz5bInKY9E9B+TeQiQ+g/44v6BskNgRCm7hakzzoOQStHcblC5osrfGxLGGxHAPxrTXifOa4QTUjisiRxbzYNImyMcSR3ZliDlCNPyu2H4194uO3hqIOYhX1/T+XIswJTOj2BIko3pMOAfDmUgQkQwyd0kops52MEfjUnpc1SS2xAMhuS3XKnfBpn7YxGnKz+5VDEZ5RehKwrY2JM5uWDAJUhpzFNHeZTCaCpl6++7Jrpn+jsX2Ix6xLciPV0UQkt0CHY6KogXIXYe5P5FBqeRfGmTWYqa/7FK8oGF/j+GE2LebI8hsCmuus+v9198HYhNAw+JXJSPA8OXUSu7EFC6JjLWzByonPAZTMuSxe7KzdRZlQgvQOGDT3RcSpqB4NSR7xSJRlXjy5I5kE+ZvhFROmvTnYurHcsz+sE9nycJthPT3+ky8G9HZKzCO/AwjilcjEvWY1IaiP2XSn1EU35EBZrISk9zRpG+atHbZNA/KJrL1qMPyN1pkVwTDr5zwyF8XEU88dilKbktIhoohTBr4JY/evKI/adHcZ9FeNkSJZkg81qAkG5j5uQpOL2bzMwGT5316UyaRJ21HeiNk6lyAX4wIMkhPG0H9kYDYkVs99ZopuoWzSYJcTO5WAFrKT29LoMHGUU3+ui+59kUIsoruosvyNzoULip6C5ogFzF5zmfjaYsg61A6r5l6O8BqmTh10fhPnZF7Y3elNfCLEgdnDWSheWWBbafP+FQeUNQfkD64/mBI4WKb2BL+Bkr8D1UgLVJkK7YfV2SuCdln51QCpWVYaviK+e+2GeU102+OGE6IOjFMKswXCwym5RkyfWn5Js+FeFWY/T5Mve1L8MdlRWYjYvPZjAjPliJBHIYyixoWxRZ94Y82yK8ETL0djKXvkjvgtAXGDBOK1n4Jnq18ZESiolj5nEOY0ky8abL5rGg/7I4ithW9PQHFSwI9dxe0DMW3FTNnIjKrom3w6jH9KfOeLb1WstG5jZD8tR7p76SYOT2ktccgvSY0bbcJzqH2j197fFA2AQWNAxZOW4Q6raMh5YdgMJugN6fY9Ud90hsRM69rgap8uRFGJDzwiQs+Xk3j7likNmOMkaTK1A8L9mv44oRTOyomC+k7BoUrXXoLHn5W0TjgUHrDprnPZP/vdsaKL8WoYOOVRwQJMReJ7bte9EJtrp5Q1B6QBJrBtCATINh05VRWqJoGtA+HlB8yaHyiz8zpPkFG+lkjgGHBoHHQoHafi9uAyqMRk+eGpDZl+JV76ZoQo6ox2Yt19O9NsvmESeKyx+2fFy83jgAAIABJREFU1XT2xjQOSEBLc79Na7eNNjWT53xxN2pqiqdtKifEgDK2oH5EUInEpmxehasjag+Ly1J6Q5PY22ZYsig/ERGmtJT0hxUrn0+LNPq2InXHYu3nQvb/6hVau22qJ5QIlQIoXolwOzGjvJzwWsHU2R5RMkZbMJgQdV5vURbM9mOO2K3fENnw/n/qUzmVxRwKfOs2Ipp7LOZ+KJyDwZRi5nBZLM1i6BwboRUMd4/I3YjZfjxLclux+jGHICXips7+kGQ5YvmbAZVH5R72ZzSVE5awKx1Fe1km+cOSIrXWJ1EWGvreQ5tkVmOGE5IVGXkw9daI1qkZ7nxK0V62iFzQJzsULo2DWp8J8GpaQnCTFgtfkc47f8kgsaPoLiiWvyEV6NKfdCVv8zsm1RNyEJojRWLdIncnpLnXoj8pqI2KoXUgxiuPK8nVmPayydpHHIZTHsU/v075lIfVFzMXcySKyv5m+n2Xn/mFL3zhP/0i/7e8/tY/+rUvuC88IvCMbeA0DRa+59NdtDEiReOQQ3dJMSwa5G+GBGmDIKuYPuvLKZo2KVwf0J+xKVzzWf+wjTVUuA0Z+rktQCvcliAFGIqtp2yKlyM6y8J207bATqa2SK8FDCYttKEYTNmkN0MG0yZTbw2onnTw85r0pia5A4WrmkRFk1mN8BrCIFSxInZkGBc5EE6E7Pn9gHYxQWzZ9GeFzZW76TOcsJh9rUeYsmnvhdwVA2uoaO8xcVuw8/FJyZ5/vMvO/jwqlKTbwvUI+jbWQDEqys8y/GiHzFmbMGHSm5PhW6IqiEl/QROkIUoqjFAwe6ej8fOK2nEDt2rhNsaw5XYClMLsm2hT/PNjRxHtHULHwvAVowlN8rpD9ZlJrL4gIFOv1ylcGdE4mhRC0GZIlDBoHotRgcPS1zsYsUVsG0SOCKASVejPMb5fWizebHsc4CksvuZhJT/PSHQg+ZWIVieL09VESUXgGqTXxeNf+ZbAnXnAFF5HshoTWRZByqC3YJG5LSeviqXEzqyLhLp+XDIXgjy097jkbkZ0dhuMzuXoLiom3hP3qCCrMUcG1ZMGqXWT9oFY3KquOPhZg+ZhTf6C8PWzt2PKj5hoTNy2QKVwN3FYJsGtfQ7Z1Zj6UWk10pua/oxoHIKUKS3yjPBBascVhctihxYmJcDGz8m8algyCU9n6eyS0Bo/r4kdxXBSEeZiWl9/cesLX/jCP/5X198HohJQgWL2FYj2DBlMa9y6prXHkbjtWszin3TIXZc+qTtrMfxwB23A6scs3JYee7klSW3ElB9wSVSEnAHjKfdeGQL15o2xHRbMvAHV4zaFa2PZ5QMDeksxXsVn60mXzKrEj2XWQrzKQPq7cTZc/hpk1kZYA01jv0XtqEl31sIIRZCkTcaBFPIzFN+wae32hJnmKlCSbdfa49A8HrD1eIrBhGLpWz5GAJtPm0S29PupTc3kWcXi/wZ7vzRgMClOSm4joHhF/n32plQixptZakdluj1z2sccCVQ0mFQkNw0SZcVwKpQyO8nY6lwzfVoz+4ZPqhwz83JVxFcxpDfk2tQfiDFCmP6qw/Ifj+geHeFVZdOcfT3AHGlyd0Jufa7EcCZF/6kulQdg9VMGw6KBXRfnpPWP5dl6whL8vQm5GzIgDJPipdg4ognS0hNL1RWQ3FQktiXsI7ZhcEjox5Pv+IQJWWRzr4j1WeqmuEL3Z0VPMH1G8HqnLeV8mJSkosZhqShTWzHOM1U5fSPN0rdCOntivPI4Cj0tdF5/bOdWeUA2Ja+m2PlwSORpcrcijKGifZ8oJt2mJrEjRrDagvYuA6srpLfGEbFYM0fSDuVvShuRvR2z/ahsik5LUX5MDEXcmnGvDUAL0zBzW0kwrz/2Q5wz6c+OeRiOuA4vf3tE8FiH7C3oLYf3nIbe7/XB2ATGopvcKx6zPxz34NsRM3+8hlePqN6fxs8KhXU4oeBclsnzYwei9SGlS0NUJO9Ruhzcw3fdVsza81C8AHZfsPBkJSS1qRllZGBVOSnDs6mvuXgVAxVJHp6fFX/+1l6bjeeyhB6UH0wS22KvdfOzLu1lk6Uvb5LckRO1O2eSuy4+/05HejttwPQfrlA9FWMOxialTXGC9bMKb8MmyMD02aEk/KQUU2/GuE1RqVkDjdOL2Xoyx8rnE+RujAVKEzZ3XrAkOzDQjPIav6CZ+0FA7mZEb9rGGkhfuvDygOmzA3rLEfn3REMx+9qARFUYkZGr2HrMYf0jGoKQ4hUfu69p7TWYf3lI6Ue8HRsHXFRHdrfuUszOKRttQuPnukSHekS/UsM6l2bqLCx9M2ZYAhR0FyWdxxwpBlNacHqg8nTA0rciyg/aJHYkS7C7IDqL3qxF7lbA7A/7TL3dp70X3JuSNBwmJUNxlFV0FkxiU91jldpdUdm5NWHJrf+csPC0KWV/nIypPBZK6OtOluSmIv9uE7c8IHPLwIjE6bg3LeYlsSO6kbvaiMnzQ3Z9SVG4KIK2/FVF9j2HRFnIW/3FCLsLM29IS4ASIxmro+gsidak9K5i6zExBAk9xb4vdSUBai4mfVPk3rkVaancpswNKg9ITobdg+y7FbQpMx+3IeY3kQedBZPqMQ9/I4WKwBgapNbFq/H9Xh+ITcAa3E2HUTjtkOY+k96Myc2/vMSoYFK60MerywmRvx7h57RM7JOa5oEE9YNi4jGYNNh5yGb2Nbn5ye2A3b8fYQ9iUluBLKpeSGcXFK8MxjHPULgRECTkBG0cSkkJPIDaAzH9Gc3iN6o0jklPaHdjgqwsZK+mufLLM+JAo6C7KDDOcFIsoEZPdTBHUP7MXmZfVWTWNJPnZfhkDgWjdhvya1S0qd1nil58Vmi6QUrch+2unGiMB4m5mxFuK2LvV0ZELqTXffLXIEzHbDxjMyyI7Xl3d0iQge1HEgRJC7cig7+Z12Oa+z3Je3CgcXC8Eb5hcutnZ/FzFoNJmUAPJm1S2+KevP6CmKyU3pHUYbtrkKjI5Np6KY9zPkX/SzMUrkc09xu0dgtfPsjFElD6Niz/QZ3MbcY5hzHLX1bUjtq4NRm8BWnN4ot9yTxcUmw9bnHrJz38vE3+CuKHeECck/OXBVoMnmozzBuMShHE3JsVbD+WJFmOMG4l2P1HfYqXY+EHDAzsmkWirNn9Jeg/0WX100W6e9JoUybyTiuUzIG6JnY1lUdimgfF6/HmX4LKCYkFH0wY9+jeuVsjNp8yWPpGjDnU7Dxo09oPg6VgbOoSo22oHZVkpURZsfhiWz5zVxJzCG7dYOaNvizasUlsf1qTuxkxc3pAfiWgcM1n5eemGRYVfl42ABWD3RU40+7KcLM3JyS11tHontv1j3t9IDaByJU+K1GNMXsBpUsB1kDotW4z4vZnkgwmRYHVWTQpXBJzhdw1qB8XbXhqU/pZtwbbjzksfPkOW0+4VE667DxssPmUjbZg/bkkQSFi/bnkvVAKqxfhdKV/KJ1tMPODJkFKGGL+vM/Kz5YovGfIjGHeong5ws/HNA6LKeXiS12sgRhniimFlhP7fEYIQBGYo1ikxRMWcSImdiC2NN1dMcmdmFHWYPG7AxhPuSNXcPLO3ojGPkcUfuuCO5dPGfSnLMonEwQpxaho4zVi3Kqw2er3RzhNxf4v+qQ2NSqUfvEu7LT+cZmMm8OYyXd8jEjku/1pGWT2Jw2CFATZmO6CSZCScj6xauNVZdZhBIrUxp9arlkDjVeRsnz7USHp3H3t+XIgKsPfe5P6A4V79mraFM783aGr09ZMvKsZzLhik70mluFzr8Z0Fiz8rKJwEaKUOAa190qic/LbGTq7ILNi0lu866sA/dmY9Y8YZG/AxjMpKg/I585/P2bmjJhxdOdsSn+UZHBoyPZj0kbu/WKD6nFPJvZziolzGm/blHivzRjntgzezL6i9N6Q4cfbpDZjdh70mHlDY/dCJt9sMFgOiBMxids2hasRtWMKryyEuOS2jznUbD+epfZ4QPWkweCxLnYHWnsStPaLLVqYFPZs5kaX8v0Jdh6yGRYtgsURu760zcwbfYKMEk1BPSZIy9yivVfaZ3MA3rZJajv+sWsPPiCbADFMvRlTeRBa+1Mk1jp4jYjBhEGQMii+J+4qyS1N+5AkAreXJVhy//E1mh8dYIQCH2XWI3I3Yq78jUWihGbigj9O95E+r3g5Yvlrgh0boSTh+nmL1l6TRDXmyi9nWH0hL+/XNzj465Jp2DogfXSYVGw8H+E2DJyWon4EVj6fxO5p/LRB+o7QoLvzCq+mGc6Iui59rUHpQk8IT1UTqycLfeZ1TeVBYUmuP5ugflQwXrsruviFlzSly0MGU4ruyaHQVrsKrcYKNw+qx0yGeYPhbEByR4t/wRC2H03SnxGTkUHJYFiS0zZ1SxKHtKHYfsQhfUdKXbeh8SoCSaIge0PswUc5oUj7eYFPW/v+NKU3URHNRvWJAK8ZMyyYFC8o3LpssE4nZvXjLnYbyn/1ETJrI6belpZl5xFxk/ILMelNSVpq7TFo7RLX6TAlLr/rH1V0dkH+hk9nl8LbthhOKErvSbx467kBxUtjOBGYektivHUxIHvdwBpKFenWpB3rLFiYQ6nGvGZEenVI7oxQds2R5s5PFMmviFGH4UNqa4RbA6cpQjS3Lht7ZlXTnXcY3c6w87gssu6cycZTCW78bIHC2xZmV9yvgpTB/Csho4IMZGtHPOoPhWJGU+yRuw6JN9IMpjTdRcXC90Qz09sTMJpKUH40Oz6wxLiEjk356Wm2Hkti9WWj92oR+StjinFTyFVGBIP5kM7CB3wmADAsGiS2DCoPweoni1RO2GTWQupHTHaeDWkd1NQfDZh/SXzxIk/IHrdeX+L6s7+FnxUaa3/KoLXXILVusPf3WlTud5h7NcTpaCbO1OhNm7SWbfw5n+68SWfRpny/xdwrPekn6xaFa5KC4zQNyg+myawFJDcNUuuycRTekiCLREWTXhMSTGo7ZJSXyXBrt0HxaiRuSddN0hsh289OsPVEmsYBg9jUJGoxS9/2yb56i/Qd4dKbI6HKtncbIm7JxOIQlLMYTGqWfs+UE8gXCBPEZ3H6zYD6MU3pjCyO/EqI2xRVY3JLvP9iV7QHQVpKbrcBVl/kztqAiQsDcdo5GeDWNalN6durj4cMJ5TYrL8t17z0nmb29aGYa8xLK5G65qC02Ka19kmZrg2Rc+euje2/FNz++Zg7n1LUD5ukbxv0nu3hNA2a+0RYoxUUr4T3vBd6MwbJVZPSBU1vVhSIw6mQ6bM+nQWD2jET60qSygMiW45tTWp9QHO/wfS3bRI1SbgeLAS4DRkGGqGmetyms0vRXrLYfjTJcEKchYjFPn2UFbjT7kHlRIJUOWI4BTNvDChcC+jPyyY9KhgU3pPqyOqLxNytw8yZGHMI8y+HtPcYdOcFQnWbUHk0lspp3cbPadqbGXGsysr9t7vglYdS7V60qR92xN58GabeGZKoxGhD5mOlS4EMm4Hyg9Ki1A9Z94R0hq/JXLMwRx/wmUDsgNWXsn7xxUiouxXN6vMm2ZuahW+YGL4i+65DZ97EbYgXW+QqCpc1B3/zr90bXIEwtDKrEeVHcsQmtHdZdBcMNj88gRloMhsh+bfce8PE3Ipm7aMp+lMKcyCCkMgTtmKQUax91GI4oUmVQ3pzcgokymLZ1TogYpA7PxsRefL5w2lJRk5vjGgfiAgyJoYvqEFqQ0sS7ptVqsddbv21ffJ9SvwBZl6PyNyJ6S0ocldMakdN1p4Xl5/WLmlpwqQEiHgNjdOQ4M84EWMNZW6w8ayBn1H3gj92fU2CWJv7bJy2vFd2NcTd6RI7MCopVj7v0ZsHb8Nm8kwDFYuvfeqGLdj/ZX0vcNSrR/RnHLy6ZvJ8iNWXBzdI3M1NUCQ3x7z9SkTzoPDd/SxkfpBEBWLh3tkbM/O7Hsv/4AKpLelrIw+2HhfJrNOWCtDuwjAvNtqFqz7ejsXtz5r0dkUEaUFQtK1Z+oa0FWsfTZPaFGuw7pwhgqCqRe2hkNYe4x7XBC2f57Q1+WsiThtOqLGnv9jMJSoxrcMhsaXIX4vpzbuYo5j0qlCJtYLaSU3prInSmtiSIZwoFJUkGI2EYTjKGeRv+HibJkYExUsyHfXKFo0TERMXIsJMTOtYQPVkmtAT/YpXl1a5+J7Gz1qECcXMqwa93SHdWYsgI3T2USkme3PsGXk+pHA1IHbE8dgavP/6+0BsAsKak8DRIGkwnNAUrg4pnpcTv71sYg4UhesBTkd6/7XnxXO/fp/o8a2BxmuKA+30i+siDkopBkvB+AIHpLYjsrd8qscs/AyMSsKOM0LpIRe+38fuQnvZZeb1ASqC7K2IxLa0JLXDdxehwulq8pcU8y+PFW3nPPwszLwO6VuyMIOURXLNpDtnMHG+w8KfNBkVFUFag2nI7KMPxUshye2Y9ecsNp80URqmzwa4TaF+5t+zSG2JEi97O2LX/34BqycLzghg9ZMG899RjPIyqJt4SwabuRWhKZcfcBgVYlCSgjsqQuOgRfNYQU67jsZuSd8/8W5E5aECpdOVe0Ers6922HlCbNEnzo/oLFgStrEM6XMbTFwYSCZATh4nt6mZ/V5FjFstRTgV0FvUjCZivEYMuQCvrFh8MWLzaZO1XzpGshyiIsjd0JjjmHZrqJk82xpTdzVePaZ6zKX0XkRy1WT6h4rMbUP8/7Mhm0+aFC6KuUd3SSqmRFU2cm3C3EsGfjEW2LIrsd5eRUuVeVSR3grp7ZMAG/l/SGuXXLPYfkJTflhO1/ohF6ej6R0f0j4YsfStiM4uQXs6e6XSGBbENKRxlHspWADlUw6Jir4HFxshZFc0y18TheLEWYOJ1yW7sj9psPz1iOYBad1GeYNhQQbo1ki+x2vGRI5AnzOvMVYnRqw9rxjlTZpHQ0rvSnrx+70+EGShv/s//b0v6L/0CIZv4XTlpOzPWHSXJBq6eUgx94OQ8gM22bUYp6MpXtK09liECcje0bT2KcDAalm0juXwmprejIGxPCDqW/hJG7cF3XmLRAVQgjFHjkHj4QC7buJnLdLb4iXQWXaYeKtNUHBQkSJKCPvK9BXTb/aJPHOcQGMw/1Kd9EZA9ZOazGUTewDZf3Ga5oeWMEJF4ZpP9WSSIOeSuxXSmzNxBzY7j9hk7sQ0DwghxGtAahtGOYNkJWL9Y2D4BqEHCkVxvLPf+isTxJ4M5xZf6kDsUj2p8OqQve3T3iNDtP48pDagu0votKlNqQZ2fbWKqR3Sd3p4TYUZijNTYtvAGkLlqRCnm2JYMsjegeZ+l7lXAsoP2mjLJPKk3/TqMFrIsfGcjd1VZDbFQDVMKvqLKVHpeYrQNVn6Ex+QisxbF4ixvdskvSYGmcOiyagkA67psyH5FZ/INVj7RAKvOoaRx+nVsaMwfcafBZl1jdGzCDOyWLLnLTKrMUHaoHlQ1IVhQkp3t66YPC/+k2FCkSpHGL7B5Ds+7V02pXNghpLmk9yJcZsRsWUweS6iP2OS3pA2xxrC3Nf7qNijcdgkd1MGudbAIHZkAwpdRW85ZjijMXyDRE2mvm5bk70zYuMjFtqUU7txwBknBWkKF9u09ySY+16N7u4UsWngdEXdOZwUY5QgaZBZ8xmWLKwB9zgw1Yc0Xtlg+nSANYjxMw6tB31mv6dYu/wBJguFSfENcNoarybQjNsW+y0jEvedrcdsMqua1GqXIGlgtwL68zGLL/mYo5jiJU16K8JtakJPTEoiT+M3PKZ31UVAMmPQPKSpHxvDKD9cJbmjcbakx3dbmmHeoHrMGufnRWx8RIZKnWf7JOoSLhqmLEw/JlGP8Kqa7aeL9JbS5F726E2bdBYNbv2vjxJbiunXWgyLFsWrAltqE4azISqUIVz9PjmlwpSicVjT2qtIliPChAGWJrUmZbLT1uycEibdgd8Zkr1uEOQ01RMCayW3FYNJxfajLqOCRIbfjarKrkDhMlQ/NBLF4J+fYPtRk/5CktpRh/IpA7cmgpvK8yO8dQe7FzP11oj+lPS75QddhrMhkS2zl/Ipg/Zug9pP9kmtC/Y9yhmULgldObMWMioq2vtlKGs3hgRpxcwZn8y6mMAEaU13CdLrI7QpaMTC94b0Zk1au1wGE4Jx231JGwpdUZRGniK34tNdFh1A5UMy/HUaMoxtHYTNF0KMADK3Rc059XbM7t9dF8jPkRlM5CgSO1Inx45Be7ecvt05g5kzQ7oLBtUTDkFaMP3kphB1ukuQ2hix9okcrb1iNFJ5SPwvrZ6m+diI3oKitV/CZxPrJkFWdAKjgvhorn8ogVaSS7D2IZtRXjY6P2PQ3ZOhdHnI9b9QpHlgnHlQMshfh+wtQIvb9mDSoTdjkL3t4x/rs/PxgOxVk8opyXq89VMibJr8rkPjwPsPBj8QCUSZ7II+8un/ltSWz8YzHulVeYDTmyHbj0ofOyxpll4cEZuK3qzDsKgoXAtoHLTp7I1Y+lbM6sdMctcNOsuaKBOhEiGJqx5GCMOi9I2zP5QpfuSIsg0lxKL+fMz0aWgcFNNGty7y3tBVFM81aB4rEIztzutHwGkLrPmjTr+1+wRiS2yP1YQNCet0OpC/EXD7s4rkqjUm8UBmTTjs1gBUpO+lJTUPaRa+J5h3f1qGOkYEuffqNE4U8TPSd9aOK1JrsjDyl0Uk4zViOksSaFq/L03tVEz2iomfF7goSgiOflckhYLsakhjv0X+RkRzv8mwqMnckQ1kOBORvWoyKsmk3O7KA1i6GFH+/ABupshfg0Q1IrHdZ+fR7L3rP/VDk9pJTe7qeIj58TbO93I0jwV4Gza5m5KUlLsVUT9sMpiLMLtyLnl1RegJIqFtuXeL34LIEeLSKCeVmd0XH4a7OHh/RpGoSEDtKGdQeSLE2bZw2oriZdHg95Y0S98asfOwJ4jTHoE77Z5YpoME0fTnNbGlSa2LT4Wfi6X9mNEkdtS9WVZmLRLR19EAu2bhNEW/H0/46L6FChWpNUGEeotinmMEmt783VxMTWu/ZvfXfOqHXEb5u+8Nsz/sceeFJHZXhrO5a+KjYQ0Uo90jsm+5lC6O6Cw5uK2Y1m6TzsGA3Hs2rcPiXAxiTnruNz7ACUTaVHj1kO1HPGbe8BlOKGpP+vRmLLQpbDhtwPbDHn7eoj8jltHbj9oEabCbBkHSIHfNoLskUt/DB9dxb3qc+ORlzIEEk7g1g9oRk8aRu4QQoeB29ofo6RGZm10GCzJBrz4cMShKmGjtVBGA1n6R6RoROG1xJ15/QSiprb0Gdk8RpWKxdXq5K9JnDZn1kI1nLRa/LWVibEnfXD8ig7bBhMLPyoaUvzHCq0oQa+2YzcQPd2jvMmjsN9h5skSQknIyTCjUnh7Tp1vECeHct/fFFN8Ri63aibTQnN8yyK8E+Dkxv3RrApW2DodYA7FtG+ZN0usxlZPyoOavyn0Jshq3bOJ0NE5DNo/WEWFcmiON+3aaMBczLCnWPqGoPJARNV0pIHPNwm1H7PvnXTq7pZR3X8qSqMakbtpMvBfROKhIbYvTUOlSSOq2SVgImX8lJLIlWGXqTZj7Pky+YdLYb9E4YDCYkNOxvUcUhfWj0lsHKYU2xeG4ctKkfkyTvWiTXhe67uaTEoAS5CN2HvSIbKFUjyYk1BQl7Z4RCDs1tSabemY9RhsQuxpzoNn7z6ooDcMJzcx3yqz+hMCD6es24YxPbMsJX/q+i7dtceA3uwymxQ3abovXQpCSnIzMeiipxo7m1qcdBtOiBXGaMkzsLSRQkUjo7bai9pyoERe+PyD7los24dZPWVSf9Rnl5Lq427bkSdywyN4J6T/epfH4fyS34f9ULymxxadeDD/BS/tUnwrIroB5uINCLnrkKBF2zMsGkdoQFlfjgCn90ghSd0wuX11gOBdw8V8exs9K5l1/n0/+RszcKyF2R2ENob8UMnnaJHkuwcazWUpnLJwmqFAReRL/1TgkJ43pK1LrmmjXkNRWRHojIHFLYrYMH8KjXZa+IQO89efS5K9H9PYGVI5bZG7B+odlmtxbjsjdCkmvCcnJ7ml6czLUqR928SpaAiw9KD8zTXJH/o+SxDwkSCgy6wHhRpJbP5Fl8g2DqbMBVk+x9VyJ0JPr1J8R0kj9kE3pvOQpmIEsnt1/EDOcUAympcQdTAhE2V0eO+fmFNZuIUHVj0Lp4ginpZl/SWTBw6LJKK9RvjAt3bJJ48kR5hCKp236s8Lqa+1Pk70pVVfjZEh3zhhnD4j7UO2Ywh5ogqSB29JYLYv15ywu/dKvow2oH1VsPSGkHbchrZmfhWQ5xDzUYVhUTL0Vy0ZakFlRkBGI062K8u5uBkT2FgS5mInTJl5dYwaCDiQ2RYo9LIphiVeTQ6OzNwYt7MEgGzP5poHbjgmLKQlVaSmu/PIEzpZNshzTPeSTfdtldHAgfP+frjGcDbnz2RxoaO0bG+N0BIIGqJwQ9IB0SO66XEttS3U+yit2HhH+i90TC/f5r9r05mOMQSjPXQiltw0mv+sQ29LmzpwOMIeazuGAnQdNJr6axF3x3nf9fSA2AbcZs/2wIQafHdkBo+tpvNsO/VlFdDVDclOJ+YevqR82MQONV5GT1u5IaRh6mtiVbLbsFYu9/zyifSgkUdWktjQHfmMcIb0oirnOkhBPenMCZ4VpqJ+MiZ9tkr1m0j4QMZwWCLB+Mia9qnG6MenTCYZFA6sXEiUEijICyL6UojtriUGJKT7wqRs2Xl0gsvnvyc924Le69GYsUjuxnEQFRVCM6T4opCcjkrI2SggjzwjFiDJZjtl8IkF3WdFesln5md/AHEk8dnOfTXJbkb/uU7wkC0U08IreAwPCJFROWjgdTWpDsf4hW8r7jkzQjVBQF7stCsPYhuRLIj81fQgyFiqGykmD3ryidkLz6HMXJQHYAzTs+h1F7qbAaaV3pdqq3q9IViK8ivAYusv2haLcAAAgAElEQVQxy18uUz1mk6j8KR/fCCTrL3dNuPBH/p9fpHSxR+4GzL8S4zSh9kiIMZIyuXqfw/z/YZNZj1CR4Plo2ayzKzJADDJS6QUpTe3+aMySVNROxYQJgQK9mmZwaCgGrXtjBjOyiRsBFC4IV2RUsEitGjjdmM6iyfW/4IyrKPBmexQvCxrg3XHEdKZr83f+8m/xG0e/yK3P/GPmnlwnc9NAHWuTuykmon4Bukuw57fWaJ70sdcdGscjooTcM23KPSidF5Zj64Bm+k2Jf8tdV4wmPNrL0tZ2FyRx+S4Xo3ZEFKnOjkXhVEWYkuH7r7//kBiyLyilNpRS58a/XviR7/nvxzFkV5VSH/+3fUZsiXtMZ9EgeyciUYvxaqIuGxUkOjpIg92N8dMG89/vj92ENKmtgNiCwWxM9hYkNxXxsiwmd6VM+qaF15AHzBgGNA4rGsdigrT0gbGjxRs/Actfb4MB4fk8rcMhb33273P45B3sXV2KbwuXfvsJxSg/1p/vTjDzRnSP05+sRkLkWRBLsdxtgQCHJZG5+mlRim0+m0PFsP6JGK8mMJVbMSl8zxMeugXD6YjCZVnIYULK3tp9JqOCRgUSMHnfP/xFhtMRbkPYjEEaqsccOouK5a+UZd4RwcH/5s44uTakud8gvRkRpmMhntRkI8qsReSvi3ApTMrC8RrSbxsjRe2oOc7kUwS5mCgVc/737iN/TSy1Yldz+7MWG88ZjPJQfiLCbiv2fKVHkDTEsfjhkOk3oP7gBNk78ZjrrmjtM+5Zgtfvj8dWWprbn0wx8VqZtU/HtA7GJG/ZLP/mDdymZu7VDluPJ2jtNvEz8v0T52O8cbUQenJP+vOa2dcjSm8L+SdMaeyG2KQldgSqy532yN8YMfGOIrtikFuJKFwLGJXUPRMTIxCHKbsr30OM0KffzDIsGjTvCyleiuguwh8+/w/5TKrPKVcSSX5l15/Q2a0Zraapf76Hn5Fnr3BJs/ORBdJXHJy2In/Rwq1D4RKMCpruiSHlxyNGBc3cqxKk29xnk1mLqJy0Se4It8b0wU+LyU7llKAUdkfh1hU7q0XsjjyP/96bABACf0NrfQR4FPglpdSR8d/9fa31yfGvb443gCPAzwBHEbPRX1dKvf9oEnlQq/crSpdDwoRB5QFx1VHA5Duazm7xlGvuFefhIGszKkloSO0+hzCpIVYEaTFjZEPy7a/98uIY79fMvjZk+2m5IHPfh9J7Pq2P9fGnA6ZeE1/CxpEMuUsmfi7mv3jyFQpmkq8f+GOG1QRRYuxO05dM+v6Mxm1LvsBd44baYYvaCU3pPWHi1e6zcToiHXUaElzpVaTnM31N/rwtJJq8YrRHqMET7/YErts0CT1531Fe5hC5GzEzb8Rjz/wOM6eHFM/LlDtyZcPw6uJYVH5ykvmXh2RWY1b/y0P4eYWfMhjORDT3mRTPG1SOe2OvO6EtBymF25T+N3cDyg8o8jdEJ5FbiVGhhJ/Ekz6Z63IvuvMKb8cQklXZpHReMVgIyb9riWferiRBSrHnD/rMvWTQOGTQOKLY/JBoKVKbMYUrEduPSdzb7MuK1gEJQc2sQvnpKXLnHQoXFfMv91n5r/diBLDxXIbMaszo/2PuvYMsvc4zv9/50s35dk7TkwMwM5gBkQmAJJhBilCgqFXWSlVeW5at4C257Fp7S7vWrl1el9clS2utVV5aWlEWRYKQSJEikQMxA8wAmBw759s3xy8e//FeDFe7BFcl2VW4VVPVM9Pdt/ve7zvnvO/7PL+nqKkdFZaj6Ylac+SNJn5GNoSR85rtvzdgUJZyIrNgkKhIoGt3clj2DDT9si09glHpd1SP2fRHNP3RiMYheW3rD3moCI7+8y1aByQABUQlmFqy2H7KJZj0OO789aP3p5MDfuPTzzD5iib9l2myyyFOW7P9ITGzlS77pFcjIlPw5v2yIoqBsetgtuXWCR0JF/VTsHvcEsv1EGraPeRiesOo+5psViMXfAajGrtu0p/2sXp/B8XgD4ghe6/HDwFf0lq7WutF4BZw3w96Dq8E0eQAN2OS2vBwmorJry2R2BTbbnoZdu6JM/LOADev2L1bRnr9WbFqvmsdfTdpNrGtsLuayZdCmvvixGs+zb0xBiU5Sm495VE/5GDcSDH3FeHkTT3XkuCRgeTIPbt9iFcHET+z/ChmVzTlzRMefinAK4fMfmdAY7/Fnmc62B2N05UOfnrZoDNpUr7UZ+rbTQYlAX3aXZlCRLbMmftFEZPYHU1/TBO/GRfl4SfT5K8onKY0Ip227PKxms/OA5rumMlg3mXlExm6Ew7aEARYckuT2BZIqdOAZDVEG4rWHkMu/pWQ1KZP4YLByHkXNURuS8IwbD1g05oXWlJ/nyfAj4qAXOy2TC26sxGNfQaJq3H8lBCd+jMSX5bYkdi1+hGYeFECOxK7Af2S+A42Hk1R+ZE+Uy+6xI41SC1ZJGoRnSmDymmDICkXdeUeReRoeU5XfArNwwHdKcXa40nK78jiG5kQrwVkF6FwTfz+QcIQqOuP5CSCvKNpzxpwU2y1QVL4FM1jPqNveZJPMBAtg58yBAKyAN0JE6elCdPiEUmvCKQk81aM+l2aa//lJJMvBoyei8jfFm9IfFeTPJdEWRE/evuJ/+Aa70UxNn/UpXaXpj1j4jQlVTm5pdj+gI2fktOGn7TIrEUydr2ihsKxiMyXXhdOBfJep9ZkAWvtURTOOtSPgumKU7U/pqmcsFG+nAjUwJT3+z0ef5cYMoBfHiYP/8G7qcT8DWPI/toPMVBYy3Eq90dsPRDD6sLC398j2vulgMZhuRFu/4zsWl5O49QVxfMW1eOaua9VSWxryasryXiuPyKNl/acojcmUWXxKkx9ZZnY5QTNowHakBVfaVj9r8VZ156XC2P17Ul+89f/ASu/dYgwE9I4rBl/1mL6WwZ23aR+UG7aWz+RIr0h3nQRkQhLwC3YbD6Wo3A9ILfoCh5sSSYHdlvhZ+Tis3ua0jvDRtBISOGalCqhWMdpHDRIbWh27o2RXDdp741IX44R2RqnJcab5JakJdXuCfETisYHXFY/rdl4NCaS1YpQayr3xIjXNdW7YvTGFZ09Mtv2s1C8HJJehdFzmvx5B6snJxg/rfDKIZuPKAqXFFMvdoVqk9Ys/4TmwBddBiVxDxauu6TWFV5adAPbp+X7xJqiatNLKUmQqqYw+7D1gEF3LiR7SxbP9FokWYUasouafllITakV6bP0ZwLqhwx6I3Jya8/a+EnBmNtdOV1l1obQlxV5TWXKIEfk3KKP3dPYNYveqFB97I6mNymnoNHzvjAOT4iBa/Q18w4YpnwxkHTgRQOrq2jutdm92yR0FLWTociv85r4lQRvvbmf+976MQDOuR4rQYevrJ0kHFiU31J09oZsPmzR2iPSZKsvjdPBqEjc+yUJrgXBtdcPmKz8dw9Jnsa6pjuhCNJQuuTitIQZkbspZVt9eEZXkSRvWz3I3RDIyXvefz/wrv93Ht8nhux3gX3ASWAT+J//pt9r+P3uZBEG/S5Tz3sYrjTotCneAdPVbN9nM/utgMSOpvCGTX9K8gL7EwLEcBoGy58tyS8TSKNLaSHSdidMRt4O7vgK4rWI6uMzZJciZr4paLDeVERrxmTkD5IkKxHFy0I2itUU6x8W+lD6pgAvAKp/r8v42ZDi5Z7QXq4q3JwpjMOa2FvrR6E7zDFs7LdY+XiM7fvFgVa61ENFULgR0p6R2LPeuMFgLCS1Ihd38ZqHnxayrPIhu+Qzel4oQk7TYORtl9JlTe2oxc4pi/q9Po0DJvnLFkFKEV+OSYilB/lbMoPf83SD/O2AnXuFgpxdjEhsGRReWcXqwO5xCTlpHJA5OEpgl53jAyafExuzNuD2jyZIbYek1hTWptS8k6+EdMdMlp50cPOycHRHLZLb0mzcfETdUf25BYWVkM42QOaWjPJ645rWvIFbilCBGJMSFXFhGh6UrgbYdckNbBwWpFuQUHh5iSmrH4GdH+/TnrYYlATekdgNiNWl7xCZUD/gEMRFW9GdEL1BkFRDCa+81zxex+oIxqxyryZIS8zc1v2mTJMmJJzW6mv8fX060wapZQs3rwj39enNBqSXDWpXyvxOY4ZfvPAzPPGH/xVbl0axt2x2HgwpnTdwWoqpl/oECWE4ho7kYQTDsjOyhpDWtrxu08/2GD3Xxc1JfR+vaFY+aZPYjeickBOyCsXeHDlgt6RJ6hZkRB2+dwDR3z6GTGu9rbUOtdYR8Pt878j/N4oh+3ezCG07RXvGIUxFpDci3PyQ1LrfILsgNa7dk1NBfNNiMAK5G4r0ekSsDr19UgeYA0Esx3c1uyflRbHbIZElXevd4/LiNucNkqtduuMGU89LM2n9g5bIjEOINyM5niZDnGEqbXZJRDjuappe2cTwQuHMTwmZx+rJbphehv1frEp24NEh46CmSG4a9CYjth5MkdySXIHIll6ICmH8FUXvRJ/upMHS5wwmXvfoTcqceveEQ+W4Q7yqUSH0xmypB6saLx+RueLgNOTNnni2QnJTrKWxuij7xs66tPdniFV90kuKqRdDWvMSrrryE3ME6eGobNdnMBZieIrKKaEEJ67H6UzK8djwYf4Zj+3TJuZAY3UUtWNJuhPibsxfU+RvRWTWQspv1OmPKGEGxiLGX2sQr0pNm3s+wfaDmjAVkVkPyd42iBxREI68CWE6wu5KQ1TGd7B92iR7GwYj0hPpTgpOy/AgtSbd/HA1iTmQ18gtR1RO2LgFEX6VrgoyHQS8kdqUQJJkJRKGwoSmPx4xcG0RYD3RJXdDEOnJTYN4RaYJk6+EGKEAZ6jEKF30BRu/rRl7Ok7xLZPuTERY8vnD3/o07tkiTkvdoQDlrllyMorBrZ+y2PMXfeyejICttoSKDEZkWhMkRUcRWbD2kSSLn03SnRL1ZPVUxOTLQh5KX4jTm4rY85UK7l73jljN9GTU3Jq1hHD0t10E3iuG7N+LG38KuDT8+BngC0qpmFJqHjgAnP2Bz6Gl/o1vWHfm1XZXRjDVk5rt0yKP7Exb0tE/0qEzC829AtmY+qaJ09GkNyLqByxJIG7JnLwzLbLP1Ks3yd+QciG3GFE/lqV7l8vWAyYqFMpLrKEFDBpT2MdaOBs2QUJGcJWTsgJHiYhELWL3ZIbBCEy/MMBPKeL1kF5ZtA5Xfz1LoqIpXFGkNiO6U1IGjJwTs47ha1KbIeNnPLGaHgqk1r6YkKbcFYv6QYf0iiZ0NIYrgpXOtCK+K8pCEQ1JOElyW8ZaG48YrH1qhHhd+hNhTGrc2tEY3XGTxc/FSG2HNPdaTL3QZfRcxNTzLbSCsbMRGw/HKb8pWQeFyzIqHIxElC8O8JMyz3eLNoVrmvYecNqyK/dGhdEXJBSN/Qa1IyabHy7SmwlJbmgyty3WnshLnd6ExsEh9mrRZPduUyYiyYjxMxFuzpCcxsca9EelJu6Na6y+3EgYmtI7orKMVzX9SVnk40cbFK7ILtqb1MQrBmNvuPSnAnrjikHRYvKVAc39Ms5VIWSXfclyuKQZPyOlSPLFNOV3eujFFPF6xKCo6U1EtA+Jsag5b1E/ArlrJlZHUb3bpl+SMrUzadCZASJFfMXBcjXe0T5hXE6MiYqiO6mp3GPQn/fIXrXxszYqkmlIf4/P+mMmo2/IhhMkoT1jEK9pBjMe8apC28JNyN4wac5ZdKc13Xv6JLYM1n7bQtVt6WfE5UTWmh+mVv+AmKG/yUngYeCngQ//e+PA/1EpdVEpdQH4EPCrAFrry0g82RXgm8B/prX+AW0JhHtfV5Qvhkw8XyWzElG47pJdCQmTYoN0y5rDP3+V8LN1st9M4TSVyE7HDLQhRzqJ/Ipwi4rePg/DE2eXm4elXz6C05Eje+godj7kYW04JDeHwZUu5Bblhq58AHJfyuCVQnKLIX5GU7gG7Qf7JNYs4jsu2RWf1LqmN+YQpGQuHcZlwUjelmNyf0Sxe0KRWTDILsl4sjcpyrTuhMnyT0Y09tnEt4RhENlQuhTQm9Akt0OCuCKxo2gd93CzUir5n2rgFkQAM/iZOvGqsAjjNS0hnAOoHjNIVAOS2xG5RZfeuKYzK4tQ7YhJf1SzeyKJ1Q1Z/VgWrxTiZg2cFhQvtoRhOExdLr+lWPlYDKsvu1Njn4nd10y+ElC65BLblYs0teExer4nISDbGqunmXhJbtzEjsbLSZjIyNsuI3ftEBZ9etMR+RsRU3+5zeSzQo3qzsiUpb+QRVsw+XKPxI7Mue2OZv8fDwhjclFrS4RhbhGi7xboj8h0qHhZdsvd4zGSaxaZZU3llGL7Vwbynk1FDAoG64/ZFK4PqN6tqJw0hLvgQJC20Ybc1Kl1cTuOvWze6fmU35HXM7UB3bsG5BZ9OjPQutsjsa3IXxPLeO2wSexSgsjW1E6GdCc1QSGQHAYgtyhW4MY+i9S6InvJZv5rfTpTJr0ZuR6MUPD6mSsOTkujJgZ09gdoQwA6Zl8x80cWI2/7BG8WSGyJjiO7LCE7pqfI3wzv8Bm+3+PvEkP2jR/wNf8U+Kf/se9956HkeNYvG5iDLIOCgd232HxYUT5rYLkRkWOQMH32FXe5nSjSm4wgEpVZ5ak+5a8l6BcN5r7hMSjbGL5DoiJpsWM3fZp7bbJXGgT5OChFe0+C7IKmMwVogXz4SYvONEy+JAzD7A0LpQPyVyGz4uK9lsDLglt2qJywKF+UtS21EVE5YeG0YPS8T2O/Te5WDy+TYvo7HWp3pWnsc8gsadCyCBWuDXDaMby0JrUlO7fdlsXB7iictrwemZWQRNWisV8x2ONR+vM8wbiwFjcOZOCugNSSJQxGW3T9ABsPW0y+EhCZitSGojem8TJq6P0XcUntiIPdBjZMsqsea4/bdGfTdCZNRt7x2T5tk78d4LxhUDts4hbEZBSZsP6FkNhCnPHvejT2OeycjtPeF5Bck5Nd/Zhm7us+KrRo7DfZ/wfrrPzIFBuPxCj/H2WKowb1uyPasyZedpTIEqnuxKshTsOjco8QcwZlUWT6CeEtDooptCngDz8p5ZLTEB3GgX+1xuJPzZC/LVLzWE1RuBHSmhU59Mw/HLD043kyiwqlRf/fmo8z8x2P5rxDa5+LEVgSE74uCtVYXZgAoSMbhZ+UsqB0QZNZGtDaF2f5sxEqiMifd4jXIixXrh+7LUThQcGkN2bhNDTNAxaJR3Yp/26O+gGLzFqINZDxZuW0Qf1wgkEJEuvCHIhVpRz202KaSm05tKctyYycNsksa/GXeHpIeRp6CwYR5sDAy2p2jxskt9+7Mfi+MBAlx2b0/M/9mmi3+2JoGRRMGgcFp1171BWBRsOBnE/yaozS5YDNn3TRq0mCbEhmvM3gSn4onVSUL8hO2pkeJu+cc2nNOTidCLsXUT1q05uMyN42KF0eUDkel4stJfNYFUngh90VgZLd1/QLBr1JyYXrjSsyK5r2jMzFU8sWxWsBO/dYpNfkiOy0hnHfAzEozX/No3osjooEEd074DL2rC0BnHmp/3ojBs1jAbkrQhOyemJA6k5rEpuK1LZ09Nc+GTH9lwb9gkFmPWDl46aUG11N9ahJel3MS93piIlXpIQIY1C62Gf1o0kJJqnJSLEzLf/njoakFk3Gzg3ol238lDEMv/TojVpsPxyRXrSweuISXPuw1MvdeZ/8BVsUa1rq1bmvR2zdJ2rJ5oGI1LqMKoP4MPob6Vl0psUW/G7oaXfMpD0fwYRL6myCICU3X39Mk9yQnkKsKaabeF3Umn5ak12QvkBvXEqmwYiSnklOFI2lKwFowX/5GTkxNU94lF+1xbXaDNm922b2axXciSyVkzHaBwKy18Xu294fUHrTpHitz8JTcVSgKF4RnUThZkii4lE5npAcgaMBmRuWaEfuDUktW4y+6bL5cIzEjrz32pBFf/orK9QfnsZPKlJbAatPmMRqoueY/boEy8Rrmp3HfdJXHQxftAEqguS2T/WYM+QmRCS3PQYlm9BWNPdJSnFyR1M9LpzGV5/+h+9fA5HVCcnfFopwZk1stPWjos2uH9WomgNaGmjWhkN/IqL+i238eoxwzMVqmfRu5rG6CnO2S+5WhJcxyKwMSK9HpDaFGqMNqZPtTkDpss/st0LSGyELPweFm75AOwsyvuuPaBr7DfolWZHdrEF3WgIrvayiP+9hehp3JKJwwSSzEtErm4yf8WXH7cs0Ag3Z5ZDkpqgF+6OikBx52yd9JUaQkMQbpyV8vUEZ0rckDTi9CtPPd0hthcR3hD1YP2zgNAKKb1h4KYPGYWjNCry0fkhRPSoThncNKmZfUF6DomJQViw/mcCd8pj+Tgsvp0ivexRuhKRXNPv+2JVd/GAML22we29E8YorQIucQeaWhd0WKW79kMXY68N8vlVbTFHNiNRWQPamSWOvuD+9jDjeYjVN4cYAq6/pj2hGzw2kWRaBlxccuJc2aB4JxUEJTP/5hgSiWDD6psBbTFfKvvqJkMopiXMrX5BTTuOgLCymr4nvSh7i6PkBTgOCuEF7WtSj6bWI5E5EYsnBT0mST3vKYlDSrH1yhI1HYqQ3ZEqhIkGrF9828dOK3eGNbrdlRl+6GlA5YdAvO7QOh8Rrkbx/CbD7msxNi9jDu1ROxZh+oY+f/p6eJbMecv1XZmhPGxSu9+mOWyS2DfozPrkrEjVWuuqhTSi/YuOWJWfxXVRY/ZBD6bJHclt4nG7eZvteg+6EQe62+ApCB0bOiyz7vR7vi0UgTJhEJpLdt9eUiPGcRE6V31LEpjscnN3ing/cwh8JiOIR07km8W2L+aldoskB8arsMNFiSvIHztWo3pWgereiPStGEqcrJpHq0TiDgsnOPTa7x01Sl+JUj9kSMDoTMv1cjyClKdyI6I8q/KQcnwd7XJLbIaNvDZj7siJ3rYUxkImD4LkFn234IvLJLvbZ83SV7oSJ2YelJx38TCRCp5Jo8Zv7YPT8ADTMPlPDHffpTUaULgXUHvC59eNJ+kWxssbrIfEdaBxwiBzR7+evy6KSvWox+50Bye2hMCmS3SKzLLFgVl9EJskNRfqaQ+VUhvIFj9WPxNh8WBpwbtmheM2ndjLECGDfl1y6v9GkfsCmOyOor9Y+6ah7GT28gWQhaB8I2XpIsXNa6METL1ZpHQqEO9hRZNYCtu9NkNoKCROaxc860sDtSBQ7QLISkLtq0pq1GP+qQ+3+ceyu7Jj1Q8ZQFQjtWUisW+Svwe490mi1+pp9f1ghjCu642L0yS5FtGdi9CakJ1C6MmBQkOlQEFfSKDwW4OaF35e7BZMvt7F60P7xFqP7qugP14nvGNTuCek/0MXLyVjaO9onfzPC6oSSWpQymHxOyEPiRhTcWv52gP9CmTAGZldAsIVbAU5LrnUR/WgWfjjO7gdCvLzGyvi4H25RvKzpjtni2GxHzH1d+iGtPQKaCWNiuGvNS3M7shXpVcX4mZ6Mz1ta8jEDSC6/dxbh+6IciE/P6COf+VXiNamDtSF4qf5YhOEpwrjmJz78KhUvzT+beJYPvvFLdCtJrIxP6BvYKzEK1wXR7JYi5v/cwy3YuFmDzozov0W1F1G9S9DbVl/ccnZbPnbamu1HxGEWa4nPXZvCxYscCJKa6eckAq01a94xeKDFcpu7KXVwakXotmFMsu4Kwws8d7tPc29CRExKvi5IiRTY9OS4HiRFttsdN6QrfrpH7GJS5uVlUZQltyK6k6LC605HpFcMvBzM/UWTnfuyDEqK4rWQfkkEIm5B4xcksdnLy1jPCGXO7HQ1didk634bdyxg6tuy4/dH5RQRJISu0zhokNiB7HJA/aBFOASYdubkvREuI4yc77L2oRTlywFrH1FYbeENDsoRe7/q4pZs1j5kEN817nAke6MSK7b1oEFkaaJkRHzLGoZqyE5md6WMiNckiKWx16R80WPzIYfkluQQRLEIbM2+PwpZ/kTsTvPNaUoDLowpAXZMS/mWXLFIbonAyHS1gEyOBhTPm9Tu8zHaFs889b9wzEmw9zu/QPxmnNAR9Fl/3gNfkSj14a0s2WUZ1XWnNYUr0DggQh0jEGyZ6UqJopXwHlCQu9ll6cmM5FGOh6SWTMK4aGS8gsh/lZYma3YlkE0qKbDYtQ9bw5BVufZSa4rWvojRs9CZlmsjvxCye5eEz9ZORiTWTa79D7/2Pi4HupIjUD9oUr/Xl3HLfIAx3WP89Bb333+dp3Ln+GcTz1Iwkxwd3eIzp9/mzUd/l28+/r8Ru7vBzgcgTGp0yWP7A3F2Tkmdm7sl47nOlBhwvGKIlx2GNQ5kFt16ZIA10BTPSxZcc96ktV/jPt7CackFn78GdtunftAkfFgirktXAkpXAuIV6V4ntgw688IF9FMSV1U6U6H1mQ7Ln0zQOChegMSOLLzagO6kQf2QNNwSuxGtOYNYQ5Nej2AjLqehcy1UIHzB1h6DwYhm9PyAzKLBoCQx31sP5YSUs6PJXtileVD4+5MvBzi7MscfeSvCK2i6UxG9cTnhyA6iSd+y6EyZdCfE3OKnpFGXXZJscy8r1Jup5xpkFyNan+iifBg5Lxjs/E2PlY+nKF4L2bnHYvR1RWaJYeKxQW/cYfu0yfzXfLQJnbtd7F4k9ez2QJp4VxV2fkByQzP+XZlqZNYiavf5lK4Kbryx1yS9HrH8KYvEjqjtonRI8W2T5IJN7UiM9MoQEtKGsTNtEVQdEvWfOQBMzWBExErtWQO7F9G+r4/dMKk94JN/y+G3P/3HHHNEYbPwxB9QfHhLMPX3NNn3xQi7ZqEvZeGeFt0Jg7FXm8RqaohhV1iDCKWFaOQ0pOzRptiDGwcN1h/LkF0Us5PVNujsDXCLMi1JLxnET9fEUHVKehWZFTmhLj0FQTakdNmjeC0ksS329MyCgVuQUJjsijTEU5tCfp79ekQUe+/77/1xEpia0WP/5JekuoMAACAASURBVJcxWhbxishkGwfBL4Y8ePdNAP7t/PPf92sve32efO4/Z/IvTVrz0gVWkTTFjECUU4KDlmZRZkX072FC31mhM6shXtaQ0I2swCwGRWH6tadFedc8AMGkR+JGjMKNkN6IQWSp4U4iKUBLT1kUzxuEcSH/xJoyw3Z/vo7zxSKDguzm1kBQZ+0jPsoJ0V2L9IJF72Qfcy3O5MuBKO4qAuIMY5q9T3tsn45TvBZgdwMqJ0S/P/VKX8qbomL6+S7rj6XILcqcGS1YMpl8GBQut1j5RI54TY71Y2dkB4zVNSqSJpu2AC2Ow9VPafIXbHJLPpXjNr09PqWzIreNtTSbj2lyV807NmBtihfByyo6M4Jj78xGxObbRO/kiDWkR9CflUZi83BIeslkUJIu/PjZPvX9cXoT8t6lVyOa+w32fnGd9c9MYbqawg2XnVNx2vsDxl8STmB6I6ByUsZ67zbevLzG6ooHAyC5I7kG9UMWnT0B5dkG3TNlvFxEWAjIXhB6cv0IBNmI0b1VXj/55b92rT168Sm2zo9jtxWz32iw+vE8mZVIQkWqIhjrj4g60i0MHaBJTXJL4uQ6M9zJP7B60Lg7IL0gPETDF19I66E+8csJ0uv6DkHKTwk70fSk7FEhNA4ZWB15junn2gzKcTYftph4NaA7YRFvRDI6roasfswkygSs/P3f/L4ngfcFaPS3/uW/+O/nYo9gelL7tuc1YTpChYpksc/PTr7GYcf7vl87atp08j3Ojo9y6NQKS2aWIGYIRiuQbnpvQuCUTksTb0Z4WQOQC6T9cJ9eyiGMCeaqeUA0C3ZXbMPZRVEvptc1sS0Luwf56136ow6RrUhWInoTBihDmpFrIrkVRJQ0M3uNFMqH6ukQ5ZtSU2cNJl4KceMxsrelaRfYivJbBp0p6WDXjinCss/+L/m09sTpTUBv3KTysGb0rKgOg4TkF/YnIoJkDNOXEVF6RebIfsrA7mlS2x6DEWGbJ3YjOjMKwxMQS5gQslFyWzMYgb1f2mX1E2mcujhW/IzJ9F9sE2+nwAAva1C62KH0pstgLEaQlBJj9LxHerWPl3coXwyo3KsYPwO1MZsgE2E3DZwuWB1JxAnu71J4WdBfqa2I9UdtsTInFE5H6mq0YvfB7LCWHrD+eEJurHWTIDVEgdVC0AbNI3KM7uwRz72KFG4JOoc8AtsmiBu4JTmWm2+lMD0Ik5C7apLa0QxKBqWrIW7GIjvX4re/9SEulWz+tL6Xp/LLTGQWeYk9dP0YtWNxDF/RnYHiZdlx+xMR8apBejOiOwVRTPIHWvMG/TFJXi5elTh2OYl+D3OXWwjYekyjfRPDlY2kfSiguz9gMBHhxxWJbUX9qGLsjQGNwxaDEU3hqmbjsZgs+ibU7g+waxYg5i8/I+PB0DSpPfdX71/QKJG6g3l2x4WQY+Y8YmM9juU2+Vzqvc3QX2oX+IO3HsLdSfLWlXnQYqaY+Y6P1QU3bzD/h2uMvO0Sr0WsPSF18rtEn9TZJPFdwTc195rkrynac9Deo8hfVTQOGMRamp2H5I2zOxqjK6im4jVPUFctzfbDEWFcmnHVx10i510XYMT0N2oSqX3RGl4oPpnVkN6YeMIjR3YPuyn24fSGMAJiNVGe7d6dwOlEjJ0THX3xDYvWnCUJNVOya069EGEPQyetnvxb7YhFrKVpHDDZORVn7WOS5DMoGpTeEdJu5GgmvtsnVhdrdumidMjju3JKilc17T0R658cI1b3ac8YtPZFLH42zWA8iZeVXS5W12zf6+AVYnSmpUE68aqcFoiFpJaGv3stIr4rzbz+bpLGPhMj0Gx/wGDfl+okahH52xHdRzoMSlJDxytQu1vTmYox9oZP8aqmMy+QleYhTXtKbMC5yyaFWx7pJYOxb69jBELZmX1afA+prQgigZQEH2ySqEQUL2rGX6xiumIa2v6ASZjQbJ0fx8+GfPvscW79r0c5fe7z/IOXfppmPUXhooSeJjfltDEoGeRuwZ4/F9RcZ8LAaSucpmL3hCm+lap8vopgUDDILkcMZj2MQEw+ax+2GXvVwNk1GXlbsjdSixYjLzrMftWg/BY0PtoXS/OhBH5axseVT7pEswPmn+6Ahsm/FKpTe05huprWIwO8rMLuvs91AqnyjD766V8V8EcArUMhOhEyNVnjVHmVfzn5xvf9uo9e/QzLO0VsR7Apxus5ehMRM9+RZtfI2yHNn22hXytgdWVMEjmKeFXqwVgrZOVTBspVxOfahJdyeGWBhNhNA7Mns/7x15osPpUlswjVD4SYXYORc1C9S5G7JSt5cisisRtQucfBT+lhs9Ag+eQW3W+MYw7kOGgEUhIYAXSnJKX34O+sUf3gFM39BvEdaVRqQ6YZWw9rUsumLNcPNkh9OStjxbIisa2pPuaRuhwjtRHRnhN8VXxXjqWxhmDLjFAx/l0Pu+1TOZViUJSuvOEL61Bpaby19kKsIfr16hGL9LpAOMdf9zE8Yf73JzTJdUXxuoeXNdl4MmD2Tw3CmMHaRzVjrxr0S6Ii9DISz92ZEbt3al2EUgDNYyGZGyZBSiS8kQXZ5Yjdk0LWMXx5nbJLEZGliLVCNj/vEX87SWojonpcYbiQ3BYprtIyZWjNKwaTAaOvmtSOQVD2QSvS121Q4kDN3oZEPWSQl6kUCO35XUKS3dE0jkZYbXk9EzvSH7G6QntymurO6DJel5HpoGSQv+nTmbJIbYUYfsTyZ010LGT0JZv6EZj75oCVj8XJXxcISJiQvESzryhf1PRGjDvuUbcgfgK0jIqDuJRbg1HRi/QmZBE48JEFLp/bI9bvbWkKHvrsDSr/fO/3xq77DYpXI17/k994/zYGQRp1yR1BeY3OVzGaFtXXxxl3vjfaeLZv8mz/r/NJjk+v41/PEvtOFqsLsapBd1ykop0JE14ukFqPyC34lC71SG/IfLk/YtAbsYhvmYweqfDUvguYdzUpnjcgFLbg6Ns+ucWA5c/kyCxBey+kFywmX5LpQXZRFoBYXY7mnSmb9GqE6SlG3hQ7cPP5cZr3yMkhdxvmvtFGhaJGO/x7Vfb/YZ3mvZMybkuKrVcEOjLOOvjFHrGGpj8W4V7L0Tho0J6T3aMzqyi+4ohN15SZdmpddnS7Kzd6dgHGzvpsPuRw+/MJYo2IPc80pFewG1G5L6JySoxQxcsi7w3ihoShzkrqTpAwaBxwyK6GaAAF6x+0SS91SV0aJjmFGqdqUjuqiDU1Ow+F5G+Laaf8tmbiVZfulJw++mMw8rpB935xYmoDUpsiWnKaBoavGMx6stP2NaEtLL5oJ05/TCS/QUZGc15WeALzX27d6a7veVo8INZAYe3aTH1TTmtCWhJeYWOfRfMA5BY9wriUI1ZPYsb8jKJ4wSCxoxh7IxSATF1GeWNnQ3oT0njzsord40KjTlQitj9gYwSw/iGD+iGHiRcgc9WhtVewaZ2pGPEdya+UQFqxCttdYQlqQ27y/EJArKFIr8gCUDspepbMWsT0cz79MZk62V24+t15okzI/Nc80qsRpSs+b5/dz+ZDJjunLEJHtBSN/e99q78vFgGtBPhg9SUeanuliC55pJc1v3/mUfZ++xf4/MJHiCufSpDl6W6aTjSgOYhz7tJeUhvqDlZq/IxL9YS+s6JGtsRHbz5ksflQisY+UzzvOeiXZXWNWwH/ZPQilx/8IxpHhD4T39VUj9rsnLYYfTMgu+Iz8WpA7naI1RcXWP2xgUBNeprOnLjSdh7SxKqyOGSXQ7rzAemrcqM0DkMYt6Rr/Kam8kCZ3XsLOO2QxG6EU5eFo3xpQHs2Rncabn0+PWT/GYyfCYdZdYr8LZ/soiaMK8KkKBcH5Qg3ryjciOhNatLrHmFcAke0pUlsChzl9hdyFK71ac8ZZG+aGIFMFdqzBvEdwVSl10UrsHMvw/GcTG9SG4qRd/rE6oruTGqoULTZfNAkf10WnciCsVcMrF6I2RdxVWy3T+F6ROWEAESySwNyLyYYfcsntxjhdMSpqQ1RCM48I6PK5rxJf0x24PwVAW3kb/kULgg52O5A6UyFpc/laBzS5G5JPkOQUmQXNNlFaO4zh6c1ub7CuJZpRyGkeleM9GaIm1G09kbsnkhgdeV3TlQiaoctgmxE4UZA+R3N2scUmUWD9nxEfyKidEmz9FSJnU+7FK9FlN5uktg0SG1FtPaY5BbEbRpvihp18sWGZAfwrmVe3jezNzyJROAnDSZebhNZsmDNfFNyFJrzBqtP2LJArEmPLLWucLYtGvtjpDc8Nh+QTSqyoXA9IkgqBh9r3QGSfL/H+2IRiGKQvm+X9U+HFK+6KF8Rux0XEIKpsVdjvHl7jn+08Dm+kKnzuVSH39x8DBA3Wmuf2C29LGw9EMPwRbgTOTD3bxaIHm9QvhCRXxBrcLwmFBulZUf95TmZPPy3O3cTJiO0BWPfWCS7FKICaOyzaM3ZNOdtuuMmg6JYLrKvJ+hMK3ZOK9IrBp0pg/SCSX7BJ7UZYrdD8pcsunMhmTWf2K6iP+qgpI8l8lEFSz8VUTkpb8Wer9ZoT8d4/X/6PSbv2yC7IGYeqw+9EZP5P6nIzXnKpnpcS+DkknSdx1/XNO/yac0ZZG/D6hOOyGYdGQ+OvO2x8SEBsmw9lCR/K8QcyPizMysYdW0CSqLf0msRTkvs1XYnIrklr9vtH3NI7kSilzAUQUpyGDKrLtWHPUJH4XQi1j6UuKNe3Hw0z9YnfGJ1EbR0p2KEjqIzaeFmFaENtSOGjCtXJYo8VpfFPLcQkRuKoqr3hphuRP6mNxQSaRa/MMr4WZ/UqkFiNyAYorcEQKMYf60nhqJ7NJlVTXpNBEjxHYvOjKZ+0MTuaca/K2Ca3qTQeTozBt25AKNvsPa5UEQ7FVNcfLcMtKWJNUKyixF7fx+2f8ilcSRLZ39A5aQsOpElExqnERA+Wef253PDJqzE0xu+JrVqEO6TvkzxskBLd+7NkFkPCGOaMGbgrDnYHUivyIlk68EY3WnZjPxpj8ZhSUgOk5raYYvcTWjsN+hNapznchJD9x6P90VPIHlgUo/8+q9idk2mnwtwC5Lf5+UlQjwa8YgPQ0S6BzziOZfwVppwZkD6jQRKQ3Inws1KI6k7IaTg7HWT/G2f7phFf0zAEoNR8QvYbUmqATHEOPNt3LU0saGQBaB/b4/Ud5PEaxG1uxWpFXVHZOS0YPRcj51TSdG39wVBFa8KwSZ0DOx2wMovhFg3k2hLC+76TYNBaRjGUdJ3eH7ZJY+VjzuULkDpXJWlHykTOmJxLl8csP5oHHevS/pCjPYhn9FXJX+hOyPBK5sPWtgdET8BNA+HjJw1cLoRu3ebw+DQiPXHbMKYpnBZEW9KvZ3cdtk+nWD89S7Ln05it6R5ml4RaIcRiJEljCsadweYbVG69Sc0I+dEKKNCmYjEGhJH3po3hQY0qvFnXDJvxbF6msYRgWZWj5kkN8WSnFkEDMk21EPlqOlKDqBANDT1o9InGP+uR3vGpj+qCFIapyGimdxtEVGlV6VfYLfld8jfgNI7HbqzSapHhU1g9WQR7t3fI3kmSX9CU7wo5UK/ZDD5fI3VTxXxM5qJVwIa+23CmGgSnJZm95QEwWaXpAEXqwMRdGYl8szqQrwekdgNaey3ac/JuFQrOe32R2VqJDRoiTRrHgopXDLwcorc7ZCNx2Vq0ZvUTD/n0Z51pM9Tl+ai4Uu5ll6Xv3emFRPfHVA5Eac3rhl7I6J21CS9qkltBez8Uo9rP/yP3789gahvkhzrMn4mYuVTBvGayFzzNwQ7VS618TMi8Mi/7TD+r+WsH7uaILMe4hZFStneK5be/E2f1JIpKbcxUV6ZA5j9ZpPElpBzgpRAQ6ee99ETA5wXs5g9CQsNElKzZ15O0DwWsHuP8An8LDQPSfqONqA1H8fqa7ysZuKl5pBzN9ylj5ls3R9j5M8lUQnkTR0MCbYzX1nH8IWynNwNae5zmHwlpD2nWH2yLEfqN0P645rqXXGCtGb0OzadkwPKr1s0DsnvZAwM1j5sktiRCUesKVCW0lsGiVrAxqOSldDcY7HxsMPEqwHzX3NxC4raIRMvpdg+nSC7EtLam8BpSMNq+oWA1HZI+YKkDocxRXs+In/BIr4rN15sV1R4jUOa2nHR/2sFtWOSwuynAQUzf2phd6QxOvGqlufNys0A0o9w2prsySpoWQxqx+TaaBwSleDI+YiRtwOqdzlU7xWQqzkYJj3VYPuxEHMg4qvcTSlJ8tehdiJi6bPpYfp0xOQrvSGwA/RGnNZxD7MvuQtuTkbLjbvyd3IFth6wAWEXvIv0nnxJU7oS4mUUYUzTPBJiDWTBDmPQPOVSP6RY+ZiJ3RE1aawugBk/rfAKEeb9dUbfEhmxn4biOwaZFQldCRKK9JJJ4YZLrK5ozjv4SUV/TEqK/ojCyyjKlwL6I4rK/RG9mYDbPymZDuNnI9rTJn7qe0Go/vXse95/74tFwBzA2L9KCNrZE6zyYEToMWjovjLC3DddVKBIbofsnHbI3RB6zCBnEA1TimJVRe2IornPpngtoDujsfqSEqsNuPHzaQwfZr/tog0IDvfojdmU/ypO67DU205LGmyTrwSkN0JyVyzy18SSGjqw98ttvLSB1dPsnpAVPXcT1j+ak3z5EGl2mbDnq7tSo1/vU7ooHvvOiQGNu32WvjAlcd4pJQlA6yH1QxbZxYjSZV+SmhMGqTUgEkip1deUn4thDcQDECRlocwsGORv+bhlzfZjQr5p7YXuqEV8iEWzepoopmnss1l/LMFgVN8Zy2bWIvol447zLLug6Y5b9EYN/LSB4WvcIiR2DBI1OYImKprc0jC5B7khYw09VADKaBEN3qQnC8VhAV0EcRkHzzwbDOt/hbt/QOOAQfdMmYnXQgrXNfFdaZYVL0n2oZs1qB+wsHqasZff/TkFG97ZE+HsWKTXpXwrXO8Tawj6Pb5pEqTlyJ/YDTDcgMaDLuNnXMpvwdjzFtkFOf53H+niZzTxWkj+Zoh7qkP+ZkT+lk93ephDOC2ybzdjYATiXsxdkYK7NyUY9Ylv2eRuQ3JDZOutx/skd3w6+wNMT7IEzG8XqB6zSVbkdWgeFDp1f96TWHkb2jMOnfmQIKXwn2iSuyEU4nhNk1kP6JVNilcDJl6AuWeEDalCmQgESXlt02sR649aWL3/DxiD/38+IhvcnMmgYJC7rmic8gjiMnvuTcjFuvKJGFZPsfWg1FrVUxFRLsAtCGk4sSNMuuSWYvIbG4QxRWYB+mWT6nExVez/Y1fsumMO8WpE5mXR8qtIs+erAell+Xnyt8Vq3J4RnbzpioYguaVZ/lRWEOABZJYU1ZMSD00kAIjuTCT+hd+5zvVfKpLeDKkdTZBad2nth9LzMUpvSHPQ6grjrvxGTWLFAtF+b3zQwstF1I4YaKXozGqclqI7bpK7LeCT5uFQmH15ReOugN6opBylbguJuXhZglKiGNTv1nh5xdjZiOYpl7E3fYqXBLzhFhWJHW+I3xYQRWterM2Nw5rgp6uktmSXdRqa2hGDsXM+nRlFEFPkbvvYHYPSBQ0RVI9Lf2H3lESRm45EgRcuywnI6UQ4bWjNWfSnxN47/RX52PChdtQSFuMVIfkYAQwKJl5O3l8/I9i51Jb8/rFWxNjrmonXArl+lgK6U3GBzAxAnWqSvWEQr2h6YzbLT2Y59C8GLH/SoXIaWnMGdj8idqTJ5P/tEN9RtOYsvIxB+ekk/bLB7glbxq739NEK1h+Tnofhy66dvy0/69gZGfsaP7dzZ/QYWZB5OcH6YzYqVBAJ/FRFcjqsnLSZfLlP7jp094QUz9o07orukIFyV0xyCwF7S1Xqj7jEqprex9usP2bQ2gc7pyw2H4UgadA8KslWbk4x8o6POYCdB0Q6bt1bf8/7733RE4hPzuixf/QrlN8QFVhvTDP/tTaLT2Xw8xHzfxZguiG3fiJG6bzBoCzNEcNX+Af6xC8k8DOa/f/nBvX7J3Cz6s4NoiI5lqbXRA+fWRPufmozuiPFDOLyea29CqsjdV9nBvb8eYfND2Yw+zDyTo/1R5MSCnlTbh4vJ7tdYkfdscUmdqXD3dpjkNgRE07kSA2aXRaQ57sNo+6UNPQSm4rpP1smmCzSmUvipwwyKx4LP2aSXrDuwFcNX24CN68ZPxNieJrlzyjylyzsnqZxWPINlIaRtz1WPmYRxTSFiwZ+5nuJO/Lciplv9wjSNis/FZB9PUFuCMBoPdXBv5WhdFGiuhI7HmHcpD1lkV0WefTI6watfXISilWFUSgKPylJtBJr79i5kN6I5BnunFbE6kOV3454/YtXfaxeSOQYrD1uo/Z1mfi/Yix/VjH3jMzKBwUTa6Cx2yEbj9jMP91i7Ykc6bWI7oS49t7F3mSXIrpjBn5myB/cFOmxf7CPWo9jdRXTz/aoHUvQmRUw59ibHqsftZh+dljD7xPjmtOQhStWE95fkBINhpf53nXlFmWBzi5E5K+1CdMOrVkhZxffEv6E4Q/LAUukxc0D37v2gylXmuCFiOwtg1gjInQkJWniJUXllMLc14FLGQAiW2jV3b0+ZsfE8BTxXWk09sYEnmq6MBgRIGp7j3hksksRZ//t+1gnoDQ4dZP2HoWfhvEzITd+OUZmEZIrpjRFRmMQSgaf05AuaulSSNgXL79XDln50Sm2n3SxxPMiqru6ZuQdEROVLw0YFAwSFTnKDwqK6jHpnu88FOKOCNcgjCmCjGbn3gzld1z6Y1C9S3zk42ejOyEn+//1OhOvCcnV6mnae8VxF6+FTL3cJ7Ma4GdkhTcH4LRDRs/L5CC7EuA0FKk1OV6u//Acfl4wXo2DsHM6Ru6qON1UJAq7ICGjvCAXiZsvYTDzLWjcJUTlIBORXo8YlKU7rk3I3hTqsR7eKP1RmTREtqa1N0FrzmL06zFSmyGtOdmFk9/KSAd/wqB21GDpSQcva9I8AEs/o5l4Qb6304DUmoiNvBw0Tnq094hduzspTL3VT0gp4ycUE69FFK+Fw9JK6uflzygWfk6xe7dD/gbEzqTZPWGTXLFY/ZhJd8yiPWNgt0OWP2XhNBXLn8nhpzXx+jC2yxXctwql3CheFcVmeiNi9x5JE574M4fUqugemvvFGJTckMZav2wx9UJEY79NkAKrK8lJ76ZhG8MSz+rIya07I4jz/O1IJOZtCQdpHM5QOxyncl+E2TFwS6K6dJpDDH0edh/xySyL2c3qKWa/ZJJZ0eSvKTpz0uSLNyOUL/b16ed8Yi9lGDvr4zTAaUipYNcsctclZcgtyKlOKyhf9MW8tqOGYTaCTNt+6O8GGo0rpc4qpd4ZxpD94+G/zyulzgzjxv5EKeUM/z02/Put4f/v+Y8+RyhNmNwtkfPWDlsUX3Voz0NmRZJZ/KQid92gO2ZTvNJnUDBoT5ns+bKiNW+QuyzNJ+dGQuS9XWn+NY7IaCmyoDvh3MkjKFyBznxEYkc+N3/JonBB1G52V5O9IS9N5VSM3G3Z8TMrEemFNvnbsqj0D44yKJoUbkgAR/GCovxOSJA08NMWjf0C1ii+LWM2qysKxdWPGvSLFkYAuQWf9oGQ5nEPp9pn/TET5nt0DntMfXWFZEVSa/2MzJHf7TnYHc0gZ7DxqMGeZ8TElFg32XlQs+frAzYfcihckt0/dOR00DniYnfkKFq4CtW7pSdRPa5oHDApXewLi+GdjozXCpr0sqb8NtQOS9Op9HwMP2XQ3A/Faz7tPYrRNzuECc3kt2Rq0DoUYneFqpS+bZFfGNDaD0pLU3DnlNif3WKEMTAovejc0dNPf6uK3RbOf3LTQCvhISz9kMHsX4V3TGFBRlM7YuMWIppHAyZfDWgfkKPw0lOSUwAwdkYz9VJEZ9IkjMHOfXLMjkyZ9ADkfmGN1R8NGZRlHGm3FMoPaR4JGT0nJ7v8gk9yN6K1X+zbflpRPygKv4lX27T2C1K+O6nI3jDJLkJnn4+fVoyc69DaYzDzbIfcO45kEH7VJbWuCVIiaW7Pw/zTPXI32piDSPoG/QgVaAZl2HzIwk/D1Itt7I6Ue/1RKY2LVzTtaRF47R63mf+jNfyMbIL1gyapNU3m1nsLBf6j5cCQNpzSWneG6PFXgP8C+DXgK1rrLymlfg94R2v9u0qp/xQ4rrX+T5RSXwCe0lr/+A96jnRxRs//7K8xeq6HW3ZoDWtxiRzTjL8uaToAO6cMsguQXvfZOeWQ2hTXmulKXFduIWT3hMHYm5JcHFmixbf6mvpBYbOltkUyWvvogPwLcTrTitLlCLsTEtlqSCCGidcC1h+1yCwLlmvlEzL3Tq3JDemnYPR8IE68pr6jIktuhzQOmHcab8WrMmM2vYilT1vM/lUIETTnbcZfqbHxoSJ+VsaMucWQQUFq3iBpEGsE9MsWW08ETH3dxOpFdKYt4esBYUJm3r1xTXJTLuzIka766BuyYzcOGEQxTWpF0TwWkp5q0e3EKbwQl+CUOWH1x+pyrDc8mPx/brH0i/tJbmtGX66w9PlRvHwEEwOMlQRmXz5/6pk1gvE8/fE4Gw+bhJmQ4nnJLcysSPlTuhTSnTAxPMGWu0XBhCUqwl3QppwWUELGDWPSB5p/usP2AxkSFRFBvVsKJYa8PKuvSe5G2K0At2hjt0Oae21yCz5WX+hEvXGH7fsFUR/ZiokXarijKZp7HfqjiuxixKBk4KdhUBbjUX9ESSp0QkbO9UMG6TW5ztDyM04/26M9F2f3HmnAeaUQu24S35VRoN3VNA9osgvD9zIm10Zrr0wtVCTGp8ZeS9Bu5YjMouRQ2J1hmtWGT/2AI47MFbnmIkdyIssXNSrUNPeZOA15HXbvMhnM+JTOiIuwuVdOyUagSVQ8nnvhv/nblQNaHu86eOzhHw18GHjXa/lvgM8NP/6h4d8Z/v9HhgvJez6ChERpbTyapHbYbZjbIwAAIABJREFUIl4XJJhWMprbPWbRnhKdd2JHMgf9jGC/3l0AvKyiOxfQHTdJbCvWH5cdvTMf0Rs1qR353piqctyiN6bY+79Ln2DiNY9ExcNPm9QPSYPNbiu6Y0L/iTU0bsnBK4eULmi603K8dprg5gySlRAj0Ow86hMkoH7YxM9oMsvyByWft/6YTeGKTAO6ExYYUPlAgcINn1gNcksh2UtV+qOKyj0W1WNSJ9cPGfD/MvfmQZZe53nf73zL3fd7e9+nZ18AzGDfCAIEIcLcJJESVbIrshNV7DhOlUk7dlJOpVJOlMjZXFY5ju1EtmRbkURREiVSlEmCxE4sgwFmMPvaPb13333/9pM/3oumKkVIimRV4VahZjDd091zv+875z3v+zy/x5NLZfcC6o/65FcDylc90lt6tMCMKoUv1kjWBJ8d64oOwDrVFrGNDQSK9G/mGf9WXIxR99uUrrpk12R6kd6OUBFs/sxBjFB2qLs/OU68DlFcM/nbcayuws8Kp2H1f8uy83CGeN2ndFmw8YVbHsPJiN6sgTPrE9mKeFNCPLQp59XIlocsjMPYe66ATuqa4rUQrxJSuqzZeDY7Oh6JZTgyoXRFjh6xjqZzEFrLJtYwJLnn4ZRM4u1IFs1HEtRPJohMSeYJkor28YC7ny3RPBLHKYudt/ZpBz8NC//yOpXziuJ1j8rFkN6cIt4W4EvlYkh3UR7OmRcapDc1zWOSTL30DZlajb9uEs07xNpyvf20YuJt0Q5sfVySpJyy9FAiWzYxN2vi5SUop3hJqtXeQsRwQq7d3ect8nd88regfSTCdKTRuPT1DqYX0Z80sXqiX3AKBmFCM/Ntg84B6M6Y9OdCmkcNCZMt2B/6/P1pw0dMpdR5YA/4LnAbaGmtPwg8/qNRY/sxZKOPt4HyH/f143su1kAeqv5CwGDcwM0ZIw6A8O3DOKR2PDJbIWFCRjQSRS2fM5yImHxNGkKxrmbqVU3tGRdd8oRbP5DVObmrWPz9FkYAuw+m6N7n4mdN9k4naC8Z5FYkWdgaSObB9KsBka0YlkwSOxbtAwbxuvjV83cD8rcHDComgzGDxHqMwq2QWAsMT9iBe4+FaAXpbZ8Dv96kdMWhP23QXZAkoDCpGExYuAXozJu07ymTvRtRuhqSWZcRVHpTk9y0yL10k9itbTJXYnTnLPbOxGgdgd6c3FzDBwZ03xpj90GDzAYkd4fk7rqM/7MEg0nF2PsOpfcVO58I6E8JYit/O6J2T0JCMGPQOK4o3vSY/l6DykV/lHWoCdIyy+7OmuRXIkxHHuDZ/8UcUaBkZ01vaayex9H/dZ3CrZDEhs3uQ9BdEKJQ65gmSMoUJ7shpXYUM0SFt+rQOG4Sq5rkbw+weyLtTm1rnAf7+PkRPWoipD+ryI921J1HUtz5CeEFosEeRPu5kr05A7srMnFMSTQyXbkfVAjFF5IUb4TU/9JhGsdh+9E4m8/I1w3iksa89Tl/RFlWdA/nhd1ni3y5cSTB/Lf7WE6EdUt6Dekt8SE0jhnkr8PE6yJ7RovPofmAT3de8gaSu9D56S7agtRuxNx3xcC2+XzIgd9xaR62R30cISQv/k6NjU/mqZ2ySNYjTF9juZrx76xh92R6ZvcUme2IiR8o3KKkPNdPfDhY/E+1CIyShu5D0oQeAo7+af7eH/f6ozFkw1TA2AWf/pymcNEiuy47a3ZNBBp+Wi5K7VQSN2cw8/0O2XWPud/fI7WraR9UZFcNnJKo/XqzCmsYcewf7DH2XUFNGb5kDaZ3QoKMZOQl6prcu3GGJUkDqlzyJYyyKyk3y7/lsP2Etd+Uy92WMm3y7JDcbWgcsWgeTTMcV4QxxcRZnyAp4RdjFyRs9Mi/7KNNxdbH4nSO5dn4RFK4+TGNnxfZbm9W3HaJhqZxTPLtjECUiSqC9G7IxFmf7Z85ytZPHMDLa8wRXMJwBVyZ2dDEL6QwAsitCHV355Essf92h/ZyjMFCQP1YAgzIX4hJ4u6YhLGWrnnEuprGAwGTb4asP2PTvK+AUzQ59H+sYQ1+mKDj5cVPYASKWE9z86/IQ+QnZQG1hprdR7Ks/NwCjSOCcsuuCOPRCODwP9+j8p7w/ty8wq1ENA/ZghqbjFG4GZHZgPZyivydALcsPIj4u2kS1dExoG3gp2VWntqN5PzbEOpyd8GgfcBk5pUhpivNMmcqJH9Lk71qU7wowaP9ObEOF2469CdNmSQhu2pqw8SZCMlsB6gQsucS5G5B616f3rRJd0GRaEVsPyFV663/VPo7hidHnURD+gvpTU39oYC9hyEY8/b1+2poUr8/ZPfpgCADzp0soS3A082nLCbOupTfEj2H5WhibTEauQXF9jMVxs77xNqw/YmQ0FY0Dxk0n5hj7tviW7B7gmUbTBgUrinyqz5e4T8QaFRr3QJeBB4FCkqpD5aXPxo1th9DNvp4Hqj/iK+1H0Omcmlayzamo8jf9dn6MYlu7s3KOa5wOyK1G2E5ooBa+XyW3myMzU+Nj+jBo3FNUcqlMKHZfdAmmCrSnxbBxOCTPUxXBDi1e1JScvUjOssR6d2Q5J4kuXYfGlI9Y9BbiNh9OEVyRxyHpqup3yNyzZ2HkqSq4ajJNlKTDTSNo+Iis3oKayCmmPaxrIAwe6L9T22L2qx0SVN+V1iFQXrUoLrtUL4i6rOdRyR3L7KhO2MRpAzKVxzyqz5+Ud6L7LqgzIo3IzoHBJoy/coAtyATB23A9tcWGVYUsapJ+4jc+LGuZvo1YRaEMSWd/2WY+p5JFFME+ZBkNaB5RLH3yXm8RYdETTrXKhJ6bf6mlMpWz6B52ERpze7D8pD25iPiLYGMdA8IZksbYuOtPjmB4Wt60zEGk4rcLcVwXJyP7QMm1fullN79eIhTNDFdWQi9vCa1I3r77CrivHtAEqKsgTyA9WM2E2+79A76tA4m6C7IvFwbmu6i2G+9gmI4FVC8rBj/5m1MJxClowF6fkj3sOgVsjdN6sflekZx6C5C4X1J9/GKEd05g8k3QvYeNFj4dUHX2X1hNzplcz9kNL1ik71tMP79GGFC4CPxqknlLZND/8qnf8IhvWGQ2QkFLnIT7n7axhpIxJyKhFWY2tGkn6iSWw1Y/QmJTRt/xcLPyfV384q7n8njZ6Fy0aH86qZkSz7q0jwkEX9/5kVAKTWmlCqMfp8EPonEk78IfHH0aT8H/N7o978/+n9GH/++/hO6jx+ck8bek7yB1J0YhYstwXZtSgx1rCcP1dgFn5lXffyUons4lPN2eZS915COaPGqHiXNpCTTLqEo/2aK/IojEMg7Ps6sR3/CYOYlvV8lxFow9+tivojiggtXEVh9OefF2uIMTO1oqqctnIpEaqWqEV5B0Vse/axd2Hrih807CUZ1ifWkMbb5lNzY3QW5+YKUlKdeXpJuI1uR2pLPcUpy1t96UrH2yThrzxvEayadAwbbH4/wc5retEGQkAXSLccwHai8H+JnYerFGlFMlJCTb0D7oEFqN6AzL30RpaF+wmTinYj2kkHtlMnyVwO2nrRJ7SrckmLshTjZjYBYN8LPaOp/ycEpG2w8JwKh1K6m9rxLlBi9T00D09GsPW+NYtY1/WV/HyEf2ZIH4Wf1yBwlZXz+TojdkV5O+U0LyxVlZKwlP789lF7CYEr+LLUj1VJv2ZcexAmX7nyM/GUbt6TIrUbUT9qUzpuUL4fk7ogHYuEbsijc/DvLtA+l8fJSimdeS2G3TIaTmumXW6Bg6rUBXlamKX4W+lOK5I7stttPmCT2FM3DMWmqxqGzLI1YL6epXPIpXQ3ozWv2HpU+R7wpAJnevMLPxUhfThCkZILljGky2wG5mwb9aYPZ74ckmhETr9Zxi4rW+xUG4yaH/o1P+aKmeRzG3vNoL4nnwBqICax+LMHKX5mjeUzuvyAtSU1/5kUAmAJeHMWNnQW+q7X+JvD3ga8opW4hZ/5fHn3+LwPl0Z9/Bfiv/qRvYLoybhqWTayhpnwlYOcXYPrlDr1pk8LVDu0lC7sXMixZ1E7FJG31pkl/WjP2rkhSDV/TPKUZTBhYQ3FjxVujRksrYOvxJN5YyLBicvBXAvqzkGh4BEmD4g1PKMNjYsxJrUt4hDbEAtwfhWQMS2JxnTjrk72r8bOSNhNvasrvGFTvHwVBbClqD4a0l0R2i6FoL8uDbQ4VTlGwT8laRHLXYDAV0VmwSNSg9G5TeHlVGf25JU1q0yBIa+yOUHmTe5rkukVqS77GwX/XpHgtYv1T0FsU269XiLjzpQqZDU1uNSS94ZDc0+ydsSXfYEOz9RQjQo5IXife8akfT5BZF0ZAkJBrVL3XZuvzPnZPMf67cQo3fcrnTLQFTkVR+Vac4kWD9gHJkuzNC5rb+kIVLysRW+nNiOnXIvpTIsNWgUiUQVSa/SlhRHYXBXnWPmAQb0cMpjTTL3VpHjbxxwKsvuRE1B/1KV8KMbsmY+8ozIZN84QWaIyGZFXCaUHgsYYP9Ud92ss27pyH3Rldh23ZBIK0jI7Hz0asPV9g4h2HwVQc+0SH/ox0/SNbSu3CLY/JN0LJr0zCxJsS35ZdlWlNmBT3X/OQheFD+ZzEt42955JfETVf7ZSNNRhVe7MGfjFkWLaIdcU9ufuQTf24ybW/WcTLCcm4cNvh7vNJUjtC4Fr9aREwzf/muqgT10KCNGgbsndAuyb94y65Z3Y+9Pn7aCgGZ+f0ws9/BdMTscPdTyty16Uzn9kKqd5n7CvPnJJi5uUea89lSDSk+xrk5EaIEhGL3wgh0uw8HMfuS2c/3onY+pjiyP/VZO+REihIVUOS20N2Hstiuh9w3wxKV30Go6lAdt3FarkM5tNsPmUw9bome7ONO5mhM2djDzQ7T0VMf9+gOycipMyGR+uQzIK9SR+zYRNridlj74zMr01PJK1ORYCemZttNj5VJrsmo7RYR3aq3B05EsU6YHgjtWBJk94QoER7WRFkIpZ/a8DNv5xEBbJLaRP8jBhWEjVpGvYXQxZ/P6S1bO9n1UcWeMeHmHcSQsgd/tBirUJRFXo5GT3O/c4GnTNT7J2WpmOQkIdGmzLSs/qKqTcd2ktx/IyifSzg8K86DKaSOEWD2gMhiT1RP6a3JHhURXo/jCOzJWNV05EdNdaGzuGIxJ4h8FgtgTDx5kjdedKj8gOb+r2aY/9kh91PTOGUFc49A6JqgrF3FKlqwOrnFHbLJIprcrdkStBbkCDXIB0RZsQUhQL36Q7Z38sSJkT81T4oqs/mmYDYjiW7eEMzrIi2JFkX4EnzuLgWB8ccktcTlK6Gkic4pTEHitJ1afZtfTbA3ItRuiRq1uyGVI7Nw3IsNF3pC4kjUZFdlUrJ7so0xAg03QWDwWzI+BsKtyDN8yApVZSXFf2Cmwe3HBGvyz058WqN3uHiRzuByO5qgpQsRsn1LoXL0mhRIex8wWXsfES87pNdD2Qs9dk0E+d8/Iwo3xZ/V9JWxt9SbPw1n42f93ErooNPNEPsXsjCtwIap4sUbkukWXfWonsgTbIa7T8UpgetQ2LqQEPjaBx1fYX+hMnMKzJ3rT1QZO90DGcEJEmP92kti1yzu6Con4yjDRg/FxHbtknuSllqDSPc8WD/Bpt4u0vujqZ6n8WNv1oisyn2296cJlUNMIfCJ1QRdJYjOgcFOWX1Fc17QprHpdEWaxhUT6dJr5nMfzskdzci1oGFbw3J3ZH3N9bRzP9BxGDckrCP2yH9Az4zLw9In02SrIpq0k/LgjH+tWvSCL0TUbgh8WC3/9ose6cNKhdFNuvnRMNhdyE6MGQ4HeKnLVkAjkss29qPZRiMyciqcMXC6kNvMSBIKOEotjVuSWM5mt1HZLHLrYVEcShfdTAcxfi7Pvm7Af1pTeV9Odem9iJKZ21qDwdU3lNc+XvjhLaSCLtXk+RvGLSOQGtZuH1LX5cJt4pkzKftiOxdjTk3YPr7BoMZzdRLdeb/kUA83Lyier8cN3rzgKHRh/oka5ra0y6lawFaKby0BNuktkS0oxoxmVY8LOEgY+/Jz7v1NGw/qYivxKVfNJTqpjdtsvOoBOtm1jVuWdNehsbpiMk3fToHpLmY3g3pLIuCUxtgNw1iPXGLRpaMXOunTFpHBM6T2dSkdgzibXF/bj43RvPwh08HPhKVQHJqTh/+wldk52pqcncdOvMi4hlOhyS3JfJbKxg+2iP/nTT1+yPiuyK5tBy9r9f3CprEniJZ0xSv9dn6WAarB1MvVtn65BipvYjQlvRgtyyleO+IR2zHFpRUWVZleyBSTMuJiLV/iPgGCR3dO2Nj98VyPPaeCI2qp2N4ec3MSz6WE1I7mSSyGY3BoHg9JNHwMIYB209mUYE0eBSih1ARZDYirKGIQPw0FG5GpHZ8AGr3xol19L6YJb3lUT8hrsLshpzz3YJIi/2MOM7i9VH4xLYo5go35Ma0XL2f1ZioSbhJoiYTB2dMHIrlS+JrN4YGYSHg6D/pcvtnixi+3PTdBVmIitdEqzAYkwCND/IDtSGVXf2ELT9TSiYKYQzChMz9vSKMvxOQObdG4+lFQNKG0luCja+8H9A6aFG+4rH5pE12DeItYRikqiEbTxuMvaOondaktgxyd0P27jeYfFtCSnJrEb0psQhHplRQnVMedtUme0dgsMmqIr0Z0TihKF4TEViQVGTXQ7p/uUP6q3nqpxTpTYXhye48nAmYekkUpmHigzGq5uD/02fr41nxGyRlGlU/KdZq0xcfQmcZxt+J8NNCG45sqVgzWy7tv9fD+/djDMelv5Ib/YwTZ2Wc2p8wSe2JcrJ+QqYY2dsmncMyrS9dkIZymFAMJyRsJrJlQTv/L/7ORxc5/o/+4f/+3yWffYzStYCdp0C5NgpZENBCcoksKQkLZy2GYwaF69C+z8dPmLRPBeBbZNYjJs657D4miGetYlgDcCYUfi6Fn5VpQ39a4RxyhNp7UFO8YIpGYcbEKyrGLnh0F2wiE2r3GdQf1ujQkLTbkqI3Z5LZkPO6n1OoUKH+4xrB1Qx2X9FdMNl7LiR/2WA4KfP08fd8dh4z0YZFoiMJyCjFxFmP0JZjQrylcSoGvVmD4vWQ0JYcAC9rsvWsrPLDox7xbWukZtNEtkh4+7OSmJTZ1AQZRbIui53EsYuktHfcR0cWQUqRW/XZ+IxATLUpXMBUPSSz7eGU7H2d/Pi5EC8rWoDBTJr0/XVi7ySJYooorrAcBVrRPqjIr46Sl2Yjilc0iZZm+4s++fMWvc91cf0Y8Zb0ENK7Ee2DAhDpzZp4MwWBY8zJGX04rvALGi9rjhZjSFUhtRfQOGbTe9jB3oox9YYruPg7mmQzYudxg0RdUqy6Dzv4UYx4R2MEinhHdBl+BrK3DDpPOoQozIFBZCoSTTF02X1oH9P4SRPWk3QXBMDavcclf9Wg8r6D/9yAxpzB3B94tA7aVC5FDCYN7L5UW0FaYLDl9x16CzYzrw5x8xaJloBH2gcN3JJC2wJLccYUew+YcDVD93BAmNTkbgl63OoLPtzLCPjUyxnUHtJMvhkRWha9hYj5b0tugZ8VBaPha/J3RA2pIrmWtVe//SOR4x+JSiA+O6fn/7MvM3YhonFExisqgplvV2mfLNE8Yu4Tc7y8yHAbx0wSDTkrq1BWWW1AohUSxgycojzwsbYYcNy8QaIZjfDLAgbtz8gZc/oVcdPtnbGZesNh56GEOP9G4RG5W5C/47H9WJxYR362wk2feN2ht5jGKSoGk4rMujR0OgdE2RikoXQ5JEgYNI+BPxaQvWajTXH5DcYtOksSnZa/LuKi2RcHbDyTkpCSvuyqgIhg+tCfFsGTV5SGnpdTpLejEdJL05k3RAtwO6R5REaShVsOg8kYmb+xCf91kd2Hs7glCI4MSJxPgYbBtJy/wwRMv+rSmxWQRfsRh8lvxfCTivSelMHpG3Wu/edjknG3ZdA95lF+0yazHbB7v838d3p0llLYw4jutMVgRvoKfmYkD0ZSho0QlA/F63qfHjz+bsTuTztM/VqcrY+Z2F2RJzsl6RNktiMSNZ+9B+KUrgQ0jlug5YgzLAmENbsmwrDIlAXf7orWItHwWftkHKWhcl7SpoOk9EKMUEg9bjnCcBWly9D78Q76fB7ThfChDvOlJnd2K/i9GBgaXAlpdUua8iWNm1PYA2EqdBbEDt2Zt+jNyWTJLUrgjQoBA1JbmlhP/u0qgERVMfXPz1H/2TP0Z0VBaPekyvBLAbP/3qC1bEpU+Ug7Yw1lbD0cl3u5PyO07SimqJ20MD0JcenNGlz5nz/CMWSJekCirqjeKyaLWEfIL2u/EKM3bY668BLPrU3x9msTijc8IlvhFeRihzHoj5s0DxskmqKt7i4q3KI0UHpzEizZPih0oVhbII+9uQTDskmsBXd+UgJFk7taNOwKko2InUfjI1WjJt7SBCmD9eey7Dwq5670hmC1cmsBUVIktUSw9YymOy9ur8x1m8oFFxVA7WSM7rzBcDpAlzzaRwS0ufNIikRNknMzWyHevX0ZsS0GpHdEDx+k5H2z+0I1soZyM+08IjeFCqF6xqD4sR06B2DjE0l6Mya3Ls7SPpwmTErKUvqNFL0D0m1XgSJRl3l0ZyFG7YEIZxymf8/GTylMXyjEKtLUHxln/G1Irxl4ObCrNs3jGqdgUr4ScvsLaYKkYudhc78MT9Qj4g1NvK2Z+5Xr5O5A7pbYtYOkIrGniJ9q0ThmcvB/cGgctcisKbJ3Na3THs5UgOnJJGYwIWlD1dMW06/06M9G9CZNwoTCGw/2TVFGKKNXPwu7DxrUTiZkTNgQw1R/WhKog6R4GYKMbCiV9+WaAUy+5YGGYTXFVieHdSlN9ppN5lqM5a8GBCmpZmLtkMajHrXTMBiTx6px1MbwYOKdiOxahN1XFK9FwkU4PEBpiUE78LUuY+/J9b75P52msyzXN7Mu1aaKIHfFpjsrG6SXk8XBGiJehowg6gq3A2ZekcmI4X4A3pWsgo88aNTPSAa8ESp2H8zgVBSFmyFT/zhG8YZPohlSvhyOfNmiBUjuQnfWJkjKmxDGoH1YOuipbTFMRLaifEkeHGdMHp7khsXEWZ+pN0KGSx52V6KcEw0R6Txw+paMLK87kvNmaoK43IwqkmpDRRLoMfUDl1jTYOy9Ic1Tmq1PaLqzFvN/EO0r5FLrFkFWU7wZ4FY0w3Gbwu2A7EZE8UZIYtdi/jdMSu/LCFJyDGV0FSQUi/9UTCczLygyKz05J96NJOoqZ1C4Ib/2pg3Gz8qOF9nCFXC+NkFuBZw5bx+OaXoCtRh/cYvMdkjpPSn1Yx3pnMdbmtZxTf6aqP2cgqgptVI0joqAJt4O6U9JZJs76ZPakhzBZF1241hbUXsoZP47LqUrPpk1ReOkGIASjYjGpw4R68j7OZhN0V4W45L17QLZuxHt4wVJBl6KsPsRhfdiLHxDPP1uWcArflozXPDYuz9D6aI0KlvHAwoXbJzKCJ46KzLywXRErKNwKuIgnPluA6+gibdknNc5HNG8J2T2BY/JNzTNIwbOZMigk5BjQk2jPAP3coEwKWPT6Ze7YmobuWIax23Kr8c48k+3MR2ZNlUuChG4cVSAOUFaKrfm/T5sJnHzioVfXyfIxLB7IdlbPbKrBtlVWPhGi/6MZCp8AChJ1iW8JUxqzKcamC5MnJOHPNGS+9zNmlTvs9n4hGxq1XuTDMYNCrfCD33+PhKLgB41LtPrmsG0zN4jS1E7laSzaFE/YTEsy/lYJMWQ3RKqkFseCW0KYvEcTEc0Tke0DsQZjskxIH/HJ72pyd3WjJ0PiDU9WssW+fMx0lvCHGgv2bQPw4WXDtNZjth5SOS9xqRD44SieVx2WKWhN2Mwdt7HqdjMvCrRWOl1AyPjyypuQOX1XYZToiosX9CYjlhUO4sGye0h/QmDzedDMnclECWyRlLPKXk4wiQkawGdpQR2XwIudx7LU7gOhfdb+Bk5KtTOaExfk9oTFv6wJLDNRGOUhnQ6ovymjTMWUbzmYviahV+6SJRO0p80UYHEZ4UxTfGGDwoq74orUSsh90S2IlkPcKZChhOa2j0W6Z2I4QGX9IpNbj0gVQ3pTVm4JUntLb1rUj+eoLNoMf5Ol8VH1lEh1E/KA9FdMOjPKOo/28fwZWf7wOa9/XGpvsJiQP2EaEH6E5JUXLoSkqhp0luQXI2hIoGTDGZDYg2TzqGIIC2NSqck95IquyTqGnfOYzipWf3xEtqQY2KYhNwNg1jdZP25GK1DsttWzhnM/Z5Je8mWyLZAvPyGJz6A2z+VYe+BuNihQ6k2UtWQxqNT0jeaF9rPvpvyVED5gkxWxl+2JbXYh/7JSZyyze4DMdyJlNyLB+HWz+YpXw6xe4rl3+5JSvW4wd5DULgK/hslIhO2HktSvBZSO2nRXrSId0NRkV4R5kWQlHF0e+nPJxb6C39ZA033mEfrmMavBGRXoLMkJXx2XSS9/VlFvC6IrcYzDs1DFpULLrG20F3HzkHxhk9yx2D6RQGClq5Ih7m9KPJSpSWQ0hmPixqvIjfeYFIMJul1RWpbuvQoyGxGVL6RYOKdCI1k+3WWZOS29bhFf8KgtRxn8at7oKHynQQzL4vqcetTk5TfMxhMiQuueSQmAaEtuPFXk/RnNFPftUjvBfvjG20oZr/niXGqB3c/azKsGCSq0J8QF6Q90Fz7WzmyaxGlqwFHf2mbIKloHjGwXE3jTIhbMPCyQvYZO2uQ2gvJrhh4eYvaKZNb/+AkzXsLZNcD+nOKzKpkGtTutenNGESjZtVgWqK7e/Oi8pv4gSJ7V86vlqNJ3oljeLD5MQO7E1J7wpd/445Nf0ZRvO5iunDnJzO0fmUOLy+BpW5JBC7WAIb1JKkdCREpXwnpLBkc/W9u0DxqkLwTI9aGhT90GEwq8qsBvRmBtUaWnK3bjzuktyMBda5AlIyIkhH5G13CbESipogxxB1LAAAgAElEQVTdSNJZBqNtjUp3OPhrXfyMLDpeXu6V9LrCz0qPTEUSePJBsGj+uij6nCWXyJIHuLcYEOUCmkflQRNhkBzRVKAYVExSu3LmT26I+Wx4ekjrqPhb4m3N3mlbkOd92H3AJtaLSG2LMKlxxCTWgd0Hs0S26AGKl0XlOf1KHy8PzpiMlrUhC9HWE5L+ZA3lXhkcd2g96O5XLD/q9ZFYBMK4Qrkm6Q2DuW+OQjznAgxf050zGUwpMnc1g1lJlp35mjDf7n7GJlHX9OdHs+afHzK8b0hn0SS9LiV1/OkamZ1QqoKClId7p+WBMgL20Ut+XmM6mng7IkpqTEfsv9qAnYcMMhuKxnGBReRWA8qX5XsOphTN+ysUbgcSSHLQJrUX0F2KyN9xSW2r/WrD7smRZPxNaXhl1obsnbYpXQmIYpJMU7snzmA6onXaZ/YFAWB2l6Sh6eWFz5+7ZpG7M6B6n8Xw0BhBQvwT3XmDwvvC0p/6QZfMmhiRnKKJV4DetEm8BWFGxDrrnxM2IsD2Y6bQeuqye5QvhcTaivaiRVDyaRy1yN3q0310iDZkPKUCWaQzdw3Wn41hxAUmEqT0fgO1fjpi7gWP3pwczfrTiiCpSTQjeoshVtMi0Yj25cuJuqbzzGEMV+jApes+q59NyPz9S66gzUsyPkvtaNRunPyNnvQkKgqza5KsDNh6Kk/+soxF7b7AYGdeikhVQ2IdTetElux6tJ9M1D4geoEPzs7DMUX+VkRmU6MtTeuoZuoHIelrceyuHAPSaxZ4BqXLo9HquEA8cisioHILivo9mulXQvysFrrwuSTJXXmQQapLuz9yLaY0mz/h42elsRxvy1QssxNiDTSxrkjNe7OKzlKSRAPyNxXli/7+k/wB8MQeRDSOKbL5Ick7ceKN/0AGor+wl4byOQPDk9U3SCkO/+shY+92ya0GZNciyuc7zH5PFHSDMRPT1xiOwk8pCtegP2liv5ojHJr05yIGj/foLkfE/3URJ2/glyLyt30SNUjUhLZjeFC+6uOUDOa+4xGkBSCZvWESb2nSOyHNzw3I3oXBhGY47xPrintsWDYY+41LzLwyBKBx1NoPLN15OEbulsHOwwkqFx0R3qw52H1Nf0HOZlEMVj6XYublIU7JxClLslB/NiK1ZVB+y6J1wKJ4VTLm+jMap6Lxf6Yh3eCJhMiKBwGRLX2C/O0QPwfBhMf241kKd3zaSzKLXvq3G4yf6wszYNXEzwG+gVeMpNHUVSSqiuazQ4YTghKPNzWTb3TJXIuRqGsaJzIUX0jgjkWoAKZfGzKsGAynxPJsmpGwDUZegJ1H4uSvm3QWY8RaorkI0prZF31ah0zslgR5dudlQjLxjk+8rcUO24edJyM2n7JY/s0OblkTu5AeQU+FmBSkFXbH4M4Xsuiyh+nC5KldXnn4X5B9bofCHR+7J3N4LycLWvOwRecAVO8XWXRuxWM4FRJvyuw+1lRk1iOGE5rsXUcmT0NF4bqQfiQ1SFO6pEnUNLnrkgodJiC5I+i2+pmI9JYitxYx8ZZm7TOQ2lZsPyZHmsxWSO62iMKSe7L5WEPN/Hdd5n/DJFkVDqRUYNCbNEnW5DpZQ8Xs98WZ2jkoU6HejMXCNzsMpwISjYj+rCQlla5oZr8iyU/ZjeBDH7+PxIgwOTGnZ778ZWJtxfg5l9ahGH5GMZyMyNyVOadTZv/s2D4eYAwMkruyU2c2NU5J0TkSkKgM4VKWRF1EJV5W5rWZdb2v/VYhJJvyBg7Lgg9P7wTsPWATJuQCR5acg4OUgZs1iPUlMDJ3N6C1bBHF5Ewer0u3tnQtpHrakCnAlmyvzcMGUz+Qf48RSMXjFmH8HZ/WIRs/I43G4g2h18Qb/JBufCzE6hiULmmaRxUHfqtJ854CzWOy6HUXJZBUJMJy85UvOVh9H7cURxsKtyhejN6UOAjTm7LQ5tZCNp7T5Ca7dFspdKiovG7jFhTOuCZzV95r05PgzPRuSLwZULsnTmo3onFSzsbxpqg94x0hCjdPaDIrsqOOvyMjs8xmQOuQJOXKwuHjlC2cooFTkUYvGgq3fKqnbYKUjLoMT65TODrToiXcpXgjpDNvjrrm0vdoPBBQescSqfZ4gNE3GTsLjVOK0iUthp5KSHpVhDReXjNxLmT3fpPS1VEY65I0R/2M3GOxtmbsXIfm8RzDMVGH9ucl6MXwNXeft1j+msPG0ymCtIyRVQRjb9Zw5vK4eZP0pkNnScJxGscU2VVo3CMxd5ajya/4NI7GUIH0xSJLPDSDcSE9ZdcjqVBmQxK7JmFCmoRGAIavSFSht6jJroCfFWXqsKwoXxziVmLsPGRy4He6dA5m0Aa8/WsfYdCo6cPCwxukdjVuUYQzVl+88ioUqWeiKp3c3pymfM5k6nVxFI697+PmFZ2jAZWzJvFXhcrqZ4RL2LzfxytE9OakY61N4dKbbiTuu7TAN+sn7BHHXmGEgs7efswivTYgssF0I/wMrH/SoHzZxT3Tx0+LLXc4F7D3RYfsioxp3JyiNyOhJ+1lWQBSVYFZqECkycXrHvk7Eekt4cNNve4S6wo7Ib0TUjpv4BckCyGy4drfzMlZfzygcUJovU5F7UthrYGmdTDOjZ9L4ZSFb2gEksPoFWDqdbHbejlQf32P8R+Y6FeLZC7GMZPCSOzd51C8DM37AsqX+tTu03gFidJefy6Gl4f2ssGDT1+lfElCMjsHYfPZERNBCXY9mnb2Cc6bT0seQOmyxquEOGWLIC6UZ6sPubWARDOSPkhfhC7dQwHDydGZdkqUcm5ZymXBvvXkCDGa1sx9U9GbE2zXxEsm42+LOCa5I7mKsTbCwhq9wuUhnXlLjmrbHs0TmuI1Tf+ES/my5A56ecXtn8rh5SQYxStoxt9UNI7Y1E7GxAQ2FkOb8n2TzYjBpOLGf1KmeTjG9sel0huOGfQnDbQtk5vsHTG3NU9G2B0JbM1uBTLhSsDdn4qo3yM5Go3jopwsnTdIb2jG3pUUazSMn5NmrOFC80xA+bLP9uOycO7dn8LwBMZ782/b9KYN3PxHPJo8fmBGH/7832U4KQEi+ZVQxiqTIoks3ApoH7BGnnT2b5jKRRFjhHFFdjOkOyNnX3MoqC6rHxGkRWlVeatG+1SZ/KUGzftKtJfFypq/KTt0f3Zki91RBMkR776smXgnojniBWpTJMMAaLj7RY3ZsoSDcFPm4YNpRbwh45z6SUVy5BSMd8QBOZiUkt/uyWzcy0uiUX/CJLsZMCyJBiLZkGAVlOz0H3D22oc1429L4zSy5KKbrtxAw5kAw5HqaPoVzWDcIEgJZ8DNS8m69G/Xufp3p7E7hsikxwSoESRlTl66BN05OfPmb0cUv3uT218+THqDfbuqVuKxL94IqJ2UEtetSMS24SvcAw7zXzUhAi8vzc3BpMZ0FIVbEa1lA3csonRBaEaRPQLBjo5C3SM+uas2E2cHrHw+SemiyJy9tDRxS9eEw/jB+zIYF1mw1ReqVHd+pOWP2Ed6pXbFgFO42uHa30qRuh0jWZWzfnrDoHPSI7EeI7JlZ83d9fBzFpGl2Pmcy/TvxEivDyCI2PixPNkRPj7WFr1GGFekqhHNwwbTrzkYvmg+tCGLb7ytqT4eMP6KRfFKh7ufyRNrS3WTWRPIqjalOYqWflT9Hk1qW67zwterVB+p0DkgR4veosjj4y05SojWQX6G3oxUzxJHptl5DOa+E/LqH/z9j24lYLWN/dHY5JsD4k0JlSxdMJj5V5eo3muRrEnSauGGiCFKVwMh0V539kU0qFE090mX6mmD3QdtnFFzb/djFUIbtp+uULzQxHRg8k2BbKR2Q3I3IbmrmP7DHTKbEf05aVYFcQm9SDQ0zkGX3rRFd86iN21ROBdj6esuxavi7Q7j4vwyHU3t80OMYDR12PGkAaekzD787/pMvS5CE68kxxL/2Tb9CZPOQXnoq/eaFG8MGUwqrL6m9Oo6E682mX5Fus2JushCK5cCStcCyldCpl6WTMD0pkHrkKT5Fm4HYs1NyK65+9wsmVVTgllKJpX3usQbmtyKJlGViUJ+JSLeFHru9peOMP1qQPG6x2BOaElj7zvEG6PodyULgN01qLwvFJzsuwnaSxLeEmtLPsLYebl+w5JBrAtLXxfSzsQrNeKtiMk3e6hI0VsKSW7YEsc+Hid3C9oHZZFoPusQb2myr9zET6tRcrKmeyhk7lsNJt7qYvcj/CND4h3JOUztaibfGpKsBzSOK+5+ukDybmwfkHL4F29KLsWNGJk1UWPG+hqvYKEijd0Pmfz9OL0pk5Ufz9BfypC9G/3QYLQQESYU7Qddth8XwMzqp+OsfjpJoi5in9RetJ8/mawF7DyeF/pPQgA4wzGFMxYx8+qQjec0jaMmkQXFq1JNGSHsPlkZBbeIKnHmpQBnXJOsR6S3fbQpFWProKg+B5OaKBXhZUR2PCx/xA1Eiek5vfDXv8L8t3sMppIkGh4bH08y8bYYdeJtGI6JgspyNIWrXboHMjglycFLVEXQ4meFXZfckxlw44Tw1sbO+7SXbGJdTf2UvKnBtIuqxaiclxs/uwLxribWCfFyJk5REcYFYjocF6+B9g0mX7AYTBhk10d20UlNvKGoXPTozdjE2xFOQRDjKpRmmNLiJEutmeTuRnRnDQxfusl2V8Ipusc80jdj+FlNZk309bkVyTHw8hGlS5I/158VfkJ622PnkQTJXTG0TL7lUL1HzP+pvUhk0Y+KLFgr8AqaA1/r4I6laB2wSdUitp/SaKVJbVhkNqRa6DzokL4kgM78SjTK6JPrFN7T48B/77H9dIl4W+6b1iEoXdV4GYVbVAyOO5ReidOfEfFT+ZL0UEB2PcOXaUwYE1yWMybsvXDJYfwbcVK7Hrd/xqRw0WbirS7dJZFl9+bZpwwPx0XtGcYEEe6npHJxyoqZF7u0D6VpnByRgUshlbfN/aPKcExCY/K3RhkMPRg732fvgTTpHXloTFdT/7RD7GKK0rWQ7qy5HzyCFq1IfsVFBZravUnahyLijVHYTEqCQPI3+tz+qQyxjmLuuz12Hs5gBHJMlftC3tP8ik9vyqJ+JmTidYP2IQMicCdClr8qz0H5coiTN7AHGqdsCPZ81SBZEyNVkJKfrTcnkyhtCJtxuOSRXIlRvhrSPGRy9Rc/wrJhw5czzvqz0sDYfiRJZl3TPmCPymH2UdV7z3lsPZXH7kWjh1RRvCmjKYDxdx2K13r4aUWiLjfN1hPWPtc+sy5RUMZunNIlRW9GJL1KiwsRINYJya5JN9VPy+4+/5sms980aR6VBWdYNsjfCSTvbTMiSJsjJ6OJNcKfd5ZkIdl5WL6u0rDzhCbziV3snsbPRWQ2RlTlPZswCShxgKW3NP1pOQ5MvS5UZGsox5fGCcVwzGbyLYf+jHSz904nKN7y8fLQOCkOstzLSdCQ3tJMvB1x97N57n7aILsVUD2jKL0r2vdQ8l3FjXguQXozIrcakVl3iHU0qV2N0pD5XpqdpyRarXUY4p0Q01XiclQjzNpmnMxOQOGWRGm1D1iCQY+LRkJFQtGpPuHvj8WSe4r45STtJYOtJxIULooSdOtjWVQorrtw0cF0Nfk7gegKChptw+7jovsP47Kb7j2YpfzaJlZP4RdCJl6TM7ifVfSnRslBxYjGCTnW2AON1RruV0qWI41CNmQnbx2U9KP87VDi3z4xJLvhs/1ogiAljcbpV8VBOPF6k2RV050zMLsOsY5i4m2P6uk02hQC1dQPhuTWpNPvp2HtpyKCpDAPhhVhJxRvREy9BM3DCXJ3NLVTksxVfUDEZDMvRky91sFPS4WU2tHUHvdx5jzqD/tElgIDJl6ysBypZsPkH/P8/UU81P+/X0oy6HIrEX7K2J+buiVZNRN1TflyyPyvrUJbsvb8rLgLsysy7vMzAtDYO5OgdSQtuLC2KMZKV/S+ZdNPw8zLPuX3xa8/cc4j0RBMldUXD3rroI3d9clshXQPB3QXBRPemzLJrEmiTHcJmkcsSlcEcdY6aNJ5ti9hpIaiuxxSuClBn8k9xdTLsvhU3jEwf7lCf1ax+I2QwRfb++BR5ctD4aeh+oSPNdDE65BZ7TGY1lhDBDLRU/SnTG5/yaJ0NcRyBVtWO2mTqIFXCahciHBKiol3HMIEdBZMUUy+LZc8d1OSbtI7EcldkRL3ZtXoLCnGmsaxJMl6QGcZhlMhsZ6MTZ28geFJgEf+dkTi9h6RLSiyKKbZecimddAgva7Jroe0jo92pylpsHkZxfKvRfSnxVDTmxtdp2vynplDoRsn6prNT8mkpfi9BF5eUb3XIt4UzFnhekT+qrlPBYq1DNqHI7qnp7B7kFkRc5FTFEakV9SUL/sULhnEOiIH7i4oWveURi7OkOYRaejG61KhTb45xE8pGj8tefXW9RRe1mSw5NOdsxlMaoZlg+IVqD5cpHNAuIbbT49h+LD+SYvcXSnd3ZxiMBVn6xlpCKe3NPmzcTLbIdnV0WTIgday/AzdRdGVaFPeR3MgKdaNoxb9ubRMOnISn7fy/P9NYi1G4b3YKOhVEprNIdTvVcQ+PIrwI7IIaCCSVXkwoYi3pJuf3tBC69kMqN1jsvofLXL4V/uoCIZlyWr38oretKTUxjoyS2+ckCSbMKFIr4tuPUjJRXdPDWgfsGkeh96MiVsQFqBW0F3U+6Eit78Up3qfQWJbSll7IEkw2Q2f4k2XKKYp3A6o3m/QWRCIhLqdJrMlDTydCcR44wlSqnVQlFzVxwPaS6aw7Gdspn5RkmjT68JCMCeHAoW4I6k8XgGqD+TI3ZEEHz8tSrswBuWzJoNxSWJK1iOxIo9BYtOmOyfCm8bROKYLnaMBg0lxKq5/JiLe1dRPCCrddDXhSHBUuCOLj1tUFK8NcQom1kBRvCSS1ep9Br15RWRrLEdK8fUvztE6GZDa0cTrBpl1zcQ7Uh00D5uMvwX9Iy6xpuLAb/doH4mon0gQP9yhdFGwWVZPkai6AupYEgm5W1AUzttk1iQQJLciMuzdJyWhx8tKQ7O7KFjt/J2I/HWD0Fb0Hx7Qn5deUfuYpCenNxTDsjkyCQV4BfGZtL7YYzCl2XzKIt74AD4i8/4gZYpSsJqU6U1WFvbEhs1gUjFxLsTwhO7s5iX3b+15mch4BU3humLzYxYzL/p0DkJvyiC5aaFHRKD+jKY/btI+Iv2DIA2VSwE7j0hT2RpC9q5MusqXNa2DBn5Gs/OoISDTbU12VfP43/4bpLelR9CblymUVjCcgCATiS3/Q15/nhiyX1FKrSilzo/+u2/050op9UujGLL3lVJn/sRFwJByv37cpHfIJ3+jT/lyiOnLQ373s5Ihl6hr3HKC3HogiOhQhBvpHRkjqRAm35Tu6tUvZ+nNi4Y8vS7RWE5FUfqOXMwPZtG5b76P83SXiXM+cy/4mK7cAHbLIFFTTL7lY42OGsmqpjdt0zoYZ+bFiNpJa9Th17gHXPxchJdWtO/1KL4dI7/i4RYU/akYiZqoEUtnLSbOOjQPSYnXPJrG6FhENky/FjL2u8l9vFZuZYjhQeNMQONJd/+I4+Wlqslu+GhD0Z+PKL2xPcpIlL+brInWwfDkHLz0NeHhJaviJchfqBHGRYwyHFe4BWm2DsZETFO54NI6lKRwpUt6xE4on5cbMbOh8SYD1n46JEyIA08F8uvYeZ/ypT6NozbpHSEd1e5VFN8WAOrac1nsrgRzpr+eI96O6H+6S5jSbD+RonVMk1mHRCtiOK7pLEe4RSjeDNl6VgjHdtOkcUosu7GOZvwdBCM+KdoDL2MQ1ePEayaFG33G35RjYXo7xM0bdBehccxiMCWBKKlvZ1n4lsPkW6E0qEMo3PbJXzXZ+IQtiddbFr05hd016B6Qhl68Ba0DFv0Z6T8U7oQi7b0oQqvSJU28Jd6CMGGMAmGk6qk9HDKcEEFP8YZLmAtxKqJUrR+3KF8Q4VluxcEpKYYVscfPvtBl/L2ImZdEJBZvizTe7kqGZmRK72TyzT7WEHIrGm3ofSDOj3p9eMvwhy8XeOaPxpAppf5w9LH/Umv9tf/P5z8PHBr99zDwf45+/dCXOPNkMchftln9rCW2y+sh6a1IstbmpTyrn4zJefeW4KP7MxGV84Ilby8ZJOuK0mXNXtoiyIYMxy2ClGbsLYNkw8fNm/SnDCrv+9RO2bQ/dw9cNqjeI7BLFWq0kvRcw4f6CZt4U1M/bpKsyflzWFRUzg+pXEwS2QoVmjhhjImzIduPQHIlRndBYzoxnLGI9LY0zdJf2KO5UyS9J+fwzEaENpVkxxswqJgMx4UalGiErHwuhbYirKbF3G9r+hMStjKcCchflvCRMCFlcOORKVI7o4bgXES8rYTDP2ORWw1Z/byFtmVnLLxv0T1eJrciycgqhLnv9qjdm6Z4w8XwY1TvixOkYTCVZzgVktySScDSc6sM/scZ3GIMq2fj5Ufiqy2TwSSEcRu7J3i46mmLxX92jcHYUcbPdlj5fJbSVZFrN48YYqk+YxC1E6R6souGmYjevEnjoZC5b2gGZZPmqYjdBwzGXzdI1gK0sklVI7rzBnZPFnoVSkM06CrSuwGtoehNItugeVzhlQLydz5gPEjFWbysyK+6tBfjbD2ZJLmnheBjKqr32pSuB7jPDCi9kICRMGnvgbg8zB1N54AmUVeMv+djDkfEpqEkMIOoFJtHxI8SxhTesQGZ9STZFXAqFsk9TXfeQIU2c9+MUGHI+o9J1RVZwiFc+Xyc5I6wB1uHIdZJk6oGtBdtTA8GFYPCrYDtxyxSO1C40WfvsRTWr27B/YcYTCjG3zDpzX24TuDPE0P2Ya/PA/9m9PfeRPIJpv6472ENNG4Z8rdE8li8JpLMzY8r7GEkcstAcM/xpjS5VMh+Q+uDePGx8x7dOZMgpZh4E6y2EIPsnkwAhmWLYUVuvs2PWeTvhOw875GoIYy8lFyszsGI0lWf1F5IsiodX8k2UHQXFIU7Ad2lNOvPsz/LN1xF64BFvCU3c6KmyK57xNoGgwlp4LT/cIrsuwkyV+qMvxuw+0REb0aRXRFtw3BcVF+toyKDjmIauyvW3K3HYwwmBHmeXLewHGnWWQNBrYMIg1LViOlX5Yas3mthBBo/ZVA5ZzD/TcCKsAea7OUaxatDDFd2tVtfSpGqRmw/mqBxSuhAhRsy1hs7a/wQcvLlEvVjMZySHgFaRQL9gc3bGkiGwOQbXVLbmpX/4ijT36+z8hNZypc18WZIb0qsuqVrsigZHYvcqvzM5Xek2VZ5zaZ6n8XEt1YovS/d/9oZzfqzJu3jIdUzElbqZRXV+0xyq2IFH4wrophi6feGcq5eSFK4Dotfl0ZybjWkvSyO1CClqN4rAJmZl/oimJo22X5KhGiDMZPSr6dZf9Zm7VM2g0mbIAH9hZDhmDgLk9URvbls0ZuJUboasPOxiEQjILseEOsq0tshTskg+W6K2tMuYVxRvBaSaGpmXh4QJBVO0WT7CZP0ukl2PaB+v0TxTb3+AahGkrJbhw26MzZ+VpBoKGgvWqS3oPPokNaRNMkNk6v/cEn6aQ3N3uPh/rPyo15/phgyrfVbow/9wqjk/8dKqQ++zX4M2ej1RyPKfuTLz8r5v3lUIqOyGy6DScXU68JUy2xA84Q0xhIt6aYHKXnYUjtSJqlQEyYMUnsRlXc7hHER8AymNf2DPom6Ir3lMfbugFhXSDfNIyb5txOYQ01mVUjGdk+T3DXwsyZ2T44ZRCL+CRIiFhqMmWx9PCJ/xdofCYUJTX4lZOb7XYxA0mN3HokTb0L5siTpjJ13yN8N2H5uAqU12VtCucWA6e/ViOKQv9kjUZWycfwsuEsuflYTb0iT6P9l772D9UzP877f89av19MbDnBQFsACWACLBXeXW9jNJlKiLHmkyIlky4mV4tjxZKR/NEziSWY8SjRyYnnkxM44VmTHdigWFXLJ5RZuBbah93J6/Xp7+5M/7m8PNbJWsa2RiTB8Z3aAPQDO+d72lPu+rt/VOGjiTUm0WWZjeE3qIhDp7klwmzGteYvelGL2+T5BUWH8zBaWp6k9bDHymk13WrH11Bj9qZQwEV8ISG8YbJ4xmPlul+JNWfpn1wPCQrLreGs/HLL68aLkAlyW1Of3gzGijGxR7L6Eq9z62Sx+ReFNRCRpm/I1KQ5ufEigLUTSOSncMkhtG2x8QiCsdl8CVWuPJoxcjNn+1F7CrGLPNz10OSDJJORvm+z/7Tqpmia/klC9LG289Q+L56C5z8Je3EYrqfaXr3ZY+rTF+rMJUVqENFZXRD6ylYGg5MhS/mZA8YrJ2lMWtdMxxl/bwq0JPr15wCBVg/HXZOVWuSJL8cy6mNOKd/rUjlpU3zZp/lKX1l7BrEdphVeRDlTqVgojEGxddmXA8scy7JyJsXti5tJK8O6GLwiy/qjBYD7cfQ5zS5rsVkR/QtObNvCq0J+W+om5kmLnEZh5vkPpskVmRwxT2fsW9vHmn20Q+OMxZEqph4FfQeLIzgAVJIfg3/j4ozFkUb9Hd1Yx++0+hXsJ9z+bwu6C24xITEVhMUJXQrwxzfYJk8ZD0o7rT4tpxvRlUGgcFFXh4meLZLYj7L5m9js+VsOShJqHXbxRl8rlLkFBpLd+CXJrIjwyQqidiaX2UFCEOYPmQWA444xeiNg8Y9OZlyvnNoZOwjERynSnTTYez+O0NJtn8gRFTVCApS/FuDWDzpxLf8TE6mlWPiIz3p6v7uC2NNf/6zxRRnP7p/MSnDqtsDxN9SWH7JrgxNyGSKzHXpPiWe24MPZTjRi/qqlcVix9xqC4GFG4n+CNysyU+o0K26cE1NKbVky/1CdxwC8qsmuK9ScFuaVNuPlXJRlIxXDn5wycusHUq2KS2vNVCAqa8W8uUTsuAyZA47TwGlI1TXfGILPuM/tcTJSCA/80YO3pAjkGEx8AACAASURBVM0DEhOXW9FktmNmvpuQXfXp7BVTTvm8BGa2FgwKdyB7T65Pf1x4iYufSlH5nsvjx24JXepomcGYYuuMdIcGE5r9/7xPdz7BDKD+9CxuU1qrS58uMPk9zf7fDvCLaleR6RcVpi9KSL9kohJY+7BoPWaeD5j9Q9j53iRj7waMvhcRu1LX2Xgmwa1JkEuY/z4HYelTWQr3pTCsvllm6utLNI4M3axNGSitAbTOenzjP/g1+r/awe6B2TUpXq5j9aTdjAKzL5Pc6LtdKuctxt6NKN1QlG96tOcs3LqiPyV/N70xFI/dhMIdxf0v5AgKcn9beyy5N98ofvC7+G8rFlJK/SrQ11r/2h/52rPA39Zaf04p9VvAi1rrfzb8sxvAs1rr9Q/6ntnRWb3nF/8Wbl0illWs6Y+Z9MfVLqc/KMjSKyhKJd/0xT/9fvx37Mq+cPztmPohC7+ssbuKOCXCksQaGo3K0kOffilk46zD5BsBtcMOhaWYzccMZr8d0JlzSIbLRTQUliM6U5IiHA5Z+4V7w7jsrGxR+lPSArQ8GUzaj3qkr6VIXGn72B1INQT8EaWlLeY2xCTS3G9QvplQO6aoXtICBtkQGXTswtTLHW7+QprqeZN0PaG5IPtzayDItcQWI5HTNKhcTciuemyfzBClZb8epWH8rWDXvrpx1mH8XECcNtg4a5LYmvSWQfFujIph/Qljl+9fvhGT2vZZ/KxoDipX5MXq7oHsipxbd48iu6p3W1NeRQ0zJOXhbB2UgFa3LozAnROK7IpYsrcetfErCWPnpJXl1hXdfRGlS5LIu/WoDA6DfT6ZWy5OEyaf32L9Y2NEWXFPxraoG/2KJiom2HVDUo2QgJXmIdH355d87n/eYfIVzdZpQYWnmkP5b1PIx+ZgeE5nBkz+rkPsKFoLkvjrNBXVKyHteaE6O23xeWhT0VwQgVhqW2MPpG3ol5FMw3vibHXrBlFaE04GqJ5FalPYmXZP77IXe9OK6hURoo1cGrD+eJrEhLAoBe7iPcmvqFwTybf1mR28l0aIHUQbcD6kM22JwG0sQVtCidImXPqNf0ex0AfEkF1/f58/jB3/InB5+E++DvzlYZfgQ0DrTxsAQF7k3HJC46imfsikdsQSPbyrpb9aEZdV7CjJehtLsDsS+128k+CNR2RXFXu/3iV2hKybXVNEGVm25pclXSfIS1prZl3R+y9apGrgbA+YeL1De49cqO60Q1CQXHrT1/RmBaWdX40kzWgioT8bicCjJ3sub2TIGGzLAxSlQRlD7foeH7sje2WvIhJmt5Ww9+t9tCEz3/jbIb1xeUCCnHDvVKJ38+jv/USOw7/RwAxg61EJXTVCqYyPn0tIrxvs+12fwh3NzglFez6F09a4dY3dleu1c8yhdsShcdDBryY09ztEKXkRStcU/cmEtWdh86w4IbUBmae28UoG9SNpCnchnAjxywbZzRi7oyjdCelPKGJHtPNGKMUsCSWRkFUzlME5KIk9188rgpFo1+VYvpFQuGWwfUpRuC3L4dSaCIy2H5EBQkVQOu/iNjSFpYitp0Z38wODnKK912Dmm3WUBntkgBHLDG9EkgUx/VKISjQbH0ox8brInY1AlIHN/UNoy4zGG48o3pUEn7l/auIXDJoHDZy26FG6CxFe1aQ/oejPRiSfaOAXDJxWJM9XUTT8g4pBd49QrLQpbevUtjHcEmqcVQftylazfCOkvRdGX90izEvtaeu0gRFoNs6kGbkQEuU0hi+ZhGYg9TC3EeFXoH2hSmZT2qPpLU3jgI225Nz3/803ZJs7IqvWDzr+LDFk/6dS6hJwCRgB/s7w7/8BcBe4DfyvwC/9v/2AxBKBzehbanc26c4o9n6lTeWy5OpZQ194uh6TXRJjzM4jmvoRqX42j0UsfyLP+lOyzyssRuz5lmgz1z8yjKMeyEsWp2Dwwij9Cc3qx4rc/0JOOG3DEI7K9YDeuElrv3w+FUHsGvglA7dmkFm28MuCdbYGQxHKxTaphmQGTH5yGfd6WuKvexbeqJCOunOawv2ArU8EbD6WFb3DdERqrS9ZBx2JOItdaBy0CIqa/FJC/h7c+vkRMlshk69ENE+E5NYSYlcyCmMXlj6ZwgzFyx8UFFvPhLQOQfOIpnpBZuTRCx6ZzZjpF8URufkhwZw3jsm/G9tXI3aGCsEEjN+p0ptRlG4HZNdjyudtBqOw/CkYuRhy70si0S5fHyYkZSVu3e6wG4zx/uqhclkx/XKEPdA42xYjFwcYoazMspsx+cUhbfk7LWlHXupSuiMzmbbAG5MBtv2L7SEdWQ8pu4L7ah4vEU4HjBa72G0J5MiuJviVhDBnYve0UHenJDotuzpMqV6VgT69qZh+XtEfM0lvaeqHnaG2QNqq9VMJ468a1I8owgXZHvWvl4YFRhPT14yfF5eqEUlbrjdpUrpi4bSEeOzWDPojBnZX4a7ZxK5m9SMWRqjoHqnS2ZeQX4nJbAiPMcrB2jMSNec2FJ09sHPMYe6bLdaecqlejXFrUg+L0sPglAo0jsj947FjjL81QEWQWw0+8P17MLwDM7P6kaf/SyH71iI6MzbeiDzcpVti+XUbctO6c5Kou/2IxeiFiN644Ka0KUs5t6HxRtWue6t0N6Z2REJKOnMSB+bnTYK80GglCFJAI5mthN6EGDDSW3o3KNXuS+hnnJJlvemLKGP7lPj9ByPiYvNLGqsvNzwoyblVrsqyrX0goXRNkncSW1E/bBIe62HeyJJblH1y5n6bjacrlO4EdKdsyfNrCb2ncdAku67Zfjqk+ppw74J5D3tZSDd7fmeJnWdnsXxNd9KgczAmu2gyft7DWWsTlzNsPpYjHlbyU3VZaTgd2X705sRFGeUT9vx+QnOfjTUQya45EB168YKD3ROqcpAz5DOUEjIbxnAgl61SdkUyDNaeMrA7AgWdfF1ewOYjAeMvWnRmDfJPbVG/OIpbl/52f0+EihWpDRNvLMbwDNx9bdS5IpNvDNh8VLYkUVqEOCjJZpx4M2DnuEPvmEe10qX71gjZZXle2ocjxl41UYlmMGpgd0Rf4HZi+iMmsSvtPsGhxax8QmN4BipWzP++T+1oSqTXW1J8TCzoPexTeNulsBQR5A3ZMhyE6Rcjmvtschsxqx8RTqFXUXT3xYy/JmKi2JUU5lRNQkFUBN0DIYWrkngc5iT4BSXosPw9g/J1H79s0ZmTnx/mpLDdOuuhag7lazLwJ7ZoXNI7srUsX9UU7g1Yf1ImnCu/9gB7B9Cw/smIwahBe9amcVgq3/YQUVW5JmqrOA0zL0SsfCmieDvZvYnFu4mo6NKSCjtyMSTKaDJbmvUn5M/7Y/LANhcsCvcGuO2E8f/7JtZAlm1uMyG9FdA+JJX3wahi68kYr6LojxlCB74hLrowJ+Qdsy9ko+xGLBLlsVAINW/3yS0LTmzto5r8WkRm1aB+JqL2Cz2sQSLMhCtZrB7kV0NqRy1WPl2hP63xqhZBUREWEiZf7VA7au6mClVfFRFO4mhGXpCGjN2DYH6U9oJiUBUwiNkzyK4lGH7Mvb80xsbZHN09YmZKHOElZNfjXaZC5fIQ2bVisnPcpnk6IMxJj9sbSxh5zSbKSAZhe4/JzhMRpg/ZFWN3YMkvDbkPA43ha0beFden6Qm1OMzB1Ldkmd0/6NN/foy5b/kU7sUSmnrdonjVZOydkMyKidNShDcLpLc0a0+khzQhiDN6d8uS2BLAMvHGgOzlFLXFMtkVmQkTG1QqlvbsAYPR9zxyGxHNh6C5IEx+I5KWpt0V++7sc9Jxyi8q1h9P0V5IUFqzcdYY+lc0lVeEI1A/bOF0pPpfug71QzJwhhlF5T2D7adD0ZZ4itZeQ8RboeDBtSEvLIDZMelPa9r7hQ2Bkj8r3lBkNmNa+xypYWwmFD+yQWZTlKi5iyncurzCXlXTOxDQPCpFbrc+VMrmbKKs1IY+6HggBgHTE4FN7EDjYU310nC0LyNU3o9YZB5uMPev1th81Gbq6zabH4mwPE2Ql+W+0xRyUOkmGEFC8bYU8aoXZQSOsuC0DDIbCXd/IkV3xmDriwfJrUXsHLOwe5rGQZfyRYPyrZj+ZMLIOZO5f7VC9bJPb8IgVQ9pHhbqjNNJCEqa9gFo7zXp7IXiRYfcWszKRzOk6zF+WTNy3iTMSNHK6Jok7xTpj1lUrwSkarJvrz8koqLuvoigKj3l8o2Q/B2Dm/+ZwEG8EUV7IaF8W6rD1UuCr86sSaH03hfd4TJcOAWGL8aR5U9kGbkYM5jUTL4qvof+VEJ+URFlDDrHfKZfaBOl1O5AULwTo6yEoCjFzMy6QfGuj9sUGjQGFC7bZDZF055d01z6m79J5WILvyyo7/UPWxRv9tAKZl4IhgVR0T+0DyRM/55IZzfPpPBLBkas8Ualm1I7YjNxzpOXoa2wfM3UawP60wnB4T5WT7Hn6zUh+ZzZpPawxc7xNKYnSdX9cZmZlYbsVZfWIdFTrD6Ton7IJqjEdPfFZNcCwqyYtTKbMUFBkX93nZGLIYkp/2bsPLQXZOZ1OuJDCQqixJQukklnX0LrAFgDYU5ufUgz/vwq1dfECGVMD8iuSesTLfdy+rstmicDshsJdtugeFMGhvaCDKhoqJ+S4JrEFr/I1llN86UJ2vvEmhw7svd/X0lq1Wxyd61dgGrhDmwfd7AfadB5xP/A9++BGASinCa3LKEemXWD9vz7J6FpHY5QEbQ7aeofmsBpyWyUv+qQqsVyYW2ZJS0PircHeCM2+SXZAxmRpnE6pHI1ZuydkO6spPaqCJoPCTU4KEnVvjMvQRTdSZP0psFgVNF5ZILawy4T32uRmDKSu+2E2lETpy0aer8i1d3i3YjNswbx4R6mJ7bm+sOazcdl+WeEsofuTkumfVAQ9Fl3T0JciShct1Chov9Ul9pRmzgF01+zmf3D1i6n397q0pvR7Dwi1yjMQ249Zva5SJaKBU16J8EIFXFKkdoRVLXVU9SOmvhlhbY0fhHqRwwK77nc/ks5wuzQX1GT7eH0V23SZ3fYfFxTuhVz9ydtwqyicAdKt2KCMrT2w85xg+xmxLH/6ZfYfLxI6U5CUJB8xsXP5vGqBs39Dt7Y+05Q6WJ0p8whxlv29mFGEZRjgqIMBhuPpRh9N5IYtpyiP+4y/gZM/kuX0QshW49XiKshjZcn8I/38UuybepPCZBz8tWYzGZC9XJI+SqMvuNTupWQW0uEQLVlsvaUKySeZ0Pa8yZBHnaemWHxZyTjoj+paS0Y5O8ZAj+xwOlKeEickvZl4Z7UB+y2AD2irKZ0xeDuX57BiKB+NiQKpJuTXRPZc+zA1mMFJp63CPLf76yEoyFhSURT6VrC/t8O2HpaoLXagvmvRYLcW5IcgdIdkdKLzFwPz1lTudKnuy8WH05LE1wok7r9wWqhB6ImULTH9J5f+hUBVryxw42/VqV0XVG56tFaSNF8SHqhdlczcqHL5pk8mW2ZMY1Aim7VC0KOGYwYxK4QZ1L1mPoRSYHpTwluaecRyN+TLILtkzaD6Rh325QUnhg6ByPyt0RXELsQ5SAoJpSvSrswvxJx/wuK6ttSi5AWlRBvsusS9xQUBdARuwK1CLPicizeS9h8TPDoZghWP2HrtEXsavaeXcY0Eg4Wtvj6pRPs/T/Ar1j0RwUUMv5qnWv/eZHp78jLDDD5eoCKNEHRorXPJL8Uk1jSgqwf/76ZJ70Ts/6kKY7LlBRG+5OCqnLrQqv1qqaEfG4J79DuSN0guxbQeMglGlpR3bqmcVRy8rKbMVY/we5H7BxLE6XlzwVwITN/YsPoxZDulIXblDpK4Tb4ZcXI5ZDOjEW6PhxUmzCY+P61C091sd/NSQ6DA2NvhySuwi+YGOH711Wq/NnNhM6MSfWyjzagcdDFiKSuMxiTgNr0ToLpJ9SO2uRWRHZsREPyz7CP77Y03WkDr6rJrijSdTFJdWekG2R3hEZUvirbkTilsDtiVfaq4I9HjH9PCtfWQFP7jEfhpfRuylH1Wkxzvzhgc8uiO6gdk0j2kUtyPfyyonxTYss3zyoO/sNtFr80Tm5FnnG7n9AfM+nOSKKREYuhzi9L1FnxNiSmIihJW10r6H6sx+2f+tUHtyYQllx6s7Jc2nh2hD2/HzIYUzQeSpHeiTEHMgDk1iISx8TpavK3u9Q/FNA6AOZCl/6YQW/SFFvmskhINx+zcVrygEy8GROllHjz81A/bJNb0Sz8i4D4UE9CKpdjnJr05rUpD0RQkiz72BGii1vzyN4XEOTI5RAz0EPYhzxUpVsxxZswctHHr8oy0RsRoMX7lJf+hIFXEnlrUEwo3IHRdJec7fMHN49SetOhM+cQpuX2RGnF9tkKky8abPx4IL3/rGb9cYe7P6PYPGNQuB/TmxBfhEokbWj6xQHdz3WoP2Rh+pLB6JcQZVo5JLsiL1tnzqJ+RFYWXllgJiqR7VR7r0N2Ixb+nyf4tLlj61IILYiycu3JNM1TwRCWoWnvAyMU2642xX8Ru0KJLt6UXrhKYOMxm9qpmO0TJpk1aWcWbg9jtjqQej1HakdeTm0I83HnqEViQm7Fpz+pyK/IwJdd6uFVobVXfA+9GfGWNB9iGOqq2Dlu0t5jMfF6X5BnM1LNR8mAX7wX0twv4FmViKgnyMkKqXQ7IbMp7bnZ52Na+0Vk1D4kRqAoDTMvepBA44ii9phwG9X9NI3HAwGAVBMyawMyG8KSANh4QjF+XhSBW6dsvIqiNxfRmTapHzbJ3zNY/MlxTB+2noxpHjDYOW6RWxNhQX9MWpRGIPWz/KLM/nFKlKq9KUHSZb6X+8D374EYBJSG8lVZnjceC2gtOIJi9mH1GSmKdfbC5s97NA6mSW9H3PoP88x+zaR6SZP5do7OQXGA2e2Y9rxJe95k8lUfty2Fmv6ISW41wi8aQ9a7EIq3j6dx38mS3hYgiFv/vqKudjYkf1cukelLJ2H5E3lmnmvR2xvhF0xWPheDAaXriv5cxPqHBVRq+gnTLyZMvioCnNgRnUPpJnQe9olTitoRselqC979xhFu7IzB/QyphhhczFBApu1jsqfuThuk300z/WKf3KJ4+UvvOcx+J5DkHE/26FoJnXnnRJrZvysPhTcpA5bdlRl+7l/IeVWvxBTvhVJtPuPRnZU9ptOW69/ZA50Zk/6k3qUjb7wyLX71GUVm0ye7pqm+ajP2jkdrv3gdBp/ssHXKpnwjZuRCQGYroTuvcbrJMPhFC2nYTTB9yG1EEomeHuY0tBIyW8mQ0qxJ1WHs3YTCYoLbSfCrtugTHGlL3vvxPHt/tykvdFqKh/mlhPK1YZG5q4e/Qm8mxdQ3NyjcNOlNJ/QnxB+y+BkpFpZuBVQva4rnUuRWJU+ifKFBf0zsu80Fm7G35TwKN0z8kqZyI2Iw6pDakFrHod/sk1iyEpr+msX2aXDaBqvP5CTNKpSVhN0y2DxtiwekITN34aZF60SAPxrTXkhwmlIwnHlOMfPdPoN9Pu05C6c9jLq7sQUGzP5BnfLNAG1A5UZIc8FCJVILez9f4k86HoxBIIHmIYFjls67hJ9uEqVF5Ve+Km6s8fMxY/8kzWBc0Z2xGH8DNs6a1I5Lf9lqGVQvabozDlFKhDStBYf6EYPcWig3+S8Kz238vEdiyU1onRRefXonIbcqQaLLH88QZWD6D03C3DDGab9oFyrXYxrHCuz5hoh/0nfk56UamtJFSyi0ZcX6k2m2TltiQrkWE6dkKRenoHDBxavKuU+8EdOdlapz/HqZKC8KtvLNmOaCQeOwovqGTX5ViLQqgcZhqZSHWcXoOz364zaD8WTYPjNoHYLplz0yWwlrT+cJMwpjYAr4oywgjcYBG6un2XjMYO1JB7epMddd8vfkXPyStJ3y96E3m5DeVnjjInCxO9A8ERI7Gq/ikF0P6eyDzUdTwy5BwvT/LC637ZMGnRmbzS/4zH99QHO/SXZVkzhiY07fdwgKgu2aerlLbiOmcrVP9bV1WnsN7J68bLnVmEHVYFCVQXznYYs4M7wH20MM+/68zJBDDX7tmHAISKQeETvS8elOGyx/cYLSnZC5b4nwqXxTALLZtYTtky6xLaskr2oy9WKL2qkK6W3JjWg9JK1BuyOFUrepiG21i41zWorFzxd3P9vmGYOZ5yXqTZsQliMsT+pBE29K2KrT0vSmRXTVPhZw+H9sYQ4MRt6V9neUVpheQvNAmsxNl/SOrEyiNDTPTNKdUew8Wmb1aQlrXfycQHViV/6zvA/e9j8QNYHM6Kw++fTfYPMxA6epKN2JWf1UQuauRIVvnkkx8caAKGOy+hGb4k2hAmXWfTbPZsgvxbQWTPKLsiQPc3JORixVcmsAnYWY0fMG+SWfzUdT9OZj3B2T0XcjWnuHoRDrMWHGYPvjPu7dFLlFjduRJeBgRKK9tAEM2QWVayF+yWTzcY3dNMiuyQu08WHN2OuK1gGDwh1N7YQmvSFah/Jtj96k7FftTszqfxTivJcVgcoxjXbls6dXTUYvhAyqFl5FUbotMdyGPxQzTUqhzh/qEbQpdKLR9wR60dkjqsninZC1pyxyy6Li609qzL5Yr41I4xVldotTwwyA4SoivSWW3/aC1GOmv7XN0hdGh0ScgJW/GuK+lWMwLu06uyeFtIk3Y3aOiYfDrcv3UxF0FhLibEJmUaK8i7dkOV28J/LosXcGhHmL2hFRvJVvxLT3mAzGRcikNNhtqF4LCLMmzQUJiMkvh6w+Y2P1RDQ0clF0Erk1ia8v3hlq8QPplgRFqSG8T6Mq34rRhrQwR97r0N2TxfQ1ax82mTiX0Bs3CPOK8s2I2hELuwvZjYStU4rs6lCPEkpKUJAzULHUKrwRcYRqBZ09ojr0RoYcgh1F5bpoXHozUixunIoovWuTW4/pzJq0D8UYfSEWeVVxUQZFETUNxjSFezIpjb8V0lwY5joMX+X3MyEG45IhkV+JWP6kyf2/8QDnDmgDcfTdkofZGiQ4mxYzL3RZ+qRLf1pMRUHBZOoliZ5u7TO589OumG2mzF0GXGZTYwaK3Iq0eNLbmt6sCGC8imL7kZTIODdMzAGs/IRU1S1PeHJosJdc5r9SJygomgviTqufSKRFVZI9KlpQZLGjyN0zKV+XJWVvwmDsDUVmM8StQXY9IM6KZDZTi2kcTNEfk5z5nRMO6m4GpWUllL9n4G6aaEvWbl7JlA7CqGbnmEWUhslXWmhTMRiR/L6x94TVl9qB3BLYHbG5mr4oydb+ckBqR7DnWsnnHrkc4bRi1p+QvXl2IxnGZkHzlKyMnI4AMcSooln95Ch2F/pjitWPOCSrGQqLMfl7MoCg5edvP2INA0O1VNePRKCk1ZZetujviXBaivqpmMlXe3hFg5FLPu35FDvHbCbeHGB6sgUp3otQMcx8t0/1skA3goJJZ8akcj3CbYtzdOGfN3AbMgMboWYwqdl8zGD0QiTXr2xQO2rQn5BVgdtMUIlU5Fc/JrWN5iEYTGRY/UxMc79FPOmz8nFNZjshON2lXzVJbKl1rH0koXhH2qdmILOsVoJqD3MiOQ9z0hWKHeEhdmc0TlOwZYkjYaXdOUHaZbYTJp838Suw9oxQlMdel7Zgd4+iek1qBk5Tkd1MyC/JwJCqQ3daJNapHdGVpLYVfkUs4GgpwG4/Yj/42wFtiTjCiEQyLCx9xeKnc5SvS2rsxJtCVt05btM+JNluufsCcEhcsHsJnT3inDICKNwP6e6N6M4qxt+EpU+Zuyq5uecC2ateDMldTJFdF0eZ05Iin9NULH6+QuLAnn+5RnrToHzJIHffoHpZU7opARX9SU2qGdPdI58tsaV3vH0aNs+4lO6GbJ12KV2xyK5IiGbplr+bgxgUNfn78qs1ULSORqTqkLtjk5zsULzVI1WXNOMwLz6JrccKrHzMJLeWYISwddImVdcY8VDFeNJh4g2fVE1CKbLfy5I4sP5hqVY7bUWYMTD9hPSWQW49GsI5ZDbf+zt66AEw8MoG1SshY+elAt2blhTfsbcSJl7T9CZMivdDcitSL/AqiqAgPezOvIR8Hvkf1infCtj5woDsumbsNQnZtJsm/ckUUVax8hGH2JVaxeaZNPkVKew2DlpUrmq6syk6syYjFxPsjkjAtx+xWH9aUztqsfV4mepVj+nvtFh/Qva/+fuK9py1W6X3x2U79T7ybDCuGMyIgmbnyZD8fSlczvyeSIxNO+Hw3xcMfOq1HM0j8hL7ZYGCdvZA7bhCK+EK9CbkvJqHNJtfDKhe0oy9qWjvh9nvhBRvixV89EKA04TNs5DeZhfDPhgRE5lbM9g6LfLkzLos5b2S5ETaPYGY9iZlZVC6HRKlZDuc2UqovGdQuSYF2u4xH6svBjWVwMh7fwaoyL+PQyXCiStf62J3Ncsfs5h43ccfjQiGUuHaERO3JcGexkCKT6U7kdhIxxIWP6cYuaSHOOiEzpxN4bqFP+ez/owEdoDgrrdOuTidhO2TthhWmjHdhYjivQhvVP6eNXST9Q6Pkl1LKN4JCApDCGQi9uCRi2Iuqr43XFrejLE8AUGoBBa/JMU1t5kQlISNcP9zDvmlgMJiTDjrg4bRdxKsgRB/oozIn7mUZ+3ZPLVjEviRXVESSTWhyKwJ789paybe8MmvSGKONhV2G7ZPurjNhKnnDJrHIsK8Zua7omyL0tB4yMDqh0PvgYXThOLdWGTC8w5GAF5F0oFqh238ooH3TIcooylfj6kdNdk6LRy95oJU+E0fsuuazIZBnNZk1oQBePM/nWH1GZvCdzI4nYStZ2Xvvf9/36b2sMx+o+8Jgry9T9KFtk4bggKrSPSbNoQ43d5rsvhjJoUhCdqpSWvNLwt9uXGsgDY1iavJrUuhuDediAfE+j6Ixq+Kd3/0TQPDU+SuOYy/0aJ5WDiOzYc0ccNl80khK6Ng4nUZHCdf8zA9COSeaAAAG31JREFURXZVtl9hXqTuUVrUjJk1A/dyGu8vNWkckiTtlZ8PqT/tU74R09jvoC2oXFI0H44IypL43NkrZKwwr8kvQvWypjsrz4Y8j4rGiRhvVCaQxIL7XxIMWlDSpBrSpYhTBpOvaia+aRM83GfzrPgk3tfe/EnHAzEIGIH4oFc+mpcIriswGLNReqj0a4t2ffuU9G33/p5HUNQMKqaMisD+fxbuOqzsboxfVBQXI478tzukV0w6ewwSU/IBL/2t32TnYZvS7YTCorSYnLqJ3QmZ+e6A/lRC9UpAe3/C1imb1oJBULKkutyTotPI9xy8spg2LE+UdpuPGriNiM6Mycx3WhTfc+gciNn8sLzkUQaqFxT3v2ARpg2mvmaLWWpqyEeYlIq229R4kxHVyyG5JemdV696mIGQZxMLDE88/42DLt1JC7cmWQtTv3uXxBbSbOyKucrwhyGugWbkYkxQSlj6ZI7KNfHyj73VEdBGX/aPrUcCsuua/phFlJOiaPq7OXRGYs+90QRrIDbtkUui7Bt716P+sKY3J3tstNzX6gVN9ZIUvOpHTcZeFGnt8ufHGD8Xkr8vttv2wYSokLD6TI44JUnKUUaTamhaBwwGB328iqZw3STKGFSvxMy84NHdG+ONDLsItkh+J1+RwWP2OwGmL92a+X8pXYLMVsKhf9QgqCQ4XVHrWX1Y/mQRt6bQhqJ8WTH6pkH9pPTq7Y5m61EDvwJB0SK/qGkd0mTWDGJXYuPF5xJL7SGnyfx2kdyyDDrWlSz5d1J4JaFQuU3NzkmN2TGZfili8oUdRt6BkcshUy/L89j88R7JUN/TmTMYTMekNiycpmLq5T7VKxG5mzadGQsjUAR5oWitPynPUmfWYPwrwokICooo94CnEqtEk1uT7ICdhy2BIewzyCyZFO/FRGlN5bzsa/y8QXNfij1/OBDgxI7ESK18NE171qK9P8GryJLObYRsPzNFf18o2urPdiTmCdl69EcMGgdNgrzMNvWH0kQZk31f8eiP2yx8RYQnKoLCS3el11+E+hFZAo5c6JNZ17s+8vSWwmlJT3j9qaKIm84bZO9bdOcjnLZm57Rm7g8SBmOK7Z8aUD8qg0N/JsZpK/yCVKVxEzbO2hSWIsy+wqsKaj23DKPvBZLmu0/owKU7Pr1p2W7c/cV9lG7FuHUpUMUOVJ7YGH7eHjvHTMpXFfklgaG4h1rc/OsOftHA6SYEeYPCJYf6CcnEm/9KHburaJyKyN2y8YuK3KLB+PmQ/D1oz7uMvWay9uEU+XsGuXvS9izeCwlzUhzdPCt5exNvhAxG1G4A5+ZZm86c6BfKlxQqlOtq9RXdL7YxIqgdg+KthNQtF8tTdOdFFKQN2Dqdwm4amAPF6schsxOTXU12Y9PrR1zGzyWMn4/ZfsSh/khMf8xg+TNVUpsGzX0mbkMUoKm6Zub5Nu1Zk8bD0j6uvm3uPqPakFblypci2nsV1mSf7oEQtwndT3fJbGrWn5Jlefmaxm3FdOal6+M2ofvogPYBedaDvCJ/z2D8XMLKR03u/eQIXsVg55jN9gmBzuZ/P8fIe5rNDwnIdvRNMWJZPbj9CxZ+wSS7LkXPxBW8nhFq7JaiM2sSp4aT0o5BUIAo/8HmAfPLX/7yn+8b/m9w/J1f//UvW59/cuh9l3qA0rLkyW4kxI5J8W5E8U5EkjJo7TcYjNokDqhY0T4SMf3dGFAUFkW7bsSK7dMWnf0x6SWb2e/6bB1wiE2LX1s/iYoNRi8EdGdMRi545Fc0RqJwWhHd2RS9KYPujM3Y2wFR2iTYU6E/oSjeS7B6IiAxY4PtRxVOQwo4k2949GbSbH4qJLVm0ZsRi7TSULkCjU96uHcdooxUw/tWluI96E/B7HdiCnd9ouzQ2NK1mDjn0522Gbvg0Z63SRxJPO5PWLT3w8hFKYy1f7FDUE8R5A0y25rmIYU/Ij8bQ+HfzdGbAr/s4o9oensjEtMkt5JgX3PJ3TWpXOqw/WiaKGXgdDWDQwGjr5goy6a9z2DyZaH4avv9ToQIqLwRBQiTMLsmwSJTr/RYfzKF0uBXEibehPphEyM0aDwaMfm9kM0Pw+xzEWFOEoa9EUXpxvuxWhrrboriXU16W9iOSg9z93oGM7+7xPIXSqQ3xTxlDRRWVww6vVmZbXuzkn0Y5gxa+wyijCa3aFK9Fsgzs18DSq6FMuk8HNI8kGL0ogwUU9/zMLRi80Mmlqdwm3KeRsciLCR89tQF/uHxf058xOPcjf0M5hLGXzGoHRfb76Bqkl8R1oQRKsy6LWE4Suy+5VuSP2kG0nq1PGEgzP3WZex0mf64SW41JLOpyGzLveztTUhvKGLTJMwrRi779CdsRt+L2D4lHoPxt0PaCybeVER2ydzVTQA0n3tu/ctf/vI//OPv3wOxEtCG7K+itBIG/UD29cV7Cf1RcVg1DtrUj7gU7vaZeDPEGxXxR1CA7H2LzLk7pGsxRii9XL8ImTUZzQdzIWtPpNj/T0KMAPK3LJwGrH/IkULeyTT9MYvWXpPmgRTp7XA3CKK1z8YMZCnljUgOYHtB9svrj5voYb/b7sDdvygJsOPfshl7u0/pJgIhOTFgUDUovJTGG5Ve++aZNOVbYlpJbSsWP2uw+VhmN1iyci1g5aMOrQOw+OkUTkeTW0mw+gluM6F0XQCrjYMG1lfLTL46TEzKKaa+F2EOxAdgRJBdTzAixeTLTUrXwN2wqVxLSGwBq3pVg80nitI2bQo3TwcG+UWP+19UTL8c4hcNBpOa7r5Iknr6mpFLA6zB0NvvKfrDrdnG41m0Bf0ZkVvvcgjTMPqqhV+2MbsGftHE9DSF+x4qETrQ9kkDrySttrVnwasY8n2V6CIAln9qThgPw6JYZ69kSnbmh2G0dxLGziM5iWXZQhXuSWt146xD48j3qUPV82LRHn/BonhDUfu5Hm5dsfpsmv6YSW5J5OL9p7r0HvJJbUsN62sXTzBn5cibHmeO3cFIi6GtelmTXwqonw1J70RkV2QmV4lY1dv7BJKyc0xi452WZvQ8RCnZ9i3/xw/TmbFINRL6YzZhxqB0oUZ7r6J4zcRpa6aG93rz0RSmp+mNW4SjIUYMS3/BJCgkuJsW6R3xtZSvi+r1g44HYhAwA6hekiKaZMWBn1c0D8iofvDvr+B0NEaoMdsezQWb0nVZ0hcWE7KrmuYnDhLmDDLrA0bfNCjekzZJ9VKP3B0bbcPtv2IOXwjo7k0o30zQSlBfXsUgVRMx0fqTLqVbyW4POHZkiZ6qidOucAdaey0O/i9L7PtXIYPhtoQEOnsTurMG2yczeBXF3q/5zP9jyaN3Wxq3LrLUoCgPQvFOSJSBwi1Bmg9GFOXrHt1pm9F3EybOxUy/ENLaJ9fCL5nsHJelu1ZDv8P8+4jsmJFLAbWjNt54xGBM7SodrQFc/+sCn5/97oCtU+J3sHwZxMxA2qbvJ/oWLjvsHM9QfcvECBI68+L5n/62JOy4rQRzEBJmwe4ootFwF/k28UafytWE1JZo6LdOGtQeFwrRuf/+H9CdMKleULTnxX25fTK966E3AsVgTNHZY+DWTNyGEHOi9BAzV5QBKL8I7QOyB5//vRBrIMtibUJrn8SBz3y7Ka3LZaifSLj/48Yw5k2z7yvermuvN6UkQCajMN4s4jY1Ixcl2yK7HhPmIfNyjuK7LmYoqxEGJsfe/Bkudmd47+WDZC6k2Tlh0vqJrhjYrjrsHHNINRMq1wS0sv50gukpUnVxYu58KCK3FjMYlQjy7JK0DGuPh9SPylau+8U2d352BIDiXekGDKoW42+F5JcTcUFuRWRvSa6D6SmSdMLct3p05iR8R5gZH9wjfCAGARJYfzahNy0z7uTrHv1JhTce0Z1RbH10hvxKiOnBYK6I2xIGe2dOUT+i2DklxqH8zRbLH8+JuOZiE7euiTK2ePe7YK87lC80KSxGpNeNYXKwCDC6cwLsdBua4u0EpxMz/dwOKoHiYkjzIU2Y0/gFg96s+Lm3PjlH/bDL+LlAOPaXDaH0riWEWQnObO5P0Z1xpII9YjD2TkhhOaR0MyE4MKA3KQVHI9RsPRMOibxptILepIlXMtk67Qz5htLztruKreHyb/6rNcrXE+wetPaarH/IIczC1Avy4gvlVmMEcOCfBPhlRZix2PfVHqkdTe3H+kQpdunFUU4UhfkVkRN35qE740iwy5tyXVp7bZb/gmLnRJ7CYoJf0eSuOUy92MH04M5fl5k2tSOFuJFLmswdB29CZrDunKQXeVVN4S5UL/tiq25K4dKIkR73qGg/tKmYfa5Fd0aTXRdTUHYjxm4ZWF3Z+2slxixtwNSrHiqGxc+WJOx1D0w/D7PfhMy60KTXn8wQu4rRd4U+FGXl53cXQrSC9pxFelvTOCgcQLeVEOQlaWjizRC7aZKcK3HhHxwncWTG9csJ+mKBQVXAIFFa7lnzx3s0H/UpXzKxBmL0AZj5pkH6m++I/8EWrYpfhtLbDlZPfA+Z3ytQvayZfb6P+1+tMxiTDs/6ExaF21268wmbp23Kt2LCLBRvgt0wSRyTwr2EOA2No0I1+qDjgRgEwoLGapvEc96wRRYRFjRzfwDTL/nUHk3oTtl4oyJ8KF/tkL8vmgK3LqYgEqidKkvfdVxz52fLdOcUrQVHFHaz4prr7S8Q5EW9l3ktS35FHsz8XYMwa2D3tERyP2Gx+IUR/JJi9RmLme8I9snuD7cGFUXjYx6lOyHrTzgERU17rzjWtk+LdPb9fLnGQ1I5BmjvsQhzYvR56FcblK/3qR/TdPZA9XWBaoY5+T75FQFETL7u4U1IO7QzL0KcxIaNJzXrz1ZJbEX/8R52V+/qLdY/LA9a6XYsZqA8NA9m8MY0zQM2O8ezDMYUzru5XV5B7CrstkKdbNHaa9I4aJNZl5nE6kF/1CD1zj3ilPj2zRCaBwQTb/qw/lReshDupagfMejslbpOe4/Yt6vvmOx77q+w76s9vIrB6HtyLdeecsluJNSPi6Xbacr5Fa/KSqE7p7n58zniXDJsCYvHIBiPsAZDIlJWsfUYJC7UjqQoLEUYMUy/3GfiXIzbCOmNSwSZX9KUb8qA3zhkMv1SwsyLIb0puWZ2XzNy2aM7LUIovwK5lYDSnYT0pmbxS1oCSFpQe0TgKelNJcnE2zKYxK6kCRkh5P4wh9GSycgIpNDs1kUK3Pnx00RDPmN7QcRtURb6e0NyS7Ja2zqtWP5EhvuvzzL2TkC6lqBixdaZPPu+6lO9GuMXDNwWlG4OGD+fsPZUisZDshWxuoqRSx9cGHwgBgGnJQir7Ltp7DYsfzxHZk2xc8xi+6RL9W1DtgIDscAGlRTNI9K37e6P6I1JAaRw38eflcq5ioRq05kTLltqxyCzrolScsoqFtbA1kkby4OpbywJ/smRG1K4LVFeUVZ+31qw8cuyHzQHkF9OMO+n2DjrMP2ST+WqqLYmznlMviIR0tZAClfZNcXK52NyqzFuS5MMnWvrn5rk/uczlG5IWnKcEjlvlBFoaX9UeHjNBZfDv16nN63JrgpGaubFiMyqiTcqAqn8ixkxDw1Tat2agdPStBbEWFS+ISKesfMJRqipnxYs+cQ5D6s/dO3VxZ8e3CmgEhh7Z0B7QXIH/Kqmuwdu/e2DOG0RaA1GFf6cz8iliNYJgaRkNhPitCZKiYouVZcAFyMQ/33xLZfa0SytA1Ilr52OCfMS5168brL5hCbVFIJynIL8fdluqFBht6RNV70ak9kKsLctvBFF60iM1ZeWnTcekaonrD9p0n/IZ+mTGTbPmGw/ksL0oXlY7tPOMRO3Iy/GxuMm6487pDc1U8+bbJ2RgURbIuhBC5AksxlIoMiaPDPaku1LZ86gPyXXePTtLu15GRidjqYzr8hsxbg7Utso3o1xOqJW7E0KtzKzHdGbEcVf/VRMmIPcDZv2o9IKn3wtEWXhumLtFwK2H5HQ3sxWwsbZNFFKUXtE/BebZzPUD5sMpiX4JJz1cRuidPyg44EYBED2c6YP1Ss++UVN56RHfzaieiWkdjJBG4r8akzhtsHq0zZWR5HdSChcsyjeD4VN/xkXZ9XGLysq12SL4DbVLveucSKh+ZNdujMC9HTamsFciNPWbHx6Vr7fYiAj/3qEEcLIJZG9RmlZeTQPSIuuflQx+k5CYkH9IVcMHj5snUqRW+pjhCLg6Mwp3EbC7NdkP1o7Li0cvyI98MJd6c23FxLyKxJiOvftELcpOXnNQ1LcW//YGHPf9uXF3g9oGIxJPcQvi1U2vTnYZTHGaY3dl7203Y3J3e+hYnFsdvfA1PPmMEjVpH3ap3U8pDNnkNlJGHtLZuL2fIrJ18TtZ7eltec2lWx9bkQ4TY217bD8uQQCgzCn6E0amJ4Evxz4R5vsHBvyEMuaVF3ksygwIhkApp5XpDcMgoLUL+ymQf9nm9hdISapRGbP1LaB3ZbZ1ysaLH08RW4ZCh/bQBtC+7E7Grtp0jwoxOTcRZfE1oy9nTCYkEEnuyzBsKYPg4osmc2BonBXUOGNAwal66JPARGxjb8V4tahvcfFL5uEcz5aia5j7HwyLAxLMO7iZ/NDebHEpY+/KYjy+d+6hRHBxuOyHWgfk0Ezux7TnrUZfzMktWVi9MUg1T0SkLuYIrMhW8DKtYjyrYB4JYPdlZVZe94UNuO4gTWkP4+945FblpV1kNdUXnIlKu5P8Qg9EINAYskyzC9Cf9yW3vbLLqPnTDYes0lPdXG6iajUihLxxcEevUmD7GbC0k/HFK+32fvVPvPf6JJdT+iPGvhVhmq/mOYhWV4GgUVqW8vDVDHY/zsRuZVg9zPEKQGV9EctUk2BhDptiUWbfKWHtmDx8yaj7yT0xwzmnuuTX4tINUSemappWgeyWH3YOi1x6509Bq15i+6Uyf5/vCUahpqwCxuHNXY7onxFsfZhg/pxTXuPjTYUbs0guywxZv1pzZ2fk9uVXZXiUGbdwPt0m/G3Q4r3Y+pHc4y81cavyN/ZeDrBH4vZOuWw8UQelcDqR8QQ1B8TcGp3ymLq9ywmnxd3X2fapDslRdLinT5OU5bcQVEz9/iKKO5GJIzV8qRIau3YGL6YdibeGBAWE6pXetz8T8YIiprsqhhZ7C6Mvid6+vmv9zE8AzPURDloH4qkQHxF07lZZuKch9JQOx2TW0nIL0mhNnYkhSqzruhNQf2NCQzPoHMgxv94m7As/EUVDfMtga1TBtkVJW3DQLN9Nsb0ZOBs/Fhfkoi1xisbQkYqCgAktS3t6pWPmsRpqD8stvSF/01LSAiQ2Qoo35TVW28uwe7AxLmQKCtqvtT2ANPT3PiVBaKU4O6sPjgbNpnNiLWnTRpHNb0Ji8JdoQZVr8TkL0v2RfWyT2ILfbp+yGHiNUmlNn3NzDdrJEP2xfhbMfe/qLjzczLBWX1xgHojIqPP3Kp/4Pv3QOgE/ru/9+tfzj3xOPklKF/toSyT/riJ5QmhRq2l6E5LdPfMdwPCvAk7LpktzdZZyF+zaRxO0Z90qB9zCQqK4v0YI1RsPxHjVUxyy+KgG/2ehGUOxhXjbw9oz6VQyKi9cwoaDwsboHyjR/1ISnThUwa9aQjzDoV7mvFzocA2thKaCy71Y4rJ55tsP5YmcWTGdPqa1gGN6RuU7sZYnmDR6idz0gbMa+K0YuJcQuOgQ+ORmOyKSfmaxgyhP2FIOk4Jxt4NCfImyjPpzouBqXRX1HvFV2xWfiIiwhHl249ZGANFfzYhd98iKCcSEZaSvMTKNagfT3AbBrk1aRNmtiI6Mxa9GWnFFZalw1E/bmP1ZcmqUGz38sSzHvsWNmnmTdrTCq9oYPcMirdh63FNYjmoxMAemHRnDKJSjNU1qVwPaBy2aB7WYCrcjiGwi3WDwr2YzpxB9VJMf8yksKhZ+ZSBCg2qFySUpLCosTxFfllcipltTftoRGpfh/K3XdJP12lt57ALPqdO3OO+V8YfS3DrJqYvq7T+XIw3F1N+16J1IiJ336BXsCjcVmyfYZjyK6rBqVd6tPc5jFyKMQcGKlFk16V415u2Kd3yQNuk6hH9cZugJGyAwWyMX5SI89aCSappEOQNnLZQjFoH5TzMgaKz16RyRQPSmYhyom7szIvrEAWxI3URM1B0joQkahi06igGk2lUrBi56FM/7DDynmbmay02nknh1hVT/+I2ZrpI/QQoI8fahT9ZJ/BAWImVUh3gxg/6c/w5HSPAzg/6Q/w5HD+s5wU/vOe2R2s9+se/+G8STf7v47jxJ/mcfxgOpdRbP4zn9sN6XvDDfW5/0vFA1AR+dPzo+NHxgzt+NAj86PjR8f/z40EZBP61YsUP0fHDem4/rOcFP9zn9q8dD0Rh8EfHj44fHT+440FZCfzo+NHxo+MHdPzABwGl1F9QSt1QSt1WSv3yD/rz/NseSql/rJTaUkpd/iNfqyilvq2UujX8tTz8ulJK/b3huV5USp36wX3yP/1QSs0qpV5QSl1VSl1RSv2N4df/P31uSqmUUuqcUurC8Lz+m+HX9yql3hx+/v9LKeUMv+4O///28M/nf5Cf/8/l0Fr/wP4DTOAOsA9wgAvAkR/kZ/p3OIengVPA5T/ytb8L/PLw97/M/9Ou2YNGFURR+LuY+EfEoEhYjCABQSxERTQBW5vUKWJjilRa2QbB3sZOiIWliIqCaST4V0dBgwrBmE5DNCAktirXYs4ujyApwiaT2Xc/GPbOnSnOebvcNzM7cFPxMPAMMGAQmMmtfx1fDeCM4n3APHCidG/S16O4G5iR3ofAqPKTwBXFV4FJxaPAg9we2v5MMn8hQ8B0pT8BTOR+KBvwcXRNEfgMNBQ3SPcgAO4Al/43b7s34ClwsZO8AXuBd8B50uWgLuVbv0tgGhhS3KV5llt7O1vu7cBh4Gul/0250ulz9yXF34E+xUX61RL4NOmtWbw3M9thZrPAMvCctBpdcfc/mlLV3vKl8VXg4NYq3lxyF4GOx9MrpNi/YMysB3gMXHP3X9WxUr25+193PwX0A+eA45klZSV3EVgEjlT6/cqVzg8zawDoc1n5ovyaWTepANxz9ydKd4Q3AHdfAV6Tlv+9Zta8Rl/V3vKl8f3Azy2WuqnkLgJvgWM6md1JOniZyqypHUwBY4rHSPvpZv6yTtIHgdXK0npbYWYG3AXm3P1WZahob2Z2yMx6Fe8hnXPMkYrBiKat9dX0OwK80gqoc8h9KEE6VZ4n7cuu59azAf33gSXgN2kvOU7aM74EvgAvgAOaa8Btef0InM2tfx1fF0hL/Q/ArNpw6d6Ak8B7+foE3FB+AHgDLACPgF3K71Z/QeMDuT20u8WNwSCoObm3A0EQZCaKQBDUnCgCQVBzoggEQc2JIhAENSeKQBDUnCgCQVBzoggEQc35B5ffgUdzwPitAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"removed = goodPSF.remove(fitPars[0],fitPars[1],fitPars[2],Data,useLinePSF=True)\n",
"\n",
"pyl.imshow(normer(removed))\n",
"pyl.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Django Shell-Plus",
"language": "python",
"name": "django_extensions"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-2.0 |
BenLangmead/comp-genomics-class | notebooks/CG_SCS.ipynb | 1 | 2926 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import itertools\n",
"\n",
"def overlap(a, b, min_length=3):\n",
" \"\"\" Return length of longest suffix of 'a' matching\n",
" a prefix of 'b' that is at least 'min_length'\n",
" characters long. If no such overlap exists,\n",
" return 0. \"\"\"\n",
" start = 0 # start all the way at the left\n",
" while True:\n",
" start = a.find(b[:min_length], start) # look for b's suffx in a\n",
" if start == -1: # no more occurrences to right\n",
" return 0\n",
" # found occurrence; check for full suffix/prefix match\n",
" if b.startswith(a[start:]):\n",
" return len(a)-start\n",
" start += 1 # move just past previous match\n",
"\n",
"def scs(ss):\n",
" \"\"\" Returns shortest common superstring of given\n",
" strings, which must be the same length \"\"\"\n",
" shortest_sup = None\n",
" for ssperm in itertools.permutations(ss):\n",
" sup = ssperm[0] # superstring starts as first string\n",
" for i in range(len(ss)-1):\n",
" # overlap adjacent strings A and B in the permutation\n",
" olen = overlap(ssperm[i], ssperm[i+1], min_length=1)\n",
" # add non-overlapping portion of B to superstring\n",
" sup += ssperm[i+1][olen:]\n",
" if shortest_sup is None or len(sup) < len(shortest_sup):\n",
" shortest_sup = sup # found shorter superstring\n",
" return shortest_sup # return shortest"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'BAAABABBBA'"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"scs(['BAA', 'AAB', 'BBA', 'ABA', 'ABB', 'BBB', 'AAA', 'BAB'])"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'ABCDBCDA'"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"scs(['ABCD', 'CDBC', 'BCDA'])"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-2.0 |
sebastianprobst/resonator_tools | examples/.ipynb_checkpoints/fitting over and undecoupled resonators in refelction-checkpoint.ipynb | 1 | 170898 | {
"metadata": {
"name": "",
"signature": "sha256:b08aebf9f313b35ed60438d2e6daff71ba00bfe7d9c7737d81b47fc27012fef2"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 1,
"metadata": {},
"source": [
"Fitting over and undercoupled resonators in reflection"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ql: loaded quality factor,\n",
"Qc: coupling quality factor,\n",
"Qi: internal quality factor.\n",
"overcoupled regime: Qc<Qi, for Qc<<Qi we have Qc~Ql and the S11 shows only a phase signal."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from IPython.display import display\n",
"%matplotlib inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 76
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Case1: Undercoupled resonator Qc>Qi"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, we generate some fake data which we can fit later:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from resonator_tools import circuit\n",
"fr = 7e9 #resonance frequency in Hz\n",
"Qi = 200e3\n",
"Qc = 400e3\n",
"freq = np.linspace(fr-0.5e6, fr+0.5e6, 1000)\n",
"port1 = circuit.reflection_port() #define a reflection port\n",
"noise = np.random.normal(loc=1.0,scale=0.01,size=(len(freq),))\n",
"S11 = noise * port1._S11_directrefl(freq,fr=fr,Ql=Qi*Qc/(Qc+Qi),Qc=Qc,a=1.,alpha=0.,delay=.0)\n",
"port1.add_data(freq,S11)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 77
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's plot the data:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.rcParams[\"figure.figsize\"] = [10,5]\n",
"port1.plotrawdata()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAFHCAYAAAAsmgFsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeYVFXysN9iyBIGRUAQGAFFwACYAzBmTODqGjCgu37G\nNaxpwQ2CbjCs/HTVNaNiWjNmQFAGM6IikhEQJYchSZSB+v6oO0zPTPdMz0znrvd5znPTuffU7e5b\nXfecU1WiqjiO4ziO4zjpT61kC+A4juM4juPEBjfsHMdxHMdxMgQ37BzHcRzHcTIEN+wcx3Ecx3Ey\nBDfsHMdxHMdxMgQ37BzHcRzHcTKEpBp2ItJXRGaJyA8iMqiCeoeISJGInJlI+RzHcSIhIk+JyHIR\nmRrh+L4i8oWIbBGRmxItn+M42UnSDDsRyQEeAvoCXYEBItIlQr27gdGAJFRIx3GcyDyN6a9IFALX\nAvcmRhzHcZzk9tgdCsxV1QWqug14Cegfpt61wGvAykQK5ziOUxGq+gmwpoLjK1X1a2Bb4qRyHCfb\nSaZh1wZYGLK9KNi3ExFpgxl7jwS7PE2G4ziO4zhOBJJp2EVjpN0PDFbLeyb4UKzjOI7jOE5Eaiex\n7cVA25DttlivXSgHAS+JCEBz4GQR2aaqb4dWEhHvyXOcLENVM+JFz/WX42Qn8dJhyeyx+xrYW0Ty\nRKQucC5QymBT1Q6qupeq7oXNs7uqrFEXUjdpZciQIVnZdra3n833nuz204xKlXcyv8d0+L4zVVaX\nM3tljSdJ67FT1SIRuQYYA+QAw1V1pohcERx/LFmyOY7jVIaI/A/oAzQXkYXAEKAOmP4SkVbAJKAJ\nsENErge6quqGZMnsOE7mk8yhWFR1FDCqzL6wBp2q/i4hQjmO40SBqg6o5PgySk83cRzHiTueeSIG\n5OfnZ2Xb2d5+Nt97KrTvJJZ0+r7TRVaXM/akk6zxQuI91psIREQz4T4cx4kOEUEzyHnC9ZfjZBfx\n1GFJHYp1nHQl8NR2EoAbPY4TW1x/JZZE6zA37BynmrjBEX/8D8hx4oPrr8SQDB3mc+wcx3Ecx3Ey\nBO+xc9IGVdi4EWrXhnr1oLIXoe+/h1mzYJ99YO+9YZddSo794Q+wfTt07QrdutmyVavKr+k4juM4\nqYwbdk5KMWIEPPGEGV3FZcsWKCy0UqcOFBVZadgwfGnQAHJy4Jtv4MgjYe5cK7vtBp07m6H3448w\nZoy1ufvutty2zQy80NK6NfzwA/z8M7Rta+d26pS8z8dxHMdxKiKphp2I9MXyweYAT6rq3WWO9wfu\nAHYE5RZV/Sjhgjox5Ztv4LPPrDdtyRIzxho1svLjj3Zs8GA44wwz0OrXN6Ns112tpw7MsNu8GTZt\nshK6Xrz9zDPQooXV374dFi6EOXOs1Klj++fMgcWLTZZGjWDmTJgxw8p779mxTp0gLw8KCqz+/PlJ\n+NBSiIKCAi666CIWLlyYbFGSiog8BZwKrFDV/SPUeQA4GdgEXKKqkxMoYimmTbOXk6ZNq3+N6dOt\nhzteqHqvuRN/Ml2HJc2wE5Ec4CHgeCxv7CQReVtVZ4ZUG6eqbwX19wdGAt5fkqIsXQoTJ5rxFVrq\n14cmTaBxYyv/+he88YYNhw4caD1yGzZYyc21YdPeveGwwyK3Vbt2yfWiISfHjLO8PDjxxNLHtm+3\n42C9d717V3yt7dutfadynnnmGYYPH84nn3ySbFHiwdPAg8Cz4Q6KyClAJ1XdW0QOAx4BDk+EYCL2\nclO/fomxtP/+cNll8PjjlZ//0UfQpQssWAA9epRcZ7/97OUrLy92cn7wAdxwgxmetWrBhAmln8GF\nC6FnT1i5EpYtg9tvh0ceqfi6q1fb/bdpExs5newlHXVYMv+eDgXmquoCABF5CegP7DTsVHVjSP1G\nwKpECugYv/4Kb75pRlTLljYXbffdS3q9ivn8c/jtb035N28OW7da2bzZjLb16+GXX6BuXav/5JNw\n/fVmyCWTYqMuXvWTRVFREbXdAo0bqvqJiORVUKUfMCKoO1FEckWkpaouj6dc27fbskEDOPNMe4ma\nNcv2bd5cUu+XX+zZXrXKes3bBjkyrrwSHnsMfvc7ePppM7Z27IC1a+343Llm2N15p+mDjh2hVy9Y\ntMjaOfFE69Xu0MF6vIuKoH17O3fDhpKpEsWMHGk9gZMm2fa0aXDIIbb//PNtruyqQPMfcoi107On\nGalgvetdupiRuGkTPPCA3fOkSXD66fB2SHbxggI44oiSnv9x4+DYY+0endTDdVg1SWIC3N8CT4Rs\nXwg8GKbeGZixtxY4NMK11Ikf69er7rmnapMmqgceqNqypWrt2qq77abarZvqsceqDhigev75qvXr\nq951V+Rr7dih+ssvqkuWqP7wg+r27Ym7j1iSqr+59u3b6913363777+/1qtXT//xj39ox44dtXHj\nxtq1a1cdOXLkzrrt2rXTb775RlVVn3/+eRURnTFjhqqqPvnkk3rGGWeoquqmTZv04osv1mbNmmnX\nrl31nnvu0T333HPnde68886wbcyYMUPr16+vOTk52qhRI23WrJmqqr777rvavXt3bdKkibZt21aH\nDh0a8X4ifc7B/lRI5J0HTI1w7B3gyJDtccBBYepFvP/q8Msvqta/FrnMm6d6xBHl9990U+RzDj/c\nlsOHmw4IPTZtmuoll5RcG1RvvTX8dTp2VH3iCdMhlcmpqvrqq7b+73+X7M/NVb3+etXBg2370ktV\n771X9bzzyl9j6lTVdetUi4pK9i1YUPw7Uv3ww5h+/GlBquovVddhsSjJVIhnRWPYhRzvBcyOcCzi\nh+rEhrlzVVu0UJ00ybaLilSXL1f9/nvVsWNVn3vOlPXPPydXzkSRqr+59u3ba48ePXTRokW6efNm\nffXVV3Xp0qWqqvryyy/rLrvsosuWLVNV1YEDB+qwYcNUVfWyyy7TTp066SOPPKKqqhdddJHef//9\nqqo6aNAg7d27t65Zs0YXLlyo3bp107Zt2+5ss6I2nnnmGT366KNLyVhQUKDTpk1TVdXvv/9eW7Zs\nqW+++WbY+8kAw+6okO1xQM8w9cLeY3VZtqy8cZOI0rBh7K/5+efljcjqlHbtSm+fckrx70j12WdV\nP/pIdfPmmH4NKUFRkerMmaanL7hA9fHH7V5TVX+pug6LRUmYAizXsM01GR2yfSswqJJz5gG7hdmv\nQ4YM2VnGjx8f9oN0omP5ctWBA1Uvvlj1sstUr7lG9cYbrbfu4YeTLV1qUJlijNUfW1XJy8vTp59+\nOuLx7t2761tvvaWqqsOHD9d+/fqpqmqXLl10+PDhet5556mqKdfJkyerqmqHDh10zJgxO6/x+OOP\nl3rbraiNp59+upxSLMv111+vN9xwQ9hjxZ/z+PHjSz3jaWLYPQqcF7I9C2gZpl5M9df8+bH7/WVq\nadFCdd99bf3RR23ZvLnqsGGqmzapLlqkOmWK6pw56TOqsHx5+X0PPWT3du+9ZT+DypVLMvSXquuw\nWJS4XDSqhm1+37xAMdYFvgO6lKnTkZJ8tj2BeRGuVeGH7lTM55+r7rKLap8+qsccUzJE84c/qD72\nmOqDD5piuP9+U3pOdIoxGeTl5em4ceN2bo8YMUK7d++uubm5mpubq7Vr19annnpKVVV/+OEHbdas\nmS5dulT32WcfXb9+vbZt21YXLFigubm5O69Rv379ncMbqqqjR48upRQraiOcUvzyyy81Pz9fd999\nd23atKnWr19fBw4cGPZ+0rzH7hTg/WD9cODLCPXC3mN1mTrVnt8mTcL/2TZuXHr72mtLhjRBdeJE\n1csvV+3Ro3S9Bx9UXbPG1vfaS/W++1RHjQrfxvHHl6x/913JcGqk8vXXFR+PVBo1qt55oaV4CLm4\nXHmlDReHfj6pzmef6U5DqqhI9YEHSobOw5fU1F+qrsNiUZI2K1FVi0TkGmAMFu5kuKrOFJErguOP\nYcO1A0VkG7ABOC9Z8mYSa9dCfr5NpN6xwyZRb9wIl19ujhE7dlg56qjSQX2d9KA4hc1PP/3E5Zdf\nzkcffcQRRxyBiNCjR49iY4JOnTrRsGFDHnzwQfr06UPjxo1p1aoVjz/+OL169dp5vT322IOff/6Z\nLl26APDzzz/vPFZZG+HS6Zx//vlcd911jBkzhrp163LDDTewalX6+UWJyP+APkBzEVkIDAHqgOkv\nVX1fRE4RkbnARuB3iZCrY0dzKBg+HIYNK33smGPg5JPNueHRR23f/feb88DAgeadeuihVhYsgBUr\n7DqPPw7XXFNynddeMwcGMC/3Zcvg+OPhtNPM+aFrV3NuuOQSOPBAKwC33WbhUnr3NseN5s3NoaJF\nC9NB9euXODL89JM5cFx2GbzyCnz4oemqtWtt/8iR8Mc/wj/+YV7qRUVw443wf/9XImdOjjmTTJ0K\nffvCwQeb7rvhhpI6zzxT+jMq/lyKeeop04PXXmtOJrm5Vf9O4s2rr9pyjz3su0h3XIfVkHhZjIks\npPDbRyqxfbvqkCGqF12k2ratvbmJWM9ctsyNixWp+pvLy8vTD4PZ4NOnT9f69evr7NmztaioSJ96\n6imtXbu2Dh8+fGf9888/X5s0aaLPP/+8qqrecsst2qRJE7333nt31hk0aJD26dNn5/yU/ffff+fb\nbmVtjBo1SvPy8vTXX3/deb0WLVroiBEjVFV14sSJ2qJFC73ooovC3k+kz5kU6bGLRYnXb6nYEWLO\nHNXRo1VD5pyrqjkyReM4UDyMV8yDD6pu3Vp1eR56yHqTqsvmzSbHjh2qt9xi6++8Y8tFi6zOjh2q\nu++uunq17uzRK2brVtVt28wZ7IMPtNo9fB9/XP17iAcrV1bnPlJTf6m6DotFcSfvLEDV3tRzcuyt\n97jj4I477E30ySdhwICSUAdO5tC1a1duuukmjjjiCFq1asW0adM4+uijS9Xp06cPGzZsoHcQOKzs\nNsCQIUNo3749e+21F3379mXgwIE732Ira+O4446jW7dutGrVihZBtOiHH36Y2267jSZNmvD3v/+d\nc889N94fRVZywQVw6aUWTuikkyzgdygiFuqjMm64wUIVFXPNNSUhi6rCH/5Qs1BBoTH5mjSxfcUj\nCsXx6kSsl7FZMwuh8u67JefXrVsS//KEEyw802efWf1x46zOjBmW/Wb8+Mhy9O4Nkydb/M1k8dVX\ncNZZdr/FmXMiccghtvzDH6wnNZ1wHVY9iuevpTUioplwHzUlNNBuWc46y2I7tWwJ554Lf/qTB++s\nCSKC/+biT6TPOdifETkKXH9VnS1bYN48M1Rmz4Z99635NZcvN/1YjIjF9Hv0UTNu77uv/Dlbt1bP\nyK0pRx9tRmkk/v1vuOUWWz//fHjxRUuL+MUXlvnnnntcfyWKZOgwN+zSkE2b4N57bR5c3boWKHjB\nAnj4YZsDsuuupUuzZjZPBqB/f0udddNNFlHeqR5u2CUGN+ycZCFic/iKDbriqVa77WZ5q6F8AORE\nUFhocxMrorhnE2wO47p1lve6GNdfiSMZOsxDOqchtWqZcffhh/Dtt2bggQ21PPecpdNZs8aWxaVt\nWxtOufdez8XoOI4TDaEvv//3fzYqkptbkvXinXfgpZdsvXfv0sZTPPjgAxtWr4gff7Tl66/bNJtd\ndnEnuGzDe+zShEmTzFOtZUsz4Lp1s964F16AUaNK6u3Y4YZbIvA33sTgPXZOqrF4MVx4oXn4Hnss\nHHSQDW927mwewfHMgHXwwdZWKFu22P/D0KHW9ujRlV/H9Vfi8KHYapINinHVKntT+/bb0vs7d7Y5\nJsW89Rb065dY2bIRV4yJwQ07J5Up+xI9bpw5p8UD1fI5bUN/NsXr0bzYu/5KHMnQYe4VmyY0b25v\nap98Unr/6NGlndjdqHMcx0kMd9xRert47l08WL269Pb06aW3RXy0xjGSatiJSF8RmSUiP4jIoDDH\nLxCRKSLyvYh8JiIHJEPOVOLgg83Dtdj79eqrkyuP42QzUeiwZiIyMtBjE0WkWzLkdOLD3/5mYaOK\nKRvcOJbMnGnL3Fzo1QuCWLuOU46kOU+ISA7wEHA8sBiYJCJvq+rMkGrzgd6quk5E+gKPY6l5soaT\nTrKYSoccYg/yJ59Y3KK//93m3BXHKHIST7iI5E72EKUO+zPwrar+RkQ6A/8N6jsZwu9+Z71nw4ZB\nXl582pg/34y5/v0t60cs5vG5/spckukVeygwV1UXAIjIS0B/YKdSVNUvQupPBPZMpIDJYtkyOOww\nM+CKJ8p+/rkVgHvusQfcSR7ZNj/lm28sltcvv1jonOJ0UllOpToM6ALcBaCqs0UkT0R2V9WViRbW\niR/33msv2o8+aqkaGzSI7fWXLLFlp06xMeqyTX9lG8k07NoAC0O2FwGHVVD/UuD9uEqURCZNsje+\nXXe1sCQ//2ylUyf45z/Nzb6w0CKOp1v0cCf9OeggmDDBwumcfDL8/vfmFRjrP7A0IxodNgU4E/hU\nRA4F2mMvqG7YZRh169roylFHlXdyqykffGDLs86K7XWdzCSZhl3Urwwicgzwe+Co+ImTXG6+GT7+\n2Navuw7+8x9zhsjPL0mg7TjJRMQSxZ90kiVE797deu/KZPjJJqLRYXcB/xGRycBUYDKwPa5SOUmh\nXTtbTp5sMeRiaYT9/e+2POKI2F3TyVySadgtBkIzlLbF3nhLEThMPAH0VdU1kS42dOjQnev5+fnk\n5+fHSs6EEPqG98ADtnziCTfqnNSjZUt45RUYORLOO88Cs/7rX/GbXwRQUFBAQUFB/BqoHpXqMFX9\nBXspBUBEfsTmDpci3fWXY9MTevWyedB33hk7w+7ll2156aWxuZ6THBKpw5IWx05EagOzgeOAJcBX\nwIDQicci0g74CLhQVb+s4FppGQfqjjtgyBBLaF1UZNkkyrJqlaWwcZxUZONGm0LwwANwySXwl79Y\nCrt4kwpx7KLUYU2Bzar6q4hcBhylqpeUuU5a6i8nPMU+CbH6SkNTg3kGicwhI+PYqWoRcA0wBpgB\nvKyqM0XkChG5Iqh2G9AMeEREJovIV0kSN2bMnl0Sb2jIENu3fr0Zdc89Z4moV6ywbVU36pzUZpdd\nbK7dtGnmWNG5s6Ve2ro12ZLFnyh1WFdgqojMAk4Crk+OtE6i+PprW65dG5vrtWtnPeRu1DnR4pkn\nEsyKFdCnD8yaVf7YsGGWLqxDh8TL5TixYPp0GDQIZsyAESNsaCoepEKPXaxIJ/3lVM4vv9goDNS8\n127sWDjxRFi0CNq0qblsTurgKcUqIR0U4/btcP/98Oc/w6+/Vlx382aoXz8xcjlOPPjvf82T7623\n4nN9N+ycVKZ4+LSmubsPPBC+/95zgGciGTkUm21s3Wqer6FG3VlnWXd9aEowVTfqnPSnf3+Lu+j2\nipONPPmkLSt7ia+IJUvMqPv8czfqnKrhhl0cueuukvl0bduWP/766/DII4mXy3HizZ57QuPG8NFH\nyZbEcRLPpZeaE9GGDdW/RnGkhMaNYyOTkz24YRcnxoyBW28t2S6bwDkvz6KVDyqXXdJxMoOHHrJ0\nS2V/+46TDaxZUzP9vmWLLRs2jI08Tvbghl2cePjhio8vWGBDs7VqlfTqiZQ8zI6T7pxyCpx5Jlx2\nmQ/JOtnJ8OHVP3fVKlu6YedUFTfs4sTVV1uQyrIMGmSOFGvXmnE3YQI8/rgZeUOGQJ06CRfVceLG\n3XfDvHnmTOE42cSzz8Lxx1fvXFW46ir7X2jVKrZyOZlPMjNPZCwVTXTdc0/rpWva1Er79ha533Ey\nkXr14LXXLOxJXh6cdlqyJXKcxNCpk4U+qQ7FMfCaNo2dPE72kNQeOxHpKyKzROQHESk3G0FE9hWR\nL0Rki4jclAwZq0K/fpV7L117rTtMONlFp07w5ps2327SpGRLE1ui0GHNRWS0iHwnItNE5JIkiOkk\ngd12g4kTbWSmqkybZsucnJiK5GQJSTPsRCQHeAjoi0VnHyAiXcpUKwSuBe5NsHhRETo3TgTeeafi\n+sVd6yeckBj5HCdVOOwwCwHRvz/ML5cpNT2JUoddA0xW1e5APjAsSEXmZDjFWYNeeqnq5xa/AB17\nbOzkcbKHShWMiOQCRwB5gAILgC9UdV0N2z4UmKuqC4J2XgL6AzvzLKrqSmCliJxaw7biwsSJ1hNx\n5532ZpWTU3Hcoq1bK3eqcJxMpX9/WLzYnCq+/BJyc5MtUY2pVIcBS4EDgvUmQGGQiszJcIp/3zt2\nVP3cNWtg6FB7IXKcqhLRsBORXsAtmEE3GUtyLZiRd4+ILADuUdVPq9l2G2BhyPYiIG1+xjNnln7o\ntm+3Eo6zz7bhqBtuSIxsjpOqXH21PTsDBsC776b9UFM0OuwJ4CMRWQI0Bs5JkGxOksnJgfPPh7/8\nxTIOVYW1a2HvveMjl5P5VNRj9xvgJlX9IdxBEdkHuBKormEX0wAIQ4cO3bmen59Pfn5+LC9fClWo\nXdtc2UeNssnhkfjHP+zBdhzHuO8+6NsXBg+Gf/87unMKCgooKCiIq1zVIBod9mfgO1XNF5GOwFgR\nOVBVS02rT6T+chJHdbMIzZ3rw7CZRiJ1WNJyxYrI4cBQVe0bbN8K7FDVu8PUHQJsUNVhEa6VsFyL\nDzwA118fff369c2z6fDD4dVXPZyJ4wAUFlqP99/+BhdfXPXzUyFXbDQ6TETeB/6pqp8F2x8Cg1T1\n65A6nis2Q9m2DerWhfXro88gUVQEu+4KP/5YMk/PyTxSLlesiPwuBm1/DewtInkiUhc4F3g7UpMx\naC8mHHssdO8eff0tW2D5cvjmm8hDtY6Tbey2m6XUu/HGZEtSI6LRYbOA4wFEpCXQGcgQ9xGnMurU\ngY4dLe9rtKxda8agG3VOdamuV+wdNW04mEB8DTAGmAG8rKozReQKEbkCQERaichC4AbgryLys4g0\nqmnbNWG//WD8+Kqf16yZ9Uxs2hR7mRwnHenSxXoy0pVodBjwL+BgEZkCjAP+pKqeZC2LaNOmaobd\n+vXQpEn85HEyn4hDsSIytYLz9lHVevERqeokYihjyxZo0KDm1xk3Do47rubXcZx0p3iu6tattqwK\nqTAUGyt8KDazGTAATj0VLrwwuvojR9r809mz4yuXk1ziqcMqUqctsPhMa8Ic+zwewqQyY8ZU/9w3\n34Tdd4fNm31CrOMUI2JzULdsgUZJ7Yd3nPhR1R67M8+MnyxOdlCRYfce0EhVJ5c9ICIT4idSanLG\nGVWrf9ddlhfWcZzIdO9ugb0HDEhcm4EzVjSoqtZ42omT3bRuDT/9VLVzLrooPrI42UHSvGJjSSKG\nMmbNsq70xYth2bLoz1u0yN7YHMcpz0cfwRVXwIwZVfMYr8kwRpDWKyqFoaojqtNGVfCh2Mzm1Vfh\nv/+FaCNdHHQQPPYYHHxwXMVykkw8h2LdsIuCL7+0IMNbtsCqVdGfV7u2eTjtskvcRHOctOf44+Gc\nc+Dyy6M/x+fYOenC0qXmdFdYGF39ffaxXuzOneMrl5NckhLuREQOEJEvRWSRiDwuIs1Cjn0VD2FS\nlXfftZ63qhh1YPGIGjWCKVPiI5fjZAL/+hfccYfNQU02MQrl5Dg7yc2NPhrCxo02ItSqVXxlcjKb\nisKdPAIMBfYH5gCfiUin4FhWhdn9+OOand+9O3yVVaaw40TPoYfaH9nkcrN5k4LPqXNiSrGD0KhR\nldedMMGGYJs2jb9cTuZSkfNEY1UdHazfKyLfAKNFJEqn7czh448ttlBhoYVm2LLFyqZNsGGDHVu3\nrmS9fXuoV8+Oq1oS6AMPTPZdOE7q0ry5PUOJoJJQTi0SI4WTLUgw2Pbss3DyyRXXXbbM/j8cpyZU\nZNipiDRV1XUAqjpeRM4E3gCaVXBe1IhIX+B+IAd4MkI6sQeAk4FNwCXhvHQTQZMmHjTSceJFkyYJ\nDVYcs1BOlekwEbkZuCDYrA10AZqr6tqqCu2kN9E4B61ZY8HsHacmVDQUew/QNXSHqn4PHAuMrGnD\nIpIDPIQp2K7AABHpUqbOKUAnVd0buBwbHnYcJ8No2jRxPXaUhHJaULYAUYdyikaHqeq9qtpDVXsA\ntwIFbtRlHwccEF0qytWrLU+s49SEiD12qvpC2X2BA8VCVf1/MWj7UGBuoEwRkZeA/sDMkDr9gBGB\nPBNFJFdEWqrq8hi07zhOitCwYeLS7anq7ys4VpWIetHosFDOB/5Xhes7GcKpp0bnHLRmjcW9c5ya\nUJFX7JDit08RqSci44F5wHIROSEGbbcBFoZsLwr2VVZnzxi07ThOCiFi81HTjGh0GAAi0hA4CXg9\nAXI5KUajRtFNNfAeOycWVDTH7lxKPMQuBgTYHdgHeBYYW8O2o1XjZeO8hD1v6NChO9fz8/PJz8+v\nllCO4ySeygy7goICCqKN8FppW3IA8Dj2kvg+MEhV1wTHvlLVQ6O8VFVM0dOBTyMNw7r+ymz228+C\nFFfG6tU+xy5TiaUOq4yKDLutIVEz+wIvqep2YKaIVDFld1gWA21Dtttib7wV1dkz2FeOUMXoOE56\nIZWE6Sxr7Nx+++01aa44lNNE4FIslFM/VZ1L1UI5RaPDijmPCoZhXX9lNm3awMqVlddbssSHYjOV\nGOuwCqnIeWKriOwvIrsD+cAHIccaxqDtr4G9RSRPROpiPYRvl6nzNjAQQEQOB9b6/DrHyTx+/bVq\nKcVqSGNVHa2qa1T1XuAPWCinw6t4nWh0GCLSFOgNvFVTwZ30pGlTy0JUGYsXewpKp+ZU1PP2R+A1\nbPj1PlWdDyAipwLf1rRhVS0SkWuAMViogOGqOlNErgiOP6aq74vIKSIyF9gIeFR4x8lAVq2Co45K\nWHMxCeUUjQ4Lqp4BjFHVFMit4SSDpk3hxx9tnl2ksFmqdtyDEzs1xXPFOo6TdI47Dm691fLGRkNN\n8iyKyAXAfFX9osz+dsBtMfL6r4o8rr8ynB07ICfHgt336hW+zubN5jiRCqn1nPiTrFyxl1Q0l05E\n6mZLXsWiIkvzIlL98nmVwp46TnaxcqVln0gEqvpCGKMulqGcHKcUtWrB2WfbUGskNmww71nHqSkV\nDcU2Aib3lLvLAAAgAElEQVSJyCxgErAM81BtBRwM7As8EXcJk8y2bXDKKfDNNzW7zhdfwJFHxkYm\nx8k0RCxdX2LakiHAK8GwaT1gNHAgUCQiF6hqTT3+HacczZtbWspIuGHnxIqKAhQ/JCL/BY4Cjg4K\nwE9YtPXPs2H84L77YNy4ml0j8z8lx6kZxx4LY8fCYYclpLl4h3JynHJUll1lyRJo4ZmKnRhQkVcs\nanyqqnep6tVBuVtVP8sGow7gT38yw0wVnnuuetcQgd9lxaC141SPk06CMWMS1lzYUE6qOpOKRzEc\np9pU5hk7Zw7su2/i5HEylwoNOwAR6SAi94nISBF5JyjlXPqzgQsvhFatqnduv36xlcVxMonevWHy\n5Oii88eAsKGcRESITSgnxylHbm7FPXbLllX//8VxQonm7fRN4EngHWBHsC8reutCufxyeKKaMwpf\nfx1+85vYyuM4mcQzz1j8rgTFsgsbygk4hRiEcnKccFQ2FLtiBbRtG/m440RLpT12wBZVfUBVP1LV\ngqBMqEmjIrKriIwVkTki8oGI5Eao95SILBeRqTVpLxacfDI0aFC9c886C/bc085///3YyuU46c6b\nb8I//gGjRlX/GasiS4ETgR7AsyLSLgh1Mg0YXLwd7IuIiPQVkVki8oOIDIpQJ19EJovINBEpiPWN\nOOlDZUOxK1b4HDsnNkTTY/egiAzFgnDu9FtT1Zq82Q4GxqrqPYFCHByUsjwNPIhNaE4q3bvXLL5Q\nsZv7jh0V13OcbOKLL+Cyy8yo69AhYc2OIPpRh2PC7RSRHMyJ7HgstdgkEXk7mKdXXCcX+C9wkqou\nEpEEBXRxUpHKhmLdsHNiRTSGXTfgIkzBhZolYRVelPQD+gTrI4ACwhh2qvqJiOTVoJ2YscsuFliy\nXj17+F58MbrzfvoJ2lX43u842cns2TZF4dlnLU5kolDV/Bhc5lBgrqouABCRl4D+wMyQOucDr6vq\noqDdVTFo10lTmjateA7p3Ln+X+HEhmgMu7OBvVT11xi22zIk5+tyoGUMrx0XWrSwqOHF/OUvcNNN\nNtn1mWcin9e+fentSZMS+yfmOKnITz/BiSfCnXfaNIc0pA2wMGR7EVA2WMveQB0RGQ80Bv6jqtX0\nrXfSncaNIxt227bBwoWwzz6JlcnJTKIx7KZi+ROXV1YxFBEZiwUzLstfQjdUVUUk7ZwxunaFP/wB\nTj+98rovvAA9e0LLltAs6kyUjpOZLF1qqcNuuimtwwBFo7PqAD2B4zBv2y9E5EtV/SGukjkpSZMm\nkQ27jRttVKhWNLPeHacSojHsmgGzRGQSJXPsVFUrDOChqidEOhY4RLRS1WUisgewImqJIzB06NCd\n6/n5+eTn59f0kpXyyy/R1bvgAti+3R9axykshBNOgEsugeuui/68goICCgoK4iVWdVgMhPowtsV6\n7UJZCKxS1c3AZhH5GMtwUc6wS4b+chJL48aWXWL7dssbG4pnnch8EqnDpLI4wyKSH26/qhZUu1GR\ne4BCVb1bRAYDuaoaznmCYI7dO6q6fwXXS0q85MLCque3/OYb671znGxj0ybo0weOO86GYKUG6a/j\nmUA7yvZrA7Ox3rglwFfAgDLOE/tiDhYnAfWAicC5qjqjzLWyJd571rPnnvDZZ+Wn6MyebaM/c+Yk\nRy4n8cRTh1XaY1cTA64C7gJeEZFLgQXAOQAi0hp4QlVPDbb/hzlZ7CYiC4HbVPXpOMhTZVaurN58\niFtvhTPPtEj7eXkxF8txUpa33jLPwJoadamAqhaJyDVYtIAcYHiQe/aK4PhjqjpLREYD32OOZ0+U\nNeqc7GKvvWDBgvKG3YYNNhTrOLEgomEnIhuIPI9EVbVJdRtV1dVYmICy+5cAp4ZsD6huG/FGFXbd\n1ebMbd5sD+wXX1R+3gcfWLnxRhg2LP5yOk6q8M47cPbZ6W/UFaOqo4BRZfY9Vmb7XuDeRMrlpC7N\nmoWPZbdunXnNOk4siGjYqaqP+FdAixYwb17pfVX5wxo/3kKmnHtu+fkWjpNpFBXB6NHw738nWxLH\nSR6RDLvVq2G33RIvj5OZ+HT+GFHVwMOTJ5tTRWFhfORxnFRhxw645RY44ABLG+Y42UpuLqxZU35/\nYaGNADlOLHDDLkbUqmXDs1Xx9AMLgSJSUnwOtZNJbNtmHrBffQUjRyZbGsdJLrm54XvsCgu9x86J\nHW7YxZibboLnnrNhp4MOiv68d9+1AJWZMv/IcTZtMkehwkIYO9ZjODpOpKFYN+ycWBJNHDunCrRr\nBxdeaOsnnVSxoXbwwTBxose3czKPtWstfENeHjz1FNSpk2yJHCf5VDQU261b4uVxMhM3KeLM0qVw\n5ZXhj339tTlhFA/DnnNOYmVznHiwdKnFq+vZE0aMcKPOcYrxoVgnEbhhF2datYIHH4S//Q2uuqr8\n8VDniVdfNZf3YkPvwQcTJ6fjxIJ58+Dooy2syf33e2+044RS0VBsVYPdO04kkqZ2RWRXERkrInNE\n5AMRyQ1Tp62IjBeR6SIyTUSq6JqQGtSuDb/9LTzySOV116+HDh0sDMopp8RfNseJFd9/D717w803\nw1//mh3zRUWkr4jMEpEfRGRQmOP5IrJORCYH5a/JkNNJDbzHzkkEyZxjNxgYq6r3BApxcFBC2Qbc\noKrfiUgj4BsRGRuatifVmT0b9t234jrPPAPHHmsP/Nq15kQxf77N13OcdODbb+Hkk+GBB+ylJBsQ\nkRwsZdjxWO7YSSLydhj9NKGy3NpOdhBpjt2qVW7YObEjmYZdPyxdGMAIoIAyhp2qLgOWBesbRGQm\n0BpIG8Nu111tWKplS+jcGbZssZheoVxySfhz//hHn5/kpD6TJsFpp8Gjj8JvfpNsaRLKocBcVV0A\nICIvAf0pr5+yoO/SiYZwQ7Hbt1vmCfcad2JFMg27lqq6PFhfDrSsqLKI5AE9sETaacPuu8Mrr5Rs\nb9tmYVDatLGeje++Kzl26qk2DAtw1lnQyHN/OCnMjh3w8stw/fUwfLh5wWYZbYCFIduLgMPK1FHg\nSBGZgvXq3ez5YrOXRo0sDFBRkU3RATPqGjUq2XacmhLXn5KIjAVahTn0l9ANVVURiRiaNxiGfQ24\nXlU3xFbKxFKnDhxzjK1PngyLFsHhh8PixfDeeyX1HnwQ7rjD3ubOPRe6dEmOvI5TFlX7rf7lL1C/\nvgUePuqoZEuVFKIJJ/4t0FZVN4nIycCbwD7xFctJVWrVgiZNzJgrHnpdv96GaB0nVsTVsFPVEyId\nE5HlItJKVZeJyB7Aigj16gCvA8+r6puRrjd06NCd6/n5+eTn51dX7IRSWGhGXThuuw2uvtqzUTip\nQ0EB/PnP9mf0z39Cv36JcZIoKCigoKAg/g1VjcVA25Dttliv3U5U9ZeQ9VEi8rCI7Kqqq0Prpav+\ncqpOsQNFqGHXpElyZXLiTyJ1mGiSrAYRuQcoVNW7RWQwkKuqg8vUEWz+XaGq3lDBtTRZ9xELrr46\nOo9ZMCeLDz+MrzyOU5avvzaDbt4860k+7zzIyUmePCKCqiZ17pqI1AZmA8cBS4CvgAGhzhMi0hJY\nEYxKHAq8oqp5Za6T1vrLqRoHHQSPP16SmejTT2HwYFs62UM8dVgyo0zdBZwgInOAY4NtRKS1iBQP\nSh4FXAgcExIuoG9yxI0fDz8MP/9sSdIjUbs29OgBhx1mThWHHw4NG5aeo+c4sWbRIhg40HrmzjwT\nZs2CCy5IrlGXKqhqEXANMAaYAbysqjNF5AoRuSKo9ltgqoh8B9wPnJccaZ1UoWzIk3XrvMfOiS1J\nm64ZDEUcH2b/EuDUYP1TsiSI8oIFFgcMLLXMgQeaJ+1XX8GXX9pk28mTrYTSoEHCRXWygI0b4Z57\n4KGHLLD27NnQuHGypUo9VHUUMKrMvsdC1v8L/DfRcjmpS9mQJz4U68Qa98NJEXr1Kj+XbvRouO++\n0vsaNzYlsG0brFhhw2IvvJA4OZ3MZuNGy+16992WFmzyZI+n6DixpGzIEzfsnFjjhl0K07evBX5d\ntcqGXQsLrQfvs89sEjvY/g8+gD32gP33T6q4ThqzYoX1zj3yiGWPGDkSDjkk2VI5TuZRdih2/XpL\nJek4scINuxSnRw8LeRIuxlGbNvDkk1YAxo6F48sNbjtOZH74AYYNs1iL55xjLw37eDAOx4kbZYdi\nfY6dE2vcsEsDcnJg2jR7q2vWzDwTr7sOvviipM5BB8HMmbB5symO3FxLKt2ypSdid0qjap7VDzxg\nv6GrrjKniBYtki2Z42Q+zZrB0qUl2+vXQ8eOyZPHyTzcsEsTunUrWW/VyjwVL7zQevO2b7c3wGnT\nYMyY0jlnf/3Vev0++yw7krI7kdm4EZ57zgy6nBzLGPHSSzac7zhOYgg3FOs9dk4sccMuDWnRAn7/\n+4rrPPig9ep17mxz9V55pcTge/NN+M9/4NBDEyOvk1ymT4cnnoDnn7f5cw8/bI4Rbug7TuIJF+7E\nPc6dWOKGXYby0Ue2bNLEAl9Om2a9d2+9ZfsHDYKuXU2h3HVX8uR04sPmzfDaa/DYYzB/vr0IfP01\n5OUlWzLHyW4aN4YNIYkxCwtLslA4TixIimEnIrsCLwPtgQXAOaq6tkyd+sAEoB5QF3hLVW9NsKhp\ny8iR5fdt3GihUbZtswTuDz9sc6u2bjUjb+BAqFcv8bI6saGoyAz6F180A/6ww+Cmm+C00yxHsRNb\ngmDp9wM5wJOqeneEeocAX2B67o0EiuikII0alTbsVq6E3XdPnjxO5pGUlGJBOrFVqnqPiAwCmpVN\nJxbUaxgkz64NfArcHAQtLlvPU/JUg8JCC5vy448Wu6xdO4ud56QPmzbB+PHw3nvwxhvQvj0MGGAe\nrq1bJ1u6+JHslGIikoOlEzseyxk7iTLpxELqjQU2AU+r6uthruX6K4uYMwdOP92CfoMZddOmmaOb\nkz3EU4clayi2H9AnWB8BFADlDDtV3RSs1sXeileXreNUn912g7POMseKP/0JfvoJOnSwHr2iIptU\n37mzZcG44w7v9UkVFiyAUaPg3Xfhk0+gZ0/rlfv0U+jUKdnSZQ2HAnNVdQGAiLwE9Admlql3LfAa\n4FEBHcB67H75xdaLHd98KNaJJcky7Fqq6vJgfTkQ9l1FRGoB3wIdgUdUdUaC5MsqjjjC3hhr1y5d\nfvnFhmovugiuvTaze4BSmbVrrVdu7Fgr69bBSSfZ0PkLL9hkbCfhtAEWhmwvAg4LrSAibTBj71jM\nsPNuOYfmzc2Y27LFdGzTpuHjlDpOdYnbz0lExgKtwhz6S+iGqqqIhFV4qroD6C4iTYExIpKvqgUx\nFzbLqVXL5tiFo3Nni5E3bBiceiosX25ZCpYvL7++Zg188w3svXdi5c80tm2z/MDFhty0aXDkkXDC\nCeYQsf/+HpswBYjGSLsfGBzoOAHcD9mhbl1o29amwKj6/Don9sTNsFPVEyIdE5HlItJKVZeJyB7A\nikqutU5E3gMOxoZtyzF06NCd6/n5+eTn51dDaiccL7wAN99sw7EtW1pp0MDyiE6ebG+bp5wCF19s\njhjTppXkvVUtvQ7W8+fBcO3zWLDA0sZ9+y1MmWLD4QsWmEF9wgnwj3/AUUdB/frJlja5FBQUUFCc\nRy81WAy0Ddlui/XahXIQ8JLZdDQHThaRbar6dtmLuf7KLlq3tiDFOTlu2GULidRhyXSeKFTVu0Vk\nMJBb1nlCRJoDRaq6VkQaAGOA21X1wzDX88nHCeaJJ6wXDyweWnFMtEjr69bBzz/b+h//CPfdl1h5\nk8HWrTbcsnWrOarMnVtSZs40o3iXXWyOXM+eNpexQwcLSeK5IysmBZwnamPOE8cBS4CvCOM8EVL/\naeCdcF6xrr+yj/PPt5fh+vXNi/0N95XOOjLReeIu4BURuZQg3AmAiLQGnlDVU4HWwDPBPLtawHPh\njDonOVx2mZXKWLsWbrvNvG6bNbP0Vb1726ThnJz4y5kIVG1YZcoU+O47W06ZAosXm+KuV8/uvVMn\nK507m1dcjx7uCZeuqGqRiFyDvXDmAMNVdaaIXBEcfyypAjopzR57WI9do0beY+fEnqT02MUaf+NN\nXebNsyHcYk/boiILmNu0Key3n83LK1tycmw+3ymnWCq1jh2t52/FCliypHxZuRJ69YILLrB0a7Fm\n0ybrbSwsLMnesWaNOZZMmQLff2+BoA880Er37rbs2DFzjNdUI9k9drHE9Vf2MWwYLFpkL3y//mpT\nLpzsIp46zA07J+EUFcGIEWYwNWtWvmzcaGnPxo+3IcvFi62Hb9ddbW5K2ZKba9kzmjWDV1+1eWo/\n/WTGWPH6hg1w8skWFqTYUCyWZdkya2PJElO2xfPcis9dv95i/DVvbm0Vl733LjHmPFxBYnHDzkln\nXnwR3n7beus6dbK8zU524YZdJbhizGw2bzYHjUhx9NassaGNX3+1nsB27SxQb/v2Jet165qxOG6c\nGZTt25sn78qVZrC1aVNS2re3eW7FyxYt3As11XDDzklnCgpsikrr1tCvn825c7KLTJxj5zhR06BB\nxcebNYMZM8xAa9Ikcr0zzrDlsmWwcKEZg61aeQwpx3ESyx572AhBnTo+x86JPf6X5mQEHTpEX7dV\nq/jMxXMcx4mG1q3NsGvY0A07J/b4AJPjOI7jJJDGjc1bfupUN+yc2OOGneM4juMkmOIg7R6s3Yk1\nPhTrOI7jOAlm7FhbRnIKc5zqkpQeOxHZVUTGisgcEflARCKmMReRHBGZLCLvJFJGx3GcyhCRviIy\nS0R+EJFBYY73F5EpgQ77RkSOTYacTurRrp0Vx4k1yRqKHQyMVdV9gA+D7UhcD8wguqTbSSGZOSyT\nnT8zm9vP5ntPhfaTjYjkAA8BfYGuwAAR6VKm2jhVPVBVewCXAI8nVsrYkU7fd7rI6nLGnnSSNV4k\ny7DrB4wI1kcAZ4SrJCJ7AqcATwIpG7PKjYvsbD+b7z0V2k8BDgXmquoCVd0GvAT0D62gqhtDNhsB\nqxIoX0xJp+87XWR1OWNPOskaL5Jl2LVU1eXB+nIgUsbM+4BbgB0JkcpxHCd62gALQ7YXBftKISJn\niMhMYBRwXYJkcxwnS4mb84SIjAXCRQv7S+iGqqqIlBtmFZHTgBWqOllE8uMjpeM4TrWJanqIqr4J\nvCkivYDngM5xlcpxnKwmKSnFRGQWkK+qy0RkD2C8qu5bps6/gIuAIqA+0AR4XVUHhrleys6/cxwn\nPiQ7pZiIHA4MVdW+wfatwA5VvbuCc+YBh6pqYcg+11+Ok4VkVK5YEbkHKFTVu0VkMJCrqhEdKESk\nD3Czqp6eMCEdx3EqQERqA7OB44AlwFfAAFWdGVKnIzA/GJnoCbyqqh2TIrDjOFlBsuLY3QW8IiKX\nAguAcwBEpDXwhKqeGuYcf6t1HCdlUNUiEbkGGAPkAMNVdaaIXBEcfww4CxgoItuADcB5SRPYcZys\nICk9do7jOI7jOE7sScuUYiJytohMF5HtwfBGpHpPichyEZmahLYrDFxag/ajCu4sIteLyFQRmSYi\n1yeh/VuDz2mqiLwoIvUS0baIdA6CwRaXdSISE0/EKtx7roi8JiIzRWRGMBcrke0vEJHvg/v/KpFt\nB3VjHlQ8yu++vohMFJHvgs/9zli1X4lslT7rIvJAcHyKiPSo7NzK7ldE2onIBhG5KZVlFZEDROSL\nQA99H60eSKScwe/mf4F8M8SmB0VFnOSM+B8jpld/CM47MVo5EyTrQSH7TxCRr4PP9GsROSaF5Cz3\nv12d5ykJ3330z5Kqpl0B9gX2AcYDPSuo1wvoAUxNZNvYsMxcIA+oA3wHdIlR+/cAfwrWBwF3hamz\nHzAVczrJAcYCHRPYfh4wH6gXbL8MXJyItsvUrwUsBdom6t6DYyOA3wfrtYGmCW7/R2DXWLRZnc8e\nuBF4AXg70e0DDUM+9y+Bo2P5OYRpr9JnHYvF+X6wfhjwZWXnVna/wGvBc3VTqsoafAdTgP2D7WZA\nrRSU8xLgf8F6g+D5aZdEOcP+x2BBsL8L6ucF51f6eSZJ1u5Aq2C9G7AoFeWs7vOUhM+zSs9SWvbY\nqeosVZ0TRb1PgDVJaLvSwKU1IJrgzvsCE1V1i6puByYAZyaw/fXANqCh2ATzhsDiBLUdyvHAPFVd\nWEm9mLUvIk2BXqr6FNg8LFVdl6j2Q0WJUZtValviF1Q8qvZVdVOwWhdToKtjKEM4onnWd8quqhOB\nXBFpVcm5Ee9XRM7AXpxmpLisJwLfq+rU4HprVDWamKSJlnMpsItYJpFdgF8xHZYUOSv4j+mPGaDb\nVHUBZhwcGoWcCZdVVb9T1WXB5gyggYhEkxU30Z9pdZ+nRMtZpWcpLQ27NCCqwKXVJJrgztOAXsHQ\nQ0PgVGDPRLWvqquBYcDPmLfgWlUdl4i2y3Ae8GIM2q1K+3sBK0XkaRH5VkSeCL6DRLUP5mg0LhgC\nuSzBbccrqHhU7YtILRH5LqgzXlWravxUlWie9Uh1Wldwbtj7FZFGwJ+AoakuK9bzoCIyWixP7i2p\nKKeqjsEMuaWYM9+/VXVtEuWMROugXlXOSZasoZwFfBMYMSklZw2ep0R/nntThWcpWV6xlSKRAxz/\nWVVjNncnTm3XyCOlgvajCu6sqrNE5G7gA2AjMJkq/NHWtH2xEA9/xLqa1wGvisgFqvpCvNsOuU5d\n4HRsyCVqYtB+baAncI2qThKR+7FcyLclqH2Ao1R1qYjsDowVkVlB73Vc25YaBhWPxb0Hb7Hdg57T\nMSKSr6oFVZWlCkT7rEfTeynhrlfmfocC96nqJhGpao9oomWtDRwNHAxsBj4UkW9U9aNUklNELsSG\nYPcAdgU+EZEPVfXHBMpZXaKVISmyikg3LArGCVGekmg5h1K95ynRctahCs9Syhp2qhrtDyEV214M\ntA3ZbkvpN61qty/mDNJKS4I7r4hwjaeAp4Jz/oX1niWq/YOBzzUIwioibwBHYvOu4t12MSdjb4kr\nK2szxu0vwuaTTAq2X8MMu0S1j6ouDZYrRWQk1vVfqWEXg7aPBPqJyCkEQcVF5FkNE1Q8Tu2HXmud\niLyH/RYLomm/mkTzrJets2dQp06Y/cVTFiLd76HAWWKxQHOBHSKyWVUfTkFZFwIfBz34iMj72EtP\nZYZdouU8EhipNm1lpYh8hv1uKjPsYilnNP8R4a4V7RSXRMtaPC3jDeCiKIzkZMlZ3ecp0XJW6VnK\nhKHYZEafj9T218DeIpIX9BydC7wdozbfBi4O1i8G3gwrmEiLYNkO+A2xG5KMpv1ZwOEi0iB4Czqe\nqs8Hqm7bxQwA/heDNqvUfjCvZKGI7BPsOh6Ynqj2RaShiDQO1nfB5mbEwis8mnv/s6q2VdW9sGHw\nj6I16mLRvog0lxJPxwZYL8HkGLUfiWie9beBgYFch2NTE5ZXcm7Y+1XV3qq6V/AZ3w/8M0qjLuGy\nYiMG+wd6oDbQh+iehUTLOQs4NrjWLsDhwM4g00mQM5TQ/5i3gfNEpK6I7IUNz0Xr9Z5QWYPn8D1g\nkKp+EaWMCZezBs9Tor/7MVTlWdIoPapSqWCGykKsS3IZMCrY3xp4L6Te/7A5XluD+r9LYNsnY1Hp\n5wK3xvDedwXGAXMwxZkbof2Pgy/+O+CYJLT/p6D9qdgE0joJbHsXYBXQOMa/u2jbPxCYhHkxvUHs\nvGIrbR/oEHzn32FzLWPy24v23kPq9yG2XrHR3PsBwLfBvX8P3BLL778C2co968AVwBUhdR4Kjk+h\ntLdbWD0R6X7LtDsEuDGVZQUuCH6HU6nEiz1ZcgL1gOcDGadTNU/jeMgZ9j8mOPbnoP4s4KQU+O4j\n/R/+FQvIPTmkNE81OWvyPCXhu4/6WfIAxY7jOI7jOBlCJgzFOo7jOI7jOLhh5ziO4ziOkzG4Yec4\njuM4jpMhuGHnOI7jOI6TIbhh5ziO4zhOViMi14rITBGZJhbgP1yd60VkalDn+pD9B4rIFyLyvYi8\nHRJyqq5YFqLvReQ7EemTiHtxw85xHMdxnKxARPJF5Oky+47BcrseoKr7AfeGOW8/4P8Bh2AhrU4T\ny7IElhv7T6p6ADASS6sIcBmwI9h/AjCsihkuqoUbdk7CEZHtIjI5eIt5QyxfX2XnXCMilwTrh4vI\nl8E1ZojIkGD/BSIyJbjuZyJyQMj5TwXZC6aWue7/iUivGN+i4zhZgIhcF+ig58Ic219EngrZ7isi\nE4Neocki8pKItA2OPSMiZ5U5f0MF7dYTkY9FxP/Dq064GG9XAXdqkM9Ww2cs2heYqKpb1LKUTADO\nDI7trSVpG8dh+XEBugDjQ665FstqElfS5kchIjnBwxDXPLFOQtikqj2Ct5j1WFDHiARvOJdiQUTB\nAh5fpqo9gG7AK8H++UDv4Lp/Bx4PuczTQN8wl3+Ekrcrx3GcqnAVcLyqXhTm2C2Yfinu7XkAGKiq\nXQLd9QKWTxvM2ChrcEQMMquqW7E0gWfUSPrsJFyP2d5A76DDoEBEwhlf04BeIrKriDQETsXShAFM\nF5H+wfrZlKQMm4KlWcwJsoUcFHJO3Egbww64HktL5RGVM4svgI4AItJRREaJyNfB22jnoM5RwCxV\nLQq2d8eicqPGzGD9C1VdF9SZSMgDFLxNrSnbuKr+AOQVp6JyHMeJBhF5FMv0MlpE/ljmWD3gcC3J\nGT0IS1c1u7iOqr4T0ssDEVJUisgdQafGZBFZHNIL+DaWOtGJguJRHuAJzNgq/kxPBGoDzVT1cMwg\nf6Xs+ao6C7gby1oyCsumsSM4/HvgahH5GmgE/BrsfwrLA/s1cB/wObA9Tre4k7Qw7MSSCZ+CjWMn\nMzesE0NEJAfLZTot2PU4cK2qHow9XMU5+47GUnQVcx8wOxjGvTxQomW5FHg/SlEmA0dUVX7HcbIX\nVb0SS1mZr6r3lzncA0sZVUxXLN1dJAT4d4ixMZmgE0NVbwt6+PKBQuDB4JzvgCNrfCNZgqoeHnyO\n/99SxZwAAB5MSURBVA9Ld9gjKB9gxtcbQb1JwA4R2S3MNZ5S1YNVtQ82rDo72D9bVU8K/rteAuYF\n+7er6o1BO2cAuVhKu7iSFoYd9kd+CyXWsZPeNAgU11Ksy/rRYJ7dEcCrwbFHgVZB/XYEPXQAqvp3\nbJ7CB8D5wOjQiwcTYX+PvSVHwxJKhkQcx3FqSntMv5VDRHYLPCRni8hNwW4Fbg4xNnoQ0okRTEd5\nARimqpNh53BsLRGpH9c7yTzCdQ69CRwLICL7AHVVtbDciSItgmU7LK/ri8H27sGyFpYnt3gIvoGI\n7BKsnwBsC3r+4krKG3YichqwIvgxe29dZrA5UFztgS1Af+y7XRuq2FS1W8g5pb57VZ2vqo8CxwEH\nikgzgMBh4gmgn6qWG3qNgOBD/I7jxA6ltM6ajs2vQlULVbU7NkIR6jhW0f/bUOBnVR1RZr/rrqoT\nbj7jU0CHwLnuf8BAABFpLSLvhdR7TUSmY8PgV6vq+mD/ABGZDcwEFqnqM8H+lsA3IjID65wKNxcz\n5ohqav8mRORf2IdRBNQHmgCvq+rAkDqpfROO48QcVfUXPSepiMiPwEGqurrM/sOAv6rq6cH2flgY\njNOLe2xE5DYAVb0jCL/xrqq+HnKNX1S1sYicjo0+HFPstRkcrwfMV9U28b1LJ91I+R47Vf2zqrZV\n1b2A84CPQo26kHopX4YMGZJ0GTJJznSS1eWMbXGcFCHSj3EK0HlnJdVpmAPgsyIyS0Q+DY6/WMG1\nirdvAFoDXwXz74YG+3tgzmeOU4rayRagGrhWdxzHcZKOqnaIsH+LiHwuIoep6sRg3/tEcOhS1d+F\n2dckWB4bofl+2Lw7xylFyvfYhaKqE1S1X7LlcBzHcZxKuBe4Mh4XDoZhj8Ym/TtOKdKxxy5tyc/P\nT7YIUZEuckL6yOpyOk52EQy/luuJi9G1twK943FtJ/1JeeeJaBARzYT7cBwnOkQEdecJx3GccniP\nneNUA4l/HmcnwF/aHMdxoscNO8epJm5wxB83oB3HcapGWjlPOI7jOI7jOJFxw85xHMdxHCdDcMPO\ncRzHcRwnQ0h5w05E6ovIxCBp8gwRuTPZMjlONlNQUEDbtm2TLYbjOI4ThpQ37FR1C5YjrztwAHCM\niBydZLEcx4mCZ555hl69eiVbDMdxnKwhLbxiVXVTsFoXyAFWV1C9xnz7LcyaBbVqVa3k5MT/nJwc\nqFPHSrY7DM6cCV26JFuK1KWoqIjatdPiEXccx3FiRFpofRGpBXwLdAQeUdUZ8Wxv9mx4913YsSO6\nsn179HVrel5REWzbZstatUqMvNq1q79evz40aFC+RNrfuDHk5kLTprasVy+e30Z4Nm2Crl1h40Zo\n2DDx7acqeXl5XH311Tz//PPMmTOHv/3tbzz99NOsWLGCtm3b8s9//pMzzjgDgPbt2zNy5Eh69uzJ\nCy+8wEUXXcT06dPp0qULw4cP591332XkyJFs3ryZq666irfffps99tiDSy65pFSbd911F08++WS5\nNmbOnMlVV13Ftm3baNy4MXXq1GH16tW89957/PWvf2X+/Pk0bdqUSy+9lCFDhiTh03Icx8k80sKw\nU9UdQHcRaQqMEZF8VS2IV3sDBlhJZVTNMCw28rZtq3i9omNbtsDmzaXLmjUl62WP//ILrF0L69bZ\nslat0obebrtBq1bQujXssUdJ6dABWrSITU/j1Kk1v0am8tJLLzFq1Ch222033n33XT799FNatWrF\nK6+8woUXXsi8efNo2bIl+fn5FBQU0LNnTyZMmEDHjh2ZMGECXbp0YcKECTvTi91+++38+OOPzJ8/\nnw0bNtC3b99S8eU6deoUto0uXbrw6KOP8uSTT/LJJ5/srN+oUSOef/55unXrxtSpUznhhBPo3r07\n/fv3T/RH5TiOk3GkhWFXjKquE5H3gIOBgtBjQ4cO3bmen5+f8TkvRazXLdkjbapm+BUbeevWwapV\nsHSplWnTYOxYWLIEfvwRfv0V9tnHyn77weGHw8EHWy9gVZg0qaR9pwQR4brrrqNNmzYA/Pa3v915\n7JxzzuHOO+9k4sSJ9OvXjz59+vDWW29x44038umnn3LrrbcyduxYrrzySj7++GNuvPFGAF599VUe\neeQRcnNzyc3N5frrr+eOO+7Yed2K2ggXxLlPnz471/fff3/OO+88JkyYUKFhV1BQQEFBQbU/F8dx\nnGwh5Q07EWkOFKnqWhFpAJwA3F62Xqhh5yQOkZIh2latKq+/ejXMmWPD3VOmwF//Ct99B507w2mn\nWTnkkMp79VLdsIvV/Mfq3F+ox+qzzz7Lfffdx4IFCwDYsGEDhYWFAPTu3Zubb76ZZcuWsX37ds4+\n+2yGDh3KTz/9xLp16+jevTsAS5YsKXXNdu3alWqvojbCMXHiRAYPHsz06dP59ddf2bp1K+ecc06F\n91T2Ze3228upAMdxnP/f3r1HW1nXeRx/f0TwAqIi6UFF8EKKGgI2iJPJVtKwMnWalpOjZDlqNSPm\nMGbqLD0rVzetqRWMNlZeJm/TWHhZiYaXbZZ3RAUULyUipOYlpkAThO/88Tzn7Iv7XDh7n/M8+5zP\na61nnef629+9cbe/fZ/n9/sZTZDYAaOAq9Pn7DYDfhoRd2Uck/XQiBFJlW7q1NK+devgoYfg1lvh\npJOSfaefDiefnJxfy/3393qodcky4Wy7Tfriiy9y2mmncffdd3PwwQcjiUmTJrVX0fbaay+23npr\n5syZw7Rp09hmm21oaWnh8ssvr+jJOmrUKFasWMH4tKfKihUr2o919Rq1pgQ74YQTmDVrFnfccQdD\nhgzhrLPO4vXXX++1z8PMbCBphuFOFkfE5IiYGBETIuKSrGOyxhoyBD78Ybj44qQ38k9+kvRMHjcO\nWluT27vlnnkm6Tyx9db5rdjlwdq1a5HEyJEj2bhxI1deeSVLliypOGfatGnMnTu3/fZooVCo2IbS\n7dXVq1ezcuVK5syZ0+3X2GmnnVi5ciXr169v37dmzRq23357hgwZwsMPP8x1113nOWHNzBok94md\nDSwSHHIIXHNNcrv1hReSBO+SS5JkDmDuXDjhhKTThnVs3333Zfbs2Rx88MG0tLSwZMkSDjmkcgjI\nadOmsWbNGg499NCa2wAXXnghY8aMYffdd2fGjBnMnDmzPRHr6jWmT5/OfvvtR0tLCzvuuCMAl156\nKRdccAHDhw/noosu4vjjj+/tj8LMbMBQrYebm42k6A/vw2p76im44AJ44IGko8Vjj8HChbDnnrBq\nFQwf3vcxSarZMcAaq6PPOd3vMp+ZWRUndtY0lixJlsMPT4ZNGT4cVq50YtefObEzM9s0TuysaQ0f\nDi+9lIyf19ec2PUNJ3ZmZpvGTylZ0/Lz9mZmZpWc2FlTc9HMzMysxImdNS3JiZ2ZmVm53Cd2kkZL\nukfSUklLJM3KOibLB9+KNTMzq9QMM0+sB86KiMclDQMWSloQEU9nHZhlzxU7MzOzktwndhHxCvBK\nur5G0tPAzoATuwEu64qdZ0swM7O8yX1iV07SWGAS8FC2kVheZFWx81AnZmaWR7l/xq5Nehv2RuDM\niFiTdTyWPRfMzMzMKjVFxU7SYODnwDURcVOtc1pbW9vXC4UChUKhT2KzbLlwNjAUi0WKxWLWYZiZ\n5V7uZ55Q8iDT1cAbEXFWB+d45okBaORIWLYs+WsDi2eeMDOrrRluxX4IOBE4TNKidJmRdVCWD87n\nzczMSnJ/KzYifkNzJKDWx/yMnZmZWSUnTNbUXLEzMzMrcWJnTctTipmZmVVyYmdNy7dizczMKjmx\ns6bmip2ZmVlJwzpPSBoKjAYCWBkRaxvVtlktrtiZmZlVqiuxk7QNcCrwD8BI4FVAwE6S3gCuBX7k\nmSKst7hiZ2ZmVlJvxe4m4Abg6Ih4tfyApBbgk8DNwPQ6X8fsPVyxMzMzq5T7mScAJF0BfBz4Y0R8\noMZxzzwxAI0aBQsXws47Zx2J9TXPPGFmVluzdJ64EvBsE1bBFTszM7NK9T5jt5yks0RXIiL26Onr\nRMR9ksb29Hrrv1yoNTMzK6krsYuIsQ2Kw2yTeYBiMzOzSs1yK9bsPXwr1szMrFLDxrGrJml+RBzV\nW+1Xa21tbV8vFAoUCoW+emnLkCt2A0OxWKRYLGYdhplZ7tXVK1bS5I4OAb+MiJYeN/7e1xoL3Ope\nsdZm9Gi4//7krw0s7hVrZlZbvRW7R4Bfd3Bs2zrbbifpemAasIOkl4ALIuLKRrVvzcv5vJmZWUm9\nid0y4PSIeLb6QJqANUREfKZRbVn/4WfszMzMKtXbeaK1kzZm1dm2WZdcsTMzMyupd7iT/+3k2Lx6\n2jbriit2ZmZmleoe7kTSeEnTJQ2r2u+ZIqzXuWJnZmZWUldiJ2kWcBNwBrBU0rFlh79ZT9tmXXHF\nzszMrFK9nSdOAw6MiDXpcCQ3ShobEd+vOzKzbnDFzszMrKTexE4RsQYgIpZLKgA/lzSGZCw7s17j\nKcXMzMwq1fuM3R8lTWzbSJO8TwA7ABPqbNusU74Va2ZmVqnexG4m8Er5johYHxEzgUPrbLudpBmS\nlkl6TtI5jWrXmp8rdmZmZiX13op9E1jftiFpH+BjwPKI+EWdbbe1OQiYC3wEWAU8IumWiHi6Ee1b\n83LFzszMrFK9FbvbgTEAkvYCHgB2B/5Z0rfqbLvNFOD5iFgeEeuBG4BjGtS2NTlX7MzMzErqTey2\ni4jn0vXPAtdFxBnAUSTP2jXCLkD59GQr0302wLliZ2ZmVqneW7Hl9ZLpwCUAEbFO0sY62671Gh1q\nbW1tXy8UChQKhQa9vOWZK3YDQ7FYpFgsZh2GmVnuKer4ZZR0LfAy8AfgHGCPiFgraXugGBEH1B2g\nNBVojYgZ6fa5wMaI+HbZOVHP+7DmNG4c3HZb8tcGFklEhGu2ZmZV6r0VeyrwBslzdkdGxNp0/3jg\nO3W23eZRYJyksZKGAMcDtzSobWtyzufNzMxK6roVGxFvUWPqsIi4H7i/nrbL2npX0r8AdwCDgJ+4\nR6yBn7EzMzOrVldiJ+nCbp4aEfG1nr5ORMwH5vf0euu/XLEzMzMrqbfzxIt03blB3TjHbJN5SjEz\nM7NK9d6KvapBcZhtMt+KNTMzq1RX5wlJJ0vqMDmUNETS5+p5DbPOuGJnZmZWUu+t2GEkU3wtAx4h\nmTdWQAvwQWAf4Ed1voZZTa7YmZmZVar3VuxcSf8JfAg4JF0gefZuLnC/B5iz3uT/uszMzErqrdiR\nJm6/SRezPuOKnZmZWaW6EzsASXNIer62/dQG8H/AoxFxcyNew6wWV+zMzMxK6p15os2WwETgWeA5\n4ABgNHCKpO/3tFFJn5a0VNIGSZMbE6r1F67YmZmZVWpIxQ6YAHwoIt4FkHQpya3ZQ4DFdbS7GDgO\n+K+6I7R+yRU7MzOzkkYldtuR9JBdnW4PA0ak04H9taeNRsQySCb8NqvmAYrNzMwqNSqxuxhYJKlI\n8pzdNOAbkoYCdzboNcwqON83MzOrVHdiJ2kzYBnJkCdTSDpOnB8Rq9JTzu7i+gUk495VOy8ibu1u\nHK2tre3rhUKBQqHQ3UutibliNzAUi0WKxWLWYZiZ5Z4aMcycpMcjYmID4umo/XuA2RHxWAfHPVze\nADRhAlxzTfLXBhZJRIRrtmZmVRrVK/ZOSX+v3n0Yzv8jbu/hfN7MzKykUYndF4CfAesk/SVd/lxv\no5KOk/QSMBX4paT59bZp/YefsTMzM6vUkM4TETFM0ghgHMmYdg0REfOAeY1qz/ofV+zMzMxKGjXz\nxKnALGBX4HGSCtsDwOGNaN+sFlfszMzMKjXqVuyZJD1iX4yIw4DJJFOKmfUqV+zMzMxKGpXY/TUi\n3gaQtGVEPA3s3aC2zWpyxc7MzKxSowYofknS9sBNwAJJfwKWN6htsw65YmdmZlbSqM4Tx6Wrrens\nE8OB2xvRtllHPKWYmZlZpUZV7NpFRLHRbZrV4luxZmZmlRr1jF2vkHSJpKclPSHpF5K2zTomyxdX\n7MzMzEpyndgBvwL2i4gDgGeBczOOx3LEFTszM7NKuU7sImJBRGxMNx8iGSfPrJ0rdmZmZiW5Tuyq\nfB64LesgLD9csTMzM6vU8M4Tm0rSAqClxqHzIuLW9JzzgXURcV2fBme554qdmZlZSeaJXUQc0dlx\nSScDHwOmd3Zea2tr+3qhUKBQKNQfnOWaK3YDR7FYpFgsZh2GmVnuKXJc8pA0A/guMC0iXu/kvMjz\n+7DeMWUKzJkDBx2UdSTW1yQREU7tzcyq5P0ZuznAMJLZLBZJujTrgCw/XLEzMzOrlPmt2M5ExLis\nY7B8c6HWzMysJO8VO7MOeUoxMzOzSk7srGn5VqyZmVklJ3bW1FyxMzMzK3FiZ03LFTszM7NKTuys\nqbliZ2ZmVpLrXrFmnWmr2K1alYxnN2wYzJwJu+2WbVxmZmZZccXOmtq6dXDkkbB2Lbz6KkyaBLNn\nwxtvZB2ZmZlZ38t1YifpIklPSHpc0l2SRmcdk+WHBPPmwfvel1Ts5syBJUvgrbdg773hoovgL3/J\nOkozM7O+k+vEDrg4Ig6IiInATcCFWQdk+XLjjXDiiaXtUaPgssvgwQdh2TLYfXf48pdh6dLsYjQz\nM+sruU7sIqK83jIM6HC+WBuYXn4Zjj76vfv32guuvRYWLoShQ+GjH02qeGefDXfcAatX932sZmZm\nvU2R826Fkr4OnAS8BUyNiPf8JEuKvL8Pa7yWluS5uu7800fAY4/BzTfDvfcmCd/YsTBxIuyzD4wf\nnyR+Y8bANtv0euhWJ0lEhAe8MTOrknliJ2kB0FLj0HkRcWvZeV8F9o6Iz9Vow4ndACTByJHw2mub\nfu369fDkk7B4cXLLtm1ZsQIGD4Zdd4VddkmWkSNhxIjKZYcdYNttk2rgsGGw1VYeV68vObEzM6st\n8+FOIuKIbp56HXBbRwdbW1vb1wuFAoVCoa64rDlMntyz6wYPhgMPTJZyEclt2pUrk2FUVq2CN99M\netm+8EKy3rasXp30xl27Ft55J0nuhg1Lkr3yhG+LLUrLkCHd295882QZNKi0Xr3d3WODBiXLZpt1\nvEi19+VFsVikWCxmHYaZWe5lXrHrjKRxEfFcun4GMCUiTqpxnit2A5AEP/4xnHJK1pHAhg1Jb9y1\na2HNmlLCt3ZtMiTLO+8kS/l6Z9sbNsC775aW8u2O1rs6LwI2bux4qT4OXSd/3UkQ99kH5s9v7Oft\nip2ZWW2ZV+y68E1JewMbgN8BX8w4HsuR9euTilQeDBqUPJvXn57Pq5UIdpUc1jonL/9GZmYDQa4r\ndt3lip3ZwOKKnZlZbbke7sTMzMzMus+JnZmZmVk/4cTOzMzMrJ9wYmdmZmbWTzixMzMzM+snnNiZ\nmZmZ9RNO7MzMzMz6iaZI7CTNlrRR0oisYzEzMzPLq9wndpJGA0cAL2YdS72aZa7LZokTmidWx2lm\nZn0h94kd8B/AV7IOohGa5UezWeKE5onVcZqZWV/IdWIn6RhgZUQ8mXUsZmZmZnmX+fTckhYALTUO\nnQ+cCxxZfnqfBGVmZmbWhBQRWcdQk6T9gbuAt9JduwKrgCkR8ceqc/P5Jsys10SE/4+emVmV3CZ2\n1SS9ABwYEW9mHYuZmZlZHuX6GbsqzZGBmpmZmWWkaSp2ZmZmZta5XFTsJM2QtEzSc5LO6eCcH6TH\nn5A0qatrJY2QtEDSs5J+JWm7qvZ2k7RG0uy8xilpgqQHJC2R9KSkLfIWp6QtJV2fxveUpK92J8Ze\njvXTkpZK2iBpclVb56bnL5NU3jEn6zgPLNt/hKRH08/0UUmH5SjOyTXa2+TvUhax9vT7ZGbWVCIi\n0wUYBDwPjAUGA48D46vO+RhwW7p+EPBgV9cCFwNfSdfPAb5V1eaNwP8As/MYJ0mP5SeAD6Tb2wOb\n5TDOk4Hr0/WtgBeA3TL+TPcB3g/cA0wua2vf9LzB6XXPZ/yZdhTnRKAlXd+PZMif3H2ePf0uZfSZ\n9uj75MWLFy/NtuShYjcFeD4ilkfEeuAG4Jiqcz4JXA0QEQ8B20lq6eLa9mvSv8e2NSbpWOD3wFM5\njvNI4MmIWJy296eI2JjDOF8GhkoaBAwF1gF/7kacvRZrRCyLiGdrvN4xJEno+ohYTpIcTMlbnBHx\neES8km4+BWwlaXDe4oQef5eyiLWn3yczs6aSh8RuF+Clsu2V6b7unLNzJ9fuFBGvpuuvAjsBSBpG\nMpNFa57jJKk6hKTbJS2UdHYe44yIO0gSuZeB5cAlEbE641g7snN63qZck0Wc5T4FLEwTmFzFWcd3\nqc9jBcbRs++TmVlTyXyAYrrf27U7Y1apVnsRESqNddcKfC8i3pK0KeNg9XWcmwOHAB8E3gbukrQw\nIu7OU5ySTiS5BTsKGAHcJ+muiHihG+03Mtae6k4MmcQpaT/gWyRzJXdHX8fZSs++S9D3sQ6mZ98n\nM7OmkofEbhUwumx7NJVVlVrn7JqeM7jG/lXp+quSWiLiFUmjgLZBjacAn5J0MbAdsFHS2xFxac7i\nfAn4daTj9km6DZgMdPVD1Ndx/i0wLyI2AK9J+i3Jj2d3ErtGxlrr2q5er/z95SlOJO0K/AI4qZtJ\nchZx9vS7lEWsPf0+mZk1l6wf8iNJLn9H8iD0ELp+iHoqpYeoO7yW5GH/c9L1r1LVeSLdfyHwr3mM\nk+Th7oUk1bDNgQXAUTmMcxZwRbo+FFgK7J/lZ1p27T0kg1q3bbd1nhgC7J5erxzGuR3Jg/7H5uG7\n1FGcPf0uZfiZbvL3yYsXL16abck8gIgAOAp4huRh9nPTfacDp5edMzc9/gSVvd3ec226fwRwJ/As\n8Ctguxqvu6k/Rn0aJ/CPwBJgMTUS0zzECWwBXJPGuJRN6BnZi7EeR1KheRt4BZhfduy89PxlwEfz\nGCfw78AaYFHZMjJvcdbzXcro375H3ycvXrx4aabFAxSbmZmZ9RN56BVrZmZmZg3gxM7MzMysn3Bi\nZ2ZmZtZPOLEzMzMz6yec2JlZQ0g6Q9LTkpZI+nYH55wpaXF6zpll+w+Q9ICkJyXdImmbdP8QSVem\n+x+XNK2v3o+ZWTNyYmdmm0RSQdKVVfsOI5nbdUJE7A98p8Z1+wP/BPwNcADwCUl7pod/DHwlIiYA\n84C2Kb9OBTam+48AvtuDWS7MzAYMJ3aWKUmzJD0l6ac1jn1A0hVl2zMkPZRWhRZJukHS6PTYVZI+\nVXX9mk5edwtJv5bk78CmqzVG0heBb0Y6p21EvFbjnH2AhyLir5HMVHIv8HfpsXERcV+6fifJHLkA\n40kGG25rczXJzCZmZlaDf9Qsa18EPhIRJ9U4djZwGbRXe34AzIyI8RExCbiWZPYBSJKN6oSjw0Ea\nI+Id4D7g2LqiH5hqVczGAYdKelBSUVKt5GsJ8GFJIyRtDXycZJowgKWSjknXP01pyrAngE9KGiRp\nd+DAsmvMzKyKEzvLjKQfAnsAt0v6ctWxLYCpEfFIuusc4OsR8UzbORFxa1mVBzqYMF7S19IK3yJJ\nq8qqgLcAn2nU++nv0qRtEfAjkmSr7TM9kmSaru0jYipJQv6z6usjYhnwbZKZS+aTzKixMT38eeBL\nkh4FhgHr0v1XkMwD+yjwPeB+YEMvvUUzs6bnmScsU5JeIJnT882q/VOB8yPi6HR7IXByRCzuoJ2r\ngEOB/yvbvWdEDC87Z1uSKt1nI2JRmjz+PiJ2aeR76u/SDgwnR8TnyvbNJ5mm6950+3ngoIh4o5N2\nvgGsiIgfVu1/P/DTiDioxjW/BU5Jk0QzM6viip3l1Rjg5VoHJO2Q9pB8RtLsdHcA/xYRk9oWyip4\n6QP31wLfjYhF0H47djNJW/bqO+l/alVGbwIOh/bEbEitpE7Sjunf3Ujmdb0u3X5f+nczkrly227B\nbyVpaLp+BLDeSZ2ZWcec2FleBZUJxFKS56uIiDciYiJwOcltuzad9ZZsJakOXV21X3TyLJ7VVOt5\nxiuAPSQtBq4HZgJI2lnSL8vOu1HSUpLb4F+KiD+n+z8j6RngaWBlRFyV7t8JWCjpKZJbvLWexTQz\ns9TmWQdg1oEXgZay7YuBeZIeLKvYDKUbSZmko4HpwGFV+7cANqSVO+um9HbrvVX71lMj6YqIP5B0\nkmjbPrSDNn9A0jmmev9ykt60ZmbWDU7sLGsdJWZPAHu3nxTRNqDtf0saDrxOkvxd2ElbbdtnATsD\nD6dDoN0cEa3AJOCBet+AmZlZXrjzhOVW2iHisoh4qJfa/wbwSETM6432zczM+pqfsbM8+w7whd5o\nOL0NewjJQ/9mZmb9git2ZmZmZv2EK3ZmZmZm/YQTOzMzM7N+womdmZmZWT/hxM7MzMysn3BiZ2Zm\nZtZPOLEzMzMz6yf+H+trbyii+LBrAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x13dcfb30>"
]
}
],
"prompt_number": 78
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"...and fit it: (since we know the electric delay, we tell it the program, this makes it more accurate)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"port1.autofit(electric_delay=0.)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 79
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"...and plot the result:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"port1.plotall()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAFHCAYAAAAsmgFsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4FNX6wPHvm15IDySUEEhAuoIgRQUiKMUCtiv2xkVR\nsSBekd+1IHqviqgoqFjQa0dsiCggqAFFQKr0DoEQakIa6dn398cspJCEQDa7KefzPPNkZ+bszLsp\nJ2dOFVXFMAzDMAzDqP3cXB2AYRiGYRiG4RimYGcYhmEYhlFHmIKdYRiGYRhGHWEKdoZhGIZhGHWE\nKdgZhmEYhmHUEaZgZxiGYRiGUUe4tGAnIoNEZIuIbBeRsRWku0BECkTkWmfGZxiGUR4R+UBEDonI\n+nLOtxWRpSKSIyJjnB2fYRj1k8sKdiLiDkwFBgHtgZtEpF056V4C5gHi1CANwzDK9yFW/lWeZOBB\nYJJzwjEMw3BtjV13YIeq7lHVfGAGMLSMdA8CXwNHnBmcYRhGRVT1d+BYBeePqOpKIN95URmGUd+5\nsmDXFNhXbD/RfuwkEWmKVdh7237ILJNhGIZhGIZRDlcW7CpTSJsMPKHWumeCaYo1DMMwDMMol4cL\n770fiCq2H4VVa1dcV2CGiACEA4NFJF9VZxdPJCKmJs8w6hlVrRMPeib/Moz6qbryMFfW2K0EWotI\nCxHxAoYBJQpsqhqjqi1VtSVWP7v7ShfqiqV12fbMM8/Uy3vX9/vX58/u6vvXMqfNvF35c6wNP++6\nGquJs/7GWp1cVmOnqgUiMgqYD7gD01V1s4jcaz//jqtiMwzDOB0R+QLoC4SLyD7gGcATrPxLRCKB\nFUAgYBORh4H2qprpqpgNw6j7XNkUi6rOBeaWOlZmgU5V73JKUIZhGJWgqjed5vxBSnY3MQzDqHZm\n5QkHiIuLq5f3ru/3r8+fvSbc33Cu2vTzri2xmjgdrzbFWl2kutt6nUFEtC58DsMwKkdE0Do0eMLk\nX4ZRv1RnHubSpljDqK3sI7UNJzCFHsNwLJN/OZez8zBTsDOMs2QKHNXP/AMyjOph8i/ncEUeZvrY\nGYZhGIZh1BGmxs6oNVTh+HHw8ABvbyjrQajQVki+LZ+8wjzWrstn87Y8WsbYaBXrQVADDzzcrG3M\naA9shR50aOdGx45C+/YQGVn2NQ3DMAyjtjCDJ4waZfr/8pn2yRFy3Q+R62lt2W6HyNQjZGsqbj7p\n2LzSUK90xDcN8U5HvdPBPRd1ywcUN/VC1BNbvhde7p4UFrhRYCtE3Atw8yhA3AoopAClANxsUOiJ\n5AcguUH4ShAB3oGE+QcRERxEw8BA8jOCyMsIJjqsER2iI+ncOoILW55vmjKcwN7BuLzjdaIYbvIv\nw9nK+7syHM8VeZhLC3YiMghrPVh34H1VfanU+aHABMBm3/6lqr+WcR2TMdYSuQW5zP5jJwtW7mLL\ngQQOZO8h1zeBHJ8EjnskkC3J6PEwGvpF0LJhBGE+ETTyi6BZSCMahwYT7h9EoHcg/p5BeGsgHoXW\nVpjnTX6OF7nZ7mRlQXY2XHQRNGpk3bewEPbtg23bSm5bt9nYfzCfpasyKPRMY93WNDbtTGdbQhq7\nD6SRnJlOcGQaviHHOJpzmGO5h8hyO4i+va7eZozx8fHcdttt7Nu3r9rvVZMLdiLyAXAFcFhVO5WT\n5g1gMJAF3Kmqa8pI45T8a8MGiIqCoKCzv8bGjdChg+NiKk3V1Jo7Q30v2NX1PMxlTbEi4g5MBS7F\nWjd2hYjMVtXNxZItVNXv7ek7Ad8BrZwerFEpBw7A8uVWM6nN4ziJ+etJyFnHvuzN7M/Zxp6MrSRl\nJuKZFU3m3lg6NIum5zktCKYrfvnR+OREI8cjyBJ3LukJgwc7LjZ3d2jRwtoGDCh+xo3CQm/c3b2B\ncLpX4rersBA83jb/fSrjf//7H9OnT+f33393dSjV4UNgCvBxWSdF5HKglaq2FpEewNtAT2cEJmI9\n3Pj4FBWWOnWCESPg3XdP//5ff4V27WDPHujSpeg6HTvC7t3W35Gj4vz5Zxg92ip4urnBokXQp09R\nmn374Pzz4cgROHgQnn0W3n674uumpFifv2lTx8Rp1F+1MQ9zZR+77sAOVd0DICIzgKHAyYKdqh4v\nlr4BcNSZARqWvDyYNQsCAiAiwuqL1rAheHpa5w9mHmTtwbV8unAtn/2yFq/maynw34tvZnt80s7F\nPaUdtiOXkLO/DXmJMYiHJ+TADm/4bj20bu3az+fuXr3pXaWgoAAPD9ONtrqo6u8i0qKCJEOAj+xp\nl4tIsIhEqOqh6oyrsND66usL114L334LW7ZYx7Kzi9JlZFh/20ePgp+fVZsHMHIkvPMO3HUXfPih\nVdiy2SA11Tq/Y4dVsHvhBSs/iI2F3r0hMdG6z4ABsGsXxMTA/v1QUADR0dZ7MzOtuIr/DX33nVUT\nuGKFtb9hA1xwgXX85pth3TorRrCOJyZaBb0RI6xjmzZZhVARyMqCN96wPvOKFXDVVTC72Ori8fHQ\nq5f18AmwcCH062d9RqPmMXnYWXLhArjXA+8V278VmFJGuquxCnupQPdyrqVG9UlPV23WTDUwUPXc\nzvka2mGVuvV8Q71uvlE9H49Sj3+HasS/+mvbh8aoZ9dP9JH/rte8grwyr2WzqWZkqCYlqW7frlpY\n6OQP4yA19XcuOjpaX3rpJe3UqZN6e3vr888/r7GxsRoQEKDt27fX77777mTa5s2b66pVq1RV9dNP\nP1UR0U2bNqmq6vvvv69XX321qqpmZWXpHXfcoSEhIdq+fXudOHGiNmvW7OR1XnjhhTLvsWnTJvXx\n8VF3d3dt0KCBhoSEqKrqnDlztHPnzhoYGKhRUVE6fvz4cj9Ped9n+/GasJB3C2B9Oed+AC4str8Q\n6FpGunI//9nIyFC16tfK33buVO3V69TjY8aU/56ePa2v06erRkSUPLdhg+qddxZdG1THjSv7OrGx\nqu+9p+rhcfo4VVW/+sp6/fLLRceDg1Ufflj1iSes/eHDVSdNUr3xxlOvsX69alqaakFB0bE9e078\nHqn+8otDv/21Qk3Nv1RNHuaIzZVF4Uo18KvqLGCWiPQGPgHaVGtURgn5hfmsO/YX176xkLd/WszO\nFiuIDoni2mYX0Sl4IDGeE/DObMWhQ0JODgx8rOjJvywi0KCBtRnVY8aMGcydO5ewsDDmzJnDH3/8\nQWRkJDNnzuTWW29l586dREREEBcXR3x8POeffz6LFi0iNjaWRYsW0a5dOxYtWnRyaZ5nn32W3bt3\ns2vXLjIzMxk0aFCJuZlatWpV5j3atWvHtGnTeP/990s0YzRo0IBPP/2UDh06sH79ei677DI6d+7M\n0KFDnf2tcobSbfbV3rFpY9JOuPt269bqVmwr2o992g1iBFqWPP/KPjf4h32/1PuXqcBQN4Z/7wbd\nS57v+LgbHu4Cg9yIvd8NBrjxwiqBy9zA5g42D7B5QqEnO20ejJjuCV08Tx4rfr74sTd/9OSp5z2h\niRf/etkXQvwg34/UbD9en+JnvQ+YPr3870enTtC8OezdW3Ts/vvhxx+t1/v3w2+/WTV5Pj7V9VNx\njcJC2L4d8vPhpZegb19oVQs6M5k8rGpcWbDbT8kFsqOAxPISq9Xs4SEiYaqaXPr8+PHjT76Oi4sz\n68WdJVVlybYtPDp1IQd8F3DYdzFBthiiCy+l2d4xPNC5F2PuD3F1mDWeozqA6xkWA0SEhx56iKb2\nzkXXX3/9yXM33HADL7zwAsuXL2fIkCH07duX77//nkcffZQ//viDcePGsWDBAkaOHMnixYt59NFH\nAfjqq694++23CQ4OJjg4mIcffpgJEyacvG5F99AyPkDfvn1Pvu7UqRM33ngjixYtqjBTjI+PJz4+\n/sy+Ga5XOo9rZj92CkfmXw2IhAUTQWwgav9q3yi178DzBeWddyuwb/ngmVX02j3f+upWUPS61LFR\nX+dDt3xwzwOPbOv9nlngmQ2ex0HdId8X8v2KttwgyA6B7FDIsb7uzQ6BoFDIbAzpzVixthnt2vkB\nVvNtv34QHg7jxsF991l99JKTrWbj2Nja0VR7+HDRYLETpk2DUaNg0iT47DNrqyxH5GFnmn9Z9zV5\nWJVVV1Xg6TasQuVOrKYML2At0K5UmliKRu6eD+ws51rlVoMap7f4jzz1afeLNh3+sPqMbaleY5sr\nQ4brgEdn6KS3DuuUKVYzx+TJqllZro62Zqipv3MtWrTQhQsXntz/6KOPtHPnzhocHKzBwcHq4eGh\nH3zwgaqqbt++XUNCQvTAgQN6zjnnaHp6ukZFRemePXs0ODj45DV8fHxONm+oqs6bN69EM0ZF9/jw\nww/14osvLhHjsmXLNC4uThs2bKhBQUHq4+Ojt99+e5mfp7zvM7WjKfZy4Cf7657AsnLSlfkZz9b6\n9VYTY2Dgqc2SoBoQUHL/wQeLmjRBdfly1XvuUe3SpWS6KVNUjx2zXrdsqfraa6pz55Z9j0svLXq9\ndm1Rc2p528qVFZ8ve7Opf2Cu4nNMCdivhG5XIv5Wmi9W2sxSOn+o9HpFueRJ5fIHlOtuVO7sqzwU\nqzzprTweqow8V6P/dZ0S97TSYYbSaL3eM7JAY2NLfn9quiVL9GTTdUGB6htvFDWdgypSoIRtsT5j\n/3E1Nv9SNXmYIzaX1dipaoGIjALmY013Ml1VN4vIvfbz7wDXAbeLSD6QCdzoqnjrktRU6NMvl+Tg\neaQ3n8nxxnPRi1vR69whDIieRQufTmg/4aKLwN/f1dEaZ+pEE0NCQgL33HMPv/76K7169UJE6NKl\ny4nCBK1atcLPz48pU6bQt29fAgICiIyM5N1336V3794nr9e4cWP27t1Lu3btANhbrE3rdPcoazmd\nm2++mYceeoj58+fj5eXF6NGjOXq09o2LEpEvgL5AuIjsA54BPMHKv1T1JxG5XER2AMeBu5wRV2ys\nNaBg+nR45ZWS5y65xBptvmuXVZsDMHmyVSN1++3W6NTu3a1tzx6rFmj6dGsk7ahRRdf5+mtrAAPA\nf/9rjVa99FK48kpr8EP79tbghjvvhPPOszaAp5+2pkvp08cauBEebg2oaNTImnzcx6eodiwhwRrA\nMWIEzJwJv/xiDfhITbWOf/edMPohL55/3guPgmAKMuDRR+HVV4vidHe3miPXr4dBg6BbN4g7D0aP\nVvA7CkH7SAjbBg03QoeZELGed/0PQ89e0KQ3bL2K6R90xN9fePBBa5BJcHB1/NSq5quvrK+NG1s/\nC1CIXAsXLYCWv0DUn3C8ERzsDIfOc2WolWLysKpx6XATVZ0LzC117J1irycCE50dV12VX1DI8Ofj\n+TPjc3YPnIXtYEfYeCN3BE7kuaeaVtg3zqh9jh8/jogQHh6OzWbj448/ZsOGDSXS9O3bl6lTp/LW\nW28BVjPg1KlTefrpp0+mOdE00aNHDzIzM5kyZUql7xEREUFiYiL5+fl42odRZ2ZmEhISgpeXF3/9\n9Reff/45AwcOrM5vRbVQ1ZsqkWbU6dI4mq+vNUr0hG3brIJcdjZcfXXR8bfesvqWnShItWsH8+YV\nnT8xPVDpWR6mTLGmPTlh3LiS5zvZZ/T74IOSx6dOtUbclh5V7udX8usJ0dHWtCsAN90EOTnWZwsM\nLOon1qOH9XXPHmtqE1X45BPYuhVCQ630GRlWml27rM+anQ0dOggDBjSErIZw4PxSAR2xCkItf4Ob\nryKr0IsXl93Mi1NHQmYkixdbo4BriqNHrcI5wMHjSdD3Pej0udWcvf1yWHkffD3DapY+6RmXxHqm\nTB52dmpBzwGjqjYc2kjUP0fj9UQzvssYS7fo9rwc+zcf9FnE9JH3MWKYKdTVRe3bt2fMmDH06tWL\nyMhINmzYwMUXX1wiTd++fcnMzKSPfeKw0vsAzzzzDNHR0bRs2ZJBgwZx++23n3yKPd09+vfvT4cO\nHYiMjKSRvQPQW2+9xdNPP01gYCDPPfccw4YNq+5vRb10yy0wfLg1ndDAgSULdWD1oerX7/TXGT0a\n0tOL9keNAi+vM4/ngQeqNlVQ8Tn5AgOtYydaFE7MVydi1TKGhFhTqMyZU/R+Ly9rOcKAALjsMvjz\nT1iyxEq/cKGVZtMm+Ojthvw2bSjMmwyTd8M3n4P/YXigHQwZTp8r9rNmjVXQdJW//oLrrrM+b8OG\nQMB+uGoE3N/RivW7j+GNHTB3ChcEXA05ITzwgFWTWpuYPOzsmCXF6pDCwqKMMys/i5kbZ/LuqndJ\nSEsgYMddbJ15OxEe5zBsGDz+uJm8syrq+8ztzlKTV55wFJN/nbmcHNi50yqobN0KbdtW/ZqHDlnz\n8p0gYtUwTptmFW5fm5YCF74MXd+FxU/C8ofJzXE7q0JuVV18sVUoRWzQ43Xo8x9YdQ/8OQayw3j5\nZfjXv6y0N98Mn39ujQpeuhRWrYKJE03+5Sz1bkkxR6lvGWNWljXKyWaznkI9Pa2miLfeAp8mO/G4\n6HWyW39KUMaFnJNxD+3cL+fD6Var+9Ch1lQjY8ZYM8obZ8cU7JzDFOwMVxGBRx6B114r2gcIbrmT\n1H63Qk4IgzO/5KdZAU6NKznZ6puIdxpce6vVV/C7jyGlaKb3EzWbYPVhTEuDJk2KrmHyL+epV0uK\nGWfPzc0q3P3yC6xeDTabQvTvRI5+lfzIJQxr9U+GNP4br5woUlKsofvRUVZzyqRJZi1GwzCMyij+\n8Pvqq1arSHBwLCPuXQyXP8jcJnG8++k8Aj0a0qdPycJTdfj5Z6tZHd8UuHUgJHWDmd9AYVG14e7d\n1tdvvrH6Jvr7m0Fw9Y2psaslVqywRqpFRFh9ZTp0gJAQZfJPP7LK/znwSYVlj5Dxx+008DZ/xdXN\nPPE6h6mxM2qa/fvh1lvhqaeU/i88gX+HRRx/8zfaxPqyYYPVj6+6dOsGq/7Ohrv6QkJv+HkSOTnC\nihUwfrx17+IDYMpj8i/nMU2xZ6k+ZIxHj1pPaqtXAyi0mQ19J+DtW0Dugqdg87Wgbnz/PQwZ4upo\n6z6TMTqHKdgZNZmIwrW3WTvffsrChdC/f/XcSxXc3BSuvtOayPmbzyj+J3DiV6gyLTIm/3IeV+Rh\nZlRsLREebnV6fe37hXBvV4h7FhY/xaaH16Abr0dtbqiaQp1hGIazTJgg8MO70GQFtP+K5FPWRHKc\nlBSg/TfQdAXMfp+NG0uWCURMNxvD4tKCnYgMEpEtIrJdRMaWcf4WEflbRNaJyBIROdcVcdYEGw5v\nYPBng5myeyQ98v4Pt/dXwZarGfWAKZsbhqtUIg8LEZHv7PnYchHp4Io4jerx1FPwwTt+1uCFyx9k\n6ntp1XavFevTYNDDNPjtXXr39CsxV6FhFOeyplgRcQe2ApdirZ+4ArhJVTcXS9ML2KSqaSIyCBiv\nqj3LuFadbcq45IojLPL8P9w7fE+340+SPH8kjcK8uOIKq8/dBRcUzelkOI9pynCOmtwUW8k87GUg\nXVWfE5E2wJuqemmp69TZ/Ku+eOwxeGXHXZwb05S/X33e4dfftQtiR/yb5h0OsPPVD6rcj8/kX85T\n30bFdgd2qOoeABGZAQwFTmaKqrq0WPrlWIto13kHD0L3Hjbczv+QhPb/B+tvpuDVbSzLsdayeXmW\nNW2JYRguddo8DGgHvAigqltFpIWINFTVI84O1qg+kyZBzGcTeHjzeSSmjKZZaJhDr785IRm6TWOA\nbVW1Ds4w6gZXtuM1BfYV20+0HyvPcOCnao3IhVasgBtvhPvvhxHjNrOvf18Swt8latF8vrz7NT7/\nIJgpU+C222rf7OGGc23dupXOnTsTGBiIu7s7//nPf1wdUl1VmTzsb+BaABHpDkRTTx5Q65sm/lEU\nbBxCj5HvO/zar8S/A1uHcve1LRx+7ZrI5GFV48qyf6XrgUXkEuBu4KLqC8e1HnsMFv9ug+5T8Bn4\nPNf7j+dCr5H0G+V+cgFtw6iMiRMn0r9/f9auXVvieHx8PLfddhv79u0r553GGapMHvYi8LqIrAHW\nA2uAwmqNynCJ5s2B5Q+RdOPVzPx6DDdc75h/rza18Vva+7BiJr16OeSSNZ7Jw6rGlQW7/UDxFUqj\nsJ54S7APmHgPGKSqx8q72Pjx40++jouLIy4uzlFxOsXK7fvgtrvAM4ucqUv5OqUVA9/DFOqMM5aQ\nkMCFF17o6jAcKj4+nvj4eFeHUdpp8zBVzcB6KAVARHYDu0pfqLbnXwacfz70bnU+vx9vxJPvL+KG\n6x0z78lTH/4COcHcPbirQ65XG5g8rGpcOXjCA6vjcX8gCfiLUzseNwd+BW5V1WUVXKtWdj6eMAGe\neQZ8z5tD9oC7YdnDsGQs2IrK20ePQphju2sYDlBTOx/369ePxYsX4+npiYeHB0OGDCEmJoZx48YR\nFhZGXl4efn5+iAjbtm0jMjLS1SFXqIYPnqhMHhYEZKtqnoiMAC5S1TtLXadW5l9G2eSiSRC2FZ39\nnmOuN3Q4HO5E5sJHHLaCRE3Nv8DkYY7gsj52qloAjALmA5uAL1V1s4jcKyL32pM9DYQAb4vIGhH5\ny0XhOszWrUXzDT0zvhAueYrs/iNhxiw+ueffHDrgweHD1pJhqqZQZ5yZX3/9ld69e/Pmm2+SkZGB\nl5cXIoKfnx/z5s2jSZMmZGRkkJ6eXuMzxJquknlYe2C9iGwBBgIPuyZaw1nmvHQDtPuWw8l5Vb5W\noa0Qt3Y/MHXU1fVmWTCTh1WdS8fXqOpcYG6pY+8Ue/1P4J/Ojqs6hYRA27awZU8qXH8jeOTAO6vg\neASHD1sLNsfEuDpKo6rkWcc8iOkzVX+qPvG0WFOf0GuzSuRhS4E2zo7LcJ0+5zWHj2OI6LoU3dO3\nStd6/bs/saU25eq4Fo4J7gw4Ig9zRP4FJg87U2bgtJMUFsLkyfB//wd5Pvvg7sGwJw7mTT7Z9Dpm\njLVlZ4OPj2vjNarGURmaYRi1S0AAsOsyiF2Aat8qrQbx4jdz4OBVNGnisPAqzeRhtZdZtsBJcnOt\nka95IX/DP3vBmru41ncKqSkeqFJiM4U6w5HE/p9FzHpDhuEUj11zGcQsIK8KrbFJSXDEfxFTx/Sr\n90uFmTzszJiCXTV68cWi/nRRUUDjVXDbAJj/Ciwdw7ffCG+/7eoojbpMVU82X0RERJCcnEx6erqL\nozKMuu35ey+ERptIPFruRA6ntWRFJjRaT49mPRwYWe1j8rAzZwp21WT+fBg3rmg/xWcF3HK5tWD0\nxmG0aGHNVj72lNUlDcNxROTkU27btm256aabiImJITQ0lIMHD7o4OsOom7w9vGH/BTzwwvKzvsb6\nY8vgYBdCA3wdGFntY/KwM+ey6U4cqSZOFzB0KMyebd+J+NuqqfvhPdg6pML3mf51tUNNni6gLqnJ\n0504Sk3Mv4yqk8uegHxfNP6Zs3r/FZOe4ad5+Rz49L84evCnyb+cp76tFVun3X8/9OoF417cCzdf\nCXOnwNYhjB0L//0vZGRAaiokJFhToGzbBv7+4Onp6sgNwzCMqnrouh58tvns5rJThZ/WrGJot386\nvFBn1H2mYFcNTvbv9E6D4ZfD0kdh4w0ANGsGbm4QFGRt0dHQp4/rYjUMwzAcr3+bHry1bwSqesad\n/lNTgci1xPp3rp7gjDrNpX3sRGSQiGwRke0ickpvMxFpKyJLRSRHRMa4IsYzMWRIsUIdClffCQl9\nYNnok2kefBAzYMIw6ohK5GHhIjJPRNaKyAYRudMFYRou0LZpEwry3Fm+KemM3/vH6iPglUmYe3Q1\nRGbUdS6rsRMRd2AqcCnWmosrRGR28eV4gGTgQeBqF4R4WhU+hF34CgQkwdczTh667z6rufWyy6o/\nNsMwqlcl87BRwBpVHSci4cBWEfnUvmqFUYeFhQGHO/LO9+vp2aHpGb33x1V/w8HO9L+6TnQjNZzs\ntDV2IhIsIoNF5D4RGWl/Qg1ywL27AztUdY+q5gMzgKHFE6jqEVVdCeQ74H4Ot3x50chXd3fw8rKf\naLISLnwZvvoKCr1Pps/NhZdfhlatnB+rYRgOd9o8DDgABNpfBwLJplBXPwQHA4c7crBwwxm/d0fm\nWnq06EyP+j3TiXGWyq2xE5HewL+AFsAarEWuBegFTBSRPcBEVf3jLO/dFNhXbD8RqDW/xps3U+KP\nrrDQ2nDPhaF3WStKpDUH4B//sApzo0eXfS3DMGqlyuRh7wG/ikgSEADc4KTYDBdzd4fuLToxb/WZ\n/4tMzF/H+QFxjg/KqBcqaoq9BhijqtvLOiki5wAjgbMt2Dl0rPX48eNPvo6LiyMuLs6Rly9BFTw8\nYPp0mDsXvv662MneL8CxGNhwIwDPPw///ne1hWK4kJkF3Xni4+OJj493dRilVSYP+z9grarGiUgs\nsEBEzlPVjOKJnJl/Gc7TiI7QaNoZv+9g/nY6Nr63GiIqYvIv53JmHuayeexEpCcwXlUH2ffHATZV\nfamMtM8Amar6SjnXcto8UG+8AQ8/XM7JwH0wsjNM+xvSmwHWnHRBQdCzp9Uya6YzMQz4Yd1irvn0\nFqa228TIuwLO+P01YR67yuRhIvIT8B9VXWLf/wUYa+9iciKNmceujjqcfoyIF6NJeyKNwMDK/boW\nFIDXk+FsfGAj7aIiqjlCw1WqMw87q1GxInKXA+69EmgtIi1ExAsYBswuJ22NebTo1w86lzcCvd+T\nsPK+k4U6gJwcOHQIVq2yN9UahsFV5/bh8rb9Gf31Kc9xtUll8rAtWIMrEJEIoA2wy6lRGi7TKDAE\nNzzYuPtopd+z5+AxcM+jbbNG1RiZUZed7XQnE6p6Y3sH4lHAfGAT8KWqbhaRe0XkXgARiRSRfcBo\n4EkR2SsiDap676ro2BF++62ME2FbofVcWPJ4me8LCYE77oCsrOqNzzBqixcvf5KcDu+QmZfp6lDO\nSmXyMOC/QDcR+RtYCDyuqimuidhwBf/cVqzas6PS6dcnbcczo7VpKjXOWkWDJ9ZX8D6HPEqo6lxg\nbqlj7xR7fRCIcsS9qionB3wrWrKv16uw4n7IDSzz9Pr11nbPPdC/f/XEaBi1SbuIVpAQxzsr32fM\nhY+4OpxNcXKoAAAgAElEQVSzUok87ChwlbPjMmqOEG3FhqQdWOMOT2/xhh14ZZqpE4yzV9HgiUbA\nIOBYGef+rJ5waq758ys46XcUOsyEqVvLPD1rFjRsaK0D269f9cRnGLWNCHivfJzXl13PQz0ewNPd\ndEA16p4mPrHsTNlZ6fSTP94O7q2rMSKjrquoYPcj0EBV15Q+ISKLqi+kmunqiqZI7jATdgyG40UV\nmS++CGNPmYfeMIziukZewNH8KObtmMdVbZxTsWUfjFUZqqpV7nZi1G8tglqxJm1B5d8QuoMLG5tm\nHePsldvHTlXvVtXfyzl3U/WFVDNt3gxdu1L2gsydPod1t5Q49MQTVo3E/v3Oic8waqPnnoOUP67j\n+y0/OPO2CcCeSmwJzgzKqJvaRrTgQHblf5UaNEvg9iEtqi8go85z2ZJitcmyZdYkwzk5cLT04Cb/\nw9BoA+w6dZ0wDw/77OOGYZSpXz9o/epVfLVuIu8OseEm1b98tar+r9pvYhh2A3tFMWH9vtMntMvx\nSqRlWLPTJzSMcpSbi4rIuSKyTEQSReRdEQkpdu4v54RXM8yZA4mJZRTqAFr8Bgl9oNDrlFMFBdCg\nAfz9d/XHaBi11eSnW5GVHMKS3atcHYqjpnIyjJPaNmmKzT+JQtvp57vKyLRR4Lufc1ue2dqyhlFc\nRY/HbwPjgU7ANmCJiJwYqlOvejkvXlzByZa/wu6KR0R07gx/1auisGFUXvfuEHpsADOWxbs6FHDA\nVE6GUVxQA2/IDmHGD4dPm/aHX47iqQFEhlU0BYNhVKyiptgAVZ1nfz1JRFYB80TkVifEVaMsXgzp\n6ZCcDLm5VpNsTo41J13isefIyvSg8FbIzLTSRUeDt7d1XhVsNjjvPFd/CsOoucK1HTtSVzjlXs6Y\nyskwThAB0qP4aNY+bhnauMK0Ww8k0kBNM6xRNRUV7FREglQ1DUBVfxORa4FvgZAK3ldpIjIImAy4\nA++Xs5zYG8BgIAu4s6xRus4QGGhtpzL/Bwyjqhq6ncPezM+cdTuHTeV0ujxMRB4DToys8gDaAeGq\nmnqmQRu1WFoUuSH7gO4VJtuXlkiwmIKdUTUVNcVOBNoXP6Cq64B+wHdVvbGIuANTsTLY9sBNItKu\nVJrLgVaq2hq4B6t52DCMOqaJdxv255Y9D2Q1ODGV057SG1DpqZwqk4ep6iRV7aKqXYBxQLwp1NU/\nYZ5RhESffgBFUmYi4V6mYGdUTbk1dqp6yuOzfQDFPlX9pwPu3R3YYc9MEZEZwFBgc7E0Q4CP7PEs\nF5FgEYlQ1UMOuL9hGDVEuE9jMm1HKbAV4OFWvYP1VfXuCs6dyVROlcnDirsZ+OIMrm/UEee2aMbR\nvMTTpjucm0jTQFOwM6qmolGxz5x4+hQRbxH5DdgJHBKRU+f2OHNNgeKPMIn2Y6dLY37rDaOOcRNB\nqHVrY1YmDwNARPyAgcA3TojLqGHCvCM5ln/6+oiU/ESaBdSIVTSNWqyiR+NhFI0QuwMQoCFwDvAx\ncAZTaZdJK5mudG5f5vvGjx9/8nVcXBxxcXFnFZRhGM4nAlpBlhAfH098fLyD7iXnAu9iPST+BIxV\n1WP2c3+pasUdoYpUNg8Da73YP8prhjX5V93WsUUkv646eNp0GewnKqSJEyIynM2RedjpVFSwy1XV\nExnXIGCGqhYCm0XEEW0l+4HijyZRWE+8FaVpZj92iuIZo2EYtYvYH9/Kq7UrXdh59tlnq3K7E1M5\nLQeGY03lNERVd3BmUzlVJg874UYqaIY1+Vfddk7TCLJWn77GLotkYhuHOyEiw9kcnIdVqKLBE7ki\n0klEGgJxwM/Fzvk54N4rgdYi0kJEvLBqCGeXSjMbuB1ARHoCqaZ/nWHUPcfzsnDHExGnNMcGqOo8\nVT2mqpOAB7Cmcup5htepTB6GiAQBfYDvqxq4UTu1DI8kz+v0NXa57sm0iQp1QkRGXVZRzdsjwNdY\nza+vqeouABG5Alhd1RuraoGIjALmY00VMF1VN4vIvfbz76jqTyJyuYjsAI4DZlZ4w6iD9mRsI7Jp\nK6csKYaDpnKqTB5mT3o1MF9Vsx36KYxao0WjcGxex0hJLSA0uOx/u6qg3im0iAhzcnRGXSNFra21\nl4hoXfgchlFfdbzxS0Iv/orFo76uVHoRQVXPqnpPRG4Bdqnq0lLHmwNPO2jU/5nEY/KvOs5mA/ex\nEXw7cC3XXFr2JMXHMnIInRiEbUKOs2quDReqSh52OhWNir2zor50IuJVX9ZVLCiAbt2sfkCnbBdP\nRFrPLftcse3PM5r21DDqlyO6hXNC2zjlXqr6WRmFOkdO5WQYJbi5QZBHJFsTy+9JlJicguSGmkKd\nUWUVtXs0AFaIyBci8qiI3Cwit4jIGBH5AqvjcZ1f0C4/HwYPhlXlrk+u0Hruaa+zdOlpkxhGvZUd\nsoKWfs5Zd88JUzkZxikCJIJ9x8rvZ5eYkoxHnmmGNaquogmKp4rIm8BFwMX2DSABa7b1P+tD+8Fr\nr8HChRUk2DkA/jGswmvU/e+SYZy9zLxMciMXk7X+U6s3WvWr7qmcDOMUQR4RHDpefo3djv3J+KgZ\nOGFUXYU9ldXyh6q+qKr327eXVHVJfSjUATz+uL1Tq8Inn5SR4GBn8MqE0O3lXkME7qoXjdaGceYW\n7FxAh6AeLP452Fm3LHMqJ1XdTMUDygzjrAV7NSQ562i557fuTSHY29TYGVV32iFoIhIjIq+JyHci\n8oN9O2VIf31w660QGVn6qMCm66DT5xW+d8iQagvLMGq177d+zy0XDGHNGkhPd8oty5zKSazOTY6Y\nyskwThHmE0ZqXnK555OOJRPsbWrsjKqrzNwCs4DdwBTglWJbvXLPPVbN28GyukisuRu6fAhiK/O9\n33wD11xTvfEZRm2UmpPKD9t+IGfNNTRtCp5nMj3w2TsxldNWik3lBFyOA6ZyMoyyhPuHkV5QfsHu\ncGYKYb6mxs6ousoU7HJU9Q1V/VVV4+3boqrcVERCRWSBiGwTkZ9FpMw2GBH5QEQOicj6qtzPEQYP\nBt/yhooc7AJZYdD6pzJPX3cdNGtmvf+nspMYRr00beU0zvW5gjdfaMbcuRX8jTnWAWAA0AX4WESa\n26c62QA8cWLffqxcIjJIRLaIyHYRGVtOmjgRWSMiG0Qk3tEfxKg9GgWEkWkrvyk2JTuZiABTsDOq\nrjL9SaaIyHisSThzTxxU1ao82T4BLFDVifYM8Qn7VtqHWDWFH1fhXg7RuTNkVzS96JKx0Od52HYF\npy5vC/vtC6HZyq7UM4x6J6cgh0m/v07hRz+zYDbExDjt1h9R+XVeLynroIi4Yw0iuxRrabEVIjLb\n3k/vRJpg4E1goKomiohZK6oeaxIcTraUX2OXlpdCZHBrJ0Zk1FWVKdh1AG7DyuCKF0vKzPAqaQjQ\n1/76IyCeMgp2qvq7iLSown0cxt8fevcGb29o1Ag+L92lbtN1cMnTELMQdhXNmJCQAM0rfO43jPpp\n4vyPydh+PrNe60S3bs67r6rGOeAy3YEdqroHQERmAEOBzcXS3Ax8o6qJ9vuWX11j1HlNQ8LIcyu/\nYJeam0xMY1NjZ1RdZZpi/wG0VNW+qnrJia2K940otubrISCiiterdo0aweLFsGABfPYZbNwIgwbB\nnXfaE6g7/PIfGPgouBWcfF90dMmJileudEn4hlGjrNuWyoTF4/lX96cZPNjV0ZyVpsC+YvuJ9mPF\ntQZCReQ3EVkpIrc5LTqjxmkWGka+Z9kFu/x8yCKZjjFm8IRRdZUp2K3nDNZPPMHeh259GVuJ8aH2\naQdq3dQp7dvDAw/A//5X7ODma+F4I+g2rUTazz6DzZshJQWn1kwYRk104AD0fnYcPUOu5vmRPVwd\nztmqTJ7lCZyPNShjIPCUiJi2tnqqecMwbD5HKWumsOPHwc0/hYb+psbOqLrKNMWGAFtEZAVFfexU\nVSucwENVy53B3T4gIlJVD4pIY+BwpSMux/jx40++jouLIy4urqqXPK2MjNJHBOa+AXfGwdarIC0a\ngFtugcJCa1kZw6jPkpPhomFL0f6zmfPIxkq/Lz4+nvj4+OoL7MztB6KK7Udh1doVtw84qqrZQLaI\nLAbOA06Z9NIV+ZfhXA1DfKDQi7TsTIL9Akqcy8wE/JIJ9TU1dnWVM/MwOd08wyISV9ZxVY0/65uK\nTASSVfUlEXkCCFbVsgZPYO9j94Oqdqrgei6ZLzk5GcLL6g590UvWMmMf/QpasjS3ahWcf75z4jOM\nmiQrC3pfks3eQRcw9R9PM6zjDWd9repcQLuS9/fAmi6lP5AE/AXcVGrwRFusARYDAW+sZRiHqeqm\nUteqL/O913sej0UTf+ciLu7YosTxLVuU9p/7kPV0Gj4ePq4JznCq6szDTluHVGyKkxJbFe/7InCZ\niGwD+tn3EZEmIvLjiUT2NWn/BM4RkX0iUmPWbzhyBFq1Kufkn49Zc9pd+PIpp8aNg3fegT17qjU8\nw6hxZs1SDnQdyWXnnssNHf7h6nCqRFULgFFYswVsAr5U1c0icq+I3GtPswWYB6zDKtS9V7pQZ9Qv\nPhrGpj2n9rM7knYcUQ9TqDMcotymWBHJpPx+JKqqgWd7U1VNwZomoPTxJOCKYvs3ne09qpsqhIZC\nSIg1DUrLlrB06YmT7vDtp/DPHtYcdzsHnHzfzz9b26OPwiv1bppnoz579Y+3cG+6lveu+hNrkYfa\nTVXnAnNLHXun1P4kYJIz4zJqLl/CSDp2asEuMTkFzwLTDGs4RrkFO1Vt4MxAaptGjWDnzpLHSvyv\nSmsOX38J//gHfPAHpJTsM/3bb9aUKcOGgbt79cdrGK4Uv/sPVgdM4Pdr/8Tfy9/V4RiGSzRwC+dg\n+qmz3iQmJ+OjZuCE4RimO7+DlDnxcEIf+O05uHUwNDhQ4tSaNdagiuTypzUyjDph46HNXPG/f9Bh\n+4dc1C7W1eEYhssEeoRxOPPUTD/pWAp+YmrsDMcwBTsHcXOzmmcfeqjUiVX3wNo74LaB4Jtyyvsi\nIkrOc2f6UBt1yeZDO+g+9TKabJzI4umXuzocw3CpIO9QUrJP/T9wMD2ZQE9TY2c4hinYOdiYMfDJ\nJzBvHnTtaj+4+EnYdSnccjl4p5X5vjlzYN++Us25hlGLbTmQQNfXLyVm3zP8/fFthJzxbJiGUbeE\n+YaRlntqwe5IZjLB3qbGznAMU7BzsObN4dZbYeDA4qtMCMx/BfZ3hzsvAX9r2r5u3az57VThiiug\nWTOXhW0YDvV3wm66TO5Ph/QxrH5vBH5+ro7IMFyvoX8o6fmnFuxSslMI8zU1doZjmIJdNTtwAEaO\nBGvy4tdh25VwVx8I3MfKldYgjBPNsDec/bRehlFjzP17Bd3evogeOprlbzyIp6erIzKMmqFRYCiZ\ntlMLdql5yTQKMAU7wzFMwa6aRUbClCnw1FNw330Cv02AlffC8AuhyYoSgye++gqCgooKelOmuC5u\nwzgb0+K/58oZl3OD/zR+e+kBs9qKYRTTJDiUbE4t2GUWptA42DTFGo7hsmxXRELt68luE5GfRSS4\njDRR9gW0N4rIBhEpPTShVvDwgOuvh7ffth9YNhp+mmr1uev0eYm06ekQE2NNg3K56Wtu1BKqytjv\n3uCBn+7jscY/8dlTQ+pFf1ERGSQiW0Rku4iMLeN8nIikicga+/akK+I0aoamoaHkup1asMsimWah\npsbOcIzKrBVbXZ4AFqjqRHuG+IR9Ky4fGK2qa0WkAbBKRBYUX7anptu6Fdq2LevEUPgoBm4awuC7\n1jL12v9wPN2T1FRrEMWuXVZ/PcOo6dJz07n+4xH8tm4Lk7sv4cHbWro6JKcQEXesJcMuxVo7doWI\nzC4jf1p0urW1jfohqmEoBR6nFuxyJYWohqbGznAMVxbshgB97a8/AuIpVbBT1YPAQfvrTBHZDDQB\nak3BLjTUmqM4IgLatIGcHPjXv+wnD3eC91Yw95rbid3YB775AlJbnHzvI49g+icZNdrqA6sZ+ukN\nHF1xKZ8MW8aN1/m6OiRn6g7sUNU9ACIyAxjKqflTPai7NCqjRUQINu9j2NSGm1gNZoWFUOCVTItG\npsbOcAxXFuwiVPWQ/fUhIKKixCLSAuiCteZirdGwIcycWbSfn29Ng9K0qdXcunZtOHw+B3pOxuuB\n7vTLmUrrvBu47jpoYNb+MGoom9qYuvxNnlw4AX6aysxxw7jqKldH5XRNgX3F9hOBHqXSKHChiPyN\nVav3mFkvtv4KDvSAPH9SjqcT3sDqfZSWBuKXTKMGpsbOcIxqLdiJyAIgsoxT/y6+o6oqIuVOzWtv\nhv0aeFhVMx0bpXN5esIll1iv16yBxETo2dON/UsfJS+hN/OuvY15h2cy5Yo3mTA2gsJCqwDYrp1r\n4zaME7Yd3c51H41g194cWq1bylsvt+Kii1wdlUtUZjrx1UCUqmaJyGBgFnBO9YZl1FRubuCWG0rC\n4ZSTBbvUNBvqc4xQX1OwMxyjWgt2qnpZeedE5JCIRKrqQRFpDBwuJ50n8A3wqarOKu9648ePP/k6\nLi6OuLi4sw3bqZKTYf9++07SBTBtLfR9Fu47l6e/nsR9F9+KqmnJMVyvwFbAA5++wgdbXyZ805N8\ncseDXDPZ3SmDJOLj44mPj6/+G52Z/UBUsf0orFq7k1Q1o9jruSLyloiEqmqJjla1Nf8yzpxHQSj7\njqbQNSYGgKTkdNwK/fF0N/1u6jJn5mGiLlrDSkQmAsmq+pKIPAEEq+oTpdIIVv+7ZFUdXcG11FWf\nwxHuv7/YiNkTGq+CoXdDVjjMex0OdwSgXz/45Rfnx2jUbx8t/IsH54+kID2c//R6h4dua4m7u+vi\nERHUxU88IuIBbAX6A0nAX8BNxQdPiEgEcNjeKtEdmKmqLUpdp1bnX8aZCRx1GS9c+S8eGDQAgJkL\ndnH7L/3JeXG3iyMznKk68zBXzjL1InCZiGwD+tn3EZEmIvKjPc1FwK3AJcWmCxjkmnCrz1tvwd69\ncO65xQ4e6ArvroLN18Id/ZDLH6ZT92P06GENqujZE/z8YO1al4Vt1APLNifQ8rGbufvna7iuyWhS\np8xn9J2uLdTVFKpaAIwC5gObgC9VdbOI3Csi99qTXQ+sF5G1wGTgRtdEa9QUvhrKgdSiCtv9x5Lx\nLjQDJwzHcdngCXtTxKVlHE8CrrC//oN6Monynj2wbp31ukMHOO88iIjw4K+/HmDp28OwxT3J+j5t\nWR//OKy4Hwqs0Ye+9WoQouEsB1LS+ccbL/Jnzjtc7Pcgfz78Lo3DzGie0lR1LjC31LF3ir1+E3jT\n2XEZNZe/eyiH0osKdofSU/DF9K8zHKdeFJpqg969rTVjVWHDBvjsMxgwAJYsAVtmOMyZBh//gkfM\nEtweaU3AJdPAPY8JE1wduVGXHD52nKsnTqLZS+eQlJ7EsjvWsXjCeFOoMwwHCfQM5UhmUcHuSGYy\nDdxMjZ3hOK6c7sQ4jUGDYPVqOHrUanZNTu7IX399y9x1K1jd9EkYNZFEfYof591C86ZedOrk6oiN\n2mpXYgYj3nuT33Jeo0leHJ9euYCb+ptfKMNwtGCvUFKy95/cT85KJsDD1NgZjmMKdjVcly7WBJYe\nJX5SFwDzCe+6iMXt/8PiBU/BsoeZ9dQ9DB0U5KJIjdpo+fojjPpoGqvcpxArl/LD9b9yxQUdXB2W\nYdRZob6h7Mhdf3I/JSeFIC9TY2c4jinY1QLu7lbzbFAQhITAzp3w0EOwdGlfWNUXItcQeuUkbv4r\nhoG7h3NzqwdpExlFeLi14oVZiN0oThXem72O5xe+TmKDbznX/xp+v3kxF7Upa+07wzAcqWGDMNYc\nLWqKTctLJjY01oURGXWNKdjVEh2KVaJERsLtt8Ott1q1eYWFXTh27DM27k9g2YHJ/JDYGd8jF1Ow\nfCS2bQM5v4sbS5ZQLxZlN8qXmp7PEx/M4ZNtb5AXuI0rY+7n99u2ER3e0NWhGUa9EREYyvHDRQW7\nzMIUwvwucGFERl1jCna1UKNGcPfdZZ2JBl7jeN7zjHhjBl/IU3gOuB+/Bvfw9me34X68GampMGsW\nvP46dO/u5MANl5i9dBPPzv6QNYWfEEIsj8aN4slrr8Pbw8vVoRlGvdM4OJRsihXsbMk09DdNsYbj\nmIJdHeTv5U/2kuEwazitL13JllbvMrrgPAKzz+Por7fCpusYOzaI9u0hIABefNHVERuOlpiSzNNf\nfMPXOz7kuGcCPX3uYMGNi+h/XhtXh2YY9VpkUCi57skn97M1haahZvCE4TguKdiJSCjwJVYV0x7g\nBlVNLZXGB1gEeANewPeqOs7JodZa33134lU3oBs5BW/wzfofmRT+KVvyRpPmOYhZv95A0uKB5OY2\noH17q3nX29uFQRtVciTjGC9+P4sv189kv/ufRGQO4MGuT/LkjQPx9TbPcI5mnyx9MuAOvK+qL5WT\n7gJgKVY+960TQzRqoMbBIeR7pKCqiAg5bsm0aGRq7AzHccmSYvblxI6q6kQRGQuElF5OzJ7Oz754\ntgfwB/CYfdLi0unMkjxnIDkrma82fcWX675l+f5ltJC+pC69mjZyFb/NaeTq8IwzsPNwEpN/+pEf\ntn3PXn4n+Fh/rmx5A08Nu5LW0XV37jlXLykmIu5Yy4ldirVm7ApKLSdWLN0CIAv4UFW/KeNaJv+q\nR7Ztg7YfNyDtqQMEeAfgNi6UjSO30y7aFO7qk+rMw1z1GD8E6Gt//REQD5xSsFPVLPtLL6yn4pTS\naYwzF+YXxshuIxnZbSSpOam89uNPTFg3iwOxY/C5vxM+CVfhkTCAwOxzadvGjfPOgwkTwNOsUe1y\nNrUxe+VK3o2fw5Ijc0h320PD9IFc1vxmZg39gs7tAlwdYn3RHdihqnsARGQGMBTYXCrdg8DXWHMU\nGQYNGoDkhJKSnYK3mx/qlU5M42BXh2XUIa4q2EWo6iH760NARFmJRMQNWA3EAm+r6iYnxVdvBPsE\n88w1NzOs3c0USg4rjv5GfNIclhwYRmrOMTJ9+zP5y8u4dvdlXHBOlKvDrXdUlRW7t/L+L7+ycNcv\nJEg8cjyCNnIlo8+bzKihFxIeappZXaApsK/YfiLQo3gCEWmKVdjrh1WwM9VyBuHhoFmhHEhLITvd\nH8kNwtvLLL5sOE61/UcQkQVAZBmn/l18R1VVRMrM8FTVBnQWkSBgvojEqWq8w4Ot59zcoH17AB86\nMZi7GQxAQmoCC3ctZOvWBfT9bCzBfgHEeF5I44KLCEy7ENvBjhw97M6hQ3DoEBw7BqtWQevWLv04\ntVp+YT6r96/jiz/+ZOHWpWzLi6cgz5PG2f3p0/wapsW9waXdm5q5CV2vMoW0ycAT9jxOADPhkIGX\nF/hoKJt2pxDh64dHvmmCNRyr2gp2qnpZeedE5JCIRKrqQRFpDBw+zbXSRORHrJEA8WWlGT9+/MnX\ncXFxxMXFnUXURnHRwdEMP384g58czpjHbOxI3Upu1J9sDF3CQa/JpDU+iC2/B5Ldk25tu/DE5Z3J\nyWnBhg3CiS5DJ9a/PfEaoEkTa8qW+s5mUxZv2MUPK1ezdM9qth5fRqrvSkiLJvR4Ly5ociljL3qO\n6/vH4Otbv8sE8fHxxMfHuzqM4vYDxauwo7Bq7YrrCsywynSEA4NFJF9VZ5e+mMm/6hd/t1ASDqVw\n3McLX5vJDOsDZ+Zhrhw8kayqL4nIE0Bw6cETIhIOFKhqqoj4AvOBZ1X1lzKuZzofO9l778FLU46S\n0/BPcsKWkxvyNznBa7F5ZOKTdh4+qZ3xTe2Mb/p5eGe0ISPFn717rfc+8gi89ppr43eG3FzIybG+\n7j6QyqJNm1i1dxNbUjayN28Nqb5rcM8PIrygC22DutA7picD2vXg3HNCCDIrw1WoBgye8MAaPNEf\nSAL+oozBE8XSfwj8UNaoWJN/1T+tRt9Dn1ZdCfUN5/P1n5H0mhksXd/UxcETLwIzRWQ49ulOAESk\nCfCeql4BNAH+Z+9n5wZ8UlahznCNESNgxIhwrHEwQ04eP3L8CH8f+pu1B9ey9uAvrE56lS1Hd2DL\nCMcjtQ3nNm1DTkwbZm+JJTa0BdHB0TTwqt2jN1Vh925YtjqTxet3s3rPDnYk7yTNbScSvh0N24x6\npxOY247GHu05J6wDw6Iv5+oeXWjfItzV4RtnQVULRGQU1gOnOzBdVTeLyL328++4NECjRgv1tfex\ny7ER5GlWfjEcyyU1do5mnnhrrp07YfyEQtJIINV9G6keW0nK3YotaBcalECGWwJuhb54ZrXALT2a\ngmNN8MiJ5LxWEfTuEkGXcyI4/5wIIho0IiPFlwMHhKQkSmxHjkDv3nDLLdZya45kUxuHUjPYuDOF\n7YeS2JuSRGJ6Egczk9ibmsShrCQyNAkNSEI88giRlrQIaEXHprF0bdmK1mGxtAtvR1RQFG5iOsY5\niqtr7BzJ5F/1z5UvTORg+hECfQLIK8znjwnPuTokw8mqMw8zBTvD6QoK4KOPICsLgoMVt4Aj5Hgn\nkOGeQKYkkZR+iFVbDrHn6EHSCg6R63kI/A+DFOJeEISXBuLnFkQDzyCCfIII9A5g03pvfDy9uGKQ\nJ9mZXmRleHE83ZOMNC/SjrmRk19AbOsCYlsV0CCogEJbAQW2AvIKC0jLyONwejrJmWmk5qSTkZtG\nVmE6uZKGzf045PvjURCMT35T/G1NCJQmhHo0IaZhEzq3asJFnZrQPqoJwT7BiFmQ1ylMwc6ozUa8\n/T6/bFtKA29fWoe24ZvHH3R1SIaT1cWmWKMe8/CA4cNP7AnQyL6VPdVXdrb1Hpvkkp6bTlpuGmk5\naSdfH0hJ56EZeaRoPp9uyyM4LJ+g0DwCQvIICMyiYdNCvNw92bbVg2V/+JGf60FIsAeZaR5kpnvQ\nwM+TsAaBNAoKpHNoEC0iA2kVFUSb6CDaxTagcaS7GYVqGIbDRIWHkr4hhQI3T5oEXezqcIw6xhTs\njO2T70YAACAASURBVBrP1/fEK28aejSkof+pfVIGfmHNDxUYePrrHTwI+/ZB48ZW062H+SswDMOJ\nWkaGcZwjFKgbUWFmVKzhWOZfmlEnxMRUPm1kpOP74hmGYVRW15iW5PjupsADOjaJdXU4Rh1jCnaG\nYRiG4URtmzSDgCQKgE7NzYo+hmOZgp1hGIZhOJGbuCEFPqgUEBlhOvAajmUKdoZhGIbhZB8O/hab\n2vD0dHUkRl3jqpUnQv+/vTsPr6ss9z7+/WXqSClthRYoM0JBoQUOk0ADiNaBweOICqIeBzwKRxAR\n9UjAF0GUF19B5aCCA9NRBESZLGIKCJSpQEfKDEXGAi0tbTPs+/1jrSQ76U6zk72zh+T3ua51Zc3P\nvXey9r7zrPU8D/C/wNakHRRHxBu97FsL3A8si4jDe9nH3QWYDSOV0t2JpFkkY8LWAr+KiB/22H4k\ncCaQSadTIuK2Hvv488tsmBnMz7By1QF/C5gdEW8H/p4u9+ZEYBH5DbpdFuUcw7Lc42cO5/KH82uv\nhPLLLf2n80JgFrALcLSkaT12uzUido+IGcBxwMWljbJ4qun3XS2xOs7iq6ZYB0u5ErsjgN+m878F\njsq1k6QtgfcDvyLp8KwiObkYnuUP59deCeVXgL2BxyPi6YhoBa4CjszeISJWZy2OBV4tYXxFVU2/\n72qJ1XEWXzXFOljKldhtFhEvpfMvAZv1st/5wCkktzDMzCrJFsBzWcvL0nXdSDpK0mLgJuCEEsVm\nZsPUoDWekDQbyNVb2HeyFyIiJK13m1XSB4GXI2KepMbBidLMbMDyejwkIq4DrpN0IPB7YKdBjcrM\nhrVyNZ5YAjRGxIuSpgD/iIide+zzA+AYoA0YCYwD/hQRx+Y4X8U+f2dmg6PcjSck7Qs0RcSsdPk0\nINOzAUWPY54A9o6I5Vnr/PllNgwN1mdYuRK7c4HlEfFDSd8CxkdErw0oJM0EvtFbq1gzs1KTVAc8\nChwK/Au4Fzg6IhZn7bM98GR6Z2IP4I8R4aEGzGzQlKsfu3OAP0j6PGl3JwCSNgd+GREfyHGM/6s1\ns4oREW2SvgrcQtLdya8jYrGkL6Xb/wf4MHCspFZgFfCJsgVsZsNCWWrszMzMzKz4qnIsE0kflbRQ\nUnt6e6O3/S6R9JKk+WUoe5akJZIek3RqEcufIGm2pKWS/iZpfC/7nShpvqQFkk4sQ/mnpe/TfElX\nSBpRirIl7SRpXta0QlJRWiL247WPl3S1pMWSFqXPYpWy/KclPZK+/ntLWXa6b21a9l+KUXa+5Usa\nKWmupIfS9/3sYpXfR2x9XuuSfppuf1jSjL6O7ev1StpK0ipJJ1dyrJJ2k3R3+jn0SL6fA6WMM/27\nuTKNb5GSx4PyMkhx9vodo+Rz9bH0uPfkG2eJYt0za/1hku5P39P7JR1cQXGu9709kOupDL/7/K+l\niKi6CdgZeDvwD2CPDex3IDADmF/KskluyzwObAPUAw8B04pU/rnAN9P5U4FzcuzzDmA+SaOTWmA2\nsH0Jy98GeBIYkS7/L/CZUpTdY/8a4AVgaqlee7rtt8Dn0vk6YOMSl/8UMKEYZQ7kvQdOAi4Hri91\n+cDorPf9HuCAYr4POcrr81on6YvzxnR+H+Cevo7t6/UCV6fX1cmVGmv6O3gYeGe6vAlQU4FxHgdc\nmc6PSq+frcoYZ87vGJJOsB9K998mPb7P97NMsU4HJqfzu5KMHFVxcQ70eirD+9mva6kqa+wiYklE\nLM1jvzuA18tQdp8dlxYgn86ddwbmRsTaiGgH5gD/XsLyVwKtwGglD5iPBp4vUdnZ3g08ERHP9bFf\n0cqXtDFwYERcAslzWBGxolTlZ4dSpDL7VbYGr1PxvMqPiLfS2QaSD9DXihhDLvlc652xR8RcYLyk\nyX0c2+vrlXQUyT9Oiyo81vcAj0TE/PR8r0dEPn2SljrOF4AxSkYSGQO0kHyGlSXODXzHHEmSgLZG\nxNMkycHeecRZ8lgj4qGIeDFdXASMkpTPqLilfk8Hej2VOs5+XUtVmdhVgbw6Lh2gfDp3XgAcmN56\nGA18ANiyVOVHxGvAecCzJK0F34iIW0tRdg+fAK4oQrn9KX9b4BVJl0p6UNIv099BqcqHpKHRrekt\nkC+UuOzB6lQ8r/Il1Uh6KN3nHxHR3+Snv/K51nvbZ/MNHJvz9UoaC3wTaKr0WElqHkLSzZIekHRK\nJcYZEbeQJHIvkDTm+1H0MnZ5ieLszebpfv05plyxZvsw8ECaxFRUnAVcT6V+P3ekH9dSuVrF9km9\nd3D87Ygo2rM7g1R2QS1SNlB+Xp07R8QSST8E/gasBubRjy/aQstX0sXDf5FUNa8A/ijpUxFx+WCX\nnXWeBuBwklsueStC+XXAHsBXI+I+ST8hGQv5eyUqH+BdEfGCpLcBsyUtSWuvB7VsFdipeDFee/pf\n7PS05vQWSY0R0dzfWPoh32s9n9pL5Tpfj9fbBJwfEW9J6m+NaKljrQMOAPYC1gB/l/RARNxWSXFK\n+jTJLdgpwATgDkl/j4inShjnQOUbQ1lilbQrSS8Yh+V5SKnjbGJg11Op46ynH9dSxSZ2EZHvH0Il\nlv08MDVreSrd/9MacPlKGoNMjq7OnV/u5RyXAJekx/yApPasVOXvBdwVaSeskq4B9id57mqwy+7w\nPpL/El/pq8wil7+M5HmS+9Llq0kSu1KVT0S8kP58RdK1JFX/fSZ2RSh7f+AISe8n7VRc0u8iR6fi\ng1R+9rlWSLqB5G+xOZ/yByifa73nPlum+9TnWN/xyEJvr3dv4MNK+gIdD2QkrYmIn1dgrM8Bt6c1\n+Ei6keSfnr4Su1LHuT9wbSSPrbwi6Z8kfzd9JXbFjDOf74hc58r3EZdSx9rxWMY1wDF5JMnlinOg\n11Op4+zXtTQUbsWWs/f53sq+H9hR0jZpzdHHgeuLVOb1wGfS+c8A1+UMTNo0/bkV8CGKd0syn/KX\nAPtKGpX+F/Ru+v880EDL7nA0cGURyuxX+elzJc9Jenu66t3AwlKVL2m0pI3S+TEkz2YUo1V4Pq/9\n2xExNSK2JbkNflu+SV0xypc0SV0tHUeR1BLMK1L5vcnnWr8eODaNa1+SRxNe6uPYnK83Ig6KiG3T\n9/gnwFl5JnUlj5XkjsE708+BOmAm+V0LpY5zCXBIeq4xwL5AZyfTZYgzW/Z3zPXAJyQ1SNqW5PZc\nvq3eSxpreh3eAJwaEXfnGWPJ4yzgeir17/4W+nMtRZ4tqippIklUniOpknwRuCldvzlwQ9Z+V5I8\n47Uu3f+zJSz7fSS90j8OnFbE1z4BuBVYSvLBOb6X8m9Pf/EPAQeXofxvpuXPJ3mAtL6EZY8BXgU2\nKvLfXb7l7w7cR9KK6RqK1yq2z/KB7dLf+UMkz1oW5W8v39eetf9MitsqNp/XvhvwYPraHwFOKebv\nfwOxrXetA18CvpS1z4Xp9ofp3tot5+dEb6+3R7mnAydVcqzAp9K/w/n00Yq9XHECI4DL0hgX0r+W\nxoMRZ87vmHTbt9P9lwDvrYDffW/fh98l6ZB7XtY0qdLiLOR6KsPvPu9ryR0Um5mZmQ0RQ+FWrJmZ\nmZnhxM7MzMxsyHBiZ2ZmZjZEOLEzMzMzGyKc2JmZmdmwJulrkhZLWqCkg/9c+5woaX66z4lZ63eX\ndLekRyRdn9XlVIOSUYgekfSQpJmleC1O7MzMzGxYkNQo6dIe6w4mGdt1t4h4B/DjHMe9A/gP4N9I\nurT6oJJRliAZG/ubEbEbcC3JsIoAXwAy6frDgPP6OcLFgDixs5KT1C5pXvpfzDVKxuvr65ivSjou\nnd9X0j3pORZJOj1d/ylJD6fn/aek3bKOvyQdvWB+j/P+X0kHFvklmtkwIOmE9DPo9zm2vVPSJVnL\nsyTNTWuF5km6StLUdNtvJH24x/GrNlDuCEm3S/J3eP/l6uPteODsSMezjdwjFu0MzI2ItZGMUjIH\n+Pd0247RNWzjrSTj4wJMA/6Rdc43SEY1GVRV80chqTa9GAZ1nFgribciYkb6X8xKkk4de5X+h/N5\nkk5EIenw+AsRMQPYFfhDuv5J4KD0vN8HLs46zaXArByn/wVd/12ZmfXH8cC7I+KYHNtOIfl86ajt\n+SlwbERMSz+7LicZTxuSZKNnwtFrJ7MRsY5kmMCjCop+eMpVY7YjcFBaYdAsKVfytQA4UNIESaOB\nD5AMEwawUNKR6fxH6Roy7GGSYRZr09FC9sw6ZtBUTWIHnEgyLJV7VB5a7ga2B5C0vaSbJN2f/je6\nU7rPu4AlEdGWLr+NpFduIrE4nb87Ilak+8wl6wJK/5t6vWfhEfEYsE3HUFRmZvmQdBHJSC83S/qv\nHttGAPtG15jRp5IMV/Voxz4R8ZesWh7oZYhKSWemlRrzJD2fVQt4PcnQiZaHjrs8wC9Jkq2O9/Q9\nQB2wSUTsS5KQ/6Hn8RGxBPghyaglN5GMppFJN38O+Iqk+4GxQEu6/hKScWDvB84H7gLaB+kldqqK\nxE7JYMLvJ7mPXc6xYa2IJNWSjGW6IF11MfC1iNiL5OLqGLPvAJIhujqcDzya3sb9Yvoh2tPngRvz\nDGUesF9/4zez4SsivkwyZGVjRPykx+YZJENGddiFZLi73gj4UVayMY+0EiMivpfW8DUCy4EL0mMe\nAvYv+IUMExGxb/o+/gfJcIcz0ulvJMnXNel+9wEZSRNznOOSiNgrImaS3FZ9NF3/aES8N/3uugp4\nIl3fHhEnpeUcBYwnGdJuUFVFYkfyRX4KXdmxVbdR6QfXCyRV1helz9ntB/wx3XYRMDndfyvSGjqA\niPg+yXMKfwM+CdycffL0QdjPkfyXnI9/0XVLxMysUFuTfL6tR9LEtIXko5JOTlcH8I2sZGMGWZUY\n6eMolwPnRcQ86LwdWyNp5KC+kqEnV+XQdcAhAJLeDjRExPL1DpQ2TX9uRTKu6xXp8tvSnzUk4+R2\n3IIfJWlMOn8Y0JrW/A2qik/sJH0QeDn9Y3Zt3dCwJv3g2hpYCxxJ8rt9I/uDLSJ2zTqm2+8+Ip6M\niIuAQ4HdJW0CkDaY+CVwRESsd+u1F8K3+M2seILun1kLSZ6vIiKWR8R0kjsU2Q3HNvT91gQ8GxG/\n7bHen139l+t5xkuA7dLGdVcCxwJI2lzSDVn7XS1pIclt8K9ExMp0/dGSHgUWA8si4jfp+s2AByQt\nIqmcyvUsZtEporL/JiT9gOTNaANGAuOAP0XEsVn7VPaLMLOiiwj/o2dlJekpYM+IeK3H+n2A70bE\n4enyO0i6wTi8o8ZG0vcAIuLMtPuNv0bEn7LO8WZEbCTpcJK7Dwd3tNpMt48AnoyILQb3VVq1qfga\nu4j4dkRMjYhtgU8At2UndVn7Vfx0+umnlz2GoRRnNcXqOIs7mVWI3v4YHwZ26twpYgFJA8DfSVoi\n6c50+xUbOFfH8teBzYF70+fvmtL1M0gan5l1U1fuAAbAn+pmZlZ2EbFdL+vXSrpL0j4RMTdddyO9\nNOiKiM/mWDcu/XlIL8UfQfLcnVk3FV9jly0i5kTEEeWOw8zMrA8/Br48GCdOb8MeQPLQv1k31Vhj\nV7UaGxvLHUJeqiVOqJ5YHafZ8JLefl2vJq5I514HHDQY57bqV/GNJ/IhKYbC6zCz/Egi3HjCzGw9\nrrEzGwAN/jjOlvI/bWZm+XNiZzZATjgGnxNoM7P+qarGE2ZmZmbWOyd2ZmZmZkOEEzszMzOzIaLi\nEztJIyXNTQdNXiTp7HLHZDacNTc3M3Xq1HKHYWZmOVR8YhcRa0nGyJsO7AYcLOmAModlZnn4zW9+\nw4EHHljuMMzMho2qaBUbEW+lsw1ALfDaBnYv2OW3PchdS5dQW1NDbU0NNarpmq+poTZrOZlqqa2p\noa625/oa6jrms7bV19Z2zdfVdDs218/62lpqa5P5hrpaRo+oZ9SIOmpqhneLwevufoSj9tut3GFU\nrLa2NurqquISNzOzIqmKT31JNcCDwPbALyJi0WCWd89jj3LDY38lExmCZMqe71xHhqCdyLEt1H2Z\nzvXtyXLW9o757J8o2ZeO9cqA2pOpthVq2iFTC+31EHUoUw+ZepTO10Q6H/XUUEcNyboa6qilnhrq\nqVUdtTTQUDOShppRjKxNp/pRjK4bxcj6kYxpGMWYhlGMHZlMG40cxaSNNmLKhI3ZYtJ4tnrbxowb\nM2Iwfx05vfLGaj70t915ZZfVTNp4dMnLr1TbbLMNX/nKV7jssstYunQp//3f/82ll17Kyy+/zNSp\nUznrrLM46qijANh666259tpr2WOPPbj88ss55phjWLhwIdOmTePXv/41f/3rX7n22mtZs2YNxx9/\nPNdffz1TpkzhuOOO61bmOeecw69+9av1yli8eDHHH388ra2tbLTRRtTX1/Paa69xww038N3vfpcn\nn3ySjTfemM9//vOcfvrpZXi3zMyGnqpI7CIiA0yXtDFwi6TGiGgerPIu+NLRXMDRg3X6oshkgnWt\nbaxZ18aallbWrGtlbUsba1pbWZvOr21tZV1rG2tbWlnb2kpLW8e6ZH5dWyvrWltY3bKW1evWsLpl\nDWta1/BW6xpeW7uctavWsDazhpbMWloya2iNNbSyhhbepLX2DdrqVhANKyBTS03rxtS2bUxDZjyj\n422Mr5vMpqOnsPm4yWwzcQo7TJ7C/tO2Z5et3laUmsbr584H3JdcLldddRU33XQTEydO5K9//St3\n3nknkydP5g9/+AOf/vSneeKJJ9hss81obGykubmZPfbYgzlz5rD99tszZ84cpk2bxpw5czqHFzvj\njDN46qmnePLJJ1m1ahWzZs3q1r/cDjvskLOMadOmcdFFF/GrX/2KO+64o3P/sWPHctlll7Hrrrsy\nf/58DjvsMKZPn86RRx5Z6rfKzGzIqYrErkNErJB0A7AX0Jy9rampqXO+sbFxyI95WVMjRo2oZ9SI\nemBU2eLIZILXV61h2SsreH75Cl54/Q2eefUVnn71BZateIGFr8znjudns/KR51lz+xMEGUav3ZG3\n1bydaZvsznt33YePH7QnUyaO7Ve5Nz9yHwDO67qTxAknnMAWW2wBwEc+8pHObR/72Mc4++yzmTt3\nLkcccQQzZ87kz3/+MyeddBJ33nknp512GrNnz+bLX/4yt99+OyeddBIAf/zjH/nFL37B+PHjGT9+\nPCeeeCJnnnlm53k3VEauxHvmzJmd8+985zv5xCc+wZw5czaY2DU3N9Pc3Dzg98XMbLio+MRO0iSg\nLSLekDQKOAw4o+d+2YmdlU5NjZg4bjQTx41m9+2n9Ln/488v5x/zl3LvE0t54Pl5fO/20/j6/Q8z\nevUu7Lnx+/ncuz7Ise/eq89avQdfuhc2gkyFZnbFGjBhIC8vu8Xq7373O84//3yefvppAFatWsXy\n5csBOOigg/jGN77Biy++SHt7Ox/96EdpamrimWeeYcWKFUyfPh2Af/3rX93OudVWW3Urb0Nl5DJ3\n7ly+9a1vsXDhQlpaWli3bh0f+9jHNviaev6zdsYZ630EmJkZVZDYAVOA36bP2dUAv4+Iv5c5Jhug\nHbaYyA5b7McX2A/4DACr1rRwyey7uGzuDXzxb5/kSzfXM2vT/+Ann/kc204Zv945IoJn+WeJI++f\ncuabHbdJn3nmGb74xS9y2223sd9++yGJGTNmdNai7bDDDowePZoLLriAmTNnstFGGzF58mQuvvji\nbi1Zp0yZwrPPPsu0adMAePbZZzu39VVGriHBPvnJT3LCCSdwyy230NDQwNe//nVeffXVQXs/zMyG\nk2ro7mR+ROwREdMjYreI+FG5Y7LiGjuqgROOaOTes37E2nOXct7BF/HIKw+y/f/bgcamM3j25RXd\n9r/xvsVk1AotYyq2xq4SrF69GklMmjSJTCbDpZdeyoIFC7rtM3PmTC688MLO26ONjY3dlqHr9uob\nb7zBsmXLuOCCC/IuY7PNNmPZsmW0trZ2rlu1ahWbbLIJDQ0N3HvvvVxxxRUeE9bMrEgqPrGz4aWm\nRnz18IN46rzLuPUT9/DcqifZ5rwd+cAPzuXVFUmvN6de81P2avg04GRgQ3bZZRdOPvlk9ttvPyZP\nnsyCBQs44IDuXUDOnDmTVatWcdBBB+VcBjj99NPZeuut2XbbbZk1axbHHntsZyLWVxmHHnoou+66\nK5MnT2bTTTcF4Oc//znf+973GDduHN///vf5+Mc/PthvhZnZsKGh0KpQUgyF12G5/eWexRz/h+/x\nQt0/mdQ2g+U1C5j/tQfY5eJtee6/nmfLt40reUyS3CK3BHp7n9P1zuzNzHqohmfsbJg7fN9pHL7v\nH/nzXYtoXriIL76nkWlbTwJ/r5uZmXXjxM6qxpH778KR++/SbZ2fsTMzM+viZ+ysirnGzszMLJsT\nO6tqfs7NzMysixM7q14hMhkndmZmZh0qPrGTNFXSPyQtlLRA0gnljskqg3wr1szMrJtqaDzRCnw9\nIh6SNBZ4QNLsiFhc7sCs/Nx4wszMrEvF19hFxIsR8VA6vwpYDGxe3qisMrjGzszMLFvFJ3bZJG0D\nzADmljcSqxR+xm59jz76KNOnT2fcuHHU1tZy1llnlTskMzMrkapJ7NLbsFcDJ6Y1dzbcuYPinM49\n91wOPfRQVq5cSXt7O9/5zncAaG5uZurUqWWOzszMBlM1PGOHpHrgT8BlEXFdrn2ampo65xsbG2ls\nbCxJbFZefsZufc888wz7779/ucMoqubmZpqbm8sdhplZxav4sWKVjDb+W2B5RHy9l308VuwwVPOt\nSSz+zyXsNHVSycuu1LFiDznkEG6//Xbq6+upq6vjiCOOYLvttuO0005j4sSJtLS0MHr0aCSxdOlS\nJk+eXO6QN8hjxZqZ9U813Ip9F/Bp4GBJ89JpVrmDssrgGrvubrvtNg488EB+9rOf8eabb9LQ0IAk\nRo8ezc0338zmm2/Om2++ycqVKys+qTMzs/6r+FuxEXEn1ZGAWsm5wiYfHTVelVjDaGZmxVXxiZ3Z\nhlRqq1idUZykM06vzNdnZmaVyYmdVa+ozOfcoLISsuQx1a6fZmY2dPkWp1UxJyp9iYjO5HezzTZj\n+fLlrFy5ssxRmZnZYHFiZ1XNjSc2TFJnTd3OO+/M0UcfzXbbbceECRN48cUXyxydmZkVW9G6O5E0\nBpgKBLAsIlYX5cT5le3uToah2lMnM+9LD7HbdqVv3Vmp3Z0MNe7uxMysfwp6xk7SRsAXgE8Ak4CX\nSO6PbSZpOXA58EuPFGGDxTV2ZmZmXQptPHEdcBVweES8lL1B0mTgCODPwKEFlmO2PlfYmJmZdVNQ\nYhcRvSZsEfEicHE6FUTSJcAHgJcj4p2Fns+Gjkrt7sTMzKwcqqXxxKWAR5uwHlxjZ2Zmlq3QZ+ye\nJmks0ZeIiO0GWk5E3CFpm4Eeb0OXn7EzMzPrUuit2G2KFIfZALhlqpmZWbZquRVrtj43njAzM+tm\n0IYUk3RTRLxvsM7fU1NTU+d8Y2MjjY2NpSrayqicjSc8RFfpNDc309zcXO4wzMwqXkEdFEvao7dN\nwA0RUbSeY9Nn7P6Sq1WsOygenupOmco/P3cX+0ybWu5QrMTcQbGZWW6F1tjdB9zey7aNCzx3J0lX\nAjOBiZKeA74XEZcW6/xWvdx4wszMrEuhid0S4EsRsbTnhjQBK4qIOLpY57KhxBU2ZmZm2QptPNG0\ngXOcUOC5zfrkGjszM7MuhXZ38scNbLu2kHOb9c01dmZmZtkK7u5E0jRJh0oa22O9R4qwQedGM2Zm\nZl0KSuwknQBcB3wNWCjpqKzNZxdybrM+uVGkmZlZN4U2nvgisGdErEq7I7la0jYR8ZOCIzPLQzn7\nsTMzM6s0hSZ2iohVABHxtKRG4E+StsYPQNkgE3LjCTMzsyyFPmP3sqTpHQtpkvdBYCKwW4HnNuuD\n/3cwMzPLVmhidyzwYvaKiGiNiGOBgwo8dydJsyQtkfSYpFOLdV6rfq6xMzMz61LordjXgNaOBUk7\nA+8Hno6Iawo8d8c5a4ELgXcDzwP3Sbo+IhYX4/xWzVxjZ2Zmlq3QGrubga0BJO0A3A1sC/ynpHMK\nPHeHvYHHI+LpiGgFrgKOLNK5rcq5uxMzM7MuhSZ24yPisXT+M8AVEfE14H0kz9oVwxZA9vBky9J1\nNty5uxMzM7NuCr0Vm11dcijwI4CIaJGUKfDcucroVVNTU+d8Y2MjjY2NRSreKpm7OxkempubaW5u\nLncYZmYVT4XcypJ0OfAC8C/gVGC7iFgtaROgOSJ2LzhAaV+gKSJmpcunAZmI+GHWPuFbcsNPw8k7\ncsMnb+SwPXcsdyhWYpKIcJWtmVlPhd6K/QKwnOQ5u/dExOp0/TTgxwWeu8P9wI6StpHUAHwcuL5I\n57Yq51axZmZmXQq6FRsRb5Fj6LCIuAu4q5BzZ52rTdJXgVuAWuDXbhFrCVfYmJmZZSsosZN0ep67\nRkScOdByIuIm4KaBHm9Dl2vszMzMuhTaeOIZ+m7coDz2MRsAubsTMzOzLIXeiv1NkeIw6zf5VqyZ\nmVk3BTWekHScpF6TQ0kNkj5bSBlmG+JbsWZmZl0KvRU7lmSIryXAfSTjxgqYDOwF7Az8ssAyzHJz\nbxdmZmbdFHor9kJJPwPeBRyQTpA8e3chcJc7mLPB5Bo7MzOzLoXW2JEmbnemk1kJucbOzMwsW8GJ\nHYCkC0havnZ80wawArg/Iv5cjDLMcgkPKWZmZtap0JEnOowEpgNLgceA3YGpwOcl/WSgJ5X0UUkL\nJbVL2qM4odpQ4VaxZmZm3RWlxg7YDXhXRLQBSPo5ya3ZA4D5BZx3PvAh4H8KjtCGJD9jZ2Zm1qVY\nid14khayb6TLY4EJ6XBgawd60ohYAsmA32brkxM7MzOzLMVK7M4F5klqJnnObibwA0ljgFuLVIZZ\nD074zczMshWc2EmqAZaQdHmyN0nDie9ExPPpLqf0cfxskn7vevp2RPwl3ziampo65xsbG2lsjGMA\nVQAAD21JREFUbMz3UKti7k1neGhubqa5ubncYZiZVTwV44tR0kMRMb0I8fR2/n8AJ0fEg71sd3d5\nw9Cok3bj9x+6jI8cuFu5Q7ESk0SEe6g2M+upWK1ib5X0EQ3uw3D+ELf1+Bk7MzOzLsVK7L4M/AFo\nkfRmOq0s9KSSPiTpOWBf4AZJNxV6ThtCXGFjZmbWTVEaT0TEWEkTgB1J+rQrioi4Fri2WOezoce3\n4M3MzLoUa+SJLwAnAFsCD5HUsN0NHFKM85vl5ho7MzOzbMW6FXsiSYvYZyLiYGAPkiHFzAaVn7Ez\nMzPrUqzEbm1ErAGQNDIiFgM7FencZjl5SDEzM7PuitVB8XOSNgGuA2ZLeh14ukjnNutVJuMaOzMz\nsw7FajzxoXS2KR19YhxwczHObdY7ufGEmZlZlmLV2HWKiOZin9MsN9+KNTMzy1asZ+wGhaQfSVos\n6WFJ10jauNwxWWVx4wkzM7MuFZ3YAX8Ddo2I3YGlwGlljscqiBtPmJmZdVfRiV1EzI6ITLo4l6Sf\nPLNOfsbOzMysS0Undj18Drix3EFYJXGNnZmZWbaiN57oL0mzgck5Nn07Iv6S7vMdoCUirihpcFbx\n/IydmZlZl7IndhFx2Ia2SzoOeD9w6Ib2a2pq6pxvbGyksbGx8OCsovkZu+GjubmZ5ubmcodhZlbx\nVMnPKEmaBZwHzIyIVzewX1Ty67DBMfbre/P/Zl3A59+7T7lDsRKTREQ4szcz66HSn7G7ABhLMprF\nPEk/L3dAVkkEOKE3MzPrUPZbsRsSETuWOwarYCFcUWtmZtal0mvszHonN54wMzPL5sTOqpYbT5iZ\nmXXnxM6qmhvNmJmZdXFiZ9XLjSLNzMy6cWJnVc3P2JmZmXVxYmdVq+MZuwcfe4H9v/tdDjvzbO5Z\n9FyZozIzMysfJ3ZW1da2tLL/z9/LyrZXeemtZez/u+ns9e1v8Niy5eUOzczMrOQqOrGT9H1JD0t6\nSNLfJU0td0xWScRv517HSMYz/+xf8Mg5P+PBLyxgTftqdrpwJw4580z+tfzNcgdpZmZWMhWd2AHn\nRsTuETEduA44vdwBWWWZ3341R2xzDFJyW3b69lNY+MNfMPvjc3lqxVK2/NE2TD/tBK69a75b0JqZ\n2ZBX0YldRGRXt4wFeh0v1oanzNjnOeWIw9dbf+iM7XnqvMu485h5jK3fmI9e+35GnPJ2/u073+D/\nXHUTT7/4ehmiNTMzG1yq9FoMSWcBxwBvAftGxBs59olKfx1WfLWnTiYz+iXi9L5/95lMcGXzPC6e\ncz0Pr5jDijH3M2LtVCZrOtuP25npW07jXTvtzD47bc0Wk8aVIHorhCQi3N+NmVlPZU/sJM0GJufY\n9O2I+EvWft8CdoqIz+Y4hxO7YUhnCK2ZROacV/p97Jp1bVzzz/k0L5rPgheX8MzqJSzXElpGPQtR\nQ8PaLRkbW7BJ3RZs0jCJCaMmMGnMBDbdaAJTNpnAVhMnMmXCxkwcN4ZNx49h4rjR1NZUdAX4kOLE\nzswst7pyBxARh+W56xXAjb1tbGpq6pxvbGyksbGxoLisOkxYu+eAjhs1oo5PHTKDTx0yo9v6TCZ4\n7uWVPPjEMhY9t4zHX36eV1a9xvK3lvPsymd487nXWJ15jbV6jdbaN8jUribqVkPdWmgbSU3bWGra\nx1CbGUN9jKWOUdQxgjqNoF4jqFMD9TUjaOiYahtoqB3ByLoRjKgbwYjaBkbWj6C+to762jrqamqp\nr0vmG2rrqKutpaGuLllXk8w31Ncl62prGdExX5fMj6hP5htqa6mtraGutoa6muRn9nJtui5ZL+pq\na6iROp9dLLfm5maam5vLHYaZWcUre43dhkjaMSIeS+e/BuwdEcfk2M81dsOQzhDHbXIJl56wXiVu\nybW2ZXh1xVu8umI1L69YxWtvrub1Vat5ffVq1rS0sKZlHW+1rGNdWwtrWtextnUda9vW0dLWwtr2\ndbS0rWNd+zpaMy20ZNaRiXbao432aCNDW7JMG5loI0N7so42omNeXcuhtnTqmkftBAHKABlCmWQ+\nXUY9p0imEERNr5OoSUcAqUEd6zvm05/j23fmlfNvKur77Ro7M7PcKj2xuxrYCWgHngCOj4iXc+zn\nxG4YamnN0FDv25+DJZMJ2jNBW3umc2rP5J5va8+QyQRtmWR9e3smmW/PMKK+jn2mFbenIid2Zma5\nVXRily8ndmbDixM7M7PcXN1hZmZmNkQ4sTMzMzMbIpzYmZmZmQ0RTuzMzMzMhggndmZmZmZDhBM7\nMzMzsyHCiZ2ZmZnZEFEViZ2kkyVlJE0odyxmZmZmlariEztJU4HDgGfKHUuhqmWsy2qJE6onVsdp\nZmalUPGJHfB/gW+WO4hiqJYvzWqJE6onVsdpZmalUNGJnaQjgWUR8Ui5YzEzMzOrdHXlDkDSbGBy\njk3fAU4D3pO9e0mCMjMzM6tCiohyx5CTpHcAfwfeSldtCTwP7B0RL/fYtzJfhJkNmojwP3pmZj1U\nbGLXk6SngD0j4rVyx2JmZmZWiSr6GbseqiMDNTMzMyuTqqmxMzMzM7MNq4gaO0mzJC2R9JikU3vZ\n56fp9oclzejrWEkTJM2WtFTS3ySN73G+rSStknRypcYpaTdJd0taIOkRSSMqLU5JIyVdmca3SNK3\n8olxkGP9qKSFktol7dHjXKel+y+RlN0wp9xx7pm1/jBJ96fv6f2SDq6gOPfIcb5+X0vliHWg15OZ\nWVWJiLJOQC3wOLANUA88BEzrsc/7gRvT+X2Ae/o6FjgX+GY6fypwTo9zXg38L3ByJcZJ0mL5YeCd\n6fImQE0FxnkccGU6Pwp4CtiqzO/pzsDbgX8Ae2Sda5d0v/r0uMfL/J72Fud0YHI6vytJlz8V934O\n9Foq03s6oOvJkydPnqptqoQau72BxyPi6YhoBa4CjuyxzxHAbwEiYi4wXtLkPo7tPCb9eVTHySQd\nBTwJLKrgON8DPBIR89PzvR4RmQqM8wVgjKRaYAzQAqzMI85BizUilkTE0hzlHUmShLZGxNMkycHe\nlRZnRDwUES+mi4uAUZLqKy1OGPC1VI5YB3o9mZlVlUpI7LYAnstaXpauy2efzTdw7GYR8VI6/xKw\nGYCksSQjWTRVcpwktQ4h6WZJD0g6pRLjjIhbSBK5F4CngR9FxBtljrU3m6f79eeYcsSZ7cPAA2kC\nU1FxFnAtlTxWYEcGdj2ZmVWVsndQTP6tXfPps0q5zhcRoa6+7pqA8yPiLUn96Qer1HHWAQcAewFr\ngL9LeiAibqukOCV9muQW7BRgAnCHpL9HxFN5nL+YsQ5UPjGUJU5JuwLnkIyVnI9Sx9nEwK4lKH2s\n9QzsejIzqyqVkNg9D0zNWp5K91qVXPtsme5Tn2P98+n8S5ImR8SLkqYAHZ0a7w18WNK5wHggI2lN\nRPy8wuJ8Drg90n77JN0I7AH09UVU6jj3B66NiHbgFUn/JPnyzCexK2asuY7tq7zs11dJcSJpS+Aa\n4Jg8k+RyxDnQa6kcsQ70ejIzqy7lfsiPJLl8guRB6Ab6foh6X7oeou71WJKH/U9N579Fj8YT6frT\ngZMqMU6Sh7sfIKkNqwNmA++rwDhPAC5J58cAC4F3lPM9zTr2HySdWncsdzSeaAC2TY9XBcY5nuRB\n/6Mq4VrqLc6BXktlfE/7fT158uTJU7VNZQ8gIgDeBzxK8jD7aem6LwFfytrnwnT7w3Rv7bbesen6\nCcCtwFLgb8D4HOX298uopHECnwIWAPPJkZhWQpzACOCyNMaF9KNl5CDG+iGSGpo1wIvATVnbvp3u\nvwR4byXGCXwXWAXMy5omVVqchVxLZfrdD+h68uTJk6dqmtxBsZmZmdkQUQmtYs3MzMysCJzYmZmZ\nmQ0RTuzMzMzMhggndmZmZmZDhBM7MysKSV+TtFjSAkk/7GWfEyXNT/c5MWv97pLulvSIpOslbZSu\nb5B0abr+IUkzS/V6zMyqkRM7M+sXSY2SLu2x7mCSsV13i4h3AD/Ocdw7gP8A/g3YHfigpO3Tzb8C\nvhkRuwHXAh1Dfn0ByKTrDwPOG8AoF2Zmw4YTOysrSSdIWiTp9zm2vVPSJVnLsyTNTWuF5km6StLU\ndNtvJH24x/GrNlDuCEm3S/I10H+5+kg6Hjg70jFtI+KVHPvsDMyNiLWRjFQyB/j3dNuOEXFHOn8r\nyRi5ANNIOhvuOOcbJCObmJlZDv5Ss3I7Hnh3RByTY9spwC+gs7bnp8CxETEtImYAl5OMPgBJstEz\n4ei1k8aIWAfcARxVUPTDU64asx2BgyTdI6lZUq7kawFwoKQJkkYDHyAZJgxgoaQj0/mP0jVk2MPA\nEZJqJW0L7Jl1jJmZ9eDEzspG0kXAdsDNkv6rx7YRwL4RcV+66lTgrIh4tGOfiPhLVi0P9DJgvKQz\n0xq+eZKez6oFvB44ulivZ6hLk7Z5wC9Jkq2O9/Q9JMN0bRIR+5Ik5H/oeXxELAF+SDJyyU0kI2pk\n0s2fA74i6X5gLNCSrr+EZBzY+4HzgbuA9kF6iWZmVc8jT1hZSXqKZEzP13qs3xf4TkQcni4/ABwX\nEfN7Oc9vgIOAFVmrt4+IcVn7bExSS/eZiJiXJo9PRsQWxXxNQ13agOG4iPhs1rqbSIbpmpMuPw7s\nExHLN3CeHwDPRsRFPda/Hfh9ROyT45h/Ap9Pk0QzM+vBNXZWqbYGXsi1QdLEtIXko5JOTlcH8I2I\nmNExkVWDlz5wfzlwXkTMg87bsTWSRg7qKxl6ctWMXgccAp2JWUOupE7SpunPrUjGdb0iXX5b+rOG\nZKzcjlvwoySNSecPA1qd1JmZ9c6JnVWqoHsCsZDk+SoiYnlETAcuJrlt12FDrSWbSGqHfttjvdjA\ns3iWU67nGS8BtpM0H7gSOBZA0uaSbsja72pJC0lug38lIlam64+W9CiwGFgWEb9J128GPCBpEckt\n3lzPYpqZWaqu3AGY9eIZYHLW8rnAtZLuyaqxGUMeSZmkw4FDgYN7rB8BtKc1d5an9HbrnB7rWsmR\ndEXEv0gaSXQsH9TLOX9K0jim5/qnSVrTmplZHpzYWbn1lpg9DOzUuVNER4e2v5M0DniVJPk7fQPn\n6lj+OrA5cG/aBdqfI6IJmAHcXegLMDMzqxRuPGEVK20Q8YuImDtI5/8BcF9EXDsY5zczMys1P2Nn\nlezHwJcH48TpbdgDSB76NzMzGxJcY2dmZmY2RLjGzszMzGyIcGJnZmZmNkQ4sTMzMzMbIpzYmZmZ\nmQ0RTuzMzMzMhggndmZmZmZDxP8HxFCieFr0ELcAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x13941b90>"
]
}
],
"prompt_number": 80
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, let us have a look at the fit results. Here, we convert the dictionary of results into a dataframe to display it in a nicer way."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"display(pd.DataFrame([port1.fitresults]).applymap(lambda x: \"{0:.2e}\".format(x)))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Qc</th>\n",
" <th>Qc_err</th>\n",
" <th>Qi</th>\n",
" <th>Qi_err</th>\n",
" <th>Ql</th>\n",
" <th>Ql_err</th>\n",
" <th>chi_square</th>\n",
" <th>fr</th>\n",
" <th>fr_err</th>\n",
" <th>theta0</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td> 3.99e+05</td>\n",
" <td> 1.24e+03</td>\n",
" <td> 1.99e+05</td>\n",
" <td> 1.11e+03</td>\n",
" <td> 1.33e+05</td>\n",
" <td> 5.89e+02</td>\n",
" <td> 9.29e-05</td>\n",
" <td> 7.00e+09</td>\n",
" <td> 9.64e+01</td>\n",
" <td> -4.21e-04</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "display_data",
"text": [
" Qc Qc_err Qi Qi_err Ql Ql_err chi_square \\\n",
"0 3.99e+05 1.24e+03 1.99e+05 1.11e+03 1.33e+05 5.89e+02 9.29e-05 \n",
"\n",
" fr fr_err theta0 \n",
"0 7.00e+09 9.64e+01 -4.21e-04 "
]
}
],
"prompt_number": 81
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, we can calculate the single photon limit, i.e., the input power necessary to maintain one photon on average in the resonator:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 'Single photon limit: %.2f dBm' % port1.get_single_photon_limit()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Single photon limit: -149.38 dBm\n"
]
}
],
"prompt_number": 82
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Or, we can compute the photons in the resonator for a given power:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 'At -100dBm, we have %.2e photons in the resonator' % port1.get_photons_in_resonator(-100)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"At -100dBm, we have 8.68e+04 photons in the resonator\n"
]
}
],
"prompt_number": 83
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Case2: Strongly over coupled resonator Qc<<Qi"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here, we study the case where internal losses become negigible, and the amplitude signal vanishes."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, we generate some fake data which we can fit later:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from resonator_tools import circuit\n",
"fr = 7e9 #resonance frequency in Hz\n",
"Qi = 10000e3\n",
"Qc = 100e3\n",
"freq = np.linspace(fr-0.5e6, fr+0.5e6, 1000)\n",
"port2 = circuit.reflection_port() #define a reflection port\n",
"noise = np.random.normal(loc=1.,scale=0.04,size=(len(freq),))\n",
"S11 = noise * port1._S11_directrefl(freq,fr=fr,Ql=Qi*Qc/(Qc+Qi),Qc=Qc,a=1.,alpha=0.,delay=.0)\n",
"port2.add_data(freq,S11)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 84
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's plot the data:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"port2.plotrawdata()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAFHCAYAAAAsmgFsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXfYFNXVwH8HEBUEEQFREVCxAKJiFLu8NsTeu1GjwZLP\nXhM0ggVbNLErKmKXJCrEhtgCwYaNqiASRSU2LIAoKvCe74+z484778zsbC/v/T3PPrs7c2fm7OzM\nvWfOPUVUFYfD4XA4HA5H9dOs3AI4HA6Hw+FwOAqDU+wcDofD4XA4agSn2DkcDofD4XDUCE6xczgc\nDofD4agRnGLncDgcDofDUSM4xc7hcDgcDoejRiirYici94jIlyIyPWJ9nYgsFJHJqdfFpZbR4XA0\nbRL0UxuLyGsi8pOInBtYN1dEpqX6rzdKI7HD4WjKtCjz8UcCNwP3x7SZoKr7lUgeh8PhCJKpn/oG\nOB04IGSdAnWq+m2RZHM4HI4GlNVip6oTge8yNJNSyOJwOBxhZOqnVHW+qr4FLI1o4vowh8NRMird\nx06B7URkqog8IyK9yi2Qw+FwZIECL4jIWyIyqNzCOByO2qfcU7GZeAdYR1V/FJE9gTHAhmWWyeFw\nOJKyvap+LiIdgedFZFbKAuhwOBxFoaIVO1X93vd5rIjcJiLtg/4qIuIK3jocTQxVrfgpTlX9PPU+\nX0RGA/2ABoqd678cjqZJsfqwip6KFZE1RERSn/sBEuWErKoV/xoyZEjZZaglOatJVidnYV8VSoNO\nWkRaiUib1OfWwAAgNLK23Oezlq6NapLVydk05VQtbh9WVoudiDwC9Ac6iMinwBBgBQBVHQ4cApwq\nIsuAH4EjyiWrw+FommTqp0SkM/Am0BaoF5EzgV5AJ+Dx1LNpC+AhVX2uDD/B4XA0Icqq2KnqkRnW\n3wrcWiJxHA6HoxEJ+qkvgHVCVi0GNi+KUA6HwxFBRU/F1hp1dXXlFiER1SInVI+sTk5HtVNN10a1\nyOrkLCzVImexkWLP9ZYCEdFa+B0OhyMZIoJWQfBEElz/5XA0PYrZh1V0VKzDUamk/KYcJcApPQ5H\nYXH9V2kpdR/mFDuHI0ecwlF83ADkcBQH13+VhnL0Yc7HzuFwOByOKmbkSPjll3JL4agUnI+dw5ED\nKf+IcotR80SdZ+dj53CkEYEJE2CnnZK2d/1XqShHH+Ysdg6Hw+FwFJh334U77ii3FI6miFPsHA5H\nVowfP5511glL2+ZwODyuuAJOPbXcUjiCNIX+yyl2DoejaNx7773suOOO5RbD4XA4sqZa+y+n2Dkc\nNcqyZcvKLYLD0WRxLmz54fqv3HGKncNRQ3Tv3p1rr72WTTfdlFVWWYVhw4bRo0cP2rZtS+/evRkz\nZsyvbbt168Y777wDwEMPPUSzZs2YOXMmACNGjODAAw8EYMmSJRx//PG0b9+e3r178+abbzY45tVX\nXx16jJkzZ3Lqqafy2muv0aZNG9q3bw/A008/Td++fVl11VXp2rUrl156adHPS1Pkiy+ccuGoLlz/\nVRicYueoCpYsgbPOgvr6cktS+YwaNYqxY8eyYMECNtpoI15++WUWLVrEkCFDOOaYY/jyyy8BK78z\nfvx4ACZMmMD666/PhAkTfv3ulee59NJL+eijj/jwww8ZN24c9913X4PcTD169Ag9Rs+ePbnjjjvY\ndttt+f777/n2228BWGWVVXjwwQdZuHAhTz/9NLfffjv/+te/SneCmghrrgm+cbBiEIGFC8sthaNS\ncf1XAVDVsr2Ae4AvgekxbW4CPgCmAn0j2qijtnn+eVVQnTix3JIYma45s5Xk/8qW7t2768iRIyPX\nb7755vqvf/1LVVVHjBih++23n6qq9uzZU0eMGKFHHHGEqqp269ZNJ0+erKqq6623no4bN+7Xfdx5\n553apUuXRMcYOXKk7rDDDrEyn3nmmXr22WeHros6z6nlFdFPARsDrwE/AecG1g0EZqX6sAsjto89\nP7kCqnfdVZRd5wWozplTbimKz2GH5XYP5wKojh+fTXvXfyU5Rr79l2p5+rByW+xGYh1fKCKyF9BD\nVTcATgJuL5VgjsripZdg9dXh738vtyTJKFTXmAv+iK/777+fvn37stpqq7HaaqsxY8YMvvnmGwB2\n2mknJk6cyBdffMHy5cs59NBDeeWVV/j4449ZuHAhm2++OQCfffZZg3127dq1wfHijhHGpEmT2Hnn\nnenUqRPt2rVj+PDhse0rgNh+CvgGOB24zr9QRJoDt6S27QUcKSI9iyVkGLleQ8XGFRSpbFz/Vd39\nV1kVO1WdCHwX02Q/4L5U20lAOxFZoxSyOSqLF1+Eq6+Gf/4TnE9tPN40w8cff8xJJ53Erbfeyrff\nfst3333HJpts4lmJ6NGjB61ateLmm2+mf//+tGnThs6dO3PnnXc2iARbc801+eSTT3797v+c6Rhh\n5XSOOuooDjjgAObNm8eCBQs45ZRTqK/gOfZM/ZSqzlfVt4ClgVX9gDmqOldVlwKjgP2LJ2mYbKU8\nWnKcYueIwvVf+VNui10m1gY+9X2fB3QpkyyOMrFwoSX7POYY6NLFMqzHtf3tb2HbbeHoo2HYMPj5\n54ZtHnwQ2rSxwUXEPr/ySnF/Qzn44YcfEBE6dOhAfX09I0eOZMaMGQ3a9O/fn1tuuYX+/fsD5rfi\n/w5w2GGHcdVVV7FgwQLmzZvHzTffnPgYa6yxBvPmzWPp0rTOs3jxYlZbbTVatmzJG2+8wcMPP1yr\nNWHD+q+1SymAU+wc1Yrrv3Kn0hU7gOAZq9CuyhHH7NkwfXpu206YANtsAyutBIcfHj0dO3UqbLkl\ntG0L110HAwfC+PFwxhm2fvlyuOACGDIEXn3VvtfXw6OPwsEHw/vv5yZfpdKrVy/OPfdctt12Wzp3\n7syMGTPYYYcdGrTp378/ixcvZqdULaLgd4AhQ4bQrVs31l13XQYOHMixxx77a0eW6Ri77rorvXv3\npnPnznTq1AmA2267jUsuuYS2bdty+eWXc/jhhxf7VJSLsvdVTrFzVCuu/8qdsteKFZHuwJOq2idk\n3R3AeFUdlfo+C+ivql8G2umQIUN+/V5XV/drRIwjNxYtgtatoXnz8PVLlsDkyWYh23lnU7ri9tW3\nLyxYAHfeaUpUEFWYMQM22ghatrTvb78N8+fDPffAFlvAn/4EH38Mv/kNfPaZtQP44Qe49Vb4y1/g\nxhvhqKPS+/3+e9h6azjxRJvO/eknm85dffWGx7/nHhg6FAYMgHbtoH172GwzUyiDbcHVWiwV3nke\nP378rxFwYJFuWsJasXH9lK/NEGCxql6f+r4NMFRVB6a+/wmoV9VrAtsVpf8Sgdtuq7zqByLwySdQ\n48n/Ofxw+Mc/SqNci9hDrM9QlaG9679KRVn6sGJFZSR9Ad2JjjbbC3gm9Xkb4PWIdqFRJ47c+PJL\n1S5dVDfZRPWpp1R/+UX16KNVjz9e9ZprVL/9VvWGG1TXXlt1662t3ZQp4fuqr1c98kjVk09Wfftt\n2++VV9pyP3feqdq2rWqHDqrHHae60UaqG26ousceqgccoDp7drrtttuqPv206g8/qF5/veoaa6ge\neqjqrFnhMrz/vuqqq6qedpr9lihefFF1+HDVa69VPf981V13VW3TRnXTTVU//rhhW3fNlYao80wJ\no2I1Qz/lazMUX1Qs0AL4b2rblsAUoGfIdoU5WY3OkeqttxZl16Hst5/qo49mbgeqn35afHnKzaGH\natVGxToKRzn6sBZF0RYTIiKPAP2BDiLyKTAEWAH7xcNV9RkR2UtE5gA/AL8rn7RNg/p6s5wtXWrT\nluedByuuaJa5P/8Z/vMf6NED1l4bTjgBLr0UHngAdtvN2rdrZ7mzfv972HtvuPlmmDYN3ngDWrWC\n11+HffeFZ581P7hu3cwHbtgwmDTJLH9PPAGDBsF224VP2RxxBFx0EXz5pe3juedg002jf9OGG5qF\nr1Wr+N++yy728rN8OVxzDRx6qP32FVfM/pw6qptM/ZSIdAbeBNoC9SJyJtBLVReLyGnAOKA5MEJV\nZ5ZS9lIaZZ54wiz8YRb5IG4qtvA4A5zDo+xTsYVARLQWfke5WbAA1l/fok/fesuUuQcfhJEjrdM4\n6SRr98kn8Le/wZ572tQlwNy5FrQwb55NmY4caT5vffvaNOdGG6WP8+OPpoxNn27tmzWD/faz/SVh\n/nwYPBj+8Afbf7FRtcFqrbXglltsmZvKKA1R5zm1vCbUg2L1XyL2YHXaaQXfdeTx9tsP4nK1qtr9\n/r//2f3kZ/586NChdpS+ww4zt49STcX++9+QdAbf9V+loxx9WFktdo7Kol07U85OOgm2394sdyNH\nmvXMT9euptj56d7dghx++cWsbiedZErb2ms37qhbtYIDDrBXLnTsCHfdldu2uSBi56FXLzjySDs3\nDkc1UOqxe/nyxsuWLLE+QSRdOSZMrk6d0oFMDocjd6ohKtZRBMaMMWtcsCMeNgzWW8864Z9+sojS\nQIR5JM2aNQyi6NKldp6+V10Vrr/erISDB5dbGocjGbNnw333JW//4IMwfHjuxwtT7Fq1Mqs9xCt2\nYPVtd90VHn88dxlqnXnzsu9XR42ybACOpoFT7JoACxean9nJJ6dTeqy+OpxyCvTpY0/Jb78NN91k\nVrfddrOUIZMnw+abN4wybcocfridr0WLyi2Jw5GMW26B449P3v7UU61fyJUwxQ7gv/+190yK3bJl\nVmWmFIpdfT0cd1zx9l8sa6kvv25iLr8cLrus8LI4KhM3FVtjfPMN7LOP+cnttJNNg/zwg/m0TJsG\nO+5oKTyOOALOOst8cA491FKH9OljCl+bNrZ9z57w8svw2mvl/lWVgYhZNMDSq1RaUkqHo9xEKXYe\nmRQ7b/tSTCEvWQL335+dRTOOn3+2WYsVVijM/qIo1Llx/Vft4ix2NUabNhZ5WldnnUzr1mk/t6lT\nzSS/997w2GOW92jxYttu991t3bhxZsHrk8rW1bw5BHJCOsguTdC4ccpDDynTpik//xzdbswYZYst\nlPr68qYgqrSXo/LxdISgYvfjj/bu/Y1JLHb+9XPmwO0hFcIvvhg6d85d3mKwwQYWMFFscrklgtv4\n76/u3RVQjjnG3vO5V3/5xfbxzTf++1fZeGPr37zvweM88EDjZfvtl1meIUPylxmUoUNrqw9zil2N\n0bKldZ633WbfO3SwznXcODjnHIs8O/lkU+xeftmS9u60Ezz9tPNrKRYDBth0dp8+6aTKYey7r/k1\nHnCApYs580zz57vqKvvfHI5S0apVWgnLhqBi9+ST9p6rYuf5tQZ5+WVLdxRFs2bwzDPxsnqyFKrM\n56efNvRHLvV4Hne8XNdlS9T/O2sWjB0bvV2Y8bBZAu2kUEbHWjNeOsWuBli2rGHnJGKVGgC+/to6\n6d694YorzE/MT12dWe5eeMHaOspHs2bw1FP2H229Nay7Lnz+ufnGeJZVh6MULFmS24AfVOyCilq2\nU7G5DriaqlwTh3esTNPH2ZBNnsujjoKJE7M/RtS5y1dBC57ruXMty0E2BP9nP8OHm0tQGGFKXJL/\nPthG1dyRsqXWJgacYlfFTJhgqUdWWMGmTE85xfLPLV9uHfM++6Tbfvhh9H5ELBLt2muLL7MjnnXX\ntQ5/0CCzVEyfDn/9qy13OIpBfb0l+g6iaiX5whgypHHKI0grch5BRS1bi12U1SbJQJypTTEUO79F\nPpNi8sgj9sqWTL9r/vzM1sokrLuu+VpnQ6b/N8pfu1AWuwcesFmqOF58MfN+qx2n2FUxq6xi5n+P\n4cMtz9oKK5hi0MIXGuNZ8BzVw5//bElc84lSdDgysWyZ+eUGUbXo+GnTGq+77DKrOhMkymLn4Q38\nzz9vPr1R2+drsUuCJ4tf5vffN6t5XPs4/IpdIZTPXLa54grzo066Tdy6775Lf772Wnj3Xft83nkW\naRsk0/R2lLIW/J9FzEiRLZ99Fr9e1bI+/PRTw+WXXmpZIGoFp9hVAQcdlM7q7p8u3XJLWG01+3zy\nyeZLN3u2daYffACjR1ukVljH7KhsXnrJInBHjKg9/w9HZRIcjL0BPzhYev6eYYN30qnYU06xh9Co\n7eMUO1X49tvGy7MlzGL3hz+Yr2uQ0aNtViQTxS45+MYbVu4xjmL1FxdeaCmxwHwfw2Z4vP8tSlmM\nki1seZK0Ltn+1uD16KGarioENgV9wgnZ7buScIpdBTNvHpx4IvzxjxZt9eSTVnVBJB2iv9lm5mR/\n2WWw8sq2zv9U5KUxcVQXZ59t02BbbQXrrGOWuzXWsKn3o4+Ge++168PhyJcwyxWkB78lSxou79TJ\n3hcvbjxVGxwwg/vMZPVKMhX79783Tpq+bFn0tHEUYYpdlKIwe3bjZcceawqOH3+qk3wtdk8/3Vie\nrbeGhx8Ob//FF2mLWhTDhqVzmQZlyNanLey/zMZit9NOJk/UscPOzQknpCOt/dtdfnmyxM2ez2CY\nfP5tZ860akPVilPsKhgRy9i+9dbwj3+Y5c7DSzo6fjzccEO6s3XUBs8/D++8Y/UfX3kF3nzT0tW8\n9JIFvDzzjCn1u+5auKg+R9PEG0CTKnb+9b17h2/jEeVjF4U3uMYpG1980XjZuefatHE2JFXsZs1q\nrAyB+XPdeWfDZdlakOIUuzfftPcbb4RXX00v//nn8PZHHw2bbBJ/vIsvzr6yyLRplkYLGsq7dClc\nckl6+TPPZPaxmzgxfY4mTkzXFfYUvjh/x622MmXrgw/Sy7x9XXJJ+NR+EE+xe+45Cxj04//vvACM\nQvpflpKyKnYiMlBEZonIByJyYcj6OhFZKCKTU6+LyyFnuVh7bRvMW7e2748/Hl5H0SsA7agdOnWC\nHj3MgblrV7sWOne2ZYMGmaL/1VdmNXnssXJLW9uIyD0i8qWITI9pc1OqH5sqIn19y+eKyLRU//VG\naSTODr9i5x/cMil20NDH17+NR5SPXRRJFLswPIua34qdyWIWZqkMsxD26hVtvQkeI9uHrCRWvbPO\nyr8+tf842cr4zjvpqPw770xXEVm6NO1n99575tfnBexF/a6ghRMsQMNTVuOmmcN87vzXR5JgC0+x\nO+ggy90atS9P/myjgiuFsil2ItIcuAUYCPQCjhSRniFNJ6hq39TripIKWQFstplVjvB4/XWLcK2v\nt5vh3ntt+S672IXpfXfUPs2bw9ChNg1fa+H6FcZIrJ8KRUT2Anqo6gbASYA/pa4Cdan+q19xxcwN\nv4Ljv46SKHb+dsHPEO1j5+cPf0gfI7h90jQY3n79fWUmwix2YcfLJvAg2/uwGMETmZThbKxQIpmV\ndUiff8+yGKc8+uUTgT/9Ke0H/te/wscfZyefR7Nmmc9NnKIWNs0cZR2tdMppsesHzFHVuaq6FBgF\n7B/SruZdx6dOhT33NNP7kCF2gV1xBSxYAGPGpNu1amV5gNZbz26Ali2t1qGqOTTvumvDKCZH7TNw\noHU+uUSQOZKhqhOBuDtrP+C+VNtJQDsRWcO3vuR9WFwibLDpxeC0WdRUbCZnff8gnouP3e23p61A\nwf2EKSlxil02ilI2PnZRRAWc+DnmGPMLDCPfxMF33mmuGdmQr1Uxqe/gzz9nVrS98+21u+giuOOO\n7OTzSGKx8ytqYZG4Ht5v/OKL6nxoLqditzbgN+TPSy3zo8B2qemNZ0SkV8mkKyHffw/PPgv9+qUL\nNf/5zxbxesAB6Xae02iHDuZ356dDB/MZOPvs0sjsqAxELLrwhhvS1tzFi6uzM6pi4voyBV4QkbdE\nZFCpBMqkjPXsmfZvyqTYLV9u6SGiUkkksc5k8rELSzQbtjxqWZwM33/fMMJy5kzbRyEUu+B9tmBB\n4zYPPRTt/5WPf+z111s2hAkTstsuShmN+u1JFLuwKemDD4Zu3Rq3DVrsoGFARFLefLPhdv6o5XHj\nzDe5X7+G7gKZLHZetLV3jnr2tHrC1UY5FbskQ887wDqquhlwMzAmQ/uqZIcdkg3Er75qT2ebbebq\ntzrSDBpkT7xnnGFW206dzC+ze3d7ABgyJFnqAEdeRKkEO6hqX2BP4P9EZMcSyhSLZyXJFBW7bBns\nuKP5eYYRZ7FLqth51pag5S2JFSZsO//nQYMaKhhz5zbcJh/F7qOPLIDEm56cMqXx8QFWXTV8+7jI\ny0xjwogR8et79bKMCcF9FcJiF6WI+79Pnpy5CkTS6f4w+vWDu+5Kf/fLNHAg7L+/KX/+HI2ZfOZW\nX93Oj//3BP1Iq4EWmZsUjf8B6/i+r4M96f6Kqn7v+zxWRG4Tkfaq2iiL0dChQ3/9XFdXR1229ukS\n0qOHTT0MHmzh2yuvHJ7s0c+QIbDNNi5IwtGYLl0aTtmDDdpffWWd0j/+AX37Wkd4yinW4VUb48eP\nZ/z48eUWI4pgX9YltQxV/Sz1Pl9ERmMuKI0KSZWz/8oUPLF8efxU/xlnNN4myA03WHqLZ58NX+8p\ncJ5zfSGnYoM574IWynwUO7DAgaipVo8oxS4XMlnYvOUzZ4bn3ovysUtqsauvt//Lv58wxS7KP81/\nHE/RittXHB07pqOkgw8B3jXxzTd2nHnzkuV0DZboDPMpzIVS9mHlVOzeAjYQke7AZ8DhQIOUlSk/\nla9UVUWkHyBhSh007BgrnfPOg1NPhSuvtFcSLr00nel93DgrLO9wRNG6tUXUrruuDahXX20Z1wcN\nsncv0rpaCCo7l4aVPSgfTwCnAaNEZBtggap+KSKtgOaq+r2ItAYGAKGCl6L/mjfPkpy/807D5d4g\n9sknDXPBRU3RBvGn/Iiy2IE9fERNawUH5bjBPS7nWdh2QeUmTrFLaiEMksniFJfc+JtvzFKULUmU\n0LDzEmWZzbQP/3e/YqcarvxFWev8ilIuip1/vT8hdPAce9f1qadaepNJkxq6EwQtj/5I2LjzlSul\n7MPKNhWrqsuwznAc8B7wd1WdKSIni8jJqWaHANNFZApwA3BEeaQtLKecYlaWXMnVudTRNJk3z9IQ\ntG7dMH2OIxki8gjwKrCRiHwqIif4+ylVfQb4UETmAMOBP6Q27QxMTPVfk4CnVPW5MvwEwKwV/rJJ\nwUE/WC82qWIXtk22RFlbkkbFxh03asCPm4r1EufmQthUZ5x8J58cvS6ObBQ7P9m4ZYRFxXqKnf97\nrtHBni9oNtfYDz+ky775LclxDwdTp2a2vPmDhfz/YSZ/1Uoko8VORNoB2wLdMb+4ucBrqrow34Or\n6lhgbGDZcN/nW4Fb8z1OpfHzz+ab4c9Snql9ixa5P006mi5PPmlWujPOsJJAScoiORqiqiHFrxq1\nOS1k2YfA5kURKgei+puoQTgXxe6LL2zgbd3aBsfzz0+2XZiS8txzyadGPRnr680FAWza99FHLYuA\nn6BCF6bYXXyxRWiGMXy4VQTy4z+H48ZZloOo9UEee8xKRQaL12f6X5Kcm/fea6xovvSSKURbbpl5\n+zA5Hnqo4TRrlMUuCd5+4vw0g4wYEe6bGPVwAKbUeddFJoIWu0JNxZaSSFVBRHYUkSeA/2CWsq6Y\ncnck9hT6hIg4F/4E1NfDnDl2sUyZAiutlFypA5s6yyVqyNG0GTwYTj/dElsPHuyUuqZOi4jH+KhB\n+I1UOuVsBrZFi2CVVay2anC7bKZXVWGPPcKVyrhlI0ZY6T2wqbd3342eivVq3mbjY7dsmc24xFm9\n9tqr4XGCn8MI+shuvDGMHRveNpNi99prDb9/913j48eVX7v11nTAQZjFLhi0ka2F0k/YVGyQqPyK\nQYLnw0uqDMmsblEWu7CkypVOnMXuQOBcVf0gbKWIbAicArxcDMFqienTYfMsn9uHDbOb68knrfRK\nmzaWw26ttYojo6P2uPtu6+TXX7/ckjgqAe9h8vHHGy6PGii90lO5WCzefdciEzMRpVR6xwwO1i+9\n1DBYI9j+xhsbr4uaovOmQP2/P5Ni5znqB5XkbP3UMhFWwixIlKz+KFBobAmEcEXK299pp5kvJoRb\n44JGiWAUqbddEjyFK87C16KFJWLPtO+4BMVJKkj4feyqvUxjpMVOVc+JUupS62er6jnFEau26JVD\n9r2LLjKlzrP0LVnilDpHdrRtW53+IY7i4CkjXmRgphQkSRMUR5FkCjcqmjVqII5SFuNk9Fvs5s9P\nz378/vf27ikxzz5rLjJxRFmYMvnJFVrxA5tmzZVMU58dO6Y/B/MXhil2wWvI+7733vFyeOczyjrp\n4fcNjcKbmQgjSQUJ//VejSlO/OTktSUivyu0ILXI99/bU1CmLPBxeDmXVlqpICI5mhC77WZ57A48\n0PI9zZuXeRtH7eIF4SW1rvjz2GWLSLLt/JGVfryku8HlQQUuyXSxX7Hr1AlOOsk+t2pl757isuee\nmRUIT95MCiBkNxWbi2KXz0Nbfb35Qvp/h98C6AVYiTQOJMnGYpfJAhqmwIediySKXVwmkWwsdtOn\nV3+i/1zd8S8rqBQ1yoMP5q6Q/eUv8PnnlnDW4ciFO+6wfImHHGKd3uabW3LrO+6o3hqIjtzxcsgl\nVey8yhS5KBAXX9y4CkPYIB+l2CXFq8ATZx0MXuuexS6XY3rHybZfVjU/uu23D19/8snJ/ahzPVfB\nfZx1VsPAkqRJjJNY7DxlOVPAXxKFC5JF8sYpkdkodrVQljPSx05Epsds16kIstQM8+fbk2GunHgi\nnHtubskyHQ4/HTrA0Ufba/ly89e89lp7Cr/gApuOWnnlckvpKCWedeu44yxZeqbUS7lahoLF3MMU\nkkyK3bhxyY4Vp+yMHp15myhrz6RJDb8njRCeP79xjrQxY6x60Lhx4aXHfvghbUWMoxDjQn19WoEJ\nO3dx5zOo2Kk2Vuy8qOBMil0uvmxRsoWd02zwIm1r4aE37rR3Ao4F9g15ZSgU0jS59FK76fJR6hYv\nNqd3p9Q5Ck3z5laS7plnbLB74QXYcEP4INKT1lGL+AeuyZMzW4D8il021owklqVgTrkg3hTc8uWW\naDbTfrLBL9/OO4e32Wabht+TKnadOjWeivVkHDgQjihzRtZglRFo+N2TNSwiNOhaVF8ffV5ySdFV\nCItkGG3mZdW2AAAgAElEQVTaJGtXqITE5SQuKvZpYBVVbTS7LSJZlh1uGmy3Xf77mDPHpsscjmKy\n5ZY21XbXXZZW4tVXoXPncktVWERkSMKmqqpNxr3Er9i1a5edYte+ffLjJFG2wnLJhRGVqiWbY0Ud\nO5v1uQ76qpm3TarQFCJi0ysLFnXcbBI+L1sW/duKkWIpV8Uv6Xk766zc9l9JRN4uqnpCzLqMCTub\nIrvvbtFEXn6kbHnoIVhttcalThyOYjFokPlyHnIIvFx7iYs+xpKqO3z4B7hVVsk84OU6FZtkAL7u\nOntP6msVRS7KTqbgjjCZyqnYTZ+erF0S6uvTY4yXwiWsvFYYwbFp3XVLW+IyV8U2H0ucXxGuBspZ\nK7YmufZa+F2OMcNHH23v++4LTzxROJkcjji6dk3m21NtqOq95ZahUth00/Tn4MB4+OHx2+aaeT/J\nADxqlL3/9FNux/DIRdnJRbHz5E1C1FRsrnj/4WOP5bcfsHrBcYpO3PkMKjiLFzfOjehRjHxwue4z\nH1mWLcsvu0Wpias8samIvC4i80TkThFZzbfujdKIVx14aU1Eclfq/Lz9dv77cDiSoGp+NOedV25J\nSktTS9k03RcKFyy15K+3GUauFrskCqEnSz4O6yLFsdiF/W6/z5mX/y6KYK64TDIWy7csjGHDrNya\nH39FiThZp8eFVQbI5X/xV4wIo9hTsWFUWz7QOOPi7cBQoA8wG3hFRHqk1mVREKv2adPGwrGff96y\ntf/pT7DLLrnt64MPrMKEw1EK7rvPnkR3373ckpScJuNTF8RvqUmifOU6qCXZzmtTV5fbMTySDNr+\n6gWQm8XOTyYFwy/TRx9VlmKXiThZf/gh+X5y+U3Dh8evz/U85TMVW231YuOmYtuoairzEdeJyNvA\nsyJyTAnkqjrWWcdeSVm2zHL9fPKJFSf+738t4mzNNYsno8Ph5+OPrUj7iy/Wpk+nS9kUjr8YehLl\nK9dBLay8V5BCpZZI4qN3990Nv+disfOTjWL34ovJLHzXXw9bbRXfLh8/7qQUSskM1sAtBPn4OeZK\ntVns4hQ7FZFVVXUhgKr+W0QOAh4HVovZLjEiMhC4AWgO3K2q14S0uQnYE/gROD4sSrcaadHCfJu6\ndi23JI6myrnn2iDhTcX16pU5+rDK6AQMBMKSdLyadCcicg+wN/CVqvaJaBPaTyXp40rNU0+lPxfT\nYvfSS5nbfFOgxFlLlmRuE0x3kWmbTGWl/OcxjKgyW3Htzzsvs/WyFHVMC3GMzp3TgRlJaNkymYKe\nq2wiuSt32USDVwJxU7HXAg2qnKrqNGAXICLlY3JEpDlwC9bx9gKOFJGegTZ7AT1UdQPgJGx62OFw\nFIDLLrPySi+9ZA70q64K224Lp58O994LM2ZU3xREAC9l09zgC8gmZdNIrJ8KJaqfStLHlZtspkvz\n5YEHCrOfMJJMDwYH9dmz49vvuGPu8kBjy1Kme8l7yE+iABabQljsgomMM5E0UXqusuUT1VpNEbEQ\nn+7koeCyVADFp6r6+wIcux8wJ9XJIiKjgP2Bmb42+wH3peSZJCLtRGQNVf2yAMd3OJo0vXrZy2PR\nIksI+/bb8NxzcNVV5u+52WZw2GFw5pnlkzUXCpWySVUnikj3mCZh/VRnYF0y93FlJYniXuXK/a+8\n/37D7wsXFvd4QQUsqYL8n//Ery9FAt18FLthw+Cii7JXhtZaK9l/kqti27x5bSQfTkJcVOwQ7+lS\nRFYUkX8D/wW+FJFCuFqvDfiN3fNSyzK1yVAAx+Fw5ELbttC/P5xzDgwZAgceaGlQRKBbt3JLV9FE\n9WVrRSwvKtkMyknSjFSLf9Hmm2fXPtMgf9hhucsCjRWQF1/Mb39R+y0G+SjznqUuW7/ddddN1q4c\nFrtqI86j5nDSkWPHAQJ0BDYE7geez/PYSf+e4OURut1QX8hTXV0ddfmGWTkcTYzFiy0FwogRFp19\n7LFmPdh443JLBuPHj2d8VEHPCERkU+BO7GHwGeBCVf0ute4NVe1XQBHzCj8pZP+VzcDnD6SIolos\ndnvsAVOmJG+fSUH6xz/yk6dYUa6liJ7NN/2M/z0pK62UrF2uiq2n2F11lWWuKDW59GG5EqfY/az6\n6yU0EBilqsuBmSJSCBfr/wH+ONJ1sCfauDZdUssaMTQYy+5wODKiaoXOR4ywxKc77GAO3Hvtlb2P\nTDEJKjuXXnppks28lE2TgBOxlE37qeocCpuyKayfmpc6RqY+Dihs/5XNwHf11ZnbVIvFLtvyVflM\ny+2yS3hwyOjRZumG4lnWSmGxyydh9Guv2Xu2il3SwK18ExSXy3KXYx+WE3E/8WcR6SMiHYE64Dnf\nukLkqX8L2EBEuotIS8xCGKy38ARwLICIbAMscP51Dkf+fPWVpVbYZBOzzPXoAe++axVP9t+/spS6\nPGijqs+q6neqeh3wf1jKpm0ybZglUf1Ukj6u4BTaopNvua9SUSzFbvvtGy+LUnbbtk1/LpYCls3/\nm2ut1nwUO0++bBW7pH1OrufV+021mNopSJyOfBbwKDb9+jdV/RBARPYG3sn3wKq6TEROA8ZhqQBG\nqOpMETk5tX64qj4jInuJyBzgB6BJZYt3OIrBRx/Bhhvak+tVV1nR6xr1PylIyiYReQToD3QQkU+B\nIaQsfnH9VFQfV8DfF0qhFYpqmYrNNlVPUsUuTDmKUnb9bYvlqJ/N/5tNwMCoUXDEEfY5n6lYry/J\npECtuio88ojNDkD+FrtmzZKdmxrt6xoQFxX7OrBRyPKnsTQCeaOqY4GxgWXDA99PK8SxHA6H0b07\nvPKKJQ+96y7461/hgAPs1b9/zVjrIJ2y6TVvgapOE5FdgEuS7iRJBG1UPxXWxxWbQlvsmvpUbFAR\n6NkzmWJXCRa7bJQYfy3UKMVu773h6Qyjf1LFrm9f2HPP9Pd8LXYtWiSzLjcFxS4uKvb4OF86EWnZ\n1OotZsu8eTZwbrVVupZsktdDjRLNOByFQwT69YMrr4SZM+GFF2DttWHwYEsqeuyx5iuUTemgSkRV\nH1LV1/zLCpyyqSIptEJRjqnYN3KoRp7E4nP00enPSc+TX1nbZBP4/e/T5ySYm6/SLHbZKDF+xSqq\nfnASpTJp8ERQkUtqsXvhhWT7i6JJK3bAKsCbIvKIiJwjIkeJyNEicm5qamISkDClYNOgvh7OOCOt\noK2zjiWAzVRkO8jcuUURz+EIZeONLUrsjTdg6lRT7g46yNJHVFL9ymwpQcqmiqQWfOxWy6G2UZIB\n258SJZep2HvuMUuT99ATVLJKYbGLk/uDD6LlyUShqs54Cl2m/yMoW77HT7q9X+HMNwl1pRJ56lX1\nFmAL4FagJbADsD02fXsLsIWq3lYKIasFVbj//ty2PeIIeOYZu2kvuqiwcjkcSXjzTYuIHTHC3l96\nqeodjQ8HZqU++1M29QeuLJdQxabQCkU5pmJzOWaSa9U/3ZjLVGyrVlZe6uuv7XucYpevgh1lmYoj\nWKIyG2UpicWrkBa7oGKXr4Uz02/dckt7X3HF9LLevfM7ZqUSq1Or8bKqXq2qf0i9rlHVV3ypUBwp\nmjeHBQty23bUKHMi/eyzwsrkcCRh2DDzd9l6awuu+MtfzOJc5YSmbEoFMNRWVVwfhVbsypGtPypg\nY5998tuvX0nLVbFbfXXL+Qjxit3UqbnJ6LHpptlvE1SW/EpMJgqt2EXhZfkIKmITQor87bpr+D5W\nX73xskzyr7ACvP66+RJ7xCmDt1dxAdOMxmsRWU9E/iYio0XkydSr6CH71cjcuXDffdlvd+CB9jr4\nYJg+veBiORwZOegg65B33LFhyoYqJzRlk4gIhUnZVJFU2iO3ZykJEjeoRil2a6wRvU0Si51fSZs/\nP3N7aKgstWoFnTqlv8cpdvmSi7U8OP3ZsWPybXMJmgorMxgWPHHSSenPv/sd3HyzVbfJdPyopMVh\nwR1JpuK33rrhdRd3DebiDlApJHlqHQPcDTwJeJdxhXUd5efHH5OXRAkyenT682OPmZ/ejjtaosc/\n/xnatSuMjA5HFD17wh13wCGHmE9ohw7llqgghKZsAvaiACmbKpWgsrHrroUrZ5Uto0ebIuTPBbfT\nTlbRpF279JRmkFxSrGSr2CWleXNT6H780QrV+6dzK02xC27jV0Iz0aZN9scLO5/eg4X/AWOllWDa\nNLNCrrACnBYSQx6m2EVZVcPy7GU6X2FTxHGKXTW7oSS5zH9S1ZtU9SVVHZ96hRhNmzatWtmFrApP\nPpnfvm66CQ491NJQJCn543AUgk02gSVLLA1KjfA5MADoC9wvIl1FpCswA/ij9z21rGYIWuwKqWy0\nb59de5HGA/awYfYe98C6xRbZHScbebKlWbP0diunwgW33treg4pdIafB81EsvNJqSY0CH3xg979H\nWCEUkcbXVpiMnjLmPxcdO6b3H2UZDFu+dKk9cAbx73uXXaJlCaMpKHZJLHY3i8hQLMnmrwZQVa3Z\nJ958ydVy5+e66+Dcc/Pfj8ORhPvus4CJK66AE08stzQF4z6Szy7sXExBSkkw8KCQ6R2yHezCFDtP\nnigL0dZbRyujcdPMSax8s2ZlbhOkefO0PMEC90FFrpCBJkn+t913h+dDqrZ7VsWkVrgePRp+Dzv/\nYYpd2P/hnRO/te3889PnLBvF7pdfLEo/jhdftH137GgpxjLhFDujN/BbrOPzX8Y10xEWmo02slx0\nffpAr17ZRSYNGACXXALbbls8+RwOsOmMxx6zJ+JvvrEo2D59yi1V4VDVunLLUA6SKnYXXZS2niUl\nl8EuOGAHrV9B4pS3uHVJ0rJE+Wy1aBGtGDZv3rgP937DIYfA//1fenmYU3+uJDnXmfwpc/WX9RS7\nf/3LSgwmlQdspumf/2yo2PmDOKLGwzBlcunS9HJvOjyMTz+16ynMhUS1oexJFbtqzneXRPRDgXVV\ntb+q7uy9ii1YNdOiBRx1lA2SzZpl5+fw3HNWiP02l0jGUWDq6+HLLy2tyfnnW2qE++6zkmJTp9aW\nUteUCSo4UQPU5ZdnP3jlMthFWeyilKw44hSZdde1JNtxRPlstW7d8Lt/8A9TODw5gn17mMN9LsmW\ngzLkSi5+c//+d1rh2WuvdCRynD+dny5d7D2uQkQYYe39il27dmlfUb+fo3fMTEq187FryHSyqKvo\naIhIbjd2If1iHE2Lr76yGrCnn26R1ttsY0rcyiub8jZokHXSr75qDxIHH1xTZcSaPEktdl4idT+Z\nHigLYbHz5MnHYnf44eHrL7ggXpakQRl+GcLOU1BGL9Ft2PnJ9d6KO9fPPhsuR5CgApSElVdOjz8t\nWqR9xps1SyuK3m+KO36Yovbf/zaWyfMHDGv/yy9p5WvFFdP+dAMHwmabZf4tYTjFzlgNmCUiz7l0\nJ7nRrRscdljy9qedZhY/hyMXFiywJMN33WVO6H/9K0ycCIsWmdI3ZQpcc01jvxpHbRC02MU9JAYH\n5uXL4cEHo9v7lcS1105/PuEE89F8//2G7UUaD+SZpmI9wiJ5vcoRo0Y1ln3p0syDcRLFbuRIGO6r\nWB6mHAWVkA03tPew4+daUSG4r7POSn/2/odMeeoyHXubbay8YJCwh4G99jI3I0gn9vX+g+uus/dD\nDkm3D1PU1luv8bLNNrPtL7648bqlS9Oy+P8HEXMdef31xtuATY9HXQvZKnYffxzdplJJotgNAQ7E\nMrVfn3r9NZ+Dikh7EXleRGanFMbQ2B0RmSsi00RksojkaNCuDB5+2J4yknDLLWZhEbF8P5MnF688\njaP22HBDePddC4S44Qb4xz/sSTubZKWONCIyUERmicgHInJhyPrVUnk+p4rIJBHp7VtX8j4sqNgl\nsTzccIO9L1/esJ5qEP++3n47/blfP0tq7U1N+hWD4PSkN+0ZNah6yoJnnfGz117RshVKsTv00IbF\n6VdcsfF+g1O6cWW0crHYXXxx42P4x4DmzWHGjMx5UzMpdnvsAZMmNV4efBh49FHzxw3+vrj/KpvE\n1ueeay5Icfh/i6pFaHvRyUFWWKFwil2hSq2VkoyKnS/FSYNXnsf9I/C8qm4IvJj6Hnp4oE5V+6pq\nyHNF9VBfH34DRbFokb2fcYZZXW6+uThyOWqTFVc0C8q771oyz403tmuoHOWhqhkRaY6VUBwI9AKO\n9OrP+hgMvKOqmwHHAjf61pW8D8slKtZLNJtJ8fHvy//ZUwTC/JhapVJB77efvfstxa+80vgYcQ+x\ncYpbkms7iWK3wgoNFZuwB6IoGXO12AWd/i+/vHHgg99C2bKlWc3i8k3usgvstlv8caPOZ1CxO/jg\n+CnpuLQnSQnuY9VVYdy4tHXQfx6TGDriXBA8/PsMVtpJWhqtEom85UVksYh8H/FalOdx98NSEZB6\nPyCmbRWe1sassAKMHWuf99nHHFSXLm341BvHWWe5qhSO7OnUyUrjvPSS+cpsuqnVJHYkph8wR1Xn\nqupSYBSwf6BNT+DfAKr6PtA9Ve3Co6R9WDZTsUEyKT5R0YXeIBpWdQBs2vXuu01Z8eRRhe22a3yM\nOIUgbpBNorRFtVm4MP15hRUaKgUrrZTZx87/fZVVGq5LYrELC1yKO2amlFotW9pUdq9e8e3CzqdI\n9DXjtfdk8f6rMCUq21mm4D5697aZq86dzS/49NPT6/IpbeYt//3vGyp2H34Y3q4aFbvIZwlVXSVq\nXQFYQ1W/TH3+EogqFKPACyKyHBiuqncVUaais/XWjS/ILbaAnXc2RS8TEyZYGZwws7fD4TFvHtx4\no/nTffNN+vX11+Z/d8IJMHNmdZfMKSFrA5/6vs8DghNAU4GDgJdFpB/QDegCzKcMfVg+eey8gfrV\nVxsrXVdcAXfemf4eFjkapdh5aSr8ClTU4Byl2M2fH1+Le4MNotd5JFH+RBqes2wsdqrw/ffJp/s8\nkijfqnDrrTaV7fdvDPL++7D++smOndRiF2zv/Xfe+QzbT76KnX+f/usul32H7ff44xvmNYxKaVNT\nil2+iMjzQFhqwYv8X1RVRSRK/95eVT9PPf0+LyKzVHViWMOhvlTZdXV11NXV5SR3qdloI5g9O1lb\n74ll+fLqzrHjKB5z5ljS0v33h7o6SwHQoYO9r766KXPVGHE9fvx4xo8fX45DJ0lwfDVwo4hMxrII\nTAY89WQHVf0sUx9WyP7rl1/sP/YUpGwGJm+gDsujKWJO7l4gWNhUbNByF0eUYhc1aHfo0FAxDLLn\nnuGlpsCiVvv0Mf+5Bx7ILJtf/mAqFGisfHq/JezeirLYrb66PXAFjxfG4YfDpZeGp/RYddWG58UL\n5IiSx0+uip2H9xDhye//T/Odio0jl6nYoKLWrFlpo2JL2YcVTbFT1d2j1onIlyLSWVW/EJE1gdDC\nWar6eep9voiMxqZFMip21cRvfwuXXZbMP+TJJ+Hzz+2JcNVViy+bo3r48Udzbv7jH60c0KBB5Zao\nsASVnUsvvbRUh/4f4Pe+WQez2v2Kqn4PnOB9F5GPgA9T6z5Lvcf2YYXsv/bay3yTPP+qMKUhrIg6\nZLZoHXqoTeXvtVf8VGw+D55hCkHSXKArrWQWq402sr7VU+KaNTNrV1I8+SdMgK22ssAQP0HFQjX6\ngTtKeejePblit8MO0XnaZs60RNNhvy9p/dQgSRU7b9q/ED523jnYbDPLqxlHkqnY/fe3sTKIX8Hz\n/hv/+V9jDcv3WWiLXSn7sHLZfZ4Ajkt9Pg5oVJ1SRFqJSJvU59ZYzcea8jL78Uf4859Nqdt5Z/O3\n8xyMw9h3XzjpJLvoHA6wQey008zx9+GH4d57a0+pKzNvARuISHcRaQkcjvVfvyIiq6bWISKDgAmq\nuricfZhfmQgOTGG5xMByGsaVMQyzeATXectGjAg/th9vcA6m2wgqBAcfnHxWA9JpVPzpQZIoAmHs\ntFN4WpZevRrWYVUNt2BC+r8I/k7/f5RJsYtTktZcE9ZaK377bOs/52qx85PtdGlwmjcOLyAnClX4\n+98b+hMHAz38FrvgQ8oWW1jAWXBdtVAuxe5qYHcRmQ3skvqOiKwlIk+n2nQGJorIFGAS8JSqPlcW\naYtEq1Z2samac/sWW1gJl0cfjd9unXXg+uvNsdR74nM0TYYNg2nTLCXO2LE2DesoHKq6DDgNq5X9\nHvB3VZ0pIieLyMmpZr2A6SIyC9gDSMWYsgZl6sPippjCcomBXTtJZgLC/Oi8Qdxb51UriMMbaCdN\nSvuE+ffl0aZNWq7gIHtho+QzjSN0w/bpseWW1u9GyeYRPO4jj8D//hfd3j99G0zm61kf/VO0mRS7\nTJbUM88062IUUVU+wpSWNdZI7mMXZ7ErlmI3a5YF4mTL1183PE6Uxa5ZMzOydOzYsH01UZYMLar6\nLdAoEDs1bbF36vOHwOYlFq0iyFT02Hta6dbNTck2dYYMsaCcaux8qgVVHQuMDSwb7vv8GrBRyHYf\nUaY+LGxg7tYtv2SrJ6Qmm8OmqLzBOCp4Igz/AB7nm+X/LXEO9sH2/rZRysK661qex+B+Mh2nZcuG\nVs/g/tdbL11RwVMePEXHX9UhuP9DDgl/sG8Xmuk1TevWZl2MIiwA5IorbLraj/c7oqolBZWvoELv\nJ9upWI9MCuFGje60xgT/r9tvTweLZVLsgtd3NfatzgW/Atl++8apTYIRjNtsY8klvQvzvfdMIfzX\nv0ojo6MyWH99y7IeN4XmaHr4lSFvYEoyIPrxJ+k9/niz5Pj35z+GNxgnHQTHjrWKKGEEB3b/cbp1\ng+efT39PqthFKQtRy1dbLbvp36Bi99RTpjD65QkGWIRNxYb9nvXXh9/9LrksYYQpdhdd1Dh3m0eS\nqdhXXkn7HhbCx86jEMn4gxbKU05Jl6HzT8V6v9N/fmpBsavCnMpNAy945p57LBP86NFwxBFmvl+6\n1EqpvP66KXOXXZbermtXM48vWJDc4dhRHdx+u/kutWhh10GLFvZautSmYd580xy9HY4wa9A556RL\nciXhqqvSuTfDAiXCFLukBKvwXHUVfPSRBf/EWexEGibdDRt0wwI4slXsIFn6lCjWXttyRkJaxqB1\nK6lit+aa+WdB6NjRfAWXLEnWPpNi17atpcOJC/7I1a+xEIpdnA+eX2ELqy4R/C+cYucoGKedZi8P\nzzk2GD3rKXV9+piV78wzrS5o167VWeOuqfO//1mHuNJK9hS50krWyQ4ebA7Qw4fbFNCyZfZautTe\nzz0XegbrITiaLP6B2UuYu8ce9sqFuEAJyH8w9lKoZFLsguQ7FXvKKcnkyzS4h+0/6BfntfF86047\nzayoN94Yr9jlavny+PFHU+p+/BH69k1PEccRFYHr4c0MFUP58c5TWIBPJi66yPyOkyp2YZbmbNwJ\nKhU3FVslvPqqvT/1lA3mxxzTcL03dTtxIhxwgOUz+/RTHFXEokXQpYs5dG+8sT2pt2plT5MTJ9rU\nR//+lmNsxx0tknrAAEs9se++jTPeO5oungVi+vSG0aHZ4E+CG1ZxIs5iFxZtmJTgvvyBFUGOP77x\nsmyCJwYMyEq0rIjKdedNE266qaUmAnOtgcbn66KLwgNEssEf1Tt5Mtx0U+ZtdtihYXCIhyefV8os\nqOTnaqXz4xkvHnkk+22vuMLew3IPBvErdv7cf8H/oBoVPKfYVQkXXmg3zXrr2RTrgw/a8hNPbNx2\nzBi7mbt2TS+bNg2++KI0sjqiWbTI/GXuuKNxCZu2bS0Q4r77LIJr8WLr5JYuhZdfzvwU7XB4eMpN\nr165WT7ABm9voA6r+BClOHkW51zxK0SLFlm97Ch69GhcjisbH7tCkY3Fzjs3zZunZTznHHsPKhFX\nXGH52ArJqadayptMhKVQyZT0N4zJk5PLBukci2tE1aPKwAknwN57J2vrXRd+v81amIp1il2VMHOm\nXWC9esF331m6k++/N7+qYBTtccelywG99ZbdoJttZhaeJDe0o3gsWQIPPWQW2O23N2vEqafC44/b\n4Hn44ZZ/yU/z5tXZuTjKh99qlSnnVya23bZhJYowJaYQlhoPv2LXpk1m/7LgscMsdoWUL4kM0Fix\n85QIT7Fr0aI8SkSLFtEpbzIRZc0K/o7HHksHdGXj1xl2jGwZMSI6KCR4HO8/8Sx8PXqYtdIvRzX2\nvc7Hrgr4y1/gggvs8+OP21Srd7GNG2cOziecYEEWN95oZXW6dLH1fmf6WbPg22/Nojd7Nlx5pbMC\nlZqOHe2/Gz7cOvgZMywx7J13mkK+1lpW43X48GTFwx2OMPzO4B06hGfgT4rnBuIRZv0qlEXsmmvM\ncp0PYT55YfLt1ijhVjS5+NgFtwmz2FVbBGaUYhdMg3LQQfDJJ9nv/8cfzQhRKoLXhT8Sulr+kzCc\nxa4KOOooM2erwoEHNrzQOne2qb36epueXbYsrdTdc49Z6bypjD59LAnpeeeZIuH5MkyYYIrhddcV\n/8m2qdOsmSlv8+bZ/9injz3ZPvusFTm/7TYLlHC1gB35ELRaFdL/spiK3QUXJA9o8Pjtb+1h1yPM\n3yso3/XX2wOVRyY/xFwUuy23hNdea9zGs37GJZGuFsICaTxyGUtWXjm63F2hEWnsB+mPlK1mxa4G\nLq3aZ+21Gzoyh+EPQ//nP+2JqVkzU/o8xW7AAEs8+eWX1mb6dItG++wzy4U2bJg9TX71FbRvn7vT\ntSOcn382pVok3FK60kqw6672cjjyIVPxd49OndLVA5JS7KnYbPFmMzyC6UUgs0Utn8H7+OPhyCPD\n9+8FRXgyqFo/cMUV4S4Wla5EZLLY+endO7djlEqxA9hll4bZJ/w4xc5RMay8smUv93PVVaakHXGE\n+eS1amX+XeusY1FXhx9uT4+9e8O118KLL1rOtJ9+ys8JuqmgCk88ASNHWmLT7t0tkWq3bjZozplj\nrxdesOird97JnEne4ciHpBbfKVOyV8qSTDtmWl4KPB+3rl0b12kNkk8/N3JksnbePe8FszRrVn2K\nXU71wpEAACAASURBVFBZi7PYDRiQm8J/wAHhEbmFRsQebG6+OXp9teIUuybAnDmWDuPrr+Hss+H8\n880puVWrhjdkXZ353Q0YYA7+zz5rT6P33WeKXufOdqN++GF8CoJa4M47bfp78OB4R9wpUywyub7e\nzu3SpTB3rtX+nTvXOvENNjCn3Ouus3NbzR2GozpIarHLJfIwrDJEWHR+ufF8VD/8MPM9N3iwPQAX\ni48/Tjvoi1gpyJYtrf/1V42p9L5h4MCGylrQqhWskJQLd9yR/z4KgbPYOSqa664zq9x550V35Kow\naJD527VvD5tsYkkoP/vMrHwjRljKlHPPNaXl559NUXzwQXudfnp05/7996ZIVhMPPWTnYfPNbZpl\n8ODw8P+zzrKglbPOcn5xjsohqWKXC0ErzI47Vp5lXzWdoD3JuVhlFcs48N574evzHdz9qaegYfqY\n667Lb9/lxG+x++gjCw6rFjL9p9Ws2JVlKBKRQ0XkXRFZLiJbxLQbKCKzROQDEckzTWPT5YEHLLI2\n7ul82DC4/35LfPzee6bYTJoE//63PWkOGmSBF7/5jVVEOPBAq3Qwc6YpjOef3zi8/8cfTeFr394U\nw5kzG+Y0mjfPitgXO8dUtixbZtOlI0eazCuuaIru2WdbkuCvvrKB4+23zRpw+ulOqatlMvVDIrKa\niIwWkakiMklEeifdtliUUrGrVLKVsxL6oWpTIvzKT/fuyRIDO4pPuSx204EDgeFRDUSkOXALsBvw\nP+BNEXlCVWeWRsSmxUcfmW/dLrukl3nRtW++aSlVRoww69vMmXDwwTBqlN3I771nQRv+weTNNy1a\n7Te/gf/8xxTDa66xPHpe0t1DDjHFqHVrOOkke8Lu06c4SpKqWRg//NCsC3Eh9TNm2G/3fGKuv96U\n1+uus/f337dBYKWV7LtLS1K7JOyHBgPvqOqBIrIRcCuwWzn7sGIqdn4F6O67GycIrhS6doWHH07e\nvhIUVn8x+mogzseu0qk2JTobyqLYqeosAIk/s/2AOao6N9V2FLA/4BS7IjBiRPS6nj3TdUjbtUvX\nCfQYN85qUIqYNWvIEMu3d/PN6RqQM2bAwoXmr9asmUXqduliyXi32gouv9w61jFjsssvlYQxY+AP\nf7BgkPXXNxm7drVp5X33tUFw4ULzlxszxpJrHnpow32suaYpeB7ffGNKYilzLjnKQpJ+qCdwNYCq\nvi8i3UWkE7B+gm2LQjEfNvwKUCX61nk0axYerQrhSlycxc5flquYnHJKeJm0SqWapytrmUr2sVsb\n8Fc7nQdsXSZZHDGMGwdbbAGXXGJ52I491qx67ds3bLdggTnX3n231T6dNMl87+bNs4Ho7LNtqna3\n3cyCeOSRplDuv79lSm/XztK++K0RS5akw+NXWaVhbqjFi22adOJES++y/fa2fNkyU96uvBLOPNOs\nh4sWmY/NPvvAM89kDtVffXWX3LmJkKQfmgocBLwsIv2AbkCXhNsWhRVXtIeVYpDNlGU1DfjHHWcP\nd2G89JK5lhST2bMt0KqaqGaLXS1TNMVORJ4HOoesGqyqTybYRVaG8aFeNWWgrq6Ourq6bDZ35MHH\nH5sFa4cdLCFnVOf03Xc22AwebMqWF1Dhhf9vvrnV7Pv6a4u+Ov54i9y9/Xb4/HM7BljC5o02gtGj\nYfz4tHWiTRvzFTzmGFMM99/frIFTpjRM0NqihQWTHHaYWRJXXdWsh65zqlzGjx/P+PHjy3HoJP3Q\n1cCNIjIZczOZDCxPuC1QnP4r3woOUVTClGUxuOii6HVJSlTlS7UpdVD7Frt8ai0HKWUfJlrGu1RE\n/g2cq6rvhKzbBhiqqgNT3/8E1KvqNSFttZy/w5GM8eOtEsaYMeGFradONd+9jh0t9UpY+oGZMy0Y\nZM4cy3e0zz7pAey118zq98svlgdp6FCb2qjVTqcpIyKoatH/2Wz6Id82HwF9gE2SbFtt/dfjj9t9\nmknkc84xK36l5WwUMX9Zf5oRR24sX24Pyj/8kH9N4lIiYr7hnotReWQoXh9WCVOxUT/sLWADEekO\nfAYcDkR4TDiqgT59LOAiTKkDu8k++QS2286mSaPaRK3bdlurazlmjE3Zbu0m7h35k7EfEpFVgSWq\n+ouIDAImqOpiEanJPizpVOxf/1pcORzlp9YtdtVKWRQ7ETkQuAnoADwtIpNVdU8RWQu4S1X3VtVl\nInIaMA5oDoxwEbHVzeqr2xRoFC1b2lTsttvm3lE0a2bl1ByOQhDVD4nIyan1w4FewL0iosAM4MS4\nbcvxOwpJtfuWXn+9uXM48qeafexqWRkt61Rsoai2qQyHw5EfpZqKLQXV2H99/TV06FBuKRyVgIgF\nsBXKF60UiJhbz8Ybl1OG4vVhVahnOxwOh6OcOKXOUc2MHm11u2sVZ7FzOBxVh7PYORyVwQormMWu\nGqdjy0mtB084HA6Hw+GoQpYuLbcEjiBOx3Y4HA6Hw+GoEZxi53A4HA6Hw1EjOMXO4XA4HA6Ho0Zw\nip3D4XA4HA5HjeAUO4fD4XA4HI4awSl2DofD4XA4HDWCU+wcDofD4XA4agSn2DkcDofD4XDUCE6x\nczgcDofD4agRyqLYicihIvKuiCwXkS1i2s0VkWkiMllE3iiljA6HwwEgIgNFZJaIfCAiF4as7yAi\nz4rIFBGZISLH+9a5PszhcJSUclnspgMHAv/J0E6BOlXtq6r9ii9WcRk/fny5RUhEtcgJ1SOrk7M6\nEZHmwC3AQKAXcKSI9Aw0Ow2YrKqbA3XA9SLilWusmT6smq6NapHVyVlYqkXOYlMWxU5VZ6nq7ITN\na6LQN1TPRVctckL1yOrkrFr6AXNUda6qLgVGAfsH2nwOtE19bgt8o6rLfOtrog+rpmujWmR1chaW\napGz2FS6j50CL4jIWyIyqNzCOByOJsfawKe+7/NSy/zcBfQWkc+AqcCZvnWuD3M4HCWlReYmuSEi\nzwOdQ1YNVtUnE+5me1X9XEQ6As+LyCxVnVg4KR0OhyMWTdBmMDBFVetEZH2sr9pMVb/H9WEOh6PE\niGqSfqtIBxf5N3Cuqr6ToO0QYLGqXh+yrnw/wuFwlAVVLfoUp4hsAwxV1YGp738C6lX1Gl+bZ4Bh\nqvpK6vuLwIWq+lZgX6F9mOu/HI6mSbH6sKJZ7LIg9IeJSCuguap+LyKtgQHApWFtS9HBOxyOJslb\nwAYi0h34DDgcODLQZhawG/CKiKwBbAR8mLQPc/2Xw+EoJOVKd3KgiHwKbAM8LSJjU8vXEpGnU806\nAxNFZAowCXhKVZ8rh7wOh6NpkgqCOA0YB7wH/F1VZ4rIySJycqrZlcCWIjIVeAG4QFW/xfVhDoej\nDJR1KtbhcDgcDofDUTgqPSo2lGpJcJyFnLEJUIuNiLQXkedFZLaIPCci7SLaleV8Jjk/InJTav1U\nEelbKtlC5MiUzLZORBamzuFkEbm4DDLeIyJfisj0mDZlP5+Z5KyEc5mSI+frM2rbTPekiHQVkcUi\ncm6lyikim4rIa2JJm6eJyIqVKKuIrCQij6RkfE9E/lhmOSPHDRH5U6r9LBEZUEFy/sa3fHexKPBp\nqfedk8pZIlkbjcUVdD/F/ffJ7ydVrboXsDGwIfBvYIuYdh8B7StZTqA5MAfoDqwATAF6lljOa7Hp\nI4ALgasr5XwmOT/AXsAzqc9bA6+X6f9OImsd8EQ55PPJsCPQF5gesb5SzmcmOSvhXOZ8fcZtm+me\nBB4F/o4Fn1WcnJj/9lSgT+r7akCzCpX1eOCR1OeVsX6uaxnlDB03sATZU1Ltu6e2z3hOyyDn5kDn\n1OfewLwKuJ9ix2Iq536KOqdZ3U9VabHTKklwnFDOJAlQi81+wH2pz/cBB8S0LfX5THJ+fpVfVScB\n7cSc2EtN0v+yrM7yauk2votpUhHnM4GcUP7kv7len50zbBt5T4rIAcCHmM9fpco5AJimqtNT+/tO\nVesrVNbPgdZiVUZaA78Ai8olZ8y4sT+mgC5V1bmYcpCkmklJ5VTVKar6Rerre8DKIrJCAjlLLitU\n1v0UI2dW91NVKnZZUA3JQZMkQC02a6jql6nPXwJRg3g5zmeS8xPWpkuR5QojiawKbJcyzT8jIr1K\nJl1yKuV8ZqISzmWu1+fawFox24bekyKyCnABMLSS5cSsDipWQ/dtETm/UmVV1XGYIvc5MBf4i6ou\nKKOcUayVapfNNuWQ08/BwNspBSYJJZW1Au+nKDYgi/upEtKdhCJVkuC4AHKWJHolRs6LGgijqhKd\nV6scyVaTnp+g5aYcUUFJjvkOsI6q/igiewJjsEGw0qiE85mJSjiXuV6fUW0a7S9wTw4F/pb6zdlY\nK0stZwtgB2BLYAnwooi8raovVZqsInIMNgW7JtAei2R+UVU/KqGcuZJEhrLIKSK9gauB3bPYrNSy\nDqX891MSViCL+6liFTtVzeZiiNrH56n3+SIyGjOBFlQRKYCc/wPW8X1fh4ZPZQUhTk4xB/XOqvqF\niKwJfBWxj6KfzxCSnJ9gmy6pZaUmo6xq1Qi8z2NF5DYRaa+WHqNSqJTzGUuFnMtcr895WGcddZ6j\n7sl+wMEici3QDqgXkSWqeluFyfkp8B/vvxBL4rwFkESxK7Ws2wGjVXU5MF9EXsEG0EyKXSHlTNLv\n53pfllpORKQL8Djw2wQKcjllrYT7KYmc2d1PUc531fDCHAx/E7GuFdAm9bk18AowoALlbAH8F3Ok\nbEn5gicuTH3+IyHBE+U6n0nODw2dVLehfM7+SWRdg3SaoX7A3DLJ2p1kwRNlO58J5Cz7uczn+ozb\nNuE9OQQ4pxLlxJy738YsYS2A54E9K1TWM4B7Up9bA+8Cm5RLTt+2DcYN0sETLYF1U9tLBcrZDnP0\nP6BS7qcoWSvtfspwThPfTyXtBAv1Ag7ENNglwBfA2NTytYCnU5/XS52wKcAM4E+VKGfq+57A+5gz\nbDnkbI8lVp0NPAe0q6TzGXZ+gJOBk31tbkmtn0pMpHS5ZQX+L3X+pgCvAtuUQcZHsCoKv6SuzxMq\n8XxmkrMSzmW+12fUvR91TwaOm3ggKoecwNGp/2c6EZH2lSArsCLwYErOd0kYGVlEOUPHjdS6wan2\ns4A9KlFO4GJgMTDZ9+pQibJW4P0U998nvp9cgmKHw+FwOByOGqHWo2IdDofD4XA4mgxOsXM4HA6H\nw+GoEZxi53A4HA6Hw1EjOMXO4XA4HA6Ho0Zwip3D4XA4HI4mjYicLiIzRWSGiFwT0eZMEZmeanOm\nb/lmIvKaiEwTkSdEpE1qeUsRGZlaPkVE+pfitzjFzuFwOBwOR5NAROpEZGRg2c5YbddNVXUT4LqQ\n7TYBfg9sBWwG7CMi66dW3w1coKqbAqMBr+TXIKA+tXx34PosK1zkhFPsHCVHRJaLyOTUU8zjqXp9\nmbY5TUSOT33eRkReT+3jPREZklp+dKpu6DQReUVENvVtf0+qwsb0wH7/KiI7FvgnOhyOJoCInJHq\ngx4IWddHRO7xfR8oIpNSVqHJIjJKRNZJrbtXRA4ObL845rgrish/RMSN4dkTluPtVOAqTdW0VdX5\nIW02Biap6k9qVUomAAel1m2g6fKaL2A1cgF6YsmGvX0uwKqaFJWquChEpHnqRkhaI9ZR2fyoqn1T\nTzGLsKSOkaSecE7EkogC3AcMUtW+QG/gH6nlHwI7pfZ7OXCnbzcjgYEhu7+d9NOVw+FwZMOpwG6q\n+tuQdedj/Ytn7bkJOFZVe6b6roew6gNgykZQ4YhMMquqP2PlHA/IS/qmSZjFbANgp5TBYLyIhClf\nM4AdRaS9iLQC9sbKhAG8KyL7pz4fSrpk2FRgv5QOsy7wG982RaMqFDvgTOA9KrMQuSM/XgPWBxCR\n9UVkrIi8lXoa3SjVZntglqouS33viGXlRo2Zqc+vqerCVJtJ+G6g1NPUd8GDq+oHQHcRaVeE3+Zw\nOGoUEbkDq8jzrIicFVi3IlYJ5c3UoguBYar6vtdGVZ/0WXkgomC8iFyWMmxMFpH/+ayATwBHFur3\n1DreLA9wF6Zseed0AFamazVV3QZTyP8R3F5VZwHXYFVLxmIVNepTq08A/iAibwGrYNVyAO7B6sC+\nBfwNq5CzvEg/8VcqXrFLFRPeC5vDLvrctKN0iEhzYAD2JARmYTtdVbfEbi6vEPMOwJu+Tf8GvJ+a\nxj0p1YkGORF4JqEok4Fts5Xf4XA0XVT1FKzkXZ2q3hBY3RcrGeXRC3gnZncC/MWnbEwmZchQ1UtS\nFr464Bvg5tQ2U4Dt8v4hTQRV3SZ1Hn8PPJGaNeqrqs9hytfjqXZvAvUisnrIPu5R1S1VtT82rfp+\navn7qrpHauwahdWCRVWXq+o5qeMcgNV8nV3s31rxih02iJ9PWjN2VD8rpzquzzGT9R0pP7ttgX+m\n1t0BdE6170rKQgegqpdjfgrPAUcBz/p3nnKEPQF7Sk7CZ6SnRBwOhyNfumH9WyNEZPVUhOT7InJu\narEC5/mUjb74DBkpd5SHgOtVdTL8Oh3bTERWKuovqT3CDERjgF0ARGRDoKWqftNoQ5FOqfeuWF3X\nh1PfO6bem2G1cr0p+JVFpHXq8+7A0pTlr6hUtGInIvsAX6UuZGetqx2WpDqubsBPwP7Y/7vA37Gp\nam/fNg3+f1X9UFXvAHYFNhOR1QBSARN3AfupaqOp1wgEN83vcDgKh9Kwz3oX869CVb9R1c2xGQp/\n4FjcGDcU+ERV7wssd31X9oT5M94DrJcKrnsEOBZARNYSkad97R4VkXexafA/qOqi1PIjReR9YCYw\nT1XvTS1fA3hbRN7DDFRhvpgFR1Qr95oQkSuxE7EMWAloCzymqscG2lXuj3A4HEVBVd3DnqOsiMhH\nwG9U9dvA8q2Bi1V139T3TbA0GPt6FhsRuQRAVS9Lpd94SlUf8+3je1VtIyL7YrMPO3tRm6n1KwIf\nquraxf2Vjmqjoi12qjpYVddR1XWBI4CXgkqdr23Fv4YMGVJ2GWpJzmqS1clZ2JfDUSFEXYxTgY1+\nbaQ6AwsCvF9EZonIy6n1D8fsy/t+NrAW8EbK/25oanlfLPjM4WhAi3ILkCWuR3c4HA5HRaCq60Us\n/0lEXhWRrVV1UmrZM0QEdKnq70KWtU297xJx+P0wvzuHowEVbbHzo6oTVHW/csvhcDgcDkcCrgNO\nKcaOU9OwO2BO/w5HA6rNYlfV1NXVlVuERFSLnPx/e3ceJVV17n38+6A0IPMQaAcmQRFQJhPQiHQZ\nguIQFWe9hpB7jdHkBhOHqMm7tNXlEENilnqJN4kGcYyaOMUpiFYDV4KIEwJOUSYVMKhoIzPP+8c5\n3VSXp5umq7rPqerfZ62z6gy79nmqTKUf9j57bwonVsUp0ryE3a9faYnLU92bgDGNUbcUvkQPnqgv\nM/Ni+BwiUj9mhmvwhIjIV6jFTqQBrPHXcZaQ/tEmIlJ/SuxEGkgJR+NTAi0ismsKZvCEiIiIiNRN\niZ2IiIhIkVBiJyIiIlIkEp/YmVlrM5sXLpq82MyujzsmkeYsnU7Ts2fPuMMQEZEIiU/s3H0jwRp5\nw4AhwBFmNjrmsESkHqZNm8bhhx8edxgiIs1G4hM7AHf/MtwtAXYDPqmjuIgAW7dujTsEERFpYgWR\n2JlZCzN7FVgNPO/ui+OOSSSJ+vTpw4033siQIUNo164d1157Lf3796dDhw4MHjyYRx7ZsQJR7969\nefnllwG45557aNGiBUuWLAHg9ttvZ8KECQBs2LCBSZMm0aVLFwYPHsz8+fNr3POGG26IvMeSJUs4\n//zzmTt3Lu3bt6dLly4APPHEEwwfPpyOHTvSq1cvrrrqqkb/XkREmouCmMfO3bcDw8ysI/CMmaXc\nPd1Y95syBV54AUpKoFWrHVvmcX32s49bt4Y99oC2baFNG2hREGm1FJr777+fp556iq5du/L3v/+d\nOXPmUFpaygMPPMDZZ5/Nv/71L3r06EEqlSKdTjNixAgqKiro168fFRUVDBw4kIqKiurlxa666ire\nf/993nvvPSorKxk/fnyN+eX69+8feY+BAwdy22238ac//YnZs2dXl2/Xrh133303gwcPZuHChYwb\nN45hw4ZxwgknNPVXJSJSdAoisavi7uvM7Ang60A681p5eXn1fiqVymnNyyOOgL59YfNm2LRpx2vm\n/rp10efr2t+4Eb78csfWqlWQ6FVtbdvWPM6+1qEDdOxY+9a+Pey2W4M/thQBM2Py5MnsvffeAJxy\nyinV10477TSuv/565s2bx/HHH09ZWRmPPvooF154IXPmzOHyyy9nxowZnHfeecyaNYsLL7wQgAcf\nfJDf//73dOrUiU6dOnHBBRdw9dVXV9db1z2iJnEuKyur3j/ooIM444wzqKioqDOxS6fTpNPpBn8v\nIiLNReITOzPrBmx198/MrA0wDvhK301mYpergw8Otsbk/tVEb/362o8rK+Gzz2DZsiCpXLcOPv98\nx/66dUGZtm2DJK9zZ/ja12pu3bvXPN5zz6CsJvfPv3x9pw1Z3CJzxOr06dO56aabWLp0KQCVlZWs\nXbsWgDFjxnDxxRezatUqtm3bxqmnnkp5eTnLli1j3bp1DBs2DIAPP/ywRp29evWqcb+67hFl3rx5\nXHbZZSxatIjNmzezadMmTjvttDo/U/Y/1tR9KyISLfGJHbAncKeZtSB4JvAud58Zc0w5Mwu6Y9u0\nga5d81Pn9u3wxRdBkvfpp/Dxx8G2Zk3w+sorO859/DF8+GGQOOyzD/TsWXPbd18YMCBI/pT47bo4\nVxur6iZdtmwZ5557Ls899xyHHnooZsbw4cOrW9H69+/PHnvswS233EJZWRnt27entLSUP/zhDzVG\nsu65554sX76cgQMHArB8+fLqazu7R9SSYGeddRaTJ0/mmWeeoaSkhJ/97Gf8+9//brTvQ0SkOUl8\nYufuC4ERccdRCFq02NEtm9WoUqt162DFiprb7Nlw553w1ltBa+H++wdJ3gEHwNChQWvm3nsr4Uu6\n9evXY2Z069aN7du3M336dN54440aZcrKyrj11luZOnUqELSM3XrrrVxxxRXVZaq6V0eNGkVlZSW3\n3HJLve/Ro0cPVq5cyZYtW2jZsiUQtOh17tyZkpISXnzxRe69916OOuqoxvwqRESaDT2+38x17AgH\nHghHHw3nngvXXAPTpsGsWbB6NSxfDlOnwvjxQdfxbbfBiBFQWgrHHAPl5VBRETxDKMkyaNAgLrro\nIg499FBKS0t54403GD265hSQZWVlVFZWMmbMmMhjgCuvvJLevXvTt29fxo8fz8SJE6tb4nZ2j7Fj\nxzJ48GBKS0vp3r07AFOnTuWKK66gQ4cOXHPNNZx++umN/VWIiDQbFvVwc6ExMy+Gz1Eo3GHlSliw\nAP75T3j+eVi8GEaNgqOOgpNOgn794o6ycZlZ5MAAya/avufwvNqMRUSyKLGTvFi3Lmi5e/JJePhh\n2GsvOP10mDQpaN0rNkrsmoYSOxGRXaPETvJu2zaYMwfuugv++lc48kiYPBkOOyzuyPJHiV3TUGIn\nIrJrlNhJo1q3LkjwfvMb6N8frr4aDj007qhyp8SuaSixExHZNUrspEls3gzTp8NVV8HYsfDrXwdz\n6RUqJXZNQ4mdiMiu0ahYaRIlJXDOOcEgi65dg5G4jz8ed1QiIiLFJfEtdmbWE5gOdAcc+IO735xV\nRi12BeaFF+DMM+G00+CGGwpvKTS12DUNtdiJiOyaQkjsSoFSd3/VzNoBC4AT3X1JRhkldgVo7Vo4\n5ZSgS/auu4K1cwuFErumocRORGTXJD6xy2ZmjwC3ZC4rpsSucG3cCGefHaxw8eijEC5OkHhRS2VJ\n41BiJyJSfwWV2JlZH6ACGOzulRnnldgVsK1bYcIE6Nw5WPWihZ78lJ1QYiciEq1g/oSG3bAPARdk\nJnVS+HbfHf7yF3j3Xbj++rijERERKVy7xx1AfZhZS+CvwN3u/khUmfLy8ur9VCpFKpVqktgkP/bY\nAx58EA4+GEaPhrKyuCOSJEmn06TT6bjDEBFJvMR3xVrwMNOdwFp3/1ktZdQVWySeegp++MNgWpR2\n7eKORpJKXbEiItEKIbEbDcwCXieY7gTgcnd/OqOMErsiMnEi9OgRTGIsEkWJnYhItMQndvWhxK64\nrFkTTGD83HPBq0g2JXYiItGU2Eki/fa3MHs2PPxw3JFIEimxExGJpsROEmnDBujfP5jb7utfjzsa\nSRoldiIi0QpmuhNpXtq0gcsug+uuizsSERGRwqEWO0msykro3RsWLIA+feKORpJELXYiItHy1mJn\nZm3N7AAzG2BmbfNVrzRf7drB978Pt94adyQiIiKFIacWOzNrD/wAOAPoBqwGDOgBrAXuAf7Y2CtF\nqMWueL33HowaBR98ACUlcUcjSaEWOxGRaLm22D0CfAF8x933dfdD3f0Qd+8LHAesBx7NNUhpvvbd\nFwYNgiefjDsSERGR5Ev8M3ZmdgdwLLDG3Q+qpYxa7IrY7bfDE0/A3/4WdySSFGqxExGJVgiJ3eFA\nJTBdiV3ztG4d9OoFS5dC585xRyNJoMRORCTa7rm82cyWsmOZr7q4u+/bkHu4+2wz69OQ90px6NgR\nUqmg1e7ss+OORkREJLlySuzcvU+e4hCp04QJ8MgjSuxERETqogmKpSAcdxzMmBGsSCEiIiLRcmqx\nq4uZPeXuRzdW/dnKy8ur91OpFKlUqqluLU2gWzcYPhxmzgySPGle0uk06XQ67jBERBIv13nsRtR2\nCXjC3UsbXHnN+/QBHtfgiebtV78K5rO7+ea4I5G4afCEiEi0XFvs5gOzarnWMce6ATCz+4AyoKuZ\nrQCucPc/56NuKSzjxsFZZ8UdhYiISHLl2mK3CJjg7m9HXFvh7j1zCW4X4lCLXTOwfTv06BGsHdur\nV9zRSJzUYiciEi3XwRPlddQxOce6RWpo0QK+/e1gEIWIiIh8VU6Jnbs/6O5v1nLt4VzqFoky8he3\n/wAAEz9JREFUbpwSOxERkdrkPN2JmQ00s7Fm1i7r/Phc6xbJ9u1vw3PPgXreRUREviqnxM7MJgOP\nAD8BFpnZiRmXr8+lbpEovXpBmzbw9lee6hQREZFcR8WeCxzs7pXhlCQPmVkfd/9dzpGJ1GLMGJg1\nCwYMiDsSERGRZMm1K9bcvRLA3ZcCKeBoM7uJYC47kbw7/HCYPTvuKERERJIn18RujZkNqzoIk7zj\ngK7AkBzrFolU1WInIiIiNeWa2E0EVmWecPct7j4RGJNj3dXMbLyZvWlm75jZpfmqVwrTgAHw5Zew\nfHnckYiIiCRLrondJ+EGgJkdYGYXmtlJ7j4nx7qr6twNuBUYDwwCzjSzgfmoWwqTmbpjRUREouSa\n2D0N9AYws/7AXKAv8GMzuyHHuquMBN5196XuvgW4HzghT3VLgRozRomdiIhItlwTu07u/k64/z3g\nXnf/CXA0wbN2+bA3sCLjeGV4Tpqxww+Hioq4oxAREUmWXKc7yZwmdizwawB332xm23OsO+oetSov\nL6/eT6VSpFKpPN1ekmjoUPjoI1izBrp3jzsaaWzpdJp0Oh13GCIiiWeewxT+ZnYP8BHwIXApsK+7\nrzezzkDa3YfmHKDZIUC5u48Pjy8Htrv7rzLKeC6fQwrTMcfAOefASSfFHYk0NTPD3TWlkohIlly7\nYn8ArCV4zu5Id18fnh8ITMmx7iovAfuZWR8zKwFOBx7LU91SwDTtiYiISE05tdg1FTM7GvgdsBtw\nu7tfn3VdLXbN0AsvwH//N7z8ctyRSFNTi52ISLRcu2KvrGdRd/erG3yjncehxK4Z2rwZunaFlSuh\nY8e4o5GmpMRORCRaroMnlrHzwQ1WjzIiu6ykBEaOhDlz4Nhj445GREQkfjkldu4+LU9xiDRI1XN2\nSuxERERyHDxhZpPMrNbk0MxKzOz7udxDpC4aQCEiIrJDrl2x7YD5ZvYmMJ9g3VgDSoGvAwcAf8zx\nHiK1GjUKXn8d1q+Htm3jjkZERCReOY+KNTMDDgNGA73C08uAOcALTTGqQYMnmrfDDoOrr4axY+OO\nRJqKBk+IiETLtcWOMKOaE24iTa6qO1aJnYiINHd5mcfOzG4hGPla9S9oB9YBL7n7oznfYOf3V4td\nM/bMM3DNNcHoWGke1GInIhIt15UnqrQGhgFvA+8AQ4GewH+Z2e8aWqmZnWpmi8xsm5mNyE+oUmzG\njIHXXoPPPos7EhERkXjl3BUbGgIc5u5bAcxsKkHX7GhgYQ71LgQmAP+bc4RStNq0gdGjYeZMOPnk\nuKMRERGJT75a7DoRjJCt0g7oEiZ6Gxtaqbu/6e5v5xqcFL/x4+Hpp+OOQkREJF75arG7EXjFzNIE\nz9mVAdeZWVvg2TzdQ6RW48fDlCngDqYnr0REpJnKObEzsxbAmwRTnowkGDjxS3f/ICxyyU7eP4Ng\n3rtsv3D3x+sbR3l5efV+KpUilUrV961SBPbfH1q2DOa0Gzo07mgk39LpNOl0Ou4wREQSL1+jYl91\n92F5iKe2+p8HLnL3l2u5rlGxwiWXQOvWwQhZKW4aFSsiEi1fz9g9a2anhJMVNxb9n7jU6dRT4YEH\ngu5YERGR5ihfLXaVwB7ANnYMlnB375BjvROAm4FuBPPiveLuR0eUU4ud4A59+8Jjj8GQIXFHI41J\nLXYiItHyktgBmFkXYD+COe0AcPeKvFS+83srsRMAfv7z4Fm7a6+NOxJpTErsRESi5avF7gfAZGAf\n4FXgEGCuu38r58rrd38ldgIEgyeOPRbefx92z9eYb0kcJXYiItHy9YzdBQQjYpe5+xHACIKuU5Em\nNWQI7LMPPPlk3JGIiIg0vXwldhvdfQOAmbV29yXAgDzVLbJLzjsP/ldrlYiISDOUr8RuhZl1Bh4B\nZpjZY8DSPNUtsktOOw3mzYN33407EhERkaaVt8ET1RWapYAOwNPuvjmvldd+Tz1jJzVceSWsWAF3\n3BF3JNIY9IydiEi0vCd2cVBiJ9k+/RT694eXXgqmQJHiosRORCRavrpiG4WZ/drMlpjZa2b2NzPr\nGHdMUhg6d4Yf/QiuuiruSERERJpOolvszGwcMNPdt5vZDQDufllEObXYyVd8/jkMHAgPPgjf/Gbc\n0Ug+qcVORCRaolvs3H2Gu28PD+cRzJMnUi8dOsCUKfDjH8PWrXFHIyIi0vgSndhl+U9As5PJLjnj\nDOjRQ12yIiLSPMTeFWtmM4DSiEu/cPfHwzK/BEa4+8m11KGuWKnVqlUwYgTcfTd8q0nWQpHGpq5Y\nEZFosS+65O7j6rpuZpOAY4CxdZUrLy+v3k+lUqRSqdyDk6JQWgp33QVnnQUVFTBAU2cXnHQ6TTqd\njjsMEZHEi73Fri5mNh74DVDm7v+uo5xa7GSnpk0LumTnzIG99447GsmFWuxERKIlPbF7BygBPglP\nzXX3H0WUU2In9TJlCkydCjNmQL9+cUcjDaXETkQkWuxdsXVx9/3ijkGKy8UXB6NlDz8c7rsPysri\njkhERCR/Et1iV19qsZNd9cwz8L3vwQUXwCWXwO6J/ieOZFOLnYhItEKa7kQkb446CubPh2efhZEj\ng6XHRERECp0SO2m2evYMEruf/hSOOw7OPBPeeivuqERERBpOiZ00a2YwcSK88w4cdBCMHg2nnALP\nPQfq3RcRkUKjZ+xEMnzxRTCR8f/8T7AM2ZlnwqmnwqBBcUcmmfSMnYhINCV2IhHcYe5ceOABeOih\nYCTtMcfA2LHBiNp27eKOsHlTYiciEk2JnchObN8OL74I//gHzJwJCxbA0KEwahR84xvB1q9f0K0r\nTUOJnYhItEQndmZ2DXA84MBaYJK7r4gop8ROmsz69UFr3ksvBSNr588PunAHD4aBA4Nt0KDgdZ99\nYLfd4o64+CixExGJlvTErr27fxHu/wQY6u7nRJRTYiexWrMGFi+GJUtqbh9/HCxf1rs39OkTvPbu\nDXvtFaxhW1oK3bop+dtVSuxERKIlOrHLZGaXAx3d/bKIa0rsJJE2bYIVK2DpUli2bMfrRx/BqlXB\n9tln0LUr9OgRJHrdu0OXLtC5847X7P3OnaFVq7g/XXyU2ImIREt8Ymdm1wLfBb4EDnH3zyLKKLGT\ngrVlS9Cyt3p1kOitXg2ffhpsn3wSvf/pp0ErX/v2wUCOqtfM/exzbdtC69bQpk2w7Wy/Zcu4v5na\nKbETEYkWe2JnZjOA0ohLv3D3xzPKXQYMcPfvR9ShxE6aFXfYuDF4tq+ycsdrbftffBE8G7hxI2zY\nsOM1cz/71X1Hkte6dbCVlARbq1Y79rO37GuDB8OkSfn9/ErsRESixb5CpruPq2fRe4Ena7tYXl5e\nvZ9KpUilUjnFJZJkZjta2Lp3b5x7bN1aM9nbuBE2b665bdq083Nt2uQeSzqdJp1O516RiEiRi73F\nri5mtp+7vxPu/wQY6e7fjSinFjuRZkQtdiIi0WJvsduJ681sALAN+BdwfszxiIiIiCRWolvs6kst\ndiLNi1rsRESitYg7ABERERHJDyV2IiIiIkVCiZ2IiIhIkVBiJyIiIlIklNiJiIiIFAkldiIiIiJF\nQomdiIiISJEoiMTOzC4ys+1m1iXuWERERESSKvGJnZn1BMYBy+KOJVeFstZlocQJhROr4hQRkaaQ\n+MQO+C3w87iDyIdC+aNZKHFC4cSqOEVEpCkkOrEzsxOAle7+etyxiIiIiCTd7nEHYGYzgNKIS78E\nLgeOzCzeJEGJiIiIFCBz97hjiGRmBwIzgS/DU/sAHwAj3X1NVtlkfggRaTTurn/oiYhkSWxil83M\n3gcOdvdP4o5FREREJIkS/YxdlsLIQEVERERiUjAtdiIiIiJSt0S02JnZeDN708zeMbNLaylzc3j9\nNTMbvrP3mlkXM5thZm+b2T/MrFNWfb3MrNLMLkpqnGY2xMzmmtkbZva6mbVKWpxm1trM7gvjW2xm\nl9UnxkaO9VQzW2Rm28xsRFZdl4fl3zSzzIE5ccd5cMb5cWb2UvidvmRmRyQozhER9SXlt1TXf/cG\n/ZZERAqOu8e6AbsB7wJ9gJbAq8DArDLHAE+G+6OAf+7svcCNwM/D/UuBG7LqfAj4C3BREuMkGLH8\nGnBQeNwZaJHAOCcB94X7bYD3gV4xf6cHAPsDzwMjMuoaFJZrGb7v3Zi/09riHAaUhvuDCab8Sdz3\nmcDfUm3fZ4N+S9q0adNWiFsSWuxGAu+6+1J33wLcD5yQVeZ44E4Ad58HdDKz0p28t/o94euJVZWZ\n2YnAe8DiBMd5JPC6uy8M6/vU3bcnMM6PgLZmthvQFtgMfF6POBstVnd/093fjrjfCQRJ6BZ3X0qQ\nIIxMWpzu/qq7rwoPFwNtzKxl0uKEZP2W6oizob8lEZGCk4TEbm9gRcbxyvBcfcrsVcd7e7j76nB/\nNdADwMzaEaxkUZ7kOAlaHtzMnjazBWZ2SRLjdPdnCBK5j4ClwK/d/bOYY63NXmG5XXlPHHFmOhlY\nECYxiYozgb+l2uxHw35LIiIFJ/YJiqn/aNf6zFllUfW5u9uOue7KgZvc/Usz25V5sJo6zt2B0cDX\ngQ3ATDNb4O7PJSlOMzuboAt2T6ALMNvMZrr7+/WoP5+xNlR9YoglTjMbDNxAsFZyfTR1nOXE/1uq\nj5Y07LckIlJwkpDYfQD0zDjuSc1Wlagy+4RlWkac/yDcX21mpe6+ysz2BKomNR4JnGxmNwKdgO1m\ntsHdpyYszhXALA/n7TOzJ4ERwM7+GDV1nN8EHnb3bcDHZvZ/BH9A65PY5TPWqPfu7H6Zny9JcWJm\n+wB/A75bzyQ5jjiT8FuqT5wN/S2JiBSeuB/yI0gu/0XwMHQJO3+Q+hB2PEhd63sJHva/NNy/jKzB\nE+H5K4ELkxgnwQPeCwhaw3YHZgBHJzDOycAd4X5bYBFwYJzfacZ7nyeY1LrquGrwRAnQN3y/JTDO\nTgQP+5+YhN9SbXEm7be0k+9zl39L2rRp01aIW+wBuDvA0cBbBA+zXx6e+yHww4wyt4bXX6PmiLev\nvDc83wV4Fngb+AfQKeK+9f5jFEecwH8AbwALiUhMkxAn0Aq4O4xxEfUcGdnIsU4gaKXZAKwCnsq4\n9ouw/JvAUUmME/h/QCXwSsbWLWlxJvC3VNd/9wb9lrRp06at0DZNUCwiIiJSJJIwKlZERERE8kCJ\nnYiIiEiRUGInIiIiUiSU2ImIiIgUCSV2IpIXZvYTM1tiZm+Y2a9qKXOBmS0My1yQcX6omc01s9fN\n7DEzax+eLzGzP4fnXzWzsqb6PCIihUiJnYjsEjNLmdmfs84dQbC+6xB3PxCYEvG+A4FzgG8AQ4Hj\nzKxfePlPwM/dfQjwMFC17NcPgO3h+XHAb3ZxlQsRkWZFiZ3Exswmm9liM7sr4tpBZnZHxvF4M5sX\ntgi9Ymb3m1nP8No0Mzs56/2Vddy3lZnNMjP9779houZIOh+43sM1bd3944gyBwDz3H2jByuVVAAn\nhdf2c/fZ4f6zBGvkAgwkmHC4qs7PCFY2ERGRCPrDJnE6H/i2u3834tolwO+huqXnZmCiuw909+HA\nPQSrD0CQaGQnG7VO0Ojum4DZwIk5Rd98RbWY7QeMMbN/mlnazKKSrzeAw82si5ntARxLsFQYwCIz\nOyHcP5Udy4a9BhxvZruZWV/g4Iz3iIhIFiV2Egszuw3YF3jazH6ada0VcIi7zw9PXQpc6+5vVZVx\n98czWniglgXjzezqsIXvFTP7IKMV8DHgzHx9nuYgTNpeAf5IkGxVfa9HEizV1dndDyFIyh/Ifr+7\nvwn8imDlkqcIVtTYHl7+T+BHZvYS0A7YHJ6/g2At2JeAm4AXgG2N9BFFRAqeVp6Q2JjZ+wRren6S\ndf4Q4Jfu/p3weAEwyd0X1lLPNGAMsC7jdD9375BRpiNBK9333P2VMHl8z933zudnag7CAQyT3P37\nGeeeIliqqyI8fhcY5e5r66jnOmC5u9+WdX5/4C53HxXxnv8D/itMEkVEJIta7CSJegMfRV0ws67h\n6Mi3zOyi8LQDF7v78KqNjBa88GH7e4DfuPsrUN0d28LMWjfqJylOUa2jjwDfgurErCQqqTOz7uFr\nL4K1Xe8Nj78WvrYgWCu3qhu+jZm1DffHAVuU1ImI1E6JnSSRUzN5WETwbBXuvtbdhwF/IOiyq1LX\nSMlygpahO7POG3U8iye1inqm8Q5gXzNbCNwHTAQws73M7ImMcg+Z2SKCrvAfufvn4fkzzewtYAmw\n0t2nhed7AAvMbDFBF2/U85giIhLaPe4ARCIsA0ozjm8EHjazf2a01rSlHkmZmX0HGAsckXW+FbAt\nbLmTXRB2t1ZkndtCRNLl7h8SDJKoOh5TS503EwyQyT6/lGA0rYiI1IMSO4lTbYnZa8CA6kLuVZPZ\nTjezDsC/CZK/K+uoq+r4Z8BewIvh9GePuns5MByYm+sHEBERSRINnpBECgdE/N7d5zVS/dcB8939\n4caoX0REJA56xk6SagpwXmNUHHbDjiZ44F9ERKRoqMVOREREpEioxU5ERESkSCixExERESkSSuxE\nREREioQSOxEREZEiocROREREpEgosRMREREpEv8fTEUqcFwqQWwAAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x13941b30>"
]
}
],
"prompt_number": 85
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here, we see that the amplitude signal completely vanishes in the noise"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Fit the signal:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"IMPORTANT: In the presence of a lot of noise, it is necessary to specify the electric delay by hand"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"port2.autofit(electric_delay=0.)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"WARNING: Lorentz fit failed, trying phase fit\n"
]
}
],
"prompt_number": 86
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"...and plot the result:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"port2.plotall()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAFHCAYAAAAsmgFsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4FFX3xz83gQCBhN5Db9KLgogoRaXaRRFRUFRsKCj6\n+lNURMX2ig0VQYEXK1YQRZolCAiI0pEqNSAtdEJJub8/boadnczszm52s9nkfp5nn92duTNzdnb3\nznfOPfccIaVEo9FoNBqNRhP9xETaAI1Go9FoNBpNaNDCTqPRaDQajaaAoIWdRqPRaDQaTQFBCzuN\nRqPRaDSaAoIWdhqNRqPRaDQFBC3sNBqNRqPRaAoIERV2QohJQoh9Qog1Dus7CyGOCiFWZD+eymsb\nNRpN4cZFP3WeEGKxEOK0EGK4Zd12IcTq7P7rj7yxWKPRFGaKRPj4k4GxwEc+2syXUl6dR/ZoNBqN\nFX/9VCrwIHCtzToJdJZSHgqTbRqNRuNFRD12UsoFwGE/zURe2KLRaDR2+OunpJQHpJR/AukOTXQf\nptFo8oz8HmMngQ5CiFVCiB+FEE0ibZBGo9EEgAR+EkL8KYS4O9LGaDSagk+kh2L9sRyoIaVME0L0\nBKYDDSNsk0aj0bjlYinlv0KIisA8IcSGbA+gRqPRhIV8LeyklMdNr2cJId4TQpSzxqsIIXTBW42m\nkCGlzPdDnFLKf7OfDwghpgHtAC9hp/svjaZwEq4+LF8PxQohKgshRPbrdoBwCkKWUub7x8iRIyNu\nQ0GyM5ps1XaG9pFP8eqkhRDxQoiE7NclgW6A7czaSJ/PgvTbiCZbtZ2F004pw9uHRdRjJ4T4HOgE\nVBBC7AJGAkUBpJTjgT7AfUKIDCANuDlStmo0msKJv35KCFEFWAYkAllCiKFAE6AS8G32vWkR4FMp\n5dwIfASNRlOIiKiwk1L287P+XeDdPDJHo9FocuCin9oL1LBZdQJoFRajNBqNxoF8PRRb0OjcuXOk\nTXBFtNgJ0WOrtlMT7UTTbyNabNV2hpZosTPciHCP9eYFQghZED6HRqNxhxACGQWTJ9yg+y+NpvAR\nzj4sX8+K1WjyK9lxU5o8QIsejSa06P4rb8nrPkwLO40mSLTgCD/6AqTRhAfdf+UNkejDdIydRqPR\naDRRzOTJcPZspK3Q5Bd0jJ1GEwTZ8RGRNqPA43SedYydRuNBCJg/Hy691G173X/lFZHow7THTqPR\naDSaELNuHbz/fqSt0BRGtLDTaDQBkZycTI0admnbNBqNwQsvwH33RdoKjZXC0H9pYafRaMLG//73\nPy655JJIm6HRaDQBE639lxZ2Gk0BJSMjI9ImaDSFFh3Cljt0/xU8WthpNAWI2rVr8+qrr9KiRQtK\nlSrF6NGjqV+/PomJiTRt2pTp06efa1urVi2WL18OwKeffkpMTAzr168HYOLEiVx33XUAnDp1ittv\nv51y5crRtGlTli1b5nXMl19+2fYY69ev57777mPx4sUkJCRQrlw5AGbOnEnr1q0pXbo0NWvWZNSo\nUWE/L4WRvXu1uNBEF7r/Cg1a2GmiglOnYNgwyMqKtCX5n6lTpzJr1iyOHDlCo0aNWLhwIceOHWPk\nyJHceuut7Nu3D1Dld5KTkwGYP38+9erVY/78+efeG+V5Ro0axbZt29i6dStz5sxhypQpXrmZ6tev\nb3uMxo0b8/7773PRRRdx/PhxDh06BECpUqX45JNPOHr0KDNnzmTcuHF89913eXeCCglVq4LpOphv\nEAKOHo20FZr8iu6/QoCUMmIPYBKwD1jjo83bwGZgFdDaoY3UFGzmzZMSpFywINKWKPz95pSvJPeP\nQKldu7acPHmy4/pWrVrJ7777Tkop5cSJE+XVV18tpZSycePGcuLEifLmm2+WUkpZq1YtuWLFCiml\nlHXr1pVz5sw5t48JEybIpKQkV8eYPHmy7Nixo0+bhw4dKh9++GHbdU7nOXt5vuingPOAxcBpYLhl\nXQ9gQ3Yf9rjD9j7PT7CAlB98EJZd5wqQcsuWSFsRfm66Kbj/cDCAlMnJgbTX/ZebY+S2/5IyMn1Y\npD12k1Edny1CiF5AfSllA2AwMC6vDNPkL375BcqXhy++iLQl7ghV1xgM5hlfH330Ea1bt6Zs2bKU\nLVuWtWvXkpqaCsCll17KggUL2Lt3L5mZmdx4440sWrSIHTt2cPToUVq1agXAnj17vPZZs2ZNr+P5\nOoYdS5cupUuXLlSqVIkyZcowfvx4n+3zAT77KSAVeBB4zbxQCBELvJO9bROgnxCicbiMtCPY31C4\n0QVF8je6/4ru/iuiwk5KuQA47KPJ1cCU7LZLgTJCiMp5YZsmf/Hzz/Dyy/DVV6Bjan1jDDPs2LGD\nwYMH8+6773Lo0CEOHz5Ms2bNDC8R9evXJz4+nrFjx9KpUycSEhKoUqUKEyZM8JoJVrVqVXbu3Hnu\nvfm1v2PYldO55ZZbuPbaa0lJSeHIkSPce++9ZOXjMXZ//ZSU8oCU8k8g3bKqHbBFSrldSpkOTAWu\nCZ+ldrbl5dHco4Wdxgndf+WeSHvs/FEd2GV6nwIkRcgWTYQ4elQl+7z1VkhKUhnWfbW97Ta46CLo\n3x9Gj4YzZ7zbfPIJJCSoi4sQ6vWiReH9DJHg5MmTCCGoUKECWVlZTJ48mbVr13q16dSpE++88w6d\nOnUCVNyK+T3ATTfdxEsvvcSRI0dISUlh7Nixro9RuXJlUlJSSE/3aJ4TJ05QtmxZ4uLi+OOPP/js\ns88Kak1Yu/6rel4aoIWdJlrR/Vfw5HdhB2A9Y/m0q9L4YtMmWLPGXdv0zHSOnTnG3hN72Xp4Kx/P\nXkeTy5fxx77fuKDPfN6c9hsLdixg4c6FLNq5iN93/c7iXYuZOn85LbpuQJTZxdMvptK12yl+TZY8\n9JDab2Ym/Oc/MHIk/P67ep+VBV9/DTfcABs3hu/zR4ImTZowfPhwLrroIqpUqcLatWvp2LGjV5tO\nnTpx4sQJLs2uRWR9DzBy5Ehq1apFnTp16NGjBwMGDDjXkfk7xmWXXUbTpk2pUqUKlSpVAuC9997j\nmWeeITExkeeff56+ffuG+1REioj3VVrYaaIV3X8FT8RrxQohagPfSymb26x7H0iWUk7Nfr8B6CSl\n3GdpJ0eOHHnufefOnc/NiNEEx7FjULIkxMbarz91ClasUB6yLl2geHHf+2p5QRqHM1MY+swu6rZM\nYdexXew9sZeDaQdJPZXKwbSD7D2aytH0g5zJPEPJoiUpSgmKEk/asRIkloindlJx0s/GsHyFpF07\nCUIFimZmSv7dK9mz7yyVqp8ktkQaaelpnDx7kiyZRdbJcpSPL0f60fLEni1H90sqUKdCNZISk6ie\nWJ3qCdX57YckXnu+At27CcqUgXLloGVLaN9exfZZ0bUW8wbjPCcnJ5+bAQdqppvMw1qxvvopU5uR\nwAkp5Zjs9+2BZ6WUPbLfPwFkSSlfsWwXlv5LCHjvvfxX/UAI2LkTCnjyf/r2hS+/zBtxLQQkJ4PJ\nUeWnve6/8opI9GH5Xdj1AoZIKXtld5JvSinb27STkf4cBYn9++H886FMGRXX1q0b3HEHFC0KjRvD\n3XfDRx/Bf/+rhkZPnlTDm42anmbLoS1sSt3ExoMb2XRIPS/fvpmM2ONULZnEgS01aJyURI+LalA1\noQoV4itQIb4Cv80uz1svVaBYVnl6dyvJ0iUCKaFOHShRAl59FRo0UPZ16ABPPQWdO6tajK++qopf\nP/88NGrk/VnOZJxh2bpD9Lz+EN2uPkS/O1M5fOYAu4/vZvex3ew+vpuUYynsPr6btDNnqBBTj7Ky\nAfGnGnBsewO2L29AnZJNmfVtOcwxt7pjzBsiUUDbwY7a+Bd2zwLHTcKuCLARuAzYA/wB9JNSrrds\nF5b+Swh49124//6Q79qWa66BAQOU99ufXbt2qb6jIHPTTSomWAu7wk0k+rAi4dipW4QQnwOdgApC\niF3ASKAogJRyvJTyRyFELyHEFuAkcEfkrC0cZGXB2rWQnq6GLR99FIoVU565p5+G336D+vWhcu1D\ndBm0gubdlzNt8QrOn7wcUXY75YvURh5oyEUNGtG9bQdKbLyD1B8bsvy3ypQsKdi9G666Cn7/ScXB\nFa0F+8/A+NGwbIHy/M2YAYPvVgLObsjm5pthxAjYt0/tY+5caNHC/vMUK1KMji2rsm9NVeLjfX/2\no6ePsuXQFjYf2szm1M1sPpRMQpcJrNr9Nw3eK8MVzVvRumpLWlVplfsTrYka/PVTQogqwDIgEcgS\nQgwFmkgpTwghhgBzgFhgolXUhZu8vHbPmKE8/P6EHeih2HCgdZrGIKLCTkrZz0WbIXlhiwaOHIF6\n9ZSX7pprYOZMFRc3cVIWe9LXcab5QjLKLCK++SL+OZ5KbGIryh1rzb2Xd+eZrP/jhWGN2bOrKE88\nAZMnw/DHoHVrmPGZGtYFqF4dFi5UYmzNGli5EmJilAfwvPNUGyMmzol+/dS299+v9u8Gf6IOoHTx\n0pxf7XzOr3a+1/LMrCx63rKNzLMrEVet4qPVH7k7qKZA4K+fklLuBWwHFqWUs4BZ4bDLDXl9sc/M\n9L3esMdO2B04ABUqaNGn0eSWiA/FhgI9FBs6hg2Dt96StL5iE+vTZ9Og+zx2iUVUjK9Ix5od6Viz\nIx1qdKBh+YbECO+5N1lZcPasJ94uJUUJuYLQUR89Ck2aqJiZiy/WQxl5RX4Zig0n4RyKffttePDB\nkO/a8Xi9e8MPP3gvP3VK9QlCKOFXpIinb7Bub0xkKgjk9VDsr7+q8BR37XX/lVcUuqFYTeSYPh1O\nnFDer9hYOHH2BPP+mcexTrMpUnQO64pkkrGhOxu+GMDcDybS+QL/6QNjYrwnURSkGJrSpWHMGOUl\n7N070tZoNO7YtAmmTIGBA921/+QTFTN7zz3BHc/OYxcfDx9+CHfe6SkJ6KQp9u6Fyy6DBx6A668P\nzoaCTkqKmngSiC6bOhXWr4d8WNZUEwaiId2JJpccPQoNG6rO2kjpUb483DP0MDWu+oi2r19Dlf9W\n44lvxxF7uBHXpf3IZat3svbFDzm/+E08NEjnhAY1y615czXLV6OJBt55B26/3X37++6De+8N/nhO\nQ7H//KOe/Qm7jAxVZebbb4O3wS1ZWe4FbzCEyyFmyq/rmuefh+eeC70tmvyJ9tgVMFJT4corVZzc\npZeqYZCTJ2H3bli9Gjp2Pk3Nbt+R2WwKGQ8u5MA/Xfl3Sh+KbptCqYZl2FleJex95WU1A3bhQli8\nONKfKn8ghPJogJptqNFovPEXY+dP2Bnb58Uo4alTKrZ3ypTQ7O/MGTVqUbRoaPbnhB5B1fhDC7sC\nRkICLFlijbWQFK+/lGWV/0f8lV9xKuZ8Sm4YSJstX/LHwlKQBd16w5tvqhmvZmJjwZITUqPRaLww\n4mitwi4tTT0bYsSNx868fssWmDcvZy6+p55Sw7t79+bO7lDSoIFKEzVtWniPE4yw02KwcKGHYgsY\ncXGq83zvPaDIKUpd+iHN3m1JhcEDuKRFTV6qtZK/n5jLson9WTy/FD//rDx7M2fmzfCHJvxs3LiR\nVq1akZiYSGxsLKNHj460SZooIz7eI8ICwSrsvv9ePQcr7Iy4VisLF6p0R07ExMCPP/q21bAlVGU+\nd+1SqaIM8lpM+TpeNAk73X/lHu2xKwBkZKiOLCZbpqcc28WSku/BwxM5kXIha8eM4dCfl1O2bM4J\nOJ07q8SWv/wCc+bkqdmaMPHqq69y2WWXsXLlSq/lycnJ3HbbbezatcthS41GcepUcGLAKuysQi3Q\nodhgZ9RLCX/9Bb16+bc1M9PTd+aWYsXct73lFuWJNNWrd4XTuYsm8eYL3X/lHu2xi2Lmz4eaNVVM\nR2ws9HvgH66ddBct32/JybOn6LL1d/j8e9h6Bdu2OfeQQqiZaK++mofGa8LGjh07aNKkSaTN0EQJ\nWVkq0bcVKeH4cfttRo6EN97IudwQcgZWoRaox85JcLkRMf7amIVdqIiL87z2J0o//1w9AsXf5zpw\nwL+3Mj+j+6/co4VdFFOqlHL/U/YfuHYgU0tdyG8zq3H4uc2seuVNSmd6AubatImcnZq8o2vXriQn\nJzNkyBASEhLo378/Tz/9NGlpafTs2ZM9e/aQkJBAYmIie/NTgJImYmRkqLhcK1JCYqKadGXluefs\nU2c4eewMDGE3b55KweG0fW49dm4wbDHbvHFjzjx81va+MAu7UIjPYLZ54YWcKZmixZun+6/QoIVd\nFHD99aqDu/pqOHjQs/yCSw5R7JqH4e4LuaBePfb83xZSv36OzOPl2bxZBfGeOWPfMWsKJr/88guX\nXHIJ7777LsePHycuLg4hBPHx8cyePZtq1apx/Phxjh07RpUqVSJtriYfYRUuhhjYs8d7+YED9u3B\n/VDsvfeqHJpO2/sSdlLCoUM5lweKncfu/vtVyUMr06apURF/BDIUGwx//KHKPfoimhPC6/4rNOgY\nu3xMSooa8vi//1PDrV9+CRUrAjHp3PzGWBjyMuWP9KHX2XWMfqIylcqq7cx/7Lg4lXtNk7eIUaHp\nXeXI3N9qG1nPdaZ5jR12nivwiKtTp7yXV6qknk+cUEO1CQk5tzGw7tOf18vNUOwXX3hPUjC2O3XK\n2xZ/2Ak7J1G0aVPOZQMGQMuWMHy4Z5k51UluPXYzZ6rUVeY2F14IdzhUTN+7F9at83280aOhTx//\ndun+K7rRwi4fIwRMmqQeoDx33/6xBK4azNRl1WD2fPYcbMwH+vee7whFh6bR5AXG9dKtsDOvb9rU\nO2Guk7CzeuycMISVL4+d3Qjc8OGqfFog1363wm7DBk9idzMffwxLl3oLu0C9Zb7sXbZMPb/1FrRt\nCx06qPdnzti3799fPQ8d6rzPp55SuU792qX7r6gmokOxQogeQogNQojNQojHbdZ3FkIcFUKsyH48\nFQk7I0X16rBqFZQsCcSd4NvTQyg+8DpY8CR8MgsONgY8dQI1GjtE9tVGRPMYTQQRQkwSQuwTQqzx\n0ebt7H5slRCitWn5diHE6uz+64+8sTgwzMLO/BPxJ+wgO8bXZl8GTjF2TrgRdnYYHrWUFGdbrNh5\nKu08hE2awOTJ9vuwHiPQ1CluhOiwYao+dW4wHydU6V3yCt1/BU7EhJ0QIhZ4B+gBNAH6CSEa2zSd\nL6Vsnf14IU+NzAe0bAknSy+De1pD3AnKfr6OrTNuJitLcOYM/O9/ql3XrqoTNN5rNKCGL4whjMqV\nK5OamsoxXRMtUCaj+ilbhBC9gPpSygbAYGCcabUEOmf3X+3Ca2ZwmAWOWQC4EXbmdtbX4BxjZ+b+\n+z3HsG5vJ7Tsru/Gfk+e9G2rGTuPnd3xAskPF+hoYTgmT/jTP6GcBRxudP8VHJH02LUDtkgpt0sp\n04GpwDU27Qq8TF+1Cnr2VK73kSPVH/OFF+DQ4SwGjH8F+veGn18kfu7/+HdrOerWhddfV/FzAweq\nP/qBAyplyeHDkf40mvyEEOLcne55551Hv379qFu3LuXKldOzylwipVwA+PpnXQ1MyW67FCgjhDAX\nWM7zPsw8O9OODRtyph5xGor1F6xvFmvBxNiNG+epJWvdj51I8SXswjEU6wunCSdmbr1VxQXakduk\nwhMmWKsM+SeaPHa6/wqOSMbYVQfMjvwU4EJLGwl0EEKsAnYDj0op/84j+/KM48dh9mz1MHj6+eM8\nve42iD8I3/wJR2uSXZ2HChVUEK2ZChXgp5/yzGRNPuZX07j8ZMsY0sSJE5k4cWJem1TQsevLqgP7\nUH3YT0KITGC8lPKDvDDInxhr3FhVmrnuOv/CLjMTTp9WM1GrVcu5L19CwTq06tTWKqiCFXZ2HD+u\nbnhr1lTv169Xw6t/Z19JciPsrOLryJGcbT79VHkS+/YNzG5/jBkDjz4a+Hb5Xdjp/iv3RNJj5+be\najlQQ0rZEhgLTA+vSZGhY0dLB1H2H7jrIjhRGab8AkdVj/T77+rurGVLXb9Vo8lnOEmCjlLK1kBP\n4AEhRIB1BsKHMWzpb1ZsRoaqjlC9uv1+fHns3Ao7YwjU6nlzWxHCzmNnvL77bqhVy7N8+3bvbXIj\n7LZtUxNIjCFnc7EEsy2lS9tv7xS7Z93eDn/6pkkTz0SKaI6x0wROJD12u4Eapvc1UHe655BSHje9\nniWEeE8IUU5KmSOL0bPPPnvudefOnekcqH86D6lfXw09PPkkDBoEJUrA889nr6y6HG65En4bAcvu\nx7hejBwJ7dvrSRKawklycjLJycmRNsMJa1+WlL0MKeWe7OcDQohpqBCUBdYdRLL/8jd5IjMT/vzT\nefuHHsq5jZU331Q1qc2jEmYMATdmjPd+QjEUa815Z/VQ5kbYgfL8OQ21GjgJu2DwN7HEWL5+vX3u\nvWiKsStI5GUfFklh9yfQQAhRG9gD9AW8UlZmx6nsl1JKIUQ7QNiJOvDuGPM7jz6qagS++KJ6nKPm\nAuh7A/zwPqy/3mubUaM8md7nzIFu3fLOXo0m0ljFzii7sgeRYwYwBJgqhGgPHJFS7hNCxAOxUsrj\nQoiSQDfA1vC86L9SUlSS8+XLvZcbomjnTu8SYk5DtFYmTMi5jYFZfEyfDh99ZL8Pq2fOl7fKKWmx\n03ZWceNL2AVbM9bfBBNfyY1TU6F8+cCP6UaE2p0XLewiQ172YREbipVSZqA6wznA38AXUsr1Qoh7\nhBD3ZDfrA6wRQqwE3gRujoy1oeXeeyEpybKwxiLoez1881kOUWfl/ffDZ5tGo/FGCPE58DvQSAix\nSwgxyNxPSSl/BLYKIbYA44H7szetAizI7r+WAj9IKedG4CMAqgLNihWe99aLvrVerFthZ7dNoFgF\nlSE23c6K9XVcq6gy9u1rKHb0aOf9+cNuqNOXfffc47zOF4EIOzPmvIOagolfj50QogxwEVAbFRe3\nHVgspTya24NLKWcBsyzLxptevwu8m9vj5DfOnFGxGeeylFdZ6RF1Wy+3bV+kSPB3kxqNJniklDbF\nr3K0GWKzbCvQKixGBYG5KoIZJ9ERjLDbu1fF7pUsqQTOY4+5285OpMyd635o1LAxKwv271evZ8+G\nr7+GunW921oFnZ2we+opGDHC/ljjx8Odd3ovM5/DOXNUlgOn9Va++UaViqxQwd02geT4+/vvnELz\nl1/8b6eJbhylghDiEiHEDOA3lKesJkrc9UPdhc4QQugQfhdkZcGWLeoPuXIlFC9u6mQTU+CW3vDj\nu7D1CtvtL78c0tJsV2k0Go0rijjcxjsF0/+RnU7ZmmTYF8eOQalSqraqdbtAhlelhO7d7UWlr2UT\nJ0Ll7EQzS5eqEltOQ7FGzdtAYuwyMtSIiy+vV69e3sexvrZjumVa4HnnwaxZ9m39CbvFi73fHz4c\nvCdVE5348thdBwyXUm62WymEaAjcCywMh2EFiTVroJXdfXuR08pTt/Qh+Nu7gN/o0bBkCXz/PSxY\noGog7t5tn25AExl0JnRNNGHcTH77rfdyp4v++Oyxk0CEncG6ddDDMaWzBydRaRzT+hf75RfvyRrW\n9m+9lXOdU/yeMQRq/vz+/tJG6jSrSPYnnAIVVnYlzKw42bpkifd7qyfQs73uvwoqjh47KeUjTqIu\ne/0mKeUj4TGrYNGkicOKHsPgSG1Y9J8cq0aMUKLO8PSdOqVFXX7CyIienx/16knWr/de9tnqz2g4\ntiEnzpyIuH1uH5rQYIiR1avVs3FqncSVsd5fTjwn3AzhOs1mPXvWvr2TWPRlo9ljd+CAZ/TjrrvU\n89VXq+fZs1WIjC8Mu6yfzV+cXKiFH3jy8AXDnDme/1e1ahKQ3HGHegbJnXeq50cekYwY4VkOkho1\nvN+npUmWLvVetnq1eu7d23u59ZGYmHPZY4/lXHbNNZ7XAwfa78vcxvooVcq3HebPvGGD5I03vNdF\nWx8WVNSWEOKOUBtSEDl+XN1V2WaBrz8L6s+GGR/iKzG9kXOpePFwWKgpyFx+uUpkfd118MEHalZk\nv+b9aJ/UnofnPBxp8zR5jDEJz3qd8RfLFYzHTgh32xkCyWrD/Pn2y60Czs1wsVnYVaoEgwer1/Hx\n6nnPHvXcs6f35BJf9voTgBDYUGww1/5gBTcoQX3ypPfnMDvwSpb0LLNOJLHGamZlOf+m/DkF7QS8\n3bnw970A+Mok4nSjYHfcNWvg4SjvHoMNx38upFYUUD75xEGQFTsGVw2G7ybBmUTbbf/7X/j3X1Um\nTKMJhvffV/kS+/RRnV6rViq5das9Y5m9ZQ7J25MjbaImDzFyyLkVdt99p56DERBPPZWzCoPdRd5J\n2LnFqMDjyzt45oz3e8NjF8wxjeME2i9LqeLoLr7Yfv0997iPow6FA0hKGDbMe2KJeb++khjbCTtr\ne0Ms+5vw50ZwgbuZvL5EZCDCriCU5XSMsRNCrPGxXaUw2FJgOHBA3Rk60vEl2HYZbOtqu/rOO2H4\n8OCSZWo0ZipUgP791SMzU8VrvvpqIiePj6H/yYfY8PByEkpGMp2lJq8xvFsDB6pk6TlSL1kI1jO0\nY4f3eztB4k/YzZnj7li+xM60af63cfL2LF3q/d7tDOEDB3Ime54+XVUPmjPHvvTYyZMeL6IvQnFd\nyMryCBi7c+frfFqFnZQ5hZ0xK9ifsAumCoaTbXbnNBCMKiDWG4FoxNdprwQMAK6yeaSG37ToY9Qo\n9afzKepK74TzJ8DP9omSTpyADz/Uok4TemJjVUm6H3+E2a/fwJkj5al5zWQ2O0bSagoi5gvXihX+\nPUBmYReIN8ONZ8maU86KMQSXmamSuvvbTyCY7evSxb5N+/be790Ku0qVcg7FGjb26AE3Rzgjq7XK\nCHi/N2w1KoGYsYYWZWU5n5dgUnSFKyQtIcFdu4KQwNnXrfpMoJSUMsfothBifvhMil46dHDRqP0b\nsGIQHLcvvLhlixou02jCSdu2gm8qPstNn9xFtx6DWLwolipVIm1VaBFCjHTZVEopC014iVnYlSkT\nmLArV879cdyILbtccnY4pWoJ5FhOxw5kfbAXfSn9b+tW0ISi1mtWlkd0Beqxs6aPychw/my+Km4E\nS7DCz+1S6wS+AAAgAElEQVR5GzYsuP3nJxz/LlLKQT7W+U3YWRi54gqoWNGTHykHxY5CqykwbrXt\n6k8/hbJl1Q9Xe+w04ebSWpdSr2pFag6YTp8+N7Cw4CUu2oGa1qYxYb7AlSrl/4IX7FCsmwvwa6+p\nZ7exVk4EI3b8Te6wsymSwm7NGnft3JCV5bnGGClc7OoE22G9NtWpk7clLoMVtrnxxJmFcDSgg2tC\nzKuvwh1Oc4abfqni6o7ZB7X076+er7oKZswIj30ajYEQgnsvuJc3Uj+iYvwNkTYn5Egp/xdpG/IL\nLVp4XlsvjH37+t42mFmxdsexY+pU9Xz6dHDHMAhG7AQj7Ax73eA0FBssxnf4zTe52w+oesG+hI6v\n82kVOCdO5MyNaBAK72Ko9pkbWzIyHLJb5FN8VZ5oIYRYIoRIEUJMEEKUNa37I2/Miw6MtCZC+BB1\noITdGv/Ozr/+Cp1tGo0vrml0LauPJTN46KFIm5KnFLaUTWtMU+HMF7iMDPjzT9/bBuuxcyMIDVty\nE7AuRHg8dnaf2xxzZuS/c8Jskxthl5fpzkaPVuXWzEyc6Hnty9Y1vqZVWgjmezlxwvf6cA/F2pGb\n1DKRwJdzcRzwLNAc2AQsEkLUz17nUHWwcJKQoKZjz5unsrU/8QR0tU54jT0LcSdgS0/bfRhs3qwq\nTGg0ecG0qYmUSr2UzFo/RdqUvKbQxNRZMXtq3IivYC9qbrYz2nTuHNwxDNxctJ991vt9MB47M/4E\nhtmmbdvyl7Dzhy9bT550v59gPtP48b7XB3uecjMUG6zXOlL4GopNkFJmZz7iNSHEX8BsIcSteWBX\n1FGjhno4Ewcshg/Vu4wMletn505VtPqff9SMs6pV88BYjQaVjuKxx2DQuEtYtGshfZvdFGmTQopO\n2WTP/v2e127EV7AXNbvyXlZClVrCTYzehx96vw/GY2cmEGH388/uPHxjxkDbtr7b+YzjDhGhEpnW\nGrihIDdxjsESbR47X8JOCiFKSymPAkgpfxVCXA98C5T1sZ1rhBA9gDeBWOBDKeUrNm3eBnoCacDt\ndrN0o5EiRaBmTfXQaCLB8OHqIlH8QAe+3/MIGVf4n30YZVQCegB2STp+d7sTIcQkoDewX0rZ3KGN\nbT/lpo/La374wfM6nB67X37x3yY1RImzTp3y38aa7sLfNrt2+V5vPo92WL1e/jx2WVnw6KP+vZfh\niFsLxzGqVPFMzHBDXJw7gR6sbUIEL+4CmQ2eH/A1FPsq4FXlVEq5GugKOKR8dI8QIhZ4B9XxNgH6\nCSEaW9r0AupLKRsAg1HDwxqNJgQ895wqr7RpSX02/LuN0qXhoovgwQfhf/+DtWujbwjCgpGyabv1\nAQSSsmkyqp+yxamfctPHRZpAhktzy8cfh2Y/drgZHrRe1Ddt8t3+kkuCtwdyepb8/ZeMm3w3AjDc\nhMJjZ01k7I8SJdy1C9a23MxqjaYZseA73cmn1mXZEyh2SSnvCsGx2wFbsjtZhBBTgWuA9aY2VwNT\nsu1ZKoQoI4SoLKXcF4LjazSFmiZN1GOorEz8iyf4Z2caG9fG89dfMHcuvPSSivds2RJuugmGDo20\nxYERqpRNUsoFQojaPprY9VNVgDr47+NCzrLdy+C2EeqNFJyrRW28lka+CsHbBwX0I8dy8+tNpQXU\nEc77c9i3+9cu953jOAKyimQ/Yk2vsx/Se9nGrCLQyrNse8ki0LAEpMc7PzKDnwppFWBuBfJvv/le\nH9BQZEyGiu2OO579fAKKpqmY7xyP9HOv1yaehY4ZIDJBZHkeMZb3NuvbXpjFsmVZHE7IgpPZ6wGE\n5Fz2IWGoM897mSjhmP068+slVYGb7Nf52i5LkJ1LzK6d6b3XMsXR019Runhplyc98vgqKTYS+FJK\nuV4IUQyYDbQEMoQQ/aWU83J57OqA2dmdAlzook0SoIWdRhMihBCULFqS2OIn6dQpnk6dYONGVWJn\n0iQ1hFGrVqStzNfY9VPVgWo2y619XMipXaYO/P4oYLmI5bgISi5sCWuX51xufp1YU3J0Fw77c963\nq9c+9+fvONlCIyYDYjKoUi2TvfsylHDJXmZe7/UQmRwulw6lT0PRk2oby0MUO4nMiIOTFSGtQvaj\nIhyrDofrwaH66nG0BueEpwmrsPv5Z9uvK2CyslCCquxWKLcFym+GMtug1D4oud/zKH5EfdazpdTj\nTIJ6zigBGcWUaM2Mg6yintfZj7SYOCgemy2OY0HGqEdGtmA23ssY7/UyhqTYWJbtiaFYuRhOHDSW\nOwh7OPe+TivBqo3268zbVS8u+Het/Tpf2xUpKpS4znGjYLedaRlQoqhLd2I+wVdETV88M8cGoj5l\nRaAh8BGQW2Hn1qFq/cfYbvesacpT586d6ZzbaVYaTSEiNiaW4yeymPmVSnuweTMMGKC8B+edF2nr\nIDk5mWSngp4OCCFaABNQN4M/Ao9LKQ9nr/tDStkuhCbmKqV4KPuv8iUqwD/uMsZWPAxs9N2mpAQ2\nBG1OnjHwcXjlC/ftazSDo2ud10skxJ2E+IMQf0A9lzwAibsgaQk0/xTKb1LiMeVC2NkRNl4DB9Uf\nJqSzXEUWVPsTGv5AWu1FUPlPOF0WUhsqcXm4Lvx7PpyoDCcrqcfpskrABfHTbFICNgQ5Ub7DTTDt\nL0isA6nb3G9XrwGs8vF9GFSpC/wduF1F4yE9TY1EPPFEYNvGhaCCRjB9WLD4EnZnpDz30+wBTJVS\nZgLrhRChCLHeDZjnkdZA3dH6apOUvSwH5o5Ro9G4Q0pV6Pzw8dO0aRXHpW1VAHevXoHHyIQTq9gZ\nNWqUm82MlE1LgTtRKZuullJuIbQpm+z6qZTsY/jr44DQ9l+BxGC9/LL/NtEyIzDQ8lX+hzSFx9t1\npLbXmq5d4Zfvst8kpiihV/tXyj98Oam7S8Oy+0kXA4FSgRllpdReVVu8zQfKjo1XU+SPRzm7tR2c\nKp+7ffsgNwmjFy9Wz4FWT3I7cSu3CYojFS8XZB8WFL4+4hkhRHMhREWgMzDXtC4+BMf+E2gghKgt\nhIhDeQit9RZmAAMAhBDtgSM6vk6jyT3796vUCs2awa2DTiBjzvL3X2WYMQOuuSZ/ibpckCClnC2l\nPCylfA14AJWyqb2/DQPEqZ9y08eFnFDnQ8ttua+8IvTCTnHxxTmXeYndY0nwdx/48V2mXrgTZr4H\ndX5h2cV1od1YiAlCGccdh65Pwf1NIWE3fPYDvLsefnqFmH96uhZ1wdZqzY2wM35/gQo7t31OsMLO\n+EyFoVynL2E3DPga5ah/Q0q5FUAI0RtYntsDSykzgCHAHJRj9YvseL57hBD3ZLf5EdgqhNgCjAfu\nz+1xNZrCzrZtUL06PPkk3HknTP91J7XLJVGtWoHr8aQQ4lzEs5TyV+B64BPAdaIhIcTnqPQojYQQ\nu4QQg9z0U059XGg+mjOhnjUZLTOjA03V41bY2YkjJ7FbtEgM7OgEX35D46U/Q6MZcHc7qLjOvWG1\nk+GBplBmO7y/En4YD/tanlsdyPcbiLAzl0vLTX5BwyPmT0CVLg0//uh5n1uPnVtPXLTNcA0GX7Ni\nlwCNbJbPRKURyDVSylnALMuy8Zb3Q0JxLI1Go6hdGxYtUslDP/gAXvj+T8q3b8NPP0GnTgXGWwee\nlE2LjQVSytVCiK7AM2534mYGrVM/ZdfHhZtQe+wK71CswioEGjd2FnZmG4ofaw4/z4U2H8IdnWD+\nM7D0QRxj3mLSocsz0GoKfDfRsUpRIN9vICLGXAvVSdj17g0z/Vz93Qq71q2hp+kj5tZjV6SIO+9y\nYRB2vmrF3u4rlk4IEVfY6i0GSkqKunC2bQsiNgPR/HOEkOfqyjo9Ps2RaEajCR1CQLt28OKLsH49\ndL9zCQ1LtufJJ1VS0QEDYNq0wEoH5UeklJ9KKRebl4U4ZVO+JNQeu0gMxf4RRDVyNx6f/v09r92e\nJ7NYa9YM7rrLc06sufnMbZVwFLD8bvhwCbT4BPr3hpI20URltsGgS6DyauWl81F6MpDvNxARYxZW\nTvWD3YhKQ9D5E3ZWIefWY/eTw6QOt8KwUAs7VNTnMiHE50KIR4QQtwgh+gshhmcPTSwFomsOcJjJ\nyoKHHvIItBo1VALYP/9ETQm//Amo6H86z/btYTdVowFASsnvB2fyyuAr+OMPWLVKibvrr4dWrfJX\n/cpAEUKMNBICCyGKCSF+Bf4B9gkhroisdeGjIMTYlQ2itpGbC3arVp7XwQzFTpqkPE3GTY9VZJnb\neq07VB8mLoJ/28C9rZUXr/hhKPUvXPyKGq5dd5OKpTvpu9qdL7s3b3a2xx+hqjpjCDp/34fVttwe\n3+32ZsGZ2yTU+RXHUy+lfAdoA7yLKnTaEbgYNXz7DtBGSvleXhgZLUgJH33ktFbA3zdA889s1958\ns4o3yMyEESPCZqJG48Ufu/8gvmg8TSs2ZdkyNSN24kT1/MsvUR9o3BdPog5zyqZOwIuRMirchNpj\nF4mh2GCO6ea3ah5uDGYoNj5elZc6eFC99yXscgjsrKLwywvw5dfQ6Dt4uKaKpau8GiYthMWPYB6m\ndfJM+cJaojIQseTG4xVKj51V2AVbA9bA32e94AL1XKyYZ1nTprk7Zn7Fp6aWioVSypellPdnP16R\nUi4ypULRZBMbC0eO+Giw4k5oPdl2ltTUqSrFxJ494bNPo7EyacUk+jXrx4svCnr2hAsvVJMr/vtf\n5XGOcmxTNmVPYChYVXFNhFrY5faCGwxOEzauvDJ3+zWLtGCFXfnycOKEeu9L2K1a5bDDXR3g8+/h\npePwyiH49lNIzRHOTosW7uxzOj54ixh/hFrYOWFk+bAKsfk2Rf4uu8x+H+VtJgX7s79oUViyBK69\n1rPMlxgcF8UFTP12bkKIusCDQG1TeymlvDqMdkUl27fb/zjPcaAJHKoHTb6BtTefW3zddeo5JgbW\nrIGkpLCaqdEAcODkAb78+0s2DtlIaiV48001NJGYGGnLQsYZIURzYC8qZdOjAEIIQWhSNuVL8tst\n9wUX2MdsFSniLOCclleu7HwcNx47s0g7cMB/e/AWS/Hx3sPEvoRdbgnGW24d/qxYEfbudbdtMJOm\nhg6Ft96yt8Fs/+DBMGGCen3HHcrraU0jY3f84sXtj2s3ucPNUPyFF0Jqque9L2EXTDhAfsHNXet0\n4EPge8D4GeezriPypKVBnTouGv72FPR4GNbdqEqzoALVDb75RsXpXXKJSvT49NNQpkx4bNYUbt5Y\n8gY3NrmRSiUrUakxvP8+9OmjLsIVKkTaupBgpGyqiCllE9CLEKRsyq9YxcZll4WunFWgTJsGlSp5\nX8QvvVRVNClTxjOkaSWYFCuBCju3xMYqQZeWpgrVm4dz85uws25TyXe4nhcJCYEfz+58GjcW5huM\n4sVh9WrlhSxaFIbYzCG3E3ZOXlW7PHv+zpfdELEvYRfNYShufuanpZRvSyl/kVImZz98+aUKJfHx\n6ocsJXz/vY+G/3SDU+Wg5ceOTd5+G268EV5/XSWS1WhCzY4jOxj/13ie6eTJ+tGsGZw6pdKgFBD+\nBboBrYGPhBA1hRA1gbXA/xnvs5cVGKweu1CKjXLlAmsvRM4L9ujR6tnXDWubNoEdJxB7AiUmxrNd\niezpghdmV/y1CrtQDoPnRlisXKme3ToFNm9W/38Du0IoQuT8bdnZaIgx87moWNGzfyfPoN3y9HR1\nw2nFvO+uXZ1tsaMwCDs3HruxQohnUUk2zzlApZQF9o43t/j23AmY/SbcciVsulIVlrbhtddg+PCw\nmKfR8Oi8RxnSdghJiWrcf8oUNWHihRdU0uICwhTcjy50CacheYl14kEo0zsEerGzE3aGPU4eogsv\ndBajvoaZ3Xj5NgRR8zY21mOP8VmM82AVcqGcaOLme7viCphnU7Xd8Cq69cLVr+/93u782wk7u+/D\nOCdmb9tjj3nOWSDC7uxZNUvfFz//rPZdsaJKMeYPLewUTYHbUB2f+WdcYDrCUNOokcpF17w5NGli\n8+PZcwGs6QfdH4Fp3tNou3WDZ56Biy7KO3s1hYupa6eyZt8axveYwqefqjvi1FQ1C7Z580hbFzqk\nlJ0jbUMkcCvsRozweM/cEszFznrBtnq/rPgSb77WuUnL4hSz5SveLzY2Zx9ufIY+feCBBzzL7YL6\ng8XNufYXTxlsvKwh7L77TpUYdGsPqJGmr77yFnbmSRxOYspOTKane5Ybw+F27Nqlfk92ISRSetvu\nVthFc747N6bfCNSRUnaSUnYxHuE2LJopUgRuuUVdJGNiHOIcfn0eqv+hklaamDsXOnaE93QiGU2I\nycqCFf+k8MD3Q7lg10ecVy+eKVNg2DA1g68gibrCjFXgOF2gnn8+8ItXMBc7J4+dk8jyhS8hU6eO\nKpPnC6eYrZIlvd+bL/52gsOww9q32wXcB5Ns2WpDsAQTN/frrx7B06uXZyayr3g6M8bkP18VIuyw\na28WdmXKeGJFzXGOxjH9iWodY+fNGiCK54dEFiEc/thnS8FXX0L3h22TFocyLkZTuNi/H156CR58\nEG64Adq3V/mtiiecot2Y64hb8TDVacfvv6sbiRtuKFBlxAo9bj12RiJ1M/5uKEPhsTPsyY3Hrm9f\n+/X/+Y9vW9xOyjDbYHeerDYaiW7tzk+w/y1f53r2bHs7rFgFkBtKlPBcf4oU8cSMx8R4hKLxmXwd\n306o/fNPTpuMeEC79mfPesRXsWKeeLoePaBly5zt3aCFnaIssEEIMVcI8X32Y0a4DStI1KoFN91k\ns2JfC5g7RsXblfLMSR8yRHn8NJpgOHJEJRn+4AMVhP766/Dbb5I+UwZzQ9d67PnicV55JWdcjaZg\nYPXY+bpJtF6YMzPhk0/s24K3SKxe3fN60CAVo7lxo3d7IXJeyP0NxRrYzeQ1KkdMnZrT9vR0/xdj\nN8Ju8mQYb6pYbieOrCKkYUP1bHf8YCsqWPc1bJjntfE9+MtT5+/Y7dur8oJW7G4GevVSYUbgSexr\nfAevvaae+/TxtLcTanXr5lzWsqXa/qmncq5LT/fYYv4ehFChI0uW5NwG1PC4028hUGG3Y4dzm/yK\nG2E3ErgOlal9TPbj9dwcVAhRTggxTwixKVsw2s7dEUJsF0KsFkKsEEIE6dDOH3z2mbrLyMGqAbDi\nDrilN8QdB+Cdd5SHRQgYOxZWrAh90lFNwaVhQ1i3Tk2EePNN+OJLyWurH+OfI5uYdM0kRDTfikYA\nIUQPIcQGIcRmIcTjNuvLCiGmCSFWCSGWCiGamtbleR9mFXZuvu4331TPmZne9VStmPf111+e1+3a\nqaTWxtCkWRhYhyeNYU+ni6ohFgzvjJlevZxtC5Wwu/FG7+L0xYrl3K91SNdXGa1gPHZPPZXzGOZr\nQGwsrF2rJj35wp+w694dli7Nudx6M/D11yoVl/Xz+fquAklsPXy4CkHyhfmzSKlmaBuzk60ULRo6\nYReqUmt5iV9hZ0px4vXI5XH/D5gnpWwI/Jz93vbwQGcpZWsppc19RfSQlWX/BwJUbrs9baF/Lyh2\nDIBj6omHHlJel7Fj88ZOTcGgWDHlQVm3DhYXeYH3583lupOzKFpw8/KGBSFELKqEYg+gCdDPqD9r\n4klguZSyJTAAMKdszfM+LJhZsUOHqmd/wse8L/NrQwjYxTHFZ//krs5OaW/2FC9alPMYvm5ifQk3\nNzNS3Qi7okW9hY2dV8zJxmA9dtag/+efzznxweyhjItTXjNf+Sa7doXLL/d9XKfzaRV2N9zge0ja\nV9oTt1j3Ubo0zJnj8Q6az6MbR4evEAQD8z6tlXbclkbLjzj+5YUQJ4QQxx0ex3J53KtRqQjIfr7W\nR9soPK05KVoUZs1Sr6+8UgWopqcbd70CZr4H+5vBbd2geM66ZMOGqaoUGo1bpJS8ueZJjtf5jJ8G\nzuWXmeVo0ULVJNa4ph2wRUq5XUqZDkwFrrG0aQz8CiCl3AjUFkJUNK3P0z4skKFYK/6Ej9PsQuMi\nald1ANSw64cfKrFi2CMldOiQ8xi+BIGvi6wb0ebU5uhRz+uiRb1FQfHi/mPszO9LlfJe58ZjZzdx\nydcx/SXDj4tTQ9lNmvhuZ3c+hXD+zRjtDVuM78pORAU6ymTdR9OmauSqShW4+24VM2yQm9JmxvK7\n7vIWdlu32reLRmHneC8hpSzltC4EVJZS7st+vQ9wKhQjgZ+EEJnAeCnlB2G0KexceGHOH2SbNtCl\nC/z6a4wSd90fgds7w2ffwzHvW4j581UZHDu3t0ZjkJICb7yVwfdZD7A/djn1lyxg8FsVOHhQxd8N\nGgTr10d3yZw8pDqwy/Q+BbAOAK0CrgcWCiHaAbWAJOAAEejDcpPHzrhQ//57TtH1wgueslBgP3PU\nSdgZaSrMAsrp4uwk7A4c8F2Lu0ED53UGbsSfEN7nLBCPnZRw/Lj74T4DN+JbSnj3XTWUbY5vtLJx\nI9Sr5+7Ybj121vbGd2ecT7v95FbYmfdp/t0Fs2+7/d5+u3deQ6eUNgVK2OUWIcQ8wC614AjzGyml\nFEI46e+LpZT/Zt/9zhNCbJBSLrBr+KwpVXbnzp3p3LlzUHbnNY0awaZNxjsBc16HDmPgrvbwxTTY\n7Rm9Me5YMjOjO8eOJnxs2QJdex9G3NiXhATB+w1/pua1iZQvr9IBlC0bnTOuk5OTSU5OjsSh3SQ4\nfhl4SwixApVFYAVgyJOOUso9/vqwUPZfZ8+q79gQSIFcmIwLtV0eTSFUkLsxEcxuKNbqufOFk7Bz\numhXqOAtDK307GlfagrUrNXmzVX83MfORX/OYbbfmgoFcopP47PY/becPHbly3vqlvo7X337wqhR\n9ik9Spf2Pi/GRA4ne8wEK+wMjJsIw37zd5rboVhfBDMUaxVqMTF5Oys2L/uwsAk7KeUVTuuEEPuE\nEFWklHuFEFUB28JZUsp/s58PCCGmoYZF/Aq7aOK22+C558x32QJ+fxRSG6oJFfNehZW3A4Lvv4d/\n/1V3hKVLR85mTf4jLU0FNw9/ZS3ituu5te1VvHLFKxSJicLIXxusYmfUqFF5dejdgNl1XgPltTuH\nlPI4MMh4L4TYBmzNXrcn+9lnHxbK/qtXLxWbZMRX2YkGuyLq4N+jdeONaii/Vy/fQ7G5ufG0EwRu\na54WL648Vo0aqb7VEHExMcrb5RbD/vnzoW1bNTHEjFVYSOl8w+0kHmrXdi/sOnZ0ztO2fr1KNG33\n+dzWT7XiVtgZw/6hiLEzzkHLliqvpi/cDMVec426VloxCzzjuzGf/8qVYd++0Hvs8rIPi5TfZwYw\nMPv1QCBHdUohRLwQIiH7dUlUzccCFWWWlgZPP61EXZcuKt7OCDBm49Uw5Vfo8BpcfxvEHeeqq2Dw\nYPWj02hAXcSGDIGkGpKXfxrP2X5d+O9VTzGm+5gCI+oizJ9AAyFEbSFEHNAX1X+dQwhROnsdQoi7\ngflSyhOR7MPMYsJ6YbLLJQYqp6GvMoZ2Hg/rOmPZxIn2xzZjXJyt6TasguCGG8yjGv4x0qiY04O4\nEQJ2XHqpfVqWJk2867BKae/BBM93Yf2c5u/In7DzJZKqVoVq1XxvH2j952A9dmYCHS61DvP6It7P\nHDAp4YsvvOOJrRM9zB47601KmzZw3nk510ULkRJ2LwNXCCE2AV2z3yOEqCaEmJndpgqwQAixElgK\n/CClnBsRa8NEfLz6sUmpcvK0aaNKuHz9dXaD/c3gg2VwtiTc0waSFgNq9s6YMSqw1Ljj0xRORo+G\nP9fv58IxfSh60TiW3rOQAS0HRNqsAoOUMgMYgqqV/TfwhZRyvRDiHiHEPdnNmgBrhBAbgO5A9hxT\nKhOhPszXEJNdLjFQdUfdjATYxdEZF3FjnVGtwBfGhXbpUk9MmHlfBgkJHrusF9nHcySfyTlD126f\nBhdcoPpdJ9sMrMf9/HPYvdu5vXn41prM1/A+modo/Qk7f57UoUOVd9EJpyofdqKlcmX3MXa+PHbh\nEnYbNqiJOIFy8KD3cZw8djExyslSsaJ3+2giIrf0UspDQI6J2NnDFr2zX28FWuWxafkCr6LH6fHw\nw3ho/A30vR7+vpH4MqPhbAK1aukh2cKMlJLWAz7nk3kPc2/iHUy79VOKFwmiTpPGJ1LKWcAsy7Lx\npteLgUY2220jQn2Y3YW5Vq3cJVsdlD3YbDdEZVyMnSZP2GG+gPuKzTJ/Fl8B9tb25rZOYqFOHfjy\ny5z78XecuDhvr6d1/3XreioqGOLBEDrmqg7W/ffpY7qxN1HGNtOrh5IllXfRCbsJIC+8oIarzRif\nw6kMmlV8WQW9mUCHYg38CcJGOf5pObF+X+PGeSaL+RN21t93NAo7HYKfD7n44pypTcruvQHeWwdx\nJ+CBpjS8agbdustzP8y//1aC8Lvv8t5eTd6z8eBGen7ak0mbX2JQ8R84OPVlLeo05zCLIePC5OaC\naMacpPf225Unx7w/8zGMi7Hbi+CsWaoiih3WC7v5OLVqwbx5nvduhZ2TWHBaXrZsYMO/VmH3ww9K\nMJrtsU6wsBuKtfs89erBHXe4t8UOO2E3YkTO3G0GboZiFy3yxB6GIsbOIBTJ+K0eynvv9ZShMw/F\nGp/TfH60sNOEDWPyzKRJKtB53DjgVDmK/jgJvpvEppqP88HpK7hn5CqEUDl/9u1Tw7Nnz6p6oZqC\nxbhx0Lr9UaoNfJxmb1zMljndqTRtOVvmt+Wrr2DZskhbqMkv2HmDHnnEfy1VMy+9lHMf4BEhdsLO\nLT16KJFmPtbLL6vXvjx2Qngn3bW76NpN4AhU2IG79ClOVK8OLVqo14aNVu+WW2FXtWrusyBUrOi/\nhJsZf8IuMVGlwzESJNvZF2xcYyiEna8YPLNgs6suYf0uolHY6ejqfMqQIephYATHpqcDWy+Hcavh\n/AlMqNQNrr6S8/aOYsMfSQwdCgsWKIEXjTXuCju7d6sOsXhxdRdZvLjqZP/z5Gk+Wv8e6Ve/TIeK\nvWjD0SkAACAASURBVLmrzhrKxFYlPV3F3wwfDo2t9RA0hRbzhdlImNu9u3oEg6+JEpD7i7GRQuX/\n/s+3sLOS26HYe+91Z5+/i7vd/q1xcUYbI7ZuyBDlRX3rLd/CLljPl0FamhJ1aWnQurVniNgXTjNw\nDYyRoXCIH+M82U3w8ceIESru2K2ws/M0BxJOkF/RHrso4fff1fMPPyhxd+stRWHZAzB2E6RVZEOX\nFtD7Phas3sG116p8Zrt2+d6nJn9x7BgkJamA7vPOU3fqJRJOE3vRu4ylIeffMJ+Fd/3KzLsnc93l\nVenSBbp1U6knrroqZ8Z7TeHF8ECsWeM9OzQQzElw7SpO+PLY2c02dIt1X+aJFVZuvz3nskAmT3Tr\nFpBpAeGU684YJmzRAowsN+3bq2fr+Roxwn6CSCCYPXUrVsDbb/vfpmNH78khBoZ9hqfOKvKD9dKZ\nMWbafv554Nu+8IJ6tss9aMUs7My5/6zfQTQKPC3sooTHH1d/mrp11ayqTz5Ry++8tTT89DKM3Qin\ny8A9bZiedRfFkzZSs6Zn+9WrYe/eyNiu8XDsmIqXef/9nCVsEhNVdZIpU2DTrkOMnPNfKo2uy5VD\n5zD/ga+YNeA7mlZqar9jjcaEIW6aNAnO8wHq4m1cqO0qPjgJJ8PjHCxmQXTsmKqX7UT9+jnLcQUS\nYxcqAvHYGecmNtZj4yOPqGeriHjhBZWPLZTcd59KeeMPuxQq/pL+2rFihXvbwJNjsbJTPSo/DBoE\nvXu7a2v8LsxxmwVhKFYLuyhh/Xr1A2vSBA4fVulOjh9XcVVVqgBpFeHnl2DsZlrWqU7sXZdC/568\n9eOPVK2WRcuWKleemz+0JnycOgWffqo8sBdfrLwR990H336rLp4d+6zioXl3U+/teqzat4of+//I\n97fMoH0NaxUrjcYZs9fKX84vf1x0kXclCjsREwpPjYFZ2CUk+I8vsx7bzmMXSvvc2AA5hZ0hIgxh\nV6RIZEREkSLOKW/84eTNsn6Ob77x5ERsFeC88Nyeg4kTnSeFWI9jfCeGh69+feWtNNsRjcJOx9hF\nAf/9ryfo+dtv4dprPT+2OXPUDLNBg6B/f3jrrXKcPj2KpNpPQLOpDJvxFPQZBsvuZ8Pq/hw6VJHp\n09WMrxdf9B9LoQktFSuq7278eNXBr10Ls+akM+qbb7lx1jvElNtGkdX3sfmLDSSVDfKWVVPoMQeD\nV6hgn4HfLUYYiIGd9ytUHrFXXlGe69xgF5NnZ9/lORJuORNMjJ11GzuPXbTNwHQSdtY0KNdfDzt3\nBr7/tDRVeSKvsP4uzDOho+U7sUN77KKAW25R7mwp4brrvH9oVaqoob2sLDU8m5Gh4rTIKM6kh26n\n86a/6FN0MlT9i5hhDegw9hoenfgtEyaePRfLMH++EoavvRb+O9vCTkyMGuLYtUuyOOV3Jux6kDEk\nUfaKcXwyZBgzr9jOc1eMoGqiFnWa4LF6rUIZfxlOYfef/7if0GBw223qZtfALt7Lat+YMarShoG/\nOMRghN0FF8DixTnbGN5PX0mkowW7iTQGwVxLSpRwLncXaoTIGQdpnikbzcKuAPy0Cj7Vq3sHMtth\nnob+1VfqjikmBu64Q/DQQxfDtIu5v+4x5pz5mpTOb1H8tnu4c/r17Jx9A2nrujDk/qKMHq3uJvfv\nh3Llgg+61thz5gzc/vgaDrf5nCtmfk7JuBLc0vwWFg1aRP1y9c+16xaAJ0GjscNf8XeDSpU81QPc\nEu6h2ECxpnCxphcB/x613Fy8b78d+vWz378xKcKwQUrVD7zwgrfHLhR25AX+PHZmmgYZDpxXwg6g\na1fv7BNmtLDT5BtKlFDZy8289JISaTffnMjmZYOIjx/EmbLb+LPt1yS0f4YjHTazss6VDHnner6e\ndBnz55Vi3Dg4fTp3QdCFBSlhxgyYPFklNq1dW+XoqlUL0k6nM3fDIhbt/5G1Z38gpuQJ7r6jH4Mu\nmE6Lyi0Q0dhraPI9bvOerVwZuChzM+zob3leYMS41ayZs06rldz0c5Mnu2tnVI8wJrPExESfsLOK\nNV8eu27dghP8115rPyM31AihbmzGjnVeH61oYVcI2LJFpcM4eBAefhgeewwSEuoQH/8YMTGPkXIs\nhWnrp/Ht+rdZeOGtlG12Pi8v6s7U+d146KbWfPxRDOPGqWFfKdVsTl8pCAoCEyao4e8nn/QdiLty\nJdx5p/IOPPywmqq/Zvu/zFk2m81//MiRcj9Rlvq0SujFKw0nM+T6tsTmNtuoRuMHtx67YGYe2lWG\nuPPOwPcTbox8cVu3+r9IP/mkd0LmULNjhydAXwhVCjIuTgkiY5KBsS4/06OHt1izerWMsl254f33\nc7+PUKA9dpp8zWuvqXIqjz5q35EnJSYxpN2D/Pneg2R+fpL05smkt57L/DL9WbQslYy4Tlyw7mLq\nbOzIxNGtSP65KGfOKKH4ySfq8eCDzp378eNqdls08emnaji6VSs1zPLkk/bT/4cOk3Trt4X6XReS\nvGsBC3cu5GCpg3Rr2Y17G1xF93rvULmUjpfT5C1uhV0wWL0wl1yS/zz7UnoStLs5F6VKqYwDf/9t\nvz63F3dz6inwTh/z2mu523ckMXvstm1Tk8OiBX/fqRZ2ASKEuBF4FjgPaCulXO7QrgfwJhALfCil\nfCXPjCxAfPyx/zajR8NHH8Gtt5bktdd6k57emz17ICFpB62vXcDE7xaxk0nEdtgOSRdw3pB2/Lui\nNT1bteaR4Q0YNjSGgQO9A4LT0lT+vfffV48OHdTwbuvWan1KCnzwAYwcmfuSOaEkIwOWL1cJns+e\nVTP1mjWDgQOh81X/kpawkq2nVvDz+r9Y2H4hW2PiuGTbJVxS8xIebv8wTSs1JUbkow+kyRX++iEh\nRFlgElAXOA0MklKuc7NtuMhLYZdfCdTOcOe6c0O0iQiz+KldO6KmaExEymO3BrgOGO/UQAgRC7wD\nXA7sBpYJIWZIKdfnjYmFi23b4OefVTCpQVISQC1WTKnFrFm3MmgQpBw8wl2jFlO95Z80ufRL/jrw\nBLN2HiTz5hYMnduaxhXOo2H5hpxKach/7q3BBW1i+e03uPtuJZD++UcNV6anq1jArVvVEMXgweoO\nu3nz8Ig8KZWHcetW5V3wNaV+7VqoWjeV9cc3sSl1E3E9N9CyyQom7FzJOz+nw97WxOxvRfEjN/B/\nV73O6EdqOe9ME9W47IeeBJZLKa8TQjQC3gUuj2QfFk5hZxZAH36YM0FwfqFmTfjsM/ft84NgNRej\njwZ8xdjld6JNRAdCRISdlHID4C9wvB2wRUq5PbvtVOAaQAu7MDBxovO6xo09dUjLlCnDko97Aj3P\nrR/9+mGWxK6kQblV/LXzb16ePp1/z24itt8Bilaox6s7G9B9TF3KxyXx/GNJLN2dxDsvJlEtqSpf\nfFGEtm3h+edVxzp9emD5pdwwfTrcf7/yFtarB/v2S6rVS6Xv3SnUbZ3CvydS2LJ/F2t27mL17s3s\nz9hEkesyeGh2QxqWb0ij8o14uOP9tKrSihqJNRBCkJqqRGJe5lzSRAQ3/VBj4GUAKeVGIURtIUQl\noJ6LbcOCEV8WDswCKD/G1hnExNjPVgV7EefLY2cuyxVO7r3XvkxafiWahysLMvk5xq46YK52mgLo\n9Pv5kAVzy9KmTRcO/diF79+DAQPgqaegeEIaWw5tYePBjWw/sp2/d29HNF9I/49T2JWYAtX2kzw1\ngXJPladOiXLs21Gex5eU5+L0sqSnleT7acWpUr4ErZuVoHrlEpRNKEGVCnEgssiSWUgkp89kcTY9\nCyklsXEZnM48ycmzJzmZfpIjJ08yd/4J9hxOpcHjqZwtepBdaakcOnWIQ5Ri9Z9JyJ9rEHM8ifRD\nSVRP6EKvloMZcE1DLmlTkZgY596qfHmd3LmQ4KYfWgVcDywUQrQDagFJLrcNC8WKwdGj4dl3IEOW\n0XTBHzhQTYay45dfVGhJONm0CRo0CO8xQk00e+wKMmETdkKIeUAVm1VPSim/d7GLgBzjzxrVlIHO\nnTvTuXPnQDbX5IIdOyA1VZViWbzY3DnF06JyC1pUbgGoTnPaYDgRB2sXQP0GmRw5fYTUU6mkpqXy\nxfepLF19iEoXHeLNCWm0aHMKiu5nzl+nOHH6NKczTyFj0qlVI4bEREFKSgz798YoASZjKBobS4e2\nJWnTrCRnT5Tk64/KUTepFM88UI6kchUoX6I85ePLU75EeYoVKYaUati1dGk17Kw7p/xLcnIyycnJ\nkTi0m37oZeAtIcQKVJjJCiDT5bZAePqv3FZwcCI/DFmGgxEjnNe5KVGVW6JN1EHB99jlptaylbzs\nw4SM4L9UCPErMNxu8oQQoj3wrJSyR/b7J4Asu+BjIYSM5OfQuCM5WdWrnT7dvrD1qlVwww1qZlXn\nzvbpB9avV5NBtmxR+Y6uvNJzAVu8WKUcOXtW5UF69lk1tFFQO53CjBACKWXYv9lA+iHTNtuA5kAz\nN9tGW//17bfqf+rP5EcegWee8eRvyy8IoWaimtOMaIIjM1NNmDt5Mvc1ifMSIdQMaCPEKDI2hK8P\nyw9DsU4f7E+ggRCiNrAH6As4RExoooHmzWHqVHtRB+pPtnOnmj374ovObZzWXXSRqms5fbqq1HGh\nHrjX5B6//ZAQojRwSkp5VghxNzBfSnlCCFEg+zC3Q7Gvvx5eOzSRp6B77KKVSKU7uQ54G6gAzBRC\nrJBS9hRCVAM+kFL2llJmCCGGAHNQqQIm6hmx0U358iqfnhNxcTBvnhJowXYUMTGqnJpGEwqc+iEh\nxD3Z68cDTYD/CSEksBa409e2kfgcoSTaY0vHjFH1tzW5J5pj7AqyGI3oUGyoiLahDI1Gkzvyaig2\nL4jG/uvgQahQIdJWaPIDQqj6rqGKRcsLhFBhPeedF0kbwteHRaHO1mg0Gk0k0aJOE81Mmwb/396d\nx0dVnfEf/zxZ2cISpAQQBcQFUQRUxA2iiGLrgm1tq1VrW1u1dWnFVlGr0f7ca+1PrfVn61r3Llr3\n3YC4ICoosrmCoKDIHgKEJM/vj3uDQ5yECTPJvZN836/XvHLn3nPPPHOTO/Pk3HvO2WmnqKNoPmqx\nE5GsoxY7kXjIzw9a7LLxcmyUWnvnCREREclCGzdGHYHUpxxbREREpJVQYiciIiLSSiixExEREWkl\nlNiJiIiItBJK7ERERERaCSV2IiIiIq2EEjsRERGRVkKJnYiIiEgrocROREREpJWIJLEzs2PNbJaZ\n1ZjZ8EbKzTezd81supm90ZIxiogAmNk4M5trZh+Y2XlJtm9jZk+b2Qwze8/MTk7Yps8wEWlRUbXY\nzQSOASZvoZwDpe4+zN1HNH9Yzau8vDzqEFKSLXFC9sSqOLOTmeUCNwHjgF2B48xsUL1iZwDT3X0o\nUApcZ2Z10zW2ms+wbPrbyJZYFWdmZUuczS2SxM7d57r7+ykWbxUTfUP2/NFlS5yQPbEqzqw1AvjQ\n3ee7+0bgAeDoemUWA53D5c7AMnevTtjeKj7DsulvI1tiVZyZlS1xNre432PnwPNm9qaZ/SLqYESk\nzekDLEx4vihcl+jvwGAz+xx4Bzg7YZs+w0SkReVtucjWMbPngJIkmy5w98dSrGZ/d19sZj2A58xs\nrru/nLkoRUQa5SmUuQCY4e6lZrYDwWfVHu6+Bn2GiUgLM/dUPrea6cXNXgImuPvbKZS9BKhw9+uS\nbIvuTYhIJNy92S9xmtlIoMzdx4XPJwK17n51Qpkngcvd/ZXw+QvAee7+Zr26kn6G6fNLpG1qrs+w\nZmuxa4Kkb8zMOgC57r7GzDoChwKXJivbEh/wItImvQnsaGb9gM+BHwLH1SszFzgEeMXMegI7Ax+n\n+hmmzy8RyaSohjs5xswWAiOBJ8zsqXB9bzN7IixWArxsZjOAqcDj7v5sFPGKSNsUdoI4A3gGmA08\n6O5zzOxUMzs1LHYFsJeZvQM8D/ze3ZejzzARiUCkl2JFREREJHPi3is2qWwZ4LgJcTY6AGpzM7Ni\nM3vOzN43s2fNrGsD5SI5nqkcHzO7Idz+jpkNa6nYksSxpcFsS81sVXgMp5vZRRHEeLuZfWFmMxsp\nE/nx3FKccTiWYRxb/ffZ0L5bOifNbDszqzCzCXGN08yGmNlrFgza/K6ZFcYxVjNrZ2b3hzHONrPz\nI46zwe8NM5sYlp9rZofGKM49E9aPtaAX+Lvhz4NSjbOFYv3Gd3GMzqfGfvepn0/unnUPYBdgJ+Al\nYHgj5T4BiuMcJ5ALfAj0A/KBGcCgFo7zGoLLRwDnAVfF5XimcnyAbwNPhsv7AK9H9PtOJdZS4NEo\n4kuI4UBgGDCzge1xOZ5bijMOx3Kr/z4b23dL5yTwb+BBgs5nsYuT4P7td4Ddw+fdgJyYxnoycH+4\n3J7gc267CONM+r1BMED2jLB8v3D/LR7TCOIcCpSEy4OBRTE4nxr9LiY+51NDx7RJ51NWtth5lgxw\nnGKcqQyA2tyOAu4Kl+8CxjdStqWPZyrHZ1P87j4V6GrBTewtLdXfZaQ3y3sw3MaKRorE4nimECdE\nP/jv1v59lmxh3wbPSTMbD3xMcM9fXOM8FHjX3WeG9a1w99qYxroY6GjBLCMdgSpgdVRxNvK9cTRB\nArrR3ecTJAepzGbSonG6+wx3XxI+nQ20N7P8FOJs8VghXudTI3E26XzKysSuCbJhcNBUBkBtbj3d\n/Ytw+QugoS/xKI5nKscnWZltmzmuZFKJ1YH9wqb5J81s1xaLLnVxOZ5bEodjubV/n32A3o3sm/Sc\nNLNOwO+BsjjHSdDq4BbMofuWmf0urrG6+zMEidxiYD5wrbuvjDDOhvQOyzVlnyjiTPQ94K0wgUlF\ni8Yaw/OpITvShPMpDsOdJGVZMsBxBuJskd4rjcR54WbBuLs1PK5WFIOtpnp86rfcRNErKJXXfBvo\n6+6VZnY48AjBl2DcxOF4bkkcjuXW/n02VOYb9dU7J8uA68P33JTWypaOMw84ANgLWAe8YGZvufuL\ncYvVzE4guATbCygm6Mn8grt/0oJxbq1UYogkTjMbDFwFjG3Cbi0daxnRn0+pyKcJ51NsEzt3b8of\nQ0N1LA5/LjWzhwmaQDOaiGQgzs+AvgnP+7L5f2UZ0VicFtygXuLuS8ysF/BlA3U0+/FMIpXjU7/M\ntuG6lrbFWD2YjaBu+Skzu9nMij0YHiMu4nI8GxWTY7m1f5+LCD6sGzrODZ2TI4Dvmdk1QFeg1szW\nufvNMYtzITC57ndhwSDOw4FUEruWjnU/4GF3rwGWmtkrBF+gW0rsMhlnKp/7W3tetnScmNm2wH+B\nE1NIkKOMNQ7nUypxNu18aujmu2x4ENxguGcD2zoAReFyR+AV4NAYxpkHfERwI2UB0XWeOC9cPp8k\nnSeiOp6pHB82v0l1JNHd7J9KrD35epihEcD8iGLtR2qdJyI7ninEGfmxTOfvs7F9UzwnLwHOiWOc\nBDd3v0XQEpYHPAccHtNYzwJuD5c7ArOA3aKKM2Hfzb43+LrzRAHQP9zfYhhnV4Ib/cfH5XxqKNa4\nnU9bOKYpn08t+iGYqQdwDEEGuw5YAjwVru8NPBEuDwgP2AzgPWBiHOMMnx8OzCO4GTaKOIsJBlZ9\nH3gW6Bqn45ns+ACnAqcmlLkp3P4OjfSUjjpW4Nfh8ZsBvAqMjCDG+wlmUagK/z5/FsfjuaU443As\n0/37bOjcb+icrPe6KX8RRREn8OPw9zOTBnraxyFWoBC4J4xzFin2jGzGOJN+b4TbLgjLzwUOi2Oc\nwEVABTA94bFNHGON4fnU2O8+5fNJAxSLiIiItBKtvVesiIiISJuhxE5ERESklVBiJyIiItJKKLET\nERERaSWU2ImIiEibZmZnmtkcM3vPzK5uoMzZZjYzLHN2wvo9zOw1M3vXzB41s6JwfYGZ3RGun2Fm\no1vivSixExERkTbBzErN7I566w4imNt1iLvvBvwpyX67AacAewN7AEeY2Q7h5n8Av3f3IcDDQN2U\nX78AasP1Y4HrmjjDxVZRYictzsxqzGx6+F/Mf8P5+ra0zxlmdnK4PNLMXg/rmG1ml4TrfxzOG/qu\nmb1iZkMS9r89nGFjZr16/2xmB2b4LYpIG2BmZ4WfQf9Msm13M7s94fk4M5satgpNN7MHzKxvuO1O\nM/tevf0rGnndQjObbGb6Dm+6ZGO8nQ5c6eGctu6+NEmZXYCp7r7eg1lKJgHfDbft6F9Pr/k8wRy5\nAIMIBhuuq3MlwawmzSor/ijMLDc8EVKdI1birdLdh4X/xawmGNSxQeF/OD8nGEQU4C7gF+4+DBgM\nPBSu/xgYFdb7R+DWhGruAMYlqf5vfP3flYhIU5wOHOLuJybZ9juCz5e61p4bgJPcfVD42XUvwewD\nECQb9ROOBgeZdfcNBNM5jk8r+rYpWYvZjsCosMGg3MySJV/vAQeaWbGZdQC+QzBNGMAsMzs6XD6W\nr6cMewc4Ksxh+gN7JuzTbLIisQPOBmYTz4nIJT2vATsAmNkOZvaUmb0Z/je6c1hmf2Cuu1eHz3sQ\njMqNB+aEy6+5+6qwzFQSTqDwv6kV9V/c3T8A+plZ12Z4byLSSpnZLQQz8jxtZr+pt62QYCaUaeGq\n84DL3X1eXRl3fyyhlQcamDDezC4LGzamm9lnCa2AjwLHZer9tHZ1V3mAvxMkW3XH9FCCabq6uftI\ngoT8ofr7u/tc4GqCWUueIphRozbc/DPgV2b2JtCJYLYcgNsJ5oF9E7ieYIacmmZ6i5vEPrELJxP+\nNsE17Ga/Ni0tx8xygUMJ/hOCoIXtTHffi+DkqpuI+QBgWsKu1wPzwsu4vww/ROv7OfBkiqFMB/Zt\navwi0na5+2kEU96Vuvtf6m0eRjBlVJ1dgbcbqc6AaxOSjemEDRnufnHYwlcKLANuDPeZAeyX9htp\nI9x9ZHgcTwEeDa8aDXP3ZwmSr/+G5aYBtWbWPUkdt7v7Xu4+muCy6rxw/Tx3Pyz87nqAYC5Y3L3G\n3c8JX2c8wZyv7zf3e419YkfwJf47vs6MJfu1Dz+4FhM0Wd8S3me3L/CvcNstQElYfjvCFjoAd/8j\nwX0KzwLHA08nVh7eCPszgv+SU/E5X18SERFJ1/YEn2/fYGbdwx6S88xsQrjagXMTko1hJDRkhLej\n3Atc5+7TYdPl2Bwza9es76T1SdZA9AhwMICZ7QQUuPuyb+xo9q3w53YE87reFz7vEf7MIZgrt+4S\nfHsz6xgujwU2hi1/zSrWiZ2ZHQF8Gf4hq7Wu9VgXfnBtD6wHjib4/a5M/GBz98EJ+2z2+3f3j939\nFmAMsIeZdQMIO0z8HTjK3b9x6bUBhi7zi0jmOJt/Zs0iuL8Kd1/m7kMJrlAkdhxr7DuuDPjU3e+q\nt16fXU2X7H7G24EBYee6+4GTAMyst5k9kVDu32Y2i+Ay+K/cfXW4/jgzmwfMARa5+53h+p7AW2Y2\nm6CBKtm9mBln7vH9mzCzKwgORDXQDugM/MfdT6pXLr5vQkSahbvrnz2JlJl9Auzp7svrrd8HuMjd\njwyf70YwDMaRdS02ZnYxgLtfFg6/8bi7/yehjjXuXmRmRxJcfTiortdmuL0Q+Njd+zTvu5RsE+sW\nO3e/wN37unt/4EfAi/WTuoSysX9ccsklkcfQmuLMplgVZ2YfIjHR0B/jO8DOmwq5v0fQCfBuM5tr\nZlPC7fc1Ulfd898CvYE3wvvvysL1wwg6n4lsJi/qAJpIn+giIhIL7j6ggfXrzexVM9vH3aeG656k\ngQ5d7v7TJOs6hz8PbuDljyK4705kM7FusUvk7pPc/aio4xAREUnBn4DTmqPi8DLsAQQ3/YtsJtta\n7LJaaWlp1CGkJFvihOyJVXGKtC3h5ddvtMRlqO4NwKjmqFuyX6w7T6TKzLw1vA8RSY2Z4eo8ISLy\nDWqxE9kK1vzzOEtI/7SJiKROiZ3IVlLC0fyUQIuINE3WdJ4QERERkcYpsRMRERFpJZTYiYiIiLQS\nsU/szKydmU0NJ02ebWZXRh2TSFtWXl5O3759ow5DRESSiH1i5+7rCebIGwoMAQ4yswMiDktEUnDn\nnXdy4IEHRh2GiEibEfvEDsDdK8PFAiAXWN5IcREBqqurow5BRERaWFYkdmaWY2YzgC+Al9x9dtQx\nicRRv379uOaaaxgyZAidOnXi8ssvZ+DAgXTu3JnBgwfzyCNfz0C0/fbb8/bbbwNw7733kpOTw5w5\ncwC47bbbOOaYYwBYt24dJ598MsXFxQwePJhp06Zt9ppXXXVV0teYM2cOp59+Oq+99hpFRUUUFxcD\n8MQTTzBs2DC6dOnCdtttx6WXXtrsx0VEpK3IinHs3L0WGGpmXYBnzKzU3cub6/W+c8U1TP/qVfKs\ngHwrJD+nkIKcQvJzCijILaQwr5CC3AIK8wppl1dIYV4B7fMLaV9QSLv8AjoUFAaPwkLaFxTQqV0h\nHdsV0rlDO4qLOrBNl44UF7WnIC8rDr9kmQceeICnnnqK7t278/jjjzNlyhRKSkp46KGHOOGEE/jo\no4/o2bMnpaWllJeXM3z4cCZNmsQOO+zApEmTGDRoEJMmTdo0vdill17KJ598wscff0xFRQXjxo3b\nbHy5gQMHJn2NQYMGccstt/CPf/yDl19+eVP5Tp06cc899zB48GBmzpzJ2LFjGTp0KEcffXRLHyoR\nkVYnqzILd19lZk8AewHlidvKyso2LZeWlqY15+XxIw9h8IIdWb+xinVVG1hfvYH1G6tYX72BquoN\nbKiuYs3GtSyrXU5VzQY21lax0TewsXYD1V5FtW+gmg3UUEUNG6ixDdTaBmpy1lObW4nnVUJeJdTm\nYdUdsJoO5NZ2IK+2I3negXw6UGDBozCnA+3yOtAhryOdCzvTtX0XunfowjZFXfhW5y707NqF3sVd\n6LNNF3p370xhflb9SiXDzIyzzjqLPn36APD9739/07Yf/OAHXHnllUydOpWjjjqK0aNH87//oZCs\nIgAAHw1JREFU/Y9zzjmHKVOmMHHiRJ577jlOO+00Jk+ezDnnnAPAv/71L/72t7/RtWtXunbtytln\nn81ll122qd7GXiPZIM6jR4/etLz77rvzox/9iEmTJjWa2JWXl1NeXr7Vx0VEpK2IfRZgZtsA1e6+\n0szaA2OBb1y7SUzs0vXjg4fzY4ZnrL5kamud1Wur+Gr1WpavqWT5mkpWVFSycm0lqyorWbVuLavX\nVVKxvpKKqkrWbKhg9frVfLb6M9ZWr6KydhUbWE2VrWJj7ipq8ldBwRqobkfOxi7kV3ejvfegKKcH\nXfN70L19D3oW9aBP1x707d6DAT17sNv2vejXs5icHI3un2mZmjBhaya3SOyxevfdd3P99dczf/58\nACoqKli2bBkAo0aN4txzz2XJkiXU1NRw7LHHUlZWxoIFC1i1ahVDhw4F4PPPP9+szu22226z12vs\nNZKZOnUq559/PrNmzaKqqooNGzbwgx/8oNH3VP+fNV2+FRFJLvaJHdALuMvMcgjuCfynu78QcUxp\ny8kxuhYV0rWoECjOSJ01Nc7i5RV89tUqFi5dwSdfLmXh8qV8tvJLvqxYyrtL3uPlhUup8KWsz1lK\nVeHnkFtFwbq+dKrtS/e8vvTq2Jd+3foypO8ARu22E3sO3FaJ31aIcraxusukCxYs4Je//CUvvvgi\n++67L2bGsGHDNrWiDRw4kA4dOnDjjTcyevRoioqKKCkp4dZbb92sJ2uvXr349NNPGTRoEACffvrp\npm1beo1kU4Idf/zxnHXWWTzzzDMUFBTw29/+lq+++qrZjoeISFsS+8TO3WdCMzeftRK5uca2PYrY\ntkcR+wzaNqV9Fi1dw1sfLGTmgoW8/8VC5q9YyKsLX+N/n9zLmtfnUZu/hvbrdqSH7UT/zrswst8e\njB+xJyN23k4JX8ytXbsWM2ObbbahtraWu+++m/fee2+zMqNHj+amm27i5ptvBoKWsZtuuomLL754\nU5m6y6v77LMPFRUV3HjjjSm/Rs+ePVm0aBEbN24kPz8fCFr0unXrRkFBAW+88Qb33Xcfhx12WHMe\nChGRNiP2iZ00ryAR3JWj99s16fYFS1bx0rsf8PqH85i5eC63T7+da2f9Gs+ppvuG4QzqMoJjhh7E\nTw/Zl66d2rdw9NKYXXfdlQkTJrDvvvuSk5PDSSedxAEHbD4E5OjRo3nggQcYNWrUpufXXXfdpucA\nl1xyCaeddhr9+/enT58+nHzyydxwww0pvcaYMWMYPHgwJSUl5Obm8uWXX3LzzTczYcIEzjjjDEaP\nHs0Pf/hDVq5c2QJHRESk9bNkNzdnGzPz1vA+soU7vPn+5zzy+lu89MHrzKx4iYqO79KtcgQjexzK\nOYd/l0OG7RR1mM3KzJJ2DJDMaug4h+vVZCwiUo8SO8mIRUvXcOvTk/nPzCeZy38pqO7BgcU/4Orj\nfsqwHfpEHV7GKbFrGUrsRESaRomdZNzG6lpueeJVbp5yD/PyHqR31UGcf9DZnHHE6C3vnCWU2LUM\nJXYiIk2jxE6a1aKlazj3rnv5z+I/UVTbl8vHXsbp387+uUOV2LUMJXYiIk2jxE5aROX6as74f/dy\n98JL2M7259EzrmO37UuiDmurKbFrGUrsRESaJivmipXs16FdHref/RMWXTCLbfL7MuTmIUy8+79R\nhyUiItKqxL7Fzsz6AncD3wIcuNXdb6hXRi12Wea2p6Zx6gs/ZI/CI3m17LqsmwpNLXYtQy12IiJN\nkw2JXQlQ4u4zzKwT8BYw3t3nJJRRYpeFPv58JXtd/QPa53Vg1qX3Z9U4eErsWoYSOxGRpon9pVh3\nX+LuM8LlCmAO0DvaqCQTBvTuyvwrHie3tgMDLz6KinUbog5JREQkq8U+sUtkZv2AYcDUaCORTOnc\nsYAPrv4n+bWd2e3ik6iuqY06pKw3b948hg4dSufOncnNzeXyyy+POiQREWkhWZPYhZdh/w2cHbbc\nSStRWJDLrMvuZXnVEsZeXhZ1OFnvmmuuYcyYMaxevZqamhouvPBCAMrLy+nbt2/E0YmISHPKijvW\nzSwf+A9wj7s/kqxMWVnZpuXS0lJKS0tbJDbJjOLO7Zh0xoPsdeueXPfwKCYcc0jUIWWtBQsWsN9+\n+0UdRkaVl5dTXl4edRgiIrGXDZ0nDLgLWObuv22gjDpPtBJXPvACf3j7J3x63mx6d+8cdTgNimvn\niYMPPpjJkyeTn59PXl4eRx11FAMGDGDixIl0796dqqoqOnTogJnx/vvvU1IS77EE1XlCRKRpsuFS\n7P7ACcBBZjY9fIyLOihpHhN/NIb+NeM44s8XRR1KVnrxxRc58MAD+etf/8qaNWsoKCjAzOjQoQNP\nP/00vXv3Zs2aNaxevTr2SZ2IiDRd7BM7d5/i7jnuPtTdh4WPp6OOS5rPY2dfzYzqh/jXlOlRh9Iq\n1LV4xbGFUUREMisr7rGTtmWX7bozvttFnPnfizj2gCeiDmer2KWZuUrolygZExGR1Cmxk1i6/de/\nYJtLr+W2Z1/l54dmX0eAOCVkwW2qX/8UEZHWK/aXYqVt6lpUyPd7XsBFT18ZdShZzd03XYLt2bMn\ny5YtY/Xq1RFHJSIizUWJncTWDaecyBcFr/PSux9EHUrWMrNNLXW77LILxx13HAMGDKC4uJglS5ZE\nHJ2IiGRaxoY7MbOOQF/AgUXuvjYjFaf22hrupJXa54IL2GgVvH35DVGHspm4DnfS2mi4ExGRpkkr\nsTOzIuAXwI+AbYAvAAN6AsuAe4G/N/dMEUrsWq8pMxcy6r6hrPzDZ3Tu0C7qcDZRYtcylNiJiDRN\nupdiHwHWAEe6+wB339fdR7p7f+AIYC3wv3SDlLbrgN370qVyGH986LGoQxEREYm9bJh54nbgO8CX\n7r57A2XUYteKnXLDP3l8wYMsue7xqEPZRC12LUMtdiIiTZMNnSfuADTTRBt26XHH8EXBFD74bGnU\noYiIiMRaWomdmc03s09SeHy8ta/h7i8DK9KJU7Jbnx6d6LXuEK79X3xa7EREROIorQGK3b1fhuIQ\nadSRA4/hsY8eBH4adSgiIiKxlQ2XYkX43fhvs7iwnKWrmrWDtYiISFZrtinFzOwpdz+8ueqvr6ys\nbNNyaWkppaWlLfXS0gIGbtuNrmv34fpHn+WKE78bdTiApuhqSeXl5ZSXl0cdhohI7KU7jt3whjYB\nT7h7yVZXvvnr9AMeU6/Ytu2Iy//Mgor3mXnlLVGHIhFTr1gRkeTSbbGbBkxuYFuXNOsGwMzuB0YD\n3c1sIXCxu9+Ribolu5y4/1hOfPyvUYchIiISW+m22M0CjnH395NsW+jufdMJrglxqMWuDaipcfIn\n9mbSSVM4cLcdog5HIqQWOxGR5NLtPFHWSB1npVm3yGZyc43tq8dy6wvPRR2KiIhILKWV2Ln7v9x9\nbgPbHk6nbpFkDul/KC99+mzUYYiIiMRS2sOdmNkgMxtjZp3qrddsEZJxvxw7hs8LJlFTWxt1KCIi\nIrGT7swTZwGPAGcCs8xsfMLmK9OpWySZvXfpRW5VN56cNjvqUERERGIn3Ra7XwJ7uvt4gp6rF5nZ\nb9IPS6Rh2zOKB15rqDO2iIhI25VuYmfuXgHg7vOBUuBwM7ueYCw7kYw7oO8oXl30ctRhiIiIxE66\nid2XZja07kmY5B0BdAeGpFm3SFLHH3AgC3MmoyFuRERENpduYncSsCRxhbtvdPeTgFFp1r2JmY0z\ns7lm9oGZnZepeiU7HTJ8AO7wyuxPog5FREQkVtJN7JaHDwDMbBczO8fMvuvuU9Ksu67OXOAmYByw\nK3CcmQ3KRN2SnXJyjN7VB/LPybrPTkREJFG6id3TwPYAZjYQeA3oD/zazK5Ks+46I4AP3X2+u28E\nHgCOzlDdkqVG9hrFpPlK7ERERBKlm9h1dfcPwuWfAPe5+5nA4QT32mVCH2BhwvNF4Tppw74/4kA+\nrlFiJyIikigvzf0T714fA1wL4O5VZpapEWRTukO+rKxs03JpaSmlpaUZenmJo+8eMJjjnlnOu598\nzpD+vaMOR5pZeXk55eXlUYchIhJ7lk7PQjO7F1gMfA6cBwxw97Vm1g0od/c90g7QbCRQ5u7jwucT\ngVp3vzqhjKuHZNvT8zdHc8KQ47nuZz+MOhRpYWaGu2tIJRGRetK9FPsLYBnBfXaHuvvacP0g4E9p\n1l3nTWBHM+tnZgXAD4FHM1S3ZLG9thnN8x/ocqyIiEidtC7FunslSaYOc/dXgVfTqTuhrmozOwN4\nBsgFbnP3OZmoW7Lbd/ccxRnP3xF1GCIiIrGR7qXYS1Is6u5+2Va/0Jbj0KXYNqhyfTUdL+vOx2d9\nTP+S7lGHIy1Il2JFRJJLt/PEArbcucFSKCPSZB3a5VG8dl9uf34KfzxBI+CIiIikeyn2zgzFIbJV\nhhaP4um5k/mjhjYUERFJr/OEmZ1sZg0mh2ZWYGY/Tec1RBpz9B6jmFOpDhQiIiKQ/qXYTsA0M5sL\nTCOYN9aAEmAvYBfg72m+hkiDTjx4b86eNofFy1fTq7hz1OGIiIhEKq0WO3e/CRgO/BUoAA4A9idI\nGG8Chrv7zekGKdKQbp0L6VyxF3e+mJFO2CIiIlktrV6xcaFesW3b/n+4GMutZkrZFVGHIi1EvWJF\nRJJL91IsAGZ2I0HP17oPWgdWAW+6+/8y8RoiDTlq91L+z+sTow5DREQkcunOPFGnHTAUeB/4ANgD\n6Av83Mz+srWVmtmxZjbLzGrMbHhmQpXW5tTD96ei3Vw+Xrws6lBEREQilanEbghwsLvf6O43AGMI\nOk58FzgsjXpnAscA6vYoDepaVEiPtaO58cnnog5FREQkUplK7LoS9JCt0wkodvdqYP3WVuruc939\n/XSDk9ZvdJ9xPDHv6ajDEBERiVSmErtrgOlmdoeZ3QlMB641s47A8xl6DZEGnTpmHB/Z09TU1kYd\nioiISGTS7jxhZjnAXIJhTkYQdJy40N0/C4v8bgv7P0cw7l19F7j7Y6nGUVZWtmm5tLSU0tLSVHeV\nVmDM8AHk3tuFBye/zfGle0UdjmRYeXk55eXlUYchIhJ7GRnuxMxmuPvQDMTTUP0vARPc/e0Gtmu4\nE2HkhReQm1fLK5deFXUo0sw03ImISHKZuhT7vJl938ya84NWH+LSqF+XHsu0yoeorVWSLyIibVOm\nErvTgIeAKjNbEz5Wp1upmR1jZguBkcATZvZUunVK6/XjMUPx2lweejlpw66IiEirl7GZJ8ysGNiR\nYEw7ANx9UkYq3/Jr61KsAMHlWMut4bXLro46FGlGuhQrIpJcRlrszOwXwCTgaaAs/HlJJuoWaYrz\nDz+RNzbczboNG6MORUREpMVl6lLs2QQ9Yhe4+0HAcIIpxURa1PgDBtFx/Y5c+uCjUYciIiLS4jKV\n2K1393UAZtbO3ecAO2eobpEmOX6n07htxv+LOgwREZEWl6nEbqGZdQMeAZ4zs0eB+RmqW6RJrjrp\neyzLn8Ezb82NOhQREZEWlbHOE5sqNCsFOgNPu3tVRitv+DXVeUI2c/All/Np5Tw+vPbuqEORZqDO\nEyIiyWU8sYuCEjupb8GSVfT/y0CeP+5VDt5jx6jDkQxTYiciklymLsU2CzO71szmmNk7ZvZfM+sS\ndUySHbYv6cKBBWdyyj3qnC0iIm1HrBM74FlgsLvvAbwPTIw4HskiD5w9gU+Zws1PTI46FBERkRYR\n68TO3Z9z99rw6VRg2yjjkezSq3tHztjxz0x44dca105ERNqEWCd29fwMeDLqICS7/PmU71FU059D\nrvhD1KGIiIg0u8gTOzN7zsxmJnkcmVDmQqDK3e+LMFTJQjk5xou/uY3XK+/hmv88G3U4IiIizSov\n6gDcfWxj283sZODbwJjGypWVlW1aLi0tpbS0NP3gpFXYrX8Prt33Xs5941h27fsSR4wYHHVI0kTl\n5eWUl5dHHYaISOzFergTMxsHXAeMdvevGimn4U5ki0696V5uW3ABr50yhb137ht1OJIGDXciIpJc\n3BO7D4ACYHm46jV3/1WSckrsJCVHX/l/eXL59Tx1/LMcMmynqMORraTETkQkuVgndqlSYidN8ZO/\n3ME9n1/AtfvdwznjG73CLzGlxE5EJDkldtImXfXQC1z45gkc3PlXPPq782lfmB91SNIESuxERJJT\nYidt1rS5n3HYLT9lXc4X/O3wWzl57D5RhyQpUmInIpKcEjtp02prnV/fcj+3zj+XPjUHcMsPL+Xb\nIwZFHZZsgRI7EZHklNiJAEuWr+Xkv/6VZyv+RK+N+3P2/r9iwjFjyM2JfKhHSUKJnYhIckrsRBIs\nXlbBuXfdx38W/pXa3Er2LTqO3x56LEeP3A0z5RFxocRORCQ5JXYiSdTWOrc98wZ/m/wQ7278N7ne\nnt3bfZsjdxvDLw8bRa/ioqhDbNOU2ImIJKfETmQLamqcu55/k3tff5a3VjzPqo7T6FS5Ozu234d9\nt9+b8XvvzcFDB+qybQtSYiciklysEzsz+yNwFODAMuBkd1+YpJwSO2kxS1dWcufzr/Pi3GnMXPYm\nS3KnUVOwkqJ1u9IrfxA7FQ9i7367cvBug9h7574U5kc+c1+ro8RORCS5uCd2Re6+Jlw+E9jD3U9J\nUk6JnURqzoKveHb6bKZ+PIfZX85h4fo5rMqfQ027L8hb34uO1duzTV4/+nTcngHdt2fgt/owsKQn\ng/qWsHPfHkr+mkiJnYhIcrFO7BKZ2USgi7ufn2SbEjuJpTWVVUybt4i3PprP7M8X8NGy+XxWsYCV\nNYuptCVsKFiCFy7HqrpRWFVCRy+hKPdbdMkvpkthN7p3KKZHp2707NyN3sXF9CnuxnY9utG/pJjO\nHQujfnuRUWInIpJc7BM7M7scOBGoBEa6+8okZZTYSdZat6GaeQu/Yt6iL/hg8RIWLPuCrypWsHzd\nClasX86a6hWsrVnBOlZQlbOcjfkr8IIVANjGInJqOpFXU0S+d6KATrSzItrldKJDXhEd8zrRsaAT\nnQuLKGrXkQ4F7ehU2J5O7drTqbAdnTu0p6h98LNLh3Z07dSeLh3b061TOzq2K4htT2AldiIiyUWe\n2JnZc0BJkk0XuPtjCeXOB3Z2958mqUOJnbQptbXO6rVVLF6+hqWrKvhy5RqWralgeUUFy9euYWVl\nBavWV7B6/RoqqiqoqFrDupq1VNWup6p2HRt9HRtZTzXrqLZ11Np6anLWUZu7Hs9dB3nrIKcaqtth\nNe2xmnbk1LYjxwvI8UJyvYBcvn7kUUieFZBnBeTnFJCXU0BBTiH5OQUM6TWY2874xmmbFiV2IiLJ\nRX5jj7uPTbHofcCTDW0sKyvbtFxaWkppaWlacYnEWU6O0bWokK5FhQxim2Z5jQ1VNaxcu54Va9ax\nunI9qyvXU7mhatNjXVUVazdsYH1VFes2VrF+02MD66ur2FBdRVV1FUWFHdOOpby8nPLy8vTflIhI\nKxd5i11jzGxHd/8gXD4TGOHuJyYppxY7kTZELXYiIslF3mK3BVea2c5ADfARcHrE8YiIiIjEVqxb\n7FKlFjuRtkUtdiIiyWmofBEREZFWQomdiIiISCuhxE5ERESklVBiJyIiItJKKLETERERaSWU2ImI\niIi0EkrsRERERFqJrEjszGyCmdWaWXHUsYiIiIjEVewTOzPrC4wFFkQdS7qyZa7LbIkTsidWxSki\nIi0h9okd8Gfg91EHkQnZ8qWZLXFC9sSqOEVEpCXEOrEzs6OBRe7+btSxiIiIiMRdXtQBmNlzQEmS\nTRcCE4FDE4u3SFAiIiIiWcjcPeoYkjKz3YAXgMpw1bbAZ8AId/+yXtl4vgkRaTburn/0RETqiW1i\nV5+ZfQLs6e7Lo45FREREJI5ifY9dPdmRgYqIiIhEJGta7ERERESkcbFosTOzcWY218w+MLPzGihz\nQ7j9HTMbtqV9zazYzJ4zs/fN7Fkz61qvvu3MrMLMJsQ1TjMbYmavmdl7ZvaumRXGLU4za2dm94fx\nzTaz81OJsZljPdbMZplZjZkNr1fXxLD8XDNL7JgTdZx7Jqwfa2Zvhsf0TTM7KEZxDk9SX1zOpcZ+\n71t1LomIZB13j/QB5AIfAv2AfGAGMKhemW8DT4bL+wCvb2lf4Brg9+HyecBV9er8N/AgMCGOcRL0\nWH4H2D183g3IiWGcJwP3h8vtgU+A7SI+prsAOwEvAcMT6to1LJcf7vdhxMe0oTiHAiXh8mCCIX9i\ndzxjeC41dDy36lzSQw899MjGRxxa7EYAH7r7fHffCDwAHF2vzFHAXQDuPhXoamYlW9h30z7hz/F1\nlZnZeOBjYHaM4zwUeNfdZ4b1rXD32hjGuRjoaGa5QEegClidQpzNFqu7z3X395O83tEESehGd59P\nkCCMiFuc7j7D3ZeET2cD7c0sP25xQrzOpUbi3NpzSUQk68QhsesDLEx4vihcl0qZ3o3s29PdvwiX\nvwB6AphZJ4KZLMriHCdBy4Ob2dNm9paZ/S6Ocbr7MwSJ3GJgPnCtu6+MONaG9A7LNWWfKOJM9D3g\nrTCJiVWcMTyXGrIjW3cuiYhkncgHKCb13q6pjFllyepzd7evx7orA65390oza8o4WC0dZx5wALAX\nsA54wczecvcX4xSnmZ1AcAm2F1AMvGxmL7j7JynUn8lYt1YqMUQSp5kNBq4imCs5FS0dZxnRn0up\nyGfrziURkawTh8TuM6BvwvO+bN6qkqzMtmGZ/CTrPwuXvzCzEndfYma9gLpBjUcA3zOza4CuQK2Z\nrXP3m2MW50Jgsofj9pnZk8BwYEtfRi0d537Aw+5eAyw1s1cIvkBTSewyGWuyfbf0eonvL05xYmbb\nAv8FTkwxSY4izjicS6nEubXnkohI9on6Jj+C5PIjgpuhC9jyjdQj+fpG6gb3JbjZ/7xw+XzqdZ4I\n118CnBPHOAlu8H6LoDUsD3gOODyGcZ4F3B4udwRmAbtFeUwT9n2JYFDruud1nScKgP7h/hbDOLsS\n3Ow/Pg7nUkNxxu1c2sLxbPK5pIceeuiRjY/IA3B3gMOBeQQ3s08M150KnJpQ5qZw+zts3uPtG/uG\n64uB54H3gWeBrkleN+UvoyjiBH4MvAfMJEliGoc4gULgnjDGWaTYM7KZYz2GoJVmHbAEeCph2wVh\n+bnAYXGME7gIqACmJzy2iVucMTyXGvu9b9W5pIceeuiRbQ8NUCwiIiLSSsShV6yIiIiIZIASOxER\nEZFWQomdiIiISCuhxE5ERESklVBiJyIZYWZnmtkcM3vPzK5uoMzZZjYzLHN2wvo9zOw1M3vXzB41\ns6JwfYGZ3RGun2Fmo1vq/YiIZCMldiLSJGZWamZ31Ft3EMH8rkPcfTfgT0n22w04Bdgb2AM4wsx2\nCDf/A/i9uw8BHgbqpv36BVAbrh8LXNfEWS5ERNoUJXYSGTM7y8xmm9k/k2zb3cxuT3g+zsymhi1C\n083sATPrG26708y+V2//ikZet9DMJpuZ/v63TrIxkk4HrvRwTlt3X5qkzC7AVHdf78FMJZOA74bb\ndnT3l8Pl5wnmyAUYRDDgcF2dKwlmNhERkST0xSZROh04xN1PTLLtd8DfYFNLzw3ASe4+yN2HAfcS\nzD4AQaJRP9locIBGd98AvAyMTyv6titZi9mOwCgze93Mys0sWfL1HnCgmRWbWQfgOwRThQHMMrOj\nw+Vj+XrasHeAo8ws18z6A3sm7CMiIvUosZNImNktwADgaTP7Tb1thcBId58WrjoPuNzd59WVcffH\nElp4oIEJ483ssrCFb7qZfZbQCvgocFym3k9bECZt04G/EyRbdcf1UIKpurq5+0iCpPyh+vu7+1zg\naoKZS54imFGjNtz8M+BXZvYm0AmoCtffTjAX7JvA9cCrQE0zvUURkaynmSckMmb2CcGcnsvrrR8J\nXOjuR4bP3wJOdveZDdRzJzAKWJWwegd375xQpgtBK91P3H16mDx+7O59Mvme2oKwA8PJ7v7ThHVP\nEUzVNSl8/iGwj7sva6SeK4BP3f2Weut3Av7p7vsk2ecV4OdhkigiIvWoxU7iaHtgcbINZtY97B05\nz8wmhKsdONfdh9U9SGjBC2+2vxe4zt2nw6bLsTlm1q5Z30nrlKx19BHgYNiUmBUkS+rM7Fvhz+0I\n5na9L3zeI/yZQzBXbt1l+PZm1jFcHgtsVFInItIwJXYSR87mycMsgnurcPdl7j4UuJXgkl2dxnpK\nlhG0DN1Vb73RyL140qBk9zTeDgwws5nA/cBJAGbW28yeSCj3bzObRXAp/Ffuvjpcf5yZzQPmAIvc\n/c5wfU/gLTObTXCJN9n9mCIiEsqLOgCRJBYAJQnPrwEeNrPXE1prOpJCUmZmRwJjgIPqrS8EasKW\nO2mC8HLrpHrrNpIk6XL3zwk6SdQ9H9VAnTcQdJCpv34+QW9aERFJgRI7iVJDidk7wM6bCrnXDWZ7\nt5l1Br4iSP4uaaSuuue/BXoDb4TDn/3P3cuAYcBr6b4BERGROFHnCYmlsEPE39x9ajPVfwUwzd0f\nbo76RUREoqB77CSu/gSc1hwVh5dhDyC44V9ERKTVUIudiIiISCuhFjsRERGRVkKJnYiIiEgrocRO\nREREpJVQYiciIiLSSiixExEREWkllNiJiIiItBL/H3wNXWtpi32iAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x13db4310>"
]
}
],
"prompt_number": 87
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, let us have a look at the fit results. Here, we convert the dictionary of results into a dataframe to display it in a nicer way."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"display(pd.DataFrame([port2.fitresults]).applymap(lambda x: \"{0:.2e}\".format(x)))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Qc</th>\n",
" <th>Qc_err</th>\n",
" <th>Qi</th>\n",
" <th>Qi_err</th>\n",
" <th>Ql</th>\n",
" <th>Ql_err</th>\n",
" <th>chi_square</th>\n",
" <th>fr</th>\n",
" <th>fr_err</th>\n",
" <th>theta0</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td> 1.00e+05</td>\n",
" <td> 3.88e+02</td>\n",
" <td> 9.57e+06</td>\n",
" <td> 3.65e+06</td>\n",
" <td> 9.90e+04</td>\n",
" <td> 5.59e+02</td>\n",
" <td> 1.64e-03</td>\n",
" <td> 7.00e+09</td>\n",
" <td> 1.36e+02</td>\n",
" <td> -2.84e-03</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "display_data",
"text": [
" Qc Qc_err Qi Qi_err Ql Ql_err chi_square \\\n",
"0 1.00e+05 3.88e+02 9.57e+06 3.65e+06 9.90e+04 5.59e+02 1.64e-03 \n",
"\n",
" fr fr_err theta0 \n",
"0 7.00e+09 1.36e+02 -2.84e-03 "
]
}
],
"prompt_number": 88
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Finally, we can calculate the single photon limit, i.e., the input power necessary to maintain one photon on average in the resonator:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 'Single photon limit: %.2f dBm' % port2.get_single_photon_limit()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Single photon limit: -152.84 dBm\n"
]
}
],
"prompt_number": 89
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Or, we can compute the photons in the resonator for a given power:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print 'At -100dBm, we have %.2e photons in the resonator' % port2.get_photons_in_resonator(-100)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"At -100dBm, we have 1.92e+05 photons in the resonator\n"
]
}
],
"prompt_number": 90
}
],
"metadata": {}
}
]
} | gpl-2.0 |
hetland/python4geosciences | materials/7_shapefiles.ipynb | 1 | 381603 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Shapefiles on maps"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"\n",
"import cartopy\n",
"import cartopy.io.shapereader as shpreader\n",
"\n",
"import shapely.geometry"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What is a shapefile?\n",
"\n",
"A shapefile contains spatial information in a particular format and is used commonly in GIS applications. It typically contains information like the polygons describing counties, countries, or other political boundaries; lakes, rivers, or bays; or land and coastline. A shapefile record has a geometry, which contains the points that make up the objects, and attributes, which store information like the name of the record.\n",
"\n",
"Shapefiles are commonly available online through local or federal agencies for geometric data on public lands and waterways."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Read and examine records from Natural Earth\n",
"\n",
"We saw in the `maps` notebook how easy it is to access shapefiles through Natural Earth and `cartopy`. Here we go into more detail.\n",
"\n",
"We can read in a dataset from Natural Earth with the following lines. \n",
"\n",
"**Note**\n",
"If we didn't re-read this each time this cell was run, we could only run through the records once. Once the states have been iterated over, the pointer is at the end of them and there are none left to show. This is like reading all of the lines of a file and reaching the end.\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"# how we tell cartopy which data we want, from the list at the end of the maps notebook\n",
"shapename = 'admin_1_states_provinces_lakes_shp'\n",
"\n",
"# Set up reader for this file\n",
"states_shp = shpreader.natural_earth(category='cultural', resolution='110m', name=shapename)\n",
"reader = shpreader.Reader(states_shp)\n",
"\n",
"# Read in the data from the file into the \"states\" generator which we can iterate/loop over\n",
"states = reader.records()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Information about the states is in variable `states` and is a generator. Without going into too much detail about generators, they are used in loops and we can see two ways to access the individual records (or states in this case) in the next few cells.\n",
"\n",
"Let's look at a few of the states by looking at the generator as a list:"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[<Record: <shapely.geometry.polygon.Polygon object at 0x7f30d9e0e160>, {'scalerank': 2, 'featurecla': 'Admin-1 scale rank', 'adm1_code': 'USA-3514', 'diss_me': 3514, 'adm1_cod_1': 'USA-3514', 'iso_3166_2': 'US-MN', 'wikipedia': 'http://en.wikipedia.org/wiki/Minnesota', 'sr_sov_a3': 'US1', 'sr_adm0_a3': 'USA', 'iso_a2': 'US', 'adm0_sr': 1, 'admin0_lab': 2, 'name': 'Minnesota', 'name_alt': 'MN|Minn.', 'name_local': None, 'type': 'State', 'type_en': 'State', 'code_local': 'US32', 'code_hasc': 'US.MN', 'note': None, 'hasc_maybe': None, 'region': 'Midwest', 'region_cod': None, 'region_big': 'West North Central', 'big_code': None, 'provnum_ne': 0, 'gadm_level': 1, 'check_me': 10, 'scaleran_1': 2, 'datarank': 1, 'abbrev': 'Minn.', 'postal': 'MN', 'area_sqkm': 0.0, 'sameascity': -99, 'labelrank': 0, 'featurec_1': 'Admin-1 scale rank', 'admin': 'United States of America', 'name_len': 9, 'mapcolor9': 1, 'mapcolor13': 1}, <fields>>,\n",
" <Record: <shapely.geometry.polygon.Polygon object at 0x7f30d9e0e6d8>, {'scalerank': 2, 'featurecla': 'Admin-1 scale rank', 'adm1_code': 'USA-3515', 'diss_me': 3515, 'adm1_cod_1': 'USA-3515', 'iso_3166_2': 'US-MT', 'wikipedia': 'http://en.wikipedia.org/wiki/Montana', 'sr_sov_a3': 'US1', 'sr_adm0_a3': 'USA', 'iso_a2': 'US', 'adm0_sr': 1, 'admin0_lab': 2, 'name': 'Montana', 'name_alt': 'MT|Mont.', 'name_local': None, 'type': 'State', 'type_en': 'State', 'code_local': 'US30', 'code_hasc': 'US.MT', 'note': None, 'hasc_maybe': None, 'region': 'West', 'region_cod': None, 'region_big': 'Mountain', 'big_code': None, 'provnum_ne': 0, 'gadm_level': 1, 'check_me': 0, 'scaleran_1': 2, 'datarank': 1, 'abbrev': 'Mont.', 'postal': 'MT', 'area_sqkm': 0.0, 'sameascity': -99, 'labelrank': 0, 'featurec_1': 'Admin-1 scale rank', 'admin': 'United States of America', 'name_len': 7, 'mapcolor9': 1, 'mapcolor13': 1}, <fields>>]"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"list(states)[:2]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Note**\n",
"\n",
"Each time you access the states, you will need to rerun the cell above that reads in the records in the first place."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Or in its natural state, we can step through the records of the generator using `next` after rereading in the records. The following cell shows the first record, which contains a single state."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<Record: <shapely.geometry.polygon.Polygon object at 0x7f30d9dbc240>, {'scalerank': 2, 'featurecla': 'Admin-1 scale rank', 'adm1_code': 'USA-3514', 'diss_me': 3514, 'adm1_cod_1': 'USA-3514', 'iso_3166_2': 'US-MN', 'wikipedia': 'http://en.wikipedia.org/wiki/Minnesota', 'sr_sov_a3': 'US1', 'sr_adm0_a3': 'USA', 'iso_a2': 'US', 'adm0_sr': 1, 'admin0_lab': 2, 'name': 'Minnesota', 'name_alt': 'MN|Minn.', 'name_local': None, 'type': 'State', 'type_en': 'State', 'code_local': 'US32', 'code_hasc': 'US.MN', 'note': None, 'hasc_maybe': None, 'region': 'Midwest', 'region_cod': None, 'region_big': 'West North Central', 'big_code': None, 'provnum_ne': 0, 'gadm_level': 1, 'check_me': 10, 'scaleran_1': 2, 'datarank': 1, 'abbrev': 'Minn.', 'postal': 'MN', 'area_sqkm': 0.0, 'sameascity': -99, 'labelrank': 0, 'featurec_1': 'Admin-1 scale rank', 'admin': 'United States of America', 'name_len': 9, 'mapcolor9': 1, 'mapcolor13': 1}, <fields>>"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"next(states)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now the next."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<Record: <shapely.geometry.polygon.Polygon object at 0x7f30d9dbc780>, {'scalerank': 2, 'featurecla': 'Admin-1 scale rank', 'adm1_code': 'USA-3515', 'diss_me': 3515, 'adm1_cod_1': 'USA-3515', 'iso_3166_2': 'US-MT', 'wikipedia': 'http://en.wikipedia.org/wiki/Montana', 'sr_sov_a3': 'US1', 'sr_adm0_a3': 'USA', 'iso_a2': 'US', 'adm0_sr': 1, 'admin0_lab': 2, 'name': 'Montana', 'name_alt': 'MT|Mont.', 'name_local': None, 'type': 'State', 'type_en': 'State', 'code_local': 'US30', 'code_hasc': 'US.MT', 'note': None, 'hasc_maybe': None, 'region': 'West', 'region_cod': None, 'region_big': 'Mountain', 'big_code': None, 'provnum_ne': 0, 'gadm_level': 1, 'check_me': 0, 'scaleran_1': 2, 'datarank': 1, 'abbrev': 'Mont.', 'postal': 'MT', 'area_sqkm': 0.0, 'sameascity': -99, 'labelrank': 0, 'featurec_1': 'Admin-1 scale rank', 'admin': 'United States of America', 'name_len': 7, 'mapcolor9': 1, 'mapcolor13': 1}, <fields>>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"next(states)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can save one to a variable name so that we can examine it more carefully:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<Record: <shapely.geometry.polygon.Polygon object at 0x7f30d9dbccc0>, {'scalerank': 2, 'featurecla': 'Admin-1 scale rank', 'adm1_code': 'USA-3516', 'diss_me': 3516, 'adm1_cod_1': 'USA-3516', 'iso_3166_2': 'US-ND', 'wikipedia': 'http://en.wikipedia.org/wiki/North_Dakota', 'sr_sov_a3': 'US1', 'sr_adm0_a3': 'USA', 'iso_a2': 'US', 'adm0_sr': 1, 'admin0_lab': 2, 'name': 'North Dakota', 'name_alt': 'ND|N.D.', 'name_local': None, 'type': 'State', 'type_en': 'State', 'code_local': 'US38', 'code_hasc': 'US.ND', 'note': None, 'hasc_maybe': None, 'region': 'Midwest', 'region_cod': None, 'region_big': 'West North Central', 'big_code': None, 'provnum_ne': 0, 'gadm_level': 1, 'check_me': 0, 'scaleran_1': 2, 'datarank': 1, 'abbrev': 'N.D.', 'postal': 'ND', 'area_sqkm': 0.0, 'sameascity': -99, 'labelrank': 0, 'featurec_1': 'Admin-1 scale rank', 'admin': 'United States of America', 'name_len': 12, 'mapcolor9': 1, 'mapcolor13': 1}, <fields>>"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state = next(states)\n",
"state"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We are seeing the attributes of the record, unique to this file, which we can access more specifically as follows:"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"{'scalerank': 2,\n",
" 'featurecla': 'Admin-1 scale rank',\n",
" 'adm1_code': 'USA-3516',\n",
" 'diss_me': 3516,\n",
" 'adm1_cod_1': 'USA-3516',\n",
" 'iso_3166_2': 'US-ND',\n",
" 'wikipedia': 'http://en.wikipedia.org/wiki/North_Dakota',\n",
" 'sr_sov_a3': 'US1',\n",
" 'sr_adm0_a3': 'USA',\n",
" 'iso_a2': 'US',\n",
" 'adm0_sr': 1,\n",
" 'admin0_lab': 2,\n",
" 'name': 'North Dakota',\n",
" 'name_alt': 'ND|N.D.',\n",
" 'name_local': None,\n",
" 'type': 'State',\n",
" 'type_en': 'State',\n",
" 'code_local': 'US38',\n",
" 'code_hasc': 'US.ND',\n",
" 'note': None,\n",
" 'hasc_maybe': None,\n",
" 'region': 'Midwest',\n",
" 'region_cod': None,\n",
" 'region_big': 'West North Central',\n",
" 'big_code': None,\n",
" 'provnum_ne': 0,\n",
" 'gadm_level': 1,\n",
" 'check_me': 0,\n",
" 'scaleran_1': 2,\n",
" 'datarank': 1,\n",
" 'abbrev': 'N.D.',\n",
" 'postal': 'ND',\n",
" 'area_sqkm': 0.0,\n",
" 'sameascity': -99,\n",
" 'labelrank': 0,\n",
" 'featurec_1': 'Admin-1 scale rank',\n",
" 'admin': 'United States of America',\n",
" 'name_len': 12,\n",
" 'mapcolor9': 1,\n",
" 'mapcolor13': 1}"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state.attributes"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"... and then each attribute individually as in a dictionary:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"'North Dakota'"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state.attributes['name']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can also access the geometry of the record:"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"100.0\" height=\"100.0\" viewBox=\"-104.39491638061642 45.654446690445575 8.158162500032645 3.653347029637061\" preserveAspectRatio=\"xMinYMin meet\"><g transform=\"matrix(1,0,0,-1,0,94.96224041052821)\"><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"0.1631632500006529\" opacity=\"0.6\" d=\"M -97.22894344764502,49.00088532164392 L -97.21413814979341,48.90244171812793 L -97.12047461626437,48.758522854194986 L -97.12734758175914,48.6421216904576 L -97.1612214831265,48.51458425556129 L -97.14850908078273,48.318782253607296 L -97.13104244666802,48.1372946233983 L -97.01515804725352,47.95420502378817 L -96.8939768135291,47.74886872007639 L -96.84423824744817,47.54619375262771 L -96.82465287960953,47.42661448830433 L -96.82041541216158,47.29220408791307 L -96.77969438351565,46.999043687521336 L -96.74582048214829,46.94452505145338 L -96.7336506823436,46.71647695574936 L -96.68548824744752,46.5132852239777 L -96.60135901567635,46.351357123391146 L -96.53890804725165,46.19948008888536 L -96.53945064979074,46.017966620460086 L -98.44178931353527,45.963447984392126 L -100.06685807981783,45.96556671811615 L -102.11686214883649,45.9613550888843 L -104.02661638061497,45.95660085711345 L -104.07741431355787,47.17156545672773 L -104.09276221394855,49.00563955341476 L -100.62989864785398,49.00300405536785 L -97.22894344764502,49.00088532164392 z\" /></g></svg>"
],
"text/plain": [
"<shapely.geometry.polygon.Polygon at 0x7f30d9dbccc0>"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state.geometry"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"(array('d', [-100.48470034126994]), array('d', [47.46271462229255]))"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state.geometry.centroid.xy # this is in lon/lat"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"and properties of the geometry like the area and centroid location:"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"21.804544852980253"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state.geometry.area # what are the units of this area?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Pull out specific records\n",
"\n",
"Find states that start with \"A\":"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Arizona\n",
"Arkansas\n",
"Alabama\n",
"Alaska\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAANsAAADnCAYAAACXOyOWAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAQ/0lEQVR4nO3d61MT1/8H8PcmIQQSAoSLIAQBgYIoAlZFtMxYldYRa6XT1unT/m99Up3pTNUZEautWvGGBVuLGJBbQ0AuIQEMue3vgd/k15QQSLI5ufB+zXRGspvdz0x5c86ePbtHkmUZRJR4qmQXQLRbMGxEgjBsRIIwbESCMGxEgmgibayurpYnJydF1UKUCSZlWa4Ot0GKNPQvSZLMWwNEOydJEmRZlsJtYzeSSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IkIgLaySDLMt4+PAhVCoVmpubkZ+fn+ySiBSRcgtrPHr0CC9fvgz+XFVVhc7OThiNRqF1EMUibRbWGBwcDAkaAExNTeHJkydJqohIOUntRi4uLmJsbAylpaVYWVnBs2fPwu43Pj6OhYUF+Hw+TExMQK/XQ6/Xo7CwEAUFBYKrJopNUrqRsizj5cuXePLkCfx+/46+U1ZWBofDgfX19eBn9fX1OH36tOL1EcUqUjdSeMu2traGu3fvwmq1RvU9m8226bPl5WVMTU2hsrISKtX/94g9Hg+ysrLirpVIScJatrW1NYyNjeHFixfY2NhQ5JgBWq0W1dXVyMrKwtTUFNbW1lBXV4eWlhaYTCZFz0UUSaSWTUjY/jvCKFJFRQVaWlpgNpuTcn7aXZIatvHxcfT398d1DCVotVoYjUbk5+cjPz8fRUVF2LdvH1QqFfx+P6xWK1ZWVtDY2Ai1Wp3scilNJS1sTqcT165dg9vtjvkYiZSXl4eKigpMTk7i/fv3AACj0YiOjg5UV1cntzhKS0kLW19fHyYmJmL+fjLt3bsXhw4dgtlsDhl8IYokaaOR8/PziTx8QlmtVlitVuh0OvT09HCgheKWsD/ZLpcr5J5YunK5XIqPntLulLCwzc7OJurQRGkpIWGbm5vDvXv3EnFoorSleNjm5+dx8+ZNeDwepQ9NlNbiGiBxuVyYmZmBx+OBx+OB2+3Gn3/+yaARhRFX2P7++288ffpUqVqIMlrM3UhZljEyMqJkLUQZLeawzc7Owul0KlkLUUaLOWylpaVobW3l7AqiHYo5KRqNBseOHUNvby/27NmjZE1EGSnuZslkMqGnpwdlZWVK1EOUsRTpA6rVanR3d/MNWEQRKHbBpdPp8Nlnn/EajmgLiiajsLAQzc3NSh6SKGMo3gy1tbVBq9UqfViitKd42HQ6HU6ePJlR3UlJCvssIFFUEpKI+vp69PT0IDc3NxGHJ0pLCWt+ysrK0Nvbyyecif5H0bBNTk5iaGgIU1NTAIDc3FycPHlSyVMQpS1F3kEyNzeHgYEBzM3NAQBaWlpQVVUFACgvL0dlZSVmZmaUOBVR2oorbHa7HU+ePNn0Bi2DwRDy89GjRxk22vViCpvP58PTp0/x8uVLhHvVncVigdVqDT5U6vV6A6/4irtgonQVddhWVlZw584dLCwsbLlPOr/CjihRogrb/Pw8rl+/Dq/Xm6h6iDJWVKORxcXF2Lt3b6JqIcpoUYVNpVLh7NmzfH6NKAZR32fTaDT4/PPPubwuUZRiuqmdnZ2NY8eOKV0LUUaLeQbJvn37dvywqEqlQkNDA44cOZJRE5SJohHzTW1JktDb24uxsTG8fv06ONyv1+thMpkwNzcHt9uNuro6HDt2DHq9Hn19fTtesJ4o08Q1g0Sr1aKpqQlNTU1wOBzQarXQ6XQAgPX1dfzxxx/o6OiASqWCzWbD9PS0IkUTpSPF+nRGozEYNODDJOTOzs5gt7GsrAzd3d1KnY4o7Qi9gNq7dy8fxKRdS2jYNBoN9Hq9yFMSpYyEhy0wICLLMh48eIDV1dVEn5IoJW07QDI2Ngaz2RzzS3zu37+P6elp6PV6vHv3LqZjEGWCbcN2584d6HQ6XLlyZdvAeTwezM/Pw+VyoaamBhaLBa9fvwaAjFhfmyge24btwIEDOHLkyI5atkePHgWXkcrLy8P79+/jr5AoQ2wbtlOnTu3oQLIshzyxzeWkiEIpNkAyPT0Nl8ul1OGIMo4iYXO73Xjw4IEShyLKWIqEbWBgIKOH9HkjnpQQd9iWlpa4tjbRDsQdtrdv3ypRB1HGY9iIBIk7bIE3HxNRZHGH7ejRo6irq1OilrhUVlbyVQ2U0uIOmyRJOHjwoBK1xKy+vh6ffvrptlPC+EoGSiZFFtZIpgMHDqCmpgZXr14NGza1Wo2PPvoIjY2NyMnJwS+//ILZ2dkkVEq7nSJ/6rVaLdRqtRKHiopOp8Px48fx119/bdmq6fV6nDp1CsXFxdDr9ejp6cHHH3/MVo6Ei6llW1xchMViweLiIkpLS9HW1obLly+jv78fdrtd6Rq3dPjwYWRlZQWXqgrH6XTC5/MF/xhIkoT29nY0NDRgeHgYIyMj275O/e3bt3A4HDAajXxBLcUsprD9888/GBoaAgDMzMygrq4OJpMJPT09+Omnn4TMJtHr9WhubobD4Yj4dIEsy3A6nZteKmswGNDZ2Yn29nb8+eefGBkZgVarhcFgQE5ODmZmZoLHHR4eDn7PbDbjxIkTfEktRU2KtIyTJEnyVtunp6fx+++/IycnB2fOnAm+7sBut+O3335DeXk5qqqqsLq6ijt37ihatMFgQE9PD4xGI0ZHR3Hv3r2w+9TV1aGqqgqlpaVRdxv9fj8mJibw6tUrWK3WkG1ZWVn48ssvUVhYGPa7sixzitcu9b+l0cL+z485bMDOf6meP3+O58+f76DU7RkMBly8eBF5eXkAgKGhITx+/Dhke1dXFyoqKhT7hbfb7RgZGcHo6GjwyQaj0YjLly8jOzs7ZF+r1YqHDx/i/PnzmxaFpMwXKWxxjRLs9JfZ5/PFc5ogg8GAL774Ihg0ACH/rqmpwVdffYXKykpFW5aCggJ0dHTgu+++g9lsBgA4HA7cv38/ZL+BgQFcv34dy8vLiv1xocwhZEhOqUETj8ezafXSwsJCHDlyBFeuXMG5c+c2tTRK0mg06O7uxr59+wAA4+PjsFgsAIDBwcGQa7vR0VHeYqAQQsL271cq1NfXo6KiYstbBZGurTY2NnD79u2QljIQtp2uOxAvtVqNc+fOoaamBgDw4MEDDA4O4tmzZyH7ybKMvr4+rKysCKmLUp+QsBmNRhgMBpw6dQqnT59Gc3Mzurq6UFBQAEmSUFNTE7wfVltbG/FYLpdLsW5prFQqFc6cOYO6ujq43e5NQQvY2NjAjRs34HA4BFdIqSiuAZJYBd4lubCwAJvNhpaWFvj9frhcLvzwww8RF9+4ePEiysvLFa8pFrIs49GjR3j16lXEmnNzc3HhwoUtRy8pcyRsNFJpw8PDGBgY2HJ7S0sLOjo6hNWzU6urqxgeHsbExAS8Xi98Ph98Pl9IAAsKCvD111/zlkCGixS2lJobGen6pqmpCUePHgXwoWVMpelWgRvknZ2dIZ+7XC44nU7cuHEDdrsdU1NTwcEV2n1SKmzhXn+n1WrR1dWF2tpabGxs4OHDhxgdHYXBYMD58+eRn5+fhEp3RqfTQafToaqqChaLBUNDQwzbLpYyzYPX6910i6CxsRHffvstamtrYbPZcO3aNYyMjMDv98PhcKTNvaxAwGw2G28H7GIp0bK5XC7cunUrZE7lmTNnsH///uDP/12Uw2Qybeq2pSqz2QyVSgW/348XL16kzAAPiZX0li1wP+rfM/c1Gs2m7ta/R/JKSkpw4cKFkMUXU5lWq0VjYyOADxO3A0si0+6S1LC53W7cvn0bNpst+JnRaMS5c+eg0YQ2um1tbTAYDGhvb8elS5eQk5Mjuty4dHZ2Bqd6DQ4OJrkaSoakDf0vLy+HzLBQq9Voa2vD4cOHt5xdkmqjkNHyeDz4+eefsbCwgMuXL6OkpCTZJZHCUu4+m81mw82bN0Me2uzt7UVxcbHi50o16+vr+PHHHyHLMjo7O9HQ0JDskkhBCZv1HwuPx4O7d++GBK20tHRXBA34MJtkz549cLvduHfvHm7dusW163YJIaORS0tLGB0dhd1ux+LiItbW1oLbioqK8Mknn4goI2WYTCZMTU0BACYnJ2Gz2XDp0iU+/Z3hEh622dlZ3Lp1C263G8CHkbn9+/fDbrdj//79aGlpSevrsFgUFRWF/LyxsYHV1VWGLcMlNGzj4+O4e/du8IU7hw4dwuHDhxP6zFk6MJvNaGhowOjoaPCzSBOZKTMkZIBkcXERjx8/xszMDACguroaJ06cCHmqmj7cc+vr64NGo8E333yTNvcNaWvCRiNlWcaLFy/w/PlzyLIMnU6Hrq4uVFdXR130bhFYmCTwMCqlNyFhc7lc6O/vh9VqRUlJCcxmM5qbm9Pu5jNRPISEzev14u3bt6isrGTAaNdKuZvaRJkqpW5qE+1WDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgDBuRIAwbkSAMG5EgmmQXQKlpfX0dS0tLkGUZsiyH3UeSJACASqVCRUWFyPLSEsNGYU1PT+PXX3/d0b5qtRrff/99gitKfwwbhRVotdKFw+HA1atXIUlS8L+AwL+1Wi10Oh26u7uRm5srvEaGjTbp7+/H+vp6ssuIisFggN/vh9/v33Ifl8sFv9+PV69eob29HSqV2CELDpDQJk6nEzabLdllREWlUsFoNG673+rqKiRJEh40gGGjMJLRxVJCdnb2jvZra2tLcCXhsRtJm6Tb9VpApC5kQGNj46ZWbWZmBiMjI8GfA9d8Bw8eRGlpqWL1MWy0SWNjIyYmJpJdRtS2C5tKpUJra+umzx0OB8bHxzd9XlhYqGjY2I2kTYqLi5GTk5PsMqLm8/kibj979mzY67rV1dWw+y8tLSlSVwDDRpuMjo7i/fv3yS4japFatpKSElRXV4fdxrBR0oTrUqWDrVou4EPYtrK2thb2c7vdDq/Xq0htAK/ZKIx0HSApLi6GyWRCTk4OJEmCWq2GRqOB3++PONS/1T1FWZaxtLSk2HUbw0Yh/H4/tFptssuIWXd3d9TfidRlnpubUyxs7EbSJk1NTTCbzWnbwkXD6/XC7XZvud1isSh2LrZsFEKlUqG2tha1tbVYW1vDmzdv8ObNGywvLye7tITYbiCovLxcsXMxbLQlvV6P1tZWtLa2YnFxEW/evIHFYkm7eZORbPX4UIBGo1xEGDbakaKiIhQVFeH48eN49+5dcJTuvzPs043IOZIMG0VFkiRFZ1UkWyBser0ep0+fRnZ2dsgfDyUHixg22tXUajXy8/PhdDqRl5eHvLy8hJ1LitRnlSRJ3q5PS5QJZFlWpDssSRJkWQ57IA79E0HMjXyGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSBCGjUgQho1IEIaNSJBtXz+ezosmECXB5FYbIr5+nIiUw24kkSAMG5EgDBuRIAwbkSAMG5Eg/wcCx7qKDZ0XlwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"pc = cartopy.crs.PlateCarree()\n",
"\n",
"\n",
"# how we tell cartopy which data we want, from the list at the end of the maps notebook\n",
"shapename = 'admin_1_states_provinces_lakes_shp'\n",
"\n",
"# Set up reader for this file\n",
"states_shp = shpreader.natural_earth(category='cultural', resolution='110m', name=shapename)\n",
"reader = shpreader.Reader(states_shp)\n",
"\n",
"# Read in the data from the file into the \"states\" generator which we can iterate/loop over\n",
"states = reader.records()\n",
"\n",
"Astates = [] # initialize list to save states that start with \"A\"\n",
"\n",
"fig = plt.figure()\n",
"ax = fig.add_subplot(1,1,1, projection=cartopy.crs.Mercator())\n",
"ax.set_extent([-170,-80,20,75], pc)\n",
"for state in states:\n",
"\n",
" if state.attributes['name'][0] == 'A':\n",
" print(state.attributes['name'])\n",
" ax.add_geometries([state.geometry], pc,\n",
" facecolor='k', alpha=0.4)\n",
" # save state\n",
" Astates.append(state)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*How could you change this loop to check for states in a specific region of the country?*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Transforming geometry between projections\n",
"\n",
"Shapefiles are often in geographic coordinates (lon/lat), and they come out of Natural Earth as lon/lat. \n",
"\n",
"Here we change a state's projection from PlateCarree (`pc`) to LambertConformal. We use the `project_geometry` method in the projection we want to transform to (`lc` in this case), and input the current projection of the shape into the method (`pc` in this case)."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"100.0\" height=\"100.0\" viewBox=\"-173.4635552564725 52.73172842850084 45.15600564669555 20.29847980202222\" preserveAspectRatio=\"xMinYMin meet\"><g transform=\"matrix(1,0,0,-1,0,125.76193665902389)\"><g><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"0.9031201129339109\" opacity=\"0.6\" d=\"M -153.0063140533369,57.11584219016598 L -154.0050902984581,56.734676825581055 L -154.51640275777007,56.99274892844678 L -154.67099280497115,57.46119578717249 L -153.76277950744148,57.81657461204376 L -153.22872941792107,57.968968410872435 L -152.5647906158351,57.90142731386706 L -152.14114722390633,57.59105866152207 L -153.0063140533369,57.11584219016598 z\" /><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"0.9031201129339109\" opacity=\"0.6\" d=\"M -165.57916419173358,59.90998688418764 L -166.19277014876727,59.7544408229889 L -166.848337368822,59.94140615502105 L -167.45527706609005,60.21306915957937 L -166.46779212142462,60.384169826897775 L -165.67442969466367,60.29360687930624 L -165.57916419173358,59.90998688418764 z\" /><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"0.9031201129339109\" opacity=\"0.6\" d=\"M -171.7316568675394,63.782515367276005 L -171.11443356024523,63.59219106714499 L -170.4911124339407,63.694975490973505 L -169.68250545965356,63.43111562769125 L -168.68943946030066,63.2975062120006 L -168.7719408844546,63.18859813094545 L -169.52943986720504,62.976931464277975 L -170.29055620021597,63.19443756779445 L -170.67138566799088,63.37582184513896 L -171.55306311753867,63.31778921167509 L -171.79111060289117,63.40584585230048 L -171.7316568675394,63.782515367276005 z\" /><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"0.9031201129339109\" opacity=\"0.6\" d=\"M -155.0677902903243,71.1477763943237 L -154.3441652089412,70.6964085964702 L -153.9000062733925,70.8899885118357 L -152.2100060699353,70.82999217394467 L -152.27000240782613,70.60000621202985 L -150.7399924387445,70.43001658800571 L -149.72000301816752,70.53001048449045 L -147.61336157935696,70.2140349392418 L -145.68998980022536,70.12000967068683 L -144.92001095907642,69.9899917670403 L -143.58944618042526,70.1525141465983 L -142.0725103487135,69.85193817817263 L -140.9859883290049,69.71199839952628 L -140.98598752156073,69.71199839952628 L -140.9924987520295,66.00002859156868 L -140.99776974812323,60.30639679629858 L -140.0129978161532,60.27683787702766 L -139.03900042031586,60.0000072292401 L -138.34087765826888,59.5621011419987 L -137.45250811073927,58.90498362897522 L -136.47972511106087,59.46386424421188 L -135.4758328991428,59.78777212181726 L -134.94498674842458,59.27054271100801 L -134.27110023312235,58.86111033795939 L -133.35554888220722,58.41028514264516 L -132.73042069566097,57.692887071353105 L -131.70782161525327,56.5521039902939 L -130.0077703457152,55.91581207948416 L -129.97999426335826,55.28499787049722 L -130.53611018946725,54.8027534043494 L -131.08581823797215,55.17890615500186 L -131.9672114671423,55.49777558045904 L -132.25001074285953,56.369996242897436 L -133.53918108435641,57.17888743756213 L -134.07806292029613,58.12306753196691 L -135.03821103227915,58.18771474876393 L -136.62806230995474,58.21220937767028 L -137.80000627968602,58.49999542910379 L -139.867787041413,59.537761542389134 L -140.82527381713302,59.727517401764885 L -142.57444353556446,60.084446519604995 L -143.9588809948799,59.999180406323475 L -145.92555681682782,60.45860972761429 L -147.11437394914665,60.88465607364463 L -148.22430620012764,60.67298940697707 L -148.01806555885076,59.978328965893624 L -148.57082251686077,59.914172675203126 L -149.72785783587585,59.70565827090563 L -150.60824337461634,59.36821116803949 L -151.7163927886833,59.15582103131997 L -151.85943315326716,59.74498403587959 L -151.4097190012472,60.7258027207794 L -150.3469414947325,61.03358755150986 L -150.62111080625706,61.28442495385443 L -151.89583919981683,60.72719798445129 L -152.57832984109558,60.06165721296427 L -154.0191721262576,59.35027944603427 L -153.28751135965308,58.86472768821979 L -154.23249243875847,58.146373602930524 L -155.30749142151012,57.727794501366326 L -156.30833472392308,57.42277435976363 L -156.5560973785464,56.97998484967063 L -158.11721655986773,56.46360809999401 L -158.43332129619714,55.99415355083853 L -159.60332739971744,55.566686102920116 L -160.2897196116342,55.6435806341704 L -161.2230476552578,55.36473460552348 L -162.23776607974096,55.0241869167201 L -163.06944658104638,54.689737046927156 L -164.7855692210273,54.40417308208215 L -164.9422263255201,54.572224839895334 L -163.84833960676568,55.039431464246114 L -162.8700013906159,55.3480431178932 L -161.804174974596,55.894986477270415 L -160.56360470278122,56.00805451112504 L -160.0705598622844,56.41805532492875 L -158.68444291891953,57.01667511659786 L -158.46109737855406,57.21692129172887 L -157.72277035218386,57.57000051536306 L -157.55027442119365,58.3283263210303 L -157.041674974577,58.91888458926172 L -158.19473120830557,58.615802313869814 L -158.51721798402306,58.787781480537305 L -159.05860612692882,58.424186102931664 L -159.71166704001732,58.93139028587634 L -159.98128882550017,58.57254914004163 L -160.3552711659965,59.07112335879371 L -161.35500342511511,58.67083771426075 L -161.96889360252644,58.67166453717737 L -162.05498653872465,59.266925360747436 L -161.87417070213542,59.63362132429059 L -162.51805904849215,59.9897236192139 L -163.81834143782024,59.79805573184346 L -164.66221757714655,60.26748444278266 L -165.3463877024748,60.5074956325624 L -165.35083187565192,61.07389516869749 L -166.12137915755605,61.50001902937622 L -165.7344518707706,62.074996853271884 L -164.91917863671785,62.633076483807926 L -164.56250790103934,63.146378485763044 L -163.7533324859971,63.219448961023595 L -163.0672244944579,63.05945872664801 L -162.2605553863817,63.54193573674117 L -161.53444983624857,63.45581696232675 L -160.7725066803211,63.76610810002327 L -160.95833513084264,64.22279857040277 L -161.5180684072121,64.40278758407531 L -160.77777767641484,64.7886038275664 L -161.3919262359876,64.77723501246214 L -162.45305009666893,64.55944468856804 L -162.7577860178941,64.3386054551688 L -163.54639421288428,64.5591604681905 L -164.96082984114517,64.44694509546868 L -166.4252882558645,64.6866720648707 L -166.84500423893914,65.08889557561454 L -168.11056006576706,65.66999705673675 L -166.70527116602196,66.0883177761394 L -164.4747096425755,66.57666006129749 L -163.65251176659567,66.57666006129749 L -163.78860165103626,66.0772073431965 L -161.67777442121016,66.11611969671242 L -162.48971452538007,66.7355650905951 L -163.7197169667912,67.1163945583701 L -164.43099138085654,67.6163382025778 L -165.39028683170673,68.04277212185025 L -166.76444068099607,68.35887685817976 L -166.2047074046267,68.88303091091625 L -164.43081051334357,68.91553538682773 L -163.16861365461452,69.37111481391288 L -162.93056616926202,69.85806183539925 L -161.9088972646355,70.33332998318764 L -160.93479651593367,70.44768992784957 L -159.03917578838704,70.89164215766894 L -158.11972286683397,70.82472117785112 L -156.58082455139802,71.35776357694174 L -155.0677902903243,71.1477763943237 z\" /></g></g></svg>"
],
"text/plain": [
"<shapely.geometry.multipolygon.MultiPolygon at 0x7f30d9e14320>"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"state.geometry # we can see the shape in PlateCarree"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"300\" height=\"300\" viewBox=\"-4292848.9745935425 2101992.698866925 2386956.897282407 2729434.353158445\" preserveAspectRatio=\"xMinYMin meet\"><g transform=\"matrix(1,0,0,-1,0,6933419.7508922955)\"><g><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"18196.2290210563\" opacity=\"0.6\" d=\"M -3398237.0903454525,3141924.198343111 L -3476108.4066980504,3143753.8701355667 L -3484303.530696251,3187515.0171946418 L -3459160.7207615445,3237299.3749765693 L -3388298.7377710748,3236569.9310390865 L -3350682.3655047007,3231239.2234891118 L -3321638.7660117825,3200418.1454706304 L -3321170.9180878033,3155223.768188445 L -3398237.0903454525,3141924.198343111 z\" /><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"18196.2290210563\" opacity=\"0.6\" d=\"M -3783087.18597724,3893707.5505169346 L -3822549.396706413,3906024.465057402 L -3835037.1460705716,3949598.3383707893 L -3837832.2304507075,3998286.7002530005 L -3781604.917297257,3971472.5838869326 L -3755325.122297959,3930775.537917494 L -3783087.18597724,3893707.5505169346 z\" /><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"18196.2290210563\" opacity=\"0.6\" d=\"M -3691710.960127151,4475633.508352396 L -3686201.6224463945,4434657.280638926 L -3653524.269394044,4418142.743867758 L -3646703.0493533798,4363268.605273811 L -3620449.431600673,4312125.717574321 L -3633286.697106265,4306060.879592375 L -3681394.11812133,4318477.15883418 L -3691125.991489925,4367759.081892349 L -3689205.1101615373,4398502.946001192 L -3727611.070129405,4429627.722304771 L -3728447.535692003,4446712.114574895 L -3691710.960127151,4475633.508352396 z\" /><path fill-rule=\"evenodd\" fill=\"#66cc99\" stroke=\"#555555\" stroke-width=\"18196.2290210563\" opacity=\"0.6\" d=\"M -2438932.8525097505,4620834.219385581 L -2450236.693403364,4552126.439865199 L -2418491.1186508117,4561402.178731234 L -2362054.1292889994,4510321.584487087 L -2382418.1995844417,4486382.825720082 L -2338872.8931438415,4427739.206232266 L -2292990.6524644224,4412962.007658086 L -2236199.2313088253,4324667.100848492 L -2168128.137634874,4267288.515273081 L -2146849.8222167394,4234010.333843771 L -2083032.7313907265,4221924.756784717 L -2042172.7047911186,4152294.298902303 L -2006982.2715703053,4111626.0301208985 L -2006982.238539226,4111626.0122882472 L -2237316.6348485486,3685692.2079830826 L -2571363.822297763,3067709.619052274 L -2521267.5806783326,3036985.6848351243 L -2484892.8309218367,2980714.087149542 L -2471079.438636057,2915021.5156320985 L -2457356.260881788,2820922.857942421 L -2374971.071480437,2854877.256627137 L -2303608.6448046495,2864007.9213421484 L -2300195.098503426,2794538.9773184 L -2282682.211861036,2733229.8066441007 L -2252556.484419555,2661557.877143544 L -2250216.1005518925,2568426.1097446876 L -2242033.919403194,2420016.9105458274 L -2167534.924280386,2310071.265452369 L -2192566.53096137,2241315.976385146 L -2247394.924254175,2203082.8600950157 L -2265021.322443384,2257038.9037861894 L -2304725.39201245,2313331.1811970696 L -2282513.4456836325,2413924.468124849 L -2321163.3174980227,2533407.7787934653 L -2307368.863252726,2648650.967239991 L -2358797.747587766,2680252.578759099 L -2447262.3446617764,2724912.4838637174 L -2497787.6946093165,2787365.8152198894 L -2554643.200645708,2954662.429415095 L -2595136.960957778,3001795.175540052 L -2666633.2400800786,3089844.887966932 L -2743664.076044428,3122197.60483668 L -2816107.5392337968,3229665.6477788915 L -2848681.607566239,3310288.9925554483 L -2917525.440011514,3324009.344901332 L -2952459.235538484,3247308.5178879877 L -2984471.2210998754,3258924.820557923 L -3056307.059346871,3276603.168410873 L -3123019.244660053,3273235.472228061 L -3192883.1122570937,3290988.263274727 L -3159533.3872849224,3353375.7401143895 L -3069976.716887429,3434237.7460294846 L -2997468.382316378,3429315.1497628693 L -2993576.9839926558,3463392.5527565307 L -3093345.6100548166,3450860.28204012 L -3172753.866281804,3409279.5536427666 L -3293055.5614891704,3391923.693904694 L -3291237.744730222,3318942.745797778 L -3388759.7540089083,3285295.0769417672 L -3472214.3454912235,3286527.8884734814 L -3544106.723043442,3296814.964879698 L -3588522.43871974,3265709.824992122 L -3704472.594708469,3281266.501008665 L -3754932.9725810178,3251926.2152214907 L -3845516.1195402113,3262692.2558965604 L -3874102.3643302717,3298645.074821919 L -3941680.4749642806,3314329.7093838025 L -4018083.3364647306,3329241.3246216923 L -4085075.3918297766,3337640.3971055835 L -4191758.8133654515,3391660.263467109 L -4186084.3827157966,3412942.9276766917 L -4096003.633167653,3402450.3482039548 L -4024149.5402088375,3385071.6027890784 L -3929730.265389986,3385694.901767391 L -3860136.7945474,3342424.39830714 L -3804807.183275462,3357894.4739487013 L -3691675.1935822032,3354311.4958128068 L -3665787.2968656803,3363377.511809292 L -3603359.6129831607,3365975.417947951 L -3538896.908884742,3428756.1312747747 L -3470701.258830094,3463748.06892212 L -3548521.133352327,3480303.658603463 L -3550995.2453176673,3508663.1200210713 L -3604198.727992068,3496806.6695559258 L -3596487.562841503,3568724.9252556846 L -3636640.457219421,3547000.0637276303 L -3615778.622726015,3606905.481422803 L -3693288.1320355115,3611215.8504475877 L -3721632.2397145242,3636334.7491491074 L -3678643.4786469024,3692665.87698955 L -3641432.1859330325,3718064.6991403606 L -3642024.793819669,3775627.288666121 L -3715212.6491781427,3811322.485622264 L -3713820.1083614924,3886907.680242014 L -3723472.070193844,3935810.877699901 L -3676479.797667225,3985322.951766145 L -3672969.9526173766,4053608.828903593 L -3608314.842080217,4088332.8262203196 L -3527676.778135039,4105649.823003458 L -3469818.684727597,4137808.266877033 L -3430701.107649496,4113677.4578110557 L -3415817.692179613,4073294.9440750782 L -3342663.9871938545,4087537.277041978 L -3319694.920410036,4052947.722316957 L -3262787.858837274,4054318.8796825497 L -3233275.2731821737,4103887.630845414 L -3241333.0618210123,4140744.2053383435 L -3179594.904802148,4150998.1699884995 L -3205319.646675908,4171497.8980821637 L -3266030.713274059,4188865.6662800773 L -3296719.077744633,4179357.6933451006 L -3309614.7656924548,4228396.979068783 L -3374911.616246458,4270162.4170309855 L -3410834.3792486168,4346441.862238618 L -3391370.745362738,4398159.47182121 L -3386499.8281828235,4497198.961538905 L -3297261.6647927263,4483092.015357038 L -3171450.5602264297,4448683.953874101 L -3140736.128728865,4420128.5025302125 L -3189149.2769446536,4377966.026178794 L -3104853.3751685168,4308544.296354821 L -3083237.9193530967,4395391.117976811 L -3096179.7013438507,4473473.939667127 L -3078073.002640967,4545049.886636902 L -3074138.3447439387,4617869.627589054 L -3093259.8624302167,4694196.512217816 L -3025678.200188213,4724672.296056493 L -2961564.2324703163,4669343.329591314 L -2876633.082556423,4673230.690326626 L -2824602.9255724098,4713960.210730078 L -2746910.27668338,4730336.89079728 L -2703388.1465565255,4712769.311093521 L -2599179.9742882513,4703498.960466541 L -2573191.0315020937,4670280.170989977 L -2474169.0820546336,4684559.290452765 L -2438932.8525097505,4620834.219385581 z\" /></g></g></svg>"
],
"text/plain": [
"<shapely.geometry.multipolygon.MultiPolygon at 0x7f30d2c03fd0>"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lc = cartopy.crs.LambertConformal()\n",
"statelc = lc.project_geometry(state.geometry, cartopy.crs.PlateCarree())\n",
"statelc # this is now the geometry of the record only, without attributes\n",
" # the shape has changed in the new projection"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Reading your own shapes and using `cartopy`\n",
"\n",
"You can read in shapefiles outside of the Natural Earth dataset and use them on maps with `cartopy`. Here we look at shipping lanes in the northwest Gulf of Mexico. You can get to the shapes or polygons themselves two different ways using `cartopy`. The first uses the `feature` interface that we've been using (with `add_feature`), but limits our ability to access attributes of the files. The second gives more access.\n",
"\n",
"\n",
"### 1st approach for using a generic shapefile:\n",
"\n",
"We start with a map:"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<cartopy.mpl.feature_artist.FeatureArtist at 0x7f30d2bbe080>"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAGzCAYAAADqqkXjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nOzdeVsayfo+8LuqaZp9RxA33GKSycycM/N9/69gfuecWU4SY6JGDaIgguzQ3fX7w+k+EjfcAOX+XNdck7AWauTmqaqnhFIKRERERESTSo57AEREREREN2FgJSIiIqKJxsBKRERERBONgZWIiIiIJhoDKxERERFNNAZWIiIiIpponpuuzOVy6vDwcFRjISIiIqIpppQSV10uburDKoRQv/3225MNioiIiIgIAP7v//7v2sDKJQFERERENNEYWImIiIhoojGwEhEREdFEY2AlIiIioonGwEpEREREE42BlYiIiIgmGgMrEREREU00BlYiIiIimmgMrEREREQ00RhYiYiIiGiiMbASERER0URjYCUiIiKiicbASkREREQTjYGViIiIiCYaAysRERERTTQGViIiIiKaaAysRERERDTRGFiJiIiIaKIxsBIRERHRRGNgJSIiIqKJxsBKRERE9DchxLiHQFdgYCUiIiL6GwPrZGJgJSIiIvqbUmrcQ6ArMLASERHR1BNCYHl5GYFAwP37S/UcX5tn3AMgIiIiGjchBIQQeP36NQCg2+3i4OAAtVrtxVVdn+PrYYWViIiIpp4QApFIxP27YRhYWVmBx/O8antO8L6OlBKZTAZSyrFWWqWUkHL4GMrASkRERFMvFotB07SBy4QQyGazz2YKXQiBXC7nLmu4ilIKMzMzyOVyUEqN7bWlUqk7VXoZWImIiGjqfR9WHclk8tkEVqUUut0uVldXEQgErqxgSinR6/VQKBTc+4ySpmmYm5tDt9sdeO7bqq0MrERERDT1rgtMmqYhlUo9m9B6dnYGXdeRzWZh2/al1xUKhVAsFmHb9ljGF4vFkM1m0e123cuEEFhYWLjxfgysRERENNWklIhGo9den8lkRjiahzFNE6VSCfF4HL/88guCwaB7nfM6x7F+VUqJYDCI+fl5AMDKygp8Ph+8Xi/W19eRSqVuvP/zWklMRERE9MjC4TBCodC113u9XgQCATSbzRGO6n5s28b+/j5CoRD8fj9SqRSazSZs24ZSCvF4HPF43K209vv9Jx2PlBKxWAzpdBrBYNANyn6/Hz/88MPwj/NUAyQiIiKadFJKJBKJW29nGMYIRvM4lFIol8sAgHg87q4V9Xg87n8zMzNYX1+HpmkQQjxZ1TUQCCCfzyMUCj3o8VlhJSIioqmllLq1ymiaJqrV6ohG9DhM0wQAWJblXvZ9iy6/34+ff/4ZrVYLOzs7AIB+v/8o61s1TcNPP/3krqHt9Xo4PT2FruswTXPgP13Xb/1AwMBKREREU0sIAa/Xe+NtyuXyyHfTCyHu/ZwXq8YXN11dXM/q6PV6+Pz5M0zThJQStm3f6bmvuq0QArqu4+PHj7BtGz6fD0opnJ2d3fg4N2FgJSIioqkWi8VuvP7k5GSsp0M5oXPYyqeU0j0EQUqJxcVFdDodZLPZgdt1u118/PjRrcY6j3/Va5VSwuPxuLf1eDzo9/tQSrlB16GUQqfTGXieYDCI9fV1FAoFt6J98Xlu+/oysBIREdHUctZw3uRiC6ZRcZr6K6UwPz8PKSX29vaGCq3fH3bw/Q58pRRarZZbWb3IOSnLeR6PxwNd193+rc64er3epft5PB6Ew2FEIhGEQiF4vd5LX9uLp4ndBQMrERERTS1d12+9jZRyYC3oqDjVy2QyCaUUvn79euPthRDI5/OXNpG1Wi2USiU0Gg30+/2B13LxKNdAIABd19FoNNwerrZto9vtugHWua0QAj6fD5FIBOFwGMFg8EmPsWVgJSIioqnl9/tvvU0+n8f29vbIlwVIKbGxsYG9vT1UKpVrbyeEgGEYSKfTiMfjAM7DbqlUwvHx8aWNVE5XgGAwiFAoBJ/PB9M0USwW0Wq13NtePHhASolAIIBoNIpQKHTtSVpPhYGViIiIptYw7apisRiCwSAajcYIRnROCIHV1VUUCgWcnZ1dG5aFEPjhhx/c1+Fsbvr69StM03TDp5QSmqYhkUig2+3i7OwMZ2dnqNfrA0sAnPZWmqYNTO8bhjHW074YWImIiGhqDTvVH4lERhZYhRDIZDLo9Xqo1+u3b0i6MBW/t7fn9mB1wqdTFa3X6zg+Ph54PGedrM/nQzgcdg9RGGapxCgxsBIREdHUurib/SbxeByHh4eXwh5w+w73+0gkEvjw4cOtjy2EQLfbRSAQAAC3YhoOh6FpGrrdLqrVqttH9uJyACegjnp6/z4YWImIiGhqDdsBwOfzIZfL4fDwcGADkmEYaLfbjzomv98Pr9frbnq6KrQ6lVHDMNDr9dBsNtHtdqHrujvl79A0DdFo1K2ejnt6/z4YWImIiGhq3eVUp2w2i2AwiKOjI3Q6HSSTSRwdHd35Oa9rtg+cN/fP5/PQNA3ZbBaFQuHKx3Du32638eXLl4HrPB4PksnkSHbvj8rzfwVEREQ0Vk85NT4sKSWUUncew12nwp1pdOD89V4XKG9yVbN9KSXevn2LVquFYrF44/pVKaW75lTXdffxgsEgAoHAs6ueDoOBlYiIiB5kZmYGXq8XjUYDrVYLvV5vYOf5U5JSwuv1YmlpCb1eDzs7O/B4PIhGo6jX6+6pSteN5yHhTgiBVCqFSqVyp9cqhIDf70ez2XRfw+LiIrxeL/78888r7+ME8kgkglQqhWg0+iKD6XUYWImIiOjOnGltIYS789zZ0KPrOmZmZtz1nneteg57lr2UEvl8HrFYzA1vUkoYhuH2V1VKwbIstNttFIvFS1XLh242WlxchK7rKBaLd3qdzi58J2yHw2Hs7OwMvHZnl38sFkMikUAoFJr4zVFPhYGViIiI7swJVc7/nROTLMtCMBjEzMwMUqkU9vf3UalUhg5z0WgU/X4f7XZ7qPt8f/xnLBYbuP7ikaGlUunSYz40AAohkMvlEAwGsb29PXSltVarAQBev34NKSU2NzfRbDbd8SaTScTj8Rc7xX9XDKxERER0Z0IIRCIR+P1+aJoGKSU8Hg98Ph/8fr/bfD6fzyOVSmF7exumaV4bQp11mUtLSxBC4I8//rj1+ZPJpNvOaRjxeNytsDqV3/uebf+9aDSKxcVF7O3t3Rpana9BOp2Grus4OTlBs9l0d/Kn0+mpraReR9z06UUIoX777bcRDoeIiIgmlbOO0u/3Y2lp6U5h0bZtFAoFHB8fD1QMlVIIBAKYm5tzNzMBQLlcxvHxMQCg3+/DsqyBqfKlpSUkEol7v5ZOp4NarYaZmZlHq2BaloXff//91sqwc+rU69ev4fV6Yds2bNt+Ebv5H+Lv5RBXfjMYWImIiKbEfXfzO+tCZ2ZmEIlE4PV67z2GXq+HbrcL27bh8/kuTelfp9FooFAooNvtIpfLIZFITMxUuVIK7XYbu7u76HQ6N1aRhRCYm5tDKpWamPFPCgZWIiKiKefxeLCxsQEA2N/fR6PRuHHq2qmmxuNxZDKZO1VTn5PT01OcnZ0hk8nA5/Nde7uDgwOYponFxUV3ut40TZTLZZRKJZimeenr6azrdarI8Xic0/03YGAlIiKaYs7ufcMwsLi4iEAggIODA3fK/eLtACAQCCCVSiEej0PTtHEM+UkopWCaJkzTRL/fR71ex9HRkdvhIBqNYnV11b29bduo1Wool8uo1+vu5VedQOWEUKUUNE1DKBRye7b6fD5WU4dwU2Cd7sUSREREt3A2D+m6DtM03bWUo+oz+hic1k6tVgunp6cIBoPuLnXgPGxJKTEzM4NkMvmgKf9JopRCq9XC2dkZarUaWq2We/lFTpjsdDruZaVSCd++fXM3aAH/C6qWZQGA26jf6/VC13Xoug6/3++2rKLHw8BKRER0Da/Xi1evXsEwjIHLTdNEs9lEo9HAycnJjbvfJ40TtnK5HMrlMrxeL5LJJEKh0IupAvZ6PXz8+NE9NMDhTM87H0AMw4DP53P/CwaDAICTkxPs7e259wkEAohGo4hGo2wzNSZcEkBERHQFj8eDt2/fDlUtazab+PLly8QHVyEE1tbWHq2V031YloVKpYJWq4Vut+u2wkomk5c+GNzX4eEhCoUCAoEAQqGQu7nLMAx4vd5b15D2ej00m014vV74/X6uOR0RrmElIiK6AyEEXr9+faeNRpZlYWdnB/V6feKWCjjLGlZWVgZaR92FUso9s/6+lFL417/+de310WgU8XgclmW5a00Nw0AymYRt22g0Gu56XCEEDMN4tJBL48c1rEREREO6T0N6ANA0DaurqyiXyzg4OJiY0CqEQCKRwMLCwr03UCml8O9//xs+nw9v37590Hjm5+fR7XbR7/fd/qpOOK3VagNrax1erxf9fh/7+/sDlxuGgXfv3j1oPPQ8MLASERFdIKXE3Nzcve4rhEAqlUK5XHY3+IyLU1VdXl6+8xKAXq+HVqsFy7Jg2zaq1SqUUpeOPb3I2Yh225gymcyNj+FsbLtYYfX7/VBKIRQKod/vu5Xel9pqiy5jYCUiIvqblBLz8/MPOnFICIF8Po8PHz6MfT3r7OzsvdarFotFlEqlgcuEEPD7/Zduu7W1hbOzMwDA69ev3Y1L9yGEcHfbX3UdA+r0YmAlIiL6WyAQQDKZfPDj+P1+zMzMuKHPqT46AXYULbGEEPcO3nNzc8hms9B1HUdHR257p6vCr2EYSCQSL/pwARo/BlYiIiLAnT5/rJZFc3NzSCQS6PV66PV68Hg8iEajEELg5OTk0jpXZzPTYwVZn8+HeDx+r/tqmuaud43FYvj27RsSicSVa2AXFxcfNE6iYbBLABERTT1N07CxsXHllPdTcc6e7/f7CIfDmJmZQafTwd7e3oNCqxO4l5aWHqVaDJyHaOeYUaKnwi4BRERE1xhHWAXOlw28efNm4LL7rHl1lhpIKd3WU87j31W9XkepVMLi4uLAcgL2IaVxY2AlIqKppWkaXr9+DZ/PN+6hAIAbOm+63ql2OrdzAne320UgEECj0QCAO68nrdVq+Pz5MwBgYWHhnq+A6GkwsBIR0VSSUk5UWAXOQ+ZVgdUwDHg8HhiGgUql4lZUvV4v1tfX4fV63dfhrFttNptDn9LU7/fdsPrTTz8NdboX0SgxsBIR0dQRQiCbzU5UWAXOgyMA6Lo+cMyraZpYXV11T3XqdDpIp9NIJBJXBtJms4mPHz9idXX1xt6pANDtdvHXX38BAH788UeGVZpIDKxERDSVbmpg/5S2t7dxdnaGcDiM5eXlgcBZLpcBADMzM+j3+zg+PoaUEpZl4f379/jHP/6B5eXlW5/D4/EgkUjceAyrbds4Pj5GoVAAAGxsbMDr9T7w1RE9Da6iJiKiqSOlHMtGom63i2q1CsuycHZ2hnq97l7X6/VQLBYBnG9+qtfrA/1aI5HI0EerGoaB5eXlG29/dnaGQqHgLi/o9XoTc5ws0fcYWImIaOqMqz2TExCB8wrn/v4+Op0OAGB3d9cNjGdnZ2i32+5tvV7vUJXVYbVaLZRKpYGx7O7u4ujoCP/973/R6/Ue/BwHBwf4f//v/7nLHIgegoGViIimjnNW/SidnJzg9PR04LJut4v379/j/fv3A9XWi6SUWF5eHurUqmq1ikKhcG3g7Ha7ODw8xObmpnucKvC/AF8oFNDpdNBut4d9WddKJBIAgD/++GPsR9TS88fASkREU8mZfh+FWq2Gr1+/XhnclFI3BkSl1NBrS3d3d1EsFvHXX3/hv//9L+r1OtrtNvb391GtVnF4eIhCoQDbtuH1eiGEwOrq6qVjYx9j41UgEMC7d+8AnAdpoofgpisiIpo6SikcHx8jGo3euDHpMZ7n6OhoYCnAsIQQkFJiZmZmqADpHBrgPE+n08GnT5/c3q3Hx8d49eoVOp0OfD4f5ufn3artysoKPn/+DF3XkUwmH+0QBaerwc7Ozr2PiSUCGFiJiGhKKaWwtbWF2dlZZLPZR1/X6qwLrdVq954S/+mnn4beHHZxiv/7cUgpYRgGQqEQXr9+fek20WgUb968ga7rj97WKpfLoVAo4PT0lKGV7o2BlYiIppZSCsViEcVi0a22Sind6qZhGHeuNiql0Gg0sLe3h263e2tYlVJC0zQkEglYloXT01N385VpmrcuB7AsC9VqFfv7+wO7/KWUbmsrTdMQDodvDOV3PRlrWIlEAoVCAXt7ewysdG8MrERENNWckHd6eopqtToQ6pRSiMVimJ+fvzI4KqXQarXQbrfRbrfdPyulhm4R5fV68ebNG7eSurCwgC9fvsA0zVurndVqFTs7OwOv46JYLIZoNHrt/S+uW30quq5DCAHTNGFZ1tCtuYguYmAlIiL628U1oA4nyHo8HoRCIYRCIei6jna7jXK5DMuyAFwdGG8jpUQ2mx2Y9pdSYn19HUqpG4OkZVnY3t6+toJr2zYajcaNgXVrawudTgc//fTTncc+LCklkskkyuUyOp0OgsHgkz0XvVwMrERERLdQSqHf7w9UYa8Kt/d97KvcVvVst9sDu/uvu81ff/0Fy7IwNzeHVCrlXtfpdFCv15FMJu838DvIZDIol8tot9sMrHQvbGtFRER0B850/2OEVdu2cXJycq/7DjO1XqvV0O12YZom9vb20Gq13Ov29vYAAOFwGJ8+fXrSJv/O1+ox+rvSdGKFlYiIaIyazSaazeZA5bHf7+Pbt28wTdPtk/q9+6wFdR6n1+uhXq9D13Xs7u661z9Vg3+nfRaPfqX7YmAlIiIaI6UUPn/+jEwmAyklWq0WKpXKrWtYhz2pa3V11T0swLnPn3/+CeA8GIdCISSTSfh8vqEPKLgrJ7AO26KL6HsMrERERGNmmiYKhQKA/1U5pZTI5/PXhtZ6vX5rRVQIgS9fvrhrXff39/H27VvMz88jHo/D4/GMJEQ6r4FHtNJ98aMOERHRBLhqE9d1az5t28bR0dGtAdC5/uIa0mKxiHg8Dq/XO7KKJ4MqPRQDKxER0QSybRvFYhEHBwcDgU8phYODA7ed1l19+/YNW1tbjzXMoXS7XQB4siUH9PJxSQAREdGEUkqhVCqhVqshHo9DKYXT01P0er0HVS3X1tYecZS3K5VKAP63lpXorviTQ0RENMFs20an08Hh4eGDH0tKOfLpedu2US6XAQChUGikz00vBwMrERHRlPD5fHj9+vWTHsX6vVqtBtu2YRgGDMMY2fPSy8LASkRE9AJ5vV6YpjnQ+7TdbsM0TRwdHUFKCV3XcXR0hLm5OcTj8ScZh7PWNpvNjjQo08vCwEo0hW47zpGInjdN07CysoLDw0PUajX3cqUU/vjjD2iaBsuy3N8F993ANYxIJAIASCQST/Yc9PKxSwDRFAkGg0in05ifn0cul4NhGKx4EL1AlmVhc3MTXq93oGl/MpkEAORyOSQSCQghIIRwQ+Vjs20bvV4Pv/zyCw8NoAdhhZVoSkgpMTs7i2g06l6WTCbdE2+I6PkTQkDTNJimCaUUyuUyZmdnUSgUkMlkkMvlkM/n3dufnJzg9PT0ydpN/fHHH7AsC7/++uuTPD5NDwZWoimhadqlKopt25BS8nxvohciFouh2+26R7A6bbAMw8DMzMyl2yeTSbfq+tgajQYsy8Lq6uqTPD5NF9bniaaAlBILCwuXpv87nc6YRkREj0EIASml+18ul4Pf7wcAzM7OIhAIoN1u482bNyPtgaqUwubmJoDzEE30UKywEk0BwzCufNNot9usrhI9Y4FAANlsFkophMNheDwehMNhVKtVpNNpzM7OotfrjXz96Pb2NgDg559/Hunz0svFwEr0wgkhsLS0dOXmqlarNYYR0X2xuwNd5MycBIPBgcu/n+Yfde/TRqOBarWK2dlZnmxFj4Y/SUQvXCQSufSG5mi32yMeDQ3L+YAhhHDXGs/OzkIphW63i0aj8eDjOen56/f74x7CJaZpIhqNIpfLjXso9IIwsBK9YEIILCwsXHmdUgq9Xm/EI6K7ePfuHc7OzlCr1TA3Nwefzwfg/IOG3+9HsVh0N9fQdLhYZbdtG1+/fkW324VlWWi329A0DQsLC9A0bSzjs20bsViM61bp0TGwEr1g4XD42unAk5OTEY+GhiWlRCAQgNfrRSqVQiqVcq+zbRubm5tP2uidJtPFsOr82TRNHBwcDNyu1+vh1atXIx/f6ekptre38dNPP0HX9ZE/P71sDKxEL9h1SwHK5TL29vY4nTxhnKMyM5nMta2GarUav29Tyvm+R6NR+Hw+1Ot1d5bEsiz3+kajgVqtNtBzeVTjm5ubY1ilJ8HASvRCOVU64PyNpNFooFKpoNFooNvtMvRMCGetajQaRTabRSAQuPH0sbt2duBGrZenVqthfn4e8/Pz7mXOEp/t7W20Wi18/vwZq6urI52a59Gr9JQYWIleML/f7x7R2O122cJqAgghEAgE3A4N4XAY+Xx+6KpUMBi8MoQ6/Th1XYeu6zAMA4ZhQEqJdruNSqXC7/8zddXhHh8/fsT6+ro7iyKEgGEYeP36NY6OjlCr1XgUKr0oDKxEL5hTWZ3EsDqNlT+/3490Oo3T01MopRAMBrG2tnZjRfV70WjUPXoTOA8z4XAYCwsLN7Yvikaj2NnZmbifA7qdruuIRqNoNBrodDpQSsG2bbRarUvLfoQQyGazyGazYxot0dNgYCV6wZrN5pP2YLxYwVFKXRm8nMuVUtB1HYFAAMFgEJqmwbZtWJaFTqeDZrPpNjhXSr24MCulRDqdRiqVQrlcRjweRz6fv1NYdaRSKRSLRRiGgfn5+aGmfaWU93ouGr9ut+v2NHWm/p1q+jiVy2VomoZ4PD7WcdB0YGAl+s7Fyp8TyJ5jgLJtG3t7e1hfX39wULn4dfD7/fD5fO7/dV2HpmnutKVt227v0F6vh16vB7/f74bU28bcbrfRarVQr9dRr9fd3fDP7ev/Pdu2cXR0hFQqhWQyiVqthn//+99IJpPI5/N3eqy5uTnMzs7eacr3uX/9ppkQAq1WC5FIxJ36H7dms4mvX78im80ysNJIiJt+iQkh1G+//TbC4RCNl3MqVLPZhKZpiEajCAaDODw8RLFYfJZv+lJK+P1+tFqtocbvVD6dN8ZQKIRQKIRAIADDMEZepet2u6jVajg9PUWz2XTD8HPknPd+cUd3Pp+/tiPAY6pUKvj69euz/dpNOykl1tfXEQqFxj0UWJaF//znPwCAX375hZV7ejR/F4yu/IFihZVeLCHEncONUgqxWOxSgMhmszg6OnqWgdVZ6wZcvW7UebOJRCJuMPX7/fB4PBPxRmQYBmZmZjAzMwPTNFGpVFAqlZ5lpwOnAg2cfzB48+bNyKplvV6PYfUZs20bOzs7ePfu3dj/Xf7xxx8AgH/84x9jHwtNDwZWerGklIhEIqhWq0MFGyEE4vH4ldPWUkoYhvFsjzJVSrlr3rrdLoD/rWlMpVLIZDJjXw83DI/H44bXTqeDUqmEk5MTdxPKc+I0fR82sDqv7747v8/Ozgb+7jzOc/u6TZJRbxw0TRPdbtc98WxULMtyu1AAwOLiIkKh0NhO06LpxMBKL1Y4HMbi4iLOzs6GCjRCiIG+ht9LJBIoFArPrqp3UTKZRLFYhNfrxdzcHCKRyLNtfePz+bCwsID5+XmcnZ2hWCyi2Ww+m++Ps8b49evXbpXq4ilGFzknCAFwN65FIhGkUqmhv3/BYBD1et39cy6Xe7SuAVe1XXrphBCIRCKo1+sje+1KKRQKBSwtLY00LP7555+IRCJYWVkBgJEsYSH6HgMrvVi1Wg2bm5tYXFxEv99HuVy+cRo5kUjcWGUMBALu+sPnyNkE9fbtW3g8nhdTHRFCIBqNIhqNotPp4Pj42D12dtJDVKfTwdnZGer1Ok5OTtxWVT/++CO8Xi9M00S1WsX+/r57n36/j1qthrOzMxwfH2NjY2Oo6ngul8Ps7CyA/1VXDcNwn/MhlFKIRqPuh8OXzvmZm5ubw/7+vlu9vs8ypLtQSqFaraJarcLv92Nubg4+nw+WZcHn8z369LxlWSgWi7AsC16v91Efm+iuuOmKXjxno8urV69gWRZ2dnbQ7/cH3lid6687yhQAqtXqRPWxdKb0b1tv2m630el0oOu6G1ZfOsuyUKlUUCwWYZrmxHzPruNMLQsh4PF4EI1GcXp6OtBx4ToejwdLS0uIRqN3DiyPtRFLCIGNjQ18/PjxQY/z3ASDQayvr+P333+HUgqvX7+GUgoHBwd3PpHsPi62gItEInfu6XuTb9++oVgsAgC8Xi/evHkzFb87aLxu2nTFwEpTwzAMvHv3Dr1eD3/99ddAYPX5fHj79u2Nv+wLhQIODw9HMdRrOeNLJpNIpVK3HuPpcILPtG2QUEqh2WyiVCqhWq0CmOyqazabRbvdvvM0s1MxjcVi8Pl88Hg88Pv9t+4oV0rhzz//RL/ff9C4vV4vVlZWsLm5ORUVVsfc3Byy2Sxs23bXUzvrPQOBwNDLkR6DEAK6riOTycDv9yMcDj/o8RqNBur1uvszNW2/O2g82CWApp6maW6vS6/Xi1Ao5K539Pl8WFlZufUXcqPRGMFIr+dskMrlcneudDzXdaoPJYRw23LZto1arYbj42M0m00Ak9Gb1Pkg4TSEv8+0uhOIKpWK+5gAsLa2hkgkcuNz+/3+awPrbWtThRDwer1YWFjA1tbWRHw9R6lQKKDf72N+fh6maQ5syuz1eu7XZ5iOFg/dBOf8/BwcHEAphV9//fVej+Nw/t0QTQoGVnrxpJSYm5sb+OW7traGer2OQCAw1Po/p1I3Dk4f1Xw+P/LdwS+JlBLxeBzxeBz9fh+VSgWVSgXtdtsNjKMIXE4wicfj8Pl8kFJC0zTouo5gMOie+PWQsTjLC2772VZKXRlWpZTuB7tKpXJtiBJCYHFxEdvb2892bfdDKKVQKpXQbrcxPz+Pk5MT9Pv9gZ+nTqeDdDrtfhhx7vf9RjvbtpHP57G7u/vgMaXT6WtPniN6rrgkgKZCMr1kkOUAACAASURBVJnE0tLSvX+Bt1otbG5ujnQ62Vl7u7i4iFgsxjefJ6KUcqfhz87O0Gw2h1o7eldOW6D5+XkkEolrq96WZeHw8BDlcvle08nO8ywuLiKRSNx423K5jK9fvw6cZBYOh5HJZBAOh/HHH3/cuinLMAz0+/2JXmrx1L4Pn7quDwRXx9u3b1Gr1dDpdJDJZAAAm5ub7qamdDr94E4kTlV8fn7efQ6i54JLAmjqnZ6eAsCdj8C8eP9RTXc61a1MJnNjsKHH4aw3DAQC7ht8r9dDo9FAs9lEq9VCr9dzN2/dZ+pWCIGZmRnMzs7e2p1B0zTMz89jbm7O7QTgtKO67WdQCIFwOIzl5eWhlo0kEgl4vV70+334/X74/f6BD0Z+v9997osbfC4+n9PXd5p9/31xwqrTjaPT6QA4D/fZbHbgtm/fvkWxWITP50OtVnvw75mLB1M4f282mzBN0z1O2Rmz05+Z6DlghZWmhhAC//znP+9cqTRNE3/++eeTVpAuThPPzMwgEAg82XPR/dm2jW63i06ng06ng1arhXa7jV6vB+By/1SlFOLxOHK53INOtDJNEycnJygUCreuKf3HP/7xqCHEeT7niNxyuewuWXB6kdZqtUd7vpdGCIF8Po9IJHLrh4hWq4WPHz+6X9v7Vvn9fj9SqRSq1SoajcZABdjr9ULXdbRaLfex//nPfzK40kRghZWmnpQSmUzmXtPqh4eHT1ZdZTX1eXHWE/v9/oHLnVOrOp0Out2uGzaGCSnD8Hg8yGQyiMfjKBQKqFQq1/5MPvbPkPN4zut2Ohlsb29D13WEw+Gp6b96V0IIJJNJxGKxob4vgUAAc3NzOD09RTgcdttK3VW323U3XwGDFeBut+tWxZ0Wajf9XuRaWJoUDKz04jlHrjpN0++i3W6jVCoNtcPXMAx4PB40Go2hpm6DweClzWD0PDkbnJwA91S8Xi/y+TxmZmawu7vr7j53KnE3dQR4TH6/Hz/88AOA838j3759G8nzPjdSSiwtLd3pPplMBplMBl+/fgXwv/WwdzFMVdY52S8ej6NSqaBareLs7AyGYWB9fR26rsM0Tfz+++9Ip9NYXFy80xiIHhsDK02Fubm5O1UJ2u02arXatZWsi62InDWHzgaXo6MjFItFd43Y92v+IpEI5ubmLlXpiIYVCATw5s0bVCoVmKaJcDh8af3pqPj9fsTj8ZGu834ubNtGo9G414fS2dlZRCIRWJaF/f39R1+SpJTC3t4ednd3B9qXtdttHB0dYX5+3q3wlkolpNNp/s6iseIaVnrxhBBYWlq60/nXpVIJe3t7A48BnE+hBQIBhEIhd6OOx+NBt9vF2dmZu0MbOA+urVbLvW8ikcDs7OyD1jISTSLLsnBwcICTkxOG1u84Hy7ua3t72900Oiq6riMUCqFarV7qcsDQSk+Ja1hpqjmVhEajgVwuN1Tf1VQqhW63i2q1Co/Hg3g8jlgsdmXYdI5sdX6xX+zBKIRAOp1GNpsd6nmJniNN07C0tIROpzP2AzYmTavVutf9bNtGuVx2T2gbpX6/f2VIfv/+PdLpNBYWFriulUaOgZWmgm3bODk5wcnJCTweDyKRCKLRKCKRyJVthpz1XfPz8zc+bqPRwPb29qVpfyEEstksZmZmeP42TQ2/3++eIEf34xxG4KwLnqSvpRACpVIJHo8HuVxu3MOhKcN3Upoazi/+fr/vhlfnLPC7Pk6v18Pp6elABwEpJYQQmJ2dRTqd5o5/miqdTsc9AvemLgaT5qr+so/52KlU6k73abfb2N/fd+9/8ffIxXWs3x9KMArO8xWLRQSDQUSj0ZE+P003BlaaOs4GA4/Hg5mZmaHvZ9s2jo+PB0Kq03hb0zTkcjkkk0lOldHUqVar2N7eBgCsrKwgl8thb28P9Xp94k/AUkphY2MDW1tbj3q8rBMoj4+P0Wq1sLa2duuhEcD5mtdffvkFlmW5/9m2jV6vh3a7jWazCcuyEAqF0Gq1xlLRdtq4EY0SAytNFSdM/vjjjwMbpG5j2zY2NzfRbrcHKqqGYSCXy/HoVJpaSins7++7H946nQ5isRhWV1dRKpUG+oFOIiklAoEAlpeX8eXLl0tr0e9LKYVkMolKpYJGowHTNAcC69evX1Eul/HmzZtLB4U4p2QNs5xoa2sLZ2dn117/FBXkYDCIYDD4aI9HNAwGVpoqzkaoVquFTqeDdDp9a9Xj+7Dq9NxcWlpCOBxmUKWp4pz25ewWr9frbrXNtm0UCgW3b2i9XserV6/w5cuXiarIOSFOCOFuIIpGo+4hCM5UvG3b96oQO2E3EAggGo0iFAq5my5rtRqazSbK5TKCwaB7VOp9LSws4MOHDwOXOWN2jh12Trt6rNDabrfx/v17rKyswOv1YmdnB5ZlIRaLYX5+nsuh6EkwsNLUUUrh5OQE1WoV3W73xsbetm3j06dPbliVUiIajWJpaWmo6T2il6bX6+H9+/dYX1+HbdvY3d0dCHXOpiEnEBqGgbW1NWxubo680iqlhM/nQzAYxOnpqTvln0gk0Gg0EAwGB9rdRSIR1Ot1AMDa2hr29vYGZlWGZRgG3rx5MxDclFKo1+v4/PkzAODXX3996MsDAPh8Pvz0009ot9vo9/uwbRu1Wg1nZ2ewLMv9oPCYX3vn+/39hlPn+37XwxKIhsHASlNHKeVOoZXLZWQymSurHE5YbbVa7ptvLBZDPp9nVZWmlvNvZWtra6Dh/EUXp9Vt23b//Yw6sNq2jU6nA9M08fPPP7sBzjCMgXXozWYTfr/f/RCqlILf78erV68GPrA6r2mYk+wuhtVWq4WdnR10Oh0AuNepezfRNG3gcIJkMgmlFNrtNjRNw+7u7pO0G7vq63DfNl5Et2HdnqbSxTfZz58/4/T09FKV6GJYBc7fqJeWlhhWaeo5Vcnbpstt24au6/j27dvYNl/Ztu3+m9U0ze2l7LSfOz09xebmJmq1GjweD5RSyOVy7mbKjY0NeL1eAOfHpg6j0+mgUqmgUqmg2Wziw4cP6HQ68Hq92NjYGElLKGc5gGEYyOfzTzZN71TRAVz7AYboMbDCSlOv2+26O5zT6TRmZ2dRq9UGqioejwfr6+tcm0WE8+BWrVaH2lXf7/cRDAbH1p9VSonFxcVrr3f6nUYiEfT7fUSj0YFgKqXE0tISPn36hGw2i6Ojo1ufUymFr1+/wrZt97Hi8TiWl5fH8oHXMAzMzc09+gcHp1+1YRg4PT1FIpG41zG0RMPguy9NPV3Xkc1m3abYpVLJ3ZQhpXTDKk+qIjrn9/vx9u1bGIZxawDb3NwcyzSxMy7btm98/l6v5x6x7Pf7sba2duk1hcNh/PLLLwOPexunsptIJLC+vj72pUTpdPrGY6EvrskfdpxKKRwcHLjHx25tbaHdbj94rERXYYWVppqU0m30HwgEsL29jaOjI8TjcczPz0PXdbasIrqC1+vF27dvsbe3h0ql4q5X/V6/33e7BoyaU1W8qbL77t27oWZOhBDo9Xp3Wovr9/svtawaFyEEVlZW3I4C33+vLlbL7/IaL7bM0nV9Yl4vvTwMrDT1nH6CTs9D5xjX09NTt8oaDoexuLjIKivRBVJK5PN5LCwsoFKp4Pj4GJ1O59rTma66/223uS9n5iQej7trUK9yU9Xxe81mc+jbOh+GJ4nP58PPP/+MnZ0dVKvVa2931++H84F+ZmaGH+7pyTCw0lSTUrr9JMPhMDKZDI6Pj6GUcn9pOzuN+YuY6GqapiGdTiOdTsO2bfT7ffR6Pfe/breLer2Ofr8/ULlzGtAXi8VHH1Ov14NS6k6B9DalUmmoMOdseJrEo0ullFd+8BZC4M2bN/j48eOdAqumaW519q7H0BLdBQMrTZ2LwXNxcRFCCJycnODw8NB9k3NIKZFIJLCwsMANV0RDcE6A+z4oOhuRTk9P3b9ns1k3rD522yunC8Bj0nUdnU7n1nH6/X6sr69P7IfcZDKJcrk8cGrf7Oys23brott2/luWBcMwkE6nhzqZi+i++NNFU0VKiVgshoWFBdi2Da/Xi36/j69fv156E3J2BycSiTGNlujlEEIgn88jnU6j1+vB7/fD5/OhVCpB13Xkcjl0u123inldKHSC7XUB1wlYT9GRYGVlBV++fEGj0bjy8Z1T8NbW1ib6A24wGEQkEnFP9VpcXEQikcCnT58GwqnP54NhGKjVapceQ0qJ169fo9FoIJVKTWw4p5dD3PSPWgihfvvttxEOh+hpzc3NIZPJuL9cu90utra2BiqrzpvO+vr6g49NJKK7sSwL+/v7l3ojO1PW1WoVrVYL9Xr9yrZauq4jHA6jUqk82mlSFyml8Oeff17aSCalRCaTQSaTeRan4Cml0O/3oes6qtUqyuUy6vX6wO9Bp1L8119/XdqUtby8jHg8Pq7h0wv19wfRKz/9sMJKU0EIgaWlpYFjGJ1jEi++KTpHrz5lo20iup6macjn8wgEAjg4OIBSCrquY3V1FX6/H0KIa9e8CiHcAz4ikciTjE8IgVAo5C5tuFhVddbDPwdCCHi9XrTbbezs7AwEVZ/Ph1gshpmZGXg8HiwsLGBvb8/9XZlKpRhWaeQYWOnFc3ohXgyrpmleGVYXFha4cYBoAszMzMDn86FQKGBubs7t5lGtVmHbtvuB0uPxIBqN4uTkBKFQyF07evHf+2Po9/sQQsDj8bhT5M7zPOc17t/3X/3hhx8urT9OJBIoFovuGtfn+lrpeWNgpRdNCIFgMIilpSX3MqUU9vb2BioKzuEAz6lCQvTSRSKRS5XSbDaLTCaDZrOJs7MzRCIRhEIhdwPlY6+l7PV6+Pz5M9rtNgKBAN68eYOlpSU0m03MzMw8aheCcbi4LPCqzXLA+e/I9fV1fPjwAaZp4vj4+NaDCIgeGwMrvWjOVJ3zJmaaJra3t91jIqWUiEQiyOfzz2LdGRH9b1r+4jGgd6n6VatVfPnyBZqmIRKJwO/3IxaLwefzDQTeZrOJjx8/AgACgQAWFhYAnFccX8JmTKUUdnZ23L/ftIzC6/ViY2MDHz9+hGVZODw8RD6fH8Eoic4xsNKLpWkaXr165QbRZrOJra0tWJYFIYS7Vi4Wi415pET0EEopNBoNBINBlEolHB0dod/v45dffrmy4ur0SK3Vajg9PcXp6SkKhQKEEHj37p170MC3b98AAG/evHmRJziVy2W02233w3smk7nx9j6fD2/evMHJyQmXTtHIMbDSi2AYBizLgmmaA7v8nSmrUqmE/f19tx1OPB7H4uIiq6pEE0YphXq9Dl3X4fF44PF4rp3mV0rh7OwMu7u7ME1z4LqFhYVr7+f1erG2tuYG3UajgWaziXq9jl6v5wbWV69ePe6LmyD1eh0HBwewbRtCCGQymRtPBHMYhoFcLjeCERINYmClF8Hj8WB+fh5fvnxBOp1GLpeDpmmwbRtfv35FtVp1qwj5fJ47XIkmVLvdxtbW1sBlGxsbA9P/wHlY/de//uX+3ePxIBaLIZFIIBQKDbWWVQiBcDiMcDj8OIN/JmzbHth0qmkastnsmEdFdDMGVnoR/H4/otEofv75Z/e0lWazie3tbbdfYiAQwOrq6lBVBCIaj0AggF9++QXNZhOWZUEpdeV0vBDCXVMaDocvrT+l613sIet0R+HOf5p0DKz07Dkbp5zd/kopfPv2DcfHx+4SgGw2i9nZWb6hET0Dzqaq28zMzIxgNC+PcxKY03eaM070HDCw0rOnlBo4heViWPV4PFhdXR3qzY+IaBp4PB4EAgEkEgmk02l+kKdngYGVnj2lFFqtFgCg0Wjg6OgIQghEo1EsLy9zYxUR0QW6ruP169fjHgbRnTCw0ovg9FXd3NwEAMzOziKbzbJyQERE9AIwsNKL0Ov13GUBi4uLSKfTYx4RERERPRYGVnoRnPWqv/7667iHQkRERI+MfSzoRWCrKiIiopeLgZWePaePIBEREb1MXBJAz5rH48H6+vqLPOebiIiIzjGw0rMkhIDf78f6+rp7shURERG9THynp2dHCIFkMonFxUW2rSIiIpoCDKz0bAgh4PV6sbS0hHA4PO7hEBER0YgwsNKzYRgG3rx5Aym5V5CIiGia8J2fngWPx4NXr14xrBIREU0hvvvTxJNSYmNjA7quj3soRERENAYMrDTRpJRYX1+Hz+cb91CIiIhoTLiGlSaWswzA7/ePeyhEREQ0RgysNHGcbgCvXr3ikatERETEwEqTwemn6vV6EQ6HMT8/D03TxjwqIiIimgQMrDR2UkqEw2EsLS1xYxURERFdwsBKYyWlxMLCApLJJE+tIiIioisxsNJYSCnh9XqxurrKDgBERER0IwZWGjkhBDKZDGZnZ1lVJSIiolsxsNLIOFXVlZUVtqoiIiKioTGw0kgIIZDNZpHNZllVJSIiojthYKUnJaWEYRhYWVnhWlUiIiK6FwZWehJSSgghkMvlkE6nWVUlIiKie2NgfSaEEFBKjXsYAP7X5P/ieIQQ7hgNw8DMzAySySSklOMaJhEREb0QDKxj4IQ427ZvvZ1hGO5tu93uk4/tKk5A9fv9CIfD8Hq9EEKg0+mg0+lA0zREIhF4vV4Eg0GeUEVERESPioF1hAzDQDweRyKRQLvdxu7u7o1VU9u20W633fuOmpQSmqYhnU4jmUzC6/XCsixUKhUcHx+j0+kAAMLhMFKp1MjHR0RERNOBgXWETNNELpeDEAJ+vx/dbheHh4e3TvVrmoZer3fr4zuVW6XUvZcPOI8Rj8eRTqcRCATcqf5yuYyDgwMopWDbNoQQmJ2dRTabvddzEREREQ2DgXWElFI4OztDNBoFcF6ZLBaLN4ZLp8n+0dERLMu6dL2U0l1asLS0hFAohK2tLbf6eVc+nw8bGxsDa0+bzSZ2d3fR6/XcoOr3+7nzn4iIiEaCgXWEbNvGzs4O3r17B4/HA7/ff+s6VqUUWq0W1tfX8enTp4HbCyEQj8eRSqUQCAQgpcTp6elQ1djreDweN6z2ej3s7++jVqu5ofpiVZU7/4mIiGgUGFhHzAmta2trkFLC4/HAtm23cvl9tVUIgUAggGAwiI2NDXz8+BFKKUgp4ff7sbS0NLBrf29v79YQfPGxpZQDU/yRSAS2baNYLA5Uf51TqlZXV1lVJSIiopFiYB0xpRQajQbq9ToikQjevn2LdruNs7Mz2LaNcrnsBlJnLerh4SEqlQpSqRQikQgajQay2SwymcxAlbPb7Q4sG3CWC3wfhKWUCAaDWFxchGEY2N/fR6lUghACrVYLf/75JyzLcschpUQul0MqlWJVlYiIiEaOgXUMbNtGq9VCJBKBruvQdR2RSAQAUKvV0O/3MTMzg6OjIwDnIbfT6aBer2N1dfXa0Ojz+ZDL5dyNXLquo9vtusFT0zSEQiGk02mEw2H3fh6PB0II2LaNSqUC4H8dAnK5HPupEhER0VgxsI6BlBK6rl953fLyMvr9Pnq9HpRSEEJA0zTk83l3s9Z16vU6CoWCW1F1+rb6/X7Mzc0hEom4Ydc0TRweHuL4+Ni9v7OZKhKJIBwOIxwOs6JKREREY8fAOiaGYaDRaCAYDA6sQf3y5QtM03Rvl81mkc1mh6pwVqtV988ejwfRaBSpVAqhUMi93DRNFItFHB8fu8sE5ubmEA6H3RZWRERERJOEgXVMNjc3B9pDGYYB27bh8XiQSCQQiUQGKqLDmJ2dRTweh8fjgWEYA/e1LOtSUA0EAlhbW7u22ktEREQ0CcQtPUDVb7/9NsLhTCcpJVKpFHK53KMfa2pZFo6OjnB0dORu4pJSIplMYmFhgRVVIiIimgh/L2m8MpiwwjoBbNtGqVRCvV7HmzdvHiVEKqVwfHyMQqHgdgoAzg8ryGQyt66HJSIiIpoUDKwTwtkkdXJyglQq9aDH6vf7+PLlC5rNJgBA13XMzc0hFos9egWXiIiI6KkxsE4Q27YfHFj7/T7++9//wrIsCCHutGmLiIiIaBIxsE4IZwOW3+/Hzs4OYrEYotHo0EGz3++j3W5ja2sLwPnU/9LSEgzDeMphExERET05BtZH4pwqdVfO8aiJRAInJydot9tQSrktqpaXlxGLxa68r1IKpVIJx8fHbs/VUCiEhYUFBAKB+78YIiIiognCwPoIhBAIBoNoNpt3Dq1KKXcpwMX7On/e3t7G4uLipWUCzWYTOzs77gEDXq8X6+vr8Pl8D39BRERERBOEgfWR1Ot1+Hw+9Hq9e4XW69qLKaXw7du3gcBaqVSwu7vrnoSVTqfZooqIiIheLAbWR+CEzW63C5/Ph06nc20AvQ/LstznKRaLODw8hFIKgUAAyWQS6XSaYZWIiIheLAbWBxBCQNd1mKYJ27ahlIKu6+j1em7IfAgpJTweDxYXFwEAe3t7KJfLEEIgkUggn88zqBIREdGLx15HD+AE1Ldv38Ln80EIAY/Hg3g8DgD3biXlBNWFhQWsra3B5/NBKYVyuQwAyGazDKtEREQ0NXg06wNJKbGwsIBkMolGo4FAIABN06CUwvv379HpdIZ+LGfzViKRQDKZdKf/PR4Pfv75Z1iWBSklgyoRERG9ODya9QnZto29vT34/X6Ew2H3ciEEDMMYKrA6FdXl5WWEQiH3cue+pmlCKcVTqoiIiGgqMbA+AqUUtra28OOPPw6EytuWBEgp4ff73b6p31dOH2MdLBEREdFzx8D6SGzbRrFYxNzcnHvZdT1RL26mikajAM6rqY1GA5ZlQdd1WJaFer0OANA0jcsAiIiIaGoxsD4SpRQqlcpAYE0mkzg6OnJbXAkhIITA/Pw8ksmkG0JLpRL29/fdx3Eqs06f1YuPSURERDRtGFgfkVMtdRiGgXfv3kEphUKhAK/Xi2w26wZS0zRxdHQ0EGqB82qtU4XN5XKXTrkiIiIimiYMrI9ECIFMJnPpcl3XAQD5fN69zDRNHBwcoFKpAMBAWJVSQtM05HK5gSosERER0bRiYH0kXq8XhmHcertut4vNzU30+333MiEEpJSIx+OIRqOIRqMMqkRERER/Y2C9g7/7g115nXO61XWtp0zTxLdv33BycjLwGEIIJJNJzM/Ps20VERER0RUYWId0W8VTCIFyuXzlsgClFD58+IB+v39p+j+fz7snYxERERHRZTyadQhSyls3Ptm27bah+v7y/f19t/m/Q9M0bGxsMKwSERER3YIV1iF4vV54vd5rrxdCQNM0LCwsuJcppXB6eoq9vT3Ytu2GVSklDMPA2trajY9JREREROcYWIfQ6/Vg2/aVa1iFEJiZmUE2m0W/38fx8TFOTk7cY1Vt2wZwHlR1Xcf8/Dw3VRERERHdAQPrd4QQCIVCl6b3DcNww+fF2y4vL6Pf7+OPP/5wA+1Vbarm5+cRj8cZVImIiIjuiIH1b860fj6fx/Hx8cB1SikcHR0NXCalRDabRSwWw3/+859LQdV5zPn5eaRSKQZVIiIionuauk1XTtC8+HdN05DNZvHjjz8iGo3CsqyB+3i9XneK3xEIBNzH+b7yCvyv+ppOpxlWiYiIiB5g6iqshmEgmUyiWCwiGo0imUwiFou5odKyLDSbTff2QggEg0H0ej3371JKLC4uuvfx+XwDgVbTNKysrCASiYzwlRERERG9TFMXWNvtNkqlEn799ddL1ymlYJomYrEY6vU6bNtGJpNBqVSCUgp+vx/hcBinp6f48OEDcrkcMpkMPJ7zL6OUEoFAACsrK+6RrERERET0MFMVWIUQiEQimJ+fv/L67e1tVKtVLC8vY2VlBaZpQtd1RKNRGIYBXdexu7vrHqtaKBSglEKj0YAQAplMBrOzs1wCQERERPSIpmYNqxAC0WgUq6urVwbKfr+Ps7MzAEClUoEQwq2ShkIhCCHw/v17VCoV9z5KKRQKBQDAwsICcrkcwyoRERHRI5uaCqvf78fKyspAoFRKodVq4ejoCNVq1b3cMIxL99/f30en0xnoBOC0sUqn00in00/7AoiIiIim1FQEVidYFgoFpFIpN5CWSiUcHBxc6psaCAQG7t9sNnF6enqpbZXH40G/38fs7OzTvwgiIiKiKTUVgVUphXa7jXa7jaOjIywtLSGRSODbt2+XQihwvsv/4n13d3cv3U7TNKyvr0PXdXfTFRERERE9vqlLWkopfP36FbquXxlWlVIDfVVPTk7cllYOKSXW19fh9/uffLxERERE025qNl1dJITAly9frrw8EAggFosBAEzTxP7+/kCAFUJgZWUFwWBwZOMlIiIimmZTV2EFrj6ZyrG2tgYpz3N8qVS6FFaXlpYQjUaffIxEREREdG4qK6zXuXgIAADEYjF4vV4A58sAcrkcksnkuIZHRERENJWmssL6PSklYrEYstnswOWapsGyLABAMpm8dD0RERERPT0GVpz3aM3n8wM9Wk3TxObmJizLgmEYWFhYGOMIiYiIiKbX1C8JcNalfn+gwObmJnq9HoQQ156ORURERERPb6orrEIIJJPJS+2pvn37hm63CyklMpkM21cRERERjdFUV1g9Hs+lqf5ms4nj42MopeD3+3mKFREREdGYTW1gFUIMtLACzpcCfPnyBUopeL1erK2tcSkAERER0ZhNfGB9isAopcTs7CwCgcDA5bVaDf1+H5qmYWNjg0euEhEREU2AiU5kQghEo1HUajUopdyTqKSUsCwLlmVBKeUenSqlhFIK4XAYuq7j9PT0ykMC/H7/lS2qjo+PAQBLS0tu/1UiIiIiGq+JDqxKKdTrdaytraFSqSAajSIejwMALMtCr9eDruv4/fffEQwGkUgkkEwmoWkaACCXy+HDhw8wTdN9TCnltbv+neUBznMQERER0fgJpdT1VwqhfvvttxEO52qapiEWi8E0TbRaLYTDYZydncE0Tfz666833vfw8BCHh4dQSkFKiXw+fymQdjodfPr0CbquI5fL8ehVIiIiohETQkApFPAIFQAAElFJREFUdeVa0ImusDosy8LJyYn790qlAmC49a2FQsH98+zs7JXV00qlgn6/DwAIh8MPHS4RERERPaJnEVivM0y4fPfuHdrtNrxe76VNVsD5soNisQgAePXq1UDXACIiIiIav2cdWIepsBqGAcMwrrzOsixsbW1BKYVcLgefz/fYQyQiIiKiB3rW5cSzszN3Kv+u+v0+Pn78iGazCcMwruwaQERERETj96wDKwAcHR3d+T6WZWFzcxOdTgdCCKysrPCAACIiIqIJ9awDq1IKx8fHKJVKuKnbwff3+fLlC3q9HoQQyGQyV65tJSIiIqLJ8KwDK3AeQA8ODvD777+jWCwO9Fy9ysnJCZrNJpRS0HUds7OzIxopEREREd3Hs9505XBOsyoUCigUCkgmk8hms5c2WymlUCgUYNu2uxSAXQGIiIiIJtuLSmtKKSilUC6X8f79+0vV1mq1CsuyIIRAOp1GMBgc00iJiIiIaFgvKrB+r91u///27qypjaON4vjp1jajXSAJEHZsk3CZ5Pt/i6yVSspJxW8ZGxsQq9A+/V5QmoARtrFhNv1/VanAzBiO7k41PU+HX19fXc3n89re3o4xGQAAAD5XZgurc06+74ffn5+fazweyxijFy9esBUAAAAgJTLZ2owxarVa+uWXX3R0dBSurjrntLa2xvGrAAAAKZKJl64+5Pu+ut2u+v2+/ve//2l/f1+j0UjWWj19+jTueAAAALiHzK2wWmu1ubmpcrksa62CINB4PJYkbWxsKJfLxZwQAAAA95G5wipJpVJJk8kkPEzAOSdrrTY2NmJOBgAAgPvKXGE1xsjzPB0eHt641ul0WF0FAABIoUwVVmuter2eJN06rnVzczOuWAAAAPgKmSqsuVxOnU5Hh4eHYVk1xqjdbiufz+T7ZQAAAJmXmcJ6fQLA/v5+eFyrxOoqAABAmmWmsOZyOTWbTZ2dnWk+n4fXW62WisVijMkAAADwNTJRWBd/9jfG3FhdNcaEe1oBAACQTpkorJLUbrc1Go00GAzCa41GQ6VSKcZUAAAA+FqZKKzWWhWLRe3v79942YrVVQAAgPTLRGGtVCqazWbq9/vhNd/35ft+jKkAAADwECIprMaYR/vZ1lp988036vf74e9ZHM8KAACA9Hv0wro4ZeoxSqsxRpubmyqVSjo4OLjxslWz2Xzw3wcAAIDoPXphdc7p8PBQGxsbj1Ja19fXNR6PNR6PJd2cGAAAAID0i2RLQBAEOjg4ULfblbUP9yvL5bKKxaKOj49vXO92uw/2OwAAABCvyF66ms/nqlQqKhQK9/p3dxVca6263a6cc3r37l04HaBSqXBQAAAAQIZEOiXg/PxcOzs7n/3nemut8vn8nfebzaaOjo7Cvau8bAUAAJA9kRbWo6MjnZ2dfdbWAGutdnd373yu2WzKGKO3b9/eKKz1ev3BcwMAACA+kRbWIAj05s0bdbvdT24NaDQaqlarSwurtVbtdlvHx8eazWaSHncaAQAAAOITaWE1xsg5p8vLy49uDWg2m+r1ehoOh0tXTJ1z8n1f/X4/XF2VpLW1tUfLDgAAgHjcvUH0ESwK6z///KNer6dOp6ODgwM558ItAKPRSO12W5K0t7en/f398N8tCu76+rry+bwuLy//+yD5vDzPi/LjAAAAIAKRFtbFaqhzThcXF9rc3NTBwYEkqVgsqlqtqlqtSpKGw6EuLi4kXRVda606nY46nY6KxaKCINB0Og1/NgcFAAAAZFMkhdX3fY1Go3CFtFAo6NmzZ8rn82q32xoOh9ra2gqf39vbC0dVGWP0/Pnz8CWrheFwKGutgiCQtVatViuKjwIAAICIPXphtdZqNBqpWCwqn89rMpkol8vp5cuXWl9f19OnT2/tZa3VauFWgZ2dHTUaDTnndHp6qkqlonw+r+FwGD7vnAtXZgEAAJAtj15YF9sAxuOxJpOJnHPhn/IXpfPDk6nq9bp++OGHsMi+f/8+HF+Vy+X0/fffazAYhD+7XC4zHQAAACCjIt3DujiN6vr3e3t7Ojk5UalUUr1eV61WUz6fl7VWp6enevXqlebz+Y39r5I0GAzCn8PLVgAAANkVaWFdJggCnZ+f6/z8XP1+PyykuVxOQRDcGFslSVtbW5pMJuHqrDFGvu9HnhsAAADRiL2wXne9nC4OBLjOGKOtrS1Np1P5vq/pdKparaZOpxNlTAAAAEQo0oMDHkqhUFCz2dRsNtPOzs4nj3kFAABAeqWq6eVyOUlX+1jfvn2rSqUScyIAAAA8ttQUVmOMNjc3JSmcMtBoNOKMBAAAgAikqrCWy2VJ0mQyiTkNAAAAopKawhoEgY6OjiT9N7/1wwkCAAAAyJ7UFFZJms/nkqTDw8OYkwAAACAqiRprdRdjjKy16vV6kq6mBEi3DyIAAABA9qSisD59+lStVkv5/FXcer2u09NTCisAAMAKSPyWAGutCoVCWFal/166orACAABkX+ILq3Pu1stVg8EgpjQAAACIWuILq6RwnNXCaDSSxAorAADAKkh8YXXOheOsrl+7/n8AAABkV+ILq3S7mDIlAAAAYHUkbkqAMUbS1ctW1lqVy+XwSNaFarWq0WhEYQUAAFgBiSustVpNu7u7H32mWq1yeAAAAMCKSNyWgM9ZNWVLAAAAwOpIXGH9cITVMrlcLoIkAAAASILEFdbpdPrJZxaHCLDCCgAAkH2JLKyLOat3WaywUlgBAACyL3GF1Tmnf//996NbAxaFdTweRxULAAAAMUlcYTXGaDAY6Oeff9a7d++WFtfF6KvxeMwqKwAAQMYlrrBKV6OtgiDQ3t6e/vjjD83n8xv3r5fU2WwWdTwAAABEKHGFtVKpaHd3V41GQ9LVKuqHe1qDIJAxRrlc7pP7XQEAAJBuiSusvu/LGKNvv/1WzWZTlUpF5XL5xjPD4VDGGAVBQGEFAADIuMSddLV4ocoYo52dHTnnwj2rC2dnZ+He1uFwGHlGAAAARCdxhfX9+/caj8eqVqtaX19fekjA9VXVy8vLKOMBAAAgYonbEhAEgY6Pj/X69Wv9+eefS6cE9Hq9G5MCAAAAkF2JK6wLzjmNx2MdHR3duud5nra2tmSM0Ww2+6zjXAEAAJBOiS2s0tVqa7/fX3pvc3NThUJBknjxCgAAIMMSXVilu1+qMsaoVqtJorACAABkWeIL63w+X3qa1WQyCbcL8OIVAABAdiW+sFprNZlMbl3P5/Oy9ir+yclJ1LEAAAAQkcQXVkm6uLi4dc1aK8/zJF2ttk6n06hjAQAAIAKJL6xBECydFCBJjUZDxhgZY3R6ehpxMgAAAEQh8YVVulphnc/nt653u11J/81uBQAAQPakorAaY3R2dnbrej6fD7cFXFxcLH05CwAAAOmWisIaBMHSwipJ9Xo9/HowGEQVCQAAABFJRWGV7p61Wq/XZa1VEARMCwAAAMig1BTWZaOtJKlWq8kYI4nxVgAAAFmUmsI6nU6X7lE1xmhrayuc18p4KwAAgGxJTWGVpNlstvT6YlqAJMZbAQAAZExqCqsxRufn53fe831fzjnGWwEAAGRMagrrp2atlstlSYy3AgAAyJrUFFZJOjs7u7OMVioVWXv1cRhvBQAAkB2pKqySdHl5ufR6pVKRc47xVgAAABmTqsIaBMGdq6ee56lUKkkS+1gBAAAyJFWFVZLevHlz570nT57IGKPpdMp4KwAAgIxITWG11qrX62ltbe3OZ+r1ujzPk3OO8VYAAAAZkZrCGgSBrLX65ptv7nzGGKPt7W1JbAsAAADIitQUVmutfN//5HP1el3SxycKAAAAID1SU1iDIFC1Wv3kc8YYeZ4nifFWAAAAWZCawmqtDeesfkqxWJQkjUajx4wEAACACKSmsAZBoJcvX955POt1i/FW/X7/sWMBAADgkaWmsErS6emp/v7770/uTfU8T8YYXVxcKAiCiNIBAADgMaSqsErSfD7XfD7/6DPFYlHGGBlj7jwZCwAAAOmQusJqjNHvv/+uv/76S8PhcOkzi2NanXMUVgAAgJRLXWF1zmk2m+n8/Fz9fl+TyeTWM4VCQaVSSc45JgUAAACkXOoK63UHBwf69ddfNZvNbt3rdDqSxAorAABAyqW2sFprNZ/PVSgUlt5fX1+XdDXaigMEAAAA0iu1hXVxVOt3332nfD5/634ul1OlUpHEPFYAAIA0S21hla72s37suNZmsymJE68AAADSLPWF9fj4WP1+f+mf/ev1uiTdOU0AAAAAyXf7b+kpYozRq1ev5JxTEARqt9s37i9OvGKFFQAAIL1Sv8K6OMlqPB7fup/L5WSM0WAw4MQrAACAlEp1YV0wxmhzc3PpPc/zJElnZ2dRRgIAAMADyURhla5K6zKLwnpychJlHAAAADyQTBRW55zevHmz9N5iigAHCAAAAKRTZgrrwcHB0nue58kYwwECAAAAKZWJwir996f/D5VKJRljwtIKAACAdMlMYV2MsFp2fTEhgMIKAACQPpkprLlc7s7r1lo55zSdTiNOBQAAgK+VmcL6sTLq+76cc5pMJhEmAgAAwEPITGG9uLjQbDZbeq/ZbEoShRUAACCFMlNY5/O5fvvtNx0cHGgwGGg4HIZ7V9fW1iTpzkILAACA5MrHHeAhzedzvX79OvzeOader6fNzU3t7u4qn8/UxwUAAFgJmVlhXQiCIPxvsW/VOafLy0vt7+/z4hUAAEDKZHrJMZfLqdvtajAY6O3btwqCQL7va2trK+5oAAAA+EyZW2GVJGOMnjx5oh9//FGe5+ny8jI85erk5CTmdAAAALiPTBZWSWq32zLGSJKGw2FYWNkSAAAAkC6ZLKye54UHCczn8xurqvP5PK5YAAAA+AKZ3MM6mUwUBIHev3+v/f39cLyVpBtfAwAAIPkyWVidc/rpp5/Cr5fdX2wXAAAAQLJlckvAYqTVsrJqjGGVFQAAIEUyWVg/xhgja1fuYwMAAKTWyjU33/fZDgAAAJAiK1dYq9Vq3BEAAABwDytVWK21qlQqcccAAADAPaxUYXXOqVwuxx0DAAAA97BShdUYo2KxGHcMAAAA3MNKFVbP83jhCgAAIGVWqrDWarW4IwAAAOCeVqaw8sIVAABAOq1MYZWkQqEQdwQAAADc08oUVuecLi8v444BAACAe1qpwnp+fh53DAAAANzTyhRWScrlcnFHAAAAwD2tTGG11qrZbMYdAwAAAPe0MoVVYoUVAAAgjVamsBpjODQAAAAghVamsAZBoHw+H3cMAAAA3NPKFFbf9+V5XtwxAAAAcE8rUViNMXr27FncMQAAAPAFVqKwlstllcvluGMAAADgC2S+sBpj1Gq14o4BAACAL5T5wipJjUYj7ggAAAD4QpkvrJ7n8bIVAABAimW6sFprtbGxEXcMAAAAfIVMF1ZJ7F8FAABIuUwX1vX1dVmb6Y8IAACQeZltc8YYdbvduGMAAADgK2W2sJbLZV62AgAAyIBMFlZetgIAAMiOTBZWY4yazWbcMQAAAPAAMldYjTHqdDoyxsQdBQAAAA8gc4VVkjqdTtwRAAAA8EAyV1hbrZaKxWLcMQAAAPBAMlVYjTHq9XpxxwAAAMADylRhbbVaKpVKcccAAADAA8pMYWV1FQAAIJsyU1hZXQUAAMimTBRWVlcBAACyKxOFtdlssroKAACQUakvrNZaPX36NO4YAAAAeCSpLqzWWj158kSFQiHuKAAAAHgkqS6spVJJ7XY77hgAAAB4RKktrMYYvXjxQsaYuKMAAADgEaWysBpj1Ol05Pt+3FEAAADwyFJZWHO5nLa3t+OOAQAAgAikrrAaY/T8+XNZm7roAAAA+AKpa331el2NRiPuGAAAAIhIqgqrtVbPnj2LOwYAAAAilJrCaq3V9vY2M1cBAABWTGoKa7FYVKfTiTsGAAAAIpaKwsrMVQAAgNWV+MK6mLlaLpfjjgIAAIAYJL6wWmvV6/XijgEAAICYJL6wNptN5XK5uGMAAAAgJokurNZaNZvNuGMAAAAgRokurM451Wq1uGMAAAAgRokurL7vsx0AAABgxSW2sBpj1Gq14o4BAACAmCW6sDYajbhjAAAAIGaJLqye58UdAwAAADFLbGGt1+ucbAUAAIBkFlZrLftXAQAAICmhhZVxVgAAAFhIZGH1PE/5fD7uGAAAAEgA45y7+6Yx/0p6FlkaAAAArKpXzrnny258tLACAAAAcUvklgAAAABggcIKAACARKOwAgAAINEorAAAAEg0CisAAAAS7f9buyeFey446AAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 864x576 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"proj = cartopy.crs.LambertConformal()\n",
"pc = cartopy.crs.PlateCarree()\n",
"land_10m = cartopy.feature.NaturalEarthFeature('physical', 'land', '10m', edgecolor='face')\n",
"\n",
"fig = plt.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection=proj)\n",
"ax.set_extent([-98, -87, 25, 31], pc)\n",
"ax.add_feature(land_10m, facecolor='0.8')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We then set up to read in shipping lane data, which is in the `data` directory:"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"fname = '../data/fairway/fairway.shp'\n",
"shipping_lanes = cartopy.feature.ShapelyFeature(shpreader.Reader(fname).geometries(),\n",
" cartopy.crs.PlateCarree(), facecolor='none')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can just add the shipping lanes onto our map!"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<cartopy.mpl.feature_artist.FeatureArtist at 0x7f30cfea00f0>"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAGzCAYAAADqqkXjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nOydd3xkdbn/P+dM75lMyqT3Tdm+NBsooqKiUlQQEQVBwXstCALS27J0bKCCYgOxYLn3Z7liwXJFLwos2zeb3SSbzSaTnun9nN8fz56TTDJJJpNJMkme9+s1ryQzc875nsmUzzzl8wiyLINhGIZhGIZh8hVxuRfAMAzDMAzDMLPBgpVhGIZhGIbJa1iwMgzDMAzDMHkNC1aGYRiGYRgmr2HByjAMwzAMw+Q1LFgZhmEYhmGYvEY7243l5eVyf3//Uq2FYRiGYRiGWcPIsiyku16YzYdVEAT55ZdfXrRFMQzDMAzDMAwAnHzyyTMKVi4JYBiGYRiGYfIaFqwMwzAMwzBMXsOClWEYhmEYhslrWLAyDMMwDMMweQ0LVoZhGIZhGCavYcHKMAzDMAzD5DUsWBmGYRiGYZi8hgUrwzAMwzAMk9ewYGUYhmEYhmHyGhasDMMwDMMwTF7DgpVhGIZhGIbJa1iwMgzDMAzDMHkNC1aGYRiGYRgmr2HByjAMwzAMw+Q1LFgZhmEYhmGYvIYFK8MwDMMwDJPXsGBlGIZhGIZh8hoWrAzDMAzDMExew4KVYRiGYRiGyWtYsDIMwzAMwzB5DQtWhmEYhmGYEwiCsNxLYNLAgpVhGIZhGOYELFjzExasDMMwDMMwJ5BlebmXwKSBBSvDMAzDMGseQRBQV1cHs9ms/r1aWYnnpl3uBTAMwzAMwyw3giBA7OhAy+bNgNGIaDSK3t5eeL3eVRd1XYnnwxFWhmEYhmHWNrKMwl//GvZvfAN47TUAgMFgQH19PbTalRXbEwRh1giqKIooLS2FKIrLGmkVRRGimLkMZcHKMAzDMMyaRgyH4TxwAOJllwGhkHq9IAhwu90rJoUuCALKy8vVsoZ0yLKMkpISlJeXQ5blZTu3oqKieUV6WbAyDMMwDLOmkcxmJNavB8JhIBBIuc3lcq0YwSrLMqLRKBoaGmA2m9NGMEVRRCwWQ19fn7rNUqLRaFBRUYFoNJpy7LmirSxYGYZhGIZZ8yQ3bgTGxoCjR1Ou12g0KCoqWjGi1efzQafTwe12Q5KkaULQarXC4/FAkqRlWV9BQQHcbjei0ah6nSAIqKqqmnU7FqwMwzAMw6xpRFGE6dRTgZ4eYHBw2u2lpaXLsKrsSCQSGBoagtPpxLZt22CxWNTbRFGEw+FYlvpVURRhsVhQWVkJAKivr4fRaIRer0dTUxOKiopm3X5lVRIzDMMwDMPkGJvNBqvbDQSDaW/X6/Uwm80IznB7PiFJEo4dOwar1QqTyYSioiIEg0FIkgRZluF0OuF0OtVIazweX9T1iKKIgoICFBcXw2KxqELZZDJh/fr1me9nsRbIMAzDMAyT74iiiMLCwokrtFogkZh2P4PBsISrWhiyLGN4eBgA4HQ61VpRrVarXkpKStDU1ASNRkOWXosUdTWbzaitrYXVal3Q/jnCyjAMwzDMmkWW5Ykoo9UKlJYC7e3ApOhfIpHA+Pj4Mq0wOxInRHcymVSvm2rRZTKZsHnzZoRCIXR1dQEA4vF4TupbNRoNNm3apNbQxmIxjI2NQafTIZFIpFx0Ot2cXwhYsDIMwzAMs2YRYzFYv/c9srPyeIDTTgN27UoRrMPDw0veTS8IQtbHnBw1ntx0NbmeVSEWi+Hw4cNIJBIQRRGSJM3r2OnuKwgCdDodDh48CEmSYDQaIcsyfD7frPuZDRasDMMwDMOsWQp+/3uYYzHA4QBKSgBZBg4dSrnPyMjIsk6HUkRnppFPURRhlyRgeBhiURGqq6sRiUTgdrtT7heNRnHw4EE1GqvsP925iqIIrVar3ler1SIej0OWZVXoKsiyjEgkknIci8WCpqYm9PX1qRHtyceZ6/FlwcowDMMwzJrF/453QHC5qBTAagXuvJNE6yQmWzAtFYqpvyzLqKyshCiK6OnpmVu0yjJqXnoJwo9+RDZdDz00rQNflmWEQiE1sjoZZVKWchytVgudTqf6tyrrisVi07bTarWw2Wyw2+2wWq3Q6/XTIqd2uz2rx4MFK8MwDMMwaxatwwE0NU1cMUN0cXIt6FKhRC9dLhdkWcbRKR6xU9END2Pdf/0XjBdfDHzyk8DwMHD//QjdeiuGhoYQCAQQj8dTzmXyKFez2QydTodAIKB6uEqShGg0qgpY5b6CIMBoNMJut8Nms8FisSzqGFsWrAzDMAzDrFlMJlPqFaIIuFzAwABFXQHU1tais7NzycsCRFFEc3Mzenp6MDo6OuP9BADFL7yAwv5+GB58ELDZIEsSAo8/jpHKSoy1t6dEZhVXAIvFAqvVCqPRiEQiAY/Hg1AopN538uABURRhNpvhcDhgtVpnnKS1WLBgZRiGYRhmzTKtO72piUTra68BZ58NgKYzWSwWBKaMbV1MBEFAQ0MD+vr64PP5ZhTLgiBg46uvQldYCFx/PWRZRmDnTgSeegq+bdvg37wZOCE8NRoNCgsLEY1G4fP54PP54Pf7U0oAFHsrjUaTkt43GAzLOu2LBSvDMAzDMGuWaan+sjIgFgMOH1YFK0C1l0slWAVBQGlpKWKxGPx+/5yRXfHss4HnngPGxuC9/XaMFxbCe+65kIqKIMiyGhX1+/0YHBxM2Z9SJ2s0GmGz2WiIgtUKnU6X+xOTJGB8HBgZoXIF5efwMOD3z7opC1aGYRiGYdYsk7vZAdDQAIuFGpYm4XQ60d/fP03sAXN3uGdDYWEhDhw4MOe+BUGA9Oij0Nx1F/DAA+i/8EKELRbYbDZoNBpEo1GMj4+rPrKTywEUgZpVej8aJcE5Oko/J1/C4fTbiCJQUEAlF0VFVHKxfj39bbMBd9894+FYsDIMwzAMs2aZ5gAQiwEGAzClttVoNKK8vBz9/f0pDUgGgwHhmQRalphMJuj1erXpKZ1oVSKjrhdfRGzbNgT//Gcky8oglpRADgRSPE81Gg0cDocaPc04vX/8OPA//0PRz6mDEwwGoLCQxKbLBTQ0AKeeSr9PrQtORyIxIXBfe42irLPAgpVhGIZhmDXLNJuoWIycAtKILrfbDYvFgoGBAUQiEbhcLgwMDMz7mDOZ7QNk7l9bWwuNRgO3242+vr60+5DjcZQ8+yziJSVo37YNFY89ht5rrwUCAWi1Wrhcrvl37yeTwEsvAS+8QIMUKiqAd70LqK+ffbtweEJ8Hjo0keofHaXHMx1aLQneoiK6zHEMFqwMwzAMwyyIxUyNZ4ooipBled5rmJYKj8dJuM0QJVTS6ACd70yCcjbSme2Looi2tjaEQiF4PJ5Z61e14TCqnngCOkGAoNGg+Oc/R/SLX0RLQwPMZvP8mqOGh4Hnnwf27QM0Gpr0de21gNlMt/f1AU8/TTW9M2EyTURaXS6gtXXid70+87XMAgtWhmEYhmEWRElJCfR6PQKBAEKhEGKxWErn+WIiiiL0ej1qamoQi8XQ1dUFrVYLh8MBv9+vTlWaaT3TxF0sRs1BRuOcxxYEAUVFRRgdHZ3XuQqCAJPJhGAwqJ5DdXU19Ho99uzZM+N5yrIMu92Oit/8Bsbt2yF84xtU96nXw5bpwSWJUvB/+APg9ZKofOc7gQ9/GBAEEuv//jfwpz8BwSA1ob3rXcBHPkK3LxMsWBmGYRiGmTdKWlsQBLXzXGno0el0qPrHPzCcTMJ32mmYb9w101n2oiiitrYWBQUFqvAURREGg0H1V5VlGclkEuFwGB6PZ1rUclqENRabNcI6lerqauh0Ong8nnlFd5UufEVs22w2dHV1pZy7YjFVUFCAwsJCWK1WWu8HP0iC88ILgZ/+lH7+/e/A3/5G/rFf+ALVlCp4vXT/nTvp761bgauvpnG0ADWY/eQnwJ49JEpPPRW45hpqPssTWLAyDMMwDDNvFFGl/FQmJiWTSVgsFjh6emBrbETgW99C16WXIplBxBIAHA4H4vE4wuFwRgJw6vjPgoKClNsnjwwdGhqats+0gjWRyFiwCoKA8vJyWCwWdHZ2Zhxp9Xq9AICWlhaIooj29nYEg0F1vS6XC06nM32Kv7UVeOop4OMfB558EujoAE4/HbjpJoqOHj5MNajPP091pA4H8Pa3AxdcQJ36skzi9PnnSaw6nWThddFFyxpFnQ0WrAzDMAzDzBtBEGC322EymaDRaCCKIrRaLYxGI0wmE4TbboPmrrvgOOMMtD39NLrOPhvBmpoZRagoijAajaipqYEgCNi9e/ecx3e5XDArtZYZ4HQ61Qir0n0/bbZ9PE6CVYk+ZojD4UB1dTV6enrmFK3KY1BcXAydToeRkREEg0G1k7+4uHhum6n6ehKjGzcC551HdlHPPw/85S9kOfWmNwGXX04pfwAIBIBf/YoErSzTdldcQY1PKwAWrAzDMAzDZIRSR2kymVBTUzO7WDQagfvuA37yE+irqtC0fz8GysvRr9OlRAxlWYbZbEZFRYXazAS/Hy2PPw5vRQXG3v9+FHznO/B89KNqaYEoiqipqUHhPMWW0+mE0+kEQP6rXq8XJSUlqXdSIqwZRoQnU1BQgKNHj855P2XqlNvtVtflcDgy7+aXZaC7m7rr3/Me4JFHSJi+9a3AQw9R85QsU8f+M89QmYDVCpx1FtW8LuFI1VzBgpVhGIZh1gjZdvPrh4ehqapCSUkJ7HY79PPp/L7oIuCllyDu2oWyv/wFrs9/HtFoFJIkwWg0TkvpAwCsVpjdbpi3bUPZD34ABIMofOEF9Jx7LqLRKMrLy1XhmS1GoxHGdKJ0njWsAD2e4XAY3d3ds95PqUmtqKhAUVFRSt3tnBHVoSHgj38E9u6lv887j37W1ACPPkq/h8MUZf2//yPR3dwMfOhDZNC/wmHByjAMwzBrAK1Wi+bmZgDAsWPHEAgEZk1dK9HUsn374HrpJejXrwc+9ansDn7aacCvfw2c6OifU/AKAnDPPcBttwFveQtw6BCMPh/WrVuX3fFnYWxsDD6fD6WlpSRgzWbyCJ0S7ezt7UUikUB1dbUqLhOJBIaHhzE0NIREIjHt8VTqepUostPpzCzdD1Ba/x//oGaqSISiqW97GwlQQSBB6vEAbjfd59e/piapM88Ebr992vpXOqvrbBiGYRiGmYYimrq6ulBdXY3Gxkb09vZicHBw2v0AwGw2o6ioCE6nE5qWForY6XRUA/ne92a3iPmmoUVxQrR+4APU5b5AZFlGIpFAIpFAPB6H3+/HwMAAZFnGyMgIHA4HGsbGSCTv2wepuRlerxfDw8Pwn5h1Pzo6mnYClRIllWUZGo0GVqtV9Ww1Go1ze6PKMnDgAJ3n4CD5l77xjcD110+UJ3R2Ak88ARw7Rmn//n7gW98CXnmFnAGKihb8GOUrLFgZhmEYZhYEQYBGo4FOp0MikUAymVQtnJbCZzQXKNZOoVAIY2NjsFgsapc6MCG2SkpK4HK5UiOgZjNF7O67j9LS5eXASSctzcIV0XrPPSTgQqEJQ/sMkGUZoVAIPp8PXq8XoVBIvX4yipiMRCJ0xcaNCP7wh+hobFQbtGg5JFSTySQAmkplNpuh1+uh0+mg0+lgMplUy6o5GRykNP++ffR3W1tqCt/rBX73OxKkySRFVO+8E6iuptvvvJN8VcvL6TYWrAzDMAyz9tDr9Vi3bh0MBkPK9YlEAsFgEIFAACMjI0gkEss65Wk+KGKrvLwcw8PD0Ov1cLlcsFqtM0cBS0uBT36SvDp//GOgpASoqpr/wbVaSmXPJ10tioDNRmvYtw845ZQ5N4nFYjh48KA6NEBBiTQrX0AMBoNay2o0GmGxWACLBSNeL0InvpwIggCz2QyHwwGHwzH/SVKTiUQoff+Pf1DKv7iY0vwXXzyR5n/1VeA736GufrudGqne+16KqN5xB4lVSQJ27waOHqVJVW43RVs3bMhuXSsAFqwMwzAMkwatVouWlpa00TJlkpLD4UBFRQWCwSCOHDmS98JVEAS1WamwsHB+XfZtbcAZZ1Da+v77KeI61RJq9oMDBQVIDg1hVKtFKBRCNBpVrbBcLte0LwYqmzdTNHLPnowE68jICOLxOMxmM6xWq9rcZTAYoNfrZ68hDYVgs9lgNhhQ2NICk8mUWc1pOhRh+cILwMgIpfbf9CbgxhsB5Vynpvlf9zrg058mkT6VoSHgllvosdy8GXjzm8kBoKyMRPAqhgUrwzAMw0xBEAQ0NTVlnNq1WCxYv349urq64Pf7865UQClrqK+vn7COmieyLEM+80yIx49TbeWtt1J3eqbR0qIiyDYb9r/0EmJporP9/f1wOBxwOp1IJpNqranBYIBr/Xrg1VcRHxpCZGxM7bY3GAxpRW5ZWRnKysqyOk+AIuswGrOb9NTbS3Wohw+TsNy0CfjYxyb8UMfHgd/8hqZOSRL5qb773RNp/tl4+GFyL1AivH//O0VW3/hGKglYxbBgZRiGYZhJZGNIDwAajQYNDQ0YHh5Gb29v3ohWQRBQWFiIqqoqaDSarPYhyzJ27twJo9GIto9+lKKrZ51FNZT33JPZdKSBAWB0FCWXXYYogHg8jng8niJOvV5vSm2tgr6qClqvF75AAJ7OTvV6g8GADYuVBs9UiPt8ZNZ/4AD9XllJaf7LLqPHJR6nprW//Y1qcAsKqJP/vPPm34g29TlZVga8+CIJ62BwfvtaYbBgZRiGYZhJiKKIioqKrLYVBAFFRUUYHh5WG3yWCyWqWldXN32a0xzEYjGEQiEkk0lIkoTx8XHIsjwx9vTGG4EbbgBOPhn461+Bt7xFbURLSygEGAwQQiGUzhJJVLr4p0ZYTQ89BHn9euh9PlhPNEKJojjvLxVzMjRE9aD0IKRv8orHgZdeIgEaDFLq/i1voSipVkvd/gcPAo89RlFPnY5sva65JruI7WwotatrABasDMMwDHMCURRRWVmZ+cShNAiCgNraWhw4cGDZ61nLysrmLVYBwOPxYGhoKOU6QRBgUsz0RZFEWiCA/t270XeizKClpYUal6bykY+Qif3YGPCf/wk8/nja4wqCoHbbAyDx99BDwOmnQ3jhBRjuvBOGLKPEGbFzJ7B+/cSaf/hD4MorKXr6xz9SlFinA049FfjsZ2l6FEDX//SnE93+LS1kxbWAsoSMsFhIVK8BWLAyDMMwzAnMZjNcSq3hAjCZTCgpKVFFnxJ9VATsUlhiCYKQtfCuqKiA2+2GTqfDwMAAjh8/DlmWU8WvKAKJBLQGAwoLC1FaWjpzxPPnP6eu+GCQ6jYzQZZpjOjb3kY1mk4n8PWvA5/5TFbnlNHx/v1vangCSGD/13+RD2xrK3DhhRPR12AQ+N//pVR/PE6uCZO7/Zmcw4KVYRiGYQA1fZ61ZdEUKioqUFhYiFgshlgspjoLCIKAkZGRaXWuSid6roSs0WjMenypRqNR610LCgpw/PhxFBYWptbA6vWAyYTiwUEU19XNvkNBoCamdKNQ05FMUlPXBz8IbNtG123ZQh31d9wxv5MRBFqrwTCxBoNh4m+DgY73u99RXanDMbHtjTdOrOeVV4Af/IC8Uc1m4PTTgZtvpn0ziw4LVoZhGGbNo9Fo0NzcPPfI0Hmg+HemizoWFxfDarWiu7sb8XgcNpsNJSUliEQi6OnpWZBoVQR3SUlJTsS30WjE1q1bp+/r9a+fqGNdyASsycgypdcffBD4xCcosjmZCy6gy3z3GYtRhDcSoYvyezRKF40GeOSR9I1W8ThwySV0ueqqVEGbT5jNFPnNdZ1snsCClWEYhlnTKGJVrc9cIkwmE1qnCLJsal6VUgNlLKiyj2zOx+/3Y2hoCNXV1SnlBGl9SC0WEqzf/CY1/lRVURR0LrxeoKsL6O6mn2NjFAWVZfpZWEhjRsvL02//5S+TdVQ6YabVUtTUZJqIps52KS+fsJvy+ciKanCQRPPgILBuHXDuuXQRhPwVqwDVy3o8QEPDcq9kUWDByjAMw6xZNBoNWlpaYMw0Vb3IKKJzttslSUqph1UEdzQahdlsRiAQAIB5d9B7vV4cPnwYAFCV6RSrmhrqjt+9m9LlpaUkJLu7Jy4jIyRGFRwOoK4OqK0l4/uCgul1n5IE9PVN7OPoUdruE58ArriCUvGf+QwdfzKJBBAOT0RSp17CYRLIkQhw6BCJ5wcfpK7+73+fuvlLS4GmJvr53/8NPPssRVcfeIAsq5QShXxBiawqjgEsWBmGYRhm9SCKYl6JVYBEZjrBajAYoNVqYTAYMDo6qkZU9Xo9mpqaoNfr1fNQ6laDwWDGU5ri8bgqVjdt2pTxwAQAVMt5+DB5iz77LInT2lq6vOENFMFMJ0j7+6n7XhGkkcjE7YJAAqy2lgTi+ecDx49T5PW++8hA/+abgY9/fKKrH6AIq82WfkrUZPbtoxGo998P7N8PfOpTNMVr587U+wkCidraWuD66+lSWgpkaXu2KLjdFFktKyPhvUphwcowDMOsOQRBgNvtziuxCpBwBACdTpcy5jWRSKChoUGd6hSJRFBcXIzCwsK0gjQYDOLgwYNoaGiY8E6dgWg0ir179wIANm7cOD+xqnD55dTRf/vtOLFgEpj795MgPXaM6kgVBIEEVk3NhCCdq4ShsRH44hdJNN5zD0VG77yTIryvf33ma+3oAL73PRKrR48C3/oWRVJnepxkGbjpJiof2L6dRPMDD0xYWi03ZWUk/ltaaIDBKkWYLfUgCIL88ssvL+FyGIZhGGbxEQQBW7ZsyX5G/ALo7OyEz+eDzWZDXV1dyhr6+/vR19eHiooKxONxDA4OqmUAALBly5aMplVFo1H09fWhurp6xvtLkoTBwUH09fVBlmU0NzfDuhAR9vTTlGYXRWpiqqggQVpbS/WtaUaoZsX4OHDLLRRhLS+naOv69SRc56K7G/jKV8jbVWnueuihuTv9YzHg2muBHTuorOC++6hJazE9YTNlzx6gvZ2a0e6+m0T8CuVEqUvaTkGOsDIMwzBrDlEUl0WsRqNRdWqUz+eD3++H40QjTywWg+fEPHi/3494PJ7i12q32zMerWowGFA3h9WUz+dTxaooiojFYpAkKfvH5dJLs9tuvhQUkFj84heBq6+miOu3vkXlCB/+8Mzb9fYCX/oSCdTRURKdmYhVgO5z111ktfXoozRM4N57JyLKy4nbTZFVUUytFV5lLP2rlWEYhmGWmVx5rc4XRSACFOE8duwYIidqN7u7u1Vx6vP5EA6H1fvq9fo5Beh8CIVCGBoaSllLd3c3BgYGsG/fPsQmp++zpLe3F6+88opa5pBTjEaKrP7gB8C//kXNWHr9jBO0MDBAJQAPPAAEAiQ+779/7jKEybhcNKXrnnuADRuoQes738nN+SwEl4sa21Y5LFgZhmGYNYcyq34pGRkZwdjYWMp10WgU+/fvx/79++H3+9NuJ4oi6urqMppaNT4+jr6+vhkFZzQaRX9/P9rb2+Hz+dTrFQHf19eHSCSCcDic6WnNSGFhIQBg9+7dizOiVqulKOcLLwDPP0+jUFta6LrJxxseplT5Aw9Qav+22yi1n035Q3MzNWc9+SRw9tnUPPaHP+TunLJhlUdWFViwMgzDMGsSJf2+FHi9Xhw9ejStcJNleVaBKMtyxgMNuru74fF4sHfvXuzbtw9+vx/hcBjHjh3D+Pi4WiMrSRL0ej0EQUBDQ8O0sbFZNV5NwWw2Y8OGDQBISC8KgkClAd3dwI9/DJx1FvDOd1KTVCJB9a533EHpf4Cuv/vuhfmpnnUWoNPRZKwrrwT+8Q9qLmMWFa5hZRiGYdYcsixjcHAQDocDtrkskBZ4nIGBgZRSgEwRBAGiKKKkpCQjAakMDVCOE4lEcOjQIbVpa3BwEOvWrUMkEoHRaERlZaUata2vr8fhw4eh0+ngcrlyNkRBcTXo6urKekxsRlx1FfDTnwLf+AZZVNlswGc/SxHQ++6jcoHrr6foqjIoYCFcfjmVBlRWUl3rtddSI1hJycL3vRA0GhLqGUTjVxocYWUYhmHWJLIso6OjA/39/YuSspYkCV1dXQva/6ZNm1BeXp5Rze3kFP/UdYiiCJPJBKvVipaWFtTW1qaUGDgcDrS2tqK1tRUVFRU5rfEtLy+HLMvTyiFyzoUXkvXVjh1k/L99+4T91I030lQutzt3x7v5ZuDb36b60XvvpbrYHJRSLIiSEprQtQphwcowDMOsWWRZhsfjwWuvvYbOzk4MDQ1hZGQEo6OjGB8fz6qWU5Zl+P1+HDhwAOPj42oj1UyIogidTofS0lIUFRVBo9GogjGTOttkMomRkRF0dXWlHEsURRQVFaGurg719fVoaWmZVYiazeaclAJMRall7enpyfm+p/H2t9P0rC9/mUa8Ohw0Ovaii8haK5doNCSK77qLIpo330zR1jn+34uCRgMkkxOerKuQ1RczZhiGYZh5oIi8sbExjI+Pp4g6WZZRUFCAysrKtHWksiwjFAohHA4jHA6rv8uyPKdQVdDr9WhtbVXtpKqqqnDkyBEkEok5BeT4+Di6urpSzmMyBQUFqm1WOibXrS4WOp0OgiAgkUggmUxmbM2VFbEYlQZcf/1EI9KVV1LtqstFTVO5xGqlfd96K1lkfeQj5O36xS/m9jhzUVxMkdWyMpp6tQphwcowDMMwJ5hcA6qgCFmtVgur1Qqr1QqdTodwOIzh4WEkk0kA6QXjXIiiCLfbneJ9KooimpqaIMvyrEIymUyis7NzxnIDSZIQCARmFawdHR2IRCLYtGnTvNeeKaIowuVyYXh4GJFIBBaLZXEOlEiQULzmGhpacOutwNgYpesffpjqVy+4ADjllNwet7ISuPhiEqw33EB+r888Q+J1qVCEalkZsHv30h13CeGSAIZhGIaZA1mWEY/HMTY2ht7eXrUbPx6PQ5KkrMTq5H2nY66oZzgczug+e/fuxa5duzA8PJxyWyQSgd/vh91un9+Cs6C0tFRdz6KQTFKk8+qrabLWXXcB738/1bPeeiv5sO7YAfzxj8Dvf5/74590ErBuHedCXvIAACAASURBVPCjHwHvfS/g8y3tmFS3m0oBSktXbYSVBSvDMAzDzAMl3Z+LRi1JkjCSpel7Jql1r9eLaDSKRCKBnp4ehEIh9TalptRms+HQoUOLZ/KPCVG+KIJVkkiUXnYZNVvt2EHWVtu20VSshx+m6OehQyRqjxwBfvKT3K/jvPOAoSHgxRfJqeBPf6JjLgVK7apeDyzS/3C5YcHKMAzDMMtIMBhEMBhMuS4ej6O7uxuHDx+eURhnUwuqRGRjsRj8fj90Oh26u7vVoQWLYvAPqI4EC4lEp0WWyWf1oouA9etJnJ5+OvC6103cx2Si67//fZqK9alP0fXf/GZu1wIAn/kM8OtfA11dtK7HHqPBBYuN201R5FUMC1aGYRiGWUZkWcbhw4fh8XgwODiI7u5u7NmzByMjIzNaVQGZOQgAQENDA0wmE/R6vbrNnj17AJAwtlqtqKmpQXNzc8YDCuaLIlgn1+ouGFkmL9T3vQ/YsgX4yleArVtpEtX0BUxMxfr970ng1teTR2suRbogUDnCo4/SCNjt20m4RqO5O0Y6DIbFP8Yyw4KVYRiGYZaZRCKBvr4+9Pb2YmRkBLIsqyNZZ6pT9fv9c0ZEBUHAkSNHEIlEEI1GcezYMQBAZWUlNm7ciK1bt6K5uRlFRUWwZjOqNEOUc8hpBPeBB2jq1Cmn0MCAxkbgbW+bbRHUlNXZSVOx3vEOuv/NN1PDVq7Q60lI33YbRXdvvJFKFtbA+NTFhAUrwzAMw+QB6RwKZqr5lCQJAwMDcwpA5fbJNaQejwdOpxN6vT63Ec8M1pEzHn0UOO004I1vBJ56ilLi55yT2bZXXw2IIoncU06h2tcvfCG3pv9OJ/C5zwF33kn+rxddRHW0S8UqFMcsWBmGYRgmD5EkCR6PB729vSmCT5Zl9Pb2qnZa8+X48ePo6OjI1TIzInoiXZ2TkoPHHqN61TPPBJ5+msawnn/+/PYxeSrWunXk2/qFL5ANVq5obKTmr8cfB04+mTxgn302d/ufiYICYHx88Y+zxLBgZRiGYZg8RZZlDA0NYf/+/ejr68Px48exb98+DA8PL6iBqbGxMYernJuhoSEASBkHmxVPPAHU1ABnn02d/oJA4jMb3v52Kgu46Sayg9q+nVL3x48vbI2TOf10mrj13/8NnHsuMDoK/O1vudv/VGSZzoUFK8MwDMMwS4kkSYhEIujv74fH40E0Gs06xS6K4qJOtUqHJEmqB+yC6mS/+12a6PTe9wK//CUQDC7cnP/kk4ErrgCuu44alxQLrPb2he13Mh/+MO3vlVeA//xPavpaDLsru538Xw8eBKqrc7//ZYYFK8MwDMOsEYxGI7Zu3QqDwbBkx/R6vZAkCQaDIfvj/vCH1MB0wQVkGzUwAHz847lZYFMTNWNdfz3VsU62wMoV119PQwWOH6e61sWwu1KmXSWTwGKOv10mWLAyDMMwzCokXVNVOBxGIpFAb28v+vr6MDQ0hL1792Isl7WbU1Bqbd1ud3bR3Z/+lIYDfOhDFJ3s6qLGqVxSVkb1rLffTqLv3nuBP/8Z+N3vcrN/QaCSg/vuI1G8GHZXlZXAgQPUgLYKYcHKMGuQpU4JMgyztGg0GtTX18Nms6VcL8sydu/ejeHhYfT39+PYsWOIRqNZN3BlgjL6tbCwcP4b//KXgN8PXHopCcg9e8icfzFwOCi6+sgjJPxuvBHo6cldo5TRSNHVO+8ELJbc210VF9N0rTPPzM3+8gwWrAyzhrBYLCguLkZlZSXKy8thMBhYvDLMKiSZTKK9vR16vT7FtN/lcgEAysvLUVhYCEEQIAiCKipzjSRJiMVi2LZt2/wttH7zG0r9X3EF8Pe/Ay+9RLWmi4nRSKL12WeBf/4T+OQnyVf1scdys//iYuDKK8mntbqaosa5srtyu6l+df363Owvz2DByjBrBFEUUVZWhurqapSUlKCsrAzr1q1btFGMDMMsPYIgqAJVlmUMDw+jpKQEAFBaWora2lqcdNJJKCkpQV1dHaqrq2G32xdtwtXu3bvR3t4+/y/Gv/89GfxffTUJ1b/8hSKSS4FGQ4LyxRdJNH/gA0BbG12Xi9Gyra3kHvDkk8BJJwEtLcAzzyx8vwUF5EiwSoMQLFgZZo2g0WimRVEkSVoy43CGYRafgoKCFPEpyzLGxsZgMBhU4ToZl8u1aBZXgUAAyWQSDQ0N89vwz38G9u6l1P+rrwK//S1wyy1LK8QEgXxZBwaAH/wAeOtbyZ3gxhuBWGzh+z/rLIrc/s//0GhZn49E+ULX/JOfLHxteQp/UjHMGkAURVRVVU2LckQikWVaEcMwuUAQBIiiqF7Ky8thMpkAAGVlZTCbzQiHw2htbV24B+o8kGUZ7SesoQoKCjLf8O9/p+78a68Fdu8Gfv5zqvlcrqjhxz9OdlFf/jKweTPwqU9RWUIgsPB9X3YZCfLdu2m/L7xAKX0mLSxYGWYNYDAY0n5ohMPhBZmPMwyzvJjNZtTV1aG2thYbN26E0WiEzWaDRqNBcXExWlpasGHDhiXPpHR2dgIANm/enPlGSur/hhuA/fupjvSee5Y/xX3eecC2bSSca2uB226jSOuJYQgL4qabgO99j5wJbr+dxsXmYr+rEBasDLPKEQQBNTU1aWvIQqHQMqyIyRZukGMmo2ROCgoK4HQ61Qiqy+XCli1boNPpIAgCDFothERiydYVCAQwPj6OsrKyzKO6r7xC6fFbbgE6OmhIwL33AvlSsnTGGVTLev315CZw//3A3XdTne1CEEWyuNq+nSyutm8nYRwO52TZq4k8eSYwDLNY2O12WCyWtLeF+U0xb1G6t5XImJLuLS8vh8vlYocHBgAQj8fnvtO3v01Rwj17Fn9BABKJBBwOB8rLyzPbYO9esq+64w4SgE88QX6l+WZ+v3Ej8NnPUkmALJP91fe/D7z22sL2azZT1PaWW+j3m28muyvOfqUgzNYhLAiC/PLLLy/hchiGySWCIGD9+vVpp8vIsoydO3eyS0CeIggCNmzYAJ/PB6/Xi4qKChiNRgD0RcPn88Hj8SCxhJEzZvkRBCHlNavVauF2u5FMJhEOh6HRaFBVVQXNVLH33HPAt74FvP3tVB+6SGJw3o2cPT3AV74CPPggcOzYxO863aKsLyeMjAAPPECPY0kJRYLf+EZqzFoIe/cCv/gFlQa89ho5FNxyS27WvEI48fxO+02cBSvDrGLsdjuamprS3jY8PIyenh4WrHmIKIowm81obm6edpskSdi9e/eiGr0z+clksTpVuE7GZrNh3bp102/weKjzPRIhUVhfn9P1jY2NobOzE5s2bYIuE8E5NkaRxUceAcbHgW9+k2o6F8liK6eEQrTWT3+aRrs+9hhQWgp88IML2+/vf0/C/YorqETC4wEuvzw3a14BzCZYuSSAYVYxM5UCsFjNT0RRhMFgQGVl5YxfNLxeL//f1ijK/93hcKCkpARmsxlarRZarTalPCQQCMDr9U7fgdsNPP008I53AFddRan3HD6XZFlGRUVFZmI1EqG09/btQCJB9aDXXbcyxCpAqftHHgG+8x3g3/8m4ZpIkOheCO94BzWZPf888K53AckkiViGI6wMs1oRRRF1dXUoKCiALMsIBAIYHR1FIBBANBpl0ZMnKELD4XDA7XbDbDbPWpva19eH/v7+ee2f/9erj/Xr16slIgCJxVgshs7OTrWZsqGhYWZLqa4uaiAyGGiyU1nZUiybkCQ69jXX0HGvu47qNktLl24NuUKWqTxg61bg7LOBP/yBBOxNNy3M3eCee6jueOPG1N9XOVwSwDBrEFEU0dbWBq1Wi/b2dkSjUbawygMEQYDZbFZFhc1mQ21tbWZRKVCE9ciRI9NEqNKgpdPpoNPpYDAYYDAYIIoiwuEwRkdH+f+/QhFFcdr/TqPRoKmpaVoWRZZlDAwMwOv1oqysbPaRq8kk8KUvUTTvyiuBiy5ajOVP5667gAsuADZsoCjrxz4GpCthWEk8+SRgsQCXXEKOBz/9KUWPs63FlSQS8jfcQEL+uutI5GfayLZCYcHKMGsQURTR2tqKaDSKzs7OvBMrazHyZzKZUFxcjLGxMfj9flgsFjQ3N8+723/Xrl1qs5UoirDZbKiqqkrbXKcwPj6Orq6uvHseMHNjMBjgcDgQCAQQiUTU101VVRWKi4sXfoB9+ygiWFpKta1O58L3OROPP05jTs88E3j0UeD1r6fLauAXvwB6e2lCV2cnNZDt2AFYrdntLxQikfrggxStvf56iuZmu78VAAtWhlmDiKKI6upqGAwGdHR0LIpQmdwNLMtyWuGlXC/LMnQ6HcxmMywWCzQaDSRJQjKZRCQSQTAYRCwWgyiKkGV51YlZURRRWVmJoqIiHDx4EAaDAbW1tVkZuh8/fhwej0etd81kkpDP50NnZyc3a61QNm/eDK1Wq6b+lWh6zojFqNv9n/+k7vd3vnPOTYaHh6HRaODMVOA+9xxFDi+6CHjmGcBmA849d4ELzzP++lcaLXv77TQA4O67yVc12y8WHg95vj7yCHDkCEVub701p0vOJ1iwMsw8mBz5U8TEShVQoiiiqakJhw8fXpBQmfw4mEwmGI1G9adOp4NGo1HTlpIkQRAESJKEWCwG4Yc/hN7phOFDH5putTMFSZIQDocRCoXg9/vh9/vVda/Ex38qBoMB69evx9DQELxeL3w+H1wuF2pra+e9r/naB3m9XnR1dbFgXYEIgoDGxsbZ0/u54l//Ij/UdetIwM4QzQsGgzh48CDcbjcqKirm3u9f/0ojSD/zGWoi6u4GPvnJ3K49X9izh6ZX7dhBXwRuvhn4/Oezd2XYu5f8XkMhqmctLMzpcvMJFqwMkyHKVKhgMAiNRgOHwwGLxYL+/n54PJ4VKZpEUYTJZEIoFMpo/UrkUxAEGAwGWK1WWK1WmM3m7Mzqb7uN0ll3353V+qPRKLxeL8bGxpDcuROCLCO0QuvdlHnvyWRS/V/U1tbC5XIt+rFHR0dx9OhRLglYoShfPq1LkQ4OhymKt28f/XzTm1JuTiaTeO2EWf62bdvSvyf8v/9HDUhf+xoJrp/9jITwa68Bv/3t6vcX7emhVP699wImEz2OF19MzVnZcOgQUFVF+1rFsGBl1iTKpKD5fkBv2bJlWiRQkiTs2rVrxX7YT/5ASdesA5BnqyJMTSbTNKucrNm+nSIDO3YseFfJr30N0d270XXNNSve6UCj0aC1tXXWutNc4vF4cPz48SU5FrM46PV6bNiwYekmnL3wAtVMbttGae0Tz9WdO3dCkqS075UAgBdfBP7v/6gWtqaGDPAfeoj8RR9/nPaZLyNXF5ORESoNuOUWshS77z7gtNOAt71tuVeWt7APK7MmEUURDocj4zd3QRBQWFiY9g1Y8cdcqSh1pPpJHoeiKEKj0aCkpAQbN25EY2Mj3G437Ha7OoM8J7S00Bt3DsSlZutWmE8+GevXr0dbWxtKSkrUcoSVhizL85pSpZRbZIvP50v5W4n2Mtmz1KNxE4kEotHo0h3wrW8FnnsO0tgY5PPPB3buBABUV1djw4YN6cXqgQNkeH/ttcC7301jYXfsoMEADz9MEce18rxzuUioP/gg0NFBwrWjA/jxj5d7ZSsSjrAyq5aCggLU1NRg7969kGV5zg97URSxYcOGGRsZPB4P+vr6VmxUTxRFuN1ueDwe6PV6VFRUwG63L75oOXiQ6q5OOw0wGskwPBIBolEy2jabgRtvzHr3siyrY0qDweCK+v+YzWa0tLSowmfyFKPJKBOEAKiNa3a7HUVFRRn//5RGLYAGSpSXl6Orqysno13T2S6tdgRBgN1uh9/vX7JzFwRBfV+bqx48l7z22mtwv/QS3D/7GXD66cCnPpW+iej4cRKlDz9Mr+3rrqNSIJOJJmzt2AE4HEu27rwhkaByiPe8hxwRnnsOGBigYQNMClwSwKxJlBrMsrIyxONxDA8Pz5pGLioqQk1NzYz7Ww1d1kVFRXC73dBqtUv3gTcyQlEGt5vGFhqNlFo0GgGtlj7QbrklJ7PNI5EIBgcHMTIyAgB5L6JEUUR9fT38fj9GRkZU8bhx40bo9XokEgmMj4/j2LFj085FiZg3Nzdn1C0+uXFQEbkHDx5EMBhc8Hko4s3n862oLwzZIggCHA4HKioqcOzYMTV6nW0Z0nyPDZBFWkVFBYxGI5LJJIxGY84jvslkEh6PBx6PB6Wlpag0myla+MorwEknAZ/73MTAgfFxeh0//DC9vm+4gRqsKisp2nrDDUAmzVmrFVmmTv+WFhKuf/4z8Le/UY3/Wok4Z8BsglW71IthmKVClmVEIhEcPXoUoihi3bp1SCaT6OrqQjweT/lgFUURRUVFs+5PkqS8+jAWRRGCIMxZbxoOhxGJRKDT6VBRUQGtdolf9gMDwObNwK5d6T+wrFYgEMhJ5MVoNKK6uhoVFRUYHR2Fx+NBIpHIW+EqSRIOHz6sOlMIggCtVov+/n6MjY2lOC5MRZZlRKNR7N+/HzU1NXOWvyhiajIlJSU5a8QqKytLPw50FSLLMsbHxxGPx9HU1IRdu3ZBlmU0NzdDlmX09vYiHA4vyvNOeQ8KhULqAAlZlmG329HY2Jgz0To5Iq/X6+F2u+kL5v33k13Tl78MXHYZmf9fdRV5jm7fTtHU7duBj3wEqK6esGCaNJVrTSIIFGX+7nfJQeCyy6hk4IYbqExiBZecLRUcYWXWDAaDARs2bEAsFlPLBBSMRiPa2tpyOhJzMVDW53K5UFRUNOcYTwVF+Cx1zR0A6hQ2GqkJ4/LLgalfDJ58EjjnnEWJvsiyjGAwiKGhIYyPjwPI76ir2+1GOByed5pZiZgWFBTAaDRCq9XCZDLN2VEuyzL27NmDeDy+oHXr9XrU19ejvb09r77ULTYVFRVwu92QJAlDQ0MYGRlBMplUp5kpEeeleM4JggCdTofS0lKYTCbYbLYF7S8QCMDv96vPqbTvHcPD1ETV2UkNVg4HCbM3vYkai/7yFxK3p59OtkwLKP1ZVfz611Qqdc01wNe/Duj1wNVXL/eq8gKOsDJrHo1Go3pd6vV6WK1Wtd7RaDSivr5+TjEXCASWYKUzIwgCioqKUF5ePu8oaUqd4z/+QRYz550HnHFG9guSZfIYjEbpotSlTv57YIA8Fx9+mFKDP/vZ9Ddmmw3w+7NfxywIgqDackmSBK/Xi8HBQTUNng/iSvkioRjCZ5NWVwTR6Oiouk8Ac3p3KhH6mQTrXLWpSllCVVUVOjo68uLxXEr6+voQj8dRWVmJRCKBcDis3haLxdTHJxNHC+U1mq24VZ4/vb29kGUZJ510Ulb7UVBeN7NSVES1mT/5CZna33ADRWEVTjuN6tc/+EHKogQCq3pKU8a85z302N11F/1+2mnLvaIVAQtWZtUjiiIqKipS3nwbGxvh9/thNpszrv/LRa1fNig+qrW1tTDmIq0WDALvfS+Jx9/+diJVN/kDVRDm7uoXBIoMGAwTNakaDfkPHjpEE20KC4HPfpZmbNfVAWNjwKuvkk2OgtW6aIJ1MqIowul0wul0Ih6PY3R0FKOjowiHw6pgXArBpQgTp9MJo9GoujUYurthvu8+JM88E74TqeVsUcoL5npuy7KcVqyKoqh+sRsdHZ1RRAmCgOrq6hVf250tsixjaGgI4XAYlZWVGBkZQTweT3k+RSIRFBcXq19GlO2mNtpJkoTa2lp0d3cveE3FxcUzTp5bFC66iCKGN95IkdZ4nF7vl11GwuzYMbr++HGguXlp1pTvvO51dGEyhksCmDWBy+VCTU1N1m/goVAI7e3tS5pOVmyHqqurUVBQkLsPn3CYIp5XXQV885tUY7aQov+uLuD55+lDSaulN+E3v5m6/6ciScAXv0hdxnV1dN1f/kLi+Mwzs1/DApBlWU3D+3w+BIPBWWtHs0UQBHU8a2FhYWrUOxSi+jYAyfvvR7/Ph+Hh4azSycpxqqurUTjHRJzh4WG1xhugx8Jms6G0tBQ2mw27d++e00XAYDAgHo/ndanFYjNVfOp0uhThqtDW1gav14tIJILS0lIAQHt7O5LJJPR6PYqLixfsRKJExSsrK9VjLBnJJL3GdTrgscfI1srlotf7O98JfPSjS7seZsXBJQHMmmdsbAwAshqBqWy/VOlOJbpVWlo6XdjkApOJRGtJCUVab7qJiv4zLTMIBKjD9d//pg+o2lr6YKqunntbUaSGjOuuo1RiURFFWJexNlipNzSbzeoHfCwWQyAQQDAYRCgUQiwWU5u3skndCoKAkpISlJWVpXdnuPtuwG4HLrsMGrsdlXY7Kioq4PP5MDg4CP+JCPRcz0FBEGCz2VBXV5dR2UhhYSH0ej3i8ThMJhNMJlPKFyOTyaQeWxTFaVFoQRCW1hc0T5n6f1HEquLGEYlEAJC4d7vdKfdta2uDx+OB0WiE1+td8PuM8rxUnmeSJCEYDCKRSKjjlJU1y7Kc2/cXjWbC7ePyy6lB6557KKr67nfn7jjMmoQjrMyaQRAEbN26dd6RykQigT179ixqBGlymrikpATmdNHJXPLCCzQi8fOfJyPrr3+dPlzSlRxIEt33T38i6xqLhaKhp5wyIXKHhqg8wGbLLFrr91Ok9cEHgd5essn58Idze46LgCRJiEajiEQiiEQiCIVCCIfDiMViAOg5pvV4kHC5AJ0OsizD6XSivLx85sET3/8+PQaNjZRaTUMikcDIyAj6+vrmrCndsmVLTkWIcjxlRO7w8DBisZiacrbb7WvGHSAbBEFAbW0t7Hb7nF8iQqEQDh48qD622Ub5TSYTioqKMD4+jkAgkBIB1uv10Ol0CIVC6r63bt26OH7MDz5IUVVBoM54brpi5oAjrMyaRxRFlJaWZpVW7+/vX7To6qJHU2firW+d8EC97TZKRyvG3nY70NdH3f2HDtGHzdatwJVXUh0aQILzt78FXn6Zoqz19YDXC0yepjT1MRME2ndtLfC+99Fxb76ZPBqXuaEtU5R6YtOUed7K1KqI3w/9jTci+uEPI/G+980tUjo7gfZ2ikrNIFYBQKvVorS0FE6nE319fRgdHZ3xOZnr55CyP+W8FSeDzs5O6HQ62Gy2NeO/Ol8EQYDL5UJBQUFG/xez2YyKigqMjY3BZrOptlLzJRqNqs1XQGoEOBqNqlFxrVY7px3agmphr7iCyo5uuYVq57npilkAHGFlVj3KyNVsaljD4TAOHDiQUYevwWCAVqtFIBDIKHVrsVimNYMtOa+9Rq4B//EfZFHzla9QRLWsDHj724F160hoShL5qP7xjxRltVonoqyZGv5LEgnd9nbgmWdILA8OAk88Qcc7UcO5ojlwgKLXo6MkyOfiiSeAo0epPGIePoyhUAjd3d1q97kSiXM4HGhsbFzACcyfTF8jaxGNRoMtW7Zkte3Ro0cxPDys1sPmGkEQUFNTA6fTibGxMYyPj8Pn88FgMKCpqQk6nQ6JRAK7du1CcXExqjMp+UnHXXeRfdPoKPCrX1ETJsPMAEdYmTVPRUXFvMRqOByG1+udMZI12YpIo9GojTQAMDAwAI/Ho9aITa35s5+oT5wapVtSZJnE1R//CJSX03VFRVRvpjAwAPzwh3Q/QSDz/8lR1vkiiuTTeOqpQFMTNXvdcw/w/vcDv/zlws8pH+juBgoKpnvNzkR/P0W652kabjab0draitHRUSQSCdhstmn1p0uFyWRSRQ+L1lQkSUIgEMjqS2lZWRnsdjuSyWTaSWcLRZZl9PT0oLu7O8W+LBwOY2BgAJWVlWqEd2hoCMXFxdm9Z11xBfDUU5RJ6esjyzs2yWeygAUrsybw+XxwuVwZ3z8QCOD48ePq34oQ0Gq1MJvNsFqtaqOOVqtFNBrF8PCw6rtYXV2NgYEBhEIhddvCwkKUlZXNXMu42IyMkEDds4cEa1sb1ZeVlNDt0ShFS7Va4KtfBTwe4NJLgUsuIcGaS5xO8mZ89VXgrLPIZWA10NNDTW0NDZndX5KyfmyVdHM+UF1dDVEUMTIywqJ1ErIs49ixY2htbZ33tnq9Hnq9Hp2dnYtWP6/sd+r+R0dHEYvF1GEbALB//360tbXNX7RWVlL2Jhym6VfPPEMilmHmCQtWZtWjRBICgQDKy8sz8l0tKipCNBrF+Pg4tFotnE4nCgoK0orN8fFxdHV1qR/Ukz0YBUFAcXEx3G53RsfNKfE48M9/0rzqcJg8Ud/2NuDCCyd8Vg8dItNvj4esaIaGgDvvpBKB226jurPFitrZ7eTLuJoIhYCdO4Gzz858m1Ug8DQaDWpqahCJRJZ9wEa+EQqFstpOkiQMDw+niMalIh6Pq84qk9m/fz+Ki4tRVVU1v2j+xz4G/OAHZKX3/e9T3XumpUQMcwIWrMyaQJIkjIyMYGRkBFqtFna7HQ6HA3a7Pa3NkCAIqKysRGVl5az7DQQC6OzsnJb2FwQBbrcbJSUl855KtWBefhn4+c8p7fa611EqTnEdGB8HfvELElWyTDWqH/gA1ZACVGN60000sWbHDhKvW7Zkbnk1H6xWWs9q4vOfp+lfen1m94/HSbivEkwmkzpBjskOZRiBkuHJp8dSEAQMDQ1Bq9WiXCklyoTmZioLSCSACy6g96cLL1y8hTKrEhaszJpBeeOPx+OqeFVmgc93P7FYDGNjYykOAqIoQhAElJWVobi4eOk6/ifzwgvAv/5FYlMQ6APi3/8mc/5AgGpIzzoLOP/89PZTNhvwyCNkcXXHHSQqI5HF6ey1WleMO8C8yFSsRqMU+d6wYXHXs0REIhF1BO5sLgb5Rjp/2VzuuyjTeuYThMNhHDt2TN1+8vvI5NT91KEES4FyPI/HA4vFAofDkfnGF15I2ZxLLgGee45Kgpah5ppZubBgZdYcSoOBVqtFiVK/mQGSJGFwcDBFpCrG2xqNBuXl5XC5XMvS+AIA+M1vgMOHyd/0wAHg2WfpL0XKiAAAIABJREFUA+GUU4BPf5rEaCYYDFRbqfwejS6eYF2Ckax5S08PiduamuVeydyEQlQ+MkPH+/j4ODo7OwEA9fX1KC8vR09PD/x+f95PwJJlGc3Nzejo6MjpeFlFUA4ODiIUCqGxsTH90IgpmM1mbNu2DclkUr1IkoRYLIaw1wvDww8jWlMD6eKLEQqFliWirdi4zYuTTwZ+9CPg4oupZOb552n6FcNkCAtWZk2hiMmNGzeqIywzQZIktLe3IxwOp0RUDQYDysvLczs6NRt+9jOyjfnc58iE/+c/pw78+daJxWIkTJRUvV5P1y0GFgsJobVKXx8NDFgJgvWBB8hj12ymMpJJKI1Fype3SCSCgoICNDQ0YGhoKMUPNB8RRRFmsxl1dXU4cuTItFr0bJFlGS6XC6OjowgEAkgkEimCVbGtam1tnTYoRJmSNa2cKBCguvLWVqCqCgDQ0dEB32T/4zTnl+sIssVigcVimf+G55xD/s3nnEPT7liwMvOABSuzplAaoUKhECKRCIqLi+eMekwVq4IgQKfToaamBjabbXmFKgA8/TT9/OQngRdfJCeAe+/NLt324x/Th+KJUZJqhHUxEMWJSO5a5E1vItFxQnjkLc8/D9TVAbt3A01N6rQvpVvc7/er0TZJktDX16f6hvr9fqxbtw5HjhyZf0RuEVFEnCAIagORw+FQhyAoqXhJkrKKECti12w2w+FwwGq1qk2XXq8XIY8H4je/CetHPqKOSs2I6mrgO99JKeepslgw9sADGLr0UiRP1EMra1bGDivTrnIlWsPhMPbv34/6+nro9Xp0dXUhmUyioKAAlZWVMwcCzjyThOp73gO84Q3kAf2GN+RkTczqhwUrs+aQZRkjIyMYHx9HNBpFzSwRLkmScOjQIVWsiqIIh8OBmpqajNJ7i86TT1L3/wc+QEL1lVeA22/PvjZMp6MpWMqEncWMsK51NBqaEJbPjIzQSF5RpGY8QUAsGsX+/fvRdEK8dnd3p4g6pWlIEYQGgwGNjY1ob29f8kirKIowGo2wWCwYGxtTU/6FhYUIBAKwWCwp1mB2ux3+E2UqjY2N6OnpScmqZIrBYEBra2uKcJNlGX6/H4cPH4bllVfQYjZTx/xJJ833pFL+NB4+jJKTToJzzx6EL7kEkiTB6/XC5/MhmUyqXxRy+dgr/++pDafK/33G91RBAM44g5xLzj+fRrWyYGUyhAUrs+aQZVlNoQ0PD6O0tDRtlEMRq6FQSP3wLSgoQG1t7fJHVQHgy18mA/5zzqEJMt3dC5/VfeqpwLe/TfsCWLCuZWSZmvc2b6ZBCMXFAKC+Vjo6OlIM51M3nUirS5Kkvn6WWrBKkoRIJIJEIoHNmzerAs5gMKTUoQeDQZhMJvVLqCzLMJlMWLduXcoXVuWcMplkN1mshkIhdHV1IXIic2F/z3uAjo7cuGRUV0Pzve9B8x//AeOJoR4ulwuyLCMcDkOj0aC7u3tR7MbSPQ5z2ni9733A9deTcF2/niL3mzblfG3M6mMZ2pgZZvmZ/CF7+PBhjI2NTYsSTRarAH1QZzPeNefIMnDfffQmf8451Hk7MAB85jML33dDA+27uZmOs5glAUx+88wzwOtfT8Lq3e9OuUmJSs6VLpckCTqdDsePH1+25itJktTXrEajUb2UFfu5sbExtLe3w+v1QqvVQpZllJeXq82Uzc3N0J9wfigtLc3omJFIBKOjoxgdHUUwGMSBAwcQiUSg1+vR3NxMllBvfjNw7rkLP8HaWioTOPnklKuVcgCDwYDa2tpFcy1RougAZvwCk4Io0pegnTvJMeDZZxdlXczqgwUrs+aJRqPo7OzEzp070dPTo9peTY6qaLVaNDU1LY9V1WQkibxR3/IWSt1/73tkXXXllbk9jhJZXaoIq1ZL58HkB93dQGcn8L//S64TUygtLc24JCYej8NisSzbFz1RFFFdXT3j7Yrfqd1uh8FggMPhSBGmoiiqKW63251RlFiWZRw9ehRdXV2qAb/T6cSGDRuyGtO6UAwGAyoqKnL+/qX4VVdVVcHlcqGhoSGzqV4XX0yOAXo9TcI64TDBMLPBgpVZ8+h0OrjdbtUUe2hoSG3KEEVRFasZTap69VWKdP7qV7lfaDIJ3Hwz1X69/vXAN75BvqqXXJL7YymR1aWKsK5WT9aVSDJJXrwuF43STNMNbjKZ0NbWBoPBMKcQbW9vz3ra00JQ1iVJ0qzHj8Vi6ohlk8mExsbGaedks9mwbdu2lP3OhRLZLSwsRFNT07KXEhUXF886FnryF5BM1ynLMnp7e9HZ2YmxsTF0dHQgHA7PvaFOR5Hhjg7g8suB7343o+MxaxsWrMyaRhRFlJWVoaKiAnV1dQCAgYEB+Hw+VFZWora2Fps2bUq1nUn3hhyLkfXPSy8BX/kKjUQdGMjdQmMxmj512WWUTnvkEercPv/83B1jMksdYbVYWLDmC1/7Go3wjUTIw3cG9Ho92traUFhYOKtFXDweh9/vXxZrq4qKCgCzNxxt2LABjY2Nc+5LEATEYrF5iU6TyQSz2Qy73b7s2RlBEFBfXz9tGIHCZA/a+ZyjLMuqm4JOp5tm0TUjl11GGSKLhaa99fdnfExmbcJNV8yaR/ETVDwPlTGuY2NjapTVZrOhuroauiNHqDNfqwXa2mh6y6FDNHbwc58DlA++m24CbrsN+NKXFj7NJRymZqrPf56iEvfeSw0LZ5yxsP3OxuQI6+jo4h1HwWZjwZoPdHTQMIc//IGa+uZAFEXU1taiqqoKo6OjGBwcRCQSmXE6U7rt57pPtiiZE6fTqdagpmO2qONUgsFgxvdVvgznE0ajEZs3b0ZXVxfGZ2n4mu//QxG4JSUlmYtdsxlwOoHjx6mk6bHH6D2TYWaABSuzphFFUfWTtNlsKC0txeDgoBo1ACY6jQVBAHbtIuP0q64CrrmG/h4ZoaaHySbfNhuJ2aeeWlh9qd9P4vfmmwG3m97Qzz131shXTljqCCuXBOQH5eVUJ33NNanP5znQaDQoLi5GcXExJElCPB5HLBZTL9FoFH6/H/F4PCXaqRjQexQbtRwSi8Ugy/K8BOlcDA0NZSTmlIaneY0uXSJEUUxb3iQIAlpbW3Hw4MF5CVaNRqNGZ+c7hhZXXkkZqTvuoL/HxkjEMkwauCSAWXMo3cGCIKC6uhqCIGBkZAR79+5VxaqCKIpwuVxobW2lCOxFF1FK/tJL6Y31S18CPvEJ4NpraXLRZN7wBhKzhw5lt9DRUWp4ufNOoKSEoqwXXbT4YnV8nNLBS1XDKsssWPMFi4XEQwYp8plQJsDZbDa4XC6UlZWhtrYWGzZsQGFhoZqSFgQBbrdbjVrmur5TeY3nEp1Ol9E+TSYTmpqalt9RZAamjpAWRRHl5eWq7dZk5iplSCaTMBgMqKysnD6Zay527aL3GIBqWZ96an7bM2sKFqzMmkIURTidTmzatAkbNmyA0+lEPB7H0aNHEY1Gp4nVmpoa1NTUTLxpx+M0naWtjWpUfT7gda+jtP0jjwC//GXqAa+9FvjqV2m7+eDxUDR1xw6K1n7hCzTJauPGBT4Cc9DfT8fdv39pIqxGIwliFqyrHkEQUFtbi3Xr1qG2thZtbW2w2+3QaDTQ6XSorq5G7auvwv3007MKPeW2me6jvFYXo2a2vr4eVqv1/7N33uFR1ekXP/dOy6T3SUIaSUggBFBAcVd3LWtZFXVdGxbsFV1F6R0EREFZXFddy7ruWlZXf3bX3nVFRVRQeic9IZX0ydzfH4c7Jb3MZFLez/PkmUy7851J5t5z33Ledl9bURSYzWZkZGT4vWa1I4KCghAaGgpFUWAwGJCSkoK4uLhWEeSAgACEhIS0uQ1VVZGdnY3k5GSMHj2azgpd3Vc4HIys7trFE/GSEmD16lb2aYLgjpQECEOK+Ph42Gw25wGnoaEBO3fu9HiMPnp1xIgRngMFfv4ZeOwx4NZbgZEjGT2dO5cTi777jml7s5m3zZvHDn6TCbj9dmDt2q6b+h84AKxZwx04QLE6axbHMvYFo0fTaqahgZ3ivhSsulANDgZ27/bd6wj9hpZz6NPT0113OhxwhIWhuakJh8xmD/Gkp6wrKipQW1uL6upqj0YhHYPBgPDwcJT5oPbaYDBgxIgR2Lx5s3P8rI6qqrDZbN2y/PIn6enpaGpqgslkQkVFBXbu3OkxXEBvpEtNTcXPP//cqikrNTUVVqvVWVKFJ57gyXxnHf/l5cCyZcxSTZjAcdKvvsra/HbEsSAAIliFIYKiKEhJSfEYw6iPSXQ/KOqjVz2Mtu12RkkNBjai6AejqCjueOfO5bz1qVM5KWrmTODuuzkv++STWfMaFdW1udk7dwKPPALcfz/T8vPnc9RqFw3Le43VSmG+ZQswZYrvSwJCQlinKxFWAQAqKqAmJSE5KgoBoaHIzc2FpmkwmUxIT0+H1WqFoijt1rwqiuIc8BEaGuqTJSqKguDgYKe/qn6Cm5GR4RJvAwA9GlxXV4e9e/d6TPIKCAhAeHg4YmNjYTQakZSUhAMHDjj3ldHR0YhwrzV96inu4zo7qd64EfjXv1h2Eh7ORiuTiSfo/bR8Qug/9N+chSB4Cd0L0V2s2u32NsVqUlKS0/rFycyZwJln0gWgZeQkJga4914K1JdfBoqLgVtu4bSo/HwK2ro64LrrgOeeY71me2zaxCjFmjUsNZg/H1i+vO/EKsCDyJIlwO9+R8Hs65IA9wirCFahtpb/d6GhiI2NRUZGBoKCgjB8+HBnVLaiosLje2s0Gp3f7eDgYOeAD/fvuzdoamqC/chwi8rKSihHGjGjoqIwevToASVW3Wnpvzp69GhkZ2cjISHBWZMaGRnp4bTgsX98+mmeeP7xj+2/iKZR1H7+ObNNisJyqUmT2MAqYlXoAhJhFQY1iqIgKCjIOakGYG3bgQMHPCIK+nCANg860dFtmqc7iYmhyJs3j01Yf/87p1C9/joPwHPmMFI5fnz7O+ZvvgHeeovit6CAgvfee/2TIouJYZNXZaXvI6wiWIWWVFWxnAacPtUyUhoXFwebzYaamhpUVVUhNDQUwcHBzgbKNutLa2vpk7xsWbeX09jYiF27dqGurg6BgYEYNWoU0kpLYfrzn2F48EFY3PYtAxH3Wl+LxdKmq4KiKBgxYgS2bt0Ku92O4uJixERHw/LSS6xDv+ii9l+gpoYn9GeeyQl9338PPPMMM0eRkT54R8JgRQSrMKjRU3X6Qcxut2PPnj2oqalxeqyGhoYiNTW1/bqzGTOY9l+3rn3BGRtL0Tp7NmtPc3KA005jVGHdOqb5Dx1i81VLS5lPPuGggbvvBvbuZTPCmjVMz/sLXaiaTL6PsFZX83W625gmDE50d4oO0NPy7mNOO2xyeuMNZj+OUFFRgd27d8NgMCA0NBRWqxXh4eEICAjwELw1NTXYtm0bACAwMBBJSUkAgLAtW/gdPzJsZKCiaRr27t3rvN5RGYXZbEZWVhZtryorUT9tGiwAp+7pJ52qyoYq/W+xbRvT/gsW0JbvyScpYNeudT1GELqICFZh0GIwGJCZmekUojU1Ndi5cyeam5ud3bGpqakIDw/veENWKyMIzzwDXHll+4+LjWXUYM4citZXXwUuvJCG/7fdxvrUu+7y7PZ/6y12ys6fz7rRp55i/WpXxsD6El2wqmrHZQy9JSTEQ0gIQ5yuTklqgaZpOHz4MIKCglBSUoKioiI0NTVh/PjxFKAlJfxf0zTAzSO1srIS5eXlKC8vR35+PhRFQU5OjjP9nZeXBwAYNWqU5wSnoiIKtO7aOPUzSktLUVdX5zx5t3VSfhQQEIBRo0ah6v33EaSqFKA7dtAhxW7nyW1FBSOn//kP923r1rHMY/Zs4JxzfDvwRBjUDOxvmyAcwWKxoLm5GXa73aPLX09vlZSU4ODBg9A0DYqiICIiAsnJyV3v5j3hBE7/KSgAOppeY7MBCxe6Iq2ffcbxqZs306Jq1SrWs55wAh9bUUGT9g0bgFdeYdqyP3QYy8AAoa/59lsgJgba/v2orqqCyWSC0WiE0Whs10ZK0zRUVVVh3759zvpSnaSkJNfzTCaeUO7bBwwf7rSe0oXu4cOHUVNTg+rqajQ2NjoFa2ZmZttrXblywNddVldXIzc3Fw6HA4qiwGazdTgRTMdisSAmK4ulG5s2AWPHMrtUV8d61pUreZJ/3HE8EdfdVRYt4t9AEHqICFZhUGA0GpGYmIjdu3cjJiYGCQkJMBgMcDgc2L9/PyoqKpxRhNTUVM8O164yaxYjqA880PHBKi6OKbDZs5naf/ddYNo0NiUMG8Z0WFkZ75s/n40In33Wvw6CfTEwABDBKrh4+WUgLg71l17aymouKyvLI/0PUKxu3LjRed1oNCI8PByRkZGtvVLT04HSUuCjjzwmzymKgpCQkHa9Rtulv3xPe4jD4fBoOjUYDIiLi+v6BjIzKU5feQV49lmWRkyZwoZTAGhu5on322/zM3d3VxGEHiKCVRgUWK1WhIWFYdy4cc7O1pqaGuzZs8fplxgYGIj09PQuRRHaJDgYOPtsprouuaTjx8bHU4zqkdZHHuGo1ltuoWgdNozNWTffTMH2/PP96yDoHmHt6efVFXRbK2Fos2sXvX/z82EdORLjNQ01NTVobm6Gpmme6fgjKIrirCkNCQlpVX/qwa9+xRpxSUcDgIeHrO6O0u1BB4GBwBVX8Pe9e3lCP3UqcOKJLnF60kncX+bnA0f+VoLQU0SwCgMevXFK7/bXNA15eXnOMav6CMj4+Pjej0r83e8YPT3lFHbTd0RCAp0D/vQn1++jR7vuf+UV+rZOnMg61xkzgP7ScRwSwpQfAKSlsdZ28mTvv47VylSiMLT55z/p4TllCgBXU1VnxHY1xRwc7BrEIcDhcDgzTmFhYT3LOOk0NzM6fuKJ/MnP58m4orDG95JLRKwKXkEEqzDg0TTNYwqLu1g1Go1IT0/v0sGvy8yeDaxYwZR+Rxw65PJjramh8NN57jmWAvzmN7S7Gj2aB9TUVEYp/B1tDQpiFPidd4BLL2V0asQIICvLu6+jKL5t6hIGBiEhwP79wA03+HslQwKj0YjAwEBERkYiJiYGyl/+wjIli4VZn67aTRUX0ytabyT96CPW+i9eTLeAkpIB76Qg9B/EV0IY8GiahtraWgDA4cOHUVRUBAAICwtDTk6Od8UqN8wJVq++2v5jXnuNhtiqSnG6di2jR0uWcFRrbS0bERITGVmtquJOPiWFTgL9oXP+iiuA9etdLgZ//Su9WQXB2+gngYLvqaiA6fXXMXLkSMTGxjLrdOgQPWqnTeOl22CGdvniC55k33MPkJ3NE/i8PPpHBwYyqi1iVfAiEmEVBgW6r+r27dsBAPHx8YiLi+t9CUB7nHUWvVlPPNEzGlFaymhkYSEF3x/+wO7nZ58FRo7kweCll4BRo/j4k05ihPXee1ke8Ic/8PqqVa7r/mThQpYr3HsvsHQpBbd4KApCz6iooNF+QID/1vDcc6ybnz+fVlRWq6t7PzwcuPpqDkCZMaPt5zscwEMPUZSuWcOT6/nzPe36BMEHiGAVBgWNjY3OsoDk5GTEdFZf6g1mz6YN1X338forr7DBICaGTVYhIYw+xMRwGMDSpXyc0cgDhU5oKB/31lsUwXPn8vq779LTdd48Hkj8gclEO5olS+gPe801vJw92z/rEYSBSEMD8PDD9CO12yn6NI3fr4kTgTPO6LsyoPJynog2NdGZRN8vAVzT5s3t+0CXlfGEfOpUYMIEupu89RZPsL2dyRKEFohgFQYFer3qhAkT+u5FIyPZffz880ydFxfTuuriizl+8OmnGZ3Ua1f1es32pjpNnkzvwhUrgN//nj/HHMPrZ5zByVn+wGZj48Rf/gLccQeNwl97zfvR35ZTcgRhMPDpp5y0NW0akJHheZ+mAe+9xzKgyZPZ1Olr9H3PTz8B48a5bq+o4L7m7LPbHpDy7bfAv/9NgRsayihsWBjLAvxdcy8MCeTIIAwKemxV1Vv+8Afgl18YNVm3jtfvuw/47jtGVd0brQwGdtS2jLC6Ex3NNFtpKWtaAwIY0Swr4/Wamr55Xy059lggIgJ4/31O/dq6lZO5vInN5r/3Jwi+4r33WEbTUqwCFHq//z3vLynhNL2+4oMPgB9+YPZkyRLur+bNY32+O5oGPPoo92lr11LwTp/Ox117rYhVoc+QCKsw4NF9BPucmhpGF8aOZVT1p5+YYrvjjrYPTrpQbS/CqqMobNDKz2dt2CWX8Mf9+q9/7bv31R5XXsnygIwMlgTceSdrcntjieOOprG2rrsm7oLQn9G0zjMHisLv9fz5vl+PXj+racCtt7J+tT3RWVnJ7/hFFzGb9OWXzK6sWMEoqyD0IRJhFQY0RqMRWVlZ3Z9U01u+/JJ+rDfeyDKA++8HvvqKUda2xCoXS8HaUYTVnYQEbm/bNgrhqCjP630xiaolixYxylJfzwPZkiWMGncXh4OpxaVLOS4ToFCVqVfCYOOSS9i02Jl928cf+/5E9JNP6HcL0KGkurp9sbpxI7M6CxYAkyYxArtlCzNAIlYFPyCCVRiQKIqCwMBAjB49us0pOD6jro5NB7t3s4br0CHWn513HqMVHY0f1COrnUVY3VEUpt0uuwyYORP48cfW1/sSs5kNG0uWsBHsppt4MO4u+kFy6VJ6zwIyplUYnBx9NN1E1qyhCCwtbVu8KgrrXb//3jfrqK4G3nyT+w4AOPNM4PHHWz9O04Ann6RP9J//zNvuvJOe0TfeKCUAgt+QkgBhwKEoCqKiopCcnOw726q2WL+eTQczZwJxcYw0ms1dn5Pd3QirO8OHM8Lx6KM0577jDl5/5BHXdWMffZ3j4pgifOghesru3El3hIsv7vo23AcG6H9DEazCYOX44/m92byZ2ZlDh1z3Wa3ACSdwet5vf0uR6HCw4dKb3HcfXUdqaoAnnqAIPf102lxdfjkfU13NzMl551Gg/u9/wP/9H0/Sw8K8ux5B6CYiWIUBg6IoMJvNSElJ6dsSgPp64IEHeMBZt45NVqtXM6I6cmTXt9OTCKs7qsrX3LaNB5tbbwVuu40NUNOn8/furKc3TJrE1/3gAzaarV7NaO9RR3V9G7pQ1TT+BAfTckcQBiPp6fxpicNBa6iHHuIY5zFjerZ/6Ij33uN302ZjWc/o0XQ3uewylhft2sVhJk8+yQxKdDRdQSwWljtJVFXoB0hJgDBgsFgsyM7O7lux+t13bDC6/HLgqqsY/fjoIwrX7opDPbIaFcVasrff9oy0dJWRI/n677zD6VOZmbz+1lv0euzKlBpvcPXVTBvu2cOo89NPM93ZVRSFJQE7d/IALRFWYSiiqsC557q+OxUV3mtk1Lf34YfAhRfyBDMnh02de/fyuzd7NvcjH3zgyhbddRfraW+6ScSq0G9QtA4KwRVF0TZs2NCHyxGEtjEajcjOzoapLUPr9etp+3TWWd57wYYGpvyjooDrr2c08dFHGdXUp1R1l3/+k2m2tDRGbX/4gWvXRWtCAn1Yx4xp37i7JT/9xKjI9OmM3vzwA/DUUzzg9MVYxMZGRntXr2bz1fz5FPVdXT/A0oapUzme9pNPOJxAEIYaS5YwHf/oo8D55zOj4w3mzKEoNRqB5csZMQV4knjnna7SJgD4+mtO4lu82H/DSoQhjaIo0DStzbMkKQkQ+j2qqmLkjh0wBQV5duDX13PnGxfHTvMJE5jy6i3upv/JyRRUisLoQ2/qRPVSgKYm+pkecwytYnTy8ylg33zTVTowZgzT78OGtb3NceNYrvDAA0zjXX89P5MHHuBn4WufRLPZNQlrzRrWtLacntMZemRVIqzCUEZvHi0v955YfO01niRHRdFjde5c130mE09s772XArW4mPWqDzwgUVWhXyKCVejXqKqKEaGhsPz8My1VjjqKDQHr17MGa8YMICWF0bnlyymaekpjI6MN4eEUqVu3UrTecguQnd37N6OXBOTnUxQfOMCDhMPB8a2TJnHKzB//yMc3NbFJ4/XXgYIC1nlGRtLEf/x41wHObObB6Jtv2Hw1axYjnV9/zcjrrFm0sPEVLZuwJk2iAfrUqV17fkgImz1iY0WwCkOX2lpeNjS4vFJ7Q0kJ9wmrVvEk+LjjeFLrTloaS4z++19mqMxm7msSEnr/+oLgZUSwCv0Wo9GIzMxMWK1WRlPnz2ed1Y03UrTpkU+AvoAnncQRiOee2/0X01Pp06dTAOvb/vOfvdd9r0dYjUZGTG+80XWffnBZvZoHLIOBpQfHHUfBrL/PsjKOSFy3jgc4RQFGjKBIPOYYDjFYs4ZWUVOnMgK7ejUfc9llvoucTJrEZrD336ddzoMP8v1MmtT5c/XIqsXCv7MgCL1D01yR00OH6BHdnv3cxRdz33rUUWy4mjOn684ngtCHiGAV+h26G0BmZqZr5OrMmcA999CaJSGBO+CW4uvss1mrdeKJXbdgaWzkzjk42DdRVXc6mnQVE8NZ4pMn83pzM9fy4YfA/v08AIWGAhMn0iLn97/n4zSNjRPffEN7GoeDNjmFhXwPixczPf/JJ4xGz5njnbKJtrjqKr5eejojrbNmsaQiPr7j5+kRVklDCoJ3ePFFnjiGhfF7uGBBx49fsIDlAuvWATfcwH3hXXf1zVoFoYuIYBX6BbqfqtlsRkhICBITE2HQz/Bra9mIYDTSP/CGGzgy8PHHPaOUAHfOa9ZwdGBn/Pgj8Pe/U1zpPqfejqq60x0fVoOB3bw5Oa7bqqvpWvDII67UeUoKo5iXXeaKiNTX06Bc09jE8dhjnPs9cSKjLOPHAxdc4P33BzBCo9fF3X03/x5r1zJ62h7BwT1zSxAEoTX5+Syfuvtu+iOfemrnNbFBQZ5Cdf16lhS519gLgp8RwSr4HVVVERISgpSUlNYuAHY7d6ALF7IO84UXGD245BL5kplsAAAgAElEQVRevvACLVp0YmLoMfjppywRaAs9qhoU5Bo3uHAhI4Q9dQDoCu4lAd0dHAAwEnnKKfwBKEj372d09eWXGV01mVgWMGlS6zGPISFsiHr3XQrJuXPZjOFN3Juw7r+fEe+lSxkdby+CGhxMMS4IQ5XmZu+k4DWNJUArVzLLsmVL1xsgx47lvuR//6N4vesu7g/FLUDoJ4hgFfyKqqpISkpCVFRU21OrjEbuMPUGoylTGFl95x2KVv33M890PWfKFKb1jz3W9Twd96hqaqqrVmvFCt9PiuqoJKAnKArfgz7aFKAY37QJeOUVHrAAfn56o1ZQEMsJJk1iFPTEE71rBwaw5GDKFJ4MTJ/O13viidbRcJ2QEGm2EoY2lZXemST1z3+yATIwkCfhy5d37/nXX8/SIb1+fv16V/mRIPgZGRwg+AVVVREQEIBRo0YhOjq64xGrs2ezdlXnxhs5berLL12/f/WV635F4U537VrXbY2NjDx89RVFan09IwhnndV3Y017G2HtCmYzU/+33sqD1fLltLaqreXkmkWLeGkw8DO12+kwUFnp3XUccwyjt++8Q1EMMOrdFmJnJQx1Kip6L1j37wdyc1nj/swz9HINDu7eNhSF+4gZMzgQRMSq0I+QCKvQ5yiKApvNhvj4+I6Fqk5kJNPbb7/NxiqAO9RlyxidmzGDaa+QEKa1ACApiTZJGzZQILpHVf/8Z9ZU9nUnbHdqWL1JRARwxhn8AWiltWwZxfq55/KzXb6cc8VPP917rzt1Kv8uGRlMMS5Y0DoiDDDqW1PjvdcVhIFGZSUzIc3NnHzVXRwOluCsWUO7vH37gCuv7NlaIiK4jwwN7dnzBcFHSIRV6DPco6oJCQldE6s6553HCF1FBa8rCjvSn3uOc7CXLGFUYfdu13OuvJIm2HpUtbaWUdVzzuHM7r62bdGFqqKw1sxfxMby4FZSws8wIIDXKyqYRvRmPemCBSwNOHzYNVygpTj19+chCP6mooKCtaqqZ5HWxx7jqGSzmd/lWbN6t56wMHHtEPodIliFPkFRFMTFxSE7O5u+qj1hzhym9XVUlc0FDz9Ms+t77mG6Oz+fzQOzZzNyeMMNFK5ffknhmpXlnTfVXbxVu+oNFIV1prfcQpH6+ef0Y7ztNorY9tL33cVkolBdvpy/L1rE7YtAFQQXlZWMaFZWsnG0O2zfzhPCCRM4pnnqVFrbCcIgQwSr4FNUVYXVakV2dnbXSwDaIzqaO+X33nPdZjJxksuqVYxOrFpFAfvzz4zsVVWxZOD881nX6U8z7L4uBegK8fFM/+3bxzKB0FDW/ublUWh6I1UfE0NxvHYtp2JNmcITB0EQiH4yGxzM4SBdxW7nhLnp05lpKi9n/bggDEJEsAo+QVVVGAwGDBs2DKNGjUKAN0YNAvQP/eADClEdq5XR1fnz+fvKlcA111C8fvMNheuIEd55/d7QnyKs7igKyyeuvZYNWOvXA5dfzoa2BQsYme4t48fTluzNN3lAjY1lTXJba5HoqzDUiIsDiopYr98dT+KHHmKWRFV5Enjnnb5boyD4GRGsA4ReRSa9jKIordajKApUVYWiKAgICEBiYiLGjh2L2NhY76+9pWtAbS2jhL/+tavuStNYzzp1as+aGHyBe4S1u927fUFSEg96W7bQ5isqip/rrl00Ia+r6932p0yhrdjWrRTEGzfyd3es1t6/jiAMNGw22tCpatdP2H76ifuU0aOBv/4VuOkm1rAKwiBFXAL8gHpEQDkcjk4fZzkyIcjhcKChocHna2sLXXBarVaEhITAbDZDURTU19ejvr4eBoMBoaGhMJvNCAoKck2o8hWxsXQD+PBDNgy99BKbDGJi6C1aVcXu9FWrGDG8//6OJy31Fe6Ctb/aOCkKcN11LBGYPZuC/+qr2Xk8dy5w6aX0Z+wp8+YxCrR8OX+/6y6KYR3d4qqlf64gDGZiY+ne0VUaG1mvum4dy580DRgzxnfrE4R+QD8JPQ0NLBYL4uLiMHLkSKSkpHQaeXQ4HKirq0OdnyJOqqrCZDIhPj4eOTk5GDVqlLMOtbi4GMXFxaiqqoLdbkd0dDRCQ0N9L1Z1Jk+mSfbu3dxpFxYCM2fSNPuGGyiGoqJcE536Q+1ofy0JaAt9qMLGjRT+Npvr4LhyJX1se4LRyFrZJUsojpctYxOWfvImnqzCUMRs7t6+4f77eeLX3EyHgD/9yXdrE4R+gkRY+xC73e60c7JarWhoaEBBQQG0TlJABoMBjY2NnW5fj9xqmtbpNjvbRkREBGJiYhAYGAhFUaBpGkpLS5GbmwtN0+BwOKAoCuLj4xEXF9ej1+oxn3/OSU6rVrERa9UqitMHH3Sl/6+9lkJoxQrg5pvZCb9qlX+tWvpj01VHqCrTjLt382Tg2ms5CUePvl55JYcUdJfISG5n9WqeWNx8M90JABGsgtAZ69czIpuWxtKo22/3bzOpIPQREmHtQzRNQ5Vbs1BISEinUVbdZF9tpw7T/faUlBSMHj3aWUbQEwICAjBu3DikpqYiKCgIiqKgpqYGW7ZswcGDB9Hc3AxN07zX+d8ddC/PAwdYW5mXR+F06aUUVu6f0ejR9G5dtYo2VhdfzDS0Pxt6BlKE1Z30dJ4MfP01RWZCAqOt33/Pz7cnpSpjxvDv8vLLQHY28OKLvF0EqzDU6ajxsLYW+Pe/Wbbz7bc0+e8PDaWC0AeIYO1DHA4H9u7dC/uRKJvVau20jlXTNNTW1mLEiBGtRKuiKIiIiEBWVhaOPvpoREZGoqampkvR2PYwGo3O12lsbMTu3buxfft21NfXe0RVvdr53xU++YQR05tuolPAypXA5s0UUsOHt/2cY49lveVf/sIu9ZNP9hzX2tcMtAirO6oKTJtGe7AZM/jZ33QTTwRmzmTpQHf54x/Z0LVpk8t7UgSrMNQJD6c9VVvcdx9P0uvrgWefZfmTIAwRRLD2Mbpo1TQNqqp6CMS2IpWKoiAwMBBBQUHIyspyPkZVVQQGBiIlJQXBwcFQVRWapuHAgQOdimD3bRsMBo/XDw0NhcPhQH5+Pn7++WdUVFQ41xoQEND3UdXqaqbzCwtp/r9vH2tSr7ySaeXO1nHKKUBKCvCPfwC/+Q0wahTw+ON9svRWDGTBqjNiBKOrX3zBOrrkZJ40fPMND6bdPVmaPRt46imXlU9wsGuamSAMRXSLq5Z8/DEzR8OGMdMxa5ZMoxKGFCJY+xhN03D48GFUV1dDURRkZ2cjPT0dNpsN0dHRHoJUrx0tKCjAL7/8gurqamdjU3x8vIeABYCGhgY0Nzc7r7cnhFVVRUhICLKzszFu3DhERUU5H1dbW4vNmzejsLDQQ1QnJiYiOzu7b6Oq77/Pbv8//Ynp/bvvBnbsoGBKTu76ds47j00NL70EnHUWIxjPP++zZbeLe0nAQD7QGAysOT3nHHb5//ILvSAvuIDR1x9/7Pq2VJWNV0uXUsyPGsUa5YFYOiEIvUG3dNMtrtypqKBv8UUXcQpdejpt6ARhCCGC1Q84HA7U1tYCAEwmE0JDQ5GYmIjk5GSYTCYoioLY2Fjn4zVNQ319Paqrq5Geno6jjjoKcXFxrYRoQEAAEhISnGLXZDI5n693/EdERCAjIwOZmZkICAiAoigwGo1QFAUOhwNlZWWw2+3O2xMTEzFmzBjExMT0XVS1ooJDAKqqGFXdvp3Xr7uOFks9WcfllzOK9+67TGPX1wNvvOH1pXeIqnKSFDA4zPGzsnjy8MknLLXQnQW++gpYs6brojMsjAJ45UqeWOi2V4IwlNCFalsR1nvvZYNidTX3W5df7p81CoIfEZcAP6CLx7YYPnw4mpqa0NjYCE3TnGn71NRUhIWFdbjd6upq5OfnOyOzum+r1WrFsGHDEBoa6hSddrsdBQUFKHbz/tPdC0JDQxESEtKlpjCv8/bbwGefMVUcEMAmqxEj2GTV27XcfDPT2MHB7Hh/8EGKrZNP9s7au4Ke7h7IEVZ3DAZ2KW/dSqF5880cgbtjB6Ov118PjBvX+XaysjgB69lngSuuAE44gbZlV13l+/cgCP0BXahmZnpGWF97jd+H6GieuM+dO3j2H4LQDSTC6icsFgsOHz7sYT+laRp2796NPXv2IDc3FwAQFxeHMWPGdCpWAaDCrfbPaDQiKioKWVlZyM7ORlhYGBRFgd1uR25uLjZt2uQUq8OGDcPIkSNx9NFHY9SoUa3EbZ9QVgbMmcO08OrVTCsvXkwBdMUV3ttBz5gBfPQR8MMPwB13sPP922+9s+3uMBgirO6MGsWTig8+4GVamqvW9dFHuxZtPessoLQU+O474PTTgcpK1sYKwlDAZqNgjYhwndgWF3P/NHky8NZbbCR1y74JwlBCIqx+Yvv27c6IZlpaGiwWCxwOB4xGIyIjIxEaGtpt0RgfH4+IiAgYjUZYLBaP5zY3N6OwsBDFxcVOkRwYGIiMjIx2o719xquvUpjMncu0+YIFnGT1wAPejyQoCrBoESMVgYFMsy1axN9zcrz7Wu29vvvlYMJoBKZP52jXlStZb3fbbcC2bYy23nAD/64dcccddB1ISmLt8qxZbJrra69fQehrbDaerOm2VprGUoClS3ki9+WXvC4IQxSJsPoBvYtft6zSPU4BYPTo0UhKSnJGRLuD0WhEcHCwszYVoFDNz8/Hpk2bUFRU5LSmio6OxsiRI/0rVouLKU4CArgjXr+etYvTpwOXXOI7UaeqHCjwt78BBw+y6efpp4E9e3zzeu7okdXBFmF1JzubJx3vv88oa0YGLz/7jCUZHUVbFYXNdcuX03Fg2TLX74IwmGk5nvXZZ4FzzwVCQlxjpgVhCCOCtR/gcDhQUlKC7du393hCVUs0TUNRURE2bdrkMU0rJCQEaWlpSE5O7vv6VNfigBdeoD/q4sXApEmMrtbXU9Donpy+xGikSF6zhtGLVatY05qf79vXHYyR1bbQo62nncba1u3bGTHVnQU2bWr/uUFBjKwuW8bI98yZFLGCMJgxmVy2d5WVwN69wEkncV951llsThSEIYwI1n6C3iR1SPej7AVNTU3Yvn07cnNz4XA4YDKZkJKSgnHjxiEzM7NL9bA+Iz+fdaQxMYxyfvwxa1Znz6YpfV9isVC03n03UFPD31eudHmC+oLBHFlti9GjWdP63nuMsqandy3amprKOtYnnuBgiJNPpl+rIAwFjj6aJ225uTzZ+93v/L0iQfA7Ilj7EQ6Ho9eCtampCb/88gtqamqcU6lycnIQFRUFgz/nTWsau74ff5wCcexY7pDNZgrFyEj/rCsoiMJ5wQLA4WCkdfFiWmr5gqESYXXHaGSUtbvR1pNO4v/NZ5/xgF1XR8ssQRjsXHUVS6X0k3lBEESw9hf0iVZWqxV79+5FeXl5lydWARSqVVVV2LRpE5qbmxESEoLRo0c7fVn9yv79TA9nZNCm6q23GGVbuJCpLn8TEUGROncuo67LlrEpq67O+6811CKs7ujR1vff56Uebf388/Z9W2+8kdHZ/fs5Gvb114G8vL5fuyD0NU88QYeUwEB/r0QQ+gUiWL1ET0Wh7rMaHR2N+vp6lJaWoqysDPv27cNPP/3kYVXVEk3TUFxcjJ9//hmbNm3Czp07ERwcjFGjRiEzMxMWi6Wnb8c7OByMqD77LKOoqam0roqNZeq9P9Vk2WyslZw7l5Ow5s3j7zJxybvota1nnMFo67ZtdBI47zxGW3/6yfPxisKTnNWrgdpankzccw/rnQVhMGG3A/qkwoMHgZIS2lgJggBABKtXUBQFQUFBPRKtmqY5SwEcDoezOcrhcMDhcGDPnj0oLS1t9byamhr88ssvyM3NRUNDA8xmM0aPHo2srCwE9ocz8p07aVE0fjyjlf/5DyMGS5YAp5zi79W1TUoKfV8XLgTi47n+efNcBxFvMBRLAtoiO9vl27p2rcu39csvKU7dXQEsFlqPLV7MNOncubT6GcrRamHw8eCDrglWe/YAxx3n3/UIQj9DBKuXqK6uhtls7pVobe++vBYp0LKyMmzfvt05ySomJgY5OTkICAjo/sK9TXMz8NBDFCIPPMDmKr0cYOlS1oz2Z7KyaKl1991s9rnmGgolb4kjfTsiXF3R1jPPZLR1yxZOyTr/fDbm/fCD67FxccCUKRS1SUksJXnsMf+tXRC8yQ8/8GRs1Chet9lcwwMEQQAggtUr6FHRhoaGVob93qD5SIRP0zQUFBRg37590DQNgYGBSExMRFJSkv8sqtz55RcKkJNOYqTyH/9gOcB99wHHH+/v1XWdo49mg9Bf/sK6yz/8gSUM3ozoSXTQxahRFKKffMKTnNRURpu+/pr/O3q09ZhjWE7y9tvAb3/LsbCffurPlQtC76mvpwPGLbdQuObmUrAeOODvlQlCv0IEay9QFMUjqqppGkwmk9eanFRVhdlsRnp6OgDgwIEDyD/iE5r64osYuX49YmNjKVbr6thN+vTTXnntbtHYSIuijz5imtdiYTp94kR23/eHyG93Of54YORI4OGHKZR+8xuKKm/RH04w+hMGA3D77RxBedddwM8/s8nqwgtZW/z993zc5Zfz923bgOuvZwPX/v3+Xbsg9Ib772dGoamJJ2jffMM6eomwCoIHIlh7gS5Qs7OzndOljEYjIiIiAPS8EUtVVRiNRiQlJSEjIwMBAQHQNM1Zy5rgcCAyJgZKcjJrLAsLeVCfPp1p1v/8x2vvsVM2bODO9txzKTAefhh44w1GyiZM6Lt1+IIzzgASEmjHdeKJQGYm8MwzvdumLlQlwto2WVmezgFJSby+YQObrRoaWBP973/TXN29IUsQBhpffMH/8dRUCtc77mCzlZzQCkIrRLD2krq6OlRXVyM7OxsjRoxAcnIyUlJSMH78eJjN5m5tS1EUBAcHIzExEWPGjEFjYyO2bNmCbdu2QVEUHHXUURg/fjziJk6EUl3NRpXbbqNgnDGD4uqKK3ggf/NNH73jI9TVMU2+cSPTt/X1rEM89VSK526+937L+ecz+vfyy8DZZzN6/NxzPd+eCNXOMRhczgEzZtA54KabgEsvpXfvxo08OVu8mCdoCxd6t85YEPqC6mrglVeAK68E/vc/NnoecwwFqyAIrRDB2kscDgcOHDiA2tpahISEOM35FUXpsq2UnvrPzMxEVlYWYmJioKoq6o9Y99jtdmiaBoPB4KpVXbiQJvcREYxqPvAApzUBwA03APv2AR9+6O23S774gp3aU6fS4Pr++xkRW7eONZ+DjSuu4PSrd94BLr6YqbvXXuvZtvS/n6KIwOqMzEzPWtaEBP6PbdrE//mrr+Z3ID4euOgiNvsJwkDh3nu5H62pYVbsmmt4AqaPZxUEwQMRrF5A0zTs3LnT2Ryl01lJgKqqCAoKQmZmJnJychAcHOxxf8vtebB9OyNRc+ey8143vj/iHIA//YmRKG9OBqqu5uvs20fhUFDAiNcFFzAi5s9JWr7mppuArVs5denqq2le//773d+OLlLlwNQ1VNWzlnXjRtauTp3KUg2zmeUBkyax7u/dd/29YkHonP/+lyVTNhtPxubMkTIAQegEEaxewuFwoLCw0OO29mym9IhqWloaRo4ciaCgIDQ0NKC0tBRFRUUoKytDSUkJqqurAcAzsgpQhL70EqNM06ezjjU6mgf0efNcQmjWLDZCbdjQ+zf47ru0pZo2jQJ1+XI2xujz4YcCd97J6PKGDbRf+vHHnp8QiGDtHunpjLZu3MhaVpuN/3uxsRSuX3zB1OrXX9MDWBD6K4cO8cT3j3/kfnXcOGYJWqIoHL4iCAIAEaxeQ9M0lJWVedwWFRUFVVWhKAoURYGqqjAYDEhKSkJOTg7Cjkx6KikpwZYtW3DgwAHk5uZi//79yM3NhaZpUBQFw4YN83yx//6XUSZVZR2r7hWanMxRlgsXckenKDRcf/VVisuecOgQI7d1dSw72LqVnf/XXgtcdx3XMFRQFL73V1+lhdesWSy72Lix+9sSwdp9VJX/35ddRkeM9esZ7X7iCUZZAf7vP/ggUFXl16UKQptoGstY5s0DysqAjz9m9qAtoqL4GEEQAIhg9SphLUaNWiwW5OTkICcnB5GRkbDZbBg7diyio6OhKArsdjvy8vJw8OBBaJrmMeUKgNMpIDo62vOFFi1iZ3RxMa/rXqH33EMrposvZgRU0yiyli8H/vWv7kWeNI2NRvffT3FwyikUa4WFnEyUmNjjz2lAoygcKvCPf3AazeLFjHZv3dq97ZhMMva1p+g+rXv38n87Kgp45BHeZzIxE7B4sUSnhP7HCy8Av/89y1d04doeNhv3t4IgABDB6jUURYHNZmt1u8lkgtlsRmpqKhISEqCqKux2O/bt24dNmzahqKjIKVQBlguYTCYkJSVh7NixiImJaT0UICCABfvLltERAGB36fHH0wd1/Hjgd79jRJQbpRXQo4927c0UFLA7OyyMO9WvvgJWrGD5waWXSq2VwcDP5S9/YS3rihXAk09SQHWG/tlJhLV3KAojrVdfzf/tL75w3RcdzazD2rV+W54gtCI3l/7Bp57KJqvTTmPTbEuCgtiIZbMBRUV9v05B6KeIYPUSZrO5S64ADQ0N2LJlCw4dOuSMqiqKAoPBgOjoaAwfPhxjxoxxRmHbJTiY0aX5810elCedxM7qJ54ATjgByMkB/vY32qQsWMDUfkdoGgcPPPYYo4jjxjHtDdATMyamS5/FkMBkYrPEvfcybbdqFU8Wjgx26BQRrN4hKYmf+7599GQ9fJi3jxvH0bqvvurX5QkCAO5bV69mc1V+Pku0Tj+97cfqkdW4OBGsguCGCNZu0JGAbGxs7LCr3263Y//+/fjll1/Q5JYKVhQFUVFRGDNmDFJSUhAeHt71MauRkSwPmDPHNb7y7LMZGX3+eaaeoqMZGb33XjaotMeePXxcVhYP/G+8wQjiwoXAOed0bT1DDT3SvXQpTxruu49lGUcGPLSJHk2XkgDvoSh0Dbj5ZpYCfPwxb7/gAka0Nm/27/oE4fHHaY9ntbpcAdpDj6xKSYAgeCCCtYt0JiIVRXFOomqJpmnYunWrM6qqo6oqhg8fjpSUFKd/a7eJi6M7wNy5rojdxRfTyP/111nQf9ppdAtoi+Zm4K9/ZYpq9WrWpt55Jz0vV6yg+BXaJziYn9OCBayZXLWKgl8v1WgPibB6n/h4lsEUF/PvUVXF+usnn2TzoCD4gx07uD849lj+L156KdP+7aFHVsPCOt+PCMIQQgRrF1BVtXXjUwscDofThqrl7QcPHnSa/+sYDAZkZWU5x7j2ipQUT3cAgCUBL75IoXr11cDBg61F688/M6r629/ywP7Pf/LnnntYXiB0jYgIlw+uyeQq1dAHObRFQIBEWH2BogBTpnDE5b330t3i7rsZBZcTBKGvsduZqbrzTja9HjoEHHdcx8/RI6tDvVdAEFoggrULmM3mDsesKori7OjX0W2uNm3ahNLSUmfnv6qqsFqtyM7ORmBgoPcWOXIkcMklPDj/9BPw97/TGeDbb4FvvuEggW++4fWGBkZTP/mE9X8WC1NU48dT9HpzXUMFm42if+5cICSEpRrugxxaoigioHxJbCxF6+LFQGgoB1usXOnvVQlDjXXr6NmsKHS2uOuuzp8TE9NxWZEgDFGM/l7AQKCxsREOhwOKonhESQGK1djYWMTFxaGpqQnFxcU4dOiQc6yqu1A1mUxITExEWFhY1+tUu8PRR7OW8p13mJpWVYqmxYspQufNY6Tp2Wd5ME9O5jhLh4NRVZPJ+2saSiQlURjNn886tVmz+PmvWcMSAHeMRomw+hqbDbj8croFzJjBlOwzz7DeVRB8QUMD+wF27gS2bKH4HDWK/4PTpnEyW2dIuZAgtIkI1hYoioLg4OBW6X2LxeIUn+6PHT58OJqamrBp0yanoG1Zp2owGJCYmIiIiAjfCFV3jj+eP65F0v7qzjt50F62jLdv3Miz/VtvZXRW8A4ZGcBVVzHCumIFD1Lz5zM97T5kwWSSg1JfMGECxcMbbwDnnsso1zffcJSrIPSEpia6Uuzc6Urz65jNHOaSmQmceCLrUH/4gVms7Gy/LVkQBgMiWI+gW0ulpqaiWDfkP4KmaShqYS+iqiri4uIQHh6OH3/8sZVQ1beZmJjYuUWVr/n4YwpX90L/F19kuqqnzV5C++TkAOefT8G6cCEjeosXs7bVYGCjm0RR+o4pU1gOkJ4O3H47I99JSWwsFIS2sNuB/fspSHftcg1pAfjdTU0FRoxgBL+t/obycmD7dj5/0yZmvHqCqjIDNpQmCgpCOww5waqqKmJjY1F4xC5EH52qp/VVVUVBQYHHc8xmszPFrxMYGIi4uDgAaBV5BVzRV680VfWU8nKmo486irWqX30FvP020//HHANs2CCRJl8xcaJrnO3Mmfx95UoKVrtdbK36mrlzmVFYsoR13rNm8W8TEODvlQn+oqmJonTXrrZFaUoKMyYXX8zUfsugQ3U1n/fxx8Du3fyO64SHU9BOnMjn91RwRkUxgise2IIw9ASrxWJBVFQUCgsLERYWhqioKA/v0+bmZtS4dXcrioKgoCA0HvE5VRQFqqoiOTnZ+ZyAgAAPQWswGJCWlobQ0NA+fGctePVVzlqfPZvpqKVLGWE69lgK1/POY9RPBKvv+M1vWFP8yCMsDaivZ7NbU5NEWPsag4HlMIsW8eRtzhx+J1atkm7swUxjIyfQ6aLUPX0fGUmHjxEj2helNTV83uefU5S6O38EB/O52dn0qrZavb9+3TFABKsgDD3BWldXh5KSEkyYMKHVfZqmwW63Izw8HNXV1XA4HLDZbCgpKYGmabBarQgJCUF5eTm2bt2KhIQE2Gw2GI801KiqisDAQKSlpcHkrwamwkJGVU87jY0/H34I/Pe/jCjFx1MkLVxI26uwMHajdmLZJfSCM87gycM//sFxoVFBTgcAACAASURBVGYzD2xGY/sOAoJvCA93uQUsWQJMnsxxxdOm+XtlQm+oraWY3L2b4rKqynWf2cyJZxkZtJOKimr9/MOH+dy2RGlQEJ87YgRw5pkd+6d6k+Bgrkv3ZB0zpm9eVxD6MUNKsCqKgtDQUCQmJrZ5/549e1BRUYHhw4cjLS0NdrsdJpMJYWFhsFgsMJlM2Ldvn3NSVX5+PjRNw+HDh6EoCmw2G+Lj4/1Tr6pptLHas4eRo+ZmNvscdRRTn+4z7KOiuBOcOpVd03fe2ffrHUqcfz4nj734Iq3HACkJ8BdZWZ5uATt28KTu1FP9vTKhI8rLKUZ37+Y+zr1EKzCQjU4ZGcDJJ7c97KSqis//7DPWlrqn7/0lSjvCfdrVd9/5ezWC0C8YMoJVURSEhYUhLS2tTUHZ1NSEqiNn5mVlZYiMjHRGSYODg2G327FlyxaP1L+macg/Mjs+KSkJMf5K2+zZw+7nSy5hh/qbbzJaMHt226mkK6/kAXvmTEZkpajf91x2Gafc6N3qUhLgP848k2bu69cD117LMoHhw1kyI/gHhwPIz3dFSg8e5Em3TkQE/z5jx7KcqWX6XdOAsjKO4t21i1387hmM0FCK0sxMjqzu717TeilATo6MZxWEIwwZwWq1WluJVU3TUFtbi6KiIlRUVDhvt1gsrZ5/8OBB1NfXezgB6DZWMTEx/hGrzc1MadbUsDayupoi9Te/YVlAe9hsLAWw25my/ugjlhAIvuX661mmccIJEmH1N3/6E78rSUms5b7zTtazhoT4e2WDl/p61pPqotS9njQigpHN9HTglFP4d2npYOJwAAUFjDju2tVa1EZFUZROmMCR1G3sxwcMcXH8jH79a88SB0EYwgwJwaoLy/z8fERHRzsFaUlJCXJzc1v5pracQFVTU4Py8vJWtlVGoxFNTU2Ij4/3/ZtoyaZNwBNPcCRrTg7w0kuccDV/Pmv1OmPyZDoGnHsuG1BEsPYNcXFARYVEWP2NotAtYOZM4P77WdO6aBEN3iXb0DM0jZ32e/bwp2WUMyCAqfu0NFc9actsV2MjO/c/+ICCrbiY2wX4d4mPp6g9+WQOPhmstnw2G5tjpSFQEJwMCcGqaRrq6upQV1eHoqIipKSkIDIyEnl5ea1EKMAuf/fn7tu3r9XjDAYDRowYAZPJ5Gy66hPq6+mfGhzMy6IiDgQ466zujZ48/nhGmM47j/Yte/cyLSr4Fl2oimD1P1Yrp78tWcLI9zXXMDMxZ46/V9Z/qavjvmLvXorS0lKXoFQUjsRNS6OdU3tRzspKitEvvqBP6eHDrvtMJnqcpqfz+bGxQ1O0RUfLeFZBaMGQEKzuaJqG/fv3w2QytSlWNU3z8FU9dOiQ09JKR1VVjBgxAlZf2Jh0xJdfMpI6fTp36v/8J6MYd99NAdsdFIVNBjt2AFdcwZq+RYt8sWrBHb0UIChISgL6A4mJbIr7619ZJrBrF/B//wdccIG/V+YfHA4gN5f7lT17mHa3212i1Grlvictjc1r0dGtBWVzM7fxv/9RmObleabuw8IoSDMymNnp7r5rKGA0en5mgiAMPcEKsERg9+7dbd4eGBiI8CMpdbvdjoMHD3oIWEVRkJaWhqC+7CStqmLaMiODUdV9+4A77uAEn6uv7vl2L7uM2126lKm7+noxUvc1EmHtf/zqV4z0vfMOhep99wE//kiHjcGG3pykR0n37vWMcKoqxWR8PPDb37KWtC2LvspKCtovvuBldbVL1BoMPBFIS6MgTUwcvKl7QRD6jCEpWNuaTKWTkZEB9UgNW0lJSSuxmpKSgrC2bFN8xVtv0Ypl5kxGM/72N9ZArl7de3EZHMyDTE0NjbNfeolWP4Lv0IWqNF31L668koMF0tLoWTxjBjBs2MA0bK+uphDdt4+XZWUuMQmwdnT4cGDkSDomtBXhbGoCDhwAPv2U28jP5zY0jRHV0FBXPeqpp/K64BtUldFWEf3CEGdICtb2cB8CAADh4eEoLS1FY2MjVFVFfHw8otoynvYFRUWMfv72t6yr27qVs+mvu867kZ8pU4AXXuB2n3nGe9sV2kYXqhJh7X8sWEC3gOXLWWYzbx6bsMxmf6/Mk5oaNibpotS9MUlRKECHD2fq/vjjOdGpZdpe02iXtGkTI6TFxTwR1jGZ2NSUlsb6+IQEaUbzF3o9q83m75UIgl8RwQrWpIaHhyMuLs7jdoPBgOYjdURRUVGt7vcJmgY8+yxrSxctYs3YAw/w7Hrt2rbTc71h1Cjgqaf4uuPHA99/T1sYwTdISUD/xWikUF28mONb77qL11es6Nt16IJ03z6gpISCUkfTWP+ckkJBOnFi241Jmkaz/b17gU8+4bZ0eyT9sXFxFLbHHMPtSTlQ/0PTPIcICMIQRgQr6NGamprq4dFqt9uxfft2NDc3w2KxICkpyfcL0QcAXHQRU/Pffw88/TTHSWZl+e51f/UrmqhfcAHToiJYfYceYZWSgP5JRARwyy3APffwhPGUUzjw4frrvfca1dUUkO6iVKelID36aArLtjrlKyv5/PXrKUzLyz1T/5GRFKSZmcDpp0vafqAREsL6Yn2IwNix/l6RIPiVIS9Y9brUlgMFtm/fjsbGRiiKgvT0dN+OW7XbOQCgtpa1qQ4HLaqioylgfZ2KO/dcYOFCCtegINa8RUb69jWHKkYjrYEkwtp/GTWK2YZnn6WDxs6drOU86aTOn6tpNMTfv9/1455qB5iyT02lKD32WNbJtrV/qaqiIP3uO17qRvu6KA0L43ZSUzksJCJiaFpADVZ+9SseBxSFJ1GCMMQZ0oJVURRERUW1sqfKy8tDQ0MDVFWFzWbzrX3Vjz8CL7/MWtKcHI5UfeUVpiOTk333uu4YjRSoxcWM7D7zDF0IBO8jJQEDg7PP5sni+vUczrFgAQVmcjIbkPbvZ1PSgQM8AdGbkQA2NaWksP7z5JM5yKMtIVlRQSH69de81JujAgLo2hES4hKkv/5120b7wuDl+OP5IwgCgCEuWI1GY6tUf01NDYqLi6FpGgIDA303xaqujjWpkZFMw9fUMAU5ciTr5/r6wHTllcC//kU3grw8RnmlycL76KUAqsrPWOhfVFdThO7fz2ar1avpy7p0Kb1aq6vZgJSSwijsH/7Q9lx6TWOqf9cuV6S1spLfa13cukdITzih7eYoQRAEAcAQFqyKonhYWAEsBdi9ezc0TYPZbEZGRoZvSgE++QR4/XVXFPXtt5lynDWLDRT+IC6Onah2O+vd3n8f+P3v/bOWwYxEVv2H3c5Z9Hpk9OBBnii6ExzM72RKCt04brqJItJs5vfVfVt5eawz16Ot7mNIAab6U1KkhlQQBMEL9HvBqihKmxOpeoOqqoiLi0Ngi8hIZWUlmpqaYDAYkJWVRYurxkba3OjC1X2edVoaD25dHc1aVkarqnHjGEUtLeV41BNOoHWVv5k8meL53HM5nlIEq/eRZivfoBviHzzoEqOlpZ5RbIOB393kZIrRc89lzXZbVFdTiP74I7dVUODZ0GQw0KdVr0O98ELpshcEQfAh/VqwKoqCsLAwVFZWQtM05yQqVVXR3NyM5uZmaJrmHJ2qqio0TUNISAhMJhPKy8vbHBJgtVrbtKgqLi4GAKSkpMBsNvMAtXgxcPPNTNsBPAAWFHDk4Oef8+Bot7tSfbqhti5oQ0J4+0svAT/8wJR7ZCTw738DW7awNq4vBxF0xPHHU0Cfdx4P6vv2ud634B0kwtozqqs57vPgQf7k57f+HCMjOZkpORmYNIkRzrbKWpqb+R3+6SeXuHWf9gS4Iq26uI2LkxIZQRAEP9KvBaumaaiurkZGRgbKysoQFhaGiIgIAEBzczMaGxthMpnw008/ISgoCJGRkYiKioLhyESQhIQEbN26FXa3A5uqqu12/evlAfpr4KGHGIVxF22qysjKsGE09W9JVRXtqXbtYlo9N5cHx5tuAlat4gFy+XLWvl12mXc+KG+hKExfbt/O5quHHqJ7gOA9RLC2pqaG3xNdkOblMbPhTnAwxWhSEsd9xse37UmsaWxmOniQ3fUHD9LD0j06qmdJkpNpFTR5ssyzFwRB6Of0a8EKUJju2bMH4eHhOHToEA4ePIiQkBBUVVXBbrdjwoQJmNCOb6jZbEZsbCwKCgqgaRpUVUVqaipMLQ509fX12LFjB0wmEzJCQniA+/prRmh+/evuLTg0lBGZMWOAJ55gTeqqVUwXPvYYGzFWreJAgP7IZZexPGHpUqC+nj+S6vQeQ60k4PBhCtCDBylI2xKjgYGcN5+YyJPAYcMAi6Xt7dXWcluffeYSty0/z/BwitGkJHoK22wSHRUEQRjg9HvBClC0HtI9CAGUlZUBQJcaovLz852/x8fHu6KnbpSVlaGpqQlwOBD6t78B2dnAxo3A7bf3bMGbNwOPP+4ao7ptG/Dww8A117CzuD+j1/TV1AAXX8xShqlT/bumwYR7hHUgd4TrkUw9MpqXx0xCy+hxUBDFY0JC52K0vp7b+vprl8Ctr+d9FgubmnRxm5REX9Rhw/rf6FRBEATB6wwIwdoeISEhnT4mJycHdXV1MJvNrZqsAJYdFBYWAgAys7KgGI2camOxcGTp669zvnh4eOcLqq9nM1VICC8dDo5VVVXfjFX1FZdeCjz/PHDDDfRkFbyHe4TVy82EXqO5mZN18vJcP6WlrdcbHu6KjObksM6zvf/xujpuRxejeXm8zR2LxbW9447jZX/NRAiCIAh9yoAWrF2JsFosFljaieg0Nzdj586d0DQNCQkJCLBa2QS1ZAlw/vkUbCUlwH338YB82WXtR8U+/RR47TVg+nTWvH77LSfl3HYb60IHEllZHEepaUypbtjAmeVC7/F3DWtVFRuWdCGan99aOBoMTKMPG+byCI2Obv9/v7qa2/rss/bT/gEB3F5SEsXosGFt+5cKgiAIQhsMaMFaVVWFpqamVjWpXaGpqQk7duxAfX09LBaLyzUgPp5m4c8/D7zxBic+rVoFfPUVf7/xRopXHd2qaswYRlVra4G772YKdN26gVs7d8IJwJdfAn/8I+tZRbB6B6PRNzWsjY1MyetiND/fNcrTHZuNkdFhw1ifnZDQvnB0OBhZzc0FvvmGl0VFbFCqqnI9Lji46zWogiAIgtADBrRgBYCioiIkJiZ26znNzc3Yvn07GhoaoCgK0tLSPKO1igJcfjkjR2vXMuJ6/PG0ynnsMeDVVyle333XZVUVFQV88AHwzjvAjBk8aA9kJk9mtPk3v2GJw6FDfI9C7zCZulfDardTJObnu36Ki1tPyTKbebKVkMCI/skndzw5qb7eZXyvR1vdRai+vuho/i8nJrL+2mZjBFYQBEEQ+pABLVg1TUNxcTEsFguio6O7VCKgT7NqbGyEoiiw2Wxt1rYCoFDThcHTTzOyeuutjGT99a9Mba5aRTE3dy6jkA88MLCbaXQMBrokFBRwbOszz7DcQegd7iUBtbW0XsrP5+dcXMz60ZaPt9koRhMTaVIfG9u+aGxu5nb27WNWID+fgrelwA0IoLgdNoyDLM48s//4AQuCIAhCCwa0YAUoQHNzc5GXl4e4uDhER0dzQlU7HDp0CDU1Nc7xq/Hx8V17oT17mMp97z1GHufPd9336KMUBDYbLwdLBOrKK9l4NmcOBVVz8+B5b76iro6fVWEhLwsKWjcsTZrEyzPOoJhMTASOOYZCtL3/XU3jiVF+Pg3vdZFrtXJGvY6qcjvDhlGQTpwoUVFBEARhwDPgBSsA5zSr/Px85OfnIyoqCnFxca2arTRNQ35+PhwOh7MUQO1qjWlJCVBeTgeBlixcSMudDz6gkD3+eOCccwZ+pDUmhtZFTU0c0/ruu8DZZ/t7VX2PLhYLC11CtLCw9XQkgJHL+Hj+jBjBms6oqLZrmX/3O57glJVRgG7e7BKiLefSKwpT/AkJ/Bk5kq8htaKCIAjCEEDROrDWURRF27BhQx8ux3uoqooxY8Z4RFvLy8uxb98+aJqGmJgYJCUldb6hJUuAZcuYZo2OZpTx0UdZ87d0qaftjqZRWHz4IfDWW8AllwC/+pX331xf8t13nKl+wQUc27pmjb9X5D1qalwiVP9pOX/eYmFDU2QkbZvi43kZF8eSkfaw23mSo0dZdZHbsuFKUShodZGbkMBLGdYgCIIgDDEURYGmaW1G+wZFhLU96urqnF6t7tFVk8mEYd1tioqNBdavp3vALbdwotWiRRRwisJmrM2baWZ+wQXAKacAL74I/N//MSo7cqT332BfMHEi8J//ABdeCKSnA7t387K/UlfHNHthIS+Liniy0VZnflAQhafNBmRkuOybOkqf6yJ30yaXCNVT/oGBrEsFuI3YWJfAHTOGl2JyLwiCIAjdZtAKVk3TYHWLflZXVztdAYYPH971UgCdJ59kfeGDD7pS/ZdcQiuru+5iBC40lLdPn07ReumltIV68kl6st56KwXMQEJR2Gy2eTOdE3TXhL5C05h614WnLkJLStr2M7VaKUBtNtaGTpxI4diR9Zndzm3rXfO62NWnLLkTGOiKtGZmAiee2H7KXxAEQRAErzAoBauiKIiIiMCmTZuQkpKCyMhI5OfnQ9M0REVFdWlCVisOHmRpgDvHHMNmrJdfBi66iHWejzzC2s+9ezkl65prKFQrK3kfwOu6uB0IXHwxcM89wPLlLImore2d6XtzM2tCdQFaXMyf8vK2pz8FBzNVHh1NI/tJk/gZdyRCm5sZ+SwqArZscYnQ6urWjzUauT091Z+dzUtJywuCIAhCv2BQClar1YrY2FiUlZXhwIEDKCwsRH19PVRV7Vrdqk5zc+fC7JJLKFjnzAFuvpmXhYXAww9zhvqnn7rKCObNY1PN6tWM0OkjYPs7VitT2ZWVjBq/8AJw7bWu+zWN95WUuMRnSQl/Wk48AhiNjI5m5DM2FjjqKEZEIyI6blTT60KLihjx1aOtLZufDAauKTqa242LowVZXBzF70BvhhMEQRCEIcagE6yqqiIuLg6BgYFQVRUOhwMNRzqubTYbDN2x92ls7Nq89wsvBM46C/jb3xjBu+02RiN37ACeeIL1q889R8F1663AihXAtm20xxo/HpgypX+llDWN7gC66CwpYRTyxRc56eu111qXBYSFuQRoair9QmNiOq/ZrKmhwN2xwyV2i4tbd8kDrkhobCyFaHo6L0WECoIgCMKgZtAJVgCwWCxobGyE7oCgaRpUVYXNZuvehhoauh4BDQxkLWtpKYcKhIQw4rpmDcda/vvfdAxYu5aRv5tu4kjX9ev5vDPPBE4/3TfCq6mJKfiSEq5Pvzx0yLMO1GTiYxWFAjQmhj/JyS4/T4CR4o5eS4+0btlC4ZubywhsW+I/KMgldIcNA44+mr8PhMizIAiCIAh9wqATrIqiICAgAAUFBR63xcTEdC+6CnRPsOpERzP6uHcva15HjgSmTmXE8e23mb4ePx5YvBgYPRq44grWZL79NoXr5ZdTHLaHw8Faz9LS1j96h3pLTCY2BkVHU4BmZ/MyKqp9o3odXYCWljIqrEdcy8tbT0/SX0sXurGxQEoKcNppFMASBRUEQRAEoQcMKsGqqioSEhIAACUlJXD3mI2Li+v+BnsiWHWGDwfuuw/44Qdg1izOdj/nHEZSn32WjwkMBKZNoxXWpZfyvueeA958s/3tqiprPaOjKTgTE1kDGh3NaGVHaBpFbUkJm8g2bnSJ0aqqtiOgJpNL6MbEMAIaE8M19KcyBkEQBEEQBi2DSrAaDAbExMR4iFVFUTod19ouvRGsOkcfzZ8PPwRmzKCbwFVX0S/0//6P/px6t7vBwHGo+gCCzmhsZFq/tJRuBXqk9dChtn1HQ0IYFY2JcYnQESN4GRoqEVBBEARBEPolg0awujsAFBYWOse1Aj2MrgLeEaw6p57aepjAFVd4PqawkLWfERGAu5vB0qX0BG25FrPZleqPjgZGjXJFXjuyfBIEQRAEQRhADBrBajAYEB4ejqqqKjQ3Nztvj4iIgLmn04W8KVgBptD1YQJ//ztLA6ZNo8coAMyfz5rS0aMpXKdNYyPSjTfSwzU2duBYYQmCIAiCIHiJQSFY9bS/oige0VVFUZw1rT1CF6xdTdF3FYuFYrSqikLU4aDd1VNPAVu3UsxmZwP/+hfvmzaNVljbtwMLFwLjxlH4dreJTBAEQRAEYQAyaLpmoqOjUV9fj5qaGudtYWFhsPQmGqkLVru98276nhAaCsydy2lY999PO6y0NP4+ciRN8TMyaIX14IO0l1qzhiNBZ8wA/vvfrvnECoIgCIIgDGAGhWBVVRVmsxmFhYUezVa9iq4CLsHq7dKAlsTHc9DA6aczgvrss7S6+vOf6SRw+DDF6pIlwNNPAxMm8D5VBe68E/j6a9+tTRAEQRAEwc8MCsEaFBQEu92OsrIy521WqxVWq7V3G9aFalsNT74gM9MzgvrOO8DkyYy4VlfzMeHhwMyZwBtvAGecwejrvn28bcsW369REARBEAShj+kTwar40C5JVVUkJyejrKzM+Tr6eNZe4x5hDQjo/fa6yrHHMoKqKIygbthAu6u77wYOHOAo0vp63ve//7Ge9Z57gM8+Y+PWwYN9t1ZBEARBEAQf4/OmK33KVEsjf29tOy4uDhaLBSUlJR7NVuHh4b1/gb4qCWgLReEggTPO4FjXl16iQ8Dtt3PM6cMP0zVg1y7g1VeBq68GbrmF5QOPPkpBO20aLa4EQRAEQRAGMEpHIlJRFG3Dhg29fhFVVREbG4uioiKvilZFUZCTkwNN0/DLL79A0zQoioLY2FgkJib2/gWefJKC8fBh4KefgClTer/NntLQwPUUFFCYDhvG3x95xOW7mpsL3Hwzx6GWlPC+4GDe1tkULEEQBEEQBD+iKAo0TWszLd8nJQEOhwMlJSWIjY2F6sVxnoGBgTCbzSgvL/e4PTY21jsv4M8Ia0ssFlpfzZ4NPPMMsHIlyxSWLwfOPhvYv5/jYP/zH2DZMj5nyRLWvH74oX/XLgiCIAiC0Av6zIe1ubkZQUFBqKioQENDQ5efp6qqx9Qq99tjY2OhaZpH5DYoKKjngwJa0p8Eq45uhVVUBKxbx6lYN90ErF4NfP89HQYmTGBZgN1Ol4HrrvP3qgVBEARBEHpMnw4OqK6uRlpaGrZt29al0gBVVWE0GtHY2Njm/eHh4Th06JBT0Hqt2Uqnvp5RzP4kWHVsNkZSd+/m6NasLDZmTZjAiOpnnzHC2ltrL0EQBEEQBD/Tp7ZWhw4dQlVVVZdKA1RVxYgRI9p9XHh4OBRFQUFBgYdgDQ0N9d6CGxsBs7l/Clad9HTgvvuA8eNZLvDKKxStZjObsrxYgiEIgiAIguAP+lTNOBwO5OfnIzY2FiaTqcPHhoWFITg4uE3BqqoqoqOjUV5eDrvdDsDlRuBVCy19JGt/Fqw6Rx1FT9bISF6uWEHRKgiCIAiCMMDpU8F6pPsLtbW1SEtLa1dchoeHIyEhAXV1dW1GTDVNg9VqRVlZmUd9a2RkpG8WrpcGDAROOomNWBER/l6JIAiCIAiCV+jTGlZdsO7ZswcJCQke/qx6CUB9fT2io6MBAHl5eSgsLHQ+Txe4UVFRMBqNqK2tdb0RoxEBvhKVAyHCKgiCIAiCMEjpU8GqR0M1TcPhw4cRFxeHkpISAIDZbEZwcDCCg4MBAHV1dTh8+DAACl1VVRETE4OYmBiYzWY4HA40NTU5t+2VQQHtIYJVEARBEATBb/SJYLVaraivr3dGSE0mE1JSUmA0GhEdHY26ujrEx8c7H5+Xl+e0qlIUBampqc4mK526ujqn5ZWqqojwZQpcBKsgCIIgCILf8LlgVVUV9fX1MJvNTosqg8GAXbt2ISoqCklJSa1qWUNCQpylAmlpaQgLC4OmaaisrERQUBCMRiPq6uqcj9c0zRmZ9QkiWAVBEARBEPyGzwWrXgbQ0NCAxsZGaJrmTOXrorPlZKrQ0FCMHTvWKWSLi4ud9lUGgwFjxoxBTU2Nc9uBgYHedQdoiQhWQRAEQRAEv9GnNawthwVomoa8vDxUVFTAYrEgNDQUISEhMBqNUFUVlZWV2L9/P5qbmz3qXwGgpqbGuR2fNVvpiGAVBEEQBEHwG30qWNvC4XCguroa1dXVKCsrcwpSg8EAh8PRaixrfHw8GhsbndFZRVFgtVp9u8jmZsBg8O1rCIIgCIIgCG3id8Hqjrs41QcCuKMoCuLj49HU1ASr1YqmpiaEhIQgJiamL5cpCIIgCIIg9CEDcm6nyWRCeHg47HY70tLSOh3zKgiCIAiCIAxcBpTSMxxJy2uahoKCgv9v725627jONo5f5/BtSEoUZb1EoiTbseMGD9CiWXTRAgUKFOi2n6Hoovt22UXRAv0M3fVLdNNN0UWBIi1gpDESI4iRoHZhy7JkS5YsUuLbzLMYDSVZpCRKpM7M8P8DCEocZuZ2VhdunXMflctlxxUBAABg3BITWI0xWlpakqTelIGZmZmbefg4R2YBAADgXIkKrKVSSZLUarVu9uFHJ24BAADg5iUmsPq+rzdv3kg6nt/6/gSBkcvnx3t/AAAAXCgxgVWSut2uJOn169c388Cb7uQCAADgjFiNtRrEGCNrrWq1mqRwSoB09iACAAAApE8iAuva2ppmZ2eVzYblVioV7e7ujjewBoE0zuNeAQAAcCmxXxJgrVUul+uFVel409VYA2urJR11cgEAAOBO7ANrEARnNlfV6/XxP7jZlDxv/M8BAADAuWIfWCX1xllFDg8PJY25w9psSoXC+O4PAACAS4l9YA2CoDfO6uRnJ9/HgsAKAAAQC7EPrNLZYHojUwIIrAAAALEQuykB5mhnvrVW1lqVSqXekayRqakpHR4eElgBAAAmQOwC6/T0tB48eHDud6ampsZ/eACBFQAAIBZityTgMl3TG10SwDxWAAAAp2IXWN8f1vxbYgAADa9JREFUYdVPJpMZfyFRYG23mccKAADgUOwCa7vdvvA70SECN9JhZWkAAACAU7EMrNGc1UGiDuuNBNbDQw4QAAAAcCh2gTUIAj19+vTcpQFRYG02m+MrhA4rAABALMQusBpjVK/X9ejRI7169apvcI1GXzWbzfF1WQmsAAAAsRC7wCqFo61839eLFy/01Vdfqdvtnrp+MqR2Op3xFEFgBQAAiIXYBdZyuawHDx5oZmZGUthFfX9Nq+/7MsYok8lcuN71yg4PCawAAAAxELvAWiwWZYzR/fv3Va1WVS6XVSqVTn3n4OBAxhj5vj++wNpshputCKwAAABOxe6kq2hDlTFG9+7dUxAEvTWrkb29vd7a1oODg/EUwpIAAACAWIhdYN3c3FSz2dTU1JTm5ub6HhJwsqvaaDTGU0izKeXz4dKA6enxPAMAAAAXit2SAN/3tbOzo+fPn+vrr7/uOyWgVqudmhQwpkKkTIYOKwAAgGOxC6yRIAjUbDb15s2bM9c8z9Py8rKMMep0Opc6zvXKCKwAAABOxTawSmG3dXt7u++1paUl5XI5SRrfxiuJwAoAAOBYrAOrNHhTlTFG00drSwmsAAAA6RX7wNrtdvueZtVqtXrLBca28UoKN1153vjuDwAAgHPFPrBaa9Vqtc58ns1mZW1Y/tu3b8dXAB1WAAAAp2IfWCVpf3//zGfWWnlHnc9Wq6V2uz2ehxNYAQAAnIp9YPV9v++kAEmamZmRMUbGGO3u7o6ngFYrnMcKAAAAJ2IfWKWww9rtds98vri4KOl4dutY+L5kE/G/CQAAIJUSkcSMMdrb2zvzeTab7S0L2N/f77s569rK5dHfEwAAAJeWiMDq+37fwCpJlUql93O9Xh/9w8dxTwAAAFxaIgKrNHjWaqVSkbVWvu+PdlpAJjO6ewEAAODKEhNY+422kqTp6WkZYySNeLxVtGb26N4AAABwIzGBtd1u912jaozR8vJyb17ryMdbjWNdLAAAAC4tMYFVkjqdTt/Po2kBkkY/3ooOKwAAgFOJCazGGL17927gtWKxqCAIxjfeCgAAAE4kJrBeNGu1VCpJOhpv9cc/Sr/+9WgezJIAAAAApxITWCVpb29v4KzVcrksezTgv7W9LRWLV39QELAUAAAAICayrgsYVqPRULnPMP9yuawgCBQEgbZ+8xutrq5e/SHttpTLXaNKAAAAjEqiOqy+7w88HMDzPBUKBUm6/jrWZlM6uhcAAADcSlRglaT19fWB11ZXV2WMUbvdvt54q5OBlaUBAAAATiUmsFprVavVdOvWrYHfqVQq8jxPQRBcb7zVycDKpisAAACnEhNYfd+XtVa3b98e+B1jjFZWViRdc1kASwIAAABiIzGB1Vqr4iV2/lcqFUnnTxS4EIEVAAAgNhITWH3f19TU1IXfM8bI8zxJGrhB60IEVgAAgNhITGC11vbmrF4kn89Lkg4PD6/2sMPDMLD6vnTJZwIAAGA8EpPGfN/XN998M/B41pOi8Vbb29tXe1izKXkenVYAAIAYSExglaTd3V19++23F65N9TxPxhjt7+/L9/3hHxQFVQIrAACAc4kKrJLU7XbV7XbP/U4+n5cxRsYYNRqN4R9CYAUAAIiNxAVWY4weP36sJ0+e6ODgoO93Th7Teq3AengYLg0AAACAM4kLrEEQqNPp6N27d9re3lar1TrznVwup0KhoCAIrjYpgA4rAABAbCQusJ60tbWlL774Qp1O58y1hYUFSWJJAAAAQMIlNrBaa9XtdpXL5fpen5ubkxSOthr6AAECKwAAQGwkNrBGR7V+9NFHymazZ65nMhmVy2VJV5jHyhpWAACA2EhsYJXC9aznHddarVYlXeHEqyio0mEFAABwLvGBdWdnR9vb233/7F+pVCRp4DSBgVgSAAAAEBtn/5aeIMYYPXv2TEEQyPd9zc/Pn7oenXg1dIc1OpKVwAoAAOBc4jus0UlWzWbzzPVMJiNjjOr1+vVOvAIAAIAziQ6sEWOMlpaW+l7zjjZN7e3tDX9jNl0BAAA4l4rAKoWhtZ8osL59+3b4m9JhBQAAcC4VgTUIAq2vr/e9Fk0RuNYBAgAAAHAmNYF1a2ur7zXP82SMud4BAgAAAHAmFYFVOv7T//sKhYKMMb3QOhTfJ7ACAAA4lprAWhgQLAuFQm9CwNCBtdGQBhz9CgAAgJuR6DmsJ2UymYGfW2sVBIHa7Xb4Ybst/f3vYRjNZM6+9vfD7w3YyAUAAICbk5rA2gujfRSLRdXrdbVarfCDv/5VevVK+s53pG5XarXC9+jV6YTfG3bNKwAAAEYuNYF1f39fnU5H2ezZf1K1Wj0dWJtN6Uc/kr773f43++yzMVYKAACAYaRmDWu329WXX36pra0t1et1HRwc9Nau3rp1S5LUiTqnjYZUKg2+GZ1VAACA2EhNh1UKQ+vz5897vwdBoFqtpqWlJT148OC4+3pRYI2whhUAAMC5VAVWSb2uaqTVaikIAjUaDTUaDa2trSmXz0u//a20tiYVi9KdO9Ldu+H7ySNe6bQCAAA4l7rAelImk9Hi4qLq9bpevnwp3/dVLBa1/MtfSk+fSn/4Q9htffYs/P3RI2ljQ7p3L7xBoSD9/vfS/Ly0vBy+arXwnfmsAAAAN8Kcd/qTMSZ4+PDhDZYzGsYYraysaHFxUcYYbW5u6vnz5wqCQKVSSf/3t79J//mP9JOfSKur0spK+D41dfZmvi+9eSOtr0svX4bvGxvhxq3TD5VmZ4+D7dJS+N7vngAAADjFGKMgCPqux0xth3V+fl7maA3qwcFB71jWdrstvX4t/elP0osX4euzz6S//EWq10/fJAjCjmr0+v73pZ/9LJzV+r4gkHZ2wlD78qX0r3+F7+/fUwrXz0aBdmkpfM3PSzY1e+AAAABGJpWB1fO83kEC3W5Xb9++7V3rdrvRl6T798PXIL/7nfTzn4dd1fV16eFDaXMznNV6/LDw96Wl42D7ve9JP/3p4ADaaIRhdmNDevJE+sc/wi5utP62UpH29sL/fm7uONRGL7q2AABggqQysLZaLfm+r83NTW1sbJzaiPX+pqxzGXMcQs9/YBg+19el//5X+uc/wy7u+8/K5Y47q8vL4VrZH/6wf8c2LDa8z8ZGeNDBp5+GPz97Jv3iF9IPfnD5fwsAAEBCpTKwBkGgzz//vPfzmevttszubhgUs9nw3drwdXKU1WXHWuXz0u3b4es8UbB9+VL63/+kf/9b2to63bGVwnoWFk6vhf344+ONXp9+GgZZAACACZDKwHpeF9UYI//HP1bmz38+Poa12w27mb5/epTVxx+PtrDLBttuNwyy0XrYx4/DDmu00WtnR/rVr0ZbGwAAQEylckrAeay1+uSTT3obsgAAAODeeVMCJm5berFYJKwCAAAkyMQF1il22AMAACTKRAVWa63K5bLrMgAAADCEiQqs0UlXAAAASI6JCqzGGOXzeddlAAAAYAgTFVg9z2PDFQAAQMJMVGCdnp52XQIAAACGNDGBlQ1XAAAAyTQxgVWScrmc6xIAAAAwpIkJrEEQqNFouC4DAAAAQ5qowPru3TvXZQAAAGBIExNYJSmTybguAQAAAEOamMBqrVW1WnVdBgAAAIY0MYFVosMKAACQRBMTWI0xHBoAAACQQBMTWH3fVzabdV0GAAAAhjQxgbVYLMrzPNdlAAAAYEgTEViNMbpz547rMgAAAHAFExFYS6WSSqWS6zIAAABwBakPrMYYzc7Oui4DAAAAV5T6wCpJMzMzrksAAADAFaU+sHqex2YrAACABEt1YLXW6oMPPnBdBgAAAK4h1YFVEutXAQAAEi7VgXVubk7WpvqfCAAAkHqpTXPGGC0uLrouAwAAANeU2sBaKpXYbAUAAJACqQysbLYCAABIj1QGVmOMqtWq6zIAAAAwAqkLrMYYLSwsyBjjuhQAAACMQOoCqyQtLCy4LgEAAAAjkrrAOjs7q3w+77oMAAAAjEiqAqsxRrVazXUZAAAAGKFUBdbZ2VkVCgXXZQAAAGCEUhNY6a4CAACkU2oCK91VAACAdEpFYKW7CgAAkF6pCKzVapXuKgAAQEolPrBaa7W2tua6DAAAAIxJogOrtVarq6vK5XKuSwEAAMCYJDqwFgoFzc/Puy4DAAAAY5TYwGqM0YcffihjjOtSAAAAMEaJDKzGGC0sLKhYLLouBQAAAGOWyMCayWS0srLiugwAAADcgMQFVmOM7t69K2sTVzoAAACuIHGpr1KpaGZmxnUZAAAAuCGJCqzWWt25c8d1GQAAALhBiQms1lqtrKwwcxUAAGDCJCaw5vN5LSwsuC4DAAAANywRgZWZqwAAAJMr9oE1mrlaKpVclwIAAAAHYh9YrbWq1WquywAAAIAjsQ+s1WpVmUzGdRkAAABwJNaB1VqrarXqugwAAAA4FOvAGgSBpqenXZcBAAAAh2IdWIvFIssBAAAAJlxsA6sxRrOzs67LAAAAgGOxDqwzMzOuywAAAIBjsQ6snue5LgMAAACOxTawVioVTrYCAABAPAOrtZb1qwAAAJAU08DKOCsAAABEYhlYPc9TNpt1XQYAAABiwARBMPiiMU8l3bmxagAAADCpngVBcLffhXMDKwAAAOBaLJcEAAAAABECKwAAAGKNwAoAAIBYI7ACAAAg1gisAAAAiLX/BwM1l7iI7I/cAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 864x576 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig = plt.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection=proj)\n",
"ax.set_extent([-98, -87, 25, 31], cartopy.crs.PlateCarree())\n",
"ax.add_feature(land_10m, facecolor='0.8')\n",
"\n",
"# shipping lanes\n",
"ax.add_feature(shipping_lanes, edgecolor='r', linewidth=0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2nd approach for using a generic shapefile"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<cartopy.mpl.feature_artist.FeatureArtist at 0x7f30d2c2d9e8>"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAGzCAYAAADqqkXjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nOzdd3hU55n38e8504s06hr1hiimuwfbGIzBgAFTTPNu6iabbDZtk2y2J9nNJpvsJnGyTrLZbJI32U3ANs0YMBhMccEt9GZEUUcS6iPNaPqc9w80EwmEkIQkBLo/16VLYjRzzjMjIf30nPu5H0XTNIQQQgghhBip1Fs9ACGEEEIIIXojgVUIIYQQQoxoEliFEEIIIcSIJoFVCCGEEEKMaBJYhRBCCCHEiCaBVQghhBBCjGj63j6ZmZmp1dbWDtdYhBBCCCHEKKZpmtLT7UpvfVgVRdEOHTo0ZIMSQgghhBAC4N57771uYJWSACGEEEIIMaJJYBVCCCGEECOaBFYhhBBCCDGiSWAVQgghhBAjmgRWIYQQQggxoklgFUIIIYQQI5oEViGEEEIIMaJJYBVCCCGEECOaBFYhhBBCCDGiSWAVQgghhBAjmgRWIYQQQggxoklgFUIIIYQQI5oEViGEEEIIMaJJYBVCCCGEECOaBFYhhBBCCDGiSWAVQgghhBAjmgRWIYQQQggxoklgFUIIIYQQI5oEViGEEEIIMaJJYBVCCCGEECOaBFYhhBBCiE6KotzqIYgeSGAVQgghhOgkgXVkksAqhBBCCNFJ07RbPQTRAwmsQgghhBj1FEWhoKAAq9Ua+/ed6nZ8bvpbPQAhhBBCiJFgc2kpyydOJMliwe/3U11djcvluuNmXW/H5yMzrEIIIYQY1dyhEF8+cYJ/fP99fnL0KAAmk4nCwkL0+ttrbk9RlF5nUFVVJT09HVVVb+lMq6qqqGrfY6gEViGEEEKMam3BIOfdHj48YQKhSCR2u6IoOJ3O2+YSuqIoZGZmxsoaeqJpGmlpaWRmZqJp2i17bikpKf2a6ZXAKoQQQohRLdNiYXJyEjUeD55QqNvnkpOTb5vAqmkafr+foqIirFZrjzOYqqoSCASoqamJPWY46XQ6srKy8Pv93c59o9lWCaxCCCGEGPWmJiXRFghQ2tra7XadTkdKSsptE1rb2towGAw4nU4ikcg1QdBut1NXV0eky0zycEpISMDpdOL3+2O3KYpCTk5Or4+TwCqEEEKIUU1VVe7PzqbJ6+V4Q8M1n09PT78FoxqYUChEQ0MDiYmJ3H333dhsttjnVFXF4XDckvpVVVWx2WxkZ2cDUFhYiNlsxmg0UlxcTEpKSq+Pv70qiYUQQgghBllcXBwfcjo5t38/vnCYNr+feJMp9nmj0YjVasXj8dzCUfZNJBKhqqoKu92OxWIhJSUFj8dDJBJB0zQSExNJTEyMzbQGg8EhHY+qqiQkJJCamorNZosFZYvFwsSJE/t+nKEaoBBCCCHESKeqKklJSWR0hqnixERO9DDLauoSYEc6TdNobGwEIDExMVYrqtfrY29paWkUFxej0+lQFGXIZl2tViv5+fnY7fabOr7MsAohhBBi1NI0jWAwiKIoTEtNRaeqHKuv5+HOS9dw5TJ761W1rSNdqHPxWDgcjt12dYsui8XC1KlT6ejooKysDIBgMDgo9a06nY4pU6bEamgDgQAtLS0YDAZCoVC3N4PBcMM/CCSwCiGEEGLUqvf7+d7bb1Pu8VDe1safjB9/TR1rY2PjsK+mVxRlwOeMzhpHP47qWs8aFQgEuHDhAqFQCFVViUQi/Tp3T/dVFAWDwcDZs2eJRCKYzWY0TaOtra3X4/RGAqsQQgghRq3/KSvjtNdLssVCstmMRa/nrc6WT1FNTU23dHeoaOjs68ynqqocdblI9vuZnJZGbm4uPp8Pp9PZ7X5+v5+zZ8/GZmOjx+/puaqqil6vj91Xr9cTDAbRNC0WdKM0TcPn83U7j81mo7i4mJqamljdbNfz3Oj1lcAqhBBCiFHrs2PGcN5oJNNupy0Q4F/efptLbjehSAR9Z1Ds2oJpuESb+muaRnZ2NqqqUllZecPQ2hII8OvKSt6sr8cbDLJl6VIe6VLeED12R0dHbGa1q+hOWdHz6PV6DAZDrH9rdFyBQOCax+n1euLi4oiPj8dut2M0Gq+ZOY2Pjx/Q6yGBVQghhBCjVmZcHHMmTAAgGA7z57t3k2Gzcb6lhQnJycCV2cWutaDDJTp7mZycjKZpVFRU9Hr/fQ0NfP/iRb5w9938z5NPsruigs/v3cvBp5+msbERt9tNMBjs9ly6buVqtVoxGAy43e5YD9dIJILf748F2Oh9FUXBbDYTHx9PXFwcNpttSLexlcAqhBBCiFHLYrHEPjbodIxPSsJhMnG8oSEWWPPz8yktLR32sgBVVRk3bhyVlZU0Nzdf936uUIjvX7jAOY+HLUuXMiMri8aODr518CBjzWbOnTvXbWY22hXAZrNht9sxm82EQiHq6uro6OiI3bfrxgOqqmK1WnE4HNjt9uvupDVUJLAKIYQQYtS6enX61NRUGr1ejtXXs2b8eODK7kw2mw232z1s41IUhaKiImpqamhra7tuWFYUhW3t7URMJk6sWkVDRwfPvvsuvz99minx8XyuoCAWPHU6HUlJSfj9ftra2mhra6O9vb1bCUC0vZVOp+t2ed9kMt3S3b4ksAohhBBi1Lr6Un9OXBzBSIQmr7fb7fHx8cMWWBVFIT09nUAgQHt7+w1ndgsSE6n1enm7poZ/fv117MAn8/J4oLOUIDor2t7eTn19fbfjRetkzWYzcXFxxMXFYbfbMRgMg/JcAuEwzT4fTV4vjV5v7H2j10tDh5cmn5cmr++a1/tqEliFEEIIMWp1Xc0O4A+HMep0lLlc3W5PTEyktrb2mrAHN17hPhBJSUl88MEHNzx2RzjMvx86xK/mz+fTu3fzlTFjeNDhIC4uDp1Oh9/vp7W1NdZHtms5QDSg9uXyvqZptAUCNHm9sQDadFUQbfL6aPJd+Xyz10ejz4s3FCLRZOrswmAhyWImpbMjQ6bdxuTUFFIsFlIsFh7q5fwSWIUQQggxal3dASDYuYWp5aoFRGazmczMTGpra7stQDKZTHhvMDvYXxaLBaPRGFv01FNoVRQFXyjEz8rKmJ2ZybazZ5nscDAnMxO3292t56lOp8PRGWL7enm/oaODXWVlvFJaSiAc5uXSUsw6Xaz9V6LZ/McAarZQnJjIg5kWksydgbTzfo4u5/IGgzT5fNfMtB6rr6dBZliFEEIIIXp2dZuoQDiMBtcEVgCn04nNZuPy5cv4fD6Sk5O5fPlyv895vWb7cKW5f35+PjqdDqfTSc1VPWGjqjwevvHBByQaDMy12/nBuXM8f//9uN1u9Ho9ycnJ/Vq9H9E0jtXXs/3iRV4pK+ODpiZm5+TyZGEBc3JzWb94MUadLnZfl9/fbZY1+vZBU3PnLGz3GddGr5ewppFiNl8Js50zrlfCrZmihIRexyeBVQghhBA3ZSgvjfeVqqpomtbvMVx9KTwYiRDpYYY1KnoZHa483+sFyt701GxfVVXuuusuOjo6qKur67V+9WR7O189cQK9qnLO46ExEuHXs2czo6gIq9Xa58VRLr+f1yoq2H7xIrvKyok3GVlQUMC/Pvwwj2Rl4Q4G2VVWxo+PHOH9urpYKUCr34/NYIjNoiaZr4TO6OzqpJTkLqH0jzOuNoOh17H9VS9jlcAqhBBCiJuSlpaG0WjE7XbT0dFBIBDotvJ8KKmqitFoJC8vj0AgQFlZGXq9HofDQXt7e2xXpeuN5+oA1dsMa0+PTUlJobm5uV/PVVEULBYLHo8n9hxyc3MxGo2cPHnyus9T0zTi4+PZVVXFXz/wAP955AgHV65kenp67H4uvx/HVZ0PojRN40xTEztKS3mltJTDly8zIzOThYWF/MODD1KUkMDxhgZ2lJbyjYMHOdXYyKycHOYXFLBq/HiSzOYrAdViiW2qMFwksAohhBCi36KXtRVFia08jy7oMRgM/KKqina3m4/l5RHXz4byfd3LXlVV8vPzSUhIiAVPVVUxmUyx/qqaphEOh/F6vdTV1V0za9nTDGtPNazXk5ubi8FgoK6url+zu9FV+NGwHRcXR1lZWbfnHm0xlZCQQFJSEna7HVVV+ZDLxRvV1Xxu+nR+eOgQfzFtGttLS9lZWkq1283P585lxdixAHgCAfZVVbHjYik7y0pRFIX5+QV89b77mJ2TQwTYW1HBd997n51lZVj0ehYWFvCNGTOYmZ2NeQg3A+iPkTEKIYQQQtxWoqEq+j66Y1I4HMZqtfJabS0FDgd/evgw354wgUl93JLT4XAQDAbxer19CoBXb/+ZcFUtZNctQxsaGq455tWB1R8Oo1OUPgdWRVHIzMzEZrNRWlra55lWV2cXgvHjx6OqKiUlJXg8nth4k5OTSUxM7PES/59Nnsy33nmHf3zwQf7fqVMcqqvjqeJinpszh72VlewpL6eyrY2dZWW8U1PDvU4nCwoKeGXFCiYkJXG+tZVXSkv50eHDvFdbywMZGTxZWMjX7r+PsUlJfRr/cJPAKoQQQoh+UxSF+Ph4LBYLOp0OVVXR6/WYzWYsFgsvp6TwxKZNTEpL4yunTvGJ/HxWZ2Ze93iqqmI2m8nLy0NRFI4fP37D8ycnJ2O1Wvs85sTExNgMa3T1/dV724ciEVDVPgfWKIfDQW5uLpWVlTcMrdHQnJqaisFgoKmpCY/HE1vJn5qa2mubKbvRyJzcXJp9Pu5KSWFJURE5cXG8WFLClvPnMak6gpEIn5k6lY1LlmBQVV6vrubnx46zs6wUXzjM/PwCPjd9OluWLiXOaOzXc70VJLAKIYQQok+idZQWi4W8vLxew2JxUhJHP/IRPr17N067nVN+P7leLzOumjHUNA2r1UpWVlZsMdOZxkbmvf02DycnsyInh19dvMjfjxtHSmewUlWVvLw8kvo5G5iYmEhiYiJwpf+qy+UiLS2t230CnRsJDORSeEJCAhUVFTe8X3TXKafTGRuXw+Ho02p+TdM42djIrvJyfjxnDh+bOJEv7ttPlt3GwsJCti1fztTUVCra2niltJS123fw5qVqpqSmsrCggE1PPcWU1NRbumvVQEhgFUIIIUaJgazmD0UinHa7mZCURHFWFvHx8Rj7OCPnMJlYv2gR3zh4kD/U1rK9tpY/f+op/H4/kUgEs9l8zSV9gHyHgySLhbDZzNdOniQSifCTS5f4wZQp+P1+MjMzY8FzoMxmM2az+ZrbA+Ewun7OsGqahtfrpby8vNf7RWtSs7KySElJ6VZ329uMarPXy97KSl4tK2dPRTka8MNZs3DabCwtLmZBQQGKovBmdTX/d/o0z5SV0ej1Mr+ggA9PvIvfPbmQxB6e6+1EAqsQQggxCuj1esaNGwdAVVUVbre710vX0dnU3S4Xv7xwkaLEBHZNmhTrxdlXiqLwl9OnM+7IEXzhMGFFic2kXo/VYODA6tXMfvFF7nM6Met0bC8rI2vJEmyDfPm6paWFtrY20tPTMZvNOK1WDDodpqueZ3V1NaFQiNzc3Fi4DIVCNDY20tDQQCgUuub1jNb1RmeRExMTb3i5HyAYDvNOTQ2vlpezp6KCs83NPJyVxbz8fL5y370UJyRwpL6edy5d4sHMTDaWlPCZPXu4KyWFhYWF/HbBAu5xOlFvs1nU3khgFUIIIe5w0dBUVlZGbm4uY8aMobq6mvr6+mvuB2C1WklJSbkyi9nYyH+WlBCKRPj07t38ev78fl9OTrVacQeDpFutNPl8ZPdhn/qsuDj2r1rF7Bdf5OMTJ9Lg9XLZ46HwJgKrpmmEQiFCoRDBYJD29nYuX76Mpmk0NTXhcDh4raqKT02ezPGGBiKRCC6Xi8bGRtrb2wFobm7ucQeq6CyppmnodDrsdnusZ6vZbO71NdM0jXMtLbxaVsbuigrerK6mKCGBuXn5fG/mTGZkZlLn8bC3spJvHDzI3spKnDYbTV4vB595hhfPnePHc+bwicmTB/zajHQSWIUQQoheKIqCTqfDYDAQCoUIh8OxFk7D0Wd0MERbO3V0dNDS0oLNZoutUoc/hq20tDSSk5O7XfK/Oz2dX8+fz5/v3k2L38+3332Xf/zQh/p1flVRSOzcprPJ6yX7BjOsUVlxcRxYvZqP7txJMBLhXGsrhf0oBdA0jY6ODtra2nC5XHR0dMRu7yoaJpvdblx+P/MLCvjzXbs4ceJEbIEWEAuq4c46V5vNhtVqxWg0YjAYMBgMWCyWWMuq3jR5veytqGBXeTl7KyqIaBpz8vL407vu4jfz52PS6zlQVcXm8+f5zJ49NHR0kGGz8df338+zs2eTFRfHjN//nlq3myy7nY7OfrN3KgmsQgghxHUYjUbGjh2L6apG7KFQCI/Hg9vtpqmpiVAodEt3eeqPaNjKzMyksbERo9FIcnIydrv9urOAi4uK+LsHHuCnR4/y38ePU5SQwNoJE/p13mSzGbvRSOMN9oy/Wqbdjkmnw6zTcbKhgfkFBTd8TCAQ4OzZs7FNA6KiM83RP0BMJlOsltVsNlMbCHC/00m+Xo8aChEIhdCrKlarFYfDgcPh6NdOUl35QyHejl7mL6/gQmsLD2Vl8UR+Pn99330UJyRwtL6ed2tqWPHyyxy5fJn7nE7m5eezftEijDodT2/dykcnTuRUYyPPnz1LeyBAk9dLht1ObecmBHcqCaxCCCFED/R6PePHj+9xtiy6k5LD4SArKwuPx8PFixdHfHBVFCW2WCkpKalfq+y/cPfdXGhp4f26Or6wdy85cXE8nJ3d58cnWywYVJUGj4eGhgY6Ojrw+/2xVljJycnX/GEQNTU1lZONjZxobOzTuZqamggGg1itVux2e2xxl8lkwmg0XreG1NfQQKPXS0piImc9HorHjsXR2ay/vzRN41RjI7s761DfrqlhfFISj+fl8ezsWTyYmUmt283uigq+fvAg+zov868oLuZv77+fmdnZ3ep1W3w+XIEAWT//OWa9nnn5+WTHxVHZ3k6GzcbbA9gi9nYigVUIIYS4iqIoFBcX9+nSLly5NDxx4kTKyspob28fcaUC0bKGwsLCGy54uh5N0/jBo4+y/OWXcZhMrNi6lYPPPMOYPl6iH5uYSJvfT2l5OcU9zLLW1tbicDhITEwkHA7Hak1NJhOTk5N5s6qKspYWWlpaYqvtTSZTjyE3IyODjIyMfj9HXyiEWa9H0emIaBoJcXH9mk2tcbt5raKC3eXl7K2oxGrQ83heHp+aMoX1ixahUxT2V1XxwtkSPvnqq7T6/czJzePJwkJ+1HmZ/3oSzWYOrF6NXlUp6twc4VvvvEON281DWVnUyQyrEEIIMXoMpCE9gE6no6ioiMbGRqqrq0dMaFUUhaSkJHJyctD1c4V/lKZpHD16FLPZzPpFi5j5/PPMyMpi4ebNvPPMMyR3boPam9cqKki1WnlmyhRSk5IIBoMEg8Fu4dTlcnWrrY0ym0yYFQW318fFixdjIdJkMjFp0qQBPaee+MJhTDod/nC41/AY1R4I8EZVFbsrKrjQ0sK7tbXMyslhbl4e//LQQ+TGx/N+bS27y8v54aFDnGho4IGMDObm5fHC4sVMTUvr10r+cVfNiGfYbBy8dIkMm01KAoQQQojRRFVVsrKyBvRYRVFISUmhsbExtsDnVonOqhYUFFyzm9ONBAIBOjo6CIfDRCIRWltb0TSNhIQE7EYj25cv56F167g3PZ3fnznDF+65J7YQrSdvVleTYrZQ2dbOjDFjyLDbe7xfdBV/1xDrA/785ZdJs1qZmuGkuLgYTdNQO2tLB1N1eztjExOxGQxY9HreunSJR7qUPYQiEf5QV9c5g1rBkfp67kt38nj+lcVS01NTKXW52FNRwZf27+eN6mry4uOZm5vHN2bM4JGsLCx9nLXviwybjTqP50oNq9s9aMcdiSSwCiGEEJ1UVSU7O7tPOw5dj6Io5Ofn88EHH9zyetaMjIx+h1WAuro6Ghoaut2mKAqWzpnUTLudpWPGUOZy8V5ZGYc77zN+/HhsNlu3x4UjEZa/tJWc+DiSzCYefeEFzv3Zn/V4XkVRYqvt4cpK+sUbN7KoqIgDVVV8a9YsHA5Hv59PXx1vaCAvPh5FUfjctGn86PBhUi0WdpeX81plJW9UV5MfH8+c3Fz+/sEHmZmdjScYZG9lJT87epR9lZWENY05uXmsGT+eX86bR9pVr8dgcnbOrKZ1tgsLRSLoB1BvezuQwCqEEEJ0slqtJCcn3/RxLBYLaWlpsdAXnX2MBtjhaImlKMqAg3dWVhZOpxODwcDly5e5dOkSmqZ1C796VSWsaRj1epKSkkhPT+9xxlOnquxYsZxmnw9PMIihj4Gq1u1m7oYNLCoq4pszZvDv77/PX+3bx68XLMBmMGDW6TDr9Zj1+kFpkH/Z4+FEfT2fv/tuAD42aRIvlJQwb8MGHs/PZ21nAI0zGnnz0iX2lJfzd2+8QanLxczsbObl5/O1++9nfFLSsG17mmG3U+fxoFdVkszmK62vrjN7fbuTwCqEEEJA7PL5YIWNrKwskpKSCAQCBAKBWGcBRVFoamq6ps41uhJ9sIKs2Wwe8PalOp0uVu+akJDApUuXSEpK6lYDazcasev11AYCZOXm9roD1v39XABV7nLx+IYNfGLSJP7+wQcB+Op999Hk8zFvwwZ84TC+UAhfKIw/HMLQ2fbKrNfH3pt0Okw6PWa9DrNOj6nzvVmv6/zcH++naRq/PHmST02ZwoLCwtjz2796NSpwpL6e1yoqWLtjB+/X1jI1NZU5eXn85PHHud/pxDDA2uCb1XVmNVrHeqcGVqW3yxWKomiHDh0axuEIIYQQw0+n0zFu3LjYJe/hEN17PhgMEhcXR1paGj6fj8rKypsKrdHAnZeXNyizxXAlREe3GY063djIrBdeYHJyMnkOx4B2wIrSNI1mn48yl4tj9fX889tv8zf338/nOmc7b/RYfzTAxoJs6MptV/+78z7Rj/2dHyebzczOzb1mURPApfZ27v7f/+XpsWOZX1jIo9nZxF+n/datkP6zn3HsIx/h47t28fnp03myqOhWD2nAOq9C9PhNJDOsQgghRrVbEVbhStnAhKua7w+k5jVaahDdFjR6jIE8n/b2dhoaGsjNze1WTtBTH9KJKSk8O3s2X3/rLRp9Pr73/vv87QMPXPfYLr+fcpeLMpeL8rY2SltbKW9ro7zz36qiUBAfT158PL9duJDHcnN7PM7yl17i1fJy4k0mzDodls6ygCuzq1dmUC1dPo7Nrur1WDrforOwk1NTmZWTA8Cxy5f54aFDXPZ4qO/o4LLHw/1OJ3/zwAPMyMrCEwqxqLBw2C7391VsZtVmo+4WL/QbShJYhRBCjFo6nY7x48djNptv9VAAYqGzt89HZzuj94sGbr/fj9Vqxd25Wry/K+hdLhcXLlwAIKczxN3In951FycaGjh46RLPHTlCnMFATnw85W1tlLlclLW6qGi7EkiDkQj58fHkOxzkx8dTmJDArJwcChwO8h0OEs1mIppGncdDucvFug8+6BZwCx0OvnrffXzpnnt469Il/v6BB1hYWIgvFMLbOYvqC4f/+PFVM66+cBhvMESLz4cvFOL9ujoADn34w/zs6FH++8QJZmVnk26zkR0Xh05V+d3p0/zh8mWeX7SIWS+8wHfee49/6CxRGCmcNhu1bvcd3ylASgKEEEKMSqqqMmHChBETVqMOHz58zW0mkwm9Xo/JZKK5uRm4Mn6j0UhxcTHGLjsiRXk8HiwWS592aQoGg5w4cQKAKVOm9HnDBLjSBWDxli3YDQZMOh3NPh958fEUOByxMJofH0+yxUJE06jtDKQVnaG23NVGRXsbFa42KtvbcJhMV4JtNNx2Pv5MUxM/OHSIbcuWYdbrWbBpE1++916+dM89fR5r1I8PH+a5o0d5Y80adly4wBf276coIQGX30+914tJpyPNaiXVYiEYDvNEQQF/OX06D/7+93z/0UdZNX58v885VD6+cycPZ2fTEQxytrmZnz7++K0e0oBJSYAQQgjRhaIoOJ3OERdWg8EgAAaDods2r6FQiKKiotiuTj6fj9TUVJKSknoMpB6Ph7Nnz1JUVERC565I1+P3+zl16hQAkydP7ldYhStdANYvWsSqbdv40ezZmHU6KtraqGhr41RjIztKS6lsa6e8zUW1202S2Uxe56X//Ph47nWms2JsMfkOB3nx8Vivc/4FhYUUJSSwYNMm1i9axJtr1vDEpk3Ud3Tw7Ycf7vOl+l8cP86zhw/z+urV7Ckv51/efZf/fOwxpqWlkWa1kma1duuV2tDRwQO//z3jkpJ4edky5m7YQL7D0e+FZEPFabNR43YzPimJ/VVVt3o4Q0YCqxBCiFEpPT39lpy3tLSUtrY24uLiKCgo6BY4GxsbAUhLSyMYDFJfX4+qqoTDYc6cOcO0adMoKCi44Tn0na2metuGNRKJUF9fT03nHvTjxo3rcaa2LxwmE3clJTHlN78hw26PhdHc+HhmZGXxzIQrATU3Ph7zTfS4XVpcTKLZzMqXX+anjz/OW2vWsHDzZho6OvivuXNv2IP0/06f5l/eeYcDq1fzfl0df/vmm+xbtYoJvSxOS7Va2b5sGbNeeIFNTz3Fr554gmUvbeXtZ9aSN4Q9Yfsqw26npLmZ2Tk5d/T2rBJYhRBCjDqqqvbpUvlg8/v9sV2j2traaG9vjzXCDwQC1HXWVba3txMMBrv1a42Pj+/z1qomk+mGwbatrY2amprYgq1AIEAkEhnw6/L9WbP490cfHfIWT4/m5LBn5UoWbt7MPzzwAPtWrWL51q2sfPll1i9adN1AvKGkhK+98Qb7Vq3ibHMzn9u7l91PP91rWI26KyWF3z35JCtffpmDzzzDV+67l0Wbt3DwmbW3vGNAhs3G61VVd3wN6525HYIQQgjRi1u10jsaEOHKDGdVVRU+nw+A8vLyWDhta2vD6/XG7ms0Gvs0s9pXHR0dNDQ0dBtLeXk5ly9f5vTp0wQCgX4fU6eq3cJqdXU1hw8fjpU5DKapaWm8uWYNzx4+zB50QD8AACAASURBVPf/8Ae2LVuGSadj/saNuPz+a+7/8oULfG7vXnatWMGl9nY+sWsXLy9bxtS0tD6fc15+Pl//0IdYtHkzH584kYeys1i1bRuhId4A4kaii66cVit1HR23fHe1oSKBVQghxKgT3at+ODU1NdHS0tLtNr/fz5kzZzhz5gzt7e09Pk5VVQoKCvq0a1Vrays1NTXXDZx+v5/a2lpKSkpoa2uL3R4N8DU1Nfh8Prxeb1+f1nUldfY0PXHixJCEqMKEBN5au5ZtFy/ypf37+b+FC5mcmsqjzz/f7dL4q2VlfPLVV9m+bBnuYJC1O3awcckSHhhADepnp09nbl4eK7dt49lZs4hoGl/Yu/eWhsRoOyub0YhBVXsM7HcCCaxCCCFGpejl9+HgcrmoqKjoMdhomtZrQNQ0rc+1peXl5dTV1XHq1ClOnz5Ne3s7Xq+XqqoqWltbqa2tpaamhkgkgtFoRFEUioqKrtk2tr8Lr3pitVqZNGkScCVID4V0m439q1dzrqWFtdu38+8zZ7Ji7FgeWreOCy0tHKis5MOvvMKWpUtRFIVlL73E7xYuZGYf23b15IezZ2PU6fjS/v28uHgxb1RX8+MjRwbxWfWP02ajzuNB07RYT9Y7kdSwCiGEGHU0TaO+vh6Hw9HrwqTBOM/ly5e7lQL0laIoqKpKWlpanwJkdNOA6Hl8Ph/nzp2L9W6tr69n7Nix+Hw+zGYz2dnZsVnbwsJCLly4gMFgIDk5edA2UYh2NSgrKxvwNrE3Em8y8cry5Xz4lVdYuHkzLy1dSrrVyox16whrGhuXLCHeaGTuhg38Yt48nrjJ0gq9qvL8okU8tG49vz51iu3LlzNj3TqKHA4WjxkzSM+q7+xGIzpFoS0QuFIe4PH0qS73diOBVQghxKikaRrnz58nIyMDp9M56HWt0bpQl8s14EvGU6ZM6fMiqK6X+K8eh6qqmEwm7HY743voIepwOJgwYQIGg2FQZle7yszMpKamhpaWliELrSa9nvWLFvGFffuY9cIL7FyxgnvS0zHpdBh0Oma/8AI/mj2bpcXFg3K+eJOJ7cuX8aF16xibmMiWpUtZtHkze+LjmdaPutjBEl1wldE523onkpIAIYQQo5amadTV1XHs2DFKS0tpaGigqamJ5uZmWltbB1TLqWka7e3tfPDBB7S2tsYWUl2PqqoYDAbS09NJSUlBp9PFwnNf6mzD4TBNTU2UlZV1O5eqqqSkpFBQUEBhYSHjx4/vNZRbrdZBD6vwx1rWysrKQT92VzpV5Sdz5jAjM5Mv79/PPU4nk1JT+cEf/sBTRUWsuWob3JuV53CwZelSPr5rF2adjp/OmcOSLVuouQUr9Z1WK3Uezx3dKUBmWIUQQoxq0ZDX0tJCa2trt1CnaRoJCQlkZ2f3WEeqaRodHR14vV68Xm/sY03TbhhUo4xGIxMmTIjNpObk5HDx4kVCodANA2RraytlZWXdnkdXCQkJsbZZPelatzpUDAYDiqIQCoUIh8N9bs01ECXNzWw5f55nZ8+mIxgkoml8dvp0nty8mSnHjvEX06YN6vkeyMjgp3PmsHjLFt77kz/hM1OnsnjzZt5YswbbAHvaDkS0dlVqWIUQQohRoGsNaFQ0yOr1eux2O3a7HYPBgNfrpbGxkXA4DPQcGG9EVVWcTme3y/6qqlJcXIymab0GyXA4TGlp6XXLDSKRCG63u9fAev78eXw+H1OmTOn32PtKVVWSk5NpbGzE5/Nhs9mG5DwXWlqYu2ED3505k5nZ2Uz5zW9wB4Os69wVa97GjdR3dPD1D31oUAP6qvHjKWlpYfGWLby+ejXnW1p4ZscONj/1FLph6vWb3hlUnTYbJxoahuWcw01KAoQQQogb0DSNYDBIS0sL1dXVsdX4wWCQSCQyoLDa9dg9uVGo8nq9fbrPqVOnOH78eGwXrSifz0d7ezvx8fH9G/AARHcVG4x2WT2pcLl4fMMG/ulDH2JBQQGPb9jAxydP5oXFi1mzbRuHL1/m4Nq1bL1wgc++9hrhQe6d+o8PPsiEpGQ+snMn/zV3Lm2BAF99/fVBPUdvMjp7sd7JM6wSWIUQQoh+iF7uH4zem5FIhKampgE9ti+X1l0uF36/n1AoRGVlJR0dHbHPRWtK4+LiOHfu3JA1+Yc/hvKhCKyX2tuZ8+IG/uqee3h67FjmbtjAsuJi/uHBB3k0J4fdK1fypX372Xz+PAdWr6akuZnV27bjH8Q+vIqi8Msn5nG5o4NvHnybTUuWsLO0lN+cPDlo5+hNpt1OXecM651awyqBVQghhLiFPB4PnqtmxYLBIOXl5Vy4cOG6wXggtaDRGdlAIEB7ezsGg4Hy8vLYpgVD1QA/2j7rZmaie3LZ42HOiy/yySmT+dikSczfuInHcnP51kMPxe4zLS2NN9eu4YeHDvGDQ4d4ZflyABZs2kzbIDbZN+n1vPTUU2w8V8JLFy6wY8UK/vbNN3m1s8Z4KEV7sUY3EbgTSWAVQgghbiFN07hw4QJ1dXXU19dTXl7OyZMnaWpqum6rKuhbBwGAoqIiLBYLRqMx9piTnTN/wWAQu91OXl4e48aN6/MGBf0VDax9bdHVF01eL3NefJE148fzuenTWbhpE/c60/nBrFnXlEp03xXrAOueXMjYxEQefeEFLg/iJfQUq5Xty5fzd2++SVVbG5ueeooPv/IKJ4e4rjTDbqfW4yHZYsETDOIb5l3choMEViGEEOIWC4VC1NTUUF1dTVNTE5qmxbZkvV6dant7+w1nRBVF4eLFi/h8Pvx+P1VVVQBkZ2czefJkpk+fzrhx40hJScFutw/68+o6Dhi8GdxWn4+5GzbwZGEhf33ffSzesoVxiUn85PHHr/t6pdtsHIjuirVjB8/OnsWSoiIeWreOi4O4E9f45GTWL1rE6u3bSbVYeHb2bBZv2TKk/VGdViu1Hg+KopDe2eLqTiOBVQghhBgBeupQcL2az0gkwuXLl28YAKOf71pDWldXR2JiIkajcVBnPPsyjsHQHgjwxMaNPJKVzT/PmMHyrVvJtNn5nyfmod5gEVq8ycTOFctRFYUFmzbz5Xvv5cv33svM9es5evnyoI3xsdxcvvPIIzy5eTPzCwr4xKRJLN68mY4hqhFOsVppDwQIhMOx3a7uNBJYhRBCiBEoEolQV1dHdXV1t8CnaRrV1dWxdlr9denSJc6fPz9Yw+wTf2et6M2WHHgCARZu2sS0tDT+/dGZrNy2jTijid8uXNDnFlImvZ7nFy3iruQkHn3+eZaPHcuPH3uMJzZuZP8gbm7wZ5Mns6y4mGUvvcTX7ruP8UnJ/MmOHUSGoE5YVRRSo5sH3KG7XUlgFUIIIUYoTdNoaGjgzJkz1NTUcOnSJU6fPk1jY+NNLWAaM8x73jd01nBGa1kHwhsMsmTLSxQlJPDcnDn8yY4dKCisW/Qk+n7OFOtUlZ8+/jjLi4t5aN06pqWl8cLixazeto2NJSUDHuPVvjtzJikWC5/es4f/mTeXJq+Prx0YmnZX0aBa4HAM2eK5W0kCqxBCCDGCRSIRfD4ftbW11NXV4ff7BxxIVFUd0l2tehKJRGI9YAdaJ+sPhVi+dStpViu/mDuXj+7cSXsgwIYlizEOcOcsRVH4+owZfO3++5n5/PM4TCZ2r1zJF/ft42dHjw7omFdTFYXfPfkkp5ua+P6hQ7y09CleLr3Ifx07NijH7yrag3VPRQW5w9Bbd7hJYBVCCCFGCbPZzPTp0zGZTMN2TpfLRSQSwWQyDei8wXCYVdu2YTUY+O3CBXx6zx4uezy8tHQpppuYsY369NSp/PTxx5m/cSNNXi9vrl3Ls4cP8/W33hqUmUqrwcC2Zcv4nxMn2FNRwSvLl/PPb7/NrkFud5Vus1HS3EyN2830tLRBPfZIIIFVCCGEuAP1tKjK6/USCoWorq6mpqaGhoYGTp06RUtLy5CNI1pr63Q6+z27G4pEeGbHDsKaxronn+QLe/dxvqWVbcuWYTEYBm2My4qL2bhkCWu3b+cPdXUcXLuW7aWlfHr3nkHZFSvDbuflZcv4/N69NHi9bFyyhI8McrurcYmJHK+v59Hs7GHbEnY43XnPSAhxQ8N9SVAIMbx0Oh2FhYXExcV1u13TNE6cOEFjYyO1tbVUVVXh9/sHvICrL6JbvyYlJfXrceFIhI++spM2f4ANixfztdff4Gj9ZV5ZsRzbEPSLnZmTw2urVvGVAwd4/uxZXl+zhlJXK0+//DLeQVjdPzUtjd8sWMCabdvJtNt5dvZsFm3ePGg7U9mNRg5fvsxjeXmDcryRRgKrEKOIzWYjNTWV7OxsMjMzMZlMEl6FuAOFw2FKSkowGo3dmvYnJycDkJmZSVJSEoqioChKLFQOtkgkQiAQ4O677+5XC62IpvHJV1+lxuNm81NL+MbBt3nzUjWvPv008UNYzjAlNZW31q7lJ8eO8W/vvseO5csx6XTM27iRVp/vpo+/sLCQv3/gfhZt3syThYX82eTJLNq8BU8gcNPHdtpsVLa381hOzk0faySSwCrEKKGqKhkZGeTm5pKWlkZGRgZjx469I1eTCjFaKYoSC6iaptHY2EhaZz1jeno6+fn53HPPPaSlpVFQUEBubi7x8fFDtsPViRMnKCkp6dcfxpqm8dk9r3G+9cql/+++9z47y8vYs3IlCWbzkIyzq3yHg4Nr17Knopy/2PMa/7twIXenpfPI889zqXML25vx6WnTeDwvj5XbtvG399/PpJSUK2UPN1l6kGQyYdMbmJiSctNjHIkksAoxSuh0umtmUSKRyLA1DhdCDL2EhIRu4VPTNFpaWjCZTLHg2lVycvKQtbhyu92Ew2GKior6/BhN0/jS/v0cra/nleXL+dHhw2w8f469K1eSbLEMyTh7kmq1sn/1ai653azYupXvPPIwz4wfz0Pr13O2qemmj//D2bMxqiqf27ePX8ybi8vv5ys32e7q0dxcGj73l3fsVTP5TSXEKKCqKjk5Odf8IPMNwiUuIcStoygKqqrG3jIzM7F0BruMjAysViter5cJEybcVA/U/tI0jZLOfqYJCQl9fszXXn+dt6qrefXpFfz38eP89vRp9q1aRZrNNpTD7ZHdaGT78mU4TCbmbtzIp6dO5ZszZjDrhRd4r7b2po6tV1WeX7yY92tr+c8jR9iydCk7y0r56ZHBaad1J5LAKsQoYDKZevyl4fV6b6r5uBDi1rJarRQUFJCfn8/kyZMxm83ExcWh0+lITU1l/PjxTJo0adivpJSWlgIwderUPj/m6wcPsruigt0rV/Lb06f5+fHj7F+9mowB9m4dDAadjv9duJAZmZk8vH49c3Jz+dUTT7Bo82Ze6XyOAxVnNLJt2TJ+fOQI+ysr2bliBf/67rvsuHhxkEZ/Z5HAKsQdTlEU8vLyerxM1NHRcQtGJAbqTr3UJwYmeuUkISGBxMTE2AxqcnIy06ZNw2AwoCgKfqCyrW3YxuV2u2ltbSUjI6PPs7r/+s47bD5/nj1PP82GkhKePXyYfatWkX1Vl4NbQVUUvj9rFp+cMoWH1q8n3+Fg27JlfGLXLn535sxNHTsnPp6tS5fy6T17aPJ62bz0KT6+axfH6usHafR3DgmsQtzh4uPjsV3ncprX6x3m0Yi+iq7ejs6MRS/3ZmZmkpycLB0eBADBPrRb+uqBA4z71a/5zrvvDsk+9lcLhUI4HA4yMzP7dP//PnaM/ztzhtdWrmR7aSnfee899q5aRZ7DMcQj7Z8v33sv//bIIzz24ouEIhH2r1rFc0eO8L333rupxav3OJ388oknWLp1K5k2Gz+ZM4fFmzdTPQgLvO4kSm8vsqIo2qFDh4ZxOEKIwaQoChMnTuxxdxlN0zh69Kh0CRihFEVh0qRJtLW14XK5yMrKwty5Qtrr9dLW1kZdXR2hUOgWj1QMJ0VRuv2f1ev1OJ1OwuEwXq8XnU5HTk4Oui7blbr8fj6+cyc7y8oYl5TES0uXkj9EYbC/CznXffABf/vGG7y1di2vV1Xxd2++yb5Vqxjbz56tw2l3eTl/tW8f33nkEe51Opm/aROP5eby7OzZqDfxR+Szhw7x61OnOLh2LT87eoz1JWd5a+1a4oaog8NI1Pn93eOLKIFViDtYfHw8xcXFPX6usbGRyspKCawjkKqqWK1Wxo0bd83nIpEIJ06cGNJG72Jk6hpWrw6uXcXFxTF27Nhrbt9UUsLHdu0irGn8aPZsPjVlyqDO0re0tFBaWsqUKVMw9GEXqn2VlazZto19q1ZR3tbGT48e5YezZzOhs1fsSHaoro4lW7bwzRkzWDVuHE+99BIZNhu/XbBgwNvFaprGZ197jTKXi23LlvHZ117jktvNy8uWoR8l3Vx6C6yj4xUQYpS6XimAhNWRSVVVTCYT2dnZ1/1Dw+VyyddtlIp+3R0OB2lpaVitVvR6PXq9vlvwdLvduFyuax6/Ytw4LnzykzzgdPLFffuY9cILXPZ4BnV8WVlZfQqrJxoaWLNtGy8uXkxHKMTHd+3imw89dFuEVYB7nU7eWLOG773/Pj8+coRdK1YQjERYuGkzbX7/gI6pKArPzZmDAnxh3z5+OmcOoUiEz+/dK//nkRlWIe5YqqpSUFBAQkICmqbhdrtpbm7G7Xbj9/vlB+AIEQ0aDocDp9OJ1WrtddarpqaG2n601OltJk7cviZOnBgrEYErYTEQCFBaWhpbTFlUVNRjdxBN0/jlyZN8cd8+dIrCr+fPZ2UPs/lDpaqtjRnr1vEfs2Zxn9PJw+vX84t581jcj36tI8Vlj4cFmzZxn9PJc489xhf37+fdmhpeWbFiwN0N2vx+Hl6/no9OnMinpkzhoXXr+eikiXz1vvsGefQjj5QECDEKqarKXXfdhV6vp6SkBL/fLy2sRgBFUbBarbFQERcXR35+fp9mpeDKDOvFixevCaHRBVoGgwGDwYDJZMJkMqGqKl6vl+bmZvn636ZUVb3ma6fT6SguLr7mKoqmaVy+fBmXy0VGRkavW66Wu1ws37qVD5qamJefz28XLBjynaRafT4eXr+ej0+axEcmTmTGunV85d57+cy0aUN63qHU5vezYutW7EYjv1+4kB8cPsz/O3WKXStWDLgWt7Iz1D83Zw73pKczY906fvzYY6zoodTjTiKBVYhRSFVVJkyYgN/vp7S0dMSFldE482exWEhNTaWlpYX29nZsNhvjxo3rdx3h8ePHY4utVFUlLi6OnJycHhfXRbW2tlJWVjbivg/EjZlMJhwOB263G5/PF/t/k5OTQ2pq6k0dO6Jp/Mf77/PNt9/Gotfz/KJFzCsoGIxhX8MfCvHExo1MS0vj2w8/zJwNG5iTm8u3H3lkSM43nALhMB/buZOq9na2Ll3KlgsX+Mc332LrsqXcn5ExoGMerqtj/qZNvLJ8OTpV5YmNG9m+fDkPDPB4twMJrEKMQqqqkpubi8lk4vz580MSVLquBtY0rcfgFb1d0zQMBgNWqxWbzYZOpyMSiRAOh/H5fHg8HgKBAKqqomnaHRdmVVUlOzublJQUzp49i8lkIj8/f0AN3S9dukRdXV2s3rUvOwm1tbVRWloqi7VuU1OnTkWv18cu/Udn0wfLB01NPLVlC5Xt7aweN46fPf44thusTm9sbESn05GYmHjD40c0jWe2byesaax78kmefvllHCYTv12w4I5pzxbRNL564ACvlpeza8UKjjc08PFdu/jtggUsLCwc0DG3XrjAZ197jbfXruX3H3zAH2pr2bJs2SCPfOSQwCpEP3Sd+YuGids1QKmqSnFxMRcuXLipoNL1dbBYLJjN5th7g8GATqeLXbaMRCIoikIkEsHn9/NXb7xBtsPBt2bO7NZqpyeRSASv10tHRwft7e20t7fHxn07vv5XM5lMTJw4kYaGBlwuF21tbSQnJ5Ofn9/vY/W3fZDL5aKsrEwC621IURTGjBnT6+X9wRAMh/mnt97iR0eOkGgys+mpJczIyurxvh6Ph7Nnz+J0Osnq4T6hSAQF0HV+j35l/37+UFfHq08/zZcPHOBCSws7VqzAeIOfCbejH/zhD/z4yBF2rlhBWyDAspde4rszZ/KxSZMGdLxnDx3iuSNHaA8EWL9oEY8P4OfF7UICqxB9FN0VyuPxoNPpcDgc2Gw2amtrqauruy1Dk6qqWCwWOjo6+jT+6MynoiiYTCbsdjt2ux2r1drvZvWappHw3HOENQ33F784oPH7/X5cLhctLS3sq6qiORBgfnr6gI51q0X3ew+Hw7GvRX5+PsnDsDK6ubmZiooKKQm4TUX/+LQPwzalh+rqWPrSSzR6vXx6yhT+Y9asbsEyHA5z7NgxAO6+++5rfiZomsaHX3mF16urOf2xj/Grkyf5nxMnOPjMM/z8+HFeOHuWN9asIb6XEpbb3e/PnOHLBw6wcckSUi0WFmzaxKemTOHvHnig3zPKmqbxWnk56XY7U26yBGSkk8AqRqXoTkH9/QU9bdq0a2YCI5EIx48fv21/2Xf9AdnTYh240rM1GkwtFss1rXIGaub69Ry6fJlLn/kMiTe5oOPR9espaW5m76xZt32nA51Ox4QJE3qtOx1MdXV1XLp0aVjOJYaG0Whk0qRJw3IJ3RcK8aX9+/nNqVNk2GxsXbYsFpaOHj1KJBLp8WclwN+98Qb7q6rIstuxGwzsq6riYOfGAP908CBvP/MMmcMQvG+1PeXl/MmOHfx87lwezMxkwcZNPJydxX8+9lhs5ll0J31YxaikqioOh6PPP9wVRSEpKanHH8DR/pi3q2gdqbFLTZqqquh0OtLS0pg8eTJjxozB6XQSHx8f24N8MExOTSXRZKKsh76Q/bVi7Fhm5eYyceJE7rrrLtLS0mLlCLcbTdP6tUtVtNxioNqu2ks+OtsrBm64ay9DoRD+Afb47C+zXs/P587l1aefxh0Mcv/vfsc3Dh4kFImQm5vLpEmTevxZ+dyRI2w+f57ty5YxNy+Pd2pq2L5sGSXNzXz19dd5ZfnyURFWAebm57Pr6af5/N59vHT+PG+sXcMHTU2s3rYNn+xQ128ywyruWAkJCeTl5XHq1Ck0TbvhL3tVVZk0adJ1FzLU1dVRU1Nz287qqaqK0+mkrq4Oo9FIVlYW8fHxQx5a/uvYMb777nsUJDjItNvxhcP4QiH8ne+dViu/eOIJki2WAR1f07TYNqUej+e2+vpYrVbGjx8fCz5ddzHqKrqDEBBbuBYfH09KSkqfv37RhVpwZUOJzMxMysrKBmVr157aLt3pFEUhPj6e9vb2YXvuiqLEfq7dqB58MB08dIjvXbjAq5cuMS09nb+5/36WFhdfsw3pxpISvrh/P2+tWUNHKMRjL77IuiefJNliYd6GDWx66ikeyc4etnGPFKWtrczfuImV48byTw8+yEd37qSuo4OXli696atOdxopCRCjUrQGMyMjg2AwSGNjY6+XkVNSUsjLy7vu8e6EVdYpKSk4nU70ev2w/cLbUFLC999/H6Nez2emTsWs12PS6TDr9Zh1Or5y4ADfeeQR5vTy2veVz+ejvr6epqYmgBEfolRVpbCwkPb2dpqammLhcfLkyRiNRkKhEK2trVRVVV3zXKIz5uPGjevTavGuCwejIffs2bN4BmGno2h4a2tru63+YBgoRVFwOBxkZWVRVVUVm70eaBlSf88NV1qkZWVlYTabCYfDmM3mQZ/xDYfD1NXVUVdXR3p6OudCIT6xezcNHR2kWK1895FHWDVuHDpV5UBlJau2bWP3ypWkWizMWLeObz/yCA9lZvLUlpf4xw89yKrx4wd1fLeTho4Onty8mYnJyfx87lz+5o03eK2igl1PP012XNytHt6I0VtgHdiGt0LcBjRNw+fzUVFRgaqqjB07lnA4TFlZGcFgsNsvVlVVSUlJ6fV4kUhkRP0yVlUVRVFuWG/q9Xrx+XwYDAaysrLQD3Cf64Fq6OhgbHIyO0pLWTF2LOarzp9uteIOBgflXGazmdzcXLKysmhubqauro5QKDRig2skEuHChQuxzhSKoqDX66mtraWlpaVbx4WraZqG3+/nzJkz5OXl3bD8JRqmukpLSxu0hVgZGRk9bgd6J9I0jdbWVoLBIMXFxRw/fhxN0xg3bhyaplFdXY3X6x2S77voz6COjo7YBhKaphEfH8+YMWMGLbR2nZE3Go04nU6y9XpKP/Uptpw7x9feeINPvvoqf/3663xy8mT+8/Bh/t/CheTFxTHrxRf5i2nTmJeXx0Pr1+MLha75fz/apFqt7F+1ipXbtrF861ZeWLyYLLudGevWsXPFCibe4PePkBlWMYqYTCYmTZpEIBCIlQlEmc1m7rrrrkHdEnMoRMeXnJxMSkrKDbfxjIoGn+h9O4JBrIPYw7E3XztwALvRyIGqKv5y+vRrdmp5Zvt2FhYW8qd33TXo59Y0DY/HQ0NDA62trcDInnV1Op14vd5+X2aOzpgmJCRgNpvR6/VYLJYbrijXNI2TJ08SvMk/GIxGI4WFhZSUlIyoP+qGWlZWFk6nk0gkQkNDA01NTYTD4dhuZtEZ5+H4nlMUBYPBQHp6OhaLhbibnLVzu920t7fHvqd66gSw9cIF/vXdd2nyenEHAgQ1DbNOx59Nnsy/Pvwwvzx5kgOVlTw1Zgw/OnKEg2vX3jE9VwcqGA7z6T17ONXYyHOPPcaXDxxgQlISv5w//1YPbUSQGVYx6ul0ulivS6PRiN1uj9U7ms1mCgsLb/iD1O12D8NIr09RFFJSUsjMzOz3LGnXOsffnznD37/1Fs+MH8+/zZzZ4/1DkQiBcBh/OBx77w+H8XfWngYikdjH0TffVf9u8fk43djI+zW1vLpqJVlxcWwoKWF5cXG319puNOIOBAb2otyAoiixtlyRSASXy0V9fX3sMvhICFddLyM3ezwE3e5+jysaiJqbm2PHBG7YuzM6Q3+9wHqj2tRoWUJOTg7nz58f72SqFgAAIABJREFUEa/ncKqpqSEYDJKdnU0oFMLr9cY+FwgEYq9PXzpaRP+PDjTcRjcUqK6uRtM07rnnngEdJyr6/+Z6FEVhaXExc/Ly+OSuXZxraWHDkiUUJSTEvv8mp6Tw7Xff5VdPPME/vPUWb1ZXMzMn56bGdbsz6HT86okn+PrBg3x5/wHmFeTzVzf5tRotJLCKO56qqmRlZXX74TtmzBja29uxWq19rv8bjFq/gYj2Uc3Pz8c8CAX6JxoaWFJYyI7SUn576hSqqhKIhdAwgciVGl2jqsOk12FUVUw6XeebHoOuy78761FNOh1GVUd7IECdx80lt5tmn4/c+Hi+N+tRJqakUJyYyM+PHeM7773HPzz4YGw8doOB9iEKrF2pqkpiYiKJiYkEg0Gam5tpbm7G6/XGLskPR+CKBpPExETMZnOsW8Nvzp3jJ/v38/nCQmYlJ9/UWKLlBTf63tY0rcewqqpq7A+75ubm64YoRVHIzc297Wu7B0rTNBoaGvB6vWRnZ9PU1EQwGOz2/eTz+UhNTSUQCMRqXbvuChf9OkciEfLz8ykvL7/pMaWmpl5357nBFmc08vzixfzk6FHmbdhAgcNBWyDAvU4nP5o9mwKHg/Vnz+K02XANU4eDkU5RFL718MN86+FbPZLbiwRWcceLRCL8f/bOOy7q+/7jz+/tA44pewuILBEX7hUXahTFLYpNutI2TTrTpCNp06bpr03SmbRpmsZt3BgFNY5oNG7cA0GWCLI3HDd/f8hdQVEPBRx8n4+HjwS877jz7nvv7+vzfr9eDQ0N9OrVy3oBt1he2Upr5aS7sNgOBQQE4NxKtXhYJgcH89qXX/KLoUN559Qp/j5+PAGOjigshadUiszGyfPrtbW3Yghzc9mVl4efxoFJQUFMCQ5mlK8vylZKsEIqJXXWLEasWYOvg4M19UWjUHRLwdoay9Kpp6cnZrPZugxfW1tLQ0PDPXtHHxRBEKzxrK6urm1U75M3b/LWyZMgCAyLiMCDW7GXD7KcbDlOQEAA6vs4L1RUVNDU1NQmyUyj0eDp6YlGo+HcuXP3PL7JZKKgoKDHKautMZvN1NfXc+XKFevrIJPJ2hSuZWVlAERGRlJTU4NWq8WzJfwiMzMTo9GIQqFos82DIpFIKCsrQ6lUWo/R1QiCwIsDBjCvTx/OlZfjqFTy2sGDrLh0iVfj40nevp14Hx8SHjCeVEQExIJVpIdQVVUF8EARmJbtu+tL2aJueXp63lHYdAYjfHy4UFbGcF9frtfVMX/7dj6fO5cQe/v7btuo13OwsJD03Fw+z8ujtLGRCYGBTA8J4a/PPHNff0UfBwfSk5IY++mneNnbMyU4GI1CwY1H2G5h6Te0s7OzfsHrdDrq6+tpaGigsbERnU5nHd56kKVbQRDw8PDA29v7DneGKq2WOdu24ahU8qNBgxjWYvvj6+tLbW0tpaWl1NXVAfdvYRAEAY1GQ3BwsE1tI66urtZCSa1Wo1ar29wYqdVq67ElEskdKrQgCN3mC/o4c/u/i6XwtLhxaLVa4FYfvZeXV5vHRkZGcvPmTVQqFTU1NQ99nbG8Ly3vM8sNu8FgsMYpW87ZbDZ36vXF08GBiS3XgF8NH87Xd+3i8te+RpirK0siI22+ERYRaQ9x6EqkxyAIAnFxcR1WKg0GA+fPn+/SwYnWy8QeHh7Y2dl12bEA3j56lK3Z2aQlJbE+M5M3jx4lPSnpjtg/s9nM+fJydubmsjsvj2PFxfT38GByUBCTg4IY6OXF9dpaLlVUoDOZcFWpcFEqcVWrcVEqUd9lSfqrGzeYuXUr6UlJnCop4eTNm/x78uQufc6dgclkorm5Ga1Wi1arpbGxkaamJnQtCrEgCJyrqiJUo8FOJsNsNuPi4oKPj0+7wRNms5nErVu5Vl1NVK9erJs+vd33p8FgoKKigqKiovv2lPbv379TixDL8SwRueXl5eh0OuuSs6OjY49xB3gQBEEgKCgIR0fH+95ENDY2WpXah7HIUqvV9OrVi+rqaurr69u0HygUCuRyOY2NjdZ9x8XFdfqNsdlsZsTatbzcEt367smTfLVoUY8fuhK5N+LQlUiPRyKR4Onp+UAXy+Li4i5TV7taTb0br8THU67VMnrdOnbPnYurSsXEDRvYPHMmYc7OfJ6fz668PD7Pz8deJmdiUCAvDhjAZn9/ZBIJB65fZ9XlyyxNT6eiqYlZoaEUNTRQpdVSqdVS1dxMVYuq5KpS4aJS4apS4axUMtDTkyVRUXw0eTIztmzhx4MGddnQVWdj6Se+fandklpVVF3Nt/fuY36fMN4dOfK+Rcrmq1e5UFaGVCrlo8mT7/r+lMlkeHp64uLiQlFREZWVlXd9T3b2e8iyP8vztjgZ5OTkIJfL0Wg0PcZ/taMIgoCbmxvOzs42/bvY2dnh6+tLVVUVGo3GaivVUZqbm63DV9BWAW5ubraq4jKZ7L52aA/aCysIAq/Gx/P64cMcX7yYnx86xIHr1xkbENDhfYmIgFiwivQABEHAxcUFb2/vDm/b1NREWVmZTRO+SqUSmUxGvQ1T3oIgYG9vf8cwWHchCAJ/HDMGhUTCL778ko8TEnBSKnl53z6uVlUxzj+ASUGBvD58OL2dnLjQorL+LSODY8XFxHl4MDk4mJVTpzLA0/OOxBsLjXr9rQLW8qe5mbOlpYxYs4a106fzq2HD+M2RI0Q/4R6ElgGnHYWFDPTx5rpWi6ur632323j1Kg4KBf83ZgyaVrG5d0OhUBAUFISHhwd5eXnW6XOLEncvR4DORK1WExUVBdz6jNy4caNbjvukIZFI7hlG0h6W3ur8/HzgVr91R23HbFFlBUHAz88PFxcXKisrqa6upra2FqVSSVhYGHK5HIPBwNmzZ3F3dyfgAQrNab178+rBg+wtKOCngwfz+2PHxIJV5IERC1aRHoGvr2+HVIKmpiZqamruqmRZluvMZjNSqdQ6SANQUlLCzZs3rT1it/f8OTo64uvre9+BmK7CbDaTVVXFztxcDhcVMaSlp25ycDBj/PyQSiTU6XTszs/nt0eOsDs/H6VUyqSgIL4XF8fmmTNxbGd5uz3s5HLs5PI2SS4zQ0MZ6efHou3b2TVnDpODgii4Lef+SSW/thYXlcrm5Jq82lpya2sZ0MHhGDs7OyIiIqisrMRgMKDRaO7oP+0u1Go1Li4u3drn/aRgMpmor69/oJtSb29vHB0dMRqN7SadPSxms5mCggLy8vLa2Jc1NTVRUlKCn5+fVeEtKyvD3d29w9csiSDwypAhvH38OLvmzOGNr74io6Skw+93EREQC1aRHkJtbS1ubm42P76+vr6NamQpBGQyGXZ2djg4OFgHdWQyGc3NzZSXl1t9FwMCAigpKaGxsdG6raurK97e3u32MnY11VotewsK2JWbx+78PAwmExMDA/lO//5M790bvdHIseJiItzccFOreWn/fs6WlPCN2FheGzqU0E50KQAYHxDA8zExrL96lRf69+e7e/Z02r4fJfm1tZjMZgJtVDpzamrQm0z0eoCbF8ty8+NAQEAAEomEiooKsWhthdls5vr160RERHR4W4VCgUKhICcnp8v65y37vX3/lZWV6HQ6a9gGwKVLl4iMjOxw0bqgb19+efgwGSUl/HDQIH5/7BgbZsx4+JMX6XGIBavIU49FSaivr8fHx8cm39VevXrR3NxMdXU1MpkMFxcXnJ2d2y02q6uryc3NtX5Rt/ZgFAQBd3d3vLy8bDpuZ2EwmTheXHyrDzUvjwsVFQzz9mFycBAvDRxApJsbuTU17MrLY/GOHXxRWEiQoyPFDQ18MmUKvx4+nEkbN1Kl1XZ6sWrB18GBksZGHOTyTotmfdSoZDLOlJbyzdjY+z5WazBQqdUScp8ewicBqVRKYGAgWq32kQdsPG40NjY+0HYmk4ny8vI2RWN3odfrrc4qrbl06RLu7u74+/vb/J6VS6X8eNAg3j52jFXTpvH2sWNcraykjw0tMyIirRELVpEegclkoqKigoqKCmQyGY6Ojjg5OeHo6HiHzRD8r7/Lr8Vi6G7U19eTk5Nzx7K/IAh4eXnh4eHR4VSqh8FsNvOP06f51eHD+GscmRgUyG9GjmSkry96k4n9BQX84/Rpdufl02DQMzEwkLnh4Xw4aRIe9vYcKSoicetW3hs3jkMLF5K8YwcXy8uJvs09oDOQSaUU1tfj8Ah8WLuKd8aO5Vp1NUNs6JcuqK2ll0pFYAf8gB931Gq1NUFO5MGw+LZaVngep9dSEATKysqQyWT4+PjYvN1zMTH89uhR8mtreaF/f94+fpyPxShSkQ4iFqwiPQbLhV+v11uLV0sWeEf3o9PpqKqqauMgIJFIEAQBb29v3N3du23i34LJbOalffv46sYNjiUn09vJiYySEnbn5/PmkSNklJQQ7+3N5KAgNs2cQT939ztUkmE+PuydO5fv79vHtN69UUql5NXWdknB6iCXU6/TPVUKq5tajZuNS6Z5tbU4KZU2tw887mi1WmsE7r1cDB432vOX7cx99+rgQGFTUxPXr1+3bt/6OmIymdpYXnX3a2w53s2bN7G3t7c5fMVOLuf7Awbwh+PHeW/cOMI++g+/GVFnc6+3iAiIBatID8QyYCCTyfDw8LB5O5PJRGlpaZsi1WK8LZVK8fHxwc3N7ZEs7xpNJr6xazeZVZXsnTePrdnZjF+/Ho1czuTgYH42ZAhj/P2xs6EtIdrdnazqaqq1WpQyGc1dFLlpUVYdFAoa9Ppui5J8XMirqUEhleL/BHxpX62s5MTNm8zp06dNepmF6upqcnJyAOjduzc+Pj4UFBRQV1fXpf7FnYHZbCY8PJysrKxOjZe1FJSlpaU0NjYSGhra7mrO7djZ2TFgwACMRqP1j8lkQqfTcebmTV4+dJj+ri78Lj6exsbGR6JoW2zcOsJ3+vcn5KOPeHPECFKio3jn5EneGzeui85Q5GlELFhFehSWgigmJsYaYWkLJpOJzMxMmpqa2iiqSqUSHx+fTo1O7Sh6o5HktDTKm5rYmZTEXzIyWH7xImmzZhHTgYIcoKa5mZUXL2I0mWg2GlFIJOi6qGDVtCirCqkUAWg2GlF1Y/vEo6amxas26DFXWBv1emZs2YLeaMRFqWRqSEibv7cMFllu3rRaLc7OzoSEhFBWVtbGD/RxRCKRYGdnR3BwMNeuXbujF/1BMZvNuLm5UVlZSX19PQaDoU3Bmp+fT3l5OREREXcEhVhSsm5vJ1I0NnJTr0Ph4IC/vz8AWVlZ1N7DZaMrFGR7e3vsbUjGa42zSsXXY2L444kTvBofT8wny/l5fDy9ujgkReTpQcxJE+lRWC7ajY2NVFRU2KSo3F6sWpwAQkJCiIyMxMXF5ZEVq1qDgdmpqTTo9WyfNYvfHj3KuitXOLhgQYeLVYCffvEFqdnZKKVStEYjSqm0SxVWSyuAg0LxxIQHdBbfi4vjvXHjSI6MfNSnck9+cuAAfhoNTUYjg729MZlMNDU1Wf++rq7OqraZTCaKioq4fv06hYWFlJeX06dPn27t47YFS/uORCKxDhA5OTmhaVG7LasmD9rWY7keWArhfv36WQc2a2pqSD9/nhcOHCBLp7NGpdrCSD8/zqSk8K9Jk6y/q1Aq+capU+Q3Nd3RQmCJHe7s1YumpiYuXbpEdXU1jY2NXLx4kXPnzlFQUHBPRf0Hgwax5soV5BIJs8JC+WtGRqedk8jTj1iwivQ4zGYzFRUV3Lhxg8LCwns+1mQycfXqVWuxKpFIcHZ2JjIyEkdHx0e6hF2v0zFt02bs5HI2zZjBj784wN6CAg4sWID3A4YRGM1m4jw9Uctk6IxGFFJplymsDnK5ddjqaepjtRW1XM6c8PDHug0iPSeH1OxsrlZV8e9Jk3C3s0On03Hp0iVqa2utrQCtixTL0FBpaSlarRalUkloaOgjeZ4W9dTd3R2ZTGbt/XR1dUWpVOLi4tLGGqz1Zzo0NBSVSvVA561UKomLi8PDwwMXFxfkcjlms5na2lqys7M5mJPDhaYmfnL2HB3VPX0cHJC2Kkp3Xr8OSiWbq6oICgoiICAAFxcXpFJpm6X7zlRYLb20OTk5XL58Ga1Wi16vp6yszNp/2x5e9vbMDw/nLxkZ/Cw+ng/Onn1qBi5Fup7H67ZXRKQbsHxxAJSXl+Pp6dmuymEpVhsbG60KhbOzM0FBQY+8yKjWapm6aTN9XV35YOIEvrn7c67VVLN33jycHsLndVlUFC/u24fBZEbf1QVrK1XVMoAl8vhQ3tjI13ftJqqXGyHOzkxraQWwfFaysrLaGM63pvWyeutBoe5uDTCZTGi1WgwGA7GxsRiNRgwGA0qlsk0fekNDA2q12rpkbzabUavV9OnTp80Nq+U52ZJk11rpbGxsJDc3F21LXPF3Bw1CU1BAuVZ715Q4W5kUFMR7p07xzX79cHFxAcDNzQ2z2UxTUxNSqZS8vLwusRtr73W4n43XTwYPZsiqVbwyZAjj/P3519mz/Hjw4E4/N5GnD1FhFemRtP6Szc7Opqqq6g6VqHWxCre+qAMDAx95sVrW2Mi4T9czyMuT9ydOYPGONIoa6tmVlPRQxSrASH9/Tqek4ONg3+UtAZrbWwJ6mML6OGM2m/nW558T5+lBXm0tfxozps3fW1TJ+w1UmUwm5HI5N27ceGTDVyaTyfqZlUql1qV5i9paVVVFZmYmNTU1yGQyzGYzPj4+1raA8PBwFC2xuZ42JjRptVoqKyuprKykoaHBqkIqFArCw8Px8/XltWHDeHfcuIe+ngz39eXmCy/w7bi4Nr+3tAMolUqCgoK6zLVEEATra3q3G5jW9HZ2ZnJwMB+cOcOr8fG8d/IUzR0c4BLpmYgFq0iPp7m5mZycHE6fPk1BQYHV9qq1qiKTyQgLC7Ppoq81GLpMSbpRV8fodetI6B3M26NGMTs1Fb3JyPZZs7C3IYveVizKqkIqRddFhYaDXG51B+iJLQGPM59cuMCl8nJOFBezaurUO95bnp6eNk28wy0bOXt7+0d2oyeRSAi4R369xe/U0dERpVKJk5NTm8JUIpEQGBgIgJeXl02fbbPZTH5+Prm5uVYDfhcXF6Kjox8opvV+qO/j/qFUKvH19e30otXiV+3v74+bmxshISE2pXr9bMgQ/pyRQYSbG/3ce/HJxYudel4iTydiwSrS45HL5Xh5eVlNscvKyqyTtRKJxFqs3i+pymAy8bujRwn76CO+uXt3p59nbnU1o9atIyUyilfj45m6eTPOSiUbZ8xo12roYbAoq0qptMvUD6lEgkIqpVGvF1sCHiNyq6v5yYEDOKtUfCcurt0QBLVaTWRkJEql8r6FaGZm5gOnPT0MlvMymUz3PL5Op7NGLKvV6nb7bTUaDQMGDGiz3/thUXZdXV0JCwt75K1E7u7u94yFbn0DYut5ms1mCgsLycnJoaqqiqysrDYDeXcjxt2dQZ6e/PfCBV6Nj+ePJ05geMztz0QePWLBKtKjkUgkeHt74+vrS3BwMAAlJSXU1tbi5+dHUFAQ/fr1s9rOGE0mLpaXU9XSi2bhYnk5w1av5sD16+yaM4e9BQVszcrqtPO8UlHBqHXr+OHAgXwzth/PrF9PHxdXVk6ditxGpasjdIfCCv+zthJbAh4PjCYTS9LSGOnrixn4+dChd32sQqEgMjISV1fXe1rE6fV66urqHom1la+vL3DvgaPo6GhCQ0Pvuy9BENDpdB0qOtVqNXZ2djg6OnZ7kMjtCIJA796973ASsNDaMaUjz9FsNmMymaztH7dbdN0NS6E6zMcHLzs7NmRm2nxMkZ6JOHQl0uOx+AlarHcsMa5VVVVWlVWj0RAQEMAH586x/OJFrtXUkBAUxIsDBnCwsJB3Tp7kzREj+FZsLIIgsHLqVJJSUxnq44NXB/0Kb+dMaSkJGzfy1qjRTO0dzNhPP2VCYCDvjB3bZYpNa4W10gbF5EGxFKr2osL6WJCanU15UxOZVVUcWbQI2X2KLIlEQlBQEP7+/lRWVlqdAW5PZ7rX9vd7zINiWTlxcXGx9qC2x71Ux9tpaGiw+bGWm+HHCZVKRWxsLLm5uVRXV9/1cR3997Bchzw8PGy+Jg339cVfo+HTzExejY/ntUOHWNC37yOfERB5fBEVVpEejUQiQd0SpanRaPD09GyzlGhRD7RaLYIgUNLYiL1czqEFCzhcVMSStDT+lpFBelIS3+7f37rtCF9fno+J4fmdOx9KWTpSVMTkDRv52zPPMCEwgFHr1jE7LKxLi1XoPoXVYm2lERXWx4IYd3d8HBx4d+xYQlsmzm1BKpXi7u5OVFQUcXFxREZGEhoaSkBAgDUBTqFQ3PGetbe371DaXEfQ6XSYzWab2hZspayszKZizjLwZGt0aXcikUjabW8SBIHIyMgOK8EW+yyz2dzhGNpX4+P5/bFjTGlZ3UprSUsTEWkPsWAV6XFYpoMFQSAgIABBEKioqODChQuUlpa2KTAlEglubm5EREQgk8l4Y/hwRvj6MmL1GhwVCi4uW8aSqCimbtrEjmvX2hznjeHDKWls5IMzZx7oPPfk5TFjyxY+SZhCfw8PRq5dx7f69eONESO6tFhNz8mhuL7emnTVVS4B0OIUoNO18WQVeXSEubiwb/58lkRFPfA+LAlwGo0GNzc3vL29CQoKIjo6GldXV+uStCAIeHl5WVVLy3u6s1oHLJ/xzkQul9u0T7VaTVhY2GOrFt4eIS2RSPDx8bHabrXmfgWs0WhEqVTi5+fXoYAIvdHI53l5uKpUSASBr8fE8O/z521/EiI9DrFgFelRSCQSXFxc6NevH9HR0bi4uKDX68nPz6e5ufmOYjUwMJDAwEDrRTu3poaDhYUEOjtxs6GBkyUlPB8djd5o5IU9e1iWnk5NczMAcqmU1dOm8avDh8msrOzQeaZmZbFoxw42zZiBv0bDmHXr+PnQeH7UxX6F269d4+eHDlHc0ICJW60BXeXDCv9rCdD0wKSrnoYgCAQFBdGnTx+CgoKs4RtSqRS5XE5AQAB/Lywk5dQpjPcoWi2F1t2KQctntSt6Znv37o2Dg8Ndj21JwQsNDX3kPav3wt7e3hqSIJVKCQwMxMvL6w4FWaVSWdO/bkcikRAZGUlAQABRUVFoXF1tbh8qqq9n/Pr1XK6sZGtiImk5Ofz26FFmhYV1yvMTeToRe1hFehTe3t5tlv2bm5vJum04ShAE5HI5YWFhVpN0o8nEXzIyeOvYMV4fNozvxsWxNz+fWampCECtXs9gb2/kEgmxy5fzyZQpjA0IINzVld+MGMHiHTs4smiRTQNSqy9d4kdffEFaUhJms5kJGzbw3rhxLLTBLuZhqdPp6OPigq+DAw06HU4ODl1bsLb0rjooFNTfo6dO5Onh9hz6kJZAAoBGQUChUnHFYCBGqWxTPAmCQEREhDUOtK6urt1oZalUirOzM5UdvEm0BalUSlhYGOfPn0d/WwuLRCLB09OzQ5Zfj5KQkBD0ej1yuZzq6mqysrLahAtYBumCgoK4cOHCHUNZQUFBqNVq1Go1TXo9Uzdt4mRJCfUvvXTP4+7Nz2dJWhov9O/PK0OG8Prhw6y6dInNM2cyomVITkSkPR7fW0ARkU7EcoG12FfBrQz0S5cutVFWLdGrUVFR1mL1amUlo9etIzU7m2OLF/PigAFIBIGJQUGsmTYNgL+OG8fBwkL2X7/OH0aNYnFaGj/avx+twcAL/fvjaWfHG199dd/z/OeZs7xy8CB75s6lUa9n2ubNfDhpUrcUqwAuKhVXKyvZlZd3a2m3C4MD4H89rBZPVpGeTa1Oh7tajc7ODl9fX+tnVS6XEx4ejlqtxsXFhdra2nYVVEEQrAEfQUFBXXKOgiC08VK1qKp9+/bFx8fniShW4X/nrdVqyc3Ntb6mgiCgVqvx8vIiLCwMmUyGv79/G8W4V69e1lQtrcHArNRUvO3t0RoM6O9yvTCZzfz2yBGS09JYkZDA12NimLRhA6dKSshYulQsVkXui1iwijz1WLwQW2eGGwwGsrOz2yg4EokEf39/q/ULQLPBQMKmTcwPD2f//PmEODu32ffEoCCWJyTw6yNH+PTZZ6nT6fjG7s9ZN3061+vqGLhyJadLS/lg4kQ+Pn+einssmf3x+HHePn6ML+bP53pdHXO2bWPt9OnMsMFyp7OYEhzM70aNItLNjWqttkujWeF/aVcOYkuACFDT3IzOZMJRocDDw4PQ0FDs7e0JDg62qrLV1dVtPrcymcz62XZwcLAGfLT+vMPDtwjo9XoMLZ7ENTU1HKusRBAE3NzciIqKsg5vPmnc7r8aFRVFZGQkPj4+1p5UV1fXNk4Lra+Ps1NTcVQoWDltGq4qFZXt9MFWNDUxffNmdubmcjI5GalEwsCVKxkXEEB6UhLuNlphifRsxJYAkacaQRCwt7e3JtXArS+ugoKCNtnglnCA2790BEHAXi7HuWUwoD0Sevfmk4QElqWns3HGDH74xReM/3Q9q6dNZabJxJSNG3FSKIn18EDTjr2O2WzmV4cOs+FqJocWLuRIURHf27uX1FmzGObj04mvhm0k9O7NmbIyqrXarldYLQWrmHQlAtTodDgqFNaIYUdHRxwdHds8xsvLC09PTxoaGqitrcXR0REHBwfrAGV7/aUnb97k1YMHSZ01C7v7BIDcjk6nIzs7m6amJuzs7IiIiGB3fT3vXsnk78+MZ0Cra8uTSOtCXqlUtmvzJQgCYWFhXL58GYPBQGlpKRIHB5bt3o2jUsnqadOQSSS4qdWUNzXh2arl43hxMfM++4zZYWH8ftQo/nTyJH8/fZqVU6cy4Ql/7US6F1FhFXmqkcvlbZJrDAYDWVlZ1NTUWD1WnZyc7qqQKKRS/jtlCj85cICb9/BgnNq7Nx9PmcKcbdt4f8IEkiMjWLhjB+fLyzm1ZAn+jhoqm5q4dlufpsls5uV9+9kLM7zMAAAgAElEQVSec42DCxawOy+Pl/btY/ecOY+kWLVgKVS7WmG1l8upbW4WgwNEAKhubkZrMOB4H29Uy7K8j4+PdXne4jzQHluuXuViRYV1+LG6uppTp05x5swZcnJyKC4ubhPFbKGhoYHz589bi1V/f38AjpSXo1Gr8L6tmH7SMJvN5ObmWn++/eagNQqFgvDwcKRSKWerqhi0ciVnysowAwcLC2/ZWrUUrJZ9/z0jg+mbN/Pu2LG8Fh9P4tatVpVVLFZFOoqosIo8tUilUvr06WNd8mpoaCArKwuj0Widjg0KCsL5tmX+2xno5cXXoqP53p49bJw5866Pmx4SwkeTJ/Psli3smD2bAZ6e/GD/fk6XlLAzKYn/XLjA6HXr+OmgQfywZdr/67t2cbWqiv3z57P84kXePXmS/fPnE+7q2nkvxAOgkEjQWaJZu7BgdVQoKGtsFKNZRahsaiLc2RmpRIJHB5fXzWYz9fX12NvbU1ZWRklJCXq9ngEDBiAIAleqqnBSKq3WaRaP1JqaGqqqqqiqqqKoqAhBEIiOjrYuf9+4cQOAiIiINglOpU1NuKpUxHaRh2x3UV5ebi3ULUNj90KlUhEREcH+Y8cwSiRkPf88qy5f5gf796M1GpELAjnV1Qzw9OSbu3ZxubKSrxYtoqypiQErV7Kgb19+N3Jkl6TziTz9iAWryFOBUqnEaDRiMBjaTPlblrfKysq4fv26dajAxcWFgIAAmwck3hg+nLgVK9iQmcnc8PC7Pm5GaChmYNrmzaQnJbF33jymbNxI3//+lxOLF+Ov0fCNXbvYnpODn4MDVc3N7EpK4r2MDFZcvMjBBQsIfAzMxpUy2f8U1q4MDhBbAkRa+MeZM8ilUq7X1eEmkdDU1IRMJkMmk91VOTWbzdTW1pKXl2ftL7Xg7+9v3c5NpcJfoyG3pobR/v5W6ylLoVtfX09DQwN1dXXodDprwdqnT592j5uamIjJbG63xedJoa6ujsLCQkwmE4Ig4Onpec9EMAtKpZJof390Z8/y4blzpERF8Z3+/fmqqIj3MzJ4ef9+3j9zhn7u7ny1cCH/PHeOPxw/futmvpUjhIhIRxELVpGnAplMhp+fH9euXcPd3d06rWsymcjPz6e6utqqIgQFBVknXG1FJZPx8ZQpzE5NZZy/P73uMSQws+WLMGHTJnYmJXH1+ecZsmoV/v/6Fw5yOX975hkqmpr47bFj/GTQIF7/6is+z8/ny4ULHzrGtbOwKKwKqZTm2wqBzsTqEiAOXfVomvR6/nH6NCHOznw/NpZr2dlt/j48PLzNZD7cKlYzMjKsP8tkMpydnXF1db3DK9VVraagtpa03FxSoqOtvxcEAY1Gc1ev0bvxpA8JmUymNkOnUqkULy8vm7efEBREamIiH1+4QJ+PP2acvz9fi47mk6lTqdfrqWluJsjJibeOHOGDs2fZO3cu0e7uXfV0RHoIYsEq8lSgVqtxcnIiNjbWOtna0NBATk6O1S/Rzs6OkJAQm1SE9hjm48P88HBe2reP1dOn3/OxiWFhGFuK1vSkJA4vWkT8qtW8NWok81ssqsYGBDBxwwaMJjOfz53z2BSrcEth1RmNOCuVuNvZ0WwwoOxAio2ttE66EhXWnssnFy/Sx8WFazU1fC02FoVUSkNDA0ajEbPZ3GY53oIgCNaeUo1Gg0qluqsSmxQWxparWXyzi6yunjRae8ha3FE6EnQgCAKj/f0Z7e9PnU7HqkuX+Nbuz3l9+DC+3b8/zi0rWxOCgvjbmTNUt4SpiIg8DGLBKvLEI5FIrKktMpkMs9nMjRs3rDGrlghIb2/vh45KfGvUKPp9spxt2dn3tZtK6tOHep2OqRs34aCQ8/KggXw9NhYAndHILw8fJszFhVF+fjyzYQN/GjuWJZGRj0WcY7CjIw16PR5qNW4qFd/du5d/T5rU6edmKVRVMhl6kwm90Sj2t/UwjCYTfzpxgt7Ozrw8YID1xuh2RbU9PGzsIR3s7c2V5597LD5bjwMmk6nN0GlHV5xaU9HUxH/PXyDe25sFffuy6epV/pqRQZPBgFQQmN67N8NFj1WRTkAsWEWeeMxmc5sUltbFqkwmIyQkxKYvP1uwk8v5aPIkktPSGO3nh3NLuEB7pOXk8OMDB6jX6Wg2GhnRMvWvMxqZ99lnnC0tpb+HBy8NGMDssDCWpqeTmp3NPydOfORLjoO9vZFLpbz8xRd8kpDA0NWr+eDMGb4TF9epx3FQKKjT6W5NfbeEBziLBWuPw8venpsNDXyz5YauKxCL1f8hk8mws7PD1dUVO2dnlqalcbasDB97e34aH8/4gACb9vNZdjZf372bnwwezItxcfzkwAG25+Sweto06nQ6TCYTk4KD72oJKCLSEcSCVeSJx2w209jYCEB9fT0lJSUIgoCTkxPBwcGdnjwzNiCAZ0NC+MH+/fw3IeGOv6/Wanlx7162ZmdjJ5fz2ezZZFdVMXfbZ8ikEuSCQD93d86mpPDmkSP0W76cf06cyInkZH556BCxy5fzwcSJzOzGwIDbkQgCyxMSiF+9mnVXrrA1MZERa9cS4+7OKD+/TjuOppWdlWUA6143ASJPH1KJhAMLFmA0mbqk7USkLadLSth89Sq/Gj4cuVTK5YoKDt24wZbERK5VV7N4xw5OJCfjd4++XoPJxGsHv2Rd5hW2zJyJj4MDo9auw8fBnlNLluAifoZFugDx6iDyVNDQ0IDZbCYzMxMAb2/vNjGsnc3/jRlDzCefsDM3lynBwdbfp+XkkJKWRrPRyKywMN4dO5a/nz7N+2fOYK+Q89fx49mSlcVAT08clUr+OHYsM0JDSUlPZ4yfH38ZP56ZLT/vyc/ntyNHWk3UuxtHpZKtiYmMWruWz2bPZkVCAvM/+4xjixfj30n+k63trERrq56LTCJB1oEeyicRs9nMsaIipBIJg7y8aNTrkUkk3V6k/+rwYW7U1bPt2jXs5HKyq6sZ6etLfw8P+nt4cKWigrnbtvHVokXtXj9v1NWxYPt27GRyTi1ZwpGiImalpvLKkCH8YOBAUckW6TKe7iuESI9Bp9NZ2wICAgI6pV/1XmgUCj6cNIlv7d5NbXMz1VotyTt2sGD7dhAE1k6fzo8HD2bSxo0cK77J6aVL8bG3x02txlGpxNDKoHyUnx9nU1KQS6X0W74cvcnE2ZQUHORyYpcvZ19BQZc9j/sR7urKR5MnMyc1lVgPD14eOJDZqak0ddKAVOvAAHHwSuRp5UxpKaPXreOl/ft5ce9eFO++S6/332fcp5/y8r59FNfXd8t51Dc3k19byxcL5vPduDhqmps5v2wZ6599FrjVj3qipAQHhaLd6+fu3FwGrVzFpMAgts1K5A/Hj99aTUpM5IeDBonFqkiXIiqsIk8Fln7VgQMHdtsxJwUF8UxgIAu3b+f4zZvojUamBgfz1/Hj+fDcOZbt3Mnbo0bxXEzMrYEwiQSDyYRcIkF/mxm/pQBOz8lhSVoas8PCeHv0aEb5+bG01c8djZXsDGaEhnKqpIQ5qansnTePjJISvv3553ySkPDQX1D2cjmNej0ms9nazyoi8rRgNpv5v+PHeffUKX4zYgRfj4kBbi2pK2Uyiuvr+cPx40R98gkvDRjATwcPRt2Fn/F6g4GSxkYclUpqmpuZEBhodSfZX1DA0rQ05oWH89aoUW22M5pM/OarI3x0/hxrpk8j1NmZsZ9+iotKRcbSpbh1MOhBRORBEBVWkaeCB7Wqelh+N3Iktc3NmMxmPp4yhV8OG8bUzZs5cL2QjCVLeL5fP2tRJ5dK0ZtMtwrX2yIgLST07s25lBTKGpvov2IFbmq19ee4FSs4VlzcnU/PyuvDh+OiUvGD/fv5z+TJXK6s5D/nzz/0fiWCgF3LsFVUr15d6vkqItLdVDQ18dbR41z+2tf4VmwsUokEaas2AG8HB/48fjwXly3jem0tC7ZvvyMetjNxVamo1Goxm80cKSriwPXrDF29mrCPPuJnBw/y0eTJvDNuXJs2hZKGBiZt3MiBwkJOLV1Kk8HA4FWrmBkayvbZs8ViVaTbEBVWkScei49gd3OsuJhl6emM9vVl/YwZLL9wkW99/jm/HTmSb7YqVC3IBOGuCmtrXNVq1j47nQ2ZmczcsoXnY2JYPjWBrVlZ1p9fHz4cRTdO00sEgVXTpjFk1So+zczk02efZdjq1fR2drZ5ovhuWHpXKxobqRL9GkWeIpxVKgwmE5llNQwLuHth5+3gwBsjRjB+/fpb14gu+mwbTSb69eqF1mCgVqdjZmgoU4KDcVOrCdRoUN2m7h64fp3FO3awLCqaXw4byuuHv2L15UtsmDGjU4cvRURsQVRYRZ5oZDIZ4eHhHU6qeRiaDQZePXiQmVu28Ovhw3l50CASt25ld34eJ5KT+VZsbLtL5ZaWAMt/78fc8HDOpKRwrqyMwatW0dfNjTMpKZxt+fl8WVlXPL274tQyhPWzgwcpa2xk9bRpLNq+nbyamg7vq7i+nmGrV+Pxj3+gkkqp1+uxb9XPKiLyNCCTSHhtaDzf3buH0oaGez72nRMnGOPn16U+xL84dIgQZ2fUcjm9nZzwsLNjuK8v4a6ubYpVk9nM744cZf5nn/HR5Mm80D+WZzZs4HRpKRlLl4rFqsgjQSxYRZ5IBEHAzs6OqKiodlNwuopTN28ycOVKrlRWkrFkCXm1tYxau5alkVHsmTePICenu24rl0jQWxRWGwpWuOVPuW3WLF4eMIBn1q/n4/Pn2TJzJt+Pi2P8+vX8/uhRjDbuqzOIcHPjw0mTmLNtG9G9evHKkCEkbt1KQwd7T69WVQFwftky7BUKmgwGa+qViMjTxGtD45kcEkDKzp28c+IEGzMzOV5czM2GBkytlv8j3dzYkpXF744e7fDnyRYOFRay9soV3p8wAYCFERH88cQJqrTaNo8rb2xk6qZNpOXmcHLJEgRg0MpVTAkKIn1O0iP3iBbpuYgtASJPHIIg4ObmRkBAQLdNpeqMRt48coR/nT3Le+PGMdDTk6Rt21BKpRxPTqa3s/N999FRhdWCIAh8LSaGZwIDWZaezrZr11iRkMDJ5GSW7dx56+epUwl7iLSajpAYFnZrCGvbNvbOncvp0lKe27WLddOn2/zvoZRKMZnNeNrbYyeToTUYcJDLxaErkacOQRB4c+RIPsvO5kBhIYeLisivqaGgro46nY7hPj6M8vPj5YEDGeXnx/f27sXPwYGU6OhOO4cGnY5l6en845lnyKqq4nt79/LPFq/nb+zaxYYZMxAEgcM3brBw+3YWhPfl1yOG8+bRo6y4eJF1z05nzCNouxIRaY1YsIo8MQiCgEKhIDAwsFtbAM6UlrI0LY0AR0dOLVnC+sxMRq5dy+vDhvPdAXE2p7i0Vlh1D6CKBjg6smfePP5x+jTD16zhl8OG8fncufwj4zTDVq/u8Pk8DL8eMYIZW7bwg/1f8K+JExm9bh1/OHacnw2Nt2l7lUxGk8FAbXMzUomEZqMRjUJB5W1qj4jI04BMImFWnz7M6tOnze+b9HouV1ay7vJlnt+5k82JiQzy8uJGJ9tc/fTAQYb5+DI5OJj+K1YQ4uTEN3bvZkVCAsPWrOFf585R29zMOydP8tGkSQz08mLKxk0oZFIylizBo8VJQETkUSK2BIg8MSiVSiIjI7utWNUbjfz68FdM2rCBHw0axDtjxjD/s+2kZmdzLDmZFwcO6FBxaFFWI9zc+LKwkB9/8QUbMzMprKuzeR8SQeDFAQM4sngx665cYcL69cwMC+WrRYtYffkyz6xfT/4D9JR2FIkgsHraND4vyGftlStsSUzkr6czSM/JsWl7XwcH1DIZvv/8Jzfq6tEZjWJwgEiPQy2XM8DTkzdHjmR7Tg5ms5nq5uZOTYrak5fHtmvZ/PWZ8bz65ZcM9vJiS2IiWVVVrLx0ibXTp/On48fZdPUqxxcvRimTMXDlSiYGBbIzKUksVkUeG8SCVeSJQCaT0adPHyS3peHojEZ+eegQfzx+vFOPd76sjCGrV3OkuIgTyclUNGkZsXYt88PD+WLBAkJsaAG4HUvBOjkoiD+OGYOLSsXyixeJW7EC/3/+kzmp23jnxAkO37hxX2P+MBcXDi1cSEJwMINXreJgYSFfLlzAxMBABq1axUfnznWpPQ7cGsJKTUzklYMHKaqvZ/2zz7Js506yWvpT74W7nR3HkpOpe+klBnl5UtPcjINCQYM4dCXSA1HKZAiCQLPRSFVTU6cVrDXNzTy/axf/njyZs6WlbLx6lb+NH49KJmPd9On8/NAhTGYzl597jv3z5/Pv8+f5WvpO1k6bxi+GDUP6lKePiTxZiC0BIo89OrOZ1OpqTly+zPMtJvxwKxN72c6d+Njbk1lVRZiLC4lhYQ91LL3RyB+OH+cvGRn8ftQoRvv5sWjHDiSCwNHFiwl9iD5RWUtLQJ1Ox978fKLd3VnYty+BGg25tbUcLS7myI0i1ly+wpXKCvq6ujHU25thvj4M9fYmxNm5TY+oVCLhlfh4pvXuTUp6OpuuZvHR5ElMDwlhaVoaW7Ky+WjyJLwdHB7qNbkXEW5u/LtlCOtEcjJvDB/OjC1bOLZ4MY42Rspa0q7EpCuRnkykmxsGo5Gq5macOymO+eV9+5gcFMwIX1/6ffIJH06ciGuLb2pfNzf+MHo08z/7jBPJyZwuKSE1K5uMpUvwFFVVkccQsWAVeayRSCTU2tuz7eJF9Dk5HL5xg/fGjeO9U6f44MwZ/jR2LEsiI/mysJBFO3Yw1t8f5wdUJy6UlZGSvhM3tYoTyclsvprF8DVr+MXQYXy/g8v/7WFRWLdkZbE7P5/MqipeP3yYep2Owd7eDPX2Zk54H94eMxqZIJBRWsrRoiK2ZmXx6sGDNBkMDGl53FAfH4Z4eeGsUhHt7s7RxYv57dGjxK1YwXvjxnFs8WJ+c+Qo/Ves4M/jxrEwIuKhzv1eJIaFkWEZwpo3jzOlpSxJS2NLYqJNr5mmZdjKw85ObAkQ6ZEYTCbOlZVhr1BQpdV2isK6/do19l+/zvlly/jRF1/wTGAg00JC2jzma9HR7MnP5+X9+/njmDE0GQ0cLCxkbnj4Qx9fRKSzEQtWkccWSxtAqFRK5f79fDBhAmsuX2bwypX0dnbmTEoKPi3q4Wh/f54NCeGnBw/y4aRJHTqOwWTi/44f571Tp/jdyJGM9fdncSepqq2xDF3JJBL6uLiwZvp0AApqazlaVMSRomJe+/JLzpWV0dvZmXgvb4b7+vCbESPo6+bGzYaGlscV8dsjRzhdWoqfRsNgLy+G+/iQGBrK1OBgnt+1i81ZWXwwYQKJoSEsTU9n89UsPpg4gV5dZEnzxogRZGzZwsv79vG3Z55h3Kef8vrhw7w5cuR9t3VosbMSFVaRnkpNczNOSiWCINzqYX1IhbWyqYlv7d7N6mnTOFRYyO68PM6lpNzxOEEQ+OfEicStWMHn+fmsnTaNaZs3M8TLi8B7WPSJiDwKxIJV5LHD4gbQp08fa+Tqn8eP56V9+8hYsoRfHznClzduoLktjvXt0aOJ/uQT9hcUMM7G9KVL5eWkpKfjpFRybPFitmZn31JVhw3j+wMeXlVtjUVhvd2HNcDRkQBHR+b17Qvc6ss906Kufp6fz++OHqWiSctAL0+Gevswxt+fnw4ZgotKxYXyco4VF3OkqIi/ZmRQUFdHrLs7BbW1hH/8MX8aM4aMJUv4xaFD9Fu+nPcnTHjoton2sAxhDVm1ilWXLrF55kwGr1pFnIcHs2+bjL4de7mcOr3e2hogItLTqG5uxqnletYZCusLe/Ywp084sR4e9Fu+nE+mTLlri46jUsm66dOZtnkzJ5KT+fHgwSzasYMDCxYgE3tYRR4jxIJV5LHA0pupUCjQaDT4+fkhbUl8OV5czOuHD+OgUJC0bRufzZrF9/fvZ9bWreyYPduae+2kVPL+hAl8Y/duzqWkYHdbzGBrDCYTfzx+nHdPneLNESMY5+/P0rS0TldVW9NaYb2XD6tCKmWItzdDvL35fsvvyhobOVZczFdFRbx36hSnbpbgqlYR7+XNUB9vXujfn39NnIjWaOTEzZscKy4mPSeH/ztxgudiYnhn3DhmhYWxLD2dzVlZ/HX8+AdunbgbliGs0evWEdWrF5tnziRh0yb6uLgQ7e5+1+0cFQrya2tFlwCRHktNS9+qxSXgYXpYN2Rmcrq0lDNLl/L9fftIDA3lmcDAe24z2Nubnw4ZwsLt29k/fz77Cgp4/fBhfjdq1AOfh4hIZyPePok8ciQSCY6OjsTExBAdHU1gYKC1WC1rbCQpNZXX4uM5kZyMo1LJkvR0/j5+PM5KJYt37GiT9PRsSAiDvbx4/fDhux7vUnk5w9esYU9+AUcXLaJBr2fm1q3Ma3EA6IpiFdoGB9iadGXB3c6O6SEhvDVqFHvnzaPyxe+xfdYsJgYFcqG8nG/u2o3r3//OpA0bSM3KJtjJieVTp3LlueesNwMj/fw4m5KCg1xOzCefsDM3t9OfY183Nz6aPJk5qan4aTS8O3YsM7dupbKp6a7bOCgU1Ol0osIq0mOpbm7GWaWiTqdDJZM9cDxrSUMDL+7dy4qEBHbl5XGmtJTf29CWA/DDQYNwVCr59ZEjLE9I4OPz59lXUPBA5yEi0hWICqvII0UikeDv74+bm1u7KUkqmQypRIKrSoVcKmVNS4/Vd/buZdXUqUzfsoVvf/45H06aZN3+L+PGEbN8OfP79mWQl5d1XwaTiT+dOME7J0/y5ogRjPX3Z2l6OjKJhB1JSQ9kVdURZBIJeqMReQeTrtpDIghE9upFZK9ePBcTA9xKszlVUsKRoiI2ZGby0wMH0LYMasV7eRPv480QLy/enziR2X368PzOnSzo25dfDBt2R3vFwzAjNJSMkhKSUlPZP38+GaWlzPvsM3bOmdPuEqOmlUuAmHQl0hOp1mpxViofqh3AbDbzjd27WRYdTW8nJ2alprJpxgwcbFRrJYLAioQE4lauZLy/P0O8vblQVsZ4G9urRES6GlFhFXkkSCQSVCoVERER9OrV666RnhqFgg8nTeKbu3dT29yMUiZjS2Ii58vK+NVXX7ElMZGzZWW8+uWX1m087O3505gxPL9rFzqjEbilqo5Ys4bP8/I5umgRdTodI1t8VffPn9/lxSrcWuq3pSXgQbFXKBjt788r8fFsSUyk8Nvf5mxKCt/o149Gg563jx0n6N//ZvH27SgkEs4tW4bOaKRfS99vZ/Kr4cNxV6t5ce9e/jhmDAICPzlwoN3HWgpVO7kcrcHQRjEXEekJVLcMXT3MwNUnFy6SW1PDG8OG8cKePSyNjGS4r2+H9uFhb8/yhAQWbt9Ofm0tX2u5GRYReRwQFVaRbkcQBDw9PfH29rYpe35SUBATAgP5yYED/GvSJDQKBWlJSYxetw43lYq02bOt//+TIUMASI6MZN2VK/z+2DFUUil/alFVx/j5kZyWhkoq43hyMr27oVC1IBOEdoeuuhJfjYZZGg2zWgatjCYTW7OyWLhjB3P79OGtUaOYEBjIkrQ0ZoWG8fboUdh3gtoqEQRWTJ3K0NWr+fj8eT59djpDWoawlkZFtXmsRWGVCAJ2cjkNer3NHq4iIk8DFpeAB1VYr9fW8tODB9gzdy4bs7LIrKxkzbRpD3QuEwIDObp4MRqFolNXXkREHhZRYRXpNlqrqj4+PjYVqxbeHTeOtJwca0+Vm1rN7jlz+OfZs2zOymL33Ln848wZ/nP+PHCrKH5p4EA+PHuW3Xl5HFm0iJrmZkatW0dyZCR758/r1mIVWnpYzeYuU1htQSqRkBQezrmUFEoaGohbsQJXtZpzKSlUarX0X7GCwzdudMqxHJVKtiYm8otDh7hSWUnqrFn86IsvOFFc3OZxrYetNGIfq0gPpMrSEvAACqvZbOZrO3fy/QED6KVW88P9+1kxdap1GPVBCHFxESNZRR47RIVVpFsQBAEvLy+8vLw6VKhacFIq+efEiXx91y7OpaTgoFDgq9Gwe+5cxqxbh7NSye45cxj76ado5HIuVVTwjzNneGvkSIb7+rJo+w40CgUnkpMJ7uZC1YJcKkVvND7SgtWCm1rN2mefZWNmJrO2bmVpVBT/mTKZtJwc5qRuY1FEX347ciTqezgt2EIfV1f+O2UKKek7+WL+PD6cOJHZqamcWLIEr5YvRE3L0BUgOgWI9Ei0RiPe9vboTSYCNJoObfv+6TPUNuv42ZAhTN+8he/0788AT88uOlMRkUeHqLCKdCkSiQS1Wk1kZKTNLQB3Y1pICKN8ffnZwYPW34W5uJCelMSL+/aRW1PD9tmz+eOJE5wqKeFkcjKlTU2M/fRTnouJZs+8uY+sWIWWlgCzuVtbAu7HnBa1NbuqmoErVhLg6Mi5ZSkU1NURt3Ilx29TQx+EaSEhfCu2H7NTU0no3ZvnY2KYtXUrzQYDQBt3ADE8QKQnYjKbaTYakQCFDQ02b5ddVcUbR75ixdQE/nP+POVNTfx86NCuO1ERkUeIWLCKdAkSiQSpVIqvry8RERGoOsnz88/jx7MlO5uD169bfxfr4cHaadNYmp5OX1dXjicns3b6dGZu3crB69c5mZzMt/v3f6hiuTN4nBTW1njY27Np5gx+Pmwo0zZv5i+nMlg9bRq/Hj6cGVu28LODB63F5YPyo0GDCHB05Dt79vDLYcPwsrfnO3v2YDab27gDWFKvRER6El729txsaMDT3p4SGwtWo8nE0rR0XouPRyGV8svDh1k5NeGBLbFERB53xIL1CeFRF1utEQThjvMRBAGJRIIgCKhUKvz8/OjXrx8eHh6deu4uKhXvP/MMz+3aRWOLEneiuJgX9+1jqLc3UkHAbDbTqNdTUFvLr0eMeGwiBmWCgLFFYfV3dHzUp9MGQRBYFBHBmaVLOVNWyqCVKwl3deVsSgpXKioYuHIlGSUlD+j6DtMAACAASURBVLX//06ZwsmbN/ngzBlWTp3K8eKb/P30aRwUChr1ekwtxauosIr0NLzs7SltbLQWrrbwpxMnUEglfC8ujpT0dF4ZMoTIXr26+ExFRB4dYg/rI0DS4kVpuo/KJpFIULY04JtMJpqbm7v83NrDUnCq1Wo0Gg0KhQJBENBqtWi1WqRSKY6OjigUCuzt7a2m/13FzLAw1mdm8sqBA2iUSv5z/jx/HjeOKDc3hq1Zg95oZMOMGaycOpXErVvZM3fuPZOWuovWwQFXKysf9em0i7eDA5/NmsWKixeZtGED3+0fx/pnn+XTzEymbNzIt2Jj+eWwYSge4N/YQaFga2Iiw9asIcbdndRZiQxfs4boXr1Qy2Q0WOJZRYVVpIfhaWdHSWOj9b/340JZGX86eZITycn8NSMDgB8MHNjVpyki8kgRFdZuRKlU4uXlRd++fQkMDLyv8mgymWhqaqLpHilBXYlEIkEul+Pt7U10dDQRERHWPtTS0lJKS0upra3FYDDQq1cvHB0du7xYtbAsOppt2TlcqqjgZHIyWVVVPLNhAy/ExvLDQYOYtHEj0b168d64cUzZtImc6upuOa978bi2BNyOIAikREeTsXQpR4qLGLpmDXEeHpxJSSGjpITBK1dxtrT0gfbd29mZVVOnsmD7dqSCwKqpU1m4fTt2Mhn1Op2osIr0SCzKqkahwGQ23/OmTWc0siQ9nbdGjqRRr+ft48dZnpCAtJ1QDhGRpwlRYe1GDAaD1c5JrVbT3NxMcXExZrP5nttJpVJ0NqhOFuXWbDbfd5/324eLiwvu7u7Y2dkhtCyzl5eXU1hYiNlsxmQyIQgC3t7eeLVKk+pqtAYDrx8+zPKLF/nruHH0cXXl2S1b8LK3J2PJEutSe41Ox8QNG/ly4QJ+PnQoEzds4MuFC/FxcOi2c72dx3Ho6l74aTSkJyXx0blzjFu/nh8MHMjWxERWXbrEhA0b+F5cHK/Fx3e4Z25iUBA/GjSIWampHFq4kFfj43nl4EExnlWkx+JpZ0dJQ8Mtj+oWldXhLh6ob351BB97B1Kiohi2Zi1vjhjR7RZ9IiKPAvGWrBsxm83U1tZaf9ZoNPdVWS0m+5K73D23/n1gYCBRUVHWNoIHQaVSERsbS1BQEPb29giCQENDA5cuXeL69esYjUbMZnOnTf53hCNFRfRfvpycmhpOLlnCxYpKJm3cyPcHDCA9KalNX+jLAweyMKIvUzZuZGHfvjwXE8PkDRvvmWnf1TwpCmtrBEHgG7GxnExOZl9BAcPXrCHe25vTS5dypKiI+NWrOV9W1uH9/mjQICJc3Xh+5y5ejIvjyKJFhLq4iLZWIj0SN7WaGp0OvdGI5z36WI8XF/Ph+XN8NHkSbx07hrudmm/Fxnbz2YqIPBrEgrUbMZlM5ObmYmiZuFar1fftYzWbzTQ2NhIWFnZH0SoIAi4uLoSHhxMXF4erqysNDQ02qbF3QyaTWY+j0+m4du0amZmZaLXaNqpqZ07+349GvZ4f7t/P7NRU3hw5klfj45m6aRMnS25yeulSnouJabdofmP4cEb6+jF9yxZeHjCAycFBJGza/MgKoidNYW1NoJMTn8+dy3MxMYz59FNWX7rE9lmzeCE2lvHr1/O7I0c7VIQL/8/eeYc3dd4N+z6SJdva3nvbGAwGs6fZO+xNmGnTpBkdydumK23f7rRf0rRvm+6kJOyYTcIeIUAYYZoVY8AG74GXbNmWJZ3vD43YrDAMZjz3dfkylnTOeY6uRL79e35DkvjPqJGcr6zgzSNH6BoSgkKS0DXrySoQPCkoFQoCfX09hVc36hRQ39TE/E2b+POQIRTW1vK3Eyd4d9Soh6ogVyC4nwhhfcC4pVWWZRQKRQtBvNEHjyRJaDQatFotycnJntcoFAo0Gg0xMTHodDoUCgWyLHPlypWvlODm51YqlS2ubzAYcDgcFBYWcvr0aaqqqjxr9fHxeeBR1b35+aS9/z6FtbUcmTuX46WljF61iu/17MlHU6YQcYsm25Ik8edhQ4kzGJm6YQO/GTCA1MBAJq5bR8M9tmm6G5oXXT0qEdbmSJLEC2lpHJ4zhy25uQxYsYL0yEiOzpvHJ3l59Fm6lDPl5bd9Pl+VirWTJvGno0fZmpMDOPuwlrdhFFwgaCuaF17dKML6xuHDDIyMZFJSEvM2beZPQ4fe8vNPIHjcEML6gJFlmdraWsxmM5IkkZKSQkJCAiEhIQQGBrYQUnfuaFFREWfOnMFsNnsKm8LCwloILEBjYyN2u93z881EWKFQoNfrSUlJoUuXLgQEBHheZ7FYOHXqFMXFxS2kOjIykpSUlAcWVa21WvnWjp3M2riRPwwaxKs9ejAiI4Mz5eWcXLCA+R073pY0KySJ/44ZjbdSybxNm/jb8GH4+/gwa+NHD1waVUolTY+wsLqJM5nYOWMGczt0YMDy5XyYlcXmqVN4NjWVwStX8ruDtx9tjTYYWDl+PPM3b+ZCZSWTEhPZcPEiX1y9ep/vQiB4uHAXXoVqtdd1Cth95Qr/OXWKNwYO5Md795IS4M/s9u3baKUCQdsghLUNcDgcWFwfSCqVCoPBQGRkJNHR0ahUKiRJIjg42PN6WZZpaGjAbDaTkJBAWlraDUec+vj4EB4e7pFdlWuspls8VSoVfn5+JCYm0q5dO3x8fJAkCS8vLyRJwuFwUFFRgc1m8zweGRlJamoqQUFBDyyquvvKFVIXvU9VYyOH585lf0EBE9au5fU+fVg3aRJhd1g45aVQsHL8eMrq63lp506WjB1Lvc3G17dsxXGXxWl3g1qhINZgeCRTAq5FIUm83K0bh+bOZcOFiwxauZKh0dF8PncuO1y5ruduUzrTIyP5ed++TFi7Dn9fX34zYACT1q2juo3auAkEbYG78OraCGtNYyPPbNnCv0aM4HR5OSu++IJ/jBghUgEETxxCWNsAtzzeiLi4OOLi4vDy8kKWZY84JiYmkpiYeMsPKbPZTGFhIeCUVHffVl9fX+Lj40lNTSU+Ph69Xo/NZiMvL4+jR496OhW40w9CQ0NJSEigc+fOBAUF3bTgq7WpaWzkm9u2M3/TJv46bCgvpDnzI3Oqa8hcsICnU1Lu+kPax8uLDZMnc6K0lJ/u28+aiRO4UFXJd3ftuuuOCneKUqHgXEXFIx9hbU6CycQns2Yys317+i1bxtrsbLZMncrCjh0ZuGIFvz90CPtt3OsLaWn0jwhn3seb+FpqKkOio5n78ccP9A8KgaAtCXaJ6rUR1u/s2sWImBgGRkWxYPMW/jlyJIEaTRuuVCBoG4SwthHe3t7U1ta2kCVZlrl48SKXLl0iPz8fgNDQUFJTUzHexrSmqma9Rr28vAgICCA5OZmUlBSMRiOSJGGz2cjPzyczM5NSVy/NiIgI2rdvT9euXenQoQMREREYDIYH+hf81pwcOi1aRJPDzqE5c9iWe9mTd7pq4gSCtdp7voZerWbLtGlsyrnEn48d4+MpU9iTn8//7v+sFe7gq/GSJGwOh6df4u2I3KOAQpL4drduHJwzh7XZ2QxZuZIRsbEcnjOHrbm5zNu06Su3+CVJ4p3hwym1WPjlZ5/x56FDqWps5H/3739AdyEQtC1hOh3FFkuLLgEbLlxgT34+fxwyhFd372ZIVBTjExLaeKUCQdsg+rC2EVlZWZ5+rPHx8Xh7e+NwOPDy8sLf3x+DwXDH0hgWFoafnx9eXl54e3u3ONZut1NcXExpaalHkjUaDYmJiTeN9j4IKhsaeHX3bnZfyePdUaNQKRSkr1hB77AwTi9cSICvb6teL8DXl23Tp5O+fDlGb2+2TZtG+ooVmHy8eaVHj1a91rV4NUsFcEdZH6dm34l+fnwyaxZ/OXaM7+zcyci4OLZNn867p04xYPlyXuvVi//p0eOm96xWKlkzaSI9Fy8mLTiYVRMm0HPJEroGBzO5XbsHfDcCwYMlRKPh86IiT5eAMouFb27fzsrx49mbn8/2y5fJXLCgrZcpELQZj89vy0cIdxW/u2WVu8cpQMeOHYmKivJERO8ELy8vdDqdJzcVnKJaWFhIZmYmJSUlntZUgYGBtG/fvk1ldcOFC6QuWoSvlxefzXma1eezmbNpE28PGcKyceNaXVbdhOt0bJ8+nd8dOsSOy5fZMX06fzp6lPdOnbov13OjapYK8DilBTRHIUl8p3t3/jxsGKvPn2dIs9zWzZdyGLB8+S2jraFaLWsmTuQb27ZRXl/P6gkTeG77ds7eQfcBgeBRJESrdUZYXd0CvrltG0936EBKQADf2LqVRaNHY7iHHtsCwaOOENaHAIfDQVlZGVlZWa2WTynLMiUlJWRmZraYpqXX64mPjyc6OrrNkvbLLRae/ugjXtm9m6VPPcXExET6LV2G1W7nzMKFTEhMvO9riDeZ2DJ1Kv/zySecLC1l2/TpvL5vH6vPn79v12wuqY9D4dWtSPLzY8+sWUxt146+S5ey4eJFts+YzhxXZ4E/HDp805SInmFhvDV4MBPXriXBZOL/DRrEpHXrqGpoeMB3IRA8OEJdRVc613jWs1ev8usBA3hh+3amJyczODq6rZcoELQpQlgfEtxFUldboZ1PU1MTWVlZ5Ofn43A4UKlUxMTE0KVLF9q1a3db+bD3A1mWycjKInXR+4RotOydNYv3T5/huW3b+OfIEbw3ZjSmB9Q2C6BTUBAbJk/m61u3Ulhby8dTpvDC9u1sy829L9dzt7WCxzfC2hyFJPHd7t05MGcOq86fZ/DKlYyKi+PzuXPZlHOJ/reIts7v2JHxCYnM/Ogj5qakMDoujtkfffzY5P0KBNcS0qzY6qW0NN4dNYp1Fy5wqryc36Wnt/HqBIK2RwjrQ4TD4bhnYW1qauLMmTPUueZSh4WF0alTJwICAlDe4cz31qS4ro6p6zfws/37WTNpIkOio+i1dCneXkpOP/MMo+Li2mRdvcLCWDFuHDM3bsTmcLB20iTmfPwx+wsKWv1a7qIrePwjrM1J8vPjk5kzmZqURN+lS1l34QI7ZsxgXoeUW0Zb/9/gQciyzA/27OGtwYOptzXx+r59bXAHAsH9J8DXlxqrFavdzltDhhBrMvGdXbtYPHYsvm2YuiUQPCwIYX1IcLeU8vX1JScnh8rKytueWAVOUa2pqSEzMxO73Y5er6djx46evqxthSzLfHDmDJ0XLSLZ34/t06bxl2PHeHX3JywZO5a/jxiBXq1us/UBDI2J4d8jRzJ+7VpM3t4sGTuWKevXc8LVRaG1uFHR1ZOCUqHglR49ODBnDquzsxm8YiUj42Kdua25OTfs2+qlUPDh+PGsu3CBlVlZZEyYwPIvvuDDL75om5sQCO4jCkki0MeHUosFWZb5+pYtvNClCz1CQ9t6aQLBQ4EQ1lbibqXQPR41MDCQhoYGysvLqaioIDc3l5MnT7ZoVXUtsixTWlrK6dOnyczMJDs7G51OR4cOHWjXrh3ebZygn1dTw1Nr1vDHI0fYPHUq3YKDGbB8BSFaLZkLFzxUOVkTk5J4c/BgRq1aRZKfH38bPpyxq1eTVVHRatd4EoquvookPz8+nTWLacnO3Na1Fy6wbdo05rv6tr5x8FCL98Xf15f1kybxyu7d5FZXs3biRF7auZPMsrI2vAuBoPXJrqwkVKfDpFazNTeXEouFn/Tp09bLEggeGoSwtgKSJKHVau9KWmVZ9qQCOBwOT3GUw+HA4XBw6dIlym9QIV1XV8eZM2fIz8+nsbERtVpNx44dSU5ORtPGTaUdDgf/OHGCbosX0zc8nA2TJvHrgwf5+WefsXLCeN4eMgTNQ7jFNTclhR/37s2IjAz6hofzmwEDGJmRweXq6lY5/5NUdHUr3Lmt7r6tg1euZERMDJ/Pncu2y7n0W7qsRVeATkFB/GvkSKasX0+YTsefhwxh0tp1XK2vb8O7EAhaD5vDwYJNm3imUyd03t4cLCxkdFwcqjZM4xIIHjaEsLYSZrMZtVp9T9J6s+cKrsmnrKioICsryzPJKigoiE6dOuHzAAuWbsbFqiqGZWSwr6CA3TNmEKXX02PJEjoEBHBs/nx6h4W19RJvyYtdu/JsaiojMjKYkJjIKz16MCJjFSXNRiXeLU9a0dVXkejqJDAjOZl+y5ax6vx5tk2bxsJOnRi0ciW/PXjQ8x5NTkri2c6dmbp+PVPbtWNKUhIzNmx84t9DwePB//v8c3xVKl7u2hVwdjERg1cFgpYIYW0F3FHRxsbG6xr2twZ2u91znaKiInJzc5FlGV9fXyIjI4mKikKSJGRZfmBjRq9bo8PB20eO0HvJEsbFx/Or/v353p49/PnoUbZOm8Zv09Px8Xo05lT8qE8fxickMH/TZr7WqRNzUjowctUqKu+xrdKTWnR1K9x9Ww/NncvGixdJX7GCodFRHJk7l11XrtBn6VJOu7b/f9q3LyFaLS/t3MkbA9NRKiS+98meNr4DgeDeOFlayh+PHOG/o0ez+MwZjhYXo1erOS16DwsELRDCeg9IktQiqirLMiqVqtWKnBQKBWq1mgTXKL4rV65QWFhIrc3GC5mZvHbuHCrXNKzjJSW0f/c9xq9Zg9UluA+Ks+Xl9F++nPUXLvDZ00/j4+VFr6VLGRARweG5c+kaEvJA19Ma/C49nSQ/ExPWruX7PXowLDqasatXU2u13vU5RYT15iSYTOyeOdPTp3VlVhabp07lG6mdGfLhh/zyswPYHQ4+GDOGQ0VF/O3ECVaMG8dHFy/wwZkzbb18geCuaLTZmLdpE28OGkR1YyMv7dzJX48f9wwPEAgEXyKE9R5wC2pKSopnupSXlxd+fn7A3RdiKRQKvLy8iIqKIjExER8fH2RZ9uSyFigUaHx8SPDzo/vixfz75ElGrVrFL/r3Q6lQMPfjjx+IDDXZ7fzqwAEGrVzJgo4d+efIkTy7dSuLz55lz8yZvN637yObgyVJEn8cMoQInY5pGzfyu/R0OgYE8Mru3TTYbHd1TqUk4XBFwb0UCmxtFA1/WFFIEi936+bsHJCTQ//ly0mPjODYvHnsL8in19KlXKyqYv2kSazNzuZkWRnrJk3ifz75hCPFxW29fIHgjvnZ/v3EG43Mat+e+Zs28XT79tTbbIRqtRS3QhqSQPA4IYT1Hqmvr8dsNpOSkkJSUhLR0dHExMTQrVs31HfYrkmSJHQ6HZGRkaSmpmK1Wjl79ixffPEFkiSRlpZGt27dGNe5M8X19XQNDuaN9HT+ePQor/XsyawOHVg5fjyVDQ18Y+tWHPdRiI4WF9NjyRI+Kyjk0Jw51Fqt9F+2jEmJSeyfPZuUwMD7du0HhUKSWDRmDF4KBfM3b+adYcOosVqZ9dFHNN1FFFuSJJSutACVQnFX53gSiDOZ2DljBs906sTAFStYfPYsH02ZwstpaQzPyOCDM2f4Qe/ezP7oI7QqFf8YMYIp69e3Sp6xQPCg2F9QwAdnz/KvkSP5xYEDROr1zEhOpriuzhNhbasUL4HgYUQI6z3icDi4cuUKFosFvV7vac4vSdJtt5Vyb/23a9eO5ORkgoKCUCgUNLhyJm02G7Iso1QqkSQJvVrN6gkTeHX3buJNJv4+fDh/+PxzPi8qwsfLi3WTJpFdWcm3du5s9Q+8+qYmfrBnD2PXrOF7PXrwh4HpzNy4kU05ORyaO5dXe/ZA2YZ9X1sblVLJh+PHU2ap56Wdu/hgzBisdjvPbNlyV38QuNMCRErArVFIEi+kpXF03jx25+XRd9kyeoeFcWL+fD4vLuG1PXuYm5LCxHXrGBUby4KUjkzdsOGBp8MIBHdDrdXKgk2b+fvw4Vyqrua9U6f496hRhOl0lFgsaNVqlJKE+R5SkASCx43HxyzaEFmWyc7O9hRHufmqlACFQoFWq6Vdu3Z06tQJnU7X4vlrz9ecLTk5qBRKxq9dS5hOx7ujRzN+7VrOlJejVav5eOpUDhUV8YNPP201ad2Xn0+XDz7gYlU1R+bOJbuyiqEZGTyb2pldM2aQYDK1ynUeNny8vNgweRKnysv40d69ZIwfT57ZzMs7dtzxe+vVPMIqhPUriTEa2TZtGs936cKQDz/k3VOnWDtxAv/TowcfnDmDBMz7+GN+3r8f/j4+fHvnrrZeskDwlXxvzx4GREYwIiaG+Zs289dhwwjValvkroq0AIGgJUJYWwmHw0HxNXl0N2sz5Y6oxsfH0759e7RaLY2NjZSXl1NSUkJFRQVlZWWYzWYAT2TVzQ8//ZT/nDrFkXlzPb1CuwQF8Zar8f2lqiqM3t5snTaNzTk5/OrAgXu6N7PVykvbdzBz40beSE/ntV49GbN6NUdLSjg+fz7Pp3Vp9c4IDxs6tZrNU6ey/fJl3vz8CBsnT+bz4mJ+tHfvHZ1HRFjvHEmS+EbnzhybN48DhYX0XrqULsHBnFywgGiDga2XL/Pi9u0sGTuWT/Pz+OfJk229ZIHgpmzJyWHzpUv8eehQvr9nD73CQpmWnAw4B2XUusazisIrgaAlj0afoUcAWZapqKggIiLC81hAQAAlJSWeKJwkSUiSRGRkJAEBAR7JKysrIy8vz3Oe5l0HJElqcU6AXVeu8D89ehBlMPC11FSqGxsZ/mEGe2fP8jS+3zt7NuE6HdunT2fgihXo1Gpe7dHjju9rS04Oz2/bztDoKA7PnctbR46w7Nw5/jh4MLM7dHjsRbU5/r6+bJ8+nfTlyzF4q9kybRqDVqzAoFbz49ucSOOOsIqiqzsnymBg09SpvH/mDCMzMnipa1cyxo/nvdOn+evx4+jUatZPnkz/ZcvoGBDAgMjItl6yQNCCivp6nt26lQ/GjuVgYSEfXbpE5oIFnucVkkSQRkNJXR0hWq3IyxYImiGEtRUxGo0tfvb29qZTp07IskxhYSFqtZrQ0FCPkNpsNkpKSlpILTijte5OAeHh4QReU8D07qhRDM/IIFynY2x8PK/06EF1YyMjM1bxyayZVDU2MjIjgz2zZhGq1bLDJa1alYrnu3S5rXupqK/nO7t2s7cgn3+PGolKoWDgihX0Cg3l1MKFBLXxNK22IlSrZeeMGaQvX45erWbb9OkMXO6U1pe7dfvK492RVVF0dXdIksTCTp0YGRvLbw8epOfSpfx39GjOuhquJ/n58f6YMczYuJFDc+YQZTC08YoFgi95YccOprZrR9fgYDovWsR/x4zBdM1OnDuyGqrRiJQAgaAZIiWglZAkiZAb9BtVqVSo1WpiY2MJDw9HoVBgs9nIzc0lMzPzOllVKBSoVCqioqLo3LkzQUFB10UxU4OCWD9pEgs3b+ZTV2T25/36MSQ6iqdWr+ZbXbsyNj6eMatXY7ZaiTYYeGvwYP51G1ulsiyTkZVFp0WL8PPxZv/s2WRkZTFv0ybeHjKE5ePHP7Gy6ibaYGD79On8bP9+9ubns336NP7w+ee8f/r0Vx7rzl0VKQH3RrhOx1+GDeNHvXvz1Jo1/PDTTz3txsbEx/Pd7t2Zv2kT9U1NbbxSgcDJii++ILOsjDfS03lpxw4mJiYyPCbmuteFNI+wipQAgcCDENZWQq1W31ZXgMbGRs6ePcvVq1c9k6kkSUKpVBIYGEhcXBypqakEBgbecru9T3g4y8eNY9qGDRwpLvb0DW0fEMCU9ev5Zb9+dA0OZuLatazPzuab27fzi/79b7m2wtpaJq9bx8/272fVhAkMj4mhz9KlSEiceeYZJiQm3vH78rjSzt+fzVOn8u2duzh79Srbpk3jh3v3svr8+Vse5xZVL1F0dc9IksTTHTqQuWABFyor6frBBxwoLATg+z170s7fn+e2bROtgQRtToHZzHd27WLx2LFsuHiRoyUl/GHQoBu+NlSrpdhiIUREWAWCFghhvQNuJZBWq/WWVf02m43Lly9z5swZmppFfSRJIiAggNTUVGJiYjCZTLedFzosJoZ/jxrFuDVrOFtejkKS+PfIkZh8fJj98cf839ChBGk0PLdtG2smTmSca2LWtciyzH8yM0l7/306BQaxbdo0/u/YMV7dvZvFY8fyr1EjMd5mi64niS7BwayfPIlntmyhuK6OTVOm8OKOHWzNybnpMe4Iq0pEWFuNEK2WVRMn8sv+/Zmyfj2v7t5Nvc3G20OGcObqVd46cqStlyh4gpFlma9t2coLXboQodPxbZe4alSqG74+2CWqoSLCKhC0QAjrbfJVEilJkmcS1bXIssy5c+c8UVU3CoWCuLg4YmJiPP1b75SJiYm8OXgwo1avJqeqCqVCwdKnnqLBZuNrW7bw/ujRdAsJ4V8nT96wb+jFqiqGfZjB30+cZNu0aST7+9FzyRIidXoyFy5kcHT0Xa3rScEd6Z6xcSNNDgdrJ05k7qZN7M3Pv+Hrm0dYRdFV6zI9OZlTCxZQYrHQ+f33PZOw3jpy5JZ/RAgE95N/nDxJZUMDP+7dm69t2crznTvTKyzspq8PdRVbiaIrgaAlQlhvA4VCcV3h07U4HA5PG6prH8/Ly/M0/3ejVCpJTk72jHG9F+ampPCjXr0YnpFBYW0taqWSMXFxfJKXx/f27GHVhAnk1tTwnV27PGuwOxy89fnn9F6yhDFxsWRMGM+P9+3ztGx6c8jgm0YABC0ZFhPDu6NGMWHtWvRqNcvHjWPq+vU3HBfqFlY/b28kIaytTqBGw9KnnuLNgQP51s6dFNXVsXLcOOZv3syFysq2Xp7gCSO7spKf7tvHB2PH8N7p05TVW/hp3763PMYtrKLoSiBoiRDW20CtVt9yzKokSXh5eREVFeV5zN3mKjMzk/Lychyu7V+FQoGvry8pKSloWrF46cWuXXm2c2dGZGTwv/v386djx/h46lQ+KyzkjcOH2Th5Mvvy8/nfzz7jVFkZfZcu46OLl/js6afRqFSMyMhgQEQER+bNpect/voX3JjxiYm8PWQIo1etIsZg8KRqnLkm6u5OCWiw27G4ioQErc+kdu34aZ8+TF2/nkQ/P37ety8TaeihNwAAIABJREFU160Tk4MEDwybw8H8TZv4Wb9+eCkU/HT/fhaPHYvqK3bT3MVW7u8iB1sgcCLaWt0GVqsVh8OBJEnXfXhIkkRwcDChoaE0NTVRWlrK1atXPWNVm4uqSqUiMjISo9F4X/qX/qh3b+qsVj4rLOTTWbOI1OvZMnUqA1euxM/Hhy3TpjFk5Ur+fuIEv0lPZ0B4OF/bsgUZ+GjKFDoEBLT6mp4kZnfogNlqZcSHGXw6exZ/HDKEUatW8cnMmSS6IukiJeDBMTEpiVPl5UxZv57dM2ZworSMuR9/zNpJk1A8Qf2DBfcfhyyTV1NDdlUV2ZWVZFVUcKa8nCBfX17o0oVBK1bw4969b+sz1l1spVGpUCkU1FitooZAIEAI63VIkoROp7tue9/b29sjn81fGxcXR1NTE5mZmR6hvTZPValUEhkZiZ+f331vtP/r9PQWPwdrtWyfNo1eS5fSOTCQUwsX0mi3848TJ0hfsYKf9+vHS127il/grcRzXbpQa21i2Icfsm/2bH7Wty8jMjL4dNYsogyGFkVXog/r/ecnffpwsqyMF3fs4B8jRjD0ww/5+b79/Cp9QFsvTfCIIcsyhbW1ZFdWkl1VRVZFBRcqK7lQVcXFqmr8fXxI8jOR5OdHOz8/BkdFMT4hgd8fPoyvSsV3une/res0L7Zyj2cVwioQCGH14G4tFRsbS2lpaYvnZFmmpKSkxWMKhYLQ0FBMJhMnTpy4TlTd54yMjPzKFlX3kzqrlbeOHMEhywRrNCgkCR8vL/6ZmcnmqVPF9v994NWePTBbrQzPyGDPzJnUNjUx3CWtIsL6YJEkiUWjR9Nv+XL+fvIkayZOpNeSJXQJDvKMwxQI3MiyTFFdnVNKm39VVXGpqgq9Wk2iyY9EPxPJ/v70CQsjyc+PRJMJrVpNfVMTF6uqyK6q4ouKCtZduMCBgkK2z5h+20EBPx8f6pqaaLTZPIVXyf7+9/nOBYKHnydOWBUKBcHBwRS7CmIUCkWLbX2FQkFRUVGLY9RqtWeL341GoyE0NBTgusgrfBl9bY2iqrtle24uz2/fTr/wcI7Om8ffTpzg+e3bWTVhAoOiotiamyuE9T7xs359qbE2Mnr1anbOmIHZamXkqlX4e3uLSVcPGK1azfpJk+i7bBmdAgNZM3Eio1evpp2/P52Dgtp6eYIHjMMVKc2pqiKrspLzlZVcqKziYlUVF6oq0anVJBhNJPqZaOfnx8z27T1SavD2xmq3c8klpecrKth++TIXKp3HllgsxBoMJLqirH3CwvhtejrhOt1tr08hSQSLaVcCwXU8ccLq7e1NQEAAxcXFGI1GAgICWvQ+tdvt1DX7gJAkCa1Wi9VVrCFJEgqFgujoaM8xPj4+LYRWqVQSHx+PoY3GQlY2NPDq7t3sunKFv48YgcnbmxEZGaQEBJDs78+/MjN5MS2N8WvX8sPevfFSiNq71kaSJN4cPJhvbt/OuDVr2DxlCjWNjbx3+jR1TU1i0tUDJtZoZIWr/dhnTz/Nn4YMYdLadRyeO4fAJ3xy2+OI3eEgz2zmQlUVF1xRUufWfRWXqqsxqNWMjI1FKUkk+vkxs33ydVKaW11NtktoP8nLc0lpFUV1tUTodCSa/EjyM9EpMJDJSUm08/Mj2mBolc9TMe1KILieJ05Y6+vrKSsro/sN8olkWcZms2EymTCbzTgcDkJCQigrK0OWZXx9fdHr9VRWVnLu3DnCw8MJCQnBy8v5NioUCjQaDfHx8ajaqCXUqqwsvr1rF5MTkzg0Zw6/O3yYD7Oy+MvQoUxLTuZ0WRkjV63i9T59iNbr2XjxIpOTktpkrY87kiTx9xEjmPfxJqZu2Mi6SRNJ8vNjSFQU5yoqaBQR1gfKoKgoft63LxPWrOXg3DmcKC1j+saNbJs27SsrtwUPH26pdIvo+YpKLlU7pfJyTQ2Bvr4kmEwkmJyR0r7h4SS6pFSnVmO128lxSWl2ZSV78vKcgltVRUGtU0oTjCaS/Ey09/dnfEICiSYTcUbjff/vxdMpwBVpFQgET5iwSpKEwWAgMjLyhs9funSJqqoq4uLiiI+Px2azoVKpMBqNeHt7o1KpyM3N9UyqKiwsRJZlamtrkSSJkJAQwsLC2iRftai2lhd37OBcRQUZEyZgtdvpv3w5fcPDOb1wIQG+vgB0Cgoiyc+PdRcu8GJaGn87cUII631EIUm8P3YM0zdsYO6mTSwfNw4vhUKkBLQRL6SlcaK0jDkff8zqCROYsHYtr+zezV+HD2/rpQluQK3VykWXkF6sqiK70h0lraKwro4InY54o4lEk1Msh8fGkGgyEW804qtSUd/UxKXqatexlRwuKuJYaSkXq5zHR+l0HqlN9vfnqfh4kvz8iDUaUbfhHzEhzaZdHb5BP2eB4EnkiRFWSZIwGo3Ex8ffUCibmpqoqakBoKKiAn9/f0+UVKfTYbPZOHv2bIutf1mWKXTNLo+KiiKoDfLhnGNVT/GTfXt5tnNn/jFiBD/dv5/Nly7x9xEjbjiO9aW0NN45fpyt06bx6iefcL6ignYiqf++4aVQsGLcOCasXcuzW7fy3ujRouiqjZAkib8OH8bQDz/kFwcOsHzcOHotXcq/T2byjS6d23p5TxyyLFNqsZBbXe3MJW22bX+xqgqz1Uq80Ui80US8yUSX4CCmtEsi0WQixmBApVRidknthcpKzpVfZcOFCx7BLauvJ8ZgIMHklNouQUEMiY4m0c+PWNfxDyMhru4AqUFBYtqVQODiiRFWX1/f62RVlmUsFgslJSVUVVV5Hve+QQuRvLw8GhoaWnQCcLexCgoKahNZvVhVxbNbt2K2Wtk+fToFtbX0XLKEUbGxnH7mmZu2QpmUlMR3d+/mQlUVz3fpwodZWbz+FdNXBPeGt5cXayZOZNrGjewvKBAR1jZErVSyZsIEei5ZQpegIDZOnkz68uV0DAygX0REWy/vscO9dX+puppLnmhpNZeqnWLqo1QyMjYWgHiTiWHR0TzninqG6XRIQHl9vasoqooDhYUsOXvWI7a1VitxRiPxLintGRrK7A4dSDAaiTYYUD6COfqhWi0Xq6oYLlICBAIPT4SwusWysLCQwMBAj5CWlZWRn59/Xd/UaydQ1dXVUVlZeV3bKi8vL5qamgh7wJX2NoeDt48c4feHD/PDXr2Z1zGFV3d/wsGiQhaNGcPQ6OhbHq9WKnk2NZV3jh/ntV696L54Ma907472FtO8BPeOVq0mVKMhu7JSRFjbmGCtlnWTJjFy1Sq2T5/Of0ePZtqGDRyaM4eoNiqWfFSRZZmKhganjLoioxerqsiprianupqiujoitDriTEYSjCYSTEb6hoeTYHJGTY2uzhn5ZrPn2I0XL7aQWi9JIt5kIt7oFNlh0dE817kziX5+hGm1bdY28H4RqtXyWUGBpw+rQCB4QoRVlmXq6+upr6+npKSEmJgY/P39KSgouOHYO2WzbSJZlsnNzb3udUqlkqSkJFQqlafo6kFwsrSUr23ZitFbzcE5czhWUkLaBx8wMzmZzAULbls6n+vShc6L3uf3gwbRPyKCZefO8Y0uXe7z6gXK5n1YRZeANqVrSAjvDBvGpHXrODxnDt/p1o1J69azb/YsfNuoaPJhpdFm43JNjSdKesElpJdcUqqQJOKMRuIMRuJNRnqHhTG7fXviTSai9XpUSiV1Vqtnq/9CVRWHiorILCsnp7qaK+Yvi6TijEYSTSZmtk/25Jf6+fi09VvwQHEXW7m/y7L82Em5QHCnPBHC2hxZlrl8+TIqleqGsirLcou+qlevXvW0tHKjUChISkrC11XI9CBosNn4388+471Tp/hdejpj4uJ4aedOsioqWDNxIn3Dw+/ofJF6PYOjolh85gwvpqXx473OHFjxoXh/cU+60qpUIiXgIWBG+/acLCtj6oYN7Jg+nZNlZXx961aWPvXUE/X/gkOWKaqtJae6msLaWs5VVDiF1CWmpfX1ROp0Tik1GkkwmegbHu7cijca8ff19ZzDLbV78vL57+nTnkhrjdVKrMHgipQaSQ0KYnBUFPEuSfV5gH/4P+y4i658VSp8lEqqGhufOGkXCK7lifyEkCSJixcv3vBxjUaDyWQCwGazkZeX10JgJUkiPj4erVb7wNb7aV4ez27bRmpAICcXLGBLTg5pH3zANzp3ZsW4cXjf5Qf9y9268u2dOzm5YAEv79zJwaKiOxZfwZ0hJl09fPxqwAAmrVvHt3bu4t1RoxiwfAW/P3SYH/bp3dZLazVkWaayocEjjznV1Vysqia3pprc6mou15gxequJMxrpEx6OVqUiPTKSBR07Emc0EqnX46VQUOuKkua4IqW7r+R5zne5phqjt/eXUms0MTI21rn1bzQSptOJEdC3SfPxrO5pV0JYBU86T6Sw3mgylZvExEQUriT9srKy62Q1JiYGo9F439cIUN3YyGt79vDxpUv8ZehQuoaEsGDzZq7W17Nt+nTSgoPv6fxDoqKwyzL7Cgr4ZpcuvHP8uBDW+4xbWEXR1cODQpJYMnYsfZct473Tp1k/eRK9lywhNSiQp27QZeNhxWy1kuuSx9yaGi5WVpHjEVJnB5RYo5E4g4FYo4mOgQGMS4gnzmgk1mBAq1ZjczjIq6khp6aGS1VVbMu9zKVqZ5Q1t7qa2qYmYgwGT2S1nb8fo+JiSXBJqsiDbx38fHywNDXRYLN50gLaBwS09bIEgjbliRTWm9F8CACAyWSivLwcq9WKQqEgLCyMgAf0obEuO5uXd+5kbFw8mQsWsDY7mx6LF/O9nj35Xs+erTJNRZIkXnS1uPrHiBEk/Oc/lFksBInJP/cNd0qAiLA+XBi8vdkweTL9li2jY0AAGRMmMGndOj6dNeuhEYU6q5XLNTUeIb1U5Yxq5lTXcLmmGovN5pFJdyungVGRxLoec0foSiwWT1T0RGkpa7OzqbVa+bykhILaWkI0Gtcxzsjo+IQEj6CGPoYFTg8jkiR5pl2JwiuBwIkQVpw5qSaTidDQ0BaPK5VK7K4oWEBAwHXP3w+K6+p4ecdOTpaVsvSppwjWaBi/di1KSWLf7Nmt/stzfseO/Gz/fhrtdiYlJvKfzEx+1KdPq15D8CVeoujqoSXBZGLZU08x66OPOPD00/wuPZ0Ja9dxaO6cB7IdW2e1kltT44mI5tbUYLXb+aywkNzqasxNTUTr9cQajMQanRLaMyzUEyENdv2hWdnQQK5LbC9VVbHz8mXPz5dratCqVMQajMS5ztErLIwkk4lfGwzEGAxt2jBf8CVi2pVA0BIhrDh7tMbGxraIHNhsNrKysrDb7Xh7exMVFXVf1yDLMu+eOsWP9+7l66mpvDdqJP93/Dh/OnqUX/Tvzwtpafcl/8vo7c2M5GT+efIkL3XtyrQNG3itV69Hsnfho4BKocBqt4uUgIeUYTEx/KRPHyasXcdnc54ms7ycWRs/4uOpU+55V6O6sdEpoi5xvFRdzZVqp5heMddQa20ixqAnxmAkxiWT7UwmZrZvT6zBQIhWi0KSqG5sJNcVZc2prmZ/foFLcL/c+o8xGDxim+zvz+i4OKfYGo3oxbb9I0GwRsOpsjKaHA4Ka2vbejkCQZvzxAurOy/12oECWVlZWK1WJEkiISHhvm6DZVdU8Pz27Z4BADaHg4ErVxKq1XJs/nyi73NfyJe7dmX0qtX8pE8fgjUaNuXkMP4Ryt17lFApFFhsNpES8BDzcteunCwrY/6mTawcP56nVq/mtT17+OOQITc9RpZlyiwWLtfUeL5yXMVMV8zOn20OBzGuKGa03kC8yUifsDBiXVv4IRoNkiRR1dDgOUduTQ17Cwq5XOMU1MvV1Vibnce99T84OsoTafXz8RHb9o8B09u140d79xKi0fDf0aPbejkCQZvzRAurJEkEBARc156qoKCAxsZGFAoFISEh9619VZPdzltHjrDq/HlmJSfzfJcu/OrAQd4/e4Y3Bw1ibkrKA/nFkxoURLzJyPoLF3gxLY2/HjsuhPU+oRJFVw89kiTxzrBhDMvI4NcHDrBy/Hh6LV1KrMFAl+BgrrhlsrqGy+Ya8mpquGI24+vlRbTBQIxeT7RLJIdGR3uE1N+VVlDpElL39v/+AmeE9IrrsVCNFqVCItpgINZgINZopH9EuOffgb6+QkifAJ5JTeWZ1NS2XoZA8NDwRAurl5fXdVv9dXV1lJaWIssyGo3mvk2xOlJczDe2biVYoyFj/HiumM10W7yYrsHBZC5YQMgDbJsFzqjSX4+fYMu0qby2Zw8XKitJ9PN7oGt4EvASRVcPHbIsU9XY6BFR9/dAHx/+mZnJ93v1YsOkSfzq4EE+zMoixmAgymCgR2gIU9slOSXVYECnVuOQZUrdkdbqarIrK9mWe5kr5i/Pq5AkzzExBgPxRiODoqJc2/gGAoSQCgQCwXU8scIqSVKLFlbg/MV18eJFZFlGrVaTmJiIJElYmpqw2u2YWqHwos5q5Wf797Pk3Dn+36BBTEhI4Ief7uWjSxd5Z/hwJiYm3vM17obJSUl8d/duLlZVsbBjJ945cYK3b7EFKrg7RNHVg8dqt5NvNnOlpoY8s5krZjOXq515o3muxxWSRLTeQLRBT5RLJGeEhPDD3r3Rq9WkBAayfNw4z7ncYnuoqJgPs7K4XGMmz3U+vVrt2vZ35qOmBAYwJj7OI6St8TkiEAgETxoPvbBKknTDiVT3gkKhIDQ0FM017Zuqq6tpampCqVSSnJyMl5cXZ8vLeWbLFs6Ul6P28iLBNeXF/RXv+jlCr//Koqhtubl8c/t2+oWHc3rhQg4WFdFp0SLGxMVxeuHCNv1FplYqeTY1lXeOH+f7PXvSc8kSfjNgABoxorJVcbe1cn8X3BsOWaakro48s9kjn1fMZvJdX7k1NVytrydMqyXaYCDKtV2fFhzEhMQEol1iafLxQZZlT2HUFde5VpeU8PbRo87z1tRQds25YgxG+oaHM6u9KzfVYBD/zwgEAsF94KEWVkmSMBqNVFdXe2YpazQaFAoFdrsdu92OLMue0akKhQJZltHr9ahUKiorK284JMDX1/eGLapKS0sBiImJQa1WU2axMH7tWn7erx/zUlIos1i46Jrwcqmqik/y8njv1CkuVldT2dDgmfASbzSS6OfnkVm9SsXr+/fzaX4+/xgxgm7BwXxr504+Ly5m8dixDImOvr9v5G3yzS5dSF30Pm8MHEjvsHCWnTvHs507t/WyHitEhPX2kWWZioYGj4zm1dR4IplOIa2loK4Wo1pNlF5PlN4tpHr6hIURrXdGS8O0WpSunOF8t9iazZwsLWPDhYvkmZ2Cmmc2AziPc0Vb44xG0oKDPTIartO1Sg9kgUAgENwZD7WwyrKM2WwmMTGRiooKjEYjfq68SrvdjtVqRaVScfLkSbRaLf7+/gQEBKB09REMDw/n3Llz2Gw2zzkVCsVNq/7d6QF+fn402mxMWb+eme3bM79jRwCCtVqCtdobToOyNDVxqaqKSy6hvVBZybacHI6XliFJMLN9e04tWMC6CxdIff995nVI4b2Fox+qaEyEXs+Q6CgWnz3Ly13T+Mm+fXw9NVXk07UiXgoFdocDL0l6oouu3KNC82trPRJ5uabGExnNM5spqK1FrVQSqdMRpdcT6YqOjoqNJcoV4YzS6/Hx8vJU6V9pdq6DhUXkec7njI6GarVE6vVE6Zxi2yU4iPGJCa7te7FdLxAIBA8rD7WwglNML126hMlk4urVq+Tl5aHX66mpqcFms9G9e3e6d+9+w2PVajXBwcEUFRUhyzIKhYLY2FhU10hiQ0MD58+fR6VSUWs0svzcOdZmZxOi0fDrAQNua50alYpOQUF0CgoCIKeqim9u30GIVsO/R44kWKNh+saNFNbW8vGUKfR4AEMI7oaXu3bl5Z07yVywgG/t3MmhoiL6iHGtrYYnJUCpfGyLrmRZ5mp9vUdGS+rqyHHJaF6Nmfxap0R6KRRE6vVE6nRE6PVE6/UMjopyCqXrS6dWe4qi3CKbZzazw1XI5Bbc/NpadCqV61gDkXodsQYDvcJCPdv3IjoqEAgEjy4PvbCCU1qvXr3q+bmiogLgtiJ/hYWFnn+HhYV5IrTNqaiooKmpifLGRmYdOkTP8HDOlJfzTMeONNnteHvd/ttkczj409GjvHHoEP/TowevdO/OvzIz+eWBA7zSvQev9eqJ6iGeJDPY1TXh0/x8vpmWxl+PHxfC2oo86ikBdoeD4ro6ClwyWlBbyxWXhBbW1lJgrqWgthZfLy8i9M7IaILRSKBGw8DISI+gRhkMngb2NY2NHhHNN5vZl5/v/Hez6Gu4VotKqSRS55JZg55h0dEtIq0P026FQCAQCFqXR0JYb4Zer//K13Tq1In6+nrUavV1RVbgjAYVFxcD0CEpCQ4f5oc9exKp1/PtXbvo8v77vDN8OMNiYr7yWsdLSnh261ZM3j4cnDMHq93OkA8/RCkp7stY1fuBJEm8mJbGO8eP86+RI0n4z38os1gIusF7J7hzHuaiK0tTEwW1tRS4RNQpozVOEXV9lVos+Pv4EK7TEaHTE+mS0tSgwC+jpTodWldktNoVGc2vrSXPbGZvXr4rwlpLfq3zOg5ZJsK17R+hc0Za+0VEeFIBogwGjN7ebf32CAQCgaANeaSF9XYirN7e3njf5Jed3W4nOzsbWZYJDw8nzGRi+VNPMW/zZuampLBi3Dh2XL7M17dupU9YGH8cMoRwne6681iamvjZ/v0sPnuWN9LTebpDB944fJi/Hj/OL/r145v3aazq/WJ+x478dP9+LDYbkxOT+HdmJj/u06etl/VY0BYRVrvDQanFQmFtLSUWC1dqalpESN1CWm+zuUTU+RWu05FgMnkioxE6HWE6HWqlEocsU26xkO86Nt9sZnvuZQpqzRQ0k1GFJLnO55TZSL2evuHhnpzUSL0ek7e3yJMWCAQCwS15pIW1pqaGpqam63JSb4empibOnz9PQ0MD3t7enq4Bw2Jj2Td7Nt//5BM6/Pe//GPECM4+8wy/PniQzosW8aPevflO9+6eXDh3q6o+YWGcWrCAS9XVdF+8mFijkWPz5hF1n8eq3g/0ajVPt2/Pv06e5KWuaUxZv54f9OqFUuT/3TOewQGSdM8RVnduZ2Ez6XRHSAtr6yisq6XIJakmb28idDp6hIYiuSSyf0SER0wjdDpPw3qr3f7l+VzR0QOFRRTWOa9jVKvZfuWKM2dUpydCryNc64yGunNQ3XJqEJFRgUAgELQCj7SwApSUlBAZGXlHx9jtdrKysmhsbESSJOLj41tEeCL1epaPH8/2nBxe27uX4/Pn89v0dBZ07MjLO3bw/pkz/GbAAD7MymJfQQHvDB/OwMhIfrx3Lxnnz/P2kCHMTE5+pKNGL6alMSwjg9f79iVMp+OjS5fabKjB44RnNKtSedMIqyzLmK1Wp4jW1VFY6xTPfHOtS0LrKHLJo1qpJEynI1yrJUyrI1Kvo31AAEOjo4nQ652Pu6Ki7jZRzeX2UFEx+WYzRa7rFNbVUtnQQIhGQ7hOR6TOWawUqdfRIzTEE2mN0OnwFTmjAoFAIHhAPNLCKssypaWleHt7ExgYeFuC6J5mZbVakSSJkJCQG+a2AvQICyOnuhqA7+7cia9KxcbJk9lw8SL/yswkyc+P0wsXsuvKFTotWsSgyEhOL1xIgK9vq95nW5ASGEgHf39Wnz/PS67iKyGs94Ysy9TbbFjtdrwUCqx2O384fNgjpEV1dR5xlCSJcK2OUK1THMN0Omd/0fAwwl1R0XCtFq2rcKnOavXIbWFtLTnV1ewrKHBGWmtrPdFWb6VXi+Mj9Hq6hQQT0UxEgzUaEU0XCAQCwUPFIy2s4JSA/Px8CgoKCA0NJTAwEK9bVPVfvXqVuro6z/jVsLCwm7620W7H21XRvzo7m2iDgZGrVvHp7NnMaN/e87o/HzuGBMQZjZit1sdCWAFe6tqVt48cYeeMGXxvzx6yKipI9vdv62U9dNgdDsrq6ymuq2spnuZaii11FLtEsthiwUuS+GX//mhVKn43YABXzGai9Hp6hYV5oqHhOp2ngr7BZqOoeaS1ro4TpaUUuqKsJm9vdly5QqPNTphO6xHRMK2OKIPzvBE3EFyBQCAQCB4lHnlhBTzTrAoLCyksLCQgIIDQ0NDriq1kWaawsBCHw+FJBVDcIpLUaLN5hNVis3H26lVe79MHWZadzd9dz22bPp0DhYVkZGUxeOVKxsTF8fN+/QjVau/THT8YJiYm8t1du/iiooKvderE346f4M/Dhrb1sh4YdVYrRS7RLK5zimdRXR1FtXUeES2uq6Osvh6TtzdhWi2hLlkM1Wpo5+/HoKhIwnQ6wrRawpoJY31TE+MTEz0RVbeIOrf7nTJaXFdHbVMTIRoNYVq3jOoI1+voEBDgiZT+a+RI/Hx8HukUFIFAIBAIboUk36J5uSRJ8pEjRx7gcloPhUJBampqi2hrZWUlubm5yLJMUFAQUa6eozfjfEUFT61ZQ/azz/LF1at4K5U02u08v20bVY2NLBozhq4hIQCeqmmlQsFvDx5k0ZkzvJSWxvd79fJEyx5F/nzkCBerq/lez550/eADLj/3HLpH+H6sdjulzQS0xGJxSmldHcV1FootdZS4nrPJMt2Cg3HIMmFaLSEu6QzT6Vxi6hTUEI0GlStHtMYluUUeua31CGlz4W2w2wjVOI8P1WoJ02k9W/LuKGuYVkuAr+8j1WFCIBAIBIK7RZIkZFm+4S+9xyLCejPq6+s9vVqbR1dVKhURERFfeXzzlIBYo5HfHjzI306c4Kd9+xKq1TJp3ToOzZ1LqFbLU6tXc7ioiElJSfyif3++3a0br+/bR9J//sPrffrwXJcuqB/igQE3Y1aHDrR/7z1+0b8/6RERLDl7lm+mpbX1slrQ5JLQEovFI5vNBbTU/d1iocZqJcjXlxAPilweAAAgAElEQVStllCNhmCNUzyT/PxIj4z0CGSoVotBrUaSJGyutlAesbVYOFFayhZXNLTE4vxuUKu5WFVFmFbnElwNoa7IaJfgYE+UNUynw19ERAUCgUAguG0eW2GVZRnfZrmkZrPZ0xUgLi7ulqkAbhqbTbmat2kTdoeDEwsWEOmS4C8qKpi8bh27Z84kJSCAM1evUmqx0HnRIp7v0oW/DBtGbk0NP9jzKX86eozfpA9genLyIxUxC9FqGRsXx39Pn+blbt14dfdunu/S5b7LVn1TEyUWi0dEK+rrKXAJY6nFQkmdhRKLM0JaY7US6ONLsFZDiEZDiMYZ9Yw26OkZFuqJgoY2i1i6K+ZLXAJaXFdHvtnM4aJiSixO2S1xRVsrGxsJ8PHxiGyIRku4TktygH+LLf9QrfaRjj4LBAKBQPCw8lgKqyRJ+Pn5kZmZSUxMDP7+/hQWFiLLMgEBAbc1IQu+jLDKsszq8+dpevXVFtXTP+3blzPl5Ty3bRv/GDGCCYmJvLZnD+E6HcdLS2n37rv8sHdvNkyexL6CAn7w6ae8+fnn/H7QIIZGR9+v2291XuralQWbN/PF176G1W5nX0EB6XfYSswhy1TU11PqklD3V1GdhVJLHWUuMS2z1FNiqcPqcBCi0RCscUpojMGAwdubOKORPuHhLjHVEHKNhFY1Nnqk1r3lf7b8KkV1ta7HnNcrsVjQqlQEazSEapzb/c5WTlpSgwJbRFqDfH1F1bxAIBAIBG3IYymsvr6+BAcHU1FRwZUrVyguLqahoQGFQvGVeavNsdrthGq12BwOFJJ0nbQoJIlFY8bwk717affuu/yif3/2z57NmuxsfrJvH4kmE+uys/m/Y8f4Vf/+HJwzh9Xnz/Pc1m0kmEz8ftBA0oKDW/v2W52+4eHo1Wq2X77MC2lp/PXYMQZERFDd2EhZfT1l10hoSZ2Fsnrnv93PX21oQK9SEeSS0CBfDSGuiGi3kBCPmAa7JNS9HW93ODyR0OYR15OlpV/+7JLQ0vp6fJRKovV6TD4+nkhriFZDv4gIT5TVLbo+t+gmIRAIBAKB4OHhsfuNrVAoCA0NRaPRoFAocDgcNDY2AhASEoLyDvJIG2w2LE1NNDTLZb0WjUrF20OHMqtDB17bs4c/HjnCGwMHcmbhQv596hS/PniQTgEB/PHIEd5yP/fMQv6dmcnoVasYERPDrwYMINZobJX7v1scskxlfT3lDQ2UNRPNMldUVK1QsP7CBd4YOJDV2dl4v/02Pl5eBPn6EqzREOj6HuSrId5kpE94mEdOnY/7onK9h/VNTS0F12LhfEUFn+blOx+rt3gk+GpDAwa12iO0btENdeWduiOjQkIFAoFAIHh8eSx/u3t7e2O1WnF3QJBlGYVCQYirov92cacENNpsnlzWm9E7LIxPZs7ko0uX+OGnn/Kmry+/HziQ7K9/nTc//5y/HD9O37AwXt6xgxij0fncs8/y1uef033xYualpPB6nz4E3mSIwZ3SYLNRXl/f4qvMYvFIaHl9PeWWesrqLZTX13O1oYEYvQFJgiCXYLolNMZgoEdICMNjYjB6e7N16lQkSfLIYZPdTnmz7X635J4uLwfgzNWrLaKwVoeDYF/fL4XWV0OQRkOUQU+P0BCP5Ia4tuNVj2CxmkAgEAgEgtbjsRNWSZLw8fGhqKioxWNBQUF3FF2FZsJqt+NzG8dKksT4hARPkdL0DRvoHRbGb9PTeSEtjV9+doCDRUV0VKkYv3YtAyMj+c2AAbyQlsavDhyg/Xvv8d3u3Xmle/cWDd6b7HauNjRQbvlSLr8U0C+F9GpDPVdd/2602wn09SXAJZ5Brn8HazR0DAggyBUVdctpgK+vp4uB1W6/LspaZrHwf8eOU+ZaQ1m9S3wtFsxNTfj7+HiirUG+LhHVaoh2NcUPbhZtdW/3CwQCgUAgENwOj5WwKhQKwsPDASgrK6N5j9nQ0NA7Pp+7S0DjLVICboRSoeDZzp15ukMH/nz0KP2WLWN6cjI/69uXV3p058d79yIB5sZGun7wARMTE1ny1FN8t3t3Xt+3j37LlqFWKrna0MDV+nosNht+3t4tBNTfx4dAX2clfLeQYAJ9fQl0SWigr69HCt1z6cvq67lqsVDqEtrLNTUcKS52yahTdN3RVovNRqCPL4Eat+w6zxui0dDdFQENahYh9fPxeaQ6HwgEAoFAIHi0eKyEValUEhQU1EJWJUn6ynGtN6N5hPVOhNWNRqXiR64erG8dOULXDz7guc6deXf0aLIqKlh9/jxeCgWBPj4AJPr5sWL8ePLNZvLNZo+gGr29PUJoaWq6bqu/vL6ei1VVrsinK9ra7DlvpZJAX196hYZSY21yya0z6prs7/9ltNUloSZvbxEBFQgEAoFA8NDw2Ahr8w4AxcXFnnGtcHfRVfhyNKtTWO/+rQrw9eW36en8//buNTiu877v+O959oKz9wVxIS4CSUGExMq2ZNmy6ErqqG3ikaxIdRJLE7Wm20j0pJ1J0pl2prWbNo0z9fRFOn3hTDvpRbKmoh2n4zFbZ5zYY8uZhImk1pFVKjIj60KFiggQJERcdxd7O+f0BbBHAAmQArCLs7v4fmY4IM853PMnX/3m2f/zf37pttv066uHCfza0aP6zXvuWXeYwIkzZzRXqeimfF6fOHgwuHf/N76hly5eVKFWX/08Z91qa2M19Na+vnWrrI1fbEQCAACdrGuSTCQSUT6f1+LiolzXDa739vYqvs1h7utWWKM73/hzKJfTiZ/5Gb186ZI+f+qUvvzSS/rSvffqF44ckZH0r/70TxUxRgezWf3qD36gL917rx47ckSfvvlmvTY3p9sHB/Uf7rsvOA4WAABgL+iKaeiNr/2NMetWV40xQU/rdqybEtDEneq3Dw7qu488ov9+//36jy++qDtPnNAP/vqvdfZzn9M/v/NOvT43p8P5vH7rhz/UR595RgezWb32xBP6uYkJPXjypP7Bt7+tt+bnm1YPAABAO+uKwCpJ/f39KpfLKhaLwbVcLqeenp5tf+ZOe1iv5+8eOKA/P3ZMn7/rLv2T739fD51cmRzw+vHjOjo8rHeWljSayeiXn31WD548qbuGhvTG8eM6sm+f7vrqV/Urzz6ri2v+vQAAAN2oKwKrtVbxeFzT09PrNlvtZHVV2v6UgK0wxugXjhzRq48/rp+dOKwHv3lS//h739PjH/ygzjz+uA5kMpqvVJSOxfT3/tf/1hPf/a4eO3JErz7xhKLW6tann9ZvPPeclqrVltQHAAAQtq4IrKlUSvV6XbOzs8G1RCKhRCKxo89tBNVyk1sCNhKLRPTLd9yhNz53XEf29emur35VX3rhBX3x7rv1fz7zmeD9FdfV3/za1/Trzz2nz991l148dkxvzc9r4skn9eUf/UiVer2ldQIAAOy2XQmsrRyRZK3VgQMHNDs7G7yncTzrTq2dErBbO+3T8bh+45679eoTT8gao7/x9NM68Zd/qaceeEDf/vmfU7FWU95x9M7ioj7w9NN68pVX9J9++qf1vUcf1ffOndORr3xFJ86ckbtmSgIAAEAna3lgbZwy1YrQaozR0NCQenp6NDMzs26zVT6f3/Hnt7qH9VoGkkn99k/9lF48dkxvzM1p4skn9fzklP7w05/Wf/nEJ3ShWNRoJqMXp6c18eST+v65c/rmpz6l//HJT+p3Tp/WHc88oz84e3bd4QkAAACdqOWB1fd9vfvuu9q/f39LQmtfX58qlYoqlYqk9RMDdmptYI2HdJ79jfm8fvehh/TdRx7RH/zVWzryla/oUqmkHx47pn999KjeWljQ4Xxev3/2rG5+6imdnZ/Xqcce07+79179y1On9Le+/nW9culSKLUDAAA0w660BHiep5mZGQ0ODsra5r0ymUwqHo9rbm5u3fXBwcGmfH553cEB4QTWhg+vjsJ66v779eWXXtKdJ06o13F05hd/UcduvVVvzM3p5t5e/efTp3X7M89Ikk5/9rMyxuhbZ8+GWjsAAMBO7NqmK9d1lUqlFIvFtvT3Ngu41loNDg7K931dvHgx+Oo7lUpt+6CAKwVTAnZh09X79XcOHND//cxn9G8+/nH90z/6I93/zW/qztVxV397bEznFhZ0MJPRF06d0p1f+5qKtZr+2Uc/GnbZAAAA27arUwKWlpY0Pj7+vr+ut9Yqeo3NTvl8XpcvXw56V5u12aohmBKwGlzbhTFGj9xyi848/rj+/pEj+vlvfUv/8Dvf0aO33KLXjh/Xrf39mlpa0r+/5x49++ijSjUpwAMAAIRhVwPr5cuXtbi4+L5aA6y1mpiY2PS5fD4vY4wuXLiwLrBms9mm1VtxXTmNKQFtssK6VtRa/dLtt+v148f1saEh3fv1r+sLp07p6NCQeqJR3dzXp307HO0FAAAQtl0NrJ7naWpqSoODg9dtDcjlckqn0xsGVmut+vv7NTc3p/rq3NFWTCNox5aAjSRjMX3h6FG9fvy4eh1H//Xll/V7Dz+sid7esEsDAADYsV39ntsYI9/3VSqVND4+rp/85Ccbjl3K5/MaGRnR8vKystmsSqXSuvu+7yuRSOjixYvB6qok7du3r6n1rm0J2K05rDvR6zj6rfvuC7sMAACApgolsL711lsaGRnRwMCAZmZm5Pt+0AJQLpfV398vSZqcnNT09HTw9xqrp319fYpGo+uCbDQaleM4Ta230kZTAgAAAPaqXQ2sjdVQ3/dVKBQ0NDSkmZkZSVI8Hlc6nVY6nZYkLS8vq1AoSFoJutZaDQwMaGBgQPF4XJ7nqVarBZ/djIMCrtQIqlUCKwAAQGh2JbAmEgmVy+VghTQWi+ngwYOKRqPq7+/X8vKyhoeHg+cnJyeDUVXGGB06dCjYZNWwvLwsa608z5O1Vr0t6NcMWgLq9baaEgAAALCXtDyFWWtVLpcVj8cVjUZVrVYViUT05ptvqq+vT2NjY1dtlMpkMkGrwPj4uHK5nHzf18LCglKplKLRqJaXl4Pnfd8PVmabiRVWAACA8LU8sDbaACqViqrVqnzfD77Kb4TOK0+mymazuu2224Ige+nSpWB8VSQS0Yc+9CEVi8Xgs5PJZEuOfQ2mBBBYAQAAQrOr33NfORHA931NTk5qfn5ePT09ymazymQyikajstZqYWFBb7/9tlzXXdf/KknFYjH4nGZvtmpoBFUCKwAAQHhCb8z0PE9LS0taWlrS7OxsEEgjkYg8z1s3tkqShoeHVa1Wg9VZY4wSLRiO7/u+qq6reKOHlcAKAAAQitAD61prw2njQIC1jDEaHh5WrVZTIpFQrVZTJpPRwMBA02upuq5i1soas3LSFZuuAAAAQrGrJ101SywWUz6fV71e1/j4+HWPed2OtW0AtAQAAACEp6MCa2Q1NPq+rwsXLiiVSrXsXQRWAACA9tAxgdUYo6GhIUkKpgzkcrmWva8xIUCSxnM5xQmsAAAAoeiowJpMJiVJ1Wq15e9bu6p6emaGHlYAAICQdExg9TxPly9flvTe/NYrJwg0U7le10hypeWAlgAAAIDwdExglSTXdSVJ7777bsvfVXVdFeorrQcEVgAAgPB0xPfcxhhZazUyMiJpZUqAdPVBBM3UCKm+76vCHFYAAIDQdERgHRsbU29vr6KrfaTZbFYLCwutD6zRqGqep4i1irRgdBYAAACur+1TmLVWsVgsCKvSe5uuWhlYG6db0Q4AAAAQrrYPrL7vX7W5qlgstvy9FdeVE4nQDgAAABCytg+skoJxVg3lclnS7vSwssIKAAAQrrYPrL7vB+Os1l5b+7MVGj2sBFYAAIBwtX1gla4Oprs5JaBMSwAAAECo2m5KgDFG0spmK2utkslkcCRrQzqdVrlcbm1gXbPpilOuAAAAwtN2SSyTyWhiYuKaz6TT6ZYfHkAPKwAAQHtou5aA97NqupstAQRWAACAcLVdYL1yhNVGIrsQIMv1uuIEVgAAgNC1XWCt1WrXfaZxiECrV1idxpQAelgBAABC05aBtTFndTONFdZWBtbqmikBDiusAAAAoWm7wOr7vs6dO3fN1oBGYK1UKi2rgx5WAACA9tB2gdUYo2KxqJdfflkXL17cMLg2Rl9VKpWWrbKuDaxxAisAAEBo2i6wSiujrTzP0+TkpF599VW5rrvu/tqQWq/XW1JDEFjrdXpYAQAAQtR2gTWVSmliYkK5XE7SyirqlT2tnufJGKNIJHLdftftKq8GVVoCAAAAwtV2gTWRSMgYo5tuukn5fF6pVErJZHLdM8vLyzLGyPO8lgXWiuvKoYcVAAAgdG33XXdjQ5UxRuPj4/J9P+hZbVhcXAx6W5eXl1tSRyOoLq8e0QoAAIBwtF1gvXTpkiqVitLptPr6+jY8JGDtqmqpVGpJHY35qxXXVTYeb8k7AAAAcH1t1xLgeZ7m5uZ0/vx5vfbaaxtOCRgZGVk3KaAVGGsFAADQHtousDb4vq9KpaLLly9fdc9xHA0PD8sYo3q9/r6Oc92qdVMCCKwAAAChadvAKq2sts7Ozm54b2hoSLFYTJJasvGqEVQ5mhUAACBcbR1Ypc03VRljlMlkJLUosNISAAAA0BbaPrC6rrvhaVbVajVoF2jFxqu1gdUhsAIAAISm7QOrtVbVavWq69FoVNaulD8/P9/09wZTAjjpCgAAIFRtH1glqVAoXHXNWivHcSStrLbWarWmvpOWAAAAgPbQ9oHV87wNJwVIUi6XkzFGxhgtLCw09b3ltZuuCKwAAAChafvAKq2ssLque9X1wcFBSe/Nbm0W3/dVZYUVAACgLXREYDXGaHFx8arr0Wg0aAsoFAobbs7ajprnKWKtItZqIJFg0xUAAECIOiKwep63YWCVpGw2G/y+WCw25X1rV1XfnJ9n0xUAAECIOiKwSpvPWs1ms7LWyvO8pk0LqNTr6kskVn5PSwAAAECoOiawbjTaSpIymYyMMZKaN96q4rqqrfbMElgBAADC1TGBtVarbdijaozR8PBwMK+1GeOt1oZUAisAAEC4OiawSlK9Xt/wemNagKSmjLe6KrDSwwoAABCajgmsxhgtLS1tei+RSMj3fc3NzWmxUtH0DjZgrQ2p5XqdKQEAAAAh6pjAer1Zq8lkUpJ0aX5eD588qQe+8Q29uc3ZrI1DAzzfV83zFCewAgAAhKZjAqskLS4ubjprNZVKyVqrpXpd04WC6r6vxDa/ym+0BFRdV/FIJNjUBQAAgN3Xcc2ZpVJJqVTqquupVEq+72sgHtf3H3hAB8bGtv2OiuvKiUbZcAUAANAGOmqF1fO8TQ8HcBxHPT09kqSFHY63agTVRmsAAAAAwtNRgVWSpqamNr13ww03yBijWq22o/FWldWgWnFdNlwBAACErGMCq7VWIyMj2rdv36bPZLNZOY4j3/d3NN6qscK68rPjuiYAAAC6SscEVs/zZK3VgQMHNn3GGKPR0VFJuuZEgesJAmu9rp4oK6wAAABh6pjAaq1VIpG47nPZbFbStScKXE9jDiubrgAAAMLXMYHV8zyl0+nrPmeMkeM4krTpBq3rCTZdEVgBAABC1zGB1Vora99fufF4XJJULpe39a51m644lhUAACBUHRNYPc/Tm2++uenxrGs1xlvNzs5u613l1ekAFcZaAQAAhK5jAqskLSws6OzZs9ftTXUcR8YYFQoFeZ635ffQwwoAANA+OiqwSpLrunJd95rPxONxGWNkjFGpVNryO9a2BBBYAQAAwtVxgdUYozNnzuj111/X8vLyhs80jmn1fX9bgbW85qQrelgBAADC1XGB1fd91et1LS0taXZ2VtVq9apnYrGYenp65Pv+tiYFVNccHBBnhRUAACBUHRdY15qZmdErr7yier1+1b2BgQFJ2l5LwLqTrgisAAAAYerYwGqtleu6isViG97v6+uTtDLaaqsHCLDpCgAAoH10bGBtHNV6+PBhRTfoM41EIkqlUpK2Po+1Qg8rAABA2+jYwCqt9LNe67jWfD4vaesnXpXrdTmcdAUAANAWOj6wzs3NaXZ2dsOv/bPZrCRtOk1gM0FLwGpwBQAAQHg6+vtuY4zefvtt+b4vz/PU39+/7n7jxKutrrCum8NKSwAAAECoOn6FtXGSVaVSuep+JBKRMUbFYnFLJ14xJQAAAKB9dHRgbTDGaGhoaMN7juNIkhYXF9/3560NrLQEAAAAhKsrAqu0Elo30gis8/Pz7/uzgsBar9MSAAAAELKuCKy+72tqamrDe40pAls5QKBMSwAAAEDb6JrAOjMzs+E9x3FkjNnSAQKV1fmrBFYAAIDwdUVgld776v9KPT09MsYEofX9aATVmLH0sAIAAISsawJrY4TVRtcbEwK2GljfLS/TwwoAABCyrkljkU1WQiORiKy18n1ftVpNklSu1fTFF15Q3FpFrFXEmOCnNea9gwNoCQAAAAhd16ywNsLoRhKJhHzfV7ValST92p/9mf7fxYuKWCvX87Rcr2uhUtFMqaR3lpaUjsXeC64EVgAAgFB1zQproVBQvV5XdIOv8PP5vIrFYhBYK66rh2+6Sb/ykY9c9WylXtfvnD4taWVagENLAAAAQKi6ZoXVdV39+Mc/1szMjIrFopaXl4Pe1X379kmS6vW6JKlUqykZi238Ob6viF35b2kc0QoAAIDwdNXyoeu6On/+fPBn3/c1MjKioaEhTUxMBKuvxVpt093/ru8rsnoIAS0BAAAA4euqwCopWFVtqFar8n1fpVJJpVJJY2Nj6ncc/aPvfEe/+cILOpTN6mA2p4O5rG7M5dTnOGqcmUVgBQAACF/XBda1IpGIBgcHVSwWdeHCBXmep0QioU8dPqznp6b0uw89pHOLizq3sKBzi4v61htv6K8WF/XYkSOSpA/29+vBkyc1mk5rOJXSSDqtkdXfD6/+7EskZDc5FhYAAAA7Z651+pMxxn/xxRd3sZzmMMZodHRUg4ODMsbo0qVLOn/+vHzfVzKZ1JfOntXzU1O6b2xMo+m0xjIZ3ZDJaDSd1g2ZjPoTCRljNFMq6bXZWV0oFjVVKKz+KupCsaDp1WvFel37k0kNpVIaSqVWgm0qrZHMarBdDbeDyaSitmtahgEAAJrKGCPf9zdcBezaFdb+/n6Z1ZXP5eXl4FjWWq2m0zMz+hcf+5h6olG9s7ioH128qN8/e1bnl5Y0WSioWKtpJJ3W4VxOvY6jkdUwe/vgoD5543srrel4XOV6XdPFoi4Ui7pQKATh9vnJyeD6dLGoy+Wy9jnOSrBNJjWUWl21zaQ1lExqOJ0OQm86FgtqBwAA2Ou6MrA6jhMcJOC6rubn54N7ruuq4rr6xKFDmujt3fDvL9dqmiwUNPHUUzrx4IOaLhY1WSjozy9c0NRqIL1QLCpqre7cv1+SNJxKayS9EmZvGxjQAzfeGLQRJGMx1T1PM6VSEGAbP1+7PKs/eecdTa/+ebpY1MeHh/X20tKacJsKfu1fvfaR/fuDaQYAAADdrCsDa7Valed5unTpkqanp9dtxPI8b2Ws1TXmqyZiMY3n85KkY7feuuEzvu9rvlIJwutUoaDJpSW9Nb+g5yanVq+v3OuJRIKe1+HV4DmaTms8l9M9IyMabqzYrq6sLlYq6wLsdKmk6WJRz09NrYTc2Vl98e679dkPfKC5/3EAAABtqCsDq+/7Or06/H+jHt1CraY/fucd5Xp6FF1zJOvaI1p937/mkFpjjHodR72Oow/091+zlrlyeaVlYE0v7LmFRb0wNaXpYinoiTXGaH8yqeFU+r1+2NVV21t6e4PQ+9/+4i905vLlnf43AQAAdISuDKxXjrZayxijf3v0qH7v1VflSnI9T67vy/N9uZ4v11/5c93z9Kt33LHjWowx2pdIaF8icd1gu1StruuFbbQi/Pjdy5ouFnWxtBJ6FysV/c+HH95xbQAAAJ2gK6cEXIu1Vh/+8Ic7elNT1XUVZz4sAADoIteaErDndu0kVkdWdTLCKgAA2Ev2XGBNp9NhlwAAAIAt2FOB1VqrVCoVdhkAAADYgj0VWBsnXQEAAKBz7KnAaoxRPB4PuwwAAABswZ4KrI7jdPyGKwAAgL1mTwXWTCYTdgkAAADYoj0TWNlwBQAA0Jn2TGCVpFgsFnYJAAAA2KI9E1h931epVAq7DAAAAGzRngqsS0tLYZcBAACALdozgVWSIhxpCgAA0HH2TGC11iqfz4ddBgAAALZozwRWiRVWAACATrRnAqsxhkMDAAAAOtCeCaye5ykajYZdBgAAALZozwTWRCIhx3HCLgMAAABbtCcCqzFGBw8eDLsMAAAAbMOeCKzJZFLJZDLsMgAAALANXR9YjTHq7e0NuwwAAABsU9cHVknK5XJhlwAAAIBt6vrA6jgOm60AAAA6WFcHVmut9u/fH3YZAAAA2IGuDqyS6F8FAADocF0dWPv6+mRtV/8TAQAAul7XpjljjAYHB8MuAwAAADvUtYE1mUyy2QoAAKALdGVgZbMVAABA9+jKwGqMUT6fD7sMAAAANEHXBVZjjAYGBmSMCbsUAAAANEHXBVZJGhgYCLsEAAAANEnXBdbe3l7F4/GwywAAAECTdFVgNcZoZGQk7DIAAADQRF0VWHt7e9XT0xN2GQAAAGiirgmsrK4CAAB0p64JrKyuAgAAdKeuCKysrgIAAHSvrgis+Xye1VUAAIAu1fGB1VqrsbGxsMsAAABAi3R0YLXW6oYbblAsFgu7FAAAALRIRwfWnp4e9ff3h10GAAAAWqhjA6sxRjfeeKOMMWGXAgAAgBbqyMBqjNHAwIASiUTYpQAAAKDFOjKwRiIRjY6Ohl0GAAAAdkHHBVZjjA4dOiRrO650AAAAbEPHpb5sNqtcLhd2GQAAANglHRVYrbU6ePBg2GUAAABgF3VMYLXWanR0lJmrAAAAe0zHBNZ4PK6BgYGwywAAAMAu64jAysxVAACAvavtA2tj5moymQy7FAAAAISg7SjADa4AAADvSURBVAOrtVYjIyNhlwEAAICQtH1gzefzikQiYZcBAACAkLR1YLXWKp/Ph10GAAAAQtTWgdX3fWUymbDLAAAAQIjaOrAmEgnaAQAAAPa4tg2sxhj19vaGXQYAAABC1taBNZfLhV0GAAAAQtbWgdVxnLDLAAAAQMjaNrBms1lOtgIAAEB7BlZrLf2rAAAAkNSmgZVxVgAAAGhoy8DqOI6i0WjYZQAAAKANGN/3N79pzDlJB3etGgAAAOxVb/u+f2ijG9cMrAAAAEDY2rIlAAAAAGggsAIAAKCtEVgBAADQ1gisAAAAaGsEVgAAALS1/w/ZHOTt/IMlIgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 864x576 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig = plt.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection=proj)\n",
"ax.set_extent([-98, -87, 25, 31], cartopy.crs.PlateCarree())\n",
"ax.add_feature(land_10m, facecolor='0.8')\n",
"\n",
"fname = '../data/fairway/fairway.shp'\n",
"ax.add_geometries(cartopy.io.shapereader.Reader(fname).geometries(),\n",
" pc, edgecolor='darkcyan')\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Great Circle Distance\n",
"\n",
"How do you find an airplane's flight path? The shortest line between two places on earth is not necessarily a straight line in the projection you are using. The shortest distance is called the Great Circle distance and it is the shortest distance between two places on a sphere. \n",
"\n",
"For example, here is the shortest path between Boston and Tokyo. It is a straight line in this rather globe-like projection because it preserves this property.\n",
"\n",
"\n",
"\n",
"However, [this link](http://web.mit.edu/dsheehan/www/MapsAPIexamples/gcr.html) shows the flight path in a different projection. Not so straight anymore.\n",
"\n",
"\n",
"Here are previously-saved latitude and longitude points along the great circle line between the LA and Newark airports (calculated using the `pyproj` package which is great but beyond the scope of this notebook).\n",
"\n",
"In particular, the LA and Newark airports have the following coordinates and are in the first and last elements of the two arrays.\n",
"\n",
" LAX: 33.9425° N, 118.4081° W\n",
" EWR: 40.6925° N, 74.1686° W"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"lons = [-118.4081, -116.53656281803954, -114.63494404602989, -112.70342143546311,\n",
" -110.74234511851722, -108.75224911337924, -106.73386144433508, -104.6881124356053,\n",
" -102.6161407277617, -100.51929657411526, -98.3991420049751, -96.25744750245255,\n",
" -94.09618490844686, -91.91751639275596, -89.72377943401308, -87.51746790832203,\n",
" -85.30120953200326, -83.07774005710772, -80.84987476165341, -78.62047790110475,\n",
" -76.39243088444343, -74.1686]\n",
"lats = [33.9425, 34.62185468395183, 35.27195983702588, 35.89163680795418, 36.47971217805657,\n",
" 37.03502459436787, 37.5564322473648, 38.042820934293715, 38.493112624072936,\n",
" 38.9062744137114, 39.281327740305926, 39.61735768834621, 39.9135222108212,\n",
" 40.169061066104604, 40.38330426236194, 40.55567979862256, 40.68572049769913,\n",
" 40.773069741323866, 40.81748594212188, 40.818845619619054, 40.77714498701483, 40.6925]"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f30c1b16358>]"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAFTCAYAAAD87l5hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nO3d65Mk13km9uecvGdVZV27ByBuxIUgAJIQSEogtaJkWitqKe1Stlb2ajcc+2Ej1g47/GG/+D/x/+AIOVaSl7umbJGyuLsUbVJBUgIggIQAggABAtOX6rpXZeXl+ENN1nT39KUuWZWZVc8vomOmZ7qrzvR0Vz315nveI5RSICIiIiLKK5n1AoiIiIiIbsLASkRERES5xsBKRERERLnGwEpEREREucbASkRERES5pt/0lx//+MfVu+++u621EBEREdH+elcp9fGr/kLcNNZKCKHiOEbyMb7vYzKZYDqdIo7jVFbWarWg6zqEEBf+XCmFfr+P4XCYyv0QERER5Ylpmmg0Gg9koLQk+S2KIkg5u6guhNjY/a1LCAGl1JWLuzWwXv77OI4hhEAURRcC7Ko0TUOr1Zp/IS/f13Q6RafTAefFEhER0a6QUuLg4ODK/JMGpRSm0ym63S6iKAIAGIYBy7LgOA40TYNSamP3v4pUA+t5SikopdDr9TAej1deYKlUQqVSuTLxK6UQRRHOzs4QhuHK90FERESUF81mE4ZhbLTaqZTCYDDAYDB44O+klLAsC7Ztw7IsKKUyr75uLLAmgiDAycnJ6ivEzf9xSTDudruYTCZr3Q8RERFRliqVClzX3Up1M6m0np2d3Xi12jRN2LYN27YvtA9s08YDaxzHOD09XasCelNrwPn7GY/H6PV6K98PERERUVY23bd6FaUU4jhGu91eKKtpmgbHcVAqlbZadd14YFVKYTweo9vtrr5KAK7rolKp3BhalVIIggBnZ2epbfwiIiIi2rRN963eZJWr1ZqmoVqtwjCMrax544EVmH0hOp3O2pfsF+npSL7o7XYbQRCsdX9EREREm6ZpGur1+pWTkbZJKYXRaLTU1WrbtlGtVjdebd1KYAVml+zDMES32125PSBpDVjki5Js+BqNRivdFxEREdEmSSlRLpfhui6A7feFXkUphTAM0W63F75aLYSA53lwHGdj/4atBVbg/syv0WiEfr+/0jgqKSVqtdpCJWilFHzf5+grIiIiyg0hBEql0tb7QBeVXK0ej8cYjUYLFxoNw0CtVoOmaan/m7YaWBNpjLyyLAu1Wu3W/+hk9FW73Z7PGiMiIiLKQrInJ49B9bIkr8VxjNFohPF4vFDVtVwupx7GMwmsiTiOEUUROp3OSm0CQoj5+IdF+lo5+oqIiIiy4DjOfPN43oPqVZLMFwQBhsPhrXlK0zQ0m01ompbK/WcaWIH7X4DhcIh+v7/SbSxagl6lmZiIiIhoVZZlwfM8SClT302fZKjk1yQDJVXRKIo2sos/qbJOJhOMRqNrN7nX63XYtp3KfWYeWBPJDLB1dvaXSiWUy+UbS9AcfUVERESbZpomPM+DpmlrBcbkKvG9wDYPouffkj+L4/iBbGMYxny2a9qV3WRtSUHQ9/35/Ugp4bouTNNM5b5yE1iBdE7F0jRtvinrptDK0VdERES0CWmdVhXHMabTKXq93lr7cDRNQ6PR2MhmqESSrc7bmR7Wy+I4Tq3P9ODgALqu3/gxaWz+IiIiIkpYloV6vb5WUEsqqZ1OB9PpNJV1CSFQr9e3Nug/bTcF1q3/a6SU8Dwvldvq9Xq3XvJPStalUimV+yQiIqL9lYzeXDWsJkG13+/j6OgotbCa3Ha73V54p3+RZBK/kyG66/J9f+H/kKxPliAiIqLiW6eyGscxfN/H8fExhsNhyiu7r9frodfr7dR8+kwCazJM9+DgYO0TE/r9/kKhVSkFy7JWvh8iIiLab6VS6dbj46+SzIs/Ozvb2obw8Xg8P8lqF4Lr1ntYLzt/0sJwOFyp4XiRXlZgdvpWt9tdZZlERES0xwzDQLPZXCqsJhlnMBhstKJ6E9M00Ww2M7nvZd3Uw3p7ytuwZHeZ67pwXRdBEGAwGMD3/YVvo9/vo1qt3tpgzAorERERLSvZzLRMWE12/3e73cz6SZN+22RkVpFlHlgTyRfSNM35F3c4HC7UODyZTBbayCWlhKZpPL6ViIiIFrZIUSyxid3/qxBCoNlsFvbUrcsybwm4SXLfk8kEw+Hwxnmqi8xDS8ZbjUaj1NdKREREu8dxnPkpVjfJw+X/RBJWi7bhPNctATdJvsi2bcOyLMRxjMFgMJ+nKoSA4zi3nnx1/vZs22ZgJSIioltpmrZQWM3D5f/z6vV64cLqbXIdWM9Lzuf1PA+e52E6ncKyLCillhqOm9bxYURERLTbkuNOr5OXy//n1et1mKa5U2EVKEBgTWaWJRumkkqqbdvz95ehlIJpmrn5xiIiIqL88Tzv2mNO83T5/7xarbaTYRUoQGBVSqHT6QCYVUcdx5mH1VWOHRNCwLIsBlYiIiK6UpI3rgurURTh9PQ0F5f/E57nwbKsQh7JuohcB1al1IV+0+l0Ou8RsSwLrusu3RaQVGf7/f6mlk1EREQFJaVEvV6/Nlckx5/mKayWy2U4jrOzYRXIeWAVQlzbc+r7Pnzfn1dMk9MnFgmvmqZtYrlERERUcLVa7dpL6kopnJ2d5Wo8puu6KJVKOx1WgZwHVmBWlr9pdqpSCpPJBJPJBFJK2LYN13XnJ19d900npczVqyMiIiLK1k1Hr8ZxjF6vl7uWQs/zdrJn9bJCxHHXdRf6uDiOMRqNcHJyguPj42s/TinFKisRERHN6bqOSqVyZaUyOUI+GauZJ/tSfMt9YE2ObV1WFEU3Hu/KwEpERETALGtcN8JKKYUgCNDr9TJY2e3CMMx6CVuR+8CacBxn6c8ZDodXvvIQQsxbBoiIiGi/XXf0ajJntd1uZ7Cqxfi+jyxPJd2WQgRWKSXK5fLSnzedTq/8T2RgJSIiIuD+aZrXVVdPT09zHQiDIMj1+tJSiMAKzELrKiFzNBpd+R/JwEpERLTfdF2/sbra6XRyNRHgKkEQcNNVniTjq5Z1XYM0e1iJiIj2l5QSzWbzyrAaxzH6/f6Ne2HyImlb2HWFCqzJCVfLiKIIQRBceXtERES0f4QQaDab17YB+L6fqyNXb7MPG68KE1gBwDCMlT5vNBo98OqDo62IiIj2U71eh6ZpDwRWpRTCMJwfCV8U+7DxqlCBVSm1Umgdj8dXvopiYCUiItovnufdeDhAnicCXGcfNl4VKrDedFTrbcbj8QP/mQysRERE+8NxHDiOc23farvdLmQ/6D5svCpcYF2ljxW4elpAEZqpiYiIaH2maV47ESCOY3S73cL2giqlWGHNm1X7WM+Xy5VS6Pf7hXwVRURERMvRdR31ev3aNoDhcIjJZJLBytJz1QbzXVK4wLpqHyswO/kqaagejUYpr4yIiIjy5rZjV6fTKQaDQQYrS9eub7wqXGBNo4+1aLv/iIiIaDXJrNWrJgJEUYSzs7OMVpauXd94VcjAumofaxzHuHv3bmF7VIiIiGhxtVoNuq7feOzqrrht41XR+1wLF1iB1ftYiYiIaD+Uy2VYlnUhxMVxDKUUgiAo7ESA69x24lVSUS4qPesFrCLpY931BmMiIiJanm3bKJfLADAPcb7vYzKZ7HSv52Qygeu6V7Y/tNttSClRq9WunJSwLcmLhmVHixYysAKzHX8MrERERHRZpVJBGIYYj8fwfX9vWgEnkwkcx3mgqtztdueZKYqizAJrsskNWH4WfiEDqxAi01cHRERElF/Hx8dZLyETSRhMxHGM0Wh0YWRXv9/PrMqqlEK3251Xv5dRyNQnhOApVURERESXnA+tQogH+lZ938+kd/f8DPykLWAZhQysAI9VJSIiIrpsPB7PA6kQApVK5YGP6fV6Ww+tURTNZ+Cvct+FDaxsCSAiIiK6yPf9Cz2sQgiUSqUHPiYMw62NulJKXZh3u8r9FrKHFWCFlYiIiOiy5ETPZASoEALlchmj0ehCSDw9PYWmabAsC7ZtwzRNKKUghLhxnuv5+1n040aj0YWNb6tUWAsbWBf5IhERERHtm/F4fOHABCEE6vU6er3eheCYXKZPLtUbhjEPsEKIeSU0eUt6T6WUCx/ilPSunsfASkRERLTnfN9HuVy+EFhN00Sz2UQQBOj3+1eOBg2CAEEQYDAYXHvbUkq0Wq2FclgyUuvy5f9V2hAK2wiaJHwiIiIiui/pTz0vGQlqmiYajQaazSZM01z6thuNxkL5K2lNOD9SKxFF0dJ9rIVOfOxjJSIiInrQ2dkZwjB84PL7+eBar9fRarVgWdZCt1mr1S60GtxEKYVOp3Pt352cnCAIgoVDq7jpA4UQKq/Hl8VxjE6nA9/3s14KERERUS45jgPP8wBcP2EpmY3a7/evrIgCQKlUQqVSWTisDgaDG1sLEp7nwXEcSCmTvtkr76CwgTU5LWE8Hme9FCIiIqLcSkZblUqlG6cAJJuq+v0+xuPxvBJr2/Z8I9YioijC0dHRwutzHAfVahVSyt0MrIumdyIiIqJ9J6VEpVKB4zgArt/AHsfx/O+W3TMUxzHOzs4eOCb2NoZh4ODg4NrAWtge1qQHg4iIiIhul+zaPz4+xnQ6vXa8VHJ5ftmspZSC7/tLh1UAV04tOK+wY60AQNcLvXwiIiKirYuiCO12G6Zpzi/FL7rzP7nynsxpjeMYYRgiDENEUbRyq2a1Wr3x7wud+FhhJSIiIlrNdDrF8fExbNuG53kPHOl6VSA9/5ZG26imaQuNymJgJSIiItpjk8kEk8kEtm1DKZVqIL2JbduoVqsLHQfLwEpERERE14602gTP8+C67sKTBwodWIH7JWsiIiIiyrekBUDTtIXDKrADgZVhlYiIiCj/LMtCrVZbqAXgssIHViIiIiLKt2VbAC4rdGC9bn4YERER0a46X6FMfn/5fWA2vioMw8zWCcz2GzUaDei6vnJYBRhYiYiIiDInpYSu6/M30zQvDPC/ynVtkcnn9Hq9zAKrYRhwXXd+pOs6YRUoeGCNoijrJRAREREtTNM0GIYBXdfnv2qadmEg/6Lh7qqPS2andjqdlU6cWoeUEo7joFQqPVD5XRcDKxEREdGWNJvNK8NcGsEujmNMJhP0er2tbkq3bRulUgmGYQBI599yWWEDazLYloiIiKgoJpPJWpuPrpJFVVXXdbiuC8dxAGx+Nn6hAyt7WImIiKhIxuMxHMdJLbAqpTAej7dSVZVSzqupt/XXpq2wgRVgSwAREREVSxAEqQTLbVZVLcuC67qwLAvAZi7536bQgZUVViIiIiqaddsClFKYTCbodrsbq6pu+5L/revJ9N7XIIRghZWIiIgKQ0oJz/NgWdZKYVUpBaUUOp0OfN9PfX1CiPkuf03T5n+WB4UNrACPZSUiIqJicBwHnuet3PcZxzF8399IVTUJ0rZtQymVeTX1KoUNrAyrRERElHeapqFWq0HX9ZWC4CarqkIIlMtllEql+ft5qaheVtjAyv5VIiIiyrNSqYRyubxyENxkr+q6Fd9tK2xgZf8qERER5ZFhGKjVapBSrnx5PZkAkHZVNY21ZYGBlYiIiCgFQghUKpVUDgaYTqephlVN0+B5HkzTLFRQTRQysPKUKyIiIsoLIQRc113r8v9Vt5mGq/pUi6iQgRVgDysRERFlS0qJUqkE13Xn76cljWAppUSz2YSmaYUNqolCBlZWWImIiCgrmqahXC7Ph+pvIgyue5u6rqPRaMyPUC26QgZWgBVWIiIi2i5d11GpVLZyROk6t20YBhqNRmEmACyisIGVFVYiIiLaBtM0UalUYBgGgHz3gdq2jWq1WsiNVTcpZGAVQrDCSkRERBsjpZwfUyqE2HoAXCUUu647n626awoZWHnKFREREW2CZVkolUowTRNAdtXUZe83rXFaecXASkRERHtN0zS4rruR3f7bUKvVYNv2zoZVoKCBlf2rREREtK7kkr+uz+JQngLfImsRQqDRaMAwjFytfRMKF1iVUgiCIOtlEBERUYF5npf7S+i6riOKoiuvLO/SjNVFFDKwTiaTrJdBREREBaXreu7DKgA0m835GqMoQhRFCIIAURShXC7vzIzVRRQusAKz83WJiIiIVlGv13Mf9C7PUNV1Hbquw7KsecU17/+GNBUusPq+n/USiIiIqKBKpVLhNlVdtk9BNVGo/7E4jtkOQERERCtJjlQtemDdR4X6HxNCsMJKREREK6nVantZndwFhQqsQRBwBisREREtzXEc6LrOwFpQhQmsSimMx+Osl0FEREQFI6WE53lsBSiwQv3PsR2AiIiIllWtVllZLbjCBNZk/hgRERHRokzThGmaDKwFV4jAynYAIiIiWkW1WmUrwA4oxP+gUortAERERLQUXdcZVndEIf4XhRAIgiDrZRAREVGBsA1gdxQisAKzYb9EREREtH8KE1gty8p6CURERFQgrLDujkIEViEEXNfNehlERERElIFCBFYAPJ2CiIiIaE8VJrAqpWDbdtbLICIiooJgoWt3FCawSikZWImIiGhhcRxnvQRKSWECK8CNV0RERLS4IAgYWndEoQKrUoqhlYiIiBY2GAwYWndAoQKrEIJtAURERLSw6452V0pBKbXl1dCqGFiJiIhop11VZVVKIY5jhtaCKFRgBbjjj4iIiJYzGo0e+DMpJSaTCcbjMVsGCqBwgZWIiIhoGUopjEajB6qplmVhOBxmtCpaRiEDK6usREREtIzhcDhvAUjaATRNg2mazBUFoGe9gFUIIdhzQkRERAuL4xhHR0cAZjlCSgkhBEqlEgNrARQusCql+I1FREREK1NKQUoJx3HgOE7Wy6EFFC6wEhEREa3CNE04jjOfOCSEYBGsIAoZWPnNRUREROfpug7btuE4DjRNA3B/1mpSUQUYUouKgZWIiIgKyTCMecU0CaLnMwLzwu5gYCUiIqJcE0JA1/X5m2EYMAxj/nfMBbuvkIGViIiIdo9pmjBNcx5MpZTzS/nJdCAG1P1UyMDKb1QiIqLdYds2KpXKfNTUVc/zfO7fb4UMrJzBSkREVGxCCDiOg3K5PJ+Lel6yWSr52PO/0v4pXGAVQiAIgqyXQURERCuQUqJUKsF13XkATU6eEkIgjmOEYYjpdIowDOdvpmmiXq+zJWBPFS6wJseqERERUbG4rgvP8yCEQBRFF4JpEAQIw/Daz51Op+j1eqhWqzxEaA8VLrCyukpERJsUxgpBFGMaKYSRwjSKEURq/jaNYoSxwjS64eNiBZwrrlxVZrlce1nkYwDA0MT9NykvvK9LAVOT0DUBQwqYmoCunfsYKWCce19uOfT5vo/T01OEYbhQ8UlKCcuyYNs2TNOc/znD6v4pVGBVSmE6nWa9DCIiyoEoVhgHMUbTCKMgwnAaYziNMJrGGAWzX2fvRxjd+7jLfz+aRveC5/0gGu/RRTxNYB5gXUPCNTW4poRjzH517/1aMjQ45953TW328ZffNzWY2oOX7A3DQBAEiKIIURTduCbTNOchNTkAgAGVChdYWWElItodSimMghjdcYjuJERn/muE7iREdzz7s94kxGB6P2SOghjjIF7oPjQJuIaGknk/hJVNDYdlE44hYWoSpn6xYmlqFyuRSdVy/ufy/p+fr3Cer24+UL28InNd/qOrYtn5m1EqqQDPqrjBuarurOo7e39W8VUI43geyJO/D89Vi4N49vF+qDAOovkLgGEQoz0KMJrGGAezr3cQLZbkk693EmD/5H/8IupeCR9++OGVH59UUR3HgWma88v9DKl0XqECKzdcERHl2ziI0LkXMmdB897798Ln+RDancxC6XVBSAqgauuoOjo8S0PTNfB47VLlz9QuVPfmf3au8mddUfErMvP2D9mIIIovVqeDiy8grvrVjwSqZRcA0Gq15rd1fte/lPKBo1OJLhM39ZAIIVSeNjhFUYSjo6Osl0FEtHemYYzTUYCTYYCTQYDj87/eezseTDGcXl31TMKnZ2uoObMQWrV11O4F0ppz/+9qtg7P0VGxtK33WFJ6DMNAs9lkAKWFCSGglLryG6ZQFVZWV4mI0hXFCmfjEMeD6b3QeT+Ang+knfGDu7d1KdAqGWiVDTzZsPHy4xU0XQMN10DVuRdM7wVShs/902g0sl4C7ZDCVFiVUuj3+xgOh1kvhYioMIIoxke9KT7sTfGL3hQf9vx7v/dxtx+gPQoe2GQkBdBwjVkYLRk4KD/4+4OyCc9mCKXrGYYB0zThOA40TXvgYACiy3aiwqqUunE+GxHRPgpjhePBvUDanQXS88H0eBBcGJekSeChiomHPQtfeMLBQdnAQel+IG2VZxVSXTKI0nqCIJhfGa1UKhmvhoquUBXWKIpwfHyc9VKIiLZGKYXTUYgPuj4+ulcZnQXTWSi9O5giOtc2KgAclg08XLXwsGfiY94snM5+b6FVZhil7Wo2mxdmqBJd56YKa2ECK3Bv/MlohF6vl/VSiIhSNQ4i/Lzj4932BO+d+Xj3bIL3OhP8/MzH6NL4pqarzwJpxcTHqrMg+tC9QHqnYsDQeOmV8uPOnTtsB6CF7ERLADD7hziOA9/34ft+1sshIlpKrBTu9qd478zHe2cTvHvv1/fOJrg7uL+pVAB4yDPxeN3GL32sjMdqNh6pziqlD3kmbJ1P/lQMul6omEE5VqgKayKOY5ycnNx6WgYRURaGfoT3OrNK6c/uBdL3znz8vDOBH95/TC2ZEo/XbTxRt/F43Zr9vmbh0brNUEo7wXVdeJ7H0Va0kJ1pCUiwn5WI8mASxHinPcbbJxO8dTLG26dj/Kw9wcnwfrVUCuBhz8ITSSC9F06fqNtouDqfyGmn1Wo1OI6T9TKoIHamJSAhhICmafA8j/2sRLRxsVL4RXc6D6Vvn8zeft7x5zvwLV3gqaaDlx+v3AulNp6oW3ikasFktZT2FDdbUVoKGViB+/2sk8kE0+k06+UQ0Y7ojkO8fTqehdN7AfWnp5P5ufUCwCNVC8+0HHzlk3U83XTwTMvBx6oWNO6+J5qTUnKzFaWmsIEVmIVW0zQZWIloadMwxrtn9y/lv3Uywdsn4wuX86u2hmdaDr72qSaebjp4uuXgqaYNx9AyXDlRMdi2nfUSaIcUPrAahpH1Mogo54Ioxk9PJ3jj7gg/Phrhx0dDvH0yQXjviCdDE/h4w8avPF6ZV0yfbjlosseUaCW6rnOzFaWq0IEV4MgMIroojBTeaY/PhdMR3joZI4hm4bRiaXju0MW/+Owhnj108HTTwWN1m8P0iW4gpYRSCotsxBZCoF6vb2FVtE8Kn/bYH0O0v8JY4d32BD8+GuGNuyP85GiEN49HmN4LpyVT4rlDF//spQM8d1jC83dcfMwzWfUhWlKpVIJt2zg9PUUcxzd+bLVahaZp/DmjVBU+sAohkjEIWS+FiDYoihV+3jl3Wf/uCG8ejzEJZ0+eriHx7KGLP3jxAM/dcfH8oYtHahYknzSJ1ub7PsrlMprN5o2h1bZtWJbFsEqpK3xgVUpB0zSEYZj1UogoRZ1xiFc/HODVD4d49cMh3jwazY8otXWJZw8c/N6nm3j+jovnDkt4rMZd+kSbMp1OEccxNE27NrRqmoZqtcorn7QRhTw44Lw4jtHpdHhUK1GBxWp2af+VD4d49RezkPpeZ/YzrUng2QMXn3qohOcOXTx36OKJBntOibatXq/Dtu35Fc0gCDAYDObPvwcHB2wFoLXs3MEB5yWHCBBRcYymEV6/O5pVUH8xxGsfDdH3Z0ctV20Nn3m4jH/8QhMvfqyM5+64PKaUaMMqlQomkwmCILj2Y8bjMUzTnFdQTdNErVbD3bt34Xkewypt1E4EVk4KIMovpRQ+6k/nl/Zf/XCAt47HuLcvCk81bfzmJ2r4zMNlfObh2aV9PukRbY8QAqVSCWEY3hhYfd9/4GdTCAHXdeE4Dn9uaaN2IukxsBLlRxDFePN4jFc/HOKVe5f3k2H8jiHxwp0S/uWvPIQXHy7hUw+V4Nn8+SXKkm3bC12tVEohDMML88+VUpy3SluxE88UpmlC13VuvCLKQBDFeOPuCD98v48fvj/AKx8O4Iez8unDnonPPVqeV0+fbjnsPSXKGdd1ASxW/On3+6jX6/OAmsxnJdq0wm+6Amav8KIowsnJCX9wiDYsjBTeOBrih+8P8MP3+3jlF8P5aKlnWg4+92gZL32sjE8/XMJB2cx4tUR0EyklDg8PIYTAdDrF6enprZ9jWdaF0EqUlp3edAXc33jleR663W7WyyHaKWGk8OOjexXUDwZ45RcDjO+Nl3q6aeNrn2ric4+W8dlHKqg6O/GQQrQ3kl3/y2xg9n0fnU6HI6xoq3bm2UUIAcdx4Ps+JpNJ1sshKqwwVvjJ0Qg/er+PH7w/C6jJ/NOnmjb+8QtNfO6RMl56pIy6a9xya0SUZ1LKC5f3F8UWPNq2nQmswCy0VqtVBEGAKIqyXg5RIYSxwptHI/zwgwF+9H4ff/OLAUbTWUB9smHjq8838PlHK3jpkTIaDKhEO2U6nc4rrAAWPjnytuNZidK2U4EVmP2w1et1nJycZL0Uotz6eWeC77/bx/fe6+GH7/cxvBdQn6hb+OonG/jsoxV87pEyGiUGVKJdNp1O52F1mZMjz4dcom3YycCqaRoqlQr6/X7WyyHKhYEf4Qfv9/G9d3v4/ns9fNCdAgA+5pn4rWcb+OXHZj2oTQZUor0TBAFMc7ZBcpnASrRNOxdYgVkfTqlUgu/7mE6nWS+HaOuieLZRKgmor304RKQA15D4/GMV/PPP3sEXnqjg0SqH9BPtu8lkAsMwltp45TgOq6y0VTsx1uo6cRzj6OiIrwRpLxz1p/jeez18790e/vrnffQmEQSATx66+MITFXzhCQ+ffqgEQ+OuXqJ9lQTS8/s8dF1Hs9mElBJxHOP09PTGKquUEgcHB5wQQKnb+bFW1xFCoFar4ezsLOulEKVuEsT40Qd9fP+92aX+d9qz6RitkoFff7KKl5/w8CuPVbiTn4jmLMuC53mI4xiTyQSTyeTClUgpJZrNJtrt9rXHtNtY3QAAACAASURBVFarVVZWaet2usIKzPpsBoMBBoNB1kshWotSCm+fTvC9d2dV1L/9xQDTSMHUBF56pIwvPOHh5cc9PN20+WRCRNfSdR21Wg2GYUApNb8Keb5iGscxzs7OHmirs22b81dpY26qsO58YAVmP3ij0YibsKhwpmGMH34wwHd+2sVfvdPFR/3Zk8dTTRtfeNzDy094eOmRMmydTx5EtBzHceB5HoQQV77IVUrh7OwMvu8DmIWJw8NDhlXamL0PrMAstI7HY/R6vayXQnSj9jDAd3/Ww3fe6eD77/UxDmJYusDLj3v4tSer+NUnPBxWeOQpEa1PCAHP8+A4zrWhtd1uYzqdwvM8uK7LKzi0MXvbw3qelBKu60JKiU6nk/VyiOaUUnjrZIy/eqeL77zTxesfjaAAHJYNfPW5Br70ZBWfe6zCKioRpU4phW63C9/3r7zUf/7YVoZVytLeBFZgltxt24bneay0Uqb8MMYP3+/jO+908d13evNL/c/fcfGvv/gwvvRUFZ9oXV3xICJK201TAXzfR71e3+JqiB60V4EVwFJz5ojSdDoM8N2fzaqof33vUr+tS7z8eAX/6uWH8GtPVjm4n4gycVX7n1IK4/EYhmHANE2+gKZM7V1gBW5+JUmUluRS/3fe6eI7P+3i9bsjALNL/b/zXANfeqqKzz1agcVL/USUsasOAVBKYTQaoV6vc6MVZW7vAqtSCnEcZ70M2lGxUnj9oxH+8q0z/Me3O/MjUF+44+J/+NWH8aUnq3iGl/qJKGeuq7Dqus6wSrmwd4FVCIFSqYThcJj1UmhHRLHC3/5igG+/1cG33+7geBBAlwK//FgF//KXH8KXeKmfiHLucmBNqque5zGwUi7sXWAF7m++mkwmWS+FCiqIYvzg/QG+/dYZ/tPbXZyNQ5iawBc/7uF/+gc1fOmpKirWXv54EdGOkFIyrFJu7OUzqpQSlUqFgZWWMgljfP/dHv7yrQ7+6p0u+n4E15D4B09W8eVnavjVJzy4Jjf0EVHxRVF07WxWoizsZWAFZqHVsqz5CR5EVxlNI3z3Zz18+60zfPdnPYyDGBVLw68/NQupLz/ucdMUEe2E8xuvOE2H8mavA6vneTg+Ps56KZQzvUmI77zTxbff6uB77/YwjRTqjo5/9MkGvvxMDZ9/tAJdY9WBiHYXK6uUN3sbWIFZaDVNE9PpNOulUMYGfoT/+HYH33rzDH/98x6ieDZ+6r/+TAtffqaGFx8uQ5N8ACei3bUrR7HTbtr7wOp5Hk5OTrJeCmVgEsT4q5918c2ftPH//mxWSX3YM/EvPnsHX36mhhfu8BhCItofSqkr57ES5YG46RWVEELt+iuuOI7RbrcRBEHWS6EtCKIY33+vj2/+pI3//NMuRkGMpqvjHz5bx29/ssGQSkR7yzAMuK4L27YhhOBjIW2dEAJKqSu/8fY+sALAdDrF6elp1sugDYlihb/5YIBvvtnGX77VQW8SoWJp+M1P1PBbzzbw2Ud4uZ+I6LyDgwPo+l5fhKUM3BRY+d0IQNd1GIbBKusOUUrh9bsjfPMnZ/iLvz/DyTCAY0j8+lNVfOXZBr7wRAWGxt39RERX8X0fmqaxykq5wcCKWaKvVCpot9tZL4XW9PbJGN98s41vvXmGD7pTGJrAr37cw1eebeBLT1ZhGwypRES38X2fc1gpVxhYMQuspmlC13WEYZj1cmhJH3R9fPMnbXzzzTP89HQCTQC//FgF/+rlh/EbT/PEKSKiZU2nU4ZVyhX2sN6jlMJkMkGn08l6KbSA3iTEt948w5+90cZrHw0BAC8+XMJXPtnAb36ihoZrZLxCIqJiu3PnDo9mpa1iD+sChBCwbRuapiGKoqyXQ1cII4X/790evvHGKb7zThdBpPBU08b//Gsfw28928BDnpn1EomIdkYcxwyslBsMrJeUy2V0u92sl0HnvHk8wjdeb+PPf9LG2ThEzdHx+59p4Xefb+LZA/ZYERFtQhiGnBRAucHvxHOEEHAcB/1+H3EcZ72cvXY6DPDnP2njG2+08dbJGLoU+NKTVfzuCw386hNVHo1KRLRhvNpIecIe1kvYy5odP4zxn3/axZ+9cYrvvdtDpIAX7rj43eeb+K1n66g6fH1FRLQtruvC8zxexaKtYQ/rEpJeVsdxMB6Ps17OzlNK4dUPh/jGG238xZtnGEwjHJYN/Hefv4Pfeb6JjzfsrJdIRLSX4jjmUa2UGwysVxBCoFqtIgxDHiawIR/2fPzZG2382RttvN/1YesSX36mht95voHPP1rhyVNERBljSwDlCVsCbhBFEU5OTtjPmhI/jPHttzr49393gh+8PwAAfO7RMn73+Sa+/EwNJVPLeIVERJSQUuLw8JAVVtoatgSsSEqJer2O09PTrJdSaG+djPH1107wf/24jb4f4WOeif/+iw/jd55v4GHPynp5RER0BRZrKE8YWG8ghIBhGKhUKuj3+1kvp1CG0wh/8eYZ/t1rJ3j97giGJvDlp2v42qea+PxjFUi+Yiciyr04jqFpvPpF2WNgvYUQAq7rIggCTCaTrJeTa0opvH53hK+/doJvvXmGURDjyYaNf/Mbj+KrzzVQ4y5/IqJCYWClvGCCWICUcr4JKwzDrJeTO91JiP/7x218/bUTvH06ga1L/MNn6/ivPt3Epx8qsf+JiKigoiiCYfCoa8oeN10tSCmFOI5xfHwMfk1mX48ffTDA1187wV++1cE0Unj+0MXXPt3Ebz/bQMniK3IioiKTUuLg4IDHs9LW3LTpioF1CUopTKdTtNvtrJeSmfYwwP/5xim+/top3u/6KJsa/tFzDfzep5t49sDNenlERJSSRqMB0zR5lYy2hoE1RUopDAYDDAaDrJeyNbFS+N67Pfy7107wnXe6iGLgpUfK+L1PNfFfPlOHbfDVNxHRLuEpV5QFjrVKkRAC5XIZQRDA9/2sl7NR3XGI//D6Kf701WN80J2i7uj45589xNc+1cITdZ5ARUS0izRNQ6VSYVilXGGFdUVxHOPo6Ggn+1lf/2iIP37lGN968wzTSOGlR8r4gxdb+C+ersHQWE0lItplBwcH0DSNgZW2jhXWDTFNc2eqrJMwxrd+coY/eeUYbxyN4BoS/+SFJv7piwd4uuVkvTwiItqCSqXCsEq5xMC6IiEEdF0vfGD9eWeCP331BP/h707R9yM82bDxv3z5MXz1Oe70JyLaJ4ZhoFTiKELKJwbWFQkhYJomhsNh1ktZWhQrfPdnXfzxKyf43rs9aBL48tM1/NMXD/DZR8p8sCIi2jNCCNTrdT7+U24xsK6haMOU26MA//7vTvF/vHqCj/pTtEoG/vUXH8bvfaqJg7KZ9fKIiCgDuq6jUqlw3irlGgPrGorww62UwqsfDvEnrxzj/3mrgyBS+PyjFfyb33gEX3qyBl3jq2kion2jaRocx4HruhBCzN+I8oqBdQ1KKei6nsvjWidhjD//cRv/9pVj/P3xGCVT4vc/08Lvf6aFjze4iYqIaN9IKechVdNmexQYUqkoONZqDUophGGIdruNOI6zXg4A4HgwxZ+8coI/ffUY3UmEZ1oO/uDFA/z2J+twTW6iIiLaJ0KIeUjVdX3+Z0R5xJOuNkgpBaUUut0uptNpZsH1jbtD/NGPjvCtvz9DHAO//nQVf/jSITdRERHtKdM0Ua/XARSjhY2IgXUL4jieB8M4jhFFEcIwRBiGiKJo/n6aX88wVvhPb3fwRz86wisfDuGaEl97oYX/5pcO8GjNSu1+iIioWAzDQKPRYFClQmFgzVBSgQVm/xGdTgeTyWSt2+z7Ib7+2in+7d8e46P+FI9UTfy3v3SIf/JCk7NTiYj2nK7raDabDKtUOAysORLHMfr9Pkaj0dKf+97ZBP/73xzjG2+cYhzE+NyjZfzhS4f4tSer0CQv+xMR7TtN09BqtbjrnwqJR7PmiJRyfvRdv9+/9eOVUvjrn/fxRz86wnd/1oOhCfz2s3X8s88e4tkDdwsrJiKiIpBSotlsMqzSTmKFNSNxHEMpNe9tPd/nGgTBfCzVH/3NEX56OkHd0fEHLx7g9z/TQqNUrAMLiIhos4QQaLVa0DSNYZUKiy0BBZB8nTujKf7XP38df/y3d9GdRPjEgYM/fOkQX3m2DlNnPxIRET2o1WpB13WGVSo0tgQUQPIgE8YK/9sPPsLLT1Q4loqIiC4QQsC2bei6DsMwoOv6fHMVnytol7HCmkMnvRGCYTfrZRARUY5omnZh9z8DKu0atgQUjFIKvu9jPB7D9/1UZ7cSEVHxJIcAcEMV7TIG1oJKDiMIggDD4XDt+a1ERFQ8tm2jVqsxqNLOYw9rQSWXfUzTnDfTj8fjjFdFRETbUi6XUS5zLwMRt50XhJQS1WoVtm1nvRQiItoCx3FQKpUYVonAwFooQgjUajWYppn1UoiIaMNKpRKPVyW6hz8JBSOEQL1eZ2glItphmqZB19m1R5RgYC0gKSXq9ToMgydeERHtIsdxsl4CUa4wsBaUlBKNRoOvwImIdoxlWexdJbqEY60KTCkFpRSOjo44q5WIqOCEEPPNtQyrtI841mpH3fuPhWVZnNFKRFRghmGgXq9DSsmwSnQFBtaCk1IysBIRFVilUmELANEt2MO6AziblYioeDRNw8HBAcMq0QJYYd0Ruq4jDMOsl0FERAtwXReVSgVCCIZVogUwsO4AIQRM02RgJSLKOSklarUaDMPgoQBES2Bg3QFCCDiOg9FolPVSiIjoGpZloVarsapKtAK+vNsRfLVORJRflmVxCgDRGphwdghPRiEiyh/btlGv1xlUidbAwLojhBAolUpZL4OIiM6xbXveBkBEq2Ng3SHJ5isiIsoewypRehhYd4gQAq7rZr0MIqK9x7BKlC4G1h0ihOAZ1EREGTNNE9VqlY/FRCliYN1BPPmKiCgbQgjUajVObSFKGX+idowQAuVyOdXb1DQt1dsjItpVnucxrBJtAH+qdpCmadD1dM6E0HUdh4eHaDabqd0mEdEuMk0TjuOwFYBoAxhYd1Ram68cx4FSCoZhoNVqoVqtsnpARHSJEIKzVok2iCWzHZQc1drv96GUWuu2LlcLHMeBbdsYDAbwfX9ezRVCYDgcrn1/RERFxE1WRJvFwLqjkoMEBoPByrdhGMYDD8DJGdiVSmXeK5t8jOu66Ha78H1/9YUTERWMZVmc0EK0Yby2u6OSwLrOA+hNvVhCCEgp5+diCyGgaRpqtRp3yBLRXmF1lWjzmCp22LrHtcZxvPTnSClh2zYODg7gOM7K901EVBR8gU60efwp22HrVll931+pJzWpvnqeh2azybFYRLSzDMNg7z7RFjCw7rh1qqxBEKx131JKGIaBZrO51u0QEeVVsumUiDaLgXXHpVFlXff++WBORLvqqs2pRJQ+BtY9sE6VdTKZrNTLeh4vlxHRrjJNM+slEO0FBtY9sE6V1fd9Vg+IiK7BEwCJtoOBdU+sWmVVSq1dIWWFlYh2kaZpfHwj2hIG1j2xTpV13ZYATdM49oWIdg4noBBtD1PEnnFdd+nPiaIok/slIsqzMAzZMkW0JQyse0RKOT9OdRnrBtZ1DzAgIsqjOI7ZEkC0JQyse0YIsXS1MwzDVB6ULcta+zaIaDcIIXZihum686qJaDHc3rhnhBCoVCoYjUYLf05SRVjniUVKiVKptPZcVyLaLNM0oWna/E3XdUgpIaWcPwbEcYwoihAEAcIwRBRF818TQogHbkfX9fn7wP0NmaPRCMPhcO1++Sz4vg/TNAsfvInyjoF1DyVV1kVDaxo9rMDsiVBKWcgnJaJdZhgGHMeB4zgAMA9f14WwJHSapnlhkogQAnEczw8MOf/nV91W8melUgmlUgmTyQSDwQBhGKb+b9yU6XS69gt6IrodA+seWrbKGkVRag/GrutiMBikcltEtB4pJZrN5rx6usrP+eXPO79zftHbSz7Otm3Yto0gCNDtdgsRXIMgYFgl2gL2sO6xRXtZk8t96/axcvMVUb4k1dDzl/uzlIRf0zTRbDZXHspvWRZqtdrW+ubTugpFRNdjYN1TUkpUKpWFP/7s7Cy13bC2badyO0S0vm63m8s2HSEEGo3GUjOcTdNEq9VCrVaD4zio1Wo4PDzc+Fg93/c5LYBowxhY99gyFc8oilJ5YpNSolqt5qKaQ0SzsBUEQe4CV1L5bTabtz5eGIaBZrOJer0OwzDmIVdKCU3T4HkeDg8PN3aAyXg8zt3Xj2jXMLDuMSEEyuXywuFxMpmkUklIemiJ9o2maTAMI+tlPCCvgSuZNNBsNq/8e13X0Wg00Gg0LgTVq25HSolGo7GRdXK0FdHmcdPVnkuqrItuhOp2u/Pd/qtWSZMpBePxmA/0tJN0XYdlWdB1fR6kpJQXds1PJhOMRiNMp9OMVzuT16seybzWRqOBdrsNYPb1rVQq8x7VRdae3E61WkW32019nePxGK7r5vbrSFR04qZX1UIIlcdX3ZSuOI5xdHS0cIVF0zS0Wq21L6+FYYjj4+O1boMoL5LRULZtzzcP3RReknFQSimMRiOMx+MLm3eklPPZpYZhwDAMaJoGIQTOzs5SnWnsui48z8t12Eoen4IgmFepV1lvHMfo9/tLzaJehGEYS/fcEtFF98bhXfmDzcBKUEphMpmg2+0uHFp1XZ+Pw1lVHMcYDAYYDocr3wZRlkzTnIdU4Pp5o7dJfu6SwHp+sP5Vt6mUwmAwSG1EXKlUQqVSyXVgTZNSCu12O/Xq9uHh4YWxXkS0HAZWulVS6VkmQKZRUYjjGMfHx7ncpUx0Hcdx4HkegNVD6rriOMZ0OkWn01m7/3TfAisw+/qdnJykOpKqUqmgVCrt1deRKE03BVZeuyAA9zcllMtl3LlzZ37izU2CIMDZ2dlaYVMIgVqttvLnE21bqVRCtVp94LjSbZNSwrIstFqttat6o9EolVnLRZKMzUrz/y+vm9eIdgEDK12QPAknY2Bu29G8boVHCAHDMLY24JtoHZVKZanJGpuW7KJvtVowTXPhz3McBwcHB6hUKvPNYKenp4jjeG8CV/K1S/MF876FfqJtYksA3SiOY5yent56RKJt26jVais/kU8mE5ydna30uUTbUK1W4ThObsLqZUqp+Wai6x63DcNAtVqFpmkXphZMJhMAsxOi9m3TUBzHGA6HqfUDl8vlXL2oISoS9rDSWhYNrUlf3ypPeEEQ4OTkZNUlEm1UvV6HZVm5DyHJUavnnZ9GkEwZuOz8uK19FMcxOp1OKpMXNE3DwcHB3n4tidbBHlZaixACzWbz1j658XiMwWCwUk8rd9ZSXjUajUKEVQDzntrzb8lpT7quX/tvyGrjWF4kbVBpiKLoxio3Ea2GgZVulTyZLTLGajgcIoqipR+sk6HeRHkhhJj3hu5zmNsXUsql+oBv0u/3GViJUsbASgs5f673baG10+msdB8cuk15IaVEq9W6sSpJuyWZkpKGZEQgQytRepgOaGHnz/W+6Uk8DEN0u92ldhxv+qxvokUZhjEfFcWwul9M00ztSs9wOOR8aaIUMbDSUhYNrePxeOljV5O2gHq9vu4yiZZmGAaazea80s+wup9KpVJqt9Xr9RhaiVLCwEpLS4LlbdXQOI4RBMHSt22aJiqVyjpLJFqYaZrzoGqaJsPqHhNCwHGc1FqTJpMJAytRShhYaSWLbpJaZbeslBKu6y502hbRqkzTRKvVQr1enwdVIqVUqt8L3W6XvaxEKeC2bFrZIg/Ck8kE1Wp16TmPUsr55yVDzYnSYFkWKpXKfHg+0WW3zZxexnQ6hVKKVXuiNTGw0soWudSllMLdu3cBAHfu3Fnq9oUQqNVqODs7S2WgN+23ZFMfgyrdhI81RPnER21a2aKXuZJTdqbT6dL3IYSYnzJEtCpN0+ZjqhhW6TpxHPOKDlFO8ZGbVrbsZoLJZLJSL1cSWtMa6k37JZlqwc1UdBshBCusRDnFwEorUUphOBwu9TnrPBEIIea7uIkWxbBKy1jllL5FcNMV0foYWGlpcRyj2+0ufYk/iqK1RrwklVbP8+A4DgzDYAihayVtAAyrtIhNbvBMNl4R0eq46YqWklRWx+PxSp8/mUzguu7KAUJKiVKpNA++QgjEcYzhcLh0xZd2VxJWhRAMq7QQpdTSc6MXNRqNYFkWvxeJ1sAKK10r2SyVHLGqlMJ4PMZgMFj5Nn3fT6XSIKWcV840TUvtDHDaDZ7nMazSUoQQsG17I7e9yoZTIrqIFVa6UhJO+/0+dF2HrusQQqxdxfR9H+PxONXTZBKGYWysQkLFoWkaq1m0NCHERqeRjEYjlEolfl8SrYgVVrpSUm1wHAfT6RSj0Si1S+69Xg/D4TDVIws3WR2hYknzLHjaP5sKrau2URHRDAMrXUtKiUqlspEjUgeDAQaDQWqhNTkDnPabEGKtHmnab8mx0JsQhiGiKNrIbRPtAwZWupEQAtVqdSNVh+FwmOoDuBACus4ul33G6iqty7KsjT2OjEYjTgsgWhEDK90qOSLVMIzUb7vb7aZaZWVbwH4zTZPVVVpbtVrdyO2yLYBodQystJDkHPa0Kw9BECAIglSqDmwLIIZVWldypWYTh5TEccyNoUQrYmClhQkh0Gw2U+8R7PV6qV0m0zSNoZWI1iKl3FiVNe0Np0T7goGVFiaEgJQSnufh8PAQnuelMpoqDEO02+35vNd11+h5HnsZiWgtUsqNtBhNJpONXglgjyztKgZWWloSXF3XxeHhIer1+tr9rUEQ4OTkJJXQKqVEuVyG53lr3Q4VD1sCKC3Ji/NNmEwmGwuWySEvDK60axhYaWXJSUKWZaHRaKxdjYiiCCcnJ4iiKJXQ6jgOarXaWrdDRPsrOQo6bePxeOXHuDiOr3xLQqoQAmEYbjQUE2VB3PQNLYRQ/IanRSml5pf2S6US+v3+Sr1aQgg0Gg0YhrF2xUwphel0ina7vdbtUDG0Wq2NTLOg/RXHMY6OjlINf6Zpol6vL9RSldxvGIaYTqcIggBhGAK4f7XrfPEgGUEYhiH6/T48z4Omabz6QIUghIBS6spvVgZWSlUSUO990+Hs7Gzlc7ST0Lpun6xSCmEYotvtcofujjs4OOAsXkqVUgrD4RD9fj+127QsC7VabeHHtuFwiF6vd+vH2baNarUKKeX8ca/dbsN1XZTLZQBsm6F8uymwsiWAUpW80k9e+TcajZX7wNrtdmrjrnRdR7PZ3MhoLsoP7r6mtAkhUCqVoGlaqre5jNtGbOm6DsdxLhzwkjzuNRoNDIdDnJycIAxDtglQYfGZm1J1+YE4OSrTsiy02+2lT7YajUYol8trVwWSzzdNE61WC77vo9/vzy+t0W7g0Ze0KZVKBZ1OJ5XbWvbxLLmkr+s6dF2HYRgwDAOaps2rqcntnr/t5HNKpRIGgwH6/T5qtRqrrFRIDKy0cUIIaJqGVquFXq+31Gkvk8kEpVIptQfY5HYsy4JhGDg6OkrldikfGFhpE5JT9AzDSKWt6HKwXOTj79y5Mw+ml1sJbrqt8/eVxr4AoqywJYC24vwM13q9vvCD5qYuYSU7aWm3pDFhgug6aY25WjY0nm+zWran//yIK8uyGFipsBhYaauklLAsCwcHBwvv5l5nBMx1lFLwfT/V26TspTHHl+gqyeX1832i69zWNiU/E5ygQUXGwEpbl7QINJvN+c7Vm2xinmAy7op2y3Q6ZQWJNiatI1uTUVTbopSCpml8MUeFxsBKmUl237ZarRsfvDcxikoIwRFXOyiOY4xGIz4x08YkG0nXkcWkktsmDRDlHQMrZUpKOR/JcpO02wK4OWd3DQaDrJdAO0xKiUqlslaFdN3Z0suqVCpwXXfr90uUJn73UuaSHbg3SbstgP2ruyuOY/i+zyorbYwQYuGTqq6yzeCYbNZi/yoVHQMr5cJtD6Zp9psqpVLZOEH5pes6e1lpY4QQME0TBwcHt77YvmyVnf5p4M8DFR0DK+XGbX1dafUmJhWHRTZ8UfGkcZwv0W2Sx5FqtbrUqL7b2p+I6Gp8VKdcSCoWNxkMBqld5k0C67qbJyh/0jxogug2yai+RYMovz+JVsPASrmwSB+rUgqdTie18+KFEKhUKjg8PGTVY0ck30cMBLRNi04O4ElTRKtjYKXcWOQyru/7CIIg1UqrpmnwPA8HBwfsbS04x3G42Yoyoev6rY9hjuMwsBKtiIGVcmPRoNHtdlMPJcl4rVqthoODA84sLKhSqcT+VcrEIps5GViJVsdHdsqNRUNoFEUYDocbqaQlwbVer6PZbGYy4JtWw81WlKWkL/6qlpSk/WgTlFK8qkB7gc/GlBvLPOgOh8ONbl6QUsI0TTSbTRwfH6fWN0ubw80slDVd11GtViGEQBRFmEwmEELMK6ub+v7sdrvzA1g0TdvIfRBljeUIyo1lQqFSCv1+f+NBMhkQTvnGzVaUF1JKCCGg6zpKpdL8hKlNfW/6vo/xeIx+v5/qJBWivGFgpdxY9oF2G2fGCyFgGAZKpdJG74fWY1kWn6gpdzZZVQVmL/LH4/H8/fO/J9o1DKyUG6tUS3u93laqrJVKhf2sOWaaJqurtHeEEBeOmVZKpX6MNVFeMLBSLiilVuq9SnrENo2tAflmWRYDK+2dq0b8bePKE1EWGFgpF5IexMPDw6XP5t7Wg7OmaahWq1u5L1oON5rQvrncDpCYTqcMrLSTGFgpN5Ih/tVqFa1Wa+FZqNvawZ+E6mUDNW2WYRh8gqa9FEXRlX++qbF/RFliYKXckVLCMAzU63XU6/VbL/Vuc+SUlBK1Wo2bsHKE/au0j6SUqNfrVx4rzc1XtIsYWCm3pJSwLAsHBwcwDOPaj7uuyrApySasWq221fulq7F/lfaVEALVavWBQwniOEYQBBmtimgzGFgp14QQ0DQNzWbz2qpmGIZQSiGO4/nbNsZd2baNZrPJsJSxM9L7UQAAAQVJREFUm17MEO06IQRKpdID/fXj8ZhtAbRTxE3f0EIIxW94ygulFIIgwNnZ2QNtAJqmQUo5fzMMA67rbjxMJkH59PR065VemnnooYf4ooH2nlIKR0dH88dG13XheR5/NqhQhBBQSl35TcsKKxVGMsT/4ODggQ1ZURQhCIL5qS+9Xm8r8wiFEJBSLrVJjNLDJ2Oi+67qZyXaFQysVChJQGw0Gg/0bV3W6XQQRdHWQmuj0eATxpYxsBLNJK0BCV4dpV1z69E9fEIgIiIioi1497q/uLGHlYiIiIgoa2wJICIiIqJcY2AlIiIiolxjYCUiIiKiXGNgJSIiIqJcY2AlIiIiolz7/wEGtYvSa5ib5QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 864x576 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig = plt.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection=cartopy.crs.Mercator())\n",
"ax.set_extent([-128, -60, 24, 50], cartopy.crs.PlateCarree())\n",
"ax.add_feature(cartopy.feature.LAND, facecolor='0.9')\n",
"ax.add_feature(cartopy.feature.OCEAN, facecolor='w')\n",
"\n",
"# add end points\n",
"ax.plot(lons, lats, transform=cartopy.crs.PlateCarree())\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Make your own Shape from points\n",
"\n",
"You can create your own Shape geometry from coordinate locations or x,y points, so that you can interact with it in a similar manner as from a shapefile. Once you have a Shape, you can change projections and look at geometric properties of the Shape, as we did above for a single state."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"100.0\" height=\"100.0\" viewBox=\"-120.17768000000001 32.172920000000005 47.778660000000016 10.415505619619047\" preserveAspectRatio=\"xMinYMin meet\"><g transform=\"matrix(1,0,0,-1,0,74.76134561961905)\"><polyline fill=\"none\" stroke=\"#66cc99\" stroke-width=\"0.9555732000000003\" points=\"-118.4081,33.9425 -116.53656281803954,34.62185468395183 -114.63494404602989,35.27195983702588 -112.70342143546311,35.89163680795418 -110.74234511851722,36.47971217805657 -108.75224911337924,37.03502459436787 -106.73386144433508,37.5564322473648 -104.6881124356053,38.042820934293715 -102.6161407277617,38.493112624072936 -100.51929657411526,38.9062744137114 -98.3991420049751,39.281327740305926 -96.25744750245255,39.61735768834621 -94.09618490844686,39.9135222108212 -91.91751639275596,40.169061066104604 -89.72377943401308,40.38330426236194 -87.51746790832203,40.55567979862256 -85.30120953200326,40.68572049769913 -83.07774005710772,40.773069741323866 -80.84987476165341,40.81748594212188 -78.62047790110475,40.818845619619054 -76.39243088444343,40.77714498701483 -74.1686,40.6925\" opacity=\"0.8\" /></g></svg>"
],
"text/plain": [
"<shapely.geometry.linestring.LineString at 0x7f30d2adecc0>"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# use lons and lats of the great circle path from above\n",
"line = shapely.geometry.LineString(zip(lons, lats))\n",
"line"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can look at properties like the length of the line, though keep in mind that any properties will be calculated in the projection being used. In this case, the line is in geographic coordinates, so the length is also in geographic coordinates, not in meters."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"45.05766262251294"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"line.length"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"### *Exercise*\n",
"\n",
"> Convert the line between these two cities to another projection, calculate the length, and compare with the actual distance. Which projection should you use for this calculation and why? \n",
"\n",
"---"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Other [shape options](https://toblerity.org/shapely/shapely.geometry.html) include:\n",
"\n",
"* Polygon\n",
"* LineString\n",
"* MultiLineString\n",
"* MultiPoint\n",
"* MultiPolygon\n",
"* Point\n",
"\n",
"and some basic information about working with shapes separately from maps and shapefiles is available in [notebook ST_shapes.ipynb](ST_shapes.ipynb)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## States Flown Over\n",
"\n",
"Consider the following: \n",
"\n",
"What states do you travel over when you fly from LA (airport code LAX) to NYC (airport code EWR)?\n",
"\n",
"First, a plot of the problem:"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<cartopy.mpl.feature_artist.FeatureArtist at 0x7f30d2a5feb8>"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAFTCAYAAAD87l5hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nOy953cTaZr+f1WplLMlBwzOAduATWhooE02wYRuaAZ6uqdnes/Z3bNndl/s/zNvvtNz2Ok4PdAJGjdNMAYbE5wwTjgH4aicVfV7wa80zpZkhZL8fM7RkV0q1XMrPXXV/dyB4jgOBAKBQCAQCASCUKETbQCBQCAQCAQCgbAaRLASCAQCgUAgEAQNEawEAoFAIBAIBEFDBCuBQCAQCAQCQdAQwUogEAgEAoFAEDTMag/m5+dzQ0ND8bKFQCAQCAQCgbBxGeI4Ln+5B6jVylpRFMWxLAt+H4/HA7fbDa/XC5Zlo2KZ0WgEwzCgKGrBdo7jYLPZ4HA4ojIOgUAgEAgEgpCQSCRIS0tbooGiBa/fAoEAaPrtojpFUTEbb71QFAWO45Y1bk3BuvhxlmVBURQCgcACARspIpEIRqMx+EYuHsvr9cJsNoPUiyUQCAQCgZAq0DSN9PT0ZfVPNOA4Dl6vFxaLBYFAAAAgFoshlUohl8shEonAcVzMxo+EqArW+XAcB47jYLVa4XK5IjZQqVRCrVYvq/g5jkMgEMDc3Bz8fn/EYxAIBAKBQCAIBYPBALFYHFNvJ8dxsNvtsNvtSx6jaRpSqRQymQxSqRQcxyXc+xozwcrj8/kwPT0duYVY/YPjhbHFYoHb7V7XOAQCgUAgEAiJRK1WQ6FQxMW7yXta5+bmVl2tlkgkkMlkkMlkC8IH4knMBSvLspiZmVmXB3S10ID547hcLlit1ojHIRAIBAKBQEgUsY5bXQ6O48CyLGZnZ0PSaiKRCHK5HEqlMq5e15gLVo7j4HK5YLFYIrcSgEKhgFqtXlW0chwHn8+Hubm5qCV+EQgEAoFAIMSaWMetrkYkq9UikQharRZisTguNsdcsAJv3wiz2bzuJftQYjr4N312dhY+n29d4xEIBAKBQCDEGpFIBL1ev2xlpHjCcRycTmdYq9UymQxarTbm3ta4CFbg7ZK93++HxWKJODyADw0I5U3hE76cTmdEYxEIBAKBQCDEEpqmoVKpoFAoAMQ/LnQ5OI6D3+/H7OxsyKvVFEVBo9FALpfH7DXETbAC/6r55XQ6YbPZIipHRdM0dDpdSC5ojuPg8XhI6SsCgRAznj59GpzYWZZFZWUltmzZkmizCASCgKEoCkqlMu5xoKHCr1a7XC44nc6QHY1isRg6nQ4ikSjqrymugpUnGiWvpFIpdDrdmh80X/pqdnY2WGuMQCAQosW1a9ewe/duKJVKjI+Pw+v14siRI4k2i0AgCBQ+J0eIQnUxvF5jWRZOpxMulyskr6tKpYq6GF9NsMYsgpaiKNA0DY1GE+xmFS4ejweTk5NwOp2rek8pigqGEshksvWYTSAQCMuSm5uLvLw8lJSUYHJyMtHmEAgEASKXy5GRkQGNRgOapgUvVoF/6TWGYaBWq5GRkQGDwbCmnrLb7Zieno5bAnz4KjJM+A/MaDTC4XDAZrOF9fz5XtrVXNC8wtfpdGEHExMIBMJq8AW1ASAtLQ02mw1erxcSiSTBlhEIBCEglUqDIjXa2fS8w46/5+ci3isaCASilsXPH1sikYBhGGi1WrjdbjidzmWT3AOBAHw+H0Qi0brHXouYC1bgX2+AQqGA2+2OKLPf5/NhamoKSqUSKpVqRRc0RVFQKBQQi8Wk9BWBQIga/HxD0zQMBgOmp6eRnZ2dYKsIBEIikUgk0Gg0EIlE6xKM/LL8/78kHhSi82/8Nj6Wfj5isThY2zVaXl3+9cjlcshksmB1AY/HExwnFgJ9JeIiWHlomoZWq11XVyyHwwG32x1MylpJtIrFYqSnp5PSVwQCIeqkp6djcnKSCFYCYQMTrW5VLMvC6/XCarVGnIfDdxxNS0uLejLUfBHMx60ufjwexFWwAm/LVslksnXVaw0EApiZmUF6evqKsbH8G2wwGNDR0YHbt29HpYrAeo6xng91reeyLAufzwepVLpg+2J7fT4fKIpa8X1bT5JdNAi1UUUsjx+vMaI5Jsuyq06aq31/Qv1eRuMYoe4fyW+Ffw5fXm+55fpIf4Nut3vBkldGRgYGBgYiOhaBQEh+pFJpMOEoUnhPqtlshtfrXbdNgUAA09PT0Ov1MSv0n8gksrgLVj4Ra70NBgDAarVCp9OteaJWKBRQKBSoqalZ95j8McMl1gKovb0dvb29uHDhwpLH5tv7888/Q6VS4fDhwyseK5bCOlrHiIeNiXgfIn3e//t//w9nzpxBZmbmksdW+/5EQ8CH892OxQXJ4v1fv36N5uZmXLp0aV3HnQ9N0wsuBjMyMtDU1BTx8QgEQvLCl96MdL7ml//tdjscDkdUbeObKvH1UhPRUStWxF2wAv8qomu329d1HI/Hs6ZnCQDy8vJgNpshkUhSNklCKpWCoiio1eo192NZFiqVKk6WEeLFap7zjURhYSEaGxvhdDqRnp4ekzHUajX8fj+sVis0Gk1MxiAQCMJEr9dHLFb55X+LxRLTHBur1QqfzxfsTpUKJER688V009PT190xwWazrfmhMwyDnJwcUooGbwOzSUwvIZVRqVTQ6/V4/PhxzMagKAq7du3CDz/8sK6YfAKBkFwolco128cvB18vfm5uLm4J4S6XK9jwJBUaKyXMV8zX/NJqtcGaZZGURXC73SF98EVFRRgdHY3E1KQhlC+kRCKJuG0uQdikwoQULUpLSzEzMxPTMSorK3HgwAH8/PPPeP36dUzHIhAIiUcsFgebAYQKH6dqs9kwOTkZlVjVcPB6vZibm0sJL2vC1w/5AF4+ztTn88Fut8Pj8YR8DJvNBq1Wu2poQFFREZqamvDuu++mxAcXKRKJhHhYUxQiWP9FIBCIS+xWYWEhNBoNbt++jaamJqjVamg0muA9fyMNTQiE5IaiqLBDAeK1/L8afLzt/FrSyUrCBSvP/GK1/JvrcDhCahHmdrvXjCNLT08Hy7Kw2+1rxnkmI6F+EaVSKWlfm4LwtfsIb5mbm1tSMSNWGI1G/P73v4fdbofVaoXNZoPNZsPg4CBsNhssFgukUimysrKCt/UkbBAIhPizllNsPtHO/o8UvlJSsnTcWgvBCNb58F8KtVoNtVoNt9sNh8OxqmfQ5XKtWg+NoigUFRVhYmIiJQVrqMhkMiJYUxQiWP/F3Nwc9Hp93Mbjq58sd+HMcRwsFgtMJhNMJhNaW1vh8XiQmZkZFLDp6elx6RRDIBDCRy6XBxObVyOW2f/hwovVaNdkTSSCFKw8/Jssk8mC2e12ux0ulyv4uFwuX7Xz1XyKiorQ0tKC0tLSmNsuVGQyGen+laIQwfovAoGAYCom8C2jdTodysrKALxtgPLmzRuYTCY8evQIZrMZ6enp2Lp1K4qLi1OqFA2BkMyIRKJgy9XVEMLy/3z0ej0YhkkZsQoIXLACb2sqDg0NYfv27cHkLI1GA6/XC6lUCo7jQp7cCwsL8eOPPyIQCKScNyPULyURrISNAMMwgk4uVCqVKCwsRGFhIYC3iRETExNoa2vDs2fPUFVVhdLSUsGIbgJho8K3O10JoSz/z0ev10MikaSUWAUELlg5jsOvv/4KrVaLa9euQS6XY8eOHdi+fTt0Oh2A8AqtKxQKGAwGzMzMICMjI1ZmCxq5XE48cSkKuRD5FwzDJFVyoUQiQV5eHvLy8mAymfDixQs8f/4clZWVKC8vh1gsDuk4/G871U5UBEIi4KsXLfd7EtLy/3x0Ol1KilVA4IJ1bGwMbrc72L1penoar1+/xl/+8hcYjUbs2LED27Ztg0KhCPmYhYWFGB8f37CCVaFQEMFKSHkkEkkwdCjZyMrKQm1tLaanp9HS0oKWlhZs27YN27dvX7b1stlsxsTEBEwmEyYmJuD1epGTk4P8/Hzk5uambLMUAiGWSCSSFevE8zVVZ2ZmBOUo0Gg0kEqlKRtSJGjB2traioqKiuAXJj09Henp6di7dy/evHmD169f486dO8jJycGOHTtQVla25uRcXFyMX375BTt37ozHS4gboWaJ8+V1QukQRkgeSJWAhUilUlit1kSbsS6MRiNqampgNpvR0tKCL7/8EmVlZcjLy8Pk5GQwiUssFiMrKwvZ2dnYs2cPxGIxhoaG0Nvbi/r6emRlZSE/Px95eXlhXdwTCBsVmqah1+tXPEfy7U+FJFZVKlXKtWJdjKAFa1ZWFrq7u5dsF4lEyM7ORnZ2Ng4cOIDR0VG0tbXh559/RnFxMXbs2IHi4uJl41SzsrIwPT2dEjXJIoGPiXO73eTklWIIafJMNFqtFkNDQ4k2IyrodDocPXoUNpsNra2taGhoQEZGBgoLC3Hw4MFl2yyXl5ejvLwcXq8XIyMjGBgYQFNTE/R6PQoKCpCfn09ayhIIK7Ba2TmO4zA3NyeoajsKhQJKpTKlxSogcMG6Y8cO3LlzBw6HA0qlctl9GIZBfn4+8vPz4fF4MDw8jIaGBty4cQMHDx5EdXX1gv2lUikYhgkmbaUK4Ypvp9NJBCshZdmxYweeP3+OgYEBFBQUJNqcqKBWq5fMZ2shkUhQVFSEoqIiBAIBjI2NYXBwEDdu3IBcLkdeXh5KS0uh1WpjZDWBkFys1nqVZVlYrVbBJFfxaDSaDeGAE7Qcl0gkqKysRE9PT0j7S6VSlJSUoLa2FpcuXcLDhw+XjWPT6/Ww2+3RNjdpoGk6aeP7CCtDPKz/QiKRICsrC83NzYk2RTCIRCLk5ubi8OHD+Pjjj2E0GvHixQs8fvw40aYRCIKAYRio1eplPZUcx8Hlcgny3LlR5n5BC1YA2LdvH16+fBl2iRqVSoXCwkK0t7cveUyn021owSqXy/HixYtEm0GIIhvh6jpcDh48CLPZvKF/64vx+/3o6OjAV199BafTiQsXLuDMmTOJNotASDgURa1YworjOPh8PsHGxQu5hF80EbxgTUtLQ3Z2NkZGRsJ+bklJybLCLBU9rOEIltOnT8NkMqG3tzeGFhHiDUm6WojBYIBCoUBTU1OiTUk4Xq8XL168wBdffIHx8XGcOnUKZ8+exaZNmxJtGoEgCFZqvcrXWZ2dnU2AVaHh8Xg2xPwveMEKvPWytre3h/2BZGRkwOl0wmQyLdiu1+sFe6UUD4xGI8rLy/HgwQPBxeIQImcjTFjhUlFRgcHBwUSbkTDcbjeam5vxxRdfYG5uDufOncOpU6eQnp6eaNMIBMHAd9Ncybs6MzMj6PnV5/MJ2r5okRSCtbi4GG63GxaLJazn0TSNioqKJV5WvV4f9rGETrhljd577z1IJBLcunUrhlYR4slGmLDCpbKyEoFAAGazOdGmxBWv14vGxkZ89dVXcLlcuHTpEo4fP460tLREm0YgCAqGYVb1rprNZkFVBFgOn8+3IcLCkkKwUhSF4uLiJZ7SUCgqKkJHR8eCGI9UFKzhlrOgaRq7du3C9PR0jCwixBsiWJfCMAwYhsHo6GiiTYkbVqsV169fh9vtxuXLl3H48GFSwopAWAaapmEwGJY9f7IsC5vNBo/HkwDLwoMPW0h1kkKwAkB+fj7Gx8fDfp5SqUR6evqCSgMajQZ2u13wV03hQNN02IKFpukNcVW2ESCNA1ZGqVTizZs3iTYjLoyPj+PGjRvYtm0bjh49umyNVgKB8HbONBgMK4YBeDweQbVcXYuNkHiVVIJ1ZGQkoquIsrKyBWEBIpEIarVakOUpIiWSgsEikQh+v39DfNE3AkSwLo9arU65FZXlePXqFe7cuYNjx45h27ZtcRnT4/Ggo6MjpS7+CRsDvV4PkUi0RLByHAe/3x8MI0qWeXUjJF4ljWBVKpXQaDQRnXg2b96M0dHRBYlWqVbaSiQShf1lLSkpgVQqxY0bN2JkFYGQeNRqNdxud6LNiBksy+LRo0doa2vDhQsXsGXLlpiPGQgE0N7eji+//BLNzc0pf6IkpBYajWbV5gB8RQCWZfHzzz/j2bNn8TYxbDZC4lXSCFbgrZc1kjhWhmFQWlqK1tbW4DaFQpFU7v61iDQk4NKlS5idnUVdXd2GiIFJVUhIwMpIpdKUXUXweDy4desW5ubmcPHiReh0upiOx3Ec+vv78c0332B0dBSbNm3C1q1bgy2fCQShI5fLIZfLV4xbnZ2dDZ4L29ra4Pf70dPTs2IDI47jMDExgcePHye09NVGSLxKOsEaSRwr8Nab2NLSAo7jMDU1hcHBwZSqQSgSiSJ6nlqtxunTpzE8PIzPP/8cAwMDUbaMEC+IYF0ehmFS8r2xWq24ceMGtFotamtrY95q2mQy4caNG3jx4gUOHTqEU6dO4c2bN6ioqIjpuARCtJBIJCtWBGBZFhaLJXhxOzMzg7a2Nhw/fhxnzpxBY2PjAv1htVrx7NkzfPnll3j48CE4jsNPP/2EqampuL2e+XAcl5Lz3HyS6rI4Ly8P33//PViWDTtmMy0tDTRNY2hoCL/99hv27dsHhUIRI0vjz3qurHJzc/HZZ5/h/v37qKurQ21tLXJycqJoHSEepPpkFSlKpTLlYiynp6dx69Yt7Ny5E9u3b4/pWGazGU+ePMHU1BT27t2LkpISUBSFvr4+6PX6mHt1CYRowDAM9Hr9imEADocjGDoUCARw9+5dvPvuu1Cr1QCAEydO4M6dO9i5cycGBwcxNzeHoqIi1NTUwGg0gqIoZGdn4+bNmzh16hSysrLi+vqAt17WWF+4JpKkEqx8HKvZbA67niBFUaioqMA///lPqNVqFBcXx8jKxBBJDOt8GIbBiRMnAAC3b9/GH//4R0gkkmiZR4gxFEWRkI4V0Ol0KSVYx8fH8euvv6K6uhqFhYUxG8fj8eDZs2fo7e1FVVUVjh8/vmDpv7OzM+ZimUCIBmu1XfV6vQtyWp4+fQqNRoPS0tLgts2bN+PAgQMYGBjA9u3bkZubu2RlMz8/HwzD4Pbt2zh+/Hhc4snn4/F4IJFIUjY0IKlCAoDI41j55/r9flRXV0eUVS9kIg0JWMyxY8cglUrx008/ReV4hPhAUVRKibJootfrU6ZO4cDAAH799VecOHEiZmKV4zh0dXXh66+/ht/vx9WrV7Fz584FYnVmZgY2mw35+fkxsYFAiCZ8rdXlKgIEAgHMzc0Ft01MTKC3txeHDh1asn9xcTFOnjyJgoKCFc+5W7ZswcmTJ/Hbb7/Fvf5zqideJZ1qKygoiDiOVSaT4ZNPPoFWq42yVYknWgKcpmmcPXsWU1NT6O/vj8oxCbGHpmn4fL5EmyFI+JWC+SelZKSzsxMNDQ04e/YsNm/eHJMxJicncf36dXR1deHMmTM4fPgw5HL5sraUlZWl3IU/IfXQ6XRgGGbVtqs8Xq8X9+7dQ3V19bLf+1DZtGkTdu7cGfeckLUSr5I9zjXpZpu8vDyMjY1F7C1J1Ql2vSEB80lLS0NRURHu37+fEl6pjQBN08TDugpyuRwvX75MtBkRwXEcnj17htbWVly4cAFGo3HJPjabDSMjIxHPAS6XC/fv38ft27exbds2fPDBB0hPT19x/6GhoWDyaqpWYCAkPyqVClKpdIGIY1kWHMfB5/MtqAgAAI8fP0Z2dnZUVg6Wq/Eaa9ZaSeI9yslKUsWwAm/LUWm1WszNzcFgMCTaHMEQbSF+7Ngx/PWvf8W9e/dw/PjxqB6bEH1omibCYRU0Gs2COszJRFNTE8bGxvDBBx8EE0X5aidDQ0MYGhqC0+mEVCqFwWDAkSNHIBaLQzo2y7J4+fIlXrx4gZKSEly9ejWk2PUPP/wQAwMD6OjowL1797BlyxYUFhYiNzeXlLgiCAKZTBbs9MaLOI/HA7fbvWyR/cHBQYyPj+Py5ctxtzWauN1uKBSKZcMfZmdnQdM0dDpdQp13/EVDuKGMSTmzZGRkwG63E8E6j2jFsPLQNI0jR47gzp072L59OzIyMqJ6fEJ0IR7W1WEYJmlDJnp7e/HBBx9AIpFgcHAQw8PDGBoagkwmQ15eHqqrq5GRkQGWZVFfX4/vv/8ep06dCmY3LwdfW7K1tRUajQYXLlyAXq8P2SaFQoFt27Zh27ZtcLlcGBwcxKtXr/DkyROcPHkyZnMz7yEiopiwFmq1Gn6/Hy6XCx6PZ9ULepfLhYcPH+LEiRNJn2zsdrshl8uXeJUtFktwDgwEAgkTrHySGxC+bknKX71KpYLT6Uy0GYIi2oIVAIqKivD69WvcuHEDhw4dQllZWdTHIEQHkUhEBOsqMAyTlN2upqen4fV6UV9fj8nJSaSnpyMvLw87d+6ERqNZsC9N0zh69Cja29tx/fp11NTULKk17fP58OrVK7S1tcFgMODYsWPrLr8jl8tRXl6O8vJy9Pb24qeffsKBAwdQUlIS0fE8Hg+sVitsNtuCm9Vqhd1uB8MwuHLlSkqVJSREn1DroXIch/r6ehQXF6dEbXZeDPKwLAun07lg/rPZbAnzsnIcB4vFEvR+h0NSCla1Wp3QjhJCJBaCFQBOnTqF5uZmPHjwAP39/dDpdJBKpdi0aROys7NjMiYhfEhIwOoolUpMT08n2oyQ6erqwqNHj+D3+6FQKFBSUoKampo1ayxSFIXKykqkpaXh119/xZ49e1BRUQGPx4OXL1+io6MD2dnZOHPmzLKxsOulpKQEaWlpqKurw9TUFPbv37/mSdHtdqO/vx99fX2YnZ0Fx3HQaDRQq9VQq9XQ6XTIyckJ/t/c3IyWlhYcPHgw6vYTNh6Tk5OYnZ0NlnVMBbxeL2QyGYDlK8h4PJ6I6tmvF47jYLPZwLJsMCwgnDjfpBSsKpUq7uUihE4sv3h79+6F0WjEkydPMDs7C7fbja6uLvzhD3+I2ZiE8CAe1tXJyspCV1dXos0ImZ6eHqhUKly8eDGiJcotW7bg/fffx61bt9DQ0ACO4yAWi3Hx4sWwlv4jwWAw4NKlS7h79y5+/PFH1NTULPGGBgIBDA8Po7e3F2NjY8jJyUFVVRUyMzOXJMksZufOnfjmm29QWVkZkZeGQJjPyMgI8vPzY+b0SQQulwsSiSRYykutVi9ZlbZarXH3sgYCgaAdkSR0J2XKvEqlgsPhSLQZgiLWX7qCggJ89NFH+PTTTyGRSJCbmxvT8QjhQQTr6mzZsgUsyyaNF5qiKMhksnXF02m1Wly8eBEymQxGoxF+vx9jY2NRtHJlpFIpTp8+jc2bN+Of//wnTCYTOI6DyWRCfX09rl27ho6ODuTm5uIPf/gDampqkJeXB5lMtqbHRaFQoLy8HM+fPw8mzjQ2NuL58+fxeGmEFGNsbCzuBf5jjcfjWfA7oigKSqVyyT5+vz9upa44jltQWjCScZPSw6pWq4lgXQQvWGPt5rdarXC73di9e3fMxiCEj0gkSsoYzXghk8nAMAxaW1uxZ8+eRJuzJtHqXCaVSvHHP/4RAPDDDz+gu7s7bt2pKIrCnj17kJ6ejrq6OjAMA5FIhJKSEly+fHld3tHKykp89913uHbtGoxGI0ZGRqDX65Gbmwu9Xp9S3jJC7PB4PJidnU1IG9VYwnEc/H5/sFoIRVHB3J/5InFmZgYikQhSqTR4gcwv04eyVB/qkj7HcXA6nQscBpHMb0kpWFUq1YI2aoT4CdbW1lYoFIolV2uExCISiUjN3DXIzc1Fd3f3hhKs8ykvL8dvv/2Gu3fvYseOHTGJYV2O3NxcXLp0CW63GwaDISq1KWUyGT7++GM4HA5MT0/DZrNBr9fj+vXrUKvVuHTpUtJnexNiz/j4ODIyMmJSdSLRBfpdLteChgkURUGv18NqtS4QjvwyPb9ULxaLgwKWoqigJ5S/8bGnNE0H42TXgo9dnc+GEawymQw+nw9Pnz6FSCQK3sRiMfLz8zf0RGU2m2N6IhobG0u5q9FUgGEYIljXYM+ePfjmm2/g9XoFP0fQNB31E15hYSEmJycxMDCA3t5eMAwDo9GIrVu3oqSkJKYXuiqVKurxprzXSKVSBQu9cxyHhoYG1NXVoba2NmUbxRCiQyqGA/B4PB6oVKoFglUikcBgMMDn88Fmsy1b6s/n88Hn863qFKRpGkajMaSLT76k1uL5LJL5LSkFK0VREIvF6OjoWHAFEAgEcP/+fZSXl+PgwYMbbrLSarVoamrCuXPnYnJ8lmVhs9lIdq4AITGsa6PX68EwDF69eoWqqqpEm7MqsRCsNE3j4MGDOHjwIPx+Pzo7O9HX14f6+nrcv38fGo0GeXl5qKqqStqSURRF4eDBg7h9+zbq6+tx+PDhuHcbIiQPo6OjOHnyZKLNiAl8fOp8+KV+iUSCtLQ0+P1+2Gy2JaWw1iItLS0kfcWHJiwXrhYIBILaLdTfaFIKVuBtJuqBAweWFKhua2vD06dP0dXVBb1ej4KCAmzfvl3wHpVosGvXLjx48CBmxzeZTACQslekyYxYLCYe1hDQ6/UYGRkRvGDlL8RjBcMwqKysRGVlJYC3S6MvX75ET08P2tvbkZ6ejvfeey8pG4bQNI0TJ07g+++/R0tLC3bt2pVokwgCxGq1wufzIS0tLdGmxIy5ublgJYD5AnO+cNXr9QgEArDZbPB4PGseU6fTLQg1WA2O42A2m1d8bHp6Gnq9HmKxOKTjJa1gVSqVcLlcS7ZXVlZi+/bt6OvrQ09PD1paWtDR0YFPP/005T2uBoMhpqLFZrMt+eIThAGJYQ0NkUiU8NiytXA6nRgdHV21U1W0yc7ODtZVHh8fx+PHj3H9+nWoVCrs27cPxcXFcbMlGojFYpw5cwY3btyAWq1OOvsJsWdsbAybN29OaQ+8z+fD1NQU5HJ5sNHI4vM3f07X6XTBVdSVEniVSmVIlTyAt4LU4XCsuvLHsixmZmag0Wggl8vX1BZJK1hVKtWKbypN0ygtLUVpaSn8fj/+9re/4d69ezh+/HicrVwdp9OJN2/eLAlq5k+ooWyf///ioOZoU1BQgPv378Nut5P6hwKDYRjBC7FYwC838e0XPR4PvF5v8N7r9cLn88Hv98Pn82FmZgZarTbRZq/Iixcv8PTpUyiVStQH0DsAACAASURBVLz77rsJsSE7OxuXL1+GzWbDw4cPcffuXTx8+BBKpTLomZHJZMjKyoppApvT6cTr168xOTkJvV4Po9EIo9EYcriCWCzGO++8g/v370OtViMzMzNmthKSj9HRUeTl5SXajLjgcrngdruhVCoX/I7nwwtXrVYLjUYDm80Gl8sFmqYhkUggk8lCFqvAWzEaanI87+1ea25OasG6nId1MQzD4NixY6irq0NFRUVCEoZMJhMsFguKiorAMAyGhobQ3NyM2dnZ4BXFcl+CxdtW+3/+EmJLSwt27twZ7ZcBiUQCsViMvr6+mByfEDkcx8Hj8eDatWvLPrba/yttW237eh5bjlCD9xdfrC0+Bl8om598+YRMvqQSX0BfaJjNZty8eRN2ux179uwRRNk4tVqN2tpa+P1+NDc3w+FwBLOEXS4Xnj17hq1bt0b14tXv92NoaAi9vb0wmUzIy8vD5s2bYTab0d7ejunp6WDCh8FggNFohEajgd1uh9lshsVigdVqhdlshs/ng0ajQW5u7oa8mCOsDMuyGB8f31D5GBzHwW63w+l0Qq1WQy6XA1g69/KaRKPRBAUkXxUgVFiWXTEUYCVcLteadbKTWrCOj4+HtG9BQQG0Wi3a29vjKlidTid+/fVXmEwm0DSN+/fvB5NjMjMz8cEHH0T9qr+jowOPHj2CXq+P+tUjy7KQSCQYHx8nglVg8AKtsLBwyYUMf7/W9sX3qz1vrWOudLzVxPJqwpqiKEil0uCNv9pnGCbkiZRlWfz9738XnId1YGAAdXV1MBgM+MMf/iC4hCeGYXDgwIEl2//617+it7d33TGiHMfhzZs36OnpwcDAAIxGI0pKSnDixIklFxf8SXdmZgbT09Po6ekJrvhotVqkp6ejuLgYWq026EkiEBYzOjoKlUq1Icsz8ln7drsdWq0WYrF42Tl0ccxrqPDOk3ATuQAsW7VgPkktWEPxsM7fP161W8fHx9HY2Ijp6elge8WMjAyYzWaMjo6itLQ0Zklg27dvx+zsLG7fvo3a2tqoJkjdvn2bNA0QKH6/HxKJZEN5DMLBZrPhhx9+gNvtRllZWaLNWcCDBw9QUFCQdNnKWVlZePr0KYaHh7Fv3z5s2rRpzefwBcSnp6eDonNqagpisRilpaVrNhTg20zysXS7d+8mMfWEsGBZFk1NTdi7d2+iTUkogUAAs7OzkEgk0Gq1IeenzF/h4ld2+S6Cfr8fgUAgLG02n5QOCVjcG3c1dDodXr9+veZ+09PTGBgYwNTUFFQqFbKzs7Fly5YlBXLHxsZQX18Pp9O5YPnR7/fD4/HAaDTi/PnzwUQG3gadThf6i4yQw4cPw+fz4eeff0ZZWRkOHz4clePabDbk5uYu8FI3NzdDLpejoqKCnDgSiM/nI919VoBlWXz99dfQaDT49NNPQy52HQ9aWlrg8/lw7NixRJsSNmfOnMHAwACeP3+OH3/8EZ999tmKF+KDg4N4+fIlZmZmACC4pF9YWIh9+/ZBq9WG5cUZHR0Nds8qKChAYWEhsrOzyRxEWJPe3l5IpdINE7+6Fl6vF1NTU5DJZNBoNMuGGi4WpPNv0Qi3EYlEIZXKSlrBqlQqw/KYVlVV4eXLlzCbzUtEo9vtxpMnT/D69Wv4fD5IpVKoVCqYzWb09PSAZVmIxWKUlZXB7XZjYmICdrsdmzZtQlVVVTDJw+fzgaZp7Nq1K+EnxRMnTqCwsBB1dXU4ePBgVDp5LK71aTKZ8OLFC9A0jd7eXly6dGndYxAigwjWlRkdHQXLsrh8+bLgBM3AwAAUCkVMOu3Eg4KCAhQUFODzzz9HY2PjshfHdrsdDx48QHV1NTIzM6FQKNa9VD8+Po5du3ahpKQEAwMDaG5uhs1mQ35+PhGvhBXx+/14+vQpampqYh4uIpPJMDU1hUAgkBRzs9vthtvthkwmC9a1j5YgXQ2ZTBa8YF3rM0nOWRJvPawOhyOs/fV6Pb7++mvI5XIolUpwHAev1wubzQaZTIZt27Zh9+7dS04eXq8Xz549Q3d3NyQSCTIzM3H+/PlgmQihUlBQAJqmMTAwgJKSknUfj6bpYFA0y7K4e/cuMjMzUV1djX/84x8YGBhAQUHBuschhA8RrCszPDwMqVQqSAFTU1ODr776CvX19Th06FCizYkYjUaDycnJJds5jkN9fT127NiBwsLCqI03NjaG9957D2q1OlhP1mazob+/PyheCwoKsHv37g0Zp0hYnvb2dmRkZMSlYkRRURH6+/vR0NCAQ4cOJU089UrVl2KBRqMJ6wI2aQWrRCIJdlEI1Ttx5coVTE1Noa+vD3Nzc8Hs4RMnTqxaIFsikeDAgQPLJh4IGb7TRSTBz8thNBrx6tUrvHr1Cq2trXC5XDh//jzUajVyc3PR2NhIBGuCIIJ1ZSorK9HZ2YmpqSmkp6cn2pwFqNVqnDhxAnV1dcjNzU3KZUqWZTE1NYWzZ88ueay3txdOpzOqjRrcbjesVuuSz1KtVqOqqgpVVVWwWq149eoVvvvuOxw7dow0OyHA5XKhra0NFy9ejMt4FEXh6NGjuHHjBjo7O7Ft27a4jJsM8CEAIpEoLCGftIIViKwXbXp6uuBOWrHi3r17kEgkUfuhVFdXQyQSob6+HnK5HL///e+DGc3bt2/HzZs3wbKsID1ZqU44F24bDY1GA4PBgJs3b+LcuXNLuuMlmoKCAkilUrx58yYpBev4+DgoiloiCp1OJ5qamlBbWxvVOWFiYgJZWVmrXqBpNBq8++67yMnJwd27d1FSUoJ33nmHzE0bFIfDgYcPHwYrSMQLiUSC06dP48aNG9Dr9QtyWjYqUqkUOp0upBCAxSTtr9ftdoNhGHKSXgGWZTE4OIh33nknqsc9cOAArl69uqT8zvwuOYT4QwTr6pw7dw5qtRr/+Mc/MDw8nGhzFsCyLDweT1SXzOPJ+Pg4OI7D559/jlu3bgW3P3r0CFu3boXRaIzaWLOzs3j+/DlycnJC2j87Oxsffvghpqam8OOPP4YVRkZIftxuNxobG/Htt99Cq9UmpDKARqPB8ePHcefOHVit1riPLyQ0Gg30en2wXna4JK1gtdlspNvSKvT29gIAysvLo35svjfxfGiahkqlQnd3d9THI6yN3+8XZEF8oSCTyXDp0iWoVCoMDQ0l2pwF8B7KaAq7eLJz505UV1dDIpHAYrEAeJtMNjMzE9USeJ2dnfjxxx9RUVER1qqRXC7H2bNnkZOTg++++w4jIyNRs4kgPDweD0ZGRnD79m189dVX8Pv9+N3vfof9+/fHrJzkWmzevBm7du3C7du316w1GiqLG6QwDAOxWAyxWAyJRBKsWS0ERwbf7GO9CZeJfyURYrfbSTD9KrS1tSErKyuuS2DZ2dkYGBgg3r4EEAgEyHseAlKpNKxyePFgZGQk4VVF1oNEIkFFRQWamppQWVkJj8eDhoYGnDhxAhRF4ZdffsHk5CQKCwvx3nvvRTQGx3F4/vx5xCEdFEVh165dyMrKwm+//UZCBFKQQCCAH374AXNzczAajTCZTDh06JBg6i5v27YNMzMzuHv3Lk6ePLmscKNpOrhyzDAMJBJJ0Bu5ktBbKTSSf47Val2zg1SsEIvFUCgUwZau6008S9pfKxGsK+P3+zE3NxfTPt/L8e6774KiKHz99dcJ+4FsVAKBAPGwhoBMJhOcYE2WsjdrwbedbmxsRH5+PjZt2oRHjx4BABQKxaqJrSvhdDphtVphsVhAURTS0tLWZeOmTZvw4YcfYmJiAh0dHes6FkFYTExMgOM4fPbZZ7hw4QIYhllQhjHRUBSF6upquFwuvHjxAjKZLFi9KD09HVlZWUhPT4der4dGo4FSqYRYLIZIJFogWhffeC/r/BtFUWBZFjMzM3EPg6FpGkqlEhkZGUhLS4NcLo84BGDJsaNgX0Kw2+2Ca2EoFF6+fAmGYULqPBNNZDIZPvroI3i9Xty9ezeuY8+HZdkFhY69Xi+8Xm+wzpzT6YTD4YDdbofNZoPNZgv2WHa73fB6vfD7/WBZNmGvIVz4trmE1VEqlfB4PIk2IyV5//33g+1S9+3bh87OTkxMTKC8vBxerxdFRUVhHW9qagrfffcdHj9+jPHxcWRnZ0flpCeXy1FSUhJ2r3OCsBkZGUFubm7Qa07TtOB+6yKRCCdPnsTLly/BsixUKlWwxfR88bme7znLsnC5XJiamopahaBQkMlkMBgMyMjIgFqtXiC0o0XSriHabDYiWFegt7c3LnXmlkMmkyE/Px8TExMxG+P777+HyWSK2fGFynI/fH4by7KC8iYIFZVKFddJfCPBe4kPHz6M2dlZPHv2DO+//z4ePXqEnTt3hrX8PjAwgPr6elRVVaGjowMikSjkRKtQUKvVGBgYiNrxNjIsy8JkMgWLzM9v3bnW3xzHwWq1rlnTPJSKQL29vaitrQ3+zzBMXGuKhopCocDWrVvR3t6Oo0ePRu24fEcqs9kctzmOYRgoFArI5XIAiHmITdIKVrvdTkpELAPLspibm0ton+RNmzaF1AY3UtxuNwoKCnDo0KEFV9P8fbR+NLynFkAwxCEQCAS3z398/hLN4v8XPzbfvsW2Lj42y7LBiYj/m+9Cwv/Nsizu3LmT1HGQ8UKj0UQt6SFa+P3+pI+lDAQCuHPnDvbu3YvNmzfj+vXrOHr0KHw+H2ZnZ3Hq1KmQjsNxHFpbW/Hy5UvU1tbCaDTixYsXGBkZwbvvvhs1e9VqNWw2W9SOt1EZGxvDo0ePQNN00IG0eA5c7W+Hw4GJiQmUlpZGND5/HLPZDLfbvSC+mWEYwXlYeUpKSlBXV4cjR45ExQPJcRxcLhesVmvMO1PRNA2ZTAalUrlmfG20SWrByqt6wr/o7e0FRVFR9UaES05ODgKBQEyTr/gfTSyZL36FntBE03TMJ6pUQKvVCi7Uw+FwQCqVJtqMddHU1ASpVIodO3bg+++/x/bt25GTk4O6ujrs2LEj5BjdV69eoa+vDxcvXgzmKBiNRthsNqjV6qjZq1KpYLfbSd3oCLFYLGhsbMTs7Cz279+P/Pz8iERLR0cHpqen1+1prKurg0ajWfBZClmw6nQ6iMViDA8Pr6v2cjy9qlKpFAqFIjhXJaJzV9L+Uu12O/EoLcLr9aKhoQE5OTkJnYQVCgXEYjFu3bqFkZGRmCRgEXG2EIqiyHsSAnq9PjjJCwWXy5XUCaR9fX0YGhrCsWPH8ODBA2i1WlRVVWFubg4mkynk0no+nw/Pnz/HkSNHFrwfRqMx6qtpDMMIMgEvGWhtbcX169eRmZmJK1euoKCgIGLx4nQ6o+IMGB8fR35+/oJtYrFYsOE/vFOpra0t4mNwHAe32x3TWFWGYaDRaJCZmQmdThe1bP+I7UnIqFGACNal3LhxA2KxGCdPnky0KTh69Cjq6+tx69YtiMVi/OlPf1qXiH7w4AF0Oh22b9+eND2Z4w0RrGvDJ6ZZrVbodLoEW/MWsViM8fFxOJ3OpIvLt9lsaGhowLlz59Dd3Y25uTl88MEHoCgKLS0t2LZtW8jVKzo6OoKZ0vPZuXNnTL7bvJeV1PMODY7j0NzcjKGhIVy+fDkq79vU1NS6L9acTic8Hg8qKysXbJdKpbDb7es6dizweDxobm7G+Pg4Pvjgg7Cfz4eCmc3mmHiQKYqCXC6HUqkMrowI5ZyblB5Wv98Pn89HsqLn8fjxY1gsFly8eFEQS1wFBQX405/+hH//938Hy7Kor6+P+FgDAwPo6upCU1NTsEwOEWdLEZLXUMjQNB0scC8Ezp07B7lcji+//DLpMtf5epG9vb1obW3F6dOnwTAMrFYrhoeHQy7w7/F40N7evmxnPplMFpPwL4/HQ84hIcJxHB49eoTR0VFcuHAhaiJ/bm4OWVlZ6zoG/xku/u1IJBJBlVfkOA6Dg4P49ttvodFo8Oc//3mJV3gtWJaF2+3G5ORk1MUqTdPQ6XTIzMyEWq0OVi4QilgFklSw8jVYhfRGJhKWZfHy5Uvs2bMnqnFe0YCmaRw6dAjd3d0rLr/x3qWVaGhoQF5eHt555x10dXXFytSkhvwWQodhGEEJVoZhcOXKFej1enz77bf45ZdfMDY2lmizQkIul+PUqVPo6elBTU1NUMi0traivLw85NjclpYW5Ofnx83rzbIs7Hb7mtnphLfv1f379zE9PY3z589HdWWT47h11yBmGAZpaWl4/vz5gu1SqVQwCZZ2ux11dXVoa2vDJ598gtOnT4d1sTQ/VtVsNkfVYUNRFNRqNTIyMoJL/kJwei1HUoYEkKYBC2ltbQUAVFVVJdiS5SkpKUFTUxPq6+tx+vRpmEwmmEymYF3FH3/8EcDbH45EIoFCoYBOpwsWPna5XDhy5AgkEgna29sxNzdHEu4WwReKJqyNWCwWXIY4TdO4dOkSHj58iPHxcfz000/YtGkTTp48KfjQp/T0dPzpT39akPnd39+Pq1evhvR8v9+Prq4ufPjhh7E0cwF8SJnQkykTTSAQwN27d+HxeHD27NmoNyeJVmLUciJLJpMlvNQfy7Lo6urCs2fP8N577+HAgQNhi0E+VtVisUR9ZVEul0Oj0QjOk7oSSflrtdlsRLDOo729HcXFxYK9KgKA/fv34+7du+jr68Pdu3fBMAyePHkC4O3E8sknn2BychImkwnT09OYm5sDRVHYvHkzysrKgiftTz75BF988YUgY5MSDQmTCA2pVBr37i+hUl1dDQB48+YN6urqcO3aNezfvx/bt29PsGWrM/9k19/fj/z8/JAvKgcGBpCenh7X1SGLxQKtVhu38ZIRv9+PX3/9FRRFBUM9oo1YLF63YO3r68Ps7OyStr+JFqyzs7N48OABVCoV/vM//xN6vT7sY/Be1Wgv/4vFYuh0uqiWgYwHSSlYSZerhXg8HmzdujXRZqxKcXExHj16hN9++w1lZWU4fPgwAASFJ8MwyM7OXjMbmGEYbN68GVNTUzG3OZkgVQJCh2EYwSwVrkRmZiY+/fRTNDc349GjR5ibm8OhQ4cSbVZImEymsGLzuru7Q64kEC2IYF0dn8+HX375BXK5HMeOHYuZqBGLxREX93c4HHjw4AFGRkZQUVGBioqKBY/L5fKErDr5fD60traiu7sbp06dwo4dOyL2Xnq93qiKVZFIBI1GA4lEklRClScpBSvpcrWUZBArx48fx8jICA4cOBDcRjJ0owMJCQgdjuOSYvkLAPbu3Quj0Yi6ujrs3r1b8CtLHMfBZDJh//79Ie1vs9kwMzMTdvLJejGbzSR+dQU8Hg9u3boFnU63oDlLLEhPT0dfX1/Yz/v2228xOzsLuVyO8+fPL+voUCgUcT0v+nw+9PX1oaWlBQUFBfjv//7vdeuUaM1TFEVBpVIF549kmf8Wk5SC1eFwCKYkjRDQarX46aefUFhYiBMnTiTanBXZsmULtmzZkmgzUpZkuGgRAhzHJZV3oaCgACqVCt9//z2uXLki6LhLq9UKmqZDvhDt7u5GcXHxuhNvwqG/vx8DAwN4//334zZmsuByufDzzz9j06ZNOHDgQMyFTXl5OTo6OsJqMjM3N4fZ2VlcvXp1VR2gVCrjMie63W50d3ejra0NhYWF+Pjjj7Fp06aoHDsa7z9N0zAYDBCJREkrVHmSZ9aeh81mI0k387h69SqOHTuG169fk/7YGxQSEhA6yeRh5bl48SK8Xi++/PJLwRZDB97G3mZmZob0/nIch56enriGMw0MDKChoQG1tbUkJGARDocDP/zwA3Jzc+MiVoG3dVjDzUofHh6GRCJZ02nF5z3EauXJ4XDgyZMn+PrrrxEIBPAf//Ef+N3vfhc1sQqsX7AyDAOj0ZgSYhVIUsFKmgYspbi4GNnZ2Whubk60KYQEQARr6CSjYFUoFPj4448BAF988QXevHmTYIuWx2QyhVxXc2JiAlKpFEajMcZWvWVwcBAPHz5EbW3tgjFnZ2cxODiY8IzyRPPy5UtoNBrs3bs3br+Pjo4OZGRkhCVYLRZLSCWheI+ty+WK2L7lMJvNqK+vx3fffQeVSoX/+Z//wblz55CWlhbVcYD1CVaxWAyDwQCappNuvlsJIlhTCJlMRkTLBobEsIZGMgpW4G0h9N///vdIS0vDjRs38PPPPwvO2xqOYJ2bm0NGRkaMLXrL4OAg6uvrcebMmQVi1WQy4ccff0RbWxv+7//+Dw0NDZieno6LTUKjoqICb968iWu72pmZmbArYMzMzIQcckJRVFReD8dxmJycRF1dHW7evInNmzfjf//3f3HixAlB5mHIZDKkpaWllFgFkjCGleM4OBwOIliXYWpqat1dQwjJCfGwhk6yClbgrdfowoULGBsbw507d/C3v/0Nly9fjqhkTrRxu91wOBwhe5pcLldcQruGhoaCYnV+29eJiQnU1dXh2LFjyMnJgdVqRW9vL3766SecP38eBoMh5rYJCZVKhby8PAwMDITcoWy98F3RQoVlWUxPT6Ompiak/dcrWF0uF/r7+9HZ2QmGYbB//35UVlbGLY48knlKoVAEa6umGknnYXU6nZBKpXEN0k8W7HZ73LNtCcKACNbwSPbJfPPmzfj0008hl8vx4sWLRJsD4K23MjMzM+TlXbfbHXPHA8dx+PXXX3H69OkFYnVsbAx1dXU4ceIEcnJyAAAajQZ79uxBQUEBJiYmYmqXUNFqtXGtUZyWloahoaGQ9+/o6ABN0ygoKAhpf5qmww4JYFkWo6OjuHPnDr755hs4nU58+OGH+POf/4zdu3fHNekx3HlKrVZDrVYn/fy2EknnYSVdrpaHb9eWl5eXaFMIBEGTbFUCVoKmaWg0GsF07eIFa6i4XK6oJqgsx/zueTyjo6P47bffUFNTs2w5pMzMTIyOjgq+WUMsUCqVGB0djdt4+fn5ePbsWcj7t7W1hVVpRiQShSxYrVYr+vr68OrVK6SlpWHXrl24evVqWC1UE4lOpwu2Vk1VklKwCjFmJNE4nU5B9wAmxBZShzV0kjkkYDFCeh0mkwn79u0LeX+32x2XkACtVguLxQKVSoXh4WHcu3cPp06dWjF8KjMzMywRlUoolcq4elh1Ol3IyW5PnjyB2+3GkSNHQj6+SCRatTFBIBDA8PAwXr16hbm5OVRWVuLf/u3f4pYIuBah/L4pikJaWhrEYrGg5oNYkHSCdXh4WDBfJgJBKKT6RBVNUsXDCggnFMTn82F2djasJCqv1xuX0C6tVou2tjaMjIygt7cXp0+fXtUTrNVq4fP54HA4NtxqXrwFa2dnZ8jlxTo7O7Ft27awwkgYhlk1MbGlpQUmkwnV1dUoKSkRZKghwzAIBALL/s5TqcZqKCTdrN3T0xOMOSL8C+Jd29gIRbgkA6n0PkkkEkFUCnjz5g2MRmNY8X1btmyJS93oqqoqbNmyBWKxGLW1tWuGLVAUhczMTMGWDosVLMtiaGgIfr8/bmPa7XZYLBZcv3591f2Gh4fh9Xqxd+/esI4vFotXbG06MzOD7u5ufPLJJygrKxOkWAUAg8GAzMxMZGVlIT09HWlpaVCr1VAoFClVYzUUksrDarFYYLFYNlz2ZqhslC8tYXnIRcva/P3vf4fdbkdPTw/6+/sXPLbS74cXuBzHLfh7/v1qf68X3q759/xNKLVDJyYmwq5QsnXrVvzwww/Yu3dvTMWCTqcLuzMiL1gLCwtjZJWwMJlMePjwIWQyGc6fPx+3cc+ePYtnz56hq6tr1f1aW1vDviAC3nonlxOsgUAA9+/fx+nTpwXd5p3/nfMwDAOGYSCVSoNzzEY67yeVYO3p6UFBQUHKLOdFEyJWNjbEwxoadrsdO3bsgEwmWzCPLCdA+f9pml5w4z0a/N/zt8/fjz/Z8OPM37bcY/zffr8/eAsEAkvu+Zvf74fT6cSLFy8wOzsbk8LloTIxMYHdu3eH9RxeSA4PD4ec9R0vMjMz8eTJk0SbsSwcx8Hj8UAsFq9b6LtcLjQ1NWFsbAz79+9HYWFhXAWQUqlEUVERuru7V93P4XCEldDH4/P5lhWkHR0dSEtLi1v5rliwkYQqT1IJ1u7ubpSWlibaDAJBcBDBGjq7du0SdB3ncL1Iw8PDqKurw0cffRQji1bH7/djeno6oiYAW7duRVdXl+AEq9FoxMzMjGAS9DiOw/T0NPr7+9Hf3w+32w2/3w+RSASpVAqJRLLgXi6XQ6vVQqPRQKPRQKlULrhAY1kWr169wrNnz1BaWoorV64kLBve6/Wu+R57PB5oNJqwj22325esyJrNZrS3t+O//uu/BPHZEkInaQSr1+vFyMgIDh8+nGhTBAkRKxsbIlg3LkePHsU//vEPzMzMJCRcanJyEnq9PiLBU1hYiMePHwuu+otEIgFFUfD5fAkva9Ta2orOzs5g/dGTJ08GP2e/3w+PxwOv1wuPxxP82+FwYHJyEn19fbBarXC73VCpVEERazKZIBaLcf78+YR65oG35/a1Vk19Pl9EzTH279+PBw8eIDMzExUVFWBZFg8ePMDx48cjEsCExJI0gvX169fIzs6GWCxOtCmChIQEbGyIYA0NiUQSjF1LFe7duweVSpWwbldzc3MRix6GYYJLwnv27ImyZetDLpfD5XIlXLAODg5i9+7dKC0tXeIRFIvFIZ0T/X4/rFZr8LZz504UFBQIwsPo8XhWFaxv3rwBy7IRNcUpKyuD0+nEw4cPUVpaip6eHshksrDDVwjCIGmCQbu7u0kXJwJhBYhgDY1Tp05haGgI4+PjiTYlarjdbuTm5iYstl+n08FisUT8/LKyMnR3dwvuopsXrIkmIyMDLpdrXeKSYRikpaUhPz8flZWVcY9VXQ2fz7fqd9dsNoNhmIi/37t374ZIJEJjYyOePXuGCxcuCOa1E8IjKQQry7Lo7e0Nq8PFRkMosVaExEEE69pkZ2eDpulVi4knG4m+WDEYDMF4z0gwGo2QyWSCu4gQg6QoKwAAIABJREFUkmCdnJxMtBkxY62QAIfDse7ksoyMDHR2dqK8vDzhIRCEyEmKkIDR0VGoVCpBl59INELzThDii8fjwdzcHP7yl78k2pSoo9PpcO7cuagUcXe73WBZdtmWnMnKWt18Yo1MJoNEIoHNZos4LtBoNMJqtUbZsvXh9XrX5TmOFhkZGXj06FGizYgZa3lYnU5n2ImIi9m3bx8ePHiAs2fPrus4hMSSFIK1u7tbcFmkBIKQkMlkyMjIiGsNxXjgdDpx8+ZN/P3vf0dVVRV27969rpNXd3c3xGKxoKsEhEtubi56enoSagPvZY1UsAYCgXWLkmhisVgwMTERVhvQWKFSqeD3++F2u1Pqe8vDVztYiZGRkYi9oj09PXjz5g2mpqZw4sQJwTYHIISGcGaIVejp6cHRo0cTbYagIR7WjQ1f11NIJ/1ooNFo8NFHH+H58+doaWlBS0sLFAoFNm/ejNHRUXg8nmAozPzC/rm5uTh58uQSz83AwEDYReSFTlVVFdrb2xOaac+XgYrUsRAIBAQjJjiOQ319Pfbv3y+ITPLh4WHQNJ2yIT9+v3/Fectut8Nms+HcuXNhHbOnpwcNDQ3w+/1BkV9RUbFuWwmJRfBnN/4Lm6gM2GSCxLASUpXdu3dj9+7dmJmZQUdHB0ZHR2EwGFBWVhZsJSmVSiGVSuF0OnH//n18/vnnqKmpCbZyZlkWU1NTOHbsWCJfStRRKBSQyWS4efMmjhw5ElE91PViMBjWLP6+GkISrL29vfB6vdi+fXuiTUFfXx8eP36M2tpayOXyRJsTExwOBywWC27cuAGRSASRSBRMsuIvOH/77TdkZWUFm28sbswxf3sgEEBjYyNKSkpQXV0Ni8WCx48fk/NjCiB4wapQKCASieB0OqMSw5aqpOrVN4EwH4PBENIybW5uLu7cuYObN29CJpNh27ZtMBqN4Dguoo45QqempgYNDQ24fv06ZDIZ3n33XWzdujVu44vF4nX1oBeKYOU7P9XW1ia8o2JnZyeeP3+Oc+fOpXSikNPphEQiCYpNr9cLlmURCATAsizkcjnMZjPsdvuq7ZHn3+fl5QVXZfludYTkR/CClaZplJaWYnR0NK4TcLJBBOvGJtGZ4kKDYRicPn0aTqcTTU1NePHiBXJycmAwGPD111/j8uXLKRUakJ2djStXrgRrTtbX16OoqChuISLrja8UimBtbGxEcXExjEZjQu1oaWnBq1ev8P777wsiLCGWOJ1OnDp1Cnl5eTE5PhGsqYPgBSvwtn1fY2MjEayrQMQKgbAUhUKBY8eOYdOmTXjw4AEqKipgsVjQ2dmJgwcPJtq8qKNQKFBTU4O//vWvuHHjRljCa/GSKf///HuapiESiUBRFEQiUXA5dr2xwWsl3sSD0dFRTExM4MqVKwmzgeM4NDc3Y3BwEO+//37KrypOT0+D47hg2E4sICUfU4ekEKxFRUX45z//CY/HA6lUmmhzBAn5URIIK1NWVgaHw4GXL1/C7/fDbDYn2qSYQdM0tm7dipcvX8LtdockBBdf8C53Acwvx86/8dtDaa+5Gon2sPr9ftTX16O6ujph3RQ5jsPDhw8xNTWF999/PyUrAiymt7cXMpksph5QlmWJhzVFSArBKhaLkZ+fD5PJFLNlg2SHeFg3NiQkYG327NmDPXv2oLGxcV0JQsnAgQMHMD4+DrPZjJqampiXBWxtbY24yD7HcfB4PAmtcNHV1YW0tDTk5uYmZHyWZXHv3j04HA6cP38+4e1g48X4+HjMwy9ISEDqkDSfYllZGQYHBxNthmAhYoVACI3Kykp4PB44HI5EmxIzaJrGlStXkJmZiefPn8dlvEhL63V1dUGpVEKr1UbZqtBgWRZtbW3YtWtXQsb3eDy4efMmPB4PamtrN4xYBd7Wu421E4phGFitVnKOTAGSRrCWlpZicHAQgUAg0aYIEvJjJBBCQ6FQQCqVorOzM9GmxJx33nkHMzMzuH79Orxeb8zGEYlEER3f5XKhubkZhw4dSlhI0+vXr6FWq+NeDszv96O9vR2ff/45JiYmcOrUqZSro7waTqcTfr8fRUVFMR2Hrw7S398f03EIsSdpBKtSqUz5nsrrgcSwbmzIZx8eUqkUNpst0WbEnOzsbFy+fBkWiwXffPNNzBqMZGdnY2RkJOzjNzY2orS0FAaDISZ2rQXHcWhpacHOnTvjNmYgEEBnZye++uorjI2NobS0FGKxOOFJZ/Gmt7c3Ll3nKIrCrl270NDQsOSx5uZmeDyemI5PiB5JI1iBt9UChoeHE22GICEeVgL5DoRObm4u+vv74Xa7E21KzDEYDPjoo4/gcrnQ0tISkzF0Oh00Gk1Y8/PY2BgmJiawZ8+emNgUCgMDA6AoClu2bIn5WCzLoqenB19//TUGBgZw8uRJnDlzJuXLVq1Ef38/aJpGQ0MDnjx5gufPn6O9vR1dXV14/fo1RkZG8ObNG8zOzsLhcMDv90d8wZWbm4uZmRmMj48v2N7Q0ID/+7//I6I1SUiq9YetW7fi7t276O3tBbC8V2ktT1Ooz1nPcfgC2vzyzkpCYjWBsVKW7kr7ulwuBAIBXLt2bUUbV3pN87eH8pz527xeb7AryVqZxvP/D+exxdu8Xi+pFrEI4mENj4MHD2JoaAjff/89rl69mmhzYo5MJgNFUVCr1TEbY+vWreju7kZ+fv6a+wYCATx8+BAHDx5MWFa+x+PB48ePceTIkZj+fnw+H9rb29Hb2wu5XI6jR49i06ZNwccpioLH41kwdwsViqKgVCpx/vz5dYcv2O12sCyLwcFBsCwLlmXBcVzwfnE1iuVs4VcW5+9TXV29pA2rSCTCzp070dDQsKBsWXZ2NsbGxnDt2jV8+umn5LwicJJKsBoMBgQCARQWFi7YvrjTxeLtK/2/eFsoxwlFSI6NjYGiKKSnpy/Yvpb4W6sO4mrH4UvLzO8lPv/1rPQaVvs7lPemv78fBoMhmDCxnM18C72VXu/8+9Wez28bGhpaV1cdAgEALly4gC+++AKvX7+OeRxdouE7B23evDlmYxQWFqKxsRFOpxMKhWLVfVtaWqDX60MSt7Hi8ePHyMvLi4l3NRAIYHR0FH19fRgeHobP58PWrVtx+PDhJfN3eXl5sLtTpKwmuEMR4yvN74sfB962i/3yyy9x9erVdSeIbdu2Dfv27Qt5f7/fD6/XG7xdv34dhw8fRkZGBqRSKW7evInBwcElghV4Wx7z6dOnmJ2dDXYO27JlC6RSKTiOw5dffonPPvtsXa+HEFuSSrDyxar37fv/2DvzoCjzNM9/MknIBJL7vuVQDhVUvPAELbzKC8Wzypru6Zrt6Iid2Y2J2Nnt2D92J2Jneo+JmO7pmN3p6prp6irLUrQKAcXyAAFvBUG8kEO5D7nvJMl8c/9wMgcEFCGTPHg/EW9k5vvm+3ufN/M9vu/ze37Ps9qig9P1NZE/+ugjc5ticurq6oiNjSU2NnbOttnf309HR8ecbU/ENlEqlXh6elJRUWHzgvX169dIJJL3CsnZ4ODgwIIFC6iqqiIhIWHK7z179oyKigr27dtnMlveR0NDAy0tLaSnpxu1XZVKxcOHD6mqqsLDw4OoqCjWrVtHRkYGbm5uk4pHfSlda2HlypVkZGQYROtMY1C1Wu0HryuTyZDJZIbjWCKR4O7ujoeHBwD+/v68evVq0nXt7e1ZunQpN2/eZNeuXchkMoKCgnjy5AkbN24kPz9/RvshMndYruqbAplMZrKBAyLWg9gFPh4xD+vMCAsL4+nTp+Y2w+TcvHlzTtJGxcTEUFRURHx8/IRzVKPRcPXqVRoaGvD19TUMgnm7Z+Xt9d4uUjB2ksvlJCcnf1CeTbVaTVFREcnJyUYLR9DpdFRXV3P37l3Cw8M5cOCAScMvzImDgwNHjx7l9OnTZGRk8Omnn84oz+lMBOtU7egJDw83FMyYrO2YmBhycnL41a9+hUwmQ6FQMDg4SEdHh0l7H0SMgyhYRURE5i0uLi42nyqvsrKSrq4ujhw5YvJt+fn50dPTw8OHDw2DqQRBoLq6muLiYrRaLZ6engiCwMDAgGG9t0Wp/nUqMat/bWhoQKVSGWIf9fGPb6MPiRAEgcHBQby8vPD39zfKPvf29nLz5k1UKhXbt2+f8/RY5kAmk5Gens7XX3+NSqWakedep9MZxeM/9v/29/fH2dmZM2fOcOTIkQmiVS6Xk56ejk6nY3R01BCK8fTpU5OWhxUxDlYpWG39BiPybkRPooixsLe3t+njSaPRcPPmTaKjo+fEw6oXlSUlJZSVlRkEpJ+fHykpKeMGGxmDL774guHhYaRS6bjpbaRSqaE7WZ//87vvvmPJkiXExMTMyNOn1Wp59OgRjx8/Zvny5SxZsmRKT6Mtph3Up4WbqZdUEAQcHR1nZYNEIhnnwJJKpRw5coTTp09z5coV9u7dO+V69vb29PX1UVdXR1VVFevWrZuVLSKmx+oEq52dnShYRWzu4i9iHhQKBVqtlurqaqKiosxtjlGpq6vj7t27SKVSNm7cOGfbtbe3Z/ny5SxevBipVDppN78x2bt374y69js7OykvL+f06dNERUWxdOnSd4p6QRDo6uqiubmZ1tZWWlpa8PPzs+nu/3fh5eWFRCKhpqaGhQsXzqgNZ2fnWdvxdo+rTCYjIiJi0kIBgiDw+vVr6urqqKmpwcnJiZiYGH7yk5/g5+c3a1tETIvVCVYxJMDymGsPlS17xGaKKOBnRmBgIOHh4RQVFVm1YBUEgWfPntHc3ExnZyeDg4PodDo8PT3Zs2fPnNdS13s054KZHvteXl6kpKQwODjI06dPycrKQi6X4+rqiouLi+G1t7eXlpYW2tracHZ2xt/fn4iICNavX28UwWWtSKVSAgICKCwspKenh8TExGkfZ/qqaMYoQ6vXAzqdjr6+PhoaGmhqamJoaIh//ud/Ri6XI5fLcXBwoK+vD09PT2JiYti4caPZClaIzAyrFKyih1VEZCKikJ8ZKSkp/OEPf+Dly5cTUuZZCwUFBdTU1ODu7o6fnx/BwcFERUXNuVC1RpydnVm9ejWJiYn09fWNm5qbm3F1dSUmJobk5ORZd2HbGrt27aKkpIRHjx7x9OlT1q1bx6JFi9673tDQEMCsjs+enh4EQUAul1NaWkp1dTWCIBATE8PevXsJCQlBEARGRkYMk1KpnLeFGmwBUbCKzArRsydi7chkMjw8PKioqLBawVpbW0tiYiIrVqwwtylW++BkZ2eHh4eHIUWSyPuRSqWsWrUKmUzGgwcPKCgooLq6mm3btr3Twz40NPRB9w59nvGBgQH6+/vp7e2lpqYGgHv37hETE8OhQ4fw9/cf166dnR329vbj8pOLWC+iYBWxSkShPB7x95gdoaGhPH/+3NxmzIi+vj40Go1FCS3xeJw/qFQqiouLWbZsGSEhIVy+fJlvvvmG1NTUKYsyuLi4oNPpePHiBdHR0Yb5Op2O169f09rayuDgIAMDA/T19dHf349UKsXT0xNPT0+8vb1Zv349vr6+BAYGztWuipgZqxOsdnZ2YgzrPMdaPTimRvxdZk5cXBxlZWVT5m+0ZPRd1levXuWTTz6Zd3GVYtiDebl69SpOTk6GilWfffYZeXl55ObmEhERwZYtW8b9R4IgUFpaCkBjYyPR0dEIgkB9fT2PHj1CEARiY2Px9fXFzc0NV1dXXF1dDQOuxfKp8xerE6zDw8Nmqz0tYjmIHhwRY6JUKpHJZLx8+XLSso6WzqZNm6ipqaGmpob4+HhzmyMyCbZ4zSovL6elpWVc1TKpVEpqair19fVcu3aNb775hh07dhhG4efn51NbW8vmzZuJjIykoqLCUKp3y5YtRERE0NXVRXt7O3V1dbS3t9Pe3k5PTw9yuZyDBw9abeiOyOywKsEqCAJtbW0W1fUlMvfY29vT2dnJF198Me4mMFWC8XdNUqmU0dFRZDKZST01s/F+Tmfd4eFhBEHgu+++m/F2xiKRSPjoo4/w9vY2SnvWgIODA729veY2Y8Y4ODjQ3t5ubjNE5gl5eXm8fPmSVatWTZoSKjQ0lM8++4zLly+TlZVFTEwMGzZswNnZ2ZAP99tvv8XHx4eoqChUKhXXrl2ju7sbV1dXvLy88PT0ZMGCBSQkJKBUKuns7OSHH34gJSXFUJhCZP5gVYK1vb0dFxcX0cM6z9m8eTOJiYlotVo0Go2hio1Go0Gr1Roq2rz9fuw8nU5nmFdVVYWTk9OEByFje0Qma2+623jf9/T7bqzussrKSlpaWuadYB0cHDS3GTOivr6ewcFBli1bZm5T5hwxJMA8dHV1ERgYyPLly6f8jkwm4+OPP6ampoa8vDx8fHwYHh5GrVZTUlKCUqlEoVAgk8kICQlh8eLFuLi4TDlgSx+7euHCBUZHR1m7dq2pdk/EArEqwdrS0mK0cnoixmOuYyelUqlRU5PU1tYSERHxzgvvfGOypNu2jlqtttq0RUVFRYSEhMyrvJLmHsugH7k+1TQ6Omq4NjY0NODk5IRGo5nQxrs+TzXPwcEBe3t7HBwcpnxvaiHv5eVFY2PjlMsVP/yAy69+hV1zMz6BgbStWYPzjh2sXLmSmJgYfH19p5WrV6VS0dLSQmNjI7W1tbi4uJCUlERkZKQxd0fECrAqwdrc3DyvPD4iIuZiPg7gUqvVVhlu1N3dzdDQEOnp6eY2xSLQaDQMDAwwMDDA4OAg/f39hvf6tEj69/r5IyMj44Tm2M/vEqRjheLbk729vUE0dnR0kJeXN+mAuLd7T6bT6zI6OjrOjsney2Qy7O3tkcvl2Nvbv/e9g4MDzs7OODs7o1QqJ7wqlUqcnJxQKpVotVrKy8tZt27dpGVnFT/8gNt/+k9Ih4cBkDU1sScnh95Nm9AcPvxOh4MgCHR2dtLU1ERdXR29vb2Eh4cTFRXFjh07xDyq8xirE6z6kYgiIiKmxRYHibwLmUxmdTGsgiBQVFSEs7Oz1WU3mAqVSkVXVxfd3d10dXWNe68Xn3rhWVNTw9mzZ8cJULVaPU5oubi4jBNdzs7OhkpWAQEBODs7j6uGNFbAvW+a7jny1VdfsWLFijkbEKfT6dBoNJMK2amErkqlYmhoaJy4b29vZ3BwcILA11dT+/Wvf40gCBOEbu6zZ0hHRsbZ5DA6isf/+T+0Hz48wd7BwUGDF7Wurg5PT0+ioqLYtWsXwcHBYtiHCGBFglVfA9jd3d3cpoiIiNggfn5+vHz5Eh8fn3HzJxMlU3Xljn3VT4IgjHudbP7bMdhvT4IgIAgCoaGhrFq1Cnhzk8/KymJ4eJidO3ea4ieZNe8Sn5N97u7uRqPRGPJtenh4jHvv6+tLREQEzs7OODo6cuPGDY4ePWoQo0qlEkdHR4t52BIEgRs3bhiE4VwhkUgM3lNTpDnLz8+nvb2dI0eOoFarJ4hav717J13PrqmJ3NzcceeJSqVCpVIRERHB4sWL2bt377xLzSYyPaxGsLa3t+Pq6ioOuBIxCfOxC1xkPGFhYdTV1VFYWDjrtqbKXjHVMqlUOm6ys7NDIpFgZ2dnqNYjlUopLS1FKpWyfPlyTp8+jVKp5JNPPplT76pOp6Orq4u2tjba2tpobW01vLa2tvL06VNGR0cZGBgwiM+xwlP/ecGCBaxYsWLCcicnp2kJTrVaTUNDg0Wn8RoeHubFixdIpVIcHBzMbY7R8PPzo7q6mosXL/Lxxx/j4OAwLpxGGxSErKlpwnraoCBSU1OBfzv2HRwc8PX1tZiHDBHLxWoEa3Nz86SpM0RERESMQVRUFEVFRSQmJlrsaPvnz59z48YNQ5aLI0eOGLX9gYEBWlpaphSjbW1tvH79GkdHR/z8/PDz88Pf3x9/f3+io6PZvHkzDx48YP369axZswZnZ2eTCRFzD7qaDs7OzoaE97bE4sWL0Wq1lJSUTLq8/5e/HBfDCqBzdET2v/4XoaGhc2WmiI1hVYL17a46EREREWMhk8lISkrizp07+Pj4EBQUZG6TJhAbG8vw8DDFxcUfLARHRkZoamqivr6exsZG6uvraW5uHidGBUEgICDAIET9/PwIDg4mMTHRIEx9fX3fmU2htbUVf39/sX67jRMZGcn9+/e5cuUK27ZtG7dMdeAAAM5/8zfYt7Yy4OFBaXo6mz75xBymitgIViNY29raLNbrISJii8zHLrqlS5fy+vVrLl26xMGDBy0ya8CKFSvo6uqioaFh3HyNRkNLSwv19fU0NDQYXvVTZ2cnAQEBhISEEBISQmhoKJs3bzYIUb3ItJb/3Ro8rPr45Omkb7I2nJ2d2b17Nzk5ORQVFbFp06Zxy1UHDhiE69OnT23Oyywy91jNWRQXF0dxcTG7du3Czs7O3OaIiIjYKFu3biUrK4sffviBY8eO4eTkZG6TgH+r9FdfX8+VK1cYHBykvLzc4C1ta2vDy8uL0NBQQkNDCQ4OZsOGDYSGhhISEoK/v79NCidLpq2tzVBRzxbx9/dn27ZtXL58GYVCMWUWn9bWVrEylcissZqr15o1a6itraW0tJSVK1ea2xwRG0McdCUylj179nDq1CmKiorYsWPHnG1Xp9PR0dFBTU0NNTU1VFdXU1NTw8uXL2lqasLV1ZXQ0FBGRkZYvnw58fHx7N+/n9DQUIKCgmxqYM/7sAYPa0VFBU5OToyOjprbFJMRFhZGQEAAjx8/nlSw6nQ6mpqa2L9/vxmsE7ElrEawSiQS9u3bxxdffIG/vz/BwcHmNknERrCWLlCRuUMqlbJ27VquX7+OWq02uhBUqVTU1tYaBOnYyc7OjoiICCIjI4mMjGT16tVEREQQEhJiqJb0L//yL3z22Wc2k3t1JljDQ2ZjYyPh4eFUV1eb2xSTUVRUREtLC9u3b590eV9fH46OjmJMs8issRrBCuDo6Eh6ejqnTp0iLS3NYnO1WcOFVETkXWi1Wu7evcvDhw/NbYpZ0el05OTkkJaW9sHdujqdjtbW1gmCtKamhra2NkJCQgyiNCkpiU8//ZTIyMj3lleVyWTIZDKqq6tZsmTJbHbPqrH066xKpWJ4eJj4+HibFKwDAwNkZ2czNDREamoqYWFhk36vvb2dkJCQObZOxBaxKsEKEBQUxIYNG8jPz7foeFbRaydizUgkEnx8fPD39ze3KWZlZGSEyspKTp48yd69e3F1dZ0gXHU6HQ0NDTx//pyKigpevHhh6MZ3dHQkKirKIEw3btxIZGQkoaGhs4ondXNzo76+fl4LVksPCSgrK8PBwcEmS4n29/eTkZGBUqnk008/faenv62tjfDw8Dm0TsRWsTrBCrB27Vrq6urEeFYRERMhlUqJiIiY14JIz5o1a7h48SIZGRkMDw8TFxdHY2MjFRUVPHv2jBcvXuDi4kJsbCwxMTGkpKTw+eefExkZiZubm0lsCggIsEmvnS1RXV1tEzlH1Wo1ly9fNlSj6u/vp6qqCm9vb/bt2/fenoempqYJGQRERGaCVQrWsfGsISEhYkEBM2PpXXPTwRb2QcR4jI6OUlNTw7Nnz6ioqOD58+c8f/6cjo4OIiIiWLlyJTExMaSlpREdHT3n6a/i4uJ48uQJr169mrfeK0v2sA4NDTE0NDRuZPzg4CCvX79+53qCICCRSCathvY2k5X5fbvkL7x5+NS3OXbSz3+7rbc/FxUVodVq8fT0pKSkBKlUyqZNm4iOjn7v76AvuyrmUBcxBlYpWOFNPGt8fDytra2iYBURMTISicSiBYGx0Ol0tLS0GLylenH66tUrgoODDV7TTz75hIULF5Kfn09iYiIrVqwwq93u7u5ERkZSUFBAWFiYxaVNmouQKEt+yGxoaMDOzs7gYXdycuLJkyc8efLknevp9+l9v59Op0MikYz7Dd4Wuu9q/0PQ6XR89tlnnDt3DqVSSXp6+rQHIdbW1hIaGiqGyIkYBasVrACenp5UVlaa2wwRG8CSb34ixkGn01FbW8ujR4949OgRjx8/5tmzZ9jb2xMTE0NcXBwbN27k3/27f8fChQsnVHO6fv06MpnMYgqYpKSk8NVXX3Ht2rUJlYbmA5Z6zmo0Gu7du4e7u7th3uHDh6e1blZWFnZ2duzevXvCMpVKZYgV7e7uJjc3l8HBQZydnRkcHMTOzo6oqCijdr+3tbWRnZ2NQqFArVazbt26aYvVnp4eiouL+dM//VOj2SMyv7Fqwerh4UFvb6+5zRARsUksVRBMB/1AKL04LS8v5/HjxyiVShISEkhISODf//t/z5IlS/D29p5Wm9XV1axdu9ZivJlSqZQdO3Zw4cIFHjx4wKpVq8xt0pyi9zJaEoIgcPbsWQD27dv3wetPtU/Xrl3j5cuXAMjlctRqNV5eXqSlpRlSnZWXl1NSUoKXlxeLFy+e3Y78KwqFwnAdsLe3p6enZ1rraTQa8vLy2LZt23uzXoiITBerFqzu7u7TPoFERERsE31i8vLy8nHeU4VCQXx8PAkJCfziF78gPj5+VjdPV1dXXrx4wdKlS41o/ewIDAxk06ZNFBUVIZfLiY+PN7dJc4alhaxoNBoyMzNRqVQcO3ZsRlkgdDqd4YFocHCQ4uJimpqaGBwcZPfu3chkMhoaGpBIJCxbtszwG8hkMlasWIFarebOnTssXLjQKLmDx/Yy+Pj4UF1dzfLly5HL5e9c78GDBwQFBZGQkDBrG0RE9Fi1YHVxcWFkZASNRiOWHBQRMSKWGsOqz22q95rqX6VSqcFz+vnnnxMfH4+vr69Rt719+3YyMjLo7Oy0KK9RTEwMIyMj3L17l4aGBnbu3GlWL7AgCHOSbtDcPQCCIJCXl8fAwAASiYT29nbkcjnp6ekzLuig97C2trZy4cIFHBwcCA4OJiEhwXDM6Y/roqIiKioqSExMNAzuWrt2LS9evOD27dskJyfPeh/t7e2BN5kCVqxYwdWrV8nNzWXnzp1T7mNdXR1NTU1E0VSDAAAgAElEQVT8/Oc/n/X2RUTGYtUqTyKR4ObmxuDgoMnSx4iIiJiP/v5+Hj58SHFxsUGcarVaEhISiI+P58SJEyQkJODv72/y7mF3d3c8PDy4efPmjLp7TUlCQgIBAQFcvHiRr7/+mp07d5plMGp7eztarXZOMheYU7AKgkBOTg7t7e34+fkhCAIbNmwgNjZ2Vu3qdDo6OzvJyckhLCyMjz76aMqHj+bmZpycnHj48CHV1dXs3r0bZ2dnAgMDqayspL6+nqSkJBYuXDhje/TnlEqlwtvbG61WS0REhEG0vh3nPTAwwI0bN/j000/nVZlgkbnBqgUrvIljFQWryGwxt7fGEpnr30Sn01FfX8+DBw8oLi6muLiY2tpa4uPjSUxM5OjRo/zt3/4tQUFBZotdTEpKIjc3l+zsbDZt2jRuYI258fX15cSJE2RlZZGXl8fx48fn3IZHjx7h4uIyJ2LFnOfsxYsX6ejo4ODBg0ZPaTY4ODjOazoVAwMDbNmyBV9fXy5evMipU6dISkqisbGRqKgo4M1AwZ6enlnFN0skElQqFa6urkRERODt7Y2TkxNnzpwhODiYuLg4AgMD0Wq1XL9+nU2bNhEQEDDj7YmITIVNCNb+/n5zmyFixVjawA1LwdSCQKVS8fjxY4M4LS4uxs7OjlWrVrFy5UqOHj1KXFycRXlqgoOD2bFjB3fu3CEjI4OlS5eSlJRkbrMMyGQyUlJSOHfu3LhR5XNFU1PTtPJzGgOtVotOp6OiogJXV1fc3d1xcnIy+XYFQaClpYU9e/YYXaxu3LgROzu794ac1NXVIQiCoWLakSNHePDgAbdv3wZg06ZNCIJAdXX1tM+fkpISIiIiJuyTXrAChIaGUllZyfHjx1m9ejXPnz8nPz+fY8eOGR5WVq9ePYM9FxF5PzYhWDs6OsxthoiITWEKEf/69WuKi4sNHtRnz56xcOFCVq5cyZ49e/jrv/5rs3pPp0toaCihoaHk5ubS2tpqbnMm4OnpiYODA48fP57zzAH29vbU1dWxdu1ak2+ruLgYiUTC7du3DeLV3d2d3bt3m0S4tre34+LiwsDAAIBJQi6mE3ddX1/PlStXiImJGTd2Y9WqVSxcuJC+vj5kMhm9vb1IJBLu379PXV0dO3bsmFK8qtVqysrKDGEvYxkrWP39/cnPz2d0dBSFQsGyZcvIz8+nurqayspKfv7zn1v8+StivVi9YHV3d6empsbcZoxDJpPR3d0tDgYTsWpm42HVarVUVFSM85729vaSmJjIypUr+S//5b+wbNkynJ2djWjx3GOpN2dHR0f6+vqANx7BuRqEtX//fk6ePMnAwABKpdKk25JKpXh7e5OWlga86SLPycnh1KlT7Nu3z6jVlXp6esjMzATeZIuQy+VmGdj2+PFj7ty5Q3R09KT5Vt3d3Q1hKm5ubvzZn/0ZtbW13Lx5k5MnT+Lu7o6Liwupqanj1mtsbESr1RrE+FikUikjIyMAODg4EBAQQFVVFXFxcUgkEoKDgyksLOSzzz6bEw+3yPzF6tVUcHAwFy5coKenx2LiybZs2cLZs2f57rvvOHTo0Jx3y4mIGIMPEayjo6M8evSIO3fucPv2bR4+fIivry8rV64kKSmJv/iLvyAyMtJicpgaA0vMA6rH0dGRxsZGcnJyaGlpQaFQcPToUZOHVzg5OeHg4MCLFy/eG4M5W2JjYykqKjIIcqVSybFjx7h48SJZWVkcPnwYV1dXo2zr+vXreHh4oFQqaWhoICQkxCjtfgj379+nrKyM1atXf1DxigULFhh6BJqbm+no6CAvL4+tW7cavlNdXU1kZCRDQ0MT1rezs0OtVhs+JyQkcPHiRZycnFiwYAHx8fGEh4cTFhY2ux0UEXkPVn/3cHFxYdu2beTl5aHRaMxtDvDmon3s2DHs7Oz47rvvxBhbEavkXYJ1dHSUkpISfvvb33L8+HEWL17ML3/5Szo6OviTP/kTbt++zY0bN/j7v/97jh8/zsKFC21KrIJlD9TbsmULXl5eqFQqtmzZgkQi4ezZs3NyjXRycqKrq8uk22hsbGR0dBRBEMaJKYCdO3fi4eHB999/b+jKng1dXV20t7ezefNm4uPjWbp0Kdu3b591u9Pl/v37fP/995SVlbF58+YZVVqTSqXjQiX0HlN4E0ve0tJCYmLipPeqsR5WeBMWsG3bNs6ePUtFRQWxsbFi3KrInGD1HlZ488RXU1NDcXHxnMROTQcHBweOHj1KZmYmGRkZ7N2716hdVCIipuRtz6FGo+Hx48fcvn2b27dv8+DBA0JDQ0lKSuLEiRP84z/+o9EHoFg6luxhVSqV48p7BgcHc/LkSR4/fszy5ctNtl1BEBgZGTG6J7eoqAidTkdQUBClpaV0d3djZ2dHYGDghB4sqVRKWloaZ86c4eTJk0RERLBu3boZ93S9evUKuVxuiC8NCgqa9f5Ml97eXsrKygyDEWc7oE0qleLq6squXbsM8+rr61m0aBFeXl6TClaZTMbo6Oi4eb6+vuzcuZNLly4RExMzK5tERKaLTQhWgI8//pjf/e53BAUFmaW7ZjL0F85Lly5x/vx5duzYYTG2GRNL9jSJzAytVkt1dTXFxcXcuXOH+/fvExwcTFJSEp988gm//e1v8fT0NLeZZsWSBevbODg4IAiCycVWQUEBIyMjRq+4VVFRgZOTE1VVVYYeLBcXlym/L5VKOXLkCI8fP6a8vJxvvvmGZcuW4e3tTWtrKy4uLsTFxSEIAk+ePKGtrY3h4WE2bdo04bgeGRkx21iEH3/8EQ8PDw4dOjSrdjQaDT/++CMDAwMT4ldVKhUuLi64urrS19c34bh+OyRAj4eHB8PDw7OyS0TkQ7AZwSqXyzl48CCnTp3iwIEDFhP8LZVK+fjjj7l+/TqXLl0iOTmZRYsWmdsso2EtN+z3Md9Ft1ar5enTpwYP6s2bN/Hx8eGjjz7i6NGj/PrXv7ao6k4iH8arV6+QSCRGr/71NrW1taxatcqo3nZ9GMPRo0c/SDiOrX726NEjHjx4ALy5V+grgwmCgEwmMxSgKSgo4MCBA+PaGRgYMLlg7evro6ioiI8++sjgCX727Bl9fX0cO3Zs1u3n5eXx+vVr9u/fP+EYCAgI4O7du6SmpiKRSBgdHR3nIZ/MwwpvhKxGo5nTQX0i8xubEazwpqsmKSmJgoICduzYYVEnUUpKCs7OzhQUFDA0NDSjOCQR02ArovtD0Ol0VFdXU1hYyI0bN7h//z5+fn4kJSVx+PBh1q1bR0JCgkXlGLU0xtZ9t3Tu379v8mTuVVVVaDQaFi9ebLQ2BwYGuHjxIlKpdFaiUS9c9QiCwIsXL/D09DSkp2prayMrK4uSkhLDgLG2tjZqa2vZsGHD7HbkPdy7d4/m5mZOnjzJhg0biIqK4sGDByxcuHDW2RYEQaChoYGkpKRJH1g8PT3p7OxkeHgYV1dXVCrVOMFqb2/PyMjIuAFZ+uPe3t4etVotDiwWmRNsSrACrF+/npcvX/LkyROjd0vNltWrV+Pk5MTt27cZGhpi3bp15jZJ5F+ZDx7Wnp4ebty4QWFhIYWFheh0OpKTkzlw4AB/93d/Ny7G+uTJk2a01DqwlpCAtrY2+vv72bNnj8m2MTg4SGFhIbGxsUb1RmZlZSGRSDh69KjR2oQ3guvtMqp+fn6sWbOGe/fu8ejRI+CNd1dfzcmUNDY2snz5ckZGRigqKqKoqAh7e3ujjMl48uQJOp2O2NhYenp6DJkc9NjZ2REcHExtbS2urq4MDQ2Ny67g5ubG8+fPp7wmmKNAhcj8xOYEq0QiIS0tjS+++IKAgACLG+i0ZMkSnJycyMvLY3BwcEI8kYiIsdBoNJSWllJQUEBRUREvXrxgzZo1bN68mZ///OdERUVZheCyVKxFsD558gQXFxeT5UUVBIGsrCxcXFzYuHGj0dotLS1laGiIEydOzJkgSkhIICQkhHPnzrFu3Tr8/PxMfg+prKxkdHSUhIQEHBwcWLZsGX19fQQGBhqlfZ1Oh06n46uvvkKj0eDv78/evXvHfSc4OJiXL1/i6uo6IRfrxo0bJ/1fX716xePHj8Wy6CJzhs0JVniT6mrv3r1cuHCBtLQ05HK5uU0aR0REBI6OjoZ8gXv27LGarkURy6ahoYGCggIKCwu5desWQUFBJCcn85//839m1apVFncuWDvWIFhbWlpMGg5QVlbG0NAQn376qVHa6+rq4sKFC6hUKhITE+fce6cfdBUVFWXybff391NYWMiSJUsMXk+lUmnUh4uEhAQiIiKoqqpCJpNx7949uru7x8UZ+/v7c+3aNbZv3052djaenp7vHFQ5PDzMrVu3OHHihFWcAyK2gU0KVoCFCxcSGxvLnTt32Lx5s8WdVAEBARw8eJDMzEzOnj3LwYMHxapYZsRaQwIGBwe5ffu2QaT29fWxefNmduzYwd/+7d+afJDNfMZaPKzh4eE8f/7cZNWnnjx5MmNxJwgChYWFrF+/3iDYrl69ikKh4MCBAyavljUZ+kFepi6yAJCTk4OHh4fJw8NcXFxYsWKFIXb33LlzODs7Ex0dTUhIiCFnr5+fH7t37yYnJ4ft27dP6V2+d+8eK1aswN/f36R2i4iMxabdeh999BF9fX08ffrU3KZMioeHB0eOHEGlUnH69GmjJLk2B9Yq9qwRQRAoLy/nt7/9Lenp6Sxbtozf//73BAQE8E//9E+UlZUZloli1bRYi2Bdv349rq6u/PDDD0a/xrS0tKBSqWYca5mfn09VVRUlJSUAvHjxgr6+Pnbt2mUWsQr/JlhNnbJJpVIxMDDAjh07TLqdsUilUg4dOsSePXuQyWTU1NRw8+ZNvv32W7RaLS9fviQmJoYDBw5w+fJlWltbJ7TR0NBAZ2cnmzdvnjO7RUTAhj2s8CYdx/Hjx/n666/RaDQkJCRY3A3G2dmZY8eOcfbsWU6fPs3BgwffmV9QZP6hH9By9epV8vLycHNzIzk5mV/84hckJSVZTAo3Ectl//79nDt3ju+++46PP/4YT09Po/ToPHjwAC8vr2l7V4eGhgzHa0NDAy9fviQ4OJgnT56gUql49eoVixYtMptYBVAoFLi4uHDlyhXS0tJMtp3CwkLs7e3Nsq/+/v6kp6dTVVXFgwcPiIuLw9fX15CnNzIykiNHjnDmzBmSk5PRarU8efKEoaEh+vv7+eyzz8QeQZE5x+aPOBcXF37605/yzTffoFarWbVqlcWJVgcHB44dO8YPP/xARkYG+/btw9vb29xmiZiRxsZGrly5wrVr1yguLmbFihV89NFH/Mf/+B/Fmt0WgrV4WOHfKu9lZWVx/vx5Q1GT2ebW7enpYcGCBXR1dRliHjs7O7lx4wZLliwhKioKeJOpoKCggN7eXpydndm2bRtXrlwhPDyc1NRUnj9/zr179wCMOnBrpmzbto3vv/+e9vZ2ow+60g9S6+jomNMSr28jlUqJjo4mLCyM0tJSbt26hbu7u6FnJjQ0lE8//ZQ//OEPjI6O4uXlRXd3N4GBgTZZAEfE8rF5wQpvalv/yZ/8CadOneL27dskJSVZ3CAnqVTKgQMHyM3NJTMzk507dxIcHGxus0TmCK1WS2lpKdeuXePq1au0tbWxdetWjh8/zu9+9zuzeN2tRYyZE2v6jfQiFSA7O5vz589z6NChcSmMPpSRkRFqa2upqKjA0dERT09PmpqacHV1JT8/n/LychYtWsTt27fx9fUlLS2NoqIiMjMzcXZ2ZuvWrQDExsYSGxtrMUnovby8cHJy4vnz50YXrNevX6erq4tDhw7h7u5u1LZngkKhICkpiZCQEAoLC8eVfw0ICMDDw4MlS5bg7+9PZmamUQoZiIjMhHkhWOHNSXnixAlOnz7Nw4cPWblypblNmoBUKmX37t3k5+eTm5trc1WxRMYzMDBg6OrPz8/Hy8uL1NRU/uf//J+sWLECOzs7c5so8g6sOXZ79+7dZGZmcu7cOfbs2TNjUabT6VCpVCxcuBCpVEpzczNbtmwhKiqKrq4uLl++zO3bt4mOjjbEPB48eJCamhqCgoImiFNLEKt6goKCqKmpYfXq1UbLFtDZ2UlNTQ2pqakWIVbH4uLiYojf1dPZ2cnQ0BAREREUFRWxdu1as4ZriMxv5o1ghTdVORISEqioqDC3Ke9ky5YtKJVKsSqWDdLQ0MDVq1e5evUqxcXFJCYmkpqayl/+5V8SGhpqbvNEPhBr8rCORe9tzc7OJjMzk/Xr139whar6+noA9u3bh4+PzwSx6enpybFjx2hsbJyQUzQyMnJ2OzAHbN68mebmZs6dO8fx48eNIqbv3r2Lm5sb4eHhRrDQuOhLrY7l0aNHREdH09nZSWtrK+np6WayTkTExrMETEZvb69VPCGuXr2adevWcf/+fe7cuWNuc2weU3nLtFotDx484Fe/+hVbtmxh165dlJeX8+mnn1JaWsrp06f52c9+JopVK8SaYlgnQyqVsn//fvz9/amqqvrg9a9fv054eDh+fn7vFHPBwcEW5TmdLlKplIMHD6JWqykoKDBKm3K53GKPGTs7O0ZHRw2fdTodjx8/Jjw8nLt377J161bs7e3NaKHIfGdeeVjhTTfsXOTXMwZLlizB0dGR/Px8hoaGDPFeIsbF2DcQtVrNrVu3yM3N5fLly3h7e5Oamsr//t//m+XLl4td/SIWRVhYGA8fPvzg9ezs7CZURbI1FAoFKSkpXL16lVevXuHg4MCJEydm3F5vb6/Fir63BWtDQwMymYz+/n4Ali5dai7TRESAeShYY2Njyc7OJjY21iqe+iMjI1EoFOTm5jI8PMyuXbuswu75xvDwMIWFheTm5nLt2jUiIyPZtWsXOTk54qh+G8XaPax6IiMjuXfv3rQHPOljr4eGhnB2dp4DC81LeHg4mzZtoqioiOHhYTo7O6eVXaGtrQ0PDw8KCwvp6OhgdHQUtVptseW4pVLpuJCA8vJyIiMjuXPnDgcOHLCJY13Eupl3gjUsLAylUklDQ4PVCImgoCDS0tLIysoiMzOTtLQ0UbRaAAMDA+Tl5ZGbm0tBQQFLly5l165d/PKXvzRpKcy5QrxBzQ/a2tqQSqXvvaYIgsCFCxdobW1FqVSyY8eOeRHKUl1dzY0bN1i0aBF1dXW8ePHivZWp9Kmr4E0+8AULFgCwYcMGi+3hs7OzQ6vVIggCgiDw7NkzFi1aRGBgoNXcK0Vsm3knWCUSCZs2beLKlSuEhoZazU3Z29ubw4cPc+7cOc6cOcOhQ4fExM1moKenhytXrnDx4kXu3LnDqlWr2LVrF3/zN38j5s6dh1jL9eNd9PT0TCtMRa1W09rayscff2xIMG/rPH36lFu3brF06VKSkpIoLS3lwYMHuLi4sHTpUnp7eykqKqK1tZUFCxbg4uJCXV0dfX19yGQy9uzZg4eHh1VcqyUSCTKZDI1Gw8uXL3FycqKyspLPP//c3KaJiADzULDCmy4wmUxGU1OTVeU6dXFx4dixY2RkZHDq1CkOHz5stHQr8513Dbpqb2/nxx9/JDc3l5KSEjZs2MCePXv4h3/4B9zc3ObQShFLwlZCApYuXUpJSQn19fWEhoYiCAJXrlzB09OT2NhYQw5ghUKBRCKZF707TU1N3Lp1i56eHlatWsXy5csBDK93796lrKyM4eFhXF1dSUxMpLy8HIlEQkBAAGvXriUkJMTqfit7e3tGR0cZGRmhu7ubVatWGQpCiIiYm3kpWCUSCRs3buTGjRsEBQVZ1U1HoVBw/Phxzp49y3fffcfBgwdnlfhbZHKam5vJzc0lNzeXZ8+ekZyczPHjx/nyyy/nRdyeyPSwpmvHVDg4OODn58etW7dob29nYGCAxsZG2traKCsrw8HBgYSEBKKjo5FIJHR2dtpEyMtkaDQazp49S39/P35+fqSnp08QbMuXLyc8PJwHDx4QHx+Pn58fACtWrDCHyUbF3t7eUMZcHz4nImIpzEvBChATE0N+fj5tbW34+/ub25wPQiaTceTIETIzMw2lXI1djeVD0Gq1qNVqBEEwxECNjYV6e9Iv0+l0CIIwZbt6MTBWFLxPIEilUiQSyaTTVMsEQWBkZIRnz55x6dIlrly5Qn19PSkpKZw4cYJ169Yhl8sBGB0dpaenZ9o2v2sf3rUvH+qZed/3xy4f6xkc+5sYm6n+23f95+/6zrvWe9eysd7zd3nS316m/zzV+lqt1qqLB4xl7dq15OTk8PDhQ3Q6HWFhYWzfvh21Ws29e/coKSnhwYMHuLq62nQxk6dPnzI4OMgnn3zyzgdTd3d3ix08NRtkMpkhU4ClFTYQEZG864IrkUh0tnJBnozy8nKKi4vZuXOnuU2ZEYIgcOnSJZqbm81WyvXLL798rwB5WwxNR7BNxocei9MRJwMDAzx79ozHjx/T0dFBbGwscXFxhIeHi+mnRN6Lv78/e/fuNbcZRqO7u5tz584hl8v57LPPDPMFQaCxsdFqc6pOB/2+x8TEsHHjRnObYxaysrKIiopi+fLl08qEICJibCQSCTqdblJxMG89rPAmz2lBQQHt7e1m9VDOFKlUyscff0x+fj6XLl0iJSWFqKioObVBJpOxbNkyq6rG1dvby6VLl8jKyqK0tJTIyEiOHz/OL37xC4sdwWss6uvruXLlyriBFDqdbtwEfFBN98m+Z6uiZixnzpyxuS5TDw8PgoOD6ezsHDdfKpXabEYAlUpFfn4+jY2NBAQEzFuxCrBx40YqKyv56quvUCqV/OxnP7OKAWMi84N5fSRKpVLWr19PWVmZVXfvbNmyxVBgYHh4eE4TPP/r09CcbW+mDA0Nce3aNc6fP8+tW7dYv349R48e5Z//+Z85f/48oaGhNi9Wp8JUIQG2jk6ns0kv/NDQ0LzJeNHW1kZ2djaOjo7zJk3Xu/D09GTt2rWsWbOG7Oxsmpub5/1vImI5zGvBCpCQkEBRURHd3d14eHiY25wZk5SUhJOTE3fu3GF4eJjVq1fP2bYtVbCq1WoKCws5f/48eXl5LFu2jP379/P3f//34uh+kVnzIV5oa0KhUDA8PGxuM0yKIAg8fvyY4uJigoKC2LVrl7lNsigkEgnBwcHU1taKglXEYpj3glUmk5GUlERZWRkpKSnmNmdWJCQk4OjoSEFBAcPDw2zevHlOtmtJglWr1XL37l3Onz9Pbm4uUVFR7N+/n//+3/+7VYZ9GBvRk2o8bM3DKggCBQUFNDU1sXjx4vd+v6+vj7NnzyIIAnK5nAULFqBWqxkZGWF0dJTR0VE0Go1hkN9YT75+sN/br/b29sjlchQKBY6Ojjg6OiKXyxkdHWV4eBiNRoNCocDJyQknJyeUSiWOjo5TPjgIgoBKpWJgYIDXr19TU1NDT08PIyMjSKVSgoODxZLXU+Dn58eLFy/MbYaIiIF5L1gBEhMTuXnzJr29vVbveVu0aBEKhYLLly8zNDRk8gFlliCAdDodpaWlnD9/npycHHx8fNi/fz+XL1+2qjy7c4El/F+2gkajoa6ujsHBwXGZKOzs7Azv3/78viwS78uIMdk8mUyGs7MzSqUSFxeXGcUcPn36lLt37wKwdetWwsPD37vO4OAgWq2WXbt2cf/+fRobG7G3tzdMSqUSBwcHQ9iQPivI2Awhb0/Dw8P09fUxOjqKVqs1ZBSRSCSG31GfaWRszLX+t9ELV/02xi57+8FaEATq6+v5wx/+MGHf3s4kAhhsnuoBfbKMJPpjYOyxMHaa7v8/neNj7O881tapJv0+6V/fzoah0Wjo6+tDq9Xa1IOZiPUiClbe5J5bs2YN5eXlNhFwHxoayr59+8jOziYzM5N9+/aZtOtyOmmKTMHLly85d+4cmZmZ2NnZsX//fjIyMli4cKFZ7LEGNBoNgiDwxRdfzPm29dWCbAWpVMrIyAi9vb3TEghTCZ3p9lC8a/23U2yNFc8ymcwgIgMDA1m7du249SsrK7l165bhc15e3rTsAQxeSnM+GGo0GgYHBw0TgJOTk0HET0fAazQa1Go1arV6nHdYrVYbzhm5XI6joyMKhYLy8nIaGxtJT083rKdf9+02xr5qtVo0Gg0ajWZS0Q1Tp1ebbN7by8YK7Hel95ts+dvz4I0XfWBgwOodOSK2gShY/5XVq1fzD//wDyxfvtwmRv76+vqSnp7ODz/8QEZGBunp6SYZ7TnXg656e3vJzs7m7Nmz1NbWkpaWxu9+9zuWLl0qeg+ngUwmQyKRcPz48Tnd7oULFwxiwlbw9PRErVaTlpZmblMMCILA0NAQ/f39BgE3NDTE8PAwIyMjlJeXTxCYdXV1uLm5ceTIkXHt6F/109jPeoGuz09sTmQyGW5ubrMSVTKZDJlMhpOT07S+r9Vqsbe3R6FQ2HS1wYsXL9pEz6OIbSAK1n9FLpezcuVKnjx5MsEDYa24u7tz9OhRQ1WsQ4cOWeXFVaPRUFhYSEZGBoWFhWzatIk///M/Jzk5GXt7e3ObZ5XMdbUuWxyc5OnpSXV1tbnNGIdUKkWpVE750H3y5EnKysrGCdampibi4uImtDP2VeQNGo2Ghw8f0tzcPC+6yZVKJX19feY2Q0QEAPFqNIY1a9ZQWVnJ0NCQuU0xGk5OThw7dgypVMrp06cZGBgwavum9LA+e/aMv/7rv2blypX8+te/Zt26ddy5c4cvvviC1NRUUayKmBV/f39GRkbMbca0yc/PR6VSsWHDBsO87u5u1Gq1VeVRNifff/89T548wcvLa84GtZoTpVJJb2+vuc0QEQFED+s4nJycWL58OaWlpaxfv97c5hgNBwcHjhw5YggPSEtL++AUXi9evGBoaAh7e3tiYmKQyWT09vYyNDRk1BJ+7e3tZGZmcvbsWbq7u0lPT+fcuXNzXhBBROR9BAQEIAgCGo3G4pOrl5eXU11dzc6dO8edrxUVFSgUinmbg3g6VFVV0d7ezu4Jzy8AACAASURBVMDAAP39/Rw7dmzOeyjMhbOzsyhYRSwGy77KmoHNmzfz5ZdfUlNTQ2RkpLnNMRoymYz09HRycnL4/vvv2bNnD35+ftNa9/nz59y4cQO5XI5Go+HOnTssWLCA0dFRnJ2diY6OnpVtKpWKa9eukZGRwf3799m+fTv/7b/9N9atWyd2SYpYLAqFAolEQktLCyEhIeY2Z0o0Gg33798nLCwMnU5HfX29YdmrV6+mfR2YL3R1deHp6cnAwACXLl2iu7sbJycnRkdHSU5OnjdiFd54WFtbW81thogIIArWCcjlco4cOcIf/vAHPDw88PT0NLdJRkMqlbJv3z4uX75MdnY227dvn1ZS6EePHhEcHGxIrv3s2TPKysoYGBggMTFxRrbodDoePnzI2bNnycnJYfHixRw6dIj/9//+37y6IYhYN3K5nNbWVosWrD09PQA0NDTQ0NAwbpkgCHNaGc+SGRgYMAwy8vX1pb29HVdXV44cOTJvBx05OTmJMawiFoMoWCfB29ub3bt38+OPP5KWlmYRI2GNyfbt2yksLOTHH38kJSXlvWmg/P39qa2tNVT2iYuLIy4ubkZdoa2trZw9e5YzZ84AcPjwYTFfqojV4uzsTGdnp7nNeCfe3t58/vnnE+a3tbWRlZVFWFiYGayyLF69esW1a9dwc3MjMTGR8vJykpKSWLJkiblNMyuiYBWxJETBOgWxsbE0NzdTUFBAamqqzXVNb968GYVCwfXr11GpVO/0smzYsIHKykpaWloICgoyzJ+uWNVoNOTn53Pq1Cnu37/P7t27+c1vfsOKFSvEVFQiVo27uzsdHR3mNuOD0Wg0XL16FX9/f1xdXc1tjllRq9Xcv38fV1dXDh8+DDDjniNbQy6XGyqXiYNcRcyNKFjfQUpKCt9++y1lZWWsWLHC3OYYnTVr1qBQKLhz5w7Dw8OsXr160u/JZDKkUilarfaD2q+vr+f06dOcOXOGwMBAjh8/zj/+4z+KXf4iNoO3t/e4mFBroLGxkStXrmBnZ8e2bdvMbY5Zef78OTdv3kQul7NlyxZzm2NxSCQSXFxc6Ovrw8vLy9zmiMxzRMH6DqRSKQcPHuT3v/89Pj4+Fh2nNlMSEhJQKBQUFhaiUqnYtGnTrNobGRnh8uXLnDp1iidPnnDgwAG+/fZbYmJijGSxiIjlEBgYyL1798xtxgdRUFBgCHuytZ6j6aIfiPbkyROWLVs25cO6CLi6uoqCVcQiEAXre3BycuLw4cOcPHmSvXv32mT3WXR0NAqFgitXrqBSqSb1ukgkElQq1ZRtVFVVcerUKc6dO0dsbCzHjh3jq6++sspCBSIi00V/E+/v78fFxcXM1kyP4eFhkpOT551YValUVFZWUldXR2trKzKZjDVr1pCQkGBu0ywaMReriKUgCtZpEBAQQGpqKleuXGHv3r02mbMwLCyMPXv2cOHCBbKzsyd4X2QyGf39/ePWGRoa4sKFC3z77bfU19dz+PBhsrOzCQ8Pn2vzRUTMglQqxc7OjqamJqvoRbhw4QISiYTAwEBzmzInqNVqMjMz6evrQ6fTIZPJcHd3Z/369ROqe4lMRKVSUV9fT1JSkrlNERERBet0WbZsGU1NTdy6dYvk5GSbHCzk7+/PgQMHyMzM5Pvvv+fgwYMG0apQKAzpcR4/fsypU6fIzs4mMTGRX/ziF2zdulUMyheZl9jZ2aFWq81txnspKiqitbWV/fv3zwvvqkajISMjA3iTGSUwMNDiCzxYEjqdjlu3bpGQkCBmcRGxCGz/qmVEduzYwfDwMM+ePTO3KSbD09OTI0eOMDg4yOnTp9FoNAA4OjqSlZXF9u3b+dnPfoavry9Xr17l66+/ZseOHaJYFZm36HQ6q6gr39nZSVBQEN7e3uY2ZU4oLCxkdHSUw4cPExoaKorVD6SmpoahoSFSUlLMbYqICCB6WD8IOzs7Dh8+zO9//3u8vLzw9/c3t0kmQalUcvToUTIyMvi7v/s72tvbycnJISwsjP/6X/8rmzZtmhceGhGR6aDT6azifLCzszM8gNoyL168oKysjN7eXpKTk20yhMvU9PX1cffuXX76059axcOYyPxAFKwfiIuLCwcPHuTs2bOkp6fbXFEBeDPSPzc3l3PnzlFVVcWqVav4H//jf6DRaEhOTja3eSIiFoW1eFitJXRhNgiCQGFhIcHBwSQnJ8+o7GxzczPFxcW0tbWh0+ne+V2JRIJEIsHBwQGFQoGzszNeXl6sXLnSaj26giBQUFBAcnLyvPHGi1gH1nlGmZmwsDB8fX3p6uoiICDA3OYYjcbGRk6ePMl3331HTEyMITY1JyeHzs5OIiMjzW2iiIjFoR/MY8n09PTQ2tqKn5/feytzyWQy7O3tkclkhhzM1oK+KpO+jPR0UalUlJSUUF1dzcjICJ6enmzZsoWwsDAEQZh00mq1CILAwMAAnZ2d9PT00N/fT3l5OeXl5VabLuvx48colUpWrlxpblNERMZh2VdZC8bX15fu7m6rF6yCIFBUVMRXX33FgwcPOHjwIN9//z1RUVGG76SlpfHHP/7RJr3JIiLGwNI9rBcvXkSr1dLc3Mz3338/q7b0XkV9qeYPXXeq18neazQaHBwckEgkSKVSw7Kx3xkrIvUhDydPnnzvNvSoVCpGRkaQy+VERUWRmJj4Qen4fHx8xmVGycrKwtnZmbKyMoKCgsZVB7R02tvbefr0KT//+c9tcmCxiHUjCtYZ4u/vT2VlpbnNmDHd3d1kZGTw9ddf4+TkxE9+8hP+7//9vzg5OU34rlQqxd/fn+bmZjNYKiJi2VhySEBPTw95eXkMDg6Smpr6wSnn9CJwdHSU0dFRNBqNYbp06RLR0dEfNIJ8Km/l25NOp0MQBMrLywkJCUEul0+6HN48LOgnqVSKWq1GoVCg0+neOWk0Gl69eoVcLmffvn0zCh+YjH379gFvUogVFRVx7Ngxo7RratRqNfn5+ezevRulUmluc0REJiAK1hni7+/PrVu3zG3GB1NeXs5XX33FpUuX+Oijj/jNb35DYmLie5+mExISuHDhAhqNxuK7P0VE5hpLFaxFRUUMDg5y8ODBGVUqkkqlODg4TDpwydvbm66uLjZu3GgMUyfl+fPn+Pj4mCS5f2ZmJo6OjnzyyScmCXtwd3enpaWFU6dOTfAK69/rtyuRSAgLCyMxMdHodkyH3t5eSkpKiIyMJDo62iw2iIi8D1F5zBBvb296enqsQsCpVCqys7P54x//SHt7OydOnODGjRsfFFAfGBiIvb09JSUlrFmzxoTWiohYH5YqWLVaLd7e3iYpq6lUKg25mU2FUqmkra3N6O0+efKEjo4O0tPTTRaju2zZMkPohN6rO9ZDPHbSarWUlJSgVqvnLEn/wMAAtbW1VFVVMTIywpIlS9i8efOcbFtEZCZYttKyYGQyGZ6envT19eHp6Wlucyalvr6eP/7xj5w5c4aEhAT+w3/4D2zdunXGN9fIyEgqKipEwSoiMgZLDQkQBIGuri6WLVtmkvYHBgZwdnY2Sdt6PD096ejoMHq73d3d6HQ6Xr16hYeHh9Hbhzdie/369dP+fnV1Nfn5+djZ2ZlssNbw8DD19fVUVlbS29tLXFwcu3fvJiQkRIxZFbF4RME6CyIjI7lz5w4pKSmTxn6aA51Ox/379/n973/PnTt3OHz4MDk5OUYpl7p69WpevHjBo0ePxPrbIh9Md3e3VfRIzARLFKyVlZUIgsDy5ctN0v7w8LDJ0x75+/tTV1dn9HY3btyIm5sb9+7do66ujtTUVLPHbUZFRRlSSkkkElatWmWUdkdGRmhsbKSqqorXr18THR3N1q1bCQ8Pt6oMECIitnfnmENSU1O5efMmmZmZbNq0CS8vLxwdHc3ypDoyMkJ2djZffvklg4ODfP755/zmN78xqgdEoVCwZMkSiouLWbx4sU0KDxHTsGbNGvLz8/nqq6+Ij49n5cqVSKVSNBoNXV1d+Pr6mtvEWWFp54IgCDx8+JCQkBCTiZKRkRGTeSf1hISEcOvWrRllJHgf8fHxBAcH8+OPP3Lq1CmCgoL4+OOPjbqND2XRokWGzC12dnasWLFiVu29fv2aH3/8kfDwcNauXcvChQst7lgVEZku4pE7CyQSCRs3biQkJIS8vDy6u7tRqVS4ubnh5uaGq6srLi4uKJVKw2TsqisdHR18/fXXfP3118TExPBXf/VXpKSkmOwmtWbNGqqqqjh//jzp6ekm2YaI7REaGspnn31GaWkppaWlVFRU4ODgYMibOZMR7JaEJVVT6unpISsrC41GY9J4SI1GY/JwKFdXVyQSCa2trQQGBhq9fU9PT44fP05bWxtZWVk0NDQQEhJi9O18CDExMQiCwM2bN5FKpTMO6eju7ubKlSscPnzYqs8tERE9omA1AgsWLOBnP/sZ8CY1SG9vL93d3fT09NDd3U1tba3hfXJyMmFhYbPe5tOnT/nyyy/58ccf2b17N6dPnyYmJmbW7b4PqVTKgQMHOH36NNevXxfrTItMG6lUSmJiIkuXLqWwsBCAzZs38/TpUwoLCwkLC7O6Lkp9aiVL8Vq9fv2a7OxsvLy82LNnj8ns0mg06HS6OamEJJfLaWpqMolg1ePn50dAQAC3bt3i6NGjJtvOdImLi0MQBG7fvo1UKiU+Pv6D1u/r6+PSpUvs2bNHFKsiNoNlXGVtCAcHB3x8fPDx8ZmwrK2tjVOnTqFSqWaUOkSr1XLt2jW+/PJLampq+MlPfsLNmzdNMgL4XehLENbW1s7pdk3J+0owihgPBwcHUlNTDZ99fHz44x//yOnTpwkNDSU2NnbOj+mZoi91aglCWxAELly4QEBAgMm7tru6ugwlSU2NUqnk9evXJt9OcnIy3333Hc3NzSYVx9NlyZIlCILA3bt3kUqlLFmyZFrrDQ0NkZuby9atW+fEiSEiMleIgnUO8fPz46c//SnffPMNKpWK+Pj4CfGuih9+wOVXv8KuuRltYCD9v/wlHdu2cfr0af7lX/4Fd3d3Pv/8c3bv3m2Wbsienh7Onz+PRCLh4MGDc759EdtDJpOxd+9eSktLefXqFc+ePUMqlaJUKvHx8cHDwwOVSmWoSKTRaNi4cSPu7u7mNt1QWckSeP78OYIgsHPnTpNvq7Ozc84Gmnl7e9PY2Gjy7bi4uODn58eNGzc4cuSIybc3HeLj48d5WuPi4t75fZVKRW5uLklJSSbLDiEiYi5EwTrHuLu786d/+qecOnWK6upq3NzcUCqVOP//9u7suakzzR/49xztkiVrsWQbY/CObWxjiG0Ws4UAIRlCCPSkOyFTU5Xpmu7pmu1mLuYPmJvf3E39LuY30zU11ZkknbCEAEnACWswkNgYYxbb2CY22MaLZO27dM7vgpEaiLEt6Wiznk+VCjDS+74sPnr0nud9HpUKq65eReG//itYnw8AIJ6YgPIf/xH/RyrF9Guv4d/+7d+WVOQ/WQKBAI4dO5b0240k9xiNRuzduxfA0yBwbGwMY2NjmJmZwfj4OEQiESQSCSQSCZxOJy5evIh33nknzav+0w5rJujt7cWqVatSsttrtVpT9oG5uLg4ZV0Fd+3ahU8//RQPHz5ERUVFSuZcTHNzczSnVSQSvfTuXCAQwLlz59DQ0IBNmzaleJWEJB9FHGmgUqnw4YcfYnZ2Fg6HI/pY9e//Hg1WI2ShEP5vQQHm/t//S9Nq/2RiYgIAMiJQIMuXWCxGZWUlKisr5/39yclJnDlzBna7HYODgxgYGIBMJsMbb7wBjUYj+Hp8Ph/sdvu8rTuDwWBG1K/86aef4Ha7cfDgwZTM53A4oFAoUjJXaWkpOI5DIBBIepCsVqtRXl6OS5cuwWAwID8/P6nzLdWGDRsQDodx+fJlMAyDmpqa534/FArhu+++w+rVq7Fz5870LJKQJKOANU1EIhGKiopQVFT0py++pEC2NAmdXuIxPT0NmUyW7mWQHLdixQqoVCp89tlnkEgkqKysxMzMDD777DM0NzdH61eGQiF8/vnnkMvlOHTo0EvHs9ls6OzsRDAYjDYBEIvFEIvFsFqtsNvtAJ7mbjc3N6OhoSG6i5kpKQGdnZ1YvXp10gv5R7jd7pTVLZXL5WBZFhMTEyk5QPTqq6/i1KlT+Pzzz7F79+6MObTU2toKnudx6dIluFwusCwLq9UaPeDb0NCAffv2ZcQHKEKSgQLWTLJqFTBPkexwBhwAAJ4etEjVGyIhC3njjTfgdDqfq7jR19eHH374Abdv34ZOp0MgEEAgEIDb7caVK1dgNBoxOTmJubk5GI1GlJSUYGBgAE+ePImm5jAMg3A4DL/fD4/Hg/z8fOzatQtqtRrXrl3Djz/+iJs3b6KtrQ1r167NiB3WwcFBeL3elLbV9Hq9KT2YJJfLMTk5mZLgUSwW49ChQ7hy5Qq+/fZbNDc3J63zVKxqa2sxODiIJ0+eoLq6GqtWrUJBQQH0ej0kEkm6l0dIUlHAmkn+5V/A//Vfg/F4ol/iFAo4//mf07ioP3E6nSkpY0PIYvR6/c9qgDY1NaGhoQHDw8N48OABQqEQfvGLX+DJkye4ePEihoaGkJeXB61Wi0ePHmF4eBg6nQ6vv/76kkrN7dq1C9u3b8e1a9dw7do13Lp1CxUVFWkPWG/cuIHKykrI5fKUzRkIBJLeNOBZGo0Gs7OzKZsPALZv3w6TyYQrV65AqVQu+ZR+sszOzqKjowN79uxJWvcyQjIZBayZ5MgRMAC4f/5nMOPjcOv1OL9rF+xqNerGx7Fy5cq0Li8VrRgJSQTLsqipqXkux6+6uhrV1dWCjC8Wi7F9+3a0tbXh4sWLuHv3bjRgjaQHsCybsjJXHMfB7/djy5YtKZkvIhQKpbT0WFFREfr7+1M2X0RtbS0mJyfR3d2N2tratB00HR0dxdWrV3H48OGMOQxGSKpRwJppjhwBe+QIACAPwD6/HyMjIzh37hw2bdqEsrKytCxrYGAAgUAgY/K5CEknuVyON954A3Nzczh+/Dj+4z/+47nfr66uTklTDc//3o1J9e4qgJTusJaXl6O3tzcpLVoXs3XrVvzxj3/Exx9/jIMHD6b0IBbP87h37x7u3buHv/zLv8z6FsaEJIIC1gwnk8lQX18Po9GIP/zhDxCLxSnfaXW73fj+++/R2NiYlFPYhGQrvV6Pv/iLv4Df74darQbLsvjss89S1ojC4XCkPCXBbDaDYZiU7jZGdnNnZ2fnrdaQTFKpFO+//z5OnTqFo0eP4p133knZ7vLDhw8xPDyMv/qrv4JarU7JnIRkqvS3ZyFLYjQa8f777+Py5ct48uRJSuf+5ptvoNFoktqXnJBsJZfLkZ+fH935CwQCKTtBX1BQAJ7nMTk5mZL5AMBut6esaUAEy7KQy+Vp664XOYil0WjQ2dmZsnkHBgawe/duClYJAQWsWaW4uBjvvvsuzp8/D/NLSmAlQ6rz1QjJZsFgMGUBq1QqhV6vx82bN1MyH/B0VzcdJ9K1Wi2mpqZSPu+zWltbMT09nZJyZi6XC1arlXJWCflfFLBmmVWrVuHw4cM4e/YsrFZrSuYsLi7GdIbUgiUk04XD4ZSmzjQ2Nqb0+9PlcqWlHnNRUVG0Jm66lJeXQyKR4OuvvwbHcUmda3R0FGvXrk35bjYhmYoC1ixUUVGBt956C9988w0cDkdK5vM8U2qLEPJyPM9Dq9WmbD65XJ6ynFngaU57Kg95RZSXl8Pn8yU9UFzMvn37YDab8T//8z+w2WxJmWN8fBy9vb1obm5OyviEZCM6dJWlamtrEQgE8NVXX+Hw4cNJbVlYUlICnufR39+Purq6pM1DSLbzer0AnjYxePEwVOTXkR/D4TBCoRCCwWD0x3A4HP06x3EIh8PRk/EikQgSiSTahUsqlUIqlWJ2djZlbVKBp61q05EilM6DV88qKirCBx98gDNnzuDo0aPYtWvXS9sIxyoYDKK7uxvj4+P41a9+ldLmDIRkOgpYs1hTUxP6+vowMzOT1MoBLMti/fr1+P777+H3++lTPyEv4fP5ADw93b0QnufBMAxEItFzD7FYDJlMBrFYHA1OJRIJQqEQ/H4/gsEgAoEAgsEgvF4vQqEQfD4fAoEAbDZbSnZ2/X5/ynJ0nxU5eDU2NpbWgBV4mjt86NAhnD17Fj/88IMgAavZbMaFCxdQVlaG3/zmN9QGm5AXUMCa5aqqqjCegqYCra2tsFgs6Ovro4CVkJeItC7+4IMPUjbn4OAgrly5krLb9MFgMG3l7bRabcqrpCxk3bp1OH36dEL1YTmOw927d3Hnzh3s378ftbW1Aq+SkOWBclizXGVlJUZHR5Oew8ZxHCYnJwXrGETIchRJzYkU10+F27dvw2g0pixgDYfDKS2e/6xMOHj1rOLiYjAMg5GRkbhe73A48NVXX8FsNuO3v/0tBauELIB2WLNcpFWq0+mMa9eD53n4fD54PB643W54PJ6f/dxmsyEYDIJlWbS2tgr9RyBk2fF4PEnNK39WY2Mjrl69CpfLlfRb9RzHged56PX6pM7zMlVVVejt7YXH44FSqUzLGl5UXFyMnp6emD7M8zyP4eFh3LhxAzt37kRra2vKG0AQkm0oYM1yDMOgsrISk5OT0YA1ktfm9Xrh8/mij2d/HQlKvV4vJBIJVCoVlEpl9KHX67Fy5UrIZDJ0dHTgzTffREFBQdp6aROSLRiGieaypkJdXR36+vrw7bff4p133knqXG63G0BqW8E+S6/XQ6FQoKurCzt27EjLGl6kUChgsViWnBbg8/nQ2dkJj8eDDz/8MLrpQAhZGEUfy0BVVRVOnz6Nnp4e+Hw+8DwPuVz+3EOhUEAul6OgoAByuRxKpRIqlQoKhWLBIHR4eBhSqRRqtTptb1KEZBOGYaLVAlJFp9OlpC6z1WqNO1dTKGvWrMG9e/cyJmCtrq7GTz/9hE8++QQHDx5ccJd7amoKFy5cwPr167Fjxw6qsUpIDChgXQZqa2uh1WrhdrshlUohkUgEu71UXFyM8vJynDp1Cvn5+VizZg0qKirS0umGkGzAsmxKd1iB1HWfstlsaQ+yNmzYgNu3b2NsbAyrV69O61qAp81cPvjgAxw7dgwXLlzAgQMH5n3e+Pg4Ll++jHfffRerVq1K8SoJyX506GoZYFkWxcXFKCwshFQqFTQXSqVSYfPmzXj//ffR1NSE0dFRfPzxx7h06RKePHmS0oLlhGQDlmXh9/tTOuf27dthNpsxNjaW1HlcLlfKcnNfRiwWw2Qyobu7O63reJZcLsf27dsxNTU174eVSLB65MgRClYJiRPtsC4TDMNApVJFc8yEJhKJUFZWhrKyMng8HgwPD+Pq1asIh8OoqalBTU1NWmozEpJpRCJRSqsEAE/zKEUiEe7evZvUXcd0tWV90caNG3Hq1CkEAoG0B9ARq1atglgsxoMHD9DU1BT9+uPHj3HlyhUcOXIExcXFaVwhIdmNAtZlhGEYSKXSpL9ZKpVKNDU1obGxEbOzsxgcHMTx48dRUFCANWvWoKysjA5nkZwlEolSnhLwxRdfQKPR4PXXX0/qPB6PJ6VdtV7m5s2b0Y5fmYRl2efuOkWC1Q8++ABFRUVpXBkh2S+zvttJQhiGgVKpTNnuDsMwMJlMMJlM2Lx5M0ZHRzE4OIjOzk5UVFRgzZo1MBqNVK6F5BSxWIxgMJiy+SJVQQ4dOpT0AM7n86Wkm9ZCbt++jcnJSRw8eDDtB8BeJBaLcfv2bYTDYej1enR2dlKwSohAKGBdRhiGgVwuB8MwKc8tFYvFqKqqQlVVFVwuFx48eIALFy6AZVlUV1ejqqoKarU6pWvKFOfPn4fNZkv3MgAgpYFUrhKLxSlNCejt7QXLsilJyQkEAmlP/RkcHERZWRmMRmNa1zGfQ4cO4dq1a7h16xYA4Ne//jUFq4QIhALWZUgul6e8rM6z8vLysGHDBqxfvx7T09MYGhrCiRMnoNfrUV1djfLy8ozIg0uV0dFRaDSatLWzfFFFRUW6l7CsyeVyzMzMwOfzJb0UXE9PD3p6erBx48akzhORzrasER6PJ2M77imVSuzcuRMnTpzA66+/TsEqIQKigHWZYRgGeXl5ggasIpEI4XA4rrUUFRWhqKgIW7ZswePHjzE0NITr169j5cqVqK6uRmlpadrL5CSb0WiE0+lMen4hyQy7du3CF198gY8//hjvvfde0joyTUxMoLu7G9u2bUNdXV1S5ngRz/Np/7AZDAYz+vDSzZs3UVZWRm1WCREYBazLkEgkglgsRigUSngssVgMo9GIQCAAu90e95jPVhnw+/14+PAh7ty5gytXrqCiogJVVVUoLCzMyHzX3t5ejI+Px/16juPgdrvR19f33OlhsjzJ5XL88pe/xEcffYTe3l5s2bIlKfPcvHkTBoMhZcEq8PRDqBDXlXiFQiHwPJ+x3aGePHmC0dFR/Pa3v033UghZdihgXaaUSiUcDkfC4ygUCvA8D4lEgoKCAni9XjidTnAcF/eYMpkMdXV1qKurg9PpxPDwMK5cuYJwOIzq6mpUV1cjPz8/4bULZWJiAitXrlwwZ26xnGGbzYaenh4UFxdnZO4dERbLsli5ciVGR0eTErByHIfp6Wns3LlT8LEXE8/dFqGIxWIwDIPHjx+jvLw8beuYTyAQwOXLl/H2229TV0BCkoAC1mWIYRgoFAo4nc6ED18pFIrndj0jLV5dLhf8fn90N5dhGLjd7pjnU6vVWL9+PZqbm2E2mzE0NIRTp05BrVajuroalZWVGXHxLygoQElJSdyvX7lyJVQqFc6dO4cDBw6kPQ+QJF9TUxO++OKLpNQKHRoaAsMwqKysFHTcxTAMk9aAFXh6zXj48GHGBaxdXV3RToCEEOFRwLpMRRoJuFyuuMeYr8UrwzBgGAZqtTp6WjjyHKVSCbvdHleXH4ZhYDQaYTQasWnTZSUrggAAIABJREFUJkxMTGBoaAhdXV0oKipCdXU1Vq9enZa6i0JVXCgvL4fb7cY333xDuzA5wGg0QiwW4969e1i/fr2gY9+/fx8FBQUpL+uUCQFr5BqUScbHxzE5OUmpAIQkEQWsy9Szna/iDbhe3F19cfwXf08kEkGr1cLv98PhcMSdNsCyLEpLS1FaWopAIIDR0VEMDAzg6tWrKCsrQ3V1NYqLi1P6piXUXA0NDXC5XDh37hz27NmTtAM5JDOsWLECAwMDggasTqcTZrMZO3bsEGzMpWIYJqF0ICFkQi3YF3V1dWH//v0Z03WLkOWIAtZlLNFd1njemFiWhVwuh0wmg8PhSLhagVQqjbZ+dbvdGBkZwfXr1+F0OqO7S5GA/MUfF/q9F5/T39+P/v7+edfAMIygZYM2btyI7u5unDhxAtu3b6fe4svY5s2b8dlnn8FiscBgMCQ8XigUwrFjx6DT6VBVVSXACmOTCTusgUAAJpMprWt4VigUgtVqTWpLXEIIBazLWqK7rH6/HyqVKubdxcjuq0ajgVKphM1mE+RNTqVSoampCU1NTfD5fOA47mc7vZGfv/i1pTxnsT+TUBiGQWtrK0pKSnDx4kWUl5ejra0t49pMksTl5+dDq9Wis7MTBw4cSHg8v9+PYDCYti5P6d5h5Tgu46oEOBwOGAyGZV+ej5B0y6y+dkRwkaA1Hol2RWJZFhKJRJCdpRfJ5XIolcroIbDIQyaTQSaTQSqVRh8SiSTad1wsFkMkEkEkEoFl2egjEtS+7JEMK1aswOHDh+F2u/Hll1/CarUmZR6SXlu2bMHU1BTm5uYSHivyvZyu/yvp3mFlWRZSqRQ9PT1pW8OLrFYrNQggJAVoS2eZE2KXVaFQJDR/ph2QyCRyuRy7d+/G4OAgTp8+jW3btmXc6WeSmJUrV0Kj0eDHH3/Evn37Eh5PIpHg3LlzUCqV0Q9hEokEEokk+gFNKpUueldBJBKhuro6pp39dAesAFBTU4OhoaGk1beNlcVioYCVkBSggDUHJJLL6vP5IJPJErr9KNQp++WKYRjU1tbCYDDg3LlzcDqdaGxspEB/GQkEAtDr9YKMFekaFwqFEAwG4ff74Xa7EQ6Ho48Xb9vP9z0YDAbBsizWrFmz5LkXSwmwWCx48OABHA4HXC4XvF4vAoEAwuGw4NeB8fFxrFy5UtAx42E2m7Fu3bp0L4OQZY8C1hyQyC6r3++nwClFjEYjDh48iLNnz8Jut6O9vT0teYpEWBzHwefzCXZIas2aNTEFmS9b0+9///uYDy8ttsP69ddfIxwOR8verVixAjqdDjqdLrqT++xdl2d/XOjrL/787NmzuHbtGt59992Y1p+oSLD+7IHPmZkZFBYWpnQdhOQiClhzRLy7rDzPg+f5hIJW2mFdury8PBw4cADnz5/HuXPn8Nprr1GpnCw3NjYGlmUF22EVwtjYGBiGibmjHMuyC34/y2QyhEIhvPPOO0n9sLVz5058/vnnmJmZSVnFgNu3b6Orqwscx6GoqAiNjY1QKBTRByEkuShgzRGJ7LJyHJfQm0/kgFO66zdmC6lUitdffx2dnZ04deoU9u3bF23SQLLP8PBw3Acfk6Wvrw8GgyHm7+vFdlgPHDiAjz/+GB0dHYLk676MVquFyWTCyZMnwbJs9CBlpPNeJK83cvBSpVJBq9VCr9c/t9sbi5GRERQUFGD9+vX48ccfcf78eXAcl3E1YQlZrihgzTFKpRJutzum14TD4YRLLimVyoS6buUalmWxdetW3LlzB2fOnMGf//mfU9mcLBQKhTA6Oor29vZ0L+Vn4q2zvNDr5HI59u/fj1OnTuH+/fuor69PZIkLOnDgAKampuDz+eD1euHz+eD3++Hz+aK5vR6PB3a7HRMTEwgGgwiFQgCeBt4ikQhSqTRacUStViM/Px96vR4FBQXzdqKTyWRYvXp1tOaqx+PB8ePHE74LRQhZHAWsOYRlWeTl5cUVsCZCiDaxuYhhGDQ1NWFychL37t1DU1NTupdEYnT37l2IRKKkBm7x2Lx5M06ePBlzULmUOqyFhYWQSqVwOp2JLnNBLMtixYoVMb8uFArBYrFgbm4ONpsNTqcTLpcLNpsNw8PDCIVC0btQkTJaLS0t8walkUoNNpsNOp1OkD8XIWR+FLDmGIZhoFQq4fF4lvyayAU80R0EmUwGv9+f0Bi5aOPGjTh9+jTWrFkDmUyW7uWQGAwNDWXkgRyTyYSWlhZcvXoVWq12yYHfUlJ7QqEQ/H4/ampqXvocnucRCATg8XiQl5cHiUQS0/oTIRaLUVhYuOC/C8dxcDgcsFgsuH//Prq6uiASiaBWq3/23BUrVuDx48cUsBKSZBSw5hiGYaBWq2MKWCPdZRIJWFmWhUqlooA1DjqdDmVlZbh16xY2bdqU7uWQGNjt9oxt2blhwwYMDg5icHAwGrCGw2HMzs7C5XLB4/HA4/HA5XJFH16vFxaLBUePHoVOp4NWq4VGo4FGo0FeXh6USiVu3boFsViMvLw82O326GudTiccDgccDgdsNhtYloVarYbL5UJDQwPWrFkDpVKZ5r+Vp1iWhVarhVarRUlJCf7whz9AIpGgpaXlZ881mUwYHx+nOyCEJBkFrDko1l1WoQqFS6VSOnwVp5aWFhw9ehT19fXQaDTpXg5ZopqaGty7dw9tbW3pXsq89Ho9LBYLQqEQHjx4gNu3byM/Px9GoxF5eXkoLS2FWq2GRqOBWq2GSqVCOByG1WrF3Nwc5ubmYLFYMDY2hrm5Obhcruj390cffRQN+nQ6HQwGA6qqqqK/juSIWq1W3LhxA8eOHUNVVRXWrl0bc/WCZJLL5dizZw9KSkrmrdhhNBpx/fr1NKyMkNzCLHRinGEYnkoSLU8cx2F6enpJzxWJRDAajQmnBPA8H91tIbHr7u6G3W7Ha6+9lu6lkCUaHBxEZ2cnPvzww3QvZV537tzB9evXIZfLUVtbi02bNiWUwhAKhTAzMwONRgOVShXTNcPr9aKrqwtdXV3RlIVsOIEfCoXw0Ucf4Z/+6Z9SmtpAyHLEMAx4np/3wkFVyXPYUm+/hcPh5w4ixCty+IrEZ926dZicnITNZkv3UsgSTU9PZ/Tp8TVr1kChUGD//v14++23E863FYvFWLFiBfLy8mL+cysUCmzfvh3/8A//gNraWnz11VdxHdzieR5TU1O4evUqxsfHk35HRywWo6CgAJOTk0mdh5BcRwFrjorkjy2V1WoVrAHAfOViyOIkEglqamowMDCQ7qWQJejp6cHAwEDG9Lyfj1Qqxa5du3Dx4kXBUn8SJRaL0drait27d+Prr7+OKd9+dnYW33zzDTo7O1FSUoLe3l4cP34cQ0ND0ZJWybBixQr89NNPSRufEEIBa06LZcczHA7DbrcnvFvBsizy8/Mzetcpk9XW1uLBgwcZE1yQ+dlsNnR3d6O9vT3hNqrJtmLFCuTn5+PHH39M91Ke09zcjJaWFpw7dw6BQGDB51osFnR0dODSpUtoaWnB7373O2zZsgW//vWvcfDgQUxOTuLEiRNJO/S5evVq3L9/PyljE0KeokNXOYxhGOTl5cHj8Sxp99Tn80Eul0MulycUcEYqFTgcjrjHyFWRwuZjY2OoqKgQbNxIC95wODzvg2VZ6HQ6+qCxRBcvXoRWq8XatWujX+M4LlrkPj8/P+FmHEJhGAZVVVUZeUu7vb0dLpcL3333Hfbu3fuzvzObzYabN29idnYW27Ztw/r1659rsMEwDFatWoVVq1bh/PnzuHDhAvbu3St4Ew6DwQC/35/SVrGE5Bo6dJXjYj0IxTAMjEYjWJZNKHjheR4WiwXBYDDuMXLV8PAwBgcH8Wd/9meCjGez2fDll18iEAhE21u+2O7S7/ejoKAAW7dupTzkRfA8j46ODkxMTKC+vj5axsnpdEKpVEKpVMJut6O6uhpVVVUoKCiI6Xsp0VbJ8xkZGcHc3BwOHDgg6LhC4HkeJ06cgM/nw44dOyASieBwOHDr1i1MTEygvb0dLS0ti34A4Hkef/zjH6FQKLBx40bB13nz5k0olUrs2rVL8LEJyRULHbqigJWA4zjMzMwsOUdVJBKhoKAg4TfNUCiE2dnZhMbIRaFQCJ988gkOHjyYcIkrjuPw5Zdfoqam5rndwBeFw2HcunUL9+/fR2trK2pra2m39RmRD2CPHj3C8PAweJ6HwWBAXV1dtIzTs7uqDocDfX196OvrQyAQQG1tLcrLy6P/njzPw+fzRYNdm82Gubk5mM1mcByHPXv2xNXl6WUGBwfh8Xjw5ptvCjamkMLhMI4fP46ffvoJhYWFmJ2dxebNm9HW1jZvqamX8fv9+P3vf4/GxkZUV1cLusa5uTlcuHABf/u3f0vfG4TEiQJWsqDIm6Pdbl9y0CoWi2EwGBIKWjmOg8vlirlVLAGuX78Om82GnTt3QqFQxD1Od3c3ZmdnsW/fviW9yc7NzeHy5csQi8XYvn17RtXLTLVIkf2xsTGMjIxAoVCgtrYW9fX1KCwsXNLfJ8/zmJ6eRm9vL+7duwe1Wg2WZWE2m6Onz41G43MPq9WKo0ePoqmpCfX19YIER/fv30c4HMbevXsTHiuZHA4HHj9+jMrKyrgPb87NzeG//uu/sHfvXhiNRsHWxvM8jh49infffRfFxcWCjUtILqGAlSwqksMYSwApkUig1+sTDlpnZ2epmUCMQqEQuru7MTQ0hPb29rjyWaenp9HR0YHDhw/H1GGI4zjcvXsXt27dQnNzMxobGwW/RZ3pRkdHceXKFRgMBtTW1qKurg4GgyGhMTmOw9jYGFiWhdFoXPDfxOFw4LPPPoNarUZ7e3vC+bD9/f2Ynp7Gr371q5zYHRwZGcHJkyfx9ttvC5ri0tvbC7FYjD179gg2JiG5hAJWsmSRwNHhcMDr9S76fKlUCp1OF3fAEukpPjc3F9frc9309DQuXboEg8GA9vb2Je+2BoNBHD9+HG1tbXEf3nI4HPj+++8RCASwf//+nCmaPjg4iFu3buHIkSNpPWATCoVw5swZPHnyBHv27Eko8AqFQujo6MCKFSuWvNue7a5fv47e3l7s379fsANwNpsNHR0d+Pu///uc+DskRGjUOIAsGcuyYFkWGo0GJpNp0SAkEAjAZrPFXaOVYRhIJBLIZLK4Xp/rCgsLcfjwYeTl5eHYsWMYHBxcUr3J69evo6ioKKFKAxqNBm+++SY0Gg26u7vjHidb8DyPvr4+3LlzBx9++GHaT4OLxWK8/fbbWL9+PU6ePImZmZklvY7neYyNjeHUqVO4ffs2fD4fxGIxdu/ejf7+/pz4twSATZs2obi4GJ2dnYLVmM7Pz4dIJMLExIQg4xFC/oR2WMmCOI6L9hpfiFwuh1arjXtXwefzwWq1xvVa8tT09DRu3rwJs9mMmpoa1NfXz3soa3R0FNevX8fhw4djOrDyMl6vF8eOHcPrr7+e9iAuWXieR1dXF6anp3HkyJGMq5Tw008/4fjx42hpaUFZWRnEYvG8pZssFku07/22bdvw8OFD3LlzJ3oAaXJyEu+9917C6Q3ZIhQK4b//+7+xevVqNDQ0CDJmX18feJ7Hvn37BBmPkFxCKQEkIUsNWhUKBTQaTVzpAcFgEGazOd4lkmfY7Xb09/djcHAQJpMJ9fX1KC0tBcuy0eBy9+7dgh4MGRoawu3bt3Ho0KFll8/KcRw6Ozvh8Xjw3nvvZezdAKvVii+++AJmszlaIF8qlUYfIpEIHo8Hu3btwrp166IfLj0eD7q6uuByubB79+6M/fMli9PpxH/+539i586dgnxPuN1unDhxAr/73e+Ql5cnwAoJyR0UsJKERA5kmc3mRTssqVQq5OXlxRy0cByH6enpRJZJXhAKhfDw4UPcv38fHo8HdXV1mJqagsFgQFtbm6Bz8TyPs2fPorCwEBs2bBB07HQKhUK4fPkyRCIRfvGLX2RVnm44HIbf70cgEIg+TCaTILvqy82DBw9w/vx5vP3224Lknt68eRMAsH///oTHIiSXUA4rSQjDMGAYZkllrNxuN8LhcMw5YQzDZEznn+VCLBajpqYGBw8exN69e+F0OsHzPF555RXB52IYBlu3bsWdO3dgs9kEHz8dAoEAOjo6oFKp8O6772ZVsAo8rZesVCqh1WphMpmwcuVKClZforq6GuFweMl5wItpaGhAf38/1ZkmREC0w0qWLNK602KxLFiGKlI/MpadCp7nwXFctDA6yU53797Fw4cP8dZbb2X1KWmfz4ezZ8+irKwsZ07N57qbN2+iv78fr732miDjDQwMYGpqCu+9954g4xGSC2iHlQiCYRiIRCIYDIYF38BDoRDsdjs4jlvyTivDMGBZFnq9XqjlkjSor68Hz/O4f/9+upcSN4vFgtOnT6O+vp6C1Ryybt06TE1NweFwCDJedXU1ZmZmMDo6Ksh4hOQ6ClhJTJYatHq93phvh0XSAnQ6XaLLJGnCsiy2b9+O7u5u+Hy+dC8nJrOzs+jo6MB3332HHTt2YMeOHRSs5hCxWIyWlhbBPmyJRCJs2rQJHR0dgpXNIiSXUcBKYhYJLBfbDeU4DsFgMOaxpVIp1Gp1IkskaaTT6VBRUYHe3t50L2VRPM9jZmYG586dw8WLF9HY2Ii/+7u/w7p169K9NJIGra2tePDgQbTKQqJKS0sBPE2VIYQkhk65kLgs9ZCUx+OBRCKJaaeKZVkolUqEQqElddsimWfDhg04duwYGhsbM65mKfA0UJ2enkZPTw88Hg+2bduGxsbGeWuXktyhVCohk8ng9/sFKe/FMAw2bdqE8+fPo76+nv5/EZIAClhJ3JZym8vn8yE/Pz/63KUGrizLRl+XbbeWydPyZjU1Nbh16xa2bt2a7uVE8TyPqakp9PT0wOfzYfv27WhoaFh2tWNJfObm5sBxnKB3eIxGI4LBILxeL9VlJSQBFLCSuC3lNH9kJwt42kY0FgzDQKvVwmq1CnaLjqROc3MzPv/8czQ1Nc3bcSvVPB4PLly4gGAwiB07dqCuro4CVfKckZERlJWVCZ67zLIs5bESkiC6WpO4LfUCHGk8EAgEYp6DYRjodLqc676zHCgUCqxduxY9PT3pXgo8Hg/OnDmDuro6/M3f/A3Wrl1LwSr5mZGREZSUlAg+LsMwVK6PkATRFZvELdYLsM/ni2uXIRK0UtHz7NPU1IRHjx7BYrGkbQ1utxunT5/Gxo0bsXXrVjr5T+YVDocxNjYGk8kk+Ni0w0pI4ihgJXHheR5utzum1yRyW59hGOj1egpas4xUKsXmzZtx7tw5uFyulM/vdrtx5swZbNmyBZs2bUr5/CR7jI+PQ6fTQS6XCz42y7IIhUKCj0tILqGAlcSM4zjY7faYb/GHw+GEbotFdlo1Gg0UCkXM1QdIelRXV2Pt2rX4+uuvU3qAzuVy4cyZM2hvb0dbW1vK5iXZaXh4GKtWrUrK2CUlJRgaGkrK2ITkCgpYSUwiO6vxlpuKNy0ggmVZqFQqaDQa6PV6FBYWwmQyZWTpJPIn69atw+rVq/HNN9/EXJs3HpFgddu2bWhtbU36fCT7TU9PJ61pSWVlJfr6+pIyNiG5ggJW8lKRw1KRFqs8z8Pr9SZ0a9fv9wuSy8WyLFiWjXbeonIxma+trQ16vR4dHR0Ih8NJnaunpwevvPIKXnnllaTOQ5aPiooKTExMJGVso9EIt9uNmZmZpIxPSC6ggJXMKxKczszMwGq1wuFwwOl0wm63JzSu3++H1+tNyolZiUQi+JhEOAzDYNu2bZBIJLh48WLSTk273W6MjY1h48aNSRmfLE9r167F8PBwUj5MsSyL2tpa3L59W/CxCckVFLCSeTEMA7lcDoVCgUAgAI/HE/Mhq5dxOBxwu92CBiyR9ZLMxrIsdu3aBZ/Ph87OzqScnL5//z42bNhApdBITNRqNUwmE6amppIyfkVFBe7cuUPlrQiJEwWs5KVYloVarYZCoRB8bJfLBZfLJdjFm2GYpKyTCE8sFmPv3r0YHx8X/Bap3+9Hf38/7a6SuDQ0NGB4eDgpY+fn50OpVGJ0dDQp4xOy3FHAShbEMAzy8/OTslvldrsFvf3GMAzEYmrelg2kUinKy8vx+PFjQccdHh5GbW2toK01Se5oamrC+Pg4bDZbUsavra2lw1eExIkCVrKoSIvUZOSI2u12QXdZKS0ge5SWlmJ8fFzQMaenp1FTUyPomCR3yGQybNu2DV1dXUkZf/Xq1RgYGIir6x8huY4CVrIkLMtCr9cLvoMZDAYRDAYFyWWktIDsUlRUBKvVKmhtVo7jIBKJBBuP5J6WlhbY7XZMT08LPrZcLkdJSQkGBgYEH5uQ5Y4CVrJkDMPAYDBAqVQKWrDf4XAIdvhGJBJR0JolRCIRiouLBd1l5XkeLEuXNRI/kUiEXbt24caNG0k5FFhdXU1pAYTEga7sZMkYhgHLstBoNDCZTNBoNIIEB6FQCHNzc9F6r4muUaPRUCOBLCF0WgDP89T9jCSsvr4eIpEIjx49EnzskpISTExMwOl0Cj42gKQE2YRkAgpYScwigatSqYTJZIJOp0s4vzUYDMJsNgsStLIsi7y8PGg0moTGIclXWlqKx48fC/Ymy3Ec7bCShDEMg7179+LGjRuC12UVi8WoqqrCnTt3BB03ItLkhQJXstzQlZ3EjWEYMAwDmUwGvV6f8IGncDgMs9mMcDgsSNCqUCig1WoTGockl0ajgVQqhcViEWQ82mElQlm9ejVMJlNSylxVVFRgcHAwrtdyHDfvIxKkMgyDUCiUcBtsQjINBawkYZEdV61WC6lUCrFYjPz8/Lh2ujiOg9lsFuQgFsuykMvl0Ov1CY1DkkvInD7KYSVC2r17N7q6ugQ/1S8SiZZ8fYsEosFgEG63Gw6HA3Nzc5ibm4PVaoXdbofD4YDD4YDf7wfwdBdXLBbDarUiFApR4EqWBbqyE8EwDAOdTgeDwQCFQgGj0QipVBrzODzPw2KxIBAIJFzyimEYSKVSFBQUUOvWDNXQ0ICJiQmYzeaEx6I3ZiIkk8mENWvW4N69e4KOGwqFlnxtZBgGHo8HZrMZDocDXq83Wl0lEAjA5/PB6/XC4/HA6/VGd1nFYjHUajUsFgtcLhelCZCsRwErEVQkTSCy66rX6+POJZ2bmxOs3JVYLIbBYEhKaS6SGKlUivXr1wtS+1IulwtaJouQV199FXfv3hWsNTXwNGCN5Tq0WHArFouhUCiea/ASue7p9Xq43W6YzWbabSVZjQJWIqhIsPrsr5VKJYxGY1z1MT0ej2BB67O7rTqdjgLXDFJXVwebzYbJycmExlEqlXC5XAKtihBArVajra0NPT09go0ZDodjuvskEonAMAwkEgkUCgU0Gg0MBgNMJhOKiopgMBig0WigUCieS4mJBK0qlQqhUAhOp5MCVpK1KGAlSccwDEQiEQoKCmKukSr0wYEXD4qRzCASidDS0oIffvghoXxBClhJMmzZsgXj4+OYm5sTZLxgMBhTwMowDAoLC6N3rFQqFaRSaTSQZVkWLMvOe+Dw2U0EiURChxJJ1qKAlaTEszVcdTrdki+aybqFFTlJSzJHVVUVtFotPv30U9y4cSOuOpUKhYICViI4qVSKnTt34ocffhDkehRrSsCzaVaxHip8NndVJpNRwEqyFgWsJKVYloVMJoPRaFzyIajIQQIh8TwfPVFLMgPDMHj11Vdx6NAhAMCJEyfw3XffxdQiU6FQwG63J2uJJIc1NzfD5/NhYmIi4bFiOXQlhMj1kw6ekmxGAStJuUiKgMFgQF5e3qLPT0Y9QZ7nBS9VQ4ShVquxadMmvPfeeygqKsKFCxdw8uRJDA8PL1o1wmg04tGjR3A4HClaLckVLMtGmwkkWr3E5/NBqVQKtLLF8TwfUyktQjIRBawkbRiGgUqlQkFBwYK3qYLBYFLmTsa4RDhSqRQNDQ345S9/iebmZvT39+OTTz7BtWvXMD09Pe+br1wuR0NDA65evZqGFZPlLpK2kmgzAY/HA7VaLdCqliaVO7qEJAMFrCStWJaNlmRZiNBpAUK3WyTJw7IsysrK8NZbb2H//v2QyWS4fPkyPv30U/zwww8wm83P/d9Yu3Yt7t69S6kBJCn27t2bcDMBt9ud0oBVrVZDqVRSUw2S1aiuD0k7hmEgl8vh8Xhe+hyfzweFQiHYgQHKX81OWq0Wr7zyCjZs2IC5uTmMjIzg22+/BcuyKCoqgt/vh9frRSgUQl9fH7Zt25buJZNlprCwEDU1Nfj+++/R3t4eV0tqp9O5pHQoIUQObFH+Ksl2FLCSjLDYxVTIfFOe558rsE2yD8MwMBgMMBgMaG1txezsLMxmM+RyORQKBUpKSlBQUJDuZZJl6s0338SlS5dw/PhxbNu2DaWlpUv+MO31euH3++NuqBIvqg5Ash2z0G1WhmF4StImqcBxHCwWy4KlptRqNVQqlSAXXo7j4Ha7qQTSMiSRSKDX6+n2J0m6iYkJnDx5Enq9Hu3t7Uvaxbx//z7cbjcOHDiQghUSkl0YhgHP8/O+ydMVnWSESBeqhUT6YQuBZVnk5eWl9KQuSQ2hPtQQspiSkhL85je/QTgcxujo6KLP53keAwMDaG5uTv7iCFlmKGAlGSGSx7oQnudhs9kSLinz7JxqtRomkynmDlwkM0X+H1HASlJFLBajpaUFDx8+XPS5NpsN4XAYpaWlKVgZIcsLBawkYyzlFq7f70cwGBR0p1UkEkGj0cBoNFJua5ZTKBRUa5KkXGVlJaamphY9zDk8PIympib6QEVIHChgJRljqYGG3W4XPCiJlNfSarUwGo1UszBLqVQqyl0lKSeRSFBZWYnx8fGXPiccDmNwcBDr1q1L4coIWT7oyk4yxlKD0HA4DLfbnZSdtEjgqtPpYDAYYur3TdJLIpFQsErSZu3atejr68OjR49+ttMaCASqmBoCAAADU0lEQVTQ19eHgoIC6HQ6QefleZ7uKpCcQFUCSMbw+XywWq1Lei7DMDCZTEkPUDiOw+zsrGB5syR5tFot5a+StOE4Dt3d3RgeHsajR4+g0+mwatUq8DyPu3fvoqqqCjt37oRerxd0Xp7nYbfbow1YRCKRoOMTkkoLVQmggJVkDI/HE1N3IqVSCbVandSgled5BINBWCyWpM1BEscwDAoLCylYJRkhHA5jfHwcIyMjCIVCaGtrg1arTcpcz37QVyqV0Gg09H1AshYFrCQruN1uOByOmF5jMpmSvqPA8zycTifcbndS5yHxk8vlyM/Pp5QAklM4joPdbofP5wNAH9xI9qM6rCQrxHPb3eFwJP12faT8FeWzZi6pVEpv0iTnMAzzXL4sz/Pw+XyU00qWJQpYSUbgeT6unVKfz5eSQIVhGMEPSxDhyGQyClhJzpmvxJ/H46GAlSxLFLCSjBAp+G4ymRZtIPCiVF2cRSIR8vPzUzIXiQ0dNCG5huM4eL3en309EAhQwEqWJQpYScaIFPHPz89HQUHBkmuhpuoEfySojjWgJsklkUjoDZrkpHA4PO/Xk1X2j5B0ooCVZByWZSGRSKDT6aDT6Ra91ZvKklMsy0Kr1UKlUqVsTrIwyl8luYhlWeh0unnbSs+380pItqOAlWQslmUhk8lgNBohkUhe+ryX7TIkS+QQVrLK1JDYUP4qyVUMwyA/Px9qtfq5r3Mch2AwmKZVEZIcFLCSjMYwDEQiEQwGw0t3NUOhEHieB8dx0Ueyb4dF0gMMBgMFS2m20IcZQpY7hmGgUql+ll/v9XopLYAsK1SHlWSNSBF/q9X6szQAkUgElmWjD4lEAqVSmfRgMhIoWyyWlO/0kqeKioroQwPJeTzPY2ZmJnptpCYCJBtRHVayLDAMA4lEAqPR+LMDWeFwGMFgEH6/H16vFw6HIyX1CBmGAcuyMR0SI8KhN2NC/mS+fFZClgsKWElWiQSIer3+Z3lbL7LZbAiHwykLWvV6Pb1hpBgFrIQ8FUkNiKC7o2S5WbR1D70hEEIIIYSQFBh72W8smMNKCCGEEEJIulFKACGEEEIIyWgUsBJCCCGEkIxGASshhBBCCMloFLASQgghhJCMRgErIYQQQgjJaP8fR4mJQQ8/RsIAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 864x576 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"fig = plt.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection=cartopy.crs.Mercator())\n",
"ax.set_extent([-128, -60, 24, 50], cartopy.crs.PlateCarree())\n",
"ax.add_feature(cartopy.feature.LAND, facecolor='0.9')\n",
"ax.add_feature(cartopy.feature.OCEAN, facecolor='w')\n",
"\n",
"# add states\n",
"# can plot states like this, but doesn't allow access to metadata\n",
"shapename = 'admin_1_states_provinces_lakes_shp'\n",
"states = cartopy.feature.NaturalEarthFeature(category='cultural', scale='110m', facecolor='none', name=shapename)\n",
"ax.add_feature(states, edgecolor='gray')\n",
"\n",
"# add end points\n",
"ax.plot([lons[0], lons[-1]], [lats[0], lats[-1]], 'ro', transform=pc)\n",
"\n",
"# add the flight path as a shape\n",
"ax.add_geometries([line], pc, facecolor='none', edgecolor='k')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Shape intersections\n",
"\n",
"An easy way to find what states the flight path intersects is looking for intersections of the Shapes."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['Arizona', 'California', 'Colorado', 'Nevada', 'New Mexico', 'Kansas', 'Missouri', 'Illinois', 'Indiana', 'Ohio', 'New Jersey', 'Pennsylvania']\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAAFTCAYAAAD87l5hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nOydaXBb13n3/7jY9437vom79n2hRe2bZceO7cTN2K3TdDJxmrTJtG++tP3Sd9qZdjqNJ2mmzdukSR0ntuM4jh1rsWSJEiVKpCiREheRIkWKi0gBXLDvwL3vB+Ui4A6AAC4Ant8MhyRwcc+D7dz/ec6z8BiGAYFAIBAIBAKBkKxQXBtAIBAIBAKBQCAsBxGsBAKBQCAQCISkhghWAoFAIBAIBEJSQwQrgUAgEAgEAiGpIYKVQCAQCAQCgZDUCJa7s6SkhBkZGUmULQQCgUAgEAiEtcsIwzAli93BW66sFY/HY2iaBnuMx+OB2+2G1+sFTdMxsSwjIwMCgQA8Hm/O7QzDwGazweFwxGQcAoFAIBAIhGRCJBJBp9Mt0ECxgtVvgUAAFPV0U53H48VtvNXC4/HAMMyixq0oWOffT9M0eDweAoHAHAEbLXw+HxkZGcEXcv5YXq8XZrMZpF4sgUAgEAiEdIGiKGRmZi6qf2IBwzDwer2wWCwIBAIAAKFQCLFYDKlUCj6fD4Zh4jZ+NMRUsIbCMAwYhoHVaoXL5YraQLlcDqVSuajiZxgGgUAAJpMJfr8/6jEIBAKBQCAQkgW9Xg+hUBhXbyfDMLDb7bDb7QvuoygKYrEYEokEYrEYDMNw7n2Nm2Bl8fl8mJ6ejt5CLP/GscLYYrHA7XavahwCgUAgEAgELlEqlZDJZAnxbrKeVpPJtOxutUgkgkQigUQimRM+kEjiLlhpmsbMzMyqPKDLhQaEjuNyuWC1WqMeh0AgEAgEAoEr4h23uhgMw4CmaczOzoal1fh8PqRSKeRyeUK9rnEXrAzDwOVywWKxRG8lAJlMBqVSuaxoZRgGPp8PJpMpZolfBAKBQCAQCPEm3nGryxHNbjWfz4darYZQKEyIzXEXrMDTF8JsNq96yz6cmA72RZ+dnYXP51vVeAQCgUAgEAjxhs/nQ6vVLloZKZEwDAOn0xnRbrVEIoFarY67tzUhghV4umXv9/thsViiDg9gQwPCeVHYhC+n0xnVWAQCgUAgEAjxhKIoKBQKyGQyAImPC10MhmHg9/sxOzsb9m41j8eDSqWCVCqN23NImGAF/ljzy+l0wmazRVWOiqIoaDSasFzQDMPA4/GQ0lcEAiFu0DQNq9UKmqZB0zQEAgE0Gg3XZhEIhCSGx+NBLpcnPA40XNjdapfLBafTGbajUSgUQqPRgM/nx/w5JVSwssSi5JVYLIZGo1nxjWZLX83OzgZrjREIBEKsGBoawq1bt6BQKEBRFMxmM1555RXw+XyuTSMQCEkIm5OTjEJ1Pqxeo2kaTqcTLpcrLK+rQqGIuRjnRLCy0DSNQCAAs9kcVZgAj8cLln8IJ66VlL4iEAixZmBgADMzM9i1axcA4MyZM9ixYwcyMjI4toxAICQTUqk0mDye7EJ1MVjN5/P54HA4VtRTfD4fer0+Zov35QRr3FO+KIqCQCBARkYGlEplxI9nvbRs2aylBDSPxwuGEqhUqtWaTSAQCEui1+tXXXuaQCCkD2KxGJmZmVCpVDHfKg/1gNI0Ped/v98Pj8cTs6pJrLdUJBJBrVYjOzs7WCVgMQKBQMKS3wWJGIR942QyGdxud1RPzufzYWpqCnK5HAqFYkkXNI/Hg0wmg1AoJKWvCARCTJi/UNbr9Xjy5AlH1hAIhGRBJBIFRepqyj6xIvQPHsbg7nToD3sbK1xDEQqFwdqusRLL7PORSqWQSCTB6gIejyc4DkVRCSvRlRDBykJRFNRq9ao8E6yLmk3KWkq0CoVCZGZmktJXBAIhJoTONRkZGeju7ubQGgKBwDWx6lZF0zS8Xi+sVmvUeThsx1GdThdzD2+oCGbjVuffnwgSKliBp/EOEolkVXGmgUAAMzMzyMzMhECw+FNgX2C9Xg+GYdDd3Q2z2Rz1mIkmnA/A/GPMZjOUSiX4fP4Cj1Do/7Ozs9DpdLExNExWEwsdSS3geI4RqyoUq0lkXAqXywWPxzMnc325z1C4E0wszhHOsdFMeMs9ZnZ2Fmq1Ouq4qvnnnpqamjPXqNVqeDweeDweiMXiqMYgEAipi1gsDiYcRQvrSTWbzfB6vau2KRAIYHp6GlqtNm6F/rlMIku4YKUoCiqVKiaJUVarFRqNZtk3hX1xb9++DbFYDIlEsuJ5E90uLRbHAMDVq1dRU1ODzMzMObeHPh+Px4PPPvsMzz33XGSGhkkiX7tYiC4uzx/L8/X398PpdGLbtm2L3h8L0R+rhUM8ys/NP2dzczPKysqQn58f8WMXg6KoOefi8XjQ6XSYnp4OawwCgZA+sPky0c797Pa/3W6Hw+GIqW1sUyW2XioXHbXiRcIFK/DHIrp2u31V52EDjcN5QwoLCyEUClFZWbmqMZOZ9vZ2VFdXo6qqasljWMHKZjsT0gOz2YypqSls2bKFa1OSguHhYajV6rh+zjMyMjAzM0MEK4GwxtBqtVGLVXb732KxxDXHxmq1wufzBbtTpQOcSG+2mG5mZuaqOybYbLaw3vSioiIYjcaox0kXxGJxMLOQkD6ky4QUKzZs2IDbt2/HdYysrCwMDQ3BZrPFdRwCgZA8yOXyFdvHLwZbL95kMiUsIdzlcgU7WaVDYyXOfMVsuSu1Wo2srKxgll2kuN3usN74wsJCTE9Pp3XVgHC/QGKxmNSqTUPSYUKKFTU1NWAYBkNDQ3EbIz8/H7W1tTh//jypGEAgrAGEQmGwGUC4sHGqNpsNRqMxJrGqkeD1emEymdLCqcFJSEAobIypTCaDTCaDz+eD3W6Hx+MJ+xw2mw1qtXrZ0ACpVBqsnZiVlRUL05OOSASr0+mEQqGIs0WEREFRFBGsIbAVSZxOZ1zHqayshEqlwrVr11BRUQG9Xg+FQgGFQrFk3UICgZB68Hi8iEMBErX9vxxsvC1bMiuV4VywsrAvpEgkCr64DocjrBZhbrc7rGYBRUVFmJycTFvBCoTnZROJRFG3yyUkJ2ztPsIfcblckMlkcR8nJycHx44dQ19fHwYHB2G322G32yEQCKBQKKBUKqFSqZCVlYWMjIwlK5sQCITkZSWnWCixzv6PFrZSUqp23ZpPUs6c7IdCqVRCqVTC7XbD4XAsW0+VvTgt94EqLCzEwMBAzO1NNUQiEQkJSDPSYTKKJX6/HzMzM8jLy0vIeEqlEtu3b59zm9PphMPhgM1mg8lkQmdnJ0wmEzQaDbKyspCVlYXMzMywKpcQCATukEqlEIvFK86z8cz+jxRWrMa6JiuXJKVgZWFfZIlEEkwWstvtQe8gj8eDVCpdtvNVKDk5OcHGA2v5IiEWi4mHNQ0hHtY/YrVaIRQKOf2es2FOoWXmWCFtNBoxMDCAlpYWSKXSoHjNzc1NiFeYQCCEB5/Ph0qlWtG7mgzb/6FotVoIBIK0EatAkgtWFrfbHawnplKpoFKp4PV6IRaLwTBM2G56Pp+PwsJCGAwGFBcXx9lqbghHtEgkkohihAnJD4/HS4pJMlkQCoVJ+XoIBAJkZ2cjOzsbwNPvq8lkwtTUFCYmJnD79m0UFBSgrq4OarWaY2sJBALb7nQpkmX7PxStVguRSJRWYhVIAcFqs9nw85//HDqdDuvWrcO6deug0WiCnpNI35CCggIMDw+npWANN46RTboipA/pVBw6FohEopRoycw2INDpdKiqqoLH40F/fz8+++wzZGdno66uDnq9nmszCYQ1CVu9aDGdkUzb/6FoNJq0FKtACgjWnp4eFBYWoqysDKOjo+jo6IBWq8W6detQWVkZ8fZZUVERWltb42RtaiAWi4mHNQ0hIQF/hN198fv9KZXkJBaLsWHDBtTU1GBgYABNTU3QarWor69fMVnU7/djamoK09PT0Gg0yM3NTannTiAkEyKRaMk68WxN1ZmZmaTayVGpVBCLxWnrwEjq2SwQCODevXtoaGiARqNBRkYGNm3ahCdPnuDRo0e4efMm8vLysG7dOpSXl0MkEq14TtZVbrFY0m7LLZKyVkSwphekrNVCJBIJHA5HSn7PhUIhamtrUVVVhaGhIVy/fh1yuRz19fXBRDKPx4OpqSkYDAYYjUaYzWbodDro9Xr09/fj+vXryMnJQWFhIQoKCiAWizl+VgRCakBRFLRa7ZLCj21/mkxiVaFQpF0r1vkktWD1er2gaXpOvVCKopCXl4e8vDz4/X48fvwY3d3duHr1KoqKirBu3TqUlJQs61koLCyE0WhMyQvZcoQrWEUiEaxWa5ytIRC4RSqVwm63p/T3nM/nBxfkjx49Qnt7OwQCQTABNSMjA1lZWdiyZQv0ev2cec/j8WB8fBxjY2Nob2+HTqdDUVERCgsLSWIXgbAMGo1myespG3ceCAQSbNXSyGQyyOXytBarQJILVqlUiuLiYgwPD2PdunUL7hcIBCguLkZxcTG8Xi/GxsZw69YtXLp0CeXl5aisrERhYeGCx6nVakxNTSXiKSSccGNYkyU4nBAbSB3WhZSUlOD27dvIz8/n2pRVQ1EUysrKUFpaisnJSYhEIuh0umUvUGKxGOXl5SgvL4ff78fk5CTGxsZw9+5dKJVKFBQUoKioKKUFPYEQa5ZrvUrTNKxWa9JdP1UqVVrGrM4n6eX4+vXrMTw8vOJxIpEI5eXlaGxsxKFDh8Dn83Hp0iU8fPhwwbEqlSqpgqRjCRGsa5O1MFlFyu7du9HZ2ZlU23arhcfjIS8vDxkZGRF5UwQCAQoLC7Fnzx689NJL2LRpE1wuFz755BP84he/gM1mi6PVBEJqIBAIoFQqF/1uMQwDl8uVlCUh02mOW46kF6wFBQUQCoUwGAxhP0Ymk6GqqgobN27E/fv3F9yvVCrXdJa8VCqFxWLh2gxCDCFlrRZSVFQEnU6H27dvc21KUkFRVLC0nVgsRllZGaRSKddmEQicwlbsWCrJyufzJW0ond/v59qEhJD0ghUA6uvrF/WUrkR2djYMBgPsdvuc21Uq1ZoWrNXV1eDxeLh27RrXphBiBPGwLs7OnTtx8+ZNrs1IGqanp9HU1IRLly5Bp9PhC1/4Avbs2UOqCRDWPEu1XmXrrM7OznJgVXh4PJ41ERKWEoK1uroaJpMpKpFZVFSE/v7+ObfJ5XLQNJ0SdRojIdw4RqFQiBdffBEXLlyAyWRKgGWERLAWJqxI2bBhQ7Cz1FrmyZMnuHjxIq5evYrc3Fw8//zzqKurg1Ao5No0AoFz2G6aS3lXZ2Zmknp+9fl8SW1frEgJwSoSiVBZWYnBwcGIH1tSUoLe3t4Fb6ZarV7geV1LlJSUYOfOnXjnnXe4NoUQA0hIwOKIxWJs3LgRN27c4NoUThgfH8e5c+fQ2tqKkpISfOELX0BVVRXxqBIIf0AgECzrXTWbzUlVEWAxfD7fmthlSwnBCgBVVVWYnJyM+HFKpRJ8Pn/BYzUaTdoJ1khFy5EjR+B0Ohd4oAmpx1qYrKKlsLAwqrkjlXE6nTh//jw6OztRXV2N5557DhUVFWlf9oZAiASKoqDX6xf9XtA0DZvNlhI1y9mwhXQnZZbZmZmZ8Hg8cLvdwbas4cAwDMrKynD//v1gwW0gPT2sFEVF9KEVCoXQarVrOp43XSCCdWmysrLWVOjL7OwsmpqaUFFRgfXr15PPBoGwCDweD3q9fskwAI/Hk1LVhPx+P/h8PtdmxJWUWW5TFIWCgoKIqgWwFBQUYGhoaE4pJ6VSmZaCNdm3LgiERJOdnQ2bzbYmPBCjo6P4/PPPsXXrVmzYsCHuYtXr9aKvr4/MO4SUQ6vVgs/nL/iOsC2dzWYzR5ZFx1pIvEoZwQoAubm5mJ6ejvhxfD4fubm5c2JgVSpVUtZTWw3RFI/Pzc1FS0tLnCwiJIpIvetrCbFYDKlUmvZe1q6uLrS3t+PgwYMoLi6O61g0TaOvrw8fffQR7t69m/YXSkJ6oVKplm0OEFoRwOv1hlULnmvWQuJVSgnWgoKCqDtUlZSUzKnJmo4eVj6fH7FoOXbsGADg448/jodJhARBYhOXRy6Xp23tYb/fj2vXrmF8fBzHjx+HXq+P63gjIyP4+OOPMTExgaysLJSVlZEkLkLKIJVKIZVKl4xbnZ2dnXMdvX37NlpaWhat6T7/sVzWQ10LiVcpdZXLyMiA1+uNyjOamZkJq9Ua9LJYLJa0W43weLyIt+aEQiFeffVVdHd34+233047Eb+WSLfPcywRCARpV8YOeJpcdeHCBTAMgyNHjkAmk8VtLKPRiLNnz6K7uxs7d+7E/v37MT09jcrKyriNSSDEEpFItGRFAJqmYbFY5ojOsbExGAwGnDp1Cr29vRgbG1vwuNnZWbS3t+PDDz/ERx99xFm9VoZh0v4akFKClY1jjaamIk3TKC0tRV9fHzweDz7//HNs27YtDlZyRzQeVgDQ6XT41re+BalUin/9139FX19fHKwjxJNowkHWEiKRKO3aEVssFpw7dw75+floaGiIm5fTarWiqakJ165dQ2VlJU6ePInc3FyMjo5CrVZDrVbHZVwCIZYIBAJotdolwwAcDgfcbnfwNpfLhba2NuzZswcajQaNjY24efMmZmZm4HK5cP/+fXz66adoamqCQCDA0aNHsWPHDly6dCmq0MVYkI6L8lBSbh8nLy8P4+PjUcVoFRcXo6mpCU6nE5mZmcjOzo6DhdwRjYeVRalU4qWXXkJVVRXeffddfOc73yEXIkLaIJfLUy6JYjnYjlWbN29GeXl5XMbwer24e/cuHj16hJqaGuzbt2+OKH7w4AFqamriMjaBEEtWarvq9XoX7C62trairKwMWVlZAAC9Xo9du3bh4sWLAJ6GKG7duhXZ2dnB86pUKlAUhcuXL6OhoQE5OTlxfmZz8Xg8EIlEaRsakFIeVmB1caxSqRQKhQJ9fX3YvHlzjC3jnmg9rKGsX78e27Ztw89//vMYWUVIBAKBgGRqL4NKpUraPuCR8vjxY1y+fBm7du2Ki1hlGAYDAwP4+OOPEQgEcPr0adTX188RqyaTCQ6HAwUFBTEfn0CINWyt1cUqAgQCgQUJmYODg7Db7diwYcOc2wsLC3Hs2DG8+OKL2Lt3L3Jychacs6CgAA0NDWhubsb4+Hh8ntASpHviVcoJ1oyMDPh8vqjiWBmGQXV1Nfbt2wexWBwH67glVmWtjh8/DoZh0NzcHAOrCIlAIBBwGvCf7CiVyrQQrENDQ7hx4wYaGxvjIhanp6dx7tw5DA4O4sCBA9i1a9eida8fPHhAGhEQUgKNRgOBQLBs29VQ7HY7Ojo6sHfv3kXrmmo0mhVbGufk5ODAgQO4du1aQkORVkq8SvU415SbbXg8HgoLC6Oqxwo8Fbysiz/diFUco0AgwPPPP4+LFy+mxUV+LSAUColgXQaNRsNZXFms6O3tRWdnJw4fPozMzMyYntvlcuHGjRu4cuUKKisrV6w2MD4+jtnZWYyNjZHPHSFpUSgUEIvFc0QcTdNgGAY+n29BRQCGYXD9+nXU1tZCq9WuauyMjAzw+fyE7nyt1PGK9SinKiknWIHo67GmO3w+P2arp5KSEmzcuBEffvhhTM5HiC8ikYgIh2Worq7GxMQE12ZEzZ07dzA4OIhjx45Bo9HMuc9sNqO7uxvnz59He3t7RGFBbD3V3//+9xCJRDh9+jTKy8tXjIE7ceIE8vLy0NfXh9/85jdobm7GyMgI+QwSkgaJRAKFQhFsWU7TNFwuFywWCwwGA6anpxckKbGlq2pra7kwOSa43e5FdQDDMJidnYXVauW8ZjdN01EJ55RLugKeCta7d+9ybUbSsZqkq8U4evQovv/976O/vx9VVVUxOy8h9hAP6/LIZLLgRSvVtrFHRkYwMTGBo0ePQiKRgKZpGI1GjI2N4fHjx6BpGgUFBairq8ODBw/w+eefo6GhYdkW1oFAAENDQ+ju7oZKpcLRo0cjSrKUyWSorKxEZWUlXC4XxsfHMTAwgI6ODuzfv3/V3qmlYD1I6d6CkrB6lEol/H4/XC4XPB7PivOjyWRCT08PTpw4kdJJS263G1KpdIFX2WKxBAV6IBDgbB5kk9wARPw9TknBqlQq55SfIDwlFklXoSgUCpw8eRLvvfce3njjDRQWFsbs3ITYQgTrygiFQni93mWFXDLi8Xig0WgwOTmJ8fFxTE5OQqlUIj8/f4E4zM/PR0dHB86ePYvGxsYFwtHn82FgYAD379+HTqfD3r17Vx0iJZVKsW7dOqxbtw5DQ0O4ePEitm3bhtLS0qifr91un/PjcDiCfwsEAjz77LNxrTlLSH0iSc4OBAJoaWnB5s2boVAo4mhV/JkfM0vTNJxO5xzNZLPZoNFoOBGtDMPAYrFE9TqnpGCVyWTw+Xwp6S2JJ7H2sALAli1b4Pf78d///d947rnnsHXr1pienxAbiGBdGbFYDIfDkTKC1Wg04tatW7h79y5EIhG2bduG/Px8bN26dUmxxuPxsGXLFmi1Wly8eBG7du1CYWEhPB4P+vv70d/fj+zsbDQ2NsalI1ZZWRm0Wi2uXLmC6elpbN26dcU52u12Y3R0FMPDw8HSYwqFAnK5HAqFAmq1Gvn5+VAoFFAoFOjs7ERPTw+2b98ec/sJa5Oenh7I5XJUVFRwbUpMCF2YL6YLPB4PJ/qJYRjYbLbgbhfDMBF5s1NSsPJ4PEilUrjdbrLKDiFWVQLms2PHDuj1erz77rs4c+YMhEIhhEIhXnvttbRNYEs1SAzryuh0OkxOTsa9dWksoGka//7v/44tW7bgueeew7p16yKqbFJaWgqVSoXLly/j17/+NZRKJdRqNY4dOxb3+sparRYnTpxAS0sLLly4gIaGhgXzdCAQwOPHjzE0NASDwYC8vDzU1dUhIyNjxQVFXV0dPvnkE9TW1kIul8fzqRDWCA8fPkRjYyPXZsQMl8sFkUgULOWlVCrhdDrnHGO1WhPuZQ0EAkE7otkNTln3pFwuj6q0VTpDUVTcREt5eTm++93v4utf/zq++MUvYmZmhiwWkgiBQLBihuhaJzs7O2USryiKAk3TePnll1FfXx9VGT69Xo8TJ07A6XRicnISXV1dGBkZiYO1CxGLxWhsbERubi7OnTsX7E5oNBrR2tqKDz/8EP39/SgoKMALL7yAhoYGFBQUhOX9ZkMQurq6grfduXMH9+7di9vzIaQvrMcvXnHXXMTDejyeOePyeLwFizs2rjdRpa4YhplT7zaacVPSwwo83TIignUu8V4pSaVSSKVSjIyMBLfoCMkDRVHw+XxpWWM4FmRnZ+PBgwdcmxE2bHbzar7Xcrkcf/d3fwcAuHr1Ku7du4f169cn5CLK4/GwYcMG6HQ6XL16FXw+H3w+H2VlZTh58uSqvKO1tbX49NNP8cEHH0Cn02FiYgIajQYFBQWcxeYRUpPJycmEd6SKNwzDwO/3B+vF8ng8KBQKOJ3OOSJxZmYGfD4fYrEYEokEIpEouE0fzhwR7pY+wzBwOp1zHGrROFdSVrASD+tCWK9MvOnq6sLGjRvjPg4hMvh8PhGsy1BfX4/PPvsMXq8XIpGIa3PCIpbZvPX19bh+/Tru3r2LysrKhO2QFBQU4OTJk3C5XDELxxCLxXjxxRfhcDhgMplgt9uhUqlw9uxZKJVKHD9+PGXeYwK3TExMoKioiGszYo7L5ZrTMIHH40Gr1cJqtc4Rjuw2PbtVLxQKgwKWre0e+sPGnlIUFXY+ABu7GsqaE6zp1Bs8FsQj6Wo+Pp8Pw8PDeOWVV+I6DiFy+Hw+iWNdBq1Wi4KCAty5cwe7du3i2pwVYT2ssUKn02HXrl349NNP8emnn6KgoAA1NTUoLy9fss96rJDJZHERyHK5HHK5fE7Xr9bWVjQ3N+PAgQPE00pYFpqmYTAYsGPHDq5NiTkejydYhxZ4Op+IRCLo9Xr4fD7YbLYFdWiBp9d4n88Hu92+5LkpikJGRkZYcwZbUmv+9n80YQgpK1hdLhc+/vhjnD9/HhRFBX9UKhWOHz+O3Nxcrk1MOFlZWejo6IjrGCMjI1CpVCQcIAmJZwxzulBbW4uenp41KVgB4MCBA2hoaMDExAS6u7vR3NyMzz77DCqVCjU1NVi3bh3y8/NXbD2ZzGzfvh1XrlxBW1tbSrzPBO6YmZmBXC5Py3wMNj41FHarXyQSQafTwe/3w2azRdw+VqfThbUYZEMTFitDGggEgl7bcBfLKStYc3JysGHDBqxfvz5YIsHn82FiYgI//vGPUVxcjH379qGsrGzNrLJramrwySefYGhoCGVlZXEZY2hoiNRjTVKIh3VlqqurcfHiRa7NCAuKouKSDCEQCFBUVISioiKcPHkSMzMzePDgAbq7u9Ha2gqpVIpt27Zh+/btKXkhpygK+/btw4ULF9DV1YX169dzbRIhSZmcnExr55bJZArGdIfqoFDhqtVqEQgEYLPZ4PF4VjynRqOZE2qwHAzDLLkTzjAMpqenodVqIRQKwzpfygpWpVIJmUy2oDh1bW0tdu7ciebmZnz00UewWCwoKSnBV77ylZSpvxgtAoEA1dXV6O/vj5tgHR0dJfGrSQoRrCuTmZmZMk1HfD5fQvp+6/V67N69G7t374bL5cKDBw/Q1NSEq1evYvPmzdi1axcyMjLibkcsEQqFaGxsxLlz56BQKKJuYkBIbyYnJ9N6QePz+TA1NQWpVAqVSgVgYXI2K2Y1Gg1omobNZltyjpTL5cHY1pVgGAYOh2PZOYymaczMzEClUkEqla7oXExZwSqXy5d8UZVKJU6ePImTJ09ienoaZ86cwW9+8xt85StfSbCViYem6bhu52k0GkxPT8ft/IToIYJ1ZdiEgWRmcnIS7777LmQyWcITh6RSKTZu3IgNGzZgZGQEly5dwg9/+ENUVFSgpKQkeHGTyWTQ6/XIz8+Pmy0ulwuPHj3CzMwM1Go1tFotdDpd2F5foVCIjRs34saNG1AoFMjMzIybrYTUw+v1wmQyrYla4i6XC263OxjzvVgVAAt/LHgAACAASURBVPa7rVaroVKpYLPZ4HK5QFEURCIRJBJJ2GIVeDrXLhcHG4rVaoXP51uxRnTKClapVBpW3EVGRgZeeOEFvPXWW+ju7kZ9fX0CrFsZmqbR0dGBjo4OeL3eJQOS53eDmH/BDa1lRtM0Jicn49oBpri4GLdv347b+QnRwzAMxsfHg3+H3g7MzcoMvX+x2+fHTi712Pn3Lfe4xVhuRT3/Pp/PB6/XC4/HA5/PB7fbHbwt9HcgEIDP54Pf74ff7w/exv4/OTm5rE1c4ff7ce7cOdy6dQsHDx7E3r17IRBwM0XzeDyUlJTgq1/9Kqanp9Hc3IyOjo5g+JXH44HD4cA3v/nNmJYECgQCGB8fx9DQEIxGIwoLC5GTkwOLxYK+vj7Mzs6Cz+cHxatWqw2W67FarbDZbMHfXq8XSqUSBQUFSb9IISQeg8GAjIwMzr5jiYZhGNjtdjidTiiVSkilUgAL68Sy865KpQoKSLYqQLjQNB1xUrzL5VrR4ZKy75RYLA4G9K70gVMqlXj++efxySefcCJYW1tbcf36deh0OlRUVMBsNuPOnTtQq9XYtm1bcMXDfiDmr37Yv+ffH5r9x/62WCz43e9+h/7+flRVVcX8uRQXF+PMmTMxPy9h9ZhMJly6dAkymWzBZwOY+/lhWez+0NsXW4kvdu6ljl3s3OEmEs0vLC0QCIIlV0QiEYRCIZRK5ZzbhUIhRCJR8H72f/a32+3GW2+9Fdb4iWR4eBjvv/8+tFot/vIv/zKpvIHsoj8UhmHw9ttv4+HDhzERrEajEUNDQxgdHYVOp0NZWRn27du36G6Rw+HA7OwsZmdnMTQ0BIfDAYVCAaVSCb1ej5KSkuAWIxdF2wmpwcTERFrHry4Fm7Vvt9uhVqshFAoXFaOLXQ/CgWEYeDyeiBO5ACxatSCUlBWswB9rsSqVyhWPrayshNVqTYBVf6Srqwuff/45AoEADh48CKvVisHBQUilUrz22mtxi6sSi8X45S9/iW9+85sx3+5ob28HAE76EBOWR6/X46WXXiLxekvg9/vR1NSUdIlETqcTP/vZz3DixImUyWrn8XioqanB+fPngw0Cwq0c4nQ6g4LTZDJhZmYGAoEAZWVlePbZZ1d8f9isbolEgvXr15N5iBAxTqcTIyMjOHXqFNemcEYgEMDs7CxEIhHUavWCxKylCHUksHVaaZoO7mAFAoGoa+SnbUgA8Mc41nAEK1sI12QyxawFm9/vR09PT/D8rOenp6cH7e3tkEgk2L17N7Zv3x70Au/fvz8mYy9HXV0dDh8+jB/96Ed44YUXYpYkZbPZcO3aNXzve98jF4kkJLSzCWEuZrMZ77zzDnw+H772ta9xbc4czp49i+rq6pQRqyzbt29HIBDAjRs30NzcjDfffHPJuXhsbAwPHjzA7OwsAAS384uKirBp06YVL1TzmZiYwNWrVyEQCFBYWIiioiLk5OSQeYkQFvfu3UNFRcWquq2lC16vF1NTU5BIJFCpVAt24BYTpKE/sQi34fP5YZXKSgvBGi5FRUXo7OzEgQMHFr3fZDLh+vXrGB4exszMDHw+HzQaDTIyMpCTk4M9e/ZArVbD7XajtbUVV65cgVarhUgkCsbQeb1e5OXl4eWXX8a6deti9VQjpqGhAZmZmfjggw9A0zQ2b9686nOyYQuhF5fW1lacPXsWNTU1+NKXvrTqMQjR4/f7SXefJbh58yakUim+8Y1vJJWocTqd6OzsxLe//W2uTYmKXbt2YefOnfif//mfYOztfBwOB27evIkdO3YgMzMzJh7uJ0+eoK6uDuXl5RgZGcHdu3dx/fp1FBYWori4GNnZ2Un1PhOSB7PZjLGxMTz//PMJGS8R3SdjgdvthtvthkQiAcMwMRWkyyGRSKBWq8NqB5vSglWhUETket68eTPOnDkDmUyGyspKiMVi+P1+DAwMoLW1NTgJPvPMM8jPz4dYLIbRaITBYMDY2Bj+7d/+DQqFAhaLBcXFxXj11Vc5FaUrUV1djX379qG7uzsmglUoFM4pUUHTNC5cuIDjx4/j5s2buHbtGvbt27fqcQjREQgEiGBdgoGBgaTsfCQSiaBQKNDd3b3kQjrZ4fF4qKurQ19fH3w+3wIvf2trK6qrq1FcXByzMQ0GQzD+v7a2FrW1tbDb7RgZGUFnZyfsdjuKioqwfv36pAsBIXBLR0cH6uvrEzJXFhUVoa2tDfv370+ZeOpElv1TqVRzci5WIqUFq1QqhclkCvv4+vp6mM1m9PT04OzZs/D7/eDz+cjMzMTWrVuxcePGBZObUqlEeXk5gKcrs6mpKRQUFAQz7JKd3NxctLW1xeRcQqEQDMNgcnIS2dnZeOedd5CZmYldu3YhOzsbP/vZz7Bt27a0r3ebrBAP69JIJBLMzMxwbcYCBAIB3njjDfzoRz9Cbm4uqquruTYpYhiGQXd3N6qrq8Hn8+fcNzQ0BJfLhbq6upiN53a7YbVaF9SGVSgUqKurQ11dHWw2GwYHB3H27Fns3r0beXl5MRufkLo8efIEZrMZzzzzTELG2759Oy5cuIB79+6R+uUhsCEAfD4/IiGf0oJVLBaH1ZmBRSAQoLGxEY2NjVGNp9FooNFoonosV9y5cycouFcLRVE4ffo0/vM//xNqtRpKpTJY27a0tBRZWVno7+8nX0yOIIJ1afbs2YOPP/6Y01JRS5GVlYVTp07hzJkzKSlY2ULjxcXFczzYLpcLd+7cibln22g0Iisra9lzKpVKbN68Gbm5uWhpaUFZWRk2bNiQdB52QuJgGAYdHR3YtGnTgoVVvKAoCs888wzOnj0LjUYT012GVEUsFkOj0YQVAjCflP72ulwuiMVirs1IWp48eYK+vj6cOHEiZufcu3cvXn/9ddTW1uKNN96YkxlcXl6O/v7+mI1FCB+2fl2yibFkoaamBnl5efiXf/kXDA4Ocm3OAgKBQMySQRONxWKBzWZDc3Mz2tvbgzFvt27dQnl5OfR6fczGMpvN6OrqCttjmpOTgxMnTmBmZgYXLlyA0+mMmS2E1GF8fByffvopRCIRSkpKEjq2VCrF/v370dbWFkw6XKuoVCpotVpQFBVViERKC1aHw5EyW/NccOfOHVRXV8c8hqu8vBzHjx9fII5KS0sxMjIS07EI4eF2u0mFgGWgKAp/+qd/iv379+ODDz7g2pwFDA8Po7CwkGszoiI/Px/bt2+H0WgMxo+OjY3BZDLFtO3lgwcPcOHCBVRWVkbkiZZKpTh48CDy8vJw5swZPH78OGY2EZKbyclJnD17Fp2dndi4cSMOHTrESSypXq/H9u3b0dTUFLMYUTYJmqIo8Pn8YD1qtuY0W7koGZwYFEUhIyMjonjVxeD+mawCh8OxJgv/hgNN0+js7MSrr76asDFLSkpgNpvhdDpJokOC8Xg8JBwgDGpra3HhwgWuzVjAkydPYpIYyQUUReHQoUOw2+0QiUQQCARoa2tDQ0MDBAIB/H4/RkZGQNM0SktLo76AdnV14fDhw1F5onk8HtavX4+srCxcv34dpaWl2LhxIwkRSDNcLheGh4cxPT2NgYEBOBwOPPfccyguLuY86amkpAQmkwlXr17F4cOHlyzWLxAIgj8ikSjojVzK/qWy+NnHWK1Wzlp2C4XCYM3kaEIA5pPS31abzUY8rEswMDAAPp+f0CLyYrEYNTU1ePvtt1OmlEe64PV6iYc1DJRKJdxud9J9Ph0OR8rFx8/H4/HAarWis7MThYWFyMrKAsMwuHbtGvr6+tDW1hZx9xuXywW73Q6LxQIej7fqsIns7GycPHkSRqMRfX19qzoXIfno6OiAwWBAQUEBKioqoFAoUFJSwrlYZdm0aROEQiFu374NiUQChUIBrVaLzMxM5OTkIDMzE1qtFiqVCnK5HEKhEHw+f45onf/DellDf3g8HmiaxszMDBwOR0KfI0VRkMvlyMrKgk6ng1QqjToEYMG5Y2AfZ5CQgKXp6uqKaWZuuLz88svg8/n46U9/mvCx1zIkJCA8BAIBJBIJbDYb16akHadOnUJXVxeuXLkS9BZ3dXXB7XYjPz8fZWVlEe28zMzM4MyZM2hvb4fBYIhJC1jgacWIsrKyhHc+JMQXhmEwMTGBbdu2oaysDHq9PqKk7ETA4/Gwd+9eWCwWGAwGKBQKSCQSCASCOeJzNeKOpmm4XC5MTU1F1R41WiQSCfR6PbKysqBUKucI7ViRsiEBbPsvUkJpITRN4/79+5x09BGLxXjttdfwj//4j3ELDaBpGufPnw9+GWmaXuAxY/9nt0tC/1/sWHZ7hv2Chf5mb1/svtBsU5qm52zPzLdhpduWGn++HfOPoygKT548SRovQrKjUCgwOzsbcXeleJPq29NyuRx/9md/hsuXLwN42t1qcHAQR44cwblz53D06NGwzzU6OorW1tZgfVeKopCfnx9TW0m8fXoxOzsLoVAY7LYmkUiSTrACT2svb9myBffu3YtpVRD22mY2mxMmVAUCAWQyWdBxGO85LGUFq8vlCsZ3EOYyPDwMPp/PWXyvWCxGVlYWxsbGUFVVFfPzm0wmtLS0YPfu3UGRFirq2P9D7wv9PX/Vx7afAxDs7BH6wwrR0L/nH7fUWOx4820MvS3UhlBBzbbDmy+2F/s9PT0Nn88Xmxc4zVEoFEnnXYt3N5lE4PV60dPTg0OHDgW7Wx08eBBjY2PIzs4Oe4HQ3d2NBw8e4ODBg9Dr9ejq6sLk5CS2bt0aM1sVCgXsdnvMzreWcTqduHfv3pya6OznObTv/FJ/P378GDKZbNULyIcPH84JgYu0E2YiycjIgNPpxMzMTEyqaDAMA5fLBavVGve5hKIoSCQSyOXyFeNrY03KClan00lKWi3B/fv3Oe/AlZ2dHTfBCjwVxSdPnozLuVOR3t7eoGeLsDzJKFi9Xm/Khze1tLQgJycH+fn5OHv2LLZs2QKNRoOmpqawu3gNDAzg0aNHOH78eHB3RqfTwW63x7Tvu1wuh8PhmLPYJERGIBBAb28v+vr6UFFRgW3bti0QL/MdB4st7N99911UVFQsSDqM9H35r//6L5SVlQX/l8lkSelhBRBMQOzv78eePXuiPk8ivapisRgymSyou7j43hDBmmawq90vf/nLnNqRk5ODgYGBuJyboqikS5rhGj6fnxZeukSgVCqTSrB6vV4EAoHgVmYq0tvbC5fLhX379uHKlSsoKChAeXk5Hjx4AJ1OB51Ot+I5/H4/7t27h8bGxjmhRDqdbk6951jA5/MhkUjgdDpjKoTXCqOjo7h9+za0Wi2OHz++qs+ux+OBXq9f1XtstVoxOzuL+vr64G1SqTRpBSvwtGrApUuXsGvXrqh2ihmGgdvthsViidvcn+gt/xXt4XT0VUDiVxdC0zQ++OAD5OXlzVlpcsHWrVvR3NyM73//+8jKysJzzz0X04sOEWcLISI+PBQKBaamprg2I4jZbIZIJILH40nJRbjBYEBvby9OnDiBu3fvgmEYbNmyBTRNo7u7Gw0NDWGdp6+vD5mZmQu2SOvq6uLyfZfJZHA4HESwRsjdu3cxPDyM3bt3xyQRzmq1rrr6Q19fH/Lz8+eU9hOJRKBpGj6fL6kSUnk8HkQiEUZGRhAIBOB0OiO6NrLhFGazOS6CnMfjQSqVQi6XB3M0kmUXImUDQF0uV8pvocWapqYmTE5O4k/+5E+4NgUKhQLf/va3ceTIEQQCAXz44YerOt/FixfxD//wD/j00085X+UlIxRFEREfJnK5PKniFzMyMpCbm4uf/exnKdmJ6f79+ygtLYXRaMTY2Bj27dsHiqIwPDwMpVKJzMzMFc/h8Xhw//79Rds6SySSuMz1Xq+X1C6OkPb2doyPj+PYsWMxE6tOpxPZ2dmrOo/BYEBWVtaC24VCIVwu16rOHUuEQiHcbjfOnz+PqakpvPLKKxGJVZqm4Xa7YTQaYy5WKYqCRqNBdnY2lEplsHJBsohVIIUFq91uJ4I1hNnZWTQ1NeGNN95ImklYpVKhrq4OL7zwAkZGRqJuiel2u3Ht2jW88MILaGtrg9FoJOJsHqGJY4TlUSqVSSUMKYrCX/zFX0AqleInP/lJUoUrhMPWrVsxPDyM9vZ27N+/HxKJBAzDoKenZ84W7XL09vaisLAwYZUbaJqGw+FI6TCMRMIwDFpbWzE1NYXDhw/H7No7OzsLpVK5aidEdXX1oiFo7M4F1/B4PIjFYnR1deHy5cvYsmULTp8+DZVKFdbjQ2NVzWZzTOd6Ho8HpVKJrKysYIH/ZHUKpWxIgN1uDysuaq3Q0tKC6urqRVeZXKNQKHDw4EGcPXsW3/rWtxbcf/PmTfT09CAzMxPZ2dnIy8tDbm4uBAIBnE4nzp49i7KyMmzevBmTk5P47W9/SzLi50HiesNHqVQmldcFePr+vf766/jNb36Df/7nf0ZGRgaOHz/OSS3lSFEqlWhsbITf7w9u7Y6OjkIoFIZVqcTv92NgYACnTp2Kt6lBHA4HJBLJnLJ0hMWhaRotLS1wuVw4fPhwTLfXJRJJTLowlZaWBr21ofHPIpGI8++6SCTC1NQUWltbUVBQgFdffTWicMZ4xqpKpVKoVKqk86QuRUoL1ljW5UtlXC4X2tvb8eabb3JtypLs2LEDTU1NGBwchFAoxPvvvw+ZTAadToehoSHU1taCoij09PSgqakJFosFIpEIfr8fOTk5eOmllwAAhw4dwuTkJIaGhlI25i8eEA9r+CgUCs4vYkvxxS9+Ec8//zy6urrw4Ycf4vbt23j22WeTfnGekZEx5//e3t6wvatjY2PQ6/UJjSW12WzEuxoGgUAAzc3NoGkaBw4ciHlfeolEEhPnw8TEBCQSyYK630KhkDMPK7sYunnzJkwmEw4dOoSCgoKIzsF6VWP9HIRCITQaTbCOd6qQsoKVXSETnsaQsR0mkhWhUIiGhgb89re/hcPhwNGjRyGXyzE9PQ2hUIjDhw/PuYD4fD5YLBZoNJo5k6RYLMaf//mf49GjR6RSRAgkhjV85HJ5UmwTLoVAIMDmzZtRV1eHTz75BD/4wQ/whS98YdH4zmTE4/HAYrGE7VAYHBxEZWVlnK2ai81mC3s7dq3i9/tx5coVCAQCNDY2xkXYSKXSVZdj6urqwkcffYRdu3YtuE8kEiW02xOLRCLBo0eP0NnZiZqaGhw7diwqse/1emM6V/H5fKhUqpStYZ+SgpVhGNKWNQSv1xuXjlKxZufOnbh58yaOHz++6OQSilAoXOC1CYVs5c0lFScfrkiV10okEuGLX/wiNm7ciF/84hdQKBQoLy/n2qwVmZqagl6vD+t1ttvtMJvNEXueVovZbCYe1mXwer24fPkylEpl1GWXwkEsFoPP58NisUQUv+z3+9HV1YW7d+9iZGQEX/rSlxbtGpXokACRSAS73Y6WlhYwDIPTp08vex1biVht0/N4PCgUiuAuRips/y9GSgpWr9cLhmGSqlQFl/D5fDx58gSDg4OoqKjg2pwlEYvF+Ju/+ZuUEQypBIlhDR+aplNqwq6oqMDevXtx6dIllJaWJv33Z2pqKuzdnqGhIZSUlCR0AToyMoKxsbGIWsWuJdxuNy5fvgydTocdO3bE/btSVlaGnp6eiArot7S0oLm5Gbt378Yrr7yypMMmER5WtkzVzMwMurq6YLPZsGXLFtTV1a36uxqL156iKOj1evD5/JSa9xYjJQUrCQeYy+bNm+F2u/Huu+9i586dOHLkCNcmLUmyX2xTFRISED6BQCDlJu79+/fj3r17eO+99/Dyyy/HPJYwlhiNRqxfv37F4xiGweDgIPbv358Aq54yOjqKW7du4eDBgyQkYBGcTicuXbqEvLw8bNmyJSFj6vV6GAyGiB4zPDyMAwcOrChyJRJJ3Nqzspn/ExMT6OrqAk3T2Lx5MyorK2O2AFvtPCUQCKDT6Ra0I09VUlI9uFwuErsYgkAgQENDA15//XVcv349JlmXhNSCJF1FRqpN3iKRCN/85jcxNTWFd955J2mrZAQCAczOzoa1DWowGCAWi2PSSz0cxsbG0NbWhgMHDsxJYjOZTBgbG0MgEEiIHcmK3+/HhQsXUFRUlDCxCjxN0Is0PttkMoXlxReLxXGpV8oK1d///vfo7+/Hzp078eqrr6KmpiamuwWrmaeEQmEwNCfV5rulSEnB6nQ6iYd1EYqKiiCRSDA2Nsa1KYQEQ0ICwicVPazAU2/Rm2++Cbfbjbfeegt9fX1cm7SA2dlZqNXqsGpBW63WVcX3RcL4+DhaW1tx4MCBOQLZaDTi4sWL6O3txYcffoi2tjbMzMwkxKZkg90yTtQCAnjqKfX7/RF3ZrRYLGF1x5JKpTHzsPL5fAiFQjx69Ai/+93vMDExgUOHDuHFF19EaWlpUs0pEokkrTyrLMm7r7QMpC3r4ng8HthsNlLui0BYBoZhUnYSFwgE+PrXv4729na89957KC8vx7PPPguNRsO1aQCeCsBwRajb7U7IPD4+Po6bN28uEKsGgwFXr17F3r17kZeXB7vdjqGhIXz++ec4cuTIqtuFpho8Hg+bNm3CvXv3EnYNmZ6ejlggP3r0KGxhLRaLYTabozUPPB4PQqEQTqcTfX19GB4eRmFh4aqTqSIZP1JkMlmwtmq6kZIeVtLlanHGxsag0WiSptMVIXHw+XziYQ2TVEu6Woxt27bhe9/7HgDg/fff59iaPxJJwlUiHA8Mw6C5uRmNjY1zBM6TJ09w9epV7Nu3D3l5eQCe1ufdsGEDioqKIo6pTBfy8vJgMpkSNl5JSQmePHkS0WM6OzvDbqghk8mi8rAKBAIIhUJMTEzg4sWLuHTpEmQyGV566SUcOXIkYTsDkc5TSqUSSqUy5ee3pUhJwUpCAhZndHQ0OPkS1h4khjU8UtnDGopEIsFLL72ER48eJc1iJRLB6vF44j6PsxncoVnkExMTaG5uxjPPPLNoJ67MzExMT0/H1a5khRVq8UpUmk9mZibEYnHYYWx+vx/37t0Lu6KATCYLO4aVTaJyOp24ffs2PvroIxiNRuzevRuvvfYadu7cmdSJehqNBnK5PK0Tm1MyJMButyfNFlgyMTU1hezsbK7NIHAAiWENn3QS9hKJBDRNg6Zpzi9UFosFfD4/7JrQbrc7IcmzCoUCVqsVMpkMjx8/RktLC/bv37+ksM7IyMDdu3fjbleyIpPJElqJp7S0FP39/SgsLFzx2EuXLkGr1YbV8hcIr0qAUCgETdMYGhrC4OAgKIpCbW0tnnnmGc7rm4ezsObxeNDpdBAKhWmxEF+OlBOsDMPAZDKhqqqKa1OSDoZhSEH9NQopaxU+6RASkIwYDAbk5OSEfbzP50tIeS61Wo3e3l48fvw4WA5puS1dtVoNv9+/oC/9WkEmkyW02P7U1FRYbXxtNhuam5vx13/912GfeyUPq0Qiwa1btzA2NoaysjIcPnw4os9wIhAIBAgEAovO7+lUYzUcUk6wmkwmuFwu4mFdAq69LARuIGWtwiddQgJYeDweAoEA57VZjUZjRBf73NxcjI6Oxj0esKamBhMTE/D5fDh48OCcklZLwYYFFBUVxdW2ZITdFk8EVqsVY2NjkMvl8Pv9y36G79y5g+Li4oiStCQSyZKClaIoPHr0CFarFa+99lrS5n7o9frgfBUIBBAIBODz+RAIBKBQKNKuEsBypJxgffToEYnTXAKyJbx2IQuV8HA6nRgZGYHL5UJ3dzeApV87Ho8HHo8X3HJnGAZ+vz/4N+v1oGkagUAgeBx7O7uAYI9n/wYQfBz7N3sfu7XP5/OX/BEIBODz+aAoCgKBADweD1NTUwlvbzofg8EQUT3NiooKfPbZZ9i0aVNcP79qtTqitp/A07CAqampNSVYnU4nOjo6YDAYEraDKZPJsH79erz99tvYu3cvDh8+vOSxbW1tOH36dETnl8vly4YEdHR04Pnnn09ascrOQSwCgQACgQBisTg4b6wVsQqkoGAdHBxEaWkp12YkLUS4rE0oilrzhc/D4datW7h48SIEAgGam5vn3BcqMtn/gacXBIqigj8AgoIx9D4ej7fgdvZiEnrhmf849n72NyuG/X4/vF5v0KvC/rCimP3b5XJhbGyMU8Fqs9kAPM1SDheVSgWVSoXx8fGkE4aZmZno6Ojg2oyEQNM0Hjx4gK6uLpSXl+P06dMJa3suEAjw+uuv49e//vWy1y673Q6z2Yzq6uqIzi8SieD3+xd4b0UiEVpaWlBfX5/QurOxZC0JVZaUEqxOpxNGozGinsNrCbIlvHYhC5XwCAQCqKurw5e//GWuTYkZ165dw61bt7Bz507OPgcGgyHs6gChVFRUYHBwMOkEq06nW1X9zngyMzOD8fFx+P1+CIVCiMViCIVCiESiOT9SqXRFUTM1NYW2tjaIRCIcOXKEs1A7r9e7rEi2WCxRxRM/fPgQmZmZc8Qqj8fDxMQEHA4Htm7dGpW9BG5IKcE6NjYWDDAmLIQkk6xdSNJVeKTja7Rv3z60trbi5s2bnC3mjUZjVBVKioqK0N7eDofDAblcHgfLooPdIvb5fAnzNi7HzMwMRkZGMDIyAh6Ph+LiYkilUni9XpjNZvh8Pni93uCPx+OB3++HQqEI1uZUKpXB//l8Pu7evYuJiQls2bKF811Ln8+37La8zWaL6vOhVCphs9nQ398fDHPg8/lob2/HyZMniZZIMVJKsD58+JDzOK1kh3ja1iZEsIaHUChMWs9ZtPj9fgCAw+HgzAaDwYDa2tqIHycQCFBcXIyHDx9iw4YNcbAsetiSSFwL1vHxcbS0tKCyshL79+8PK2kMeCoCbTYb7HY7bDYbTCYTRkdHYbVa4Xa7UVlZidOnTydF/OZKgnV8fDyqrfucnBy8/PLLePfdd/G1r30NJSUluHXrFiorK0kJyBQkZQSr3+/H8PAwTpw4wbUpSQsRLGsXUoc1PLZt24YbN27gfZhKzAAAIABJREFU1q1b2L59O9fmxITJyUl4vV4cOnSIMxtWs7Ozbt06NDU1Yf369Um1QySRSOByuSKKy40HCoUCIpEImzZtiuhxQqEQOp0ubIHLJV6vd9mavI8fP8a6deuiOnd9fT0ePnyI1tZWKBQKzMzMLJvcRUheUsYdNzk5CYVCQVqyLgPDMMTDukYhHtbwkMlkOHLkCFpaWrg2JaawyV5codPpom7pqdPpIJFIMDk5GWOrVodUKk1Yx6flUKvV8Hg8SWFLvPD7/ct6WN1u96oWDnV1dbh//z5+9atfobGxkXOvOSE6UsbDOjQ0RMpZEQjL4HA4cPHiRa7NiDlqtRpbt26NmSBzuVxJ3WIxUgQCAefeda1WC5PJFHUspF6v5zSkYTG8Xm+w+gGX8Hg86PV6TE9Pp21InM/nW9bD6nA4VuWsWrduHfLz86HT6dL2NVwLpIRgZRgGAwMD2Lt3L9emJDXpVhCdEBk+nw/T09Np52W/c+cO7ty5gxdffBGZmZmrPt/Y2FhYbSBTBa1WC4fDAZvNxtn2tVarRX9/f9SPDwQCSfW5tVqtwT7yyYBer8fs7Gzaiq3lQgL8fj9sNtuqKhjweDxkZWXh5ZdfjvocBO5JCcE6PT2NQCBAuluFARGsaxetVouXXnqJ845HsYamaZw9exY//OEPsX79elRVVaGiogIA8ODBg2A9U7/fD5/PB5/Ph8zMzOAx8xkeHk6rxa9EIkFeXh56enqwa9cuTmzQ6XSYnZ2N+vF+vz+pMrZbW1uxdetWzuNXWUQiESwWC9dmxI3lqjF0dnZCqVRG3BHNarWira0NHR0dkMlkeOaZZ9JqZ2UtkhJXtpGRERIOEAakrBUhHaEoCqdOncL27duDhf/fe+89SCQSyGSyYNcXHo8HoVAIoVCI8+fPo76+HidPnpxTv3F0dBRerzetPKwAUFtbi/7+fs4EK/saO53OqOpl0jSdNIL14cOH8Pl8Cev2tBKjo6Po7e1FY2Mj16bEDa/Xu6SH3Wg0RixWnzx5gh//+McoKCjAiy++iPv370edtEVIHlJCsLrdbkgkEq7NSAmIYCWkK1lZWTh16hROnToFp9MJg8GwZMyk3W7H+++/j7feegv79+/H5s2bIZVKcffu3ajKLyU7mzdvRlNTE37wgx9g+/bt2LhxY8ITVFUqFaxWa1SCNVlCAtxuNzo6OnDgwIGksOfhw4fo7OzEwYMHU7Yj00p4PB4YDAb80z/9EwDMaUEsFAoRCAQwNDQEo9G4aCc59jf7N/C0IcKePXtw+PBh8Pl8GI3GtNt5WoukxDtYXFyMpqYm1NfXc21KUkOyxAlrBZlMtmyCj0KhwFe/+lV0d3ejqakJ58+fx549eyASidDb2wuLxRJxf/lkRqVS4e///u/R0dGBGzdu4LPPPsM3vvGNmMT8hksgEIg6+zoQCCSFh/X27dsoLS1NCnHY19eH3t5eHD58OK0+q/MZHR1FVVUV/vZv/xY0TQdbErPhPYFAAE6nM1gJhW1NDGDBb7YmsVgsnrMwJRV00oOUEKz5+flwuVxRbzetFUhIAIEwl/r6etTX12N6eho//OEP8dWvfhU+nw8//elP8Z3vfIdr82IKRVHYunUrtm7dil//+tdobm7Giy++mLDxV7MTFggEOPeATUxMwGAw4PTp05zaAQD37t3D0NAQjh07llQdwOLB6OhoMOSPoqhga9lYQhKS04OUEKwURaGkpGRVxYPXCmQVubYhXvbFycjIwKFDh/CTn/wEGo0G4+PjXJsUV44ePYr/893v4v6tW+F7Lnk88IJ/8ubcTv3hfx5F/XFb9g9/8ygKFJ+Px6sQe1yHBPj9frS1tWHHjh2c1+hsb2/HkydPcPTo0TXhoBkZGUFdXV1cxyAe1vQgJQQrAJSWlqKjo4MIVgJhCYgHYXkaGhpQW1uL0dFR/OpXv4LZbE7byiNqtRqNBw9i8tNPcaq2FtlabViPo+cteNj/mZDfNMPAzzAI0PTTLVyfD4zXi0uI7jPIMAy8Xi+nIQGDg4PQaDSclo1iGAY3b96E2WzGkSNHlq1Lmi7QNI2RkRG88MILcRuDx+OR3cc0IWUEa3FxMS5evLhs+Yu1Dk3TZBW5xuG6gHyyo9frodfr0dPTgzt37uDgwYNcmxQ3Xv7Sl3BercbH77+Pvz98GLw4zw13x8ej+vwNDg5CKpVyVnKIpmn09vbimWee4WR84KmH+fr16/B6vTh8+PCaucZNTk5CKBRCG+aCKhoYhiE7T2lCyqgbkUiEgoKCpGvfl2yQVSSBsDJVVVWrKnSfCggEApx69lkEsrNxo68v7uNRiHzB5HK50NnZiZ07d3I2dz169AgKhSLi0kmxYmZmBj/+j/+Ay+XCgQMH1oxYBZ6GA+Tk5MR1jEAggIyMDAwPD8d1HEL8SRnBCgAlJSWYmJjg2oykhQSWr23Iex8+JSUlMBqNXJuREL705ps47/fj7evXEfhDFnU8UOBpsfZIuHPnDsrKyqDT6eJjVBj09vbGPYZyMUwmE66eO4fm//f/YL11C8XFxUlRKSGRjIyMoKSkJO7jVFRUoLu7G16vN+5jEeJHyglWo9FItj2XgGx7EAjhIZFI4Pf7MTMzw7Upcae0tBTf/b//FxNFRfi4oyNu45Tz+XjY0xP28U+ePIHBYMCGDRviZtNKjIyMAHhaiSZRWK1WXL94EU0//jHyu7rwcm4uNAmumZssPHr0KCENGsRiMXJzc9Ez7/PZ29uLjz76CD6fL+42EFZPysSwAoBSqYRKpUJfX9+cmJelPEuh8ZxLHRN6+1Lxn6HHhDsW6+0MFZFLCe35QnMx4Tn/sYsdY7PZYDQaMTw8HCykPN+20P9Dj5n/3JZ6zGLHLWVb6O3s34u9HqExRuzf8+OO5p/T4/EseP4EsmgJF6VSiYaGBvzv//4v/uqv/irtY79FIhEOPPssbvzgB3Ebo1yvR2dHB3z79q24rR0IBNDa2sppVr7X68Xt27cT1h3Mbrej69YtTLa1YT2Ph/05ORCGeFQNBkNcEq3CnROW26EJ/X5QFIX8/PxVf2fMZjMePnyIX/7ylxAIBBAIBBCJRBAIBODz+cGudWwDAfbv0B+GYeBwOAA8be/q9/uRl5eH7du3LxivqqoK165dw4YNG4KebIVCgfHxcfz+97/HqVOnYl5OixBbUkqwAoBYJMKH//EfEPD5i26Bz89yZQDMOYLHm3NM8Ms8r4zLYmIJ87/QoeIr9BiGwbjBgAI2NucP91HzxljsXHMEJLD4MRQ1Z2x22jAYjaC7utDzh0lvsddiudvn38csccxTU57eYnO7YVIokFdcvMD+xSa0ULHMwv69lIBe7Jwmk4mIs0Ugr0n4HDx4EENDQzh79ixOnTrFtTlxx2AwIDuOHQNlIhFyPZ7/z957R8d113n/r7lTNZJGGvVRs9WLm5rlblkuiZ04cYoTkwRCFkICCWxg4Vl+PPuc82PP8nvKAsvSgoE8lJBNQiAGh2CcxHGJu2TZcpNk9Wr1NhpJU+/9/WFpkGzZltVmRrqvc+bozq2fGc3ceX8/30+hoaGB5OTkO+579epVgoKCPJqVX1JSQkxMzKy2/XY6nbS0tFBeUsKVw4fZGR/PushItDfVnF2k13PpjTe4NNULzeT3fuR+e/O9ZPS3we5yYVixgue/8pVp1c4dHh4mNjaWZ599FqvVitPpxOFwYLPZblkebSYwPDw8rqFAXV0darWa9PR01Go1oihy8ODBCQWrv78/QUFBVFZWkpGRAeCOn9VoNLz//vvs3LlTFq1ejM8J1kWLF/N4XBw5HrzR3Q2n08n/s28f/+6hvt5zSUljI6cMBp7/8pfn9Lrf/va3571X7F6RY1jvDZVKxfbt23njjTcWhGDtbGtj0Sz/GKf6+1N64cIdBWtlZSXV1dXcf//9s2rLnWhpaaGtrY2dO3fO+LklSaK1tZWGigpaLl4kwmZDZzYTNDBA9m3E8aN5eTNux2zhdDr53enT7P3BD3jhlVemLPBsNhv+/v6YTKYp23Lo0CH6+vrYvXs3cGMGrrS09Lad7NLS0jh//jzp6ekoFAo0Gg1Go5HExETKy8upra0lPT19yvbIzC4+J1hVKhVyBKuM7EmUmQni4+MRRZGOjg4iIiI8bc6sIYoizWVlrJrlurOxwcGcrKnBbDZPWKbq4sWLXL58mZSUFBoaGsbNqkz0d6JwobHLGo3mnmtz2+12zp49y5o1a2Y8HKGnp4fiQ4egupoUtZrVoaHoNRqutLZS3dIyo9fyFCqVimfXrOGNM2f4+Q9+wItf+9qURKvVap12CIQgCO62rKPPo6Ojqa6uJjc395b9Q0JCUKlUfPzxxxiNRnQ6HX5+fvT19eFwOOZtXeb5gs8JVqVSiUv2rMnITIgs5O8NQRAwmUw0NTXNa8F69MgRgtvbySwomNXrCILAIlHk3JkzbL7vvnHb+vv7uXj2LI1Xr9J68SJwI9RIUCiQRmcHbgoPGhWm7rkDSQJJuhGiJIr0Wq3ct3s3YWFhiKKIJEnufvJjGe1R73A46OnpITw8fFqevZtxOBxcKimh4dgxVqrVpMTFzesZD6VKxadXr+a3p07x3p/+xO49e+75HFarddrteG/OEwFITEzk2LFjLFmy5JZWwZIkkZWVRXNzM+3t7dhsNhwOB35+fvT393ustJnM5PA5wSoIAq677yYzz5Fb7cnMFGq1ekKRM1/o7+/n+O9/z8tLlsx68wAAweXi+NtvExIejnIkMcbS00Pb2bOsFQSey852x/O7Paa3WYYR8Xqb5b0nTvDB668TGhqKNCJYBSYOj1ELAmpBwOV0YjEaEWw20rOzCQ0NndbrbW5u5tyBA8R2d/NYVBR+t/PazrPBpFKlItTPD+sU46LtdvuMeFhvTvotLCyks7OTvXv38tWvfvWWYwwGA5mZmQDu5K6WlhaMRuO0BbTM7OJz/x2lUsn8/WmRmSyyJ/FW5rNHZzZRKpXzuj7jO7/7Hav9/IibIw+yn1qNcXgY1QcfIIwIyEiVinUREehmeAreZDCQ4HCwfelSBIVi0oNYu9PJtQsXOFFcjH9aGun5+cTExEz6O2Sz2ejo6KD26lUsJSUUBAcTHRc3nZfik2iUSnpHsvTvFavVOu0EJ0EQbvktUKlUfOpTn+I73/kO3d3dtwxIlEolKpWK7u5uGhsbaWxsRKfTTZioJeNd+KRgFeUf5gWPLM4mRhby905aWhp/+ctfyMzMnLa3zRuwWq3U19dz9fJlqs6cwdDdzQNz3HY0UKtl5RwlxgoKBap7LLivUalYZjKxRBSpb2zkckUFF0wmkvLzCQoOJjAwkICAALcAHh4epqOjg/bmZrqqqxlsayMSiBUEMuLiUC7Q2Z6lsbF8cuoUXffdd8/T6Xa7/ZYp+3tFoVCM87AKgoBarWZoaIjQ0FCuXLlCQkKCuzSWQqHg+vXrNDc3ExQURGJiIrm5uXLsqo8gC1YZn0UWrbciC9Z7Jz8/n8bGRo4ePcrjjz/uaXOmzL7f/55rp09j7ekhUqslSa/n2ZgYElesmJNQAE8wLr51CgiCQGJYGIlAm9lM3V/+QrVCgRkYBPyCgxGUSmydnUQpFJiUSjIDAwk1me4pJGm+NruJi4igoKWFV//5n0nfto2du3ah1+sndazVasVvmg0ThoaG0Ol06HQ6+vv7aWxspKmpCafTSW5uLuHh4TidToaGhrDb7YiiSExMDGvXriUwMHBa15aZe3xSsMoxrDKyMLsVWcBPnby8PN58801PmzFlOjo6KDtwgC9lZWHKykIpx+LdM1EGA1FjKhuIoojFbscligTHxk7/+zVPv5/bs7NZZbHw9gcf8C9//SvPfPWr5E2iTJfVap2w9NSdUCqVCIKAIAjYbDZqamqIjY1l//79aDQaEhMT2bZtG+Hh4fL9cB7ic3c1lUolC1YZGZkZJT4+HrvdPmHMmy9w/NgxcgwGYsPDPW3KnDNbyZeCIGCYxUYL8wmX00nzwAC5EREcfO01aisr2fnII3f0trpcrgljx0djTB0OB1arlaGhIYaGhhgcHGRgYMD9UCqVGAwGVqxYQWpq6rjulzLzE58TrIIgIM7T6S2ZySN7WCdGfl+mhiAIJCUlcenSJQoLCz1tzj0TER7OqYEB8js65iy5ymuQP/MeZ//58+QlJPBoVhZDdjtvFhXxo4oKHn3mGdLS0iY8JjExkT/96U9s27bN3ZLV5XJRVlZGdXU1CoUCf39//P39MRgM+Pv7ExUVRVBQEMHBwbPSxlbGu/E5wapQKHDN03ggmXtDnvKRmUmSk5O5fPmyTwrWDZs2YR4c5NiBA3x6AQlW+ZfA81ytr6dxaIjPjiT26TUans/Lo6Sxkd//8Ics37KFHTt3jhOYf/3rXykqKmLz5s0EBAQwODhIaWkp169fJz09nT179hAYGIgkSQwNDdHT00NfXx/t7e2EhITIYnWB4nOCta+vjyCXHBQgA+fOnUOj0SAIAkqlEqVSiWKktM1oPb3R9aP7jMY/je47uh1mVgBP1dM5neQMl8tFb28vNpttyucYi16vn3QCxXzAZDJx4sQJT5sxZTIzM9n37rueNkPmNszH4XVRRQX7KyrYnZt7Sw3T3Ph4UiIi+K9jx/jx1as8/pnPkJCQcOO4oiJefvll9Ho9x48fp6+vj5SUFNLS0hgeHqakpISuri66urpwuVwEBga6vaz79+9n06ZNJCUleeIly3gQnxOs7c3NhMghAQue1atX09jY6O5u43K5EEURl8vl7o4zuk6SJERRHPcYu85ms9Hd1IRpglaSMylibznX7UTtBOsnk+Xd19nJb/7932ckps/pdBK/fDmf++IXp30uXyEgIIChoSFPmzFlWlpa8JfvjTJzRFdfH3+4epWXCgpIuE1JK4NOx5fy8zlVW8vr3/sehU88wdb77sNgMPCLX/yCiIgIwsLCUCqVnD9/HoPBgMFgICgoiISEBLKzs28ZNMfHx/PJJ5/Q399PTk7OXLxUGS/B9wRrVRXL/P09bcZdWUjT1ZIHQjR27tw5Y+eqqanhvR/9iP8uF452c7G5mSMz5Kn1FZRKpc/GAFutVg6//TafT0nxtCmIc/geSqLouZJdI21gXS4XTqcTp8uFy+l0rxsdPAO0dnS4yy7dfI7xTyf33o3ODKlUKpQq1Y3l0eejs02z/L4YAwLQKZXob1P8X33+PLqDBxH6+rg/OJjo3Fz+cvUqq9asISgoiPj4eDIzMwkODiY4OBj/2/yuKxQKVCoVCoWCjo4OWlpaALh69SpLly6ddvMBGd/BpwSry+Wis6GBkAk8YTIyMjLToa+v77Y/mt7O8ePHSXE4SI6J8bQpHkd0ubDZbO6H1Wq9sWy3Y7Nasdps2Ee3jSw7R4Smc0RoOh2O2wrRsfvdLBRHBaRqTIgSwHW7nebhYd5rbb3V4JucG5NxdbhcLrddozaNiuRR+5QjoU9jRey4ZbXavaweWa/VatFotei0WjQaDVqdDq1Gg1arRavTodFo0Gm1aLVa+oeHcbpcE84Iqc+fR//uuygcDgCUfX0sPXqUzpgYtFotzz///B1f36itFouF1tZWWlpa6O7uJiIigkWLFpGTk0NISMgk3imZ+YRPCdbe3l70djsaucagzAyykLzhMrdnaGgI9Qy3Dp0ryk6fZsc8EatOh4PBwUF3KaOxy27xOfI43dlJgMtF6UcfYbXZsFmtuFyuccLrZtGl1WjcxeaDgoJuZKir1W7RNirmbidEx66bbG3Vi83NnCgv5+Vt22b53RtBknCJ4i0e37EC/Gah63A4sNvt495fi8UyTuyPLtttNkoGBlA7nfxncTEarfbv77FWy1daW1E4xzdRV7lcrD1wAPP//t+3mDvqRZUkiY6ODpqbm7l+/ToqlYrFixeTk5NDTEyMz34/ZWYGn1J+XV1dhMgJVzIzjCxYZeBGbFxXVxdOp/OWBBJP43Q63TUrx8b0OZ1O/vDWW7hqasgoKPCUebflTuJzcHCQwaEhhm76K7pc7nJGer3+xl9/f/z1egINBsLHeP/M9fVEaTRsWbHi715AtdrrivT3DQ/PWDLkpBiTUKqZpYz6f92/ny8WFhKm12Oz2bDb7e5Bg+HVVyc8Rt/dTbPZ7A59GP3b29tLS0sL/f39REVFER8fz6pVq+SWqTLj8K678l3oaG4mVE4qkJkFfDNycfaYyzhEbyEwMBC9nx/f/X//X4LuJexoTAy3+12TJCRRRBxpHSqJ4t8fI9tGkwMlSUJ0OpFGPF6jy6NeMEkUUQJKhQKXUsmOL3yBtevW0d3dzW9+/GMiWlp4Zd26uYvlkyQGBwcxm82YBwYw9/ffWDab6Tebqejqoq6/n+tHj7rF56jwHCs+Q8PCiB8VpGO2azSaSQvO0qEhQpVKwry4YcJfy8o40NtL/Eg1kvmCAjhbX8/Dy5ejV6nQjwmnEYODUfb13XLMcFgYFRUVbifB6N+QkBBWr16NyWTyusGijPfgU5+MtqoqlvtojJmMjM/hZV6quSA1OZm+v/2NTXfwSonARMPmm5NcFCPrBIUChUp14+/IA7jxXBAQuNG4QKVUohIElCoVakFAKQg3pqkFwX3upo4O9r72GoagIMouXyalrY0nN2yYsQQbm9VKf38/5oEBBsxm9/JYUTowMIBarXZndBsMBgxBQURGRpKamkrk8DDhbW18edu2G/UyZ/FzJIkieLkQdLlcRCUk4F9T42lTZpRnVq7kjaIiMkwmUm4aMFi3bx8XwwqAXo/+Bz9g165dc2ypzHzBZwSry+Wiq7GR0HvsPSwjIyMzWdasX89rZ86gCwy85UfYG4iLiOC5tDR+9YMfIJhM7AwJmbRYdToc9PX10dPTQ29vLz09PfT3998QpSNiVJIkgoKCxolRY3Awi+LjMQQFEWQwEBgYiPoO3lx7UxP1ZjPauWhrOmYA4K3EBQdzpKOD+dY4NCk6mgSjkfMNDbd8Vxw5OQwB6gMHUJvNWIKCqHzqKVIeegg5ZVpmqviMYB1NuFJ7+WhaRma+sBCDb2JiYnjkuef41c9/zjf8/AgNCPC0SbeQEhvLCyoV//Ojj9Dk57vXiy4X/f394wSpe7m3l0GLhaCgIIwhIYQYjYSEhJCSmkrQmNqXs+0RnWk8UVLvXum0WAgyGmFgwNOmzDgP5eby6uHDHCwrY3tm5rhtjpwcHCN1UiWFgqudnSTKOSgy08BnBKvL5UKpVmNzOtHKMS5eg+BDP263w9s9NDJzy4oVK+h+/HF+9Mc/8vXcXAxz4SmcBJIoYh4YoKenh67uboZ6eykvKaHk6FF6enowm834BwQQEhJCSEgIxuBgkpOT3c8NBgPCPBvwiwqF19+D2gcHCVm0CG6uwToPMAYE8OLGjfzk6FH0ajUbb1MHWKlSIRkMchKVzLTwGeUXGRlJ4v33U/z++6yPivK0OTIy85qFmHQ1ls1btjA4MMAvDx3i66tXz92FJQmLxUJnZyednZ10dHTQ2dlJV1cXfX196HQ6QkJCGNTpCBIEUpOSMI54S4ODg1EutMH8SFKbN3NdFIkLD6fH04bMEmHBwXxh/XpePX6cCIOB9MjIW/bptFiITEmRnQMy08Kn7m5rCgr4U10d165dI+02reBkZGRkZoLtDz7Id8+epaazk6QZjmd1Ohx0dXfTOSJIxz4EQSAsLIzw8HDCw8NJSEggLCwMY0iIuxLAH86fJ8PhIH/Vqhm1ayYQJen2bYdnGG8fVlmsVroUCtbFx89bwQrQ2deHpFBg9PO7ZZtSEGgbHCQyOdkDlsnMJ3xKsAqCwH1PPMG7P/whYYODhMoVA2RkZgVJkugfGKC5uXnOry16UVxiWm4u7x0+zNemIlgliX6z+RZB2tnZyYDZjNFodIvSxMREVq1aRXh4OP6TiJsN0OnoHxycwiuaX4iShODFpQ7PNzeTkJk5b9uHupxOPrp4kePNzXx+3ToiJygHp1Sp6BAEVkdHe8BCmfmETwlWuFErseCZZzi1dy9btVo5nlVmRvDVHvKzxbDDQc3Fi7zZ0eFpU+7KbMoVlyhS39TEn8+cYWde3sQ1IiWJnt5e2lpbaWtro629/cY0fmcnao2GiBFRGh4eTkpyMuHh4YSEhEwrnjQ9IoK3a2un8crmCZLk1Ulil3p6yLz/fk+bMStYhob4zYkTDAsC/7Rlyx0TFHuVSsK9sOqGjG/hk2ovISGB69u3y/GsMjKzRIBWy6rgYL60cqWnTfE45hUr+PXp0/zoww9JMRoxKJWoHQ7a2tpobW2lvb0drU6HKSqKqKgo0tLSWL9+PeHh4fhNMEU6EywKCaHPbsc8OIhBnmnySqx2Ow2SxJNLl1JfX+9pc6ZNR28voYGBKFUqWrq6eKe4mNCQEF5aufKOXu5eq5WQ+Hi5IYDMtPHZT5A7nrWigjR55OZRvGcCV2YmWcheZ5fLRWdnJ63Xr9PW1oahrY3TjY0ctloxBQayIz2dqKgosrOziYyMHNflZy4QBIGI4GDKm5pYlZ4+p9f2Jm7XxMEbKGpsZFFGBoGBgZ42ZVq4nE7+6+xZrjidqG02Qm02Op1ONqalseOmUlY3IygUtA8MELl27RxZKzOf8VnBKggCWx9/nLf/7d9I87QxMj6NIAhePa3oCby9VNCMIUn09/e7vaWjf7u6ujAajZhMJqKiosjPz2fXrl102u28V1rKYzt2eNpydmRk8M7ZsyxfvBg/Lym95Qm8NYb1Sm/vuHCAruFhfl9UdNfj+vv6CBop/3S3b+HooFIcWRa5UfN0bNtfBAGFJCHw9xJ+o8sKhQLFmHPASCLbyLkA2ru7saSk8PVvfIOffu97OGtq+Na2bZMq96ZSq2kVRTJjY++6r4zM3fBZwQoQFBSEEBCA1eFAp1Z72hwZmXnFvPOwShLd3d00NTfT3NRES0sLra2tKJVKoqKX1iobAAAgAElEQVSiMJlMJCcns2HDBiIiIibs5rTv1ClSjN7RsyjTZCI2IoIDFy7w+Jo1njZnHHMlIr31M2p3OmlzONgYEQFASkoKK5977q4JhZIkceDdd9n98MMTbhuLKIqUl5dTX1+PWq0mOjqalJQUgoKCUCgU4/4Hoij+XdyKotsOSZLcy6P7j4raUUFbW1RETnY25eXlhDU38/K2bZMqn6YUBLqGhugPDycmJuau+8vI3A2fFqwAwZGRDLS1yYJVZlp46w+fp1AoFL4d6jGSCNXc1ERzczPNLS20tLSg02qJjY0lNjaWwsJComNiCJhkN6uqzk4aOzp4Zvv2WTZ+8jyZk8P/+fBDFldWkpua6mlz5hyRu3sh5xpRFNl77hxx+fkkJCQAoNPp2Lx5812PdTqdHD58mK1bt96y7cKFC3R1dREREUFQUBB//vOfAfjiF7/I4OAgpaWlnD17loceeoj8MR3Qpkt3dzeiKGIwGJBUqkmJVQWASsWxnh62PvfcvK2SIDO3+LxgNUREYGloINwLWyjKyPg0viLiJYm+vr4bwnTk0dLSgkqtJjYmhtjYWAoKCoiNiZlUyajbcb2vjzCdDp0X/fgadDqeX7uWXx4/TpC/P8kLzJPljYXoXzt3DsWSJex55pl79jS7XK5bjrHZbJw9e5bDhw+Tnp5OZWUl3d3dZGVlsXPnTvf+ubm51NXV8frrr7s7nM0EGo0Gu91OVFQU/ZKE3elEcxfRqtPp+LCpiSW7d2MymWbEDhkZnxesQVFRWGw2T5sh4+t44Q+fJ/HWuMDR2qajU/pNzc20NDejUChueE7j4li/fj0xMTEETlATcjpsSErieHU1F+vqyEpKmtFzT4eEsDCeyMvj18XFPDY4uKA8rZIX1OzttlgIDQigrquLv1RXY09M5HPPPYd6CrN+LpfLLcLNZjP79u2jqqqK4OBgXnzxxXHir6Ojg3fffZf8/HwWLVoE3Kigk5mZycGDB3n66adn5PVpNBoGBgYICwsjcMUKDra2cr/JdNuSkmqViisdHZCVRbZcZURmBvF5wRoQFESTp42QkZmHeEOYhM1qpbGxkfqGBrdIFUXRPa2/etUqYnfvJshgmPVBhyAIbElL42hlpVcJVoDsuDgMOh2vnzlDTVcXD+flecwT3NLXR/AcXVsURY8Ort68cIHzTicuux1DaCg5Dz3Eho0bp1zOTBRFFAoFbW1tvP766yQkJPAv//Iv6PX6W/bt6+ujqqqKK1eusG7dOgoLC1Gr1axdu5Z//dd/JTg4mNWrV0/b06rRaLBarbhcLtYVFNDZ2srRK1fYFBJyi2gVFAr67XbK/P15bNcur/SAy/guPi9YDQYDlmkU4JaZAbxA2MjMLAIeKFcmSfT09FBfX09DQwMNDQ10dXcTGxPDokWLWLlyJY8++ijBwcEe84ivWryYg2VllNbUeJ1oTQoP579t28Yb587xnx98wD/df79HYgfL2tp4aK68vCOJQZ7gzQsXaIiI4J9fegmFQjHpWOg7IYoiLpeLvXv3UlBQQGFh4W33bW5uJjU1lcLCQt566y0qKyt57LHH6OjoICkpic7OTn74wx/yxBNPsHTp0inbpNFocDgcAERHRzM0NETcE09wdN8+lut0ROj1KEf+ByqNhiPXr1Pw0kv4y/WBZWaY+SFYPW3EAmbBlD+SmXGcDgctLS3UNzTQMCJSBUFg8eLFboFqMpkmleQxVwiCwCMrVrCvtJQT1dVsTk8nc2Q61hsI0On44vr1/PuhQ1xrbmZZYuKcXr9naAizxULaHJUx8tQsQFF9PXVGI1946aUZrbOq0+mIjIzkoYceIvEO/7uhoSE6OztJSEggNDSUl19+mSNHjrB3714CAgJYv349a9as4Uc/+hEnT56clGBVq9V0dnbeGBDetH5UsIaGhnLq1Cl27NiBMSyM6tJSTpWUsF6pZHF4OEdbWkjcsYP4+PjpvREyMhPgPb8EU8RgMDCsVHp8akhGZj4xG9+lAbOZhoYGtwe1tbWViIgIFi1axPIVK3j44Yc96j2dLNlxcayIieFUXR2/KSrif8bEeF0Xn+XR0ZR6QLBea2sjVKtFOQf3YlEUqe7poWtggLLubgJVKqIDAlidno5ilq9f293N0u3bZ7wpgEaj4ZVXXrnjPkNDQ5SUlDAwMOAWhgqFgs2bN7NkyRLOnDnDsmXLcDgcOJ1Ourq6uHjxIsuWLbvj97qlpYVz587xwAMP3GKT3W53P4+KiqKpqYnk5GQSExMpMpno3LcPR1cXg6mpbF2/fhrvgIzM7fGuu+wUEASBgJAQBu12Ar2seLYkirN+45SZGTyfuuF9TMd7JYkibW1t47ynw8PDLFq0iEWLFrF9+3bi4uLQaLUzaPHcIQgC65OS2H/hgqdNmZAlJhOv19TM+XVz4+M5Wl3NmYoK1tylC9J06bRYkKKj2fa5zzE4OIjZbOajU6e4dPw4e3JzCZ7hyjFlra0cb25mWWgobZLEqsjIGT3/ZDCbzZw7d466ujoKCgqIuqk1eWRkJLt27XI/f+mllygtLeWjjz6iuLiYJ554ArvdTvhN3SHVajX19fUMDw/fck2tVovL5XI/j4mJoa6ujuTkZAAiTCbOiCK1KhW7Hn8cpRyiJzNL+LxgBTDGxNB99arXCFaVSkV4cDBvnTzJnjVrvGpKU0ZmMii4NxHvcrlobmqitraWmpoaGhsbCTQYWLxoEYlJSWzevJnw8PB5N4CTJMnr6oACBPn5MeRw4HI6aenupqq1lYKlS2fdE6xRqchftIiq9nZmu5VBpMGA3unEaDSyYsUKALZu3cqf332XvQcO8OV16wiYIFlpquyrryf5vvv4wwcfoFYo5nzau7e3lzNnztDa2sq2bdsmdX29Xs/atWtZvXo1+/bt49vf/jYqlYqdO3dSUFDg3k8URbq6uhAEAbvdPi72Wa1WYxtTiScsLIzS0lI6OjqIiIjAZDLRHxrK5t27CQoKmtkXLSMzhnmhpHI3b+bDq1eJtNvx85Iaif9YUMDekyf51bFjfGbDBq+q3SgjMxnuJMRcLhctzc3U1NRQW1tLQ0MDISEhJCUlsWbNGp566qlp1TyVmR4BGg1Gg4Fv/+UvSEol/lotjT09PLtx46wPoNMjIzlRUTGr1xglWa2m8to1t3hTqVTs3rOHd0SRX374IV+aoXtvUX09QkwMDz30EA1VVSSkpMxYndO70dvbS1tbGw0NDXR0dPDwww8TFhZ2T+cQBIHdu3e7z3XgwAHS0tKIiopCoVDQ1NREXFwcnZ2dDA4OjhOsGo1mnIdVo9GQk5PD+++/z3333UdsbCyfevllWazKzDrzQrBGR0ez9JFHOPvOOxRERnpFKQ2dRsOXN2zgV2fP8ovDh/ncxo0zOtqXkZlNBEFgbECA6HLR0tJCTU0NNbW1NNTXExISQmJiIqtXr+app55Cv0Czgr0xdl4QBL6xdSstfX1Ejgwc/vPoUfYXF/PYLLdx1ahUzGYqlCiK/K28nMrhYTrsdnaGht6yz5NPPcVvBgb49alTPJmdTeg0xdQnHR0UPPccgiDwj9/4xrTOdS84HA7Onz/PiRMnMJlM7Nq1657F6liWLl3KxYsXeeyxx9zhBGq1mrq6OvLy8rBarQwNDWEc035Yq9W6k65GiYqKIj8/nw8//JAHH3yQSA+ER8gsPOaFYAXIWbmSlqoqKi5eJGOkf7OnUalUvLBuHW8VF/OTjz/mxYICjDNczFxm+nij4PA0osuFub+fY0ePUltbS11dHUajkcTERFbl5/PUpz61YAXqWERJ8uowh5gxGd/rk5O5MAdxrYfKy4mY4cH56dpa/tDSQqhOBw4HupQU1m3ejE6nIyUlZcJjnn3+ef4YEMB3jxwhTalkR2YmUXfwirqcToAJPdCDCsW0hOJUaWxspKGhgT179hAVFXVLBv9kkSSJK1euUFJSwrp168a1iXW5XHR1dREXF0dtbS1DQ0Pjjr3ZwzpKeHg48fHxdHZ2yoJVZk6YN4JVEAS2PPIIf2xoIGJwkFAv+jF9auVK3r98mR8fOcLn160jxgM3Ppm74AUdczyJJIpcv379hge1poYLtbVcV6nI0WrJW7mSJ598Up7i93Eq29tJHuM5mw1a+/spa27mm/ffP6PnbbdYyN22jeVZWQwMDLBs2bK7xuMKgsCTTz/N0COPcPjQIX64fz9LtVp6XS7MDgfLg4JYZDRS3tlJhcVCv8NBvFbLKxPUPrWL4pSbAUwGh8PB9evXiY2NdSctDQwMcOnSJSIjI0lLS5vWzGFFRQVHjx7FZDJNWNtVp9MxMDBAQEAAPT0947aNrcM6FkmSxpW8kpGZbeaNYAUICAhg41NPcXrvXrZptXftdzyX7Fy2jECtlp+fOMFn8/NJio72tEkyCxlJoqOjg8qqKqqrqqirr8cQGEhiUhJ5eXnkbdnCwbIydu3Y4WlLvRZRFPFe3+p4nE4nVR0dbMzPn9XrnK6rIysqakbDn0RRpNlsJiEkxJ2Zfi/o9Xp2PvwwuStXcuXKFZIiIvD396fo5Eku19WRfN99PJ2TQ2RkJN/71rcoa2gYV1u3qrMTl1Y7I40Bbkd3dzdvv/02Op2Op556irCwMOrq6ujo6GDPnj3TDnMrLS3FYDCwa9euW1rGulwuTCYTzc3NBAQE0NLSMm67Tqeb0MMqSRIajWZcQpaMzGziPYpuhkhMTKRp2zbOHzzI6ptKfniagtRUAnQ6flVUxFNZWSxdvNjTJsksIIaHhqiqqqKyqoqqykokSSI1LY3s7Gx2795NwJiaknVdXV7RmtWbGW2j6Qscrqwk1s+PxbM4ddtpsVBSX8+LMxgj63Q6+e7Zs/hlZpKdnT2tc5lMJkwmk/v5ROJ36549/O5nP2Nzby9xkZF0DA7yUXs7D7/wwqx6WJubmzEajcTExLB3714yMjIYHBwkLS1tymEAo7S1tdHa2ur2rE5UszwiIoLm5mYyMjKwWq3jtgmCgFKp5I033nB/3hUjHcZsNhtpaWnTsk9GZrLMO8EKsK6wkHerq6lrbCRhjjI5J0tufDwBWi2vnznDw1Yrq9LTPW2SDHh9sfqpILpcNDU1ce3aNaqqqmhvbychIYGU1FQ2bthARETEHV+3r4gxTyGCz3xuzjc3z2q7VKfTyWunTlG4aBHxMyiK37t6FUN2Ns89//ycxJrn5eUR853v8L1/+zeCe3pYnJxMwZYt0xbLd8JisVBXV0dmZibr168nLy+PixcvkpGRMSWP8s1IkkRbW5u75Jxer7+lOUB4eDglJSXk5eVNWIv10UcfxWIZ31NSqVRSUVExq0JeRmYs81KwqlQqtu3Zw3v/+Z+EDg9j8LIvVFpkJC9u2MAvTp7EYrWyJSvL0yYtaOaTMOvt6aGyspLKykqqa2owBgeTmprK/du3s3jRIlQ3TQfKTB1RFBF8wAtttlrpHxiY1Xap+y5eJEypZMtIPdTpYrZaKW5ooMjh4KVHH53TxEiTycTaLVvQ6/XsmOWQGKfTyaVLl+jv73cnQkVGRnLffffN2DVMJhOvvPIKp06dQqvVcu7cOVavXj2uLJdarUav12O1WnE6nfT19Y3z7Obl5Y07p0KhYHh4mMHBwQljYmVkZoN5KVgBQkJCyNu9mzO//S1btVqvywSPDwnhlcJCXj12jAGbjV0rV3p1trGMd2K32aipqXGL1GGrldSUFJYsWcIjjzxCoFyVYlbxhcHOgNWKIAgMDA3NSpWSIbudC42N/POWLTNyDxNFkf84d46InBx2r1t3S1emuWIuOjbV1NRw7do11q5dS+gE5blmipiYGJ544gkkSaK/v5/f/va3bNiwgYyMDAwGgzuOtb29nS1btnDs2DFWrVp121qzGo2Gjz/+mI0bN6LzkoY9MvOfeStYAZYuX07zunVcPnOGFR666d2J8IAAvrZlCz/95BMGT57kU77aFcsHvEx3xQeEB/w9m39UoDY3NxMXH09qSgrPPPMMJpNJHvjMESK+IVhjgoPJTUjgzTNn+OLmzTN+jzlWVUWa0ThlMfz6+fPYJIkv5OYC8EFFBcFLlvAPL7wwk2beEw6HY9a7grlcLioqKoiKiiJzltvYjqJQKHjmmWcoKyvj1KlTnD59mri4OJKSklCpVDQ3N5Obm4tareajjz5i5cqVtwwYVCoVV69edTcKkZGZK3xQHd0bmx54gD+1tqJuaiJzFkewU8Wg0/G1TZv42YkTclcsmQmx22xUVlZSXl5O+UjMWFpqKgUFBSQmJY3rSiMzd4g+VArtkeXL+cmxY7NyjylubGTP0qVTOraksZFqvR7rwAB1XV2EBgRwzGzm8y+9NGP2TYXQ0FCqq6vH1SudaTo6Oujv72fNLDdyuBlBEFi6dCmZmZnU1tZSWlpKW1sb/v7+7vjV+Ph4duzYwcGDB8nOzsZgMNDb2+uu0VpdXc2ePXvm1G4ZmXkvWHU6HY987nP85Xe/w1lTw3IvrIGq02j4ysaNclcsDyJ6mZe4r7eXsrIyysvLaWhoID4+nvSMDLZs2UKIFw68FiIiIPiAhxVuiJSXRjrv/fSjj0iLiGB9RgbB0yzV1NLXh2izkRoTM2690+lEhHGlBUVR5EhVFQN2OzszMhhyOvljczNP/uM/0tfbyy/27UPo6mL5gw8SO4vxtpOhsLCQ4uJiLly4MOMJV5Ik0dTURHFxMUqlkpib3ru5QhAEkpOTiYmJoby8nM7OTjZt2uTeHh0dzc6dO3njjTdwOBxYLBaam5uJiIjg+eefx9+Lap3LLAzmvWAF8PPzY9dnP8uBt9+m5OpVcsLCvG4qb7Qr1pvFxfz0yBFe2LBB7oq1gJBEkcbGRsorKigvK8NsNpOekUF+fj6f/vSn0cpxYt6Jl91H7sToPeZETQ0V7e388tgxvlRYOK3BccfAACF6PT89e5Z0o5G1iYk09vbyVnU1NoWC+8PCKExN5WJzM+82NhKSloZap+P/O3sWrSSR88ADpI9USlm+YgXnzp0jJydnpl7ylFGpVGzZsoWioqIZF6wdHR2cPn0ajUbDo48+it7Dzgk/Pz9ycnJoaWmhuLiYxWPKLUZERGA0GjGbzaxbt45r167x9NNPy5UBZDzCghCscKMf8s6nn+bgH//ImZISVoWHe10iFsDTK1fy3qVLclesBYDNaqWyqorysjIqrl0jwN+fjIwMHnvsMeLj4+VYVC9HFEV8R67+nfVJSaxPSuLN4mJeO3aMFwsL8ZvigKi2q4v6gQE0kZGoFy/mgwsX0Pr788ALL2A0GnnvnXcoPn2aHoWCx770JZYtWwbA6VOnqK+tZfuY8kp6vZ6NGzfOyGucCZYsWcJ7773H8PDwjAk0m83GpUuXcDgcPProo14VzhMQEIBzpD3tKP39/QDs3r2b4uJisrKyZLEq4zEWjGCFG6U7HnjySd5obqbXy9q3juXh5csJ0unkrlhzxFwOXHp7eigvL6esrIyGhgYWLVpERkYGW7dtu21Groz34ouCdZSnV67k/54+zU8PH2Z7ZuaUGpkIgkDYunXk5OVRsGkTAwMDKJVKt9fwpX/6J06eOIHocrnFKsCatWtZs3btTL2UWSEgIIDk5GTeeustnn322RlJwurs7KS2tpbt27d7lViFG1URbu5ode3aNaKjo+nt7cVsNrNihsqWychMhQUlWOHGl9I+NISfl9ejHNsV6+msLJbIXbF8EvdUf3k5ZeXlWAYGSE9PZ9Xq1XzmM5+Rp/p9GF9qHHA7/mHVKk7V1fHH0tJ7FqwWq5WioSGe2rWLlJQUAALHdEuDG1PrBWPiIn2Nz3zmM7z66qv89a9/ZdeuXdM+n0qlwmw2eyxu9U4olcpbPKzXrl0jJyeHS5cusXbt2lmvnCAjcycW3KfP4XDgGBjALyLC06bcldz4ePy1Wl4/fZpHrFby5a5Ys8ZMtiF1OZ1U19Rw5fJlrpaVERAQQGZGBo/LU/3zCslHQwLGIggC65OS+ODqVTp6e4kwGid9bElTE8EJCW6xOh9RqVQ899xzfP/73yc4OBi1Wk1+fv6UhZvVakWn02G3271O/AmCME6wtrW1ATc6calUKrmElYzH8a5vzBygUCjQBwczYLNh8AHvVnpkJF/cuJGfnzjBkN3OpuXLPW3SOBQKxfyowzpNHHY7lZWVXLlyhfLycsLDw1m6bBlffvlln8zq97aqCd6Kr1QJuBvRRiM1ra33JFiD/fy4PtL2dz6LVoPBwI4dO3jzzTexWCy4XC42bNhw1+NsNhtqtZr29nY6OzuRJIlr164RFBTk8USriVCpVOMEa2VlJdHR0ZSXl7N9+3avS1SWWXgsOMGqUqnI3LKF8j/8gVUmk6fNmRTxISH846ZNvPrJJwzabDy4cqWnTZp3TOVmbLNaqaio4MqVK1y7do2YmBiWLVvG9h07CAoKmgUrZbwJ36nCenc0KhWOm+IXb0dJYyMfX7/OYEgIjz3//Lz3vHV3d1NdXc3WrVtpamqiu7t7UscdO3aMhoYG9Hq9O3kpPT2dVatWzaa5U0apVCKKIpIkIYoi1dXVmEwmoqKiiIqK8rR5MjILT7ACLM/O5s0PPsBisxGg1XranEkRaTDwtc2b+cknnzB46hRPrF4tTy3PEPciVoeHhigrK+Py5cvU1tayaPFili1dyq5HHiFgmjUtZWQ8RYfZTEF8/F33+9Ply1zx96fgs58lOzvb66a1Z5qOjg4OHDhAeHg4q1ator+/n9dff50VK1aQkJCAw+Ggvb2da9euERkZiclkore3l/r6epqbm9Hr9aSkpJCVleV1SVYTMZp41dzcjEql4vr16zzxxBOeNktGBligglWn05FeWEjF/v3k+YiXFSBYr+efNm/mp598wu8++YSn16+f9z8Y3oBlYICrV69y+fJlGhsbSU5OZvny5ez51KfkEi8LGF8tazURBj8/rvf0kHy3ZCBRJG3FClbO81megYEBysrKuHTpEnFxcaxatQqj0UhYWBi7du3i9ddfZ+3atTidTlpbWxEEgTNnzhAeHo7D4SAyMpKcnBzS0tJ86h4xmnhls9kYHBxk+fLlGOR64DJewoJVO1krV/LWoUMscTi8vmLAWPQaDa9s2sTeEyd47cgRnisokFu5zgL9fX1cvnKFK5cv09raSmpqKvn5+Tz77LNofMQrLzP7zJe4voKUFN4rKWHDkiUoBIFflZRQbrcTo1SSotezITkZg05HVGAgpe3tnjZ31hBFkZMnT1JWVobRaCQnJ4fU1NRx1Q9ycnKIjo7mwIEDBAUFUVhYyKJFi7Db7XR0dBAeHu5TInUso4I1LS2N6Ohor4y1lVm4LFjBqtfrSd20iYq//pVsH/Kywo14sy9v3MivTp9m78cf87mNGzF4aU1ZX6Kvt5eLFy9y+fJluru7ycjIYGNBAakpKah8aFAjMzfMp8S0pSYTfxIE/uPgQeKMRio0Gr70P/4Hra2tVF69yneKilimUnHdZiMmLc3T5s4a7e3tXLlyhTVr1pCYmHhb72JUVBSf+9znxq3T6XTETyKswpsZm3h1c4kyGRlPo7hTOR+FQiHNZLkfb8NisfDO//pfPBgQgNZHp9Z/f+4cda2tvFhQ4JFWrqWNjfx+YID8DRsQJQnR5UISxb8vu1yIgORyIUkSrtHtoujeTxL/nr5yt7jc22Vljz1utBHA6DpBobixrFCgABRK5Y31gN3hoLqmhhPvv09oezsxMTHExMQQPtVOaDdXTRix92a7b3kVN20fd+UJvoO3vE8373Pz9cY87xsawk+jwW/MZ979Xo087x4aoqypiY0jpdQmcx+4OQlp7P/11hegmPCYCY8d+1pGj5vgPZYmWDfhue/wXk103luuM2KbxW6nor6eV59++rbX8iVqOjvpHhzkr1eu0KbT8X9+/nO0I7MJPT09HD92jAB/fwq3bvXKLoHTxWq18t5776HT6di6deuC9C4ePnyYpKQkMjIy5MRRGY+gUCiQJGnCG/iCFqwARw4eRPnRRyz34SzI9y9f5nxtLV9Yvx7THJdQKm9s5KenTrEpNRVBEFAoFCgUClSCgIIb4lHBDcGmFAQEheKGgBz5q5zElOpEn8DbebdG149+bkVJGrdOlCRsdjv19fXU1tbS1dVFUGQkfYLA8xs2IIyI2RnhJhvF2wi4u33D7tWTd7fv7OH2dhbddx/R0dHufcceI7pciJLEoMVyWy+LW7DcbgAxwfrJTp/f67G3E0/Tud5ktlksFj56+21+tm3bpK7jK3RbLHz144/579/97ri+8vMVp9NJRUUFxcXFBAYGsnbtWqIXaHfBnp4e6uvr6ejoICAggMceewzlTN4TZWTuwp0Eq2+6FWeQnDVrePfYMTJcLtQ++sXcuWwZ/hoNPztxgs+tXs3iyMg5u7ZGpSIuNJTdOTlzds2pYLfbqSgvp7S0lOrqapKTk3musJCMzEzaLBb+69QpNi2QtoMVJSUsXbqUHC//n3k7PT09FB844GkzZhx/jYZIk8kruzHNNIODg7z33ns4nU63ZzE8PNzTZnmMkJAQQkJCkCSJo0eP0tnZKZe0kvEaFrxgDQoKIm7NGqo++YTMORR6M01hWhr+Wi2/PH2az+TkkD5HsVTCjdHQnFzrXnE5nVRWVlJaWkpFRQVxcXFkZWXxxJNP+mxShIz34HK5mH8T46ASBERRnNeeNUmSaGtro7i4GLVazYYNG4iOjp6XoQ5TQaFQEBoaSktLiyxYZbyGBS9YAXLWreMvJ0+S6nKh8uGbdP7ixei1Wn535gyP22zkzEH3GYUgeJVglUSR2tpaSktLuXLlCuHh4WRlZfHQQw8RICcRABPEz8pMifkqWCs7O0GhwGaz3XVg19TURH19PQDZ2dnuWsSiKDI0NITVasVms7nDhQRBcC+rVCqUSiUqlQpBENx/Z4v+/n6qq6tpb2+noaEBUTESItsAACAASURBVBSJiIggLy+P2NjYWbuurxIWFkZra6unzZCRcSMLViA0NJSo/Hxqz54l1ceng5aaTDy/YQOvnTzJkM3G+qVLZ/2aHperkkRjUxOlpaVcuniRwMBAsrKyeOWVVwi+h1aTCwYvGmD4Mi6Xa960ZoUbyXh/LCujwc+PJ59/flKzEB988AF2ux2FQsGhQ4dQKBQ4HA5cLhdqtRqdTueuFe0a6aQ12k3JNSYRUxRFXC4XCoUCtVqNWq1Gq9Wi0WjQaDQoFArsdjsOhwNBEMZt0+l06PV6/Pz88PPzQ6fTYbVaGR4eZnh4GKvVitVq5dKlS5jNZiRJQqvVEhQUxMDAAA0NDW7BrFQqUavVCIKAWq12P1coFDidTux2OzabDZvNhtlsxs/PD61Wi1qtRqVSoVKp0Gg07uXRx9jto8uj1xnL2Jjpm+Onb7dt7LIkSbd9jG4XR5JeR5+PXT/2HFarla6uLlwu17z2tsv4DrJgHSF7/XoOnj1Lsij6/LRQQlgYX960iVePHWPQbuf+WYxVFMBjAqirs5Pz589z4cIFBEEgKyuLF154gQgfDu2YCyxWK8XFxVy/fn1OrxscHMz69evn9JqzidPppKajg299+OGNhEJuiAcBUI4mF44su7ePHKsYU03iZmEy9u5zS9LXBN81QaFAKwj4K5XoBQE/lQq9VotWrcZPo0Gv06HXaNBrtfhpNCgnqIjy50uX2N/cjCE2lsyMDCorK6murnbbMDahcqy3tLOzk8LCQvLz82lvb0er1aLT6dDpdFO6jzqdTrfIHCs4JUlCp9Oh1WpxuVzYbDaGh4ex2Wzuffv7+2lra8Nut6PRaNziNSQkBK1WS0ZGhnvdqEAbFcujIttut+N0OnE6nTgcDhwOB06nE1EU0el07vNqtVqOHTtGSkoKERERbjE99hiHw8HQ0NC4c7lcLvd2p9M5qcTA0X0mu+9EiZQ3z4K5K6mM/E/HXmPsQ6vVcu7cOa9tJyuzsJAF6wiRkZGE5eRQe/48yT7uZQUwBQXxta1b+fHRowyePs2jq1bNSitXhUIxpx7W4eFhLl28SElJCV3d3WRnZfHpT3/6RoLIPPJ2zSYuSZrzQZnD4eCDDz6YV4I1PDyc0MWLeeVb3wJuiK2xHsNRoTMqjEY9iqPcXDXiZq/XZBntTGSxWBgaGqLLYsE6MIDVYsExNIStsxP74CD24WFcViufSU1lRWLiuHOcNZvZ/NhjGI3GW7xyox7RsV640deXkZHB4sWLEQQB0wzUs1apVAQGBvpEDdBDhw6xdu1awsLCpnyOUa8z3F5g3vx5uNM2uFV03vy4Fzo7O+WwABmvQRasY8jeuJFD586ROA+8rAAhej1fH2nl+l/Hj/PUunUTelemy2zHsIouF5WVlZSUlFBZWUlKSgqFhYWkpqXJU1VTwODnx4rsbPLy8ubsmmazmfPnz8/Z9eYCvV5PQEAANpuNiIgIT5szKS5fvsxfvv99li9e7B7AdlssiH5+7Nq1C7XcIGNSiCO/EQ6HY1rn8fb7l5+fH4ODg542Q0YGkAXrOKKjowlavpyGsjIS5rie6WwRoNPxyqZN/OzECX597BjPbtiAZgZbuc5ma8rW69cpKSmhtLT0RpvE3FweffRR9HJXLxkvYTQxxVcEa21VFf6CMG625Ux9PRm5ubJYnQSiKLJ//34uXryISqVCp9N52qRZxc/PD7PZ7GkzZGQAWbDeQvamTZy8fJnFkjRv+oTrNBq+snEjr50+zS8OH+YfCgrwn6GyTsM224x6WC0DA1y4cIGSkhKGhobIyc3lxRdfJNxHBIHMwiIiIoLW1lZW+EAN3zNnzlD53nt8ZfXqcesrhodZOwfJmfOBI0eOUF1dzVe+8hVC54lT406MJrCJ82TWUca3kQXrTcTHx3MxO5uy0lKWzINY1lFUKhUvrFvH74qL2XvkCJ/fuJHgkRI0k6Ho2jXOjJSviQ4MZH16OlEhIRy5do28RYumZZvT4aC8vJxz585RX19P5pIl7HzoIZISE2cl7lZGZqYIDQ2lsbHR02bclba2Nj785S95aflyjGO+906nkzaXi6SkJA9a572IokhRURHHjx9Hr9fT0dGxYMQq4E52Gxwc9Im4Ypn5jSxYJ2DLI4+wr7UVY18f0QaDp82ZMQRB4LOrVvHHCxf42ZEjfGHDBsKCg+96nN1u5/3ycnYsX06gnx9lra388NgxFhkM1PX38+yGDfdujCTR2NhISUkJly5dwhQdTW5uLs888wyakf7lMjLeTlhYGKWlpZ4246589Le/ETg8zJHaWqitda/vHR5GFx0ti5ERRFHk5MmTBAQEEBUVxf79++nv7+ehhx5CFEWMRuO0kqx8DUmS8Pf3x3KHNs0yMnOFLFgnQK/Xs+3Tn+bgj3/MFpuNgHkmoHZnZ/M3rZZXjx3j8+vWEXOXG/Cg3Y5NFFkWHU2ATsdSk4mHly7lXFMTaU4nunuIiTX391NSUsK5c+cAyM3Lk+ulyvgsERER9PX1edqMu7J+0yZaJmgk0nnpEjFyTDhwwwu9b98+LBYLFosFhULBmjVruO+++xbsdLgoiuj1eiwWi6dNkZGRBevtiIyMJG/PHk789rdsDQvz6Q5YE7EjMxO9SsXPT5zgH1atIuEOJWmMAQHkRERwoKyMJ0dquuo0GtZPchpRdLmouHaNoqIi6uvqWL58OXv27CE+Pl4uRSXj0xiNRux2O1ar1asTcBISEkhISBi3zul0cvToUQoKCjxklXfxm9/8hqVLl/LAAw9QW1tLcHDwgvKmTsSoh1WuFCDjDciC9Q4sWbaMji1bOHfoEKvnYT/lgtRU9Fotr509y2dyckiPj7/tvsmRkZy5x3p8PT09nCsupvjcOYKDgsjPz+fpp56Sp/xl5g0qlQqj0Uhra+stgtCbMZvNvPHGG8TGxrJkyRJPm+NR2traOHToEMPDw2zduhVBEEhOTva0WV6Dv78/AwMDnjZDRkYWrHdjw7Zt/KmlhcrqalLnYaD9ykWL8NNoeP3sWZ6028ma5o3a6XBQVlZGUVERLS0tZOfk8PnPf56oeSj4ZWTgRgMBXxKsZrOZ//iP/yA7O5vt27d72hyP0tjYyK9//WuysrL41re+5dVeck/h5+dHZ2enp82QkZEF691QqVRs37OHfT/5CUaLhfB7yKz3FZaaTHx+3Tr+78mTDNvtrMnMvGUfBXduENDR3k5RURHnz58nymQif+VKnnvuOVRybUeZec6oYPUVqqqqMJlM7Nq1y9OmeIy2tjZOnDjBpUuXePDBB+XWo3dAr9fLHlYZr0AWrJMgMDCQzZ/+NEdefZWtdjv6GSy87y0khYfz8qZN/Oz4cYbsdrZkZY3b7q/TMXxTVxe73c7lS5c4e/YsPT095OXl8fLLLxPqY3Ff86XeroxnCAsL4+LFi542Y9JcuXLlRivjBYLT6aS6upqOjg5aW1upq6tjaGiIFStW8PWvf52goCBPm+i1jLZztdvtnjZFRkYWrJMlLi6OpY8+yqnf/57CiAiU8zBrNCY4mK8WFvKTY8cYtNl4eIzXIcDPjyGbDYCWlhaKioq4dPEi8fHxFBQUkJ6R4fVtBmVkZgOj0egzHqj9+/fT1dW1YLyrTqeTN954g7a2NqKjozGZTKxdu5a4uDhPm+YTaDQaDh8+TH5+vqdNkZGRBeu9kL1yJZ0tLZSePEluZKSnzZkVwgIC+KctW/jxsWMMnzjB7tWrUapUBGq11DU08P0f/AD78DD5+fl89atfJWgSdVxlZOYzoij6hJfearVy5swZvvnNbxK8QL63f/7znxkYGOAb3/gGKpX8c3cvaDQaLl68SGhoKGlpaZ42R0ZGFqz3gkKhoPDBB9l3/Tp1zc0khIR42qRZwaDT8bXCQl49fpyfHjhAlM3G1StXwN+fJRs3cn9+vtyBSkZmBEmSfGJ2QaVSoVAoFoRYdTqdXLlyhcuXL/PNb35TFqv3iEKhoLu7m6amJp588klPmyMjA8iC9Z7RaDTc//TT7P/RjwgaHCRkHhbddjocXLtyBU1ZGR93dJAWG8t/+8pXeOv8eSJjYmSxKiMzBpfL5ROF5VUqFaIo4nQ657WAu3btGu+88w5arZaHH34YvV4/pfM0NjZSVVWFJEkIgoAgCO6YToVC4X6uUqkwGAwEBwdjNBrRzoOyfSqVipMnT7Jt2za5coKM1zB/71qziNFoZOXjj3P5V7+iYB4J1r7eXs6cPUtxURFRUVFsKSzkpbQ0flVUxH8VFdFssZAxT0MhZGSmiq+EBJjNZuCGwJ7PgrWmpobMzEwef/zxez7WYrFw4cIFSkpKMJvNJCUloVarEUURSZKQJAmXy4UkSYiiCNzw5losFgYGBhgaGsLPz4/09HQyMjJYtmzZTL+8WUer1XLq1CnS0tKIjY31tDkyMm7m711rlomJjaXIB7wqd0MSRaqqqjh1+jQN9fVk5+TwxS9+kfCICPc+L6xbx2uffMJQf/89tWGVkVkIuFwurxesTqeTb3/72wQHB3PgwIG77q9SqVAqlahUKrd3cXTd6EOSJPf2yTLqmRw9RqlUjls36rUc3T66rFarUSgU7v1H/yoUCiRJwul04nK5cDqdtLe3ExQURGtrq/v/MtY7Ovbco4/r169z4cIFysvLiY2NpbCwkGXLlt2z51wURT788EMO/f/t3XlwVOeZL/7vOaf3fVFrQxLaASEJSQgECouByMZxgoODTRJjx4ljz9TYmcmdO/7Nrbp/zMyt3EyqJrcqMzW5SaXiuRPHzmQcLzEGYzYDBsQiwGyyAG1oQ2jtRb0v5/z+IK1BWIC6+5xepOdTpTIS3e/7Ckunn37P8z7PoUO4evUq9Ho9iouLYxojlTiOQ39/PzweDx5//PFUL4eQGShgjZPRaERIo0EwHIYiA3crvB4Pzp8/j1OnTkGhUKC5uRnf/va3obhPQLqjoQFdExPz/nYiIbHieT6tUwJ4nsfRo0ehUqmwZs2aOT0+EokgFArB5/NNpxFEA8JogDg8PAyn04mKiopZx5hNtJbz3TuU0R3L6NeifxYEAaOjo2AYBmaz+Qt/F/387mCXZVnY7XZotVpcu3ZtxuOj8979eSQSwejoKHJyctDc3IzXXnsNBoMhrn9n4E5g/OUvfxnNzc3o6OjA73//e/zVX/0V1Gp13GMmUyQSwYULF/Dkk09mRF42WVgo8ogTwzDIKijA5MAAchO4wCXb0OAgWltbcbW9HcuWLsXOnTuxePFi4CE7RCadDtlqNa4MD6OeSsIQMi0SiaT1i/tPf/pTqFQqfO973xO15ejQ0BBef/11/Pmf/7loY97rxIkT6O3txXPPPSfJ+P/6r/+KmpoaPPXUU6K9EY/mtDY1NeHgwYPo7e2FzWabkfd695+ju8UymQzyFDVaYVkWCoUChw4dwsqVK2Gdh10dSeajgDUBWSUlmLx+Pe0D1nAohEuXLuHUqVOYmprCmjVr8Nprr0EXY9euhrw8nOnro4CVkLuk86GrYDAIh8OBH//4x6KPvWjRIgiCgImJCckCnMLCQpw6dUqSsQ8dOoRIJILt27dLdtcoKysL77333owdYWDmTm/0g2EY7NixA3X3NG2RCsMwUCgU8Hq96OzsRF9fHywWC2pra5MyPyGxooA1AZa8PAzc59ZXOpicnMSpU6dwrq0NBYWF2LxlC5YtXRr3Kf+G8nJ8vH8/3H4/dHRylBAA6V3WyuFwSHbKm+d5BAIB6PV6ScYH7gTFdrsdgUBA1NP34XAYn3zyCZ555hlJdzVj2X3u6enBb37zG3AcJ9lhLYZhIJfLEQwGcfPmTfT29iIYDKK8vByPPfYYsu86u0BIuqGANQFZWVm4rFAgHIlAli4vWIKA3ps3ceL4cfT09GDlypV49dVXRWmXatBqsdxqxceff44dDQ0iLJaQzHe/fM10cOzYMcl2zFwuFziOu2/euxhkMhn0ej1GRkZQVFQk6riPPfYY3n//ffh8Pqxdu1a0seNVWlqK5557Dr/97W/BsiyWL18u2tgKhQKRSAR9fX24efMmpqamUFZWho0bNyIvLy/tDw0SAlDAmpCcnBwUPvooDuzfj3UGA0wqFfg/3fJJtnAohEuXL+PEiRMIBgJYt24ddu7cCYXINQEfX7EC/+fIEWyqrIQ1xpQCsnAplUqo1Wr8+te/xrZt2+bVTk665rBGi+dLlWPqcDhiTiuKh9VqFT1gBYCNGzeitLQUv/3tb3H16lU0NzeLGiTGo7y8HLt27cKbb76JnTt3oqqqKqHxOI7D1NQUTp06BbvdjsWLF6OpqQkFBQVpm8ZCyP1QwJoAhmGwfssWdBUV4ZPf/Q6LHA7oeR46uRxahQIauRxauRwMAF4QwEciEDucdbvdOH3qFE6fPo3c3Fw89uijWLJkiWTF/bNMJnxp0SK82daGv9q0SZI5yPyjVCrxwx/+EJ9++il+/vOfo7q6Go8//jg6Oztx5coVVFVVobGxMdXLjEs65rB6vV688847WLRoEfLy8iSZw+l0JiVgtdlsGBkZkWTswsJC/M3f/A1OnjyJd999dzrHP5UqKirw7W9/G7/73e/wrW99C0uXLo1rHI7j4Ha7cezYMaxfvx4lJSVU4YVkNPrpFUF5RQVy//t/x8jICKZcLkyOjaFvdBRT4+OYmpiAkuehB2BgGBSwLHJEyPkavnULJ06cwNX2dtTW1OD7L72E3NzcxL+ZOdja0ID/e+gQ/nDhAp6m1AAyRxqNBlu3bkVTUxP27t2LH/3oRygsLERxcTE+/PBDLF26NCkBkNgikUjKTnfPZmJiAr/61a9QXFyMbdu2STaP0+lMqATUXBUUFODy5cuSja9QKLBp0ybk5ORgz549aGxsTHlgt2TJEuzcuRP/8R//gWeffRaVlZUxPZ9lWfj9fhw7dgwtLS0opIOyZB6ggFUkOp1u1hdbQRDg8XgwNTUFp9OJMx98gBqHAyVx9PMWeB4dHR04ceIExsbGsLa5Gf/fa69Bm+QXeZlMhufXrcM/7d+PJTk5qF20KKnzk8xmNpuxa9euGQdpPB4P3n//fXzrW99KebAQq3A4nDYpAXa7HT//+c+xdu1atLS0SDqXy+WC0WiUdA7gzi7owYMHJZ+nqqoK+/btw2effYZVq1ZJPt9c1vP000/jd7/7HXbt2jXnkmQMwyASieDw4cNYv349Batk3sisV4YMxDDMdDCbl5eHvLw87Pl//w+B27exdJZSMPILF6D6+GOwDgd4kwn+rVvhrqpC27lzaD15Emq1GuvWrUNtbS24FL2wB4NB7Dl/HmqtFgVmc0rWILb0PTYzf9196nvr1q1444038Hd/93fIzs5GcXExKioqUFpaOusp93Qq1h8Oh9Nmh/XgwYOorq6WPFgF7gTHJSUlks+TnZ0Nj8cDt9st+Q78o48+iv3792PlypVp8fNVXV0NQRDw5ptv4rnnnkNZWdkDHx+t8Xrw4EE0NTWJWneXkFSjgDXJjEYjtr/8Mva8+SYCPT0oNhigksmgkcuhOH8einffBRMKAQA4hwPKt9/GexwH17Jlcy7yLyW7y4V/P3kSKq0Wf7N5M7VqJaIwGAx49dVX4Xa70dvbi56eHhw+fBhvvfUW9Ho9GIZBIBBAKBRCKBSC1WrFa6+9luplA7iTEiDlSfm5CgaDaG9vxyuvvJKU+ZxOJywWi+TzsCwLk8mEkZERyQPWmpoaHDhwAGfPnk15LmtUTU0NwuEw3nzzTXznO995YKtXjuNw4MAB1NbWJnxgi5B0QwFrCmg0Gnz9hRdw9vhxXBkagsduh9tux84PP4TyT8FqlIzn8S2dDu5du1K02pkOX70Ks8mEF9KgDAyZf3Q6HWpqaqbrUAYCgekDN2q1GiqVCmq1Gj/72c9w5coV1NTUwO12o7OzEzU1NSlJJ0iXKgHHjh3D4sWLk1aBweFwIEuEcnlzkZWVhZGRkYfuMIph27Zt+M///E+sWLEibVqq1tfXIxKJ4De/+Q2++93vzloxQalU4uDBgygrK0N9fX0KVkmItChgTRGFQoF1W7bM+Jrwv/7XrI/lXK5kLGlORjweNMd5apWQWCmVyllfnNetW4ePPvoIZ8+exc2bN2EymXDgwAF8+9vfnpGzFw6HcerUKaxfv/6hc4XD4elUg2jgGw6HcfHiRVy6dAn5+fnYuHEjNBrNjOeFQqGU5936/X6cPHkSL7zwQlLmC4fD8Hg8SdlhBYDc3FzJKgXcq6KiAkVFRfj1r3+NZ599Nmnf48M0NjZCEAT8+7//O1566SUUFxfD7/fD4/HA6XSip6cHubm5abMzTIjYKGBNI0xREdDX94Wv83Ec0JLKmMeD/CQctCDkQVauXIlr166hqKgITz/9NHQ6HU6fPo3XX38dVVVVaGhoQGlpKf7t3/4NAwMDcDqd+OpXvwrgzq1zv98/fcL9888/x4cffgin0wmGYabbaEZzGBctWoTq6moMDAzgJz/5Caqrq7F169bp56dDDuuhQ4dQWlr6wNvFYnK5XFAqlUkL1PPz89Ha2pqUuQDg+eefx+7du/GLX/wC3/zmN5OyszsXq1evBs/zeP3117FixQrI5XKYzWaYzWZUV1dj2bJlqV4iIZKhgDWd/O//Dbz8MuD1Tn9JkMvh37o1hYv6L8FgEJ5wGLYMLD1E5he5XP6F3cTm5mZUVlaitbUVf/zjH2G325Gfn49XXnkFv/rVrzA0NITJyUm43W6wLIusrCx4PB4wDIPHHnsMdXV100FqOBxGKBSCIAgzdlTHxsZw7Ngx/PSnP0VjYyO2bt2a8oDV6/Wira0NL7/8ctLmtNvt0Gq1SZuvqKgI7733XtLmA+6kBuTn5+ONN97Ak08+iYYUl/DjOA5erxd2ux3PPfcc6uvrRW1XS0i6o4A1nTz7LAAg8j/+B9jBQXgMBnQ/8gjklZXIEQRwKW6fN+p0QqdWp8XpWUJmk5WVNV17dHJyElqtFkqlEi+88AKGhoamC+mHw2F0dHTAYrGgqKjoCz/TMpls1t1Dm82GHTt2YN26dThw4AB+/OMfA0BKD7icPHkSFRUVWJTE8nLJahoQZf5TNZLJycmk3qJvbGyE1WrFG2+8gWXLlqUsp1Umk2FiYgKtra3YtGlTUqozEJJuKGBNN88+C+5PgavM74e6vx997e04ffEi6kMhlKSwjFT/6ChMSdxVISQRdwc2RUVFM3Jh5XJ5Qjtmubm5eP7559Hd3Y233noLp0+fxuDgIAKBADiOg9FoxKOPPprQ+ufKbrcnrWlIlMPhSErTgLvZbDYMDQ0lPae0pKQEubm5eO+997Bjx46k72oqlUr09PSgvb0dX/3qV+dVW2NCYkFbZWlMpVKhsrISLdu34xt//de4ajZjwOFIyVrsLhf2dXbiKynutU1IOikrK8MPfvADFBQUQKVSwWazQavV4tNPP03aGrxe7xcOgknN5XIlPXDMycnB0NBQUueM+s53vgOPx4Nf/epXsNvtSZtXLpfjypUr6Orqwvbt2ylYJQsaBawZwmg04okXX8RnOh2Gk1w1QOB5/MeZM6hfvBgVNltS5yYk3ZnNZmzfvh2PP/44tmzZgsbGxlmbHUgpGAwmdb5kdbm6W3FxMW7dupXUOaNUKhVefvll5Ofn46233kravOFweDpYTfaONiHphgLWDGKxWLD1xRdxRi7HmNudtHkHx8cx6PXi6ytWJG1OQjLV1NRUUnMdV65ciYsXLyZtPuDO92hKcvWSkpISDA4OJnXOe23fvh2Tk5O4efOm5HMxDIO+vj6Ul5fT4SpCQAFrxsnOzsZjL72EkwAm76omIKU8iwWRUAj+cDgp8xGSydxud1J3WJcvXw6Hw5HU2+Vut3v6IFSyZGVlIRKJYHJyMqnz3o1lWdTV1eHMmTOSz6VQKNDT04OKigrJ5yIkE1DAmoHy8vKw5fvfx/FQCE6/X/L5ZDIZCg0GdNy+LflchGQ6j8eT1JJPLMuisLAQPT09SZtzamoq6SkBwH8dvEqljRs34vr16/jjH/+I0D2dCcUik8lgt9sRCoWQl5cnyRyEZBoKWDNUYWEh1r3wAo55vXD6fJLPt9hoRO/4uOTzEJLpvF5vQgGr3++Hy+XC+Pg4hoeH0dvbi56eHgwPD2NychL+Wd6kOhyOpFUK8Pl84Hk+6Qe9gNQevIoyGo3467/+awwNDeGXv/wlxsbGRB1fpVKhq6sLx44dw/r168GkuJwhIemCylplsLLyckw9/TQuvvkmNkqcM1dVWIjXz55FZU4OapNY75GQTHP79m20tbWhs7MTAB4YcITDYUQikRkf0Rqwcrl8+gO40wI2EAggGAwiHA6D4zjI5XJwHIeBgQEoFIqkfH9utztl9UiLiorQ3t6ekrnvptPp8Morr+Djjz/GL37xC/zt3/5twnmmHMeB53kcPnwYcrkczzzzTFJr3RKS7ihgzXBLli1Dm1w+o5WkFMry8/GdlSvxRlsbTGo1itKkvzYh6cZgMGD16tV45JFHZv17QRCm/6xQKKaDU4VCAblcPqffY57n4ff7EQwGEQwG8c477+DcuXNYvHixWN/GfblcrqRXQYgqKyvD/v37UzL3bLZu3YqrV6+iu7s7oeYRSqUSAwMDOH/+PBoaGrBixQraWSXkHhSwZji1Wg1zaSlGBweRK3HZkzyLBYIgQJeiFytCMoFarUYoFJK08xTLstBoNNBoNPD7/RgZGcGTTz4p2Xx3m5qaSmqO7t3uPniV7Dqw91NSUoKenp64AlaGYSCTydDa2gqPx4Mnn3wSVqtVglUSkvkoh3UeKKiuxm2PR9Qxw5EIXH4/Rqam0Ds+jlPXruHDc+dQlpsLSwpy16TEMAxw164XIYlQKBSz5plKhef5Gbu2UvN4PCnJX42y2Wzo7+9P2fz3WrFiBa5cuYJwjFVUFAoFXC4XPvzwQ5jNZnzjlwqeUAAAIABJREFUG9+gYJWQB6Ad1nmgqKQER1kWdXN4bDAchj8chi8Ugi8YhDcUgi8chodh4AXgAeAVBEQ4DiqDARqzGT6eR8/168hWKLCtpkbi7yb56MYbEZNcLpfs9PhsNBoN1q1bhz179uDP/uzPJJ9vamoKer1e8nnuZ+nSpbh06RLq6uZyxZNeeXk5wuEwBgYGUFJS8tDHMwwDuVyOixcvYmhoCC0tLSgoKEjCSgnJbBSwzgO5ubnw6XToGhtDKBJBIByGH4CfZeEThDt/BuAXBHAKBRRaLVRGI9RGI1QmEzRGIyxqNRap1VCr1dBoNDMOEBzfvx/by8uxNCcnVd8iIRlDpVIlvfPUl7/8Zfz93/89hoeHJS+D5Ha7U1LSKqq5uRn/+I//CIfDkfTmBfcTDAbR0dGBwsJCyGT3f1mVyWTwer04fPgwbDYbdu7cSU0BCJkjCljnAZZlUbd1K3o6OiDXaqHS6aBUq2FQKqFUKqFSqaBSqaBUKsFxXMzje6am0BEMIjw8jLKsLKj/dGqZEPJFyd5hBe7sevI8D1sSWie7XK6kHO66H41Gg+LiYly8ePG+B9uS7Yc//CHeeustDA8P48UXX5z1MTKZDGNjYzh9+jTWrVuHysrKJK+SkMxGAes80dDUhIqqKnhEzmUFgMe+8Q2Mjo6ip70dn128iLxAAJVaLQpMJkkrExCSiRQKRdJ3WLVaLVQqFTo6OlAjcdqO2+1OeV/7L33pS9i9ezc2bNiQFtcgq9WKV199FT/60Y/Q29v7hdQAmUyG0dFRnD17Ftu2bUNWVlaKVkpI5kr9bzoRBcMwkp3cZRgGOTk5WLt5M578wQ+Q8/TTuJiXh/+8dQttg4OwJ6lFLCGZQKlUJn2HVSaT4YknnsDu3bslnzsVbVnvtXTpUvA8jxs3bqR0HXdjWRarVq3CqVOnZnz97mD1a1/7GgWrhMSJdljnEYZhJN/dkcvlKC8vR3l5OVwuF3o6O7GvrQ26gQFUKhQosVqhfEAOFyHzXSoCVrfbjQMHDqCioiKutJ+54nkebrc7LXJHjUYj+vv7sXTp0lQvZVphYSFu3rw5/blMJsPIyAja2tqwbds2qgJASAIosphHGIaBRqNJ2u1Ig8GAupUrsaKhAcPDw+i5ehVtly+jMBRChV6PfKORil+TBScVAWtbWxtycnLwzDPPSDqPx+MBx3FJ66p1P5988gk8Hg/WrVuX0nXcSxAEBINBhEIhqNVqClYJEREFrPMIwzBQqVRgGCapdRkZhkF+fj7y8/MR2LgRfTdv4uy5cwj096OSYVBmtcKYolaO6cKdxLqcD8NTzVlJKRSKmGtyJmquJZUS5Xa7U9blKioYDOLw4cN49dVXU1oPdjYlJSVgWRY//vGPUVtbC4VCge3bt1OwSogIKGCdh1QqFXw+X0rmViqVqFyyBJVLlsBut6Pn+nXsvXAB2vFxVMjlKLFaF1yVgdM3b+L3Q0NQpknQziiVWE89yiWjUqkQDocRDocfWOJILJcuXUJPTw9aWlokn8vlcqU8SBweHobZbJa8fFc8dDodfvCDH2BsbAzvvPMOXnzxRQpWCREJBazzDMMw0Ol0ogasHMchEonE/Dyz2YyVa9agoakJw8PD6Lt2DecvXkROIIBytRpFZjNkEubbpQuTWg1Lbi7+2//8n0kJYEhqyWQyLFu2DP/8z/+M73//+5LWLD1//jz27NmDXbt2JSWA8/l8Ka8bevv27bQ+uKRSqdDZ2YmnnnoqpeW/CJlv6NVzHuI4DjKZTJTbkjKZDDabDcFgEE6nM64x704ZCG/YgIGBAXRcvoyT166hRBBQqtcjz2BI23xXQRAw5nYj3hvpJrUa3PXr+PTTT7F582ZR10bS03PPPYfdu3fjrbfewl/8xV9INs/+/fvx9NNPo7y8XLI50k06B6wcx6GzsxMsy2LFihWpXg4h8woFrPOURqOBy+VKeBy1Wg1BECCXy5GVlQWfzzddpDweMpkMJSUlKCkpge/RR3GztxenP/sMgYEBlAMoM5thkag8V7zGPR587PXCtGhR3GOUNzfjysWLWL58OXKoY9i8x7IstmzZgp/85Cfw+/2S5H329PSAYZiknpLnOC6p+fGz4Xk+LWqvziYYDOLq1avYsWNH2r4BJyRTUcA6DzEMA7VajampqYRfXNRq9YwLr1qthkqlgtvtRiAQmN7NZRgGHo8npvnUajWWVVVhWVUVnE4neru6sP/cOagHB1HGcSi1WqFN8Wlk4M4hJWNeHlq++c2ExhkeHsbx48fR0tKS0taWJDn0ej0KCwtx5coVrFq1SvTxT58+jfr6+qQGbyzLxpUeJKYlS5bg0KFDKV3DbJRKJQ4ePIjVq1envLECIfNRer5NJQkTo5GAXC7/wi4BwzBgWRZ6vR5WqxUmkwl6vR46nQ42my3u/Daj0Yi6lSvx5Msvo+6738X46tV4b2oK+wYH0Tk6imCST11LIS8vD/X19fjkk0/gpWYLC0JVVRUuX74sydhdXV2orq6WZOz7kbLG61wVFBRgbGws1cuYQSaT4fr169BoNFi+fHmql0PIvEQ7rPNUNGCNddfzbvfurt47/r1/x3EcTCYTAoEAXC5XXGkD0a5aOTk5iKxbh6GhIXRfvYrT7e0oDIdRptNhkdGY9FuCjEjzlZWVwePx4OjRo2hpaYF8gVVMWGiqqqpw8OBB0SsGdHV1QaVSoaCgQLQx5yLeA5himpiYSLs7FIFAAB0dHXjmmWcoFYAQiVDAOo9Fg1a32x3X8+MJOFmWhUqlglKphMvlSqhaAcdxKCoqQlFREfybN6O/rw8XLl7E8Z4elAIwKRTTwfjdIfm9X5stYJ9+jCBgwutFiOdxaXBw1nW4AwFAxFaUtbW18Pl8+Pjjj7Fu3bqUt7kk0snKykJhYSFOnz4tWpF7r9eLd999F6tXrxZlvFiwLBt3/rpYJiYm0u535tatWygvL4eOysURIhkKWOexRHdZA4EAtFptzDsG0d1Xg8EAjUYDh8OR8K6MSqWaru86NTWF3u5u3J6amjEn8KedUIZBdMXTO6N37QgzDDPjc6UgoKapCb77HKriACwVuZZiU1MTuru7cejQIdTW1mLJkiWijk/Sx9q1a/HRRx+JFrDu3r0bixcvxqZNm0QZLxbpELCOjIykVZUAjuMwOTlJJawIkRgFrPNcIrusibaXZFkWcrkcVqsVo6OjCY11N71ej9q6OtHGS5WysjLYbDacPHkSt27dwtq1a1PeRYiIb/ny5di3bx+uXLmCmpqahMdTKpUpq4XKcVzKA1aWZeFPo85xLMvC4XCgoaEh1UshZF6jQ1fzXDRgjTevKhAIJDw/5XTdn8FgwGOPPQaTyYS9e/fi9u3bqV4SERnLsmhpacGePXtEGc9ms2FkZARutzvhN5WxSocd1ubmZly9ehVTd91hSSWGYeByuWCxWFK9FELmNdphXQAS2WX1+/1QKpUJHXJKdd3GdMeyLOrr65GTk4MTJ06grq5uQRWCXwiKi4tFqwxRUlKCgwcP4ic/+cl0Iw+5XA6lUgm5XA65XA6FQgGO42a8WZyt4kd5eXlMzSxi2WENh8OYnJzE+Pg4JiYmZuSz3z3G3deH6NfvvWbc+/VAIICzZ89iy5Ytc167VNxuN/R6PXWxI0Ri9Bu2ACSSyxoIBGiHNEny8/PR0tKCI0eOwO12Y8WKFfRvP0/09fUhOztblLEWLVqEf/iHf5j+PBwOw+/3IxAIIBgMwufzIRgMIhwO3zfwA4CrV69ieHg4prkf1jjA5XLh17/+NVwuFwKBAPR6PYxGI0wmE9RqNQDMGkTf+3MefYMc/Xr08+h/q6urcebMGWzatCnlTQQcDkda5dQSMl9RwLpAxLvLKggCBEFIKHCiHda5MxqN2Lp1K44ePYqpqSk0NzenRe1LkpiBgQEUFRVJMrZMJoNOp4v5hHpHR0fMt7EZhnngDmt/fz+CwSBeeeUVmM1mSXcd/+mf/gmXLl1CfX29ZHPca2hoCNevX5/u1scwDCYnJylgJSQJKId1gUgklzXRnDWO41K+C5JJVCoVWlpaAAAHDx5MqwMmJD59fX0oKytL9TJm6OrqQmVlZUzPeVhKwNKlS6FSqXDmzBnJb5Fv3rwZn3zyCS5cuID29nZ0dXVhcHAQY2NjmJqaEj2/NxQK4Ze//CX6+/vx29/+Fv/yL/+CP/zhD2hra0u7MluEzEe0w7rAaDQaeDyemJ4TiUQSfvHRaDRx14NdiDiOw7p163Dp0iV8/PHHaGlpSbhzGUmN27dvY2RkJK3ykicmJhAIBGLe9WVZ9oF3TGQyGb73ve/hZz/7GXJzc9HY2JjoUu9r5cqV6O3txdmzZxEOhxEIBBAKhabTIYLBIFiWhVKphEqlgsFggMFggNFonE5VuDtl4WHXuHA4jEgkghdeeAE8z6O9vR2jo6OYmppKeTMFQhYCClgXEJZlodPp4gpYE5FoA4OFimEY1NXVgWEYnD9/Hhs2bEj1kkgcWltbUVdXl1Yly6xWK7RaLdrb22MqtTWXQ1cGgwE7duzA7t27JQ1YAWDHjh0P/PtoTq/X68XExATsdjvsdjv6+/sxNTUFj8cDr9cLn88HrVY7HdDeG9Tm5OTM+P/Hsuz0v1tnZyfGx8fTbgedkPmGAtYFhmEYaDSamE4sRw9vJHoASKlUJlwmayFavnw5du/ejbGxMdhstlQvh8QguhP30ksvpXopX/DEE0/gvffeg06nQ0lJyZye87BDV1EOhwO5ubkPfZzUZbIUCgUUCgWMRiPy8vLu+zie52G32zE5OYnJyUnY7XaMj4+jt7cXbrcbTqcTf/mXfznrNdBqtaKrq0uy74EQcgcFrAsMwzDQ6/UxBaw8zyccsLIsC61WSwFrHGQyGVasWIHz589j69atqV4OiUFvby/kcvmcgrdkq6mpgdPpxN69e/Hqq69Ofz2ac86y7HQFgugupdvtBsdxGBgYgE6ng1arhUajAXDnTkw0mI0eTIqOE81hj47j8XjgdrvhcrkgCAKKi4uRlZWVsgOaLMvCarXCep+Odr/4xS/w+9//HgaD4Qt/ZzabMTo6Cp7nKVefEAlRwLoAxbrLKlZ+lkKhSIvC45motLQUHR0d6O/vl+y0ORGfXC6H1+vF7du30zJobWhowL59+yAIAtRqNZxOJzo6OjA+Pg6fzzedzhP90Ol0+PrXv45AIIDbt2/D6XTC6/VCo9FAr9dDr9dDoVBgYGAA9fX1+Oyzz6aDU5/PB41GM51LajAYkJOTg3A4jEuXLgEAlixZ8sCd0FTZuHEjWltb8corr3zh72QyGdRqNex2+30DXkJI4ihgXYBi3WWNRCKi1QOlw1fxYRgGDQ0NaGtrQ0FBAe3kZIiioiIUFxdjcHAwLQNWrVYLvV6P9vZ2OBwO+P1+1NTUYM2aNdBqtVAoFA8dIxKJYGpqCk6nE06nE8PDw1i9ejUsFgsMBsN0IKvT6e5bom3ZsmUYGBjAZ599hsuXL2PJkiUoLCxMm5JuVVVVqKqqmvXvIpEIsrKyMDIyQgErIRKigHUBm+suayQSQTgchkwmSyhwpcNXicnPz4dOp0NnZyeWLFmS6uWQORLzDZ/YBEFAYWEhzp8/j2eeeQbFxcUxvxniOA4mkwkmkwkAUFtbG/M6GIZBUVERioqKMDY2hosXL+LAgQNYu3bt9LixkMlk4HkeoVAoKUFvVlYWbt++fd+glhCSONqmWaBYloVer5/z4+12u2j5Zel0WjrT1NTU4Pr166leBpmj9vZ2DAwMYNGiRaleyn099dRTyMrKQnZ2dlrs3NtsNrS0tGDDhg04ffp0TFVNOI6DXC7H559/jj179mDfvn24cuWK5LWMLRZLzF3DCCGxSf3ViaRMdMdzLiKRCJxOZ8L5pyzLwmg0pu2OU7qLtvccGRlJ8UrIw/T39+Ptt9/Gs88+m5bpAFFqtRrl5eU4efJkqpcyQ3l5OVatWoWTJ0/C5/M98LHRQLWzsxO7d+8GAOzcuRO7du2C2WzGkSNH0NbWFtNh01hotVoEg0E4HA5JxieEUMC6oDEMA51ON+fgMdqvPNGd1mgOLYlPRUUFldFJczzPY/fu3XjkkUdmpG8wDJM2eZl3W7p0KQYHB9MuXae6uhrLli3D6dOnZ+1cxbIsFAoFuru7sXv3bvj9fuzYsQMbN26ETqeDWq3GqlWr8PzzzyM3NxenTp0SvQMWcOf/d1FREf1eEiIhymFd4GLNK3U6ndOn/ePdJY1WKfD5fJK8eMx3JSUluHz5MgKBAJRKpShjTk5OYmBgAJFIBJFIBDzPg+f5GZ9brVYsX748LQOudOP1ejE8PIwXX3wRwWBw+qR89EMmk6GwsBA2my1lpZzuJpPJ5lxjNdlWr14Nr9eLs2fPYu3atdNlsuRyObq7u3H16lXk5+dj+/bt922RKpPJpsc5d+4c1qxZI/pdnsLCQpw7d07yZgmELFS0w7rARQPWuV68BUHAxMSEKLus8RymIHdygPPz89Hb2yvKeIFAAEePHkU4HIZCoYBOp4PZbEZWVhby8/NRXFyM8vJyTE5OYu/evRgdHRVl3vmG4zioVCr4/X7cunULBQUFePPNN9Ha2oqenh4EAgFYrVZUV1dj8eLFuHHjBj766CO0t7fD7XZ/4XcwuhsbLX4fDAYxNjaG7u5u2O12UdfOMIwoLZilsmHDBmi1Wpw5cwaTk5MYGhqabqbxta99DY899th9g9W7rV+/HgDQ0dEh+hpNJhOCwSAmJydFH5sQAjAPCjwYhhHS8R03EZcgCPD7/XA6nXMORGUyGaxWa0KHNHieh9vtjrlVLLnTn/7cuXP4yle+kvBBmePHj0OlUmHVqlUPfWx/fz/a2tpQWFiI+vp6yOXyhObOdBzHQSaTYWJiAv39/RgYGIBCoUBZWRlKSkpgs9ke+GbQ6XTixo0buHbtGliWRXFxMXJzc6e7KzkcDjidTvh8Puj1+ulSUR0dHVi+fLloNXkVCgXeffddvPDCC3MqZZUK4XAYHR0d6O7uhkwmw6pVq5CTkxPzOD6fD3/4wx+wbNkyFBQUiLrGa9euQavVYvXq1aKOS8hCwTAMBEGY9aJJASsBcCdoFQQhpgBSLpfDYrEkHLSOjY1RM4EYCYKAY8eOwePxYO3atbBYLHGN09vbiytXruArX/nKnHfXAoEALly4gOHhYTQ1NaX1CXipyOVyOBwOdHV1YWhoCEajESUlJSgtLZ3TTt9sbt++jRs3bmB0dBRGoxEWiwVmsxlmsxlGo3HG75nD4cDevXuRlZWF6urqhN+0KBQKvP3223j55ZcXRMrH+Pg4PvjgAzQ3N4t6p8ftduPMmTPYtWuXaGMSspBQwErmLBo4ulyuh57MBe680JnN5rhfMAVBoNtoCeju7saFCxewZMmSmAMXj8eDjz76CJs3b46r4PmtW7dw5swZZGdno7GxUbR82nSnUCjQ29uL9vZ21NfXo6SkJCWHCIPBIA4ePAifzyfKv//Jkydhs9mwceNGkVaY3m7cuIHW1lZs3LhRtFJ7LMti//79ePzxx2Gz2UQZk5CFhAJWEjOe5yEIAux2+0MPRimVSpjN5rgPMfA8D4fDgUAgENfzFzqv14vTp0/D5/PNebdVEAQcOnQIeXl5qK6ujnvucDiMc+fOwePxYMuWLXGPkymUSiWuXbuGnp4ebNu2bdbe8skkCALOnDmDa9euYc2aNTAajXN6nlwuh8/ng8fjgclkmn7j2NraiuLiYqxdu1bilaeH06dPo7+/H1/60pdEq0F748YNKBSKBfNvSIiYHhSw0qErMiuWZcFxHCwWy0NvFQcCATgcjrgPYrEsC41GE9dzyZ2OZZs3b8aSJUtw+PBhHD9+/KF1Wjs6OsDzPJYvX57Q3NHT14FAAN3d3QmNle7UajUuXbqEwcFBPPXUUykPVoE7F/c1a9Zg/fr1aG1txdDQ0AMfH61XevHiRRw8eBDnz5/H0aNHMTIyAr1ej9zcXHR2di6YFJ2mpiZotVpcvnxZtDELCgrQ2dmZlhUXCMlktMNKHorneUxMTCAcDj/wcWq1GgaDIa6dilAohPHx8XiXSP4kGAyip6cHN27cAMMwqKysRElJyYyDNHa7HYcOHcLjjz8OnU4nyrwTExM4cuQInnjiCajValHGTCcqlQpnz56Fx+PBE088kZbpDxMTE/joo49gNpuh1Wohk8mgUCimg1SO4+DxeNDe3o6KigqsWrUKSqUSfX19+OyzzzA2Nobs7Gw8+uijC+oNZDAYxDvvvIPi4mKUlJQkPB7DMPjkk0+wYcMG0Q91ETLfUUoASUj0QNb4+DgikcgDH6vVaqHT6WIOWnmep+5NIose4hkeHkZxcTEqKipgNBqxb98+LFu2DGVlZaLOd+HCBbjdbmzYsEHUcVNNqVTixIkTYFkWW7duTdvST8Cd5h69vb0IhUIIBoMIhUIz/sxxHBobG2dNG3E6ndDr9WnRnjXZnE4n3n77bWzevFmUYP327dvo7OzE008/TV39CIkBBawkYYIggOd5jI+PP/R2YVZWFmQyWUwX6mhA/LBdXBI7r9eLrq6u6S48FosFjzzyiOjzhMNh7NmzB42NjfNmZ0mpVOLIkSPQ6/XYsmXLgjhBv1AdP34cbrcbdXV1ooz36aefoq6ubkanM0LIg1EOK0kYwzBgWXZOtVfj7aedaIksMjuNRoPa2lp8/etfR1NTE5qbmyWZRyaTYc2aNTh79iyCwaAkcyQLwzCQyWQ4cOAAsrKy0NLSQsHqPFdXV4eBgQHRuu/V1tbizJkz9CacEJFQdEDmLNp5x2q1PnD3NBwOw+l0TlcamOvYLMvGXU+UPBzLsli0aJGkheFzc3ORn5+Pzz77TLI5pMZxHBiGwf79+1FSUoKNGzfSbd0FQK/XY/Hixejp6RFlPJPJBLPZjCtXrogyHiELHQWsJCZzDVp9Ph/GxsZiHlsmk8VdeJ2kh4aGBgwODmZcC9doG9Suri7s3bsX1dXVaGpqSvWySBLV1dWhu7tbtCoJVVVVuHDhAvx+vyjjEbKQUcBKYhYNLB+2G8rzfMy31xiGgUKhSEkhdiIOhUKBhoYGnD9/PtVLmZPoKfrOzk588MEH8Hq92L59u2i5jCRz5OTkwGw2Y3BwUJTxNBoNFi9ejHPnzokyHiELGQWsJC7RoPVhvF5vzPUIo3VZ52N5pIWiuLgYkUhEtBd+KUQD1evXr2P37t0IBoP4xje+gS9/+cu0y7+AVVVVobe3V7TxKisrcf369bhz+wkhd1DASuI2l0A0eissWhprrliWhdFoFK1lIkkuhmGwYsUKXLx4Me0KqMtkMshkMnR0dOCDDz4Az/PYsWMHNm3aNOdOUWT+cjqdojaFkMvlqKiowOeffy7amIQsRBSwkrjNJc9LEASMjIzEVWOVYRiYTKa0LNJOHq6wsBAcx6Gvry/VSwHwX3cF2tvbsXv3brAsi2eeeQYbN25Mi65VJD309vYiLy9P1DE1Gg1VCyAkQRSwkrjNdecsursaT6kjhmFgNpspaM1QK1aswKVLl1Le6jN6QHDfvn1gWRY7d+7E+vXrKVeazBA9LGqz2UQdl2GYlP8OEJLpKGAlcYv1Auz3++O6PRwNWqUsx0SkkZ+fD41GI1qpoHj8qRA19u/fj7q6OmzYsEG0lrRkfrl16xasVqvoNXejP4OEkPhRwEriIggCPB5PTM8JBAJxz8cwDCwWCwWtGaiurg6XLl3C1NRU0ueO7mzt378fDQ0NqK2tTfoaSObo6+sTPR0AoICVEDFQwEpixvM8nE5nzLf4I5FIQrfFojutBoMBarUacrmcCrpnAJvNhpqaGhw+fBherzdp80aD1QMHDmDVqlWoqalJ2twk8wiCIEn+KnDn4JXT6RR9XEIWEgpYSUyiO6s+ny+u58ebFhDFsiy0Wi0MBgMsFgtycnKQnZ0NrVYb95hEepWVlSgtLcWRI0eS0raVYRhEIhEcOHAAq1evxvLlyyWfk2Q2h8OBUCgkSaWIrKwsTE5OpuQuAyHzBQWs5L6ih6WiLVYFQYDP54Pb7Y57zEAgIMqtMZZlwbLsdOctyklMf7W1tcjOzsaRI0ckPzGtUChw8OBBNDU1oaqqStK5yPwgl8sBxJ6bPxeCIKCoqAg3btwQfWxCFgoKWMmsosHp6Ogo7HY7XC4XpqamEr6tFQgE4PP5JHlRiL7gkPTV2NgIrVaLEydOSHZqmmEY3Lx5EzabDcuWLZNkDjL/6HQ6ZGdn49atW5KMX1RUhGvXrkkyNiELAQWsZFYMw0ClUkGtViMYDMLr9cZ8yOp+XC4XPB6PqAFLdL0kvTEMg+bmZvA8j1OnTklyEEWhUODzzz9HfX296GOT+a28vFyy7mwmkwk8z2N0dFSS8QmZ7yhgJffFsiz0er0kLVLdbjfcbrdoQSvDMNTKNUOwLIsNGzZgamoKV65cEX38kZERqFQq5Ofniz42md/Ky8sxMjIiScoKz/MoLi7G9evXRR+bkIWAAlbyQAzDwGg0SlK43+PxIBKJiDZetJMRSX8ymQyrV68WvT6rUqlEe3s77a6SuGg0GhQUFODmzZuSjF9YWIjOzk5qIkBIHChgJQ8VbZEqRY6o0+kUdZeV0gIyh8ViQSQSEfXktNvthsfjQUlJiWhjkoWlqakJN27cQCgUEn1slUoFvV6P/v5+0ccmZL6jgJXMCcuysFgsou9ghkIhhEIhUXIZKS0g8+Tl5Yl6yCUcDkOj0YBl6dJG4mOz2SQ70S8IAkpKSigtgJA40FWdzBnDMLBardBoNKIW7He5XKIdvuE4joLWDLJo0SJRA1ZBEChYJQlbs2YNbt68GXe96QfJy8tDf39/Qp3/CFmI6MpO5oxhGLAsC4PBgOzsbBgMBlGCg3A4jMnJyel6r4mu0WAwUCOBDJGbm4uRkRGQsItHAAAKaElEQVTRcpkFQaDuZyRher0eS5cuxeeffy762CzLIi8vT/T87ShqAUvmKwpYScyigatGo0F2djbMZnPC+a2hUAjj4+OiBK0sy0Kn08FgMCQ0DpGeUqmEyWQStdQP7bASMTQ2NmJkZAQul0v0saWsyRpt8kKBK5lv6MpO4sYwDBiGgVKphMViSfjAUyQSwfj4OCKRiChBq1qthslkSmgcIr38/HzR0gLo9DURi0qlQn19Pdrb20UfOycnB5OTk3EFwzzPz/oRDVIZhkE4HE64DTYh6YYCVpKw6I6ryWSCQqGATCaD0WiMa6eL53mMj4+LchCLZVmoVCpYLJaExiHSWrRoEfr7+0UJNiklgIiptrYWU1NTGB8fF3VchmFgNpvn1DkwGoiGQiF4PB64XC5MTk5icnISdrsdTqcTLpcLLpdrOi9WJpNBJpPBbrcjHA5T4ErmBQpYiWiiF2Gr1Qq1Wg2bzQaFQhHzOIIgYGJiAsFgMOEghmEYKBQKZGVlUevWNGW1WmEwGNDV1ZXwWHToiogpWi9Y7AYXDMMgEonMqeoKwzDwer0YHx+Hy+WCz+ebrq4SDAbh9/vh8/ng9Xrh8/mm37TJZDLo9XpMTEzA7XZTmgDJeHRlJ6KKpglEd10tFkvcuaSTk5OilbuSyWSwWq2SlOYiiaurq8OVK1cSrn0ZDQQIEcvSpUvBcZzoLVvD4fCc30Q/7I2/TCaDWq2e0eAlet2zWCzweDwYHx+n3VaS0ShgJaKKBqt3f67RaGCz2cBxXMzjeb1e0YLWu3dbzWYzBa5pxGq1Ijs7Gx0dHQmNo1KpJClFRBYuhmHQ3NyMq1evitrkJBwOz/kaxHEcGIaBXC6HWq2GwWCY/p3Jzc2dvkuhVqtn3GGIBq1arRbhcBhTU1MUsJKMRQErkRzDMOA4DllZWTHXSBX74MC9B8VI+qirq8P169fh9/vjHkOhUMDr9Yq4KkLutFTNyspCd3e3KOPFkhIQfXxOTs70HSutVguFQjEdyLIsC5ZlZ83fvnsTQS6XU443yVgUsJKkuLuGq9lsnvNFU6pbWNEdDpI+9Ho9ioqKcOzYsbirBigUCgSDQfp/S0TX3NyMGzduIBgMijJeLDusd6dZxZqjfXfuqlKppICVZCwKWElSsSwLpVIJm8025/yt6EECMQmCQJ1m0lBjYyNKS0tx/vx57NmzB52dnTHlpPI8D7VaTWkBRHRWqxVlZWUJp60AdwLQUCiUtIOg0esnHTwlmYwCVpJ00RQBq9UKnU730MdLUU9QEATRdkqIeDiOQ0VFBb72ta+hoaEBg4ODeP/993Hp0qU5BaGRSAR6vR5jY2NJWC1ZaJqamjA4OAi3253QODzPg2XZuPL64yEIAjiOo/xVktEoYCUpwzAMtFotsrKyHnibKtGT4/ebW4pxiXjy8/OxadMmtLS0wO/348MPP0RraytGR0fv+8IrCAIqKyvR1tZGL85EdBqNBrW1tbh69WpC4wQCgZjz+RMVT4lBQtIJBawkpViWnS7J8iBipwVQ6aPMYTQa0dTUhG3btsFgMODs2bN4//33cf78eUxMTHzh8TabDYIgoLe3NwWrJfNdfX09nE7nrD97cxUIBOZ0d0kser0eGo2GahSTjEZ1fUjKMQwDlUr1wNPdfr8farVatAMDlL+aeVQqFaqrq1FdXQ2Hw4G+vj6cOHECgiBg8eLFWLx4MeRyOfx+P6xWK86ePYvS0tJUL5vMM3K5fLqZwPr16+O6Jnm9Xmg0GglW90XRA1uUv0oyHQWsJC087GIqZr6pIAgzCmyTzGMymWAymbBixQpMTEygr68Pn376KQRBgEqlQnZ2NgoKCqhVK5HEsmXL0NfXhyNHjmDlypUwGo1zfi7DMPB4PEndYY3OS0gmYx50m5VhGIHywEgy8DyPiYmJB5Yj0uv10Gq1olx4eZ6Hx+NJ+PAEST9yuRwWi4VufxLJ3bhxAydOnEBpaSkqKirm9DOnUChw+PBhrFmzBkVFRUlYJSGZg2EYCIIw64s8XdFJWoh2oXqQaD9sMbAsC51Ol7TbciR5xHpTQ8jDVFZW4pvf/CY8Hg9aW1vn9By/3w+fz4eCggKJV0fI/EIBK0kL0TzWBxEEAQ6HQ9T2iHq9HtnZ2Uk/sUukEf05ooCVJItGo8HWrVtht9sfWnqN4zh0d3ejsrKS7gAQEiP6jSFpYy4X8EAggFAoJOpOK8dxMBgMsNlslNua4dRqNZWzIknHcRxKSkowODj4wMfJZDL09PRgyZIlSVoZIfMHBawkbcw10HA6naIHJdHyWiaTCTabjWoWZiitVks7VyQlSktLMTQ09MDHTExMQKvVwmKxJGlVhMwfdGUnaWOuQWgkEoHH45FkJy0auJrNZlit1jn3+iapJ5fLKVglKbN48WK43e77HhxVKpXo7OwUfXdVEAS6q0AWBLq6k7QRy0VXqoA1imVZKBQKWK1WCoIyBB22Iqkkk8mwfPlyfPzxxzh79iz6+/vh9/uhUqngcrlw9OhRTE5OorKyUvS5nU4n3G43NUQh8xqVtSJpw+v1wul0zvnxGo0Ger1e0oBSEASEQqGEutoQ6TEMg5ycHApYScr5/X7cunULAwMD6OvrQyAQgMFgQH19PcrLy0W/Xvn9ftjtdgB3rokGg4F+D0jGelBZKwpYSdrweDxwuVwxPSc7Oxscx0m0ojsEQcDU1BQ8Ho+k85D4qVQqGI1G2g0nacfj8UCj0UgSRPI8D6fTCb/fD4DeuJHMR3VYSUaIp1yVy+USrczV/UTLX1E+a/pSKBT0Ik3SkpSpKgzDzGgzLQgC/H4/5bSSeYkCVpIWBEGIa6fU7/cnJVBhGAZms1nyeUh8lEolBaxkwZmtxJ/X66WAlcxLFLCStBAt+J6dnf3QBgL3StbFmeO4mHqGk+SROi2EkHTD8/ysjQqCwSAFrGReooCVpI1oEX+j0YisrKw510KVOiUgKhpUxxpQE2nJ5XJ6gSYL0v2qAkhdRYWQVKCAlaQdlmUhl8thNpthNpsfeqs3WQErcGdtJpMJWq02aXOSB6P8VbIQsSwLs9k8a1vph7WIJSQTUcBK0hbLslAqlbDZbJDL5fd9XLJrD0YPYZlMpqTOS2ZH+atkoWIYBkajEXq9fsbXeZ5HKBRK0aoIkQYFrCStMQwDjuNgtVrvu6sZDochCAJ4np/+kPp2WDQ9wGq1UrCUYg96M0PIfMcwDLRa7Rfy630+H6UFkHmF6rCSjBEt4m+327+QBsBxHFiWnf6Qy+WS1T68d008z2NiYoK6zKRIbm4uvWkgC54gCBgdHZ2+NlITAZKJqA4rmRcYhoFcLofNZvvCgaxIJIJQKIRAIACfzweXy5WUeoQMw4Bl2ZgOiRHx0IsxIf9ltnxWQuYLClhJRokGiBaL5Qt5W/dyOByIRCJJC1otFgu9YCQZBayE3BFNDYiiu6Nkvnlo6x56QSCEEEIIIUnQd7+/eGAOKyGEEEIIIalGKQGEEEIIISStUcBKCCGEEELSGgWshBBCCCEkrVHASgghhBBC0hoFrIQQQgghJK39/5ZDe7BQH45yAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 864x576 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Set up reader for this file\n",
"states_shp = shpreader.natural_earth(category='cultural', resolution='110m', name=shapename)\n",
"reader = shpreader.Reader(states_shp)\n",
"\n",
"# Read in the data from the file into the \"states\" generator which we can iterate over\n",
"states = reader.records()\n",
"\n",
"# Note that if we didn't re-read this each time this cell was run, we could only run it once.\n",
"# Once the states have been iterated over, the pointer is at the end of them and there are\n",
"# none left to show. This is like reading all of the lines of a file and reaching the end.\n",
"\n",
"# Remake map here\n",
"fig = plt.figure(figsize=(12,8))\n",
"ax = fig.add_subplot(111, projection=cartopy.crs.Mercator())\n",
"ax.set_extent([-128, -60, 24, 50], cartopy.crs.PlateCarree())\n",
"ax.add_feature(cartopy.feature.LAND, facecolor='0.9')\n",
"ax.add_feature(cartopy.feature.OCEAN, facecolor='w')\n",
"\n",
"# add end points\n",
"ax.plot([lons[0], lons[-1]], [lats[0], lats[-1]], 'ro', transform=pc)\n",
"\n",
"# add the flight path as a shape\n",
"ax.add_geometries([line], pc, facecolor='none', edgecolor='k')\n",
"\n",
"# Loop through states and see if they intersect flight path\n",
"# deal with shapes differently if want to dig into them more\n",
"\n",
"visible_states = [] # initialize for storing states\n",
"\n",
"for state in states:\n",
" # pick a default color for the land with a black outline,\n",
" # this will change if the flight intersects with a state\n",
" facecolor = '0.9'\n",
" edgecolor = 'black'\n",
"\n",
" if state.geometry.intersects(line):\n",
" facecolor = 'red'\n",
" # also save to list if intersects\n",
" visible_states.append(state.attributes['name'])\n",
"\n",
" ax.add_geometries([state.geometry], pc,\n",
" facecolor=facecolor, edgecolor=edgecolor, alpha=0.4)\n",
"\n",
"print(visible_states)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"### *Exercise*\n",
"\n",
"> _What additional states could a passenger in this airplane see? Assume he or she can see 100km from the airplane's position, on either side of the plane._\n",
"\n",
"> Make a buffer away from the flight path.\n",
"> * What should the units of the projection be? \n",
"> * First you will need to convert projections. \n",
"> * _What is a good choice for a projection and why?_\n",
"> * Once you set up your buffer, add it to the map.\n",
"\n",
"---"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"### *Exercise (continued)*\n",
"\n",
"> _What additional states could a passenger in this airplane see? Assume he or she can see 100km from the airplane's position, on either side of the plane._\n",
"\n",
"> \n",
"> What states are visible?\n",
"> * Save the names of the visible states and print them out \n",
"> * Color differently on the map the states that are visible from the plane but that aren't actually flown over.\n",
"\n",
"---"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"### *Exercise (continued)*\n",
"\n",
"> Find the length of the flight track and area of the flight buffer region.\n",
"\n",
"> \n",
"> What projection should we use to get a good approximation of the real values?\n",
"> * Compare your length with the actual distance\n",
"> * Compare your buffer region with an appropriate estimation\n",
"\n",
"---"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
yhat/ggplot | docs/examples/Linear Regression.ipynb | 1 | 138477 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from ggplot import *"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<ggplot: (274454201)>"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtsAAAIACAYAAABTiaBEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXmQbVld5/v5rbX3PufkcKcaEAufDYrwLEJ4iGHZShvg\ngAyK8uAZij5En+1AACI+upFGGYvCtrApC6HpoqEtEQGlBAMDm34+EdoywlAEH4o4IMhkVd1762ae\nPMPea63f+2Ptfc7Okyene3O8uT4RN+49mefsYe19M7/rt7/r+xNVVRKJRCKRSCQSicSeYw77ABKJ\nRCKRSCQSiauVJLYTiUQikUgkEol9IontRCKRSCQSiURin0hiO5FIJBKJRCKR2CeS2E4kEolEIpFI\nJPaJJLYTiUQikUgkEol9IjuMnV66dIm77rqLtbU1RIRHP/rR3HTTTQyHQ9797ndz6dIlzpw5wzOe\n8Qy63S4AH/7wh/noRz+KMYbv+q7v4qu/+qsB+MIXvsDv/u7v4pzjoQ99KE984hMBcM5x11138cUv\nfpGFhQWe/vSnc+bMmcM43UQikUgkEonECeVQKtvGGJ7whCfwnOc8hx/7sR/jz/7sz7j33nv5yEc+\nwkMe8hCe+9zn8uAHP5gPf/jDANxzzz184hOf4DnPeQ7PfOYzef/7308TD/7+97+fpz71qTzvec/j\n/Pnz/P3f/z0AH/3oR+n1ejzvec/jpptu4oMf/OBhnGoikUgkEolE4gRzKGJ7eXmZBz7wgQB0Oh2u\nvfZaVlZW+OQnP8mjHvUoAB75yEfyyU9+EoC//du/5RGPeATWWs6ePcs111zD5z//eVZXVxmPx9xw\nww0bPtPe1td+7dfy6U9/+qBPM5FIJBKJRCJxwjl0z/bFixf50pe+xIMe9CDW1tZYWloCoiBfW1sD\nYHV1lVOnTk0+s7y8zMrKyoavnzp1ipWVlQ2fMcbQ7XYZDAYHdVqJRCKRSCQSicTheLYbxuMx73rX\nu3jiE59Ip9PZ8H0R2bN9zXalX1lZod/vr/va0tLSOvGeSCQSiUQikUhcCYcmtr33vOtd7+KRj3wk\nD3/4w4Eodvv9PktLS6yurrK4uAhMK9kNKysrnDp1atOvtz9z6tQpQgiMx2MWFhYm7/3zP/9zPvSh\nD607pm/91m/lcY973L6dcyKRSCTWc/fdd/PUpz6Vl73sZfzkT/4kxhz6A9dEIpHYUw5NbL/3ve/l\nuuuu46abbpp87WEPexh/+Zd/ybd8y7fwsY99jIc97GGTr7/nPe/hpptuYnV1lQsXLnDDDTcgInQ6\nHT73uc9xww038LGPfYxv/MZvXLetBz3oQXziE5/gwQ9+8Lr9f/3Xf/1k+w1LS0tcvHgR59w+n/3R\nodPpMB6PD/swDowsyzh79uyJu86QrvVJ4rhc6/Pnz/OCF7yAxz72sTzpSU/i/Pnzl7Wdk3qtj8t1\n3kvStT4ZNNf5auFQxPZnP/tZ/uqv/orrr7+eN73pTQB827d9G9/8zd/Mu9/9bj760Y9y+vRpnvGM\nZwBw/fXXc+ONN/KGN7wBay1PfvKTJxaTJz/5yeui/x760IcC8OhHP5r3vOc93HbbbfR6PZ7+9Kev\nO4ZTp07NtYzce++9VFW1n6d/pMiy7ESdb4Nz7sSdd7rWJ4fjcK2rquK2227j3nvv5dZbb6Uoiis+\n5pN2rY/Ddd4v0rVOHCdEZ83MJ5yTJrZ7vR7D4fCwD+PAyPOc66677sRdZ0jX+iRxHK71Bz7wAV7w\nghdw66238qQnPemKtnVSr/VxuM57TbrWJ4PmOl8tJHNcIpFIJA6Uf/qnf+Lmm2/mB37gB/iO7/iO\nwz6cRCKR2FeS2E4kEonEgTEcDrn11ls5e/YsP/VTP0We54d9SIlEIrGvHGr0XyKRSCRODqrKu9/9\nbv7oj/6It7zlLVfVY+JEIpHYjFTZTiQSicSB8PGPf5zXve51PPe5z+Uxj3nMYR9OIpFIHAhJbCcS\niURi37n//vu5+eabecxjHsMzn/nMlKedSCRODMlGkkgkEol9xTnHHXfcwWc+8xl+4zd+Y9KwLJFI\nJE4CSWwnEolEYl/54z/+Y97ylrdwyy238FVf9VWHfTiJRCJxoKTneIlEIpHYNz7/+c/z6le/mqc9\n7Wk88YlPnDQkSyQSiZNCEtuJRCKR2BfG4zGve93r6HQ6PP/5z6coisM+pEQikThwko0kkUgkEnuO\nqvLe976XD3zgA7z5zW/m+uuvP+xDSiQSiUMhVbYTiUQisef87d/+La997Wv5yZ/8SW666abDPpxE\nIpE4NJLYTiQSicSe0u/3ufnmm7nxxht59rOfjbX2sA8pkUgkDo1kI0kkEonEnhFC4K1vfSt//dd/\nzdvf/naWlpYO+5ASiUTiUEmV7UQikUjsGXfffTdvfOMbedGLXsTXfM3XHPbhJBKJxKGTxHYikUgk\n9oR77rmHV77ylTzpSU/ie7/3e1PMXyKRSJDEdiKRSCT2gKqqeP3rX49zjhe+8IUp5i+RSCRqkmc7\nkUgkElfM7//+73PXXXfxa7/2azzwgQ887MNJJBKJI0OqbCcSiUTiiviHf/gHbr75Zn70R3+Uxz72\nsYd9OIlEInGkSGI7kUgkEpfNYDDgNa95DQ9+8IP5iZ/4iRTzl0gkEjMkG0kikUgkLosQAnfeeSd/\n/ud/zp133sny8vJhH1IikUgcOVJlO5FIJA6CUIIfxr+vEv7iL/6CX/3VX+WFL3whN95442EfTiKR\nSBxJUmU7kTghhHIVylUwOWTbNBoJJagHsWB2kSpxuZ/bB/z4An51hB8PwCxPxa5bA1WwBdhePNbt\njvdKzyuUiOtPtqHZ0qGPz5Vy8eJFXv7yl/P4xz+eZzzjGZvH/B2heyKRSCQOgyS2E4mTgOtjxGHC\nGMKYAJsL7lAiTfVVPQo7E0mHISg3E3LlBaS8lxAccuk82Ougew4pz2P9KmpyQtWBrAd2IR6v7c0f\nk8sdjzZ+tH4bfrRxG/stSrfa/i737ZzjtttuY2VlhRe96EV0Op1N93nFY5dIJBLHnCS2E4nD4iAr\nfm5ACGNwY7AdCNXm71W/9et5hBLKi4i2hJUG6Fx7+ce8g31uKuRcHxl/ARvWyEareH8vUl4HWQ5a\ngQawFtxK3E62iCLx87PXYvb8/Sj+QWNl3BQ7uJa69euditLN9rPd/rfa/mUI4g9+8IP81m/9Frfd\ndhsPetCDNn/j5dxLl0EIgTBaIYwvQmD7JzdXCerH8WlNemqQSBxpkthOJA6Dvar47USwhxJCiZEh\nJoxRHNjFzbcpdr0okm3SJepzUQ3g1xAAyaOgD+X+iYCthJwC5SXElFBdBF+AUYzrgDrITwEZiEUM\n8Voo8Vyz1vYai4n62oYyAvUYk8dTVw+mQFrHMPda2h7Bj6bjYXs7P5eGze6ZeV9nF9vfbt8z99hn\nP/tZXv3qV/PDP/zDPP7xj994nG12ey9dLn6ACZ5Mx6irtn5yc7UQSkQNoj49NUgkjjhJbCcSh8Fe\nVPx2KtjrKqyXAmcA6WwUe21MEbe106p7I0RRgh8jYmo/dGffKpnA1kKuOI2T05TlP+OcQ0RRFFWH\nJ4sebrsIkqEC4ocgVTxXp1E8myKO62Q8AiBAiNVxyePXQhV98O3xmIfJa/E+Z136TkSpH0EYT69J\n8/6d3EtbbX+r783cY8PRiFtuuYXrrruOn/7pn94+5m+399LlEiqgM/P6Kkc96zIO9vP/WiKRuCKS\n2E4kDoO9qPjtsBqKOgSwNsdYi9pFdC8rjOpjZRuPkKHqEQ1x3/tZXdxKyImFYolQdvEoBA9+jLFC\nyE9D7xyQR+2sHsIK0EGyEnVDkGyyj2b7YruoGMS7+mt5FM5tod3sexb1dfU71p119lrNngustwc0\n17FdxWzGdif30lZjtdX3WttVVX7rne/kIx/5CL/+67/OmTNnNu5nHgdQbVXJUFeibhQnQGbp6l+Y\nOXud9+upQSKRuGKS2E4kDuOX8l5U/HYismqbg5oKr4GgGkXaNskbu7K4iCWYApxDs14tdrKY+LFT\nLvcabPZeseD75LbC2C54R3BjNF/GSEC9Q/OF+n1rQIZQIdUlFAv5UpxA+LX4JMBkEz+3QrTMmHzi\n2VbXn1a45x1TPSFp/q3t42ze3/ZQNwtNwwiVThT1thvtERo2fG5H99JW47rVONb32F/9f5/gdb/y\nqzz/+c/nkY985ObbOgykg1ohmIxQD+5VvzDTFKgYVKqrd0KRiIQSdeyvLS+xrySxnTjZHGZawpXu\nZyciSyzihwiKzXsQwvbb3a3FRSxiCjQD4xxqckRytG112Ir9uAZ+CL5CdYD1l/ChgOIUHjMVq/mp\n+MurchgdEwIxJSQ/F6v/bgWCQ7Ic/BparUZxnS2st3G4fm1DiZMdnfcLsZmQaIif86NYpZ6X2lKt\nIL6P+jFWS7ztRcGvblLN1tnt72M8o6pnZWWVl73ql/imb/omfvAHf3DzmL9DwojHFGcxxRipKnSn\n1p5jjtgO2B38n04cX+qfj4KpnyCSBPcxJIntxMnmgNISdsVuxNAOvq9i42N2KcCEHYln/HB6DNtZ\nQZrKrh8TyAATK7+hnJ9h3a4CZ0v7cw1CtHqE4AgIwQioo/B9nGRxYaMf1uLXEco+4BDpolkZLR91\nZV78GmiFasCIotUYtYtxguGHUThT2ztMF/LT9TG0rqPYqY0kjACDqGFDDGAoIVSIejQMif7wHtgc\nxUwrzY1PfpPkkU2rYLuZ2NTv9QHe9J/fyhe/+EVe97pfodfbwu9/WMw+1dmJtSeROA4cxd9RiV2T\nxHbiZHNQaQk7ZT+qvLaHiEVsgTCa+rW3EPW1zNzZ9l0f49eiuNUAFIBDvEMRROz0PFwf4/r1/uu8\n79kK+F5cg2oFdETAoDELLlaRTQ7iwQ/AL8WFk2GE+CEmjAhFTFHR8gJgMSJxUaJfQ2QBMT7GrdEs\nUgyx+k1ckKdhPBHCs9dxMqYqM2skW3Yb9WA7BHWodAl+AFYRrdD8bBTtjdied39sVwXbzS/u+nsf\n+uP/yVvvfDu//B9fw1d+5Vfu8AIcMCZHpSBgURMjHPVq92wnTgZH7XdU4rJIYjtxsjmotISdsh9V\njMZnTBbtB5vFxTXnrh5pjcOGxXyzuEFd/fUY9QTTQ0yBESGEIYR8+gtiNiUiVJAtRWG0led5t4iA\nG5NpHxsqQhhAtoyYDlD7ydVDeR7GFxAdI6bO4AbAQtYjBAdGIAhipa5Kt35sqgdiBR2R2l/d+uXY\nCD5VJFuIHxGDVv3otZ2NAazvQc2orSedWkjmGyclk/3v4vW8X9ybiVKxfPELn+cVr34t/8fTn8YT\nvvMJ24/7ISEiSNZBst70Gh72/+VEYi+Y9/M7cexIYjuROEo/vParimGKKEQaLdnYEFo2hw3H0Hx/\nq5jAelvSiOjgo9ix3bpga9cnbJg8Voonx5VH4d/8m008z/PYqnKpgAmoLOArD2YBVCm9QB6tLrj7\noVoFBbWLeDxBLUgB2QIGjRYcuwxSoGGElwxMB2x3ukgy5AgjgnQQk0VrSW3FkcnhSB2PSIzwqxc8\nbogBbM6juSb5qek2mnPdIqavaUkfRmOoxnWe+Prtz6aebDbpKh3ccuttLCwu8jM/83yyYmH7a5JI\nJPae2Z/fiWNHEtuJxCyH+fj5oCrts+kYs1Fwoaz9zCF6m2Fz73a2gCsN6AikC8UZ1BR4KeI52O70\nPLKlaB1pe7ab7beObVu2s9vky2DOITLEkEF5H6GzgA1r+JDX1epxbSvJ0DCOFu3O9ZAvgMkJLnq1\nkcX6HFo52fUERNSgMo6VZ2pRrSGOocZs7+b81Y/qgxPEZHVsYDE3BjC+zU7PsX696f0xaSwULTKB\nAJWLdpn8TBTds6knsOXY33XXXXzwg/8Pb33rWzl7zQO2vyaHSFVVVBc/TXXpn4EuLGzR1TKRSCQO\nmCS2E4k2bRHnh9Hf3LTkPigOYl/tdAwxczN7RQyi9ULDZhHfJrF2xmTAAmAIjbhuC+o2s68vp5q/\nnV0iW4DeOVQ9bm0EMgZ3L4bTeNvDhCFql5FwgUCGGgtmGYrTkC3GBZaSISZHUIL6ullPN+6u8U37\nIYKLlpm6yY2aPMZ32070V9djpiaPCx9RRB2qduvz3UxYb3INAKTOODfqMToAp3hAxGxMPWn2PWfs\nP/nJT3LLLbfw3Oc+l2/4hm/Y/DocFcovkds1Ov4SwZ2PBcAkuBOJxBEhie1Eok3LayuhRCVbv8Dv\nuDKbUFHH9TVV/A3V1VkRph7cWvyJsWEcJFaINQpUgovbbttCmm3Mq9ZfTjV/O4GeLYF28VoBgaw6\njzE9JPQheIIY6BpUe8QmfAVSLECsu6NiiE1k3KR5jdre+v2KjSks6vGSQ9YDdGP+dWMJCSXiVurx\nDqjpbT6BaY3NjmiOSyygqCr42q5TT5jmPjGYM/aDwYBXvOIVPOpRj+JZz3rWkYv5m4vrs25Br187\ntENJJBKJWZLYTiTaNLF3fsA64TQrVI5T0sEmCRUTq0g7naQtFG0vWh/UI7HZ+SY5r1qnkUSx7c2M\nx9uPYlUYNn9asNsx3E6guz4wopAAfoyzBSCIG4Ptx2N1A8jPIowwbkgYjdDel0eRqg4JAzRUqF2I\nVoymIu+HsWLt+nUyyBjBxbTB4po4IvMiD/0o5j83k5Lme+1OkTtl9v5rCXstriHQx8sAI4Ig633z\nc8ZystkQePOb38zf/d3f8c53vvNoxvzNI1sCWgLbLh7aoSQSicQsSWwnEjPEIDaz5UK0Y9Wdrj4P\n9eU0W7qpbte2CJiTOtLYDtxa9B5vNvHQQFBDHLOZBX/xDfGvvX5asNVnQwVhgPNrYHPscESQjEz7\nVKGHHX0Bny1B6GNCwIQRSohiuLm+GjB4vGlsMdOnAvhhFPRaoiGgOkaNh/xMPLe5E4A1TKiFtZb4\n8X1IcWaSMrLj8djs/ms+a3uI5lA4QgjRUrNDK9Tdd9/Nm9/8Zm6++WYe8pCHbH8sR4Xiy6iKMWNb\ne+SThSSRSBwhkthOJNrUsXfaVH6RjXFLx63JQJOMoSZ6htVNG85sFwNnihhRPbtQr40GjLVRU4vF\ni512j5zN9IZpAsd+jlsoYbSG0fvAr0RhXfSoQg9cBWYYK9j2NJobvKuvc115NmFtarWpG9I0Vf6p\nwM2hvBchRs8FbNymKeqc7xAjCG1vku6ixMWY4kdgukilMT97XqzfZmx3/9V2FeP6YAvUdqMFZhvu\nu+8+Xvayl/E93/M9POUpT9nZsRwR8jwnP/vl5G6JqkqRDYnE1YCqHg8b2w5IYjuRaFML0BhFV8zP\nNT1uTQZM3UWSelFkI+xsb2cxcNtZNkyGqhAr2wIm2/CexrKiyPp4uythSyuPQGbxbgFsFe283kV7\ndtaJVhdZgO61EFbjaYQxnqLu1hgXj2ogiuWms2MYo34NkQI1HdQso7oGdBEb/dJUF5HyAgaJmdp2\nIXaWFIOaHHWDaD/BYvwgxglmy1Nv93YV6O3uv/F9GLNWW13WCFyYnsMm23bO8cu//MuICD/3cz9H\nlqVfDYlE4pDxJWSdwz6KPSH9RE0k2uxksd5exvMdlPfb9kBcFGChjMkUs/veKoJvq2OzPUJ+Zpo+\nMltFrXO0NVus9xnQdhzg5bCdlUcE8OQZZGQ4qSA/S6AEbIwG7CyCEYLLo/UgGLA2xv7ZBcCBdCA/\njbo1REtwI0wYo6YTn4DkC6ALYEyccJgCygsYLTEaCNGAE6vYJo8JJKZCyZGsSwgODa4+ZrveEx/K\nmMmNrreBbHf/BRcDZkwWowuDm3Sd3Myq8nu/93u8733v44477uDaa6+9/OuSSCQSe8VRf2q8C5LY\nTiQuh70Qxofg/dYmsaFpJNPed+NFbkTcZrnas4iN3RfrCMFJO3jXr20ZHiRaWCYt06/0PHfUKdEw\n9uAQIAcKjIDU2d9BK7RaA/FY6UBe4Ou27rHSbNb51o1fQ/0IIRC0F1NKQjWtLHeuif92A8T3gQCq\nEKJnXZG4PdtFq/tj/J/J686WMzalUCLlBSRE60owvZiV3VyTDQK7NXHKl1AJBPHRytK+jrPNjEzB\nP/7jP3LzzTfzEz/xE9x0001Xdl0SiURirzjqT413QRLbiUSbgxTAB+n9Vo/YArF1tF1ThW7vu1m0\nyO49chs+5/rRMwyoH8Tv2gU2NNC5XLazUlT3Q6gIZYmU51GzCJ0OaMCbLpKfY7IIVhWjq6gLSHYa\nzWvRPDMpUBWUutGMcYAHTO0ptNMJS76EV4cPo7iPRrC3croJ1fQazD4JEBsr2mEMYYQJVcyC8TPd\nJWca2sSD9Gi2RDBdgrtUTxhayRzqawtL/PdgOOIVr3gFD33oQ/nxH/9xjJm3wDWRSCQOAXuEgwd2\nSRLbiUSbgxTAB+n9nt12W2i3jkXWicvWsW1ld/GjSdV60hExtBapiUGDopLNb6BzOWxnpagGmPHn\nKMI9WNcnGEfIzmCyHsH20GwhxsPlZwBHNezHKnBQ0BLxBtBp63iTR791GBKCAga8Q2yONN0jQxWF\ndbZUn6MAOllg2R5TaQlgbZ4GNJaR+NU4VhomL2MTnVFMkGlPBOfcs7Z3DbHJENE21IxTK29bVXnb\n297Gxz/+cd7xjnewsHAZ7diPUwRmIpE4VlwtiyMhie1EYj0HKYD30vu9k32JQaWaiuK2Jxg2P/et\nqv2hJDZ/qT3Boawb25SAB8ljFF5WTGIGdadjup2Q27IZTJcw7lNVX0BdFr3YjHHZ9XFhpOlBcQ5M\njqn6iCjYBbwEjO+jYpFgYgJJE/cXKsQNMOrxKJg8Nr2px2Vdh8d5Vef2mM4Z50kWeSijALeLqAZC\nqKa2FmlVnlvNdba8Z9vj5PqTXO+/+OgnuP3X3sQv/uLLeNjDHrb5WG7GcYvATCQSiUMiie1Eos1B\nCuB6fweGKUBGU98uMwKvSV+ZPffZCneopp0ka5EZoLY+VFH7iYkZz2KgjrbT3YzplQq58hJQQfB4\nBbDA6djEJstjK3WTRTFLDmYBIxIryd4Ba2Cq6Lk2eWxIowEjFkFBRyDLsUW7X6u3z8bEj3n3U1Np\nRqKtZN7i1MYz38QGzgrq5j2b7WOTMYU42bn/4kVe+oqb+c7vfALf933ft/NxbXPcIjATiUTikEhi\nO5GY5ShU5/b68Xwo8cNVZHQhLuyz3amto6GOA9xAI/SapjSmmKZmiJ16gAmoVkhQRCzB9qJfeAcZ\nzxu4EiEXSqjuA6NocQ7GVTyGYgmMINJFTRZNHmLjwkbbJYQx+IoYUOjQagRhFLtnhirmaWcLdXpI\nVkccdjCtpj2hqYRvdlxN98n6nFTMtHI+W52et522JWSLDpyquvEeqiMtvVp+5fY7GKwNePGLX0ye\nz1iKdspxi8BMJBKJQyKJ7UTiqLHXj+dDGVuLh4vY8gLB9FBORytFq4PkVu28FeKivrZFosnqbtq+\nK4g6JLgo6JVYFb6cCcOVCDn1QIYVpZtDv4KQL8cYPykItZc6+BJsJ1bkNdpIyPOYJhIGqDhMGKJ+\nDUwXNTmeHAzR1pGfjs1rwqhetJgz9VzXNNey/jtoAOocd8mnNpVNKuAbJlw7Hcd591A9pv/9f/wh\n7/rtu3jTG9/A9ddfv/NxneWgnwIlEonEMSWJ7cTJ5igu8Nqsqnu5x9osrMMhGpAwRH0HslPzbSPz\nMAWYEqlWozi13WmknNgYY6cjVB0+AKJgs43Z0TvlSoScWFi4AT+4njUtCN1RrGznHcRalNh0R9Sh\n3tVrEU1t7cgBiQtFQ4kEh/oxYrtofhpMB5rca4iLP7F1lbrYWMVvVbHrD9SLHjWKczHzq/a7nXDN\n3BsaaquQH8d9ZUuQn+Jzn/88L3/Va3n2s5/FY//N43Y+pptxVP7PJBKJxBEmie3EyeWoLvDapI36\njo51niBvqsK2IEhBEDsVhu2FjvXCuWYfs/FyzWJI8GhoVZr9cJJBbapLeLuIGEHxUw/z5fh52+e3\nk4nGTNY0+fUUWrKmgnEXCNUq1giuWMKYbqxI+zHYTszebjpc2g7ea0wrIYvfV+J4NROMUIJbi0PV\nVKHnHVtzLcXG/RE7eU7sI5PFlyXi+tMIxnkWn82Yd2+oQfza5OveW0pvePkrX8MNNzyI5zzneSnm\nL5FIJA6IJLYTJ5cr9QXvsad6XWWyOZ6ddHdsbWOzduvkpwis4a2LrzvXzE3MUD+ctKqfjZcT9bF5\nDXn0OreqtSE41I9i/xaxqPTi4st2YsYVjM3kvPww7rs9UZh37mEEnS5Gl6AcEMwCeI/THHBR+Kqv\nIxBbgrjJwrbdWIF2a4BGQT2TzqJonGQAYnKCmC0WSIY4wWn2UY/bRKS7tXXJJiphZxaf+v2zr5Wc\nELSOZMxQDG9/+2/yp3/6p7zjHe9gcXFx/rYSiUQisecksZ04uVyuL3gfPNXbbm8nx7rN5MHYvF6w\n2F1fsS4vRmFpO1OLw+w2mkYqk9dmnfi0WqJiEKkdydlCrBKbznRfTeV8t2PVstFIKFHJYpwgzE9M\nASBDqj5Un6czvIiagrL3Fdg8x6shSKe2unTBj1FfgonHJoDaHoQSY5ofkUpo9lGtgFsFiZMMAM2K\nzSv4zWSlEdmuHxdcmhyBmOQSKmJ7+Hqxosk3t/jMTvRkTudPP0R0jCFez49/4hO87j/dxr/7d/+e\nG2+8cXfjn0gkEokrIontFqPRiDzPybKTMyzGGHq9y0iLOKaICIPBgDzPsfZULVzqiDpT7ChEXx0I\n00fwSoZklz+GO9meanfbY1VvEJ1mOqsUiO2gfhxT5kyGWVioLSR1R0PnQAQJARVHkBxBiIozthM3\nuUFlOXYwbKwOdhHJFxERnHYxsoiqR805jFkgK06D7SK2E0WyllCfo4qJX9/p+NTn1YxTPK9i3TjN\nnvvInEYvCJfcEGcFjAFfYUyGdhbJe0uIsXjvyToG1R5oSRAwxakYZ1gNkcxBcGAy1C4iOLBjDLED\npFogP4PJO9Eaki3OPbfJOfgyjq3pQBONaAuUaGuRutOk2kVM1p2znTGiZt1YqnbicdY2mKAOw5C8\nGzt2rg6CpkHnAAAgAElEQVQcv/iqX+Fxj3s8P/IjP7Jt+sg0yWR3/y8Ok/b/6/Tz++omXeuTwVH/\nmbNbTs6dugO63S6rq6tUVbX9m68Ser0ew+Fw+zdeJeR5zpkzZ1hbW5u5zgEY7WwjM41K1BQwe8vs\nxmayk+2t/8DmxxpCa78BGMaqpy/pdQzj4QiVCs2z+D43QDRACChjsLX1o7o3LiAsziJVNWmxLgEg\ndjvUsrZiVKvY+nzVGEJnAR86sRtjNVofdweoDnafUhIC+BAFoAkIozpho1XR9UNA4rZdBeo4I4EL\nPkA1IuQlVVmB3k8VALtICB5vpk8Jgqmm4+vWMK4ZZ0fIsjhero+EClUXJy5IzOY2Eo+TTf4/hQBu\nDEEQAmiFqI/bNQVQQKifIASF8aWN99DsWEq8UaTpNBnGqBtgewV+PMKTcevr/yv33Hsft7/hjTjn\ncM5tM9Zz7sejsJZhCzb/f311c9J+fkO61ieFy44kPaIksZ1I7JbtkjJ2azPZywi1eZ+ttxnU1d0I\ni2m0nJi4+M/k8Tj8GOP7oEMMgnerU6vCzDlOW4mX+PFKtGVkcywPzcSj2SfE6uxuLDimdczqp63k\n/RATSkKseU8mBZO26OSIjMAKSIEwRssRQRTsUqzwt60f7Tb2YgmmmFZ4fT1xCBUGJUiGmm7sjNk0\nBNowRq1raor4EzfkdVxiFqvhtjfXKjL3HtrMTtROPTF5jDiUgj/80N3c+Zu/za++/nV8+Zddu/04\nt7e12etE4jhzFBOoElc9SWwnEpfDVj+kL0es7OcPfVPbP0JYL1pNAdkSoakIi4npHFohwYOWoBK/\n1qRwtEVd3cLcVBcxjBEpcOrQagU617Y81jaKXw1T7zds7EbZZrNfiDMVXp1UdMsoMpvjyxagOIvn\nAXgWIHjQVfJRINguEPBSoMsPJ7j+JJVkXdpIKONiURstPOrWQLROdBEwC5D1oje9fWz15zddrArT\ncWheu35cjGnyeAzz7qFmojHn85PJWhM9aAxfOr/Ky25+PT/4A8/g2x73LTuPYEzNahJXK0c1gSpx\n1ZPEdiKx1xyUWNlphaauQhubYXCo66OmA6ZOwmiSPfwQbIcQunUGdew0OUnPaFfgG1GnnkAGwSM6\nBslaFe+mulx/thaI7SYv67pRzklH2XbBqJioNE0B6HSsxUJxHU4vRCuLFLHa69bqqrKgZiE2+2lN\nQLS6FI8R4iShbkGPW4UwxuoYTIdgltDiNG1XobaTSPwIwnh6bbaacLk+xvXrcx/HBZOzn6nTYCYv\nt+ogGUqqILz6l27nzJnT/Oxzf3wa87dJis3EgtNU6Zv3pupf4moiPbVJHBJJbCcSe40povAK1cSe\nsefspkKjHvyQMBhDOajzogUTxhM/rjbCHSA/E5uiZBo7JWaL0++19+H6dbU6q5M1AlJeios5TRYr\ntNWlegVoBsW5qZCb142yfbyzxz9Ls53G6iE2poU0FV8/Ah2RySriRhgCXk4DHgkhLo6UDMoL0P2y\ndUknUEV7DSBaEtwI8at1d8yKYBU1y1N7yexx1nnkon56bZqKuesjrVSWZizWX9sKsqX1glf9+rHM\nT8+/1vXYvPNd7+AP/98P8fb/9iaWF4rpRKC+F9Z1qXR9TBP9qA7NlnZ/z7r+9H5vzjWROGqkpzaJ\nQyKJ7URir2nsB7X/d13Fc6/YTYXGD5HyXlTGUA7R4svANlVhP6l8x2zp2u6Rn0JQBEVDGQVYm/oc\nNVsEN8Cj4PsYUZAhdvxFfLkQRTcemoSLlne5vQhv3S+9nf5C3GpMqxUY/wuZVhgDVH3gIq44DZqB\nWUTyTuwmCbV9ZgymN7WjBIf4tdh9Ux0aAmq7qOnGpjntiMTqYlzUmC9Nqv5BQ7TiNEkzoay31RLh\nYuP+wrh1Xk38X+v8ygsYv1a/GOPNnG6VNZ/61Kd41c238LPP/bd83SO+NlpeWjX4dftvrndD/b1t\naT9VCeXGynwS3ImjSHpqkzgkkthOnEim8Wb78EP3IB5V7qZC4wZIqJAsICFAWAPOTD9Xt/SWOuZN\nQwW2izaWC8k2jk/LIqLZAgYPYYiVAEERE8BfQjrXgMQIO21XcLf6pbfTX4jbXb/gceMvwWiNEAx0\nliC/Ni6KzLqgJnqu/RBqIStSouQxZ9vfj6qA5Bgd40yB2h5qlyaTBgUY34dxA8RkSHUR7wYxYhCP\nUY9HY9W8qYQ3Gr05dtubZm1vWhkWghSABywwPxZrMBjwH/7DS/jGb3g0/+cPPA0bBrFjZX4q2mNa\n3u/JBKt9TG1P/WbMPlVxg5nvn5yEiMQxJAnsxCGQxHbiZBKqzW0YVyrCD+JR5a4qNIKIYEQwNsP7\nWL0MthuFtFSxit3yTsd4u1G0Z8zrjNg+R5MTsECOuiEiJbAA2QOikDfNMc6IyG0SWrZkOxtNqEAt\nPk4D6qSUZaTooiEublQpIAyjnz0MY5VbqKvbRbS6VCtgM5za6Ge3y7H75roxF8S0fpRqFTtWOkdA\nQKt17dxDqMAPwLTyuDerBE/sPTrp3gmgZmMslqryxje+kc985jO84XffRVYUaBjW1hgmTzGkZRlp\n9h1mPNtbMjt5FFlX5GfOsSUSicRJJontxMlks+rzXqxWP6hHlTvdbnEaX17E6ZgKjd5p24tVaT8E\nk6NQV15rL7HW6qldhZ3Zt4YS3CD6kG0eG7OMDcFXqAnQsQSVSVOYA316IBZo7DyAF3Bj1AcwGVYH\naDUghCUQi3UX8XYBMafwoYLRvyDVBWwY4J3GxjPZOYzJpt7wpmsjGgV10/3RLiCmQFnDuD5BsmjH\nyc/G74cmK9ujrh+F9tzKfDlZTKrqo3A3xabV7z/5kz/hjjvu4NbXvoqv+PJrGQ9WEdONi1CpF3yK\njeK7foqxoRPlTq7R7GQyP01or1FIFpJEIpFYRxLbiZPJbLV5Nq+44XItIEfpUaUp6s6GBYQC8l6d\nbuFQVUydCoLtTluE2w4SaquC+ph+0aYWgkIgEJDqElJewFqDy85gKPH9zyGL1yNZtKwEP9q7cZnX\norxNFrsnFoywIYCAD+O6uusxZUmlBsnGMZnFjwnSwajExZU4RBQkQ00Vq/2TdusDJJuOQbBdvAYg\nxOMozkURrVWs+IchYVwB8TiF+JSBUOKxm3qv25VoAYJkcbHqnDE8f/48L33pS/nfn/a9POE7/k30\n2WuJSqtSXVtWpHUttZ1ystPJ5bzJ5CHf76HqE4ZCqPrAzruTJhKJxEGQxHbiZGLyqbBsV/SuxtXq\nfoRkPaRYBHcB3BCyDHCAJWBgUjWdZnAHmPp653m2m3ESE1u1a47VCtExmY7xLJJVl6KNIzvDeq/B\nlRO3tklL32wJ8msYV9fh8/vABTCKcfdH+4RdBNMF7YAGgumB7aF2ATCgimiIQjcAWTYVqTKdhMS/\nA1KciROSRjiLBTKMDjBhTDA9vB8wyTNvD8XchkF+42LFZkHrDN57brnlFjpFzoue/2PkjBBZQkwn\nPq0IVbSdzGZyN/d6e5t+tLMnMkdpMun6ZDLGaIfM9/Fapep6IpE4UiSxnTiRiMh8wXBVrlaPbVcE\nMCYnkIOWqB8htoNgCaZVMd2s8Uqb5nvqETGoXYbFM1TlGrjzlPQgP0XQkhACE1G8V8ks6mM+dvNy\n3hOIbBnb6WFCF6pVAor1q7igeBXonorHYhdiYoddjOkqpgC3hjcDvFHIFyFbRKUTK+bQspAwjf9r\ni2b1YIQQQFRjhdt0QCxqOrGijUC+vCEje+KpprZ+NAK9sXrM8L73vY/3v//93Pm2/8yp5UUkDOKa\nBK1Qstrr3UrFmdnfushC2H13z8MmVHHNaPt1IpFIHCGS2E4kZtkvgbFX6Se73Y7tEdSjhLgoMFsE\nP0Klil5eZX38G+zMSpAtxaYvkkFWi8E65k60XxeI89r6kE8a2uyJiNvuCUQoITMYvQYdl9DJAa39\nyiEu+pROtJDkSygGTL2NpoNjfhrJT8enII2FQyy4/iRZRW03VsRnr4XYKN6Ls3g/RG0PMTmaLdQC\nf06Ldlh3TgIxFaVdgW7SROrPffrTn+ZVr3oVz/mp/4uv/7qHAXWHS18RgovJK3O2PWF2cjk7YTgO\nmByYE52YSCQSR4QkthOJg2Cv2gRfznbq71euTtcI41j5zJeQelGfbmbx2ErYt20nfgjVSqymZjmh\njFYJVQO+RGRt+vm9EHHbPYFQD1rgqlWMDgkugLWorxc05qeg6IJZBIhpIiaPLdlrMSx+GBNZlGg5\nqpvlmFBOqtlBsqkYdv2pYBUbF0l2vyxuE4lCO1uaVJDn0vaiT86tQ9Nkp/m6AqWDX/iFX+DGG/9X\nfvzZz8QQYjUckKwHPi7MnIjz7fLKm+6e7WM5DmRLOHKCFDi7RPJsJxKJo0YS24nEQbBXCy8vZzt1\nh0BT3YMZ/DMuW4LiOrRcQbMOSCcmlMyyE2HfvEcsGkaIlogGTNbBqScTwQePrUbRu52f3TsRt9Uk\nQyxUK7jRP6PDPqoWOucI0UyCcWsE56BrQLJ43L4kmMU4ITF53dJHwNc2BVPEZjl1JCKSx/MXg4Zy\nutDUFGj9B/VQnF0XK7ndmE66SvoRYnNEfWyQ0/LOa3Dcccfb+Ju/+Rt++513UnQXYyKIBjAm+tHF\nR89224+/zXgeVwuVyZcwvWsxfcVXyUaSSCSOFklsJxIHwV4tvLyc7YQK3P3Y8l8g9MEFgskJdhGR\nWNmd2+VyJ8J+3dcskxbm6qNIzYrJYksNbr3o26+mQhC31/8MnfEFhqHCBsWX92E614NI7MBoBOxS\nzM8efwEJCjmIWUR9wIiiYpCsE8Wu69eLQUOM4zPEZBeoFxaWtSeHuuX64sakka3GNJTg1qJ9xBRI\nGCDVpVo4FzGvvOYvPvoxbr/9dm6++Wb+1YO/CnH9yViqGAwlRn1MRFHDjjlGAjuRSCSOC0lsJxIH\nwV5VDS9nOyYHt4ZWDhnfg0gX8SM49SjEzOnu2LATX3QjmE0B+TLBxfcEA2Se4FYRXEzyyE/vqsJ7\nRbg+MMD6VYwfQ1BCeCA29MH0CFhUFmJ79VAiFKB9GJ+H3EFxXWx4g0TztJjpwjvJ4+vGQuL6iB8g\nOFQCEgao6cVs7dkM7c3GtB4PbZoL+QGUlxA8ghKsib5wsaz2B7zkpS/nKU95Ct/93d8N+PXJLJKh\nkhF0gMSe8HvnlU8kEonErkliO5E4KPZK6Ox2O9kSQZZwfA4owDtCltdt20/V22wtKmtVnOfGI9bv\nkVDGtAw/mlZyi2La3MQUhJGNtgvTXR/Htt8t7cf3QHaOQX4NVbUGLEFxhkqy6COP/dGhvAQCKoox\nBYQ6DxyNcYDqJ9YQIPq4606OcWxCbABkMnwwoA7FIGJq0Tyanl/TMGjm9brzbzpMakDtYoyxkzyO\nn+0RpMNr/+OrqaqSF7/oZ7Di5yaziC0QkyNq0CYt5bgseEwkEomrjCS2E4njym5sGMUpGBUY6UCR\nEzrLsdqLiXF2ppgszJPWttX25mcW18ItNlzRuFCw5d8mKFrnT08+MlvR3c8886BgHOTXQA9wXcBi\nJMNLDzKLhCFS/gshO4cJVbSNZAtAJ9pBOuem59oSyjGBpd2B0WC8A5SgghiDuFWiildE3XTyslm3\nyCZGEaJVJVtGQonRekJju6hYPvCBD/A7v/PbvO2//BrnzpyKdpbZbdkeKgVqOjFTvB3leJWiqqgb\no24IIaQKfiKROFIksZ1IHEd2Y8Oo7R5CjgkDUIvxQ8LC2Zjz3EqhUD8CdZNWMVqtRKFoe/PtEK3u\ng7j4XsmW4zFJvaiv/ZmGpt17qwq+p4gBHdK1HfqyCN0lMCY2rRGNscxuBTVnwBqCOUNwl2IV2Vow\n2eQ419GI5UaAuz7i6oQXsaAZGhyCBwz4NWI3yjyOyWZdNNsV79rnrSHH+5iSQrbE5794Ly9/+cv5\n8R97Ft/4mEdMU0Y01GkyMllEKbYTE1eaSdMxW/C4a0KFaInBI6FKlplEInGkSGI7caJQX6LVAPUl\nm3YfPA7sxoZRL5TToqCyp8EN0GDAZnMqzAaCi35krRCNfm4Ru17ATMRhQP0w+pM1xNbfE+vDJl06\noRb/TOwrcxdoXgm2C+YchAtYmxG0RO1XELIF8A6RmEoSW5UbKE5H4a9jcB7sIjI+j5psg9d8cj7N\n+SNxfEwnLmRsUkmwoC4unjTNZ7boojnbbKZpQ28KqqriF3/xF/lXX/m/8NP/9kcw1Is0/RpgkVpk\nb9j6dmO6n4tUD5L9tiUlEonEFZDEduLkEEqMKILHaAlhky6SrfcfWSGyGxuGWPBjMjdErUGLB+Cy\nXmzb3pnZVmOV0AAaEGOmHRJnBczEy6xxgWW2XMfPEZupzFbD2+y3OPIjMA6XL+M9wGno1BnXCi4U\n0OmBvTbGEfoRxloIGcat4AdDTLFE0GjfaKw0Esq4+LL2ZmO7sQtniF0eY1v0POZbE90o6msJrOzc\nyjEzbnfeeSd/9md/xu+86+10F+px9qM4ccjy6QLIevvqx9EWtNW9u9+LVA+S2XG9ii0ziUTi+JHE\nduLk0FQx173ehKMuRHaTShJiFT/4psraQbJl1HQntoV122oar/gR2jRYCeV87zbEBjBN5dtNj2/b\nHOxm2y0xu2foGKEgy3rRURIMDO+LkXg4VE5hZAknFeoGdV527Suv7gcFEQ+ZAGux0g9QXcCEuOjR\nhwAs1wsZA2DrbpkFwddJJijIaFq5vwwR+PGPf5xbb72VX/iFX+CrH/o18b6snxio2Imwn4xlKBE1\n9VOGLe7dq6kabHJUipgyY7aZRCcSicQBk8R24uQw+xh/K+FzHITITgWFG4AEtHOKUA1jgxeTg+1M\n7Qpzt9WMlWxlfpgKfz+a+K8F0PICsaFKPldMa6jWtR7fU7wns2CLU2Rra1Q40BIbVtEQ8ORxLEw3\nprIohFCirg8hoGRotRb97HYhTjoA/DhG+9HkcTswAbLl6XlDtJ5AbCiE1nYZrUU4c2018yZOg8GA\nl7zkJXz7t387T3/608HYDd7uSTObpumNH7JuUlmt1NuduQ47iXY8qk92ZhARJOvEzpmamtokEomj\nRRLbiZODKQiiKJYgdVOTzdjvtIyDRAQTKqyxSLGI0yyKszqub0MGcygR10fdGkZATazWxsWTrTbi\nbRFWV1qlaaDi+ojvI3UWdYD1Qs+PZkToJgsHL5fOWaphh/Hwizi/BmYR4wbgL2JUyIozqFslFKcR\nVYJWUThjwC5C1iX4Iap5rFZrABS1i4QwiH5vk9ULLm0dBzg9t/YYhXoRYxy7sLHiPO8pCqDBcesv\nvYpL91/kpS9+Idba6Vg3NJOl9rUQG9ck+CGEEaLE4wvj9ddhq6cjR/3JTiKRSBwjkthOnCjEFpD1\ngItbe1qvpAnNbEXwsCuE+WnC+H5gRJAOJusQJEdwrUSL1sTCjxC/BmEcG7WQ1ecQYn40EEyBNGPU\nnGO7wU11CQmjmIoheayur6tuz9bK59TOr2TcbBc0RIGNwvg+AlnMzs6WQBfALIIIIor1Q7xdBrqI\nEHOrzQJky/E86wWdWpyJglVL1C7GyYK6OmqwHgeIk47qEho8YmqbjB9OM6+bJJaMjU9N/AgRwx/+\nj//O29/x29xx+2u4/kxBcP2NTwi2GJfYat4htvVjfrZ50Xae+tqfjulC59rNxzuRSCQSm5LEduLk\n4WN+8bae1ssRxrMVwSZ1o3l9udu9EkwBvesJ2iW4L9VV2jCttsL6yn0oo9hWH9NbAtGXbTt1xJ0B\nzSbntK7BjfpY2SWLMWzl/aixUbi2sT1CXelFzMa25ldaWQ0OqMgzgVJB46RC8mXAIrkh5MugluBL\n0AJMrBD7sBCj/2xshNMskJxMvrrXx334UT1hM9ES03SUrCMBjV/D14tTtWn6A1CtIHjUtp4qrEO5\n9977eOkrXsuP/tDTeOy/fnT88vgeqFaj/ac4t/m5N01tbIgNbsIwTnhgkv6y7URGLFSXMH4tvl01\nWmz22lufOFocdmEgkbhKSWI7cfLYTz/27LaaHOn92NduUI8RC5JjjceLjQLQ9eP3Z36xqgrtJisi\nBtEqVmbrRi7AOruN1NvRUEG+RBhcQMKIwEIdKdjyZ5uirjBv8ov9Sq5RKMGt1U17PFnVJ2iFzzKM\ndPEqqD0LWQeyU7UNJERRTYii2Ham27O9+U8r/DCm2hCvb6jfK6GM1WBANGC0jAsoQw5ITHppIzbu\nu96+c46XveI1XH/9dTz/p34IMRm4+xHvMbYE5/Ghgu4D5p9/e+KULRLq/U482zuZyJgCxRDEArXf\ne7Yqnri6SNahRGLfSGI7cfLYz5iw2ZSN2V9Wh+H9dn3ErxHcBRh/KXZQ7OV1VVkw6qcWBVPEZAe7\nEKMRqaP8BAJ1F8W6Eq0zwnPdObsVQBHbjQsJ2w1wGrZLK7kcz3xTZbddyJap/DJVUQEF2DN4qT3Z\n3bMQPIjUot/VAtmCEUw9mQh1u/V1TycaS4mGuC9DXTlWJs16VAlItN6EKlbVwxit88clDMGPpwkl\nrbF457vfzYc+/D9512/+VzpL10XPtytj0bwRvG4VwtnNLVBiUKnmJ73sdCKTLSBuOjHQ9qQxcfVx\nHBaFJxLHlCS2EycK9SXBVzhfosGxH90Loy2glmdX4v3eK9wAGd+L8fdTVOfxZCgjND9de47XYtVS\nsnh8thcXQ4ZhPIusxyQ7Oz819xzWJYuYArTuZhhG0fcd3O4mGpc7bhNbjAHj0ZAD3fi6cxpMB+xp\nyOs28mJj5R4m8X7qxyBVc2LxT7YwrW6rxte2Q1CHtnPFW2JfvYCOcGYxvl8r8IO4sFIDKjo514ZP\nfepTvPa1t/B//+xP87UP/+o4DnWWuRl/sTU+3S3FkNgO2LDZN3c2kcmWYrW+eTqTLCRXN1fTovBE\n4oiRxHbi5FA3tTE6IteSxk29p90L1cfFdc3LVkTboaE+2kXCChpGBHsaDQrBYcIQAwQr9UK/+jGy\nycEsEIg+ZLXdzZvUzCaLuAHkSyiO4ASVbL0tY6dczjVpBINbgbJPIZewrKHaJTiFhWug6GLyRVTy\nuIjQFIRYno6iXAqCHyCSIcbEVuiuH+8WrdBQe96zpWhdl2zalr68iGhzZ3mCXZxYaGLTmSJ+VvL4\nmZagGY1GvPjF/55//Y2P5oee/p2IX5s2qinOReuIW41Cuzhz+WJoNxOZYyKwVRV1Y9QNIYRkf7gc\njkJhIJG4SkliO3FyaJraNNWb2b/3gv2sDl3u4iWTE7wnlCPEjTEyxmeLIDmhWiOIAdNbl0oipkAz\nMCGb2EV003OZWeInTVORWmSbhTo+7wAeSzeCIThwfcbuIpRrhLAEdgXLGbwuRHuItYCvO4lmk0mS\nmiIuemzEtylQN0DVIQrYDqpaV7xrMeqHiPpoLalFskgeF2Y2E5VQAa6uokPTlAaiWLz99tv5whe+\nwBtvfSO5lVqgZ9N9dB8QrSPb3QOhjI6Ylv92w/uvNiEVKkTLuCg3VMfTb3wUFicegzFTX6LVIMZb\nTg1eicSRJontxMlBLOrHqMviD2rpTL6+Z+xXdehKFi+5NUxW4DkD40uoC1AY8H3ELJAZxYURuD7a\npFzUEX4BpvaSzfZne4TRv4Bfi37ozrVQXqoTQHpxgV8o0YOqkpoi+rHdKgw+h1R9RM6i3VPYURcf\nBIqzUK1hRNHOtXUjm3guzXWTUEJ1EcoLqKnbsmsdfWg7k4WvTSa5CHUXwwxFESlAMkRiW3et01cU\nOxXa9ZjefffdvOUtb+H2//RaHvBlDySECnQc7Ty1b3zbrpwwyUjHFlCuxXztpttks42rkePuN06L\nE3dG/XRS8HFxckjdQhPHgyS2EycLAWxOsAUathGRl8vs9rarWO2konVFYkIQu4C1juCuxZte7UH2\naJbjVGIVFzPZ/2TC0Cya3IrRPdjqPIgQxqMosrMlRGQq1g+6WmcsuBKDwdGLkYWDC7HKXFUY8WAs\nRgyhNJCfRjFQTC0/Wl7EuD7xacg42rVtd5rEUqeeiNYZ5KpgMjRbjoKpsZY0iAHTjSK7FXd48eJF\nfv7nf57v//7v5/Hf/gTUr9VecQMmw/hYVdedXAs/QkKJYOIiTG1ZKo6bAN0N+7no+SA47pOFg6J5\nOrnudSJx9EliO3FyqPOHTb6IyYbgDsDbuV3FaqcVrSuxp+RLaPkltBrENIviOmy2RPAlRkMtipVg\n6h8Hrj9dFNf4zTebEIQS3MokvUN1AFVAJY9NbUwB2SJ60L51KcD18eW94DKMyQiMULcSF0SW98Uc\nbdFoobYdIIPq0tSbrmFiLRGImdn5qdj+PJRRMPtBXAQqEv3t1rQsM3GR6Gx79ebBt4rFe88rX/lK\nFhcXedGLXlQ3AZL6XVI3HhrFRZk7GsO2pceuf33cBOhuMHn9VMGi5hhWO9PixJ0hJ+ieTlxVJLGd\nODns5Af1Xvsmt6pYNXnQdWQcsL7V94zH9krsKcF7AgaqEYR78Qs5LNyAL8/XwlFiBdr162ou4PsE\nP4zZ0a3jXzchUB/93sPP1ucikF+HVBfje/NronDfalz3w6vqR1CcIvPnIDiC5pDlOFWQEeKzOm97\nETqnYhVZy9hwRn2sItsOhMF0m61FngaPViux4qwekdrTbvLak117sdvt1Ou0Em2d63vf8x7+4A/+\ngHe8/b+x0K1/HJsi/mQOJcbHiZiK21kVr24WFNROvOdoiBX94yZAd4GIIFkHyXox9eW4kRYn7gxT\nEERRLEEKMMmznTgeJLGdODls94N6L3yTs8Jxs4pVExGHbugiKGrm7/9yfwG7PtaADWOgj3OKhCX8\neIEsy6iVHc6tTVM1tKqbs9RVVjHMtSOohzDEhRATTpqEDbGxupwvIhpQP0Jsd+N57ZdXVUuwOdXi\nNaCjWkwX2DDCYXByPWTLYJYg62H8AIKi2Smkuhi7JRbn8HYpVq+lrvJXK7V1ZFgffxUFuy3ipKO9\nYI/1kRkAACAASURBVKtpcT/vvIF/+qd/4pWvfCUveN5P8chHPHyaWNJYm2w3NsOhNa6zTOII/XTc\nsyUwCqbO92bDEtbEUSQJ7B0htkDyBcSupUZLiWNDEtuJE8WWP6iv1DfZCMdaAKntrW/z3a5YNdtu\nFiFOYudagmqv/IiSxXSO8X2IX8MUS0CA0CfItfHfNPvWaFsIrk4VyWu7xHh6Ds1Cx0Yk+xGZzQn2\nHILDiWKyU9Gi0SwElE18lvvlVZVu1Kh+hPEjQrYA1hKsicJZ8njOWQF+SHBriOSIrEWrTXYKGd8z\n8VYLEMbnkTBCwwBVjc1msjO1T3tx3QQiTkJcPXbDqRCuqaqKl7zkJfxvj/o6nv2sH5p//raHtD6z\nIQ2mmbCFEhPKWMmuc7nFdhDTur+TtzWRSCQOjSS2E4l2dbDNbv2A6tdVatWPNl+AWVe8Jy3OG29w\nI2B3uv+dWDDyU3h7Gs85rAxRrTB+BMVXxK6A6urEkbhgNJge6FqsTGeLseIqdQ71zPkKoGYRkfMI\ndXVbOnW+dN3me8NCQbv+3/vhVS2WwZzDcT+h14exnywIhYXpREIrcB5MB9US3CpaN4wRvxo7PmZ1\nBrn6eI7laiz4Z0vQe8D0CUbbOoLU5+UQ8jjpaF2fN73pTXzqU5/id9/z7vrpwpzz385aMImuDDOv\n/frJzex2E4lEInGgJLGdONm0xXH9ZyKcdvtYd4NwNJtXFDcRUrvybe5mcWVxBk5/JX5VIHiCOQ2d\nM1Fsu0sxKs/XCxpNjsoysdreWBOK6cK+SZfG+nw7ZyhdHxiD6UQBarvxT6sKPmnZ/v+z9+7RsmVX\ned9vrrX3rqrzuvf2bUm2umXACGQbCEgKz0QGmRALZFAcC4YTx/HwI7EtOSJEWHIDRsKYx0CAAVs4\ndgjYEggS64UdNHB4mIcHsQlYyCAjYzFEMHpAd9/HeVXV3mutmT/m2vW6dc6pcx99b/dZ3xg9bled\nXXuvtXbdc7819ze/L29K+o3IvbFKDOAmbKcjxt2YJB6qESLbaNUgTtBqC9GAuhrvBA1KUhAiIhMr\nzPdjixPAI+E6XrCgHpylTfZ2iWB+2/29TJ1Vzb1fkoH80i/9Et/7vd/Ld3zHd/DI8z4+x7ufMP/T\n1qNff3E20J5Q977ovW960QAXFBQU3FcUsl1wIaGqtzQoCvlR/e06Z7gG7aPOe43zaRXFdQToPKRo\nUwmGRiTuU4UbJBI62EPrS2g8RGQbJx4E4sxZwyHi59VpP1pfce+JsuuMYOfPqh8gfrgse3CNbQ4W\nCPeSPvksnLeJst4GRnRZpOPEZB++uUJCQPIYc9R6DMc4UaguGZHWSKxGVsxPLUoDVU3sGpzrULeD\nVAtzXH06klpzEnG1rQn23To4OOCxxx7jT/7JP8nLXvay+drcDvr1F2+SloVNosjT0JGjoKCg4BmK\nQrYLLiZSd2uD4lnkeBP0XsjnIYa368axqQSj20e6m6TpPow/gobLuHqXqA7a6+ZJnRsaNbZQDecd\nddmy7sTqs2vAtThXoQxw2pIWK9+Lc7tdffbtNFHWl8CN6PCWkOm3gC1CfQlkaBprqWHQh/gkJAYE\nG5P9vEKIqNuyBkgERg+Twhh8BdlX+5anI6k1jbs04GtUkxFiKr75m9+AiPDYY4/hnFs79HOhEOqC\ngoKCBx6FbBdcTKxrUDytynoeQpyruEtyiZNwJ24cm0ow4hg3vYboTTu+fZx4OILdBpUtlAQqpkeu\ndizxsR/PQhX7RMwqqxVRm6V1vGVuK5/bCKuk/CR7xEWEQwhH1CTj+SLgty0h029Z2qPfwhpCg30P\nUpMlHckaLJ2aZtt5nHaoG6LNVeAGpIlpu11j48kaaUmtkWs/sKZFMK9t1/DjP/7jvPvd7+aHfuiH\n2N3d3WzuBQUFBQVPexSyXXAxkYneUoPiKUT7XIT4PMffqRvHJsRcapJ2VNMbaHsNV+2RiOj0SRhU\nJEbgLN2Qeo8UjrLTSAA5AmeJkCduOMTPdMrAfC3jeGUc3nTbfWDOppuKxap4XtcT7RF7tNeAA5y2\nuKTga2KzC83DkMam1U7HeAKRCpMSmWuLU0cSI+GSDsBvoeJRl+VFfojLGxINh5Y8mZtLF9cnpc4q\n3K7hIx97gje84Q38tVf/FV706X/47E3YeXAvfMoLCgoKCu4aCtkuuJhw9eYNZOclxJscfx4HlDsl\nU9UWyW0T1aPOA11uVuygexzvnkVyl9F6b2kMTqdoUMTVpNTOCfUqyXW5IrxKosUb4V4Yu21uajvN\npoRztYK/iT1ie2C6a2lQnZDqPRg+F0eLhgMcAY2NyUH8ZVCHOkuRFNchKdg6pYBzwRosZ7ro3JCo\nnVW1/XZ2YalmwTXSPoGkQKp2ie0xX/PY6/jk5/9B/vJf/O9nuvW74im+ycbuqSLjhfQXFBQUrEUh\n2wUFZ+G89nRnHX8eB5S7Efriaqi3SVvPRY/AkSDcRJxH3Q7EIxQP1SVr6PNDa3ZUUCJQzyq0MyzO\nL7UnkmiTjmQfE00n+22fOYc5gZdwOCd1vdvJLcdXuZK+TRqI6bO7A5QpqhHVhEpn86swK8AkUI2I\nqSHnsyNVg7gaEY+i86o1QDcGvDWUmhjHxhmO0NQiqhCP+IF//A7e929/lR/9P76PmjEknVfB7xRn\nbezuVWjQKp6q65wHhfwXFBQ8IChku+BCQmO7RNq0b2xch/Pa023qjwxnO6DcjdAX8UBDRUcQb8Ta\nXUZxSDjA4U1KEQ7nsd5SAVMjyGkCbrTmnKyPnF/we16Sl9ypj3l/HvvwGXNuQBK1a3CaSFTQXUdk\ny8ZbbUG1TaquggbA2WbBb0PlbP7dTTRNSajps/1ouWqvEem90vuR5aq1pITolF/7d7/O3/l7/zvf\n9MbH+LhHfx9oh8RojjX9k4SzcBppPGFjp3FqTxVSd/sbnPPgXoUT3S4eRPJfUFBwYVHIdsHFRJos\n/2PcB9CchHNXk09ptOzJ0yJxOwmrUoyTKrmnITfsxakHnSDUqAhOIBFJSSGYE4dqypXpATEF0BZV\nC4DR/lx9q+Ni5Hx33bTLfjT3nV4jIzHCLXNSf17Eickwls63Br6xDYVOkAS2cQj49gnQjkQCt4fQ\nmuGKr0gyAHHW4JgmJhMRl6v+CwmRfQOsa9Buf07keglJmuDoOD4+5vVv+G5e9kVfwJd96ctAFE0B\nNGSfbjZroD1tU7huYxcOzSI95gZNZbPv2p3gXoUT3S4eNPJfUFBwoVHIdsGFg6qSYouEA4z4DZh7\n3S3gbj+G7slp3yioaSPSuVEl94zromOcBJSES/ukUJHYNj231NAMEY0z8mo+2S5HmNeQWpImk5h0\n12H6uAXiNFfzBiKgIkjqK+SjBQcSsQorzANfbnseYVnzfNLmIwWkGQGX0XAA1OAgxRbwRL8Nwz00\nJqiGNm8BwoGdP9zExymxvoLUW6Q+pTGPQ3JIj2iX5zIns+qGhBT51jd/P8fjwBu+/mtx1QjVYDIY\nrSxSnTXV/lXEDTaFi69Ta5+pKxuja+zJyaLWvY+Pv5uV3nsVTnS7eNDIf8FdQ0qJNNknTa9D4vYK\nEAUFTzEK2S64eIgtTqyKCwlN7lRd9bkfQ59E0nsim8+lm5CSs6QYm4wDIAaku4nGluRrYAQkcAGH\nIya1mHZxy7KDOAGX54KD7jq+u2E/imMQhyCIqxBpzFIvHBuR7G4g4qHatYDDxbGvaL43blTt9dLZ\nu/q0450bIvVVmCTwl/IcKsQLUm1bU2Szh7gKjcdoOLJ1ciBxgktTYjwwyQm6YOfYQTxGuus4tSZI\n0ZbUXodqG/FD/sXP/gI/8vb38APf93fZu/KceTU8TkgazlFpXt2WnLFN0eWodolTtNqau+/cS2nF\n/SbYi3jQyH/B3UM8xqVIpVM05NiqQrgLHnDcN7L9oz/6o/zGb/wG29vbvOpVrwLgZ37mZ/jlX/5l\ntre3AfjCL/xCPumTPgmAn//5n+e9730vzjle9rKX8fznPx+Aj3zkI7z73e8mhMAnfdIn8cVf/MUA\nhBB417vexUc/+lG2trZ45StfyeXLl+/DTAseOGhEpCL5LSCisibM5l4EsNxOtW3dZzYhp4tNmBoh\nKaqV8TCN4Kfgr4IMiX4L3CCfK5O5OAaiSSjIb/sK2v35NVxjLhzViKRqmuc0ASqIR7jUAUbIVZpZ\nA+VsHuEQwjFCsn8szyKA4o2w99Xx0whUtUViQHf8O0i4Bl0Hux9HbBpQB37Xgm6qLbS9ZjpuPwJX\n4eINVDwJQZNmp5F5Y6Z2hzimpNTh0piEIPmzAI9f2+dr3vgm/oe/+Of4nM/7gmX5yYIH+9Jm66R7\n6kcWEtQ3l56VbtrLa8SR9HhW0Z75fz8V+u0HBYVgPzOROmCw8rqg4MHGfSPbn/EZn8FnfdZn8a53\nvWvp/c/93M/l8z7v85bee/zxx3n/+9/Pq1/9avb393nLW97Ca17zGkSEH/uxH+MVr3gFjzzyCD/4\ngz/IBz/4QZ7//Ofz3ve+l9FoxGte8xp+7dd+jZ/4iZ/gy7/8y5/KKRY8oEgqaBgj6dga4aqVaHG4\n/cfQp5H026m2rX6GDauTS2N3IEoaXiFFBzoB2cVVA6iGOF8RpEZcPbPw01wFpuplCEb0tNoltceg\nijhF6x1oHkInvwvx2EJg/ADiMbiKpLUR9WqIZmlJv2Fw4RBNE5zGeXXqNAK46fqlFnyDHv1HJP0W\nGiLiAnpU4UbPQb1HJa9LOIZ4hMRDRCKpukxMO6DHJBlCvZvnM0E02NLSkRKo3yLEKRqOTIpTD0gx\n8nVv+CYeefR5/LWv/Or1Y7xF9jGebyLW2CrO1mXTQCUwzXrVGdGe/XClKl6kFQVPRyxu2te9Lih4\nAHHfyPbHfdzHcePGjY2O/cAHPsCnfuqn4r3nypUrXL16lQ9/+MNcunSJ6XTKI488AsCnf/qn84EP\nfIDnP//5fOADH+ClL30pAH/kj/wR3vOe99yzuRQ8zRBbnECHB80EZI0O9rYeQ59E0hcrl2dVJ1er\nnIvXXg2KOYmcLozDtNhKlcYkadF6h1g/DGJR5okaqtH8WPFzzbZG05WTXVOaKxbWkibghkYEwyEO\nncW6q6a8dor4xnyoF508IDuYAFjTJt01uxf1GcmKZ92HXk/dXod0gA+HuDaBBMJwD+iowoRu0uuX\nJ3idInEM4RBtoqVEpoHZAbpBrtiHhYtUiExApzhRomybdjvs88P/5P/mF/6ff8W73vVummbDsabO\nQnb6+a3e002+eyvfGalG4BeessDs/jzl0opiwVdwN+G3SG5EkENSNSgSkoKnBR44zfYv/uIv8r73\nvY/nPve5/PE//scZDoccHBzw6KOPzo7Z3d1lf38f5xx7e3P7rL29Pfb37TH3wcHB7GfOOYbDIcfH\nx2xtbT21Eyp44CB0OFfj8i/pdFLz4W0Sg1scN86j/z7r2E0r7oubBVWQrMtO+ZzDh1BxgIMqV28X\nz7codVj0AI9jpJnLsVSjVYfTxKqoUqOI6bTjFHpLwFs2MzWkqfVOpoBSWeW4d2u5XVLWr830Yzad\nFJF0hKqD+hJ2wSkSb6JHYyAYMU0TQvLgO5Ns1Hu2gchz1GqL1Ee5V9uk1EDYJ7ltqIaQAv/hN36T\nb3nTd/M3v/YxPvETP3Hzsc5CcvrXp1Sc1xHXcGibhV5CAsDowdAtFwu+grsM5xxuuIcbTIldkZAU\nPD3wQJHtz/zMz+TzP//zERF+6qd+in/+z/85r3jFK+7KuVWXH6Hu7+9zeHi49N7Ozg5V9UAtyT2H\n9566vjiP4arKwk5c5elnHfwW7i6sgcYWJzqrBCepEV+jIeB8bd/B1JFoEVeDqxFZJvr9sT0SDqnm\nr1UrSLVZyJEAhzhdey7yDLtwE3EtdeUJ9YjghqBT6uYKsdrDiRBEcd6h1SWEgE8T1NJeUFHE16ZJ\ndkOczqulUUHw+OAARUUJvqGqRsB2noNfmgNAkF0LmJke2v2od6mcIzkB7245fuN74BSnLS0VVMqY\n30fHk9B8IoyeheiUGFq81mjVELUhhgOcCL4awOAhXFWTvOCqLdBEckPwW7YZ0IimFicejSN8OCKl\nji56Xv/Gv8Mf+4I/yn/zp78CX8/v95zsLt+jfqyqNWht6+RHJ9zLhe8XttZJsteLiziZv6feLfy9\nvr9/t8/6Pt8t9L+3y+/vZz7Kvb4YeKbd3wdqNn1jJMCLX/xi3va2twHzSnaP/f199vb2Tnx/8TN7\ne3uklJhOp0tV7V/+5V/mZ3/2Z5eu//mf//kz6UnBMxcpJS5deRS0tfCTZgfn3NkfPAPaHSPMq86K\nR+otNEwRbed/ugbxA1QapBosnyMfM3u95pjzHAfQ1seEaU0VJ6RqQqx20O1LjC4/gqrH1xXqh7h6\n2xoZNZrndj9e8Ui1ZT/zDcR5ddV8ox+CcEQKE1KMIDVeglWH6yG4wWxsqgqxJU2v4+IuKTS4cAN1\nHlfvkNw2Mnr4xLmceQ/y+Q91Sjf5EHU45NLgeXTbD6HDEcPmMnHcUPtIlAFOFJGH8ZLQehvZuoQb\nXbX1aPay7KdZJsl5XVLK8+6mfP03fxdPXrvJj/3Td/LQw78fqQZn3qN+rHN5UbOWZM+OX/P9AiAO\nFhJJPTSXb3v97jbO8z297WvkddTumMu7W2euY8EzA1euXLnfQygo2Bj3lWyvVpsPDg7Y3TXN5q//\n+q/z7Gc/G4AXvOAFvPOd7+RzPudzODg44Nq1azzyyCOICIPBgN/5nd/hkUce4X3vex+f/dmfPfvM\nr/zKr/Doo4/y/ve/n0/4hE9YutaLX/xiXvCCFyy9t7Ozw/Xr1wkhcFEwGAyYTqf3exhPGaqq4sqV\nK1wfR0JQYJr/u330FUyNY5xGVEwSkcQqlf1rDUdWmZQGkYNc8R0tnUdjBynrst0QOYE4pO4YlyYz\nopbcEFevl0h140M4nuAP90GPSF5Rf5OJXCEheF+T3BTkeOYn7TSiKeAlkVyDuGMS3qr2C9VaVavO\nkjpiu4/EQxwgKMHvIMNnIdX2bA4aW5y2pPYGPk2JKSIkok5xjSc5hxvfvGOy1IUO3A67o0tcmya0\nCyQ6OrdHSgP85PfopM2688aSJTuB7iau2wZf46qjW8677h79y1/4N7z5H/wA//Af/F1CDPze40/Y\nk4A4wS2Q49X7vQ6nVcP7tZudT0yOIam1jWOuwkslDIfDB+Lv9VnV/btyjdhS+8iVy1e4fv0Juuit\nV+AC4KL9/oaF3+Hl3+pnNPr7/EzBfSPbb3/72/mt3/otxuMx3/md38lLX/pSPvShD/Gxj30MEeHy\n5ct86Zd+KQDPfvaz+ZRP+RTe/OY3473n5S9/+ewX9stf/vIl67/eKvBFL3oR73znO/me7/keRqMR\nr3zlK5euv7e3t6T37vH444/TXSAdWFVVF2q+PUIId2/esyRFiKkDnZoO1wkSj8yizjVAk0NV7Lrq\nBLS75Tw9VIPZ1K2dgLlgzD5aCfEkyUCMEKYIAVTwKRLShDaa/CREARUkHc80tTF1ECeEFMBNrWGy\n2jF/6cUxusaSJuMUuiNcPERFUKlJdBATsPAPYk6A1AgajtEUEedJ1RWUEUpFuhv/gHYt+MvE+Lum\n2Z4K1M8z5xAVhAHoAGSEiMM7R5ABuBEx2b2LXbeskYa5cwiARq4f3uD1r389f/a/+zO85HM/hxQT\nxCM09kR4fn9n93v1nIua6tXvwJLeXSDJwvGZtCYBrfL5GgiBGOMD9PdagMp06ekekKM4weW/JzFE\nQuhsTS4ALurvb7jLv8OfBrjI9/qZgPtGtlfJL8ALX/jCE49/yUtewkte8pJb3n/uc5878+leRFVV\nfMVXfMWdDbKgYBOshtWkzjTZKz8/s2HtPN7e4kmuYea/fKaNW4vQoeEAbQZGwOs96+RfaYbsaYqC\nEfQ4MY/mddZ8eS4izvow++ZQqe1nqV2ea9/g6WoiDXgwHz7ubvOcHwAma0l0JHKFtR1DaE3nXu8g\n1RBNnuBH4M3GcLFJdCbPiOOc+JiQNM6uK543vvFvcfnyJV77Vf/TcsU2TphF3C82mC6S6WjnkUXL\nv7O+A2dZCZ6G00j+0xniYdHWsFgaFhQUPGB4oDTbBQVPS6w6hKz6vq4G0Zxk/Xceb2/xy8mSpzpY\ndEBNTMdG8GJrxHnRy7k/54JzBCmYI4d4EsGiwv3Q7Af7uWSyLqlFq5FdA4DaXE76QJX+Ov2GI3WQ\nXU1cak1yA+bzfTfIn2sgBmpJuCQ4vUY4/iiydRlEULcF4nBSEwe7OD8wmUeOOCeObYx9CIymvI4K\n4QBwvOOf/Rw/+dM/xzve/sMMhlsW0pOj5HENkqutS+E1cZJdWPK9XpRY9P+d9h24HRu9VS/vdST/\n6Uy4XWONoXiT1riLUdUuKCh4+qCQ7YKCTXAayVlTsdaVKuJSNbMn3Hfi7X2eYzVZyEycQGiBGzB9\nIldfFz63eE4/MiI4k0HMq4fZA2P+ucUqe7Vn5+z1ubMxLIf7UOU16X3DZ6T2LqUapg78gMoPce4A\nujH4CT5eI8guIgPw28TqUiZrdW747PJwmizjYe59nWyTobHlQx++xt/61u/h9V/9al7w/I83j+44\n6RdkeSz9nFILGoz0hn00TCzmvr5k53XN6V7Yt2Ojl20BNXX29GE2noUxPgOSJMU3SL2F+KOSKFhQ\nUPDAoZDtgoKzqoWbkJzTXveEsq8AS4WIP/s8Z41r46AdB9113PQ6Eq4DU7rj34HJxyCH0awdR71H\n7MA8wwd2nMblinovI0mt6blFSJU1asppFdoZsU9GahdlJncDrobhVbrY0aLZY7sidmOoaqJu5cr8\nNvghkq+rcYKEg1xlriyMJ1ecVSyOvguRv/GG7+KzP/OF/Ldf/gpbkxzKI35Ikmb93HNlOYUjXGpR\nEQRIaWKblP64hUj3Jc/xTWVGqUUDVmnPGnk7NoL6W9e4yC4KCgoK7ikK2S642NiESPekZ/Fx/3nQ\nSwMWQ0z6856EdUEld/ioP8o2+AhsgUsQD6EbWcNiDvhZWgvXwODhZcIfDm3z0L/uJTLxGE0tQgK/\nDdXOrXrlVfTNf4ua8duZ4+qmJBxadbO+RBo4aAXGv2vzTRHXHZLqh6HaMlK+KPMJB0jKPuhMibna\nTGpxaQx4/v73v4MP/faHec87vgVf1Uh3A4kTEEGSA1eh1fatcxdv9zRNTd+drQeTVHaP12jFl76T\nm8iM8mcFZ08uZv0CtTnNuME8EfSZotkuKCgoeMBRyHbBxcYm1UKNc/KTJucnKeet4qZ2qSKppx27\nCeLEyG/jYNwgrjKJR5hCNUUiqFS3as17OcniuMga5GwRiGugvYFDUT8wt4m+Gru6Pvcitnu14bC3\n25OeXHpAIFoIkOg+XgekdGTWiq6Zx8tjrizJNYg4wNt8skY9pcAvve/XefP3v503f+ff5urDDyEo\naEJQIo1VyF11YoS0EecajRGqmqSgbri8Xid9JzeRDuVjU3to2nJxpGo3S3yGJdq6oKCg4D6gkO2C\nCwXN4RcaW8w1w9/a8LeKXpMcJ1honyw3/W2C81RxNTKL8J69vgOynYK5g3QOGKD1NvirqBOc2FxI\n7frmx5Vx9Y4rsNCUmV047GfVnKAvVsBPqtbeaZx333CYx6ZZyqIO6K7j4zWq8CRJ96GboE1NooGU\noLsOoiAD24D4IarRKtjizYUldTlGfsz+/iGv+7pv5yv+1Jfxx77oi4FkGy+/RcQZia62Tya0ve1h\ntWuplJrQZvfW40+rYJ+1NuKhfQKJLU47kmYtfb1XKtgFBQUF9wmFbBdcHCSLuxZiDmJZsJxbbWpb\nRO/8oRFRh95JM98mhCcT1ARGlPzwzoiSq2F6HecicEgKFbRPQryKdvuo35pVtTUcgU4BN5dXLDpl\nrCPj9SVinEKaWEiMH91KoE+q1p7H7nAVCw2Hmnpvc4uiRyN0h0hlgTsqijY7CI7kt2dyE3ENKgFx\nYhXmasesoFMHKogeQfskjsg3vukfMWgavua1/6PJQNxo7l7ihyDVyfdqYaySJTq66AizdL/O0fy6\nBhrDzFJRqvr25TkFBQUFBXcFhWwXXBxoBNzKa25t+FtFT356v+kep8lAeo32qm53EynFosxkE6J0\n1jnrbXAOpwraIfEmUY+MnArZPzpCt4/XFk0Bpx2hTTiXLfHEoeJt/uvmXW2BDm0c7Q07d9YGk7r1\ndoj9n5vaHa6ibzgEqxKnANWQGMlVc2iPPwbtPsIQ9c8mDnaAMJOPiLZmBcgIjccza0apttHJx6i6\nm4Qw4T0/+a/4v97z07z9Ld/BcLRra5b/m7lfrM7xlLGucxpZuoe3S441QrWF+IC4Sd7s6PJThoKC\ngoKCpxSFbBdcHJwUfrEp2fPDLO9IJ8sdellE/tOizpvZVTeWTJzDQ/nMc9aXgCGxPYbQQT0EHIQJ\nOnhWrmAvJvtF0A7aNsdeO5zzRGlwfst053izuusr/jNJyJiUpjgRc9kAqzajVgFe3UCsq+LOLAHl\n9Kq++Jl3tKl7OvtMtZUr00olEcX02owehsFlCGOEgLraminrgZHu2KEcgE9GnDWhKfKRjz7J13zb\nD/NVf+VP8al/+JNJ/ZONOMl2emruIovz6eek0ch1mmY9d5bg3Kml30nIDivJB6JYQqh5fsfTbScL\nCgoKCu4ZCtkuuDg4Ifxio0f2J+mV1xzXu3OAglbz9+HOXE1Out5prwFu/HvgEB1tw1jA9zrhgBMQ\nESJGzFIUNIasUwaXrpNkgGQ7v9nTgGrXSHcvM+mJZZxCCiQUxdwvRJxtPOSExsHVCm84xKUWtEPD\nIdonXa753NK9q5p5+mV3E3Q/q4MqlAVJzOhhUgwgiRglz3uCJ6BJSK5F1XzCu+R4/be8hU/7wx/P\nX/gz//Vyc2hPq+MEtAVVm0tPwlOLxCOrgkudnwqskZrciZTmhLWUegeGW1n6FDezndwU96LRmmcc\nzgAAIABJREFUtaCgoOAZjEK2Cy4U1oZfbKqj3qQCnp1LFLVqpSxIQlYrmHeDqGwyrvA4vr0O0wl+\n+v8Bv49WxyC75tiB2DlCh0oD1TYx1uACMQoqQkoBqhFzmimzqjZ+hIZD6PbR9gbeKSKeoBXi3YIa\nXm8d2yr6SrB2M3I4C985zWt8Mf0SIAZ8UioveB0jUhOc4InE7hBXbyEyINYN9mtQ0WzbJ5qs6l3t\n8n0//JO8/9//Nu/5wW/EN30K5BHaN4KGQyQe5wj3senF/Y4Rak2ZmCsivXa6vnUedyKlWQfXINUI\nOpYlTbCZ7eRpuJtV+IKCgoILgkK2Cwo2waZNa7M0xYooRhC1J4oa50mL4jYnVauVxJXXZ44reqR9\ngjD9PSI7UF0BdVAPkZSQdB06SNU2rtomVbuIMycO3ACcJ6UsSVAQgslMUmtNfu01XNgnaYcQSQkj\nm36EuqERZnEnx9SvrJ9VyPOTAddk6c4Z5HB1HeodYn2ZKUorAs6kHHQ3wO/ZGKvKPMHFgw7Q7gZo\nQMUCfN7/q7/K3/lff4Tv+MbX8pzf/1x7UCEOh5JSB+LROAWBlCLqFFINLj/d6MedJraxq/by3Fb0\n03fYELkOqT2A9sAcUvJ37q6EB93NKvxdhKqiYYqGsTnNlA1AQUHBA4RCtgsKNsWGFfCZOKW3glus\nvi42Yy6EmJxItFYrialdikDfqLI4ukzYei50+5AiBAHMjUO7A9Mru37cCZpnmTOH1KRe7qLRjksT\nJE1NEgKmeW6vIQQkdTgNucmwJvots5w7rdFz3dxdTZKhEfq8YdmIHK5IMyqnVM0OHO6DJHw8xKUj\nYqVQ7+LcwJocc2iNuiHktMzJZMJrH/sGvuzlX8QXf/EXmTzGmQRD1PTtvauIKDhfowjqBtZIKubv\nrdKgkp8HJNug9M4296wq3F5DfIuLHaSaVO3YfbjT8CC4+1X4u4XUIdriiEjqSsW9oKDggUIh2wUF\ndxknWgme0Ax46mP51crhqrPHJpXFyRMwvYZLB0iaAJ6Ypta0h+LjEcREFG+2eAg0V+bnz57TdNYE\nKFKD1CbzCIegCQk3IUxJRLR5FpC1yeu01gvShls2DrnZUgdXc4iO3LY7R4yg2oGYVCa6HZT8Oh6S\nUKs2Nw/Zdes9G4oq3/It30oXIn/zsdeazrrKKY8aSSw4rXiPJkfSDk0JIUs2vFWxxWcPb7Bq+KKb\nzYKOf+Z1rtHI/+2Gz6QWwjHisxe843xyqbNwD6rwdwUPaMW9oKCgAArZLii4u+idOfqXZ/2jfxZJ\nWK0knmShdxryMam6Aq6F+iGoRuB20LhP1NwcSW5gXKzG94jjPrsGEc1BOQo4RMfEGFHngG2od4zE\nrpONLGwuNE6yN/ZCcmJfRYdlCc55kQJeOjwRTyAhuHSEF0cbxlTuJhHAb6Httfk6u4af/pmf4/98\n+zt52w/+I7Z3L81lP7nC3ieIzp5M9BsFjlCV+T1aeCqwOP/Fc83mvboutztvjfn6YeX1XcSDQrAX\nsfr34EGpuBcUFBRQyHZBwXrcruPCaYmU66rYZyVYrqkk6nnH5naAATABFah2oXoI6h2EMZK8NUY2\nV+2c4SgnSi5YxIlHFdTVxORBnDUROoV2DFUDDHFVlaPfGyOjq57jqZs36a1qsTfVoG8CPyDEQJze\nREmoDInaEF1tuuxwjEqD1C10HVS7qCaeePImj33tN/CqV72KF37Gf4LEMf2ziplt3irCoQUmOav4\nK3mT5UdotWPkObW2RuEI7a6ZI8xwZz7vpXXYQKN+Elat/6qtixHR7mpUGhIedfJgbggKCgouLArZ\nLihYRWqRcDgjfCcm/Z2AE2Uk66rYvQ3baQmWq9c+L5HwwOhZ4A8hqDVIDvaAiPpLRDcAGYCvrYKt\nUyR5kkYjan2DnXg7WTNcaGScoOIRGSHVMHs5z11BJLVoas2HekakmVVuZxuOlYbBuwVRtZUNU6hT\nrpoLiOIFdPxhtLqE05ZEw9d83TfwCX/w43nVX/7z0O0jfXS71OvdY1Kbj5uad7ffBl2wdewr1HGM\ndDctuRQhpbFJcPL6qh8tV/pvtzK7av13QUiniCDVwFxYtLvfwykoKChYQiHbBQWriJPlCnT/WB/O\nrngvBLzc8tlVJ4peMnEe2cntIJiHtKhCPCSkMRAhBdxgD3SP5DxoBXqE61pAoepMrwygAZcr0kqu\n8mbZBdUlNI6tyTAF8AkJhxYDn0OAZvP3o5kM4xZ3ldTePXIYJziXZTHxJqgiXnE6JbkBUfaMlEVB\n/BQ/vclb3/Hz/OIv/Rv+2TvfRkWLpjFJU/bJXiHA/ZjDkUWwi5hHdwpQrwmNEQ+6GBzk51pqWNjU\n3AUt9KL1X0FBQUHBfUch2wUFt2DVDzq/3sRjOMtCZvrbPvglpyJq72vdf7YnbYufv9uoLs+cMhCL\nbGf6JIw+jqSA82aBF6f47ggXDhEikQrqyzOf66Wo8QVnFdWIOA8xUaVDYhuROpgWvN7NhJuZU4uu\nkNbZmp6VcHge+YxrUKnNYVEcOI+6IVHyGtQDJB6jOXDn33/wt/mW73oL3/i1r+Z5z72aK+AeRBA3\nMNlMP+5waPIS8Wg4Am2zw4efu6csjjenYapi7i70ftv1LWMuKCgoKHjmoZDtgoJV+JFJKPrGuF6n\nu4njQdYqz7ylc6IgqcXl43WRuN0NjfJZJHR0leRy46N6i2sXAabgL89j6MMxCoSUcCSIbba8S8hC\n6uFMTtFrzcM+qtjnVcApkjpwaRbRbrVtmVWvJeu4tV/jsxIOzxumUo1Q8UQagtuiD8mhqlGx0BnV\nCtF92vERX/WGf8AX/dEX8V99yX9mvthEIKJkDXo//9Tak4/sn61Eq+bTIlLBYDSTzkhqIezj0oTk\ntlFXo+RQG1dfDC11QUFBQQHufg+goOCBg2vmrhyLeu1NHQ/8CPFDBKwC2jtQ9JhFm4/n0omTqrln\nIZM6ycmVLKYo9ohHUO/ix/u49gYyOYLqshFp1OLUXQMIIjXiKiPLqcWn4xm5VfFL7iAKaDxCYouo\nxbRrnKKqJAT83CNbXIO42mwCl8ao83h7XWiePGtjc5bcRiqgxkkEJ6Y5Dx1KBd7hicjANh9v+vvv\n5Pr+MW98/Z9Fchy7qqBuBIS8TgvX7YNq4jRLaQa5QW/BN719EolHEKe2ljq1X7bOEjr7RNF7BVWd\nPU25l9cpKCgoKDgbpbJdULAO64jvplXomWNImhPy1OZo9Pm5Z9Xdk663CTYhoeEYmT5J9AFpj0xO\ncvwh85UO+0g6Qv0e+AFRt0E7kjrwtZHmPu1y0Ymj15pLhXiPBkt8jJgbhspw7rRyhgOJ6dRdrihP\n7P3Vqu95w1RSCzJF2yOqbj9LYhpq6Wi7m6Q0gTryC7/4b/nH/+Sneet3/lUu72zj6IhxCs1DSDzC\nxSOSGyAhV+dTi4QDNHWoCFAj9VbeLEQIB4gboCq2rrEFCaD92ulTE3d+3icBt+u+U1BQUFBwJgrZ\nLig4DzYlIuJNegGZeC9Ej0u17D0SJ+cjOovEaBMS6rbwx0+g04+iMaDNFdMZd/sgitMJqVYYPARu\naETTTcF50zsvekovXkejzSVmAhonJDeyc/htq2JrNN36SQ4kfYgN5KpxukUxb3M4p9wmddBOgAPQ\nMY7aNhY6RWSIuiE3fvfD/PVv/D7+0p/+Aj7v0x6ma/dJ1da86hyOEU1IisCRxb2jtkmSXk5TofE4\nj3FotoI5hVK7MVqNCEnBDfPxcykN/XzuBRbDc866znmJeUFBQUHBuVBkJAUF9wIL5FQ0gh/MpCW9\nhhvIxDmcLgNZxKpsBCN9qxKP5c90hGYLsM+46eOAQ9IRlU6o4gTCTbO5A2uoHDyMVpdIsuCXvShJ\nyIEzWl8iJoemqRmYMDXphLh5Nbsfn6a5g0kvm8nrJHFq6YuunsWZ34LzyG3Eg3SQOpIIURyxE6bq\n0eoyrh7xN7/jB3nO1T1e++f/CxQFSYgfZT/sQ1Q8SRprqExTUIEUEFGTxfSBMW6EpKndV6lmc1e/\nZZuO4cNQ79n96m4g3fX5Ot6r8BVZ+dV+2nVK+mJBQUHBPUWpbBcU3Auk1qQVvQRDo7lYwILf9NzZ\nY4bbSZxcF7SyNJYDqBri8FFwx+B3ALUQkNghKZi1n8bsuZ3HjFXjJbVIHJNcM69CLxJ7X+Fah0pE\nYzCi2jw0G5eQHUtmeud2HkneS25QwCO9hvuOmwct3dL5AcIRXjti1eBdjUrk7f/sX/Azv/Br/Nj3\n/3Wa4Q4pViA7KBUONZLtG7PyS5McPb8F8YgUyf7oFfgBdDfw8ZDkBqCOpLYp0FyBF0C7A1yyBlRS\nQLsbFiJ0r9Cnb27yJOC8Ep2CgoKCgnOhkO2CgkWEQ5MgbOoWsU7r2l7DtdcwQust6MTVaDhAyQSs\nT1gUv9wwuI7onFc2soouIOEGhAOTCVQVNM+DepeUpiRnFdiZPlvNfUS7fSROADH3kkW/7KWxgRDR\n7ggnSuwOkfFvo/4yuv3oTB5CmiyE28icsIs3d5A4mW9ANvU1PwmuAXeZ6fR3SNNje4S3tYWmKR/6\nzd/ijW96K1/3ulfzB57/QjrGkCoY7KG+D9apbN7VNrjLC+No0Hpk349Zxf8YTcHurc/z8sPs1pJQ\nP5xX8CHbL4o1Y6b2nsg2RM6Roni3UjsLCgoKCtaikO2Cgh7hEBcO7f/T1BriTiPc67SuAN0NXBqD\ndsQUoY5IX8VMYyQ6O7av7ObPryU6q9c4T8WyR7OFVpdguGtBJ9VDUA2NEPoRUEM1QN3QyK5Gk7ak\niTX+4c3Rw+8ZGV9cE41QbRH8HqpK7I4QPaKOQtBA6vag3rs13KZvlEytrXuagJjvdFpoKr1tLbGr\nIdyA9iYwhdjB4W+C3+K13/wj/Oef/Wl8xZ/6kjx/AdTWQ5P5pItDLOg9j7Obb2xcPZezTJ8AKtCE\nS2M0eLS+bOPOx9u93iKlKegUUoRqwWP7rKcZT0XzYiHYBQUFBfcMhWwXFPRI3emvV3Gi1tVnX+cO\n0YSm7FLRyxN6f+nFUJtTEilveX2WbOSWcwCa8BFUhVTVVrmVymz+fEPqfxVkkkk4mOmUVTo0OpvW\n6rnFg6uQwUOoHyLpw/jYAgfgnZH15ooNQyGhZqmXNwyi0QJ3FJSUPb/9Geu7AcIRjJ+kYYKmSEoK\nccp3/dD/y4d/9xo/8N2vM436zNpRbV1Th+aNgfYVeU04FNWAACl1cy9wALE5gJDUr29OrHZMLhPE\nNjquWtZtn3T/S/NiQUFBwdMehWwXFPRwdXacWHi9ik0kHX5A6DwiCfVXoLlkDYTSIL7Ouu0628gd\nzs6ni57ei+e8Yz2tgtRoNUTTBDo15iuVeUT3wTKIyV1m1xVcNUTSdFZRF9csR8q7Buq9/BRgD23H\npOl/BBKOA1I3gSbb/1Xb9lk/J9t9lVt6WUYvr7nTuYd9qBtox1TdPornX3/gcb73R/41//Bb/xyX\nLu2RtJpp010OolFNOXGyyaE12PdAAQ22Zn3zYZzkQB4QPzBLxerSrWR79r0YzTXvfbS9q2ZSorVE\nujQvFhQUFDztUch2QUGPaid7Ka/RbGc3DundNE6SdPS2bs1lNHVQ7Zrul+2Z97b2qZRxMq9apokd\n31xZJlw9OYsT1tSVN4MfQjUicRWqFmQXfB6v82hMIEZ6XTxC8eakIQ1KQN0wk+HeK3uB9PYa9/69\nZkhKe2icoAzAKYQjnLg87+GscXC2cemj4KWa67jzz5ZsAs9T0VUHEgjuWYRh4OgQvvrbf4I/+2Uv\n5o9+1gtJ1RVreBRnaxstdl38tjV5+i2QGtEWjdGkLW5oc5iNI9s51pfQ6HI8fI1WW+ulPr3VYX9f\nxZtuezbmNUS6NC8WFBQUPO1RyHZBwSLWabT7KPHUIRrmFch1ko7eN7q5mmUCcguBnBGwbt+cLmYE\nrDqxwik90b2dhjo/BKmoidCN6ZoIYQrpGPWXczOgVXg1dahObZPQXM5VbDGvbBOYzK8dDnHd9bxp\nmBCjIu11Kp3iHAQJxHAIWEAOixXrfJ6ZXn2xqr8onYA5Oc/X3KiBtdqC6gohHaLVVd7wv/0M21tD\nXvfX/jQMngXNQzMph8RjCDdwVNbQ2v9a1Nbukauhediul1qTmmTdtqQWrbZI/X2tdk4e16o+P891\nhrUe6aV5saCgoODpjkK2Cy4cVNWS/eLkVgKzTkPdVxbFZTlB/3oNOcqpiTKThmzPz7N4nXBoxFlT\nli54s5FbvN5swHcoJRCF+ipddx30ELpjGEVoD21M1WXEVRDHlpiIQ6KQ/AjqS7eS3756H46NbMZj\nXJoQwxRHIMRIJZHIEFd1JAIkscp9femWyv0tOGm+52lg1QTTfXz8CO/5yd/kPT/3H3j3m/8qo9Eu\noRohBCPVcYq6CmWEMLWqdtVAPMbpFKdTUgzo9HE0HJoHeCbdqnGu6653l+0QT8LKzzdNJC0oKCgo\nePqikO2Ci4fY4rS9NS79pGa0/lH+OrnDGpjYQ9b+DMiSlEkOP7GKr0q9LDdYxJ1KCWKH757AhRvQ\n3iA1U9J4B0bPRSeKDBIqTZaqtDhXId2xNU2Kg+7ArP9mOuvc3Cn9HAW0s8AXDagfEl0Ffo9U7WXP\n5+H5AmnWzXe1YTUcr5eYpBamT0K4zu89Mebr/v6/5vV/4bP55E94DsHvQtUYqXZiriMCqd6C0Ddo\n1hAnpDwfoTN7P72C8x1JO0RqVOzXpyxIS/S8G6F7QaTDIWkyhhDvgl95QUFBQcGdopDtgouHkyqn\nJ71/ktxhEX1FPHVW/exPsY589U2BijUkijciKj5XSuNcXtBXyF1z+7ptqYjdMdLegHgAU4AP27l2\nPhnXPUl026anDgEhoTKAeIx0Vs133Q0SHql354mS9SVidutI3RGINzeOZicT8govieSHRk7XNZyu\nrl/fJLkw9/mTgYUGVu2s4XR1wzT7XCS5IX/5236O//QFV/nz/+UjJBep0z4hNOjoqm0kXE3SZPuF\n+qG5Pzaa9xI1Go9JbsdkJ9rZEwG/bVIbV9/ZRuhu2/rl6r+rh7gwOdu+sqCgoKDgnqOQ7YKLh3WV\n4/7Pk4jTaURooSKuGowPr1apV11MwEgezHW+aV5tJ45RmEWXK3eg2xYHbpuEMws8PQD3bNMkxwNE\nBog0qI5yhb0CtwUqmeBD6m7OQnjw23O9enPFNhj1HpqOkXZqenAn4GuimquJ1qdomTe1t1tsYFW/\nrJdfvW/S8A//yS/w737rJj/2976QtPVsUE+cHqA6gpHma8mCnr5DomnCtRqhASJjcLtI3aDiTFKi\nHtFozZPUloa5SRPnKrG+F7Z+57WvfIZAY4t2xyYPO+2pUkFBQcF9QCHbBRcPviFJg8pKWuHtNqOt\nWOFpnMyb+E4iVflYZjZzrXlD9w4XuTFxhv586655FvL5k+YodLdjwSpUph0XMTeSpjYnEtfLW5IF\n26QJPk6IfgunLTEcmE1hf27X4KohqWtx2hHDEb5qUBRXDYi9zvm09VuzGVmL/jwrOvLVjdGv/uY1\nvvsHfpbvf8OX8vBz/gC0+4g8Qd38fqZ00N2wpsd8fSEicULC1kUE8B4NHga7lg5JQv0eNE1uJGXe\nFHkW1n0H7oWt3yb2lfcKT0X4zgnXdaIIEactpHOkZxYUFBQ8BShku+DCQUQQ39g/yqs46x/pdYRi\noSIuuXFOUEia7f7i8mdVkWprdkrN+m1F524kq4RzlTSdy3P62Ih8OsjE+wiCwgCQEcFfgvqyadEH\n2yZxSWNUPck5iC1aXbIoc6mssXBxnaotUjy0OPo0BRzSXsvNhKMFbfcJa6jxlpTME7Hw2SV7PTD5\nh3gmbeJ/+etfzyu/5LN4xUs/mWsHN0ixJUlH6vahfggUi6SPE2tojQdIHjv1NprUpDB+C3GDuf+3\nRlxqZxspPS1gaHGe64j1vbD1y9X/hCdV1VMnIbmf4TsaAbfyuqCgoODBQSHbBRcbMwK8UFU9iSSc\nRCgWK+KaEHSuJY6TmQ54JjVB5n7c+R3yuUxYItmbO2u+ex1zbqw8t247HUFV4WSLpNetsl1X4EYw\nvErtHUHUCKy3kBtxQzS2OOdI1SWEYJ7cMoDm0vLaAeq3gcoq5mmMxrEF2nQTcBbJjmtu9SoH03q7\nhlm4zkmkc010vaU+Lr//TX/7mxESX/uaV5L0SaKokeJ6YI2R7RHs9Bsll+UjE5x2qDSmP88hO+Jr\nJE1QVRiYnWNKgaXY+kzy++v3/7/2aUaP07Tpd4pqBzccgY7vzvk2wf0M38nBRMuvCwoKCh4cFLJd\ncHHRk7T8Z+oTEuF8lnSLx6cWCeM5gceBODQFS2+UZh7ssiiZSO087OQUp5Pb0m2nCtIU1UyO622o\nr8DoeeA9kQYlS0fiEaQAOgW/jaqHqsmhLs3c33pRpx4nFuZSXyF1T+DiOLubTC32vdlB2tyEqFbo\nXvIqF7/cVHoSWdqgsfUnfupf8PZ3vJO3v+V7GG0lkAByBFVE3BDIBN2N5v7dmohURA1GnL1Z+Uk6\nQkMAn1Mzu5tm0ZifSmh/zwCN49n9QyM6S+Xsb5yfVcZXpUvnxv2Sa5yG+xm+4xqSKIonSWP9AgUF\nBQUPEArZLrhwmPls9xrpGWnLDYvrqnLh0OQYpHlFs3flWCQ+4lG1RkmXIkiLC4mUOrxGkphkIlU7\nc4LS+zUjVgU/iUDdbvWwslh2HeyCjAAHSc1rWmuoB1BdscbI7oa5i4QxDCpz6Oirzq5eruD2EAft\nkxCPSTHhaBDXgUs4nUKcoNIBFssu3QHqji1cJru7bFThPYnQ5fefePIaf+Nr38hX/c+v4VM+9dPQ\n/V8jaUCpwTmcGyH1tlXm+41OHAOOSsegHYkEWqPaZinJFBWHeI/GKeIqe8Ig3nYOvRxIE8tPHFZq\n2Wc8MdmYPN9PucZpuM/hO+IbpN5C/NGFaQotKCh4+qCQ7YKLh+yzzaJGGlgbRw4zOzUFc6qIE6j3\n7NBbmt5SrmA6k2T0Zxch0aAqpn3WlFMp21lEOn54ukCkJ4c9odlYj6tQX6IaBzReBxkSmaDdPjTP\nItGAq5A4RjTgUNQ5UpxAjVXRU2eaZvHWHLk4lnAAsc0OJEOSq0goUJFUcdqZvMQPQXNkfbZJXCKa\np+mf4RRLwIakyuse+3r+0B/6Q/ylv/gXoH0CNOA94BuIgRgCcbhtwTpYjDxxAtUWIQxN9qsDnE9I\ndx3B/M9FpxAD6nZAuyyzGSzLgcRl//Tx7N4o3Cr7uVNHkvsp1zgLDwLpLygoKHgAUch2wYWDpmCV\nbY2kbP2mrg+XWVOVy5UykwnU82O6fXN+6F/HCWjAYTIC0SNURqYJltrkE71UpSdJcWKkWyokOSPy\np5CWWwJzNqmKir0fEqY/rq8YOZYKml1EPBoOURVEk0lINKFpYJIScaZDz9HyqgnqvflYYoswnUWX\na+oQEVQEZEjCmye1eKsU+y1rPNRkEhQ/3LxKe8LP//Fbf5h/89738ePv+ad4wozMq0tU2hLwMLhk\nTZEpzHzMRSOSxuAr0G2S30LDGBXyBqCx+QL4ASl18+bM/j4u6a/T8tL3JDxbJ87kMrfrSHJi4M8D\nKC0pKCgoKAAK2S64iEhmEeYyaUm9DvkkrLNTSy1oWA5VycRHFVQyJ6r70BQxQu9Hc01yOLTzagcI\npIkR4JOgcVnb3KdQ5p+tJauptcpuN7YxsGeSDxkaMYxTXDUiuQGqiRQSGo+QJDC6YuNLLUJnFF+j\nTS5vGgAUh+tu2k4gTQmyhdYjiAkGl6C6ZHHmcQxRMxm3T/ae4mda/p2CD37wg3zbt30b3/7t385z\nnv1wHmMH6kjdIXTXcNqQmiv49iYxTkHUiLQboupMRqPm46GDh8HVSDxCNKJ+K/txD6z6Hg6ReGwV\n/+aheePnaphR6uxYIkiNxqn9xl0K3zmn1nlddX+tteQZTwkKCgoKCp4yFLJdcPHgzP0iiZ7uftFj\nMUzFPOOsit27h2iaySBk8lEkHBgZqnYBQVxFylVNXSBIRo4HxNCBJKCeyxHWVSdvsZBbEZ2sq4pq\nhHAT0iHS3kDjGHwNdQNRIRyYA6JMIHSgLSoN4pMRRUkoFRqOjST7ITCxqn61ZeP0NUH2rLGwxfTR\nfoRWFSIVyQ8QmIW/aJzO1nHJuWUT28U4ZlHb3rYtX/mVX8mf+BN/gi/5ki9ZrvBWHkm7BH8A7QRp\nH7dmVbeLQ/CDywSO0eZZNq9cqRbxaF5djRPA2VyrHVuT1AFm4TiXkazcG42gwZ5qaEAdNu54bD/v\nP3M7WufVYx5kaUlBQUFBQSHbBRcP4irENYg3OcaJ7hc9+oY4x6y6qxpy3Hqu7vYEOk5xaQopoXKc\nK7aDuR58wUFDeueRvkrqB/azcLRcAe3R2//1ATfZ9m4+sTXzEI8cfQwNR0jax7VT8A1xJOAOISm0\nN3ECCUXiGPw23tUkjSb18AOUxpw9VPFxnygeZSs3Tg5wdYPECSqRJKMs4RDUbc2r+X1lvl+z1KHo\n3LnjtPuQzD7QLSR1arXDm970Jo6OjviGb/iG+RqBbXRSwlWKkwatBKUj6RA4QsINEoo2zwFhrt2v\nduZrnNdZ+icW+X1xNSZmBw39PfYzTf+skdRZ5TzFAzSMoRqZS0svNbkTR5KVe3zfnEAKCgoKCs5E\nIdsFFw8nJUiuw4I9oIYjY9tuONd3L3pzhyPwAyOQPpltnhuafKRPiVz8jEYkHCIaAA/pCO06tL48\nJ38LloJLHtXkyutisMu6ebgGdeZ/nbgKehOqxpxVks/j7dB4bBVssnbd7eSmzspkEN6haQf02HTc\nyWQlJo0ZotNICkdIrvaKRBthfcXG128MluwS66Vg7VM3PdnD3OQhVlX+l//qV3jrW9/K2972Nkaj\nBdmEa3Llexf0hhXRdQq6jegxXgF/GSVZld8Nzdqw98cGiIfmzIIg1Q7qhtZYuSgp0g5pNx91AAAg\nAElEQVSkManJovUf5GCjvD5pAM42Z+rr+ROOu4WzquNFz11QUFBwX1HIdsGFw6kJkmvSDWeEWzsk\njtHKjCuSG2bP5r5CWSPirHKuHdENLJwmN0/2um5JLdpXtVVzIAym2U5xds0lD+7eEUTDnITHyVIV\n9US4HfO8ZgpVDf5hGF6BamgNnXGCoHjviCGAVqjzUO1ZoySA3wM9sEq4eETEzukaCAcIiroal6bE\n1Jq7inpLooy5mr2GFOqmRFAjhCNExyA1Nw+u89Wve4xXvepVvOhFL1pzHzsYjOgmQ5P6yCXbPIii\nDCElYGA6bFcbYe4rxOEQCfsQxjid2uapyiL8RUmRLjioaMrvzZ1VVLxV+HNAkSxuNu529fm8QUwF\nBQUFBU8ZCtkuKOixjpgsPqIXN5NIIDUgyxXobPcW2xum5+0bKXMYjOhKpLQfQb2L667Te22ra6xx\nc1HDHCe5kTJXdmOYnVfUnU2iBjuw9QiE3zXNc/fbEC9Z2I2rSX47V4yn4B14j9NA0hbnhrYxSG22\n7xuQ1Fu1vEfs8N0TaNci6QDcZUTAEbMLRzNLxJxV+PsNxUahPO3sszF2KJ7Xv+E7ed6jj/LqV7/6\n5Hs5fhzXfZiqfZKkiVRdwvktEgmtd2C4Z/cpHKBSz4ly+0S2NZySZJifIAznBHlBoz3brmkEApI7\nY2fpltVcomKkv5ptPJ4SFD13QUFBwX1HIdsFFw6zUJs4Wa6oriMmfoT6UbbkGyHONMYiDl3VYYM1\n0WnCBQVtIUaSVLPI9qUqbrQ47SSNkV23ZWRW/FzDvOB68v+z9+5Blq1ned/v/b611r70ZS7nIgkJ\nhAhKxQoGOX9QUC4SVyAxoijLIRBcoMTBKYerDoiSMDcRAQoyka0YX+IUIAOVAKJAFsiWXIWCTUVK\nyjYxSpUhJS6GWETSuc6lu/dtre973/zxfmvv3T09c2bO6XOm5/R6quac6em1116XntnP96znfR6z\nzn3OYewk8eSx3haVZ2BXl93SEMc+8CdzaOfIdEoIE6y7gYSASiTkGZpX0FwGM8RaTATJK/eWhylU\nU7dKWIepYST3doeIWsnhjjuAbo7vuSitvSUjjggi/NI//BAf+z/+BR/+0AeJ8XYKsWCzxzH7/7Cc\nsFwaMqNhcqk8kbgEsfYhTTKSF2QzrD1EdO4pJaOAVZd9sVDux7o5s/xyJXuMWX2r/3xbzS8FPi8q\nBj/3SxfaYom7X7QOGDDgvmEg2wMuHkqpzbHYvl6tzItSRCIeVwcbkmTZi2AsoSbHmyS3cYJQ9k2V\nVjKa17ndoaGvOqfa8fpvK+UvsLE19KknKRXv8L6/x51I1LGymMYtD5W5mo2ARIJEFM8GzylBDggL\n0ETIN6B+FLoDLHQggSCKSLXJlt4e0Kx2EKkQDCxAAJOp+727uZPuave5Ka1b1+H//eSf8MM/9h7e\n+SPv4FWf85rbv2b5JOgRtWQkrRAqt7Yw8tjDOEJixDMItwhpOiLGsC76MaYweviWBRJ+Ff0exYkv\nCNaDtCc82feTCN3nZseXJM6DB778GyOEW+c7BgwYcO4wkO0BFw93IHzui27xgcV2ywbSeBoGVpJH\nvEnS6v1TUkNqV6vJm+QJ7fy1EqBP4Oj3bx3EqQ8mlni8YxnKRRG34CoseYGdtm2Pk+qxZQjR3yPO\n3c+QWgTxIULtC252CIvr5G5BFoM8R0IA2cE1XMFCdPW6LwMCqC+RTbE6o6sbIJW3ZKIEy2hUP+Z0\ntPHB97ibUpbyPqlb8V1v++/48i//Ct74n33ts9zkDM0lLD1Caq57zGG95wuZer9YfoL70sEXPbYE\nhUDni4dQk6r9482WpynFvdIt8dakkZO4V6J2FsTutNedB8L4IOK8eOAHe9CAAQ8UBrI94OLhpArc\nf13Ih4Tx+mvb/hDbbpIUsDx3XzYc/8CNE39dT6jjqETJLd3+Ub72YceMaQbpIMZT/bzrSDntipJa\nbd7ztA/6kx+8eQGhIXYLcjeDsANNTbYIoymibk/xtJPOY6zFMLz8J2tan5NITejr2PuFyOSzsDiG\ndITmAJLd9lKO3Sy6gKzdpsb82UpZTiHcP/F3/hZPPPkkP/ez/8AHNO+EuAOjy6xiyclmpxDrBKHy\nm1hfWqvSfm0bGF+hmy+AziMbm0vl3m/I6S0JMCeTSG5n1bhXovZCEbvzQhgfRJwXkjvYgwYMeKAw\nkO0tLJdL6rqmqi7OZQkhHI9Ne4lDRJivErGZEqrs/trQeL14DpCsKNtsBvsKIVRqgnaYGZITFhtC\nZZgkqMZIyclWHUEKTuBsCt6xCCYerxf3wIxA69YRCSAVUo0xKqTa3A9L+L4tYGmJYRAqJFSYGNKM\nbyGelsP6HACWeR9r9shNGQjUAJoJdJ4BHXapQwvdgiBzcpxiKKqJGCqq8S6hHpO7SIyVE9S4i6AQ\nSgvk9CqWGqgEyQeQlZwyod4ljP18cxBijds4yjUH0M4QTb44keCpJvXxn8l/8c8/xk//9D/gfT//\nMzz68D4mYX29T8OSV2OzTzJvPwWUJwBhDFGI0RAxQkhQV4hEVI8IepNWlaqZYNWY0OyhVSCGFglp\nvbAyE88LLz876PHr7aVAtx6bJRA2Q7In7/Xz3X4bd/p7/Xz2e14hIszn8xf83++Tf7dud69faJiN\nS8SmMZo2x/4+vdTxYt3r84aL+Fn9UsLF+Um9C4zHYw4PD+m67n4fyouGyWTCYrF49g1fIqjrmsuX\nLzOfz+m6jHsqlpsNtIJc6tNj5RFxerDxRSYrySABNBK6JSoJKvEGRbhliM494GySKDSVCEDnl0GX\nrpZ2+P8XR5tylNAg3QzRpQ9pmkJskTBCQwNJbmMT0I36ajWYEOIYSY8jdOhqgjYLSIo10LUtECCP\nIS/RAIRA6loszpEsmNSYCaYG3WGx3GSE7IkmeQWrp4jtTRAlhx33RC9XfiHCISlpyf7eGkrNi3VZ\njd8C9fMq13J2dMC3f8dj/Dff9F/y+i/60ywXS0y6zfU+Dd0CdMUuBxx117EUySNFJlfQDnK1gOUM\nbIzkObZ4nCbfQPIS4pgsr0BXS3T5aVKcEiSsj9lMS5MmW4kx282WCpzyd2orsx3LbgO63b/Ap+Wq\nl5+Ru8Ed/15vK9v3uN/ziv7v9Ww2e+H//d7+u3W7e/0iYTKZsFwsOPZv2EscL+q9Pke4iJ/VLyUM\nZHvAADjuYa0vHf9eeVwr4IOMNnaS2futTcHGt2zfv8a2WgiBdWW7aQuIk+bef60tIR2VY1qh1e56\nUNLCeF2oYr2F5HaPsU/YWpAx2rYgU3/NaA9MnNTnJVEyqkoIQrYaCeZqewiYrpBQYxJRAsVDU4Yh\n3Q7jVowE7SGBhKkieIJJCDWWDkEVyWUBYrp+nWm3KZXZTvIopPDtP/TDXL18ibe8+a9uzuluWj8X\nTzBJn2HetpgG8uiV5QnClICgoQasSL0JzR2qgoh5xT0KYQ8JI9x/H/0csY2qnZflyURpmbzTMYXG\nfetptrk/20kS/c9gn74icWNHKnXyZ4JhaPL54UTR1HANBwwY8GwYyPaAAdoi6WjjyT0Z0bbtj0xH\nQMBChUm18WCX/awJ8PaHcJxsyE3/Kx0Vn2+xJmy3UNpWOYp2W6/XkpoS3MbQv+6U8zlGpNrrnh0t\nR2DL4hk3DyUJEdIhWQ3qqf8/qHNJEpYjSIaQIGQCwf3apoh1PvCpHeSy8Ai1x+fhA50gaHsNVAnN\nqDwhqPw9LPnxWgZkncW9PifL/No//jC//pF/yoc++MvEeuSDpXemtBvEhrmO6fqnFCGS4q7HNlZX\n/Dr0sY7qcY6xrsnZICsWJwRRzFrPV/cL5lGB/ZOOk9f/Th5ebcGUIIAusGRYvfGEr5+G5OXmHvfJ\nJmdN5gZy+Pww+N4HDBhwDxjI9oABeXn8gzMvj39w9ip0ex2xDolTRFvU1GP7CqwvasGtBuSl/w3r\nIwJ1K24wL4uiulXf7q9E8mxDlqPnO0v5nvXkfMtmcgynkYC8gPYZwvwG0j0BzcvJKlA/7E2R3cz9\nzNUeUu1gCl0+8oVFrKCalNrxDrVVOa4pZk6Ms9Vgc8gdov44W+IIzDBLCIIImCYsjrwQJ9SQNrnj\nFqpbklU+88RTvP2H3skPft9b+dxXf07JQ9mc5x0JTqiBmpw6P46iUodqhMoU6umm/bPeh9HL6aQq\nvnGFepcQep+9+Tb9E4Y0858Hqfzebi3U1vf6NPSqdf8zoqsNOT827BaG4bfzjvMyKDlgwIAHAgPZ\nHjDgFqW0fH3ysb51hO6aZ21XY2DkFgLLTr6iq59iyS0WoUb7RJKTlg/LoCu3KGy3RUpFpgFJeP1g\ntXVEsvZyy5p0nyi06Al/T/4kuurcHWL5JtYBcVWONRPbQ0I+IEWPvFMLTvaokHoHIWB5jqSbWJgQ\nSBB3XdnvrSyaiNqhuLqtYQfqh93DLWAyxhcKpQK+2nWy3F92owxdboZ/cs685bu/hy/90i/h6//S\n1zsZ75s0e0J+J4LTHUI+oqovY3oD5KofS9UX2kw3xNgyYMTopTTWzYsHe+QpK/XV9TFLXmzurYQN\n6ecuhnmKTaaPhTzWSrn99KS3eZwW6zjgfGBIAxkwYMA9YCDbAwbECdp7YyWsy1qOPda3BGlBTEeo\nRFSX0Dzqfuu+BKfPXM4roPiYw2TzoXyi+t3C2C0C2z5ljFBN14fmlo28to2QF8VK0W9+q8J2TNkO\nDeQ5xBqrHgG9DnIFrAU1cjQ07mJSk9sDJ8P1rltCNHuxiy2L08NVYkKL2AhCwKodSHPQhOgKkZpc\n7xHqHaw0M0Ln1pHq8vGCoGpnc81PkJWf/Mmf5I/+6I/4yEc+glTTY02aa8X+TiqyLqBqGGelkQbT\nGR2JGAQNxQrTN3r2L0lzLC3X0YpOohtorvoGxdJhUm0lkXSbewPHoyJPYm0pks3rT2uaHAj2+cdw\nvwYMGHAPGMj2gAGh2bQb9h+c3cFGRZXgg3GxIuUdVzRlBLFxomXZEyr6shkoirgiusByvbEglKHI\n/mvRJUjlPnEAia6Ggw/F9WrvNmHfxslSGFNfAGyTWKmh2kVoEVsB11EeJehNlClN9ySdjAnskMLE\n1fo4Kv5086i+ZozYCimDlCbN5ti0LRnk4uU5YYTmpc8eIm7psLDJJC/HvSap2hZbhl/73/md3+En\nfuIn+Kmf+ikuXbq0Of++SdP02QmONFBfoo2P0uoN4BLUD5NWByU5Zt+zwMuAo+U5la1IolR5TpJA\niJfJod60ZPY57JLXTxDs5DE8m8K5tdi45RzOirCdrPEeCmxeGAzXcsCAAXeJgWwPuJBQVSeTvfd5\ny1fN6mlIs9KeWGOhwcSH/agmhDhxK0CcFmU6ejpJ+aWhxiwg2RM4SAfr9w2FoHmJzLz4c21D6MBJ\ndj8M2Q9CghOmcpy2TZ62VXhLbmjYrnyv9wHDmn0sJU9b0Q5lF7oVrXkCh5oUBf8Q01T8yuX8RDFG\nKD44SGnOFG0xCVheoWWY0wlnROyAmGZoarDxox4V2C9GemVwHYsYEW1ZLJd853d+J9/wDd/Al33Z\nl22uSbnGx2Lw7oTJK2D5NCktYSm+4JBMw4ou34A09WskwZ9EmGJETCKJgFGhVlJH+sQR3LZj2j0/\nRfqFJGkna7y13RhchkG+AQMGDLgvGMj2gIuJPD8esQdOHtMR5CPPjtai1JqWcpsaTYdA5c2CWzYG\nb0rcqMmSOgICgjcwbg9dWvYqdG2RascJfXujkFrZEOptlfROBGnbuhCaDRFfp6FEYOx17U32aPEw\nhhig3kGyEPIBqqtSxFNBEKTZ88HIMHKSXtXuM24uFy948VCnQyKGxBoJkaQrJFZIe4jYApWM5LkP\ne24fb1F4Jad1esuP/Ohfp2kavu/7vu/4Od4rqQ0N2IomZqp6BNaSVtcwuYQF2cQV9m2f9S4Z3BrT\nraAeQxghWFHdQ3kSkTzKsV/MlH0cw1kqyfe6r5M2ln4xebvvDxgwYMCAFxwD2R5w4WBmWJp5fXpv\ns0hzCF3xW0eE7NnYoXZyBU52modKZfoWwdq2REBRrlvUXOGFbmNJgfVAnoCrjzYDGiTUBG3XxH9N\nmHubxrYCv40tL7iAK8/bxKw9IIREWF3HVo9D8yg5BD//8DB0LZY7JO75wgJFgEhCLbg1JgohVCBO\nPr2y3D3UVoYE14uD3CE6R2KA3DhZN/F958Vx+0k6Klaamo/8xm/ygV/9R3zwgx88vdDgXojr8glY\nPQX2NHQLTCNEQTQRo5JVIYw2Tw/iBNMMtoR6D0ZXNosn062SouSWmO1rv42zjIR7Lvs6ObgX6lu/\nP2DAgAEDXlQMZHvAxUNuCWKlMCRjtBB3cX06eegHjcfFwe190luwvHA7yHqYz8ogY++/nrofW0op\nDIIS8bKU2qPoKOV0vddWYokbbBGpNwr8ScL9bKqvJjQdoFLSTaTxAUiZlHSMGuJe8XaP8YHGhkR0\nb7opxNH6PWzLM63aARXZknfAkGD0EGojEMWqiZ+beG39mpCXnHFDMIOnnvkMb/uBd/LX3voYr33t\na+/1jt6K1RNIvoHYDPKMrPsweZSummJhBNVesdfg96s7QMTjAQ1fBG1bdtTCxtojcW0fuuVan2Uk\n3HPZV/lZMDZpMTZ4tgcMGDDgvmIg2wMuHixD3CXHtDXYVxciCT4UWJcIPDaDcNsEaysWEG0JhQhp\nyeLGMpKOUGmQklMtfUGJZUI+AvH3URFCr7KXpkYp72H50FXxkrftx7uFbSK1rRhvkyupIHVIXnhZ\nS1ogKTnpTCvEErW0qDQoqeRQjyGnUoCTkV7dt2KXKecn6nX1pgq6IAeB7iZUDYRdNASorvgiZJ0X\nziYnvBQAvfV7f4wv+tOv4y+/6b843qr4XNG1BOmQah/rDKqHYXSZ0OyjUmNxtE4jEW2xPPcSnzBy\nWw9hc7/h1nrz2x3fWUbC3WlfdyLQwX/m1hXsA8EeMGDAgPuKgWwPuHiQSBDcL40ryaFUr4vOyDIB\nWgIBcEKofYEJ3BoL2Ht6wb3YpJI9PUNJhBjRvNqo1do52bTk5L7a9YZC7SA266IUH3BTQpphmrwo\npvc9g2+z1VTZx1bfYj0oudCm834LrN6D1RzCNaLNyGFMNoPRFZg8SmifxPIKoUXjflGgM6Kd+9jT\nDOsjDttDajqSdTTdAavcUtdTuuZlSPWQv1fvhz852InxM7/wa/zr/+f3+fV/9EulDOcMfMXjh8nL\nfbp8HWQXRpehukSWCCobC0x3AGQgIHnu17m+hNVXjlmF7tovfpaRcLfb17M1ng4YMGDAgHOFgWwP\nuHCwUJPUsDQHEY+qC0C3IJhAMI/6A6h6z+tW8c3Jtr9tSCzpIgtEU2ladKK69gd3BwTMiZItUU3I\nyC0NfTX3Os85jMlSouIs0JfceJ738nju9GkqqmW3jKAQH4L0lKdwpAXIE6AgdojGR2Cy6xnbaYZ2\nS4JkJCuElcf/4akeIsHrxgmIleFQbT2RBM/mdruKN2y6it0vBoq2XQY5/+DffJIf/1vv5e/+zXfw\n8NVSdnOn/Oy7RaggXiKEhHZHfpBKGQqdENINt/5IiSSMNTmPSob2Kcr1KU2dd1KWzwyn7evZGk8H\nDBgwYMC5wkC2B1w4iHbEnoAaaF54I2MYIShCxELJu+4LTE4MRK4LUSx7SgmyzuvWNAOgzR2IOMmM\nY0/vyAuATYugTJwYbu8bIE58QDPPiCGiMkFCJKeZk0PtyvBeeV1P/Prfb+/PjeAICyzi9hDtwFZI\n7rCYUZ1B6sAWoBWiM4IYxCkhzdBQbCDWgva+bUFxsurnk3yhYdm36/95CfVmYdAvJizTacWbv/sH\n+Zq/+NV8xZ/7s27dOLObHKGeEJurxJWRmIEeULFPTploK1LISBhjGiAE93BXO273uZO6fpZDkM8J\nt2k8HTBgwIAB5xID2R5w4WCaXNXUZSGpxUtd7ZJz8eluN/xtebPXOc/aQZ75kF992Qlar1z3kXaa\nIQTEOqw7JFRO2BXZeMCrsFayj6mkvRIcxqTQ78eHLcUyZq68rwts4nhtzXCiKJs/q/egvoR1T0On\nUFUeB5iOsHq3eMIjsILFM0iMBEC7JWKGVlehj8rThAYrg5PF217teSNjmNDpLlQjWiYQG1+EWHay\nXdow+/bHd/34u+lS4oe+/61Y5ddN4M5E924RRwgQJBFthsgOnanbYEzRMPYa+bjjqSRx7Ne09+Pf\nqSr9LIcgnwtOazwdMOD5YBiiHTDgBcVAtgdcPGgmkFFdEvIck4mT3zguhTJbKnFeuCILThSL5zpY\ni0kkWCL3j/G386PjBOoMZC+I4YTaHOoNmS/7Pn6M5cOv5HuTl5itnFz139O0OeZq91Yv73pfHbQz\nyC3oIeSRK/b1JSCR4kObQcpooEu3riCAk+neDmJxymagVAkiaKip6gkpNFTWkoiEaoJKIFiLtjME\nQ6nWr/vYxz7KL/zCL/D+97+f0c7VYwOIZxJPV+1i4RKr7pBVioTK00VS2MGAHCdQTX1RUU3X14+8\nXFtypEQa3kI+znII8rmQnNMaTwcMeK64709qBgx46WMg2wMuHkIkhSman8LSAquil5fk5bE4OOnb\nAnVxvIXPBCGVpOwtHCNdhtCnhEQsd5v682of4n6JnDtE0DV56mPa+rbENWEuxFyshW62sWTEkb9b\nOvLWS2tdbT7m5fWBTfIMskCcQ+d510GMoEeYBnK6BJohTokxQ6xQiV7yYwGTCRICFqeurofaowjr\nfVIrEBM5A3HkJDytSkZ4Jkomxz0gcOPGDb77rd/LWx77Vv79P/Xasx0q3LpPRKEyCFVNH+too4eh\nubLOLtc+u7wnvXAsM/12qvUtTw+eC54PyTkvZGhQRB983O8nNQMGXAAMZHvAhYOEimAJw6jE0DzH\n0g0vg+nRf+CUuu4yXVeKUCpUM4aSZVxU1K2huvYa5LlXwvd+bImotpsBx3Tk1e26JFhGrfP9g9sp\nLHnec2gwBIljH0Jc3QRdgNSEkEsiCG4pKOUrFnDC3VP11LlfefkEmq9j8rnYjleRKxFl7se+OoJJ\ng8WGLAomfv4ClhNU2Yt6pFrXpUv/LuEITLy8hkgygA7JSwiTMiQKUPHXfvDtfP6/8xq++a/+leNP\nA7bxfEmcZWivIXKTaHM07PrgY3NlY/XZeq/tunts63huV1rTD6b2dqPngged5JwjRdRyi3VzLLdw\nchE84M44yyc1AwYMOBUD2R5w4aBSkdICuplbQKoR2s1LlXm7qSEvHzpGxESA4Mpx8U4TphsbR08y\n0hGSDjx3W0DFXAm3lqArLKj7bbOyVpx1sbaECGHjWV4T0dqzvLXFLBFMUVGCZnJoi0PF001UGie1\nsdl4eYN/O9kjwC5YBUmg8nxtWR2hjWKxgjxCU0MMwYlziKjWSBhhEpBQbYp1en94d0hM1yGvEO1I\nMRDiDpo7MhMII38KUO3wvn/4Yf75v/xtfv3Dv4qIHK+kX9+gMyBxeeltoLLyS0Na9wudfC/SzC9Q\nXwLTk/zbldacjH68U+72yfc6ln/+gJOc87JYUC+pEjLBWo92HFT2u8cL8WRpwIABxzCQ7QEXD90R\nMc3A5k6es6HVQ+tINbEOs4xR+QdPc9lfl5fuv5YABCfHPTnriVSau12ku+ZKan0JiNA+Q7AVWu14\nAoY0xfIhqBmGZ+h5wWRw+4ZUGwLY3fRYuriDSsQkeMNjboEWCQHiTvGeT44vALpDoAW9hq8AKmgq\nH2hEYPJZBDtEQ4OQsdSScX+2aIelJTJqWCvvvWLe7z8viOkAy0uPOzTDJmNv5Sw2Fw0Nn/zU0/zo\nj72Hd//4u3j05a/YqndfHP+QvxOJuxvFuxBoaSYgL0MXT5PDPsQKWT3jud+9x11bDFv7syU0t9bd\nb+9X20Lii3oq4e5I5m0WEA80yTkviwXznPTjXw+4JzxoP3sDBjxgGMj2gAsHbQ8xW2I5I2mO1Q+5\nEpyXYB0SKoTSfSLjjYc3r9bkSMIWybLs5TKWseUzhPQMIS/BDsmdwmgM1qFpRZYR1BVUO+S2BVsW\nh0qJy0sKITkZ3C4rKVGAJgFS2BAd9SFFNKGyhPrKxne+hoE1nryRs+eIdwnqBOERPzZGIBO3i4Q5\njazoqBFdkcPU68olbsi8X8hyDIZZQE2IeQ5MiLYk9YQ/TsjUvPm7/1ve8IY38FVf/RfWr18T0Lxw\n8h0nx6MVS0rMLdvfSfFe+90rcghorAvpz4R8k9yr2FsWlpLzcnuVuifm5R6Y5c2C5m5I5u0WEA8y\nyTkviwWJHIs/fNCeEAwYMOAlj4FsD7h4SEuqdASiWAik7hDaQxhdKpnUXfE8l/r00BPxTCgd2KoC\noSigWyUjFjJZvbERJiDJC2TSypM5xCAIlmZE2tImeYDqBKoS5xai+7jT0YZw98RmnTIi0N7w35lX\nn4tUx33nPWTsKvnoCiyPoHnERWoDRrt+rtq5vURvQF55BXtunaSGBgmVK+v98Wwln1is6dSgW5Et\nQFOTU4JYCGm9z3ve/W6uX7/Oj/7oj26OqyecayJb+YICNue4jbu1LUgEXVDlBaFy+w8EhIykQ6Da\nEETL/i7b0Y2noR+eBKzaWRP6uyaZ50UFPmuch8VCaNyuhduoCINne8CAAecLA9kecPFQTdFqj5xa\nt19XFQQnQlbtka11Ih1HrrT2ZFtwH7MEz5mudsr3Fls7bwgSCCGABHIKSMhIrDFVLOua0JtJsY8I\nVCAhuvK8LqrRY4S0H8qTPk8b81QUTRgZi7ep7a7GMN6FdBPqCdgRhEuIrbDUIaMpVRS6rqMKDdk6\nzAKWOqxpIFYEjGzZz7VU1EvJ+rY0I9BiQYi5JeUlVbNL0g6TyG/91m/x3ve+l/e9731MJieGULsD\n98eHanPs2h1LBFl72O+WsIamxBxmEEHK4kbyqEQX4ucRJ0WZVY4po6dh670Fbk5aX5MAACAASURB\nVG81uR3Oiwr8EoXEBqmnSJz5wnHAgAEDzhEGsj3gwiHUO0hzBUktAchqxDTHpEbHnwXx8vEBOW3B\nEoIRMLcSxNGG7G2XjDSXUMQbGalgMsHyHNOZ87l6igiYCiLmyi+K5YAGAWmQ4nN2Uh839gltsTQr\ngq+AGJZcnSfsOvnfKt5Zo8TvEWtoj0AuQdti0wZiREhkVZBIzi1GhRpe3V5aNVUT0BKyq4aaVxBC\niRlc4KU3qaRzeLSixR1m8xXf9V3fxbd8y7fw+te//tiiof+9FSvK2hIe6uPH31/neyKsFZEVlWYq\nndGyh+Lqv8cgLrcWLRz7/an7PQuyPBDsAQMGDLiQGMj2gAsFy65ap/oyVq9ADQluAVHtfPit2j1O\nqFZPQ55jEshhshXfN4PQbvzVPYGcFtLbK6a5QdoWlZXvJ+9DHJFXhxAiMPYmSaHYGSZYqLdU9cWG\ncOc5oguMmkqUJBUxNOTSmHh6+2IkdIdo97jHANJBHehtMiKhDIN6OkgUXGmONViL5BUaIlRbZDHU\nTsClg66lSjf9/FfXvIUz7sHoEX7g+9/By1/+ch577LFbUzy0RULtVh1T6Js1Q7POG7+F2N4tYa13\n6Fa7JOlIQT3XvJp6OY+1xU4C64KezQ/I7fd5r2T5buMLtxcgd2quHDBgwIABDyQGsj3g4qBEhMVg\nBCI5jIsnwNA4BWrQOZJGxYs8gbwkpEOPFANyqLEwJvSDerry4bqtXGbpEyswrN6H7mbJ6oaIkHXu\ng5FAEEMXTyFBCKMrIJDzwocct7OeLZdSmpnr68FIUjK/pS4xJpxurYhjlAwr82HMnIs6nsE8a9vq\nXV9ESIWxcNtF+wQW91yBryflPYrdQoLbbCRCPaVtx9A+heA19rF7mve//7f5jd/4Z/yTf/KPCaTj\nEXuySY+QcozW23K2r+dzRTVFcyYtr/k5NxHSyn3kNARmaNdBnB47ljPzUt/tMOe6PKlEO2778wfC\nPWDAgAEvCQxke8DFQYkIMzN09SSy/DTWtQRbFpITIXcgh8WjrJDnoDNUM0jA1HDpt99nB+0zSLW3\nVmQtzT3XmehDjN0Blbal1GbsfNUyYnPCaomlG0RbYe11ZHQZxp+DpKNNOgd4VXpeItIQxMjSEGKD\nVvtlcLK6/YDf6hm3keQF0HvGC8EMFSaelkKYwuQKusiQrkFWqrDC2gOoroCpRxJaKup+KdFJC2pW\nZF1R5QO60WWeePxxfvBdf493vP37+OyX7XvDpXauyofxetBSz6KJ8TQsnqTKN6hCRtoboGPYcUsM\n4vnmFsdug5FYlPVn8W2fhtup13c7zNk/DentQRbvvP2AAQMGDHjgMJDtARcHJSLM0gpWT1B1N7FQ\nkbN4fnZ1FQlSfM81nkmthHSESABVlGlRmr3MxNXLGskzJ8Ne/I6EsavQ7TVPOmGFdEduvYiXETGP\nB0wHTrR0iYSESvbjEMWkJJ30iShhgol64keo0dCwtkH08Xg9tklgdxO6Fci++6vDVSfc7lgnsECT\nQOxg1XmGdHMJuoykGVbXvo9qF6n3EQmotgQ98lRBW5JzRsMYNW+6/LZ3/DL/0Zd8If/5G7/SFyyW\nPF+c6Ncabj3mk3g+LZJ6BLrEVjeJeoPcjSF8VkleSe65r/cIgOal399n822fcnx9IgsSse2oxrzw\n8+4TXG6nmFteK+CeyFIsLS+VtJIBAwYMGDCQ7QEXCCUiTHOLdYqkmwQzrNpDq0vY6CqkGRYrlLDO\nZk75MrBydZgZaIWaga2g2gNA8pFH40lwlbg7IOgKzR1BZ+TUuWUkTCFGz4CuH4WUQY6wUGMmKA3Y\nkpDBovh7mkIcIdXUFdjehhGadTiepaON3xeOk0CJBMmoXccXENltFaZeeNOuiNpCd4jWYyzuEVDo\nzEX4/j+WS7Omq+JKBbRAhcQKbEriKn/vF/5vPvn4AT/999+D6IJ1lbx0myjFZyOTdyKyd4McCN0z\nxDh30lt1fm/Hj0DcdYVeu0KsJ+tSm2P528/6HsvjVpG+TTIdlUp3A1ti2hzLCj/ZIqmhAanI1mxy\nvgcLyYABAwa8ZDCQ7QEXChIbjA6iotlTMHIQyAZp7kQQnNRKBXGKjBLBMtY+46kZ1iFhRJYxUu1g\neeE16T3ZtZUX55RmRAtjLEKQ2jOATbwUp9nF7KESA5ixWFJFVNDgBNXzvm1zTKFxP7dlpLvplg7M\nCWMcr0lfH8uHZWz0ENq8AhKwyjCaQI5uW8hzSIfEfJNsLSIvxwi+mGCENleg3vGByXWKiOeQiwSg\nwWKNyAgC/O7v3+Tv/Pw/42f/p/+evb2pK8VSQRj7PmNzd0UwtyOyd4vRPm3zSjpu0Fb70ExBajSM\nfYEUam/7XNd22oZk37WqfNJ2Ur7WrmR310DtVfVwuo9b4vGYw4FoDxgwYMBLDgPZHnChYLlFV4eF\nBEbQZYnFy4R85Hwr7pTUioRVuxiQ0xzYIYR5SRkBYilCMfV9hQZpn/F9ojS2pLXKCb4K6CFoQnSG\nyWWQxonfzhjNR2WIMnjkHgmzBFYXtVU3vmZtXTnPByA1pkssdDhxjJvjW580niMeOmDmJTuMPQIv\nLTA8bSSbuFpvU39RvYtUk6JGTyFOMRQjQrXjySemEPfI9YLl6hrf8SO/wn/9l/5TvvTPvBpLc0Kz\nCxhZItR795C2cTsie5fWktAQmoeomxGV3SDJPowegeYqIH5/q966EVzplureVOXtyEcJm2bNUPsT\ngPWxFGvIaT7uddb3kL89YMCAAS9VDGR7wMVBSSMRTVRp6ekPlXrNeZpBZf7oP46BeqPkNlfX1g3t\narc6m2yIb6h94FDcHiKWASXJyFXtMIHRCu0ikLB2BpMpUu87SV89BWHsyRiagIyaQKzWtgbRZfEb\nF6XY1EtxxDC8AVLK8VpfP96TwDWRV6CCZs+r22UEJERXWJqD7LitJRoSawIV2cxf0ye3qEE1chUd\nyoKlQ7qneMf/+Cvs7ox46zd/zTrXuz9G4N5i7U4jsneb8AFQTdB6QqoCOQYYvRxGV5E+6aO8VqE8\nwXgOA5qh2UQ+bp9XaMogqUE13VhItkt5tB1i/gYMGDDggmAg2wMuDkoaSTIl6REhzTCrsMkE0QXS\nJc+bri/59j0ZUq9VJ479V17612lG0AVaLBxW7UI1gdYQUwRzC4aMIAkSV9Tmed6a5tBdL+9TEYKV\n4cmKIAICpiuMGtElQkIk+jbVJVfRrfLji3gRTe8Zj5MNsSvpIbF7ipxnwArio75AkArIbi0ODZ67\nHYCWiBXCvAthAiRCnkNuMZ37+6wH/4xf/81/xQf/t4/z6z/zFqoqetIHgom45zuONosBeHaCeRqR\n7dsm+6/v5K02JYZd4mhMHAmp8oFXO6km36sX/LTj3Ea/IOhTZE5khBusYyD7mMgh5u/5w3KLdXPP\n0UeedfsBAwYMeDExkO0BFweFGEp3RNTkSRQV5M6HG3MzdqJt4rXeRb2VUo2+zkGmVLbnGSEforJE\n2C8DkhUmNUZErXMxWZYQhNx1IEaOHhPI6hkI3hYpIu6BtoQSfchSmnUetiqEYL4YQCHUZHb9WErV\n+XpY8qRaGsfk5mHPmRactE4fBZYEMiKBIBVdNSZUI5SKZOIqdjMByZATFgIisRDG+ZrwPvPEH/O2\nd/4sb3/z1/C5r7pKyq0PYELxd4+O34e7HUDcPoe+xXObsN8pzcQUYwap9acCaQFphtR7/nQgNBvb\nx1ni2SL/+icVFm6/zYB7Q//Eiux5+CrD4mXAgAHnCgPZHnBxUNJI2tyheQG2RDo8Aq5uiMFQUXK1\n40OIULKpy2vTrHwdPSIwzRCdIzGu69TRjooVSqYKSpuOqKqKJDWECWorJDaItSgNsbsGeYmGEVZf\nApl4U2OZb6TUp0s0rxqXQvbzyj3QWykX1tte+uzmnnDUV3zwsrriX1djJ9KIRxmGKSoJZIKEkf+/\nEswESYdYtQ8IYoEQKx80JPoQoyW+63vfzRd/4at50xu/2D3fUkFukSAYI1e182pju7kb+8RJb7bl\nje3D9K5eH9ojkBWyugZRYXQF0dF6MPEFwbZV5HbvczfbDLh7WHa7UlphaQEaBrI9YMCAc4WBbA+4\nUDBtseV16vYzbknoEshVxMTLblTdZ9ujECNJRwRrUQTLc1d6gayGxYBK49aM7hDLK08XUQUWSK4I\nomgMWG4Ac2sFLaQDLCevT5fK86114YOUwZCw4+8pkSzuGxcMK0r2OvKvkGwppPSYXaMouMGuoaaQ\nd8H2geDEO9Y+wDm6Qg57IAlLHVJVBBNyANhBbYWuS30U0gHv/V9+hU/8mz/hn/7iD5SinSmEimBL\nRMHixAc4466TZO1A/DhvG+d3u9SO/tw4Yc84DRJJFpA+3k9nnj5S7W8WJCUt5kyJWW8VudPA491s\n83wyxi8aJIKuEGsJFJ//9mJzwIABA+4zBrI94OIgHVHJCpNEJ1NAsdEexEyOEyTWWH35uD2htEKS\nF6gmJFQgpRhHKqzaAwkey7cmR2NYXiPnI4iXyBKwmBEDMx/CFEtYXhKLB1lNSXnllgcEYgAFK7F+\nNFd832lW/qyoxKaIBERbtPz+lrxoyVCNUI2ebuImbSQYljKVzknVVR/AFJAgxDzDUnQ7jQIx+XFY\nKu9r/MEf/B7v/ts/x0+++zvZv3QVk8oTVHTpmeEyhth6kEi172pzH7G3HedXri99k+RZpHZIQMQ8\nCzxnj/4L442vHe7NQ34vuJt9PYsqf9eDoAP8iYclrM8sNxmsOQMGDDhXGMj2gIsD7SBCrRlNNyAt\nUBZ0csVJdXUFRg9tbe8kUCxjcepDlH25Cz7EKJox61NDvHwmr7IrbNUOhOhqeQzQHhJsCWHfmwJN\naMMegeQkViKWS4QfNUFWrsY2o40Pu8LLXrKr38TRFrEoru2TedHLp6G9Dql1e0p8BKrgVpKwIugc\nSRWEgNV7EHZRC6h2ngseatDsoSuqiBmrlPi2t72br/+L/zFf9me/GOsO3SurSyQ0RIkkMb+G1RSx\nFtMAom6BwVzJ1xbSEaGQS7N0q2rdn8e9EM44wRghskCbSz742ccn9ip5j7MgZmepRN9t1fsLgQdU\nUZc4QaopEuZI7vzvy4ABAwacEwxke8DFQaiBFew+ymr02VDNgAqqGsjQXN4Qu6IumnauQkNpd8wQ\n99wLrEss1O5NlrApRxFB4ggQIgnNc0KeQbrm6nBXORlsHgJr0e6GR/HFkZNCiZA9js/CxBcJW4/F\nPbquqHd56cdu2T3hfcrIdl60LsvCIfnr8gHo1UKqdtFgSIhevpKWhOK31jAGESencezXoeTm/dh7\n3ouEwA+87TtASk29dD6sGSs07pe88UCQjOQZWaaYJUTnrq6HyWaR0mOr9fJ5kT5tiZNLyHgXaR8H\nm0C979abk+T1+RKzs1ai75en+0FW1EONSYMSsTAMSA4YMOB8YSDbAy4Oql3atGJCBaNHqFZGyDMy\nGV09A83D7iOGLXU4lEHIzotcpLQfao1pVewPNX19OtpC3MV4mpCO0M4HDLMuCRZQyyWmu0T05QzN\nQ0hswJzcw9izsaUi1DsI5qU6JQpP1vnelfvDpaSUrNXvEykdBhARW7kFJRmkBJUrvaqCmZamx4ac\nO1fm45RQjVFtsVCTZQTB+N//z/+L973/w3zwF/8+9WQfliuqkMlZkTx30l4HCJfLAiRgJhAiZiBS\nrhfFkiKhX0FshiefL4IPpEplSNxFiE6ySyzf8ybz2zhrJfpuPN0vBO6nov48ISLeTiolyWfwbA8Y\nMOAcYSDbAy4O0hGNQJy+EuInSfk6yI6rymbQHUKfBrelLqq55UEMiLWT5C670hsn7nVGNiptsY5Y\n7jAaxJaIBKIkNOygcQxhD4IQaNC8QrRDETeCVBEzjzIT64qXWo4fl2VXaUNDEB+gJI5Pf3weKqDG\nmldAO3NPuYnbZsI+ygwf1jyCZh/qXYIeorqAzrzlUjto9rh5MOMt3/8/8D1v+VZe+7rXl/O9ibYt\n1i2c+IddCDte0iOCkYEIsUG0Q3ASJEQs+PXUbc82PH+FNU7IrdG1c7q0cs94cG/7mcf+vRBK9P0g\nig96SkpuCda+cF78AQMGDHiOGMj2gIsD7TBapD2ijpluvEfdXQdRLDakEmcH+Ie1tsVfHJAQnO9a\n3kTsERDUyVu146/rbiLzf0tcPU60llV1GbRFwwiNV3278ed42U2auXc75DL0uIsJgEF9xaMGTVkT\n+bWv2T3ja29zH6cHpxOkuO/7DDgBHl1yAh8nUDeEbk7o5iQNbomZ7KDZYHUTRi2h3sGsxfIRb/3e\nH+F1/95r+aa//CZvY8zLYl8PiHVIqMkxEkLlLYrVxIdHSwmOaUvu8HOKIz+GkxXpfdxij+eisKYj\nYvc0VQWVZBIGmtB65/Yk8rn6le+XEg1n67G+n+dxFjhNmX9APegDBgx4aWEg2wMuEMyV4vYQSQcg\nDV3cBZtC/UiJ3Ws90UNbgrbF9tFiqxkmAWsegeBtiEEErEPzDKt2XP3trmPtAZJuokREjrCw7yRb\nSjtl1XjjJLiv2bIT0hAJtsKIQOt2DCsui+yV8lLsKtb7LuLEs6f74chTo+Zqb7ZcHnoGsWYYfxaw\ngvYG1erTSD6A5gop1zB72stsmjFRE7k9RJp9fv6XPsi/+vi/5jc+9L+uEz3cB195xF8N0l2D9hoh\nBHT0St9GYrF1NJtfdyJAZ6GwtteQ9gCTBWF1RIgtNnrYfwpO29/z9SvfDyJ3nj3W94PknryvfRRm\n+f25uj4DBgy4UBjI9oCLgzghY54XLTtQCxIbLO7D+FFXWvsP7H5ozzqsPUR0hsQpOR8W32+NmpR2\nyVAGEFdOfiRh1BiGydStGUC0lry65gOAjSeXgPumJc+xtEBD5ZaR3AKKGEi3xFAvtcmdR/1JLNne\njXu46Q/7FK+qzqCOMHolyNNQXwWyp5nIihaIsSZngaYp8Xvm3mZLGMq//ZNP886/8dP87Xf/EFeu\nXPXYw/59qh1INdihR+1Jg1rwvHAbI8Uasj62u6hqf94Ka+oIqZDs7ibK7p0V8gfRr3zWx3xW5P1+\nLQJig0qDiR6zW63xINzTAQMGvCQxkO0BFwcSERpkdBWqTyO5g3rq6SLWAcXW0Kty3TPQzpHuKYJE\n0K6UsVxxEp5nxcfdEtqnUBMsTIExJoJSkkVUifkGMc0J1YSumxBtQQ677gHv87FjRZRIJiDSEOwQ\nrMJ0BbmDagQ6B50hUiFh6op4v0jYztbeRl4i3Ryjc1VbKIuDGWjE/SU1gQ7NhxCmrrCnOanaJduI\nb/2ed/HGr/5y/vyf+w/IukBSSWCpdkEieXEN2uuEANQ+WGmafJseLybZafZJqz20TmgT18cpobk1\njQTuTU0/L9aEs/ZYnxV5v08LFxFfPKPlKU9/n9YbPGAe9AEDBrxkMJDtARcL4pm8JmMsVp6CEUBQ\nL4bRFkszmP0Jlg5d4daMiboFRW3jgVbFtKWyOUiNysTtEvU+1u5gofLtVtcQWnI+QlDQJwijXXJl\nVIxIVITY9A3qfkAhojbxBA/xynOrdkoyivox68wHKUO1URCr3VvJYJg4AbHO1WzC5v82I3TX0Gri\n/nGpgA7tDrAsUE35G//z+5kvVvzw9/wVLC2Q2BBUivcamH+Gxg7IQRGdk2ZPk/Z3vZ1yuzr+bsnO\nWSijzSWYvIywY4TuJlkmnlhxu7r426npJ6/lebJunLXH+qzI+3kZtHzQPegDBgx4yWAg2wMuDiw7\nUawCod5B0xzTjOgCdAzSQXsDuhvE9AxVntOaQajJYacMTwZXllEsTDFdYGmFBYPRZTAnyrGqibqk\na68DE6QOWA6QD6G6jOQZhB20ajALJAWiebxevY/lBdgBYD7QGPrEkzFWe126aefteX0KSiE1t5BB\nxGP9iCAjjxtMHcgR1DuEWKNq3qYZakgHVHmOYvzL3/4UP/OLH+YDP/cumtEOokesw7aRkgG+QMgE\nyW6BibEMPlZg6t5zuHuycxbKaLWLTl+DThOpvQFWY8XOgsRi/+EWwn0MpxHr82Y3ebGr5l/M/ZwF\nBoI9YMCAc4CBbA+4OJAIGKYrxFZuqcgrjECo3X9NVtDVethRpEbkElQTL34xRdIcRaAeIVQYLYQR\nQQyt92H5ZLFoZCflUckycltJ/UoYv5w2LzyqD6CaEDBP7wh9ZneNhAiWXGlvLiOhxqoJZPVhzTCC\nuLP2bNtpNhLLEL2iXHSFdUcQO9BXIHnhNpoQUaYlYtAr2zMwmy/49nf8It/5TV/Fn/p3Px9iQ7Yp\nhAqRppTw1FBdQdsnyjHU0DxaSn2yn8vtIgnvdJ/OQhmt9lA7xNICLEHlmeXHrk2P06whp13L/tj6\n7c8yQvA84KzI6UByBwwYMGCN+0a2f+3Xfo3f//3fZ2dnh2/7tm8DYLFY8Mu//MvcvHmTy5cv83Vf\n93WMx65GffSjH+XjH/84IQS+8iu/ks///M8H4NOf/jS/+qu/SkqJ1772tbzhDW8AIKXEBz7wAT7z\nmc8wnU752q/9Wi5fvnx/TnbA+UBoyLYir+ZYWiKCW0mk8SztMIZKIN3wiDoqNOxBfBgKTZN6WkjY\n2AcIqz0sZ4jiqnGowRKq2avcqysgActGqHbRqkGqEVbtQb3jg4Sh7Fu8Uty0Q/KKgLkfum+KLBGD\n3lZZrRM+7ITN4RaimjpIN510YqATH9KsrgBCkkvl9TteDBKULIG3vfNn+OxXPMQ3/1dfBSEicepW\nE9SJPriiPr5Clz4bbO7XZedR1kU1d4ok3Ca4cIzsGpQnCXbr6+4W7eM0ccZID7BuSasJGV/ZKNon\n2kL7Yzj2/ZPXMjQ+6Ln1JGEoUBkwYMCAAXdCePZNXhi8/vWv501vetOxP/vYxz7G533e5/HmN7+Z\n17zmNXz0ox8F4Mknn+R3f/d3+fZv/3a+8Ru/kQ996ENYeZT9oQ99iDe+8Y089thjPPPMM/zhH/4h\nAB//+MeZTCY89thjfMmXfAkf+chHXtwTHHD+UOL8gikihkgk4GQ3VLuEULn1QQIaxuS45xXuIx+c\nDHHinuswgWYXqS8Tql23j8RdT+XoDoFMiGPfFvX87GYfHT3iBD0tYfIKaB7ySL50RFg+Tlh8CtJN\nJ2+6LEObHCOqAh4f2Fxxf/Y2KSykz0KDSXSlOzRgC38faYBp2W8GW0LzMi+tiXtQj51sxxEf+Mjv\n8pu/9cf83Xe9mdDsQ9zxYUxTV79DheQZoRxvGO8iO58N04d8wRAmWLWDaeexhSfuA91NpL2GpCNY\nPoGsnkbywklvIb596sr2n90T0pH/f10Hv0JDg/UZ5XdSsOH0a1nuh8QxEhq/H/fbSjJgwIABA841\n7hvZfvWrX81kcvwR7Cc+8Qle//rXA/BFX/RFfOITnwDg937v9/iCL/gCYoxcuXKFhx56iE996lMc\nHh6yWq145Stfectrtvf1ute9jj/+4z9+sU5twHlFXmKrJ7B0zX9PhYUx0KCm7n3WDjGF3BHzDNIM\ncgIUE1AiVu1D8xBWX0I1uQ/bskfm5QXkI3K3RNFCwidUAUZBaMRApog58RddQHuErZ6G5VPY/DOg\nS0xqsirZDOrL7uM+SfpgrcqK5Q0p7RsSe6U7rwjLp5DlNeApyOZ527GGWBGrMVUUomViPuLTT17n\n7X/zl/jr3/P1PProo07uxQjixT6iS+huuPJs2UuBSglQyHNIc2T1JCyfJKRDgi6Q9hqsnoLV006w\n04yQZ5AOCfkI0g3PPk9Ht0a2lXtHXtwb6e5r69eZ4MVyU+0cv4YSy3VaHC8IguPXcnv7bZzDlAsz\nO35OAwYMGDDgvuFcebZnsxm7u/4Bube3x2w2A+Dw8JBXvepV6+329vY4ODgghMD+/v76z/f39zk4\nOFi/pv9eCIHxeMx8Pmc6nb5YpzPgvKG9TtSbhMkOllt0dc3j9OpEaBNW72PtIaG7Bqxcmbbi4Q5G\nIHgNu+k69UNIBASsRbvrWHdElY4QFmAtObdQB1LqyKsjLI5g0mHtdazaBVXQOXU+cEKXb5BXTyGT\nV7nXuVdle+J4Es82sGcZVjNUAzD1XxZZ179bJNcTYARVQNsF3/H9P8F/8h9+IX/hK/4MKslTVcIE\nlQpIBFtgOfkuJHgWuK48+o8lVu0SNKEY0lwCrTFxGwqASMS02EN6K4kpErLHHFo+HmPYK90W7i0B\npHkZK55iJTN/irDzKveOn/LafpD0rnCeBgBvh/OUmjJgwIABFxznimyfhMhdfvjdBcyOez8PDg44\nOjo69me7u7tU1bm+JGeOGCN1Xd/vw3hR0FUNohNy13le9WpFNMHsClWzQxLBghEDWKyRGIj1JbTa\nQaT+/9l792DL0rLM8/d+37fWvp1LXqoK6gZBN0iI0faE2FxmoB2cMHSi6Mbp8DqtOGPYQ2MLgYKi\n7Y1RBtu2mx5xUFCEbhUZHSQYLx2O3WIbjjjaoYIT6jA9ChQUFJmVeTLPZe+91vq+950/3rXPyczK\nrDwnK7Mqs3L9IjIyz86z915r77w8693P+zyEAEEEiwIsKbogCQQxkIpsSqlG5DRB2kiQBLbt+4hh\njSS7/RR0z5ccqzGkiJLRaoKoeWpI3iPkMwSpoV6DFLFgniF8CRaMYAeTS5UaidVFv5/LDuQF8Agw\nBlvDy3TWYXycWK2hsSZIxU+862c59cgWv/SvXkmwBaozoIPxCaoglKYlqZ8nYUQJNZQlUSssCaGb\no0WIsUYsEGN0PzxK6MU5iNfEK5iAWETiiBjcnmFx7MuXxUA7TAIxjr2x0x8JSY/9Z9ZKS2LBaP0u\nJlqTS8TS2EuMzB93JZYNIY5mB6/hIR4fbu6/MzGUi/5eH+6cbl1W/24P/34/9Rne69uDp9r7e+Sz\n+dSnPsVDDz3Ei170out+MGtra+zu7rK2tsbOzg6zmf8HuJpkr9je3mZj7RV4IwAAIABJREFUY+OK\nt194n42NDVSVpmkummr/8R//Mb/7u7970fN/yZd8CS972cuu+3kN3By040Lc61hu/T9syHm6SWBs\nC9oQGM3uQEfrbjFoayTveRLI6Gk+qUUJNN4HUx1D0hTTCtEp5DmGUdIxul0lLhdY3SEqzKUiVjXE\nTAyAZNIoEibryOQkVFO6ykjlHJYXWKyR+gRVAAsjZHISGa1BnPpy5iWYmbdNrqassb7oItXM+Own\n1n3xsztJpKGkYyCRtcmUtLFBqqeoCh/58wd5+7t/hV9/zz/laceniIFNx8T148jGSUII2LIQdLzf\nBGn1JqXZIbYT8nJEaIRCIo03KWFMrDfRYkiMxOQXC4rH8IVgHgtYGiAS6t6u0S9fivn5WmnAQJLf\nblLv//pKWDeH7PnjxzePYUSo1pFqiuUGufACpRghXvCaHeLxb3b8HA8uIJ4K5/RYmBmWG46tjUCm\nj/p7MPDU4/jx40/2IQwMHJpDi+0HH3yQr//6r+cjH/kIIsLu7i7vf//7+c3f/E3e9a53XdOTXzpt\nfu5zn8tHPvIRXvKSl/DRj36U5z73ufu3f+ADH+BFL3oROzs7nD17lnvvvRcRYTQa8elPf5p7772X\nj370o7zwhS+86LHuu+8+/vzP/5xnPetZFz3X85///P3HX7G2tsbW1hY552s6n1uR0WhE0zRP9mE8\nIXTNLmn3PON2we7uEpPMsuySwwK6hE4VxveCzCCDl8tsQEmwPIXkbQLiQjqMKHGGtGeQvIPKCEYB\n5tuwTND2sX8skLykwuh0G5MJ2kWkjZRyJzFCzhOk2cWaJaAwE1J3HhXF9gKhbiCcQ6KX5hxZRMgE\nqpOweJjChovy0Ql22yWyvUUdzrDbVnzDq7+b/+GVD/B5n/dMdhafgdKQyxpIJuRTPnUuhdDugnZo\nHGOjhLZnqRcfJ3dzpCwp1Z1gtaeztBkQsEzQXSREtDpGCB1R3CZiBmoNEgykgbCEsiRw4e8X91v3\n8YhXew1Wk+0TG1O2zp8jl4jGDpEtLO950kv/OMViH7NYDv34Nzt1XdMsdp9S5/RYRCmc2JyxdW6L\nkkv/Cc9T3zZzO/37vSKlxPHjx4f/q5/irN7npwqHFtuvetWreOCBB/i93/s9Tp48CcCXfdmX8frX\nv/6anvj9738/n/jEJ1gsFrz1rW/lZS97GS95yUv45V/+Zf70T/+Uzc1NvvqrvxqAu+66iy/4gi/g\n7W9/OzFGHnjggf3/OB544IGLov+e85znAPBFX/RFfOADH+Btb3sbk8mEr/qqr7ro+Tc2Ni7ye684\nffo0Xdc96vanKiml2+d8Fw8TpaWeHGOx82lUlS5sYIzdx9zuguzA5E5IvWc4N5BPEXSBtru4+zXC\nyJNHpCw93USXaPMI1p0nSCZQgS3JAmZCSwFZ7+MFNyCeAItkS9D5sqDKCLEWmX8G0gi1EZQlpas8\nI7rsPXpB8lBEb76sTkC3C+MpdA2MKo/EI/M9b/43nNiY8Lr//iuw3KAWEEkYgpQ9Sl6HbgFljq7s\nF5a8ibJkurbFugVRgDgihDFqEBQ07xFpsTjDzP3aBUX14M+dZ4T3jZ6aQRV5rN+/KuIXNmHCMu/5\ndLx9xC+AyhzLu+6ZH92FBcH/KTzK49/cpJTI2p/XU+ScHguTDMwoudB1HSZ6UNt+JS6XrX6LcVv9\n+30JOefb6txv5/f6qcChxfYf/dEf8Ru/8RuEEPaF7ubmJufPn7+mJ75U/K74pm/6psve/tKXvpSX\nvvSlj7r9nnvu2c/pvpCUEl/zNV9zTcc28BRFe6/ueIZVx6BRLAVINZW0KIViO0gegRWCLil5iZQ5\noSxJZYcSRmiaYdaCGkqEdsf/TliBMEUNhAiy4dNdKVQWCOqCOqd1qKa+LCkR0WU/aYVSek+eTKA6\niPbblw3XEjOXl/io/ixgnrtdG+DlPb/57/8Dv/mhP+G33/tGQkhYs+MXFdUxX9Is/uyiS6w9D1Kw\n6g633FiBsiDFgDImaKZo8deFfrkzBFSTF0/Gel/cXG3J0Kz4+xWu0acY+tbMskvodjGJhOYUWhpE\ngrd/Sg3T+676UAM3OUdNiBkWSAcGBp5ADh3997SnPW0/w3rFX/zFX/CMZzzjuh/UwMANoVpDi+dR\nW9yAyV1QH/cIPgNQb5DsziG68Bi7svSkkbKHauftk3iLpCdxZAQhaONiMlQgM0wmGArWgiY6SzQy\nodPg+dNSuSCQ6N9rhhAJQSAdI6aamHeRbvvKbYpXina79PYYibZN6M4TOAN2vp8eZx45fYrv+rFf\n5Ydf++Xcc2LkOeFVRRUSCZAw8ozu5hRh7xPEvEWwjOjSxYpEkArT4o9pGQhe0NOLZMEXICXNDqwg\ncPlYvf74pZ86BssXxxpeicu9FmVO0F1i3vE88OYMtGcJ3TmizhHE88yHaLxbn1BhUns052E+/bla\nis/AwMDAdeTQYvsNb3gDL3/5y3nPe95Dzpn3ve99fO3Xfi1vfOMbb+TxDQxcPyRicQYWkSDe+phq\nNByjlQklrEM1wYqgeemV7GmGUaFhhkpCLWDdjk9E0wxjRKk36dJxjxEUgfEdWJi6mDNByhmi7ZLo\nXATknf3jcf/0MXL1NHK1icYTYB1l72E0b7twAMz0YhFxuXxtgLyLdOcvLogJI4qcQOM6ykmwEaQK\nkxGv+aFf4KVf/Gy+9r/+W35hQPapc+yFi9QuWpcPE/I5YnsWbfcw4yBGL03J1BQCHQmCJ3yQZmic\neB55nGGasbK4+vu0Ej6r2MP9r68giK7wWlhpsdxipUPKHHSBWvT3sI8RJIxvLaE1ZGdfFhFB0ghJ\nl7l4u+wdbv6s9IGBgacOh7aRfPM3fzMnT57kne98J/fffz8/93M/xw//8A/zlV/5lTfy+AYGrh+l\n8aU8bajaz9HomDoKbXUHkjawOHFfshho8Zr0dMybFyOorRGCp2n4KNyg3iDmglC8GMciEowgS6Jk\nSqhdkGtHimNiLKhlL66x4pPdOIFRb0NpTxObHYK0UDJZl5gc269m3+dSgdht95ngc6QXkAYH7ZKS\n3JpC4z9n413v/yP++pOP8K73fSdZgi95hgnBGoIIqubZfCgQKBaJKCbiBT77deUdMY1ROpJ2dBQC\nhpr6uZUF0p1DygJE/Pb6+JVF0f4xH6Ly/XKvRf+1WkHnD2P5HCW3WJjC6ASUQhcFQt8QeqsIrSfb\n+vAU8DjvcytkpQ8MDDxlOFL03yte8Qpe8YpX3KhjGRi4Ng4rAqxglkFbtHjihZUAVmH1CUBBl0Qx\nrDSo1EBBYoXllkADWkE9chEYJ5DWKO02WOgtEWBbp93rrUtfFpSEVusQFJMZFtddwK9E3qp2Pe8B\nCY0zWOlH0150ujd6/xxXghR8mq1ewS6lL4WJs4PXRISkW5T8aY/AK4GPfXybf/muD/Gv/+c3MJtt\noiIwuhtijbbnaKX3XItHC4YYUJugllykppkfW1ng9ewVJgmjAy1Q9kAzYhnL20hzmmAdEiqvS7+c\nfWTFSghJ9FbP1ScAVxPnF34Nfgx5TrDOHy/WhDRDq+gT7WpjP8LwluDJtD482UL/RnCrH//AwMAt\nw6FtJK997Wv58Ic/fNFtH/7wh3nd61533Q9qYODQXMlOcTniGEvHIK2hYYo3Bvo0OHRnoN0h6JJI\nJpC9REUCIUbQhqgdQkOk87uuRF21RqzWiSHCzl8T288CLUV9Oq3pGIzvJssmGteh3oRq/UBAryrW\n0wyxQii7mAglTvs6eefSSnYLtVe4s/JHRwgJJaCSDgRtHJOrDSzdCUxpFx2v/tH/k1e+4gt58fM2\niDp333oQkEiYnCSONoiCF+bESO46VAslrsPkzt5T7X5qMEw94s9zs5fQnu0vAlooHVjnTZzW9faQ\ni2M/H8XKz53WLu/rvuR791+LlXjWFul2CFIIsb9NElod88XPav1AbN8qPJnWh8HjPDAwMHDNHFps\nv+997+OLv/iLL7rt+c9/Pr/4i7943Q9qYODQHEUEpClSbyLTe9C0CWHsk1MLaGlBAiaBnFuyengJ\nUiGlBQRNU4pVlKz9MmBx+waGlgXabcPyNEF3qOcPUS0fAi0EKdCeR+ox1Bt4IsjcowPbLaQ9C915\naLewkChhDbUAcQ0m94DpwVRRW5+ArwR6P7kW6/aXxEi9kOwr5ZEAYeLxhkx483s/waiqeOM3/G1o\nzyC65zX0ZQlhhMZNCoEiNZb3YP4593OPNtwTS+kFfi9UJfpFQbVOCRMQl92UHWgf8YVUVYoJxfCL\ngDg5+nv9WH7lS5cty9JFtiTAvHK+PuFLmnF8bc//ZHO5i4onisHjPDAwMHDNHNpGIiKo6kW3lVIe\nddvAwBPKlSwElyOt0eWGztRFqTYYBQkKZdwLGbA47e0F65Am5NxBbLGupQqFQoNphzVnEAwrewTt\nKNpAmqDN0nOizYCO0J5FZUaVlC6tIyiazxGt+EQ4jrDqBJQ5UQzGJzBtMe2gO+flT3G8P8W3UPvP\n2iK4eFVTQNwLndYOztmKT5rzEkrhd//sFP/b732Wf/tjL6KyHSzcRbBMsG2s24DRHR5raAHa81S2\nS9aWEGo0TwijCcUMS9P9OELB3FYCBOvQ0hHKHFVzu059EkubEKS/GLiGifKRbQwGcUIJY0po0bQB\n47v8guJqU/WbmSdrEj94nAcGBgaumUNPtl/60pfyfd/3ffviWlV505vedNns64GBJ4yjTPvyLrVA\nkiWSt4lkwAWvId5YaECaEepNGG8gYQKjTRidQEMiF0NVQBTKLnRnYXEKs37xcHScUt1BqcfksAbq\nE2yCINp4lF+3B92ckM8TyjZSdn1SfmEyRnHBHrQhWOtpJIhP4vcTSbreLrGNmLogv1Bow8Hkuyw5\nv7vNt7/z/+V7v/5ennV3jdYnsbBOqwm0w2wJe5+AxSlEz0PZpeQWZYJKhUpAMczk4te92sCsw/IO\nRf3TAS/FMcQDBIn1GiFOCWnMNXFUG4NEgnaEakKoNmF0shfszeEsRwOP5kpRjQMDAwMDj8mhJ9s/\n/uM/zstf/nLuvvtunvnMZ/Lggw9y991382u/9ms38vgGBq7OYf/z1w4isDxPtDlBwKxDSVCtYbFv\nkoxjAoZZvyCYpkizgxGJqUJjjXRblCJUzMkmxK5F6zGu1g1ygTiCWJHjcYg1nfZCXcWXJbsG0+zp\nJiFBtUFpcV8zY6gqFPNinJWn+yKBaFD2CP1tpQQX3Be+HqGGsIalEa97xyf5z/7GBt/wX32ei8/6\nGMTk2eJkyEskdB7p1zVI3kMCSHUMo4K0iYYZ1Bv7E3bixLOryxys89K+AlpNMasIMWCSUAQT68t+\nwoHQPeyk9CifYIBbb2KNVGMkNn7xgvveL0pqGRgYGBgYuMEcWmzfd999/Mmf/Al/+Id/yKc//Wnu\nv/9+XvCCFxDCoYfjAwNPLqFCu7NoaTDMp8QlQLXpPufVQp4Esva2jFB5TJ8qVCNy9hxprIbYUUqF\nkem0X3Y0tyhINKQ0qG56Z3m37bnb1TFfriwNqq0neZTiArssXNgDZkagRajc2tJH/130Ub7EPjWl\nwErEXm7im2re+1sP8Wcf3+VD//xFgEKY+sWHBYjJk0LoMDVot4gBTFo/X2lh41leAoQdCOML0lBC\nPod1C6oAXboTiRMseKY11YZbYiwffPpQll580z/OVW0hV7IxXDGJxpBQIWmChDmU4hc0KwfJ6j4D\nAwMDAwM3mCNF/4UQePGLX3yjjmVg4IZj2mHVBqV6OuQWUoDqJFSbWBhBteGZGtb592YvQyEkyBFJ\nAdI6ZiBdR7SGWJaotmSiZ0pbJnTLvjRlB6r1PqejQ9pTWJp4MopEoiQ00OdkF0KoMBLECm2XEDLQ\nt01eanuQCHGEqOx/bZcRkB//+P/Hm9/1f/HO13whm7MAbPo0uywgmg/IS3IhLAYkSrtDQElVolQj\nLFUQqj5dpI8gXFlWujmx23EPeVGId3h8oXWevJLWoN0iWAFrMa0efZyHSbe4UtNkf/+LBHucUHQH\nzS3FgDT1u/gfgkd/AjAwMDAwMHCDeEyx/fmf//n85V/+JQD3338/InLZ73vwwQev/5ENDFxv8pxg\nLTEGYvAo66gLStkiNIpO7vdJM4blBUEUIyJlCbqHheCFLlJDCJhl2vlZWO566EVcQHcWy0tMkgt0\nAnRb1PQ+b1Nyt+NRJ7ECy4T2HFrmMLkPSVPMGgIZRBHtKIgLXHwoTqgPxKUVVHvLyiqv+wJKKXzr\n9/wkX/2ye/m7XxiBs/iZC8g6aAQMqzahGvcT4BqjwUoGmWBpw2P72nNexBMqiBeI5VjRWvBrizQB\nMYIuUBn5lL7b9kVSYp91rgdJKSuuZcp8FR+320gmbiOxg+SUYcFvYGBgYOCJ5DHF9s/8zM/s//oX\nfuEXbvjBDAzcUMoSaR9BrCMsH6ZkCOxiXSTkE2hMIE8nxBEmgaCNtz2WXSgdQcQXAnVBCAnNC6It\nKNZQ5V2KGCXOoNpAE9CeA6lAC21VIaFCWYMwgzDxpcLSQD5DyokiEZ0+E4sTLOd+uq7uoy7LXiD2\nPghtPd5OgtejS/DfucRW8aM/+qO0bcf3f8t/DvNP9PdfeiReWnfhLDWkiRfhpP7x8xzVBSIQpMO6\nPay0RBE0rflk3oo/nypJwFJCNUM7BxGCzEF3MZn0NdoVUO1fJOz7pq9V/D6Wj3u/4n31o9yacX8D\nAwMDA7c8jym2X/KSlwA+HXv3u9/NT//0TzMajZ6QAxsYOBRHqZC2ghK84dA6yAuC7fURdoosxlhc\nd6tBacir8hgLHm9n5hPr0pezyGpCHFCrPKt7fALsLmgzUnWYjEGmGDOMOVRrkKLnbatStEFkgoWE\nlAVaFjC6E7QlasKkw0qLhaY/x2r/XEAuOrdLfdB/+Ef/kZ//+Z/nV9/1XVTxPwF34pF4FciGf19I\nJDqy1FBN3VrTbROTUJhhucOaJUzWEGsIZlgBC72/3QrERA4TKHNMDEQJ7RlEApqmkGoUuaiGXXox\nbI9nyvxYcXRWes978WIeu/yncgMDAwMDAzeaQ203xhj5rd/6rWEZcuDm4ijtkbA/GS7mP0hjcoDO\nDNW5L/EtThGWnyXSECV4+2Gaul85b3sZTajdEpE7RIB66n5pZvSjYCBiYQ3kJIQRSIvQp3CoIKJQ\nrRHCiBQiEfHoP+kLX8KYTKRIhYaJP0aoDuL24sStIyvE7SArdnd3+bbXvo7Xv/71POdvPtv/pkeA\nFqhg1NthNO8X0RDGUJ+ENEZKS7SOKhpIQXSOWEFN0eJRhPvPa4UkSrSOpG65Ie+gee6LpX2LJWnm\nP8NBOc3jbSK8UhxdX/VuF1a+DwwMDAwMPAkcWj1/+7d/Oz/4gz9I13U38ngGBg7PkSukDRCKRG8M\n1zlFJli9QQmbniRS9tB229scoRfaIxeXBiLm6STNFlhH7jKUSBndCZMTkEHyHlUMVBKAzhcmrSWw\n10/VM5YV4giNJ+jiGh3iMX/R/dgSEpLWD7Kzqw1kJRpXqSmhPqhmX9Wa97zhu7+f5zz72XzLN78S\nKoF61FtEKpAdaAvB5oRynlp3CGUB7VY/sa9AOyTv+gRaKiwv0ZL9k4EwhpAOlhOlJlORqbypkYDJ\nmBL6pkbxghnixCfOeRvRZV/5foNqvyUioUbS1M/HypXbJ4/CY7VYXun7DnufgYGBgYGnJIdOI/mJ\nn/gJHn74Yd761rdy5513IiKYGSIyLEgOPDkcNXtZIioVeXEK0S1MhSCgNvVlyHYL4g7Ud5C6llwy\nTO4HXUJZYiF5TfliC2yBWEss22TWifUapVrHbAcphmkEknubKUhpCFpAdtC8g9Rrbhmpa8g1Es3b\nFaX0z9VXjYfabRcrYboS1H175CplY5XEYcAHPvABPvwHf8iHPvQ7fp9mB9rzhPwICgQVNK+jZQNE\naMoWJPUIxOYUAFkm+JXDBFIFVsHoOEbfZrl6ra1AHCOjO7BYQ14AAY0jr35PU4h+jHTn/dxWi5Jy\nDRPnw9qGQo2KL2Vqb7e5KGP7WqwreRdZJbGsLCyXe5wLU1LKwi/xLlxqHZYzBwYGBm4rDi22hwXJ\ngZuOUGPael50n0P9mJQliYao26T2LDlMiHmBBkVGFUXGfWBIJlugkKHZAmsIpSV1D1PEq9GjZI/z\nkwKiaOij5MIYzUtEt31SbhsgcwIF67Ypo6e55UTVPdZWECkkCWiAkudY3EB6u4VBnwKy9HKbOIG8\n6+e8yrxevQYJHvrsab7/B3+Yt771rZw8ebKfpgqkKSobQIfKpE9CqcH2qPHvyXkXFS/sETIq6v70\nUmB8BxLdyiJW0JU3XCKkKaYNhIiGqdfP0xfs9BF70tfP+/kCMgYJl40qvCJHrGz3NJIpIhHhgk/k\nrmWa3i+kHqoU58LHv5y3fmBgYGDgtuLQYvvFL34xb37zm3nf+97HZz7zGe655x6+7uu+ju/93u+9\nkcc3MHBlVtPdfmnQ+oXGKxLHNItMs2gIXUbZBsswvQstDRITImB5hzg6DrGi6A5SFlhZoLmhhAqq\nGZq3CIbH+6VjLralhuD52lZ2Pc85zMCETAWjO/CkZyN0Z1EJmFSYCVmzV5trC5inj+wnaiyJ2oBk\ndDHHQgQZIaHybGtwL3de8k++9dU88MADfPmXf7nfN9QQJkDVL0Du9tGBFbBFKGNP/+siVjVuY9EF\noSwIlsnphJ9jSJ7/bf1yZJwcLDeuprzaYZXt20X2k0Z6gYoELxYy9an9UbOuj2gbMjMsN/0F2QV/\nNq41ZlDC4UpxLvzE5dLvGbzjAwMDA7cdhxbbr371q/nYxz7G2972Np75zGfyyU9+kre85S089NBD\nvPvd776RxzgwcHmO6tluzjFqP0u2c6i1Hr+HQLsgyhKTQInHQdboSIhE0EywjFkmCEiqsZBQWUPD\nyNsh6w0Y3+3T4uUpku4Rl6fAljQ2IvYLlcF2ydVJpMxRnQB7vjWR99AwQULC6MVu8Mm25h2vTaeP\nCZRAqE5CaPGSy4RFr3P/8bf9JGfOnuWHfuiHLj7verPX+AEIUFrIO1CmmM3ReAKNU5CZv4xhCt05\nTBKBBq1PgGYv2AmzvlWzvThKb+UnLwvodlyYrpYhV+9LqH0JVeKBF/0oHNU2pB1iLUEiBR5fmU1/\nYXGoUpwLU1L6c7TDJuYMDAwMDDzlOLTY/uAHP8hf/dVfcezYMQCe97zn8cIXvpBnP/vZg9geeHI4\nqviyPUqoCFZTZORTbVMIgVwfw1bT6ekdXsKiHYQpJa7D8hGyLDAzf57RSZ8UlwzVugvaPrNaS+6t\nHQVyQxnVEAU6wBoXrqMKkYy0e55nXUVC2KDEwKryHYCSXWiTUJtjKkhsfMEwjLH6BAJ85KP/N+/4\n6Z/lV97/y4zrcNDyGGrP++Y8NJ8A1j0tJG5AbrDJHQTdBdagnoFFQt7q88RbVKu+QXMdCRXkbYSC\nhhlixRczAWnPeiV9+0j/OkSsOobF2YFdxPTA480hPom4lMeK+rvc210WWOefFkifTPJ4Ygb9RA+Z\nCz6I6oGBgYGBnkOL7ac//enM5/N9sQ2wWCy4++67b8iBDQxclSOKL7QixppQ16g0FKZ9I2Twqnb6\nrGkiVk09sSSMoD0DUdBS+3RYRlDPiH1dumrjk+DRnZA20FChadOLGusE1i9LiiClg8oIvVgO0iIh\nYhSsLCBuQn3BxDhN0RJ9Am4RTzcpYA2mAqljvjjHt77mdXzbt76KL3je5x/4mrvz7p22BeQINgUW\nwBoQ/VytQBAvzlmegtGdqAWCmkcOxv6cU410572OngJ178MuS9CWUPbQ7iyp+RxZRoSYKGWO1CeR\nOOlztisv4dH28p7nwyw/HlbEakuQcpCzrXL0Sfq1PvftyFHy7gcGBgZuMw4ttr/xG7+Rr/iKr+A1\nr3kN9913H5/61Kd4+9vfzitf+Uo+9KEP7X/fl37pl96QAx0YuCxH+Y99/X7a89sE2aHM7vepdF5A\n1XuawzqkTa9JDzUEsLyAfJ6gXe8zjmiowPA0EcQXAq34kmIUiFNPHtE9tIkwmvhzUbA0AZti8SSI\nUrTr9+ei+4FDgrSGdtv9dDr51FwixBbynCIKuYKgSLfF973prdz9tLv4tlf/IyhLt3DkXRfAErH5\nDnSnYX9JUCAXiAXqSZ//7ZGEtFugmRggxATWkKVGTDFtsdK4YN7/RMF8Yl3m0GwhZQ7RCKWiKITY\nZ4/3FxvE/v261PN8xOXHq2IFCxWqUEqHWRpE4I3ier93AwMDA08xDi223/nOdwLwlre85aLb3/GO\nd/COd7wDABHhr//6r6/j4Q0MHIIjxMGFyV2M0pLl8iHodolljy5OGOU9yiShpUbDOtpsISEiZU7Q\nhlB2wVpUk0+fwxiLE8SyC+Q4RiR4ygiKWW/lqI77c8sIIggJG/dxeNIBG6ANSEKqTSBje58iBEUk\nYoDmuUf89ekeQVuws0jp+PV///v8H7/9+/z2r7/X4zhLA5g/N/TWjTnYMVzVL4Dafzl9OsQJUrZI\nkslljkkFIewLVZME1aRPKKeP8ct+sbEqlClL0IzFMVlHqNW0cQKMUCvuF0+j/aKZy3qej5yZfhUk\nQvYYxoD5BchRbSuXcqtMb7XFMo//fA/L9X7vBgYGBp5iHFpsf/zjH7+RxzEwcG0cZaqW56RqAvGE\nLxdag1FBNtrRDCutT6ZHU5/SttsoEaSjM4iqlLQGkgGF+i4XypjXpEv0CXE392xty1DUWyfFCCMB\nCjl3EFpCGmGeXN0vDE4I1lJKRszrzUUqt7J4R7oL1jgFzTxy+pN815vexj/7vlfxtLtO7CeNmHaQ\nlygtxBm0p6F5ENgDRsDYp/nVCajW6bqx+6yrdRfFzVmQKRoCpBN9s6X74wX1C4oLinUINSXOIGWK\ntqDmFpMghK6lSIBw3Bskr+R5Pqr//nB/OPwKQcQ/NXg8IvBWmd6H+OvZAAAgAElEQVSuWlXxbPYn\n5DhvyHs3MDAw8NTh0GJ7YOCm5ChTNRGf9s1Pk8o2ph2l2wNTLAQvmOnOE+cPoab9Ql1CZRMQlAWE\niiBuJREJWJpBtwu5gdD5FDlWEKJPiXUJ6Q5IxykIFsdesy6BkPcI2tLSi5O84+koYQNYesY1LcSA\nhIJYQLUDBOsW/JM3/E986d/9O/z9L38JasWXN7UlWIelGisCGKQAPA2YAyMIay62tQMRwmiDIFDi\nCFAsjLGYXUzXa/0UuuoXShsXsBdNpo0YIhqEKJClIN2uL1nWJwD1afZjeaaP6r+/GlaQOEbSBGQP\nyY2/n9f62LfK9PbJOM7r/d4NDAwMPMUYxPbArc1RpmpxQu7OQrtN7hpfYNQlhBNIdxqTQAyeOBLq\nKSVsQLWOlQJVhPYUEfOlyrTu4rY0SAhIMLR9xL9ensaW55G8xKq7ICtMNgji9ouiBjGSM6TSeMEL\nc8zGvqg5GlE0Ab3POCRPEMkF0Q6JI37qX/8SDz70Wd7zv3y3/77gTZPWgRUCoGmGxYnH9XEa37Lc\nBTag3YN0HibHUElobiD0SShxjIWA1Osg0k/eJ1i3jZQG+gbIfZtCnLj3vJtTZIQIhCAEMYiCSX24\n8pqrLrgewcYhsV98rVEzrP/k4ZqnvbfK9PbJOs5BYA8MDAxckUFsD9zaHGWqVpYEa8lWkcoCy6eh\nNJRihJAoeUmZnoS0gaQZxHWoTwAJ8jYWJpTS0YdjQzoO3Vli3sGseBTf7mcwnYN1mIwhRKjXPdc6\nVD7Zrtahm0O36C0pC0Z5STO6l5DGaF5A2nCrRhz3S4sLTxbROX/5nz7Ov/rJ9/JL7/geZrUQyw4q\nFRLXvLTSFEH6CL4A4Q6YPgPmO8AYdBdkCrSEPCdYi6B0XU2qx2RVAhltd9Dx+n5pEKZul0HA+iSS\nPl9b0gwb3+WLkhRy8k8DvO59bb9W/po5qo0j1FgwiFP/9EFWpe1c27T3Vpne9sdpJKy3+AwMDAwM\nPLkMYnvg1uewgqLbIdASQ2ZZT0HudiGbC4wC1GskM3JMBKBYAQJSTbDuLEnULRkxkVVBFz7pzdsE\nxFscWfZiLILu4NuBuV+uBKuOQTDQACkiBSit21JMCdaiVEAmlgVqnfu6g+dVt4s5//g7foR/9I1/\nj7/9tz4fCxWdVJ6Iop0LdJm6EBZPNsFa/8FpPx5ZA1uHsI6WjHY7pJCBCikbPolnicY1RMyTVqxA\nqBGyC+q28UbJaqP3ibsQtt4Hjup+sgr1sccfu3cN9oj9uvY4Qcrehb9xbcdwo4Tr9V68DLXbZ7qr\nf+vAwMDAwI1nENsDtw+hxtpMLI0vDqap20PSJiXdAeEYOXmxTVkJVW2wtrdLaAsl+4Q53en15GlG\nzvPex7wBYYPUPOS2jK5BZULIu2hoqXWPLAVLIyzOfAotLaQ1chBMM7m0MDqO6MLtD5ZBaiT4wuSb\n/sW/YW024zte/fVu+6iPEzFP+UAwCX1s4QUlLtW4j9+bAgFGT4fxnRBrghRCMEQzAKW0/TR8TAgR\nM8Un1H2meHeGkLdd/FveX8oUwCQi9br7ziX2S5ebV34/jmoLuVZ7RKh8yvtETqUPe243YvHyiU4j\nGRgYGBh4TAaxPXD7EBKGYKNNorVo0xB1mxxPkGxJqcaQxpgqUZdYOY/F5BnNlilFifk8Km6jQGZI\nEGxyD5Td/TzpPLkPmt1+yhxQzSBGF8R/nQ2SINUIxFsbXcDXnjyiC7eBYBAmWBxjpvzO73yID/7G\n7/DvPvhOYj1FiwvhEmcXC9GV0FvVqVdrnrCSd6ANELIng6SIakbi1B8jTFAZeYyhLYkUSmmwUO2n\njhgJjT7NFuGgfl1bF44UTy+JYxe4VxKd12IL6b/3qIJZRA6+X9uL2zVvBEc5t+u90Hgj00hulejD\ngYGBgZuMQWwP3EYICpRYUao7wR4idxvQLcnVJuTsRS9lm9Q+Qk5rBCvk+i7Pkg7RrRmavQI9TX2C\nWBZAgBiB1hM+2AV9BC3PgDQmGS5ERdCqhngCi0YOG2BzAr0gtA4tHVbNMIv7UXlb2w3f/j0/wg/9\n02/lGU/f8JKZWHnFfJz4lDnUkPfc9hHHfsraT6otuOWjbPvEeXkW6juhOoHS+jQ6Td1iUlXkJnt2\nNtWBsDKP/AsGSML64hisuLiUgJWlt81LhLL02/vkkouE30pUrgSc6dUF3HWY+D4h8X1HSsi5zguN\nNyqN5FaJPhwYGBi4CRnE9sDtQ7dNyucY5dPY/CGyKrGcwqq7MDIaQPIOppmOhOY9aLZ6MVsjlgkB\nQlDasgvzU8S6phiEWGPWYfUm7PXlNivRGceUrkHqgJpAPAHViBAShIzmXoiHhOYOqk2s2jiwYoSa\n173+NbzwBX+Hr/oHX0kp8/72kQvkUCEW/BwluJ0DoCzcBiIVWIuUz3qyio4gbPp5je/ElqfdBpPW\noT4JzWlEDGSMpQTdtgt1yxACviNavLAnrUFZuI2lLD0XHCW0Z1ArhFCh9ILvQiEp0avfV15vyzfe\n9vBExeIdRUBf78XLG5VGcqtEHw4MDAzchAxie+D2wTJKpMugljHmqFV4TsUIwggzCGIEWsSEQEvX\nnIXqJBpqtDOKZhh7XXpA0LxAdIGFAtUIqjv7ZcXeylEMm9yBCb1wn4NOUekFcrVGabe8/Cauw+ik\n+657G8DP/fwv8Bd/+TH+w7/7dYj4ZF0ErPMs7n55EegtHZ0X6tCLWASkxnIEdv15rIHFljdSSoPE\nKYhRaIFIiCNPH8k7lDBz2wkghlttZHSw9NhH6lHmCNkn22Xugl+mYKmfXpeLLBwm0RsqJfRT/Rss\n4HqBvy9sH+/S5pU4qoC+nhcYNyqN5FaJPhwYGBi4CRnE9sCtzVF8pGGMlSU571IIkNZcaMdpv0g4\nA5ug7RlPBJEA0lebWwNqFCKW1np7x7gXj4Yy9oVEFUgVlNoj9ko/rZWaSgy1jrL8HMQRIRxDJUJp\n3VdMwEShLPuJdODjn/w0P/LP/iXv+dmfYjab9mJxAfNzboqZ3O3+aDhodSwLL7/ZF7F9hbsmYAZt\ngW4J1TloZ4Qk6CrGD18MtW7Rt0VmL78pC8QKEirggoXD1XugnYu8PAeCi30raElY3NgXZ9KL7tXx\nygWi7VBZ3I8T86O44c9zaJF7I3zQNyKN5FaJPhwYGBi4CRnE9sCty1F9pNpBmRNN6WKATsH2oCRg\nAvSRfXHW+7AzFipEKqzskWwONGRb96KY8V10zZZH+VUb3gzZ7rq1ox1DamF8HOQExIhZ56kioSbq\nLlZqQkhonhMDXtyuC0rZBZtQVHjVq1/LP/xvv4YXvehFAEjzOVLZQ21OLAvyMiKjYxSTPhPckdXS\nYlm4YM7n+ijCDhh5eY21UM57EmFch9Ed+D8JmWJG0NYvBkLwC4A47pNGwn6+9up1lVB56odmP4cw\nA9SXJXtLjFw4Ge0XOJ9QAWfFPzFYfflkWyFuNR/0zXxsAwMDAzcxg9geuHU5qo9U95C8Qy4ZugZC\nRErn0+R8FnQDTEjSeQRgMVRmnhedC6GbY2QiuxQ9BnnpE+qUEIlemV5tQLsJ9TlgDHKXC+68JGvn\ngrjexDDUDIp666SpCy6pISgS4Ed+7G0I8D3f9R0XCNvs9hEtfvGgy/6+euB5DjWWdyHv+dfzbZ/Q\no7gPxSvfIUMY04bK7R5hBjFAyRDHaFkiYZUTXtzykcYH4hj6ixKDfA4prTc1xnUkJiD2hTLxyjaE\nJ1LA3WxWiMEHPTAwMHBbMIjtgVuXo4qn5TlC+zBSlqgt0LKGqUC3A7H3MncNgW0iAdI6pZoBAWxO\nhxK0oXRTqAvYghAEXS6gnkB1EiqFMAFmBAoqGenOepukKbQNxCUaZ32Odwdpna7s+bSZANWMP/iD\n3+e9v/RB/u0H3kWsp/ui1NI6pTuDhhHFABmjKhCtT0xZxe0pIVSAoZz3iEHWcLGdfHof+wk9/rRB\nFFMvsYlpgmrj9pC8REYzPIrwIEJvf7kxz9G8dCuMiXu64/jiCfiq+Ea7/aXPG42qostttNny64y0\ndnNZIW428T8wMDAwcEMYxPbArcuRF9ECXTpB4iwqGz6NtSUWTnjxSzcHm6MYUNyaIb1tIiZCC0IN\nNIguXZS2510kl4LKGHQOi4dI7cOgoGkdi1OkCkQ9Q9YtQnsvOq76Ipxpby3pz0cDu+dO8Zo3/Ajf\n+7p/yN+8e4IuT8H0vn5yXaHphIv6Zg7JXR6Q0bLwmL3VMqKu2iwn0J3HrTJ7MLkLggAC1hBp0FbQ\nMIbx3Z5ogmJp3QV1qA+SVVZclOu9JIggIYFEisQ+veSC90Vbd0r31e922OSRx+Fp1uYUzIXQ7mLU\nKNy4pchrYfBBXzc0N+hiC23P+0Lu8FoODAzcRAxie+DW5ij/qaYTRIkUa72EJhzD9Ix7rUMF0iCW\nERKGImW7t3gs0ZKxOPL0j7iOlRaas1g5B2GGSAuch+1PkNqHoDnl7YqT+xFdkLotAntQHUdsD8oc\ny3vY6GnQLjCpkDCCasZ3vO4HeN7n3cd/99/8F2ANms/BskIkYN0WkQajwsYzrFuAdZhWkOK+0BYM\no/96dBLqNbegNDNozkMtYOvQfg6RRBIj5zXMjkM6jloDNsfCFNLswA6yn4tdLsrIFiseP2h9pf2l\n78u1WCYej6c575K6cwSbEXSPYp1HJd5sDKLw8aMtgYZggaQLShG/qBpe24GBgZuEQWwP3D6kEdkC\nJlNgBnnrQPS1u1CtgwglVJguvTky+6IkIj4MjglJNSYTyKtK9R1CWHmq91BVn3ZrB6XFqOgkIrEi\ndguIc4gtVsTr4Ak+ntaO93/wV/iPf/Ln/N7/+p2E7gywAbIOzWeR3PST+AkqnRfVmBJKhxJ84a+f\nPluovYBHQl/Gk92XjoEG0DEst5A4I8QODMxmMFqAmk/FQySkmfuw8YVC6aPzzMpBLXtap0gFq/bI\nauPRr/21WCYej6dZO0wqrKziERVG1eHvP3DrYAW44M9Gv/8wMDAwcLMwiO2B24d8lhQrShaUHY/Q\nM4MSfDEwbWBlG9MGiAQ7D2VCSjWt1WRN7kkOoz49LhGLolooeQlxE+IGod0j54bU7aF18WbJ0Z0Y\nkDHQykXpaM2n3wISNvj0pz/JD7z5x/mpt343a8fuIjdn0QiU80ipEFsQyy5dUKiOAR0SK7S0aMns\ntzDmXU/+2M+zHvsCZEoeSUjndpOUsGpGtkWf3d0QmlNYGJPoKFJhRCxO/bHzHlJ297O8LVRIdDEu\n1dp+Pfx+hN8lFpCrWiYutYw8Hk/zKqJQAioVKtMbM+kcKsyffCTiuwirr8Pgfx8YGLipGMT2wM3L\n9RYyWQndaXTvFLR7IAEpS0x2oKwTdY9CAS0EXSLiIroLI6AjVmPQTOkyRPUJt1aoVFh1HGIFaUKe\nPQt2A3m04Yt5BKhO9I9f+wTdMqE701s9DLPEq173P/IP/t6X8V++4DmE5hHP/Y6VD+3GI7TtiJox\nKf0kfIaEgjBDYi9m8y7QC15TP+96E8YnoL3HIwDThmeEyx0Abk+JmxCnfcFPAIRoLUXnblORGeQ9\nQpmjoXJxrhkJ44PnW/1YCf5uGxCII88mv/Q9vPD9hctaRq7Z05zW/AJkPMUmCWx0/aedN2t0n7ZY\n5sY3ct4shBqVhMqEHCb+ic7tcN4DAwO3DIPYHrg5uSFCJtBpi0qBXNyLbBniGgiotcDKDlEgtxA7\nt3nECdaeJpSF2zqqkxgTciiQElLPXDjr0qfeYsAehGMwPumCgBYJNSKGimKlwSyAFf7FT76Pvb0F\nP/Ddr8XsDBpqghUv3EknEBo0JnKZ9WJ5AlXwKXzAbS1xdEHmdZ9eItEn8XkB2ttIokIaubeaMUaH\n0NelW+UtkKVBiWg18el/qH05U2uU4HGIUqErq0qc7E+2ac9Cc5pgLcQpRvbYwAvfv0vf377EZ5+V\nMH4c73moNgnjDUIypOsOX5pz2Iu8mzG6r39dhYD0DaS3g/AMaUSYHCfUmdJdzzafgYGBgcfPILYH\nbk5uhJAp5xAMqFys0kft4T5j4ziwAxiy3MLqDaB4K2Q5R2oe9mKY6h4o6zA67gU2ZliY9A9XwfIc\nqX0QtKPEMVbclmIyQbRxUSw1poYE5U//7GO86+f+d371l99JPVmH1VRSGz/u0TFUM6iiVYTRBiLR\nlyTDKtnjCnF6En3arUuwpf+cC+RjsH7S77dYUlCojkMaYaUjEwkh+EXHSrjF8YEvXCKEar8kxlZV\n7N02ks9D2SNY54N9if5aXyhiH/V+2qOP+/ESKkxqlIj1ZUJX5SgXeTdjdN/NeAEwMDAwcJsziO2B\nm5PDCpm8e5DdfLVYN1Nit43mHbDPYuUOsLmLxHYXpnf0leZCqTYBgbTunuvlHlkMKR2EOaxyscd3\ngCoiiqn6dDdAjncAc7AxtNsw7SBEzCa9h9qfZ7l3nle/8Sf4zm/5Cp57d8DKEiG7LSREiBv9ZLmC\nepOgHWjjU/i01l88BMz6aV5ac/F9YfGMLkAVmqZfqsyQxoTuLBo2vfa9OkaKgawLF/M2JbRn0W4O\nI/XJM/TLnPX+EqStkknyLlIWWN4GM0Qb1BSN+IWIxEeL2Au5AW2SIoKkkVeX2yGnnUcRqzdjdN/N\neAEwMDAwcJsziO2Bm5PDCJm8S+g9ymhz9RzlMKYLNRYnwD0+1C6117V356DdQnSBiRFNIY4xEVQM\nYiQ2e1A6JOyQ8zYUJZY9ioyA4JncIbk/evFgb33ehfo+0I5AwQTMJggBk4rvevN7eOa9J/jHX/MC\nOl1Aexor5vtecQ2iuLAnEGgxxHczFejOEQWQikK9L4gveq3KAro9b5yMY59q23EwQ4sL5SIzAi3B\nI0kIeYkIRN2hlBGxfYRsRkhrnmxiGdX24LVuHiHmc1hZesJJKJA2PKEkTPrs70tsIhJ7X/lNJFTh\n6GL1ZjnuFf3fGyN5Is3NdnwDAwMDtyGD2B64ebmaUNDusb++FDEXfuMA1RJ0G1BYfoYgYzSeIegu\nFipKaSDNoMtQTyEs6YhQz/z2XgiX3IA0ng4SItLtYHnP2xnl/2fv3YMs26/6vs/6/X57n1d3T8/j\n3qurK8tYFlg2VCxKDlUKUJjClEUSh8QOwRVCBZtCIuGVkFC2iYkhJjEPy2A7fkBiG4RwFVAuRBli\nYgcEkUwZKtgxMSBswAKkqyvdufPo7vPa+/dbK3+sfbp7erpnpufOzJ259/epmpo+p/c+Z7+6+7vX\n+a7v6nxCo4wQW6BaiBglXSbEwI/9k5/j/T/3y7z/738DhNYrw/0NaC8SuhtouQ5phowvux+cgpkh\nMqSndPt+I9DsDkL2tnqxi8UYfd9D8v2V69C1hKbBSO7FtkQXZhAnqATI+yB+s0FZgSxuvZHZHGvt\noL+BdFex3BF0n8KOZ4bLxIf2aOc3AsetLo+TwD7O41itPi+h9Wp+tS5XKpXKY0EV25Unl9Ac+Zo3\nj++E9qTuBn0WyHtuqQDPxrYRSKZIC/0K0bmL5nYX1vuQFwg90ndY3MViA5KQvIdYfzia3Iguxie7\nLlgnn+SWEYtIbIfmycCLV/f5s9/6Pbz7L3wlly8/4znYVpCSsdU1gu6DGkXXSD6A6bPDJMcAYkhZ\nEsgoI/dvb6rax6wah2LREgzBg5ChjCEkdD0ntJEQJ2icuvCOhtnGkz0ixDhYXlq3Yhy+7tahv9k0\nI3mNURAZQZpAcwksHw27gaEJMj7+IvZx3rZKpVKpPHFUsV15cklbbh3ZeLZD67aJs8ScGUWze5gt\n4OPLV8DIv9aGmF9AMKT7GDlMIYzcHlFWiHXeQIiBtf6+ukbWL2HLq1i6AM2YEFrol4NVYwHtc1jw\nKYumGUvGO//MX+Mdn/dZ/NF3vAPWL9LnJWCeEmIdlt3KEG2B5gOs30ZGl4b8acVCRm2KxS3PwZb2\nsBlSwK0nZY2lbZg+A5PXweLasJ8ZrAETNI4xBJMtKEuECTQN2BorHRanlDiD0QWveFsPMhzrY4kh\nJe1g1qOpgTgbauzx8AZIAAvNUWJJpVKpVCqvEarYrjzZbKwN95Iiob1nVlsCrgMLoIfmsldjDUr7\neig3IF4CW3uM3XgEtkDUsChuDWmmEATymlBuugC1hPYZKz0ixX3Xpj4IR8agc0wSf/P7f5IXPvES\n7/3fvw3J+6Ad0eaeFWwtyBaFmwT6IelkZ1CrBQQX1yEissLiGJEWiyNfxBT660RdDbvco6s9mH8E\nuut4dXtIWRlfBM2kNCYnsOiV7KKFIBFtdpBmCwtjSFPkmH/ZjqeKpJmL8BCxvD668QkNpkPk3iYe\n8EmhDqupVCqVygMi3H2RSuUJ4F5SJLoVUm5CboDx8C8AU4+4m15y0d1nb+wz80mP3f4weMagmA+l\nCRO8Mp6HIRojrLkwTGwcxphrJAaF0EMaE0X4td98gb/+936cv/XtX8M4KdbfxLrrkFdQOtA5xOAV\nZU2UdBHaraGaPAYRz9Y2Q6UFCZ4+ctw+khfH0jcC7P/msJ8Z76x8EeihX0EYoxYw2fYKtYzd8xtH\n0F5Gmt0hkeWEUN5MhRySSTTO/HhJhGbbmy1hmFQ585uiJ0W0brKqrfgN3ObYViqVSqVyH9TK9jFW\nqxVN05DSa+ewhBCYTJ6giuMZWAlu89g8FheMZpt8Z2UVCxp3oF8DF4YlA5QD0G1PJEm7sP06WL0I\nJEitWzTo0HYXGARjG91S0r4OKwdARyzXyXLJh8hoDxhFO4gXEBH6suIr/of38tVf8u/x1t//Rq9O\npwC5O0wDMSK53CQ0IyQmLI0wmRCmlwmS0JCIYl69L+Yj2AleQWZFGI/o5RJh+dtga0KzQ8dN6A9w\noZ1AnvL9HF2C9mksFmgScfY01mwhZUG0bWJskDDG2meQxidIHsUszjyHmwllvUeQFsvZ3yJkwmgL\ntQhxgoR06GkXkUd0RXj032KxoGkaYoyed15WbKZaShyduj2WQY7VIYzkDYdPEK+Wn+t75fi5rr+/\nX93Uc/3a4FH+rXgUvHau1HtgPB6zv79P/xqaQDaZTFgul6/0Ztw/JzOlDz/6V2B5q70kjL1PUApw\nFRfcB5Augu4hnWEm0F6EcYT+qo/51hUhCKFborJCmRHmH0ObAiGR02WvJmcBuwmLF9Dcg3WeR72+\nhsll/txf/jEuXRjzVV/ymZR+DtIgRMympO6ALOrTHUshSkHjlKItxBFa8EzxIJQwAVO3oMR2aJAU\nNPSEPMXWe/TrJSaATYGhOs820EG8DGUNNIQIyYyuW1FWB6ABmos+tj73EFvPHl/uHx1HCtbrUaV6\ndZ1Y9r1R0jqK4PniohCGqEJ45FF0TdOwu7vLfD6nX8+RfHC4Dxras6vtx68Zhu1+wn4lPPE/1+fk\nlnNdf3+/qqnn+rVB09wl8OAJo4rtypPLSZ92aG+3O9xiJ4nuuW63YbkC1kCB/iaMtj1/O+0iGBZa\nZPQcNghU1RsQG7d6BCGUOdoWxDpiFMLoGXI/R2/+BqKfIK4/AggqE1T2+Kmf/lf8+Pt/lZ/9u19C\nTHGYrNhgMoLUUewCkHw4jmVMM0UERjvul9big2vWS4hLJLRoXkJeImGovBYBu4Hk6zQxodJgMVDG\nVzzNZP8FYBvKvqeFAJqz68gkBOmxPIjmZhfSFNt44u9k09lUIELCFLeONDuernJ8uVdymuFm+M7h\nYz17e14N8X+VSqVSeWyoYrvy5GLl1sr2aQNIjg8pkR4ZXcLmK9yvPQK2YDxMiwwt0PuUxNJhcQaj\ny1CuQd5B24h3PaonmpQeCy1K655qEZAeywnV6KK1nXPtxY/w9d/+Y3z713wGT18aI5pRC9BccJ9z\nbBB2PPUkdyAJNRkaCyOUNZEVZkrRHmOY6Gh58IZ3WJ9hPHMBzhhlDhS3TcSpV6jp8KmWBt0FaDOQ\nICgSGyyvsJggmKeR6LGWjs049o34PH6smwueS64riDMYP+3Pa3e0jsS7T/h8wJgZltdYXh5dI4fX\nQrjzwJoqsCuVSqXygKhiu/JkcFo6xKaBbfjaThNIt1QpZ8T1DXK5CewBM+AmdHFIDpl5+kho3GpS\nFiAjoHiuNBHRjDEhh8YHxaQGZRdtRhB2oHkJ+DDKFrBCZZuv+c6f4bM//fX8sbdfonQL90tvBsyQ\nQWYQMuQOswWEHc/kRofJixHTDisdYh2mLUFc25c49RRDSy74G7ed5L4BmwMTKFd9CE57yRNJ4kXc\nj34RxhexvPExT5EQsDBGgk99tDyH4E2Cpj3QD0kjJ4+1eWIK7pH3ZJQC2mOiPljnEWN5Dp1nkoNg\nocVkyByPk1dGUG9uQBD/BKCK+kqlUnnVU8V25fHnrFg/iSjiAuZktfU4G0ETIhmDsD18owca9xbH\nHTAhlAWxrDHrKWkXs6WLY4xgCYmRknahmYEWwuoq2ioiE6wZ8q5j4+JZRnz/T/xrfv13bvD+v/2Z\nYAc+fh2gzIl5HyRQAiBTiB2Ye7xDSsQmUMoKJHslu3Q+KCYEtM8EDAktog2aRkiaDf7iYTKmjnw7\nF/8W+s6H7NDAuIHpU9Be8ibImMjFhnSRKaTpsTQTg34PoSDiHjrdDNDZ0O8RdT7c0GRKJz4MyBQJ\nzVFyyaO0kWiHlD3o1b3ajAab0KOtrp/cJvIBYbiWzbLbdKrgrlQqlVc1VWxXHn/O8gtb8Yg5AXR5\nNK39LJ/t4iVSd5Wsl4CP45XtbhDaPWiHKmBGMIiyRtVHo6sKWKaUAqwIZYmJ0ticdVmTuhfp4w70\n10BdUP/G8zf4tvf8K37wf/pcpuMA2g5NkYZZwXTl1eisSOgAQboXsTx3ISYR4i40LWpATIOAngCG\nqg453M3g/06+33GM5D1CALSjLBeg+0NCSgZ52rPFmy2KNN54KSMXou0lKGvUzFNVQutWFFNgM0Hy\nxK+NskbK4lij6ng4D2FoSI1H5+VRUVYEit8kWD8EsbwCQuCyOFgAACAASURBVPv4JzJWhuM4cNJH\nXqlUKpVXJVVsVx5/jnttN4+H/xXxyYzmPmopXn11oXrCKmD73hxoUzyZYwSEocEvQTsDbdEsqBjE\nbRelcRvyHlqWRFtRSo9qBi2o7kHaR+IUuOmZ2jGQS+Zd7/4V/tR/8Gbe9qnP+lTIMIYUsbjtzYfd\nATHv+aj4YNCvsNIDS7TrUdmHcUYYY6IEazAxoq0pJK/IS0tILSoFK8tB4ComLaYHPu2SfWAG4Zon\nizBkejcXwVZIaAjB0HwAceQj5yURrMO0weIY64aGUhli/DafJoBnfZv4sTQZHrso19S+QiPazYfq\nhBaTiIX06CvIp30is7kBgbP7DCqVSqXyqqKK7crjz1npEBIRCe4v1jWemb1GRDBJHok3rO+05LA7\nxLjt+vIY0IG10K28WVIzMPepjzb4pmMhLV8i0KFphixfQqVAf0BoLnhiSPM6yPtYiXzrD/wWbdvw\nDV/6ViDC+BIWxO0izRWQEdZfR/J1KD1BhKINcf0SoVxDQsLyFM0ZGU0wDC0rUChmh8cjJKAsfIpk\nmA1V6ILEBmyESfCbhXIdbBgJH6fD8Jkd6DNiGSkgsWDddSRtDYJZ3UMeR4MwDL4vm3OxIU0peeZR\nhyYQmsNpk4867u+QOMFkDWmCNTse4fgo0c5zybFbrlfSFlo925VKpfKaoortypPBWc2PcYL1e96f\nF2DwLWwe3CoK48SztmOHT1O8APTD0Jq1N/HNn0faKUJAY+Pf769ByeQ0JXULWF5HynUI22TAiHTN\nRbddMObnfulX+aH3P88//iufTYg6VIMTUaJPaEyNV+HzPtLdJFk/iNMtigQ0bUMoWNqB0Pp0RgGR\n5EMaLWPWATtoHPn+hsZFse80ZtEfhwmMLsD4uaGj0oAIo6eGaD4lioJmrCyxOHMvuBWwnkIExG9q\nBLe9WPFPDjZIROIEaDHNR8f+5PF/lIQWlYTRopyoHt9tFPv9jmrfrGfFG0QxRLtbegxOby6tVCqV\nyquZKrYrTzaDR/mwAU+iV3PBUx+O5263Y2jGUMbAR/AovI9DtwOygn4EgtsmbAT9AUJAtHcvN2ty\nexlypoiCKtGWZFOiCKXdZW//gK9+9z/jm7/sU/hdl7O/bzPxxsbcEZsxRTeRhR1qGdMebWcuZNNT\nPmDHehe0za4LuDDySEJdEG0FJDQOcYVhGOUe2qPR4qHFhtHrpBlMn4E0h7XBaNdHwCNYGJFzwaVh\ngmaKWecDcRisFxIgNN4YKen2iqxELM0GP/LKU1x06T7wZptXChHxRtMQ0b47cm+c1my74axm3Ltx\nbD0rKzYTM92hLVVkVyqVymuYKrYrTzZWkGMixjb+7rI6qr4e+osDIQx+bMa4jeQ5wKCbI7okNBco\n+jTBDghlQclLoMBoF8krLBefMMkSckdun4bp6ynt66DZ5b/9tr/Fp3/KJb74jzzredYhQhAIMwqK\nWPZ4wdEu1lwmW3+URU0aPNNDJnZ7xb3cyCCmfRBLb0PsoCR/Pk19/zbNd8dvMCQOaSp446aoN1pa\nAQmILUmxAZTecCtI8LhDQ9kYjC20R37tIdv7FjvPRuiLYaVHbDXkj7+CQvNOg3judZl7rczf0lMQ\nDqvbnvBShXalUqm8lqliu/JkU5ZDHnbytIlBYEscHy5ig4+ZOEKlhVCAgle2FcIbfYhLHPso9CBo\njuhgzbB+BSUTBDQmjAbaZ6DtgNYruHGLH/rxn+f//dBHef/3/scgH4ei7lbp5gQWSApD6kdE+gPQ\nOdE6zApSVuQ4coE+ftpzuEWhvwHNDhIaLE1du4pgusYsDOuuhySSBrEjC8dhk+j4AsgMaWfAPuQV\n1h8M+d2Rgg5V6MlRlTrvHSWJmB5Ws+WYVeKw6rvx1GsPRBAhmLjw1rUf/7uJzfu1btyJk82Hcorf\n/LRl7vT9O73XZr3N8bhTY+jD2N9XglfLflQqlcpDpIrtyuPFef545wOkzKGs3f4RWhfcm9fYvB4g\nFrDVPrE/oMgE2MHV5NoFbjS3mGgAXRLzPiI9pfiUxlDmBNxGUVJwa0ackayjmPI7L1zjm//y9/F3\nv+2/ZGd8QFwuQfdQHWPdGk2JuBasvQBasDSBPpBlDLImCPjwnNYr4bGl0RU9DaHMMZ1CnPkUSevA\nAkggkBHNlBJu9UrDMXEJkoy4WkJeo9PG4wLLEmJDsCmgqPqwFw8uHBodMUzC0ScGxzn+OLR4QMra\nGwN15RVySUfWljuc8/uybtwFM9CSKVpuqS7fcRT73Ua1n3V9nmfE+0Pa30fOq2U/KpVK5SFTxXbl\n8eG8f7zzglCGYSpEig4e6Y3wKashWcTtF+Qb7nvOAHP88p9DvonYHpZnpFDIvQyvlWC8DRIpcUTR\nOcQtoIF4GfS6x/+Z8RV/5n/jT37h5/D2t70Jbv5rSnwdyBV/DYmQZmi3j6yug32MEJ7CpJAwWN/E\nohCbEZkJVrYxXdFHjyNUaV05lvXg3x5746N2mNgwur33yL84PkXwGdb3ZMtgDXRzyL1bPNKUbAqC\nxxymLazfByIS0uG5OBTu5djo81Nyq22wvGTtcJUfb48KvG2l+7Ru3AntCKwRTQQrHpW44W6C8Kzv\n3+36vFeh+TD295Xg1bIflUql8pCpYrvy+HDeP95WkM0kG9PblhcJGEbMNw4TKYIu0HwDV9zbeJ0z\nYfJ6H3N+KFxXHpm3aT7UnoCLRk1x8Fkncl7xHX/np+j7NX/+6/4zWHwYOIDuY34zMNlF4zPI+hrB\nDsDGEDK6vgHtFr12ML7ithFa0AJtJJU9WC8RW5PHr8cIiBQCoGEXkxasR8oasTUatzFp3O4RJz6o\nJs99+/sboHugILbC5CKENXQLYttAasEKxaUyFkdDioYMVpSj5kt3cMut52FT7dXe/dutj6M3zG8K\nQnvnc3m/1o07UVaE0CMUgnX4VCBenuXhQYnLh7G/rwSvlv2oVCqVh0wV25XHh/P+8U5Tch55U5+0\n3ii44XDKpGImmLhFIus2NOJimI8CKyBD6SFfAhTSCIiIKJZ7pE2YrYjdNSzM0DCHpIQ44p//ym/x\n9/7BP+P/+L6v9wi9vIAugzZgO2h6CmyMWfGGwTQdvM0B6XtSWZPJwA4WAhIiZmvQJYXoA2Z6H1YT\nJBJ0jlqBOAMiaoVQeiyYWz7Kyqu6+cD3X9fo8uPEvCDkq5BXaHOJErYgRYo1wHqIBDyA7N73Q1Gd\nZkfC9GQzqpVbUzgsHzUGDjGEFkcu4O90Ls9jwbhnDDPDcodlPyZyLA7yviwPD0pcPpT9fQV4texH\npVKpPGSq2K48PoQW087FaGju/sdbBqtDcZFnJ4WQFQRDQvKhL+uriF3H9Fl8VPsYr2y3YJ/wuLrR\n5cHsu/JGyPE2pglsSbbo+db9AcQJ8+WCd33LP+Abv/LzedMb3+jV6ZQI64960yYvouspjCJML2Ir\n8QqrGKQZJh0ljEGX7imOM3/P/gCxTEpjNE0pIQIBrMNK74NmLCHNBOLUGyY3VenN8SN7lCCA9ZQQ\nKNNnYNW7FSYEr3THTMgHiPUUbY+SRU5L0ThNbFrhFh9zHA9xd9PD5BK7FyH2oIVanPiUT4onwqjd\namW5n6r0OX3Zd1zu1SJMXy37UalUKg+RKrYr98+DTiLQbohLG0au38nn6wsAnqcM4bCqe0tCRtqi\nlE0qhEK3B7oDXAQUn4hYIA7i3iLYyj3cbHlcHiuk33cLMmDNFkjmG/7SP+TNn/R6vvSL/xNCE1Fp\nIM9RuTC89tNelW5byDNoJ175lpEL+9AOEzB3KJv9lgA29Rg+GXsFO0yhzCm6RGyI4wsdkguWtlBp\nPRt8M8xHAlI6LOCCO+wg6ZJXyccrSDt4zGD0pJX+GiCENKGUCWfmQp8mNvPBYWVbrKBp61Qv9wPj\nXq+50KKMMWlRgt/g3K0qnQ+ObvTO2odzZm7XxsFKpVKpVLFduT+0Q/LBofCxtPXyBcW5PbE2iNXN\n+8rtCRmboTdW3EesCnoNj/67AiyALfc0y5bbKUyhFP+/uw4xEk0xWUCZUgR+7Kd+lQ/84r/hZ370\nu5HJZZTGM7HDzJsQycP2BBfLCGSDNAE6kBkgFMwjAjfTKhVIY2KaUvolrBcw2wJ8JL1ZIUZDpaCM\nQRpsM07d9HCfC/jjtAW7n4L1H0fWBVKLNbsQAkFXqAwTNHXpFf3NNMqzzuXJ5yWim4zvTQb3w+Kc\nIlZCIsRIDJFShiFBZ8Xx5YNbrTdwvpuG4zcBtXGwUqlUKseoYrtyf5TVrcLnXrKU78Z5PbFxgpYV\noks833lIvTgllm1YASZvhD7C+gZwAzgALoItQZ4GOtD5MAxxDyYRuo4cE9gUmikvvLjPN777H/I3\nvvUruXTxAmZKTIppQfPCq+cbi0rzlAvu2BLzTZ8OHwKFNRYbUtknt9uEXtAw8huYXokSCc0OvR0g\nXUSaHWi30fWeJ6yELaSZYtIQxBsWTXuvzqYtt6kcr043l5FuH7M9Qr6B5gsu/MMWlnpUvTpOc+F8\ngnljOxm4ozf75XJOEatlRVn35LzCwsQbR48P/IEjkZwXJ57v73278gGyGUy0qf4fpzYOPnSsdFi/\nwErHbQ28lUql8gpTxXblPjkpKW6TGOfnvA1XwyhyywxV3cbFXz44Guhyi+jeJZYXKP0fwBsjl8An\n4X+ct6BfQTuCdAFWS2AN/WJIIyleRQ6Jr/zmH+M/+rxP5w9/xnPE1QvkuE3Rxj3b7RjaXej2h2Ni\nYGsoa0pM/tRo24W8rQj5BhRIAp29hKUEZmh/033fs23PEkexYWBNCVtIHLktRCIMLmlC49GGJ6u3\neQFixKbH1h2YoKVHLUAzRnOCRiHu+LafRxwej1l8ENfAnTjPzVg+oLElMWyRKKh2/unLcY43d2Ke\nQrPxuQ9Wpruind94Hh/0EydHueS1cfDhox1B7FjyjNRjXqlUHiuq2K7cH3HiqRgb+8DJiuH9cp4/\nkhuxZAXT9eDdxmPrJCESb7UaNFuU9jlogL1Ng6QAg1Bu2kFsdSBrd4LEBJOZ2y4k8N1//19yfX/F\nt3zdOwj9ApoAepWgY6S9RCGAvgjsDa99xR0rZc/TQuKWPz++CMuPoaqI3aQ02/gbNr5fNnfbSdlD\nwwQwSNFvBOIYixNodlzMDfYHASyc8iNdVtBfx4pPzrSwC3GT3tLAeNeF4eYcbpoe7/VcaOfDbIYx\n7g/No3yuBsUeYoOFFpPoNyonlz8u3NMMLcGH8NzJs32SYez94X1GFdiPHitAOPG4UqlUHh+q2K7c\nH5tpjY9CXJzVFFdWUOYE7TDNHj0Xt3xYy7GYt0PWNwjdJ9AcgX+Di22AN0DqPaEjTFxgp22QlStY\naYDI//dbN/mbP/wved/f/hratiGEgFgPuUe1ECV5RXv0HHAJ8sr9293z0D7lH3EHAZJbTZoJWXch\nQtEAMSCrawiFEiM62oYsMBJoJkRdQTlA0wzi1AV3aL2urT3eONm6paGshoST8RCNOEZN8VST3vdz\nGPYjQ1OllSWy8WvfyRN9/HwM50F05euEwYrysLjX6yw0CGsktkgcQxjd3gB5rFLuja8X7i8OcHMO\njo21rzxCJHLLpyrVtlOpVB4zqtiu3D8PS1ScEHNnN8XZYSKJNz8C1mMyOlrmlj+8NwnLF1A+GXgT\nXnJugNEgkhLQwXIYaNNcgu1nIS9Z2Yx3fsuP8t/8qT/KW97yKYOv2y0EvlE6+KXHg0Dv8CmVS2+2\n1IAgmO7D2kB6iGMvihaIrCirG1izjTXR7xesYDGAGWH1AlGX9GELk4k3NW5E7aYKW5aD0PYbELXO\nt9EMYgAElQREt8WUta9b5i42ScMwG44G0Zy80TnZpDgMEzq0Y+j68agspi16NUoprK2FPHfLjiSI\ns8MGyLtWyjf7v1nmrH6AsxovKw+f0KJiGNGnrYbq2a5UKo8XVWxXHi9OE3NyxkfEcYKtX0J1AYiL\nzzjz75UVdpvv1shMca92BjqgB2YglyCvPRVkFCC3QPDovtEV/vx3/CNe/9Q27/qTnzlE9iml71yw\nIqSy9pfC/BNtycAKyr5/berCVwLEOTAhZBDt0XyAiZFCQ9YZ2ASkYDJzD3VZonlOCcmzxG3pUXab\nZsjjgq+sfXKk4IJ8OGay+jhRbxD6go6maFA/BnmOhTg0ELa+/YcDgYp7kTfn4uTxH44ppqh5LqIR\nvXp8HhvKcN4fdIxkDA0hTdynv75KkAB0LrSDD925W1a2qN+wBO0OG07ve0z7w+bYMTQb3335VxES\nW6SZInF+vubWSqVSeQRUsV15vDhNzB3neKVauyOBZ9kXDe1hdVZu8xB3eGPkCr/0m+H117D+bVJb\nKHIBbAsTgfE2pF3+yT/9DX7ygx/iA9/3XxBsgZW5N2Fucrp1gVj2qpoNDYrxCq6+bYjjC0Ok4Nob\nJK1BZQLponuw+yVqcpj3LbZE6FBdDyPWE0EMbInlJWZ6WFW+5WiJ+47NigvuOIb1S1juMV1CXhPV\n0HiFJFBMCLZGwwxGisatIyF6zJpyeG5Oa1KU4J8smCJiPmDnPN7th5FLbQU0I9YRdEXRAsGbXLF8\nbw2Qx6aQ3vr4Majcn+TEMWTzdaVSqVRecarYrjxenBRzcXL2R/15QSxzsIwZ7tk+vuyGw9fLwAQX\nwQ0e+7cGLkIxsu2AbCPlgIBgXcvV/Zav/45/yF/+hv+Qy5euoKGBfo6GSIiCqFEEVBJFZiD77onu\nbwACKUDz9OAlH8a508DoArAF1sLyI0SWFEa+LoaJYCTP1pYJpOTZ2bpCSYh1p+9nmkFo0H4fSudJ\nKmWJsMBKwSyjMgJRTHtseRVJgjUjr96ycnvL5oalzD3WMY4Pq+i3nI/hPU0byAtPQznvlMaHkUst\n0VNgwLenmZIVv+lJF+6tAfIwUWRogNwc68fRE3zbMdRXZjsqlUqlchtVbFceL86TOFFWhOL5yAZk\n1aGqfCIZ5VAcGX7JDwkk7AzPD+PQi0HYwUZbmB5gZcR//Rd/kM97++/jHZ/9yQQWiCaP8AsTRFdY\nbMCMQuMWFuuOqtg0buUQcW+39p4A0s4gXnYBvtr39dsL0F4BE2R9jYaMjhJFEtZOwQKqa/eRNxNv\ntox66/GReGj7kBAwa32qYz8f7DjFD0HTApFQFiiRWJSSdj3NxRS0Ryx7cKExVPBvPUeHaOfvGVos\nnUg4vldRet589dM4aUMJLYphEtF2129qED/+p0QAnnq9ba7FzeCex9mXfdsxDHDyvFUqlUrlFaGK\n7crjx72KmTgmy8grmDKCZvtIaGs3WCmOi6MxMHixKbg0/ATwe4bv7UBZEcscCZHved8/57efv873\n/aUv9pfUDrU5kKC9RAljb3ZMF6BJPmxmtYZcoNz09yjPQBuBwcMsM0hvhGYGtnJxKwY6NC6GhKUp\nbgKIg92hcZ2YfMy79oYNUx9t49sejpv3avaYGiLq1e00BhmhEv2+op9DM8fCGJMpOQYstCjJxehQ\nyRXLiIARvIFyI+ZOiNPDm6N7aTg843zf13obzrChSJpBcwEJa89PP6MB8o4WlsdRWJ/Gqcdw9Qpv\nVKVSqVSgiu3Kk0xISJwAIyAcZUyf2WwXh2U3l30LPIWLkqugK8gXKM2Yf/Phl/jO9/4SP/zu/5Tt\nkZHzkrh6npC2KG3AFiNoZoRgKB1tv0fH2F8rb/yyg6e6myNNIdicMn7WGxhHW8j+C8TVR8iafdNM\nvZQcjIChRL+JSF6JLmSs6GEWdMCw7sbg0e05HE0fGiQIQT1/3Js4IcgY1X1oGlAjx21otynig3is\nvXR4vBR8jLwVJAS3lZyWRgIPRpC+nNc4w4YiIkgaIWky2HOOsblGtD+7AfdJ49gx3GTOVyqVSuWV\np4rtypNLnKBx5iI5jL2qfZYY1M0Y54R7txPu17559HwxCFP6XHjnt/0C7/zjv49/5y3PkAke9Yf6\nVMd+H2gQeoItUe2xEIbXNdAFsIWnkWxDs8ZkSjGFnH3ozSJDdx2xjqQdKgHFhbZYRlBv5itLn7ET\nGlI7paQhNSS0nvGthmAEczFsljFJWJxRiC7e0xiaXWz1cSwEgnVoMx3E+RakYXJknAwxd4MdJ225\nD950aLyMt8cBPg7+5fPaUI5PjjzWWHtP61YqlUqlck6q2K48XpwnAs6KJ3SEBGJoWQ6xc5vR4eLD\nW9rdwTNtwIvA7x1eYIx7t5NPY2x8fPm3/I2fZmcifMMXvZFig8e7nVHKBDG8YbDpwRagex5yMt72\n7dDkr8eNYRvmEC4B2YV6mXsOcGvY+AL94hrICAnBRW8cY0UpdERbosxBDYtX6GXqdpUwGvzhxYW3\nrb1yW4abiBSRTUxdaKBbQD5ASk/Q4u8TNn7yBnTtg2mGmxIDJLSYdu7Bjh4jZ0O6yy03M5tzdEoe\n9z2fx5cb+3evNpTNUBsrh/tEaI/sRo+rH7tSqVQqTzRVbFceH85rUTDFbPNlD7aPWCHkG1jJSEho\nswvZY+nQqxw1R2Y8jWQEtBCvwmiXD/ziR/jRn/kY/9df/8OUtOMxcfH1UK5i7SXM1pCehm4PQ7Cy\nB6PX+Zj2MBqE/gW8ag4QXOQnQfJ6qBJfG4bIXIHmoscXpksw+l2+XuwIfUdggqohwbAQic2UEiZH\nVXwJLlT7JaL9kCuePWd5M5QmTiAaiFDabZAlkAZ7yoQoCrqi5DhMm9x42TldiFrxZsFN/vlpAnwj\n0u/lPD4oW8rd1skHhGGsvV8rGdKWn4dhEmelUqlUKg+DKrYrjw/njoAzROfeBCh4RJ51aF5h1iMy\nG3zQg4AMW0T+rSeH8Hr88t+8x4wbeyu+5t0f5C/+V3+IZ1930UVyiFA+hgvyKbDjw290iQTxQTWr\n6+j0KRfB7RXoP4yXu+fAJdBrUC5ipTlseLS+h7Qi2pLSXPJ1UYg7EAJqLUr2hsXYgrTDNMhhlHxo\nDm0zppm8aaaM49srtEURzQTrQaAgPiGz3cWsd4vIZpjNMRvFqUJ0M+hm0xx50sIBRyPR7+U8PozY\nv8OX6rB+4cktxwedhMYjCms1u1KpVCqPgCq2K4+WO1kGzuu9LSuk3xssFAULPSEKWI+VgkTFyEN1\nNgELCm8HppuNwdNIEtgBX/edv8DbP/Uyf/wPvxEpHWKG6gGxL5S4Q9QlYnOyTJGyxrIiunJbSD+F\nMKQ/SAM2BmbARYgy2BdsSCm5CGELCIhFYrfAZA+NU2jGhBDQxoU0zQUsjADzFJE2+ij2zbELLbS7\niE4PD4udPG7SYEEwnUDKMH4WRpcJIoi0EMBk5O+zsYycdo42PmeJt+Y4b87p4TadGBhzp/NoxX3p\nm/d6UJ5p7QhiCIVgHRwbjiSApentEZGVSqVSqTwEqtiuPDruIWbtXBFwunYR2+9hZpCM0jwFwVzg\nhpF7tg/jABX4TeDTGCQXcBGY8YM/+f/wKx/e52f+2lshRA+v0CWy+BghJIoKodx0YZ0mPvjGVlhe\nEtNFpL9GiWMs3/BcbYZKqnS+HSUAEcZvhLaB6XNewdaAdmtiWSK2gKWPng+hhZDQ0hODUEgEy2i3\nj4aJj6a/1+MWEzRPQWdHDZPjS6gEfyzDqPt78MjLsXNmpp5SInEYI69DGsqmCn+X83iaeH9QVWYr\neMTjQJz4Dcqm6n4vQ20qlUqlUnkAVLFdeXTci2XgeHOddncZatMTFr9DKDcxAl2+TDDDYoukHSxO\nEAwdMqAJ27i4LnjsXwQKv/Xxq3zrD/467/mmtzObzdwmsvyYZ1lPtulp3NfsodOQMypTSBMfliIt\nYh0m6jF9ZY57wjOMngIa6F/AowBvQvsWSJdBOzQEiAvU1lh3090ccUYsS2+ojCvK1rNuJwGCFKws\njjKvjx+3M0nEdgtCQdY3UUtHgvM8x/s2y4gdDbWR6J7x4xX3u3FSvD/IJBCJHK9mnzrsqFKpVCqV\nR0AV25VHx73YRM7TMGcdxQzLHcUyFEXbLbeUkIbq5fGq6QiP5Bs8ymSKvshXfPev8KWf9wb+3U97\nDrJ6BbwYcABlAmxDG9CMe7jDUK3NxYe+SPT/uwVIxm0q2d+7JNDlYGNZD4I/D/nOI4IdoJKRbo4o\naJpCt0dgjujCReyyYOPXQzMFEmbBs7qHxJHTjuEtVeXRBcoykZoJKhNodzx7u710vuN9soKuHVKW\nR+uetyr9ICZHnkVoyVYo6zm5nwNnHKuHzctNWqlUKpXKE08V25VHx73YRM7TMGcg2hNsQSiZLAKa\nCe2Mgg4V18F/XFa4AF7iaSEKJL79h55HRPkzX/w66FdeedZhtDdjwEelozbEcU8h7YLeBBSjwOQS\nqiuQKayfx7O7C9BBfwCy75F9UiB0w8TIJbBHWN+AsiAEpYTGhXwcoWWJxm2E7JV5IjluQRgjaXRk\n4RiO6yGniec4gbRLiNFzpeMxb/R5GxRPNEvelkxyHs66Hh6UQNUFoSSSrsna+aCeR2kfeVgDgCqV\nSqXyRFHFduXRcjexcbdq5y0DVRJFFGRKSQZhNoi+gDF1QSotgmF5GLPOYvhX+IUPHfADP/Xb/J//\nyx8jhs71d3gK2HOvd2hcmIKLeAztV9AGJEwwDGQFqyVhuo3mQcgieHVb3R+tCvRgS8gT6ObQBIQ1\nll9EwzYA1rTABOLTFCLBrvqUyNBg7VNIe8EzvhGII9+uu4nlzbFqtt1+Qgd5f8gd785XXT4pgmXI\n8x6+Z5vXO4+gPLnsgxKo2hHKAmHmw39Mbk0kedCcdoPwEJNWKpVKpfLkUMV25fHiTtXv40KsLDF6\nSE9BNkgjr1o2u2i65I2MJu4DDi1odi82AZgyX2a+6n99P9/0JW/ljU9vAR+GnKB9Gka7Ls4seHNh\nXoAkn4kz2gJdI6XDYkTWHSa990OmZ2G5j6v2jsNBNswhXPGqdnsFmjH0C0wyRaYgLZrGwMgH8Eye\nhlWDrhs0ttBMcLGug8g9lvZxW/LIKeJZO7e3mEFe67vwGwAAIABJREFUAQ1Yh+QDLG0dZXLfpZnx\nNBFsMHxq4O91arX9PDwogWrFhwzd8rg5e/mXw1k3CA/TJlOpVCqVJ4YqtisPl8VHvGEwzmD6hntb\n50yP9iBcBnFjJRNYYtJ5PF/7tMfaiXk1WTz2zTRgaQvCHB9iE/nvvvfn+NRPush//rlvxsXx9Og9\nzKC/6SkdeoGge6jOiHnpI9fHlwndddQiob9OiVuIGYR9vKr9HD7UZnSYXoJ00KinpMQR9CuiFsT2\nyYxJoj4W3sS3od1BwpCoEZKPig+jISNaAHGRfPJYbZJANqkboXUxnDsfLy8FoaOU5bCv5d4aB88S\nwYNQFwtnL3se7legnlJ1J2yhaUQJc1QeYgLJHY7NudJ1KpVKpfKqpIrtysNj8RGa9Uf963zDw/Du\nVXCfxkaIHYqbDMsXCXodZOwVZx2EvRhmEQOPBQwthEsEfp0f+eCL/PyvfYKf/c5/H/dWj/y1tHFv\nttpQLW9AIyoXwTKlzKH03nwHwBq1DvqrFHmWo0E2H8MFvEJ5CsICxpehSy6m1z1MnqWEAmUHbEJJ\nLioDC6+go0SKC3MJZBkjAqIrz8ROszObI+UwXcQG4d3h3ZeCaEaDwSlDbO7p2B9/fC/fOy/3I1DP\nqiwHQ9pdGBmo3OkVXh532v8qsCuVSuU1TxXblYdHmd/58Xk5FGLqjX7ddWK5hqyvDhXhKTZ9zsU2\nAUkTT9Pe2CSY85GX/gDf9P3/N9/zdW9nZxbxke1DagkK5QBsAbpAerDRCCyBFujFB9foCqwHmYBm\n9y3nm1h3AUIABtsHK+C6W0ckQnPZq9zjpz2dxMLgvTbEekwyVjIu2oUcZtDs4tMrG6ysveEz3KES\nXVa3Cs+NxUMLilLiDEu7PiznPGPK7ySCH3QF97zrn1FZltgizRSJ85fv175T02atYFcqlUrlDlSx\nXXl4xBnkG7c+vhfuImwOs6FL9pHcukIsQ96D7gbSbGFhjEnyUeSDrUB1wrv+6j/lT3zm7+KzP+11\nuH/7AtDgo9IbKPugU6DDZAY6jFHv90H3QUcemycjIGCWgF23h7Rj6PLwmtfxLO8WyhRkSbQbqDyN\n5Y4mLunDDLFNGvQKmCKWsaIwuuT7O77k27kZHb8Zy36mVcP8RuCwam2Q54T+BoI3eZZ2F9rL5xeF\nd1r+lRSYD9MbrR2UpSfbDDdtp3rSq8CuVCqVyhlUsV15eEzfQJ+XUPYg7tybhUS9cW8jFm0zeOUk\noYV0gRxGngxi+ECZfh/p97BR8mmGEg9F+3e/559ysBT+wpd+Bu6tLsP/ADsuYrWFoFB2vRExJV9m\nFXERPQfb8tUkQPsMNDLYTxRKAa4de91LwEtgjTcnlk9AGqFhCywSCJRuTmwCgqBh7Akm7QV/PQOa\nbTBFdDkMvixnD4CR6McCfF0r0N8k6RxSRBSwfHZG95PIw6osb3oDtPeboOG9aqpIpVKpVM5DFduV\nh0c+ILTbgEfbaT64e5PaaTaIs8RTe8GtHGaICaYrECXSo3npDYnD+/3SL/0S3/vDv8CPf/Onk6Lg\nVe2CK9Il0IGtXIgWt5xQxh7VJ+MhF/vAl8tAWkCaIjrHdIcQFA3FGyLjFSjX8R+vF0GeAowi2/4e\nZY0sVkirRCmUtAUiWNrB0iUwCN01t47IJaysETI2DOexOwlKie7n3mRfI/61FujXoMF3+WXlVz+G\ng1oexnZsRLWEoxsXqKkilUqlUjkXVWxXHh4nfbLHH28E22Fm9ka42a3r3Pb4GN0NCD34UHYXlAa6\nqSqXFcQxy3XhXe96F9/wpz+TNz/3YeBZvClyM0kSoIew60kmsgKN+FCaG7gdZIb7urO/blIIARuy\nvS2IV9Jj71YUDnB7yvaQCtLDcu5xdN0BuZlBiHTpIpDo0wVodtzfTU/oXoIQUVMs7QwV1YzJ5M7p\nIcezrzd7JwnVzvOmET/293LjcxqnNSMOXz9W4vtBsLGnhNYH4kh6dX0iUKlUKpVHQhXblYdHaEDX\ntz6GI8GmHVLmKBGJY7eMxIlPTNxUZu8YS9cTFzeg/zhmI7TdhW6PMrrgUx5DQrTjz/3Zb+R3/+43\n8qf/xFvgefAGRmUoV+IV7gV0Y+CaWz44AEaeUGKTobq5AhLoDeCKe9D1AGLAmhmkK1AE+Lf49MkO\n2Dp2v9B6fJ9Ef50QhvSRmQvf6bP+vdUNYr4JCKYFxi0huZhV1CdinnnMT7FUhBE5TIjqkYGI+g3D\n/QjHk+9dVoiEw+89MeL7Xqrzx4/lWXamSqVSqVTuQhXblYdH2vKK4CbzeVNJ3Qi2ska0QyQiGtwy\n0uz4cvci1nIHegNZ77k4by5D2yN5gfX7MLrCP/rJf8xP/fT7+Zmf/knk+vuA38SF9kVcENvw+PWQ\nDPQNoM9zmCiSBcIaornwxqC56F7unJFygDEDixDnLr6Z4iPbG+AlWAcYzRC9CWWExcsARC2EskLF\nCN3HCFLIaQekoOL52KUoUDAmnsJCPN3GcBfxmNKUGBLWrSmlH24eyt3XPy2/+hbBbbcuY3q7+H7c\nROp5plQ+btteqVQqlSeOx1Jsf9d3fRfj8RgRIYTAO9/5TpbLJT/yIz/CzZs32d3d5Yu+6IsYj8cA\nfOADH+Bf/It/QQiBd7zjHbz5zW8G4Pnnn+d973sfOWc++ZM/mS/4gi94JXfrtclxq0I+GKwkdsIy\nshGPw+NjI8Apy7NFt2SKTICJNzPqEnRJU+b066tcPTD++z/7TfzV73o3ly8/BdevAm/DRfAYHzyz\ned8V5IILZRmeG2wjuob0BuDDHAppvQx2AN0epOhOEz1wZwpr3Acegct+DHQPY+QV93YHJq+jhIwW\nQVgTuxcI0pH53RBHlDBGwtiXl5HbZKQ5stwc527iMU0HX3iHxgaaC0fC+U7r32lq5EZca4eU5dEy\nom6n2fA4NhPWMeqVSqVSeYQ8lmJbRPiyL/syJpMjC8EHP/hB3vSmN/FZn/VZfPCDH+QDH/gAn//5\nn88nPvEJfvmXf5mv+qqvYm9vj/e85z187dd+LSLCT/zET/CFX/iFPPfcc7z3ve/l13/91w+FeOUR\n010j5D1v4JPGBVvaopQ4PHfCMnIHAXgo9FZzJL8E2mFiHscnPaYrNEx419d+I+/4I5/N533+O/x1\nwgjh5zH+EC6oFVfHEXgJF+EF2ME93Uv8R2QxbNQW0IPM3C4SVpCXCIbkiFhD0THEpz3ujzUw9qp+\n3IHpzC0ccTTkdF/B0gJZX8MiXsUOEdL2IMLxJJLYeCJGaoamxxNYufW4nBTjaQJxCrFBSwPNsYE4\nZek3QHLKBMg7TY089pyG9sj2c9r4+HvhUTZd1jHqlUqlUnmEnPKX+/HADvPLnA996EO89a1vBeAP\n/sE/yIc+9CEAfu3Xfo1P+7RPI8bIxYsXuXz5Mh/96EfZ399nvV7z3HPP3bZO5QGzqUBvxPHJ7/U3\nobuKlLn/2zTqxbH/C+3tntjThF4+QPqbSFl6PGBZYOkSFseeShJakBFFe773vT/JCx9/if/5f/xa\n6K75NpAwfi9HzZE7eAW7xYW0Afu4CP8oPg1yI8Jv4h7sftDpcyiCFcPKCLW1p6HodVywD7GCsfG3\nasbAwj3bZe37O7kC6TI22kbTFIveBAl+4yGxcXFu6o2VXlI+9diIdsjw/23fl4RJQ5AWaWbDpwAe\nsejH8cS524jPexHOQ0OmxLE3ZsYJFlpM4unj5E9juLE63P7TrqO7rH/a9Welw/oFVk68XmjPv42V\nSqVSqdwnj2VlG+A973kPIQTe9ra38ba3vY35fM7WllsStre3mc99GuH+/j5veMNRfvP29jZ7e3uE\nENjZ2Tl8fmdnh729vUe7E68F7mRh2OQUL34HWX4UMYXpMxgJ4szXGwScHXu9w5SSk9XOskKs+BAb\nwNoZ5B4XxxmaBCgf+o0X+a6/84/40e//DkajMeSFi3rtcOG8uew3NpIEfAIX31N8+uNlvKLd+nMF\nvGkyQ6/eLNls7lVHEJ9CxyMoI5j/NnADF9vb/hJk/zpfhckl6K+79zskCJdRFMLEK+ApkCxhNGDe\n1BhC4xo/73v03/EKsMQ7V5e1I9gCMYimZO0hLxBbH+WZWzyRCsO95Vc/iIzrl2PruMMnIEEMoRCs\n83HtJ6ZeViqVSqXyKHgsxfaXf/mXHwrqH/iBH+DKlSu3LSMip6x57+zt7XFwcHDLc1tbW6T0WB6S\nh0aMkaZp7nt9y5kQj9ZXgtsdgNK70E6L30R0DxiT8z42fobQ7pCk3LIeYgQxIFByD3SIACFQgpDi\niKDiExbN6MTHmB9WfNcdnWW+4s//fb76Sz+P3/+pv58gYCEheoBqD+wBm+tpSOegw38UdqAdQbfG\nhfhsiHsbQ3lpWDd5ZZoG5IIvpyvoPwH974XU+Mj2UvCYwBvQX4FUQG8iUnwke1ToO0hrCEpqLlHS\nBWxyEVFFpMcsEpoWlYbYTIfkjwYLEGyBYkiaQRgT0tGHVCqtV8UH+rUStSOwxjQA6tPjy3CTYh1d\nGBNH26f8XN3LtXH/1w+ABXNBfMb233HdM64/y5k4/CjHFElweF2+Fni5P9dPGpvf2/X396ufeq5f\nG7zazu9juTfb2z4EZTab8Za3vIWPfvSjbG1tcXBwwNbWFvv7+8xms8Nlj1es9/b22NnZOfP5Db/4\ni7/Iz/7sz97yvp/zOZ/D537u5z7MXXsiMTMox6rMsT0UZZbXyDGhZNIiaQRAmYOuO2TWEPpEiS06\nuUB4+vcQY4voEts4mULy99EGyhJdLhAxwugSklrUItJMoJ9j/fz/Z+/dgy3L7vq+z2+ttfc+j/vs\n7umeB0ggSxnFQHBAiSgbATYuhyo52FUGV0HZRZWNhQFh4/AwhAIHUgY5GBs7FlgBpxKMjWwwKWIn\nhlhGIANxQaqkCebhIPGSNKN+TN++j/Pae631yx+/de65t6dnpiWmm9Hc9am6un3O3Weffc4+d/Td\nv/td3y9I4PqtmU2c4wzoID7N3/iBX+Hq5W2+6S1fSNMp2jR46XHac9OeCPNoJ2yCTfn3Y3a3JnCz\nUmIzgLtqaSQJLMHkqGx/ZGkolOl8+5iV37T70BxAumyP7y6Di6CJlhXqPTrq6MIIHfdMw4gkHW6y\nS+4ew40uQ864/jrqOmT0COo6fFv87DmV4bXZIGh2wbfnzo+6BsmbyvZenqXprtg2AkOzg99+HLd6\nFslLEEdudnHj3dNz9zB5oc/Xiz72eT5/Z+/f39s/97msvHLZ39///T6EykOinuvKxxMvO7Hd9z2q\nStd19H3PBz7wAT73cz+XJ598kve973189md/Nk899RRPPvkkAE8++SQ//uM/zmd91mdxfHzM7du3\neeKJJxARuq7jQx/6EE888QRPPfUUb3zjG0+f5zM/8zNP97Fma2uLg4MDYowP9TX/ftJ1HavV6gW3\n0dTfY/Jof4Y3gTycsRE0p0IprQ7Is0wzP4Z0CMwYhsvgb9KEEWhvcX84CFO0v4PEIyRbxbigaHMH\n9RNSs424BqcJnEd1BYsbMPsN1naQd7+v5V/+9K/ynn/y1cz7OXL7t0l+SpBMlo7STILF+q2wifb6\n9qFNo1XBTaxpkWAtlP16Aq/ANsge6Kjs7wiSR/rraDeB/sDsJcsl0EDSYhVx9HK1tLhfIudMXiwZ\nGiXJjvmHc4bhGJdXuJTAD8gwIzcelvYaJZ7gnDdLiWtRt0LC+Szyu89XvziijT1N4xmGRN9GfF4i\n/Ryng9lQwhxOrj9nX6f7fIHz/PvJ8x2XqhJcZn93h4PDI2JevCyO92FxP7/XryRCCOzv79f/fl8A\n6rm+GKzP8yuFl53Yns1mvPOd70REyDnzaZ/2abz2ta/l8ccf50d/9Ed573vfy+7uLl/8xV8MwNWr\nV/mUT/kU3v72t+O9581vfvPp/6m++c1vPhf997rXve70eXZ2ds5NutfcvHmTYRiec/8rlRDCi7/e\n4pVeo5LNA3u3p1qBfOY/fhnodhiWU1w/Jzc7JjxXzxK5CgiaBCFDnqNxBcMSicdoTibohxM0A34b\nTStLLdFwpo1yCzjh4HjB1/7dX+Nvfe3ncW1/BIvfITWPQOesxyUdFXE8Xb8KNhF/nPl3B/EQE+PJ\nIv/6AZuCN8AYxtswtDAsyvNPUUnWOjlEUFcefweGE2geN2uJc2Ux6IQs26CeRCD7El1Ii6QlqKIq\naBbIGU0ZXbcX6hJWs7Kfznzaetf5u+t8IR09U8Q5ejK4KUkFZGIWGJylq9xrX6fn8ow3Gl5mCwsF\nCM/5/EnTIM2EpDNivDi/03Cfv9evQGKMF+p1X9TzDPVcVz6+eNmJ7f39fb7yK7/yOfdPJhO+7Mu+\n7J6PedOb3sSb3vSm59z/+OOP81Vf9VUv+TFeOO4VlXY/xSBhC4ZjaC+hPuAloE7JKW2SI3J/Gjsn\npTlSymQ2+xHqpxZbdzb2rzynWUIcqlu89e3v53M+/VHe/LmfSs5KklER5EImmycc2FhI1uJ6Pe1s\nzJtNMjuIZmAPBg96p2yTgWB+66TQRBiKsHbTsr8Ey9tABEbWKrm2eUhfIviuwORxQMk62CS9vQTN\nFE0elWj3AfitTVJL7ovIphzfPd7ze52vZtdiFRsPkjbZ5+v93s/ixppNXalUKpXKx8TLTmxXXobc\nK3FiXWSy5vnEV5jA+BqyEiQvyFmhG6NrsehHZd9FyK6tJarQOgg7ECYmjdfHId7EY47ANj/0rmd4\n/9M97/7GPwzpGGnWkX5TECEjJo6JwHXg0fLzCZY4EoEGcodVrSfMYjKH/hh0giWRZPuePhGCwBCw\neMAJ+CWMniiZ1VMsjSSCzEB3wIHgSqRlKHnaE7x4knhEe7S/ZV5sAoiYSG4vbd7LtETyqrz+kXm2\n7/d8ARKK6L9r2/uiZlNXKpVKpfIxUcV25f64W5Tdr/gSD25ElhFZEoRds5IAcqZpUMVbHF1a4osf\nPK6zuMMWuo4DXMfT+TG4zG8+c4vveudv8M5veR0TN7MJc38Lpy25m8DiCBlN0NZDDpjQ7jgV04D9\nGmTgGNxjJSt7BAjo2nbSYosjr5YpcwJdAdvQBXtdMYGT8vjW9hmuWqkNPaquWB3mltOdR6isQBvE\nNyiKLufgA+KnqB9vptm5B41l+p9OS4Hu63zlHlldR6MgSdHu2kdvAflYIv4eZlFNpVKpVCovU6rY\nrtybFxNK9yO+1gUleYBQ8qp9y6l142wV+3pa67ewxYpLSHN77Lo6fC24i9iMcclb/t7/y1/8gif4\nQ695BNiGYQ55gUiwAplutzzPWth7TGiXCTMJE9pl0p2fLtvF8rXEhPO4PPY6rMagHzEPtqwgfBL4\nAN0ezG6D34N0YI9RBRagjqBzUCGmA1i2MGotH9uZbUQ0ITqHQXE6kPICzb1Nt8v7lKHkaX8UAnZ1\nC9/fBN/g+0PisDAbywuJ9Xvx0Qjm+7EZVSqVSqVyAahiu/Jc7lcovZh4SktcqVIXvHmz3QjVjDqr\nICct7VMYtsxy4jpyP+A0Q4qwumGPa+5azKqJv/mOn6MLga/7M5+MLV5UiBnSLfAdLm+R+wW0gmtb\nsoAJ62JZIdpjcJiYnpX71/nbe2XbCXDAqSDXhUUCdsHys53YRUBcwKiDflH2OQe3D9rBeI+oC8ha\npt8ziDNcEyzWULPZYuIK55w1ZRJQP8FFE+VSXjfibep9v6SFRQFygl/dJqrHxR0T7h+t4L5fqse7\nUqlUKhWgiu3KvXjJhNI66cODC+R1TJvYx86h4Bqy5s2CSWnIfoKmFeIcQiTHw/Izdyo2/+9f+mX+\n2f/5a/yb73wDzjWYKG5AF8QhQdgvLZQr1D9mDYkezEIyYuPBXi+QXJSvS+VnHrgF7GL2kREmoHuI\nEbo5yFXQQ5BL4D14B8uFtUC6GzZNdwEmj1o7JBNEZyitTbzjHbzLZPcIyZQvuCnZg8Ql6hsT4DpA\ndqgLZ473ebjXXyT8mDyICW5p7LXpcCbR5QFQPd6VSqVSqQBVbFfuxUsllPyYXBJGNKm1PQbzQEta\nmXdZS/KGayGeILoAVTwDiDMbRRrADaWsZcnRLPHVf+Xr+Pav+SyeuPIYJo6nmEDu7NhTjySPioIm\nRJwl8gEmqseY2F77tlvMUlLKbDgBHim394BDTHQ31jLZ7pv27vZBHeJGqEb7jVqcYCsixab1zTaM\nHoN+hupg70M6NLE7lEKeZhcklGAWNQ+7KiIgaQZEpN01DzuYh/1unu8vEt0VUpwjriOlOXQ75fzq\neSvPS8lLUeNeqVQqlcorgCq2K8/FtSZy82CL+z5WobR+3OompDnSbEPYtlSR4aQIQ2cxf/0B5BV+\nOCDnlZUVyKjYRyLEE/Ad4gJ/7Ru/lTd8xh/ii7/gtfDhp9gsXnydWU/8NoTO7NIA8cBeD2CT7TKh\nPp28A/xu2c+6DvcR4BjkMmiLCe4dYFGOqbcJti5AvS1+TFjOdl6Yrzrb5B4/sTSU0WVLIckDDGrW\nET+y7Zc3IYxwoiRpoJ0ADSqOpA7CCMn9RkDf6wLo+f4i4VoYP4oLEMViDHM5r+cWXJ6NV3wpBHIV\n2JVKpVKpVLFduQe5N7OCM+Gp60SMj2E/zH6XdvVBq2VPJ0RxyPhVqB+hIpBOzLeNB10iOeHJ5NCW\nxBFvKR8h4dKMf/5jP8l7n/pl3vPTPwm33gF8AlYg0wEZ0h1wpWCmaRCdExZHpLBj/S08C7wGm17P\nzxzs42U/HjjGIgCfsMSRcALqbRrt90GP7Pkc0EdrjHRqFwdyx0Q2S1sUmhc2PW62cXlOZmyTbjyw\nIudsKSNEXF7hGchuCwlTcpojcY64huyvmMcasXNxP/naZwV52EJ8tL8suAbEny++0VQXNVYqlUql\n8gCoYvuCo2n1XCvBS+XZHo6gv46sroMmkttG3RTaq+AC0t/AxUOQQPT7EBOqJviExnzFGoE5Opvz\nwWc+wrd91//E//yO72G6tWWWak4wkRyBsdkxcJYO0owg9QwxQduYOEYwoR0p7TDrF4lZUUoZDZeA\nbMJ0tG33r8Ymqhtn71dcElgQo+LahhwE+hZksN0pJeYwIXmF14EsvsQfbqPpNinbgk3NQvItKbXg\nO3Q4RvLS2lBVIc2QZv/5mxvLRPo0h/zuyXQ8MUtKeb3PsaHcLdShLmqsVCqVSuUloIrti0zuEXXP\ntRJ8tJ7ttfVgbT9Yf+9vQ3+ELj9iCxWba9BexQ0HZPHkaDYS4gpkDuKIMsJpRtPMFvO5gMw+hPQH\nfMU3/CBf8qc/h896w6dsGhTZxqwfHazLa9wcZNdsHZ0gtFYmY+HUmIUENjGA2GM5ZFPn3mKiWyEl\nkCXoTYgO0lV7qARy7HEScark0SfBONi0PsxAOpAW8IQ8w6UZoooOJzDaB3fZ4g01Q9vaIfgAzdSm\n/b4B6VBnCyVfSGifTqRzb37vs2kluYfhCMUhwwx1Y8su96PzlpGzDZ33c94rlUqlUqm8KFVsX2RO\nK8/P3uaFPdt3e3rjCTIcg64Q8WRpceipLxvtiX4XuGNNjjqD4QCRgPoWl+Y4XRATZL8HOUN/gNMB\nXCYvrADmu//Ru1n1A9/y1i+EvLKJdwZTqCVhg6a0sAdIAo1DpYEwBj8tduxdTJgHzEay9mh35fs2\nm2jAARhBWkEjoCMgQj40oUwih23QSG73zS8uJds7n9hUWzz4CUOK+JhQ7yDfgT7g2y1yVpsyi020\ncZ2952EHl48QF1ARUrP7/JaO9XkrolslIOI3F09pieQlDD0uzkk+ny60PCfK66LGSqVSqVRecqrY\nvsjcPblc315PSjVB1o1nO/dIPNlkPbsWhiNcXqB5WewLgy0I1HRaYOPjHegPyS7jnUfdBNpHoL9N\njIf4tCSPtiAdIqvrhGypHSkGcIH3/spv84M/9u951z/6crxGNLu7hKDDxthAPwOdQxch9zidIvmE\n5PfKdcUzwBOYoHZsfgWWd705xZ4iybza7rJNuEmgzmIImYA7NHHv8qZZsj/Ex0PwJyS9bGkrPiI+\n4AVSjNAkco5Ijqg0ON+QJZy2amq7Q4qNPV/YPl/bfq/zuP7LApRj47wIR0EEVbXFnK69t02kCuxK\npVKpVF5Sqti+yLgWFYfKcH6SmZbnF8qlIkQXH7YYOm+TYs2xbDOYyCTaFBmKcBeIc5ImlAweUlqV\ndshF8WR7HAM5HqF5hqaBnFdFuGfmi8xXfOuP8t++5fN51WM7ZGmAiAwHxX0smD+k5E/nFXBkCyRx\nZV+NLXTMYJNtxSbZDbYYci0wGxAFXQvvAE0L+oTZPdZlN65UzuuCNh2gGYZ210RuOgFpSGEHpBTG\nuAaaR2DxW6W4MgEju4jxI3Bjs364Dg1bJoJdW+IA72PCfDqRzhY/uN5+ffHkGlRaCA3qgTC2d63a\nRCqVSqVSeeBUsX3BEd+Bz3fdq+dv5h6GQ6S/hdcVWUsEXdgBHKpijZDqIUzJfrRZpBemaBwjeYEO\nC2tFXN0A1yB+grg5aFMEfQN6AnpCXiWywjd814/zuk9+nC/702/ESQ/xFrnfNQ/26YLHdQsktg/E\nEkzcAU221JPotovYdphV5ITNNNuVryWQzTedsl1UNC2sSnX8aVqJ2HS726KXDnKxgHhX9LiUtscD\nlCu2vcvEZseaMWViz0GDkBFn75WGyabe3jUbi8fzxfHdff8Z37XeVWqjwxE5RisWcu3z+78rlUql\nUqm8pFSxXXkuZ8porLUxQ16azzr35Jwsyq/ZheHIMpvxFmnnx2d8wAGXl7h4jC5nBBdR3+DSCcNy\nYaWKFGHqtyEfQ1yRhwOywr969zP8/C/9Oj/zT78WaT0uKpDRdIKGaRHP6xbI9QVCDywgm287ScSE\ndJnCs8BE9bh8j6fHCncsN5uMZWxvW5Z2Qymf8cCoLFy0KXeQQFTFO09Ksbz2FnUdMC1Wmgw5I6WO\n3jXbqA5oe4WcljZ1V2e2l9OFjity7jcRfcVftEgVAAAgAElEQVT2cTYP+54xfc+XVJIWOBKORNb4\n3G0qlUqlUqk8EKrYrpxnPS1dp5KIP40GFBdQJjYVbXZte3E4PwFK2t05a0IkSyA3WxCXp9uDQoDE\nGFxPooFmAicfIfQ3kXTEzVs93/Q9P8v3f8efZW9nSs6ewXm8gOKtxjyDJYbM2XyUr7BZMLm0fOx1\nDp+jbDcCrJVxU39ehGtzCeS4TJfVLjRUQPuyzTHEKYQtCFsm1duG5NoirGcw2oO+VL5LMFtKnuKl\nJ2c7HnWTEsOXcDqQyBDnZmOREnsYI/gRonEjptc+67v91mn5/Asb49yEtve4GNG0uHcDZaVSqVQq\nlZecKrYrG+4VIbcWz35KwpvlpNm1BXtpAa4l58FEuoTzQk88pExz8kFSTIh3iAsIkZQHJC3wjYlD\nG1p7svfkNOHL3/Zz/Nef82o+7zM+geT3odtF04KoCs0+uFERz2txv57WOmyyPbNjK1UwxMOyicPE\nuQATNsU2UpohTyyfO98Gv2ui1wk0ezAcAnuWHNJMwe2wtp1415BoQVaWKDJ6rOx3XBYwLsmqZJeB\nETTbaJxBXqIE2w/r2MSmXPCMy18WOLP40W++n1kACSDq7l1GIwLx2M5TUltwWf3alUqlUqk8FKrY\nrmy4O0JOM04c2bUbD7EfbbzBuUfS4rRtMotZITYLLSPMP4zGO+RhbgsNQwZ2wIlFAy5PSM0URlcg\nNIg6/sE//zVuHye+461/jOR2oB3Zwst2C5dX5LBlHvAMG7G8Fo8Jm5yXEhvpbErdH9pEmjEmtFtO\nE0wAOAEvIFPbVXsNpLeqdufArUtwbkPehf4WjD7RhHiMNpl2Cn4XR0RjQhjI7SPm584DXiD7FpEB\njbNSMuMRUUQc6jqyTLi7JdISDs9cyJS/NOh60n32oujseTy9nc1XLw0pDybuq1+7UqlUKpWHQhXb\nF5xzDZJ3R8gVi4VoskV2Z8pPpEy+VRVFN7nNcWafKleaFEdj4kKADvQQ2n1AcXFOjku83sINI5L2\nJG355Q/O+Qc/+uv8xPd8Po1PIBEfD2yq3u2R/S5Ig6bjMqkeY4sd18fcAyvQY8g74DKiK9Tt2lSX\nZ4DHynaBzcJKLVncwV53q+AvQzuFxRy6S5A+DDwCfrDbccB1Y7JPtCyJOZJdIGePQ1C3bXXzGciK\n6BLxU0tucWaHUZESHVguZMLW5uSsLT1h697Ri2HLLoDEb/4iAc+dWmtGmh1cFxCJNYWkUqlUKpWH\nSBXbF5m7GyTXKRXrCLmyzTnrApyKcQHUd/Z4QHJPdq0JcTBxq4pPi2JLmZJXS4g3IIxARiQS2Wdy\nmrNaRN7ybf+a/+ZLX8+Tn7iLX123zG7nwA2IKrBEc7ZpcQArnjnLCLNjbNkRSrDFiu0E+gG4XI7c\nYW2RR+VxbfFXA20HseSFuzF0HnoP46t2YRLGtqDRYz5tHdBhRZZkWdx5gROHukASypTak1KyuEQF\ndLAkmKQocSOqz3L39PlekYxlAv6CZTS+Q5I1aIqovXeVSqVSqVQeClVsX2TubpBMy2IXGZ3+PJ9d\nKAklH/uMV3gdM4ecj5PTBM0WyJg0eTWsesu+7o+QNpLDNcgLGE5wbo50Hd/yvT/B45dbvupPPkpM\nz5LCZTs8LRnUaWYit3FlsSbnjx+weL7eimjyxGwe0phoDgOb1JJcvtaPWUHubHs/QeISFWe53c5B\nUBueS7R9qAe/R3YT0B7VRHCZmOw5RAdEHSmXCxHfAGNLMnENSIumE3O6uIDmBRpPniu4z5+w57/9\nQraQsEWKc5woCWfn8qzdp1KpVCqVygOjiu2LzFk7Qcl3llIoc2pRWBNPkCK0zT6SNyK8iDY5u29N\ntrhQuqJr5xBXIAPqPIQT8LukMII449+85z/wk//u1/iZd3wh0Q+gnSVzECylY3WDxjs0bBPZZfPR\nbbE4vzWDffldWxjYtOD2rAHSHWGWkzGWWDLD7CQeiJuowzSzY/SNHT8Jsti2zbaJ72YLpmYlAY/6\nspjRLUFHJOnI2tqiS9+ZfxtnCzv9FJotpL9tk+a8RN3YvOUvxN2RjGfPzwuhCQkTXACXZuQ8nK9z\nr1QqlUql8sCoYvsic7ZBUjOCbiwla4sCQH8bhtuQI65E72XxiJ8ANiXVtaf7rOdbM6xuIv0ddFmi\n8FjhwhG5n0DXIjpw+86Cv/Y97+J7vvaPcGWvhZjBDeCmJYO6gf422uyQ87MQttFwtQy1Tyjej/Ki\nplgde2uPLdnWtrAT7H8a7ApA2cQEJshHyGATes+KvLiBjK+RS/uixOKbVshxhpx8BC890bU4v03O\nEdREe9AVuWmJpDIF97ZgNK1YJ6eogmoP0iEU7/uLnC/WDZP30yy5RpNZe5YHyOIW+D2YPFETSSqV\nSqVSeQjc/Tf4ygXDGiTH1uh47idF+MUTJB7hckKGO8hwaBPrHCEeI0XInWZzrxfsASxuWATf4g4b\nUTwm51EpcVF08Sx/+W0/z+f/F4/xX/2Xj5kwZAUScJpoJCDJHit5huRkgvU0+m+dLrK2iCTgNrg5\njC+D2wbZgW7XrCBslcdYQc7Gv30FaFGmJs6LfSSnTcukilhiyOgSeI8ON03Qi2MIW6SwC90TECZE\nzcR+YYraZyus8a7se2nT+naP7LbIriFLZ8dydqHjvVi/xx/NRFo8eThC+2dxcY5Pd2B147mpJZVK\npVKpVF5y6mS7YjyfRSGbTQIXyNIAkexGIA5NEc3DpgBnzWkG9BJWC/S04XEBjCylJLQg8IP/+wf4\n3Y+c8L9865swK4dDZQIqZDzqsCk2GU09VpUubHK1Z2dehGAf6QZkZKkfORP8MVmvkhHgBjYFH3Ea\nE4gCvSWP7HwysCT1pQ1SHawOEOkRXSFpIEmLNA5tdsrzlozs9jLoCX74CB5ryxzSAoYO9QEnLdJM\nUWnLBYvD+QYlICJkdLO49KW0d2hC8hIXGnIf0FKnUyfblUqlUqk8eKrYrhjPZ1FwtqBPM9DskjVv\nGg59h3MNoCbUz+xLoRQ0HmLT5AG4BCSL1Etz3v/bN/nuH/kNfvzb/gAjP8esHwrDgU2k2wnKBPIW\nNAnVjLgitIfD8mQNp+2PgAnfJXDHxKx2JN1B86JsFsqB9Wf+nbHmx0fsPnkEWiuIYbXE5yObpscT\n8CMcvVlGEEg9ogu0uQJNB/2MLFNwPSpjcAHCFPVbJMlouVCBkq2dE0pC/eT84tKXEvGojG0Rpgvl\nrxnTKrYrlUqlUnkIVLFd2XCvaWrYMuGcB8hn6sIlgDiyeBOPdws318KwANllk219bN9Xc4Y28Je+\n85f4y29+jD/46sfKdNxB/yx+OIB8h8yAi3PSeIZLlxBRqzvPqdhYwCwhZ8S2G4HuWO26KioeoUeH\nvnza15aTdW17BBa2fRzAHVtqSUrgFdoJaXliFxjSQbDFjTSXgZaMR5xDJJFRCJfQdkVyocQT7lu2\neLtvi0oRW7i5XmQa7K8CcvdfBl5KNEG7jfqGmO/YRdXoWl0cWalUKpXKQ6CK7cqGtff6bCvheuKd\nexgSrni5M4KIK+kdK/Rei/bSMcwPgVJrzqPAAcRDvuMfH7A9bfmrX/KG4h8ewSqCtKTcmphe3bLH\n+o4cFWm30WDtis46G9nYSIrj3Js9g5SgCWheoa4I5H4LE+Zlkk0EngUeh/xhSHvIaoHLu/jco9kz\nNI+Y31uANIU04JodsrNFj945RCHqYG6U0FjDpGLCfPoqW6Sp2RZpFnvO2RIafbGc7N8rZZ/STKD1\ndqFUo/8qlUqlUnkoVLFdMUorJPEEWV0nxx5pxujocWgvFSHoNtHOmk1g68wqx1U2OdGnIq6HeFz+\nvcBsJM/yc/9B+Rfv/i3e9X1fiLQN5Mtl3wdWj54BJhBXqO+tan3rMXtat2WLE5/voysBmlSysUcQ\ndm3C7Dz0J5jgn9qxocBVYAThCmiD4klhhGRQ1wDOptM04FbQJLK7BM0IcKRmbHnksgNhG/IC7z06\nvkJeL2RcRyPmHoZDS245W7X+oEXvesFqf4gfDqzuPoq9zS+Y612pVCqVSuX3ShXbF5zcH0N/XCba\nERYfxC8/QgA0jRlUz3mJM3Ju8i1pQMpQWTXf5TeO2FS7x5obO45mE77m+/413/Xln8HjuycwL15o\nt2/Z2i4AHeBBWnIYWZMjPY4RSY9hmGJebTij/u2bGyDslCzsEQ7I5E3oCL9TjslsILZIcmmJId7B\n9NXAiuj27QHN45bV7cdl8p+hGbNunMze23btJQgTZBgQLNIwp6VN2jUjGk+n2aexivebk/0SoHkA\nLCddtLc4xRfL9a5UKpVKpfJ7porti8zyOjDHxRWa1RY9plWJvQtANkEW5xsrRJpZGkgYb2wnaPE0\nn/Fu5x4TsifluwM8f+X7f443vn6LP/XGHdBdiLeBFobS1Jgs8QSctTW6kRXJxExuDmHwtlgyzsuL\nWDdBlhTLpkyKRaCfo6MdE9+0EC5hEX9SHrMCnga5ZgU63VWbjLNtr7UdwWTXmi+bMcgIpwtLZZGm\n5He3IG0pu2lRzcQh2fsmJc97HZfoms379DBj98rFkYQp0q8sR12THU+lUqlUKpUHShXbF5V4AvEQ\nmOEXd4h4VBVSJEqLF4/KqORCD0g8gTTHDc+S4oALI7KfoGmFSgOjrY2FJPdIPEFZAdegRP/9yLs/\nwK/8zhE/8z98tgn2GIE7QII0NstHPuLUV52LjSMqTFokLwksSP0BGsZlXaQle5ySMa9404ATRDOo\noM0WEG2YHSeQFVso2dqFQ9dYt41mGE1BFe8bVAVtt+298Q05JfAjBLHWSD+yr7Udo92372JTehGb\n+CuhtG8WW4mmkqgipXDnAVpJ1otY/ZToViUhcadaSCqVSqVSeQhUsX1RyWVBXz7BpWNkWCCuJTd7\nqE6Jfgrd5VJSIzA8C8MJPi9Qhbw4QAi4dovcXrJJ6XrSHWeIRpSMiekdfuf6nO/4J0/xj7/xc5mO\nr9hCwnSAKdw5MDWRHNe51xmIVvPutiBaJbsGNRtGu3vvSqZ+RhN/l0hE3SVkuEP2rdWtuw7SHCQD\nY5CJtTt23mwVCohD0hIRj4sn5LCLuEByWzbtd5PT6D58h/iRNWeuX7t4E9yuweXeCmxKNbqmUgZU\nJspubSvRiJ7zur/ErBe5OqBzD17cVyqVSqVSOaWK7YuKa8C35NShKmRp8Vhlu+sukcI2hG2c9lbp\nnjLEOTkvkDjH5SW0l/A6oPHYims0mfjsD4Ae8gLYI+XEW7735/nzf/xJ3vCfXAYG82fLDhtf97al\niDgtj+uAucUNxmPIoG0isWflMem4LKTM51+X7jDItu1PPZqT7csN9lx+AkwgLYqPe2bikww6KZ05\nDRrGZHbNPoPVvUs6QaUrbZu6scxospr78m8t4janhdlS0gKXZzgdyLTkeLyxk5THPHBbiWtx3dje\nz0qlUqlUKg+NKrYvKiXOb4g3LalCE85ZJbnkpdk6fC5V7DMQRVNChkOSmh9Zs5JzgnxoE2Ickheg\nK5s+k4GWt/2z/wcE/vqf/YOYj+MINGBqd4ZNtg/BPQaxwRY/LmxbXVpudjslBTGBHqYmzBWeU2qz\nbqd0DjSSG2/7SAn6JU38XQa3a8/trpQp8wh8LP5rARcI3SWyn5D9FpBg8SEgWr62C2Q/MiGtyfal\n8Xxk4tlK9eUNNC/I0tp0PGcb6J8es68FM5VKpVKpvEKpYvuCE8QW+MUQGBSQhuy2oZlaaQ2Cxjmi\nCg5Ss4WmjIQWpCEOK/AenEd0Cf0Sp5msFlHyi//xaX74376fn/rOP4F3Y05r1rPHFk96LBlkbBF7\n8RngECuccWb1GD4CfkQrgb5Vs4G40XnBuqaZgHvUvueliWBR277dYWg/0VoqY7LGx9VtiHs25O6U\n5KbgpiTU/NvDEULE5zku9ww4CNuoBMsZBzTOQHtEms1kO/c2PS9+dUEQKVP4MIEwLa2bD8GzDRBP\nyMuFve7q1a5UKpVK5aFRxfZFJq0Q36Eu4HUgqUCzB25sC/vEoWlljY1Y4YyXFYz3IS5RPDRbBJfJ\n2pMHRdOCQML7hsOTnq/+H3+Bb/3ST+dVVy+VJ12yiQM8KfeV+vTVvPxsvQ1AA7IHDgbpzD4y7NsC\nSGCTl71OI0llkeQC2g7nR2S3ZRcP/go0+5BnsCoRg34LUBQhZaC7BN1jaD4qxS8dxDmSV2YdSXOI\nR8WGMype7QHNGQ2hJI1kiCe43KN5QAWyG4P24MbF013E9drr/SBLZuIJLp6Ab3GrA3J/aJ73Kror\nlUqlUnngVLF9kfEdEtdeYS0JISe4LqBZTDRqwhEh9qhGBg0WDygjaLdxuoLhGE2HVuoSdtF0iOL4\n+r/zHj7lky7zpX/s9Vj837omfR29dwU4wqbYasUz6aj8rEQK5gOzhQC+v012AzkcQrhWPr2h7Lck\nksQFTq+Tm0eRpDg6su8sni/1Ng0PE5hdh3gHP9wmNRkXrpLdHnRPQDfBDwOKI0uLEojebCvqJiaY\nxVkB0Pq9W7dputYsNGtPOAmnoH4Kfs8WU54R2qdNkprsFTwIwb3O044LXJqTXcJFX0ttKpVKpVJ5\nCFSxfZEJWwxpivqJ5Vu3zia22RZFIlYG4zST86IIyBaJEZUIKYCuyGll0XZxYeUwruF/+6lf5N8/\n9Qw/+7e+qDxZwpobV+Xf68n0CjjmdNEifblvF4gmwN0IU8mCYyATbYDs1vtN2EdZi1hPJoxHe0Qm\nVkzTboMkvK5Iydu2XCORgMvk7jJM/wBMrlrMIfZeiB+hPIJ6D3FpXvDS4qOpR10APy2vpbT7xCOk\nv2PHGPZKvnbxvJz1Zt+9KPJBLZJ0jWWnn5bYlF/7WmpTqVQqlcoDp4rti0qZqoZ2gvYdCTUrSV7h\n8gyVMerGiJ6gqTexlnqafNvsJWGLlEbWkpgj+IZGjxmy8OFbM775v/+H/MB/90fZmUZMKK/FdWQz\n3e4x+8clYFy2e7ZsM7NtsuVl44REKKJ+QLW1CTMl+WS9z2aP7HZLycwl2Ho9bD9hSSDthNRuwZAt\nWzsI+EvQBSu2mV6FHFGKd7vZBhSm10pJz21cXqLDAZJn5LCPQ08n0upaWN3CpxkqUsR4Qrurp38l\nOIf48/c9qEWSYYucexKRKF1JWKGW2lQqlUql8hCoYvuiUkSeaiZlRaUhqoPhyGrXA5CXaFyRnSWR\nEI8RlrgiMZPbQnIkpEOyzhFpyK7hL3393+GL/tQf54985lX48ByzhSgmoteCMmNCufi1mWJe7R4T\n4qWyXUtCSAZtJ5bfLY2ljlCq0nHlMcmiA7vWvOejazB5BPDkdaNjswPtwp5KBhy3yexDiLA6wolD\nwxQcqCvbuxb6A8R3JaZvaeU2bVPSB+OZ5syI6ICQrATHdeBam5aXiL/TTG3XmlBfp5g8KM927hHX\n4rsdYn4WEHKYVAtJpVKpVCoPgXvVglQuAuJhOMCtbuGJSBjb9HqYIcNtQrqDSzNwAXVTK6HxU2JW\nVtnTK5AGVHsyQsqOhPL3fuDHmM0WfNs3/dUSgT3CbB7COpnD4v8W5UAaTFivsEWRj5evEXBSynR6\n8J3FC/o9CKNSnrNeYHkMLE0wh21ongCm4BuczpF8AmmwRsesMARbKBkacvt48YSPS0TgDNGErK0f\nawHsGiStECIiHglj2w5KU6QvMYnJWjU1oSp23GmJ5N62zz2k5eY8uPZ8TOCDoFxYOQcSysS+Cu1K\npVKpVB4KdbJ9Uck9mlZkVfLqDhpvweo2Tua4PCfHEzTsIaO21J4rOS4RHJCs6THfQoiWex3GvPc/\nXucdP/Sv+D/+6d8mBCliO2JiuscWMvry1WHie4VZSE7Kv+fYxLsDGiu/CQ1IJsRjJK2IfoTEETk7\n4DY2pi7WkO6a2UuaKWhEFjfIMoJmBPPr+NVNojQw3IZRqVYPE2ABecClJbm0PqJ+kxLiWjLeYgOl\nNZ+26+BsuU3uwTUkv2vCXbrT+vrz6PnGyQcd+/ew7CqVSqVSqVSeQxXbF5U8IOKQ1U1C/zT9co7T\nGeKUlAdSitA+YtPu4yPU9aArJB8BAZci6jt8npHSHouh4yv++tv5hrf+OZ58zaPEtDjzZBGbaI8x\nMT0v9wdMKC+wSfZR+ZkHtjgV4wMwysRmBMlDSmjXlYWTE+wPNE0R2M5aIuOMNp8gaUGWXRg/isYb\n0B+YVzktTSdrRPMC4jbk4mnGF0E9RnJvVo+0LNP/ACRLFWl2zKKxtohkyxD33qHJg0RyEeBZpZTX\nOFhPweHBppCsKXYVJZivvFa1VyqVSqXy0Khi+6LiGjQeE1c3kP7I1iL2CzwDGYV2YuJxdWyRecMx\nDAdIPMSJx6ee2G6jJFThm9/2w7z6E6/xF77si9Dcm1h1YJaRVXlSAbbPHMSKjb2kxWwkh5i1ZISp\n7FL7vvJ4F0l+Fy+QcjRfBAtsKi4Qd+2+bg8WPSnOEQV1K6t8dxZ3F3BEXUDWUg+fgYwQUSJIZ3aL\nNWoxhFLeN2jMz73+cR7K9Np846qCmsncFka6djPBXk+Zz06aH3RVO5hvPIztLa1UKpVKpfLQqGL7\nohK2oI/I8gC3vImQyDmRRiaGJc/RxdM06ZDkxkiekfDEMAI/IfZHqCjZBX7y3/06P/0Lv8rP/Iu/\njWiyWvLWLBqt/izKTRwLVF4H2tLLozjtESKBpxnkE8hcxqsSeBZYMsi0WFZ6RLaJoUP9FuJGlpvt\nvHmlR7uwMN+3ujHQWetk2MbnAWjNKa4R3Bjd/iQSS2BiCx7bDq9K9mMkzdBhHyYjmzbn3sSyH4Ef\nW+OjZptO+7G9j2mJQ+3iBdBoE3+VBtHBLhRyZ+/33UU2a6qto1KpVCqVVyxVbF9E1mJvOCTkQyTN\nIC/om32kz0ia0RBZNSukP8aFES6uSM5B2LX4azdFs+PWnZ6v/9s/xd//9r/AlUeuklXBSyl4OcQi\n/BKbpJEF0CCsyu0PEohEZth0+xZwA8c1HInkL4FfgTpCUgZnNgxiAg20+n5wR+BaVu1nINIgviG3\nV+iH4rH2LfhtyA0+3sLTkgKkdhtkCs0Wzo9wYUr26+QUkLWnen1P2LqHz1pP31YBtJlamks2q4y4\n8V1b8fBSSCqVSqVSqfy+U8X2RaPka2vuQWcwzIFkPmc8uIgfFkUsiiV5xCUyLKC5jB+O0U6Q3JFH\nV/iKb/xBvuBzPpXP/7w/DOJwAiKOdFqYcjbwpmVTr74WtWsRvo4FnJfbS6AB14PbhXYbyQNCi9LB\n5DKsPlR2k84sxlRcvE1mBze+aq9NWvLoMUsn4ZbVqHOL5HZxoz1wU+hKu2NzeWP3WE+vKc9x9vaa\nuyfeJeZPJSESUF8WSd5tFakCu1KpVCqVC0EV2xeNtegbboP2xNAhMZB1hIZt6A/Q4YhID36bldux\nyXc6ARTxU/IQoO34hz/yHj5y85gf/t63mk9ZHJ6ExGPso7VLL5/NRlxvgzwN7JNkASxI7GDT7g7c\nFklfg5XcNPY4/7hdCOSeLIKO9tDRo2XKDNpumZ5XB3T4xuPjEVEytI/C6NHymrOlpmz/p4zDiuM7\nv4W6bbS9RNYxjC5ZBX2YbBof78fq4drzE++0NG+3dIha4supeL8Xp1GA+uAjACuVSqVSqTx0qti+\naKxFZH8E+ZicrZVduwkkW8gYvQeusP54KA1xlcB5kr9O9lP+v/d/mL/7v76Hn/j7f45RJ6guYXDQ\nTkrj5EF5wi0sB7tUmXMJSxDpznwHGMFoDKsjyFvYdNvbw1wD3pFkgkoH7WXIM2iv0E9eDxyB7EBz\nlUiDYH5u+uuQeiQ00F6Ddo9hEHKzIocDkCkORx5dMXuMH9lzlQzq+7Z6nP3ZOoXFNeSM1d4/XwJI\nSTJZJ5NkTee93ZVKpVKpVD7uqWL7lc7dec6nfmEPy0P86lkk3iZKaWFUReIAHKDuiinO4RjHs+Qc\n0Jzplz1f/h3/F2/9kv+MT30V5NVNUtizSvWckNQjXtC8PoiW0yxsSlU4DrONRCwScADZthQTDjlt\nnJRHISdQwfmG7LdscWQS6LZKZF8AtwfdJyAhoC4AmZwb0Dk+dhCWECZIt4UbXyOfzCEvSNKA91Y+\nE6bnhe7HInrP2kpC+8LieZ1KokP5nu9tValUKpVKpfJxSxXbr2SKPxuwPOdYIvJcA76xdkgBhpNS\ni95CGFsdegayBw3gRmReDShKw994xy9yZbflq7/o9dDfxuVM7h5F/TbEQ0QyToUY1weyrlNfl9ro\nma+1uG6gn20sFSWkz44dcB16WiYzgdZBfxNPh2qPoqgMqL9GDAJxiWsyOWWcy+S8QrTDNVOa0YRm\ncol+dWSLMHO6t6/6Y+FuW8kLCfbyV4b1ORIS+jBiACuVSqVSqTw0qtg+w3K5pGkaQnhlvC0aKfF5\nkPsTxPWIHwGRhQwQtshJkFymqjpAaiFFE73OPMjkFiuc2ebdT93kX/78df7t2/8EkiLJteQ0h+Wz\n0I0R2cLLHCGXRYuwqWZfV7c7Ngskj8r9DWQHPI2J8inIFjiB8WVoLuEmj6DTfaQdE9yEYdhGFmZz\nCbIk6ZI8GdGOH2VYPIMfjvCjKT4t0GaEG+8i4jhZnEAeCKK2oNMlHDMIe7imLHKUte2lvJe6bn08\nsxDyrm02247ua1vVEdmD5HUlvMUquubBTLedc4zHF2dyLiLM5/NX1O/0/VLP9cXgop1nqOf6ovB8\n///68crF+aTeB6PRiOPjY4bhZdD8ca8672gi8ayv+MX2cTrZHk7stpQq8piLGBQ0BvMr5wWwhH4J\nXIdlMD3sPfAqDo5XfO33f4C3fcWncW1vgou3kLzCh0skPcId/ha5e5TY7dqQ+HSoq2zKazwmsBvs\n47f+j0csz38JE+fOxGfwNslOS3RYkReHoLukZguaR8n8Fi49W9oR5zA7ILpdVFuGPILoGVYZ8jHk\nBro9trenzJ89RleHeBLJDzZV7+aIH/XiHTcAACAASURBVKNhq7Q9nnnvz76XsGlivNcCx/mHkHho\nt7urL9zamM+I7ZTN7x7vvenvlfF4zGKxePENXyE0TcPe3h6z2ezl8Tv9EKnn+mJw0c4z1HN9UWia\n5sU3+jiiiu2XI3fbP8p9Lp6Un69saPxigtu1Zh1JK0gDTtSyo/MShoXF/mVAT8xSzQDpNdjHYr/Y\nKsagAdVjvub73sebPnWbP/mGbUgNeXQJ4so81asF0iiyvI5Lc1Kzf9fBrJOmBzYfuyUmvkO5vwXX\nlQn3lv1cWhjuQHMJ4gxJPaod4sSmzc4uFDIOLZpeNCHDzFJU+oFGZ/Spw8ltss9o3EXiDDfcwTtI\nmnGsQAT8GM0rpL18vkr9bntHWkJaIGlxuvQza4I4x/fXcRohnZhuHj32wueonOeauV2pVCqVyiuP\nKrZfjtwt7DTZRDvNijckmCh9MeIJLs1AE1kSWV1pXnEgK1jdgNUtLBGkBfYg3cFE8LTcdwnyB/ih\nd32E3/jwMe/+7jdaUUy8DsMeTT4EBnJsyWyhXQPpDo60cZEAm7ztUL7WedoL7KACcAJu2y4GUJAE\nugKdgpsSs+B8j8oCt7pFWh1YYEksFx3tJfATcu6tRh4POiehILEsCr1BlkP8cIOkPSQFAqIdqgnJ\nC4je4gbX0204HwV4eiGUIa/MKiKN3U6zM68VSyd5sYbIKrArlUqlUnnFUsX2y5F7ZTznHpfm5Y7e\nUjlejDg/nZC7nFASSIOTTIpLs1asZsABGzvHgI27nwWuAc/wm884vuudT/Mj3/wmJt0BsGWCtO0Z\ndAuaCXRTiAHyDB97cujJ59T2+sbar11ytImYZ/vY7gsZYinasQBt8AHxivPgVYlJwWdQxWNFOgom\nkNs9VARocG1HRnDDDTQuwQ2I34EcUU1kVbIEYETyU0sriSvQFZKXII1ZQOC5E+hyThBX7mtKjfsU\ndP3aMxp2q5iuVCqVSuUCU8X2y5F7WQtcS5QOtDdrxf0IuLMLDERRbQBBVWB+A+ZLTOjuYnaOBhO/\n29hk+wox3eYt3/s+/uIXfBL/+WsvwWmtugcdw/JDkI5w7JH9CL8CWOGGE5C1lUTYTHvXItqzSRwR\ni/0bd7Zpuwspg3dWNONGaO5Ifpfse1TUsrTDDinPUBfJLlhWdrNr71tIqK6gndDrtXIxAH68jQtL\naLZBILsOmivQXQIHGko8oiZLPzk7lV6/5+KthbOcJ9VcEl7G0F4iLRtIcxP/o2sfzZmvVCqVSqXy\nCqOK7ZcrzxHTinee9QQ6nXqgX4Bml6TZLCgZELWpblpAvgn9LSz3egRcZbNgcb2gMfA3f+R36Frh\n6/7MazExvs9pbF90gIMMOVuRTHJKooPuMgzrlX7rPO1YnmNl+xcBnWPtkdFyrrsG4p5t6sRui4O2\ng/E+Oiwg7KLtFXALGG6AbxA/QkOHiENLA6SmpXmrt63QhjiDeBttnYn7bmQCubkEYWwWndAhaGmB\ndFbhfo9zc3oxdK8c7SqwK5VKpVKpFKrY/njBj0l52KSR3E/5iWuh3S/xfbfw6RBNK3SYY+p7DNzC\nRPQR1hoZMTF9wC/86jHv/Jnf5F1v+3Scu4VNu0eY1zrCcJvADTQFJCWifwJwOAVWx2R3Jmnk1Jdd\nrCPOW1b2chdcgtGWZX/Tgt8BPQIyPkWSV5Ap4jvwE7S9gjQ76HBEEMG5gJIZ4spksngILeIa1DVI\nWcKoFtiNuI4ctq2ARhoIrXnMVUF7FG9i+oUKaao1pFKpVCqVyn1QxfbHC+KRMD29ec+J671YJ2mI\ngAqqA0JEc8QSP6aY2F7H7NwEEsfzjre+/b18+5//dJ648ipOi2dYYOJ5As4T82sgjGA8Bp0AS7Jm\naNy5dYKbNBIBjsq2ArzfcrzzBHg1uC2rYi/WkxxaaC7D5DHUj4svelReW0cK2/9/e/ceJFd53nn8\n+77n9Onume4ZaTSjC7ohkAwYCDZKCCY4voCX2OskFcveYJtdXOUsMd6yWce7WcebLOwm2YpxLpsl\ndig2hBh7N4Q4kVmnIFR8iey1HeMQJwGMhcDIQkJXRnPpnunLOe+7f7ynp2eEkMGo1dLM71PlUl9O\nd5+eM1T95vXzPg+u80HxQFgdN1F3DLqxIYC3noPmBN428H45kc1wxubdT5p5JxMLWTuUf0QlBWoR\nERF52RS2zxQv1CLueP24j2UiTHsa057AuBbWRLi5FnyWUIfd6RAyCEzy72//Ry7dXOFfvW4zISiP\n0m3bVwIqUGhDczJ0R8kA08D6Jrb9HM6uxLlOx5T5Q2zawDLCCwjvG5swbt3E4dAsDn8cJIN4OwLF\n1aEsJQ/SmCj8sVFcjsmmsCZ8hosGws8iKuNNhDdxHqDr2GwGl9UpNA9g7DS2VQ8r6cUSJmthozLe\nzeJtOfw/B3ndtoiIiMjLobB9Jjk2TB+vH/fxAndaw2c1svZM6MKRLCME3zqhJKTzmiowy707DvLt\np6b4ym+/OX9+im4JSacvdgbpJDCd14SXoDiE8ymOMXDzpz85ukNtCkATzDj4vJc21dBdBAekRLHF\nx8tDx5XSWSFoJ8u7XVo6q/pRGecMrt0MK9HJ8ILnTOd2azzvi13HpbO0GxbnMogdhjbeF3Amwpsy\nxtiF7f5EREREXgaF7dPdiVaufbbwee+Ov/I9u5dCOgmRxTnIWp0yjVFCmIbQazvjmcMtbv70t/nj\nX7qSSnmMbps+mx9zmLCpMu+Bjc8bjJhQh53mrfDwL/DblYX3jJZD1A7vmx4Cf3a4bZeRYcJxyWjY\nbFiohAEy+XfynUEy7QlsNoW1YExK2jqM65Ta2ATvWvkfAp7It/BpHeNmsPEIoTefwZsyJCV8VALv\n8MaGengNmBEREZGTQGH7dPaDVq59FqYk+iw8H1XCyqzv9ioxaQ3fqmHTabxrYdMZMl/Nqzg6Gxbb\nQIZzCb/4+1/h2tedy2teuTZ/h1nCarYndBEpAA2Il4XhOJjweh9Bq4b1Tbxv4KNq3lq7s6qddzDB\nQWzBt8EXw/sXiuEPheIyKI6FGnCTQGEobFKMB/P36HzvvCQlmwVrcC7GmCisVndWo10rvMIW8HGZ\nNCtBPEgaJZjySCgRKSwPXUps8vzx7CIiIiIngcL26ezYletjyxq8Cxv7IIwuz6ZDiDVx2OSXzWJ8\nC28j2vVnMa2DYAehaEK+7gRlwu3f/uy3aaWeX333FYTyjjohaBcJQ2c60x/bkE6Fdn1MhOfTNiQl\nXFQEF3f3Q9Jm4ebIfKJiZCDyMLAWkjjUZSdDYAtYG+OSUWxSxZsYg8fhw88ia4Z/o2IoFWlbsBZj\nY0yh2t046jNIa6Gdn2thCyVctIY4myBOluPbGSQrTtxxRERERORlUtg+HXUCdja7cGX7eDXbdEpI\nGtA8gjUx3tjQh9oD6QTM7MOkhyGdxJsmYXUZ5gbK4PmHXZP88YOPcv9vvJXIxoQ67jYhaEN4s3yk\nOg6ohMDrmvnTzTBV0s5ifRuiCs53Xgfdlel8+mOxGFr++RhMOaxe2wGwBSI8zs3gXRkfl8P39i6U\ngdAGUwwdRpJR0nYTsikwFSiv6wbnbBabToRR9d7hfAGspcUg3ia4OAor5wraIiIi0kMK26ebeaUj\n3jscpju63c+bf57WwLXC9ELAp3WscxgzC+0atBswuC70jm6O49MGUXoUb8t4k+DjEiEAl5lpTHLj\nbV/kV669jHPWjOUfMJv/2wnJncE0w/ljE+ANYQXcQeZD6UdSwZGBjfMykvmr8fn0yHIBSiN50G0C\nFUjGoDAIcQnnUvB5e8OoFKY1pjMYMqyxeAPORJDWiApJmAAJZGkNkpH855ji01l8NpM3OKlCu0kc\nW6Jihbjdpp01FLZFRESkpxS2Tzfz280Zi3HtUIcNuLwkAteC1tEwjd0U8tKJBMs4tlXHu1kcEaTT\nobzEFMEbMjsIWHxpJaTT+YdE/PIf/T1b1i7j31z9yvyxGqE2eyC/3yIE5U7ddRQe80NAI4Ts2EAU\ngS1hXR3nbP7b1aZbs10Pq/ClFVB+RV633Q4rzNEQ4DAGTFTIe2nbEJq9B1vAZPl5+Ci09HOdCZW5\nrDnvdoMonQybKbMGWZZi44Qoa0N7GlIT+nKLiIiI9JDC9umm094O5no9h6mINqzCZo25zX/WtfLS\nEoO3BVzWxqcNfOs5PJOYtAGVDVA5G+fHoeHC8Ji5VWf4v3/3GF999CB/+/F3YExnFTshBOzO2PZO\nSUlnEuQAcBbErfB+SQUSE8aeF8qhv7YphNV1CnTrwodCd0E7ApVN4a0ah0M5SmkMiPBpnRQXgrDN\nQ7WNMVmKMzF4D1El1FoDtI92f3ZRsXvbZzjn8M7nP08X+nOTd2yxRbX2ExERkZ5T2D7dHGd4zVzd\nNvnIcWPBFnCOMAkySiBOwmp2Yx9RYx+Rj7DZEdpZCoVhrGuAB2dnIAth/sDRGr9y58N84t9dzvLq\nvKBKSli9zuj+ijhC+z+fP56FoTCmDr4GfkUoc7ERcQbYlNRBGJTTCe0Z2DYwG8pgisswpRVYMjLv\nQp/seADjw/t7WwoDZnxG+NpxGDrTqbVORsII+2wmbAjtlJAAYPLx7gVcOwFbwkVDuMjji2N4Z8Ep\nbIuIiEhvKWyfjo6pI14QviHUakPoOoIPfaFbR4lmn8Wlz2Fa4+Bmwa3ExCP4tIXLUqwH4y0+m8Jn\nnvf9/hf5mdds4PWvWnPMp5U6J5L/2yKE5RJhwM0RoAH+LCiUQxeR6kpCPbcjLSwLGzfjWuilnc3m\n52nz/tYWXBPjW1gb4YnnuotgInzW6K7k2wSy2e6o9s74+fznYOLBuUDu01p3xbswSJYtA1J85MMY\n+LiET0rYwbOwzfG85lxERESkdxS2zwTH28Q3rxWgcS28icgMEBVxvo31LYyrQ9qEKCNpT4MLPblb\nhQq3/em3OVpr8l//9U8RNjlmdPtpW0KrP0cI0Alhw2TK3ARIBsBPhlrtOAI7GoKud1if4Uwezodq\n0IzCKnIhhsHlUCiBHcCbAbzJ8KYAhWUhbHcC9jHDecy8ko8F7f3mbyjtbHi0CRSGw+bRrB6+Uqef\ndlzA2ALOJORz3kVERER6RmH7TDR/OmRngE1Ugmgl1B7BsQJnqzB8QXi8uIoWtZCVqfLo96b5xF/8\nE/fd/LMkhU6Hk84qtiH0164QwnZnVTsmhPE8aBcMDA5AkoDdAAPrwYSg7knBDELJhNrogWehPRM2\nQUajUFgLg2shHsBlzbAyPb/f9bF/XByntCac6rz6dggr3/Pq3UmWQ5oAPpTjEEK7KQxgonqYLiki\nIiLSQwrbZ6K0BukMxjdh/DvQPIKPh6H2HWhNQXsyjEOf2QsDZ0N7mqj+fUinqPuU993yIB+6/nLO\nXz9C6DwC3V+FGt12fTa/PU1YHi4As1CqQDGCQhJCdXlV2IhJBNl0GLSTjOTlHXWoOSjMhqA9sBaG\nt4Qg7LMXP1TmeMfYBB+VF5adzN/0aBOIWVDzrk2RIiIiciopbJ8JXCsEaB9a71k8vn0UjjxMMvtd\nSCdJ2w2yLMG0vgZswKf74OiFcPSvYNVPkNWfhbTJr/7Rt1g9WuQXf/Z8GIfu0JnOBsiI0D0kH1zD\nbH4/AiaBMmQWWg0wbSI7SWZHYXhz2OCYFQETarCzBsQD2IEVkLVwhSEYXJ2PXyeUjRzvux67gn0i\nnbD+Qq953qp44aX85EVEREReFoXt013jIDQOE/kZiAfJXApZK6xut/dDcz80D2NMATO7hoQp4Fm8\nmaXFuRT9fppThym2dvLgw+M8+FCLL33yX2KyKYr+73CmifUHSHkVmALGzxLxNJDQNufiKBH5CWK+\nC1RxZiXt9ihJexpnhomimCxbB81DgMdEZcJEmjj0uDaWgjV470kJ0xwN4OeXf3TMq7+eK4/phOfW\neOijHRXnDa6ZF8yPF9w75gXwbntDERERkd5T2D6dtcax7XF881ni9jhplobV7XYTOzBClrZxzQlM\n8wD4FXgzRJPXElaknwPyHtQzGc9OWT7wv1p8/Bc2MDZcgbRK01wDTINx5A2wwUyScjYwSKfXdmbW\nkDFK6K99BLC0SfB+GT6rQdqAxnjojhI1iYzHRQN4W8S7lMwbvCnhTRwG0bhWt2vIfMcG8M791jhR\n61A+wj4iA4grLxzMX4qXupIuIiIi8hIobJ/OsiY0DmNnvg9T3yVmFlcI49Rd/Si4Nm1/NhCBWQcU\ngXWEoDwERDTNhXjf5v1/MMVVrxrlp35sC7RL3f2Qc2UknQcSQm12ie60SPJ/Izrt/XwUg/VkJgzV\nwTdDiz4T4azFOQfFAYgGSF0z/JFQWAZxee4Tn8dEoU1gJ/x2Anlaw2Qz3cfT2vNXso+3Uv6DnGgl\nXUREROQkUNjut7QWumJ0OnLMf3z2OTj6KH72KbLGs7h2G19oETGNG1wXxrG3jmDYg2eMsLmxSqit\nhrDCfYA/euAJ9hxu8Sf/4QpgIExdtCvzY6qE3tnT+e1y/vo2IVhDqNvuROR8ImSUQmyBGGwG6QyW\ngzgMNqngbQSt5/DWEhUG8L6Ndw181sTYeuibfRzhU8zzHjSdziHe5TNyju1E8kNsfHyhlXQRERGR\nk0Rhu5/SGjbNu4G4ZpigHlfC4429uOkn8fUnMfVnSLOUiGcgOwtvHC5ykFYJMyUn6fbJniKE1UEg\n5Yl9bX7nL57kz/7zj1IuJkATnJkb1573A2Thr0JMWOmu5bfj8Do8cBSiagjbNsakDp/OYtNxXLwe\nbExqKmBL0J7GTj8N2Tg+dfjSCiLjML5CapJuYO6UcPgMM29lea6uOxmmnTUIZS1J2Ij5Qu0AX4qT\nEdhFRERETkBhu5+O7fPcud88RHTgS7jmQaKpx3AUgBoZ64ESmQfqe4H1hJC9gVBPXaa7Ml2j1a7w\ni//jG/zbt1zAJedszD9kFuJlIY+32yzsr82825buePZ2/phhrsd2IQYX4SOADIcJpR3xMDYZwpsI\nP3OQePofwM1inafNOdi4SOY8RNNh+iN0SzheKPxGZSiNhlVtY7slJC+35ONkBHYRERGRE1DY7idb\nANdceB/g4LexR+6H9mocBkcEjOUH+fx/RULAhtDDr9PSbjK/PcCv/5+vUSknfOjnfhSYIYTlMvhC\nXordWb2G7oh2R3dSZIEw4MZ0nysZqAxCsQqtaTCz4JJuC77CMM7EYZjO7EF88yD4Ns5FWA5jB9fi\nXGPeynrna2UQlY8ffm3+/r0IxQrYIiIi0kMK2/0UV3Cu1W1p16nZdrtxzX3AKhwVQuit0N202CSE\n6meBlcAIYWMj+TEJX/nn7/MX/+8J/ua3fgZrC4R0a4BZyDKIRuhufpyvQfi1aAOt0BPb1MLLywaK\ng1AcBWMgKWCp4xiCwioorYXiim4gzmYw7UN4b8A53MDZtG0ZZ4chSsJmyM6xnVXsFwq/CsUiIiJy\nBlLY7qe0hvFZCNo2wbtWHipreFp0NykO0Q3BhhCsy/n9zkp351I2mKjN8ME//Aq/cf3lrF2xgu7A\nGk8oO6lDOkK3Xns+SwjzRTAliCZD2Uh2BOK1UDoL4jEolCEyuHYDChUor4PqOQtDcVSkFa0NUySj\n5ZAM48obQ9C2BbyJQmkIKEyLiIjIoqSw3S+uBVkjhO35Ncu5lPOB1YSAXCKE4JgQsg0hfJdgLpR3\nJNz0yS9w+flreNuVF+SPdeqgO+37OuUnnY2QnZoOx4L6jkoG0XAoHcksJKthcB2UVoOPIM5LTwrD\nUKg+PzBHRYjziZLeAENQGJp7rrMZ0mtjooiIiCxSCtv94rOw2c/Pu++zUFoBhBDcCcWdftedVWyT\n/+sIq9zduu/PfPFxvvPMBF/+2DXzPyx/vwJz9deWvF7c0S0n6RzThmEHAxWwndHqK8BWiWwB5xr4\nwljoCmKiUJ99vCE1yRAMbiS0FUygPJqXjNiFwVxhW0RERBYphe1+yWuVnWuHVe50GtwBzPh38A0I\nnUaadFevBwmr2dOE0pL5farDpsbdB2b4zT/9Zz71H3+SykDeJg/oBvWU0CO7GvZXpvNXtAmPFfOw\nn5TDqnZxVXhpoQTekRkTzikZwhgLUemFV6bLa7HpBDSnIE5wpXWYzvEmCq391AVEREREFjGF7X6x\nSXdUeFqD/X+Dbewmqn+Hdvqa/KBOh5AmIXBX5j1Wy+8HmTPc8Pt/w3VvPJfLzltNd1UcukNpEmAY\nYg8FD3EEkQnTHQeBgWp4niKYFTC0AaICkJFkk6TOYkxMFpexvo3vhOQXCtvVc3DeQ/ko+BJU13eP\nV8AWERGRJUBhu5+yBvbgV/CNJ+Hg4+CngX3zWl53pjoOEbqPdEpIIJR7dAbZRPzWPX+PMfCRay+i\nu6JdJ6ToCjBBCN0NSKpQjPLPy+tYShUonRPqr+MKDKyF8lnQOAjpJK2GhUI7vF9hAEcc+l2fKDjb\nBIbO7ZbImCisaitoi4iIyBKhsN0vR74N41+kcPgBWmwA6jgTYeY2Mxq6tdSdx2bormYndIL3Qzv3\n85kvPc4Dv/E2IhsRQnaFELQhrIwfAoqQlMDEEC8Pi9823zBZ3AJDr4C4HPp9J8vDS0urIB0EWwSX\nQTwQyr2jcne4zIkoWIuIiMgSprDdD+OPED97D+nkfrz7Hp5NhF7ZR8j4kfygzhRHCKHbEEK3n3cb\najOO99/2TX71XT/O2as7K+CdriOdln8OWA4UoWigehYU1oBZDVEGPoHqJqhsPP7gmM7AmrQG3uHm\nT3EUERERkReksN0Pzb2QHg152QDsBl4LLKNbJlJhYUu+EnMbHEkIl26SX7rjm1y4cZR3v7HT5m+I\nEMin6K5s5725B4tQXQaDF0CynLi9H2tSnI9JbfHEq9C9nOIoIiIiskgpbPeDj0mztWAmafFzdC/D\nMCEkd9TyxywLR6gDNPjsVw/yrScO8re3vnnea6by4zuhGyiXYKAVWvUNXgLLL4TGOKbZgMhgXNod\nLnMiCtgiIiIiL4nCdj/MHIHZSYr+XjqBuGl+HusPUeD7NM2PUfR/Nnd40/w8Rf9Z4Gya5lKK/mn2\nPdfmv9z9CLd/4McZG5yiRRnjO2PZ23hTBUxY3F42ApwbJjyOXBT6YqdTZNFy4mKYFj9XsSIiIiIi\nJ43Cdl/sITTT9vMemyVsgJw45nHm3XfAQZw7wnv/537e8ROOn/yRaYyfINSkFImpYWnTpACVIRhe\nBaNXQHEMiqPd1WmTECUDREkR75s4o1VrERERkZNNYftUcy1wB+n2y+4o0x0+Y455rnM/THj87e0T\n1GYdv/5uQgs+muF1tokt1QEHpRTKY5iRH8MPrIdk5JiPW0PbO7AZ7cIwlNec5C8qIiIiIgrbp8qh\nb0H9KchSQh12KA8JCsAAzgzTZAMwNO+5ChDRNG8HBvjHJw/yhw/U+fx/uxxXAGjRNGugAL48gDMr\nMMQwcA5UX4kpLseb41xmm8DAWqJiQrvZUj22iIiISA8obJ8Kh74FU9+kWPsn8ClNfzZF/zXCinST\nprmC2D+NNxGRb9EyntiPAwUsk7TMMNbPUG8NcONtX+XD27ayZe35hM2QAzBYgGXLoLw5rFabKKxk\nV9aCKfD8spScTTBxOTQ4EREREZGTTmH7VEgPARPgU3CNcJsGISzXgeeIOIAnwTAJVIn4Bp4ChqMY\nrqbAI3zkzowNqwb4hTdfDMsbUCqDLQMbYM1PdsemmwiMBROpJ7aIiIhIHylsnwp2GCiG2x4wBmgR\nNkTOEMpKniFscjwMUTF0+ptT4K8eOsKX/9nw5T+5FrNiJQyeC6mD6oYwjMZEC/tfu5Z6YouIiIj0\nmcL2qbDyslA+wgidqY7N4jC0J8PdeJhm+efAThFCeYFm+h6wR4BVHBo/wofuivmd//RWVlz4Pqhs\n+sGfqYAtIiIi0ncK26eCTWDVFZBdCviw4nz472F2H1CEkfNCjbWNwHuIB2FqN5hZfBpx4y//Ote8\n6Y1cc91/D1McRUREROSMsOjD9q5du/jrv/5rvPdceumlXHnllf05EZssXG1e+y9OfPzYKACf/MQn\nOHhkmv99zx9AfGy7QBERERE5nS3qsO2c4/777+f666+nWq1yxx13cN555zE2NtbvU3tRHnvsMW67\n7Tb+/M//nFJJQVtERETkTLOoh3Tv27ePFStWsGzZMqIo4qKLLmLnzp39Pq0XpdlscuONN/L+97+f\niy++uN+nIyIiIiI/hEUdtqenpxkaGpq7PzQ0xNTUVB/P6MX7tV/7NUZGRvjABz7Q71MRERERkR/S\noi4jOZGpqSlqtdqCxyqVCnHc/x/JF77wBe6//3527NhBkvS2q0gURRQKhZ5+xumkc31Ph+t8qula\nLx261kvDUrvOoGu9VCy267u4vs0xqtUqk5OTc/enpqbmVroffvhhduzYseD4jRs3sm3bNpYvX35K\nz/NY73znO3nnO9/Z13NYrKampvjyl7/M1q1b+36dpbd0rZcOXeulQ9d6aZh/nedXKJypFnXYXrt2\nLePj40xMTFCpVHj00Ud5+9vfDsDWrVs577zz5o49fPgw27dvp1arLYoLK8dXq9XYsWMH5513nq7z\nIqdrvXToWi8dutZLw2K7zos6bFtrectb3sKnP/1pvPe8+tWvnutEMjQ0tCguoIiIiIicvhZ12AbY\nsmULW7Zs6fdpiIiIiMgStKi7kYiIiIiI9FN0yy233NLvkzgdeO9JkoSzzz6bYrHY79ORHtF1Xjp0\nrZcOXeulQ9d6aVhs13nRl5G8GPNHuhcKhf6NdJeeuu+++3jiiScYHBzkDW94Q79PR3pocnKS7du3\nU6/Xefzxx7n00ku5/PLL+31acpKlacpdd91FlmU45zDG8PrXv77fpyU9VKlU2LlzJ/v37+dd73pX\nv09HeuTOO++kVCqxc+dOrLXccMMN/T6ll2XJh+0zfaS7vHivetWruOyyy9i+fXu/T0V6zFrLNddc\nw5o1a2g2m9xxxx2ce+65+u96BXy6jAAABglJREFUkYnjmOuvv54kSXDOceedd7J582bWrVvX71OT\nHvnmN7/J2NgYzWaz36ciPWSM4T3veQ/lcrnfp3JSLPma7TN5pLu8NBs3blw0/+HKiVWrVdasWQNA\nsVhkdHSU6enpPp+V9EJn8FeapnOr27I4TU5OsmvXLi699NJ+n4qcAt77fp/CSbPkV7aPN9J93759\nfTwjETmZjh49yoEDB1i7dm2/T0V6wDnHHXfcwfj4OJdddpmu8yL24IMP8qY3vUmr2kvE3XffjbWW\nrVu3snXr1n6fzsuy5MO2iCxezWaTe++9lze/+c2LYpONPJ+1lve97300Gg3uueceDh06xMqVK/t9\nWnKSdfbbrFmzhqeffrrfpyM99t73vpdqtUq9Xufuu+9mdHSUjRs39vu0fmhLPmyfaKS7iJy5sizj\n3nvv5ZJLLuH888/v9+lIj5VKJTZt2sSTTz6psL0I7dmzh507d7Jr1y7SNKXZbPKXf/mXvO1tb+v3\nqUkPVKtVAAYHB7ngggvYt2+fwvaZ7EQj3WXxWUw1YHJi9913H2NjY+pCsojV63WiKKJUKtFut3nq\nqafUTWqRuvrqq7n66qsB2L17N1//+tcVtBepVquF955isUir1eKpp57ida97Xb9P62VZ8mH7RCPd\nZXH57Gc/y+7du5mdneV3f/d3ecMb3sCrX/3qfp+W9MCePXt45JFHWLlyJbfffjsAV111labJLjK1\nWo3t27fjvcd7z0UXXcQrXvGKfp+WiLwM9Xqde+65B2MMzjkuvvhiNm/e3O/TelmM11KfiIiIiEhP\nLPnWfyIiIiIivaKwLSIiIiLSIwrbIiIiIiI9orAtIiIiItIjCtsiIiIiIj2isC0iIiIi0iMK2yIi\nIiIiPaKwLSIiIiLSIwrbIiIiIiI9orAtIiIiItIjCtsiIiIiIj2isC0iIiIi0iMK2yIiIiIiPaKw\nLSIiIiLSIwrbIiIiIiI9orAtIiIiItIjCtsiIiIiIj2isC0iIiIi0iMK2yIiIiIiPaKwLSIiC3zq\nU5/ita99bb9PQ0RkUVDYFhFZQrIs+4HHeO8xxpyCsxERWfwUtkVEziB79+5l27ZtrFy5krGxMT74\nwQ/yve99j6uuuorR0VFWrlzJddddx9TU1NxrNm3axK233soll1xCpVLBOcfHPvYxNm/ezNDQEBdd\ndBGf+9znAPjud7/LjTfeyDe+8Q2q1SojIyP9+qoiIouCwraIyBnCOcdb3/pWNm3axJ49e9i3bx/X\nXnstAB/96Ec5cOAAjz/+OHv37uWWW25Z8Np77rmHBx54gImJCay1bN68ma997WtMTU1x8803c911\n13Hw4EHOP/98br/9dl7zmtcwPT3N+Ph4H76piMjiobAtInKGeOihh9i/fz+33norpVKJJEm44oor\nOOecc7jqqquI45gVK1bwoQ99iB07dix47U033cRZZ51FsVgEYNu2baxatQqAd7zjHWzZsoWHHnro\nlH8nEZHFLu73CYiIyIvzzDPPsHHjRqxduE5y6NAhbrrpJr761a9Sq9XIsux55R/r1q1bcP/uu+/m\n937v99i9ezcA9XqdI0eO9PT8RUSWIq1si4icIdavX8+ePXtwzi14/KMf/SjWWh577DEmJib4zGc+\ng/d+wTHzNzzu2bOHG264gU9+8pMcPXqUo0ePcuGFF869RpsjRUROHoVtEZEzxGWXXcaaNWv4yEc+\nwszMDM1mk69//evUajUqlQrVapV9+/bx8Y9//ITvU6/XsdYyOjqKc4677rqLRx99dO75VatWsXfv\nXtrtdq+/kojIoqewLSJyhrDW8vnPf55du3axYcMG1q9fz7333svNN9/Mww8/zLJly/jpn/5ptm3b\ntuB1x65UX3DBBXz4wx/m8ssvZ/Xq1Tz22GNceeWVc8+/8Y1v5MILL2T16tWsXLnylHw3EZHFyvhj\n/79GERERERE5KbSyLSIiIiLSIwrbIiIiIiI9orAtIiIiItIjCtsiIiIiIj2isC0iIiIi0iMK2yIi\nIiIiPaKwLSIiIiLSIwrbIiIiIiI9orAtIiIiItIj/x/0xOMRZ+a4/gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1100c7e50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ggplot(diamonds, aes(x='carat', y='price')) + \\\n",
" geom_point(alpha=0.05, color='orange') + \\\n",
" stat_smooth(method='lm') + \\\n",
" xlim(0, 5) + \\\n",
" ylim(0, 20000)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-2-clause |
kialio/gsfcpyboot | TestInstall/TestTestInstall_ipy2.2.ipynb | 2 | 24578 | {
"metadata": {
"name": "",
"signature": "sha256:eda572be091f41c414dd2995a852bde3751bc4416060e1577cb37d3acfe0338d"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"success = True # We'll use this to keep track of the various tests"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"try:\n",
" import numpy as np\n",
" import scipy\n",
"except:\n",
" success = False\n",
" print \"There was a problem importing numpy or scipy. You will definitely need these!\""
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"try:\n",
" import matplotlib\n",
" import matplotlib.pyplot as plt\n",
" %matplotlib inline\n",
"except:\n",
" success = False\n",
" print \"There was a problem importing matplotlib. You will definitely need this\""
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.plot([1, 2, 3], [1, 4, 9], \"ro--\")"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 4,
"text": [
"[<matplotlib.lines.Line2D at 0x106d258d0>]"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAW0AAAEACAYAAAB4ayemAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFHlJREFUeJzt3XmwXHWVwPHvyUJCYAZFBIYRQWLpLKKCirIYu0owyjYz\nlAIuQ6k1EowgI0q5hMCzXKbUUQlIuSSDIgIlJY4CCTEQ7YA4bCPIqiWvHEGLgII+CRjIcuaP7hcf\nL2/pfq+7b9/u76eqK/363tw+XG5Obn6/8zs3MhNJUjnMKDoASVLjTNqSVCImbUkqEZO2JJWISVuS\nSsSkLUklMmnSjojTI+KuiLg7Ik7vRFCSpLFNmLQj4iXAvwGvAl4GHB0R8zsRmCRpe5Pdaf8dcHNm\nbszMLcA64Lj2hyVJGstkSftu4LURsWtEzAOOAp7X/rAkSWOZNdHGzPx5RHwGWAM8AdwObO1EYJKk\n7UUzvUci4tPAA5n5lRGf2bxEkqYgM6PZ39NI9cju9V+fD/wLcOkYX+yrRa9zzjmn8Bh66eX59Hx2\nzeuPf2TJ3nuTwHTudBup0/5ORNwDXAkszsw/TeP7JKn/DA7CwQfzhv33Z8n86RXgTZq0M3NBZv5j\nZr48M380rW+TpH6zbh0ceiiceioLVq5k4bJlLF24cMqHc0Vkl6lUKkWH0FM8n63l+WzSihVw/PHw\nrW/B4sUALDjqKD6xevWUD9nUROSYB4jI6R5DknrSJz9ZS9ovetF2myKCnMJEpElbkgow1aTt8Igk\nlYhJW5Ja4emnO/I1Jm1Jmq7ly6FSgQ4MFU+4jF2SNIHNm+HMM2HVKrjqKoimh6ibZtKWpKkYGoIT\nT6wl7ptugmc/uyNf6/CIJDVrwwY4+GCYP792l92hhA2W/EnS1PzkJ3DIIVP+7dZpS1KJWKctSX3A\npC1JExkagvvuKzqKbUzakjSeektVvv3toiPZxqQtSWOpVre1VGVgoOhotrFOW5JGW74cliyBSy+F\nww8vOppnsHpEkka6447aopkrrxyzpWqrWPInSa3y1FMwZ05bv8KSP0lqlTYn7Olo5GnsH42IeyLi\nroi4NCK6979GknrchEk7IvYF3gMcmJn7AzOBE9sfliR1wIoVteXoJTLZnfafgE3AvIiYBcwDftv2\nqCSpnTZvhg98AD73Odhtt6KjacqEJX+Z+VhEfB54APgz8IPMvK4jkUlSOxTUUrVVJhsemQ/8O7Av\nsBewc0S8vQNxSVLrDa9wfOEL4ZprSpewYfLFNa8EfpKZjwJExHeBQ4BLRu40MGK1UKVSoVKptDRI\nSWqJX/yitsJx8eKOf3W1WqVarU77OBPWaUfEy6gl6FcBG4FvALdk5gUj9rFOW5Ka1JY67cz8GfBN\n4DbgzvrHX2s+PElSK7giUlJv2rIFZs4sOopxuSJSkoYNDsKBB9bGsHuMSVtSbxluqbpoEbz4xUVH\n03K2ZpXUO5Yvh7POgksu6bqWqq1i0pbUG84+u/aEmRtuaGtL1aI5ESmpN9x6a23RTEkWzNhPW5JK\nxOoRSeoDJm1J5XP33UVHUBiTtqTyGG6pevzxsHFj0dEUwuoRSeUwsqXqjTfC3LlFR1QI77Qldb/h\nlqrz58OqVaWpEGkHq0ckdbetW2tL0k8+uZCWqu1iyZ+k3vXEE7DTTkVH0VImbUkqEeu0JakPmLQl\ndY/BQfjyl4uOoquZtCV1h+GWqpqQddqSitcHLVVbxaQtqTibN8OZZ9Zqr3u8pWqrTDo8EhEvjojb\nR7yGIuL9nQhOUo/7wx/gscfgpptM2A1qquQvImYAvwUOyswH659Z8idJTepUyd/hwOBwwpYkdVaz\nSftE4NJ2BCKpD/iv8mlreCIyInYAjgE+PHrbwMDAtveVSoVKpdKC0CT1jOEJxz33hA9vl0L6QrVa\npVqtTvs4DY9pR8Q/Ae/NzDeO+twxbUnjG9lS9fLL+7pD30idGNN+K3BZs18gqY/ZUrXlGkraEbET\ntUnI77Y3HEk949ZbayscTz0VvvQlmD276Ih6gl3+JLXHo4/CXXeBc1xjsjWrJJWIrVklqQ+YtCVN\n3wMPwKZNRUfRF0zakqZn3Tp49atrT0hX25m0JU3dihVw/PFw8cVOOHaIrVklNW/LFvjQh2ypWgCT\ntqTmffrTcPfdtZaqLpjpKEv+JDVvwwaYM8cFM9NgnbYklYh12pLUB0zaksa3ZQssWwYbNxYdiepM\n2pLGNjQExxwDV18NTz1VdDSqM2lL2t5wS9X99quV9e2yS9ERqc6kLemZ1q2Dww6D006zpWoXsk5b\n0jNdfnlthePhhxcdicZgyZ8kFcCSP0nqAyZtSSoRk7bUr9atgze9CbZuLToSNWHSpB0Rz4qI70TE\nfRFxb0S8phOBSWqj4ZaqH/wgzPDerUwaqR5ZBqzKzDdHxCxgpzbHJKldbKlaehNWj0TELsDtmbnf\nBPtYPSKVwcaNcNxxtceCXX65LVUL1q7qkRcAv4uIr0fETyNieUTMm1qIkgo1Zw687W21u2wTdmlN\nNjwyCzgQODUzb42Ic4GPAGeP3GlgYGDb+0qlQsXHDkndJwLe8Y6io+hb1WqVarU67eNMNjyyJ/A/\nmfmC+s+HAR/JzKNH7OPwiCQ1qS3DI5m5HngwIoZnKw4H7plCfJI6acsWWL++6CjUBpMuY4+IlwEr\ngB2AQeBdmTk0Yrt32lI3GRqCt74V9tkHvvzloqPROHzcmKRaS9VjjoHXvx6++EWYZU+4bmXvEanf\njWypev75Juwe5Z221Avuuw8qFbjkEluqloTDI1K/e/hh2GOPoqNQg0zaklQijmlLUh8waUtls24d\n3ONyiX5l0pbKZLil6u9/X3QkKog1QVIZ2FJVdSZtqdsNr3DctAluuskOfX3O4RGp2113Hey3H1xz\njQlblvxJUhEs+ZOkPmDSlqQSMWlL3WJoCN78ZmuwNSGTttQNBgfh4INrvUMs59METNpS0datg0MP\nhVNPhQsugNmzi45IXcw6balI3/gGfPjDtlRVw0zaUpF2390VjmqKddqSVICp1mk3dKcdEf8H/AnY\nAmzKzIOa/SJJ0vQ1OjySQCUzH2tnMFJPe/RReM5zio5CJddM9UjTt/GS6lasgAMOgCeeKDoSlVwz\nd9rXRcQW4KuZubyNMUm9Y7il6sqVtcZPO+1UdEQquUaT9qGZ+VBEPBe4NiJ+npk3DG8cGBjYtmOl\nUqFSqbQ0SKmUhluqPv003HyzHfr6XLVapVqtTvs4TVePRMQ5wIbM/Hz9Z6tHpNEy4ZBD4MAD4dxz\nXTCj7bTtaewRMQ+YmZmPR8ROwBrg45m5pr7dpC2N5de/hn32KToKdal2lvztAfx3RAzvf8lwwpY0\nARO22sDFNZJUAB+CIBVlaAiuuqroKNQnTNrSdAy3VL3uuqIjUZ8waUtTNbKl6rJlRUejPmGXP2kq\nVqyAJUtsqaqOM2lLzXr0UbjwQluqqhBWj0hTkQlhOx5NndUjUieZsFUQk7YklYhJW5rIihVw3nlF\nRyFt40SkNJaRLVWvvrroaKRtTNrSaENDcOKJsGmTLVXVdRwekUb61a9qKxz32w+uucaEra5jyZ80\n0oMPwurV8J73FB2Jelzb+mk38MUmbUlqknXaktQHTNrqXxs2wNatRUchNcWkrf40OAgHHQSrVhUd\nidQUk7b6z8iWqkcfXXQ0UlOs01Z/saWqSq6hpB0RM4HbgN9k5jHtDUlqkwsuqD2swJaqKrGGSv4i\n4gzgFcBfZeaxo7ZZ8qeuc/3Klaw57zxmPfUUm+fM4Q3vfz8LXvUqmD3bBTPqClMt+Zv0Tjsingcc\nCXwKOGMKsUkddf3Klfzg9NP51ODgts+WDA7CsmUsOOqoAiOTpq+RicgvAmcC1kapFNacd94zEjbA\npwYHufb88wuKSGqdCe+0I+Jo4JHMvD0iKuPtNzAwsO19pVKhUhl3V6m9Mpm1fv2Ym2Zu3NjhYKS/\nqFarVKvVaR9nwjHtiPg08K/AZmAu8NfAFZl50oh9HNNW8TLhhz+EgQHO+ulP+eSTT263y9KFC/nE\n6tUFBCdtry3L2DPzY5m5d2a+ADgR+OHIhC11hRtugAULYPFiOOUU3nDZZSyZP/8Zu3xs/nyOOO20\nggKUWqfZOm1vqdV9HnoITjml1gN75kwWAMycydLzz2fmxo1smTuXN552mpOQ6gl2+ZOkAtjlT70t\nE6rV2tNkpD5m0lZ3y4S1a2tj1osWwQMPFB2RVCiTtrrTyGS9eHEtYd9zD4yaYJT6jQ2j1J3WroX3\nvQ+WLq1NMM7yUpXAiUh1q61bay+TtXqUE5Eqp0zYsmX7z2fMMGFLYzBpqxgjx6y/8pWio5FKw1sZ\nddaI5eY88gicfXZtzFpSQ0za6pzHH4cjj3xmsp45s+iopFJxIlKdtXo1HHGEyVp9b6oTkSZtSSqA\n1SPqDsMTjE4uSm1h0lZrjF7BuOuuRUck9SQnIjV9a9duXw3imLXUFiZtTd+11z6jn7Wk9nEiUpIK\n4ESk2iuz1mVPUqFM2prYyAnG448Hn2guFcqkrbGNrgY55RS4806YO7foyKS+NulEZETMBdYBc4Ad\ngO9n5kfbHZgK9oUvwNe+ZjWI1GUamoiMiHmZ+WREzAJ+DHwoM39c3+ZEZC/asAF23NFkLbXJVCci\nGyr5y8wn6293AGYCjzX7RSqZnXcuOgJJY2hoTDsiZkTEHcDDwI8y8972hqW2Gx6zfu1r4ZZbio5G\nUoMavdPeCrw8InYBfhARlcysDm8fGBjYtm+lUqFSqbQ2SrXOWP2sX/GKoqOSel61WqVarU77OE0v\nromIpcCfM/M/6z87pl0W998P73qXy82lLtC2Me2I2A3YnJl/jIgdgSOAj08hRhXtuc91ublUcpPe\naUfE/sBF1Ma/ZwAXZ+bnRmz3TluSmuRDEFQzPGY9Zw4cdljR0Ugah71H+t3oFYwbNhQdkaQ2sDVr\n2Y33dHPHrKWe5PBI2T39NBx1FLzznSZrqUQc05akEnFMu9dl1oY/JPU1k3a3GznBeNJJRUcjqWAm\n7W41uhpk0SK4+uqio5JUMKtHutXJJ8P118PSpbUJxln+r5LkRGT3euAB2Gsvk7XUo6wekaQSsXqk\nbIbHrI89Fh5/vOhoJJWESbvTRk8wnnACzJtXdFSSSsIB00669VY44wyXm0uaMse0O+mWW+CXvzRZ\nS3IiUpLKxInIbjE8Zr1+fdGRSOpBJu1WGT3B+JvfFB2RpB5k0p6u0cn6lFPg3nvhla8sOjJJPaiR\nZ0TuDXwT2B1I4GuZed6I7f09pj04CMccA0uWOMEoqWFtm4iMiD2BPTPzjojYGfhf4J8z87769v5O\n2lC7246mz72kPta2icjMXJ+Zd9TfbwDuA/ZqPsSSy4Q//3nsbSZsSR3S1Jh2ROwLHADc3I5gutLI\nMeuzzio6Gkl9ruEVkfWhke8Ap9fvuHvbeA/MlaQCNZS0I2I2cAXwrcz83ujtAwMD295XKhUqlUqL\nwivI1q2wcGGtParLzSW1QLVapVqtTvs4jUxEBnAR8GhmfmCM7b05EXnbbXDAASZrSW3RzuqRw4Dr\ngTuplfwBfDQzV9e392bSlqQ2svdIs4bHrNesgc98puhoJPUZe480avQKxpe+tPaZJJVAf/XTXreu\nVrZnP2tJJdVfwyPLl9eeEmOyllQwx7QlqUQc0x6WCTfe6Di1pJ7UO0l75ATju98NDz1UdESS1HLl\nT9rj9bPeq/96WknqfeWvHrniilova6tBJPWB8k9EbtoEM2aYrCWVylQnIstzp51Ze80YNaIze3Yx\n8UhSAbp/THvkmPVllxUdjSQVqnuT9ugJxkWL4IQTio5KkgrVncMjv/sdHHdcbbn50qW1CcZZ3Rmq\nJHVSd05Ebt0K3/9+7SnnJmtJPchl7JJUIuVbxj48Zu3koiQ1rPNJe/QE45w5HQ9BksqqswPGa9du\n/3RzF8VIUsM6O6Z98snwuteZrCX1vXY+2PdC4Cjgkczcf4ztTkRKUpPaORH5deCNDR8xE+6/v9k4\nVFetVosOoad4PlvL81m8SZN2Zt4A/GGifc5auJDrr776LxOMb3kLbNnSsiD7iX8oWsvz2Vqez+K1\nZCLyk2vWsOT662HXXVnw2c86Zi1JbdKykr9PbdzItS95Cbz97SZsSWqThqpHImJf4KrxJiJbH5Yk\n9b5C+mlP5UslSVMz6fBIRFwG/AR4UUQ8GBHvan9YkqSxTHtxjSSpcxqaiIyICyPi4Yi4a4J9zouI\nX0bEzyLigNaF2HsmO58RUYmIoYi4vf46q9MxlklE7B0RP4qIeyLi7oh4/zj7eY1OopFz6fXZuIiY\nGxE3R8QdEXFvRPzHOPs1fm1m5qQv4LXAAcBd42w/ElhVf/9q4KZGjtuvrwbOZwW4sug4y/IC9gRe\nXn+/M/AL4O9H7eM12rpz6fXZ3DmdV/91FnATcNio7U1dmw3daefkC2yOBS6q73sz8KyI2KORY/ej\nBs4ngBO8DcrM9Zl5R/39BuA+YK9Ru3mNNqDBcwlenw3LzCfrb3cAZgKPjdqlqWuzVXXafws8OOLn\n3wDPa9Gx+1ECh9T/qbQqIv6h6IDKol6eegBw86hNXqNNmuBcen02ISJmRMQdwMPAjzLz3lG7NHVt\ntrI16+i/eZ3hnLqfAntn5pMR8Sbge8CLCo6p60XEzsB3gNPrd4nb7TLqZ6/RcUxyLr0+m5CZW4GX\nR8QuwA8iopKZ1VG7NXxttupO+7fA3iN+fl79M01BZj4+/E+qzLwGmB0RuxYcVleLiNnAFcC3MvN7\nY+ziNdqgyc6l1+fUZOYQsBJ45ahNTV2brUraVwInAUTEa4A/ZubDLTp234mIPSIi6u8PolaaOXoc\nTHX1c/VfwL2Zee44u3mNNqCRc+n12biI2C0inlV/vyNwBHD7qN2aujYbGh6pL7B5HbBbRDwInAPM\nBsjMr2bmqog4MiLuB54AXIAzgcnOJ/Bm4L0RsRl4EjixqFhL4lDgHcCdETH8B+JjwPPBa7RJk55L\nvD6b8TfARRExg9pN8sWZuTYiFsHUrk0X10hSiRT3NHZJUtNM2pJUIiZtSSoRk7YklYhJW5JKxKQt\nSSVi0pakEjFpS1KJ/D/TljdGaeZa8gAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x105018ad0>"
]
}
],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"try:\n",
" import pandas, PyQt4, enaml\n",
"except:\n",
" success = False\n",
" print \"There was a problem importing pandas, pyqt, or enaml. You will need these for Days 2 and 3.\""
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"try:\n",
" import h5py\n",
" from mpl_toolkits.basemap import Basemap\n",
"except:\n",
" success = False\n",
" print \"There was a problem with h5py and/or Basemap. You will need these for Day 2.\""
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"There was a problem with h5py and/or Basemap. You will need these for Day 2.\n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Basemap Test\n",
"try:\n",
" f = plt.figure(1, figsize=(14.0, 10.0))\n",
" f.suptitle(\"Basemap - First Map\")\n",
" f.text(0.05, 0.95, \"Mollewide\")\n",
" f.subplots_adjust(left=0.05, right=0.95, top=0.80, bottom=0.05, wspace=0.2, hspace=0.4)\n",
" f.add_subplot(1, 1, 1)\n",
" b = Basemap(projection=\"moll\", lon_0=0, resolution='c')\n",
" b.drawcoastlines()\n",
" b.drawparallels(np.arange( -90.0, 90.0, 20.0))\n",
" b.drawmeridians(np.arange(-180.0, 181.0, 20.0))\n",
"except:\n",
" success = False\n",
" print \"There was a problem creating a Basemap plot. You will need this for Day 2.\""
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"There was a problem creating a Basemap plot. You will need this for Day 2.\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA7MAAAK5CAYAAABt8nm9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X2UbXdd3/HPlxsQQRA1lmrAgpCFgEIDEiJSHQvSKy5I\nUTQGfAIWYttQW61GtNXpUsQsrbWIspBGllZLaBElVAwLLVMoDQ/BkBBJaCKyTIKLIs8iaEK+/WP2\nhcnk3jszuec+fG9er3/m7L1/s8/v3LXXvfO+v33OVHcHAAAAJrnT8Z4AAAAA7JWYBQAAYBwxCwAA\nwDhiFgAAgHHELAAAAOOIWQAAAMYRswCMUlWfqarLq+qdVfWOqvq64z2nVaqqjaq6ZnmNl1fVt1fV\nS6vqwXs4x9mHGl9V61V1S1U9YMu+f7Xse8QqXgMAHAunHO8JAMAe/U13n5EkVfWEJC9IsnZcZ7Ra\nneRp3f0nW/b97sEGVtWduvuWgxx6SpLXJLn6EOd/V5LvSvL8Zd93JLnqds8YAI4DK7MATPaFST6c\nJFX1BVX1R8tq7ZVV9eRl/92r6g+Wldx3VdV3LvsfuayCXlZVl1TV31/2b1TVL1XV26vq6qp6VFX9\nXlX936r6mQNPvOy7rKquqqpnb9n/18v3X7XM59Tb8brqVhubc3rElvP/YlW9M8nXVdXPV9WfVtUV\nVfULy0r1k5L8wrKy+5UHOf/vJzl7Od8Dknw0yYe2PN+vLa//qqpa37L/fVV1wfLn+9atq7sAcKxZ\nmQVgms+vqsuT3DXJlyX5x8v+TyV5Snd/YgnIS5NcnGR/khu7+1uTpKruWVV3TvIrSZ7U3R+qqnOy\nuUr5rGyuXP5tdz+qqv5lklcnOSPJR5L8WVX9Und/JMkzu/sjVfX5Sd5WVa9c9t8tydu7+4er6t8l\n+ekkz93D66skv1NVn1rm8vjl6wF3S/KW7v43VfUlSS7s7q868Nq6++NVdXGS13T3qw7xHB9P8hdV\n9dBsRu0rkjxjy/GfXF7bviR/VFVf3d1XLfP4aHc/rKq+J8kvZzOcAeCYszILwDSf6u4zuvvB2QzV\n31r23ynJC6rqiiSvT/LlVfX3klyZ5JuXFczHdvfHkzwoyUOzGWqXJ/nJJKdteY6Ll69XJbmquz/Q\n3X+X5L1J7rsc+6FldfTSZd/py/5bshmHSfLbSR67x9d34DbjM7r7Ed394W3HP5PP3Xb8sSSfrqoL\nq+op2Qz6AyqH94ok5yb5p0l+b9uxc6rqHUn+JJt/Tg/Zcuzly9eLkpxU71cGYBYrswCM1d1vqapT\nq+pLk3xrklOTPKK7P1NVf57krt19bVWdsRz/2ar642zG259292MOceq/Xb7esuXxge1TqmotyeOS\nnNXdn66qN2RzpXi7yq1XVbOsdl62bL66u9cP8X2H8unu7uX131xVZy5zeWqS85bH2f6823SS/5Hk\nF7K5ivyJqjowv/sn+ZEkX9vdH6uqlx3ite30HABwVFmZBWCsqvqqbP5b9qEk90zy/5aQ/aYk/2AZ\n82XZDMDfSfKL2bxl+D1JvrSqzlrG3LmqHnKw5zjY0y7P9ZElZL8qyVlbjt8pmx+olCRPS/Kmrd/c\n3Z9ZVl3POETIJruMxKq6e5J7dfcfJvnhJA9fDn1imeMhv7W7P5Xk/HzuQ6AOuGeSTyb5eFXdO8m3\nbDt+zpav/2c38wSAo8HKLADTHHjPbLIZlt/X3bdU1e8keU1VXZnNlc8Dn+T7Ndn8MKRbktyU5Ae7\n+6aqemqSF1bVF2bz38P/mOTd256rc9uw7CSXJPnBqnp3NsP40i3HP5nkzKr6t0k+kM/F36psnc89\nkry6qu6azT+Lf73svyjJS6vquUm+o7vfe7BzdPcrsv1A9xXLn+81Sa5P8r+3Dfmi5VbuT2fzNmUA\nOC5quVMJAFiBqvpEd9/jeM/jaFhu3X7kQd7HCwDHnNuMAWC1Tub/JT6ZXxsAw1iZBQAAYBwrswAA\nAIwjZgEAABhHzAIAADDOMYvZqrqlqv7Llu1TquqDVfWaHb7v+6vqV5bH61X1I0c4jydV1fmHOPbX\nR3JuAAAAjo1j+XtmP5nkoVV11+7+dJJvTnJDdv5kxD7E49ulu1+T5FAB7dOwAAAABjjWtxm/Nsm3\nLo/PTfLybP6S91TVF1fV71fVFVV1aVV9zeFOVFUPqKo/rKrLquqNVfWgqtpXVe9djt+rqj5TVY9d\ntt9YVQ/cttJ7/+W5rqyqn912/h+tqrct81lf6Z8CAAAAR+RYx+wrknxXVX1ekq9J8tYtx/59knd0\n98OT/ESS31r217ZzHFg9/fUkz+3ur03yo0l+rbs/k+Q9VfWQJI9N8o4k37A83326+7pt5/pPSX61\nux+W5P0HdlbVE5I8sLvPTHJGkkdW1T86khcOAADA6hzL24zT3e+qqvtlc1X2D7Yd/vok37aMe0NV\nfUlV3eNg56mquyd5TJL/XvXZ1r3L8vVNSb4hyf2TvCDJs5P8ryRvP8ipHpPkKcvj305ywfL4CUme\nUFWXL9t3T/LA5dwAAAAcZ8c0ZhcXJ/nFJN+Y5Eu3HTvUKux2d0ryke4+4yDH3pjknyf5siQ/lc1V\n27Vl/168oLt/fY/fAwAAwDFwPH41z28kWe/uP922/01Jnp4kVbWW5IPdvf3ThStJdfcnkvx5VT11\nGV9V9fBlzNuyueL6me7+2yRXJHlODh6zb07yXcvjp2/Z/7okz1xWgFNVp1XV9vAGAADgODmWMdtJ\n0t03dveLtuw7sPq6ns33pl6R5OeSfN9Bxmx9/PQkz6qqdya5KsmTlvP/XZK/SPKWZdwbk3xBd7/r\nIOf4oST/oqquTPLlW+b4+iT/Ncmly7H/luQLjvD1AwAAsCLV7bfRAAAAMMvxuM0YAAAAjoiYBQAA\nYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4\nYhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQs\nAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAA\nAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACM\nI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfM\nAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUA\nAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADA\nOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHE\nLAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkA\nAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAA\njCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMbZMWar6jeq6gNV9a7D\njHlhVV1bVVdU1RmrnSIAAADc2m5WZl+WZP+hDlbVE5M8sLtPT/IDSV68orkBAADAQe0Ys939piQf\nOcyQJyf5zWXsW5Pcq6ruvZrpAQAAwG2t4j2zpyW5fsv2DUnus4LzAgAAwEGdsqLz1Lbtvs2Aqtvs\nAwAAgO7e3pQ7WkXM3pjkvlu277Psu41uPcvJY319Pevr68d7GrBSrmtONq5pTkaua042VXvu2CSr\nuc344iTfu0zirCQf7e4PrOC8AAAAcFA7rsxW1cuTfGOSU6vq+iQ/neTOSdLdL+nu11bVE6vquiSf\nTPKMozlhAAAA2DFmu/vcXYw5bzXTgTnW1taO9xRg5VzXnGxc05yMXNewqY7V+1irqr1nFgAAgK2q\n6nZ9ANQq3jMLAAAAx5SYBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhH\nzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgF\nAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAA\nwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBx\nxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZ\nAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAA\nAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAY\nR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6Y\nBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsA\nAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACA\nccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYJwdY7aq9lfVNVV1bVWdf5Djp1bV\nJVX1zqq6qqq+/6jMFAAAABbV3Yc+WLUvyXuSPD7JjUnenuTc7r56y5j1JJ/X3c+rqlOX8ffu7pu3\nnasP91wAAADc8VRVurv2+n07rcyemeS67n5fd9+U5KIkZ28b85dJ7rk8vmeSD20PWQAAAFilU3Y4\nflqS67ds35Dk0dvGvDTJ/6yq9ye5R5LvXN30AAAA4LZ2itnd3Bf8E0ne2d1rVfWAJK+vqod39ye2\nD1xfX//s47W1taytre1hqgAAAEy3sbGRjY2NIz7PTu+ZPSvJenfvX7afl+SW7r5gy5jXJnl+d795\n2f7jJOd392XbzuU9swAAANzK0XrP7GVJTq+q+1XVXZKck+TibWOuyeYHRKWq7p3kQUneu9eJAAAA\nwG4d9jbj7r65qs5L8rok+5Jc2N1XV9VzluMvSfJzSV5WVVdkM45/rLs/fJTnDQAAwB3YYW8zXukT\nuc0YAACAbY7WbcYAAABwwhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAA\nAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADG\nEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNm\nAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIA\nADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABg\nHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhi\nFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwA\nAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAA\nxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwj\nZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wC\nAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGGfHmK2q/VV1TVVd\nW1XnH2LMWlVdXlVXVdXGymcJAAAAW1R3H/pg1b4k70ny+CQ3Jnl7knO7++otY+6V5M1J/kl331BV\np3b3Xx3kXH245wIAAOCOp6rS3bXX79tpZfbMJNd19/u6+6YkFyU5e9uYpyX53e6+IUkOFrIAAACw\nSjvF7GlJrt+yfcOyb6vTk3xxVb2hqi6rqu9Z5QQBAABgu1N2OL6b+4LvnOQRSR6X5G5JLq2qt3T3\ntdsHrq+vf/bx2tpa1tbWdj1RAAAA5tvY2MjGxsYRn2en98yelWS9u/cv289Lckt3X7BlzPlJPr+7\n15ft/5zkku5+5bZzec8sAAAAt3K03jN7WZLTq+p+VXWXJOckuXjbmFcneWxV7auquyV5dJJ373Ui\nAAAAsFuHvc24u2+uqvOSvC7JviQXdvfVVfWc5fhLuvuaqrokyZVJbkny0u4WswAAABw1h73NeKVP\n5DZjAAAAtjlatxkDAADACUfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAA\nAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAY\nR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6Y\nBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsA\nAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACA\nccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOI\nWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMA\nAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAA\nGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCO\nmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDEL\nAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYJwdY7aq9lfVNVV1\nbVWdf5hxj6qqm6vq21Y7RQAAALi1w8ZsVe1L8qIk+5M8JMm5VfXgQ4y7IMklSeoozBMAAAA+a6eV\n2TOTXNfd7+vum5JclOTsg4x7bpJXJvngiucHAAAAt7FTzJ6W5Pot2zcs+z6rqk7LZuC+eNnVK5sd\nAAAAHMQpOxzfTZj+cpIf7+6uqsphbjNeX1//7OO1tbWsra3t4vQAAACcLDY2NrKxsXHE56nuQ/dq\nVZ2VZL279y/bz0tyS3dfsGXMe/O5gD01yd8keXZ3X7ztXH245wIAAOCOp6rS3Xv+7KWdYvaUJO9J\n8rgk70/ytiTndvfVhxj/siSv6e5XHeSYmAUAAOBWbm/MHvY24+6+uarOS/K6JPuSXNjdV1fVc5bj\nL7ldswUAAIAjcNiV2ZU+kZVZAAAAtrm9K7M7fZoxAAAAnHDELAAAAOOIWQAAAMYRswAAAIwjZgEA\nABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAw\njpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwx\nCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYA\nAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA\n44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYR\nswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YB\nAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAA\nMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAc\nMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIW\nAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAA\nAOOIWQAAAMbZVcxW1f6quqaqrq2q8w9y/OlVdUVVXVlVb66qh61+qgAAALCpuvvwA6r2JXlPkscn\nuTHJ25Oc291XbxnzdUne3d0fq6r9Sda7+6xt5+mdngsAAIA7lqpKd9dev283K7NnJrmuu9/X3Tcl\nuSjJ2VsHdPel3f2xZfOtSe6z14kAAADAbu0mZk9Lcv2W7RuWfYfyrCSvPZJJAQAAwOGcsosxu743\nuKq+Kckzk3z9wY6vr69/9vHa2lrW1tZ2e2oAAABOAhsbG9nY2Dji8+zmPbNnZfM9sPuX7ecluaW7\nL9g27mFJXpVkf3dfd5DzeM8sAAAAt3I03zN7WZLTq+p+VXWXJOckuXjbk39FNkP2uw8WsgAAALBK\nO95m3N03V9V5SV6XZF+SC7v76qp6znL8JUl+KskXJXlxVSXJTd195tGbNgAAAHdkO95mvLIncpsx\nAAAA2xzN24wBAADghCJmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYR\nswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YB\nAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAA\nMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAc\nMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIW\nAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAA\nAOOIWQAAAMYRswAAAIwjZgEAABhHzAIAADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADG\nEbMAAACMI2YBAAAYR8wCAAAwjpgFAABgHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNm\nAQAAGEfMAgAAMI6YBQAAYBwxCwAAwDhiFgAAgHHELAAAAOOIWQAAAMYRswAAAIwjZgEAABhHzAIA\nADCOmAUAAGAcMQsAAMA4YhYAAIBxxCwAAADjiFkAAADGEbMAAACMI2YBAAAYR8wCAAAwjpgFAABg\nHDELAADAOGIWAACAccQsAAAA44hZAAAAxhGzAAAAjCNmAQAAGEfMAgAAMM6OMVtV+6vqmqq6tqrO\nP8SYFy7Hr6iqM1Y/TTjxbGxsHO8pwMq5rjnZuKY5GbmuYdNhY7aq9iV5UZL9SR6S5NyqevC2MU9M\n8sDuPj3JDyR58VGaK5xQ/EPCych1zcnGNc3JyHUNm3ZamT0zyXXd/b7uvinJRUnO3jbmyUl+M0m6\n+61J7lVV9175TAEAAGCxU8yeluT6Lds3LPt2GnOfI58aAAAAHFx196EPVn17kv3d/exl+7uTPLq7\nn7tlzGuS/Hx3v3nZ/qMkP9bdf7LtXId+IgAAAO6wurv2+j2n7HD8xiT33bJ932yuvB5uzH2WfUc8\nOQAAADiYnW4zvizJ6VV1v6q6S5Jzkly8bczFSb43SarqrCQf7e4PrHymAAAAsDjsymx331xV5yV5\nXZJ9SS7s7qur6jnL8Zd092ur6olVdV2STyZ5xlGfNQAAAHdoh33PLAAAAJyIdrrNeM+qan9VXVNV\n11bV+YcY88Ll+BVVdcaq5wCrtNM1XVVPX67lK6vqzVX1sOMxT9it3fw9vYx7VFXdXFXfdiznB7fH\nLn/+WKuqy6vqqqraOMZThD3Zxc8fp1bVJVX1zuWa/v7jME3Ytar6jar6QFW96zBj9tSJK43ZqtqX\n5EVJ9id5SJJzq+rB28Y8MckDu/v0JD+Q5MWrnAOs0m6u6STvTfIN3f2wJD+T5NeP7Sxh93Z5TR8Y\nd0GSS5L4AD9OaLv8+eNeSX41yZO6+6uTPPWYTxR2aZd/V5+X5PLu/odJ1pL8h6ra6cNd4Xh6WTav\n6YO6PZ246pXZM5Nc193v6+6bklyU5OxtY56c5DeTpLvfmuReVXXvFc8DVmXHa7q7L+3ujy2bb43f\ns8yJbTd/TyfJc5O8MskHj+Xk4HbazXX9tCS/2903JEl3/9UxniPsxW6u6b9Mcs/l8T2TfKi7bz6G\nc4Q96e43JfnIYYbsuRNXHbOnJbl+y/YNy76dxvjhnxPVbq7prZ6V5LVHdUZwZHa8pqvqtGz+0HTg\nf0R9uALL8sbQAAACQUlEQVQnut38XX16ki+uqjdU1WVV9T3HbHawd7u5pl+a5KFV9f4kVyT5oWM0\nNzha9tyJq74VYbc/8Gy/Zc0PSpyodn1tVtU3JXlmkq8/etOBI7aba/qXk/x4d3dVVdxmzIlvN9f1\nnZM8IsnjktwtyaVV9Zbuvvaozgxun91c0z+R5J3dvVZVD0jy+qp6eHd/4ijPDY6mPXXiqmP2xiT3\n3bJ932wW9eHG3GfZByei3VzTWT706aVJ9nf34W6fgONtN9f0I5NctNmxOTXJt1TVTd29/feMw4li\nN9f19Un+qrs/leRTVfXGJA9PImY5Ee3mmn5MkucnSXf/WVX9eZIHJbnsmMwQVm/Pnbjq24wvS3J6\nVd2vqu6S5Jwk23/4uTjJ9yZJVZ2V5KPd/YEVzwNWZcdruqq+Ismrknx3d193HOYIe7HjNd3dX9nd\n9+/u+2fzfbP/TMhygtvNzx+vTvLYqtpXVXdL8ugk7z7G84Td2s01fU2SxyfJ8r7CB2XzQylhqj13\n4kpXZrv75qo6L8nrkuxLcmF3X11Vz1mOv6S7X1tVT6yq65J8MskzVjkHWKXdXNNJfirJFyV58bKS\ndVN3n3m85gyHs8trGkbZ5c8f11TVJUmuTHJLkpd2t5jlhLTLv6t/LsnLquqKbC5Q/Vh3f/i4TRp2\nUFUvT/KNSU6tquuT/HQ23wJyuzuxur1dFQAAgFlWfZsxAAAAHHViFgAAgHHELAAAAOOIWQAAAMYR\nswAAAIwjZgEAABhHzAIAADDO/we0gYMqsKEZagAAAABJRU5ErkJggg==\n",
"text": [
"<matplotlib.figure.Figure at 0x108bdb7d0>"
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"if success:\n",
" print \"Congratulations! Your python seems to be working properly. We look forward to seeing you at the Boot Camp!\"\n",
"else:\n",
" print \"There was a problem somewhere along the line. Please let us know where and we will try to help you get to the bottom of it.\"\n"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"There was a problem somewhere along the line. Please let us know where and we will try to help you get to the bottom of it.\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | mit |
danlamanna/scratch | tests/integration/add_layer.ipynb | 1 | 3692 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from matplotlib import pylab as plt\n",
"from matplotlib.colors import LinearSegmentedColormap\n",
"from geonotebook.wrappers import RasterData\n",
"from IPython.display import display, Image"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Unstyled RGB Layer"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"EXPECTED=\"https://data.kitware.com/api/v1/file/586a8f688d777f1e3428d849/download\"\n",
"# Set the center of the map to the location the data\n",
"M.set_center(-120.32, 47.84, 8)\n",
"\n",
"# Clean up any layers that might already exist\n",
"for l in M.layers:\n",
" M.remove_layer(l)\n",
"\n",
"rd = RasterData('data/WELD.tif')\n",
"\n",
"M.add_layer(rd[1, 2, 3])\n",
"\n",
"display(Image(EXPECTED, format=\"png\"))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Unstyled NDVI Layer"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"EXPECTED=\"https://data.kitware.com/api/v1/item/586a8fc98d777f1e3428d84b/download\"\n",
"\n",
"M.set_center(-120.32, 47.84, 8)\n",
"M.layers.annotation.clear_annotations()\n",
"for l in M.layers:\n",
" M.remove_layer(l)\n",
"\n",
"rd = RasterData('data/WELD.tif')\n",
"M.add_layer(rd[4])\n",
"\n",
"display(Image(EXPECTED, format=\"png\"))\n",
"# TODO: Add image for comparison"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Winter Colormap w/ NDVI Layer"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"EXPECTED=\"https://data.kitware.com/api/v1/item/586a902c8d777f1e3428d84e/download\"\n",
"\n",
"M.set_center(-120.32, 47.84, 8)\n",
"for l in M.layers:\n",
" M.remove_layer(l)\n",
"\n",
"rd = RasterData('data/WELD.tif')\n",
"\n",
"# Create Colormap\n",
"cmap = plt.get_cmap('winter', 10)\n",
"\n",
"M.add_layer(rd[4], colormap=cmap)\n",
"\n",
"display(Image(EXPECTED, format=\"png\"))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Custom Colormap w/ NDVI Layer"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"EXPECTED=\"https://data.kitware.com/api/v1/item/586a90a08d777f1e3428d851/download\"\n",
"\n",
"M.set_center(-120.32, 47.84, 8)\n",
"for l in M.layers:\n",
" M.remove_layer(l)\n",
"\n",
"rd = RasterData('data/WELD.tif')\n",
"\n",
"cmap =LinearSegmentedColormap.from_list(\n",
" 'ndvi', ['blue', 'beige', 'green'], 20)\n",
"\n",
"M.add_layer(rd[4], colormap=cmap)\n",
"\n",
"display(Image(EXPECTED, format=\"png\"))"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Geonotebook (Python 2)",
"language": "python",
"name": "geonotebook2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
chenyuqing/rfe-frame | code_deploy/rfe_svm_mic.ipynb | 1 | 3916 | {
"cells": [
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn.svm import SVR\n",
"from minepy import MINE\n",
"import pandas as pd\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"filename = \"./data/nci60.csv\"\n",
"df = pd.read_csv(filename)\n",
"X = df.iloc[:,2:]\n",
"y = df.iloc[:,1]"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Define the rfe-svm function\n",
"def rfe_svm_mic(X, y, num_feature_to_selected):\n",
" import time\n",
" clf = SVR()\n",
" model = clf.set_params(kernel='linear')\n",
" X_new = X\n",
" record = {}\n",
" del_ = X.shape[1]-num_feature_to_selected\n",
" start_time = time.time()\n",
" for i in range(del_):\n",
" # get the column name\n",
" names = list(X_new)\n",
" # fit the svm and get the weights of features\n",
" fit = model.fit(X_new, y)\n",
" # compute the mic scores\n",
" mine = MINE()\n",
" mic_scores = []\n",
" for i in range(X_new.shape[1]):\n",
" mine.compute_score(X_new.iloc[:,i], y)\n",
" m = mine.mic()\n",
" mic_scores.append(m)\n",
" sum_cor = {}\n",
" # sum_cor = (1-0.3)*svm_coef + 0.3 * mic_scores\n",
" for i in range(X_new.shape[1]):\n",
" sum_cor[names[i]] = 0.5 * fit.coef_[0][i] + 0.5 * mic_scores[i]\n",
" # get the column name with the samllest value\n",
" min_colname = min(sum_cor, key=sum_cor.get)\n",
" # print(min_colname)\n",
" # get the column number with the samllest value\n",
" min_colnum = X.columns.get_loc(min_colname)\n",
" # print(min_colnum)\n",
" # print(sum_cor[min_colname])\n",
" # remove the feature with the smallest weight\n",
" X_new = X_new.drop(min_colname, axis=1)\n",
" # record the index and value of the deleted feature\n",
" # record.update({min_colname:sum_cor[min_colname]})\n",
" record[min_colname] = sum_cor[min_colname]\n",
" elapsed_time = time.time() - start_time\n",
" return X_new, record, elapsed_time"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"20999.64202952385"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Do the feature selecltion and get the selected features\n",
"X_new, record, elapsed_time = rfe_svm_mic(X, y, 50)\n",
"#for key,value in record.items():\n",
"# print(key,':',value)\n",
"len(record)\n",
"elapsed_time"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# combine the label and write to the local destination\n",
"X_new.insert(0, \"IC50\", y)\n",
"X_new.to_csv(\"./selected_features/rfe_svm_mic_out_50_with_50percent.csv\")"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
snotskie/teaching | 4176-157-10Z2/Studio3.ipynb | 1 | 6397 | {
"cells": [
{
"cell_type": "markdown",
"source": [
"# Studio 3: Responsive and Material Design\n",
"In this Studio assignment we will be introduced to two concepts, responsive design and material design. This assignment will cap off our studies into web design as we move into the end of the semester.\n",
"\nThis Studio will be due Sunday, April 22nd, 11:59pm Eastern"
],
"metadata": {
"deletable": true,
"editable": true
}
},
{
"cell_type": "markdown",
"source": [
"# Grading and Submission Instructions\n",
"To submit, write your responses to the following questions in a Word document, then upload it to Blackboard under this week's folder in Current Assignments.\n",
"\n",
"Studios are due the Sunday after they are assigned, at 11:59pm eastern time.\n",
"\n",
"Studios are each worth 3% of your final grade. Scoring on your submission will be based on the following rubric:\n",
"\n",
"0% - Student does not submit on time or submits plagiarized or unacceptable work. Double check that you have attached the right file, as usually students get zeros because they upload a previous week's Lab by accident.\n",
"\n",
"1% - Student answers all questions for Parts 1 and 2, but not Part 3, with sufficient and accurate responses.\n",
"\n3% - Great work, maximum points! Student answers all questions with sufficient and accurate responses."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"# Part 1\n",
"First, watch our first \"studio video\" for this assignment, listed below (~5 minutes). As you watch, there almost certainly will be technical terms mentioned that are not defined or questions you may wonder that the video does not answer. When you come upon one of these, jot them down. Then, after completing the video, answer the questions below.\n",
"\n",
"**[Responsive Web Design Tutorial and Explanation](https://www.youtube.com/watch?v=BIz02qY5BRA)**\n",
"\n",
"1. Was the speaker clear in their demonstration? Was the sound and video quality clear? Was the speaker professional in their delivery and did they provide sufficient background information/links to the tools they are using?\n",
"1. Summarize what skills, techniques, concepts, etc. we are learning in this course that the speaker demonstrated. How did they use these skills, etc. to accomplish their goals? Be specific in your examples.\n",
"1. What is the \"final product\" that the video teaches us how to make? How would you rate this final product: Good? Bad? Amazing? Total Loser? Needs Improvement? Just \"Meh\"?\n",
"1. What technical terms/questions did you jot down while you watched the video? Pick at least two, then do online research to find answers to them yourself (as always, include links to your citations)."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"# Part 2\n",
"\n",
"To provide background information to the information presented in the second video, you may read through the following spec:\n",
"\n",
"- [Material Design Spec](https://material.io/guidelines/)\n",
"\n",
"Next, do the same as before for this video (~7 minutes), taking notes and jotting down questions as you watch, and afterwards answer the questions below.\n",
"\n",
"**[Bootstrap and Material Design Lite Project Tutorial](https://www.youtube.com/watch?v=ijRFjD-Ao4E)**\n",
"\n",
"1. Was the speaker clear in their demonstration? Was the sound and video quality clear? Was the speaker professional in their delivery and did they provide sufficient background information/links to the tools they are using?\n",
"1. Summarize what skills, techniques, concepts, etc. we are learning in this course that the speaker demonstrated. How did they use these skills, etc. to accomplish their goals? Be specific in your examples.\n",
"1. What is the \"final product\" that the video teaches us how to make? How would you rate this final product: Good? Bad? Amazing? Total Loser? Needs Improvement? Just \"Meh\"?\n",
"1. What technical terms/questions did you jot down while you watched the video? Pick at least two, then do online research to find answers to them yourself (as always, include links to your citations)."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"# Part 3\n",
"\n",
"Finally, answer these two general questions:\n",
"\n",
"1. For this question, write a post to the Studio Discussion forum (under the \"Ask the Instructor and Other Discussion Boards\" tab on Blackboard), and title your post something like \"Bryan Knowles, Studio #1\". First, post your answer to Part 1 Question 4 and Part 2 Question 4 (the research questions). Then, choose one:\n",
" - Look for a video tutorial that is on the same or similar topic and is about the same length as these videos, share the link in your post, and then briefly summarize that video in your post.\n",
" - Get the example from the video to work for your computer/setup, and post a screenshot of your code and website and discuss any difficulties/successes you had in getting this example to work.\n",
"1. What skills, techniques, tools, lines of thinking, designs, etc. from all videos you watched in today's Studio would you like to \"steal\" for your own work, or how do these things compare to the work you are researching in this class? How do the skills, etc. that the speakers demonstrate compare? How do their \"final products\" compare?"
],
"metadata": {}
}
],
"metadata": {
"kernelspec": {
"name": "node_nteract",
"language": "javascript",
"display_name": "Node.js (nteract)"
},
"language_info": {
"name": "javascript",
"version": "8.2.1",
"mimetype": "application/javascript",
"file_extension": ".js"
},
"kernel_info": {
"name": "node_nteract"
},
"nteract": {
"version": "0.8.4"
},
"gist_id": "5262272c40c19be30ac5042db00ef74b"
},
"nbformat": 4,
"nbformat_minor": 2
} | mit |
SamLau95/nbinteract | notebooks/Using_Interact.ipynb | 1 | 81692 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Using Interact"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `interact` function (`ipywidgets.interact`) automatically creates user interface (UI) controls for exploring code and data interactively. It is the easiest way to get started using IPython's widgets."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"from __future__ import print_function\n",
"from ipywidgets import interact, interactive, fixed, interact_manual\n",
"import ipywidgets as widgets"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Basic `interact`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"At the most basic level, `interact` autogenerates UI controls for function arguments, and then calls the function with those arguments when you manipulate the controls interactively. To use `interact`, you need to define a function that you want to explore. Here is a function that prints its only argument `x`."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"def f(x):\n",
" return x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When you pass this function as the first argument to `interact` along with an integer keyword argument (`x=10`), a slider is generated and bound to the function parameter."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "f033f0e3edcf43ccb1a2acd6d425f76b",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(IntSlider(value=10, description='x', max=30, min=-10), Output()), _dom_classes=('widget-…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=10);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When you move the slider, the function is called, which prints the current value of `x`.\n",
"\n",
"If you pass `True` or `False`, `interact` will generate a checkbox:"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "15163972fb56426aa3ae2c77f72d0242",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(Checkbox(value=True, description='x'), Output()), _dom_classes=('widget-interact',))"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=True);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you pass a string, `interact` will generate a text area."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "222e7059bc3b42e7ad87230fcdf76ad7",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(Text(value='Hi there!', description='x'), Output()), _dom_classes=('widget-interact',))"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x='Hi there!');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`interact` can also be used as a decorator. This allows you to define a function and interact with it in a single shot. As this example shows, `interact` also works with functions that have multiple arguments."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "55fb76f8e64f42bc9bc2a4340644955c",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(Checkbox(value=True, description='x'), FloatSlider(value=1.0, description='y', max=3.0, …"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"@interact(x=True, y=1.0)\n",
"def g(x, y):\n",
" return (x, y)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Fixing arguments using `fixed`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are times when you may want to explore a function using `interact`, but fix one or more of its arguments to specific values. This can be accomplished by wrapping values with the `fixed` function."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"def h(p, q):\n",
" return (p, q)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When we call `interact`, we pass `fixed(20)` for q to hold it fixed at a value of `20`."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "9ff68d35b29643b3bfb83d9b87296b44",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(IntSlider(value=5, description='p', max=15, min=-5), Output()), _dom_classes=('widget-in…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(h, p=5, q=fixed(20));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that a slider is only produced for `p` as the value of `q` is fixed."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Widget abbreviations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When you pass an integer-valued keyword argument of `10` (`x=10`) to `interact`, it generates an integer-valued slider control with a range of `[-10,+3*10]`. In this case, `10` is an *abbreviation* for an actual slider widget:\n",
"\n",
"```python\n",
"IntSlider(min=-10,max=30,step=1,value=10)\n",
"```\n",
"\n",
"In fact, we can get the same result if we pass this `IntSlider` as the keyword argument for `x`:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "223ad088ced145819dd25d13e14f4e00",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(IntSlider(value=10, description='x', max=30, min=-10), Output()), _dom_classes=('widget-…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=widgets.IntSlider(min=-10,max=30,step=1,value=10));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This examples clarifies how `interact` proceses its keyword arguments:\n",
"\n",
"1. If the keyword argument is a `Widget` instance with a `value` attribute, that widget is used. Any widget with a `value` attribute can be used, even custom ones.\n",
"2. Otherwise, the value is treated as a *widget abbreviation* that is converted to a widget before it is used.\n",
"\n",
"The following table gives an overview of different widget abbreviations:\n",
"\n",
"<table class=\"table table-condensed table-bordered\">\n",
" <tr><td><strong>Keyword argument</strong></td><td><strong>Widget</strong></td></tr> \n",
" <tr><td>`True` or `False`</td><td>Checkbox</td></tr> \n",
" <tr><td>`'Hi there'`</td><td>Text</td></tr>\n",
" <tr><td>`value` or `(min,max)` or `(min,max,step)` if integers are passed</td><td>IntSlider</td></tr>\n",
" <tr><td>`value` or `(min,max)` or `(min,max,step)` if floats are passed</td><td>FloatSlider</td></tr>\n",
" <tr><td>`['orange','apple']` or `{'one':1,'two':2}`</td><td>Dropdown</td></tr>\n",
"</table>\n",
"Note that a dropdown is used if a list or a dict is given (signifying discrete choices), and a slider is used if a tuple is given (signifying a range)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You have seen how the checkbox and textarea widgets work above. Here, more details about the different abbreviations for sliders and dropdowns are given.\n",
"\n",
"If a 2-tuple of integers is passed `(min,max)`, an integer-valued slider is produced with those minimum and maximum values (inclusively). In this case, the default step size of `1` is used."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "1ed79e95f9d344b8b6474a0049d49ab1",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(IntSlider(value=2, description='x', max=4), Output()), _dom_classes=('widget-interact',)…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=(0,4));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If a 3-tuple of integers is passed `(min,max,step)`, the step size can also be set."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "00c6df02e73342ca8f2183ea15025d52",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(IntSlider(value=4, description='x', max=8, step=2), Output()), _dom_classes=('widget-int…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=(0,8,2));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A float-valued slider is produced if the elements of the tuples are floats. Here the minimum is `0.0`, the maximum is `10.0` and step size is `0.1` (the default)."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "bd0e5dc04aa345bd85d34f192d278031",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=5.0, description='x', max=10.0), Output()), _dom_classes=('widget-inte…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=(0.0,10.0));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The step size can be changed by passing a third element in the tuple."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "482ed7eb581c42c296a6a45c41e5ed24",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=5.0, description='x', max=10.0, step=0.01), Output()), _dom_classes=('…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=(0.0,10.0,0.01));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For both integer and float-valued sliders, you can pick the initial value of the widget by passing a default keyword argument to the underlying Python function. Here we set the initial value of a float slider to `5.5`."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "6401a9e7e52f46868e5a042861d48f27",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=5.5, description='x', max=20.0, step=0.5), Output()), _dom_classes=('w…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"@interact(x=(0.0,20.0,0.5))\n",
"def h(x=5.5):\n",
" return x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Dropdown menus are constructed by passing a list of strings. In this case, the strings are both used as the names in the dropdown menu UI and passed to the underlying Python function."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "f4360071d1004580bf5408bf785e1c9d",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(Dropdown(description='x', options=('apples', 'oranges'), value='apples'), Output()), _do…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=['apples','oranges']);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you want a dropdown menu that passes non-string values to the Python function, you can pass a list of (label, value) pairs."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "93d5b89bdbac438f8fd1dfffa3b2fad2",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(Dropdown(description='x', options=(('one', 10), ('two', 20)), value=10), Output()), _dom…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(f, x=[('one', 10), ('two', 20)]);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## `interactive`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In addition to `interact`, IPython provides another function, `interactive`, that is useful when you want to reuse the widgets that are produced or access the data that is bound to the UI controls.\n",
"\n",
"Note that unlike `interact`, the return value of the function will not be displayed automatically, but you can display a value inside the function with `IPython.display.display`."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here is a function that returns the sum of its two arguments and displays them. The display line may be omitted if you don't want to show the result of the function."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"from IPython.display import display\n",
"def f(a, b):\n",
" display(a + b)\n",
" return a+b"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Unlike `interact`, `interactive` returns a `Widget` instance rather than immediately displaying the widget."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [],
"source": [
"w = interactive(f, a=10, b=20)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The widget is an `interactive`, a subclass of `VBox`, which is a container for other widgets."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"ipywidgets.widgets.interaction.interactive"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"type(w)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The children of the `interactive` are two integer-valued sliders and an output widget, produced by the widget abbreviations above."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(IntSlider(value=10, description='a', max=30, min=-10),\n",
" IntSlider(value=20, description='b', max=60, min=-20),\n",
" Output())"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"w.children"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To actually display the widgets, you can use IPython's `display` function."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "05b0702daf424ad789fe8d9d6e83336a",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(IntSlider(value=10, description='a', max=30, min=-10), IntSlider(value=20, description='…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"display(w)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"At this point, the UI controls work just like they would if `interact` had been used. You can manipulate them interactively and the function will be called. However, the widget instance returned by `interactive` also gives you access to the current keyword arguments and return value of the underlying Python function. \n",
"\n",
"Here are the current keyword arguments. If you rerun this cell after manipulating the sliders, the values will have changed."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"{'a': 10, 'b': 20}"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"w.kwargs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here is the current return value of the function."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"30"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"w.result"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Disabling continuous updates"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When interacting with long running functions, realtime feedback is a burden instead of being helpful. See the following example:"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [],
"source": [
"def slow_function(i):\n",
" print(int(i),list(x for x in range(int(i)) if \n",
" str(x)==str(x)[::-1] and \n",
" str(x**2)==str(x**2)[::-1]))\n",
" return"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1000000 [0, 1, 2, 3, 11, 22, 101, 111, 121, 202, 212, 1001, 1111, 2002, 10001, 10101, 10201, 11011, 11111, 11211, 20002, 20102, 100001, 101101, 110011, 111111, 200002]\n",
"CPU times: user 578 ms, sys: 5.41 ms, total: 583 ms\n",
"Wall time: 586 ms\n"
]
}
],
"source": [
"%%time\n",
"slow_function(1e6)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice that the output is updated even while dragging the mouse on the slider. This is not useful for long running functions due to lagging:"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "d829e71d520f45c2babd61343c8c3403",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=100000.0, description='i', max=10000000.0, min=100000.0, step=100000.0…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from ipywidgets import FloatSlider\n",
"interact(slow_function,i=FloatSlider(min=1e5, max=1e7, step=1e5));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are two ways to mitigate this. You can either only execute on demand, or restrict execution to mouse release events."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### `interact_manual`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `interact_manual` function provides a variant of interaction that allows you to restrict execution so it is only done on demand. A button is added to the interact controls that allows you to trigger an execute event."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "2825044603bc4ca88b4e31fad6323de1",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=100000.0, description='i', max=10000000.0, min=100000.0, step=100000.0…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact_manual(slow_function,i=FloatSlider(min=1e5, max=1e7, step=1e5));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### `continuous_update`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you are using slider widgets, you can set the `continuous_update` kwarg to `False`. `continuous_update` is a kwarg of slider widgets that restricts executions to mouse release events."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "6ab91396cf5b48c18091a483ab74becb",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=100000.0, continuous_update=False, description='i', max=10000000.0, mi…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"interact(slow_function,i=FloatSlider(min=1e5, max=1e7, step=1e5, continuous_update=False));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### `interactive_output`\n",
"\n",
"`interactive_output` provides additional flexibility: you can control how the UI elements are laid out.\n",
"\n",
"Unlike `interact`, `interactive`, and `interact_manual`, `interactive_output` does not generate a user interface for the widgets. This is powerful, because it means you can create a widget, put it in a box, and then pass the widget to `interactive_output`, and have control over the widget and its layout."
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "cd9df478fc9745bda1a3e291e467fa73",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"HBox(children=(IntSlider(value=0), IntSlider(value=0), IntSlider(value=0)))"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "37204ea492d94bb5a437b781194d4af0",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Output()"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"a = widgets.IntSlider()\n",
"b = widgets.IntSlider()\n",
"c = widgets.IntSlider()\n",
"ui = widgets.HBox([a, b, c])\n",
"def f(a, b, c):\n",
" print((a, b, c))\n",
"\n",
"out = widgets.interactive_output(f, {'a': a, 'b': b, 'c': c})\n",
"\n",
"display(ui, out)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Arguments that are dependent on each other"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Arguments that are dependent on each other can be expressed manually using `observe`. See the following example, where one variable is used to describe the bounds of another. For more information, please see the [widget events example notebook](./Widget Events.ipynb)."
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "0786b892519440d09487064cb11d907f",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=0.0, description='x', max=10.0, step=0.05), FloatSlider(value=5.0, des…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x_widget = FloatSlider(min=0.0, max=10.0, step=0.05)\n",
"y_widget = FloatSlider(min=0.5, max=10.0, step=0.05, value=5.0)\n",
"\n",
"def update_x_range(*args):\n",
" x_widget.max = 2.0 * y_widget.value\n",
"y_widget.observe(update_x_range, 'value')\n",
"\n",
"def printer(x, y):\n",
" print(x, y)\n",
"interact(printer,x=x_widget, y=y_widget);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Flickering and jumping output\n",
"\n",
"On occasion, you may notice interact output flickering and jumping, causing the notebook scroll position to change as the output is updated. The interactive control has a layout, so we can set its height to an appropriate value (currently chosen manually) so that it will not change size as it is updated.\n"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "d2074ce69c7949b6a33b7ac5f333bc8b",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(FloatSlider(value=0.0, description='m', max=2.0, min=-2.0), FloatSlider(value=0.0, descr…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"from ipywidgets import interactive\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"def f(m, b):\n",
" plt.figure(2)\n",
" x = np.linspace(-10, 10, num=1000)\n",
" plt.plot(x, m * x + b)\n",
" plt.ylim(-5, 5)\n",
" plt.show()\n",
"\n",
"interactive_plot = interactive(f, m=(-2.0, 2.0), b=(-3, 3, 0.5))\n",
"output = interactive_plot.children[-1]\n",
"output.layout.height = '350px'\n",
"interactive_plot"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
},
"widgets": {
"application/vnd.jupyter.widget-state+json": {
"state": {
"00c6df02e73342ca8f2183ea15025d52": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_5c990ddbb95046389664cec7035382ae",
"IPY_MODEL_9bcfe85dc67940ba8a33fb3b7738f0f4"
],
"layout": "IPY_MODEL_d38ecb1814784d69a206c6dbf149a91a"
}
},
"01bf1a39bf26433a9734c0d0a3fb1ea7": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"027fdc4bd5074e66adfbb6732874ef49": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "m",
"layout": "IPY_MODEL_7d522b95d9f5405c970cd20c796cade2",
"max": 2,
"min": -2,
"step": 0.1,
"style": "IPY_MODEL_76066491075142a5a5374c5c3861aed4"
}
},
"0594a48a01524ecfb03b75430870ff01": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"05b0702daf424ad789fe8d9d6e83336a": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_087925f1efc04e72ac42e1d74d0b46ff",
"IPY_MODEL_d81e4389c79d4208bf378ae04d2e688b",
"IPY_MODEL_bb2355a3b29846418b505e3251267762"
],
"layout": "IPY_MODEL_a7161c5f033d43a9b0c74045f911075f"
}
},
"05ffb5b9ba8042e8b0aae2e8db329a65": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"075b550d7071452080eef4557538b33a": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "TextModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_a6e5164f75ee4be2abe454ee41afe4b8",
"style": "IPY_MODEL_5e5636faeb0145fa9528712f44b39e8b",
"value": "Hi there!"
}
},
"0786b892519440d09487064cb11d907f": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_d708c16ad4e645a5bedad7c85a666544",
"IPY_MODEL_fd767d0532654a2abbbf19cb575bf0a9",
"IPY_MODEL_3fdfc934d2224cd581a8360a7518d8b6"
],
"layout": "IPY_MODEL_f5f267b9582e4bdbb80f5e5313b94e8f"
}
},
"087925f1efc04e72ac42e1d74d0b46ff": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "a",
"layout": "IPY_MODEL_e10eb4630aee47699d6870f9d69653b6",
"max": 30,
"min": -10,
"style": "IPY_MODEL_be62be2500db4f7199ff51d0c98925b4",
"value": 10
}
},
"0915bed033034002ac2481442b52dfc2": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"0958092831da4984b8ea57cec45d84c0": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"095ee59539354749ab8e28dd9c18cf9a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"09ad3046bcec4f739c1aec28f8bb8596": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"0cb23651e77d410eb17b687f8cb8c865": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DescriptionStyleModel",
"state": {
"description_width": ""
}
},
"0eafa181aecd4b9bba70484857aef6dd": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_4e71ebc08b2f4f1d94344830ec314ff9",
"outputs": [
{
"data": {
"text/plain": "(True, 1.0)"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"1071d6ed008d4d31b50eb45324e3268a": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "ButtonStyleModel",
"state": {}
},
"10e9bcf4b16e4f6b8c5d81cabaeeee55": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_db7d7fab789b40faa0f44d9d489ebda1",
"outputs": [
{
"data": {
"text/plain": "5.0"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"124088a0e8eb49768f3a1ee5e2b6b5e7": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_d1841751618b4f64a5d8aff7437d9146",
"outputs": [
{
"data": {
"text/plain": "'Hi there!'"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"12574ead8f1e4246861ef090c5a3cc64": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_9cdd3bd3158c4249ad1a08090297ac19",
"max": 20,
"step": 0.5,
"style": "IPY_MODEL_2c63cad5cb7541e2b8fcecb7317587b1",
"value": 5.5
}
},
"15163972fb56426aa3ae2c77f72d0242": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_e47d8ed3d8b64c33b7be6d6fbb5c8043",
"IPY_MODEL_efa6dff08d4042cfa4cad4ea2cd9b0d3"
],
"layout": "IPY_MODEL_f0c2430c49964174b2b98c396ab47f8e"
}
},
"1561ec3b83544f6da52b54b81e03424b": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"16cdb235cc554822b97329b63e94d4d5": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DropdownModel",
"state": {
"_options_labels": [
"one",
"two"
],
"description": "x",
"index": 0,
"layout": "IPY_MODEL_331fa54206594f1481f3193dd3e56767",
"style": "IPY_MODEL_f558da4bd74747df81d36c9a44e28df3"
}
},
"18cbb06d65eb4a16908365899cb0aba3": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"19a38ad4e60f4e7ca1290008f58ebd40": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"1c4e17ab4e1c427cb043fcdba1f29ed2": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"1d0fc2407f4c423c92d0f341cb067f40": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"1ed79e95f9d344b8b6474a0049d49ab1": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_a8c5697bdc98492994605224daf22010",
"IPY_MODEL_758d3373c7a2426dbf14648ce970fbab"
],
"layout": "IPY_MODEL_8a86b279718b47e5bad34a004e806b9b"
}
},
"222e7059bc3b42e7ad87230fcdf76ad7": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_075b550d7071452080eef4557538b33a",
"IPY_MODEL_124088a0e8eb49768f3a1ee5e2b6b5e7"
],
"layout": "IPY_MODEL_bbd17a2eb5cb42dca9a9722623351b98"
}
},
"223ad088ced145819dd25d13e14f4e00": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_f8d77c653f4f4719b1071872033e862a",
"IPY_MODEL_afbdafa5ee9044158749a7434202dec5"
],
"layout": "IPY_MODEL_a89852a28fe84286b257911d1c2e997f"
}
},
"24b23d4021b944a7a66d653aa197c6e0": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"25382077986c42c68b02a22931922636": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"2709f5bc99e44625976cab25175f3c2c": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"2825044603bc4ca88b4e31fad6323de1": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_2c1fcf1b2837474190e7f56c93ceac80",
"IPY_MODEL_f66e2484398441d29868e1b00d491c5d",
"IPY_MODEL_7636ebc78f1247b8bc797daa8679eb98"
],
"layout": "IPY_MODEL_4178fb9cbcfe48c78c373c9a13793021"
}
},
"2c1fcf1b2837474190e7f56c93ceac80": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "i",
"layout": "IPY_MODEL_2709f5bc99e44625976cab25175f3c2c",
"max": 10000000,
"min": 100000,
"step": 100000,
"style": "IPY_MODEL_663c0ff472394a05b9c5becc4abcd761",
"value": 100000
}
},
"2c63cad5cb7541e2b8fcecb7317587b1": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"30679fd7912545b4a192d91923c76831": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"331fa54206594f1481f3193dd3e56767": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"34e9eca67d87423a8019bb5e7cddea7f": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "y",
"layout": "IPY_MODEL_afc0cae1f84640fdaeb2123fb2d15fb5",
"max": 3,
"min": -1,
"step": 0.1,
"style": "IPY_MODEL_cfbe54fefdb44343a95023cfa476dac9",
"value": 1
}
},
"37204ea492d94bb5a437b781194d4af0": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_f7aa92f05c1b4b85b0ac310426f58d7c",
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": "(0, 0, 0)\n"
}
]
}
},
"39ed90ded9044c25a02236de2b3a5037": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"3bc54f2937d143a5ab3e3f507a6ad73f": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"3c3b6f95c8ff431981adbd153763c180": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "CheckboxModel",
"state": {
"description": "x",
"disabled": false,
"layout": "IPY_MODEL_5c4fe49015e34e8d9c834639ef3a1cfb",
"style": "IPY_MODEL_0cb23651e77d410eb17b687f8cb8c865",
"value": true
}
},
"3d464c0255e343eaad35ed5675bc1fe0": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"3fdfc934d2224cd581a8360a7518d8b6": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_c295641d02b248809e00419c126c8da1",
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": "0.0 5.0\n"
}
]
}
},
"4046bb590921472cad4270ec31b603ed": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_f13e3a632d434d6d9c213c394081e6a8",
"outputs": [
{
"data": {
"text/plain": "5.0"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"40ea12aed26a4ddf9b396783ac1f3633": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"41293c7f1fc24d7f84c5f39c829f5645": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_05ffb5b9ba8042e8b0aae2e8db329a65",
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": "100000 [0, 1, 2, 3, 11, 22, 101, 111, 121, 202, 212, 1001, 1111, 2002, 10001, 10101, 10201, 11011, 11111, 11211, 20002, 20102]\n"
}
]
}
},
"4178fb9cbcfe48c78c373c9a13793021": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"482ed7eb581c42c296a6a45c41e5ed24": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_958d785b53ff44fc98ada61785387748",
"IPY_MODEL_4046bb590921472cad4270ec31b603ed"
],
"layout": "IPY_MODEL_cb02d590e2a24a339ce5b4bc6bbf03ef"
}
},
"4c52785e0a6346579b52fbdc7d900e2f": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"4e71ebc08b2f4f1d94344830ec314ff9": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"50bf5db6aa694760b3d2ac80d03ac4bb": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_80ce329e08794806b56a112e7a6d2e9b",
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAADaNJREFUeJzt3W2MXOdZh/HrxtsEQUOTYIe82GYTEVW4gNSwMoXwUiUhdUxIAAFyJSAiSFZBkRKJqk2wVAr9VCoKQhQi00a8RSRAG2oiR4nTJkJ8SOja2E5cJ80muNS1m2woJEWRWqzefJhjNFrP7M7OOTNr31w/abQz5zzznHuec/yfZ86c9UZmIkmq41vWugBJUrcMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGJm1mKj69evz9nZ2bXYtCSds/bv3/9qZm5Yqd2aBPvs7Czz8/NrsWlJOmdFxBdHaeepGEkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGI6C/aIWBcR/xoRD3fVpyRp9bqcsd8JHO2wP0nSGDoJ9ojYCPwU8PEu+pMkja+rGfsfAu8DvtlRf5KkMbUO9oi4GXglM/ev0G5nRMxHxPzi4mLbzUqShuhixn4tcEtEHAMeAK6LiL9e2igzd2fmXGbObdiwoYPNSpIGaR3smXlPZm7MzFlgB/DZzPyl1pVJksbideySVMxMl51l5pPAk132KUlaHWfsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklSMwS5JxRjsklRM62CPiE0R8UREHI2IIxFxZxeFSZLGM9NBH6eA38zMAxFxAbA/IvZl5uc76FuStEqtZ+yZeTIzDzT3vwYcBa5o268kaTydnmOPiFng7cDTXfYrSRpdZ8EeEW8GPgnclZmvD1i/MyLmI2J+cXGxq81KkpboJNgj4k30Qv3+zPzUoDaZuTsz5zJzbsOGDV1sVpI0QBdXxQTwCeBoZn60fUmSpDa6mLFfC/wycF1EHGxu2zvoV5I0htaXO2bmPwPRQS2SpA74m6eSVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFdBLsEbEtIp6PiIWIuLuLPiVJ42kd7BGxDvgYcBOwBXh3RGxp268kaTxdzNi3AguZ+VJmfgN4ALi1g34lSWOY6aCPK4Av9T0+DvxQB/2e4Xf+8QifP/H6JLqWpKnYcvl38Ns//baJbqOLGXsMWJZnNIrYGRHzETG/uLjYwWYlSYN0MWM/Dmzqe7wROLG0UWbuBnYDzM3NnRH8o5j0u5wkVdDFjP1zwNURcWVEnAfsAPZ00K8kaQytZ+yZeSoi7gAeBdYB92XmkdaVSZLG0sWpGDJzL7C3i74kSe34m6eSVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVIzBLknFGOySVEyrYI+Ij0TEcxFxOCIeiogLuypMkjSetjP2fcD3ZeYPAF8A7mlfkiSpjVbBnpmPZeap5uFTwMb2JUmS2ujyHPvtwCMd9idJGsPMSg0i4nHg0gGrdmXmp5s2u4BTwP3L9LMT2AmwefPmsYqVJK1sxWDPzBuWWx8RtwE3A9dnZi7Tz25gN8Dc3NzQdpKkdlYM9uVExDbg/cBPZOYb3ZQkSWqj7Tn2PwYuAPZFxMGIuLeDmiRJLbSasWfm93RViCSpG/7mqSQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjEGuyQVY7BLUjGdBHtEvDciMiLWd9GfJGl8rYM9IjYBPwn8e/tyJEltdTFj/wPgfUB20JckqaVWwR4RtwBfzsxDHdUjSWppZqUGEfE4cOmAVbuA3wJuHGVDEbET2AmwefPmVZQoSVqNyBzvDEpEfD/wGeCNZtFG4ASwNTO/stxz5+bmcn5+fqztStL/VxGxPzPnVmq34ox9mMx8Brikb4PHgLnMfHXcPiVJ7XkduyQVM/aMfanMnO2qL0nS+JyxS1IxBrskFWOwS1IxBrskFWOwS1IxBrskFWOwS1IxBrskFWOwS1IxBrskFWOwS1IxBrskFWOwS1IxBrskFWOwS1IxBrskFWOwS1IxY/8x61YbjVgEvjjm09cDZ+PfVbWu1bGu1bGu1Tlb64J2tX13Zm5YqdGaBHsbETE/yl/pnjbrWh3rWh3rWp2ztS6YTm2eipGkYgx2SSrmXAz23WtdwBDWtTrWtTrWtTpna10whdrOuXPskqTlnYszdknSMs7KYI+IX4iIIxHxzYiYW7LunohYiIjnI+JdQ55/ZUQ8HREvRMSDEXHeBGp8MCIONrdjEXFwSLtjEfFM026+6zoGbO+DEfHlvtq2D2m3rRnDhYi4ewp1fSQinouIwxHxUERcOKTdVMZrpdcfEec3+3ihOZZmJ1VL3zY3RcQTEXG0Of7vHNDmnRHxWt/+/cCk62q2u+x+iZ4/asbrcERcM4Wa3to3Dgcj4vWIuGtJm6mNV0TcFxGvRMSzfcsujoh9TRbti4iLhjz3tqbNCxFxW+tiMvOsuwHfC7wVeBKY61u+BTgEnA9cCbwIrBvw/L8FdjT37wV+fcL1/j7wgSHrjgHrpzh2HwTeu0Kbdc3YXQWc14zplgnXdSMw09z/MPDhtRqvUV4/8BvAvc39HcCDU9h3lwHXNPcvAL4woK53Ag9P63gadb8A24FHgADeATw95frWAV+hd533mowX8OPANcCzfct+D7i7uX/3oOMeuBh4qfl5UXP/oja1nJUz9sw8mpnPD1h1K/BAZn49M/8NWAC29jeIiACuA/6+WfQXwM9MqtZme78I/M2ktjEBW4GFzHwpM78BPEBvbCcmMx/LzFPNw6eAjZPc3gpGef230jt2oHcsXd/s64nJzJOZeaC5/zXgKHDFJLfZoVuBv8yep4ALI+KyKW7/euDFzBz3Fx9by8x/Ar66ZHH/cTQsi94F7MvMr2bmfwL7gG1tajkrg30ZVwBf6nt8nDMP/O8E/qsvRAa16dKPAS9n5gtD1ifwWETsj4idE6yj3x3Nx+H7hnz0G2UcJ+l2erO7QaYxXqO8/v9r0xxLr9E7tqaiOfXzduDpAat/OCIORcQjEfG2KZW00n5Z62NqB8MnV2sxXqd9V2aehN4bN3DJgDadj91Mmye3ERGPA5cOWLUrMz897GkDli29rGeUNiMZscZ3s/xs/drMPBERlwD7IuK55p19bMvVBfwp8CF6r/lD9E4T3b60iwHPbX151CjjFRG7gFPA/UO66Xy8BpU6YNnEjqPViog3A58E7srM15esPkDvdMN/N9+f/ANw9RTKWmm/rOV4nQfcAtwzYPVajddqdD52axbsmXnDGE87Dmzqe7wROLGkzav0PgbONDOtQW06qTEiZoCfA35wmT5OND9fiYiH6J0GaBVUo45dRPwZ8PCAVaOMY+d1NV8K3Qxcn83JxQF9dD5eA4zy+k+3Od7s57dw5sfszkXEm+iF+v2Z+aml6/uDPjP3RsSfRMT6zJzo/4sywn6ZyDE1opuAA5n58tIVazVefV6OiMsy82RzauqVAW2O0/su4LSN9L5fHNu5dipmD7CjuWLhSnrvvP/S36AJjCeAn28W3QYM+wTQ1g3Ac5l5fNDKiPj2iLjg9H16XyA+O6htV5ac1/zZIdv7HHB19K4eOo/ex9g9E65rG/B+4JbMfGNIm2mN1yivfw+9Ywd6x9Jnh70ZdaU5h/8J4GhmfnRIm0tPn+uPiK30/g3/x4TrGmW/7AF+pbk65h3Aa6dPQUzB0E/NazFeS/QfR8Oy6FHgxoi4qDl1emOzbHzT+LZ4tTd6gXQc+DrwMvBo37pd9K5oeB64qW/5XuDy5v5V9AJ/Afg74PwJ1fnnwHuWLLsc2NtXx6HmdoTeKYlJj91fAc8Ah5uD6rKldTWPt9O76uLFKdW1QO884sHmdu/SuqY5XoNeP/C79N54AL61OXYWmmPpqimM0Y/S+wh+uG+ctgPvOX2cAXc0Y3OI3pfQPzKFugbulyV1BfCxZjyfoe9qtgnX9m30gvotfcvWZLzovbmcBP6nya9fo/e9zGeAF5qfFzdt54CP9z339uZYWwB+tW0t/uapJBVzrp2KkSStwGCXpGIMdkkqxmCXpGIMdkkqxmCXpGIMdkkqxmCXpGL+F6/JAyRQbGLGAAAAAElFTkSuQmCC\n",
"text/plain": "<Figure size 432x288 with 1 Axes>"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"525209fdbe0a4b86b145ff2c3ba991cd": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"55fb76f8e64f42bc9bc2a4340644955c": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_3c3b6f95c8ff431981adbd153763c180",
"IPY_MODEL_34e9eca67d87423a8019bb5e7cddea7f",
"IPY_MODEL_0eafa181aecd4b9bba70484857aef6dd"
],
"layout": "IPY_MODEL_d4c26ee816c04fcbb3e3369a47670386"
}
},
"5a4b3d367a3e44ee923d3eefcad4d578": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"5b8dc227a94a42d09651a0531ea6818a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"5c4fe49015e34e8d9c834639ef3a1cfb": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"5c990ddbb95046389664cec7035382ae": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_7914ff4848834b62b7ff3d1228483323",
"max": 8,
"step": 2,
"style": "IPY_MODEL_8529cd039b0c4a9199879e2cb87f918a",
"value": 4
}
},
"5df256ac024a47cabfeccc867a788523": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DescriptionStyleModel",
"state": {
"description_width": ""
}
},
"5e5636faeb0145fa9528712f44b39e8b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DescriptionStyleModel",
"state": {
"description_width": ""
}
},
"613f1639b6a5475ab2c9f690f592c673": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"6401a9e7e52f46868e5a042861d48f27": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_12574ead8f1e4246861ef090c5a3cc64",
"IPY_MODEL_d24e5412fe314b0bbcae4b1b1b13a37d"
],
"layout": "IPY_MODEL_dc5e6dbaaa0a4a3380c8140720430d2e"
}
},
"640e6be17c28412e843a168b0aa558b6": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"663c0ff472394a05b9c5becc4abcd761": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"6ab91396cf5b48c18091a483ab74becb": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_f8f53a5d93ea4866a46b0ff106fca80c",
"IPY_MODEL_41293c7f1fc24d7f84c5f39c829f5645"
],
"layout": "IPY_MODEL_39ed90ded9044c25a02236de2b3a5037"
}
},
"6c709a42ad54487c86967820d027da2a": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"758d3373c7a2426dbf14648ce970fbab": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_c03ec0712e674c5c918861c668b25d14",
"outputs": [
{
"data": {
"text/plain": "2"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"76066491075142a5a5374c5c3861aed4": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"7606fe77ccab4bc6afd865978bc7e5be": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_1561ec3b83544f6da52b54b81e03424b",
"outputs": [
{
"data": {
"text/plain": "'apples'"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"7636ebc78f1247b8bc797daa8679eb98": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_7a5251fb0bc249daac117d2c1528dedb"
}
},
"7914ff4848834b62b7ff3d1228483323": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"7a5251fb0bc249daac117d2c1528dedb": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"7b9939a164ec4fd696a024e553a24273": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_3d464c0255e343eaad35ed5675bc1fe0",
"outputs": [
{
"data": {
"text/plain": "10"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"7d522b95d9f5405c970cd20c796cade2": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"7d9f82e664c143e0b45a9df5ed8ce416": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DescriptionStyleModel",
"state": {
"description_width": ""
}
},
"80ce329e08794806b56a112e7a6d2e9b": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {
"height": "350px"
}
},
"80da7e7f1c144043bcf5fcc60af65e77": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"8529cd039b0c4a9199879e2cb87f918a": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"8600e512e6064e3189d44e5e4194e44f": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"87c33f3da654486387892ab6bb7409f6": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"8a0d71b4b8594ad18d4cd6e4fa3d3ff8": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_5b8dc227a94a42d09651a0531ea6818a",
"max": 10,
"step": 0.1,
"style": "IPY_MODEL_6c709a42ad54487c86967820d027da2a",
"value": 5
}
},
"8a86b279718b47e5bad34a004e806b9b": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"8ed5704fb133455a820148311537430a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"9204c17374944ccb81ed6edd080f62a8": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "i",
"layout": "IPY_MODEL_957eb9f559574281a4939e760931dcb7",
"max": 10000000,
"min": 100000,
"step": 100000,
"style": "IPY_MODEL_8600e512e6064e3189d44e5e4194e44f",
"value": 100000
}
},
"934beb95bef145d6b97c248dc615544d": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"93d5b89bdbac438f8fd1dfffa3b2fad2": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_16cdb235cc554822b97329b63e94d4d5",
"IPY_MODEL_98f347e7f6fd49b78035d2292d1e804b"
],
"layout": "IPY_MODEL_c34a38797d774dd8874442fede13873a"
}
},
"93e45d43537d4b9aae925b665bcf7a5b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"950683eaca0e4eb0bf5d8dc3c1413435": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"957eb9f559574281a4939e760931dcb7": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"958d785b53ff44fc98ada61785387748": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_3bc54f2937d143a5ab3e3f507a6ad73f",
"max": 10,
"step": 0.01,
"style": "IPY_MODEL_e6e3abd3ef084d7e8a86f101db541446",
"value": 5
}
},
"95e8d18ca86d408a99f6fbc95a96edfe": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"983cd3aa2dae439b9a2c451b63cfa372": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"98f347e7f6fd49b78035d2292d1e804b": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_ecb567d1db1c4676a924ebbb2de0d6c8",
"outputs": [
{
"data": {
"text/plain": "10"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"9bcfe85dc67940ba8a33fb3b7738f0f4": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_40ea12aed26a4ddf9b396783ac1f3633",
"outputs": [
{
"data": {
"text/plain": "4"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"9cdd3bd3158c4249ad1a08090297ac19": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"9ff68d35b29643b3bfb83d9b87296b44": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_f60a4790a75d47b1ba6c6a675ea2e36b",
"IPY_MODEL_bfe48e65e4bb48e3a8774a5acb40abae"
],
"layout": "IPY_MODEL_c6f7d10328ce40e6a72f754da78e9734"
}
},
"a267f58ff8324debabccb0279bf2a287": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"a6e5164f75ee4be2abe454ee41afe4b8": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"a7161c5f033d43a9b0c74045f911075f": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"a89852a28fe84286b257911d1c2e997f": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"a8c5697bdc98492994605224daf22010": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_5a4b3d367a3e44ee923d3eefcad4d578",
"max": 4,
"style": "IPY_MODEL_93e45d43537d4b9aae925b665bcf7a5b",
"value": 2
}
},
"adb6797e127b47e29a348f69e2387165": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"afbdafa5ee9044158749a7434202dec5": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_1d0fc2407f4c423c92d0f341cb067f40",
"outputs": [
{
"data": {
"text/plain": "10"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"afc0cae1f84640fdaeb2123fb2d15fb5": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"b1f9e0d181bf46d8baea0a962bedaf6a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"bab43214a622472ea72d93065f73d2d2": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DropdownModel",
"state": {
"_options_labels": [
"apples",
"oranges"
],
"description": "x",
"index": 0,
"layout": "IPY_MODEL_f1688f748fe44bc3956d8b4c6da2989a",
"style": "IPY_MODEL_5df256ac024a47cabfeccc867a788523"
}
},
"bb2355a3b29846418b505e3251267762": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_8ed5704fb133455a820148311537430a",
"outputs": [
{
"data": {
"text/plain": "30"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"bbd17a2eb5cb42dca9a9722623351b98": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"bd0e5dc04aa345bd85d34f192d278031": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_8a0d71b4b8594ad18d4cd6e4fa3d3ff8",
"IPY_MODEL_10e9bcf4b16e4f6b8c5d81cabaeeee55"
],
"layout": "IPY_MODEL_613f1639b6a5475ab2c9f690f592c673"
}
},
"bd889a0f1bd74b859f8940863b54fe9e": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"be62be2500db4f7199ff51d0c98925b4": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"bfe48e65e4bb48e3a8774a5acb40abae": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_30679fd7912545b4a192d91923c76831",
"outputs": [
{
"data": {
"text/plain": "(5, 20)"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"c03ec0712e674c5c918861c668b25d14": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"c295641d02b248809e00419c126c8da1": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"c34a38797d774dd8874442fede13873a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"c6f7d10328ce40e6a72f754da78e9734": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"c806bd5b0c3041c0b38f59cf53b42144": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_da142600dede46f7bc26976165f42142",
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": "100000 [0, 1, 2, 3, 11, 22, 101, 111, 121, 202, 212, 1001, 1111, 2002, 10001, 10101, 10201, 11011, 11111, 11211, 20002, 20102]\n"
}
]
}
},
"ca32ae2961354694bfb56c867b485397": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"caeff6c6e28b4e6bb08a96ce112de9d4": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"cb02d590e2a24a339ce5b4bc6bbf03ef": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"cd9df478fc9745bda1a3e291e467fa73": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "HBoxModel",
"state": {
"children": [
"IPY_MODEL_ffb3c03d22994d4eac5132b72351d57b",
"IPY_MODEL_d18caf1f35394938b1e9d91994a047fa",
"IPY_MODEL_e075b1152e294fd38d838c3a333cca6d"
],
"layout": "IPY_MODEL_1c4e17ab4e1c427cb043fcdba1f29ed2"
}
},
"cf5aaa2d5b0847b3864a940a8009c291": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "b",
"layout": "IPY_MODEL_e941a4ad85d8474a8872aaeebf14b684",
"max": 3,
"min": -3,
"step": 0.5,
"style": "IPY_MODEL_0594a48a01524ecfb03b75430870ff01"
}
},
"cfbe54fefdb44343a95023cfa476dac9": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"d0d66c4182ad4fe687e3388819f8de3e": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"d1841751618b4f64a5d8aff7437d9146": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"d18caf1f35394938b1e9d91994a047fa": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"layout": "IPY_MODEL_caeff6c6e28b4e6bb08a96ce112de9d4",
"style": "IPY_MODEL_01bf1a39bf26433a9734c0d0a3fb1ea7"
}
},
"d1b68543684b4119a2be3076732ca200": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"d2074ce69c7949b6a33b7ac5f333bc8b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_027fdc4bd5074e66adfbb6732874ef49",
"IPY_MODEL_cf5aaa2d5b0847b3864a940a8009c291",
"IPY_MODEL_50bf5db6aa694760b3d2ac80d03ac4bb"
],
"layout": "IPY_MODEL_0958092831da4984b8ea57cec45d84c0"
}
},
"d24e5412fe314b0bbcae4b1b1b13a37d": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_24b23d4021b944a7a66d653aa197c6e0",
"outputs": [
{
"data": {
"text/plain": "5.5"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"d38ecb1814784d69a206c6dbf149a91a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"d4c26ee816c04fcbb3e3369a47670386": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"d708c16ad4e645a5bedad7c85a666544": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_950683eaca0e4eb0bf5d8dc3c1413435",
"max": 10,
"step": 0.05,
"style": "IPY_MODEL_18cbb06d65eb4a16908365899cb0aba3"
}
},
"d81e4389c79d4208bf378ae04d2e688b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "b",
"layout": "IPY_MODEL_095ee59539354749ab8e28dd9c18cf9a",
"max": 60,
"min": -20,
"style": "IPY_MODEL_525209fdbe0a4b86b145ff2c3ba991cd",
"value": 20
}
},
"d829e71d520f45c2babd61343c8c3403": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_9204c17374944ccb81ed6edd080f62a8",
"IPY_MODEL_c806bd5b0c3041c0b38f59cf53b42144"
],
"layout": "IPY_MODEL_b1f9e0d181bf46d8baea0a962bedaf6a"
}
},
"da142600dede46f7bc26976165f42142": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"db7d7fab789b40faa0f44d9d489ebda1": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"dc5e6dbaaa0a4a3380c8140720430d2e": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"de09bf16808749f7960dae91bd70a1a3": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"e075b1152e294fd38d838c3a333cca6d": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"layout": "IPY_MODEL_87c33f3da654486387892ab6bb7409f6",
"style": "IPY_MODEL_ca32ae2961354694bfb56c867b485397"
}
},
"e10eb4630aee47699d6870f9d69653b6": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"e47d8ed3d8b64c33b7be6d6fbb5c8043": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "CheckboxModel",
"state": {
"description": "x",
"disabled": false,
"layout": "IPY_MODEL_983cd3aa2dae439b9a2c451b63cfa372",
"style": "IPY_MODEL_7d9f82e664c143e0b45a9df5ed8ce416",
"value": true
}
},
"e6e3abd3ef084d7e8a86f101db541446": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"e941a4ad85d8474a8872aaeebf14b684": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"ecb567d1db1c4676a924ebbb2de0d6c8": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"efa6dff08d4042cfa4cad4ea2cd9b0d3": {
"model_module": "@jupyter-widgets/output",
"model_module_version": "1.0.0",
"model_name": "OutputModel",
"state": {
"layout": "IPY_MODEL_d1b68543684b4119a2be3076732ca200",
"outputs": [
{
"data": {
"text/plain": "True"
},
"metadata": {},
"output_type": "display_data"
}
]
}
},
"f033f0e3edcf43ccb1a2acd6d425f76b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_fc0ac8c971d84732aa5f5ea820588ec3",
"IPY_MODEL_7b9939a164ec4fd696a024e553a24273"
],
"layout": "IPY_MODEL_934beb95bef145d6b97c248dc615544d"
}
},
"f0c2430c49964174b2b98c396ab47f8e": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"f13e3a632d434d6d9c213c394081e6a8": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"f1688f748fe44bc3956d8b4c6da2989a": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"f4360071d1004580bf5408bf785e1c9d": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "VBoxModel",
"state": {
"_dom_classes": [
"widget-interact"
],
"children": [
"IPY_MODEL_bab43214a622472ea72d93065f73d2d2",
"IPY_MODEL_7606fe77ccab4bc6afd865978bc7e5be"
],
"layout": "IPY_MODEL_a267f58ff8324debabccb0279bf2a287"
}
},
"f5296e817f674bd5bdaa5a7b8bd29ca9": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "SliderStyleModel",
"state": {
"description_width": ""
}
},
"f558da4bd74747df81d36c9a44e28df3": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "DescriptionStyleModel",
"state": {
"description_width": ""
}
},
"f5f267b9582e4bdbb80f5e5313b94e8f": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"f60a4790a75d47b1ba6c6a675ea2e36b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "p",
"layout": "IPY_MODEL_25382077986c42c68b02a22931922636",
"max": 15,
"min": -5,
"style": "IPY_MODEL_09ad3046bcec4f739c1aec28f8bb8596",
"value": 5
}
},
"f66e2484398441d29868e1b00d491c5d": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "ButtonModel",
"state": {
"description": "Run Interact",
"layout": "IPY_MODEL_95e8d18ca86d408a99f6fbc95a96edfe",
"style": "IPY_MODEL_1071d6ed008d4d31b50eb45324e3268a"
}
},
"f7aa92f05c1b4b85b0ac310426f58d7c": {
"model_module": "@jupyter-widgets/base",
"model_module_version": "1.0.0",
"model_name": "LayoutModel",
"state": {}
},
"f8d77c653f4f4719b1071872033e862a": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_0915bed033034002ac2481442b52dfc2",
"max": 30,
"min": -10,
"style": "IPY_MODEL_bd889a0f1bd74b859f8940863b54fe9e",
"value": 10
}
},
"f8f53a5d93ea4866a46b0ff106fca80c": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"continuous_update": false,
"description": "i",
"layout": "IPY_MODEL_adb6797e127b47e29a348f69e2387165",
"max": 10000000,
"min": 100000,
"step": 100000,
"style": "IPY_MODEL_19a38ad4e60f4e7ca1290008f58ebd40",
"value": 100000
}
},
"fc0ac8c971d84732aa5f5ea820588ec3": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"description": "x",
"layout": "IPY_MODEL_de09bf16808749f7960dae91bd70a1a3",
"max": 30,
"min": -10,
"style": "IPY_MODEL_640e6be17c28412e843a168b0aa558b6",
"value": 10
}
},
"fd767d0532654a2abbbf19cb575bf0a9": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "FloatSliderModel",
"state": {
"description": "y",
"layout": "IPY_MODEL_4c52785e0a6346579b52fbdc7d900e2f",
"max": 10,
"min": 0.5,
"step": 0.05,
"style": "IPY_MODEL_d0d66c4182ad4fe687e3388819f8de3e",
"value": 5
}
},
"ffb3c03d22994d4eac5132b72351d57b": {
"model_module": "@jupyter-widgets/controls",
"model_module_version": "1.2.0",
"model_name": "IntSliderModel",
"state": {
"layout": "IPY_MODEL_80da7e7f1c144043bcf5fcc60af65e77",
"style": "IPY_MODEL_f5296e817f674bd5bdaa5a7b8bd29ca9"
}
}
},
"version_major": 2,
"version_minor": 0
}
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| bsd-3-clause |
gabrielhpbc/CD | Projeto 1 - CD.ipynb | 1 | 397813 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"___\n",
"# Ciência dos Dados - PROJETO 1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Gabriel Heusi Pereira Bueno de Camargo"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Título\n",
"O comportamento da segurança alimentar no território brasileiro."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"___\n",
"## Introdução\n",
"\n",
"A diversidade do território brasileiro se apresenta em diversos fatores, entre eles há um negativo que deve ser destacado: a insegurança alimentar, ou melhor, a segurança alimentar restrita para uma parcela baixa da população. A partir disso buscou-se realizar uma análise de como isso se comporta, observando a diferença entre as regiões, entre a zona urbana e rural e ainda um destaque para a distribuição desse problema de acordo com a renda familiar. Dessa forma com auxílio de uma ferramenta do IBGE, a PNAD, os dados serão analisados e explicados ao longo da análise para então uma conclusão ao final. Vale destacar ainda que será tratado com a base de dados de 2009 e 2013, a última divulgada que involve questões de âmbito alimentar. A orientação do projeto como um todo vai ao encontro de responder a seguinte pergunta sobre segurança alimentar: ao comparar as pesquisas de 2009 e 2013, qual é a faixa de renda familiar em que se concentra maior número de pessoas que já passaram por situação de insegurança alimentar? A comparação será feita apenas para as 2 regiões que demonstram maior disparidade desse problema entre zona rural e urbana. "
]
},
{
"cell_type": "code",
"execution_count": 175,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import os\n",
"from numpy import zeros_like"
]
},
{
"cell_type": "code",
"execution_count": 176,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Esperamos trabalhar no diretório\n",
"C:\\Users\\Gabriel Camargo\\Documents\\Insper - Engenharia\\Ciência dos Dados\\PNAD DOM2013\\DOM2013csv\n"
]
}
],
"source": [
"print('Esperamos trabalhar no diretório')\n",
"print(os.getcwd())"
]
},
{
"cell_type": "code",
"execution_count": 177,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base = pd.read_csv('DOM2013.csv',sep=',')\n",
"base9 = pd.read_csv('DOM2009.csv',sep=',')"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## MUDANÇA DA VARIÁVEL INICIAL QUE MOSTRA O ANO DE PESQUISA."
]
},
{
"cell_type": "code",
"execution_count": 178,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base.V0101=base.V0101.astype(\"int\")\n",
"base9.V0101=base9.V0101.astype(\"int\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## DEFINIÇÃO DAS REGIÕES E TRANSFORMAÇÃO EM UMA CATEGORIA;"
]
},
{
"cell_type": "code",
"execution_count": 179,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base.loc[(base.UF<18),\"REGIAO\"]=\"NORTE\"\n",
"base.loc[(base.UF>20)&(base.UF<30),\"REGIAO\"]=\"NORDESTE\"\n",
"base.loc[(base.UF>30)&(base.UF<36),\"REGIAO\"]=\"SUDESTE\"\n",
"base.loc[(base.UF>35)&(base.UF<44),\"REGIAO\"]=\"SUL\"\n",
"base.loc[(base.UF>43)&(base.UF<54),\"REGIAO\"]=\"CENTRO-OESTE\"\n",
"base.REGIAO=base.REGIAO.astype(\"category\")"
]
},
{
"cell_type": "code",
"execution_count": 180,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base9.loc[(base9.UF<18),\"REGIAO\"]=\"NORTE\"\n",
"base9.loc[(base9.UF>20)&(base9.UF<30),\"REGIAO\"]=\"NORDESTE\"\n",
"base9.loc[(base9.UF>30)&(base9.UF<36),\"REGIAO\"]=\"SUDESTE\"\n",
"base9.loc[(base9.UF>35)&(base9.UF<44),\"REGIAO\"]=\"SUL\"\n",
"base9.loc[(base9.UF>43)&(base9.UF<54),\"REGIAO\"]=\"CENTRO-OESTE\"\n",
"base9.REGIAO=base9.REGIAO.astype(\"category\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## DIVISÃO EM ZONA RURAL E URBANA, A SEGUNDA VARIÁVEL DE ANÁLISE"
]
},
{
"cell_type": "code",
"execution_count": 181,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base.loc[(base.V4105<4),\"ZONA\"]=\"Urbana\"\n",
"base.loc[(base.V4105>3),\"ZONA\"]=\"Rural\"\n",
"base.ZONA=base.ZONA.astype(\"category\")"
]
},
{
"cell_type": "code",
"execution_count": 182,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base9.loc[(base9.V4105<4),\"ZONA\"]=\"Urbana\"\n",
"base9.loc[(base9.V4105>3),\"ZONA\"]=\"Rural\"\n",
"base9.ZONA=base9.ZONA.astype(\"category\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# CRIACÃO DA VARIÁVEL INSEGURANÇA ALIMENTAR:\n",
"A SEGUIR MODIFICA-SE AS VARIÁVEIS (PERGUNTAS SOBRE INSEGURANÇA ALIMENTAR) CRIANDO UMA ÚNICA CHAMADA \"INSEGURANÇA ALIMENTAR\". O MOTIVO PARA ISSO É QUE AS 4 PERGUNTAS FEITAS REPRESENTAM SITUAÇÕES DE DIFICULDADE PARA SE ALIMENTAR, PORTANTO PARA SE CONSIDERAR UMA PESSOA QUE PASSOU POR SITUAÇÃO DE DIFICULDADE ALIMENTAR DEVE SE TER PELO MENOS UMA PERGUNTA RESPONDIDA COM \"SIM\". HÁ AINDA A CARACTERIZACAO PARA CATEGORIA DAS 4 PERGUNTAS."
]
},
{
"cell_type": "code",
"execution_count": 183,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base.loc[(base.V2103==1) | (base.V2105==1) | (base.V2107==1) | (base.V2109==1),'Insegurança_Alimentar'] = 'Sim'\n",
"base.loc[(base.V2103==3) & (base.V2105==3) & (base.V2107==3) & (base.V2109==3),'Insegurança_Alimentar'] = 'Não'\n",
"base.V2103=base.V2103.astype(\"category\")\n",
"base.V2105=base.V2105.astype(\"category\")\n",
"base.V2107=base.V2107.astype(\"category\")\n",
"base.V2109=base.V2109.astype(\"category\")"
]
},
{
"cell_type": "code",
"execution_count": 184,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base9.loc[(base9.V2103==1) | (base9.V2105==1) | (base9.V2107==1) | (base9.V2109==1),'Insegurança_Alimentar'] = 'Sim'\n",
"base9.loc[(base9.V2103==3) & (base9.V2105==3) & (base9.V2107==3) & (base9.V2109==3),'Insegurança_Alimentar'] = 'Não'\n",
"base9.V2103=base9.V2103.astype(\"category\")\n",
"base9.V2105=base9.V2105.astype(\"category\")\n",
"base9.V2107=base9.V2107.astype(\"category\")\n",
"base9.V2109=base9.V2109.astype(\"category\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## CRIAÇÃO DO \"PROBLEMA ALIMENTAR\":\n",
"EM SEQUÊNCIA HÁ MAIS 4 PERGUNTAS DESTINADAS APENAS ÀQUELES QUE APRESENTARAM INSEGURANÇA ALIMENTAR. PORTANTO UTILIZOU-SE O MESMO\n",
"PROCESSO DO QUADRO ACIMA. ESSAS PERGUNTAS REFLETEM ALGUNS PROBLEMAS PELOS QUAIS AS PESSOAS PODERIAM TER PASSADO CASO RESPONDESSEM PELO MENOS UM SIM NAS 4 PERGUNTAS INICIAIS."
]
},
{
"cell_type": "code",
"execution_count": 185,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"base.loc[(base.V2113==1) | (base.V2115==1) | (base.V2117==1) | (base.V2121==1),'Problema_Alimentar'] = 'Sim'\n",
"base.loc[(base.V2113==3) & (base.V2115==3) & (base.V2117==3) & (base.V2121==3),'Problema_Alimentar'] = 'Não'\n",
"base.V2113=base.V2113.astype(\"category\")\n",
"base.V2115=base.V2115.astype(\"category\")\n",
"base.V2117=base.V2117.astype(\"category\")\n",
"base.V2121=base.V2121.astype(\"category\")"
]
},
{
"cell_type": "code",
"execution_count": 186,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"base9.loc[(base9.V2111==1) | (base9.V2113==1) | (base9.V2115==1) | (base9.V2117==1) | (base9.V2119==1) | (base9.V2120==1) | (base9.V2121==1),'Problema_Alimentar'] = 'Sim'\n",
"base9.loc[(base9.V2111==3) & (base9.V2113==3) & (base9.V2115==3) & (base9.V2117==3) & (base9.V2119==3) & (base9.V2120==3) & (base9.V2121==3),'Problema_Alimentar'] = 'Não'\n",
"base9.V2113=base9.V2113.astype(\"category\")\n",
"base9.V2115=base9.V2115.astype(\"category\")\n",
"base9.V2117=base9.V2117.astype(\"category\")\n",
"base9.V2117=base9.V2119.astype(\"category\")\n",
"base9.V2121=base9.V2120.astype(\"category\")\n",
"base9.V2121=base9.V2121.astype(\"category\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## FILTRAGEM INICIAL:\n",
"TRANSFORMACÃO DAS SIGLAS EM NOME DAS VARIÁVEIS DE INTERESSE E POSTERIOR FILTRO PARA RETIRAR PESSOAS QUE NAO RESPONDERAM (NaN)\n",
"AS 4 PERGUNTAS INICAIS E RENDA. VALE DESTACAR QUE NAO SE UTILIZOU PARA A VARIÁVEL \"PROBLEMA_ALIMENTAR\" POIS AQUELES QUE NÃO \n",
"TIVERAM INSEGURANÇA ALIMENTAR NÃO FORAM CHEGARAM A SER QUESTIONADOS SOBRE E PORTANTO PERDERIA-SE DADOS."
]
},
{
"cell_type": "code",
"execution_count": 187,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>ANO</th>\n",
" <th>REGIAO</th>\n",
" <th>ZONA</th>\n",
" <th>RENDA</th>\n",
" <th>Insegurança_Alimentar</th>\n",
" <th>Problema_Alimentar</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.500000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.780000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.234000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.300000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.400000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.100000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.300000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.780000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.178000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.978000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.410000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.606000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.356000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.800000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.200000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.780000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.606000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148657</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148659</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148661</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148663</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.100000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148664</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148665</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.200000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148666</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.020000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148667</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148668</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148669</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.350000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148670</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148671</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148672</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.500000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148673</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148677</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.300000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148678</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.400000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148679</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.520000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148680</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.615000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148681</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148682</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.300000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148683</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.500000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148684</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.000000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148687</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.780000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148688</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.870000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148689</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148690</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.550000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148692</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.400000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148693</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148694</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.550000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148695</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>116543 rows × 6 columns</p>\n",
"</div>"
],
"text/plain": [
" ANO REGIAO ZONA RENDA Insegurança_Alimentar \\\n",
"2 2013 NORTE Urbana 3.500000e+02 Não \n",
"3 2013 NORTE Urbana 6.780000e+02 Não \n",
"4 2013 NORTE Urbana 8.000000e+02 Não \n",
"5 2013 NORTE Urbana 8.000000e+02 Não \n",
"6 2013 NORTE Urbana 1.234000e+03 Não \n",
"7 2013 NORTE Urbana 4.000000e+03 Não \n",
"8 2013 NORTE Urbana 3.500000e+03 Não \n",
"9 2013 NORTE Urbana 1.300000e+03 Não \n",
"10 2013 NORTE Urbana 1.400000e+03 Sim \n",
"11 2013 NORTE Urbana 1.000000e+03 Não \n",
"12 2013 NORTE Urbana 1.100000e+03 Não \n",
"14 2013 NORTE Urbana 1.300000e+03 Não \n",
"15 2013 NORTE Urbana 6.780000e+02 Não \n",
"16 2013 NORTE Urbana 3.000000e+03 Não \n",
"17 2013 NORTE Urbana 5.000000e+03 Não \n",
"18 2013 NORTE Urbana 1.178000e+03 Não \n",
"19 2013 NORTE Urbana 5.000000e+02 Não \n",
"20 2013 NORTE Urbana 2.000000e+03 Não \n",
"21 2013 NORTE Urbana 2.978000e+03 Não \n",
"22 2013 NORTE Urbana 1.500000e+03 Não \n",
"24 2013 NORTE Urbana 2.410000e+03 Não \n",
"25 2013 NORTE Urbana 4.606000e+03 Não \n",
"26 2013 NORTE Urbana 1.356000e+03 Não \n",
"28 2013 NORTE Urbana 4.800000e+03 Não \n",
"29 2013 NORTE Urbana 3.200000e+03 Não \n",
"30 2013 NORTE Urbana 6.780000e+02 Não \n",
"31 2013 NORTE Urbana 5.500000e+03 Não \n",
"32 2013 NORTE Urbana 2.000000e+03 Não \n",
"33 2013 NORTE Urbana 2.606000e+03 Não \n",
"34 2013 NORTE Urbana 6.000000e+03 Não \n",
"... ... ... ... ... ... \n",
"148657 2013 CENTRO-OESTE Urbana 0.000000e+00 Não \n",
"148659 2013 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"148661 2013 CENTRO-OESTE Urbana 8.000000e+02 Não \n",
"148663 2013 CENTRO-OESTE Urbana 1.100000e+03 Não \n",
"148664 2013 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"148665 2013 CENTRO-OESTE Urbana 3.200000e+04 Não \n",
"148666 2013 CENTRO-OESTE Urbana 2.020000e+04 Não \n",
"148667 2013 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"148668 2013 CENTRO-OESTE Urbana 8.000000e+03 Não \n",
"148669 2013 CENTRO-OESTE Urbana 2.350000e+04 Não \n",
"148670 2013 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"148671 2013 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"148672 2013 CENTRO-OESTE Urbana 2.500000e+04 Não \n",
"148673 2013 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"148677 2013 CENTRO-OESTE Urbana 1.300000e+04 Não \n",
"148678 2013 CENTRO-OESTE Urbana 1.400000e+04 Não \n",
"148679 2013 CENTRO-OESTE Urbana 5.520000e+04 Não \n",
"148680 2013 CENTRO-OESTE Urbana 1.615000e+03 Não \n",
"148681 2013 CENTRO-OESTE Urbana 6.000000e+02 Sim \n",
"148682 2013 CENTRO-OESTE Urbana 1.300000e+03 Não \n",
"148683 2013 CENTRO-OESTE Urbana 7.500000e+02 Não \n",
"148684 2013 CENTRO-OESTE Urbana 3.000000e+03 Sim \n",
"148687 2013 CENTRO-OESTE Urbana 1.780000e+03 Não \n",
"148688 2013 CENTRO-OESTE Urbana 4.870000e+03 Não \n",
"148689 2013 CENTRO-OESTE Urbana 4.500000e+03 Não \n",
"148690 2013 CENTRO-OESTE Urbana 1.550000e+03 Sim \n",
"148692 2013 CENTRO-OESTE Urbana 2.400000e+03 Sim \n",
"148693 2013 CENTRO-OESTE Urbana 1.000000e+02 Sim \n",
"148694 2013 CENTRO-OESTE Urbana 1.550000e+03 Não \n",
"148695 2013 CENTRO-OESTE Urbana 8.000000e+02 Sim \n",
"\n",
" Problema_Alimentar \n",
"2 NaN \n",
"3 NaN \n",
"4 NaN \n",
"5 NaN \n",
"6 NaN \n",
"7 NaN \n",
"8 NaN \n",
"9 NaN \n",
"10 Não \n",
"11 NaN \n",
"12 NaN \n",
"14 NaN \n",
"15 NaN \n",
"16 NaN \n",
"17 NaN \n",
"18 NaN \n",
"19 NaN \n",
"20 NaN \n",
"21 NaN \n",
"22 NaN \n",
"24 NaN \n",
"25 NaN \n",
"26 NaN \n",
"28 NaN \n",
"29 NaN \n",
"30 NaN \n",
"31 NaN \n",
"32 NaN \n",
"33 NaN \n",
"34 NaN \n",
"... ... \n",
"148657 NaN \n",
"148659 NaN \n",
"148661 NaN \n",
"148663 NaN \n",
"148664 NaN \n",
"148665 NaN \n",
"148666 NaN \n",
"148667 NaN \n",
"148668 NaN \n",
"148669 NaN \n",
"148670 NaN \n",
"148671 NaN \n",
"148672 NaN \n",
"148673 NaN \n",
"148677 NaN \n",
"148678 NaN \n",
"148679 NaN \n",
"148680 NaN \n",
"148681 Não \n",
"148682 NaN \n",
"148683 NaN \n",
"148684 Não \n",
"148687 NaN \n",
"148688 NaN \n",
"148689 NaN \n",
"148690 Não \n",
"148692 Sim \n",
"148693 NaN \n",
"148694 NaN \n",
"148695 Não \n",
"\n",
"[116543 rows x 6 columns]"
]
},
"execution_count": 187,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"base=base.loc[:,[\"V0101\",\"REGIAO\",\"ZONA\",\"V4614\",'Insegurança_Alimentar',\"Problema_Alimentar\"]]\n",
"base.columns=[\"ANO\",\"REGIAO\",\"ZONA\",\"RENDA\",'Insegurança_Alimentar',\"Problema_Alimentar\"]\n",
"base=base.dropna(subset=[\"RENDA\",\"Insegurança_Alimentar\"])\n",
"base"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## TABELA 1 - 2013"
]
},
{
"cell_type": "code",
"execution_count": 188,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"writer = pd.ExcelWriter('Tabela1-2013.xlsx',engine='xlsxwriter')\n",
"base.to_excel(writer,sheet_name=\"Projeto_1\")\n",
"writer.save()"
]
},
{
"cell_type": "code",
"execution_count": 189,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>ANO</th>\n",
" <th>REGIAO</th>\n",
" <th>ZONA</th>\n",
" <th>RENDA</th>\n",
" <th>Insegurança_Alimentar</th>\n",
" <th>Problema_Alimentar</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.280000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.160000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.300000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.650000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.940000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.950000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.512000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.260000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.242000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.650000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.580000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.700000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.350000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.395000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.200000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.250000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.200000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.730000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.070000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.500000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.200000e+01</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.300000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.500000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>37</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.500000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>39</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.345000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>40</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.250000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>41</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.000000e+02</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153787</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.264000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153789</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.600000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153790</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.500000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153791</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153792</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153794</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153795</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.800000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153796</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.900000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153797</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153798</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.200000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153799</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.300000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153800</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.110000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153801</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.600000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153802</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153807</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153808</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153809</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153810</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.530000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153811</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.740000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153815</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.552000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153817</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.200000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153818</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.700000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153819</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.910000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153823</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.728000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153830</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153831</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153832</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153834</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.500000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153835</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.150000e+04</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153836</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.500000e+03</td>\n",
" <td>Não</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>121163 rows × 6 columns</p>\n",
"</div>"
],
"text/plain": [
" ANO REGIAO ZONA RENDA Insegurança_Alimentar \\\n",
"2 2009 NORTE Urbana 8.280000e+02 Sim \n",
"3 2009 NORTE Urbana 3.160000e+03 Não \n",
"4 2009 NORTE Urbana 9.300000e+02 Não \n",
"6 2009 NORTE Urbana 4.650000e+02 Não \n",
"7 2009 NORTE Urbana 9.940000e+02 Não \n",
"8 2009 NORTE Urbana 2.950000e+02 Sim \n",
"9 2009 NORTE Urbana 6.512000e+03 Sim \n",
"10 2009 NORTE Urbana 5.260000e+02 Sim \n",
"12 2009 NORTE Urbana 1.242000e+03 Não \n",
"13 2009 NORTE Urbana 0.000000e+00 Não \n",
"14 2009 NORTE Urbana 5.000000e+02 Sim \n",
"15 2009 NORTE Urbana 9.650000e+02 Não \n",
"16 2009 NORTE Urbana 6.580000e+02 Não \n",
"18 2009 NORTE Urbana 7.700000e+02 Não \n",
"19 2009 NORTE Urbana 3.350000e+02 Sim \n",
"21 2009 NORTE Urbana 1.395000e+03 Não \n",
"22 2009 NORTE Urbana 4.200000e+03 Não \n",
"23 2009 NORTE Urbana 5.250000e+02 Não \n",
"24 2009 NORTE Urbana 8.200000e+02 Não \n",
"25 2009 NORTE Urbana 1.730000e+03 Sim \n",
"26 2009 NORTE Urbana 4.070000e+03 Não \n",
"27 2009 NORTE Urbana 3.500000e+02 Sim \n",
"29 2009 NORTE Urbana 9.200000e+01 Sim \n",
"30 2009 NORTE Urbana 7.000000e+02 Sim \n",
"31 2009 NORTE Urbana 9.300000e+02 Sim \n",
"33 2009 NORTE Urbana 1.500000e+03 Sim \n",
"37 2009 NORTE Urbana 8.500000e+02 Não \n",
"39 2009 NORTE Urbana 1.345000e+03 Não \n",
"40 2009 NORTE Urbana 2.250000e+03 Não \n",
"41 2009 NORTE Urbana 6.000000e+02 Não \n",
"... ... ... ... ... ... \n",
"153787 2009 CENTRO-OESTE Urbana 3.264000e+03 Não \n",
"153789 2009 CENTRO-OESTE Urbana 6.600000e+03 Não \n",
"153790 2009 CENTRO-OESTE Urbana 1.500000e+04 Não \n",
"153791 2009 CENTRO-OESTE Urbana 5.000000e+03 Não \n",
"153792 2009 CENTRO-OESTE Urbana 9.000000e+03 Não \n",
"153794 2009 CENTRO-OESTE Urbana 1.500000e+03 Não \n",
"153795 2009 CENTRO-OESTE Urbana 2.800000e+03 Não \n",
"153796 2009 CENTRO-OESTE Urbana 4.900000e+03 Não \n",
"153797 2009 CENTRO-OESTE Urbana 8.000000e+03 Não \n",
"153798 2009 CENTRO-OESTE Urbana 1.200000e+04 Não \n",
"153799 2009 CENTRO-OESTE Urbana 3.300000e+03 Não \n",
"153800 2009 CENTRO-OESTE Urbana 2.110000e+04 Não \n",
"153801 2009 CENTRO-OESTE Urbana 2.600000e+04 Não \n",
"153802 2009 CENTRO-OESTE Urbana 4.500000e+03 Não \n",
"153807 2009 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"153808 2009 CENTRO-OESTE Urbana 8.000000e+03 Não \n",
"153809 2009 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"153810 2009 CENTRO-OESTE Urbana 4.530000e+03 Sim \n",
"153811 2009 CENTRO-OESTE Urbana 6.740000e+03 Não \n",
"153815 2009 CENTRO-OESTE Urbana 1.552000e+04 Não \n",
"153817 2009 CENTRO-OESTE Urbana 7.200000e+03 Não \n",
"153818 2009 CENTRO-OESTE Urbana 4.700000e+03 Não \n",
"153819 2009 CENTRO-OESTE Urbana 1.910000e+04 Não \n",
"153823 2009 CENTRO-OESTE Urbana 9.728000e+03 Não \n",
"153830 2009 CENTRO-OESTE Urbana 4.000000e+03 Não \n",
"153831 2009 CENTRO-OESTE Urbana 1.000000e+12 Não \n",
"153832 2009 CENTRO-OESTE Urbana 5.000000e+03 Não \n",
"153834 2009 CENTRO-OESTE Urbana 2.500000e+04 Não \n",
"153835 2009 CENTRO-OESTE Urbana 2.150000e+04 Não \n",
"153836 2009 CENTRO-OESTE Urbana 7.500000e+03 Não \n",
"\n",
" Problema_Alimentar \n",
"2 Sim \n",
"3 NaN \n",
"4 NaN \n",
"6 NaN \n",
"7 NaN \n",
"8 Sim \n",
"9 NaN \n",
"10 Sim \n",
"12 NaN \n",
"13 NaN \n",
"14 Sim \n",
"15 NaN \n",
"16 NaN \n",
"18 NaN \n",
"19 Sim \n",
"21 NaN \n",
"22 NaN \n",
"23 NaN \n",
"24 NaN \n",
"25 Sim \n",
"26 NaN \n",
"27 Sim \n",
"29 NaN \n",
"30 Sim \n",
"31 NaN \n",
"33 NaN \n",
"37 NaN \n",
"39 NaN \n",
"40 NaN \n",
"41 NaN \n",
"... ... \n",
"153787 NaN \n",
"153789 NaN \n",
"153790 NaN \n",
"153791 NaN \n",
"153792 NaN \n",
"153794 NaN \n",
"153795 NaN \n",
"153796 NaN \n",
"153797 NaN \n",
"153798 NaN \n",
"153799 NaN \n",
"153800 NaN \n",
"153801 NaN \n",
"153802 NaN \n",
"153807 NaN \n",
"153808 NaN \n",
"153809 NaN \n",
"153810 NaN \n",
"153811 NaN \n",
"153815 NaN \n",
"153817 NaN \n",
"153818 NaN \n",
"153819 NaN \n",
"153823 NaN \n",
"153830 NaN \n",
"153831 NaN \n",
"153832 NaN \n",
"153834 NaN \n",
"153835 NaN \n",
"153836 NaN \n",
"\n",
"[121163 rows x 6 columns]"
]
},
"execution_count": 189,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"base9=base9.loc[:,[\"V0101\",\"REGIAO\",\"ZONA\",\"V4614\",'Insegurança_Alimentar',\"Problema_Alimentar\"]]\n",
"base9.columns=[\"ANO\",\"REGIAO\",\"ZONA\",\"RENDA\",'Insegurança_Alimentar',\"Problema_Alimentar\"]\n",
"base9=base9.dropna(subset=[\"RENDA\",\"Insegurança_Alimentar\"])\n",
"base9"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## TABELA 1 - 2009"
]
},
{
"cell_type": "code",
"execution_count": 190,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"writer = pd.ExcelWriter('Tabela1-2009.xlsx',engine='xlsxwriter')\n",
"base9.to_excel(writer,sheet_name=\"Projeto_1\")\n",
"writer.save()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## PRIMEIRA OBSERVAÇÃO:\n",
"OCORRÊNCIA DE PESSOAS QUE JÁ PASSARAM POR SITUAÇÕES DE INSEGURANÇA ALIMENTAR (\"Sim\") PARA POSTERIORMENTE ANALISAR AINDA A DIFERENÇA ENTRE AS REGIÕES E ZONAS."
]
},
{
"cell_type": "code",
"execution_count": 191,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Não 76.2\n",
"Sim 23.8\n",
"Name: Insegurança_Alimentar, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAATwAAAFICAYAAADNtkLRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAF4hJREFUeJzt3XuQpXV95/H3xxkMOlxH2tkRvCWiqGxAbRHUeBuwvEXY\naKFGpU3ITjarrtFsucRExURT5GZlK2V2a9bbqGBEgWXWEMLsLLhaWuqAqNwUZUGRuTTIdTQq+t0/\nnqf10HRPn+k+Pd3j7/2qOnWey+95zvc5fc7n/J7LOZ2qQpJa8IClLkCS9hYDT1IzDDxJzTDwJDXD\nwJPUDANPUjMMPKkRST6e5JQRru+NSf5yVOvbK6qqiRtwI/BD4G7gDuDzwH8AHjDQ5sPAu/vhRwEF\n3DNw+2o/73XA56at/7eBrX27bcA/A8+cvt6B9lPrXzlQ34kz1P0c4GcDNdwMnAs8dYa2AW4Arplh\n3mXAv/bbfxdwOXAG8CsDbc4EfjJtm++Y43k9oG/3z7M857Nt083TaivgmGntLuinP2eY+vq2X5/2\nN313//z/xsAyu2b42z5i2uvgXmDttHoGH3/qNXTCbp6bFwOf69tuB94PHDgw/1eAD/Z/j+3AW6Yt\nvwH4Rv/3f920ea/s590F7AQ2AgftppZfB64BMjBtLfA/gFv6bbqh3/ajhqxh//71+NClfn8Pe2ut\nh/ebVXUg8EjgLOC/AB+YY5lDquqA/nbMTA2SvAX4O+AvgDXAI4D3AS8dUd23VNUBwIHA8cB1wGeT\nrJvW7lnAQ4FfTfLUGdbzhn771wJ/RPemuShJBtp8YmB7D6iqQ+ao7WXAj4CTkvybPd+0n/smcNrU\nSJKHACcAk9PazVXfw+i26z6q6rNTywBP7CcP/m2/0z/uqn6b7gReM0Odn+jXcRhwKfDJ3WzTwXSB\n+zDg8cDhwF8PzD8TOJLu9fhc4K1JXjAw/6vAfwSumGHdnweeXVUHAb8KrOwfaza/D5xdfVL1z+/n\ngQfTfRgcCDwZ+Axw0jA1VNW/0n2wnzZ93nLVWuABUFV3VtUm4BXARJKj57uuJAcDfwa8vqrOr6pd\nVfWTqvp0Vb11VDUDVOfmqnoHXW9h+u7EBHAhcFE/PNt6dlXVZXSBfAJdT2S+JoD/DnyNmQNiWGcD\nr0iyoh9/FV0P78d7uJ6/At6VZOU863gZXY/sz9j9c3gvXc2HJxmbpc05VXVxVf2gqm6n6009Y6DJ\nBPDnVXV7VV1L15t63cDy76uqLXQ98+nr/k5VbR+Y9FPgMbvZrhfShdmUN9P1Dl9bVd/uX1t3VNWH\nqurvh6mhdxkLe/3sVU0G3pSq+hJdl/w3FrCaE+i69heMpKjhnQ88ue+RkOTBwMvp3oRnA69M8sDd\nraDv1Wxlntuf5JF0u6dTj7mQT/pb6Ha5nt+PnwZ8ZB7rOZ/ujfy6edYxAXwc+EfgqCRPmalR/9ye\nBtwG3D7kup8FXN0vfyhdT/urA/O/yi96n3NK8swkd9IdpngZ3V7GTO1WAY+m2zWdciJwQVX9bNjH\nm8W1wIx7PstR04HXuwVYvZv5tya5o7/95xnmPwS4tf/E35tuoTtmN7VL91t0u5aXAP8E7Mdwn7zT\nt//Uge29I8mlu1n2tcDXquoauoB4YpIn7eF2DPoIcFqSo+h2N78wQ5u56ivg7cDb5wr86ZI8gm7X\n8pyq2gFs4f4hfmqSO+iOB/974OXD/O2TnEQXpu/oJx3Q39850Owuul3LoVTV56rqYOAIul3lG2dp\nOvUauXtg2mF0xw2n6ntp/3zeneSSYWvo13nwHrRfUgZed1zl+7uZf1hVHdLf/maG+bcBh82xC3Uv\nXQAN2o/uQPB8P2EPp3tz39GPTwDnVtW9/bGV89jNLtm09Qxu/7kD23tIVT13N8ueRtezo6q+R7fL\nNMxjzuZ84HnAG4CPztJmzvqq6iK6nvvv7+Hjvxa4tqqu7MfPBn47yeDf7tz+uOEa4Cpgxh7goCTH\nA+fQheM3+8n39PcHDTQ9mPuG0lD65/5iug+dmUy9RgbD9Da6HubUOjb12/VmYE8+KA7kvqG9rDUd\neP2B/cPpzqTN1xfoela7O93/HbqzsoMeDXx3AbsU/w64oqp2JTmCLihek2R7ku10u7cvSnLYbCtI\n8nC6N+xn9/TBkzyd7oD7Hw885tPoAmJex8+q6gd0B8H/gNkDb1h/AryN7qD8sE6jO+EztT3vpesJ\nvWiGWm8F1gNnJlk7ff6Uvse7Cfjd/ljY1PK3053NH9wdPIZ+l3ceVgK/NtOMqtoFfBt47MDkLcAp\nSRaaAY/nvrvly1qTgZfkoCQvoftE/FhVfX2+66qqO+l2U96X5JQkD06yX5IXJvmrvtl5wIuTPD/J\niiQPA/6U+38i75dk/4HbfYIjncOTvBP4Pbo3NHQ9k28CjwOO7W+PpevlvGqG7X9wkmfTneD4Et1J\njj01AWwGnjDwmEcDD6I7QD7UNs3gbXRnH2+cR00/15+UuYohe5xJTqALjOO47/acwyzHJqvqG8C/\nADOenOpPhl0MvLGq/tcMTT4C/GmSQ5M8nm4X+cMDyz8wyf50hy6mnscH9PNe3e+CTx1LfQ9diM3m\nIuDZA+PvBQ4FPprk1/rX1oH9dg9uw6w19J5N9yG1bxj1dS7L9cZ9r8O7k65n9npgxUCbD3P/6/BW\nzrCu13H/6/BeTXcCYBfdsZF/Ap4+MP836a59uxO4ie6Yy4Om1VfTbu/mvtfh7aI75vYp4PiBZa+j\ne1NNr/OtwNZ++DJ+cR3e3cBX6HpB+w+0P5P7X+d2D9Ous6I7SXM73WU+0x/zH4BPDbFN06/D+71Z\n/m43s/vr8H5eX7/+xwws+7R+2oenrfN+f1u6M83nzfD4x9H14Ff3j/+xafOf1v9d7nctGvAh7nsN\n5T3A1QPzB6/D28H9r8O7bIbnb+q5eE//3Ozq7zcAD9nN6/9out7j4HV4D6O7LGtbX9u36a7ne/yQ\nNUxdh7dmqd/fw97SFy7pl1ySc+iOQf7PEa3vjcDDa8SXXy0mA09SM4Y6hpfkzUmuTnJV/328/ZOs\nTrI5yfX9/aGLXawkLcScgZfkcOA/AeNVdTSwgu6rO2cAW6rqSLqDpWcsZqGStFDDnqVdCTyoP8P2\nYLoD5yfTHeCkvx/ZrzBI0mKY83qpqvpekr+hu5bsh8AlVXVJkjVVta1vtp3uQsz7SbKe7nolVq1a\n9ZSjjjpqNJVLUu/yyy+/tapm/E7zoDkDrz82dzLdhbJ3AJ9Mcp8viVdVJZnx7EdVbaA7Zc74+Hht\n3bp1iPIlaXhJbhqm3TC7tCcC/6+qJqvqJ3Rf/3k6sGPqCvP+fud8i5WkvWGYwPsOcHx/dX6AdXS/\nkLCJX1zFPvWzRJK0bA1zDO+LST5F9wOA99Jdob+B7tcezk1yOt03B05dzEIlaaGG+pJ3Vb0TeOe0\nyT+i6+1J0j6hyR8PkNQmA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzZjvPyve5yVLXcHy5O/B6peZ\nPTxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDw\nJDXDwJPUDANPUjMMPEnNmDPwkjwuyZUDt7uS/GGS1Uk2J7m+vz90bxQsSfM1Z+BV1Teq6tiqOhZ4\nCvAD4ALgDGBLVR0JbOnHJWnZ2tNd2nXAt6vqJuBkYGM/fSNwyigLk6RR29PAeyXw8X54TVVt64e3\nA2tmWiDJ+iRbk2ydnJycZ5mStHBDB16SBwIvBT45fV5VFTDj/7uqqg1VNV5V42NjY/MuVJIWak96\neC8ErqiqHf34jiRrAfr7naMuTpJGaU8C71X8YncWYBMw0Q9PABeOqihJWgxDBV6SVcBJwPkDk88C\nTkpyPXBiPy5Jy9bKYRpV1S7gIdOm3UZ31laS9gl+00JSMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDw\nJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPU\nDANPUjMMPEnNMPAkNcPAk9QMA09SM4YKvCSHJPlUkuuSXJvkhCSrk2xOcn1/f+hiFytJCzFsD++/\nAhdX1VHAMcC1wBnAlqo6EtjSj0vSsjVn4CU5GHgW8AGAqvpxVd0BnAxs7JttBE5ZrCIlaRSG6eE9\nGpgEPpTkK0nen2QVsKaqtvVttgNrZlo4yfokW5NsnZycHE3VkjQPwwTeSuDJwH+rqicBu5i2+1pV\nBdRMC1fVhqoar6rxsbGxhdYrSfM2TODdDNxcVV/sxz9FF4A7kqwF6O93Lk6JkjQacwZeVW0Hvpvk\ncf2kdcA1wCZgop82AVy4KBVK0oisHLLdG4GzkzwQuAH4HbqwPDfJ6cBNwKmLU6IkjcZQgVdVVwLj\nM8xaN9pyJGnx+E0LSc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QM\nA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8\nSc1YOUyjJDcCdwM/Be6tqvEkq4FPAI8CbgROrarbF6dMSVq4PenhPbeqjq2q8X78DGBLVR0JbOnH\nJWnZWsgu7cnAxn54I3DKwsuRpMUzbOAV8L+TXJ5kfT9tTVVt64e3A2tmWjDJ+iRbk2ydnJxcYLmS\nNH9DHcMDnllV30vyUGBzkusGZ1ZVJamZFqyqDcAGgPHx8RnbSNLeMFQPr6q+19/vBC4AjgN2JFkL\n0N/vXKwiJWkU5gy8JKuSHDg1DDwfuArYBEz0zSaACxerSEkahWF2adcAFySZan9OVV2c5MvAuUlO\nB24CTl28MiVp4eYMvKq6AThmhum3AesWoyhJWgx+00JSMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDw\nJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPU\nDANPUjMMPEnNMPAkNcPAk9QMA09SM4YOvCQrknwlyaf78dVJNie5vr8/dPHKlKSF25Me3puAawfG\nzwC2VNWRwJZ+XJKWraECL8kRwIuB9w9MPhnY2A9vBE4ZbWmSNFrD9vD+Dngr8LOBaWuqals/vB1Y\nM9OCSdYn2Zpk6+Tk5PwrlaQFmjPwkrwE2FlVl8/WpqoKqFnmbaiq8aoaHxsbm3+lkrRAK4do8wzg\npUleBOwPHJTkY8COJGuraluStcDOxSxUkhZqzh5eVf1xVR1RVY8CXgn8n6p6DbAJmOibTQAXLlqV\nkjQCC7kO7yzgpCTXAyf245K0bA2zS/tzVXUZcFk/fBuwbvQlSdLi8JsWkpph4ElqhoEnqRkGnqRm\nGHiSmmHgSWqGgSepGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiSmmHg\nSWqGgSepGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpoxZ+Al2T/Jl5J8NcnVSd7VT1+dZHOS6/v7\nQxe/XEmav2F6eD8CnldVxwDHAi9IcjxwBrClqo4EtvTjkrRszRl41bmnH92vvxVwMrCxn74ROGVR\nKpSkERnqGF6SFUmuBHYCm6vqi8CaqtrWN9kOrJll2fVJtibZOjk5OZKiJWk+hgq8qvppVR0LHAEc\nl+ToafOLrtc307Ibqmq8qsbHxsYWXLAkzdcenaWtqjuAS4EXADuSrAXo73eOvjxJGp1hztKOJTmk\nH34QcBJwHbAJmOibTQAXLlaRkjQKK4dosxbYmGQFXUCeW1WfTvIF4NwkpwM3AacuYp2StGBzBl5V\nfQ140gzTbwPWLUZRkrQY/KaFpGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiS\nmmHgSWqGgSepGQaepGYYeJKaYeBJasYwPwAqNS3vylKXsCzVO2f8NzbLmj08Sc0w8CQ1w8CT1AwD\nT1IzDDxJzTDwJDXDwJPUDANPUjMMPEnNmDPwkjw8yaVJrklydZI39dNXJ9mc5Pr+/tDFL1eS5m+Y\nHt69wB9V1ROA44HXJ3kCcAawpaqOBLb045K0bM0ZeFW1raqu6IfvBq4FDgdOBjb2zTYCpyxWkZI0\nCnt0DC/Jo4AnAV8E1lTVtn7WdmDNLMusT7I1ydbJyckFlCpJCzN04CU5ADgP+MOqumtwXlUVMONP\nJ1TVhqoar6rxsbGxBRUrSQsxVOAl2Y8u7M6uqvP7yTuSrO3nrwV2Lk6JkjQaw5ylDfAB4Nqqeu/A\nrE3ARD88AVw4+vIkaXSG+QHQZwCvBb6e5Mp+2tuAs4Bzk5wO3AScujglStJozBl4VfU5YLaffF03\n2nIkafH4TQtJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1Iz\nDDxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzZgz\n8JJ8MMnOJFcNTFudZHOS6/v7Qxe3TElauGF6eB8GXjBt2hnAlqo6EtjSj0vSsjZn4FXV/wW+P23y\nycDGfngjcMqI65KkkZvvMbw1VbWtH94OrJmtYZL1SbYm2To5OTnPh5OkhVvwSYuqKqB2M39DVY1X\n1fjY2NhCH06S5m2+gbcjyVqA/n7n6EqSpMUx38DbBEz0wxPAhaMpR5IWzzCXpXwc+ALwuCQ3Jzkd\nOAs4Kcn1wIn9uCQtayvnalBVr5pl1roR1yJJi8pvWkhqhoEnqRkGnqRmGHiSmmHgSWqGgSepGQae\npGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiSmmHgSWqGgSepGQaepGYYeJKa\nYeBJaoaBJ6kZBp6kZhh4kpph4ElqxoICL8kLknwjybeSnDGqoiRpMcw78JKsAN4HvBB4AvCqJE8Y\nVWGSNGoL6eEdB3yrqm6oqh8D/wicPJqyJGn0Vi5g2cOB7w6M3ww8bXqjJOuB9f3oPUm+sYDH/GV1\nGHDrUhcBkCx1BZrD8nmtnLmsXiyPHKbRQgJvKFW1Adiw2I+zL0uytarGl7oOLX++VhZmIbu03wMe\nPjB+RD9NkpalhQTel4Ejkzw6yQOBVwKbRlOWJI3evHdpq+reJG8A/gVYAXywqq4eWWVtcZdfw/K1\nsgCpqqWuQZL2Cr9pIakZBp6kZhh4kpph4ElqhoG3xJIckOSApa5DaoGBt0SS/NskXwGuBq5JcnmS\no5e6Li0/SV6S5CtJvp/kriR3J7lrqevaF3lZyhJJ8nngT6rq0n78OcBfVNXTl7QwLTtJvgX8FvD1\n8g27IPbwls6qqbADqKrLgFVLV46Wse8CVxl2C7foPx6gWd2Q5O3AR/vx1wA3LGE9Wr7eClyU5DPA\nj6YmVtV7l66kfZM9vKXzu8AYcH5/G+unSdO9B/gBsD9w4MBNe8hjeNIyl+SqqvKE1gi4S7tEkozR\n7ao8ke6TG4Cqet6SFaXl6qIkz6+qS5a6kH2du7R7WZJ/6AfPBq4DHg28C7iR7ie3pOn+ALg4yQ+9\nLGVh3KXdy5JsrqqTklxeVU9J8rWq+vV+3per6qlLXaP0y8pd2r3vx/39T/r7bUleDNwCrF6akrQc\nJTmqqq5L8uSZ5lfVFXu7pn2dPby9LMl+VfWTJC8BPkv3M/l/DxwEvKuq/NVoAZBkQ1WtT3LpwOSf\nv2E93rvnDDxpmUpyHPCdqtrej08AL6M73ntmVX1/CcvbJxl4e1mSd+xmdlXVn++1YrSsJbkCOLGq\nvp/kWXT/+/mNwLHA46vq5Uta4D7IY3h7364Zpq0CTgceAhh4mrJioBf3CmBDVZ0HnJfkyiWsa59l\n4O1lVfW3U8NJDgTeBPwO3af33862nJq0IsnKqroXWMcv/qE9+N6dF5+0JZBkNfAW4NXARuDJVXX7\n0lalZejjwGeS3Ar8kO4kF0keA9y5lIXtqzyGt5cl+Wu6n/rZALyvqu5Z4pK0jCU5HlgLXFJVu/pp\njwUO8LKUPWfg7WVJfkb3ixf3MnCJARC6kxYHLUlhUgMMPEnN8Lu0kpph4ElqhoEnqRkGnqRm/H9j\netpc/txfPQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4faa04e0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"g1 = (base.Insegurança_Alimentar.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"plot = g1.plot(kind='bar',title='DIFICULDADE ALIMENTAR 2013 (G1)',figsize=(5, 5),color=('b','g'))\n",
"print(g1,\"\\n\")"
]
},
{
"cell_type": "code",
"execution_count": 192,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Não 68.3\n",
"Sim 31.7\n",
"Name: Insegurança_Alimentar, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAATwAAAFICAYAAADNtkLRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAF0xJREFUeJzt3XuwpHV95/H3JwyKAgojx9kRREyCeGEFzIigiTfE0niB\njRZqVMZIdrIpb4nZcolGxURTbLJx3Vi6W7NeGBVQVjDMGkJgJ+DqaqmDonJTlAJFZpjhDoNR0e/+\n8TwHmkOfOX3O6XMZf+9XVVf38zy/5+nv05dP/55Ld6eqkKQW/NpSFyBJi8XAk9QMA09SMww8Sc0w\n8CQ1w8CT1AwDT2pEkjOTHD/G5b0pyX8e1/IWRVU1cQGuBX4C3AncBnwZ+A/Arw20OQ14b3/7IKCA\nuwYu3+qnvQ740pTl/z6wuW+3Bfgn4LenLneg/eTyVwzU97whdT8b+OVADdcDZwFPHdI2wDXAFUOm\nXQz8a7/+dwCXACcDDx5ocwrw8ynrfNsMj+tefbt/muYxn26drp9SWwGHTWn3uX78s0epr2/7nSnP\n6Xv7x/93BubZMeS5PXDK6+AeYPWUegbvf/I1dPROHpsXAV/q224FPgLsPTD9wcDH+udjK/DWKfMf\n3j9Pd/fXh0+Z978CNwC3Ah8Gdt9JLU8GrgAyMG418D/7ZdzVv3ZOAx7fT38ccC6wHbgF+GfgkIH5\n96B7PT5yqd/fo15a6+G9pKr2Bh4DnAr8J+CjM8yzT1Xt1V8OG9YgyVuBDwB/DawCDgQ+BLx0THXf\nUFV7AXsDRwFXAV9McsyUds8EHgn8epKnDlnOG/v1Xw38GfBK4LwkGWjzmYH13auq9pmhtpcBPwWO\nTfJvZr9q9/oecOLkQJJHAEfTvdkGzVTfo+jW636q6ouT8wBP6kcPPrc/7O93z36dbgdeM6TOz/TL\n2A+4CPhfO1mnh9MF7qOAJwD7A387MP0U4GC61+NzgLcleUFfx4PowuZTwL7ABuDcfjx0H1ZrgEPp\ngukpwF/spJY/Ak6vyU/G7vH9MvBQug+DvftlfAE4dvLxATYCh9C9rr/W1wRAVf0r3Qf7vc/bctda\n4AFQVbdX1UbgFcDaJIfOdVlJHg78JfCGqjqnqnZU1c+r6vNV9bZx1QxQneur6l10vYWpmxNr6V6Q\n5/W3p1vOjqq6mC6Qj6briczVWuB/AN9meECM6nTgFUl264dfRdfD+9ksl/M3wHuSrJhjHS+j65H9\nJTt/DO+hq3n/JBPTtDmjqs6vqrur6la63tQzBpqsBf6qqm6tqiuB9XRbD9D1glcAH6iqn1bV39P1\n4J/bT38J8MGquqWqtgN/D7x+J+v1Qrowm/SndD3L11bVD/rX1m1V9fGq+mBf/9eq6qP9ffycrkd5\nSB+Wky5mfq+fRdVk4E2qqq/Rdcl/Zx6LOZqua/+5sRQ1unOAp/Q9EpI8FHg53ZvwdOCVA72Bofpe\nzWbmuP5JHkP3xpy8z/l80t9At8n1/H74ROATc1jOOXRv5NfNsY61wJnAp4HHJ/mtYY36x/ZE4Ga6\nTcpRPBO4vJ9/X7qe9rcGpn+L+3qfTwK+PdkjGzL9ASUBB/QfwFNr3RN4LPDdgdHPAz5XVb8csfbJ\n+rdW1c0D464Ehm75LEdNB17vBmDlTqbflOS2/vIfh0x/BHBT/4m/mG6ge5FPbtL9Ht2m5QXAPwK7\nM9on79T1P2FgfW9LctFO5n0t3ZvyCrqAeFKSI2a5HoM+AZyY5PF0m5tfGdJmpvoKeCfwzpkCf6ok\nB9JtWp5RVTcCm3hgiJ+Q5Da6/cH/Hnj5KM99kmPpwvRd/ai9+uvbB5rdQbdpOTl9cNrU6ecDb0ky\n0e9KeHM//qFD7n7yNXLnwLj96PYbTtb30v7xvDPJBUPqP4BuN81bp0y6k27TfZdg4HX7VW7ZyfT9\nqmqf/vJfhky/Gdhvhk2oe+gCaNDudAcjZvMJO2h/ujf3bf3wWuCsqrqn37dyNjvZJJuynMH1P2tg\nffepqufsZN4T6Xp2VNWP6TaZRrnP6ZxDt8n2RuCT07SZsb6qOo+u5/5Hs7z/1wJXVtWl/fDpwO8n\nGXzuzur3G64CLgOG9gAHJTkKOIMuHL/Xj76rv37YQNOHc18o3TVl2tTp7wO+CVxKty/uH+gOqNw4\npITJ18jeA+NuputhAlBVG/v1+lPgfh8U/Sb7BcCHq+rMKcvemwcG87LVdOD1O/b3pzuSNldfoetZ\n7exw/w/pjsoOeizwo1luUgz6d8A3qmpH/+n7XOA1SbYm2Uq3efu7SfabbgFJHk33hv3ibO88ydPp\ndrj/+cB9Po0uIOa0/6yq7qbbCf7HTB94o3oH8HaG93imcyLdAZ/J9Xk/XU/od4fUehOwDjglyeqp\n0yf1Pd6NwOuratPA/LfSHc0f3Bw8jH6Tt79+8pQDSk+enF5VP6mqN1bV/lX163QBdsmw11NV7QB+\nQHdwY9Im4PgkO82AftP7AmBjVb1vSJMncP/N8mWtycBL8rAkL6bbDPtUVX1nrsuqqtvpNlM+lOT4\nJA9NsnuSFyb5m77Z2cCLkjw/yW5JHkV3RO3TUxa3e5I9Bi73C4509k/ybuAP6d7Q0PVMvkd3NO3w\n/vI4ul7Oq4as/0OTPIvuAMfX6A5yzNZa4ELgiQP3eSjwELod5COt0xBvB55VVdfOoaZ79QdlLmPE\nHmeSo4HfAI7k/utzBtPsm6yq79KdqjH04FR/MOx84E1V9b+HNPkE8BdJ9k3yBLpN5NP6aRcDvwDe\nnOTBSd5M16P/l37Z+yd5VP+aOIpuM/7dO1nF84BnDQy/n+7o7yeT/Ea/nL379Z6s/2H9+v2/qjp5\nmuU+i+5Datcw2/NYdtUL9z8P73a6ntkbgN0G2pzGA8/DWzFkWa/jgefhvZruAMAOun0j/wg8fWD6\nS+jOpboduI7u9ISHTKmvplzey/3Pw9tBt8/ts8BRA/NeRfemmlrn24DN/e2Lue88vDvpNofeAewx\n0P4UHnie211MOc+K7iDNrXSn+Uy9zw8Dnx1hnaaeh/eH0zxv17Pz8/Dura9f/m8OzPu0ftxpU5b5\ngOeW7kjz2UPu/0i6HvzK/v4/NWX60/rn5QHnogEf5/7nUN4FXD4wffA8vBt54Hl4R/SvmZ8A3wCO\nGJj2zP7xvZvuYMSrZ3j9H0rXOxw8D+9RdKdlbelr+wHd6S9P6Kev7R+nHQw5Z5H7zsNbtdTv71Ev\n6QuX9CsuyRl0+yD/YUzLexPw6Brz6VcLycCT1Iwm9+FJapOBJ6kZBp6kZsz1+4Zzst9++9VBBx20\nmHcpqQGXXHLJTVU19DvNgxY18A466CA2b968mHcpqQFJrhulnZu0kpph4ElqxoyBl+SQJJcOXO5I\n8idJVia5MMnV/fW+i1GwJM3VjIFXVd+tqsOr6nC6L5rfTffbbycDm6rqYLovIk/3XTtJWhZmu0l7\nDPCDqroOOI7ue3f012P7cxBJWgizDbxX0v0aLHRfGN7S395K9/tgD5BkXZLNSTZv3z717wkkafGM\nHHj9r8e+lCF/WlLdF3KHfim3qtZX1ZqqWjMxMeNpMpK0YGbTw3sh3Q9OTv6i6o2TP3zYX28bd3GS\nNE6zCbxXcd/mLHS/4jr544qT/5YlScvWSIHX/+vRsXT/OTDpVLr/Ir2a7h+QTh1/eZI0PiN9tay6\n38R/xJRxN9MdtZWkXcKifpd2ObnfX6PoXv4erH6V+dUySc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXD\nwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPUDANP\nUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzRgq8JPsk+WySq5JcmeToJCuTXJjk\n6v5634UuVpLmY9Qe3n8Dzq+qxwOHAVcCJwObqupgYFM/LEnL1oyBl+ThwDOBjwJU1c+q6jbgOGBD\n32wDcPxCFSlJ4zBKD++xwHbg40m+meQjSfYEVlXVlr7NVmDVsJmTrEuyOcnm7du3j6dqSZqDUQJv\nBfAU4L9X1RHADqZsvlZVATVs5qpaX1VrqmrNxMTEfOuVpDkbJfCuB66vqq/2w5+lC8Abk6wG6K+3\nLUyJkjQeMwZeVW0FfpTkkH7UMcAVwEZgbT9uLXDuglQoSWOyYsR2bwJOT/Ig4BrgD+jC8qwkJwHX\nAScsTImSNB4jBV5VXQqsGTLpmPGWI0kLx29aSGqGgSepGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4\nkpph4ElqhoEnqRkGnqRmGHiSmmHgSWqGgSepGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4Elq\nhoEnqRkGnqRmGHiSmmHgSWqGgSepGQaepGYYeJKasWKURkmuBe4EfgHcU1VrkqwEPgMcBFwLnFBV\nty5MmZI0f7Pp4T2nqg6vqjX98MnApqo6GNjUD0vSsjWfTdrjgA397Q3A8fMvR5IWzqiBV8D/SXJJ\nknX9uFVVtaW/vRVYNfbqJGmMRtqHB/x2Vf04ySOBC5NcNTixqipJDZuxD8h1AAceeOC8ipWk+Rip\nh1dVP+6vtwGfA44EbkyyGqC/3jbNvOurak1VrZmYmBhP1ZI0BzMGXpI9k+w9eRt4PnAZsBFY2zdb\nC5y7UEVK0jiMskm7Cvhcksn2Z1TV+Um+DpyV5CTgOuCEhStTkuZvxsCrqmuAw4aMvxk4ZiGKkqSF\n4DctJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXD\nwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPUDANP\nUjMMPEnNMPAkNWPkwEuyW5JvJvl8P7wyyYVJru6v9124MiVp/mbTw3sLcOXA8MnApqo6GNjUD0vS\nsjVS4CU5AHgR8JGB0ccBG/rbG4Djx1uaJI3XqD28DwBvA345MG5VVW3pb28FVo2zMEkatxkDL8mL\ngW1Vdcl0baqqgJpm/nVJNifZvH379rlXKknzNEoP7xnAS5NcC3waeG6STwE3JlkN0F9vGzZzVa2v\nqjVVtWZiYmJMZUvS7M0YeFX151V1QFUdBLwS+Jeqeg2wEVjbN1sLnLtgVUrSGMznPLxTgWOTXA08\nrx+WpGVrxWwaV9XFwMX97ZuBY8ZfkiQtDL9pIakZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiSmmHg\nSWqGgSepGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiSmmHgSWqGgSep\nGQaepGYYeJKaYeBJaoaBJ6kZBp6kZqxY6gKk5S7vyVKXsCzVu2upS5g1e3iSmmHgSWrGjIGXZI8k\nX0vyrSSXJ3lPP35lkguTXN1f77vw5UrS3I3Sw/sp8NyqOgw4HHhBkqOAk4FNVXUwsKkflqRla8bA\nq85d/eDu/aWA44AN/fgNwPELUqEkjclI+/CS7JbkUmAbcGFVfRVYVVVb+iZbgVXTzLsuyeYkm7dv\n3z6WoiVpLkYKvKr6RVUdDhwAHJnk0CnTi67XN2ze9VW1pqrWTExMzLtgSZqrWR2lrarbgIuAFwA3\nJlkN0F9vG395kjQ+oxylnUiyT3/7IcCxwFXARmBt32wtcO5CFSlJ4zDKNy1WAxuS7EYXkGdV1eeT\nfAU4K8lJwHXACQtYpyTN24yBV1XfBo4YMv5m4JiFKEqSFoLftJDUDANPUjMMPEnNMPAkNcPAk9QM\nA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8\nSc0w8CQ1w8CT1AwDT1IzDDxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9SMGQMvyaOTXJTkiiSX\nJ3lLP35lkguTXN1f77vw5UrS3I3Sw7sH+LOqeiJwFPCGJE8ETgY2VdXBwKZ+WJKWrRkDr6q2VNU3\n+tt3AlcC+wPHARv6ZhuA4xeqSEkah1ntw0tyEHAE8FVgVVVt6SdtBVZNM8+6JJuTbN6+ffs8SpWk\n+Rk58JLsBZwN/ElV3TE4raoKqGHzVdX6qlpTVWsmJibmVawkzcdIgZdkd7qwO72qzulH35hkdT99\nNbBtYUqUpPEY5ShtgI8CV1bV+wcmbQTW9rfXAueOvzxJGp8VI7R5BvBa4DtJLu3HvR04FTgryUnA\ndcAJC1OiJI3HjIFXVV8CMs3kY8ZbjiQtHL9pIakZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiSmmHg\nSWqGgSepGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4ElqhoEnqRkGnqRmGHiSmmHgSWqGgSep\nGQaepGYYeJKaYeBJaoaBJ6kZBp6kZhh4kpph4ElqhoEnqRkzBl6SjyXZluSygXErk1yY5Or+et+F\nLVOS5m+UHt5pwAumjDsZ2FRVBwOb+mFJWtZmDLyq+r/ALVNGHwds6G9vAI4fc12SNHZz3Ye3qqq2\n9Le3Aquma5hkXZLNSTZv3759jncnSfM374MWVVVA7WT6+qpaU1VrJiYm5nt3kjRncw28G5OsBuiv\nt42vJElaGHMNvI3A2v72WuDc8ZQjSQtnlNNSzgS+AhyS5PokJwGnAscmuRp4Xj8sScvaipkaVNWr\nppl0zJhrkaQF5TctJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1Iz\nDDxJzTDwJDXDwJPUDANPUjMMPEnNMPAkNcPAk9QMA09SMww8Sc0w8CQ1w8CT1AwDT1IzDDxJzTDw\nJDXDwJPUDANPUjMMPEnNMPAkNWNegZfkBUm+m+T7SU4eV1GStBDmHHhJdgM+BLwQeCLwqiRPHFdh\nkjRu8+nhHQl8v6quqaqfAZ8GjhtPWZI0fivmMe/+wI8Ghq8Hnja1UZJ1wLp+8K4k353Hff6q2g+4\naamLAEiWugLNYPm8Vk5ZVi+Wx4zSaD6BN5KqWg+sX+j72ZUl2VxVa5a6Di1/vlbmZz6btD8GHj0w\nfEA/TpKWpfkE3teBg5M8NsmDgFcCG8dTliSN35w3aavqniRvBP4Z2A34WFVdPrbK2uImv0bla2Ue\nUlVLXYMkLQq/aSGpGQaepGYYeJKaYeBJaoaBt8SS7JVkr6WuQ2qBgbdEkvzbJN8ELgeuSHJJkkOX\nui4tP0lenOSbSW5JckeSO5PcsdR17Yo8LWWJJPky8I6quqgffjbw11X19CUtTMtOku8Dvwd8p3zD\nzos9vKWz52TYAVTVxcCeS1eOlrEfAZcZdvO34D8eoGldk+SdwCf74dcA1yxhPVq+3gacl+QLwE8n\nR1bV+5eupF2TPbyl83pgAjinv0z046Sp3gfcDewB7D1w0Sy5D09a5pJcVlUe0BoDN2mXSJIJuk2V\nJ9F9cgNQVc9dsqK0XJ2X5PlVdcFSF7Krc5N2kSX5cH/zdOAq4LHAe4Br6X5yS5rqj4Hzk/zE01Lm\nx03aRZbkwqo6NsklVfVbSb5dVU/up329qp661DVKv6rcpF18P+uvf95fb0nyIuAGYOXSlKTlKMnj\nq+qqJE8ZNr2qvrHYNe3q7OEtsiS7V9XPk7wY+CLdz+R/EHgY8J6q8lejBUCS9VW1LslFA6PvfcO6\nv3f2DDxpmUpyJPDDqtraD68FXka3v/eUqrplCcvbJRl4iyzJu3YyuarqrxatGC1rSb4BPK+qbkny\nTLr/fn4TcDjwhKp6+ZIWuAtyH97i2zFk3J7AScAjAANPk3Yb6MW9AlhfVWcDZye5dAnr2mUZeIus\nqv5u8naSvYG3AH9A9+n9d9PNpybtlmRFVd0DHMN9f2gPvnfnxAdtCSRZCbwVeDWwAXhKVd26tFVp\nGToT+EKSm4Cf0B3kIslvArcvZWG7KvfhLbIkf0v3Uz/rgQ9V1V1LXJKWsSRHAauBC6pqRz/uccBe\nnpYyewbeIkvyS7pfvLiHgVMMgNAdtHjYkhQmNcDAk9QMv0srqRkGnqRmGHiSmmHgSWrG/wdPzbgx\n8MtsSQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4c2ff940>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"g2 = (base9.Insegurança_Alimentar.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"plot = g2.plot(kind='bar',title='DIFICULDADE ALIMENTAR 2009 (G2)',figsize=(5, 5),color=('b','g'))\n",
"print(g2,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## APROFUNDAMENTO NAS REGIÕES:\n",
"GRÁFICO DE FREQUÊNCIA SEGUIDO DE UMA TABELA QUE POTENCIALIZA A ANÁLISE DOS VALORES, JÁ QUE MOSTRA OS VALORES ABSOLUTOS E VISA BUSCAR MAIOR COMPREENSÃO E COERÊNCIA DOS VALORES."
]
},
{
"cell_type": "code",
"execution_count": 193,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>INSEGURANÇA ALIMENTAR</th>\n",
" <th>Não</th>\n",
" <th>Sim</th>\n",
" <th>All</th>\n",
" </tr>\n",
" <tr>\n",
" <th>REGIÃO</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>NORTE</th>\n",
" <td>10870</td>\n",
" <td>5886</td>\n",
" <td>16756</td>\n",
" </tr>\n",
" <tr>\n",
" <th>NORDESTE</th>\n",
" <td>20899</td>\n",
" <td>11470</td>\n",
" <td>32369</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SUDESTE</th>\n",
" <td>30085</td>\n",
" <td>5313</td>\n",
" <td>35398</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SUL</th>\n",
" <td>16760</td>\n",
" <td>2811</td>\n",
" <td>19571</td>\n",
" </tr>\n",
" <tr>\n",
" <th>CENTRO-OESTE</th>\n",
" <td>10233</td>\n",
" <td>2216</td>\n",
" <td>12449</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"INSEGURANÇA ALIMENTAR Não Sim All\n",
"REGIÃO \n",
"NORTE 10870 5886 16756\n",
"NORDESTE 20899 11470 32369\n",
"SUDESTE 30085 5313 35398\n",
"SUL 16760 2811 19571\n",
"CENTRO-OESTE 10233 2216 12449"
]
},
"execution_count": 193,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAFaCAYAAAD7Oy2lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xu8VFX9//HXhzsBIjcRQQXNKwgYF/WnEYkXvMI3DTRN\nLIWvt1KzC/g1JEsz00yzUtQSL2GkokhlIKGmeQkUBUHD9Kgg9zsoIvH5/bHWHIZhzjnDOTNn5uzz\nfj4e53H2dfZn75n57DVrr72XuTsiIpJMDYodgIiIFI6SvIhIginJi4gkmJK8iEiCKcmLiCSYkryI\nSILVepI3szvN7Id5eq19zGyjmTWM48+Y2YXVfK2rzeyeHJedbmbPx+0/Vp3tFZqZ/dXMRtTCdtzM\nPp/jsuPM7MFCxyS5S39PMr9Pkj9mdqiZzTIzy9PrNTWzt8ysQ1XL5jXJm1mZmX1iZhvMbK2Z/dPM\nLjKz8u24+0Xu/uMcX+u4ypZx9w/cvaW7/7emsbv7De5e5QnCzNoCi4BrgUeB31d3mzFBbopfrMVm\n9ot8fcHc/SR3n5CP1yoFuXwepGJmdp+ZbTWzThUtk8/v067alcJCjq/X1MzuNbP3Yz6aY2YnZSwz\nKCbKj81sppntmzbvy3HaOjMry/L6M81shZmtN7PXzWxIFSH9GLjZ025MMrOzzOzlmAOWx+FLUicC\nM7vSzN6N2/jIzG41s0YA7v4p8DtgdFXHohAl+dPcvRWwL3Aj8APg3nxvJLWztc3dV7v7N9x9hrv3\nc/cna/iSvdy9JfAlYDjwzZpHKcVkQclUhZpZC+AMYB1wbpHDybsKjncj4EPC96o1cA0wycy6xnXa\nA48BPwTaArOAP6atv4mQRL9XwWavALq4+27AKODBik6gcfqXgcfTpl0F3Ab8HNgT6AhcBBwNNImL\nTQH6xW30AHoB30576T8AI8ysaQUxBu6etz+gDDguY1p/YBvQI47fB/wkDrcHpgJrgdXAPwgnngfi\nOp8AG4HvA10BBy4APgCeS5vWKL7eM8BPgVeA9cATQNs4byCwqKJ4gXHAg2nzjgH+GWP7EDg/Tj8F\neC2+/ofAuIzXPB14M673DHBIJcfLgc+njU8Cfp023ppwglwCLAZ+AjSM8xoCtwArgfeAy7Iciwvj\ncAPCh/x9YDlwP9A6zksdwxHxuK4E/i/j/Xsx7s8S4A6gSUX7kLF/3YBngQ3A9Lhu+jE+Mu0Yvw4M\nzOWzBZwPPA/cDKyJ+39S2rLnA+/G7b4HnJM275vAgrje34B90+adALxNSIa/ibGnjmHm5yN13NKP\n9/XAC4TP7eeBb8RtbYjx/G/a+gMJvwiviu/JEuAbafObx/f3/RjP80DzOO9PwNI4/TmgexXfy/MI\nn9XLgXkZ88r3q4J9+kl8jzYCTwLtgIcIn/9/AV3TXuvg+D6vjsdxWNq8+4BfA3+Ox+NlYP8477m4\n3U1xO8OBNoTcsCK+V1MJSZWKjncO+ekN4Iw4PAr4Z9q8FvF1Ds5Y5zigrIrX7Q9sBvpXcvyfzvhe\nb0rFkmNubQc8DfwmY/pC4EuVrpvrRnIMpIyMJB+nfwBcnPZmp5L8T4E7gcbx74uAZXuttA/g/fEN\naV7Bh3Ix4azXglCdkvoADyTHJE/4FbIBODvG1Q7onfY6hxESZ09gGTA0zjswvnnHx/W+D7xDWlLM\n2H55giR8QZYAV6bNnwzcFfdlD8LJ63/jvIuA+UAXwhfi6SzHIpWgvhnj2A9oSSjBPJBxXO+Ox7QX\n8Cnx5AT0ISTjRnHZBcAV2fYhy/69CPwCaAoMiMc0dYw7A6uAk+OxPD6Od6jqs0VI4p8BIwknu4uB\njwCLx2o9cFBcthMxCQJD4nE4JO7PNcQvOqHAsR74Spx3edzGriT5D4Ducf3GhALB/jGuLwEfA19I\n+xxtBa6Ly54c57eJ838dX7Nz3Mf/BzRNez9bxeP6S2BOFd/LGcBNhNLiVqBP2rzy/apgn96J+9Ca\n8Hn7NyHxNSJ8F3+fliQ/JJzYGgGHEwoMh6Z971cREmIjwoni4Yo+R4Tv3BnA5+K+/gl4PG3+Tse7\nimPQkZCID47jtwG/zVhmLhmJl0qSPOHEsznG/hTQoILlfs6OhbfB8X1olENO/Rrhc+mEE16vjPlT\ngG9X+hq5JO9c/6g4yb9ELB2yY5K/jlDa3ilJZL5W2gdwvyq+aDemzT8U2EL4kgwk9yQ/Bpic4z7/\nErg1Dv8QmJQ2rwHhpDOwgnU9voGb4vBEtn+ROxKSbfO05c8GZsbhv7NjyfC4LMcilaBmAJekLXsQ\nIYGlErezYynpFeCsCmK+Iv3YUEGSB/aJH+QWadP+kHaMf0A80aTN/xswoqrPFiHJv5M273Mxjj0J\nyWYtIUE0z3iNvwIXZLw/HxNO6ucBL6bNM0LS2pUkf10Vn5XHgcvj8EBCybFR2vzlhBNqgzivV2Wv\nF9fZPcbRuoL5+xB+FacKKX8DbkubX75fFexT+q+6W4C/po2fRjzBEErf/8jY9l3AtWnf+3vS5p0M\nvFXV5yhtfm9gTdp4lcc7bdnGhELQXWnT7iUtV8RpLxB/sWd8r8qqeO2TgO9Usszd7JiXzgWWZiyT\n+kX7CTAgy2scQKjX3zNj+kPA2Mr2v7bqDTsTfsJl+jmhpDAtXmCo8iIC4YuX6/z3CW9C+5yi3G5v\n4D/ZZpjZEWkXXdYRStSp198rbhMAd98W4+lcyba+QChdDweOICQpCImnMbAkXsReS/jS7JG2rfR9\nrey47BBXHG5EOJGkLE0b/jjGhJkdaGZTzWypma0HbiC347kX4Uu5KWO7KfsCX03tW9y/Ywgl71yU\nx+vuH8fBlnF7wwnvyxIz+7OZHZy2zdvStreakMw7k3E8PXyDFuUYS8oO74GZnWRmL5nZ6ri9k9nx\n2K1y961p46nj3h5oRpbPoJk1NLMbzew/8f0oi7Mqek++Dixw9zlx/CHga2bWOMd9WpY2/EmW8ZZx\neF/giIz38xzCiTcl62csGzP7nJndFS+cridU6eye0TChqlxArKt/gFDYuyxt1kZgt4zFWxN+bebM\n3T9z978CJ5jZ6RUstobwayRlFdA+/bqiu/8/d989ztspL7v7QkI18G8yZrUinBwqVPAkb2b9CF+i\n5zPnufsGd7/K3fcj1GV/x8wGpWZX8JIVTU/ZO214H0KJdSWhtPy5tLgaAhU1P/qQ8BM1mz8QfiLt\n7e6tCdVNqWZRHxE+7KltWIxncWUBezCJUL0xNi2GT4H27r57/NvN3bvH+UsIVTUp6fudaYe42F7K\nXpZ98R38FngLOMDDBaCr2b6/lVkCtIkX/dK3m/IhoSS/e9pfC3e/MYfXrpS7/83djyecMN4ilKRS\n2/zfjG02d/d/knE843uXfnx3+PywY/Iq33Ta+k0J1YU3Ax3jF/gv5HbsVhKqAbJ9Br9GqHY6jpCU\nuqY2WcFrnQfsF0/SSwnVZ+0JJ5x8+hB4NuPYtnT3i6v5elcRfnEeET93A+L09P2sNBfE9/BeQmHm\nDHf/LG32m4SqydSyLQjH+81qxtuIinPGG4Sq3JQXCd/tqlrk5LKNQwjXsypUsCRvZruZ2anAw4Sf\ng3OzLHOqmX0+vhnrgP8SflpCSED7VWPT51pok/o5QnXQIx6ahP0baGZmp8RSzDWEOs1sHgKOM7Nh\nZtbIzNqZWe84rxWw2t03m1l/wpcuZRJwSmya1ZjwQf2U8FMsFzcCI81sT3dfAkwDbonHsoGZ7W9m\nX0rb1uVm1tnMdidUf1RkInClmXUzs5aE0vgfM0qRFWlFqFLaGEvEOX1p3f19QouFH5lZEzM7hvDz\nPuVB4DQzOzGWTpuZ2UAz65L1BXNkZh3NbEj80n5KKLGlPlN3AmPMrHtctrWZfTXO+zNwmJkNjSWs\nS9kxkc8BBlhoS96aUKVXmSaEz9cKYKuF5nsn5LIP8Rfg74BfmNle8fgcFU8creJ+rSKcdG6o5Fgc\nRUgK/QnVHb0J16v+QEj++TQVONDMvm5mjeNfPzM7JMf1M7/vrQi/FNZaaLZ8bTVi+i0hCZ7m7p9k\nzJsM9DCzM8ysWXz91939LQi/AOL0xmHUmplZkzjv4PgrrXncz3MJJ6FnK4hjOvCF+Hq4+1rgR8Bv\nzOxMM2sVt9eb7b/kMbMLzWyPOHwo4TM3I21+Z0LLoJcqOwiFSPJPmtkGwpn9/wglh29UsOwBhLqy\njYSz22/cfWac91PgmvjT77u7sP0HCPV/Swk/eb8N4O7rgEuAewgl601U8HPc3T8glHSuIvwSmMf2\ns/4lwHVxH8cSkm1qvbcJ9W2/IpTGTiN8wLbkEng8ET7H9mZb5xGSxXzCT75H2F6dcTfhJPAGobXP\nXwil82xtnH9HOC7PEVqbbAa+lUtMwHcJJ7INcZt/rHzxHXyNUAW1mvAluj81w90/JJRkriYkwg8J\n+13Tz2QD4DuEXy+rCRc8L47bnAz8DHg4VgHMI9Sn4u4rga8SLlCuIlzPmUVIqLj7dMK+vwHMJiS1\nCrn7BsJnbxLhvfsa4Rdgrr5LuBA4h/C+/izu2/2Eaq/FhM9FZV/wEcAT7j7X3Zem/ggXHU+NyTMv\n4v6eAJxFOPZLY8yVN+/bbhwwIX7fhxGudTUnfI9eIlzYzJmFNu//SzixLbVwL8pGMzsnxruCcN3m\nesL70z/GnjKAcJL5C+EX6CeE7xuEXxPjCNdQVhAu0g9391ezxeLuywjX0IakTbuJ8Dn9PuEEt4xQ\nHfsDthcKjwbmmtmmGMdfCN+XlK8BEzy0ma/4WMTKe6mAmX2d0Dom72398ymWFO90932rXFiqFOty\nFxGaX86savkCxmGE5DLYi3CTkuRHLIlPIDSzrHHSjb/qXidcpF1e2bIlc8NGKYpVGx8QbmQoKfGn\n4smxOqkzoaQ8udhx1WWx6mj3+AVKXXuo9KdwgeNpTmgZ1pBwz4HUUe4+38PNk3kpVbv7p+5+cFUJ\nHnJM8mZ2uZnNM7M3zeyKOK2thWe4LIz/29Q08BL0e8INIH8tdiBZGKFebw2humYB2y/aSvUcRWjR\nkqpqG5qlLrc2HUK4VtWKHFqSiGRTZXWNmfUgXDztT2iG9BShedoowgXIGy00fWzj7pVd/BMRkVqW\nS0n+EOBld/84tsZ4lnBX4BBCHRPx/9DChCgiItWVS5KfB3wxNiP8HKHVyd6Etr9L4jJL2fHGGhER\nKQFVPsnR3ReY2c8IV/g3EZp0/TdjGTezrPU+ZjaKULVDixYt+hx88MHZFhMRkQrMnj17pbtX+ez4\nbHa5CaWZ3UBoWnY54ZksSyw8SvMZdz+osnX79u3rs2bNqk6cIiL1lpnNdve+1Vk319Y1qbuu9iHU\nx6du7R8RFxlBeNCYiIiUkFw73njUzNoR7v681N3XmtmNhIfwX0C4A29YoYIUEZHqySnJu/sXs0xb\nBQzKsriIiJSIonShl+6zzz5j0aJFbN68udihSAE0a9aMLl260Lhxrk+2FZF8KnqSX7RoEa1ataJr\n165YfjoylxLh7qxatYpFixbRrZvuyhcphqI/u2bz5s20a9dOCT6BzIx27drpV5pIERU9yQNK8Amm\n91akuEoiyWdq2bLCXsHqlaFDh3LkkUfuMG3cuHHcfPPNAIwdO5ann366oDHcd999fPTRRwXdhogU\nTtHr5OuCrVu30qhR7R6qtWvXMnv2bFq2bMm7777Lfvvt3EnWddddV/A47rvvPnr06MFee+2V8zrF\nOF5SGF1H/7la65XdeEqeI5HqKsmSfMozzzzDwIEDOfPMMzn44IM555xzUj2UM3r0aA499FB69uzJ\nd78bOo5asWIFZ5xxBv369aNfv3688MIL5dOPP/54unfvzoUXXsi+++7LypUrKSsro0ePHuXbu/nm\nmxk3bhwAAwcO5IorrqBv377cdtttPPnkkxxxxBEcfvjhHHfccSxbFrpHHTduHN/85jcZOHAg++23\nH7fffnv5691///307NmTXr16ceGFFwJw9913069fP3r16sUZZ5zBxx9/TDaPPfYYp512GmeddRYP\nP/xw1mXOP/98HnnkEQC6du3KmDFj6N27N3379uXVV1/lxBNPZP/99+fOO+8sX+fnP/85/fr1o2fP\nnlx7behRraysjEMOOYSRI0fSvXt3TjjhBD755BMeeeQRZs2axTnnnEPv3r355JNPuO666+jXrx89\nevRg1KhR5e9H5vESkdJQ8sWt1157jTfffJO99tqLo48+mhdeeIFDDjmEyZMn89Zbb2FmrF0bOiu/\n/PLLufLKKznmmGP44IMPOPHEE1mwYAE/+tGPOPbYYxkzZgxPPfUU996bWydPW7ZsIfUYhjVr1vDS\nSy9hZtxzzz3cdNNN3HLLLQC89dZbzJw5kw0bNnDQQQdx8cUX8+9//5sbbriBF154gXbt2rF69WoA\nvvKVrzBy5EgArrnmGu69916+9a2de+KbOHEiY8eOpWPHjpxxxhlcffXVOy2TaZ999mHOnDlceeWV\nnH/++bzwwgts3ryZHj16cNFFFzFt2jQWLlzIK6+8grtz+umn89xzz7HPPvuwcOFCJk6cyN13382w\nYcN49NFHOffcc7njjju4+eab6ds33FF92WWXMXZseGz917/+daZOncppp5220/GqL1TSlVJX8km+\nf//+dOkS+nbu3bs3ZWVlHHnkkTRr1owLLriAU089lVNPPRWAp59+mvnz55evu379ejZu3Mjzzz/P\n5Mmh06TBgwfTpk1u/ZsMHz68fHjRokUMHz6cJUuWsGXLlh2aBJ5yyik0bdqUpk2bsscee7Bs2TL+\n/ve/c+aZZ9KuXTsA2rYN3WnOmzePa665hrVr17Jx40ZOPPHEnba7bNkyFi5cyDHHHIOZ0bhxY+bN\nm7fDr45sTj/9dAAOO+wwNm7cSKtWrWjVqhVNmzZl7dq1TJs2jWnTpnH44YcDsHHjRhYuXMg+++xD\nt27d6N079FXep08fysrKsm5j5syZ3HTTTXz88cesXr2a7t27lyf59OMlIqWhpKtrAJo23d4PcMOG\nDcvre1955RXOPPNMpk6dyuDBgwHYtm0bL730EnPmzGHOnDksXry40ou4jRo1Ytu2beXjmU39WrQo\n7zidb33rW1x22WXMnTuXu+66a4dls8VYkfPPP5877riDuXPncu2112ZtXjhp0iTWrFlDt27d6Nq1\nK2VlZUycOLHC18yMo0GDBjvE1KBBA7Zu3Yq7M2bMmPLj884773DBBRfkvA+bN2/mkksu4ZFHHmHu\n3LmMHDlyh/jTj5eIlIaST/LZbNy4kXXr1nHyySdz66238vrrrwNwwgkn8Ktf/ap8uTlz5gBw9NFH\nM2nSJACmTZvGmjVrAOjYsSPLly9n1apVfPrpp0ydOrXCba5bt47OnTsDMGHChAqXSzn22GN55JFH\nyqtpUv83bNhAp06d+Oyzz3jooYeyrjtx4kSeeuopysrKKCsrY/bs2RXWy++KE088kd/97nds3LgR\ngMWLF7N8eeVdRLZq1YoNGzYA20+C7du3Z+PGjeXXA0SkdJV8dU02GzZsYMiQIWzevBl35xe/+AUA\nt99+O5deeik9e/Zk69atDBgwgDvvvJNrr72Ws88+mwceeICjjjqKPffck1atWtG4cWPGjh1L//79\n6dy5M5U9637cuHF89atfpU2bNhx77LG89957lcbYvXt3xowZw4ABA1izZg2nnHIK48eP58c//jFH\nHHEEHTp04IgjjihPoCllZWW8//77OzSd7NatG61bt+bll1+uwVELJ8EFCxZw1FFHAaGp6oMPPkjD\nhg0rXOf888/noosuonnz5rz44ouMHDmSHj16sOeee9KvX78axSMihbfLz5OviWzPk1+wYAGHHHJI\nQbf76aef0rBhQxo1asSLL77IxRdfXF7Krw0jR45k/Pjx9fbGoNp4j4sl6Rdek75/dUVNnidfJ0vy\nu+qDDz5g2LBhbNu2jSZNmnD33XfX2rYHDBjA+vXr2bZtW6UlZhGRQqgTSf6NRWurtV7PLrsDcMAB\nB/Daa6/lM6ScPffcc0XZrogI5N4z1JVm9qaZzTOziWbWzMzamtl0M1sY/+fWLlFERGpNlUnezDoD\n3wb6unsPoCFwFjAamOHuBwAz4riIiJSQXJtQNgKam1kj4HPAR8AQINWWcAIwNP/hiYhITVSZ5N19\nMXAz8AGwBFjn7tOAju6+JC62FOhYsChFRKRacqmuaUMotXcD9gJamNm56ct4aIeZtS2mmY0ys1lm\nNmvFihV5CDmZzIyrrrqqfDz9YWlbtmzh5JNPZtCgQVx00UVFilBE6qJcWtccB7zn7isAzOwx4P8B\ny8ysk7svMbNOQNZbJ919PDAeQjv5/IRdWNVtG1yRXNoMN23alMcee4wxY8bQvn37HeY1adKEv/zl\nL3mNSUTqh1zq5D8AjjSzz1m4m2cQsACYAoyIy4wAnihMiPVDo0aNGDVqFLfeeutO8yp6zPHq1asZ\nOnQoPXv25Mgjj+SNN96o7bBFpMTlUif/MvAI8CowN64zHrgRON7MFhJK+zcWMM564dJLL+Whhx5i\n3bp1O0w/5phjeOmll3jttdc466yzuOmmmwC49tprOfzww3njjTe44YYbOO+884oRtoiUsJxuhnL3\na4FrMyZ/SijVS57stttunHfeedx+++00b968fHpFjzl+/vnnefTRR4HwQLRVq1axfv16dtttt6LE\nLyKlp04+hTLJrrjiCu699142bdpUPq2yxxyLiFRGSb7EtG3blmHDhu3Qe1VFjzn+4he/WP644mee\neYb27durFC8iO1CSL0FXXXUVK1euLB9PPea4T58+O7S8GTduHLNnz6Znz56MHj06p+fci0j9Uice\nUFbbivGY1FRHHhA6M0nv4HvIkCEMGTJkp3Xatm3L448/XivxiUjdpCQvIvVWfXhevqprREQSTEle\nRCTBlORFRBJMSV5EJMGU5EVEEkxJvoRcf/31dO/enZ49e9K7d29efvllLrzwQubPn1/s0ESkjlIT\nymzGtc7z662rcpEXX3yRqVOn8uqrr9K0aVNWrlzJli1buOeee/Ibi4jUKyrJl4glS5bQvn17mjZt\nCkD79u3Za6+9GDhwILNmzQKgZcuWfO9736N79+4cd9xxvPLKKwwcOJD99tuPKVOmFDN8ESlRSvIl\n4oQTTuDDDz/kwAMP5JJLLuHZZ5/daZlNmzZx7LHH8uabb9KqVSuuueYapk+fzuTJkxk7dmwRohaR\nUqfqmhLRsmVLZs+ezT/+8Q9mzpzJ8OHDufHGHR/R36RJEwYPHgzAYYcdRtOmTWncuDGHHXYYZWVl\nRYhaREpdlUnezA4C/pg2aT9gLHB/nN4VKAOGufua/IdYfzRs2JCBAwcycOBADjvssJ0eONa4cWNC\n51zQoEGD8qqdBg0asHXr1lqPV0RKXy49Q73t7r3dvTfQB/gYmAyMBma4+wHAjDgu1fT222+zcOHC\n8vE5c+aw7777FjEiEUmCXa2THwT8x93fB4YAqaLmBGBoPgOrbzZu3MiIESM49NBD6dmzJ/Pnz2fc\nuHHFDktE6rhdrZM/C5gYhzu6+5I4vBTomLeoii2HJo/51qdPH/75z3/uNP2ZZ54pH05/HHHmCSB9\nnohISs4leTNrApwO/Clznrs74BWsN8rMZpnZrBUrVlQ7UBER2XW7Ul1zEvCquy+L48vMrBNA/L88\n20ruPt7d+7p73w4dOtQsWhER2SW7kuTPZntVDcAUYEQcHgE8ka+gREQkP3JK8mbWAjgeeCxt8o3A\n8Wa2EDgujldLqO2RJNJ7K1JcOV14dfdNQLuMaasIrW1qpFmzZqxatYp27dqVtwGXZHB3Vq1aRbNm\nzYodiki9VfQ7Xrt06cKiRYuo7KLssjWfVOu1F2xoXt2wJE+aNWtGly5dih2GSL1V9CTfuHFjunXr\nVukyJ9WDznZFRApBDygTEUkwJXkRkQRTkhcRSTAleRGRBFOSFxFJsKK3rpHk61qN1lFqGSWSH0ry\nJaA6SRCUCEWkaqquERFJMCV5EZEEU5IXEUkwJXkRkQRTkhcRSTAleRGRBMu105DdzewRM3vLzBaY\n2VFm1tbMppvZwvi/TaGDFRGRXZNrSf424Cl3PxjoBSwARgMz3P0AYEYcFxGRElJlkjez1sAA4F4A\nd9/i7muBIcCEuNgEYGihghQRkerJpSTfDVgB/N7MXjOze2Kfrx3dfUlcZinQsVBBiohI9eSS5BsB\nXwB+6+6HA5vIqJrx0Ftz1h6bzWyUmc0ys1mVdfEnIiL5l0uSXwQscveX4/gjhKS/zMw6AcT/y7Ot\n7O7j3b2vu/ft0KFDPmIWEZEcVZnk3X0p8KGZHRQnDQLmA1OAEXHaCOCJgkQoIiLVlutTKL8FPGRm\nTYB3gW8QThCTzOwC4H1gWGFCFBGR6sopybv7HKBvllmD8huOiIjkk+54FRFJMCV5EZEEU5IXEUkw\nJXkRkQRTkhcRSTAleRGRBFOSFxFJMCV5EZEEU5IXEUkwJXkRkQRTkhcRSTAleRGRBFOSFxFJMCV5\nEZEEU5IXEUkwJXkRkQTLqdMQMysDNgD/Bba6e18zawv8EegKlAHD3H1NYcIUEZHq2JWS/Jfdvbe7\np3qIGg3McPcDgBlxXERESkhNqmuGABPi8ARgaM3DERGRfMo1yTvwtJnNNrNRcVpHd18Sh5cCHbOt\naGajzGyWmc1asWJFDcMVEZFdkVOdPHCMuy82sz2A6Wb2VvpMd3cz82wruvt4YDxA3759sy4jIiKF\nkVNJ3t0Xx//LgclAf2CZmXUCiP+XFypIERGpniqTvJm1MLNWqWHgBGAeMAUYERcbATxRqCBFRKR6\ncqmu6QhMNrPU8n9w96fM7F/AJDO7AHgfGFa4MEVEpDqqTPLu/i7QK8v0VcCgQgQlIiL5oTteRUQS\nTEleRCTBlORFRBJMSV5EJMGU5EVEEkxJXkQkwZTkRUQSTEleRCTBlORFRBJMSV5EJMGU5EVEEkxJ\nXkQkwZTkRUQSTEleRCTBlORFRBIs5yRvZg3N7DUzmxrH25rZdDNbGP+3KVyYIiJSHbtSkr8cWJA2\nPhqY4e4KhH/7AAAVKUlEQVQHADPiuIiIlJCckryZdQFOAe5JmzwEmBCHJwBD8xuaiIjUVK4l+V8C\n3we2pU3r6O5L4vBSQl+wIiJSQqpM8mZ2KrDc3WdXtIy7O+AVrD/KzGaZ2awVK1ZUP1IREdlluZTk\njwZON7My4GHgWDN7EFhmZp0A4v/l2VZ29/Hu3tfd+3bo0CFPYYuISC6qTPLuPsbdu7h7V+As4O/u\nfi4wBRgRFxsBPFGwKEVEpFpq0k7+RuB4M1sIHBfHRUSkhDTalYXd/RngmTi8ChiU/5BERCRfdMer\niEiCKcmLiCSYkryISIIpyYuIJJiSvIhIginJi4gk2C41oZQSM651Nddbl984RKRkKclLadIJTCQv\nVF0jIpJgSvIiIgmmJC8ikmBK8iIiCaYkLyKSYEryIiIJpiQvIpJgufTx2szMXjGz183sTTP7UZze\n1symm9nC+L9N4cMVEZFdkUtJ/lPgWHfvBfQGBpvZkcBoYIa7HwDMiOMiIlJCcunj1d19YxxtHP8c\nGAJMiNMnAEMLEqGIiFRbTnXyZtbQzOYAy4Hp7v4y0NHdl8RFlgIdCxSjiIhUU05J3t3/6+69gS5A\nfzPrkTHfCaX7nZjZKDObZWazVqxYUeOARUQkd7vUusbd1wIzgcHAMjPrBBD/L69gnfHu3tfd+3bo\n0KGm8YqIyC7IpXVNBzPbPQ43B44H3gKmACPiYiOAJwoVpIiIVE8ujxruBEwws4aEk8Ikd59qZi8C\nk8zsAuB9YFgB4xQRkWqoMsm7+xvA4VmmrwIGFSIoERHJD93xKiKSYEryIiIJpiQvIpJgSvIiIgmm\nJC8ikmBK8iIiCaYkLyKSYEryIiIJpiQvIpJgSvIiIgmWy7NrREQk3bjW1VxvXX7jyIFK8iIiCaYk\nLyKSYEryIiIJpiQvIpJgufQMtbeZzTSz+Wb2ppldHqe3NbPpZrYw/m9T+HBFRGRX5FKS3wpc5e6H\nAkcCl5rZocBoYIa7HwDMiOMiIlJCqkzy7r7E3V+NwxuABUBnYAgwIS42ARhaqCBFRKR6dqlO3sy6\nEroCfBno6O5L4qylQMe8RiYiIjWWc5I3s5bAo8AV7r4+fZ67O+AVrDfKzGaZ2awVK1bUKFgREdk1\nOSV5M2tMSPAPuftjcfIyM+sU53cClmdb193Hu3tfd+/boUOHfMQsIiI5yqV1jQH3Agvc/Rdps6YA\nI+LwCOCJ/IcnIiI1kcuza44Gvg7MNbM5cdrVwI3AJDO7AHgfGFaYEEVEpLqqTPLu/jxgFcwelN9w\nREQkn5L9FMo69KQ4EZFC0GMNREQSTEleRCTBlORFRBJMSV5EJMGU5EVEEkxJXkQkwZLdhFKkVKl5\nr9QSleRFRBJMJXkRyT/9UikZKsmLiCSYkryISIIpyYuIJJiSvIhIginJi4gkWC49Q/3OzJab2by0\naW3NbLqZLYz/2xQ2TBERqY5cSvL3AYMzpo0GZrj7AcCMOC4iIiWmyiTv7s8BqzMmDwEmxOEJwNA8\nxyUiInlQ3Tr5ju6+JA4vBTrmKR4REcmjGl94dXcHvKL5ZjbKzGaZ2awVK1bUdHMiIrILqpvkl5lZ\nJ4D4f3lFC7r7eHfv6+59O3ToUM3NiYhIdVQ3yU8BRsThEcAT+QlHRETyKZcmlBOBF4GDzGyRmV0A\n3Agcb2YLgePiuIiIlJgqn0Lp7mdXMGtQnmMREZE80x2vIiIJpiQvIpJgSvIiIgmmJC8ikmBK8iIi\nCaYkLyKSYEryIiIJpiQvIpJgSvIiIgmmJC8ikmBK8iIiCaYkLyKSYEryIiIJpiQvIpJgSvIiIgmm\nJC8ikmA1SvJmNtjM3jazd8xsdL6CEhGR/Kh2kjezhsCvgZOAQ4GzzezQfAUmIiI1V5OSfH/gHXd/\n1923AA8DQ/ITloiI5IO5e/VWNDsTGOzuF8bxrwNHuPtlGcuNAkbF0YOAt6sf7i5rD6ysxe3VtiTv\nX5L3DbR/dV1t79++7t6hOitW2ZF3Tbn7eGB8obeTjZnNcve+xdh2bUjy/iV530D7V9fVpf2rSXXN\nYmDvtPEucZqIiJSImiT5fwEHmFk3M2sCnAVMyU9YIiKSD9WurnH3rWZ2GfA3oCHwO3d/M2+R5UdR\nqolqUZL3L8n7Btq/uq7O7F+1L7yKiEjp0x2vIiIJpiQvIpJgSvIiIgmmJJ8AZlbw+x1EqsPM9ip2\nDPVdIpK8mf0ybfjyjHn31XpABWBmz6cNP5Ax+5VaDievkv7+mdm5acNHZ8y7bOc1EuWlYgdQE2b2\npJlNqeiv2PHlIiklwAFpwyOA29LGe9ZyLIXSIm24e8Y8q81ACiDp7993gAfj8K+AL6TN+yZwR61H\nVHvq+mfz5mIHUFNJSfJWwXCSVNbWta63g036+1fZ/iVxf9PV6c+muz9b7BhqKilJvoGZtSFUP6WG\nU1+ehsULK692N7P/Iezj7mb2lTjdgNbFCysvkv7+eQXD2cbrHDP7Fdn3w4DdazmcvDKzuVS8b9vc\nvVcth7TLEnEzlJmVAdvIXipyd9+vdiPKPzP7fWXz3f0btRVLviX9/TOzj4F3CPu3fxwmju/n7i0q\nWrcuMLMRlc139wm1FUu+mdm+2SYTnts1xt1PruWQdllSkvy+7v5+seMoJDP7irs/Vuw4CiHp718F\niaJckvc9SczscOBrwFeB94BH3b3kr6ckJcm/6u5fqHrJuivJ+5jkfQMws2nufkKx4ygUM3uSnauk\nVgIz3f3B7GvVDWZ2IHB2/FsJ/BH4rrtXeuIuJUmpk0/6xaukS/r7V63OHuqQbC1Q2gLnmlkPd6/L\n/T+/BfwDONXd3wEwsyuLG9KuSUpJfjmh+8Gs3P3btRhOQaTV6+40i1BvXWebGib9/TOzd4HvVjQ/\nwdVwDYHZ7t672LFUl5kNJTxG/WjgKcLn9B5371bUwHZBUkrynwCzix1Egb0HnFbsIAok6e9fa+BU\nKriwDCQyybv7f83q9o80d38ceNzMWhD6sL4C2MPMfgtMdvdpRQ0wB0kpySe6ThfAzF5z98OLHUch\nJP39qwf71zbL5DbAecDn3f2cWg6poGIT368Cw919ULHjqUpSSvJbih1ALXih2AEUUNLfv7pdnK3a\nbMIvktR+bgNWAc8AFxcppoJx9zWETkPqRMchiXh2DXCWmZXfEGRmXzaz28zsO7FrwiT4W3pTPDMb\na2avx2do1Jn6wWzc/chs083sQDO7u7bjKYCvp4+YWTsz+x8z61OsgPJsOHC0u3eLddXXAUuBZiSn\nIFlnJSXJ/5H4bBcz6w38CfgA6AX8pohx5dP1wAoAMzsVOJfw3JMpwJ1FjKvGzKynmU0zs3lm9hMz\n62RmjwJ/B+YXO748uNHMegCYWSdgHuG9e8DMrihqZPlxJ/ApgJkNAH4KTADWUUdKu0mWlCTf3N0/\nisPnEvqbvQX4BtC/eGHllbv7x3H4K8C97j7b3e+h7jfRuxv4A3AG4UQ2B/gPoT731mIGlifd3H1e\nHP4GMN3dTwOOICT7uq6hu6+Ow8OB8e7+qLv/EPh8EeMSkpPk0+s8jwVmALj7tuKEUxBmZi3NrAEw\niLiPUbMixZQvTd39Pnd/291vAza5+/fdfXOxA8uTz9KGBwF/AXD3DYT667quYVqfBoMIv8BSVF1T\nZEl5A/5uZpOAJYSr+n+H8p/GSbmo90tCCXc9sMDdZ0H5rdZLihlYHjSL+5E6WX+aPu7urxYtsvz4\n0My+BSwiPGb4KQAzaw40LmZgeTIReNbMVhKaw/4DwMw+T6iykSJKShNKI/xM7ARMcvfFcfrhwB7u\n/rdixpcvZtYZ2AN4PfUrJZ7IGrv7B0UNrgbMbGYls93dj621YArAzPYgXIzsBPw61bbazL4M9HH3\nOv/McjM7krB/09x9U5x2INAyASfpOi0pSf5gd38rDjd190/T5h3p7nW6dxoIvQulngNiZke7+wtp\n8y6rCw9Kkp2ZWSN331rsOCS5klIn/4e04Rcz5iWldc130oZ/lTGvzl+8M7M9zOxHZvZI/PtRLAHX\neUnuulFKX1KSfH3oeSex+xj7Pf1XHL0//gG8ktknah2V5K4bpcQl5cJronveiZK8j7cAQ939tbRp\nU8xsMnAXoalhXZbkrhulxCUlyXcxs9sJpaLUMHG8c/HCyquDzewNYu9CcZg4Xqd7TgJ2y0jwALj7\nHDNrVYyA8izJXTdKiUtKkv9e2vCsjHmZ43XVIcUOoIDMzNrEZ4KkT2xLMqoUnwVOTxtOf5roc7Uf\njtQniWhdk87MWgK4+8Zix1IIZrY7cEAc/be71/l2yGY2ChhJeOZ6qrldH+BnhLuX7ypWbCJ1XWKS\nvJldDIxh+0WujcDP3D0RrWvMrCmhfnoo4dnyBuwLTAYucvc6fdNXfB7P99l+YfJN4Ofu/mTxosof\nMzsIGAUcHCctINz+/+/iRSX1QRJ+CmNm1xB+Ag9093bu3g74MnBSnJcE1xDujtzb3Q+Pve3sQ6hy\n+2FRI8sDd5/q7gNS718cTkqCP4rw2N2NhAd23Q1sAp6JNxGJFEwiSvJm9jbQK/NZJ/G28dfd/cDi\nRJY/ZjYP6J/2kLLU9JbAS+7eoziR1ZyZja1ktrv7j2stmAIws78SflU+kzH9S8Bodz+pKIFJvZCI\nkjwhEez0MCt3/4RkPAAKYFtmgofyaw91/Uy9KcsfwAXAD4oVVB7tn5ngAdz9Wep+yygpcUlpXbPY\nzAa5e/qTGTGzY6n7D+9K8djtWLabZ+r0iSw+FhqA2GTycsIjeR8mtKGv6zZUMm9TJfNEaiwpSf7b\nwBPx9vFUh9B9CT2sDylaVPnVmrBvibxDMjaX/A5wDqHDiS9kNqmsw/ZOu3cjXZLu45ASlYg6eQAz\nawZ8je2tM+YDDyXomeSJZWY/J3SEMp7wlMZENX81sxGVzXf3CbUVi9Q/iUnymczsVHefWuw4Ci0+\nzvV77j6y2LFUl5ltI3Qft5Udry8Y4XrLbkUJTCQBklJdk811QGKSvJn1BG4G9gIeB34N3EF4rkud\nrrd296Q0AMjKzJ5k52cPrQRmph4fLVIoSU7ySau7vhv4LeFRyoMJvURNAM5RlVTJy9YpSFvgXDPr\n4e6jazsgqT+SXF3T390T86xuM5sTb4BKjb/r7mp+V4eZWUNgdvr7KpJviSnJxw4mLiXttngze9/d\nlxUxrHxKej+o9Y67/zf0XClSOIkoyceOJf4A3Mf2JpR9gBGE6owXKli1zkh6P6hJFpuHZmoDnAd8\n3t3PqeWQpB5JSpJ/Cbg485nkZtYbuMvd63qnE1KHmdl7hIutqWL7NmAV4Xk2P3H39UUKTeqBpFTX\nJL3TCSB7lRShXfny4kUlORgOfOjuS6C83fwZQDOS8x2UEpWUpmsWb/nPnJiUTifqQz+oSXYn4T4A\nzGwA8FNCy6h1hBvARAomKaWIW4FpZpat04lbixZVfiW9H9Qka+juq+PwcMJz5B8FHjWzOUWMS+qB\nRCR5dx9vZh8BPyZUZTjhsQY/ScozyaknVVIJ1dDMGrn7VmAQofOQlER8B6V0JeYDFh9hsNMdrmbW\nwt2T8KS/pPeDmmQTgWfNbCXwCfAPADP7PKHKRqRgEpMczKyzmfU1syZxfA8zuwFYWOTQ8iVVJfUl\nM2sV/wYCfyU5VVKJ5O7XA1cRmvge49ubtDUAvlWsuKR+SEoTyiuA/wPeAZoCvyHUx98P3JRq1VDX\nJb0fVBHJv6Qk+fmEEtJqM9sH+DdwtLvPrmJVEZFES0qd/OZU6wV3/8DM3k5agk96P6giUhhJSfJd\nMnre6ZQ+7u7fLkJM+Zbt4nELQj+o7Qgti0REdpCU6pp61fNOWj+oFwCTgFt016uIZJOUkvxB7n51\nsYMotIT3gyoiBZCUJpSDix1AocV+UP8FbAAOc/dxSvAiUpWkVNe8Dgykgt6g0m4pr7PUD6qIVEdS\nkvynwGKyJ3lXD0oiUl8lpU5+vrsfXuwgRERKTVLq5EVEJIukJPnbih2AiEgpSkqd/O/Z8WJkOnf3\nC2ozHhGRUpGUOvmdHjEM7A1cCTSs5VhEREpGIkry6cxsP+BqYADhEbz3uvuW4kYlIlIcSamTx8wO\nNrMHgSeB54FD3f23SvAiUp8loiRvZn8i9Ol6C+FZLv9Nn5+Em6FERKojKUm+jO0XXlP/UzdG6WYo\nEam3EpHkRUQku0TUyZvZuWnDR2fMu6z2IxIRKQ2JKMmb2avu/oXM4WzjIiL1SSJK8uz4YLLMh5Rl\nfTKliEh9kJQk7xUMZxsXEak3klJd8zHwDqHUvn8cJo7v5+4tihWbiEgxJeWxBr2AjsCHGdP3BpbW\nfjgiIqUhKdU1twLr3P399D9gXZwnIlIvJSXJd3T3uZkT47SutR+OiEhpSEqS372Sec1rLQoRkRKT\nlCQ/y8xGZk40swuB2UWIR0SkJCSldU1HYDKwhe1JvS/QBPgfd9fFVxGplxKR5FPM7MtAjzj6prv/\nvZjxiIgUW6KSvIiI7CgpdfIiBWFmvczsj2b2+/QH4YnUFSrJi4gkmEryUqeZ2X/NbI6ZzTOzJ81s\n9zi9q5l9Euel/s6L81qa2W/N7D9m9qqZzU61zorrzcvYxi/NbLGZNciYPtTM3jCzBWY218yG1tZ+\ni+QqKY81kPrrE3fvDWBmE4BLgevjvP+k5mW4B3gXOMDdt5lZB+Cb2V48Jvb/ITwy40vAzDi9F3Az\ncLy7v2dm3YDpZvauu7+Rv90TqRmV5CVJXgQ6V7aAme0P9AeucfdtAO6+wt1/VsEqA4E3gd8CZ6dN\n/y5wg7u/F1/jPeCnwPdqsgMi+aYkL4lgZg2BQcCUtMn7Z1TXfBHoDryeSvA5OBuYSLgP4xQzaxyn\nd2fnG+1mxekiJUNJXuq65mY2h/C00Y7A9LR5/3H33ml//8hc2cz+L54APsoyrwlwMvC4u68HXgZO\nLMxuiBSGkrzUdak6+X0J/QdcWsXy84FeqYuo7n59XH+3LMueSHgu0lwzKwOOYXuVzXygT8byfQhV\nOyIlQ0leEsHdPwa+DVxlZhU2KHD3dwjVKj+JVTyYWTOydxN5NnChu3d1965AN+B4M/sc4aLrGDPr\nGl+jK3A1cEt+9kgkP5TkJTHc/TXgDbaXtjPr5L8dp18ItAPeMbNZhCqe76e/Vkzkg4E/p73+JuB5\n4DR3nwP8AHjSzN4CngS+H6eLlAzdDCUikmAqyYuIJJiSvIhIginJi4gkmJK8iEiCKcmLiCSYkryI\nSIIpyYuIJJiSvIhIgv1/pJCvACW+KT4AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4b77b9b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"tb1= (pd.crosstab(base.REGIAO,base.Insegurança_Alimentar,margins=True,rownames=[\"REGIÃO\"],colnames=[\"Insegurança Alimentar\"],normalize='index')*100).round(decimals=1)\n",
"plot = tb1.plot(kind=\"bar\",title=\"Distribuição Regional de Insegurança Alimentar 2013 (G3)\")\n",
"\n",
"abs1=pd.crosstab(base.REGIAO,base.Insegurança_Alimentar, margins=True, rownames=['REGIÃO'], colnames=['INSEGURANÇA ALIMENTAR'])\n",
"abs1=abs1.loc[['NORTE','NORDESTE','SUDESTE','SUL','CENTRO-OESTE']]\n",
"abs1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Nesse caso pode-se observar uma clara coerência entre os dados percentuais e absolutos, isso porque as regiões Norte e Nordeste mostram a maior frequência e número de pessoas que já passaram por situação de insegurança alimentar."
]
},
{
"cell_type": "code",
"execution_count": 194,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>INSEGURANÇA ALIMENTAR</th>\n",
" <th>Não</th>\n",
" <th>Sim</th>\n",
" <th>All</th>\n",
" </tr>\n",
" <tr>\n",
" <th>REGIÃO</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>NORTE</th>\n",
" <td>8570</td>\n",
" <td>5903</td>\n",
" <td>14473</td>\n",
" </tr>\n",
" <tr>\n",
" <th>NORDESTE</th>\n",
" <td>20348</td>\n",
" <td>16167</td>\n",
" <td>36515</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SUDESTE</th>\n",
" <td>28235</td>\n",
" <td>8639</td>\n",
" <td>36874</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SUL</th>\n",
" <td>15895</td>\n",
" <td>3722</td>\n",
" <td>19617</td>\n",
" </tr>\n",
" <tr>\n",
" <th>CENTRO-OESTE</th>\n",
" <td>9655</td>\n",
" <td>4029</td>\n",
" <td>13684</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"INSEGURANÇA ALIMENTAR Não Sim All\n",
"REGIÃO \n",
"NORTE 8570 5903 14473\n",
"NORDESTE 20348 16167 36515\n",
"SUDESTE 28235 8639 36874\n",
"SUL 15895 3722 19617\n",
"CENTRO-OESTE 9655 4029 13684"
]
},
"execution_count": 194,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAFaCAYAAAD7Oy2lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xm8VVXdx/HPl0EgwQFBQknBoVQUMcHh0YyccwhLc0hT\nS+WxtLRs0B4fRSszs0ybDLPEMosccqinJHPIcgJFBdEwRcUQGQRBcSB+zx9rncvhcu69h8u599y7\n+b5fr/u6++zh7N/e+5zfXnvtfdZSRGBmZsXUpd4BmJlZ23GSNzMrMCd5M7MCc5I3MyswJ3kzswJz\nkjczK7B2T/KSrpT0vzV6r80kLZHUNb++W9LJrXyvr0n6WZXzTpR0X17/Ta1ZX1uT9H+STmiH9YSk\nraqcd6ykX7V1TFa98mPS+PtktSNpO0mTJKlG79dD0lOS+rc0b02TvKSZkpZKWixpoaR/SDpVUsN6\nIuLUiPh6le+1b3PzRMQLEdE7Iv6zprFHxEUR0eIJQlJfYBZwPnAj8IvWrjMnyNfzF+slSd+r1Rcs\nIj4cEeNr8V4dQTWfB2uapGskLZM0sKl5avl9Wl2rU1io8v16SLpa0vM5H02R9OFG8+yTE+Ubku6S\ntHnZNEn6tqT5+e/b5Qla0n9Jeii/9+OS9mwhpK8Dl0bZD5MkHS3pwZwDXsnDn218IpC0jqTpkmaV\nxkXEW8DPgbNb2hdtUZI/NCL6AJsDFwNfBa6u9Uokdav1e1YjIhZExKci4s6IGBkRt63hW+4YEb2B\nDwJHAZ9e8yitnnKC6DBVoZLWBQ4HFgHH1Tmcmmtif3cDXiR9r9YHzgUmSBqcl+kH3AT8L9AXmAT8\ntmz5McBhwI7AMOBQ4L/zsn2B24DvABsAlwC3SdqwifgGAh8Cfl827izg8vwe7wYGAKcCewDrNHqL\nLwNzK7z1r4ETJPWotN4GEVGzP2AmsG+jcbsAy4Ht8+trgG/k4X7A7cBCYAHwN9KJ55d5maXAEuAr\nwGAggJOAF4B7y8Z1y+93N/At4CHgNeAWoG+eNgqY1VS8wFjgV2XT9gT+kWN7ETgxjz8YeDS//4vA\n2Ebv+RFgWl7ubmDbZvZXAFuVvZ4A/Kjs9fqkE+Rs4CXgG0DXPK0r8F1gHvAccHqFfXFyHu5C+pA/\nD7wCXAusn6eV9uEJeb/OA/6n0fG7P2/PbOCHwDpNbUOj7RsC3AMsBibmZcv38W5l+/gxYFQ1ny3g\nROA+4FLg1bz9Hy6b90Tg2bze54Bjy6Z9Gpiel/szsHnZtP2Bp0nJ8Mc59tI+bPz5KO238v39TeDv\npM/tVsCn8roW53j+u2z5UaQrwrPyMZkNfKpseq98fJ/P8dwH9MrTfge8nMffCwxt4Xt5POmzegYw\ntdG0hu1qYpu+kY/RElJi2wi4jvT5fxgYXPZe2+TjvCDvxyPLpl0D/Aj4Q94fDwJb5mn35vW+ntdz\nFLAhKTfMzcfqdmBQ2futsr+ryE+PA4fn4THAP8qmrZvfZ5v8+h/AmEafmwfy8CHAk43e+5/ASc3s\n/780+l6/XoqlhZiH5M/Qh2mUv/L0GcAHm32PllayOn9USPJ5/AvAZ8oOdinJfwu4Euie/z4AqNJ7\nlX0Ar80HpFcTH8qXgO3zPDeWfYBHNd5JNJHkSVchi4FjclwbAcPL3mcHUuIcBswBDsvT3psP3n55\nua8Az1CWFButvyFBkr4gs4EvlE2/Gfhp3paNSSev/87TTgWeBAaRvhB/qbAvSgnq0zmOLYDepBLM\nLxvt16vyPt0ReIt8cgJ2JiXjbnne6cCZlbahwvbdD3wP6AHslfdpaR9vCswHDsr7cr/8un9Lny1S\nEn8HOIV0svsM8G9AeV+9BrwvzzuQnASB0Xk/bJu351zyF51U4HgN+FiedkZex+ok+ReAoXn57qQC\nwZY5rg8CbwDvL/scLQMuzPMelKdvmKf/KL/npnkb/wvoUXY8++T9+n1gSgvfyztJpc0BeZ07l01r\n2K4mtumZvA3rkz5v/wT2zdt4LfCLsiT5IunE1g3YiVRg2K7sez+fVGjoRjpR/KapzxHpO3c48K68\nrb8Dfl82fZX93cI+GAC8yYokfjnwk0bzPMGKk8AiYNeyaTsDi/NwpSQ/A7isiXV/h5ULbwfm49Ct\nipx6O/BRKuSvPP1W4PPNvUd7XVL+m3RJ1Ng7pC/h5hHxTkT8LXLkzRgbEa9HxNImpv8yIqZGxOuk\nS7EjW1HP/QnSmff6HNf8iJgCEBF3R8QTEbE8Ih4Hrid9gSGVQP4QERMj4h1SSbMX6QvalEckvU5K\nnneTSpBIGkD64p+Zt/cV4DLg6LzckcDlETErIl4lVY015VjgexHxbEQsAc4Bjm5U5XVBRCyNiMdI\npeod8/ZOjogHImJZRMwknXQ+SAskbQaMBP43It6KiHtJJcGS44A/RsQf876cSLpkPqil986ej4ir\nItUfjyd9jgbkacuB7SX1iojZETEtjz8V+FZETI+IZcBFwPBcF3sQMC0ibsrTriCVllfHNRExLe+r\ndyLiDxHxr0juAe4gFWRK3gEuzPP+kVSKfV+uevg0cEZEvBQR/4mIf0SqhyUifh4Ri/PrscCOktav\nFFA+Dh8Cfh0Rc0gJ//jV2KZf5G1YBPwf8K+I+EveR78jJXNIiW9mRPwib/+jpELWx8ve6+aIeCgv\nex0wvKmV5u/cjRHxRkQsJpXaG3/uVtrfTb2XpO55feMj4qk8ujcpkZd7jXRCqTT9NaB3ri+/HxiY\n69S75wcctiSdkCrZgFTAKekHzMv7oRTjP/J9zKWS9srjPkq6cr+5qW3L77tBM9PbLclvSrqEa+w7\npJLCHZKeldTiTQRSaaHa6c+TSkn9qopyhfcA/6o0QdKu+SbNXEmLSImj9P6b5HUCEBHLczybNrOu\n95M+UEcBu5JKRJCuJroDs/PBX0hKsBuXrat8W5vbLyvFlYe7sSIpwsoJ7Y0cE5LeK+l2SS9Leo2U\nGKvZn5sAr+aTbfl6SzYHPl7atrx9e5KSdTUa4o2IN/Jg77y+o0jHZbakP0japmydl5etbwGplL0p\njfZnLmw03Oiq0krHQNKHJT0gaUFe30GsvO/ml3/RWbHf+wE9qfAZlNRV0sWS/pWPx8w8qalj8klg\neqmQQkp2n8iJrxpzyoaXVnjdOw9vDuza6HgeS6pvLqn4GatE0rsk/TTfOH2NVKWzQaMCW0u5gHzC\n/CXwNqlKs2QJsF6j2ddnRTJuPH19YEk+Yc8n1defRdofB5KupJv6vLzKipMHpCuafuWFrIj4r4jY\nIE/rku+jXAJ8voVN7EOq7mxSmyd5SSNJX6L7Gk/LpZGzImILUl32FyXtU5rcxFu2VNJ/T9nwZqTS\n0jxSNUrDmTZ/WJp6/OhF0pm5kl+TLpHeExHrk6qbSnfD/036sJfWoRzPS80FnD84E0glhPPKYngL\n6BcRG+S/9SJiaJ4+m1RVU1K+3Y2tFBdpvyxj5S9sU34CPAVsHRHrAV9jxfY2ZzawYf6wlq+35EXS\nVdcGZX/rRkRzVyRViYg/R8R+pBPGU6SqqNI6/7vROntFxD9otD/zsSvfvyt9flg5eTWsumz5HqSS\n7KXAgPwF/iPV7bt5pKqFSp/BT5CqnfYlJZ7BpVU28V7HA1vkk/TLpOqzflR/xVStF4F7Gu3b3hHx\nmVa+31nA+0hVJuuRqvtg5e1sNhfkY3g1qTBzeKPS/jTy1Wqed13S/p5WaXoeLk0jIu6J9OBFX9KJ\ndBtSdWolj5OqckvuJ323RzcT/takY/u3fNxuIl09vFy6eZxtS7ryblKbJXlJ60k6BPgNqc7viQrz\nHCJpq3wwFgH/IV1qQ0pAW7Ri1ccpPZP6LlJ95w35kv6fQE9JB+dSzLmkOs1KrgP2lXSkpG6SNpJU\nurTsAyyIiDcl7UL60pVMAA5WejSrO+mD+hbpJk41LgZOkfTuiJhNurz/bt6XXSRtKal0yToBOEPS\nppI2ID3F1JTrgS9IGiKpN6k0/ttGpcim9CFdqi7JJeKqvrQR8Typ+uUCpUfA9iQ9oVDyK+BQSQfk\n0mlPSaMkDar4hlWSNEDS6PylfYtUIit9pq4EzpE0NM+7vqRSdcIfgB0kHZZLWKexciKfAuyl9Cz5\n+qQqr+asQ/p8zQWWKT2+t38125CvAH8OfE/SJnn/7J5PHH3yds0nnXQuamZf7E5KXLuQqkaGk+5X\n/ZrVq7Kpxu3AeyV9MldhdJc0UtK2VS7f+Pveh3SlsFDpaZbzWxHTT0hJ8NBYtXr3ZlKV3uGSeub3\nf6ysOudaUqFzU0mbkr7L15QWlrRT3sb1SCfyFyPiz03EMRF4f14PEbEQuAD4saQjJPXJ3+/hrLiS\nn0oquJWO28mkfTScfAWT4+oLPNDcTmiLJH+bpMU5kP8hlRw+1cS8W5Muc5aQzm4/joi78rRvAefm\nS78vrcb6f0k6GC+TLnk/D5DrFD8L/IxUsn6dJi6vIuIFUknnLNKVwFRWnNU/C1yYt/E8UrItLfc0\nqa75B6TS2KGkD9jb1QSeT4T3kh6ZgvRFXId0w+tV4AZWVGdcRToJPE562uePpNJ5pWecf07aL/eS\nnjZ5E/hcNTEBXyKdyBbndf62+dlX8glSFdQC0pfo2tKEiHiRVJL5GikRvkja7jX9THYBvki6ellA\nqsf9TF7nzcC3gd/kKoCppKcWiIh5pPrjS0gJdDvSSapUDz6RtO2PA5NJSa1JuR7586TPx6ukfXHr\namzHl0g3AqeQjuu387ZdS6r2eon0uWjuC34CcEuke0gvl/5INx0PycmzJvL27k+6Z/Rv0vfv2zRd\nkGpsLDA+f9+PJN1Q7kX6Hj0A/Gl14lG6z/LfpKT4stJvUZZIOjbHO5d0Y/ebpOOzCyvud0GqGr2N\ndAyeIB3vn5ZN/0qO7UXSd/KjTcWS74X8lbKSe0RcQvqcfoWUvOfk9/8q6WGAZY2O2QJgeX5d+o5/\ngnSf4a1m90W0eJ9z7Sbpk6SnY2r+rH8t5ZLilRGxeYszW4tyXe4s0uOXd7U0fxvGIdLJ/MCow4+U\nrDYkbUd6QGCXqEHSzVd1jwF7RXooo0kd5gcbHVGu2niB9HRChyKpl6SDcnXSpqSScnN34a0Fuepo\ng/wFKt17aPZSuI3j6UV6fLIr6Xlp66Qi4slch1+TUnWkJ9a2aSnBg5N8S35BumT7v3oHUoFI9Xqv\nkqprprPipq21zu6kJ1pKVW2HVajLbU/bku5V9aGKJ0nMKnF1jZlZgbkkb2ZWYE7yZmYF1q4tOfbr\n1y8GDx7cnqs0M+v0Jk+ePC8iWmw7vpJ2TfKDBw9m0qRJ7blKM7NOT9LzLc9VmatrzMwKzEnezKzA\nnOTNzAqsLl3olXvnnXeYNWsWb775Zr1DsTbQs2dPBg0aRPfu1bZsa2a1VPckP2vWLPr06cPgwYNR\nbToytw4iIpg/fz6zZs1iyBD/Kt+sHupeXfPmm2+y0UYbOcEXkCQ22mgjX6WZ1VHdkzzgBF9gPrZm\n9VVVkpf0BUnTJE2VdH3u4KGvpImSZuT/G9YqqN69m+wVbK1y2GGHsdtuu600buzYsVx66aUAnHfe\nefzlL39p0xiuueYa/v3vf7fpOsys7bRYJ5+bsf08qdf1pZImkBrX3w64MyIuVuqb9Wya752o01q2\nbBndurXv7YuFCxcyefJkevfuzbPPPssWW6zaSdaFF17Y5nFcc801bL/99myyySZVL1OP/WVtY/DZ\nf2jVcjMvPrjGkVhrVVtd0w3olbtFexep55fRpEbwyf8Pq3Vwd999N6NGjeKII45gm2224dhjj6XU\naubZZ5/Ndtttx7Bhw/jSl1LHUXPnzuXwww9n5MiRjBw5kr///e8N4/fbbz+GDh3KySefzOabb868\nefOYOXMm22+/fcP6Lr30UsaOHQvAqFGjOPPMMxkxYgSXX345t912G7vuuis77bQT++67L3PmpO5R\nx44dy6c//WlGjRrFFltswRVXXNHwftdeey3Dhg1jxx135OSTTwbgqquuYuTIkey4444cfvjhvPHG\nG1Ry0003ceihh3L00Ufzm9/8puI8J554IjfccAOQfk18zjnnMHz4cEaMGMEjjzzCAQccwJZbbsmV\nV17ZsMx3vvMdRo4cybBhwzj//NSj2syZM9l222055ZRTGDp0KPvvvz9Lly7lhhtuYNKkSRx77LEM\nHz6cpUuXcuGFFzJy5Ei23357xowZ03A8Gu8vM+sYWkzyEfESqQ/DF0idHS+KiDtInRPPzrO9TOos\nt+YeffRRvv/97/Pkk0/y7LPP8ve//5358+dz8803M23aNB5//HHOPfdcAM444wy+8IUv8PDDD3Pj\njTc2JNYLLriAvffem2nTpnHEEUfwwgsvVLXut99+m0mTJnHWWWex55578sADD/Doo49y9NFHc8kl\nlzTM99RTT/HnP/+Zhx56iAsuuIB33nmHadOmcdFFF3HXXXfx2GOPNcz/sY99jIcffpjHHnuMbbfd\nlquvrtzh1PXXX88xxxzDMcccw/XXX19VvJttthlTpkzhAx/4QMMJ4IEHHmhI5nfccQczZszgoYce\nYsqUKUyePJl7770XgBkzZnDaaacxbdo0NthgA2688UaOOOIIRowYwXXXXceUKVPo1asXp59+Og8/\n/DBTp05l6dKl3H77il7wyveXmXUM1VTXbEgqtQ8BFgK/k3Rc+TwREZIqNkwvaQwwBlISWl277LIL\ngwalvp2HDx/OzJkz2W233ejZsycnnXQShxxyCIcccggAf/nLX3jyyScbln3ttddYsmQJ9913Hzff\nnDpNOvDAA9lww+puHxx11FENw7NmzeKoo45i9uzZvP322ys9EnjwwQfTo0cPevTowcYbb8ycOXP4\n61//yhFHHMFGG20EQN++qTvNqVOncu6557Jw4UKWLFnCAQccsMp658yZw4wZM9hzzz2RRPfu3Zk6\ndepKVx2VfOQjHwFghx12YMmSJfTp04c+ffrQo0cPFi5cyB133MEdd9zBTjvtBMCSJUuYMWMGm222\nGUOGDGH48NRX+c4778zMmTMrruOuu+7ikksu4Y033mDBggUMHTqUQw89dJX9ZWYdQzXVNfsCz0XE\n3Ih4B7gJ+C9gjqSBAPl/xW6oImJcRIyIiBH9+69+I2o9eqzoB7hr164N9b0PPfQQRxxxBLfffjsH\nHnggAMuXL+eBBx5gypQpTJkyhZdeeqnZm7jdunVj+fLlDa8bP+q37rrrNgx/7nOf4/TTT+eJJ57g\npz/96UrzVoqxKSeeeCI//OEPeeKJJzj//PMrPl44YcIEXn31VYYMGcLgwYOZOXNmVaX5UhxdunRZ\nKaYuXbqwbNkyIoJzzjmnYf8888wznHTSSVVvw5tvvslnP/tZbrjhBp544glOOeWUleIv319m1jFU\nk+RfAHaT9K7cqfA+pK7mbiX1Bk/+f0vbhLiqJUuWsGjRIg466CAuu+wyHnvsMQD2339/fvCDHzTM\nN2XKFAD22GMPJkyYAKQqi1dffRWAAQMG8MorrzB//nzeeuutlaoeGlu0aBGbbropAOPHj29yvpK9\n996bG264gQULFgA0/F+8eDEDBw7knXfe4brrrqu47PXXX8+f/vQnZs6cycyZM5k8eXKT9fKr44AD\nDuDnP/85S5YsAeCll17ilVea7yKyT58+LF68GFhxEuzXrx9LlixpuB9gZh1Xi9U1EfGgpBuAR4Bl\npP5ExwG9gQmSTgKeB45sy0DLLV68mNGjR/Pmm28SEXzve98D4IorruC0005j2LBhLFu2jL322osr\nr7yS888/n2OOOYZf/vKX7L777rz73e+mT58+dO/enfPOO49ddtmFTTfdlG222abJdY4dO5aPf/zj\nbLjhhuy9994899xzzcY4dOhQzjnnHPbaay9effVVDj74YMaNG8fXv/51dt11V/r378+uu+7akEBL\nZs6cyfPPP7/So5NDhgxh/fXX58EHH1yDvZZOgtOnT2f33XcH0qOqv/rVr+jatWuTy5x44omceuqp\n9OrVi/vvv59TTjmF7bffnne/+92MHDlyjeIxs7bXrn28jhgxIhq3Jz99+nS23XbbNl3vW2+9Rdeu\nXenWrRv3338/n/nMZxpK+e3hlFNOYdy4cWvtD4Pa4xhb2/AjlB2DpMkRMaI1y64VDzO/8MILHHnk\nkSxfvpx11lmHq666qt3Wvddee/Haa6+xfPnyZkvMZmZtYa1I8ltvvTWPPvpoXdZdekTRzKweOkTb\nNWZm1jac5M3MCmytqK4xayu+MWkdnUvyZmYF5iTfQUhaqc2X8sbS3n77bQ466CD22WcfTj311DpF\naGadkatrKmjtJXhTqrk079GjBzfddBPnnHMO/fr1W2naOuuswx//+MeaxmRmaweX5DuIbt26MWbM\nGC677LJVpjXVzPGCBQs47LDDGDZsGLvtthuPP/54e4dtZh2ck3wHctppp3HdddexaNGilcY31czx\n+eefz0477cTjjz/ORRddxPHHH1+PsM2sA3N1TQey3nrrcfzxx3PFFVfQq1evhvFNNXN83333ceON\nNwKpQbT58+fz2muvsd5669UlfjPreFyS72DOPPNMrr76al5//fWGcc01c2xm1hwn+Q6mb9++HHnk\nkSv1GNVUM8cf+MAHGporvvvuu+nXr59L8Wa2Eif5Duiss85i3rx5Da9LzRzvvPPOKz15M3bsWCZP\nnsywYcM4++yzq2rn3szWLq6Tr6Aev0YsdeQBqTOT8g6+R48ezejRo1dZpm/fvvz+979vl/jMrHNy\nSd7MrMCc5M3MCqzFJC/pfZKmlP29JulMSX0lTZQ0I//fsD0CNjOz6rWY5CPi6YgYHhHDgZ2BN4Cb\ngbOBOyNia+DO/NrMzDqQ1b3xug/wr4h4XtJoYFQePx64G/hq7UJb4fFZC1u13LBBG9Q4EjOzzmV1\n6+SPBq7PwwMiYnYefhkYUGkBSWMkTZI0ae7cua0M08zMWqPqJC9pHeAjwO8aT4uIAKLSchExLiJG\nRMSI/v37tzrQtcE3v/lNhg4dyrBhwxg+fDgPPvggJ598Mk8++WS9QzOzTmp1qms+DDwSEXPy6zmS\nBkbEbEkDgVdqH16djF2/xu+3qMVZ7r//fm6//XYeeeQRevTowbx583j77bf52c9+VttYzGytsjrV\nNcewoqoG4FbghDx8AnBLrYJaG82ePZt+/frRo0cPAPr168cmm2zCqFGjmDRpEgC9e/fmy1/+MkOH\nDmXffffloYceYtSoUWyxxRbceuut9QzfzDqoqpK8pHWB/YCbykZfDOwnaQawb35trbT//vvz4osv\n8t73vpfPfvaz3HPPPavM8/rrr7P33nszbdo0+vTpw7nnnsvEiRO5+eabOe+88+oQtZl1dFVV10TE\n68BGjcbNJz1tYzXQu3dvJk+ezN/+9jfuuusujjrqKC6+eOXz5jrrrMOBBx4IwA477ECPHj3o3r07\nO+ywAzNnzqxD1Gad29rQEbvbrulAunbtyqhRoxg1ahQ77LDDKg2Ode/eHUkAdOnSpaFqp0uXLixb\ntqzd4zWzjs/NGnQQTz/9NDNmzGh4PWXKFDbffPM6RmRmReCSfAexZMkSPve5z7Fw4UK6devGVltt\nxbhx4zjiiCPqHZqZdWJO8pVU8chjre2888784x//WGX83Xff3TBc3hzx2LFjV5qvfJqZWYmra8zM\nCsxJ3syswJzkzcwKrEMk+dT0jRWRj61ZfdU9yffs2ZP58+c7GRRQRDB//nx69uxZ71DM1lp1f7pm\n0KBBzJo1i+aaIZ7z6tJWvff0xb1aG5bVSM+ePRk0aFC9wzBba9U9yXfv3p0hQ4Y0O8+H14KfHpuZ\ntYW6V9eYmVnbcZI3MyswJ3kzswJzkjczKzAneTOzAqu2Z6gNJN0g6SlJ0yXtLqmvpImSZuT/G7Z1\nsGZmtnqqLclfDvwpIrYBdgSmA2cDd0bE1sCd+bWZmXUgLSZ5SesDewFXA0TE2xGxEBgNlLouGg8c\n1lZBmplZ61RTkh8CzAV+IelRST/LHXsPiIjZeZ6XgQFtFaSZmbVONUm+G/B+4CcRsRPwOo2qZiI1\nPFOx8RlJYyRNkjSpuaYLzMys9qpJ8rOAWRHxYH59Aynpz5E0ECD/f6XSwhExLiJGRMSI/v371yJm\nMzOrUott10TEy5JelPS+iHga2Ad4Mv+dAFyc/9/SppFapzW4FW0Pud0hs9qotoGyzwHXSVoHeBb4\nFOkqYIKkk4DngSPbJkQzM2utqpJ8REwBRlSYtE9twzEzs1ryL17NzArMSd7MrMCc5M3MCsxJ3sys\nwJzkzcwKzEnezKzA6t6Rt7Xux0LgHwyZWctckjczKzAneTOzAnOSNzMrMCd5M7MCc5I3MyswJ3kz\nswJzkjczKzAneTOzAnOSNzMrMCd5M7MCq6pZA0kzgcXAf4BlETFCUl/gt8BgYCZwZES82jZhmplZ\na6xOSf5DETE8IkrdAJ4N3BkRWwN35tdmZtaBrEl1zWhgfB4eDxy25uGYmVktVZvkA/iLpMmSxuRx\nAyJidh5+GRhQ8+jMzGyNVNvU8J4R8ZKkjYGJkp4qnxgRISkqLZhPCmMANttsszUK1szMVk9VJfmI\neCn/fwW4GdgFmCNpIED+/0oTy46LiBERMaJ///61idrMzKrSYpKXtK6kPqVhYH9gKnArcEKe7QTg\nlrYK0szMWqea6poBwM2SSvP/OiL+JOlhYIKkk4DngSPbLkwzM2uNFpN8RDwL7Fhh/Hxgn7YIyszM\nasO/eDUzKzAneTOzAnOSNzMrMCd5M7MCc5I3MyswJ3kzswJzkjczKzAneTOzAnOSNzMrsGpbobSO\naOz6rVxuUW3jMLMOyyV5M7MCc5I3MyswJ3kzswJzkjczKzAneTOzAnOSNzMrsKqTvKSukh6VdHt+\n3VfSREkz8v8N2y5MMzNrjdUpyZ8BTC97fTZwZ0RsDdyZX5uZWQdS1Y+hJA0CDga+CXwxjx4NjMrD\n44G7ga/WNjxba/mHXmY1UW1J/vvAV4DlZeMGRMTsPPwyqcNvMzPrQFpM8pIOAV6JiMlNzRMRAUQT\ny4+RNEkOtYbCAAAUz0lEQVTSpLlz57Y+UjMzW23VlOT3AD4iaSbwG2BvSb8C5kgaCJD/v1Jp4YgY\nFxEjImJE//79axS2mZlVo8UkHxHnRMSgiBgMHA38NSKOA24FTsiznQDc0mZRmplZq6zJc/IXA/tJ\nmgHsm1+bmVkHslpNDUfE3aSnaIiI+cA+tQ/JzMxqxb94NTMrMCd5M7MCc5I3MyswJ3kzswJzkjcz\nKzAneTOzAnOSNzMrMCd5M7MCc5I3MyswJ3kzswJzkjczKzAneTOzAnOSNzMrMCd5M7MCc5I3Mysw\nJ3kzswJbrU5DzMwMGLt+K5dbVNs4qtBiSV5ST0kPSXpM0jRJF+TxfSVNlDQj/9+w7cM1M7PVUU11\nzVvA3hGxIzAcOFDSbsDZwJ0RsTVwZ35tZmYdSItJPpIl+WX3/BfAaGB8Hj8eOKxNIjQzs1ar6sar\npK6SpgCvABMj4kFgQETMzrO8DAxooxjNzKyVqkryEfGfiBgODAJ2kbR9o+lBKt2vQtIYSZMkTZo7\nd+4aB2xmZtVbradrImKhpLuAA4E5kgZGxGxJA0ml/ErLjAPGAYwYMaLiiaDNdKI74GZmbaGap2v6\nS9ogD/cC9gOeAm4FTsiznQDc0lZBmplZ61RTkh8IjJfUlXRSmBARt0u6H5gg6STgeeDINozTzMxa\nocUkHxGPAztVGD8f2KctgjIzs9pwswZmZgXmJG9mVmBO8mZmBeYkb2ZWYE7yZmYF5iRvZlZgTvJm\nZgXmJG9mVmBO8mZmBeYkb2ZWYE7yZmYF5iRvZlZgq9WevJnViPs6sHbikryZWYE5yZuZFZiTvJlZ\ngTnJm5kVWDV9vL5H0l2SnpQ0TdIZeXxfSRMlzcj/N2z7cM3MbHVUU5JfBpwVEdsBuwGnSdoOOBu4\nMyK2Bu7Mr83MrANpMclHxOyIeCQPLwamA5sCo4HxebbxwGFtFaSZmbXOatXJSxpM6tT7QWBARMzO\nk14GBjSxzBhJkyRNmjt37hqEamZmq6vqJC+pN3AjcGZEvFY+LSICiErLRcS4iBgRESP69++/RsGa\nmdnqqSrJS+pOSvDXRcRNefQcSQPz9IHAK20TopmZtVaLzRpIEnA1MD0ivlc26VbgBODi/P+WNonQ\nzDofN9vQYVTTds0ewCeBJyRNyeO+RkruEySdBDwPHNk2IZqZWWu1mOQj4j5ATUzep7bhmJlZLfkX\nr2ZmBeYkb2ZWYE7yZmYF5iRvZlZgTvJmZgXmJG9mVmBO8mZmBeYkb2ZWYE7yZmYF5iRvZlZgTvJm\nZgXmJG9mVmBO8mZmBeYkb2ZWYE7yZmYF5iRvZlZgLSZ5ST+X9IqkqWXj+kqaKGlG/r9h24ZpZmat\nUU1J/hrgwEbjzgbujIitgTvzazMz62BaTPIRcS+woNHo0cD4PDweOKzGcZmZWQ20tk5+QETMzsMv\nAwNqFI+ZmdXQGt94jYgAoqnpksZImiRp0ty5c9d0dWZmthpam+TnSBoIkP+/0tSMETEuIkZExIj+\n/fu3cnVmZtYarU3ytwIn5OETgFtqE46ZmdVSNY9QXg/cD7xP0ixJJwEXA/tJmgHsm1+bmVkH062l\nGSLimCYm7VPjWMzMrMb8i1czswJzkjczKzAneTOzAnOSNzMrMCd5M7MCc5I3MyswJ3kzswJzkjcz\nKzAneTOzAnOSNzMrMCd5M7MCc5I3MyswJ3kzswJzkjczKzAneTOzAnOSNzMrMCd5M7MCW6MkL+lA\nSU9LekbS2bUKyszMaqPVSV5SV+BHwIeB7YBjJG1Xq8DMzGzNrUlJfhfgmYh4NiLeBn4DjK5NWGZm\nVguKiNYtKB0BHBgRJ+fXnwR2jYjTG803BhiTX74PeLr14a62fsC8dlxfeyvy9hV528Db19m19/Zt\nHhH9W7Ngt1pH0lhEjAPGtfV6KpE0KSJG1GPd7aHI21fkbQNvX2fXmbZvTaprXgLeU/Z6UB5nZmYd\nxJok+YeBrSUNkbQOcDRwa23CMjOzWmh1dU1ELJN0OvBnoCvw84iYVrPIaqMu1UTtqMjbV+RtA29f\nZ9dptq/VN17NzKzj8y9ezcwKzEnezKzAnOTNzArMSb4AJLX57x3MWkPSJvWOYW1XiCQv6ftlw2c0\nmnZNuwfUBiTdVzb8y0aTH2rncGqq6MdP0nFlw3s0mnb6qksUygP1DmBNSLpN0q1N/dU7vmoUpQS4\nV9nwCcDlZa+HtXMsbWXdsuGhjaapPQNpA0U/fl8EfpWHfwC8v2zap4EftntE7aezfzYvrXcAa6oo\nSV5NDBdJc8+6dvbnYIt+/JrbviJub7lO/dmMiHvqHcOaKkqS7yJpQ1L1U2m49OXpWr+wamoDSR8l\nbeMGkj6WxwtYv35h1UTRj180MVzpdacj6QdU3g4BG7RzODUl6Qma3rblEbFjO4e02grxYyhJM4Hl\nVC4VRURs0b4R1Z6kXzQ3PSI+1V6x1FrRj5+kN4BnSNu3ZR4mv94iItZtatnOQNIJzU2PiPHtFUut\nSdq80mhSu13nRMRB7RzSaitKkt88Ip6vdxxtSdLHIuKmesfRFop+/JpIFA2KvO1FImkn4BPAx4Hn\ngBsjosPfTylKkn8kIt7f8pydV5G3scjbBiDpjojYv95xtBVJt7FqldQ84K6I+FXlpToHSe8Fjsl/\n84DfAl+KiGZP3B1JUerki37zquiKfvxa1dlDJ1LpCZS+wHGSto+Iztz/81PA34BDIuIZAElfqG9I\nq6coJflXSN0PVhQRn2/HcNpEWb3uKpNI9dad9lHDoh8/Sc8CX2pqeoGr4boCkyNieL1jaS1Jh5Ga\nUd8D+BPpc/qziBhS18BWQ1FK8kuByfUOoo09Bxxa7yDaSNGP3/rAITRxYxkoZJKPiP9InfsiLSJ+\nD/xe0rqkPqzPBDaW9BPg5oi4o64BVqEoJflC1+kCSHo0InaqdxxtoejHby3Yvr4VRm8IHA9sFRHH\ntnNIbSo/4vtx4KiI2Kfe8bSkKCX5t+sdQDv4e70DaENFP36duzjbssmkK5LSdi4H5gN3A5+pU0xt\nJiJeJXUa0ik6DilE2zXA0ZIafhAk6UOSLpf0xdw1YRH8ufxRPEnnSXost6HRaeoHK4mI3SqNl/Re\nSVe1dzxt4JPlLyRtJOmjknauV0A1dhSwR0QMyXXVFwIvAz0pTkGy0ypKkv8tuW0XScOB3wEvADsC\nP65jXLX0TWAugKRDgONI7Z7cClxZx7jWmKRhku6QNFXSNyQNlHQj8FfgyXrHVwMXS9oeQNJAYCrp\n2P1S0pl1jaw2rgTeApC0F/AtYDywiE5S2i2yoiT5XhHx7zx8HKm/2e8CnwJ2qV9YNRUR8UYe/hhw\ndURMjoif0fkf0bsK+DVwOOlENgX4F6k+97J6BlYjQyJiah7+FDAxIg4FdiUl+86ua0QsyMNHAeMi\n4saI+F9gqzrGZRQnyZfXee4N3AkQEcvrE06bkKTekroA+5C3MetZp5hqpUdEXBMRT0fE5cDrEfGV\niHiz3oHVyDtlw/sAfwSIiMWk+uvOrmtZnwb7kK7ASlxdU2dFOQB/lTQBmE26q/9XaLg0LspNve+T\nSrivAdMjYhI0/NR6dj0Dq4GeeTtKJ+u3yl9HxCN1i6w2XpT0OWAWqZnhPwFI6gV0r2dgNXI9cI+k\neaTHYf8GIGkrUpWN1VFRHqEU6TJxIDAhIl7K43cCNo6IP9czvlqRtCmwMfBY6Soln8i6R8QLdQ1u\nDUi6q5nJERF7t1swbUDSxqSbkQOBH5WerZb0IWDniOj0bZZL2o20fXdExOt53HuB3gU4SXdqRUny\n20TEU3m4R0S8VTZtt4jo1L3TQOpdqNQOiKQ9IuLvZdNO7wwNJdmqJHWLiGX1jsOKqyh18r8uG76/\n0bSiPF3zxbLhHzSa1ulv3knaWNIFkm7IfxfkEnCnV+SuG63jK0qSXxt63insNuZ+Tx/OL6/NfwAP\nNe4TtZMqcteN1sEV5cZroXveyYq8jd8FDouIR8vG3SrpZuCnpEcNO7Mid91oHVxRkvwgSVeQSkWl\nYfLrTesXVk1tI+lxcu9CeZj8ulP3nASs1yjBAxARUyT1qUdANVbkrhutgytKkv9y2fCkRtMav+6s\ntq13AG1IkjbMbYKUj+xLMaoU7wE+UjZc3prove0fjq1NCvF0TTlJvQEiYkm9Y2kLkjYAts4v/xkR\nnf45ZEljgFNIba6XHrfbGfg26dfLP61XbGadXWGSvKTPAOew4ibXEuDbEVGIp2sk9SDVTx9Galte\nwObAzcCpEdGpf/SV2+P5CituTE4DvhMRt9UvqtqR9D5gDLBNHjWd9PP/f9YvKlsbFOFSGEnnki6B\nR0XERhGxEfAh4MN5WhGcS/p15HsiYqfc285mpCq3/61rZDUQEbdHxF6l45eHi5Lgdyc1u7uE1GDX\nVcDrwN35R0RmbaYQJXlJTwM7Nm7rJP9s/LGIeG99IqsdSVOBXcoaKSuN7w08EBHb1yeyNSfpvGYm\nR0R8vd2CaQOS/o90VXl3o/EfBM6OiA/XJTBbKxSiJE9KBKs0ZhURSylGA1AAyxsneGi499DZz9Sv\nV/gDOAn4ar2CqqEtGyd4gIi4h87/ZJR1cEV5uuYlSftERHnLjEjam87feFdJ5G7HKv14plOfyHKz\n0ADkRybPIDXJ+xvSM/Sd3eJmpr3ezDSzNVaUJP954Jb88/FSh9AjSD2sj65bVLW1PmnbCvkLyfy4\n5BeBY0kdTry/8SOVndh7yn67Ua5Iv+OwDqoQdfIAknoCn2DF0xlPAtcVqE3ywpL0HVJHKONIrTQW\n6vFXSSc0Nz0ixrdXLLb2KUySb0zSIRFxe73jaGu5OdcvR8Qp9Y6ltSQtJ3Uft4yV7y+IdL9lvboE\nZlYARamuqeRCoDBJXtIw4FJgE+D3wI+AH5LadenU9dYRUZQHACqSdBurtj00D7ir1Hy0WVspcpIv\nWt31VcBPSE0pH0jqJWo8cKyrpDq8Sp2C9AWOk7R9RJzd3gHZ2qPI1TW7RERh2uqWNCX/AKr0+tmI\n8ON3nZikrsDk8uNqVmuFKcnnDiZOo+xn8ZKej4g5dQyrloreD+paJyL+k3quNGs7hSjJ544lfg1c\nw4pHKHcGTiBVZ/y9iUU7jaL3g1pk+fHQxjYEjge2iohj2zkkW4sUJck/AHymcZvkkoYDP42Izt7p\nhHVikp4j3WwtFduXA/NJ7dl8IyJeq1NothYoSnVN0TudACpXSZGeK3+lflFZFY4CXoyI2dDw3Pzh\nQE+K8x20Dqooj64p/+S/8ciidDqxNvSDWmRXkn4HgKS9gG+RnoxaRPoBmFmbKUop4jLgDkmVOp24\nrG5R1VbR+0Etsq4RsSAPH0VqR/5G4EZJU+oYl60FCpHkI2KcpH8DXydVZQSpWYNvFKVNctaSKqmC\n6iqpW0QsA/YhdR5SUojvoHVchfmA5SYMVvmFq6R1I6IILf0VvR/UIrseuEfSPGAp8DcASVuRqmzM\n2kxhkoOkTSWNkLROfr2xpIuAGXUOrVZKVVIflNQn/40C/o/iVEkVUkR8EziL9IjvnrHikbYuwOfq\nFZetHYryCOWZwP8AzwA9gB+T6uOvBS4pPdXQ2RW9H1Qzq72iJPknSSWkBZI2A/4J7BERk1tY1Mys\n0IpSJ/9m6emFiHhB0tNFS/BF7wfVzNpGUZL8oEY97wwsfx0Rn69DTLVW6ebxuqR+UDciPVlkZraS\nolTXrFU975T1g3oSMAH4rn/1amaVFKUk/76I+Fq9g2hrBe8H1czaQFEeoTyw3gG0tdwP6sPAYmCH\niBjrBG9mLSlKdc1jwCia6A2q7CflnZb7QTWz1ihKkn8LeInKST7cg5KZra2KUif/ZETsVO8gzMw6\nmqLUyZuZWQVFSfKX1zsAM7OOqCh18r9g5ZuR5SIiTmrPeMzMOoqi1Mmv0sQw8B7gC0DXdo7FzKzD\nKERJvpykLYCvAXuRmuC9OiLerm9UZmb1UZQ6eSRtI+lXwG3AfcB2EfETJ3gzW5sVoiQv6XekPl2/\nS2rL5T/l04vwYygzs9YoSpKfyYobr6X/pR9G+cdQZrbWKkSSNzOzygpRJy/puLLhPRpNO739IzIz\n6xgKUZKX9EhEvL/xcKXXZmZrk0KU5Fm5YbLGjZRVbJnSzGxtUJQkH00MV3ptZrbWKEp1zRvAM6RS\n+5Z5mPx6i4hYt16xmZnVU1GaNdgRGAC82Gj8e4CX2z8cM7OOoSjVNZcBiyLi+fI/YFGeZma2VipK\nkh8QEU80HpnHDW7/cMzMOoaiJPkNmpnWq92iMDPrYIqS5CdJOqXxSEknA5PrEI+ZWYdQlKdrBgA3\nA2+zIqmPANYBPhoRvvlqZmulQiT5EkkfArbPL6dFxF/rGY+ZWb0VKsmbmdnKilInb9YmJO0o6beS\nflHeEJ5ZZ+GSvJlZgbkkb52apP9ImiJpqqTbJG2Qxw+WtDRPK/0dn6f1lvQTSf+S9IikyaWns/Jy\nUxut4/uSXpLUpdH4wyQ9Lmm6pCckHdZe221WraI0a2Brr6URMRxA0njgNOCbedq/StMa+RnwLLB1\nRCyX1B/4dKU3z4n9o6QmMz4I3JXH7whcCuwXEc9JGgJMlPRsRDxeu80zWzMuyVuR3A9s2twMkrYE\ndgHOjYjlABExNyK+3cQio4BpwE+AY8rGfwm4KCKey+/xHPAt4MtrsgFmteYkb4UgqSuwD3Br2egt\nG1XXfAAYCjxWSvBVOAa4nvQ7jIMldc/jh7LqD+0m5fFmHYaTvHV2vSRNIbU2OgCYWDbtXxExvOzv\nb40XlvQ/+QTw7wrT1gEOAn4fEa8BDwIHtM1mmLUNJ3nr7Ep18puT+g84rYX5nwR2LN1EjYhv5uXX\nqzDvAaR2kZ6QNBPYkxVVNk8COzeaf2dS1Y5Zh+Ekb4UQEW8AnwfOktTkAwUR8QypWuUbuYoHST2p\n3E3kMcDJETE4IgYDQ4D9JL2LdNP1HEmD83sMBr4GfLc2W2RWG07yVhgR8SjwOCtK243r5D+fx58M\nbAQ8I2kSqYrnK+XvlRP5gcAfyt7/deA+4NCImAJ8FbhN0lPAbcBX8nizDsM/hjIzKzCX5M3MCsxJ\n3syswJzkzcwKzEnezKzAnOTNzArMSd7MrMCc5M3MCsxJ3syswP4fQ508btQ/Y6QAAAAASUVORK5C\nYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4b5965f8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"tb19= (pd.crosstab(base9.REGIAO,base9.Insegurança_Alimentar,margins=True,rownames=[\"REGIÃO\"],colnames=[\"Insegurança Alimentar\"],normalize='index')*100).round(decimals=1)\n",
"plot = tb19.plot(kind=\"bar\",title=\"Distribuição Regional de Insegurança Alimentar 2009 (G4)\")\n",
"\n",
"abs19=pd.crosstab(base9.REGIAO,base9.Insegurança_Alimentar, margins=True, rownames=['REGIÃO'], colnames=['INSEGURANÇA ALIMENTAR'])\n",
"abs19=abs19.loc[['NORTE','NORDESTE','SUDESTE','SUL','CENTRO-OESTE']]\n",
"abs19"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## OBSERVAÇÃO DA SITUAÇÃO NA ZONA URBANA E RURAL:\n",
"ASSIM COMO NA CELULA SUPERIOR, UM GRÁFICO INICIAL PERCENTUAL SEGUIDO DE UMA TABELA CONTENDO VALORES ABSOLUTOS QUE POSSIBILITAM OBSERVAR A DIFERENÇA ENTRE AS DUAS ZONAS"
]
},
{
"cell_type": "code",
"execution_count": 195,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>INSEGURANÇA ALIMENTAR</th>\n",
" <th>Não</th>\n",
" <th>Sim</th>\n",
" <th>All</th>\n",
" </tr>\n",
" <tr>\n",
" <th>ZONA</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>Rural</th>\n",
" <td>10427</td>\n",
" <td>5745</td>\n",
" <td>16172</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Urbana</th>\n",
" <td>78420</td>\n",
" <td>21951</td>\n",
" <td>100371</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"INSEGURANÇA ALIMENTAR Não Sim All\n",
"ZONA \n",
"Rural 10427 5745 16172\n",
"Urbana 78420 21951 100371"
]
},
"execution_count": 195,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAExCAYAAACQ43JGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYFOW59/HvzY4yKpuIIJtBZZElDgbjEiIuuEIiUYhG\nSFCORo0xJgaNQfSckxjjG416EqPGiMaNiMTlGIOiHKNRERRZRIPRUUfZZB8WEbnfP55nhqaZpWem\ne3pm6ve5rr669rq7qvqup57azN0REZFkaJLvAEREpO4o6YuIJIiSvohIgijpi4gkiJK+iEiCKOmL\niCRIzpO+md1uZj/P0rS6mVmJmTWN7bPN7LwaTusqM7srw2GfMbMX4/wfrcn8ZHdm5mb2pXzHITul\nrpNs/ndlV2b2oJmNyuL0LjGzX2U0sLvX+AMUAVuAjcA64J/ABUCTGk7ruGqOMxs4rza/IYN5tAP+\nBAwHXgNOy+X8ahjjVUBJ2mcT4MC5+Y6vkrgd+FINxhsPvJjv+BvqB+gJ7AB+n611kuX4pgB/zvI0\nTwFejHlqOXAXUJDSvyVwN7Ah9v9R2vh3AO/E5TY+rd+Y2G8DsBKYCuxVSSwDgLcAS+nWGbgT+CT+\nf98D7gEOSVs3m1L+43el9GsFFAP7VrUsslHSP83dC4DuwPXAT4E/ZmG6uzCzZtmeZibcfY27f9fd\nZ7n7EHd/Ih9xVMbdf+HubVI/wE2EDWt6nsNLvHxtu5U4F1gLnGVmLfMdTLZVsLz3Bv4L2B/oA3QB\nfp3SfwrQm5DHvg5cYWYjUvq/CXwfeL2caf8T+Jq77wX0AprFeVXkP4D7PWZrM2sfp7EHcDRQAHwZ\n+D/g+LRxB6b8z8tqOdx9K/A3wrqtXC33nkWklc6Bwwl7w/6x/R7gv2JzB+BJwt52DfAPQhXTfXGc\nLYQ92BVAD8KebQLwIfBCSrdmcXqzgV8Ccwh72ceAdrHfMKC4onhJK00AR8UFvw74iLg3J5QQ3ojT\n/wiYkjbN04HFcbzZQJ9KltchwDPxt78DnJnS7x7gd3HFlQAvAfsBNxP+oG8DgzNcLyfHePukdOsT\n41sX4z09bd7/A/wv4ajtVeDAlP6/jb99AzAPODptfc+N/VYAv6kkrp8Aywilme+RUqoklLRujOt6\nBXA70LqC6YwnpaQf1+uPgQXAeuBhoFVl21zstz9hp7gKeB/4Qco0WxNKbGuBJYRtsjil/y4lYnbd\nzocRSl0/JZQa7wPaxjhWxWk+CXRNGX828J9xvW8EZgIdart9lrPsDPg3cGFczqPT+qeuk/J+0xWE\n0uwyYBRhW/tXXLZXpUynCTApzms1MI2d/80ecT7j4vr+FPhZ7DcC2AZ8TvgfvBm7fzeuh42EUvB/\npMxrt+WdwX/km8DClPZPgBNS2q8DHipnvBdJK+mn9W8D3As8Vckw7wFHpbT/F2GnUmkNSfo2V07/\ns4Hnq/ztmSSRSmZSRDlVMnFFXljOhvNLwp+5efwcTTzESZ9WyoZxL7An4U9Y2i016X8M9I/DTCcm\ncqqR9Al7943A2BhXe2BQynQOjRvxAMIfZVTsdxDhcOv4ON4VwLtAi3KWyZ6EP+V3CSWBwYSNvW/K\ncvoUOIxwqPYcIRGdCzSNG0bVKzQso9XAWSndmse4rgJaAMfG33twyrxXExJ4M+B+UjZ44Jy4TJoB\nlxP+WKVJ9WXgOykb/NAK4hoRl13punqAXRPMTcDjhOq0AuAJ4JcVTGs8uyf9OYQk3o6QHC6obJuL\n63MeMDkuk16EP+OJcbzrCSWttkBXwg6lOkl/O/Arws6sdVx+ZxBKcwXAX4C/pow/m5AgD4rDzwau\nr832WcGyOxr4LP6uW4EnKkosFfymyTGG8wk7sAfi7+lHKLT1jMNfCrwSl11L4A/Ag2n/7Tvjbx0Y\nY+qT/t9MiesU4MC47r4GbAa+XNHyzuB/cjNxG4/LwoFOKf3PIGWnkNK93KRP2CmvZ2cVzAkVzHfP\nOEzHlG6vUMXOOmXdfEL4/z0K9Ejr/2VgTZXTqWqAKoIoovyk/wo799ypG851hNL4bnur9GmlbBi9\nyumWmvSvT+nfl1BKaEr1kv6VwIwMf/PNwE2x+efAtJR+TQg7oWHljHcW8I+0bn8ArklZTnem9LsE\nWJLSfiiwrorYWhJK3bekdT86bihNUro9WLqhxXmn1g+eDLxdyXzWEg4zIRyBXUtKqbSCce5OW1cH\nxXX5JcIfeRO7Hl0cAbxfwbTGs3vSPyel/Qbg9sq2OeArwIdp3a4E/hSby3YAsf08qpf0txF3jBX8\nhkHA2pT22cDVKe3fB56uzfZZQf+7iDubuIw/J6UemMqT/hagaWwviMN+JWXceewsEC0Bhqf06xzn\n1Yyd/+PUI505wJj0/2Ylv+OvwKWZLu+0cY+P2/BBsf2AGE+rtGGKyhm3qpJ+lxj/QZX0T5/Xu8RC\nSmw/nXBEtxGYmdL9GEIBZR/gNmARMRfG/r2BL6r6/bm6eqcL4XAv3a/jD5xpZu+Z2aQMpvVRNfp/\nQCiFdMgoyp0OIJSydmNmXzGz581slZmtJ5yoLp3+/nGeALj7jhhPl3Im1R34ipmtK/0QDsf2Sxlm\nRUrzlnLa21TxO35L+GNdntZ9f+CjGF+pD9LiXJ7SvDl1Xmb2YzNbYmbrY9x7s3MZTCAk8LfN7DUz\nO7WC2PZn93VVqiOhBDwvZdk8HbtnqqL4K9rmugP7p62Pq4BOFcRb1XaYbpWHelYAzGwPM/uDmX1g\nZhsIO8t9Sq9Eq+I31HT7TB+2NfAtwpEc7v4y4aj82xn+ptXu/kVs3hK/K9pGuwMzUpbtEuALdi5f\nqGSbKyf2k8zsFTNbE6d3Mrv+zl2WdyXTGUo4Ohnt7v+KnUvi914pg+5NSLrV4u4fE7bdhyoYZF38\nLkjptpqwUyydxuPuvg9wGSHJl3Z/wd23ufs6wpFUD0K1bakCwtFGpbKe9M1sCCGZvJjez903uvvl\n7t6LsDf7kZkNL+1dwSQr6l7qgJTmboSk9ymh5LhHSlxNqTiJfEQ4dCzPA4RqhwPcfW9CVYHFfp8Q\nNu7SeViM5+MK5vF/7r5PyqeNu19Yxe/LiJl9h3BIeqa7f57W+xPgADNLXd/dKogzfbpHE6qtzgTa\nxo1xPXEZuPtSdx8L7Es4vH7EzPYsZ1LL2H1dlfqUkDD6pSybvT2ckK6VSra5jwhHEqnro8DdT06J\nt2vKpA5Im/RmUrYvdt15w+7b7eXAwYSS8V6EUhvs3JYqU9PtM903CIntd2a23MyWE/6r4zKIobo+\nAk5KW76tYlKsyi7LLp5snk4459MpboNPsevvrCpPYGaDCcvqe+4+q2xE97WE9T0wZfCBhHNfNdGM\nCtaXu29iZzVeqVnAqLT/Z6ZSl0EfwrmBSmUt6ZvZXrGU9xDh0GxhOcOcamZfislxPWHPX1r6XEGo\nV62uc8ysr5ntQTiUfySWRv4FtDKzU8ysOXA1ofqjPPcDx5nZmWbWzMzam9mg2K+AUE+21cwOZ9dS\n0TTgFDMbHudxOaFu8p/lzONJ4CAz+46ZNY+fIWbWp5xhq8XM+hNOAp/t7uWVSF8lJKkr4nyHAadR\ncWkkVQGhvnQV0MzMJpNSIjKzc8ysYzyKKC3F7Nh9MkwDxqesq2tKe8Rx7wRuMrN943S7mNmJGcRX\nqUq2uTnARjP7qZm1NrOmZtY/FlpK473SzNqaWRfg4rRJzwe+HccbQahnrkwBYce2zszakfL7M1DT\n7TPdOEI126GE6qVBwJHAQDM7tBrxZOJ24L/NrDuAmXU0s5EZjrsC6JGSBFsQ/rurgO1mdhJwQnWC\nif+Rp4FLvPwr8O4Fro7ruw/hnMU9KeO3MLNWhCTb3MxalcZnZmebWbfY3B34b0Iir8hT7Lq9/IZw\nXuE+MzvQggLC+imdfz8zGxS3tzZxnI8JR1Clvka4EKRS2Uj6T5jZRsKe/WcxmO9WMGxv4FnC4dTL\nwO/c/fnY75eEhb7OzH5cjfnfR1g5ywknQH8A4O7rCfWidxEWzibCGf7duPuHhMPFywlHCovYudf/\nPnBd/I2TCcmgdLx3CCc5byWUVk8jXMK6rZx5bCRsqGPYeTKm9MRTbf2IcILoUQs3r6V+rorxnAac\nFOP8HeH6/bczmPbfCX+WfxGqZLaya1XHCGCxmZUQqpfGuPuW9Im4+98I9c3PEapbnksb5Kex+yux\n+uNZQsm4tsrd5mLB4FTCH+t9wnK5i3BYD6EAURz7PQs8Qtihl7qUsExLq+n+WkUcNxNOWn5KOOf1\ndKY/oKbbZ6q44xoO3Ozuy1M+82Is2S7t/5ZQqp4ZY3uFcB4lE3+J36vN7PX43/kB4betJezYHq9m\nPJcTjvT/mPLfSC3JX0MogX9AOL9yg7unrqOZhJ32VwnX7G9h59FaX+CfZraJcPXVO4SdRkXuAM6O\nBRHc/VNgKOG/9SKhWmk+YYdeWhPQiXBV2gbC+abuwKmlR/Vxh3Qy4YqzSpVeOSNRrCZp4e5Zv9dA\nGi4zu5CwQ6uqRJ/rOLR9NgJm9gDhIpCqCguZTu8SQhXfFVUNq2fvpIiHTR8Sbs6QBDOzzmZ2pJk1\nMbODCSXFGXmOSdtnI+Hu385Wwo/TuzWThA9K+un+RLg+vMp6MWn0WhAuqd1IqIp6jFAtlk/aPqXW\nVL0jIpIgKumLiCSIkr6ISILU6dP/OnTo4D169KjLWYqINHjz5s371N2rc4d6heo06ffo0YO5c+fW\n5SxFRBo8M/ug6qEyk1H1jpldZmaLzWyRhTe+tDKzdhbeKLU0frfNVlAiIpIbVSb9eCffD4BCd+9P\neILlGMKzsme5e2/CLceZPDxNRETyKNMTuc2A1hbeSLMH4TECI9l5y+9UwgsVRESkHquyTt/dPzaz\n0jcabSE833mmmXVy92VxsOXs+sjUMmY2EZgI0K1bt/IGEZEMfP755xQXF7N1a5VPEJYGqlWrVnTt\n2pXmzZvnbB5VJv1YVz+S8DLldcBfzOyc1GHc3c2s3Lu83P0OwgOGKCws1J1gIjVUXFxMQUEBPXr0\nID6rSxoRd2f16tUUFxfTs2fPnM0nk+qd4wjPHV8Vn+j2KOFJcyvMrDOE55QQ3pspIjmydetW2rdv\nr4TfSJkZ7du3z/mRXCZJ/0NgqIU3/xjh8axLCI82LX0c6zjCs0lEJIeU8Bu3uli/VSZ9d3+V8Czx\n14GFcZw7CC+OPt7MlhKOBq7PYZwiUo42bWr9crFGYdSoUQwdOnSXblOmTOHGG28EYPLkyTz77LM5\njeGee+7hk08+yek8siGjm7Pc/Rp2f9PPZ4RSv0jW9Zj0v3U6v6LrT6nT+TVW27dvp1mzOr3nk3Xr\n1jFv3jzatGnDe++9R69eu7+A77rrrst5HPfccw/9+/dn//33z3icfCwvPXtHpBGYPXs2w4YNY/To\n0RxyyCGcffbZlD5Bd9KkSfTt25cBAwbw4x+Hl9KtWrWKM844gyFDhjBkyBBeeumlsu7HH388/fr1\n47zzzqN79+58+umnFBUV0b9//7L53XjjjUyZMgWAYcOG8cMf/pDCwkJ++9vf8sQTT/CVr3yFwYMH\nc9xxx7FiRXh3+pQpU/je977HsGHD6NWrF7fcckvZ9O69914GDBjAwIEDOe+88wC48847GTJkCAMH\nDuSMM85g8+bN5f72Rx99lNNOO40xY8bw0EPlvwF0/PjxPPLII0B4MsCVV17JoEGDKCws5PXXX+fE\nE0/kwAMP5Pbbby8b59e//jVDhgxhwIABXHNNKPMWFRXRp08fzj//fPr168cJJ5zAli1beOSRR5g7\ndy5nn302gwYNYsuWLVx33XUMGTKE/v37M3HixLL1kb686pqSvkgj8cYbb3DzzTfz1ltv8d577/HS\nSy+xevVqZsyYweLFi1mwYAFXX301AJdeeimXXXYZr732GtOnTy9LtNdeey3HHnssixcvZvTo0Xz4\n4YcZzXvbtm3MnTuXyy+/nKOOOopXXnmFN954gzFjxnDDDTeUDff222/z97//nTlz5nDttdfy+eef\ns3jxYn7xi1/w/PPP8+abb5YN/81vfpPXXnuNN998kz59+vDHP5b/srAHH3yQsWPHMnbsWB588MGM\n4u3WrRvz58/n6KOPLtshvPLKK2XJfebMmSxdupQ5c+Ywf/585s2bxwsvvADA0qVLueiii1i8eDH7\n7LMP06dPZ/To0RQWFnL//fczf/58WrduzcUXX8xrr73GokWL2LJlC08++WS5y6uu1e1xhYjkzOGH\nH07Xrl0BGDRoEEVFRQwdOpRWrVoxYcIETj31VE499VQAnn32Wd56662ycTds2EBJSQkvvvgiM2aE\nF4SNGDGCtm0ze7rKWWedVdZcXFzMWWedxbJly9i2bdsulx+ecsoptGzZkpYtW7LvvvuyYsUKnnvu\nOUaPHk379u0BaNeuHQCLFi3i6quvZt26dZSUlHDiiSfuNt8VK1awdOlSjjrqKMyM5s2bs2jRol2O\nSspz+umnA3DooYdSUlJCQUEBBQUFtGzZknXr1jFz5kxmzpzJ4MGDASgpKWHp0qV069aNnj17MmhQ\neGf5YYcdRlFRUbnzeP7557nhhhvYvHkza9asoV+/fpx22mm7La+6ppK+SCPRsmXLsuamTZuW1RfP\nmTOH0aNH8+STTzJixAgAduzYwSuvvML8+fOZP38+H3/8caUnhZs1a8aOHTvK2tMvK9xzzz3Lmi+5\n5BIuvvhiFi5cyB/+8Iddhi0vxoqMHz+e2267jYULF3LNNdeUeynjtGnTWLt2LT179qRHjx4UFRVl\nVNovjaNJkya7xNSkSRO2b9+Ou3PllVeWLZ93332XCRMmZPwbtm7dyve//30eeeQRFi5cyPnnn79L\n/KnLq64p6Ys0YiUlJaxfv56TTz6Zm266iTfffBOAE044gVtvvbVsuPnz5wNw5JFHMm3aNCBUcaxd\nuxaATp06sXLlSlavXs1nn322S1VFuvXr17O52V4sKF7HTb+7k02fbWdB8TpWbNjKsnVbWFC8jgXF\n69j6+RcsWbaBLn0Luf+hafxj4fssKF5X9r1u/QbW+B7Me38Vf7h7Kms3bSsbt/Tzx6n3cdu9f6Go\nqIiioiLmzZtXYb1+dZx44oncfffdlJSUAPDxxx+zcmXltyIVFBSwceNGYOdOsUOHDpSUlJSdT6gP\nVL0j0oht3LiRkSNHsnXrVtyd3/zmNwDccsstXHTRRQwYMIDt27dzzDHHcPvtt3PNNdcwduxY7rvv\nPo444gj2228/CgoKaN68OZMnT+bwww+nS5cuHHLIIRXOc8qUKVx04Xj22nsfDv/q0XzyUeVPBf7S\nwX2YcNFlfHf0yWxYv55jhp/A5F/dzEU/vopzTj+Otu06cOjgw9gcE3Cpjz/6kE+Kixnw5SFl3Xr2\n7Mnee+/Nq6++WoulFnaKS5Ys4YgjjgDCpbF//vOfadq0aYXjjB8/ngsuuIDWrVvz8ssvc/7559O/\nf3/2228/hgwZUuF4da1O35FbWFjoep6+ZEKXbO5uyZIl9OnTJ6fz+Oyzz2jatCnNmjXj5Zdf5sIL\nLyw7CqiOBcXrajT/a6+4lMm/urnaNykN6LpPjeZXH5W3ns1snrsXZmP6KumLSJkPP/yQM888kx07\ndtCiRQvuvPPOOpv3d884mU0lG9mxY0elJWqpHSV9ESnTu3dv3njjjbzM+0/Tn8rLfJNGJ3JFRBJE\nSV9EJEGU9EVEEkRJX0QkQZT0RaRBGXhAW2687uqy9qm331r28Ldt27Zx8sknM3z4cC644II8RVi/\n6eodEamxbN9P8fjFR1Y5TIuWLZn19BNMuPgy2rZrv2u/Fi146ildBVQZlfRFpEFp2rQZo789jj/f\n+bvd+lX0WOc1a9YwatQoBgwYwNChQ1mwYEFdh11vKOmLSINz1rjzeOqvf2HjhvW7dK/osc7XXHMN\ngwcPZsGCBfziF7/g3HPPzUfY9UKV1TtmdjDwcEqnXsBk4N7YvQdQBJzp7muzH6KIyK7aFOzFqWeM\n4YG776BVq1Zl3St6rPOLL77I9OnTATj22GNZvXo1GzZsYK+99spL/PmUyTty33H3Qe4+CDgM2AzM\nACYBs9y9NzArtouI1IlzJlzIXx++jy1bdr5Rq7LHOktQ3eqd4cC/3f0DYCQwNXafCozKZmAiIpXZ\nu21bTjh1FDMeuq+s2/r16+nSpQsAU6dOLet+9NFHc//99wPh1ZIdOnRIZCkfqp/0xwClbyjo5O7L\nYvNyoFPWohIRycC5Ey9m3Zo1Ze1TpkzhW9/6FocddhgdOnTYpfu8efMYMGAAkyZN2mWHkDQZP1rZ\nzFoAnwD93H2Fma1z931S+q91993erWZmE4GJAN26dTvsgw8qf7a2COjRyuWpi0crZ0tNH61cU3q0\ncuaqU9I/CXjd3VfE9hVm1jkG1Bko97Uy7n6Huxe6e2HHjh1rF62IiNRKdZL+WHZW7QA8DoyLzeOA\nx7IVlIiI5EZGSd/M9gSOBx5N6Xw9cLyZLQWOi+0iIlKPZfQYBnffBLRP67aacDWPiIg0ELojV0Qk\nQZT0RUQSRElfRBqcO2+5kW8MP4LRxx/JmScezauvvsp5553HW2+9le/Q6j09WllEam7K3uV2HlDD\nyS04r+r7eN6cN4cXZs3k4adm06JlS9auWc0BHVpz11131XCuyaKSvog0KKtWrmCfdu1o0bIlAG3b\ntWf//fdn2LBhzJ07F4A2bdrwk5/8hH79+nHccccxZ84chg0bRq9evXj88cfzGX7eKemLSIPy1WO+\nzopPPua0Ywr576suZ+7LL+02zKZNmzj22GNZvHgxBQUFXH311TzzzDPMmDGDyZMn5yHq+kPVOyLS\noOyxZxsefGo2r895mdf++Q+uuOh7NNn0q12GadGiBSNGjADg0EMPpWXLljRv3pxDDz2UoqKiPERd\nfyjpi0iD07RpU4YccRRDjjiK3of0Zfr0R3bp37x5c8wMgCZNmtAyVgU1adKE7du313m89Ymqd0Sk\nQSn691I+eP/fZe3vLF5I9+7d8xhRw9KoS/p6UqNI47N50yaun3wFGzdsoGnTphzQoxcP3/cnRo8e\nne/QGoRGnfRFJMemrC+3cy4frdx3wCDu/evMXbp16LAPs2fPLmsvKSkpa54yZcouw6b2SyJV74iI\nJIiSvohIgijpi4gkiJK+SAOS6etNpWGqi/WrpC/SQLRq1YrVq1cr8TdS7s7q1atp1apVTuejq3dE\nGoiuXbtSXFzMqlWr8h1KlVas3VKn81uysXWdzi9XWrVqRdeuXXM6DyV9kQaiefPm9OzZM99hZOQk\n3SNTb2X6jtx9zOwRM3vbzJaY2RFm1s7MnjGzpfG7ba6DFRGR2sm0Tv+3wNPufggwEFgCTAJmuXtv\nYFZsFxGReqzKpG9mewPHAH8EcPdt7r4OGAlMjYNNBUblKkgREcmOTEr6PYFVwJ/M7A0zu8vM9gQ6\nufuyOMxyoFN5I5vZRDOba2ZzG8IJKBGRxiyTpN8M+DLwe3cfDGwirSrHwzVk5V5H5u53uHuhuxd2\n7NixtvGKiEgtZJL0i4Fid381tj9C2AmsMLPOAPF7ZW5CFBGRbKky6bv7cuAjMzs4dhoOvAU8DoyL\n3cYBj+UkQhERyZpMr9O/BLjfzFoA7wHfJewwppnZBOAD4MzchCgiItmSUdJ39/lAYTm9hmc3HBER\nySU9e0dEJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRBlPRFRBJESV9EJEGU9EVEEkRJX0QkQZT0RUQS\nRElfRCRBlPRFRBJESV9EJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRBMnpzlpkVARuBL4Dt7l5oZu2A\nh4EeQBFwpruvzU2YIiKSDdUp6X/d3Qe5e+lrEycBs9y9NzArtouISD1Wm+qdkcDU2DwVGFX7cERE\nJJcyTfoOPGtm88xsYuzWyd2XxeblQKesRyciIlmVUZ0+cJS7f2xm+wLPmNnbqT3d3c3Myxsx7iQm\nAnTr1q1WwYqISO1kVNJ394/j90pgBnA4sMLMOgPE75UVjHuHuxe6e2HHjh2zE7WIiNRIlUnfzPY0\ns4LSZuAEYBHwODAuDjYOeCxXQYqISHZkUr3TCZhhZqXDP+DuT5vZa8A0M5sAfACcmbswRUQkG6pM\n+u7+HjCwnO6rgeG5CEpERHJDd+SKiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiCKOmLiCSI\nkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+\niEiCZJz0zaypmb1hZk/G9nZm9oyZLY3fbXMXpoiIZEN1SvqXAktS2icBs9y9NzArtouISD2WUdI3\ns67AKcBdKZ1HAlNj81RgVHZDExGRbMu0pH8zcAWwI6VbJ3dfFpuXA53KG9HMJprZXDObu2rVqppH\nKiIitVZl0jezU4GV7j6vomHc3QGvoN8d7l7o7oUdO3aseaQiIlJrzTIY5kjgdDM7GWgF7GVmfwZW\nmFlnd19mZp2BlbkMVEREaq/Kkr67X+nuXd29BzAGeM7dzwEeB8bFwcYBj+UsShERyYraXKd/PXC8\nmS0FjovtIiJSj2VSvVPG3WcDs2PzamB49kMSEZFc0R25IiIJoqQvIpIgSvoiIgmipC8ikiBK+iIi\nCaKkLyKSINW6ZFOqMGXvOp7f+rqdn4g0eCrpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohI\ngijpi4gkiJK+iEiCKOmLiCSIkr6ISIJUmfTNrJWZzTGzN81ssZldG7u3M7NnzGxp/G6b+3BFRKQ2\nMinpfwYc6+4DgUHACDMbCkwCZrl7b2BWbBcRkXqsyqTvQUlsbR4/DowEpsbuU4FROYlQRESyJqM6\nfTNrambzgZXAM+7+KtDJ3ZfFQZYDnXIUo4iIZElGSd/dv3D3QUBX4HAz65/W3wml/92Y2UQzm2tm\nc1etWlXrgEVEpOaqdfWOu68DngdGACvMrDNA/F5ZwTh3uHuhuxd27NixtvGKiEgtZHL1Tkcz2yc2\ntwaOB961wM0IAAAKoUlEQVQGHgfGxcHGAY/lKkgREcmOTN6c1RmYamZNCTuJae7+pJm9DEwzswnA\nB8CZOYxTRESyoMqk7+4LgMHldF8NDM9FUCIikhu6I1dEJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRB\nlPRFRBJESV9EJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRBMnngmohI/TZl7zqe3/q6nV8WqaQvIpIg\nSvoiIgmipC8ikiBK+iIiCaITuSKgE4GSGCrpi4gkSCYvRj/AzJ43s7fMbLGZXRq7tzOzZ8xsafxu\nm/twRUSkNjIp6W8HLnf3vsBQ4CIz6wtMAma5e29gVmwXEZF6rMqk7+7L3P312LwRWAJ0AUYCU+Ng\nU4FRuQpSRESyo1p1+mbWAxgMvAp0cvdlsddyoFMF40w0s7lmNnfVqlW1CFVERGor46RvZm2A6cAP\n3X1Daj93d8DLG8/d73D3Qncv7NixY62CFRGR2sko6ZtZc0LCv9/dH42dV5hZ59i/M7AyNyGKiEi2\nZHL1jgF/BJa4+29Sej0OjIvN44DHsh+eiIhkUyY3Zx0JfAdYaGbzY7ergOuBaWY2AfgAODM3IYqI\nSLZUmfTd/UXAKug9PLvhiIhILumOXBGRBFHSFxFJECV9EZEEUdIXEUkQJX0RkQRR0hcRSRAlfRGR\nBFHSFxFJECV9EZEEUdIXEUkQJX0RkQRR0hcRSRAlfRGRBFHSFxFJECV9EZEEUdIXEUkQJX0RkQTJ\n5B25d5vZSjNblNKtnZk9Y2ZL43fb3IYpIiLZkElJ/x5gRFq3ScAsd+8NzIrtIiJSz1WZ9N39BWBN\nWueRwNTYPBUYleW4REQkB2pap9/J3ZfF5uVApyzFIyIiOVTrE7nu7oBX1N/MJprZXDObu2rVqtrO\nTkREaqGmSX+FmXUGiN8rKxrQ3e9w90J3L+zYsWMNZyciItlQ06T/ODAuNo8DHstOOCIikkuZXLL5\nIPAycLCZFZvZBOB64HgzWwocF9tFRKSea1bVAO4+toJew7Mci4iI5JjuyBURSRAlfRGRBFHSFxFJ\nECV9EZEEUdIXEUkQJX0RkQRR0hcRSRAlfRGRBFHSFxFJECV9EZEEUdIXEUkQJX0RkQRR0hcRSRAl\nfRGRBFHSFxFJECV9EZEEUdIXEUkQJX0RkQSpVdI3sxFm9o6ZvWtmk7IVlIiI5EaNk76ZNQX+BzgJ\n6AuMNbO+2QpMRESyrzYl/cOBd939PXffBjwEjMxOWCIikgvNajFuF+CjlPZi4CvpA5nZRGBibC0x\ns3dqMc96zaAD8GmdzfBaq7NZNXZadw1bAtZf92xNqDZJPyPufgdwR67nUx+Y2Vx3L8x3HFJ9WncN\nm9Zf5mpTvfMxcEBKe9fYTURE6qnaJP3XgN5m1tPMWgBjgMezE5aIiORCjat33H27mV0M/B1oCtzt\n7ouzFlnDlIhqrEZK665h0/rLkLl7vmMQEZE6ojtyRUQSRElfRCRBlPRFRBJESV9EJEFyfnNWY2Vm\nP6qsv7v/pq5ikZozs1OAfkCr0m7ufl3+IpLKmNkTQIVXn7j76XUYToOkpF9zBfkOQGrHzG4H9gC+\nDtwFjAbm5DUoqcqN+Q6godMlm5JYZrbA3QekfLcB/ubuR+c7NpFcUUm/lsysFTCB3asIvpe3oCRT\nW+L3ZjPbH1gNdM5jPFIFM1tI+dU7Buxw94F1HFKDo6Rfe/cBbwMnAtcBZwNL8hqRZOpJM9sH+DXw\nOiGZ3JXfkKQKp5bTzQjPAbuyjmNpkFS9U0tm9oa7D06pImgO/MPdh+Y7NsmcmbUEWrn7+nzHIpkx\ns8HAt4FvAe8D0939tvxGVf+ppF97n8fvdWbWH1gO7JvHeKQazOyrQA/if8HMcPd78xqUVMjMDgLG\nxs+nwMOEwuvX8xpYA6KkX3t3mFlb4GrCU0bbAD/Pb0iSCTO7DzgQmA98ETs7oKRff70N/AM41d3f\nBTCzy/IbUsOipF8LZtYE2ODua4EXgF55DkmqpxDo66rjbEi+SXiM+/Nm9jThNa16DVk16I7cWnD3\nHcAV+Y5DamwRsF++g5DMuftf3X0McAjwPPBDYF8z+72ZnZDf6BoGncitJTO7np11i5tKu7v7mrwF\nJRkxs+eBQYQbsj4r7a67OhuWWL36LeAsdx+e73jqOyX9WjKz98vp7O6uqp56zsy+Vl53d/+/uo5F\npK4o6YuIJIhO5NaSmZ1bXndd9lf/mdlQ4FagD9CC8NrPTe6+V14DE8khJf3aG5LS3AoYTri7U0m/\n/ruNcCXIXwhX8pwLHJTXiERyTNU7WRZv63/I3UfkOxapnJnNdffC0rupY7c33H1wvmMTyRWV9LNv\nE9Az30FIRjabWQtgvpndACxDlzFLI6ekX0tpL3VoAvQlVBdI/fcdwjq7GLiM8NCuM/IakUiOqXqn\nltIu+9sOfODuxfmKR6onlvQPIey433H3bXkOSSSnlPSzLD6aYay735/vWKRy8VWJtwP/JtzK3xP4\nD3f/W14DE8khJf0aMrO9gIuALoQHrT0T238MvOnuI/MYnmTAzN5m1wd3HQj8r7sfkt/IRHJHdfo1\ndx+wFngZOA+4ilBaHOXu8/MZmGRsY2nCj94DNuYrGJG6oJJ+DZnZQnc/NDY3JVz50c3dt+Y3MqmK\nmX0zNh4PdAemEer0vwV86O7fz1dsIrmmkn7Nlb48BXf/wsyKlfAbjNNSmlcApSfjV5HynmORxkgl\n/Roysy/Y+VRNA1oDm2Oz61b++i0enf3A3W/KdywidUlJXxLLzOa4++H5jkOkLinpS2KZ2U1Ac3Z/\nF8LreQtKJMeU9CWx4ktUYOcd1aVVc8fmKSSRnFPSl8Qxsx+VNsZvJ5zEfdHdy3spjkijoYdLSRIV\nxE+b+CkgPFr5b2Y2Jp+BieSaSvoikZm1A5519y/nOxaRXFFJXySKL7O3KgcUacCU9EUiM/s64dEa\nIo2W7siVxDGzhey8YqdUO+ATwisTRRot1elL4phZ97RODqx2903lDS/SmCjpi4gkiOr0RUQSRElf\nRCRBlPSlUTGzb5jZ/LTPDjM7ycz6mdlzZvaOmS01s5+bmcXxxsfhBqRMa5GZ9UhpH2RmbmYj6v6X\niWSHkr40Ku4+w90HlX6A3wH/AF4gvNbyenc/GBgIfBVIfWFKMfCzSiY/Fngxfos0SEr60miZ2UHA\nZOA7wBjgJXefCeDum4GLgUkpozwJ9DOzg8uZlhHerDUeON7M9LIVaZCU9KVRMrPmwAPA5e7+IdAP\nmJc6jLv/G2gTX3IPsAO4gfC+43RfBd6P48wGTslR6CI5paQvjdV/Aovd/eFqjvcAMNTMeqZ1Hws8\nFJsfQlU80kDpjlxpdMxsGHAGkPrgtLeAY9KG6wWUuPuGeD4Xd99uZv8P+GnKcE3j9Eaa2c8Iz+dp\nb2YF7r4xl79FJNtU0pdGxczaAn8Czk1LyPcDR5nZcXG41sAthOqcdPcAxwEdY/twYIG7H+DuPdy9\nOzAd+EZufoVI7ijpS2NzAbAv8PvUyzaB04GRwNVm9g6wEHgNuC19Au6+jbBD2Dd2GgvMSBtsOqri\nkQZIj2EQEUkQlfRFRBJESV9EJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRBlPRFRBJESV9EJEH+P4yY\nzrRerGInAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4c07b080>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"tb2 = (pd.crosstab(base.ZONA,base.Insegurança_Alimentar,margins=True,rownames=[\"ZONA\"],colnames=[\"Insegurança Alimentar\"],normalize='index')*100).round(decimals=1)\n",
"plot = tb2.plot(kind=\"bar\",title=\"Distribuição em Zonas de Insegurança Alimentar 2013 (G5)\")\n",
"\n",
"abs2=pd.crosstab(base.ZONA,base.Insegurança_Alimentar, margins=True, rownames=['ZONA'], colnames=['INSEGURANÇA ALIMENTAR'])\n",
"abs2=abs2.loc[['Rural','Urbana']]\n",
"abs2\n"
]
},
{
"cell_type": "code",
"execution_count": 196,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>INSEGURANÇA ALIMENTAR</th>\n",
" <th>Não</th>\n",
" <th>Sim</th>\n",
" <th>All</th>\n",
" </tr>\n",
" <tr>\n",
" <th>ZONA</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>Rural</th>\n",
" <td>11392</td>\n",
" <td>6251</td>\n",
" <td>17643</td>\n",
" </tr>\n",
" <tr>\n",
" <th>Urbana</th>\n",
" <td>71311</td>\n",
" <td>32209</td>\n",
" <td>103520</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"INSEGURANÇA ALIMENTAR Não Sim All\n",
"ZONA \n",
"Rural 11392 6251 17643\n",
"Urbana 71311 32209 103520"
]
},
"execution_count": 196,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAExCAYAAACQ43JGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmcnfPd//HXJ7vKIJEI2UODyF4TYm0qlliTFpHYEqUp\nRVWphhJpbm1V3Sh+rQoqdhoNobhDyK1xhzQhYglNMRhkkX2yiMjn98f3O5MzJ7OczJwzJzPX+/l4\nnMe59utzbZ/re33Pda7L3B0REUmGRvkOQERE6o6SvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISILk\nPOmb2R1mdk2WptXZzErMrHFsn2Fm59VwWleZ2V0ZDvu8mc2M8/97TeYnWzMzN7Nv5zsO2SJ1m2Tz\n2JXyzOxhMxuWxeldbGa/z2hgd6/xBygC1gNrgJXA/wHnA41qOK0jt3GcGcB5tVmGDObRGvgrMBj4\nF3BiLudXwxivAkrSPmsBB87Od3xVxO3At2sw3mhgZr7jr68foBuwGfhztrZJluMbDzyQ5WkeD8yM\neWoRcBdQkNK/OXAPsDr2/3na+P2AucC6+N0vbdybgc+BFcCfgKZVxNIHeBewlG57ABPjNEqAD4F7\ngX1ThmkMXBeHWQO8AewS+7UAioHdqlsX2Sjpn+juBUAX4Hrgl8DdWZhuOWbWJNvTzIS7L3f3c9x9\nursPcPen8hFHVdz9t+7eMvVD2AnfBR7Pc3iJl699twpnE5LTaWbWPN/BZFsl63tnQsJsD/QAOgB/\nSOk/HuhOyGPfA64wsyFxes2AJ4EHgFbAJODJ2B1gLFAI9AL2Br4DXF1FiD8GHvSYrc1sV0KB+VvA\nYUBBnMb/AkeljPdr4GDgIGAn4CxgA4C7bwCeJWzbqtXy7FlEWukcOIBQiugV2+8FrovNbYCnCWfb\n5cA/CVVM98dx1hPOclcAXQmljnOBT4CXU7o1idObAfwOmE04Qz8JtI79BgHFlcVLWmkCODSu+JXA\np8DolBLCG3H6nwLj06Z5EvBOHG8G0KOK9bUv8Hxc9veB4Sn97iWUEJ6N6+AVYHfgFsIB+h7QP8Pt\nclyMt0dKtx4xvpUx3pPS5v3/gH8QShCvAXul9P9jXPbVhFLOYWnbe07stxi4qYq4fgF8QSip/JCU\nUiWhtHRj3NaLgTuAHSqZzmhSSvpxu14OzAdWAY8CLara52K/9oST4lLgI+CnKdPcgXBwrwAWEPbJ\n4pT+5UrElN/PBxFKXb8klBrvJySLp+O8VsTmjinjzwD+K273NcA0oE1t988K1p0BHwAXxPV8Slr/\n1G1S0TJdASyJ23EYYV/7d1y3V6VMpxEhGX4ALAMeY8ux2TXOZ1Tc3l8Cv4r9hgAbga8Jx8Gbsfs5\ncTusIZSCf5wyr63WdwbHyA+At1LaPweOTmmfADwSm48GPqN8yfwTYEhsnkP5Y/l04NMq5v0hcGhK\n+3XAm1RRQxL3nxJSjssKhjkDeKnaZc8kiVQxkyIqqJKJK+SCCnac3xEO5qbxc1jpikyfVsqOcR+w\nI+EgLO2WmvQ/I5xhdyQcwA+k7giVxUtK0iec3dcAI2NcuxIv3+J0ehN24j6EA2VY7Lc3oRrlqDje\nFcB/gGYVrJMdCQflOUAToD9hZ98vZT19CexPuFR7kZCIzmbLZV31GzSso2XAaSndmsa4rgKaAUfE\n5d0nZd7LCAm8CfAgcYeP/c+M66QJcBnhwCpNqrOAs2JzS2BgJXENieuudFs9RPkEczMwlVCdVgA8\nBfyukmmNZuukP5uQxFsTksP5Ve1zcXvOBcbFdbIn4WA8Jo53PaGk1QroSDihbEvS3wT8nnAy2yGu\nv5MJpbkC4G/AEynjzyAkyL3j8DOA62uzf1ay7g4DvorLdRvwVFr/qpL+pri+mgI/IpzAHorL05NQ\naOsWh78EeDWuu+bAX4CH047tiXFZ+8aYeqQfmylxHQ/sFbfddwnVLN+pbH1ncJzcwpak3irG0y6l\n/8nEkwJwKfBs2vhPAZfF5vSkf0ac3s6V5AEH2qZ0e5XqT9aHE074pSe2fwMXpg3zHWB5tcte3QDV\nBFJExUn/VbacuVN3nAmE0vhWdYbp00rZMfasoFtq0r8+pf9+hFJCY7Yt6V8JTMlwmW8Bbo7N1wCP\npfRrRDgJDapgvNOAf6Z1+wtwbcp6mpjS72JgQUp7b2BlNbE1jzvgrRUc6ItIKUkAD5fuaHHed6X0\nOw54r4r5rAD6xuaXCZedbaqJ7Z60bbV33JbfJhzIayl/dXEQ8FEl0xrN1kn/zJT2G4A7qtrngAOB\nT9K6XQn8NTaXnQBi+3lsW9LfSDwxVrIM/YAVKe0zgKtT2n8CPFeb/bOS/ncRTzZxHX9NSj0wVSf9\n9UDj2F4Qhz0wZdy5bCkQLQAGp/TbI86rCVuO49QrndnAiPRjs4rleAK4JNP1nTbuUXEf3ju2d4rx\ntEgbpig2X0NKISh2e5Atx891hCu0toSr89fi9PaoYN4dKpjXf4iFlNh+EiHBrwGmxW6nx/HuJpwo\n+xBOukeljNcd+Ka65c/V3TsdCJd76f4QF3CamX1oZmMzmNan29D/Y0IppE1GUW7RiVDK2oqZHWhm\nL5nZUjNbRfihunT67eM8AXD3zTGeDhVMqgtwoJmtLP0QSgS7pwyzOKV5fQXtLatZjj8SDqzL0rq3\nJ1xubk7p9nFanItSmtelzsvMLjezBWa2Ksa9M1vWwbmEBP6emf3LzE6oJLb2bL2tSrUllIDnpqyb\n52L3TFUWf2X7XBegfdr2uApoV0m81e2H6ZZ6qGcFwMy+ZWZ/MbOPzWw14WS5S+mdaNUsQ033z/Rh\ndwBOJSQs3H0W4ar89AyXaZm7fxOb18fvyvbRLsCUlHW7APiGLesXqtjnKoj9WDN71cyWx+kdR/nl\nLLe+q5jOQMLVySnu/u/YuSR+75Qy6M6EpFvaP7Vfev/fEKrY5hGq4J4gHIeL2drK+F2Q0m0Z4aQI\ngLtPdfddCFcYpb8blK7vCe6+3t3nA48Q1kOpAkL1ZpWynvTNbAAhmcxM7+fua9z9Mnffk3A2+7mZ\nDS7tXckkK+teqlNKc2fCyv6SUHL8Vkpcjak8iXxKuHSsyEOEaodO7r4zoarAYr/PCTt36TwsxvNZ\nJfP4X3ffJeXT0t0vqGb5MmJmZxEuSYe7+9dpvT8HOplZ6vbuXEmc6dM9jFBtNRxoFXfGVcR14O4L\n3X0ksBvh8nqyme1YwaS+YOttVepLwk7dM2Xd7OzhB+laqWKf+5RwJZG6PQrcvfQg+oJQNVGqU9qk\n15Gyf1H+5A1b77eXAfsQSsY7ES7XYcu+VJWa7p/pvk9IXn8ys0VmtohwrI7KIIZt9SlwbNr6beHu\n1e5zpK27+GPz44TffNrFffAZyi9ndXkCM+tPWFc/dPfpZSO6ryBs774pg/cl/PZF/O4Tj+9SfUr7\nxyR8kbt3iPvZMmBuWiGrdF5r2VKNV2o6MCzt+Ew3v4LlTF/mHoTfBqqUtaRvZjvFUt4jhEuztyoY\n5gQz+3ZceasIZ/7SFbOYUK+6rc40s/3M7FuES/nJsTTyb6CFmR1vZk0Jv6ZXdqfCg8CRZjbczJqY\n2a5m1i/2KyDUk20wswMoXyp6DDjezAbHeVxGqJv8vwrm8TSwt5mdZWZN42eAmfWowTKXY2a9CD8C\nn+HuFZVIXyMkqSvifAcBJxK2VXUKCPWlS4EmZjaOlFKPmZ1pZm3jDl5aitlqZyesq9Ep2+ra0h5x\n3InAzWa2W5xuBzM7JoP4qlTFPjcbWGNmvzSzHcyssZn1ioWW0nivNLNWZtYBuCht0vOA0+N4Qwj1\nzFUpIJzYVppZa1KWPwM13T/TjSJUs/UmVC/1Aw4B+ppZ722IJxN3AL8xsy4AZtbWzIZmOO5ioGtK\nEmxGOHaXApvM7FjCj6sZi8fIc8DFXvEdePcBV8ft3YPwm8W9sd8Mwn7zUzNrbmY/JSTcF+O0O5hZ\newsGEqqDqtq+z1B+f7mJ8LvC/Wa2V5xOAWH7AODuHxBuQvhVjKEHMIKQV0p9l3AjSJWykfSfMrM1\nhDP7r+ICnFPJsN2BFwiXS7OAP7n7S7Hf7wgrfaWZXb4N87+fsHEWEX4A/SmAu68i1IveRSjRriX8\nwr8Vd/+EcJl0GeFK4W22nPV/AkyIyziOkAxKx3uf8CPnbYTS6omEW1g3VjCPNYQddQSh5L2ILT88\n1dbPCT8Q/d3Cn9dSP1fFeE4Ejo1x/olw//57GUz7fwgHy78JVTIbKF/VMQR4x8xKCNVLI9x9ffpE\n3P1ZQn3zi4TqlhfTBvll7P5qrP54gVAyrq0K97lYMDiBcGB9RFgvdxEu2yEUIIpjvxeAyYQTeqlL\nCOu0tJruiWriuIVQF/sl4Tev5zJdgJrun6niiWswcIu7L0r5zI2xZLu0/0dCqXpajO1Vwu8omfhb\n/F5mZq/HY+enhGVbQTixTd3GeC4jXOnfnXJsvJPS/1pCCfxjQpK/wd2fA4jHzzDCTRUrCb8pDUs5\nzvciFPTWEu74Guvu06qI5U7gjNIrB3f/EhhIOLZmEqqN5hFO6Kk1ASMJNQvLCHfaXVN6xWJmLQj7\nyKTqVkTpnTMSxWqSZu6e9f8aSP1lZhcQTmjVlehzHYf2zwbAzB4i3ARSXWEh0+ldTKjiu6K6YfXs\nnRRm1pLww9b38h2L5JeZ7WFmh5hZIzPbh1BSnJLnmLR/NhDufnq2En6c3m2ZJHxQ0k/3V8L9t9XW\ni0mD14xwS+0aQlXUk4RqsXzS/im1puodEZEEUUlfRCRBlPRFRBKkTp/+16ZNG+/atWtdzlJEpN6b\nO3ful+6+Lf9Qr1SdJv2uXbsyZ86cupyliEi9Z2YfVz9UZlS9IyKSINUmfTPbx8zmpXxWm9nPzKy1\nhdcILozfreoiYBERqblqk767v+/u/dy9H+FZ7+sIf1IZC0x39+6EBwZl8sRMERHJo22t0x8MfODu\nH8eHJw2K3ScRnlfxy+yFJiKpvv76a4qLi9mwodonCEs91aJFCzp27EjTpk1zNo9tTfojCC/fgPCI\n0y9i8yLKPydbRLKsuLiYgoICunbtSvmn/EpD4O4sW7aM4uJiunXrlrP5ZPxDroWXAJ/ElifglfHw\nt94K/9prZmPMbI6ZzVm6dGmNAxVJug0bNrDrrrsq4TdQZsauu+6a8yu5bbl751jgdXcvfRvMYjPb\nA8LDqQgvS96Ku9/p7oXuXti2bVZuMxVJLCX8hq0utu+2JP2RbKnagfA869JncI8iPJBKROpQy5a1\nfrlYgzBs2DAGDhxYrtv48eO58cYbARg3bhwvvPBCTmO49957+fzzz3M6j2zIqE7fwuvvjgJ+nNL5\neuAxMzuX8OKB4dkPT5Kq69h/1On8iq4/vk7n11Bt2rSJJk3q9D+frFy5krlz59KyZUs+/PBD9txz\n6xfwTZgwIedx3HvvvfTq1Yv27dtnPE4+1ldGJX13X+vuu8a3UZV2W+bug929u7sf6e4VvQhdROrA\njBkzGDRoEKeccgr77rsvZ5xxBqVP0B07diz77bcfffr04fLLw0vpli5dysknn8yAAQMYMGAAr7zy\nSln3o446ip49e3LeeefRpUsXvvzyS4qKiujVq1fZ/G688UbGjx8PwKBBg/jZz35GYWEhf/zjH3nq\nqac48MAD6d+/P0ceeSSLF4ca4fHjx/PDH/6QQYMGseeee3LrrbeWTe++++6jT58+9O3bl/POOw+A\niRMnMmDAAPr27cvJJ5/MunXrKlz2v//975x44omMGDGCRx6p+A2go0ePZvLkyUB4MsCVV15Jv379\nKCws5PXXX+eYY45hr7324o477igb5w9/+AMDBgygT58+XHttePthUVERPXr04Ec/+hE9e/bk6KOP\nZv369UyePJk5c+Zwxhln0K9fP9avX8+ECRMYMGAAvXr1YsyYMWXbI3191bW6PcWISM688cYbvPPO\nO7Rv355DDjmEV155hR49ejBlyhTee+89zIyVK8NrjC+55BIuvfRSDj30UD755BOOOeYYFixYwK9/\n/WuOOOIIrrzySp577jnuvjuzF3Rt3Lix7BErK1as4M7Jz2Fm/P3h+/jFNf/F5eOuY/HqDbw+/23u\nevQp1q4tYeh3B3DIiSP5+MP/cO2E65g05Tl2adWaVStWML94JfsMHMzdx54KwO03XMeE/76d088Z\ns9W8J957Pzf8ZgLt2rXj5JNP5qqrrqo23s6dOzNv3jwuvfRSRo8ezSuvvMKGDRvo1asX559/PtOm\nTWPhwoXMnj0bd+ekk07i5ZdfpnPnzixcuJCHH36YiRMnMnz4cB5//HHOPPNMbr/9dm688UYKCwsB\nuOiiixg3bhwAZ511Fk8//TQnnnjiVuurrinpizQQBxxwAB07dgSgX79+FBUVMXDgQFq0aMG5557L\nCSecwAknnADACy+8wLvvvls27urVqykpKWHmzJlMmRJeEDZkyBBatcrsj/annXZaWXNxcTHnX3gJ\nXy5ZxNdff02HTl3K+h12xNE0a96cZs2b07pNW5Z/uYTZ//dPjjruJHZp1RqAneM8//PeAm7/w3Ws\nWb2KdevWcvB3j9hqvsuWLuGTjz7g0EMPxcxo2rQpb7/9drmrkoqcdNJJAPTu3ZuSkhIKCgooKCig\nefPmrFy5kmnTpjFt2jT69+8PQElJCQsXLqRz585069aNfv3CO8v3339/ioqKKpzHSy+9xA033MC6\ndetYvnw5PXv2LEv6qeurrinpizQQzZs3L2tu3LhxWX3x7NmzmT59OpMnT+b222/nxRdfZPPmzbz6\n6qu0aNEio2k3adKEzZs3l7Wn31a44447ljVffPHFjBw9hkFHH8e/Zs3kjpuuL+vXrNmWGBs1asSm\nTd9UOs9rLvsJt9z1APvs15snH3uIObNmbjXM/zz9BKtXrSy7r3316tU8/PDD/OY3v6lyeUrXVaNG\njcqttxDTJtydK6+8kh//+MflxisqKtpqPa9fv36r6W/YsIGf/OQnzJkzh06dOjF+/Phy6yx1fdU1\nPXBNpAErKSlh1apVHHfccdx88828+eabABx99NHcdtttZcPNmzcPgEMOOYTHHnsMgGnTprFixQoA\n2rVrx5IlS1i2bBlfffUVTz/9dKXzXLVqFbvtHn7MnPq3hysdrtQBBx/G889MZVWcV+n3upIS2uy2\nO19//TXPPLHV34MAeO7Jyfzp/skUFRVRVFTE3LlzK63X3xbHHHMM99xzDyUlJQB89tlnLFlS4V3p\nZQoKClizZg2w5aTYpk0bSkpKyn5P2B6opC/SgK1Zs4ahQ4eyYcMG3J2bbroJgFtvvZULL7yQPn36\nsGnTJg4//HDuuOMOrr32WkaOHMn999/PQQcdxO67705BQQFNmzZl3LhxHHDAAXTo0IF999230nmO\nHz+eCy8YzU4778IBBx/G559W/VTgb+/Tg3MvvJRzTjmO1atWcfjgoxn3+1u48PKrOPOkI2nVug29\n++/PupiAS3326Sd8XlxMn+8MKOvWrVs3dt55Z1577bVarLVwUlywYAEHHXQQEG6NfeCBB2jcuHGl\n44wePZrzzz+fHXbYgVmzZvGjH/2IXr16sfvuuzNgwIBKx6trdfqO3MLCQtfz9CUTumVzawsWLKBH\njx45ncdXX31F48aNadKkCbNmzeKCCy4ouwrYFvOLV9Zo/r++4hLG/f6Wbf6TUp+Ou9Roftujiraz\nmc1198JsTF8lfREp88knnzB8+HA2b95Ms2bNmDhxYp3N+5yTj2NtyRo2b95cZYlaakdJX0TKdO/e\nnTfeeCMv8/7r48/kZb5Jox9yRUQSRElfRCRBlPRFRBKkQdfp6w4QEZHyVNIXkXqlb6dW3Djh6rL2\nSXfcVvbwt40bN3LccccxePBgzj///DxFuH1r0CV9EcmtbF9NT73okGqHada8OdOfe4pzL7qUVq13\nLd+vWTOeeUZ3AVVFJX0RqVcaN27CKaeP4oGJf9qqX2WPdV6+fDnDhg2jT58+DBw4kPnz59d12NsN\nJX0RqXdOG3UezzzxN9asXlWu+6GHHsqrr77KG2+8wYgRI7jhhhsAuPbaa+nfvz/z58/nt7/9LWef\nfXY+wt4uqHpHROqdlgU7ccLJI3jonjvLPSm0uLiY0047jS+++IKNGzeWPX1z5syZPP744wAcccQR\nLFu2jNWrV7PTTjvlJf58UklfROqlM8+9gCcevZ/167e8Ueviiy/moosu4q233uIvf/nLVo+AFiV9\nEamndm7ViqNPGMaUR+4v67Zq1So6dOgAwKRJk8q6H3bYYTz44INAeLVkmzZtElnKByV9EanHzh5z\nESuXb3k99/jx4zn11FPZf//9adOmTbnuc+fOpU+fPowdO7bcCSFpVKcvIjVW2R8Sa/po5Uy8+n5x\nWfOubXfjtYWflz1aeejQoQwdOnSrcVq3bs0TTzyRs5jqk4xK+ma2i5lNNrP3zGyBmR1kZq3N7Hkz\nWxi/M3uZpoiI5E2m1Tt/BJ5z932BvsACYCww3d27A9Nju4iIbMeqTfpmtjNwOHA3gLtvdPeVwFCg\ntGJsEjAsV0GKiEh2ZFLS7wYsBf5qZm+Y2V1mtiPQzt2/iMMsAtrlKkgREcmOTJJ+E+A7wJ/dvT+w\nlrSqHA8v2q3wZbtmNsbM5pjZnKVLl9Y2XhERqYVMkn4xUOzupa+Xn0w4CSw2sz0A4veSikZ29zvd\nvdDdC9u2bZuNmEVEpIaqTfruvgj41Mz2iZ0GA+8CU4FRsdso4MmcRCgikmbirTfy/cEHccpRhzD8\nmMN47bXXOO+883j33XfzHdp2L9P79C8GHjSzZsCHwDmEE8ZjZnYu8DEwPDchish2a/zOFXbuU8PJ\nzT/v42qHeXPubF6ePo1Hn5lBs+bNWbF8GZ3a7MBdd91Vw7kmS0a3bLr7vFhF08fdh7n7Cndf5u6D\n3b27ux/p7surn5KISO0sXbKYXVq3plnz5gC0ar0r7du3Z9CgQcyZMweAli1b8otf/IKePXty5JFH\nMnv2bAYNGsSee+7J1KlT8xl+3ukxDCJSrxx8+PdY/PlnnHh4Ib+56jLmzHplq2HWrl3LEUccwTvv\nvENBQQFXX301zz//PFOmTGHcuHF5iHr7occwiEi98q0dW/LwMzN4ffYs/vV//+SKC39Io7W/LzdM\ns2bNGDJkCAC9e/emefPmNG3alN69e1NUVJSHqLcfSvoiUu80btyYAQcdyoCDDqX7vvvx+OOTy/Vv\n2rQpZgZAo0aNaB6rgho1asSmTZvqPN7tiap3RKReKfpgIR9/9EFZ+/vvvEWXLl3yGFH9opK+iNQr\n69au5fpxV7Bm9WoaN25Mp6578uj9f+WUU07Jd2j1gpK+iNTc+FUVds7lo5X369OP+56YVq5bmza7\nMGPGjLL2kpKSsubx48eXGza1XxKpekdEJEGU9EVEEkRJX0QkQZT0ReqR8EBbaajqYvsq6YvUEy1a\ntGDZsmVK/A2Uu7Ns2TJatGiR0/no7h2ReqJjx44UFxdTH95LsXjF+jqd34I1O9Tp/HKlRYsWdOzY\nMafzUNIXqSeaNm1Kt27d8h1GRo4d+486nV/R9cfX6fzqM1XviIgkiJK+iEiCKOmLiCSIkr6ISIIo\n6YuIJIiSvohIgijpi4gkiJK+iEiCZPTnLDMrAtYA3wCb3L3QzFoDjwJdgSJguLuvyE2YIiKSDdtS\n0v+eu/dz98LYPhaY7u7dgemxXUREtmO1qd4ZCkyKzZOAYbUPR0REcinTpO/AC2Y218zGxG7t3P2L\n2LwIaJf16EREJKsyfeDaoe7+mZntBjxvZu+l9nR3N7MKn/caTxJjADp37lyrYEVEpHYyKum7+2fx\newkwBTgAWGxmewDE7yWVjHunuxe6e2Hbtm2zE7WIiNRItUnfzHY0s4LSZuBo4G1gKjAqDjYKeDJX\nQYqISHZkUr3TDphiZqXDP+Tuz5nZv4DHzOxc4GNgeO7CFBGRbKg26bv7h0DfCrovAwbnIigREckN\n/SNXRCRBlPRFRBJESV9EJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRBlPRFRBJESV9EJEGU9EVEEkRJ\nX0QkQZT0RUQSRElfRCRBlPRFRBJESV9EJEGU9EVEEkRJX0QkQZT0RUQSRElfRCRBlPRFRBJESV9E\nJEEyTvpm1tjM3jCzp2N7azN73swWxu9WuQtTRESyYVtK+pcAC1LaxwLT3b07MD22i4jIdiyjpG9m\nHYHjgbtSOg8FJsXmScCw7IYmIiLZlmlJ/xbgCmBzSrd27v5FbF4EtMtmYCIikn3VJn0zOwFY4u5z\nKxvG3R3wSsYfY2ZzzGzO0qVLax6piIjUWiYl/UOAk8ysCHgEOMLMHgAWm9keAPF7SUUju/ud7l7o\n7oVt27bNUtgiIlIT1SZ9d7/S3Tu6e1dgBPCiu58JTAVGxcFGAU/mLEoREcmK2tynfz1wlJktBI6M\n7SIish1rsi0Du/sMYEZsXgYMzn5IIiKSK/pHrohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuI\nJIiSvohIgijpi4gkiJK+iEiCbNM/cqUa43eu4/mtqtv5iUi9p5K+iEiCKOmLiCSIkr6ISIIo6YuI\nJIiSvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIgewyAi9Z8egZKxakv6ZtbCzGab2Ztm\n9o6Z/Tp2b21mz5vZwvjdKvfhiohIbWRS0v8KOMLdS8ysKTDTzJ4FfgBMd/frzWwsMBb4ZQ5jFckd\nlRQlIaot6XtQElubxo8DQ4FJsfskYFhOIhQRkazJ6IdcM2tsZvOAJcDz7v4a0M7dv4iDLALa5ShG\nERHJkoySvrt/4+79gI7AAWbWK62/E0r/WzGzMWY2x8zmLF26tNYBi4hIzW3TLZvuvhJ4CRgCLDaz\nPQDi95JKxrnT3QvdvbBt27a1jVdERGohk7t32prZLrF5B+Ao4D1gKjAqDjYKeDJXQYqISHZkcvfO\nHsAkM2tMOEk85u5Pm9ks4DEzOxf4GBiewzhFRCQLqk367j4f6F9B92XA4FwEJSIiuaHHMIiIJIiS\nvohIgihpv8T9AAAKgklEQVTpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+\niEiCKOmLiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohI\ngijpi4gkiJK+iEiCVJv0zayTmb1kZu+a2Ttmdkns3trMnjezhfG7Ve7DFRGR2sikpL8JuMzd9wMG\nAhea2X7AWGC6u3cHpsd2ERHZjlWb9N39C3d/PTavARYAHYChwKQ42CRgWK6CFBGR7NimOn0z6wr0\nB14D2rn7F7HXIqBdJeOMMbM5ZjZn6dKltQhVRERqK+Okb2YtgceBn7n76tR+7u6AVzSeu9/p7oXu\nXti2bdtaBSsiIrWTUdI3s6aEhP+gu/89dl5sZnvE/nsAS3ITooiIZEsmd+8YcDewwN1vSuk1FRgV\nm0cBT2Y/PBERyaYmGQxzCHAW8JaZzYvdrgKuBx4zs3OBj4HhuQlRRESypdqk7+4zAauk9+DshiMi\nIrmkf+SKiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohI\ngijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo\n6YuIJEi1Sd/M7jGzJWb2dkq31mb2vJktjN+tchumiIhkQyYl/XuBIWndxgLT3b07MD22i4jIdq7a\npO/uLwPL0zoPBSbF5knAsCzHJSIiOVDTOv127v5FbF4EtKtsQDMbY2ZzzGzO0qVLazg7ERHJhlr/\nkOvuDngV/e9090J3L2zbtm1tZyciIrVQ06S/2Mz2AIjfS7IXkoiI5EpNk/5UYFRsHgU8mZ1wREQk\nlzK5ZfNhYBawj5kVm9m5wPXAUWa2EDgytouIyHauSXUDuPvISnoNznIsIiKSY/pHrohIgijpi4gk\niJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiS\nvohIgijpi4gkiJK+iEiCKOmLiCSIkr6ISIIo6YuIJIiSvohIgijpi4gkiJK+iEiC1Crpm9kQM3vf\nzP5jZmOzFZSIiORGjZO+mTUG/h9wLLAfMNLM9stWYCIikn21KekfAPzH3T90943AI8DQ7IQlIiK5\n0KQW43YAPk1pLwYOTB/IzMYAY2JriZm9X4t5btcM2gBf1tkMf211NquGTtuufkvA9uuSrQnVJuln\nxN3vBO7M9Xy2B2Y2x90L8x2HbDttu/pN2y9ztane+QzolNLeMXYTEZHtVG2S/r+A7mbWzcyaASOA\nqdkJS0REcqHG1TvuvsnMLgL+B2gM3OPu72QtsvopEdVYDZS2Xf2m7Zchc/d8xyAiInVE/8gVEUkQ\nJX0RkQRR0hcRSRAlfRGRBMn5n7MaKjP7eVX93f2muopFas7Mjgd6Ai1Ku7n7hPxFJFUxs6eASu8+\ncfeT6jCceklJv+YK8h2A1I6Z3QF8C/gecBdwCjA7r0FJdW7MdwD1nW7ZlMQys/nu3ifluyXwrLsf\nlu/YRHJFJf1aMrMWwLlsXUXww7wFJZlaH7/XmVl7YBmwRx7jkWqY2VtUXL1jwGZ371vHIdU7Svq1\ndz/wHnAMMAE4A1iQ14gkU0+b2S7AH4DXCcnkrvyGJNU4oYJuRngO2JV1HEu9pOqdWjKzN9y9f0oV\nQVPgn+4+MN+xSebMrDnQwt1X5TsWyYyZ9QdOB04FPgIed/fb8xvV9k8l/dr7On6vNLNewCJgtzzG\nI9vAzA4GuhKPBTPD3e/La1BSKTPbGxgZP18CjxIKr9/La2D1iJJ+7d1pZq2AqwlPGW0JXJPfkCQT\nZnY/sBcwD/gmdnZASX/79R7wT+AEd/8PgJldmt+Q6hcl/Vows0bAandfAbwM7JnnkGTbFAL7ueo4\n65MfEB7j/pKZPUd4TateQ7YN9I/cWnD3zcAV+Y5DauxtYPd8ByGZc/cn3H0EsC/wEvAzYDcz+7OZ\nHZ3f6OoH/ZBbS2Z2PVvqFteWdnf35XkLSjJiZi8B/Qh/yPqqtLv+1Vm/xOrVU4HT3H1wvuPZ3inp\n15KZfVRBZ3d3VfVs58zsuxV1d/f/retYROqKkr6ISILoh9xaMrOzK+qu2/62f2Y2ELgN6AE0I7z2\nc62775TXwERySEm/9gakNLcABhP+3amkv/27nXAnyN8Id/KcDeyd14hEckzVO1kW/9b/iLsPyXcs\nUjUzm+PuhaX/po7d3nD3/vmOTSRXVNLPvrVAt3wHIRlZZ2bNgHlmdgPwBbqNWRo4Jf1aSnupQyNg\nP0J1gWz/ziJss4uASwkP7To5rxGJ5Jiqd2op7ba/TcDH7l6cr3hk28SS/r6EE/f77r4xzyGJ5JSS\nfpbFRzOMdPcH8x2LVC2+KvEO4APCX/m7AT9292fzGphIDinp15CZ7QRcCHQgPGjt+dh+OfCmuw/N\nY3iSATN7j/IP7toL+Ie775vfyERyR3X6NXc/sAKYBZwHXEUoLQ5z93n5DEwytqY04UcfAmvyFYxI\nXVBJv4bM7C137x2bGxPu/Ojs7hvyG5lUx8x+EBuPAroAjxHq9E8FPnH3n+QrNpFcU0m/5kpfnoK7\nf2NmxUr49caJKc2LgdIf45eS8p5jkYZIJf0aMrNv2PJUTQN2ANbFZtdf+bdv8ersp+5+c75jEalL\nSvqSWGY2290PyHccInVJSV8Sy8xuBpqy9bsQXs9bUCI5pqQviRVfogJb/lFdWjV3RJ5CEsk5JX1J\nHDP7eWlj/HbCj7gz3b2il+KINBh6uJQkUUH8tIyfAsKjlZ81sxH5DEwk11TSF4nMrDXwgrt/J9+x\niOSKSvoiUXyZvVU7oEg9pqQvEpnZ9wiP1hBpsPSPXEkcM3uLLXfslGoNfE54ZaJIg6U6fUkcM+uS\n1smBZe6+tqLhRRoSJX0RkQRRnb6ISIIo6YuIJIiSvjQoZvZ9M5uX9tlsZseaWU8ze9HM3jezhWZ2\njZlZHG90HK5PyrTeNrOuKe39zMzNbEjdL5lIdijpS4Pi7lPcvV/pB/gT8E/gZcJrLa93932AvsDB\nQOoLU4qBX1Ux+ZHAzPgtUi8p6UuDZWZ7A+OAs4ARwCvuPg3A3dcBFwFjU0Z5GuhpZvtUMC0jvFlr\nNHCUmellK1IvKelLg2RmTYGHgMvc/ROgJzA3dRh3/wBoGV9yD7AZuIHwvuN0BwMfxXFmAMfnKHSR\nnFLSl4bqv4B33P3RbRzvIWCgmXVL6z4SeCQ2P4KqeKSe0j9ypcExs0HAyUDqg9PeBQ5PG25PoMTd\nV8ffc3H3TWb238AvU4ZrHKc31Mx+RXg+z65mVuDua3K5LCLZppK+NChm1gr4K3B2WkJ+EDjUzI6M\nw+0A3Eqozkl3L3Ak0Da2Dwbmu3snd+/q7l2Ax4Hv52YpRHJHSV8amvOB3YA/p962CZwEDAWuNrP3\ngbeAfwG3p0/A3TcSTgi7xU4jgSlpgz2OqnikHtJjGEREEkQlfRGRBFHSFxFJECV9EZEEUdIXEUkQ\nJX0RkQRR0hcRSRAlfRGRBFHSFxFJkP8P701VkIt3uIsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e511852b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"tb29 = (pd.crosstab(base9.ZONA,base9.Insegurança_Alimentar,margins=True,rownames=[\"ZONA\"],colnames=[\"Insegurança Alimentar\"],normalize='index')*100).round(decimals=1)\n",
"plot = tb29.plot(kind=\"bar\",title=\"Distribuição em Zonas de Insegurança Alimentar 2009 (G6)\")\n",
"\n",
"abs29=pd.crosstab(base9.ZONA,base9.Insegurança_Alimentar, margins=True, rownames=['ZONA'], colnames=['INSEGURANÇA ALIMENTAR'])\n",
"abs29=abs29.loc[['Rural','Urbana']]\n",
"abs29\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## CRUZAMENTO DE DADOS: \n",
"SUB-DIVISÃO MAIS COMPLEXA, CADA ZONA DIVIDIDA POR ESTADO E A FREQUÊNCIA DE CADA UM DESSES, O OBJETIVO DESTE GRÁFICO É ANALISAR EM UMA ÚNICA IMAGEM AS DIFERENÇAS NOTÁVEIS ENTRE OS FATORES TERRITORIAIS ANALISADOS E ASSIM FOCAR DIRETAMENTE NAS REGIÕES QUE PRECISAM DA ANÁLISE PARA RESPONDER A PERGUNTA"
]
},
{
"cell_type": "code",
"execution_count": 197,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Insegurança_Alimentar Não Sim\n",
"REGIAO ZONA \n",
"CENTRO-OESTE Rural 79.4 20.6\n",
" Urbana 82.5 17.5\n",
"NORDESTE Rural 50.4 49.6\n",
" Urbana 68.2 31.8\n",
"NORTE Rural 59.5 40.5\n",
" Urbana 66.3 33.7\n",
"SUDESTE Rural 83.5 16.5\n",
" Urbana 85.1 14.9\n",
"SUL Rural 85.1 14.9\n",
" Urbana 85.7 14.3 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAGMCAYAAADQnrmpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xm8HFWZ//HPNwlL2BMMIQIhgOxLkERAFNkdVAR0EEWQ\noCI6giOowyIMiyjCoIyO/lwQFVBAcQBBcFRAwBUwIci+KTsJRCAkrBLy/f1xTkOlc5e+91bVza37\nvF+vfqWrqrueU7c6p0+fOs8p2SaEEELzjBjsAoQQQqhGVPAhhNBQUcGHEEJDRQUfQggNFRV8CCE0\nVFTwIYTQUMOugpe0rqQHJa1VWHeipB/n5xMlPStpZMXleEDSrlXGCH1TPCeSPi/prMEuUxNJ+rKk\nw0vc37sl/bSs/TXJkKvgJV0r6WlJy/RzF98BDrH9cFcbbT9kewXbr/S/lNWRtKOkRwa7HEOVpBXy\nF/j/9fQ626fYPriucrVIOkjSH0re57aSrpT0lKQ5kn4maUJhuySdJunJ/DhNkgrbT5Z0q6QFkk5s\n2/dOedvc/N5LJK3RQ1nGAQcC3y2sW1HSGfkL9jlJD0n6X0nb5O2tRlfxYUmfBbD9C2BTSVuU9Tdr\niiFVwUuaBGwPGNizH+9fC/iB7V+XW7LQHUmjBrsMbf4VeAnYTdLqg12YsnXz9x4DnAlMAtYG5gM/\nLGw/BNgbmAxsAbwb+Hhh+33AkcAVXez7DuCdOcbrgXuBb/dQxIOAX9p+IZd3GeC3wObAHsBKwMbA\nT4B3wCKNrhVsr5BfuxC4qLDfC/JxhCLbQ+YBHA/8ETgDuLxt29nA/yN9COcDNwDrFbZ/HXgYmAfM\nALYvbDsR+HF+Pon0BTIqLx8E/D3v835g/8L7PgLcCTwN/BpYu4eyfwh4EHgSOBZ4ANg1bxsBHA38\nLW+/EBjbzX52BB4pLF8LnJz/LvOB3wCvy9uWBX6c9zkX+AswPm9bGfg+MAt4FPgiMDJvGwl8FfhH\nPubD2v4mr5a9h7/fR4GHgN/l9T8DZgPPAL8DNu3DudsUuBJ4Cngc+HxevzXw53xss4BvAkv38hn6\nLfAl4Cbgc23biuekq2P6MOkz9DTwCeBNwC05/jfb9tXtZyPv6xOkynBuPnaRKrYXgVeAZ4G5+fXv\nAmaSPrsPAycW9tXl37uXv8FWwPzC8p9Iv2qLZb++i/f9uBi7i+3LAF8G7ujl739AYfngfO6W70M9\ncAJwTdu6twD3V1n/DMXHoBegT4VNLYlPAlOAl8mVVd52Nqki2xoYBZwH/KSw/UBg1bztc6TKZtm8\nrav/zKOA5fN/qg3ztgnkignYK5dn4/za44A/dVPuTfJ/2Lfl/wRnAAsKlcmngeuBNfP27wIXdLOv\nHVm8gv8bsAEwOi+fmrd9HPgFsByp0p4CrJS3XZLjLA+sBtwIfDxv+wSpZbYmqWV2FX2v4M/N+x6d\n138EWDEf39eAmzs5d/k9s4DPkr6wVgS2ydumANvm90wiVaiH9/D5WZvU8tsk7++Wtu2vHlc3x/Sd\nXIa3kyrin+e/3RrAE8AOnXw28r4uB1YBJgJzgN3ztoOAP3RxzjcnNQS2IH3J7d3T37uX/0eHU6jA\nSV+62xSWp1D4Aiis77KCz8cwN/9tXwYO6iH2HOBNheWfAGf3oQ4Q6fN+UNv6sfnvsNJg11NL0mPQ\nC9CHE/vW/OFptU7vAo4obD8bOKuw/E7grh72NxeYnJ939Z+5VcHPJf2sH932/v8DPlpYHgE8Txet\neNIvj+KXzfLAPwuVyZ3ALoXtE/KxjupiXzuyeAV/XGH5k8Cv8vOPkFpnW7TtYzypm2J0Yd1+5FYR\nqZX18cK2Xel7Bb9uD3/7VfJrVu7t3OVyzezwM3I4cEkP248jf7GQKuVXgDcWtr96XN0c0xqF1z4J\nvL+wfBH5y6W3z0be11sL2y8Ejs7PD6Ktgu/iOL4G/Henf++2925B+iVU/AX7CrBRYXn9vE+1vbe3\nFvxY4Chg2x5e83JbrKvIDZK8vCXp/9w84O4u3r89qbG0Qtv6pXKZJ3bydxguj6HUBz8N+I3tf+Tl\n8/O6otmF588DK7QWJB0maaakhyU9kLe9rqeAtp8D3k9q0c6SdIWkjfLmtYGv54tLc0n/aUSqONq9\nnvTTurjfJwvb1wYuKezrTtJ/uvE9la+gu+P+Eal74CeSHpP0X5KWyvGWysfUivldUmt0sfK2Pe/U\nq++RNFLSqZL+JmkeqSKFRf/+3R3DWqQW22IkbSDpckmz835PoedzeiDp1wG2HwWuY/HPUE8eLzx/\noYvlVpk7+Wx0+1ltJ2kbSdfkC6TPkD6P7cfZ6zmS9AbSl8+nbf++sOlZUt93y8rAs841Z6dsPwWc\nA1zaw7WXp0m/wlqeJDVoWvu42fYqwHtJv/baTQMusv1s2/rWPuf2pcxNNyQqeEmjgX2BHfJ/5tnA\nEcBkSZM7eP9bgP8E9rW9lu1JpA+1enwjYPvXtncjfQjvAr6XNz1MauWuUniMtv2nLnYzi1RRtcqz\nHKm7qOVh4B1t+1o2V0L9Zvtl2yfZ3gTYjnQR68Ac7yXSr6FWvJVsb1oo75qFXa3Fop4jdfu0dHWx\nslg5fJDUbbErqfKYlNf3+vfPZV23m23fJp2T9W2vBHy+u31K2o7UMj2m8BnaBvhgBReC+/LZaNdV\npXo+cBmwlu2VSV1F7cfZY2UsaW1Sa/lk2z9q23w76QJry+S8rj9GkRoKK3Wz/RZSd2LL1cDbJS3f\n245zPfA+0pdIu42BB2zP61txm21IVPCkK/yvkPpOt8yPjYHfkyqs3qxC6h98TtLSko5n0VZElySN\nl7RX/vC9RPpSWJg3f4dUWWyaX7uypPd1s6v/BfaQ9FZJSwNfYNG//XeAL+X/hEgaJ2mvDo6rt/Lv\nJGlzpTH980g/jxfankW6GPtVSStJGiFpPUk75LdeCHxa0hqSViH97C66GfiApKUkTQX26aUoK5L+\nfk+SvhhO6cNhXA5MkHS4pGXykLptCvudBzybf1n9Ww/7mUa6UFv8DG1Gum7xjj6UpxN9+Wy0exxY\nM39OWlYEnrL9oqStSV+YHcvDFn9LuhD8nS5eci7wmXy+1yBdnzi78P6lJC1L+syOkrRs/kwh6b2S\nNsyfoXGk60szc2u+K78Edigsn0tqUFwiabP8a29ZYGoX730P6RfANV1s24H06yQUDJUKfhrwQ6fh\nUrNbD9Koif07aIH9inTy7yKNZHmRzrodRgCfAR4j/czegVyJ2L4EOI3U/TEPuI1uKgrbtwOHklpi\ns0gf0uJY9q+TWmi/kTSfdMF1m/b99MPqpC+XeaRun+tI3TaQvhiXJl1MfTq/rvVT+XukL4BbSKM3\nfkm6KNzKDfhPYL38vpPycfXkXNLf/dEc7/pOD8D2fGA30tC9F/M+dsqbP0eq7ObnMneZ7JIrjH2B\nbxQ/P7bvJ/09+tJN00mZO/5sdOG3pNbzbEmt7shPAl/In43jSV/AfXEw6VfQicWx5IXt3yVdjL81\nPy6nME6d9Ld9gXQ95Nj8/EN52xqk/1/z83sXkiri7pwLvDO3xrH9Iul83kEaRTUPuJs0QmnftvdO\nA37UTdfRfm1lDuSLKCH0RNI7gO/YXnuQy7E98Hbb/zmY5QgDI+kU4AnbXytpf+8GPmS7/Qth2IsK\nPiwmt652IrXix5NGiFxvu7T08n6UaQXSdYvzbL91sMoRwlBSaReNpE9Luk3S7cpzT0gaq5Q2fW/+\nd0yVZQj9IlLXy9OkLpo7SV0Dg+kk0s/4ywe5HCEMGZW14CVtRkpi2Jo05vtXpOFdh5AuGJ0q6Whg\njO32i3ghhBAGqMoW/MbADbaft72AdIHvvaThcq1hTueQRsiEEEIoWZUV/G3A9pJWzeO+30kaTz0+\nD9ODlOzRaTJPCCGEPqhspj/bd0o6jXSh7jnS2OlX2l5jSV32EUk6hDw73PLLLz9lo4026uplIYSw\niBkzZvzD9rjBLseSoLZRNHlo1COkibV2tD1LaU7qa21v2NN7p06d6unTp9dRzBDCECdphu2uEqWG\nnapH0ayW/51I6n9vpVy3EkumAZdWWYYQQhiuqr4Zw0WSViWlyB9qe66kU4ELJX2UlN0YyQkhhFCB\nSit429t3se5JYJcq44YQQhg6c9GEEELoo6jgQwihoaKCDyGEhooKPoQQGioq+BBCaKiqh0mGEEKP\nJh19RZfrHzj1XTWXpHmigg9hiOiuIoTyK8M6Y4XqRBdNCCE0VFTwIYTQUFHBhxBCQ0UffAgDEH3V\nYUkWLfgQQmioqOBDCKGhooumQ/FTPIQw1EQLPoQQGqrqOzodIel2SbdJukDSspLGSrpS0r353zFV\nliGEEIaryip4SWsA/w5Mtb0ZMBL4AHA0cLXt9YGr83IIIYSSVd1FMwoYLWkUsBzwGLAXcE7efg6w\nd8VlCCGEYamyCt72o8BXgIeAWcAztn8DjLc9K79sNjC+qjKEEMJwVmUXzRhSa30d4PXA8pIOKL7G\ntgF38/5DJE2XNH3OnDlVFTOEEBqrymGSuwL3254DIOliYDvgcUkTbM+SNAF4oqs32z4TOBNg6tSp\nXX4JQEw1GkII3amyD/4hYFtJy0kSsAtwJ3AZMC2/ZhpwaYVlCCGEYauyFrztGyT9L3ATsACYSWqR\nrwBcKOmjwIPAvlWVIYQQhrNKM1ltnwCc0Lb6JVJrPoQQQoUikzWEEBoqKvgQQmioqOBDCKGhooIP\nIYSGigo+hBAaKir4EEJoqKjgQwihoaKCDyGEhooKPoQQGioq+BBCaKio4EMIoaGigg8hhIaKCj6E\nEBoqKvgQQmioqOBDCKGhqrwn64aSbi485kk6XNJYSVdKujf/O6aqMoQQwnBWWQVv+27bW9reEpgC\nPA9cAhwNXG17feDqvBxCCKFkdXXR7AL8zfaDwF7AOXn9OcDeNZUhhBCGlboq+A8AF+Tn423Pys9n\nA+NrKkMIIQwrlVfwkpYG9gR+1r7NtgF3875DJE2XNH3OnDkVlzKEEJqnjhb8O4CbbD+elx+XNAEg\n//tEV2+yfabtqbanjhs3roZihhBCs9RRwe/Ha90zAJcB0/LzacClNZQhhBCGnUoreEnLA7sBFxdW\nnwrsJuleYNe8HEIIoWSjqty57eeAVdvWPUkaVROWAJOOvqLbbQ+c+q4aSxJCKFtksoYQQkNFBR9C\nCA0VFXwIITRUVPAhhNBQlV5kDWGwdHfxOC4ch+Gkxwpe0rLAHsD2wOuBF4DbgCts31598UIIIfRX\ntxW8pJNIlfu1wA2kjNNlgQ2AU3Pl/1nbt9RQzhBCCH3UUwv+RtsndLPtDEmrARMrKFMIIYQSdFvB\n216sEzO32pe2Pc/2E3Qzj0wIIYTB1/FFVkkHA/sAIyVNt31MdcUKIYQwUN0Ok5S0Z9uqXW3vbns3\n4J3VFiuEEMJA9TQOfnNJl0raMi/fIuksSd8DYgRNCCEs4Xrqg/+SpNWBL0gS8J/AisDoGDkTQghL\nvt764J8DDgfWB84EpgP/VXWhQgghDFxPffBfBC4CLgd2sr0ncDPwS0kH1lS+EEII/dRTH/wett9O\nmrv9QADblwFvB8bUULYQQggD0FMXzW2SzgRGA9e1VtpeAHy9k51LWgU4C9iMdHPtjwB3Az8FJgEP\nAPvafrofZQ8hhNCDni6yHiBpc+Bl23f1c/9fB35lex9JSwPLAZ8HrrZ9qqSjgaOBo/q5/xBCCN3o\ncbpg27f2t3KXtDLwNuD7eV//tD0X2As4J7/sHGDv/uw/hBBCz6qcD34dYA7wQ0kz8xj65YHxtmfl\n18wGxnf1ZkmHSJouafqcOXMqLGYIITRTlfPBjwK2Aj5l+wZJXyd1x7zKtiW5qzfbPpM0NJOpU6d2\n+ZowtMQc7SHUq6MKXtIWpIuir77e9sW9vO0R4BHbN+Tl/yVV8I9LmmB7lqQJxIRlIYRQiV4reEk/\nALYgTU+wMK820GMFb3u2pIclbWj7btJwyzvyYxpwav730v4XP4QQQnc6acFva3uTfu7/U8B5eQTN\n34EPk/r9L5T0UeBBYN9+7juEEEIPOqng/yxpE9t39HXntm8GpnaxaZe+7iuEEELfdFLBn0uq5GcD\nLwEiXR/dotKShRBCGJBOKvjvAx8CbuW1PvgQQghLuE4q+Dl5DpoQQghDSCcV/ExJ5wO/IHXRAB0N\nkwwhhDCIOqngR5Mq9rcX1vU6TDKEEMLg6rWCt/3hOgoSQgihXL3ORSNpA0lXS7otL28h6bjqixZC\nCGEgOpls7HvAMcDLAPl+rB+oslAhhBAGrpMKfjnbN7atW1BFYUIIIZSnkwr+H5LWI11YRdI+wKye\n3xJCCGGwdTKK5lDStL0bSXoUuB/Yv9JShRBCGLBORtH8Hdg136xjhO351RcrhBDCQHXbRSPpAEmv\nbrf9XLFyl7SepLdWXcAQQgj901MLflVSFusMYAbp9nvLAm8AdgD+QdsdmkIIISw5uq3gbX9d0jeB\nnYG3kG768QJwJ/Ah2w/VU8QQQhiYGTNmrDZq1KizgM2o9l7UdVoI3LZgwYKDp0yZ0uWd8Xrsg7f9\nCnBlfvSZpAeA+cArwALbUyWNBX5KugXgA8C+tp/uz/5DCKETo0aNOmv11VffeNy4cU+PGDGiEfd4\nXrhwoebMmbPJ7NmzzwL27Oo1dXyT7WR7S9utG38cDVxte33gaqKbJ4RQvc3GjRs3rymVO8CIESM8\nbty4Z0i/SrrU0U23S7YXsGN+fg5wLXDUIJRjiTXp6Cu63fbAqe+qsSQhNMaIJlXuLfmYum2oV92C\nN3CVpBmSDsnrxttuJUrNBsZ39UZJh0iaLmn6nDlzKi5mCCFUS9KUj33sY2u2lo8//vjxn/nMZ14P\n8OKLL2qHHXZ4w5vf/OYNPvjBD04sK2ZHLXhJ7wI2JY2iAcD2Fzp461ttPyppNeBKSXcVN9q2pC6/\nVW2fSUqwYurUqY375u23E1fuYdsz9ZUjhCFs0tFXTClzfw+c+q4Zvb1m6aWX9i9/+csxs2bNmj1h\nwoRFpntZdtllfd11191XZpmgs9kkvwO8H/gU6X6s7wPW7mTnth/N/z4BXAJsDTwuaULe9wSgy6u/\nIYTQJCNHjvSBBx4455RTTlms1+L8889feYstttho44033mS77bbb4OGHHx4F8Pjjj4/cdddd19tg\ngw02mTx58kY33HDD6L7E7KSLZjvbBwJP2z4JeDOwQW9vkrS8pBVbz0k3DLkNuAyYll82Dbi0LwUO\nIYSh6j/+4z+euPjii8c++eSTI4vrd9ttt2dvvvnmu+6888479tlnn6e+8IUvrA5w5JFHvn7y5MnP\n33PPPXecfPLJj06bNm2dvsTrpIvmhfzv85JeDzwJTOjgfeOBSyS14pxv+1eS/gJcKOmjwIPAvn0p\ncAghDFVjx45d+L73ve/JU089dbXRo0cvbK2///77l957773XnDNnzlL//Oc/R6y11lovAdx4440r\nXnTRRfcB7LnnnvMPOeSQUU899dSIsWPHLuwuRlEnLfjLJa0CnA7cRBq7fn5vb7L9d9uT82NT21/K\n65+0vYvt9W3vavupTgoaQghNcMwxxzx+/vnnv+655557tf497LDDJn7yk5984p577rnjm9/85oMv\nvfRSKQNget2J7ZNtz7V9EanvfSPbx5cRPIQQhpvx48e/8u53v/vp888//3WtdfPnzx85ceLElwHO\nPvvsVVvrt9lmm/k//OEPVwW4/PLLVxwzZsyCTlvv0NlF1lskfV7SerZfsh1DNUIIYQCOPfbY2XPn\nzh1VWH5sv/32W2/TTTfdeNVVV311hM1pp5322MyZM5fbYIMNNjn22GPXOPvss+/vS5xO+uDfTRpF\nc6GkhaRpBi6MuWhCCENVJ8May/b888/PbD1fa621FrzwwguvLh9wwAFzDzjggLnt7xk/fvwrV111\n1d/6G7OTLpoHbf+X7SnAB0mTjvXpWySEEEL9Ok10WpvUin8/aeKwI6ssVAghhIHrtYKXdAOwFPAz\n4H35Dk8hhBCWcJ204A+0fXflJQkhhFCqbit4SQfY/jHwrjwXzSJsn1FpyUIIIQxITy345fO/K3ax\nLSb/CiGEJVxPt+z7bn56le0/FrdJekulpQohhIY56qijVr/oootWHTFihEeMGMG3vvWtB7/73e++\n7sgjj3x8ypQpL1YRs5M++G8AW3WwLoQQhoYTVy51umBOfKbHcfVXXXXV8r/+9a9XufXWW+8YPXq0\nZ82aNeqll17ST3/60wdLLUebbsfBS3qzpM8C4yR9pvA4ERjZ3ftCCCEs6tFHH11q7NixC0aPHm2A\nCRMmLJg0adLLW2+99Ya/+93vlgNYbrnl3vjxj398zTe84Q2bbrfddhtcc801y2299dYbrrnmmpuf\nd955PdwIons9JTotDaxAauWvWHjMA/bpT7AQQhiO9t5773mPPfbY0pMmTdrsgAMOmHjFFVes0P6a\nF154YcQuu+wy77777rt9+eWXf+W4445b4/e///09P/vZz+47+eST1+hP3J764K8DrpN0tu1Kf0aE\nEEKTrbzyygtvu+22O371q1+tePXVV684bdq09Y4//vhHiq9ZaqmlvM8++8wD2HTTTV9YZpllFi6z\nzDLeeuutX3j00UeX7k/cTvrgn5d0Oovfsm/n/gQMIYThaNSoUeyxxx7z99hjj/lbbLHFCz/60Y9W\nbdvuESNSp8qIESNYZpllDDBy5EheeeUV9SdmJ3MOnwfcBawDnESaD/4vnQaQNFLSTEmX5+Wxkq6U\ndG/+d0w/yh1CCEPGX//612VuvfXWZVrLM2fOHL3mmmv+s+q4nVTwq9r+PvCy7etsfwToS+v908Cd\nheWjgattrw9cnZdDCKGx5s2bN/LAAw9cZ7311tt0gw022OSuu+4afdpppz1WddxOumhezv/Oyhmt\njwFjO9m5pDWBdwFfAj6TV+8F7JifnwNcCxzVWXFDI53YwwCBE+P2A6ECvQxrLNv222///MyZM+9q\nX3/jjTe+Og1McTrhM844Y5HKv7itLzqp4L8oaWXgs6Tx7ysBR3S4/6+RZp4sZsOOtz0rP59Nunfr\nYiQdAhwCMHHixA7DhRBCaOm1grd9eX76DLBTpzuWtAfwhO0ZknbsZt+W1OW0B7bPBM4EmDp1akyN\nEEIIfdTTZGPfoIc5Z2z/ey/7fguwp6R3kkbfrCTpx8DjkibYniVpAvBEP8odQgihFz214KcPZMe2\njwGOAcgt+M/ZPiAPuZwGnJr/vXQgcUIIoQMLFy5cqBEjRjSqN2DhwoUCur0Jd0+JTucUlyUtZ/v5\nEsp0Kun+rh8FHgT2LWGfIYTQk9vmzJmzybhx455pSiW/cOFCzZkzZ2Xgtu5e08kdnd4MfJ80bcFE\nSZOBj9v+ZKcFsX0tabQMtp8Edun0vSGEMFALFiw4ePbs2WfNnj17MzobHj4ULARuW7BgwcHdvaCT\nUTRfA/4FuAzA9l8lva2c8oUQQvWmTJnyBLDnYJejbh19k9l+uG3VKxWUJYQQQok6acE/LGk7wJKW\nYvHM1BBCCEugTlrwnwAOBdYAHgW2zMshhBCWYJ0kOv0D2L+4TtLy3bw8hBDCEqLHFrykNSRNlbR0\nXl5N0inAvbWULoQQQr/1dMu+w4GbSfPPXC/pYFLf+2ig3PsZhhBCKF1PXTSHABvafkrSROAe4C22\na52FLYQQQv/01EXzou2nAGw/BNwdlXsIIQwdPbXg15T0P4XlCcXlDiYbCyGEMIh6quD/o205Wu9h\n6Iubi4RhpOPJxkIIIQwt/Zp0J99tKYQQwhKsv7OqqdRShBBCKF0nc9EsxvZ3yy5IWAJ1118dfdUh\nDAmdzAf/mZ622z6jm/ctC/wOWCbH+V/bJ0gaC/wUmAQ8AOxr++m+FTuEEEJvOumimQr8G2mysTVI\nk49tBayYH915CdjZ9mTSBGW7S9oWOBq42vb6wNV5OYQQQsk66aJZE9jK9nwASScCV9g+oKc32Tbw\nbF5cKj8M7AXsmNefQ7rT01F9LHcIIYRedNKCHw/8s7D8z7yuV5JGSroZeAK40vYNwHjbs/JLZne6\nrxBCCH3TSQv+XOBGSZfk5b1JLe9e2X4F2FLSKsAlkjZr225JXd4ANw/FPARg4sSJnYQLIYRQ0GsL\n3vaXgA8DT+fHh22f0pcgtucC1wC7A49LmgCQ/32im/ecaXuq7anjxo3rS7gQQgh0Pg5+OWCe7a8D\nj0hap7c3SBqXW+5IGg3sBtxFunn3tPyyacClfS51CCGEXnUyTPIE0kiaDYEfki6W/hh4Sy9vnQCc\nI2kk6YvkQtuXS/ozcKGkjwIPAvsOoPwhhBC60Ukf/HuANwI3Adh+TFJPwyPJr7slv699/ZPALn0s\nZwghhD7qpIvmn3nIoyHuxxpCCENFJxX8hZK+C6wi6WPAVcD3qi1WCCGEgeq1i8b2VyTtBswj9cMf\nb/vKyksWQghhQHqs4PMF0qts7wREpR5CCENIj100OVFpoaQeboMTQghhSdTJKJpngVslXQk811oZ\n92QNIYQlWycV/MX5EUIIYQjptoKXNNH2Q3Fv1hBCGJp66oP/eeuJpItqKEsIIYQS9VTBF++7um7V\nBQkhhFCunip4d/M8hBDCENDTRdbJkuaRWvKj83Pysm2vVHnpQggh9Fu3FbztkXUWJIQQQrk6nQ8+\nhBDCEBMVfAghNFRlFbyktSRdI+kOSbdL+nReP1bSlZLuzf+OqaoMIYQwnFXZgl8AfNb2JsC2wKGS\nNgGOBq62vT5wdV4OIYRQsk6mKugX27OAWfn5fEl3AmsAewE75pedA1wLHFV6AU7sYX60E58pPVwI\nISxpaumDlzSJdPu+G4DxufIHmA2Mr6MMIYQw3FRewUtaAbgIONz2vOK24q0Au3jfIZKmS5o+Z86c\nqosZQgiNU2kFL2kpUuV+nu3WjJSPS5qQt08AnujqvbbPtD3V9tRx48ZVWcwQQmikKkfRCPg+cKft\nMwqbLgOm5efTgEurKkMIIQxnlV1kBd4CfIh0s5Cb87rPA6eSbuT9UeBBYN8KyxBCCMNWlaNo/sCi\nM1IW7VJyKxhOAAAgAElEQVRV3BBCCElksoYQQkNV2UUzfMSY+xDCEiha8CGE0FDRgg+hKvHLLgyy\naMGHEEJDRQUfQggNFRV8CCE0VPTBh9AEdfb3dxcrrisscaKCDyEsmeIi9YBFF00IITRUVPAhhNBQ\nUcGHEEJDRQUfQggNFRV8CCE0VFTwIYTQUFXe0ekHkp6QdFth3VhJV0q6N/87pqr4IYQw3FXZgj8b\n2L1t3dHA1bbXB67OyyGEECpQWQVv+3fAU22r9wLOyc/PAfauKn4IIQx3dffBj7c9Kz+fDYyvOX4I\nIQwbg3aR1bYBd7dd0iGSpkuaPmfOnBpLFkIIzVB3Bf+4pAkA+d8nunuh7TNtT7U9ddy4cbUVMIQQ\nmqLuCv4yYFp+Pg24tOb4IYQwbFQ5TPIC4M/AhpIekfRR4FRgN0n3Arvm5RBCCBWobLpg2/t1s2mX\nqmKGEEJ4TWSyhhBCQ0UFH0IIDRUVfAghNFRU8CGE0FBRwYcQQkNFBR9CCA0VFXwIITRUVPAhhNBQ\nUcGHEEJDRQUfQggNFRV8CCE0VFTwIYTQUFHBhxBCQ0UFH0IIDRUVfAghNFRU8CGE0FCDUsFL2l3S\n3ZLuk3T0YJQhhBCarvYKXtJI4P8B7wA2AfaTtEnd5QghhKYbjBb81sB9tv9u+5/AT4C9BqEcIYTQ\naLJdb0BpH2B32wfn5Q8B29g+rO11hwCH5MUNgbv7GOp1wD8GWNyIVU+sJh5TxBq8OGvbHld2YYai\nym66PVC2zwTO7O/7JU23PbXEIkWsIR4nYg2tWHUeU1MNRhfNo8BaheU187oQQgglGowK/i/A+pLW\nkbQ08AHgskEoRwghNFrtXTS2F0g6DPg1MBL4ge3bKwjV7+6diFV7rCYeU8QaOnEaq/aLrCGEEOoR\nmawhhNBQUcGHEEJDRQUfQggNtcSOg+8rSW8GDgC2ByYALwC3AVcAP7b9zFCMleONAV6f4zxge2GZ\n+687VlPPlaRlgT1yrNbf8DbgijIHEtQVp8mxhotGXGSV9H/AY8ClwHTgCWBZYANgJ+DdwBm2Bzwc\ns65YklYGDgX2A5YG5uQ444HrgW/ZvmYgMQYpVuPOVY51EqlyuhaY0UWsZYHP2r5lKMRpcqzhpCkV\n/Ots95jS3MlrlqRYkq4EzgV+YXtu27YpwIeAW21/fyBxBiFW485V3s+7bF/Rw/bVgIm2pw+FOE2O\nNZw0ooIPIYSwuEb0wUuaD3T1TSXAtleqIOa2wDeAjUndGiOB58qKJWmrnrbbvqmMOF3EHQOsT/pJ\n3Ir1uxL337hzlWP8gq6PCwDbe5YVK8cbBxxFmnK7eK52LjFGrceUY1Z+XMNJIyp42ysOQthvkqZZ\n+BkwFTiQ1F9Ylq/2sM1A6R94SQcDnybND3QzsC3w5zJjNfRcAXyl5P315jzgp8C7gE8A00jXTspU\n9zFBPcc1bDSyiyb31xW//R+qIMZ021Ml3WJ7i7xupu03lh2rLpJuBd4EXG97S0kbAafYfm+FMeNc\n9YOkGbantB3TX2y/abDLNhBNPa7B0ogWfIukPUkt39eTrsKvDdwJbFpBuOfzZGk3S/ovYBYV5RVI\n2ozFf7KeW0GoF22/KAlJy9i+S9KGFcRp8rlaH/gyi5+vdUsO9XL+d5akd5FGC40tOQZQ6zFBjcc1\nHDQt0elkUrfCPbbXAXYhDfOrwodIf7/DgOdIUyD/a9lBJJ1A6j/+Bmm42H8Bpfd9Zo9IWgX4OXCl\npEuBByuK1bhzlf0Q+DawgHS+zgV+XEGcL+bhrZ8FPgecBRxRQRyo75ig3uNqvEZ10RR+iv8VeKPt\nhZL+anvyYJetv3K3yWRgpu3JksaTEnR2qzjuDsDKwK/yrRXL3n/jzhUs0sVwq+3Ni+sGu2z91cRj\nGi4a1UUDzJW0AvA74DxJT5BabKWT9BbgRFLXwqt/xwp+tr6QK78FklYidWes1dub+ivfFH08cH9e\ntTpQer84zTxXAC9JGgHcm6fFfhRYoewgebTJx4BJLHpMHyk7FjUdE9R+XI3XtBb88qT05hHA/qQW\n6Hm2n6wg1l2kn44zgFda68uOJelbwOdJo0A+CzwL3Gz7w2XGybE+BZwAPA60pihw62JXybEad65y\nrDeRriWsQuqGWgk43Xap3U+S/gT8nsWP6aIy4+RYtRxTjlXbcQ0Hjangc8vzKts71RTvBtvbVBxD\nwJq2H87Lk4CVqkrXlnQf6QbopVd8bXEad65ynJHAabY/V0Osm21vWUOc2o4px6vluIaLxlxktf0K\nsDBfoKnDNZJOl/RmSVu1HmUGcPr2/WVh+YGK5+J4GCh1orSuNPFcwavH9day99uNyyW9s+ogNR8T\n1HRcw0VjWvAAedTHG4ErKfTn2v73CmJ1NfmWy864k3QO8E3bfylzv93E+j6wIWmmxZda622fUUGs\nxp2rHOvbwBqkpKricV1ccpz5wPKk8/Qy1WYC13JMOVZtxzUcNO0i68X5Ubm6uheAbYD9JT1I+s/V\n+sCX3i9Oupj6ECmdf+kK9l/UxHMFaZz4kyya/WtKPtaaM4JrOSYYtEznxmpUC75uORFjUxZN/vhC\nyTHW7mq97arGpzdSHeeqblXPGzRYmnpcg6FRLXhJ99PF5EhVDIeT9B1gOVLix1nAPsCNZcehh8me\nypaHqB3J4hVhFV0ZTTxXSPohXR9XqcP86pg3qBCrlmPKsWo7ruGgURU8aSKplmWB91FdmvN2trfI\nc2acJOmrwP9VEOcK0n8ukY5pHeBuqknpb030tAfVT/TUxHMFcHnh+bLAe0jp9mX7NK/NG7RTa96g\nCuJAfccE9R5X4zWqgu9ieN/XJM0Ajq8g3Av53+clvZ7URzmh7CCtzMGWPPrjk2XHyVa1/X1Jn7Z9\nHXCdpEou7jbxXMHi47UlXQD8oYJQtc0bVOMxQY3HNRw0qoJvG/o2gtRKrOoYL8/ztpwO3ERqZX+v\nolivsn2TpKrGdNc5gVXjz1W2PrBaBfttnzfoaaqbN6hdVccEg3tcjdOoi6xtw+EWAA8AX7F9d8Vx\nlwGWdck32877/kxhcQSwFaml/S8VxNqDlEW4Fmlys5WAk1zCPUu7iNW4c5X3335Dk9nAMVVmYqr6\neYNqP6Yct9LjGg4aVcHXSekO8J8kJYGY9JP127ZfLDnOCYXFVkV4Udlxmqyuc1W3/CuodUx/dEV3\n+apbU49rMDQmk1XSSEmvKywvLekQSXdWFPJc0oXOb5DuGLQJ8KOyg9g+qfD4ku3zqOjnsaR1Jf1C\n0j8kPSHpUklVjGpp5LnqiqQNJJXeHSTpeOAcYFXgdcAPJR1XdpxuYldyTHnfg3ZcjWR7yD9IE3E9\nQ+ozvg54O/AIcAmwVUUx7+hk3QBjvJk0pG+1vLwFcD7wcEXHdD1p7vRR+XEAcEOcq45ibAH8BrgN\n+CLpIu5F+diOqOCY7iZ1NbWWRwN3D+Vjquu4htOjKS3444Aptl9PmjXwF8C/2X6Pq/t5d5PSzZwB\nyBc+p5e1c0mnAz8g3ZjiCklfJP1nu4F0kasKy9n+ke0F+fFjCuPhS9K4c5V9j/Tl+6+koaU3A38D\n3mD7v0uOBekLsnhuliFN41umuo8J6jmuYaMRffCSbrK9VWH5NtubVRTrVlLf4FKkeVseystrA3fZ\n3qSkOHeQWrQv5sy+h4HNbD9Qxv7bYrVGyhwFPA38hHRM7wfG2D6mxFiNO1c51iKzIEr6u6tJ2voG\n6RgmksaLX5mXdwNudIn3z63rmPK+azuu4aQpwyRXaxttskpx2eVOlrVHifvqyYvOFwFtPy3p3ioq\n92wGryVTAXy8sM1AaRU8zTxXAMtKeiOv/Q1fKi6X+Ouk9ctjBqlbq+XakvZfVNcxQb3HNWw0pQV/\nQk/bbZ9UcryRwO22Nypzv20x5pLudtTytuKy7VLvy6p0x5432/5jmfvtIk7jzlWO09WMlS12idM9\n5GM61/b+Ze2zmzi1HVOOV8txDSeNqOAHg9J0t5+yXcXt7FpjgLvllGladsyZtt9Y9n4HW9XnajBI\n+gOwsxs2PrypxzVYmtJFMxjGALdLupFF58gupWVdRQXegasl/StwsZv1zV/puRokfwf+KOkyFj2m\n0ufur1lTj2tQRAXff/852AWowMeBzwALJL1Ic2620MRz9bf8GAE0aQ71ph7XoIgumhBCaKhGt+Al\n7QXMtn1Diftsn5fDwD+Aa4CjXPENq6ugxe9PauAfzjf7rqkMjTxXkiYAT9l+qdcXd7a/X9DNMeW8\nhcqVfUx5n4N+XE3U6Ba8pFOAzYFRtt9RYZwxwEGkecffV1WcHOsUUiboWWVVUN2MlhhLum3ffrZv\nLiNOL2Vo3LnK8a4C1iPNH/S5EvbX1cX3saSs43ttHz3QGB2UodRjyvsc9ONqokZX8HVrT+KpKMbe\npP9ck20fWHGsqcAZtt9WZZzBUMe5KsQSsInt2yuMMRKYUUxMqlIdx5Tj1HpcTdOIqQokHVl4/r62\nbbXcDUbSUtTQ5WX757a/WnXlnmNNB1Yoc59NPVeSdi48X6dt83uqrghtv1Ll/rvwYNXHBINyXI3S\niBZ8sTXWRSp8qS01SV2lTI8hpfX/wSXdyFnShbb3zc9Ps31UYdtvbL+9jDi9lGE88EvbU0rcZ+PO\nVY5Vy3EVppUoGgMcSJojppYkIUkP216rxP0tEcfVNE25yKpunne1PFDvbls26RZwX7d9RYlxihOK\n7UaaJ6ZlXIlxivOAFI0FtiPdI7PUcN0872p5oOo6V1DfcbVPK9G6GHkt8G8lxulN2S3DJeW4GqUp\nFXz71ffutg08kP3hMvfXU6h+buuP9pkVWxXhZ2w/UXKsJp4rqOm4bLd3/1Smbc6gRTZRctddncc1\nnDSlgp8saR7pgzc6Pycvlz3dbV2WyxM7jSAdU2uSJ5HmyC6N7XPK3F8vmniuANbN2ZcqPCcvD9XK\nq6dEo6/XVorQb03pg1/K9su9v3Lo6GWiJ2zvVFdZytTEcwWDM3dQCL1pSgVf25C3ukja1vb1g12O\nsjXxXAFIOtv2QYNdjjJJ+p+2VcXkoz8MQpFCHzVimCTlX5zrewGkvfKdgsryrRL3tSRp4rmCdHu7\nQSNpgqRlSt7tjLbHTcCzwOmSDi85VpcqOq5hoyl98ON6uCBU10x02wCbSyorE3NJqAhLz5qlmecK\nXrtm0uV5K/nmGF35EbCepNKyS7u7NiPpO8CfgK+VEacXpR/XcNKUCn4k6ar+oFWKtj9f8i7XKVyo\n6ypeHVPd3kjKmv1v0njkMjTxXAGsAXyVro/LQKk3x1gsgL1rK7u0yjg51gspVPXqPK4makoFP6vM\npJWeSDrS9n/l5++z/bPCtlNKrDzmkCqMQWP75xXstonnCuC+su9w1BVJO9v+bX6+ju37C5vfY/vi\niuOPAj4EPFJlnDYP2p5YY7zGiD74vvtA4Xn7vUp3LzHOs7av6+5RYhwkXVh4flrbtt+UGYtmnqs6\nfaXw/KK2bceVGUjSfEnzCo/5wKPAO1j0vr1VG/TuyqGqKRX8Xnl+EQAkbSjpiG5S1QeqrozF+3t/\nSWnas2aLSs2aBXbpaqWkVSQdW3KsOrNmi5nGSFpK0hslrVZynNqOyfaKtlcqPFa0Pd72vrYfKzNW\nb0WpMVajNKWL5sfAR4F7Jb0B+DNwHrCHpDfZbm+9DURdmZhflrS67dkAkg4E/hV4EDjR9lMlxqoz\na3Z5SacCrwd+DlwAfIH0s/+CkmPVljULvFfSo7Zvl7Qy6TP4CjBW0udsl3VstR2TpLWBubafycs7\nAXuTPoPfdIn3Ta0za3Y4aUoFP8b2vfn5NOAC25+StDRpeFeZFXxdmZjfBXYFkPQ24FTgU8CWwJnA\nPiXGqi1rFjgXuI7UvbA7aZqEm4EtWl9mJaoza3Z725/Izz8M3GN7b0mrA/9HeV9edWbMXgi8B3hG\n0pbAz4AvA5NJw3gPLjFWZM1WoCmJTrfY3iI//yNweusCoaS/2p5cYqxaMjGL5Zb0/4A5tk/MyzeX\nOT92nVmz7edD0iPARNsLy4pR2HdtWbOSZtp+Y35+BfAz22e3byshTm0Zs23/r74CLLR9pKQRwM2t\nbWHJ1ZQW/C35A/go8AbgN5D6dSuIdQNQRybmyDxOewGp3/qQwrayz9sxdWbNKt1VqdVf/CSwch4K\nR8ldT3WdK4C5kvYgfQbfQuoybI06KfNX0IdrzJgt9unvTP4lbHth2cMkI2u2Gk2p4D9GmtZ2EvB2\n28/n9Zuw6KiDMtR1Rf8C4DpJ/wBeAH4PkK8xPFNyrG9RX0W4MqnbrPh3bCUBGVi3xFh1jr74OPA/\nwOrA4YXupl2AMqcmrrPV/Ns8wmoWaW721vDMCUBp/e/ZjC7WjSVlzf7Udh1JVY3TlC6alWzP62bb\nRNsPlRjrEaDbbMsyMzElbQtMAH5j+7m8bgNghTIzI8vsQliS1Hmu6iLpLmA/asiYzb+q3k/6DF5o\n+9G8/o3AarZ/XVasHsowGvhTEz+fdWhKC/5acgtU0tW2i0Pxfk65rdNaMjHbE1rIwyZt35OHf5aZ\n+l5r1my++L0/sGledTtwvu2XyoxDjVmzqu8OXLVmzNr+SRfrZraeS5IrbCXWmTXbRE2p4IufgPZb\nf5X96agrE/MrvPbFdBGLfkkdB5SZsVhb1qykTYDLgD/y2s/yHYFjJe3lcu/zWVvWLPXdgauWjNns\nGkkXAZcWfwXnL+i3kkasXQOcXUXwQcqabZSmVPB1jneuqzlRZ5LOszXOV/4N4N9sX1lcKWlX4JtA\nmfPc19n0qzOXoC67Ax8BLsi/IueShpeOJA1k+FqxNT8QOUu2+HcS8DxpSG2dWbON0pQKfrWcKKHC\nc/Jy2ZmYexWH30naEHgnab6MMlvVdX5p1Zk1u0Z75Q5g+yqle8OWqdusWeBQ218qMVZduQSLZcwC\nmwGPuuTbK9p+kXQB/ls5zuuAF2zPLTNOjtXTOPjQT02p4L/Ha4kSxecAZ5Ucq66s2ToTWurMmh0h\naZn2/nZJy1L+57HOrNlZvHZBdzaLXtwtM4GrrozZReQGzawq9g31Zs0OJ40YRVMnSbfa3jw/PxkY\na/vQVtZsa1sJcepMaLkJ2NX2Uzlr9ie8ljW7se3SsmYlHQdsS2pBP5jXTSINMZxeZp95TuC6jlQJ\n7p4fNwNHVJA1WwtJt9veND8/HNixmDE7VEebSLqBNBvmYzlr9ipS1uwWwMu2y8yaHTaa0oJH0jtI\niRiteaNvB06z/cuSQxW/EXcGTgew/U9JpWVjFitwSePyujll7b/NyEIr/f3AmbYvAi6SdHOZgWx/\nUdJhwO8lLUf6RfIs8BXbZXfRjG1l/wK/lvQ+YP8qsmYBJK0KfBDYKK+6kzQ6qMxfQMWW7G6k6QOw\nPXuIjzYZXZjA7ADgB7a/2sqaHcRyDWmNmE1S0seAk4ETSYky6wInASdKOqSHt/bHLZK+IukIKsya\nVXJCTnS6G7hH0hxJx5cZJxuZRyxA6rf+bWFb6Y0A2990mt97HWCS7bUrqNyBlDUraayksbyWNdta\nLjPOxsBtwBTgHuBe4E3AbZI26um9fTRX0h65j/8twK9y/LIzZuvWnjV7NaSs2cEpTjM0pQV/BPDW\ntpbSb3Or/g+kybnKUlfW7BGkoWhvcr6pg6R1gW9LOsL2f5cYq7as2dy/377u1ee2zy0xXJ1ZsycD\nn7Z9YXGlpH8FvkS6plGGujJm61Zn1uyw0Yg+eEl32t64r9v6GauWrFlJM4HdbP+jbf04UmZrqX2t\nNWbNdtdS35M0wmZINjok3W17w75uC8mSkDXbRI3oogHmSVpsxsi8bn7Jsa4t7P/qtm1l3uJuqfbK\nHV7th1+qi9f3W86avd72JcCrN6iwfQ/pl0ppbH+q9QD+nTQh2I7A9VQwH46kpSV9OHerfSU/X6bs\nOMBz/dzWJ6r37lu1sv0T2//dqtzzupmtyl1D/CLDYBiSraUufBa4TNIPeS07ciop0+6AkmPVlTXb\n08/Ssn+y1pk12+ovPgj4HKli38f23WXGyHHqzJot5l8sUgzKzcWoK2O2boOaNdtUjajgbf9B0tbA\noaSKA9Iomm0rGA5XVwJS62YV7aq4WUVtWbOSDiVdw7ga2N32A2Xuv02dWbPt+RdFZeZiNDFjFmrM\nmh1OGlHBA9h+HHh1hImkrSoa61xL1qztkWXtq5Nw3TzvanmgvgE8QWqVvaXwq1uAXe5NJGrLmrV9\nUpn760Gdd9+qTZ1Zs8NJIy6ydkXSTbar6NM9oaftVf9HVwVp9pLmAr8jVRLb5+fk5bfaHlNirLV7\n2t5Kfiop1j3A5t1kzd5qe/2u39mvWLXcsEI13n0rDH1NruCH9BznktYC/pPF0+wPJCXPfLrEWHVm\nzfY6vWwnr+kwVp1Zs9O6WD0W2BeIG1aEQdHkCn5v5/uyVrDvyrNmByvNvuqsWUnXki7k9ngxzfl+\npiXEOww4Eqg6a7a7+KXfsKKmjNnQAI2p4FXTTSRy1uzHSZXG9Lx6KnAqcJbtUpKqVO/NqUW6fvEp\nUt+ugAXAN8ps5eZYy5Iupu1PymRtv5j2rSoupklaEcB22cNmO4ld5k23NyYlAf0amEk6V28kjajZ\n2fZdZcQJzdCICr6b4XBTSKnce9q+o8RYd7B41myrVfWHspKqJP2VNKSvdRXymuJyma21fKH4HcAh\n7VmzwK9Kzpotxq30YlpXWbNFJWfNdhW/dcOK99p+d0n7/F9SIlBXGbMftF1WxmxogKZU8FcDp3Yz\nHO7YMi881ZU1K+kBYCFdD1O07dLS7OvOmq1LnVmz6vmGFYcXJtIaaJzImA0da8owyTpvIjFP0mTb\nfy2uLDtr1vaksvbVgW6zZnMre0jK2bLAq91Q+5MSg64nzQ9TZqy6blhRS8ZsaIamVPB13kSitqzZ\nuq4rUG/WbK1qzJqt64YVdWXMhgZoylw055LmLn91jHUeDnch8KMyA+UxzVuT/nYH5YdIWbNljnfe\nBLiD1O/+UH7sCNwuadPu39kvkyXN6+IxHyjlBiaDIWfN3kG6HrO77YOqqNyzC4Hlc9wtSfO0PwRM\nJiXwlKWVMdv+WIHy714WhrhG9MHDYsPhIP1crWU4XM6aLW3GxbzP2q4rNJXSDVieAOaweP94qVmz\nkm5p7U/SV4CFto9UvmFFyRm6IXSkMRV8y2AMh6sia1bSXba7vFFEmRdzeylDFTenrk3NWbPFWzne\nBBxTmAXxlrIq+LoyZkMzNKUPHkkjgTGti4W5//ogUmJQ1ZVhFdOY1nZdobes2TJj1eyhurJmqe+G\nFTO6WDcWOF1SZMyGRTSiBS/pA8B3Sd0y95JGSPwA+AtwctndJ13ELz1rtuY0+8bdnBrqzZrNo3QG\n7YYVVWTMhqGvKRX8bcDetu+TtBWpotrH9i8qildX1mwtafZ1Zs3Wqc6s2Trn2Olh/0N6/qVQvqZU\n8Iv0gUu6zfZmFcWqLWu2ELPS6wp1Zs0OlhqyZq+lxjl22mKXnjEbmqEpFfwjwBmFVZ8pLts+Y7E3\n9T9WLaNb6kyzrzNrtqnq+rVQV8ZsaIamVPC1zdFe1+iWOtPsQ7mq/rUQQqeaUkk8afubNcWqZXRL\nnWn2OUZdWbONZ/tl0mia0tWYMRsaoCmZrB+pMVZtWbOSRkk6mDTf966kC8fvt31LyXHqzJoNA1NX\nxmxogKa04Gtj+4t5dMvvJVWWNavm3pw6DMzoQj/7AcAPbH+1lTE7iOUKS6Cm9MEvIF1oWmwT6SLh\nShXFrWx0S81p9oOeNRs6U1fGbGiGprTgb61z/G9NWbPrlLSfTtQ5G2cYmLoyZkMDNKUPvjY5a/Yp\n4BZJ10l6O/B30h2R9i8x1EO2H+zukctS1hQJtV1XCAN2OHAx8ADpzmIv5/WrA8cOVqHCkqkpXTSf\nt31KTbFqyZqtO3GmrqzZMDBLQsZsGDqaUsGfwKL91EW2fXKJsWrJmq0zzb4t7qDdnDr0bjAzZsPQ\n05QK/rNdrF4OOBhY1fYKJcaqLWu2ELPRN6cOnRusL/4wNDWigi/KLdBPAx8l9SF/1fYTJe6/tqzZ\nukTW7NAUGbOhN435jytpLKk1vT9wDrCV7acrCFVn1mwt6s6aDeWoMmM2NEMjRtFIOp009/t8YHPb\nJ1ZUuUO9WbO1qStrNoRQn0Z00eSkoJeABXSdFFRaolP7RdYmaMuaPa3irNkQQk0aUcHXabCyZqtU\nZ9ZsCKE+jeiDl7Sz7VZG3zq27y9se6/ti0sMV2vWbE3qzJoNIdSkES34YrdJF+PUS+1SaeJt0SJ5\nJoRmasRFVha9E1F7+n5Z6fwtPyt5f0uCayR9StLE4kpJS0vaWdI5pASaEMIQ0oguGhbtN25vZZbd\n6lxK0vHdlaPMrNka7U4aHXSBpK6SZ74WyTMhDD1N6aKZC/yO1FrfPj8nL7/V9pgSY9WWNTsYInkm\nhOZoSgW/Q0/bbV9XUdxKs2ZDCGEgmtJFcwcwzvYdxZX5VnRzyg5WY9ZsCCH0W1Musn6D1K3QblXg\n62UGqjlrNoQQ+q0pXTTTbU/tZlup0/nWmTUbQggD0ZQumhV72LZUmYFsN+VXTwih4ZpSWd0n6Z3t\nKyW9g3Q7vdJI2rnwfJ22be8tM1YIIQxEU7poNgAuB/4EzMirpwJvBvawfU+JsWrLmg0hhIFoRAs+\nV+CbA9cBk/LjOmCLMiv3rM6s2RBC6LdG9MHneVJeAn7Yy2vK+LlSZ9ZsCCH0WyMqeNJcKr3eiBg4\nu4RY60q6jNRabz0nL8esjCGEJUZT+uC7uhHxaFIXVKk3Ih6srNkQQuirRlTwRVXPpSJpHD1kzdou\nPXM2hBD6oxEXWYtsv2x7VoUTZdWWNRtCCAPRuBZ81erMmg0hhIFoXAu+BrVlzYYQwkBEBd93tWXN\nhhDCQEQXTR/VmTUbQggDERV8P0haBvgg0Opvvx043/aLg1eqEEJYVFTwfdRJRmyJWbMhhNBv0Qff\nd/xQjNIAAAO9SURBVNdI+pSkicWVkpaWtLOkc0iZsyGEMKiiBd9HdWbNhhDCQEQFPwBVZ82GEMJA\nRAUfQggNFX3wIYTQUFHBhxBCQ0UFH/pM0iuSbpZ0m6RfSFolr58k6YW8rfU4MG9bQdK3Jf1N0k2S\nZkj6WOF9t7XF+JqkRyWNaFu/t6RbJN0p6VZJe3dTxl+3leMxSTfkbZJ0nKR7Jd0j6RpJmxbe+0C+\nv0BreR9JZ7ft/+eSrh/QHzKEijXlhh+hXi/Y3hIgDws9FPhS3va31rY2Z5Gmcljf9sI87fJHutp5\nrtTfAzwM7EC6WQuSJgNfAXazfX++6fmVkv5u+5biPmz/S2F/y5Oyjo/Lqw4FtgMm235e0tuByyRt\nWkhWmyJpk/ZpofP+VgGmAM9KWtd2TFERlkjRgg8D9WdgjZ5eIGk9YGvgONsLAWzPsX1aN2/ZkZQd\n/G1gv8L6zwGn2L4/7+N+4MvAf/RSxq8Dv7R9ZV4+CjjM9vN5P78hTT2xf+E9XwWO7WZ/7wV+AfwE\n+EAvsUMYNFHBh36TNBLYBbissHq9tq6R7YFNgb+2KvcO7AdcAFwCvCsPRyXvZ0bba6fn9d2V8b2k\nuYKOycsrAct30epu38+FwFaS3tBD+S5g0S+gEJYoUcGH/hgt6WZgNjAeuLKw7W+2tyw8ft/+ZknH\ntvrFu9i2NPBO4Oe25wE3AP/S/rpOSFqD1Hr/YL4pe1+8ApxO/mIo7HM8sD7whzyx3MuS4h4AYYkU\nFXzoj1Yf/Nqkm40f2svr7wAmty6Y2v5Sfv9KXbz2X4BVgFslPUC6afp+hf1MaXv9FFJ3ziIkCTgH\nOLXYj56/NJ6TtG4H+/kR8DZgrcK6fYExwP25fJOIVnxYQkUFH/ot92H/O/BZSd1esLd9H6kL5Iu5\nW6c15YO6ePl+wMG2J9meRJoOYjdJy5EusB4jaVLexyTg86T+ciQdJumwvJ/PAS/a/n9dxDgd+B9J\no/P7diV9kZzfVu6Xgf8Gjmgr3+6F8k0h+uHDEipG0YQBsT1T0i2kiu/35D74wkt+YPt/gINJFet9\nkp4EXgCOLO4rV+K7A58o7P85SX8A3m37p5KOAn6R++VfBo603Yq3EfDH/PyLwCNtZXna9k6k++qO\nIf1KeIXU1bSX7Re6OMTvk0ff5C+UtYFXh0fm0TzPSNrG9g0d/MlCqE1MVRAaQ9LlwHtt/3OwyxLC\nkiAq+BBCaKjogw8hhIaKCj6EEBoqKvgQQmioqOBDCKGhooIPIYSGigo+hBAaKir4EEJoqP8Pu4HF\nVZUhyFsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4b6f2ef0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ct1=(pd.crosstab([base.REGIAO, base.ZONA],base.Insegurança_Alimentar, normalize='index')*100).round(decimals=1)\n",
"ct1\n",
"print(ct1,'\\n')\n",
"plot = ct1.plot(kind='bar',title=\"Análise de Insegurança Alimentar 2013 (G7)\")\n",
"ax = plt.subplot(111)\n",
"box = ax.get_position()\n",
"ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])\n",
"ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))\n",
"plt.ylabel('Freq.Relativa (em %)')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 198,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Insegurança_Alimentar Não Sim\n",
"REGIAO ZONA \n",
"CENTRO-OESTE Rural 79.1 20.9\n",
" Urbana 69.4 30.6\n",
"NORDESTE Rural 52.3 47.7\n",
" Urbana 56.6 43.4\n",
"NORTE Rural 57.4 42.6\n",
" Urbana 59.7 40.3\n",
"SUDESTE Rural 76.1 23.9\n",
" Urbana 76.6 23.4\n",
"SUL Rural 85.4 14.6\n",
" Urbana 80.3 19.7 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAGMCAYAAADQnrmpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xm8HFWZ//HPN2ELewIxhCUEEFC2sEQUENkVFQEVUQSJ\nC6KjOID6YxFkVQYGZXR0XBAVUEBBUBDcIAKCIzAJCfuq7CQQ1rCEJeT7++OchkrnLp17q+rm1n3e\nr1e/0lXVXc+pW53Tp0+d55RsE0IIoXmGDXQBQgghVCMq+BBCaKio4EMIoaGigg8hhIaKCj6EEBoq\nKvgQQmioIVfBS1pb0gOS1iisO07SL/PzcZKelzS84nLcL2nnKmOEhVM8J5K+JumMgS5TE0n6D0mH\nlLi/D0j6dVn7a5JBV8FLukrS05KW7OMufgQcaPuhrjbaftD2srZf63spqyNpe0kPD3Q5BitJy+Yv\n8D/29DrbJ9k+oK5ytUj6pKRrS97nOyRdLukpSbMkXSBpbGG7JJ0i6cn8OEWSCtvHS7pS0ouS7iw2\nTPJ7j5L0oKTZkn4lafkeyjIa2B/4cWHdcpJOy1+wL+R9/UbS2wuv2VTSNZKelfSwpK+3ttn+PbCh\npE1K+YM1yKCq4CWNB7YFDOzeh/evAfzM9p/LLVnojqTFBroMbT4MvAzsImmVgS5M2br5e48ETgfG\nA2sCzwE/L2w/ENgTmABsAnwA+Fxh+3nANGAl4CjgN7mihlRZfwLYBlgVGAF8r4cifhL4g+05ubxL\nAn8FNgZ2A5YH3gr8Cnhv4X3nAn8DRgHbAV+QVKwDzsvHEYpsD5oHcAzwd+A04NK2bWcC/wNcRvoA\nXw+sU9j+XeAhYDYwFdi2sO044Jf5+XjSF8hiefmTwL/yPu8D9i2879PAHcDTwJ+BNXso+yeAB4An\nSf9J7gd2ztuGAUcA/8zbzwdGdbOf7YGHC8tXASfmv8tzwF+AlfO2pYBf5n0+A/wfMCZvWwH4KTAD\neAT4BjA8bxsOfBt4Ih/zQW1/k9fL3sPf7zPAg8Df8voLgJnAs6T/qBsuxLnbELgceAp4DPhaXr8l\n8I98bDOA7wNL9PIZ+ivwTeBG4Ktt24rnpKtj+hTpM/Q08HngbcDNOf732/bV7Wcj7+vzwD35vf8D\niFSxvQS8BjwPPJNf/35SBTs7xz+usK8u/969/A02B54rLP8v6VdtsezX5efrkb4Qlyts/xvw+fz8\nN8BhhW1b52NYuoe//36F5QPyuVumlzK/CGxQWL4AOLKwvA1w30DWT4viY1C14EmthXPy4z2SxrRt\n/xhwPKnFci/pP3LLVGBTUgvgPOACSUv1FEzSMsB/A++1vRzpwzs9b9sD+BrwIWA0cE3eb1f72QD4\nIamSX5XUElq98JIvkVpQ2+XtT5P+03fq46TK503AEsBX8/pJpIp8jRzz88CcvO1MYC7wZmAz4N2k\n/2wAnyW1njYlVQZ7LkRZWrYjVVjvyct/BNbNZbyRdA6Lujx3kpYDrgD+RPrbvBmYnN/zGnAosDKw\nFbAT8IXuCiRpTdIXZOsztP9CHtPb8zF8FPgO6Yt6Z9IX0N6StstxOvls7Eb6gtgE2Bt4j+07SOfo\nH07dhCvm176Qy7oiqbL/N0nt56T9792TdwG3FZY3BG4qLN+U17W2/cv2c91sbydgSdLfqSsbA3cV\nlncG/mz7hV7K/B1gf0mLS1qfdL6vKGy/AxjfU/fQkDTQ3zCdPoB3Aq/yRuv0TuDQwvYzgTMKy+8D\n7uxhf88AE/Lz4+iiBQ8sk1/3YWBE2/v/CHymsDyM1MpYs4tYxwC/KiwvA7zCG63FO4CdCtvH5mNd\nrIt9bc+CLfijC8tfAP6Un3+a1DrbpG0fY0itshGFdfsAV+bnfwU+V9i2Mwvfgl+7h7/9ivk1K/R2\n7nK5pnX4GTkE+G0P248Gpufnq5G+IDYrbH/9uLo5ptUKr30S+Ghh+ULgkE4+G3lf7yxsPx84Ij//\nJHBtL8f5HeC/Ov17t713E9IvoeIv2NeAtxSW1837FKlRcl3bPr4JnJmfHwDcncuxAnBJfu9W3cR/\ntS3WFcDJheVNSf/nZgN3FdZvTfrin5v3f3zbfhfP68d18ncYKo/B1IKfBPzF9hN5+dy8rmhm4fmL\nwLKtBUkHSZom6SFJ9+dtK/cU0KlV8VFSq2qGpMskvSVvXhP4rqRnJD1D+k8jUsXRblXST+vifp8s\nbF8T+G1hX3eQ/tO1/0LpTnfH/QtS98CvJD0q6T8lLZ7jLZ6PqRXzx6TW9QLlbXveqdffI2m4pJMl\n/VPSbFJFCvP//bs7hjVIXVcLkLSepEslzcz7PYmez2nrFyC2HwGuZsHPUE8eKzyf08Vyq8ydfDa6\n/ay2k/T2fJFzlqRnSZ/H9uPs9RxJejPpy+dg29cUNj1P6vtuWQF43qnmbN/W2t5q0f+M9OvkKtKv\ngivz+u4GAjwNLFdYfpLUoAHA9nSnXy4fIv0SQNIo0i+4E0jdjmuQfsEXf6219vlMN3GHpEFRwUsa\nQfoZu13+zzyT9NN8gqQJHbx/G+DrwN6217A9nvTBVY9vBGz/2fYupA/hncBP8qaHSK3cFQuPEbb/\nt4vdzCB9KFvlWZrUZdLyEKkbqLivpXIl1Ge2X7V9vO0NSC2g3UiV3EOkFvzKhXjL22797J7B/F1I\nazC/F4ClC8tdXax04fnHgT1IvwRWILX2oIO/fy7r2t1s+yHpnKxre3lSt0iX+5S0NallemThM/R2\n4OMVXAhemM9GO3ex7lxSy3gN2yuQRoK1H2dX73td7p66AjjR9i/aNt9GusDaMoE3unBuA9bOXWUL\nbLc9z/axtsfbXj2vfyQ/unIzqV+/ZTLw7twd2p21gddsn217ru2HSRdh31d4zVuB+23P7mE/Q86g\nqOBJfcCvARuQfsJtSjqh19BZP+qKwDzgBUlLSDqG+VsRXZI0RtIe+cP3MulLYV7e/CNSZbFhfu0K\nkj7Sza5+A+wm6Z2SliC1RIp/+x8B38z/CZE0Ovfj9oukHSRtrDSmfzbp5/E82zNIF2O/LWl5ScMk\nrdPqQyZ1GRwsaTVJKwKHt+16OvCx3B86Edirl6IsR/r7PUn6YjhpIQ7jUmCspEMkLZmH1LWGzy2X\nj+v5/Mvq33rYzyTShdriZ2gj0qiP9/bwvr5YmM9Gu8eA1fPnpGU54CnbL0nakvSF2TFJq5G63b5v\n+0ddvORs4Mv5fK8GfIXUbYbtu0nn+1hJS0n6EKkf/cK871H5s6N8rek04ATb87qIA/AH0vWCYuwZ\npF+wG+Vfe0sBEwuvuTuF0sfzZ3UV0i/rmwuv2Y706yQUDJYKfhLwc6cx6jNbD9KoiX07aIH9iXTy\n7ySNZHmJzrodhgFfBh4l/czejlyJ2P4tcAqp+2M2cCvdVBS2bwO+SGqJzSD9TC3+hP0uqYX2F0nP\nAdeRWpf9tQrpy2U2qdvnalK3DaQvxiWA23N5fsMbP5V/QvoCuJk0euMPpL7PVm7A14F18vuOz8fV\nk7NJf/dHcrzrOj0Ap4t7u5CG7r2U97FD3vxVUmX3XC5zl8kuucLYG/he8fNj+z7S32Nhumk6KXPH\nn40u/JXUCp4pqdUd+QXghPzZOIb0BbwwDiC1go9TygF4XtLzhe0/Bn4P3JIfl1IYp066AD6RdL7/\nA9jL9qy8bWXS5+MF0v+xn9k+vYeynA28L/8qx/ZLpPN5O2kU1WzSRdi3kc4ZuVX+IdKv9qdJXzi3\nkkZ+tezTVuYAKHWzhdA9Se8FfmR7zQEux7bAu21/vdcXh0WWpJOAx21/p6T9fQD4hO29y9hfk0QF\nHxaQW1c7kFrxY0g/x6+zXVp6eR/KtCzpusU5tt85UOUIYTAZLF00oV4idb08TeqiuYPUNTCQjif9\njL90gMsRwqARLfgQQmioaMGHEEJDRQUfQggNtajN9NellVde2ePHjx/oYoQQBoGpU6c+YXt0769s\nvkFRwY8fP54pU6YMdDFCCIOApAcGugyLiuiiCSGEhooKPoQQGioq+BBCaKio4EMIoaGigg8hhIaK\nCj6EEBoqKvgQQmioqOBDCKGhBkWiUwihXuOPuKzbbfef/P4aSxL6I1rwIYTQUFHBhxBCQ0UFH0II\nDRUVfAghNFRU8CGE0FBRwYcQQkNFBR9CCA0VFXwIITRUVPAhhNBQlVbwkg6VdJukWyWdJ2kpSaMk\nXS7pnvzvyCrLEEIIQ1VlFbyk1YB/Byba3ggYDnwMOAKYbHtdYHJeDiGEULKq56JZDBgh6VVgaeBR\n4Ehg+7z9LOAq4PCKyxFCWER1N+9NzHnTf5W14G0/AnwLeBCYATxr+y/AGNsz8stmAmO6er+kAyVN\nkTRl1qxZVRUzhBAaq8oumpHAHsBawKrAMpL2K77GtgF39X7bp9ueaHvi6NGjqypmCCE0VpVdNDsD\n99meBSDpImBr4DFJY23PkDQWeLw/QeLnXQghdK3KUTQPAu+QtLQkATsBdwCXAJPyayYBF1dYhhBC\nGLIqa8Hbvl7Sb4AbgbnANOB0YFngfEmfAR4A9q6qDCGEMJRVOorG9rHAsW2rXya15kMIIVQoMllD\nCKGhooIPIYSGiptuhzBIxI2ww8KKFnwIITRUtOBD6IdoVYdFWbTgQwihoaKCDyGEhooKPoQQGioq\n+BBCaKio4EMIoaGigg8hhIaKCj6EEBoqKvgQQmioqOBDCKGhooIPIYSGqvKerOtLml54zJZ0iKRR\nki6XdE/+d2RVZQghhKGssgre9l22N7W9KbAF8CLwW+AIYLLtdYHJeTmEEELJ6uqi2Qn4p+0HgD2A\ns/L6s4A9aypDCCEMKXVV8B8DzsvPx9iekZ/PBMZ09QZJB0qaImnKrFmz6ihjCCE0SuUVvKQlgN2B\nC9q32Tbgrt5n+3TbE21PHD16dMWlDCGE5qljPvj3AjfafiwvPyZprO0ZksYCj9dQhn6Leb9DCINN\nHV00+/BG9wzAJcCk/HwScHENZQghhCGn0gpe0jLALsBFhdUnA7tIugfYOS+HEEIoWaVdNLZfAFZq\nW/ckaVRNCCGECkUmawghNFRU8CGE0FBRwYcQQkNFBR9CCA0VFXwIITRUj6NoJC0F7AZsC6wKzAFu\nBS6zfVv1xQshhNBX3Vbwko4nVe5XAdeTMk6XAtYDTs6V/1ds31xDOUMIISyknlrwN9g+tpttp0l6\nEzCugjKFEEIoQbcVvO0FJl/JrfYlbM+2/TiDZB6ZEEIYijrOZJV0ALAXMFzSFNtHVlesEEII/dXt\nKBpJu7et2tn2rrZ3Ad5XbbFCCCH0V0/DJDeWdLGkTfPyzZLOkPQTIEbQhBDCIq6nPvhvSloFOEGS\ngK8DywEjYuRMCCEs+nrrg38BOARYFzgdmAL8Z9WFCiGE0H899cF/A7gQuBTYwfbuwHTgD5L2r6l8\nIYQQ+qinPvjdbL+bNHf7/gC2LwHeDYzsZOeSVpT0G0l3SrpD0laSRkm6XNI9+d+O9hVCCGHh9FTB\n3yrpdOBs4OrWSttzbX+3w/1/F/iT7bcAE4A7gCOAybbXBSbn5RBCCCXr6SLrfpI2Bl61fefC7ljS\nCsC7gE/m/b0CvCJpD2D7/LKzSFMhHL6w+w8hhNCzHmeTtH1LXyr3bC1gFvBzSdPyEMtlgDG2Z+TX\nzATG9HH/IYQQelDlPVkXAzYHvmT7eknfpa07xrYluas3SzoQOBBg3LiY8iYsnPFHLDDTBgD3n/z+\nmksSwsCpcj74h4GHbV+fl39DqvAfkzQWIP/b5Xw2tk+3PdH2xNGjR1dYzBBCaKaOWvCSNgHGF19v\n+6Ke3mN7pqSHJK1v+y7SaJzb82MScHL+9+K+FT2EEEJPeq3gJf0M2IQ0PcG8vNpAjxV89iXgHElL\nAP8CPkX61XC+pM8ADwB796HcIYQQetFJC/4dtjfoy85tTwcmdrFpp77sL4QQQuc66YP/h6Q+VfAh\nhBAGTict+LNJlfxM4GVApAEwm1RastA4MbIlhHp1UsH/FPgEcAtv9MGHEEJYxHVSwc/Kc9CEBuqu\nVQ3Rsg5hsOukgp8m6Vzg96QuGqD3YZIhhBAGVicV/AhSxf7uwrpOh0mGEEIYIL1W8LY/VUdBQggh\nlKvXYZKS1pM0WdKteXkTSUdXX7QQQgj90ck4+J8ARwKvAuT7sX6sykKFEELov04q+KVt39C2bm4V\nhQkhhFCeTir4JyStQ7qwiqS9gBk9vyWEEMJA62QUzReB04G3SHoEuA/Yt9JShRBC6LdORtH8C9g5\n341pmO3nqi9WCCGE/uq2gpe0H3Cu7XkAtl9o274OMNb2tdUWceiJ7NIQQhl6asGvRMpinQpMJd1f\ndSngzcB2wBO03YIvhBDCoqPbCt72dyV9H9gR2IZ00485wB3AJ2w/2NvOJd0PPAe8Bsy1PVHSKODX\npDtE3Q/sbfvp/h1GCCF0b+rUqW9abLHFzgA2otpbldZpHnDr3LlzD9hiiy26vPVpj33wtl8DLs+P\nvtrB9hOF5SOAybZPlnREXj68H/sPIYQeLbbYYmesssoqbx09evTTw4YN80CXpwzz5s3TrFmzNpg5\nc+YZwO5dvWYgvsn2AM7Kz88C9hyAMoQQhpaNRo8ePbsplTvAsGHDPHr06GdJv0q6fk3FZTBwhaSp\nkg7M68bYbo2jnwmMqbgMIYQwrEmVe0s+pm7r8aor+Hfa3hR4L/BFSe8qbrRtcgJVO0kHSpoiacqs\nWbMqLmYIIVRL0haf/exnV28tH3PMMWO+/OUvrwrw0ksvabvttnvzVltttd7HP/7xcWXF7CTRCUnv\nBzYkjaIBwPYJvb3P9iP538cl/RbYEnhM0ljbMySNBbq8OGD7dFKCFRMnTmzcN28IYeCMP+KyLcrc\n3/0nv39qb69ZYokl/Ic//GHkjBkzZo4dO3a+6V6WWmopX3311feWWSbobDbJHwEfBb5Euh/rR4A1\nO3jfMpKWaz0nzSd/K3AJMCm/bBJwcZ9KHkIIg8jw4cO9//77zzrppJMW6JY+99xzV9hkk03e8ta3\nvnWDrbfeer2HHnpoMYDHHnts+M4777zOeuutt8GECRPecv31149YmJiddNFsbXt/4GnbxwNbAet1\n8L4xwLWSbgJuAC6z/SfgZGAXSfcAO+flEEJovP/3//7f4xdddNGoJ598cnhx/S677PL89OnT77zj\njjtu32uvvZ464YQTVgE47LDDVp0wYcKLd9999+0nnnjiI5MmTVprYeJ10kUzJ//7oqRVgSeBsb29\nKU9xMKGL9U8COy1MIUMIoQlGjRo17yMf+ciTJ5988ptGjBgxr7X+vvvuW2LPPfdcfdasWYu/8sor\nw9ZYY42XAW644YblLrzwwnsBdt999+cOPPDAxZ566qlho0aNmtddjKJOKvhLJa0InArcSLoo+pOF\nPrJQjuNW6GHbs/WVI4TQJ0ceeeRjm2+++QYf+9jHXs8POuigg8YdfPDBM/fdd99nL7300uVOOOGE\nVcuI1WsXje0TbT9j+0JS3/tbbB9TRvAQQhhqxowZ89oHPvCBp88999yVW+uee+654ePGjXsV4Mwz\nz1yptf7tb3/7cz//+c9XArj00kuXGzly5NxOW+/Q2UXWmyV9TdI6tl+2Hc3EEELoh6OOOmrmM888\ns1hh+dF99tlnnQ033PCtK6200usjbE455ZRHp02btvR66623wVFHHbXamWeeed/CxOmki+YDpFE0\n50uaR5pH5vxO5qIJIYRFUSfDGsv24osvTms9X2ONNebOmTPn9eX99tvvmf322++Z9veMGTPmtSuu\nuOKffY3ZSRfNA7b/0/YWwMdJk44t1LdICCGE+nWa6LQmqRX/UdLMkIdVWagQQgj912sFL+l6YHHg\nAuAjefhjCCGERVwnLfj9bd9VeUlCCCGUqsdb9tn+JfD+PBfNfGyfVmnJQggh9EtPLfhl8r/LdbEt\nJv8KIYRFXE+37PtxfnqF7b8Xt0naptJShRBCwxx++OGrXHjhhSsNGzbMw4YN4wc/+MEDP/7xj1c+\n7LDDHttiiy1eqiJmJ33w3wM272BdaJrupkWIKRHCYHfcCqVOF8xxz/Y4rv6KK65Y5s9//vOKt9xy\ny+0jRozwjBkzFnv55Zf161//+oFSy9Gm23HwkraS9BVgtKQvFx7HAcO7e18IIYT5PfLII4uPGjVq\n7ogRIwwwduzYuePHj391yy23XP9vf/vb0gBLL730Zp/73OdWf/Ob37zh1ltvvd6VV1659JZbbrn+\n6quvvvE555zTwyRU3esp0WkJYFlSK3+5wmM2sFdfgoXQpeNW6P4RQgPsueeesx999NElxo8fv9F+\n++037rLLLlu2/TVz5swZttNOO82+9957b1tmmWVeO/roo1e75ppr7r7gggvuPfHEE1frS9ye+uCv\nBq6WdKbtSn9GhBBCk62wwgrzbr311tv/9Kc/LTd58uTlJk2atM4xxxzzcPE1iy++uPfaa6/ZABtu\nuOGcJZdcct6SSy7pLbfccs4jjzyyRF/idtIH/6KkU1nwln079iVgCCEMRYstthi77bbbc7vttttz\nm2yyyZxf/OIXK7Vt97BhqVNl2LBhLLnkkgYYPnw4r732mvoSs5M7Op0D3AmsBRwP3A/8X6cBJA2X\nNE3SpXl5lKTLJd2T/x3Zh3KHEMKgcdNNNy15yy23LNlanjZt2ojVV1/9larjdlLBr2T7p8Crtq+2\n/WlgYVrvBwN3FJaPACbbXheYnJdDCKGxZs+ePXz//fdfa5111tlwvfXW2+DOO+8cccoppzxaddxO\numhezf/OyBmtjwKjOtm5pNWB9wPfBL6cV+8BbJ+fnwVcBRzeWXFD6Ke4I1aAXoc1lm3bbbd9cdq0\naXe2r7/hhhtenwamOJ3waaedNl/lX9y2MDqp4L8haQXgK6Tx78sDh3a4/++QZp4sZsOOsT0jP59J\nujn3AiQdCBwIMG7cuA7DhRBCaOm1grd9aX76LLBDpzuWtBvwuO2pkrbvZt+W1OW0B7ZPB04HmDhx\nYkyNEEIIC6mnyca+Rw9zztj+9172vQ2wu6T3kUbfLC/pl8BjksbaniFpLPB4H8odQgihFz214Kf0\nZ8e2jwSOBMgt+K/a3i8PuZwEnJz/vbg/cUIIoQPz5s2bp2HDhjWqN2DevHkCur0Jd0+JTmcVlyUt\nbfvFEsp0Mun+rp8BHgD2LmGfIYTQk1tnzZq1wejRo59tSiU/b948zZo1awXg1u5e08kdnbYCfkqa\ntmCcpAnA52x/odOC2L6KNFoG208CO3X63hBC6K+5c+ceMHPmzDNmzpy5EZ0NDx8M5gG3zp0794Du\nXtDJKJrvAO8BLgGwfZOkd5VTvhBCqN4WW2zxOLD7QJejbh19k9l+qG3VaxWUJYQQQok6acE/JGlr\nwJIWZ8HM1BBCCIugTlrwnwe+CKwGPAJsmpdDCCEswjpJdHoC2Le4TtIy3bw8hBDCIqLHFryk1SRN\nlLREXn6TpJOAe2opXQghhD7r6ZZ9hwDTSfPPXCfpAFLf+wig3PsZhhBCKF1PXTQHAuvbfkrSOOBu\nYBvbtc7CFkIIoW966qJ5yfZTALYfBO6Kyj2EEAaPnlrwq0v678Ly2OJyB5ONhRBCGEA9VfD/r205\nWu8hhDCIdDzZWAghhMGlT5Pu5LsthRBCWIT1dVY1lVqKEEIIpetTBW/7x2UXJIQQQrk6mQ/+yz1t\nt31aN+9bCvgbsGSO8xvbx0oaBfwaGA/cD+xt++mFK3YIIYTedNKCnwj8G2mysdVIk49tDiyXH915\nGdjR9gTSBGW7SnoHcAQw2fa6wOS8HEIIoWSdTBe8OrC57ecAJB0HXGZ7v57eZNvA83lx8fwwsAew\nfV5/FulOT4cvZLkXLcet0MO2Z+srRwghFHTSgh8DvFJYfiWv65Wk4ZKmA48Dl9u+Hhhje0Z+yczu\n9iXpQElTJE2ZNWtWJ+FCCCEUdNKCPxu4QdJv8/KepJZ3r2y/BmwqaUXgt5I2attuSV3eANf26cDp\nABMnTmzETXJDCKFOncwH/01JfwS2zas+ZXvawgSx/YykK4FdgcckjbU9Q9JYUus+hBBCyTodJrk0\nMNv2d4GHJa3V2xskjc4tdySNAHYB7iTdvHtSftkk4OKFLnUIIYRedTJM8ljSSJr1gZ+TLpb+Etim\nl7eOBc6SNJz0RXK+7Usl/QM4X9JngAeAvftR/hBCCN3opA/+g8BmwI0Ath+V1NPwSPLrbs7va1//\nJLDTQpYzhBDCQuqki+aVPOTREPdjDSGEwaKTCv58ST8GVpT0WeAK4CfVFiuEEEJ/dTKK5luSdgFm\nk/rhj7F9eeUlCyGE0C89VvD5AukVtncAolIPIYRBpMcumpyoNE9SD7n4IYQQFkWdjKJ5HrhF0uXA\nC62VcU/WEEJYtHVSwV+UHyGEEAaRbit4SeNsPxj3Zg0hhMGppz7437WeSLqwhrKEEEIoUU9dNMX7\nrq5ddUFCaJy4T0AYYD1V8O7meQhhURNfJqELPVXwEyTNJrXkR+Tn5GXbXr7y0oUQQuizbit428Pr\nLEgIIYRydToffAghhEEmKvgQQmioyip4SWtIulLS7ZJuk3RwXj9K0uWS7sn/jqyqDCGEMJR1ksna\nV3OBr9i+Md8gZGqe7uCTwGTbJ0s6AjgCOLz06DGqIIQwxFXWgrc9w3brLlDPAXcAqwF7AK3s2LOA\nPasqQwghDGW19MFLGk+6fd/1wBjbM/KmmcCYOsoQQghDTZVdNABIWha4EDjE9mzpjQRZ25bUZRKV\npAOBAwHGjRtXdTFDCIua6Gbtt0pb8JIWJ1Xu59huzUj5mKSxeftY4PGu3mv7dNsTbU8cPXp0lcUM\nIYRGqnIUjYCfAnfYPq2w6RJgUn4+Cbi4qjKEEMJQVmUXzTbAJ0g3C5me130NOJl0I+/PAA8Ae1dY\nhhBCGLIqq+BtX8v8M1IW7VRV3BBCCElksoYQQkNFBR9CCA0VFXwIITRUVPAhhNBQUcGHEEJDRQUf\nQggNFRV8CCE0VFTwIYTQUJVPNhZCaJjuJgGLCcAWOdGCDyGEhooKPoQQGioq+BBCaKio4EMIoaGi\ngg8hhIZ6+/tLAAAgAElEQVSKCj6EEBqqyjs6/UzS45JuLawbJelySffkf0dWFT+EEIa6KlvwZwK7\ntq07Aphse11gcl4OIYRQgcoqeNt/A55qW70HcFZ+fhawZ1XxQwhhqKu7D36M7Rn5+UxgTM3xQwhh\nyBiwi6y2Dbi77ZIOlDRF0pRZs2bVWLIQQmiGuiv4xySNBcj/Pt7dC22fbnui7YmjR4+urYAhhNAU\ndVfwlwCT8vNJwMU1xw8hhCGjymGS5wH/ANaX9LCkzwAnA7tIugfYOS+HEEKoQGXTBdvep5tNO1UV\nM4QQwhsikzWEEBoqKvgQQmioqOBDCKGhooIPIYSGigo+hBAaKir4EEJoqKjgQwihoaKCDyGEhooK\nPoQQGioq+BBCaKio4EMIoaGigg8hhIaKCj6EEBoqKvgQQmioqOBDCKGhooIPIYSGGpAKXtKuku6S\ndK+kIwaiDCGE0HS1V/CShgP/A7wX2ADYR9IGdZcjhBCabiBa8FsC99r+l+1XgF8BewxAOUIIodFk\nu96A0l7ArrYPyMufAN5u+6C21x0IHJgX1wfuWshQKwNP9LO4EaueWE08pog1cHHWtD267MIMRpXd\ndLu/bJ8OnN7X90uaYntiiUWKWIM8TsQaXLHqPKamGogumkeANQrLq+d1IYQQSjQQFfz/AetKWkvS\nEsDHgEsGoBwhhNBotXfR2J4r6SDgz8Bw4Ge2b6sgVJ+7dyJW7bGaeEwRa/DEaazaL7KGEEKoR2Sy\nhhBCQ0UFH0IIDRUVfAghNNQiOw5+YUnaCtgP2BYYC8wBbgUuA35p+9nBGCvHGwmsmuPcb3temfuv\nO1ZTz5WkpYDdcqzW3/BW4LIyBxLUFafJsYaKRlxklfRH4FHgYmAK8DiwFLAesAPwAeA02/0ejllX\nLEkrAF8E9gGWAGblOGOA64Af2L6yPzEGKFbjzlWOdTypcroKmNpFrKWAr9i+eTDEaXKsoaQpFfzK\ntntMae7kNYtSLEmXA2cDv7f9TNu2LYBPALfY/ml/4gxArMadq7yf99u+rIftbwLG2Z4yGOI0OdZQ\n0ogKPoQQwoIa0Qcv6Tmgq28qAba9fAUx3wF8D3grqVtjOPBCWbEkbd7Tdts3lhGni7gjgXVJP4lb\nsf5W4v4bd65yjN/T9XEBYHv3smLleKOBw0lTbhfP1Y4lxqj1mHLMyo9rKGlEBW97uQEI+33SNAsX\nABOB/Un9hWX5dg/bDJT+gZd0AHAwaX6g6cA7gH+UGauh5wrgWyXvrzfnAL8G3g98HphEunZSprqP\nCeo5riGjkV00ub+u+O3/YAUxptieKOlm25vkddNsb1Z2rLpIugV4G3Cd7U0lvQU4yfaHKowZ56oP\nJE21vUXbMf2f7bcNdNn6o6nHNVAa0YJvkbQ7qeW7Kukq/JrAHcCGFYR7MU+WNl3SfwIzqCivQNJG\nLPiT9ewKQr1k+yVJSFrS9p2S1q8gTpPP1brAf7Dg+Vq75FCv5n9nSHo/abTQqJJjALUeE9R4XENB\n0xKdTiR1K9xtey1gJ9Iwvyp8gvT3Owh4gTQF8ofLDiLpWFL/8fdIw8X+Eyi97zN7WNKKwO+AyyVd\nDDxQUazGnavs58APgbmk83U28MsK4nwjD2/9CvBV4Azg0AriQH3HBPUeV+M1qoum8FP8JmAz2/Mk\n3WR7wkCXra9yt8kEYJrtCZLGkBJ0dqk47nbACsCf8q0Vy95/484VzNfFcIvtjYvrBrpsfdXEYxoq\nGtVFAzwjaVngb8A5kh4ntdhKJ2kb4DhS18Lrf8cKfrbOyZXfXEnLk7oz1ujtTX2Vb4o+Brgvr1oF\nKL1fnGaeK4CXJQ0D7snTYj8CLFt2kDza5LPAeOY/pk+XHYuajglqP67Ga1oLfhlSevMwYF9SC/Qc\n209WEOtO0k/HqcBrrfVlx5L0A+BrpFEgXwGeB6bb/lSZcXKsLwHHAo8BrSkK3LrYVXKsxp2rHOtt\npGsJK5K6oZYHTrVdaveTpP8FrmHBY7qwzDg5Vi3HlGPVdlxDQWMq+NzyvML2DjXFu9722yuOIWB1\n2w/l5fHA8lWla0u6l3QD9NIrvrY4jTtXOc5w4BTbX60h1nTbm9YQp7ZjyvFqOa6hojEXWW2/BszL\nF2jqcKWkUyVtJWnz1qPMAE7fvn8oLN9f8VwcDwGlTpTWlSaeK3j9uN5Z9n67camk91UdpOZjgpqO\na6hoTAseII/62Ay4nEJ/ru1/ryBWV5NvueyMO0lnAd+3/X9l7rebWD8F1ifNtPhya73t0yqI1bhz\nlWP9EFiNlFRVPK6LSo7zHLAM6Ty9SrWZwLUcU45V23ENBU27yHpRflSuru4F4O3AvpIeIP3nan3g\nS+8XJ11MfZCUzr9EBfsvauK5gjRO/Enmz/41JR9rzRnBtRwTDFimc2M1qgVft5yIsSHzJ3+cUHKM\nNbtab7uq8emNVMe5qlvV8wYNlKYe10BoVAte0n10MTlSFcPhJP0IWJqU+HEGsBdwQ9lx6GGyp7Ll\nIWqHsWBFWEVXRhPPFZJ+TtfHVeowvzrmDSrEquWYcqzajmsoaFQFT5pIqmUp4CNUl+a8te1N8pwZ\nx0v6NvDHCuJcRvrPJdIxrQXcRTUp/a2Jnnaj+omemniuAC4tPF8K+CAp3b5sB/PGvEE7tOYNqiAO\n1HdMUO9xNV6jKvguhvd9R9JU4JgKws3J/74oaVVSH+XYsoO0Mgdb8uiPL5QdJ1vJ9k8lHWz7auBq\nSZVc3G3iuYIFx2tLOg+4toJQtc0bVOMxQY3HNRQ0qoJvG/o2jNRKrOoYL83ztpwK3EhqZf+koliv\ns32jpKrGdNc5gVXjz1W2LvCmCvbbPm/Q01Q3b1C7qo4JBva4GqdRF1nbhsPNBe4HvmX7rorjLgks\n5ZJvtp33/eXC4jBgc1JL+z0VxNqNlEW4Bmlys+WB413CPUu7iNW4c5X3335Dk5nAkVVmYqr6eYNq\nP6Yct9LjGgoaVcHXSekO8F8gJYGY9JP1h7ZfKjnOsYXFVkV4Ydlxmqyuc1W3/CuodUx/d0V3+apb\nU49rIDQmk1XScEkrF5aXkHSgpDsqCnk26ULn90h3DNoA+EXZQWwfX3h80/Y5VPTzWNLakn4v6QlJ\nj0u6WFIVo1oaea66Imk9SaV3B0k6BjgLWAlYGfi5pKPLjtNN7EqOKe97wI6rkWwP+gdpIq5nSX3G\nVwPvBh4GfgtsXlHM2ztZ188YW5GG9L0pL28CnAs8VNExXUeaO32x/NgPuD7OVUcxNgH+AtwKfIN0\nEffCfGyHVnBMd5G6mlrLI4C7BvMx1XVcQ+nRlBb80cAWtlclzRr4e+DfbH/Q1f28u1HpZs4A5Auf\nU8rauaRTgZ+RbkxxmaRvkP6zXU+6yFWFpW3/wvbc/PglhfHwJWncucp+Qvry/TBpaOl04J/Am23/\nV8mxIH1BFs/NkqRpfMtU9zFBPcc1ZDSiD17SjbY3LyzfanujimLdQuobXJw0b8uDeXlN4E7bG5QU\n53ZSi/alnNn3ELCR7fvL2H9brNZImcOBp4FfkY7po8BI20eWGKtx5yrHmm8WREn/cjVJW98jHcM4\n0njxy/PyLsANLvH+uXUdU953bcc1lDRlmOSb2kabrFhcdrmTZe1W4r568pLzRUDbT0u6p4rKPZvK\nG8lUAJ8rbDNQWgVPM88VwFKSNuONv+HLxeUSf520fnlMJXVrtVxV0v6L6jomqPe4hoymtOCP7Wm7\n7eNLjjccuM32W8rcb1uMZ0h3O2p5V3HZdqn3ZVW6Y89Wtv9e5n67iNO4c5XjdDVjZYtd4nQP+ZjO\ntr1vWfvsJk5tx5Tj1XJcQ0kjKviBoDTd7ZdsV3E7u9YY4G45ZZqWHXOa7c3K3u9Aq/pcDQRJ1wI7\numHjw5t6XAOlKV00A2EkcJukG5h/juxSWtZVVOAdmCzpw8BFbtY3f6XnaoD8C/i7pEuY/5hKn7u/\nZk09rgERFXzffX2gC1CBzwFfBuZKeonm3Gyhiefqn/kxDGjSHOpNPa4BEV00IYTQUI1uwUvaA5hp\n+/oS99k+L4eBJ4ArgcNd8Q2rq6AF709q4Annm33XVIZGnitJY4GnbL/c64s729/v6eaYct5C5co+\nprzPAT+uJmp0C17SScDGwGK231thnJHAJ0nzjn+kqjg51kmkTNAzyqqguhktMYp02759bE8vI04v\nZWjcucrxrgDWIc0f9NUS9tfVxfdRpKzje2wf0d8YHZSh1GPK+xzw42qiRlfwdWtP4qkoxp6k/1wT\nbO9fcayJwGm231VlnIFQx7kqxBKwge3bKowxHJhaTEyqUh3HlOPUelxN04ipCiQdVnj+kbZttdwN\nRtLi1NDlZft3tr9ddeWeY00Bli1zn009V5J2LDxfq23zB6uuCG2/VuX+u/BA1ccEA3JcjdKIFnyx\nNdZFKnypLTVJXaVMjySl9V/rkm7kLOl823vn56fYPryw7S+2311GnF7KMAb4g+0tStxn485VjlXL\ncRWmlSgaCexPmiOmliQhSQ/ZXqPE/S0Sx9U0TbnIqm6ed7XcXx9oWzbpFnDftX1ZiXGKE4rtQpon\npmV0iXGK84AUjQK2Jt0js9Rw3Tzvarm/6jpXUN9xtU8r0boYeRXwbyXG6U3ZLcNF5bgapSkVfPvV\n9+629T+Q/aky99dTqD5u64v2mRVbFeGXbT9ecqwmniuo6bhst3f/VKZtzqD5NlFy112dxzWUNKWC\nnyBpNumDNyI/Jy+XPd1tXZbOEzsNIx1Ta5InkebILo3ts8rcXy+aeK4A1s7Zlyo8Jy8P1sqrp0Sj\n79ZWitBnTemDX9z2q72/cvDoZaInbO9QV1nK1MRzBQMzd1AIvWlKBV/bkLe6SHqH7esGuhxla+K5\nApB0pu1PDnQ5yiTpv9tWFZOPrh2AIoWF1IhhkpR/cW7hCyDtke8UVJYflLivRUkTzxWk29sNGElj\nJS1Z8m6ntj1uBJ4HTpV0SMmxulTRcQ0ZTemDH93DBaG6ZqJ7O7CxpLIyMReFirD0rFmaea7gjWsm\nXZ63km+O0ZVfAOtIKi27tLtrM5J+BPwv8J0y4vSi9OMaSppSwQ8nXdUfsErR9tdK3uVahQt1XcWr\nY6rbG0hZs/9FGo9chiaeK4DVgG/T9XEZKPXmGAsEsHduZZdWGSfHmpNCVa/O42qiplTwM8pMWumJ\npMNs/2d+/hHbFxS2nVRi5TGLVGEMGNu/q2C3TTxXAPeWfYejrkja0fZf8/O1bN9X2PxB2xdVHH8x\n4BPAw1XGafOA7XE1xmuM6INfeB8rPG+/V+muJcZ53vbV3T1KjIOk8wvPT2nb9pcyY9HMc1WnbxWe\nX9i27egyA0l6TtLswuM54BHgvcx/396qDXh35WDVlAp+jzy/CACS1pd0aDep6v1VV8bifb2/pDTt\nWbNFpWbNAjt1tVLSipKOKjlWnVmzxUxjJC0uaTNJbyo5Tm3HZHs528sXHsvZHmN7b9uPlhmrt6LU\nGKtRmtJF80vgM8A9kt4M/AM4B9hN0ttst7fe+qOuTMz/kLSK7ZkAkvYHPgw8ABxn+6kSY9WZNbuM\npJOBVYHfAecBJ5B+9p9XcqzasmaBD0l6xPZtklYgfQZfA0ZJ+qrtso6ttmOStCbwjO1n8/IOwJ6k\nz+D3XeJ9U+vMmh1KmlLBj7R9T34+CTjP9pckLUEa3lVmBV9XJuaPgZ0BJL0LOBn4ErApcDqwV4mx\nasuaBc4GriZ1L+xKmiZhOrBJ68usRHVmzW5r+/P5+aeAu23vKWkV4I+U9+VVZ8bs+cAHgWclbQpc\nAPwHMIE0jPeAEmNF1mwFmpLodLPtTfLzvwOnti4QSrrJ9oQSY9WSiVkst6T/AWbZPi4vTy9zfuw6\ns2bbz4ekh4FxtueVFaOw79qyZiVNs71Zfn4ZcIHtM9u3lRCntozZtv9X3wLm2T5M0jBgemtbWHQ1\npQV/c/4APgK8GfgLpH7dCmJdD9SRiTk8j9OeS+q3PrCwrezzdmSdWbNKd1Vq9Rc/CayQh8JRctdT\nXecK4BlJu5E+g9uQugxbo07K/BX0qRozZot9+juSfwnbnlf2MMnImq1GUyr4z5KmtR0PvNv2i3n9\nBsw/6qAMdV3RPw+4WtITwBzgGoB8jeHZkmP9gPoqwhVI3WbFv2MrCcjA2iXGqnP0xeeA/wZWAQ4p\ndDftBJQ5NXGdrea/5hFWM0hzs7eGZ44FSut/z6Z2sW4UKWv217brSKpqnKZ00Sxve3Y328bZfrDE\nWA8D3WZblpmJKekdwFjgL7ZfyOvWA5YtMzOyzC6ERUmd56ouku4E9qGGjNn8q+qjpM/g+bYfyes3\nA95k+89lxeqhDCOA/23i57MOTWnBX0VugUqabLs4FO93lNs6rSUTsz2hhTxs0vbdefhnmanvtWbN\n5ovf+wIb5lW3AefafrnMONSYNav67sBVa8as7V91sW5a67kkucJWYp1Zs03UlAq++Alov/VX2Z+O\nujIxv8UbX0wXMv+X1NFAmRmLtWXNStoAuAT4O2/8LN8eOErSHi73Pp+1Zc1S3x24asmYza6UdCFw\ncfFXcP6CfidpxNqVwJlVBB+grNlGaUoFX+d457qaE3Um6Txf43zl3wP+zfblxZWSdga+D5Q5z32d\nTb86cwnqsivwaeC8/CvyGdLw0uGkgQzfKbbm+yNnyRb/TgJeJA2prTNrtlGaUsG/KSdKqPCcvFx2\nJuYexeF3ktYH3keaL6PMVnWdX1p1Zs2u1l65A9i+QunesGXqNmsW+KLtb5YYq65cggUyZoGNgEdc\n8u0Vbb9EugD/gxxnZWCO7WfKjJNj9TQOPvRRUyr4n/BGokTxOcAZJceqK2u2zoSWOrNmh0lasr2/\nXdJSlP95rDNrdgZvXNCdyfwXd8tM4KorY3Y+uUEzo4p9Q71Zs0NJI0bR1EnSLbY3zs9PBEbZ/mIr\na7a1rYQ4dSa03AjsbPupnDX7K97Imn2r7dKyZiUdDbyD1IJ+IK8bTxpiOKXMPvOcwHU1qRLcNT+m\nA4dWkDVbC0m32d4wPz8E2L6YMTtYR5tIup40G+ajOWv2ClLW7CbAq7bLzJodMprSgkfSe0mJGK15\no28DTrH9h5JDFb8RdwROBbD9iqTSsjGLFbik0XndrLL232Z4oZX+UeB02xcCF0qaXmYg29+QdBBw\njaSlSb9Inge+ZbvsLppRrexf4M+SPgLsW0XWLICklYCPA2/Jq+4gjQ4q8xdQsSW7C2n6AGzPHOSj\nTUYUJjDbD/iZ7W+3smYHsFyDWiNmk5T0WeBE4DhSoszawPHAcZIO7OGtfXGzpG9JOpQKs2aVHJsT\nne4C7pY0S9IxZcbJhucRC5D6rf9a2FZ6I8D2953m914LGG97zQoqdyBlzUoaJWkUb2TNtpbLjPNW\n4FZgC+Bu4B7gbcCtkt7S03sX0jOSdst9/NsAf8rxy86YrVt71uxkSFmzA1OcZmhKC/5Q4J1tLaW/\n5lb9taTJucpSV9bsoaShaG9zvqmDpLWBH0o61PZ/lRirtqzZ3L/fvu7157bPLjFcnVmzJwIH2z6/\nuFLSh4Fvkq5plKGujNm61Zk1O2Q0og9e0h2237qw2/oYq5asWUnTgF1sP9G2fjQps7XUvtYas2a7\na6nvThphMygbHZLusr3+wm4LyaKQNdtEjeiiAWZLWmDGyLzuuZJjXVXY/+S2bWXe4m7x9sodXu+H\nX7yL1/dZzpq9zvZvgddvUGH7btIvldLY/lLrAfw7aUKw7YHrqGA+HElLSPpU7lb7Vn6+ZNlxgBf6\nuG2hqN67b9XK9q9s/1ercs/rprUqdw3yiwwDYVC2lrrwFeASST/njezIiaRMu/1KjlVX1mxPP0vL\n/slaZ9Zsq7/4k8BXSRX7XrbvKjNGjlNn1mwx/2K+YlBuLkZdGbN1G9Cs2aZqRAVv+1pJWwJfJFUc\nkEbRvKOC4XB1JSC1blbRroqbVdSWNSvpi6RrGJOBXW3fX+b+29SZNduef1FUZi5GEzNmocas2aGk\nERU8gO3HgNdHmEjavKKxzrVkzdoeXta+OgnXzfOulvvre8DjpFbZNoVf3QLscm8iUVvWrO3jy9xf\nD+q8+1Zt6syaHUoacZG1K5JutF1Fn+6xPW2v+j+6Kkizl/QM8DdSJbFtfk5efqftkSXGWrOn7a3k\np5Ji3Q1s3E3W7C221+36nX2KVcsNK1Tj3bfC4NfkCn5Qz3EuaQ3g6yyYZr8/KXnm4BJj1Zk12+v0\nsp28psNYdWbNTupi9ShgbyBuWBEGRJMr+D2d78tawb4rz5odqDT7qrNmJV1FupDb48U05/uZlhDv\nIOAwoOqs2e7il37DipoyZkMDNKaCV003kchZs58jVRpT8uqJwMnAGbZLSapSvTenFun6xZdIfbsC\n5gLfK7OVm2MtRbqYti8pk7X9YtoPqriYJmk5ANtlD5vtJHaZN91+KykJ6M/ANNK52ow0omZH23eW\nESc0QyMq+G6Gw21BSuXe3fbtJca6nQWzZlutqmvLSqqSdBNpSF/rKuSVxeUyW2v5QvF7gQPbs2aB\nP5WcNVuMW+nFtK6yZotKzprtKn7rhhUfsv2Bkvb5G1IiUFcZsx+3XVbGbGiAplTwk4GTuxkOd1SZ\nF57qypqVdD8wj66HKdp2aWn2dWfN1qXOrFn1fMOKQwoTafU3TmTMho41ZZhknTeRmC1pgu2biivL\nzpq1Pb6sfXWg26zZ3MoelHK2LPB6N9S+pMSg60jzw5QZq64bVtSSMRuaoSkVfJ03kagta7au6wrU\nmzVbqxqzZuu6YUVdGbOhAZoyF83ZpLnLXx9jnYfDnQ/8osxAeUzzlqS/3SfzQ6Ss2TLHO28A3E7q\nd38wP7YHbpO0Yffv7JMJkmZ38XgOKOUGJgMhZ83eTroes6vtT1ZRuWfnA8vkuJuS5ml/EJhASuAp\nSytjtv2xLOXfvSwMco3og4cFhsNB+rlay3C4nDVb2oyLeZ+1XVdoKqUbsDwOzGLB/vFSs2Yl3dza\nn6RvAfNsH6Z8w4qSM3RD6EhjKviWgRgOV0XWrKQ7bXd5o4gyL+b2UoYqbk5dm5qzZou3crwROLIw\nC+LNZVXwdWXMhmZoSh88koYDI1sXC3P/9SdJiUFVV4ZVTGNa23WF3rJmy4xVswfrypqlvhtWTO1i\n3SjgVEmRMRvm04gWvKSPAT8mdcvcQxoh8TPg/4ATy+4+6SJ+6VmzNafZN+7m1FBv1mwepTNgN6yo\nImM2DH5NqeBvBfa0fa+kzUkV1V62f19RvLqyZmtJs68za7ZOdWbN1jnHTg/7H9TzL4XyNaWCn68P\nXNKttjeqKFZtWbOFmJVeV6gza3ag1JA1exU1zrHTFrv0jNnQDE2p4B8GTius+nJx2fZpC7yp77Fq\nGd1SZ5p9nVmzTVXXr4W6MmZDMzSlgq9tjva6RrfUmWYfylX1r4UQOtWUSuJJ29+vKVYto1vqTLPP\nMerKmm0826+SRtOUrsaM2dAATclk/XSNsWrLmpW0mKQDSPN970y6cPxR2zeXHKfOrNnQP3VlzIYG\naEoLvja2v5FHt1wjqbKsWTX35tShf0YU+tn3A35m+9utjNkBLFdYBDWlD34u6ULTAptIFwmXryhu\nZaNbak6zH/Cs2dCZujJmQzM0pQV/S53jf2vKml2rpP10os7ZOEP/1JUxGxqgKX3wtclZs08BN0u6\nWtK7gX+R7oi0b4mhHrT9QHePXJaypkio7bpC6LdDgIuA+0l3Fns1r18FOGqgChUWTU3povma7ZNq\nilVL1mzdiTN1Zc2G/lkUMmbD4NGUCv5Y5u+nLrLtE0uMVUvWbJ1p9m1xB+zm1KF3A5kxGwafplTw\nX+li9dLAAcBKtpctMVZtWbOFmI2+OXXo3EB98YfBqREVfFFugR4MfIbUh/xt24+XuP/asmbrElmz\ng1NkzIbeNOY/rqRRpNb0vsBZwOa2n64gVJ1Zs7WoO2s2lKPKjNnQDI0YRSPpVNLc788BG9s+rqLK\nHerNmq1NXVmzIYT6NKKLJicFvQzMpeukoNISndovsjZBW9bsKRVnzYYQatKICr5OA5U1W6U6s2ZD\nCPVpRB+8pB1ttzL61rJ9X2Hbh2xfVGK4WrNma1Jn1mwIoSaNaMEXu026GKdeapdKE2+LFskzITRT\nIy6yMv+diNrT98tK52+5oOT9LQqulPQlSeOKKyUtIWlHSWeREmhCCINII7pomL/fuL2VWXarc3FJ\nx3RXjjKzZmu0K2l00HmSukqe+U4kz4Qw+DSli+YZ4G+k1vq2+Tl5+Z22R5YYq7as2YEQyTMhNEdT\nKvjtetpu++qK4laaNRtCCP3RlC6a24HRtm8vrsy3optVdrAas2ZDCKHPmnKR9XukboV2KwHfLTNQ\nzVmzIYTQZ03poplie2I320qdzrfOrNkQQuiPpnTRLNfDtsXLDGS7Kb96QggN15TK6l5J72tfKem9\npNvplUbSjoXna7Vt+1CZsUIIoT+a0kWzHnAp8L/A1Lx6IrAVsJvtu0uMVVvWbAgh9EcjWvC5At8Y\nuBoYnx9XA5uUWblndWbNhhBCnzWiDz7Pk/Iy8PNeXlPGz5U6s2ZDCKHPGlHBk+ZS6fVGxMCZJcRa\nW9IlpNZ66zl5OWZlDCEsMprSB9/VjYhHkLqgSr0R8UBlzYYQwsJqRAVfVPVcKpJG00PWrO3SM2dD\nCKEvGnGRtcj2q7ZnVDhRVm1ZsyGE0B+Na8FXrc6s2RBC6I/GteBrUFvWbAgh9EdU8AuvtqzZEELo\nj+iiWUh1Zs2GEEJ/RAXfB5KWBD4OtPrbbwPOtf3SwJUqhBDmFxX8QuokI7bErNkQQuiz6INfeFdK\n+pKkccWVkpaQtKOks0iZsyGEMKCiBb+Q6syaDSGE/ogKvh+qzpoNIYT+iAo+hBAaKvrgQwihoaKC\nDyGEhooKPiw0Sa9Jmi7pVkm/l7RiXj9e0py8rfXYP29bVtIPJf1T0o2Spkr6bOF9t7bF+I6kRyQN\na+UmnBUAAANISURBVFu/p6SbJd0h6RZJe3ZTxj+3leNRSdfnbZJ0tKR7JN0t6UpJGxbee3++v0Br\neS9JZ7bt/3eSruvXHzKEijXlhh+hXnNsbwqQh4V+Efhm3vbP1rY2Z5CmcljX9rw87fKnu9p5rtQ/\nCDwEbEe6WQuSJgDfAnaxfV++6fnlkv5l++biPmy/p7C/ZUhZx0fnVV8EtgYm2H5R0ruBSyRtWEhW\n20LSBu3TQuf9rQhsATwvaW3bMUVFWCRFCz701z+A1Xp6gaR1gC2Bo23PA7A9y/Yp3bxle1J28A+B\nfQrrvwqcZPu+vI/7gP8A/l8vZfwu8Afbl+flw4GDbL+Y9/MX0tQT+xbe823gqG729yHg98CvgI/1\nEjuEARMVfOgzScOBnYBLCqvXaesa2RbYELipVbl3YB/gPOC3wPvzcFTyfqa2vXZKXt9dGT9Emivo\nyLy8PLBMF63u9v2cD2wu6c09lO885v8CCmGREhV86IsRkqYDM4ExwOWFbf+0vWnhcU37myUd1eoX\n72LbEsD7gN/Zng1cD7yn/XWdkLQaqfX+8XxT9oXxGnAq+YuhsM8xwLrAtXliuVclxT0AwiIpKvjQ\nF60++DVJNxv/Yi+vvx2Y0Lpgavub+f3Ld/Ha9wArArdIup900/R9CvvZou31W5C6c+YjScBZwMnF\nfvT8pfGCpLU72M8vgHcBaxTW7Q2MBO7L5RtPtOLDIioq+NBnuQ/734GvSOr2gr3te0ldIN/I3Tqt\nKR/Uxcv3AQ6wPd72eNJ0ELtIWpp0gfVISePzPsYDXyP1lyPpIEkH5f18FXjJ9v90EeNU4L8ljcjv\n25n0RXJuW7lfBf4LOLStfLsWyrcF0Q8fFlExiib0i+1pkm4mVXzXkPvgCy/5me3/Bg4gVaz3SnoS\nmAMcVtxXrsR3BT5f2P8Lkq4FPmD715IOB36f++VfBQ6z3Yr3FuDv+fk3gIfbyvK07R1I99UdSfqV\n8Bqpq2kP23O6OMSfkkff5C+UNYHXh0fm0TzPSnq77es7+JOFUJuYqiA0hqRLgQ/ZfmWgyxLCoiAq\n+BBCaKjogw8hhIaKCj6EEBoqKvgQQmioqOBDCKGhooIPIYSGigo+hBAaKir4EEJoqP8Ph8n1Fjvp\nJh0AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4bf1c550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ct2=(pd.crosstab([base9.REGIAO, base9.ZONA],base9.Insegurança_Alimentar, normalize='index')*100).round(decimals=1)\n",
"ct2\n",
"print(ct2,'\\n')\n",
"plot = ct2.plot(kind='bar',title=\"Análise de Insegurança Alimentar 2009 (G8)\")\n",
"ax = plt.subplot(111)\n",
"box = ax.get_position()\n",
"ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])\n",
"ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))\n",
"plt.ylabel('Freq.Relativa (em %)')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## SEQUÊNCIA DE ANÁLISE PARA CADA ANO:\n",
"Observando os dois últimos gráficos pode-se perceber precisamente as duas regiões que apresentam maior disparidade entre zona urbana e rural. No caso de 2013 (1°gráfico) Norte e Nordeste são as duas regiões que serão analisadas a fim de responder a pergunta-guia do projeto, já na situação de 2009 apresenta-se o Centro-Oeste e o Nordeste. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## ANÁLISE QUANTITATIVA:\n",
"OBSERVAR COMO SE COMPORTA A INSEGURANÇA ALIMENTAR DE ACORDO COM A RENDA FAMILIAR.\n",
"O PRIMEIRO HISTOGRAMA DEMONSTRA A FREQUÊNCIA ENTRE AQUELES QUE RESPONDERAM PELO MENOS UM \"Sim\" NAS 4 PERGUNTAS INICIAIS E SÃO CONSIDERADOS PORTANTO, EM INSEGURANÇA ALIMENTAR."
]
},
{
"cell_type": "code",
"execution_count": 199,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 9.4\n",
"[350, 700) 17.0\n",
"[700, 1050) 19.2\n",
"[1050, 1400) 14.9\n",
"[1400, 1750) 12.0\n",
"[1750, 2100) 8.0\n",
"[2100, 2450) 5.0\n",
"[2450, 2800) 3.3\n",
"[2800, 3150) 2.3\n",
"[3150, 3500) 2.2\n",
"[3500, 3850) 1.6\n",
"[3850, 4200) 1.3\n",
"[4200, 4550) 1.1\n",
"[4550, 4900) 0.5\n",
"[4900, 5250) 0.7\n",
"[5250, 5600) 0.4\n",
"[5600, 5950) 0.4\n",
"[5950, 6300) 0.2\n",
"[6300, 6650) 0.1\n",
"[6650, 7000) 0.2\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAGDCAYAAAA8mveiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xm8HFWZ//HPl7BDJEACsoUAsgw6ghAjKCKIQciA6LgR\nQRaXKIoK6jjggujouCLiD9lBVpFFQNSwBEQRhYEEwhKWgBCEEEhYQgggS/L8/jinSaXTfW/VTfft\nvrnf9+vVr1t9anu6bnc9dU5VnVJEYGZmVtZynQ7AzMwGFicOMzOrxInDzMwqceIwM7NKnDjMzKwS\nJw4zM6tkmU8ckqZJ2qXTcdjgI2kXSY8W3vu7aC0jaWtJkyWpRct7s6S/l5l2QCcOSTMkvaeu7CBJ\nN9TeR8QbI+LPvSxnlKSQtHybQu1qks6U9L1OxzFQ5e9cSPpoT9OV+S62g6Q/S/pUP6+ztk2+Vlf+\naDF55p3f5ZKelfScpOskvb0wvvbbnJ9fMyQdURg/v/BaKOnFwvv9JB0t6ZW66eb28TOtJOl0SQ/n\nWKdK2rNumt0k3SvphfxZNi6M2zWXPStpRoPlXydpjqR5km6XtE8vIf0P8NPIN+OV2R9KOjQnm5ck\nnVmcNiLuAOZK2ru3bTGgE8dAMVgTUrt04fY8EHgaOKDTgbTDUmzvp4GvSRraZLmbAX8D7gQ2AdYH\nLgWulrRj3eTDImJ14EPAtySNBYiI1Wsv4J/A3oWy8/K8FxSni4hhffw8ywOPAO8C1gC+CVwoaVT+\nPMOBS4BvAWsBk4ELCvM/D5wB/FeT5R8GbBgRrwMmAOdKWq/RhLl8V+Cyip/hMeB7OY5GzgM+09tC\nlvnEUczCksbkbDtP0hOSfpYnuz7/nZuPSHaUtJykb+aji9mSzpa0RmG5B+RxT0n6Vt16jpZ0saRz\nJc0DDsrrvlHSXEmzJB0vacXC8kLS5yTdn49m/kfSZpL+nuO9sDa9pDUl/SEfnTyThzds0faqHeEd\nKOmfkp6U9I3C+GbbEEk75Hjn5iOmXQrjNpF0ff5s10j6paRz87jFmnQa/N/6uj0/m7fn3Lw+FcZ/\nWtI9OZ67JW2Xy4+Q9I9C+Qd62V4bk3YkE4D3Snp9D9PWf6aL8md6TtKdkraQdGT+vj0iaffCvGso\nHe3OkjRT0vckDcnjDpJ0g6Sf5u/DQ8pHwpK+D7wTOD5/t4/P5cfldcyTNEXSOwvrWmJ797QNenAP\ncCPw5SbjjwZujIhvRMTTEfFcRPwCOAf4UaMZImIyMA3Yto8x9VlEPB8RR0fEjIhYGBF/AB4Cts+T\n/CcwLSIuioh/kT7fNpK2yvPfHBHnAA82Wf7tEfFS7S2wArBRk3DGArfm9VT5DJdExGXAU00m+TOw\nm6SVelrOMp846hwHHJcz+mbAhbl85/x3WD4iuZH0YzmIlNU3BVYHaj+6rYETgP2A9UhHHxvUrWsf\n4GJgGCmLLwAOB4YDOwK7AZ+rm+e9pC/hDsDXgFOA/UlfnjcB4/N0ywG/AjYGRgIv1mJroZ2ALXOc\nR0n6t1zecBtK2gD4I+loZi3gq8BvJY3I8/0auBlYm/SD+njFePqyPfcC3gq8GfgIafsi6cM5hgOA\n1wHvY9EP6R+kHe0awHfo4agvOwCYHBG/Je0o96vwmfYm7STXBG4DriL9bzcAvgucXJj2TOBV4A3A\nW4DdgWLz09uA+0jb48fA6ZIUEd8A/gocmr/bh+bpbyHtfNci/W8ukrRyYXn127uvvgUcJmmtBuPG\nAhc1KL8QeIekVepHSNqB9Ft4YCliaglJ6wJbkBIZwBuB22vjI+J5UpxvrLDMP0j6F/B/pJ345CaT\n/jvp/91SETETeIX0229qWUgcl+UjyrlKbZcn9DDtK8AbJA2PiPkRcVMP0+4H/CwiHoyI+cCRwL5K\n1fYPAb+PiBsi4mXgKNIRQtGNEXFZPjJ5MSKmRMRNEfFqRMwg7RTeVTfPjyNiXkRMA+4Crs7rfxa4\ngrTDICKeiojfRsQLEfEc8P0Gy1pa38lx3076MWyTy5ttw/2BiRExMX/mSaQv/ThJI0k78KMi4uWI\nuAG4vGI8fdmeP4yIuRHxT+A6Fh2lfoq0rW+J5IGIeBggHy0+ltdzAXA/MKaHuA4g7XjJf6s0V/01\nIq6KiFdJO9AROeZXgN8AoyQNyzuoccBh+ah3NnAssG9hWQ9HxKkRsQA4i3RAs26zFUfEufl79GpE\nHAOsxOI7i8W2d4XPVL+eqcAk4L8bjB4OzGpQPou0byommyclvUiqwZxAtSaajxT3EZKuqzBvQ5JW\nICXUsyLi3ly8OvBs3aTzgIZNdY1ExF55+nGk3//CJpMOA55rUF5lf9jMc3n5TS0LieP9ETGs9mLJ\no86iT5KOEO6VdIukvXqYdn3g4cL7h0ltnOvmcY/URkTECyxZ9Xuk+CY3Q/xB0uO5+v+/pB9O0ROF\n4RcbvF89L2tVSScrNZXNIzW1Das1XdStdz8tOil4RQ+ft97jheEXauum+TbcGPhw3Zd2J9IObH3g\n6bydahbbPiX0ZXs2+wwbkWoWS1Bqgpxa+AxvarDc2rTvILXN/yYX/Rr4d0llm1Hq/79P5h1/7T05\n5o1JzRazCnGdDKxTmP+1z1rYzqvThKSv5qa6Z/Py1mDxz9n0/yNpZOE7Nb/njwikA6tDcgIsepL0\n/ai3HrAQeKZQNpz0eb4C7ELaHmVdWNxHRMSujSaSdFLhc3292cIkLUeqKb4MHFoYNZ9Ugy1ag8Y7\n+KYi4pWIuALYXdL7mkz2DI0TUpX9YTNDgR4vIFgWEkdpEXF/RIwn/eB+BFwsaTWWrC1AOom0ceH9\nSFJTwROkI6LXzinkKvXa9aure38icC+weW7m+TrQ18vovkI6OnxbXlatqW2J5UXEeYWTgnvWj6+q\nh234CHBO3Q90tYj4IWl7rSVp1cKiim23zwOvjcsJcASLa+X2fITUzLaYfL7iVNLOYO38w7urh+Ue\nmMdNlfQ4qXmhVt5KjwAvAcML2/Z1EVG2CWSxbZfPZ3yN1Hy3Zv6cz7L452zabXZE/DMWPynd88rT\nEfklwDfqRl0DfLjBLB8h1XiKBxpExIKI+BnwL/q2Q+wtzs8WPtf/NppGkoDTSQeQH8y1w5ppLKqZ\nk38Xm7GoKauq5WnwPc3uIB3AtVRucl6RXprBBlXikLS/pBG5+lfLqAuBOfnvpoXJzwcOVzqpuzrp\niPaC3KxwMbC3pLcrnZA9mt53WkNJ1db5+WTZIUvxUYaSjkjn5rbjby/FsirpYRueS9om75U0RNLK\nSie9N8zNQJOBoyWtqHTFTPGSv+nAypL+IzcBfJPUdNKTpdmepwFflbS9kjfkpFE7iJiTP+vBpBpH\no+2wMmkHN4HUBFZ7fQH4mFp45VdEzAKuBo6R9DqlCzc2k1S2efIJFv9uDyUdBM0Blpd0FEseKbfa\nd4CDWbwJ5DvA2yV9X9JakoZK+gKpua9R01bND0lXa63cwzTtciLwb6Srt+qb8C4F3iTpgzm2bwO3\n15qy8v9tZVJtSfk3UrvgZStJe0paRdIKkvYnHRD+pUkck4Dtqm4DScvneYYAtd9p8bv6LuBPsegk\nfUODKnEAewDTcvX6OGDf3F7+Auk8wd9yU8AOpMvVziE1Az1EOsr5AkA+B/EFUhPFLFIVdTbpqLCZ\nrwIfI1VbT2Xxy/Sq+jmwCqmqfxNw5VIsq6pm2/AR0gnVr5N2SI+QLjusfcf2I53Efop0Av0C8vbK\n53A+R9qhzyTVQBa7yqqBPm/PiLiI9P/+NSnpXQasFRF3A8eQ2tGfIJ2A/FuTxbyflLzPjojHay/S\n92Z50nZqpQNIR4J3k5opLqZxM08jxwEfUrri6hekk/BXkhL2w6TvdtWmw0oi4iHS72m1Qtn9pObM\nbYAZpN/SB4H3RkSz7Q7pIoxngE+XXP1Htfh9HPMlrdP7bIvLBxefIR0gPF5Y1n7588zJ8X8/xzeG\nxc9D7Uz6zkxk0UUtV9cWTzoAnU36/XwJ+GhE3Nooloh4AvgT6TdXxTfzeo8gnZd8MZfV7Aec1NtC\nFH6Q01LLNZK5pGaThzodz0Ag6QLg3ojot9pSkzhOBo6JiOmdjMOsKqWrO88CxkQLduSS3gycHBH1\n99AsYbDVOFpG0t5KJ6lXA35KuolpRmej6l6S3pqbV5aTtAfpSKnqzUutjml10rmsnXub1qzbRMTd\nEfHWViSNvLw7yiQNSFVq65t9SFVvkdrv923VP3AZ9XrSCdK1Sc1Qh0TEbZ0NiX+Qmqp263AcZgOK\nm6rMzKwSN1WZmVklThxmZlbJMnWOY/jw4TFq1KhOh2FmNqBMmTLlyYiov+m2qWUqcYwaNYrJk5v1\nCWZmZo1Ierj3qRZxU5WZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVeLEYWZmlThxmJlZJU4cZmZW\niROHmZlV4sRhZmaVOHGYmVklThxmZlaJE4eZmVWyTPWOO1AdO2l6n+c9fOwWLYzEzKx3rnGYmVkl\nThxmZlaJE4eZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVeLEYWZmlThxmJlZJU4cZmZWiROHmZlV\n4sRhZmaVtLWTQ0lnAHsBsyPiTbnsAmDLPMkwYG5EbNtg3hnAc8AC4NWIGN3OWM3MrJx29457JnA8\ncHatICI+WhuWdAzwbA/z7xoRT7YtOjMzq6ytiSMirpc0qtE4SQI+Ary7nTGYmVlrdfIcxzuBJyLi\n/ibjA7hG0hRJE5otRNIESZMlTZ4zZ05bAjUzs0U6mTjGA+f3MH6nfO5jT+DzknZuNFFEnBIRoyNi\n9IgRI9oRp5mZFXQkcUhaHvhP4IJm00TEzPx3NnApMKZ/ojMzs550qsbxHuDeiHi00UhJq0kaWhsG\ndgfu6sf4zMysibYmDknnAzcCW0p6VNIn86h9qWumkrS+pIn57brADZJuB24G/hgRV7YzVjMzK6fd\nV1WNb1J+UIOyx4BxefhBYJt2xmZmZn3jO8fNzKwSJw4zM6vEicPMzCpx4jAzs0qcOMzMrBInDjMz\nq8SJw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6ukrd2qDybHTpre\n6RDMzPqFaxxmZlaJE4eZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVeLEYWZmlThxmJlZJU4cZmZW\niROHmZlV4sRhZmaVOHGYmVklThxmZlaJE4eZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVdLWxCHp\nDEmzJd1VKDta0kxJU/NrXJN595B0n6QHJB3RzjjNzKy8dtc4zgT2aFB+bERsm18T60dKGgL8EtgT\n2BoYL2nrtkZqZmaltDVxRMT1wNN9mHUM8EBEPBgRLwO/AfZpaXBmZtYnnTrH8QVJd+SmrDUbjN8A\neKTw/tFctgRJEyRNljR5zpw57YjVzMwKOpE4TgQ2BbYFZgHHLM3CIuKUiBgdEaNHjBjRivjMzKwH\n/Z44IuKJiFgQEQuBU0nNUvVmAhsV3m+Yy8zMrMP6PXFIWq/w9gPAXQ0muwXYXNImklYE9gUu74/4\nzMysZ8u3c+GSzgd2AYZLehT4NrCLpG2BAGYAn8nTrg+cFhHjIuJVSYcCVwFDgDMiYlo7YzUzs3La\nmjgiYnyD4tObTPsYMK7wfiKwxKW6ZmbWWb5z3MzMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqaetV\nVdZ+x06a3ud5Dx+7RQsjMbPBwjUOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAz\ns0qcOMzMrBInDjMzq8SJw8zMKnHiMDOzSkr3VSVpTWB94EVgRkQsbFtUZmbWtXpMHJLWAD4PjAdW\nBOYAKwPrSroJOCEirmt7lGZm1jV6q3FcDJwNvDMi5hZHSNoe+LikTSOi4XPEzcxs2dNj4oiIsT2M\nmwJMaXlEZmbW1So9j0PSCOBLwCrASRFxf1uiMjOzrlX1qqpjgKuAS4Fftz4cMzPrdj0mDklXSdq5\nULQiMCO/VmpfWGZm1q16q3F8BNhb0vmSNgO+BfwAOA74XLuDMzOz7tPbyfFngf+StCnwfeAx4ND6\nK6zMzGzw6O0+js2AQ4CXga8AmwEXSPoj8MuIWND+EM3MrJv01lR1PnAJcB1wTkT8NSLeC8wFrm53\ncGZm1n16uxx3JeAhYHVg1VphRJwt6aJ2BmZmZt2pt8RxCHA8qanqs8UREfFiu4IyM7Pu1dvJ8b8D\nf++nWMzMbABwt+pmZlaJE4eZmVXS1sQh6QxJsyXdVSj7iaR7Jd0h6VJJw5rMO0PSnZKmSprczjjN\nzKy8UolD0ui8k7817/DvlHRHiVnPBPaoK5sEvCki3gxMB47sYf5dI2LbiBhdJk4zM2u/sr3jngf8\nF3AnUPrJfxFxvaRRdWXF+z9uAj5UdnlmZtZ5ZRPHnIi4vA3r/wRwQZNxAVwjaQFwckSc0ob1m5lZ\nRWUTx7clnQZcC7xUK4yIS/q6YknfAF4l1WYa2SkiZkpaB5gk6d6IuL7BciYAEwBGjhzZ13DMzKyk\nsonjYGArYAUWNVUFqTuSyiQdBOwF7BYR0WiaiJiZ/86WdCkwBlgiceSayCkAo0ePbrgsMzNrnbKJ\n460RsWUrVihpD+BrwLsi4oUm06wGLBcRz+Xh3YHvtmL9Zma2dMpejvt3SVtXXbik84EbgS0lPSrp\nk6QuTIaSmp+mSjopT7u+pIl51nWBGyTdDtwM/DEirqy6fjMza72yNY4dgKmSHiKd4xAQ+ZLapiJi\nfIPi05tM+xgwLg8/CGxTMjYzM+tHZRNH/b0YZmY2SJVqqoqIh4GNgHfn4RfKzmtmZsuWsneOfxv4\nbxbd5b0CcG67gjIzs+5VttbwAeB9wPPw2vmIoe0KyszMulfZxPFyvt8i4LXLZc3MbBAqmzgulHQy\nMEzSp4FrgFPbF5aZmXWrUldVRcRPJY0F5gFbAkdFxKS2RmZmZl2px8QhSbUuQXKiWCJZFKcxM7Nl\nX29NVddJ+oKkxXoPlLSipHdLOgs4sH3hmZlZt+mtqWoPUtfn50vaBJgLrEJKOFcDP4+I29obopmZ\ndZMeE0dE/As4AThB0grAcODFiJjbH8GZmVn3KdvlCBHxCjCrjbFYPzt20vQ+z3v42C1aGImZDSTu\nNsTMzCpx4jAzs0qcOMzMrJKynRzuIOkWSfMlvSxpgaR57Q7OzMy6T9kax/HAeOB+0uW4nwJ+2a6g\nzMyse5VuqoqIB4AhEbEgIn6FH+5kZjYolb0c9wVJK5IeH/tj0mW5Pj9iZjYIld35fzxPeyjpmRwb\nAR9sV1BmZta9ytY4tgf+GBHzgO+0MR4zM+tyZWscewPTJZ0jaS9Jpe84NzOzZUupxBERBwNvAC4i\nXV31D0mntTMwMzPrTpX6qpJ0BenxsasA7yddlmtmZoNI2RsA95R0Juk+jg8CpwGvb2NcZmbWpcrW\nOA4ALgA+ExEvtTEeMzPrcmWfOT6+3YGYmdnA0Nszx2+IiJ0kPUc6t/HaKCAi4nVtjc7MzLpOb08A\n3Cn/Hdo/4ZiZWbcre3L8nDJlZma27Ct7A+Abi2/yDYDbtz4cMzPrdj0mDklH5vMbb5Y0L7+eA54A\nftcvEZqZWVfpMXFExA/y+Y2fRMTr8mtoRKwdEUf2U4xmZtZFynY5cqSkNSWNkbRz7dXbfJLOkDRb\n0l2FsrUkTZJ0f/67ZpN595B0n6QHJB1R/iOZmVk7lT05/ingeuAqUu+4VwFHl5j1TJZ84NMRwLUR\nsTlwbX5fv74hpCcM7glsDYyXtHWZWM3MrL3Knhz/EvBW4OGI2BV4CzC3t5ki4nrg6brifYCz8vBZ\npD6v6o0BHoiIByPiZeA3eT4zM+uwsonjXxHxLwBJK0XEvcCWfVznuhExKw8/DqzbYJoNgEcK7x/N\nZWZm1mFl+6p6VNIw4DJgkqRngIeXduUREZKi9ymbkzQBmAAwcuTIpQ3JzMx6Ubavqg/kwaMlXQes\nAVzZx3U+IWm9iJglaT1gdoNpZpIeT1uzYS5rFNspwCkAo0ePXqokZGZmvevtPo616l/AncANwOp9\nXOflwIF5+EAa3w9yC7C5pE0krQjsm+czM7MO663GMYXUuaEKZbX3AWza08ySzgd2AYZLehT4NvBD\n4EJJnyQ1d30kT7s+cFpEjIuIVyUdSrp6awhwRkRMq/jZzMysDXrr5HCTpVl4D92x79Zg2seAcYX3\nE4GJS7N+MzNrvbL3cUjS/pK+ld+PlDSmvaGZmVk3Kns57gnAjsDH8vvnSDfomZnZIFP2cty3RcR2\nkm4DiIhn8klrMzMbZMrWOF7J3YAEgKQRwMK2RWVmZl2rbOL4BXApsI6k75Mux/3ftkVlZmZdq+wN\ngOdJmkK6GkrA+yPinrZGZmZmXanXxJGbqKZFxFbAve0PyczMulmvTVURsQC4T5I7gjIzs9JXVa0J\nTJN0M/B8rTAi3teWqMzMrGuVTRzfamsUZmY2YJQ9Of6XdgfSacdOmt7pEMzMBoSyl+OamZkBThxm\nZlaRE4eZmVVS6hyHpM2BHwBbAyvXyiOix+dxmJnZsqdsjeNXwInAq8CuwNnAue0KyszMulfZxLFK\nRFwLKCIejoijgf9oX1hmZtatyt7H8ZKk5YD78yNdZ9L3Z46bmdkAVrbG8SVgVeCLwPbAx4ED2xWU\nmZl1r7I3AN6SB+cDB7cvHDMz63Y9Jg5JP4+IwyT9nvwQpyL3VWVmNvj0VuM4J//9absDMTOzgaHH\nxBERU/LgZODFiFgIrz2jY6U2x2ZmZl2o7Mnxa0knx2tWAa5pfThmZtbtyiaOlSNifu1NHl61h+nN\nzGwZVTZxPC9pu9obSdsDL7YnJDMz62ZlbwA8DLhI0mOAgNcDH21bVGZm1rVK38chaStgy1x0X0S8\n0r6wzMysW5WtcQC8FRiV59lOEhFxdluiMjOzrlW2W/VzgM2AqcCCXBykXnLNzGwQKVvjGA1sHRFL\n3D1uZmaDS9mrqu4inRA3M7NBrmyNYzhwt6SbgZdqhe6rysxs8CmbOI5u5UolbQlcUCjaFDgqIn5e\nmGYX4HfAQ7nokoj4bivjsL47dtL0pZr/8LFbtCgSM+tvZS/H/YukjYHNI+IaSasCQ/q60oi4D9gW\nXuv3aiZwaYNJ/xoRe/V1PWZm1no9nuOQtE7++2ngYuDkPGoD4LIWxbAb8I+IeLhFyzMzszZqmjhy\nFyP/k99+HngHMA8gIu4H1mlRDPsC5zcZ93ZJd0i6QtIbW7Q+MzNbCj3VOLYCbs/DL0fEy7URkpan\nwYOdqpK0IvA+4KIGo28FRkbEm4H/R5MajqQJkiZLmjxnzpylDcnMzHrRNHFExK9J5x4A/izp68Aq\nksaSdvS/b8H69wRujYgnGqx/Xq1H3oiYCKwgaXiD6U6JiNERMXrEiBEtCMnMzHrS4zmOiPhdHjwC\nmAPcCXwGmAh8swXrH0+TZipJr5ekPDwmx/pUC9ZpZmZLoexVVQuBU/OrJSStBowlJaJa2Wfz+k4C\nPgQcIulVUhfu+/rOdTOzzivbV9VDNDinERGb9nXFEfE8sHZd2UmF4eOB4/u6fDMza48qfVXVrAx8\nGFir9eGYmVm3K9VXVUQ8VXjNzHd4/0ebYzMzsy5Utqlqu8Lb5Ug1kCrP8jAzs2VE2Z3/MYXhV4EZ\nwEdaHo2ZmXW9sldV7druQMzMbGAo21T15Z7GR8TPWhOOmZl1uypXVb0VuDy/3xu4Gbi/HUGZmVn3\nKps4NgS2i4jnACQdDfwxIvZvV2BmZtadyj46dl3g5cL7l3OZmZkNMmVrHGcDN0uqPWzp/cBZ7QnJ\nzMy6Wdmrqr4v6Qrgnbno4Ii4rX1hmZlZtyrbVAWwKjAvIo4DHpW0SZtiMjOzLlYqcUj6NvDfwJG5\naAXg3HYFZWZm3atsjeMDpCf1PQ8QEY8BQ9sVlJmZda+yiePl/CyMgNeepWFmZoNQ2cRxoaSTgWGS\nPg1cQwsf6mRmZgNH2auqfpqfNT4P2BI4KiImtTUyMzPrSr0mDklDgGtyR4dOFmZmg1yvTVURsQBY\nKGmNfojHzMy6XNk7x+cDd0qaRL6yCiAivtiWqMzMrGuVTRyX5JeZmQ1yPSYOSSMj4p8R4X6pzMwM\n6P0cx2W1AUm/bXMsZmY2APSWOFQY3rSdgZiZ2cDQW+KIJsNmZjZI9XZyfBtJ80g1j1XyMPl9RMTr\n2hqdmZl1nR4TR0QM6a9AzMxsYKjyPA4zMzMnDjMzq8aJw8zMKnHiMDOzSpw4zMysEicOMzOrpGOJ\nQ9IMSXdKmippcoPxkvQLSQ9IukPSdp2I08zMFle2d9x22TUinmwybk9g8/x6G3Bi/mtmZh3UzU1V\n+wBnR3IT6Xnn63U6KDOzwa6TiSOAayRNkTShwfgNgEcK7x/NZWZm1kGdbKraKSJmSloHmCTp3oi4\nvupCctKZADBy5MhWx2hmZnU6VuOIiJn572zgUmBM3SQzgY0K7zfMZfXLOSUiRkfE6BEjRrQrXDMz\nyzqSOCStJmlobRjYHbirbrLLgQPy1VU7AM9GxKx+DtXMzOp0qqlqXeBSSbUYfh0RV0r6LEBEnARM\nBMYBDwAvAAd3KFZrg2MnTe/zvIeP3aKFkZhZVR1JHBHxILBNg/KTCsMBfL4/4zIzs9518+W4ZmbW\nhZw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAzs0qcOMzMrBInDjMz\nq8SJw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAz\ns0qcOMzMrBInDjMzq8SJw8zMKnHiMDOzSpbvdABmVR07aXqf5z187BYtjMRscHKNw8zMKnHiMDOz\nSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKySjiQOSRtJuk7S3ZKmSfpSg2l2kfSspKn5dVQn\nYjUzs8V16gbAV4GvRMStkoYCUyRNioi766b7a0Ts1YH4zMysiY7UOCJiVkTcmoefA+4BNuhELGZm\nVk3Hz3H0tiSXAAAKMElEQVRIGgW8Bfi/BqPfLukOSVdIemO/BmZmZg11tK8qSasDvwUOi4h5daNv\nBUZGxHxJ44DLgM0bLGMCMAFg5MiRbY7YzMw6VuOQtAIpaZwXEZfUj4+IeRExPw9PBFaQNLzBdKdE\nxOiIGD1ixIi2x21mNth16qoqAacD90TEz5pM8/o8HZLGkGJ9qv+iNDOzRjrVVPUO4OPAnZKm5rKv\nAyMBIuIk4EPAIZJeBV4E9o2I6ESwZma2SEcSR0TcAKiXaY4Hju+fiGyw8LM8zJZex6+qMjOzgcVP\nADQrybUVs8Q1DjMzq8SJw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4z\nM6vEd46b9YOluescfOe5dRfXOMzMrBInDjMzq8SJw8zMKnHiMDOzSnxy3GwAcJfu1k1c4zAzs0qc\nOMzMrBInDjMzq8TnOMyWcT4/Yq3mGoeZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVeKrqsysLdyV\n/LLLNQ4zM6vEicPMzCpxU5WZNbW0zU22bHLiMLOu5Dveu5cTh5ktc5x02svnOMzMrJKO1Tgk7QEc\nBwwBTouIH9aNVx4/DngBOCgibu33QM1sUOlUbWUgXb7ckRqHpCHAL4E9ga2B8ZK2rptsT2Dz/JoA\nnNivQZqZWUOdqnGMAR6IiAcBJP0G2Ae4uzDNPsDZERHATZKGSVovImb1f7hmZr0bLFehdeocxwbA\nI4X3j+ayqtOYmVk/G/BXVUmaQGrKApgv6b4+Lmo48GRrouoXAynegRQrDKx4B1KsMLDiHUix8uWl\ni3fjKhN3KnHMBDYqvN8wl1Wdhog4BThlaQOSNDkiRi/tcvrLQIp3IMUKAyvegRQrDKx4B1Ks0L/x\ndqqp6hZgc0mbSFoR2Be4vG6ay4EDlOwAPOvzG2ZmndeRGkdEvCrpUOAq0uW4Z0TENEmfzeNPAiaS\nLsV9gHQ57sGdiNXMzBbXsXMcETGRlByKZScVhgP4fD+GtNTNXf1sIMU7kGKFgRXvQIoVBla8AylW\n6Md4lfbPZmZm5bjLETMzq8SJg9T9iaT7JD0g6YgOxXCGpNmS7iqUrSVpkqT78981C+OOzPHeJ+m9\nhfLtJd2Zx/0id93S6lg3knSdpLslTZP0pS6Pd2VJN0u6Pcf7nW6ON69niKTbJP1hAMQ6I69nqqTJ\n3RxvvpH4Ykn3SrpH0o5dHOuWeZvWXvMkHdYV8UbEoH6RTs7/A9gUWBG4Hdi6A3HsDGwH3FUo+zFw\nRB4+AvhRHt46x7kSsEmOf0gedzOwAyDgCmDPNsS6HrBdHh4KTM8xdWu8AlbPwysA/5fX2ZXx5vV8\nGfg18Idu/i7k9cwAhteVdWW8wFnAp/LwisCwbo21Lu4hwOOk+y06Hm/bPuhAeQE7AlcV3h8JHNmh\nWEaxeOK4D1gvD68H3NcoRtLVaTvmae4tlI8HTu6HuH8HjB0I8QKrArcCb+vWeEn3LF0LvJtFiaMr\nY83LnsGSiaPr4gXWAB4in9vt5lgbxL478LduiddNVd3dtcm6sejelceBdfNws5g3yMP15W0jaRTw\nFtJRfNfGm5t+pgKzgUkR0c3x/hz4GrCwUNatsQIEcI2kKUo9OXRrvJsAc4Bf5WbA0ySt1qWx1tsX\nOD8PdzxeJ44BItKhQlddAidpdeC3wGERMa84rtvijYgFEbEt6Wh+jKQ31Y3vingl7QXMjogpzabp\nllgLdsrbdk/g85J2Lo7soniXJzUHnxgRbwGeJzX1vKaLYn2N0k3S7wMuqh/XqXidOEp2bdIhT0ha\nDyD/nZ3Lm8U8Mw/Xl7ecpBVISeO8iLik2+OtiYi5wHXAHl0a7zuA90maAfwGeLekc7s0VgAiYmb+\nOxu4lNT7dTfG+yjwaK5tAlxMSiTdGGvRnsCtEfFEft/xeJ04ynV/0imXAwfm4QNJ5xJq5ftKWknS\nJqRnltycq6/zJO2Qr5o4oDBPy+Rlnw7cExE/GwDxjpA0LA+vQjofc283xhsRR0bEhhExivRd/FNE\n7N+NsQJIWk3S0NowqS3+rm6MNyIeBx6RtGUu2o30KIeui7XOeBY1U9Xi6my87TyhM1BepK5NppOu\nQvhGh2I4H5gFvEI6MvoksDbpJOn9wDXAWoXpv5HjvY/CFRLAaNIP9x/A8dSdCGxRrDuRqsd3AFPz\na1wXx/tm4LYc713AUbm8K+MtrGsXFp0c78pYSVcj3p5f02q/ny6Od1tgcv4uXAas2a2x5vWsBjwF\nrFEo63i8vnPczMwqcVOVmZlV4sRhZmaVOHGYmVklThxmZlaJE4eZmVXixGFmZpU4cdiAJmlB7nL6\nLkm/r93o14LljlKhi/uS86wi6S+ShrQihlaSNLGnbSPpN5I278+YbOBy4rCB7sWI2DYi3gQ8Tf8+\nbrjeJ4BLImJBu1YgqU+Pe46IcZG6W2nmRFLHima9cuKwZcmNFHr9lPRfkm6RdIcWPbxplNIDfE5V\neqjT1bkbktrDbm6XdDuFBJTn+aukW/Pr7U3Wvx+Frhx6WP+9ks6UNF3SeZLeI+lvSg/mGVO/UEkH\nSbpc0p9Idww3XHYuv0ypl9ppWtRTbe1hS8NzFyF/zJ/zLkkfzZP8FXhPXxOTDS5OHLZMyM1Du5H7\nGZO0O6mvnjGkbia216JeWzcHfhkRbwTmAh/M5b8CvhAR29QtfjYwNiK2Az4K/KLB+lcENo2IGSXW\n/wbgGGCr/PoYqRuXrwJfb/IRtwM+FBHv6mXZn4iI7UldTHxR0tp1y9kDeCwitsm1tCsBImIh8ABQ\n/9nNluDEYQPdKkrP2ag9l2BSLt89v24jPbhpK9LOFuChiJiah6cAo3L7/7CIuD6Xn1NYxwrAqZLu\nJHVtvXWDOIaTklBNb+u/M++spwHXRur7507Sw7wamRQRT5dY9hdzjekmUk+p9ect7gTGSvqRpHdG\nxLOFcbOB9Zus3+w1rpbaQPdiRGwraVXSE88+T6oRCPhBRJxcnFjpwVMvFYoWAKv0so7DgSdIR+PL\nAf9qFAewcnFVJde/sPB+Ic1/k8+XWPYuwHuAHSPiBUl/rouJiJguaTtSp5Tfk3RtRHw3j145fw6z\nHrnGYcuEiHgB+CLwldxOfxXwCaWHTSFpA0nr9DD/XGCupJ1y0X6F0WsAs3IN4eOk5z/Xz/8MMERS\nbUddaf0VNVv2GsAzOWlsRXrG9GIkrQ+8EBHnAj8hNYHVbEHqQdWsR65x2DIjIm6TdAcwPiLOkfRv\nwI3pEQTMB/Yn1TCaORg4Q1IAVxfKTwB+K+kA0jmB5xvNnOfZCbgmIq7uw/pL6WHZVwKflXQPqVvt\nmxrM/u/ATyQtJHXhfwiApHVJtbfHlzY+W/a5W3WzFslNQIdHxMc7HUtVkg4H5kXE6Z2Oxbqfm6rM\nWiQibgWu68YbAEuYC5zV6SBsYHCNw8zMKnGNw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwq+f8b\nwTOQ9B8aDAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e522e3f60>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"faixa = np.arange(0,7350,350)\n",
"frenda = pd.cut(base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")], bins=faixa, right=False)\n",
"t1 = (frenda.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t1,\"\\n\")\n",
"\n",
"plot = base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")].plot.hist(bins=faixa,title=\"Histograma - Insegurança Alimentar - NORTE - 2013 (H1)\", weights=zeros_like(base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")])+1./base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")].size*100, figsize=(6, 6), alpha=0.5)\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()\n"
]
},
{
"cell_type": "code",
"execution_count": 200,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 14.6\n",
"[350, 700) 20.1\n",
"[700, 1050) 20.7\n",
"[1050, 1400) 14.5\n",
"[1400, 1750) 10.7\n",
"[1750, 2100) 6.5\n",
"[2100, 2450) 4.0\n",
"[2450, 2800) 2.6\n",
"[2800, 3150) 1.8\n",
"[3150, 3500) 1.2\n",
"[3500, 3850) 0.9\n",
"[3850, 4200) 0.7\n",
"[4200, 4550) 0.3\n",
"[4550, 4900) 0.3\n",
"[4900, 5250) 0.4\n",
"[5250, 5600) 0.1\n",
"[5600, 5950) 0.2\n",
"[5950, 6300) 0.2\n",
"[6300, 6650) 0.1\n",
"[6650, 7000) 0.1\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAGDCAYAAAAWKgYNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Wm4XFWZ9vH/bSCMkYCJyBQCiCjaghARBZVBFBDEWSIK\n4hBBULEdGqTF0K3tCK/agICCTMosiBrFQKOCgpBAgITBIINkIAlDCAEUQ573w1pFdipV59QZ1qmq\nw/27rrrO3mtPT+1TVc9ea+1BEYGZmdlge0G7AzAzs+HJCcbMzIpwgjEzsyKcYMzMrAgnGDMzK8IJ\nxszMiujaBCNplqTd2h2HPf9I2k3SnMq4P4vW0ST9SdJrBnF9N0p6ZW/zdWSCkXS/pLfUlX1E0nW1\n8Yh4ZUT8vpf1jJcUklYrFGpHk3SWpK+1O45ulT9zIekDPc3XymexBEm/l/TxId5mbZ98qa58TjXJ\nStpW0hWSHpf0hKRrJL2hMr323VyaX/dLOrpunfdLejovv1jSnyUdJukFlXnOkvRMZT1LJd1amf4x\nSXfldSyQNEXSKEm/qcz/r7p1nJoPIpbXrXeppNf3c799UdLMHMd9kr5YN3183kdP5XjfUpm2Ud6X\n8/I+G1+37LclPShpiaQHJH25bvr+wBMRcUsenyzpvAYxhqSX5uFDJE3P65yTt1H9Hf0u8F+9ve+O\nTDDd4vmauErpwP15CPAocHC7AylhAPv7UeBLkkY1We9WwJ+A24EtgI2By4DfNfiBHh0R6wLvBb4i\naa+66ftHxChgc+CbwH8AZ9TN8+2IWLfy2i7H8Wbgf4CJeR2vAC4EiIh9avMDP61bx2F5vfPq1rtu\nRFzfpz1V2S2kz9H6wN7AkZIOrEw/H7gFeBFwLHCJpLF52nLgt8B7mqz7TOCVEfFC4A3AQZLeXZl+\nGHBuH+NdGzgKGAO8DtgT+EJl+hXA7pJe0tNKujbBVGs5knaSNC1n2wWSTsyz/TH/XVw7+pD0Akn/\nmTP9QknnSFqvst6D87RHJH2lbjuTJV0i6TxJS4CP5G1fn4+w5ks6SdLIyvpC0qckzc5HL/8taat8\nNLZE0kW1+SWtL+lXkhZJeiwPbzpI+6t2xHiIpL9LeljSsZXpzfYhknbO8S6WdKtWPlLdQtIf83u7\nStLJtaMj1TUlNfi/9Xd/Hpb35+K8PVWmf0LSnTmeOyTtkMuPlvS3Svm7etlfmwNvBiYBb+vpi9Tg\nPV2c39MTkm6X9DJJx+TP24OS3lpZdj1JZ+T3OlfS1ySNyNM+Iuk6Sd/Nn4f7JO2Tp30deCNwUv5s\nn5TLv68VR7PTJb2xsq1V9ndP+6AHdwLXA//eZPpk4PqIODYiHo2IJyLiB6QfuW81WiAipgGzgO2b\nTH88Iq4APgAcIulVLcT52hzHLXkdj0bE2RHxRAvLDqqI+HZE3BwRyyLibuAXwC4Akl4G7AB8NSKe\njohLgdvICSUiFkTEKcBNTdZ9V0QsqRQtB2o1kZHAHsAf+hjvDyPi2oh4JiLmkpLwLpXp/wCmA2/r\naT1dm2DqfB/4fs7gWwEX5fI35b+jK0cfH8mv3YEtgXWB2pdzW+AU4CBgI2A9YJO6bR0AXAKMJu30\nZ4HPkTL960mZ/lN1y7wN2BHYGfgScDrwIWAz4FXAxDzfC4CfkI7WxgFP12IbRLsC2+Q4j5P0ilze\ncB9K2gT4NfA1YAPSUcylWnF09TPgRtKR12Tgw32Mpz/7cz/Sj8ergfeTP+SS3pdjOBh4IfAO4JG8\nzN9IP8jrAccD50naqIe4Dgam5S/7naTPRKv2J/2Yrk86Kr2S9L/dhNSscFpl3rOAZaQfhNcAbwWq\nzV6vA+4m7Y9vA2dIUkQcC1wLHJk/20fm+W8i/UhvQPrfXCxpzcr66vd3f30FOErSBg2m7QVc3KD8\nImAXSWvVT5C0M+m7cE9PG42IG4E5pP9lb/5COjg4XtIuktZoYZni8gHRG0kJFeCVwL11ie/WXN7q\nOo+WtJS0b9Yh/e8BtgaWR8Scpgu35k2VeGvuBLbraaFOTjCX5yPUxZIWk374m/kX8FJJYyJiaUTc\n0MO8BwEnRsS9EbEUOAY4UKm54L3ALyPiuoh4BjgOqL9Z2/URcXlELM9HG9Mj4oZ8ZHI/6cfjzXXL\nfDsilkTELGAm8Lu8/ceB35B+WIiIRyLi0oh4Kn/Yvt5gXQN1fI77VtKHuPYBabYPPwRMiYgp+T1P\nBaYB+0oaR/qhPy4f6VxHqjr3RX/25zcjYnFE/B24hhVHvR8n7eubIrknIh4AiIiLI2Je3s6FwGxg\npx7iOpgVX9Kf0bdmsmsj4sqIWEb6oR2bY/4XcAEwXtJoSRsC+wJHRcSTEbEQ+H9AtenkgYj4UUQ8\nC5xNOvDZsNmGI+K8/DlaFhEnAGuQDihqVtrffXhP9duZAUwlNVnVGwPMb1A+n/SbU01KD0t6mlQj\nOgW4vIXNz6tbxxeqvxWSzs4xXgu8m1Q7+DXwiKQTazXEFmxct97FktZpcdmeTGbFwSSkg9zH6+ZZ\nAjRsgmwkIr6Z59+BdHBTW99ooFGN7f31763ZuiV9FJhA6nepeiKvv6lOTjDvjIjRtRerHsVWfQx4\nGXCXpJsk7dfDvBsDD1TGHwBWI31pNwYerE2IiKdYcQRc82B1JDd//ErSQ7nZ4X9IX7CqBZXhpxuM\nr5vXtbak05Sa6JaQmvhGN/pCSDpIKzoef9PD+633UGX4qdq2ab4PNwfeV/dB3JX0Q7cx8GjeTzUr\n7Z8W9Gd/NnsPm5FqKqtQavqcUXkPr2qw3tq8u5D6Di7IRT8D/k1Sw+abBur/vw/nBFEbJ8e8ObA6\nML8S12nAiyvLP/deK/t5XZqQ9AWlJsLH8/rWY+X32fT/I2lc5TO1tOe3CKQDsMNzoqx6mPT5qLcR\nqfnmsUrZGNL7+TywG2l/9GYTUj9QzXervxURcUhtQkT8JiL2JyWkA0itF62eGDGvbr2jI+LJ+pn6\n8l2UdCTpYOXtEfHPXLyUVOOuWo/GiaGpfFB1C+kzdnwufozGieqi+vfWJN53At8A9omIh+smjwKa\nJibo7ATTsoiYHRETSV/Mb5E6yNZh1doHpKOfzSvj40hNFAtIR1jP9XnkqvyL6jdXN/5D4C5g69y8\n9GVSh15/fJ50tPm6vK5aE98q64uIn8aKjsd9+rm96vqa7cMHgXPrPozr5COm+cAGktaurGqzyvCT\npM7C9CZSohzLygZzfz5Iat5biVJ/yo+AI4EX5S/TzB7We0ieNkPSQ6Smllr5YHoQ+CcwprJvXxgR\nrTaNrLTvcn/Ll0jNhuvn9/k4K7/PprdPj4i/Vz5TTZNYZf67gJ+TOqWrrgLe12CR95NqUNUDEiLi\n2Yg4EfgHPR9IIum1pARzXU/zNYh1eURcDfwf6eBi0LT6Xcw1gaOBPWPlJqtZwJZa+aSJ7Vi1SapV\nq7Hie3BP2rTqm/p7JWlv0vdm/4i4vcEsryC1gjQ1LBKMpA9JGhsRy1mRUZcDi/LfLSuznw98Tqlz\nel3SEfKFuTnjEmB/SW/InWOT6f3HbRSpOrtU0suBwwfwVkaRjj4W57btrw5gXX3Swz48j7RP3iZp\nhKQ1lTrvN83NT9OAyZJGKp0htH9ltX8F1pT0dkmrA/9JarLpyUD2549JzSU7KnlpTi61g41F+b0e\nSpMfGaX+iveTOve3r7w+DXxQg3imW0TMB34HnCDphUonoGyldPZTKxaw8md7FOlgaRGwmqTjWPXI\neLAdDxzKyk0lxwNvkPR1SRsonRb8adKRe6MmtZpvks5OW7N+Qt4/+5Fqlec1+cGrX+YASQcqnTwj\nSTuRmlt7akIvQtJBpN+avSLi3uq0iPgrMAP4av5+vRv4N+DSyvJrsuK7s0ZtH+XPzCfr3uMRwNV5\n3c+QEn6fmtol7UHqo3tPpH6v+ulrkvqVp/a0nmGRYEin/c3K1frvAwfm9vynSP0Yf8pNEDuTTuk7\nl9T8dB/pqOnTAJH6SD5N+hDPJ1VdF5KOMpv5AvBBUnX2R+TTIPvpe8BapCaGG0inJg6VZvvwQVLT\nwpdJP1wPAl9kxWfnIFJn/COkEwEuJO+vSH1MnyL98M8l1Wh662zs9/6MiItJ/++fkZLj5cAGEXEH\ncAKpnX8B6cv7pyareScpyZ8TEQ/VXqTPzWqk/TSYDgZGAneQmjMuoXHzUiPfB96rdIbZD0gnE/yW\nlNgfIH22+9pk2ScRcR/p+7ROpWw2qRl1O+B+0nfpPcDbIqLZfofUT/IY8IlK2S8lPUF6H8cCJ5IS\nWtWXtPK1KrWmnNq6ZpMOWs4DvhMRrZ7csLFWvQ6m2anCvfkaqTXkpsq6Tq1MP5DUz/EYqUnqvRGx\nqDL9adLvEaQafrX/7F2kpuEnSO/xf/Or5jT6fvLNV0jNdFOaNP/tD/w+Iub1tBKFHzjWVK7hLCY1\n19zX7ni6gaQLgbsiYshqX03iOA04IR8dmj2vSfoT6YzDWwZpfX8BPhYRM3uab7jUYAaNpP2VOtvX\nIZ01cTvpKMwakPTa3KzzgtxmewCtnQlUMqZ1SX1tb+ptXrPng4jYZbCSS17f63pLLpCq/LayA0hV\nfpH6Fw4MV/N68hJSR++LSM1fhw/mB7mf/kZqItuzzXGYPa+5iczMzIpwE5mZmRXhBGNmZkUMqz6Y\nMWPGxPjx49sdhplZV5k+ffrDEVF/EfSADasEM378eKZNm9buMMzMuoqkB3qfq+/cRGZmZkU4wZiZ\nWRFOMGZmVoQTjJmZFeEEY2ZmRTjBmJlZEU4wZmZWhBOMmZkV4QRjZmZFOMGYmVkRxRKMpM0kXSPp\nDkmzJH02l28gaaqk2fnv+k2W31vS3ZLukXR0qTjNzKyMkjWYZcDnI2JbYGfgCEnbAkcDV0fE1sDV\neXwlkkYAJwP7ANsCE/OyZmbWJYolmIiYHxE35+EngDuBTUhPjDw7z3Y28M4Gi+8E3BMR90bEM8AF\neTkzM+sSQ3I3ZUnjgdcAfwE2jIj5edJDwIYNFtkEeLAyPgd4XcEQ22vy5PYsa2ZWUPFOfknrApcC\nR0XEkuq0/Kz7AT2zWdIkSdMkTVu0aNFAVmVmZoOoaIKRtDopufw0In6eixdI2ihP3whY2GDRucBm\nlfFNc9kqIuL0iJgQERPGjh305+WYmVk/lTyLTMAZwJ0RcWJl0hXAIXn4EOAXDRa/Cdha0haSRgIH\n5uXMzKxLlKzB7AJ8GNhD0oz82hf4JrCXpNnAW/I4kjaWNAUgIpYBRwJXkk4OuCgiZhWM1czMBlmx\nTv6IuA5Qk8l7Nph/HrBvZXwKMKVMdGZmVpqv5DczsyKcYMzMrAgnGDMzK8IJxszMinCCMTOzIobk\nVjHPC75li5nZSlyDMTOzIpxgzMysCCcYMzMrwgnGzMyKcIIxM7MinGDMzKwIJxgzMyvCCcbMzIpw\ngjEzsyKcYMzMrAgnGDMzK8IJxszMinCCMTOzIpxgzMysCCcYMzMrwgnGzMyKcIIxM7MinGDMzKwI\nJxgzMyvCCcbMzIpwgjEzsyKcYMzMrAgnGDMzK8IJxszMilit5MolnQnsByyMiFflsguBbfIso4HF\nEbF9g2XvB54AngWWRcSEkrGamdngKppggLOAk4BzagUR8YHasKQTgMd7WH73iHi4WHRmZlZM0QQT\nEX+UNL7RNEkC3g/sUTIGMzNrj3b2wbwRWBARs5tMD+AqSdMlTWq2EkmTJE2TNG3RokVFAjUzs75r\nZ4KZCJzfw/Rdc9/MPsARkt7UaKaIOD0iJkTEhLFjx5aI08zM+qEtCUbSasC7gQubzRMRc/PfhcBl\nwE5DE52ZmQ2GdtVg3gLcFRFzGk2UtI6kUbVh4K3AzCGMz8zMBqhogpF0PnA9sI2kOZI+licdSF3z\nmKSNJU3JoxsC10m6FbgR+HVE/LZkrGZmNrhKn0U2sUn5RxqUzQP2zcP3AtuVjM3MzMrylfxmZlaE\nE4yZmRXhBGNmZkU4wZiZWRFOMGZmVoQTjJmZFeEEY2ZmRTjBmJlZEU4wZmZWhBOMmZkV4QRjZmZF\nOMGYmVkRTjBmZlaEE4yZmRXhBGNmZkU4wZiZWRFOMGZmVoQTjJmZFeEEY2ZmRTjBmJlZEU4wZmZW\nhBOMmZkV4QRjZmZFOMGYmVkRTjBmZlaEE4yZmRXhBGNmZkU4wZiZWRFOMGZmVoQTjJmZFVE0wUg6\nU9JCSTMrZZMlzZU0I7/2bbLs3pLulnSPpKNLxmlmZoOvdA3mLGDvBuX/LyK2z68p9RMljQBOBvYB\ntgUmStq2aKRmZjaoiiaYiPgj8Gg/Ft0JuCci7o2IZ4ALgAMGNTgzMyuqXX0wn5Z0W25CW7/B9E2A\nByvjc3LZKiRNkjRN0rRFixaViNXMzPqhHQnmh8CWwPbAfOCEgawsIk6PiAkRMWHs2LGDEZ+ZmQ2C\nIU8wEbEgIp6NiOXAj0jNYfXmAptVxjfNZWZm1iVaTjCS1pf0SklbSup3YpK0UWX0XcDMBrPdBGwt\naQtJI4EDgSv6u00zMxt6q/U0UdJ6wBHARGAksAhYE9hQ0g3AKRFxTQ/Lnw/sBoyRNAf4KrCbpO2B\nAO4HPpnn3Rj4cUTsGxHLJB0JXAmMAM6MiFkDeaNmZja0ekwwwCXAOcAbI2JxdYKkHYEPS9oyIs5o\ntHBETGxQ3GzeecC+lfEpwCqnMJuZWXfoMcFExF49TJsOTB/0iMzMbFjorQazEkljgc8CawGnRsTs\nIlGZmVnX62tn/QmkfpHLgJ8NfjhmZjZc9JhgJF0p6U2VopGkjvn7gTXKhWVmZt2utxrM+4H9JZ0v\naSvgK8A3gO8DnyodnJmZda/eOvkfB74oaUvg68A84Mj6M8rMzMzq9XYdzFbA4cAzwOeBrYALJf0a\nODkini0fopmZdaPemsjOB34OXAOcGxHXRsTbgMXA70oHZ2Zm3au305TXAO4D1gXWrhVGxDmSLi4Z\n2JCbPLndEZiZDSu9JZjDgZNITWSHVSdExNOlgrI+GEhidFI1s4J66+T/M/DnIYrFzMyGkXY9cMzM\nzIY5JxgzMyvCCcbMzIpo6WaXkiYAxwKb52UERES8umBsZmbWxVq9m/JPgS8CtwPLy4VjZmbDRasJ\nZlFE+JHFZmbWslYTzFcl/Ri4GvhnrTAifl4kKjMz63qtJphDgZcDq7OiiSxIt5ExMzNbRasJ5rUR\nsU3RSMzMbFhp9TTlP0vatmgkZmY2rLRag9kZmCHpPlIfjE9TNjOzHrWaYPYuGoWZmQ07LTWRRcQD\nwGbAHnn4qVaXNTOz56eWkoSkrwL/ARyTi1YHzisVlJmZdb9WayHvAt4BPAkQEfOAUaWCMjOz7tdq\ngnkmIoJ07QuS1ikXkpmZDQetJpiLJJ0GjJb0CeAq4EflwjIzs27X0llkEfFdSXsBS4BtgOMiYmrR\nyMzMrKv1mGAkKTeNkRPKKkmlOk+DaWcC+wELI+JVuew7wP7AM8DfgEMjYnGDZe8HngCeBZZFxIQ+\nvC8zM2uz3prIrpH0aUnjqoWSRkraQ9LZwCE9LH8Wq15DMxV4Vb5I86+sODOtkd0jYnsnFzOz7tNb\ngtmbVIM4X9I8SXfkq/lnAxOB70XEWc0Wjog/Ao/Wlf0uIpbl0RuATfsbvJmZda4em8gi4h/AKcAp\nklYHxgBPN2rS6qePAhc22zxwlaRngdMi4vRB2qaZmQ2BVm8VQ0T8C5g/WBuWdCywjPS0zEZ2jYi5\nkl4MTJV0V64R1a9nEjAJYNy4cfWTzcysTdpyuxdJHyF1/h/U7ASBiJib/y4ELgN2ajLf6RExISIm\njB07tlDEZmbWV0OeYCTtDXwJeEdEPNVknnUkjaoNA28FZg5dlGZmNlBFE4yk84HrgW0kzZH0MeAk\n0m1mpkqaIenUPO/GkqbkRTcErpN0K3Aj8OuI+G3JWM3MbHC11AcjaWfgf4FXACOBEcCTEfHCnpaL\niIkNis9oMu88YN88fC+wXSuxmZlZZ2q1BnMS6bTk2cBawMeBk0sFZWZm3a/lJrKIuAcYERHPRsRP\n8EPIzMysB62epvyUpJGkxyZ/m3S6sh84ZmZmTbWaJD6c5z2S9EyYzYD3lArKzMy6X6s1mB1JZ3It\nAY4vGI+ZmQ0TrdZg9gf+KulcSftJavkOAGZm9vzUUoKJiEOBlwIXk84m+5ukH5cMzMzMuluf7kUm\n6Tekm1CuBbyTdLqymZnZKlqqwUjaR9JZpOtg3gP8GHhJwbjMzKzLtVqDOZh0W/1PRsQ/C8ZjZmbD\nREsJpsktX8zMzJrqMcFIui4idpX0BKnv5blJQPR2LzIzM3v+6u2Jlrvmv6OGJhwzMxsuWu3kP7eV\nMjMzs5pWL7R8ZXUkX2i54+CHY2Zmw0WPCUbSMbn/5dWSluTXE8AC4BdDEqGZmXWlHhNMRHwj9798\nJyJemF+jIuJFEXHMEMVoZmZdqNXTlI+RtD6wNbBmpfyPpQIzM7Pu1uojkz8OfBbYFJgB7AxcD+xR\nLjQzM+tmrXbyfxZ4LfBAROwOvAZYXCwqMzPreq0mmH9ExD8AJK0REXcB25QLy8zMul2r9yKbI2k0\ncDkwVdJjwAPlwjIzs27Xaif/u/LgZEnXAOsBvy0WlZmZdb3e7kW2QYPi2/PfdYFHBz0iMzMbFnqr\nwUwn3eRSlbLaeABbForLzMy6XG83u9xiqAIxM7PhpdWbXUrShyR9JY+Pk7RT2dDMzKybtXqa8inA\n64EP5vEngJOLRGRmZsNCq6cpvy4idpB0C0BEPCZpZMG4zMysy7WaYP4laQT5qZaSxgLLi0VlQ2Py\n5PYsa2bPC602kf0AuAx4saSvA9cB/9PbQpLOlLRQ0sxK2QaSpkqanf+u32TZvSXdLekeSUe3GKeZ\nmXWIlhJMRPwU+BLwDWA+8M6IuLiFRc8C9q4rOxq4OiK2Bq7O4yvJtaWTgX2AbYGJkrZtJVYzM+sM\nvTaR5R/7WRHxcuCuvqw8Iv4oaXxd8QHAbnn4bOD3wH/UzbMTcE9E3JtjuCAvd0dftm9mZu3Taw0m\nIp4F7pY0bpC2uWFEzM/DDwEbNphnE+DByvicXGZmZl2i1U7+9YFZkm4EnqwVRsQ7BrLxiAhJMZB1\nSJoETAIYN26wcqCZmQ1UqwnmK4O4zQWSNoqI+ZI2AhY2mGcusFllfNNctoqIOB04HWDChAkDSlZm\nZjZ4Wr2b8h8GcZtXAIcA38x/f9FgnpuArSVtQUosB7LiIk8zM+sCrZ6m3C+Szic9WnkbSXMkfYyU\nWPaSNBt4Sx5H0saSpgBExDLgSOBK4E7gooiYVTJWMzMbXK02kfVLRExsMmnPBvPOA/atjE8BphQK\nzczMCitagzEzs+evlmowkrYmXWS5LbBmrTwi/DwYMzNrqNUazE+AHwLLgN2Bc4DzSgVlZmbdr9UE\ns1ZEXA0oIh6IiMnA28uFZWZm3a7VTv5/SnoBMFvSkaRTh9ctF5aZmXW7VmswnwXWBj4D7Ah8mHQN\ni5mZWUOtXmh5Ux5cChxaLhwzMxsuekwwkr4XEUdJ+iX5YWNVA70XmZmZDV+91WDOzX+/WzoQMzMb\nXnpMMBExPQ9OA56OiOXw3DNi1igcm5mZdbFWO/mvJnXy16wFXDX44ZiZ2XDRaoJZMyKW1kby8No9\nzG9mZs9zrSaYJyXtUBuRtCPwdJmQzMxsOGj1QsujgIslzQMEvAT4QLGozMys67V8HYyklwPb5KK7\nI+Jf5cIyM7Nu15fnwbwWGJ+X2UESEXFOkajMzKzrtXq7/nOBrYAZwLO5OEh3VTYzM1tFqzWYCcC2\nEbHK1fxmZmaNtHoW2UxSx76ZmVlLWq3BjAHukHQj8M9aoe9FZmZmzbSaYCaXDMLMzIafVk9T/oOk\nzYGtI+IqSWsDI8qGZmZm3azHPhhJL85/PwFcApyWJ20CXF42NDMz62ZNE0y+Ncx/59EjgF2AJQAR\nMRt4cfHozMysa/VUg3k5cGsefiYinqlNkLQaDR5AZmZmVtM0wUTEz4C5efT3kr4MrCVpL+Bi4JdD\nEJ+ZmXWpHvtgIuIXefBoYBFwO/BJYArwn2VDMzOzbtbqWWTLgR/ll5mZWa9avRfZfTToc4mILQc9\nIjMzGxb6ci+ymjWB9wEbDH44ZmY2XLR0L7KIeKTymhsR3wPe3t+NStpG0ozKa4mko+rm2U3S45V5\njuvv9szMbOi12kS2Q2X0BaQaTV+eJbOSiLgb2D6vewTpbLXLGsx6bUTs19/tmJlZ+7SaJE6oDC8D\n7gfeP0gx7An8LSIeGKT1mZlZB2j1LLLdC8ZwIHB+k2lvkHQbqYbzhYiYVT+DpEnAJIBx48YVC9LM\nzPqm1Sayf+9pekSc2J+NSxoJvAM4psHkm4FxEbFU0r6ke59t3WDbpwOnA0yYMMF3FzAz6xCtPnBs\nAnA46SaXmwCHATsAo/Krv/YBbo6IBfUTImJJRCzNw1OA1SWNGcC2zMxsCLXaB7MpsENEPAEgaTLw\n64j40AC3P5EmzWOSXgIsiIiQtBMpGT4ywO2ZmdkQaTXBbAg8Uxl/Jpf1m6R1gL1It56plR0GEBGn\nAu8FDpe0DHgaODAi3ARmZtYlWk0w5wA3SqqdSvxO4OyBbDgingReVFd2amX4JOCkgWzDzMzap9Wz\nyL4u6TfAG3PRoRFxS7mwzMys27XayQ+wNrAkIr4PzJG0RaGYzMxsGGgpwUj6KvAfrDideHXgvFJB\nmZlZ92u1BvMu0vUqTwJExDwGdnqymZkNc60mmGfyGVwBz50BZmZm1lSrCeYiSacBoyV9ArgKP3zM\nzMx60OpZZN+VtBewBNgGOC4iphaNzMzMulqvCSbfTv+qfMNLJxUzM2tJr01kEfEssFzSekMQj5mZ\nDROtXsm/FLhd0lTymWQAEfGZIlGZmVnXazXB/Dy/zMzMWtJjgpE0LiL+HhEDuu+YmZk9//TWB3N5\nbUDSpYVjMTOzYaS3JjJVhrcsGYh1mcmT27u8mXW83mow0WTYzMysR73VYLaTtIRUk1krD5PHIyJe\nWDQ6MzPrWj0mmIgYMVSBmJnZ8NKX58GYmZm1zAnGzMyKcIIxM7MinGDMzKwIJxgzMyvCCcbMzIpw\ngjEzsyJuuibFAAAMc0lEQVScYMzMrAgnGDMzK8IJxszMinCCMTOzIpxgzMysCCcYMzMrom0JRtL9\nkm6XNEPStAbTJekHku6RdJukHdoRp5mZ9U9vz4MpbfeIeLjJtH2ArfPrdcAP818zM+sCndxEdgBw\nTiQ3AKMlbdTuoMzMrDXtTDABXCVpuqRJDaZvAjxYGZ+Ty1YiaZKkaZKmLVq0qFCoZmbWV+1MMLtG\nxPakprAjJL2pPyuJiNMjYkJETBg7duzgRmhmZv3WtgQTEXPz34XAZcBOdbPMBTarjG+ay8zMrAu0\nJcFIWkfSqNow8FZgZt1sVwAH57PJdgYej4j5QxyqmZn1U7vOItsQuExSLYafRcRvJR0GEBGnAlOA\nfYF7gKeAQ9sUq5mZ9UNbEkxE3Ats16D81MpwAEcMZVxmZjZ4Ovk0ZTMz62JOMGZmVoQTjJmZFeEE\nY2ZmRTjBmJlZEU4wZmZWhBOMmZkV4QRjZmZFOMGYmVkRTjBmZlaEE4yZmRXhBGNmZkW0627K9nw3\neXJ7ljWzIeMajJmZFeEEY2ZmRTjBmJlZEU4wZmZWhBOMmZkV4QRjZmZFOMGYmVkRTjBmZlaEE4yZ\nmRXhBGNmZkU4wZiZWRFOMGZmVoQTjJmZFeEEY2ZmRTjBmJlZEU4wZmZWhBOMmZkV0ZYEI2kzSddI\nukPSLEmfbTDPbpIelzQjv45rR6xmZtY/7Xpk8jLg8xFxs6RRwHRJUyPijrr5ro2I/doQn5mZDVBb\najARMT8ibs7DTwB3Apu0IxYzMyujXTWY50gaD7wG+EuDyW+QdBswF/hCRMxqsPwkYBLAuHHjygVq\nnWPy5PYsa2Z90tZOfknrApcCR0XEkrrJNwPjIuLVwP8ClzdaR0ScHhETImLC2LFjywZsZmYta1uC\nkbQ6Kbn8NCJ+Xj89IpZExNI8PAVYXdKYIQ7TzMz6qV1nkQk4A7gzIk5sMs9L8nxI2okU6yNDF6WZ\nmQ1Eu/pgdgE+DNwuaUYu+zIwDiAiTgXeCxwuaRnwNHBgREQ7gjUzs75rS4KJiOsA9TLPScBJQxOR\nmZkNNl/Jb2ZmRTjBmJlZEU4wZmZWhBOMmZkV4QRjZmZFOMGYmVkRbb8XmdmQ8n3MzIaMazBmZlaE\nE4yZmRXhBGNmZkU4wZiZWRFOMGZmVoQTjJmZFeEEY2ZmRTjBmJlZEb7Q0qxVvkjTrE9cgzEzsyKc\nYMzMrAgnGDMzK8J9MGZDYaB9MO7DsS7kGoyZmRXhBGNmZkW4icysG/gUaetCrsGYmVkRTjBmZlaE\nE4yZmRXhBGNmZkU4wZiZWRE+i8xsuOvWs8i6NW57TttqMJL2lnS3pHskHd1guiT9IE+/TdIO7YjT\nzMz6py01GEkjgJOBvYA5wE2SroiIOyqz7QNsnV+vA36Y/5qZ9czXDXWEdjWR7QTcExH3Aki6ADgA\nqCaYA4BzIiKAGySNlrRRRMwf+nDNbMi164e+XclpGN6vrl0JZhPgwcr4HFatnTSaZxPACcbMOlMH\n/si3U9d38kuaBEzKo0sl3d3PVY0BHh6cqIZEN8XbTbFCd8XbTbFCd8XbTbHC8ccPJN7NBzOUmnYl\nmLnAZpXxTXNZX+chIk4HTh9oQJKmRcSEga5nqHRTvN0UK3RXvN0UK3RXvN0UK3RmvO06i+wmYGtJ\nW0gaCRwIXFE3zxXAwflssp2Bx93/YmbWPdpSg4mIZZKOBK4ERgBnRsQsSYfl6acCU4B9gXuAp4BD\n2xGrmZn1T9v6YCJiCimJVMtOrQwHcMQQhjTgZrYh1k3xdlOs0F3xdlOs0F3xdlOs0IHxKv2Om5mZ\nDS7fi8zMzIpwgqH329YMUQxnSlooaWalbANJUyXNzn/Xr0w7Jsd7t6S3Vcp3lHR7nvYDSSoQ62aS\nrpF0h6RZkj7b4fGuKelGSbfmeI/v5HjzdkZIukXSr7og1vvzdmZImtbJ8eYLti+RdJekOyW9voNj\n3Sbv09priaSjOjXehiLief0inWTwN2BLYCRwK7BtG+J4E7ADMLNS9m3g6Dx8NPCtPLxtjnMNYIsc\n/4g87UZgZ0DAb4B9CsS6EbBDHh4F/DXH1KnxClg3D68O/CVvsyPjzdv5d+BnwK86+bOQt3M/MKau\nrCPjBc4GPp6HRwKjOzXWurhHAA+Rrlfp+Hifi3soNtLJL+D1wJWV8WOAY9oUy3hWTjB3Axvl4Y2A\nuxvFSDob7/V5nrsq5ROB04Yg7l+Q7ivX8fECawM3k+4c0ZHxkq75uhrYgxUJpiNjzeu+n1UTTMfF\nC6wH3Efue+7kWBvE/lbgT90Sb+3lJrLmt6TpBBvGimt/HgI2zMPNYt4kD9eXFyNpPPAaUq2gY+PN\nTU4zgIXA1Ijo5Hi/B3wJWF4p69RYAQK4StJ0pTtrdGq8WwCLgJ/k5scfS1qnQ2OtdyBwfh7uhngB\n98F0jUiHHh11yp+kdYFLgaMiYkl1WqfFGxHPRsT2pNrBTpJeVTe9I+KVtB+wMCKmN5unU2Kt2DXv\n232AIyS9qTqxg+JdjdQM/cOIeA3wJKmJ6TkdFOtzlC5Gfwdwcf20Toy3ygmmxVvStMkCSRsB5L8L\nc3mzmOfm4fryQSdpdVJy+WlE/LzT462JiMXANcDeHRrvLsA7JN0PXADsIem8Do0VgIiYm/8uBC4j\n3S29E+OdA8zJtVeAS0gJpxNjrdoHuDkiFuTxTo/3OU4wrd22pl2uAA7Jw4eQ+jpq5QdKWkPSFqRn\n5tyYq81LJO2czxI5uLLMoMnrPgO4MyJO7IJ4x0oanYfXIvUX3dWJ8UbEMRGxaUSMJ30W/y8iPtSJ\nsQJIWkfSqNowqa9gZifGGxEPAQ9K2iYX7Ul6REjHxVpnIiuax2pxdXK8KwxFR0+nv0i3pPkr6ayL\nY9sUw/mkRxH8i3Sk9THgRaTO3tnAVcAGlfmPzfHeTeWMEGAC6Qv+N+Ak6jo0BynWXUnV8tuAGfm1\nbwfH+2rglhzvTOC4XN6R8Va2tRsrOvk7MlbS2Ze35tes2veng+PdHpiWPwuXA+t3aqx5O+sAjwDr\nVco6Nt76l6/kNzOzItxEZmZmRTjBmJlZEU4wZmZWhBOMmZkV4QRjZmZFOMGYmVkRTjDW1SQ9m29l\nPlPSL2sXVA7Ceser8uiEFpdZS9IfJI0YjBgGk6QpPe0bSRdI2nooY7LhzwnGut3TEbF9RLwKeJSh\nfcx2vY8CP4+IZ0ttQFK/HnMeEftGuk1OMz8k3WDTbNA4wdhwcj2Vu8RK+qKkmyTdphUPGRuv9KCp\nHyk9fOx3+fYxtYcy3SrpViqJKi9zraSb8+sNTbZ/EJVbcPSw/bsknSXpr5J+Kuktkv6k9ACpnepX\nKukjkq6Q9H+kK7gbrjuXX650V+NZWnFn49pDwcbkW7v8Or/PmZI+kGe5FnhLfxOYWSNOMDYs5Gap\nPcn3kZP0VtK9mHYi3R5kR624y+/WwMkR8UpgMfCeXP4T4NMRsV3d6hcCe0XEDsAHgB802P5IYMuI\nuL+F7b8UOAF4eX59kHT7nS8AX27yFncA3hsRb+5l3R+NiB1Jtwb5jKQX1a1nb2BeRGyXa32/BYiI\n5cA9QP17N+s3JxjrdmspPeel9lyMqbn8rfl1C+kBYy8n/SgD3BcRM/LwdGB87p8YHRF/zOXnVrax\nOvAjSbeTbpm+bYM4xpCSVU1v2789/6jPAq6OdM+m20kPnWtkakQ82sK6P5NrYDeQ7qxb369yO7CX\npG9JemNEPF6ZthDYuMn2zfrM1WHrdk9HxPaS1iY9we8IUg1DwDci4rTqzEoPSPtnpehZYK1etvE5\nYAHp6P4FwD8axQGsWd1Ui9tfXhlfTvPv5JMtrHs34C3A6yPiKUm/r4uJiPirpB1INyf9mqSrI+K/\n8uQ18/swGxSuwdiwEBFPAZ8BPp/7Ea4EPqr0UDQkbSLpxT0svxhYLGnXXHRQZfJ6wPxc4/gw6fno\n9cs/BoyQVPtB79P2+6jZutcDHsvJ5eWkZ7CvRNLGwFMRcR7wHVLTW83LSHfcNRsUrsHYsBERt0i6\nDZgYEedKegVwfXoEBkuBD5FqLM0cCpwpKYDfVcpPAS6VdDCpz+LJRgvnZXYFroqI3/Vj+y3pYd2/\nBQ6TdCfpdu03NFj834DvSFpOejTE4QCSNiTVBh8aaHxmNb5dv9kgyU1Pn4uID7c7lr6S9DlgSUSc\n0e5YbPhwE5nZIImIm4FrOvFCyxYsBs5udxA2vLgGY2ZmRbgGY2ZmRTjBmJlZEU4wZmZWhBOMmZkV\n4QRjZmZF/H9jmJYJR1hmWQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e52bd7c18>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"faixa = np.arange(0,7350,350)\n",
"frenda2 = pd.cut(base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")], bins=faixa, right=False)\n",
"t2 = (frenda2.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t2,\"\\n\")\n",
"\n",
"plot = base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")].plot.hist(bins=faixa,title=\"Histograma - Insegurança Alimentar - NORDESTE - 2013(H2)\", weights=zeros_like(base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")])+1./base.RENDA[(base.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"red\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 201,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 9.0\n",
"[350, 700) 24.4\n",
"[700, 1050) 21.0\n",
"[1050, 1400) 15.5\n",
"[1400, 1750) 9.7\n",
"[1750, 2100) 6.9\n",
"[2100, 2450) 4.1\n",
"[2450, 2800) 2.5\n",
"[2800, 3150) 1.8\n",
"[3150, 3500) 1.3\n",
"[3500, 3850) 0.9\n",
"[3850, 4200) 0.9\n",
"[4200, 4550) 0.7\n",
"[4550, 4900) 0.3\n",
"[4900, 5250) 0.3\n",
"[5250, 5600) 0.1\n",
"[5600, 5950) 0.2\n",
"[5950, 6300) 0.2\n",
"[6300, 6650) 0.1\n",
"[6650, 7000) 0.0\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGDCAYAAAAfwaZ3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XfYHVW59/Hvj0BIIEAICTHSQhMElRYQjshBioIHEF6O\nCNLEggVUsFKUcl49Kkp9QQ4gSEc6AkoLBwsKQkIxdFCCAUISSgiBSEnu94+1tplsnjJP2bMLv891\n7euZvabdM8/ec89as/aMIgIzM7NGW6zZAZiZ2TuDE46ZmVXCCcfMzCrhhGNmZpVwwjEzs0o44ZiZ\nWSUalnAkPShp60Yt36w7kraW9HThvT+LZpmkMZIekTR8kJY3VtLDkpbsbdp+JRxJUyVtV1f2GUm3\n195HxPoR8bteljNeUkhavD9xtDtJ50r6QbPjaFf5MxeSPtXTdGU+i40g6XeSPt+E9Y6TdLak6ZJe\nyQeXYyUtnceHpFclzS28vpPHHZPH71FY3uK5bLykGwrzvCnpjcL7/8nJfkF+/4qkRyUdUBefJH1b\n0uOS5kn6h6Qf9XbAkjRS0umSnpP0mqQpXSx7al5mcdtOzeOGSjpe0tO5fKqkk/K44vQL6paxd94v\nb9ZNN7uf/58l8//nqbyP7pO0Y9002+b/22uSbpO0Wt3++4mkF/LrJ5JUGP9vku7Ky/6rpC3rQjgM\nODci5uXp3/Y51dtP2o6TNE3SnBz3EbVxETEDuA04sLdt7+gmtXdqImuUFtyf+wMvAvs1O5BG6M/+\nljQKuAMYDmwREcsA2wPLAWsWJt0gIkYUXscVxr0IHCtpSP3yI2LH2jzARcBxhWV8KU/2bB6/LHAo\ncJakdQqLOYV0cNoPWAbYEdgWuKyH7RoKTARWA7bI2/Nt4MeSvlE3+c5123ZwLj8cmABslte7NXBP\n3q4Rhe36R90yLsrzX1q33JHdxduLxYFpwL/n7fgecJmk8XlbRwNXAd8HRgGTgEsL8x8I7ApsAHwA\n2Bn4Yp53FHAd8FNgJHAccJ2k5fP4JUnfmwv7GPM5wPoRsSzwb8Dekv5PYfxFtRh6FBF9fgFTge3q\nyj4D3N7VNKR/8CRgDjADOCGX/wMIYG5+bUFKgt8DngJmAucDyxWWu18e9wLpH1JczzHAFaSdOQf4\nfF73HcBsYDpwKjC0sLwAvgI8DrwC/F/SF/PPeRmX1aYHlgeuB2YBL+XhlfuzD/PyzgV+kIfH51j2\nz/vleeDIwrRd7sM8bvMc72zgfmDrwrjVgT/kbZsInAZcmMdtDTzd3f92APvzS3l/zs7rU2H8F4CH\nczwPARvn8sOAvxXKd+tl360GLAB2B94C3lUYt8h2dbFNl+dtegWYAryHdDCaSToQfLQw73LA2Xlb\nnwF+AAwpfuaBn+XPw5PAjnncD4H5wD9Jn+1Tc/nJeR1zgMnAhwvretv+7sdn6gd5mxbrYZoA1upm\n3DGkg8f9wP65bPE8z/juPr/d7ftcNhP4ZB5eO++XzeqmWQV4Hdimm7g+l5ezdF35p/L+Xba7Y1Nh\n2uuBQ/p5fDuG/L1pxAv4K7B7Hj4Q+HNh3NLAPGDd/P7PwIGF8Z8F7szDOwEP1S37MeBzeXgr4Im6\n8b+r/6x19X8sjFspf8a+UyhbHHgNWK2n7ayqhnMycHKk7LgmC89ktsp/R0Y6Y7iD9CX+DPARYA1g\nBOmghqT1gJ8DewPjSAeDlerW9QnSl3Yk6Yszn3SWNZqU0LYlJZiijwGbkA7c3wHOBPYhfQneB+yV\np1sM+CXpYLcq6UNwap/3Rs+2BNbJcR4l6b25vMt9KGkl4DekA80o4FvAlZLG5PkuBu4CViB9afbt\nYzz92Z87AZuSzr72IO1fJH0yx7Af6ex3F9KJA6Rk82HS//RY4EJJ43qIaz9gUkRcSUpge/dhm3YG\nLiCdQNwL3ET6364E/BdwRmHac0kJbS1gI+CjpMRb80HgUdL+OA44W5Ii4kjgj8DBsehZ9t3AhqT/\n1cXA5ZKGFZZXv7/7ajvgqohY0I95a4J0Mne0pCX6uxBJi0nahbRvnsjF25IOZHctssKIacCdpNpY\nV7YHboiIV+vKrwSGkT6LvbkT+Iakr0h6f7EZqpkkjSWd9DyYi9YnJXwA8jY/kcvfNj4Pr0/3RDqO\nAbyf9HntT5yHSZoLPE1KghcXYnwrx7hBT8sYSMK5RtLs2ouUCLrzJrCWpNERMTci7uxh2r1JZ+9/\nj4i5pDPPPXPzwn8C10XE7RHxBnAU6ctRdEdEXBMRCyJiXkRMjog7I+KtiJhKOpj8e908x0XEnIh4\nEHgAuDmv/2XgBtKBhoh4ISKujIjXIuIV0lls/bIG6tgc9/2kD1LtH9jdPtwH+G1E/DZv8y2kmtDH\nJa1KOvAfFRFvRMTtwLV9jKc/+/PHETE7Iv5BatvdMJd/nrSv747kiYh4CiAiLo+IZ/N6LiXVkDbr\nIa79WPiBv5i+Nav9MSJuyl+Sy4ExOeY3gV8B4/P1grHAx0lnxa9GxEzgRGDPwrKeioizImI+cB7p\nRGhsdyuOiAvz5+itiDgeWJJ0glGzyP7uwzbVrECqjfXmnuL3V9LH6uK8llST7881qHfnY8I84Grg\nGxFxbx43uof4pufxXelyvvw/fL5uvmvqtu0LufxHwE9Ix5hJwDOS9u/Ddu1Rt9zb+jBvl3JCvwg4\nLyIeycUjgJfrJp1DagbsavwcYEROoHcA4yTtKWmJvH1rAkvlaUeSavb1Tqk7nl9fP0FE/DjHsDHp\nhK0+xlfy8rs1kISza0SMrL14+1lu0edIGfwRSXdL2qmHad9NajKreYpUXRubx02rjYiI11h4hlwz\nrfhG0nskXa90oXEO8N+8/UM9ozA8r4v3I/KylpJ0Rr5oNofUVDWyq7bufKGxdnHxhh62t95zheHX\nauum+324GvDJug/LlqQD37uBF/N+qllk/5TQn/3Z3TasQqrJvI2k/fLF09o2vK+L5dam/RCpqfBX\nuehi4P2SNuxq+i7U/3+fzwmj9p4c82rAEsD0QlxnACsW5v/Xthb28wi6IelbSj16Xs7LW45Ft7Pb\n/4+kVQufqbndTPYC6X/fm42L39+IuKmLab4HHEmqQfTFs/mYsCzpes02hXHP9xDfOOD5brazy/ny\niejoPL5m17ptOwsgIuZHxGkR8SHSgfGHwDmFVoTeXFa33I90NZFS54la/Ed0NU2ebjHSgfsN4ODC\nqLmkfVe0HAsTRf345YC5+STuBdL1nW+SPuc7kJrSax0AXmJh4ir6Wt3xvMtjdF7HvaTvybF1o5ch\nNaN3q5ImtYh4PCL2In1RfwJcodRjpqtbVT9L+qLXrEpq0phBOsNZuTZCqVvfCvWrq3t/OvAIsHZu\njjqCVMXsj2+SzkY/mJdVaxJ82/Ii4qJYeHFxx/rxfdXDPpwGXFD3RVg6n41MB0ZJWqqwqFUKw6+y\n8MyHnDjHsKjB3J/TWPTCdW29qwFnkb50K+QP/AM9LHf/PO4+Sc8BfymUD6ZppOsKowv7dtmI6Kn5\nomiRfSfpw6Qm2z2A5fN2vsyi29nt7dsj4h+x6MXtrkwEdssHswHJteUn6Plksqf5Xwe+SzoZ2DUX\n/y+wiqRFaq+SViE1ad/azXZOBHbMn/mi3Un/o55aTbqKbV5EnEY6AK/Xpw3rfdlfKsT/311Nk2sj\nZ5NOpHfPteuaByk0TeVtXpOFTW6LjM/DtXFExO8jYtOIGEVqQl+X1KwO6VrRewayfdniFL7LOfGv\nxaJNfW9TScKRtI+kMZHalWsZcAGpyr6AdK2m5hLgUEmrSxpBOoO+NFedrwB2Vur2N5R0PaC3g90y\npCrnXEnrAl8ewKYsQ8rss5V6gxw9gGX1SQ/78ELSPvmYpCGShil1aVw5N1dNAo5R6hK6Ben6Rc1j\nwDBJ/5Gr9t8jNfH0ZCD78xfAtyRtomStnGxqJx+z8rYewMI25/r9MIx0wD6Q1FRXe30V+LQGsSdd\nREwHbgaOl7Ss0jWJNSWVbUadwaKf7WVIJ0+zgMUlHcXbz2QH6oS8zPPyvkXSSpJOkPSBfizvSFKS\n7JdITd/Hk5q/iYjHgP8BLpK0ef7Mrk+6FjMxIiZ2s6gLSGfplyt1z15CqRnwFOCYSM3fPZJ0SP5u\nDFfq6r0/6X9yb2/zNsDpwHtJveHqm06vBt4naff8eT8auL/Q5HY+6VrUSkrXcL9JutYIgKSN8v5Z\nltShZVqhBnsXqVWm/tp3t/Ln/ouSls/f282Ag4BbC5NtBkytNZF3p6pOAzsAD+bq8cnAnvkM4zVS\ntfZPuclic1L3uwtIzVVPknr5fBUg0jWWr5KaUqaTqpYzSWc43fkW8GlSdfQsFu1e2FcnkbqbPk86\no7pxAMvqq+724TTSheYjSAeyaaTuorX/7d6kC6ovkDoWXEreX/lL+hVSIniGVOP5V9/7bvR7f0bE\n5aT/98WkZHkNMCoiHiIdlO4gHaTfD/ypm8XsSkr650fEc7UX6XOzOGk/Dab9gKGknnMvkU56yjRZ\nQfo//aeklySdQuqccCMp0T9F+mz3tYmzRxHxIqnb6pvAXyS9QjowvMzCC/cA92vR35Sc1M3y/sTC\ns+P+OgdYVVLtZOdg0mfuQtJ3+EZST6ndu1tAri1tR9pffyGd9JxA6sn507rJr6vbtqtz+Wukz9lz\npO/wQaTaxd9Lbsen6pY7V9KKvc+2qHwi8EXSidJzhWXtnbd1Fmlf/JD0mduMRa8bnkHq+jwlv65n\n0Y4u38nbN430Wd2tNiKfAJxLuvbbF7uxsBfphcD/y6+avUknEj1SRPs+gC3XgGaTmneebHY87UDS\npcAjEVFZ7aybOM4Ajs9nvGZWEaUerH8ENupnx5T65a0I/D4v7589Tdt2P/yUtLPSxfulSdXFKaR+\n89YFSZvmZqDFJO1Aqg1d0+SYRpCu1W3V27RmNrgiYlZErDsYySYvb2ZEvLe3ZAOpCaLdfILU5CbS\n9Yk9o52raY33LtKvllcgNZd9udBFtVn+RmpS27bJcZhZhdq6Sc3MzNpH2zWpmZlZe3LCMTOzSrTF\nNZzRo0fH+PHjmx2GmVlbmTx58vMRUf9j7qZpi4Qzfvx4Jk2a1OwwzMzaiqQef4hZNTepmZlZJZxw\nzMysEk44ZmZWCSccMzOrhBOOmZlVwgnHzMwq4YRjZmaVcMIxM7NKOOGYmVklnHDMzKwSTjhmZlYJ\nJxwzM6uEE46ZmVWiLe4W3Uwzrj+x3/OO3enQQYzEzKy9uYZjZmaVcMIxM7NKOOGYmVklnHDMzKwS\nTjhmZlYJJxwzM6uEE46ZmVXCCcfMzCrhhGNmZpVwwjEzs0o44ZiZWSWccMzMrBJOOGZmVgknHDMz\nq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOzSvgR0w3kx1ObmS3kGo6ZmVXCCcfMzCrhhGNmZpVwwjEz\ns0o44ZiZWSWccMzMrBJOOGZmVgknHDMzq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOzSjjhmJlZJZxw\nzMysEk44ZmZWCSccMzOrhBOOmZlVomEJR9Iqkm6T9JCkByV9PZePknSLpMfz3+UbFYOZmbWORtZw\n3gK+GRHrAZsDB0laDzgMuDUi1gZuze/NzKzDNSzhRMT0iLgnD78CPAysBHwCOC9Pdh6wa6NiMDOz\n1lHJNRxJ44GNgL8AYyNieh71HDC2m3kOlDRJ0qRZs2ZVEaaZmTVQwxOOpBHAlcAhETGnOC4iAoiu\n5ouIMyNiQkRMGDNmTKPDNDOzBmtowpG0BCnZXBQRV+XiGZLG5fHjgJmNjMHMzFpDI3upCTgbeDgi\nTiiMuhbYPw/vD/y6UTGYmVnrWLyBy/4QsC8wRdJ9uewI4MfAZZI+BzwF7NHAGMzMrEU0LOFExO2A\nuhm9baPWa2Zmrcl3GjAzs0o44ZiZWSWccMzMrBJOOGZmVgknHDMzq4QTjpmZVcIJx8zMKuGEY2Zm\nlXDCMTOzSjjhmJlZJZxwzMysEk44ZmZWCSccMzOrhBOOmZlVwgnHzMwq4YRjZmaVcMIxM7NKOOGY\nmVklnHDMzKwSTjhmZlYJJxwzM6uEE46ZmVXCCcfMzCrhhGNmZpVwwjEzs0o44ZiZWSWccMzMrBJO\nOGZmVgknHDMzq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOzSjjhmJlZJZxwzMysEouXnVDS8sC7gXnA\n1IhY0LCozMys4/SYcCQtBxwE7AUMBWYBw4Cxku4Efh4RtzU8SjMza3u91XCuAM4HPhwRs4sjJG0C\n7CtpjYg4u1EBmplZZ+gx4UTE9j2MmwxMHvSIzMysI5W+hgMgaQzwdWA48D8R8XhDojIzs47T115q\nxwM3AVcDFw9+OGZm1ql6TDiSbpK0VaFoKDA1v5ZsXFhmZtZpeqvh7AHsLOkSSWsC3wd+BJwMfKXR\nwZmZWefordPAy8C3Ja0B/BB4Fji4vseamZlZb3r7Hc6awJeBN4BvAmsCl0r6DXBaRMxvfIhmZtYJ\nemtSuwS4CrgNuCAi/hgRHwNmAzc3OjgzM+scvXWLXhJ4EhgBLFUrjIjzJV3eyMDMzKyz9JZwvgyc\nSmpS+1JxRETMa1RQZmbWeXrrNPBn4M8VxWJmZh3MjycwM7NKOOGYmVklnHDMzKwSpW7eKWkCcCSw\nWp5HQETEBxoYm5mZdZCyd4u+CPg2MAXwkz7NzKzPyiacWRFxbUMjMTOzjlY24Rwt6RfArcDrtcKI\nuKohUZmZWccpm3AOANYFlmBhk1qQbntjZmbWq7IJZ9OIWKehkZiZWUcr2y36z5LW6+vCJZ0jaaak\nBwplx0h6RtJ9+fXxvi7XzMzaT9kazubAfZKeJF3DKdst+lzSvdjOrys/MSJ+1pdAzcysvZVNODv0\nZ+ER8QdJ4/szr5mZdZZSTWoR8RSwCrBNHn6t7Lzd+Kqkv+Ymt+UHsBwzM2sTpZKGpKOB7wKH56Il\ngAv7uc7TgTWADYHpwPHdrPNASZMkTZo1a1Y/V2VmZq2ibC1lN2AX4FWAiHgWWKY/K4yIGRExPyIW\nAGcBm3Uz3ZkRMSEiJowZM6Y/qzIzsxZSNuG8ERFB+u0Nkpbu7woljSu83Q14oLtpzcysc5TtNHCZ\npDOAkZK+AHyWVDvpkaRLgK2B0ZKeBo4Gtpa0ISl5TQW+2I+4zcyszZRKOBHxM0nbA3OAdYCjIuKW\nEvPt1UXx2X0L0czMOkGPCUeSclMaOcG8LckUp7HBM+P6Ewc0/9idDh2kSMzMBkdv13Buk/RVSasW\nCyUNlbSNpPOA/RsXnpmZdYremtR2IF2vuUTS6sBsYDgpUd0MnBQR9zY2RDMz6wQ9JpyI+Cfwc+Dn\nkpYARgPzImJ2FcGZmVnnKNtLjYh4k/RDTTMzsz4byO1pzMzMSnPCMTOzSjjhmJlZJcrevHNzSXdL\nmivpDUnzJc1pdHBmZtY5ytZwTgX2Ah4ndYv+PHBao4IyM7POU7pJLSKeAIbkOz3/kn4+lM3MzN6Z\nynaLfk3SUNJjpo8jdY/29R8zMyutbNLYN097MOmZOKsAuzcqKDMz6zxlazibAL+JiDnAsQ2Mx8zM\nOlTZGs7OwGOSLpC0k6TSdygwMzODkgknIg4A1gIuJ/VW+5ukXzQyMDMz6yx9upeapBtIT+ocDuxK\n6h5tZmbWq7I//NxR0rmk3+HsDvwCeFcD4zIzsw5TtoazH3Ap8MWIeL2B8ZiZWYcqlXAiYq9GB2Jm\nZp2tx4Qj6faI2FLSK6RrN/8aBURELNvQ6MzMrGP09sTPLfPfZaoJx8zMOlXZTgMXlCkzMzPrTtkf\nfq5ffJN/+LnJ4IdjZmadqseEI+nwfP3mA5Lm5NcrwAzg15VEaGZmHaHHhBMRP8rXb34aEcvm1zIR\nsUJEHF5RjGZm1gHKdos+XNLywNrAsEL5HxoVmJmZdZZSCUfS54GvAysD9wGbA3cA2zQuNDMz6yRl\nOw18HdgUeCoiPgJsBMxuWFRmZtZxyiacf0bEPwEkLRkRjwDrNC4sMzPrNGXvpfa0pJHANcAtkl4C\nnmpcWGZm1mnKdhrYLQ8eI+k2YDngxoZFZWZmHae3e6mN6qJ4Sv47Anhx0CMyM7OO1FsNZzLppp0q\nlNXeB7BGg+IyM7MO09vNO1evKhAzM+tsZW/eKUn7SPp+fr+qpM0aG5qZmXWSst2ifw5sAXw6v38F\nOK0hEZmZWUcq2y36gxGxsaR7ASLiJUlDGxiXmZl1mLI1nDclDSE/9VPSGGBBw6IyM7OOUzbhnAJc\nDawo6YfA7cB/NywqMzPrOGV/+HmRpMnAtqQu0btGxMMNjczMzDpKrwknN6U9GBHrAo80PiQzM+tE\nvTapRcR84FFJq1YQj5mZdaiyvdSWBx6UdBfwaq0wInZpSFRmZtZxyiac7zc0CjMz63hlOw38vtGB\nmJlZZyvbLdrMzGxAnHDMzKwSTjhmZlaJUtdwJK0N/AhYDxhWK48IPw/HzMxKKVvD+SVwOvAW8BHg\nfODCRgVlZmadp2zCGR4RtwKKiKci4hjgPxoXlpmZdZqyv8N5XdJiwOOSDgaeAUY0LiwzM+s0ZWs4\nXweWAr4GbALsC+zfqKDMzKzzlP3h5915cC5wQOPCMTOzTtVjwpF0UkQcIuk68sPXinwvNTMzK6u3\nGs4F+e/PGh2ImZl1th4TTkRMzoOTgHkRsQD+9YycJRscm5mZdZCynQZuJXUaqBkOTBz8cMzMrFOV\nTTjDImJu7U0eXqqH6QGQdI6kmZIeKJSNknSLpMfz3+X7HraZmbWbsgnnVUkb195I2gSYV2K+c4Ed\n6soOA26NiLVJNafDSsZgZmZtrOwPPw8BLpf0LCDgXcCnepspIv4gaXxd8SeArfPwecDvgO+WjMPM\nzNpU6d/hSFoXWCcXPRoRb/ZznWMjYnoefg4Y28/lmJlZGylbwwHYFBif59lYEhFx/kBWHhEh6W2/\n7wGQdCBwIMCqq646kNWYmVkLKPt4gguANYH7gPm5OEh3je6rGZLGRcR0SeOAmV1NFBFnAmcCTJgw\nocukZGZm7aNsDWcCsF5EDMaB/1rSfdh+nP/+ehCWaWZmLa5sL7UHSB0F+kTSJcAdwDqSnpb0OVKi\n2V7S48B2+b2ZmXW4sjWc0cBDku4CXq8V9nYvtYjYq5tR25Zcr5mZdYiyCeeYRgZhZmadr2y36N9L\nWg1YOyImSloKGNLY0MzMrJP0eA1H0or57xeAK4Az8qiVgGsaG5qZmXWSbhNOvpXN/81vDwI+BMwB\niIjHgRUbHp2ZmXWMnmo46wL35+E3IuKN2ghJi9PFA9nMzMy6023CiYiLgWfy299JOgIYLml74HLg\nugriMzOzDtHjNZyIqP0o8zBgFjAF+CLwW+B7jQ3NzMw6SdleaguAs/LLzMysz8reS+1JurhmExFr\nDHpEZmbWkfpyL7WaYcAngVGDH46ZmXWqUvdSi4gXCq9nIuIk4D8aHJuZmXWQsk1qGxfeLkaq8fTl\nWTpWsRnXn9jvecfudOggRmJmlpRNGscXht8CpgJ7DHo0ZmbWscr2UvtIowMxM7POVrZJ7Rs9jY+I\nEwYnHDMz61R96aW2KelpnQA7A3cBjzciKDMz6zxlE87KwMYR8QqApGOA30TEPo0KbDAN5AK6mZkN\njrKPmB4LvFF4/0YuMzMzK6VsDed84C5JV+f3uwLnNSYkMzPrRGV7qf1Q0g3Ah3PRARFxb+PCMjOz\nTlO2SQ1gKWBORJwMPC1p9QbFZGZmHahUwpF0NPBd4PBctARwYaOCMjOzzlO2hrMbsAvwKkBEPAss\n06igzMys85RNOG9ERJAfUSBp6caFZGZmnahswrlM0hnASElfACbih7GZmVkflO2l9jNJ2wNzgHWA\noyLiloZGZmZmHaXXhCNpCDAx38DTScbMzPql1ya1iJgPLJC0XAXxmJlZhyp7p4G5wBRJt5B7qgFE\nxNcaEpWZmXWcsgnnqvwyMzPrlx4TjqRVI+IfEeH7ppmZ2YD0dg3nmtqApCsbHIuZmXWw3hKOCsNr\nNDIQMzPrbL0lnOhm2MzMrE966zSwgaQ5pJrO8DxMfh8RsWxDozMzs47RY8KJiCFVBWJmZp2tL8/D\nMTMz6zcnHDMzq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOzSjjhmJlZJZxwzMysEk44ZmZWibLPw7F3\nkBnXn9jvecfudOggRmJmncQ1HDMzq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOzSjjhmJlZJZxwzMys\nEk44ZmZWCSccMzOrhBOOmZlVwgnHzMwq4YRjZmaVcMIxM7NKNO1u0ZKmAq8A84G3ImJCs2IxM7PG\na/bjCT4SEc83OQYzM6uAm9TMzKwSzUw4AUyUNFnSgfUjJR0oaZKkSbNmzWpCeGZmNpiamXC2jIgN\ngR2BgyRtVRwZEWdGxISImDBmzJjmRGhmZoOmaQknIp7Jf2cCVwObNSsWMzNrvKYkHElLS1qmNgx8\nFHigGbGYmVk1mtVLbSxwtaRaDBdHxI1NisXMzCrQlIQTEX8HNmjGus3MrDncLdrMzCrhhGNmZpVw\nwjEzs0o44ZiZWSWccMzMrBJOOGZmVgknHDMzq4QTjpmZVaLZz8OxDjPj+hP7Pe/YnQ4dxEjMrNW4\nhmNmZpVwwjEzs0o44ZiZWSWccMzMrBJOOGZmVgknHDMzq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOz\nSjjhmJlZJZxwzMysEk44ZmZWCSccMzOrhBOOmZlVwgnHzMwq4YRjZmaVcMIxM7NKOOGYmVklnHDM\nzKwSTjhmZlYJJxwzM6vE4s0OwKxmxvUn9nvesTsdOoiRmFkjuIZjZmaVcMIxM7NKOOGYmVklfA3H\nOsJArv+ArwGZVcE1HDMzq4QTjpmZVcIJx8zMKuGEY2ZmlXDCMTOzSjjhmJlZJZxwzMysEk44ZmZW\nCSccMzOrhBOOmZlVwre2McOPRjCrghOO2QAN9D5u/eVEZ+3GTWpmZlYJJxwzM6uEE46ZmVXCCcfM\nzCrhTgNmbcoPnbN24xqOmZlVwgnHzMwq4YRjZmaV8DUcM+sz35nB+sMJx+wdqll3SLB3rqYlHEk7\nACcDQ4BqN7ULAAAITklEQVRfRMSPmxWLmbWHZiZJ18wGrikJR9IQ4DRge+Bp4G5J10bEQ82Ix8ys\nN75n3sA1q4azGfBERPwdQNKvgE8ATjhmHc5Nee9czeqlthIwrfD+6VxmZmYdqmU7DUg6EDgwv50r\n6dEBLG408PzAo6pEO8UK7RVvO8UK7RVvO8UKbRXvNwYS62qDGclANSvhPAOsUni/ci77l4g4Ezhz\nMFYmaVJETBiMZTVaO8UK7RVvO8UK7RVvO8UK7RVvO8Xam2Y1qd0NrC1pdUlDgT2Ba5sUi5mZVaAp\nNZyIeEvSwcBNpG7R50TEg82IxczMqtG0azgR8VvgtxWtblCa5irSTrFCe8XbTrFCe8XbTrFCe8Xb\nTrH2SBHR7BjMzOwdwDfvNDOzSnR0wpG0g6RHJT0h6bAmxnGOpJmSHiiUjZJ0i6TH89/lC+MOzzE/\nKuljhfJNJE3J406RpAbEuoqk2yQ9JOlBSV9v1XglDZN0l6T7c6zHtmqshfUMkXSvpOvbINapeT33\nSZrUBvGOlHSFpEckPSxpi1aMV9I6eZ/WXnMkHdKKsQ66iOjIF6kzwt+ANYChwP3Aek2KZStgY+CB\nQtlxwGF5+DDgJ3l4vRzrksDqeRuG5HF3AZsDAm4AdmxArOOAjfPwMsBjOaaWizcvd0QeXgL4S15f\ny8VaiPkbwMXA9a38OcjrmQqMritr5XjPAz6fh4cCI1s53ryuIcBzpN/LtHSsg7K9zQ6ggf/ILYCb\nCu8PBw5vYjzjWTThPAqMy8PjgEe7ipPUk2+LPM0jhfK9gDMqiPvXpHvetXS8wFLAPcAHWzVW0u/N\nbgW2YWHCaclY87Kn8vaE05LxAssBT5KvS7d6vIXlfxT4UzvEOhivTm5Sa/Xb54yNiOl5+DlgbB7u\nLu6V8nB9ecNIGg9sRKo5tGS8uYnqPmAmcEtEtGyswEnAd4AFhbJWjRUggImSJivd+aOV410dmAX8\nMjdZ/kLS0i0cb82ewCV5uNVjHbBOTjhtI9LpSUt1F5Q0ArgSOCQi5hTHtVK8ETE/IjYk1R42k/S+\nuvEtEauknYCZETG5u2laJdaCLfO+3RE4SNJWxZEtFu/ipGbr0yNiI+BVUrPUv7RYvCj96H0X4PL6\nca0W62Dp5ITT6+1zmmyGpHEA+e/MXN5d3M/k4fryQSdpCVKyuSgirmr1eAEiYjZwG7BDi8b6IWAX\nSVOBXwHbSLqwRWMFICKeyX9nAleT7vLeqvE+DTyda7gAV5ASUKvGCymR3xMRM/L7Vo51UHRywmn1\n2+dcC+yfh/cnXSuple8paUlJqwNrA3flqvYcSZvnnij7FeYZNHnZZwMPR8QJrRyvpDGSRubh4aRr\nTY+0YqwRcXhErBwR40mfxf+NiH1aMVYASUtLWqY2TLrW8ECrxhsRzwHTJK2Ti7YlPe6kJePN9mJh\nc1otplaNdXA0+yJSI1/Ax0m9rP4GHNnEOC4BpgNvks7EPgesQLqA/DgwERhVmP7IHPOjFHqdABNI\nX/q/AadSd4F0kGLdklSV/ytwX359vBXjBT4A3JtjfQA4Kpe3XKx1cW/Nwk4DLRkrqXfn/fn1YO37\n06rx5vVsCEzKn4drgOVbNV5gaeAFYLlCWUvGOpgv32nAzMwq0clNamZm1kKccMzMrBJOOGZmVgkn\nHDMzq4QTjpmZVcIJx8zMKuGEYy1L0vx8+/YHJF1X+5HnICx3vAqPiig5z3BJv5c0ZDBiGEySftvT\nvpH0K0lrVxmTWVeccKyVzYuIDSPifcCLwEFNjOWzwFURMb9RK5DUr0e+R8THI93apzunk24aatZU\nTjjWLu6gcCdcSd+WdLekv2rhg9fGKz146yylB7LdnG95U3tQ1f2S7qeQuPI8f5R0T379Wzfr35vC\nbUN6WP8jks6V9JikiyRtJ+lPSg/V2qx+oZI+I+laSf9L+pV5l8vO5dco3bn5QS28e3PtQWmj8+1o\nfpO38wFJn8qT/BHYrr8JzWywOOFYy8vNWNuS74Un6aOk+0ltRrqdySZaeCfjtYHTImJ9YDawey7/\nJfDViNigbvEzge0jYmPgU8ApXax/KLBGREwtsf61gOOBdfPr06TbBX0LOKKbTdwY+M+I+Pdelv3Z\niNiEdDuTr0laoW45OwDPRsQGuVZ4I0BELACeAOq33axSTjjWyoYrPeum9myQW3L5R/PrXtJD19Yl\nHaQBnoyI+/LwZGB8vr4xMiL+kMsvKKxjCeAsSVNIt4lfr4s4RpOSV01v65+SD/IPArdGun/UFNJD\n+LpyS0S8WGLZX8s1tDtJdw+uvy4zBdhe0k8kfTgiXi6Mmwm8u5v1m1XCVWxrZfMiYkNJS5GecngQ\nqQYi4EcRcUZxYqUHxr1eKJoPDO9lHYcCM0hn/4sB/+wqDmBYcVUl17+g8H4B3X/fXi2x7K2B7YAt\nIuI1Sb+ri4mIeEzSxqSbrf5A0q0R8V959LC8HWZN4xqOtbyIeA34GvDNfB3iJuCzSg+JQ9JKklbs\nYf7ZwGxJW+aivQujlwOm5xrJvqRnzNfP/xIwRFLtAN+n9fdRd8teDngpJ5t1Sc+xX4SkdwOvRcSF\nwE9JTXU17yHdVdisaVzDsbYQEfdK+iuwV0RcIOm9wB3pMSDMBfYh1Wi6cwBwjqQAbi6U/xy4UtJ+\npGser3Y1c55nS2BiRNzcj/WX0sOybwS+JOlh0i3q7+xi9vcDP5W0gPQojC8DSBpLqi0+N9D4zAbC\njycwKyE3VR0aEfs2O5a+knQoMCcizm52LPbO5iY1sxIi4h7gtlb84WcJs4Hzmh2EmWs4ZmZWCddw\nzMysEk44ZmZWCSccMzOrhBOOmZlVwgnHzMwq8f8BfP3zw0MKz3YAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e52c59518>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"frenda9 = pd.cut(base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base.REGIAO==\"CENTRO-OESTE\")], bins=faixa, right=False)\n",
"t19 = (frenda9.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t19,\"\\n\")\n",
"\n",
"plot = base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"CENTRO-OESTE\")].plot.hist(bins=faixa,title=\"Histograma - Insegurança Alimentar - CENTRO-OESTE - 2009(H3)\", weights=zeros_like(base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"CENTRO-OESTE\")])+1./base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"CENTRO-OESTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"chocolate\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 202,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 19.9\n",
"[350, 700) 33.0\n",
"[700, 1050) 20.4\n",
"[1050, 1400) 11.1\n",
"[1400, 1750) 6.1\n",
"[1750, 2100) 3.4\n",
"[2100, 2450) 2.0\n",
"[2450, 2800) 1.0\n",
"[2800, 3150) 1.0\n",
"[3150, 3500) 0.5\n",
"[3500, 3850) 0.4\n",
"[3850, 4200) 0.3\n",
"[4200, 4550) 0.2\n",
"[4550, 4900) 0.1\n",
"[4900, 5250) 0.2\n",
"[5250, 5600) 0.1\n",
"[5600, 5950) 0.1\n",
"[5950, 6300) 0.1\n",
"[6300, 6650) 0.1\n",
"[6650, 7000) 0.0\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAGDCAYAAAA8mveiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Wm4HVWZ9vH/TSAQIBAgEZnDJIi2TAFBwAYBGRSQVpEw\niigNgoKNA8irQrdTo9BiozQgyhCIzIgKMjU2gigkEiRhCkqQQEiCEEIAGZLn/bDWJpXNGapOTmXX\nSe7fde3r1FzPrlO7nlqrqlYpIjAzMytrqU4HYGZmA4sTh5mZVeLEYWZmlThxmJlZJU4cZmZWiROH\nmZlV0rjEIWmSpJ07HYcteSTtLGlqod/7ojWapLskbdmPy7tH0rt6m26RJg5JUyTt1jbsk5LubPVH\nxLsi4re9LGekpJC0dE2hNpqkCyV9s9NxDFR5nwtJn+hpujL7Yh0k/VbSpxfxOlvb5Mttw6cWk6ek\nzSRdL+kFSS9Kul3S+wrjW7/NOfkzRdJJbcucIumVPP8sSb+XdLSkpQrTXCjptcJy5ki6vzD+SEkP\n52VMl3SDpKGSbixM/3rbMv4nnxzMa1vuHEnb93G7fUnSxBzH45K+1DZ+ZN5GL+d4249/B0l6QtJL\nkq6TtGph3FqSfiHpufx/OLpt3n2AFyPivtx/qqQxXcQYkjbqYvhtXRxHvw/8e2/fu3EljiZYUhNS\nXRq4PQ8HngMO63QgdViI7f0c8GVJQ7tZ7obAXcADwPrAmsC1wM1dHHiHRcSKwMeAr0navW38PhEx\nFFgP+C7wFeCCtmlOj4gVC5/Ncxz/DHwbGJ2X8U7gcoCI2Ks1PXBp2zJaB96n25a7YkTcXWlLFTYL\naT9aBdgTOE7SgYXxY4H7gNWAU4CrJI3I3+NdwLnAocDqwMvAjwvzjgEez+M+BHxb0i6F8UcDl/Qp\naOlgYJkuRl0P7CLp7T0uICIW2QeYAuzWNuyTwJ1dTQNsC4wDZgPTgTPz8L8BAczJn+1JSfD/AU8A\nM4CLgZULyz0sj/s78LW29ZwKXEX6R80GPp3XfTcwC5gGnA0MLiwvgM8Ck4EXgf8ANgR+n5dxRWt6\n0k71K2Am8HzuXnshtuOFwDdz98gcy+F5uzwLnFKYtsttmMdtl+OdBdwP7FwYtz5wR/5utwI/Asbk\ncTsDU7v73y7E9jw6b89ZeX0qjP8M8FCO50Fgqzz8JOAvheH797Lt1gPmAR8F3gDeXhi3wPfq4jtd\nmb/Ti6SD5zuAk0n725PABwvzrkw6EE4DngK+CQwq7vOks7vnSQeHvfK4bwFzgX+Q9u2z8/Cz8jpm\nA+OBnQrresv27sM+1Yrpl8A3CsOntvYL0kHqhi7mPQe4o21/XLow/h7gS70cB7bN/5d3t+/jXazv\ni8B1VX4n3f2P+/sD/BD479z9DuBVYGhh/B3A0bn728BlhXEbAq8BQ4EV83Z8W2H8ecAluXsw8AqF\n40jeD8Z0EVMAG7Xtm4+Sfv8L/K/y+FuAw3v6nk0vcZwFnBURK5E26hV5+Pvz32Ex/2zhk/mzC7AB\nacOfDal4TcrkBwNrkDbcWm3r2o/04xtGOlOZC3wBGE5KTLuSEkXRHsDWpH/Al0n/2EOAdYB3A6Pz\ndEsBPyMdtNYl/cPPrrw1erYjsEmO8+uS3pmHd7kNJa0F/Jp0QFuV9GO8unU2BFxG+sGvRtohD60Y\nT1+254eBbYD3AAeQti+SPp5jOAxYCdiXdAIAKWnsRPqfngaMkbRGD3EdBoyLiKtJiejgCt9pH9LB\ncxXSWeRNpP/tWqTi/bmFaS8kJaaNgC2BD5ISaMt7gUdI2+N04AJJiohTgN8Bx+V9+7g8/b3AFqT/\n1WXAlZKWKyyvfXv31deAE4pVJgW7k5JnuyuAHSQNaR8haTvSb+GxnlYaEfeQktROJWL8I7CHpNMk\n7SBp2RLz1E6SSPFPyoPeBfw1Il4sTHZ/Ht4a/2b1W0T8hZRo3kEqybxlFaRtCbAxMC8ipnYxXW++\nTUr2z3Qz/iFg854W0InEcV2u15wlaRYLFs3avQ5sJGl4RMyJiD/0MO3BpLPpv0bEHNKZ4IG52P4x\n4JcRcWdEvAZ8nZRpi+6OiOsiYl5EvBIR4yPiDxHxRkRMIR0U/rltntMjYnZETAImAjfn9b8A3Eg6\nYBARf4+IqyPi5bwTfauLZS2s03Lc95N2xtY/vrtteAjp7PGG/J1vIZVM9pa0LukA/vWIeC0i7iQV\nYavoy/b8bkTMioi/AbeTDpSQDrinR8S9kTwWEU8ARMSVEfF0Xs/lpBLLtj3EdRjpwEv+W6W66ncR\ncVNEvEE6gI7IMb8O/BwYKWmYpNWBvYETIuKliJgB/BdQrMJ4IiLOj4i5wEWkE5rVu1txRIzJ+9Eb\nEXEGsCzpRKFlge1d4Tu1r2cC6YzzK12MHk4qQbWbRjqWFJPNs5JeIZUyfwxcV2L1T7ct44vFY4Wk\ni3KMvwP+BdiKdPLzd0lnShpUYh0Aa7Ytd5akFUrO25NTmX+SCOnk9YW2aWaTShQ9js/HibtI1XzL\nSdqKVEpePk83jFTybXdA+3crjpQ0CtgB+O8evseLefnd6kTi+EhEDGt9eOtZZ9GRpOz7sKR7JX24\nh2nXJFVFtTwBLE36Ma5JKuYDEBEvM/+MteXJYo+kd0j6laRnJM0mZenhbfNML3S/0kX/inlZy0s6\nN18Em00qrg7rakeXdHDhgt2NPXzfdsWzh5db66b7bbge8PG2HWxH0gFsTeC5vJ1aFtg+JfRle3b3\nHdYhlSzeQtJhkiYUvsO7u1hua9odSFVwP8+DLgP+SdIWXU3fhfb/77P5wN/qJ8e8Hqn+eFohrnOB\ntxXmf/O7FrbzinRD0hclPaR0UXoWqYRV/J7d/n8krVvYp+b0/BWBdGJ1TE6ARc+S9o92a5CqmZ4v\nDBtO+j4nkqqHuqpPb7cW6TpLy/eLx4qIOLw1IiJujIh9SIlmP1JtQ9kbCp5uW+6wiHipfaIqv0VJ\nx5FOQj4UEa/mwXNIJeSilZl/wO9t/MGk/fVJUglhDKlUBmlbd3Ut6or271aIcSlSEj8+n/x0Zyip\nurhbja6qiojJETGa9IP7T9KFpRV4a2kB0tnKeoX+dUlVBdNJZ0Rrt0bkIvVq7atr6z8HeBjYOFfz\nfJWui49lnEg6O3xvXlarqu0ty4uIS2P+Bbu9+ri+4vK624ZPkupLizvZChHxXdL2WlXS8oVFrVPo\nfon5Zz7kBDiCBfXn9nySVM22AEnrAecDxwGr5R/JxB6We3geN0HSM6Qqj9bw/vQkqcpheGHbrhQR\nvd7mmC2w7STtRKoKPQBYJX/PF1jwe3bbzHVE/K2wT3WbnArTPwxcQ7qYW3Qr8PEuZjmAVOIpnmgQ\nEXMj4kzS9ZqeThCRtA0pcdzZ03RdxDovIm4D/pf51Tj9ouxvUdKnSNfadm2rOpoEbNB2s8HmzK/K\nmkShSijffDCYdP2BiHgiIj4cESMi4r2kZHxPnvyxNIvaq9x7shIwCrg87//35uFT8z7W8k4KVWhd\naXTikHSIpBERMY/5GXAe6SLzPNK1jJaxwBckrS9pRdIZ7eU5s14F7CPpfZIGk4qUvR20hpKKjXMk\nbQocsxBfZSjpjHRWrjv+xkIsq5IetuEY0jbZQ9KgXBzeWdLauRpoHHCqpMFKd8zsU1jso8Bykj4k\naRnSTQm91TMvzPb8CanaYmslG+Wk0TqJmJm/6xF0c/BQuh5wAHAUqQqs9fkccJD68c6viJgG3Ayc\nIWklSUtJ2lDpbqAyprPgvj2UdBI0E1ha0td565lqfzsNOIIFqyxOA94n6VuSVlW6/fVzpDPtrqq2\nWr5LultrufYReft8mFQKHBMRD/QWmKT9JB0oaZW8P2xLqvbsqSq7Fkp3J30b2D0i/locFxGPAhOA\nb+Tf178A/wRcnSe5lPQb3CmfzP0HcE2upkLSO/M2HizpENJ1sjPzsl8jJfIqVd4vkGoTWvv+3nn4\n1uSTqPw/2ppUXdmtRicO0u1tk3Lx+izgwFxf/jLpOsFduSpgO+CnpAuXd5DuUvkH6aBApGsQnyPt\nnNNIRcQZpLPC7nwROIhUbDyffLtfH/0AGEIq6v8B+M1CLKuq7rbhk6Qi/ldJB6QngS8xf584mHQR\n+++kC+iXk7dXpGs4nyUd0J8ilUB6u0jX5+0ZEVeS/t+XkZLedcCqEfEgcAapHn066Ud5VzeL+Qgp\neV8cEc+0PqT9ZmnSdupPh5HOHh8kVStcRdfVPF05C/iYpOcl/ZB0Ef43pIT9BGnfrlp1WElEPE76\nPa1QGDaZVJ25OenOqGmkevc9IqK77Q7pOsTzpDvjWn4p6UXS9ziFdEA8om2+L2vBZy2ezcNby5pM\nOhkZA3wvIsreFLCm3vocx0dLztvum6Tai3sLy/qfwvgDSWf5zwPfAT4WETPhzePS0aQEMoO0rYsl\nsz2Av+Z5jwb2bM2btW7lLSVfHyzu+61lTc+JCNIJ4m8j4umelqWIJe9FTrlEMotUbfJ4p+MZCCRd\nDjwcEYustNRNHOcCZ+SzObMlmqS7SHfg3ddPy/sjcGRETOxpuqaXOPqNpH2ULlKvQLp//gHSWZN1\nQdI2uXplKUl7kkonZe6MqTOmFUnXst7f27RmS4KI2KG/kkZe3nt7SxqQiuhLiv1IRW+R6u8PjCWx\nuFXe20kXSFcjVUMd0587aB/9hVRVtWuH4zBboi2RVVVmZtZ3S0xVlZmZ9Q8nDjMzq2RAXOMYPnx4\njBw5stNhmJkNKOPHj382Itofzl1oAyJxjBw5knHjxnU6DDOzAUXSE71PVZ2rqszMrBInDjMzq8SJ\nw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAzs0qc\nOMzMrJIB0TpuJ50zdmyf5z1m9Oh+jMTMrBlc4jAzs0qcOMzMrBInDjMzq8SJw8zMKnHiMDOzSpw4\nzMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAzs0qcOMzMrBInDjMzq8SJ\nw8zMKnHiMDOzSpw4zMysEicOMzOrpLbEIWk5SfdIul/SJEmn5eGrSrpF0uT8d5W6YjAzs/5XZ4nj\nVeADEbE5sAWwp6TtgJOA2yJiY+C23G9mZgNEbYkjkjm5d5n8CWA/4KI8/CLgI3XFYGZm/a/WaxyS\nBkmaAMwAbomIPwKrR8S0PMkzwOp1xmBmZv2r1sQREXMjYgtgbWBbSe9uGx+kUshbSDpK0jhJ42bO\nnFlnmGZmVsEiuasqImYBtwN7AtMlrQGQ/87oZp7zImJURIwaMWLEogjTzMxKqPOuqhGShuXuIcDu\nwMPA9cDhebLDgV/UFYOZmfW/pWtc9hrARZIGkRLUFRHxK0l3A1dIOhJ4AjigxhjMzKyf1ZY4IuLP\nwJZdDP87sGtd6zUzs3r5yXEzM6vEicPMzCpx4jAzs0qcOMzMrBInDjMzq8SJw8zMKnHiMDOzSpw4\nzMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAzs0qcOMzMrBInDjMzq8SJ\nw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAzs0qc\nOMzMrBInDjMzq8SJw8zMKnHiMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vE\nicPMzCpx4jAzs0pqSxyS1pF0u6QHJU2SdHwefqqkpyRNyJ+964rBzMz639I1LvsN4MSI+JOkocB4\nSbfkcf8VEd+vcd1mZlaT2hJHREwDpuXuFyU9BKxV1/rMzGzRWCTXOCSNBLYE/pgHfU7SnyX9VNIq\niyIGMzPrH7UnDkkrAlcDJ0TEbOAcYANgC1KJ5Ixu5jtK0jhJ42bOnFl3mGZmVlKtiUPSMqSkcWlE\nXAMQEdMjYm5EzAPOB7btat6IOC8iRkXEqBEjRtQZppmZVVDnXVUCLgAeiogzC8PXKEy2PzCxrhjM\nzKz/1XlX1Q7AocADkibkYV8FRkvaAghgCvCvNcZgZmb9rM67qu4E1MWoG+pap5mZ1c9PjpuZWSVO\nHGZmVokTh5mZVeLEYWZmlZS+OJ6f8F4TeAWYkp/DMDOzJUyPiUPSysCxwGhgMDATWA5YXdIfgB9H\nxO21R2lmZo3RW4njKuBiYKeImFUcIWlr4FBJG0TEBXUFaGZmzdJj4oiI3XsYNx4Y3+8RmZlZo1V6\nAFDSCOB4YAjwPxExuZaozMyssareVXUGcBNwLXBZ/4djZmZN12PikHSTpPcXBg0mtS81BVi2vrDM\nzKypeitxHADsI2mspA2BrwHfAc4CPlt3cGZm1jy9XRx/AfiSpA2AbwFPA8e132FlZmZLjt6e49gQ\nOAZ4DTgR2BC4XNKvgR9FxNz6QzQzsybprapqLHANcDtwSUT8LiL2AGYBN9cdnJmZNU9vt+MuCzwO\nrAgs3xoYERdLurLOwMzMrJl6SxzHAGeTqqqOLo6IiFfqCsrMzJqrt4vjvwd+v4hiMTOzAcDNqpuZ\nWSVOHGZmVokTh5mZVVKqkUNJo4BTgPXyPAIiIt5TY2xmZtZAZVvHvRT4EvAA4Df/mZktwcomjpkR\ncX2tkZiZ2YBQNnF8Q9JPgNuAV1sDI+KaWqIyM7PGKps4jgA2BZZhflVVkJojMTOzJUjZxLFNRGxS\nayRmZjYglL0d9/eSNqs1EjMzGxDKlji2AyZIepx0jcO345qZLaHKJo49a43CzMwGjFJVVRHxBLAO\n8IHc/XLZec3MbPFS6uAv6RvAV4CT86BlgDF1BWVmZs1VttSwP7Av8BJARDwNDK0rKDMza66yieO1\niAjSsxtIWqG+kMzMrMnKJo4rJJ0LDJP0GeBW4Pz6wjIzs6YqdVdVRHxf0u7AbGAT4OsRcUutkZmZ\nWSP1mDgkKVdRkRPFW5JFcRozM1v89VZVdbukz0latzhQ0mBJH5B0EXB4feGZmVnT9FZVtSfwKWCs\npPWBWcAQUsK5GfhBRNxXb4hmZtYkPSaOiPgH8GPgx5KWAYYDr0TErN4WLGkd4GJgddLdWOdFxFmS\nVgUuB0YCU4ADIuL5hfkSZma26JR++jsiXo+IaWWSRvYGcGJEbEZq6+rY3FDiScBtEbEx6f0eJ1UN\n2szMOqe2ZkNykvlT7n4ReAhYC9gPuChPdhHwkbpiMDOz/le2kcOFImkksCXwR2D1iJiWRz1Dqspa\nLJ0zdmyf5z1m9Oh+jMTMrP/U3lChpBWBq4ETImJ2cVzxafQu5jtK0jhJ42bOnFl3mGZmVlLZRg63\nk3SvpDmSXpM0V9LsEvMtQ0oalxbeTz5d0hp5/BrAjK7mjYjzImJURIwaMWJEuW9jZma1K1viOBsY\nDUwm3Y77aeBHPc0gScAFwEMRcWZh1PXMf/bjcOAXVQI2M7POqnJX1WPAoIiYGxE/o/eXO+0AHAp8\nQNKE/Nkb+C6wu6TJwG6538zMBoiyF8dfljSY9PrY04Fp9JJ0IuJO0itmu7Jr+RAX3sJcpDYzswWV\nLXEcmqc9jvROjnWAj9YVlJmZNVfZEsfWwK/zXVGn1RiPmZk1XNkSxz7Ao5IukfRhSYvk+Q8zM2ue\nUokjIo4ANgKuJN1d9RdJP6kzMDMza6bSJYeIeF3SjaQH9oaQmgr5dF2BmZlZM5V9AHAvSReSnuP4\nKPAT4O01xmVmZg1VtsRxGKkp9H+NiFdrjMfMzBqu7DvH3eKemZkBvb9z/M6I2FHSiyzYGKFIbRSu\nVGt0ZmbWOL29AXDH/HfoognHzMyaruzF8UvKDDMzs8Vf2QcA31XsyQ8Abt3/4ZiZWdP1mDgknZyv\nb7xH0uz8eRGYjptDNzNbIvXWwu138vWN70XESvkzNCJWi4iTF1GMZmbWIGVvxz1Z0irAxsByheF3\n1BWYmZk1U6nEIenTwPHA2sAEYDvgbuAD9YVmZmZNVPbi+PHANsATEbELsCUwq7aozMysscomjn9E\nxD8AJC0bEQ8Dm9QXlpmZNVXZtqqmShoGXAfcIul54In6wjIzs6Yqe3F8/9x5qqTbgZWB39QWlZmZ\nNVZvbVWt2sXgB/LfFYHn+j0iMzNrtN5KHONJjRuqMKzVH8AGNcVlZmYN1Vsjh+svqkDMzGxgKNvI\noSQdIulruX9dSdvWG5qZmTVR2dtxfwxsDxyU+18EflRLRGZm1mhlb8d9b0RsJek+gIh4XtLgGuMy\nM7OGKlvieF3SIPJbACWNAObVFpWZmTVW2cTxQ+Ba4G2SvgXcCXy7tqjMzKyxyj4AeKmk8cCupFtx\nPxIRD9UamZmZNVKviSNXUU2KiE2Bh+sPyczMmqzXqqqImAs8ImndRRCPmZk1XNm7qlYBJkm6B3ip\nNTAi9q0lKjMza6yyieNrtUZhZmYDRtmL4/9XdyBmZjYwlL0d18zMDHDiMDOzipw4zMysklLXOCRt\nDHwH2AxYrjU8Ivw+DjOzJUzZEsfPgHOAN4BdgIuBMXUFZWZmzVU2cQyJiNsARcQTEXEq8KHeZpL0\nU0kzJE0sDDtV0lOSJuTP3n0L3czMOqFs4nhV0lLAZEnHSdqf9M7x3lwI7NnF8P+KiC3y54aSMZiZ\nWQOUTRzHA8sDnwe2Bg4FDu9tpoi4A3iuz9GZmVnjlH0A8N7cOQc4oh/W+zlJhwHjgBMj4vn2CSQd\nBRwFsO66bibLzKwpeixxSPpB/vtLSde3f/q4znOADYAtgGnAGV1NFBHnRcSoiBg1YsSIPq7KzMz6\nW28ljkvy3+/31wojYnqrW9L5wK/6a9lmZla/HhNHRIzPneOAVyJiHrz5jo5l+7JCSWtExLTcuz8w\nsafpzcysWcpeHL+NdHG8ZQhwa28zSRoL3A1sImmqpCOB0yU9IOnPpGdCvlAxZjMz66CyzaovFxFz\nWj0RMUfS8j3NkKcb3cXgC8oGZ2ZmzVO2xPGSpK1aPZK2Bl6pJyQzM2uysiWOE4ArJT0NCHg78Ina\nojIzs8Yq/RyHpE2BTfKgRyLi9frCMjOzpipb4gDYBhiZ59lKEhFxcS1RmZlZY5VtVv0SYENgAjA3\nDw5SK7lmZrYEKVviGAVsFhFRZzBmZtZ8Ze+qmki6IG5mZku4siWO4cCDku4BXm0NjIh9a4nKzMwa\nq2ziOLXOIMzMbOAoezvu/0laD9g4Im7NT40Pqjc0MzNrot6aVX9b/vsZ4Crg3DxqLeC6ekMzM7Mm\n6jZx5CZG/iP3HgvsAMwGiIjJwNtqj87MzBqnpxLHpsD9ufu1iHitNULS0qTnOMzMbAnTbeKIiMuA\np3LvbyV9FRgiaXfgSuCXiyA+MzNrmB6vcUTEL3LnScBM4AHgX4EbgP9Xb2hmZtZEZe+qmgecnz9m\nZrYEK9tW1eN0cU0jIjbo94jMzKzRqrRV1bIc8HFg1f4Px8zMmq5UW1UR8ffC56mI+AHwoZpjMzOz\nBipbVbVVoXcpUgmkyrs8zMxsMVH24H9GofsNYApwQL9HY2ZmjVf2rqpd6g7EzMwGhrJVVf/W0/iI\nOLN/wjEzs6arclfVNsD1uX8f4B5gch1BmZlZc5VNHGsDW0XEiwCSTgV+HRGH1BWYmZk1U9lXx64O\nvFbofy0PMzOzJUzZEsfFwD2Srs39HwEuqickMzNrsrJ3VX1L0o3ATnnQERFxX31hmZlZU5WtqgJY\nHpgdEWcBUyWtX1NMZmbWYKUSh6RvAF8BTs6DlgHG1BWUmZk1V9kSx/7AvsBLABHxNDC0rqDMzKy5\nyiaO1yIiyE2rS1qhvpDMzKzJyiaOKySdCwyT9BngVvxSJzOzJVLZu6q+n981PhvYBPh6RNxSa2Rm\nZtZIvSYOSYOAW3NDh04Wi8g5Y8cu1PzHjB7dT5GYmS2o16qqiJgLzJO08iKIx8zMGq7sk+NzgAck\n3UK+swogIj5fS1RmZtZYZRPHNfljZmZLuB4Th6R1I+JvEeF2qczMDOj9Gsd1rQ5JV1dduKSfSpoh\naWJh2KqSbpE0Of9dpepyzcysc3pLHCp0b9CH5V8I7Nk27CTgtojYGLgt95uZ2QDRW+KIbrpLiYg7\ngOfaBu/H/CbZLyI10W5mZgNEbxfHN5c0m1TyGJK7yf0RESv1YZ2rR8S03P0M3bwQStJRwFEA6667\nbh9WY2ZmdegxcUTEoDpXHhEhqcuSTEScB5wHMGrUqMqlHTMzq0eV93H0l+mS1gDIf2d0IAYzM+uj\nTiSO64HDc/fhwC86EIOZmfVRrYlD0ljgbmATSVMlHQl8F9hd0mRgt9xvZmYDRNknx/skIrpraW/X\nOtdrZmb16URVlZmZDWBOHGZmVokTh5mZVeLEYWZmlThxmJlZJU4cZmZWiROHmZlV4sRhZmaVOHGY\nmVklThxmZlaJE4eZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVeLEYWZmlThxmJlZJU4cZmZWiROH\nmZlV4sRhZmaVOHGYmVklThxmZlaJE4eZmVXixGFmZpU4cZiZWSVOHGZmVokTh5mZVeLEYWZmlThx\nmJlZJU4cZmZWiROHmZlV4sRhZmaVOHGYmVklS3c6AKvHOWPH9nneY0aP7sdIzGxx4xKHmZlV4sRh\nZmaVOHGYmVklThxmZlaJE4eZmVXSsbuqJE0BXgTmAm9ExKhOxWJmZuV1+nbcXSLi2Q7HYGZmFbiq\nyszMKulk4gjgVknjJR3VPlLSUZLGSRo3c+bMDoRnZmZd6WTi2DEitgD2Ao6V9P7iyIg4LyJGRcSo\nESNGdCZCMzN7i44ljoh4Kv+dAVwLbNupWMzMrLyOJA5JK0ga2uoGPghM7EQsZmZWTafuqloduFZS\nK4bLIuI3HYrFzMwq6EjiiIi/Apt3Yt1mZrZwfDuumZlV4sRhZmaVOHGYmVklThxmZlaJE4eZmVXi\nxGFmZpU4cZiZWSVOHGZmVokTh5mZVeLEYWZmlXT6DYDWQOeMHdvneY8ZPbofIzGzJnKJw8zMKnHi\nMDOzSpw4zMysEicOMzOrxInDzMwqceIwM7NKnDjMzKwSJw4zM6vEicPMzCpx4jAzs0qcOMzMrBIn\nDjMzq8SKXsRSAAAIzklEQVSNHFq/cgOJZos/lzjMzKwSJw4zM6vEicPMzCpx4jAzs0qcOMzMrBIn\nDjMzq8SJw8zMKnHiMDOzSpw4zMysEj85bo2xME+dLyw/tW5WnkscZmZWiROHmZlV4sRhZmaV+BqH\nGW7V16yKjiUOSXsCZwGDgJ9ExHc7FYvZwnDSsSVNRxKHpEHAj4DdganAvZKuj4gHOxGPWac46dhA\n1KkSx7bAYxHxVwBJPwf2A5w4zEpa2NuXFybxOOEt2TqVONYCniz0TwXe26FYzJZInXpuppPP6wxE\nTUy0jb04Luko4KjcO0fSIwuxuOHAswsf1SIxkGKFgRXvQIoVBla8AylWGEDxfvaggxYm1vX6M5aW\nTiWOp4B1Cv1r52FviojzgPP6Y2WSxkXEqP5YVt0GUqwwsOIdSLHCwIp3IMUKAyveJsbaqec47gU2\nlrS+pMHAgcD1HYrFzMwq6EiJIyLekHQccBPpdtyfRsSkTsRiZmbVdOwaR0TcANywiFbXL1Vei8hA\nihUGVrwDKVYYWPEOpFhhYMXbuFgVEZ2OwczMBhC3VWVmZpUs1olD0p6SHpH0mKSTOhjHTyXNkDSx\nMGxVSbdImpz/rlIYd3KO+RFJexSGby3pgTzuh5JUQ6zrSLpd0oOSJkk6vqnxSlpO0j2S7s+xntbU\nWAvrGSTpPkm/GgCxTsnrmSBp3ACId5ikqyQ9LOkhSds3MV5Jm+Rt2vrMlnRCE2PtVkQslh/SRfe/\nABsAg4H7gc06FMv7ga2AiYVhpwMn5e6TgP/M3ZvlWJcF1s/fYVAedw+wHSDgRmCvGmJdA9gqdw8F\nHs0xNS7evNwVc/cywB/z+hoXayHmfwMuA37V5P0gr2cKMLxtWJPjvQj4dO4eDAxrcrx5XYOAZ0jP\nWzQ61gXiXhQr6cQH2B64qdB/MnByB+MZyYKJ4xFgjdy9BvBIV3GS7jzbPk/zcGH4aODcRRD3L0ht\nijU6XmB54E+kFggaGSvpeaXbgA8wP3E0Mta87Cm8NXE0Ml5gZeBx8nXbpsdbWP4HgbsGQqzFz+Jc\nVdVVsyZrdSiWrqweEdNy9zPA6rm7u7jXyt3tw2sjaSSwJelMvpHx5qqfCcAM4JaIaGyswA+ALwPz\nCsOaGitAALdKGq/UkkOT410fmAn8LFcF/kTSCg2Ot+VAoNUGS9NjfdPinDgGjEinC426vU3SisDV\nwAkRMbs4rknxRsTciNiCdDa/raR3t41vRKySPgzMiIjx3U3TlFgLdszbdi/gWEnvL45sWLxLk6qD\nz4mILYGXSNU9b2pYvCg9/LwvcGX7uKbF2m5xThy9NmvSYdMlrQGQ/87Iw7uL+6nc3T6830lahpQ0\nLo2Ia5oeL0BEzAJuB/ZsaKw7APtKmgL8HPiApDENjRWAiHgq/50BXEtq1bqp8U4FpuYSJ8BVpETS\n1HghJeQ/RcT03N/kWBewOCeOpjdrcj1weO4+nHQtoTX8QEnLSlof2Bi4JxdhZ0vaLt85cVhhnn6T\nl30B8FBEnNnkeCWNkDQsdw8hXYt5uImxRsTJEbF2RIwk7Yv/GxGHNDFWAEkrSBra6ibVxU9sarwR\n8QzwpKRN8qBdSa9paGS82WjmV1O1YmpqrAtaFBdSOvUB9ibdFfQX4JQOxjEWmAa8TjozOhJYjXSh\ndDJwK7BqYfpTcsyPULhLAhhF+vH+BTibtguB/RTrjqQi8p+BCfmzdxPjBd4D3JdjnQh8PQ9vXKxt\nce/M/IvjjYyVdDfi/fkzqfX7aWq8eT1bAOPy/nAdsEpT4wVWAP4OrFwY1shYu/r4yXEzM6tkca6q\nMjOzGjhxmJlZJU4cZmZWiROHmZlV4sRhZmaVOHGYmVklThzWWJLm5manJ0r6Zethv35Y7kgVmrgv\nOc8QSf8naVB/xNCfJN3Q07aR9HNJGy/KmGzx5sRhTfZKRGwREe8GngOO7WAsnwKuiYi5da1AUp9e\n5RwRe0dqcqU755AaVzTrF04cNlDcTaHlT0lfknSvpD9r/gucRiq9wOd8pRc73ZybImm98OZ+SfdT\nSEB5nt9J+lP+vK+b9R9MoTmHHtb/sKQLJT0q6VJJu0m6S+nlPNu2L1TSJyVdL+l/SU8Nd7nsPPw6\npZZqJ2l+a7WtFy4Nz82E/Dp/z4mSPpEn+R2wW18Tk1k7Jw5rvFw9tCu5rTFJHyS117MtqZmJrTW/\n5daNgR9FxLuAWcBH8/CfAZ+LiM3bFj8D2D0itgI+Afywi/UPBjaIiCkl1r8RcAawaf4cRGrG5YvA\nV7v5ilsBH4uIf+5l2Z+KiK1JzUx8XtJqbcvZE3g6IjbPpbTfAETEPOAxoP27m/WJE4c12RCld220\n3k1wSx7+wfy5j/Typk1JB1uAxyNiQu4eD4zM9f/DIuKOPPySwjqWAc6X9ACpeevNuohjOCkJtfS2\n/gfywXoScFukdn0eIL3Mqyu3RMRzJZb9+Vxi+gOptdT26xYPALtL+k9JO0XEC4VxM4A1u1m/WSUu\nulqTvRIRW0hanvTWs2NJJQIB34mIc4sTK7146tXCoLnAkF7W8QVgOulsfCngH13FASxXXFXJ9c8r\n9M+j+9/bSyWWvTOwG7B9RLws6bdtMRERj0raitQo5Tcl3RYR/55HL5e/h9lCc4nDGi8iXgY+D5yY\n6+lvAj6l9LIpJK0l6W09zD8LmCVpxzzo4MLolYFpuYRwKOkd0O3zPw8MktQ6UFdaf0XdLXtl4Pmc\nNDYlvWd6AZLWBF6OiDHA90hVYC3vILWiarbQXOKwASEi7pP0Z2B0RFwi6Z3A3ek1BMwBDiGVMLpz\nBPBTSQHcXBj+Y+BqSYeRrgm81NXMeZ4dgVsj4uY+rL+UHpb9G+BoSQ+Rmtb+Qxez/xPwPUnzSE34\nHwMgaXVS6e2ZhY3PDHCz6mZl5CqgL0TEoZ2OpSpJXwBmR8QFnY7FFg+uqjIrISL+BNzexAcAS5gF\nXNTpIGzx4RKHmZlV4hKHmZlV4sRhZmaVOHGYmVklThxmZlaJE4eZmVXy/wEyS5cnbdQgAAAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e55ebd2b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"frenda29 = pd.cut(base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")], bins=faixa, right=False)\n",
"t29 = (frenda29.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t29,\"\\n\")\n",
"\n",
"plot = base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")].plot.hist(bins=faixa,title=\"Histograma - Insegurança Alimentar - NORDESTE - 2009(H4)\", weights=zeros_like(base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")])+1./base9.RENDA[(base9.Insegurança_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"darkslategray\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## ANÁLISE INICIAL E NOVA FILTRAGEM:\n",
"COM A PRECISÃO DOS VALORES MOSTRADOS ACIMA, PODE-SE OBSERVAR ONDE HÁ MAIOR CONCENTRAÇÃO EM CADA UMA DAS REGIÕES DE INTERESSE DE ACORDO COM A DISPARIDADE ANALISADA ANTERIORAMENTE NOS GRÁFICOS. DESSA FORMA A PARTIR DE AGORA A ANÁLISE SE CENTRARÁ APENAS ÀQUELES QUE PASSARAM POR SITUACÃO DE INSEGURANÇA ABRINDO PARA UMA NOVA VARIÁVEL, CHAMADA DE PROBLEMA ALIMENTAR E PAUTADA EM PERGUNTAS QUE DEMONSTRAM FALTA DE COMIDA OU ALIMENTAÇÃO RESTRITA POR CONTA DE FALTA DE DINHEIRO."
]
},
{
"cell_type": "code",
"execution_count": 203,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>ANO</th>\n",
" <th>REGIAO</th>\n",
" <th>ZONA</th>\n",
" <th>RENDA</th>\n",
" <th>Insegurança_Alimentar</th>\n",
" <th>Problema_Alimentar</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.400000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>53</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>60</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.134000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>61</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>80</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.134000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>81</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.780000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>91</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.020000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>93</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.878000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>94</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>95</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.300000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>96</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>106</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>107</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.148000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>117</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.348000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>120</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>123</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Rural</td>\n",
" <td>1.428000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>125</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Rural</td>\n",
" <td>1.678000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>128</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Rural</td>\n",
" <td>1.816000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>129</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Rural</td>\n",
" <td>4.840000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>135</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Rural</td>\n",
" <td>3.600000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>140</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.500000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>142</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.380000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>143</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.434000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>150</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.740000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>167</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.808000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>170</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.100000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>177</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.178000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>184</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.988000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>216</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Rural</td>\n",
" <td>6.780000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>224</th>\n",
" <td>2013</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148570</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.512000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148574</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.000000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148581</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.200000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148582</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.878000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148584</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148586</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148587</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.150000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148591</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.320000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148596</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148605</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148607</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.000000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148608</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.678000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148613</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.100000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148616</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.200000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148619</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.200000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148621</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.678000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148624</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148629</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.400000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148630</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.780000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148637</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.200000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148644</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.157000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148645</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148651</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148656</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.506000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148681</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148684</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.000000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148690</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.550000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148692</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.400000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148693</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148695</th>\n",
" <td>2013</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Não</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>27696 rows × 6 columns</p>\n",
"</div>"
],
"text/plain": [
" ANO REGIAO ZONA RENDA Insegurança_Alimentar \\\n",
"10 2013 NORTE Urbana 1.400000e+03 Sim \n",
"53 2013 NORTE Urbana 0.000000e+00 Sim \n",
"60 2013 NORTE Urbana 1.134000e+03 Sim \n",
"61 2013 NORTE Urbana 5.000000e+02 Sim \n",
"80 2013 NORTE Urbana 2.134000e+03 Sim \n",
"81 2013 NORTE Urbana 6.780000e+02 Sim \n",
"91 2013 NORTE Urbana 1.020000e+02 Sim \n",
"93 2013 NORTE Urbana 1.878000e+03 Sim \n",
"94 2013 NORTE Urbana 1.000000e+12 Sim \n",
"95 2013 NORTE Urbana 1.300000e+03 Sim \n",
"96 2013 NORTE Urbana 1.000000e+12 Sim \n",
"106 2013 NORTE Urbana 0.000000e+00 Sim \n",
"107 2013 NORTE Urbana 2.148000e+03 Sim \n",
"117 2013 NORTE Urbana 1.348000e+03 Sim \n",
"120 2013 NORTE Urbana 8.000000e+02 Sim \n",
"123 2013 NORTE Rural 1.428000e+03 Sim \n",
"125 2013 NORTE Rural 1.678000e+03 Sim \n",
"128 2013 NORTE Rural 1.816000e+03 Sim \n",
"129 2013 NORTE Rural 4.840000e+02 Sim \n",
"135 2013 NORTE Rural 3.600000e+02 Sim \n",
"140 2013 NORTE Urbana 1.500000e+03 Sim \n",
"142 2013 NORTE Urbana 7.380000e+02 Sim \n",
"143 2013 NORTE Urbana 1.434000e+03 Sim \n",
"150 2013 NORTE Urbana 2.740000e+03 Sim \n",
"167 2013 NORTE Urbana 1.808000e+03 Sim \n",
"170 2013 NORTE Urbana 1.100000e+03 Sim \n",
"177 2013 NORTE Urbana 2.178000e+03 Sim \n",
"184 2013 NORTE Urbana 2.988000e+03 Sim \n",
"216 2013 NORTE Rural 6.780000e+02 Sim \n",
"224 2013 NORTE Urbana 9.000000e+02 Sim \n",
"... ... ... ... ... ... \n",
"148570 2013 CENTRO-OESTE Urbana 1.512000e+03 Sim \n",
"148574 2013 CENTRO-OESTE Urbana 3.000000e+03 Sim \n",
"148581 2013 CENTRO-OESTE Urbana 1.200000e+03 Sim \n",
"148582 2013 CENTRO-OESTE Urbana 2.878000e+03 Sim \n",
"148584 2013 CENTRO-OESTE Urbana 1.000000e+12 Sim \n",
"148586 2013 CENTRO-OESTE Urbana 3.000000e+02 Sim \n",
"148587 2013 CENTRO-OESTE Urbana 1.150000e+03 Sim \n",
"148591 2013 CENTRO-OESTE Urbana 2.320000e+03 Sim \n",
"148596 2013 CENTRO-OESTE Urbana 7.000000e+02 Sim \n",
"148605 2013 CENTRO-OESTE Urbana 8.000000e+02 Sim \n",
"148607 2013 CENTRO-OESTE Urbana 3.000000e+03 Sim \n",
"148608 2013 CENTRO-OESTE Urbana 4.678000e+03 Sim \n",
"148613 2013 CENTRO-OESTE Urbana 2.100000e+03 Sim \n",
"148616 2013 CENTRO-OESTE Urbana 1.200000e+03 Sim \n",
"148619 2013 CENTRO-OESTE Urbana 1.200000e+03 Sim \n",
"148621 2013 CENTRO-OESTE Urbana 1.678000e+03 Sim \n",
"148624 2013 CENTRO-OESTE Urbana 1.000000e+12 Sim \n",
"148629 2013 CENTRO-OESTE Urbana 2.400000e+03 Sim \n",
"148630 2013 CENTRO-OESTE Urbana 6.780000e+02 Sim \n",
"148637 2013 CENTRO-OESTE Urbana 1.200000e+03 Sim \n",
"148644 2013 CENTRO-OESTE Urbana 1.157000e+03 Sim \n",
"148645 2013 CENTRO-OESTE Urbana 0.000000e+00 Sim \n",
"148651 2013 CENTRO-OESTE Urbana 0.000000e+00 Sim \n",
"148656 2013 CENTRO-OESTE Urbana 3.506000e+03 Sim \n",
"148681 2013 CENTRO-OESTE Urbana 6.000000e+02 Sim \n",
"148684 2013 CENTRO-OESTE Urbana 3.000000e+03 Sim \n",
"148690 2013 CENTRO-OESTE Urbana 1.550000e+03 Sim \n",
"148692 2013 CENTRO-OESTE Urbana 2.400000e+03 Sim \n",
"148693 2013 CENTRO-OESTE Urbana 1.000000e+02 Sim \n",
"148695 2013 CENTRO-OESTE Urbana 8.000000e+02 Sim \n",
"\n",
" Problema_Alimentar \n",
"10 Não \n",
"53 Não \n",
"60 Não \n",
"61 Não \n",
"80 Sim \n",
"81 Sim \n",
"91 Não \n",
"93 Não \n",
"94 Não \n",
"95 Não \n",
"96 Sim \n",
"106 Não \n",
"107 Sim \n",
"117 Sim \n",
"120 Sim \n",
"123 Não \n",
"125 Sim \n",
"128 Não \n",
"129 Sim \n",
"135 Não \n",
"140 Não \n",
"142 Não \n",
"143 Não \n",
"150 Não \n",
"167 Não \n",
"170 Não \n",
"177 Não \n",
"184 Não \n",
"216 Não \n",
"224 Não \n",
"... ... \n",
"148570 Sim \n",
"148574 Não \n",
"148581 Não \n",
"148582 Não \n",
"148584 Não \n",
"148586 Sim \n",
"148587 Sim \n",
"148591 Não \n",
"148596 Não \n",
"148605 Não \n",
"148607 Sim \n",
"148608 Não \n",
"148613 Não \n",
"148616 Não \n",
"148619 Não \n",
"148621 Não \n",
"148624 Não \n",
"148629 Sim \n",
"148630 Não \n",
"148637 Não \n",
"148644 Sim \n",
"148645 Sim \n",
"148651 Sim \n",
"148656 Não \n",
"148681 Não \n",
"148684 Não \n",
"148690 Não \n",
"148692 Sim \n",
"148693 NaN \n",
"148695 Não \n",
"\n",
"[27696 rows x 6 columns]"
]
},
"execution_count": 203,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"base=base[(base.Insegurança_Alimentar==\"Sim\")]\n",
"base"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## TABELA 2 - 2013"
]
},
{
"cell_type": "code",
"execution_count": 204,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"writer = pd.ExcelWriter('Tabela2-2013.xlsx',engine='xlsxwriter')\n",
"base.to_excel(writer,sheet_name=\"Projeto_1\")\n",
"writer.save()"
]
},
{
"cell_type": "code",
"execution_count": 205,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>ANO</th>\n",
" <th>REGIAO</th>\n",
" <th>ZONA</th>\n",
" <th>RENDA</th>\n",
" <th>Insegurança_Alimentar</th>\n",
" <th>Problema_Alimentar</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.280000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.950000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.512000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.260000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.350000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.730000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.500000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.200000e+01</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.300000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.500000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>45</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.800000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>48</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.800000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>49</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.600000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>61</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.565000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>65</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.115000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>68</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>8.680000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>70</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.590000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>81</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.650000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>86</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.660000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>93</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.620000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>100</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.200000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>109</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.500000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>120</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.330000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>126</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.240000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>127</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.565000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>139</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.150000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>142</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.658000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>146</th>\n",
" <td>2009</td>\n",
" <td>NORTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.250000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153551</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.050000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153552</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>7.500000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153553</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>3.260000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153555</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.800000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153562</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>5.600000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153564</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.016000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153566</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.650000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153568</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>6.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153572</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>9.800000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153573</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>1.230000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153574</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>7.300000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153575</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.658000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153577</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.300000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153599</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>6.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153601</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>6.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153610</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>6.800000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153611</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>1.200000e+03</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153616</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>0.000000e+00</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153618</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.150000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153622</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>1.000000e+12</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153632</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>5.000000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153639</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Rural</td>\n",
" <td>9.650000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153643</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>2.465000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153652</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.750000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153664</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.800000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153667</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.300000e+02</td>\n",
" <td>Sim</td>\n",
" <td>Sim</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153732</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>6.400000e+02</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153766</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>1.765000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153769</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>9.900000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>153810</th>\n",
" <td>2009</td>\n",
" <td>CENTRO-OESTE</td>\n",
" <td>Urbana</td>\n",
" <td>4.530000e+03</td>\n",
" <td>Sim</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>38460 rows × 6 columns</p>\n",
"</div>"
],
"text/plain": [
" ANO REGIAO ZONA RENDA Insegurança_Alimentar \\\n",
"2 2009 NORTE Urbana 8.280000e+02 Sim \n",
"8 2009 NORTE Urbana 2.950000e+02 Sim \n",
"9 2009 NORTE Urbana 6.512000e+03 Sim \n",
"10 2009 NORTE Urbana 5.260000e+02 Sim \n",
"14 2009 NORTE Urbana 5.000000e+02 Sim \n",
"19 2009 NORTE Urbana 3.350000e+02 Sim \n",
"25 2009 NORTE Urbana 1.730000e+03 Sim \n",
"27 2009 NORTE Urbana 3.500000e+02 Sim \n",
"29 2009 NORTE Urbana 9.200000e+01 Sim \n",
"30 2009 NORTE Urbana 7.000000e+02 Sim \n",
"31 2009 NORTE Urbana 9.300000e+02 Sim \n",
"33 2009 NORTE Urbana 1.500000e+03 Sim \n",
"45 2009 NORTE Urbana 1.800000e+02 Sim \n",
"48 2009 NORTE Urbana 4.800000e+02 Sim \n",
"49 2009 NORTE Urbana 6.600000e+03 Sim \n",
"61 2009 NORTE Urbana 1.565000e+03 Sim \n",
"65 2009 NORTE Urbana 2.115000e+03 Sim \n",
"68 2009 NORTE Urbana 8.680000e+02 Sim \n",
"70 2009 NORTE Urbana 5.590000e+02 Sim \n",
"81 2009 NORTE Urbana 6.650000e+02 Sim \n",
"86 2009 NORTE Urbana 1.660000e+03 Sim \n",
"93 2009 NORTE Urbana 7.620000e+02 Sim \n",
"100 2009 NORTE Urbana 1.200000e+03 Sim \n",
"109 2009 NORTE Urbana 5.500000e+02 Sim \n",
"120 2009 NORTE Urbana 2.330000e+02 Sim \n",
"126 2009 NORTE Urbana 2.240000e+03 Sim \n",
"127 2009 NORTE Urbana 1.565000e+03 Sim \n",
"139 2009 NORTE Urbana 5.150000e+02 Sim \n",
"142 2009 NORTE Urbana 1.658000e+03 Sim \n",
"146 2009 NORTE Urbana 5.250000e+02 Sim \n",
"... ... ... ... ... ... \n",
"153551 2009 CENTRO-OESTE Urbana 5.050000e+02 Sim \n",
"153552 2009 CENTRO-OESTE Urbana 7.500000e+02 Sim \n",
"153553 2009 CENTRO-OESTE Urbana 3.260000e+03 Sim \n",
"153555 2009 CENTRO-OESTE Urbana 1.800000e+03 Sim \n",
"153562 2009 CENTRO-OESTE Urbana 5.600000e+02 Sim \n",
"153564 2009 CENTRO-OESTE Urbana 1.016000e+03 Sim \n",
"153566 2009 CENTRO-OESTE Urbana 4.650000e+02 Sim \n",
"153568 2009 CENTRO-OESTE Rural 6.000000e+02 Sim \n",
"153572 2009 CENTRO-OESTE Rural 9.800000e+02 Sim \n",
"153573 2009 CENTRO-OESTE Rural 1.230000e+03 Sim \n",
"153574 2009 CENTRO-OESTE Rural 7.300000e+02 Sim \n",
"153575 2009 CENTRO-OESTE Urbana 2.658000e+03 Sim \n",
"153577 2009 CENTRO-OESTE Urbana 1.300000e+03 Sim \n",
"153599 2009 CENTRO-OESTE Rural 6.000000e+02 Sim \n",
"153601 2009 CENTRO-OESTE Rural 6.000000e+02 Sim \n",
"153610 2009 CENTRO-OESTE Rural 6.800000e+02 Sim \n",
"153611 2009 CENTRO-OESTE Rural 1.200000e+03 Sim \n",
"153616 2009 CENTRO-OESTE Rural 0.000000e+00 Sim \n",
"153618 2009 CENTRO-OESTE Urbana 6.150000e+02 Sim \n",
"153622 2009 CENTRO-OESTE Rural 1.000000e+12 Sim \n",
"153632 2009 CENTRO-OESTE Rural 5.000000e+02 Sim \n",
"153639 2009 CENTRO-OESTE Rural 9.650000e+02 Sim \n",
"153643 2009 CENTRO-OESTE Urbana 2.465000e+03 Sim \n",
"153652 2009 CENTRO-OESTE Urbana 1.750000e+03 Sim \n",
"153664 2009 CENTRO-OESTE Urbana 4.800000e+02 Sim \n",
"153667 2009 CENTRO-OESTE Urbana 6.300000e+02 Sim \n",
"153732 2009 CENTRO-OESTE Urbana 6.400000e+02 Sim \n",
"153766 2009 CENTRO-OESTE Urbana 1.765000e+03 Sim \n",
"153769 2009 CENTRO-OESTE Urbana 9.900000e+03 Sim \n",
"153810 2009 CENTRO-OESTE Urbana 4.530000e+03 Sim \n",
"\n",
" Problema_Alimentar \n",
"2 Sim \n",
"8 Sim \n",
"9 NaN \n",
"10 Sim \n",
"14 Sim \n",
"19 Sim \n",
"25 Sim \n",
"27 Sim \n",
"29 NaN \n",
"30 Sim \n",
"31 NaN \n",
"33 NaN \n",
"45 Sim \n",
"48 Sim \n",
"49 NaN \n",
"61 NaN \n",
"65 Sim \n",
"68 NaN \n",
"70 Sim \n",
"81 NaN \n",
"86 NaN \n",
"93 NaN \n",
"100 Sim \n",
"109 NaN \n",
"120 NaN \n",
"126 Sim \n",
"127 NaN \n",
"139 NaN \n",
"142 Sim \n",
"146 NaN \n",
"... ... \n",
"153551 NaN \n",
"153552 Sim \n",
"153553 Sim \n",
"153555 NaN \n",
"153562 Sim \n",
"153564 NaN \n",
"153566 Sim \n",
"153568 Sim \n",
"153572 Sim \n",
"153573 NaN \n",
"153574 Sim \n",
"153575 NaN \n",
"153577 NaN \n",
"153599 Sim \n",
"153601 Sim \n",
"153610 Sim \n",
"153611 Sim \n",
"153616 Sim \n",
"153618 Sim \n",
"153622 NaN \n",
"153632 NaN \n",
"153639 NaN \n",
"153643 NaN \n",
"153652 NaN \n",
"153664 Sim \n",
"153667 Sim \n",
"153732 NaN \n",
"153766 NaN \n",
"153769 NaN \n",
"153810 NaN \n",
"\n",
"[38460 rows x 6 columns]"
]
},
"execution_count": 205,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"base9=base9[(base9.Insegurança_Alimentar==\"Sim\")]\n",
"base9"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## TABELA 2 - 2009"
]
},
{
"cell_type": "code",
"execution_count": 206,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"writer = pd.ExcelWriter('Tabela2-2009.xlsx',engine='xlsxwriter')\n",
"base9.to_excel(writer,sheet_name=\"Projeto_1\")\n",
"writer.save()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Caracterização dos problemas alimentares:\n",
"Os próximos gráficos tem como objetivo avaliar, além do comportamento da variável \"problema alimentar\" de acordo com a renda mensal familiar comparar com a distribuição de \"insegurança alimentar\" ou seja se a distribuição analisada anteriormente se mantém de certa maneira nessa variável que por sinal é dependente da inicial, \"insegurança alimentar\"."
]
},
{
"cell_type": "code",
"execution_count": 207,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 12.7\n",
"[350, 700) 20.6\n",
"[700, 1050) 21.0\n",
"[1050, 1400) 14.9\n",
"[1400, 1750) 11.3\n",
"[1750, 2100) 6.6\n",
"[2100, 2450) 3.9\n",
"[2450, 2800) 2.5\n",
"[2800, 3150) 1.8\n",
"[3150, 3500) 1.7\n",
"[3500, 3850) 1.0\n",
"[3850, 4200) 0.4\n",
"[4200, 4550) 0.6\n",
"[4550, 4900) 0.2\n",
"[4900, 5250) 0.4\n",
"[5250, 5600) 0.2\n",
"[5600, 5950) 0.1\n",
"[5950, 6300) 0.1\n",
"[6300, 6650) 0.0\n",
"[6650, 7000) 0.0\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAGDCAYAAAA4byefAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYHVWd//H3x7BDZJGILAkBJ6LACIQ2oiKGTZOIgstP\niWziElFQcNxAZySOo8y4jeMDsiOrYZFVDUtAoyIgJBAgLCERgmSBRFmSsJrw/f1Rp0Nxc7v7pLur\nb3Xn83qe+3TVqVNV39vp1LfOObUoIjAzM+vKa1odgJmZ9Q9OGGZmlsUJw8zMsjhhmJlZFicMMzPL\n4oRhZmZZnDAGGEkTJV3YyfK5kvbry5i6Q9JUSZ9J04dIuqHVMdnAIWmSpIN6cXuXSxrbW9urKyeM\nGkgH8eclLZP0hKRzJW3U6riqpsLDku7vrF5EXBQR7+2ruNpJGi1pXgv2O1fSIkkblso+I2lqaV6S\nviZpdvrb+ZukkyStW6pzrqSX0t/Vk5KmSHpzWvbNVL5M0guSVpTm70t1QtKzpfJlkr7eze/0fkk3\nS3pa0uOSzpI0uLR8XUnnSFqSlv9bw/pnSJol6WVJn2xYdnBatiT93s6T9NpOYnkrsAtwdZr/pKSb\nm9RbeXKV/hZebvhdHFGq/j/Af3XjV9OvOGHUxwciYiNgJNAG/HtjhXSQGEj/ZnsBrwe2l/S2VgfT\n2ySt1YPVBwHHdrL8Z8AE4HBgMDAW2Be4tKHeD9Lf1dbAfOBsgIj4fkRslJYdBdzaPh8RO5XW36VU\nvlFE/KCb32djigPqVsBbUjw/LC2fCIwAtgX2Br4uaUxp+d3AF4A7m2z7FuA9EfFaYHtgLTo/eH8O\nuChW/67lBQ2/i/PaF0TE7cBrJbWt5jb7lYF08BkQImI+cC2wM6zsmvmepD8Dz1EcXLeSdE06a5wj\n6bMNm1lP0iWSlkq6U9IuzfYl6TWSjpf0V0n/kHSppM3SsuHpDPNISY9JekrSUZLeJumedKZ4cmlb\nb5T0u7Sdv0u6SNImXXzdIyjO8ian6aYazwBTXF9IZ9dLJX037f+WdJZ5qaR1SvUPkDQjxXxLOsNs\nXzZX0lfTd3om/d7WU3F2fy2wVemMcitJoyTdmra1UNLJDfsKSUdLmg3M7uL7d+aHwFeb/Q4ljaA4\neB4SEbdGxPKIuA/4CDBG0j6N60TE8xTJZNcexNRtEfHLiLguIp6LiKeAM4F3laocAXw3Ip6KiAeA\nM4BPltY/JSJuAl5osu2/RcTjpaIVwL90Es5Y4A/d/zYdmgq8v4Lt1oYTRs1IGgqMA+4qFR9GcTY5\nGHgUuBiYR3G29lHg+w0HiQOBy4DNgF8CV0lau8nuvggcBLwnbesp4JSGOm+nOPP7OPBT4FvAfsBO\nwMckvac9dOAkXjmDHEpx1tjR99wgxX5R+hxcPvBmeB+wO7AH8HWKA8yhab87A+PTfnYDzqE4q3wd\ncDpwjUpdN8DHgDHAdsBbgU9GxLMUB5byWeUCioPRl4HNgXdQnNV/oSG2gyh+bzuuxvdpNI3iAPTV\nJsv2Beals9qVIuIx4DZg/8YVUgIcD8zpQUy9aS+gvetrU2BLilZEu7sp/saySNpT0jPAUorE+dMO\n6m1I8e88qxsxv15Fl/Ejkv5XpS7D5AGKrq4BywmjPq6S9DRwM8XZz/dLy86NiPsiYjnwBoozs29E\nxAsRMQM4i6Jrot30iPhVRPwT+AmwHsWBtdFRwLciYl5EvEhxgP9oQ1fKd9N+bgCeBSZFxKLUEvoT\nsBtARMyJiCkR8WJELE77fQ8d+zDwInAD8FtgbVbv7OwHEbEknVnPBG6IiIcj4hmKlsFuqd4E4PSI\n+EtErEjdCC82/D5+FhELIuJJ4Nd0chYeEdMj4rZ0Vj+XIgE1fs+TIuLJdFbfE98GvihpSEP55sDC\nDtZZmJa3+2r6u1oK7Elx8rE67kytqfbP+1Zz/VVI2p+iRfHtVNQ+XvdMqdoSihOkLBFxc0RsDGxD\n0Tqb20HV9hbb0obyPRq+59PAsNLyByn+LrYE9qE4WflJwzaWlrY/IDlh1MdBEbFJRGwbEV9oONg8\nVpreCngyIsp/8I9S9AmvUj8iXuaV1kijbYErS/9BHqA4g96iVOeJ0vTzTeY3ApC0haSLJc2XtAS4\nkFcfuBodAVyaDrwvAJfTSbdUE1lxUXzHrzQcCIby6t9HuTvjudK6q5D0Jkm/UTEwu4QisTd+z8ea\nrNq+/mmlLq5vdlQPICJmAr8Bjm9Y9HeKA1czW6bl7X4UEZsAwyl+Lzt0ts8mRqa/y/bP9Y0VJA0r\nfadlnW1M0h4Urd6PRsRDqbh9nfJA9caselDvUjqRuY6iFd7M0+lnYzK6reF7bgL8rbTdxyPi/oh4\nOSIeoWjVfqRhG4NL2x+QnDD6h/Lg3AJgM5WuMKE4E5pfmh/aPqFikHybtF6jx4CxDf9R1kv/6VbX\n91Oc/5oGHw+l6KZahaRtKM7SDk0H3scpuqfGSeosyXTHY8D3Gr7jBhExKWPdZoOip1KcbY5I3/Ob\nrPo9OxxMjYijSl1c3++oXsmJwGd59QnB74ChkkaVK6buzD2Am5rs928Ug+j/J2n9jP1mS2MIKweD\nO6qXugevAT6VxiPa13+KomVU7s7ZhdRl1Q1rAW/sINZngb8Cb+rmtlduilWPn2/h1d1qA44TRj+T\n+qlvAU5Kg7NvBT5NcUbfbndJH05dS8dRdMHc1mRzpwHfk7QtgKQhkg7sZmiDKc4Un5G0NfC1Tuoe\nBjxEcba7a/q8iaIlNL6b++/ImcBRkt6uwoYqLvHM6e54AnidpI1LZYMpukuWqbhE9fO9HO+rRMQc\n4BLgS6Wyhyj+7S6StIekQZJ2omil3RgRN3awrSkUJw4Tqoy5GUk7U5z5fzEift2kyvnAv0vaVNJb\nKJLkuaX115G0HkVyXjv97b8mLTtE0rA0vS3wPZokzZLJdN5d2iz+vSVtm/6GhlJcRnt1Q7X3UHSH\nDlhOGP3TeIouhgXAlcCJDQeJqykGqZ+iODh/OI1nNPo/ijO+GyQtpUgqb+9mTN+huCT4GYoxiSs6\nqXsE8PPUzF/5oTgIrk63VJciYhrFwedkit/HHEpX33Sx7oPAJODh1J21FcUg9CcoukvOpDiYV+0/\ngcYB1mMoxq4upEjU11EMkjd2kzT6IcUlq+t2Ua/d3Xr1vQdNB5MzfAUYApythvs9khMpzvwfpfge\nP4iI60rLb6DoUnsnxQUOz1MMnENxccEtkp4F/kwxoN145WDZGcAhkpq2gDuwG8WJ2rPp5z2UkriK\ny8KXNV6IMNBo9S9FNjPr3yT9kmIM7ape2t7lwNkRMbk3tldXThhmZpbFXVJmZpbFCcPMzLI4YZiZ\nWRYnDDMzy9KTp2nWzuabbx7Dhw9vdRhmZv3K9OnT/x4RjY+gWcWAShjDhw9n2rRprQ7DzKxfkfRo\nTj13SZmZWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZWRYnDDMz\ny+KEYWZmWZwwzMwsixOGmZllGVBPq+2vpk6c2u11R08c3WtxmJl1prIWhqShkn4v6X5J90k6NpVv\nJmmKpNnp56YdrD9G0ixJcyQdX1WcZmaWp8ouqeXAVyJiR2AP4GhJOwLHAzdFxAjgpjT/KpIGAacA\nY4EdgfFpXTMza5HKEkZELIyIO9P0UuABYGvgQOC8VO084KAmq48C5kTEwxHxEnBxWs/MzFqkTwa9\nJQ0HdgP+AmwREQvToseBLZqssjXwWGl+XiozM7MWqTxhSNoIuBw4LiKWlJdFRADRw+1PkDRN0rTF\nixf3ZFNmZtaJSq+SkrQ2RbK4KCKuSMVPSNoyIhZK2hJY1GTV+cDQ0vw2qWwVEXEGcAZAW1tbj5JP\nT/TkSiczs/6gyqukBJwNPBARPyktugY4Ik0fAVzdZPU7gBGStpO0DnBwWs/MzFqkyi6pdwGHAftI\nmpE+44D/BvaXNBvYL80jaStJkwEiYjlwDHA9xWD5pRFxX4WxmplZFyrrkoqImwF1sHjfJvUXAONK\n85OBydVEZ2Zmq8uPBjEzsyxOGGZmlsUJw8zMsjhhmJlZFicMMzPL4oRhZmZZnDDMzCyLE4aZmWVx\nwjAzsyxOGGZmlsUJw8zMsjhhmJlZFicMMzPL4oRhZmZZnDDMzCyLE4aZmWVxwjAzsyxOGGZmlsUJ\nw8zMsjhhmJlZFicMMzPL4oRhZmZZnDDMzCyLE4aZmWVxwjAzsyxOGGZmlsUJw8zMsjhhmJlZFicM\nMzPL4oRhZmZZ1qpy45LOAQ4AFkXEzqnsEmCHVGUT4OmI2LXJunOBpcAKYHlEtFUZq5mZda7ShAGc\nC5wMnN9eEBEfb5+W9GPgmU7W3zsi/l5ZdGZmlq3ShBERf5Q0vNkySQI+BuxTZQxmZtY7WjmG8W7g\niYiY3cHyAG6UNF3ShI42ImmCpGmSpi1evLiSQM3MrLUJYzwwqZPle6axjbHA0ZL2alYpIs6IiLaI\naBsyZEgVcZqZGS1KGJLWAj4MXNJRnYiYn34uAq4ERvVNdGZm1kyrWhj7AQ9GxLxmCyVtKGlw+zTw\nXmBmH8ZnZmYNKk0YkiYBtwI7SJon6dNp0cE0dEdJ2krS5DS7BXCzpLuB24HfRsR1VcZqZmadq/oq\nqfEdlH+ySdkCYFyafhjYpcrYzMxs9fhObzMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbF\nCcPMzLI4YZiZWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZWRYn\nDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZWRYnDDMzy+KEYWZmWZww\nzMwsixOGmZllccIwM7MslSYMSedIWiRpZqlsoqT5kmakz7gO1h0jaZakOZKOrzJOMzPrWtUtjHOB\nMU3K/zcidk2fyY0LJQ0CTgHGAjsC4yXtWGmkZmbWqUoTRkT8EXiyG6uOAuZExMMR8RJwMXBgrwZn\nZmarJTthSNpU0k6StpfU00TzRUn3pC6rTZss3xp4rDQ/L5U1i2uCpGmSpi1evLiHYZmZWUc6PfBL\n2ljSNyXdC9wGnA5cCjwq6TJJe3djn6cC2wO7AguBH3djGytFxBkR0RYRbUOGDOnJpszMrBNrdbH8\nV8D5wLsj4unyAkm7A4dJ2j4izs7dYUQ8UdrGmcBvmlSbDwwtzW+TyszMrEU6TRgRsX8ny6YD01d3\nh5K2jIiFafZDwMwm1e4ARkjajiJRHAx8YnX3ZWZmvaerFsarSBoCHAusD5wWEbO7qD8JGA1sLmke\ncCIwWtKuQABzgc+lulsBZ0XEuIhYLukY4HpgEHBORNy3OrGamVnvWq2EQTHecCbFwf6XwNs6qxwR\n45sUN+2+iogFwLjS/GRglUtuzcysNboa9L5e0l6lonUoWgVzgXWrC8vMzOqmq8tjPwZ8QNIkSW8E\n/gM4Cfg/4AtVB2dmZvXR1aD3M8DXJG0PfA9YABzTeMWUmZkNfJ0mjNSq+DzwEvAV4I3AJZJ+C5wS\nESuqD9HMzOqgq0HvScBxwIbABRGxL/A+SYcDNwD7VhyfdWHqxKndXnf0xNG9FoeZDXxdJYx1gUeA\njYAN2gsj4nxJl1UZmJmZ1UtXCePzwMkUXVJHlRdExPNVBWVmZvXT1aD3LcAtfRSLmZnVmN+4Z2Zm\nWZwwzMwsixOGmZllyXqWlKQ24FvAtmkdARERb60wNjMzq5Hchw9eBHwNuBd4ubpwzMysrnITxuKI\nuKbSSMzMrNZyE8aJks4CbgJebC+MiCsqicrMzGonN2EcCbwZWJtXuqQCcMIwM1tD5CaMt0XEDpVG\nYmZmtZZ7We0tknasNBIzM6u13BbGHsAMSY9QjGH4slozszVMbsIYU2kUZmZWe1ldUhHxKDAU2CdN\nP5e7rpmZDQxZB31JJwLfAE5IRWsDF1YVlJmZ1U9uK+FDwAeBZwEiYgEwuKqgzMysfnITxksRERT3\nXiBpw+pCMjOzOspNGJdKOh3YRNJngRuBM6sLy8zM6ibrKqmI+JGk/YElwA7AtyNiSqWRmZlZrXSa\nMCQpdUWREsQqSaJcx8zMBq6uuqR+L+mLkoaVCyWtI2kfSecBR1QXnpmZ1UVXXVJjgE8BkyRtBzwN\nrE+RaG4AfhoRd1UbopmZ1UGnCSMiXgB+Dvxc0trA5sDzEfF0zsYlnQMcACyKiJ1T2Q+BDwAvAX8F\njmy2PUlzgaXACmB5RLTlfikzM+t92XdrR8Q/I2JhbrJIzmXVx4pMAXZOz6F6iFduBmxm74jY1cnC\nzKz1Kn28R0T8EXiyoeyGiFieZm8DtqkyBjMz6x2tfh7Up4BrO1gWwI2Spkua0NEGJE2QNE3StMWL\nF1cSpJmZtTBhSPoWsBy4qIMqe0bErsBY4GhJezWrFBFnRERbRLQNGTKkomjNzCz34YN7SLpD0jJJ\nL0laIWlJd3cq6ZMUg+GHdHQPR0TMTz8XAVcCo7q7PzMz67ncFsbJwHhgNsVltZ8BTunODiWNAb4O\nfDAinuugzoaSBrdPA+8FZnZnf2Zm1jtW5yqpOcCgiFgREb8g46VKkiYBtwI7SJon6dMUyWcwMEXS\nDEmnpbpbSZqcVt0CuFnS3cDtwG8j4rrV+mZmZtarct+495ykdShe0/oDYCEZySYixjcpPruDuguA\ncWn6YWCXzNh6xdSJU/tyd2Zm/U5uC+OwVPcYindiDAU+UlVQZmZWP7ktjN0puoWWAN+pMB4zM6up\n3BbGB4CHJF0g6QBJuYnGzMwGiKyEERFHAv8CXEZxtdRfJZ1VZWBmZlYv2S2FiPinpGsp7sBeHziI\n4vJaMzNbA+TeuDdW0rkU92F8BDgLeEOFcZmZWc3ktjAOBy4BPhcRL1YYj5mZ1VTuO72b3U9hZmZr\nkK7e6X1zROwpaSnF2MXKRUBExGsrjc7MzGqjqzfu7Zl+Du6bcMzMrK5yB70vyCkzM7OBK/fGvZ3K\nM+nGvd17PxwzM6urThOGpBPS+MVbJS1Jn6XAE8DVfRKhmZnVQqcJIyJOSuMXP4yI16bP4Ih4XUSc\n0EcxmplZDeReVnuCpE2BEcB6pfI/VhWYmZnVS1bCkPQZ4FhgG2AGsAfFi5H2qS40MzOrk9xB72OB\ntwGPRsTewG7A05VFZWZmtZObMF6IiBcAJK0bEQ8CO1QXlpmZ1U3us6TmSdoEuIriXdxPAY9WF5aZ\nmdVN7qD3h9LkREm/BzYGrqssKjMzq52uniW1WZPie9PPjYAnez0i6zNTJ07t9rqjJ47utTjMrH/o\nqoUxneKhgyqVtc8HsH1FcZmZWc109fDB7foqEDMzq7fchw9K0qGS/iPND5M0qtrQzMysTnIvq/05\n8A7gE2l+KXBKJRGZmVkt5V5W+/aIGCnpLoCIeErSOhXGZWZmNZPbwvinpEGkt+5JGgK8XFlUZmZW\nO7kJ42fAlcDrJX0PuBn4fmVRmZlZ7eTeuHeRpOnAvhSX1B4UEQ9UGpmZmdVKly0MSYMkPRgRD0bE\nKRFxcm6ykHSOpEWSZpbKNpM0RdLs9HPTDtYdI2mWpDmSjs//SmZmVoUuE0ZErABmSRrWje2fC4xp\nKDseuCkiRgA3pflXSeMlpwBjgR2B8ZJ27Mb+zcysl+ReJbUpcJ+k24Fn2wsj4oOdrRQRf5Q0vKH4\nQGB0mj4PmAp8o6HOKGBORDwMIOnitN79mfGamVkvy00Y/9GL+9wiIham6ceBLZrU2Rp4rDQ/D3h7\nL8ZgZmarKXfQ+w9V7DwiQlL0ZBuSJgATAIYN606vmZmZ5ci9rLY3PSFpS4D0c1GTOvOBoaX5bVLZ\nKiLijIhoi4i2IUOG9HqwZmZWaEXCuAY4Ik0fAVzdpM4dwAhJ26U7yg9O65mZWYtUmjAkTQJuBXaQ\nNE/Sp4H/BvaXNBvYL80jaStJkwEiYjlwDHA98ABwaUTcV2WsZmbWuawxDEkjgJMoLnFdr708Ijp9\nH0ZEjO9g0b5N6i4AxpXmJwOTc+IzM7Pq5bYwfgGcCiwH9gbOBy6sKigzM6uf3ISxfkTcBCgiHo2I\nicD7qwvLzMzqJvc+jBclvQaYLekYiiuWNqouLDMzq5vcFsaxwAbAl4DdgcN45UonMzNbA+TeuHdH\nmlwGHFldOGZmVledJgxJP42I4yT9mvTypLKuniVlZmYDR1ctjAvSzx9VHYiZmdVbpwkjIqanyWnA\n8xHxMqx8/Pi6FcdmZmY1kjvofRPFoHe79YEbez8cMzOrq9yEsV5ELGufSdMbdFLfzMwGmNyE8ayk\nke0zknYHnq8mJDMzq6PcG/eOAy6TtAAQ8Abg45VFZWZmtZN9H4akNwM7pKJZEfHP6sIyM7O6yW1h\nALwNGJ7WGSmJiDi/kqjMzKx2ch9vfgHwRmAGsCIVB8VTa83MbA2Q28JoA3aMiB69f9vMzPqv3Kuk\nZlIMdJuZ2Roqt4WxOXC/pNuBF9sL/SwpM7M1R27CmFhlEGZmVn+5l9X+QdK2wIiIuFHSBsCgakMz\nM7M66XQMQ9Lr08/PAr8CTk+LtgauqjY0MzOrkw4TRnoUyHfT7NHAu4AlABExG3h95dGZmVltdNbC\neDNwd5p+KSJeal8gaS2avFDJzMwGrg4TRkT8EpifZqdK+iawvqT9gcuAX/dBfGZmVhOdjmFExNVp\n8nhgMXAv8DlgMvDv1YZmZmZ1knuV1MvAmeljZmZroNxnST1CkzGLiNi+1yMyM7NaWp1nSbVbD/h/\nwGa9H46ZmdVV1rOkIuIfpc/8iPgp8P6KYzMzsxrJ7ZIaWZp9DUWLY3XepWFmZv1c7kH/x6Xp5cBc\n4GPd3amkHYBLSkXbA99OLZf2OqOBq4FHUtEVEfGf3d2nmZn1TO5VUnv35k4jYhawK4CkQRT3e1zZ\npOqfIuKA3ty3mZl1T26X1L91tjwiftKDGPYF/hoRj/ZgG2ZmVrHcFyi1AZ+neOjg1sBRwEhgcPr0\nxMHApA6WvVPSPZKulbRTswqSJkiaJmna4sWLexiKmZl1JHcMYxtgZEQsBZA0EfhtRBzak51LWgf4\nIHBCk8V3AsMiYpmkcRRPxx3RWCkizgDOAGhra/PzrczMKpLbwtgCeKk0/1Iq66mxwJ0R8UTjgohY\nEhHL0vRkYG1Jm/fCPs3MrBtyWxjnA7dLah+YPgg4rxf2P54OuqMkvQF4IiJC0iiK5PaPXtinmZl1\nQ+5VUt+TdC3w7lR0ZETc1ZMdS9oQ2J/iYYbtZUel/Z0GfBT4vKTlwPPAwRHhLiczsxZZnZvvNgCW\nRMQvJA2RtF1EPNLlWh2IiGeB1zWUnVaaPhk4ubvbNzOz3pU1hiHpROAbvDI4vTZwYVVBmZlZ/eQO\nen+I4mqmZwEiYgE9v5zWzMz6kdyE8VIaPwhYOf5gZmZrkNyEcamk04FNJH0WuBG/TMnMbI2Se5XU\nj9K7vJcAO1A8KHBKpZGZmVmtdJkw0sMBb0wPIHSSMDNbQ3XZJRURK4CXJW3cB/GYmVlN5d6HsQy4\nV9IU0pVSABHxpUqiMjOz2slNGFekj5mZraE6TRiShkXE3yKiN54bZWZm/VhXYxhXtU9IurziWMzM\nrMa6ShgqTW9fZSBmZlZvXY1hRAfTtoabOnFqj9YfPXF0r8RhZn2nq4Sxi6QlFC2N9dM0aT4i4rWV\nRmdmZrXRacKIiEF9FYiZmdVb7rOkzMxsDeeEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPM\nzLI4YZiZWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpalZQlD0lxJ90qaIWlak+WS\n9DNJcyTdI2lkK+I0M7NCVy9QqtreEfH3DpaNBUakz9uBU9NPMzNrgTp3SR0InB+F24BNJG3Z6qDM\nzNZUrUwYAdwoabqkCU2Wbw08Vpqfl8peRdIESdMkTVu8eHFFoZqZWSsTxp4RsStF19PRkvbqzkYi\n4oyIaIuItiFDhvRuhGZmtlLLEkZEzE8/FwFXAqMaqswHhpbmt0llZmbWAi1JGJI2lDS4fRp4LzCz\nodo1wOHpaqk9gGciYmEfh2pmZkmrrpLaArhSUnsMv4yI6yQdBRARpwGTgXHAHOA54MgWxWpmZrQo\nYUTEw8AuTcpPK00HcHRfxmVmZh2r82W1ZmZWI04YZmaWxQnDzMyyOGGYmVkWJwwzM8vihGFmZlmc\nMMzMLIsThpmZZXHCMDOzLE4YZmaWxQnDzMyyOGGYmVmWVr/T29ZQUydO7fa6oyeO7rU4zCyfWxhm\nZpbFCcPMzLI4YZiZWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZ\nWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsLUkYkoZK+r2k+yXdJ+nYJnVGS3pG0oz0+XYr\nYjUzs0Kr3ri3HPhKRNwpaTAwXdKUiLi/od6fIuKAFsRnZmYNWtLCiIiFEXFnml4KPABs3YpYzMws\nT8vHMCQNB3YD/tJk8Tsl3SPpWkk79WlgZmb2Kq3qkgJA0kbA5cBxEbGkYfGdwLCIWCZpHHAVMKLJ\nNiYAEwCGDRtWccRmZmsuRURrdiytDfwGuD4ifpJRfy7QFhF/76hOW1tbTJs2rVvxTJ04tVvrWf8y\neuLoVodgVjuSpkdEW1f1WnWVlICzgQc6ShaS3pDqIWkURaz/6LsozcysrFVdUu8CDgPulTQjlX0T\nGAYQEacBHwU+L2k58DxwcLSqOWRmZq1JGBFxM6Au6pwMnNw3EZmZWVdafpWUmZn1D04YZmaWxQnD\nzMyyOGGYmVkWJwwzM8vihGFmZlla+mgQs77Wkzv6fZe4rencwjAzsyxuYZhlcuvE1nRuYZiZWRYn\nDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZWRbf6W3WB3pylzj4TnGr\nB7cwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZWRZfVms2wPnFT9Zb3MIwM7MsbmGY9QM9\nvfGvFXw3OYrLAAAIlUlEQVSz4sDjFoaZmWVpWcKQNEbSLElzJB3fZLkk/Swtv0fSyFbEaWZmhZZ0\nSUkaBJwC7A/MA+6QdE1E3F+qNhYYkT5vB05NP82sj7SyK8yD9fXTqjGMUcCciHgYQNLFwIFAOWEc\nCJwfEQHcJmkTSVtGxMK+D9fM1hROVB1rVcLYGnisND+PVVsPzepsDThhmFmnWtUyamWLrC+SVb+/\nSkrSBGBCml0maVY3N7U58PfeiapP9Kd4+1Os0L/i7U+xQv+Ktz/FCt/pUbzb5lRqVcKYDwwtzW+T\nyla3DhFxBnBGTwOSNC0i2nq6nb7Sn+LtT7FC/4q3P8UK/Sve/hQr9E28rbpK6g5ghKTtJK0DHAxc\n01DnGuDwdLXUHsAzHr8wM2udlrQwImK5pGOA64FBwDkRcZ+ko9Ly04DJwDhgDvAccGQrYjUzs0LL\nxjAiYjJFUiiXnVaaDuDoPgypx91afaw/xdufYoX+FW9/ihX6V7z9KVbog3hVHJfNzMw650eDmJlZ\nFicMun5MSR/FcI6kRZJmlso2kzRF0uz0c9PSshNSvLMkva9Uvruke9Oyn0lSBbEOlfR7SfdLuk/S\nsTWPdz1Jt0u6O8X7nTrHm/YzSNJdkn7TD2Kdm/YzQ9K0OsebbgD+laQHJT0g6R01jnWH9Dtt/yyR\ndFxL442INfpDMej+V2B7YB3gbmDHFsSxFzASmFkq+wFwfJo+HvifNL1jinNdYLsU/6C07HZgD0DA\ntcDYCmLdEhiZpgcDD6WY6hqvgI3S9NrAX9I+axlv2s+/Ab8EflPnv4W0n7nA5g1ltYwXOA/4TJpe\nB9ikrrE2xD0IeJzifomWxVvZF+wvH+AdwPWl+ROAE1oUy3BenTBmAVum6S2BWc1ipLja7B2pzoOl\n8vHA6X0Q99UUzwWrfbzABsCdFE8WqGW8FPcc3QTswysJo5axpm3PZdWEUbt4gY2BR0hjt3WOtUns\n7wX+3Op43SXV8SNI6mCLeOXek8eBLdJ0RzFvnaYbyysjaTiwG8VZe23jTV08M4BFwJSIqHO8PwW+\nDrxcKqtrrAAB3ChpuoonL9Q13u2AxcAvUnffWZI2rGmsjQ4GJqXplsXrhNFPRHFqUKtL2iRtBFwO\nHBcRS8rL6hZvRKyIiF0pzt5HSdq5YXkt4pV0ALAoIqZ3VKcusZbsmX63Y4GjJe1VXlijeNei6PY9\nNSJ2A56l6NJZqUaxrqTi5uYPApc1LuvreJ0wMh9B0iJPSNoSIP1clMo7inl+mm4s73WS1qZIFhdF\nxBV1j7ddRDwN/B4YU9N43wV8UNJc4GJgH0kX1jRWACJifvq5CLiS4mnUdYx3HjAvtS4BfkWRQOoY\na9lY4M6IeCLNtyxeJ4y8x5S0yjXAEWn6CIqxgvbygyWtK2k7ineG3J6aqUsk7ZGugji8tE6vSds+\nG3ggIn7SD+IdImmTNL0+xXjLg3WMNyJOiIhtImI4xd/i7yLi0DrGCiBpQ0mD26cp+tpn1jHeiHgc\neEzSDqloX4pXKtQu1gbjeaU7qj2u1sRb5UBNf/lQPILkIYqrCr7VohgmUTy6/Z8UZ0KfBl5HMfg5\nG7gR2KxU/1sp3lmUrngA2ij+w/4VOJmGAb5einVPimbwPcCM9BlX43jfCtyV4p0JfDuV1zLe0r5G\n88qgdy1jpbi68O70ua/9/0+N490VmJb+Fq4CNq1rrGk/GwL/ADYulbUsXt/pbWZmWdwlZWZmWZww\nzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YVi/JmlFevTzTEm/br9Brxe2O1ylR81nrrO+pD9I\nGtQbMfQmSZM7+91IuljSiL6MyfofJwzr756PiF0jYmfgSfr2tb6NPgVcERErqtqBpG69VjkixkXx\nWJSOnErxwEOzDjlh2EByK6WncEr6mqQ7JN2jV16aNFzFi3POVPEypRvS40LaXzJzt6S7KSWetM6f\nJN2ZPu/sYP+HUHrkQif7f1DSuZIeknSRpP0k/VnFC3FGNW5U0iclXSPpdxR3+Dbddiq/SsVTY+/T\nK0+ObX/J0ebpUR6/Td9zpqSPpyp/AvbrbkKyNYMThg0IqRtoX9JzwCS9l+JZOqMoHgexu155iuoI\n4JSI2Al4GvhIKv8F8MWI2KVh84uA/SNiJPBx4GdN9r8OsH1EzM3Y/78APwbenD6foHjcyleBb3bw\nFUcCH42I93Sx7U9FxO4Uj4L4kqTXNWxnDLAgInZJrbLrACLiZWAO0PjdzVZywrD+bn0V77lofy/A\nlFT+3vS5i+KFSW+mOMgCPBIRM9L0dGB46t/fJCL+mMovKO1jbeBMSfdSPGJ6xyZxbE6RfNp1tf97\n00H6PuCmKJ7Rcy/FS7SamRIRT2Zs+0uphXQbxZNLG8cl7gX2l/Q/kt4dEc+Uli0Ctupg/2a4+Wn9\n3fMRsaukDSjeMHY0RQtAwEkRcXq5sooXPr1YKloBrN/FPr4MPEFx9v0a4IVmcQDrlXeVuf+XS/Mv\n0/H/yWcztj0a2A94R0Q8J2lqQ0xExEOSRlI8LPK/JN0UEf+ZFq+XvodZU25h2IAQEc8BXwK+kvrh\nrwc+peIlT0jaWtLrO1n/aeBpSXumokNKizcGFqYWwWEU71duXP8pYJCk9gP0au1/NXW07Y2Bp1Ky\neDPFO5xfRdJWwHMRcSHwQ4qurnZvoniiqVlTbmHYgBERd0m6BxgfERdIegtwa/EKAJYBh1K0KDpy\nJHCOpABuKJX/HLhc0uEUff7PNls5rbMncGNE3NCN/WfpZNvXAUdJeoDi8da3NVn9X4EfSnqZ4lH6\nnweQtAVFa+3xnsZnA5cfb27WS1JXz5cj4rBWx7K6JH0ZWBIRZ7c6Fqsvd0mZ9ZKIuBP4fR1v3Mvw\nNHBeq4OwenMLw8zMsriFYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbl/wPvvxahcV49awAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e52c16d30>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"frenda3 = pd.cut(base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")], bins=faixa, right=False)\n",
"t3 = (frenda3.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t3,\"\\n\")\n",
"\n",
"plot = base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")].plot.hist(bins=faixa,title=\"Problema Alimentar - NORTE - 2013 (H5)\", weights=zeros_like(base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")])+1./base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"purple\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 208,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 21.1\n",
"[350, 700) 22.3\n",
"[700, 1050) 21.8\n",
"[1050, 1400) 13.1\n",
"[1400, 1750) 8.7\n",
"[1750, 2100) 5.1\n",
"[2100, 2450) 2.9\n",
"[2450, 2800) 1.5\n",
"[2800, 3150) 1.1\n",
"[3150, 3500) 0.7\n",
"[3500, 3850) 0.6\n",
"[3850, 4200) 0.4\n",
"[4200, 4550) 0.3\n",
"[4550, 4900) 0.2\n",
"[4900, 5250) 0.1\n",
"[5250, 5600) 0.1\n",
"[5600, 5950) 0.0\n",
"[5950, 6300) 0.0\n",
"[6300, 6650) 0.0\n",
"[6650, 7000) 0.0\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAGDCAYAAAAmphcsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmcXFWd/vHPY1jCEgkYiOwBB0FglCUg/MQNBAEFQR01\no4i4oAKCjjoDOkrQQRx1HGUABQVZRVFZ4goBcQcxYZEgYECCQIAEIYQlgITv749zSm4qvdzu9K2q\n7vO8X6969a27fqu6u557zr11ryICMzMr13O6XYCZmXWXg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DM\nrHAOgi6TNF3SuQNMnyfpNZ2saTgk/ULSe/Pw2yVd1u2azPoj6bWSLh7B9e0n6bsjtb5OcxAMQ/5w\nXiLpUUn3SzpT0prdrqtpSv4i6U8DzRcR50XEXp2qq0XSqyTd3YXtzpO0QNIalXHvlfSLynNJ+rik\nuflv56+STpC0amWeMyU9lf+uHpQ0U9JWlenvkrQ0T39U0h2SviXphZV5pkiKyjytx1vz9I0k/UDS\nA5IeljQnr/fllXkf62Mdm+Swf6Jt/A+H+Z69UNIlkhbm13qppC3b5vmIpPskLZZ0Rtt7dYSkWZKe\nlHRm23Jb52kP5cflkrZuK+F44POVZULSP7WtZ7mdNElH5ff9MUk3t977iPghsI2kFw/n/eg2B8Hw\n7RcRawI7AFOB/2yfIf/zj6X3+BXAesDmknbqdjEjTdJKK7D4OOCoAaafCBwKvBOYAOwD7AFc0Dbf\nF/Lf1YbAPcDpbdOvytPXAl4DLAFmS9q2bb6JEbFm5dHaWz0HuAvYFHgecBBwf0T8ujUvsE0f6/hr\nHndE23r3G+R96c9EYAawJTAZuAa4pDVR0muBo0nv0abA5sBxleXnA/8FnNHHuucDbwUm5ccM4DuV\nde8ErBURVw+l4NzifQ/wOmBN4PXAA5VZzif9jkedsfQh1RURcQ/wU2Bb+EcXyfGSfgs8TvrQ3EDS\njLznc5uk97WtZryk70p6RNK1kl7S17YkPUfS0ZJul/Q3SRdIWidPa+0JHiLprrwn9AFJO0n6o6RF\nkk6qrOsFkn6e1/OApPMkTRzk5R5M+mf9SR7uU97D/E3leUg6LO8NPyLps3n7v8t7exdIWqUy/+sl\nXZ9r/l11L0tp7/tj+TU9nN+38Up74z8FNqjsrW4gaWdJV+V13SvppLZthaTDJc0F5g7y+gfyReBj\nfb2HkrYADgPeHhFXRcTTEXET8CZgb0m7ty8TEUtIIbFdXxuLiKURcXtEHAb8Ephes86dgDMj4rFc\nx3UR8dOay46YiLgmIk6PiAcj4u/A/wJbSnpenuVg4PSIuCkiHgI+A7yrsvyFEXEx8Lc+1r0ovzdL\nAQFLgere/j6k96y2vEN3LPCRiPhTJLdHxIOV2X5BColRx0GwgiRtDOwLXFcZfRBpz2ACcCdpb+Ru\nYAPgzcDn2v753wB8D1gH+DZwsaSV+9jch4ADgFfmdT0EnNw2z0uBLUh7RF8BPknac9wGeIukV7ZK\nB07I63kRsDEDfJhIWj3Xfl5+vK36gVrDa4EdgV2AfwdOA96Rt7stMC1vZ3vSXt77SXuspwIzqt0C\nwFuAvYHNgBcD74qIx0j/4PMre6vzSR8CHyHtGe5K2sM8rK22A0jvW3v3wVDMIn0QfKyPaXsAd0fE\nNdWREXEXcDWwZ/sCOdimAbfV2PaFwMtr1nk1cLKkt0napOYynfAK4L6IaH2wbwPcUJl+AzC5EhSD\nkrQIeAL4P+BzlUn/DNw6xPo2yo9t847WHZKOa2vx3wxMkfTcIa676xwEw3dx/kP7DWnvovqHdmbe\nk3kaeD7wMuA/IuKJiLge+Capi6BldkR8P+8ZfRkYT/rAbPcB4JMRcXdEPEn64H5zW5fGZ/N2LgMe\nA86PiAW55fJrYHuAiLgtImZGxJMRsTBv95X0743Ak8BlwI+BlRna3s8XImJx3hOeA1wWEX+JiIdJ\ne/Lb5/kOBU6NiN/nvd6z8nar78eJETE/7439kH72mvPrnB0RV+e933mkYGl/nSfkPdMlQ3g9ffk0\n8CFJ67aNnwTc288y9+bpLR/Lf1ePALuRdioGM5+0E1H1QG4FtR4vyuP/hfR38CngjtzyGko334lt\n6/3sEJbtk6SNSDs0/1YZvSbwcOX54vxzQt31RsREUhfaESy7ozaR9P62u7b62khdUy0b5Z97kYLk\n1aSgfk9lntY6B2tZ9xwHwfAdEBETI2LTiDis7UPkrsrwBsCDEVH9w7uT1Ae83PwR8QzPth7abQpc\nVPlDvZm0xzu5Ms/9leElfTxfE0DSZEnfkXSPpMXAuSz7gdTuYOCC/IH6BPADBuge6kOtukiv8aNt\n/5Abs+z7cV9l+PHKsstROij5I+WDjqTAbn+dd/WxaGv5r1e6mj7R33wAETEH+BHLfoBA6kdev5/F\n1mfZfuYv5Q+wKaT3Zcu+FmqzIfBg27hJ+e+z9bg51/hQRBwdEduQ/m6uJ+3UqMZ2AI5sW++n+ppJ\n0k2V963f1koOzcuAUyLi/MqkR4HqnvVa+WdfH+D9yi3FrwNnS1ovj36IvgNlh+pro3IwmfS7gLRD\ns6iyU7FvZZ7WOhcNpcZe4CBoRvWSrvOBdSRV//A2IR0IbNm4NZCbmhvl5drdBezT9o84Pu/tD9Xn\ncp3/HBHPJXXT9PlhkPfYdgfekT9Q7yN1E+0raaDwGI67gOPbXuPqbR8S/enrUrpfA24Btsiv8xMs\n/zr7vQRvRHyg0tX0uf7mqzgWeB/LBv3PgY0l7VydMXcr7gJc0cd2/0o6+PxVSasNss0DSXv5QxIR\nDwBfIoVse4tihUTENpX3rc/aJK1NCoEZEXF82+SbgOqxspeQDmovd0yghucAq/Ps7+SPwAv7n71P\ntwJPsezfSvvfzYuAeRGxmFHGQdCw3A/8O+CEfFDzxaTmZPW0tB0lvTF38XyY1BXS1xkNXweOl7Qp\npL0pSW8YZmkTSHtdD0vaEPj4APMeBPyZtHe6XX68kNRymTbM7ffnG8AHJL1UyRqSXtcWpP25H3ie\npLUq4yaQuhUeVToV84MjXO8yIuI24LvAkZVxfyb97s6TtIukcZK2IbWqLo+Iy/tZ10zSDsFyZ6Lk\ndWwm6f+AV7HsGTX9kvTfkraVtFJ+Tz8I3DbMD9hhy/3olwK/jYj2FhTA2cB7lE4FXZvUlXVmZfmV\nJI0nna01Lv9vrZSn7Slp+/wePZfU7fkQqQUN6WSHgbpBlxMRj5N+r/8uaULeOTqU1AJseSWpm3PU\ncRB0xjRSU38+cBFwbNs//yWkg7sPkT5035iPF7T7KulUuMskPUIKi5cOs6bjSKe+Pkzq879wgHkP\nJjXd76s+SB9uQ+keGlREzCLtUZ9Eej9uo3K2yCDL3kI6he8vuVtpA9LB238ldSl8g/TP3LTPAGu0\njTuCdGzoXFIA/4x0cPlNg6zri6QPn9bB8l0lPUoKt1+Quk92iogb25ZbpGXP92/1v69O+htcBPyF\n1BW3/xBe20lt6509hGWrDiSdwXRI2/o2AYiInwFfAK4kdaXeQWpttfwnqbvmaFJrdgnPnsI9kfR3\n8DBwO/ACYO/cpUlEXEvaARrq/84RpN/dfOAq0okd1dNXp5G6i0YdhW9MY2aFkbQXcFhEHDBC69sP\nOCgi3jIS6+s0B4GZWeHcNWRmVjgHgZlZ4RwEZmaFcxCYmRVuRa622DGTJk2KKVOmdLsMM7NRZfbs\n2Q9ERPslT5YzKoJgypQpzJo1q9tlmJmNKpLurDOfu4bMzArnIDAzK5yDwMyscA4CM7PCOQjMzArn\nIDAzK5yDwMyscA4CM7PCOQjMzArnIDAzK5yDwMyscA4CM7PCOQjMzAo3Kq4+2k3TZ0wf/rL7D39Z\nM7NOcYvAzKxwDgIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCufvETTI30Ews9HALQIzs8I5\nCMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCucgMDMrnIPAzKxwRXyhbEW+2GVmNta5RWBmVjgHgZlZ\n4RoLAkkbS7pS0p8k3STpqDx+HUkzJc3NP9duqgYzMxtcky2Cp4GPRsTWwC7A4ZK2Bo4GroiILYAr\n8nMzM+uSxoIgIu6NiGvz8CPAzcCGwBuAs/JsZwEHNFWDmZkNriPHCCRNAbYHfg9Mjoh786T7gMmd\nqMHMzPrWeBBIWhP4AfDhiFhcnRYRAUQ/yx0qaZakWQsXLmy6TDOzYjUaBJJWJoXAeRFxYR59v6T1\n8/T1gQV9LRsRp0XE1IiYuu666zZZpplZ0Zo8a0jA6cDNEfHlyqQZwMF5+GDgkqZqMDOzwTX5zeKX\nAQcBN0q6Po/7BPB54AJJ7wHuBN7SYA1mZjaIxoIgIn4DqJ/JezS1XTMzGxp/s9jMrHAOAjOzwjkI\nzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAO\nAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyuc\ng8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK\n5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOz\nwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyvcSnVnlLQ2sAGwBJgXEc80VpWZmXXMgEEg\naS3gcGAasAqwEBgPTJZ0NXBKRFzZeJVmZtaYwVoE3wfOBl4eEYuqEyTtCBwkafOIOL2pAs3MrFkD\nBkFE7DnAtNnA7BGvyMzMOqr2MQIASesCRwGrAV+PiLmNVGVmZh0z1LOG/ge4FLgI+PbIl2NmZp02\nYBBIulTSKyqjVgHm5ceqzZVlZmadMliL4C3AfpLOl/QC4FPACcBXgcOaLs7MzJo32MHih4GPS9oc\nOB6YDxzRfgaRmZmNXoN9j+AFwAeBp4CPAi8Avivpx8DJEbG0+RLNzKxJg3UNnQ9cCFwJnBMRv46I\n1wKLgMuaLs7MzJo3WBCsCtxBOji8emtkRJwNvH6wlUs6Q9ICSXMq46ZLukfS9fmx7/BKNzOzkTDY\n9wg+CJxE6hr6QHVCRCypsf4z8/Jnt43/34j4Us0azcysQYMdLP4d8LvhrjwifiVpynCXNzOz5nXr\nMtQfkvTH3HW0dpdqMDMzuhMEXwM2B7YD7iV9W3k5kg6VNEvSrIULF3ayPjOzonQ8CCLi/ohYmu9n\n8A1g537mOy0ipkbE1HXXXbezRZqZFaTWReckTQU+CWyalxEQEfHioW5Q0voRcW9+eiAwZ6D5zcys\nWXWvPnoe8HHgRqD2nckknQ+8Cpgk6W7gWOBVkrYDgnRa6vuHUK+ZmY2wukGwMCJmDHXlETGtj9G+\niY2ZWQ+pGwTHSvomcAXwZGtkRFzYSFVmZtYxdYPgEGArYGWe7RoK0uUnzMxsFKsbBDtFxJaNVmJm\nZl1R9/TR30nautFKzMysK+q2CHYBrpd0B+kYwbBPHzUzs95SNwj2brQKMzPrmlpdQxFxJ7AxsHse\nfrzusmZm1ttqfZhLOhb4D+CYPGpl4NymijIzs86pu1d/ILA/8BhARMwHJjRVlJmZdU7dIHgqIoL0\n3QEkrdFcSWZm1kl1g+ACSacCEyW9D7icdOVQMzMb5WqdNRQRX5K0J7AY2BL4dETMbLQyMzPriAGD\nQJJylxD5g3+5D//qPGZmNvoM1jV0paQPSdqkOlLSKpJ2l3QWcHBz5ZmZWdMG6xraG3g3cL6kzYBF\nwGqkALkM+EpEXNdsiWZm1qQBgyAingBOAU6RtDIwCVgSEYs6UZyZmTWv7iUmiIi/k242b2ZmY4gv\nE2FmVjgHgZlZ4RwEZmaFq3vRuV0k/UHSo5KekrRU0uKmizMzs+bVbRGcBEwD5pJOH30vcHJTRZmZ\nWefU7hqKiNuAcRGxNCK+hW9WY2Y2JtQ9ffRxSauQblf5BdJppD6+YGY2BtT9MD8oz3sE6Z4EGwNv\naqooMzPrnLotgh2BH0fEYuC4BusxM7MOq9si2A/4s6RzJL1eUu1vJJuZWW+rez+CQ/K1hvYhnT10\nsqSZEfHeRqsr2PQZ01ds+f1XbHkzK8eQrjUk6aek21WuBhxAOo3UzMxGsbpfKNtH0pmk7xG8Cfgm\n8PwG6zIzsw6p2yJ4J/Bd4P0R8WSD9ZiZWYfVPUYwrelCzMysOwa7Z/FvImI3SY+Qjg38YxIQEfHc\nRqszM7PGDXaHst3yzwmdKcfMzDqt7sHic+qMMzOz0afuF8q2qT7JXyjbceTLMTOzThswCCQdk48P\nvFjS4vx4BLgfuKQjFZqZWaMGDIKIOCEfH/hiRDw3PyZExPMi4pgO1WhmZg2qe/roMZLWBrYAxlfG\n/6qpwszMrDNqBYGk9wJHARsB1wO7AFcBuzdXmpmZdULdg8VHATsBd0bEq4HtgUWNVWVmZh1TNwie\niIgnACStGhG3AFs2V5aZmXVK3WsN3S1pInAxMFPSQ8CdzZVlZmadUvdg8YF5cLqkK4G1gJ81VpWZ\nmXXMYNcaWqeP0Tfmn2sCD454RWZm1lGDtQhmky42p8q41vMANm+oLjMz65DBLjq3WacKMTOz7qh7\n0TlJeoekT+Xnm0jaudnSzMysE+qePnoKsCvwr/n5I8DJjVRkZmYdVff00ZdGxA6SrgOIiIckrdJg\nXWZm1iF1WwR/lzSOfJcySesCzzRWlZmZdUzdIDgRuAhYT9LxwG+AzzVWlZmZdUzdL5SdJ2k2sAfp\n1NEDIuLmRiszM7OOGDQIcpfQTRGxFXBL8yWZmVknDdo1FBFLgVslbdKBeszMrMPqnjW0NnCTpGuA\nx1ojI2L/RqoyM7OOqRsEn2q0CjMz65q6B4t/2XQhZmbWHXVPHzUzszHKQWBmVjgHgZlZ4WodI5C0\nBXACsDUwvjU+Inw/AjOzUa5ui+BbwNeAp4FXA2cD5zZVlJmZdU7dIFgtIq4AFBF3RsR04HWDLSTp\nDEkLJM2pjFtH0kxJc/PPtYdXupmZjYS6QfCkpOcAcyUdIelA0j2LB3MmsHfbuKOBKyJiC+CK/NzM\nzLqkbhAcBawOHAnsCBwEHDzYQhHxK5a/wf0bgLPy8FnAATVrMDOzBtT9Qtkf8uCjwCEruM3JEXFv\nHr4PmNzXTJIOBQ4F2GQTX+bIzKwpAwaBpK9ExIcl/ZB8U5qqFb3WUESEpOXWm6edBpwGMHXq1D7n\nMTOzFTdYi+Cc/PNLI7jN+yWtHxH3SlofWDCC6zYzsyEaMAgiYnYenAUsiYhn4B/3KFh1mNucQTq+\n8Pn885JhrsfMzEZA3YPFV5AOFresBlw+2EKSzgeuAraUdLek95ACYE9Jc4HX5OdmZtYldS9DPT4i\nHm09iYhHJa0+0AJ5vmn9TNqj5nbNzKxhdVsEj0naofVE0o7AkmZKMjOzTqrbIvgw8D1J80k3r38+\n8NbGqjIzs46p/T0CSVsBW+ZRt0bE35sry8zMOqVuiwBgJ2BKXmYHSUTE2Y1UZWZmHVP3MtTnAC8A\nrgeW5tFBugqpmZmNYnVbBFOBrSPC3/A1Mxtj6p41NId0gNjMzMaYui2CScCfJF0DPNkauaLXGjIz\ns+6rGwTTmyzCzMy6p+7po7+UtCmwRURcnr9VPK7Z0szMrBMGPEYgab38833A94FT86QNgYubLc3M\nzDqh3yDIl5T4bH56OPAyYDFARMwF1mu8OjMza9xALYKtgBvy8FMR8VRrgqSV6ONGNWZmNvr0GwQR\n8W3gnvz0F5I+AawmaU/ge8APO1CfmZk1bMBjBBHRumnM0cBC4Ebg/cBPgP9stjQzM+uEumcNPQN8\nIz/MzGwMqXutoTvo++b1m494RWZm1lFDudZQy3jgX4B1Rr4cGynTZ0wf/rL7D39ZMxt9al1rKCL+\nVnncExFfAV7XcG1mZtYBdbuGdqg8fQ6phTCUexmYmVmPqvth/j+V4aeBecBbRrwaMzPruLpnDb26\n6ULMzKw76nYN/dtA0yPiyyNTjpmZddpQzhraCZiRn+8HXAPMbaIoMzPrnLpBsBGwQ0Q8AiBpOvDj\niHhHU4WZmVln1L1V5WTgqcrzp/I4MzMb5eq2CM4GrpF0UX5+AHBWMyWZmVkn1T1r6HhJPwVenkcd\nEhHXNVeWmZl1St2uIYDVgcUR8VXgbkmbNVSTmZl1UK0gkHQs8B/AMXnUysC5TRVlZmadU7dFcCCw\nP/AYQETMByY0VZSZmXVO3SB4KiKCfClqSWs0V5KZmXVS3SC4QNKpwERJ7wMuxzepMTMbE+qeNfSl\nfK/ixcCWwKcjYmajlZmZWUcMGgSSxgGX5wvP+cPfzGyMGbRrKCKWAs9IWqsD9ZiZWYfV/Wbxo8CN\nkmaSzxwCiIgjG6nKzMw6pm4QXJgfZmY2xgwYBJI2iYi/RoSvK2RmNkYNdozg4taApB80XIuZmXXB\nYEGgyvDmTRZiZmbdMVgQRD/DZmY2Rgx2sPglkhaTWgar5WHy84iI5zZanZmZNW7AIIiIcZ0qxMzM\numMo9yMwM7MxyEFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4\nB4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEGu3l9YyTNAx4B\nlgJPR8TUbtViZlayrgVB9uqIeKDLNZiZFc1dQ2ZmhetmEARwuaTZkg5tnyjpUEmzJM1auHBhF8oz\nMytDN7uGdouIeyStB8yUdEtE/Ko1MSJOA04DmDp1anSryBJNnzF9+MvuP/xlzaw7utYiiIh78s8F\nwEXAzt2qxcysZF0JAklrSJrQGgb2AuZ0oxYzs9J1q2toMnCRpFYN346In3WpFjOzonUlCCLiL8BL\nurFtMzNblk8fNTMrnIPAzKxwDgIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCucgMDMrnIPA\nzKxwDgIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCucg\nMDMrnIPAzKxwDgIzs8I5CMzMCucgMDMr3ErdLsDGlukzpg9/2f2Hv6yZDZ9bBGZmhXMQmJkVzkFg\nZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEcBGZmhXMQ\nmJkVzkFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY437PYeobvd2zWHW4RmJkVzkFgZlY4B4GZWeEc\nBGZmhfPBYhsTVuRAM/hgs5XNLQIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8L5rCEzfHkLK5tbBGZm\nhXOLwGwFuTVho51bBGZmhXMQmJkVzl1DZl3kbiXrBV0LAkl7A18FxgHfjIjPd6sWs9HI11eykdKV\nIJA0DjgZ2BO4G/iDpBkR8adu1GNWIrdGrKVbLYKdgdsi4i8Akr4DvAFwEJiNAg6RsaVbQbAhcFfl\n+d3AS7tUi5l10Ip2aZWmE8HZsweLJR0KHJqfPirp1hVY3STggRWvqiNGU60wuuodTbXC6Kp3NNUK\no6je4zhuRWrdtM5M3QqCe4CNK883yuP+ISJOA04biY1JmhURU0diXU0bTbXC6Kp3NNUKo6ve0VQr\njK56O1Frt75H8AdgC0mbSVoFeBswo0u1mJkVrSstgoh4WtIRwKWk00fPiIibulGLmVnpunaMICJ+\nAvykQ5sbkS6mDhlNtcLoqnc01Qqjq97RVCuMrnobr1UR0fQ2zMysh/laQ2ZmhRvTQSBpb0m3SrpN\n0tFdrOMMSQskzamMW0fSTElz88+1K9OOyTXfKum1lfE7SroxTztRkhqodWNJV0r6k6SbJB3Vq/VK\nGi/pGkk35FqP69VaK9sZJ+k6ST8aBbXOy9u5XtKsUVDvREnfl3SLpJsl7dqL9UraMr+nrcdiSR/u\naq0RMSYfpIPQtwObA6sANwBbd6mWVwA7AHMq474AHJ2Hjwb+Ow9vnWtdFdgsv4Zxedo1wC6AgJ8C\n+zRQ6/rADnl4AvDnXFPP1ZvXu2YeXhn4fd5ez9VaqfnfgG8DP+rlv4O8nXnApLZxvVzvWcB78/Aq\nwMRerjdvaxxwH+l8/67V2siL64UHsCtwaeX5McAxXaxnCssGwa3A+nl4feDWvuoknVm1a57nlsr4\nacCpHaj7EtI1oXq6XmB14FrSN9R7slbS92WuAHbn2SDoyVrzuuexfBD0ZL3AWsAd5OOevV5vZf17\nAb/tdq1juWuor8tYbNilWvoyOSLuzcP3AZPzcH91b5iH28c3RtIUYHvSnnZP1pu7Wq4HFgAzI6Jn\nawW+Avw78ExlXK/WChDA5ZJmK33Tv5fr3QxYCHwrd719U9IaPVxvy9uA8/Nw12ody0EwakSK8546\nfUvSmsAPgA9HxOLqtF6qNyKWRsR2pL3tnSVt2za9J2qV9HpgQUTM7m+eXqm1Yrf83u4DHC7pFdWJ\nPVbvSqTu169FxPbAY6TulX/osXpR+jLt/sD32qd1utaxHASDXsaiy+6XtD5A/rkgj++v7nvycPv4\nESdpZVIInBcRF/Z6vQARsQi4Eti7R2t9GbC/pHnAd4DdJZ3bo7UCEBH35J8LgItIVw3u1XrvBu7O\nLUKA75OCoVfrhRSw10bE/fl512ody0HQ65exmAEcnIcPJvXFt8a/TdKqkjYDtgCuyU3GxZJ2yWcG\nvLOyzIjJ6z4duDkivtzL9UpaV9LEPLwa6VjGLb1Ya0QcExEbRcQU0t/izyPiHb1YK4CkNSRNaA2T\n+rLn9Gq9EXEfcJekLfOoPUiXte/JerNpPNst1KqpO7U2dRCkFx7AvqSzXm4HPtnFOs4H7gX+Ttpz\neQ/wPNKBw7nA5cA6lfk/mWu+lcpZAMBU0j/j7cBJtB0YG6FadyM1Sf8IXJ8f+/ZivcCLgetyrXOA\nT+fxPVcguRbWAAADwElEQVRrW92v4tmDxT1ZK+lsuxvy46bW/0+v1pu3sx0wK/89XAys3av1AmsA\nfwPWqozrWq3+ZrGZWeHGcteQmZnV4CAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8B6lqSl+TK9\ncyT9sPXlsRFY7xRVLglec5nVJP1S0riRqGEkSfrJQO+NpO9I2qKTNdno4iCwXrYkIraLiG2BB4HD\nu1jLu4ELI2JpUxuQNKxbx0bEvpEusdGfr5EudmfWJweBjRZXUbmyoqSPS/qDpD/q2RvSTFG6Ick3\nlG5Uc1m+9ETrBh43SLqBSqDkZX4t6dr8+H/9bP/tVL6+P8D2b5F0pqQ/SzpP0msk/VbpZiM7t69U\n0rskzZD0c9K3Svtcdx5/sdKVQG/Ss1cDbd1AZlK+LMSP8+ucI+mteZZfA68ZbtDY2OcgsJ6Xu2P2\nIF8rStJepOut7Ey6rMCOevbKmFsAJ0fENsAi4E15/LeAD0XES9pWvwDYMyJ2AN4KnNjH9lcBNo+I\neTW2/0/A/wBb5ce/ki7b8THgE/28xB2AN0fEKwdZ97sjYkfSZQWOlPS8tvXsDcyPiJfkVtTPACLi\nGeA2oP21mwEOAuttqynda6B1bfaZefxe+XEd6WY0W5E+PAHuiIjr8/BsYEruP58YEb/K48+pbGNl\n4BuSbiRdDnjrPuqYRAqVlsG2f2P+8L0JuCLSdVxuJN2cqC8zI+LBGus+MrdoriZdjbK93/9GYE9J\n/y3p5RHxcGXaAmCDfrZvhXNT0XrZkojYTtLqpLsyHU7aYxdwQkScWp1Z6UY6T1ZGLQVWG2QbHwHu\nJ+0tPwd4oq86gPHVTdXc/jOV58/Q///bYzXW/SrgNcCuEfG4pF+01URE/FnSDqSLBP6XpCsi4jN5\n8vj8OsyW4xaB9byIeBw4Evho7ue+FHi30s1zkLShpPUGWH4RsEjSbnnU2yuT1wLuzXvwB5HuIdu+\n/EPAOEmtD94hbX+I+lv3WsBDOQS2It2ndhmSNgAej4hzgS+SupxaXki6SqXZctwisFEhIq6T9Edg\nWkScI+lFwFXpMuw8CryD1ALozyHAGZICuKwy/hTgB5LeSepTf6yvhfMyuwGXR8Rlw9h+LQOs+2fA\nByTdTLoU8dV9LP7PwBclPUO65PkHASRNJrWu7lvR+mxs8mWozWrIXS4fiYiDul3LUEn6CLA4Ik7v\ndi3Wm9w1ZFZDRFwLXNmLXyirYRFwVreLsN7lFoGZWeHcIjAzK5yDwMyscA4CM7PCOQjMzArnIDAz\nK9z/BxF+4oGwyjq6AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e51134438>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"frenda4 = pd.cut(base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")], bins=faixa, right=False)\n",
"t4 = (frenda4.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t4,\"\\n\")\n",
"\n",
"plot = base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")].plot.hist(bins=faixa,title=\"Problema Alimentar - NORDESTE - 2013(H6)\", weights=zeros_like(base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")])+1./base.RENDA[(base.Problema_Alimentar=='Sim')&(base.REGIAO==\"NORDESTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"darkgreen\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 209,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 12.7\n",
"[350, 700) 26.2\n",
"[700, 1050) 22.2\n",
"[1050, 1400) 15.4\n",
"[1400, 1750) 6.8\n",
"[1750, 2100) 7.7\n",
"[2100, 2450) 3.2\n",
"[2450, 2800) 0.9\n",
"[2800, 3150) 1.8\n",
"[3150, 3500) 1.8\n",
"[3500, 3850) 0.0\n",
"[3850, 4200) 0.9\n",
"[4200, 4550) 0.5\n",
"[4550, 4900) 0.0\n",
"[4900, 5250) 0.0\n",
"[5250, 5600) 0.0\n",
"[5600, 5950) 0.0\n",
"[5950, 6300) 0.0\n",
"[6300, 6650) 0.0\n",
"[6650, 7000) 0.0\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAGDCAYAAAAmphcsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYHVWdxvHvK/sS2RKQPcAgiA5LiAgDowiigBsug6IC\n4oIoiyijAi40o4Cj4sIIDqvsCMqqIrIIKoJiAoGAgICGYQkkSEIg7OE3f5xzpbjc7q7u9F26z/t5\nnvt03Vp/dXNTb9WpulWKCMzMrFyv6HYBZmbWXQ4CM7PCOQjMzArnIDAzK5yDwMyscA4CM7PCOQhG\niKQ+SWcOMHyGpLd0sqbhkHSNpE/k7g9LurzbNZn1CklHSTpwBOd3tKRPj9T8hqvoIMgb56ckPSHp\nYUmnSlq223W1m5K/SfrLQONFxFkR8dZO1dUgaVtJ93d6uXnZH5I0JX8nZkr6laRt8rA+Sc/lYY3X\n3Mq0IWm6pFdU+n0jf6/+vTLN/DxudT5r5RB+Or9/RNIFklZtqm8jSZdIekzS45KulvRvNdbrHZJu\nyMv+h6SzJK1RGf5RSQuaanpC0mp5+DaSrsvLfVTSHyS9XtKhlXGfbprHbZXPZX7TfL84zH+ft0u6\nVtJcSQ9JOknSuMrwJSSdImleHv75puk3lTRV0pP576ZN035P0oOS5kg6TtJileETgD2A4/P7lt/T\nFjtT1fV+Mn8em+fRvwMcKmnx4XweI6XoIMjeGRHLApOAycBXmkfIG86x9Fm9EVgZWFfS67tdzEiT\ntOgwp/s88H3gSGAVYC3gWOBdldHOjYhlK6/lm2azGvDB5nlHxO8b0wCvzb2Xr8zn/3K//fI4/wIs\nS9pQNOpbD/gDMB1YJy/rQuBySVsNsF7vB87O6zY+L/8Z4FpJK1RGvb5p3ZaNiAclvRL4BfA/wIrA\n6sDhwDMRcWRlvfZpmsdrK/PepGm+3+qv3kEsB3wjr/trci3frgzvA9YH1gbeDHxR0o75c1gcuBg4\nE1gBOA24uLIRPpi0DXgd8GrSNqG6PfgocGlEPFW32LwztWzlM/oM8Dfgxjx8JnAHL/2OddxY2rgt\nlIh4APgV6UvQSPUjJP0BeJK00Vwt7409KuluSZ9sms2Sks7Ne2o3Stqk1bIkvULSwZLuyXtn50la\nMQ+bmPcY9pJ0X94z2Sfvfd2S94R+WJnXepJ+k+fzSN7Ta944NduT9B/i0tzdUt5LvLbyPiR9RtJd\neR2/npd/Xd4DO6+6Z6O0Fzot13ydpI0rw2ZI+s+8To/lz21JScvkf4fVKntRq0naQtL1eV4zJf2w\naVkhaV9JdwF3DbL+rdZ1OeC/gH0j4oKImB8Rz0XELyJiKHuv3wIOH24YNUTEXOAiYNNK7z7ShvbL\nEfFoRDweEccAZwD/3Wo+kgQcDXwjIs6OiKci4iHgE8ATwOdqlPPqXNM5EbEgz+PyiLhl2Cs4THkd\nLouIJyNiDnAisHVllD2Br0fEnIi4HTiBtAEH2BZYFPh+RDyTPzsB2+Xh7wT+J3+2s4FjgI9V5r0T\n8NuFXIU9gdPjpbd0uAZ4+0LOd6E4CDJJawI7AzdVeu8O7A2MA+4FfgLcT9obeT9wpKTtKuO/G/gp\naa/pbOCi6qFlxf7ALsCb8rzmkPY8q95A2rP5AGlP7svAW0h7c7tKelOjdOAoXtxDWpO0wehvPZfO\ntZ+VXx8c4mHp24DNgS2BL5L+o30kL/d1wG55OZsBpwCfAlYiHU5fImmJyrx2BXYk7d1uDHw0IuaT\n/sM9WN0rBRaQNlrjga2A7Ul7V1W7kD63jYawPg1bAUuS9rAXxgXAPF7c+AyLpJWA9wJ3V3rvQPp+\nNTsP2FrSUi2GbUA6snnJdBHxAnB+nudg/goskHSapJ2ajiK67Y1AowlqBWBV4ObK8Jt58QjstcAt\nTRvh6vBmAtbIOwkA/wrcOdxCJa2d6z29adDtQMudxk5xEKSN9VzgWlLaH1kZdmpE3BYRzwOvIu15\nfCkino6IacBJpDbDhqkR8bOIeA74LmnDsmWLZe4DfDki7o+IZ0gb7vc37UV+PS/ncmA+cE5EzMpH\nLr8HNgOIiLsj4oq8hzM7L/dN9O+9pGaBy4FfAosxtL2Rb0XEvIi4DbgVuDwi/hYRj5H25DfL4+0N\nHB8Rf8p7kafl5VY/j2Mi4sGIeBT4OS/d+32JiJgaEX+MiOcjYgYpWJrX86i8N1f70L1iJeCR/G89\nkF3zUUnjdXVzqcBXga8Os933GEmPAY+QQm//yrDxwMwW08wk/V9escWw8ZVxWk03vvJ+y6Z1uwcg\nIuYB25DW7URgdj4yXmUI63Vj07zfNoRpW5K0A2kP+2u5V+P83mOV0eaRduQaw6vDmodfBnxW0gRJ\nrwIOyP2Xzn+XBx5vmn61pvWaS/qsWtkD+H1E/L2p/+N53l3jIIBdImL5iFg7Ij7TtBG5r9K9GvBo\nRFS/CPeS2ihfNn7e42ocPTRbG7iw8sW5nbTHW/2P9XCl+6kW75cFkLSKpJ9IekDSPFL7Z/U/d7M9\ngfPyBvVp0l5hv81DLdSqi7SOBzX9B1mTl34eD1W6n6xM+zKSXi3pF0onAOeRArt5Pe9rMWlj+v+t\nNDUd2mKUfwDjazTpnJe/L43Xm5tHiIhLSf/2nxpkXq0cEBHLkY6QVgDWqAx7hLTH22xV4AVgTov1\nfKQyTqvpHqm8/2PTuq1XWafbI+KjEbEG6chvNdKRal2Tmub96+YRlE6Y//PE6kAzk7Ql6aj7/RHx\n19y7Mc0rK6Mux4sb7yeahjUPP4LUIjANuI7UNPccL37H5/BiaDQ82LRey5N2KlvZg3Reotk4YG6L\n/h3jIBhY9RDyQWBFVa5QIB1yP1B5v2ajQ+nk8hp5umb3ATs1fYGWzHv7Q3VkrvNfI+KVpGYatRpR\n6SqR7YCP5A3qQ6Rmop0lDRQew3EfcETTOi4dEefUmLbVLXF/RDqptn5ez0N5+Xr2eyvdiNin0tR0\nZItRricdsexSo746vpxrXHqwEVuJiOmkk6LH5nZ+gCuB/2gx+q6kcwdPtljPO0mh9JLp8vfzfcBV\nw6jtDuBU8vm0kRIR/xcvPbHaUm52vAT4WERcVZl+Dukop9rMsgm56Sj/3bjyeUIK3Nvy9E9FxH4R\nsXpErEvaOZiad+oAbiGfLxkqSVuTwvNnLQa/hpc2Z3Wcg6CmiLiPtJdwVD6puTHwcdIeeMPmkt6b\n9yoPJG1Y/thidv8LHJHbDMmHou8eZmnjSHs6j0laHfjCAOPuTmrv3YDUDLMp6Yt9P7ltfwSdCOwj\n6Q1KllG69K95j6qVh4GVKm2zkNZzHvCEpA2BEb32OjdtfY204d1F0tKSFstt4kO+wiUiriE1nQ3l\naKvZaaSjxMYVJYcD/6Z0EcOKksZJ2p+0p/mlfuoI4D+BryhdGrtkbvY4ibR3/L3BipC0oaSD8o5E\n43zabrT+breVpNeRmnD2j4iftxjldNK6riDpNcAnSaEF6aTsAuAApUtFDyDtPPwmz3t1pQsTlI84\nvgocVpn3pQzc7DqQPYHzm1oUGt5EalbtGgfB0OwGTCTt5V8IHBYRV1aGX0w6uTuHtNF9bz5f0OwH\npD2ayyU9TvoP9YZh1nQ46TK3x0ht/hcMMO6ewHER8VD1RQqmhdlgvUxETCH9J/wh6fO4m5onUPMe\n5znA33Kz0mqkjdmHSIfxJwLnjmS9eblHA58nXTI4m3RUsx+piaDhA3r5tfYr9zPLr9C63b5uPc+S\nvitfze/vIrU/bwLMIO39vg94W0T8YYD5nEv6Pn6OtJf7F2ApYOuI+Edl1K1arNvrSZ/5G4A/SZpP\n+r7eChw0hNW5uWm+Q2lWqjoImACcrKbfK2SHAfeQmm2vIZ3Tugz++XnuQgrOuaTv4y65P8B6pJ29\n+aQQPjifo2s4nXT03OqkfL8kLUk6antZs5DS70Q24qXfsY5T+ME0Zma1SDoSmBURww2y5vkdDdwT\nEceNxPyGXYeDwMysbG4aMjMrnIPAzKxwDgIzs8I5CMzMCrdQN8bqlPHjx8fEiRO7XYaZ2agyderU\nRyJiwmDjjYogmDhxIlOmTOl2GWZmo4qke+uM56YhM7PCOQjMzArnIDAzK5yDwMyscA4CM7PCOQjM\nzArnIDAzK5yDwMyscA4CM7PCOQjMzArnIDAzK5yDwMyscA4CM7PCjYq7j3ZTX19fV6Y1M+sUHxGY\nmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwE\nZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgH\ngZlZ4RwEZmaFcxCYmRXOQWBmVri2BYGkNSVdLekvkm6T9Nncv0/SA5Km5dfO7arBzMwGt2gb5/08\ncFBE3ChpHDBV0hV52Pci4jttXLaZmdXUtiCIiJnAzNz9uKTbgdXbtTwzMxuejpwjkDQR2Az4U+61\nv6RbJJ0iaYVO1GBmZq21PQgkLQucDxwYEfOAHwHrApuSjhiO7me6vSVNkTRl9uzZ7S7TzKxYbQ0C\nSYuRQuCsiLgAICIejogFEfECcCKwRatpI+KEiJgcEZMnTJjQzjLNzIrWzquGBJwM3B4R3630X7Uy\n2nuAW9tVg5mZDa6dVw1tDewOTJc0Lfc7FNhN0qZAADOAT7WxBjMzG0Q7rxq6FlCLQZe2a5lmZjZ0\n/mWxmVnhHARmZoVzEJiZFa6dJ4uL19fX15VpzcyGwkcEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaF\ncxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ\n4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBm\nVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCYmRXOQWBmVjgHgZlZ4RwEZmaFcxCY\nmRXOQWBmVjgHgZlZ4RwEZmaFW7TuiJJWAFYDngJmRMQLbavKzMw6ZsAgkLQcsC+wG7A4MBtYElhF\n0h+B4yLi6rZXaWZmbTPYEcHPgNOBf4+IudUBkjYHdpe0bkSc3DyhpDXztKsAAZwQET+QtCJwLjAR\nmAHsGhFzFnZFzMxseAYMgojYYYBhU4GpA0z+PHBQRNwoaRwwVdIVwEeBqyLim5IOBg4GvjTkys3M\nbEQM6WSxpAmSviHpaEnrDzRuRMyMiBtz9+PA7cDqwLuB0/JopwG7DL1sMzMbKUO9auho4NfAhcDZ\ndSeSNBHYDPgTsEpEzMyDHiI1HZmZWZcMGASSfi3pjZVei5Pa9WcAS9RZgKRlgfOBAyNiXnVYRATp\n/EGr6faWNEXSlNmzZ9dZlJmZDcNgRwS7Au+UdI6k9YCvAkcBPwA+M9jMJS1GCoGzIuKC3PthSavm\n4asCs1pNGxEnRMTkiJg8YcKEemtjZmZDNtjJ4seAL0haFzgCeBDYr/kKolYkCTgZuD0ivlsZdAmw\nJ/DN/PfiYdZuZmYjYLDfEawHfBp4FjgIWA84V9IvgWMjYsEAk28N7A5MlzQt9zuUFADnSfo4cC/p\nqMPMzLpksN8RnAMcCCwDnBER2wNvk7QHcDmwfX8TRsS1gPoZ3O90ZmbWWYMFwRLA34FlgaUbPSPi\ndEk/bWdhZmbWGYMFwaeBH5KahvapDoiIp9pVlJmZdc5gJ4uvA67rUC1mZtYFvg21mVnhHARmZoVz\nEJiZFa7Wg2kkTQa+DKydpxHpDhEbt7E2MzPrgLpPKDsL+AIwHfCTyczMxpC6QTA7Ii5payVmZtYV\ndYPgMEknAVcBzzR6Vm4kZ2Zmo1TdINgL2BBYjBebhgJwEJiZjXJ1g+D1EbFBWysxM7OuqHv56HWS\nNmprJWZm1hV1jwi2BKZJ+jvpHIEvHzUzGyPqBsGOba3CzMy6plbTUETcC6wJbJe7n6w7rZmZ9bZa\nG3NJhwFfAg7JvRYDzmxXUWZm1jl19+rfA7wLmA8QEQ8C49pVlJmZdU7dIHg2IoL02wEkLdO+kszM\nrJPqBsF5ko4Hlpf0SeBK4MT2lWVmZp1S66qhiPiOpB2AecAGwNci4oq2VmZmZh0xYBBIUm4SIm/4\nX7bxr45jZmajz2BNQ1dL2l/SWtWekhaXtJ2k04A921eemZm122BNQzsCHwPOkbQOMBdYihQglwPf\nj4ib2luimZm104BBEBFPA8cBx0laDBgPPBURcztRnJmZtV/dW0wQEc8BM9tYi5mZdYFvE2FmVjgH\ngZlZ4RwEZmaFq3vTuS0l/VnSE5KelbRA0rx2F2dmZu1X94jgh8BuwF2ky0c/ARzbrqLMzKxzajcN\nRcTdwCIRsSAifowfVmNmNibUvXz0SUmLkx5X+S3SZaQ+v2BmNgbU3Zjvnsfdj/RMgjWB97WrKDMz\n65y6RwSbA7+MiHnA4W2sx8zMOqzuEcE7gb9KOkPSOyTV/kWymZn1troPr98L+Bfgp6Srh+6RdFI7\nCzMzs84Y0r2GJP2K9LjKpYBdSJeRmpnZKFb3B2U7STqV9DuC9wEnAa9qY11mZtYhdY8I9gDOBT4V\nEc+0sR4zM+uwus8s3q3dhZiZWXcM9sziayNiG0mPk84N/HMQEBHxyrZWZ2ZmbTfYE8q2yX/HdaYc\nMzPrtLoni8+o08/MzEafuj8oe231Tf5B2eYjX46ZmXXagEEg6ZB8fmBjSfPy63HgYeDijlRoZmZt\nNWAQRMRR+fzAtyPilfk1LiJWiohDOlSjmZm1Ud1bTBwiaQVJW0h6Y+M12HSSTpE0S9KtlX59kh6Q\nNC2/dl6YFTAzs4VT63cEkj4BfBZYA5gGbAlcD2w3yKSnkp5udnpT/+9FxHeGVKmZmbVF3ZPFnwVe\nD9wbEW8GNgPmDjZRRPwOeHT45ZmZWbvVDYKnI+JpAElLRMQdwAYLsdz9Jd2Sm45WWIj5mJnZQqob\nBPdLWh64CLhC0sXAvcNc5o+AdYFNSY+8PLrVSJL2ljRF0pTZs2cPc1FmZjaYuvcaek/u7JN0NbAc\ncNlwFhgRDze6JZ0I/KKf8U4ATgCYPHlytBrHzMwW3mD3GlqxRe/p+e+yDKP9X9KqETEzv30PcOtA\n45uZWXsNdkQwlXSzOVX6Nd4HqYmnX5LOAbYFxku6HzgM2FbSpnn6GcCnhlO4mZmNjMFuOrfOwsy8\nn9tXn7ww8zQzs5FV93cEAj4MrBMRX5e0FvCqiLihrdUVrK+vr6vTm1k56l41dBywFfCh/P5x4Ni2\nVGRmZh1V91GVb4iISZJuAoiIOZIWb2NdZmbWIXWPCJ6TtAj5KWWSJgAvtK0qMzPrmLpBcAxwIbCy\npCOAa4Ej21aVmZl1TN0flJ0laSqwPenS0V0i4va2VmZmZh0xaBDkJqHbImJD4I72l2RmZp00aNNQ\nRCwA7syXjJqZ2RhT96qhFYDbJN0AzG/0jIh3taUqMzPrmLpB8NW2VmFmZl1T92Txb9tdiJmZdUfd\ny0fNzGyMchCYmRXOQWBmVri6dx9dHzgK2AhYstE/IgZ8HoGZmfW+ukcEPyY9a/h54M3A6cCZ7SrK\nzMw6p24QLBURVwGKiHsjog94e/vKMjOzTqn7O4JnJL0CuEvSfsADpGcWm5nZKFf3iOCzwNLAAcDm\nwO7Anu0qyszMOqfuD8r+nDufAPZqXzlmZtZpAwaBpO9HxIGSfk5+KE2V7zVkZjb6DXZEcEb++512\nF2JmZt0xYBBExNTcOQV4KiJegH8+o2CJNtdmZmYdUPdk8VWkk8UNSwFXjnw5ZmbWaXWDYMmIeKLx\nJncvPcD4ZmY2StT9HcF8SZMi4kYASZsDT7WvrJHV19fX7RLMzHpW3SA4EPippAdJD69/FfCBtlVl\nZmYdU/t3BJI2BDbIve6MiOfaV5aZmXVK3SMCgNcDE/M0kyQREae3pSozM+uYurehPgNYD5gGLMi9\ng3QXUjMzG8XqHhFMBjaKiJf9utjMzEa3upeP3ko6QWxmZmNM3SOC8cBfJN0APNPo6XsNmZmNfnWD\noK+dRZiZWffUvXz0t5LWBtaPiCslLQ0s0t7SzMysEwY8RyBp5fz3k8DPgOPzoNWBi9pbmpmZdUK/\nQSBpEvD1/HZfYGtgHkBE3AWs3PbqzMys7QY6ItgQuDl3PxsRzzYGSFqUFg+qMTOz0affIIiIs0kP\nqQe4RtKhwFKSdgB+Cvy8A/WZmVmbDXiOICIuzp0HA7OB6cCngEuBr7S3NDMz64S6Vw29AJyYX2Zm\nNobUvdfQ32n98Pp1R7wiMzPrqKHca6hhSeA/gBVHvhwzM+u0Wvcaioh/VF4PRMT3gbe3uTYzM+uA\nuk1DkypvX0E6QhjKswzMzKxH1d2YH13pfh6YAew64tWYmVnH1b1q6M3tLsTMzLqjbtPQ5wcaHhHf\n7We6U4B3ALMi4nW534rAuaTHXs4Ado2IOfVLNjOzkVT3wTSTgU+Tbja3OrAPMAkYl1/9ORXYsanf\nwcBVEbE+cFV+b2ZmXVL3HMEawKSIeBxAUh/wy4j4yEATRcTvJE1s6v1uYNvcfRpwDfClmnWYmdkI\nq3tEsArwbOX9s7nfcKwSETNz90MLMR8zMxsBdY8ITgdukHRhfr8LaW9+oURESGp5F1NJewN7A6y1\n1loLuygzM+tH3R+UHQHsBczJr70i4shhLvNhSasC5L+z+lnmCRExOSImT5gwYZiLMjOzwdRtGgJY\nGpgXET8A7pe0zjCXeQmwZ+7eE7h4gHHNzKzNagWBpMNIJ3QPyb0WA86sMd05wPXABpLul/Rx4JvA\nDpLuAt6S35uZWZfUPUfwHmAz4EaAiHhQ0kCXjZLH262fQdvXXK6ZmbVZ3aahZyMiyLeilrRM+0oy\nM7NOqhsE50k6Hlhe0ieBK/FDaszMxoS69xr6Tn5W8TxgA+BrEXFFWyszM7OOGDQIJC0CXJlvPOeN\nv5nZGDNo01BELABekLRcB+oxM7MOq3vV0BPAdElXAPMbPSPigLZUZWZmHVM3CC7ILzMzG2MGDAJJ\na0XE/0XEQt9XyMzMetNg5wguanRIOr/NtZiZWRcMFgSqdK/bzkLMzKw7BguC6KfbzMzGiMFOFm8i\naR7pyGCp3E1+HxHxyrZWZ2ZmbTdgEETEIp0qxMzMumMozyMwM7MxyEFgZlY4B4GZWeEcBGZmhXMQ\nmJkVzkFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4B4GZWeEc\nBGZmhXMQmJkVzkFgZla4wZ5ZbKNUX19fV6Y1s9HHRwRmZoVzEJiZFc5BYGZWOAeBmVnhHARmZoVz\nEJiZFc5BYGZWOAeBmVnhHARmZoVzEJiZFc5BYGZWOAeBmVnhHARmZoVzEJiZFc5BYGZWuK49j0DS\nDOBxYAHwfERM7lYtZmYl6/aDad4cEY90uQYzs6J1OwisB/npZmZl6eY5ggCulDRV0t5drMPMrGjd\nPCLYJiIekLQycIWkOyLid42BORz2BlhrrbW6VaOZ2ZjXtSOCiHgg/50FXAhs0TT8hIiYHBGTJ0yY\n0I0SzcyK0JUgkLSMpHGNbuCtwK3dqMXMrHTdahpaBbhQUqOGsyPisi7VYmZWtK4EQUT8DdikG8s2\nM7OX8i+LzcwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyuc\ng8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK5yAwMyucg8DMrHAOAjOzwjkIzMwK\n5yAwMyvcot0uwMaWvr6+rkxrZsPnIwIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCucgMDMr\nnIPAzKxwDgIzs8I5CMzMCucgMDMrnIPAzKxwDgIzs8I5CMzMCufbUFvP8C2szbrDQWBjwsIGgYPE\nSuamITOzwvmIwAw3S1nZfERgZlY4B4GZWeEcBGZmhXMQmJkVzkFgZlY4XzVktpC6dcWRfzthI6Vr\nQSBpR+AHwCLASRHxzW7VYtYt3hhbL+hK05CkRYBjgZ2AjYDdJG3UjVrMzErXrSOCLYC7I+JvAJJ+\nArwb+EuX6jErjn9EZw3dCoLVgfsq7+8H3tClWsxsiEoMgrG8zj17sljS3sDe+e0Tku5ciNmNBx5Z\n+Ko6YjTVCqOr3tFUK4yuekdTrTCMeg8//PA2lTKohfls164zUreC4AFgzcr7NXK/f4qIE4ATRmJh\nkqZExOSRmFe7jaZaYXTVO5pqhdFV72iqFUZXvZ2otVu/I/gzsL6kdSQtDnwQuKRLtZiZFa0rRwQR\n8byk/YBfky4fPSUibutGLWZmpevaOYKIuBS4tEOLG5Empg4ZTbXC6Kp3NNUKo6ve0VQrjK56216r\nIqLdyzAzsx7mew2ZmRVuTAeBpB0l3SnpbkkHd7GOUyTNknRrpd+Kkq6QdFf+u0Jl2CG55jslva3S\nf3NJ0/OwYySpDbWuKelqSX+RdJukz/ZqvZKWlHSDpJtzrYf3aq2V5Swi6SZJvxgFtc7Iy5kmacoo\nqHd5ST+TdIek2yVt1Yv1Stogf6aN1zxJB3a11ogYky/SSeh7gHWBxYGbgY26VMsbgUnArZV+3wIO\nzt0HA/+duzfKtS4BrJPXYZE87AZgS0DAr4Cd2lDrqsCk3D0O+GuuqefqzfNdNncvBvwpL6/naq3U\n/HngbOAXvfw9yMuZAYxv6tfL9Z4GfCJ3Lw4s38v15mUtAjxEut6/a7W2ZeV64QVsBfy68v4Q4JAu\n1jORlwbBncCquXtV4M5WdZKurNoqj3NHpf9uwPEdqPtiYIderxdYGriR9Av1nqyV9HuZq4DteDEI\nerLWPO8ZvDwIerJeYDng7+Tznr1eb2X+bwX+0O1ax3LTUKvbWKzepVpaWSUiZubuh4BVcnd/da+e\nu5v7t42kicBmpD3tnqw3N7VMA2YBV0REz9YKfB/4IvBCpV+v1goQwJWSpir90r+X610HmA38ODe9\nnSRpmR5rNBcxAAAFZklEQVSut+GDwDm5u2u1juUgGDUixXlPXb4laVngfODAiJhXHdZL9UbEgojY\nlLS3vYWk1zUN74laJb0DmBURU/sbp1dqrdgmf7Y7AftKemN1YI/Vuyip+fVHEbEZMJ/UvPJPPVYv\nSj+mfRfw0+Zhna51LAfBoLex6LKHJa0KkP/Oyv37q/uB3N3cf8RJWowUAmdFxAW9Xi9ARMwFrgZ2\n7NFatwbeJWkG8BNgO0ln9mitAETEA/nvLOBC0l2De7Xe+4H78xEhwM9IwdCr9UIK2Bsj4uH8vmu1\njuUg6PXbWFwC7Jm79yS1xTf6f1DSEpLWAdYHbsiHjPMkbZmvDNijMs2IyfM+Gbg9Ir7by/VKmiBp\n+dy9FOlcxh29WGtEHBIRa0TERNJ38TcR8ZFerBVA0jKSxjW6SW3Zt/ZqvRHxEHCfpA1yr+1Jt7Xv\nyXqz3XixWahRU3dqbddJkF54ATuTrnq5B/hyF+s4B5gJPEfac/k4sBLpxOFdwJXAipXxv5xrvpPK\nVQDAZNJ/xnuAH9J0YmyEat2GdEh6CzAtv3buxXqBjYGbcq23Al/L/Xuu1qa6t+XFk8U9WSvparub\n8+u2xv+fXq03L2dTYEr+PlwErNCr9QLLAP8Alqv061qt/mWxmVnhxnLTkJmZ1eAgMDMrnIPAzKxw\nDgIzs8I5CMzMCucgMDMrnIPAepakBfk2vbdK+nnjx2MjMN+JqtwSvOY0S0n6raRFRqKGkSTp0oE+\nG0k/kbR+J2uy0cVBYL3sqYjYNCJeBzwK7NvFWj4GXBARC9q1AEnDenRsROwc6RYb/fkR6WZ3Zi05\nCGy0uJ7KnRUlfUHSnyXdohcfSDNR6YEkJyo9qObyfOuJxgM8bpZ0M5VAydP8XtKN+fVv/Sz/w1R+\nvj/A8u+QdKqkv0o6S9JbJP1B6WEjWzTPVNJHJV0i6TekX5W2nHfuf5HSnUBv04t3A208QGZ8vi3E\nL/N63irpA3mU3wNvGW7Q2NjnILCel5tjtiffK0rSW0n3W9mCdFuBzfXinTHXB46NiNcCc4H35f4/\nBvaPiE2aZj8L2CEiJgEfAI5psfzFgXUjYkaN5f8LcDSwYX59iHTbjv8EDu1nFScB74+INw0y749F\nxOak2wocIGmlpvnsCDwYEZvko6jLACLiBeBuoHndzQAHgfW2pZSeNdC4N/sVuf9b8+sm0sNoNiRt\nPAH+HhHTcvdUYGJuP18+In6X+59RWcZiwImSppNuB7xRizrGk0KlYbDlT88b39uAqyLdx2U66eFE\nrVwREY/WmPcB+Yjmj6S7UTa3+08HdpD035L+PSIeqwybBazWz/KtcD5UtF72VERsKmlp0lOZ9iXt\nsQs4KiKOr46s9CCdZyq9FgBLDbKMzwEPk/aWXwE83aoOYMnqomou/4XK+xfo///b/Brz3hZ4C7BV\nRDwp6ZqmmoiIv0qaRLpJ4DckXRUR/5UHL5nXw+xlfERgPS8ingQOAA7K7dy/Bj6m9PAcJK0uaeUB\npp8LzJW0Te714crg5YCZeQ9+d9IzZJunnwMsIqmx4R3S8oeov3kvB8zJIbAh6Tm1LyFpNeDJiDgT\n+Dapyanh1aS7VJq9jI8IbFSIiJsk3QLsFhFnSHoNcH26DTtPAB8hHQH0Zy/gFEkBXF7pfxxwvqQ9\nSG3q81tNnKfZBrgyIi4fxvJrGWDelwH7SLqddCviP7aY/F+Bb0t6gXTL808DSFqFdHT10MLWZ2OT\nb0NtVkNucvlcROze7VqGStLngHkRcXK3a7He5KYhsxoi4kbg6l78QVkNc4HTul2E9S4fEZiZFc5H\nBGZmhXMQmJkVzkFgZlY4B4GZWeEcBGZmhft/Rd7ZVs30Z+cAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4b702240>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"frenda39 = pd.cut(base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base.REGIAO==\"CENTRO-OESTE\")], bins=faixa, right=False)\n",
"t39 = (frenda39.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t39,\"\\n\")\n",
"\n",
"plot = base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base9.REGIAO==\"CENTRO-OESTE\")].plot.hist(bins=faixa,title=\"Problema Alimentar - CENTRO-OESTE - 2009(H7)\", weights=zeros_like(base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base9.REGIAO==\"CENTRO-OESTE\")])+1./base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base9.REGIAO==\"CENTRO-OESTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"black\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 210,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0, 350) 12.7\n",
"[350, 700) 26.2\n",
"[700, 1050) 22.2\n",
"[1050, 1400) 15.4\n",
"[1400, 1750) 6.8\n",
"[1750, 2100) 7.7\n",
"[2100, 2450) 3.2\n",
"[2450, 2800) 0.9\n",
"[2800, 3150) 1.8\n",
"[3150, 3500) 1.8\n",
"[3500, 3850) 0.0\n",
"[3850, 4200) 0.9\n",
"[4200, 4550) 0.5\n",
"[4550, 4900) 0.0\n",
"[4900, 5250) 0.0\n",
"[5250, 5600) 0.0\n",
"[5600, 5950) 0.0\n",
"[5950, 6300) 0.0\n",
"[6300, 6650) 0.0\n",
"[6650, 7000) 0.0\n",
"Name: RENDA, dtype: float64 \n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAGDCAYAAAAmphcsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYHGW99vHvbQgQFglIjGEJAU8EgQMBAsIrKrIooLLo\nOWpUjChGBVk86jmgolFfxKO4viAKguwoyiqyBcQFBTGBEBJZghIkEJIghCQQQMLv/eN5WopmlprJ\nVHfP1P25rr66utZf9/T0XfXUpojAzMzq62XtLsDMzNrLQWBmVnMOAjOzmnMQmJnVnIPAzKzmHARm\nZjXnIGgTSVMlndfD8HmS9m5lTf0h6TeSDsvd75d0XbtrMuuOpLdKumwA5/cOST8bqPm1i4OgD/KP\n8wpJyyUtlHSWpHXaXVfVlPxN0l96Gi8izo+It7SqrgZJe0ia34blzpO0SNLahX6HSfpN4bUkfVbS\n3Pzd+bukEyWtURjnLEnP5u/VY5KmSdqqMPxDklbm4csl3S/pJ5JeUxhnnKQojNN4vCcP30TSxZIe\nlfSEpNl5vm8ojPtkF/MYm8P+6ab+v+znZ/YaSZdLWpzf67WStmwa51OSHpG0VNKZTZ/VBpIuzbU+\nIOl9TdMeJum+XOM1kjZqKuEE4OuF8UPSvzXN40UraZImSPp9/tzmSzq+MSwifglsI2m7/nwencJB\n0HfviIh1gB2BicAXmkfI//xD6bN9I/BKYAtJO7e7mIEmabVVmHwYcHQPw78PTAE+CKwL7AfsBVzU\nNN438vdqY+Ah4Iym4Tfn4esBewMrgBmStm0ab2RErFN4NNZWzwUeBDYDXgEcAiyMiN83xgW26WIe\nf8/9Ptk033f08rl0ZyRwBbAlMBq4Fbi8MVDSW4FjSZ/RZsAWwJcL058CPJunfT9wqqRt8rR7AF8D\nDgQ2AO4HLizMe2dgvYi4pY81XwD8Ls/zTcDhkg4oDL+Q9DcetIbSj1VLRcRDwNXAtvCvJpITJP0B\neIr0o7mRpCvyms99kj7aNJs1Jf1M0jJJt0navqtlSXqZpGMl/VXSPyRdJGmDPKyxJniopAclPS7p\n45J2ljRL0hJJJxfm9WpJv87zeVTS+ZJG9vJ2J5P+Wa/K3V3Ka5g3FV6HpMOV1oaXSfpqXv4f89re\nRZJWL4z/dkkzc81/LK5lKa19fya/pyfy57am0tr41cBGhbXVjSTtIunmPK8Fkk5uWlZIOkLSXGBu\nL++/J98EPtPVZyhpPHA48P6IuDkinouIOcC7gH0l7dk8TUSsIIXEhK4WFhErI+KvEXE48Ftgask6\ndwbOiogncx23R8TVJacdMBFxa0ScERGPRcQ/ge8AW0p6RR5lMnBGRMyJiMeBrwAfAsh/63cBx0fE\n8oi4ifS9PCRP+3bgF3naZ4GvAm+U9Oo8fD/SZ9ZX44DzG589cBMvhCbAb4C39WO+HcNB0E+SNgX2\nB24v9D6EtGawLvAA8FNgPrAR8B/A15r++Q8Efk5a07gAuEzS8C4WdyRwEGltZCPgcdKaUdHrgPHA\ne4DvAp8nrTluA7xb0psapQMn5vm8FtiUHn5MJK2Vaz8/P95b/EEt4a3ATsCuwH8DpwEfyMvdFpiU\nl7MDcCbwMdIa64+AK4rNAsC7gX2BzYHtgA9FxJOkf/CHC2urDwMrgU8BGwK7kdYwD2+q7SDS57Z1\nH95Ps+mkH4LPdDFsL2B+RNxa7BkRDwK3APs0T5B/7CYB95VY9iXAG0rWeQtwiqT3ShpbcppWeCPw\nSET8I7/eBrijMPwOYHQOitcAz0XEvU3Diz/KRcrPja2mfwfu6UeN3wU+KGm4UjPWbsD1heF3AeMk\nvbwf8+4IDoK+u0zSEtJawW9Jm6INZ+W1keeAVwGvB/4nIp6OiJnAj0lNBA0zIuIXec3o28CapB/M\nZh8HPh8R8yPiGdIP9380NWl8NS/nOuBJ4MKIWJS3XH4P7AAQEfdFxLSIeCYiFuflvonuvRN4BrgO\n+BUwnL6t/XwjIpbmNeHZwHUR8beIeIK0Jr9DHm8K8KOI+FNe8zo7L7f4eXw/Ih6OiMeAX9LNWnN+\nnzMi4pa89juPFCzN7/PEvGa6og/vpytfBI6UNKqp/4bAgm6mWZCHN3wmf6+WAbvzwlpuTx4mrUQU\nPZq3ghqP1+b+/0n6HhwP3J+3vPrSzPf9pvl+tQ/TdknSJqQVmv8q9F4HeKLweml+XjcPW8qLLc3D\nAK4B/lPSdpJGkP4uAayVh48kfb7Nbiu+N1LTVNGVpJWhFcDdpC2WPxeGN+bZ25Z1x3IQ9N1BETEy\nIjaLiMObfkQeLHRvBDwWEcUv3gOkNuCXjB8Rz/PC1kOzzYBLC1/Uu0hrvKML4ywsdK/o4vU6AJJG\nS/qppIckLQXO48U/SM0mAxflH9SngYvpoXmoC6XqIr3HTzf9Q27Kiz+PRwrdTxWmfQmlnZJXKu90\nJAV28/t8sItJG9P/sNDU9LnuxgOIiNmkH4vmH5BHgTHdTDYmD284KSJGkpohVpDa0HuzMfBYU78N\n8/ez8bgr1/h4RBwbEduQvjczSSs1opyjmuZ7fFcjSZpT+Ny63VrJoXkd8IOIuLAwaDlQXLNeLz8v\n62JYY/iy/B6vJ60kXQzMy49lpP8rSFvS6/JSOxbfGy/embwBKWC+QlpR2xR4q6Ti1mVjnku6e7+d\nzkEwsIqXcn0Y2EBS8Ys3lrQjsGHTRofSzuVN8nTNHgT2a/pHXDOv7ffV13Kd/x4RLyc103T5Y5DX\n2PYEPpB/UB8hrRntL6mn8OiPB4ETmt7jWk0/Et3p6hK6p5LW3sbn9/k5Xvo+u730bkR8vNDU9LXu\nxiv4EvBRXhz0vwY2lbRLccTcrLgrcEMXy/07aefz9/JabU8OJq3l90lEPAqcRArZ5i2KVRIR2xQ+\nty5rk7Q+KQSuiIgTmgbPAYr7yrYn7dT+B3AvsFre91IcPqew/FMiYnxEjCYFwmqkLVGAWaTmpb7Y\nAlgZEefklaH5pCbf/QvjvBaYFxHNWyuDhoOgIrkd+I/AiXmn5nbAR0hr4A07SXpnbuI5htQU0tUR\nDT8ETpC0GaS1KUkH9rO0dUlrVk9I2hj4bA/jHkL659uS1AwzgfSPNJ/ctj+ATgc+Lul1StaW9Lam\nIO3OQuAVktYr9FuX1GywXOlQzE8McL0vEhH3AT8Djir0u5f0tztf0q6Shikd4XIxcH1eg+1qXtNI\nKwQvORIlz2NzSf8P2IMXH1HTLUn/K2lbSavlz/QTwH2FtvmWyO3o1wJ/iIjmLSiAc4CPSNo6B8bx\nwFkAeX/QJcBX8vdjd+AA0hFR5P+zbfP3Zyxpf9T38k5nSAc79NQM2pV706z1PqWDNl5F2g83qzDO\nm0jNnIOWg6Bak0ib+g8DlwJfavrnv5z0pXqc9KP7zry/oNn3SIfcXSdpGSksXtfPmr5MOvT1CVKb\n/yU9jDuZtOn+SPFB+nHrS/NQryJiOmmN+mTS53Ef+WiREtPeTTqE72+5WWkj0s7b95GaBk4n/UhX\n7SvA2k39PknaN3QeKYCvIe1cflcv8/om8N+FneW7SVpOCrffkJpIdo6IO5umW6IXH+/faH9fi/Qd\nXAL8jdQUdwDlndw03xl9mLboYNIRTIc2zW8sQERcA3wDuJHUlHo/aWur4XBgBLCIdIDFJ/L+J0hN\nNxeQPudbgZtJQUKe922kFaDS/zt5Lf+dpAMPHic1qc0G/m9htEmkfVCDlsI3pjGzmpD0FuDwiDho\ngOb3DuCQiHj3QMyvXRwEZmY156YhM7OacxCYmdWcg8DMrOYcBGZmNbcqV11smQ033DDGjRvX7jLM\nzAaVGTNmPBoRzZc+eYlBEQTjxo1j+vTp7S7DzGxQkfRAmfHcNGRmVnMOAjOzmnMQmJnVnIPAzKzm\nHARmZjXnIDAzqzkHgZlZzTkIzMxqzkFgZlZzDgIzs5pzEJiZ1VxlQZBvJH2rpDskzZH05dx/qqSH\nJM3Mj/2rqsHMzHpX5UXnngH2jIjlkoYDN0m6Og/7TkScVOGyzcyspMqCINLNkJfnl8PzY/DdIHnW\n1P5Pu90qTGtm1iKV7iOQNEzSTGARMC0i/pQHHSlplqQzJa1fZQ1mZtazSoMgIlZGxARgE2AXSdsC\npwJbABOABcC3uppW0hRJ0yVNX7x4cZVlmpnVWkuOGoqIJcCNwL4RsTAHxPPA6cAu3UxzWkRMjIiJ\no0b1eoMdMzPrpyqPGholaWTuHgHsA9wtaUxhtIOB2VXVYGZmvavyqKExwNmShpEC56KIuFLSuZIm\nkHYczwM+VmENZmbWiyqPGpoF7NBF/0OqWqaZmfWdzyw2M6s5B4GZWc05CMzMas5BYGZWcw4CM7Oa\ncxCYmdWcg8DMrOYcBGZmNecgMDOrOQeBmVnNOQjMzGrOQWBmVnMOAjOzmnMQmJnVnIPAzKzmHARm\nZjXnIDAzqzkHgZlZzTkIzMxqzkFgZlZzDgIzs5pzEJiZ1ZyDwMys5hwEZmY15yAwM6s5B4GZWc05\nCMzMas5BYGZWcw4CM7OacxCYmdWcg8DMrOYcBGZmNecgMDOrOQeBmVnNOQjMzGrOQWBmVnOVBYGk\nNSXdKukOSXMkfTn330DSNElz8/P6VdVgZma9q3KL4Blgz4jYHpgA7CtpV+BY4IaIGA/ckF+bmVmb\nVBYEkSzPL4fnRwAHAmfn/mcDB1VVg5mZ9a7SfQSShkmaCSwCpkXEn4DREbEgj/IIMLqbaadImi5p\n+uLFi6ss08ys1ioNgohYGRETgE2AXSRt2zQ8SFsJXU17WkRMjIiJo0aNqrJMM7Naa8lRQxGxBLgR\n2BdYKGkMQH5e1IoazMysa1UeNTRK0sjcPQLYB7gbuAKYnEebDFxeVQ1mZta71Sqc9xjgbEnDSIFz\nUURcKelm4CJJHwEeAN5dYQ1mZtaLyoIgImYBO3TR/x/AXlUt18zM+sZnFpuZ1ZyDwMys5hwEZmY1\n5yAwM6s5B4GZWc05CMzMas5BYGZWcw4CM7OacxCYmdWcg8DMrOYcBGZmNecgMDOrOQeBmVnNOQjM\nzGrOQWBmVnMOAjOzmnMQmJnVnIPAzKzmHARmZjXnIDAzqzkHgZlZzTkIzMxqzkFgZlZzDgIzs5pz\nEJiZ1ZyDwMys5hwEZmY15yAwM6s5B4GZWc2tVnZESesDGwErgHkR8XxlVZmZWcv0GASS1gOOACYB\nqwOLgTWB0ZJuAX4QETdWXqWZmVWmty2CXwDnAG+IiCXFAZJ2Ag6RtEVEnFFVgWZmVq0egyAi9ulh\n2AxgxoBXZGZmLVV6HwGApFHA0cAI4IcRMbeSqszMrGX6etTQt4BrgUuBCwa+HDMza7Ueg0DStZLe\nWOi1OjAvP9boZdpNJd0o6S+S5kg6OvefKukhSTPzY/9VewtmZrYqemsaejfwBUmfAL4AHA+cSGoa\nOryXaZ8DPh0Rt0laF5ghaVoe9p2IOGkV6jYzswHS287iJ4DPStoCOAF4GPhk8xFE3Uy7AFiQu5dJ\nugvYeNVL7odZU9uyWDOzwaC3pqFXSzoJOAz4NHAZ8DNJR0kaVnYhksYBOwB/yr2OlDRL0pn5RLWu\nppkiabqk6YsXLy67KDMz66PedhZfCFwC3AicGxG/j4i3AkuA68osQNI6wMXAMRGxFDgV2AKYQNpi\n+FZX00XEaRExMSImjho1qtSbMTOzvustCNYA7iftHF6r0TMizgHe3tvMJQ0nhcD5EXFJnnZhRKzM\nl6g4Hdilf6WbmdlA6G1n8SeAk4FngY8XB0TEip4mlCTgDOCuiPh2of+YvP8A4GBgdl+LNjOzgdPb\nzuI/An/s57xfDxwC3ClpZu73OWCSpAlAkLY0PtbP+ZuZ2QDo05nFfRERNwHqYtBVVS3TzMz6zvcj\nMDOrOQeBmVnNlWoakjQR+DywWZ5GQETEdhXWZmZmLVB2H8H5wGeBOwHfmczMbAgpGwSLI+KKSisx\nM7O2KBsEX5L0Y+AG4JlGz8ZJYmZmNniVDYJDga2A4bzQNBSky0+YmdkgVjYIdo6ILSutxMzM2qLs\n4aN/lLR1pZWYmVlblN0i2BWYKel+0j4CHz5qZjZElA2CfSutwszM2qZU01BEPABsCuyZu58qO62Z\nmXW2Uj/mkr4E/A9wXO41HDivqqLMzKx1yq7VHwwcADwJEBEPA+tWVZSZmbVO2SB4NiKCdO4Aktau\nriQzM2ulskFwkaQfASMlfRS4nnSbSTMzG+RKHTUUESdJ2gdYCmwJfDEiplVamZmZtUSPQSBJuUmI\n/MP/kh//4jhmZjb49NY0dKOkIyWNLfaUtLqkPSWdDUyurjwzM6tab01D+wIfBi6UtDmwBBhBCpDr\ngO9GxO3VlmhmZlXqMQgi4mngB8APJA0HNgRWRMSSVhRnZmbVK3uJCSLin8CCCmsxM7M28GUizMxq\nzkFgZlZzDgIzs5ore9G5XSX9WdJySc9KWilpadXFmZlZ9cpuEZwMTALmkg4fPQw4paqizMysdUo3\nDUXEfcCwiFgZET/BN6sxMxsSyh4++pSk1Um3q/wG6TBS718wMxsCyv6YH5LH/STpngSbAu+qqigz\nM2udslsEOwG/ioilwJcrrMfMzFqs7BbBO4B7JZ0r6e2SSp+RbGZmna3szesPBf4N+Dnp6KG/Svpx\nlYWZmVlr9OlaQ5KuJt2ucgRwEOkwUjMzG8TKnlC2n6SzSOcRvAv4MfCqCusyM7MWKbuP4IPAZcCW\nEfGhiLgqIp7raQJJm0q6UdJfJM2RdHTuv4GkaZLm5uf1V/E9mJnZKii7j2BSRFwWEc/0Yd7PAZ+O\niK2BXYEjJG0NHAvcEBHjgRvyazMza5Meg0DSTfl5maSlhcey3q41FBELIuK23L0MuAvYGDgQODuP\ndjZpX4OZmbVJb3co2z0/r7sqC5E0DtgB+BMwOiIaN7h5BBjdzTRTgCkAY8eO7WoUMzMbAGV3Fp9b\npl83064DXAwck09I+5eICNJRSC8REadFxMSImDhq1KgyizIzs34ou7N4m+KLfELZTr1NlO9zfDFw\nfkRcknsvlDQmDx8DLCpfrpmZDbTe9hEcJ2kZsF1x/wCwELi8l2kFnAHcFRHfLgy6Apicuyf3Nh8z\nM6tWj0EQESfm/QPfjIiX58e6EfGKiDiul3m/nnSxuj0lzcyP/YGvA/tImgvsnV+bmVmblDqzOCKO\ny8f7jwfWLPT/XQ/T3ASom8F79aVIMzOrTqkgkHQYcDSwCTCTdF7AzcCe1ZU2BMya2v9pt1uFac3M\n+qDszuKjgZ2BByLizaRDQZdUVpWZmbVM2SB4OiKeBpC0RkTcDWxZXVlmZtYqZa8+Ol/SSNL1hqZJ\nehx4oLqyzMysVcruLD44d06VdCOwHnBNZVWZmVnL9BgEkjbooved+Xkd4LEBr8jMzFqqty2CGaRL\nQBQPA228DmCLiuoyM7MW6e2ic5u3qhAzM2uPshedk6QPSDo+vx4raZdqSzMzs1Yoe/joD4DdgPfl\n18uAUyqpyMzMWqrs4aOvi4gdJd0OEBGPS1q9wrrMzKxFym4R/FPSMPK9AySNAp6vrCozM2uZskHw\nfeBS4JWSTgBuAr5WWVVmZtYyZU8oO1/SDNJVQwUcFBF3VVqZmZm1RK9BkJuE5kTEVsDd1ZdkZmat\n1GvTUESsBO6R5DvIm5kNQWWPGlofmCPpVuDJRs+IOKCSqszMrGXKBsHxlVZhZmZtU3Zn8W+rLsTM\nzNqj7OGjZmY2RDkIzMxqzkFgZlZzpfYRSBoPnAhsDazZ6B8Rvh+BmdkgV3aL4CfAqcBzwJuBc4Dz\nqirKzMxap2wQjIiIGwBFxAMRMRV4W3VlmZlZq5Q9j+AZSS8D5kr6JPAQ6Z7FZmY2yJXdIjgaWAs4\nCtgJOASYXFVRZmbWOmVPKPtz7lwOHFpdOWZm1mo9BoGk70bEMZJ+Sb4pTZGvNWRmNvj1tkVwbn4+\nqepCzMysPXoMgoiYkTunAysi4nn41z0K1qi4NjMza4GyO4tvIO0sbhgBXD/w5ZiZWauVDYI1I2J5\n40XuXquH8c3MbJAoGwRPStqx8ULSTsCKakoyM7NWKntC2THAzyU9TLp5/auA91RWlZmZtUzp8wgk\nbQVsmXvdExH/7G06SWcCbwcWRcS2ud9U4KPA4jza5yLiqr4WbmZmA6PsFgHAzsC4PM2OkoiIc3qZ\n5izgZNJF6oq+ExE+JNXMrAOUvQz1ucCrgZnAytw7eOkP/ItExO8kjVuF+szMrGJltwgmAltHxEvO\nLu6nIyV9kHR+wqcj4vHmESRNAaYAjB07doAWa2ZmzcoeNTSbtIN4IJwKbAFMABYA3+pqpIg4LSIm\nRsTEUaNGDdCizcysWdktgg2Bv0i6FXim0bM/1xqKiIWNbkmnA1f2dR5mZjZwygbB1IFaoKQxEbEg\nvzyYtLVhZmZtUvbw0d9K2gwYHxHXS1oLGNbbdJIuBPYANpQ0H/gSsIekCaSdzfOAj/WzdjMzGwC9\nXYb6lRGxSNJHSTtuNyAdPbQx8ENgr56mj4hJXfQ+o5+1mplZBbrdWZwvKfHV/PII4PXAUoCImAu8\nsvLqzMyscj0dNbQVcEfufjYinm0MkLQaXdyoxszMBp9ugyAiLiDdpB7gN5I+B4yQtA/wc+CXLajP\nzMwq1uN5BBFxee48lnRtoDtJO3evAr5QbWlmZtYKZY8aeh44PT/MzGwIKXutofvp+ub1Wwx4RWZm\n1lJ9udZQw5rAf5IOJTUzs0Gu1LWGIuIfhcdDEfFd4G0V12ZmZi1Qtmlox8LLl5G2EPpyLwMzM+tQ\nZX/Mi1cIfY50aYh3D3g1ZmbWcmWPGnpz1YWYmVl7lG0a+q+ehkfEtwemHDMza7W+HDW0M3BFfv0O\n4FZgbhVFmZlZ65QNgk2AHSNiGYCkqcCvIuIDVRVmZmatUfZWlaOBZwuvn839zMxskCu7RXAOcKuk\nS/Prg4CzqynJzMxaqexRQydIuhp4Q+51aETcXl1ZZmbWKmWbhgDWApZGxPeA+ZI2r6gmMzNroVJB\nIOlLwP8Ax+Vew4HzqirKzMxap+wWwcHAAcCTABHxMLBuVUWZmVnrlA2CZyMiyJeilrR2dSWZmVkr\nlQ2CiyT9CBgp6aPA9fgmNWZmQ0LZo4ZOyvcqXgpsCXwxIqZVWpmZmbVEr0EgaRhwfb7wnH/8zcyG\nmF6bhiJiJfC8pPVaUI+ZmbVY2TOLlwN3SppGPnIIICKOqqQqMzNrmbJBcEl+mJnZENNjEEgaGxF/\njwhfV8jMbIjqbR/BZY0OSRdXXIuZmbVBb0GgQvcWVRZiZmbt0VsQRDfdZmY2RPS2s3h7SUtJWwYj\ncjf5dUTEyyutzszMKtdjEETEsFYVYmZm7dGX+xGYmdkQ5CAwM6u5SoNA0pmSFkmaXei3gaRpkubm\n5/WrrMHMzHpW9RbBWcC+Tf2OBW6IiPHADfm1mZm1SaVBEBG/Ax5r6n0g0DhT+WzgoCprMDOznrVj\nH8HoiFiQux8BRrehBjMzy9q6s7h4+8tmkqZImi5p+uLFi1tcmZlZfbQjCBZKGgOQnxd1NVJEnBYR\nEyNi4qhRo1paoJlZnbQjCK4AJufuycDlbajBzMyyqg8fvRC4GdhS0nxJHwG+DuwjaS6wd35tZmZt\nUvbGNP0SEZO6GbRXlcs1M7PyfGaxmVnNVbpFYKtg1tRVm367VZzezGrDWwRmZjXnIDAzqzkHgZlZ\nzTkIzMxqzkFgZlZzDgIzs5pzEJiZ1ZyDwMys5hwEZmY15yAwM6s5B4GZWc05CMzMas5BYGZWcw4C\nM7OacxCYmdWcg8DMrOYcBGZmNecgMDOrOQeBmVnNOQjMzGrOQWBmVnMOAjOzmnMQmJnVnIPAzKzm\nHARmZjXnIDAzqzkHgZlZzTkIzMxqzkFgZlZzDgIzs5pzEJiZ1ZyDwMys5hwEZmY1t1q7FixpHrAM\nWAk8FxET21WLmVmdtS0IsjdHxKNtrsHMrNbcNGRmVnPtDIIArpc0Q9KUNtZhZlZr7Wwa2j0iHpL0\nSmCapLsj4neNgTkcpgCMHTu2XTWamQ15bdsiiIiH8vMi4FJgl6bhp0XExIiYOGrUqHaUaGZWC23Z\nIpC0NvCyiFiWu98CfKUdtQxZs6b2f9rtVmFaMxt02tU0NBq4VFKjhgsi4po21WJmVmttCYKI+Buw\nfTuWbWZmL+bDR83Mas5BYGZWcw4CM7OacxCYmdWcg8DMrOYcBGZmNecgMDOrOQeBmVnNOQjMzGrO\nQWBmVnMOAjOzmnMQmJnVnIPAzKzmHARmZjXnIDAzqzkHgZlZzTkIzMxqzkFgZlZzDgIzs5pr183r\nrZPNmtr/abdbhWnNrC28RWBmVnMOAjOzmnMQmJnVnIPAzKzmHARmZjXnIDAzqzkHgZlZzTkIzMxq\nzkFgZlZzPrPYBpbPSjYbdLxFYGZWcw4CM7OacxCYmdWcg8DMrOa8s9g6h3c0m7VF24JA0r7A94Bh\nwI8j4uvtqsWGgFUJEXCQWK21pWlI0jDgFGA/YGtgkqSt21GLmVndtWuLYBfgvoj4G4CknwIHAn9p\nUz1Wd26WshprVxBsDDxYeD0feF2bajFbNavaLNUuqxJgDs4hpWN3FkuaAkzJL5dLumcVZrch8Oiq\nV9USg6lWGFz1DqZaofJ6vzyQM+tDrQO63P4aTN+FVal1szIjtSsIHgI2LbzeJPf7l4g4DThtIBYm\naXpETByIeVVtMNUKg6vewVQrDK56B1OtMLjqbUWt7TqP4M/AeEmbS1odeC9wRZtqMTOrtbZsEUTE\nc5I+CVxLOnz0zIiY045azMzqrm37CCLiKuCqFi1uQJqYWmQw1QqDq97BVCsMrnoHU60wuOqtvFZF\nRNXLMDOzDuZrDZmZ1dyQDgJJ+0q6R9J9ko5tYx1nSlokaXah3waSpkmam5/XLww7Ltd8j6S3Fvrv\nJOnOPOz7klRBrZtKulHSXyTNkXR0p9YraU1Jt0q6I9f65U6ttbCcYZJul3TlIKh1Xl7OTEnTB0G9\nIyX9QtLdku6StFsn1itpy/yZNh5LJR3T1lojYkg+SDuh/wpsAawO3AFs3aZa3gjsCMwu9PsGcGzu\nPhb439z8m58OAAAGf0lEQVS9da51DWDz/B6G5WG3ArsCAq4G9qug1jHAjrl7XeDeXFPH1Zvnu07u\nHg78KS+v42ot1PxfwAXAlZ38PcjLmQds2NSvk+s9Gzgsd68OjOzkevOyhgGPkI73b1utlby5TngA\nuwHXFl4fBxzXxnrG8eIguAcYk7vHAPd0VSfpyKrd8jh3F/pPAn7UgrovB/bp9HqBtYDbSGeod2St\npPNlbgD25IUg6Mha87zn8dIg6Mh6gfWA+8n7PTu93sL83wL8od21DuWmoa4uY7Fxm2rpyuiIWJC7\nHwFG5+7u6t44dzf3r4ykccAOpDXtjqw3N7XMBBYB0yKiY2sFvgv8N/B8oV+n1goQwPWSZiid6d/J\n9W4OLAZ+kpvefixp7Q6ut+G9wIW5u221DuUgGDQixXlHHb4laR3gYuCYiFhaHNZJ9UbEyoiYQFrb\n3kXStk3DO6JWSW8HFkXEjO7G6ZRaC3bPn+1+wBGS3lgc2GH1rkZqfj01InYAniQ1r/xLh9WL0sm0\nBwA/bx7W6lqHchD0ehmLNlsoaQxAfl6U+3dX90O5u7n/gJM0nBQC50fEJZ1eL0BELAFuBPbt0Fpf\nDxwgaR7wU2BPSed1aK0ARMRD+XkRcCnpqsGdWu98YH7eIgT4BSkYOrVeSAF7W0QszK/bVutQDoJO\nv4zFFcDk3D2Z1Bbf6P9eSWtI2hwYD9yaNxmXSto1HxnwwcI0AybP+wzgroj4difXK2mUpJG5ewRp\nX8bdnVhrRBwXEZtExDjSd/HXEfGBTqwVQNLaktZtdJPasmd3ar0R8QjwoKQtc6+9SJe178h6s0m8\n0CzUqKk9tVa1E6QTHsD+pKNe/gp8vo11XAgsAP5JWnP5CPAK0o7DucD1wAaF8T+fa76HwlEAwETS\nP+NfgZNp2jE2QLXuTtoknQXMzI/9O7FeYDvg9lzrbOCLuX/H1dpU9x68sLO4I2slHW13R37Mafz/\ndGq9eTkTgOn5+3AZsH6n1gusDfwDWK/Qr221+sxiM7OaG8pNQ2ZmVoKDwMys5hwEZmY15yAwM6s5\nB4GZWc05CMzMas5BYB1L0sp8md7Zkn7ZOHlsAOY7ToVLgpecZoSk30oaNhA1DCRJV/X02Uj6qaTx\nrazJBhcHgXWyFRExISK2BR4DjmhjLR8GLomIlVUtQFK/bh0bEftHusRGd04lXezOrEsOAhssbqZw\nZUVJn5X0Z0mz9MINacYp3ZDkdKUb1VyXLz3RuIHHHZLuoBAoeZrfS7otP/5PN8t/P4XT93tY/t2S\nzpJ0r6TzJe0t6Q9KNxvZpXmmkj4k6QpJvyadVdrlvHP/y5SuBDpHL1wNtHEDmQ3zZSF+ld/nbEnv\nyaP8Hti7v0FjQ5+DwDpebo7Zi3ytKElvIV1vZRfSZQV20gtXxhwPnBIR2wBLgHfl/j8BjoyI7Ztm\nvwjYJyJ2BN4DfL+L5a8ObBER80os/9+AbwFb5cf7SJft+AzwuW7e4o7Af0TEm3qZ94cjYifSZQWO\nkvSKpvnsCzwcEdvnrahrACLieeA+oPm9mwEOAutsI5TuNdC4Nvu03P8t+XE76WY0W5F+PAHuj4iZ\nuXsGMC63n4+MiN/l/ucWljEcOF3SnaTLAW/dRR0bkkKlobfl35l/fOcAN0S6jsudpJsTdWVaRDxW\nYt5H5S2aW0hXo2xu978T2EfS/0p6Q0Q8URi2CNiom+VbzXlT0TrZioiYIGkt0l2ZjiCtsQs4MSJ+\nVBxZ6UY6zxR6rQRG9LKMTwELSWvLLwOe7qoOYM3iokou//nC6+fp/v/tyRLz3gPYG9gtIp6S9Jum\nmoiIeyXtSLpI4P+VdENEfCUPXjO/D7OX8BaBdbyIeAo4Cvh0bue+Fviw0s1zkLSxpFf2MP0SYImk\n3XOv9xcGrwcsyGvwh5DuIds8/ePAMEmNH94+Lb+Pupv3esDjOQS2It2n9kUkbQQ8FRHnAd8kNTk1\nvIZ0lUqzl/AWgQ0KEXG7pFnApIg4V9JrgZvTZdhZDnyAtAXQnUOBMyUFcF2h/w+AiyV9kNSm/mRX\nE+dpdgeuj4jr+rH8UnqY9zXAxyXdRboU8S1dTP7vwDclPU+65PknACSNJm1dPbKq9dnQ5MtQm5WQ\nm1w+FRGHtLuWvpL0KWBpRJzR7lqsM7lpyKyEiLgNuLETTygrYQlwdruLsM7lLQIzs5rzFoGZWc05\nCMzMas5BYGZWcw4CM7OacxCYmdXc/wfnev5ZlzK8pgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20e4b1b1b38>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"frenda49 = pd.cut(base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base.REGIAO==\"CENTRO-OESTE\")], bins=faixa, right=False)\n",
"t49 = (frenda49.value_counts(sort=False, normalize=True)*100).round(decimals=1)\n",
"print(t49,\"\\n\")\n",
"\n",
"plot = base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")].plot.hist(bins=faixa,title=\"Problema Alimentar - NORDESTE - 2009(H8) \", weights=zeros_like(base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")])+1./base9.RENDA[(base9.Problema_Alimentar=='Sim')&(base9.REGIAO==\"NORDESTE\")].size*100, figsize=(6, 6), alpha=0.5,color=\"orange\")\n",
"plt.ylabel('Frequência relativa (em %)')\n",
"plt.xlabel('Renda (em reais)')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Em comparação com os primeiros histogramas pode-se dizer que se mantém o ideal da distribuição, ou seja os primeiros 4 intervalos (350 cada) concentram a maior parte das pessoas que já passaram por alguma situação de insegurança alimentar e também apresentaram algum tipo de problema com alimentação."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Conclusão "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" Inicialmente deve-se destacar que as variáveis selecionadas foram apenas aquelas que existem nos 2 anos de pesquisa para que assim houvesse maior coerência no momento de comparação. Em termos de efeito conclusivo é válido observar primeiramente uma melhora percentual nos números de insegurança alimentar no país, os primeiros gráficos (G1 E G2) mostram isso a ponto de que em 2009 31,7% da população já havia passado por alguma situação de insegurança alimentar e 2013 mostrou que 23,8% apresentou essa falta de segurança. \n",
" Em termos direcionados a pergunta-guia, o gráfico G3 já apresenta as regiões com maiores problemas quanto à insegurança alimentar e coincidentemente as mesmas que apresentam a maior divergência nos valores entre zona urbana e rural, lembrando que trata-se dos dados de 2013. Em relação a 2009, G4 nâo apresenta grande coerência entre os dois tipos de valores, porém o Nordeste já se mostra em destaque negativo pelos altíssimos números. Partindo disso deve-se partir para o foco diretamente, os gráficos G7 e G8 apresentam enfim as duas regiões de cada análise, primeiramente Norte e Nordeste, como já dito anteriormente, no ano de 2013, e Centro-Oeste e Nordeste em 2009. A partir daí vale observar os histogramas relacionados àqueles que tiveram insegurança alimentar de acordo com a renda mensal familiar, sendo assim H1,H2,H3 e H4 apresentam um certo padrão de concentração dos entrevistados nas 4 primeiras faixas de renda, sendo um intervalo de 350 entre cada uma. Isso mostra que basicamente a população mais pobre com rendas até aproximadamente 1500 sofrem mais com falta de alimentos nessas regiões de análise, que retomando apresentam maior disparidade entre zona urbana e rural para insegurança e segurança alimentar.\n",
" Com o aprofundamento das questões, partiu-se para \"Problema Alimentar\" que pode ser descrito como problemas relacionados a falta de comida ou alimentação restrita devido basicamente a falta de capacidade monetária, e novamente pode-se observar uma concentração na margem esquerda (menor renda familiar), ou seja isso mostra que apesar de uma melhora ao longo dos 4 anos entre as duas pesquisas manteve-se um padrão negativo nas regiões, apesar do centro-oeste ter melhorado seus valores percentuais a região Norte se mostrou em decadência e \"tomou\" esse lugar no que se observou em 2013 tanto para \"problema\" quanto \"insegurança\" alimentar.\n",
" Há uma possível demonstração de que as áreas centrais ainda se mostrem mais desenvolvidas e cada vez mais distantes de regiões periféricas, primeiro que na maioria dos casos observados a região urbana apresentava maiores problemas percentuais para acesso a alimentação e as próprias regiões de maior problema nessa questão, a manutenção do Nordeste e a passagem do Centro-Oeste justamente para outra região mais distante do centro desenvolvido do país, o Norte."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
ehsteve/ipython-notebooks | HEXITEC Determining Gain.ipynb | 1 | 236297 | {
"cells": [
{
"cell_type": "code",
"execution_count": 414,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from hexipy.exposure import LongExposure\n",
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"from astropy.modeling import models, fitting\n",
"from astropy.utils.console import ProgressBar\n",
"import scipy.interpolate as inter\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
".data[1451833:?] | No valid checksum found, possible end at :1451905\n",
".data[1799093:?] | No valid checksum found, possible end at :1799138\n",
".data[2303749:?] | No valid checksum found, possible end at :2303813\n",
".data[2664978:?] | No valid checksum found, possible end at :2665041\n",
".data[2998749:?] | No valid checksum found, possible end at :2998751\n",
".data[3709991:?] | No valid checksum found, possible end at :3710046\n",
".data[3942252:?] | No valid checksum found, possible end at :3942254\n",
".data[4369474:?] | No valid checksum found, possible end at :4369569\n",
".data[5003331:?] | No valid checksum found, possible end at :5003380\n",
".data[6674902:?] | No valid checksum found, possible end at :6674952\n",
".data[9292542:?] | No valid checksum found, possible end at :9292613\n",
".data[9618462:?] | No valid checksum found, possible end at :9618524\n",
".data[9696258:?] | No valid checksum found, possible end at :9696300\n",
".data[10683828:?] | No valid checksum found, possible end at :10683915\n",
".data[10771562:?] | No valid checksum found, possible end at :10771618\n",
".data[11029872:?] | No valid checksum found, possible end at :11029914\n",
".data[11206177:?] | No valid checksum found, possible end at :11206276\n",
".data[12073202:?] | No valid checksum found, possible end at :12073264\n",
".data[12073266:?] | No valid checksum found, possible end at :12073335\n",
".data[12073337:?] | No valid checksum found, possible end at :12073399\n",
".data[13172292:?] | No valid checksum found, possible end at :13172405\n",
".data[13994512:?] | No valid checksum found, possible end at :13994553\n",
".data[14128741:?] | No valid checksum found, possible end at :14128804\n",
".data[15691895:?] | No valid checksum found, possible end at :15692022\n",
".data[15798175:?] | No valid checksum found, possible end at :15798223\n",
".data[18286778:?] | No valid checksum found, possible end at :18286780\n",
".data[18442941:?] | No valid checksum found, possible end at :18442997\n",
".data[18951407:?] | No valid checksum found, possible end at :18951450\n",
".data[20055557:?] | No valid checksum found, possible end at :20055599\n",
".data[21964736:?] | No valid checksum found, possible end at :21964800\n",
".data[22150558:?] | No valid checksum found, possible end at :22150560\n",
".data[23030873:?] | No valid checksum found, possible end at :23030959\n",
".data[23546372:?] | No valid checksum found, possible end at :23546463\n",
".data[23922898:?] | No valid checksum found, possible end at :23922946\n",
".data[24259243:?] | No valid checksum found, possible end at :24259298\n",
".data[25320513:?] | No valid checksum found, possible end at :25320576\n",
".data[25702318:?] | No valid checksum found, possible end at :25702370\n",
".data[26019088:?] | No valid checksum found, possible end at :26019178\n",
".data[26046469:?] | No valid checksum found, possible end at :26046510\n",
".data[26181294:?] | No valid checksum found, possible end at :26181349\n",
".data[26391029:?] | No valid checksum found, possible end at :26391121\n",
".data[26521552:?] | No valid checksum found, possible end at :26521554\n",
".data[26610369:?] | No valid checksum found, possible end at :26610426\n",
".data[27003810:?] | No valid checksum found, possible end at :27003859\n",
".data[29543581:?] | No valid checksum found, possible end at :29543654\n",
".data[30603538:?] | No valid checksum found, possible end at :30603602\n",
".data[30955732:?] | No valid checksum found, possible end at :30955803\n",
".data[34504271:?] | No valid checksum found, possible end at :34504349\n",
".data[34809782:?] | No valid checksum found, possible end at :34809855\n",
".data[37558178:?] | No valid checksum found, possible end at :37558198\n",
".data[38471717:?] | No valid checksum found, possible end at :38471801\n",
".data[39553167:?] | No valid checksum found, possible end at :39553294\n",
".data[40590579:?] | No valid checksum found, possible end at :40590644\n",
".data[41173324:?] | No valid checksum found, possible end at :41173365\n",
".data[41391967:?] | No valid checksum found, possible end at :41392044\n",
".data[43983615:?] | No valid checksum found, possible end at :43983617\n",
".data[44280263:?] | No valid checksum found, possible end at :44280334\n",
".data[44820113:?] | No valid checksum found, possible end at :44820200\n",
".data[46052917:?] | No valid checksum found, possible end at :46052980\n",
".data[47360895:?] | No valid checksum found, possible end at :47361003\n",
".data[48046444:?] | No valid checksum found, possible end at :48046529\n",
".data[48046531:?] | No valid checksum found, possible end at :48046588\n",
".data[48046590:?] | No valid checksum found, possible end at :48046711\n",
".data[52775582:?] | No valid checksum found, possible end at :52775584\n",
".data[53396844:?] | No valid checksum found, possible end at :53396907\n",
".data[53772562:?] | No valid checksum found, possible end at :53772662\n",
".data[55362614:?] | No valid checksum found, possible end at :55362616\n",
".data[55389772:?] | No valid checksum found, possible end at :55389774\n",
".data[55474305:?] | No valid checksum found, possible end at :55474347\n",
".data[55779748:?] | No valid checksum found, possible end at :55779796\n"
]
}
],
"source": [
"e = LongExposure('/Users/schriste/Data/hexitec/hexitec_packets_20160603_212356.dat')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"HEXITEC Exposure <8,567,071±2,926 counts 557.033448 s 15,379±5 cps> "
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"e"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<Table length=13>\n",
"<table id=\"table4735894096\">\n",
"<thead><tr><th>parameters</th><th>value</th></tr></thead>\n",
"<thead><tr><th>str20</th><th>float64</th></tr></thead>\n",
"<tr><td>Percent Read</td><td>99.9999982752</td></tr>\n",
"<tr><td>Integration Time (s)</td><td>557.033448</td></tr>\n",
"<tr><td>Total counts</td><td>8,567,071.14776</td></tr>\n",
"<tr><td>Total counts error</td><td>2,926.95592724</td></tr>\n",
"<tr><td>Counts Rate</td><td>15,379.8143195</td></tr>\n",
"<tr><td>Counts Rate Error</td><td>5.25454250144</td></tr>\n",
"<tr><td>Counts per Frame</td><td>9.7315259297</td></tr>\n",
"<tr><td>Channel Low</td><td>2,679.0</td></tr>\n",
"<tr><td>Channel High</td><td>16,383.0</td></tr>\n",
"<tr><td>X Low</td><td>0.0</td></tr>\n",
"<tr><td>X High</td><td>79.0</td></tr>\n",
"<tr><td>Y Low</td><td>0.0</td></tr>\n",
"<tr><td>Y High</td><td>79.0</td></tr>\n",
"</table>"
],
"text/plain": [
"<Table length=13>\n",
" parameters value \n",
" str20 float64 \n",
"-------------------- ---------------\n",
" Percent Read 99.9999982752\n",
"Integration Time (s) 557.033448\n",
" Total counts 8,567,071.14776\n",
" Total counts error 2,926.95592724\n",
" Counts Rate 15,379.8143195\n",
" Counts Rate Error 5.25454250144\n",
" Counts per Frame 9.7315259297\n",
" Channel Low 2,679.0\n",
" Channel High 16,383.0\n",
" X Low 0.0\n",
" X High 79.0\n",
" Y Low 0.0\n",
" Y High 79.0"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"e.describe()"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAaAAAAEZCAYAAADR8/HkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X24VWWd//H3B5CDAiJkcAp8wBTDHlQsbLLyJOVDM6FW\nGk4zYtFv5spKpmeYpuE0128mdZqJmhmdpkyRKckskyZT8oenpvKBfAhTVCYDAeVYEqjkEOL398e6\nNyy252Efzl5n7bPP53Vd+zpr3+tea3332nuf777vda+1FBGYmZkNtGFlB2BmZkOTE5CZmZXCCcjM\nzErhBGRmZqVwAjIzs1I4AZmZWSmcgMzMrBROQNYtSb+WdEpV2VxJ/517vk7S7yU9Jenp9PdLad6H\nJN0naUSu/l9JukvSMEmHSXo+Td+YW/4Pknbknl8m6eRU96mqbZ2YW/dpkn6Uyjsl3Srp7d28tvMl\n/VzSNkmPSrpE0rDc/PGSrpf0TNoP5+Xm7SfpW6n8eUlv6mL9M1IsT0t6XNKHe9nXl0j6raTfSLq4\ni/nzJT2S4rlf0pE9rOswSSslbZf0gKRZuXltklZL+l3a1rclvbSb9YyU9NX0Hm+TdLek0/uyH6rW\n9/H0eXhK0q8kfbxq/kpJT0jaKukeSbN7WNfJknZVfRb+vKrOW9Jn7Zn0Hr+rp/isBBHhhx9dPoBf\nA6dUlc0FflxV583dLC/gx0B7en4EsBU4Nj0/DNgFDKta7krg76rKTgYe7SHWdwHbgPcCY1PZG4Ev\nd1P/L4GTgBHAS4CfA5/Mzb8mPfZP9bYC09O8/YCLgNcDm4A3Va37RUAnMCetfzRwdA+x/yWwJsXx\nEuB+4C9y898P3FtZBzAVOKiH9f0M+EegBXgH8DvgRWnei4HJuddxCXBDN+s5APhb4JD0/I+Bp4BD\na9kPXazv48BxZD98pwHrgHNz818F7JemZ6ZtTepmXb19Ho5J78GpaXvjgallf6f8qHqfyg7Aj8Z9\nUHsCOqWHdUxL/7xfCdwC/N/cvHomoPXAR/vxWj9S+Uec/vHuAF6Wm78E+IcultvQRQL6e2BJH7b9\nU+D9uefvBX6WpgU8SjdJvot1HQU8C4zOlf0on9By5S3A54Bf9iHWXwBn17IfaljXF4EvdjNvJvB7\n4DXdzO/t8/B14LP7+nnwY2Ae7oKzvlJfKkfEw2T/5G4FJgN/V/eApKOBKcC3+7GaN5G1PCBLmjsj\n4le5+b8AXlHjul4H/E7ST1NX4A2SDumh/ivS+rva1iFkr+1VqRvpV5Lae1nXIxGxvbvYJR0i6Xdk\n/+A/StYK6pWkSWQJ7v7e6qb650m6t4cqb6xel6TvSXoWuB3oiIif52LeImlKrvrE1L35K0n/LOmA\n3LzXZYtptaRNkq6WNL6WuG3gOAFZb76bvvhbJG0B/q2HOr9Lf+dVzf8JMAG4LiL+0I9YJudiqWxr\nf7IuL4DH92Wlkt4HnAB8PhWNIev+yXsKGFvjKqcA5wMfJksg68i687ozhqz7ML+tMWl6cvr7VrIk\ncgpwXhf7uLt1vSD2iNgQEePJ9tvfAA/3/HJA2XG8/wSuSj8qehUR10TEcd2s77NkP2aurFrm7ek1\nnAGsqIp5QkRsTEVrgOMi4iVk++QE4J9zq5oC/BlwNlnSPAD4l1ritoHjBGS9OTN98SdExATgwh7q\njE9/r6jMkLQf8GWyL/+HJB3ej1g25WKpbOtZ4Mk0/yV9XaGks8i6zE6PiC2p+BngwKqq44Cna1zt\ns8D1EXF3SrifBf5I0lhJC3MHzS/rZnvjUlllXQCXRMTTEbGebH++LcX/y9z6TupL7BGxFbgauCE/\nAKOaJJElnx1kSbVfJH2ILDm8LSJ2dhHXroi4GThN0p90tY6IeCIiHkzT64FPAu/MVXkW+FpE/Coi\nfg/8A1lSswbiBGS9qaXLrac6fwt0RsRfkf3j/I+6RJUTEQ+RHYN4Z29189KIri8DfxIRD+RmPQyM\nkPSyXNmx1Nj1BKwGurzMfER8LiLGRsSBEVFJ5ven9Vccl9vWQ0B1q3H3uiPilbn1/TQtd4Sk0TXG\nvh/ZwITqpJV3BXAw8I6I2NVDvV6l1uYnyY4b9tZiHQG8rJc6e60+N726r7HZwHMCssJIOhb4ENko\nLoB24DBJF+Sr9WWVPcz7GPAZZcPExyrzBklf7ia2U8h+1b8zIu7Kz0u/mL8D/J2kAyS9AXg7sDS3\n/EhJo9LTFkktuVVcCZwt6dWpBfgZ4CcR0V0L6mrgo5JeKmky2XGZK1MszwLLgE9KGpOOgfwF8L2u\nVhQRa8lGzC2S1CLpHWQDQL6d4j5b0rS0f15M1m11d2oNdbWf/h14OTC7q+7TXvZDdd33kLU235pa\nLfl5R0s6XdIoSSMk/RnZMaIfdbOuNkmHpulDgIuB7+aqXAm8V9LUdGzoU3Szz6xEZY+C8KNxH8Aj\n1DYKbjvZcYbK49tkP25WAR+rWv5k4AmyX93djYL7Gl2Pgnsut42n09+zc3VOJRv2/RTZENyVwBnd\nvLaVZC2L/Lq+n5s/HrierEtrHfDuquV/nWLPPw7Nzf9LYCNZ9+ANpKHPPezri1Pd3wKfq5o3luwY\n0lNko/0+3cu6DiUb9PF7smMlb87N+1B6X58GHgO+QRpm3c16nk/reTq3n86rZT8AfwrcV/V52lG1\nzy9L815ONvBgG7AFuIMs6VWWPSTVn5KefyTt32fSPvkCuZF/qc6i9FnrBK4CxpX9nfJj74fSG1UY\nSfPZ8wv4KxHxpTQa5Ztk/4DWkZ0LsC3VXwi8j+yfzfyIWJHKZ6QP0Sjgxsi6dJA0kuwX5AlkX953\nR8Sjhb4oMzPrt0K74CS9ApgHvIasX/tPUr/6AuCWiDia7JfowlT/GOBcYDrZAcPL0gFQgMuBeREx\nDZgm6bRUPg/YEhFHAYuBS4t8TWZmVh9FHwOaDtwRETsiO3j5Y7Izs2eTndhH+ntWmp4NLIuI5yJi\nHbAWmCmplezs9lWp3tW5Zc7Mres6YPdlR8zMrHEVnYB+CbxR2XW1DiAbOnoI2eU1OgEiYjMwMdWf\nTDaaqWJTKptM1t9bsZE950fsXiYlua2SJhTzcszMrF5G9F5l30XEg5IuAX5IdrDwHrKDlC+oWsfN\n9ulMfTMzK0ehCQggIq4kDSmV9PdkrZVOSZMiojN1rz2Rqm8iayFVTEll3ZXnl3lM0nDgwNhzQuFu\nkoodbWFm1qQiopAf9oWfB5TONSCN2T+bbNjncuCCVGUu2TBVUvmcdG7BVOBI4M7UTbdN0sw0KOH8\nqmXmpulzyAY1dKnsIYe1PBYtWlR6DI7TMTpOx1l5FKnwFhDw7XRMZidwYUQ8lbrlrk1nRa8nG/lG\nRDwg6VrggVz9yh74IHsPw74plV8BLJW0luw8ijkD8JrMzKyfBqIL7gU3qYqsi+wt3dT/HNnVk6vL\n7yK7X0h1+Q5SAjMzs8HDl+JpMG1tbWWHUBPHWT+DIUZwnPU2WOIsUuFXQmgUkmKovFYzs3qRRAzW\nQQhmZmZdcQIyM7NSOAGZmVkpnICGmNbWwxkz5qCywzAz8yCEoaZycXHvCzOrhQchWF20th5edghm\nZru5BTSE7Lm1kltAZlYbt4DMzKzpOAENSS3ujjOz0rkLbgjJd8GBu+HMrHfugjMzs6bjBGRmZqVw\nAjIzs1I4AZmZWSkG4pbcH5H0S0mrJX093W57vKQVkh6SdLOkcbn6CyWtlbRG0qm58hlpHQ9LWpwr\nHylpWVrmtnTrbzMza3CFJiBJLwU+DMyIiFeT3YH1PGABcEtEHA2sBBam+seQ3d10OnAGcJn2DN26\nHJgXEdOAaZJOS+XzgC0RcRSwGLi0yNdkZmb1MRBdcMOB0ZJGAPsDm4AzgSVp/hLgrDQ9G1gWEc9F\nxDpgLTBTUiswNiJWpXpX55bJr+s6YFaBr8XMzOqk0AQUEY8B/wQ8SpZ4tkXELcCkiOhMdTYDE9Mi\nk4ENuVVsSmWTgY258o2pbK9lImIXsFXShEJeUFPxyahmVq4RRa5c0kFkLZTDgG3AtyS9B6g+A7Ke\nZ0R2e8JUe3v77um2trYhfk/2HXR2ri87CDNrMB0dHXR0dAzItgpNQMBbgEciYguApOuB1wOdkiZF\nRGfqXnsi1d8EHJJbfkoq6648v8xjkoYDB1a2Vy2fgMzM7IWqf5x/9rOfLWxbRR8DehR4naRRaTDB\nLOABYDlwQaozF7ghTS8H5qSRbVOBI4E7UzfdNkkz03rOr1pmbpo+h2xQg1Vxd5uZNZrCrwUnaREw\nB9gJ3AO8HxgLXEvWclkPnBsRW1P9hWQj23YC8yNiRSo/AbgKGAXcGBHzU3kLsBQ4HngSmJMGMFTH\nMaSvBVd9HbiKobxPzKx3RV4LzhcjHSKcgMxsX/hipGZm1nScgMzMrBROQGZmVgonIDMzK4UTkJmZ\nlcIJaEjz5XjMrDwehj1EdDcMGzwU28y652HY1i9u5ZhZI3ILaAjoqfUDbgGZWffcAjIzs6bjBGRm\nZqVwAjIzs1I4AZmZWSmcgMzMrBROQGZmVgonoCbnc4DMrFEVmoAkTZN0j6S7099tki6SNF7SCkkP\nSbpZ0rjcMgslrZW0RtKpufIZklZLeljS4lz5SEnL0jK3STq0yNc02HR2ri87BDOzLhWagCLi4Yg4\nPiJmACcA24HrgQXALRFxNLASWAgg6RjgXGA6cAZwmfacRXk5MC8ipgHTJJ2WyucBWyLiKGAxcGmR\nr8nMzOpjILvg3gL8KiI2AGcCS1L5EuCsND0bWBYRz0XEOmAtMFNSKzA2Ilalelfnlsmv6zpgVqGv\nwszM6mIgE9C7gW+k6UkR0QkQEZuBial8MrAht8ymVDYZ2Jgr35jK9lomInYBWyVNKOIFmJlZ/YwY\niI1I2o+sdfOpVFR98bF6Xoys22sWtbe3755ua2ujra2tjps1Mxv8Ojo66OjoGJBtDcjFSCXNBi6M\niNPT8zVAW0R0pu61WyNiuqQFQETEJaneTcAiYH2lTiqfA5wcER+o1ImIOyQNBx6PiIldxDAkL0ba\n24VIwRcjNbPuNcPFSM8Drsk9Xw5ckKbnAjfkyuekkW1TgSOBO1M33TZJM9OghPOrlpmbps8hG9Rg\nZmYNrvAWkKQDyFowR0TE06lsAnAtcEiad25EbE3zFpKNbNsJzI+IFan8BOAqYBRwY0TMT+UtwFLg\neOBJYE4awFAdh1tA3RiK+8XMalNkC8j3A2pyTkBm1h/N0AVnZma2FycgMzMrhRNQE/N14MyskfkY\nUBOr5fgP+BiQmXXPx4CsQC1uKZlZKdwCamK1toDArSAz65pbQGZm1nScgMzMrBROQGZmVgonIDMz\nK4UTkJmZlcIJyMzMSuEEZGZmpXACalI+udTMGp1PRG1SfTkJFXwiqpl1zSeiWp+49WNmg0HhCUjS\nOEnfkrRG0v2STpQ0XtIKSQ9JulnSuFz9hZLWpvqn5spnSFot6WFJi3PlIyUtS8vcJunQol9To+vs\nXF92CGZmvRqIFtAXyW6hPR04FngQWADcEhFHAyuBhQCSjgHOBaYDZwCXaU9f0uXAvIiYBkyTdFoq\nnwdsiYijgMXApQPwmszMrJ8KTUCSDgTeGBFXAkTEcxGxDTgTWJKqLQHOStOzgWWp3jpgLTBTUisw\nNiJWpXpX55bJr+s6YFaBL8nMzOqk6BbQVOC3kq6UdLek/5B0ADApIjoBImIzMDHVnwxsyC2/KZVN\nBjbmyjemsr2WiYhdwFZJE4p6QWZmVh8jBmD9M4APRsTPJX2BrPuteshVPYdgdTtao729ffd0W1sb\nbW1tddxsYxgz5uCyQzCzQayjo4OOjo4B2Vahw7AlTQJui4gj0vM3kCWglwFtEdGZutdujYjpkhYA\nERGXpPo3AYuA9ZU6qXwOcHJEfKBSJyLukDQceDwiJnYRS9MPwx4z5mC2b39yn5Zt9n1jZvtm0A7D\nTt1sGyRNS0WzgPuB5cAFqWwucEOaXg7MSSPbpgJHAnembrptkmamQQnnVy0zN02fQzaoYUja1+Rj\nZlaGwk9ElXQs8FVgP+AR4L3AcOBa4BCy1s25EbE11V9INrJtJzA/Ilak8hOAq4BRZKPq5qfyFmAp\ncDzwJDAnDWCojqPpW0B9Pfl0jxYmTWpl8+Z19QzHzJpAkS0gXwmhiex7Aso0+/4xs74btF1wNnB8\n9QMzG2zcAmoS/W39gFtAZvZCbgFZj9z6MbPByC2gJlCP1g+4BWRmL+QWkJmZNR0nIDMzK4UT0CDn\n4z9mNlj5GFAJKkmjHid+1uv4D/gYkJm9kE9ErYNGSkCVpFGPeJyAzKxIHoRgZmZNxwnIzMxK4QQ0\niHkAgpkNZj4GVILsuE0Lo0eP4plntvZzPfXTKPvHzBqHjwE1kT2tlh1s3/6/bsWY2ZDlFtDAx/GC\nsn2Jq7X1cDo719cjpH7FYWbNbVC3gCStk/QLSfdIujOVjZe0QtJDkm6WNC5Xf6GktZLWSDo1Vz5D\n0mpJD0tanCsfKWlZWuY2SYcW/Zrqq2WfWkH1Tj5mZgNtILrgngfaIuL4iJiZyhYAt0TE0WS30F4I\nIOkY4FxgOnAGcJn2NBkuB+ZFxDRgmqTTUvk8YEtEHAUsBi4dgNdURzucTMxsSOpzAkqtl1f3ZZEu\ntnMmsCRNLwHOStOzgWUR8Vy6rfZaYKakVmBsRKxK9a7OLZNf13XArD7EZmZmJakpAUnqkHSgpAnA\n3cBXJP1zjdsI4IeSVkl6fyqbFBGdABGxGZiYyicDG3LLbkplk4GNufKNqWyvZSJiF7A1xTmI7Fs3\nnJnZYDaixnrjIuKplECujohFklbXuOxJEfG4pBcDKyQ9RJaU8up59LuQg2XFcjecmQ09tSagEZJe\nQnZ85tN92UBEPJ7+/kbSd4GZQKekSRHRmbrXnkjVNwGH5Bafksq6K88v85ik4cCBEbGlq1ja29t3\nT7e1tdHW1taXl9JvbuWYWaPr6Oigo6NjQLZV0zBsSe8C/hb4SURcKOkI4B8j4p29LHcAMCwinpE0\nGlgBfJbsOM2WiLhE0qeA8RGxIA1C+DpwIlnX2g+BoyIiJN0OXASsAr4PfCkibpJ0IfDKFNcc4KyI\nmNNFLKUPw+75xNEWJk1qrekK2UUMwe7L9s1s6Cj9atiSToqIn/ZW1sVyU4HrybrYRgBfj4iL0zGa\na8laLuuBcyNia1pmIdnItp3A/IhYkcpPAK4CRgE3RsT8VN4CLAWOB54E5qQBDNWxNHgCytT4ftQj\nnH3evpkNHY2QgO6OiBm9lTUyJ6DalL2PzKyxFJmAejwGJOmPgNcDL5b00dysA4HhRQTUrHz8x8xs\nb70Nwx4JjCFLVGNzj6eAdxUbWnOp7ZhN78Oxx4w5uC7xmJmVrdYuuMMiYlCPEy67C64v3WbdxVnM\n4IPatm1mQ1MjHAOaBnwcOJxct11EnFJEUEUYPAmo+9FoRR77qXACMrO8RkhAvwD+HbgL2FUpj4i7\nigiqCIMnAUF3ScgJyMwGWiMkoLsi4oQiAhgogysBZarjdQIys4HWCLdj+J6kCyW9RNKEyqOIgOyF\nWlsPZ/jw0WWHYWZWV7W2gH7dRXFExBH1D6kYZbaA9m3wwJ5uuIFo+VS4BWRmeaV3wTWDMhPQvieQ\nLAkN5IVKh8rnwcxqU3oCknR+V+URcXXdIyrI4ExAAC3AjnqF0isnIDPLK+1KCDmvzU2PIruY6N1k\nN4azQg1c8jEzG0j71AUn6SCyO5eeXv+QijF4W0ADyy0gM8trhFFw1bYDU+sZiJmZDS01dcFJ+h57\n7lo6HJhOdjsFMzOzfVLrIISTc0+fA9ZHxMbCoiqAu+Bq4y44M8srvQsuIn4EPEh2JezxwB+KCMbK\n1vvVuM3M6qWmBCTpXOBO4BzgXOCOdJvumkgaJuluScvT8/GSVkh6SNLNksbl6i6UtFbSGkmn5spn\nSFot6WFJi3PlIyUtS8vcJunQWuOyajsG9JwjMxvaah2E8GngtRExNyLOB2YCn+nDduYDD+SeLwBu\niYijgZXAQgBJx5AluOnAGcBl2tN/dTkwLyKmAdMknZbK5wFbIuIoYDFwaR/iMjOzktSagIZFxBO5\n50/WuqykKcDbgK/mis8ElqTpJcBZaXo22fDu5yJiHbAWmCmpFRgbEatSvatzy+TXdR3ZOUpmZtbg\naj0R9SZJNwPXpOfvBm6scdkvAJ8AxuXKJkVEJ0BEbJY0MZVPBm7L1duUyp4D8oMeNqbyyjIb0rp2\nSdoqaUJEbKkxPjMzK0GPCUjSkWTJ4hOS3gG8Ic26Dfh6byuX9MdAZ0TcK6mth6r1HHo1eIacmZkN\nYb21gBaTjs9ExHeA7wBIelWa9/Zelj8JmC3pbcD+wFhJS4HNkiZFRGfqXqt0720CDsktPyWVdVee\nX+YxScOBA7tr/bS3t++ebmtro62trZfw+8+jysxsMOno6KCjo2NAttXjeUCSVkXEa7uZd19EvKrm\nDWXnEn0sImZLuhR4MiIukfQpYHxELEiDEL4OnEjWtfZD4KiICEm3AxcBq4DvA1+KiJskXQi8MiIu\nlDQHOCsi5nSx/VLOAxpM5wBV+FwgM6so82KkB/Uwb/9+bPdi4FpJ7wPWk418IyIekHQt2Yi5ncCF\nuazxQeAqsouh3hgRN6XyK4ClktaSDY54QfIxM7PG01sL6BpgZUR8par8/cBbI+LdBcdXN24B1c4t\nIDOrKO1+QJImAdeTXfngrlT8GmAkcHZEbC4iqCI4AdXOCcjMKhrhhnRvBl6Znt4fESuLCKZITkC1\ncwIys4rSE1AzcAKq3VD5TJhZ70q/GKmZmVm9OQFZFV8R28wGhrvgit/ugG+zHobK58LMeuYuODMz\nazpOQGZmVgonIDMzK4UTkJmZlcIJqEAeTWZm1j2Pgit2mwO6vXoaKp8LM+uZR8GZmVnTcQIyM7NS\nOAGZmVkpnIDMzKwUhSYgSS2S7pB0j6T7JC1K5eMlrZD0kKSbJY3LLbNQ0lpJaySdmiufIWm1pIcl\nLc6Vj5S0LC1zm6RDi3xNZmZWH4UmoIjYAbw5Io4HjgPOkDQTWADcEhFHAyuBhQCSjiG7Pfd04Azg\nMu0ZSnY5MC8ipgHTJJ2WyucBWyLiKGAxcGmRr8nMzOqj8C64iPh9mmwBRgABnAksSeVLgLPS9Gxg\nWUQ8FxHrgLXATEmtwNiIWJXqXZ1bJr+u64BZBb0UMzOro8ITkKRhku4BNgM/TElkUkR0AqTbek9M\n1ScDG3KLb0plk4GNufKNqWyvZSJiF7BV0oSCXo6ZmdXJiKI3EBHPA8dLOhC4XtIryFpBe1Wr4ya7\nPWGqvb1993RbWxttbW113KyZ2eDX0dFBR0fHgGxrQK+EIOkzwO+B9wNtEdGZutdujYjpkhYAERGX\npPo3AYuA9ZU6qXwOcHJEfKBSJyLukDQceDwiJnaxbV8JoQ98JQQzg0F8JQRJB1dGuEnaH3grsAZY\nDlyQqs0FbkjTy4E5aWTbVOBI4M7UTbdN0sw0KOH8qmXmpulzyAY1mJlZgyu6C+4lwBJJw8iS3Tcj\n4kZJtwPXSnofWevmXICIeEDStcADwE7gwlyz5YPAVcAo4MaIuCmVXwEslbQWeBKYU/BrMjOzOvDF\nSAvS2no4nZ3rB2x79TZUPhdm1rNB2wU3lA3m5AMtvpWEmRXOLaDitjdg2yrKUPlsmFn33AIyM7Om\n4wRkZmalcAIyM7NSOAGZmVkpnIDMzKwUTkBmZlYKJ6AC+BwaM7PeOQEVYHCfhFrhk1HNrFg+EbWY\nbQ3IdgbCUPl8mFnXfCKqmZk1HScgMzMrhROQmZmVwgnIzMxK4QRkZmalKPqW3FMkrZR0v6T7JF2U\nysdLWiHpIUk3V27bneYtlLRW0hpJp+bKZ0haLelhSYtz5SMlLUvL3Cbp0CJfk5mZ1UfRLaDngI9G\nxCuAPwI+KOnlwALglog4GlgJLASQdAzZ7bmnA2cAl2nPmObLgXkRMQ2YJum0VD4P2BIRRwGLgUsL\nfk1mZlYHhSagiNgcEfem6WeANcAU4ExgSaq2BDgrTc8GlkXEcxGxDlgLzJTUCoyNiFWp3tW5ZfLr\nug6YVdwr6p1P3jQzq82AHQOSdDhwHHA7MCkiOiFLUsDEVG0ysCG32KZUNhnYmCvfmMr2WiYidgFb\nJU0o5EXUoDmugmBmVrwRA7ERSWPIWifzI+IZSdWn19fzdPtuz9htb2/fPd3W1kZbW1sdN2tmNvh1\ndHTQ0dExINsq/FI8kkYA/wX8ICK+mMrWAG0R0Zm6126NiOmSFgAREZekejcBi4D1lTqpfA5wckR8\noFInIu6QNBx4PCImdhHHgFyKp5kuwwO+FI/ZUDfYL8XzNeCBSvJJlgMXpOm5wA258jlpZNtU4Ejg\nztRNt03SzDQo4fyqZeam6XPIBjWYmVmDK7QFJOkk4MfAfWTdbAH8NXAncC1wCFnr5tyI2JqWWUg2\nsm0nWZfdilR+AnAVMAq4MSLmp/IWYClwPPAkMCcNYKiOxS2gPmth0qRWNm9eV3YgZlaSIltAvhp2\n/bdT+DYG2lD5jJjZCw32LjgzM7MXcAIyM7NSOAGZmVkpnIDMzKwUTkBmZlYKJyDrRYuvb9eL1tbD\nGTlyVNlhmA06HoZd/+0Uvo0yDJXPyb7I3nOfM2XNycOwBwm3FIaePe/5Dl+I1qyP3AKq7zYKXX+Z\nhsrnpK/2fs/dCrLm4xaQlczHgbrywn3iVpBZX7gFVN9tFLr+sg2Vz0qtunu/vZ+smbgFZGZmTccJ\nyKyu3F1pVisnILN90H2S8XEgs1r5GFB9t1Ho+ss2VD4rtejtvfa+smbhY0CDgLtdhg6/12b1UWgC\nknSFpE5Jq3Nl4yWtkPSQpJsljcvNWyhpraQ1kk7Nlc+QtFrSw5IW58pHSlqWlrlN0qFFvp6eNH+3\ni49tVPT+XntfmdWi6BbQlcBpVWULgFsi4mhgJbAQQNIxwLnAdOAM4DLt6ee4HJgXEdOAaZIq65wH\nbImIo4DFwKVFvpihzcc2aud9ZVaLQhNQRPwE+F1V8ZnAkjS9BDgrTc8GlkXEcxGxDlgLzJTUCoyN\niFWp3tVCF9QkAAALXklEQVS5ZfLrug6YVfcXYWZmhSjjGNDEiOgEiIjNwMRUPhnYkKu3KZVNBjbm\nyjemsr2WiYhdwFZJE4oL3YY6d62Z1c+IsgMA6jlcqMeRGu3t7bun29raaGtrq+Omh4Ls2MZQvtaZ\nu9as2XV0dNDR0TEg2yp8GLakw4DvRcSr0/M1QFtEdKbutVsjYrqkBUBExCWp3k3AImB9pU4qnwOc\nHBEfqNSJiDskDQcej4iJL4yi+GHYzT4EO2+oDjFubT28TwloqO4nay6DfRi22Ltlshy4IE3PBW7I\nlc9JI9umAkcCd6Zuum2SZqZBCedXLTM3TZ9DNqjBBrn29vbdrdN8q7VsfWv9eCScWW8KbQFJ+gbQ\nBrwI6CRr0XwX+BZwCFnr5tyI2JrqLyQb2bYTmB8RK1L5CcBVwCjgxoiYn8pbgKXA8cCTwJw0gKGr\nWNwCqpOi9uOYMQezfft29vTKDgOep/IbZtKkiaV1//W19VPhVpANdkW2gHwlhPqtv7B1N5b63vOm\ntfVwfvOb3/D88wE822v9RYsWldIq2tf3d6h8v6x5OQHVQZEJaF9/HQ9m/d2XexLP7/uwVEv6O4zR\no0fyzDNb+xVDrfrz/g6V75c1LyegOigyAQ2d1k9FC6NHj9rnBJB1tT3Z7ygG4rPb3x8XQ+X7Zc1r\nsA9CsKazg+3b/5cxYw7q01KtrYcj7V+X5AMtSAcUeqC/vb29ny1bD0Qw64lbQPVZdyHrbXwtVH7D\njB49ko9//K+APSPXxow5mDFjxrBlyxZ27nyOWo7x7EsM9TwmVZG10p4BdvR7XUPlO2bNyV1wdeAE\nVLSW3HSlYf1sKu//P/Hetj1s2HBe/OIX9ysRtbe38/nP/2saife/dYtuqHzHrDk5AdWBE9BQkB2b\nghGMGTOmx2SUHdt5gmzIt9LfoIhkOVS+Y9acnIDqwAloqKi0uCrdg5UEA3snm/q1cHqLp4guQrOB\n4gRUB05AVqah8j2z5uNRcGZm1nScgMzMrBROQP3k8zysdz4fyKwrPgbU//XWfZ3WnIbKd82ai48B\nmZlZ03EC6gd3q1jt3A1nVs1dcP1bZ13XZ81vqHzfrHm4C64Xkk6X9KCkhyV9qux4zLrW0ucLuJo1\ns0GfgCQNA/4VOA14BXCepJeXG5VZV7q+inhHR0c54fSR46yvwRJnkQZ9AgJmAmsjYn1E7ASWAWcW\nvVH359u+yZKQdAAjR44CBs8/IsdZX4MlziIN+mNAkt4JnBYRf5Ge/xkwMyIuqqpXt2NAQ/EOqFaE\nyvXq/gCMTGX569V1dQ276rJ9WWZf1/McsF8DxdNd2U5gRJ3j2fcYhw0Tzz//PKNHt/CHPzzPyJHD\ndt+65POf/9e9Lpzb3t5eyi3ne+JrwfVgIBPQnisoF3FfGzNrbvkL5UKW0Hel50qP58nfY2ugbjvf\nkyIT0IgiVjrANgGH5p5PSWUv4FFrZlaeHVV/q8v3tn37s03/P6sZWkDDgYeAWcDjwJ3AeRGxptTA\nzMysR4O+BRQRuyR9CFhB1na9wsnHzKzxDfoWkJmZDU6Ddhi2pCmSVkq6X9J9ki5K5eMlrZD0kKSb\nJY3LLbNQ0lpJaySdmiufIWl1OpF1cUHxDpN0t6TljRqnpHGSvpW2e7+kExs0zo9I+mXaxtcljWyE\nOCVdIalT0upcWd3iSq9zWVrmNkn5Y5/9jfPSFMe9kr4t6cAy4+wqxty8j0l6XtKEMmPsKU5JH06x\n3Cfp4kaMU9KxaZ33SLpT0msGPM6IGJQPoBU4Lk2PITsO9HLgEuCTqfxTwMVp+hjgHrJux8OB/2FP\nC/AO4LVp+kayUXX1jvcjwH8Cy9PzhosTuAp4b5oeAYxrtDiBlwKPACPT828CcxshTuANwHHA6lxZ\n3eICPgBclqbfDSyrY5xvAYal6YuBz5UZZ1cxpvIpwE3Ar4EJqWx6g+3LNrJDAiPS84MbNM6bgVPT\n9BnArQP9ntftn1fZD+C76Uv0IDAplbUCD6bpBcCncvV/AJyY6jyQK58DXF7n2KYAP0wfzEoCaqg4\ngQOBX3VR3mhxvhRYD4xPX5DljfS+A4dVfcnrFhfZP94T0/Rw4Df1irNq3lnA0rLj7CpG4FvAq9g7\nATXUviT7UXRKF/UaLc4fAOek6fOA/xzoOAdtF1yepMPJsvvtZF/2ToCI2AxMTNUmAxtyi21KZZOB\njbnyjamsnr4AfILszLSKRotzKvBbSVcq6yr8D0kHNFqcEfEY8E/Ao2mb2yLilkaLM2diHePavUxE\n7AK25ruh6uh9ZL9uGypOSbOBDRFxX9WshokxmQa8SdLtkm6VdEKDxvkR4POSHgUuBRYOdJyDPgFJ\nGgNcB8yPiGfY+588XTwfUJL+GOiMiHvZc6p0V0qNk6w1MQP4t4iYAWwn+yXUaPvzILJLLR1G1hoa\nLek9XcRV9v7sTj3jqvtJIpI+DeyMiGvqudp+r0DaH/hrYFH/w+l6E3Vc1whgfES8DvgkWautXuoZ\n5wfI/m8eSpaMvlbHddcU56BOQJJGkCWfpRFxQyrulDQpzW8Fnkjlm4BDcotXTljtrrxeTgJmS3oE\nuAY4RdJSYHODxbmR7Nflz9Pzb5MlpEbbn28BHomILemX1vXA6xswzop6xrV7nrLz3w6MiC31ClTS\nBcDbgD/NFTdKnC8jOx7xC0m/Ttu7W9JEuj8Zvax9uQH4DkBErAJ2SXpRA8Y5NyK+m+K8Dnht9TaL\njnNQJyCyjP1ARHwxV7YcuCBNzwVuyJXPSaM1pgJHAnembpFtkmZKEnB+bpl+i4i/johDI+IIsj7T\nlRHx58D3GizOTmCDpGmpaBZwPw22P8m63l4naVRa/yzggQaKs3JNlYp6xrU8rQPgHGBlveKUdDpZ\nN/HsiMifml9mnLtjjIhfRkRrRBwREVPJfjAdHxFPpO29u1H2Jdnx6FMA0vdpZEQ82YBxbpJ0copz\nFrA2t82Bec/39YBW2Q+ylsUu4F6yERt3A6cDE4BbyEbFrQAOyi2zkGxExxrS6I9UfgJwX3oDvlhg\nzCezZxBCw8UJHAusSvv0O2Sj4BoxzkVpm6uBJWRXyCw9TuAbwGNk11Z5FHgv2WCJusRFdtGwa1P5\n7cDhdYxzLdngjrvT47Iy4+wqxqr5j5AGITTgvhwBLE3b/TlwcoPG+foU3z3AbWQJfUDj9ImoZmZW\nisHeBWdmZoOUE5CZmZXCCcjMzErhBGRmZqVwAjIzs1I4AZmZWSmcgMz2gaRJkq5Jl59fJem/JP0f\nSd8rMaZbJc0oa/tmfeUEZLZvrie7qsVREfFashP3JtG416AzazhOQGZ9JOnNwB8i4iuVssiu0Pzf\nwFjtuanf0twyn5F0R7qZ17/nym+VdHGa96Ckk1L5XGU3hvuBspvZXZJb5q2Sfibp55K+ma5abjbo\nOAGZ9d0rgbu6mXcccBHZTb1eJun1qfxfIuLEiHg1cEC6SnrF8Ig4keyKxO258mPJrqv1arJriE1O\nF7X8G2BWRLwmxfHROr0uswE1ouwAzJrMnRHxOICke8mu4PwzYJakTwAHkF0f7pfA99My30l/7yK7\nzUTF/4vsFiNIuj/NG0+W3H6aLgi5X1q/2aDjBGTWd/cD7+pmXv5K0ruAEZJagH8DZkTEY5IWAaO6\nWGYXe38n8+t6Ps0TsCIi3tOP+M0agrvgzPooIlYCIyW9v1Im6VXAG7tZZBTZ4IQn0w0Uu0te0PuN\nvG4HTpL0srTdAyQdVXPwZg3ECchs35wNvFXS/0i6D/gH4PGqOgEQEduAr5K1nH4A3Fldp4fn1ev6\nLdn9ha6R9Auy7reje1nWrCH5dgxmZlYKt4DMzKwUTkBmZlYKJyAzMyuFE5CZmZXCCcjMzErhBGRm\nZqVwAjIzs1I4AZmZWSn+P0aVor91qWuFAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11af40cd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"e.plot_spectrum()"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"pixel_index = (23, 34)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAEZCAYAAACEkhK6AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH2pJREFUeJzt3XmYZFWZ5/HvryohWQqKQqQSqYIClIJWBFGBFrVCFkVt\nUVxQ3ECHbp/uQW1Rocpum8RnWsHp0WFsHbVVRFQERTZbGpopUruxkU22YlFZSkBIVCgW4UEt3vnj\nnihuBnEjTmbGlpm/z/PEkxHn3nPOmzcy4417zo0TigjMzMzamdfvAMzMbGZwwjAzsyxOGGZmlsUJ\nw8zMsjhhmJlZFicMMzPL4oRhZmZZnDBmGUl3SDqgoexISf9RenynpMckPSzpkfTz/6Rtx0i6QdJQ\naf+/lXS1pHmSdpT0ZLr/w1L9P0h6ovT4C5JWpH0fbuhr31Lbr5L0o1Q+LulSSa+r+N3eLekqSQ9J\n+pWkkyXNK21fJOkcSY+m43BEadtGkr6byp+U9PIm7e+dYnlE0r2S3t/mWJ8s6beSfiPppCbbPyjp\n9hTPGknPbtHWjpJWS/q9pJskHVjaVpN0vaQHU19nS3pWRTsbS/pKeo4fknSNpEMmcxwa2vtI+nt4\nWNJtkj7SsH21pPslrZP0M0mHtmhrhaT1DX8L72rY56D0t/Zoeo7f3Co+67GI8G0W3YA7gAMayo4E\nftywzysq6gv4MTCaHu8MrAP2TI93BNYD8xrqnQp8oqFsBfCrFrG+GXgIeA+wRSp7GfCliv3fB+wP\nDAHbAVcBx5W2n5Fum6b91gG7p20bAR8AXgLcA7y8oe1nAOPA21L7mwPLW8T+PuDmFMd2wBrgr0rb\njwaurbcB7ARs1aK9nwD/ExgG3gg8CDwjbXsmsH3p9zgZOK+inc2AfwCWpsevBR4Gdsg5Dk3a+wiw\nF8Wby12BO4HDS9v3ADZK9/dJfS2uaKvd38Ofpefglam/RcBO/f6f8q30HPU7AN86/ITmJ4wDWrSx\na3qxfR5wCfA/Sts6mTDWAsdO43f9UP2FM71QPgHsUtp+GvDJJvXuapIw/hE4bRJ9XwYcXXr8HuAn\n6b6AX1GRlJu09RzgcWDzUtmPygmoVD4MfAq4cRKxXgcclnMcMto6BTilYts+wGPAiyq2t/t7+BZw\n4lT/Hnzr/s1DUnODJrNzRPyc4kXpUmB74BMdD0haDiwBzp5GMy+neGcPRZL7Y0TcVtp+HfDczLb2\nAx6UdFkaGjtP0tIW+z83td+sr6UUv9seaVjlNkmjbdq6PSJ+XxW7pKWSHqR4QT6W4iyjLUmLKRLS\nmnb7pv2PkHRti11e1tiWpAskPQ5cDoxFxFWlmB+QtKS0+7ZpuO82SZ+RtFlp235FNV0v6R5J35C0\nKCdu6w0njNnp3PSP+oCkB4DPt9jnwfTzvzVs/09ga+B7EfGHacSyfSmWel+bUgwBAdw7lUYlvRd4\nIfBPqWgBxXBI2cPAFplNLgHeDbyf4gX/TorhrSoLKIbTyn0tSPe3Tz8PpnjRPwA4oskxrmrrabFH\nxF0RsYjiuP098PPWvw6omIf6JvD19CagrYg4IyL2qmjvRIo3H6c21Hld+h1eDVzcEPPWEXF3KroZ\n2CsitqM4Ji8EPlNqagnwTuAwiiS3GfC5nLitN5wwZqfXp3/UrSNia+BvWuyzKP38an2DpI2AL1H8\nsx4jadk0YrmnFEu9r8eB36Xt2022QUlvoBhCOiQiHkjFjwJbNuy6EHgks9nHgXMi4pqUIE8E/lzS\nFpJWlSZpv1DR38JUVm8L4OSIeCQi1lIcz9ek+G8stbf/ZGKPiHXAN4DzyhP+jSSJIlk8QZEEp0XS\nMRQv5q+JiD82iWt9RFwEvErSXzRrIyLuj4hb0v21wHHAm0q7PA58LSJui4jHgE9SJCEbEE4Ys1PO\nEFSrff4BGI+Iv6V4oftyR6IqiYhbKcbQ39Ru37J0xc+XgL+IiJtKm34ODEnapVS2J5lDMcD1QNOl\nmyPiUxGxRURsGRH15LsmtV+3V6mvW4HGs7INbUfE80rtXZbq7Sxp88zYN6KYCG9MMmVfBbYB3hgR\n61vs11Y6mzuOYt6r3RnhELBLm30mNF+6f/1kY7PecsKwCSTtCRxDcZUPwCiwo6SjyrtNpskW2z4M\nfFzFZb9bqPBSSV+qiO0AinfNb4qIq8vb0jvS7wOfkLSZpJcCrwNOL9XfWNIm6eGwpOFSE6cCh0l6\nfjrD+jjwnxFRdYbyDeBYSc+StD3FvMKpKZbHge8Ax0lakMbw/wq4oFlDEfELiiuqTpA0LOmNFBcc\nnJ3iPkzSrun4PJNiGOeadLbR7Dh9EdgNOLTZcGKb49C47zsozuYOTmcF5W3LJR0iaRNJQ5LeSTHH\n8aOKtmqSdkj3lwInAeeWdjkVeI+kndLcxvFUHDPrk37PuvvW2RtwO3lXSf2eYpy8fjub4g3ElcCH\nG+qvAO6neFdbdZXU12h+ldSfSn08kn4eVtrnlRSX8T5McUnlauDVFb/baop37uW2/rW0fRFwDsUQ\nz53AWxvq35FiL992KG1/H3A3xXDZeaRLWVsc65PSvr8FPtWwbQuKOZCHKa4G+7s2be1AcZHBYxRj\n/a8obTsmPa+PAL8Gvk26bLainSdTO4+UjtMROccBeDtwQ8Pf0xMNx/wLadtuFBPdDwEPAD+lSFL1\nukvT/kvS4w+l4/toOiafpXRlWNrnhPS3Ng58HVjY7/8p3566KT1JXSNpIfAVindMTwLvpRg+OJPi\nxedOiuu6Gyf9zMxsgPRiSOoU4IcRsTvFuOwtwErgkohYTvGucVUP4jAzs2no6hmGpC2Bn0XELg3l\ntwArImJc0gjFtdu7dS0QMzObtm6fYewE/FbSqSrWtPlymsxaHBHjABFxH7Btl+MwM7Np6nbCGAL2\nBj4fEXtTTLSu5OmXL3Z3IsXMzKZtqP0u03I3cFekpQIorsRZCYxLWlwakrq/WWVJTiRmZlMQEZNa\nEihHV88w0rDTXZJ2TUUHUnwY6XzgqFR2JMUljFVtDPzthBNO6HsMjtMxOk7HWb91S7fPMKBYSvlb\n6cNQt1Os6jkfOCt9gnQtcHgP4jAzs2noesKIiOuAFzfZdFC3+zYzs87x0iAdUKvV+h1CFsfZOTMh\nRnCcnTZT4uyWrn/SezokxSDHZ2Y2iCQRM23S28zMZg8nDDMzy+KEYWZmWZwwzMwsixOGmZllccIw\nM7MsThhmZpbFCcPMzLI4YZiZWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPM\nzLI4YcwgIyPLGBlZ1u8wzGyO8jfuzSBS8QVaPiZm1oq/cc/MzPrKCcPMzLI4YZiZWRYnDDMzy+KE\nYWZmWZwwzMwsixOGmZllccIwM7MsQ93uQNKdwEPAk8AfI2IfSYuAM4EdgTuBwyPioW7HYmZmU9eL\nM4wngVpEvCAi9kllK4FLImI5sBpY1YM4zMxsGnqRMNSkn9cDp6X7pwFv6EEcZmY2Db1IGAH8u6Qr\nJR2dyhZHxDhARNwHbNuDOMzMbBq6PocB7B8R90p6JnCxpFspkkiZV9MzMxtwXU8YEXFv+vkbSecC\n+wDjkhZHxLikEeD+qvqjo6Mb7tdqNWq1WncDNjObYcbGxhgbG+t6P11d3lzSZsC8iHhU0ubAxcCJ\nwIHAAxFxsqTjgUURsbJJfS9vXuLlzc0sR7eWN+92wtgJOIdiyGkI+FZEnCRpa+AsYCmwluKy2nVN\n6jthlDhhmFmOGZkwpssJYyInDDPL4S9QMjOzvnLCMDOzLE4YZmaWxQnDzMyyOGGYmVkWJwwzM8vi\nhGFmZlmcMMzMLIsThpmZZXHCMDOzLE4YZmaWxQnDzMyyOGGYmVkWJwwzM8vihGFmZlmcMMzMLIsT\nhpmZZXHCMDOzLE4YZmaWxQnDzMyyOGGYmVkWJwwzM8vihGFmZlmcMMzMLIsThpmZZXHCMDOzLE4Y\nZmaWxQnDzMyyOGGYmVmWniQMSfMkXSPp/PR4kaSLJd0q6SJJC3sRh5mZTV2vzjA+CNxUerwSuCQi\nlgOrgVU9isPMzKao6wlD0hLgNcBXSsWvB05L908D3tDtOMzMbHp6cYbxWeCjQJTKFkfEOEBE3Ads\n24M4zMxsGoa62bik1wLjEXGtpFqLXaNqw+jo6Ib7tVqNWq1VM2Zmc8/Y2BhjY2Nd70cRla/V029c\n+iTwTuBPwKbAFsA5wIuAWkSMSxoBLo2I3ZvUj27GN9NIAsDHxMxakUREqNPtdnVIKiI+FhE7RMTO\nwNuA1RHxLuAC4Ki025HAed2Mw8zMpq9fn8M4CThY0q3AgemxmZkNsK4OSU2Xh6Qm8pCUmeWYkUNS\nZmY2ezhhmJlZFicMMzPL4oRhZmZZnDDMzCyLE4aZmWVxwjAzsyxOGGZmlsUJw8zMsjhhmJlZFicM\nMzPL4oRhZmZZnDDMzCyLE4aZmWVxwjAzsyxOGGZmlsUJw8zMskw6YUhaJOn53QjGzMwGV1bCkDQm\naUtJWwPXAP8i6TPdDc3MzAZJ7hnGwoh4GHgj8I2I2Bc4qHthmZnZoMlNGEOStgMOB37QxXjMzGxA\n5SaME4GLgF9GxJWSdgZ+0b2wzMxs0Axl7ndvRGyY6I6I2z2HYWY2t+SeYXwus8zMzGaplmcYkv4c\neAnwTEnHljZtCczvZmBmZjZY2g1JbQwsSPttUSp/GHhzt4IyM7PBo4hov5O0Y0Ss7UE8jf1GTnxz\nhSQAfEzMrBVJRIQ63W7upPewpC8Dy8p1IuKATgdkZmaDKfcM4zrgi8DVwPp6eURc3abeMPBjiqGt\nIeB7EXGipEXAmcCOwJ3A4RHxUJP6PsMo8RmGmeXo1hlGbsK4OiJeOKUOpM0i4jFJ84HLgA8AbwJ+\nFxGflnQ8sCgiVjap64RR4oRhZjm6lTByL6u9QNLfSNpO0tb1W07FiHgs3R2mOMsI4PXAaan8NOAN\nkwnazMx6L/cM444mxRERO2fUnUcxlLUL8PmIWCXpwYhYVNrngYh4WgLyGcZEPsMwsxx9nfSOiJ2m\n2kFEPAm8QNKWwDmSnktxljFht6r6o6OjG+7XajVqtdpUQzEzm5XGxsYYGxvrej+5ZxjvblYeEd+Y\nVGfSx4HHgKOBWkSMSxoBLo2I3Zvs7zOMEp9hmFmOfs9hvLh0exkwChzarpKkbSQtTPc3BQ4GbgbO\nB45Kux0JnDeZoM3MrPeyzjCeVknaCvhORBzSZr89KCa156XbmRHxj2nC/CxgKbCW4rLadU3q+wyj\nxGcYZpajr5fVNglmI+DGiFje6YAa+ulbwhgdHZ0wfzIInDDMLEe/P4dxAU9NTM8HdgfOavbZiU7q\nZ8JIB7wvfVdxwjCzHP1OGCtKD/8ErI2IuzsdTJN+nTBKnDDMLEdfJ70j4kfALRQr1i4C/tDpQMzM\nbLBlJQxJhwNXAG+h+F7vn0ry8uZ9MczIyLJ+B2Fmc9BkFh88OCLuT4+fCVwSEXt2NTgPSU1QH5IC\nD0uZWbV+fw5jXj1ZJL+bRF0zM5sFcr8P498kXQSckR6/Ffhhd0IyM7NB1HJIStKzgcURcZmkNwIv\nTZvWAd+KiNu6GpyHpCbwkJSZ5ejLZbWSfgCsiogbGsr3AD4ZEa/rdEAN/ThhlDhhmFmOfs1hLG5M\nFgCpbFmngzEzs8HVLmFs1WLbpp0MxMzMBlu7hHGVpL9sLJR0NMWXIpmZ2RzRbg5jMXAOxSe76wni\nRcDGwGERcV9Xg/McxgSewzCzHP1eS+oVwPPSwzURsbrTgVT064RR4oRhZjkGannzXnHCmMgJw8xy\n9PuT3mZmNsc5YZiZWRYnDDMzy+KEYWZmWZwwzMwsixOGmZllccIwM7MsThhmZpbFCcPMzLI4YZiZ\nWRYnjD4ZHR2d1P4jI8u6EoeZWS6vJVXdd1fXa5ps++V1pMBrSZlZNa8lZWZmfdXVhCFpiaTVktZI\nukHSB1L5IkkXS7pV0kWSFnYzDjMzm75un2H8CTg2Ip4L/Dnw3yXtBqwELomI5cBqYFWX4xhIufMY\nnr8ws0HQ0zkMSecC/5xuKyJiXNIIMBYRuzXZf1bPYUDeXETj/EVuPTObm2b8HIakZcBewOXA4ogY\nB0hf87ptr+IwM7OpGepFJ5IWAN8DPhgRj0pqfHtc+Xa5PGxTq9Wo1WrdCNHMbMYaGxtjbGys6/10\nfUhK0hDwA+DCiDglld0M1EpDUpdGxO5N6npICg9JmdnkzOQhqa8BN9WTRXI+cFS6fyRwXg/iMDOz\naejqGYak/YEfAzdQDDsF8DHgCuAsYCmwFjg8ItY1qe8zDHyGYWaT060zDH/Su7pvJwwzm5Fm8pCU\nmZnNAk4YZmaWxQnDzMyyOGFUGvaSHGZmJZ70ru4b6N7ksie9zaxbPOltZmZ95YRhZmZZnDD6Zrjf\nAZiZTYoTRt880e8AzMwmxQnDzMyyOGFkKC+xvmDBNr7c1szmJF9WW903UFy+Wl5XqlOX2/qyWjPr\nFl9Wa2ZmfeWEYWZmWZwwWurc8iAjI8uatDXMggVbtayz8cabdKR/M7Pp8hxGdd8THk93DqOxXrn9\nqraazV20q2Nm5jkMMzPrKycMMzPL4oTRIc3nKMzMZg/PYVT3PeFxuzmMdnMbnsMws17xHIaZmfWV\nE0Zbk19VtryUSE775aGsydU1M+sdD0lV9z3h8WSGpMpLiTTb3q79qn2a7W9m1shDUmZm1ldOGGZm\nlsUJY4q6OdcwOjrqS3TNbOB4DqO67wmP210O28k5jByD/LyZWX95DsPMzPqqqwlD0lcljUu6vlS2\nSNLFkm6VdJGkhd2MwczMOqPbZxinAq9qKFsJXBIRy4HVwKoux9ABxWclms1bjIwsa7pE+ejo6Ia5\niKfmI4bT/tt0NVozs27o+hyGpB2BCyLi+enxLcCKiBiXNAKMRcRuFXUHZg6jmfp8RbuyHJ7DMLNO\nmU1zGNtGxDhARNwHbNuHGMzMbJIGYdLbb5XNzGaAoT70OS5pcWlI6v5WO5fnDWq1GrVarbvRTUvr\nr1xtZWRkGY8+um5DO/DEpOrX50zMbO4ZGxtjbGys6/30Yg5jGcUcxh7p8cnAAxFxsqTjgUURsbKi\n7oybw+iVZp/z8LyGmUH35jC6mjAkfRuoAc8AxoETgHOB7wJLgbXA4RGxrqK+E0aLvsucMMysbkZO\nekfE2yPiWRExHBE7RMSpEfFgRBwUEcsj4pVVyWIw5S51Plzxcyrt59f1ciKT4yE8s8nx0iDVfbfd\nZ9DOMJqVWzWfldlsNSPPMMzMbPZwwjAzsyxOGFNSzCuUl/zoRHvWa1O/DNpsLvIcRnXffek3l+cw\nps/HzGYrz2GYmVlfOWGYmVkWJ4xsgzfP4M8RmFkveQ6juu++9Jur8atgPR4/eT5mNlt5DsPMzPrK\nCaPnOj+05SVBJs/femg2eR6Squ67L/3mKg9JlWMd5OdzkPiY2WzmISkzM+srJwwzM8vihDFlVXMR\nvVkmJOeS2pGRZX2f3xiEGBr5cmSzqfEcRnXffel3slrNYQzCZaODEEOjxud2kGIz6wTPYZiZWV85\nYZiZWRYnjK7pzVIiE+cHqpfrbjVuP50x/XLdXs8NTHZ+ZHR0NO0/eMu8mM0EnsOo7rsv/XZCs+VC\nWn0d6XS+qrRxeZJeLrs+2barntNB/h8wmwrPYZiZWV85YZiZWRYnjBlpmOmMw+fOZ9TnCJrNFTy1\n3/CEbSMjyzbMo5S/wra8T71us77Kym2VLViwzdP2rdVqlb9TY19mNjWew6juuy/9dkK7OYzGuYaq\nba0+r9C4jlWzz4NU1S/XbbU8e9UcRbN2283DtHo+B/l/wGwqPIdhZmZ95YQx6ww3DO88NRzUOMTT\neElszrBN1dBPY912l7vW928ciqrH0ay9icNTTx+SazbUNbGdZsN4w1NaumQQlzzppmZ/Gx7mm3s8\nJFXdd1/67ZWq5dHr26D10E9V3XZ9Nms3N9bG+622Nxv+yokt1yAuedJNVZdMz5Xff6bxkJSZmfVV\n3xKGpEMk3SLp55KO71ccZmaWpy8JQ9I84J+BVwHPBY6QtFs/YpmdWl1yW1ySW18iY/78zZ9Wb8GC\nbZA2e1q9eln9603Ll9a2v9S3WLbkqa9Gbbb/cJP7w5WX59aVv261/ns91Vf1cimNms19tJurqG+v\nuhx5/vzNN9Qvz7HkzhnlxNxqLuqoo46a0Hfj/cZLlMsxVl3W3CqG0dHRCW3W26g6JnVjY2PUarWm\n81DtdGI+qer5aIx3bGysst6cmNeKiJ7fgP2AC0uPVwLHN9kv+gXwbQ7d6s95+fkv/x3k/H2029bY\nZrN2p/p32upx1e/Wbv+qY1O1b1W9Vse87oQTTmjbX+4xmIqc57keZ1W9Tj2nnZDi6Phrd7+GpLYH\n7io9vjuVmZnZgPKkt5mZZenLZbWS9gNGI+KQ9HglxSnUyQ379T44M7NZILpwWW2/EsZ84FbgQOBe\n4ArgiIi4uefBmJlZlqF+dBoR6yUdA1xMMSz2VScLM7PBNtCf9DYzs8HR00lvSUskrZa0RtINkj6Q\nyhdJuljSrZIukrSwVGeVpF9IulnSK0vle0u6Pn3w7393IdZ5kq6RdP6gxpj6WCjpu6nvNZL2HbRY\nJX1I0o2p/W9J2nhQYpT0VUnjkq4vlXUstvS7fifV+S9JO3Qoxk+nGK6VdLakLfsZY1WcpW0flvSk\npK0HNU5J70+x3CDppEGMU9Keqc2fSbpC0ot6Gmc3rtWtugEjwF7p/gKKeYzdgJOB41L58cBJ6f6f\nAT+jGDpbBvySp86Kfgq8ON3/IfCqDsf6IeCbwPnp8cDFmNr9OvCedH8IWDhIsQLPAm4HNk6PzwSO\nHJQYgZcCewHXl8o6Fhvw18AX0v23At/pUIwHAfPS/ZOAT/Uzxqo4U/kS4N+AO4CtU9nugxQnUKMY\nIh9Kj7cZ0DgvAl6Z7r8auLSXz3tHX7ymcEDOTX/4twCLU9kIcEu6P+EDfcCFwL5pn5tK5W8D/m8H\n41oC/Hv6I6onjIGKMbW5JXBbk/KBiZUiYawFFqU/5vMH7TkHdmz4p+xYbBQvlPum+/OB33QixoZt\nbwBO73eMVXEC3wX2YGLCGKg4Kd7IHNBkv0GL80LgLen+EcA3exlnP9eSWkaRPS+n+OccB4iI+4Bt\n026NH/C7J5VtT/Fhv7pOf/Dvs8BHKT65WTdoMQLsBPxW0qkqhs++rGL9joGJNSJ+Dfwv4Fepv4ci\n4pJBirGJbTsY24Y6EbEeWFcelumQ91K8cxy4GCUdCtwVETc0bBqoOIFdgZdLulzSpZJeOKBxfgj4\nJ0m/Aj4NrOplnP1aS2oB8D3ggxHxKBNfmGnyuGckvRYYj4hrgVbXMfctxpIhYG/g8xGxN/B7inca\ng3Q8twJeT/FO6VnA5pLe0SSmQTieVToZW0evjZf0d8AfI+KMTjbbkUakTYGPASd0or1mXXSwrSFg\nUUTsBxxHcVbUKZ2M868pXjd3oEgeX+tg223j7HnCkDREkSxOj4jzUvG4pMVp+whwfyq/B1haqr4k\nlVWVd8L+wKGSbgfOAA6QdDpw3wDFWHc3xbu3q9LjsykSyCAdz4OA2yPigfQu5hzgJQMWY6NOxrZh\nm4rPH20ZEQ90IkhJRwGvAd5eKh6kGHehGE+/TtIdqc9rJG2b+ixPsvb1WFK80/4+QERcCayX9IwB\njPPIiDg3xfk94MWNfXYzzn6cYXyNYkztlFLZ+cBR6f6RwHml8rel2fydgGcDV6Rhgock7SNJwLtL\ndaYlIj4WETtExM4U432rI+JdwAWDEmMp1nHgLkm7pqIDgTUM0PGkGIraT9Imqe0DgZsGLEYx8d1V\nJ2M7P7UB8BZgdSdilHQIxbDpoRHxREPs/YpxQpwRcWNEjETEzhGxE8UbnBdExP2pz7cOQpzJucAB\nAOn/aeOI+N0AxnmPpBUpzgOBX5T67P7zPtXJmClO4OwPrAeupZjRvwY4BNgauITiqqmLga1KdVZR\nzPjfTLo6IJW/ELghHbBTuhTvCp6a9B7UGPcErkzH9PsUV0kNVKwUQxI3A9cDpwEbDUqMwLeBXwNP\nUCS391BM0HckNop12s9K5ZcDyzoU4y8oLia4Jt2+0M8Yq+Js2H47adJ70OKkGJI6PfV7FbBiQON8\nSYrvZ8B/USTgnsXpD+6ZmVkWr1ZrZmZZnDDMzCyLE4aZmWVxwjAzsyxOGGZmlsUJw8zMsjhh2Jwh\nabGkM9JyzldK+oGkv5R0QR9julTS3v3q32wynDBsLjmH4pP7z4mIF1N80Gkxg72OldnAcMKwOUHS\nK4A/RMS/1MuiWEH1P4At9NSXUJ1eqvNxST9NXz7zxVL5pZJOSttukbR/Kj9SxZcZXajiy5dOLtU5\nWNJPJF0l6cy0qrDZjOKEYXPF84CrK7btBXyA4ktodpH0klT+uYjYNyKeD2yWVjKumx8R+1KsGDpa\nKt+TYl2e51OsQbR9WsTu74EDI+JFKY5jO/R7mfXMUL8DMBsAV0TEvQCSrqVYYfUnwIGSPgpsRrG+\n1I3Av6Y6308/r6ZYur3u/0WxZD+S1qRtiyiS0WVpAbiNUvtmM4oThs0Va4A3V2wrr/a6HhiSNAx8\nHtg7In4t6QRgkyZ11jPx/6jc1pNpm4CLI+Id04jfrO88JGVzQkSsBjaWdHS9TNIewMsqqmxCMRn+\nu/SFX1XJBtp/8czlwP6Sdkn9bibpOdnBmw0IJwybSw4DDpb0S0k3AJ8E7m3YJwAi4iHgKxRnJhcC\nVzTu0+JxY1u/pfh+jTMkXUcxHLW8TV2zgePlzc3MLIvPMMzMLIsThpmZZXHCMDOzLE4YZmaWxQnD\nzMyyOGGYmVkWJwwzM8vihGFmZln+P5+Z/WZ0TXDYAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11beb3f10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"e.plot_spectrum(pixel_index=pixel_index)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Defining the fit function"
]
},
{
"cell_type": "code",
"execution_count": 167,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from astropy.modeling.models import custom_model\n",
"def step_function(x, mean, bkg1, bkg2):\n",
" return (bkg2 - bkg1) * 0.5 * (np.sign(x - mean) + 1) + bkg1\n",
"\n",
"@custom_model\n",
"def emission_line(x, amplitude=1., mean=1., stddev=1., bkg1=1., bkg2=1.):\n",
" return (amplitude * np.exp(-0.5 * ((x - mean) / stddev)**2)) + step_function(x, mean, bkg1, bkg2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Fit the 30.9 keV line"
]
},
{
"cell_type": "code",
"execution_count": 332,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hist, bins = e.spectrum(pixel_index=pixel_index)\n",
"width = 1 * (bins[1] - bins[0])\n",
"center = (bins[:-1] + bins[1:]) / 2\n",
"m, argmax = (hist.max(), bins[hist.argmax()])\n",
"g = models.Gaussian1D(amplitude=m, mean=argmax, stddev=30)\n",
"fit_t = fitting.LevMarLSQFitter()\n",
"t = fit_t(g, center, hist)\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 333,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Parameter('mean', value=5098.54298882)\n",
"Parameter('stddev', value=46.598968279)\n"
]
}
],
"source": [
"print(t.mean)\n",
"print(t.stddev)\n",
"#print(t.bkg1)\n",
"#print(t.bkg2)"
]
},
{
"cell_type": "code",
"execution_count": 334,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x158a9a2d0>"
]
},
"execution_count": 334,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEZCAYAAACU3p4jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VNX5+PHPkz0RAgE0IAIqIK2ILOICFIksYRMQUSu2\nFZRav61L69KKtUWw1YpVa/Vnq1arKC6oiIKySgiLLIqAFRQQBESQqIAEyEaS8/vj3uAYMslkmJkz\nM/d5v173lZm7PnMy88ydc889R4wxKKWUin8JtgNQSikVGZrwlVLKIzThK6WUR2jCV0opj9CEr5RS\nHqEJXymlPEITvlJKeYQm/DgjIttEpG+1eWNEZKnP8+0iUiQihSJy0P37qLvsRhH5WESSfNb/nYh8\nKCIJItJGRCrdx7N9ti8TkVKf5/8SkT7uuoXVjnW+z74Hishid36BiCwSkWF+XtvVIrJaRA6IyBci\nMllEEnyWZ4nIDBE55JbDaJ9lySLymju/UkQurGH/3dxYDorIVyJyUx1lPVlEvhWRb0Tk/hqW/1ZE\nPnfj2SAi7WrZVxsRyRORwyLyiYj081mWIyL/E5H97rGmi8jJfvaTIiJPu//jAyKyRkQG1accqu3v\ndvf9UCgiW0Xk9mrL80TkaxH5TkTWisjwWvbVR0Qqqr0XflFtnf7ue+2Q+z++rLb4VD0ZY3SKownY\nBvStNm8MsKTaOhf52V6AJcBE9/npwHdAZ/d5G6ACSKi23bPAPdXm9QG+qCXWy4ADwDVAQ3deb+BJ\nP+tfD/QCkoAWwGrgDz7LX3andHe974Afu8uSgZuBnsAu4MJq+24KFABXuvs/AehQS+zXA5+6cbQA\nNgC/8ln+S2Bd1T6A04DGtexvOfB3IBW4FNgPNHWXnQi09Hkdk4G3/OwnA5gAtHKfDwUKgdaBlEMN\n+7sd6IJzcngGsB24wmd5JyDZfXyee6xsP/uq6/1wpvs/yHWPlwWcZvszFU+T9QB0CvE/NPCE37eW\nfZzhJsuzgHeBv/osC2XC3wHcehyv9ZaqxOcmulKgrc/yKcB9NWy3s4aEfy8wpR7Hfg/4pc/za4Dl\n7mMBvsDPl2oN+2oPFAMn+Mxb7PsF4jM/FfgbsL4esX4EjAykHALY1z+Bf/pZdh5QBHT3s7yu98OL\nwKRg3w861T1plY43SH1WNsZsxkkqi4CWwD0hD0ikA3AKMP04dnMhzpk1OF9SR4wxW32WfwR0DHBf\nFwD7ReQ9t2rpLRFpVcv6Hd3913SsVjivrZNbLbFVRCbWsa/PjTGH/cUuIq1EZD9OQr0V5yy/TiKS\njfOFsqGudd31R4vIulpW6V19XyIyS0SKgZVAvjFmtU/M+0TkFJ/VT3Kry7aKyMMikuGz7AJnM/mf\niOwSkedFJCuQuFVgNOHHpzfdD9o+EdkHPF7LOvvdv+OqLV8GNAFeN8aUHUcsLX1iqTpWOk4VCsBX\nwexURK4FzgEedGc1wKlO8FUINAxwl6cAVwM34STs7TjVQ/40wKmO8j1WA/dxS/fvAJyk3RcYXUMZ\n+9vXMbEbY3YaY7Jwyu1PwObaXw6Icx1mKvCc+yVeJ2PMy8aYLn72Nwnn5OHZatsMc1/DYGB+tZib\nGGO+dGd9CnQxxrTAKZNzgId9dnUK8HNgJM6XVAbwWCBxq8Bowo9PI9wPWhNjTBPgN7Wsk+X+faZq\ngYgkA0/ifNhuFJFTjyOWXT6xVB2rGNjrLm9R3x2KyCU4VTCDjDH73NmHgMxqqzYCDga422JghjFm\njfsFNwnoISINReROn4uM//JzvEbuvKp9AUw2xhw0xuzAKc8hbvzrffbXqz6xG2O+A54H3vK9YF2d\niAhOsi/F+RI7LiJyI04yHmKMOVJDXBXGmHnAQBG5uKZ9GGO+NsZsdB/vAP4AjPJZpRj4rzFmqzGm\nCLgP50tEhYgm/PgUSBVObetMAAqMMb/DSVRPhSQqH8aYTTh1yKPqWteX2+LkSeBiY8wnPos2A0ki\n0tZnXmcCrMoA/gfU2HWsMeZvxpiGxphMY0zVl+cGd/9VuvgcaxNQ/VfR0X0bY87y2d977nani8gJ\nAcaejHMht/qXhK9ngGbApcaYilrWq5P7a+oPONd96vpFlgS0rWOdH+ze5/H/6hubqifbFxF0Cu3E\ncV60xUk0+3FbRwBpOAlsrPu8DVBJ4Bdtd9YS6yj3WGNwqi8E+An+W+n0Bb4FfuJn+Us4F/4y3P3s\nx22l4y5PcV/PTpzqllSfZRfh/Oo4Gyeh/gNYXEvs1+Mk5JNxqnA2ANf5LH8OmIlT1XEKTnXG2Fr2\ntxx4gO9b6ezj+1Y6I3GuUQhOon8V+KCWfT3h7i/Dz3K/5VDDuj/DqXY7psUS0AEY5O4rCecXQAlO\ntU1N+8rh+9ZCrXCuET3ts/waYCtOi6YMYBpOdZT1z1W8TNYD0CnE/1D4PMCEfxinnrhqmo7zi+8D\n4LZq2/cBvnaTjb9WOv/1k/DLfY5x0P070medXJxmoIU4TfLygMF+Xlsezpmz777e8VmeBczAqSLZ\nDvy02vbb3Nh9p9Y+y68HvsRJ/G/hNoWspazvd9f9FvhbtWUNca4BFOK0Rrqrjn21dhNgEc6Xw0U+\ny250/68Hgd04X2ytatlPpbufgz7lNDqQcgCuAj6u9n4qrVbm/3KX/QjnQu0BnC+oVcBwn21bueuf\n4j6/xS3fQ26Z/AOflknuOne777UCnC/NRrY/U/E0iVvIYSMijYCncZr4VQLX4vz8noaTPLbjtOut\nftFKKaVUCEWiDv+fwGxjzI9xqgs2AuOBd40xHXDO2u6MQBxKKeVpYT3DF5FMYK0xpm21+RuBPsaY\nAhFpjtN290dhC0QppVTYz/BPA74VkWfdPj2ecm+0yDbGFAAYY/YAJ4U5DqWU8rxwJ/wkoBvwuDGm\nG86FwvEc2/wtvBcSlFJKkVT3KsflS5xmeavd59NxEn6BiGT7VOl8XdPGIqJfBEopFQRjzDH32oQ1\n4bsJfaeInGGcW7v74bRX3gCMxekPZAxOEzh/+whniEycOJGJEyeG9RixLBrLZ8uWLWRkZNS9Yhid\n3LIlt916K7fddpvVOIqKimjXzm+vy1ZF43snmoSzfJwbrY8V7jN8cLpifdG9Xf9znJsrEoFX3Tv4\ndgBXRCAOpZTytLAnfGPMR8C5NSzqH+5jK2VDbu4w9u0Lqk84mjRpwfz5s0IckVKOSJzhR7WcnBzb\nIUQ1LR//evToUeN8J9mvrnFZXfbt634cEUUXfe/Uzkb5hP1O2+MhIiaa41N2REsd/u5du2pc1r17\nd4JN+NCd1asD3zaa6/CVPSIS+Yu2SikViFNPPZUdO3bYDiPmtGnThu3btwe8viZ8pZR1O3bsCHuL\nvHjkrzWOP9ofvlJKeYQmfKWU8ghN+Eop5RGa8JVSqg6bN2+ma9euZGZmkpSUxL333ms7pKBowldK\nqTo88MAD9O3bl8LCQsrLy7nrrrsAWLx4Ma1atbIcXeA04SulVB127NhBx44dj5lvjKl3SxmbNOEr\npVQt+vXrx6JFi7jxxhvJzMzkZz/7GRMmTKCoqIghQ4awe/duGjZsSGZmJnv27LEdbq004SulVC0W\nLlxI7969efzxxyksLCQlJQWAjIwM5syZw8knn8zBgwcpLCykefPmlqOtnd54pZSKCaGqOgn2Bq94\nuDFME75SKibEQ8K1Tat0lFIqSLF0wRY04SulVNCys7PZu3cvhYWFtkMJiCZ8pZSqg78z+Q4dOjB6\n9GhOP/10mjRpEvWtdLQ/fBVztD/878VLf/hu/+22w4g5/srNX3/4eoavlFIeoQlfKaU8QptlKhWg\njRs38tBDD7Fv3z5WAKNGjaJTp07ccsstNGrUyHZ4StVJz/CVqkNhYSF33303l19+Oeeffz633347\nALfddhtFRUXk5OQwbdo0KisrLUeqVO30DF+pWnz00Udcc8019OvXj/z8fJo2bXp0Wc+ePenZsycf\nffQRd911F6+88govvPCCxWiVqp2e4Svlx65du7j22mu59957+fvf//6DZO+rc+fOzJw5k/bt2/Pr\nX/9aW5uoqKUJX6kaHDx4kDFjxvCrX/2KwYMH17l+QkIC9957L+Xl5TFzE47yHk34SlVTXl7Or3/9\na7p3786vfvWrgLdLTk7miSeeoKysjMOH/xvGCJUKjiZ8paqZPHkyxhj++te/1ruvlEaNGpGVlcWh\nQ/+P0tIVYYpQqeDoRVulfGzevJlXXnmF/Px8kpKC+3gkJSWRmXkPhYV30azZfET0Y6aiQ9jP8EVk\nu4h8JCJrReR9d16WiMwXkU0iMk9EtBGzss4Yw4QJE/jd737n9wJtoNLSBpOQcCJFRc+HKDqljl8k\nqnQqgRxjTFdjzHnuvPHAu8aYDkAecGcE4lCqVvPmzePrr7/m6quvBiA3dxjdu3evcQJqXSYiZGbe\nw6FDj1BZuc/aa1Khcdppp/Hggw/SuXNnGjZsyHXXXcfXX3/NkCFDyMzMJDc3lwMHDgCwcuVKevXq\nRVZWFl27dmXx4sVH9/Pcc89x5plnkpmZSbt27XjqqaeOLqsaEP3hhx8mOzubli1b8txzz4X0dUQi\n4UsNxxkBTHEfTwEuiUAcSvlVUlLCpEmTmDRpEsnJyQDs2/cVTidoNU3UsQySkzuQlnYJBw9OjtTL\nUGH0xhtvsHDhQjZv3szMmTMZMmQI999/P99++y0VFRU8+uij7N69m4svvpgJEyawf/9+HnzwQUaN\nGsXevXsBpzvl2bNnU1hYyLPPPsstt9zCunXrjh5jz549HDx4kN27d/P0009zww03HP0iCYVIJHwD\nLBCRD0Tkl+68bGNMAYAxZg9wUgTiUMqvJ598krPOOovevXuHdL8NG95KSck8jhxZH9L9epJIaKYg\n3XTTTTRr1owWLVrQu3dvzj//fM4++2xSUlIYOXIka9asYerUqQwdOpSBAwcCzgDo3bt3Z/bs2QAM\nHjyYU089FYDevXuTm5vL0qVLjx4jJSWFP//5zyQmJjJ48GAaNGjApk2bgi+zaiJxNamXMeYrETkR\nmC8im3C+BHzpnSrKmn379vHUU08xZ86ckO87IaExDRrcRmHhvTRt+nLI9+8plm9oy87OPvo4PT39\nmOeHDh1ix44dvPrqq8yaNQtwrguVl5fTt29fAObMmcM999zD5s2bqayspLi4mLPPPvvofpo2bUpC\nwvfn4RkZGRw6dChkryHsCd8Y85X79xsReRM4DygQkWxjTIGINAe+9rf9xIkTjz7OyckhJycnvAEr\nz5kyZQqDBw+mdevWYdl/RsZPOXToEY4cWU9y8llhOYayT0Ro3bo1V199NU8++eQxy8vKyrjsssuY\nOnUqI0aMICEhgZEjR4bkzuz8/Hzy8/PrXC+sCV9EMoAEY8whETkByAUmATOBscBkYAzwlr99+CZ8\npUKtpKSEKVOm8Nprr4XtGCIpnHDCOA4depKsrMfCdhxl389//nO6d+/OqFGj6N+/P2VlZaxatYr2\n7duTmZlJWVkZzZo1IyEhgTlz5jB//nw6dep03MetfjI8adKkGtcLdx1+NrBMRNYCK4FZxpj5OIl+\ngFu90w+4P8xxKFWj119/nc6dO9O+ffuwHicj4+eUluZRUVHzKFkqulW/Ac/fDXktW7Zk5syZ3Hff\nfZx44om0adOGBx98kMrKSho0aMCjjz7K5ZdfTpMmTXjllVcYMWJEvY57vHSIQxVzQjXEYWVlJX36\n9OGBBx6gR48exyyvbajC3V+15OQW/pJ3zdsVFk4ChMzMCbVEpUMcqsDpEIdKBejdd9+lYcOGXHDB\nBRE53gkn/JKiomlUVmrnasoOTfjKs5544gmuv/76kP9s9icxsSWpqRdRVPRiRI6nVHWa8JUnrV27\nll27djF06NCIHrdBg+s5fPhpjDkS0eMqBZrwlUdNnTqVMWPGBN1BWrCSkzuRmNiK0tKFET2uUqAJ\nX3nQ4cOHmTNnDqNGjbJy/IyMKykqmmbl2MrbNOErz3n77bc599xzf3CnZCSlpV1MWdlKKir83m+o\nVFhowlee8+qrr/LTn/7U2vETEhqQljaI4uI3rMWgvEkTvvKUbdu28dlnn9G/f3+rcaSn/5Ti4mna\n9lxFlCZ85SmvvvoqI0eOJCUlxWocKSnnY0wZR46sq3tlFbMmTZrEL37xC9thHKVjrynPqKio4LXX\nXuP55+2PQiUipKdfQXHxNFJSutoOJyrt3LmT0tLSsO0/NTWVVq1aBb39pEmT2Lp1a53vp0jd5xEI\nTfjKM5YuXUqzZs0488wzbYcCQEbGZXzzTS6ZmXcjkm47nKhTWloaki40/CkqKgrbvqOVJnwV13Jz\nh7kjV8H+/ftJSUk5OgyhbYmJLUlJ6UJJyVzS00faDkfVYvLkyTz22GMUFhbSsmVLHnroIe677z4A\nZsyYQbt27Vi7di3bt29n7NixrF27lgsuuIAzzjjDcuQ/pAlfxbWqYQorK4soLe1Go0bvAU0C3Dr8\nXwxpaZdSXPyWJvwotnnzZh5//HE+/PBDsrOz+eKLL6ioqOCPf/zjMVU6V111Fb169WLBggWsXLmS\noUOHcskl0TOCqyZ85QmlpQtJTu5GQkKgyT4y0tIGUFh4F5WVhSQkZNoOR9UgMTGRsrIy1q9fT9Om\nTf0OlLNz505Wr17NwoULSU5Opnfv3gwbNizC0dZOE77yhJKSWaSnX2w7jGMkJGSSktKDkpL5ZGRc\nBtSvyikjI4OtW7eSnd2GPXu2hy1OL2vbti2PPPIIEydOZMOGDQwaNIiHHnromPV2795NVlYW6enf\nX49p06YNX375ZSTDrZU2y1Rxr7LyMKWlS0hLG2Q7lBqlpw+jpGSW+6wMpy/9QKe5gKGgYEekw/aU\nK6+8kqVLl/LFF18AcMcddxzT+qZFixbs37+f4uLio/Oq1o8WmvBV3CstfZeUlHOirjqnSmrqAMrK\nVlFZecB2KKoGmzdvZtGiRZSVlZGSkkJ6ejqJiYk0b96c7du3H715rnXr1nTv3p27776bI0eOsGzZ\nsqODmUcLrdJRca+k5G3S0qKrLtVXQkJDUlJ6UlIyjzC2Qow5qampYW06mZqaGtB6paWljB8/no0b\nN5KcnEzPnj156qmnSElJ4YUXXqBp06acfvrprF69mhdffJExY8bQtGlTevTowZgxY/juu+/C9hrq\nSxO+imuVlZWUli6lUaMHbIdSq/T0YRQXz9CE7+N4booKpU6dOrFq1aoaly1duvQHz0877TSWLFkS\nibCColU6Kq6VlpaSknIuCQlZtkOplVOt8z6VlZW2Q1FxTBO+imvFxcWkpUVf65zqEhIakJLyE0pK\nSmyHouKYJnwVtw4dOkRZWRlpaQNthxKQ9PSLNeGrsNKEr+LWokWLSElJISGhse1QApKa2p+ysjIq\nKw/aDkXFKU34Km7Nnz8/4JYY0cCp1kmhtDTfdigqTmnCV3HpyJEj5OXlkZaWZjuUeklNTaWkZL7t\nMFSc0maZKi598MEHtG7dmm+++cZ2KPWSlpbGwYN5GHMEkWTb4URMmzZtoqrf+FjRpk2beq2vZ/gq\nLs2bN4/c3FzbYdRbYmIiSUmtKSt733YoEVV1x6pO9Zu2b99er3LWhK/ijjGG+fPnx2TCB0hNzaW0\nVKt1VOhpwldxZ9OmTVRWVkbNyFb1lZaWS0nJfB3gXIVcRBK+iCSIyBoRmek+zxKR+SKySUTmiUij\nSMShvKHq7D5W64STks4EKikv32Q7FBVnInWG/1vgE5/n44F3jTEdgDzgzgjFoTwglqtzwBn0OjV1\nICUl82yHouJM2BO+iJwCDAGe9pk9ApjiPp4CRM8YYCqmFRQUsG3bNi644ALboRyXtLQBlJYusB2G\nijOROMP/B/B7wLdCMtsYUwBgjNkDnBSBOJQHLFiwgJycHJKTY7tJY0rKBZSXb6OiYo/tUFQcCWs7\nfBEZChQYY9aJSE4tq/q9OjVx4sSjj3NycsjJqW03yusWLlzI8OHDbYdx3ESSSU3tQ2npIjIyRtsO\nR0W5/Px88vPz61xPwtkSQETuA34OlAPpQENgBtAdyDHGFIhIc2CRMebHNWxvtKWCqm7Lli1k1NBx\nfElJCV26dGH58uU0aeKMbuWMD7s6yCP533b3Vy05ucWuem9Xn2MWFb1OSclcmjR52u/aGRlFbN3a\nDhBt1aOOEhGMMce0WghrlY4x5o/GmNbGmNOBK4E8Y8wvgFnAWHe1McBb4YxDecOqVavo0KHD0WQf\n61JTcygrW4YxZbZDUXHCVjv8+4EBIrIJ6Oc+V+q4LFy4kL59+9oOI2QSE5uRlNTOc3fdqvCJWMI3\nxiw2xgx3H+8zxvQ3xnQwxuQaY6Jn0EcVs/Ly8ujXr5/tMEIqNbUvpaULbYeh4oTeaaviwueff05R\nUREdO3a0HUpIpab2o6Qkz3YYKk5owldxYdGiRfTt2zdm7671Jzm5E8Z8R3n5DtuhqDigCV/FhXir\nv68ikkBq6kWUli6yHYqKA5rwVcwrKipi9erV9O7d23YoYaH1+CpUNOGrmLds2TI6d+5Mw4YNbYcS\nFqmpfSgrW4UxxbZDUTFOE76KefHYOsdXQkIjkpM7UVq63HYoKsZpwlcxzRhDXl5eXNbf+9JqHRUK\nmvBVTNuyZQsA7du3txxJeKWm5lBauth2GCrGacJXMW3RokXk5OTEXXPM6pKSzsSYIsrLt9kORcUw\nTfgqpuXn53PRRRfZDiPsnEFRcigtzbcdiophmvBVzCouLmb16tX06tXLdigR4SR8bY+vgqcJX8Ws\nFStW0KlTJzIzM22HEhGpqb3d5pkltkNRMUoTvopZ+fn5nhoQJyGhCUlJZ2jvmSpomvBVzFq0aJEn\n6u99Od0saGsdFRxN+Com7dixg4MHD3LmmWfaDiWi9MKtOh6a8FVMys/Pp0+fPiQkeOstnJzcmYqK\nAioqdtsORcUgb31aVNzwSnPM6kQSSU29UKt1VFDqnfBFJEtEzg5HMEoFoqysjBUrVnDhhRfaDsUK\nbZ6pghVQwheRfBHJFJEmwBrgPyLycHhDU6pma9asoW3btnEzWHl9OQl/GcaU2w5FxZhAz/AbGWMK\ngUuB540x5wP9wxeWUv4tXbrUU80xq0tMPInExJYcObLWdigqxgSa8JNEpAVwBfB2GONRqk5Llizx\ndMKHquaZ+bbDUDEm0IQ/CZgHbDHGfCAipwOfhS8spWq2Z88edu/eTdeuXW2HYlVqah+9cKvqLSnA\n9b4yxhy9UGuM+Vzr8JUN8+fPp0ePHiQlBfrWjU8pKedSXr6Fior9tkNRMSTQM/zHApynVFjNnTs3\nbseurQ+RFFJSLqCo6D3boagYUutpkoj0AHoCJ4rIrT6LMoHEcAamVHWVlZUsWLCA//u//7MdSlRI\nTc2huHgp8DvboagYUdcZfgrQAOeLoaHPVAhcFt7QlPqhNWvWcOKJJ3LyySfbDiUqpKb2oahoGWBs\nh6JiRK1n+MaYxcBiEXnOGLMjQjEpVaO5c+cycOBA22FEjaSk0xBJAz62HYqKEYHW4aeKyFMiMl9E\n8qqmsEamVDXz5s3ThF9NRkZvnAZ0StUt0KYOrwFPAE8DFYHuXERSgSU4VUNJwOvGmEkikgVMA9oA\n24ErjDEH6hG38pgDBw6wbt06LrzwQnbv1o7DqmRk9Kaw8DXbYagYEWjCLzfG/Lu+OzfGlIrIRcaY\nIhFJBN4TkTnAKOBdY8wDInIHcCcwvr77V96xcOFCevbsSUZGhu1Qokp6+vnA7bbDUDEi0CqdWSLy\nGxFpISJNqqZANjTGFLkPU3G+YAwwApjizp8CXFKfoJX3aHVOzRISGgDdbYehYkSgCX8M8HtgOfCh\nO60OZEMRSRCRtcAeYIEx5gMg2xhTAGCM2QOcVN/AlXcYY5g7dy6DBg2yHUqU0nJRgQmoSscYc1qw\nBzDGVAJdRSQTmCEiHTm2HZnfdmUTJ048+jgnJ8fzfah40caNG/nyy1107NgRgLZt21JUVFTHVl4y\nCK0R9bb8/Hzy8/PrXC+ghC8iV9c03xjzfKABGWMKRSQf591ZICLZxpgCEWkOfO1vO9+Er7xp7ty5\nVFZW8P15wRYg0Lp8L1R3OL2ebNmyhXbt2lmORdlQ/WR40qRJNa4XaJXOuT5Tb2AiMLyujUSkmYg0\nch+nAwOAT4GZwFh3tTHAWwHGoTxozpw5tkOIcgI4X4xK1SbQKp2bfJ+LSGPglQA2bQFMEZEEnC+X\nacaY2SKyEnhVRK4FduB0u6zUMQ4fPsyKFStshxET5s6dy4033mg7DBXFgu1y8DBQZ72+MeZjoFsN\n8/ehA6ioACxevJhu3bqxZMkS26FEvSVLllBSUkJaWprtUFSUCnSIw1kiMtOd3gE2ATPCG5pSaOuc\nejjrrLNYtmyZ7TBUFAu0Dv9B4CF3ug+40BijzQJU2GnCD9ygQYO0Hl/VKqCE73aithGnp8wsoCyc\nQSkFsHXrVg4ePEiXLl1shxITBg8erAlf1SrQKp0rgPeBy3EusK4SEe0eWYVVVe+YImI7lJhwzjnn\nUFBQwM6dO22HoqJUoFU6dwHnGmPGGGOuBs4D/hy+sJTS6pz6SkhIIDc3V8/ylV+BJvwEY4zvzVF7\n67GtUvVWWlrK4sWLGTBggO1QYsqgQYP0vgXlV6BJe66IzBORsSIyFngHmB2+sJTXLVmyhI4dO9K0\naVPbocSUgQMHkpeXR1mZXmZTx6o14YtIOxHpZYz5PfAkzj3cZwMrgKciEJ/yqNmzZzN06FDbYcSc\nk046iQ4dOvDeezq4uTpWXWf4j+CMX4sx5g1jzK3GmFtx2uA/Eu7glHe98847DBkyxHYYMWnIkCG8\n8847tsNQUaiuhJ/t3i37A+68U8MSkfK8zz77jEOHDtG1a1fbocSkoUOHMnu21riqY9WV8BvXsiw9\nlIEoVWX27NkMHjxYm2MGqVu3buzdu5dt27bZDkVFmboS/moRua76TBH5Jc4gKEqFnNbfH5+EhAQG\nDx6sZ/nqGHUl/N8B14hIvog85E6LgXHAb8MfnvKaw4cPs3z5cvr31771jodW66ia1NpbpjsMYU8R\nuQg4y52xS6v/AAAUmUlEQVT9jjEmL+yRKU9auHAh5513HpmZmbZDiWkDBgxg3LhxFBUV6cDv6qhA\n+8NfBCwKcyxKMXv2bG2dEwKNGzema9eu5Ofna3mqo/RuWRU1jDFafx9CWq2jqtOEr6LG+vXrSUpK\nokOHDrZDiQtV7fGNMXWvrDxBE76KGlU3W2lzzNDo2LEjlZWVfPLJJ7ZDUVFCE76KGjNnzmT48OG2\nw4gbIsKwYcOYNWuW7VBUlNCEr6JCQUEBn3zyCX369LEdSlwZPnw4M2fOtB2GihKa8FVUeOedd8jN\nzSU1NdV2KHGlT58+fPLJJxQUFNgORUUBTfgqKmh1TnikpqaSm5urnakpQBO+igLFxcXk5eVpe/Ew\n0WodVUUTvrIuLy+Pbt260aRJE9uhxKUhQ4awaNEiiouLbYeiLNOEr6zT6pzwatKkCV27diUvT3tE\n8TpN+MqqyspKZs2axbBhw2yHEte0WkeBJnxl2Ycffkjjxo1p37697VDiWlV7/MrKStuhKIs04Sur\ntDonMtq3b0/jxo358EMdxsLLwprwReQUEckTkQ0i8rGI3OzOzxKR+SKySUTmiUijcMahotdbb72l\n1TkRMnz4cN58803bYSiLwn2GXw7caozpCPQAbhCRHwHjgXeNMR2APODOMMehotDmzZv59ttv6dGj\nh+1QPOHSSy9l+vTp2pmah4U14Rtj9hhj1rmPDwGfAqcAI4Ap7mpTgEvCGYeKTtOnT2fkyJEkJGjN\nYiSce+65FBUVaWdqHhaxT5qInAp0AVYC2e5oWhhj9gAnRSoOFT2mT5/OqFGjbIfhGSJy9CxfeVNA\nI14dLxFpALwO/NYYc0hEqv+m9Psbc+LEiUcf5+TkkJOTE44QrWve/FQKCnYEtW12dhv27NkesWMG\ne7yajtmvX7+g9qOCM2rUKG688UYmTJhgOxQVQvn5+eTn59e5noS7Pk9EkoC3gTnGmH+68z4Fcowx\nBSLSHFhkjPlxDdsar9Q3On3AB/taJah62eCPGdzxfnjMh4FPgKcDPmZVrG3bbqGoKNBxWrsDq+sZ\nZd3b7v6qJSe32BXRY9YkI6OIrVvbEej/pKKigpYtW7Js2TLatWsXZIwq2okIxphjBpaIRJXOf4FP\nqpK9ayYw1n08BngrAnGoqDId0OqcSEtMTGTkyJFareNR4W6W2Qv4GdBXRNaKyBoRGQRMBgaIyCag\nH3B/OONQ0WY3zvV7rc6x4bLLLtOE71FhrcM3xrwHJPpZ3D+cx1bRbAYwFEixHYgn9enTh23btvHF\nF1/QunVr2+GoCNL2cMoCrc6xKSkpieHDh/PGG2/YDkVFmCZ8ZcGHwEDbQXjaqFGjeP31122HoSJM\nE76yYDCQbjsIT+vfvz8bN25k586dtkNREaQJX1nwM9sBeF5KSgqXXnopr7zyiu1QVARpwlcRs2NH\n1Q1XWp0TDa666ipeeukl22GoCNKEryLm+7NJbZ0TDXr37s0333yjfet4iCZ8FTF6NhldEhMTufLK\nK3n55Zdth6IiRBO+ioj169ezd+9e22GoaqqqdbzShYnXacJXEfHyyy8zevRo22Goarp27UpycjLv\nv/++7VBUBGjCV2FnjOGll17iqquush2KqkZE9OKth8R1wm/e/FREpN5T8+an2g49rqxcuZK0tDS6\ndOliOxRVg9GjRzNt2jTKy8tth6LCLK4TvtPvuqn3FGy/9KpmU6dOZfTo0W7XyCratG/fntatW7Nw\n4ULboagwi+uEr+wrKSlh2rRpjBkzxnYoqhZjx47l2WeftR2GCjNN+CqsZsyYQbdu3WjTpo3tUFQt\nRo8ezdy5c7UlVZzThK/C6plnnuHaa6+1HYaqQ1ZWFkOHDuXFF1+0HYoKI034Kmy2bdvGunXruOSS\nS2yHogIwbtw4nnnmGW2TH8c04auwee6557jqqqtIS0uzHYoKQE5ODgcPHmTNmjW2Q1FhoglfhUVF\nRQXPPvss48aNsx2KClBCQgLXXHMNzzzzjO1QVJhowldBSK3zXoakpCR27txJly5dfjBfRbexY8cy\nbdo0iouLbYeiwkATvgpCKXXfz3AF8HgN81U0a9WqFeedd54OfxinNOGrMCgA5gPalUIsGjduHE8+\n+aTtMFQYaMJXYfAUzhl+Y9uBqCCMGDHiaAsrFV804asQKwP+DdxkOxAVpOTkZH7zm9/w2GOP2Q5F\nhZgmfBVi04EfA2fZDkQdh+uuu4433niDb7/91nYoKoQ04asQexQ9u499zZo149JLL+U///mP7VBU\nCGnCr1HdzQ6jq2vl4OINvfeBr4BhYdi3ql1w74Ha3q833XQT//rXvzhy5EjkXoYKK034NQqk2WE0\nda0cbLyh9hhwI5AYhn2r2gX3Hqjt/dqlSxdOP/103nzzzfCGriJGE74KkT3A24DeWRtPbr75Zh59\n9FHbYagQCWvCF5FnRKRARP7nMy9LROaLyCYRmScijcIZg4qUx4ArgSzbgagQGjFiBF9++SUrVqyw\nHYoKgXCf4T8LDKw2bzzwrjGmA5AH3FnXToIdqlBFyn7gCeAO24GoEEtKSuKOO+7g3nvvtR2KCoGw\nJnxjzDKcbOBrBDDFfTwFqLPv3GCHKlSR8hgwHDjVchwqHMaOHcvatWu1F804YKMO/yRjTAGAMWYP\ncJKFGFTIHMRJ+HX+UFMxKi0tjd///vd6lh8HouGirZ6Kx7R/A/2BM2wHosLouuuuY9myZWzYsMF2\nKOo4JFk4ZoGIZBtjCkSkOfB1bSt/Xxc/EchxJxUdioCHgXdtB6LC7IQTTuCWW27hvvvuO+5hEJs3\nPzWo5svZ2W3Ys2f7cR07XuXn55Ofn1/nehLu4cxE5FRgljGmk/t8MrDPGDNZRO4Asowx4/1sa5wf\nAEJwPwQivZ2zbTBl6nyxBX9MO+XzKJAP1Kcr3eOPtW3bLRQVZQS4XXdgdRDHq33b3V+15OQWuyJ6\nzJpkZBSxdWs7jqdcA32/FhYW0rZtW5YvX0779u2DOJZ7xKDf68F9trxIRDDGHNNyJdzNMl8ClgNn\niMgXInINcD8wQEQ2Af3c5yrmHAT+BvzZdiAqQjIzM7n55puZMGGC7VBUkMJapWOM8dchev9wHldF\nwt+BAUBX24GoCLr11ls544wzWLVqFeeff77tcFQ9RcNFWxWTHgf+ajsIFWEnnHACf/nLX7j99tu1\neiUGacJXQboeaG07CGXBmDFjOHDggPaxE4M04at6+sj9W+N1duUBiYmJPPjgg9xxxx3ak2aM0YSv\n6ukP7t9Mq1Eou3Jzczn99NN17NsYowlf1cMbwE7bQago8fe//5177rmHPXv22A5FBUgTvgrQfpyR\nrHQEJOXo1KkT48aN47e//a3tUFSANOGrAP0Bp5+7XrYDUVFkwoQJrF27lpkzZ9oORQVAE37IRctw\ng6G0CJiHc6OVUt9LT0/nP//5DzfccAMHDhywHY5fwXaxbmfI0vDRhB9y0TLcYKgUA9cB/0Iv1Kqa\n9OnTh8GDBzN+fPS23Aq2i3U7Q5aGjyZ8VYfxwLnAxbYDUVHsgQceYNasWSxYsMB2KKoWmvBVLd4A\nZuKc3SvlX+PGjXnhhRe4+uqr2b17d5iOElx1afRXmUaOJnzlx1bg/4BX0XFqVSAuuugifvOb3zB6\n9GjKy8vDcIRgq0ujuco0sjThqxqUAFcAf8KpzlEqMH/84x9JTU3VHjWjlCZ8VYNbgdNw2t0rFbjE\nxESmTp3K888/z+zZs22Ho6qxMeKVimoP4QxqshxnUA2lalbXyFVDhw6NYDQqkJHE9Axf+XgJeASY\nCzS2HIuKdnU3dZwOtMC5HqT16eH2w/9HzfQMX7neBX4H5KHdHqvQuBQoAAYC7wEn2Q1H6Rm+AlgJ\njAZeA86yHIuKL78GfgoMxemPSdmkCd/zFgDDgSlAH8uxqPj0F+BCnPfXV5ZjiX7BdgMRCE34nvcz\nnLrWIbYDUXFLgAeBK4GfWI4l+gXbDUQgNOF7kgH+7T6eB/S2GIvyBgH+CNzuPv/QYizepQnfcw4D\nY/i+u4SuFmNR3vNr9+9g4Em01U5kacL3lE+A84BEYJXlWFR0sNU/zTLgceDnwKHjfxkqIJrwPeEI\nTh3qhcBtwLNAhtWIVLSw1T/NGTitw1KBLjiNB1S4aTv8uLccpxO0FjgfsHZ2w1HqqAzgv8DbwK+A\nHsDDQHObQcU1PcOPW58CVwGXA3fh3D2ryV5Fo4uBDUAboBMwEfjOZkDHLdimleHuylkTftz5GKf5\nWw5wNrAR58YX7RdHRbMMnCE0VwA7cE5OJgDf2gwqaME3rQzvRWxN+HHjWaAnzm3s3XD6LxkPNLQZ\nlFL11A7nvbwK2O0+Hw0stBlU3LCW8EVkkIhsFJHNInKHrThi1wHgFZwPA8AMnAT/BfAHoIGluJQK\nhbbA08A2nBOZW9z5t+D05hqOAVbin5WELyIJwP/DOR3tCIwWkR/ZiMV588SCQpybpP6Ec4t6K+AF\n4CJ3+UycLhJCfR0+P8T7ix+lpctthxDl8kOwjyyccRk+cp83wbl5Kxunc7Z/AKsJ3xdAcM1WA5Mf\nppj9s3WGfx7wmTFmhzHmCM6p6gg7oeTbOaxfB4A1OEML/gW4DGiP08rmPpw6vjtxfu6+g9O6IZzy\nw7z/2FVWtsJ2CFEuP4T7qkqif8ZJ8P/D+WxsBsYCmcA5wLU4XXy/g3P9qvQ4jxtss9VA5B9nbPVn\nq1lmS2Cnz/Mvcb4E4oTBeaMU4dzZehg4iJPMC3F6DfwW2At8g5O8wTl7KcP5OdsWp63yKOAe97G2\nolXK0RKnFdpV7vNDwHqcXwIf47RK24pTxdnUXWcEzolTM3deU5xxHxrhfGE0xLl4fIL7N/4+bzHw\nii6u9rcmtX2j+nYK5vvtW/V4C05f3Qao9Fl+oc+8Cp+/FTg/H6v+HnGnMncC54dTCt+/cTJw3lCZ\nOG+uxjhvumZAB+BkYD7O2UpTtEWNUvXVALjAnXyVA3twqkDH4vTWuRfYjvNLoeok7ADOl0bVSVoR\nzmcenGqlFCDZ/ZvkMyW6U4LP36qKkxycz3KC+9d3AucLqeqO9+qfeX+jhdWVG2rLkyDGRL4vCxG5\nAJhojBnkPh8PGGPM5GrraUcbSikVBGPMMd8OthJ+IrAJ6Ifzlfs+MNoY82nEg1FKKY+wUqVjjKkQ\nkRtx6jESgGc02SulVHhZOcNXSikVeXF5p62IJIjIWhGZ6T7vLCLLReQjEXlLRBr4rHuniHwmIp+K\nSK7P/G4i8j/3xrBHbLyOcBGR7W5ZrBWR9915WSIyX0Q2icg8EWnks75nyshP2VwmIutFpEJEulVb\n3zNlA37L5wH39a8TkekikumzvpaPyD0+8+aKSHOf9SNbPsaYuJtwbsebCsx0n78P/MR9PBa4x318\nJrAWp2rrVJwmO1W/elYB57qPZwMDbb+uEJbP50BWtXmTgT+4j+8A7vdiGfkpmw44N0PkAd185v/Y\nS2VTS/n0BxLcx/cDf/Pie6eW8mng8/gm4N+2yifuzvBF5BSctphP+8w+wxizzH38Lk7jdnBuTX3F\nGFNujNkOfAac534DNzTGfOCu9zxwSdiDj5yqtmK+RuCMZI77t+r1eq2MjikbY8wmY8xnHNsmbgTe\nKhuouXzeNcZUtWFcCZziPvbaewdqLh/fEV5O4Pv2nhEvn7hL+Dj3Wv+eHzbOXy8iw93HV/D9G7L6\nDWC73HktcW4Gq/KlOy9eGGCBiHwgIr9052UbYwoAjDF7gJPc+V4rI9+yua6Odb1WNlB3+VyLc0YK\nWj5Hy0dE/ioiX+DcKTbBnR3x8omrhC8iQ4ECY8w6fng2Ng64QUQ+wPmGLatpew/pZYzphvNL6AYR\n6c2xd6959Wp+9bL5ie2Aoozf8hGRu4AjxpiXrUVnX43lY4z5kzGmNfAiTrWOFXGV8IFewHAR+Rx4\nGegrIs+7P8kHGmPOxem3Z6u7/i6cW/CqnOLO8zc/LhhjvnL/fgO8idOtRYGIZAO4Pym/dlf3VBlV\nK5sZ1N7lh6fKBvyXj4iMxUlyV/msruVz7PvnJZxe38BG+di+yBHGiyd9+P6i7Ynu3wSc+umx1S6a\npACn8cOLJivdf5bg/EQdZPs1hahcMnAvIuH82nkPyMW5aHuHO7+mi7ZxX0b+ysZn+SLgHJ/nnimb\nOt47g3CGrGpabX0tH6d82vmscxPwqq3ysV5IYSx834R/M86dvRuB+6qtd6db0J9W+3Cfg9ML02fA\nP22/nhCWy2nAOveN9jEw3p3fBOeC9iacG+Iae62MaimbS3DqWotx7gyf47WyqaN8PsMZpmqNO/1L\ny+cH5fM6Tvee64C3gBa2ykdvvFJKKY+Itzp8pZRSfmjCV0opj9CEr5RSHqEJXymlPEITvlJKeYQm\nfKWU8ghN+MozRCRbRF52u6P9QETeFpHrRGSWxZgWVe9yWalw0YSvvGQGkGeMaW+cbjbuBLLxbr9B\nymM04StPEJGLgDJjzH+q5hljPgaWAg1F5DV3EIoXfLb5s4iscgeieMJn/iIRud9dtlFEernzx7gD\ngMxxB5KZ7LPNAHEG4VktItNEJCMiL1wpH5rwlVecBXzoZ1kXnO43zgTaikhPd/5jxpjzjTFnAxlu\nb6xVEo0x5+MMtjPRZ35n4HLgbOCnItJSRJoCfwL6GWO6u3HcGqLXpVTArAxirlSUed+4vRyKyDqc\n0YeWA/1E5Pc4nWJlAeuBd9xt3nD/fgi08dnXQuMOeCEiG9xlWThfJu+JiADJ7v6ViihN+MorNgCX\n+VlW6vO4AkgSkVTgcZwhDXeLyN1AWg3bVPDDz5HvvirdZQLMN8b87DjiV+q4aZWO8gRjTB6Q4jPC\nFyLSCejtZ5M0nIu5e8UZ9N7flwUcO/RhdSuBXiLS1j1uhoi0Dzh4pUJEE77ykpHAABHZIiIfA/fh\ndHfsywAYYw7gjIu8AZgDvF99nVqeV9/Xt8BY4GUR+QinOqdDHdsqFXLaPbJSSnmEnuErpZRHaMJX\nSimP0ISvlFIeoQlfKaU8QhO+Ukp5hCZ8pZTyCE34SinlEZrwlVLKI/4/Il7Wjnuds/UAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1464c7650>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"e.plot_spectrum(pixel_index=pixel_index)\n",
"fit_x = np.linspace(t.mean - 5 * t.stddev, t.mean + 5 * t.stddev, 100)\n",
"plt.plot(fit_x, t(fit_x), label='fit', color='black')\n",
"plt.axvline(t.mean, color='red', label='mean')\n",
"plt.axvspan(t.mean - t.stddev, t.mean + t.stddev, color='grey', alpha = 0.2, label='std')\n",
"plt.xlim(t.mean - 5 * t.stddev, t.mean + 5 * t.stddev)\n",
"plt.legend()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"t."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Find the 80.9 keV line"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"([80, 283, 495, 627],\n",
" array([ 5077, 9137, 13377, 16017]),\n",
" array([15, 4, 1, 0]))"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from scipy import signal\n",
"peakind = signal.find_peaks_cwt(hist, np.arange(30,40))\n",
"peakind, center[peakind], hist[peakind]"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAEZCAYAAACEkhK6AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XmYZFWZ5/HvryohWQqKQqQSKaAApaAVQVSwRa2QRVFb\nFBcUN9Ch26d7UFtUqLLbJvGZVnB6dBhbR20VERVBkc3WppopUruxkU22YlFZSkBIVHbhQS3e+eOe\nLG4FsdzMjBtxb+Tv8zzxZMRdznnvyYh4455z44QiAjMzs27mDToAMzOrBycMMzMrxAnDzMwKccIw\nM7NCnDDMzKwQJwwzMyvECcPMzApxwhgykm6TdEDTsiMl/Ufu8e2SHpX0kKSH09//k9YdI+k6SSO5\n7f9W0pWS5knaSdIT6f4Pcvv/QdLjucefl7Q8bftQU1375cp+paQfpeWTki6W9No2x/YuSVdIelDS\nrySdLGlebv0iSedIeiS1wxG5dRtJ+k5a/oSkl7Uof58Uy8OS7pb0vi5tfbKk30r6jaSTWqz/gKRb\nUzxrJD2zQ1k7SVot6feSbpB0YG5dQ9K1ku5PdZ0t6RltytlY0pfT//hBSVdJOmQ67dBU3ofT8+Eh\nSbdI+nDT+tWS7pX0gKSfSTq0Q1nLJa1rei68s2mbg9Jz7ZH0P35Tp/iszyLCtyG6AbcBBzQtOxL4\ncdM2L2+zv4AfA+Pp8S7AA8Be6fFOwDpgXtN+pwIfb1q2HPhVh1jfBDwIvBvYIi17KfDFNtu/F9gf\nGAG2A64AjsutPyPdNk3bPQDskdZtBLwfeDFwF/CyprKfBkwCb03lbw4s6xD7e4EbUxzbAWuAv8qt\nPxq4eqoMYGdgqw7l/QT4n8Ao8AbgfuBpad3Tge1zx3EycF6bcjYD/gHYIT1+DfAQsGORdmhR3oeB\nvck+XO4G3A4cnlu/J7BRur9vqmtxm7K6PR/+LP0PXpHqWwTsPOjXlG+5/9GgA/Ctx//Q4gnjgA5l\n7JbebJ8DXAT8j9y6XiaMtcCxszjWD069caY3yseBXXPrTwM+0WK/O1okjH8ETptG3ZcAR+cevxv4\nSbov4Fe0ScotynoW8BiweW7Zj/IJKLd8FPgkcP00Yr0GOKxIOxQo6xTglDbr9gUeBV7QZn2358M3\ngRNn+nzwrfybu6TmBk1n44j4Odmb0sXA9sDHex6QtAxYApw9i2JeRvbJHrIk98eIuCW3/hrg2QXL\nehFwv6RLUtfYeZJ26LD9s1P5reragezY9kzdKrdIGu9S1q0R8ft2sUvaQdL9ZG/Ix5KdZXQlaTFZ\nQlrTbdu0/RGSru6wyUuby5J0gaTHgEuBiYi4IhfzfZKW5DbfNnX33SLp05I2y617UbabrpV0l6Sv\nS1pUJG7rDyeM4XRueqHeJ+k+4HMdtrk//f1vTev/E9ga+G5E/GEWsWyfi2Wqrk3JuoAA7p5JoZLe\nAzwf+Ke0aAFZd0jeQ8AWBYtcArwLeB/ZG/7tZN1b7Swg607L17Ug3d8+/T2Y7E3/AOCIFm3crqyn\nxB4Rd0TEIrJ2+3vg550PB5SNQ30D+Fr6ENBVRJwREXu3Ke9Esg8fpzbt89p0DK8CVjXFvHVE3JkW\n3QjsHRHbkbXJ84FP54paArwDOIwsyW0GfLZI3NYfThjD6XXphbp1RGwN/E2HbRalv1+ZWiFpI+CL\nZC/WYyQtnUUsd+VimarrMeB3af120y1Q0uvJupAOiYj70uJHgC2bNl0IPFyw2MeAcyLiqpQgTwT+\nXNIWklbmBmk/36a+hWnZVFkAJ0fEwxGxlqw9X53ivz5X3v7TiT0iHgC+DpyXH/BvJklkyeJxsiQ4\nK5KOIXszf3VE/LFFXOsi4kLglZL+olUZEXFvRNyU7q8FjgPemNvkMeCrEXFLRDwKfIIsCVlFOGEM\npyJdUJ22+QdgMiL+luyN7ks9iSonIm4m60N/Y7dt89IVP18E/iIibsit+jkwImnX3LK9KNgVA1wL\ntJy6OSI+GRFbRMSWETGVfNek8qfsnavrZqD5rGx92RHxnFx5l6T9dpG0ecHYNyIbCG9OMnlfAbYB\n3hAR6zps11U6mzuObNyr2xnhCLBrl202KD53/9rpxmb95YRhG5C0F3AM2VU+AOPATpKOym82nSI7\nrPsQ8DFll/1uocxLJH2xTWwHkH1qfmNEXJlflz6Rfg/4uKTNJL0EeC1wem7/jSVtkh6OShrNFXEq\ncJik56YzrI8B/xkR7c5Qvg4cK+kZkrYnG1c4NcXyGPBt4DhJC1If/l8BF7QqKCJ+QXZF1QmSRiW9\ngeyCg7NT3IdJ2i21z9PJunGuSmcbrdrpC8DuwKGtuhO7tEPztm8nO5s7OJ0V5Nctk3SIpE0kjUh6\nB9kYx4/alNWQtGO6vwNwEnBubpNTgXdL2jmNbRxPmzazARn0qLtvvb0Bt1LsKqnfk/WTT93OJvsA\ncTnwoab9lwP3kn2qbXeV1FdpfZXUn3J1PJz+Hpbb5hVkl/E+RHZJ5WrgVW2ObTXZJ/d8Wf+aW78I\nOIesi+d24C1N+9+WYs/fdsytfy9wJ1l32XmkS1k7tPVJadvfAp9sWrcF2RjIQ2RXg/1dl7J2JLvI\n4FGyvv6X59Ydk/6vDwO/Br5Fumy2TTlPpHIezrXTEUXaAXgbcF3T8+nxpjb/fFq3O9lA94PAfcBP\nyZLU1L47pO2XpMcfTO37SGqTz5C7Mixtc0J6rk0CXwMWDvo15duTN6V/UmkkLQS+TPaJ6QngPWTd\nB2eSvfncTnZdd/Ogn5mZVUg/uqROAX4QEXuQ9cveBKwALoqIZWSfGlf2IQ4zM5uFUs8wJG0J/Cwi\ndm1afhOwPCImJY2RXbu9e2mBmJnZrJV9hrEz8FtJpyqb0+ZLaTBrcURMAkTEPcC2JcdhZmazVHbC\nGAH2AT4XEfuQDbSu4KmXL5Y7kGJmZrM20n2TWbkTuCPSVAFkV+KsACYlLc51Sd3bamdJTiRmZjMQ\nEdOaEqiIUs8wUrfTHZJ2S4sOJPsy0vnAUWnZkWSXMLYro/K3E044oZyye3z8pcVZl/bsYZu6LXvb\nxrVpz5q8J5Wl7DMMyKZS/mb6MtStZLN6zgfOSt8gXQsc3oc4zMxsFkpPGBFxDfDCFqsOKrtuMzPr\nHU8N0gONRmPQIRTiOHunDjGC4+y1xqADGLDSv+k9G5KiyvGVToK5fPxlcJuWb5jbuCbHJomo26C3\nmZkNDycMMzMrxAnDzMwKccIwM7NCnDDMzKwQJwwzMyvECcPMzApxwjAzs0KcMMzMrBAnDDMzK8QJ\nw8zMCnHCMDOzQpwwzMysECcMMzMrxAnDzMwKccIwM7NCnDBqZGxsKWNjSwcdhpnNUf7FvSpr+nUv\nKfsBrTndJrNVk19Mq7VhbuOaHJt/cc/MzAbKCcPMzApxwjAzs0KcMMzMrBAnDDMzK8QJw8zMCnHC\nMDOzQpwwzMyskJGyK5B0O/Ag8ATwx4jYV9Ii4ExgJ+B24PCIeLDsWMzMbOb6cYbxBNCIiOdFxL5p\n2QrgoohYBqwGVvYhDjMzm4V+JAy1qOd1wGnp/mnA6/sQh5mZzUI/EkYA/y7pcklHp2WLI2ISICLu\nAbbtQxxmZjYLpY9hAPtHxN2Sng6sknQzWRLJq/5sXmZmc1zpCSMi7k5/fyPpXGBfYFLS4oiYlDQG\n3Ntu//Hx8fX3G40GjUaj3IDNzGpmYmKCiYmJ0uspdXpzSZsB8yLiEUmbA6uAE4EDgfsi4mRJxwOL\nImJFi/09vbmnN++tmkxPXWvD3MY1Obaypjcv+wxjMXCOpEh1fTMiVkm6AjhL0nuAtcDhJcdhZmaz\n5B9QqjKfYfReTT4h1towt3FNjs0/oGRmZgPlhGFmZoU4YZiZWSFOGGZmVogThpmZFeKEYWZmhThh\nmJlZIU4YZmZWiBOGmZkV4oRhZmaFOGGYmVkhThhmZlaIE4aZmRXihGFmZoU4YZiZWSFOGGZmVogT\nhpmZFeKEYWZmhThhmJlZIU4YZmZWiBOGmZkV4oRhZmaFOGGYmVkhThhmZlaIE4aZmRXihGFmZoU4\nYZiZWSFOGGZmVogThpmZFdKXhCFpnqSrJJ2fHi+StErSzZIulLSwH3GYmdnM9esM4wPADbnHK4CL\nImIZsBpY2ac4zMxshkpPGJKWAK8Gvpxb/DrgtHT/NOD1ZcdhZmaz048zjM8AHwEit2xxREwCRMQ9\nwLZ9iMPMzGZhpMzCJb0GmIyIqyU1Omwa7VaMj4+vv99oNGg0OhVjZjb3TExMMDExUXo9imj7Xj37\nwqVPAO8A/gRsCmwBnAO8AGhExKSkMeDiiNijxf5RZnyVJ0Hu+CUBMKfbZLaa2tRKMMxtXJNjk0RE\nqNflltolFREfjYgdI2IX4K3A6oh4J3ABcFTa7EjgvDLjMDOz2RvU9zBOAg6WdDNwYHpsZmYVVmqX\n1Gy5S8pdUj1Xky6FWhvmNq7JsdWyS8rMzIaHE4aZmRXihGFmZoU4YZiZWSFOGGZmVogThpmZFeKE\nYWZmhThhmJlZIU4YZmZWiBOGmZkV4oRhZmaFOGGYmVkhThhmZlaIE4aZmRXihGFmZoU4YZiZWSFO\nGGZmVsi0E4akRZKeW0YwZmZWXYUShqQJSVtK2hq4CvgXSZ8uNzQzM6uSomcYCyPiIeANwNcjYj/g\noPLCMjOzqimaMEYkbQccDny/xHjMzKyiiiaME4ELgV9GxOWSdgF+UV5YZmZWNSMFt7s7ItYPdEfE\nrR7DMDObW4qeYXy24DIzMxtSHc8wJP058GLg6ZKOza3aEphfZmBmZlYt3bqkNgYWpO22yC1/CHhT\nWUGZmVn1KCK6byTtFBFr+xBPc71RJL6hJUHu+CUBMKfbZLaa2tRKMMxtXJNjk0REqNflFh30HpX0\nJWBpfp+IOKDXAZmZWTUVTRjfAb4AfBlYV7RwSaPAj8m6tkaA70bEiZIWAWcCOwG3A4dHxIPTiNvM\nzPqsaJfUlRHx/BlVIG0WEY9Kmg9cArwfeCPwu4j4lKTjgUURsaLFvu6ScpdUb9WkS6HWhrmNa3Js\nZXVJFb2s9gJJfyNpO0lbT92K7BgRj6a7o2RnGQG8DjgtLT8NeP10gjYzs/4reoZxW4vFERG7FNh3\nHnAlsCvwuYhYKen+iFiU2+a+iHhKAvIZhs8weq4mnxBrbZjbuCbHNtBB74jYeaYVRMQTwPMkbQmc\nI+nZZGcZG2zWbv/x8fH19xuNBo1GY6ahmJkNpYmJCSYmJkqvp+gZxrtaLY+Ir0+rMuljwKPA0UAj\nIiYljQEXR8QeLbb3GYbPMHqrJp8Qa22Y27gmxzboMYwX5m4vBcaBQ7vtJGkbSQvT/U2Bg4EbgfOB\no9JmRwLnTSdoMzPrv0JnGE/ZSdoK+HZEHNJluz3JBrXnpduZEfGPacD8LGAHYC3ZZbUPtNjfZxg+\nw+itmnxCrLVhbuOaHFtZZxgzTRgbAddHxLJeB9RUz8ASxvj4+AbjJwPhhNF7NXnB19owt3FNjm2g\nCUPSBTw5MD0f2AM4q9V3J3ppkAkjNfhA6s4F4YTRazV5wdfaMLdxTY5t0Aljee7hn4C1EXFnr4Np\nUa8ThhNGb9XkBV9rw9zGNTm2gQ56R8SPgJvIZqxdBPyh14GYmVm1FUoYkg4HLgPeTPa73j+V5OnN\nB2KUsbGlgw7CzOagol1S1wAHR8S96fHTgYsiYq9Sg3OXVMsuKXC31IzVpEuh1oa5jWtybIP+Hsa8\nqWSR/G4a+5qZ2RAoOr35v0m6EDgjPX4L8INyQjIzsyrq2CUl6ZnA4oi4RNIbgJekVQ8A34yIW0oN\nzl1S7pLqtZp0KdTaMLdxTY5tIJfVSvo+sDIirmtavifwiYh4ba8DaqrHCcMJo7dq8oKvtWFu45oc\n26DGMBY3JwuAtGxpr4MxM7Pq6pYwtuqwbtNeBmJmZtXWLWFcIekvmxdKOprsR5HMzGyO6DaGsRg4\nh+yb3VMJ4gXAxsBhEXFPqcF5DMNjGL1Wkz7oWhvmNq7JsQ16LqmXA89JD9dExOpeB9KmXicMJ4ze\nqskLvtaGuY1rcmyVmt68X5wwnDB6riYv+Fob5jauybEN+pveZmY2xzlhmJlZIU4YZmZWiBOGmZkV\n4oRhZmaFOGGYmVkhThhmZlaIE4aZmRXihGFmZoU4YZiZWSFOGAMyPj4+re3HxpaWEoeZWVGeS6p9\n3aXO11So/Ny8Nfl5pMBzSc1YTeYCqrVhbuOaHJvnkjIzs4EqNWFIWiJptaQ1kq6T9P60fJGkVZJu\nlnShpIVlxmFmZrNX9hnGn4BjI+LZwJ8D/13S7sAK4KKIWAasBlaWHEclFR3H8PiFmVVBX8cwJJ0L\n/HO6LY+ISUljwERE7N5i+6Eew4AuYxGpv7R5/KLrftZeTfqga22Y27gmx1b7MQxJS4G9gUuBxREx\nCZB+5nXbfsVhZmYzM9KPSiQtAL4LfCAiHpHUnKLbpux8t02j0aDRaJQRoplZbU1MTDAxMVF6PaV3\nSUkaAb4P/DAiTknLbgQauS6piyNijxb7ukvKXVK9VZMuhVob5jauybHVuUvqq8ANU8kiOR84Kt0/\nEjivD3GYmdkslHqGIWl/4MfAdWTdTgF8FLgMOAvYAVgLHB4RD7TY32cYPsPorZp8Qqy1YW7jmhxb\nWWcY/qZ3+7qdMIZRTV7wtTbMbVyTY6tzl5SZmQ0BJwwzMyvECcPMzApxwmhr1FNymJnleNC7fd1A\neYPLHvQekJoMWtbaMLdxTY7Ng95mZjZQThhmZlaIE8bAjA46ADOzaXHCGJjHBx2Amdm0OGGYmVkh\nThgF5KdYX7BgG19ua2Zzki+rbV83kF2+mp9XqleX2/qy2gGpyWWRtTbMbVyTY/NltWZmNlBOGGZm\nVogTRke9mx5kbGxpi7JGWbBgq477bbzxJj2p38xstjyG0b7uDR7Pdgyjeb98+W3LkmjXCVnl/1ul\n1aQPutaGuY1rcmwewzAzs4FywjAzs0KcMHqk9RiFmdnw8BhG+7o3eNxtDKPb2IbHMCqiJn3QtTbM\nbVyTY/MYhpmZDZQTRlfTn1U2P5VIkfLzXVnT29fMrH/cJdW+7g0eT6dLKj+VSKv13cpfv6+7pHqv\nJl0KtTbMbVyTY3OXlJmZDZQThpmZFeKEMUNljjWMj4/7El0zqxyPYbSve4PH3S6H7eUYxvpl4DGM\nXqtJH3StDXMb1+TYPIZhZmYDVWrCkPQVSZOSrs0tWyRplaSbJV0oaWGZMZiZWW+UfYZxKvDKpmUr\ngIsiYhmwGlhZcgw9kH1XotW4xdjY0pZTlI+Pj68fi3hyPGI0bb9NqdGamZWh9DEMSTsBF0TEc9Pj\nm4DlETEpaQyYiIjd2+xbmTGMVqbGK7otK8JjGH1Skz7oWhvmNq7JsQ3TGMa2ETEJEBH3ANsOIAYz\nM5umKgx6Vz9dm5kZIwOoc1LS4lyX1L2dNs6PGzQaDRqNRrnRzUr3n1xtZ2xsKY888sD6cuDxae0/\nNWZiZnPPxMQEExMTpdfTjzGMpWRjGHumxycD90XEyZKOBxZFxIo2+9ZuDKOXpjOG0eq7H9ZCTfqg\na22Y27gmx1bWGEapCUPSt4AG8DRgEjgBOBf4DrADsBY4PCIeaLO/E0aHuvOcMAqqyQu+1oa5jWty\nbLUc9I6It0XEMyJiNCJ2jIhTI+L+iDgoIpZFxCvaJYtqKjrV+WibvzMpv/i+nk5ketyFZzY9nhqk\nfd1dt6naGUar5dYk9wnRZ2Ulqcmn8BmpybHV8gzDzMyGhxOGmZkV4oQxI9m4Qn7Kj16UZ/0288ug\nzeYij2G0r3sg9eZ5DKMETWMY4DbruZr0889ITY7NYxhmZjZQThhmZlaIE0Zh1Rtn8PcIzKyfPIbR\nvu6B1JvXbQwj/z0C98cX5DGM8tWkn39GanJsHsMwM7OBcsLou953bXlKkOnzrx6aTZ+7pNrXPZB6\n84p2SW3wK30V/n9WQupScJuVqCbdNjNSk2Nzl5SZmQ2UE4aZmRXihDFj7cYi+jNNSJFLasfGlg58\nfKMKMTTz5chmM+MxjPZ1D6TevE5jGOu36dAfX4XLRqsQwwakp7RpZWIbFjXp55+RmhybxzDMzGyg\nnDDMzKwQJ4zS9GcqkQ3HB9pP192p3342ffr5ffs9NjDd8ZEn46veNC9mdeAxjPZ1D6TevCJjGC33\nazH1RaefI53NT5U2T0/Sz2nXp1u2pJZtWuXXQC3VpJ9/RmpybB7DMDOzgXLCMDOzQpwwammU2fTD\nFx3PmBojaDVWkB8PyK8bG1u6fhwl/xO2+W2m9m1VV16+rLwFC7Z5yraNRqPtMTXXZWYz4zGM9nUP\npN68ssYwmsca2q1rboNW+zTXkd+23f75fTtNz95ujKJVud3GYdaXhccwSleTfv4ZqcmxeQzDzMwG\nyglj6Iw2de882R3U3MXTfElskW6bdl0/zft2u9x1avvmrqipOFqVt2H31FO75Fp1dW1YTqtuvNEZ\nTV1SxSlPytTqueFuvrnHXVLt6x5IvXkz7ZIqVHab6dGn1kHnrp92+3ars1W5RWNtvt9pfavuL2jf\nptN9nlVuypOStbtkuuXx16TbZkZqcmzukjIzs4EaWMKQdIikmyT9XNLxg4rDzMyKGUjCkDQP+Gfg\nlcCzgSMk7T6IWIZTp0tus0tys/73UebP3/wp+y1YsA3SZk/Zb2rZ1M+bbjjVRrdLfbNpS578adRW\n24+2uD/a9vLcKfmfW506rifraj9dSrNWYx/dxiqm1re7HHn+/M3X758fYyk6ZlQk5k5jUUcdddQG\ndTffb75EOR9ju8uaO8WQb7epvwsWbNW2TaZMTEzQaDRajkN104vxpHb/j+Z4JzrsNxfGtQYyhiHp\nRcAJEfGq9HgFEBFxctN2HsMYdBBDptMYRsexjy6X9ua3abeujJ/UbY6v1eNOl1V32r5V7M11txw/\nImvjbmNc+fLGx8c58cQTO9ZXtA1mosj/OSIYlxhvc+l3lca1hm0MY3vgjtzjO9MyMzOrKA96m5lZ\nISMDqvcuYMfc4yVp2VNUoWtoUObukZenXZtOPc/yz7d299uW3WGbVuUXLbeITuV2O7ai61rF2rKe\nNuV0i7lIfTMpr1dlTK07sWA7DKNBjWHMB24GDgTuBi4DjoiIG/sejJmZFTKQM4yIWCfpGGAVWbfY\nV5wszMyqrdLf9DYzs+ro66C3pCWSVktaI+k6Se9PyxdJWiXpZkkXSlqY22elpF9IulHSK3LL95F0\nbfri3/8uIdZ5kq6SdH5VY0x1LJT0nVT3Gkn7VS1WSR+UdH0q/5uSNq5KjJK+ImlS0rW5ZT2LLR3r\nt9M+/yUpP3Y3mxg/lWK4WtLZkrYcZIzt4syt+5CkJyRtXdU4Jb0vxXKdpJOqGKekvVKZP5N0maQX\n9DXOiOjbDRgD9k73F5CNY+wOnAwcl5YfD5yU7v8Z8DOyrrOlwC958qzop8AL0/0fAK/scawfBL4B\nnJ8eVy7GVO7XgHen+yPAwirFCjwDuBXYOD0+EziyKjECLwH2Bq7NLetZbMBfA59P998CfLtHMR4E\nzEv3TwI+OcgY28WZli8B/g24Ddg6LdujSnECDbIu8pH0eJuKxnkh8Ip0/1XAxf38v/f0zWsGDXJu\neuLfBCxOy8aAm9L9FcDxue1/COyXtrkht/ytwP/tYVxLgH9PT6KphFGpGFOZWwK3tFhemVjJEsZa\nYFF6Mp9ftf85sFPTi7JnsZG9Ue6X7s8HftOLGJvWvR44fdAxtosT+A6wJxsmjErFSfZB5oAW21Ut\nzh8Cb073jwC+0c84BzmX1FKy7Hkp2YtzEiAi7gG2TZs1f8HvrrRse7Iv+03p9Rf/PgN8hOyLwVOq\nFiPAzsBvJZ2qrPvsS8rm76hMrBHxa+B/Ab9K9T0YERdVKcYWtu1hbOv3iYh1wAP5bpkeeQ/ZJ8fK\nxSjpUOCOiLiuaVWl4gR2A14m6VJJF0t6fkXj/CDwT5J+BXwKWNnPOAc1l9QC4LvAByLiETZ8Y6bF\n476R9BpgMiKupvNXIQYWY84IsA/wuYjYB/g92SeNKrXnVsDryD4pPQPYXNLbW8RUhfZsp5ex9fQi\nfUl/B/wxIs7oZbE9KUTaFPgocEIvymtVRQ/LGgEWRcSLgOPIzop6pZdx/jXZ++aOZMnjqz0su2uc\nfU8YkkbIksXpEXFeWjwpaXFaPwbcm5bfBeyQ233qC37tlvfC/sChkm4FzgAOkHQ6cE+FYpxyJ9mn\ntyvS47PJEkiV2vMg4NaIuC99ijkHeHHFYmzWy9jWr1P2/aMtI+K+XgQp6Sjg1cDbcourFOOuZP3p\n10i6LdV5laRtaf/l3YG0Jdkn7e8BRMTlwDpJT6tgnEdGxLkpzu8CL2yus8w4B3GG8VWyPrVTcsvO\nB45K948Ezsstf2sazd8ZeCZwWeomeFDSvpIEvCu3z6xExEcjYseI2IWsv291RLwTuKAqMeZinQTu\nkLRbWnQgsIYKtSdZV9SLJG2Syj4QuKFiMYoNP131MrbzUxkAbwZW9yJGSYeQdZseGhGPN8U+qBg3\niDMiro+IsYjYJSJ2JvuA87yIuDfV+ZYqxJmcCxwAkF5PG0fE7yoY512Slqc4DwR+kauz/P/7TAdj\nZjiAsz+wDriabET/KuAQYGvgIrKrplYBW+X2WUk24n8j6eqAtPz5wHWpwU4pKd7lPDnoXdUY9wIu\nT236PbKrpCoVK1mXxI3AtcBpwEZViRH4FvBr4HGy5PZusgH6nsRGNk/7WWn5pcDSHsX4C7KLCa5K\nt88PMsZ2cTatv5U06F21OMm6pE5P9V4BLK9onC9O8f0M+C+yBNy3OP3FPTMzK8Sz1ZqZWSFOGGZm\nVogThpmZFeKEYWZmhThhmJlZIU4YZmZWiBOGzRmSFks6I03nfLmk70v6S0kXDDCmiyXtM6j6zabD\nCcPmknPIvrn/rIh4IdkXnRZT7XmszCrDCcPmBEkvB/4QEf8ytSyyGVT/A9hCT/4I1em5fT4m6afp\nx2e+kFt+saST0rqbJO2flh+p7MeMfqjsx5dOzu1zsKSfSLpC0plpVmGzWnHCsLniOcCVbdbtDbyf\n7EdodpXbXoT0AAABUklEQVT04rT8sxGxX0Q8F9gszWQ8ZX5E7Ec2Y+h4bvleZPPyPJdsDqLt0yR2\nfw8cGBEvSHEc26PjMuubkUEHYFYBl0XE3QCSriabYfUnwIGSPgJsRja/1PXAv6Z9vpf+Xkk2dfuU\n/xfZlP1IWpPWLSJLRpekCeA2SuWb1YoThs0Va4A3tVmXn+11HTAiaRT4HLBPRPxa0gnAJi32WceG\nr6N8WU+kdQJWRcTbZxG/2cC5S8rmhIhYDWws6eipZZL2BF7aZpdNyAbDf5d+8KtdsoHuPzxzKbC/\npF1TvZtJelbh4M0qwgnD5pLDgIMl/VLSdcAngLubtgmAiHgQ+DLZmckPgcuat+nwuLms35L9vsYZ\nkq4h645a1mVfs8rx9OZmZlaIzzDMzKwQJwwzMyvECcPMzApxwjAzs0KcMMzMrBAnDDMzK8QJw8zM\nCnHCMDOzQv4/zZm2bbomdwQAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x12daac550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"e.plot_spectrum(pixel_index=pixel_index)\n",
"for peak in center[peakind]:\n",
" plt.axvline(peak, color='red', label='mean')"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"9137"
]
},
"execution_count": 65,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"center[peakind][1]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Fitting the 80.9 keV line"
]
},
{
"cell_type": "code",
"execution_count": 329,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "IndexError",
"evalue": "index 1 is out of bounds for axis 0 with size 1",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mIndexError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-329-ca208a2f0674>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 3\u001b[0m \u001b[0mcenter\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m(\u001b[0m\u001b[0mbins\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m-\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m+\u001b[0m \u001b[0mbins\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;34m/\u001b[0m \u001b[0;36m2\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 4\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 5\u001b[0;31m \u001b[0mg\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mmodels\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mGaussian1D\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mamplitude\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mm\u001b[0m \u001b[0;34m*\u001b[0m \u001b[0;36m0.2\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mmean\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcenter\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0mpeakind\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mstddev\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m30\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 6\u001b[0m \u001b[0mfit_t\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mfitting\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mLevMarLSQFitter\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 7\u001b[0m \u001b[0mt\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mfit_t\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mg\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcenter\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mhist\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mIndexError\u001b[0m: index 1 is out of bounds for axis 0 with size 1"
]
}
],
"source": [
"hist, bins = e.spectrum(pixel_index=pixel_index)\n",
"width = 1 * (bins[1] - bins[0])\n",
"center = (bins[:-1] + bins[1:]) / 2\n",
"\n",
"g = models.Gaussian1D(amplitude=m * 0.2, mean=center[peakind][1], stddev=30)\n",
"fit_t = fitting.LevMarLSQFitter()\n",
"t = fit_t(g, center, hist)"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Parameter('mean', value=9254.37467207)\n",
"Parameter('stddev', value=69.3977526117)\n"
]
}
],
"source": [
"print(t.mean)\n",
"print(t.stddev)"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x12f469850>"
]
},
"execution_count": 75,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEZCAYAAABiu9n+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8FfW9//HXJwkJCQEMW8IOAlpxt1SLiqYguBcR7S22\nLu217e+6tFZvK9giwa3S2tZ6a6+ltKi1tdpWiyhWZAlqudoixbogiGWRLYgIYU0g+fz+mAkcQyY5\nCTk554T38/GYR+bMfOc7n7PkfM58vzPfMXdHRESkLhnJDkBERFKXkoSIiERSkhARkUhKEiIiEklJ\nQkREIilJiIhIJCUJERGJpCTRypjZSjMbXmvZ1Wb2cszjVWa2y8zKzWx7+PeBcN0NZvammWXFlL/J\nzF43swwz62tm1eH8rJjtK82sIubxL8zs7LBsea19nRZT97lmtiBcXmZm883s4ojndpWZLTKzbWa2\nxsymmFlGzPoCM3vazHaEr8O4mHVtzOyP4fJqMzurjvpPCWPZbmYbzOzGBl7rKWa22cw+NLN761j/\nLTP7dxjP22Y2sJ66+prZPDPbaWbvmNmImHXFZvYvM/s43NefzaxHRD3ZZjYtfI+3mdliMzuvMa9D\nrfr+O/w8lJvZ+2b237XWzzOzTWa21cz+aWafr6eus82sqtZn4cpaZc4JP2s7wvf4svrikxbg7ppa\n0QSsBIbXWnY18FKtMp+L2N6Al4CS8PGRwFbgxPBxX6AKyKi13XTgjlrLzgbW1BPrZcA24CtA+3DZ\nMOCXEeW/AZwBZAHdgUXAd2PWPx5OuWG5rcAx4bo2wDeB04F1wFm16u4MlAFfDOtvBxxdT+zfAJaG\ncXQH3ga+HrP+WmBJTR1Af+CIeupbCPwIyAEuBT4GOofrugI9Y57HFGBGRD15wO1A7/DxhUA50Cee\n16GO+v4bOIngB+VRwCrgCzHrjwfahPOnhvsqjKiroc/D4PA9GBXurwDon+z/qcN9SnoAmpr5DY0/\nSQyvp46jwi/Y44A5wF0x65ozSawGbj6E5/rtmi/L8MuxAhgQs/4R4J46tvugjiRxN/BII/b9N+Da\nmMdfARaG8wasISIR11HXIGA30C5m2YLYpBOzPAf4AfBWI2J9AxgTz+sQR10/A34Wse5UYBcwJGJ9\nQ5+H3wGTm/p50JSYSc1NhwdrTGF3X07wRTQf6Anc0ewBmR0N9AL+fAjVnEXwCx6CxLbX3d+PWf8G\ncGycdX0W+NjM/hY2e80ws971lD82rL+uffUmeG7Hh00m75tZSQN1/dvdd0bFbma9zexjgi/hmwmO\nJhpkZoUESejthsqG5ceZ2ZJ6igyrXZeZzTSz3cCrQKm7L4qJeYuZ9Yop3i1synvfzH5iZnkx6z4b\nbGb/MrN1ZvaomRXEE7ckjpJE6/SX8J9zi5ltAR6sp8zH4d//rLX+FaAT8Cd3rzyEWHrGxFKzr1yC\n5h2ADU2p1My+CnwauC9clE/Q1BGrHGgfZ5W9gKuAGwm+5FcRNF1FySdoKovdV3443zP8O5Lgi344\nMK6O1ziqroNid/cP3L2A4HX7PrC8/qcDFvQrPQY8HCb+Brn74+5+UkR9kwl+cEyvtc3F4XM4H5hd\nK+ZO7r42XLQUOMnduxO8Jp8GfhJTVS/gy8AYgsSWB/xPPHFL4ihJtE6jw3/OTu7eCbiunjIF4d9f\n16wwszbALwn+QW8ws36HEMu6mFhq9rUb+Chc372xFZrZJQTNQ+e5+5Zw8Q6gQ62iHYHtcVa7G3ja\n3ReHSXEyMNTM2pvZhJiO1l9E7K9juKymLoAp7r7d3VcTvJ4XhPG/FVPfGY2J3d23Ao8CM2I77Wsz\nMyNIEBUEie+QmNkNBF/gF7j73jriqnL3F4Bzzeyiuupw903u/m44vxr4LjA2pshu4Dfu/r677wLu\nIUg8kkRKEq1TPM1L9ZW5HShz95sIvtymNktUMdx9GUGb+NiGysYKz9T5JXCRu78Ts2o5kGVmA2KW\nnUiczSzAv4A6h0R29x+4e3t37+DuNQn37bD+GifF7GsZUPvoa3/d7n5cTH1/C7c70szaxRl7G4LO\n7NqJJdavgS7Ape5eVU+5BoVHbd8l6Mdq6MgvCxjQQJlPVB8z/6/GxiaJpyQhn2BmJwI3EJydA1AC\n9DWza2KLNabKetbdAky04BTd9hY408x+GRHbcIJfx2Pd/fXYdeEvz6eAO8wsz8zOBC4GfhuzfbaZ\ntQ0f5phZTkwV04ExZnZCeCQ1EXjF3aOORB4FbjazHmbWk6CfYHoYy27gD8B3zSw/bJP/OjCzrorc\n/T2CM6EmmVmOmV1KcNLAn8O4x5jZUeHr05WgiWZxeFRR1+v0EPAp4PN1NRU28DrULvslgqO2keGv\n/9h1R5vZeWbW1syyzOzLBH0WCyLqKjazPuF8b+Be4C8xRaYDXzGz/mFfxa1EvGbSgpLdc66peSfg\n38R3dtNOgnbvmunPBD8a/gHcUmv7s4FNBL9eo85u+g11n920L2Yf28O/Y2LKjCI45bac4PTHecD5\nEc9tHsEv9Ni6notZXwA8TdB8swr4j1rbrwxjj536xKz/BrCWoClsBuFpp/W81veGZTcDP6i1rj1B\nn0Y5wVlc32ugrj4EJwrsImi7/1zMuhvC93U7sB74PeEprhH1VIf1bI95ncbF8zoAVwBv1vo8VdR6\nzX8RrvsUQWf1NmAL8BpBYqrZtndYvlf4+Nvh67sjfE1+SswZXWGZSeFnrQx4GOiY7P+pw32y8I1J\nGDPrCEwj+GVUDXyVoGngCYIvnFUE513X7rgTEZEka4nmpp8Bs9z9GIJ21neB8cAcdz+a4NfhhBaI\nQ0REGimhRxJm1gH4p7sPqLX8XeBsdy8zsyKCc6s/lbBARESkSRJ9JNEf2Gxm0y0YQ2Zq2CFV6O5l\nAO6+EeiW4DhERKQJEp0ksoBTgAfd/RSCztLxHHyqYWI7RkREpEmyGi5ySNYCH3h4mT7BGTTjgTIz\nK4xpbtpU18ZmpuQhItIE7t6o4XiiJDRJhEngAzM7yoNhAUYQXCD0NnANwfgzVxOcbhhVRyJDbHYl\nJSWUlJQkO4wmS4f4V6xYQV5eXp3rfvzjH3PLLbckPIYePXuyft26Zq+3sfHv2rWLgQMjRyBPinT4\nDNWnNcQ/efLkZqsv0UcSEAxL/LvwAqV/E4yWmQk8GV7JuRr4QgvEISIijZTwJOHubwCfqWPVOYne\nt4iIHBoNy9HMiouLkx3CIUn3+IcOHZrsEA5JuscP6f8ZUvyflPArrg+FmXkqxyfJUV+fREtJVJ9E\nY6Vin4Qkn5mlR8e1iEg8+vXrx+rVqxsuKJ/Qt29fVq1aldB9KEmISNKtXr067c5kTAXBbUMSS30S\nIiISSUlCREQiKUmIiEgkJQkRkQYsX76ck08+mQ4dOpCVlcXdd9+d7JBajJKEiEgDfvjDHzJ8+HDK\ny8vZt28f3/ve9wBYsGABvXv3TnJ0iaUkISLSgNWrV3PssccetNzdW+QMo2TSxXSSdnQx3QGt5WK6\n8OKvZIdRpxEjRrBgwQKys7PJysri4osvZsCAAYwfP54uXbpQWVlJbm4uZsby5cspKipqsdiiXrfm\nvJhORxIiIvWYO3cuw4YN48EHH6S8vJzs7GwA8vLyeP755+nRowfbt2+nvLy8RRNES9HFdCKSFpqr\nWaepRyypeqSTaEoSIpIWDtcv6WRTc5OISBO19k5rUJIQEWmywsJCPvroI8rLy5MdSsIoSYiINCDq\niOHoo49m3LhxHHnkkXTq1ImNGze2cGSJp1NgJe3oFNgDdArs4U2nwIqISFIpSYiISCQlCRERiaQk\nISIikZQkREQkkpKEiIhEUpIQEZFIShIiIhJJSUJERCIpSYiISKSEDxVuZquAbUA1sNfdTzWzAuAJ\noC+wCviCu29LdCwiItI4LXEkUQ0Uu/vJ7n5quGw8MMfdjwbmARNaIA4RkSbp378/9913HyeeeCLt\n27fna1/7Gps2beKCCy6gQ4cOjBo1im3bgt+5r776KmeccQYFBQWcfPLJLFiwYH89Dz/8MIMHD6ZD\nhw4MHDiQqVOn7l+3YMECevfuzU9+8hMKCwvp2bMnDz/8cEs/1YO0RJKwOvYzGngknH8EuKQF4hAR\nabKnnnqKuXPnsnz5cp555hkuuOAC7r33XjZv3kxVVRUPPPAA69ev56KLLuL222/n448/5r777mPs\n2LF89NFHQDC0+KxZsygvL2f69Ol8+9vfZsmSJfv3sXHjRrZv38769euZNm0a119//f7kkywtkSQc\neNHM/mFm14bLCt29DMDdNwLdWiAOEUlnZs0zNdGNN95Ily5d6N69O8OGDeO0007jhBNOIDs7mzFj\nxrB48WIee+wxLrzwQs4991wARowYwZAhQ5g1axYA559/Pv369QNg2LBhjBo1ipdffnn/PrKzs5k4\ncSKZmZmcf/755Ofns2zZsqa/Zs2gJW5feoa7bzCzrsBsM1tGkDhiaYxgEalfkocSLyws3D+fm5t7\n0OMdO3awevVqnnzySWbOnAkEt1zdt28fw4cPB+D555/njjvuYPny5VRXV7N7925OOOGE/fV07tyZ\njIwDv93z8vLYsWNHop9avRKeJNx9Q/j3QzP7C3AqUGZmhe5eZmZFwKao7UtKSvbPFxcXU1xcnNiA\nRUSawMzo06cPV111Fb/85S8PWl9ZWclll13GY489xujRo8nIyGDMmDHNch+N0tJSSktLD7meuiQ0\nSZhZHpDh7jvMrB0wCpgMPANcA0wBrgZmRNURmyRERFLZl7/8ZYYMGcLYsWM555xzqKys5LXXXmPQ\noEF06NCByspKunTpQkZGBs8//zyzZ8/m+OOPP+T91v4BPXny5EOus0ai+yQKgVfM7J/Aq8BMd59N\nkBxGhk1PI4B7ExyHiEiT1b59adTtTHv27MkzzzzDPffcQ9euXenbty/33Xcf1dXV5Ofn88ADD3D5\n5ZfTqVMn/vCHPzB69OhG7TcZdPtSSTu6fekBun3p4U23LxURkaRSkhARkUhKEiIiEklJQkREIilJ\niIhIJCUJERGJpCQhIiKRlCRERCSSkoSISIJMnjyZK6+8MtlhHJKWGAVWRKTRPvjgAyoqKhJWf05O\nDr17927y9pMnT+b999/n0UcfrbdcKgytcSiUJEQkJVVUVCR0+JVdu3YlrO7WRM1NIiINmDJlCr16\n9aJDhw4cc8wxzJo1i3vuuYcnnniC9u3bc/LJJwOwatUqiouL6dixI+eeey6bN29OcuSHTkcSIiL1\nWL58OQ8++CCvv/46hYWFrFmzhqqqKm677baDmpuuuOIKzjjjDF588UVeffVVLrzwQi65JL3vzqwk\nISJSj8zMTCorK3nrrbfo3Lkzffr0qbPcBx98wKJFi5g7dy5t2rRh2LBhXHzxxS0cbfNTc5OISD0G\nDBjA/fffT0lJCd26deOKK65gw4YNB5Vbv349BQUF5Obm7l/Wt2/flgw1IZQkREQa8MUvfpGXX36Z\nNWvWAHDrrbcedNZS9+7d+fjjj9m9e/f+ZTXl05mShIhIPZYvX878+fOprKwkOzub3NxcMjMzKSoq\nYtWqVftv+tOnTx+GDBnCpEmT2Lt3L6+88gozZ85McvSHTn0SIpKScnJyEnqaak5OTlzlKioqGD9+\nPO+++y5t2rTh9NNPZ+rUqWRnZ/Pb3/6Wzp07c+SRR7Jo0SJ+97vfcfXVV9O5c2eGDh3K1Vdfzdat\nWxP2HFqCbl8qaUe3Lz1Aty89vOn2pSIiklRKEiIiEklJQkREIilJiIhIJCUJERGJpCQhIiKRdJ2E\niCRd37590/6+C8nQEsN+KEmISNKtWrUq2SFIBDU3iYhIJCUJERGJ1CJJwswyzGyxmT0TPi4ws9lm\ntszMXjCzji0Rh4iINE5LHUl8C3gn5vF4YI67Hw3MAya0UBwiItIICU8SZtYLuACYFrN4NPBIOP8I\nkN739xMRaaVa4kjip8B3gNihCgvdvQzA3TcC3VogDhERaaSEngJrZhcCZe6+xMyK6ykaOUZwSUnJ\n/vni4mKKi+urRkTk8FNaWkppaWlC6k7o/STM7B7gy8A+IBdoDzwNDAGK3b3MzIqA+e5+TB3b634S\nchDdT+KA1nI/CWleaXM/CXe/zd37uPuRwBeBee5+JTATuCYsdjUwI5FxiIhI0yTrOol7gZFmtgwY\nET4WEZEU02LDcrj7AmBBOL8FOKel9i0iIk2jK65FRCSSkoSIiERSkhARkUhKEiIiEklJQkREIilJ\niIhIJCUJERGJpCQhIiKRlCRERCSSkoSIiERSkhARkUhKEiIiEklJQkREIilJiIhIJCUJERGJpCQh\nIiKRlCRERCRSo5OEmRWY2QmJCEZERFJLXEnCzErNrIOZdQIWA78ys58kNjQREUm2eI8kOrp7OXAp\n8Ki7n4buUS0i0urFmySyzKw78AXg2QTGIyIiKSTeJDEZeAFY4e7/MLMjgfcSF5aIiKSCrDjLbXD3\n/Z3V7v5v9UmIiLR+8R5J/E+cy0REpBWp90jCzIYCpwNdzezmmFUdgMxEBiYiIsnXUHNTNpAflmsf\ns7wcuCxRQYmISGqoN0m4+wJggZk97O6rWygmERFJEfF2XOeY2VSgX+w27j48EUGJiEhqiDdJ/BF4\nCJgGVMVbuZnlAC8RNFtlAX9y98lmVgA8AfQFVgFfcPdtjYhbRERaQLxJYp+7/29jK3f3CjP7nLvv\nMrNM4G9m9jwwFpjj7j80s1uBCcD4xtYvIiKJFe8psDPN7Doz625mnWqmeDZ0913hbA5BUnJgNPBI\nuPwR4JLGBC0iIi0j3iOJq8O/34lZ5sCRDW1oZhnA68AA4MHwiu1Cdy8DcPeNZtatETGLiEgLiStJ\nuHv/pu7A3auBk82sA/C0mR1LkGA+USxq+5KSkv3zxcXFFBcXNzUUEZFWqbS0lNLS0oTUbe6R388H\nCpldVddyd3+0UTszmwjsAq4Fit29zMyKgPnufkwd5T2e+OTwsmLFCvLy8pIaQ4+ePVm/bl1SYwDY\ntWsXAwcOTHYYkmLMDHe35qgr3j6Jz8RMw4AS4PMNbWRmXcysYzifC4wElgLPANeExa4GZjQmaBER\naRnxNjfdGPvYzI4A/hDHpt2BR8J+iQzgCXefZWavAk+a2VeB1QRDkIuISIqJt+O6tp1Ag/0U7v4m\ncEody7egmxaJiKS8uJKEmc3kQOdyJnAM8GSighIRkdQQ75HEfTHz+4DV7r42AfGIiEgKiavjOhzo\n712CkWALgMpEBiUiIqkhriRhZl8A/g5cTtDJ/JqZaahwEZFWLt7mpu8Bn3H3TQBm1hWYA/wpUYGJ\niEjyxXudREZNggh91IhtRUQkTcV7JPFXM3sBeDx8/B/ArMSEJCIiqaKhe1wPBArd/TtmdilwZrjq\n/4DfJTo4ERFJroaOJO4nuNcD7v4U8BSAmR0frrs4odGJiEhSNdSvUBheNf0J4bJ+CYlIRERSRkNJ\n4oh61uU2ZyAiIpJ6GkoSi8zsa7UXmtm1BDcSEhGRVqyhPombCG4U9CUOJIUhQDYwJpGBiYhI8tWb\nJMJbjJ5uZp8DjgsXP+fu8xIemYiIJF2895OYD8xPcCwiIpJidNW0iIhEUpIQEZFIShIiIhJJSUJE\nRCIpSYiISCQlCRERiaQkISIikZQkREQkkpKEiIhEUpIQEZFIShIiIhJJSUJERCIpSYiISKSEJgkz\n62Vm88zsbTN708y+GS4vMLPZZrbMzF4ws46JjENERJom0UcS+4Cb3f1YYChwvZl9ChgPzHH3o4F5\nwIQExyEiIk2Q0CTh7hvdfUk4vwNYCvQCRgOPhMUeAS5JZBwiItI0LdYnYWb9gJOAV4HC8K53uPtG\noFtLxSEiIvGL6850h8rM8oE/Ad9y9x1m5rWK1H68X0lJyf754uJiiouLExGiiEjaKi0tpbS0NCF1\nm3vk93Pz7MAsC3gWeN7dfxYuWwoUu3uZmRUB8939mDq29UTHJ+lnxYoV5OXlJTWGHj17sn7duqTG\nALBr1y4GDhyY7DAkxZgZ7m7NUVdLNDf9BninJkGEngGuCeevBma0QBwiItJICW1uMrMzgC8Bb5rZ\nPwmalW4DpgBPmtlXgdXAFxIZh4iINE1Ck4S7/w3IjFh9TiL3LSIih05XXIuISCQlCRERiaQkISIi\nkZQkREQkkpKEiIhEUpIQEZFIShIiIhJJSUJERCIpSYiISCQlCRERiaQkISIikZQkREQkkpKEiIhE\nUpIQEZFIShIiIhJJSUJERCIpSYiISCQlCRERiaQkISIikZQkREQkkpKEiIhEUpIQEZFIShIiIhJJ\nSUJERCIpSYiISCQlCRERiaQkISIikZQkREQkUkKThJn92szKzOxfMcsKzGy2mS0zsxfMrGMiYxAR\nkaZL9JHEdODcWsvGA3Pc/WhgHjAhwTGIiEgTJTRJuPsrwMe1Fo8GHgnnHwEuSWQMIiLSdMnok+jm\n7mUA7r4R6JaEGEREJA6p0HHtyQ5ARETqlpWEfZaZWaG7l5lZEbCpvsIlJSX754uLiykuLk5sdCIi\naaa0tJTS0tKE1G3uif0hb2b9gJnufnz4eAqwxd2nmNmtQIG7j4/Y1hMdn6SfFStWkJeXl9QYevTs\nyfp165IaA8CuXbsYOHBgssOQFGNmuLs1R12JPgX298BC4CgzW2NmXwHuBUaa2TJgRPhYRERSUEKb\nm9z9iohV5yRyvyLJMmrUxWzZsqHBcp06dWf27JktEJHIoUlGn4RIqxUkiEVxlBuS+GBEmkEqnN0k\nIiIpSklCREQiqblJJCmyGTKk4SanjIy2VFfviVyfl5fHjh372LhxVTPGJnKAkoRIHPbs2cNHH33E\n5s2b2bx5M1cCDz30EEVFRfTv35/+/fvToUOHRtRYSTx9F9XVQxoot4uyskGN2K9I4yhJiISqq6tZ\nsmQJc+bMYfny5Xz44Yds3ryZjz76iIqKCjp37kyXLl3o0qULVwLr169n8eLFrFy5kpUrV5Kfn8/W\nrVvJyrqFrKwjyczsT1bWkWRl9cOsbbKfnkiTKEnIYW3nzp289NJLvPjii8ydO5fOnTszcuRIxowZ\nQ9euXencuTNdu3alffv2mMVcm9SzJ3fcccf+h+7Oxo0bGTVqFPv2nURV1UoqK//Bvn0rqa4uIyfn\nc+TmXkJOTjFmOUl4piJNoyQhh521a9cyZ84cXnzxRRYtWsQpp5zCyJEjuemmm+jTp0+T6jQzunfv\nTk5ODjk5V35iXXX1FnbvfpadO3/F1q0307btueTmVpCdvQ8z/QtKatMnVA4LO3fu5IknnuD3v/89\nZWVlDB8+nHHjxvHQQw/Rvn37hO47I6MT7dpdRbt2V1FVtZ7du59l+/anqKr6NG3bXkRu7mjatBmC\nmU42lNSjJCGt2vr165k+fTqPP/44Q4cO5c477+TUU08lMzMzKfFkZvYgP//r5OdPZd++P7F79wy2\nbRtPdfV28vKuoF27a8jIKEhKbCJ1SfgAf4dCA/xJXeIZ4O+NN95g3LgvUV6+lby8PPLy8sjKqvs3\nUUOnmdZVbv2GDfTo3j2iZMNnLcEnz1rau/cddu78NXv2/JW8vMtp1+7rZGb2OKhcbXl5u3j//UHo\n/0RiNecAfzqSkFajqqqKOXPmMHXqVNasWUN19T66dXuHjIz6T01t+DTTusr1jNimacNttGkzmCOO\n+DFVVbewc+c0PvxwJG3bnku7dntp06ZJVYo0CzWCStrbs2cPDz/8MGeddRYPPPAAV111FQsXLiQ/\nP7/BBJFqMjN70KHD7XTr9gqZmX3YsmULW7b8J5WVi5MdmhymdCQhaWvPnj08/vjj/PznP+e4447j\n/vvvZ8iQIZ88VTVNZWQU0L79TeTn/5Zdu85k69b/IjOzN/n5N5CdfXareI6SHpQkJKUUFfWjrGx1\nvWX69+/P7t17gX0cf/zxTJ8+nRNOOKFlAmxhZka7dl8hL+/L7N79DOXld2CWS37+zeTkDE92eHIY\nUJKQlBIkiKhO2D3ANNasuYusrK385S9/abXJoTazNuTljSU3dwx79sxi+/Z72LHjJ8D1yQ5NWjn1\nSUga2AP8HBgIvEj37g/RqVOnwyZBxDLLIDf3Irp0eZF27f6LLVt+BMBzzz2nM5wkIZQkJIXtBH5G\nTXKAGcAMcnKOS2pUqaAmWfTqFdzdbsKECZx66qlKFtLs1NzUysTTpg9QWNi32YaXbv59biE4cvg5\ncBZBcvh0rTLxDbXd2tVcpb1kyRKefvppJkyYQElJCRMnTuSiiy4iI0O/A+XQ6BPUyhxo069/iudL\nvaX3uXbt2nBuELAGeBn4EwcnCDgw1HZ90+EjIyODsWPHsmTJEsaPH8/kyZMZPHgwv/rVr9izp+EL\nBUWiKElI0i1btoxrr702po/hDWAacHQSo0pPNcli0aJFPPTQQ8yYMYN+/fpx5513snnz5mSHJ2lI\nSUKS5vXXX+eyyy5j2LBh9OnTh/feey9c0yupcbUGZkZxcTHPPvss8+bNY/Xq1QwaNIjrr7+eFStW\nJDs8SSNKEglUVNQPM2twKirql+xQW0x5eTlTp07ltNNOY8yYMZx55pmsXLmS22+/nc6dOyc7vFZp\n8ODBTJs2jaVLl1JQUMDQoUO59NJLWbhwYbJDkzSgJJFAyegfSE1O0L8Affv25YUXXmDSpEmsXLmS\nm266iXbt2iU3vMNEUVERd911F6tWrWL48OFceeWVnHjiidx3332sW7cu2eFJitLZTZJAG4FHgN8A\nwdDcy5Yto1u3bskM6rDXrl07brjhBq677jpeeuklHnvsMY4//nhOOeUUrrzySi699NKE32ND0kfa\nH0moSaepchp8zTIz28X12n7SduBp4BLgGGA5MB14G0AJIiEafi/r+h/IyMiguLiYadOmsW7dOr7x\njW/w1FNP0atXL8aNG8dzzz3H3r17k/OUJGWkfZJQk05TVdDQa1ZdvavBMlAd1vdDYDjQA3gQuJjg\nNNZfA6cDGpAucRp+Lxv6H8jNzeXyyy9nxowZvP/++wwbNoy7776bXr16ccMNN/Dss8+ybdu2xD8V\nSTlpnyS9lP4EAAAJ3UlEQVQkGbYSXL9wLdA7XLYauBnYAMwB/hNQk0U66tKlC9dddx0LFy5k4cKF\n9OjRg5/+9Kf07NmT0047jQkTJjB79mx27tyZ7FClBSQtSZjZeWb2rpktN7NbkxWHNKQKWAY8CdwG\nDCNIDL8GTgDmheUeBC4C8pMQoyTKgAEDuO2225g7dy6bN29mypQpZGdnc+edd1JYWMiwYcOYNGkS\npaWlumivlUpKkrBgLIGfA+cCxwLjzOxTEWUb0R5en/jabeNph6+vf6O0tLQRMcUfW8v0qewg+LJ/\nCPh/4bKOwHnA40AO8D1gE/A88E3gqEbU3/DzPFQVFel9Wmcqx9+2bVuKi4uZPHkyL7/8MmVlZUyc\nOJHKykpuvfVWCgoKOOqoozjzzDO57bbbeOyxx1i8eHGzHXG0VP9j0/6HW159r0dzStbZTacC77n7\nagAz+wMwGnj34KINDVYW7wtS025bv+pqa7BcWVn0PktLSykuLo4zphoNx1bfPuPjBM1Ea8MJ4PaY\nxyuBdcARwPnASWGZteGy5hDPe3Boz7Oy8v/IyTn9kOpIpnSKv127dowaNYpRo0YBsHfvXlasWMGk\nSZPIzc3lueee40c/+hHLly+nqKiIwYMHM3jwYPr27UtRUdH+qXv37nGdBl3/MPKx5Q7tM9S0/+GW\nF/16lACTm20/yUoSPYEPYh6vJUgcchAnGKcINm3aREVFBXv27KGiooKdO3eybdu2/dPWrVvDbb4J\nbAunrQSnoq4lOA21FweuaM4g6FTuBfQhGDPpboIPWU09zZUgpLVr06YNxxxzDIMHD2bixIn7l+/b\nt4+VK1fyzjvvsHTpUpYuXcr8+fPZuHEjGzduZMOGDWRmZn4icRQWFtKhQwfat29P+/btyc+vacac\nTdDXlR/+bQdkx0yZLfukDwNpcJ3EiJj52lmz5vHn4igDcHYcZQDOrCOOT5Y5/fSDf+25Ox988AEv\nvPBCzNLP1qqjmqCdf1/4typc17/W8gqC+yhUUvM2HXvsseTk5NC2bVtycnLIy8vjiCOOoGPHjvun\nwACCZqKaqTtBXo6937NxIBmIJE5WVhaDBg1i0KBBjB49+qD17s727dv3J42NGzdSVlZGeXk527Zt\nY926dWzfvj0s/SOC06y3EzSP7gT2EvyfVFBzJNqxY0eys7P3T5mZmWRkZJCRkYGZ7Z+vPZkZ69ev\nZ/bs2ZHrG9Okk/hyF9RR6r06ljWdJWPseTP7LFDi7ueFj8cD7u5TapXTwPgiIk3g7s3SOZGsJJFJ\ncMrMCIJzJv8OjHP3pS0ejIiIREpKc5O7V5nZDQQNjBnAr5UgRERST1KOJEREJD3oius4mNm3zOzN\ncPpmuKzAzGab2TIze8HMOsaUn2Bm75nZUjMbFbP8FDP7V3gB4f1Jjv8yM3vLzKrM7JRa5dMh/h+G\n8S0xsz+bWYeY8ukQ/x1m9oaZ/dPM/mpmRekUf8y6W8ys2sw6pWr8Uc/BzCaZ2VozWxxO56Xqc6gV\n/7dilt8Yxvimmd2bkPjdXVM9E8HFfv8iuJIsk6CJbAAwBfhuWOZW4N5wfjDwT4KmvH7ACg4csb0G\nfCacnwWcm6T4jyS47dsggkumT4kpf0yaxH8OkBGWuRf4QZq9/vkxZW4E/jdN4n8RODJc1wv4K8FF\nNp1S8fNTz3swAJgE3FxH+ZR6DvV8horD+aywXJdExK8jiYYdA7zm7hXuXgW8BFwKfJ5gHGzCv5eE\n858H/uDu+9x9FcH5aKeGvxTbu/s/wnKPxmzT4vG7+zJ3f4+Dr14bnSbxz3H3mtEFX+XAxR/p8vrv\niCnTjgMjJaZ6/AsIPv8APwW+U6t8qn1+IPp/GOq+ejPVnkNd8Y8F/ovgx+k+AHevuT9ts8avJNGw\nt4BhYfNSHsGJyb2BQncvA3D3jUDNGNi1LxRcFy7ryYFLnQnneyY4doiOP0o6xv9Vgl9FkEbxm9ld\nZrYGuILg8ndIk/jN7PPAWnd/s1b5VIsf6n4OvQguXLohbLKcZgeajFPtOUR9hgYBZ5nZq2Y238w+\nHZZv1vjT4GK65HL3d81sCsFh9g6Cw7iquoq2aGBxakT8Kamh+M3se8Bed388SSHWq7743f37wPct\nGODyRlLw6saI+NsSjPY4Mpmxxaue9+B/gTvd3c3sLuDHBEMbp5R64m8DFLj7Z83sM8AfCZqhmpWO\nJOLg7tPdfYi7FxOMc7EMKDOzQoDwMG5TWHwdn/yl2ytcFrU84eqIf3k9xdMmfjO7huBX1RUxxdMm\n/hi/50DzRzrE/xZBW/cbZrYyjGWxmXULY+pTR5xJix/qfg/c/UMPG+eBX3FgaKB0eA+WERwtPBWu\n/wdQZWadae73INGdLq1hArqGf/sA7xCMbzEFuDVcXlfHdTbBWBuxnUavEnwQjaB55LxkxR+zbj7w\n6ZjHaRE/wdC0bwOda5VNl/gHxqy/EXgyneKvtX4lwS/alIy/nvegKGb9t4Hfp+pziIj/G8DkcPlR\nwOpExN8ib1C6TwQdRW+FL3xxuKwTwd11lhGcYXBETPkJ4RuzFBgVs/zTwJsEHUk/S3L8lxD8EtlN\ncNX782kW/3sEdzpaHE6/SLP4/0RwxsoSYAbQPZ3ir7X+34RnN6Vi/PW8B4/GvAd/IehnTMnnEBF/\nG+C3YTyLgLMTEb8uphMRkUjqkxARkUhKEiIiEklJQkREIilJiIhIJCUJERGJpCQhIiKRlCTksGFm\nhWb2eDiE8j/M7Fkz+5qZzUxiTPOt1lDtIqlESUIOJ08D89x9kLt/huCCo0JSdNwtkVSgJCGHBTP7\nHFDp7r+qWebBCKYvA+3N7I/hDVp+G7PNRDN7LbxJy0Mxy+eb2b3hunfN7Ixw+dUW3ADpeQtuRjUl\nZpuRZrbQzBaZ2RPhaJ4iKU9JQg4XxwGvR6w7CfgmwZg3A8zs9HD5/7j7ae5+ApBnZhfGbJPp7qcR\njPlTErP8ROBy4ATgP8ysZzjo2veBEe4+JIzj5mZ6XiIJpaHCReDv7r4BwMyWEIxwuhAYYWbfAfKA\nAoKxc54Lt3kq/Ps60Demrrke3lDIzN4O1xUQJKC/mZkRjLmzMJFPSKS5KEnI4eJt4LKIdRUx81VA\nlpnlAA8S3Np1vZlNIriPQu1tqvjk/1FsXdXhOgNmu/uXDiF+kaRQc5McFtx9HpBtZvtvKmNmxwPD\nIjZpS9Ch/ZGZ5ROdYKDuW2DGehU4w8wGhPvNM7NBcQcvkkRKEnI4GQOMNLMVZvYmcA/BMOmxHMDd\ntwHTCI5Angf+XrtMPY9r17UZuAZ43MzeIGhqOrqBbUVSgoYKFxGRSDqSEBGRSEoSIiISSUlCREQi\nKUmIiEgkJQkREYmkJCEiIpGUJEREJJKShIiIRPr/9dVvo2GULjUAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x12cef8590>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"e.plot_spectrum(pixel_index=pixel_index)\n",
"plt.plot(center, t(center), label='fit', color='black')\n",
"plt.axvline(t.mean, color='red', label='mean')\n",
"plt.axvspan(t.mean - t.stddev, t.mean + t.stddev, color='grey', alpha = 0.2, label='std')\n",
"plt.xlim(t.mean - 5 * t.stddev, t.mean + 5 * t.stddev)\n",
"plt.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Putting it all together"
]
},
{
"cell_type": "code",
"execution_count": 605,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def fit_line(x, y, guess):\n",
" g = models.Gaussian1D(amplitude=guess[0], mean=guess[1], stddev=guess[2])\n",
" #g.bounds = {'mean': (guess[1] - 0.1 * guess[1], guess[1] + 0.1 * guess[1])}\n",
" fit_func = fitting.LevMarLSQFitter()\n",
" fit = fit_func(g, x, y)\n",
" return fit\n",
"\n",
"def guess_peak_index(x, y, search_range=None):\n",
" this_y = y.copy()\n",
" if search_range is None:\n",
" result = (y.max(), x[y.argmax()])\n",
" else:\n",
" this_y = y.copy()\n",
" this_y[x < search_range[0]] = 0\n",
" this_y[x > search_range[1]] = 0\n",
" result = (this_y.max(), x[this_y.argmax()])\n",
" return result\n",
"\n",
"def find_pixel_gain(spectrum, verbose=False):\n",
" # fit the strong line first\n",
" hist, bins = spectrum\n",
" x = (bins[:-1] + bins[1:]) / 2\n",
" # find the location of the strong line\n",
" m1, x1 = guess_peak_index(x, hist)\n",
"\n",
" # find the location of the high energy line\n",
" m2, x2 = guess_peak_index(x, hist, search_range=[8000, 10000])\n",
" \n",
" if verbose:\n",
" print(peakind)\n",
" # first line\n",
" guess = (m1, x1, 30)\n",
" fit = fit_line(x, hist, guess)\n",
" \n",
" result = np.zeros(2)\n",
" \n",
" result[0] = fit.mean.value\n",
" # second line\n",
" guess = (m2, x2, 30)\n",
" fit = fit_line(x, hist, guess)\n",
" result[1] = fit.mean.value\n",
" return np.clip(result, 0, 2**14)\n",
"\n",
"def is_bad_pixels(spectrum):\n",
" hist, bins = spectrum\n",
" return (bins.max() - bins.min()) < 5000\n",
"\n",
"def find_all_gains(e):\n",
" \"\"\"Returns an array with channel number of line\"\"\"\n",
" lines_locs = np.zeros((80, 80, 2))\n",
" bad_pixel_count = 0\n",
" bad_fit_count = 0\n",
" with ProgressBar(80 * 80) as bar:\n",
" for ix in np.arange(0, 80):\n",
" for iy in np.arange(0, 80):\n",
" bar.update()\n",
" try:\n",
" spectrum = e.spectrum(pixel_index=(ix, iy))\n",
" except:\n",
" print(ix, iy)\n",
" bad_pixel_count += 1\n",
" pass\n",
" if not is_bad_pixels(spectrum):\n",
" try:\n",
" result = find_pixel_gain(spectrum)\n",
" lines_locs[ix, iy, 0] = result[0]\n",
" lines_locs[ix, iy, 1] = result[1]\n",
" if (result[0] == 0) or (result[1] == 0):\n",
" bad_fit_count += 1\n",
" except:\n",
" print(ix, iy)\n",
" \n",
" else:\n",
" bad_pixel_count += 1\n",
" \n",
" print(\"{0}% bad pixels\".format(bad_pixel_count/(80*80)))\n",
" print(\"{0}% bad fits\".format(bad_fit_count/(80*80)))\n",
" plt.imshow(lines_locs[:,:,0])\n",
" return lines_locs\n",
"\n",
"def check_pixel(pixel_index):\n",
" result = find_pixel_gain(e.spectrum(pixel_index=pixel_index), verbose=True)\n",
" e.plot_spectrum(pixel_index=pixel_index)\n",
" plt.axvline(result[0], color='red', label='mean')\n",
" print(result)\n",
" plt.axvline(result[1], color='red', label='mean') \n",
"\n",
"def pixel_gain_function(pixel_index):\n",
" return np.poly1d((m[pixel_index], offset[pixel_index]))\n",
"\n",
"def pixel_energy_axis(pixel_index):\n",
" hist, bins = e.spectrum(pixel_index=pixel_index)\n",
" center = (bins[:-1] + bins[1:]) / 2\n",
" return pixel_gain_function(pixel_index)(center)\n",
"\n",
"def calculate_fwhm(sigma):\n",
" return 2 * np.sqrt(2 * np.log(2)) * sigma\n",
"\n",
"def plot_corrected_spectrum(pixel_index):\n",
" hist, bins = e.spectrum(pixel_index=pixel_index)\n",
" width = 1 * (bins[1] - bins[0])\n",
" center = (bins[:-1] + bins[1:]) / 2\n",
" energy = pixel_gain_function(pixel_index)(center)\n",
" plt.plot(energy, hist)\n",
" plt.ylabel('Counts')\n",
" plt.xlabel('Energy')\n",
" \n",
"def get_fwhm(line_energy, pixel_index):\n",
" energies = pixel_energy_axis(pixel_index)\n",
" hist, bins = e.spectrum(pixel_index)\n",
" guess = (50, line_energy, 1)\n",
" bounding_box = (energies < line_energy + guess[2] * 3) & (energies > line_energy - guess[2] * 3)\n",
" fit = fit_line(energies[bounding_box], hist[bounding_box], guess)\n",
" return fit\n",
"\n",
"def find_all_fwhm(line_energy=30.9):\n",
" fwhm = np.zeros((80, 80))\n",
" for ix in np.arange(0, 80):\n",
" for iy in np.arange(0, 80):\n",
" try:\n",
" f = get_fwhm(30.9, (ix, iy))\n",
" fwhm[ix, iy] = calculate_fwhm(f.stddev)\n",
" except:\n",
" pass\n",
" return fwhm\n",
"\n",
"def calculate_gain_and_offset(channel_list, energy_list = [30.9, 80.9]):\n",
" result = np.zeros((80,80,2))\n",
" # calculate the slope (i.e. the gain)\n",
" result[:,:,1] = np.clip((energy_list[1] - energy_list[0]) / (channel_list[:,:,1] - channel_list[:,:,0]), 1e-4, 2)\n",
" # calculate the offset\n",
" result[:,:,0] = energy_list[0] - m * result[:,:,0]\n",
" return result\n",
"\n",
"def plot_total_spectrum():\n",
" pass\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 324,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(30, 0)\n",
"0% bad pixels\n",
"0% bad fits\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP4AAAD/CAYAAADRymv0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXuU3UWV7787hkd4BElGGk0DCUOiSQR5aNDFuMiID9QR\nnbnjc8Y1aUdHB73iVa/iYxZwdeaCa2YUR/H67FYcfOALucMoKguvTyQICZOAaSRREqCVRNJCABNS\n94/fr87v+zu9d1f9Tp9zQnP2Z61ep7pO/arq9zq1a9euvSWEAMdxBos5+7oDjuP0H3/xHWcA8Rff\ncQYQf/EdZwDxF99xBhB/8R1nAJnRiy8iZ4rIrSKySUTe2a1OOY7TW6TTdXwRmQNgE4AzANwJ4HoA\nrwgh3Nq97jmO0wtmMuKvAjAeQvhVCGE3gC8CeHF3uuU4Ti+ZyYu/CMAd9P/WMs9xnEc4c3vdgIi4\nTbDj7CNCCKLlz+TF3wbgaPp/uMybwulDwOoji/TqI4HVj6++k7GdVSfXHJZsdPNY8blkjV3m/BuB\n809KVtU1vD1v75HQ3rV3AdfeXf1/wTq77Exe/OsBHCcixwC4C8ArALxSLTlR/J2/ZupXOS87c9zd\n9wEAHj73kEbHOc6jndWPrw+qPXnxQwgPi8ibAFyNQlfw6RDCLZ3W5zhO/5jRHD+E8C0AT0yVWzyT\nRjogTiu8PW/P29PpeB0/uwGREFX/w2umL7v761V6vz/Xy4yPFZ9LE3UBwK2jx7TSTxr5VfoAx3kU\nIWO2cs9Ndh1nAOnLiB/WdL/eV49+opW+dOTvqi+WUKHN3W8XAC4f/bNW+qUj/7ejOt45en4rfdHI\n+Wa5mRClIyBPQnIeXfiI7zhODX/xHWcAmbWifjTkAaY35olcMfpcAMCLR65Olv3L0Utb6a+MvLph\nz2YXrx/9EADg4yNv2cc96Q1xStWr6dS+IEcJDrio7zhOG/7iO84A0ldR/2ujz2/lfw6FCP25A1/V\nypuvG/wWtoGRQmLHi0a/3Mq6cuRl1fdXUdkX5NXVTtNpRCfkimu9poldxGzmjNErW+nvjbxoH/ak\nf7io7zhODX/xHWcA2Wcmu+Gb5fdnUeEMMbxTdl1efB700mbH9UMr3A9jHtB13v2sKr1fqcyf/EKV\nZ065HmG8ffR9rfQ/j/yDWmbrWPH5d+GrrbyrRv5bL7s1hYtHKwOzc0Yqw7P4TALNn8scXNR3HKeG\nv/iOM4D0Vau/vbKLwcLSLsYUd75Had48fHrx8bzRb7SyPi0vaaWf/OBdrfS9byCvBLOM/zH6T630\nB0fenX1cnEIBbdOoHvGR0b9tpd808uneN9hvMqafnxz961b6dSOf721/GuCivuM4Nfo64vPofvCP\ninbDc+kH6QA68Iz8Nmqj3NOr9O4fVWl1rZzW/Md/U6V5TTvWvefhKu8r91ZexF85ckV+Rw00u4HF\no5Uzoy0jy2fcRopvjZ7eSp858v3eNRSvuWZj8QinUymsL7BUvKf48BHfcZwa/uI7zgCSFPVF5NMA\n/gzARAjhhDLvcABfAnAMgC0AXhZC2GkcH/5QOtKtidtRaUIKE9NUlkR2lK3Ij/e2sm4/rvr9OvaH\n1fmET1VSzvtH3wYAeO+if6nqymhbtTfI4NTRawEAh+D3rTzLVHT16H+20teOlGbNpFR67bZ/a6U/\nfMh/b6U7XvtVzJpz1pQ/Nvo3rfTfj3x22iY2jlXp5QuqdOo6/mr0ca30MSO/nb5wBtE0OscsemKs\nSg+tKROGcq8bTk7OHq2exRtwCgDgupHVnVWmMFNRfxTA89ryzgXw3RDCEwFcA+BdM+qh4zh9Jfni\nhxB+COB3bdkvBhB/8j8L4CVwHGfW0Kl77SNCCBMAEEK4W0SOmK7w1lI8Z3d4Z28rxJyLH/u2Vt6c\nUIl5WKSLeUdMFN5yw6LqN4td67F4z2Lamw8s2gsHV3ksA1m78DTRNJqBAsDwUfQFrURcN7QaAPD2\nifdBhewUWuI9t3tVNWV5By5opVkMZ3Hzw+EiAMC/jWREK1c06j+6709a6eeM/FA9LCXe13ZM4mXT\nlLRh8b5TM+IvjNKqC4pVl2tGn9HKe9bIT9TjWuI9kFx9eMKDNGa+Ya9eqORfR/++lX7ryMda6UtG\nqmf/BaNfRT/plnLP4+M5ziyi0xF/QkSGQggTInIkgN9MV/hD5efhN06Nnec4Tndoj503HVkGPCKy\nGMCVIYTjy/8vArAjhHCRiLwTwOEhhHONY1sGPDUR+bQysZQKk93I2bdXGs9LFlUi0eT24vNQEtkf\neKhKT9yvn8OScp4xeWeVVxMfLQcesWlaDOjUUYflfIPFvLhzjNt4gOpYQe3JubSCcaGqvJ0xlrZf\n05azJn8/qqMfTj4uGH1HK33eyAda6Q+MvgkA8Cr5SCsvFdgFAOT95VXf85hWXjh//5l1MgNe4XkC\nqof1spG/1YpPy4y0+iJyGYAfA1gmIr8WkREAFwJ4joj8AsXM9sLGvXIcZ5+RFPVDCK8yvnp2l/vi\nOE6f6K8jDtb9l3b5uyerrP3I0GMrqeo10Yyj2ZwoVTSbZVv+0EqzaBbtrDu1sa7tLByiL4wdW1GT\n+4ZDKi2uZRjDU6AFB08ty9rtufRTvYWmNa0pgGFwkty1R9sB/vUduhZag+u9bUeV3k1lzg6KgVIG\n7KBkCBPT9yfla5Hge/n+PdPb3+fsPuT7c96DynPWQyOgFsr5u62+4zg1+jLi316mF9Luu+0PTS17\n7BdJWfVB+qG6o0rKNUWZDU+qvmdFEo8085X8PZTHv7KPH/1lK33Xoj9upU/cVqz53rSoWgeOCkYA\n+KsHdW+/j/0/hV8A9gnAyr0tZOD8pLvva6UfPvcQAPVRaQftDFz6hCq9i+rYU54YKyxrirlPVunJ\nkSody+d4/dWkBsutVI3EaBzNqQHgvSP/MrUAKsXha0NlAPHjEX0LJ5/LS++9DADwjaFqxiqfIBuJ\nF1c2Euz2bM3oJQCAsZGz1TZ4FB8nhbE2clseoZN2GBdRJYZ5RlQCa0pmH/Edx6nhL77jDCB9EfXv\nKZdCWWSNOqqaiGIoQWqi0tGFqDRO4j+LV7K6Op871kyVcoZPpH8oXbMxWDM1v6ZgZLdgJG3y2nuc\nUtREPxZ5K+kW8jua4nym7DOJxCwS/jKQw4xFisMMnstQHfKSqo1NL6muS7wP86vlasw7sEqzkjHu\nOASqXWSW0vDQj1Q2XdcdUml1W0pI2nEpH6O+Pbvq2wLq07by2TmeFMA3kzLxJGW6BFQ2EuxZl+0N\n2C6idn/ihcnw9lxT0sVTpWv/8tGqwJdGuMGp1HYIsjK8A8clLuo7jlPDX3zHGUD6IupvKtOaxv0B\n6Cy7turXH15MGvyDlcKGeMsiXWyP+8BOOzb9yVTxF6CpiKXFpd15cimJ7K9SJCwWG1msPJrSTy4+\nuO/zptYEoH7al4XCZJXNVWtTJ4L7H69HzcSWVg5YA77zzMouYt7C4kheAVhPff5o+FArfa5UIbgX\nl6K60H2cpJ0eE7TaM0SrQFsfmtpPvpfMCuq/KqrTtd9KbT8t0MrO0cXKDk8p+Znk+yuvovzPTZ2q\naVNAoD4NHB8dLvJGtiodrsOrNd+5zw7/7qK+4zg1/MV3nAGkrwY8KTGNxSDFWzAAYNmbSrfcV5Co\nNUQi+9rpd6ktJU3pJBnAaAZFQCWa8g7AHWQqe9R3Scz7fNV21PQuu61y0rCOfAM+5Z+pz2+fOs2w\nrgWz5Bz65/Kp35+y7Qet9BXyzFaaTaflN+cBAO55TGXIMkmrL5XHwHo/oh+9OeQwBE8fayXDEZWV\n0MZpN23bDCui/sq30PW+d+r1Buoi9GMurLT9kYdPrrT+cklV3wZa7Yja/g2jx1Zl5XZofCFUnufe\nN/K/i77xagddOMuN++tHi6nRx0eqaZFlVJUbNMVFfcdxaviL7zgDSF935zGaNj9lZw9UIjCLnQcZ\nZbmNqBlnQxwWD62phQZPF/hA1pa3yj5hap5Vlqvjvi89jI6j6cnK40js3VVKdGT0ApqebCYRc4g0\n6nGH30pc3MrbBJ5DUD9qU4RCNb6B1NesTd9I58dTvEklj+H7sJKMsdZdW5zfCbzi8I7q+73/q5Jo\nOerR/veXezv2kBh/WvX9ZjIk0qZXS+icAxWwdiKuiKs8vI2gQcQmS3TvxPmLi/qO49Toq3JPQxuV\ngUqp1k78peWRgUePeTTisZIqNYpba+WxfznOCbU2aqPkKrrWw1Uy/Ef1o7yrPD/ea88BKW6hkWYx\njdwHf7Uc2c7UlZt8fmo/2R7hJ9VdWTdcHckjW7zmJ5BJ7/avVemJh6eW5Tos5aWlAF5RXsf1NGIu\nonvN7a2gax5HWH7OTqDvWRLiPsW2V95EUtWH6NqurZLr/6tKx6tVswUhKcXcycd2HbEs9Y3NlzV/\nEFE5CFQKQh/xHcep4S++4wwgObHzhgF8DsAQgL0APhlC+HBu/DwW9TVRikW7TsXpJsdZCkTLdDjW\nbYmg3B+uI9UnFr216Y4lCvMUSFMwWdezZiqqiMJMTUylsrto+hGnItZUzSL2z7pWixXFIzNkiPfW\nVC7WrdkEWH1jama1Y/pxrMCdKEV58ihn22FQ3VHU301947V70+xX2Q0oc8t3+lMyI1F/D4C3hhBW\nAngGgDeKyJPg8fMcZ9aSEzvv7hDCTWX6PgC3oFBNefw8x5mlNNLql4E1rkWxh+yOEMLh9N2OEMIU\nXTzvzkutlVvir1YmtV7flPmJ1YCcdX4u83slL2ftWjvvnHOKx1micm0F4P7KsmIdjprShqa9b8+P\nWFOS5YbDjFTZOSeQCe21U6VU7g9XezydX82k+u1FfXs/U9V1m9KfdrRz5batZ06bcjF83D+GsVb6\n/bIGgG33sfDX1a697a8d1gu10RWtvogcAuArAM4pR/72XwyPn+c4s4Ss2HkiMhfFS39pCOGKMjs7\nft6Hy885AJ5e/jmO0116ETvvcwDuCSG8lfKy4uexya6lDY9Y4iYTRaghw4zVMlTRfuGs6YSm7U+J\ndu3tpcRzPo7LxvNjrTD3h/MZrT3uc44Di4ilAdfuWc4qiTaFs6ZO1kjU6ZQrhWUcpa2upJ5JoNKy\ns6GRNd1jRyOH7VfuOv1L2nU6VkWm23lA9WqpMR8Vn3zTifrJayQipwH4KwA3i8iNKET6d6Pw+v1l\nEXkNgF8BHQZEdxyn7+TEzvsR6ls/GI+f5zizkL7Y6sdpR45RQyQlKlqia0rEbioeaoY/OW1r/bTa\n06YcrIXfRlrqJv200K6RdV1SRknW+aX6kSPea+Ut+3yenkwoBjqp6w2kjcmsa8TnuvK9xfu06f2V\nhM3Xm9+B1HTXakObzi5Wpr4r4bb6juMQffWyqyk5+BcwtUOOy+SY0HZKagTK+eWPIzavpeeMjrFM\njhIrZb9gSSm5fWjPZ6Iiz1I2NlEmWqM/n98CJY/h859vSAVa3xYY9hta35aeTv/QltNacJdSucem\n0Nb5L1fMr5vcMy5fCwxS4rvzHMep4S++4wwgfXW9xZaSh5af1lqzRRMvtBo5YnpOPzqpI2f3Xqpt\nVuLMJTF1S3lxrd2COTYSqT6kplQ5DjW09XjL9kK7Xtb9S+125CnJfsr37f3UrgF/fwYF3/i2VGHV\nl5f3Z5Kc+1oOYbT7sJDSFI3dDHgSHXFonndd1Hccp4a/+I4zgOwzrb62zm1psrU1TGunlIUm8jFN\nxHtL85xy9pCzNh/ry9mpqJkI87XStMbtRLNRyzlFk1WSnOlE6r7zNbpNccTBpGwa2vsUWURtTCTa\nYHKmpbFurte6hiyyb75zalk26WUz3Rj6G6iH/27HRX3HcWr4i+84A0hftfrajrNuGIDkmMVqNNHw\nW3WlphmW2GmdU/Qpx4YnlmHTQsVMNWcHmYY1feH+H2qU0cqmdt/lGGBp7VkrAJbWXrtvrDnfpbTB\ndeQYUmluwDVfhu1lmzzjPAXaQx057Ibi/b3nKWQifGDxefD9Luo7jkP4i+84A0gT25eO0cT5mGeJ\nsZaInDIcYXGNjV227pz6fY7mXBPBci5arLvJigMA7FDsxa1Q1ZYmPrKCouOsJ3vylGMMXp3Y8tDU\nsgyLq5YozDvqtj2cf5x23g8Y3/O0YI+S5nNmw6ehA6v0bcq+Cmt1iZ2OMDEkuPXM1gxx1tBxY1Pr\n4rIHLanS8gYKsf7kQpLnd2xhjG6k1BnxEd9xBpC+jPi5ihJrFKiN4qWSY1vGOim75NKULjnrsrvb\nPoE8z7lNJJMUOevVmgn0Llq7t+rQTGFZksjZ36+1wf3Y9rBeJpKzK1Mz9TXCKybNbWuBOOg50vrB\nI+kCI19TXuZIChygQzs/TreCZAAIFBl4XGkvBx/xHWcA8RffcQaQnNh5BwD4fwD2RyF9fCWEcEGT\n2HkblHqbrCs3EaVSa/pNxHsg7W01FTiBxUd2+sBKvFTwhl+GygPEjTiplX6hVKGR4/nleOTVyFmD\nZ5rEPmyyPt7EJVs3dnPymj5frya2I1w21me5mWsyxbMUhHyP4w6+FUoo7mWYwTp+COEhAH8aQjgJ\nwIkAni8iq+Cx8xxn1pIl6ocQooHTASh+wAI8dp7jzFpyA2rMAXADgD8G8NEQwrtE5HdNY+cxcecR\ne0TNERWj+JOzhqtpU7kuTp9A4aA3KuaWTaYF3A9LZFzx19Te56v0sLJbzjJjbaLJ1eL6Wd936s+w\nyRIRX3sWXZu0x2VPoXXu9ZunlrVsNqwYfrcouxmbeEy2pkDWVOXe8GQAwNOG/quVd8Nv9LJ8LnGH\n38Y7q7zof2/Gu/NCCHtLUX8YwCoRWQmPnec4s5ZG6/ghhEkRuRbAmeggdh4AnFr+OY7TXX4G4HoA\nj7sxXTZHq/9HAHaHEHaKyDwA3wZwIYDTkRk7b22Z1gwkLBEsJValHHW0k4q91mlgDCtYgqa9bhLL\nzoqxlnKYcQJpd1n8W2rEGtTas6YF3bD26mbgjxzDJg3rXq+g6d5keY3mUiNsNGb1f+Vji/dpw716\nQA1r52NsxnLWUnPKQfdyOzvmK1n46uJzRrHzADwewGfLef4cAF8KIVwlIj+Fx85znFlJTuy8mwGc\nrOTvgMfOc5xZSV8ccdyeLgYgL6JKFEm1qDVAXTzSsIxvUiI7k2PgorWXo4XXfOfV/LBRWjM4yVl9\nWKz4nLP2Rlh1aFOZFc+t0uuv1uvQRhoWsa3w0p1qy6drt71savqRE4J9SXkuvDLEqwVbDN+Hsf98\nbzgKE9cR3WcDaIXJ5vZiP4+FO+JwHIfoq5ddTVmTY8KojTTWWqy15j1cKkS2KIqt9jaYJko6rb6m\n0WQ1icYalbS18KbmoanryaSiuy4yRqtUHRapiLU5ktfiUim2xbAXsaSpaLFmKeMsN2orTiw+N96k\n98eSWLRYkjlRmTVlaXwWjoKP+I7jEP7iO84A0ldRn0mJcUzKRVaOZ1lN9G7iZCJVb3u+tjvPUtjl\nOPbQSO0izDlOa9fqZ2o6kCOGa9O9Joo3zrNCrKcCjeSYQMd18+2G6XTKBJrrHTKmQJqtBk9JjstQ\nWkf3XRw7b0+583P/nS7qO45D+IvvOAPIPhP1m3ih1TTVTXesxTqGMsQnFgujqatm5tpOKjR2KpQz\n5+dMEbQyKdPcHFLXENDv23Ij7p1mRtwk+AZjXTcrlmIThyHaeS/vwvXkfs5/jF4mOmbJmX5qz0Bt\np+ma4tNj5zmOU8NffMcZQPriXjuSCuRgGcZoIlhThxSxjBWemqkFrSjFu1RQj/bjNJGdqQV4UNJW\n31YYDkPi9dq6c2oekBYhmxrGxP6zzzorrPV62iWYeuCaxNxjLA2/hjVd0ure//HVVHjdTlVqThqm\n1YyADF+L0VTXMtO9mUx9oygPAJvHis+mL7KP+I4zgPiL7zgDyD7bnRe1m5abaUsLu6T0NL35+1We\nNUXQxB82tsiJ4NKkrGaIY4nYLG5qmuMcY6Ym4jtPjTTnGpYIzZvJFlN6ou343La1zWnWPUtp+JvE\n6rP6aU3h4rW1dg4y2n1fSsfJX1AUnP+gKDgUz7CJMRlfr2WvKOree3VV723lRZ6Re23HcR599HUd\nv0mQAkYzTdXi6QF57pFS7TFNXH012Zuf6lPO7rwmcB0c2GNeGS32NkPpaZ23Vi+T8m/ACqobxvTj\nUrBiUfFABSDtci1lssuwOW0TvwjW88LSj3Zd1oxe0kq/R85W62tJGGQrsauUGg++30d8x3EIf/Ed\nZwDJFvVLZ5trAWwNIZzVJHaeJupH8XweiVS3GW6Jln6ySo+/rjyOvrfMfjXxzjL5TK1dN4mXx/Xl\n7HrTFHY50xDNKQdHNLEUmSnT26Y74DS4Xk2cPuGCKm/jeXq9qSleToCLFKnnyJoicahtq3yEz2NI\nUTwC+pTSCvLC6/vRLoDNieMU6Eh0R9Q/B8BG+t9j5znOLCXrxReRYQAvAPApyvbYeY4zS8mNnXc5\ngH8EcBiAt5WifnbsvLiO38TfWopUAIz2fE27C+X79jJRXG6ys47zm2rhNVPfFUaQDI2U04t2Uv1L\nTRea7rJLPQMnfI/69hdV+pZSlK1NFzNE75RWv9b2miq9cWzq9yym70cVanEOLXsLayVCW80ZajC1\n4FWIGI9yRuv4IvJCABMhhJsA6MbKBR47z3FmCTl6kNMAnCUiL0DxQ3aoiFwK4O7c2HkfKj/3wmPn\nOU6v+MFe4Id7gfsyyjYy4BGR01GJ+h8AsD0ndt50BjyWMYWlqY+izSIlKET7cU3E3pz4exqpfqZM\netvzNf9tTcx0tT60H8f50RWzJna2tz2B6WniL5CxzumpqFy4rMOyKWVzpl8pUs9IjiFVyjcgG9fs\npmeVXb13apgVTYrHadiN97RbWv12LgTwHBH5BYAzyv8dx5kFNA2T/X0A3y/THjvPcWYpfXXEoYmC\nKbfIgC5O7yCRiY9rIm6yCDZO2nLNiCTHeKVT19ja+S1WtLRNSRnRAJX4btmed2rAYz1YUVNtaan5\nvDc8tCy7Pevap1ZzrKlDLJ/jEzK12sGOSI6ndS+uO2bnOBThuneV70FtNWBNmRgzKoCb7DrOQLLP\nvOymdjFpCiigUkI1GX3a69basEj98jddN480CU5h1avFS7Nir1m7wrS2c0x2I5YJbcpLcI7vhW7a\nfVhwe03Md5lOFXO8ph+vM/dhHq3js8suaydiZLiUmg57yHfnOY5D+IvvOANIX5R704nZc41ynNZE\nG0sMTAVcsJRqC4x8rZ0cpxwaLDZbu+hagT8oj9fPU0EkrKkTT5c0ewJrKsPtaf20plw8ndCUX00f\nPE1pZonm2vlxf443HLekXK6ZobiVQCI556c58KjtnCTxnu1Wdil9XrGmyrtuLN22j/iOM4D4i+84\nA0hftPobynRKbGIx54n3VPaM9x5TuaGNAQdyHHFo2mJLTLc02VHkzlnPTYWtbhIXzTLvTXntzQlP\nnRJpm8YzjDT1v6eR42hDI7VKYMXWs7T6nfZnqWJCm2NOnDJnT4VS185pJVyr7zgO4S++4wwg+yyg\nRsqQI8fHXcTSoGoiVs7uvSYBNSwDF20VIRUggskR7zudyvD5xakMr5zwefBeazb7jeTsrkxN63jF\ngfuZ2g3YxKlKE6MkrsMyREr54rOepybPAGPdvxg8ZCFZA0X/fC7qO45Tw198xxlA+ro7r1Pba03E\nssRfS/u5p+0TsMW8lEOQHKOdWKbJdAJI7w1o4iZ7mHa6sV84Pi6KvdxPNtTRxHtur7angkTeB4zd\ndxFuz9L0aysUiww/dCnte04Idm3VqcmUk+vIuX9Ll1Tp9ZuLTyvGIR/Hxl1RxB83/V/p+IjvOANI\nX0b86Ub6pkosrYx1nPZrbZ1wty9E/IVeclSVx9FRU0qjnJ1gmuKQz2OcRvmUZJKzH7/mTuqAqW1o\nASKAunmyJmGseD39Q/WNj1XpWJ6927JUccrpVXo9RVKerg/t/UhJctb6P0d8nq+UtexX4ijP9Vlt\nHEu+bMOppK9bXh43ph9n4SO+4wwg/uI7zgCSG1BjC4CdKDxk7w4hrOokdl6nNImh1lQZ06TtFJqi\nKGcdv0kY7FTMvSZmnkB1Ha2ylug5UycZOQ4wmrj3sspGZRnXy+n5Rr52/6z7ZClRUyytLNFbHneX\n/nmVN/51Kktu4ibJ6GK70l5UCj4FM1/H3wtgdQjhpBDCqjLPY+c5ziwl98UXpazHznOcWUquqH87\ngHsBPAzg4yGETzWJnRdF/SZhqzsNHNGNcNdMKkacFgAD0EVMS7urnasl/qamNU12wrXXF5mv5AHA\nVuW4HA2y1n9Lg54S7y0HJam4fdb943PVorTnPJNDim88NoHWHHW09yNa3GrOOQBgxYuq9OYrqe7y\njbuZOp+zOy93Feu0EMJdIvI4AFeXQTTafzHMX5APl59zADy9/HMcp7tcD2At8sT4rBc/hHBX+flb\nEfkGgFUAJnJj5725SWOO43TE08q/+J5dMk3ZpKgvIgcBmBNCuE9EDgZwNYALUITN2tEkdh6jiWDM\ncTRpuIXEmCgq8o4oNqDI0cJGLBFT03Bb2vnU1MESQVn8TRmOWH7vmJT22jrXBUpZayqTcgPONFkB\nsKYn85X8nGldk9UOZqGSZ8UUTO18tFYtuB+LSas/Xmr1tXOeDs1gaCjDvXbOIDwE4OsiEsry/x5C\nuFpE1gL4soi8BsCvALwsoy7HcR4BJF/8EMJmACcq+R47z3FmKX2NpLNYMVioxfwyxHcmik2WDTn/\nkg0ZbpQjqWg2XDeLYLsobYmxWqSgJtFstD5wvYB+vXK05SmDqJRLba6vqVFPbJuXf6ydetp5c99y\nxGLNfTif/8nUkW10U2Iy9Vy0E6egvI/AutdcR3SfvUV5TtvLatPOBUrZXoXJdhxnlrLPYuelXCKl\nTExzXCI1WdNn88mtZHgc27NGM2tXm9ZG07X5mdIkrl+OPYVm3poKnJHTNyYlseRIGNq5NnXxpkls\nlv8D7bjhjGjHHCRDG+lZ2ZiKl8f3Zr7HznMcR8NffMcZQPoi6q8r06n1cUsU1pRYlthliViaEivH\nS2skR2kVmvutAAARWklEQVSW2t2VI+pHFhmKySZTAUtU1MTXnKAk2lQmx9w25XIsZ6eiFgbcWptP\nXduc9lIu3lJei/k4awqrPYuWCXHKdFhTyHZjd57jOI8i/MV3nAGkL+bzcY2RRZ4o5rBW3AphrZnk\nWh23NKhavSlNN5PjIVfzAMui3UGUTompVvjmmp0CtbdNsXuwAkdwP+IUIMfHn4Zm/gvUxVSuI+Vb\nzqo77sRrarIbyZnK7FHyramANYWL19za4cicQM41xu8sPvm6WX4CNdhm5feGLQDjI77jDCD+4jvO\nANIXUV8zuoli1dCaKu+U0R+00l+UZ7bS3EnNsCLHR1zKuCbllEMTA9vr0MyMrf5YYqOWZ2mhub3U\ntIWPYw3/HuV7aydiyqCGHWOwqKvV18T5Rnv/ItZUR6vPaq9J2GrLpNy6Xhr8PEzcOfV76xmxTL9j\nGcvBh4WP+I4zgPiL7zgDSF8MeDaU6U4NR1J+5FLabW4vx89eKkKNhab5T+05aD8uYhmkrFhapdeP\nTz2OV0k0kb6d1BSBRfZU2OocYxcNayqT0mTPM9JazLmmuxZjP7gPrGW3di3G4xYZWna+hlqMxpy+\nWS7B28t6mGzHcWr0dcRP/VIx1ugRfxFz3F+l1orZpJX32GujsTVipkbuJiMmUPWziXkv0Pl6e5P7\noI2qlsfa1E5LSyGWilTcNJBHysVbyhYgRwGsPWeWxMpoEg0/k+zVmCU5zZRXu0/Hwkd8x3EIf/Ed\nZwDJWscXkcMAfArAk1GE03oNgE3IiJ0H6DudNNHUWpvnslHEnGeUtbybalg71lJrzDmmvrHPLK5Z\nyiGuL7pu4nXiJiJmDpqIabXRZPehpYDK8RartZHjGVdDU4xaz0iKnOmLNl2wnmUrCEgsYz2TnF5M\nO1Df8+BFAIC3yjtbeanpG5A/4l8M4KoQwnIUu/1uhcfOc5xZS/LFF5H5AJ4ZQhgFgBDCnnJk99h5\njjNLyQmo8RQAnwCwEcVovxbAWwBsaxo7T9M8WtrWBcpON4tOfdlZ4tr8RNtNfLYxfK6Wr76lo8Xn\n+IhSAWxxOmp6Lb93qeuSsxqiHZez2zFVJkernwpsYtl6aDEFU3H2rL7l2AIMkRjeOo4KTBhTuFj3\niqOqvI13KB1qQzu/OJ14KmYWUGMugJMBvDGEsFZEPohCzG8cO28vihA/q6yCjuN0zE/Kv/syyua8\n+FsB3BFCWFv+/1UUL37j2Hnd9CDrOE6dZ5R/ccT/5DRlc8Nkfx/A60IIm0TkPFS+HBrFztNEJUvE\nZDF2Lonek6WolOOeWcNaDbDa3q7kWcEZmojQKR9qOabFKcMR7TyAtHib0+eU7zxLDNdiy1miPpNy\nc271I4aotvwWWtMzbSrK58z95DLxmrNBWBMzZCYVz5HztWnRMsw8TPabAfy7iOwH4HYAIwAeA4+d\n5zizktww2etQTM/b8dh5jjML6YutflROaj71mjpkiNRiqJEmdTv53NPEtJxfOraXjqJZzs6zlDto\ndv29VXH9zVgrC01WKppgOc6w/CBqWnauY57Rfy3WGxu1WP3vNDKPdnzOqkwKaxql1WFdW82/3jzD\n2QfHnZy8Ty8TiffJ3Ws7jlOjr663mPgraCk+LEXS7rZPAJik0dMKIjGv7bO9vdSvfc6aP//6xj5z\nf7QAH1wWqHwLaKNkTv+a7lSM/bBis1nK0Eklj0cwGLYXUSlm3esmZrqWh1xtxyD3zTou5ZKLr61l\nequVPcKIyKsF3dhtuPTaQcbw3LYWKMZSkDI+4jvOAOIvvuMMIH0R9bU17eHSNHGczBKHjLh3LPIs\nVPJYjEvFiMsxu9QwA3gYirfpXCK1Y3nO1dq2dotpDjwsJV1q95ql0NM8DbNYyfdhccIdWupaWeWb\nxqTTXKflBMbQAr5oInZ7e9r323YoBaBPOZru6ov9n2Irn8BHfMcZQPzFd5wBpK/r+CyaLVTKWppl\nJoq6lomt5TtPI2c9VzPBtHZsMdr5pTTBQLXWz+v8TXwV5oQP57q13V2a45P2MjFtSLGmKBzjCz5A\n4j/XkTLltUJHM9o1snZDpuwiLJqI+ow1JYlpSyPP9+F4kut/U14QbZXkKPg6vuM4hL/4jjOA9EXU\nv71Ms7HLvAOLzwcerPIWkny8kTb5WmJq6zhKa0Y7QFp7baGJbEtOrdLj1+nHxbpznG9oO+Bq5q90\n/myslFo5yImHd6iSZ00XtGvxeyWP6wX06YAlKlt+CSPW+eWsfEQ6jZ2Xg7b6wM/noRRoY4sSzjrH\nqYw2TWy6O89HfMcZQPzFd5wBpK+RdFL+1iyNNYuN0QNIKvJNOzP12WaJbly2yU4vy7Y6NSVJGRpZ\nBiepmHo5llxNdudxfTuUMjnOTBYoZfj8c7TzsT3ujzU9YTTHJk2mUSlHHYBugDVfcTrT3l5quhqv\nrYv6juPU6IvJrrYTT1uztzysWr/yEWu3FZR864StfdCpPnS6n5v7cZDyvSWNpGL4cX8sZSKTihFn\nKZgOVb63zF/nK/mWCTHDkoK2zm1JB5oy0dqduJwOvM3YORexRmtNIWfZmTCaEnUPPXs1uwl6Pvej\nA6Oyt+mL7CO+4wwg/uI7zgCSlBBEZBmKGHkBgKCIvvsPAC5FZuy8beXnEcp3ljIuZRKZ46IppTis\nKWBIxNIcVdTCTCd2nnH/rDVqbkMTwy2x2XJccqjyvWUCnfIGbF371K4+S0Gq3QdLKcj5KfGdsewi\n4nTH2tXH4n3K8zGTml5ayjgmFY7dcin3QMJJS05sx+SIH0LYFEI4KYRwMoBTANwP4Ovw2HmOM2tp\nKuo/G8AvQwh3wGPnOc6spaky8OUALivTQyGECQAIIdwtIpokDwA4dU3xuXWsytvT9tnemRxNvYYl\nVkWx0VotsAIgRFgcZfGeNeeaOJkjdlnn3V7XdPXF47hszq6+VAhzSzsfbQRyHHho2nBLrDaDqijf\n5/jcY1uGyHLyWMu+7HZNLYrjaL7xc5oWWNMTDWsViIkrOzw9266YpwP6NEKLnTcd2S9+GUzjLAAx\nEHd27Lzzbyw+J1GF+XEcp7t0O3Ze5PkAbggh3FP+nx077/yTis+t6xq05jhOI7oeOw8AROQLAL4V\nQvhs+f9FaBg7T9P6sgHFlpTqFpVIZ4lM3AYbxkQxLmfaoJlgNtH4ArrInnL2AVSiXs4OMk3jzubE\nLLqymSpry7UVBUurr4nTOe7RtXDeOaGqtSlCU1NmzWCIqRkB0WpN1JxbBkqp2IBMjmGa5jNPc9TR\n3p72bMRrtRIzNNkVkYNQKPa+RtkXAXiOiPwCwBkALsypy3GcfU9u7LxdAB7XlrcDHjvPcWYlfbHV\nj6T8xVnfa7bOlujD4r1mwGJp/S1xTYvAY/VzkRIvLmeKwGHAoyERrxZY/v5YPNQMYxirvtg/ngrw\nNbQizWhY11bTMufsKdBiy3Fdlg281k6OoZEWCUnbIQhMs+dDKWutVGiivDVFspyjRJf0vAKwYk2Z\nGDM6CTfZdZyBpK9edpt4iLVGF+2XNkcRFkcPVrRYe5+5n1FZZpmEptbgLQ/A1p5wzd4gR5Gp7T7k\nNqwRSlvHZ5oosXLcacV8vp484vM11CQd67qkdiJqCsb2OprYDaSuRRNFbnsZrSy7X5tLN/OgjxSf\n4yNT++PRch3HqeEvvuMMIH11vaUpNixFC5OjWIusIA+4m8kDrjZ1sBQmne5eY+Jx1tQj5fYrZ/dh\nyrzXInV+1jmlAmqkFF5AekrCpKZ1luJNu9dLyaB8nEzNLBdocRrI5tn8vRVoJD7jlrdnRrMzsaZn\nQwlHMdpUbcbr+I7jPLrwF99xBpC+ivqMJvJZ4q0mxrD4ZJmjNvGHl9JqW9r51MpAzvqx1l4TsZnJ\nOedUmRyTZK1tyxRYm0bxeVjnmopRaJn6avlaEJH2/JS3ZmsFgM91cRkwY9v96bLas59z7TW7gOEX\nVXlbryw+PXae4zg1/MV3nAGkL6L+pmm+t0ToWsw5xfdYjmGFFXBBI+WrL0eDrDmqyInNltKyW+1x\nn6OhUU6Y8JTBUxO/hRZNQljnTGs0RyNLyaHGVnKowVM/zedek92Vlvhv+RSMZSwDpk6nnDWDJ2UX\nIeMBNRzHUfEX33EGkL6I+n8oRbItJI6lRNqFRn4TUTi1GpDjlEMzNNK+B9J7DbQYgEDdDjuGAc+J\nypMygsmZZmiiKWNNqVLkONrQSK1E5ISRni6eXHtZa1Up5g/TdIKfXysSUjTc4ee3CUNkaLSZDI34\n/vJzpBGvt4v6juPU6MuIf7uSn1qDZrTdTTmeS1OjQM7e/B1KHpNq2/JYy/CIEcunTIEBfSTN8ayr\nKRZzAlxo+8ebSAFcX85e+pwoyJGULYAWZAOwd8g1iZ3XRKKxziOO6FZswN1KWaDyGDxJHjajLwg3\n2XUcp0ZfXvyf9qMR4mfeXlfp9/27Ll2kqzzar6dGX1xv/RjAU9vyNCVdjpgaRTP25X0cpScBXA9g\nFZqJh1Z7UfSaThEY29PEXj7O2gF3C6UXlZ/WFGE3tdepyScT67Biy81D8aA+HXb/NVI72aw18Xko\nzu801M8v5RiD0RS8VqzC+QDWo3AemYplZ7WdmiK02yNcD+CZRnvMbZQ+xigbA4I0ve8u6jvOAOIv\nvuMMIH3R6ve0AcdxTCytfs9ffMdxHnm4qO84A4i/+I4zgPT8xReRM0XkVhHZVAbX7Hb9nxaRCRFZ\nT3mHi8jVIvILEfm2iBw2XR0N2xsWkWtEZIOI3Cwib+5VmyJygIhcJyI3lm2d16u22tqdIyI/F5Fv\n9ro9EdkiIuvKc/xZH9o7TEQuF5Fbynt4aq/aE5Fl5Xn9vPzcKSJv7vX9y6GnL76IzAHwEQDPQ2FB\n+EoReVKXmxkt62fOBfDdEMITAVwD4F1dbG8PgLeGEFaiiEr8xvKcut5mCOEhAH8aQjgJwIkAni8i\nq3rRVhvnANhI//eyvb0AVocQTgohrOpDexcDuCqEsBxFzIlbe9VeCGFTeV4nAzgFwP0Avt6r9pp2\nrmd/KOw+/pP+PxfAO3vQzjEA1tP/twIYKtNHAri1h+f4DRT2Hz1tE4VJ/1oAT+tlWwCGAXwHwGoA\n3+z19QSwGcDCtryetIfCXueXSn7PnxcAzwXwg361l/rrtai/CMAd9P9WVMZpveSIEMIEAIQQ7gZw\nRKJ8R4jIYhQj8U9R3Miut1mK3TcCuBvAd0II1/eqrZIPAvifAHi5p5ftBQDfEZHrReS1PW5vCYB7\nRGS0FL8/UYaA7+X5RV4O4LIy3Y/2pmVQlHtdX7MUkUMAfAXAOSGE+5Q2utJmCGFvKET9YQCrRGRl\nr9oSkRcCmAgh3ARAXf/tZnslp4VCFH4BimnTM5X6u9XeXAAnA/ho2eb9KKTQXrUHABCR/QCcBeBy\no/6+r6n3+sXfBuBo+n+4zOs1EyIyBAAiciTqpv0zRkTmonjpLw0hXNGPNkMIkwCuBXBmD9s6DcBZ\nInI7gC8AeJaIXArg7l6dWwjhrvLztyimTavQu/PbCuCOEMLa8v+vovgh6Om9A/B8ADeEEO4p/+91\ne0l6/eJfD+A4ETlGRPYH8AoA3+xBO4L6CPVNAGvK9N8AuKL9gBnyGQAbQwgX97JNEfmjqPEVkXkA\nnoNiT09Pzi+E8O4QwtEhhGNR3KtrQgivBnBlL9oTkYNKyQkicjCKefDN6N35TQC4Q0SWlVlnANjQ\nq/aIV6L4IY30ur00vVYioBihfgFgHMC5Paj/MgB3AngIwK8BjAA4HMB3y3avBvDYLrZ3GoCHAdwE\n4EYAPy/PcUG32wRwfFn/TSg2kb2nzO96W0rbp6NS7vWkPRRz7ngdb47PRy/PD4Um//qy3a8BOKzH\n7R0E4LcADqW8nt+/1J+b7DrOADIoyj3HcQh/8R1nAPEX33EGEH/xHWcA8RffcQYQf/EdZwDxF99x\nBhB/8R1nAPn/Qz6VSE/uXcQAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x156947810>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"result = find_all_gains(e)"
]
},
{
"cell_type": "code",
"execution_count": 591,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x16df5b510>"
]
},
"execution_count": 591,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAClCAYAAABSvzbeAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXl4VdXV/z/LG3JNMCEmNNFAahCQguIA/nCuWKktWqda\nbZ21tZO12vG1dgq37Vu1k9UOb21pxYpDHYpDC5WixuKEgiJYkEmCgWhSEgMxiQm57t8fezzJTXID\nMQn0rufJk5Nz99lnn5N91177u9b6LlFKkZGMZCQjGdlzZa/BHkBGMpKRjGTkvZWMos9IRjKSkT1c\nMoo+IxnJSEb2cMko+oxkJCMZ2cMlo+gzkpGMZGQPl4yiz0hGMpKRPVx2K0UvIhUicsdgj6OziMgT\nIvLpnbz2iyLypohsF5F9O312gIi8KyJ7mb/ni8jF/THmjAwdyczrzLx+r2XIKXoRuUBEXhCRJhHZ\nIiJ/F5FjgyZ7TOC/iGQBPwdmKKXylVJvpWjmnlcpdapSqt8VgogcLCL/EJH/iEiyv/vPSGZep2g2\nEPP6EhFZKiLbROR1EbnRLi7/bTKkHlpEvgb8AvgRUAy8H/gNcMZgjus9lP2AOLB6kMexA/gLsFPW\nW0Z6lsy8HjTJAa4BioCjgJOBbwzqiAZJhoyiF5F8IAFcqZR6SCnVqpRKKqXmK6W+FTSNi8jtZku4\nUkSmBH1cKyLrzWeviMhZwWeXishiEfmpiDSIyAYR+Wjw+RMi8gMRecpc/w8RKQw+P1pEnhaRt0Tk\nJRE5Mc3nyhaRXxorbrOI3CQiw0RkPPCqafaWiCxKoy+3lU7jefJFZLaI1IhItYj8UEQkVb9KqbVK\nqduAVek8U0bSl8y8HtR5fatS6mmlVIdS6g3gTuC4dJ5vT5Mho+iBY9BWwIO9tDsduAsYATyCtoys\nrAeOU0rZL9dcESkJPp+GtjKKgJ8Cf+zU9/nApcD7zFi+ASAio4C/AT9QSu1rzj8gIkVpPNd3zX0P\nBQ4zx99VSq0DDjZtRiilZqTRV2fp6XluB9qBA4EjgA8DV+zEPTKya5KZ132X92pefxD4906MZ/cX\npdSQ+AEuAGp6aVMBLAz+ngg099D+JeB0c3wpsDb4LAd4Fyg2fz8BfDv4/IvAfHP8P8Dtnfr+B3Bx\ncO2nuxnDeuAjwd+nABvNcTmQBPbq5toDws/D+/T0PObnHSAefP4p4PFe3u9YIDnYc2FP+snM68Gf\n16bdp4HXgcLBnhOD8ZPF0JF6YKSI7KWUereHdm8Gxy3A3vYaEbkE+Cp6ogEMB0amulYp1Wp2fPsA\ndd30vY85PgA4T0RON38LkAU8lsZzlaInmJVNwP52GGlc35N09zxFwDDgDXNOzM/rKfrIyHsrmXnd\nd+nXeW2grv8FTlZKNezi2HZLGUqK/lmgDTgL+GtfLxaR9wO/B05SSj1rzr2Engi7KtXAn5VSn9+J\na7egv1DWMXUAUNMPY+pJqtGWT5Ey5kxGBk0y87r/pM/z2uD7twKnKqX+a31QQwajV0ptR29hfyMi\nZ4pIjohkichMEbmhh0vthB+O3uJtFZG9RORy4JB+Gt5c4HQROcX0vbeInCgipWlcew/wXREZKSIj\nge8BYShZb1/YPn+hlVJvAguBm0QkT7QcKCIf7PYmInE0fisiEheR7L7eNyNdJTOvu5X3fF6LyIfQ\nz3iOUmpZX++3J8mQUfQASqlfAF9DO3rq0FuyK+nZkaXMtavRsbvPobd+BwNP9XbLbo47j2szcCbw\nbeA/6G3qN/Dvryfr4kfAUmAF8LI5/t907tuXMab4/BIgGx1J0wDchw576yIicgDQCqw0fbTiIycy\nsouSmdc7P8YUn6c9r9HvOx+YLzp/YbuI/L2Xe+2RIpmdfUYykpGM7NmySxa9iHxURF4VkbUicm1/\nDSojGRlsycztjOxJstMWvehU4rXobLMa4AXgU0qpzJY/I7u1ZOZ2RvY02RWLfhqwTim1SSm1A+2c\nObN/hpWRjAyqZOZ2RvYo2RVFPwod7mRlszmXkYzs7pKZ2xnZo+Q9j6MXkYy3979ElFL9Edu920hm\nbv93yJ4wr3dF0W9Bs/BZGW3OdZEDgE1YrqRyfIJfOlIJTO/r2Ab52sG890BdW2V+rDy5k/cckpL2\n3K4ogERj73NblSWQ6opOZysZ+v/noXLtQN27ij1xXu8KdPMCME50EYFsNOfEw6kaTq2YgH7J07Ff\nhI+pg/mYOjjSrlIt2IXhZGRgpRz/P50+iON4TyTtuf0dBZ3nthqTQI1JRNptrCal/JtE6g8yMkhS\nzp44r3faoldKJUXkKnSm2l7AH01yR0YysltLZm5nZE+T9zxhSuOYl9I3uCaUqiF17WNqIQAnyykD\nfu+hfW1ij8Ay+yJ6bneGY7qX9hHaes/eVoG6KEHlm3DSovSvB9gWTzCirYKe/ldvml3Cft2OLfW1\nb5Lo4Zqer01PduXawbr3njGvB0jRpz+Z7zWUFOfJ1PdqSBnZRfmYOpi/SWda7+6/EAUialvqrjYp\npcr7d3QDJ7ui6ENRxfq81EXPv1uoz+/V0LfFoL/EwkoH9+EZ+0teI8GBA3xfdVECmdv5nj0r+t1l\nbg8l9sqM7KGyDbgxxflrtZ8+IxnZbWV3mduDQmr2FRWP/D1aXchodSGgLXlrzY9XZzNenR1pu5+6\nhP3UJZFzC1U69NlROVNN4Ew1oc/XpZL/NidyV2u+d8lJ8bOnyM9J0Dxc/6jzo85VdWoCdao+t/1t\n/QPAg7P0D9qSl7oKZ/FbqWvQP32VO0hwRz84eYvMz2DIgVSwmASLB9BZ3dWaT092h7k9INDNXepM\nLpDDOUZpNtFn5V9OWb8pf06rn4uUzleZKymj3AZd7OL1S2kb0PveoV7hYukv1lotlypdpe52qe3D\nVd1vcUVE/SHF+c+ye8coi4h6E42Fq4sM/DK3gubh+nh4c3qKQ51rrr0vdXtVnOgC66Qj/ybRZ9jF\nLkqMALlbXzufBKe+hzDKWqPMDwruoYoTLDNlU47chXtvi+u+R7RV9PqeU0vP0M3uMrcz0E1GBkSG\nopWTkYz0h+wOc3vAnLGzVCuzRL+SS1WJsxaHbf0aO94xNS5G+zoMd6nlXCCHv6dj66tMUyfxvDwx\n2MPos+ynLkl757Tz0rNFnyoI/QxSWz0i8lXgM+iCGyuBy9EFOP6Cxj6rgPOU0n4wEbkOXRO0A7hG\nKR0aJSJTgDnA3ug6qV/ZhQdM+VxQwUx1KAtkBRB16KkxCWdKyboK59ycWAgdSX2+s2P2vZJqEpR1\nYxlXm3F193lv8jIJDhsEh6063Fjoy/2915KI7Ax2XXq36PsytwdLelX0IvJH4GNArVLqUHNuX7r5\n0qW4XkFFRLlPUTPY0DYOgG17/y7lfbVS1RmH56nbuVc2Rj4/RJ3Gr7kKgOky08FCpdTwgKzv5bG9\nPKIWA3C6nJD2Nf0ph6mPAvCy/GNQ7t9/0rOi/2eK8x+m65fBVDd6CviAUqpdRP4CzAcmAfVKqZ8Y\n2uB9lVLfEpFJwJ3A/0NnsC4CxiullIgsAa5SSr0gIvOBm5VSjwb36pe5rU5PUPuIPldyGbpECCCv\ndgPFXJFgx336eNj+0XY2NHIHXvGqKxKu1MjmV9NXyD4UU0fw7Gz0zs4qz4GKnAmfs79EHZVAllSQ\njqLvw9y+BrjC/PkHpdQtPc23/jRg0nHG3gZ8pNO5bwGLlFITgMeB69LoJyP/xdJHh1UMGC4iWabp\nFjR75O3m89vRNVhBG0/3KKU6lFJVwDpgmojsB+QppV4w7f4cXGMlM7czssuSztwWkYPRu9QjgcOB\nj4nIWLqZb8aAOQ+YCMwEfiumIjrwf8BnlFIHAQeJSOc53EV6xeiVUk+ZUnOhnAmOvOZ2NJHEt7rr\n40w1gdtlDQeoTwHwotzDAvVdAGYyHSpnAXDIiS/wiqn0dS03cg4aJrk3WBffpz4NwCvyJ1qVf6Ux\n9F64L9Y8RC35A9W5ALwm9/EZNRKAP8rWbq+domaY51nUJ2fxMnUvANdxPQt30ZI/U03gIVnT5fyN\nqp5rRcdMHKA+xSa5B9AJX70ne/W/5KXZTilVIyI/R5fbawEWKqUWiUiJUqrWtHlTRIrNJaPQBbit\nbDHnOtCsk1a6MFD2x9xWVySQ2RVsjRkYYU6Fs8ohcAb+RfHyWXoiW2setDVvIZ1JV4DMrvDXWb9+\nR/e7A9C7gBwTyBZatjs6gvucClvv1vc5pWMxL8qibvsDUB9IuHuOPx+4O/r51liCkcmuY3o5ePbO\n1ryNoDkhDStfnZhAnuzaTn3evOdbKyJ5Bvb9pxqTu9bkKyyr693Bq6359CTNuT0RWKKUagMQkX8B\nH0cbKtNNm3C+OQMGqBIRa8BsIrUB43aqqWRnnbHF3XzpUsrlzOEhjnHK5hw1jplGee+nLiHJ6wC8\nIn930Ti5VLrrD1TncoahGlmBxkIfB2bKdNfmKXnaHf9RrQXgS9t+zTsFtwAa6nklKBdZ2PFZABqy\nvM/8NfHfQKvgn1UPcox0NgS1hF+WvkQDTZXzzNFL3bb5utL/mp9LR7dtgJRKHuBaKQoWonvc+cFQ\n8pC+w0pECtDK9gB0mPJ9InIhXeuKvlfOpT7N7Y2zOw3q1ATbTbSvmpjQX2+g/VJh2Pn6uP5er5Cq\nSTB6jD4vs1phtvZThQpb5gTRKGUJMKW7rTIqORHWBdxbqRKtaudCibn/i7LILS6j46SEPcKFpSUF\nCN1ZoS41/fWE1VsF350SD/uRJzUkBiCPBO/iVn8cPl9VMvU9VZnpo7rCRS691s8hm2nO7VeAHxmo\npg04FV1nt98NmFTSX1E3GbrWjPQoucAzRGduNzIDeE0p1QAgIvOAY4Faa9UbWMYE37EFKAuut0yT\n3Z3vq2TmdkZ6lNw02iilXhWRG4F/Am+jrbxUy9N7Mt92VtF396VLKWdJG2dW3MdDc8+Fwuk8IJWw\nWe+G35QbHBzzRZXPckMROo+zecT4s7OoZOYm7fL43AG/BbRFf4g6DSBiqYN2yALOmu/cRkdJdI1+\nfUA9D8AE1nCIXAzQrTXfk3SOQw+jMl5Rd7AVDQtNl5nd9tGbJR/KXWo5QJcopd6257smVUTpXHuW\nnCxdl+/k4NxNqR/xdeBoEdkbbfmcjGaTfBu4DJ2IeCnwkGn/MHCniNyEtmzGAc8bZ+w2EZlmrr8E\nuIXepU9z+0BOpGJygl81wfR94aT53srctjpBvnnGYWfjoJii8bBto3G6dqBtNEB9MwcxVm8YyaIO\nSSCv6OPtdTCiE91xaB2rsxPIPP13CK8UjoBlAfzSan6n48QM8wHUZR6istZ3CIP0FN2TaryhhHH/\nL5OAN7rvo31EwkFTw5sruoViulJDa0jJQj0NSTo5mqvoy7wGPbefeheeDlV0CnWtlLoN7RdCRP4X\nXdxmQAyYtMIrRaQceEQpNdn8fSPQoJS6MYyA6OZadZc6kx/zHarb9PiOjT/Do7XafzC35MKUYZSV\nakGPirA7uU69y11cAOCgIiupcHQL8/yLE5xi/pza131+Nbc4pT9aXchmuROAE9XRPCnPpT2uE9XR\nANzAt8ijCcD121eZomakVOLXqXe5Xnr3r1+ltA3ya2lx5+xi+x/5k8v0Tef9+5DTnqNu2kd0PZ+9\nrdvwygo0NfAOtOVzBRoKvRc9yTehoxMaTfvr0I6uHUSjE6YSjU64JsW9ytmFua3OBeKw3aB+Ozqg\nyKaTZoHUeCUy3yjGKWjnA2il0x0HTiiW9rilrmsi1rZ4gnwzlSzGDwa2MN4GmeuhEPaGZWa8R3a6\nvzrSKPKl0cXjqXn6OBW+rk5PsNFEHTUAJeZ8Twr/CfMuTiK6iIQwVXj/jeb+Ie6fCpdXVyRYZ+C0\ngzolsvUljNQTvPUedZPu3BaR9yml/iMi7wf+ARwNfIcU8y2IJjsKbcD8Ex9N9hxwNdqA+Ttwi1Kq\nR2dfrxa9iNyFdhYUicjraBanG9DY6acxX7re+snIf7cMi/fexopSKgFdgNQGNKyTqv31wPUpzi8D\nJnd3n8zczkh/SB/m9gMiUog2SK5USm03hsW9neebUmqViNwLrAraW6v8S0QNmF4jOgYkYeoBNZNF\nzGAG2grNps1Hu3xhFqP/bx0Am+VOF5HSQg5x2gFYxSSK0M7RkdQDUUjlQHWuc6SOVhdyAXcB8JNu\nKr3NVIdyraEiCq3WHypNRHIsz3AhcwE4jfkuouf38lYkGsda/r+Xt1wRlZAH5kPqSAAel6Upx9HZ\nQZxK1qo/cpB8pst5y9PzkKzpUyz+AepT3IeOLpom56RsY7mDTpGTU34OHuY6R6aZMz1b9Or9Kc6/\nPrSSSvoqIqK2xWF7GxQO1+c6OiDLmE+5R6GXJ2DHRlhtovFz0N9cgEllGo4BqG/zFuubJHRMPrBj\nHgw71d+31kAw+wVt7bE6P8GO+frzzdt8f+rzCWpv1eezYlB0uensUQ9vqLMTrDOWcyvesZrK0l5K\nwsElnemNQ3jHSueY+ufMOp5HlB1THafPb34alphz44FCc2yt8c79dQfFhM5Y26aoyDOFqg8lkMd9\n+670Fb1b9LvD3M5QIGRkYGT4YA8gIxl5j2Q3mNsDouiXciQXcCd1Br07XU5wMfWbZBabTXLs3o1X\n00RXfPgutdxf+3PLVDmL36sNAHxO7guO7+TWd75g2vzO8dsX0Ogs1GrKuuDPh6jT+J6xrh9Tnmzt\nUXWhs+gPU438MbCaL9d+FU5XRSwxu488NY67RYeLhpb88eo4IBoGOpcLOdz4E6icBdNnmfsv5BmO\n1f3R5LJ+/8rHAdhfvhIJq7SW/Go1h4lyGQAT1Rm0mHiA0FexSe6hTWW7NgCrJRo/F1ryNyq9g/oL\nn4z4Bbwln6b0AbrZnSS/FGqDpO0RbRWoImNFPu5j6kvOhUKDi5dR4eLraYN8E1CXfzhgM2zHe4tY\njU84grF3C731bLH17W8Tid+oNTuH8kJY2ODjzu1Yis4HmnWbG6uJ4Ng2NLOqwecAAF1CHUvwUlKG\ndiuiLe0Vc/xnlkhsyX0+67fkMvinaXPUuTD/Pn1+FCBP6/4XkuATgWPWZQmbsbIEnRpnJAxXDQuv\n7NjetQ11PgR11eNEJF0iuojsBnN7QKCbxWoKubSy0sClE1hDBzEATpDTHQyxOPlBcmPaTVVAo4M1\nlql72cBYALKNQj1LjnFOw0YKOEuOAXRc/sOcCcAHtz3pIm8OUJ8iae65We70MebXHa8HesMslisN\n+WxgHNkmRKKARk6Q093z2KSqdrIdBJJDC41oGOdc7uM/8qfIOzhPjXEUDnXq5xTL1wF4UD3LjVwL\nwJrkBC6J6cXldB7hEfQ9P8+tbDVksdaJm0WS09DvJlTi09RJfJlfAXCxHMI+b38JgH8O/7CDusLk\nqRDysQvi/tREnjeVfEaNTJFI1gt0c3SK88+ldFgdhE4JV4AABwLfA+5gCHLdrEXDHIea2PZVNTDM\nfJ4PlJiE99rZUGIYt+VXrY7X6WUSTDa4REcS1m3z11o4aHizXxhq22C8nnb80ywcH74MF7kjcyu4\nxyi6T17mF4vwPg3bYLtZGMYUBzDGFQnXz7o5YHVkCTDaxOCvMLDRoecG95xXoa8FVs2G8cY5Oexc\ndCYEQJaHnEpOhyVmQSsHA8bq7g41aR6yMOoMxthMLQYKyz0ONi40z1AGt5iF5pNAiYntkOXRhcvB\nWKcmkPldFbo6JQHLzbV1fYBu0p/bg8bhNCh89Bn5L5ThKX5SiFJqrVLqCKXUFGAq2vacxwClimck\nI32WNOa24XD6MjDF8CplAeczVCgQ+kPqKKGFXOdQbaTAWeYLVCX7mP3qQ1lraNr6NQA2j7yTZ9WD\ngLaei0146f/wEwCuUktoNTlpcdqYpk4CYDLz3c4hjKO/h085q1Zb1fr8s0oTo9VeX0K72YPFgn3w\nCXK6K4oC8JoJr7xLLefTaMt9tTzsHLl/5hIOUmvMuHV/n+UPgLboi+XrDjIp5y7+gM7QJebvGyPZ\nZQyhPK8e6BI6ClBDqeOmf0XdwSHmGY/hLOfkzuOPHIR27lrIZ5o6iR+gcxJ+wde69AtRqoVVTAL+\nlbJdt7Jz29sZwAalVLWIdEdN0K+p4n2V8hE66mK7MUtLYtBq/nVZMVyoXz6AKS++bWyOS20cBmwx\nVmorMMnsDLbXa8cuaOqAfGNR5z8JtcaSP8VYqGvnJBhvrrufBEeZvtfN8c7FqmbPmJmzN3QY6IaT\nQb1tQjfvhlyjpMafCy3GqVvVrLN5wVv5S+6Doy7Tx2tJ8JR5zuOPhBXG+t7RKWvYpk2UFHnFU4t3\n+r5GwlnyS0nodwbabjUb7/VmV3DYwgrHXrlquQ5ZtePbz7BZriXhCreESU3L5vvjkGt/yUI4emdI\n2NKf25bD6V08h9N1DMC8HhBFb7HiPLQyTBKjgEZAK40286Yq1QLq0BDCVlVkFAocxBpq2B/A0QTf\nrB6kkQJAwys/NwoqSRZf4+cAHKBG8id0fHgHMaewj+ZcKk3ceJtT7h0OGrmDi/keP3DjtzBTa1uu\nS9LKYzGHm33e7eoBF8HymGqnGu2Gv4abAa1QraI9k4e43WDtdZRwbNszADTGC5xyr6XYJUx9WbVE\nOHgAvsuPOMUgbgvlJZ5XDwAwbeYsFw1TQykPqmdd+2vQPoIEFa79cfVPm3f6Cwdl2QUY4Bj1QZ4V\nrdAfkjWuv7N2JpZg7524Ru/E7zLHA5Iq3lfJ0lODepMMlYtWXgBTSyDHQBcNzbDDJADlvx8mvaOP\n11XDKAOp7NVQwdoarbwKYx5eGQVsnqOPd+ChIRsXvgPAQB7nZGmYyIpdLMJCVaubcUq0pBaH7+ee\n4ekOcodrBQ/6RdrFq9xcN/psqDRjKsZHxaxb6vH7SvxxK/7l187BfNNgejG822Hw/4+Aekcfr5jn\nI5PW3Q3jzA1sf+8WJjQ1GDBpol+ItiQ1Tw9oGgeL6W+e65//5HfeAMOae2rgL9lpBsw05vZAcjil\nkl6hGxEZLSKPi8i/RWSliFxtzu8rIgtFZI2IPCoiKdIGMpIRI/EUPz2IiAxDWzWWgKjfuW4yczsj\n/SJpzO1OHE6laMt+wDic0rHoO4CvKaWWi8g+wDIRWYh2JCwK+MGvoxuWvwLeIkkW7ehojyLqnYV+\nK593luxP+SY5WGdsjLVoJ20eTYwxacmLVbXr9y1j0W9lJOUGGmliH/6X75qBx1zf7cSdxb5aHmY6\nOupmhInQOSs+j2/ys0i/YIukaCfpK+oOZ92/QSlf5SbXzvZzssAb6pcA/Cupo2VaVC77i4ahfqhu\njUA0a+ITzDvZSo1hq0oSY7WaA8DH+SuPo2Gpu8yO5Gyu4Vyj/55VFQ4Sm7LgKedwzqbdUUGEsfon\nz3mGzZdq5+7TRdrKr1XFfNrsfOKOMlFDbHYH8398gcXo5wnzFtKW4VBZA5U9pLV3kpnAMqWU9fq+\nF6niuzy3G7ZpKMRa2ZuBcmvl10KRMUG3NEOrseKHbYONZvTlI2C9MbdDsq3CEVBkvp0b61LH6TcY\nizsX+Msc0x/euh5/KjxlYIp8/O4DYPxl5mA+rmQfwdir5vhzh14EG41FvNKce3qe3xXkAGNMnP+q\n+f4+k5P+hY/DK5vNwPSL9PFTcz2kk3c3TDXjysNfe/xxRCJsAFY2QKEZY5mpLwt6p5Dzqj6/LZ5w\nlnwQfMOf997fcs2xA1htprznoNeQV9oROOnN7UHlcOpz1I2IPAj82vycGAywUin1gRTt1QJ1IgU0\nOrhmK0XUG76XGB0Oyy6mlqSZDvUUOcXcQq5TWjYaZhWTKMMrfRt+mSQWLBaNTEBTHNSwv+s7lxbW\nmygeu4BspNyN723y+AHfB+BHfNcp0ibyeMMo4/2p4Yvo7d8f+CxNhqy0Kbj2SBMqcC03uj7qKKHN\nLHhJspxiLqeKavP/+xnf4PsGOmohl/nob9HZzHPPFcI8d6EXgAu40z1jkpiDzKbLTJcElU07F5lk\nMJs0NpmV1JvInlxaHCvoRHUGY9Fhq3+Tf7NAVbr7a79DuIj0EnVzVYrzv+4+qURE7gb+oZS63fyd\nkpqgP1PFd2Zuv4mOGrHQSAlQYiy6HR2Qv48+rtrmWQ5LRugFAiAvgEhagalm474xUL6jR3jl2dqm\nFw1wkL+DU0ArtEPN/de1wXhzXNsGo8xikXuuhk9AK12rsMcV6ugU0Ip7nVkkCmP+OVzi1ts+cmZz\nMIaQyXFYMMZxwCQTdbRsnm9ngWr7/Fbpj8K/01S4RD4+YWxrLOGgpbJXFS9/QE+pEqDYrHpNzR6a\nWUuCD7ypYeR39/upC8fcjoeLDqbCJIL1nPiU7tw2nEt/RBfIaUNz3rwAvJ+hQIHQ6aHK0cjYc3SP\nmWYkI12lD85YEclFW0CfC06/p6nimbmdkZ2WNOa2Uup5Ebkfzd1kOZx+j+FwGjIUCGZrWwn8UCn1\nkIg0KKUKg8/rlVJFKa5TlWoajRQ4ixmgytgAk1jlzq1nrLPiS3nDtQFvybcaKzWbdpdUdBRLKDYu\nsEYKnNM3RgdvG0t7KsuoQ39fm8hzTtgm9nH3s1JNmYOZsmlnHLqYyQ18i2/wUwB+y5f4vbwFwAZ1\nq9tRFNBIrTkeaaz4DmKOuqGFXGcN38OnaDG2TSu5LorneXmCteqPgLbMbX8fbNCO1ssLf8tJhq//\nMpnoIo6u5zq3Q4iRdO87TpuDo0qpcWO1jtckMefYPog1lMuVACxWj3ARd7r+eoZrerHov5/i/A+G\nRpr4rszt14D8INKmFVwEzIoab0lNKoZ6E5mzJQnjghA86zDN2dsXC2l9x1vRm7dBiWnf0OytziKj\nYP7ZpvfvoLVGTvD5ZgNLdODvmRPXOwPQjlnr4GzAx7HvWAJPm13HKLyDudz8tn/b6+yu4Kjz4WET\nGZMfjOWoU2CFiXvfjoe6RgGjTZjQsiWeVbMDmH6ZaX93tIgKQG3Sty3E4x2FeAqEtUHkzgqIwDW2\nu/GlsFGDBd2UPUwjjn4Iz20r6bJXZgF/AxYopW4251YD04Pt7RNKqYkprlVnVkxib94hTjuHTc/n\nhOl7RZTyKPXBAAAgAElEQVS4Ve5vUcBf+CQAP+V/IklSFhrJNbCMhXIAXuII9/cE1rDGYPtlVLsF\nwoZ4WrFK2MIl1ZS5KJo1TOAow7TRRJ4bay4tLswz5OLJpcUpzdlcwSVoTD9c2AraTJRRfBLlBi7a\nwFj2N+NuJde1r6HUvZNQYmZ6xml3z9JEnnsnMZJuEfkNX3LvoYj6SH92cfmcafs3TnMLaC0lzDMV\n90J2S4gWQyl/Yj+aK5fxn4QFT5/sWdH/OMX5bw/+l2FX53ZFEayr18ryGPSWYFyhb2MhmqJgmXiq\nDiZaKCbp8ffWd6IFNKaaBWNzjYdADsXD1fY/GuLfwwhw8ZhWiFYmFfv7WwU4cYT3HWxu84q5Cb+g\ntBJVqhCN4mkAbJ70SrxC3YLvrwHthbT9hXo7vI9ddEbF/LvoAKYYd/gK8z6nFkOt0e4h5JKDTqAC\nqKz29x8FjDZRypsfiXLmjDH+AplbwV0keA64xUU8dj+vYWjP7VDShW7+BKyyXwQjD5OaH7yLnD3r\nEApoDJRNVyWWkd1L9pk+lX2mT+U/CYvRP9nzBUM3TXyX5vas98GCek+R2dpdw4zsFnK0+bnFVffr\nZV7DUJ7bTnq16EXkOHR2zEp06I8Cvg08Tzf84J2uV79Vl3IEy11USYyks0KLqHeQSjF1kdj4VNCN\ntXqTZLm2ubS4RSSHFufcBVybUmocfJEkyyVbWQs9lxbnRL2c25zDNIskOebrm0uLG3cLuc6BGSPp\nLPoYHc7Ba3chMZKurX4Ww4tDk7OuR1LvqA6ygoSpIuq5lc8DcLoppziHy/kkfwE0LGSt8TKq3XX1\nFDnIJ5eWSKSP3f1YVsxKtcC968msdI5j8DueOO3uf1BNmfs//Ixv8B1+zDR5pWeL/tcpzl81uFZP\nf8xtVQrraryjE7yFXJvUpfpAW8t2BtQShW5s++2B9V0U93BFbdJbwKFlVmJ2BeuTYJ0Iw4Acc35L\nMrrwjAuibqyE96zD1z8tH+7H1Rr0YysyF+PPlQTjasJHuBTidxcleKvb3gu0pW2v7SDKoWMd0KuT\n3jK3O4rRIwzHD36MoDkEjjdu8/p1PuppVY2/Zyt6F4QZk32O8iB3YcxlsGIOHEYaztghOLc7y4Bx\n3dhoFYDDWe6yV2MkmYDPuAwVs1Ww7WRHFJX+3eEiTFrJcZh7kpjD65NkUYDG0X/Md0hYLz1FbjGw\nCquFHIfn70OT67uUGqfsNO6t+2siz/WRTZvD4JvIc4uOXSyWcaSDgrJpdwveSLa6cE3ARRFtYByT\n2rTvYnH8BAfvWKhoPWNZhqZAvoC7IhE/lcYSmcxKp5jzeJvpJ+j7F1Zu4a8xnbBlE8t+wdcpMe+s\niTy+ZajdE1S4eyaDUNUWct0z+vq3vWD0t6U4f/nQ+jL0VSzXzajhMMxoq6e3wbQgFHKFwcKPGgHD\nDF5SX+MVyjCiYpXhMDykMyzLK30bUgkeJw8V6ih8FmgtXnGXDPfROgTtJ+KLoDQF7YcFYwkXALsX\nzwqO8/DKcjxEsn6tVOEhnReBmcECaPuZPFxHx2D6sNeHi8Ros6K1NPu2tcChJhpo43wY8yHTx+O+\nVlQhftGtbfPjDRfOYfhFylesSgOjT2NuDzaHU4brJiMDI3un+OlGRGSEiNwnIqtNMtNRPSUxich1\nIrLOtD8lOD9FRFaIyFoR+eV793AZ+a+WNOb2YHM4DYhFP0edx3SeYLWhNCij2lmh4CkGGilwFmQb\n2WQZC7KNuHNEjnRcdx4CaaQgEm1iLc+QaiGMyy+iPnJ/8A5K0NCJhXHqKXI7gWzaGWs2r28EDtNw\nfI3s645zjd1QxFb3XDWUunvl0hrh/7G7ngIaXfx6HcUuL8D2t56xjDOfV1HOQWZHFMb559DiIJ0O\nYuxr3sMhcjF1SlvyV6H3nAexxu04Ql9KkiwWmSqvM3jM7bYu5XZXUvEUdQQL5SV6tej/muL8x7st\nJTgHeFIpdZtxlg5HQyr1QRJT53jj/4cOPlmEjzdeAlyllHpBROYDNyul+o3rRkRU83BY1AzHBTBK\nYYq2JUGkS5i4lLN3FLqxEE3omAwhj1Cs9VkUHNfiHa1AZJZbK/Yjai1L5SA3Fgt7rMZDGnVEY+Kj\n3xbdl4VCtgfX5QT3CaNxxg2HWmOBr8RH72zHW/QfAF617fEO6Hx8LH1npzDoZ7ZRR5XAjOD92p1W\nfZt3IIeWe37Q1+iLtEMWNL/QCWmWEuzL3DbXnAJ8Tyl1goi8SoqcDRH5FqCUUjeaaxYAs9BQ4uNK\nqUnm/KfM9V/sbowwQFw3k1jFMo500Sa1lLjwxQIanQKro8SF/k1mpVPeLeQ6+MQqOI2W66kYjSjJ\ndfj7/tQwG80TezlzHL5+I9dyBZoQxCqvMGGpmFp+yjcBrdzt+RJqOR9NJvYTvukw/0c4w/WXJMvB\nIHYhaiHHLT5hmGkuLeybNNBvDLew3cLVXIumsdUwkn4PFucfSb179g5ijhNoDpdzKvNd3+E7KTFf\ny8fUQofH2/EdybJIhNBH0WG5f+ZSPshiQPPR+4pdd7q2WsmnIWkWZxCRfOAEpdRlAIbUaZsMUVKz\nLc0wY7gOUwSNXecbRRNGvOTs7XnnV1UHVMbNhs8dWF3tlU4eBCaNV7r5QTTKl00S3Gw52Smxa9Ri\n7jHV20riHjqaGNPVlwAelINc5E55kL167jtv8NLe+7vnsItOGEppj1vxzzAM73+oxyvu2qCP1c3+\nuJBo1I5V4g34BSUH7+Aehk4yA78ogn6noJPRrEzBv/fRcc9BBDD1ODOup4Ow1/NxXP9r5/rM5FS1\ncbuVvhceGXAOp0yFqYwMjKRPajYG2Coit6F9YUuBrzBESc0ykhH2hsqXoHJ5703Fczhda04NCNfN\ngEA3d6hzmMwK50A8gcXOIm0iz1mbYWx6LSXOkm0iL+Bw0Ut0nHZnhWbT5nYCbWS7PoqodzBKkiwH\nk1Qxxlnd1tK+jctd/LulRwB4jBmcw/2A3jm0B05fC//k0eSOS6lxkTxLTHTxODa4z4vY6oqUlFHt\nIo5ayI1EFlmen2JqHRyzj7GVDk2u5K2Y3k20E3fv5lE+4hzb+1Pj7tkaOE/biLuom4+j95w3c417\nD3nBDiKXFhevX0Aj3+VHgN79WOv+OvUu1ZQxVz7XM3TzXIrzR6cszjAVnZ16jFJqqYjchDYSr0qV\nxCQivwKeVUpXjRGR2cB89Bb3eqXUKeb88cD/KGU4ovtBRES9WwgvNsDUIHbbWqX5eGs5dFiW4+GY\nkk6JU6kibUrQVAmgLVprsYax6NZCHhfccwd+h9CEdnba+1hLdxjeSs/BW+mFwQ6gMKYhKYK20+Oe\nIyaPaBTN6uA4hH9smylx7RAF7ci2kM6L+J1BDlGaBEsrsc5cVxKMNYS2tgTPGTquW4N2TUTj+6eb\nQi5kBeydZ+sBy8I0om7SnNum/RnoLNePmr9T5mykgG7+gS5ev4kgr2NIQTcZyQh7Q+ULUJm6Tnoo\nm4FqpZRt+QAaohkQ8qeMZKTP0jcK7vOBu4O/u8vZeBi40xg6o9Br+PPG97TNcOe8AFwC3EIvMiAW\n/Vo1OkKyVU+RszbLqE4Zj97EPg6P/y4/chi4tZbrKaLIoJihRa0pA4pd3zZMso5iF764lZEuTLKK\nMYDG3+29S6lxIZChxOjg+GbN4f7K8IMddl9KjSNpu59P8A3DghnGztu25VS5sd7PJ/gSvwFgPeMo\n43X3HuLuPfjdzAfqNgHwavEBEQftGrRj7VE+4nY213KDe7Ywc3clk51D2e6k1nCQO04ScwVaQrbO\nduJMu9VwF35hlisK00SeqTHbizN2XYrz47u1ep4EPquUWisiFfiIwfec/KkvIiJqsTm2FuJoNMUA\nRGPnIcjejOnYcPAEZKCtVetUrCXqMLQW2eg4VAW4M2hH50pjvYZkYBNHePy6FR9qWE40jDNVfPu4\noJ88fHnABaa/MN69HJ+tGzpJ6/AhlauD8zvwTtosdNIC6Oxai++34ouJ1OMLslSahPiJ+PezIxj3\nAWiTF/TOYXOwc7HUCEsDltAcYJLx/Cx7MtjRYLNn03DGpjm3DYfTJuBApVSTOVdINzkbJrzyM+YR\nw/DKqUTDK6/pbnzu3mkkTMXRSSXZ6P/L/UqphIjsSzfxn51fxGPqGJrIc9DJ2+Q5RTqJVU5p3cRX\n+QK3AtFIkTbiXMrtgKbLBa3crVLLoykCPVilmkOLc3A2kRehHphoOHZsJFCYSGTvCZpi2To7x1DF\nTXwVgC9zi4tqyaPJwUhN5EV4d/TnbzulnyRGeZseR2282EFBnaOA7Fg6iLk24cIRVqAKndF2HFWU\nu4X1yORSnolpXqD9qXGRSzahqoUcp+iXc7hbTMvZ6J5hLRM4T6YCMEXN4Gb83NIVsHpR9K+nOP/+\nbhX9YcBs9PfuNTRtcIx+/kL0x9yuRse72xj1whgUGaW0rjqqrMM0/brgeJRx3jYkffvRRBWZ/Q9P\nDByMFrrJxyvaiTF40UyNKUH0SVUABeXglfiUAIIJYZawTQNegYex+yFjp12IVhNlsgwjgNxY8Ao1\nB5/sFUoHUYethb2skyUfvaIDnBEsfluCNjnBeI8LmDk34Z91igvS1TVubUWwHWgGy7QUfR/m9mBJ\nr9CNUqpNRE5SSrWISAx42oT6nEOanN0ZyUhftrdKqZfR4ZKdZUY37a8Hk+UVPb8MH7yR6rrM3M7I\nrsvOVU8bUOkTdGO2Hv8CvojO6OoS/5niGrVcjSeLZKSgR6vbjXsrtJZixzwZwjExOpxlaeGcWkqc\no3VfGllvInkLaHTWcDVlztotp8pZ5o/yEc4wdAJh6TzrIA5rtG5Qtzr4ZwlHObbNGB0OXtGx+97p\n2/m58prfpn54oRu3j+ff6p5Lk5O1Bsc+PLKsTUNOtfFidz+7U9lKkWPerKOYf6FD645gubu/zdAF\nHedvYavHjN6cyjLH4jnGbfCjZHIh7cESpjEDHdp3Gn9jHh/nGHm5R4v+neau5/cePnSsnp2d28+h\nraXQcrXWYujoLA8s8TADFbxD9sXmKLe8vXbicO9YrMK3sVbuavxqVoe3vlvxllwOMMaYzpvrPJSS\nAxxvzocFSMLwyRDaseca8OGfJXgruikYdxij3hoch0VA1hOFgey9QkbKYvyOJgzFDHcg4Y4jJHvL\nD5y4dkezI7h2fOAY3oL/v0wt0zuyg+jdGTvU5zakz165F7AMGAv8Ril1nYi8pZTaN2gToXYNzqtn\n1WF0EONBdOWBT3C/U3CAw9prKWayqWHzPEc5TD2bdodD23Ol1Lh473s431VGqqHUQUFx2t19sml3\nyjObNg4XHSf/itLx6rdxORcHrJMW0gnpEMLqS7WUcDg6hjwZ8M28RYGDnGyUTC6tbhFppMAp6Wza\nXT7B2ObXWDn8kOCdaJgrj7ddG/tcRf9u5Y2D9XO1ke0grGJqHY3Dl/iNLzxOFPaxnDp2gainyME8\nZVS7d3aynMJhOjiA55qPoXG43ueuZLJjyfwHH2WiXEZv0M22juwu50dktQ/6l2FX5/Zac1wYwC+h\n0g8V/dNm+ny00FeV2g5MMT1XNXh8OY+oorXYfQsBx0zAgNkQtLXSgYdFGvCKc1oQUZNFVAGWm0Xn\n6WZ//yyiitw+lx1HfnCfDqL0ArYi1YlE4/JDKgWr+GcO1/e1Um5+b8Er8nKjuFe3+WcdRYCtD4f1\npo8SvL+kqi266Fgq6Tk1XrlPBCbptBsqZ8NJaUI36c5tk809GzgEeBdNb7CWAaBASCvqRin1LnCE\nSWaZJyIH04f4z9mz3uRdhFd5nLLpY3DEcBnZbeWdyud5p/J5fk0jGG78nqQ91vXLQLCbGizZ1blt\nwx1y3oXjBGMeZGR3FVsSsEr/ldY1fZjbN6MV87mdMr67wISdKBBGA4tEZLzSlrmlQHhBROaLyEd6\ny/jemVKC30MbFleQJmd3vdqbKsY4eGMD45xjNLTsk8QcrKHJv3SWXpz2CK0BRAtrVFHudgI1lDrL\nfSWTHcd8O9nO+VhGdZes2iySbDWRMw9yFlfyW0DDObbNh1nEP9AW7nVc76gRWgyvpb2PhXdC/ns7\n7lDayHZO0NxkC7EO84xZMWpjvjSivb99VzGS7lwHMbdDKG1oYE2hZv2+kLkcyzOAhoIu4Q5ARxdZ\nR7MlJHtF3RGJCgqhtN/yJQCuYDa3cTkAy5jKKSbBNJdWvi0j6M2i36S6utwOkLpBt+hD2Zm5fT+a\nyMtalxODLNlwC5CLhzpa8bVZATqsdR3QETSgo2YAlmyLUgZM0sFUrNBlkrVD11ji65s9LBHGjhcC\nl6sFAPxIZkZ45a0FPgyYbpiCliyMMkZai3kF/p6dCdkIPgNtiVsAsoMgcogo22Ve0MbuTEJYpgof\ngTMq2MV8TOk8uUflmAiRmn2eHDxL6IvNUfqEicH7OvQyfVw5B6Ybi37WbMz3u3eLPp25bQyJl5RS\nYztdPyAUCOlE3YwEdiiltolIDjqF/Ab0bqxLuFuqF7FAnRhReuAhmFqKHYQQYtO/4UouZ45rbxWl\nhTTaibvCGpNYFVkwQi6ZkFbYJkkVBRQCVqoY45RnMbWuAMqRLHOYf3iPAhq5wSS3XchdDlYppcYn\nbDXraVs7/H0OUjkkZwObWz2MEvZ5iYks+isfd+cnbVtH9Yj93Pux7y5U+jYqp4WcSCSQVegxOlwC\nVjlVLvz0a/wCgHl83EExCSrc/6qUGkeRfCW/ddw4z8q/GK80DHcf51JNGafL4z0q+nVqdJfz42Vz\nd1E3VcA29PZ2h1JqWk+RMDu7xe2Pub015lPxrdgasGEoZB4eruhM2Wsl5KkZX6qpdTHnXJRKHLab\nPkOFtiVFHzvQhUrseYf5d3PPMLonpHJoSEbruoJetCy2XoiHZUL8PXzOfKLY/YvmeFxw/yr84hgu\nDGGlqjCKaXtw3fHmOCcO+SYBatlcr9CbmnXBdYDVQfxUWG3qaCp42YRe7gAOHQHZ23rH6NOZ2yaS\n7Pfo0oBhxveWVDBhfycCpsNeuT/whIgsB5YAjyql5qMD/D8sImuAk8GQs2QkIymkjXiXnx7kXbRF\nfYRSyhYvei9Y/jJzOyO7LGnO7Sz0xuQ3SjNYNqPn9IBQIKQTXrkSv3MKzzfQTbhbZ4mRjMSJh0lD\nebztLOkw1v5b3OgoATYwjlu4GoDv8wNAwx6WcTG0itvJdjuERgpcwk8RW13UT8inbq3XkPWyijGc\nZsjBypLVrIpNcv1Zbvg2srmaX5k+cly0ylaKnFXUNlxjd7m08oZ53vNb/+QgJDsuK39F88Qnibld\nwaoR4x28Y6318F3+iqu50iRdZZF043uEM1yt2/2pYSo60bSa97v+1t18mB7nNXFu51JA77Ds7mkV\nkxyE1U62c+5WqzIKeNCcj0dqDXQn7aTCMbsVoasR0u+kZv0xtzuSGqqxZf821ngLNWRMDOPOt+Ot\nyNC6DveYlTXR+HLLeBk6Fe2XtxbfNo/oPcOdQ7n5vQUfd38U3pG8Jen7bMVDSus79W/HGkIh1okc\nkgltwe9Emoj2PSVoY99XPv69zFILmCUzwTyD3Q249zYcWpv9dfY5t7fB9rn6eBg+kSwHyDGEaKuJ\nvnf7HG+SiOxIhh0HRg30KO1ks7SymaWVLT01G9SM7wHJjH1WHUYLuZHsVQuHNAXJU2NZ7/DmkE2x\nhlLX3rYtpSZQ0j7UURf+1koljybHK1PORqeQYiQddGTHFEaeZNMWKTxi2R7DJKVs2txiEUb35NDi\nFOl+dXqPuL3Io5l523bQNEL/nf/6DjaNeZ/7zPaRJMuNq4C3nIKflNTYf02s1C2CVYxxz5JLiwsh\nzaGFu7gQgLOZF1lMrQ/BLoKrmcQ9Bqr6Jj9zC+Jf+CTf4cfm/E9ddjLAdPMlPFEdTS4tLJBzeoRu\nnlJTu5w/XpZ1B928BjQCSeBWpdTs7iJh+nuL2xcRUxx8GD6MLyvLQzdFeGbKddVeGYWJQOX4jNXx\nwXEeUcriEC+3Ss+aC2GS0g58FajCoE24iOzAK+aJnc6HxUbCqBZrvFiNshm/4AwjmkVr20whdRWq\nouAZ8vCZseXBPScG/DoN6Egh8ItPSVAztgUPM72Y9IvL5Bic3KFx/FvlmAgHkYWOCvGLUwc+e1aN\nT7BsHRxJ79BNunN7MDO+M1w3GRkQ6aNFf5xS6g0ReR+w0EAoA7LFzUhG+ip9mNtXo/lrumR8i8in\nMRnfAEqpVSJyLxrT34EmQrNz/ktEfU+90noMqEVvnYDj2BBxJtrjsax3SUNrOChi1Vtr/FE0zHqx\niSIBbblXGCfKj/iOs8ZzaXE7gFxaHKxRTZmzgq2Tcizrqeb9gLbirQW8iknOiVtBgu8Z6AiIxMOH\njlKbfGTPjWvb4K75Qvx3JExRk+N4mif4kOmjLTJuG+sep53yZm1/VQ/XTp9GClzUUjzZRkss150P\nSy1auYZbXIRQkphzUNu2YSz+MxzrMMYZLHL/g7C/Ut5weQ1jqGK0fJneom4WqOmsqHyLFZX+f3pn\nYlOvUTfG8nmbbiJhUkQn7BLLX1/ExtHnA8XGvF3d4PltduB51Fds81bxlE486eXBtWEMfirYJyzh\nZy3R7Xgrehy+eMe0GKxM+rbWim5Am4lgSvx1YoYEbd2GjtSq4Bg0lGOt4hy8M3Rd0KaVaEx9aN3b\nvlfidxWF+N3IDqK8M6mc1+PN71qiUTxWsvD5B1WkZhUNpQoPKa0HTk0z6maBmt7l/EypHFoRZQOh\n6B9Tx1BDqaPQraE0Ap3YRKQcWpzCiZF0WHEBjQ5Wsed0qWo9Q+O0RRwgPjGqPVKExMI4YfuwSLgN\nMSxiK1/kdwDczqUBpOIrVmXTFslktdmm7cRdBI6NtImRdAuUrvG6jxlnawSKsgthSKn8NnmuP7sQ\nFLHVkahl0+YWHMBlCMdpc9DMCXI6G9St5ny7i1ayir6cjS5yp5ZiBz39jG9wtYkUv5qbHUY/Vj7P\ngya0bRKrTJHxnhX9A2pml/PnyILuiJ/2Ukq9LSLDgYVAAu0UHXKkZq+hM05XGRihc6RNGI1ilU6o\nxLYTzaS1WHz+Pr74df4+nr64qTlKjgaaxyZMBgqLlGwxU2NcwMdTRTRixo6lHq+Mm4hmm4bKu/Oz\nNRDQLuOjYUbhFXc5XhnX4TH/OqK+BvuOwtDQDnzmbxhpZO9TF5yfgg/pXB882yj8YhVm6ZYE50+h\nAnWZNhgXzElf0ac7twdTMtBNRgZE2oOFuBcpQScuKfT8vFMptVBEljIAW9yMZKSv0oe5PWgyIBb9\nAnUiHcRYzhGAhgQsx0xIK3z6EY/x4Eva8i1no4M+GilwL9NG2qxhgrNIy3jdOWPXM85Z/RNY4yJc\nQms8Scw5M20s+ff5oYNowNMKF9DonLthsZPlHO5qtbaS6xyYSbI4sUa7l24u/RygrfiQ08Za/8s5\nghnJRQB0xDxLZQ2lbiyNFLh3ZcecRZI/cwkAl/Bn13cHMbcjyjFFFUHXeLWJXnYMtm+AL/A7Xhat\nA/d685s8XXKce/awnKOFs7ZS5PiAjlfHcT3f4gR5sUeLfo46r8v5y+TeIWX19FVsHD14SoEdRK3O\n0YEOyDJm1epmbyGXxP35J5ujDGzWGg6jVADzDfB1WsGHaoQQyTiiTtSs4HzInmkt4wZ87duVSb8z\nGIW3ru1KOTnou5BoktZ96ocAHCPfi5QbtOOtwu8oQss9hHqGEY0uGm/eY20AL42/TP9eMCeaGGb7\nXkEUUgqTxEL2TPv8IefO+Mtg3Zz0uG7SndsDlR+ScpzpKnrDCbIU2KyUOqOnAXa6Ti1WU8ijyUEM\nMZIOg06S5RRIPUUuuuYmvsrnDWVxLi1dYlM7V52yMImuKpV0/YWkZRZnLnHT3CdXhZWutHL1SjUV\nLLSVIkcKVkOpw8CrKXP4eW6bD7dqivuIo40mRiKsFFUuV1KvYWaqKYvAQnbci/kgAB/hUaesS6h1\n7zKPJhd1M5J6l/TVQYzvo798t3EZR5k4B7uYbKXIURevYQIn8C8z1iyK5evuGRarR1zfdiH8LH/g\nWJ7hbvlMj4r+9+riLuc/J3cMuqLf2XltrlVriUbRhFWdcgjw9ICDPsyYDasdhZ+FmHRRwKveQdei\n4WHST6jQc4L+NhEN1wwVanguLzhv24TUv1VB2xCusTIOj92X4GuvPkQiQsYWZsOGit6Od0vQbwPa\nrwE+WawwyEAOQzTDCluhb2NiHBbY4uzAJ8y4XiMR4eCxYxx9mf4tc3pX9OnObRNNNlUp9VZw7kYG\noOh9OglTVq4BE5enJWUCS0YykkpayOnyM0QkM68zskvSh7ndXX7I7eb4dnSuBwT5IUqpKvSmZJoJ\nREiVH9KjpIXRi8ho4FTgf4GvBQNMlcDSReK0E6edH5hok1qKXXw2eM6Vx9RCVpjN6wXc5SCTkG7Y\nVkdqIs+FNXV2kvoY9MZIEZAw4Sh0noK28q2VGsbfj2QrE9o0RLM4foLj1NlKkYORwipZ4HcONfFS\nNya7m+kgxvF12ub5d/GBrsgH+GpXpdS4HUU72S5a6FT+7t5nZ/hFv4coRbLdEdVSwmw0iccMFnXh\nzgmvW8JR7rmayKNK6YSpM3mYfU2k0xf4ndvZ/JMPM4+zIrXRUslQxDF3dV6Dt2yPM6ZoXYN3Bg7D\nc600NMPxJqZ+Y7W/fvwI73RdGThV82M+Zry2LZqcZAFGa7kW4y3akGohpEYYR5Q+wLZZDcwMYtCd\nkzIoSBJCM1bKiVridmfwIt4qbgDmm2i4sPJTSBO8jmiUkpVw1xPe21E9NHvH7TC8IguphsM+V7dF\ncxHsuIqC5zz+ChzdZuUcOC4oStKT9GFuK+CfIuLyQxigovfpOmNvAr4JhI/e3QAzkpEu0ta3OPqB\nksy8zsguSx/m9qDlh/Sq6EXkNKBWKbVcRKb30LTbAdZQSh5NzsIMY7nBY7/txF3WZjVlLsSwnpEO\nd57R3OUAACAASURBVN9gXDqdS/aNNcdVjHFW/xuUOidtK7kRZ2wYsw46ZNFuuc7kYR5CJ1Bm086a\nuA5HnMoyNjDWjdXHmCfdPztGkn0bdK51e6HPRk0aK7+dOFuKvb1idyUb1K2u6EqxfJ0zlb7nb7jK\ntbWZrp/gfncuDD3No8m9v7HyeZbrZFEKeMs9221c7kImrS9hPWPd+At4y4V8NlLgcPxP8hd3z9/x\nBecXuIUvRz7rTsJCM71JX3DzXSA02+V5DXDoRbB5ri9TF2LbHfgs2XxgmbHky4Owxx0dnrFyIj4e\nv6pBW5ugLU7ryFyNN9/C0oShn8BKE94CzkGTdIGO6bdjPBR42oZg4q3ezW1RB6dt78MVPIYe4vwh\njYG9L2hrvsocf/F8WBBsAUO83kpdcL4JeNFY3ScFdV/tWHKIxtFbJ/bkYGyt+J1GYTCWF9v8tZWz\nvR9j+nhYl6IWbCppJZdNlVVsqtzUYzul1Bvm939E5EF0mdyhQYEgIj8GLkL/H3LQ738eOjs4LSrX\nKyreR5x2djCMqdNz+cj0VlfYo5wq51TdykgHMZzBw45iOJs2B6uEYgt8bHT/Qi1ZLhqn2jljayl2\nfDS1lDgFaxXWZFa6RaGKche73k7cwSi5tDqIJocWB++sYiInGe7qRgpcnPrZyXkAjn4YtFM2ZNcM\n6YsL2kxFqHg2RaKZMTerX7nzVXH9nPtT42CekP6hhVy3OG5gnFvE8mhy0Ud6YdD3t87nKsq5kDsB\nHdV0reHw6sz+GdIonFd5FW9XvsjH+BvVlLEwsbRHZ+zXTSRGKD+X73VHgfBVYCqQbxR9vzusdnVe\n2+f6AtAGxM2F78fXal3v/+2MIqh7OlzT5kJUAYVFQBrwiUydZUWnmrHFeOU2Cq9cy4NCHh3oVRKi\nDuAwSigsLF6I1x7D8ArQqrL64P478PBLZ+jISpjUNCz4rIFoNI590Z0LmDinqu07pvMHQC+ctUl/\nz5DeYb/lWr9VHy6uv+1EI6PsePPQC+kSc/+SSZBY1bszNp25Pdj5IemQmn0bTY6PiJwIfF0pdbGI\n/AS4DM30dynwUHd9fG6WLp/nqYpbu2uakd1E9pk+hX2mT+EKlvIM/4+FiaU9tk8Xx+wjbr4rhGa7\nPK9B1x3cjsfIa3tom5GhL0eZn1bg0IO1ou9N0pzbg5ofsisJUzekGmAqaSIvwkdfR7GztKsod1my\nSWKulmsxdZGs0XgQdw9wLvc5tscCGp11v4pJrr8OYrQYh2P4z4jRQZ6x0q2jE3QmKMDpPBKhX7A7\nhCQxxpqatcuY6kogfoIHuJ9zAJjEalfwoyamx58T8zBVLq0OxmgnzjxTXvFU/k5bXO8yfsXVrDaZ\nrB3E3Hn7zuoZ6azrGB3OMRsPiNaSxJyztdxtVHUfK43D22bXFrGV50xS/KX82YW4PsYMprJMPwv7\n02pgqyLqHUSUQwtfTwPG7lyPoAfpC27erw4rI2nPa9BWYFj2b1RQPKQcgjcP4wwss6XBD2YT0TDJ\ng1/V3+W1HxBHk1AHTAtoEsJMWojy1XfgLdSnm73VPZmoeRVmnVpZiY+jr036Raso6D9kr7TO3WFE\nHb1hCcSQ0uF7GlXjejklYlHbMZTgLfcw1JKgf5sNPCwL6sx7/nLHY9wkJwPRUMzaNlh4uLj+tgR9\n2V3E6LivJ1C7zYdVLpkDcp/OjO1N0pnbSqmNwOEpznfLlKp2suh9KhkwrpsOYi42PExYqmcky83z\nT6eSOrNJzKHVRa9kBRWVvLIrcin+IXtkSIEcMk+GsfBx2pyCt9fl0urusZLJkbqzVjEeznIHe6xm\nEqcaDtOwUHkruS6RysJNSbJc5E5LPNf1V0a1u2dB8zZXQHwrRZGFpnN1qjjtkYSzMKnJPnsN+zu6\n5uhi0B7xVYBeiO3/I047i8y8m8xK9wxrOMgtAB9ksRtLNu3M5gp+IrN6hG4uVr/vcv4O+Vzn7e1p\nwEyl1FUGN/+agW46M1fWK6WKBpO50j7Xy0Qpe8OEpUK80t2BT/rZ3hZVumG915AR0kphpxh8C9OM\nS9E2ZKYsxCvI7fjkoe1EWSrtPfPwAHEDfjHKIhpVA1HWyxV4hf6S+h8+Kj9xfVgTJx+P6dd2GrOV\nVqIRS2FSk13ZbQJaVScfQhgLT4rzrfj3PBmfdFZOtH5tOJYPnw9yd+/QTTpze7AlQ4GQkQGRNrKp\nq1xNXeWrPTU7DjhDRE7F4OYicgfw5kA4rDKSkZ2RIRpRFpEBseifV4eQTZtzXtZT5OLRw/KBuvaq\ntpiTZFHG66b9SGeRWmdjHk0sMXDDGKqcxT6Srexj1uh9k40siek22bQ7q/vQ5EqeiR0LwEQDQTRS\n4DJPT+dh5+zMpSXCNW8hpKVMZQaPATqqqJyNrh+7cxlfrdGD5uK9XEx9Li2UNmjbYmPhfu6d5NEU\nqYdrLf2QZCys62rHVEsxx9doO+uK0l+5yKYCGiPWvR1THk38hisBXDZvGIsPHuaKkXQ7rAIaXc3Y\nGSxyENZUOQ/1WgI5sHvLR0TUWaprpP2Dcn5P11jc/AyDm9cPJUIz+1xL0VajszhHwNMmjza0qHPw\nVm8OUc74kDzMWpfTi2FdnW8fwg72eGZwzsoS4MPmeEXQ9/rg/h8gYJKMRekbwh3IqOBaa43bez0f\nfB46mqvw5QvDIighRBNmoFbhdwerg/GWA381xx+na9RPId66D3dIObhQeIqJRt2EzmH7PC149tCO\npI5IAjiSCn6p3uAr8vteLfq+zO2BiChLOc6BUvSNFERYGK1yOUuO4Xyl6YGv5QanzMqodiGQIR+O\nhR32pdHxy0xilWOHHMcGh5nFaXP3rKbMpfkX0Nil2HgOLQ6zbiHHKcZck+sGesGxiVZVjHHK3X4G\nut5sSPUAUfpgTW+g+1vDBLfg5dHkIoH2p8bh+G1ku2utAi5iq1Pi7cRdJFAxte58NWVuUSqlxp0P\ni4l/mj8B8Cc+HQm1tGLfF+jIJ89wWRIJS20ij8NlXY+K/hTV1ae5UM5MV9EXAveirfRN6C9Do2l3\nHfAZtG4KvwxTiX4Zrkl1n10REVH/RivQEIopCRSQLUiyui1KBxxCF6EStYqxGF+Q47xCjc1DFCay\nv8OoE59+F6U0LsYrug68wm7CK+xaPBwUBgoWB/2G2H6Iods+WvGL2AFEFX2VOc4lqnSt1BKlj7Dv\nZUtwvjzwe1pa5dAPEDKDgl48QHMF2bFvIXUIaOcw0nzgaHqHbvoytwcioiyVZKCbjAyI9LHwCEqp\nJ4EnzfGAOKwykpGdkXTn9kBFlKWSAVH0oeMUtOVpLcLVao6L8W5kX2eFrmWCs6RtFA14KzObNme5\n1zPSwSgrmRyhS7AFS0ZS7/qLhnpqeTsgSRtJvfu8kQLn0C2g0Vm1eTS5sd7JBa7G7Gom8dHqJwFY\nV6aTtFvIdTuBeorc+E7gX27n0EgBSznSHV+ATnYKa9laK/8NSh08lSTmYatkPfWxke6d2d1PuJup\npYT5nAb4GrVVlLud1ATWuh1CWBOgiTwHM01gjYN/HuEM7jSJXD1JL8XAd1spwnDIW7oCYIexNJuC\n42I8IdfE4dBhTEqbfg/a0rRWZx7eov1rg2evbMJbqeXmd20yWo/WWrgdRItthMVLbN/jicJLIXQT\nsj1ONl/f2eY5jyMaC2+t+OLgnpuC4y1E4RorLXgqg3HBGIcFz/EiHhqzXP+1eIioCr+jiNA+xGCc\nGe+S4Jlt4gTodxHex47xw2fDsnmkJX2Y24MWUTYgir6DGCOpdy8kSVaQSZoboeS1x2GSTxN5LmvU\nRofUBFmvyznchfvl0uLavEGpW2AKaHTnQ4ZJ6xNoJ+7ONbGPC+0MC38DLqHrYv7skq0+yGLHWVNM\nHa+WHWCezRf2sDDUKiY5uCZUpHk0ubBM+y7s89h72iifsFDI2+S5gi5vxQrcohhCNyXUBRW9Olyh\nlxDzt+NYw0GcWKvZK18veb+LEJrIKtf+fj7hmDF/xxfTmuitKTfru79kBRg3RGGDLKIRMFaJjWrW\nSVMAhW1RjL3c/G7FhwmubosmJ5UTldDLXI4v/B1CGmFkzEQ8pLQi4IApJ4qB2/ZbgErzjNOD8dkF\nJ/Q/NBCFsUIqY3u+CP/M4bNUQcT8spExqYqPt+KfM4SQ8uMwzCwGIdXyUfgFZjt+4Xo+6ReaHOCo\ni/TxxrnwpPoiyP/Rm6Qzt/srE3tnJV1Ssyr6wKOckYx0lqFq0WfmdkZ2VdqI01y5lJbKHpMGBzWi\nLC1nbF94lFNcqyrVtEgseOjgBO/ILKDRWZvZQWx8jKTDwWySUjVlkT6tNR5y5OTS6iz2aso4v/ke\nAB4f/qEInzvAWxREGCYtpBKjw0Eg9Yx0Dtg6SiLwzyJ0wsaRLOPYZr3jqhm+H6AToGyt2Xbi7rlC\npsgcWiiXK11/z6sH3DuxFv3323Qf+3w0yYYn9gc0nGMhnyNZ6nYW9RS5+7QFHEKNFLjdyhKmAXAG\njzgnbJx217aWkgjn/+FygR7cVbPg17MAzdGTJIuDZHOPztix6pUu5zfIIYMea7yrc/tluib2hFw3\ndh/ehLdiQ0dm6DwM6QAIzq/G0xfUEU1OAm0V55kdwvpm33cVUe76sHxhSLVgreSQRycnaP8DdQe/\nFM25vii4p02A+oqc4r4JnSONQqen5an5NwmnzX6oHuFiU8RmHP7dhVBTMVGOeYhy4K8I/i4P2u4A\nJhoV0Zr0OQCjiEbj2HtOvwhkrh7jcyTYDpxC787Yvs7twYgoS1fRbwSOVErVB+deRRdbtitRpVLq\nA6lexGI1hVZynXLPCnDnNrKdUq2i3CnsEMappSSg7dWWYS4tDpbJIhlZOELCMouHV1PmkoxKqHXK\nLoROPLQUc4Rpb1Dq+h5JvYNr6hnp/AxhtEsj+zLOIJZW0RZRHwmdDBcoOybNkaMLbo9jQyRhysJc\nFqMP+WpWcqhLZJqQXMOamObZKaPaQS25tDgYrIxqt3BcYPhtwgUxiyTf4UcAfIOfcYJoauLn1Sf5\n/+2dfXxdVZX3v9ub9pqUtGlTc2lKhtSG1lZbC2WIU6gEqSA4IIgOiuiAgo6j4ujMiOPLA47yjDzj\nPCozOjMKAwLCMIAgPAMDFIhAq8W+2WpKaWujaYM3NCU0bUJCLvv5Y++99jrpTXPTl6SUsz6ffHp7\n7nnZ52RnnbV/67d+672e8HYO9yckk2exkXrz/D4d/TF2b4Wobea4Ys0ZssATwHjcivMua+3XDhUN\n7UDn9kpcSBWcm4YtdPXonAnOCUNSVKuepOPW1aYBr+8mqROj8XiIwC0kHbe+fvg/JBuJdJN0qLr3\nbHCYE0m+PMI9aCE13chEV/pq5oxm9+hiKC0foT8H2uVqYo4iXF/j+fUUZ/p0kxRMu9A6sOlxMyfx\ncp3/fve55c5I2eztc9c9m+EdfalzWx0z6oyyUjH6kegop5baXtb7SmkYvbW2zxhzmrW2xxiTAZYZ\nYx4ELsA1BAlR9t8BIfL5M5xfOAZYaow5zuuC/CvwsUBDM8acWYSGls7t1A7ISp3bwcaCUVaqoz8g\nHeVeKiiQkeRgDXmRG9aRax1tCrrpk6i7nB6BVSarKD+sCsooSK/UKrokkq6jjW6OAlzEHGQPWpir\nGpW4MWUoCLtGs3XG0y+riKUskYRpGXlZUXSQk9VAC3MkgfmRws2AS5L2q9WCJGlf3Eb7pDfI58Ik\nd75qOmXclezmbt4HIEycLqoEwppLi6wstmbqBYKpIS+Rvu5B6xLbbpUTCsQWsZzvexbNl7iGa/gK\nAP/N2TTbS/04utlm3O/sfHsPV3kNkFv5UEkSxH0vlY7RW2vD8iyLm6OWQ0dDO6C5HRJ5uu1eCP07\niH9goe0duCi7Xn0Otp3i7f6mq/1yRVoSHkOMdE8gKXsQIv1Wdc0cyQIjzZ7RkbleGYSI+WZf7n+m\n+bgoVupzQJIVFD7PJ1JFcsSkb24f20OcPI+kkia40DfAWZpn30HyGYbtzwC3mjl7HbsLWHdn3Hei\nn2HLHi7O9S9mI5nbY2UlOXo7Mh3lvez2qzfzCq9jgHHMb6ritKaI/X6Sf+UHXA44Pmqg6p3G4wkY\nJziz4FD7GS/OupvKRBNwLZgWYI9yegXKmEqnOMEAyzxHrWDTG5nNAtbI+VZ5DLyRFeQKbipuzdSL\nlsxSThe2Sx1tHO/llbdm6gEEmoIktbN90hvkObROOkbgn/o9v6N1gjs219fBhdk75DmAe5lpvZxw\nvxX0yrUf4GyBsJawVM5dSTeLvVZNqDzuJysa9+3Ucq1vqPQ1rhIdoqns4Nc2IsiLmv+Bjc15vgGs\nZzbJEpu9rf+l0nn0vnpwFTAT+J6PyA8JDe1A5/Y3/L/jgD8B3kx0Rg3KKWvnOpHoAKeTlPWd6FG9\n7arb0zE1kPcj2FmIOH5wRLv8tcJxwUEOqBuuJxZsLVOUziWqknc78dx5kloyjf7YAfNxGXeASLRG\nTiXxhTIOR98M51jnP88hvjjyxJdlHnytu/te69QECOYU96fIupVJSeXwOUey6jiEIA3AOz10c7eZ\nI/voYrdW4K6HYS0wAXhDFag4dEgbydweKyul8chgHeUzcJJu91GinOtHr66lQJmiIXUOtWtqrxKb\n3XQ0s5uOZg4t3MaZrPzaw/vcv393Bfz8Z/CLnw17bmvtK8DxxpiJOGnXN3MIOvEcjLl9hf9XO93U\nXr22wP/UAHMnw9dKcfS7h1/RjnbuabCVEtGPSEe5mPWT5fv8JX/DtwAXVd6Hy7R/l88K7NJKPRfi\nmDHdVEpy8jY+xKXcCERu+hxa2O3f8+Uq6bqCRuGV9zFeotqp7BBYaCOzBcYJUX6AlcCV9Qeo5TYu\nEv56DxWikeN6VBXkfoIeTS8VsooI59Rw0nj6BfKpoJdswY1paWaJrDJ6JrxeksGFsowkgNf7EpG5\ntAgU00l1Qo7gT32S9C/5Pot5QsYUktl5xVe4gw8AblWwiGXy3P+XZwj9O5/gL/mef5ZZSdhW0s0Z\nHgF5lCXyvPdpL5XB8ae7n2Df2bthgzZr7S5jTDPwLg5NJ54DnttlwIwPwjovd5InJvS29SX7p+rG\nF6E5ycSjYKePqHuI3Z5yKN53R4xup6virGA7gZdVwZZmwOjEaN5H8pXE8216Ma4c5qj9xxFXCesL\nUO2P1S80Ha6FF1wZSXZRcDC6r+3v1HlaSbKHpCcscVzbgXM8q8j+Nm7THaj0Uu17vrPah81FEulP\nBB7w0E01SdOwT1hdDQDbtlKavTS8Gx2D3FPCRlWmWGvJzOZZ+RxsNs8KJFHNDtm/n/GCSQcnWkEv\nf89XAbiM66Wo6ShVsXoP5wmUARGP76BGRLkCLl9MoyZcL7wssvRJReoWGhL7BaZNG3UCKQXRtbm0\n8MdbHQXrDzMmKdpjXPLV8pzg8rV7/kDLBDcpq3ghwbYJ42sVFxLhp36ySgwtx1RPM32BKrlmA1vk\nc9j3Oq7gw7h8QoEyYeV8kW8KVLaU0zmzSJX1Wo5nLQv4jvnSPlk3/KrIPHurKca6mYrjs79ojCnH\nYerfxOHzh7wTz0jMKJniKcpxB2EsTVFcR4QlNBZfQcSltY5NDl9xi+tUpaWMNXYOSQpjjggLNahz\n96r9ykjiz+Ga3cT8grb1REgnjCNPhGV+QmTF6EKrXiJ2VqE+N5Ks0g3OtYdkhyn90tEMI0i2Gsxl\n3MsofK+ZTttVbuTlIsdqppN+ji8DJ0yACXuGZ92UOrfVMRW46P6TwC0UYXgZY74IWGvttf6YB4Gr\nce/Jx6y1c/32D/jjPznUGCHVuklttGx3yXtOA37kcfrXAXdYax/wTvuQd+JJLbURW4lzezRzT4Nt\nVBx9DXm6mEy/f3fX0UY70+Rz0F7J0p8oZLrLs00u5UZhk+SkIGgqH/IslBwdchzA074f7TzWC0Tj\nGoW79afmsocouZcKiWQv4UaJdiFGvgUy3O+bhi9hqdLoqZIE63j6Zfs5vltWWaHA6hlz5H4jtz/K\nIbjzu1/HigknCTTzKEskeRpWEO3UMrfgEsc9mQq1fZrqDfuCUvHsl2RxN5WS5A7PdxHLZUy9VPAN\nviz3FZKxF3KHSDfnyMu5q+jib/gW32EYe2m4HZxZa9cTA0S9/bAUNtuJiw7LfES5+cUIeWwuxL/A\n44jyubojVR6Y7/+0t3Z4aAbX9Sjw7suJEWjjJGj1KwbNbglRqYZrdqrrzJ8E21TSNUSvu9Q+byJC\nJzmiCufEviQDKIw7JFffq8YyuCF5uE4l8Ze3nWRdQKBY1ROLmvSKo57Ix+9Q34dzb1aJ63XElcb6\nPfE6mjmU08eSTEBrCYsH1Wpgn1b63B6V3FMxSyP61EbHSvxjSC21V529BKxrhvXNJe0+CrmnvWxU\nMPrb7HuYzbMiTXA/50okPY91ieYbQTmxlvZE4nCLj+hDYnQr9YLFa6y7g5xEyT2Uy2rhfO5JSA8s\nxOlShG0OI3dx02w2SpL2Ac7mEp8Ihpi87SAnq4zTaJbvC2Tk3moLbjUxkMkIzv4Ei4WLr3u/1va1\nszHrqlpd1O0yQZMLXezIVMt2cPRQvYIJidteKqT2oIa8ROAFMvLsC5SJnETA39eygCYel3OEvr0/\n4fyi/WPDygjgH/kbruErHGN27hujv7vIPLtgaBzz1WDGGPtpey2XmCvlr3MKsb/rsp3JClTdYETL\nJoS1YysRo9aNMl4mJnhX98XoTGPu4S8lrDDAYdfb/Uqjkhgt1xMpjbk6eNCLwx6rrtPZh1rTxmsG\nbF17lnLgEQclc7a5MiH70Oo/n6DGtZkkX14nQ7U0RNingvgcRZlSjUnXK4xT19GVu+XA3Le4z1t/\nHcnAg7nyYTV0yjlw3/2ueGNYjL6EuT3WuadRS8Z2UylJw8Ve2wKg2T4otMs62ljnV9oFysTJdFEl\ncENwWP1kpRmJZsxoeYEqusQxVyvu/AoaBcoITmtwT9nQ1CRLf+KcASZZzzzRqdHXqaQ70WDFHRN7\ntjb0baElO3evfTvIJYrHQjesSgUAfpvPAfApvqfUPwvCPqqiS/q91tMq8E8PFdKYZTFPSCP1owRC\nqhOuf468KFMuYK08s83MlLG0Ui/nnsd6uqjiLea3+3b0Pyoyz/781e/oQ+ORAJ28mauwx7lisk2b\nYmJyEw52AZdkbfVeqDobG2h0kGyCEayMpFMPL5VQ9KNlgicSE72DuyrpRG/4rM8NSTmG4FS1rEAx\nqYMpRFjqJJISBNrpB2fcSzIBHaCWVpKNxcPLaxuRKRPuWUsgTyQJV0lDFjWWbcSX6ETi85pDUr4i\n3HOPv/5iSnD0JcxtY8w8XKGfzj1dc7hJIKSW2oFZidCNcc0Zbsb9nb0C/NBae91o8Y1TS23EVsLc\nHuvcU6miZpOA64G34P74Pgo8SwlSrsYYu9YeRydTJTJ2jUfce7edWulLOo/1ss9/ciF/4fufQoQt\ndAVsgD0q6BHVxg5qJOp2zTL2FhYrkEkkaYMF2GMuLcxZ0erO11gptMeHOJMTPXxRzY6EGFtYEVTQ\nIwnMwDXXq4LKQjfjX3LxR1C3hKDQ6c7RSbUkW8e/9DL9r3dxTlvGrRo2Mlvgn1bqhTbazjRJVlfQ\nI6uSxhdX8+gkV9s9hxZ5JgFO+jc+wXwfk13AXWzwyewaOhL00/C8V3GiVBH3kaWW9mHVK/lukXn2\n2aL0yqOBo63T7T4Kx1J4D3Aph6Dl2oHO7V+Q7E26naTWeohcddR8QhaafRSvI9cpxAhci43lSerU\nh0hWV5RqOKfVf9ZKmPUTYLVK7urqUa1wGVYLmuqox69pnuE+K4ic+l41Vn1cOTG6X02EhSoH7a+F\nykKUfrf9Kh8wX098X4MXi8Elg1er7eEZTiRq2lcQPeN2ksll3e4wWJnfrxT1ylLn9lhaqY7+JuBn\n1tobjTFluArhL1GilOsGeyzLWcQsX1jTT1ac8VR2iJNsZ5rAFxX0inOv4/d76ak8wWIaPBe+lnaB\nTqrokvPV8XvBqTMUWMVCAM4jto4J8Eo3lcIEamCLXLuP8dKdaTAs9ABnA+4FFe6nhwrhr2/EYe6L\nWC4w09M00uQx/XbFBKqkW15Wq1go0FKGgtQQhOv3UC5wVRdVCcgnFFdNpVNeXBX0CEumhwrh/Id7\n7KZSXk5H0S01DhDlly/jesl3LGKZFLlV0k07tZxhntq3o7+myDz78vB/DF6W4F/8z0HnGx/o3H4c\n5yyLLY0166WepAaNbtqtHUzYPpHosOdnXfEV/nytap9wTLj+M4PGIr1WM46dgr/eYMydQf/PkcwR\nTBz0/U4iW6YDvOC12x7uc4v9NKeafwEcdBXgF80MCi9C/PfhhaF1b8ap+9AvgmJ6PVqyWEsddxJf\njGEM4F4QU4ps78a95d9ICY5+P+f2aNrrhtvBU4EWW2tvBLDWDvjo5j04zAn/73mHbJSpvfrtpSI/\nw5gxph5Xkf4LBilKEgPE6aB6TUa+8XSG4Runczu1g2L7MbdH20rB6GcAO4wxNwJvBVYCf8UIpFy7\nqKKGvEShFfQKfKCTtPNYL1BKF1USwXYyVXHCXWhzIqskIemajbhYoIcKgYIKZEQeoJweLitcDzi5\ngcC6aeOPAGimSSLtPDk5rpZ2iXx10jdDgZP8wjCrmqRA5OYHaYDNzJQE6DTaeZLFAJLMDRYgomm0\nyzPRK5nwPPTzqyu08UKmSp5TMM1EWsc8gZy6qZSoP0BPBTIiy/B2npTve6mQXrzdVAoj6p+5gu8Y\n93u41/68NAmE3uF30eZhm7twmPtuL1Og7WCwCA54btfgIlH9Rpmi/g0QxVPEpONEYqSvI2fdBAO1\nf2tfhGs6iJBM2HcnkceuE61zUJG74prvItnIQydmQ6Qdzgsofley1WBIjB5HciUQov+c+Rc5XzXx\nzbyT5ComzPBOYtS/mfhW1hG3XmWEc/eqsejeANNJJo+DVap9ytX5c8AxXpv+qTuHk+lTVsLcfWF2\n/AAAIABJREFUHuvcUymOvgyXRPiUtXalMebbOHnYkv/w+shSR5ss97V0wFKWCGWylwpxkl3E/qc7\nVJMPjb8Hx7OR2Zzv4ZgMBXkZVNMp+2Tppz3jXiILWSmFTwFrvtqU86gNjrRHrqO7QHWQEydYy3Mi\n31BBhzjKWtoTjtJ93ys5gQEyono5jXZ5sfVQISyYVmbEPrBUybkDRt7JVGYX3Pc7MtXi4NuoE6pl\nO9ME859Bq4y1m0p5lqFALEu/vCjz5IR+WU4Pp/Y5vZxfZN8mFMwCZVzkn1ULc6nfU8KfRB+wrRm2\nNw+7q4dQ7gJusdYGQbFDwTc+4LkdoJQa9f/ggDQur/ukagneHEkhtOB0qrPwsj/BrkI8ZznRAWl2\njZYoCBk/7bTLSHa+Cs57F9Gh7iTCG4OdYasaL/7/weluJuLsL6t7qycph/Bf9moAzjFXy3nKiS+J\n40h2gQr73Gy/zkeNkzsJGkHjymKj8F245wXQ3Rfve2IGBgpxXDr/oRusBNsJ5O+M/2+6DJe9Gc76\nht8F99g/r3NPxpiHcbmnQ651U4qj3wa0WWtDQ8S7cX8MJUu53nj1Nl7PS+zhJd7aNIkTmiqH2jW1\nV4mtat7NquY9PM8rbOoffn92A1VN7ifY018bau//AFqstd9V24ZSlLwP+LF30tNxPu9pn4x90Rhz\nEo5v/BHgukHXOeC5fR3OWUwA3gZ+rZbaq9VW4rL/A8DSVSUeVIIEgocb/+A/7zbGbMA58EPVZyFh\nwzp6P9nbjDGzrLXPAqcDv/E/l1CClOulVx9DFS9I9NrOVOFnj6dPSvEbWSER/VGy6HXl/AE2CUVK\nXUyWoqLNzBRoZz3zZCWgk5QFMsLYqWerROkhcl9l/0si2QEyDPj3/yKWJ+CTcA+1PCf3oMXE2qmV\ncYXjqtkhSd8yChLRtzBXxNj6yKp2gwNyn3W0STI4RPY15IWBcw1f5nN8G3ANU2ICu02auwyQETbO\nc9TKeULStZ6tcpwu+CqQYVn2ZCCsJtw+O6ikpqmes5rcNbs4iWv+4Wn2aaXTK08GPgSsN8aswUXT\nX8LNs4OqdXMw5vYVJHXcp0yAnZ7dMv8tsMm3E81lXRESOIhCSyCEyL+BGDn39iXb7S305LCt7TEC\n1tx6XZilE5zBBid8A+tGh1zX2+/zGd+3WCtMdhMj9nDcLuLbTzuRzUTxtg3qHANAk7lazqdb+QVr\nRT1HYrR9no/mIer7dxeSjUfqlbqmyB68Hq7b7Qq5LjFXJq6lC79CdD8dl3x9ox/f9DUwZCiibYSY\n/L5yT4dK66ZU1s1bcYuYccBvccuNDEMQ/Qcda2+z76GSbnFwW5gpUEGF5O4dfBHofGtYIBWntbSL\n2mRgxmjn+iSLpaCqTuXlNCNlOYtEM+Y6PsNlfk0W4KRuKmnxtMIzeUicbjWdAnvoPrF9ZAUi6qFC\nWCtVdMm9BXbLDqZKgdF65rGG4wH4CDcLFr+cRZy/x/mTrgmT5PpdCrrRDct1M5PgpDuplmt3Up2A\nuXSh12kegtHVtWv8+CvZLfLGy1kkrKXTeJy/538BrpAqKFlmGHC/H/OHfbNuzi8yz+4Ze2bCgc7t\nPb4XrODiyqHrylKtTFlJhBpa+5INOYJp6V3dqKSMvRkw+twnT4LVngg6HffigaibEyy8DCaShG7C\njNDFVt0klSTBOfpm+9cANJl/kjHpgq5dJOEdDW9p3F1DSj1qezjndCLmNl0dM0Udt7PI9jIizFWp\n9pmCYzKBe/7zP+g+b709vjxf9seW0jOW8y083ww7muMXz3yt6HEetmkGvm6t/akxZqe1dor6vtNa\nW22M+Wfg59Y6zWVjzPXAA35Y/2CtPcNvPwX4grX23KHGGJ7FsGat/RWOpzzYihL9U0ttL+sefpex\nsHRup3bA1g28vgmOaYrbntl7LTCKuae9rz0aEghPWycyESLmLqpY4HXitzBTEqKVdAsHPsMAj/q/\ntdNZKonFoFe/kJUSka7leIFieqgQCGYFjVJYNJ4+aQm4gLUiuxC46w9xpiR0y+mRBGeWPoF8cuSF\nmz6LjbJPBzWSbM3Sn2jzBzCvbz3d2cjLD1ZGgZV+TLW0qwYincKq0T1mw7ZptMvzWMsCWam0MJeZ\nfhVRQa80bsnSL6uf8fQJjBTOl6HAZ3Fw+KXcKHUGz1Er9Ql1tIm8wnncIxBWNZ20MJfzzMP7jugX\nF5lnT459RH8gZrwefR54p2pxp6NizYwJEarWlNc6Laj9BxdPhc9a475HfV/sOA3hdBM56vXE9+50\ntd90opTBdGJitpVkIhncKkQrUwZwUyeAxxGjeI035NQ+A8QIvJUk1BPubz5xRRPGcQLJZ6uvqeGo\nhT5af+r26A3rSa6GdE1BvRpLI3A0JUT0Jc5tY8zNwA5r7efVtmsZBa2bUZFAqKKLPDV8eo8rnnhw\nwruk4fV53CuVnY9zmmjZLGK50B17qUhUuIJr/BEx8vECdfQqNPJ87hHHXEs7Zf5lUE5Poko2XE87\n4QDFLGCt7LOcReK8Jxe66MgEzL9VmDbQLYVhwbl2ZasEGlmy5zG+NcEteS/jeoF/CmQkL1EgI2Pp\nJysvgAV7fuXON2ESuT3Pu2c7oUvgrCq6lARynTyfezmfC3xP2FZmSA5Byxt/wlch91IuL9Cj6BZH\nnycnssv9ZAVyWsnCkpqDj5Re+WoxceDKq+Y8XLJdQTr1wHS/feme6KzLSBbylCtIIZiunoUI9Wh5\nXS1qprmg4eUyQLLASleshrGMI1mQFJxrDUkqIyTZQroa9yF7Gx82F8k+4a/xd8Aq67D2M8zXEzmD\nQDLOkazYrfefd6lrBcqpziHsIsJeugBtOs7Bh/PpSuPwotUvoAp1f+U4wbdEhcZQVhq9ctRyT8Us\n1bpJbXSsVG3v1FJ7tVkJc9tauwxUaX3SDg+tmwMxY4z9gb2YRSwXBcUBMpLMK6MgcM1GZknE/LRS\nmAzQTjgWXCIxRK/dVAosM5cWiTYr6JV97uE8Ye5cxG0SBYf2gf/GJyRB28JcpW7ZL9F1BzlJ+t7G\nRVzkG58UyMgKYBrtMt5QjNXONIGWKtktEFYDm7mRSwG3KghJ0h4qEj1wTyu47aEOQGv1lBUK3JWJ\nrCUNMw3IqqVMVg4tzJUVR7j3Nurkd9BDuSTN6/i9PNfx9LOANQD8OTdztu9NexrNrGUBHze37hu6\nmVFknm0tury9AfhTIG+tne+3HZaCZsYYa98EnZsg79kgAyQj3coinyHKAa9TkfvgUv+wv466dxFh\nF10YFL5fTVIX52SvmLn6xaSUr+blH6NWEXP8/iteTMJFYb0aeO6dwLn+uBV9MVreRVxdNJCUTNDK\nlKjtWpOnVY19pXXtbD5o/iqhWgl7J6V1IVWweuIK4W57LfPNlYBbQen9w+rmrItxPFlg1b+7VoQl\ntRIscW6PpY2Ko7/fvoNVnCjaL/NYz11cAMB/8FFu8s7uw9wiMMV9nMO7fSHVRmaL8wwQTjk9CT36\nwJ7pYzznXO6qOZ/84UIZx2S65AXwAO8Wxxsc93rmCabdwlwacXTBBjaLE6ziBYE1JtMlUMsqTpQX\nQxdVApkE2KOHCnGSlexmOa7B+JK+pfRl3Uukk6nU9rnjHsqeKftnKAhM0znBuYFuKgUKOp618iLK\n0SG0zH6yCZqk7pKl2TjgcPvwEm5hLl/kWhl3KDirIS/776ZSPofnd5L59b4d/bQi8+y5oo7+FBwz\n+Wbl6K/lEAiaHagZY+yzwHFngH+ns+56mO9VuJ+6P7I7NvRFx9xAxIvnZ53GPCQphZr1Mp3oABsn\nuYbe2jrUcScpDfoNRA2aASJ0tGFPkrqpK2C1xPAUtY/G0cP3WkitWDFYORGW2kSEXXqJDln3z61W\n59T3v51YBKY16IPpLlnhPsK49GeNy4dranrl4ApngBMpwdGXOLfH0obVukkttYNiJeqBWGufAl4Y\ntHko7RkpKrHWtuL8yUmevVCsqCS11A6+lTi3jTE3GGPyxph1attkY8zDxpiNxpiHvJpq+O7vjDGb\njDEbjDFnqO0nGGPWGWOeNcYM28UTSojojTGzcMtmCxhcPcFXcd3LS5Jy/bV9IxuZzXgPH1TRpQqF\nxrOe+YCDbsL2mWyRiLhARgqigjKkbvYxky0qWbtDImbd1apzkIxCiMBX+PKOBjZL4raONtU8JMJq\nD/BugSwe4kze7tkumqUznj7huIdrd1PJ1D6XRF6RbZSxNvF4gglU0eeuuSNbzcM+wq6iSyLzxoJb\nhbyQqWJywW1bl5knq5mFrBQ4ZoDY1WowzBUi+sDtX8MCaSqygpPkvrqp5Alf63kiq2Tcmq+focBs\nNg4f0ZcVmWcDxaMeY8yxwP0qoh/MNd5prZ1yoFzjgzG3HwfmqVL7bcSodxxwsp8+OwuxB+u6vhjd\nlmddtA8uMq332+snwTp/xSkke7mGqDZsy5PsTBXgiiWZWGA0nQh76Aj4ZSLY+wzJIqRgOvEayuKm\nEyNuDZ2Uk4zuQ45aF101EBO9mpmkE6YnqTHoFUAY90SSnaQ0pz5E5U0Z+KuBHwDwd+bjAtFMUWOc\nuwBWrY3nDueccRmsur7EiL7EuT2Wq9VhI3pr7bPW2uOttScAC3Gph3twZbpLrbWzgcdwGg2ppVbc\nBor87L8dFLwxndupHRQrcW6P5Wp1pKybJcAWa22bMWYojYa9bAWN9DFeOO1lFCQhWUNeItbTaE6U\n4ucUZy0kFgN/+yi6pe1gUKIEFwGHnrFT6ZTk5Hj6JJLtY7ysBkIlri7938xMkR3IUBDMvYouwbJn\n86yMqZUZcmw3lQlhNnBU0M6sO5/rhesQwhbmCi2zk2o6sjV+rP3StOTYjuf5Tc0bAUSl8knezmmZ\nx+VZBu58Bzk+jaOw/hOfT+joh1VOIyvY6u85rHAa2CIrm0q6E3x9nScJz6qLKukf281RiVXPvq3Z\n/4zYRqOoZL/mdtOnoOV7MUHaS8STf0dM0vYCm33kXoNiYyplyoQi40tJqYNw/hx7i5rpiLscJSMw\nCY7zJ9EURE1X3E58mDopWk6yT2tIfOrq3TK1TStghvNoqQMtqrZO3YNuPVhOfBY/Iz7HwdW74J5f\nWEXk1PY56t5WF+BvzceBZMXsZnWddWtV/9xLoOUm/58NBxqLlGw1oyGBMFJHfyF4qskIpFw/2nY7\nj9SdIkU+raqr03PURgaJUrWE2E2qkm5RcwxOdxUniiPrYrI47i6qxGldxI8FsuihXKCU5ZwsLJRQ\nuJWlT/Zdw/HyQmmiWRKfXVQJW6if8fJSqmaHfG5lhujKhMItLXWsC5zG0ydQVTk9POuT1dV0imMu\nq3lSsWfcv/NYx/Q2N7XvqTtfxr2ANXwX1z6yjTqRRh4gI8fmyclzC9blAaIwpvD7cPeSl3EHldFa\nJaPsCrNmM7z14mo/GtW2IZVEjP8JdigEzQbbfs1tdjqHExzxHFxPWICGQpJFohUTtXMNgO1EXCco\ngPyeZBOM4Dy1wwzX3ERkumiZ4tadcZ+dFE+6NhLHuJnoEDRcpOWWg3PVjkNz4ncRYZmJxBfafGIx\n1uB+ejoxvMx/fq+6D90oXPPctVxB8HS6SGwKyYbkxejuOSDni6oeuSmec/Wy5Ezdtx3UIpFDwo4p\n2dEbY8bhlhNXDjGgQ0vfSe1VbqX9MRhjbgOagGpjzO+Bq4BvAnceqqKSdG6ndmDWi+s4sGy4HYvZ\nqEggjCSiPwtYZa3dMcwA9zLzR6dy7lWdTORF3to0iVOa8hJB5slJZWwFPRK9AgkYJ5Tfh8i+ms4E\nTTBErC3M5SJ+DMDdvE+ShotYLgnTJMXQNftopT7B298iNMUYuc+lhWaaAEcRDbRLDdcczxqBOAI8\ndR73yOqkhjx1e9zKa+2EtwqnvYOcjDVXyEtpxQ6qZVxhRZSln5d8uHc2/y338mm+J1x8Pb4v8I/8\nP98GcAsNCaolBPqnW9nkyMv2Nurk2rpyuJtKHmvOsKa5mxc5mlmvROhsaOsZfhfAWnvREF8dyqKS\n/Z/bt5/K5fyMblzT2SVAjV+Y7iQJOejINUTBrUT5gBxR+bI66xQsg2moJcAnL6vjiomEVRAj8WPV\nTQyosawjrhYqSVbMblefwzk1RTTALzuJK4oN6nPAGiAJtWwjSbvUkg5a7z7cXyNwjA+vt/oy2g5g\nvhNW5aZl8ZkMTgzr8CLcm5Z9yAObbo/bf46TKs4thM39xGXIPq0Ht07Ra5X/M9TOY7FaLZ1Hb4y5\nHfgfa+2P/P+LajQUOc4+bd/CRmYzzy9SP8//5W/5FuCcjNZ4iVBLhTjbNupEvVJrtvQLv71LIIaN\nzE7wx4MT1A7bNQdxTn+FZxqfy/0CR2xRaOVsNspL6XFOE/mAubQIY2YWGwV2aqdWnKNmugQsfi4t\nAgstZxHncS/gMPrASuqlQqCbJpqFyx6ZLgNSQ9BObUKOOYx1KUtkrDk6ZJ8qXkjIQrjnVCb6PLPZ\nKM9hBY1yX9Nol/230CDnyFCgkRXDNwdXfWijzTosuMYHMrd/A8yZAss8FnLKO2DTY+7zRJJ8cY1j\na6cfnNsukuwS7dzDG6vYG0fz3LVKZC7jcOpw7vnq+qHwqZrItFlPdJJaJkE3NtFsmYDb1xDZOPVA\nkx/AHR3x3npJFoxpKYXgdDcQmTnTB91ruCet/6OLy8I56okvqDK1v8bbpwA32v8NwOXmS8JSmoOC\ntN4P/AxMRwmsmxLntl6t+iFfBdwL3EkRpVRfDPgx3LTQxYALSa5WPzvU+IKVFNEbYypwwcrH1eai\nGg2ppVbcDk/5ynRup3bgVtrcHqPVKlC6THEP8IZB23YONcDB1kMFDWwWfnkvFZLwAyQy7qFCGDTd\nVErUuJgno0CYj1j7yErEfzYPCJMkT42wULL0i8TA2fy3RNUZ3yUVIhxSTg8PcDbgePQhofoAZwus\nUal+oQ9xJg1+lfEss2Xca1ggq4gAM2UoCKdd68tf8uKtcr7sUX08lHGMnrm0SOLzCRZzbt/9AKzP\nut+t08h3v7oKeuQ5dVAjUNBpPC5tBZs5TSqB+8lKlB749+X0yCpkJSfKuHXzklWcyG6/vZ5W7uF8\nAJawlFnmYwzfouHwVDU70Lk992JYdav6U38jbPcR/XZiFNuQgWYfXdcD9R6a216IUXIlMUrWfV0b\niOffRnyS7/T/arhEl/Sj9m0kriK2EXn8L6tzNxIVLnXFbK86tt7/u06de7u6fhlwnQrFw6pkDrDW\nfgyAN5gbZP9lwMnsbVpt8xh1Ld2wpVgVrU56v6z2H9wb9wLzJSD5rFqBdzreBSvuhLdxFaW1Hjk8\n57a2UZFAuMVekGgI4gqg3K+mUvXh6qRaYJwqutjsnUwv5UI33OBxb93L1TXcfjvgmCehc1I70+hi\nslwzSBzU0SYUzIBHP8oSZvnjqnghoQMTpA56qRAphnZqxaHrJuShPy4gL6J6WhONP8KLyF3TOc+5\ntPCAx9G7OUrBP7ulgUmAVO7lfKGqZigIy6iRFQ7fBzZmIh1yJluEAaRx9zCmCnoE1lpBo7CCCoqt\ns4YF4vTz5LjVODf0pL2fOtqoN88PA908UuSbdx4W0M3+mjHG/pa9G4y0+s87SRYy6ebYumQ/7D8O\nOFWxbnQHp+DI1hNxb61oGWwiLi0IDqMPxx1Lstl1gGJ0c5CniY5cWy/RqYax6h64ZSSx/eBoNVxV\nT1IBUztdLZmsrxlsgzpngJ/mqEKzciJ0s4uI/+uX5akUh710XmL+xUj/1133wedf+mduMJ8pAbo5\n/Od2KoGQ2ijZriI/xc0Y8y5jzDO+xPvKIXdMLbXDwkqb22M5r0clol9l5ySUKduok8i4jILALkE1\nERyv/S2XO2jkwR82STIxMEl6KRf4p5cKiXY7mZpINga4JUOBDh9TZSgI0+dZH+UvZJVEtRkGVLn/\nVEmSzuZZgXzKKPCC3ydHh0TPLnp3+4RxtFEnsgJdVEkk3Uq9JFhbqeckv0LJ0i9FVRX0yr0v5XQg\nCLT1ynP6lC+S+ke+IAnYLTSIfMFf8O/CAJrFRoFsQsL3TB6SZKzm889ki6ya2qnlDi4EHFQWWy26\nfrgLzYZhIvpbi3xzcbGE1etw2a3TgXYcs+AD1tpnip17LM0YY5/0n3XST0euIXLW/LcBoOkS9/mR\nm2JkXk6yl6uGcXSjEp2EhCSPfDNJTn2rOl+IXDUbZrAcgpYJCFFyA04eQdt0ojvTevi96hw9g+5B\nR/fhs2Ym6ZaFE4nP6Nab4vm10uTdfkrp1ZFW8lxhL+Y4c6vcQxhvN1F4rRe43KGQtNwTz7Ma9/t4\nH6UkY4ef22M9r0dNj/541orDnEyXONUBMglYJziZhazklh++T7ZvTtTtORZN0L+poEdeAC3MFWe3\nnEWCNy9grbBX8uQ4XtQk3Yugmh2J/rXB0dfRJvvoqtFe1XC7nVp50YTvASlMqqNNXizLWSSwy+K+\nJ9mRdWMqkBFYChBHXqBMnGp4WWgZ4zw13Mn75dkFCuksNiYalgfGzKMsEWhGQz6B/tnICoGt8uRY\nyUIZRxh3Jd0iy3y6Wcot9iNEpHkoKxnHPAnYZK39HYAx5j9xZeKHnaOHCDsEpziR6Nw0RXGApDbM\nZ250CqFX3nRl4iVwrNpH49668jacP2jnLOuLT1cXKe0aNC5dYKQx7eAANUVzuxpLNxF2CmwdDddo\nDL+XWLY5heQLRXesCjmCAZKFWXosd98Uxx7uOZx71a3xfPplsR04y9c095pbZdx5InSju2eVAffd\nE68ZxnXxJcAk8I3XhrGS5vaYzuu08Uhqo2RDQzWDbDrJvj7biGq7qaV2GFpJc3tM5/WoOPpuKhMR\n+BZmCmRRQ1706M/kIeHLt1MrkWwdbQJ36H+jNn2vRPGt1AvHfBHLBZJYxHKJqmtpl88hktXslTra\nBFrqJ8vjvkiqgS0y7gp6Eiyc2Ic1Rtta/yawe87gIeHRr8kukMTxTLYkmqGEFUwr9QKfXM4PAfgc\n35aE7nIWSUJbrzhcM5HxMu516jkEaOlzfFvuN8Bny1mUSDLrz2EcN3KprJRusJdJsnjfdvgzE/bH\njsVFvDr6bfCMmnwBFnpt+m33RxilHrjCQ7QbSGrQaKkBXxvEOJKJSkmCDiT/Dw6i0XIBIRKuh8Rv\nKYwlR1KbvZjEQJnaP5QEaaaP5sJrSKeXuAI4Tp17HMk2gRc6shubHojXnAjcZv8JgHPMXyfkI8I5\ngulkLMCKn/nzqW1TSDKT8mp7gMBOuQzsT9zndTfB/Mso0Q7/uT0qGP2f2Zu4jOuF7tfFZJEbfpzT\nBDLRzcFz5BN6KkGbJmjaVNEl+wIJbDrYXFoSuHt4AaxhAa3MAGL16hVcJ05SS/l2Ui2QhW5wMkBG\n6KKt1MuLIUNBNHWCcw/nAqe5s9uPScsbD6Z86uKu0EwkQFydTBUoJkNBGpZ0ZauEQtpPVl5ct/Bh\n6QkLscF60O1ZqpiEuhAN4GY+DMA1fEVopmtZIBTRLP1kKHC6+fm+MPpWoi/UlrfWHj1o37cBV1tr\n3+X//0XAWmuvLXbusTRjjD3OruVbZkGiH2uAIt5EUrBLY+QaotFVpwE60NDIBqKDfZlYrBmuqWuO\nNY0ydzE8cmscV4Aujh10bt3gRHeyCts7iNh5uB89Pog00moiLbKXJI1TSy3rwjBdpNWqjtWQTnjR\n6a5STb5a9qkVxfMcgwWKvmFvkM+3Xe6onk9dH6958fnQfE+8/lmXgbl+WIy+lRLm9ljP61Fh3XQ0\nD4ffDm1rmve/0GZ58/7rz61t3kt+fET2VHNh+J2GsFXNu4ffaQj7ZXNpUgPFbFNz+/A77YdZa+ut\ntabIz9FFdv8l0GCMOdYYMx74APiu5EeYPT38LkPab8bougcCKB/ImAGfVds/O5B73peNYG6P6bwe\nFehmevN/0tM0W6LhSrolIlzCUomkV3IiJ/rCoxDN/6a5k/lNUZ8lMG26iQXV7UyTiF5zwh9rLmNm\nk4sXNDOnjILADSGKXs88Ofd4+nm2+Q+c3vQys9ko51vJiXKdMgqyyqghL7DUeuZRSTd3NG9iTpNr\nNVO3ZxvtE4721ytQo9QtZxccBLIi0yhQz8rmXZzV5Mb3HLUCzYSiqx7KEzLP47NuHA9wNr9pvpdT\nmsroYrJE/V/l71Wf2i3S6zY89yUsJUOBTc1dTG1aLM96Di2yitjBVGHpLOZJkUPWxV0Hw6y1BWPM\np4GHcYHIDdba/Y8UDrHdZRaQJ6m0GCLUZ0jKEWz27/6zfOTYjIvUQyij1akaKC7xW4mLcLcCoeXQ\ndCJEsoHI9MnfGiPhAWLk/wQxAp9IDEd7STKGQvQcrgnOMwWpgACN1JOMxMO4uweNewvwJyRZRAtn\nwB3uTypR4KTrDo7DQS1PE7Wjy4Fmj21p+GUTsb+tTnIvBz5uXBTfSbLdYX3YaUKUb1jRASuu56DZ\nWM/rUXH0GQpeCNdp7ncxOUH3C3YmD3Hcwy6v/qMz/kwYIM8yK0FrBAdfaOce2Dqum6n703kFI066\njIJsb6FKqJyffMBp/j919gki69tGHa/jFcoosINqgTKmsiPRwSlAMl1UCQOnkRW0Ucd4+iLNsyxG\nyln6hbGygLVszsQipOCYeyin1wsmdlElfVkDbKX7webokPE1sIX/oY7lzGMmW4RldBTdMj53/3P9\nsXm5l43M5nk2MUBGCsS20CCw2nsffpCfnuFcy0ZmSSXwDFqFTXWwzCtNlqJ9POamnRPAg/av+cof\nO2z5KaX11lyACzyNL3+PO64AzP8gvHx73C84aa3fckz8WjTeMyRpluHzdKJzXWYv4ARzt7smMRfw\nYyLU0U180QzWhtHiZGGfoA3f+A5Y5yuANfxyHJF/NZ3o0FuB31/1dp68+lQWmq/LM7tja6yMPeaS\nqAffC/zeV9JecPkN8CgsewF6vaxTOdF56a5Wc4jQje6CpQXOLng/9PjYZOKeyORZd2uYA1IdAAAE\nUklEQVSUjG6kBEnIEdpYzuu0YCq11FJL7Qi3UUnGHtILpHbY2OFU8j0als7t14YdCfP6kDv61FJL\nLbXUxtZS6Ca11FJL7Qi31NGnllpqqR3hdkgd/UjV2owxNxhj8saYdWrbZGPMw8aYjcaYh4wxk4Y4\n9hhjzGPGmN8YY9YbY64o9XhjTNYYs8IYs8Yfe9VIru33fZ0xZrUx5r4RjrvVGPMrf+2nR3jsJGPM\nncaYDf6+G0dw7Cx/zdX+3xeNMVeM5J5fyzaSuf1anNd+31Gf2+m8HsKstYfkB/cS2Yyj6Y4D1gJv\nGuaYU4AFwDq17VrgC/7zlcA3hzj2aGCB/3wUsBFXnFjq8RX+3wzwC5wORUnH+u8/h5Oxu2+E4/4t\nrlUd+3HPNwGX+s9lOBmmksc86HfVjmtnNuLjX2s/I53br8V5fTjM7XReq2dxyE4MbwMeVP//InBl\nCccdO+gP4hkg5z8fDTxT4vXvxXUJGtHxuH4NK4E/LvVYHNX5EVw/yPtGMm5c7Uv1oG3DHoujNG8p\nsn3EzwtXe/PkgTzv19LP/szt19q89t+P6dxO53X8OZTQTTG1tulD7Lsvq7HW5gGstX9gbwmLvcwY\nU4+LoH6B++UOe7xfoq4B/gA8Yq39ZanHAt8G/hbQFKZSj7XAI8aYXxpjLhvBsTOAHcaYG/0y9QfG\n9T8t9braLgRfLrt/x7/W7GDM7SN9XsPYz+10Xnt7NSZj98kHNcYcBdyF65q+u8j+RY+31r5irT0e\nF8WcZIx5cynHGmPejRMwWgvsi2871LhPttaeAJwNfMoYs7jEMZfhKui/54/fg4ssS7pfNf5xwLm4\nTvTF9k/5t6NjR9q8hjGc2+m8TtqhdPTbgT9S/9dSHiOxvDEmB2CMOZrirR/x35fh/hhusdb+dKTH\nA1hrd+FkSN5V4rEnA+caY34L3A68wxhzC/CHUq5rrX3O//s8bll+UonX3Qa0WWtDof3duD+OEd0v\ncBawylq7w/9/pMe/Fu1gzO0jel77a47l3E7ntbJD6ej3V63NkIwg7gMu8Z//HPjp4AOU/QfQYq3V\nfWGGPd4YMzVk4Y0x5cA7cZIdwx5rrf2StfaPrLVvxN3jY9baDwP3l3DdCh+pYYyZgMMU15d43TzQ\nZoyZ5TedjhMIHMnzAvgg7g852EiPfy3a/szt18y89tcb67mdzmtthzIBgIseNuLE4r5Ywv634bLk\nfcDvgUuBycBSf56Hgaohjj0ZpxO1Fqdoutpff8pwxwPz/P5rcbpGX/bbhz120HlOJSatSrnuDDXe\n9eEZlXpd4K04p7MW+AmOmVDymHEJuueBSrVtRPf8Wv0Zydx+rc3rsZ7b6bze+yeVQEgttdRSO8Lt\n1ZiMTS211FJLbQSWOvrUUksttSPcUkefWmqppXaEW+roU0sttdSOcEsdfWqppZbaEW6po08ttdRS\nO8ItdfSppZZaake4pY4+tdRSS+0It/8POvq6Utw3xmkAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x16dbdb5d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"f, axes = plt.subplots(1, 2)\n",
"cs = axes[0].imshow(result[:,:,0], vmin=0)\n",
"f.colorbar(cs, ax=axes[0], shrink=0.5)\n",
"axes[0].set_title('Channel of line 1')\n",
"cs = axes[1].imshow(result[:,:,1], vmin=0)\n",
"f.colorbar(cs, ax=axes[1], shrink=0.5)\n",
"axes[1].set_title('Channel of line 2')"
]
},
{
"cell_type": "code",
"execution_count": 603,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(0, 10000.0)"
]
},
"execution_count": 603,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEKCAYAAAAMzhLIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGiBJREFUeJzt3X+QZWV95/H3B0ZAQQhimI6MzuAiCuwaJOVgwlZsg8uP\nbClWtpagluCvKgtxZbXcCJZbM7pakUpUTK1YSUQdVBaRJDJEHEcWprJaIqiQQRgB4/Jj0Gl1IRgS\nl+XHd/84p4c7Pd2nu6fvvd1z+/2qunDuc348z7n9nPme5zk/nlQVkiTNZJ/FLoAkaWkzUEiSOhko\nJEmdDBSSpE4GCklSJwOFJKmTgaJDknVJPr/Y5ZgqyQ1J3ryH656bZEeSXyY5dMq81UmeTLJP+/3a\nJG/oR5m1dFivrdfztewDRZLXJbk5yT8leSDJV5P8Ts8iI/OgSZIVwEeBV1bVwVX10DSL7dzfqvr9\nqur7PyhJjkuyKcnPkzzR7+3Lej3NYsOo12cn+W6Sh5Pcl+SiyeC0txuJndhTSd4NfAz4EHA48Dzg\nk8CrF7NcAzQG7A9sW+RyPAZ8Cdijs0d1s14vmqcD5wOHAScCJwPvWdQS9cmyDRRJDgY+ALy9qq6u\nql9V1RNVdW1VXdCz6P5JNrRN2tuSnNCzjfcm+VE77wdJXtMz75wk/yvJnyR5MMk/JDmtZ/4NST6Y\n5Jvt+puSPKtn/suSfCvJQ0luSfLyOe7Xfkkubs8ityf5eJKnJXkB8MN2sYeSXDeHbe3sCpjD/hyc\n5NNJfpLk/iT/LUmm225V3VVVnwXumMs+ae6s14tar/+8qr5VVY9X1U+BLwInzWX/lrplGyiA36Y5\nC/nKLMu9CrgcOAS4hubMbNKPgJOqavLg/EKSlT3z19Kc5RwG/Alw6ZRtvxY4B/j1tizvAUhyBPC3\nwAer6tA2/a+SHDaH/Xp/m++Lgd9sp99fVXcDx7XLHFJVr5zDtqbq2p8NwP8Dng+8BPh3wFv3IA8t\njPV6/gZVr38XuH0PyrP0VNWy/ACvA34yyzLrgM09348B/rlj+VuAV7XT5wB39cx7OvAkcHj7/Qbg\nfT3zzwWubaf/CNgwZdubgDf0rPvmGcrwI+DUnu+nAP+7nV4DPAHsM8O6q3vn9+bTtT/t5/8C+/fM\nPwu4fpbf918BTyx2XRilj/V68et1u9ybgfuAZy12nejHZwXL1/8Bnp1kn6p6smO5HT3T/wIcMLlO\nkrOBd9FUVIADgWdPt25V/aptsR4E/GyGbR/UTq8GzkzyqvZ7gBXA/5zDfj2HpoJOuhf4jclizGH9\nLjPtz2HA04CftmlpP/dNsw0NlvV6/vpar9uuug8DJ1fVgwss25KwnAPFt4FHgdcAfz3flZM8D/gL\n4BVV9e027RaairRQ9wOXVdXb9mDdB2gOyMkLe6uBn/ShTF3upznzOqza0yktGut1/8y7XrfXN/4c\n+P2qGplrcMv2GkVV/ZKmCf7JJGckeXqSFUlOT/KRjlUnD5gDaZqov0iyT5I3Af+6T8X7AvCqJKe0\n2z4gycuTPGcO614BvD/Js5M8G/ivQO+tgLMd8PP+B6GqdgCbgY8neWYaz0/yuzNmkuxP03+dJPsn\n2W+++Wp31usZDbxeJ/k9mn38D1X1vfnmt5Qt20ABUFUfA95Nc6HsZzRNyrfTfSGw2nW30dy7fSNN\n0/U44JuzZTnD9NRybQfOAN4H/Jymmf0envp7dZ3dfAj4LrAV+Pt2+sNzyXc+ZZxm/tnAfjR3Mj0I\nfJnmtsXdJFkN/Aq4rd3Gr3jqzhUtkPV6z8s4zfw512ua3/tg4No0z6/8MslXZ8lrr5DZWlTtmd/f\n0fxYK4CrquoDaZ5+/BJNE/Ae4Myqerhd50KaizmPA+dX1eY2/QTgc8ABNBe4/vMA9kmakySrgMuA\nlTRn0X9ZVX9m3ZZ2NWuLoqoepemvfAlwPHB6krXABcB1VfVC4HrgQoAkxwJn0txJcTpwSc99x58C\n3lJVRwNHJzm13zskzcPjwLur6jia20rPS/IirNvSLubU9VRV/9JO7k/TqiiaJuSGNn0DzcUzaJ7+\nvKKah07uAe4G1iYZA55ZVTe3y13Ws440dFW1o6pubacfoblQugrrtrSLOQWK9sLTLTR9lt9oD4iV\nVTUBOy/6HN4ufgTN3QKTHmjTjgC296Rvb9OkRZdkDU2L+Uas29Iu5tqieLLtelpFcwZ1HLtfEPK2\nSO2VkhwEXEVzzeERrNvSLub1HEVV/TLJFuA0YCLJyqqaaJvekw/bPAA8t2e1VW3aTOm7SeKBqYGq\nquYJqubNo1cBn6+qq9vZA6nb1msN2mS97rdZWxTtfcuHtNNPp3nXyTZgI/DGdrFzgMmDbCNwVpqX\neB0JHAXc1DbhH06ytr0AeHbPOrtZjMfU161bN/A8YHB5r1y5esa/48qVqxdtn5dSvs3fYBefAe6o\nqk/0pA2sbi/WPi/Hv/Mw8+49rhdrnwdpLi2K3wA2pHmv+j7Al6rq2iQ3AlemeQvjvTR3g1BVdyS5\nkua+48do3mI5uRfnsesthJv6ujfL3MTEvczUSzIxMZATjb1akpOA1wO3tdfgiuYe/4uwbks7zRoo\nquo24IRp0h8Epn1TY1X9MfDH06R/D/g38y+m1H9V9S1g3xlmW7el1rJ+Mnuq8fHxZZf3cst3uVqO\nf+e9dZ/HxtaQZOdn330P3Dk9NramL2Wcr1mfzF4MSWoplqsfEhjUrjXd4zNtPAPvx9xbJKEGdNFv\nlnxHtl4vd/08rnc/jnu/z3wcD7Je26KQJHUyUEiSOhkoJEmdDBSSpE4GCklSJwOFJKmTgUKS1MlA\nIUnqZKCQJHUyUEiSOhkoJEmdDBSSpE4GCklSJwOFJKmTgUKS1MlAIUnqZKCQJHUyUEiSOhkoJEmd\nDBSSpE4GCklSJwOFJKmTgUKS1MlAIUnqZKCQJHUyUEiSOs0aKJKsSnJ9ktuT3JbkP7Xp65JsT/L9\n9nNazzoXJrk7ybYkp/Skn5Bka5K7klw8mF2SJPVTqqp7gWQMGKuqW5McBHwPOAP4Q+CfqupjU5Y/\nBrgceCmwCrgOeEFVVZLvAO+oqpuTXAt8oqq+Pk2eNVu59lYJDGrXkgAzbTyM6m86X0moqixCviNb\nr5e7fh7Xux/Hvd9nPo4HWa9nbVFU1Y6qurWdfgTYBhwxWbZpVjkDuKKqHq+qe4C7gbVtwHlmVd3c\nLncZ8JoFll+SNGDzukaRZA1wPPCdNukdSW5N8ukkh7RpRwD396z2QJt2BLC9J307TwUcSdISNedA\n0XY7XQWc37YsLgGeX1XHAzuAjw6miJKkxbRiLgslWUETJD5fVVcDVNXPexb5S+CadvoB4Lk981a1\naTOlT2v9+vU7p8fHxxkfH59LUaXdbNmyhS1btix2MaS91qwXswGSXAb8oqre3ZM2VlU72ul3AS+t\nqtclORb4InAiTdfSN3jqYvaNwDuBm4GvAn9WVZumyW9kL/p5MXvxeTFb/TbqF7NnbVEkOQl4PXBb\nkltoSvw+4HVJjgeeBO4B3gZQVXckuRK4A3gMeHvP0XEe8DngAODa6YKEJGlpmVOLYthG+czLFsXi\ns0Whfhv1FoVPZkuSOhkoJEmdDBSSpE4GCklSJwOFJKmTgUKS1MlAIUnqZKCQJHUyUEiSOhkoJEmd\nDBRatpJcmmQiydaeNIf4laYwUGg5+yxw6jTpH6uqE9rPJtg5xO+ZwDHA6cAlaV7KA/Ap4C1VdTRw\ndJLptinttQwUWraq6pvAQ9PMcohfqYeBQtqdQ/xKPeY0wp20jFwCfLAdaOtDNEP8vrVfG3fkRvXL\nMEdudDyKIXM8isXX+97+JKuBa6rqxdMst3NekguAqqqL2nmbgHXAvcANVXVMm34W8PKqOnea7Y1s\nvV7uHI9CGm2h55pEe81h0h8AP2inNwJnJdkvyZHAUcBN7XDADydZ217cPhu4ejhFl4bDrictW0ku\nB8aBw5LcR9NCeIVD/Eq7sutpyOx6WnwOhap+s+tJkrSsGSgkSZ0MFJKkTgYKSVInA4UkqZOBQpLU\nyUAhSepkoJAkdTJQSJI6GSgkSZ1mDRRJViW5PsntSW5L8s42/dAkm5PcmeTrPe/td8hISRohc2lR\nPA68u6qOA34bOC/Ji4ALgOuq6oXA9cCFAEmOxSEjJWlkzBooqmpHVd3aTj8CbANW0QwNuaFdbANP\nDf/4ahwyUpJGxryuUSRZAxwP3AisrKoJaIIJcHi7mENGStIImfN4FEkOAq4Czq+qR5JMfddtX9+f\n7JCR6pdhDhkpjaI5jUeRZAXwt8DXquoTbdo2YLyqJtpupRuq6hiHjOzmeBSLz/Eo1G+OR9H4DHDH\nZJBobQTe2E6fw1PDPzpkpCSNkFlbFElOAv4OuI0mrBXwPuAm4ErguTSthTOr6h/bdS4E3kIzZOT5\nVbW5Tf8tdh0y8vwZ8hzZMy9bFIvPFoX6bdRbFA6FOmQGisVnoFC/jXqg8MlsSVInA4UkqZOBQpLU\nyUAhSepkoJAkdTJQSJI6GSgkSZ0MFJKkTgYKSVInA4UkqZOBQpLUyUAhSepkoJAkdTJQSJI6GSgk\nSZ0MFJKkTgYKSVInA4UkqZOBQpLUyUAhSepkoJAkdTJQSJI6GSgkSZ0MFJKkTgYKSVInA4UkqZOB\nQpLUyUAhSeo0a6BIcmmSiSRbe9LWJdme5Pvt57SeeRcmuTvJtiSn9KSfkGRrkruSXNz/XZHmZ4a6\nfWiSzUnuTPL1JIf0zLNua1maS4vis8Cp06R/rKpOaD+bAJIcA5wJHAOcDlySJO3ynwLeUlVHA0cn\nmW6b0jBNV7cvAK6rqhcC1wMXAiQ5Fuu2lqlZA0VVfRN4aJpZmSbtDOCKqnq8qu4B7gbWJhkDnllV\nN7fLXQa8Zs+KLPXHDHX7DGBDO72Bp+rpq7Fua5layDWKdyS5Ncmne5rnRwD39yzzQJt2BLC9J317\nmyYtNYdX1QRAVe0ADm/Trdtatlbs4XqXAB+sqkryIeCjwFv7VyxYv379zunx8XHGx8f7uXktI1u2\nbGHLli17unr1sSjWa/XNAuv1vKRq9uMgyWrgmqp6cde8JBcAVVUXtfM2AeuAe4EbquqYNv0s4OVV\nde4M+dVcyrU3SmBQu9Z0mc+08TCqv+l8JaGq0k7vUreTbAPGq2qi7Va6oaqO6UfdHuV6vdz187je\n/Tju/T7zcdxbr/ttrl1PoeeaRHsATfoD4Aft9EbgrCT7JTkSOAq4qW3CP5xkbXsB8Gzg6gWXfhka\nG1tDkmk/2iO71G2aOvzGdvocnqqn1m0tW7N2PSW5HBgHDktyH81Z1CuSHA88CdwDvA2gqu5IciVw\nB/AY8PaeU6jzgM8BBwDXTt4ppfmZmLiXrlaD5m6Guv0R4MtJ3kzTWjgT+le3x8bWsGPHPQPZH2lQ\n5tT1NGyj3ERfaBN1tu4lu55mN8gm+iz5FuDfYQTZ9SRJWtYMFJKkTgYKSVInA4UkqZOBQpLUyUAh\nSepkoJAkdTJQSJI6GSgkSZ0MFJKkTgYKSVInA4UkqZOBQpLUyUAhSepkoJAkdTJQSJI6GSgkSZ0M\nFJKkTgYKSVInA4UkqZOBQpLUyUAhSepkoJAkdTJQSJI6GSgkSZ0MFJKkTgYKSVInA4UkqdOsgSLJ\npUkmkmztSTs0yeYkdyb5epJDeuZdmOTuJNuSnNKTfkKSrUnuSnJx/3dFkjQIc2lRfBY4dUraBcB1\nVfVC4HrgQoAkxwJnAscApwOXJEm7zqeAt1TV0cDRSaZuU5K0BM0aKKrqm8BDU5LPADa00xuA17TT\nrwauqKrHq+oe4G5gbZIx4JlVdXO73GU960iSlrA9vUZxeFVNAFTVDuDwNv0I4P6e5R5o044Atvek\nb2/TJElL3Io+baf6tJ2d1q9fv3N6fHyc8fHxfmehZWLLli1s2bJlsYsh7bVSNfu/8UlWA9dU1Yvb\n79uA8aqaaLuVbqiqY5JcAFRVXdQutwlYB9w7uUybfhbw8qo6d4b8ai7l2hslsJBday75zLSB7nmj\n+pvOVxKqKrMv2fd8C/DvMIIWelzvuq2px3Hv95mP40HW67l2PaX9TNoIvLGdPge4uif9rCT7JTkS\nOAq4qe2eejjJ2vbi9tk960yfYcLY2Jo5Fk+SNCizdj0luRwYBw5Lch9NC+EjwJeTvJmmtXAmQFXd\nkeRK4A7gMeDtPU2D84DPAQcA11bVpu6ci4mJoZ/0SZKmmFPX07A1TfRiFLtL7HpafHY9qd/sepIk\nLWsGCklSJwOFJKmTgUKS1MlAIUnqZKCQpEU2NraGJDz1DtWlxdtjh8zbYxeft8eq3/p7XHt7rCRp\nL2OgkCR1MlBIkjoZKKRpJLknyd8nuSXJTW3avIcAlkaBgUKa3pM0r9J/SVWtbdP2ZAhgaa9noJCm\nF3Y/PuY1BPAwCikNg4FCml4B30hyc5K3tmkr5zkEsDQS+jUUqjRqTqqqnyb5dWBzkjvZ/SGVPbpz\nfnKYX4f41UIMc4hfH7gbMh+4W3zzfTApyTrgEeCtzGMI4Kr6zpTt+MDdiBreA3cHAI/unLNy5Wp2\n7Lhn5zZ84E4akiTPSHJQO30gcApwG/McAniohdYy8ShN0Gg+ExP3DiVXu56k3a0E/qZtAawAvlhV\nm5N8F7hynkMAS3s9u56GzK6nxee7ntRvw3zX09R5k/XJridJ0qIxUEiSOhkoJEmdDBSSpE4GCklS\nJwOFJKmTgUKS1MlAIUnqZKCQJHVaUKBwFDBJGn0LbVE4CpgkjbiFBgpHAZOkEbfQQOEoYJI04hb6\nmvGBjQImSVoaFhQoquqn7f9/nuQrNF1JE0lW9owC9rN28QeA5/asvqpNm8H65r/r1ztkpBZkmENG\nSqNoj8ejSPIMYJ+qeqQdBWwz8AHgZODBqrooyXuBQ6vqgvZi9heBE2m6nL4BvGC6AV4cj6Jrfcej\nWCjHo1C/jfp4FAtpUTgKmCQtA45wN2S2KBafLQr126i3KHwyW5LUyUAhSepkoJAkdTJQSJI6GSgk\nSZ0MFJKkTgYKSVInA4UkqZOBQpLUyUAhSepkoJAkdTJQSJI6GSgkSZ0MFJKkTgaKJWhsbA1Jpv1I\n0rA5HsWQzeW99QsZc8LxKGbneBTqN8ejkCQtawYKSVInA4UkqZOBQpL6pPdGlLGxNYtdnL7xYvaQ\neTF78XkxW/02eVxPvSg917+1F7OXselucwVG7mxD0mizRTFA3S2DA4BHO9bud4ti+vxWrlzNjh33\ndJRj9NiiUL/ZotCAPErzB5/uM7z8JibuHVB+kmYytbdhqTNQSNJA7L9LMOjtbm5O0AZ9ctg/Kxa7\nAJI0miZb8Y2JiaXfcpiJLQpJUicDhSSp09ADRZLTkvwwyV1J3jvs/KVBsW5rVA01UCTZB/jvwKnA\nccBrk7xomGXosmXLlsXMfRHzHr7F/a37z7q9tPJd3Lxnynf/AdzlNIht7m7YLYq1wN1VdW9VPQZc\nAZwx5DLMaE8qVv/Gjph/3nuzUQsUjGDd3pvzXdy8Z8q39xb1fhnENnc37EBxBHB/z/ftbdpea/fb\n3PaeW97UVyNXt6VJXszu8ad/evGMrQNfuSE1praie4+NqfM+8IEP75zed98Dd5nX9b1rnsfi8A31\nFR5JXgasr6rT2u8XAFVVF01ZztNxDVS/X3Uwl7ptvdagDeoVHsMOFPsCdwInAz8FbgJeW1XbhlYI\naQCs2xplQ30yu6qeSPIOYDNNt9elHkgaBdZtjbIl+fZYSdLSsaQuZvf7gaUkq5Jcn+T2JLcleWeb\nfmiSzUnuTPL1JIf0rHNhkruTbEtySk/6CUm2tmW7eI7575Pk+0k2DjnfQ5J8ud3W7UlOHEbeSd6V\n5AftOl9Mst+g8k1yaZKJJFt70vqWV1v2K9p1vp3kebP/8p2/jXXbur331u2qWhIfmqD1I2A18DTg\nVuBFC9zmGHB8O30QTR/yi4CLgD9q098LfKSdPha4haZLbk1bnslW13eAl7bT1wKnziH/dwFfADa2\n34eV7+eAN7XTK4BDBp038Bzgx8B+7fcvAecMKl/g3wLHA1t70vqWF3AucEk7/YfAFdZt6/ZyrduL\nHiB6foiXAV/r+X4B8N4+5/EV4JXAD4GVPQfcD6fLE/gacGK7zB096WcBn5olr1XAN4BxnjqYhpHv\nwcA/TJM+0Lzbg+le4NC20m4c9G9N8w/v1kHsI7AJOLGd3hf4uXXbur1c6/ZS6noa6ANLSdbQROkb\naX7wCYCq2gEcPkMZHmjTjmjLM5+yfRz4L+z65N0w8j0S+EWSz7ZdA3+R5BmDzruqfgJ8FLiv3cbD\nVXXdkPZ50uF9zGvnOlX1BPCPSZ41x3JMZd3uT77W7f7kNe+6vZQCxcAkOQi4Cji/qh5h98emp35f\naH7/Hpioqltpxi6cSV/zba0ATgA+WVUnAP9Mc9Yx6H3+NZpXVqymOQM7MMnrB53vLPqZ15IcTMC6\nbd3ug1nr9lIKFA8AvRdVVrVpC5JkBc2B9PmqurpNnkiysp0/BvyspwzPnaYMM6XP5CTg1Ul+DPwP\n4PeSfB7YMeB8oTlzuL+qvtt+/yuag2vQ+/xK4MdV9WB7lvI3wO8MId9e/cxr57w0z0gcXFUPzrEc\nU1m3F54vWLcXrW4vpUBxM3BUktVJ9qPpU9vYh+1+hqav7hM9aRuBN7bT5wBX96Sf1d4VcCRwFHBT\n29R7OMnaJAHO7llnN1X1vqp6XlU9v92P66vqDcA1g8y3zXsCuD/J0W3SycDtg95nmmb5y5Ic0C5/\nMnDHgPMNu54N9TOvje02AP4jcH3Hvs/Gum3d3rvr9mwXMYb5AU6juXvjbuCCPmzvJOAJmrtMbgG+\n3+bxLOC6Nq/NwK/1rHMhzZ0D24BTetJ/C7itLdsn5lGGl/PUBb+h5Av8Js0/TrcCf01zZ8jA8wbW\ntdvYCmygucNnIPkClwM/oXl95n3Am2guNvYlL2B/4Mo2/UZgjXXbur1c67YP3EmSOi2lridJ0hJk\noJAkdTJQSJI6GSgkSZ0MFJKkTgYKSVInA4UkqZOBQpLU6f8Dme50rcC5WIAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x185305fd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"f, axes = plt.subplots(1, 2)\n",
"axes[0].hist(result[:,:,0].flatten(), bins=100);\n",
"axes[0].set_xlim(0)\n",
"axes[0].axvline(result[:,:,0].flatten().mean())\n",
"axes[0].set_title('Channel of line 1')\n",
"axes[1].hist(result[:,:,1].flatten(), bins=100);\n",
"axes[1].axvline(result[:,:,1].flatten().mean())\n",
"axes[1].set_title('Channel of line 2')\n",
"axes[1].set_xlim(0)"
]
},
{
"cell_type": "code",
"execution_count": 607,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"gain_offset = calculate_gain_and_offset(result)"
]
},
{
"cell_type": "code",
"execution_count": 583,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"m = np.clip((80.9 - 30.9) / (result[:,:,1] - result[:,:,0]), 1e-4, 2)\n",
"offset = 30.9 - m * result[:,:,0]"
]
},
{
"cell_type": "code",
"execution_count": 609,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0.31483410500574482"
]
},
"execution_count": 609,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"gain_offset[:,:,1].mean()"
]
},
{
"cell_type": "code",
"execution_count": 617,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(0, 0.05)"
]
},
"execution_count": 617,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEKCAYAAAD9xUlFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH7FJREFUeJzt3X+wXGWd5/H3J0R+hIQYRRJNgIASCKgb4hpUUK8lv90B\n1pliorMCgqPDj4WVXSUw6yaoVRinBMdyoHaEgQRhIFLDEjSGkEourgyECAlEkkmyQwWSQK4iyBjD\nKCHf/eM8fdK5P7tvn+57b5/Pq6rrnn76nH7O6X76fs/znOc8jyICMzMzgFFDvQNmZjZ8OCiYmVnO\nQcHMzHIOCmZmlnNQMDOznIOCmZnlHBSGMUkHSnpQ0m8l3ZvSvinp15JeHOr9M2sVSYdL+jdJGup9\naXcOCsPbnwHvACZExJ9LOhy4GjguIt412DeVdKGk/1vUTprVStJsSY9L2ilph6THJF060HYRsTUi\nDgnfWNV0DgrD25HApqofwpHAyxHxmwbfV4B/XNZSkv47cBMwH5gYEZOAvwI+IuktQ7pzlnNQGAYk\nHSdppaRXJa2T9CeS5gH/C5idqs1fBJYB70rP/0HSAZJ+KOnltO0qSe9I73mIpFslvShpq6RvKHMc\ncAvwYUm/k/TKkB24lYakQ4DrgUsj4v6I+D1ARDwdEZ+LiDcknS3pKUmvSXpe0tyq7Y+UtEfSqPR8\npaSvS/p5+j0slfS2oTm69jJ6qHeg7CSNBh4EbgVOAz4KPAB8gOxs/t0RcUFadyNwZ0QckZ5/ERgH\nTAb+CMwAXk9vvQB4CTgaGAv8GHghIn4g6a+ASyLiYy05SDP4MLA/sLifdXYCn4uIZyW9F3hY0pqI\nqGzTvXb7GeBMYBuwFPgfwHXF7nb5uKYw9D4EHBwR8yNid0SsJAsSn61h2zeAtwPTIrMmInZKOgw4\nC/hyRPx7RLwMfJfsR2Q2FA4la/rcU0mQ9Giq4e6SdEpE/CwingWIiF8C9wAf7+c9b4+If42IPwCL\nyE6KrEGuKQy9dwFbu6W9kNIH6mG0EJgC3CNpPPBD4K/Jrj28BXgpddZQerxQ3G6b1eU3wKGSRlUC\nQ0ScDCDpBWCUpFnAt4D3ktUq9gd+1M977qha3kVWI7YGuaYw9F4EDu+WdgSwfaANI+LNiPhGRJwA\nfAT4E+ACsiDz78DbI+JtETEhIt4aEe+vbFrc7pvV5DHgD8C5vbxW6WZ6N/B/gMkR8Vbgf1e9Zi3i\noDD0VgG7JH1V0mhJHcB/Iqs690tSh6T3potvO8mak96MiB1kF6VvkjQuXWA+WlLlGkIXMMU9PqxV\nIuI14OvAzZL+VNLYVC5nAGPSamOBV9NF51n0bEJ1gGgBB4UhFhFvkJ3hnw28DHyf7GLbpho2nwTc\nB7wGPAusJGtCgqzGsD+wHniFrBo+Kb22Iq2/Q9KvijkSs/5FxN+Q3WfzVbKmnx1kPeG+CvwzcBnw\nDUmvAf8TuLf7W/SxbAXSQPeCSJpG9uUEWaQ+GvgacGdKPxLYApyfzgaQdC1wMbAbuCoilqX0mcAd\nwIHAkoj4b4UfkVkdUi3rSWBrRJyTukH+JVAJltdFxNK0rsu1tb0BawoRsSkiToyImWTdJH8P3A/M\nAZZHxLFkZ57XAkg6HjgfmE7WA+bmqlvTbyHrCjkNmCbpjKIPyKxOV5HVmqrdGBEz06MSEKbjcm0l\nUG/z0anAv0bEVrILRgtS+gLgvLR8DnBP6l65BdgMzJI0CRgXEavTegurtjFrOUlTyJrtbu3+Ui+r\nn4vLtZVAvUHhz8l6CEB2m3oXQLqweVhKn8y+XSy3p7TJZDeZVGxLaWZD5SbgK/Rsn75C0tp0R/j4\nlOZybaVQc1BIPVXOYW+/4e4/JF/4sRFD0qeArohYy741g5uBoyNiBtmF0O8Mxf6ZDZV6bl47C3gy\n3R0L0CVpYkR0pSp05cLcdvbtdz8lpfWV3oMkBxhrthuAcySdDRwEjJO0sDKkSPIDsrvLweXaRoiI\naKjrbj3NR58B/rHq+WLgorR8Idl4PZX02ZL2l3QU8B7gidTE9JqkWekC3QVV2/QQEU19zJ07ty3y\nGEw+0D7HMphHKl/XRcQREXE0MBtYEREXpBOcik8DvxxJ5Xqov7/hkm8Zjzm5vq+yV6uaagqSxpBd\nZP5iVfJ8YJGki4HnyXpmEBHrJS0i6x//BnBZ7N3jy9m3697SRg/ArGDfTjdU7SHrav0lcLm28qgp\nKETELrLJXqrTXiELFL2tfwNZ9bx7+pPA++rfTbPmiYhHgEfS8gX9rOdybW2vtHc0d3R0tEUercqn\nnY6ljIbqcx3K77OMxwx0NvoGA97RPBQkxXDcr3YhQZk/XklEgxfjBpmvy7U1TVHlurQ1BTMz68lB\nwczMcg4KZmaWc1AwM7Ocg4KZmeUcFMzMLOegYGZmOQcFMzPLOSiYmVnOQcHMzHIOCmZmlnNQMDOz\nnIOCmZnlHBRKShKTJk0d6t0ws2HGQaG0gq6u54d6J4acpFGSnpK0OD2fIGmZpI2SHpI0vmrdayVt\nlrRB0ulV6TMlPSNpk6TvDsVxmBXFQcHK7iqyKTYr5gDLI+JYYAVwLYCk48mmnJ0OnAXcnOZkBrgF\nuCQipgHTJJ3Rqp03K5qDgpWWpCnA2cCtVcnnAgvS8gLgvLR8DnBPROyOiC3AZmCWpEnAuIhYndZb\nWLXNsDdp0lQk9Xi4abG8apqj2axN3QR8BRhflTYxIroAImKHpMNS+mTgsar1tqe03cC2qvRtKX1E\nyJoQe84G19XV8onpbJhwULBSkvQpoCsi1krq6GfVQufPnDdvXr7c0dEx1PP52gjW2dlJZ2dn4e/r\nOZpLKG8JR5Txc06XAm4A/gvZmf5BwDjgfuA/Ah0R0ZWahlZGxHRJc4CIiPnpPZYCc4HnK+uk9NnA\nxyPi0l7yHXblOvssetuncpaNkcxzNJs1ICKui4gjIuJoYDawIiI+BzwIXJRWuxB4IC0vBmZL2l/S\nUcB7gCciYgfwmqRZ6cLzBVXbmI04NQUFSeMl/Sh1xXtW0knuumdt6lvAaZI2Ap9Mz4mI9cAisp5K\nS4DLqk77LwduAzYBmyNiacv32qwgNTUfSboDeCQibpc0GjgYuA74TUR8W9I1wISImJO67t0FfBCY\nAiwHjomIkLQKuCIiVktaAvxtRDzUS37DrprdTtx8VEw1exD5Drty7eaj9tGy5iNJhwAfjYjbAVKX\nvNcoWdc9M7MyqKX56CjgZUm3pzs//17SGLp13QOqu+5trdq+0nVvMiO4656ZWRnU0iV1NDATuDwi\nfiHpJrK7PrvXLd11z4alZnXdM2tHA15TkDQReCz10kDSKWRB4d2UqOteO/E1BV9TqPA1hfbRsmsK\nqYloq6RpKemTwLNkXfQuSmnuumdm1gZqvaP5SuAuSW8BngM+D+wHLJJ0MVkt4HzIuu5JqnTde4Oe\nXffuAA4ElrjrnpnZ8OI7mkvIzUduPqpw81H78B3NZmZWOAcFMzPLOSiYmVnOQcHMzHIOCmZmlnNQ\nMDOznIOCmZnlHBTMzCznoGBmZjkHBSstSQdIWiVpjaR1kuam9LmStqWh4p+SdGbVNp5V0Nqah7ko\nIQ9zsXc4AEljImKXpP2AR8nG+ToL+F1E3Nhtu+nA3QxyVsHhWK49zEX78DAXZgWIiF1p8QCyASIr\n/wl7+3Gdi2cVtDbnoGClJmmUpDXADuDhqn/sV0haK+lWSeNTmmcVtLZX69DZZm0pIvYAJ6a5yO+X\ndDxwM/D11Cz0TeA7wBeKyM8zClpRmjWjoK8plJCvKfTe9irpa8Dvq68lSDoSeDAi3t/orILDsVz7\nmkL78DUFswZJOrTSNCTpIOA04F/SNYKKTwO/TMueVdDanpuPrMzeCSyQNIrsBOneiFgiaaGkGcAe\nYAvwJfCsglYObj4qITcfeea1CjcftQ83H5mZWeEcFMzMLOegYGZmOQcFMzPLOSiYmVmupqAgaYuk\np9Nokk+ktAmSlknaKOmhqqEAPJKkmdkIVWtNYQ/QEREnRsSslDYHWB4RxwIrgGsB0jAB5wPTyUab\nvDnd0ANwC3BJREwDpkk6o6DjMDOzAtQaFNTLuucCC9LyAvaOCnkOHknSzGxEqjUoBPCwpNWSKgOD\nTYyILoB0m/9hKd0jSZqZjVC1DnNxckS8JOkdwDJJG+l5G2Shtz96NEkrSrNGkzRrR3UPc5GmLNxJ\nNpRwR0R0paahlRExvdGRJNNrw244gHbiYS48zEWFh7loHy0b5kLSGElj0/LBwOnAOrIRIy9Kq13I\n3lEhPZKkmdkIVUvz0USyyUcirX9XRCyT9AtgkaSLyWoB54NHkjQzG8k8SmoJufnIzUcVbj5qHx4l\n1czMCuegYGZmOQcFKy1JB0halYZvWZd61nkIFys1BwUrrYj4A/CJiDgRmAGcJWkWHsLFSsxBwUot\nInalxQPIetcFHsLFSsxBwUpN0ihJa4AdwMPpH7uHcLHSqnWYC7O2FBF7gBMlHUJ2P84JNHEIFw/f\nYkVp1vAtvk+hhHyfQu/9uSV9DdhFk4ZwGY7l2vcptA/fp2DWIEmHVnoWSToIOA3YgIdwsRJz85GV\n2TuBBZJGkZ0g3RsRSyQ9jodwsZJy81EJufnIw1xUuPmofbj5yMzMCuegYGZmOQcFMzPLOSiYmVnO\nQcHMzHIOCmZmlnNQMDOznIOCmZnlHBTMzCznoGBmZjkHBTMzyzkomJlZruagkGaoekrS4vTck5ub\nmbWZemoKV5ENGVzhyc3NzNpMTUFB0hTgbODWqmRPbm5m1mZqrSncBHyFfQde9+TmNqJJmiJphaRn\nJa2T9F9T+lxJ21Jz6VOSzqzaxk2j1tYGnHlN0qeArohYK6mjn1ULnZHDE5xbUfqZ4Hw3cHUq22OB\nJyU9nF67MSJurF5Z0nT2No1OAZZLOibNnFNpGl0taYmkMyLioWYdk1mz1DId58nAOZLOBg4Cxkm6\nE9ghaWLV5Oa/SutvBw6v2n5KSusrvVfVQcGsEd1PKq6//nogr+HuSMs7JW1gb+21txmsziU1jQJb\nJFWaRp+n96ZRBwUbcQZsPoqI6yLiiIg4GpgNrIiIzwEP4snNrU1ImgrMAFalpCskrZV0a1XPOjeN\nWttr5D6FbwGnSdoIfDI9JyLWA5XJzZfQc3Lz24BNwGZPbm7DQWo6ug+4KiJ2AjcDR0fEDLKaxHeG\ncv/MWqmW5qNcRDwCPJKWXwFO7WO9G4Abekl/Enhf/btp1hySRpMFhDsj4gGAiPh11So/IKsVQwFN\no75WZkXp51pZQ7T3JH74kBTDcb/aRX7XCKKMn7MkIkJpeSHwckRcXfX6pNTciaQvAx+MiM+me3Du\nAk4iax56GDgmIkLS48CVwGrgJ8D3uteEh2O5zlpye9uncpaNkay6XDeirpqCWTuRdDLwF8A6SWvI\n/jteB3xW0gxgD7AF+BJkTaOSKk2jb9CzafQO4EBgiZtGbaRyTaGEXFMo5oxqEPkOu3LtmkL7KKpc\ne0A8MzPLOSiYmVnOQcHMzHIOCmZmlnNQMDOznIOCmZnlHBTMzCznoGBmZjkHBTMzyzkomJlZzkHB\nzMxyDgpmZpZzUDAzs5yDgpmZ5RwUzMws56BgZmY5BwUrLUlTJK2Q9KykdZKuTOkTJC2TtFHSQ5LG\nV21zraTNkjZIOr0qfaakZyRtkvTdoTgesyI4KFiZ7QaujogTgA8Dl0s6DpgDLI+IY4EVwLUAaY7m\n84HpwFnAzVI+j90twCURMQ2YJumM1h6KWTEcFKy0ImJHRKxNyzuBDcAU4FxgQVptAXBeWj4HuCci\ndkfEFmAzMEvSJGBcRKxO6y2s2sZsRHFQMAMkTQVmAI8DEyOiC7LAARyWVpsMbK3abHtKmwxsq0rf\nltLMRpwBg4KkAyStkrQmtbvOTelud7W2IGkscB9wVaoxdJ+x3jPYW2mMHmiFiPiDpE9ExC5J+wGP\nSvop8Kdk7a7flnQNWbvrnG7trlOA5ZKOiYhgb7vraklLJJ0REQ817ejMBiBpNFlAuDMiHkjJXZIm\nRkRXahr6VUrfDhxetfmUlNZXeg/z5s3Llzs6Oujo6CjgKKyMOjs76ezsLPx9lf2vrnFlaQzwM+BS\n4E7g41U/nM6IOE7SHCAiYn7a5qfAPOB5YEVEHJ/SZ6ftL+0ln6hnv6w++aVRRBk/Z0lEhNLyQuDl\niLi66vX5wCsRMT+d8EyIiMoJz13ASWTNQw8Dx0RESHocuBJYDfwE+F5ELO2W77Ar19l18t72qZxl\nYySrLteNGLCmkDIbBTwJvBv4u3Smv0+7q6TqdtfHqjavtLvuxu2uNoxIOhn4C2CdpDVk/x2vA+YD\niyRdTHYycz5ARKyXtAhYD7wBXFb1X/5y4A7gQGBJ94BgNlLUFBQiYg9woqRDgPslnUCT211dzbai\n9FXNjohHgf362OzU3hIj4gbghl7SnwTeN/i9NBse6mo+ApD0NWAX8AWgo6r5aGVETO+l+WgpMJfs\njGtlRExP6W4+GiJuPiqmmj2IfIdduXbzUfsoqlzX0vvo0ErPIkkHAaeR9edeDFyUVrsQqFykWwzM\nlrS/pKOA9wBPpK59r0malW74uaBqGzMzGwZqaT56J7AgXVcYBdwbEUvShTW3u5qZtZG6m49aYThW\ns9uJm4/cfFTh5qP20bLmIzMzKw8HBTMzyzkomJlZzkHBzMxyDgpmZpZzUDAzs5yDgpmZ5RwUzMws\n56BgZmY5BwUzM8s5KJiZWc5BwczMcg4KVlqSbpPUJemZqrS5krZJeio9zqx67VpJmyVtkHR6VfpM\nSc9I2iTpu60+DrMiOShYmd0OnNFL+o0RMTM9lgJImk42PPx04Czg5jQvCMAtwCURMQ2YJqm39zQb\nERwUrLQi4ufAq7281Nvww+cC90TE7ojYAmwGZqVZB8dFxOq03kLgvGbsr1krOCiY9XSFpLWSbq3M\nOghMBrZWrbM9pU0GtlWlb0tpZiNSLTOvmZXJzcDXIyIkfRP4Dtl85IWYN29evtzR0UFHR0dRb20l\n09nZSWdnZ+Hv65nXSsgzr+2doUrSkcCDEfH+XtbLX5M0B4iImJ9eWwrMJZuKdmVETE/ps4GPR8Sl\nvbzfsCvXnnmtfXjmNbNiiKprCOkaQcWngV+m5cXAbEn7SzoKeA/wRETsAF6TNCtdeL4AeKA1u25W\nPDcfWWlJuhvoAN4u6QWyM/9PSJoB7AG2AF8CiIj1khYB64E3gMuqTvsvB+4ADgSWVHosmY1Ebj4q\nITcfFVPNHkS+w65cu/mofbj5yMzMCuegYGZmuQGDgqQpklZIelbSOklXpvQJkpZJ2ijpoar+3B4O\nwMxshKqlprAbuDoiTgA+DFwu6ThgDrA8Io4FVgDXAkg6Hg8HYGY2Ig0YFCJiR0SsTcs7gQ3AFLLb\n/hek1Raw99b+c/BwAGZmI1Jd1xQkTQVmAI8DEyOiC7LAARyWVvNwAGZmI1TN9ylIGgvcB1wVETsl\nde+vVmj/NQ8HYEVp1nAAZu2opvsUJI0Gfgz8NCL+NqVtADoiois1Da2MiOntOhxAO/F9Cr5PocL3\nKbSPVt+n8A/A+kpASBYDF6XlC9l7a7+HAzAzG6EGrClIOhn4GbCO7JQigOuAJ4BFwOFktYDzI+K3\naZtrgUvIhgO4KiKWpfQPsO9wAFf1keewO6NqJ64puKZQ4ZpC+yiqXHuYixJyUHBQqHBQaB8e5sLM\nzArnoGBmZjkHBTMzyzkomJlZzkHBzMxyDgpWWpJuk9Ql6ZmqNI/+a6XmoGBldjvQfaRej/5rpeag\nYKUVET8HXu2W7NF/rdQcFMz2dZhH/7Uyq3mUVLOS8ui/Niw1a/RfD3NRQh7mYu9wAJKOBB6MiPen\n56Ua/dfDXLQPD3NhVgylR4VH/7VSc/ORlZaku4EO4O2SXiA78/8W8CNJF5NG/wWIiPWSFgHryUb/\nvazqtP9y9h39d2krj8OsSG4+KiE3H3mU1Ao3H7UPNx+ZWc0mTZqKpB4Ps+5cUygh1xTKV1Por0bg\nmkJ7cE3BzMwK56BgZmY5BwUzM8s5KJiZWc5BwczMcg4KZmaWc1AwM7PcgEHBs1OZmZVHLTUFz05l\nZlYSAwYFz05lZlYeg72m4NmpzMzaUFFDZxc+SIpnqLKiNGuGKrN2VNOAeK2cnSq97gHxmsgD4nlA\nvKpX+kwvY9kYyVo9IJ5npzIzK4FauqTeDfwzWY+hFyR9nmx2qtMkbQQ+mZ4TEeuByuxUS+g5O9Vt\nwCZgs2ensuFM0hZJT0taI+mJlFZ3V2yzkcbzKZSQm48GrmZLeg74QES8WpU2H/hNRHxb0jXAhIiY\nk7pi3wV8EJgCLAeO6V6I3XxkzeT5FMyaS/T8fdTVFbsVO2lWNAcFs94F8LCk1ZK+kNIm1tkV22zE\nKapLqlm7OTkiXpL0DmBZun7WvT2l7vYVd7W2ojSrq7WvKZSQrynU1/YqaS6wE/gCdXTFjohV3d7H\n1xSsaXxNwaxJJI2RNDYtHwycDqyjzq7YLd1ps4K4+cisp4nA/ZKC7DdyV0Qsk/QLYJGki8luyDwf\nsq7Ykipdsd9g367YZiOKm49KyM1HvqO56pU+08tYNkYyNx+ZmVnhHBTMzCznoGBmZjkHBTMzyzko\nmJlZzkHBzMxyDgpmZpZzUDAzs5yDgpmZ5RwUzMws57GPzFpo6dKes9COGTOGj33sY0OwN2Y9eeyj\nEvLYR0M39tG4cR9j1KiD9kl//fXHWLXqEWbMmNFwHpMmTaWr6/k+XvXYR+2sqHLtmoJZC/3udwuB\nI/dJGz9+Fn/84x8Lef8sIPT1z99sYL6mYGZmOQcFMzPLtTwoSDpT0r9I2iTpmlbnb9YsLtvWDloa\nFCSNAr4PnAGcAHxG0nGt3IeKZkx4PRR5tCqfdjqWZhhOZXs4Gcrvc6jyHspjltTR6Hu0uqYwC9gc\nEc9HxBvAPcC5Ld4HwP9Ih2MercynCRoq22ed9Z+R1OMxadLUZu1vSzgotFxHo2/Q6qAwGdha9Xxb\nSjMb6Roq26+88iJZr6F9H313LzVrjtJ2Sb3vvvs49dRTOeWUU4Z6V6xExo27GGnMPmmvv76pny0O\nSPMr72vUqDHs2bOr4L0bfL4TJx7Jjh1bmrg/1iotvXlN0oeAeRFxZno+B4iImN9tPd81Y01V9M1r\ntZRtl2trhUbLdquDwn7ARuCTwEvAE8BnImJDy3bCrAlctq1dtLT5KCLelHQFsIzsesZt/tFYO3DZ\ntnYxLMc+MjOzodGy3keSDpC0StIaSeskzU3pEyQtk7RR0kOSxvey7RRJKyQ9m7a9shn5VL3HKElP\nSVrcjDwkjZf0I0kb0jGd1IQ8vizpl5KekXSXpP3rPJY/S9u/KWlmP5/VgDdsNZJHrd99o8eR1u33\nex9g21o+h+9J2ixpraQZ9WxbYL4nVqXfJqlL0jP15NlA3jNSWs2/54Lz7bWMtCLvqtcGVcYa/J63\nSHo6HfcTA2YWES17AGPS3/2Ax8n6ds8HvprSrwG+1ct2k4AZaXksWdvtcUXnU7X9l4EfAoubkQdw\nB/D5tDwaOKTgz+tdwHPA/un5vcAFdR7LscAxwApgZh/bjQL+H9kIb28B1vb1vTSQR83f/WDzqOd7\nH+znAJwF/CQtnwQ8Xu9nWGS+6fkpwAzgmUH8lhs55rp+zwUfc48y0opjbqSMFXDMzwETas2vpfcp\nRESlL9sBZP8Mg+wGnwUpfQFwXi/b7YiItWl5J7CBfvqADzYfyM5igLOBW5txLJIOAT4aEben99kd\nEf9W9HGQFfqDJY0GxgAv1nMsEbExIjbT//CaNd+wNdg86vnuGziOmr/3PtTyOZwLLEz7uQoYL2li\njds2I18i4ufAq/UdauN51/t7Lirf9Ly331StGsq7gTLWUL5kZb/m//UtH+ZC0hpgB/BwRKwGJkZE\nF2T/AIDDBniPqWRnN6ualM9NwFcYoLA0kMdRwMuSbk/VyL+XdFAv6w06j4h4EfgO8AKwHfhtRCyv\n81hqUfMNWw3kUf0eU+nnu28wj5q+9z7U8jn0tU4jN70NJt/tdbx/0/Ou5fdcZL4NlpFGj3mwZazR\nfAN4WNJqSX85UGatrinsiYgTgSnALEkn0PMD6vMDkzQWuA+4Kp1hFJqPpE8BXeksRvR/BjvYYxkN\nzAT+LiJmAruAOQUfx1vJzhyOJGtKGivpszUey0mSju9r3cFqNI9avvvB5lHP916g0k9wUOvvuUit\nKOu9GaIyVnFy+l9zNnC5pH7v2B2SobNTc0kncCbQVVW9mgT8qrdtUjPIfcCdEfFAk/I5GThH0nPA\nPwKfkLSw4Dy2AVsj4hfp+X1kQaLIPE4FnouIVyLiTeCfgI/0l0dVPitTPrXYDhxR9XxKSisyj7q/\n+0HkUff33k0tn8N24PBe1qn7Mywo30Y1lPdgfs9F5FsxmHLYYN6NlLGGjjkiXkp/fw3cT9Yc1bda\nLz40+gAOBcan5YOAn5FFrvnANSm9v4uzC4Ebm51P1ft8nD4uBhVwLI8A09LyXGB+kXmkL30dcCDZ\nGckdwOX1HEvV6yuBD/Sx7X7svQC2P9kFsOlF5lHrd99oHrV87/1sM+DnkL67yoXAD7H3omtNn2HR\n+Va9PhVYV8/xFpF3Ld9pEz7rfstIKz7vwZSxBo95DDA2LR8MPAqc3m9+9X4pg30A7wOeSgf0DPDX\nKf1twHKyHgjLgLem9HcCP07LJwNvpm3XpPc5s+h8av3iGs0D+A/A6rT9P1UKasF5zCW7gPcM2QXp\nt9R5LOeRtVG+TnaH7k/7yOfMtC+bgTlF51Hrd9/ocQz2B9vf5wB8Cfhi1TrfJ/txP01VT6haPsMm\n5Xs3WQeEP5Bdf/p8k/M+sd7fc5HH3FcZadXn3UgZa+CYj6r6nNfVUr5885qZmeU8HaeZmeUcFMzM\nLOegYGZmOQcFMzPLOSiYmVnOQcHMzHIOCmZmlnNQMDOz3P8HXS1Ni9Oj3hUAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x166d35ad0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"f, axes = plt.subplots(1, 2)\n",
"axes[0].hist(gain_offset[:,:,0].flatten(), bins=100);\n",
"#axes[0].set_xlim(0)\n",
"axes[0].axvline(gain_offset[:,:,0].flatten().mean())\n",
"axes[0].set_title('offset')\n",
"axes[1].hist(gain_offset[:,:,1].flatten(), bins=1000);\n",
"axes[1].axvline(gain_offset[:,:,1].flatten().mean())\n",
"axes[1].set_title('Gain')\n",
"axes[1].set_xlim(0, 0.05)"
]
},
{
"cell_type": "code",
"execution_count": 618,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.colorbar.Colorbar at 0x165199f90>"
]
},
"execution_count": 618,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAADcCAYAAACPmTFaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXm8XFWV778/kojMgyhTSKJixJHho4CNygW1BZoGX0+K\nfmzARvt1o/CkX4sir0Ne81pAfYqtPUADAorQ4gD6QMCGq4DMJJAGAiIyhSQa0dAQhgzr/bF3cavq\nnlNn1zlVdc+tWt/P53xy6tTe++y6+dWqfdbeey2ZGY7jOM5wsNFUd8BxHMfpHW7UHcdxhgg36o7j\nOEOEG3XHcZwhwo264zjOEOFG3XEcZ4hwo+44jjMFSJot6VpJ90haIum4nHJfkfRzSYsl7VHU7sze\nd9VxHMdJYB1wgpktlrQ5cIekq81saaOApIOBV5vZayTtA/wLsG+nRn2k7jiOMwWY2QozWxzPnwbu\nA3ZuK3Y4cEEscwuwlaTtO7XrRt1xHGeKkTQP2AO4pe2tnYHHml4vY7Lhb8GNuuM4zhQSXS+XAsfH\nEXsl3Kg7fWdryZR2PDzVfXWcbuhC2yuy6kuaSTDoF5rZZRlFlgG7NL2eHa/l4hOlTt9ZDZyaUO5k\nmNvvvjhOL+lC23l+8HOBe83szJz3LweOBS6RtC/wOzNb2elebtSdgTBrqjvgOH2irLYl7Qd8CFgi\naRFgwEmEwY2Z2VlmdoWkQyQ9CDwDHF3Urht1ZyC40Jxhpay2zexGYEZCuY8Poj+O0xWbTHUHHKdP\n1E3bbtSdgeDuF2dYqZu23ag7A8GF5gwrddN23frjDCl1e0R1nF5RN237OnVnIMxKOLKQtLGkWyQt\nikGPFsTr/1vSXfH6jyTtkFN/K0nflnRfDJy0T88/nDPSlNV2v/CRujMQygrbzJ6XdICZrZE0A7hR\n0pXAGWb2dwCSPgEsAP4qo4kzgSvM7E/jRo9NS3bFcTJxn7ozklQRmpmtiacbx6asbTv1ZsCG9nqS\ntgTeYWZHxXbWAU9V6IrjTKJuRrRu/XGGlCp+R0kbAXcArwa+Zma3xeunAn8O/A44IKPqK4FVks4D\ndgduJ8TXeLZCdxynBfepOyNJFb+jmW0wsz0JcS/2kfT6eP1kM5sDfBP4REbVmcBehB+CvYA1wKd7\n84kcJ+A+dWckyRLaHcCdXbRhZk9Jug44CLi36a2LgCuAU9qqPA48Zma3x9eXAid2cUvHKaRuRrRu\n/XGGlKzRyr60pnA5J6OMpO2AtWa2WtImwHuA0yTtamYPxmLvIyQYaMHMVkp6TNJ8M3sAeBetPwaO\nUxmfKHVGkgp+xx2B86NffSPgkhjk6FJJ8wkTpI8A/x1A0o7A2WZ2aKx/HPBNSbOAh0gIiOQ43VBW\n25LOAQ4FVprZmzPe3xL4BjCHECPmi2b29cJ2zaxklxwnDUn2QEK5+YCZqd/9cZxeUUXbkt4OPA1c\nkGPUPwNsaWafiU+s9wPbx1VcufhI3RkIdXtEdZxeUWEPxg2SOuUQMGCLeL4F8Jsigw5u1J0BUbdl\nX47TK/qo7a8Cl0t6AtgceH9KJTfqzkCYlaK0wjGI49SPPmr7vcAiMztQ0quBayS9uSiPqRt1ZyDM\ndKPuDClZ2r5+PdwwaY9z1xwNfA7AzH4h6ZfAboRNdPn9qXxbx0lgVmF+F8eZnmRp+8AZcGDT69Oe\nya2ueGTxCPBuQryj7QnzrQ8V9cdXvzh9R5LZyxLK/cZXvzjTiyralnQRMAa8DFhJCEr3EmJ+0rg8\n9+uEZb0AnzOzbxXey426028kmb0iodyv3Kg704s6atvdL85gcKU5w0rNtO0BvbpA0ksl/UDS7yRd\nEq+dKunXcdmRk8fMhMOZNki6QtKHp7oftaBm2vavUnf8CfByYBszM0m7ACcAu5jZb8o2KulI4Bgz\ne0eP+lk/Np7qDji9xMwOmeo+1IaaaduNenfMBR6wiYmIucCqKgY9IsLuseHFleYMKzXTtrtfMpC0\nm6TrJP025sX8Q0mnAH8HfEDSU5I+BlwN7BRfnxvzaX5D0qpY9xZJL49tbinp3yQ9ESMH/r0CuwH/\nDLxN0n9JenLKPng/qdkjqhOQtJekOyWtlvTvki6O+V+3jq7GX0n6TTzfuanedZI+Es+PlHS9pM9L\nelLSLyQdNHWfasDUTNtu1NuIeSx/APyI4Go5jpCE4ZvAPwAXm9mWZnYWcDDwRHz9EeBIQoyGnYFt\nCZEDG1l2zgdeAF4F7EkIIXuMmS2N5W4ysy3MbNvBfNIBs3HC4QyUGLnyu8C5BL1+C/hvjbfj9V0I\nUQLXELat57E3Ifzxy4DPkx1JeTipmbbdqE9mX2AzMzvdzNaZ2XUEI//BhLprCaKeb4FFZva0pFcQ\nfgA+aWbPmdkq4MvAEf36ELWjZqMZBwhan2FmXzWz9Wb2PeBWADP7rZl9z8yeN7NnCDsb39mhrUfM\n7Nzomjwf2CHqfvipmbb9qzSZnYDH2q49Gq8XrXC5gJBy7WJJWxFiIX+W4HufBSyXBBO7yB7tXbdr\nju8orSM7Acvarj0GEBOSfJkQf2Rrgl43l6SmOaVmVjROzOxZBaFvDvyqHx2vFTXTthv1yTxBeORs\nZg4hlnHHzQNmth74e+DvJc0Broz1rgSeA16W84UY7klScKXVk+UEV2EzuwAPAn8DvAZ4q5n9WtLu\nhOyDwz+p3y0107a7XyZzC7BG0qckzZQ0RshOcnFRRUljkt4Ys/Q8TXDHrDezFYRJ1S9J2iJOkL5K\nUuNxdiUwO/o4h5OXJhzOoLkJWC/pWEkzJB0OvDW+twVhPugpSdsyOf+r06Bm2naj3oaZrQX+EDgE\nWEWYHPpwzHFZxA6E5MargXuA6wguGIA/J8R1uBd4Evh2LA9wbSy/QtJwPq7OSDgyiCuKbpG0KK5E\nWhCvnyHpPkmLJX0npv7Kqv9JSf8p6W5J35T0kt5/uOlJ1PofAccAvyXMG/0QeB74ErAp4TvwM0Ji\n75bqRc33tLN1pqS2+4XHfnH6jiSzwxLKXZ4dH0PSpma2RtIM4EbCiqQtgWvNbIOk0whBkD7TVm8n\n4AZgNzN7Ie4C/n9mdkH1TzWcSLoZ+GczO3+q+zIdqKJtFeQojWXGCD+ws4Bfm9kBRfeqNFKXdJCk\npZIekHRilbacIafCCgEzWxNPN44lzcx+bGaNiNU3Eyaos5gBbBaXqm5K8WQ3MDralvROSdtH98uR\nwJsIy3mdVMpr+zzCRHQmcbHF14BDzeyNwJ+mdKe0UY9+46/GTr0BOCJupHGcyVRYyytpI0mLCCss\nrjGz29qKfIQwGd2CmT0BfJGwymgZ8Dsz+3FRV0dM268F7iK4Xz4J/LGZrZzaLk0zSmrbzG4g/N3z\n+CDwHTNbFsuvSulOlZH63sDPzeyR6Ju7GDi8QnvOMFNtpL7BzPYkjMb3kfT6xnuSPgusNbOL2utJ\n2pqgybmE5XubS0rZbzAy2jazs81sh7iBbg8z81F6t/Rvnfp8YNu4e/c2JQZQq7IYZ2da13M/Tvgy\ntCDJnfYjQsd40RmTRePLYXzF5Osd2n9K0nXAQcC9ko4iTGgfmFPl3cBDZvYkgKTvAr8HTPoBaMO1\n7bxIYRz0/k2EzgT2Iuh7M+AmSTeZ2YNFlfrOnP13Ye7YXADmjs1hXjxP4SenXM/+p5QLXjhVdafy\n3oOq+/D4IzwyPrF36vqFN3SukLGsa+yV4Wiw8K7JZSRtRxiJr44bYt4DnBZji/wt8E4zez7nro8C\n+0p6KWFFx7uAdtdNJfZvOp8XjywWsoAFLGy5Nk5Ie1OGUas7qHs/HI8GP0lpPEPb48tgvHow7scJ\nAQOfA56T9FNgd8I+glyqGPVlhE05DWYzeXcaAHPH5lYykE79mDc2t+XHudCol1fajsD50c+9EXCJ\nmV0h6eeEJaLXxF26N5vZXyukADvbzA41s1slXQosIuwZWASclXDPZG3/hFNZwMkt1xZyKkDb9ewt\nCFnG3pk65tH6w5xk1DO0PTY3HA0W3pFbu1OO0suAf4yrvjYG9gH+b4nuJHMbsKukuYSdaR9glGKZ\nON1R8hHVzJYQHkHbr78mp/xywjKxxuuF0LXVdG076ZTUtppylEp6lLYcpWa2VNJVwN3AeuAsM7u3\nqN3SRt3M1kv6OGGn5EbAOWZ2X1bZuWNzsi4nMR3rTuW9p/Izd6RmW6k70Y2220fpna4tZEE8XxjP\nH+56lN4Y2c8rKNO4TxZ5dRdmPHWk1k2hSt2pvndHSmrbzAon7c3sC8AXumm375uPJNnJrXtCnCHk\nVH0ud0JJktlJxW3oH6ZX4mlJtqCL8tlumXwjXGSc+81U3n8q3FJZP2oL6azJOmp7Go2fnGmNK80Z\nVmqm7Zp1xxlahlhpjRFtYFbLaK91dL52Up0FLHxxRDp5pFguvlveE0H3TF18uQkX1eCeFEr/vWqm\nbXe/OD2h0P1yenEbOnH6uV+IhrjZkHZrVIvKl3VFlKnX/AOV/2PTW7KMd/ibrJ10vUrbZX7sktwv\nNdN2zX5jnKHFleYMKzXTto/UnZ5QOFI/s7gNHT/9RuoLaB0RN49qGyNDaF39Etwa1Ueh3dBp1F7V\nXTNVa+2z+t3rviSN1GumbTfqTk8oNOqdUhY3yn18uhr1CVdBsx86353SWj7LB99cv/karE02Wq0/\nMOWNXXn3T3/dNhP36f2PSqPNJKNeM20XBvSSdI6klZLubrq2jaSrJd0v6aoYItJx8qlZdhhwbTs9\nombaTvEGnQf8IyGpcoNPAz82szNirOnPxGuOk03NkvNGKmt7YYeJ0sb7gbUZtSe7ZbJH551dI1mT\nm5PvOatDuaw2m0fZk1fB5I2Os5402vuZMqrOG+XnTUinuJC6+fxdjfxrpu1Co25mN8Tt0s0czkQs\no/MJ8XLcqDv51GwyCXqt7WBAm10r7Ya51TWzMKPM2qb3T848zzaaEz765jKtBq657YUtPzZZBiyv\nbnv/J+7ZMNj5RjVlNU1zO1k/Aq3upM59bG2veeloN1vGEqiZtst25xWNQPpmtkLSK3rYJ2cYqZnw\nO+DadrqjZtruVXc6zrb+5JTrXzzvNvSuU0/aQ+8W0iGzUc3pqO39OZmFHEAY0M9jAec3jQTXMjE6\nb3VhTB7Ft5bpNMnZPsptH8ln12t3oaSvvpm8fjzL5TFr0v3z2ytejx/+hp03P2WNwjv1vflanivm\nYVpD7yZRUtspOUpjubcSkn+/38y+W9huyuqX+Ij6g8aNJd0HjJnZSkk7ANeZ2ety6vrqlxGgcPXL\n5cVt6LDBr36pqm0yjfME7cvtAq1LGlN8zcW+6lkZ92tfUjm5rym+6SJf9OR2O/9g5G0s6uxHzypf\nvGmp7KawibmShNUvJbUt6e3A08AFHRJPbwRcAzwLnJti1FPT2bXH/L0cOCqeH0mI++s4+fQv5VdV\nXNtONUpqOyFHKcAngEuBX3XTnY7kxPw9Dfi2pI8AjwB/lnpDZ0Spofulf9qePGnZ6oqBZndFc9lm\n18lE+dZJwM4TiNlr2rPdPVmbpdZOut6+ln7y+2szRsvt95lwrTSPmvOut/69Jk+CtrukWp9K8lYA\nTa6b105X6+v7pG1JOwHvM7MDJE1Kp5hHyuqXvJi/7069iePUbTIJXNtOj+iftr8MnNj0Osk1WcOv\nmjOUlM8OszHwU0JGmJnApWa2UNIZwB8Sco/+AjjazJ7KqH8Q4cvRSHaREH6pPJN91M1+dDpeb6V1\nzXrreefRd97yxrxRcHZ/Jz9FNMq036N1grd1uWDzPfMmh1uXV05espgXeqGZ5vfzRtt58w15ZZLJ\nSqp+J4wv6r6pNt4CXKyQr3E74GBJa63Ai+9hApyeUDhRenNxG9o3e1JK0qZmtibmarwROA7YErjW\nzDZIOo2QAuwzbfU2Ah4gJJx+gpCm7gNmtrS7T5fT38KJ0naXy8T1fMOcHW4g2wgVly0yhikumux7\nTtw33PO0eO1ZehGyN98AT/7Mk10szf3K+lt02jjVOiGbNFFaTdvzCBP1b+pYXzovliucKPWRujMY\nKmyVNrM18XRjgmbNzH7cVORm4I8zqu4N/NzMHgGQdDFhc1FPjLrjAKW1XZSjtK148ujbjbozGCps\npY4j7juAVwNfM7Pb2op8BLg4o+rOwGNNrx8nGPoB0T6abF2HXlwnr2z7aLJ9F+vEaLbYRdPq/sge\nAU+e4G3t3wLCCD37/c60Pim0ThRn9xc6ubDWJjydNPe9dRllqcBg5ZOqF+YobSr7kdSybtSdwVBB\naWa2AdhT0pbA9yW9vpFVXdJngbVmdlFP+tk3OhtG6ORmyW6rtWxx+6ntTn6d70Yqd7/WTVnZfvz2\n1S8pm7ca7WXH4cmiTFKTSdTMitasO87QkqG08VvCkYqZPSXpOuAg4F5JRwGHAAfmVFkGzGl6PTte\nc5zeUTMrWjhRKmk2IYrd9sAG4Gwz+4qkbYBLgLmEnbV/ZmarM+r7ROkIUDhRmhBRQHMyd91tRxiJ\nr5a0CXAVYS35BuCLwDvN7Dc5950B3E+YKF0O3AocYWb3xfcra7toR+ngyV6V0rl8arm8NlPb6DWT\nd+V26keKW6Z9MjVporSktvtFyo7SdcAJZvYG4G3AsZJ2YyJE6WuBawkhSh0nm/I7SncErpO0GLgF\nuMrMriCEzN0cuEbSnZL+CUDSjpJ+CGBm64GPA1cD9wAXNwx6ZAi1PavpSC3fTbtV2ugtjZgvwUg3\n+pcdrXEya2n2vzdoLIlsjw/TkZrtlk7ZfLQCWBHPn46xMWbj4XedbigpbDNbAuyVcf01OeWXE4Ik\nNV7/CHhtTlnXtlOd6eZ+aSkc1lSOA28EHjOzbZree9LMts2o4+6XEaDI/bJ2kvNiMrO2mrp0dmW1\nXT/3S6/oh0slz4XTsIrrenT/vPt0vp69dr3Y/VI3bSf/xkjanBBY5vg4qmn/NejvLiZnWrO+ZqOZ\nZlzbWfTDpZLX5rqMa1XuX+Qmal5G2Rrit8xKmLppO6k7kmYSRH+hmTWi1q2UtH1TiNLcKGIeT334\n6Dae+roZKdM3G8p3qCRVtQ3/0XT+SuBV/eqqMxAeAn7JeBc16qbt1HjqFwCrzOyEpmunA0+a2ekx\nl+M2ZjbJ7+jul9GgyP2yet1LCtvYauYLUxFPvZK2h9f9Mp0pu34+i5ML3S9103ZK6N39gA8BSyQt\nIjyKngScDvy7h991UnhhRrHw4YW+96MZ1/awkB3WuAoTSxuLqZu2U1a/3Ej+RlgPUeoksa5uKddx\nbTu9oW7arpmL3xlW1rvUasRUbRbqF83r06t9rqxwv0XUTdup6ewcpxLrmVF4ON2ylsmbbVI23+QZ\nvtSNO3Wkmw1XrSzg5GjA17ZcS6WstiWdI2mlpLtz3v+gpLvicYOkjuF5G9TrJ8YZWl4gxe/oONOP\nCto+j7Az+oKc9x8ihMFYHZO9nA3sW9SoG3VnINTN7zgcZI1M+7G+e7hpzfDUHkOmeMReVttmdoOk\n3PXd1pp+42ZCKOlC3Kg7A6FufkfH6RUD0vYxwJUpBf2b5gwEd784U01Kar/JqQGLydL27ePPcPv4\nmozS3SPpAOBo4O0p5VPWqecl/k0KT+o4UE/3i2t7tEjJAlWGLG3vMbYle4xt+eLrsxauKtW2pDcD\nZwEHmdlvU+oUrn4xs+eBA8xsT2APQkbrvZnW4UmdQbOemYXHoHFtO72gorYVj8lvSHOA7wAfNrNf\npPYnaUljVuJfQnjS8+P184H3pd7UGT3quqRxtLS9luxlkKNO9nLItNSClZY0XgT8DJgv6VFJR0v6\nS0kfi0X+F7At8E+SFkm6NaU/qQG9JiX+bQQ8ghCXWtIrUtpyRpO6+tSHU9t57oTRXN0ymbTNV1V8\n6ikUJZ42s48CH+223SSj3pb493uS3sDkcKQjGJ7USaWOPnVwbTvVqZu2u3JkxsS/44TEvx56d4Tp\nNvRuWZ95h8nMPwFOAV4HvNXM7syom5mDNOs+ZbVdz9C72aPQlByd04tuk2FQcB0aoXeB5PC7dVuu\nm5J4Oi/x7/546F0nUhR694f2rsI2DtV/ZLYhaVMzWxMTSd8IHAesJhjqfwX+Z45R3wHYwcwWx0QY\ndwCHm9nS+H5lbXvo3Qa9DHc7NQR3S/v/Z3Ho3Sra7gcpPzE7AudH3+NGwCVmdoWkm/HwpE4iz1fw\nqWdNZprZ/QCScr8oOTlIdwaWxiKubacyVbTdD1JC7+Yl/n0SD0/qJFLlETVrMrNEG/MIyxZvaVxz\nbfeSfuQz7XWO0s6UdUvVzf1Sr944Q0uVJYttk5nfl/R6M7s3tX57DtLSHXEGSK9i2HRn4MvMO9Qt\nwqgbdWcgZD2i3jf+K5aOd5iDbCNOZl5HmMxMMuo5OUgdp2dMO/eL4/SCrEfU+WM7MX9spxdfX7Zw\nsp3OmMx8D2Eys6VYh1ufC9xrZmeW6LYz7Snvgkldp14394snyXAGQoUdpTsC10laTPCHXxUnM98n\n6TFCfOkfSroSQNKOkn4Yzxs5SA+MO/LujHGpnaGgt7tjg+tlJt2Odeu2W7pePzHO0FJW2B0mM78P\nfD/j+nLg0HjeKQep4/QE96k7I0nd/I6DZ9jygnZiUGvWU9pP70twvTz7YvnwujhJRt20nex+kbRR\nfHy9PL7eRtLVku6XdJWkrfrXTWe6U8cojTBIXY+KQYfmAFkT+T+nvi/NZOUl7VS+E2W1XZSjNJb5\niqSfS1osaY+U/nTjUz+e1hUHHp7USaZufscmXNdOJSpo+zzgvXlvSjoYeLWZvQb4S+BfUvqTGqVx\nNnAI8H+AE+LlwwnbqSGEJx0nfCEcZxJ18zvCoHQ9/bfPV2Ei52e96GX8mwrzRR1zlBK0eEEse4uk\nrZojiOaR+sz7JeBvgeZH0WkentQZJM+z8VR3IQvXtVOZPmp7Z+CxptfL4rVqRl3SHwArY1CksQ5F\nPTypk0vdRuq90/VMYF2H90dzhD5B+d2dWdQx0mSWtkMU00emoDdpI/X9gMMkHQJsAmwh6UJghYfe\nHV26D71bL6NOD3QduKrpvC6hd+tKw5iXXwnUvTHv9odkIvRuKlna3mXsVewyNqGFny68oas2I8uA\nXZpez47XOpIS0Osk4CQASfsDf2NmH5Z0BnAUcDpwJJC7BXv/U95RdBtnmjFvbG7Lj/P1BaKt27Kv\nXug6UBx21ZlOvIrWH+brCmtU1HZujlLgcuBY4BJJ+wK/K/KnQ7V16qfh4UmdROq2lboDU6zrYZ5Y\n7ddn6zTyr+bq6WeYgJijdAx4maRHgQWEZDBmZmfFndOHSHoQeAY4OqXdbjMf/QT4STz38KROMjV0\nv7xIvXQ93Y15fwxsZ/rTburmowqrXzrmKI1lPt5tu9Nm+ORMb+ps1B2nCnXTtgf0cgbC82xceDjD\nwHR/0ghk7zbNpm7a9pG6MxDqNpoZDKMU72W48CQZjlNA3YTvOL2ibtp2o+4MhLotaRwMPkofBeqm\nbTfqzkCYRksaHSeS5lOvm7br1RtnaKnbI6rj9Iq6aTs1SuPDwGpgAyFf5N6StgEuAeYCDwN/Zmar\n+9RPZ5pTVviSNgZ+StiUMRO41MwWdqM/SRsBtwOPm9lhbe89jGu7gLwJ3242E61lQdzK0zoJ2dz2\nVE0sT3yO1tgyaX2ZlkadIPgxM/tt07VG3OkzJJ1IiDvtoXedTMou6zKz5yUdYGZrJM0Aboz5SP+Y\ndP01YqZvmfGea7uQXmwmmpWzomRWznk/aP4Raj6fuG+ZQGF1W46buk5dGWUPJ8SbJv77vl51yhk+\nqiTJMLM18XRjwkDESNRfU8z0f8tp3rXtVKJuCWBSjboB10i6TdIx8VpL3GnA4047uVQRfkw5twhY\nAVxjZreRrr9GzPS8ELqu7a5YS+oEYv1oHpU3n1f7THUz6qnul/3MbLmklwNXS7qfyV+S3LjTHnp3\n+Og29O66CsI2sw3AnpK2BL4n6Q0k6C8jZnpWNLxK2ob/aDofhdC703mZZt4cQPPr7kPvVtG2pIOA\nLxMG2OeY2elt728JfAOYA8wAvmhmX+/UZpJRN7Pl8d9fS/o+sDewMjXutIfeHT66Db37Qobf8anx\nRTw1vjj5nmb2lKRx4CDS9JcVM/0CM/vzpjYradtD7w4b3YfezdJ2CnEC/6sEET0B3CbpMjNb2lTs\nWOAeMztM0nbA/ZK+YWa5mVkK3S+SNpW0eTzfDPh9YAkh1u9RsVhC3GlnlMl6JN1s7C3seMoxLx5Z\nSNpO0lbxfBPgPcB9JOjPzE4yszlm9irgA8C1zQbdtT2s5LlTWidFe0UF98vewM/N7BEzWwtcTJjP\nacaALeL5FsBvOhl0SBupb0945LVY/ptmdrWk2/F46k4iFfyKOwLnx1HNRsAlMc70zWToT9KOwNlm\ndmhC267toWSwLqIK2m7PQfo4wdA381XgcklPAJsD7y9qNCXz0S+BPTKuezx1J5kKSxqXAHtlXM/U\nX3SnTDLozTHTm665tp3KZGn7mfHbWTN+ey+afy+wyMwOlPRqwqT+m83s6bwKvqPUGQh126DhOL0i\nS9svHduHl47t8+LrVQvPyqq6jDAB2iArB+nRwOcAzOwXkn4J7EbYTJeJG3VnILhRd4aVCtq+DdhV\n0lxgOWHe54i2Mo8QnhpvlLQ9MJ+wRCcXN+rOQKiy7KveeMz0wDDnVu1MWW2b2XpJHweuZmJJ432S\n/pKYpxQ4Ffi6pLtjtU9F92AubtSdgVB22Vf9aTViIVnxgsz3hptR+qytVNG2mf0IeG3btX9tOl9O\n8Ksn40bdGQjufnGGlbpp2426MxDWb6iX8PtFmYBQg2e6uYzq3d+6aTs19O5WhIBIbyREtfsI8AAe\nntRJZN26egm/wWhqe1AGslfGuL4GHeqn7dSAXmcCV5jZ64DdgaVMhCd9LXAtITyp42TywnMbFx5T\nhGvbqUTdtF04Uo8BZd5hZkcBxC2qqyUdDuwfi50PjDPSMaedTqyv2WgGXNv9p94j7Gy6X8VTN22n\nuF9eCaySdB5hJHM78D9oC08qycOTOrmsW1sv4UdGQNt1WmpYti+D9Kk33ydtyrFu2k7p9UzCNu1j\nzex2SV/35RcVAAAOyUlEQVQijFq6CE/qjDobnq/lkkbXtlOZumk7xag/DjxmZo1tqd8hCD85PKnH\nUx8+uo2nTs0eUSOVtV3/eOrdjHD7PSIu23aVPnX7dNB9PPW6aTsloNdKSY9Jmm9mDxBi/94Tj6OA\n0ykIT+rx1IePbuOpsy4rP8XU0gttD1c89TJukTL1Bkm3fes+nnrdtJ26Tv044JuSZhF+yo4mZOHw\n8KROGh0jQE8prm2nGjXTdmrmo7uAt2a85eFJnTSem+oOZOParkKdR+gDpGbaTl2n7jjVWJtwOENA\np//IIf2PrqBtSQdJWirpAUkn5pQZk7RI0n9KKvQHeZgAZzCsn+oOOE6fKKntlBylccfz14DfN7Nl\nMU9pR3yk7gyGdQlHBpJmS7pW0j2Slkg6Ll7fXdLPJN0l6bJGrtGM+ltJ+rak+2Ib+2SVc3pFJ5dM\ndzlCF3AyCzi5co8CfXxCKKlt0nKUfhD4jpktAzCzVUXd8ZG6MxjK+x3XASeY2eJouG+XdA1wdrx+\ng6SjgE8Bf5dRvxEG4E8lzQQ2Ld2TWlDv4Fa9pLfB0fr4Nyuv7ZQcpfOBWdHtsjnwFTO7sFOjbtSd\nwVByhYCZrQBWxPOnJS0lfBleY2aNdZQ/Bq6izajnhAF4qlxPHCeH/q5+aWyQOxDYDLhJ0k1m9mCn\nCo7Tf3ogfEnzCImibwbukXSYmV1OWHI4O6NKVhiA483s2eq9mSpGY5TeOwawlj5L20vG4T/Hi2qm\n5Ch9HFhlZs8Bz0n6KUHLuUa90KcuaX6ceb0z/rta0nGStpF0taT7JV0VHfqOk82zCUcHouvlUoJR\nfhr4C+BYSbcRRjAvZFRrjHK+ZmZ7AWtoCszl2nZ6QpaWdx2D950ycWTzYo5SSS8h5Ci9vK3MZcDb\nJc2QtCmwD3Bfp+6k7Ch9ANgTXpytfRz4HhPhSc+IS3E+g0eyc/LIWiFw7zjcN15YNfrCLwUuNLPL\nAMzsfmKaL0mvAf4go2p7GIBLgReXjbm2R4EBPNmUXP2SkqPUzJZKugq4O97pLDO7t1O73bpf3g38\nwswe8/CkTldkPaLOHwtHg+8uzKt9LnCvmZ3ZuCDp5Wb262iMTwb+pb1SThiAvC9ESW3PzPlwzvSh\nYQZL/j9W+O8vylEaX38B+EJqm90a9fcDF8XzIQpP6vSdksKXtB/wIWCJpEWEiIknAfMlHRtff9fM\nvh7L7wicbWaHxiaywgBk4dp2ylGz3/Rkox6/FIcx8fjq4UmddEou+zKzGyEzs++PgK9klF8OHNr0\nOi8MwItU0fYCPj1N8pI6+WRZ5S7GuzULE9DNSP1g4I6mxe8eeneE6T70bv/60gNKa3shBzARfreO\noXedbPJWxZQJvduD7vSQboz6EcC3ml5fjofeHVm6D73b5w5Vo7S2hyv0rlMu9G6/+lKOpDABcSnN\nu4HvNl0+HXiPpPsJyj6t991zhoaaBvSqrm3f6pFOnQJ6FYcsSA5RUDNtp4beXQO8vO3ak3h4UieV\n56e6A9lU13bNhmm1ZjpsnJpwyyxkAZC7ImuCmmnbhxnOYHDb5wwrNdO2G3VnMNRM+M4oUCb42ayc\n8w7UTNtu1J3BULNlX1PPdMjvOd2pmrB6k7SiNdO2G3VnMNRsNOM4PaNm2naj7gyGmgl/6vERejFT\n+TTTxT1rpm3PfOQMhpot++od07bj04DuMiUV0yex9TlHaSz3VklrJf1RUXcGYtQfHn9kpOpO5b2n\n8jN35PmEY+R4yOtOm3t3oKS2m3KUvhd4A3CEpN1yyp1GSARTyECMelfbyYeg7lTeeyo/c0fK53Gs\nOWVGkg2vZ5fb0VsYtbq9uPcsOo/+273RiaLsb45SgE8Qwkbnhqtoxn3qzmAYGS9Fp2V0jdUUg0q8\nVLd8phvo3Kf2MMYN0WxCb3/1m+/TfF7yHuW1XZijVNJOwPvM7ABJ7flLM3Gj7gyGkXSvOCNBf7X9\nZZoSuwAqqiCz/kbMleQheUcEM8sUnCTj4AQZXKncNuqIa3s06KTJXG3/ZhyeHJ94/eDCSe1I2hc4\nxcwOiq8/HW5npzeVaUwGCNgOeAb4WMzNm92nfht1x5FkvDtBZz+eXkbdcapoW9IMoBE0bjlwK3CE\nmWXmII0J1H9gZt/Ner+Bu1+cwVAyj6Pj1J4+5ihtr5LSro/Unb4jyXhbgs5uyhzNzAYuALYnzLSd\nbWZfkbQ7IS/pSwlTVX/dlGC6uf4ngb+IdZcAR5vZC9U+keMEqmi7X/jmI2cwlN+gsQ44wczeALwN\n+GtJrwPOABaY2Z7AAuDz7RXjyoFPAHuZ2ZsJT6Yf6N2Hchxqt7Gur0Y9dbdUU/lzJK2UdHfTtW0k\nXS3pfklXSdoqp+5sSddKukfSEknHpdaXtLGkWyQtinUXdHPvWHYjSXdKurzLfj8s6a5471u7rLuV\npG9Lui9+7n26qDs/3vPO+O9qScd185m7Yn3CkYGZrTCzxfH8aWApsBNh5N3o29bAspw7zwA2kzQT\n2BR4ovqH6U7bo6jrWHbg2h64rqG0tvuGmfXlIPxgPAjMJSxMXQzsVlDn7cAewN1N104HPhXPTwRO\ny6m7A7BHPN+cMAGxWxf1N43/zgBuJqwXTaob3/8k8A3g8i77/RCwTdu11LpfJ7gTIIxCt+qmz23/\nV08Au5Spn9C+8SYrPoIfsVM784CH4//vbsAjwKOEtb675NQ5DvgvYCVw4VRoexR1XQdt91vXvdR2\nL4/+NQz7Alc2vf40cGJCvblt4l8KbN8k8KWJ9/8+IXtNV/UJo7nbCRnok+oCs4FrgLEm8afW/SXw\nsrZrhXWBLYFfZFzv+u8F/D5wfZW/d0H7xq5WfHQQPsGg3Q4cHl+fSdiUAfAnwDUZdbYmZIXelmDU\nvgd8cCq0PWq6roO2+63rXmm710c/3S9Zu6V2LtHOK8xsJYRHceAVRRUkzSOMjG4m/EcW1o+PmYuA\nFQQDcVtqXeBLwN/SOjudWteAayTdJumYLuq+Elgl6bz4qHmWQr7N1Ps2837goi773R1Zj6RPj8Oq\nUyaOHKLr5FLCSLuRBPpIM/t+7OeltO3Ei7wbeMjMnjSz9YQ8pL/Xg0/TC20Pu65h6rXdf11D7dwv\n03GitONUs6TNCQbgeAs+2PbymfXNbIOFSbfZwN6S3pBSV9IfACst+H07zW7n9Xs/M9sLOAQ4VtI7\nEvs8E9gL+Fqs/wxhxJj0eZv6Pws4DPh2TvneLI/Kiocxawy2OGXiyOdc4F4zO7Pp2jJJ+wNIehfw\nQEa9R4F9Jb1UkgjrgTPXANeAYdM1TKG2B6ZrqF1co34a9WXAnKbXs8mfzOrESknbA0jagQ5BbXJG\ndMn1AczsKWAcOCix7n7AYQo7v74FHCjpQmBFyn3NbHn899eER+u9E+/7OPCYTSzj+w7hi9DV5wUO\nBu4ws1Xxdbf103g24chA0n7Ahwh/18YE2EHAR4EvxlHoqcDHYvkdJf0QwMxuJehhEXAXwTi1r/0t\nQy+0PdS6jvecSm0PRtdQWtv9op9G/TZgV0lzJb2EsJQsd2trE6J1ZHA5cFQ8PxK4rL1CE1kjusL6\nkrZrzIZL2gR4D2FEV1jXzE4yszlm9irCZ7zWzD4M/CDhvpvGERiSNiP4AJck3ncl8Jik+fHSu4B7\nUuq2cQThS9ug2/pplF/9cqOZzTCzPcxsTzPby8x+ZGY/M7O3xGtvM7NFsfxyMzu0qf5CM3udmb3Z\nzI60EA2vKmW0PTK6jvebam0PRtdQO/dLXx32hFHB/cDPgU8nlL+IMFv9POHR+WhgG+DHsZ2rga1z\n6u4X/3yLCSOzO+P9ty2qD7wpll8M3A18Nl4vrNvWzv5MTCil3PeVTf1d0vgbpd4X2J1gYBYT/MVb\nddNnwuTZr4Etmq519ZkTdWBsYcXHACeTBqntUdP1VGt7ULquq7Z9R6nTdyQZmyTo7FmP/eJML+qo\nbY/94gyGmmVcd5yeUTNtT8fVL850xBIOx5mOVNC2CnYmS/qgwq7cuyTdIOlNRd1x94vTdyRZmtV2\n94szvaiibYXcow8QJoKfIMwhfMDMljaV2Re4z8xWx1Vfp5jZvp3u5CN1x3GcqaEwR6mZ3Wxmq+PL\nm0nY5OY+dWdAjEySUmfkKK3twhylbRwDXFnUqBt1Z0AMeFud4wyM/mtb0gGEpbBvLyrrRt0ZED5S\nd4aVLG1fD9xQVDFpZ7KkNxN2Qh9kZr8tatQnSp2+EyaTViSU3MEnSp1pRRVtKyFHqaQ5hEijHzaz\nm1P65CN1Z0D4SN0ZVspp29JylP4vwm7Yf4pB6daaWSe/u4/Unf4TRjO/TCj5Sh+pO9OKOmrbR+rO\ngPCRujOs1EvbbtSdATHg+KOOMzDqpW036s6A8CWNzrBSL227UXcGRL0eUR2nd9RL227UnQFRr9GM\n4/SOemnbY784A6Jczi9JsyVdK+keSUskHRev7y7pppji7lZJb8mp3zEKnuNUp1757Hyk7gyI0o+o\n64ATzGxxTI92u6RrgDOABWZ2taSDgc8DBzRXjFHwvkpTFDxJlzVHwXOc6rj7xRlJyj2imtkK4pY9\nM3ta0lJgJ2ADIcUZwNZkJ35+MQoegKRGFDw36k4PqZf7xY26MyDWVG5B0jxgD+AW4JPAVZK+SEjo\n/HsZVbqNguc4Jaiu7V7iPnVnQKxLOPKJrpdLgePN7Gngr+L5HIKBP7dvXXecjlTTdq/xkbozILL8\njktJ8YRImkkw6Bea2WXx8pFmdjyAmV0q6ZyMqklR8BynGu5Td0aSrNHKrvFocFlGGSCMwu81szOb\nri2TtL+Z/UTSuwhpwdq5DdhV0lxCFLwPAEd03XXH6Yj71J2RpNyyLkn7AR8ClkhaREgIeRLwUeAr\nMXzpc8DHYvkdgbPN7NC8KHiVP4rjtOBhApyRpHR40huBGTlvT1qbbmbLgUObXv8IeG2pmztOEu5+\ncUaSej2iOk7vqJe23ag7A6JeoxnH6R310rYnyXD6jqSHgbkJRR8xs3n97Y3j9I46atuNuuM4zhDh\nm48cx3GGCDfqjuM4Q4QbdcdxnCHCjbrjOM4Q4UbdcRxniPj/t+f9VvpvX5kAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1334ee990>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"f, axes = plt.subplots(1, 2)\n",
"cs = axes[0].imshow(gain_offset[:,:,0])\n",
"axes[0].set_title('offset')\n",
"f.colorbar(cs, ax=axes[0], shrink=0.9)\n",
"cs = axes[1].imshow(gain_offset[:,:,1])\n",
"axes[1].set_title('gain')\n",
"f.colorbar(cs, ax=axes[1], shrink=0.9)"
]
},
{
"cell_type": "code",
"execution_count": 556,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.28779546489\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEPCAYAAABBUX+lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd8lGW2wPHfSQhIkQ4JEBAQ6RBECBbUKBZ0V2HVRVFE\nveqqu27Rvd61LrhFXXd1da1rWcWCqKg0FRQlK0UICAmgNOkEAoQiJQghOfePZwaGkDJJZuadyZzv\n5zMfZt55ywGSM8+c9ymiqhhjjKn5ErwOwBhjTGRYwjfGmDhhCd8YY+KEJXxjjIkTlvCNMSZOWMI3\nxpg4EZGELyIJIrJIRCb5Xo8SkU0istD3GByJOIwxJp7VitB1fgt8CzQM2Pakqj4ZoesbY0zcC3sL\nX0RSgUuBV0q+Fe5rG2OMOSoSJZ1/AvcAJYf03iki2SLyiog0ikAcxhgT18Ka8EXkJ8BWVc3m2Bb9\n80BHVe0D5AFW2jHGmDCTcM6lIyKPACOAw0Bd4ETgQ1UdGbDPScBkVe1dyvE20Y8xxlSBqh5XNg9r\nC19V71fVdqraEbgG+FJVR4pISsBuVwBLyznHkceoUaOOeR2tD4vT4ozWRyzEaHFW/1GWSPXSKelx\nEekDFAPrgNs8isMYY+JGxBK+qv4X+K/v+cgKdjfGGBNiMTXSNiMjw+sQgmJxhpbFGTqxECNYnOES\n1pu21SUiGs3xGWNMNBIRNNI3bY0xxkQPS/jGGBMnLOEbY0ycsIRvTAU+/RSuvdbrKIypPkv4xlRg\n2jR45x2YOdPrSIypHuulY0wFzjwTunaFVavgq69AbJ5XE+Wsl44xVVBYCDk58OSTsHOnK+8YE6ss\n4RtTjiVLoEMHaNwY/vIXuP9+OFxUTFZultehGVNplvCNKUdWFqSnu+dDh0Lt2jDkuXsY8MoAxmSP\n8TY4YyrJEr4x5QhM+CLQ91dPMn3tVDKvn8U9n9/DV+u/8jZAYyrBEr4x5QhM+OOWjuPjnf+k34qp\nrPziLN6+4m2GvT+M73d+722QxgTJeukYU4a9eyElBXbvhpmbvuSa8dfwxcgvKFjXi6uugpUrYcy3\nL/LU3Kf4+uavaVK3idchGwNYLx1jKm3hQkhLg2U7F3PN+Gt47+fv0Su5FwMGQL9+8PzzcHu/27mk\n0yVc9f5VFBYVeh2yMeWyFr4xZfj732HZ5g183u4snrjoCYb1GHbkvW+/hfPOg++/h/oNihj67lBS\n6qfw0mUvIdZR33jM0xa+iCSIyEIRmeR73UREPhORFSIyTUQaRSIOYypjXlYx01v+lLtPv/uYZA/Q\nowcMHgxPPAGJCYmMvWIsWZuzeGruUx5Fa0zFItLCF5G7gNOAhqp6uYj8Ddihqo+LyB+AJqp6bynH\nWQvfeCbltPnUHzGS1XctK/X9tWtdaWf5cmjRAlbvXE36K+nk/T6PpMSkCEdrzFGetfBFJBW4FHgl\nYPMQwN+JeQwwNNxxGFMZeXnwQ8oEft6r7B/NDh1g+HB49FH3+uSmJ9OhcQdmb5wdoSiNqZxIlHT+\nCdwDBDbVk1V1K4Cq5gEtIxCHMUGbPx8Se07gZ13Lb4s8+CCMGQMbN7rXQ7oMYeLyiRGI0JjKC+si\n5iLyE2CrqmaLSEY5u5ZZtxk9evSR5xkZGTG3hqSJTVOzViF1d9G/Tf9y90tJgV/8Ah5+GF55BS7v\ncjk/e/dnPHnxk3bz1kRMZmYmmZmZFe4X1hq+iDwCjAAOA3WBE4GPgH5AhqpuFZEUYIaqdivleKvh\nG090uekfdOz3PZ/+6sUK9921Czp3hlmzoHNnpcPTHZhy7RR6tuwZgUiNOZ4nNXxVvV9V26lqR+Aa\n4EtVvR6YDNzo2+0GwL4Dm6ihCqtrT2BkenC3lpo0gbvvhocecr9oVtYx0cqrgVePAReKyApgkO+1\nMVFh7pKtFDdbyhWnnhf0Mb/5jWvhL1zoyjqTVk4KY4TGVE1Ya/iBVPW/wH99z3cCF0Tq2sZUxquz\nJtPmwGDq1KoT9DH168MDD7jHxMnnsGrHKjbv3UzrE1uHMVJjKsemVjCmhC9yJ3B2yyGVPu7WW113\nzvPOTaJ3vUuYtGJyGKIzpuos4RsTYN+hfWxM+Irr0i+t9LG1a8OCBa68s3bq5fzfq5N45x04fDgM\ngRpTBZbwjQnw8fJp6MYzOHdA1Wb7SEyEq6+GxR9cwuHWM/nXi/vo2hVefhkOHgxxsMZUkiV8YwKM\nyZpA8q6hNGhQvfM0OqEhZ3c4g/99YRqvvQYffggdO7q5d/btC02sxlSWJXxjfAqLCvnv5o85J/ny\nkJzv8s6ut87ZZ7vFz6dMgXnz3JQMo0e7efaNiSRL+Mb4fLX+K+r92InzTmsTkvNd3uVyPl75MYeL\nXRH/1FPhvfdg9my3ktaf/xySyxgTNEv4xvhMWD6BhJVDjyxpWF1tG7WlXaN2zNk455jtnTvDzTfD\nmjWhuY4xwbKEbwygqkxYPpG984fSM4QzIpQ16rZtW9i0KXTXMSYYlvCNARblLYLDJ9AntRtJIZzK\nfkjXIUxcMZGSc0Klph6dYdOYSLGEbwyunHNy4VAGpId2hsu05DQKiwtZln/sIirJybBzJxw6FNLL\nGVMuS/jGAFNWToEVl4esfu8nIlze+fLjyjqJidCqFWzeHNrrGVMeS/gm7u0/tJ8VO1aw+qv+IU/4\nAJeccgmfr/n8uO1W1jGRZgnfxL2FWxbSpXFPCvbWoWPH0J9/QJsBfLPlG4q1+JjtduPWRJolfBP3\nsnKzaK3p9O8P4Vikqlm9ZrSo14IV+SuO2Z6aagnfRJYlfBP35uXOIzFvQFjKOX7pbdLJys06ZpuV\ndEykWcI3cS8rN4v8nPSIJ3wr6ZhIC2vCF5E6IjJPRBaJyBIRGeXbPkpENonIQt9jcDjjMKYsW/dt\n5YeDP/DtzE70L3+98mpJb5NO1mZr4RtvhXXFK1U9KCLnqWqBiCQCs0XkU9/bT6rqk+G8vjEVycrN\nomfjdDY2SiA5OXzXOTXlVL7b/h0/Hv6RE2qdAFgL30Re2Es6qlrge1oH9wHjH3IYhttjxlROVm4W\nzQ6Gt5wDUDepLl2adSEnL+fItuRk2LHDBl+ZyAl7wheRBBFZBOQBn6vqfN9bd4pItoi8IiJVW23C\nmGrK2pxF0frwJ3w4vo6fmAgpKTb4ykRO2BcxV9Vi4FQRaQh8JCLdgeeBP6mqishfgCeBm0s7fvTo\n0UeeZ2RkkJGREe6QTZwo1mKycrPouCCd9AhMVZzeJp0Z62Ycs81f1mnfPvzXNzVXZmYmmZmZFe4n\nJSd1CicReQjYH1i7F5GTgMmq2ruU/TWS8Zn4snLHSi568yK2P7COrVup9ipXFVm6bSlXvnclK+48\n2h//6qth6FAYPjy81zbxRURQ1ePK5uHupdPcX64RkbrAhcByEUkJ2O0KYGk44zCmNFm5WZxSL52T\nTw5/sgfo1rwbW/ZuYdeBXUe22eArE0nhLum0AsaISALuw+VdVf1ERN4QkT5AMbAOuC3McRhznHmb\n5tFw7wBOikD9HiAxIZG+rfqyYPMCLjz5QsCVdNaujcz1jQl3t8wlQN9Sto8M53WNCUbW5iyarRrG\nxRFK+HD0xq0/4aemwldfRe76Jr7ZSFsTlw4ePsjSbUtZO6dvRHro+JUcgGV98U0kWcI3cSlnaw4n\nNz6FjWvq06NH5K6b3iadeZvmHVkBy0bbmkiyhG/iUlZuFu0S00lLI6RLGlakbcO2AGza45r1KSk2\n+MpEjiV8E5eycrOokx+ZAVeBROSYAVj+wVdbtkQ2DhOfLOGbuDQvdx4/fBfeKZHLUnLErZV1TKRY\nwjdxZ9eBXWzeu5m1Wd059dTIX7/kjVvri28ixRK+iTsLNi/g1OS+5G5MDMuShhXp17of32z+hqLi\nIsB66pjIsYRv4s683HmcUm8A7dpB7dqRv37Tuk1JaZDC8vzlgJV0TORYwjdxJys3i+YH0+nc2bsY\nAuv41sI3kWIJ38QVVSUrN4uELel06eJdHIEJ31r4JlIs4Zu4suGHDYgI275v630Lf/PRhG8tfBMJ\nlvBNXMnKzSK9TTorV4inLfw+KX1Ynr+cA4UHaNUK8vOhsNC7eEx8sIRv4kpWbhbprdNZuRJPW/gn\n1DqBbs27kZ2XTWKiW+7QVr4y4WYJ38SVBVsW0LVRPwoKoFUrb2NJb5POvNx5gN24NZFhCd/EDVUl\nOy+benv60LkzyHHrAUXWaa1OY1HeIsBu3JrIsIRv4sbGPRs5odYJ5K9L9rR+75eWkkZ2XjZgN25N\nZIR7icM6IjJPRBaJyBIRGeXb3kREPhORFSIyzb8MojHhlJOXQ1pymuf1e78eLXqwcsdKDhUdspKO\niYiwJnxVPQicp6qnAn2AS0QkHbgXmK6qXYAvgfvCGYcxANl52fRJ6cOKFURFC79uUl06NunIsu3L\nrKRjIiLsJR1VLfA9rYNbUlGBIcAY3/YxwNBwx2FMztboauEDpCW7so6VdEwkhD3hi0iCiCwC8oDP\nVXU+kKyqWwFUNQ9oGe44jMnZmkOvlmmsWhVdCT9naw5t21oL34RfWBcxB1DVYuBUEWkIfCQiPXCt\n/GN2K+v40aNHH3mekZFBRkZGGKI0Nd3eg3vZvHcz9X/sTKNGcOKJXkfk9Enpw99m/42UQUcHX0Vy\nBS5TM2RmZpKZmVnhfuJfWzMSROQhoAC4BchQ1a0ikgLMUNVupeyvkYzP1FxzNs7ht1N/y6Md5vPX\nv8KMGV5H5OTty6PH8z3Ivyefdu2E2bOhXTuvozKxTkRQ1eM6Hoe7l05zfw8cEakLXAgsAyYBN/p2\nuwGYGM44jPH30FmxInrKOQApDVKolVCL3L25duPWhF24SzqtgDEikoD7cHlXVT8RkbnAeyLyP8B6\nYFiY4zBxzt9DZ+UX0dFDJ1CflD6+G7epduPWhFVYE76qLgH6lrJ9J3BBOK9tTKCcrTmM6D2CKSvg\nwgu9juZYaclp5OTl0LbtTy3hm7CykbamxisqLmLptqX0Tu7NypXR18L399Sxko4JN0v4psb7fuf3\ntKzfkjo0YvNmaN/e64iOdbSkY33xTXhZwjc1Xs7WHNJS0li92iX7aOv22KV5Fzbt2UTzVvuthW/C\nyhK+qfGitYeOX62EWnRr0Y299ZZYC9+ElSV8U+PlbM1xPXSisH7v1ye5D5sOZ7N9u618ZcLHEr6p\n8bLzsqO6hQ9uquSl23No2RK2bPE6GlNTWcI3NdqOgh3sPbSX9o3bR3ULP7CnjpV1TLhYwjc1mn+G\nTBGJ+hb+km1LSG1bbDduTdhYwjc1mr+cs2OHq40nJ3sdUekan9CYZnWb0aDdamvhm7CxhG9qNH+X\nTP8c+F6vY1uePil9KG6ZYwnfhI0lfFOj5eRFfw8dv7TkNPbVz7aSjgkbS/imxjpUdIgVO1bQo0WP\nqFnWsDxpKWlsE2vhm/CxhG9qrGXbl9GhcQfqJtWNqmUNy9InpQ9rD+RYC9+EjSV8U2P5B1wBMdHC\nb9+4PXsLd7Nt704bfGXCwhK+qbH8PXSKi2H1ajjlFK8jKl+CJNA7uTeNOueQl+d1NKYmCveKV6ki\n8qWIfCsiS0Tk177to0Rkk4gs9D0GhzMOE5/8PXQ2bIBmzaB+fa8jqliflD7U72RlHRMe4V7x6jBw\nt6pmi0gD4BsR+dz33pOq+mSYr2/ilKoe6aGzeE701+/90pLTmJIy227cmrCodAtfRJqISO9g9lXV\nPFXN9j3fh1vPto3/VJW9tjHByt2bS2JCIikNUmKifu+XlpJGwYnWU8eER1AJX0QyRaShiDQFFgIv\ni0ilWuci0h7oA8zzbbpTRLJF5BX/QufGhIp/SmQgJnro+PVs2ZPdtVawbuMhr0MxNVCwLfxGqroH\nuAJ4Q1UHUIk1aX3lnPHAb30t/eeBjqraB8gDrLRjQirWeuj41UuqR4vaJ7Fs+3KvQzE1ULA1/Foi\n0goYBjxQmQuISC1csn9TVScCqOr2gF1eBiaXdfzo0aOPPM/IyCAjI6MylzdxKjsvmyFdhgCx1cIH\n6NYkjTUFOUBQlVNjyMzMJDMzs8L9RFUr3knkKuCPwCxV/aWIdAT+rqpXBnHsG0C+qt4dsC1FVfN8\nz+8C+qvqtaUcq8HEZ0xJXZ7twgfDPuDkE3vStCns2weJiV5HFZx7pzzGc6/ls/eDf3gdiolRIoKq\nHnefNNgW/hZVPdLcUNU1wdTwReQs4DpgiYgsAhS4H7hWRPoAxcA64LYg4zCmQvsP7WfjDxvp0qwL\ny7+DDh1iJ9kDnNUpjcdPfILDh6FWuPvRmbgS7I/TM0DfILYdQ1VnA6X9qk0N8rrGVNqSbUvo1qIb\nSYlJMVW/9zutTRqSksPmzUq7dtaZzYROuQlfRM4AzgRaiMjdAW81pPREboznYrWHjl+rBq1ISBCy\nV2+hXbvWXodjapCKeunUBhrgPhhODHjsAa4Kb2jGVE2s9tDxExGaHkrj67XZXodiaphyW/iq+l/g\nvyLyuqquj1BMxlRLdl42V/e4GnAt/Ftv9TigKkhNSmPx1hzgUq9DMTVIsDX8OiLyEtA+8BhVPT8c\nQRlTVcVazJJtS+id3BvV2GzhA3Ru1IeFe6d4HYapYYJN+O8DLwKvAEXhC8eY6lmzaw3N6jajSd0m\n5OeDKjRv7nVUlde3VRof7/mL12GYGibYhH9YVV8IayTGhEB2XjZpKe6Grb91H83r2JYlvWNX9q/e\nQEFhAfWS6nkdjqkhgp1aYbKI/FJEWolIU/8jrJEZUwWx3kPHr327JBJ3dWXptqVeh2JqkGAT/g3A\nPcAc4BvfY0G4gjKmqmK9h45f69ZwODeNb3Ktp44JnaASvqp2KOXRMdzBGVNZ/lWuILZb+ElJcOL+\nNOauy/E6FFODBFXDF5GRpW1X1TdCG44xVbfzwE52/7ibDk06ALHdwgdondCH7C3jvQ7D1CDB3rTt\nH/D8BGAQbl58S/gmaizeupjeyb1JkASKimDNGujUyeuoqq7TiWl8sWcxxVpMgtjy06b6gkr4qvrr\nwNci0hgYF5aIjKmiwHLO+vXQsiXUi+EOLh1bNWGWNmbtrrWc3PRkr8MxNUBVmw37gQ6hDMSY6vIv\nWg6unBOr9Xu/tm2h6aE+ZOfZjVsTGsEucThZRCb5Hh8DK4CPwhuaMZXjX7Qc3A3bWK7fA6SmQp3d\naeRstRu3JjSCreEHrsRwGFivqrbMsokahUWFLM9fTs+WPQHXwu/a1eOgqik1FQ5vSiNn65teh2Jq\niGC7Zf4XWI6bKbMJYCssm6iyPH857Rq1OzIqtSa08Nu2hb2rrKRjQifYks4wIAv4OW5d23m+ZQ8r\nOi5VRL4UkW9FZImI/Ma3vYmIfCYiK0Rkmog0qs5fwpjAAVdQM2r4rVtD/qqO7Dywk10HdnkdjqkB\ngr1p+wBu3dkbVHUkkA48FMRxh4G7VbUHcAbwKxHpCtwLTFfVLsCXwH2VD92YowJ76OzfD/n50K6d\nx0FVU1IStGieQJfGvVi8dbHX4ZgaINiEn6Cq2wJe7wjmWFXNU9Vs3/N9wDIgFRgCjPHtNgYYGnTE\nxpQisIfOqlWu/30srWNbltRUOKmOlXVMaAR703aqiEwD3vG9vhr4pDIXEpH2QB9gLpCsqlvBfSiI\nSMvKnMuYQKp6XA+dWC/n+KWmQrPDaeRsned1KKYGqGhN20645HyPiFwBDPS99TXwdrAXEZEGwHjg\nt6q6T0S0xC4lXxsTtC37tqAorRq0AmJ/SoVAbdsCP6Qxi5e8DsXUABW18J/CV19X1Q+BDwFEpJfv\nvcsquoCI1MIl+zdVdaJv81YRSVbVrSKSAmwr6/jRo0cfeZ6RkUFGRkZFlzRxxj8lsvgmvl+5EgYN\n8jioEElNhY15vVh2aBmFRYUkJSZ5HZKJQpmZmWRmZla4n6iW3bgWkfmq2r+M95aoaq8KLyDyBpCv\nqncHbPsbsFNV/yYifwCaqOq9pRyr5cVnDMBjsx4jvyCff1zkhoukp8PTT8MZZ3gcWAiMGwcffgg5\n53Thg2EfHBlnYEx5RARVPW7pn4puvDYu5726QVz0LOA64HwRWSQiC0VkMPA34EIRWYGbiO2xis5l\nTFkCe+io1rwa/qZNkJacRk6ejbg11VNRwl8gIreW3Cgit+AWQSmXqs5W1URV7aOqp6pqX1Wdqqo7\nVfUCVe2iqhep6u6q/gWMCeyhs20b1KoFzZp5HFSIpKbCxo3QJ8V66pjqq6iG/zvgIxG5jqMJvh9Q\nG/hZOAMzJhgFhQWs372ers3dPAqLF8f+lAqBWrd2H2I9mqfx3IKnvQ7HxLhyE76v6+SZInIe4C8e\nfqyqX4Y9MmOCsHTbUro070LtxNoAvP8+DBnicVAhVLu266nTsCCN7LxsVPXIzWljKivY+fBnADPC\nHIsxlRa4aPnBg/DBB5Bdwyof3bvDznVtKNZi8vbl0erEVl6HZGKULaNjYtr8zfPp17ofANOmQc+e\nvr7rNUi3brBsmVgd31SbJXwT07Jys0hvkw7A2LFw7bUeBxQG3bvDsmXQv3V/5m+e73U4JoZZwjcx\nq6CwgFU7V5GWnMa+ffDpp3BVhXO4xh7Xwof0Nulk5WZ5HY6JYZbwTcxatGURPVr0oE6tOkycCGef\nXXO6Ywbq1s1NF9GvVTrzcudhgxFNVVnCNzErHso5ACeeCE2bwuFdbaidWJt1u9d5HZKJUZbwTczK\n2uwS/vbtMHs2XH651xGFT/fu8N13VtYx1WMJ38SsrNws+rfuz/jxcOml0KCB1xGFz5E6fmtL+Kbq\nLOGbmJRfkE9+QT5dmnep0eUcv2Na+Jst4ZuqsYRvYtL8XNf/fuOGBJYtg4su8jqi8PK38Pu17sei\nLYs4XHzY65BMDLKEb2JSVm4W6a3TGTfOdcWsXdvriMLL38JvWKcR7Rq149tt33odkolBlvBNTJq/\neT7pbdIZOxaGD/c6mvBr1gzq1IEtW+zGrak6S/hxTtU9YomqkpWbRaP96ezY4frfx4PAOv68XFvj\n1lSeJfw49/DD8OCDXkdROet/WE9SYhJfTmjD8OGQECc/xTbi1lRXWH9VRORVEdkqIosDto0SkU2+\n1a/8K2AZj4wfD1984XUUleOv38dD75xA/hZ+7+TerN61mn2H9nkdkokx4W4bvQZcXMr2J32rX/VV\n1alhjsGUYe1a2LoVliyBggKvowleVm4WycX9qVMH+vTxOprI8bfwayfWplfLXizcstDrkEyMCWvC\nV9VZwK5S3rIVHKLA5Mlw2WXQqxdkxVCFICs3i7xv0rn2WointUC6dXMtfLCyjqkar6qfd4pItoi8\nIiKNPIqhSg7XoO7P/oQ/cCDMmuV1NME5XHyYhVsWMvu9fnHROydQ69ZukZf8fBjQZoAlfFNpQa14\nFWLPA39SVRWRvwBPAjeXtfPo0aOPPM/IyCAjIyPc8ZVJ1fUIuf9+lyhj2Z49MG8efPSRayW/+KLX\nEQXnu+3f0SQxlVatGtOpk9fRRJZIwI3b7uk88OUDXodkokRmZiaZmZkV7hfxhK+q2wNevgxMLm//\nwITvta+/hrlz3bqpsZ7wp02Ds85y88+cdRbceCMUFUFioteRlW9+7nxqb0+Pq5u1gfyLoQwc2Ik9\nB/ewdd9Wkhskex2W8VjJxvDDDz9c6n6RKOkIATV7EUkJeO8KYGkEYgiJZ5+Fu+6CTz5xyTGW+cs5\nAC1aQEoKLI2B/4k5G7LYsiCdq6/2OhJv+Fv4IkL/Nv2trGMqJdzdMscCc4DOIrJBRG4CHheRxSKS\nDZwL3BXOGEJlyxaYOhX++Edo08a19mNVUZFbHeqnPz26LVbq+F+uyKJH43Raxek63v6umWAzZ5rK\nC3cvnWtVtbWq1lHVdqr6mqqOVNXeqtpHVYeq6tZwxhAqL78Mw4ZB48auZTy53EJUdPv6a/eh1a7d\n0W1nnRX9Cb+gsICNBSu55bI0r0PxjL+FDzZzpqm8OBmjWD2FhfDvf8OvfuVex3rCDyzn+A0cCDNn\nRvc0C1+tWoRu687VV9bxOhTPnHQS7NgBe/dC/zb9mZ8735Y8NEGzhB+ECRPglFNcf3WA/v1h505Y\nvdrbuKqqtITfqZP7YNuwwZuYgjHm8yxOqpVO48ZeR+KdxETo3BmWL4eUBimcWOdEvt/5vddhmRhh\nCT8Izz4Ld9559HVCAvzkJ7HZyl+9Gnbtgn79jt0uEv11/Bmrsrg0Ld3rMDwXWMe3/vimMizhV2Dx\nYpckhww5dvvll8dmwp882X1YlTbhWDQn/C1bYHtSFjcPtoR/XB3fEr4JkiX8Cjz3HNx+OyQlHbv9\nggtg/nz44Qdv4qqq0so5fqFK+AUFoe+2+tq4HSQ2zCetTZfQnjgGHdNTx27cmkqwhF+OXbvgvffg\n1luPf69+fTfqdmoMTf32ww/uQ+qCC0p/v08fWLfO/b2r48Yb4S9/qd45ShrzxTx6NO5HgtiPbGAL\nv2+rvizeuphDRYe8DcrEBPvtKcfrr8Oll0JyGQMZY623ztSp7kOqfv3S309KgvT06o0x2L0bpkyB\nt94KXY+f1athY9KXDO2TEZoTxrhOnWDjRvjxR2hQuwGnND2FbzZ/43VYJgZYwi9DcbEr5wTerC3p\npz91A5hiZUK18so5ftUt63z0EQwe7G4CL1hQ9fMEeucdqN/zCy7sNCg0J4xxSUnQsSOsXOleD+ow\niC/WxtiiBsYTlvDL8Nln0KgRnH562fukprp+0XPmRC6uqjp8+PjRtaWpbsIfOxauu84tTDJ2bNXP\n46cKY8Zv58AJa+jfun/1T1hDBNbxL+h4AdPXTPc2IBMTLOGXwd8Vs6L51mOlrDNnjvtwSk0tf7/T\nT4eFC900vJW1ZQt8840rgw0fDuPGVf/mbU4O/NBkBud1OIekxKSKD4gTgXX8s086mwWbF7D/0H5v\ngzJRzxJ+KVavdlMHX3NNxfvGSsIPppwDcOKJ0KWLS9yV9d57rrtq3bruHK1bQxAztpZr7Fhoc/YX\nDOpo5ZxAgS38BrUbcFrr05i5Yaa3QZmoZwm/FC+8ADfd5BJXRfr2dXPLr1oV/riqI9iED1Uv65Rc\nY7a6ZZ1k9PtAAAAcq0lEQVTiYle/z284nQs6ltG1KE4FtvABLuhgZR1TMUv4JRQUuN45d9wR3P4J\nCa4uHs2t/FWr3IdS377B7V+VidS+/x7Wr4fzzz+67eqr3U3cH3+s3Ln8Zs2C+m3WUsh+erToUbWT\n1FBdurhvov4OA1bHN8GwhF/C2LFw5pnQoUPwx0R7WWfyZPehVNro2tKcdRbMnu1a2MF65x03m2it\ngCV1UlMhLc3dLK6KsWOhx2WunCPxtHhtEOrWdSUz/3xO/dv0Z93udWzbv83bwExUs4QfQPX4eXOC\nMWiQq3lXd8BSuFSmnANu6uRGjdwEXcFQhbffptRVqK691n0YVNahQzB+PBSmfsGgDla/L01gHb9W\nQi3ObX8uM9bO8DYoE9Us4QeYPRsOHCh7JGpZ6tWDc8+NzlG3u3a5D6NBlcyZlanjZ2e7BD1gwPHv\nXXmlW05xz57KXf/zz6FL12LmbvvC6vdlKFnHH9RhkJV1TLnCveLVqyKyVUQWB2xrIiKficgKEZkm\nIo3CGUNlPPcc/PKXwZc+AkVrWWfqVPdhVK9e5Y4bONB9AAbjnXdcS760qkvTppCR4aaYroyxYyFj\n2FIandCIdo3aVXxAHDruxm3HC/h8zec2P74pU7hb+K8BF5fYdi8wXVW7AF8C94U5hqD4lzC84Yaq\nHf/Tn7rjCwtDG1d1Vbac4xdsC9/fk6a8RcUr21tn/374+GM4obuVc8oTWNIB6Na8G4eKDrFm1xrv\ngjJRLdxLHM4CSla2hwBjfM/HAEPDGUOwXnrJ9buv6uIarVu74e7BtoojobDQfQhVNLq2NF27unlx\nNm8uf79Zs1wrvnv3sve57DKYOxe2BrmY5aRJcMYZMHebdccsT9eu7j6L/+a6iFhvHVOuWhXvEnIt\n/evYqmqeiLQM14W++y74Van+/W83nUJ1+Ms6GRnVO0+ozJ7tPoRat678sQkJR3vr/PznZe9Xsu99\naerVcx86778f3A3xsWNh2PBCfrdhFm8MfaNygceRRo2gSRO3Sln79m7bBR0vYPLKydzW7zZPYzPR\nyYuEX1K5BcfRo0cfeZ6RkUFGENl0zhx49FF3s/K004IL4qaboGfP4PYty+WXu66J//hHxVMyREJV\nyzl+/rJOWQnf35MmmFG5117rpkyuKOHv2AFffQW//vs8On3ViWb1mlU+8Djir+P7E/6gDoO4a9pd\nFBUXkZiQ6GlsJnIyMzPJDGZYu6qG9QGcBCwOeL0MSPY9TwGWlXOsBqu4WHXqVNVzz1Vt3171hRdU\nDxwI+vCQKC5WTU1VXbYsstctyymnqH7zTdWPnz1btW/fst+fPFl14MDgznXokGrz5qqrV5e/34sv\nqg4bpjp6xmi957N7gg82Tv3mN6r/+Mex27o9200X5C7wJiATFXy587icGolumeJ7+E0CbvQ9vwGY\nWN7BgwbB9Ollz61eVORamf36we9/7xYrWbXKrVJ1wgnVD74yRKJn1O2KFW7U8KmnVv0cp53mzrN3\nb+nvB1PO8UtKct8Uxo0rfz//Oaevtfp9MEr21AEbdWvKFu5umWOBOUBnEdkgIjcBjwEXisgKYJDv\ndZlGjoRf/9r18Z4w4egNqkOH4LXXoEcP+Pvf4Y9/dOvPXnfdsaM9Iy1aumf6R9dWp7RUp46bjmHu\n3OPf27cPPvmk/Pp+SRUNwtq4EZYuhYHn72PRlkUMbDew8kHHmZI9dcCX8NdawjfHC3cvnWtVtbWq\n1lHVdqr6mqruUtULVLWLql6kqrvLO8cNN8C338K997oacK9e8MADbtWfsWPh+eddQhoypGr950Pt\n/PPdlL47dngbR3Xr935ldc+cNMnd1G3ePPhznXmmG4C1ZEnp77/7LlxxBczL+4p+rftRL6mSgwfi\nkL+FH/gN+NyTzmXuprkcKDzgXWAmKkVBiqxYQoJLBPPnw1NPuaQxfrwbjXn++dFxg9TvhBPgvPOq\nPn9MKHzyiVubNnAis6oqayK1ypRz/BIS3Dz5ZfXJ95/zizU2ujZYLVq4b7R5eUe3NTqhET1b9mTO\nxhhYmcdEVEwkfD8RuPBCeOYZt/ZqtPKyrLN9O9xyC4wZE9z0zhU580zIyjp2QNmOHe5DYMiQyp9v\n+HBX1ik5MduyZS5pnXMOfLHWBlxVRql1fJsu2ZQiphJ+rPjJT1yf/kOHIntdVfjFL2DEiNCNBWjS\nxHX5y8k5um38eLdubYMGlT9f795uEfWSC6W/844b+Lbjx22s272O/m1sOcNglVXHt3VuTUmW8MMg\nJQU6d4aZEV6A6D//gbVr4c9/Du15S9bxq1LO8RM5fqoF1aPn/OC7DxjcaTC1EqJhiEhsKK2Ff3rq\n6azcsZK8fXmlH2TikiX8MLnsstJLF+Hy/ffuxvbbb7veNaEUmPD9PWkGD676+YYPd6Nu/WWi+fNd\nff+00+CtJW9xfe/rqx90HCmthV+nVh2GdB3CO0uqMDe1iRkFBfDWW67HYuCjLJbww2TkSLcYeO/e\nLgn7VyYKh8OHXRnnwQddN9VQ8yd8VdeP/soroXbtqp+vY0c4+WQ3vgKOtu7X7FrNqh2ruOjki0IT\neJworYUPMLL3SN5c/GbkAzIRsWcPXHIJvPqqG50e+CiLaBRPpSoiGs3xVUTV1fIfecS1jO+5x03h\nEOoBYX/6k0vIU6eGp2uqKrRrBzNmuH73//xn9e8RPPOMa9m/9ppbGSszE97N+xPb92/nmUufCUXY\ncUPVzauzbp2byM6vqLiIk546iakjptKzZTXnDTFRZedO9y37tNPctO4lf+9FBFU9rv+itfDDSAQu\nvhj++1/3teuTT1zr9vHHK78gSFnmzXP/4a+/Hr5xCCKulf/SS64X0NlnV/+cw4a5nkyffOJW2Orc\nWXlr8Vtcn2blnMoSKb2Vn5iQyHW9ruPNHGvl1yR5eW6Ni3PPdeOQKvN7bwk/Qs480yW4qVPdClEd\nO7rRwfn5VT/nvn2ulPPcc1WbEbMyBg50YyCuuQYSQzAnV3Ky61r7y1+6cs78zfMB6N/aeudURWl1\nfIDr067n7SVvU1RcFPmgTMht2OC6Lg8b5hqOlR2DZAk/wnr3djXruXPdJ3XnznDXXbBpU+XPdffd\nLhFfdVXo4yxp4EB3k3X48NCdc/hwyM2Fq6+GN3PeZETvEbZYeRWVVcfv2bInLeq3IHNdZsRjMqG1\napVL9nfcAQ89VLUBp5bwPdKpkyuRLFnivpL17u0GTK1cGdzxkya5m55PPx3eOP169nQt/L59Q3fO\nn//c1fBbphTy7rfvcl2v60J38jjTvXvpCR/g+t7X283bGLd0qbtv9sADroFYVZbwPdamDTzxhPv0\nTk11UxlcfbUr+5QlLw9uuw3eeAMaNoxMnImJ8NvfhnYai/r13VxJn63+jFOancLJTU8O3cnjTLdu\npZd0AK7tdS0TV0ykoLAgskGZkFiwAC64wK2zceut1TuXJfwo0awZjB4Na9a42vZPfgKXXnr84C1V\nuPlm9xhYQyaTfHPxm4zoNcLrMGJa+/buhvq+fce/l9IghdNTT2fC8kquJG88N3OmywMvvRSacqol\n/Chz4oluXv81a2DoULjxRtcr5tNPXbJ/8UXYtg1GjfI60tDYc3APn37/KcN6DPM6lJiWmOjuBy1f\nXvr7VtaJPZ995sa8jB3rVtMLBUv4UapOHTcvzooVrifLH/7gFjP54x9dF8+kJK8jDI0Pl31IRvsM\nW8owBLp1c1OJl2Zo16HM3TTXplqIAUVF7t7WiBHw0UeunBMqlvCjXK1a7qtcTo5bD+CNN6BLF6+j\nCp03F79pUymEyFVXubWcC0op1ddLqseQLjbVQjQ7eBBeeQW6doWXX4Zp09w9vVDybKStiKwDfgCK\ngUJVPW7C41gfaWvKt2nPJnq/0JvNv9/MCbUivB5lDTVihBt1+9xzx7/3xZovuOfze1h428LIB2bK\ntH+/q9E/8YTrDXfffa77ZXU6SETjSNtiIENVTy0t2Zua750l73BFtyss2YfQs8/Cxx+7EcwlZbTP\nYHvBdpZuWxr5wMxxdu5006J06ABz5sDEiW5g5rnnhm9RJy8Tvnh8feMxmxkz9Bo3dovf3HKL67UT\nyKZaiA5btrh5tTp1cvMfffWVmz32tNPCf20vE64Cn4vIfBGpZu9SE2umr5nOgcIDnH1SCCbmMcc4\n91y4/nrXZ7tkRXRkmptBs6atd/vhh640Es3WrIHbb3cz2h486Mba/Oc/rmYfKV6uMnGWqm4RkRa4\nxL9MVY9bPXX06NFHnmdkZJARqqWcjGeKtZh7p9/LX87/CwliX/LC4U9/gtNPd1Pn3nLL0e3dW3Tn\nzLZn8q95/+IPA//gXYAhtHatu2H9i1+4bsvRZskSeOwxdxP2tttc19mWLUN7jczMTDIzMyvcLyqm\nRxaRUcBeVX2yxHa7aVsDvfftezw++3Gybs2yhB9G333nWvtff+3KB34r8lcw8LWBLP/V8hrRHfb/\n/g9274bPP4d//cstPhQN5s51U6NnZbnpEG6/3d1Qj4Sybtp6kvBFpB6QoKr7RKQ+8BnwsKp+VmI/\nS/g1TGFRId2f784LP3mBCzqGsIOxKdW//uUG7sya5br4+t0x5Q7qJdXjiYuf8C64ECgogJNOcsl1\n82Y3i2R2tpuN1Quqbo6rRx5x3zzuuQf+53+gbt3IxhFtvXSSgVkisgiYC0wumexNzfTKwldo37i9\nJfsIufNO16r861+P3T4qYxSv57zOut3rPIkrVMaNgwED3ApqZ5/tkuvNNx9/7yLciovdfYT+/d2c\nUzfd5ObH+tWvIp/syxMVJZ2yWAu/Ztl/aD+nPHMKk4dP5rTWEeiSYADX8j31VNft7/TTj24fNWMU\na3av4c2fxWavHVU3e+ujjx5dY/nQIbf2xC23uBJKuBUWum9Qf/sbNGjg+tAPGRK+xYiCFW0tfBOH\nnpr7FOecdI4l+whr3dqtjDRixLGTq/3vmf/L9DXTyc4rZ2rWKPb11+7vc1HAEsi1a7upRx56yE1L\nEi4HDrgxD6ec4ka//+tfbvW5n/3M+2RfHmvhm4jIL8in67NdmXvLXDo17VTxASbkbrrJzcH00ktH\ntz2X9RyTVk5i2ohp3gVWRdde62aW/d3vjn/v+efdfDRz5oR23qkffnDnfvpp923pvvtcSSnaWAvf\neOqRmY8wrMcwS/Yeevppd0Nx4sSj235x2i9Ys2sN09dM9y6wKsjLczPI3nhj6e/fcQe0aOG6p4bC\ntm1w//3uXsF337l/xwkTojPZl8cSvgm79bvXMyZnDH88949ehxLXGjaEN990fcHzfJNmJiUm8dfz\n/8ofpv+BYi32NsBKePll1yOncePS3xdxg5peecW18qtq/Xr49a/d4Kjdu2H+fPdv2LNn1c/pJSvp\nmLC7ccKNtG3Ylj+f/2evQzHAgw+6QUD+1qmijG88gLQDd9H5YNVX2ejRw7Wsw62w0C348umnbmnQ\n8kyc6NZ+zs52a00Ea9kydyN28mR3A/h3v4NWraoVdkSVVdLxcqStiQNjssfw1fqvWHTbIq9DMT6j\nRkHHjoHTKAvDC//B63uHc1ajM2iW2L5K5/37311SHDo0VJGWbsIEN5CsomQPrsfMlCmuq+R//lPx\n/gsWuF4/M2e6lv3330OTJtWPOWqoatQ+XHgmVn255ktt+feW+t2277wOxQTh6blPa7dnu+nOgp1V\nOn7WLNXkZNUtW0IcWAnnnKP63nvB7793r2qnTqrjx5f+fnGx6owZqhddpJqaqvrPf6ru2xeSUD3j\ny53H5VQr6ZiwWLZ9GRljMhh35TjO63Ce1+GYIN097W4WblnItBHTqFOrTqWPf+gh+OYbN0VzOKb4\nXbwYLrnEzTJZmd43c+e61v6iRa6bKrjBUh9/7EbF7tgB997ruq7Wrh36uCMtqqZWCJYl/Ni0dd9W\nznj1DEadO4ob+tzgdTimEoq1mGHvD6N2Ym3euuKtSs91VFjoBj7ddJNbmjPUbrsNUlPdB0tlPfyw\nu4E7ZYqbjvjRR910E/fd59aOTUwMfbxesYRvIqKgsIDzxpzH4JMH8/B5D3sdjqmCA4UHGPTGIDLa\nZ/DIoEcqffzKlW5pvpkzQzv17+7dbrGQZcsgJaXyxx8+DAMHwurVbv3f++5zI3TDtdiIlyzhm7Ar\nKi7i5+//nPq16/PG0DeQmvibFCfyC/I589Uz+f0Zv+e2frdV+vgXX3RdJ7/+OnQlkqeect0i3367\n6ufYvBk2bDh2iomayBK+CatDRYf43dTf8e32b/lsxGdVqv+a6LJ652oGvjaQ5y59jiu6XVGpY1Xd\nNMVpacdP3FYVxcXQpYtbzevMM6t/vprORtqasMnOyyb95XTW/7Cej67+yJJ9DXFy05OZdM0k7pp2\nF7dMuoXdP+4O+lgRt/jKf/7jSjvV9dlnrh/9GWdU/1zxzBK+qbJDRYcYNWMUF715EXedfhdThk+h\nad2mXodlQqh/m/4suWMJtRNr0/P5nkxeMTnoY5OT3bw9I0e6OWiq49ln3VTPViWsHivpmCpZtGUR\nN050I2j//dN/06ZhG69DMmGWuS6TWybdwoDUATw9+Gma12se1HG33+5mlxwzpmrXXb3a1dw3bIiu\nueWjWdSVdERksIgsF5GVIlIzFtes4VSV7Lxsfjf1d1z81sX8/ozfM3n4ZEv2cSKjfQY5t+eQXD+Z\nXi/04pl5z7Bt/7YKj3viCXfz9v33q3bdF15w3Twt2VefJwlfRBKAZ4GLgR7AcBGpsANXMIv0RoOa\nFue63et4ZOYj9HyhJ0PHDaVeUj2yb89mZNrIiPTEqWn/nl6qboz1a9fnyYufZMLVE5ibO5fOz3Tm\n4rcuZkz2GPYc3FP6MfXdHPV33gm5uZWLs6DAfTOIxBw9VREL/+eBvGrhpwOrVHW9qhYC44AhFR0U\nK/+4sRynqrJ+93qmrJzCozMfZeB/BtL/5f5s2rOJf//036z57RoeGfQIrU9s7Wmc0SgW4gxVjANS\nB/D2FW+Te3cuN/W5iQ+Xf0jbf7blqveu4oX5LzBz/Ux2Hdh1ZP/0dJfwb7zR9bgJNs533nE3ajt0\nCEnYIRcL/+eBvJo8rQ2wMeD1JtyHgAmjw8WH2XdoH9v3bye/IJ8V+St4deGrbC/Yzrrd61iybQlL\nty2lflJ9eif3plfLXtw78F4uOvkiaifWgPHmJuTq167PNT2v4Zqe17DzwE4+WvYRczfN5Y3Fb7B0\n21Ia1mlIr5a96NGiB63OT2VddgvueKI5v7iuBc3rNad5vebUS6pX6jdFVXez9rHHPPiL1VBRP1vm\n4LcGH3n+/eLvmfvW3GPeVyq+qRvMjd9QnmdNzhpmvlF+X7RQxlSkRRwuPkxRsfvT/zhw+AAHCg9w\n4PABCgoLKCouokHtBrSo34IW9Vqwc8tO6m6sS4t6LejRogfX9LyGXi170axeswqva0xJTes25ea+\nN3Nz35sBN03Dhh82sHTbUpZuW8rGPevofvkCXvtqO+OeyudQ0nYO1cqnWA6SoHVILD6BhOK6JBbX\n5fDMvTxR8BGF5yRw/7oEHno5kQRJIDHB/ZkgCSTK0W2ChKS8KFTuHKsWryLr7axjz+FBHEGf14te\nMCJyOjBaVQf7Xt+Lm93tbyX2sy46xhhTBVEz0lZEEoEVwCBgC5AFDFfVZREPxhhj4oQnJR1VLRKR\nO4HPcDeOX7Vkb4wx4RXVA6+MMcaETtROrSAiqSLypYh8KyJLROTXvu3jRGSh77FWRBZGUYy/8W1P\nE5GvRWSRiGSJSD+vYgwizjkikiMiE0Wkgcdx1hGReb5/tyUiMsq3vYmIfCYiK0Rkmog0itI4rxKR\npSJSJCJ9vYyxgjgfF5FlIpItIh+ISMMojfNPvp/NRSIyVUSqMClyeGMMeP/3IlIsItE9t0hpy2BF\nwwNIAfr4njfA1fy7ltjnH8CDURTjcqAbMA24yLf9EmBGlP1b+uPMAgb6tt8I/CkK/t/r+f5MBObi\nuuv+Dfg/3/Y/AI9FaZxdgFOAL4G+XsdYTpwXAAm+7Y8Bj0ZpnA0C3v818EK0xeh7nQpMBdYCTb3+\ntyzvEbUtfFXNU9Vs3/N9wDJc//1Aw4B3Ih2bXykxLgdaA8WAvxXaGAhyfGF4lBFnG+AUVZ3l2206\ncKVHIR6hqv6ltevg7jEpblCefyaWMUCYl8muWGlxquoKVV0FYepTVwVlxDldVf3Dn+biEpanyohz\nX8Au9XG/V54p42cT4J/APZ4EVUlRm/ADiUh7oA8wL2Db2UCeqq72KKxjlIjxLuAfIrIBeBy4z7vI\njhUQ51zgWxG53PfWMKLgF19EEkRkEZAHfK6q84FkVd0K7sMLaOlljFBmnFEniDj/B/g08pEdq6w4\nReQvvt+ja4E/RluMvt+fjaq6xMvYghX1Cd9XVx4P/LbEJ/5wPGzdByolxjt8z9vhkv9/vIzPr5Q4\nbwZ+JSLzcS2oQ17GB6Cqxap6Ku7DJ11EesBxI9A872lQIs4BItLd65hKU16cIvIAUKiqYz0L0Kes\nOFX1Qd/v0du4sk60xJguIr2A+4HAen7UfLsrTVQnfBGphUtQb6rqxIDticAVwLtexRYQS2kx3qCq\nEwBUdTxRMG1EaXH6ShAXq2p/3HxGUfFtCUBV9wCZwGBgq4gkA/hu3FU8RWOE+OKcgYszapWMU0Ru\nBC7FtZyjRjn/nmOJgpIjHPOzOQRoD+SIyFrcB8E3IuL5N9CyRHXCx7WMv1PVp0tsvxBYpqqbPYip\npNJizBWRcwFEZBCw0pPIjnVcnCLSwvdnAvAg8KJHsfnjae7vgSMidfH9PwOTcDeVAW4AJpZ6gggp\nI87lJXeLeGAlAygjThEZjKs5X66qB72MEcqNs1PAbkNxPwueKCPGhaqaoqodVbUDbk6wU1U1ahok\nJUXtXDoichZwHbDEVzdT4H5VnQpcTRSUc8qKEbgV+Jfvm8iPwC+8i7LcODuLyK98rz9U1de9ixKA\nVsAY3wdQAvCuqn4iInOB90Tkf4D1uPsNXiorzqHAM0BzYIqIZKvqJVEY5yqgNvC5uHlf5qrqL6Mw\nzvEi0hl3s3Y9cHu0xVhiHyUKPujLYwOvjDEmTkR7SccYY0yIWMI3xpg4YQnfGGPihCV8Y4yJE5bw\njTEmTljCN8aYOBG1/fCNCScRKQJycP2mFRinqo97G5Ux4WX98E1cEpE9qhrSeeBFJFFVi0J5TmNC\nyUo6Jl6VOiJS3KI6o0XkG9/iG5192+uJyKsiMtf33mW+7TeIWzzmC2C6OM+LyHfiFm35WESuEJHz\nROSjgOtcICIfRuRvaoyPJXwTr+qKWzVtke/Pnwe8t01VT8PNLfS/vm0PAF+o6unA+bjpr+v63jsV\nuEJVz8NN6tdOVbsD1wNnAKjqDKCLiDTzHXMT8Go4/4LGlGQ1fBOvClS1rGUI/S3xb4Cf+Z5fBFwm\nIv6FLmoD7XzPP1fVH3zPBwLvA6jqVhGZEXDeN4ERIvI6cDruA8GYiLGEb8zx/DNIFnH0d0SAK30r\nWh0hIqcD+4M87+vAZN/53w9YdcqYiLCSjolXlZ3VcBrwmyMHi/QpY7/ZwJW+Wn4ykOF/Q1W3AJtx\n5aHXKnl9Y6rNWvgmXp0gIgs52i1zqqreT9mraf0ZeEpEFuMaSmuAy0vZ7wNcjf9bYCOuLPRDwPtv\nA81VdUVI/hbGVIJ1yzQmxESkvqruF5GmuDWOz/IviiEiz+AWzrAWvok4a+EbE3pTRKQxkAT8KSDZ\nLwD2AXd7GZyJX9bCN8aYOGE3bY0xJk5YwjfGmDhhCd8YY+KEJXxjjIkTlvCNMSZOWMI3xpg48f8u\nBmzu/N69AQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1628610d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"line_energy = 30.9\n",
"pixel_index = (45, 50)\n",
"plot_corrected_spectrum(pixel_index)\n",
"f = get_fwhm(30.9, pixel_index)\n",
"x = np.linspace(10,80,500)\n",
"plt.plot(x, f(x))\n",
"plt.xlim(line_energy - 1 * 4, line_energy + 1 * 4)\n",
"print(calculate_fwhm(f.stddev))"
]
},
{
"cell_type": "code",
"execution_count": 498,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"pixel_index = (60,40)\n",
"energies = pixel_energy_axis(pixel_index)\n",
"bins, hist = e.spectrum(pixel_index)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"fwhm = find_all_fwhm()"
]
},
{
"cell_type": "code",
"execution_count": 569,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x1338e8150>"
]
},
"execution_count": 569,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEPCAYAAABBUX+lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAG61JREFUeJzt3XuQnNV55/HvTwhxNbJ80UwigSSbiyWnHGBtgY29bgcj\nAzaSgmMC6yRcnNRWiAsSZ71I3mw0ZC+xWBKvYxfZctkmY6+wLOzFyJigQUZdXmOQMAhzkawMSyQU\nxdP4EkgAm0jw7B/vGdFqzUxfprvfnnl/n6qufvvtc973mTMzT58+/fY5igjMzGz6m5F3AGZm1h1O\n+GZmBeGEb2ZWEE74ZmYF4YRvZlYQTvhmZgXRUMKXdK2kR9PtmrRvjqQhSbskbZI0u6r8aknDknZK\nWtap4M3MrHF1E76kNwMfAd4KnA58QNIbgVXA5og4DbgHWJ3KLwEuARYDFwA3SVJnwjczs0Y10sNf\nDGyNiBcj4iXgO8DFwHJgMJUZBFam7eXA+og4EBG7gWFgaVujNjOzpjWS8B8D3pWGcI4FLgROBPoi\nogIQESPA3FR+HrC3qv6+tM/MzHI0s16BiPihpLXA3cBzwHbgpbGKtjk2MzNro7oJHyAibgZuBpD0\n38h68BVJfRFRkdQPPJ2K7yN7BzBqftp3CEl+gTAza0FEtPS5aKNX6bw+3Z8E/DpwC7ARuCIVuRy4\nPW1vBC6VNEvSIuBkYNs4Qffcbc2aNeM+19e3oJU2BqCvb0FHYurFdnJMvR1Tr8blmBq7TUZDPXzg\n65JeA+wHro6If07DPBskXQXsIbsyh4jYIWkDsKOq/LTozVcqe2h15KpS8YVKZpavRod0/u0Y+34G\nvHec8n8O/PnkQjMzs3byN21rlEqlvEM4jGNqjGNqXC/G5Zg6T3mNtkiaciM92ffHWo1Zkx5/MzOT\nRHTyQ1szM5v6nPDNzArCCd/MrCCc8M3MCsIJ38ysIJzwzcwKwgnfzKwgnPDNzArCCd/MrCCc8M3M\nCsIJ38ysIJzwzcwKwgnfzKwgnPDNzAqi0SUO/0jSY5IekbQuLV84R9KQpF2SNkmaXVV+taRhSTsl\nLetc+GZm1qi68+FL+mXgu8CbIuJfJX0VuBNYAvw0Im6QdB0wJyJWSVoCrAPeRraA+WbglNrJ7z0f\nvplZ87oxH/4RwHGSZgLHAPuAFcBgen4QWJm2lwPrI+JAROwGhoGlrQRnZmbtUzfhR8Q/An8BPEWW\n6J+NiM1AX0RUUpkRYG6qMg/YW3WIfWmfmZnlqO4i5pJeTdabXwA8C9wq6cMcPrbR9HjFwMDAwe1S\nqTTt1o80M5uscrlMuVxuy7EaGcP/DeB9EfF76fFvA2cDvwaUIqIiqR/YEhGLJa0CIiLWpvJ3AWsi\nYmvNcT2Gb2bWpE6P4T8FnC3paGUZ71xgB7ARuCKVuRy4PW1vBC5NV/IsAk4GtrUSnJmZtU/dIZ2I\n2Cbpa8B2YH+6/xzwKmCDpKuAPcAlqfwOSRvIXhT2A1dPua68mdk0VHdIp2Mn9pCOmVnTunFZppmZ\nTXFO+GZmBeGEb2ZWEE74ZmYF4YRvZlYQhUv4/f0LkdTSzcxsKivcZZmTvbTSl2WaWZ58WaaZmdXl\nhN81R7U8lNTfvzDv4M1sGvCQTnO1c6vr4SAzAw/pmJlZA5zwzcwKwgnfzKwgnPDNzArCCd/MrCCc\n8M3MCqJuwpd0qqTtkh5K989KukbSHElDknZJ2iRpdlWd1ZKGJe2UtKyzP4KZmTWiqevwJc0A/gE4\nC/go8NOIuEHSdcCciFglaQmwDngbMB/YDJxSe9G9r8Nvrq6vwzcz6O51+O8F/l9E7AVWAINp/yCw\nMm0vB9ZHxIGI2A0MA0tbCc7MzNqn2YT/m8AtabsvIioAETECzE375wF7q+rsS/vMzCxHMxstKOlI\nst77dWlX7RhD02MOAwMDB7dLpRKlUqnZQ5iZTWvlcplyudyWYzU8hi9pOXB1RJyfHu8EShFRkdQP\nbImIxZJWARERa1O5u4A1EbG15ngew2+irsfwzQy6N4Z/GfCVqscbgSvS9uXA7VX7L5U0S9Ii4GRg\nWyvBmZlZ+zTUw5d0LLAHeENE/Eva9xpgA3Bieu6SiHgmPbca+AiwH7g2IobGOKZ7+E3UdQ/fzGBy\nPXxPj9xc7dzqOuGbGXh6ZDMza4ATvplZQTjhm5kVhBO+mVlBOOGbmRWEE76ZWUE44ZuZFYQTvplZ\nQTjhm5kVhBO+mVlBOOGbmRWEE76ZWUE44ZuZFYQTvplZQTjhm5kVhBO+mVlBNJTwJc2WdKuknZIe\nl3SWpDmShiTtkrRJ0uyq8qslDafyyzoXvpmZNarRHv6ngTsjYjHwq8APgVXA5og4DbgHWA0gaQlw\nCbAYuAC4SdkyU2ZmlqO6CV/SCcC7IuJmgIg4EBHPAiuAwVRsEFiZtpcD61O53cAwsLTdgZuZWXMa\n6eEvAn4i6WZJD0n6XFrUvC8iKgARMQLMTeXnAXur6u9L+8zMLEczGyxzJvAHEfF9SZ8iG86pXVW7\n6VW2BwYGDm6XSiVKpVKzhzAzm9bK5TLlcrktx1LExHlaUh9wX0S8IT1+J1nCfyNQioiKpH5gS0Qs\nlrQKiIhYm8rfBayJiK01x4165+6E7OOEVs+bX9082srMeo8kIqKlz0XrDumkYZu9kk5Nu84FHgc2\nAlekfZcDt6ftjcClkmZJWgScDGxrJTgzM2ufRoZ0AK4B1kk6EngSuBI4Atgg6SpgD9mVOUTEDkkb\ngB3AfuDqXLryZmZ2iLpDOh07sYd0mqrr10wzgw4P6ZiZ2fTghG9mVhBO+GZmBeGEb2ZWEE74ZmYF\n4YRvZlYQTvhmZgXhhG9mVhBO+GZmBeGEb2ZWEE74ZmYF4YRvZlYQTvhmZgXhhG9mVhBO+GZmBdFQ\nwpe0W9IPJG2XtC3tmyNpSNIuSZskza4qv1rSsKSdkpZ1KngzM2tcoz38l8nWrz0jIpamfauAzRFx\nGnAPsBpA0hKy1a8WAxcANylbdcTMzHLUaMLXGGVXAINpexBYmbaXA+sj4kBE7AaGgaWYmVmuGk34\nAdwt6QFJv5v29aUFzomIEWBu2j8P2FtVd1/aZ2ZmOWp0EfNzIuJHkl4PDEnaxeELtHrRVTOzHtZQ\nwo+IH6X7H0v6BtkQTUVSX0RUJPUDT6fi+4ATq6rPT/sOMzAwcHC7VCpRKpWajb8gjqLVj0H6+hYw\nMrK7veGYWdeUy2XK5XJbjqWIiTvmko4FZkTEc5KOA4aA64FzgZ9FxFpJ1wFzImJV+tB2HXAW2VDO\n3cApUXMiSbW7uiJLnK2ed2rWzaOdzawzJBERLfUAG+nh9wG3SYpUfl1EDEn6PrBB0lXAHrIrc4iI\nHZI2ADuA/cDVuWR2MzM7RN0efsdO7B5+1+r69dZs+phMD9/ftDUzKwgnfDOzgnDCNzMrCCd8M7OC\ncMI3MysIJ3wzs4JwwjczKwgnfDOzgnDCNzMrCCd8M7OCcMI3MysIJ3wzs4JwwjczKwgnfDOzgnDC\nNzMrCCd8M7OCaDjhS5oh6SFJG9PjOZKGJO2StEnS7KqyqyUNS9opaVknAjczs+Y008O/lmzZwlGr\ngM0RcRpwD7AaIK1pewmwGLgAuEmtrsBtbZAtgN7srb9/Yd6Bm1mbNZTwJc0HLgQ+X7V7BTCYtgeB\nlWl7ObA+Ig5ExG5gGFjalmitBS+SLY/Y3K1S2ZNLtGbWOY328D8FfJxDF1bti4gKQESMAHPT/nnA\n3qpy+9I+MzPLUd2EL+n9QCUiHiZbTXs8XinbzKyHzWygzDnAckkXAscAr5L0ZWBEUl9EVCT1A0+n\n8vuAE6vqz0/7DjMwMHBwu1QqUSqVmv4BzMyms3K5TLlcbsuxFNF4x1zSu4E/jojlkm4AfhoRayVd\nB8yJiFXpQ9t1wFlkQzl3A6dEzYkk1e7qiuzz41bPW6S6Io/fj5lNTBIR0dKFMI308MfzSWCDpKuA\nPWRX5hAROyRtILuiZz9wdS6Z3czMDtFUD7+tJ3YPv8fruodv1osm08P3N23NzArCCd/MrCCc8M3M\nCsIJ38ysIJzwzcwKwgnfzKwgnPDNzArCCd/MrCCc8M3MCsIJ38ysIJzwzcwKwgnfzKwgnPDNzArC\nCd/MrCCc8G0cRyGppVt//8K8gzezMXg+/OZqF6ju5M7pufTNOqOj8+FLOkrSVknbJT0qaU3aP0fS\nkKRdkjZJml1VZ7WkYUk7JS1rJTAzM2uvhnr4ko6NiBckHQHcC1wDfJBsTdsbxlnT9m1kC5hvxmva\nTsG67uGb9aKOr3gVES+kzaPI1sENYAUwmPYPAivT9nJgfUQciIjdwDCwtJXgzMysfRpK+JJmSNoO\njAB3R8QDQF9EVAAiYgSYm4rPA/ZWVd+X9pmZWY5mNlIoIl4GzpB0AnCbpDdz+Pv9pt/DDwwMHNwu\nlUqUSqVmD2FmNq2Vy2XK5XJbjtX0VTqS/jPwAvC7QCkiKpL6gS0RsVjSKiAiYm0qfxewJiK21hzH\nY/g9Xddj+Ga9qNNX6bxu9AocSccA5wE7gY3AFanY5cDtaXsjcKmkWZIWAScD21oJzszM2qeRIZ1f\nAgYlzSB7gfhqRNwp6X5gg6SrgD3AJQARsUPSBmAHsB+4OpeuvJmZHcJfvGqudoHqekjHrBd1/LJM\nMzOb+pzwzcwKwgnfzKwgnPDNzArCCd/MrCCc8M3MCsIJ38ysIJzwzcwKwgnfzKwgnPCtA7werlkv\n8tQKzdUuUN384vW0DGbj89QKZmZWlxO+mVlBOOGbmRWEE76ZWUE44ZuZFUQjSxzOl3SPpMclPSrp\nmrR/jqQhSbskbRpdBjE9t1rSsKSdkpZ18gcwM7PG1L0sMy1Q3h8RD0s6HngQWAFcCfw0Im6QdB0w\nJyJWSVoCrAPeBswHNgOn1F6D6csye72uL8s060UdvSwzIkYi4uG0/RzZAubzyZL+YCo2CKxM28uB\n9RFxICJ2A8PA0laCMzOz9mlqDF/SQuB04H6gLyIqkL0oAHNTsXnA3qpq+9I+MzPL0cxGC6bhnK8B\n10bEc5Jq33c3/T58YGDg4HapVKJUKjV7CDOzaa1cLlMul9tyrIamVpA0E7gD+NuI+HTatxMoRUQl\njfNviYjFklYBERFrU7m7gDURsbXmmB7D7+m6HsM360XdmFrhi8CO0WSfbASuSNuXA7dX7b9U0ixJ\ni4CTgW2tBGdmZu3TyFU65wDfAR4l67YF8AmyJL4BOBHYA1wSEc+kOquBjwD7yYaAhsY4rnv4PV3X\nPXyzXjSZHr5ny2yudoHqOuGb9SLPlmlmZnU54VuP8eIpZp3iIZ3maheo7lSLN6vr4SCb7jykY2Zm\ndTnhm5kVhBO+mVlBOOGbmRWEE76ZWUE44ZuZFYQTvplZQTjhm5kVhBO+mVlBTMmE39+/sOWv35uZ\nFdWUnFrB0yN0o+5Uizer66kVbLrz1ApmZlaXE76ZWUHUTfiSviCpIumRqn1zJA1J2iVpk6TZVc+t\nljQsaaekZZ0K3MzMmtNID/9m4H01+1YBmyPiNOAeYDWApCXAJcBi4ALgJvmTUjOznlA34UfEd4F/\nqtm9AhhM24PAyrS9HFgfEQciYjcwDCxtT6hmZjYZrY7hz42ICkBEjABz0/55wN6qcvvSPjMzy9nM\nNh2npWvhBgYGDm6XSiVKpVKbwjEzmx7K5TLlcrktx2roOnxJC4BvRsRb0uOdQCkiKpL6gS0RsVjS\nKiAiYm0qdxewJiK2jnFMX4ff03WnWrxZXV+Hb9NdN67DV7qN2ghckbYvB26v2n+ppFmSFgEnA9ta\nCczMzNqr7pCOpFuAEvBaSU8Ba4BPArdKugrYQ3ZlDhGxQ9IGYAewH7g6l5XKraCOann6jL6+BYyM\n7G5vOGY9xlMruG4PnTPfuu6b2FTgqRXMzKwuJ3wzs4JwwjczKwgnfDOzgnDCNzMrCCd8M7OCcMI3\nMysIJ3wzs4JwwjczKwgnfDOzgmjX9MgtefLJJ/M8vZlZoeQ6l87xxy9qut6BA8/zi188zVScq2Vq\n1Z1q8U6+rufSsalgMnPp5JrwW/vnvAO4iKmYUKZW3akW7+TrOuHbVODJ08zMrC4nfDOzguhYwpd0\nvqQfSvo7Sdd16jxm7ZEtntLKrb9/Yd7BmzWkIwlf0gzgs8D7gDcDl0l6UyfO1X7lvAOYIsp5B9Bm\nL5KN/zd/q1RGcnmx6O9f2PJ5Z8w4uude3Nq1UHc79WJMk9GpHv5SYDgi9kTEfmA9sKJD52qzct4B\nTBHlvAPoIRO9WKyZ4LnJvVhUKnsmPPZEt4jWXuCyc3ZGLybXXoxpMjqV8OcBe6se/0PaZ2aHaP2d\nhXXejTf+z2k11JfrF69OOOGipuscOFDhhRc6EIyZNaD1heJnzDiWl1+e+J/3+uuvb7nuZM47sdZe\nXCuVo1tuq76+BYyM7G6p7kQ6ch2+pLOBgYg4Pz1eBURErK0q4y6KmVkLeuqLV5KOAHYB5wI/ArYB\nl0XEzrafzMzMGtKRIZ2IeEnSR4Ehss8JvuBkb2aWr9ymVjAzs+7q+Ddt630BS9K7JT0j6aF0+5Mu\nxPQFSRVJj0xQ5q8kDUt6WNLpeceUUzvNl3SPpMclPSrpmnHKda2tGomp220l6ShJWyVtTzGtGadc\nN9upbkx5/E2l885I59s4zvNd/d+rF1OO7bRb0g/S73DbOGWaa6uI6NiN7AXlCWABcCTwMPCmmjLv\nBjZ2Mo4x4noncDrwyDjPXwB8K22fBdzfAzHl0U79wOlp+3iyz2Vqf39dbasGY8qjrY5N90cA9wNL\ne+Bvql5MXW+ndN4/Av73WOfOo50aiCmvdnoSmDPB8023Vad7+I1+Aau1a5daFBHfBf5pgiIrgC+l\nsluB2ZL6co4Jut9OIxHxcNp+DtjJ4d+n6GpbNRgTdL+tRq/7O4rss7HasdI8/qbqxQRdbidJ84EL\ngc+PU6Tr7dRATNDldqo650Q5uum26nTCb/QLWG9Pb0m+JWlJh2NqRG3c++iNL47l1k6SFpK9A9la\n81RubTVBTNDltkpDAtuBEeDuiHigpkjX26mBmKD7f1OfAj7O+Be35/H3VC8myOd/L4C7JT0g6ffG\neL7ptuqF2TIfBE6KiNPJ5t/5Rs7x9Krc2knS8cDXgGtTrzp3dWLqeltFxMsRcQYwHzirFzouDcTU\n1XaS9H6gkt6hiXx6zYdoMKa8/vfOiYgzyd59/IGkd072gJ1O+PuAk6oez0/7DoqI50bfekbE3wJH\nSnpNh+OqZx9wYtXjw+LutrzaSdJMssT65Yi4fYwiXW+rejHl+TcVEf8MbAHOr3kqt7+p8WLKoZ3O\nAZZLehL4CvAeSV+qKdPtdqobU15/TxHxo3T/Y+A2siHyak23VacT/gPAyZIWSJoFXAoc8il49ZiT\npKVkl4r+rMNxwcQ9jI3A76SYzgaeiYhKnjHl2E5fBHZExKfHeT6Ptpowpm63laTXSZqdto8BzgN+\nWFOsq+3USEzdbqeI+EREnBQRbyDLBfdExO/UFOtqOzUSUx7/e5KOTe9ikXQcsAx4rKZY023V0bl0\nYpwvYEn699nT8TngNyT9PrAf+Dnwm52MCUDSLUAJeK2kp8imNJw1GlNE3CnpQklPAM8DV+YdE/m0\n0znAh4FH01hwAJ8gu+oql7ZqJCa631a/BAwqmxZ8BvDV1C4H/85z+JuqGxM5/E2NJed2qhsT+bRT\nH3CbsiloZgLrImJosm3lL16ZmRVEL3xoa2ZmXeCEb2ZWEE74ZmYF4YRvZlYQTvhmZgXhhG9mVhBO\n+HYISS+lKWC3p/v/mHdMAJK2KJtm+2Fl0/6+pc3HXyPpY3XK/KqkC6oeX9Su9pF0tKSyMgskvVDz\ne5gl6cdVX6bql/SypHdUHeNpSXPG+lkk/f3ot0NTvS9VPXdEOvbG9Pj9ksZeXNamNCd8q/V8RJwZ\nEWek+xsme0BlS162w2VpPpO/Bm5s0zGbcTrZvCYARMQ329E+yVXA1+OVL8Y8UfN7+FfgPuDt6fl3\nAA+leySdCvwkIsabcbX6CzfPA78i6aj0+DyqJuGKiG8BH5B0dDt+MOsdTvhWa7ypHf5e0oCkB5Ut\nynBq2n+sssVb7k/PXZT2Xy7pdknfBjannutNknZIGlI26+DFkt4j6baq87xX0v+pE9t9wC9X1TlP\n0vckfV/SVyUdm/Z/UtJj6V3BDWnfAknfTvvuVjY1bu3PukXSmWn7telnnwn8GXBJ6nF/KP2Mn5no\nuJJulvRpSfdKekLSxeP8bB8GqucFGuv3cB8pwaf7T3HoC8C94xx7rOPdCbw/bV9GNo9MtTLwgQmO\nZ1OQE77VOqZmKOFDVc89HRH/BvhfwH9I+/4T8O2IOBv4NeBGZXO3AJwBXBwR7wEuJptxcAnw26RE\nFRFbgNMkvTbVuRL4Qp0YzyfNWJjq/QlwbkS8lWxmw4+l4YuVEfEr6V3Bf011PwPcnPbdkh7XExFx\nAPhTsikKzoyIW0efa+C4/RFxDnARsLb24JKOBBZFxFNVu9+oV1ZYGj3WvbyS8JeSTag1OnnWO4Dv\nVdX/WFX97WRTLRz8ecjWprgs9fLfwuFTTD8IvGu8BrGpqaNz6diU9EKaknUsoz3xB4FfT9vLgIsk\nfTw9nsUrM6TeHRHPpu13ArcCRERF0paq434Z+C1JfwOcTfaCMJZ1KUEdRza8Qiq/BLhXkshWVvse\n8Czwc0mfB74F3JHKv70q9i8zRgJu0UTH/QZAmkdq7hh1Xwc8U7PviTF+Dw8AZ6R3MDMj4gVJT0p6\nI1nCrx7m+suI+MvRB8pmgzwoIh5Ttp7AZWTtU/sO4Gmq3kXZ9OCEb814Md2/xCt/OwI+GBHD1QWV\nzd73fIPH/Rvgm+n4t0bEy+OU+3cRsT0Nz3wW+GA6/1BEfLi2sLKZDc8FPgR8NG034gCvvPttdBx7\nokmpXqzaHmuo5ueNnCcifi5pmGy8/6G0+36yzxVeHxF/N0H1sc67EfgfZJP2va7muaNTXDaNeEjH\najW7KMUm4OBC4hp/IeV7gQ+msfw+siQDHJz3+x/JhodubiC2PyVb0ONUsoR3Turljn6mcIqyKWVf\nHRF3AR8jG7YYjeOytP1bwP8d4zy7gbem7eohrX8BThgntu81cNzqn+GgiHgGOELZFOLjlkvuA/4w\n3UP281+b7hs1euwvAtdHxONjlDmVw6fjtSnOCd9qHV0zhv/f0/7xerD/hWxBiEckPUb2weZYvk62\nxOXjZOtwPkg27DJqHbA3InaNU//g+SPiF8BfAB+PiJ8AVwBfkfQDssR7GvAq4I607ztki1RD9uJ0\npaSHyT4ovXaMc90I/L6kB4HqhS62AEvG+GxjouPWttt47ThENuxVr9y9wCJeSfgPkS1rN9EHtrXH\nC4CI2BcRnx2n/HvIhnpsGvH0yNY1ko6LiOfTB6pbyZZwezo99xngoYiYqIc/bUk6A/jDiLi8B2KZ\nSzb/+nl5x2Lt5TF866Y7JL2a7IPVP6tK9t8HniMbeimk9NnEFkmK/HthJwF/nHMM1gHu4ZuZFYTH\n8M3MCsIJ38ysIJzwzcwKwgnfzKwgnPDNzArCCd/MrCD+PxNshh0ZjEzmAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1337a8990>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(fwhm.flatten(), bins=np.arange(0.5,5,0.2));\n",
"plt.xlabel('Energy Resolution (FWHM)')"
]
},
{
"cell_type": "code",
"execution_count": 328,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"9985.0"
]
},
"execution_count": 328,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"result[:,:,1].max()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
" "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
kinshuk4/MoocX | misc/deep_learning_notes/Ch2 Intro to Tensorflow/005 - Tensorflow Intro.ipynb | 1 | 50321 | {
"cells": [
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting MNIST_data/train-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/train-labels-idx1-ubyte.gz\n",
"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"import numpy as np\n",
"import tensorflow as tf"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[8]]\n"
]
}
],
"source": [
"x = tf.constant([[2, 2]])\n",
"y = tf.constant([[1], [3]])\n",
"\n",
"with tf.Session() as sess:\n",
" result = sess.run(tf.matmul(x, y))\n",
" \n",
"print(result)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"you can evaluate the result with `foo.eval()`."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-2 -1]\n"
]
}
],
"source": [
"x = tf.Variable([1, 2])\n",
"a = tf.constant([3, 3])\n",
"\n",
"with tf.Session() as sess:\n",
" x.initializer.run()\n",
" sub = tf.sub(x, a)\n",
" result = sub.eval()\n",
" \n",
"print(result)"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import math"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0\n",
"1\n",
"2\n",
"3\n"
]
}
],
"source": [
"state = tf.Variable(0, name='Ge')\n",
"one = tf.constant(1)\n",
"\n",
"new_state = tf.add(state, one)\n",
"update = tf.assign(state, new_state)\n",
"init_op = tf.initialize_all_variables()\n",
"\n",
"with tf.Session() as sess:\n",
" sess.run(init_op)\n",
" print(sess.run(state))\n",
" \n",
" for _ in range(3):\n",
" sess.run(update)\n",
" print(sess.run(state))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now implement something similar."
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"60\n",
"120\n",
"480\n",
"960\n",
"3840\n",
"7680\n",
"30720\n",
"61440\n",
"245760\n",
"491520\n"
]
}
],
"source": [
"some_state = tf.Variable(15, name=\"awesome\")\n",
"two = tf.constant(2)\n",
"\n",
"update = tf.assign(some_state, tf.mul(two, some_state))\n",
"\n",
"with tf.Session() as sess:\n",
" some_state.initializer.run()\n",
" \n",
" for _ in range(5):\n",
" sess.run(update)\n",
" print(update.eval())\n",
" \n",
" # eval executes the update twice. Same with `run`.\n",
" print(update.eval())"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[array([ 21.], dtype=float32), array([ 7.], dtype=float32)]\n"
]
}
],
"source": [
"input1 = tf.constant([3.0])\n",
"input2 = tf.constant([2.0])\n",
"input3 = tf.constant([5.0])\n",
"intermed = tf.add(input2, input3)\n",
"mul = tf.mul(input1, intermed)\n",
"\n",
"with tf.Session() as sess:\n",
" result = sess.run([mul, intermed])\n",
" print(result)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# some explorations"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAEKCAYAAAAB0GKPAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsfXm8XsP9//tzkwiRhFiySIRaErUVJdWNa19qp0XVUlXa\nWmr7Fj9ViVZbpdqi1FbVfutrTVElRImlVGLfSZSQSCLElkTkJnd+f5xn+swzzyyfmTPnWW7O+/W6\nr3uec2Y7c2bmPZ9lZkgIgRIlSpQoUcKHjmYXoESJEiVKtAdKwihRokSJEiyUhFGiRIkSJVgoCaNE\niRIlSrBQEkaJEiVKlGChJIwSJUqUKMFCSRg9HER0OBE9VHAelxHRmUXmoeRV+PukBhF9hYheShGW\niNYkoo+IiBhpbUtEbym/nyeibXil5oGIriGic5hh1yKibiIqx502RfnhegAqg8y/iOgDInqXiB4i\nos8rQQpdbCOE+L4Q4tzU6ToGmLZaPCSEeFgI8dmYsET0OhFtrzx/SwgxUPAXUP03nBBiYyHEg+yC\nFwNWuXWyK9Ea6N3sApTIByIaAODvAI4BcBOA5QB8FcCnzSxXIhCyAcY7m06SGVEvIcTSRuRVwgv5\n7Uu0EEoJo/0xCoAQQtwoMnwqhLhXCPG8EoaI6HwimkdErxHRrsqDYUR0GxG9R0SvEtFRlft9iWgh\nEa1S+X0mEXURUf/K73OI6MLK9X/VEnJmSEQnE9EcIppJREco+a1CRH8nog+J6DEi+qlDxfRA5f8H\nFTXMFxjvM5CIriKityvl+KlNfUNEZxPRTUT0FyL6AMDhRLQVET1CRO9Xyn4xEfWuhB9LRBdVrnsT\n0XwiOq/ye3ki+oSIVjbko6uGXieiU4jomUo+/0dEy+lhiejPAEYC+Hvl/U/VpS4iOoKIXqw8n0ZE\nR1vqskZaqeT7UeVvfiXNkZVnexDRU5UwDxPRJkoamxPRE5Xvdz2A5R35dRDRBUQ0l4imAfia9txY\ndiLqB+BOAGsQ0ceV50Nd36ZEgyCEKP/a+A/AAABzAfwJwK4AVtaeHw5gMYAjkc3avgdgpvL8QQAX\nA+gD4HMA3gHQWXk2CcC+leu7AUwFsEvl9wMA9qpcXwPgnMr1tgC6AJwNoBeA3QAsALBS5fn1AK4D\n0BfAZwG8CeBBy7utBWApAAp4n78BuBTZQLYagH8D+K4l/bORSWJ7Vn73BbA5gDGVtEcCeAHACZXn\n2wF4pnL9RQDTADxa+b09gKcs+WwL4E3l9+uVcg0BsDKAFwEc7Qi7naFOOiq/dwOwduX6q5W63syR\n1vaG8p0L4P7K99ocwBwAW1bq4NBKvD6VvzcAnFAJu3/lW5xjee/vVd5tjcp73hdb9sq9LWzfpvxr\nzF8pYbQ5hBAfA/gKgG4AVwB4pyIxrK4Ee0MI8UeR9bprAQwjosFENALZwHeaEKJLCPEMgKsAHFaJ\n9yCAbYmoF4BNAVxU+d0XwFYAbJLBYgA/FUIsFULcBWA+gNGVWfF+AH4iMknopUp5fNAlBNv7DEY2\nCJ0khFgkhHgXwG8BHOxI+1EhxN8BoFKmp4QQk0WGN5HV6bYyLID1iWgQgG0AXA1geGVGvA2qEhEH\nvxNCzBFCfIBMpbhZwPv/F0KIu4QQb1SuHwJwD7LBlwUiOhBZ/ewvMnXcdwH8QQjxeKUO/oKMVLeu\n/PUWQlxU+ba3AJjiSP7rAH4rhHi78p6/yFN2IcSTjm9TogEoCaMHQAjxihDiSCHESAAbI5vR/VYJ\nMlsJ+0nlsn8l3DwhxEIl7HQAwyvXDyCbVW8B4FkAEwF0Ihs4pgoh3rcU6T0hRLfye2Elv9WRzUxn\nKM9iDJu291kL2Sx4VkVd9T6APyCTNGyoyZ+I1q+ozGZV1FTnyvhCiEUAHkdWB9sgk8AeQUbY2yKM\nMOYo17J+gkFEuxHRo5SpFN9HRpiu91Xjbo5MutxHCDGvcnstAKdU6k/W4QhkbWUNADO1ZKY7slgD\ntfVbEza07K5vU6IxKAmjh0EI8Soy9dTGjOBvA1iFiFZU7o1EdVB4BMBoAPsCeEAI8XLl+e4IGxwl\n5gJYgmwAkljTET7U6PkWgEUAVhVCrCKEGCSEWFkIsWlAHpcBeAnAukKIlQGcidoZ/oPI1E+bIZtd\nPwhgF2QSVxEeSNY6qNg9bgbwKwCrCyEGAbgLDolEiTsYmfru+0KIZ5VHbwE4t1J/sg77CyFuADAL\n1cmExEhHNrNQ+33XCii76b1936ZEwSgJo81BRKMpMzAPr/xeE5mK4VFfXCHEDGSk8AvKjNybAvgO\ngL9Unn8C4AkAx6JKEI8g000HE0ZF6hgPYCwRrUBEG6Cq/jJhLjJV27rM9GcjU2v8hogGUIZ1KGzt\nwQAAHwkhFlbK933t+QOVMr8ohFiCTMo4CsDrQoj3AvLhYjaAdbR7cpBcrvL3rhCim4h2A7CzL8GK\nivFmAH+pqJVUXAnge0Q0phJ2RSLavTKpeBTAEiI6vmL03w+ZTcGGGwGcQETDK2q805RnvrLPAbAq\nEQ1U7vm+TYmCURJG++NjAF8A8BgRfYxsQH8WwKmOOOrs7WAAn0EmbdwC4CwhxP3K8weQqZEmK7/7\nI2w2reZ3PDID6Cxk9ofrYHEBrhDWuQD+VVGP2AYnNf3DkA1ELwKYh8zVeGhAWU8FcAgRfQTgcmRG\nehWPIDOoP1Ap44sAPkEYgYZITr8EcFbl/U9W4wsh5iMzQN9ERPMAHATgNka+IwB8GcCJFQ8k6Yk0\nQgjxBDI7xiWVNF9F5mgAIUQXMhvUtwG8h8xGoROOiiuROUs8g0yV99+wvrILIV4B8H8A/lN596Hw\nf5sSBYMyu2HORDK3xt8iI6CrhRDnac+/iers4mMAP5BisC9uiZ4NIvolgCFCiG83uywlSpRwI7eE\nUfF8uQSZHncjAAdXxEUV/wGwjRDicwB+hsy7gRu3RA9CRYW2SeV6DDIV2PjmlqpEiRIcpFBJjUHm\nMTO9IrJeD2BvNYAQ4t9CiA8rP/+NquHMG7dEj8MAAOOJaD4ylcP50q21RIkSrY0UqySHo9Z1bgbc\nhrCjkHlDxMQt0eYQQjwOYP1ml6NEiRLhaOiyeiLaDpnB7CuNzLdEiRIlSuRHCsKYiVpf7BGoX9yD\nisvmFQB2VRZ8seJW4pcbkZUoUaJEBIQQSdarpLBhTAGwHmWboi2HzD3udjUAZZua3QLgUCHEayFx\nVcTuf9LT/s4+++ym5PvGGwJA898/pi5++cvWK3sRdbHffgI339z8sjT7r5F9ZNEiga4uXlhAYNVV\niynHzJkCr75qyjMdchOGyPafOQ7ZgqkXAFwvhHiJiI6h6s6ZZwFYBcCllO2COdkVN2+ZShSDN99s\ndgni8ckn/jA9AePHA9dd1+xSLFtYYw3giCOaXQpgxx2BUaOKzSOJDUMIMQHZFhLqvcuV6+8iWwzE\niluihMQRRwDXXAP4z5dzI/FEq0SJ/2LePOCZZ/jhi2qL8+cXk66KcqV3G6Kzs7Mp+TZj0L32WmCp\n40gjbl0sC4Qh62JZeFcfmtVHejpKwmhDNLozdHUBixc3NEsA1YHPlXczCaO7G3jyyfTpxqIcJKto\ndF2EtK9GEfrSpcDbb6dNsySMEl7suSewqWu/14LAIYzQtFJiwgTg85/3hytRQkWjCOPdd4HNXKes\nRKA83rCEF5MnA+/bTr5oAFqVMD7tCaeml0iCvDa2lJg5E/joI2DQIKAjsUhQShglWhZFSBgPPdTz\ndfw9/f1aEXPnNrsE1e++887AhhtmKtPURFYSRomWRRGEsc02wPPP50+vRAkVc+YA011nDyrQCf2p\np9IO7IsWVfMpCaNEw9HsGetLCVbmqO/Q3W0PVyIMS5YATz/d7FK0BhYu9IcB6vvTyy+nL4vMp1RJ\nlUiGxYuBu+7yh5NoNHHI/PbYI11a+nWJfPjLX4DNN292KdobffoUk26pkiqRFOPHA7vv3uxS2JFy\nYG8WSXR3A5MmNTbPRr6rVH+U4EP/PqkJQ5JEKWGUSIplaaatvmsjPVomTwa2265x+aXEppsCxx7b\n7FIUjyVLgI8/zp9ObLsqJYwGYPvtgQMPbHYp2hut5ApoQlGE1kiidK1Sb3U89xxw333NLkXxGDsW\nGDiwefmnIgy9XZcShoL7788WTpUoHjEDrBDAHXc0Pt9GpLUsodUnFSnwn/80Nr+iVVISpYShoRwE\n8qHIweC117IV4nnQ6oSxLAym5TumR2nDKFFCQ6uReRHlabV3tGHaNODqq5tditZFs0mxN3O/jTff\nBFZd1R9OtstSwiiRFEV2lBSDqUwjxQysWYN7swcjAPjFL4Cjjmp2KVoXqb4RNx29Lfbqlf332bte\nfDHbSp2bbilhaGiXGV67o1n1LPPdccd0aaVEK5CBCSnf1feOrVoHIWj2O8jv1dXFC8dFKWFoaMRA\n9v3vF3+KVbMQOyNScfTRwKuvhsUJRUppJVV6JXoOUg2q3HZlC+fbAoebvmrDKAmjgejqAu6+G5g6\nNSzelCnABx8UU6ZWw5VXAn/7m/357NnxezfJDpKaMHo6SgmjFl1d2e6tNjTb6F2UhFGqpBqMb30L\neP318HhjxgCnn56+PK0KU4eTjfuAA4BNNolLtyjCaOQA0QoDap4ytEL5bfjb34BzzvGHO/FEYKWV\n7M9b5R19EoZvDzS9n7SsSoqIdiWil4noVSI6zfB8NBE9QkSLiOhk7dkbRPQMET1FRJND8i161vjs\ns/FxlyxJV45WQUx9pzgzolRJlTBh3Djg7LP94Rq1ziJ2cOZKGKHlKELCyH2AEhF1ALgEwA4A3gYw\nhYhuE0KoezC+B+B4APsYkugG0CmEaOIRPWa0ysyjKBT5finSLlVSaZDn3Vu5D3B3HfYNmq2ikkpl\nw5BoVQljDICpQojpQoguANcD2FsNIIR4VwjxBADTvJsSlcOL997L9q3noqeK8qGIXemdKt+SMJoH\nUzveemvgiCMaXpQ6cL9pqxOGhE8rwSVItd+0og1jOIC3lN8zKve4EAAmEtEUIvpuSMahg8AXvwis\nv35YnJ6MdiE1znd+553iyxGDVqjj1GV47DHgnnvSphmDdpUwurpqyYE7MQp9XoSE0Qpnen9ZCDGL\niFZHRhwvCSEeNgUcO3as8quz8mdGV1e2rfROO1Xvvf02sGABv2Ct0NnbAS6jdx6oK1Z9GDIkkyBX\nWcWdVqvg+OOzv1Z32W7lPhDqZhr7PDWEyLbN0c+iyUsYEp98MgnAJFx+OTBrVkwJ7UhBGDMBjFR+\nj6jcY0EIMavyfy4R/Q2ZistLGOPGudO9805gn32ap79t5Y4mYSrjnDnAkUcC//hH48ujI1Ql5TIa\ntprR+5JLgKFDgTPPbHZJ2hfNkDB++9vM62+HHfKlM2VK9Zo7MeK22379OgF04qijgGeeAWbN8gyW\nAUihkpoCYD0iWouIlgNwEIDbHeH/W61E1I+I+leuVwSwMwC2176rAps9KLQDYZjw2GMZ2apolg0j\nZVrNbg8mFNVG9Hd15fPyy9n23ja0cjtuBmGcdBLw4x/zw9uglilWJfX22/4xsOWM3kKIpQCOA3AP\ngBcAXC+EeImIjiGiowGAiIYQ0VsATgJwJhG9WSGKIQAeJqKnAPwbwN+FEGztaNGDQCt3lhQIfb9m\nHdHaU9dhNKocrvq7+mq3tN7KfYDbLuReTTY0ox+kUOMOHw7ccEN2vWRJvZdVS7rVAoAQYgKA0dq9\ny5XrOQDWNESdD2CzFGVQ8eijwCOP1N8P/SChDWmTTdyztZSYMQNYcUVg0KC06cZ0BlM9tbJbbSri\ny/uOjZIwXPANpr48mkkorWb0Dql3Nc88Kim5GeEBB1SvZdqt6lbbcvjyl4Hzz+eHnzLF7wMNZDry\nn/3M/vz556uHOhXdkdZcM7PRpIapUS4LbrVEwBtvpE3ThzPPzM4NaSZSz0AB4OmngRdeSJ+uDi5h\npO6LzZIwXO/76KPm9FrRrbZpsFVwaCWNGZPtiaRD/6gvvgicdZY7LflRGzHzeu+99Gm2oq4/hTcM\nJ42ZbFeNNOjuBq67rvh8XPWSWl0DAJtvnvWpotHOEkYKGwZQLbvJ4aOUMJiIYVWThKFX9rvv+tPh\nNuJWQCuchyEEcO217jTy7gLKTaMIlWUr2wCAYggD4B8KlAdFLNwjql9At9ZatVvc2PJthkrKRRil\nhMGErZLyzp45M/pG6na5eTz6aPgqUd+9VPjoI/uq4ZQqqVaF/g0/+KCxJFOESgpoDGHINn333W4V\nNJcwJFHofeXNN9273UrEEgY3vuu5iTA+/bSUMGpgq8CiTtDiSBi+U7NSgvueX/oS8LBhZUuqBXdF\nLdzjppVaenj9deDAA/nh80Cvuw8/bEy+Ej1BwjjrLOBHPzKHue66bMB3Qb7jJ5/UphtbHg5MKqk8\n6zBMhHHJJaWEwUKKSiICnnqq9t7Chf54po++9dbF6KqLmIm20mw+VLfLVUn50ps4EbjxRn/5ikBR\nM34b8npJ2dBICcNVZ4ccAtx/vzudVIQRAt8ka8EC4Kqr7M/1dEzjzsKFpYTBQkynS234UtN77DHg\ndtdSxkiElNk0MLSCfp0zyKcmDB+aWS8pCCOlW62si0WLsnacKt0UkO+Zt87kO8oJYaxEm9eGoca/\n6y7gu9rOei7CsN0rJQwGbB2+ESvDbV5SqVxD58+v/g4Z2LgzvkbbMDhITRi+ekvZyUL3MWo0WXEJ\n48YbM0mZi1aRMDjgSBimAV5HSpWUSWJQ05eq70bvk9VWhHH++cA111R/p3KrTYkivaSuugoYMKD6\nuwgJI5UNQ+Lxx+vvLVkCfOc7/nR1Inj8cfOutKlUUq2wGK2ItpvHrVZi2LDsP/eQn0baMBpNGL7y\nhORpi++buHHql2gZJ4wf/Qg4TTnPLyVhpGoQRUoY06fX/s5LGCakkiZc6cybB/zxj/5w+sxrq62A\no4/2hwstTyuh0ZMdbn59+2b/586tvW9rg+0oYbSSSsonYZjSMaFUSTFQxAxx7ly7J4aKIiWMPOqL\n0A5smu00a9A1ieIqZJ2nUjlyOtm++6ZZ6Gf7pnnqWo/rSourktJJmWP0DjlKIAaNlDBSw9R31bGD\nqxouVVIBaKRK6n3mAbI2tYarER57LI9oYghD5hsqYXR0AA88wIvjSicPWtnofeutwL/+xU8ztD4a\ntQCU2y64RCHRuzfQv795y4pUaKQNQ0UeCUPm5VvpzZUwfFjmJQxOpbWCDSOEMC69tNpYXYiZLbiM\nYz496ltv1T4zreWILZcpP9uzPIRx5ZXAffeFrdVI2X5ipTPbep6Y7WBSbA3CXSsgISXat9/mhY9B\naglDLtyLla7zqqRk3Z59dnUjQRWmuvfthpxawmiFE/eSo4iV3ty4oTNDrreDKQwnjqkTuKCGW265\n2nvPPcdLIySPFOFdnfroo7NdhDfaiJ9eyk7mG3BsEwtTO5o/H1httbQqk1DC4ObtWh+QCj4JY/x4\nXjqyrLIvFkkYRFk412TtnHOA3XazP/d5/JVutRY0UiVVFGHIPaxCxFnbbxWXXALcdJObMHwSRp8+\n/jKlgktn66sbWee2uhciXl3ACc9BCgnDt6NyHh08d5Vx6DcpcucDn4Sx//68dHRyK5owAL9KyvSt\nQ9WCan6p0HaE4aqADz7I/rcCYXBVUtJNMfVM7PjjgVNPraYfI2HohFGEMVCmedFF9md5bRg6Yahr\nWYQAPv64Nj63k4XYkFJIGD6cckr9vc03N6c1blx2sqLMz+YuGythyHBLl2b2vyKOok1twzANyC4S\nyQNTmdXvZNt9Vs+/9JLywPax7r23ephQEW61eSUMW3w5k+AMEPp7+cq8wgpVCcO0fkGPv9tutfvu\nSJVUDEIHlhNPtD/LSxjd3bXPttsu2y8KAP76V2DgQF5ZdRRJGDEzc93lFcjOpjDZx8aOBX7xi2q7\n03do1csXShiqhHHvvcDPf86LFwKbhPHgg2HpNFIlpedpy0OOC/PmVe1WMYSxzEsYNqgDYsxK71QI\nlTBCCCPUhrHCCtWZCufQ+gkTag3beSQMrsdSio4YKmEAVZ97k6eTacLx2mtx7SfW6N3dDVx/fa3R\nWJ/5qltux8InYejhYgijqIWQJgnjnXeAbbcNSydUJSUEsMUW9XvLhaikfOpg+T3GjAE23DC7loSm\njhUuG8Yyv3BPh4lp77+/uSopm1qjCJVUiIQRA0kYMYNejApMxTvvVAdErr48hDDku6mn7LlUUuut\nB0ya5C6HCzESxsEH127braZxxhnA8svz8nZNoLh68VjCsLVrqQbMAxNhxLR3E2EceSRw8832937q\nKWDOnNp7eW0YJpXUW29VJ8MxNoyWVEkR0a5E9DIRvUpEpxmejyaiR4hoERGdHBJXh6/jbb99c91q\nQ1UJIUbvUJXU8su7O1CRRu+8hDFkSHWhZBESxj33ZB3QtAOxrf3oqp0UKikbfBMIjscaxybjyyfW\nrdZl9J48macGXLrU7elkIow8Ey91QL7mmswl2/TdXO0sNE81Xiqjd4jKKhS5h1Yi6gBwCYBdAGwE\n4GAi2kAL9h6A4wGcHxGXWY7qdSsYvbnxG6WSajTyEgZQVceYOsCHH9aTbYiX1PHHZ/p9U1ux1avu\ngloEYeQxesfkHWsn8pGRSyVlsqeZ8NRTbk8nkw0jT73ltWFw4FJJmSQMNZypfO1o9B4DYKoQYroQ\nogvA9QD2VgMIId4VQjwBQJ/veuNyoVZcETYMm9599mzgmWfqn3GZvZVVUtz6Cp3FpLBhrLxytkJe\nfa6HkwZ8E2EAdh0vlzA4CDV6S8jBIWZ7DdvgLqHumeSbtaYwetvK5wPXEaUICUPPg9NmY1VFpjxc\nXlJcG4bteR6kIIzhANQ1wTMq9wqJy+l4RUsY6vUhhwCbbVb9HWL0PvTQzLCpxnMhRiWlNrxYaaMZ\nNgwVtrp59tna53pal15avW/Kp6MjTMKIaVd5JYwrr6x/FpqnHm/cOH6aRRAGF9zBLpYwbrwR2GWX\n+HUY+r2URm+uSsq30jv1WNhmK73HYuHCzCUQ6Kz8ZWgWYeiDsPyov/41cMEF5jgS//u/2UxZjedC\n6Gyho6NWwliwoJqfLb1U4jhXDRIrYQDV2betnOrgayOMEAkjlLBNZTHh1VeBUaNq7+WZmUvYiFSu\nV3KFseXNbRMulZQt7k9/CsyYAVx+efabU7866YfU0U03ZbYsec6HSeUTYmiOJQyTGtKkkuKWZcGC\nSQAmYdq09FuzpCCMmQBGKr9HVO4VEHcs+vXLCEOdJQHFimE6XAwfKhJzPYFM4Ijsanl0wvAhlQrP\n9qxowlDjhxCGbcJRhErq9deB0aPrw7k2n3Op2Dh5q6v/bWG22642zUZIGBddBLz7bpUwOBM/fRY9\ndSo/PzUNoH5AdtWPCUWrpLg2jP79OwF0Yv31gcGDgeeeG1cfKBIp5uJTAKxHRGsR0XIADgLgOpBU\nfcXQuLlUUnrcDz/MXBcBf8Pm6qBDjd6SMIpQSekDizqzVONfe60/b5keFxzC4KTR0WEPL1ds+yQM\n17czzfRSGL0ffzxz8faVwbaWwiVh6Gntvz/wj3/Uh9cHQLlYUR2MbLNW6UKcd6V3HiM0V8JQw5n2\nYOLm4yNp/V4e+KR7vV0sXcq3YfjyyYPchCGEWArgOAD3AHgBwPVCiJeI6BgiOhoAiGgIEb0F4CQA\nZxLRm0TU3xaXk6/LY8g3M5ErQZ95pmpDOOWUqk7chxgJw9bIXP7qRLXbqod6Sen52s5vOPJIc3hu\nx/A1ftszjoRBVBtm0aKqMVsnDL0OU6mkbHYpVzvbbbfMxTvlQGtLa/z4ajt2hT/qqOy/qqYsigAk\n4YWo1vT7nPadR0+vTxB08lTbXrNVUjff3BrrMJLYMIQQEwCM1u5drlzPAbAmN24M1IrxVdLLLwPb\nbFN/37WYyDaQ5lVJSTzyCPCZz9TfX7CguuWJjlAJY8YMc3yuV1lqCYNDGLqEMXEisNZaWZkXLcru\nxSzck2mb2op+z7Yfl6vsLr09px59EgZncNXrRRpSORKGK28OYrykYgjD9g1DIPPRVT42lRS3/K68\nfJMsfRz59FOzSoqbXyq09UpvFTFGb73iuYO9Gk/mNXy4OU0uvvWt2k3xTIgxuqrl0VemcpFCBDel\nF0MYEuo+V7EqKV3CsKmk5Iw8ZDLgUuW4Bh/XTN6Vv6nN63lLwlAljKLcamUeIVuDyLLMmZOdXV+0\nhKGmoeZv+j6m984zofKt9NbLRhSukrK5jedB2xGGT88M8BtQyNJ+n4QhvRFCVVIqTD73LmkmVMLw\nbTDnyjsUMXVpgq6ScqUXY8MIkTD0b+vrrLYycIgnxIYB8AhD6sVVCSNUJcUNL8kpRsIYOjSbPOnu\nsqb2GyJh+Mqedx3GvvtW+/Ds2eYwuoTxu98BV1wRVr6vf70+PRtaceFeUxBiw5g7t/6D33MPcOCB\nteFcHZk7yOUhDNM2FXnAJYzQ2a+OomwYQriN3qb0OPcluAv3iiQMm+pKDaOnwSUMm0oqpYRhqwNJ\nTqlUUkccAay7rrl8eQnDppICwuwG8+ZV9yYbNixTfdsg8zzxROCOO/x5CFEtn7qnWdsZvVsFLrfa\nwYMzLxL5QaZPzxbs6MgjYUgUKWHk9ZLSCYMjZsciBWEAdsIwdWqX0dsGU7uJJQwXEcycaS6n7f3z\nEIYtvE4Yav0LkeWpn13/7rvZvkq2NG1lUre84Q5aLsJ47LHarfcl8kgYurbCJ2GEHo+r9+cnn6ze\n852HIWFahxGCZV7CsKmkfK60775bvWdzoY2RMPR81bRDB1+fhJHXSyp0mxDOQMXJ15WuK9zcudlg\nXZSEIYTbhiF/c7ZvefbZWrdbPY3NNgP+/Gd/OjK8qR2pA5r+ThyduJz12ySMyy4DVlmlNs4zz2Re\ndKF1rNowdHAlDIkjjghXK4aAQxhAdn4IALz4Ylw+999fvXapEE1lU8tne25CKWFYYKvYkFl0jKrJ\nZiANSVvCJ2H48vbly5EwQp7HxuWq9958MxvkYgnDl4dUefnSsw1+av3rK2p1wgCqNjPOTFENw1GL\nmFyEbRKKTW6sAAAgAElEQVSGzYZhmsHb0nLd79u3eh2ycM+WtmudkI0wQvo9V8KI3b1Z1rc6IezX\nj18+CVNd+rzjSsJgwDfL56gBXHFcH9bm416ESsoHn0pq1135ZQsJZwv78MPZYskQlZQtLVun5saX\n910dSrYHjoRhUxea6j9UwjCtQPblr8aT/+UusapKSk3bNbibpBxbmVRJK2RrEJtKUS2zjpSE4dut\nNvRAMfl8ueWyFejSDRwwE0YqlZT63UvCsEBtNDbCiB1YALvUojfW6dN56Zlw3nn1J8CpadhUUuPH\n20X/UJWUq75s9aeX68ADs62pdXz1q8A556QhDBW2GThHlWZSSemDo48wJk6s38rB1FFN6XAGT1P9\nu1RStnhAdqaHScJQycMEPa33388MvKY81Os8Kin1t75LgYpGSRj6kcW+AVxN5/33a89TMR1+xW3n\nKlwOJ6WEocClzzcRBme2H6NGcX2QUAnj4YeBn/zEH07Pe//9zavUuYShhvnnP8331d8/+hGwzz72\nct14I3DrreZn3d3hK1a5HTOUMLgShs2oLuPuvHO2Etf0TM2bI6m4JAxXvZmcA0zhdfdUDnmpz9Qw\n22xj719yQEyhkgKqxvipU2sJL6WXlIswZs2q30HWlJ6tPfXqZT5bXYWvnXPrUj3KNTVhtNlutXb4\nCIMD1wezdSzuB7n3Xh7ju8R3/dmECVVjPmf/LBdhhNTTDTdkR0e64CpPKJFyRf9QLynb97CpX1wq\nk5D65xBGCrda22BuU0mFSBhAlo4tj379MhVMnlmu6T1Hjcp2gj5ZObeTK2HYwnDcanfYIS4Pid69\na1VSXAlInXiEqqRKCQO1OnAVasX4/MxTShgu6OE4KiH9A++3n/0ZANx9d/Y/D2Ho4Wz35G+X8U/m\n4Zr1pVZJ5ZEwXIONvhuuq8PqdSLTDZUwJEJtGKY1JTLcnXfWpmUjo1DCUKUaE2HYyhqjklKhb+HD\ndVHlShgffWSPs9Za/vRM0CWMkHqR4L5TacPQ8O9/h6uk1Gvbh+FKGCeeWL3mDIwStp1JVejvpZ7m\nZ/r43/qW/RlXJQXwGqP83VuTS9W85cDJUdXlIQzTLDCUMHzlHDy4Nr6rfbjqRMIkYchwd9yRLfyy\nDcD6PR3crSb0Os8jYej2n3nzqmlKfX/IwOiS4Fz3TX0wxHZy3321+Z9+uj3Oxhv70zOBQxgxKilX\nOqWEUYFJF+hzqzUZN3W4ZiDqM9XNj2vDAMynaIUgZjuUPIRhS4vjXsgl0iIlDPW5beDKM6CpsBGG\nScIwedLtuSdw4YXmMpgkDM6g6XtnG3mYYCMM+fv224FVV62GUSUsV7v9y19qT0b0lV+HzYZhauu2\n9KQEJgdk1f1Vj6N6N3HKJ+u0o6N2whiqklLT4uZZShgKYozevpmi7X5HR9wqSx0hEoav8eiwzTC5\nhPHQQ/X3YlRSEo2UMPKopHz5339/rRHRBkkYrkFPEobrqFyXhGGSpF54IfvPVcvobcK1GNBULjVN\nVSWl7p2kE4YLxx5bfza7nqcPeSUMCdW2Y4uzwgrVa44zhrrTsUz/0EMbo5IqJYwKfIOpiTBMAyIn\nXZm2i0xsWLoUWHvt6m91u4SYsnD2LlLjzpxZu52BizB23NFcBrk3jopUEkYewrClx7lvS9sUfvvt\nM7dZgGf0VmeUehgTYdi+qU/CkJAqkhgJQ0+Tsw7DJmHoaboIwzYgp5QwYgjDtI29HkddlMjpo6rd\nSrXvcVVStnHNVYZSwtBgYk4fYXz4Yf09Ha7V3Hqcn/60Pl8dixfXrsuQhNGrl71zxkoYKmTcyZOB\nQw6p3g/dGgSoPfJSpsvR1zeDMFzeULb7IWsiOEQv69j0HeXWIK7FnS4Jw0WAXBuGTcJQr11rSGII\nw+X5l5cwAD5h6NDT56yTMW2rr+LHP7anqbaNIiUMub1LKWEwYeqQnIEhRMKQ6yU4fvwSPh2mml4o\nYdgGARUxe0mZOrROGCbksWFMnmwPb4LP6O0iEr0sW21lPzeEMwhx6tilkjKB4+nn2hrEdY+rkjKd\nPW8iDPmfq5LiSn+2+6p3mK8PcCUMFXo6Pglj/Hhzmqp6irOhpukZVy0+YkSmOislDCZMEgans7vU\nTtzZjq0cAM/oHUsYHEJMRRgxKqlLLqlPxzRILVkCfOEL9eXwldMULoYwHn8ceP55ezrvvAMcc4y9\nLEuWAGecUZXM9DJdfDHwve/Vp+16l9iFezZ1RYxKSq4h4BKGqx37JgycZyao37lZKilbmo1WSfXu\nXYyE0bYL9/SKNPmtA9nRpwCvkYZIGBKumbQ+QHM20uPaKXQUIWHo6foIY+7c6rVe1uOPr09n8eJs\nF1cVMTNDH2GErsZ3OUXcd1/1wBsTliypfa6X6Xe/A157jV8W9ZqrklLLa8rD1FZ8M1g52bERhpq+\nPuvn7iVlKqsPahnU9SZFEYZPJWVLs7u7WqaiVVKyzltWwiCiXYnoZSJ6lYhOs4S5iIimEtHTRLS5\ncv8NInqGiJ4iosmmuDrkYjWJL3+5upEeUFuJu+9efy9U1237wPKZDS4JI0ZU50oYKVVSJtgIY489\nqtcclZS6QEoipFPo15wZtv48pOPaZucqfDsCu6QztTy2Qd1WblUl5SIW9R1sEqQJJsKwSTU2NZEJ\neSUMtU/stVf1Og9huKR1VcLo7nYfSaCqodRrWz/2qZxMz2fPBtZYoz5fOWa1HGEQUQeASwDsAmAj\nAAcT0QZamN0ArCuEWB/AMQAuUx53A+gUQmwuhBjDyfOCC2p/P/aY/9hJjsrm17/O9t43wWUQt8FE\nGK7OrKbnIozY9wsljOeey1Q0eh42o7dcuKXe06EOUqY65XZ0eW/SpDCjtK0sapoxhCHzPvfc2nrQ\nwd3xNFTCIMq2bNHLa0rXVO5Ro+pXUKswuRbbVFI6ebkkDO5iWVt8029b3CJUUvpYZEuTo5LyTRJN\n7/Tqq9k+V3o6Mo+WIwwAYwBMFUJMF0J0AbgewN5amL0B/BkAhBCPAViJiIZUnlFMOVwbecUOqI8/\nbt573zYTBdwfxKSS8pWBMzPzvZ+to4UaW087DTjrrPp85aCnDxbqYM+RMEzlNG2i6BpUttsun4Rh\nahcxhCHf/X//110GnTBsrrqmQdVlwzDBJ2HoYfSBR4Vsyy+9VL1nkrylGoQrYUhMmGAuqw826T+P\nl5S8P3Ei8Mtf1obRVVIuu6QuYeT1kuJuPtjSEgaA4QDUrehmVO65wsxUwggAE4loChF9N0F5ohuQ\nK70UEoZqw4ghDJ+qAQB+9jO7mDx/vr2sIdA9YEwEwLEbmL7Jl75kD+9Lz0YYeW0Y6n3bYCsHA52U\nfYRhSy9E8gHMdWmbZdvsFq4+Ip/ZNv2TZTv//KwOQo3epvU+MX22o6PqIeTK1wSThKETmS5h+AZk\n2S5efbVewvjmN2vDxqikbPUb66jjQysYvb8shJhFRKsjI46XhBAPm4OOVa47K3/1iJUwBg4069VD\nCGPffYG//S271hv8AQeYG6UpPVdHczWcs87KXENNmDcv8wBS98MJgW8Gn0LC4ORrex4jYbgG5mHD\nslm3tJl1d9vbEZcwdHWercwmCcNFHCbpkTOL5aqHTOpMk0pKSqRclRRnEuSD/g62dU5CZCrMzk5z\nOqa+qZdBlzB8hCHTlHu+AdXB/P/+r758OtR65BLG++9PwsKFk/D227wFyyFIQRgzAYxUfo+o3NPD\nrGkKI4SYVfk/l4j+hkzFxSAMO2IJw3Wfq5JSTxtz7WeTRyVlW5DlQkdHtup7k03iZx562V0SBied\nVIQRqqpR07VJGFtuma2UB6qedq5Fb3KA8tmJUtkwbOoUX9qcdzDBdjyorz1/+KHbNhIqNelxZs8G\nxo2rLZNtK58PPqhVYeowGfb1MoR6SfnqTUWMSsoUZ+DATgwc2InVVwe23RZ46KFx9YEikUIlNQXA\nekS0FhEtB+AgALdrYW4HcBgAENHWAD4QQswhon5E1L9yf0UAOwPQvODd+Mc/6u/FEoargXIlDHUG\nGeOp4QrHnY2ZnptO+AqFbzZsc21WsWAB8MUvusOY8t1mG3+5UkoYvXrVl8+mqgKqA7b+zUNVUvL3\nAQfU5+siRhNR+YzeISopU/outYfsF3femZ3AaIPrG02aZH9mg5ywmd5F3Sbnww+BF1+sfW6SMPST\n/nQvKZ+EYfoGIeswQp5LdHVl7awIt9rcEoYQYikRHQfgHmQEdLUQ4iUiOiZ7LK4QQtxJRLsT0TQA\nCwB8uxJ9CIC/EZGolOWvQoh7QvJ3NUYVHMLgLvBSEUoYvtkwEXDRRcB665nLYSsn5/3yIkTCsNWl\nal8JMeK5RGtbvZjIwBZXvRbCPEt1zc5n6jK1JV+X0dtXRq5KyjexsNWLa0AKmSnLZzZwvgtQ3X4n\nBNJDy1Re6b0mBHDmmbXb3gC8A65UwnjySf972tRMXAlDpn/GGcD66/PiLFmStTOOyiwUSWwYQogJ\nAEZr9y7Xfh9niPc6gM30+/nLU3+vURKGqpKKIQwA+OEPgc03tz9vVcJQ39dWlyqh5lFJcfXgAM/F\nV4XUg+vlW7rUXs9yg0JXOYHa9iHzcoVXw4SqpELcam3hJXzH++rl4RJGavTqleW95Zb1z6SEMWOG\neXsbjhehqpI64QRg7Fh3+FQSxpw5wDrr+MsHVAmjJSWMZoPL1I2SMFRjr0tNkGdmxh1Ai4aeD0cl\npdZP6LoJG2x1qv421as+EQiVMGLq2UUYvnbpyi+FhFGESsoHH9mHwrSnloQkjJEjzYRhsmHo4Gy8\nqSKEMFwShi0tE6RKSvVWS4UeuZdUSsL4/e+z++qurypCjd4pCCPG6J0CITYMjsEyj6uzqxymvGwd\n1BTGJmHEEIYeRvcec5VZv8dVSUmE2jBcBvtQo3eREsbs2cArr5if6YSsQq0j07v6PBiB+u8XQxhF\nbw1SpITR9oQRI2GEpOWrcJeEEWvD8IGjklJF51RIYcNoFmH44urpFEEY0oNHT9OHWKM3px+oYVyE\nwXWrVZ/ZEDNYqrjqKmCDDczPXBKGz4ONc+Z6CsKINXpznWi6urJNMqdOLQmjDilVUib4KlxvQFzC\nCMG4cVlj50oYQtQeJZkK+uAwY0btb45KSgWXMHzfwFUvvng2CSPU6O0rG5CpM/QZcJEShk+q0jfV\ndOnwU0gYjVCVqqvMdfjaW6MkjKJVUkuWVM//KQmDAZ/olpIwQiUMUwe77LLqClqZnpru2LGZF46M\n45tNNoowdtqp9jlHwuC6cargEoZt8OUavX02DD18CsLQid412VHLp4fTB/tDD7Wvmo9RSdlsGDa4\nCCOvhOGCq0y+78UxeocQhu17NkIlJTUMJWFoaLaEoSPGhiE9O1z5qfdN+9fo7+c7syKmg+px9EN1\nirJhcGdxoSopH2GY0oudeAAZYejvEuNWa4I+2Ol7WgFVicL2DnkkDNMzHY2QMFwqqUZJGDZCVtOI\nUUlx608avW3ly4O2JwwgXO+fsuG6BgCuDUNt5C7CkHF8hCHTdJUzD2HI/+qeUn/4Q34bhm2XV9es\n0VQuvQyudzW1C5vRWx8AQm0YoYsB9TCu9+HOjl1SkiuNFDaMRkgYeVRSS5eav5GKIgnDp5LixpFG\nb1v58qAkjJxpywYkw6lnhzeLMOQM2YUYW4peb1KaEgK48MLaZxwJQx+E9POQJWJVUj7CsKkMhLAT\nRqiEoX9nF2FwJYxYwpDvZFNtFW305khKeZFHwgCyOgqRMEzwEQYR8LBh86MYCaNUSQVCiOYShnwu\nB09180KuSopDGGpD5RAGd5DNA1XCsA3Wrnz1MDbPrkYRhiph2GwYpvQ5ZQPMM8tUC/dM59jrkIOh\n7Rvkcas1PdMhBPD//h9w0knmZyGwDdz6ffVgtSIIw0WM3d12CWPBAns8G0JUUiVh5ERRKikJuaBH\n3WjNZZw+8sjqPdNpaTp8EoYer6MD+NWv7A0nj4Qh/6v2Gp+qxVROvQOvuKI5DteGoedpOvTHVB5V\nUlLvhUoYe+5Zn/73v1+9Ng1GIaTDlTBchMEhKBP++c/6ezESxgUXmAfLUKhbdOj55pEwevd2fxM9\n7ViVlAk+lZS+lYktTqmSciBGwuCkKcFVSUmvJK5K6p13qvdMxlAdo0eHqaSIgJVXtntq2QaKlVay\nl8Flw+AOhK4ZbSxh+CQM3dCrxjMRhm3Bk8+GseaaqIO6dxZHJVWkDUOXMGwDGhcqYejpcOpPfxYC\nG2GkUEm5wCEMqZ61fU9b+WK8uFyTA1desWh7wgDSq6RiVFaDBmX/f/ObKnm4CEMd9Pv390sYquRi\nIwy5+lXaMDo67GUwNc6RI+0raE1liyEMFXrZbK7AsYQh0/eppKR0KMMvXWpeZNfVVTvT1t/RN9j4\nCMMGE1G4VFI2fPghcM454XYYF0IljFTSvW335aJtGDpMef3hD9n/FBKGryyTJ9ff69273raaCm1P\nGEXYMNSw3AqXhLHuusBuu2XXXMIYMIBXNpeEce651dWvS5f6O44pn1VWAVZbzZ+/rpIydYwYt9q8\nEoZtMPZJDJIwZHhZLr1j33wzcPvttfFV+AyiPi8p24AaopIaNszdhv7xj9rJRx4JQ5dWVIS61aaS\nMFxtJQVhcMaDlCqpOXPceb36av091aW+JAwNeiWbFisBxRGGfL7yyvXhXUbvxYszyQLITvoLaYgm\nwnjiieq1bYasPrcNFCHlMB3RKRGzcC/W6G1T1XDPddbPUJD1p+ernyOv58eRMGIkMZPRW4ckjPXX\nDxt88xCGq0wcCSOPtOEyere6DcOlkkohgakq7pIwDJCVsuee9plHyLYVIR9NNlwpYcQQxoABfpWU\nCtfB8zIPqZIyQd1mJAS2AdI0M+Z0TtOZ5ybESBhLlvjVNLpKSpUwbCopFTEqKRdh+CQMlw1DqhJ1\nlZMLKVVEMYTx9NP2+LFotEpKtpGNNqreU79TqISRijA47r8xaHvC0FVSsQYlW1jfYCVnxWusUVsm\nwL01yOLFVVUUlzDkM/U0NhOkCsZWL7ESRghhxHhJHXNMeJnUNNW0R4yotTdwjN6qhAH4CSO1SsoG\njoQh0bt3a0sYKrbYov7ZGWfw8nW1iTxjQKhKKqWXVN5vIdGnTylhWKF+XK5LXUqVVJ8+wE9+Auyw\nQ314nw1D6uylpKHnrYM7EPgkDJsNg5OuWg6X0buRW4OYJAyf7lfGM0kYknD1+tMlO/3QpBQqKY4N\nwxYOcK+N0PHss/aDn7hIZcOQdjdfHYYitL35CNe2Y4Lp2/gkRtP9VBKGREkYBthm0mrFcRY2SXCZ\nXjbAvn3NXglqA91449q05eDzpz+ZCSPPh5adz6WSSmHDUDt3CgnDhth1GEB2Fvjw4fY0bCopU74+\nVWCMlxRnIhMiYYQQRl6oA5z+LUMJY8mSrP64qhQ9/V/9yp23qYwqPvOZ7H+oSsrV9mwShqtvpFZJ\nlYShQVVJudQwOmFsuKE7TVMaOtTZiOkD+WwYQgCbblqbp2tQ4jYmm9FWfZ7ChqFKGNwFYUVLGD/6\nEXDLLdVnRx9dP7MfMQLo7KyW2+ZWq8NXXh9hxO4lNW9e7Tez1e2GGzaWMIB6kpUIJQyfVKwjRiXl\n+n7SsyhUJWUiDJ9KylaOVEbvlldJEdGuRPQyEb1KRKdZwlxERFOJ6Gki2iwkrj//6n8uYay6atWz\nSUeISkoSFneA0QlDj3fXXe68OOCopFKs9B4xovqbq5JS81W3UXGBu/lgdzdw/vnZWhgJ0wAgv5du\nw9CN3qGdLUbC4KiZvvGNbAatShqmsJde2njCWLQo+5+XMOTGf7EqKdUGGEMY0hYZSxgmpxobYfjO\nR8+LlvaSIqIOAJcA2AXARgAOJqINtDC7AVhXCLE+gGMA/IEbN7w85mudMFwDQuiqcFXfrabZ3V21\nU8j7Lk+XVLDp4CVsEoavTLqtYOjQjHTHjq1dua6GceVx9tnu/CRCbRiqH7pNJ60Shi5hvPwyL18d\nLmK77Ta/DeOdd+wLJ6dN80sYffq4z9kuAtKzjbvS2wZJGLHePZxv5fKak23G51arw0QYPgnDtGJb\nbY8urLeev0ytLmGMATBVCDFdCNEF4HoAe2th9gbwZwAQQjwGYCUiGsKM6wVHwtD32uESBqfC1bTU\nGZ4Q7iM51dkQp5OHShi2srtsGNz0AeAvf7HPCDlGby5C12HohGEazNR61yWMefOAJ5/ML2Go8ffa\ny6+SuvFG4LDDzGl/+qmfMOTMMpW3jQ9CNE/CSO0lJScNoVuDmFRSPgnD1Dek9OnrH3ffXStBm6Da\nblMjBWEMB/CW8ntG5R4nDCeuFzaSUK85or/pOXd2a5oZyYFbTUcvhy1903qSEBuGSyUVqyvVZ/If\nfWTvYBwJg4s8EoZNJSXjqYShdmTbeh4XXIQBmLdq4Q7uixb5607OLJuhksorYYQavXXkVUnF2jDk\nlvwrrFC95/OSsp1eyJEw+va1b4sioUrVqdtCgVzkRKSgNFa57qz88SSMugI4nsWopEwioIkwuBIG\n1yBsgm+lt23mwx2Y1bK61F6uNEIQShjqDEt2Hn0SYFJJqXXi65Qm+La+zkMYn37qV2f27p1J0u1s\nw0ix4MxWpxzCMKkw99kHuPVWe9xddslIQN3LTZaDq5Iy2bdM4NjWFi6chA8/nAQAuPNOf5ohSEEY\nMwGMVH6PqNzTw6xpCLMcI66Csca7oYQhGT6lSkolBnVg9Z3hbLpWy6gilUrKRhihNgzALmHMmuVO\nIwQpbBgmKUP3kuLMkl3wSRi9elW/6/HHZ6ov0+ZxJqgShm0m2qdP/Cr+GAiRzoYhJQxunevh1N82\nYuBKGK53MZVvwIDa0yJ9Now8EoarX0usumonVlqpEzNmALvvDkyYMM4dIQApVFJTAKxHRGsR0XIA\nDgJwuxbmdgCHAQARbQ3gAyHEHGZcLzgqKRUTJgCTJqUhDPmBbRKGfl/XdfpIzZSXDyYJQ1fPmdLy\nSTUhhOFLIwS+b/DGG9l/m4Ths2E0gzBGjMjW5oRIGK1mwwDSSxh5jbS2QRoA/v1vezyXSso3puj9\nyUcYNhsGhzA4Eoba/lNPHnIThhBiKYDjANwD4AUA1wshXiKiY4jo6EqYOwG8TkTTAFwO4AeuuLFl\nCVFJuZ6HVLLuJaU/c6mkurrMZSDibVdtg8+tNqQh6/Fk+hKpV+Zuumm995TvO8rwJqO36ZQ5lw1j\n6NDqs5ReUkDWkdXvSsRXPeoShikvacPIo840wbYppCxX375pCIMze7alr35T9QwSFR98YE9Pthm9\nXvfe218m/d1jvKS4Rm9O/fTpU5yUmcSGIYSYAGC0du9y7fdx3LihCJUwfMizDkNVSak2DDW8xOLF\nZhtGnz7ufag45XfNREKMcbb4EqE6Z987dHf7Z+quuIDZS0rd0lumabJh5Gk/vnJLG4P6PMTo7Vtp\nLiWM1ITRu7c970WLMoNvKsLgtqfXX7c/cxGDDTYbxgUX1O5vZXov29qaGJWUDy7bpESre0k1HTFG\nb8D+gfK61arpuyQMlTBUyJmobnhN5SUVK2GYXAhDJQzfAKkO4BJ5CKNXL+D992vVEbrRW5Uw1NXr\noeCs9NYljBCVlJw5u2wYjZQwpk0DnnsuHWFw1C0SOoHZnEe4sKmkOGOKnqfP1rTHHvX3lhmVVCsh\nlDBsCFVJAfaFez7CMEESRmz5f/KTTK8fuo1yjEoqtEFyDOupJQwdLhuGej/UU8rnJRUjYXz729l/\nnTBM8YqSMGR99u0L3Hdf9f6772b/hw6tlmerrYCLLjKnk5IwUsNGGByJR9ck+NZhDBsGrL567T2u\nSopTHrX9p0aPIIxYkuAYvTkDnK2hm3TNNglDzad379rZLrcsKubODfeS4g40atxQWwtHJZVXwlAJ\nx0YYsiwqYeh1rm4KyUGISkq2Gx9hqGnKA5waTRiyfj7zmdpt/AHg17/OttmReXZ3A+usY/5m669v\nz+Oaa/IRRl57pHxHXTWk21VM+UgPLx3f+IbdG9HmtZdawkiNHkUYemXG+nSHEIa+DYea/wUXxKmk\npHuk/iyEMHwqqTwShhrXZMDjpGGDiTC4kHWrznBtaiLZQVWbiS5h2I6MtSHES0rCVx9qmhyVlO0c\n9zyQKimTV5/umeXy/NNPLDQhxcI9ib0D94yYODGTovIShhq/uzsjDikpyuf690u5DqMkDA+KNHpz\nBjg1Lz1Pl5Rg85KySRgh8Bm983hJ5SEMX6fIQximb2VKS+7qKuPYJIxQwuCopEJtGDbCcEkYeTzs\nTJCEYWofcrGdutNvnkE/lUpq662zxXbc9IQAdtyx1mmFWyYfYYwalW2xr+enwuTNZwKnPKqXVGnD\ncKAIG0aohKHHcUkYtjzlwJJHJVWkhFG0SirWVVct16qrZv9NhHHDDdWyqDYTXcLIq5LSEWPDMBGG\nLJ8p/SJVUqNGmaUm9T3y2CJSqqRijeA6YaSQMEzvZZIwSpVUg5CCJFSYNhJzhbV5SQFuG4YavtGE\nwXX3M+WvryUJAccTK68NAwAGD7aH69u3VmesGr1VL6lQwvBJGDFeUuoxuC4J4/nnq+3QVMcHHugv\nvw1Swhg/3vxOqoTxwgv5Bv28/Ve20dh0evWqrT8OYXR11RKGrqEw9WObSiq10buUMAyw2TBSqKR8\ncHlJme5zVhNLG0ZKlZR6nVLCaCWVlJq2HORs5VMJwyRhAOEqKdssV8IkYYQcyjR/fvZfJ4wLLwQ2\n2sidZp6BQw5AJq8xebqbSoQhC/BU6JJ6aFwVsSfO+dxqVay0UvbfJ2FwJn66ZGNDqIRREoYBqY3e\nm2xSveaqpNQyhKikbBJGXi+pIlRScn+oadOq9xohYcSk3dEBfPObmQujCT4bhnqfC86CKp0w5NYa\nNqgSxuuvA/361X+/ww+vTbMowpDp6+XTJaVmShh6GbjvLcPp39wlYch6PuAAe1ux7etWpEpqpZXS\nE5HAajsAACAASURBVIVEjyAMiddf50sYXD25b0bs2xnWN+jbjN55VVKuMtlEX66EoXq76GqszTd3\np9HdDXzuc+7nsTYMvSx//at7LYUQ2TvbvIBCy6HG3X57YOeda5/rs9cXX+SfE750KfCf/2QH6OgS\nht7mUxOGunDPp5KSYZplw8irkgoljNVWy1aCh0oYJqM3d2sQ07utqWztajtJNAV6BGHICnz5ZX5D\nSbHRGcC3Ycj7HINkCi8p3261MYSRAjErvbmw7dFjgpQElyyp9QJSJYzQ+lfr+7bbgNGVDW9eeCH7\nr7+XXPjmghyIFi7M4ks1ma42Ua/V73jssdXwY8b48zMhVMJoBS+plIRx003msKoqykcYukrYpGmQ\nExgXbHXUr1/1WiWMUiWlYaWVqhWoHk0IuBsNt1H7Klyf0cTaMNR8ZAfl+uybZsKtTBiu7xIrYXR0\n1Kt71P86TIShly0PYRBV32PgwOy/PhhdfLE/TRmnq6t6LQcck55eJ4xLLqnGeewx4IQTeO9iKoPt\nWUoJI7UNw4Xrrqu/Z1pLo6oN1XxUwlDrSHea4dSHVEltt507nC0t9QCnQYNKlZQRt92WLbGXFbjc\ncmFGb06lcr2kfG61EtdfX/vbppIC6s/JtpXXdDqcq5HaCGPUKHP4lHj2WeDpp+3PYyWMXr3sZyWb\noEp8Ngkjj0pKtSHJ+3p66qzQBhmnq6v2RL3u7mq59W3sbauLQ6CW9eCDge99r5q+Hk7mKSc6rWTD\ncOErX6m/Z5Iw1HPWdUnBJ2GEekm9+KK7zLaJoKp6lcb4ItDWhKEv45fukhKuRpOKgUNVUrfcUvvc\nVEbXXjCmmZNpc7hQCeO73wUef9yeb6OgSxg/+xkvXihhAG4JI4Yw9HxlfJmmaTDyQSUMuc5Cfj/T\nAO365ip8BzepZdtgA+Cyy8zpqzYME4GFopE2DJM3kekbjRoFnHqqOQ35rrZ3fvppPmHk8ZJSCcN0\nXGwq9AjCiJEw1HgucFVSNjc+Xx4mlZRthm3Tq5sII1TCGDgwOzms2dC9pA46yBzuiitqf+urqCU4\nNgwpoemOBnkJQ28T+gAVQhiSIFQJw0QYLs84Fb681eeusFLCUAkjVlLg9kkOOOmYJmY+UjcRpvpf\nx7331k/eTO7aebcGUUkiD2H70HaEsd9+1WvdFS3EhgFkZ/H6wPWS4koYHIQShqnhhxJGio5q26U0\nBDph2Mqli92mfZpc8Ysweqvo6KiXMPRBJYQwgFrCUCUMXSVlQh7CUMvAkTBi25LJo0jHDjuY78fY\nMEwL3Hz7gdkIw6VGVfN54w1gyy3zSRgmlIRhgSoays5jMnbq1zqEAP78Z39++kc8/fTa3yYbhgrf\nLNVlw+CGt92T9/feG/jXv6rPdtqp/sxtV12dfLL92S23ZOosANhmG3s4LriEode3bvT2QdX1q04G\neYzeevouCQPgSTD6zruq88ScObXp69cqfBME14DrIgzV6K0SWAxp+BwigNpN/FTkVUnZ7qkTCBPk\nc9e3VAljrbWy//pENKVKymZPTYG2IwzdoCxErS97iIRhgk4iMQv3VPgkDJNKymbDCJn1quL9lltW\nVwIDmdeHbq9w1dU669ifDR4MrL12NY3YBnrooZlajOslpdeDzYbhgrQLyLTyGr318qW0YQDVdqFL\niJw279thwDWz5qikVCN8HgnDF5fb/lMThi1dn0pKpsl5L5s24zjlrFIbYXz/+7VplV5SBuiEoetA\nYxruFlvU/o6xYZi8pEIII1QlpUJdpW4jMaDehdaVru+ZPjDGoKMjG3B0LylfvUnoq6h9IKoShiy/\nKmHk9ZIyTSLyqqRUo7dr4R4HJsJVoabDVUmpNpWiJAxue/Cl89vfmuvft49ZXpWUhEklpUv9EvoC\nUNO7qXaRllVJEdEgIrqHiF4horuJyOjQRUS7EtHLRPQqEZ2m3D+biGYQ0ZOVv12DCl9h5RjC8ImY\nvnASPgkjpuO4Gp+vMZg6t6kMnD2tOHmmIgxZhyaVFEcNFyphSMKQAx5Qv1gytdFbHzg49WWzYdgW\nysWqpFzqMhdhSPWTzc03BBwbhu+5rpKy9d8f/rD2XWw2DJtK6o47asNzVVJ6fmo+Npdazphikwhb\nTSV1OoB7hRCjAdwH4Aw9ABF1ALgEwC4ANgJwMBFtoAS5UAixReVvgi9DtQJWXLFquJTP8koY+ofn\nEoatITdKwpCLkLiEwTmDmfMsFWHI+LE2jBjCWLKkViWlSxh5Z2p62eUCPttzE9S60N1qTenEEgZX\nJWVKnyNhDBhQa5g1IY9KKsaJwxSGK2Ho7rQuD0PdGQcId0IIQctKGAD2BnBt5fpaAPsYwowBMFUI\nMV0I0QXg+ko8iehhZtgwd0NJSRhf+II5vOkAJbVMMj2bXcJUxlAbBlHtmcR62hwJw9XIGk0YsTaM\n0LM5JGGoKimbO2nMAKTXf8weP2oZ1IGnuxs499z6fE3lPOqoqmOCKV1TvBBJi8i/DoOj4pMeh768\nOLC1fZe0BPAJQ1cz/vCH9rKYJoAhBOf6NqYwrWzDGCyEmAMAQojZAEynEAwH8Jbye0blnsRxRPQ0\nEV1lU2nZICtG2h1C/LhDVVJbbWUO75sVyfQuvdTcYTiNVi2LT1JR/fZdeaRSSakqnSIIg6uzNp01\n4ctLN3rntWHo0OvFRximMyvUule3BhEC6OysTV+/lrjySmDffatxTeFMXmcSvu9hcqu1hdOx/PLA\nSy9l13klDKKqHcCmklJPvgvte6ZyyLox7bYgwVFJuQZ4n0pq9dVrf9tWnaeAlzCIaCIRPav8PVf5\nv5cheGjxLgWwjhBiMwCzAVzoDj4WV189FsBYnHfepP/O5uVOjfqAKj+quv2zDzYJw9aQfXvFyPur\nrQZ8/vP25xyVlGtDQpOHRSqVlJ7n0UfXPnPlEwL5PVOopHwdRSUMdUfYkIHSh1AJ409/sqcB1Nsw\npKEzRqr2DUJcSUv2OZ+XFJGZgHv1ylaSA/mM3kJkq6onTKgvs4qLLgJmzqxPy2bDsOWvq6Rc4Kik\nQs7g0fHaa7XpT5kyCTNnjgUwFhMnjo1P2ADvrj1CiJ1sz4hoDhENEULMIaKhAN4xBJsJYKTye0Tl\nHoQQc5X7VwL4u7s0Y/Gd7wDXXJNJFbr6JytT/XXITDEFYZi8pELg2lvf9i6ywcm8VfI0lV3f+C7E\nS0on5ZSEwZUwirJhyJmirv6LUUnpEsagQWHx1TSAbOCRW2B3d5v3ouIOuPL/vfdWz7K25evrP7qE\nEaKS0k+qyyNhbLpp9gfY0+nXD1hjDXv6PgnDppJywbXVj54+Byb7kHrvi1/sxPDhnZg1K1tz9c9/\njuMn7kFeldTtAI6oXB8O4DZDmCkA1iOitYhoOQAHVeKhQjIS+wF4PiRzSRimQVI+B3g6RAmbSkre\nX201Xjp6elzVCmBvYHffbZ+9SYnB5G4ZM9i5numEkVIlBaSRMDhlcUkY+gCXQsJwnc1hy0NXSalt\n3nSELHeCos+QXYSxyir+Mi5dWjVq2yRu267KEpxZdt51GC4JBeBvfCnL8dBD/rCc8cf17qEG/VY2\nep8HYCciegXADgB+CQBENIyI7gAAIcRSAMcBuAfACwCuF0JUtJb4VUW99TSAbQGcxM1YNkoXYZgM\nwRK2gd4lYcycWW/cMh16r177DMIhKqlnn7U3BkkYJttF0YThykdddMQtQ69e1XMcfGH32KMahyNh\nPPFENb7LhgHk73j6YOxzd7RNBiRMu9WGDia2mbLrG6v6eVsZu7ur27XYysAhjFiVFDecL76PMEzf\n0geTSkpHHglDv1ekW23kUTUZhBDzAOxouD8LwB7K7wkARhvCHRaeZ/Xa5A2gVpycgYUQhk3CIDKL\nsnlVUiEShis9nTB8KiluuqZnIRJG7Mx8yJDqtZrGiBHAjBn1KoFQLympkurVy+wlFSJhrLde7bG1\nepyYQUbCJGHI8vm8ZVzwEYZM+4ILeGVcurRqo1EnERI2lVQqCYPrpuqrH64NQ/6/6ip3eKB4lZR+\nTx0XW20dRlMhZzY2CUMnDM7eUaE2DN9z36BtkjBcjdZn9G41CSNkkFTTsaUpVQC6lwqXMNT0XOsw\n1LRN5VCx7bbm+y4Jw1c20z3bAUq+NFxls5G9fPdTTrGnf8MNwNZbV/uhXGfCld7V/IH8Rm9OuLwS\nhkSo0dtXFtfAHjroF6mSyiVhNBOSHFyLmCRhyEbAqUg9jL7OQgfXrTZEJOWkp0J2WDWdUAkjJE8X\nYcQsoNLD2tR7pjKphPHee2F5+PaS4hq9bQvSQiUMH+HqW4Pkkeh8ZeMMuN/4RjXu0qXVfjZ/vjl+\nXqP3iivyJYxQwuDaMPT64hi9OXtJhZACZx1GTLqsvNMm11joA5QuYUi3Q/lRYwjDdl/q2ItQSYWo\nhySKtGE0SiVlkjBsYUyEEZqHby8pdSt9F1ZdtTZtCb1eYnYu1t1b1UlSCpWUWsaNNzbn60ufqHbR\n3fz59WE4KinfEcHz54cb9U1ldSHUS6ooCWPCBPsz3zu0stG7qdAlDBthhHjxmHSvpvvDh2e7uPrW\nYcQYvUPUQxJ5vaRSudXaBk0fbGooX73J+pVrcTj5yP+LF9slDKBKBD7YwrkGF9NZLD7ClXU9bRqw\nYEE+gtb7BBEwZUr9c25akjDuuSfb5p4rYYTaMIpWSXEnHiEShs3ord7T351zVo8tLZNtNxXaljDk\nAMNRSenE4UtXhU0lpS5Y0p9vvnl9enp812AeqpJSy+myZbgQQlI2wjA1VO7Ao6vQfPWmd9jNNjOv\nlAaAN9803//008wDyCZhmPLVvb6GDKl3tdbjSMgy33BD/a7IpvBqHHlNBJx4Yv0zVxqustnIPlTC\n6OrKvLZ22sk+SzelyVWF+crVKBuG3v64Eoavn8cavW+6qf5eqZJSoA+ELgljdMUva+21s/95VFIu\nwtCfyT1+XOn5PKEOs/iPtaJbbZEqKX0g099JdnCi7HAt9VwAPc4551TVLkRVwlCN3r7vv/32tfef\nfz7bfvqYY/wqqRhVgZqmPHtCT98WnpOuOvCFSHYqZBqudSY2FVooYRQlYfhsGJyFezZXcFuaalkW\nLTKHUfM2xTvggPrwpUrKAkkYEiphLFhQPTRIXVDESVOFywtKJYxVVgF+//v6sLbBVD+PWR/oTYuy\n1PT0cjTTrTYkHxtCVVK6hEGUHRR16aX2sHvtVfs9Fi3iSxh6WhKrrZappP7wB/M7qf9DVKOm/Do6\n7OdguO650g2VMFxp+dZrmNLUzznn5hUbzhffNrh/9rPmdFTCuNCysRHHhmGy+9jg++69epUqKSNc\nEkZHB/DFLwJPPplvpi07qO4Jo3ppyfx+8IP69GwN1LXvTkdHVSripteqbrWx8M0Q9Rmei9RsHezT\nT7PvYLNhuPLlwCZh5CEM1TCc2ujNSSdWwrDF9Z2hLbH//rV56UglYdhsEscck6ndUqqkVCxY4E9H\nwkcYpUrKAqkztw2SHR2ZPSHk45rCPPlkvT+6SyVlSk8P49uo7eSTgXnzeOUDqhu4tZqXVAhCJAy9\nbDbJ0JYuEGfDiFWxAXHbwNvI2ZZOKGGoAyBHwnAN+iphmL4HR8Kwlf/mm+35c8vJie9SH6nusSaV\nlC1tjoThIgy9Leq70+ooVVIK9IFAFdFtahh9VuCCqaFvvnm9hCEXTvn28I9RSXV0ZA3RtFmd7R32\n2MNNnj646qZREoZJPWLLO2TW7pMwpPpPX4fhypcDk9onFLqEYXvmumeCqf50tQYXJsJw5amCu1BO\nIlTCCHVJ5ZbHNKbY0ubYMEIkgc99LvMKtG1jXhKGBT6VlEQeCcNkVFLz50oYOlxG79D01PAmHXcM\nUXLD+ggjz4zcFT9EpWJLV9owNtkE+OMfM5WDr65COqOtXmI9YnQvtJj6VlWorjKGzNBNZ0K4VFem\nuFxwCSNEQlKRZ+GeLW3bO6rhR440h7HhiSdqvf9sWyYt8yopWcmDBtUThvrcN2D40pfYYANzON2G\nYYNtBuezYfjSs6GIld4+CaMIlZRvwNI7LkdC0tuElDCIqlJGHpWU/sxWLyFnH6jvxRlcY1VSep3n\nVUnpiFFJffJJ7YFHtvxd5eQSoc+GYUuXOxlzkfuttwL33WePbxpjVl+9dm87m4TBXZ/ERdsRhhDA\n++/XnofhGySLmGkLAbzwQnZaGFcl5SKM0IV7e+9tft4uRu+TT7bnw5EwJGx2AU59ShsG4CeemHdM\nIWG4VFKuPLnhbG61qW0Ytnsuwlh+eTsJ62i0SipEwrBBhu/b1+4VCfDai40wQg6P46DtCAOo7oqp\nz/BthBGikuIiZu8nLmG44JvNF2HDMOnOTz21eq2WifsehxxSf88027WRlfzPMSSb6kyqpPRDf3zf\no9GE4VJJ+cK7kNetVhqh1bB5jd4cqOkefzwvnPo7tUqKY8PwpaXbI2JgG4/ySv062pIwJEwqKfWZ\nfp268jjwGb1j01Ohpm3SXRYhYRx0ULU8eWbfpnuuBm9TCbikIJdKyiZhcNdh2PI0/ZaIVUmlnPD4\n6s8nYaiqDq4NwyWdADwiVdPYSzkk2qdCnDzZXgYVXMIwaS1C+pCEENl6MVe+oRJGkWg7wvCt9DZB\n7xShsxpOOWywqaRcXlIu+CQM1U+/SJWU2mFss9QQ6FKFr+yumZ4trH5P2jDU+L78XO8n7V0DBrjD\n5lFJnXNOdq2eqx4D18Bn+q3HUyEHfVmXtnAcCcPXfmyTCZ9KitsXUhnhQ+Oq9fCPf4Sn1SjCaNvt\nzYHs43d3A/ffn/32qRFaSSWlEwYXvoFNXcCXSiXlI4wYlZRLTcMhL/lfzmpD4kgsXFg9w8EnYXDq\ncq210s8GdTXRF76QXYdIKSbo78uVjkzP5SCrDnp6e7KtseCuwzDlq+bhs1X4vp9vaxBbOnm0FqY6\nBMx154PeHsqV3gaYKrZRTBs6MOoNS7dhfO1r2dYWPnAJY+21eY06JIz622QsTamS4qT50Uf+2bye\nrn5v2LDsP1fCiHGr1ZHCSypvO/cNfDEShu8s9hi32hg1j+kZt43mUUlx4kmsuGK17en55iGhotHW\nhJFH/dGocvgWRsl7++xT3V7adXKcr+FLldTddzdHJWXDOedkW19z0nTdV/MaMCCO8NR7Q4dm//Ut\nRjhG7x12sOfpQh4JQ2L99ePy1tONJYxQCcN2jztA+5751mGkIgxXGULw2mvAww9Xf7skDA7awoZB\nRIOI6B4ieoWI7iailSzhriaiOUT0bEx8iauvzo6EdJep/l4RlclVobgW7fzmN+YGOnOmPT2bx4+E\nnL327x82mMYac1VpwzUw9+tXO6PSw+rbLvjKHqIacEkYgwdn/0NtGFdfDdx7rz1PV1p53WoXLgT+\n53/scV54IVv5z0nXZgMKGQgbqZKylVGt09//HjjpJHNYX/pFrMMwYciQ2nNUXM4NMSqpopBXwjgd\nwL1CiNEA7gNwhiXcNQBMR4Jw4wMAjjyy1hNDh811rwjkNXoTZecamOJOn25Pz+RGqpYl9AClWJUU\nNw3TGhk97NprA+edF1deW8e1SSU6pCtoChsGF3m9pFZYwd3ON9yw6npug49wfcRpKmOIhCEPCMpj\n9LbZMH7wA2Dddc3xfCSeSiV15JHmeBzYwl59tT2O3l5b1YaxN4BrK9fXAtjHFEgI8TCA92Pjc2Ej\njNDFO9y8OLARhg0XX1xd42CCL41QL6lYwjARpo+sbYQxZkw2wIVIGHo6ejjf3joyvK6KkvdtbcYn\niZji6FDT/va3+WmkmAzpXkMhtgr1vk8l5ZI2gepW4KE2DFsb4qJRKinX4O5Dj1VJARgshJgDAEKI\n2QAGNzh+DXwSRspKDfXq8YWTOO64qieMCandajkDoI8wXGnYzol2SQCuOuNKGK446rUcILiLO1NI\nGqqE8cc/AiNG2MPGrsPgLvALVa2Y3jvGhmGSSkLh8pKS2HHHzN7DlTBCv78vvL61CQcxKqmWcasl\nookAhqi3AAgAPzYEz1tsZ/yxY8f+97qzsxOdnZ11YfLM/EIQo5JKAa4NQ73PIYM8C9Js+SxZkg0m\nhx7qVkmZ0vGpSvIShkSohJFCtRBr9M67GliFz602RFqU5fJtk2GaMKRah2HDaadlf88/X18GX/qu\n59z2MH48L1xIGUxQ29SkSZMwe/YkAIAyZCaBlzCEEDvZnlUM2UOEEHOIaCiAdwLzD4o/1vP2XBtG\nM1RSqfLlutWqYVKTqE0l5SIW/dvklcp8hOFLQ5/h2g5ikrCd7R6DEH1z6pXepgFv6NDssDFTOFt8\nFbqaC3CrAdVr7gFKvrKESlSp4PsmMd8sJs7aa1evOzs7MXRoJ955JyOMcePGhSdoQd4meDuAIyrX\nhwO4zRGWKn+x8b1olNF7m22ydRMSpkb4yiv1z/LqXwH/+6kqKU5enI5kmm3bVFIuyctXFyYJw1Ze\n/bdLjDe9o40obBKGdHVOaUfgIJYwfNKNWidvvw387ne8+Ka69G3NI8PI8o8dW0/Y3P5ga0ONIowQ\nCeP++4HPfz483xiV1ODBmatu0cjb/M8DsBMRvQJgBwC/BAAiGkZEd8hARHQdgEcAjCKiN4no2674\nedAIwnjgAUDVhpkag/TSyEsYemPxrRCPlTD0ettxx3rXRDXdlBKGqxPGShi2ckjohCFdHG1eUpIw\nUkhtIV5Svll7CpgIOmSA4xCGeu/UU812D1M8VzliCDSFmtBXhn79sv+dnWlVmT6ssw6weHF2XZRN\nI9fWIEKIeQB2NNyfBWAP5fc3Q+LHl8ctMkukFktdKo8+fbLBNxV8u7OGEoYcyPUwcuX5b35TH8em\n73ZJBi4bhkvCIDITTYxKSr2n6919xkmdMDjgDk62zn3MMelVUlyELNwzEaDL6E1kJ4wQtIJKypSe\nuiAvBnm+c+ymplw0sAkWD65bbSOgDmQTJ9beywOTCK9ex2w+aBvoXaudbRIGVx8fooJwzVZDJAwX\nicgjeN+vOH/r7yHrtQgJw1ZnF1/cGAnDBK5KEOCrpNS60wnbVq+77Va7WNdWH61kw0il9pIw2Yia\nhbbefNCERhm9uemFbjPuQ8imhSGEEbLSl6uSUuFaxesjBBfRxKqkbGWZP998X7dh5PmW+uBmU1Hp\n7x7iJZVqrynOc1NePglDTnx8Esall8aXwRcnBUImPlw02k4Wgh4nYTSDhRtJGBwjoT6oxUgYIbpj\nziDK8ZKyxXfN4mIJwwZJDJy9pHzgqqRcNo1mqaR85K6+QwxhcG0YrnLFfItG2DBicfnl5jSboSGx\noccRRiM7lYSr4abe44VDGD4xX4UkWRNhxKikXPDZMGyqjRgbhgm+1d+A2ctML09ecG0Y+ndJ4SUV\nG84FDmFwVVI+2NpQs1RSrqNVQ7Haatn/VlA92bBMEIa6nxFg/yATJsTly1UVpJQwXOmmkDAA90Am\nd3nl5sMxeqvkahvc8xCGCltZGyFh6JMIrkqqiMmQ7T3zrio3vbtLwuC21XXWAXbemRfWVB6OhPHS\nS7w0P/64dkNNPS/fPVuYZkx6uWjhosUhz6C8i2l7RAa425HEitMq9HM0XOXhdsKOjnAbxsiRZp9+\nF0IIQ73Oq5IKgZQwfANpShuGi5xSL/wsQtfP9ZIySRihhNG3L3D++fV5pJQwRo/2hwHCpIsvfAEY\nNMgdxtaWY1RSpQ2DiZiB44QTgGnT4vN0SRg2wth//7i85O6qqVRS8nmemTMnLse12UYYLqKNVUn5\nJAwbUgzaXAlDz6+rK3/eOmyDnu89fTYMPb4q/btsGCEoSiVVhEpozBhg3jx3GNtkpLRhFITY3WrX\nWKN+O2QOHngg+8+VMFR861v8fAYMyPbPB6runy6Ebrdgs2FIpFjH4krDZ0gtQsKwvYNPwkihkoq1\nYXzyCT9vTpmEqB5R6wqXN58VVwQOO8xMGHpbVc8F96WdYuHed7+b/f/61/lpFYWi7CwpsUwQho5U\nH0TmFSNhhGDuXOCqq7JrKWGoSGHDMKmkUgyaJsybF6+SSmXDsIErYeSpgw03rP3tmkHGEkbRbrUq\nPvvZ+nvye+y6a7ZNzrXX8ozeW23FL1sKCeOKK7K43zQuLY5DbNuQ8XSpq5UkjB61DqPRbrX6jp8m\npCCMvn2r6y+khCHzPO64+g4bQhguLykThg/nb1Rnw6BBwIIF9fFtRm+XEdFGGKY4ISopWyeVKpxY\n1YYpXa4nXQoJo4jB56tftUuQd91Vf09tb6bvtsYa2f5WPqQ0ercCZNlS7kqcGj2OMEyD97bbAr/6\nVfV3qkbD+cCp1mHIPHQbxsUX28PmtWGYBpcZM3jhfGF8+fkkDP03x1DI+RZLlwK33JKpUUxQj9X0\ngfu9uTaMEMLI28bzSmzcFdAx5YyRMGLyeyd07+2csGksZFtsBbLrUSopwNxQ+/d3n4GcN68YG0Yo\ndAnDhaK9pGLAsWE00q3WhiVLgP32s3vMyY3lOGgmYcTi8MPr841BKpuSK2zRW4O4joMuAqYJ6Nln\nA3vvHZ5W6SXFgE8llVon3yiVFFAlDI6XVKqV3jGztjwzPY6XlH4vhDC4EoYJV1zhjpcHnDrr3x/Y\nYov8efnK/6c/8cL5yhwqYeSRNDjliZlYxA66KW0Yo0a1hmQh0aNUUkBjjd6NVElJ7xEpYdjSevDB\nqudLETaMPBg0qLrgr2gJg0OSJpiM3ssvD2y3HbDeevz0uWEAntH74495aeXJy5RvLLjxYwgjZvBv\npA0jL9Go48mAAfnLkxI9ijBitwZpJwnDRxhf/Wp9frE2DC5McXWVjhDZwDtrVm2cyy+vrtwNkTAk\nON9ALYMvTdsBVOutB0yd6s8jBqm3j0mBIlRSqSdqMRJGK83WdeiEMW1atrK9ldDjCKORDSLUqyGF\nhGFyq80LovQ2DH2bFdd6FGkX4KzDSGXDCJEwuFtfxISxpR+aRmr4bDXcATrmHhc9jTB0o3fM7tzy\nlgAADhhJREFU2jCJ0obBQLPWYTTD6J3qHYYPz2/DiIGpA6faGmTFFYFNN62Pw3kf3+aDRYBr9G4U\nZs/Otn7Jg0YYvVUUQRgx2opf/ALYYIPweED4BLQZ6FESBtDYjbs4C/e4qhUfJGHI/1/7GjB9enx6\nEk88kS0kcxFGzGxSh81Lyubp4tuDy0UY771n3nJCTfOQQ8xeRyuvXH8v9cy41SF3FciDIiWMPHG4\ncadNi7MfnH56eBwJk9G71ZBreCWiQUR0DxG9QkR3E9FKlnBXE9EcInpWu382Ec0goicrf7vmKU+j\nbRih6pAUKilJTptuCtx5Z1y+srwrrpitKzC51aaGjTCKkDD69vXP0tZcExg3rvbeW28B99/vjheC\nFKRi27qj1VEkocbYMPS4PuRRB8WiHSSMvMPE6QDuFUKMBnAfgDMs4a4BYNsL9kIhxBaVv8gNxjMI\nAey7L3Drre5wqVVSjfCSkpKFzCvPRnR//nPt72aqpDgSRt4T9yR8M8YRI4DVV/enw0XImg1b+fv1\na62tISRawa02BO1gw/ARRiuUPS9h7A3g2sr1tQD2MQUSQjwM4H1LGkmq4StfAU47LZtd2ha6yEa+\n2mpmNUcoGmnD0CWMlYyynBnq+/Xvn6lj1LLldavNo5LiSBihKikTFizICCEGsUbvrbbK9lHiILWE\nN3x42vRC0YiV3ip8C1pTEoaUzFMj1oGjkcirLRsshJgDAEKI2UQ0OCKN44joUACPAzhFCPFhTEF+\n/vNal1IXHn4YWLw4JpdacETI1DaMXr3SzziL8JLi5Knnw1mHYYvv62Qhs/1UIMoWXnHDpsRPfwqc\nckr9/UZJK400ej/3nF+FlJIwbOe+54Vs/ynK2DQvKSKaSETPKn/PVf7vZQgeWsxLAawjhNgMwGwA\nFwbG/y9CvFsGD3bPNm+/nZdOyBoAIK1KKiVMEgaQttGFShjN2hrEBFPdpF5QlZow+vRJq14LRSPc\namUb2XjjxkoYRcG3HqcVjOHeIgghdrI9qxiyhwgh5hDRUABB23UJIeYqP68E8HdX+LFjx/73urOz\nE52dnTjhBOCii9K6Q66xBi8cR8JIvflgEQ0+rw0jRiVlihuzcK8ZYvzUqemNoo0qf6MGzCIljBi0\nO2E8+iiw5Za8dCZNmoS5cycBAJQhMwnyctbtAI4AcB6AwwHc5ghL0OwVRDRUCDG78nM/AM+7Mhtr\nePvf/S4jjJSrZbmNqpE2DFmmIlYFd3Tks2Go4L6vbzdZk5fU2ms3R8LQoW4RkgqtNpD5vmOKhXv7\n7gtsv709vC/vkL7V7oSx9db8dDo7O7H66p14772MMMbp7oA5kLebnQdgJyJ6BcAOAH4JAEQ0jIju\nkIGI6DoAjwAYRURvEtG3K49+VVFvPQ1gWwAnxRaEI2Fwj6O0bW2tI5QwZOfIg5SSlGr01t9h5ZX5\n2xKk6oQ+t9rXX6/Psx0MhRw0qvytZMMYPz6bBOj45z+ByZP98ZclwghFUd85l4QhhJgHYEfD/VkA\n9lB+G8+zEkIclid/FZyB9Etfqh10bBg9OvN//+gjd7hQldT3vgdcf331aNdQDB6ceXilhq6Smj49\nW6cg1VK+tQkx52H4JIw8C/faEa08kJng++Y77pi1dxXcd+SulC4Jo/Fo826W4aSTMjLwgcg8ozE1\nIo5bYoxKKk+DnTOnmN0rdcIYOTJsURTHEM/p3CEL9ySku3G7E4YsvzyDYZNNmleWFBg6FLjsstp7\nHFsUBzEqqZh8Go12IIwWsLvnx4XRvlX5ELpwT43TSPg6iUklFYJNNwXuvTcsju+oUq6EoR9Z266Q\n737rrcCbbwJHH93c8vQ0LGsSRkuqpHoyOBXOUYeklDCKgs2tNiT+Dju4w+j1MGhQ7bG5QK3boO+I\nVp0wWnk7BQ7kyv1dc22O09pIJWHIsDEqqVaeWLSDhNHC1df6aBcJwwZZNpOXVFF5SXR01B+bq/rS\nq+FtzgpAdbv3VqrXGOTZ6mVZg2wbI0dmR5hysKxJGEWhzbtZGsQ2op4kYbTCgKsShtp5LrwwW83r\nitMK5Y8FUXsMFnnhmljF9Is+ffjrDErCSIM27mbNR4yY24oNNq9KigOO+kA9HEoNP3BgtppXRU+y\nYchV/O2EGB25a6VyuXCvJIy2Rox+lJNOKw1ssmyf/SywyirF5fOjHwFHHOEPZ5MwOHFaqV5D0YqE\nUYTRNJWdKY93VEkY+VAavVHsqma9EbRSg5XlHz++2HzOO48XzmbDMKGUMNoPzdwLqRW3iNfxta8B\nl1ySJq3yiNYGI2YxGidMOw9sRSNGwpDrMNphQLBBvkM7Iaa+U9swehoGDACOPbbZpXCjlDByoKct\nHPLh5z/3h8kzcO++O/DGG2HpyPoscpZe9DdrpITRTGJthd1WS+RDOd/NAd+WykB7eEn5IN/hDNt5\niolw8snZWcpAmD5XiGLPuyh6kF1WBlLXe26xBfCZzzSuLCXisIw0VTdMg/gBBwBTprjjrbwysGiR\nO8yyppJKRYjtrGIKRTuqpGLgUkndcUexRt9lxU4kUa70bjDOPZcXTu79Y0MrGL1Ned52WzGdKFVD\nbQePkVQYOTI7Y6OV4DvONrVbbdGkudxyy9YkpCiUhIHGDuKtopLay3ReYgthWerc48dnZ463Eo48\nMpOyU6KZbrUl0qCHK0iaj55gw2gGfBKGT7JLiaK/2cCBwLBhxeYRCiJgpZXSprms2GpaAaNGFWPX\nW+Y/4W9/Cxx0UHHpl4QRBxdhNHqGWc5o6xGz0DOVhFH2IT9uuQVYvDh9uss8Yfzwh8Wmv6wZvVNh\nWbJhtBs++aR2GxcuUkkYJYH7sfzycd/Ih3L4Khh64/7855tTjnZDKw0K5Yy2FrEDUSoJY/DgNOmU\nCEdJGAVDH/j+53/ab/bs85hRse66aaSoPfcExozJn06JWpx5JnDDDc3JO5WEMWhQa00oliXk6tpE\nNIiI7iGiV4jobiKqM5MR0Qgiuo+IXiCi54johJD47Q59dtqInWFtWHvtbKPBUIweze+gN9wAvPde\neB46Dj8ceOyx/OmUqMWIEcA3vtGcvNv9kKsS+SWM0wHcK4QYDeA+AKa1wEsAnCyE2AjAFwEcS0Qb\nBMRvW/zrX8D556dPd9KkSVHxnnsOiIzKxgorZAsaG4XYuuiJaPW6aKSXVKvXRbsiL2HsDeDayvW1\nAPbRAwghZgshnq5czwfwEoDh3PjtjC99CVhttfTpxnaG/v2L3UKjGSh6YHj0UeDBBwvNIhlafZBs\npITR6nXRrsjL+YOFEHOAjBiIyGmOIqK1AWwG4N8x8UvEoTTaxmPrrZtdgp4D/RCsEu0HL2EQ0UQA\nQ9RbAASAHxuCWzXdRNQfwM0AfiiEsK1rLU1ZiXHMMdnGbiVKNBuf/WxprG53kMjxBYnoJQCdQog5\nRDQUwP1CiDqzKhH1BnAHgLuEEL8LjV8JWza1EiVKlIiAECKJniGvSup2AEcAOA/A4QBus4T7I4AX\nVbIIjJ/shUuUKFGiRBz+f3tn92JVFYbx3xM59KWWF2k5OikS0k0xlUVTBAUqKV6GEAX+CV6YjX9B\nN1FddNMHRvZh3zBBREgXkRd9oDJilickGyeaiGyiLvqQp4u1Tp6ZnGmfpuPZ7PX+4MBe67DZ633O\nZr9nrfU+5yx0hrEMeA1YBZwC7rf9k6RrgGdsb5U0AnwIHCUtORnYY/u9uc5fUERBEARBT1hQwgiC\nIAjKofZOb0mbJX0h6YSk3f0eT6+Zy+g4n8lR0qiklqTjkjb2b/S9QdJFkg5JGsvtIrWQtFTS6zm2\nY5JuK1iL0azBuKSXJA2UooWk5yRNSRrv6Os6dknDWb8Tkp6odHHbtX2REtpXwBCwCDgCrO/3uHoc\n8wrgpnx8BfAlsJ60z/Nw7t8NPJqPbwAOk/ajrst6qd9x/M+a7AReBMZyu0gtgOeBHfn4YmBpiVrk\n58FJYCC3XyXtgRahBXAnyZ4w3tHXdezAx8Ct+fhdYNO/XbvuM4wNQMv2Kdt/APtJZr/G4vMbHQeZ\n2+S4Ddhv+0/bXwMtkm6NQNIgcB/wbEd3cVpIWgLcZXsvQI5xmgK1AH4GfgcuzxWYlwKTFKKF7Y+A\nM7O6u4o9V6Uutt3+I+oXqGCcrnvCWAlMdLRPc84l3nhmGR2Xu8PkCLRNjrM1mqRZGj0O7GKmR6dE\nLdYAP0jam5fnnpZ0GQVqYfsM8BjwDSmuadsHKFCLDq7uMvaVpOdpm0rP1ronjGKZZXT8hX+aGhtf\nrSBpCzCVZ1zzlVU3XgvSksIw8JTtYeBX0m+xlXhfrCUtUw4B15JmGg9QoBbz0JPY654wJoHVHe3B\n3Ndo8jT7DWCf7bY3ZUrS8vz+CuD73D9JKktu0ySNRoBtkk4CrwD3SNoHfFegFqeBCduf5fabpARS\n4n1xC3DQ9o+2zwJvA3dQphZtuo39P2lS94TxKbBO0pCkAWA7yezXdM5ndGybHGGmyXEM2J6rRNYA\n64BPLtRAe4ntPbZX215L+uw/sP0g8A7laTEFTEi6PnfdCxyjwPuCVAhyu6RLJImkxeeUpYWYOevu\nKva8bDUtaUPW8CHmMU7/Tb93/CtUBGwm3SAt4JF+j+cCxDsCnCVVhB0GDmUNlgEHshbvA1d2nDNK\nqn44Dmzsdww90uVuzlVJFakFcCPpS9QR4C1SlVSpWuwiJcxx0ibvolK0AF4GvgV+I+3j7ACu6jZ2\n4GaSoboFPFnl2mHcC4IgCCpR9yWpIAiCoCZEwgiCIAgqEQkjCIIgqEQkjCAIgqASkTCCIAiCSkTC\nCIIgCCoRCSMIgiCoRCSMIAiCoBJ/AWv5pBwdRVYsAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x106c92940>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEACAYAAACwB81wAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAADi9JREFUeJzt3W+MZXV9x/H3h91ipJtSqrLbsPgnpUFtbJDarQk2O7YI\n4xOX9AFBmxY0pibEaGIahbYJu21TpEmb2Bge1KLZEgmlNgVa22UlZDalLeKfXUF3S9em/HErg4rS\nGGMDu98+mAO5GWa5d+49d+7M/N6vZMK5Z8793d8vF95zOPfemVQVkqTN74xZT0CStDYMviQ1wuBL\nUiMMviQ1wuBLUiMMviQ1Ymjwk+xMcl+SbyR5OMmHuv3nJDmY5JEk9yQ5e+A+1yc5nuRYksumuQBJ\n0mgy7H34SXYAO6rqSJJtwFeAPcB7ge9V1Z8m+RhwTlVdl+SNwGeBXwZ2AvcCP1++4V+SZmroGX5V\nPVlVR7rtHwLHWAr5HmB/d9h+4Ipu+13A7VX1XFU9ChwHdvU8b0nSKq3qGn6S1wIXAQ8A26tqEZZ+\nKADndoedBzwxcLcT3T5J0gyNHPzucs7ngA93Z/rLL9F4yUaS1rGtoxyUZCtLsb+1qu7qdi8m2V5V\ni911/qe6/SeA8wfuvrPbt3xMf0BI0hiqKuPcb9Qz/E8DR6vqEwP77gau6bavBu4a2H9VkjOTvA64\nAHhwpUGratN+3XDDDTOfg+tzfS2ubzOvrWqy8+ShZ/hJLgF+E3g4yWGWLt38HnATcEeS9wGPAVd2\nET+a5A7gKPAscG1NOktJ0sSGBr+q/hXYcppvX3qa+9wI3DjBvCRJPfOTtlMyNzc36ylMlevb2Dbz\n+jbz2iY19INXU3vgxCs9krRKSagpv2grSdrgRnpbprSezR862et4B3af7iUraWPzDF+SGmHwJakR\nBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+S\nGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHw\nJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakRBl+SGmHwJakR\nBl+SGrF11hOQ1qv5Qyd7He/A7i29jietlmf4ktSIocFPckuSxSQPDey7Icm3kny1+5of+N71SY4n\nOZbksmlNXJK0OqOc4X8GuHyF/X9eVRd3XwcAkrwBuBJ4A/BO4OYk6W22kqSxDQ1+Vd0PfH+Fb60U\n8j3A7VX1XFU9ChwHdk00Q0lSLya5hv/BJEeS/FWSs7t95wFPDBxzotsnSZqxcd+lczPwh1VVSf4Y\n+DPg/asdZO/evS9sz83NMTc3N+Z0pI3Dd/9oNRYWFlhYWOhlrLGCX1XfGbj5KeAfuu0TwPkD39vZ\n7VvRYPAlSS+2/GR43759Y4816iWdMHDNPsmOge/9BvD1bvtu4KokZyZ5HXAB8ODYs5Mk9WboGX6S\n24A54BVJHgduAN6e5CLgFPAo8AGAqjqa5A7gKPAscG1V1XSmLklajaHBr6r3rLD7My9x/I3AjZNM\nSpLUPz9pK0mNMPiS1AiDL0mNMPiS1AiDL0mNMPiS1AiDL0mNMPiS1AiDL0mNMPiS1AiDL0mNMPiS\n1AiDL0mNMPiS1AiDL0mNMPiS1AiDL0mNMPiS1Iihf+JQ6sP8oZO9jndg95Zex5Na4Bm+JDXC4EtS\nIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+\nJDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC\n4EtSI4YGP8ktSRaTPDSw75wkB5M8kuSeJGcPfO/6JMeTHEty2bQmLklanVHO8D8DXL5s33XAvVV1\nIXAfcD1AkjcCVwJvAN4J3Jwk/U1XkjSuocGvqvuB7y/bvQfY323vB67ott8F3F5Vz1XVo8BxYFc/\nU5UkTWLrmPc7t6oWAarqySTndvvPA/594LgT3T5JUzZ/6GTvYx7YvaX3MTU74wZ/uRrnTnv37n1h\ne25ujrm5uZ6mI0mbw8LCAgsLC72MNW7wF5Nsr6rFJDuAp7r9J4DzB47b2e1b0WDwJUkvtvxkeN++\nfWOPNerbMtN9Pe9u4Jpu+2rgroH9VyU5M8nrgAuAB8eenSSpN0PP8JPcBswBr0jyOHAD8HHgb5O8\nD3iMpXfmUFVHk9wBHAWeBa6tqrEu90iS+jU0+FX1ntN869LTHH8jcOMkk5Ik9c9P2kpSIwy+JDXC\n4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDWir1+PrE2i79+p7u9Tl9YPz/AlqREG\nX5IaYfAlqREGX5IaYfAlqREGX5IaYfAlqREGX5IaYfAlqREGX5IaYfAlqREGX5IaYfAlqREGX5Ia\nYfAlqREGX5IaYfAlqRH+xasNyr9MJWm1PMOXpEYYfElqhMGXpEYYfElqhMGXpEYYfElqhMGXpEYY\nfElqhMGXpEYYfElqhMGXpEYYfElqhMGXpEYYfElqhMGXpEYYfElqhMGXpEYYfElqxER/4jDJo8Az\nwCng2araleQc4G+A1wCPAldW1TMTzlOSNKFJz/BPAXNV9eaq2tXtuw64t6ouBO4Drp/wMSRJPZj0\nj5iHF//Q2APs7rb3Awss/RCQtEHNHzrZ63gHdm/pdTyNZtIz/AK+kORLSd7f7dteVYsAVfUkcO6E\njyFJ6sGkZ/iXVNW3k7wKOJjkEZZ+CAxafvsFe/fufWF7bm6Oubm5CacjSZvLwsICCwsLvYw1UfCr\n6tvdP7+T5E5gF7CYZHtVLSbZATx1uvsPBl+S9GLLT4b37ds39lhjX9JJclaSbd32TwKXAQ8DdwPX\ndIddDdw19uwkSb2Z5Ax/O/D3Saob57NVdTDJl4E7krwPeAy4sod5SpImNHbwq+q/gYtW2P80cOkk\nk5Ik9c9P2kpSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+\nJDXC4EtSIyb9i1d6Cc+dKk71ON7WwBlJjyNKaonBn6LrHjrF15/pb7zff+MZ/Oqr+htPUlu8pCNJ\njTD4ktQIgy9JjTD4ktQIgy9JjTD4ktQI35YpaWbmD53sdbwDu7f0Ot5m4xm+JDXC4EtSIwy+JDXC\n4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtS\nIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSIwy+JDXC4EtSI6YW/CTzSf4jyX8m+di0HkeSNJqp\nBD/JGcAngcuBXwDeneT103is9WphYWHWU5iqpw8vzHoKU+Xzt3Ft9uduEtM6w98FHK+qx6rqWeB2\nYM+UHmtd2uz/0j195NCspzBVPn8b12Z/7iYxreCfBzwxcPtb3T5J0oxsnfUENrOdLw8/Plm9jbfN\nZ0vSBFLVX5BeGDR5K7C3qua729cBVVU3DRzT/wNLUgOqKuPcb1rB3wI8Avw68G3gQeDdVXWs9weT\nJI1kKhcJqupkkg8CB1l6neAWYy9JszWVM3xJ0vqzZp+0TXJOkoNJHklyT5KzVzjmZUm+mORwkm8k\n+ZO1mt+kRlzfziT3dWt7OMmHZjHXcYyyvu64W5IsJnloree4WqN8ODDJXyQ5nuRIkovWeo6TGLa+\nJBcm+bckP07ykVnMcRIjrO89Sb7Wfd2f5E2zmOe4Rljfu7q1HU7y5SS/NnTQqlqTL+Am4KPd9seA\nj5/muLO6f24BHgAuWas5Tnt9wA7gom57G0uvc7x+1nPv+fl7G3AR8NCs5zxkPWcA3wReA/wEcGT5\ncwG8E/h8t/0rwAOznnfP63sl8EvAHwEfmfWcp7C+twJnd9vzm/D5O2tg+03AN4eNu5a/S2cPsL/b\n3g9csdJBVfWjbvNlLC36+9OfWi+Grq+qnqyqI932D4FjbJzPJ4z6/N3PxnjORvlw4B7grwGq6ovA\n2Um2r+00xzZ0fVX13ar6CvDcLCY4oVHW90BVPdPdfICN898ajLa+Hw3c3AZ8d9igaxn8c6tqEZbC\nB5y70kFJzkhyGHgSWKiqo2s4x0mMtL7nJXktS2fCX5z6zPqxqvVtAKN8OHD5MSdWOGa92uwfflzt\n+t4P/PNUZ9SvkdaX5Iokx4B/AoZeIu71XTpJvgAMngEFKOAPVjh8xVeLq+oU8OYkPwUcTLK7qtbF\n58D7WF83zjbgc8CHuzP9daGv9UnrSZK3A+9l6XLjplJVdwJ3JnkbcCtw4Usd32vwq+odp/te90Le\n9qpaTLIDeGrIWP+b5PPAW4B1Efw+1pdkK0uxv7Wq7prSVMfS5/O3AZwAXj1we2e3b/kx5w85Zr0a\nZX0b2UjrS/KLwF8C81W1ES41Pm9Vz19V3Z9ka5JXVNX3TnfcWl7SuRu4ptu+GnhR7JK88vl3fyR5\nOfAOll6s2AiGrq/zaeBoVX1iLSbVo1HXB0v/ZzDWJwHX0JeAC5K8JsmZwFUsrXHQ3cBvwwufHv/B\n85e1NoBR1jdovT9fyw1dX5JXA38H/FZV/dcM5jiJUdb3cwPbFwO8VOzpDlirV51/BriXpXemHAR+\nutv/s8A/DrzS/FXgMPA14Hdn/Wp5z+u7BDjJ0g+xw91a52c9977W192+Dfgf4P+Ax4H3znruL7Gm\n+W49x4Hrun0fAH5n4JhPsvRuia8BF896zn2uj6XLd08APwCe7p6vbbOed4/r+xTwvYGmPDjrOfe8\nvo8CX+/W9y/AW4aN6QevJKkR/olDSWqEwZekRhh8SWqEwZekRhh8SWqEwZekRhh8SWqEwZekRvw/\nKZKj47Fk1noAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1200b09b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"initial = tf.truncated_normal([1000], stddev=0.1)\n",
"with tf.Session() as sess:\n",
" result = initial.eval()\n",
" # print(result)\n",
" plt.plot(result)\n",
" plt.title('Showing the raw initialized data')\n",
" plt.show()\n",
" \n",
" plt.hist(result, np.linspace(-0.2, 0.2, 11), \n",
" ec='none', rwidth=0.9, color='#47c0fc')\n",
" plt.xlim(-0.3, 0.3)\n",
" plt.ylim(0, 200)"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([-0.2 , -0.16, -0.12, -0.08, -0.04, 0. , 0.04, 0.08, 0.12, 0.16])"
]
},
"execution_count": 58,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
""
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [python3]",
"language": "python",
"name": "Python [python3]"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3.0
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | mit |
mauriciogtec/PropedeuticoDataScience2017 | Alumnos/Luis Puente/Tarea 1- Luis Federico Puente 103108.ipynb | 1 | 43204 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 1: Imprimir como matriz"
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de matrices\" \n",
" def __init__(self, list_of_rows): \n",
" \"Constructor\"\n",
" self.data = list_of_rows\n",
" self.shape = (len(list_of_rows), len(list_of_rows[0]))\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz"
]
},
{
"cell_type": "code",
"execution_count": 110,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"A = Array([[1,2,3],[4,5,6]])"
]
},
{
"cell_type": "code",
"execution_count": 111,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1, 2, 3]\n",
"[4, 5, 6]\n",
"\n"
]
}
],
"source": [
"print(A)"
]
},
{
"cell_type": "code",
"execution_count": 112,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 2, 3]\n",
"[4, 5, 6]"
]
},
"execution_count": 112,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 2: Validador de tamaño"
]
},
{
"cell_type": "code",
"execution_count": 113,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" "
]
},
{
"cell_type": "code",
"execution_count": 114,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"A = Array([1,2,3])"
]
},
{
"cell_type": "code",
"execution_count": 115,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1]\n",
"[2]\n",
"[3]\n",
"\n"
]
}
],
"source": [
"print(A)"
]
},
{
"cell_type": "code",
"execution_count": 117,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1]\n",
"[2]\n",
"[3]"
]
},
"execution_count": 117,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "code",
"execution_count": 118,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"A = Array([[1,2,3],[4,5,6]])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 3: Indexing and item assignment"
]
},
{
"cell_type": "code",
"execution_count": 125,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" def __getitem__(self, idx):\n",
" return self.data[idx[0]][idx[1]]\n",
" \n",
" def __setitem__(self, idx, new_value):\n",
" self.data[idx[0]][idx[1]]= new_value"
]
},
{
"cell_type": "code",
"execution_count": 126,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"A = Array([[1,2,3],[4,5,6]])"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"5"
]
},
"execution_count": 128,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A[1,1]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 4: Iniciar una matriz en ceros y crear matriz identidad"
]
},
{
"cell_type": "code",
"execution_count": 166,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" def __getitem__(self, idx):\n",
" return self.data[idx[0]][idx[1]]\n",
" \n",
" def __setitem__(self, idx, new_value):\n",
" self.data[idx[0]][idx[1]]= new_value\n",
" \n",
" def zeros(x,y):\n",
" \"Matriz de ceros\"\n",
" zeroarray= Array([[0 for col in range(y)]for row in range(x)])\n",
" return zeroarray\n",
" \n",
" def eye(x):\n",
" \"Matriz identidad\"\n",
" identidad= Array([[0 for col in range(x)]for row in range(x)]) \n",
" for a in range(x):\n",
" for b in range(x):\n",
" if a==b:\n",
" identidad[a,b]=1\n",
" return identidad "
]
},
{
"cell_type": "code",
"execution_count": 167,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Ceros=Array.zeros(2,3)"
]
},
{
"cell_type": "code",
"execution_count": 168,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[0, 0, 0]\n",
"[0, 0, 0]"
]
},
"execution_count": 168,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Ceros"
]
},
{
"cell_type": "code",
"execution_count": 169,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Identidad=Array.eye(4)"
]
},
{
"cell_type": "code",
"execution_count": 170,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 0, 0, 0]\n",
"[0, 1, 0, 0]\n",
"[0, 0, 1, 0]\n",
"[0, 0, 0, 1]"
]
},
"execution_count": 170,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Identidad"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 5: Transpuesta"
]
},
{
"cell_type": "code",
"execution_count": 191,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" def __getitem__(self, idx):\n",
" return self.data[idx[0]][idx[1]]\n",
" \n",
" def __setitem__(self, idx, new_value):\n",
" self.data[idx[0]][idx[1]]= new_value\n",
" \n",
" def zeros(x,y):\n",
" \"Matriz de ceros\"\n",
" zeroarray= Array([[0 for col in range(y)]for row in range(x)])\n",
" return zeroarray\n",
" \n",
" def eye(x):\n",
" \"Matriz identidad\"\n",
" identidad= Array([[0 for col in range(x)]for row in range(x)]) \n",
" for a in range(x):\n",
" for b in range(x):\n",
" if a==b:\n",
" identidad[a,b]=1\n",
" return identidad\n",
" \n",
" def transpose(self):\n",
" \"Matriz transpuesta\"\n",
" nrow_t=len(self.data[0])\n",
" ncol_t=len(self.data)\n",
" transpuesta=Array([[0 for a in range(ncol_t)]for b in range(nrow_t)])\n",
" \n",
" for a in range(nrow_t):\n",
" for b in range(ncol_t):\n",
" transpuesta[a,b]=self.data[b][a]\n",
" return transpuesta"
]
},
{
"cell_type": "code",
"execution_count": 192,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 2, 3]\n",
"[4, 5, 6]"
]
},
"execution_count": 192,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = Array([[1,2,3],[4,5,6]])\n",
"A"
]
},
{
"cell_type": "code",
"execution_count": 193,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 4]\n",
"[2, 5]\n",
"[3, 6]"
]
},
"execution_count": 193,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"trans=A.transpose()\n",
"trans"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 6: Suma de matrices"
]
},
{
"cell_type": "code",
"execution_count": 212,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" def __getitem__(self, idx):\n",
" return self.data[idx[0]][idx[1]]\n",
" \n",
" def __setitem__(self, idx, new_value):\n",
" self.data[idx[0]][idx[1]]= new_value\n",
" \n",
" def zeros(x,y):\n",
" \"Matriz de ceros\"\n",
" zeroarray= Array([[0 for col in range(y)]for row in range(x)])\n",
" return zeroarray\n",
" \n",
" def eye(x):\n",
" \"Matriz identidad\"\n",
" identidad= Array([[0 for col in range(x)]for row in range(x)]) \n",
" for a in range(x):\n",
" for b in range(x):\n",
" if a==b:\n",
" identidad[a,b]=1\n",
" return identidad\n",
" \n",
" def transpose(self):\n",
" \"Matriz transpuesta\"\n",
" nrow_t=len(self.data[0])\n",
" ncol_t=len(self.data)\n",
" transpuesta=Array([[0 for a in range(ncol_t)]for b in range(nrow_t)])\n",
" \n",
" for a in range(nrow_t):\n",
" for b in range(ncol_t):\n",
" transpuesta[a,b]=self.data[b][a]\n",
" return transpuesta\n",
" \n",
" def __add__(self, other):\n",
" \"Suma de matrices o suma de un escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape != other.shape:\n",
" raise Exception(\"Las dimensiones son distintas!\")\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] + other.data[r][c]\n",
" return newArray\n",
" elif isinstance(2, (int, float, complex)): # en caso de que el lado derecho sea solo un numero\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] + other\n",
" return newArray\n",
" else:\n",
" return NotImplemented # es un tipo de error particular usado en estos metodos\n",
" \n",
" __radd__ = __add__\n",
"\n",
" def __sub__(self, other):\n",
" \"Suma de matrices o suma de un escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape != other.shape:\n",
" raise Exception(\"Las dimensiones son distintas!\")\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] - other.data[r][c]\n",
" return newArray\n",
" elif isinstance(2, (int, float, complex)): # en caso de que el lado derecho sea solo un numero\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] - other\n",
" return newArray\n",
" else:\n",
" return NotImplemented # es un tipo de error particular usado en estos metodos"
]
},
{
"cell_type": "code",
"execution_count": 213,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[[-4, -4], [-4, -4]]"
]
},
"execution_count": 213,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = Array([[1,2], [3,4]])\n",
"B = Array([[5,6], [7,8]])\n",
"C = A - B\n",
"C.data"
]
},
{
"cell_type": "code",
"execution_count": 214,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[-9, -8]\n",
"[-7, -6]"
]
},
"execution_count": 214,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"D = A - 10\n",
"D"
]
},
{
"cell_type": "code",
"execution_count": 215,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[2, 3]\n",
"[4, 5]"
]
},
"execution_count": 215,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"1 + Array([[1,2], [3,4]])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ejercicio 7: Multiplicación de matrices"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" def __getitem__(self, idx):\n",
" return self.data[idx[0]][idx[1]]\n",
" \n",
" def __setitem__(self, idx, new_value):\n",
" self.data[idx[0]][idx[1]]= new_value\n",
" \n",
" def zeros(x,y):\n",
" \"Matriz de ceros\"\n",
" zeroarray= Array([[0 for col in range(y)]for row in range(x)])\n",
" return zeroarray\n",
" \n",
" def eye(x):\n",
" \"Matriz identidad\"\n",
" identidad= Array([[0 for col in range(x)]for row in range(x)]) \n",
" for a in range(x):\n",
" for b in range(x):\n",
" if a==b:\n",
" identidad[a,b]=1\n",
" return identidad\n",
" \n",
" def transpose(self):\n",
" \"Matriz transpuesta\"\n",
" nrow_t=len(self.data[0])\n",
" ncol_t=len(self.data)\n",
" transpuesta=Array([[0 for a in range(ncol_t)]for b in range(nrow_t)])\n",
" \n",
" for a in range(nrow_t):\n",
" for b in range(ncol_t):\n",
" transpuesta[a,b]=self.data[b][a]\n",
" return transpuesta\n",
" \n",
" def __add__(self, other):\n",
" \"Suma de matrices o suma matriz y escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape != other.shape:\n",
" raise Exception(\"Las dimensiones son distintas!\")\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] + other.data[r][c]\n",
" return newArray\n",
" elif isinstance(2, (int, float, complex)): # en caso de que el lado derecho sea solo un numero\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] + other\n",
" return newArray\n",
" else:\n",
" return NotImplemented # es un tipo de error particular usado en estos metodos\n",
" \n",
" __radd__ = __add__\n",
"\n",
" def __sub__(self, other):\n",
" \"Resta de matrices o resta matriz y escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape != other.shape:\n",
" raise Exception(\"Las dimensiones son distintas!\")\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] - other.data[r][c]\n",
" return newArray\n",
" elif isinstance(2, (int, float, complex)): # en caso de que el lado derecho sea solo un numero\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] - other\n",
" return newArray\n",
" else:\n",
" return NotImplemented # es un tipo de error particular usado en estos metodos\n",
" \n",
" def __mul__(self, other):\n",
" \"Multiplicación de matrices o multiplicación de matriz por escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape[1]!=other.shape[0]:\n",
" raise Expeption(\"Las dimensiones de las matrices no permiten hacer la multiplicación\")\n",
" rowA=self.shape[0]\n",
" colA=self.shape[1]\n",
" rowB=other.shape[0]\n",
" colB=other.shape[1] \n",
" newArray = Array([[0. for l in range(colB)] for i in range(rowA)])\n",
" for i in range(rowA):\n",
" for l in range(colB):\n",
" for j in range(rowB):\n",
" newArray[i,l]= newArray[i,l] + self.data[i][j]*other.data[j][l]\n",
" return newArray\n",
" elif isinstance(other, (int,float, complex)):\n",
" rowA,colA= self.shape\n",
" newArray = Array([[0. for c in range(colA)] for r in range(rowA)])\n",
" for i in range (rowA):\n",
" for j in range(colA):\n",
" newArray.data[i][j]=self.data[i][j]*other\n",
" return newArray\n",
" else:\n",
" return NotImplemented\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[17.0, 22.0, 27.0]\n",
"[22.0, 29.0, 36.0]\n",
"[27.0, 36.0, 45.0]"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = Array([[1,4], [2,5],[3,6]])\n",
"B = Array([[1,2,3], [4,5,6]])\n",
"A*B"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(3, 2)"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.shape"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(2, 3)"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B.shape"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 4]\n",
"[2, 5]\n",
"[3, 6]"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[2, 8]\n",
"[4, 10]\n",
"[6, 12]"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A*2"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Matriz triangular"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Array:\n",
" \"Constructor de Matrices\"\n",
" def __init__ (self, list_of_rows):\n",
" \"Constructor\"\n",
" \n",
" #Obteción de dimensiones\n",
" self.data = list_of_rows\n",
" nrow=len(list_of_rows)\n",
" \n",
" #Caso vector: redimensionar correctamente\n",
" #Si list_of_rows=[1,2,3] entonces list_of rows[0]=1 es un entero (no una lista)\n",
" if not isinstance(list_of_rows[0],list):\n",
" nrow=1\n",
" self.data = [[x] for x in list_of_rows]\n",
" #Con esto, self.data=[[1],[2],[3]]\n",
" \n",
" #Se calcula en número de columnas y la dimensión\n",
" ncol=len(self.data[0])\n",
" self.shape=(nrow,ncol)\n",
" \n",
" #Validador \n",
" if any ([len(r) != ncol for r in self.data]):\n",
" raise Exeption(\"Las filas deben ser del mismo tamano\")\n",
" \n",
" def __repr__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz\n",
"\n",
" def __str__(self):\n",
" matriz=\"\"\n",
" for x in self.data:\n",
" matriz = matriz + str(x)+\"\\n\"\n",
" return matriz \n",
" \n",
" def __getitem__(self, idx):\n",
" return self.data[idx[0]][idx[1]]\n",
" \n",
" def __setitem__(self, idx, new_value):\n",
" self.data[idx[0]][idx[1]]= new_value\n",
" \n",
" def zeros(x,y):\n",
" \"Matriz de ceros\"\n",
" zeroarray= Array([[0 for col in range(y)]for row in range(x)])\n",
" return zeroarray\n",
" \n",
" def eye(x):\n",
" \"Matriz identidad\"\n",
" identidad= Array([[0 for col in range(x)]for row in range(x)]) \n",
" for a in range(x):\n",
" for b in range(x):\n",
" if a==b:\n",
" identidad[a,b]=1\n",
" return identidad\n",
" \n",
" def transpose(self):\n",
" \"Matriz transpuesta\"\n",
" nrow_t=len(self.data[0])\n",
" ncol_t=len(self.data)\n",
" transpuesta=Array([[0 for a in range(ncol_t)]for b in range(nrow_t)])\n",
" \n",
" for a in range(nrow_t):\n",
" for b in range(ncol_t):\n",
" transpuesta[a,b]=self.data[b][a]\n",
" return transpuesta\n",
" \n",
" def __add__(self, other):\n",
" \"Suma de matrices o suma matriz y escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape != other.shape:\n",
" raise Exception(\"Las dimensiones son distintas!\")\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] + other.data[r][c]\n",
" return newArray\n",
" elif isinstance(other, (int, float, complex)): # en caso de que el lado derecho sea solo un numero\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] + other\n",
" return newArray\n",
" else:\n",
" return NotImplemented # es un tipo de error particular usado en estos metodos\n",
" \n",
" __radd__ = __add__\n",
"\n",
" def __sub__(self, other):\n",
" \"Resta de matrices o resta matriz y escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape != other.shape:\n",
" raise Exception(\"Las dimensiones son distintas!\")\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] - other.data[r][c]\n",
" return newArray\n",
" elif isinstance(other, (int, float, complex)): # en caso de que el lado derecho sea solo un numero\n",
" rows, cols = self.shape\n",
" newArray = Array([[0. for c in range(cols)] for r in range(rows)])\n",
" for r in range(rows):\n",
" for c in range(cols):\n",
" newArray.data[r][c] = self.data[r][c] - other\n",
" return newArray\n",
" else:\n",
" return NotImplemented # es un tipo de error particular usado en estos metodos\n",
" \n",
" def __mul__(self, other):\n",
" \"Multiplicación de matrices o multiplicación de matriz por escalar\"\n",
" if isinstance(other, Array):\n",
" if self.shape[1]!=other.shape[0]:\n",
" raise Expeption(\"Las dimensiones de las matrices no permiten hacer la multiplicación\")\n",
" rowA=self.shape[0]\n",
" colA=self.shape[1]\n",
" rowB=other.shape[0]\n",
" colB=other.shape[1] \n",
" newArray = Array([[0. for l in range(colB)] for i in range(rowA)])\n",
" for i in range(rowA):\n",
" for l in range(colB):\n",
" for j in range(rowB):\n",
" newArray[i,l]= newArray[i,l] + self.data[i][j]*other.data[j][l]\n",
" return newArray\n",
" elif isinstance(other, (int,float, complex)):\n",
" rowA,colA= self.shape\n",
" newArray = Array([[0. for c in range(colA)] for r in range(rowA)])\n",
" for i in range (rowA):\n",
" for j in range(colA):\n",
" newArray.data[i][j]=self.data[i][j]*other\n",
" return newArray\n",
" else:\n",
" return NotImplemented\n",
" \n",
" def forward_subs (self,Y):\n",
" \"Método para resolver una matriz triangular inferior\"\n",
" if isinstance(Y,Array):\n",
" if Y.shape[1]!=1:\n",
" raise Exeption (\"Y no es un vector\")\n",
" if Y.shape[0]!=self.shape[1]:\n",
" raise Exeption (\"Las dimensiones de las matrices no permiten hacer la operación\")\n",
" \n",
" rowA,colA= self.shape\n",
" for i in range(colA):\n",
" for j in range(rowA):\n",
" if i>j:\n",
" if self.data[j][i]!=0:\n",
" raise Exeption (\"La matriz no es triangular inferior\") \n",
" \n",
" colY= Y.shape[0] \n",
" newArrayX = Array([[0.] for l in range(colY)])\n",
" \n",
" for j in range(colY):\n",
" if j==0:\n",
" newArrayX.data[0][0]=(Y.data[0][0])/(self.data[0][0])\n",
" \n",
" if j>0:\n",
" for i in range(j):\n",
" newArrayX.data[j][0]=newArrayX.data[j][0]-(self.data[j][i]/self.data[j][j])*newArrayX.data[i][0]\n",
" newArrayX.data[j][0]=Y.data[j][0]/self.data[j][j]+ newArrayX.data[j][0]\n",
" return newArrayX\n",
" \n",
" \n",
" def backward_subs (self,Y):\n",
" \"Método para resolver una matriz triangular superior\"\n",
" if isinstance(Y,Array):\n",
" if Y.shape[1]!=1:\n",
" raise Exeption (\"Y no es un vector\")\n",
" if Y.shape[0]!=self.shape[1]:\n",
" raise Exeption (\"Las dimensiones de las matrices no permiten hacer la operación\")\n",
" \n",
" rowA,colA= self.shape\n",
" for i in range(colA):\n",
" for j in range(rowA):\n",
" if i<j:\n",
" if self.data[j][i]!=0:\n",
" raise Exeption (\"La matriz no es triangular superior\") \n",
" \n",
" colY= Y.shape[0] \n",
" newArrayX = Array([[0.] for l in range(colY)])\n",
" \n",
" for j in range(colY):\n",
" c=colY-j-1\n",
" if j==0: \n",
" newArrayX.data[c][0]=(Y.data[c][0])/(self.data[c][c])\n",
" \n",
" if j>0:\n",
" for i in range(j):\n",
" q=c+1+i\n",
" newArrayX.data[c][0]=newArrayX.data[c][0]-(self.data[c][q]/self.data[c][c])*newArrayX.data[q][0]\n",
" newArrayX.data[c][0]=Y.data[c][0]/self.data[c][c]+ newArrayX.data[c][0]\n",
" return newArrayX"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"A = Array([[1,0,0], [2,3,0],[4,5,6]])"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 0, 0]\n",
"[2, 3, 0]\n",
"[4, 5, 6]"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Y =Array([[1],[2],[3]])"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(3, 1)"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Y.shape"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"X=A.forward_subs(Y)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1.0]\n",
"[0.0]\n",
"[-0.16666666666666663]"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"A = Array([[1,2,3], [0,4,5],[0,0,6]])"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[1, 2, 3]\n",
"[0, 4, 5]\n",
"[0, 0, 6]"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [],
"source": [
"X=A.backward_subs(Y)"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"[-0.25]\n",
"[-0.125]\n",
"[0.5]"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.125"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"1/8"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
phasedchirp/Assorted-Data-Analysis | exercises/SlideRule-DS-Intensive/Inferential Statistics/sliderule_dsi_inferential_statistics_exercise_2.ipynb | 2 | 117775 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"### Examining racial discrimination in the US job market\n",
"\n",
"#### Background\n",
"Racial discrimination continues to be pervasive in cultures throughout the world. Researchers examined the level of racial discrimination in the United States labor market by randomly assigning identical résumés black-sounding or white-sounding names and observing the impact on requests for interviews from employers.\n",
"\n",
"#### Data\n",
"In the dataset provided, each row represents a resume. The 'race' column has two values, 'b' and 'w', indicating black-sounding and white-sounding. The column 'call' has two values, 1 and 0, indicating whether the resume received a call from employers or not.\n",
"\n",
"Note that the 'b' and 'w' values in race are assigned randomly to the resumes.\n",
"\n",
"#### Exercise\n",
"You will perform a statistical analysis to establish whether race has a significant impact on the rate of callbacks for resumes.\n",
"\n",
"Answer the following questions **in this notebook below and submit to your Github account**. \n",
"\n",
" 1. What test is appropriate for this problem? Does CLT apply?\n",
" 2. What are the null and alternate hypotheses?\n",
" 3. Compute margin of error, confidence interval, and p-value.\n",
" 4. Discuss statistical significance.\n",
"\n",
"You can include written notes in notebook cells using Markdown: \n",
" - In the control panel at the top, choose Cell > Cell Type > Markdown\n",
" - Markdown syntax: http://nestacms.com/docs/creating-content/markdown-cheat-sheet\n",
"\n",
"\n",
"#### Resources\n",
"+ Experiment information and data source: http://www.povertyactionlab.org/evaluation/discrimination-job-market-united-states\n",
"+ Scipy statistical methods: http://docs.scipy.org/doc/scipy/reference/stats.html \n",
"+ Markdown syntax: http://nestacms.com/docs/creating-content/markdown-cheat-sheet\n",
"\n",
"****"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from __future__ import division\n",
"import matplotlib\n",
"matplotlib.rcParams['figure.figsize'] = (15.0,5.0)\n",
"import pandas as pd\n",
"import numpy as np\n",
"from scipy import stats"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Total count: 4870\n",
"race == 'b': 2435\n",
"race == 'w': 2435\n"
]
}
],
"source": [
"data = pd.io.stata.read_stata('data/us_job_market_discrimination.dta')\n",
"print \"Total count: \",len(data)\n",
"print \"race == 'b': \",len(data[data.race=='b'])\n",
"print \"race == 'w': \",len(data[data.race=='w'])"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>id</th>\n",
" <th>ad</th>\n",
" <th>education</th>\n",
" <th>ofjobs</th>\n",
" <th>yearsexp</th>\n",
" <th>honors</th>\n",
" <th>volunteer</th>\n",
" <th>military</th>\n",
" <th>empholes</th>\n",
" <th>occupspecific</th>\n",
" <th>...</th>\n",
" <th>compreq</th>\n",
" <th>orgreq</th>\n",
" <th>manuf</th>\n",
" <th>transcom</th>\n",
" <th>bankreal</th>\n",
" <th>trade</th>\n",
" <th>busservice</th>\n",
" <th>othservice</th>\n",
" <th>missind</th>\n",
" <th>ownership</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>b</td>\n",
" <td>1</td>\n",
" <td>4</td>\n",
" <td>2</td>\n",
" <td>6</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>17</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>b</td>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>6</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>316</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>b</td>\n",
" <td>1</td>\n",
" <td>4</td>\n",
" <td>1</td>\n",
" <td>6</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>19</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>b</td>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>4</td>\n",
" <td>6</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>313</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td></td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>b</td>\n",
" <td>1</td>\n",
" <td>3</td>\n",
" <td>3</td>\n",
" <td>22</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>313</td>\n",
" <td>...</td>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>0</td>\n",
" <td>1</td>\n",
" <td>0</td>\n",
" <td>Nonprofit</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>5 rows × 65 columns</p>\n",
"</div>"
],
"text/plain": [
" id ad education ofjobs yearsexp honors volunteer military empholes \\\n",
"0 b 1 4 2 6 0 0 0 1 \n",
"1 b 1 3 3 6 0 1 1 0 \n",
"2 b 1 4 1 6 0 0 0 0 \n",
"3 b 1 3 4 6 0 1 0 1 \n",
"4 b 1 3 3 22 0 0 0 0 \n",
"\n",
" occupspecific ... compreq orgreq manuf transcom bankreal trade \\\n",
"0 17 ... 1 0 1 0 0 0 \n",
"1 316 ... 1 0 1 0 0 0 \n",
"2 19 ... 1 0 1 0 0 0 \n",
"3 313 ... 1 0 1 0 0 0 \n",
"4 313 ... 1 1 0 0 0 0 \n",
"\n",
" busservice othservice missind ownership \n",
"0 0 0 0 \n",
"1 0 0 0 \n",
"2 0 0 0 \n",
"3 0 0 0 \n",
"4 0 1 0 Nonprofit \n",
"\n",
"[5 rows x 65 columns]"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data.head()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Callback count for black-sounding names: 157.0\n",
"Callback proportion for black-sounding names: 0.064476386037\n",
"Callback count for white-sounding names: 235.0\n",
"Callback proportion for white-sounding names: 0.0965092402464\n"
]
}
],
"source": [
"# number of callbacks and proportion of callbacks\n",
"print \"Callback count for black-sounding names: \",sum(data[data.race=='b'].call)\n",
"print \"Callback proportion for black-sounding names: \",sum(data[data.race=='b'].call)/len(data[data.race=='b'])\n",
"print \"Callback count for white-sounding names: \",sum(data[data.race=='w'].call)\n",
"print \"Callback proportion for white-sounding names: \",sum(data[data.race=='w'].call)/len(data[data.race=='w'])"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"The outcome variable here is binary, so this might be treated in several ways. First, it might be possible to apply the normal approximation to the binomial distribution. In this case, the distribution proportions is $\\mathcal{N}(np,np(1-p))$\n",
"\n",
"There are a number of guidelines as to whether this is a suitable approximation (see [Wikipedia](https://en.wikipedia.org/wiki/Binomial_distribution#Normal_approximation) for a list of such conditions), some of which include:\n",
"\n",
"* n > 20 (or 30)\n",
"* np > 5, np(1-p) > 5 (or 10)\n",
"\n",
"But these conditions can be roughly summed up as not too small of a sample and an estimated proportion far enough from 0 and 1 that the distribution isn't overly skewed. If the normal approximation is reasonable, a z-test can be used, with the following standard error calculation:\n",
"\n",
"$$SE = \\sqrt{\\hat{p}(1-\\hat{p})\\left(\\frac{1}{n_1}+\\frac{1}{n_2}\\right)}$$\n",
"\n",
"where $$\\hat{p}=\\frac{np_1+np_2}{n_1+n_2}$$\n",
"\n",
"giving\n",
"\n",
"$$z = \\frac{p_1-p2}{SE}$$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"z-score: -4.108 p = 4e-05\n"
]
}
],
"source": [
"xb = sum(data[data.race=='b'].call)\n",
"nb = len(data[data.race=='b'])\n",
"xw = sum(data[data.race=='w'].call)\n",
"nw = len(data[data.race=='w'])\n",
"pHat = (nb*(xb/nb) + nw*(xw/nw))/(nb+nw)\n",
"se = np.sqrt(pHat*(1-pHat)*(1/nb + 1/nw))\n",
"z = (xb/nb -xw/nw)/se\n",
"print \"z-score:\",round(z,3),\"p =\", round(stats.norm.sf(abs(z))*2,6)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So, the difference in probability of a call-back is statistically significant here.\n",
"\n",
"Plotting the distribution for call-backs with black-sounding names, it looks fairly symmetrical and well-behaved, so it's quite likely that the normal approximation is fairly reasonable here."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.collections.LineCollection at 0x7f0ff397bf50>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/matplotlib/collections.py:590: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison\n",
" if self._edgecolors == str('face'):\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3sAAAE4CAYAAADinuoIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHM5JREFUeJzt3X+MZWd5H/DvExsnqSJ1S5BsYzs1KkbBaVI7TZyVkMIA\nodrsHzb5J9RpREIjYZUYIlS14FRNdts/EicFUYvWsYRBVqJiEEmpaZwYCzEo/WUgNYbENrAKbm0D\nS4sgCtAodnj6x5w1d8Yz987Ozuyce+7nI412znnec+e90rv33ue+73mf6u4AAAAwLd9x2B0AAABg\n/0n2AAAAJkiyBwAAMEGSPQAAgAmS7AEAAEyQZA8AAGCCFiZ7VXWsqh6tqs9V1Zt3aHPbEH+oqq4d\nzn1XVT1QVZ+sqoer6tdm2p+oqieq6sHh59j+PSUAAAAunBesqguSvCPJTyR5MsnHq+qe7n5kps3x\nJC/s7quq6seS3J7kaHf/ZVW9rLu/WVUXJvkvVfWS7v6vSTrJ27r7bQf1xAAAAFbZopm965Kc6u7H\nuvupJHcnuWFLm+uT3JUk3f1AkiNVdfFw/M2hzUVJLkjy1Znr6hz7DgAAwA4WJXuXJXl85viJ4dyi\nNpcnGzODVfXJJKeTfKS7H55p94Zh2eedVXVkT70HAABgW4uSvd7l42ydpesk6e6/7u5rspH8/XhV\nrQ3x25O8IMk1Sb6Y5K27/DsAAADswtx79rJxn94VM8dXZGPmbl6by4dzz+juP6+q30/yI0nWu/vL\nZ2JV9c4kH9zuj1fVbpNNAACASeruPd0CtyjZ+0SSq6rqyiRfSPLqJDduaXNPkpuT3F1VR5N8rbtP\nV9Xzkjzd3V+rqu9O8sokJ5Okqi7t7i8O1/9Ukk/v1IFu+R6LnThxIidOnDjsbrAkjBd2y1jhbBgv\n7Jaxwtmo2vtWJ3OTve5+uqpuTnJfNjZYubO7H6mqm4b4Hd19b1Udr6pTSb6R5LXD5ZcmuauqviMb\ny0V/u7s/PMRuraprsrHc8/NJbtrzMwAAAOBZFs3spbv/IMkfbDl3x5bjm7e57tNJfniHx3zN2XUT\nAACAs7GwqDosg7W1tcPuAkvEeGG3jBXOhvHCbhkrnC815nviqqrH3D8AAICDVFV73qDFzB4AAMAE\nSfYAAAAmSLIHAAAwQZI9AACACZLsAQAATJBkDwAAYIIkewAAABMk2QMAAJggyR4AAMAESfYAAAAm\nSLIHAAAwQZI9AJbGiRMn9hQDgFVU3X3YfdhRVfWY+wfA+VVV2el9YV7sxIkTkkEAltLw/lZ7udbM\nHgCjchBJ2cmTJ/f9MQFg7MzsATAqe52922sMAMbMzB4AAACbSPYAOO/GdP/cmPoCAPvJMk4Azrvz\nvVTTEk8AlpVlnAAAAGwi2QMAAJggyR4AAMAESfYAYAc2bwFgmUn2ADgQU0iUFGMHYJnZjROAAzGm\nXTXt1AnAsrIbJwAAAJtI9gAAACZIsgcAADBBkj0A2IMpbEADwLRJ9gDYs1VOeOzUCcDYLdyNs6qO\nJXl7kguSvLO7b92mzW1JfjLJN5P8fHc/WFXfleSjSb4zyUVJ/lN33zK0f26S9yb520keS/LT3f21\nbR7XbpwAIzam3THHFAOA/XJgu3FW1QVJ3pHkWJKrk9xYVS/e0uZ4khd291VJXpfk9iTp7r9M8rLu\nvibJDyV5WVW9ZLjsLUnu7+4XJfnwcAwAAMA+WbSM87okp7r7se5+KsndSW7Y0ub6JHclSXc/kORI\nVV08HH9zaHNRNmYGv7r1muHfV53LkwAAAGCzRcneZUkenzl+Yji3qM3lycbMYFV9MsnpJB/p7oeH\nNhd39+nh99NJLt5D3wEAANjBomRvtzcjbF1D2knS3X89LOO8PMmPV9Xas/7Axg0PbnoAAADYRxcu\niD+Z5IqZ4yuyMXM3r83lw7lndPefV9XvJ/n7SdaTnK6qS7r7S1V1aZIv79SB2Z3e1tbWsra2tqDL\nAAAAy2l9fT3r6+v78lhzd+OsqguTfCbJK5J8IcnHktzY3Y/MtDme5ObuPl5VR5O8vbuPVtXzkjzd\n3V+rqu9Ocl+Sk9394ar6jSRf6e5bq+otSY5097M2abEbJ8C4jWkHzDHFTpw4sdJlKQDYP+eyG+du\nSi/8ZL5deuHO7v61qropSbr7jqHNmR07v5Hktd39P6vqB7Ox+cp3DD+/3d2/ObR/bpL3Jfm+KL0A\nsLTGlGAtSwwAzsaBJnuHSbIHcPjmzVKNKYlalhgAnA3JHgAHZkyJ0hRiAHA2DqyoOgAAAMtJsgcA\nADBBkj0AAIAJkuwBAABMkGQPAABggiR7AHAeKbYOwPmi9AIAc42pbMHUYwCwldILAAAAbCLZA8DS\nQgCYIMs4ARjVUsZVjgHAVpZxAgAAsIlkDwAAYIIkewAAABMk2QMAAJggyR4AAMAESfYAAAAmSLIH\nACOh3iEA+0mdPQBGVWtOzPseAN+mzh4AC5k1AoDVYmYPYEWMaZZKzMweALtjZg8AAIBNJHsAAAAT\nJNkDAACYIMkeAADABEn2AAAAJkiyBwAAMEGSPQAAgAmS7AHAEjhx4sRhdwGAJaOoOsCKGFOBcDEF\n1wHYHUXVAQAA2GRhsldVx6rq0ar6XFW9eYc2tw3xh6rq2uHcFVX1kar606r6k6p640z7E1X1RFU9\nOPwc27+nBLC6LPUDAM6Yu4yzqi5I8pkkP5HkySQfT3Jjdz8y0+Z4kpu7+3hV/ViSf9vdR6vqkiSX\ndPcnq+p7kvxxkhu6+9Gq+tUkf9Hdb5vbOcs4Ac7KmJYWilnGCcC5O8hlnNclOdXdj3X3U0nuTnLD\nljbXJ7krSbr7gSRHquri7v5Sd39yOP/1JI8kuWy233vpMAAAAIstSvYuS/L4zPET2Zyw7dTm8tkG\nVXVlkmuTPDBz+g3Dss87q+rIWfQZAACABRYle7tdL7J1lu6Z64YlnO9P8kvDDF+S3J7kBUmuSfLF\nJG/d5d8BAABgFy5cEH8yyRUzx1dkY+ZuXpvLh3Opquck+d0kv9PdHzjToLu/fOb3qnpnkg/u1IHZ\nzQbW1taytra2oMsAAADLaX19Pevr6/vyWIs2aLkwGxu0vCLJF5J8LPM3aDma5O3DBi2VjXv5vtLd\nb9ryuJd29xeH39+U5Ee7+2e2+fs2aAE4C2PaNETMBi0AnLtz2aBl7sxedz9dVTcnuS/JBUnu7O5H\nquqmIX5Hd99bVcer6lSSbyR57XD5S5L8bJJPVdWDw7lbuvsPk9xaVddkY7nn55PctJfOAwAAsL25\nM3uHzcwewNkZ02yTmJk9AM7dQZZeAABGbvb+dgA4w8wewISMabZJbBwxAJabmT0AAAA2kewBAABM\nkGQPYMm4PwsA2A337AEsmTHdDyY2/hgAy809ewAAAGwi2QMAAJggyR4AAMAESfYAAAAmSLIHAAAw\nQZI9AACACZLsAcCEqcsIsLrU2QNYMmOq4Sa23DEAxk+dPQAAADaR7AEAAEyQZA8AAGCCJHsAI2RT\nDQDgXNmgBWCExrSJh9h0YwCMnw1aAAAA2ESyBwAAMEGSPQAAgAmS7AEAAEyQZA8AAGCCJHsAAAAT\nJNkDgBWlniPAtKmzBzBCY6rFJraaMQDGQZ09AAAANpHsAQAATJBkDwAAYIIkewCHxOYYAMBBWpjs\nVdWxqnq0qj5XVW/eoc1tQ/yhqrp2OHdFVX2kqv60qv6kqt440/65VXV/VX22qj5UVUf27ykBLIeT\nJ08edhcAgAmbm+xV1QVJ3pHkWJKrk9xYVS/e0uZ4khd291VJXpfk9iH0VJI3dfcPJDma5Ber6vuH\n2FuS3N/dL0ry4eEYAACAfbJoZu+6JKe6+7HufirJ3Ulu2NLm+iR3JUl3P5DkSFVd3N1f6u5PDue/\nnuSRJJdtvWb491Xn/EwAAAB4xqJk77Ikj88cP5FvJ2zz2lw+26CqrkxybZIHhlMXd/fp4ffTSS7e\ndY8BAABY6MIF8d1WWt1a5O+Z66rqe5K8P8kvDTN8mxt2d1Xt+HdmNzBYW1vL2traLrsEAACwXNbX\n17O+vr4vj1XdO+dzVXU0yYnuPjYc35LkW91960yb30qy3t13D8ePJnlpd5+uquck+c9J/qC73z5z\nzaNJ1rr7S1V1aZKPdPf3Z4uq6nn9A1hmVZWdXuPExA47BsA4DK/VWyfXdmXRMs5PJLmqqq6sqouS\nvDrJPVva3JPkNUNHjib52pDoVZI7kzw8m+jNXPNzw+8/l+QDe+k8AAAA25ub7HX300luTnJfkoeT\nvLe7H6mqm6rqpqHNvUn+rKpOJbkjyeuHy1+S5GeTvKyqHhx+jg2xX0/yyqr6bJKXD8cAwEioAwmw\n/OYu4zxslnECUzamJXtiYmcTA+D8OchlnAAAACwhyR4AAMAESfYAAAAmSLIHAAAwQZI9gANkR0MA\n4LDYjRPgAI1pB0Uxsf2KAXD+2I0TAACATSR7AAAAEyTZAwAAmCDJHgAAwARJ9gAAACZIsgcAnBUl\nRQCWg9ILAAdoTNvli4mdjxgA+0vpBQAAADaR7AEAAEyQZA8AAGCCJHsAAAATJNkD2Ad2JwQAxsZu\nnAD7YKfdCce0S6KY2PmIAbC/7MYJAADAJpI9AACACZLsAQAATJBkDwAAYIIkewDAvrEzLcB42I0T\nYB/YjVNMbHEMgLNnN04AAAA2kewBAABMkGQPAABggiR7AAAAEyTZAwAAmCDJHsAu2VIeAFgmC5O9\nqjpWVY9W1eeq6s07tLltiD9UVdfOnH9XVZ2uqk9vaX+iqp6oqgeHn2Pn/lQADtbJkycPuwsAALs2\nN9mrqguSvCPJsSRXJ7mxql68pc3xJC/s7quSvC7J7TPhdw/XbtVJ3tbd1w4/f3gOzwEAAIAtFs3s\nXZfkVHc/1t1PJbk7yQ1b2lyf5K4k6e4HkhypqkuG4z9K8tUdHntPhQEBAABYbFGyd1mSx2eOnxjO\nnW2b7bxhWPZ5Z1Ud2UV7AAAAdunCBfHe5eNsnaVbdN3tSf7V8Pu/TvLWJL+wXcPZDRHW1taytra2\nyy4BAGNy4sQJGx0BLLC+vp719fV9eazq3jkvq6qjSU5097Hh+JYk3+ruW2fa/FaS9e6+ezh+NMlL\nu/v0cHxlkg929w/u8Dd2jFdVz+sfwPlUVdnpNWmn2F6uERNbxRgA2xteO/d0C9yiZZyfSHJVVV1Z\nVRcleXWSe7a0uSfJa4aOHE3ytTOJ3pwOXzpz+FNJPr1TWwAAAM7e3GWc3f10Vd2c5L4kFyS5s7sf\nqaqbhvgd3X1vVR2vqlNJvpHktWeur6r3JHlpku+tqseT/Ep3vzvJrVV1TTaWe34+yU0H8eQAAABW\n1dxlnIfNMk5gTCzjFBM7uBgA2zvIZZwAAAAsIckeAADABEn2AAAAJkiyBzBDDTAAYCps0AIwY783\nnhjTBhhiYmOOAbA9G7QAAACwiWQPAABggiR7AMChc78swP5zzx7ADPfsiYmNLwawytyzBwAAwCaS\nPQAAgAmS7AEAAEyQZA8AAGCCJHsAAAATJNkDAACYIMkesHLU8wIAVoE6e8DKOZ81wsZUq0xMbFlj\nAKtMnT0AAAA2kewBAKNm6TXA3ljGCawcyzjFxKYTA5g6yzgBAADYRLIHAAAwQZI9AACACZLsAQAA\nTJBkDwAAYIIkewAAABMk2QMmSV0uAGDVqbMHTNJY6oCNpR9iYlONAUydOnsAAABsItkDAJaWJdsA\nO1uY7FXVsap6tKo+V1Vv3qHNbUP8oaq6dub8u6rqdFV9ekv751bV/VX12ar6UFUdOfenAgCsmpMn\nTx52FwBGa26yV1UXJHlHkmNJrk5yY1W9eEub40le2N1XJXldkttnwu8ert3qLUnu7+4XJfnwcAwA\nAMA+WTSzd12SU939WHc/leTuJDdsaXN9kruSpLsfSHKkqi4Zjv8oyVe3edxnrhn+fdXeug8AAMB2\nFiV7lyV5fOb4ieHc2bbZ6uLuPj38fjrJxQvaAwAAcBYWJXu73ed461agu94feaitYD9lAACAfXTh\ngviTSa6YOb4iGzN389pcPpyb53RVXdLdX6qqS5N8eaeGs7tsra2tZW1tbcFDAwAALKf19fWsr6/v\ny2PNLapeVRcm+UySVyT5QpKPJbmxux+ZaXM8yc3dfbyqjiZ5e3cfnYlfmeSD3f2DM+d+I8lXuvvW\nqnpLkiPd/axNWhRVB/ZqLEWfx9IPMbFVjAFMwYEVVe/up5PcnOS+JA8neW93P1JVN1XVTUObe5P8\nWVWdSnJHktfPdOw9Sf5bkhdV1eNV9doh9OtJXllVn03y8uEY4KyorwUAsLO5M3uHzcweMM+YZhDM\n7ImJjS8GMAUHNrMHALCszP4Dq87MHrC0xjSDYGZPTGy5YgDLwsweAAAAm0j2AAAAJkiyBwAAMEGS\nPQAAgAmS7AEAAEyQZA8AAGCCJHvAqKmTBQCwN5I9YNROnjx52F0AJsgXScAqUFQdGLUxFWFWVF1M\nbDViAGOiqDoAAACbSPYAAAAmSLIHAAAwQZI9AACACZLsAQAATJBkDwAAYIIke8ChU+8KGBOvScBU\nqLMHHLox1ddSZ09MTEwNPmBM1NkDAABgE8keAADABEn2AAAAJkiyBwAAMEGSPQAAgAmS7AEAAEyQ\nZA8AYJfU4AOWiWQPOC98QAKm4OTJk4fdBYBdU1QdOC/GVBRZUXUxMTEF14Floag6AAAAm0j2AAAA\nJkiyBwAAMEELk72qOlZVj1bV56rqzTu0uW2IP1RV1y66tqpOVNUTVfXg8HNsf54OAAAAyYJkr6ou\nSPKOJMeSXJ3kxqp68ZY2x5O8sLuvSvK6JLfv4tpO8rbuvnb4+cN9fE4AAOedXYeBsVk0s3ddklPd\n/Vh3P5Xk7iQ3bGlzfZK7kqS7H0hypKou2cW1e9pRBhgvH3SAVaYsAzA2i5K9y5I8PnP8xHBuN22e\nv+DaNwzLPu+sqiNn1WtglHzQAQAYj0XJ3m4LyZztLN3tSV6Q5JokX0zy1rO8HgAAgDkuXBB/MskV\nM8dXZGOGbl6by4c2z9np2u7+8pmTVfXOJB/cqQOzy8LW1taytra2oMsAAADLaX19Pevr6/vyWNW9\n8+RdVV2Y5DNJXpHkC0k+luTG7n5kps3xJDd39/GqOprk7d19dN61VXVpd39xuP5NSX60u39mm7/f\n8/oHjEtVZaf/s6saG0s/xMTEDjcGsFfDa8ue9juZu4yzu59OcnOS+5I8nOS9Q7J2U1XdNLS5N8mf\nVdWpJHckef28a4eHvrWqPlVVDyV5aZI37aXzAADLwAZWwGGYO7N32MzswXIZ07foY4mNpR9iYmLj\njQHMc2AzewBb+XYaAGA5mNkDzsqYvg1fhthY+iEmJjbeGMA8ZvYAAADYRLIHAAAwQZI9AIBD5F5o\n4KC4Zw84K2O6z2UZYmPph5iY2HLGANyzB+wr3zIDACw/M3vAs4zpW+1lj42lH2JiYssZAzCzBwAA\nwCaSPQCAkbKsHjgXlnECzzKmJUzLHhtLP8TExKYXA1aDZZzAWfNtMQDAtJnZgxU1pm+npxwbSz/E\nxMSmFwNWg5k9AIAVYnUGsBtm9mBFjenb6SnHxtIPMTGxacXM+MHqMLMHbMs3vwAAq0uyBxN28uTJ\nw+4CAOeZL/qAMyzjhAkby3KjVY6NpR9iYmLTitnUBVaHZZwAAABsItmDJWe5DgAA25HswZJzXx4A\nu+ULQlgt7tmDJTeW+0fE3LMnJia23K8twDi5Zw8mzjexABw07zUwPWb2YAmM5ZtksXF8+y4mJiZ2\nvvsBHB4zewAAAGwi2YORsHwGgLHyHgXLyTJOGImxLA0SW+6lVmJiYqsRG0s/gINnGScsCd+MAjA1\n3ttgvCR7cB6piQfA1Mx7b5MIwuGS7ME+88YGABt8yQmHS7IHezAvofPGBgCL+XIUDt7CZK+qjlXV\no1X1uap68w5tbhviD1XVtYuurarnVtX9VfXZqvpQVR3Zn6cD54eEDgDOjeWfcPDmJntVdUGSdyQ5\nluTqJDdW1Yu3tDme5IXdfVWS1yW5fRfXviXJ/d39oiQfHo5hz9bX1/f9Mb3RAMDhmHoieBCfW2A7\ni2b2rktyqrsf6+6nktyd5IYtba5PcleSdPcDSY5U1SULrn3mmuHfV53zM2GlzXvRnPemYDkmACyX\nvSaCY0oSJXucL4uSvcuSPD5z/MRwbjdtnj/n2ou7+/Tw++kkF59Fn1lR816k571ozntTkNABwHTs\n9T1/WZJEOFuLkr3dVs/cTZG/2u7xhqrpqnSO1F5f/A4iNu9F+qMf/eiOMQCAec53kngQK5IkpWyn\nNnKtHYJVR5Oc6O5jw/EtSb7V3bfOtPmtJOvdffdw/GiSlyZ5wU7XDm3WuvtLVXVpko909/dv8/cl\ngQAAwErr7t1Mrj3LhQvin0hyVVVdmeQLSV6d5MYtbe5JcnOSu4fk8GvdfbqqvjLn2nuS/FySW4d/\nP7DdH9/rkwIAAFh1c5O97n66qm5Ocl+SC5Lc2d2PVNVNQ/yO7r63qo5X1akk30jy2nnXDg/960ne\nV1W/kOSxJD99AM8NAABgZc1dxgkAAMByWlhU/aBU1buq6nRVfXrm3I7F1qvqlqE4+6NV9Q8Op9cc\nhh3Gym9W1SNV9VBV/V5V/c2ZmLGywrYbLzOxf1pV36qq586cM15W1E5jpareMLy+/ElVzd6jbqys\nsB3ei66rqo9V1YNV9fGq+tGZmPGyoqrqiqr6SFX96fA68sbhvM+5PMuc8bIvn3UPLdlL8u5sFFyf\ntW2x9aq6Ohv3/F09XPPvq+ow+875td1Y+VCSH+juv5fks0luSYwVkmw/XlJVVyR5ZZL/NXPOeFlt\nzxorVfWybNSC/aHu/rtJ/s1w3lhhu9eW30jyL7v72iS/MhwbLzyV5E3d/QNJjib5xap6cXzOZXs7\njZd9+ax7aAOpu/8oyVe3nN6p2PoNSd7T3U9192NJTmWjaDsrYLux0t33d/e3hsMHklw+/G6srLgd\nXluS5G1J/vmWc8bLCtthrPyTJL/W3U8Nbf7PcN5YWXE7jJcvJjnzbfuRJE8OvxsvK6y7v9Tdnxx+\n/3qSR7JRa9rnXJ5lh/Hy/P36rDu2bw12Krb+/GwUZT9ju+LurK5/nOTe4XdjhWepqhuSPNHdn9oS\nMl7Y6qokP15V/6Oq1qvqR4bzxgrbeUuSt1bV/07ymxm+eY/xwmDYlf7abHxY9zmXubaMl1l7/qw7\ntmTvGbsotm5nGVJV/yLJX3X3f5jTzFhZYVX1N5L8cpJfnT095xLjZbVdmORvdffRJP8syfvmtDVW\nuDPJG7v7+5K8Kcm75rQ1XlZMVX1Pkt9N8kvd/RezMZ9z2WoYL+/Pxnj5+sz5c/qsO7Zk73RVXZIk\nQ7H1Lw/nn0xyxUy7y/PtpRKsqKr6+STHk/yjmdPGClv9nSRXJnmoqj6fjTHxx1V1cYwXnu2JJL+X\nJN398STfqqrnxVhhe9d1938cfn9/vr2UynhZcVX1nGwker/d3WfqSfucy7ZmxsvvzIyXffmsO7Zk\n70yx9WRzsfV7kvzDqrqoql6QjWU2HzuE/jESVXUsG9+639DdfzkTMlbYpLs/3d0Xd/cLuvsF2fgw\n/8PDUhrjha0+kOTlSVJVL0pyUXf/3xgrbO9UVb10+P3l2dhEITFeVlpVVTZmfR/u7rfPhHzO5Vl2\nGi/79Vl3blH1g1RV70ny0iTPq6rHs7GL1bbF1rv74ap6X5KHkzyd5PWtQODK2Gas/Go27ou4KMn9\nG/9H8t+7+/XGCjPj5XvPvLZ097tnmjwzHoyX1bbdWMnGMrx3Ddvr/1WS1yTGCjt+bnldkn9XVd+Z\n5P8Nx8YLL0nys0k+VVUPDuduic+5bG+78fLLSW7LPnzWVVQdAABggsa2jBMAAIB9INkDAACYIMke\nAADABEn2AAAAJkiyBwAAMEGSPQAAgAmS7AEAAEyQZA8AAGCC/j9TPp07Ef9fMAAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f1003634510>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"pb = xb/nb\n",
"x = np.arange(110,210)\n",
"matplotlib.pyplot.vlines(x,0,stats.binom.pmf(x,nb,pb))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Alternatives"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Because the normal distribution is only an approximation, the assumptions don't always work out for a particular data set. There are several methods for calculating confidence intervals around the estimated proportion. For example, with a significance level of $\\alpha$, the Jeffrey's interval is defined as the $\\frac{\\alpha}{2}$ and 1-$\\frac{\\alpha}{2}$ quantiles of a beta$(x+\\frac{1}{2}, n-x+\\frac{1}{2})$ distribution. Using scipy:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Interval for black-sounding names: [0.055, 0.075]\n",
"Interval for white-sounding names: [0.085, 0.109]\n"
]
}
],
"source": [
"intervalB = (stats.beta.ppf(0.025,xb+0.5,nb-xb+0.5),stats.beta.ppf(0.975,xb+0.5,nb-xb+0.5))\n",
"intervalW = (stats.beta.ppf(0.025,xw+0.5,nw-xw+0.5),stats.beta.ppf(0.975,xw+0.5,nw-xw+0.5))\n",
"print \"Interval for black-sounding names: \",map(lambda x: round(x,3),intervalB)\n",
"print \"Interval for white-sounding names: \",map(lambda x: round(x,3),intervalW)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The complete lack of overlap in the intervals here implies a significant difference with $p\\lt 0.05$ ([Cumming & Finch,2005](http://www.apastyle.org/manual/related/cumming-and-finch.pdf)). Given that this particular interval can be interpreted as a Bayesian credible interval, this is a fairly comfortable conclusion."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Calculating credible intervals using Markov Chain Monte Carlo\n",
"Slightly different method of calculating approximately the same thing (the beta distribution used above the posterior distribution given given the observations with a Jeffreys prior):"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pystan"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"modelCode = '''\n",
"data {\n",
" int<lower=0> N; \n",
" int<lower=1,upper=2> G[N];\n",
" int<lower=0,upper=1> y[N];\n",
"} \n",
"parameters {\n",
" real<lower=0,upper=1> theta[2];\n",
"} \n",
"model {\n",
" # beta(0.5,0.5) prior\n",
" theta ~ beta(0.5,0.5);\n",
" # bernoulli likelihood\n",
" # This could be modified to use a binomial with successes and counts instead\n",
" for (i in 1:N) \n",
" y[i] ~ bernoulli(theta[G[i]]);\n",
"}\n",
"generated quantities {\n",
" real diff;\n",
" // difference in proportions:\n",
" diff <- theta[1]-theta[2];\n",
"}\n",
"'''\n",
"\n",
"model = pystan.StanModel(model_code=modelCode)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"dataDict = dict(N=len(data),G=np.where(data.race=='b',1,2),y=map(int,data.call))\n",
"fit = model.sampling(data=dataDict)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Inference for Stan model: anon_model_8b4f1e02e3c6136d2cb318fc285607be.\n",
"4 chains, each with iter=2000; warmup=1000; thin=1; \n",
"post-warmup draws per chain=1000, total post-warmup draws=4000.\n",
"\n",
" mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat\n",
"theta[0] 0.06 1.5e-4 5.0e-3 0.06 0.06 0.06 0.07 0.07 1152.0 1.0\n",
"theta[1] 0.1 1.8e-4 5.9e-3 0.09 0.09 0.1 0.1 0.11 1117.0 1.0\n",
"diff -0.03 2.3e-4 7.7e-3 -0.05 -0.04 -0.03 -0.03 -0.02 1166.0 1.0\n",
"lp__ -1358 0.03 0.98 -1361 -1358 -1358 -1357 -1357 834.0 1.0\n",
"\n",
"Samples were drawn using NUTS(diag_e) at Mon Nov 9 20:23:03 2015.\n",
"For each parameter, n_eff is a crude measure of effective sample size,\n",
"and Rhat is the potential scale reduction factor on split chains (at \n",
"convergence, Rhat=1).\n"
]
}
],
"source": [
"print fit"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/matplotlib/figure.py:387: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure\n",
" \"matplotlib is currently using a non-GUI backend, \"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA34AAAFCCAYAAACuDg/rAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXd4HOXVsH8fSZaLXOTejXHFNgZjbDBddNsvmG5ikkD4\nQcKXhJIeIM3kl7yp5A2EN/lIISEJCIMxtgEDNgZjYtNcwHKVe5EsWS4qVi/n+2N2VrO7s7uzq12t\nJD/3denS7swzz5wpO3POc85zjqgqBoPBYDAYDAaDwWDouKSlWgCDwWAwGAwGg8FgMCQXY/gZDAaD\nwWAwGAwGQwfHGH4Gg8FgMBgMBoPB0MExhp/BYDAYDAaDwWAwdHCM4WcwGAwGg8FgMBgMHRxj+BkM\nBoPBYDAYDAZDB8cYfgZDkhGRkSLSJCLm92YwGAwGg8FgSAlGETUYkoCI7BORKxLQjzEaDQaDwWAw\nGAwtxiiTBkNyUEAS2F8i+zIYDAaDwWAwnGIYw89gSDAi8i9gBPCqiFQAt/lWfUFE9otIiYg86mgv\nIvKwiOwSkaMiskBEevtWr/b9LxWRChE5X0RGi8g7vrYlIvJvEenVekdoMBgMBoPBYGhvGMPPYEgw\nqvpF4ABwnar2AF70rboIGAdcCfxYRMb7lj8IzAEuBQYDJ4D/9a27xPe/l6r2UNWPfN9/7ms7ARgO\nzE/aARkMBoPBYDAY2j3G8DMYko8dpvmYqtaq6ibgM+Bs3/L/A/xQVQtVtR54DLjVN68vJMRTVXer\n6kpVrVfVo8D/AJcl/zAMBoPBYDAYDO2VjFQLYDCcQhQ5PlcB3X2fTwNeEZEmx/oGYKBbJyIyEHgC\nuBjogTWAczzh0hoMBoPBYDAYOgzG42cwJAeNoe0BYKaq9nb8dVPVw2H6+W+gEThTVXsBX8T8lg0G\ng8FgMBgMETDKosGQHIqB0R7b/l/gv0VkBICI9BeROb51JUBTUF/dgUqgXESGAt9NjMgGg8FgMBgM\nho6KMfwMhuTwC+CHInIcuIXIHsAngKXAchEpBz4AzgNQ1SqsRC5rROS4iJyHNQdwKlAGvAq8HKV/\ng8FgMBgMBsMpjqgmT18UkYeAe7ESVPxFVZ8QkT7AAqx5TfuAuapamjQhDAaDwWBoRURkJvB7IB34\nq6r+Kmj9GcDfgXOAH6jq477lXYD3gM5AJrBEVR9pTdkNBoPB0HFJmsdPRM7EMvqmY2UvvE5ERgMP\nAytUdRyw0vfdYDAYDIZ2j4ikA08BM4GJwDwRmRDU7BjwAPBb50JVrQEuV9UpwFnA5SJycfKlNhgM\nBsOpQDJDPc8APlLVGlVtxBrFvAWrXtmzvjbPAjcmUQaDwWAwGFqT84BdqrrPV57lBeAGZwNVLVHV\ndUB98Ma+8G6wPH7pmIy9BoPBYEgQyTT8NgOXiEgfEekGzAaGAQNVtdjXppgwKesNBoPBYGiHDAUO\nOr4f8i3zhIikicinWO/Hd1V1a4LlMxgMBsMpStIMP1XdDvwKWA68AXyKlYLe2UYxSSkMBoPB0HFo\n0TtNVZt8oZ7DgEtFJCchUhkMBoPhlCepBdxV9RngGQAR+TnWyGexiAxS1SIRGQwccdtWRIxBaDAY\nDKcIqiqpliFBFADDHd+HY737YkJVy0TkdWAasMq5zrwfDQaD4dQiUe/IpJZzEJEBvv8jgJuB57HS\n1t/la3IXsDjc9qra5v9+8pOfpFyGjiRne5LVyHlqytmeZG0vcnYw1gFjRWSkiGQCt2O999wIeJGL\nSD8RyfZ97gpcDWx02zDV1+xUuC87muxGfiP7qSp/e5ZdNbHvyKR6/ICFItIXawL719Qawfwl8KKI\n3IOvnEOSZTAYDAaDoVVQ1QYRuR94Cys5y99UdZuI3Odb/7SIDAI+AXoCTb7SRxOBIcA/RCQNa2D2\nX6q6MiUHYjAYDIYOR7JDPS91WXYcuCqZ+zUYDAaDIVWo6htYc9udy552fC4iMBzUZhMwNbnSGQwG\ng+FUJamhnqcCOTk5qRbBE+1FTmg/sho5E0t7kRPaj6ztRU7DqUV7vi/bs+xg5E8l7Vl2aN/yt2fZ\nE40kOnY0UYiItlXZDAaDwZA4RATtOMldko55PxoMBsOpQyLfkcbjZzAYDAaDwWAwGAwdHGP4GQwG\ng8FgMBgMBkMHxxh+BoPBYDAYDAaDwdDBSXYdv0dEZIuI5InI8yLSWUT6iMgKEckXkeV2zSKDwWAw\nGDoKIjJTRLaLyE4R+b7L+jNE5AMRqRGRbzuWDxeRd33vzs0i8mDrSm4wGAyGjkrSDD8RGQl8GZiq\nqpOx6hl9DngYWKGq44CVvu+GNspLL8Gtt8Ls2ZCXl2ppDAaDoe0jIunAU8BMrPp880RkQlCzY8AD\nwG+DltcD31TVScAM4Osu2xoMBoPBEDPJ9PiVY73AuolIBtANKATmAM/62jwL3JhEGQwt4N134f77\n4eabLcPvyivhnXdSLZXBYDC0ec4DdqnqPlWtB14AbnA2UNUSVV2H9Z50Li9S1U99n08C27AKuyeN\no1VHk9m9wWAwGNoISTP8fIXaHwcOYBl8paq6AhioqsW+ZsXAwGTJYIifggKYNw9yc+GOOywDcMEC\nuP12OHAg1dIZDAZDm2YocNDx/ZBvWUz4ImfOAT5KiFRhWLF7BZV1lcnchcFgMBjaAMkM9RwNfAMY\niTVa2V1EvuBs4ytEZIoRtUF+9zvL4LviiuZll18O3/423HknNDamTjaDwWBo47T4vSYi3YGFwEM+\nz5/BYDAYDC0iI4l9TwPWquoxABFZBFwAFInIIFUtEpHBwJFwHcyfP9//OScnh5ycnCSKa7ApLYW/\n/x0++yx03Xe/C8uWwRNPwLe+1fqyGQyG9s+qVatYtWpVqsVIJgXAcMf34VheP0+ISCfgZeDfqrrY\nrY15PxoMhpagqpRUlTAga0CqRTEEkcx3pFhOtyR0LHI28BwwHagB/gF8DJwGHFPVX4nIw0C2qoYk\neBERTZZshsj8+tewaRP8+9/u63ftghkz4KOPYPTo1pXNYDB0PEQEVZVUy5EofPPadwBXYk11+BiY\np6rbXNrOBypU9XHfd8Ga/35MVb8Zpv+Evh9z83KZM34OWZlZCevTYDC0bUoqS3h7z9vMmzwv1aIY\nopDId2TSPH6q+pmI/BNYBzQBG4A/Az2AF0XkHmAfMDdZMhhip6kJnnoKliwJ32bMGHjkEfjyl+Ht\ntyHNVIM0GAwGP6raICL3A29hZbT+m6puE5H7fOufFpFBwCdAT6BJRB7CygA6BfgCsElENvq6fERV\n30ymzA1NDcns3mAwJIHGpkbS09Lj2lZTONNKVbHGuAytTdI8fi3FePxSw+rV8MAD7mGeThob4ZJL\nrAQwDzzQOrIZDIaOSUfz+CWbZHj8ADPybzC0M3LzcrnhjBvo1qlbzNseqTzCyj0rU/K7z83LZe6k\nuXEbracaiXxHGl+NIYDnn7eMuWikp8M//wk//SlsCwleMhgMBoPBYDAkm/rG+uiNUkz+sXx2HN0R\nsKxJm1IkzamNMfwMfurqYOFC+NznvLUfMwZ+/nP4/Oehtja5shkMBoPBYHDnZN1JymrKUi3GKU1j\nU2NKQqbbQ8jkhsMb2HB4Q6rFMGAMP4ODFSvgjDNg5Ejv23z5yzBiBPzwh0kTy2AwGAyGuHll2yvU\nNdalWoyksmL3CpbtXJZqMU45KmorsMOu39v/Hkt3LE2xRG2Pspoy3ELTUznH8FTGGH4GPwsXwtwY\nU+2IwF//ahV6f/fd5MhlMBgMBkO81DTUUF1fHXZ9fWM9hysOt6JEiceEzaWG1/JfY8+JPYBlBNY2\nmPCnYCrqKlItgsGBMfwMADQ0wGuvwY03xr5tv37wpz9Z3r+qqsTLZjAYDAZDLGwq3hQw9ymSd2Hb\n0W2s2reqFaQydETqm6z77FTwYNU21CZskMEkcEwNSTX8RGS8iGx0/JWJyIMi0kdEVohIvogsF5Hs\nZMphiM6aNVbI5ogR8W1//fUwfTr85CeJlctgMBjaGyIyU0S2i8hOEfm+y/ozROQDEakRkW8HrXtG\nRIpFJK/1JO54bDmyhaNVR1t9v7UNtRyrOtbq+zUkhyOVR6IaKKfS3MpF2xbxadGnMW1jDLy2RVIN\nP1XdoarnqOo5wLlAFfAK8DCwQlXHASt93w0pZPHi+Lx9Tp54Av7+d8jPT4xMBoPB0N4QkXTgKWAm\nVl2+eSIyIajZMeAB4LcuXfzdt21U6hrrTIhfBJxJL1pL+Vx/eD3Ldy9vlX3FQpM2caTySEL7PFJ5\nhBW7VyS0z2RS31hPQXlBTNus3LOS4sriiG3sUE+hZUlWCsoLIv6e1xxYw9aSrS3aRyKoqjehXe2Z\n1gz1vArYpaoHgTnAs77lzwItNDkMLUE1MYbfgAHwne/Ao48mRi6DwWBoh5yH9a7bp6r1wAvADc4G\nqlqiquuAkDzsqvo+cMLLjl7e+jKfFHySAJFPbRJpFLZVQ3x/6X5W7lmZ0D4PVxxOiVc1XnYd38Xq\n/as9t6+sqwRab9Bg9f7VEeU7UHaAz4qiFFlOMEcqj/DO3ncS2qd9Pk+F0NhwVNdXp+xZ0ZqG3+eA\nXN/ngapqD6EUAwNbUQ5DEJs2WUlazjyz5X099BB89BF8+GHL+zIYDIZ2yFDgoOP7Id+yhGJnqTxZ\ndzLRXSeMmoYaCisKQ5bn5uW6Kj3lteWU15ZH7LOgvCCssdHY1NiimmZN2tRq57OksiSm9puKN1F0\nsiju/SVDyW4PZQScOOWNdp+U15b7M3R6PXfxnuPik8V+L1pbSzJ0qPwQxScjezxjZX/ZfiD5BvV7\n+95j85HNLe5nw+ENLNu5jNqGWnYe29ni/lSVxdsXxxwymyhaxfATkUzgeuCl4HVqXflT1+xvA7z6\nKsyZYxl/LaVrV/jRj+Cxx1rel8FgMLRDWuV9Znsj4t02UpZLN2oaamIeoc4rzuO9fe+5rnPr6/X8\n13k9//WIfa7ev5q1B9e6rntxy4ss3LowJhmd7Di6g1d3vApYhsEHBz+IuQ8vyuyJ6hO8veftmOYC\nbjmyJaQANlhyFp8sdjU6ymrK/HXlWqO+XHV9NY1NjWHXHyo/1CreM7d7q6Gpgd3Hd/u/L9y60B+i\n6UZr1uN7Z+87rC9cH/f2LQ0xdVJ8spgT1c0BB259t+Qaqqr/d5WMwYijVUf917+wopD9pZaRWddY\n53lQ6O09bwccY/HJYspqythbupd1hev8y+MdJMo7Yk3frmmoiWv7lpLRSvuZBaxXVXuIq1hEBqlq\nkYgMBlwDz+fPn+//nJOTQ05OTrLlPCVZuhR++cvE9XfnnVaSl7w8mDw5cf0aDIaOwapVq1i1alWq\nxUgWBcBwx/fhWF6/hPKzn/6MfaX7yMrMIv2mdBpGNNCvWz+mDJoS0K6qvopunboFLFu6Yyk9Ovfg\nunHXhfS7r3QfQ3sMpVN6p4Dlr2x7hbMGnsWkAZNaJLetUCVSWQ3HsapjDOo+KGT5ybqTdM/s3iyT\nTwG1szMCnKg5wb7SfVww/IKAbStqK+jRuUfYfXpRZu02y3cv55aJt5CZnhm4XpUPDn3AhcMvjNrX\n1pKtbC3ZGnK9AJbtXMaE/hOYMmhKiwwLVaVRG8lIi6wyLt6+mFG9R3H+sPNd17+//30Axvcbz9TB\nU+OWJ5Kcdmji7WfeTpo0+zYKygtCvMm2ly3aNfWKl8GU6vpqDpQdYHy/8S3eXzJ4Z+87ZGVmMWf8\nnKT0/8LmF/yfVZWq+iqOVx9nWM9hru1z83KZM34OWZlZEfutrq+mc0ZnVuxeQd9ufblm9DUB61/d\n8SpZmVnMHBN9+nRJZYl1v0vg/e58ZhWUF7B6/2rmTZ4Xtb9g7GRATuOysamRI5VHGNxjMJDcd2Rr\nhXrOoznME2ApcJfv813AYreN5s+f7/8zRl9yKCyEXbvgkksS12eXLvDAA/Bbt7QFBoPhlCcnJyfg\n+d7BWAeMFZGRvmiX27HeeW7Ebf3M/vJsbv3ardz50J3k5ORQUlnimrhiyfYlHCg7ELK8pqHGNdzw\ng4Mf+EOxgqluaFZsS2tKPYc9bT+63f+5ttGqc+bFQDpccZjcvNyQ5V49DpuKN/mVrIKKAo5XHwcs\nJTBako9whulr+a8FeES84CWE1Bmm2qRN7C/dj6oGHKuXc7bh8IaQfuPF9pxsLNrIS1tCArZcsa9v\nJJKV9fRo1VH/fLRgr1+4sNTcvFxey38toXJsOLwhbKbPxdsXh1yjYN7Y+UaAd9ILDU0NvLLtFdd1\ndlh4OOzfhZN3974b8TqV1ZSxqXiT6zpVJf9Yc5a/SPdtXnGef0AgHMH3lNvvf/H2xWwr2Qa43191\njXWcrDvpeqzx4BwkihfnedlzYk9ASZlkviOTbviJSBZWYpdFjsW/BK4WkXzgCt93Qwp4/XW49lro\nFDpY2CK++lUrhLQgtgRahnZMkza1aniMwdAWUdUG4H7gLWArsEBVt4nIfSJyH4CIDBKRg8A3gR+K\nyAER6e5blwusBcaJyEERudvrvoOVXdtoWnNgjS2bv8B0fWM9b+95O+7j3HJkS0DYUyQ2Ht7o/xxu\nbltpTWnIMrvwc0sSiNjnJK84LyB00/msshVJr/PuKusr/X0GK6FuSumWI1v8IaTheG//e7yab7Wx\nFcKlO5bySWHk5D22QWMbjXY4aLT5Q5V1lRypPBIwKFBdX+2/P07WnWTB5gWA5RHzSjye3A2HN/DR\noY9i3i6ZBBjcMYY27ji6g32l++Led2lNKYdPep/rV3SyiNqGWtfQwZLKEl7e+nLE7d3CxotOFoWV\nQVF2Hd/FliNbXNdX1Vd58jDHG+q5YMsC131HG3Sob6znrV1vhSxPld6SqjIXSTf8VLVSVfupaoVj\n2XFVvUpVx6nqNaoa+sQ3tApLl1o1+BJN795w++3wt78lvm9D2+L1/NeZ/pfp9PxFT4b9bhi/Xfvb\nFs0/MhjaCiLSTURijslS1TdUdbyqjlHVX/iWPa2qT/s+F6nqcFXtpaq9VXWEqp70rZunqkNUtbOv\nzd9d9+GiNDmXBXt6mrSJFza/wKJti4I3C6G8tpy84shlBCMl9gg3l2bj4Y3858B/QpYfrTrKGzvf\nCFluh+olKuGF8/y4ye8sdxC8vqK2wn9O39//Pg1NDWw+sjnACxq8D5tIHhfb81haU+o3umxDuaq+\nKqp3LJyhZXs2wl2npTuWsnLPSv+gAMCr+a+yYo9VniHcNaxvrKe6vpqq+ip/qGRVfVWLkuLsPr47\nYL7d4YrDMZddiERecV6AUeSlHEG0Eg5A2LmmQIsS8QSzvnB9xKRH6wrXUVLVPGhRWFHI8t3LqW2o\n9RtDkTy/4QwwQVqUwKe8tjyicePVuA6+x1WVEzWRve5e5yPvPr47ojd7+9Ht/kEpe8Cnqr7K0wDH\nsp3LIq6P9jxKFq2Z1dPQxqishPfeg1mzktP/ffdZhl9j/JEmhjbOXzf8lXuW3sNjOY9R+O1CVnxx\nBWsPruX8v57f5rKTGQyxICJzgI1YnjtE5BwRCReymTLc5om44UURshXi3cd3tygb3sKtC129gU7l\n1Cl3uLA22/ALVori9RTUNtT66845DZ5oNGkTr+W/xmfFzan07fDAgvKCAKXaPi6nxy2SUvdp0afU\nNNT4jT6A3Se8h/m59b3z2M64UsU3NjX6DaT0tPSQ9WsPruW1/NdYvH0xy3YuY++JvQC8uevNqB5N\nJ8HXL9jj8v6B96OWXahtqPUbn/b24c7z5iObOVTePM3WvjaRBjfClU1YumMpx6qOUXSyyJ84xI1o\nIYXRvMu2YVFYUUj+sfyQpEfByUqcXutD5Yc4VnWMJTuW+Ne73Q/h3tH2wK3zfObm5YY1Pmsbal0N\ny9fzX6egIrwB77wPPjzkLRW8fR2r6qto0iZqG2pdIwJsb3U0okUTuNVNXLK9+bwWVhS63iuqSllN\nGUUni8LWXgx+drcWxvA7hVmxAqZPt7xzyWDKFBg4EJa3vVq2hgTwwuYX+Pn7P2f13auZPXY2PTv3\nZPLAybw892XumHwHl/z9khaFuxgMKWY+cD6+mnqquhEYlUqBnPgTBDiUp5qGGlbuWRlTSQOn8mcb\nfs6seOEU4OAR74amhoD5eDuP7QwI36xrrHP1Xu0r3eca5uncR5M2BSjSsYRIOc9PXWOdq6IXbIjY\nmTJtbA+c87zaiTzWFa7jjV2h3sptJdtC5LQ9IE4jD0JDKZ1JSaLh5nlYV7jOf5xumUCDcZ6T+sZ6\n1heuD+jXPj/7S/f7DUPnuXAeTzjjK1wUSLyZDRdtW8SS7UtYsn2Jp1qWLSk6bh9/bUMtlXWVHCw/\nyLt73w1sE+ae3HJkCyeqT7CpeFPAPVzTUBPg1Qw3mOGWFTc3L5fX818PW1/PvnYBAxIu/dsGiaqS\nm5fLwbKDIW2c2AazU+6ymjIWbVvERwXuobpewyj3le4L690ury33P5Ps+YDHqo6xYPMC1h9e7x/M\niYdw8kV7xtjy2MmVgrHvt81HNgc8Q3Pzcv37VJQVu1eQm5fbqmV5jOF3CrNkCdxwQ/R2LeErX4Gn\nn07uPgytT2FFIQ++8SAv3fYS4/qOC1gnIjx6yaM8cN4DXPnPK43nz9BeqXeZhtBmqnPb4YPhRoq9\nesWcCQXsvmylZvvR7a5KjZ2ZEJrnEbqFMzqVKmeCF1u+yrpKPjj4QYh3RFUDjmv38d2uc3OatInc\nvNywJSMA1+2isaVkiz9xRfHJ4pBwzmAqaiv8yp3zvAdfg9fzX+eFzS8EnHNw9yrYnKw76bq+SZs8\nh9FFI3h+nTMxR6xU1Fbw4aEPA5LVnKw76a+JB833RWFFYUBCEjsBhy17WU0ZS7YvYV3hOnYd3wVY\npTCCQyz3le4LGewIrj0XyzzFcNhy20lEnLh5tqrrq9lUvImdx3ey5cgW/zGAdayr968O66GHyNew\npqEmcDDEd6+FM7yPVh3lQNmBABls7DDbjws+DlguSMCxuoXf2s8KeyDkRPWJqMlk/DIHHV84L/Xa\ng2vDDmC0xGBavnt52JDR8tryiMdheyjDeW7f3PUm4D4wY89dVlX/oMux6uQkPHKjtco5GNoYjY3w\n2mtW2YVkcvvt8J3vwNGj0K9fcvdlaB1UlS+/+mW+Ou2rTBsyLWy7h2Y8REVdBdf++1re+9J79O6a\nJNeywZActojI54EMERkLPIiVdKVN4WbgiUhciQOCPQhuSsuaA2tCsoQ2NjW6jpxH8+aEM6jslO8z\nhs1w7aemocYyLHyZ9QorCsMmmojE+sL1nDvk3IgK6Dt732Fk9kiAiHXftpZsZfLAyQF9NWkTaZIW\ncT6QoiHeKGcfDU0NfqOysq6S3LxcumR0oVN6J3p17hUQwhiOF7e8GHF9pPmiwZlFo1FaU0ppTSn1\njfUcPnmYuZPmuno+IdTbsvbgWg5XHPZ7PO05UjuP7aRn556M6TOGQ+WHXEMsS2tKAzyldqhoz849\nPcldVlNGry69PB5lKG4DMIu3Wwnr3a6/bYCt3LMybJ+xeCntcxzOW+wcHBnTZ0zAunjmI9qDA8HZ\nLd/c9SYDuw/01EfwfXf45GH6Z/VHVWloaggoUVLfVO8ayRBtDmxVfVXY2qDB21bWVbKlxHqOLN+9\nnBG9RgR4s71kMW7SJpq0yW80uhn2tvfb7byraoDxXlFb4Wm+aSwYj98pygcfwJAhMHJkcvfTo4c1\nh3Bh/DV1DW2MBVsWUFBewA8u/UHUtj+45AdcefqVzHpuVtj01gZDG+UBYBJQi1WOqBz4RkolcsEO\ntXJS21AbYpzFk3DJViJtpbayrtK1NER5bblf0XaOwDdqszIcbJipatSyCLbCYytCTu/d4ZOHA0bk\nw6WWj4TbsYD3xBDBLNi8IEDR82owBXtpwu3fTi5R01BDRW2F59T0TqPknb3vhBhcwcXN7WUQ/hxF\no6KuORlOOGMkXQLnEdoGfrjjP1Z1LGCeqBfc5qW5XZdoiTiiESnRi23kOc9xtGt3oOxAgJc0GrYR\nlS7pAdk4w92DbtMwgu9DL/eXbbgq6vf+e52vFpzQyX5G7Dq+i4VbA5VGVfU8D9BJQ1NDyD3wccHH\nrmViDpQdCLhGzucXeHsurCtc57n0iRPbCFU0YD+fFH7iKZQ5FlqjnEO2iCwUkW0islVEzheRPiKy\nQkTyRWS5iGQnWw5DIIsXJz/M0+aOO+C551pnX4bkUl1fzcNvP8wTM58IKTrshojwu2t/x7Qh05j5\n3Exj/BnaDb6M1I+q6jTf3w9U1dOEJBGZKSLbRWSniHzfZf0ZIvKBiNSIyLdj2daN4Dlj+cfyQ8K2\nYlWYndjKf2FFoet6O2wTCEjyEWmu4aJti6KWg7CTh9g4FdH3978fdiTfq+KpWAW/gz0Pwc+peOcq\neyrmHqSYRwr9CyaeeWvFJ4v9iqSdwKW6vjrkfrFLfaw9uDZiRslolNaUhibn8R1zJE9nMOW15Szf\nvTwkhLM1SFXa/Viwf2sFFQUBgzxuWXQraisCSpvYBHsmYzH6nfN0g+fRxnL+Nh7e6B88coZ35h/L\n9+Td9oJbMqnPij4LKYESS2bZitoKmrQp4m/FDoeNRF1jHQs2L/Abp8m431vD4/cEsExVJwBnAduB\nh4EVqjoOWOn7bmglVOGVV+Dmm1tnf9deC9u3w/7wCbAM7YTff/h7pg6eymUjL/O8jYjwh1l/4NzB\n53L5s5cnNM21wZAsRORdlz/3bAqB26UDTwEzgYnAPBGZENTsGJZH8bdxbBsVew6Jk3iUV9vQ85Kg\nIV4vmRdilT1aaKNNbUMtK/esDDG2YjG+ImF7JCMVe1YCPZ+RQv8ShW3IRjKQneviMTBt4/mNnW+4\neo7Kaso814H0gqJJT4kfbzZZL8SSkMkN22jx8lsJZ9DFm2gH4pc/+Nmyv2y/X0dwFrpP9jMo0jxb\nL7yW/xo7j+2MeP7t0N9I2HNew2U6TgRJNfxEpBdwiao+A1ZhW1UtA+YAz/qaPQvcmEw5DIFs2gRN\nTXD22a2zv8xMuPVWyA31rBvaEcUni3n8g8f59dW/jnlb2/i76YybuPBvF7YoeYDB0Ep81/H3I+BT\nIHpVYjjSBb8gAAAgAElEQVQP2KWq+1S1HngBCIivUNUSVV0HBGtLUbf1gttI9f6y+EfeoinoLVWa\nUk2yjNZXd7zqGkbpJBajtjVTvicSN7ndQivDZXf1QiwGc6QacFX1Va4hyHWNdSGe9USSqMEGt0Gf\nYOIJi04WbvOF470PvMzBSybB4edOopWNaE2iJncRkfXAM8Dzqho5ID+U04ESEfk7cDbWS/MbwEBV\ntf2XxYC3maCGhGB7+1qxXiS33gqPPgoPG99uu2X+qvncefadIRPDvSIi/OiyHzGkxxBy/pHDa3e8\nxtTBUxMspcGQGHyGmZP/iIiXyRZDAWde9ENYZSG80JJtIxKtblhLiJYGvq3TEk9HNKLN9/Ga7r49\nk0xvsBOvxl+kDJ/OGm02irJ89/KEZAZNNsHh0W2BSPMfg/GaEbQtEimDeUtKTiQaLx6/z2G9jD4R\nkRdE5Frx7k/PAKYCf1TVqUAlQWGdag13tf0A6g7EokVw002tu89LL4Vdu+Bg+9YPTlm2lmzl5W0v\n88NLf9jivu6Zeg9PzX6Kmf+eGZJG3GBoK/jmott//URkJuAlRWBL3mfmXZgCWhpmZ4jMjmPRawkm\ngpYa0eGyth4qP9QujL62SGvWpzN4I6rHT1V3Ao+KyA+B67C8f00i8gzwhKpGSvtzCDikqvYo6ULg\nEaBIRAapapGIDAZcfdzz58/3f87JySEnJyf6ERkikp8PR47ABRe07n47dYLrr7eSyjzwQOvu29By\nvrfiezxy8SP06donIf3dPOFmOqd35qYFN7Hm/1vD6b1PT0i/hvbBqlWrWLVqVarFiMYGmg2xBmAf\ncI+H7QqA4Y7vw7HehV7wvO3CPzZnvZs4fSITp0/0uAuDoXWJlr21rRBuINKtfITBG3nFeakWoV2y\n9ZOtbP0kOSH04iW+XETOBu4GZgFvAc8DFwNfUNUpUbZdDdyrqvkiMh/o5lt1TFV/JSIPA9mq+nDQ\ndtoeMim1N37+czh8GJ56qvX3vWQJPPEEvBM1PYKhLfHWrrf4+rKvs+VrW+ic0TmhfT/18VP88ZM/\nsvaetWR3Mcl9T1V8dedaMfg8eYhIBrADuBIoBD4G5qlqSNVn3zuxQlUfj2VbEdHnNz2fzMMwGAwG\nQxvhjrPuSNg7Mqrh55vjVwb8FXhZVWsd615R1YhBgz6j8a9AJrAby4BMB14ERmCNos5V1dKg7Yzh\nlwTOPhv+8Acr9LK1qa6GQYNgzx7o27f192+IndqGWib/aTL/c+3/8F/j/isp+7jv1fuob6rnmRue\nSUr/hrZPWzL8ROQWIoRcquqicOscfcwCfo/1rvubqv5CRO7zbf+0iAwCPsEKHW0CKoCJqnrSbVuX\n/o3hZzAYDKcIrW34jVJV98DnJGIMv8SzYwdcfrk1zy49PXr7ZHDjjTB3rlXbz9D2+e/3/5sPD33I\n0nneC8nGSkVtBZP/NJk/X/9nrhl9TdL2Y2i7tDHD7x9ENvzubj1p3DGGn8FgMJw6JNLwizrHD7hX\nRH5te+REpDfwbVVteZYHQ6vy0ktWds1UGX0As2fD668bw689sPfEXh7/4HE++bKXRIbx06NzD/58\n/Z/5yqtfYfPXNtM9s3tS92cwREJVv5RqGQwGg8FgSAZesnrOdoZh+ko6JCfmy5A0VK06enPnplaO\nWbPgrbegsX2WIzplUFW+8tpX+N6F32NU71FJ3981o6/hohEX8du1v43e2GBoJUTkOhH5noj82P5L\ntUwGg8FgMMSLF8MvTUS62F9EpCvWfD1DO2LTJqishAsvTK0cw4fD0KHw8ceplcMQmX98+g+OVx/n\n2xd+u9X2+bPLf8YfPv5DwgrZGgwtQUSeBuYCDwLi+3xaSoUyGAwGg6EFeDH8ngNWisg9InIv8Dbw\nz+SKZUg0zz8P8+ZBmpcrnmTscE9D26SwopDvv/19/jbnb2SkeYkGTwyn9z6dL0z+Aj9b/bNW26fB\nEIELVfVO4LiqPgbMAManWCaDwWBIOulpKZwTZEgqUc0AVf0V8DNgInAG8FPfMkM7oanJCvP8/OdT\nLYnFrFnwxhuplsLghqpy79J7+dr0rzFlUMRKLUnhB5f+gOfynmNf6b5W37fBEES173+ViAzFquU3\nKIXyGAwGQ6sgtIlcW4Yk4Mn/o6pvqOq3VfU7qvpWsoUyJJb//Aeys+HMM1MticUFF8Du3VBSkmpJ\nDMH8bePfKDpZxA8u+UFK9j8gawBfmfoVfrPmNynZv8Hg4DVfMrPfAOuxSg/lplSiIM4aeFbC+po6\neGrC+koUV5x+RapFMLRDMtPbx2yk/ln9Uy2C4RQkquEnIreIyE4RKReRCt9fudcdiMg+EdkkIhtF\n5GPfsj4iskJE8kVkuYiYys1J5F//gi98IdVSNNOpE+TkwIoVqZbE4GRf6T4eWfkI/7zpn3RK75Qy\nOb4x4xvkbs6l6GRRymQwGFT1p6p6QlVfBkYCZ6jqj7xsKyIzRWS77935/TBtnvSt/0xEznEsf0hE\n8kRks4g8lJCD8UCXjC7RGwUxacCkJEjSTI/OPZLaf6ro07VPqkXo0HgZEElFREs44vntGVqXjvQs\n8uLx+zUwR1V7qmoP31/PGPahQI6qnqOq5/mWPQysUNVxwErfd0MSqKmBl19ue+UTrrkGli9PtRQG\nmyZt4u4ld/PdC7/LmQNS6xoe2H0gd0y+g99/+PuUymE4tfENWD4qIqNVtcaZ3TrKdunAU8BMrCkS\n80RkQlCb2cAYVR0LfAX4k2/5mcC9wHTgbOA6ERmdsIMKYnCPwU6ZYt5+XN9xce23W6duntolI9xs\neK/hCe/zVMer4TKoe+tESnu5l9uLV9CQGk7LDszjlSZtIEFGgvByJEWquq2F+wn+Fc4BnvV9fha4\nsYX9G8Lw6qswdSoMG5ZqSQKxDT8NWybZ0Jr878f/S21DLd++oPWyeEbiOxd+h79s+AulNZ50bYMh\nGcwBGoEXRWSdiHxHREZ42O48YJeq7lPVeuAF4AaXvp8FUNWPgGwRGQRMAD7yGZqNwHvAzeF21Dmj\nc8wHBTCx/0QA+nXrF9f2/v2nx7f/Xl16RVxvG4YiwoxhM+LaRzi6ZnRNWF/ByiF48wzEY2S3ZdzO\ngxtK8l74I7NH+j87Bww+d+bnom578YiLQ5a1JLnJGf3OiKl9Ms9LPGR3aXkQ3oT+E6I3ioHW9oqe\nM+icgO/p0nGS3Xgx/NaJyAIRmecL+7xFRMK+iFxQ4G3fi/PLvmUDVbXY97kYGBiL0AbvtLUwT5sx\nY6BrV9i8OdWSGPKP5fPT1T/l2RufbTOZvEZmj2TWmFn8dcNfUy2K4RTFZ7j9SlXPBeYBZwF7PWw6\nFDjo+H7ItyxamyFAHnCJbzpEN6yauWGH7Ub3js8ZaBsnqfbuh8Nv+CEJHWlPdE3SVCfAcBrFrf3s\n7p7Z3f9Z28AIbkuMabepDcGKv1fmTprbqtmwwxHr/EHnIJKbVzzWY4rV+G0tenb2FrAY7BHuSB4/\nL1eyF1Z2s2uCli/yuI+LVPWwiPQHVojIdudKVVURcX1qzJ8/3/85JyeHnJwcj7s0ABw9Cu+9B889\nl2pJ3LnmGquY++TJqZbk1KWxqZG7Ft/FTy77CWP7jk21OAF8c8Y3uWnBTTx0/kMpnXNoSDyrVq1i\n1apVqRYjKiIyErgdq4ZfI/A9D5t51YJDNFVV3S4ivwKWA5XARqDJbeOFf1zIjoE7yCvOY+L0iUyc\nPjHsjnp07kGfrn3YX7qf8f3G07tLb48iNjNv8jxy8wJz20RTti897VJW718d875sIyZc/xcOv5C1\nB9fG3K+iIX2mSRpN6nqK4+K0Xqex+chm1/NlE81gvHXirSzcupDOGZ2pbagN2875XMzqlEV5ref0\nC4CVPOedve+ELM/KzKKyrjLitlMHT2X1/tVMGzKNkdkjyT+W71930YiLWHNgTUyyAAztOZSC8oKY\ntwvGvsYDsgZEvUdzRua4hqDGa0imp6XH7MFLhuHcq3MvSioDM+iNzB4ZNmN28D2ZkZZBQ1NDwLJY\nrk88HrpRvUex58QeenftzfCewzlRc4KDZdb4WKK85Nldsj39ToINvd5de3O06mhM+xrbdyw7j+2M\naRubrZ9sZesnW+PaNhpeyjl8yfd3t/PP6w5U9bDvfwnwClYYTLEvrAURGQy4VmyeP3++/88YfbHz\n0ktWzbwebXRO6jXXmAQvqeY3a39D14yufG3611ItSgjnDjmXUb1H8fK2l1MtiiHB5OTkBDzf2yIi\n8hHWOysNuE1Vz1PVxz1sWgA4h8yHY3n0IrUZ5luGqj6jqtNU9TKgFNjhtpOvfverzJ8/n1u/dmtE\now+gU1onf6jS1MFTycrMCmnjxXs1vl9sZQyH9BgScX24kM/zhp4XIpPTuxUtxNV5fM62qhpynNOG\nTIvYVyREJCRJiNu5jaU/aDbohvX0PkfDS9jvtCHTuPGMG/0e1YHdQ4Otrhx1JXPGz4nal33tBvcY\nTKf0TsybPI8Lh1/oWV6bS0+71P95aI9gx3gzzut04xnNs4NumXhLSFv7Gp8zOLLXbt7keQHzXKPR\nP6t/gCco3lDrYMJ53u3fAURORhN8DuZNnudqzF4w/AIArh9/fcg6p7E6rOewAI9urNw8ITQosG+3\nvv7P4bxu9rlNkzQmDZgUEILr5fnUu2v0AS03A3L60OlR2507+FzX44rEpP7xJ7+aOH0it37tVv9f\nIvGS1XO8iKwUkS2+72eJyA+9dC4i3USkh+9zFpbXMA9YCtzla3YXsDge4Q2R+fe/207tPjcuvxzW\nroXq6uhtDYlnU/EmHv/gcZ654Zk2G8bwrQu+xeMfPN4mQokMpxx3+ZKS/UJV98Sw3TpgrIiMFJFM\nLI/h0qA2S4E7AURkBlBqT38QkQG+/yOAm4Dn3XbSkt9sZnom8ybPi3t7J04lHELn9swZP4cBWQNc\ntx3Ve1SIZ6BH5x7+uYNO5WtIjyF+xbBTWuQIAKeSaCuwg3sMDglh82Lg2Fw16irX/Thl9HpNvHgv\nxvYdy7i+4wLOXazX3L42tgHePbM7XTsFznEMNr7DXatg3BRxW7l3W3fxiItDnuNTBk3x7MlxGllO\n48stSYuXPoO9clMGTQkwANyO4dLTLvVvN6THEG4YHzx1N5RIyYT6detH3259/QMqwYMGTk+025y5\nWWNnMWnAJP856NetH/817r9C2jmNLmgO27Sz8gafw+wu2a7n0IvxddOEm1wNYmeUwRWnX8H146+P\nOjAUCz0796RX59CBpOD5im7zmqMd1/BewxGJPezcjlwY3Sdp+bniwstR/AV4FKjzfc/Dmu/ghYHA\n+yLyKfAR8JqqLgd+CVwtIvnAFb7vhgSyZw/k58O116ZakvBkZ8NZZ1l1Bg2tS21DLV985Yv8+qpf\nB0yKb2tcN+46SmtKWXMw9rAhg6ElqOr26K1ct2sA7gfeArYCC1R1m4jcJyL3+dosA/aIyC7gacDp\ncl/oG2hdCnxNVT3H7104/EJmjZ0Vc6r6jLSMACUsOEHJZSMvA6B/t9B5Q8GGhFO5FxGyMrNcR/hv\nnnCz6zwgp5fLqZB1zujMLRNv4aYJN9G3W1/P8/XsPnJG5oR40LIyszyF5WWmZ9I/qz83nBGo6IuI\nX9nM7pLt96h4wenpshnde7T/uKYNmRaigHsNIRza0/Kcde3UlQFZAwI8R7bcNk5lNljZDzdP7JrR\n17h6Nu1rP6znMK4ZHTg7yE1pjiUBSLqk++WJZtjZ1zyWOZgT+k9wzTabJmn+5Znpmf5jvGzkZZ7m\nVV484mJyRub4vzsz4XbP7O4/T1MHT+XqUVcHbFtRV+H/7dmcPehsv+GW3SU7oHRF54zOUeew3X7m\n7f7BFvvejWTQjO07lj5d+4QYjzbnDzs/4Hu0EM+5k+bStVPXAI9iuL6dDOw+kJyROVw04qKwbdx+\nH1eOujLge3Am4lG9R4VsZ+/DljEeA/W2Sbf5DepEJpRKBF4Mv26+rGOANScPqPfSuaruVdUpvr8z\nVfUXvuXHVfUqVR2nqtd4TZNt8M7zz8PcuVbNvLaMPc/P0Lo89t5jjMweyZemfCnVokQkTdJ44LwH\nePKjJ1MtisHgGVV9Q1XHq+oYx3vvaVV92tHmft/6s1V1g2P5pao6yffefDfCPoDApAtZmVlkd8lm\nQv8JnjN2npZ9GpeedmmAEitIQL+24jO813BunWiFHYUzctyUr2BDMl3Sw4bJDes5zK/Yuyn4tmLp\nVDBjmf9je1FsgzWSUnbduOsAy7MCoWUoBGFwj8HMmzyPWWNnMaLXCE/zBQVxDbOcPnR6iCLtxL7m\ntlxu6wAGZjX3feWoK0OM82BZ3D5DaOjl0J5DueS0S/yK+vnDzierk0vYsAh9u/UNe12cXsVo3lub\nnp17+o8xTdIiZp4Mvn/csnZ6NQpFhItGXMTkgVYygmvHXMvssbMD2kTzkjp/E3ZG3WDG9xsf8Js4\na+BZnD3wbM+lTyLu33FvuBl5kX4/04ZM4+rRV5MzMse1ndcBmBG9RjCs57CA58yE/hOYPHByVE/a\n9KHTmTFsBoN7DA64t4NxiwyKVLZjUPdBrr83+96wQ2KD7xW3324wzudn8HkLF20RPLB0xelXuIah\nthQvhl+JiIyxv4jIrcDhhEtiSCgvvND2ave5ce21pp5fa/PhoQ95ZuMz/Pm6P7eLtOJfmvIl3t7z\ntn+St8FgaOa2Sbf5P8cTEn3h8AtDFBkRCVFubez5XOEiBdwMzvF9x/sNtdljZwcoW04FaUDWgACP\nhVflPJZsnfb+7DDIoT2H+j0yTgNpUPdBdO3UlT5d+4Qo32P6jGFc33Gu+41k+Dm9MxlpGX6lLmdk\nTlgvrfMcTB86nYtHXByxZESk4uW2ARJg7EV4BwQrzemSHuA1HdV7VMTtP3fm5wK8OX269iEjLSNg\nLlb/rP7MHDMzopd69tjZIcccXEJCEIb2HMoFwy/wy2gfp1u4pdsAhdML5TceEfp16+efh9ezc8+A\n8NhbJt7C5adfntAw35sm3MSkAZNIT0snu0u2p5IUEH+SmGi/szRJI03S/O3iCRMf2H0gl5x2ScCy\nAVkDOHPAmc0e2hboI4msyxh8bwTPve3TtY/rduHqVGamZ3LLxFv8gwc2wc+Pbp26MXPMTP93LwZm\nPHjJ6nk/8GfgDBEpxEpn3YZnjhk2b4bycrjAe9RJypg2DQ4dgoICGBp+XrchQVTXV/OlxV/iD7P+\nkLSHSqLp2bknd559J//7yf/yy6tMVLihdfDNS/8WMEJVvywiY4HxqvpaikUDoitJLakNJog/lC+a\nN2PvXivsbVD3QX7ld9iZw1iweUGArPZIf/CcsitHXUl1fTXLdy/3h2XZ2QQjHaN9fFeOupJunbqx\n+/huLjntEtYVriO7SzZ1jXXUNdbRu2vvgHqgZw44M2TOzeAeg7lt0m2sObCG6npr0vnlp18OWB6e\nYNLT0pk6eKq7XBGU70kDJnGs+pjfkzamzxjG9BnjlyEafbv2DTCagvd13bjr6J7ZPSDDphPbgD29\n9+mU1ZSFrHeG0V0//nqyOmVR31RPmqSxvnB9XPdc98zuHKs6xuAegxnSYwhTBk2hvqk+wJvYu2tv\nenftzfHq4577H9FrBJ8VfRaw3i181ub03qez98RehvQYQmFFoaunsmfnnhGzsbrhxeBwXqdIZRFs\nAyi4TTwGkbOP3l17U1kfmqVVRLh4xMV0zujM5iObOVZ1LCSTp5PsLtkcKDsQsyzRaOkA9I1n3Eh6\nWjofF3wcsZ39W7OvsZeamxBqGIczlM/odwa9uvRix9HQfFyZ6ZmMzB4ZMDBkD3L1z+rvz8AanKAm\nGfkNohp+qrobuNL3EkxT1YqES2FIKC+8ALffDmltM19HABkZVrjnm2/CPfekWpqOzw/f+SFTBk0J\n8BK0Bx447wFm/G0GP77sxwkJfTEYPPB3YD1gpyosBBYCbcLwcyNRhaBtA87LyP6HH8K8eYFzYNIk\njRG9vNS6t4wRr+F+bgzIGkBNQw1ghYkO6zmMJm1CVamsr6RHZo8AIy09Ld01Y6HXOmWzx86OmLlz\ndJ/REbMLRjJO3HAqxdEUZFuRdbsPnNfSmUXSqcQ6E3DY58ieh7m+cH0sYofg9Ihlpme6Djz26dqH\nYT2Hcaj8EDOGzaB/Vn9e3fGqa39ZnbKiZhF1nq/pQ6ZzzqBz6JzR2cruGuFczhg2g+G9hvPRoY8S\nEhXjvB5pkhazcWnTr1s/BnUfxJYjW6K2HdxjMAOyBnCk8gjTh0wPm73W9oZedtpl1DbWsmT7EsDd\nuJk0YJI/VNWtDEqwIXXN6GtYvjt6SFek4uin9z6dwd1DB0V6denlH7yIFMrsxBk2eduk2/z3pG1c\nDeo+iKKTRSHbBd8Dzu9XjbqKjLQM3tz1ZtTnb/fM7q4e+eDjnz50OntOxJJPLDa8ZPX8iYj8GPgO\n8E0R+bHvu6ENomoZfp/zFhnQJpg9G5YtS7UUHZ/Pij7jX5v+xVOzn0q1KDEzus9oLhh2Ac/nuSY4\nNBiSwWhV/RW+xGaqGrmwWQqxlfpwo8NeDUI7hMmrsmvvzm23wUkYIo1cx6NcR+ovTdJIT0unZ+ee\nMWXj8zIvsleXXhGNxIy0DL+XdOaYmVww/AJmDJsR91wd50BXsDLuNEDjNfqdyrrXpCnh6NapW9hw\nN69cctolnDP4HIb3Gh5ioA/tMTQgwYsd7nnh8Av9GSrDyZue1jyvNNpxnt779JgLlns9/17Cl8O1\nuXr01fTp2idsUplgGWyPkpffQHpaekQDzC+b79zNGT8noI7ktCHTAsIUoTlpS7SSKecPO5+ZY2b6\n9+8cmJgxbIbrQItbKLptiI7qPSrg+TN77OyQJDkZaRkh58T28nsJfbVJT0v3D/R0z+zu6kl2e1Z1\nzujsf94EX7cxfcb4k/4kajDPiZc7u5LmgrRdgeuwMpUZ2iAbfCkCprpHobRJrr0WHnwQ6uvbfjKa\n9kqTNvH1ZV/nZ1f8zHPSh7bGg+c/yLfe+hb3nHNPu5ibaGj31IqIfyhZREYD4atptwFa6g2/dsy1\nlFSWeB5Bj4Xzhp7n98wFk5GWEaDIZaRluKalTzZ2avxEKVt2CGNLOHfwuZw98GwWbVsU8NwL9sY6\nk4a4KZ/hOG/oeUwbMo2XtrwUVeGN9tzNSMvwK882fbv2jTk80JntNWdkjj88eNKASa4GXvB8v0TR\nKb2T54yMWZ2y/IZHcFmBcIMU4a5TtPN87ehrPd2jyYyO6dqpqz/RE1jX3s1YvuGMG6Kewy4ZXeiS\n0YUenXswtOfQsHPo7P2Eww5TPX/Y+VTVV/mX9+rSK2zNUC8493n16KvJ7pJNdX01u47v8peesX+P\nPTJ7hMzdc7tWzpqAkQaxnF74ROEl1PO3zu8i8hvAczoOEUnHqmt0SFWvF5E+wALgNGAfMNdk9Uwc\nL71kZfNsT3rxwIEwdiysWQM5OamWpmPyr8/+RV1jHfec037jaa88/UoamhpYtW9ViHJhMCSB+cCb\nwDAReR64CPiSlw1FZCbweyAd+KvPcxjc5klgFlAFfElVN/qWPwJ8AWjCKp90t6qGGJzBykKwITB5\nwGRKa0r5tOjTqKFtTsKl8I+EavR3TrQ5bMGKWbS09MkYCQcrfX1bIj0t3e/hCWeYjes7LiDpyvBe\nw5k7aa6n/u3EHRDZ4BjUfVBMBeVtxvcb769TFw/2fXPwoFX6aZ7HvCJpkha1tEA0rh93veffjXMu\n6GnZpzGo+yBW718d0s7u73Nnfi5iCGEkwoUaBz8TJvafGFK+IGB/wXPXYggrDiZclt5YjM+MtIyI\nRh9Yvwf7WdevWz+OVh31rxuQNSDA4IuHXl16BQzWzB47O+DZZA+cTx86PWzhd6cn1Avj+40P+9zt\nn9WfeZPncQeJy9YYzyywLCCWNBwPYXkI7TvyYWCFqo4DVvq+GxKAqmX43da+pm8BVrjn66+nWoqO\nSV1jHT9690c8OetJT3WH2ioiwoPnP8iTH5vSDobk46s5ewtwN1YR9XMjlVew8Q12PgXMBCYC80Rk\nQlCb2cAYVR0LfAX4k2/5SODLwFRVnYxlOMYVuD+4x+CAOmkDsgZEnJvW3ujfrX9YZbMjMn3odNe5\nibdOvJVzBp8TsjyeZ32kcMDLT788LsMvUZTG6B64/czbY1bAg+mc0dlztsjM9MyAtp0zOnP1aKsu\nn9t1i2RYxVJ/MBKxGiFOr90Fwy4IMGarq+F4mNw7N0+4OaHF2L0ybci0gHmeZw4401/qpGtG15As\nml6YPXZ2wPVqiafQJlqCloFZAyNm4000Xub45Tn+tgA7gCe8dC4iw4DZwF/BfyfPAZ71fX4WuDFm\nqQ2ufPqp9X9KbLV72wTXXQevus/hNrSQZz99lon9JzJj2IxUi9JivnjWF3l///vsPbE31aIYOigi\ncq6ITBWRqcAIrPJFh4ERvmXROA/Ypar7VLUeeAG4IaiN/z3oq5ObLSIDgXKsOrndRCQD6AYUhJHT\n0/FkZWbRr1s/RmaPZM74OZ628UqkOX7JZniv4QHhUh2dMX3GuF7zTumdPM9hjMTNE25OaEp8QzO9\nu/ZulYRqsXjBM9MzQ2ohpkmaX067lInNBx+Er7mcqgGY3l17hw3zFZGAuYKRSFb0gFcS8fuNBS9z\n/K53fG4Ain0vMy/8D/BdwBmzMVBVi32fi4H2kVO+HWB7+9pTmKfNtGlQWQnbtsGECdHbG7xR31jP\nL/7zC/51079SLUpCyMrM4u4pd/PUx0/x+LWPp1ocQ8fkcYioCUSLMx4KOItOHgKCqwS7tRmqqhtE\n5HHgAFANvKWqb7vtxGua70Qbe24k0/Ab1nOYawFuJ16SUhigocHSE9zCJU8l72kqiOX3Gs8c9qtG\nXRWTR/+WibfE1H+w+C++CGedBWec4d6+PTG853B/GZdkEMmwjKcmYkvxYviVB33v4bwpVdXV+Ssi\n17z5E/oAACAASURBVAFHVHWjiOS4tVFVFZGwZ2T+/Pn+zzk5OeSYCWBhUYWFC+H5dpr0UARuvBFe\necUYfonkubznGJk9MiTDXnvm/vPuZ+qfpzI/Z77nOjyGtsWqVatYtWpVqsVwRVVzWtqFx3Yh2p0v\ngcw3gJFAGfCSiHxeVZ8LbvvsE8/yfu/3gY79fkxPS3ctwO3ELirfGuTmtp9yScHUex2yN6SMeMOx\n45mb64WmJmhsDHUoNDbCsWNJ2WXSyM21nCMZQZZP105dOXvQ2UnZZ1ZmFv27xX5tkvmO9GL4bcAK\ndznh+94bazRSfX+jwmx3ITDHN5ehC9BTRP4FFIvIIFUtEpHBwJFwO3YafobI5OVZD/Vzz021JPFz\n443wyCPw6KOplqRjoKo88dET/PLKjlX0/LTs07h85OU8+9mz3H/e/akWxxAHwYbKY489ljphwuDL\n6Pk14GKsd937wJ9U1T01ZTMFgNNSGY7l0YvUZphvWQ6wVlWP+WRYhPUuDTH87nroLn/B81TTmqGe\nu3fDoUNw2WXR29rU1cGRIzAsQVPUwh1vRYWVgGTWLOt7YyOkG2dki2lshKLQ8modFtvYagtZztet\ns35zA+OIzSsvt+YFjhyZcLHiprEx1PBLJvFGXCTzHellzGoFcJ2q9lXVvsB/ActV9XRVDWf0oaqP\nqupwVT0da3L6O6r6RWApcJev2V3A4pYdggEsb9+tt7bPME+bSy+1HjAHD0Zva4jO+sPrKa0p9U8w\n70h8Y8Y3ePKjJ0MKyBoMCeSfWMlZnsRK1jIJ8BIzvQ4YKyIjRSQTuB3rvedkKXAngIjMAEp9UyB2\nADNEpKtYoTVXkaLySQ0N0dukYm7f/v1QWBjbNvn58P77yZHHydGjgUlIXnzRUnybUvyYqvIlOkz0\n9Tp40PKiJJu9e61z257JSMvwnGxk3TpLp2sLnDxp/S8uDl1XVRX+3v7oI2tO4AcfJE+2ZFBdbU07\nSgRFRfDJJ4npK5F4MfwuUFV/eW1VfQNrBDJW7EfOL4GrRSQfuML33dBCbMOvPdOpE8yZ03YeeO2d\nv6z/C/eec2+rTxxuDS4afhG9uvTi9XyTCtaQNCap6j2q+q6qvqOq92IZfxFR1QbgfuAtLKNtgapu\nE5H7ROQ+X5tlwB4R2QU8jeVZRFU/xTI41wGbfF3+2W0/GWmxuwNOnPCm/FdVWXPBmo8pcvtUGIDh\nKCpKjjESr/FWWwsLFljnPhUUFMCSJcnpu7WOKd77K5wC39gYWz9VVXD4cHwy2MSSbKSiomX7ai2O\nHoWtQcNSa9bAe+/Bnj3eBo8SiRevcLR7aeVKWBo8TBcnu3ZZf7GwaVPyz5sXjbBQRH7oG708XUR+\nQJgsY+FQ1fdUdY7v83FVvUpVx6nqNaaGX8vZutUalTnvvFRL0nK+8AX4979TLUX752TdSV7c+iJ3\nn3N3qkVJCiLCt2Z8i8c/MAleDEljg4hcYH/xeebWe9lQVd9Q1fGqOkZVf+Fb9rSqPu1oc79v/dmq\nusGx/NeqOklVJ6vqXeGSqa15t3uI0hWNN9+0DIFoBCseL7wAByLU4K6paR3Pjxfe9RXcqA2pfBg/\n1dWW8daSLKY1NVaI6v79LZNl3TpLHrCUxJUrI7evq2v+HE7uxsb4jLi2FGHU1ARbtjR/LywMr8C/\n+GLguaipgZKS8H2vXw+rVln3eGt4HlvrvBYXt/x3a//O8vOt58ahQ7F75GNh48bm+z+Yd9+1rmW8\nlJUF/l7ipakp/n62bAlfNiNReDH85gEDgFeARb7PrZ+GxhCWl16Cm29uWw/heMnJsUZtYlVoDIG8\nsPkFLjvtspTU1mktbp14K3tO7GF9oSdd3GCIlWnAGhHZLyL7gLXANF9po02RN20d4lHW4/VcRfJC\nJLMGa0WFpZDZeH3PLV8e/z5VLUXWJtYR+PLglHg+1q61/lrCzp2w2DdB5tAha+5iS9m50xoUiBWv\n16KoKHAKx+uvRza0glm3LnqbykrLELYJl8jGzQu4YQO87Zo718J5nHboYzI4ciTQIK2oaL73SkoS\nn0zFS23EYENKNfD3aLN+fexe0cZGa06szfbtkZ8lublWm3gMS9vLu327FTrsxrJlsQ8Yvf126HX5\n7DN4+eXma5mfHz2x0vvvJ8bo9EJUw09Vj6nqg8DFqnqOqj4ULpOnITW8+KKVZawjkJ4Od9wBz4Wk\nMjDEwj8/+yd3T+mY3j6bTumdePD8B/ndh79LtSiGjslMrORll2ElXRkFzMIqcZT8GglRyM4YHPA9\nmsJie8K2bbOUn6YmSxnZsSO0rVeFPtiD1NKQz4aG0D5WrLAUsljxMvJfUxOotFVVWefx5ElLkQ1H\ntON0GorJVObCyVFWZq1zrt+8ObzCG2voo43X+2TNmkAFv7w8MQZrJFnCnRs3L2CiBs0PHQo0+svK\nYvOorVwZaDy99po1V66kxDIw3nknMXKGIzfXui7r1jXL7Wbkbd7svr3zGnuhpiZwQKCoyDp/W7aE\nv1fj5cUXrf/btllew0RRUhIaYho8uLB+vZWAMRKHDjUP5CU7dN5LAfcLRWQrsN33/WwR+WNyxTJ4\nZcsW64dyfnCVqHaMHe4Z78voVOdA2QG2lGxh1thZqRYl6dw79V7e3PUmB8oixKEZDHGgqvuwSir0\nBPrYf77C7PtSKBoAvTMGB4RfLloUeVTZTs5w/Lil+CxYYCmZGzaE36a1eeklSzFzEs2gra1191w0\nNMDHH1ufwyn2n3wS6BlcssQyNMO1j6SQ1dTAhx82f7c9Q3ZoYDIicoLfkYcPW0bWsmVWSOmKFc0y\n5eWFV9hjIZnz+ioro8+JiuYprKiIrmRD4LVs6bUpKLAS073/fuDvyc1oipUDByJ7I22amhJjMJSX\nWx7gcOzaFTlqwG1dOI+5syRKaWnzddi0KdB7G0yk4wxet2iR5YELbhMt5D3R4apero3d5p13mgcQ\nwoW1tgQvoZ6/xxr5PGoJpp9hjYAa2gAvvmjVJWmPNYXCcfbZMGgQvPFGqiVpnyzYvIBbJtxCZnpm\nqkVJOtldsrl7yt38/sPfp1oUQwdDRP5/rAQrf8Aq6m7/tTlsAzCSchFJuQ3O2BevIpwIxdM5Wu7s\nzzl/y8nHH4d/V0QzEtzkdTM0gz0Zbts5DaKCAnj11fD7PXrUfWCzvt7q+733LKNh587wYaPQfK6q\nqy0PzapVzfeCW501W+5I3pT8/FDju6rKMqgqK62QUNsbGu56L1oUPTx206ZA+ZqarH6jZUFctcry\ngoVjzx7LwLVl8xLO2FLDb90690GGeH8P8Qw8vPmmdd9EoqEh8v0UbR9gHWssYbpgDehUVoYaU/Zx\nqlq/4XgH+6urw3v4a2tDfwd1dbB6tfW5rMw9fPe991ruYT0UXMTHR0GBuyd4zZrmz/Z9u3hx4gdb\nPJkLqho8nN7KuXoMbqhaht/cuamWJPHcfz/84Q+plqJ98vzm57lj8h2pFqPVeOj8h/jHp//gRHWK\n0uYZOiq3A6NV9TJVvdz+S7VQwRw9Gjnxik0k5TacguM0gg4dsrwZtmL+9tvuI+nR2LvXfQ53sKGw\naVNghue8PMv4cIZVnTjRrFzFooy+8UZ4w0Q1MMyzoaFZCbPnH735ZqiB6Dx2N+PRadCuWNHsVXF6\nSBYutIyWwkLrONets4ycRYsiH0+sc7+cnklovjcaGqxj//TTwPVLllhhh7as+fmWgeUMY92929q+\noMA6/tpa65iDa1A7j+XgQes+2r7dCkX2mnhozx5LcfeSaOWNN6xrs317+DbO38Yrr1hyl5U1ew6d\n64N/R/X1zeUy3NaDdd7cyiHEw+bN7kZOWZnl8bVl2bw5MDPv4cPWd+ccOjdvv5ffcDyGcnFxqGFq\n78u+r4L3vWtX9Pmd9fWWceQ20GLfn5HkXbYs/HxgO/mN0/DauzdUzkhlLYKpqrJ+KzbOvsKFhSc6\ny6cXw++AiFwEICKZIvIdYFuUbRCRLiLykYh8KiJbReQXvuV9RGSFiOSLyHIRyW7ZIZy65OVZD6iO\nFOZpc9tt1svHbf6JITxbS7ZSUlnCJSMuSbUorcbwXsO5btx1/N91/zfVohg6FluA3vFsKCIzRWS7\niOwUke+HafOkb/1nInKOb9l4Edno+CsTkQcj7csZmhhp7oqb8uNUNBobLUW6qKhZMXEq6cePW8/j\nXbss5aWkJDABilc++6zZYFy/PtBr5ZRzy5ZAhUfVMj6cOA0st3A4u69gg6K0NFBZd6Ia6JlwKmm2\nZ6CyslnRXL7cktWpwLkZobZHyKapyVLGFyywlEvbMLDPh62Ul5Y2H2e40EG3GoVelPPg/lasaP5c\nXh46d8mphH/0EezbZ33OzbWOr6io2ZOiap2H4IQfzmu2bZvVZuPG2Of8FRQEXtdIYZX19dY+woVC\nO89VTY3V165dlvFUW+tuaNlzKIPLT7l5/AoKEjM/r7HR0vsWO6pfHz4ceL/Zht2xY4G/H6cBnpsb\n3sCLNLfVJtERZuHKbnzyiTVA4uYJ/OSTwGO0/zuNWTshVTRjtrExcu2+igrr3snNtQZNgp8du3YF\nRiS47U/Ver4uWdJ83+7fb2VMjubpjObJjRUvl+//AF8HhmKVcTjH9z0iqloDXK6qU4CzgMtF5GLg\nYWCFqo4DVvq+G+IgNxfmzesY2TyD6dIF7r0Xnnwy1ZK0L3Lzcrl90u2kp6WnWpRW5bsXfpcnP36S\nmoYW5HI2GAL5b2Cjb4DyVd9f1ApPIpKOVfB9JlYB+HkiMiGozWxgjKqOBb4C/AlAVXf4kqidA/w/\n9s47Tqryavzfs7ssvapUUSyAYomgYgnqqhgRK8ZGmvr6WpIYTfmZaBITiCmW12iMKcYW9Y2IYkOj\nIpa1vIogKiKIFDUCIiJKF9hyfn88c5m7d+/M3JmdmTuze76fz3xm7p1bzn1ue85z2v7AJlxG7bR4\n7lvZxqX43eo++MB1/GfPzpxVOVXcXViHZ+7c1KPhCxcmY7q891g+32eeYutZxNauddaidPhlTVf0\nva7OWZFWr3bWSf+xp3Iv9HfwVJt2NqN0uLPJCJqpM6maTJoT5hY5Y4azwvnLRQQVwXTxl489lmzL\nbBPceGUTMmVC9OReujSpcHr4rZqeHP7O+UcfOfmXLElvrXnooaZK6apVbp3nnmuqKHt4yy5dmixe\nHrb9NWvCB7YzXZ/Q9FqrrW167PX1bn+ZFGm/tXTr1miZU8P2H9Wd1XPP9bs/eut6yqpf5uCgj59Z\ns9xzI8xl+aOP3PXz2GPJsgiZrK2NjZlLKPiVf7+LqkeUazx4v3jP7bBz/n//l3QHzXQfZEtaxU9E\nqoA/qeo3VLW3qu6gqt9U1UiOBarq6cXVQCXwBS4b2l2J+XcBp+QmetumsTGp+LVWLr3UHWMqP2mj\nKarKpHcmtSk3T499+uzDAf0P4J9v/TNuUYzWw93A1YlPNjF+I4HFiSQwdcB9wMmBZba9B1X1NaCH\niPQJLDMaWKKqS8mA12H3dzDXrm2aDTOTQuWN4kdxWUrV2Qub/847ziqRKrvh/PlNO6HBbJSpCKa+\nDyOYGOHtt5MdUNXwY/XPW7YsfUfcb2HNNp7Ls5Z55CMRiJ+oHflNm9In0sjGEhe8xoLtm02Gy+nT\nnWXLy0abjkzZJD0l2B+7+OqrTvGaOTNcMUh1vyxa5Nb57LNwF1tPAfAPwngWHr/18913m1qnvGt1\n6dJobe5XbIPXnr94epTsmC++mD6hSxD/eY3inuvnpZecfJnureAgSTDuFNw5SqUUbdiQ+R7wjiPT\nMy84KONdL+nOQRjBa8o759ko3fkgreKnqvXAziLSPpeNi0iFiLwFrASeV9V5QB9V9W6zlUDwZWdE\n4NVXoVMnlwiltdK7N5x3Hlx9ddySlAezPp5FZUUlI/qNiFuUWLhi1BVc+3/XUt9oIchGXtigqjep\n6nOqWpv4RHG6GQD4lbVliXmZltkxsMxZwL3ZCBzskK1dm3RTyjRq7Cl+hahTFmYZ8tcF9HceFy2K\nltjro4+ax6qFuWulShbz/PPR6o5FSQ4S3HYUMiXZKDSehePRR8P/z6UMRVCZzZSoJRP19c2tjJlY\nGjJMkmrw2FOKghacfMe5/ec/7nvGDOeurJqc5+EfRIgy+OJX6IL3tn/94D2SDank8N/PqVym0/Ha\na055TncP+BW/xsbmcaceLakhOnly8rmX7nx67r8eM2Y4efzX+6ZN6a+bMMXa70ZeTKoiLPM+8HLC\nxcU7xaqqGYtnqWojsJ+IdAemiciRgf9VRFI21YQJE7b9rqmpoaamJoK4bYNJk1y9u9bo5unnsstg\njz3gpz+FnXaKW5rS5t659zJ+7/FIa78oUnDowEMZ2H0g98+7v01aPcuJ2tpaaoNZH0qPlxKx6VOB\nbV0dVc1UACGqChC8UbetJyLVuHqBofGBAFOmTNj2e9iwGoYNq9nmCeJnyZJoFgTPLS1INm5GqTo+\nYckM/PF6Ik07elGsX5s3N4+9Cioe0LRum9+y47cGvvceDB2aeZ+5kM7NLEwxSpU0JhtrWRQyFbj3\nK+ZRiZJkqNCEyZ2qZImntHiDHV5M64svtux6mDo1fBDCu2bDSi/ks3ZbMJFNWHxhpoQ00DymNp9s\n2dJc+U1F1MQpuVBREa0URtDtO6i0LV/u3E8HD87PuZw/v5b582tbvqEQUip+InKPqn4b55JyA846\n2CWXnajqWhH5Ny5mYaWI9FXVT0SkH5DyleRX/IwkdXUum2eqF3VrondvuOQSpwBOnhy3NKVLQ2MD\nk+dNpvbs2rhFiZUrRl3BZdMv46y9z6JCWlGNk1ZGcCBv4sSJ8QmTmhE4ZezgwPxMmT2XAwN90wNx\nFr10y+yYmOdxHDBbVVPmqjzttAnN5qXqILXEjTCbosypOjx+V86wRBnz5qUu15CKXOpbpcqO9957\n0L9/9tuLsu1s2z7YhlbPNjVecph84bdyZor5SqeMpEsUAsli4n5yUZpTXRvB/YcNPkSJF810HB6F\nVMzSbT+X5FJBUiWAirqen61bndt0tlbqMLzBPI+HHsrfOzJdz2h/EekPfISrY3Rz4JMWEdney9gp\nIh2BY4A3caOnZycWOxt4JHwLRiqeesqNKuy2W9ySFIef/tS5BkTx9W+r1H5Yy4CuAxi6fYGGrcuE\nY3c7lg5VHXhkgT1WjJahqjX+Mg5ZlHN4HRgsIoMSlrszce89P1OB7wCIyMHAGl8IBMB4IC82nvr6\nlqUDD+vETJsWvmwwuUzQWtgSt7MgubiYpWLjxpZbN9LVlsuGKO6nAA8+mJ/9lTtRSjrkQi41IHMl\n12svTIGMg2ziA3NhasaUWrnjPaOyHWBJVbJl3rzSH6xJ5+r5d1zWzV2BYL4pTcxPRz/gLhGpwCmY\n96jqsyLyJnC/iJwHfAi0wip0heWee+Db345biuLRqRNcf72r7ffmm1Dd+uuSZ81dc+7im/t8M24x\nYkdEuPLwK/l17a8Zt8e4Nuv2auQHETkBl5mzgzdPVX+Tbh1VrReRi4FpuKRmt6vquyJyYeL/W1T1\nCREZKyKLgY3Aub59dsYldjk/H8dQ6E6ZnxkzoF075xZ1+OHN6/xFSTQRlTDFry2V/8klBs8oPfLt\nwpsL6bKzRqEQccHlSFwxe9kimmHYQkT+rqoXFUke/341k2xtkTVrYOed3Qu0V6+4pSkeqnDSSbD/\n/mAewE1Zs3kNg24cxOJLFrN9p+3jFid2VJXhtwznqiOv4sShJ8YtjhEBEUFVS0pLF5FbgI7AUcCt\nwOnAa6p6XqyC4d6P995b2u/Hbt3iT2BiGEbh6dAh3IW7nNh++8JZj/PBN76Rv3dkxiCYOJQ+IzVT\npsDRR7ctpQ+cP/Xf/w5/+YurC2UkuXfuvRy7+7Gm9CXwrH4TX5iIDR4ZLeBQVf0O8LmqTsTF+rVt\nX+osMKXPMNoG5a70QWkrffnGsh+UGXfeCeecE7cU8TBgAPzhD3DuuS2LWWlt3P7m7Zw3PHYjREkx\nbs9xNGgDj76XIle5YWTGSx+ySUQGAPVA3xjlMQzDMIwWYYpfGfHee86H+Ljj4pYkPs47D7bbDq69\nNm5JSoM3V7zJ6k2rGb3r6LhFKSkqpILf1PyGK5+/kkYtcMoxo7XyuIj0BK7Dxbl/SJ4SrhiGYRhG\nHJjiV0b885/wrW+54Pm2igjceivccAPMnx+3NPFz08ybOH/E+Va6IIQThpxAp3aduH9eiaQ+M8oK\nVf2Nqn6hqg8COwNDVfXKuOUySofttotbAsMwjOyw3mKZ0NAAd9/t3BzbOjvtBBMnwgUXFL5+TCmz\nbN0yHl3wKN898Ltxi1KSiAi/O+p3/Or5X1HXkEUVasMAROR0EemWmPwpcKeIjIhTJqO06NYt8zKG\nYRilREEVPxEZKCLPi8g8EXlHRC5JzO8lItNFZKGIPO3V+zNS8+STMHAg7LVX3JKUBhdd5JS+f/wj\nbkni48YZN3LOfufQq2Mby/STBaN3Hc2gHoO49Y1b4xbFKD9+parrRGQUcDRwB67MUUZEZIyILBCR\nRSLysxTL3JT4f46IDPfN7yEiU0TkXRGZn6jzZ5QgbSkhhGEYrYNCW/zqgB+p6l64jGjfF5E9gcuB\n6ao6BFcr8PICy1H23HILXHhh3FKUDhUVTum78sq2+fJds3kNd751Jz86+Edxi1LyXDP6Gq568So2\nbLViQ0ZWeGV4TwBuVdXHgYyO9iJSCdwMjMHVAByfeO/5lxkL7K6qg4ELgL/5/v4T8ISq7gnsC7zb\n0gMxCkM5eZwMGRK3BIZhlAIFVfxU9RNVfSvxewPuBTYAOAm4K7HYXcAphZSj3Fm6FF55Bc6wUvdN\n2HtvGD/eKX9tjT+++kdOHHIiA7sPjFuUkmd4v+EcvcvR/M8r/xO3KEZ5sVxE/gGcCfxbRDoQ7Z05\nElisqh+qah1wH3ByYJlt70BVfQ3oISJ9RKQ7cJiq3pH4r15V1+bpeLLisMPi2Gt5ISVVeTI9u+xS\nvH117ly8fbUmOnWKWwLDT0XMwXCFciUv2mGJyCBgOPAa0EdVVyb+Wgn0KZYc5cjttzsFxx6mzZk4\nER56CObMiVuS4rF83XL+Musv/ObI38QtStnwu6N+x80zb2bZumVxi2KUD2cA04CvqeoaoCdwWYT1\nBgBLfdPLEvMyLbMjsAuwSkTuFJE3RORWEYmlO9iWO6EHHRRtuXJS/HKR9dRTc9vX0UfDbrvltm5b\nJmofL64Ef1/5Sjz7zTeVldGW69IlfP4OO+RPlnQU6vlSVZjNNkVEugAPApeq6nrxHY2qqoiEVlme\nMGHCtt81NTXU1NQUVtASZOtW59I4bVrckpQmPXs6i9/ll7s4yLbAlc9fyQUjLmCn7jvFLUrZsHOP\nnblw/wv5+bM/5+5xd8ctTpuntraW2trauMVIi6puxL23vOkVwIooq0bcRfC1rrh38gjgYlWdJSI3\n4kIhfhVcecqUCdt+DxtWw7BhNaE7OeooeO65pvP22gvmzcsgXExKTXW1e+/FSVXEnlGUNurYEb78\nMvNy6ejbFz75JDm93XawenXLthmF9u0zyxJG586gUe+CCFRVpa7de/DBMGNG/vZVTMaOhSeeSE5H\nvefy2bZBhgyBhQvD/+vevXD7LSY9e0YLEUp1PophCZw/v5b3369l8+b8b7vgip+ItMO9PO9R1UcS\ns1eKSF9V/URE+gGfhq3rV/zaKg88AHvuCfvsE7ckpcsFF7jyDrW10NrHBt5c8SZPLHqChT9I8WQ2\nUnL5qMsZevNQZi2fxYEDDoxbnDZNcCBv4sSJ8QmTf5YDfh/sgTiLXrpldkzME2CZqs5KzJ9Cihj4\n006bEEmYsNHpDh3glFPgkUea/5cNhxwC/fo5r4tMHHEEvPBC5uW22w5WrHByr1rVMvkKQWUlnHyy\nO+YoHfUBA2Dx4pbts1cvp2xVVrr23rQp+230KHIKvV69XJhKXQsSKnuDAL17u2Nes6b5MumOa6+9\n3DX0aWgPMzWDB8OiRan/32cfmDs3u22G0bVrbut17gxr8+AAftppMGVKcvrww3MfUDj22HADRUsH\nKfbfH2bPjr58lIGJQYNalhuistI9QwuhlHkMG1bDqFE1fP65m37oofy9Iwud1VOA24H5qnqj76+p\nwNmJ32cDLXz9tE5U4cYb4dJL45aktKmuhquucla/Qo6ExU19Yz3//dh/84ej/0C39pZHPFu6tu/K\nb4/6LZc+dakVdTcKyevAYBEZJCLVuBjBqYFlpgLfAUhk7VyjqitV9RNgqYh4qThGAxlsc6kZP96N\nTp92WvP/OnZsPm9gliHD3buHW4XCiGrN8DJXe8ufkiEDQO/e4fOjJjM588ym0/36pV++qip5zFGO\nKd0yfbIIchk1yimc6WIvhwyBXXfNXo6ojB6d2g026No5eHD4dZcNfpkPOCD79aNaboOE7SuTe1+2\n1rAzz2x+Tvz9l513dt8dOrhv/7WSratnVNkGDMh/H2rUqNzX7dUre3mC7pnt2jllsKUcckjyd//+\nTWNmjz469Xr+52OqZ1Xv3uFutIWyLBbaYPlV4FvAkSLyZuIzBrgaOEZEFgJHJaaNAK++Cl98Accf\nH7ckpc9ZZzl3mscei1uSwvHHV//Idh2345z9zolblLLlnP3Ooa6xjn+9/a+4RTFaKapaD1yMiw+c\nD0xW1XdF5EIRuTCxzBPA+yKyGLgF+J5vEz8A/iUic3BZPX8fZb9eh6e6unlh8agdRX9Hw+s0h3Xc\nBg3KbrseJ52U/J0qBszrYHuytG/vFNiDD4YRIVUUu3WDE05oOu+rX3X1XtPRs6f7zlYh8i/v/33G\nGbD99snp009339l0Ov3Wq2HDmv43cGB6JXu77Zx15KCDmm7nsMOSsuSCf1s77OBiP/3XhKdohg0k\nQObzkIqxY+FrX3O/VVO7enrnIGzQQrXpOYo6SAHNlfIdd2y6XY9eiWpKe+yRelv9+rn//W1UhUlU\nhwAAIABJREFUUdH82gtrw3Hj3H1zxBFu2p/ww5uXjlGjnMKeD/zyprv3vVjFM85oWaywv809Mt1P\nHTo0VdJPPBGOPLLlXnP+4x08OPn8gNQKHbh9e+fJWy543o8+uvn9DslnYL4TbRU6q+fLqlqhqvup\n6vDE5ylV/VxVR6vqEFX1AueNAH/4A/z4x9EDUdsyFRXO6nflleWVYjsqCz5bwHWvXMc/TvwHUk4Z\nBUqMCqng5uNu5vJnL2fdlnVxi2O0UlT1SVUdqqq7q+ofEvNuUdVbfMtcnPj/K6r6hm/+HFU9MDH/\n1ExZPb1O3QBf+piRI+HAEG/mPfZwnbJUliavo7Hzzm658eObd5b79nVKGDTtDKUanfY6qiJum55F\nb//9nXtYWIfHW97/vcsuMHRo+LJ+l7kDD3TKRpi1p2/fpCISJfmIp0z7rYD+Y/a/mysrmyvO48c3\nVQYzUVWV7DQPHZpaafIUD3+H02+R8LPjjuFtsd12rgPrLeOXwc9xxzlL4/jxyXn+49x33/D9ZsOI\nEc2vn+7dk+2vmlmB8Nb3BiXC8L86/Rbh3XZrrlAcdVTTab9iN3hwsu08BSBdv6OmBoYPh/32S70M\npL6+O3dOXmv+66+6uvmywft+xx3Dl8sF/3Y6dnTTY8c2X66mxintwb5rWF82lavu6aeH163O1B+u\nqAhXdPfeO7t7EZoq+FVVzgjjJTzyLLKpOPbY5O/+/Zv+53kxZOrKDRjgFMcwBbglxJys1EjFnDnO\nr/m//ituScqHE090nRS/z3prYEv9FsY/OJ6rjryKQT0GxS1O2XPQjgfxtd2+xsTaVhVXZrRB+vVL\njm57nZSuXV1navfdmy/ftauzHmRy/Ro5MtmRDrpaHXlkssPi74Sl6sSEdQy9dXv1copDmEXK60gH\nt3vwwc6K4XWGgv970365DzzQKReHH+6sgTU1yY6bt3yYi6Tn1ugpIL17h7t1BS2OwemoVFS4dU87\nzVkuvvpVZ6mI4r7pV34zucd57eG5NIokcwnsvXfz5YNKl9+i4lmpPAU/6KEUPD/euif7CpwMHZrZ\nepXqmg0OEPgVYNXULpp+uTp1ajpwkokOHVz7HXigUwiHD2/e5jU1zS3v3j79SrRfcfbLFHYO/ZY/\naL59aD6gkeq+HDo0/L9018722yevxWOOcddq9+7Nz3m3bk1lO+00t6x3n4fJ7V2/xx3njjGVm262\n7o9RBqeisMMO7riiWI3Hj3fPtt13Dy/JUFXl2u/445teC0EqKvLjptpsu/nfpJEPfv97Z+3z/LuN\nzIjA737nrH6p3ELKkcufuZxde+7KhftfGLcorYZrRl/DPW/fw5xP2lAdEKPV4bcQeJ24oKXCTyaF\nIN0IdFgiiijeKN42U6VGF3EdoeC7bvvtw107d9nFufWlct3y9tejh+uYn3ii6wwPHZqUt1+/5p3A\ndu3cPv0KgKfUeO22007h7njBtkmVtKOmxoUlBPEsKb16Obn8ndW9926+vUznsVs3t51g7V/P4rH7\n7k2tHyLOGrX33tHcd6urm64/fnxSkQ5eE8ESBZ4S2amTa4uvf73pMdXUNB+08M5VOotZWKde1V0n\nYTUMg204eHB2bokVFcmO/R57OIXIf73269fcTbpnz+bt612vBx/szr9nWRwypLn7aOfOTRWP4P16\n1lmZrUgDBzqL04gR7r4bO9YpIWGEXesHHOAUlurqpCyZ6s21a+euYU+2sHg277rp0aOphSxorcyk\neHn7OP541x7+68I758E2Gjmy+eDTMccklx8wILPSGBb7euCBTe+Higp3r1RVufsn1+Q+LcUUvxLk\nnXdchsoLrZ+fNaNHu5HgO+6IW5L88MiCR3howUPceuKt5uKZR3p37s3vjvodF/37Ikv0YpQlXbs2\ntYL06uWef+kSWuSSuCGVwjZ+fHi8W1gtsvHjk9sZOtRZstJx6qmuw57K9S0Vw4YlLYFex7xLl/DO\ncJil8JhjnALQp4/bt18RGD8+6d6XDR06JJXUfv3CZdl1V5fsI5MroIe/49y+ffM2P/RQp1AFlbBU\nik2qc5yOVDF9wY76Pvs4Wbz4Tn8HWiS5fO/ezv23X7+m7opjxiQ71Xvu6a6N9u1dW40a1dziB0lF\nJjiYEOY66JclykBGKgWgsjLz9dqtW+qEN7vs4mTwLJQ77OAsiZkQcet+7WvJNkh3nY4a1fTcde/e\nVBn1PyMOP9wNnPitkpWVLS8sLuKuYf92BwwId8UcNKjpYNbw4U6mIMFz161baiV4hx2SsZngrj3/\nc7N//2huoUcemfztWULDBnY8onThihHaZYpfCfLLX8JPfxrfaEA5IwJXX+0Ku+eS8rqUeHfVu5z/\n2Pk8cPoD9OrYK/MKRlacN+I8KqSCv836W9yiGEbWnHBCehe8luDvoHixfsOHh1vgwCmcXszUccel\n33b79pkTfrRvn7mT1LWrs6B4nccTTnCdyajxTBUVqV0o27d3x+p1wqIqzP36hccshblr9e+fVEQ8\nC13UsT3PIiLiXCaD7rQVFeEDAGFKy9e/nluc3iGHJK11HuPHN7doVVS4c+LFqaVy2aysDM/E2rNn\nUwWufXun/O25Z9OELv622357t0zQcjhkSHrXur33burqesQR7hz5ZQ5zoQ6SjUuhP0kIRLsG/Of2\n9NOdYux3nwyLm03nPda9e7hC2qGDGxTYY49kop2WMmyYU7qGDXNt6/Vz99033PIo4hQzT1mtqnIy\njRjRNI6uUyd3TaR7tnj3cffuTdfNtHwuGWWDDBqUOVZv8GDXJmPGuOlCefwVpYC7EZ0ZM1xs36RJ\ncUtSvhx4oMuCdPXV8JvfxC1NbqzZvIZTJp/CtaOvZeSAkXGL0yqpkApuO/E2DrvzMMbsPobdekXI\n9mAYJUomN7WamvTZ57ykL++/H/5/uhioHXZI1krzd/xTxfflg8rKZAcJsh8oFWnqnhVmqfTvK4wu\nXZq6ng0bFt7pDuvMDxvm2i2Ke146srEQ7L9/c/fBXBN/VFZmb5044wxYvjy3/WUiaIH0n5eoinsw\nMUz//u6TrWLs7S/Kfvv1a6qMRrkWvvpV2LLF/Q47B506pVdww/Du2z32cIMXs2Ylr43KyvC4vDAy\n7Tfo5nnIIalLhHiIOCufv26eZ139+tfhwQedjFEt5h4nnODqMQbvfW9AxmuTqC7AfqtrkFTJl/x4\nCuaGDe4714y4mSh0Hb87RGSliMz1zeslItNFZKGIPC0iRS4rWrqows9+Br/6VWo3CiMa118Pf/0r\nLCzDOudbG7Zy6uRTGbPbGM4dfm7c4rRq9txhT35x2C84+5GzaWhsiFsco5UgImNEZIGILBKRn6VY\n5qbE/3NEZLhv/oci8nai/NHMKPs766z0Sh24DmaqjnqfPs4VL11GxEyEdXKzLfcQF6edlto97vjj\nw2OSwFkfDj888/bTJdFoidKX7brV1c0tTMUm3xEL3vYGDUrtstorxGGmf//kec1GpkJHXETZfnV1\n4TzCOnZ0rqNnnJFdHcRcE6dUVkZ7TlRWhg/OVFc7Ba6mJvt9d+3q3KL9su+6a9LNM5MiucMOLj7Q\nI6pyHDeFdvW8ExgTmHc5MF1VhwDPJqYN4KGHYM0ay+SZDwYMgF/8Ar773fIq76CqnDf1PHp06MEf\nj/1j3OK0CS49+FLaVbbjty/+Nm5RjFaAiFQCN+PefcOA8SKyZ2CZscDuqjoYuADw+xsrUJMofxTJ\n3J9rZ3S//ZybZjAhTC7bC8b91NRklyxjxAhnkYqDdu1SH3O3brkXAvfo3LlwxZgLRaY4zFKjS5fw\n2C9w1iG/JWrYMDdQMmyYc90MqwEYFz17Zh7EyYW9905dOiUf9OiR2c27UHTtGs1YcuihqRPZeP/7\nXX379ElfA7GyMlpZmGwpdJxfoev4vQR8EZh9EnBX4vddwCmFlKFc2LwZLrsMbrjB6vblix/8wMX5\n/c//xC1JNFSVS5+6lPe/eJ//PfV/qaywC6EYVEgF9556L7e9eRsPvftQ3OIY5c9IYLGqfqiqdcB9\nwMmBZba9B1X1NaCHiPir6xUlk9Oee+YvLnCnnZKJDUaPzj4N+c47h8d4lTJRY3Dat3fJW/JNIaxP\nvXs7y0Wh3MyyKaIehVza4CtfSfazDjwwu2Ql2SjwuSRT6tAhvGRISxk8OLXlOl+kqslXKnTunD5p\ni1e/1MOfbKeYdOwI48YVbvtxxPj1UdWVid8rgRSlZNsW113nbsp0qbiN7KiqgsmTnSn+oIMy1wmK\nE1Xl8mcu55Wlr/Dsd56lU7sshsqNFtOvaz8ePvNhjvvXcezUfScO6J+HaG6jrTIAWOqbXgYEo1jC\nlhmAeycq8IyINAC3qOqtBZQ1r3id8Dg6S8Vm3Lj8FcYuJbp1y18ijzC22655UpiW0KlT+myd+eSY\nYzLXwITcFD7D8FPIUm6xOh+oquJecm2axYvhT39yHyO/7LQT3HOP81efGSlapvioKj95+ic8teQp\npn1rGt07RHizGHnngP4HcMdJdzD2X2N54cMX4hbHKF+ivtNS2SpGqepw4Djg+yJyWH7EMvJJhw4t\nc99sy8pBPhXmiorcspLmwvbbl0/cqmGkIg6L30oR6auqn4hIP+DTVAtOmDBh2++amhpqconeLHFU\n4Xvfc0ldCuVa0dY55hi4/XYXAHzffaVlVa1vrOeixy9i3qp51J5dS8+OMUfet3FOHHoi9512H6c/\ncDrXHnMtZ3/lbKufWABqa2upra2NW4xCsRzwRw0NxFn00i2zY2Ieqvpx4nuViDyMcx19KbiTQr0f\nzzyz/OLR2iIVFeFJS4zSwcJ2jFwp5DtStMDDTiIyCHhMVfdJTF8LrFbVa0TkcqCHqjZL8CIiWmjZ\nSoFbboFbb4VXX7WRpELz3HPwzW/CJZe4OolxP5Q3bN3AWVPOoq6xjgfPeJAu1TlU0TUKwtyVc/nm\nQ99k916785exf6Ff135xi9SqERFUtVVo2CJSBbwHHA18DMwExqvqu75lxgIXq+pYETkYuFFVDxaR\nTkClqq4Xkc7A08BEVX06sI828X5srUya5AYg+7Qg0EW18BkmjezxSnF5yWTq61ueHMgw8vmOLHQ5\nh0nAK8BQEVkqIucCVwPHiMhC4KjEdJtkyRKXefKee0zpKwZHHeVq0zz1lMs4t2RJfLIsX7ecI/55\nBH279OXx8Y+b0ldi7NNnH2adP4s9tt+Dff62D1e/fDWb6zdnXtFo86hqPXAxMA2YD0xW1XdF5EIR\nuTCxzBPA+yKyGLgF+F5i9b7ASyLyFvAa8HhQ6TMMMKWvVDnkkKY120zpM0qNglv8cqW1j2hu3Aij\nRrnSDT/4QdzStC0aG1085e9+B7//PZx/fnFforOWz2Lc5HFcPPJifvbVn5krYYmz+PPF/OTpn/DO\np+9w3THXMW6PcXbO8kxrsvgVg9b+fmztTJoERx6ZfeZTwzDaJvl8R5riFwONjS7tdceO8M9/2shd\nXMybB9/6lqvDctttxUlFfPecu/nJ0z/hthNv4+Q9ghnejVLmmfef4YdP/ZCduu/EX8b+hV167hK3\nSK0GU/yyozW/H9sC77/vUsfHHW5gGEZ5UDaunkZzGhvhoovg449dfJ8pffGx114utrJvX1c8+I03\nCrevrQ1bueTJS7jqxauoPbvWlL4yZPSuo3nzwjc5fOfDOfDWA/nza3+mURvjFsswjDJj111N6TMM\nIx7M4ldEvvzSuRUuXQqPPw5du8YtkeFx//3w/e/DVVfBhRfmVyH/aO1HnPHAGfTu3Ju7x91Njw4l\nXuXUyMjC1Qs599FzaVfRjttPup3deu0Wt0hljVn8sqM1vh8NwzCMcMziV4a8954L+G1ogCeeMKWv\n1DjjDHj5Zfj7393v1atbvk1V5d6593LAPw7g63t+nUfPetSUvlbCkO2G8OI5L3LS0JM46LaD+NOM\nP9HQ2BC3WIZhGIZhGCkxi1+B2bwZrrvOJRP57W/zb00y8svmzXDFFTB5Mtx4I5x+em7n66O1H/Gj\naT9iwWcLuPuUu9m///75F9YoCRauXsgFj13Aui3ruHnszRw68NC4RSo7zOKXHa3l/WgYhmFkplVY\n/ERkjIgsEJFFIvKzuOQoFI2Nrlj4nnu62LE33nCxfab0lTYdOsANN8CUKS7j5+GHw0vNSienZvWm\n1Vz53JWMuGUE+/bel9kXzDalr5UzZLshPH/28/y/Q/8fZzxwBidOOpFZy2fFLZYRI1HebyJyU+L/\nOSIyPPBfpYi8KSKPFUdiwzAMoy0Qi+InIpXAzcAYYBgwXkT2jEOWllJbW9tkur7eWYuGD4c//hHu\nuAMefhh22ike+TyCcpYypSDroYfC7Nmu3Ma557rSG/fe6yyCHn453175Npc8eQmD/zyYFRtWMPuC\n2fy65td0qOpQfOEDlEJ7RqFc5ITmsooI39jnGyy+ZDHH7nYspz1wGiNvHcnfX/87K9aviEdIyqtN\nWwtR3m+JAu67q+pg4ALgb4HNXIqrAdgqzXrlfF2Ws+xg8sdJOcsO5S1/Ocueb+Ky+I0EFqvqh6pa\nB9wHlGWaw9raWrZuhRkz4Gc/c9m6/vIX59b52muuVk8pUE4XfanIWlnplL4FC+CHP3SlN/r1g298\nA/5xx5fcfM9d/OLZX7Lv3/bl+HuPp3v77sy5aA63nXQbO/fYOW7xt1Eq7ZmJcpETUsvaoaoDF4+8\nmPcveZ8JNROo/bCWYX8dxv7/2J8fPPED7nrrLl5d+ior1q+grqEuNjmNghLl/XYScBeAqr4G9BCR\nPgAisiMwFrgNaJU+IuV8XZaz7GDyx0k5yw7lLX85y55vqmLa7wBgqW96GXBQTLKgCitWwJYtyc/m\nze6zaZP7bNzoPhs2wPr18PnnsHKlSwhy/fWuFtxxx7lsnfvuG9eRGJnYuHUjjdpIgza478YGGrSB\nhsYG6hvrqWusY2vDVrbUb2FT3SY21m1k7ea1fLbzZ4y8fDldVnzAyx/O5/7/LETf7kG7ld9m98a/\ncfh2B9OwqpKH34HttoPu3V0Cn86doVMnV7OxQwdo3x6qq6GqKpnOW9W5BnshO+3bQ4WlXSprKisq\nGTt4LGMHj2Vrw1ZmLp/JjGUzePr9p/nLrL/wn7X/4fMvP6djVUe6VHehU7tOtK9qT4eqDnSs6ui+\n23WkY1XH5HdVRzq160THdh3p3K4znas706W6C12ru9Klugudqzu7/6s6Ul1ZTXVlNZvqNrFm8xoq\npZIKqUBEqJRK2le1j7uJWjNR3m9hywwAVgI3AJcB3Qooo2EYhtEGiUvxKyn3lfp6OOAA1yFv3959\nOnRwn06d3KdzZ+jSxX137QpDh8Jhh7mi39dfD93sFV0W9L2+LwAVUrGtM1xZUUmlVNKush1VFVW0\nr2xPdWX1tg52z4496dWhFwO6DeDkvb7Gz4/8EcN2GMa1ci3f//4EFiyAJUtg+XJYtMhZf9eudQME\n3qCBN5CweTPU1blPQ0My5rOiwv0WcZZiGzxoPVRXVjNqp1GM2mlUk/mN2si6LevYuHUjm+o2sbl+\nM1satvBl3Zdsrt+8bd6X9V/yZd2X27431W3is02fsWHrBjbWbWT9lvVsrNvIhq0b2FS3iS/rvmRr\nw1a2Nmxl/cz13HLjLdsGORRln977MPP8mTG1Rpsg6vstaM0TETkB+FRV3xSRmvyKZRiGYbR1Ysnq\nKSIHAxNUdUxi+gqgUVWv8S1TUsqhYRiGUThaS1bPiO+3vwO1qnpfYnoBUANcAnwbqAc64Kx+D6rq\ndwL7sPejYRhGGyJf78i4FL8q4D3gaOBjYCYwXlXfLbowhmEYhpEnorzfEsldLlbVsQlF8UZVPTiw\nnSOA/6eqJxZPesMwDKM1E4urp6rWi8jFwDSgErjdlD7DMAyj3En1fhORCxP/36KqT4jIWBFZDGwE\nzk21ueJIbRiGYbQFSraAu2EYhmEYhmEYhpEfip47sJwK27ZEVhH5UETeTsha0EwKLZSzh4hMEZF3\nRWR+wu2opOQUkaGJdvQ+a0XkklKTMzH/ChGZJyJzReReESlo+sQWynppQs53ROTSOOUUkT1E5FUR\n2SwiP8lm3RKS8w4RWSkicwspY0tlFZGBIvJ84jp9p5D3Ugvl7CAir4nIW4ln0x8KKWe5UMz7IVfC\n3n8i0ktEpovIQhF5WkR6+Ja/InE8C0TkazHI2+zezUVeEdk/8UxdJCJ/ilH2CSKyzPfOPK4UZU/s\nN/R5VA7tn0b2smj/VM/YMmn7VLKXRdv79t1EpylK26tq0T44t5fFwCCgHfAWsGdgmbHAE4nfBwEz\nAv//GPgXMLWUZQU+AHqVepviakn9V+J3FdC9FOX0LVMBrAAGlpqciXXeB9onpicDZ5fiuQf2Bubi\nEkhUAtOB3WKUcwfgAOC3wE+yWbcU5Ez8dxgwHJhbqHOepzbtC+yX+N0FF49Wqm3aKfFdBcwARhW6\nbUv5U8z7oYVyNnv/AdcCP038/hlwdeL3sMRxtEsc12KgosjyNrt3s5TX856aCYxM/H4CGBOT7L8G\nfhyybEnJnthX6POoHNo/jezl1P7NnrHl0PZpZC+btk/sr4lOU4y2L7bFr5wK27ZI1gTFyFKXs5wi\n0h04TFXvSPxXr6prS03OwDKjgSWqupTC0BI51wF1QCdxCR46AcsLJGdLZO2Lezm9pqqbVbUBeAE4\nNS45VXWVqr6Oa7+s1i0ROVHVl4AvCiRbkJxlVdVPVPWtxO8NwLtA/1KTM/HfpsTPapzS83mB5CwX\nink/tJTg+2/bsyjxfUri98nAJFWtU9UPcR2akUWRMEGKezcbeQ8SkX5AV1X1PHzu9q1TMNI8d8L6\nHyUlO6R8Hg2gDNo/jexQPu0ffMZ+QRm0fRrZoUzaPoVOU/C2L7bil6pobdRlvMK2jYUSMKIcUZZR\n4BkReV1Ezi+YlLnLuSOwC7BKRO4UkTdE5FYR6VSCcvo5C7g379KllyHSeVfVz4HrgY9w2fzWqOoz\nJShrf5y177CEW0En4Hiat3Ux5SzEutlSzH21lLzIKiKDcNaC1/IiVXNaJKeIVIjIW7jC5s+r6vw8\ny1dulMs1Gvb+66OqKxO/VwLeoF5/3HF4lMoxZStvcP5y4j2OH4hz77/d5y5W0rIHnkdl1f4+2Wck\nZpVF+4c8Y+dRJm2fQnYok7YnXKcpeNsXW/HLS2HbkP8LQa6yeoxS1eHAccD3ReSw/IjVjFzlVJx5\nfATwV1Udgcsud3keZQvuLwphcro/RKqBE4EH8iVUCDmfdxHZDfghzgzfH+giIt/Mn2jNyFlWVV0A\nXAM8DTwJvEnhBlRakkGqmNmnyinTVYtlFZEuwBTg0sRodSFokZyq2qiq++EGJQ4XK2peLtfoV9O9\n/9T5JKU7lpI6zgjylhp/ww3s7ocLjbg+XnEyk3gePYh7Hq33/1fq7R/yLC2b9g95xh4Z+L9k2z7F\n+6Es2j6KTlOoti+24rccGOibHkhTTTVsmR0T8w4FThKRD4BJwFEicneJyoqqfpz4XgU8TOFcV1oi\n5zJgmarOSsyfglMES01Oj+OA2Yk2LRQtkfMA4BVVXa2q9cBDuOu2FGVFVe9Q1QNU9QhgDS4+IS45\nC7FuthRzXy2lRbKKSDtcJ+t/VfWRPMvmJy9tmnBB/zfuHmvLlMU1qqorEt/+99/KhJs5CfekTxOL\nZ3rux0U28i5LzN8xMD+W41DVTzUBzo3M63+UpOy+59E9vudRWbR/2LO03Nofmjxj96dM2t7D/34o\no7YP02nuoQhtX2zF73VgsIgMSlhvzgSmBpaZCnwHQFyGyTUJP+qfq+pAVd0F5+73nKp+pwRlXSki\nnUSka2J+Z+BrONe6kpJTVT8BlorIkMRyo4F5FIac5fT9Px53gxSSlsj5HnCwiHQUEcG1Z0rXNBH5\np4hcJSKjRGSBb/5QcZmq1onIxeKyVz0mImtEZHKeZEVEeie+dwLGUTgX2ihyegRHvrJZN045i03O\nsiauzduB+ap6Y2HFbJGc23tuOiLSETgGZ5luyxTzfsiJNO+/qcDZicXOBrwO/lTgLBGpFpFdgMG4\nZAVxk5W8iffpOhE5KHGPfdu3TlFJdBg9xpHsf5Sc7GmeRyXf/qlkL5f2T/OMLYe2D5XdU5oSlGzb\np9Bpvk0x2l6LlLnG++CsNu/hAhOvSMy7ELjQt8zNif/nACNCtnEEBc7q2RJZgV1x2XfeAt7x1i01\nORPzvwLMSsx/iAJl9cyDnJ2Bz3BBrCV53hPzf4pTnufiAnPbpdnPncBvQubfDlzvm/42LuahWaa7\nFsr6YkLWt4Aj42xTXHa0pcBaXID2R0CXVOuWqJyTcLGdWxLLnFuKsuIynzUmzvubiU/Bspi1QM59\ngTcScr4NXFbI9iyXTzHvhxzl24WQ9x/QC3gGWIhzMe/hW+fnieNZABwbg8zevbvVu3dzkRdnLZmb\n+O+mmGT/L1yCh7dxz/xHcHFDJSd7Yr+hz6NyaP8Ush9XLu0P7BP2jC2Ttk8le1m0feBYtuk0xWh7\nK+BuGDEhInfiXG2vDMx/Bpe96fbE9C+BoepGgwzDMAzDMAwja4pewN0w2ioiMlxc9tR1InIfroYe\nIlIjIksTv58DaoCbRWS9iNwLXAmcmZg+Ny75DcMwDMMwjPLFFD/DKAKJeJxHcO6fPXGZSb+Oy9i0\nzeyuqkcBLwHfV9WuqvoN4PfAfYnpO4suvGEYhmEYhlH2VMUtgGG0EQ4GqlT1T4npB0VkVprlJfA7\n7mQihmEYhmEYRhljFj/DKA79aZ5i9z+kVugs+NYwDMMwDMPIG6b4GUZxWAEMCMzbmWgKnimBhmEY\nhmEYRoswxc8wisMrQL2IXCIi7UTkVODAxH9hVr+gq6dhGIZhGIZh5IwpfoZRBFS1DjgVOAdYDZwB\nPOj9TXOrngZ+m9XPMAzDMAzDyJmC1/ETkR7AbcBeuM7rucAiYDLO1e1D4AxVXVNQQQxKPUptAAAg\nAElEQVTDMAyjCIjIGOBGoBK4TVWvCVnmJlyx503AOar6ZmL+HcDxwKequk/xpDYMwzBaO8Ww+P0J\neEJV9wT2xVWcvxyYrqpDgGcT04ZhGIZR1ohIJXAzMAYYBowXkT0Dy4wFdlfVwcAFwN98f9+ZWNcw\nDMMw8kpBFT8R6Q4cpqp3AKhqvaquBU7C1TMj8X1KIeUwDMMwjCIxElisqh8mXLzvA04OLLPtHaiq\nrwE9RKRvYvol4IsiymsYhmG0EQpt8dsFWCUid4rIGyJyq4h0Bvqo6srEMiuBPgWWwzAMwzCKwQBg\nqW96Gc0z+kZZxjAMwzDySqEVvypgBPBXVR0BbCTg1qkuyNASVxiGYRitgajvs2C2XnsPGoZhGAWl\nqsDbXwYsU9VZiekpwBXAJyLSV1U/EZF+wKfBFUXEXoKGYRhtBFVtLWVLlgMDfdMDce/CdMvsmJgX\nCXs/GoZhtC3y9Y4sqMVPVT8BlorIkMSs0cA84DHg7MS8s4FHUqxflp9f//rXscvQVuUvZ9lNfpO9\nrcrfyngdGCwig0SkGjgTmBpYZirwHQARORhYo8nwh0jEfc7a6rVazrKb/CZ7W5W/nGVXze87stAW\nP4AfAP9KvACX4Mo5VAL3i8h5JMo5FEEOwzAMwygoqlovIhcD03DvuttV9V0RuTDx/y2q+oSIjBWR\nxbgQiHO99UVkEnAEsJ2ILAV+pap3Fv9IDMMwjNZGwRU/VZ0DHBjy1+hC79swDMMwio2qPgk8GZh3\nS2D64hTrji+gaIZhGEYbphh1/NocNTU1cYvQIspZ/nKWHUz+OCln2aH85TfaDuV8rZaz7GDyx0k5\nyw7lLX85y55vJN++o/lCRLRUZTMMwzDyh4igrSe5S8Gx96NhGEbbIZ/vSLP4GYZhGIZhGIZhtHJM\n8TMMwzAMwzAMw2jlmOJnGIZhGIZhGIbRyjHFzzAMwzAMwzAMo5Vjip9hGIZhGIZhGEYrxxQ/wzAM\nw8gjIjJGRBaIyCIR+VmKZW5K/D9HRIZns65hGIZh5IIpfoZhGIaRJ0SkErgZGAMMA8aLyJ6BZcYC\nu6vqYOAC4G9R1zUMwzCMXDHFzzAMwzDyx0hgsap+qKp1wH3AyYFlTgLuAlDV14AeItI34roA1NcX\nSnzDMAyjtWKKn2EYhmHkjwHAUt/0ssS8KMv0j7AuAO+802I5DcMwjDaGKX6GYRiGkT804nLSkp00\nNrZkbcMwDKMtUhW3AIZhGIbRilgODPRND8RZ7tIts2NimXYR1gXgllsm0K+f+11TU0NNTU1LZDYM\nwzBKhNraWmprawuybVGNOjiZ4w5EPgTWAQ1AnaqOFJFewGRgZ+BD4AxVXRNYTwstm2EYhhE/IoKq\ntsgCViqISBXwHnA08DEwExivqu/6lhkLXKyqY0XkYOBGVT04yrqJ9XX2bGXEiOIck2EYhhEf+XxH\nFsPVU4EaVR2uqiMT8y4HpqvqEODZxLRhGIZhlDWqWg9cDEwD5gOTVfVdEblQRC5MLPME8L6ILAZu\nAb6Xbt0YDsMwDMNohRTD4vcBcICqrvbNWwAcoaorE5nMalV1j8B6ZvEzDMNoA7Qmi18xMIufYRhG\n2yGf78hixPgp8IyINAC3qOqtQB9VXZn4fyXQpwhyGEaszJsHb70Fmza5z+67w9FHQ4cOcUtmGIZh\nGIZhtHaKofh9VVVXiMgOwPSEtW8bqqoiEmramzBhwrbfFrxulCMNDfD443DTTfDuu1BTA507O2Xv\nwQfhm9+EY4+FH/4QDjkkbmkNozgUMnC9rWAOMYZhGEa2FNzVs8nORH4NbADOx8X9fSIi/YDnzdXT\naG188AF84xuu0PKPfgSnnQbV1U2X+fRTpwD+7ncwejRccw30Mfu30cYwV8/sEBF9/XVl//3jlsQw\nDMMoNGWT3EVEOolI18TvzsDXgLnAVODsxGJnA48UUg7DKDaTJ8PIkXD66fDaa04BDCp9AL17w3e/\n66yBO+wAe+/t1jUMw0iHlIiaPH163BIYhmEYUSm0q2cf4GFxb6gq4F+q+rSIvA7cLyLnkSjnUGA5\nDKMobN0Kl14KzzwDTz4JBxwQbb2uXeG665yCOG6ciwecMAEqipF31zAMI0c++yxuCQzDMIyoFFTx\nU9UPgP1C5n8OjC7kvg2j2Kxc6dw5e/aE11+H7t2z38bw4TBzJpx6KrzzDtxzj4sJNAzDKDW8aAzV\n0rFAlhKbN1vyLsMwSguzJxhGHnjpJTjwQJel85FHclP6PHr3hmefhY4dnfVv8+b8yWkYRuvAQuBL\nn4cfNouoYRilhSl+htEC1q+Hiy+Gs86Cv/41f+6Z7dvDXXdBjx5wxhlQV9fybRqGUXhEpJeITBeR\nhSLytIj0SLHcGBFZICKLRORnvvmni8g8EWkQEavUF5FSVYTt2W0YRilhip9h5MCGDfCPf7hkLJs2\nObfME07I7z6qquB//9d1aL71LVcawjCMkudyYLqqDgGeTUw3QUQqgZuBMcAwYLyI7Jn4ey4wDngx\n3U5KybUybqWrrg7uuy9eGQzDMMoBU/wMIyLr1rmELd/9Luy0k/t9991wxx0urq8QVFfDAw+4sg+/\n+EVh9mEYRl45Cbgr8fsu4JSQZUYCi1X1Q1WtA+4DTgZQ1QWqujDTTuJWtkoJGxRrOQsX2jVVKBoa\nYOnSuKUwDIcpfoaRgi1b4Lnn4IorXGmG/v3h6qthxx1h7lwXv3HEEYWXo0MHp/zddx9MmVL4/RmG\n0SL6qOrKxO+VuOzWQQYA/q7gssQ8o8T58su4JWgZW7eGz589O/V/bR1VV483V5Yvh5dfzp88RvFY\nvz5uCfKPKX6GEWDJEvj+912SlZ//3LlcXnedC9J/4QVneRtQ5C7a9tu7Qu/f/S7Mn1/cfRtGayVR\na3ZoDutNF5G5IZ+T/MupqgJhdpS821bisNb4s3rGSTH3/8gj0NhYvP3lk61b3XskFXGfx1Jlzhw3\n+NpSJk1q+TbiYvFiqK2NW4ri8/jjsGJF3FLkl0LX8TOMsuHjj10NvtpauOACWLAA+vWLW6ok++/v\nFNBTTnHlIrp1i1siwyhfEkradUB7YJCIDAcmqupJ6dcEVT0mzXZXikhfVf1ERPoBn4YsthwY6Jse\niLP6ReaWWybQv7/7XVNTw4oVNZx+uhuoMowwzCU2NzZsiFuC+PnPf1zISVukJdbeXKmtraW2QJq2\nvSIMA5g+Hc4+G84/H+68E7p0iVuicM45x7mM/OhHcPvtcUtjGGXNBOAg4HkAVX1TRHbNw3anAmcD\n1yS+HwlZ5nVgsIgMAj4GzgTGhyyXMoXLRRdNYIQv5+ekSa5jb4qfkYpSt+ipwtq1Lpt1KfDxx1BZ\nGbcURlukpqaGmpqabdMTJ07M27bN1dNo06i6EgznnAP/+hdMnFi6Sp/HDTc4q+Sjj8YtiWGUNXWq\nuiYwLx9OfFcDx4jIQuCoxDQi0l9E/g2gqvXAxcA0YD4wWVXfTSw3TkSWAgcD/xaRJ8N2Ukqd+FKS\nxShfPvrIJU0rFV54wdXoLaUMuvlixYrmLsuPPQZffBGPPEbxMMXPaNNMmOAedrNnw5FHxi1NNLp2\ndTX+Lrqo7bpeGEYemCci3wSqRGSwiPwZeKWlG1XVz1V1tKoOUdWvecqlqn6sqsf7lntSVYeq6u6q\n+gff/IdVdaCqdlTVvqp6XPR9J39v3AirV7f0aIrL559nX/duTVB1b+XU1eUeb5ZJQY9bgY/Dpa6c\neOON1G6nDQ3Znb/aWpd0xs+GDfE/M559FubNi1eG1o4pfkab5bbbXJ28J56Avn3jliY7Ro1yVsoL\nLoj/ZW0YZcoPgL2ALcAkYB3ww1glyoIwK4T/WfB//wdPP11YGfL97Jk2Dd56K/ryn37qLESPBJxp\n16+PvwNbKDZvbpsK0sqVzc9zsSgVi9977zmraBj33+8Uw5aSr3t69uzcBqY//bS5QpoPNm3K/zbz\nSV1d6ozBW7bkd1+m+BltkieegF/+0nUa+oQlWy8DJk6E99+3wsWGkQuqulFVf66qByQ+v1DVzXHL\nFZWWdtA25/FI86kAZrOtVMlKamsLo/TGPci2dauz5Hps2hRu8Vy1Ch56qPn8uOVvCZ9+Wv6lNArN\n2rVxS5Bk4UKXIT0bCpl86NFHSzdJz5IlrlRX2MDGwoXh93JLKLjiJyKVIvKmiDyWmO6VSIW9UESe\nFpESCeM12goffeQSuTz8MAwZErc0uVNd7ayWP/5x6x3dNoxCISLPh3yei1uuqGTq5KXr5G/a5J5/\n5czatS7Nfqnz5ZfOkpkPXnoJnn8+Of3ii+ExcZ991txKsGpVeSt+cVIqFr9sWb4cnnkm9f8NDfkP\nF2loaKrAffCBy0Iehdmzs9vXxo3uus7EO++475Ur0y+XCv99k+s20pHOwpltm0ShGBa/S3HB617T\nXQ5MV9UhwLOJacMoCqquFt4PfwiHHBK3NC1n5Eg480z4yU/ilsQwyo7LfJ8rgbeAArxmC0NYJz5q\nx97fMVu/vuX1xYqlUHzySVLWJUuaJ6LYsgU+/LDwHfVsXC2/+MLFLn7wQcvbOVhgPZt6gs8849om\nHS09j6qZ9wGus56tdSfbc/r228n2aWgo7xp6flaujH7ely9PrxgtXuxi6vwsWJCdLEGefRaeeio5\nvWiR+0QheH1nYsaM9Iqtx9y57nvmzOz34aeuDp7Lcmhw5szsi8CvXl1Y63ZBFT8R2REYC9xGMi31\nScBdid93AacUUgbD8DNpEixdCpddFrck+eO3v3WuTVEegIZhOFT1dd/nZVX9EVATt1z5IthR/uwz\nePPN5v/l0sFQhWVZVR3MD5kyDi5eDK++Wng53n47+rKeMjVjRmFkycSWLcmOr2f5yIaFC11Zgyis\nXx+t/Z95xsWrBcmnwj5vXjKuKxslMywWLJ1c77+fuWOfz+P65JPUcX6p9rtoUfh5CVP0g+6QweeD\nt86aNeFK0OrVsG5dNPk8Vq50/bKKIpiiim31XrLEHVs2PP00vPZaYeSBCIqfiMwWke+LSM8ctn8D\nbjTVPz7RR1W9cYKVQJlGWBnlxmefObfI225zbpKthS5d4K9/hQsvtBgIw4hKIuzA+2wvImOAbnHL\nlQtex9PfqfF+v/6663xMn57daH461qxxbodtDa9N/Ra/zz5rWlpn0iSnPDz+uJuOau3w8/HH4VbF\noAIRpRP78cfpFb66uqbKzrp1Td2IZ892CXc++sid9/nzw7eTbcKZYnTAH3ssu+VXrWpeJimTnK+9\n5mrrRlUu83HcqbaRav6SJdEssWE88ohzBw1u2+9y3FJeecW1YbYKciGuoUWLshvYKRSqhevPRSn1\nehZwLjBLRF4H7gSeVk3f5CJyAvBpoihuTdgyqqoiknI7EyZM2PY7WMzQMLLlJz+Bb3zDuUe2NsaO\nhX/+E37/e7jqqrilMYz01NbWUltbG7cYb5AMQagHPgTOi02aHFFNKhlhLFoUvSD2hg3OLbFTJ9h+\nezcSny75ldcLiCN2rBD73LrVWSy6dYPOnaOts2qVU5zWrYN//9vN27w5tRWosTGzZeOFF2DECBg6\nNPUy/iQvLeHVV5MxRo2NyWMYPz65zNq1LktsdbVro2HDmm/ngQfgsMPyIxO486uaHytQ1GslVSmR\nMIXk1VeTyp6nEO+zT/i+c83KuH49dOwIVYGeeioFKRiv5y3nfa9e7c7lrrsmZYtCWLvkMzlUUM5C\nu2ovXOjKYvXr1/y/d95xx7bvvpm3M3cu7Lgj9MzSLLZsmRs4899jYWTrVhqVjIqfqi4Cfi4ivwRO\nAO4AGkXkDuBPqvp5ilUPBU4SkbFAB6CbiNwDrBSRvqr6iYj0A1KGlvoVP8NoCXPmOPN5LqOv5cIN\nN8BXvgLf+lb6DoNhxE1wIG/ixIlFl0FVBxViuyLSC5gM7IxTJs8IKRRPwsJ4I1AJ3Kaq1yTmX4d7\n124FlgDnqmqkfH1ROnIrVzZVavwxQJ6FpKoKTj/ddTxOPtkpgnExZYpTNMKUjXyxYYOLTdp+e2fZ\n8o7fz+bN6T1FoipiTz8NY8ZEl62hwcm0005N50+dGn0b6fArJQsXpl+2sjL6tjzmzXPK2557ZifX\nK684ReWkk7Jbr1h89FHTWLtUFs933mlqca2ri+5x9PjjTkk76KCm83NVjLxMt9ttl/26/kGefGff\n9I4nU+zipEnu3kmlaG3Z4lyI0ylts2fDf/7jBsPCFL8wUj1X33nH7fOAA6JtxyNd7VH/PZRtTdOo\nRBpLEZGvAH8ErgMeBE4H1gMp9dFEmuyBqroLzmr4nKp+G5gKnJ1Y7GwgpsosRltiwgT46U+dW2Rr\nZcAAV6Lie9+z7G2GkQoR+bqInJrqk4ddZExgJiKVwM3AGGAYMF5EvK7x08BeqvoVYCFwRdQdR7nv\ng53zMLcmv4XhP/9x3y+/nD8rUzqCx1BXl8xa7P23YkV22/zgg/R1vNascf97nfewTvzDD6fvmPrl\nfvfd1MtlilMM8vHHLj7w/vszr7tihVOY/GSjJGTqaEa1vtXXu20tXequLy/GMBs+/zz76y1TbNln\nnzWf549pC7t/6utdHF+uBK+7bF0ks+38++/vVOf+iSeaTmdrvcs0QBBGWFKVhoamsYfe/eU/T0El\nc9as1BbU5cszF3/P9tmRC6pJ7wFIfw+qNs3q6S/dUKh+XKQYP1ys3kxgX1W9RFVnqOr/AB9ksS/v\nEK4GjhGRhcBRiWnDKBhvvOEyK110UdySFJ6LL3YvzNaSwcwwCsCJGT4tJUoCs5HAYlX9UFXrgPuA\nkwFUdbqqeirGa8CO6XYWFtfXUkSSnV2voPrSpS6xRNh+8tlBCeucBxPJRPUS9p6DM2ZkH9/oj6/x\nOqRhxxnWqYuafKOhwXX6nnoqdfHtbFwdP/wwqainI1VKev/xTZrU3HUw6nl+/nlnrXr55abz6+sL\nF7e0cWPSTdXPpElJuadPd+/H2bOTCtljjyXbw1sulwGOqG0TpZD4u+8mS4CEDTakUyT8bZDJddKT\n+dln0yeoCSb3CTvWTZvSt1uYcrlpU+YsvPff33T/q1c3fx605PmzZUv2ynWm/c2bBw8+GK2W6Oep\nfCYLSJQYv9NVNXS8Q1XHRdmJqr4AvJD4/TkwOrKEhtFCJkyAyy93vvKtnaoq+PvfYdw4F/cXNbbH\nMNoKqnpOgXcRJYHZAMCf620ZcFDIcv8FhA7jbNzoFIcoFp1ckiZ4Sh5kzlq4Zg307ZvdPvw0NsLk\nyemXmTmzqcdGrnFT3rrV1c3bxW/pe+SRpFtZFEtfLp3PDz5wFgxovg9ve7m49XnH8cwzsPvuzf9/\n7rlkfFG6gYMondKPP04mg/HWX78+/PzMnBlNMf3gg+a10zJZpaKWOKircxar7t2TbRO08E6dCqNG\nha+/bp2794Jt9f777lzttVd6V07VzLGzH3+cbHv/feixciW0axfuqpjLfVFXlz4r+OLFmbfx1FPZ\nl0qIem2nUpa9+arRtxU8b1OnupjeY4+NLn99vWv/VES16keJ9y0EUXb53/4i6yLSU0R+W0CZDCNv\nvP66G0k9//y4JSkeBx0EJ5wAv/pV3JIYRmkjIieIyE9F5FfeJ+J600VkbsinSURSIglamEqQUU0Q\nkV8AW1X13rD/N25MlmdI7i+K9NmTKnmMt7/nn09ahzZudKPd2RB051Jtns78g4B/UToFIlOGyYce\nauqu5rkIesfgdSI9uTylIp0LZ0uTXaTquC5Zknnd+vqmLm6edTNKcWs/maxRYdfXnDlJq7BHUPlo\naHDvYr+174svUlv/Zsxoaj167rnw+PytW5Od9agdf79rp3deRZxl0B97FWYFmjbNKUhhFue6Otfu\nnnLrWZuDbqJeLbj581MraWHt/OKLyd+LFzeVIcxKDpnbJBdrk5d0x+O991w7btmS+/Mn16Qu3jUS\ntt+6unDPJ++8+t26N21y8x98sOl9HFzf24/fe2DVqqZZcBcvzlzqxjvOxYub1jwsFlEsfmNV9efe\nhKp+ISLHA78snFiGkR8mToSf/xw6dIhbkuLyhz+4ZAjnngvDh8ctjWGUHiJyC9ARF3JwKy52PVL1\nJFU9Js12oyQwWw4M9E0PxFn9vG2cg6uBe3Sq/UyZMoEePVxWucbGGoYNq8mb4pdqO+k6ZgsWQO/e\nrhO0davrlEXJjDltWtPns2oyrsqf1KKxMXrH0q9QpFIC/UrOnDnpt+ft11OuVq1ySqA/YcnMmdFk\n89iwIWntS0eUGnqrV7tYukGD3LRfkc7GjS3o2hmFdIkq/Cxa5K4Pj6VLXSd7dA7+X6pw333u+lLN\nnADGf91450k1aWX2Yqz8ymbYtRZFUaqvb6oIBPHuoTlznNVo8ODkfwsWpE7M5o8DCzJ9ema50iGS\nu9L2xhupBxg8hTDI+vWundJ5EtTVpbeq+Qmzume67oOW7qAyny7Jit+6vGaNi5kcOtRl4g2z0L71\nVnhyo9mzU8v31lu1zJhRm3WZlChEUfwqRKSDqm4GEJGOQCuqgma0VhYscC/WBx6IW5Lis912rrTD\nd7/rgv3jcCcwjBLnUFXdR0TeVtWJInI9kI/xVy+B2TWkTmD2OjBYRAYBHwNnAuNhW7bPy4AjvPdu\nGKedNoFeveCQQ5JxPdl23tJ1jrKNewl2TKdOde6EGzY4F826OqeQ+JW8l192nelM2SKjEqaYRi0+\nHtyOP94raNHasMHNGzCg+X9RCSoHqRSoKC6M6WIuX389O7n8BF3f8m1RXrXKdf47dXLXQBSLz+ef\nOzdNSCpq992XVKDef795DGOmNvRiMgsRL5sNb77ZPHtrQ0Nqhfy+++Css1JvLxtLmn+ZdK6Tmzc3\nT9aTqkB5qljXZ591gzO9eqWWr7YWjkkxvCbS1OrmnV9/nGym8+ff55YtzRVUf3zqrFlNXabDtr14\nsXu2pSvWvmqVcx2PMljSt28Np5xSs236oYfyl/k6SnfwX8CzInKeiPw38Axwd94kMIwCcdNNrqh5\nW7P2eZx7rlP47rgjbkkMoyTx7EKbRGQArpZfCyLVthGawExE+ovIvwFUtR64GJgGzAcmq6rnSPhn\noAswXUTeFJG/ptrR5583TeaQbWd1ypTw+Vu2hCtMnkuk52YZxWL12GNOUXr+eZcZ84svXMd84cJk\nJylfneywDrKX5TJs5HzatPBaWf74umXLUndg043YpyNVzNTs2fDkk9lvL5e4ruXLm7vPBsmUITFI\nLufx8cez28+0aeFWFU+Rfu215sXKs1EC4ubRR5vL++yz4ctGPa4oVqOw+LawQfOWlhFZuzZpkfey\nB4dZ/jK5Hfvd3L128I7zvfeS/+VauD7MDdnbT5jLt2p6z4GGBucmPHdu9ORPhSJKHb9rRORtXEIW\nBX6jqtMKLplhtIAvvnCjYfPnxy1JfFRUwF//6oKWx43LrXaPYbRiHheRnrgyRV4X/taWbjRVAjNV\n/Rg43jf9JNCsm6+qg4Pzou871zWj8e67zrXUG20Pxtl9+WV4J9qrDwiuOLl/tB+iJ+YIKz3hJ12q\n9iVLYOTIpm2UynXPv0w6pSBXT4pZs2DvvZvPX7y4aQbRqPXSsnUzhaYxY1Ep1PXlKR1h10FYvFSY\n7OncVMPkDjvH2Vj8cm0L/zndssVd0/vu21TRyGbbYW6lkyY1LQ6eycIUVLI8i18h3Az91thMCrcX\nu9jY2DTeLmjFDrbX3LnOGg+pnxmbN6e/vzIltMo2PvL++913VNfoQhLF1TPlC8owSpXbbnMJTlqS\naa41sN9+cOaZcMUV8I9/xC2NYZQOqvqbxM8HE5a4DmGF1suNSZPgsMMKt/108USPZFGVN4rS5dXB\nagnBTqGntEbpXGfqmGaqG5cOf1HvVHidxUzku6B2Kjz330mTnEtiukLZ2bByZeoSRKlKT2RDpoEF\nT4H3J/YohqvnihVOudl33+zuHT/Bmnx+SsmS6ZGuXYOW3FTPmrBkUH7q6pommwqjvj63AROPoBU2\n6uBVmLW62GRU/ETk6zhXlT6AdxmpqnYrpGCGkSv19fDnPzu3IgOuusoFFs+YAQcfHLc0hlEaJDxZ\n7sO5WS4BWpiXMX68DtBLLzUtfRC2TKniz7oYpQ5WNixZkntMXhh+WeOkWOfU37n96KOmyVpaQrp2\nzKVYeJCweFV/m3mKn79THrUjH4ancKWL90pHPutxxrn/IFOmpI8dzrYcRDqCWYHDaEkm3kJYQ4tF\nFEeFa4GTVLWbqnZNfEzpM0qWhx922c323z9uSUqD7t3h2mvhe98r3siwYZQBJwENwP0i8rqI/D8R\n2SnTSqWMv8NWKkpJkDg7TP64RX8cUCrWr8/sXppP/MpGlNppQVKl9S8UQcUi11i6lihZUQizHPmv\nwzC5gqVSciFYwD6I117B2LBcCsgHWbgwmlU5jM8+y/+1pNpc6cuHNRfSl1lJR7YeBQ89lNt+So0o\nit8n/7+9Mw+Xorr29rs4cIDDKDIjo4KIYkQNIqgcBLwIKDhFyeSnJmocrjHGiJoBNDdCbkwco4lT\n0MQpTjHGiagnMZNTZFAk6I0ToGicZ0HW98eu4tSpU91dPVRXd5/1Pk89XXP9endV1157r71WYNC5\nYVQ8F10Ep5yStorK4ktfcklKL7ssbSWGURmo6guqulhVd8NF1NwZyBHuorKJE+Tjb38rzkWxWOJE\nC80UdKZYcuXXCvO3v+Uf3bRUFGK4l9vYD99vuYLdlKqiXwqSMugL6WULG/mFBOsJU4xL4YMPFp8i\nolhyBXcJEqcRJ4q0nu20iTPG73ERuQkXktrviFVVrRHb16glVqxwkcrmzElbSWUh4gK9TJ4MhxwC\nAwakrcgw0sdLp3A48AVc79930tRTLA8/HL0+XBktNtl4XEoxRs+oXMrZG5okpR4LV2hPWy1TTBnH\nMdAyjRE1WhPH8OuBC3u9X2i9GX5GxXHZZXDssc1hgo1mxoyBr30NTjsNrr8+bfLSlusAACAASURB\nVDWGkS4i8gguJ+3NwGGq+u+UJSVGnDE7hSTvzkWpx+gZRhJEhe4vJ0mMqcuW8L3aqIQGhnDuwmom\nTjqH/1cGHYZRNO++CzfdZK1t2fje92DHHV0+mWmtAs4bRpviSFVdnXu32iOqovnWW+XXYRiVQCld\n/qLyX5bz+pVKnJyflUwt1StzjvETke1F5AERedpb3llEvhvjuE4i8oiILBORVSJynre+l4gsFZE1\nInK/iPQs/msYBvz61zB1KgwcmLaSyqWhwUU8PeGE8rl7GUYlkpTRF/cdJyIzRGS1iDwrImcE1p8r\nIsu9d+cDIjK4WE3h8TJRYcwrMfS7YdQybckVOgmPAqMw4gR3uQI4i+bxfStxA+GzoqofA1NUdRfc\noPkpIrIXMB9YqqqjgAe8ZcMoClU3hu2EE9JWUvnMnu2SBy9alLYSw6hJcr7jRKQOuASYAYwB5onI\nDt7mH6vq57x35x3AD4oVFCdYhBl+hmEYtU8cw69BVbdkxFBVBWJ1TKuq385YD9QBb+FCaC/x1i8B\n5sZWaxgZ+MtfXKqCxsa0lVQHF14Il1xSeBhkwzAyEucdNx54zossuhGXT3AOgKq+F9ivK1DmIP2G\nYRhGrRLH8HtdRLbzF0TkUOCVOCcXkXYisgzYADykqk8D/VTVD+q7AZcY3jCK4uc/h+OPt1bruAwe\nDD/4ARx3XPI5lAyjEhGRLiLyPRG5wlseKSKzS3DqOO+4QUAwvfNab52v7X9E5CXgSKAsffOPP16O\nqxiGYRhpEif24UnAL4HRIrIel+foS3FOrqqbgV1EpAdwn4hMCW1XEckYz2jBggVb5hsbG2m07hwj\ngvXr4b774PLL01ZSXZxwAvzmN3DllS4SqmGUi6amJpqamtKWcQ3wBDDRW14P3ALcletAEVkK9I/Y\ndHZwIcs7LmscP1U9GzhbROYDPwOOCu9zyy0LtsyPGdPImDGNuWQbhmEYVcCqVU2sWtWUyLlFY8aR\nFZEuQLuQG0r8C4l8D5cW4mtAo6q+KiIDcD2BoyP217jajLbN97/vBklfemnaSqqPlSth331duGTL\n7WekhYigqmXtrxeRJ1R1NxF5UlXHeeuWq+rnijzvanK840RkArBAVWd4y2cCm1V1cWi/IcDdqrpT\naL1ef729Hw3DMNoCX/xi6d6ROXv8ROQHuNZJAVQ8XzpVPSfHcb2BTar6toh0BqYDC4E7ce4ri73P\nO4r5Akbb5pNP4Je/hIceSltJdTJ2rHP3POkkuPXWtNUYRln5xHs3ASAi2wIxwqDkJM477nFgpJdA\nfj0uifw8T8dIVX3W228O8GQJNBmGYRhGrDF+H3jT+8BmYCYwLMZxA4AHvTF+jwC/V9UHcOMVpovI\nGmBfyjR+wahNbr4Zdt4Zdtgh975GNN/9LqxaBbfckrYSwygrC4B7gW1E5HrgQeCMrEfEI/IdJyID\nReQPAKq6CTeM4j5gFXCTqvqhls4TkZXeu7MROK0EmgzDMAwjvqvnlgNEOgL3q+rkZCRtuY65ehpZ\nUYXx452r5wEHpK2muvn73+Hgg53rZ+/eaasx2hppuHp61+0NTPAW/6GqVRFB01w9DcMw2g6ldPWM\n0+MXpguB6GOGkRaPPAJvvgkzZ6atpPrZc0+YNw9OOSVtJYaRLCKym4jsKiK7AkNwUapfAYZ46wzD\nMAyjJokzxm9lYLEd0BfIOr7PMMrBhRfCiSdCXV3aSmqDH/7Quc3+7ncwZ07aagwjMc4ne1TNKVm2\nGYZhGEbVEiedQ9CJbhOwwUs4axip8dxz8Mc/usAuRmloaICrr3Y9f3vvDb16pa3IMEqPqjamrcEw\nDMMw0iCOq+e7gelDoJuI9PKnRNUZRgZ+/GOXh65bt7SV1Bb77OPG+p16atpKDCNZRKSziJwmIreL\nyG0icqqIdEpbl2HUAh07pq3AMIwo4vT4/RM3DuItb3kr4CWcq4wCI5KRZhjRrFvnIlA++2zufY38\nOe885/J5110we3baagwjMa7FNWhehEtX9EXgOuCwNEUZRi3wSSkSoxiGUXLiGH5LgdtV9W4AEdkf\nOEhVj01UmWFk4Cc/gaOOgq23TltJbdK1K1x1FXzlK/DUU9CzZ9qKDCMRdlTVMYHlB0VkVWpqjJqk\nXz/YsCFtFYZhGI44rp57+kYfgKreA0xMTpJhZOb112HJEjjNMlslypQpLsDLt76VthLDSIx/isie\n/oKITACeSFGPUYN07562AsNo22y1VdoKKos4ht96EfmuiAwTkeEicjawLmlhhhHFBRfAYYfBwIFp\nK6l9Fi2CBx5wQXQMowbZHfiriLwoIi8AfwN295KnryjkhN7Y96UiskZE7heRyP5yEZkhIqtF5FkR\naZU03ht7uNnG0bdk223Lc52+fctznUqkQ4e0FRhGafn859NWkJsePcp3rTiG3zxcCofbgdu8+XlJ\nijKMKNatg8svh7PPTltJ26BbN7jsMjjuOPjww7TVGEbJmYEboz4ZaPTm98dFsj6wwHPOB5aq6ijg\nAW+5BSJSB1ziXX8MME9EdghsHwxMB14sUEPNsuOO5blO+xiDYL7wheR1pEGpDL8hQ0pznraEGd2V\nQbscltGgBDKZi5eaPc5/T7HkNPxU9Q1V/W9gL1Udp6qnqOqbyUszjJZ873vOCLEXSvmYORMmTIDv\nfz9tJYZRWlT1BeAdoDvQy59U9QVvWyEcCCzx5pcAcyP2GQ88511nI3AjEMyc+VPgOwVev+xss03a\nCtIhrfyx06blP769XD2lQUaNap7fddf4x43xRt127lxaPcWSa6x7v37FX6MUcQsqrXfr4IPz23+/\n/Zrn00oplavHv74+uWvvuWfufYolp+EnIhO9Ae+rveXPicjPE1dmGAGWL4e774b5rdrPjaS54AK4\n7jp47LG0lRhG6RCRc4EVwMW4pO7+VAz9VNUP5bEBiKoODgJeDiyv9dYhInOAtapakKtpGvgV9HKP\nZStFRbsc+C35pWDoUOjTp7ly3Lt37mO23hrGj49/DdXCtIXp0wcGDHDzcctg3jz43OfyO8ana9f8\n9s9EJgOvktJT9OmTtgLYfvt4+8Upt112aZ7femt3H5SbYONIrh6/JIkqr1L/18XpVLwA55LyOwBV\nXS4ik0srwzAyowrf/rbrdbKB8uWnTx8XSfW44+DRR8vjimAYZeBwYFtV/TSfg0RkKdA/YlMLJ3RV\nVRGJqkZHVq1FpDNwFs7Nc8vqTDpuuWXBlvkxYxo59dRG7rsvs+44iORf8ff379UL3n03837DhsEL\nL8Q/74wZcO+90du6dIF994Ubboh/vrSoNve9gQPh//6vuHPsvbf7nDwZbryxMOM332N694b338//\nOmH237+w+6pQg3nMGFiVZyzhUhnnhTJwYOvfp3172LTJze+0k4sIHpck6xT9o/6pI+hU4gyuPXrA\nO+/E33+bbeDtt91/G8CqVU2sWtXEdtuVXlssu1ZVXwqt2hTnOBEZLCIPicjTIvKUiPy3tz7WAHjD\nAPfyf/ll+PrX01bSdvnyl11L6M+tr9+oHZ7G5aXNC1WdrqpjI6Y7gQ0i0h9ARAYAr0WcYh0wOLA8\nGNfrty0wDFguIs8D2wBPiEik49Ghhy7YMo0Z05jv14gkV9CsqLEtfo9fror6hAn5aYkymPI1BqZM\nibdfuLcoU6/PsGHZzxPlqldXB7vvHk9HEuQTNGLevNy9C3HO51dU/d+rHIZfEN/N9MADk3XLy4ep\nU1sujx7tPrfbrvxaCmXkSPcZ1UAUdI/M9ZyEyeQ2XYre8riGXz5kM7wPP9x9Bl1Ww0T9v/j/dw0N\n7nPMmEYOPXQBixcvYOHCBQXpzEQcw+8lEZkEICL1IvJt4JmY598InKqqOwITgBO9Qew5B8AbBrig\nIiedBD/9afW1nNYSIs7oO/dcWL8+bTWGURJ+BDzpNT7+3pvuLPKcdwJHevNHAndE7PM4MNKLlF2P\n63m8U1WfUtV+qjpcVYfjjMFdVTXKeEyEXBUtv1ISrKzGrdxHbZ80KXrfmTOzXz8ucXpG+vVrPaZn\n553dZ9jIyWVERH3HQnpR8zl/FMEeglKPRezWLf9jymH4Bff3NXbpUpjb3owZrdflcq+M+o2DPVnh\nxoVCx/PlMrxL6VocJqphyDeyd9qpsHPOmgXDh2fePm5cYecFdx+kERMi6KrquzsHiVuXTcrlNc4j\ncTxwIm4MwjpgnLecE1V9VVWXefPv4wzGQcQbAG8YLFzoBitnqggY5WP0aDj2WMvtZ9QM1wKLvKlU\nY/wWAdNFZA2wr7eMiAwUkT8AqOom4CTgPmAVcJOqRjWmlsyhK+6YoEyVxuC4k4aGlr1Cfut11LEj\nRrRcjjMmDVzlNni+bC7+fi/EHns0r/uv/4p/vSlTWo+r8a8drpCq5j+WbMSI4g2/fIOzJOUKuM8+\nLvhELmMybJwUYowEjaawYe4bc0Edma5RSFlE5X0bOzb/YzZvbp4PN1oUM47Mb5iIIp8Gct8lN1+C\nZT1iREsDZbvt8vu9u3dPzlgdO7bZdTJI3PGJmYjT6+1/p6jfOWzMzprVcrnUrp1hst56ItIeuFBV\nv6iqfVW1j6p+SVXfyPdCIjIMZzQ+QrwB8EYb58kn4Zpr4MIL01Zi+Jx9thvnd//9aSsxjKJ5X1Uv\nUtUHVbXJm/5UzAlV9U1Vnaaqo1R1P1V921u/XlVnBfa7R1W3V9XtVPW8DOcaUWgE7bDB5UdKLJRg\n5XnOnOZW9D32aHb/jFN5K9QgyWT4bLedM87Gjm3phtqli0v9EK4ER1UCIb+KZzajJ3yeI45wlbig\nAZCLqVNbX8MPzhI+fz7lGfceCJ7Td1vzGTTIGWS5Kqbhcs+3Yj97thsfGCTK+A9WwIPXCH6HvfaK\nvkZjY3w9flRSP4JtlHvmbru1Xpftdw/erwce6PITxyWbO25427Rp0fvtuWfr5yEft9NM9165A88E\nG3wgu1HsU2isCN9g22GH3O7b/v0Yda1g41HPnq33STq4TNbTey2TQ0WkqHhGItIVuBU4RVXfC11D\nKWHLplEbbNrkxvQtWlQ90dvaAg0NcNFFcPLJ8MknaasxjKJ4WETOE5E9RWRXf0pbVCkIh8KPqnhH\nVd79/UrlVl9MMK6g5v79o0Osf/7zzmVup51a9tqJRFcAM7lixtEQxQ47ZN4WDICRzUCrr2/pJte3\nb7Ph17FjYWPUoq4XDI0fNlIyBdfIVAHNN9l0rnIMG7rdurW8h0Va94qAC/ATRbbeQp+OHeO70vn3\nll/xj5tPMqr8fDfUYJl06eI0l6KnNo6Rvddebhxe+HrhVBBDhzaPRQxfI+zC6F83yrUyk0t3rlQw\nQX2Z0nuE7504379379wuy1E9uMFrhH9bP69n+Ppjx8Jcz6dx6NCW2/r0ccGEoLyRROPE0vk38Bdv\n7IOfxllV9adxLiAiHXBG33Wq6o932CAi/VX11SwD4FmwYMGW+cbGRhrzaaIxqpoLLnCVhqOOSluJ\nEWb2bLj8cvcbnXFG2mqMaqSpqYmmpqa0ZeyKa3QMhx2JGRKksvArSZ07R1d+OnSAjRtbr+/bF17L\nMYpwwgT485+z7xN1zXCjXbjy5lfwP/oo+7l79mwdHCMbSUY9DBqYw4bBM8844+zTT1uWQbDHKpue\n/v1d5TAYBbF9e3c+v1LoE7fnzD8+SFDD4MHwxBPNy506uXW5tPrsuqsb673bbq53+Xe/a329IOFK\n7cSJ7je9++7m7Z991vq40aNh9erM5w02UITdD+O6FQfJFdzIp6HBGZ0PPph9v06dXJyCIKNGtcxx\nWGqi7pFc5ZiJurrm326rrVqee+BA99/h9175900+BoyfusMnWyP/3LmuLH/3O7c8YgT8+9/uXt9j\nD3jkkWbNmejTB15/3d17s2e3jN46ZIj7H/r3v93yjBnunP5yLjIZoO3aNf/vbbUVvPhi633C80mT\n0fATketU9Su48Xg/w/UO5uXdLiICXAWsUtULApv8AfCLyTwAvoXhZ7Qdnn4aFi92D105HwYjPhde\n6P5sv/SltpvA2SiccEPewoULy65BVRtz7lQFhIOHRFXcReDQQ50nxW9/23JbsKKWqYcqKpontOz5\n8XtZMhmY4NzL3n0X7rvPtZDX1bmeqHXrojUXSvA7DRkCL4XjkuMq32vWZD+PiNP51782a9x77+aw\n9T4jR7r31vjxcNddrc+TzeUvymXMr0TGTWI+frxzwQfXi/WHPzRvy3SOqVPhX/+CtWtdeQVzqeWi\nWzc3jtLvRcz2W02Z0ty74hsgXbu6eyeX8TRuXLTBEnW9cI9v8N6cONEZKi++mD0fbdi9NBtRBkbX\nri1TSnTt2tLwGzYsmSiTQaLKJlyO2Yz7HXZwjRlhevduNvL8nu58GmOiCGrdd9+WvbP77ON6Ql99\ntXldQ4PrEHj3XdfoMHy4M+aef755n6j7vVcv99xmM3579nR1mihDL1vj1JQp8J//ZD5vIf9jEycm\n61GVrcdvNxEZCLyES3BbyN/wJODLwAoRedJbdyZuwPvNInIM8ALwhQLObdQgn34KX/kKnHde63Eq\nRuWw7bbwjW+4/Io33pi2GsMoDBGZDYwBtjg+quo56SnKn6iokdtsA2++2ToCb5RLXyY30Pffdy3w\nGza03g6t3eTq6+GQQ5yW226LPqZ9+9bpHzJVQovptQv2BE2a1NLwmznT9TQFXR+zVc7CFfz6+mb3\nS/+4HXd0blzdujkDI1zu+X6XUoW3P/jgaFfR9u1dJbtv39w564YMccZh2HgNll+Q8Lix/v2bjZ+w\ne10pI3X36+d6VP7yl9bbwi52+VKoG15jI9x8c/Pynnu23idTgvMBA+CVV5qXhw5t2VsEbkzec8+1\nXJfPONDgtgMOyL1Pt26Z3WOLcZmG1r19fmNT+/YtjWn/fvbvYWg2SIcNix5jKOL+E6MM2jh0797a\n8PO/U//+0ca8SO6Gm0wBrJIeJ5nN8Lscl2phBPBEaJt667Oiqn8h8zjCDENOjbbMD3/oXpzHHJO2\nEiMXZ57pAgY89FD8fFmGUSmIyC+Azrjom1cAh+GCj1UlwaiBW23lxvH4lc64lTJ/fvvtnevf3/+e\nn4Z8xqPlqkwXYvjNnZu5txFa9gS1a+fcvUpBXV3zeaPKOp/gLuAqvVHlk6nM4kRj9cszXHGfMCF7\nmoxJk5ybb1SvbBRh99Tgtf0KbT4G7LBhrceTdeoEH3zQfL177nHnzCcaYtzeVGgu91yueeF7Nlf0\n02xjDNu3d8GB/IbVqOchjkHqp40I9lpFaQ+7bPrEfQ6D+5XSU6tr15a94pMnt+5x9w3A8O9fKpdv\nv5c/bHiHOeCAlt99bh75Cvr1Sy59Q5iMhp+qXgRcJCKXq+rx5ZFjtGUefRR+8QtYtsxcPKuBhgb4\n2c/gxBPdb1YpiXINIyYTVXWsiKxQ1YUicj5wb9qi8mXrrZ2xk09FFpr/Y6Mqy/64lLg9HZMmZW71\nzsWYMdG5QQuptHXunF85+D1Qfs/T1lvDG4GY5XGCs8Qh3+N33jk6OE2mcUTFvC+z5VDLl0wVV9/w\nLSTNQ7iXTMT12vq9QMFk2LnKOZPxm4tiAm9Mm1ZckKMwQSN60KDW7srhMi0mj2Ox7/SoRoAghdy3\nwR73YombY7NDh3i909lSvXTs2HrcaSnvi3zIeTub0WeUgw8/dC6eF18cnfDSqEzmznUtshdckHNX\nw6g0fOedD0VkELAJKHoEjoj0EpGlIrLGSw7fM8N+M0RktYg8KyJnBNYvEJG1IvKkN0Wkk25m332b\n89a1PH9urXPntmxNDx8zYULLZNaZelSGDMleGQv+p4crWn36REfQSzJAS5jtt3e9f2HjNey2GEdT\nnJ6gTGSKrukTLie/Uh++Zr6J7nORS3+uSnHnztEJywupwA8Y4MqpZ+RTVRgjRmTOFTxoUOHJ1sHd\n35ncOXOR7RmeNi1zY0uuZ9//vfL5Xf18mZmIumYpf6M45Po+223XMmXFmDHOBTQqcmmc8+XDwQe3\ndOE86KDmNCHlJk5UT8NInPnzXQXkCzbas6oQccb6Hns4t5SoUM6GUaHcJSJbAf9L83CGK0pw3vnA\nUlX9sWfQzfemLYhIHXAJbsjDOuAxEbnTS+SuwE/jRs4O90b4lZU4rleZ0j745+zUqdnYmzu3sArs\n5MktW7qj3B633971tD37bPO6Uhsv2WjXrvX4s8MPL6ynJ1Mi+2efze7yOXly9t6ZcC/V8OHOKNmw\nobmH1nfl23vv6CiZcYiq7OZKWj9tWvbv1r497Ldf6/VdurhyvvXWeNoOOSR7GfmpPTKRqSLf0JA5\nRcU++8TTlu385WDXXeGf/8z8rI8f7wKG9OuX/dnadltn8K1c6Za33rqlK3MpKbdn1/DhLXu4o3rV\nu3XLHF20b9/sLt35kHSS9myY4Wekzh//CLffDitWpK3EKIRtt3V5/U49Nf4L3DDSJhDE5VYRuQvo\npKrvlODUBwJ+fMAlQBMhww8YDzynqi8AiMiNwBzADz9QdJUoV8UkUyV1//2jK3n5upL6hEPkNzS0\nbmH3K2Tvv9+su67ONSaFw+EnSdDQC87nU6GPMkx69nQGzscfu+nhh1sGrID4qQR8JgSSkIRd1tq3\nb917WIxRMm5c9sTY+dwbQ4a0dHHLx7jO1UNYV+dSY+RLpQ0t6d69uTdv3jznztmnT3R0Wp+gITF5\nsvu9g1Ey495f3bs749k3/IYMqd4G3ULu+Wzjfnv1ytwzXE2UMWWgYbTm7bfh6KPhqquyJ8w0Kpsz\nzoDly1uGETeMSkZEDhMRvwr6HeCaEiVw76eqfizMDUBU+/Eg4OXA8lpvnc/JIrJcRK7K5Cqai3bt\nnAfFhAnxc5qJOCMlyYpwu3bNibDDNDa2DKkv0trdMklGj47umcrWixRmt91auscG6dTJlW8wgmIp\nyjrp3oN27UoXgXPSpNwurUmRdI9c0EAqJDJjz57OeJ01q6VL4qhRuetHwe82YIAz9HKVs39MrrF4\ncSjEbbfSDO62ghl+RqqccoprYYl62RrVQ6dOLqn7N77hcuwYRhXwfVV9V0T2AqYCV+OiWefEG8O3\nMmI6MLifqirOdTNMtiroZcBwYBfgFeD8qJ3CronN2prn6+pcT1q4V6VbN2egBBkxovSJpSutYpdL\nT/v20eO58kkGXl8fvxGzY8fiA1UceqgzMuIGNonL+PGFa0qDUt9re++d/zWCDRpRqRtyMW6c+z3L\nTSnG4nXt2jxUp1On9AKXlJLBgzPHnBg0qLDeZUiv4WPL9dO9vNGWueMOlxh32bK0lRilYNo0F2Ti\nO99xRqBhVDj+KKjZwBWqepeInBvnQFWdnmmbiGwQkf6q+qqIDABei9htHTA4sDwY1+uHqm7ZX0Su\nBH4fdZ077ljAW2+5JNyNjY00NjYya1Y817mxY1u7b+24Y+6xXJVCWgZlKXuM9tuvcPfZIKXMhRdk\n222TOW8UU6fmn/IiaXI9C127urLfuBF22aXltnbtCuupjhOYJRPFRB4tFb6bs99r6RP8TvX1Ll9z\nNTBoUHM+wTD19fl5AvjEjSjb1NREU1NT/heIgRl+Riq8/rrrHfrtb6unsmHk5ic/cX+GltvPqALW\nicgvgenAIhHpRGm8YO4EjgQWe593ROzzODBSRIYB64HDgXkAIjJAVf3UzQcBK6MuctxxC3juuZYV\niTit7AcdlLxr4OGHw003JXf+NINolIpiIkVGMXRoacZDplG2mZLBl5p8vlvPnq09kYJGdseOrnfu\nhhvyS5qeBJMm5dcrnSaHHOLKDJJtwBkxIjrqabXgN+b5LFy4sGTnNsPPKDuqcPzxLn3DXnulrcYo\nJT16wGWXwde+5oL1lHN8jmHkyReAGcD/qurbXu/c6SU47yLgZhE5BnjBuw4iMhDXszhLVTeJyEnA\nfUAdcJUX0RNgsYjsgnMHfR44LuoihVaayhFNLirhddqMGZN/AJUgw4e71DVB8sl1mDRh1922Rpye\nz3zfR2HjvEOH8iXZzodCXTXLZaAW89zlQ329M8iHDXORxo1ozPAzys5vfgOrV7tPo/aYPRtuvhm+\n+U24ohTB8Q0jAVT1A+DWwPIruDF1xZ73TVyahvD69cCswPI9wD0R+321WA1Ga4YObVlBzjexdTCK\npk99vevdrAYKzSVXDRx8cLzvN3hweVJG1UKPNJSu4aZdO/e8hVOMlLJhaM4c16jVrl1h4yvbEhXS\nVmW0FZ5/3oX9/81v0s1jYiTLpZfCn/4E11+fthLDqE2GDHHJh438mTUr89idWmXgQOdmV4vkY9Tm\na/BXCw0NLSPixqFHj5YpH4JMneryayZJKQ2/hobK6X2vdKzHzygbmzY5987581sPhjZqi27dXK/f\n9Omw++6ljxZoGG2dvn0zV9oqhaQq2YVUGIPH1ELEwUIoNoKoUdnk61LZsaMz8KIo9X9LrfSC1gKJ\n2scicrUX4WxlYF0vLxT2GhG5v9AcRUb1sWiR6+U79dS0lRjlYJdd4JxznGvNxx+nrcYwjHJy4IHJ\nBO7q0iX/nK+jR1sQsbhYr0n+ZEqtYkRTzUFXaoGkH/FrcIPng8wHlqrqKOABb9mocf76V7j4Yliy\nxF4sbYnjj3dBFY48svLCdRuG0UypA7EkFdhp9mwXxTAfxo2rXRe/UjNsmEvLY8Rj3ryWbsONjW4y\nMuO7pFZS8Ke2RKJVcFV9GHgrtPpAYIk3vwSYm6QGI31efhkOOwx+9au2N66irSMCV18Nr7zi8vsZ\nhlF5NDZWTwTedu2swpgkIuVLr1CLDBiQOel3KUg7+XcpsOc3XdK4hfqp6gZvfgPQLwUNRpn46COX\nN+qUU2D//dNWY6RBp05wxx2ulX7oUDj55LQVGYYRJMmKqmFUOtViiBxwQLy0FdVCtZR7rZFq24Gq\nqojYkM8aRRWOPRZGjrTenrZOr15wzz3O+Ove3bl+GoZhGEaa1Ne3ztdXkop1jwAAEL5JREFUqdg4\nVaMUpGH4bRCR/qr6qpcw97VMOy5YsGDLfDiLvVHZqMLpp8Mzz8Cf/2wtO4YbO/LAAy7S5wcfwAkn\npK3ISIumpiaamprSllFyRKQXcBMwFC95u6q+HbHfDOACXPL2K1V1cWDbycAJwGfAH1T1jDJIN4w2\nSa2muKhk/Pqg1QvTQTThGKsiMgz4vaqO9ZZ/DLyhqotFZD7QU1VbBXgREU1am5EMqvCtb8HDD8P9\n99t4AaMlzz8P06a53uAzrEprACKCqlZ9NcB7v/1HVX8sImcAW4XfbyJSB/wLl+R9HfAYME9VnxGR\nKcBZwExV3SgifVT19Yjr2PvRMAxuuAFmznQ5+SqZd991n34qlRtucLEfamHMYjko5Tsy6XQONwB/\nA7YXkZdF5ChgETBdRNYA+3rLRo2weTN885suiufSpWb0Ga0ZPtz1Al93HXz965bqwagp4gQvGw88\np6ovqOpG4EZgjrftG8B53nqijD7DMIwg1RCxtnv3tps/s9JIOqrnPFUdqKr1qjpYVa9R1TdVdZqq\njlLV/aLcYIzq5M03Xe6mJ55wPX355loy2g6DBsHf/w5vvw377OMivxpGDRAneNkgIHjHr/XWAYwE\n9hGRf4hIk4jsnpxUwzCqnTlzbOyfkR+WUc0oCY89BrvtBqNGwUMPQc+eaSsyKp1u3eDmm12C9/Hj\n4dZb01ZkGLkRkaUisjJiOjC4n+eLGeWPmc1Hsz3OPXQCcDpwc+mUG4ZRazQ0pK3AqDbMu9Yoio8+\ngh/9CH7xC7j8cjj44LQVGdWECHz72zBxIhx9NNx0E1xyCfTtm7Yyw4hGVadn2iYicYKXrQMGB5YH\n43r98D5v867zmIhsFpGtVfWN8Eks+JlhGNXK8OHV4aKaFkkGQEs8uEuh2OD1yufee+HEE11P3wUX\nwMCBaSsyqpmPPoIFC2DJEjjnHDjmGHsxtBVqLLhL1uBlItIeF9xlKrAeeJTm4C7HAQNV9QciMgr4\no6oOibiOvR8NwzDaCKV8R5rhZ+TN00+7vHz/+hdcfLElZjdKy7JlcMop8M47rkHBOjJqnxoy/Hrh\n3DOHEEjnICIDgStUdZa33/40p3O4SlXP89Z3AK4GdgE+BU5T1aaI69j70TAMo41ghp+RCq+8AgsX\nwm23wZlnujxsHTumrcqoRVTdmL/TT4exY+G882DHHdNWZSRFrRh+5cLej4ZhGG2HqknnYNQG77wD\n3/0u7LQTdOkCq1fDqaea0Wckhwgceqi716ZMcdMxx8DatbmPNQzDMAzDMFpjhp+RkY8+gp/8BEaO\nhHXr4Mkn4fzzLTefUT46dnSNDGvWuIAvn/sczJ/v0kAYhmEYhmEY8THDz2jFJ5/AZZfBdtu5XGsP\nPQTXXANDWoUYMIzy0LOnc/dcsQLeeMOlDTn/fEv+bhiGYRiGERcz/IwtfPwxXHqpM/juvBPuuMON\ns7KxVUalMGgQXHEFNDXBn/4Eo0fDr38NmzenrcwwDMMwDKOyseAuBv/5j8vDd+mlLjXD978Pn/98\n2qoMIzd//rOLMPvhhy6f5KxZbnygUV1YcJf8sPejYRhG28GiehpFowqPPgpXXQW33AIHHeTGUu20\nU9rKDCM/VF0P9VlnQY8ecPbZMHOmGYDVhBl++WHvR8MwjLaDGX5GwaxZA7ffDtdeCxs3wlFHwdFH\nQ79+aSszjOL47DPXiPGjH7nl00+HQw6Bzp3T1WXkxgy//LD3o2EYRtuhJgw/EZlBcwLbK1V1cWi7\nvdhKwHvvwV//6gK03HUXvPkmzJ0L8+bB3ntbr4hRe6jC3XfDxRfDY4/BEUfAl78M48dDXV3a6owo\nasnw85K43wQMJZDEPWK/yHegiNwIbO/t1hN4W1XHhY6196NhGEYboerz+IlIHXAJMAMYA8wTkR3S\n0JIETU1NqVz3jTeckXfZZfD1r7vxegMGuGiInTq5oBjr1rnt++yT2ehLS38pqGbtYPpLgYgb63fv\nvS4FSb9+cNxxLh3EEUfAz3/unpN33215XCVoL4Zq119DzAeWquoo4AFvuQXZ3oGqeoSqjvOMvVu9\nqaao5nu1mrWD6U+TatYO1a2/mrWXmrSieo4HnlPVF1R1I3AjMCclLSUnqRts40Z48UUX0OLaa2Hh\nQvjqV2HSJOjTB0aMgNNOg8cfh3HjXLCW11930Q8XLoSJE6FdjF+8mh+QatYOpr/UDBnighWtWOGm\n/faDZcvcczJwoJv22AMOOwzmz29i0SL41a/gvvtg+XJ47bXqiRhaaWXfhjkQWOLNLwHmRuyT8x0o\nIgJ8AbghQa2pUM33ajVrB9OfJtWsHapbfzVrLzXtU7ruIODlwPJaYI+UtCTC5s3w6adu2rjRTcH5\nTz5pnj76yEUl/OADeOcdN739tqt0vv46vPqq66l74w3XazFsGAwdCsOHw5Qp8LWvuRQMAwaY66Zh\nZGLQIDee9eij3fJnn7ln66WXXIPKNdc4V+inn3brX3nFTe+9B/37OyOxf3/Xg9ivH/TuDb16ual7\nd+ja1U2dO7se9k6dXAL6ujp7LtsY/VR1gze/AYgaQR3nHbg3sEFV/6/0Eg3DMIy2SFqGX80OTpgw\nwUXLPOcc6NAB6uvdZ3i+Y0c31ddDly6ustjQ4KIS9ujhElaPGuV68vr1c5XW/v2hfVq/mGHUGHV1\n7rkaNAj23BNWr4YFC1rv9/HHzhBcv959btjgpmefdYbim2864/C99+D9993+H3/sGnQ+/dQ1AnXs\n2Pwf4P8PBP8P2rd3n3V1bmrXzhmL/uQP51J159u82Rmun30Gmza55fXr4be/dfOqblq82I3pNUqL\niCwF+kdsOju4oKoqIlHvuzjvwHnA9QXIMwzDMIxIUgnuIiITgAWqOsNbPhPYHAzwkuFlaRiGYdQg\nNRTcZTXQqKqvisgA4CFVHR3aJ+s7UETa43oBd1XV9RHXsPejYRhGG6JU78i0+o8eB0aKyDBgPXA4\nrnVzC7VSCTAMwzDaFHcCRwKLvc87IvbJ9Q6cBjwTZfSBvR8NwzCMwkgluIuqbgJOAu4DVgE3qeoz\naWgxDMMwjBKyCJguImuAfb1lRGSgiPwBYr0DD6cGg7oYhmEY6VKxCdwNwzAMwzAMwzCM0pBWOgdE\npJeILBWRNSJyv4j0zLDfDBFZLSLPisgZgfU3isiT3vS8iDxZPvXF6/e2nSwiz4jIUyKyOOr4JChB\n2S8QkbWB8p9RLu3e9Ysue2/7aSKy2Uu4XDZKUP7nishyEVkmIg+IyOAq0v6/3j2/XERuE5Ee5dLu\nXb9Y/YeJyNMi8pmI7FomzVnvY2+fi7zty0VkXD7HJk2R+q8WkQ0isrJ8iiubSvhNcyEiL4jICu/9\n8Ki3LuOzJyJnet9ntYjsl4LeVvdZIXpFZDcRWeltuzBF7eF39P6VqN277mARecj7X31KRP7bW1/x\n5Z9Fe1WUv4h0EpFHxNUlVonIed76aij7TNqrouwD167zdP7eW06+7FU1lQn4MfAdb/4MYFHEPnXA\nc8AwoAOwDNghYr+fAN+tJv3AFGAp0MFb7lNF2n8AfKua7x1gMHAv8DzQq5r0A90C+50MXFlF2qcD\n7bz5RVHHV7j+0cAo4CFc4I2k9eb8DwRmAnd783sA/4h7bCXr95b3BsYBK8upu1KnSvhNY+ps9b+a\n6dnDJbBf5n2fYd73a1dmva3uszz1+t5TjwLjvfm7gRkpaY98R1eadu9a/YFdvPmuwL+AHaqh/LNo\nr6byb/A+2wP/APaqhrLPor1qyt673reA3wB3esuJl31qPX5Uf5LbYvV/AzjPW4+qvp6w3iClKPs0\ngwuUQv9Pge8kqjIzRelX1fcC+3UF/pOg1jDFal+qqn5K9EeAbRLWG6ZY/atVdU1ZlObQEmDLd1LV\nR4CeItI/5rFJU4x+VPVh4K0y6q10KuE3jUv4HZHp2ZsD3KCqG1X1BVyFZnxZFHpkuM/y0buHuAiu\n3VT1UW+/a4n+fykpWZ6RqHd0RWkHUNVXVXWZN/8+8Awuz2XFl38W7VA95f+hN1uPa1h6iyoo+yza\noUrKXkS2wTV8Xkmz5sTLPk3Dr9Akt4NC+6SV5LZY/SOBfUTkHyLSJCK7Jye1FaUo+5PFuWVdJRnc\n5RKkKP0iMgdYq6orElWZmaLLX0T+R0RewkUNXJSU0AhK9dwCHI1rnSonpdRfDuJoybTPwBjHJk0x\n+o3WVEtZKfBHEXlcRL7urcv07A3EfQ+fSvlO+eoNr19Hut8j6h1d0drFRbkdh2sUrKryD2j/h7eq\nKspfRNqJyDJcGT+kqk9TJWWfQTtUSdkDPwNOBzYH1iVe9ommc5AqT3KbsP72wFaqOkFEPg/cDIwo\nWGyIhLVfBpzjzZ8LnA8cU4jOTCSlX0Q6A2fhXA63rC5UZyaSvvdV9WzgbBGZj/vzOKpQrWHK8dyK\nyNnAp6pa8me3TP875SKulkoN71+o/kr6DSqJaimXSar6ioj0AZaKy224hSzP3pZdkpWXHzH0VhqJ\nv6NLjYh0BW4FTlHV95wzl6PSy9/TfgtO+/siUjXl73ng7CJuvP19IjIltL1iyz5CeyNVcu+LyGzg\nNVV90tPdiqTKPlHDT1WnZ9ombjByf21OcvtaxG7rcGOxfAYTsGzFJbk9CEgkyELC+tcCt3nXeUxc\nkJGtVfWNSteuqlv2F5Ergd+XQnOQBPVvi/OPXu69WLYBnhCR8cHvVcH6w1xPiXvNyvDc/j+ce8PU\n0ihuSRnLvhzE0RLeZxtvnw4xjk2aQvWvS1hXtVJJ92ZGVPUV7/N1Ebkd57qZ6dmr1N8/H71rvfXb\nhNan8j2yvKMrUruIdMAZfdepqp/3sirKP6D91772ait/AFV9R1y6md2okrL3CWjfXVWb/PUVXvYT\ngQNFZCbQCeguItdRhrJP09XTT3ILMZLcikg9LrfRnYHtWZPcJkyx+u/A5XhCREYB9aUy+mJQlHbv\nZvQ5CCh3xL2C9avqU6raT1WHq+pw3IOzaymNvhgUW/4jA/vNAcoZ0bZY7TNwrg1zVPXjMugNU4r/\nHZ9y9LLF0XIn8FUAEZkAvO25isT9HklSjH6jNZXwm2ZFRBpEpJs33wXYD/eOyPTs3QkcISL1IjIc\nNwziUdInL72q+irwrojsIa5V8StE/78kTpZ3dMVp9653FbBKVS8IbKr48s+kvVrKX0R6i+cKKc4b\najquPlENZR+pXbzx4R4VW/aqepaqDvbqoUcAD6rqVyhH2WuZIteEJ6AX8EdgDXA/0NNbPxD4Q2C/\n/XGRkp4Dzgyd4xrg2GrUj2uNvw53Uz4BNFaR9muBFcBy7wbrV01lHzrXvyl/VM9iy/8W775Zhmtp\n7FtF2p8FXsS9XJ4Efl5lZX8QbozVR8CrwD1l0NxKC3AccFxgn0u87csJRBuN8wxUuP4bgPXAJ165\nH5XGd6ikqRJ+0xz6hnv/TcuApwK/eeSz5207y/s+q4H/SkGzf5996t9nhejF9Zas9LZdlJL2o8ny\njq4k7d5198KNcVoWeC/MqIbyz6B9/2opf2As8E9P/wrgdG99NZR9Ju1VUfah7zKZ5qieiZe9JXA3\nDMMwDMMwDMOocdJ09TQMwzAMwzAMwzDKgBl+hmEYhmEYhmEYNY4ZfoZhGIZhGIZhGDWOGX6GYRiG\nYRiGYRg1jhl+hmEYhmEYhmEYNY4ZfoZhGIZhGIZhGDWOGX6GYRiGYRiGYRg1jhl+hmEYhmEYhmEY\nNc7/B5DbBL9cIxJxAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f0fee73f3d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"samples = fit.extract(permuted=True)\n",
"MCMCIntervalB = np.percentile(samples['theta'].transpose()[0],[2.5,97.5])\n",
"MCMCIntervalW = np.percentile(samples['theta'].transpose()[1],[2.5,97.5])\n",
"fit.plot().show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Estimating rough 95% credible intervals:"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.055, 0.075]\n",
"[0.085, 0.109]\n"
]
}
],
"source": [
"print map(lambda x: round(x,3),MCMCIntervalB)\n",
"print map(lambda x: round(x,3),MCMCIntervalW)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So, this method gives a result that fits quite nicely with previous results, while allowing more flexible specification of priors.\n",
"\n",
"Interval for sampled differences in proportions:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[-0.047, -0.017]\n"
]
}
],
"source": [
"print map(lambda x: round(x,3),np.percentile(samples['diff'],[2.5,97.5]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And this interval does not include 0, so that we're left fairly confident that black-sounding names get less call-backs, although the estimated differences in proportions are fairly small (significant in the technical sense isn't really the right word to describe this part)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Accounting for additional factors:\n",
"\n",
"A next step here would be to check whether other factors influence the proportion of call-backs. This can be done using logistic regression, although there will be a limit to the complexity of the model to be fit, given that the proportion of call-backs is quite small, potentially leading to small cell-counts and unstable estimates (one rule of thumb being n>30 per cell is reasonably safe)."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"Index([u'id', u'ad', u'education', u'ofjobs', u'yearsexp', u'honors',\n",
" u'volunteer', u'military', u'empholes', u'occupspecific', u'occupbroad',\n",
" u'workinschool', u'email', u'computerskills', u'specialskills',\n",
" u'firstname', u'sex', u'race', u'h', u'l', u'call', u'city', u'kind',\n",
" u'adid', u'fracblack', u'fracwhite', u'lmedhhinc', u'fracdropout',\n",
" u'fraccolp', u'linc', u'col', u'expminreq', u'schoolreq', u'eoe',\n",
" u'parent_sales', u'parent_emp', u'branch_sales', u'branch_emp', u'fed',\n",
" u'fracblack_empzip', u'fracwhite_empzip', u'lmedhhinc_empzip',\n",
" u'fracdropout_empzip', u'fraccolp_empzip', u'linc_empzip', u'manager',\n",
" u'supervisor', u'secretary', u'offsupport', u'salesrep', u'retailsales',\n",
" u'req', u'expreq', u'comreq', u'educreq', u'compreq', u'orgreq',\n",
" u'manuf', u'transcom', u'bankreal', u'trade', u'busservice',\n",
" u'othservice', u'missind', u'ownership'],\n",
" dtype='object')"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data.columns"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>race</th>\n",
" <th>b</th>\n",
" <th>w</th>\n",
" </tr>\n",
" <tr>\n",
" <th>computerskills</th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>408</td>\n",
" <td>466</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>2027</td>\n",
" <td>1969</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"race b w\n",
"computerskills \n",
"0 408 466\n",
"1 2027 1969"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# The data is balanced by design, and this mostly isn't a problem for relatively simple models.\n",
"# For example:\n",
"pd.crosstab(data.computerskills,data.race)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import statsmodels.formula.api as smf"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Checking to see if computer skills have a significant effect on call-backs:"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Optimization terminated successfully.\n",
" Current function value: 0.277880\n",
" Iterations 7\n"
]
},
{
"data": {
"text/html": [
"<table class=\"simpletable\">\n",
"<caption>Logit Regression Results</caption>\n",
"<tr>\n",
" <th>Dep. Variable:</th> <td>call</td> <th> No. Observations: </th> <td> 4870</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Model:</th> <td>Logit</td> <th> Df Residuals: </th> <td> 4867</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Method:</th> <td>MLE</td> <th> Df Model: </th> <td> 2</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Date:</th> <td>Mon, 09 Nov 2015</td> <th> Pseudo R-squ.: </th> <td>0.007469</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Time:</th> <td>20:23:07</td> <th> Log-Likelihood: </th> <td> -1353.3</td> \n",
"</tr>\n",
"<tr>\n",
" <th>converged:</th> <td>True</td> <th> LL-Null: </th> <td> -1363.5</td> \n",
"</tr>\n",
"<tr>\n",
" <th> </th> <td> </td> <th> LLR p-value: </th> <td>3.779e-05</td>\n",
"</tr>\n",
"</table>\n",
"<table class=\"simpletable\">\n",
"<tr>\n",
" <td></td> <th>coef</th> <th>std err</th> <th>z</th> <th>P>|z|</th> <th>[95.0% Conf. Int.]</th> \n",
"</tr>\n",
"<tr>\n",
" <th>Intercept</th> <td> -2.4772</td> <td> 0.132</td> <td> -18.728</td> <td> 0.000</td> <td> -2.736 -2.218</td>\n",
"</tr>\n",
"<tr>\n",
" <th>race[T.w]</th> <td> 0.4324</td> <td> 0.107</td> <td> 4.025</td> <td> 0.000</td> <td> 0.222 0.643</td>\n",
"</tr>\n",
"<tr>\n",
" <th>computerskills</th> <td> -0.2418</td> <td> 0.129</td> <td> -1.875</td> <td> 0.061</td> <td> -0.495 0.011</td>\n",
"</tr>\n",
"</table>"
],
"text/plain": [
"<class 'statsmodels.iolib.summary.Summary'>\n",
"\"\"\"\n",
" Logit Regression Results \n",
"==============================================================================\n",
"Dep. Variable: call No. Observations: 4870\n",
"Model: Logit Df Residuals: 4867\n",
"Method: MLE Df Model: 2\n",
"Date: Mon, 09 Nov 2015 Pseudo R-squ.: 0.007469\n",
"Time: 20:23:07 Log-Likelihood: -1353.3\n",
"converged: True LL-Null: -1363.5\n",
" LLR p-value: 3.779e-05\n",
"==================================================================================\n",
" coef std err z P>|z| [95.0% Conf. Int.]\n",
"----------------------------------------------------------------------------------\n",
"Intercept -2.4772 0.132 -18.728 0.000 -2.736 -2.218\n",
"race[T.w] 0.4324 0.107 4.025 0.000 0.222 0.643\n",
"computerskills -0.2418 0.129 -1.875 0.061 -0.495 0.011\n",
"==================================================================================\n",
"\"\"\""
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"glm = smf.Logit.from_formula(formula=\"call~race+computerskills\",data=data).fit()\n",
"glm.summary()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The effect might be described as [marginal](https://mchankins.wordpress.com/2013/04/21/still-not-significant-2/), but probably best not to over-interpret. But maybe the combination of race and computer skills makes a difference? Apparently not in this data (not even an improvement to the model log-likelihood or other measures of model fit):"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Optimization terminated successfully.\n",
" Current function value: 0.277831\n",
" Iterations 7\n"
]
},
{
"data": {
"text/html": [
"<table class=\"simpletable\">\n",
"<caption>Logit Regression Results</caption>\n",
"<tr>\n",
" <th>Dep. Variable:</th> <td>call</td> <th> No. Observations: </th> <td> 4870</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Model:</th> <td>Logit</td> <th> Df Residuals: </th> <td> 4866</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Method:</th> <td>MLE</td> <th> Df Model: </th> <td> 3</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Date:</th> <td>Mon, 09 Nov 2015</td> <th> Pseudo R-squ.: </th> <td>0.007645</td> \n",
"</tr>\n",
"<tr>\n",
" <th>Time:</th> <td>20:23:20</td> <th> Log-Likelihood: </th> <td> -1353.0</td> \n",
"</tr>\n",
"<tr>\n",
" <th>converged:</th> <td>True</td> <th> LL-Null: </th> <td> -1363.5</td> \n",
"</tr>\n",
"<tr>\n",
" <th> </th> <td> </td> <th> LLR p-value: </th> <td>0.0001133</td>\n",
"</tr>\n",
"</table>\n",
"<table class=\"simpletable\">\n",
"<tr>\n",
" <td></td> <th>coef</th> <th>std err</th> <th>z</th> <th>P>|z|</th> <th>[95.0% Conf. Int.]</th> \n",
"</tr>\n",
"<tr>\n",
" <th>Intercept</th> <td> -2.5702</td> <td> 0.193</td> <td> -13.340</td> <td> 0.000</td> <td> -2.948 -2.193</td>\n",
"</tr>\n",
"<tr>\n",
" <th>race[T.w]</th> <td> 0.5794</td> <td> 0.240</td> <td> 2.418</td> <td> 0.016</td> <td> 0.110 1.049</td>\n",
"</tr>\n",
"<tr>\n",
" <th>computerskills</th> <td> -0.1268</td> <td> 0.213</td> <td> -0.595</td> <td> 0.552</td> <td> -0.545 0.291</td>\n",
"</tr>\n",
"<tr>\n",
" <th>race[T.w]:computerskills</th> <td> -0.1850</td> <td> 0.268</td> <td> -0.690</td> <td> 0.490</td> <td> -0.711 0.341</td>\n",
"</tr>\n",
"</table>"
],
"text/plain": [
"<class 'statsmodels.iolib.summary.Summary'>\n",
"\"\"\"\n",
" Logit Regression Results \n",
"==============================================================================\n",
"Dep. Variable: call No. Observations: 4870\n",
"Model: Logit Df Residuals: 4866\n",
"Method: MLE Df Model: 3\n",
"Date: Mon, 09 Nov 2015 Pseudo R-squ.: 0.007645\n",
"Time: 20:23:20 Log-Likelihood: -1353.0\n",
"converged: True LL-Null: -1363.5\n",
" LLR p-value: 0.0001133\n",
"============================================================================================\n",
" coef std err z P>|z| [95.0% Conf. Int.]\n",
"--------------------------------------------------------------------------------------------\n",
"Intercept -2.5702 0.193 -13.340 0.000 -2.948 -2.193\n",
"race[T.w] 0.5794 0.240 2.418 0.016 0.110 1.049\n",
"computerskills -0.1268 0.213 -0.595 0.552 -0.545 0.291\n",
"race[T.w]:computerskills -0.1850 0.268 -0.690 0.490 -0.711 0.341\n",
"============================================================================================\n",
"\"\"\""
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"glm2 = smf.Logit.from_formula(formula=\"call~race*computerskills\",data=data).fit()\n",
"glm2.summary()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But, there's still rather a lot of stuff left to explore in this data."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-2.0 |
analysiscenter/dataset | batchflow/tests/notebooks/tfmodel_test.ipynb | 1 | 11953 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2019-08-19T09:50:07.420782Z",
"start_time": "2019-08-19T09:50:00.419642Z"
}
},
"outputs": [],
"source": [
"%load_ext autoreload\n",
"%autoreload 2\n",
"import os\n",
"import sys\n",
"import warnings\n",
"\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import tensorflow as tf\n",
"\n",
"sys.path.append(\"../../..\")\n",
"from batchflow import *\n",
"from batchflow.opensets import MNIST\n",
"from batchflow.models.tf import *\n",
"\n",
"tf.logging.set_verbosity(tf.logging.ERROR)\n",
"warnings.filterwarnings(\"ignore\")\n",
"os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Setup"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2019-08-19T09:50:08.741769Z",
"start_time": "2019-08-19T09:50:07.423134Z"
}
},
"outputs": [],
"source": [
"mnist = MNIST(batch_class=ImagesBatch)\n",
"\n",
"if __name__ == '__main__':\n",
" MICROBATCH = None\n",
" DEVICE = None\n",
"\n",
"print('\\nMicrobatching is: {}'.format(MICROBATCH))\n",
"print('\\nDevice is: {}'.format(DEVICE)) "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2019-08-19T09:50:08.791975Z",
"start_time": "2019-08-19T09:50:08.744078Z"
}
},
"outputs": [],
"source": [
"def get_classification_config(model_class, config):\n",
" default_config = {\n",
" 'inputs/images/shape': (28, 28, 1),\n",
" 'inputs/labels/classes': 10,\n",
" 'initial_block/inputs': 'images',\n",
" 'loss': 'ce',\n",
" 'microbatch': MICROBATCH,\n",
" 'device': DEVICE,\n",
" }\n",
"\n",
" pipeline_config = {\n",
" 'model': model_class,\n",
" 'model_config': {**default_config, **config},\n",
" 'feed_dict': {'images': B('images'),\n",
" 'labels': B('labels')},\n",
" }\n",
" return pipeline_config\n",
"\n",
"def get_segmentation_config(model_class, config):\n",
" default_config = {\n",
" 'inputs/images/shape': (28, 28, 1),\n",
" 'inputs/masks/shape': (28, 28, 1),\n",
" 'initial_block/inputs': 'images',\n",
" 'body/decoder/blocks/combine_op': 'softsum', # for some reason `concat` is not working from within pytest \n",
" 'loss': 'mse',\n",
" 'microbatch': MICROBATCH,\n",
" 'device': DEVICE,\n",
" }\n",
" \n",
" pipeline_config = {\n",
" 'model': model_class,\n",
" 'model_config': {**default_config, **config},\n",
" 'feed_dict': {'images': B('images'),\n",
" 'masks': B('images')},\n",
" }\n",
" return pipeline_config"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2019-08-19T09:50:08.839789Z",
"start_time": "2019-08-19T09:50:08.798160Z"
}
},
"outputs": [],
"source": [
"def get_pipeline(pipeline_config):\n",
" \"\"\" Pipeline config must contain 'model', 'model_config', 'feed_dict' keys. \"\"\"\n",
" pipeline = (Pipeline(config=pipeline_config)\n",
" .init_variable('loss_history', [])\n",
" .multiply(multiplier=1/255., preserve_type=False)\n",
" .to_array()\n",
" .init_model('dynamic', C('model'),\n",
" 'MODEL', config=C('model_config'))\n",
" .train_model('MODEL', fetches='loss',\n",
" feed_dict=C('feed_dict'),\n",
" save_to=V('loss_history', mode='a'))\n",
" )\n",
" return pipeline"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2019-08-19T09:50:08.871723Z",
"start_time": "2019-08-19T09:50:08.842370Z"
}
},
"outputs": [],
"source": [
"def run(task, model_class, config, description, batch_size=16, n_iters=10):\n",
" if task.startswith('c'):\n",
" pipeline_config = get_classification_config(model_class, config)\n",
" elif task.startswith('s'):\n",
" pipeline_config = get_segmentation_config(model_class, config)\n",
" \n",
" train_pipeline = get_pipeline(pipeline_config) << mnist.train\n",
" _ = train_pipeline.run(batch_size, n_iters=n_iters, bar=True,\n",
" bar_desc=W(V('loss_history')[-1].format('Loss is {:7.7}')))\n",
" \n",
" print('{} {} is done'.format(task, description))\n",
" return train_pipeline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Classification"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-04T09:12:20.455897Z",
"start_time": "2020-02-04T09:12:19.224361Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'initial_block': {'layout': 'S>>r' + 'fa'*2,\n",
" 'units': [64, 128],\n",
" 'attention_mode': 'scse',\n",
" 'reshape_to': (28, 14, 2)},\n",
" 'body': {'layout': 'fa'*2,\n",
" 'units': [256, 512]},\n",
" 'head': {'layout': 'faf',\n",
" 'units': [600,10]},\n",
"}\n",
"\n",
"ppl = run('classification', TFModel, config, 'simple fc')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-03T07:40:59.308835Z",
"start_time": "2020-02-03T07:40:44.695229Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'body/block/se_block': {'ratio':8},\n",
" 'head/layout': 'f'\n",
"}\n",
"\n",
"ppl = run('classification', ResNet18, config, 'ResNet18')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-03T07:06:11.018342Z",
"start_time": "2020-02-03T07:05:52.039725Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'head/layout': 'f'\n",
"}\n",
"\n",
"ppl = run('classification', XceptionS, config, 'Xception')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"ppl = run('classification', MobileNet_v3_small, {}, 'MobileNet_v3_small')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Segmentation"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-04T09:12:51.059150Z",
"start_time": "2020-02-04T09:12:20.791711Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'initial_block/filters': 4,\n",
" 'body/encoder': {'num_stages': 3},\n",
" 'body/decoder/blocks/combine_op': 'attention',\n",
"}\n",
"\n",
"ppl = run('segmentation', UNet, config, 'unet')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-03T07:37:10.920096Z",
"start_time": "2020-02-03T07:36:57.661643Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'initial_block': {'layout': 'cna', 'filters': 2},\n",
" 'body/encoder': {'base': ResNet18,\n",
" 'filters':[4]*4,\n",
" 'downsample': [[]] + [[0]]*4},\n",
" 'body/embedding': [{'layout': 'cna', 'filters': 16}]*4,\n",
"}\n",
"\n",
"ppl = run('segmentation', EncoderDecoder, config, 'encoder-decoder with ResNet18 backbone')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-03T07:38:10.811772Z",
"start_time": "2020-02-03T07:37:10.921740Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'initial_block': {'layout': 'cna', 'filters': 4},\n",
" 'body/encoder': {'base': ResNet,\n",
" 'num_blocks': [2, 2, 2, 2, 2],\n",
" 'filters': [2, 4, 8, 16, 32],\n",
" 'downsample': [[]] + [[0]]*4},\n",
" 'body/embedding': {'filters': 32},\n",
" 'body/decoder': {'num_stages': 5,\n",
" 'factor': 32,\n",
" 'skip': True,\n",
" 'upsample': {'layout': 'X'},\n",
" 'blocks': {'base': DenseNet.block,\n",
" 'num_layers': [2, 2, 2, 2, 2],\n",
" 'growth_rate': 2,\n",
" 'skip': False}},\n",
"}\n",
"\n",
"ppl = run('segmentation', EncoderDecoder, config, 'encoder-decoder with ResNet, DenseNet blocks')\n",
"\n",
"config['body/encoder/block/resnext'] = True \n",
"ppl = run('segmentation', EncoderDecoder, config, 'encoder-decoder with ResNeXt, DenseNet blocks')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-05T12:42:13.259519Z",
"start_time": "2020-02-05T12:41:47.454064Z"
}
},
"outputs": [],
"source": [
"ppl = run('segmentation', DeepLabXS, {}, 'DeepLab XS')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"end_time": "2020-02-05T13:21:49.768970Z",
"start_time": "2020-02-05T13:21:39.807243Z"
}
},
"outputs": [],
"source": [
"config = {\n",
" 'initial_block': {'layout': 'cna', 'filters': 4},\n",
" 'body/encoder/num_stages': 3,\n",
" 'body/encoder/blocks': {'base': ResNet.block,\n",
" 'filters': [8, 8, 8],},\n",
" 'body/embedding/filters': 32,\n",
" 'body/decoder': {\n",
" 'skip': True,\n",
" 'upsample': {'layout': 'X'},\n",
" 'blocks': {'base': DenseNet.block,\n",
" 'num_layers': [2, 2, 2],\n",
" 'growth_rate': 2,\n",
" 'skip': False}},\n",
"}\n",
"\n",
"ppl = run('segmentation', EncoderDecoder, config, 'encoder-decoder with ResNet blocks, DenseNet blocks')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.1"
},
"varInspector": {
"cols": {
"lenName": 16,
"lenType": 16,
"lenVar": 40
},
"kernels_config": {
"python": {
"delete_cmd_postfix": "",
"delete_cmd_prefix": "del ",
"library": "var_list.py",
"varRefreshCmd": "print(var_dic_list())"
},
"r": {
"delete_cmd_postfix": ") ",
"delete_cmd_prefix": "rm(",
"library": "var_list.r",
"varRefreshCmd": "cat(var_dic_list()) "
}
},
"types_to_exclude": [
"module",
"function",
"builtin_function_or_method",
"instance",
"_Feature"
],
"window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
mne-tools/mne-tools.github.io | 0.17/_downloads/f44d9c0360e7806c2f8988ccd7a3b432/plot_point_spread.ipynb | 1 | 9726 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n\nCorrupt known signal with point spread\n======================================\n\nThe aim of this tutorial is to demonstrate how to put a known signal at a\ndesired location(s) in a :class:`mne.SourceEstimate` and then corrupt the\nsignal with point-spread by applying a forward and inverse solution.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import os.path as op\n\nimport numpy as np\nfrom mayavi import mlab\n\nimport mne\nfrom mne.datasets import sample\n\nfrom mne.minimum_norm import read_inverse_operator, apply_inverse\nfrom mne.simulation import simulate_stc, simulate_evoked"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, we set some parameters.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"seed = 42\n\n# parameters for inverse method\nmethod = 'sLORETA'\nsnr = 3.\nlambda2 = 1.0 / snr ** 2\n\n# signal simulation parameters\n# do not add extra noise to the known signals\nnave = np.inf\nT = 100\ntimes = np.linspace(0, 1, T)\ndt = times[1] - times[0]\n\n# Paths to MEG data\ndata_path = sample.data_path()\nsubjects_dir = op.join(data_path, 'subjects')\nfname_fwd = op.join(data_path, 'MEG', 'sample',\n 'sample_audvis-meg-oct-6-fwd.fif')\nfname_inv = op.join(data_path, 'MEG', 'sample',\n 'sample_audvis-meg-oct-6-meg-fixed-inv.fif')\n\nfname_evoked = op.join(data_path, 'MEG', 'sample',\n 'sample_audvis-ave.fif')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load the MEG data\n-----------------\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"fwd = mne.read_forward_solution(fname_fwd)\nfwd = mne.convert_forward_solution(fwd, force_fixed=True, surf_ori=True,\n use_cps=False)\nfwd['info']['bads'] = []\ninv_op = read_inverse_operator(fname_inv)\n\nraw = mne.io.RawFIF(op.join(data_path, 'MEG', 'sample',\n 'sample_audvis_raw.fif'))\nevents = mne.find_events(raw)\nevent_id = {'Auditory/Left': 1, 'Auditory/Right': 2}\nepochs = mne.Epochs(raw, events, event_id, baseline=(None, 0), preload=True)\nepochs.info['bads'] = []\nevoked = epochs.average()\n\nlabels = mne.read_labels_from_annot('sample', subjects_dir=subjects_dir)\nlabel_names = [l.name for l in labels]\nn_labels = len(labels)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Estimate the background noise covariance from the baseline period\n-----------------------------------------------------------------\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"cov = mne.compute_covariance(epochs, tmin=None, tmax=0.)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Generate sinusoids in two spatially distant labels\n--------------------------------------------------\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# The known signal is all zero-s off of the two labels of interest\nsignal = np.zeros((n_labels, T))\nidx = label_names.index('inferiorparietal-lh')\nsignal[idx, :] = 1e-7 * np.sin(5 * 2 * np.pi * times)\nidx = label_names.index('rostralmiddlefrontal-rh')\nsignal[idx, :] = 1e-7 * np.sin(7 * 2 * np.pi * times)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Find the center vertices in source space of each label\n------------------------------------------------------\n\nWe want the known signal in each label to only be active at the center. We\ncreate a mask for each label that is 1 at the center vertex and 0 at all\nother vertices in the label. This mask is then used when simulating\nsource-space data.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"hemi_to_ind = {'lh': 0, 'rh': 1}\nfor i, label in enumerate(labels):\n # The `center_of_mass` function needs labels to have values.\n labels[i].values.fill(1.)\n\n # Restrict the eligible vertices to be those on the surface under\n # consideration and within the label.\n surf_vertices = fwd['src'][hemi_to_ind[label.hemi]]['vertno']\n restrict_verts = np.intersect1d(surf_vertices, label.vertices)\n com = labels[i].center_of_mass(subject='sample',\n subjects_dir=subjects_dir,\n restrict_vertices=restrict_verts,\n surf='white')\n\n # Convert the center of vertex index from surface vertex list to Label's\n # vertex list.\n cent_idx = np.where(label.vertices == com)[0][0]\n\n # Create a mask with 1 at center vertex and zeros elsewhere.\n labels[i].values.fill(0.)\n labels[i].values[cent_idx] = 1."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Create source-space data with known signals\n-------------------------------------------\n\nPut known signals onto surface vertices using the array of signals and\nthe label masks (stored in labels[i].values).\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"stc_gen = simulate_stc(fwd['src'], labels, signal, times[0], dt,\n value_fun=lambda x: x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Plot original signals\n---------------------\n\nNote that the original signals are highly concentrated (point) sources.\n\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"kwargs = dict(subjects_dir=subjects_dir, hemi='split', smoothing_steps=4,\n time_unit='s', initial_time=0.05, size=1200,\n views=['lat', 'med'])\nclim = dict(kind='value', pos_lims=[1e-9, 1e-8, 1e-7])\nfigs = [mlab.figure(1), mlab.figure(2), mlab.figure(3), mlab.figure(4)]\nbrain_gen = stc_gen.plot(clim=clim, figure=figs, **kwargs)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Simulate sensor-space signals\n-----------------------------\n\nUse the forward solution and add Gaussian noise to simulate sensor-space\n(evoked) data from the known source-space signals. The amount of noise is\ncontrolled by `nave` (higher values imply less noise).\n\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"evoked_gen = simulate_evoked(fwd, stc_gen, evoked.info, cov, nave,\n random_state=seed)\n\n# Map the simulated sensor-space data to source-space using the inverse\n# operator.\nstc_inv = apply_inverse(evoked_gen, inv_op, lambda2, method=method)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Plot the point-spread of corrupted signal\n-----------------------------------------\n\nNotice that after applying the forward- and inverse-operators to the known\npoint sources that the point sources have spread across the source-space.\nThis spread is due to the minimum norm solution so that the signal leaks to\nnearby vertices with similar orientations so that signal ends up crossing the\nsulci and gyri.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"figs = [mlab.figure(5), mlab.figure(6), mlab.figure(7), mlab.figure(8)]\nbrain_inv = stc_inv.plot(figure=figs, **kwargs)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Exercises\n---------\n - Change the `method` parameter to either `dSPM` or `MNE` to explore the\n effect of the inverse method.\n - Try setting `evoked_snr` to a small, finite value, e.g. 3., to see the\n effect of noise.\n\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.8"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | bsd-3-clause |
gfeiden/Notebook | Daily/20160910_low_mass_polytrope_lum.ipynb | 1 | 182048 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Determining initial $T_{\\rm eff}$ and luminosity for DMESTAR seed polytropes\n",
"\n",
"Currently, we are having difficulty with models in the mass range of $0.14 M_{\\odot}$ -- $0.22 M_{\\odot}$ not converging after an initial relaxation. There are several potential candidates for why the models are not converging. The first is FreeEOS is running with a set of plasma properties (pressure, temperature) that are outside of it's typical working range. I suspect this is not the case, as lower mass models converge properly, despite having cooler temperatures. Other potential candidates are the seed luminosity and $T_{\\rm eff}$ supplied to $\\texttt{newpoly}$ for computation of an initial polytrope model that DMESTAR then relaxes before a full stellar evolution run. To test this idea, we can compare model properties for the seed polytropes with the final relaxed quantities determined by DMESTAR."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Current seed values\n",
"\n",
"Scripts used to generate a new polytrope for DMESTAR models rely on a piece-wise function to generate an appropriate combination of $T_{\\rm eff}$ and luminosity for a model based on the requested stellar mass and solar composition. That piece-wise function is \n",
"\\begin{align}\n",
" \\log(T) & = 3.64 & M \\ge 3.9 \\\\\n",
" \\log(L) & = 0.2\\cdot (M - 5.0) + 2.6 & \\\\\n",
" & \\\\\n",
" \\log(T) & = -0.028\\cdot M + 3.875 & 3.9 > M \\ge 3.0 \\\\\n",
" \\log(L) & = 0.55 \\cdot M + 0.1 & \\\\ \n",
" & \\\\\n",
" \\log(T) & = 0.039\\cdot M + 3.5765 & 3.0 > M \\ge 1.5 \\\\\n",
" \\log(L) & = 1.7 & \\\\\n",
" & \\\\\n",
" \\log(T) & = 0.039\\cdot M + 3.5765 & 1.5 > M \\ge 0.23 \\\\\n",
" \\log(L) & = 0.85\\cdot M + 0.4 & \\\\\n",
" & \\\\\n",
" \\log(T) & = 0.614\\cdot M + 3.3863 & 0.23 > M \\\\\n",
" \\log(L) & = -0.16877\\cdot M - 0.117637 & \\\\\n",
"\\end{align}\n",
"While models with masses below $0.23 M$ are found to converge, the greatest issues occur right in the vicinity of the final piecewise condition. We can view this graphically,"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f21b0673210>]"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsAAAAKvCAYAAABkjXlgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xt83HWZ9//XNTlMmrYEKJaChZZDS9sUikmL4CogaGXd\nnwdYHkpkb1fUdWEPYr3dZWVxUbhlV12t667gHu4F+lOzt4/bXQERWaG6rhzbpLQ0bWlLz/RAKTS0\nTWZymOv+4/tNOqc0yWQmM5l5Px+PPOx8D5+5htj2ytXre33M3RERERERqRSRYgcgIiIiIjKelACL\niIiISEVRAiwiIiIiFUUJsIiIiIhUFCXAIiIiIlJRlACLiIiISEVRAiwiIiIiFUUJsIiIiIhUFCXA\nIiIiIlJRlACLiIiISEUpqQTYzG42s7Vm1hl+PW1m1wxzz+fMbJOZdZnZLjP7lplF0675YzPbbmbd\nZvasmS0p7CcRERERkVJVUgkwsBu4DWgCmoGVwENmNj/bxWb2MeCvgTuBecAngY8CX0265qPAN8Nr\n3gasBR43s9MK9zFEREREpFSZuxc7hhMys0PAF9z9/izn/h6Y5+7vTTr2t8Al7n55+PpZ4Dl3vzV8\nbQSJ9nfc/evj8RlEREREpHSUWgV4kJlFzOwGoB54ZojLngaaB1oazOxc4P3Ao+HrGoJK8pMDN3iQ\n8T8BXFa46EVERESkVFUXO4B0ZraQIOGtA44A17r7pmzXuntr2Mrwm7CyWwV8z92/Fl5yWnjsQNqt\nB4ALChG/iIiIiJS2kkuAgU3AIqABuB5YYWaXZ0uCzexK4HbgZuB54HzgO2a2z93/V64BmNk04H3A\nDiCW6zoiIiIiUjB1wGzgcXc/NJobSy4Bdvc+YFv4co2ZXQLcCtyS5fK7gBVJ/cEdZjYF+EfgfwGv\nAf3A6Wn3nQ7sP0EY7wN+kNsnEBEREZFxdCPww9HcUHIJcBYRIDrEuXogkXYsAcHDbu7ea2ZtwNXA\nwwPHw9ffOcF77gD4/ve/z/z5WQdQSJlZtmwZy5cvL3YYMk70/a4s+n5XFn2/K8fGjRv5vd/7PQjz\nttEoqQTYzO4BHgN2AVMJMvorgKXh+RXAHne/PbzlEWCZmb0APAfMIagKP+zHx1t8C3ggTISfB5YR\nJM4PnCCUGMD8+fNpamrK2+eT0tXQ0KDvdQXR97uy6PtdWfT9rkijblctqQQYmA48CJwBdALrgKXu\nvjI8PxPoS7r+boKK793AW4GDBJXeOwYucPcfhQ/K3UXQ+vAC8D53P1jYjyIiIsXWt/dVEkeOkeiK\nEamvK3Y4IlIiSioBdvdPD3P+qrTXA8nv3cPcdy9w75gDFBGRCeON5St4/Z5/pvvNDWyfvZTqs2ZQ\nc/7Z1M6dRe3cWdTMmU3tnLOpmnZysUMVkXFWUgmwiIhIPiRicd749v9//IA7fbv20bdrH90rn0u5\nNjKtgdo5s8Ok+Gxq58ymZu4sqt86HYuU7Lh8ERkDJcAiQEtLS7FDkHGk73f5Sxw6jHcFbYEfiL5l\nmGs7iR1aS+zZtSnHrb6OmvPOonbubGrnhMnx3NnUnDsTq60pWOwyNvr9LSNR8lshF4OZNQFtbW1t\naqQXEZmAel7exe5LbyzM4lVV1Mw6g5qBxHjuLGrD5DgydXJh3lNEMrS3t9Pc3AzQ7O7to7lXFWAR\nESk73t2TeiASYfp9X6J38w56Nu+kZ8tOerftgZ7e0S/e30/vtj30bttD189/k3KqasZpQSvF+WGf\n8dxZ1M6ZRdXp0wimcIpIKVACLCIiZcdj8ZTXVhdl6nXvSb2mr4/enfvo3bKTns07g//dspPezTtJ\nHDmW0/v273+N7v2v0f3rtpTjkZOmhP3Fs6iZM/AQ3ixqZp2BVeuvYpHxpt91IiJSdjIS4PrM/ZSs\nupra886i9ryzmHzNO4/f607/gUODyXDP5p30bg3+t3//aznFk3jzKPG2DcTbNqSeqK2h5tyZ1CYl\nxbVzZlFz/tka2yZSQEqARUSk7CS6UxPgSN1QG4pmMjOqZ5xG9YzT4F3NKef63zwaVop3Bcnxlp30\nbt5B7469kEjfmHQEenrp3bSd3k3bSak5m2WObQvbKjS2TWTslACLiEjZ8e7UjaFsFAnwiVSdNIWq\n5kbqmhtT3y/eQ+/2V+jZvIPeLbvo2bIz+PXWXXhaMj4iIxjbFkylmKWxbSI5UAIsIiJlJ1sPcCFZ\ntJbaeedQO++c1DgSCfpeeTWsFofJcfjrxKHOnN5LY9tExk4JsIiIlB2PpU6BsEmFTYCHYpEINWfN\noOasGdRf/faUc/2HDgetFFvCyRSbd9K7dRd9u/bl9F7eFaPnxS30vLgl9cQQY9tq5syi6qQpuX40\nkQlNCbCIiJSdzB7g2iJFMrSqaSczadrJTLr0opTjia4YvVt30bN11/iMbZtzdrAttMa2SQVRAiwi\nImUnowVi0sSZqBCpryN60VyiF81NOV7QsW3/nbqHgMa2SbnT/4tFRKTsjHcP8HjQ2DaR/FECLCIi\nZSdRoCkQpUhj20RGTwmwiIiUnfStkCNFegiu2Ep2bNucs6meebrGtknRKAEWEZGyk9kCUXoPwRVT\nqY1tG+g31tg2GS9KgEVEpOyUYw/weCiVsW21887h1Nv/gMlL35HrRxE5ISXAIiJSdjKnQCgBHqvx\nHNvW07GVA5/8ErM3PUJkSn2ePoHIcUqARUSk7GTMAZ5AY9AmmkKNbfN4Dz2bd1DXtKBQoUsFUwIs\nIiJlJ/1BLrVAjL98jG1L39FPJF+UAIuISNnRQ3Cl60Rj23Y0foj+V18ffO25tFCIjIDmj4iISNlJ\nqAd4QrJo6g8q3qMKsBSGEmARESk76RXgiFogJoT08WceVwVYCkMJsIiIlB31AE9MFk1LgNUCIQVS\nUgmwmd1sZmvNrDP8etrMrjnB9b80s0SWr0eSrrk/y/mfjc8nEhGRYsgcg6YpEBOB1aa1QMTVAiGF\nUWoPwe0GbgO2AAZ8AnjIzC52941Zrr8WSP7dchqwFvhR2nWPhWtZ+DqHfR5FRGSiyByDpgrwRJDR\nAqEKsBRISSXA7v5o2qE7zOwW4FIgIwF298PJr83sY8Ax4P+mXRp394P5jFVEREqT9/dnbMCgKRAT\nQ0YLhHqApUBKqgUimZlFzOwGoB54ZoS3fRJodffutONXmtkBM9tkZvea2al5DVZEREpGttmx6gGe\nGDKmQKgFQgqkpCrAAGa2kCDhrQOOANe6+6YR3HcJ0AjclHbqMeDHwHbgPOCvgZ+Z2WXu7vmMXURE\nii+9/xeUAE8UGoMm46XkEmBgE7AIaACuB1aY2eUjSII/Bbzo7m3JB909uR+4w8xeBF4GrgR+mbeo\nRUSkJGRNgNUDPCFoDJqMl5JLgN29D9gWvlwTVnZvBW4Z6h4zqwc+CtwxgvW3m9lrwPkMkwAvW7aM\nhoaGlGMtLS20tLQM9zYiIlIk6ZtgAEQ0BWJC0ENwMpTW1lZaW1tTjnV2dua8XsklwFlEgOF+dP8I\nwTSIHwy3mJnNBKYB+4a7dvny5TQ1NY0kRhERKRHelZYAV1VhNRPhrztRD7AMJVsBsr29nebm5iHu\nOLGS+hPBzO4h6NndBUwFbgSuAJaG51cAe9z99rRbPwX8xN3fSFtvMnAnQQ/wfoKq79eAzcDjhfsk\nIiJSLBkzgDUBYsJQBVjGS0klwMB04EHgDKATWAcsdfeV4fmZQF/yDWY2F3gH8N4s6/UDFwEfB04G\n9hIkvn/l7vpdJSJShtJbINT/O4FoDJqMk5JKgN3908OcvyrLsc1A1RDXx4Ahd5ITEZHyk74NckQT\nICaM9J3g0BQIKZCSnQMsIiKSi8wWCCXAE0UkrQc4oR5gKRAlwCIiUlYyEmC1QEwcaoGQcaIEWERE\nykpCLRATVnoLhB6Ck0JRAiwiImUlvQdYFeCJw9IqwKgFQgpECbCIiJQV9QBPXBqDJuNFCbCIiJQV\nJcATV8ZGGEqApUCUAIuISFnJmAOsBHjCyKgAqwVCCkQJsIiIlJX0rZAj9UqAJwolwDJelACLiEhZ\nUQvExJW+bbVaIKRQlACLiEhZUQI8cWWMQdMcYCkQJcAiIlJW0nuANQd44kgfg+baClkKRAmwiIiU\nFc0Bnrgye4B7cfciRSPlTAmwiIiUFY+lVg3VAjFxpI9Bwx36+osTjJQ1JcAiIlJWvDuW8loV4Ikj\nvQIMmgQhhaEEWEREyop6gCeurAmwJkFIASgBFhGRspIxBUIV4AkjowUCVYClMJQAi4hIWcl4CE4V\n4AkjewKsCrDknxJgEREpK3oIbuJKH4MGGoUmhaEEWEREykpGD7BaICYMq6qCqqqUY6oASyEoARYR\nkbLh/f2Q9tCUeoAnFm2GIeNBCbCIiJSN9P5fUAvERJNtMwyRfFMCLCIiZSN9AgQoAZ5oMhJgjUGT\nAlACLCIiZSMRy/zncvUATyzpkyDUAiGFoARYRETKhirAE19GBTjLDzUiY1VSCbCZ3Wxma82sM/x6\n2syuOcH1vzSzRJavR9Kuu8vM9ppZl5n9wszOL/ynERGR8ZbRA1xVhdVUFycYyYnVpVeA1QIh+VdS\nCTCwG7gNaAKagZXAQ2Y2f4jrrwVmJH0tBPqBHw1cYGa3AX8CfAa4BDgGPG5mmdO2RURkQvPuWMpr\nTYCYeKw2LQHWQ3BSACX1Y7G7P5p26A4zuwW4FNiY5frDya/N7GMECe7/TTp8K3C3u/80vObjwAHg\nwyQlyiIiMvFpBvDEl/kQnFogJP9KrQI8yMwiZnYDUA88M8LbPgm0unt3uMY5BJXhJwcucPc3geeA\ny/IbsYiIFFt6D7D6fyeejDnAqgBLAZRUBRjAzBYSJLx1wBHgWnffNIL7LgEagZuSDs8AnKDim+xA\neE5ERMqId2sb5IlOY9BkPJRiBXgTsIigX/c+YIWZzRvBfZ8CXnT3tkIGJyIipSuzAqzHPSYajUGT\n8VByFWB37wO2hS/XhJXdW4FbhrrHzOqBjwJ3pJ3aDxhwOqlV4NOBNcPFsmzZMhoaGlKOtbS00NLS\nMtytIiJSBBk9wKoATzjaCU6yaW1tpbW1NeVYZ2dnzuuVXAKcRQQY7k+wjwC1wA+SD7r7djPbD1wN\nrAMws5OAtwPfHe6Nly9fTlNTUy4xi4hIEWRMgaivK1IkkqvMBFgVYMlegGxvb6e5uTmn9UoqATaz\ne4DHgF3AVOBG4ApgaXh+BbDH3W9Pu/VTwE/c/Y0sy36bYJrEVmAHcDewB3ioEJ9BRESKJ30OsHqA\nJ57075kqwFIIJZUAA9OBB4EzgE6Cqu1Sd18Znp8J9CXfYGZzgXcA7822oLt/PWyR+EfgZOC/gd92\nd/1IKSJSBjyRoHfLTmKrN3DsF6lDg5QATzwagybjoaQSYHf/9DDnr8pybDNQNcx9Xwa+PJbYRESk\nNPR3HiHetoHY6g5iqzuIt28g0Xk067URPQQ34WSMQdMUCCmAkkqARUREknkiQe/mncRWrQ8S3rYO\nel/aMeL7a+bMKlxwUhDaCU7GgxJgEREpGf2HB6q7QcIbb9tA4sixnNaKvm0+U1ven+cIpdDUAiHj\nQQmwiIgUhff30/PSDuJtHcRWBe0MvVt25rxe1ZnTqVvcSN2SRuqaG4k2zceqTtghJ6VIO8HJOFAC\nLCIi46L/jTeDqm7YyhBr24Af7cptsdoaoosuCBLe8Kv6zOn5DViKIqMFQj3AUgBKgEVEJO+8v5+e\nTduDhHfVemJtG+jduivn9apnnk60uXGwwhtdOCdjxzApDxkPwWkOsBSAEmARERmz/kOHiYWTGeKr\n1xNr34gf685pLYvWEl10AdGB6u6ShVTPOC3PEUupytgKWQmwFIASYBERGRXv66Nn4/agjWFVkPD2\nbtuT83rVZ82gbnEj0cULqVu8IKjupj0IJZVDY9BkPCgBFhGRE+p/7Y3B6m4wd3cj3pVjdbeuluii\neUEbw+KF1DUvUHVXUqT3AKOH4KQAlACLiMgg7+ujZ8O2MNldT3z1Bnq3j6G6O+sM6sLe3eiShUQb\nz8dq9FePDE1j0GQ86E8hEZEK1nfwjXAMWTh394VNeFcsp7VsUpToxfMGpzJEmxupPn1aniOWcqcW\nCBkPSoBFRCqE9/bRs+HlwepubHUHfTv25rxe9ewzw2R3IXWLG6ldcJ6quzJm2glOxoP+pBIRKVN9\nr74eTGRYHeysFn9hE94dz2ktq687Xt1dspBo0wKqp5+a54hFslWA1QIh+acEWESkDHhvH/GOrcHM\n3XCjib6d+3Jer3r2W4Md1Qaru+di1forQwovowc41oO7Y2ZFikjKkf40ExGZgPoOHDo+c3dVB/G1\nm/BYbpUyq59EtGk+dc0LqFsSTGaoOu2UPEcsMjJWl2WDk94+0Gg8ySMlwCIiJc57eol3bB2cuRtb\n3UHf7v05r1dz7sxgBNmSRuqaG6mdf46qu1IyMsagEfwe0GxoySf9iSciUmL69r8WTGVo6yC+qoP4\nupdyr+5OnkRd0/xwk4nGoLo77eQ8RyySP9kSXY/3wJT6IkQj5UoJsIhIEXlPL/EXNwfV3bZgo4m+\nPQdyXq/m/LOpa15AdEnYuzvvHKyqKo8RixRW+lbIoFFokn9KgEVExlHfvoPHZ+6u7iC+bnNQ3cqB\nTakP+nabG4kOVHdPbchzxCLjK3sFWAmw5JcSYBGRAvF4D/EXtwQzd1cF1d3+va/mvF7NnFnHN5lY\n3EjtBbNV3ZWykz4GDTQKTfJPCbCISJ70vXIgSHTDVob4us2Q4z/dRqZOJtq8YHBHtbrmBVSdclKe\nIxYpPVZVBVVV0N8/eEwVYMk3JcAiIjlIxOL0rNsc7qoWVnf3Hcx5vZq5swZn7tYtWUjNnLNV3ZWK\nZdEavCs5AVYFWPJLCbCIyDDcnb5XXk3ZZCK+bnMwmzQHkZOmBHN3wwfVos0LqGqYmueoRSYui9bi\nXbHB10qAJd+UAIuIpEl0x4mve4n46o6wd3c9/QcO5baYGTUXzA5HkDVSt6SRmjmzsEgkv0GLlJGM\n3eA0BULyTAmwiFQ0d6dv9/7Bmbux1R3E12/JvbrbMCXo2Q03mYg2L6DqpCl5jlqkvKWPQlMCLPmm\nBFhEKkqiO078hU3EVq8n3raB2Kr19L/6em6LmVE775xgBNlA7+55Z6m6KzJGGRVgtUBInpVUAmxm\nNwO3ALPDQx3AXe7+8xPc0wDcA1wLnArsAD43cI+Z3QncmXbbJndfkNfgRaTkuDt9u/YFfburgoQ3\nvn4L9PUPf3MWkZOnBlXdJY3BA2tN84lMnZznqEUkfRSaKsCSbyWVAAO7gduALYABnwAeMrOL3X1j\n+sVmVgM8AewHrgP2ArOAw2mXrgeuDtcEyO3fNkWkpCW6YmF1N+jbja/eQP/BHKu7kQi188+hbvHC\nYBzZQHXXbPh7RWRMrDatBUJj0CTPSioBdvdH0w7dYWa3AJcCGQkw8CngZOBSdx8o6ezKcl2fu+c+\nn0hESo6707djbzBzN3xQrafj5ZTZoaMRObUh2FVt8UKiixdQ17SAyJT6PEctIiOR+RCcWiAkv0oq\nAU5mZhHgI0A98MwQl30gPHevmX0IOAj8EPiauyeSrptjZq8AsfD6L7r77oIFLyJ5lzjWnVTd7SDe\n1kH/wTdyWywSoXb+ucGDamHCW3OuqrsipSKjBUI9wJJnJZcAm9lCgiS1DjgCXOvum4a4/FzgKuD7\nwG8D5wP3EXyuu8NrniVopXgJOAP4MvBrM1vo7scK8ylEZCzcnb7trwRbCIcJb8+GbblXd6c1BCPI\nwgfVohfPU3VXpIRlTIFQC4TkWcklwMAmYBHQAFwPrDCzy4dIgiPAAeAz7u7AGjObCXyBMAF298eT\nrl9vZs8DOwmqy/efKJBly5bR0NCQcqylpYWWlpacPpiIZJc42hVUd5M2mkgc6sxtsaoqahecGyS7\ni4MKb/U5b1V1V2QCyegB1kNwFa+1tZXW1taUY52dOf49QQkmwO7eB2wLX64xs0uAWwmmQ6TbB/SE\nye+AjcAMM6sO10pfv9PMNhNUi09o+fLlNDU1jfoziMjQ3J3ebbuJr94QVHhXddCzcRskEsPfnEXk\ntJOPbyG8uDGo7k6elOeoRWQ8qQVC0mUrQLa3t9Pc3JzTeiWXAGcRAaJDnHsKSC/HXgDsy5b8ApjZ\nFOA8YEXeIhSRISWOdhFr33A84W3bQOL1MVR3G88LEt5wo4nq2WequitSZrQTnBRaSSXAZnYP8BjB\nJIepwI3AFcDS8PwKYI+73x7ech/wx2b2HeDvgbnAF4FvJ635DeARgraHtwJfIRiDllpHF5Exc3d6\nX949OHM3tno9PRu351zdrXrLKeEmE0GFN7roAlV3RSqAeoCl0EoqAQamAw8SPKzWCawDlrr7yvD8\nTJJm+Lr7HjN7H7AcWAu8Ev7660lrziSYDDGNYErEbwjGph0q7EcRKX+JI8eItW8MZu6u6iDWvoHE\nG2/mtlh1FdGFcwZn7tYtbqT67DNU3RWpQBqDJoVWUgmwu396mPNXZTn2HPCOE9yjJ9ZE8sATCXq3\n7jo+hmx1Bz2btkNKC/7IVU0/NZjIMDB7d9EFROrr8hy1iExE6T3AR3+ykthTLxQpGilVh5ecl/O9\nOSfAZnYywfbD7yLYfa2eoMK6Bnjc3Z/OOSoRKbr+N48GbQzhRhPx9g0kDh/JbbHqKqIXzg3aGMKH\n1arPmqHqrohklTEF4mgXvUe7ihSNlKrEnOk53zvqBNjMzgTuIujP3Qs8D7wAdAOnAu8GvmBmO4Gv\nuPv/yTk6ERkXnkjQu2VnsKNaW1Dh7X1pR+7V3dOnDT6oFl3cSPSiC4hMGupZVhGRVFWnTyt2CFLm\ncqkAryHo02129w3ZLjCzScCHgc+Z2Vnu/rdjiFFE8qy/80j4kFpH8MBa+0YSbx7NbbGaaqIXzR3c\naCK6ZCHVb52u6q6I5GzyB67k8H3/Rt+OvcUORcpULgnwguEeIHP3boIpC61mph/jRIrIEwl6N+88\nvsnE6vX0bt6Z83pVZ7wlaZOJRmovmkukTtVdEcmf6recwlm/eoDY6g78mFofJLuDRw7BD7+T072j\nToDd/ZCZLRiq+jvAzP7M3b+haQsi46v/8JHBEWSx1R3E2zaQOJLjrt+1NUF1d3Ewc7duSSPVbz09\nvwGLiGQRmTyJ+isWFzsMKWG17e0535vrQ3CPm9lvufuubCfN7AvAV4Fv5ByZiAzL+/vpeWkH8XAy\nQ2x1B71bxlDdPXN6kOwuCWbvRi+ckzGPU0REZKLLNQH+DfBEmAQfTD5hZv8TuAf4+FiDE5FU/W+8\nOTiCLNbWQaxtA57rk9G1NUQXXZDSzlB9Zu5P1IqIiEwUuSbA/4Ngd7XHzexKd38TwMyWAX8D/L67\n/1ueYhSpSN7fT8+m7UHCG/bv9r68O+f1qmeeHjykFrYyRBequisiIpUppwTY3fvM7DrgCeCnZrYU\nuJmg5eET7v7DPMYoUhH6Dx0mFk5miK9eT6x9I36sO6e1LFpLdNEFRJcM9O4upHrGaXmOWEREZGLK\neSMMd+82s/cD/wW0AXOBm9z9+/kKTqRceV8fPRu3hw+qbSC+ej292/bkvF71WTPCTSYWUrd4QVDd\nTdtKVERERAI5JcBm9sGkl/cBfwf8BOhMPufuD48tPJHy0P/aG0F1d9V6Ym0biLdvxLtyrO7W1RJd\nNC/cZGIhdc0LVN0VEREZhVwrwD/Jcux3w68BDlTluL7IhOV9ffRs2DY4cze+egO928dQ3Z11RrCr\nWvMCoksWEm08H6vJ+R9vREREKl6uPcCRfAciMlH1HXyDeFvH4EYT8Rc24V2xnNaySVGiF88LEt7F\nC4g2N1KtLUFFRETySmUkkVHw3j56Nrw8WN2Nre4Y01ad1bPPDEeQLQx2VVtwnqq7IiIiBaa/aUVO\noO/V14OJDOEmE/EXNuHd8ZzWsvq6sLobTGWINi2gevqpeY5YREREhqMEWCTkvX3EO7YOztyNre6g\nb9e+nNerOWcm0cULkqq752LV+i0nIiJSbPrbWCpW3/7XgokMq9cTW9VBfO0mPNaT01pWP4lo03zq\nmhdQtyR4YK3qtFPyHLGIiIjkQ65j0M519235DkakULynl/j6LYMzd2OrO+jbvT/n9WrOnRmMIAs3\nmqidf46quyIiIhNErn9jrzOzHcDDwEPu/lz+QhIZu779rx2fyrC6g/i6l3Kv7k6eRF3T/HCTicag\nujvt5DxHLCIiIuMl1wT4NOC9wIeAh8zMgZ8SJMS/cPfcZkCJ5MB7eom/uJnYqvBBtbYO+vYcyHm9\nmvPPHpy5W7e4kdp552BVGmktIiJSLnKdAxwDHgEeMTMDLgM+CHwNaDWzJwiS4Ufc/WC+ghUB6Nt3\ncLC6G1vdQc+6zXg8x+rulPqgb7e5kehAdffUhjxHLCIiIqVkzE2L7u7A0+HXX5jZHIJk+BPAfWb2\neXf/7ljfRyqTx3uIr9tMrK1jsMLbv/fVnNermTMrHEPWSLS5kdoLZqu6KyIiUmHy/tSOu28Bvgl8\n08ymARp0KiPW98qBMNFdH0xoWLcZenpzWisydTLR5gWDG01Em+ZTdcpJeY5YREREJpqCPrbu7oeA\nQ4V8D5m4ErE4Pes2B60Mq4KEt39f7h0zNXNnDc7crVuykJq5s7CIdu0WERGRVCU1t8nMbgZuAWaH\nhzqAu9z95ye4pwG4B7iWoNq8A/hc8j1m9sfAF4AZwFrgT919VQE+ggzB3enbc4B42LcbW72e+Itb\noLcvp/UiJ01Jqu42Em1eQFXD1DxHLSIiIuWopBJgYDdwG7AFMII+4ofM7GJ335h+sZnVAE8A+4Hr\ngL3ALOBw0jUfJWjJ+AzwPLAMeNzM5rr7awX9NBUs0R0nvvYl4oO9u+vpP5DjPwaYUXPB7HAEWdC/\nWzNH1V0RERHJTa4bYVwOPO3uuZXvhuDuj6YdusPMbgEuBTISYOBTwMnApe7eHx7blXbNMuAf3X0F\nDFaZfwf4JPD1fMVeydydvt37B2fuxlZ3EF8/hupuwxSiYaI72Lt70pQ8Ry0iIiKVKtcK8C+BM4Dc\nH8cfhpkhIZ6YAAAgAElEQVRFgI8A9cAzQ1z2gfDcvWb2IeAg8EPga+6eCCvEzQQtEkAwtSIc03ZZ\noWIvd4nuOPEXNgVtDG0biK1aT/+rr+e2mBm1884JRpAN9O6ed5aquyIiIlIwuSbAltcokhc2W0iQ\n1NYBR4Br3X3TEJefC1wFfB/4beB84D6Cz3U3wYYdVUD6rggHgAvyHnwZcnf6du0bfFAtvrqDeMdW\n6Osf/uYsIqecFGwyEU5mqGuaT2Tq5DxHLSIiIjK0sfQAe96iSLUJWAQ0ANcDK8zs8iGS4AhBMvuZ\ncB7xGjObSfDA291jDWTZsmU0NKRuitDS0kJLS8tYly5Zia5YWN0NH1RbvYH+gzlWdyMRauefE7Qx\nNC84Xt21gv38JCIiImWotbWV1tbWlGOdnZ05r2dB3jjKm8wSwGNA/ETXuft1OcaV/F6/ALa6+y1Z\nzv0K6HH3pUnHrgEeBaIEleou4Hfd/eGkax4AGtz92iHeswloa2tro6mpaawfoWS5O3079gYzd1dv\nILZ6PT0dL0N/jtXdUxuCXdUWLyS6eAF1TQuITKnPc9QiIiIi0N7eTnNzM0Czu7eP5t6xVICPAN1j\nuH+kIgTJbDZPAenl2AuAfQMP6JlZG3A1wdbMhFs3Xw18pyDRlrDEse6gujuwjXBbB4nXDg9/YzaR\nCLXzzz3+oNriRmrOnanqroiIiJS8sSTAn3X3vD4EZ2b3EFSWdwFTgRuBK4Cl4fkVwB53vz285T7g\nj83sO8DfA3OBLwLfTlr2W8ADYSI8MAatHnggn7GXGnenb/srYXU3GEXWs3Fb7tXdaQ3BCLLwQbXo\nxfNU3RUREZEJKdcEuFD9v9OBBwkmTHQC64Cl7r4yPD8TGJyt5e57zOx9wHKCDS5eCX/99aRrfmRm\npwF3AacDLwDvc/fctxwrQYmjXZnV3UM59sZUVVG74NxwV7WgpaH6nLequisiIiJloaSmQLj7p4c5\nf1WWY88B7xjmvnuBe8cWXelwd3q37Sa2qmNwo4mejdsgkchpvchpJx/fQnhxY1DdnTwpz1GLiIiI\nlIZcE+B3AzmOBpDRShztIta+gfiqoLIba9tA4vUxVHcbzwsS3rB/t3rWGaruioiISMUYdQJsZje4\n+7+N8NqzgLPd/alRR1ah3J3el3cPztyNtXXQs3F7ztXdqreccnzm7kB1t74uz1GLiIiITBy5VIBv\nMbM7gfuBR9w9ZYtiM2sAfgv4PeC9BNsVyzDi6zbz+jfuJ/bsWhKHj+S2SHUV0YVzBmfu1i1upPps\nVXdFREREko06AXb3K8zsg8CfAn9tZscINqOIAacAM4DXCKYsLHT39F3YJE1/5xFe+f/+CO8+4Vjl\nDFXTTw0mMixupK65keiiC1TdFRERERlGTj3A4aYSD4fTFd4JzAImESS+a4A17p7bv9lXoO5ftw2f\n/FZXEb1wbtDGsCRIeKvPmqHqroiIiMgojWUOMO7+GvCTPMVSsbK1PFSdPm3wQbXo4kaiF11AZNJQ\n+4GIiIiIyEiNKQGW/EgcPZbyetK7mjjjx99WdVdERESkAMaUAJvZG2TfFMMJeoK3Ag+4+/1jeZ9y\nlzjSlfI60jBVya+IiIhIgYy1AnwX8JcE2xc/Hx67BLgG+C5wDnCfmVW7+z+P8b3KVuJIagU4MnVy\nkSIRERERKX9jTYDfCdzh7t9LPmhmf0iwhfHvmtk64LOAEuAhKAEWERERGT+RMd7/PuCJLMefDM8B\n/Aw4d4zvU9YyWiCm1hcpEhEREZHyN9YE+HXgA1mOf4DjWyVPBnLc2aEyqAIsIiIiMn7G2gJxN0GP\n77s53gO8BHg/cHP4+r3Af43xfcpa4mhqBdimqAIsIiIiUihjnQP8z2a2AfgT4Lrw8EvAFe7+dHjN\nN8cWYvlTBVhERERk/Ix5DrC7PwU8lYdYKpanJ8CqAIuIiIgUzJgTYDOrAj4MzA8PdQAPu3v/WNeu\nFJkPwakCLCIiIlIoY90I43yCKQ9vJWh9APgisNvMfsfdXx5jfGXP3dUCISIiIjKOxjoF4jvAy8BZ\n7t7k7k3A2cD28JwMw491g6dupqcxaCIiIiKFM9YWiCuAS919YOQZ7n7IzP4C9QWPSPoECFAFWERE\nRKSQxloBjgNTsxyfAvSMce2KkN7+AHoITkRERKSQxpoA/xT4JzN7ux13KfA94OGxh1f+0hNgq6vF\namuKFI2IiIhI+RtrAvxZgh7gZ4BY+PUUsBW4dYxrVwRNgBAREREZX2PdCOMw8CEzmwPMCw9vdPet\nY46sQmRMgJiiBFhERESkkMY8BxjA3bcAW/KxVqXJaIHQBAgRERGRghp1Amxm3xrpte7++VGufTNw\nCzA7PNQB3OXuPx/i+t8H7gccsPBwzN3rk665H/j9tFt/7u7vH01shaIWCBEREZHxlUsF+G0jvM6H\nvyTDbuA2gmqyAZ8AHjKzi9194xD3dAJzOZ4AZ3vfx8K1Bq6J5xBbQWRsg6wEWERERKSgRp0Au/u7\nCxFIuPajaYfuMLNbgEuBoRJgd/eDwywdH8E1RZE4mp4AqwVCREREpJDGOgWiYMwsYmY3APUEUyaG\nMsXMdpjZLjP7iZktyHLNlWZ2wMw2mdm9ZnZqYaIevYwWCD0EJyIiIlJQeXkILp/MbCFBwlsHHAGu\ndfdNQ1z+EvBJYB3QAPwZ8LSZLXD3veE1jwE/Jtie+Tzgr4Gfmdll7p5Lm0ZeZUyBUAVYREREpKBK\nLgEGNgGLCBLa64EVZnZ5tiTY3Z8Fnh14bWbPELRK/CFwZ3jNj5Ju6TCzFwlmF18J/LJAn2HE0rdC\nVg+wiIiISGGVXALs7n3AtvDlGjO7hGBTjVtGcq+ZrQHOP8E1283stfCaEybAy5Yto6GhIeVYS0sL\nLS0tw4UyYpkVYCXAIiIiIslaW1tpbW1NOdbZ2ZnzeiWXAGcRAaIjudDMIsCFQPrDdMnXzASmAfuG\nW2/58uU0NTWNMMzcZI5BUwuEiIiISLJsBcj29naam5tzWq+kEmAzu4egZ3cXMBW4EbgCWBqeXwHs\ncffbw9dfImiB2AqcDPw5cDbwL+H5yQStED8G9hNUfb8GbAYeH6/PdSKZUyBUARYREREppJJKgIHp\nwIPAGQTzfdcBS919ZXh+JtCXdP0pwD8BM4A3gDbgsqR+4X7gIuDjBAnyXoLE96/cvbewH2Vk1AIh\nIiIiMr5KKgF2908Pc/6qtNefB4bcbc7dY8A1+YmuMLQTnIiIiMj4Ktk5wJXA4z3Qk1qItinqARYR\nEREpJCXARZTe/gCqAIuIiIgUmhLgIkpvfwAlwCIiIiKFpgS4iDIqwNVVWF1tcYIRERERqRBKgIso\n2wQIMytSNCIiIiKVQQlwEWkbZBEREZHxpwS4iDIrwJoAISIiIlJoSoCLKCMBnqIKsIiIiEihKQEu\nosxNMFQBFhERESk0JcBFpG2QRURERMafEuAiUgIsIiIiMv6UABdReguEqQVCREREpOCUABeRH1UF\nWERERGS8KQEuIk2BEBERERl/SoCLqO/gGymvI1PUAiEiIiJSaEqAi6Rv/2v0btqecqzm3JlFikZE\nRESkcigBLpKulc+lvI5MnUzd4sYiRSMiIiJSOZQAF0nXk6kJ8KQrFmM11UWKRkRERKRyKAEuAu/r\no/tXq1KO1V99aZGiEREREaksSoCLILaqg8SbR1OO1b9HCbCIiIjIeFACXARdTz6b8rq28XyqZ5xW\npGhEREREKosS4CLoeiI1AVb1V0RERGT8KAEeZ337DtLTsTXlmPp/RURERMaPEuBxlj79IXLSFOqW\naPyZiIiIyHgpqQTYzG42s7Vm1hl+PW1m15zg+t83s4SZ9Yf/mzCzrizX3WVme82sy8x+YWbnF/aT\nDC29/3fSlUuwao0/ExERERkvJZUAA7uB24AmoBlYCTxkZvNPcE8nMCPpa1bySTO7DfgT4DPAJcAx\n4HEzq8179MPw3j66/2t1yrH6q98+3mGIiIiIVLSSKj26+6Nph+4ws1uAS4GNQ9/mB0+w7K3A3e7+\nUwAz+zhwAPgw8KMxhjwqsedfJHHkWMqx+quUAIuIiIiMp1KrAA8ys4iZ3QDUA8+c4NIpZrbDzHaZ\n2U/MbEHSGucQVIWfHDjm7m8CzwGXFSj0IaX3/9ZeOEfjz0RERETGWcklwGa20MyOAHHgXuBad980\nxOUvAZ8EPgjcSPB5njazM8PzMwAnqPgmOxCeG1ddK9PGn2n6g4iIiMi4K6kWiNAmYBHQAFwPrDCz\ny7Mlwe7+LDCYVZrZMwStEn8I3Dk+4Y5M395X6el4OeWY5v+KiIiIjL+SS4DdvQ/YFr5cY2aXEPTx\n3jKSe81sDTAw5WE/YMDppFaBTwfWDLfesmXLaGhoSDnW0tJCS0vLcLdmyBh/1jCFuuYFQ1wtIiIi\nIgNaW1tpbW1NOdbZ2ZnzeiWXAGcRAaIjudDMIsCFwKMA7r7dzPYDVwPrwmtOAt4OfHe49ZYvX05T\nU1OOYafKHH92icafiYiIiIxAtgJke3s7zc3NOa1XUhmYmd0DPAbsAqYS9PVeASwNz68A9rj77eHr\nLxG0QGwFTgb+HDgb+JekZb9NME1iK7ADuBvYAzxU+E8U8J5eutLHn6n9QURERKQoSioBBqYDDwJn\nEMz3XQcsdfeV4fmZQF/S9acA/0TwQNsbQBtwWXK/sLt/3czqgX8kSJL/G/htd+8p8GcZFFu1Hj+a\nuj+Hxp+JiIiIFEdJJcDu/ulhzl+V9vrzwOdHsO6XgS+PJbax6HoidYpbdNEFVE8/tUjRiIiIiFS2\nkhuDVo7SH4DT+DMRERGR4lECXGB9rxygZ+O2lGPa/lhERESkeJQAF1jG+LNTTiKq8WciIiIiRaME\nuMDSx5/VX7kEq6oqUjQiIiIiogS4gLKOP1P/r4iIiEhRKQEuoO7n1uHHulOOTdL4MxEREZGiUgJc\nQOntD9GL51H9llOKFI2IiIiIgBLggup6Iq3/V7u/iYiIiBSdEuAC6d1zgN6XdqQcU/+viIiISPEp\nAS6Q9PaHyKkNRN82r0jRiIiIiMgAJcAFktH+8O5LNP5MREREpAQoAS4Aj/fQ/eu2lGPa/U1ERESk\nNCgBLoDuZ9fhXUnjz8yof/clxQtIRERERAYpAS6AjPFnb5tH1WkafyYiIiJSCpQAF0DG9sea/iAi\nIiJSMpQA51nvrn30bt6Zckzzf0VERERKhxLgPMsYfzatgejFGn8mIiIiUiqUAOdZ15PPpbyuf/cl\nWET/mUVERERKhTKzPErE4nT/d9r4s/dcVqRoRERERCQbJcB5FHt2Hd4VO37AjPorlxQvIBERERHJ\noAQ4j7qeeCbldbRpPlXTTi5SNCIiIiKSjRLgPMro/9X0BxEREZGSowQ4T3p37KV3666UY5r/KyIi\nIlJ6lADnScb4s9NOJrrogiJFIyIiIiJDUQKcJxm7v131do0/ExERESlBJZWhmdnNZrbWzDrDr6fN\n7JoR3nuDmSXM7N/Tjt8fHk/++lk+407E4nT/pj3lmNofREREREpTdbEDSLMbuA3YAhjwCeAhM7vY\n3TcOdZOZzQa+Afx6iEseC9ey8HU8L9GGYk+/gHcnLRmJaPyZiIiISIkqqQTY3R9NO3SHmd0CXApk\nTYDNLAJ8H/gr4HKgIctlcXc/mM9Yk6VPf4g2L6Dq1GxhiIiIiEixlVQLRDIzi5jZDUA98MwJLr0T\nOODu95/gmivN7ICZbTKze83s1HzGmt7/O1ntDyIiIiIlq6QqwABmtpAg4a0DjgDXuvumIa59J3AT\nsOgESz4G/BjYDpwH/DXwMzO7zN19rPH2bn+F3pd3pxzT/F8RERGR0lVyCTCwiSChbQCuB1aY2eXp\nSbCZTQFWAH/g7m8MtZi7/yjpZYeZvQi8DFwJ/PJEgSxbtoyGhtRWhpaWFlpaWgZfp1d/q95yCrUX\nzjnRsiIiIiIyCq2trbS2tqYc6+zszHk9y0MRtKDM7BfAVne/Je34IqAd6Of4w20DLR39wAXuvn2I\nNV8F/tLd/3mI801AW1tbG01NTSeMb98Nf5aSBE/96DVM/4e/HPZziYiIiEju2tvbaW5uBmh29/bh\nrk9WihXgdBEgmuX4RuDCtGNfBaYAnyWYKJHBzGYC04B9Yw0s0R2n+ymNPxMRERGZSEoqATazewh6\ndncBU4EbgSuApeH5FcAed7/d3XuADWn3HwZ8YGSamU0meEjux8B+4Hzga8Bm4PGxxht7+gU81nP8\nQCTCJI0/ExERESlpJZUAA9OBB4EzgE5gHbDU3VeG52cCfaNYrx+4CPg4cDKwlyDx/St37x1rsF1P\npA6nqFvcSNUpJ411WREREREpoJJKgN3908Ocv2qY8zelvY4BI9pJLhfp83/V/iAiIiJS+kp2DnCp\n63l5N73b96Qc0/gzERERkdKnBDhH6dXfqumnavyZiIiIyASgBDhH6fN/6696O2Y2xNUiIiIiUiqU\nAOcg0RUj9tSalGP177msSNGIiIiIyGgoAc5B91Nr8HjS+LOqKiZdubh4AYmIiIjIiCkBzkF8bcqu\nzMH4s4apRYpGREREREajpMagTRSnfuEmpn7kGrqefJauJ55l0ruaix2SiIiIiIyQEuAc1Zx9Bg03\nXUvDTdcWOxQRERERGQW1QIiIiIhIRVECLCIiIiIVRQmwiIiIiFQUJcAiIiIiUlGUAIuIiIhIRVEC\nLCIiIiIVRQmwiIiIiFQUJcAiIiIiUlGUAIuIiIhIRVECLCIiIiIVRQmwiIiIiFQUJcAiIiIiUlGU\nAIuIiIhIRVECLCIiIiIVRQmwiIiIiFQUJcAiQGtra7FDkHGk73dl0fe7suj7LSNRUgmwmd1sZmvN\nrDP8etrMrhnhvTeYWcLM/j3LubvMbK+ZdZnZL8zs/PxHLxOZ/sCsLPp+VxZ9vyuLvt8yEiWVAAO7\ngduAJqAZWAk8ZGbzT3STmc0GvgH8Osu524A/AT4DXAIcAx43s9p8Bi4iIiIiE0NJJcDu/qi7/9zd\nX3b3re5+B3AUuHSoe8wsAnwf+Ctge5ZLbgXudvefuvt64OPAmcCH8/8JRERERKTUlVQCnMzMImZ2\nA1APPHOCS+8EDrj7/VnWOAeYATw5cMzd3wSeAy7Lb8QiIiIiMhFUFzuAdGa2kCDhrQOOANe6+6Yh\nrn0ncBOwaIjlZgAOHEg7fiA8N5Q6gI0bN448cJnQOjs7aW9vL3YYMk70/a4s+n5XFn2/K0dSnlY3\n2nvN3fMbzRiZWTVwNtAAXA/8AXB5ehJsZlOAdcAt7v54eOx+oMHdrwtfXwb8BjjT3Q8k3ft/gIS7\ntwwRw8eAH+T7s4mIiIhI3t3o7j8czQ0llwCnM7NfAFvd/Za044uAdqAfsPDwQEtHP3BB+OuXgYvd\nfV3Svb8C1rj7siHecxrwPmAHEMvLBxERERGRfKoDZgOPu/uh0dxYci0QWUSAaJbjG4EL0459FZgC\nfBbY7e59ZrYfuJqgWoyZnQS8HfjuUG8Y/kcc1U8SIiIiIjLuns7lppJKgM3sHuAxYBcwFbgRuAJY\nGp5fAexx99vdvQfYkHb/YcDdPbl599vAHWa2laCiezewB3iosJ9GREREREpRSSXAwHTgQeAMoJOg\narvU3VeG52cCfaNZ0N2/bmb1wD8CJwP/Dfx2mECLiIiISIUp+R5gEREREZF8Ktk5wCIiIiIihaAE\nOAsz+2Mz225m3Wb2rJktKXZMkn9m9i4ze9jMXjGzhJl9sNgxSeGY2RfN7Hkze9PMDpjZf5jZ3GLH\nJYVhZjeb2Voz6wy/njaza4odlxSemf1F+Gf6t4odixSGmd0Zfo+TvzYMf+dxSoDTmNlHgW8S7DD3\nNmAt8LiZnVbUwKQQJgMvAH9EsGGKlLd3AX9PMAXmPUAN8J9mNqmoUUmh7AZuA5qAZmAl8JCZzS9q\nVFJQYcHqMwR/d0t5Ww+cTrCx2QzgnaO5WT3AaczsWeA5d781fG0Ef5B+x92/XtTgpGDMLAF82N0f\nLnYsMj7CH2pfJdho5zfFjkcKz8wOAV9w9/uLHYvkX7hBVhtwC/Algnn/ny9uVFIIZnYn8CF3b8p1\nDVWAk5hZDUGl4MmBYx78hPAEcFmx4hKRgjiZoPL/erEDkcIys4iZ3QDUA88UOx4pmO8CjyRNjpLy\nNidsYXzZzL5vZmeN5uZSG4NWbKcBVcCBtOMHOL6znIhMcOG/7Hwb+I27j6pvTCYOM1tIkPDWAUeA\na919U3GjkkIIf8C5GFhc7FhkXDwLfAJ4iWB07peBX5vZQnc/NpIFlACLSCW6F1gA/FaxA5GC2gQs\nAhqA64EVZna5kuDyYmYzCX6gfY+79xY7Hik8d3886eV6M3se2Al8BBhRi5MS4FSvAf0ETdXJTgf2\nj384IpJvZvYPwPuBd7n7vmLHI4Xj7n3AtvDlGjO7BLiVoEdUykcz8BagPfzXHQj+NfdyM/sTIOp6\n4KmsuXunmW0Gzh/pPeoBThL+5NgGXD1wLPzNdDU57jUtIqUjTH4/BLzb3XcVOx4ZdxEgWuwgJO+e\nAC4kaIFYFH6tBr4PLFLyW/7CByDPA0Zc1FAFONO3gAfMrA14HlhG8ODEA8UMSvLPzCYT/LQ4UDE4\n18wWAa+7++7iRSaFYGb3Ai3AB4FjZjbwLz2d7h4rXmRSCGZ2D/AYsAuYCtwIXAEsLWZckn9hz2dK\nL7+ZHQMOufvG4kQlhWRm3wAeIWh7eCvwFaAPaB3pGkqA07j7j8LxSHcRtD68ALzP3Q8WNzIpgMXA\nLwkmATjB/GeAB4FPFisoKZibCb7Pv0o7fhOwYtyjkUKbTvB7+QygE1gHLNWEgIqhqm95mwn8EJgG\nHAR+A1zq7odGuoDmAIuIiIhIRVEPsIiIiIhUFCXAIiIiIlJRlACLiIiISEVRAiwiIiIiFUUJsIiI\niIhUFCXAIiIiIlJRlACLiIiISEVRAiwiIiIiFUUJsIiIiIhUFCXAIlIRzOyXZvatUVw/y8wSZnZR\nnte9Ilz3pJHeU2qSPkO/mf17seM5kTDOhJm9XuxYRKR0KAEWkUpxLfClUVy/C5gBrIcTJq6jXReg\nHPagd2Au8ImBA2b2QPjf6N70i83su+G5fx3HGCH4Hn5unN9TREqcEmARqQjuftjdj43ienf3V909\nER4ygqTPxrJumTno7m8mvXaCHxxuMLPowMHw1y3AznGOD3d/Fegc7/cVkdKmBFhEKkJ6q4KZbTez\nL5rZ/zazN81sp5n9QdL5wRYIM5sFrAxPvRH+0/+/DrHu75nZqnDNfWb2AzN7yyhjTZjZZ8zsETM7\nZmYbzOxSMzsvfL+jZvaUmZ2TdM+5ZvYTM9tvZkfM7Hkzuzpt3T8ys81m1h1e96Okc9eb2Toz6zKz\n18zsP81s0mjiDq0BdgPXJR27jiD5XZMWz5Dvma21xMz+I7mCPNz3UERkKEqARaSSfR5YBVwM3Avc\nZ2Zzks4PtCrsAn43/PUc4Azg1iHWrAbuAC4CPgTMAu7PIbY7gAeARcBG4IfA94CvAs0Eleh/SLp+\nCvAo8O7w8zwGPGxmMwHMrBn4u3DducD7gF+H52aE6/8LMA+4Avh30qrdI+TAvwKfTDr2SYL/BoPr\n5fE9h/seiohkqC52ACIiRfSou38v/PXXzGwZQQK5JTxmELRDJD1Elf7P/inc/YGklzvM7HPAc2ZW\n7+5do4jtX939xwBm9nXgGeAr7v5EeOzvCBLNgfddB6xLuv9OM7sO+CBBYng2cDT8zMcIqrRrw2vP\nAKqA/3D33eGxjlHEmu4HwN+Y2VkEhZZ3AB8l+G87IF/vOdz3UEQkgyrAIlLJXkx7vR+YPpYFzazZ\nzB4O/zn+TeBX4amzxxDbgfB/16cdqzOzKeH7Tjazvw3bJd4wsyMEldWB9/0FQRvCdjNbYWYfS2px\nWAs8Caw3sx+Z2afN7ORRxjvI3V8DfgrcRPCQ3KPunj6FIV/vmffvoYiUPyXAIlLJetNeO2P4c9HM\n6oGfA4eBjwGLCaZEANSOITY/wbGBeL9J0HLxF8A7CVon1g+8r7sfBZqAG4C9wFeAtWZ2krsn3H0p\ncA1BFfZPgU1h73Ou7idIfj8O/O/0k0O850tJ75kgsx2iJsv75PV7KCKVQX9IiIiMTE/4v1UnuGYe\ncCrwRXd/yt03A6fn6f2HG532DuABd3/Y3TuAV4HZKQsESedKd/8LggR5NnBV0vln3P0rwNsIEstr\nyd3PCZLvauA/h7oo7T17kt7zIEGbBABmFgEWjiEeEZFB6gEWERmZnQRJ6AfM7GdAd5bxZ7sIkrjP\nmtn3gAsJHjpLl8vDZdnuST62BbjOzH4avr6L1IfOfgc4l+DBtzeA3wnPv2RmlwBXEySqrwKXAqcB\nG3KIEwiSbTObF/46I3kfwXuuBL5pZu8HXiZ42C3ntgwRkWSqAItIpUhPwrJVVIe8xt33AncCf0PQ\nZ/r3GTcHva+fAK4n+Gf9Pwf+5wjeZyTnhzv2eYLE9ingIYIKbHvS+cME48ieJEgyPwPc4O4bgTeB\nywmmSLxEkDx/3t2HrNyOhLsfDVsvshnuPf8VeDD8+hVBErwybY2R/ncS+X/t3Xd83WXd//HXJ0l3\nSzpYRRDECQ6kdeBAbkFAUcGBSsCJg+EstxNHAW/HT2/AWUCRdSNVBBQUGSKiIuBoGSpDVKAIBTrT\nka4kn98f5xSS9KRN0pyV83o+Hnm05/pe3+/5wKHlnSvXkHqJEt+YS5LUr4jYj0IYnZqZNX/IRES8\nGzgtM6dWuxZJtcEpEJKkoXowIn6emUdVu5D+FHfDaAbWVLsWSbXDEWBJ0qAUjzZ+UvHlquJxwzUp\nInYv/rYrMyt+FLOk2mQAliRJUkNxEZwkSZIaigFYkiRJDcUALEmSpIZiAJYkSVJDMQBLkiSpoRiA\nJUmS1FAMwJIkSWooBmBJkiQ1FAOwJEmSGkrdBeCIODYibo+I9uLXTRHx6i3c85aIuCsi1hTvfU2l\n6jD47/kAACAASURBVJUkSVJtqbsADDwIfAqYAcwErgcuj4g9SnWOiJcCFwHfB54PXA78LCL2rEy5\nkiRJqiWRmdWuYatFxBLg45l5bolrPwLGZ+ahPdpuBm7NzOMrWKYkSZJqQD2OAD8uIpoi4ghgPHBz\nP91eAlzXp+2aYrskSZIaTEu1CxiKiHgOhcA7FlgJvDEz7+6n+47Ao33aHi22S5IkqcHUZQAG7gb2\nAlqBw4ELIuIVmwnBgxIR04CDgfuBtcPxTEmSJA2rscBuwDWZuWQwN9ZlAM7MTuDfxZe3RsSLgI8C\nx5Xo/giwQ5+2HYrt/TkY+OHW1ilJkqSyO4rChgcDVpcBuIQmYEw/124GDgC+1aPtQPqfMwyFkV8u\nvPBC9tij5OYSGmFmzZrF6aefXu0yVCF+3o3Fz7ux+Hk3jrvuuou3v/3tUMxtg1F3ATgivgxcBSwA\nJlFI/fsBBxWvXwD8JzNPLN7yTeCGiDgBuBJoo7B92vs38zZrAfbYYw9mzJhRjn8M1ZjW1lY/6wbi\n591Y/Lwbi593Qxr0dNW6C8DA9sD5wHSgHbgDOCgzry9e3xno3Ng5M2+OiCOBLxW/7gUOy8w7K1q1\nJEmSakLdBeDMfN8Wru9fou1S4NKyFSVJkqS6Udf7AEuSJEmDZQCWgLa2tmqXoAry824sft6Nxc9b\nAzEijkIebhExA5g3b948J9JLkiTVoPnz5zNz5kyAmZk5fzD3OgIsSZKkhmIAliRJUkMxAEuSJKmh\nGIAlSZLUUAzAkiRJaigGYEmSJDUUA7AkSZIaigFYkiRJDcUALEmSpIZiAJYkSVJDMQBLkiSpoRiA\nJUmS1FAMwJIkSWooBmBJkiQ1FAOwJEmSGooBWJIkSQ3FACxJkqSGYgCWJElSQzEAS5IkqaEYgCVJ\nktRQDMCSJElqKAZgSZIk1ZVct57uteuHfH/LMNYiSZIkbbXs7qbrkcVseGAhGx54mM4FC9nwwMLi\nrw/T9chiOj70xiE/3wAsSZKkispMupevLATa+x9mw4IeIfeBh9nwn0dh/YbNPqNz4aIhv78BWJIk\nScOue806Oh8sBNzOBQvZsGDh44G3c8FCuleu3qrndz2yeMj3GoAlSZI0aNnVRefDiwojthunJyx4\n+PFR3K7Hlpb1/TsXNlAAjojPAG8EngWsAW4CPpWZ/9jMPe8CzgUSiGLz2swcX+ZyJUmS6lJm0r1k\nORseeLgwevtAcRR34+v/PAqdXWWtIcaNoeXJ0xn15OmFX3fbqfj7nVi27FF4xU+H9Ny6C8DAvsC3\ngb9QqP8rwLURsUdmrtnMfe3AM3giAGdZq5QkSapx3as6npia0GOR2cbX2bG5aDUMmptpedL2j4fc\nUbvuRMuuTwTe5u2nEhElb22av2LIb1t3ATgzD+n5OiLeDTwGzARu3PytOfTZ0pIkSXUmN3TS+Z9H\niyH34V7zcTcsWEj34uVlr6F5uylPjOLuWhzB3XU6o568Ey1P2p4YVfk4WncBuITJFEZztzTRZGJE\n3E9h7+P5wImZeWeZa5MkSSqbzKTr0SVPhNoHHn5iqsKChXQ+9Bh0d5e1hpgwjlG7FqYl9P51OqN2\n2ZGmibU347SuA3AUxsS/Ady4hTB7D3A0cAfQCnwCuCki9szMh8tfqSRJ0tB0rVjVe/7tA8XR3GLI\nza04EGJAWppp2XlHRu1anKLw+Ghu4XXT1NZ+pynUqroOwMAcYE/gZZvrlJm3ALdsfB0RNwN3AccA\ns8tZoCRJ0ubkuvVs+M8jhZBb4tCH7uUry15D8w7TCqH28UVmG+fj7kTL9G2J5uay11BJdRuAI+I7\nwCHAvpm5cDD3ZmZnRNwKPG1z/WbNmkVra2uvtra2Ntra2gZbriRJalADOdWMLO/a/KZtJvYItb13\nVWjZeUeaxo0p6/tvrblz5zJ37txebe3t7UN+XmSZ/4WXQzH8Hgbsl5n/HsL9TcDfgSsz8+Mlrs8A\n5s2bN48ZM2Zsdb2SJGnkGo5Tzbba6FGM2mXHwiKzjfNve4ziNk+eVN73r4L58+czc+ZMgJmZOX8w\n99bdCHBEzAHagEOB1RGxQ/FSe2auLfY5H3goM08svv48hSkQ/6SwaO6TwJOBsytcviRJqkPlPtVs\niyJonr5dYR5ur90UCoG3eYdpRFNTeWsYQeouAAPHUtj14YY+7e8BLij+fheg587MU4DvATsCy4B5\nwEsy8+6yVipJkupCtU81A2iass0Ti8x27TEP98nTGbXzDsSY0WWvoVHUXQDOzC1+e5OZ+/d5fQJw\nQtmKkiRJNa0mTzV7fFeFwihu06QJZX1/PaHuArAkSVIpVT/VrKmJlp13eGL+bZ9dFTZ3qpkqywAs\nSZLqQs2datZrV4XqnWqmwfNTkiRJNafzkcWs/PHVbPjXg9U71azHIrNaPtVMg2cAliRJNaXzkcUs\nePGR5Zmy0ONUs40juI+favbk6TRNm+w0hQZgAJYkSTVlxfmXb1X4ffxUs55H9xZ/bdlpuxF3qpkG\nzwAsSZJqytp5d272+hOnmvXYD3fj612m1/ypZqo+A7AkSaoZmcm6W+/q1bbNuw5j3CtmjuhTzVRZ\nBmBJklQzOu97iO7lK3u1Tf7YOxi18w793CENnmfmSZKkmrG2z+hv83ZTaXnS9lWqRiOVAViSJNWM\ndfN7B+AxM/ZwVwYNOwOwJEmqGWvn914AN3bvPapUiUYyA7AkSaoJuX4D6/96b6+2MTMMwBp+BmBJ\nklQT1t/1b3Ld+l5tY57/rCpVo5HMACxJkmpC3+kPo3bfmeYp21SpGo1kBmBJklR12dnJmt/P79Xm\n9AeVi/sAS5KkqshM1t12N6su+RWrfnodXYuW9bo+Zu89q1SZRjoDsCRJqqgN9z3EykuvZdUlv2LD\nvx7st9/YmY4AqzwMwJIkqey6Fi9j1c+uZ+Wlv2LdX/6+xf5jX/RcxsxwBFjlYQCWJEll0b16Dauv\nvpFVl1xLx2/+DF1dW7xnzN57MPHwg9jmna/3AAyVjQFYkiQNm+zsZM3v5rHykmtZfeXvyY41W7yn\nZbedmHT4QUw8/EBGP/XJFahSjc4ALEmStkrvxWy/pmvR0i3e0zStlYmHHcCktxzEmJl7OtqrijIA\nS5KkIRnoYraNYtwYJrxmXyYefhDj/+uFxChjiKrD//IkSdKADXYxG01NjNvvBUw6/EAmHPIKmiaO\nL3+R0hYYgCVJ0mZ1r17D6mv+wKqfXDO4xWxvPpCJb9iflh2mVaBKaeAMwJIkaRMuZtNIZgCWJEmA\ni9nUOAzAkiQ1OBezqdH4X6wkSQ3IxWxqZAZgSZIahIvZpAIDsCRJI9hWLWZ784GMfpqL2TTy1F0A\njojPAG8EngWsAW4CPpWZ/9jCfW8BTgF2A/4BfDozrypvtZIkVZ6L2aTNq7sADOwLfBv4C4X6vwJc\nGxF7ZGbJb2sj4qXARcCngCuBo4CfRcTemXlnZcqWJKm8XMwmDUzd/ZeemYf0fB0R7wYeA2YCN/Zz\n20eAqzLztOLrL0TEgcCHgOPLVKokSWXnYjZp8OouAJcwGUhgcz/feQlwap+2a4DDylWUJEnlMqTF\nbM9/FhMPP8jFbBJ1HoCjMEHpG8CNW5jKsCPwaJ+2R4vtkiTVvMcXs136K1b/4ncuZpO2Ql0HYGAO\nsCfwsnI8fNasWbS2tvZqa2tro62trRxvJ0lSLy5mkwrmzp3L3Llze7W1t7cP+XmRmVtbU1VExHeA\n1wP7ZuaCLfR9ADg1M7/Vo+0k4LDM3LtE/xnAvHnz5jFjxozhLVySpC1wMZu0ZfPnz2fmzJkAMzNz\n/mDurcs/IcXwexiw35bCb9HNwAHAt3q0HVhslySp6lzMJlVO3QXgiJgDtAGHAqsjYofipfbMXFvs\ncz7wUGaeWLz2TeCGiDiBwjZobRR2jXh/RYuXJKmH7o61rL76RhezSRVWdwEYOJbCrg839Gl/D3BB\n8fe7AI//LZKZN0fEkcCXil/3Upj+4B7AkqSKcjGbVH11F4Azs2kAffYv0XYpcGlZipIkaTNczCbV\nlroLwJIk1QsXs0m1yT9ZkiQNo67Fy1h1+W9Yecm1LmaTapQBWJKkrfT4YrZLrqXjN3+CThezSbXM\nACxJ0hC4mE2qXwZgSZIGKDNZd/s9rPrJtS5mk+qYAViSpC3YcN9DrLzsV6z6ybWDW8z25gMZ/8oX\nuZhNqjH+iZQkqQQXs0kjlwFYkqQiF7NJjcEALElqaNnZyZrfz2flJde6mE1qEAZgSVLDcTGb1NgM\nwJKkhuFiNklgAJYkjXAuZpPUlwFYkjQidT6ymMWfOo3V197kYjZJvRiAJUkjTveqDh567fF0Lli4\n2X4tu+3EpDcfyMTDD3Ixm9RABh2AI2IM8GJgV2A8sAi4NTPvG+baJEkakqX/7wf9ht/HF7MdfiBj\nXvBsF7NJDWjAATgiXgZ8FHg9MApoB9YAU4ExEfFv4HvAmZm5sgy1SpK0Rev+ei/t37ukV5uL2ST1\nNKC/ASLiCmAGcBFwEPCXzFzT4/ruwL5AG3BCRLwzM39VhnolDYMNCxay7PQL6PzPo9UuRRp2G+59\nALq7H38dY0az82/OZfRTd6liVZJqyUC/Bb4SeHNmbih1MTP/DfwbOD8i9gSmD1N9koZZ19J2Hj70\nQ3Q+9Fi1S5EqYvLH3m74ldTLgAJwZp410Adm5p3AnUOuSFLZZCaPffSrhl81jFFP3YUpHz6q2mVI\nqjFDngQVEaOB7YGmnu2ZuWBri5JUHit+cBkdV99Y7TKkioixo9nuG58mxoyudimSasxQdoF4OnAO\n8NK+l4AEmoehLknDqGvFKpZ/80KWn/HjXu1N205mykeOAlfBa4SJ0aMZt99MRj/Vrc0kbWooI8Dn\nAZ3A64CFFEKvpBqU6zew4vzLWXrqeXQvad/k+vbf/iwTXrVPFSqTJKl6hhKAnw/MzMy7h7sYScMj\nM1n9i9+y9ItnseG+/5Ts03r8EYZfSVJDGkoAvhPYdrgLkTQ81v7l7yz5wndY++e/le7Q0kzrMW9h\n2ueOqWxhkiTViKEE4E8BX4uIE4G/Ar22RsvMFcNRmKTB2XDfQyz5n7NYfcVv+u0z4bWvYOrnj3Fe\npCSpoQ0lAF9X/PXXfdpdBCdVQdfSdpadej7t5/4UNnSW7DNm5p5MO+mDjNvneRWuTpKk2jOUAPzK\nYa9C0qB1r11H+9mXsvz0/6N7xaqSfVp224lpnz2GCYe9knCnB0mSgCEE4Mz8bTkKkTQw2d3Nqsuu\nY+mXv0/ng4+U7NM0eRJT/vvdtL7nDe6BKklSH0PZB/gVm7uemb8bejmSNmfNH25lyezvsu72e0p3\nGD2K1ve/mSkfeyfNkydVtjhJkurEUKZA3FCiredewGWdAxwR+wKfAGYC04E3ZOYVm+m/H9B3VVAC\n0zPT82BVF9b/436WnHwGHdfe1G+fiW96FVNPfD+jdt2pgpVJklR/hhKAp/R5PQrYG/gi8NmtrmjL\nJgC3AT8ALhvgPQk8A1j5eIPhV3Wg89ElLPv6uay48BfQ1VWyz9iXPp9pJx3P2L33qHB1kiTVp6HM\nAd70OCn4VUSsB06jMDJbNpl5NXA1QAxuVc8it2hTvehevYblZ/yI5d+eS3asKdln1NN3ZdoXjmX8\nwS9zgZskSYMwlBHg/jwKPHMYnzecArgtIsYCfwNOysz+f5YsVUl2dbFy7lUs/erZdD26pGSf5u2m\nMOWTR7PN219HtAznH2FJkhrDUBbB9d1INCjMxf00hakJtWYhcAzwF2AM8H7ghoh4UWbWYr1qQJlJ\nx6//yNJTzmD9Xf8u2SfGjWHycUcw+cNH0jRxfIUrlCRp5BjK8NFtFObU9v2Z6y3A0Vtd0TDLzH8A\n/+jRdEtEPBWYBbxrc/fOmjWL1tbWXm1tbW20tbUNe51qXOv+ei9LTp7Dmt/+pXSHCCa1HcLUT7+X\nlunbVbY4SZJqwNy5c5k7d26vtvb2UrNyByYyc8u9et4QsWufpm4K82vXDrmKIYqIbrawC0Q/930N\neFlmvqyf6zOAefPmzWPGjBnDUKm0qc6HH2Ppl7/PyouvgX7+HI575YuYNvs4xjz7aRWuTpKk2jZ/\n/nxmzpwJMDMz5w/m3qEsgnugb1tETAYqHoC3wvMpTI2QKq575WqWffNC2s+6mFy7vmSf0c9+KtNm\nH8/4V76owtVJkjTyDWUO8KeA+zPzx8XXFwOHR8RC4JDMvH2Ya+z7/hOAp/HEFIzdI2IvYGlmPhgR\nXwF2ysx3Fft/FLgP+DswlsIc4FcCB5azTqmv3NDJiguuYOnXz6F7Sekf2zRP346pn3kfk956MNFc\n1i21JUlqWEOZA3wscBRARBxIIUi+Gngr8HXgoGGrrrQXUDjYIotfpxbbz6cwB3lHYJce/UcX++wE\ndAB3AAd4Yp0qJTNZ/cvfs/SLZ7LhXw+W7BMTxzPlI0fResxbaRo/tsIVSpLUWIYSgHcENv5f/HXA\nxZl5bUTcD/xxuArrT2b+FmjazPX39Hn9dQrBXKq4tfP+zpLZc1j7xztKd2huZpt3HsqUT7yHlu36\nnjEjSZLKYSgBeBmFEdYHKYz8fq7YHpT5GGSpXmy4/2GW/M9ZrL78+n77jH/Ny5n2+WMZ/fS+60ol\nSVI5DSUAXwZcFBH3AtOAq4rtewP/HK7CpHrUtWwFy047n/YfXAYbOkv2GbP3Hkw76XjGvfT5Fa5O\nkiTB0ALwLOB+CqPAn8zMVcX26cB3h6kuqa50r13Hih9cxrLTL6C7fVXJPi1Pns7Uz32AiYftTzT1\nO4tHkiSV2VC2QdsA/G+JSz8E3rfVFUl1JLu7WfWz61n6pe/RuaD0znpNkycx5YR30nr0m4gxoytc\noSRJ6msoI8D9mQ58EfjyMD5Tqllr/nArS06aw7rb7i7dYfQoWt/7JqbMeifNU7apbHGSJKlfwxmA\npYaw/t4HWHLKmXRcfWO/fSa+8QCmfvYDjNp1pwpWJkmSBsIALA1Q52NLWfa/57Ligp9DV1fJPmP3\n2YtpJx/P2Bl7Vrg6SZI0UAZgaQu6O9bSfsaPWfbtH5Kr15TsM+qpuzBt9nGMf/XLiYiSfSRJUm0Y\ncACOiNO20GW7raxFqinZ1cXKH1/N0q+cTdcji0v2adp2MlM/cTTbvOP1xCi/n5QkqR4M5v/Yew+g\nj8cLa0TouP6PLDl5Duvv/HfJ6zF2NK3HHcGUDx9J06QJFa5OkiRtjQEH4Mx8ZTkLkWrBur/9kyUn\nz2HNDX8u3SGCSW97NVM/8z5adtq+ssVJkqRh4c9sJaDz4cdY+pWzWfnjqyGzZJ9x//VCps0+njHP\neVqFq5MkScPJAKyG1r1yNcu+fRHtZ/6YXLOuZJ/Re+7OtNnHM37/F1e4OkmSVA4GYDWk3NDJiv/7\nOUu/fg7di5eX7NO847ZM/fT7mHTEq4nm5gpXKEmSysUArIaSmXRcfSNLTjmTDf9cULJPTBjHlA8f\nReuxb6VpwrgKVyhJksptMNugHQ1ckZml94OSatza+XeyZPYc1t5ye+kOzc1s847XMeUTR9Oy/dTK\nFidJkipmMCPAbwfmRMR84HIKYfiu8pQlDZ8NDzzM0i99j1U//XW/fca/+uVM+8KxjH76rhWsTJIk\nVcNgtkHbPyKmAK8FDgU+GxGPAldQCMQ3ZmZ3ecqUBq9r2QqWnX4B7T+4DNZvKNlnzPOfxbSTjmfc\nywayzbUkSRoJBjUHODOXARcCF0bEaGB/CmH4h8C4iPglhUB8VWauHu5ipYHIdetpP+cylp12Ad3L\nV5bs07LLjkz93DFMfMP+RFNThSuUJEnVNORFcJm5Hri6+HV8RLyAQhj+PLAH8MVhqVAaoMxk9c+u\nZ8mXzqLzgYUl+zS1TmTKrHeyzXvfRNPYMRWuUJIk1YJh2wUiM/8C/AX4QkSMGq7nSgOx5ubbWXLS\nd1k3v59p6aNaaH3vm5gy6500T22tbHGSJKmmlGUbtMwsPeFSGmbr/7mAJaecQcdVN/bbZ8Jh+zPt\nsx9g1FOeVMHKJElSrXIfYNWlzkXLWPb1c1lxwRXQ1VWyz9gXPZdpJ3+QsS94doWrkyRJtcwArLrS\n3bGW9rMuZtm3fkiu6ijZZ9TuOzP1C8cx4ZB9iYgKVyhJkmrdsAXgiJgMHJKZFw3XM6WNsquLlRdf\nw9KvnE3XwkUl+zRNa2XqJ45mm3ceSozyeztJklTacKaEXYH/AwzAGlYdN/yZJSfNYf3f/1nyeowd\nTesxb2XyR46ieZuJFa5OkiTVG4fJVLPW/f2fLDn5DNb85k+lO0Qw8S0HM+3E99HypB0qW5wkSapb\nBmDVnM6Fi1j6lbNZ+aOrILNkn3GvmMm02ccz5nnPqHB1kiSp3hmAVTO6V3Ww/NsXsfyMH5Fr1pXs\nM3qP3Zn6heMYf8CLXeAmSZKGZMABOCI+soUuFdlkNSL2BT4BzASmA2/IzCu2cM9/AacCzwYWAF/K\nzPPLXKoGKDs7WXHhL1j2tXPoWrSsZJ/mHaYx9dPvY1Lba4jm5gpXKEmSRpLBjADPGkCfBUMtZBAm\nALcBPwAu21LniNgN+AUwBzgSeBVwdkQ8nJm/Kl+Z2pLMpOOaP7DklDPZcO8DJfvE+HFM/nAbk487\ngqYJ4ypcoSRJGokGHIAz8ynlLGSgMvNq4GqAGNjPwI8D/p2Znyy+viciXk4h0BuAq2TtbXezZPZ3\nWXvTbaU7NDWxzTtez5RPvIeWHaZVtjhJkjSiNcIc4H2A6/q0XQOcXoVaGt6GBQtZ+qXvseqyvh/J\nE8Yf9FKmfeFYRj+zJr7nkiRJI8yAAnBEHJGZPxpg312AJ2fmH7aqsuGzI/Bon7ZHgW0iYkxmll5t\npWHVtXwly75xAe3fvxTWbyjZZ/TznsG2J3+QcS+fUeHqJElSIxnoCPBxETEbOBf4eWbe1fNiRLQC\nLwPeDhwIvHdYq1TdyvUbaD/npyw77Xy6l60o2adl5x2Y+tkPMPFNryKamipcoSRJajQDCsCZuV9E\nHAp8GPhKRKymMIq6FphCYZR1MXAe8JzM7DviWk2PAH1PSdgBWLGl0d9Zs2bR2traq62trY22trbh\nrXAEykxWX/4blnzpLDrvf7hkn6ZtJjJ51jtofd+baRo7psIVSpKkejF37lzmzp3bq629vX3Iz4vs\n56CBfm+I2BZ4OYWjj8dRCL63ArdmZveQKxmCiOhmC9ugRcRXgddk5l492i4CJmfmIf3cMwOYN2/e\nPGbM8Mfxg7XmljtYctJ3WTfvztIdRrXQ+p43MuW/30Xz1NbSfSRJkjZj/vz5zJw5E2BmZs4fzL2D\nXgSXmYuBnw32vuESEROApwEbd4DYPSL2ApZm5oMR8RVgp8x8V/H6mcAHI+L/AecABwCHAyXDr4Zu\n/b8WsPSLZ7H6yt/122fC6/+LaZ87hlG771zByiRJkp5Qj7tAvAD4DZDFr1OL7ecDR1OYjrHLxs6Z\neX9EvJbCrg8fAf4DvDcz+9+GQIPStXgZS79+HisuuBw6u0r2GfvC5zDt5A8y9oXPqXB1kiRJvQ06\nAEfEMgrBs6+kMCf4n8B5mXnuVtZWUmb+Fuh3pVRmvqdE2+8onBynYdS9Zh3tZ13Msm9eSK7qKNln\n1FN2Zurnj2HC6/bz6GJJklQThjICfArwWeAq4E/FthcBrwa+CzwFOCMiWjLz+8NSpWpKdnez6ifX\nsvQr36fzocdK9mma2srUj7+bbd51GDF6VIUrlCRJ6t9QAvDLgc9l5pk9GyPiGOCgzHxzRNxBYbqB\nAXiE6fjtX1hy0hzW/+3ektdjzGhaP/AWJn/s7TRvM7HC1UmSJG3ZUALwwcCnSrT/mifm4/4S+OpQ\ni1LtWXfXv1l68hl0/PqWfvtMfOvBTP3M+xm1c99d5yRJkmrHUALwUuD1bHqU8OuL1wAmACu3oi7V\niM5HFrP0q2ezcu5V0F16l7tx+85g2uzjGbPXMytcnSRJ0uANJQB/kcIc31fyxBzgF1LYVuzY4usD\ngd9ufXmqlu5VHSz/7lyWz/kR2bG2ZJ9Rz9yNabOPZ/yr9nGBmyRJqhtD2Qf4+xFxJ/Ah4E3F5nuA\n/TLzpmKfU/u7X7UtOztZedEvWfrVH9C1aGnJPs3bT2Xqp9/LpLZDiJZ63ElPkiQ1siGll8z8A/CH\nYa5FVZSZdPzqJpacfAYb/vFAyT4xfiyTP3Qkk497G00Tx1e4QkmSpOExpAAcEc3AG4A9ik1/B67I\nzNKnIKimrbv9HhbP/i5r/3Br6Q5NTUw66rVM/eTRtOy4bWWLkyRJGmZDOQjjaRR2eXgShakPAJ8B\nHoyI12bmv4axPpXRhgcfYemXv8eqS37Vb5/xr9qHabOPZ/SznlLByiRJkspnKCPA3wL+BeyTmUsB\nImIacGHx2muHrzyVQ1f7SpZ/4/9o//6l5Lr1JfuMfu7TmXbyBxm/rwfoSZKkkWUoAXg/eoRfgMxc\nEhGfxnnBNS3Xb6D93J+x7NTz6F62omSflidtz9QT38/Eww8imvo9cVqSJKluDSUArwMmlWifCJQe\nTlRVZSarf34DS754Fp33P1SyT9OkCUz+2Dtoff/hNI0bU+EKJUmSKmcoAfgXwPci4r08sQ/wi4Ez\ngSuGqzANj7V/+iuLT5rDuj//rXSHlmZa3/0Gpnz83TRPm1zZ4iRJkqpgKAH4I8D5wM3Ahh7PuQL4\n6DDVpa20/l8PsvR/zmL1L/o/j2TC6/Zj6ueOYfRTd6lgZZIkSdU1lIMwlgOHRcTTgWcVm+/KzH8O\na2Uakq4ly1n2v+fRft7PoLP0rnRjXvBspp10PONe/LwKVydJklR9Qz7GKzPvBe4dxlq0FbrXrKP9\n+5ew/Bv/R/fK1SX7tOz2JKZ9/hgmvP6/PLpYkiQ1rAEF4Ig4baAPzMwThl6OBiu7u1l1ybUs/fL3\n6XzosZJ9mqZsw5T/fjet73kDMXpUhSuUJEmqLQMdAd57gP1yqIVo8Dp+P48lJ81h/R3/KHk9163o\noAAAFJNJREFUxoym9QOHM/mjb6e5tdTGHZIkSY1nQAE4M19Z7kI0cOvvvo8lJ8+h47pb+u0z8fAD\nmXriBxi1y44VrEySJKn2DXkOsCqv85HFLP3aOaz84ZXQ3V2yz9iX7c22J3+QMXs9s8LVSZIk1QcD\ncB3oXtXB8jk/Yvl3f0R2rCnZZ9QzdmXa7OMYf+BLXeAmSZK0GQbgGpadnayc+0uWfvUHdD22tGSf\n5u2mMuVTR7PNUa8lWvw4JUmStsTEVIMyk47rbmHJKWew4e77SvaJ8WOZfPwRTP5gG00Tx1e4QkmS\npPplAK4x626/hyUnz2HN7+eX7tDUxKQjD2Hqp95Ly47bVrY4SZKkEcAAXCM6H1nMki+eyaqLr+m3\nz/gD9mHq7OMYs8fuFaxMkiRpZDEA14DuVR089Nrj6VywsOT10c95OtNOOp7x+72gwpVJkiSNPAbg\nGrDmljtKht/mnbZn2onvZ+JbDiKamqpQmSRJ0shjAK4B3UuX93od48Yw5YR30XrMW2kaN6ZKVUmS\nJI1MBuAa0L1mXa/XY577DKZ87B1VqkaSJGlkq8ufq0fEByPivohYExG3RMQLN9P3XRHRHRFdxV+7\nI6KjkvVuSd/DLWL82CpVIkmSNPLVXQCOiLcBpwKzgb2B24FrImJze4K1Azv2+Nq13HUORnb0HgFu\nMgBLkiSVTd0FYGAWcFZmXpCZdwPHAh3A0Zu5JzNzUWY+VvxaVJFKB6h7zdper2OcAViSJKlc6ioA\nR8QoYCbw641tmZnAdcBLNnPrxIi4PyIWRMTPImLPMpc6KNnRNwC78E2SJKlc6ioAA9sCzcCjfdof\npTC1oZR7KIwOHwocReGf+aaI2KlcRQ5W3xHgpvHjqlSJJEnSyDfid4HIzFuAWza+joibgbuAYyjM\nI646R4AlSZIqp94C8GKgC9ihT/sOwCMDeUBmdkbErcDTttR31qxZtLa29mpra2ujra1tYNUOkCPA\nkiRJ/Zs7dy5z587t1dbe3j7k59VVAM7MDRExDzgAuAIgIqL4+lsDeUZENAHPBa7cUt/TTz+dGTNm\nDL3gAco++wDHeEeAJUmSNio1ADl//nxmzpw5pOfVVQAuOg04rxiE/0RhV4jxwHkAEXEB8J/MPLH4\n+vMUpkD8E5gMfBJ4MnB2xSvvR67usw+wu0BIkiSVTd0F4My8uLjn7ykUpj7cBhzcY2uznYHOHrdM\nAb5HYZHcMmAe8JLiFmo1oe9JcO4DLEmSVD51F4ABMnMOMKefa/v3eX0CcEIl6hqqTU6CcwRYkiSp\nbOptG7QRaZMRYAOwJElS2RiAa0D2PQnOKRCSJEllYwCuAd0dfbdBMwBLkiSViwG4yrKzE9Zv6NXm\nCLAkSVL5GICrrO8ewOAiOEmSpHIyAFdZ3+kPAE0ehSxJklQ2BuAqKzkC7FHIkiRJZWMArrLuPnsA\nE0GMHV2dYiRJkhqAAbjKNtkCbdxYIqJK1UiSJI18BuAq6zsHOMY7/1eSJKmcDMBV1ncE2FPgJEmS\nyssAXGXZ0XsRnHsAS5IklZcBuMr6LoJzBFiSJKm8DMBV1ncbtHAPYEmSpLIyAFfZJiPA7gEsSZJU\nVgbgKnMEWJIkqbIMwFW2yT7AjgBLkiSVlQG4yrpX99kGzX2AJUmSysoAXGWlToKTJElS+RiAq6zv\nSXBN7gMsSZJUVgbgKnMEWJIkqbIMwFXWvckuEAZgSZKkcjIAV1lusg+wAViSJKmcDMBVtsk+wAZg\nSZKksjIAV9mmJ8EZgCVJksrJAFxl2eEcYEmSpEoyAFdZd59dIJo8ClmSJKmsDMBVlJlkh0chS5Ik\nVZIBuJrWb4Du7l5N4QiwJElSWRmAq6jvKXAATRMcAZYkSSqnugzAEfHBiLgvItZExC0R8cIt9H9L\nRNxV7H97RLymUrVuTt9T4MARYEmSpHKruwAcEW8DTgVmA3sDtwPXRMS2/fR/KXAR8H3g+cDlwM8i\nYs/KVNy/vgvgAJrcBUKSJKms6i4AA7OAszLzgsy8GzgW6ACO7qf/R4CrMvO0zLwnM78AzAc+VJly\n+5er+wTglmZi9KjqFCNJktQg6ioAR8QoYCbw641tmZnAdcBL+rntJcXrPV2zmf4Vs+kWaI7+SpIk\nlVtdBWBgW6AZeLRP+6PAjv3cs+Mg+1fMJlugOf9XkiSp7FqqXUAtmzVrFq2trb3a2traaGtrG5bn\n910E5x7AkiRJm5o7dy5z587t1dbe3j7k59VbAF4MdAE79GnfAXikn3seGWT/x51++unMmDFjsDUO\nWPea3scgN413BFiSJKmvUgOQ8+fPZ+bMmUN6Xl1NgcjMDcA84ICNbRERxdc39XPbzT37Fx1YbK+q\n7FjT67UjwJIkSeVXbyPAAKcB50XEPOBPFHaFGA+cBxARFwD/ycwTi/2/CdwQEScAVwJtFBbSvb/C\ndW+iu6PPCLBzgCVJksqu7gJwZl5c3PP3FApTGW4DDs7MRcUuOwOdPfrfHBFHAl8qft0LHJaZd1a2\n8k1tMgfYXSAkSZLKru4CMEBmzgHm9HNt/xJtlwKXlruuwep7FHLTeAOwJElSudXVHOCRxhFgSZKk\nyjMAV9Gm+wAbgCVJksqtLqdA1ILlZ/2E5u2m0LLT9rTstB0tO2476GOMNzkJboIBWJIkqdwMwEPQ\n3bGWJZ/71ibtzdtNpWWn7WjeaTtapheD8U7bFULy9O1onr5dr50ess8uEI4AS5IklZ8BeAg6Fy4q\n2d61aCldi5bC7ff0e2/T1FZapheC8bq//bP3NRfBSZIklZ0BeAi6+gnAA9G9tJ31S9tZ//d/bnLN\nEWBJkqTycxHcUIxqYdy+Mxj11F2IYTy8IhwBliRJKjtHgIdg3Iufx7jLvglAZtLdvorOhx+j8+FF\ndD382OO/71y4qPD7hx4jV6/Z/EMjGLfPXhWoXpIkqbEZgLdSRNA8eRLNkycxZs+n9tuve+XqJ4Lx\nw4voXLgxMC+C5ia2eeehjNptpwpWLkmS1JgMwBXSNGkCo5/5FEY/8ynVLkWSJKmhOQdYkiRJDcUA\nLEmSpIZiAJYkSVJDMQBLkiSpoRiAJUmS1FAMwJIkSWooBmBJkiQ1FAOwJEmSGooBWJIkSQ3FACxJ\nkqSGYgCWJElSQzEAS5IkqaEYgCVJktRQDMCSJElqKAZgSZIkNRQDsCRJkhqKAViSJEkNxQAsSZKk\nhmIAliRJUkOpqwAcEVMi4ocR0R4RyyLi7IiYsIV7boiI7h5fXRExp1I1qz7MnTu32iWogvy8G4uf\nd2Px89ZA1FUABi4C9gAOAF4LvAI4awv3JPA9YAdgR2A68Mky1qg65F+YjcXPu7H4eTcWP28NREu1\nCxioiHgWcDAwMzNvLbZ9GLgyIj6emY9s5vaOzFxUiTolSZJU2+ppBPglwLKN4bfoOgojvC/ewr1H\nRcSiiPhrRHw5IsaVrUpJkiTVtLoZAaYwfeGxng2Z2RURS4vX+vND4AHgYeB5wNeAZwCHl6lOSZIk\n1bCqB+CI+Arwqc10SQrzfockM8/u8fLvEfEIcF1EPCUz7+vntrEAd91111DfVnWmvb2d+fPnV7sM\nVYifd2Px824sft6No0dOGzvYeyMzh7eawRYQMQ2YtoVu/wbeAfxvZj7eNyKagbXA4Zl5+QDfbzyw\nCjg4M3/VT58jKYwcS5IkqbYdlZkXDeaGqo8AZ+YSYMmW+kXEzcDkiNi7xzzgA4AA/jiIt9ybwqjy\nws30uQY4CrifQsCWJElSbRkL7EYhtw1K1UeAByMifglsDxwHjAbOAf6Ume8oXt8J+DXwjsz8S0Ts\nDhwJ/JJCyN4LOA1YkJn7V+EfQZIkSVVW9RHgQToS+A6F3R+6gUuAj/a4PorCArfxxdfrgVcV+0wA\nHgR+AnypQvVKkiSpxtTVCLAkSZK0teppH2BJkiRpqxmAJUmS1FAMwCVExAcj4r6IWBMRt0TEC6td\nk4ZfROwbEVdExEMR0R0Rh1a7JpVPRHwmIv4UESsi4tGI+GlEPKPadak8IuLYiLg9ItqLXzdFxKur\nXZfKLyI+Xfw7/bRq16LyiIjZxc+459edg3mGAbiPiHgbcCowm8KWabcD10TEtlUtTOUwAbgNOJ7C\n1nga2fYFvk3h6PRXUVg0e61Ho49YD1I4ZGkGMBO4Hrg8IoZ8sJJqX3HA6gMU/t+tke1vwA4UTgPe\nEXj5YG52EVwfEXEL8MfM/GjxdVD4i/Rbmfm1qhansomIbuANmXlFtWtRZRS/qX0MeEVm3ljtelR+\nEbEE+HhmnlvtWjT8ImIiMI/CVqmfB27NzBOqW5XKISJmA4dl5oyhPsMR4B4iYhSFkYJfb2zLwncI\n1wEvqVZdkspiMoWR/6XVLkTlFRFNEXEEhS0yb652PSqb7wI/z8zrq12IKuLpxSmM/4qICyNil8Hc\nXG/7AJfbtkAz8Gif9keBZ1a+HEnlUPzJzjeAGzNzUPPGVD8i4jkUAu9YYCXwxsy8u7pVqRyK3+A8\nH3hBtWtRRdwCvBu4B5gOnAT8LiKek5mrB/IAA7CkRjQH2BN4WbULUVndTeEE0FbgcOCCiHiFIXhk\niYidKXxD+6rM3FDtelR+mdnz6OO/RcSfgAeAtwIDmuJkAO5tMdBFYVJ1TzsAj1S+HEnDLSK+AxwC\n7JuZC6tdj8onMzuBfxdf3hoRL6JwMuhx1atKZTAT2A6YX/zpDhR+mvuKiPgQMCZd8DSiZWZ7RPwD\neNpA73EOcA/F7xznAQdsbCv+YToAuKladUkaHsXwexjwysxcUO16VHFNwJhqF6Fhdx3wXApTIPYq\nfv0FuBDYy/A78hUXQD4VGPCghiPAmzoNOC8i5gF/AmZRWDhxXjWL0vCLiAkUvlvcOGKwe0TsBSzN\nzAerV5nKISLmAG3AocDqiNj4k572zFxbvcpUDhHxZeAqYAEwCTgK2A84qJp1afgV53z2mssfEauB\nJZl5V3WqUjlFxNeBn1OY9vAk4GSgE5g70GcYgPvIzIuL2yOdQmHqw23AwZm5qLqVqQxeAPyGwk4A\nSWH/Z4DzgaOrVZTK5lgKn/MNfdrfA1xQ8WpUbttT+LM8HWgH7gAOcoeAhuGo78i2M3ARMA1YBNwI\n7JOZSwb6APcBliRJUkNxDrAkSZIaigFYkiRJDcUALEmSpIZiAJYkSVJDMQBLkiSpoRiAJUmS1FAM\nwJIkSWooBmBJkiQ1FAOwJEmSGooBWFJDiIjfRMRpg+i/a0R0R8Tzhvm5+xWfu81A76k1Pf4ZuiLi\nsmrXsznFOrsjYmm1a5FUOwzAkhrFG4HPD6L/AmBH4G+w2eA62OcCjIQz6BN4BvDujQ0RcV7x39Gc\nvp0j4rvFa+dUsEYofIYfq/B7SqpxBmBJDSEzl2fm6kH0z8x8LDO7i01BIfTF1jx3hFmUmSt6vE4K\n3zgcERFjNjYWf98GPFDh+sjMx4D2Sr+vpNpmAJbUEPpOVYiI+yLiMxHxg4hYEREPRMT7e1x/fApE\nROwKXF+8tKz4o/9z+nnu2yPiz8VnLoyIH0bEdoOstTsiPhARP4+I1RFxZ0TsExFPLb7fqoj4Q0Q8\npcc9u0fEzyLikYhYGRF/iogD+jz3+Ij4R0SsKfa7uMe1wyPijojoiIjFEXFtRIwbTN1FtwIPAm/q\n0fYmCuH31j719PuepaaWRMRPe44gb+kzlKT+GIAlNbITgD8DzwfmAGdExNN7XN84VWEB8Obi758O\nTAc+2s8zW4DPAc8DDgN2Bc4dQm2fA84D9gLuAi4CzgS+BMykMBL9nR79JwJXAq8s/vNcBVwRETsD\nRMRM4JvF5z4DOBj4XfHajsXnnw08C9gPuIw+o90DlMA5wNE92o6m8O/g8ecN43tu6TOUpE20VLsA\nSaqiKzPzzOLv/19EzKIQIO8ttgUUpkP0WETV98f+vWTmeT1e3h8RHwP+GBHjM7NjELWdk5mXAkTE\n14CbgZMz87pi2zcpBM2N73sHcEeP+2dHxJuAQykEwycDq4r/zKspjNLeXuw7HWgGfpqZDxbb/j6I\nWvv6IfDViNiFwkDLS4G3Ufh3u9FwveeWPkNJ2oQjwJIa2V/7vH4E2H5rHhgRMyPiiuKP41cANxQv\nPXkranu0+Ovf+rSNjYiJxfedEBH/W5wusSwiVlIYWd34vr+iMA3hvoi4ICKO7DHF4Xbg18DfIuLi\niHhfREweZL2Py8zFwC+A91BYJHdlZvbdhWG43nPYP0NJI58BWFIj29DndbIVfy9GxHjgamA5cCTw\nAgq7RACM3oracjNtG+s9lcKUi08DL6cwdeJvG983M1cBM4AjgIeBk4HbI2KbzOzOzIOAV1MYhf0w\ncHdx7vNQnUsh/L4T+EHfi/285z093rObTadDjCrxPsP6GUpqDP4lIUkDs774a/Nm+jwLmAp8JjP/\nkJn/AHYYpvff0tZpLwXOy8wrMvPvwGPAbr0eUAid12fmpykE5N2A/XtcvzkzTwb2phAs38jQXU0h\nfLcA1/bXqc97ru/xnosoTJMAICKagOdsRT2S9DjnAEvSwDxAIYS+PiJ+Cawpsf3ZAgoh7iMRcSbw\nXAqLzvoayuKyUvf0bLsXeFNE/KL4+hR6Lzp7LbA7hYVvy4DXFq/fExEvAg6gEFQfA/YBtgXuHEKd\nQCFsR8Szir/fJLwP4D2vB06NiEOAf1FY7DbkaRmS1JMjwJIaRd8QVmpEtd8+mfkwMBv4KoV5pt/e\n5ObC3Nd3A4dT+LH+J4H/HsD7DOT6ltpOoBBs/wBcTmEEdn6P68spbEf2awoh8wPAEZl5F7ACeAWF\nXSTuoRCeT8jMfkduByIzVxWnXpSypfc8Bzi/+HUDhRB8fZ9nDPTfkyT1EiW+MZckqV8RsR+FMDo1\nM2v+kImIeDdwWmZOrXYtkmqDUyAkSUP1YET8PDOPqnYh/SnuhtEMrKl2LZJqhyPAkqRBKR5t/KTi\ny1XF44ZrUkTsXvxtV2ZW/ChmSbXJACxJkqSG4iI4SZIkNRQDsCRJkhqKAViSJEkNxQAsSZKkhmIA\nliRJUkMxAEuSJKmhGIAlSZLUUAzAkiRJaij/H0Z1AJH1XYV6AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21b036ac50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(2, 1, figsize=(8, 8))\n",
"\n",
"masses = np.arange(0.08, 5.0, 0.02)\n",
"\n",
"# compute and plot temperature relationship\n",
"p1 = [3.64 for m in masses if m >= 3.9]\n",
"p2 = [-0.028*m + 3.875 for m in masses if 3.9 > m >= 3.0]\n",
"p3 = [0.039*m + 3.5765 for m in masses if 3.0 > m >= 0.23]\n",
"p4 = [0.614*m + 3.3863 for m in masses if m < 0.23]\n",
"tr = p4 + p3 + p2 + p1\n",
"\n",
"ax[0].set_xlabel(\"initial mass [Msun]\")\n",
"ax[0].set_ylabel(\"log(T / K)\")\n",
"\n",
"ax[0].plot(masses, tr, '-', c='#dc143c', lw=3)\n",
"\n",
"# plot luminosity relationship\n",
"# compute and plot temperature relationship\n",
"p1 = [0.2*(m - 5.0) + 2.6 for m in masses if m >= 3.9]\n",
"p2 = [0.55*m + 0.1 for m in masses if 3.9 > m >= 3.0]\n",
"p3 = [1.7 for m in masses if 3.0 > m >= 1.5]\n",
"p4 = [0.85*m + 0.4 for m in masses if 1.5 > m >= 0.23]\n",
"p5 = [-0.16877*m - 0.117637 for m in masses if m < 0.23]\n",
"lr = p5 + p4 + p3 + p2 + p1\n",
"\n",
"ax[1].set_xlabel(\"initial mass [Msun]\")\n",
"ax[1].set_ylabel(\"log(L / Lsun)\")\n",
"\n",
"ax[1].plot(masses, lr, '-', c='#dc143c', lw=3)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Relaxed model values\n",
"\n",
"We can compare the relationship(s) quoted above with model values for temperature and luminosity after the model has relaxed to a stable configuration. This takes only a couple time steps to achieve, so we will look at the model relationship during the third time step for all models with masses between 0.08 and 5.0 Msun. Models are taken from a recent study where we used the most up-to-date version of the Dartmouth models for young stars (Feiden 2016)."
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model_directory = \"../../papers/MagneticUpperSco/models/trk/std/\"\n",
"\n",
"# get all file names\n",
"from os import listdir\n",
"all_fnames = listdir(model_directory)\n",
"\n",
"# sort out only those file names that end in .trk\n",
"fnames = [f for f in all_fnames if f[-4:] == \".trk\"]\n",
"\n",
"# sort numerically\n",
"fnames = sorted(fnames)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To select which model time step is most representative of a relaxed model, we can step through the first 50 iterations to find if there are any noticable jumps in model properties."
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArMAAAKgCAYAAACIpfUuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xm81VW9//HX53BAwOEoDliiplKIeh2gNPI6l2nOZhSp\n5FiSJmH8br+Ge7u3wfu7pWFWZmqppGJZzuZsZgqml4M4BCaOIIIgeECZzrB+f5xNHY5n2GfP+5zX\n8/E4D93f71rr+9nI1/1msfb6RkoJSZIkqRrVlLsASZIkKVeGWUmSJFUtw6wkSZKqlmFWkiRJVcsw\nK0mSpKplmJUkSVLVMsxKkiSpahlmJUmSVLUMs5IkSapahllJkiRVrZzDbEScExGzI6Ih8zM9Io7o\nov2fIqKlg5872rX7bkQsjIhVEXF/RAzPtUZJkiT1bvnMzM4Hvg6MAkYDDwG3RcTITtqfAGzb5mcP\noBn43foGEfF14Dzgi8C+wLvAvRExII86JUmS1EtFSqlwg0W8BUxOKV2dRduvAv8JvC+ltDpzbCHw\no5TSlMzrzYDFwBdSSr/rbCxJkiT1TQVZMxsRNRHxOWAwMCPLbmcA09oE2Z1onbF9cH2DlNIK4K/A\nmELUKUmSpN6lNp/OEbEHreF1ILASOCGlNDeLfvsCuwOntzm8LZBonYlta3HmnCRJkrSBvMIsMBfY\nC6gDTgKmRsSBWQTaM4FnUkoz87w+EbEl8EngFWBNvuNJkiSp4AYCHwDuTSm9VciB8wqzKaUm4KXM\ny1mZGdeJwITO+kTEYOCzwLfbnVoEBDCUDWdnhwKzuijjk8D1PatckiRJZXAycEMhB8x3Zra9GmCj\nbtqMBQbQLoCmlF6OiEXAYcDT8I8vgO0H/LyL8V4BuO666xg5srONFHqnSZMmMWXKlHKXsYFS1FSM\na+Q7Zq79e9ov2/aFbtfbVNr7LlU9hb5OIcbLZYxi3TfZtq203z+lVGnvva/eO5X2mZNN2zlz5nDK\nKadAJrcVUs5hNiIuBO4GXgM2pTVpHwQcnjk/FViQUvpmu65nAremlJZ3MOwlwLcjYh6tb/Z7wALg\nti5KWQMwcuRIRo0alevbqUp1dXUV955LUVMxrpHvmLn272m/bNsXul1vU2nvu1T1FPo6hRgvlzGK\ndd9k27bSfv+UUqW9975671TaZ04P2xZ8SWg+M7PbANcC7wMaaJ1NPTyl9FDm/DCgqW2HiPgQ8DHg\nEx0NmFL6YWYZwi+BzYG/AEemlNblUWevNW7cuHKX8B6lqKkY18h3zFz797Rftu0r8fdGJam0X59S\n1VPo6xRivFzGKNZ9k8vYfU2l/fr01Xun0j5zchm7kAq6z2w5RMQoYObMmTMr6k+LUjU49thjuf32\n28tdhlRVvG+knquvr2f06NEAo1NK9YUcuyD7zEqSJEnlYJiV+rBK+ytDqRp430iVxTAr9WF+KEs9\n530jVRbDrCRJkqqWYVaSJElVyzArSZKqTmNzM00tLeUuQxWg0E8AkyRJKoqGtWv5/uOP89u5c5m/\nciUBDN98cw7eYQeO+MAH+PiOO7LZRt09iFS9jWFWkiRVtKaWFi6bNYv/+8gjrG5u/sfxBLzw9tu8\n8PbbXPn00wDsOmQIp+62G+fstRdDBg0qU8UqJcOsJEmqWHe/9BJn3HMPi1atyqr93GXL+Najj/Kt\nRx9l1NZb86ODD+bQHXcscpUqJ8OsJEmqOC8uX85n77yTmYsX5zxG/ZIlHHbTTQwZMIDrjzqKI3bZ\npYAVqlIYZiVJUsVY3djIVx96iCueeaZgYy5bt44jb7mFzfr354lTTmHEllsWbGyVn2FWkiRVhN88\n9xxn3Xsv64q0S8GKxkZ2vfpq9tl6a5489VT61bipU2/gf0VJklRWC1asYKdf/pLxd99dtCDb1qwl\nS6j98Y+596WXin4tFZ8zs5IkqSxSSnzrkUf47yefLMv1j7j5ZraureXNr361LNdXYTgzK0mSSu6F\nZcuou/TSsgXZ9ZY0NREXXcSaNWvKWody58ysJEkqmZQSp9x5Jzc8/3y5S9nAoJ/9DIA3zj6bbevq\nylyNesIwK0mSSuKVhgaGX3klzd03LZv3XXkltRE0nHceg32aWFUwzEqSpKL70j33cMWzzxZkrKN3\n2ok7Pv1pABqbm7nv5Ze599VXmbloES83NLBs7VrWNTeTchy/KSU2/ulPefLzn+fD739/QWpW8Rhm\nJUlS0axat45NLr0052DZ1oQ99+Syww/f4Fj/fv04avhwjho+vNv+KSX+d+FCvnjffTz11lvdtv/I\nDTeQJk/OuV6VhmFWkiQVxU+feILzH3kkrzG2HDiQJ085hZ023zzveiKCj2y3HbNOP/2fxy66KO9x\nVV6GWUmSVFApJQZefDHrcuxfE8EVn/gEZ+65Z0Hr6kiaPJkTfvc7bn3ttaJfS8VhmJUkSQXz1Btv\nsM/11+fU91M77cQdJ5xATYmfzHXL2LFc/uSTTPjzn0t6XRWGYVaSJBVELn9lv/WgQcw+9VTet9lm\nRagoe+d85COG2SplmJUkSXlZtWoVG192Wdbta4CpRxzByXvsUbyi1GcYZiVJUs56Mhu746ab8vcz\nz2RAbfXEj9cbGtjOhyhUtOr53SRJkirGETfeyL0LFmTVdvKHP8yPDj64uAUVyeSHH2bacceVuwx1\nwTArSZKy9vclSxhx7bVZtb316KM5btddi1xRcd320kvlLkHdMMxKkqRupZQYOGUK61paum07Zb/9\n+OoBB5SgquJb3dz9w3cbm5t5t7GRVU1NrG5qoiUlWlKiuaWl9Z+Zn5aUGFBTw6D+/RlUW8ug2loG\n9uvHoP79qYkowbvpnQyzkiSpS1974AF+/NRTWbWt5idmDQTWdHB85K9/zfI1a3insZG1zc00t7QU\n5IlmHamJoH9NDQP79WOTAQPYfKON2GrQILbdeGOGbbopJ48cyT5Dhxbp6tXJMCtJkjr0zpo1bPaz\nn2UV3B48/ngOzeKRspXscyNGcM3zz7/n+Nxly0pWQ0tKrG1uZm1zMw3r1vH6O+9scP62efN44ayz\nSlZPNTDMSpLUh7y1ejUn3Horf33jDXauq6N+/HgG9e//nnYn3nILt7z4YlZjVvNsbFv/uf/+HYbZ\nSvJqQ0O5S6g4hllJkvqAxuZmzrn/fn797LP/ODZ3+XK2/+UvWXreef849npDA8OuvDKrMT+90078\n/tOfLnit5bLjkCHlLqFbjalYCxyql2FWkqReLKXEFbNnc96DD9LUQRB6a80arn36ab6w55587Lrr\nmLFoUVbjNkyYwGYbb1zocqUeM8xKktRLPb5wIZ+6+WaWr+noa03/dNp993HaffdlNebGwDu9ZFmB\negfDrCRJvcyid9/lyN//nqeWLCnouDceeSSf3X33go4p5cswK0lSL7GmqYmz772X6+bMKfjYzRdc\nQE1NTcHHlfKV8+/KiDgnImZHREPmZ3pEHNFNn7qI+HlELIyINRExt22fiPhORLS0+/lbrjVKktQX\npJT4ycyZbPKTnxQ8yB72/veTJk82yKpi5TMzOx/4OvACEMBpwG0RsXdK6T13UkT0Bx4AFgEnAguB\nHYG32zV9FjgsMyZAUx41SpLU66xtamJtczMRwRMLF3LSHXfw9tq1Bb/OvNNOY5ettir4uFIh5Rxm\nU0p3tTv07YiYAHwU6OiPhWcCmwMfTSmtfzbcax20a0opFXaRjyRJVWzBihXcMHcuv//733lmyRLW\nZPGI1XwMBFb30S953XTMMXzmjjvKXYZ6oCBrZiOiBhgLDAZmdNLsmMy5yyLiOGAJcAPwPymltg96\n/mBEvE7rE+VmAN9IKc0vRJ2SJFWDlevWcfPf/87ls2dTv3gx61pauu9UIN8bM4Zv779/ya5XaU4a\nMYK/b7UVlz71FKsbGxlYW8uAmho2qq1lYL9+NKfEqqYmVjU28u66dbzb1MTba9eydPVqlq1ezYp1\n61jd1ERjER95qw3lFWYjYg9aA+dAYCVwQkppbifNdwYOBa4DjgSGA7/I1PC9TJvHaV2u8DzwPuA/\ngUciYo+U0rv51CpJUqVKKTFz0SIufOIJ7n/lFd5pbCz6NR8fN47Df/tbVrQJyivPO49NBg4s+rUr\n3Qe33JKfHnZYQcZa3djIaytXMvvNN3ly0SJmLV7Mc2+9xZurVpHLH1EGFKSq3iXfmdm5wF5AHXAS\nMDUiDuwk0NYAi4EvppQSMCsihgGTyYTZlNK9bdo/GxFPAK/SOut7dZ61SpJUMVJKPDJ/Pt+ZPp1H\nX3+d5hI92WmL2lremjiRiKDhggv+UUtEdNNTuRjUvz8jhgxhxJAhjN111w3ONTY3M3fZMu548UVu\nfeEFnl26lNXdLCE5Z++9i1luVcorzKaUmoCXMi9nRcS+wERgQgfN3wDWZYLsenOAbSOiNjNW+/Eb\nIuLvtM7idmnSpEnU1dVtcGzcuHGMGzcuuzcjSVIBvfT225z/4IM8NH8+TS0tDN14Yz4ydCgHDhvG\n1Oee46klS0r+19AXH3AAF+y333uOG2TLo3+/fvzL1lvzL1tvzTc/+lGgdSb38YUL+c2cOdz90kss\nWrVqgz7/feCB5Si1R6ZNm8a0adM2ONbQ0FC060Uq4J8EI+JB4NWU0hkdnPsBMC6ltHObYxOB/5NS\nGtbJeJvQOjP7nZTSzzppMwqYOXPmTEaNGlWItyFJUk6aWlq45tln+dZf/sKbq1eXu5wNrJo4kUH9\n+5e7DPVQY3Mzf1mwgF898wyvrFjBY5//fLlLykl9fT2jR48GGJ1Sqi/k2DnPzEbEhcDdtO5IsClw\nMnAQcHjm/FRgQUrpm5kuvwDOjYhLgZ8CHwK+AVzSZswfAXfQGmC3A/6L1q25Noz3kiRVkPkrVjDx\nT3/itnnzaCnRcoFsjR8xgmuPOabcZShH/fv149Add+TQHXcsdykVK59lBtsA19L6Ra0G4Gng8JTS\nQ5nzw2izR2xKaUFEfBKYAswGXs/8+w/bjDmM1h0OtqR1t4NHad3K66086pQkqeBSStw+bx5ffuAB\nFr5bmd9RXnD22WzXbgme1Nvks8/sWd2cP7SDY38FPtZFHxe4SpIq2rrmZi5+8kn+a8YM1hZ5v9dc\n7Tt0KH899dRylyGVREH2mZUkqbd7a9Uqzrn/fv7wwgsVvX/o9M99jjHDOvwqitQrGWYlSerCs0uW\n8Nk77uBvy5aVuxQ2ra1lh802Y7tNNuGB117bYJ/SYYMH8+o551BTU1O2+qRyMMxKktROSombnn+e\nL953Hw3r1pX02pvV1nLw9ttz7qhRHLbjjvTrJpy+uWoVG9fWsvEAt9NX32SYlSQpoyUlvvvYY3z/\nr38tyUMM+gFfGz2a7x9wAP1rc/tI3mbw4MIWJVUZw6wkqc9b09jIF++7j+vmzCn4etgAztlzT0YP\nHcqIIUPYqa6O922yicsBpAIxzEqS+qzlq1dz4m238fCCBQUdd4v+/Xnk859nj623Lui4kt7LMCtJ\n6nNebWjgk7//Pc8vX16wMbccMICnxo9n2OabF2xMSd0zzEqS+oxXGho4+MYbeXXlyoKMV1dby7On\nnWaAlcrIMCtJ6vVea2jgwAKG2PtPPJGP77xzQcaSlB/DrCSp11qwYgUH3Hgjr6xYkfdY40eM4Npj\njilAVZIKyTArSeqVvvHII/y/J57Ia4y6CBacdx6bbLRRgaqSVGiGWUlSr3Pe/ffz89mzc+4/eZ99\n+NFhhxWwIknFYpiVJPUaKSU+MnUqM5csyan/K2edxY5+mUuqKoZZSVKvcPIdd3DD88/3uN+wQYN4\ndcIEH2IgVSnDrCSpqn3/scf49xkzetzv+J124pZPf7oIFUkqJcOsJKkq/fnVVzn4ppt63O/i/ffn\ngjFjilCRpHIwzEqSqsrba9awzWWX0djS0qN+Nx11FCeNHFmkqiSVi2FWklQVUkp86KqrmNfQ0KN+\ndxx7LEd/6ENFqkpSuRlmJUkVb9IDD3DJU0/1qM8fjz+eI4cPL1JFkiqFYVaSVLFmLVrEqOuu61Gf\n333qU3xmt92KVJGkSmOYlSRVnKbmZob87GesbGzMus9/ffjD/MfBBxevKEkVyTArSaooX7r3Xq54\n5pms2x+3/fbc+tnPFrEiSZXMMCtJqggvL1vGzr/+ddbtt99oI177yleKWJGkamCYlSSVVUqJ9//i\nFyxatSrrPi1f+xoRUcSqJFULw6wkqWyueOopvvTAA1m3f/Pss9m6rq6IFUmqNoZZSVLJNbe0MHDK\nFJpSyqr9pQceyFf23bfIVUmqRoZZSVJJfevPf+bCJ5/Mqu0HBg3i5XPPLXJFkqqZYVaSVBJrGxsZ\n9JOfkN1cLDRfcAE1NTVFrUlS9TPMSpKKbsI993D5s89m1fa+447jEx/8YJErktRbGGYlSUXT3NxM\n/ylTspqNHda/P/MnTix6TZJ6F8OsJKkofvLEE3z1kUeyarv6K19h4EYbFbkiSb2RYVaSVHADLr6Y\nxix2Kvjy7rvz8yOPLEFFknorw6wkqWDuf/FFDr/llqzapsmTi1yNpL7AMCtJKogdfvEL5r/7brft\n7jjmGI4eMaIEFUnqCwyzkqS8NDY1MeCSS7Jq62yspEIzzEqScvajxx/n3x59tNt2fzjiCE7cY48S\nVCSpr8l5N+qIOCciZkdEQ+ZnekQc0U2fuoj4eUQsjIg1ETG3fZ+IODciXo6I1RHxeER8JNcaJUnF\nM+jHP84qyKbJkw2ykoomn5nZ+cDXgReAAE4DbouIvVNKc9o3joj+wAPAIuBEYCGwI/B2mzafBS4G\nvgg8AUwC7o2ID6WUluZRqySpQJa98w5bXn55t+1+deihnDFqVAkqktSX5RxmU0p3tTv07YiYAHwU\neE+YBc4ENgc+mlJqzhx7rV2bScAvU0pToXX2FzgKOAP4Ya61SpIK49t/+hM/mDmz23aujZVUKgVZ\nMxsRNcBYYDAwo5Nmx2TOXRYRxwFLgBuA/0kptWRmbkcDF67vkFJKEfEAMKYQdUqScrfJlCm829zc\nZZsP19Xx5Nlnl6giScozzEbEHrQG1IHASuCElNLcTprvDBwKXAccCQwHfpGp4XvAVkA/YHG7fosB\n93CRpDKKiy7qts2KL3+ZTQcPLkE1kvRP+c7MzgX2AuqAk4CpEXFgJ4G2htZg+sWUUgJmRcQwYDKt\nYVaSVGGee+MN9rj++m7buaxAUrnkFWZTSk3AS5mXsyJiX2AiMKGD5m8A6zJBdr05wLYRUQssBZqB\noe36DaX1S2NdmjRpEnV1dRscGzduHOPGjcvmrUiS2jnwN7/hL4vb/2XZhq466CDO/Iibzkj6p2nT\npjFt2rQNjjU0NBTteoXeZ7YG2KiTc48B7ZPlCOCNTCgmImYChwG3Z15H5vWl3V14ypQpjPJbs5JU\nENksK2j52tdo/d+0JP1TR5OJ9fX1jB49uijXy2ef2Qsj4oCI2DEi9oiI/wYOonVNLBExNSIubNPl\nF8CQiLg0Ij4YEUcB3wB+1qbNj4GzI2J8ROwKXE7rl8quybVOSVLPZBNk0+TJBllJFSGfmdltgGuB\n9wENwNPA4SmlhzLnhwFN6xunlBZExCeBKcBs4PXMv/+wTZvfRcRWwHdpXV7wFPDJlNKSPOqUJGVh\nwdKlbH/NNV22+crIkVx61FGlKUiSspDPPrNndXP+0A6O/RX4WDf9LgMuy7UuSVLPnXXrrfxq3rwu\n26w9/3wGDBhQoookKTuFXjMrSaoy/S+66J9/jdYJdyuQVKlyXjMrSap+0U2Q3blfP4OspIrmzKwk\n9VHdfdFr+vHHM2b48BJVI0m5McxKUh/z1Lx57HPrrV22cTZWUrUwzEpSH/Kp667j7kVdP4fGICup\nmhhmJamP6O6LXoOAVQZZSVXGMCtJfUB362Ov/tjHOO1jXe6cKEkVyTArSb1YSomaiy/uuo2zsZKq\nmFtzSVIvtbqx0SArqddzZlaSeqG7HnuMo2fM6LKNQVZSb2CYlaReZv+rrmL62293er4f0GSQldRL\nGGYlqZdoSYl+3SwrOHGHHfjD2LElqkiSis8wK0m9wPI1axjys5912ab+sMPYZ599SlSRJJWGYVaS\nqlz94sWM/s1vumzj+lhJvZW7GUhSlUopceXTTxtkJfVpzsxKUhVa1djIlx94gGufe67LdgZZSb2d\nYVaSqszfly3jpNtv55mlS7tsZ5CV1BcYZiWpivz++ec54957WbluXadtBgBrDbKS+gjDrCRlqbG5\nmUvr65mzbBmn7b47/zpsWMmu/e66dXzz0Ue5tL6+y3a71NUx7+yzS1SVJJWfYVaSsvSDxx/nvzJP\n1fr1M88w9VOf4pTddiv6dW+fN4+vPPggr61c2WW7s4cP54rjjy96PZJUSQyzkpSlm1944R//noAv\n3H03tTU1fG7XXYtyvVcbGjj/oYe4/cUXu237P/vsw78ddlhR6pCkSmaYlaQspJSY1+4RsS0pccpd\nd9Evgs+MGFGwa61tauIn9fX81/TprGpq6rb9bz/+ccbuvXfBri9J1cQwK0lZeOPdd1ndQbBsTolx\nd95JbU0NJ3zwg3ldo7G5mauffZbvP/4487tZUrDeIyecwAG77JLXdSWpmhlmJSkLL7ablW2rOSXG\n3nEHfzj2WI4dPrzHYze1tHDd3/7Gd2fM4OWGhqz7PfP5z7PH+9/f4+tJUm9imJWkLMxbvnyD10Hr\nutn1mlpaOOn227nluOM4KouZ0qaWFv721ltMf/11psycyd/bjd+dV04/nR233LJHfSSpNzLMSlIW\nXmw3Y3rUzjuz3aab8svZs/9xrLGlhRNvv53/d8ABbLvxxgzo14+N+vVjQL9+DKip4fV33uHJRYt4\nctEiZr35ZofLFrKx5ItfZKvNNsvr/UhSb2GYlaQstJ+Z/eAWW3DRwQfT1NLCr5555h/H1zU3c8HD\nDxetjoYJE9hs442LNr4kVRvDrCRlof1OBsM335yaCK44/HCaW1q45rnnil7Dqq98hUEbbVT060hS\nNakpdwGSVOk62pZrl803B6Amgqs++cmcH57wgc02Y+yIEezQr1+X7dZOnGiQlaQOODMrSd1YtmYN\nDWvXbnBs+BZb/OPf+9XUcM0RR7D7llvyx5dfZlVjI+uam1nX0sLapibWtbSwrrmZgbW17LPNNnxk\n2235yLbbMnroULYePJh9r7yS15qbO71+06RJ9Osm7EpSX2WYlaRutN+Wq7amhh3bfQGrX00N/3e/\n/fi/++3Xo7HHXHUVT3axHVfjV79qkJWkLrjMQJK60X6JwY6bbUZtTf7/+zzgV7/i8S72r107cSK1\ntc45SFJXDLOS1I32M7PDM+tl8zHh1lt5tIu9ZVeffz4D+vfP+zqS1NsZZiWpG+235dolzzB72YwZ\nXD5vXqfn3znvPAYOGJDXNSSprzDMSlI32j8wIZ+Z2duffZZzH3us0/Nvf/nLbDxwYM7jS1JfY5iV\npG4Uamb20Zdf5rh77un0/JIvfYm6wYNzGluS+qqcw2xEnBMRsyOiIfMzPSKO6KL9FyKiJSKaM/9s\niYhV7dpc3ebc+p8/5lqjJOXrnXXrWLxqg/9V5TQz+9eFCzngD3/o9PycU09lq0037fG4ktTX5fM1\n2fnA14EXgABOA26LiL1TSnM66dMAfCjTHiB10ObuzFjr26ztoI0klUT7L38B7FRX16MxHnv9df51\n2rROz9959NHsOnRoj2uTJOURZlNKd7U79O2ImAB8FOgszKaU0pJuhl6bRRtJKon223IN23RTBvVg\nl4GHX3uNQ373u07P/78xYzhq111zrk+S+rqCrJmNiJqI+BwwGJjRRdNNIuKViHgtIm6NiI6e/3hw\nRCyOiLkRcVlEDClEjZKUi/Yzs7v0YFb2gVdf7TLIfv6DH+Tr+++fc22SpDyfABYRe9AaXgcCK4ET\nUkpzO2n+PHAG8DRQB/wfYHpE7JZSWphpczfwB+BlYBfgv4E/RsSYlFJHSxIkqajaz8y2fYxtV/74\n0kscdfPNnZ7fZ8gQrj/uuLxqkyTl/zjbucBetIbTk4CpEXFgR4E2pfQ48Pj61xExg9blCF8CvpNp\n03YK47mIeAZ4ETgY+FOetUpSj+XywITb5s3j+Ftv7fT8VhttRP0ZZ+RdmyQpzzCbUmoCXsq8nBUR\n+wITgQnZ9I2IWcDwLtq8HBFLM226DLOTJk2irt1f/40bN45x48Z1V4okdaqn23Ld9PzzjL3jjk7P\n1wBLvvKVQpQmSRVp2rRpTGv3pdeGdvt1F1KhH/pdA2yUTcOIqAH+BWj/RbK2bYYBWwJvdDfelClT\nGDVqVJZlSlL31jY1MX/lyg2OdTUze8OcOZx8V6f/SwOgefLkgtQmSZWqo8nE+vp6Ro8eXZTr5Rxm\nI+JCWte4vgZsCpwMHAQcnjk/FViQUvpm5vW/07rMYB6wOfBvwA7AVZnzG9O63OAPwCJaZ2P/B/g7\ncG+udUpSrl5uaHjP/oEdzcy+u24d3/jLX/jprFldjpcMspJUcPnMzG4DXAu8j9b9Y58GDk8pPZQ5\nPwxoatN+C+AKYFtgOTATGNNmfW0zsCcwntawu5DWEPsfKaXGPOqUpJy0Xy+79aBBbLbRhn/59JcF\nCzj9nns63I+2rcavfrXg9UmS8ttn9qxuzh/a7vUFwAVdtF8DdPoEMUkqtfY7GbSdlV3V2Mi3Hn2U\nn8yc2eHTX9p66fTTqa0t9KouSRIUfs2sJPUa79nJILMt1/TXX+e0e+7hhXZfDuvI5QcfzE5bblmU\n+iRJhllJ6lT7mdmdNtuM//Pww1z8v//b7WwswEHbbsuXPvzh4hQnSQIMs5LUqfZhdvaSJdz+4otZ\n9R1UU8PDp5xSjLIkSW0U5HG2ktTbNLW08Eq7fRGnL1zYSev3WnVBp18RkCQVkGFWkjowf8UKGlta\nNji2dPXqrPq6BZcklY5hVpI68GK7WdmN+vXLqt8qn+4lSSVlmJWkDrR/jG2/iG77PHjiiQzaKKuH\nIEqSCsQwK0kdaL8t16qmpk5atvrMzjtz6M47F7MkSVIHDLOS1IH2Oxl0ZbPaWn534olFrEaS1BnD\nrCR1oLtsyTMzAAAgAElEQVTH07bV4KNqJalsDLOS1E5KKeuZWXcukKTyMsxKUjtvvPsuq7tZIwvw\n4mmnFb8YSVKXDLOS1E62Swx23mqrIlciSeqOYVaS2mm/LVdHhg0aVIJKJEndMcxKUjvtH5jQkfnn\nnluCSiRJ3THMSlI72czMSpIqg2FWktrpbs3sY5/+dIkqkSR1xzArSe10ty3Xx3baqUSVSJK6Y5iV\npDaWrV7N22vXdnq+toS1SJK6Z5iVpDa6m5Vt9CEJklRRDLOS1EZPHmMrSSo/w6wktdHVzOyl++1X\nwkokSdkwzEpSG11ty/WVAw4oYSWSpGwYZiWpje7WzEqSKothVpLaeH7Zsg6PJ7/4JUkVyTArSRnv\nrFvHW2vWlLsMSVIPGGYlKaOznQwO3WqrElciScqWYVaSMs665ZYOjz942mmlLUSSlDXDrCQBS5cu\n5X9Xrix3GZKkHvLJjJL6vFNuuonrX321w3PrJk4scTWSpJ4wzErq0+Kii7o8379//xJVIknKhcsM\nJPVZ3QXZhSefXKJKJEm5cmZWUp/UXZB1X1lJqg6GWUl9yltvvcVWV1/dZRuDrCRVD8OspD7j5Ftu\n4YYXX+yyjUFWkqqLYVZSn9DdsoK6fv14e9KkElUjSSqUnL8AFhHnRMTsiGjI/EyPiCO6aP+FiGiJ\niObMP1siYlUH7b4bEQsjYlVE3B8Rw3OtUZKg+yD7iwMOMMhKUpXKZ2Z2PvB14AUggNOA2yJi75TS\nnE76NAAfyrQHSG1PRsTXgfOA8cArwPeBeyNiZEppXR61SuqDZs2axagHH+yyTcvXvkZEdNlGklS5\ncg6zKaW72h36dkRMAD4KdBZmU0ppSRfDTgS+l1K6EyAixgOLgeOB3+Vaq6S+Z7OLL2ZlSl22cX2s\nJFW/guwzGxE1EfE5YDAwo4umm0TEKxHxWkTcGhG7tRljJ2Bb4B/TKCmlFcBfgTGFqFNS3xAXXWSQ\nlaQ+Iq8wGxF7RMRKYC1wGXBCSmluJ82fB84AjgVOzlx7ekS8P3N+W1qXHSxu129x5pwkdam5ubnb\n9bET99rLICtJvUi+uxnMBfYC6oCTgKkRcWBHgTal9Djw+PrXETGD1uUIXwK+k2cdkvq4w6dO5f43\n3+yyjetjJan3ySvMppSagJcyL2dFxL60rnudkE3fiJgFrN+tYBGtXwwbyoazs0OBWd2NN2nSJOrq\n6jY4Nm7cOMaNG9ddV0lVrrvZWHBZgSSVyrRp05g2bdoGxxoaGop2vUjdrCvr0WARDwKvppTOyKJt\nDfAccFdKaXLm2ELgRymlKZnXm9EabMenlG7qZJxRwMyZM2cyatSoAr0TSdWiuyC7ff/+vDZxYomq\nkSR1pL6+ntGjRwOMTinVF3LsnGdmI+JC4G7gNWBTWtfBHgQcnjk/FViQUvpm5vW/07rMYB6wOfBv\nwA7AVW2GvYTWXRHm0bo11/eABcBtudYpqffqLsi+MnYsO+6wQ4mqkSSVQz7LDLYBrgXeR+v+sU8D\nh6eUHsqcHwY0tWm/BXAFrV/mWg7MBMa0XV+bUvphRAwGfklr4P0LcKR7zEpqr7sg67ICSeob8tln\n9qxuzh/a7vUFwAVZjPufwH/mWpek3s8gK0laryD7zEpSqRhkJUlt5bs1lySVREqJmosv7rqNQVaS\n+hxnZiVVvLVr13YZZAdikJWkvsowK6miLX77bQb+9Kednt+lpobVBllJ6rMMs5Iq1uOvvsq2V13V\n6fkjt96aeRd0+71SSVIvZpiVVJGeX7SIMTd1+KwUAL61++788QtfKGFFkqRK5BfAJFWcpqYmdr3u\nuk7P/+GQQzix9UkykqQ+zjArqeL0v+SSTs89N3Ysu/lUL0lShmFWUkXpah/Zt848kyFbbFHCaiRJ\nlc41s5IqRm0XQXbOZz9rkJUkvYdhVlJF2PtXv6K5k3Of3GYbdt1++5LWI0mqDoZZSWV38YwZzF6+\nvNPz94wfX8JqJEnVxDArqaxeWLqUyY891ul5n+wlSeqKYVZS2TQ2NfGha67p9LxBVpLUHcOspLIZ\n0MUWXE2TJpWwEklStTLMSiqLrrbgeujoo+nXr18Jq5EkVSvDrKSS23TKlE7P7VdXxyG77lrCaiRJ\n1cwwK6mkDrr+et5p7mwTLnj87LNLWI0kqdoZZiWVzCVPPMEjb7zR6Xm/8CVJ6inDrKSSuHzmTCY9\n8kin5w2ykqRc1Ja7AEm93xl33cXVc+Z0ev7dc88tYTWSpN7EMCupqEZfcw31S5d2en7qoYcyeNCg\nElYkSepNDLOSimbIpZeyfN26Ts9/aPBgTh01qoQVSZJ6G8OspKKovegiOt+zoNXzX/5ySWqRJPVe\nfgFMUkGllIhuguywAQP8wpckqSAMs5IKZm1jIzUXX9xlm0/vsAPzzz+/RBVJkno7lxlIKoil77zD\n1pdf3mWbi/ffnwvGjClRRZKkvsAwKylvjy9YwJgbb+yyzZ3HHMNRI0aUqCJJUl9hmJWUl8vr65nw\n0ENdtnl47FgO2mGHElUkSepLDLOScnbanXdy7dy5Xbb5k0FWklREhllJOdnz17/mmWXLumzz4Nix\nHGyQlSQVkWFWUo+saWxkk5/8pNs9ZO//zGc41CArSSoyw6ykrLS0tLDNz3/OW2vXdtv23pNO4uM7\n7liCqiRJfZ1hVlK39vvNb3hi8eKs2t796U9z+Ac+UNyCJEnKMMxK6tSE++7j8qefzrr9XSeeyBE7\n7VTEiiRJ2pBhVtJ7/Obppxl/33096nPHCSfwqZ13LlJFkiR1LOfH2UbEORExOyIaMj/TI+KILPt+\nLiJaIuLmdsevzhxv+/PHXGuU1DNPL15MXHRRj4Js/5oabjv+eI7eZZciViZJUsfymZmdD3wdeAEI\n4DTgtojYO6U0p7NOEfEB4EfAI500uTszVmRed/9tE0l5eXvVKoZcdhmph/322GorLj30UA5x1wJJ\nUpnkHGZTSne1O/TtiJgAfBToMMxGRA1wHfAfwIFAXQfN1qaUluRal6TsNTU3s9mll7K6ubuNtv5p\nAHDW3ntz+h57MHroUCKi2z6SJBVLQdbMZkLqWGAwMKOLpt8BFqeUro6IAztpc3BELAaWAw8B304p\ndb0zu6QeSSmx3eWX88a772bdZ+TGG/OfhxzCscOHM7DW5faSpMqQ1ydSROxBa3gdCKwETkgpdfhs\ny4j4V+B0YK8uhrwb+APwMrAL8N/AHyNiTEqpp38DKqkDJ918M3946aWs2w8fNIiHx49nu003LWJV\nkiTlJt/plbm0htM64CRgakQc2D7QRsQmwFTg7JTS8s4GSyn9rs3L5yLiGeBF4GDgT3nWKvVpU558\nkgv+/Oes2w8A1nztay4jkCRVtLzCbEqpCVg/xTMrIvYFJgIT2jXdBdgRuCP++clYAxAR64ARKaWX\nOxj/5YhYCgynmzA7adIk6uo2XII7btw4xo0b17M3JfUyd8ybx3G33tqjL3c1XXAB/Wpy3uxEktSH\nTZs2jWnTpm1wrKGhoWjXi0L+7X1EPAi8mlI6o93xAbQG0rZ+AGwCnA+8kAnG7ccbBrwKHJdSurOT\na44CZs6cOZNRo0YV4F1IvcOTb7zBATfeyNoefLnrtTPOYPshQ4pYlSSpL6qvr2f06NEAo1NK9YUc\nO+eZ2Yi4kNY1rq8BmwInAwcBh2fOTwUWpJS+mVJaB/ytXf+3gbR+G6+I2JjWL4j9AVhEa/j9H+Dv\nwL251in1NfOWL+ej11/PW2vWZN3nykMP5Sz/MChJqkL5LDPYBrgWeB/QADwNHJ5SeihzfhjwntnW\nLjQDewLjgc2BhbSG2P9IKTXmUafUJ7yxciUH3HgjL/bgr3IGAGsnTy5eUZIkFVk++8ye1c35Q7s5\nf3q712uArJ4gJum99rjmGpatzf4ZI6d+8INMPe64IlYkSVLxuVmk1Ev0JMg+9rnP8bFhw4pYjSRJ\npWGYlfqYNRMnslH//uUuQ5KkgjDMSn3ERsAa18dKknoZN5KU+oBDttvOICtJ6pUMs1Iv8c0Pf7jD\n47889FAe8uEhkqReyjAr9RI/OPhg9tliiw2OvXjmmXzR/WMlSb2YYVbqRerPPJP1X+1adf757Nwu\n3EqS1Nv4BTCpl1nn2lhJUh/izKwkSZKqlmFWkiRJVcswK0mSpKplmJUkSVLVMsxKkiSpahlmJUmS\nVLUMs5IkSapahllJkiRVLcOsJEmSqpZhVpIkSVXLMCtJkqSqZZiVJElS1TLMSpIkqWoZZiVJklS1\nDLOSJEmqWoZZSZIkVS3DrCRJkqqWYVaSJElVyzArSZKkqmWYlSRJUtUyzEqSJKlqGWYlSZJUtQyz\nkiRJqlqGWUmSJFUtw6wkSZKqlmFWkiRJVcswK0mSpKplmJUkSVLVyjnMRsQ5ETE7IhoyP9Mj4ogs\n+34uIloi4uYOzn03IhZGxKqIuD8ihudao6SuTZs2rdwlSFXH+0aqLPnMzM4Hvg6MAkYDDwG3RcTI\nrjpFxAeAHwGPdHDu68B5wBeBfYF3gXsjYkAedUrqhB/KUs9530iVJecwm1K6K6V0T0rpxZTSvJTS\nt4F3gI921iciaoDrgP8AXu6gyUTgeymlO1NKzwLjgfcDx+dapyRJknqvgqyZjYiaiPgcMBiY0UXT\n7wCLU0pXdzDGTsC2wIPrj6WUVgB/BcYUos7ephJnB0pRUzGuke+Yufbvab9s21fi741KUmm/PqWq\np9DXKcR4uYxRrPsml7H7mkr79emr906lfebkMnYh5RVmI2KPiFgJrAUuA05IKc3tpO2/AqcDZ3Uy\n3LZAAha3O744c07tVNr/VMAwW+x+htnCqLRfn776gZzrGL31A7kaVNqvT1+9dyrtMyeXsQupNs/+\nc4G9gDrgJGBqRBzYPtBGxCbAVODslNLyPK/Z3kCAOXPmFHjYytfQ0EB9fX25y9hAKWoqxjXyHTPX\n/j3tl237QrfrbSrtfZeqnkJfpxDj5TJGse6bbNtW2u+fUqq0995X751K+8zJpm2bnDYw6wKyFCml\nwg0WcT8wL6U0od3xvYB6oBmIzOH1s8LNwIjMv78I7J1SerpN34eBWSmlSZ1c8/PA9YV6D5IkSSqa\nk1NKNxRywHxnZturATbq4Pgc4F/aHfsBsAlwPjA/pdQUEYuAw4CnASJiM2A/4OddXPNe4GTgFWBN\nPsVLkiSpKAYCH6A1txVUzmE2Ii4E7gZeAzalNVAeBByeOT8VWJBS+mZKaR3wt3b93wZSSqnt+oBL\ngG9HxDxaw+n3gAXAbZ3VkVJ6CyhowpckSVLBTS/GoPnMzG4DXAu8D2igdTb18JTSQ5nzw4CmngyY\nUvphRAwGfglsDvwFODIThiVJkqQNFHTNrCRJklRKBdlnVpIkSSoHw6wkSZKqVq8PsxExLCL+FBHP\nRcRTEXFSuWuSqkVE3BwRyyLid+WuRaoGEXF0RMyNiOcj4sxy1yNVi3w+b3r9mtmI2BbYJqX0dEQM\nBWYCH0wprS5zaVLFi4gDad2t5AsppbHlrkeqZBHRj9adew4CVtL6eTOmCA8LknqdfD5vev3MbEpp\n0fqHMKSUFgNLgSHlrUqqDimlR4B3yl2HVCX2BZ7NfO68C/yRzHaVkrqWz+dNrw+zbUXEaKAmpfR6\nuWuRJPU67wfafr4sBLYrUy1Sn1FxYTYiDoiI2yPi9YhoiYhjO2hzbkS8HBGrI+LxiPhIFuMOoXVf\n3LOLUbdUbsW6d6S+wPtHyk0l3DsVF2aBjYGngC8D71nQGxGfBS4GvgPsA8wG7o2Irdq0+XJEzIqI\n+ojYKCIGALcAF6aU/lqKNyGVQcHvndKULVWEvO8fWmdih7V5vV3mmNSbFeLeyUtFfwEsIlqA41NK\nt7c59jjw15TSxMzrAOYDl6aUftjJONOAOSml75agbKnsCnXvZNodDJybUvpMcauWKkOu90+bL4Ad\nTOsXwJ4EPuYXwNRX5PvZk+vnTSXOzHYqIvoDo4EH1x9LrWn8AWBMJ332Bz4DHN9mxmn3UtQrVYpc\n7p1Mv/uB3wJHRsRrEbFfsWuVKk22909KqRn4GvAwUA9cZJBVX9aTz558Pm9qC1NuyWwF9AMWtzu+\nGBjRUYeU0mNU3/uUCq3H9w5ASukTxSxKqhJZ3z8ppTuBO0tUl1TpenLv5Px5U1Uzs5IkSVJb1RZm\nlwLNwNB2x4cCi0pfjlQ1vHek3Hn/SLkpyb1TVWE2pdRI6xNVDlt/LLOQ+DBgernqkiqd946UO+8f\nKTeluncqbi1pRGwMDAcic2jniNgLWJZSmg/8GLgmImYCTwCTgMHANWUoV6oY3jtS7rx/pNxUwr1T\ncVtzRcRBwJ94715l16aUzsi0+TLwb7ROUz8FfCWl9L8lLVSqMN47Uu68f6TcVMK9U3FhVpIkScpW\nVa2ZlSRJktoyzEqSJKlqGWYlSZJUtQyzkiRJqlqGWUmSJFUtw6wkSZKqlmFWkiRJVcswK0mSpKpl\nmJUkSVLVMsxKkiSpahlmJUmSVLUMs5IkSapahllJkiRVLcOsJEmSqpZhVpIkSVXLMCtJkqSqZZiV\nJElS1TLMSpIkqWoZZiVJklS1DLOSJEmqWoZZSZIkVS3DrCRJkqqWYVaSJElVyzArSZKkqmWYlSRJ\nUtUyzEqSJKlqGWYlSZJUtQyzkiRJqlpFDbMRcU5EzI6IhszP9Ig4ops+n4mIORGxOtP3yGLWKEmS\npOpV7JnZ+cDXgVHAaOAh4LaIGNlR44j4GHADcCWwN3AbcGtE7FbkOiVJklSFIqVU2gtGvAVMTild\n3cG5G4HBKaVj2xybAcxKKX25hGVKkiSpCpRszWxE1ETE54DBwIxOmo0BHmh37N7McUmSJGkDtcW+\nQETsQWt4HQisBE5IKc3tpPm2wOJ2xxZnjkuSJEkbKHqYBeYCewF1wEnA1Ig4sItA2yMRsSXwSeAV\nYE0hxpQkSVJBDQQ+ANybUnqrkAMXPcymlJqAlzIvZ0XEvsBEYEIHzRcBQ9sdG5o53plPAtfnW6ck\nSZKK7mRav+xfMKWYmW2vBtiok3MzgMOAS9sc+wSdr7GF1hlZrrvuOkaO7HCThF5r0qRJTJkypdxl\nbKAUNRXjGvmOmWv/nvbLtn2h2/U2lfa+S1VPoa9TiPFyGaNY9022bSvt908pVdp776v3TqV95mTT\nds6cOZxyyimQyW2FVNQwGxEXAncDrwGb0prGDwIOz5yfCixIKX0z0+UnwMMRcQFwFzCO1i29zu7i\nMmsARo4cyahRo4rxNipWXV1dxb3nUtRUjGvkO2au/XvaL9v2hW7X21Ta+y5VPYW+TiHGy2WMYt03\n2battN8/pVRp772v3juV9pnTw7YFXxJa7JnZbYBrgfcBDcDTwOEppYcy54cBTesbp5RmRMTngR9k\nfl4Ajksp/a3IdValcePGlbuE9yhFTcW4Rr5j5tq/p/2ybV+JvzcqSaX9+pSqnkJfpxDj5TJGse6b\nXMbuayrt16ev3juV9pmTy9iFVPJ9ZgstIkYBM2fOnFlRf1qUqsGxxx7L7bffXu4ypKrifSP1XH19\nPaNHjwYYnVKqL+TYJdtnVpIkSSo0w6zUh1XaXxlK1cD7RqoshlmpD/NDWeo57xupshhmJUmSVLUM\ns5IkSRVuVWNjuUuoWIZZSZKkCpVS4vCbbmLzSy9lybvvlrucimSYlSRJqkApJf71hhu4/9VXaUyJ\n7X7xC5avKfgzB6qeYVaSJKnCtKTEqKlTmf7GG/841ghsd9llNDY3l6+wCmSYlSRJqiDNLS2M/NWv\neGrJkvecW93Swsq1a8tQVeUq9uNsJUmSlKWmlhZ2vuIK5r/zTrlLqRqGWUmSpAqwurGR7S6/nOXd\nzLxGRIkqqg6GWUmSpDJbvmYN7//5z1mTUrdta7Jo05cYZiVJkspowYoV7HjFFbRk2d552Q35BTBJ\nkqQy+dvSpWzfgyALgMsMNmCYlSRJKoNH5s9n92uuKXcZVc8wK0mSVGLXP/ccB/32tzn1dV52Q66Z\nlSRJKqFvPfIIFz7xRM79/frXhgyzkiRJJXLCzTdz60sv5TeIuxlswDArSZJUZC0psefVV/PcsmV5\nj2WU3ZBhVpIkqYhWrVvHdpdfztvr1uU91vjddmOzQYMKUFXvYZiVJEkqkgUrVvCBK66guQBjXXvk\nkYzfffcCjNS7GGYlSZKK4IFXXuETv/993uMMqKnhqfHjGbnVVgWoqvcxzEqSJBXY96ZP5z+mT897\nnJ3r6pj9hS+wyYABBaiqdzLMSpIkFUhKiSN+/3vue/XVvMc6bffd+fURRxA+8atLhllJkqQCWNPY\nyM5XXMEbq1fnPdZvjz6asbvuWoCqej/DrCRJUp5ea2hg5yuvzPuLXoNra3nu9NP5QF1dQerqCwyz\nkiRJebj5+ef59B135D3OnlttxZOnnsqAfv0KUFXfYZiVJEnK0fi77uI3c+bkPc7XRo/mokMOKUBF\nfY9hVpIkqYfWNjUx/IorWLBqVV7j1AAPfOYzHLLjjoUprA+qKebgEfGNiHgiIlZExOKIuCUiPtRN\nny9EREtENGf+2RIR+f1OkSRJKpC5S5cy8JJL8g6yQwcPZul55xlk81TUMAscAPwU2A/4ONAfuC8i\nunsOWwOwbZsf/ytLkqSyu2zmTEZec03e45y86668MWECWwwcmH9RfVxRlxmklD7V9nVEnAa8CYwG\nHu26a1pSxNIkSZKy1pISh06bxp8XLsxrnABuO+EEjtlll8IUppKvmd0cSMCybtptEhGv0DpzXA98\nM6X0tyLXJkmS9B4LVqxglyuvZF1KeY0zZOBA5p5+OltvvHGBKhMUf5nBP0Tr4ysuAR7tJpg+D5wB\nHAucTGuN0yPi/cWvUpIk6Z8umzWL7a+4Iu8ge8Lw4Sw991yDbBGUcmb2MmA3YP+uGqWUHgceX/86\nImYAc4AvAd8pZoGSJEnQuqxgzHXX8cTixXmPdeOnPsVnd9utAFWpIyUJsxHxM+BTwAEppTd60jel\n1BQRs4DhXbWbNGkSde2eljFu3DjGjRvX03IlSVIf9tLbbzPiqqtoynOcLQcO5LnTT2doH5uNnTZt\nGtOmTdvgWENDQ9GuFynPafNuL9AaZI8DDkopvZRD/xrgOeCulNLkDs6PAmbOnDmTUaNG5V2vJEnq\nu5558032nDo173HG77Yb1xx5JK2rLFVfX8/o0aMBRqeU6gs5dlFnZiPiMmAcretf342IoZlTDSml\nNZk21wKvp5S+mXn977QuM5hH6xfG/g3YAbiqmLVKkiR95De/yat/vwgeGjuWA7ffvkAVqTvFXmZw\nDq27Fzzc7vjpwPo/9mwPNLc5twVwBa37yy4HZgJjUkpzi1qpJEnq89bm8TfWI7bYgvpTT2XwgAEF\nrEjdKfY+s93ulpBSOrTd6wuAC4pWlCRJUoF9f//9+daYMeUuo08q9T6zkiRJvcag2lqeHj+e4UOG\nlLuUPsswK0mSlIPjd9mFPxx/PDV+yausDLOSJEk90C+CP40dywF+yasiGGYlSZKytN+22/LIuHEM\n6Nev3KUowzArSZLUjQBuPOooxo4cWe5S1I5hVpIkCVi1dm2Hx3euq+OpL3yBTd1yqyIZZiVJkoAb\nnnuuw+Mvnn12iStRT3S7D6wkSVJf8LOZM8tdgnJgmJUkSQJmNzSUuwTlwDArSZKkqmWYlSRJ6sQW\n/fuXuwR1wzArSZLUiROGDy93CeqGYVaSJKkT3x4zptwlqBuGWUmSpE7sNGRIuUtQNwyzkiRJqlqG\nWUmSJFUtw6wkSZKqlmFWkiT1eUdNm1buEpQjw6wkSerz/vj66+UuQTkyzEqSpD5tq4suKncJyoNh\nVpIk9WlvdXL8nD32KGkdyo1hVpIk9VnRxazsL444ooSVKFeGWUmS1CetWrWq03Orzz+/hJUoH4ZZ\nSZLUJ2182WUdHj91xAgGDhhQ4mqUK8OsJEnqcza5+OJOz0095pgSVqJ8GWYlSVKfct3s2bybUofn\n0uTJJa5G+TLMSpKkPmPJihWcev/9HZ67/MADS1yNCsEwK0mS+oTGpia2ueKKTs9/ad99S1iNCsUw\nK0mSer2WlhYGXHJJp+ebL7ighNWokGrLXYAkSVIxNTc3UztlSqfn31dbS02N83vVqqj/5SLiGxHx\nRESsiIjFEXFLRHwoi36fiYg5EbE6ImZHxJHFrFOSJPVOTd0EWYCFX/1qiapRMRT7jyEHAD8F9gM+\nDvQH7ouIQZ11iIiPATcAVwJ7A7cBt0bEbkWuVZIk9SJNzc307ybIXnnIISWq5v+3d+fxUdX3/sff\nn5nsCQlrEhBkLa4tkIjiAoiICCJwXYDEWm69tbba1mJ77b3e++t2H61dXKoiVmoVcYnWpe4bLoio\nSE0ENy6CaNmURTAsEsjy/f2R4A0xk2XmnJkzyev5eOTx6Hznez7nA/Vk3h6/8z3wi6/LDJxzkxu/\nNrN/lbRVUrGkpREO+5Gkp51z1zW8/rmZTZD0A0mX+tQqAADoQA7U1Ci9hTWyB32nuDgO3cBP8V4g\n0lWSk7SjhTknSnq+ydizDeMAAAAtqqqublOQ3fq978WhG/gtbl8AMzOT9CdJS51z77cwtVDSliZj\nWxrGAQAAIvpi/35l33RTq/OG9eypXjk5cegIfovnbgbzJB0t6eQ4nhMAAHQSbQ2ykvTW7Nk+d4N4\niUuYNbO5kiZLGu2c+6SV6Z9KKmgyVtAwHtGcOXOUl5d3yFhJSYlKSkra2S0AAEg27Qmyd5xxhur/\ngzH8UFZWprKyskPGKisrfTufuQjPJvbsBPVBdpqksc65dW2Yf5+kTOfctEZjr0pa6Zz7yhfAzKxI\nUnl5ebmKioo87BwAACSD9gTZ7mlp+uxHP/K5IzRVUVGh4vov2xU75yq8rO3rnVkzmyepRNJUSXvN\n7OAd10rnXFXDnDslbXLOXdXw3g2SFpvZFZKebDi+WNLFfvYKAACSz74DB9ocZCVp7cXEiY7G790M\nvpf+bCAAACAASURBVCcpV9JiSZsb/cxoNKefGn25yzn3uqRSSd+VtELSOZKmtfKlMQAA0MnU1NYq\n68Yb2zz/qpEj1S0z4lb3SFJ+7zPbalh2zp3WzNhDkh7ypSkAAJD0nHNKa+WBCI3lpabqN2PH+tgR\nEoUHEQMAgKST9ac/qT3f+nn729/2rRckVjy35gIAAIiJc049585VVW1tm4/5+ahROjw318eukEiE\nWQAAEGjOOT22Zo0uXrRI2/bta9exA3Jy9MuT2eK+IyPMAgCAQPpo506dct992rx3b9Q1XvvmN9lT\ntoMjzAIAgECZV16uHy5erLoY98K/a9Ik9eaRtR0eYRYAAATCzxYv1h/efNOTWtMGD9Y3jznGk1oI\nNsIsAABIGOecZj72mB5Ys8azmj0zMnT/2Wd7Vg/BRpgFAABxV1Nbq1PuvVdvbNniaV2TtKSkROkp\nRJzOgv+nAQBA3FRWVenYBQu0cc8eX+rfceaZOqpHD19qI5gIswAAwHfrduzQsXfeqX3t2B+2vb59\nzDGafeyxvtVHMBFmAQCAb365dKl+tWyZ7+c5pkcPzZ840ffzIHgIswAAJKnrli/Xfy9dqv11dYc8\n2rUtG1qZpAFduuiVkhId5vHTsT7Yvl3D77rL17uwjWWnpuqFGTOUEgrF5XwIFsIsAABJaO6bb+on\nS5ZEfbyT9NHu3eo7f74kKSclRSlmSg2HlRoKKTUUUkY4rKzUVGWmpio7HFZ2Sooy09KUmZqqrHBY\n2ampyklLU2ZKim5//329/9lnHv3p2ufZc89VQXZ2Qs6NxCPMAgCQZKqqq/XDxYs9rbmnpqb+f1RX\ne1rXT2FJd06erJP79k10K0ggwiwAAEmmx403JrqFhBuen6+7Jk3Ssb16JboVJBhhFgCAJPKrpUv1\nRYyPeU02meGwju3ZU6P79tXxvXtrZGGhBublycwS3RoCgDALAECS+HDnTv0yDjsDJEpGKKTCnBx9\nrVs3ndC7t47v3VvDevVSvy5dCK6IiDALAEASWLphg0bff3+i22hV3/R09c7LU5fUVGWmpSkvNVVZ\n6elKD4WUnpKijJQUFWRlqTAnR4fn5KhnVpZy09LUNSNDaeFwottHEiLMAgAQcAvffVezn3km0W18\nKTslRWcNGqRrxoxRv65dE90OOjnCLAAAAfbfS5boN8uXx+VcITNlhsMqzM7WiPx8TejfXxMGDNAA\n1qciwAizAAAE1HmPPKKH1q71/TzdMzK0/bLLCKxISoRZAAACaPgdd2hlHB5CkB4Oa+MllxBkkbQI\nswAABIhzTvk33aTtBw74fq4hXbtq8cyZykxN9f1cgF8IswAABERVdbUyb7jBl9ohM/Xr0kVj+/bV\ntCFDNLZfP/XIzPTlXEA8EWYBAAiAjz//XANvu82zerlpaSrKz9fkQYN0xoABOrZnT4VDIc/qA0FB\nmAUAIMGeWrtWZz3ySEw1hnTtqjF9++rswYN1Up8+ys/O9qg7INgIswAAJNBVL7+sq//xj5hqXH3K\nKfqPUaM86ghILoRZAAAS5NR779XLmzfHVONbRx9NkEWnRpgFACDOnHMquOkmbYtxx4KT+vTRgkmT\nPOoKSE6+rgQ3s9Fm9piZbTKzOjOb2sr8sQ3zGv/Umlm+n30CABAvB2pqFL722piD7IwjjtCSWbPY\nHxadnt93ZrMlrZD0V0kPt/EYJ2mopN1fDji31fvWAACIr027dqnv/Pkx15k3fry+P2KEBx0Byc/X\nMOuce0bSM5Jk7ftXx23OuV3+dAUAQPwtXb9eo//2t5hqZITDWjJrlkb27u1RV0DyC+KGcyZphZlt\nNrPnzOykRDcEAEAsyt57L+YgOzA3VxsuuYQgCzQRtDD7iaRLJJ0r6RxJGyQtNrPhCe0KAIAo/erV\nV1X69NMx1Thv6FB98J3vqGdWlkddAR1HoHYzcM59IOmDRkPLzGywpDmSZiemKwAAovOtxx/XXatX\nx1Tj5vHjdSnrY4GIAhVmI1gu6eTWJs2ZM0d5eXmHjJWUlKikpMSvvgAAiKj/Lbdo/d69UR+fnZKi\nV0tLNSyfDX2QXMrKylRWVnbIWGVlpW/nM+ecb8UPOZFZnaTpzrnH2nncc5J2OefOi/B+kaTy8vJy\nFRUVedApAADRq6quVuYNN8RU4+s9e+rV0lJ1SUvzqCsgsSoqKlRcXCxJxc65Ci9r+3pn1syyJQ1R\n/Ze6JGmQmQ2TtMM5t8HMrpbUxzk3u2H+5ZI+kvSepAxJF0saJ2mCn30CAOCFNz/5RCPvuSemGpeP\nGKHrTzuN/WOBNvJ7mcFxkl5S/d6xTtK1DeN3SrpIUqGkfo3mpzXM6SPpC0lvSxrvnFvic58AAMTk\nB88/r5tXrIj6+LCZHpk2TVOGDPGwK6Dj83uf2ZfVwo4JzrlvN3n9R0l/9LMnAAC81veWW7QphvWx\n+VlZKr/wQvXt0sXDroDOIRm+AAYAQCBVVlWp69y5MdWYNHCgHp0+XanhsEddAZ0LYRYAgCg8tHq1\nznv88ZhqXHfqqZpz3HEedQR0ToRZAADa6fT77tMLGzfGVGPJrFka3bevRx0BnRdhFgCANqqprVX2\n9dfrQIx1fjZyJEEW8EjQHmcLAEAgLV6/XqkeBNkju3fX1WPGeNITAO7MAgDQqskPPKCn//nPmOuk\nhkJ6vbSUPWQBDxFmAQCIoLqmRtl/+pOqPar37HnnqWtGhkfVAEgsMwAAoFlPrFmjNA+D7O9Gj9a4\nww/3qBqAg7gzCwBAEyMXLtSbW7d6UisjHNYT55yj8f37e1IPwKEIswAANNi0e7f63nqrZ/W+0auX\nXjj/fPXMyvKsJoBDEWYBAJD005de0rXl5Z7V+/eRI/W7MWMU4stegK8IswCATq26pkbdbrhBe53z\npF7YTI9Mn64pgwd7Ug9AywizAIBO68k1azTl0Uc9q9c9I0NvXHCBhnTr5llNAC0jzAIAOqWiBQv0\n1vbtntUbWViol2bMUHZammc1AbSOMAsA6FQ2VFbq8L/8xbN6qaGQ/jBmjC4vLuZhCEACEGYBAJ3G\nRU8+qTtWrfKs3lmDBmnhpEnqnpnpWU0A7UOYBQB0eJX79qnrzTd7Vi8tFNK9U6bo3KFDPasJIDqE\nWQBAh/a9Z57Rre++61m94oICPX3uuerF3rFAIBBmAQAd0q6qKuXNnetZvZCZrjv1VP2oqIi1sUCA\nEGYBAB3O5YsW6caVKz2rNyA3Vy/OmKGBXbt6VhOANwizAIAOY+/+/epy003y5vEH9f595EhdPXq0\nwqGQh1UBeIUwCwDoEH7ywgu67q23PKvXIyNDz51/vooKCjyrCcB7hFkAQFLbu3+/cm+6SXUe1rzg\nqKP014kTlZ7CxyQQdFylAICk9cNFizTXw7Wx2ampenjqVJ0xcKBnNQH4izALAEg6m3btUt/58z2t\nOW3IEN09ebJyeBwtkFQIswCApHLiwoVatnWrZ/WyUlL04NSpmjRokGc1AcQPYRYAkBRe/Oc/Nf6B\nBzytefagQbp3yhTuxgJJjDALAAi02ro6Fcydq88OHPCsZlZKih6YOlWTuRsLJD3CLAAgsH7/2mv6\nj9de87TmWYMGqWzKFHXhbizQIfi6A7SZjTazx8xsk5nVmdnUNhxzqpmVm1mVmX1gZrP97BEAEDyV\nVVUKXXNN1EE2LRRSSpNHzmampOjx6dP1xDnnEGSBDsTvO7PZklZI+qukh1ubbGYDJD0haZ6kUkmn\nS7rNzDY75xb51yYAICjOfughPfHRR1EfP+uII3T3WWdp0549+tZTT2nltm2aMmiQbj79dOWmp3vY\nKYAg8DXMOueekfSMJJk1+Vfk5n1f0jrn3JUNr1eb2SmS5kgizAJAB/b6xo066b77oj4+Ny1N/7jg\nAg3t0UOSdHhurhbPmuVVewACKmhrZkdJer7J2LOSrk9ALwCAODhQU6PCm2/WzurqqGv87PjjdfXo\n0WrbfRMAHUnQwmyhpC1NxrZIyjWzdOfc/gT0BADwyXeeekp/ff/9qI/vl5OjNy+8UPnZ2R52BSCZ\nBC3MAgA6gTc2btSoGJYUmKQ/T5ig7w4b5l1TAJJS0MLsp5IKmowVSNrV2l3ZOXPmKC8v75CxkpIS\nlZSUeNshACBq1bW1Kpw7VztiWFIwIj9fr8yapWx2JAACqaysTGVlZYeMVVZW+nY+c875VvyQE5nV\nSZrunHushTm/kzTJOTes0di9kro65yZHOKZIUnl5ebmKioq8bhsA4JFLnnlG8999N+rjU0IhPTZ9\nOo+dBZJQRUWFiouLJanYOVfhZW1f78yaWbakIar/L0KSNMjMhkna4ZzbYGZXS+rjnDu4l+yfJV1m\nZr+XdLuk8ZLOk9RskAUABN8bmzZpVJO7NO11cLutcMjX7dEBJCG/lxkcJ+klSa7h59qG8TslXaT6\nL3z1OzjZOfexmZ2l+t0LfiRpo6R/c8413eEAABBwB2pqVDh3rnbW1ERdo1dmppaVlmpQt24edgag\nI/F7n9mX1cJTxpxz325mbImkYj/7AgD4a9ajj+r+NWuiPt4k3XjaafoBy8cAtCJoXwADACSxpz/8\nUJP//veYapzUp48WnXeesviCF4A2IMwCAGJWuW+f8m++WQdiqJGZkqIXZ8zQqD59POsLQMdHmAUA\nRM05p+KFC/XWtm0x1flxUZGuGzeOJ3gBaDfCLAAgKn9ctkxXLl0aU41BeXlaVlqqXjzBC0CUCLMA\ngHZ5f+tWHbNwYUw1UkMhPTxtmqYMHuxRVwA6K8IsAKBNqmtqdNgtt2jb/hYfyNiq737jG7plwgSF\nWFIAwAOEWQBAq2Y98ojuX7s2phpDunbVayUlLCkA4CnCLAAgovtXrdKsJ5+MqUZaKKRHeAwtAJ8Q\nZgEAX7GhslL9//IXuRjrfH/YMM09/XSWFADwDWEWAPClmtpaDZo/Xxv27o2pzhHduumVWbNYUgDA\nd4RZAIAk6cLHH9fdq1fHVCM9HNaj06dr4sCBHnUFAC0jzAJAJ3ffqlUqiXFdrCT9YPhw3TB+PEsK\nAMQVYRYAOqn1n3+uAbfdFvO62KO6d9eSWbPUMyvLk74AoD0IswDQyVTX1mrIrbdq/RdfxFQnIxzW\n4//yLzp9wABvGgOAKBBmAaATmfnoo/rbmjUx1/nZ8cfr6tGjZSwpAJBghFkA6AQWvv22Zj/3XMx1\nji8s1KLzz1dueroHXQFA7AizANCBrd2xQ1+7/faY6+SmpenFGTNUXFjoQVcA4B3CLAB0QFXV1Tps\n3jztqK6OqY5J+uPYsbriuONYUgAgkAizANCBOOc07r779PKmTTHXOnPAAD08bZoyU1M96AwA/EGY\nBYAO4o/LlunKpUtjrlOQlaUlM2dqaI8eHnQFAP4izAJAknvrk09UdM89MdcJm+mvZ5yh2V//ugdd\nAUB8EGYBIEntqqpS77lzFdtusfUuOOoo3XHmmUoNhz2oBgDxQ5gFgCRT55xOXLhQy7dti7nW4Lw8\nLSkpUZ+cHA86A4D4I8wCQBL5+Suv6H/eeCPmOunhsB6aOlVnDR7sQVcAkDiEWQAIuN0HDui2FSt0\nxZIlntT7cVGRrh03TiG22gLQARBmASCAqmpq9PRHH+nu997Tw2vXxlwvPRxW6ZFH6rpx49Q1I8OD\nDgEgGAizABAgH+zYoXkrVujO997T5/v3x1QrZKZJAwbo2nHjdET37h51CADBQpgFgASrqavTk+vW\n6ea33tKif/7Tk5r/duyxmj9xIksJAHR4hFkASADnnN7dvl0Pr1mj2995R+t37/ak7tCuXfVaaal6\nZGV5Ug8Ags73MGtml0n6qaRCSSsl/dA5948Ic2dLukOSU/0jwSWpyjnHb2UASa+2rk6vb96sR9au\n1SNr1+rDzz/3rHZ6OKynzzlH4/r396wmACQDX8Osmc2UdK2k70paLmmOpGfNbKhzbnuEwyolDdX/\nhVnnZ48A4BfnnNZ+/rmWbtyoJRs36sl167Rt3z7Pz/Mfxx+v344eLWNJAYBOyO87s3Mk3eqcWyhJ\nZvY9SWdJukjSHyIc45xzse8EDgAe233ggK58+WVVbNmirhkZKszKUu+cHBVmZ6t3w09aOKxln3yi\npRs3aummTdryhRfP52reyIICvThzpnLS0nw7BwAEnW9h1sxSJRVL+u3BMeecM7PnJZ3YwqE5Zvax\npJCkCklXOefe96tPAGir/3rlFf155cpEt6EuaWlaMmuWhufnJ7oVAEg4P+/M9pQUlrSlyfgWSUdE\nOGa16u/avi0pT9K/S3rNzI52zm32q1EAaIvnPdppIFom6dpTT9Wc445LaB8AECSB2s3AObdM0rKD\nr83sdUmrJF0i6ReJ6gsAnHP6eNeuqI7NDYe1q7Y2pvNP7N9fj0yfrozU1JjqAEBH42eY3S6pVlJB\nk/ECSZ+2pYBzrsbM3pI0pLW5c+bMUV5e3iFjJSUlKikpaVu3ANCCrV98oX01NYeMXfyNb2jX/v36\nZO/e+p89e7SnulpDu3XTKYcdplG9e+uK55+PKcjmZ2bq1dJSDenWLdY/AgDERVlZmcrKyg4Zq6ys\n9O185px/mwWY2TJJbzjnLm94bZLWS7rROffHNhwfkvSepCedcz+NMKdIUnl5ebmKioq8ax4AGlm2\nebNOvPfeL1+nhkLa9+MfKxwKHTKvzjmFzHTFokW6Pob1tWEz3XHmmbrwmGOirgEAQVFRUaHi4mJJ\nKnbOVXhZ2+9lBtdJWmBm5fq/rbmyJC2QJDNbKGmjc+6qhtf/T/XLDNZK6irpSkmHS7rN5z4BoEUf\nNbmr0D839ytBVpLWfPaZjlywIKZzlRx5pBZOnqyUZuoDAA7la5h1zv3NzHpK+rXqlxeskDSx0dZb\nfSU1/u923STNV/0DFnZKKpd0onPuf/3sEwBa03S97MAmy5o27t6t8WVl+iDKdbWSNDA3V6+Wlqp3\nTk7UNQCgs/H9C2DOuXmS5kV477Qmr6+QdIXfPQFAezW9MzsgL081dXV6at06XbN8uV7ZHP2GKzmp\nqXrw7LM1cdCgWNsEgE4nULsZAEBQNQ2za3fuVP/587V5z56oa6aHw7p94kSVHn10rO0BQKdFmAWA\nNmgaZl/asCHqWilm+tNpp+nS4cN5BC0AxIgwCwCtqK2r0/oY1sIeZJJ+fuKJ+sVJJxFiAcAjhFkA\naMXmPXtUXVcXU41pgwfrgalTlRoOe9QVAEAizAJAq5ouMWiPwXl5eq20VPnZ2R52BAA4iDALAK2I\nJsxmp6TohRkzdEKfPj50BAA4iDALAK1ousdsa64dO1ZXjBzpUzcAgMYIswDQirbemR2cl6cVs2cr\nJy3N544AAAcRZgGgFa2FWZNUNmWKZh55ZHwaAgB8iTALAK1oKcweX1ioV2bNUloKv04BIBH47QsA\nLThQW6tNEZ7y9c0jj9RdU6bEuSMAQGOhRDcAAEG2Yfdu1TnX7Ht/njAhzt0AAJoizAJAC1paYpCd\nnh7HTgAAzSHMAkALYnlgAgDAf4RZAGjBx4RZAAg0wiwAtCDSndm0EL8+ASAI+G0MAC2IFGa/P2xY\nnDsBADSHMAsALVj3+efNjv9uzJg4dwIAaA5hFgAi2Fddra379jX7XkZqapy7AQA0hzALABF8vGtX\nolsAALSCMAsAEbAtFwAEH2EWACKIFGZTzeLcCQAgEsIsAEQQKcz+eMSIOHcCAIiEMAsAEUR6YMJv\n2MkAAAKDMAsAEayJsC1XakpKnDsBAERCmAWACN7eti3RLQAAWkGYBYBmVO7fn+gWAABtQJgFgGZE\nWi/LAgMACBbCLAA0I9JOBv95/PFx7gQA0BLCLAA0I1KY/fnJJ8e5EwBAS3wPs2Z2mZl9ZGb7zGyZ\nmY1sZf75ZraqYf5KM5vkd48A0NSHEXYySAmH49wJAKAlvoZZM5sp6VpJv5A0QtJKSc+aWc8I80+S\ndK+kv0gaLulRSY+Y2dF+9gkATb3y4YeJbgEA0AZ+35mdI+lW59xC59z/SvqepC8kXRRh/o8kPe2c\nu845t9o593NJFZJ+4HOfAHCIt3fvTnQLAIA28C3MmlmqpGJJLxwcc845Sc9LOjHCYSc2vN/Ysy3M\nBwDP1f+q+iq+ZAAAwePn7+aeksKStjQZ3yKpMMIxhe2cDwCe275vX7PjvzjhhDh3AgBoDTcaAKCJ\nSHvM/jc7GQBA4Pi5//d2SbWSCpqMF0j6NMIxn7Zz/pfmzJmjvLy8Q8ZKSkpUUlLSpmYB4KBI23KF\nQvz7PwC0pqysTGVlZYeMVUb4veoF38Ksc67azMoljZf0mCSZmTW8vjHCYa838/6EhvEWXX/99Soq\nKoqpZwCQpIqNGxPdAgAkreZuJlZUVKi4uNiX8/n9ZMbrJC1oCLXLVb+7QZakBZJkZgslbXTOXdUw\n/wZJi83sCklPSipR/ZfILva5TwD40u9XrEh0CwCANvI1zDrn/tawp+yvVb9cYIWkic65bQ1T+kqq\naTT/dTMrlfSbhp81kqY55973s08AaI0lugEAQLP8vjMr59w8SfMivHdaM2MPSXrI774AoD3+Z9So\nRLcAAGgG32YAgEbqIuwxexU7GQBAIBFmAaCRT/bsaXa8/vurAICgIcwCQCPrfNw+BgDgPcIsADTy\n7YdYsg8AyYQwCwCNfFhdnegWAADtQJgFgFb8hp0MACCwCLMA0IqrTjkl0S0AACIgzAIAACBp+f7Q\nBADwUl1dnapqarTnwAHt2L9flVVV+qyqSlv27lWNczr3a19T96ysqGrX1NV53C0AwG+EWQCBsbuq\nShc99ZQeXLcu6hrfXbQo4ntdzDRt6FD9bvRoHda161fe/8/nnov6vACAxCDMAkiIpevXa/aTT2rd\n3r1xO+du53T36tW6e/XquJ0TAOAvwiwA3zjn9PrGjfrJSy9p2datiW4nKr8sLk50CwCAFhBmAcTs\ns717dc2bb2rBO+/o06qqRLfjqV+MG5foFgAALSDMAmiTdTt36taVK/XgBx/o4127xFelAABBQJgF\nIEnaVVWle1et0l/feUfvbN2q/YluCACANiDMAp3Mtj17NOXvf9fyLVsS3UqLslJSdM6QIbp67Fj1\nycnRxt27tfyTT/Ta5s1auXWr1lVW6rN9+7SvpkY1zkWsY5JCZgqZKWymlFBIVa0cc9CZ/fp5+CcC\nAPiBMAt0As98+KFmPv64dtXUJLqVZpmkPjk5unzECF06YoSy09K+Mufw3Fwdnpur8444otkazjlV\n1dQoIyVFZtbuHvZVV2vpxo26Z9Uqrd+1S38YM0bH9enT7joAgPgizAIdUE1trX784ou6eeXKRLfS\nrJRQSEX5+fqvE07QWYMHKxyK/WGEZqbM1NSoj89MTdWEgQM1YeDAmHsBAMQPYRboID7dvVtnPPig\n3vnss0S38hVd0tJ01sCBumrUKB3bs2dUd04BAGgOYRboIPrfeqsOJLoJ1S8Z6JuTo3/9+td12fDh\nKsjOTnRLAIAOjDALdBBhM6kNX2ryWmoopGG9eukHw4fr/COOUFYz610BAPALYRboIHLS0rRvv38b\naqWYqWdmpooKCjRl8GCdOXCgBuTmsmQAAJBQhFmgg8hNT9c2D8JsejisPjk5Oql3b00ZMkSn9eun\nfJYKAAACijALdBBDu3fXh7t2tXl+yExHde+ucf36acrgwRrVp4/y0tN97BAAAO8RZoEO4u7Jk9Vj\n3rwW54TMNPqww3Tt2LEq7t07Tp0BAOAfwizQQXTPymp2PGymU/v10x/GjlVRQUGcuwIAwF+EWaAD\nOS4/X29u3aoUM43v31+/HzNGw/LzE90WAAC+IcwCHcgLM2dq/a5dOrZXr0S3AgBAXMT+DEkAgZGb\nnk6QBQB0Kr6FWTPrZmb3mFmlme00s9vMrMX9fcxssZnVNfqpNbOWv9ECIGplZWWJbgFIOlw3QLD4\neWf2XklHSRov6SxJYyTd2soxTtJ8SQWSCiX1lnSljz0CnRofykD7cd0AweLLmlkzO1LSREnFzrm3\nGsZ+KOlJM/upc+7TFg7/wjm3zY++AAAA0LH4dWf2REk7DwbZBs+r/s7rCa0ce4GZbTOzd8zst2aW\n6VOPSS+Idwfi0ZMf54i1ZrTHt/e4ts4P4j8bQRK0v5949eP1ebyoF00Nv66baGp3NkH7++ms107Q\nPnOiqe0lv8JsoaStjQecc7WSdjS8F8k9kr4p6VRJv5V0oaS7/Gkx+QXtl4pEmPX7OMKsN4L299NZ\nP5CjrdFRP5CTQdD+fjrrtRO0z5xoanupXcsMzOxqST9rYYpT/TrZqDjnbmv08j0z+1TS82Y20Dn3\nUYTDMiRp1apV0Z42aVVWVqqioiLRbRwiHj35cY5Ya0Z7fHuPa+t8r+d1NEH7c8erH6/P40W9aGr4\ndd20dW7Q/vmJp6D92TvrtRO0z5y2zG2U0zLa3EAbmXOu7ZPNekjq0cq0daq/o3qNc+7LuWYWllQl\n6Tzn3KNtPF+WpD2SJjrnFkWYU6r6O7oAAAAItgucc/d6WbBdd2adc59J+qy1eWb2uqSuZjai0brZ\n8ZJM0hvtOOUI1d/t/aSFOc9KukDSx6oPywAAAAiWDEkDVJ/bPNWuO7PtKmz2lKR8Sd+XlCbpdknL\nnXMXNrzfR9ILki50zr1pZoMklUp6SvWBeZik6yStd86d5kuTAAAASGp+Ps62VNJc1e9iUCfpQUmX\nN3o/VdJQSVkNrw9IOr1hTrakDZIekPQbH3sEAABAEvPtziwAAADgNz+fAAYAAAD4ijALAACApNXh\nw6yZ9TWzl8zsPTNbYWbnJbonIFmY2cNmtsPM/pboXoBkYGZTzOx/zWy1mf1bovsBkkUsnzcdfs2s\nmRVKynfOvW1mBZLKJX3NObcvwa0BgWdmYyR1kTTbOTcj0f0AQdawn/r7ksZK2q36z5sTnXM7E9oY\nkARi+bzp8HdmnXOfOufebvjfWyRtl9Q9sV0BycE5t0T1Dy4B0LrjJb3b8LmzV/VbTZ6R4J6A7iJq\njwAAArlJREFUpBDL502HD7ONmVmxpJBzblOiewEAdDh9JDX+fNks6bAE9QJ0GoELs2Y22sweM7NN\nZlZnZlObmXOZmX1kZvvMbJmZjWxD3e6S7pR0sR99A4nm17UDdAZcP0B0gnDtBC7Mqv6BCSskXar6\nR9kewsxmSrpW0i9U/7jblZKeNbOejeZcamZvmVmFmaWbWZqkv0v6rXOuPY/TBZKJ59dOfNoGAiHm\n60f1d2L7Nnp9WMMY0JF5ce3EJNBfADOzOknTnXOPNRpbJukN59zlDa9N9U8Lu9E594cIdcokrXLO\n/ToObQMJ59W10zDvVEmXOefO97drIBiivX4afQHsVNV/Aewfkk7iC2DoLGL97In28yaId2YjMrNU\nScWSXjg45urT+POSToxwzMmSzpc0vdEdp2Pi0S8QFNFcOw3HLZJ0v6RJZrbezE7wu1cgaNp6/Tjn\naiX9RNJiSRWSriHIojNrz2dPLJ83Kd60Gzc9JYUlbWkyvkXSEc0d4Jx7Vcn35wS81u5rR5KccxP8\nbApIEm2+fpxzT0h6Ik59AUHXnmsn6s+bpLozCwAAADSWbGF2u6RaSQVNxgskfRr/doCkwbUDRI/r\nB4hOXK6dpAqzzrlq1T9RZfzBsYaFxOMlvZaovoCg49oBosf1A0QnXtdO4NaSmlm2pCGSrGFokJkN\nk7TDObdB0nWSFphZuaTlkuZIypK0IAHtAoHBtQNEj+sHiE4Qrp3Abc1lZmMlvaSv7lV2p3PuooY5\nl0q6UvW3qVdI+qFz7s24NgoEDNcOED2uHyA6Qbh2AhdmAQAAgLZKqjWzAAAAQGOEWQAAACQtwiwA\nAACSFmEWAAAASYswCwAAgKRFmAUAAEDSIswCAAAgaRFmAQAAkLQIswAAAEhahFkAAAAkLcIsAAAA\nkhZhFgAAAEmLMAsAAICk9f8BoVpYnOatO5QAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21b1c6ca10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(2, 1, figsize=(8, 8))\n",
"\n",
"model_props = np.empty((len(fnames), 3))\n",
"for j in range(0, 50):\n",
" for i, f in enumerate(fnames):\n",
" model_props[i, 0] = float(f[1:5])/1000.0\n",
" \n",
" try:\n",
" trk = np.genfromtxt(model_directory + f, usecols=(0, 1, 2, 3))\n",
" except ValueError: \n",
" model_props[i, 1] = 0.0 # temperature\n",
" model_props[i, 2] = 0.0 # luminosity\n",
" continue\n",
" \n",
" model_props[i, 1] = trk[j, 1] # temperature\n",
" model_props[i, 2] = trk[j, 3] # luminosity\n",
"\n",
" ax[0].semilogx(model_props[:,0], model_props[:,1], '-', c='#008b8b', lw=3)\n",
" ax[1].semilogx(model_props[:,0], model_props[:,2], '-', c='#008b8b', lw=3)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can now iterate through these filenames and save the third timestep to an array."
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"model_props = np.empty((len(fnames), 3))\n",
"for i, f in enumerate(fnames):\n",
" model_props[i, 0] = float(f[1:5])/1000.0\n",
" \n",
" try:\n",
" trk = np.genfromtxt(model_directory + f, usecols=(0, 1, 2, 3))\n",
" except ValueError: \n",
" model_props[i, 1] = 0.0 # temperature\n",
" model_props[i, 2] = 0.0 # luminosity\n",
" continue\n",
" \n",
" model_props[i, 1] = trk[1, 1] # temperature\n",
" model_props[i, 2] = trk[1, 3] # luminosity"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Plotting these two relations, we can compare against the function used to generate the polytrope seed model."
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f21b231ced0>]"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsgAAAK1CAYAAADVFxhpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xd8VfX9x/HXN3tBBmEP2XsoKEtEUcFZK64atUodqLWt\npbVaLXW22NoqrXXValWqpvVXWwcqKmJBZAlBiOy9ZyABsnPv9/fHvWDuyCC59+YkeT8fjzzIPd/v\nOedzlauffPM5n6+x1iIiIiIiIh5RDR2AiIiIiIiTKEEWEREREalECbKIiIiISCVKkEVEREREKlGC\nLCIiIiJSiRJkEREREZFKlCCLiIiIiFSiBFlEREREpBIlyCIiIiIilShBFhERERGpxFEJsjHmDmPM\nCmNMgfdrgTHmwhrO+akxZq0xpsgYs90Y85QxJt5vzl3GmC3GmGJjzCJjzBnhfSciIiIi0lg5KkEG\ndgD3AUOBYcAc4F1jTL9gk40x1wGPAw8BfYGbge8Bv60053vAk945pwErgI+NMZnhexsiIiIi0lgZ\na21Dx1AtY0wecI+19pUgY38B+lprx1c69kdguLV2rPf1ImCxtfZu72uDJxF/2lr7RCTeg4iIiIg0\nHk5bQT7BGBNljLkWSAIWVjFtATDseMmEMaY7cDHwgfd1LJ6V6M+On2A9PxHMBkaFL3oRERERaaxi\nGjoAf8aYgXgS4gTgKDDRWrs22Fxrbba3VGK+d2U4GnjBWvt775RM77F9fqfuA/qEI34RERERadwc\nlyADa4EhQCpwFTDDGDM2WJJsjDkHeAC4A1gC9ASeNsbssdb+pq4BGGNaARcAW4GSul5HRERERMIm\nAegKfGytzQvlhR2XIFtrK4DN3pfLjTHDgbuBO4NMfxSYUak+eZUxJgX4K/Ab4CDgAtr6ndcW2FtN\nGBcAb9TtHYiIiIhIBF0PvBnKCzouQQ4iCoivYiwJcPsdc4PnYTxrbbkxZhlwHvDe8ePe109Xc8+t\nAK+//jr9+gVtoNFkTZkyhenTpzd0GD4iEVOo7xGK69X1Gid7Xm3nh3peU+O09x2peJz22XHa56a2\nc5329yeSnPbe9dkJ73mh/OysWbOGG264Abx5Wyg5KkE2xkwDPgK2Ay3w/ERwNjDBOz4D2GmtfcB7\nyvvAFGPM18BioBeeVeX37LftOZ4CXvUmykuAKXgS61erCaUEoF+/fgwdOjRk768xSE1Nddx7jkRM\nob5HKK5X12uc7Hm1nR/qeU2N0953pOJx2mfHaZ+b2s512t+fSHLae9dnJ7znhfqz4xXyclhHJchA\nG+A1oD1QAKwEJlhr53jHOwEVleY/hmfF+DGgI3AAz0rx1OMTrLVveR/kexRPacXXwAXW2gPhfSuN\nU1ZWVkOHECASMYX6HqG4Xl2vcbLn1Xa+E/9uOInT/vlEKh6nfXac9rmpy7WbG6f989FnJ7znNZbP\njuP7IDcEY8xQYNmyZcsc9VOtSGNw2WWX8d577zV0GCKNij43Da905XoOP/kqJj6OtLuyiB+iZldO\nl5OTw7BhwwCGWWtzQnltp60gi4iIiESUdbnYc+0vcB04BMCx9/5H+s9uJH3KjZhYpUrNkWM3ChGR\nxslpvy4VaQz0uWlYFdv2nEiOAXC5OPyHV9h54e2Urd3ScIFJg1GCLCIhpf/Ri5w8fW4alnW5gh4v\nW7meneffSv6z2VXOkaZJCbKIiIg0by7/jrHfsqVl5D38HLsv+zHl23ZHMChpSEqQRUREpFmz7qoT\n5ONKluSyc9zNHPvvZxGISBqaEmQRERFp3tx+Hb2ioki961owxnfa0UL2TX6Y/T/9He7C4ggGKJGm\nBFlERESaN/8V5OgoMh++iw7vPUNM1w4B04++8QE7z7+V0twNEQpQIk0JsoiIiDRvfntCmGhPepQ4\ncjCdP3+FlGsuDDilfON2dl54O/kv/hvtKdH0KEEWERGRZi2gQ0XUt+lRVEoSbZ/9FW2em4pJTvSd\nV1ZO3q/+zL6bf437aGEEIpVIUYIsIiIizZt/DbJf7TFAi6svoPOcvxN/at+AscKZc9k5/jb1TG5C\nlCCLiIhI8+ZXg2yigqdHsd070fGD5zwP8Pkp37SDnRdM5ujbn4YlRIksJcgiIiLSrNmALhaBK8jH\nmbhYMh++i/b//CNR6S19r1NUwv47HuXAL6djy8rDEapEiBJkERERad78a5Cjo2s8Jem8EXSa/RLx\nQ/oEjB15+T/suvwnVOzLC1WEEmFKkEVERKR58+9CUc0KcmWxXdrTYeaztLzxsoCx0q++YeeEyZSu\nXB+KCCXClCCLiIhIs+a/k54xtU+PohLiaf3kL2j99P2YhDifMdfu/ey69Icce/fzkMQpkaMEWURE\nRJq3k6hBrkrLrIvp+OELxHRp73PcFpey79YHOfTE32u1pbU4gxJkERERad5cfolrFV0sahI/qBed\nPv4rCSOHBIwd/sMr7LvlQW1R3UgoQRYREZFmLaDEIrru6VF0Zjod3p5OixsuDRgrnDmXfZMfrvO1\nJXKUIIuIiEjzZkOzgnyciYul9VP30uq3dwdcq+iTBbjyj9br+hJ+SpBFRESkeQtBDbI/Ywxpk6+i\n3T8eDxizhUX1vr6ElxJkERERad7q0cWiJomjAuuR/bvKifMoQRYREZFmzfo/pFePGuQAJshqtLpZ\nOJ4SZBEREWnewlBicUKwBFlLyI6nBFlERESaN/8V3Xo+pOcjaIIcustLeDgqQTbG3GGMWWGMKfB+\nLTDGXFjN/M+NMe4gX+9XmvNKkPEPI/OORERExOms34quCeUKcrBrqcTC8WIaOgA/O4D7gA2AASYB\n7xpjTrXWrgkyfyJQeV/HTGAF8JbfvI+81zr+t7Q0dCGLiIhIo+Zy+b4O4UN6JsgKsn9CLs7jqATZ\nWvuB36Gpxpg7gZFAQIJsrc2v/NoYcx1QCPzbb2qptfZAKGMVERGRJsK/BjncD+mpxsLxHFViUZkx\nJsoYcy2QBCys5Wk3A9nWWv99HM8xxuwzxqw1xjxnjMkIabAiIiLSaAXspBfKGuSgJRZKkJ3OUSvI\nAMaYgXgS4gTgKDDRWru2FucNBwYAP/Ab+gh4G9gC9AAeBz40xoyy+h2HiIiIqIuF+HFcggysBYYA\nqcBVwAxjzNhaJMm3ALnW2mWVD1prK9cjrzLG5AKbgHOAz0MWtYiIiDROEe9ioQTZ6RyXIFtrK4DN\n3pfLvSvDdwN3VnWOMSYJ+B4wtRbX32KMOQj0pIYEecqUKaSmpvocy8rKIisrq6bbiIiISCMR1hKL\nYA/pqcTipGVnZ5Odne1zrKCgIGz3c1yCHEQUEF/DnGvwdLN4o6aLGWM6Aa2APTXNnT59OkOHDq1N\njCIiItJYhXEFOVgXC60gn7xgC5Q5OTkMGzYsLPdzVIJsjJmGp2Z4O9ACuB44G5jgHZ8B7LTWPuB3\n6i3AO9baw37XSwYewlODvBfPqvHvgfXAx+F7JyIiItJohLMGGTyryJWTYiXIjueoBBloA7wGtAcK\ngJXABGvtHO94J6Ci8gnGmN7AaGB8kOu5gMHAjUAasBtPYvygtbY8HG9AREREGplw1iAfv17lXssq\nsXA8RyXI1tpbaxg/N8ix9UB0FfNLgCp34hMRERGxLv8a5FCvIPvfUAmy0zm2D7KIiIhIRNgwryD7\n1yErQXY8JcgiIiLSvAXUIIc2PQppVwyJCP0bExERkWYtsM1beEss/O8nzqMEWURERJq3MK8gq8Si\n8VGCLCIiIs2b30N6RIc6Qfa7nhJkx1OCLCIiIs2atWHcSQ8Cu1iozZvjKUEWERGR5s0/YQ22+119\nqMSi0VGCLCIiIs1bmDcK8V+RtkqQHU8JsoiIiDRrEd8oRCUWjqcEWURERJo3/xXk6KAb9NadSiwa\nHSXIIiIi0rwFtHkL8Qqyf8mGEmTHU4IsIiIizZv/VtP+bdnqyz/fVoLseEqQRUREpFmzfivIoa9B\n9r2eHtJzPiXIIiIi0ry5XL6vQ93FQhuFNDpKkEVERKR5869BDvlOejXcTxxHCbKIiIg0a9Yd7p30\n1MWisVGCLCIiIs2buliIHyXIIiIi0rz590EOeRcLv4f0VGLheEqQRUREpFkLKLEIcQ2yf4WFVpCd\nTwmyiIiING/+K8gqsWj2lCCLiIhI8xZQg6yH9Jo7JcgiIiLSrFlXmFeQVWLR6ChBFhERkebNqs2b\n+FKCLCIiIs1bmEss/HfSUxcL53NUgmyMucMYs8IYU+D9WmCMubCa+Z8bY9xBvt73m/eoMWa3MabI\nGPOpMaZn+N+NiIiINAoBD+mFeSc9rSA7nqMSZGAHcB8wFBgGzAHeNcb0q2L+RKBdpa+BgAt46/gE\nY8x9wI+AycBwoBD42BgTF6b3ICIiIo2I/4quCXkNskosGpuYhg6gMmvtB36Hphpj7gRGAmuCzM+v\n/NoYcx2eBPjflQ7fDTxmrZ3pnXMjsA+4nEqJtIiIiDRTLpfv61CvIPtfTyUWjue0FeQTjDFRxphr\ngSRgYS1PuxnIttYWe6/RDc/K8mfHJ1hrjwCLgVGhjVhEREQaJf8V3RBvFKISi8bHUSvIAMaYgXgS\n4gTgKDDRWru2FucNBwYAP6h0uB1g8awYV7bPOyYiIiLNXMBOemHealoJsvM5cQV5LTAET73w88AM\nY0zfWpx3C5BrrV0WzuBERESkiQnoYhHaGmT/tnFWCbLjOW4F2VpbAWz2vlzuXRm+G7izqnOMMUnA\n94CpfkN78fxioy2+q8htgeU1xTJlyhRSU1N9jmVlZZGVlVXTqSIiItJYhLsGWSUW9ZadnU12drbP\nsYKCgrDdz3EJchBRQHwNc64B4oA3Kh+01m4xxuwFzgNWAhhjWgIjgGdruvH06dMZOnRoXWIWERGR\nRiKgL7G6WDhOsAXKnJwchg0bFpb7OSpBNsZMAz4CtgMtgOuBs4EJ3vEZwE5r7QN+p94CvGOtPRzk\nsn/C0w1jI7AVeAzYCbwbjvcgIiIijYx/DXLIH9Lzu54SZMdzVIIMtAFeA9oDBXhWfSdYa+d4xzsB\nFZVPMMb0BkYD44Nd0Fr7hLcE469AGvAFcJG1tiws70BEREQaF/+ENeQP6fm9Vps3x3NUgmytvbWG\n8XODHFsPRNdw3sPAw/WJTURERJoeW16B66DfL6BDXoPsmyHrIT3nc2IXCxEREZGwcx8rYs9191K2\napPPcRMfG9L7+HexUImF8zlqBVlEREQkEir2H2JP1i8oW7ne57iJjyNxTIgf0Pd/SE8lFo6nFWQR\nERFpVsrWb2XXxXcEJsdJCbT9+2PE9egc2huqzVujoxVkERERaTaK5i5l382/xn3kmM9xV1oLlj42\nmeL2Lei7axf9W7UiPSEhNDdViUWjowRZREREmoWC197l4H3TAzYG2ZmWxKSrh7N150bYufHE8XbJ\nyfRv1Yrh7dpxZseOjO7QgYzExJO/sfogNzpKkEVERKRJsy4XeQ8/R8ELbwWMrWyXxuQrR3AwJXC1\neG9hIXsLC5mzfTvgqZQY3bEj3+3Rg4m9etEzPb1W9w+ssFCC7HRKkEVERKTJch8rYt8dj1L08ZcB\nY7N6t+eeS4dSElu7dMgCX+7axZe7dnHvvHmc07kztw8ZwsSePYmPqeYaKrFodJQgi4iISJNUtmUX\nm66/l7gN2wPGnh/Zi6fG9sN6yx9ioqIYmJlJaUUFG/PzKffbXS+Y/+3Ywf927KBDSgr3DR/ObYMG\nkRgbpEWculg0OkqQRUREpEmpcLuZ/Y//0P7XL5BSXOozVhZlmHrhqfxnUBcAOrdowe1DhnDLoEG0\nS04GoNzlYlN+Pqvz8li2bx9f7trFkr17Ka6oCLgXwO5jx7h7zhweX7yYh0aN4tbBg4mpvGqsLhaN\njhJkERERaRJKKyr4e24uO558hR98vDygl+3hhFjumjicJV0yuaBrV+489VQu6d7dN5kFYqOj6duq\nFX1bteKK3r1PXHvO9u28s3Ej/9mwgYPFxQH331tYyJ2zZ/PM8uX86dxzOf+UUzwDKrFodJQgi4iI\nSKNW5nLx99xcnpo3n5+89QW3rNsdMGdDqxb8Mussxp89ijeGDKn1A3bHxcfEcFH37lzUvTtPn3su\n/924kee+/povdu4MmLsqL4/x//d/XN+vH9PHjQvcalolFo6nBFlEREQapXKXi9dWreI3ixYRvWUX\nz7zzFb0PHg2Y98WALpRN+zELzhhGUrAa4ZMUHxPDtX37cm3fvszfuZNHFy7k023bAua9sWYNH23Z\nwuyiIlpWHtAKsuMpQRYREZFGxW0tb6xezUMLFrCloIDLv9nBI5+sILnct7+x28CeyVdwwyM/ISY6\nOiyxjOnUiU+uvprPt29nyuefs+LAAZ/xQyUlrMzLY0zlg0qQHU8JsoiIiDQan2zdyn3z5vH1/v0k\nlFfw+Ke5XJ0b2KXC1SKJjn97hF7njYxIXOO6dGHZ97/Py7m53DdvHvmllR4ODHhIr+YOGdKwlCCL\niIiI4y3ft497581jtreUoefBIzz97tKgJRVx/bvT7tVpxHbrGNEYo6OimDxkCJf17MmPP/uMf69f\nD3j6J/vQArLjKUEWERERx9paUMDU+fN5Y80azwFrueKbHTz86UqS/EoqAFp8/ztk/vZuohLjIxzp\nt9olJ/N/l13GG6tXc+fs2bi11XSjowRZREREHCevuJhpixbxzNdfU+byJMKpxWU8+skKLlkb2KXC\nJCfS+slf0OLK8ZEOtUrX9+/P/3bswJq5PsdtLTYhkYalBFlEREQco7i8nKdzcnh8yRIKKtXxnrll\nP7//cDntjpUEnBM3oCdtX36EuB5dIhlqrbRLTsb6FyFrAdnxlCCLiIhIg3Nby+urVzN1/nx2HP22\nrji+3MUv5q5m0rLNQc9rOem7tHrsx0QlNFxJRXXaJSdjtZNeo6MEWURERBrU7G3b+MXcuXy9f7/P\n8QF783ly5jJ65h0LOCcqvSWt/3gPKZeNi1SYddIuOZk8/xpklVg4nhJkERERaRC5Bw5w79y5zNq6\n1ed4rMvNHQvX88OF64kNsutc4jln0OYvDxDTLjNCkdZdu+RkDvof1AKy4ylBFhERkYjafewYD375\nJa988w1uv3KDgXsO87uPvqbvgSMB55mEOFo99ENa3nIFxn9V1qHaJSez0i/U0oqKhglGak0JsoiI\niETE0bIy/rBkCU8uXUqRX5IYX+7i7vlrueWrTUQHqdGNH9KHNs//mrhep0Qq3JBom5SE9Uvmj5aW\n0q6B4pHaUYIsIiIiYVXhdvPSypU8tGAB+4uKAsZP35HHEx+voEte4KYfREeT9pPrybhnEiYuNgLR\nhlZKXBzRUVE+x46VlVYxW5xCCbKIiIiEhbWW9zdt4r5581h76FDAeFpxGffPW8OVX28Nen7cgJ60\n+fMviR/SJ8yRhld8jG+6VVhaduJ7ay1uazHGENVIykaaA0clyMaYO4A7ga7eQ6uAR621s6o5JxWY\nBkwEMoCtwE+Pn2OMeQh4yO+0tdba/iENXkREpJnafewYv1+yhP/t2MFpbdowZdgwylwu7pk7l3k7\ndwbMN9Zyde52pn6xjqRjxYEXjIsl4+eTSPvxdZhYR6UqdRLv9x7eXrees598MqD+OtoY4qKjiYuO\nJt771TIujtT4+G//jI8nPT6etsnJtE1Kol2lP1slJjaa2mync9rfuh3AfcAGwACTgHeNMadaa9f4\nTzbGxAKzgb3AFcBu4BQg32/qN8B53msCqDpeRESkng6XlPDEkiX8OSeHYm9N8coDB3ht1aoqz+m7\nv4C/zF1Ht817go7Hnz6ANn+6j7g+3cISc0NI8FtBxrtq7M9lLcUVFSf+WZ6sxJgYurZsSfe0NLql\nptI9NZVe6ekMysykS8uWSp5PgqMSZGvtB36Hphpj7gRGAgEJMnALkAaMtNYe35B9e5B5FdbaA6GL\nVEREpPkqLCvjzzk5PPHVVz673VUnpbSc3+Zs5+L5qzBBWreZ5EQyfnkrqbddiYmODnXIDSol3ncT\nk3ClqcUVFaw5dIg1QcpZWsbFMTAzk4GZmQzKzGRw69ac2qYNLeOducFKQ3NUglyZMSYKuAZIAhZW\nMe073rHnjDHfBQ4AbwK/t9ZW7sLdyxizCyjxzr/fWrsjbMGLiIg0QaUVFby4ciW/XbSIfUEetgsm\n2u3mjvX7+dHc1cTmB3kID0i+bByZj/2ImA5tQhmuY/RMT6dyUmIaoBHykbIyFuzezYLdu32O90pP\n55HRo8nq1y/iMTmZ4xJkY8xAPElsAnAUmGitXVvF9O7AucDrwEVAT+B5PO/rMe+cRXhKNdYB7YGH\ngXnGmIHW2sLwvAsREZGmw+V28/rq1Ty0YAHbjgT2JwZP/ex3e/Zk3s6dHCz21BVP2HmYx+evJ3Xb\n3qDnxHbrRObvfkrSuSPCFrsTJMXFUXkvwFsGDOSmm75PFBDlfTjPbS3lbjdlLhelLhdlbjfF5eUc\nKSujoLTU58+84mL2FRWxt7CQvYWFHCopqXNsGw4fJsavy4Y4MEEG1gJDgFTgKmCGMWZsFUlyFLAP\nmGyttcByY0wn4B68CbK19uNK878xxiwBtuFZnX4lfG9DRESkcbPW8t8NG5g6f37QX9sfd3Xv3vxm\nzBh6Z2RQWFbGJ3Pm0/GZt2i1OHgtsomPI+2nN5D2o+uISmgGv+KP8i2qaJuYRKvWrUN2+TKXi72F\nhWwtKGBLQQGbvX9uys9nVV5ejWUww9q2DVksTYXjEmRrbQWw2ftyuTFmOHA3nu4W/vYAZd7k+Lg1\nQDtjTIz3Wv7XLzDGrMez2lytKVOmkJqa6nMsKyuLrKys2r0ZERERB3O53RwqKWF/URGHS0romJJC\nV+//92Zv28YDX3zB0n37qjz/om7d+O2YMZzmTbBcBw9T/ORrDH7lHXC5gp6TdOEYMh/9EbHdOob+\nDTlVwMNxoS2xiIuOpkvLlnRp2ZKxnTv73sladh49yjcHD5J7/OvAAVbn5VHudpOekEA3v1zHibKz\ns8nOzvY5VlBQELb7OS5BDiIKqOrHyy8B/2y1D7AnWHIMYIxJAXoAM2q68fTp0xk6dOhJhCoiIuIM\nLreb3ceO+awobi4oYNfRo+wvKmJ/URF5JSUB3RTaJCXRPjmZFQeqfrZ9TMeOTDvrLM7q1AkA99FC\n8p/7J/nP/wtbGKRtGxA3oAetHv0RSWNPD92bbDR8E2TrdlcxLwx3NobOLVvSuWVLLure/cTx0ooK\nvjl4kN2FhY2iu0WwBcqcnByGDRsWlvs5KkE2xkwDPsLTiaIFcD1wNjDBOz4D2GmtfcB7yvPAXcaY\np4G/AL2B+4E/VbrmH4D38ZRVdAQewdPmzffHEBERkUbCbS1F5eWUVFRQ6nJxtKyMVXl5rNi/nxUH\nDrDm0CG2FhRQXodE7HjyHMypbdowbcwYLuzWDWMM7uJSjrzyXw7/+XXch4Kv5kW3ziDj/ltpcd3F\nTa47RW0ZvxKLBnhGL0B8TAzD2rUjPOll4+eoBBloA7yG52G6AmAlMMFaO8c73olKPYyttTuNMRcA\n04EVwC7v909UumYnPJ0tWuHpcjEfT1u4vPC+FRERkdA4XFLCwt27mb9rF/N37WLJnj2UVlHCEA69\n0tN57MwzubpPH6KMwZZXcCT7Qw798VVce4KvNJv4OFLvuIb0n36fqJSkiMXqSP4rtEF6IIuzOCpB\nttbeWsP4uUGOLQZGV3OOCoZFRKRR2X7kiCcZ3rmT+bt28c3Bg2FfdEyMiQnYoKJTixY8NGoUkwYO\nJCYqCltWzpF/fcThP79OxbbgG31gDClXTyDjvluI7dI+zFE3En4JcmnuBgpe/k/IbxN/ah8Shg0I\n+XWbozonyMaYNDzbO5+FZ/e6JDwrtMuBj621C0ISoYiISBN3sKiIOdu3M3v7dj7bto3NIXz4KCkm\nxrOrmnd3tVNatqRdcjJtkpJonZhIm6QkMhMTiYmKYnNBAYt27yb34EF6pKXx/f79SYiJwV1SSsEb\nH5D/lzeo2LW/ynslX3wWGfffRlzfprMLXkj4lViUzM+hZH5OyG+T/rOblCCHyEknyMaYDsCjeOqD\ndwNLgK+BYiADGAfcY4zZBjxirf1X6MIVERFp/FxuN0v27uXDzZv5cMsWcqrpFFFbmYmJnNqmDUNa\nt2Zw69b0Tk+nW2oqbZKSav0QVo+0NHqkpZ147S4qIf+l/5D/zJu49lVdmZg4dhgZv5pMwtD+9X4f\nTZGJddQv7KUW6vJvbDmeOuFh1trVwSYYYxKBy4GfGmM6W2v/WI8YRUREGr2DRUV8vHUrH27Zwqwt\nW056c4eEmBiGt2vHmI4dOatTJ/pmZJAQE0NCdDTx0dEkxsaGLFbXoQKOvPIOBS+/jevA4SrnxZ8+\ngIz7b22mnSlqL2HUEI688k5DhyEnoS4Jcv+aHnCz1hbj6RKRbYxpVafIREREGrmNhw/z9vr1vLNx\nI4v37DmpOuKMhATGdOzo+erUiaFt2hAfE96VyPItu8h/4S2OZn+ALa56c4mEkUNIv2cSiWOHNYoW\nYQ0t5fLzcB8+SuGs+djSsrDdJ6Zzu7Bdu7k56U+atTbPGNO/qtXj44wxv7DW/kHdIkREpDlZk5fH\nv9ev5+3166vtJewvOTaWsZ06cf4pp3Bely4Mat2aqAglnyVLV5H/bDaFH8yrtsNC4thhpP/sJhLP\nPC0icTUVxhhSb55I6s0TGzoUqaW6/ij6sTHmTGvt9mCDxph7gN8Cf6hzZCIiIo2AtZaVBw6cSIqr\n25LZ38DMTC7u1o2LunVjdMeOxEWwT7Atr6Dwwy8oePH/KFmSW+3cxHNHkPHzm0gYPihC0Yk0rLom\nyPOB2d4k2efHY2PMz4FpwI31DU5ERMSpth85whtr1jBj1SrW1jIpToqJ4fxTTuHi7t25qFs3urRs\nGeYoA1XsOcCRf7zPkRnvVfvgHdHRpEw8l7Q7ryV+cO/IBSjiAHVNkL+PZ3e6j40x51hrjwAYY6YA\nvwNustb+M0QxioiIOMKR0lLeXr+ef6xezf927KhVTXHrxEQm9urFFb16cXbnziSEuY44GGstJQu+\npuDl/1CuZMWUAAAgAElEQVT44RdQzSYjJiWJljdeRtrkq4jp2DaCUYo4R50+pdbaCmPMFcBsYKYx\nZgJwB56SiknW2jdDGKOIiEiDqXC7mb1tGzNWreKdjRsDNtMIpkNKClf26sWVvXszpmNHoqOiIhBp\nIFfBUY79+1MKXvkv5eu2Vjs3ukMb0m6/mhY3XEp0y5TIBCjiUHX+MdZaW2yMuRiYCywDegM/sNa+\nHqrgREREGsrGw4f528qVvLZqFfuKimqcf0rLllzVuzdX9u7NiPbtI/aAnT/rdlP85XKOvvkBhTPn\nYkuq75qQcMZAWt5yBSmXjVO/XhGvOn0SjDGXVXr5PPBn4B2goPKYtfa9+oUnIiISOWUuF+9s2MCL\nK1fy2fagz6H7SI2P53t9+nDjgAGM7tChQVuele/cx9F/fsjR7I+o2F7FNtBeJimBFldNoOWky4kf\n1CtCEYo0HnX9UTFYt+srvV/HWSByj+OKiIjU0fHV4le++YYDxcXVzo2JiuKibt24sX9/Lu3Ro0Fq\nio9zHyuicNZ8jv5rFsVzl1bbog0gtmcXWv5gIi2+dwHRqS0iFKVI41PXGuSGKaYSEREJEZfbzYdb\ntvB0Tg6zt22rcf7pbdty44ABXNu3L62TkiIQYXC2rJyiOYs59vanFH78ZbUbegAQG0PyBWfS8geX\nk3iWNvYQqQ0VG4mISLNSUFrK33NzeWb5cjYXFFQ7Nz0hgZsGDOC2QYPon5kZoQgDWbebkoUrOPr2\npxS+/z/c+UdrPCeuX3daXHcJLa4aT3RmegSiFGk6lCCLiEizsO7QIf6Sk8Orq1ZRWF5e7dyzOnXi\n9sGDubJ37wYrobAuFyWLVlL4wTyOzZyLa0/Nu/JFtUwh5crzaXHdJcQP6aPVYpE6UoIsIiJNlrWW\nj7du5c/LljFr69Zq5x5fLZ48eDD9WrWKTIB+bFk5xV/kcGzm/yicNR/3wfyaT4qOJmncGaRcNYHk\ni8cSlRgf/kBFmjglyCIi0uSUu1z8a906nliyhNyDB6ude2qbNtw9dCjf69OHxNjYCEX4LXdRCUVz\nFlP4wVyKPlmI+8ixWp2XMGIwKVeeT8p3zlEJhUiI1bXNW3dr7eZQByMiIlIfReXlvJyby5NLl7Lt\nyJEq50UbwxW9evGToUM5s2PHiJcilG/dTdGnCyicvYiSL5djS6vvVXxc3IAepFwxnpSJ5xHbuV2Y\noxRpvuq6grzSGLMVeA9411q7OHQhiYiInJy84mKeWb6cvyxfTl41bdoyEhKYPHgwd556Kl1atoxY\nfLasnOJFKyj6dCFFsxdRvrHmHsvHxQ3sRfKlY0m55Gzi+nYLY5QiclxdE+RMYDzwXeBdY4wFZuJJ\nmD+11paEKD4REZEqbT9yhKeWLuVvK1dSVM0W0H0zMvj56adzfb9+ESujKN++h+K5Syn6bBFF//sK\nW1h9f+XK4s8YSMolY0m+5Gxiu3YIY5QiEkxd+yCXAO8D7xvP76VGAZcBvweyjTGz8STL71tra37s\nVkRE5CRsP3KEaYsX8/fcXMrd7irnjerQgfuGD+c7PXqEfetnV14+xfOXUzxvKUXzllGxdVftT46O\nJnH0EJIvPYfki88ipl3DtZQTkRA8pGettcAC79cvjTG98CTLk4DnjTE/s9Y+W9/7iIiI7PAmxi/X\nkBhf3K0bvxwxgjFhrC92HyuiZEkuRfOWUjxvGWW5G07q/OjW6SSdO4Kk80eROO4M7Wwn4iAh72Jh\nrd0APAk8aYxpBWSE+h4iItK87DhyhMcXL+alahLjaGPI6tePe884g0GtW4c8BldePiWLV1K8aCUl\nC1dQmrsBXK6Tukb8af1IOn8kSeNHefoUR2ljWhEnCmubN2ttHpAXznuIiEjTdaCoiN8uWsTzK1ZQ\nVkUyGh8dzW2DB/Pz00+na2pqyO5dvmMvJYtWULJoJcWLVlC+vubtqP1FZaSSOGYoSeNHkXTuCGLa\naM1IpDFwVB9kY8wdwJ1AV++hVcCj1tpZ1ZyTCkwDJuJZrd4K/LTyOcaYu4B7gHbACuDH1tqvwvAW\nREQkBI6WlfHU0qX88auvOFbFrnfx0dHcPmQI9w0fToeUlHrdz32siNIV6yjJWU3psjWU5Kyu1c51\n/kxSAgkjBpN09ukknjWMuIE9tUos0gg5KkEGdgD3ARsAg6eO+V1jzKnW2jX+k40xscBsYC9wBbAb\nOAXIrzTne3hKPiYDS4ApwMfGmN7W2uq7x4uISESVVlTwwooV/GbRIg5W0a4tPjqayYMH88sRI+qU\nGFuXi7K1WyjN8STCpTmrKVu7Faqpaa5STDQJp/UjcewwEseeTsLpAzBxkd9sRERCq64bhYwFFlhr\nq+6pUwfW2g/8Dk01xtwJjAQCEmTgFiANGGmtPf67N//mklOAv1prZ8CJVepLgJuBJ0IVu4iI1J3b\nWl5fvZoHv/yyyg0+4o4nxsOH07FF7R5os2XllK3fRmnuesq+2Uhp7npKV6zHFtW+5VplJimBhNMH\nkDByCAkjB5MwtD9RyYl1upaIOFddV5A/B9oD+0MYiw9jTBRwDZAELKxi2ne8Y88ZY74LHADeBH5v\nrXV7V5iH4SnBADxdN7xt6EaFK3YREam9eTt28NPPP2f5/uD/SzHAjQMG8PDo0dXWGLuPFlL6zUbK\nvtlAae4GSr/ZQNm6rVAWvESjNqIyUkkYMYhEb0IcP6g3JtZpv3wVkVCr66c8bM0kjTED8SS9CcBR\nYKK1dm0V07sD5wKvAxcBPYHn8byvx/BsaBIN7PM7bx/QJ+TBi4hIrW3Oz+feuXN5e0PV7dEu69GD\n344Zw8BKXSlsRQXlW3ZRtnYLZeu2ULZ6M6W5G06u73AwMdHE9e9BwrD+xJ/Wj4Rh/Ynt2UU1xCLN\nUH1+DLYhi8LXWmAIkApcBcwwxoytIkmOwpPsTvb2Y15ujOmE54G8x8IUn4iI1MOR0lKmLV7M9GXL\nquxMMaZjR3535hjOKIfyr9ZweO1HlK3d7EmIN+6o16rwcTFd2nsT4X7ED+1P/OA+RCXG1/u6ItL4\n1SdBftUYU1rdBGvtFSd7UW9d82bvy+XGmOHA3Xi6W/jbA5R5k+Pj1gDtjDExwEHABbT1O68tngf7\nqjVlyhRS/X6dl5WVRVZWVm3eioiIVOJyu3nlm2/41fz57C8qOnE8rbiMboeO0e3QMU4vdnEhcbTa\nu5KKe19iR0lZSO4d06U98YN6ETewJ/GDehN/Wj+1XBNpRLKzs8nOzvY5VlBQELb71SdBPgrU7SmH\nkxMFVPUj/ZeAf7baB9hz/AFCY8wy4Dw8W1/j3Rr7PODpmm48ffp0hg4dWsewRUTkuEVrN/DEf96n\nePNOrjx8jK7ehLjboWOklwSuBtd5fTgmmrg+XYkf2Iu4gb1OJMXapU6kcQu2QJmTk8OwYcPCcr/6\nJMg/sdaG9CE9Y8w04CM8nShaANcDZwMTvOMzgJ3W2ge8pzwP3GWMeRr4C9AbuB/4U6XLPoVntXsZ\n37Z5SwJeDWXsIiLNmS0rp2LnPsq37aZ8+x4qtu2mfOtuirfuonDzDloXlvCHEN8zuk0GcX27Eden\nG3EDehI/sCdxfbth4uNCfCcRaW7qmiCHq/64DfAang4ZBcBKYIK1do53vBNworWctXanMeYCYDqe\nDUB2eb9/otKct4wxmcCjeEorvgYusNaefAd4EZFmynXkGK7dB6jYtZ+K3fs8f+7aT/mOvVRs203F\n7gNV9hGubxO0qMw0TxLcpxtxfbt6/+xGdEbods0TEanMUV0srLW31jB+bpBji4HRNZz3HPBc/aIT\nEWma3EUlVOze701691X6fv+J7+2xopovVB+xMcR27Uhsj87E9exMbPfOnu97n0J0Znp47y0i4qeu\nCfI44FAoAxERkdCxLheuvAJc+w/h2p9Hxf5Dnu/35QW8dh8tjEhMbqA0M420Pt2I79WF2B6die3R\nhbgenYnp0g4To/7CIuIMJ/1fI2PMtdbaf9Zybmegi7X2y5OOTEREfNiyclyHCnDl5eM6VID7YD6u\ng4c9ye6+PFz7D1Gx3/On62A+VNFCLZwK4mPZkZbEztQktqcle79PZsiwQfzy8kvo1UqdI0TE+ery\n4/qdxpiHgFeA9621PltAG2NSgTOBG4DxeLaDFhGRKrjyj1KyaAWug57E13Uo35P8Hio4kRC78woi\nttJbnajMNGI6tCGmYxtiOrQhv1VL/pq3l1kVxexIS+JIgu8Dcv1bteLZ887jnC5dGihiEZGTd9IJ\nsrX2bGPMZcCPgceNMYV4NusoAdKBdnj6D78KDLTW+u9iJyIiXkWfL2HvpF9hi0oaOhSi0loQ06G1\nNwFu+20i7E2Gozu0JirB03Wz3OXiD199xaMLF1KaGY9/N86U2FgeGj2au4cOJTY6ugHejYhI3dWp\n4Mta+x7wnrc7xBjgFDwPKh8ElgPLrbXBH2cWEZETDv3+5fAmx8YQnZlGdJsMotu0Isb7Z3SbDGLa\nev6MbtuKmHaZRKUk1eqSi/fs4baPPyb34MGg41f37s30cePo2EK9h0WkcarXExHW2oPAOyGKRUSk\nWbHlFZTmbjj5E40hKr0l0Rmpnq+2rb5Ndv2T38y0kD38drSsjF998QXPLF8etNdnlxYteO7887mk\nR4+Q3E9EpKHokWERkQZSvmUnlPnuGZd4zhmeFd9WaURnpBHVKtX7farneEYqUWktIt7xYeamTfxw\n9mx2HD0aMBZlDD8ZOpTHzjyTlDht0iEijV+9/gtrjDlM8E1DLJ6a5I3Aq9baV+pzHxGRpqhszRaf\n19HtMunwf081UDTBFZSWcvecOby2alXQ8SGtW/O3CRM4o337CEcmIhI+9V2CeBT4FZ7toZd4jw0H\nLgSeBboBzxtjYqy1f6vnvUREmpSytZt9Xsf17dZAkQT32bZt/GDWrKCrxgkxMTw8ahQ/O/10PYQn\nIk1OfRPkMcBUa+0LlQ8aY27Hs0X0lcaYlcBPACXIIiKV+K8gx/Xr3kCR+CoqL+e+efN4ZvnyoOPn\nn3IKL4wfT4+0tAhHJiISGfVNkC8A7gty/DPgSe/3HwK/q+d9RESaHCeuIC/avZubPvqI9YcPB4y1\njIvjT+PGMWngQIwxDRCdiEhk1DdBPgR8B5jud/w7fLsVdTIQ+Ps5EZFmzF1cSvmWXT7HGnIFuczl\n4pEFC/jdkiW4beCjJed16cLfL7yQLi1bNkB0IiKRVd8E+TE8Ncbj+LYG+QzgYuAO7+vxwNx63kdE\npEkpX78V3L7t4uN6d22QWFYeOMCNH37IigMHAsYSY2L4/dix3HXaaURp1VhEmon69kH+mzFmNfAj\n4Arv4XXA2dbaBd45T1Z1vohIc1W21rf+OKZrB6KSEyMag8vt5o9ffcWvv/yScnfg3k4j2rdnxkUX\n0TsjI6JxiYg0tHo30rTWfgl8GYJYRESajcD648iWV+w+dowbPviAz3fsCBiLjYri4dGjuXf4cGKi\noiIal4iIE9Q7QTbGRAOXA/28h1YB71lrXfW9tohIUxXQwSKCD+jN3LSJSbNmkVdcHDA2KDOTf1x8\nMUPatIlYPCIiTlPfjUJ64ulS0RFPaQXA/cAOY8wl1tpN9YxPRKRJClhBjsADeqUVFdw3bx5/zskJ\nGIsyhnvPOIOHR48mPsK79ImIOE19/yv4NLAJGGmtPQRgjGkFvO4du6Se1xcRaXJcR45RsWu/z7Fw\nryCvP3SIa2fOZPn+/QFjnVu04M1LLmFMp05hjUFEpLGob4J8NpWSYwBrbZ4x5peoLllEJKhyvwf0\niIkmrmeXsNzLWsuMVau467PPKCwvDxif2KsXL02YQEZiZB8QFBFxsvomyKVAiyDHU4Cyel5bRKRJ\n8u9gEdujMyYuNuT3OVJayg9nz+aNNWsCxuKjo5k+bhx3DBmiTT9ERPzUN0GeCbxojLmFb/sgjwBe\nAN6r57VFRJqksjXh72Dx1Z49ZH3wAZvy8wPG+rdqxT8vvZRBrVuH/L4iIk1BfRPknwCvAQuB47+7\ni8GTHN9dz2uLiDRJpX4ryHH9Qld/7LaWp5Yu5f4vvqAiSG/jyYMHM33cOJJiQ79iLSLSVNR3o5B8\n4LvGmF5AX+/hNdbajfWOTESkiQpXD+R9hYVM+ugjZm3dGjCWGh/P3yZM4Oo+fUJyLxGRpiwkvXys\ntRuADaG4lohIU1Zx4DDug75lD6HoYPHp1q18/8MP2VdUFDA2qkMH3rzkErqmptb7PiIizcFJJ8jG\nmKdqO9da+7OTvPYdwJ1AV++hVcCj1tpZVcy/CXgFsMDxp0xKrLVJlea8Atzkd+osa+3FJxObiEgo\n+K8em4Q4Yrt2qPP1yl0ups6fzxNffRUwZoD7R4zg4dGjiY2OrvM9RESam7qsIJ9Wy3m2DtfeAdyH\nZzXaAJOAd40xp1prAx/D9igAevNtghzsvh95r3V8TmkdYhMRqTf/HfRie3fF1DF53ZyfT9bMmSzZ\nuzdgrH1yMq9fcgnndglP+zgRkabspBNka+24cATivfYHfoemGmPuBEYCVSXI1lp7oIZLl9ZijohI\n2IWq/vifa9dy+yefcKQssKPmxd268epFF9E6KSnImSIiUhPH7idqjIkCrgGS8HTJqEqKMWYrEAXk\nAA9Ya1f7zTnHGLMPOAzMAaZW3txERCRS/Hsgn2wHi8KyMn4yZw5//+abgLHYqCieOPts7h46VL2N\nRUTqwXEJsjFmIJ6EOAE4Cky01q6tYvo64GZgJZAK/AJYYIzpb63d7Z3zEfA2sAXoATwOfGiMGWWt\nrUsZiIhInVhr69UD+ev9+7l25kzWHQr8+b5Xejr/vPRShrZtW+84RUSaO8clyMBaYAiehPcqYIYx\nZmywJNlauwhYdPy1MWYhnlKM24GHvHPeqnTKKmNMLrAJOAf4PEzvQUQkQMWu/dhjvl0m4muxgmyt\n5Znly7ln7lzKXK6A8Rv79+eZ88+nRVxcyGIVEWnOHJcgW2srgONLLMuNMcPxbDpyZ23ONcYsB3pW\nM2eLMeagd061CfKUKVNI9WuLlJWVRVZWVk2hiIgE8F89jmqRTHSHNtWek1dczM2zZvHepk0BYymx\nsTw/fjw39O8f0jhFRJwmOzub7Oxsn2MFBQVhu5/jEuQgooD42kz01i0PAvwf9qs8pxPQCthT0/Wm\nT5/O0KFDaxmmiEj1Ah/Q61ZlrXBJRQV/W7mSaYsXs7ewMGB8WNu2/PPSS+mZnh6WWEVEnCTYAmVO\nTg7Dhg0Ly/0clSAbY6bhqRneDrQArgfOBiZ4x2cAO621D3hf/xpPicVGIA24F+gCvOQdT8ZTavE2\nsBfPqvHvgfXAx5F6XyIiEOwBvcD649KKCl7KzeXxxYvZdexY0Ov8/PTTmXbWWcSpt7GISFg4KkEG\n2gCvAe3x9DdeCUyw1s7xjncCKirNTwdeBNrh6VCxDBhVqV7ZBQwGbsSTQO/Gkxg/aK0tD+9bERHx\nFfiA3rf1x6UVFfz9m2+YtngxO48eDXp+68REXrvoIi7qHpqtqUVEJDhHJcjW2ltrGD/X7/XPgCp3\n67PWlgAXhiY6EZG6sy4X5eu3+RyL69cday0v5eby2MKF7KgiMQZPb+OXLriA9ikp4Q5VRKTZc1SC\nLCLSVJVv3YUt9d3UI65vNx5esIBHF1bd6v3cLl14ZPRoxnTqFO4QRUTESwmyiEgE+G8xHd06ndLU\nFP60bFnQ+ed07swjo0cztnPnSIQnIiKVKEEWEYmAYB0s3lq3LmCr6LGdOvHI6NGc06VLJMMTEZFK\nlCCLiESA/wpyXN/uvLhypc+xC7t25cMrr9Q20SIiDSyqoQMQEWkO/FeQ93dqzcLdu32O3T5kiJJj\nEREHUIIsIhJmtrSM8k07fY69Y3xLK9onJ3OJ2reJiDiCEmQRkTAr27gdXC6fY88VHvJ5/YOBA4nV\nxh8iIo6gBFlEJMz8d9ArbZvBLtw+x24dNCiSIYmISDWUIIuIhJn/DnprW/lu9jGha1e6paVFMiQR\nEamGEmQRkTDzX0Fe1CLO5/XkwYMjGY6IiNRACbKISJj5d7DYkNnyxPdtk5K4rEePSIckIiLVUIIs\nIhJG7mNFVGzb43NsXetvE+RJejhPRMRxlCCLiIRR2fqtPq9dBjZVqkHWw3kiIs6jBFlEJIz8d9Db\nmp5CWYxnxfi8Ll3omZ7eEGGJiEg1lCCLiISJu7iUo//8yOfYhswWJ77Xw3kiIs6kBFlEJAzcxaXs\nvfF+Shat8Dm+qp2nnVvrxEQu79WrIUITEZEaKEEWEQkxd4knOS7+31c+xw8nxJJ9alcAbhowgDg9\nnCci4khKkEVEQsiWlrFv0tSA5LggPpZJ3xtNfqKnB/JtKq8QEXGsmIYOQESkqbClZez9wVSKPlvk\nc7woMY4brxl1orzinM6d6Z2R0RAhiohILShBFhEJAVtWzt5bHqTo04W+x1OSuP6K008kx6CH80RE\nnE4JsohIPdnyCvbd9hBFH3/pc7w8KZ4fXD2C3DbfbgzSKjGRiXo4T0TE0ZQgi4jUgyc5fpjCD7/w\nOV4cH8uNE4ezvFJyDHBj//4kxOg/vSIiTqaH9ERE6siWlnmS4w/m+hwvjI1m0lUjWN7Jt864V3o6\nU0eOjGSIIiJSB1rGEBGpA/exIk8rty9yfI4XxkZzy9WjWNaplc/xWwcN4vdjx5KRmBjJMEVEpA4c\ntYJsjLnDGLPCGFPg/VpgjLmwmvk3GWPcxhiX90+3MaYoyLxHjTG7jTFFxphPjTE9w/tORKQpqzhw\nmN2X/yQgOS6Kjea2q0aytPO3yXG/jAzmXXstf7vgAiXHIiKNhNNWkHcA9wEbAANMAt41xpxqrV1T\nxTkFQG/vfABbedAYcx/wI+BGYCvwG+BjY0w/a21ZqN+AiDRt5dv3sOfqn1G+eafP8WNx0dx+5UiW\ndMkEID46mqkjR3Lv8OHaEEREpJFxVIJsrf3A79BUY8ydwEigqgTZWmsPVHPZu4HHrLUzAYwxNwL7\ngMuBt+oZsog0I6VrNrPnmp/j2nvQ53heUhw3X/1tn+PzunTh+fHj6ZWe3hBhiohIPTkqQa7MGBMF\nXAMkAQurmZpijNmKp1wkB3jAWrvae41uQDvgs+OTrbVHjDGLgVEoQRaRWipevJJd192LOVLoc3xH\nahKTrhnFtowUMhMTmT5uHNf364cxpooriYiI0zkuQTbGDMSTECcAR4GJ1tq1VUxfB9wMrARSgV8A\nC4wx/a21u/EkxxbPinFl+7xjIiI1OvDhXPJue4TYsnKf4+syW/CDa0ZxoEUikwcPZtpZZ9FKdcYi\nIo2e4xJkYC0wBE/CexUwwxgzNliSbK1dBJzY09UYsxBPKcbtwEORCVdEmiq3tXz01Ev0fOIfxLp9\nHm9gaccMJl81gkE9ujHr3HM5rW3bBopSRERCzXEJsrW2AtjsfbncGDMcTx3xnbU51xizHDjepWIv\nnof32uK7itwWWF7T9aZMmUJqaqrPsaysLLKysmo6VUQauXWHDvHPe3/HDe8GVnjN6dGWx687h+fH\nn0dW374qpxARCbPs7Gyys7N9jhUUFITtfo5LkIOIAuJrM9FbtzwI+ADAWrvFGLMXOA9PGQbGmJbA\nCODZmq43ffp0hg4dWsewRaQxstby8vKv2ffAn7hh2eaA8XcGdeHQr29j5ZmjSYmLa4AIRUSan2AL\nlDk5OQwbNiws93NUgmyMmQZ8BGwHWgDXA2cDE7zjM4Cd1toHvK9/jafEYiOQBtwLdAFeqnTZP+Hp\nhrERT5u3x4CdwLvhf0ci0pjkFRdz99vvcNH0t7h2+8GA8c/HD+PyZx6kR0ZGkLNFRKSpcFSCDLQB\nXgPa4+lvvBKYYK2d4x3vBFRUmp8OvIjngbvDwDJgVOV6ZWvtE8aYJOCveJLoL4CL1ANZRCr7bNs2\nHn7lTR57/X90LgjYb4gDP/4etz74owaITEREIs1RCbK19tYaxs/1e/0z4Ge1uO7DwMP1iU1EmqYy\nl4up8+fz9Rvv8ezMZSSXu3zGy2NjaD39Pnp8r8pNPUVEpIlxVIIsIhJJ6w4d4vqZMxn53y94fn5g\nN8ny1ul0ffMJEk7t2wDRiYhIQ1GCLCLNjrWWl3Nz+eWsT3jova+4eN3ugDlRp/Wl54zHiWmX2QAR\niohIQ1KCLCLNyqHiYm775BMWLV3BK/9ZQv/9gW2CUq69iNZ/+DlRCbVqoCMiIk2MEmQRaTY25edz\nwb//TXruJv77zhJaFfk+q2ujosh85Iek3n6NehuLiDRjSpBFpFlYvm8fF/3735y3YDVTZ+cS57cz\nnklNof3fHiFp3PAGilBERJxCCbKINHmfb9/O97Pf4sH3lnDB+j0B47G9TqHdPx4nrkfnBohORESc\nRgmyiDRpb69fz/TnXuVf735Fu2MlAeNJ40fR5oUHiW6Z0gDRiYiIEylBFpEm68VlOax75FleWbie\nqCDjaT++joxfTcZER0c8NhERcS4lyCLS5FhreeqdDzjl4Rf54e7DAeNRGam0+cv9JE84swGiExER\np1OCLCJNisvt5rnH/sx5L75Hi7KKgPGEscNo++xU9TcWEZEqKUEWkSajOP8IM2+6l4sXrAoYc0dH\nkfmr20m761pMVLCCCxEREQ8lyCLSJBxaspK1kx5g6IHAjT8KO7Sm92vTtGW0iIjUipZRRKRRs243\nO558lQPf+RFtgyTHBy8cxcAvX1dyLCIitaYVZBFptMrWb2XH3b+DpasC/mN2ND6G4l9PZtTtWQ0S\nm4iINF5KkEWk0XGXlHJ4+j849PTrRFW4AsZzO7XilL89wqjThzRAdCIi0tgpQRaRRqVo3lL2/vwP\n2K27A2rE3MCb5wziumcfoVeb1g0RnoiINAFKkEWkUXAdPMzBB5/l2P99HHR8e2oSL2adw5P3/ZgO\nKdoVT0RE6k4Jsog4mrWWo29+yIGHn4X8owHj5VGGl4f3JO/m7/LCxReSGh/fAFGKiEhTogRZRByr\nbC6ZnyEAACAASURBVP1WDtzzR0oWrgg6ntMhnT9NHMUvv38N3+nRI8LRiYhIU6UEWUQcx11SSv6f\n/sHhp9+A8sDd8I7Ex/CHs/sTm3Ux7593LhmJiQ0QpYiINFVKkEXEUYq+WMbBe/5I+eadQcdn9u3I\nS98ZzrQrv6tVYxERCQslyCLiCBX78sh79AWOvTUr6PiO1CT+n737jq+yPP84/rkyICRA2ENBcY9a\n0cQ6GS4UQcWBI2qddVstzrptrdZRbdVqrdZZNf25RQTBBSKKg4ATFFFkbwgjkHWu3x/noOckJ5Bx\nZvJ9v155wbnv+3nON4GHXLm5n/u5edDu9DnqIN4/+GA65uQkOKGIiLQUKpBFJKmqS9ew6oHnKH30\nRbxsQ63+KjMe23s7XhhUwP1HDtGssYiIxJ0KZBFJikDZBkr/8xIr738GL10bdczULTpyw+F92efA\n/SjRrLGIiCSICmQRSSivrGL1M6+z9O4nsKUro47ZeBPehP1/xb8HH86RmjUWEZEEqvkgqqQyswvM\n7HMzKw19fGhmg+t57MlmFjCzl2u0PxFqD/8YHZ/PQETq4oEAq14Yy/S9TmTZ1fdGLY6rzPi/3bfm\n8N8dQvapQ/nqnLNVHIuISMKl2gzyXOAaYCZgwJnAa2a2h7tPr+sgM+sD3A28X8eQMaFzWeh1eUzS\nishmuTvzX3+PRbc+TMfZC6nrMR5v7LwF/+i3M2127MPjAwaoMBYRkaRJqQLZ3d+o0XSDmV0I7AtE\nLZDNLAN4BrgJGADkRxlW7u5LY5lVRDbN3fnk9XdY+9f/0Of7+XSsY9z723Tj7wN3Zcd+e/HYnnty\nYO/emFkdo0VEROIvpQrkcKHC90QgF/hoE0NvBha7+xNmNqCOMQea2WJgJfAucIO7r4hpYBEBYG1F\nBa+9/hZZ/3iGvWbMo0sd46Zu0ZHHDtuT3wwbxOi+fenVrl1Cc4qIiNQl5QpkM9uNYEGcA6wBjnX3\nGXWM7QecBfTdxCnHAC8BPwLbAX8FRpvZfu7uscwu0pL9uGoVT45+i26PvMLgr+fWOe7bLu0Yc2w/\n9j/tGF7baSdaZWYmMKWIiMjmpVyBDMwgWPDmA8OBp81sQM0i2czaAk8D57p79FvhAXd/Puzl12b2\nJTALOBB4L8bZRVqc8qoqHvm/1yh//GWKvppLdiD6z53z8nOZesogDrzwVB7o2TPBKUVEROov5Qpk\nd68Cfgi9nGpmewOXARfWGLodsDXwuv2yYDEDwMwqgJ3c/cco5//RzJYB27OZAnnEiBHk50cuaS4q\nKqKoqKhhn5RIM+RVVXz831dZ9K//MeTHxXWOW9E2h3mnD2XgFecwsL2WUYiISMMVFxdTXFwc0VZa\nWhq397NUX2VgZu8AP7n72TXaWxEscsPdBrQFLgVmhortmufrBfwEDHP3UXW8ZwEwZcqUKRQUFMTg\nsxBpPqpXrmbB4y+z5NEX6LB8dZ3j1rdpTdlZR1Nw1e/IapubwIQiItISlJSUUFhYCFDo7iWxPHdK\nzSCb2e0E1wzPAdoBpwIDgcNC/U8D89z9OnevAL6pcfwqwDduCWdmeQRv4nsJWESwoL4T+A4Ym4jP\nSaS5qJjxI6seeYFVz79JZnklHeoYV5WdRdZZw9jlyrPJ7Ng+oRlFRERiIaUKZKAb8BTQEygFvgAO\nc/d3Q/29gFqzwptQDewOnA50ABYQLIxvcvfKWIUWaa48EKDsrY8offRF1k/4DIC6bqlb2T6XNqcf\nxU4XnUpW17o2dRMREUl9KVUgu/vvNtN/8Gb6z6rxegNQryfxicgvqlevZc1zoyl97GWqZs/f5Niv\ntuhE4IyjOOqi35KVU9djQERERNJHShXIIpJcFbPmUProS6z53xh83fo6x1VmGGN22oJFww9hxDmn\n0CMvL4EpRURE4ksFskgL5+6sf+8TSh99kbK3J29y7PLcVhT37cNHB+3BX447mhFbb52glCIiIomj\nAlmkhQqsLWPN82Mp/c9LVM78aZNjv+mWz5N7bcu43bbiiv33Y/w++5CTpX8+RESkedJ3OJEWxquq\nWH7rv1nzzCgCq9fWPTAjg7wh/bEzjubsrz6hb7duTDn0UHbs1ClxYUVERJJABbJIC2NZWZR/9nWd\nxXFGh3a0/+1RtD/rWLJ79wDg0z13Yuv27fnlmTwiIiLNlwpkkRYo/7wT2PDJlxFt2TtvQ4dzh9P2\n+EFk5LWJ6OtT44mSIiIizZkKZJEWKG9IfzK36Eb1wqXkHrY/+ecNp03/Qs0Qi4iIoAJZpEWy7Cy6\nPXAt2b16kL1tr2THERERSSkqkEVaqNwBeyU7goiISErKSHYAEREREZFUogJZRERERCSMCmQRERER\nkTAqkEVEREREwqhAFhEREREJowJZRERERCSMCmQRERERkTAqkEVEREREwqhAFhEREREJowJZRERE\nRCSMCmQRERERkTAqkEVEREREwqhAFhEREREJowJZRERERCSMCmQRERERkTApVSCb2QVm9rmZlYY+\nPjSzwfU89mQzC5jZy1H6/mxmC8yszMzeMrPtY59eRACKi4uTHUEk7ei6EUktKVUgA3OBa4ACoBB4\nF3jNzHbZ1EFm1ge4G3g/St81wCXAecDewDpgrJm1imVwEQnSN3qRhtN1I5JaUqpAdvc33P1Nd5/l\n7t+7+w3AWmDfuo4xswzgGeAm4McoQy4DbnX3Ue7+FXA6sAVwTOw/AxERERFJdylVIIczswwzOxnI\nBT7axNCbgcXu/kSUc2wD9ADe2djm7quBj4H9Ypu4eUjFWYxEZIr1e8TifI09R0OPq+/4VPy7kUpS\n7euTqDypdu2k2nXTmHO3NKn29dG1E9/j0uXaSbkC2cx2M7M1QDnwEHCsu8+oY2w/4Czgd3Wcrgfg\nwOIa7YtDfVJDqv1DBSqQ432cCuTYSLWvj77Jx/e4dPkmnw5S7eujaye+x6XLtZOVtHeu2wygL5AP\nDAeeNrMBNYtkM2sLPA2c6+4rY5whB2D69OkxPm3qKy0tpaSkJNkxIiQiU6zfIxbna+w5GnpcfcfH\nelxzk2qfd6LypNq1k2rXTX3Hptrfn0RKtc9d1058j4vltRNWp+XUO0A9mbvH+pwxZWZvAd+7+4U1\n2vsCJUA1YKHmjTPi1cBOod/PAvZw9y/Cjh0PTHX3EXW85ynAs7H6HEREREQkbk519+diecJUnEGu\nKQNoHaV9OvDrGm23AW2BS4G57l5lZouAQ4AvAMysPbAP8OAm3nMscCowG9jQlPAiIiIiEhc5QB+C\ndVtMpVSBbGa3A2OAOUA7gkXqQOCwUP/TwDx3v87dK4Bvahy/CnB3D18b8Q/gBjP7nmDBeyswD3it\nrhzuvhyI6U8iIiIiIhJzH8bjpClVIAPdgKeAnkApwVnfw9z93VB/L6CqISd097vMLBf4N9ABmAgc\nESqwRUREREQipPwaZBERERGRREq5bd5ERERERJJJBbKIiIiISBgVyI1gZr3M7D0z+9rMppnZ8GRn\nEkkXZvayma0ws+eTnUUkHZjZkWY2w8y+NbNzkp1HJF005fuN1iA3gpn1ALq5+xdm1h2YAuzg7uuT\nHE0k5ZnZAIK71Jzh7icmO49IKjOzTII7Ng0E1hD8frNfHB6QJdLsNOX7jWaQG8HdF2188Ii7LwaW\nAZ2Sm0okPbj7+8DaZOcQSRN7A1+Fvu+sA0YT2vpURDatKd9vVCA3kZkVAhnuPj/ZWUREpNnZAgj/\n/rIA2DJJWURajBZRIJtZfzMbaWbzzSxgZkdHGXOxmf1oZuvNbLKZ/aYe5+1EcN/mc+ORWyTZ4nXt\niLQEun5EGicVrp0WUSADecA04CKg1qJrMzsJuAe4GdgT+BwYa2ZdwsZcZGZTzazEzFqbWSvgFeB2\nd/84EZ+ESBLE/NpJTGyRlNDk64fgjHGvsNdbhtpEmrNYXDtN0uJu0jOzAHCMu48Ma5sMfOzul4Ve\nGzAXuN/d76rjPMXAdHf/cwJiiyRdrK6d0LgDgYvd/YT4phZJDY29fsJu0juQ4E16nwL76yY9aSma\n+r2nsd9vWsoMcp3MLBsoBN7Z2ObBnxreBvar45gDgBOAY8Jmxn6ViLwiqaIx107ouLeA/wOOMLM5\nZrZPvLOKpJr6Xj/uXg1cAYwHSoC/qTiWlqwh33ua8v0mKzZx01oXIBNYXKN9MbBTtAPcfRL62ok0\n+NoBcPdB8Qwlkibqff24+yhgVIJyiaS6hlw7jf5+0+JnkEVEREREwqlADu5hXA10r9HeHViU+Dgi\naUPXjkjj6foRaZyEXDstvkB290qCTyY6ZGNbaLH3IcCHycolkup07Yg0nq4fkcZJ1LXTItbRmlke\nsD1goaZtzawvsMLd5wL3Ak+a2RTgE2AEkAs8mYS4IilD145I4+n6EWmcVLh2WsQ2b2Y2EHiP2nvp\nPeXuZ4fGXARcTXCKfhrwe3f/LKFBRVKMrh2RxtP1I9I4qXDttIgCWURERESkvlr8GmQRERERkXAq\nkEVEREREwqhAFhEREREJowJZRERERCSMCmQRERERkTAqkEVEREREwqhAFhEREREJowJZRERERCSM\nCmQRERERkTAqkEVEREREwqhAFpEWwczeM7N7GzB+azMLmNnuMT7vwNB529f3mFQT9jlUm9nLyc6z\nKaGcATNbkewsIpI+VCCLSEtxLHBjA8bPAXoAX8EmC9uGnhfAGzg+FTmwI3DmxgYzezL0NXqo5mAz\nezDU93gCM0Lwz/APCX5PEUlzKpBFpEVw91Xuvq4B493dl7h7INRkBItCa8p5m5ml7r467LUT/MHi\nZDNrvbEx9Psi4KcE58PdlwCliX5fEUlvKpBFpEWouRTCzH40s2vN7DEzW21mP5nZuWH9Py+xMLOt\ngXdDXStDSwser+O8p5nZp6FzLjSzZ82sawOzBszsPDN73czWmdk3ZravmW0Xer+1ZjbJzLYJO2Zb\nM3vVzBaZ2Roz+8TMDqlx3ovM7DszWx8a93xY33Az+8LMysxsmZmNM7M2DckdMhWYCxwX1nYcweJ4\nao08db5ntKUrZvZK+Az05v4MRUQaSwWyiLRklwOfAnsADwH/MrMdwvo3LoWYAxwf+v0OQE/gsjrO\nmQXcAOwODAO2Bp5oRLYbgCeBvsB04DngYeA2oJDgTPY/w8a3Bd4ADgp9PmOAkWbWC8DMCoH7Qufd\nETgceD/U1yN0/v8AOwMDgZepMVteTw48Dpwd1nY2wa/Bz+eL4Xtu7s9QRKTBspIdQEQkid5w94dD\nv7/TzEYQLDBnhtoMgsstwm7yqrmsIIK7Pxn2craZ/QH42Mxy3b2sAdked/eXAMzsLuAj4E/u/nao\n7T6ChejG9/0C+CLs+JvN7DjgaIKF41bA2tDnvI7gLO/nobE9gUzgFXefG2r7ugFZa3oWuMPMehOc\niNkfOIng13ajWL3n5v4MRUQaTDPIItKSfVnj9SKgW1NOaGaFZjYy9N/9q4Hxoa6tmpBtcejXr2q0\n5ZhZ29D75pnZ30LLMVaa2RqCM7Mb3/ctgsscfjSzp83slLAlFJ8D7wBfmdnzZvY7M+vQwLw/c/dl\nwCjgLII38b3h7jV3kYjVe8b8z1BERAWyiLRklTVeO034d9HMcoE3gVXAKcBeBHe5AGjVhGy+ibaN\nee8huKTjj0A/gkszvtr4vu6+FigATgYWAH8CPjez9u4ecPfDgMEEZ3F/D8wIrb1urCcIFsenA4/V\n7KzjPb8Ne88AtZdbZEd5n5j+GYqIgP4RERGpr4rQr5mbGLMz0Am41t0nuft3QPcYvf/mtobbH3jS\n3Ue6+9fAEqBPxAmCRem77v5HggV0H+DgsP6P3P1PwJ4EC89jabw3CRbnWcC4ugbVeM+KsPdcSnAZ\nBgBmlgHs1oQ8IiL1pjXIIiL18xPBIvUoMxsNrI+yvdscgkXepWb2MPBrgjfF1dSYm9+iHRPeNhM4\nzsxGhV7/mcib4oYC2xK8MW8lMDTU/62Z7Q0cQrCQXQLsC3QBvmlETiBYjJvZzqHf1yru6/Ge7wL3\nmNkQYBbBm/EavexDRKQhNIMsIi1FzSIt2oxsnWPcfQFwM3AHwXWuD9Q6OLj29kxgOMFlA1cDV9Tj\nferTv7m2ywkWvpOA1wjO4JaE9a8iuN3aOwSL0POAk919OrAaGEBwF4xvCRbXl7t7nTO/9eHua0NL\nO6LZ3Hs+DjwV+hhPsEh+t8Y56vt1EhFpEIvyg72IiEidzGwgwWK1k7un/EM4zOxM4F5375TsLCKS\nHrTEQkREGmuumb3u7qcmO0hdQrt5ZALrk51FRNKHZpBFRKRBQo+O3jL0cm3occ4pycy2Df222t0T\n/qhrEUlPKpBFRERERMLoJj0RERERkTAqkEVEREREwqhAFhEREREJk3YFspldYGafm1lp6ONDMxu8\nmWNOMLPpZrY+dOwRicorIiIiIukl7QpkYC5wDVAAFBLci/M1M9sl2mAz2x94DngU2IPgBvqvmtmu\niYkrIiIiIumkWexiYWbLgSvd/Ykoff8Dct396LC2j4Cp7n5RAmOKiIiISBpIxxnkn5lZhpmdDOQC\nH9UxbD/g7RptY0PtIiIiIiIR0vJJema2G8GCOAdYAxzr7jPqGN4DWFyjbXGoXUREREQkQloWyMAM\noC+QDwwHnjazAZsokhvEzDoDhwOzgQ2xOKeIiIiIxFQO0AcY6+7LY3nitCyQ3b0K+CH0cqqZ7Q1c\nBlwYZfgioHuNtu6h9rocDjzb1JwiIiIiEnenEtyQIWbSskCOIgNoXUffR8AhwP1hbYOoe80yBGeO\neeaZZ9hll6ibYzRbI0aM4O9//3uyY0RIRKZYv0csztfYczT0uPqOj/W45ibVPu9E5Um1ayfVrpv6\njk21vz+JlGqfu66d+B4Xy2tn+vTpnHbaaRCq22Ip7QpkM7sdGAPMAdoR/KlhIHBYqP9pYJ67Xxc6\n5D5gvJldDrwBFBHcHu7cTbzNBoBddtmFgoKCeHwaKSs/Pz/lPudEZIr1e8TifI09R0OPq+/4WI9r\nblLt805UnlS7dlLtuqnv2FT7+5NIqfa569qJ73GxvnZCYr4cNu0KZKAb8BTQEygFvgAOc/d3Q/29\ngKqNg939IzM7Bbgt9DETGObu3yQ0dZooKipKdoRaEpEp1u8Ri/M19hwNPa6+41Px70YqSbWvT6Ly\npNq1k2rXTWPO3dKk2tdH1058j0uXa6dZ7IMca2ZWAEyZMmVKSv1UK5IOjj76aEaOHJnsGCJpRdeN\nSMOVlJRQWFgIUOjuJbE8d1rvgywiIiIiEmsqkEUkplLtv0tF0oGuG5HUogJZRGJK3+hFGk7XjUhq\nUYEsIiIiIhJGBbKIiIiISBgVyCIiIiItzBuzZnH1hAloN7Po0nEfZBERERFppBe//ZaiN96gKhAg\nOyOD2/r3T3aklKMZZBEREZEW4plvvuGkUaOoCgQAuP3jj7lt8uQkp0o9KpBFREREWoBHv/iC00eP\nJlBjWcX3K1dqqUUNKpBFREREmrn7pkzhvHHjqFkGX9i3L48NHoyZJSVXqtIaZBEREZFmyt255cMP\n+fNHH9Xqu2Kvvbh74EAVx1GoQBYRERFphgLuXPrOOzw4bVqtvhv33Zc/HXCAiuM6qEAWERERaWYq\nq6s5Y8wYimfMqNX31/79+eM++yQhVfpQgSwiIiLSjJRVVjJ85EjG/PhjRLsBDw8axHl9+yYnWBpR\ngSwiIiLSTKzcsIGjXnmFSfPnR7RnZ2TwzJAhnLjzzklKll5UIIuIiIg0A3NWr+aIl17im+XLI9pz\ns7J4edgwDt9mmyQlSz8qkEVERETS3LQlSxjy0kssXLcuor1jTg6jjzuOfbfYIknJ0pMKZBEREZE0\n9tbs2Rw/ciRrKioi2nvm5TFu+HB269o1ScnSlwpkERERkTT15Fdfce64cT8/OnqjXTp1Yszxx7N1\nfn6SkqU3FcgiIiIiacbd+cvkydw0aVKtvgG9evHqMcfQMScnCcmaBxXIIiIiImmkorqaC996i8e/\n+qpW34k77cRTRxxBTpZKvKbQV09EREQkTSwrK+P4kSN5f968Wn1X7LUXdw0cSIaejtdkKpBFRERE\n0sA3y5Zx5Cuv8GNpaUS7AfcdfDC/LyhITrBmSAWyiIiISIob88MPnDxqFKtr7FSRm5XFM0OHcuwO\nOyQpWfOkAllEREQkRbk7/5gyhSsnTCDgHtG3Zdu2jDz2WHbPaJWkdM1XRrIDiIiIiEhtFdXVnP/W\nW1w+fnyt4njvHj349LTT2PGzb5mz14msHfleklI2T5pBFhEREUkxC9auZfjIkXy0YEGtvpN33pnH\nDz+c8sdeYfFN/wR3llz8F7J6diXnN7slIW3zoxlkERERkRQycd48Cp5+OmpxfOsBB/Ds4MGsu/kh\nlt/4AIRmln1DBQt/+0cq5y5KdNxmSTPIIiIiIinA3Xlg6lSuGD++1pPx2mRl8fQRR3Bcr61YfPaN\nlI35oNbxeYP7kdWjS6LiNmtpVyCb2bXAscDOwHrgQ+Aad/9uE8ecATwBOMHdUAA2uHtunOOKiIiI\nbNa6igrOe+stnps+vVZfn/bteXnYMH5t2Sw49jLKp9Ye0+m6c+nwh99i2gM5JtKuQAb6Aw8AnxHM\n/1dgnJnt4u7rN3FcKbAjvxTIvomxIiIiIgkxa9Uqjn31Vb5ctqxW3+F9+vDc0KHk/biA+b+9lqo5\nCyMHtMqm2/3X0u74QQlK2zKkXYHs7kPCX5vZmcASoBCo/f8NEYf60jhGExEREWmQ12fN4vTRo1lV\nXl6r74Z99+WW/fdnw5sfMP/Cv+BlkfOAGR3a0ePJ22hzwJ6JittipF2BHEUHgrPBKzYzrq2ZzSZ4\nY2IJcJ27fxPnbCIiIiK1VFRX88f33+fvU6bU6mvfqhVPDxnC0dttx6p7n2bFHf+pNSZrq570/N/d\ntNph60TEbXHSukC24EKbfwAfbKbY/RY4G/gCyAeuAj40s13dvfYtoiIiIiJx8uOqVZw0ahSfLqq9\n48SunTvzyrBhbJ+Ty+Jzb2Hda+/WGtN6r1/R46nbyerWKRFxW6S0LpCBh4BdgQM2NcjdJwOTN742\ns4+A6cD5wM3xDCgiIiKy0Yvffsvvxo2jNMqSihN32onHDj+c1ktWMn/4RVR8ObPWmHYnDabL364k\nI6d1IuK2WGlbIJvZP4EhQH93X7i58eHcvcrMpgLbb2rciBEjyM/Pj2grKiqiqKiooXFFRESkBdtQ\nVcUV48fz0LRptfpaZ2by94MO4oK+fVk//lPmXfBnAitKIwdlZND5lgvJv+CkFrlTRXFxMcXFxRFt\npaWldYxuOnNPv80cQsXxMGCgu//QiOMzgK+BN9z9yij9BcCUKVOmUFBQ0OS8IiIi0nKVlpdzyPPP\nM2Xx4lp9O3TsyPNHHUXfLl1Yee9TrLzriZ8f/rFRRvu2dH/kFnIP2SdRkdNCSUkJhYWFAIXuXhLL\nc6fdDLKZPQQUAUcD68yse6ir1N03hMY8Bcx39+tCr28kuMTie4I39V0NbAXUXvUuIiIiEkMPTp0a\ntTg+ZZddeHjQIHLXrmdh0dWsf/fjWmOyt+1Fj2fvpNX2WyUiqoSkXYEMXEBw14rxNdrPAp4O/b43\nUB3W1xF4BOgBrASmAPu5+4y4JhUREZEWb8aKyI222mRl8cAhh3D2brtRPnU68865iap5tQvovCH9\n6Xr/tWTmt0tUVAlJuwLZ3TPqMebgGq8vBy6PWygRERGROtS8Ie+avffm7N12o/TfL7D81oehojLy\ngMxMOt1wHh0uLmqR641TQdoVyCIiIiLppOZDQHpsqGRR0dWUvTO51tjMrp3o/ugtevhHkqlAFhER\nEYmj8Bnkfj8uYcAjd1G2cnWtcTn79qX7o7eQ1aNLIuNJFCqQRUREROKotLyc7OoAV0z4ht99Oivq\nmA6XFNHpuvOwbJVmqUB/CiIiIiJxVLl6LcXPfsAeC1fW6svs2oluD15P7kF7JyGZ1EUFsoiIiEic\nuDtHTf42anGce+i+dL3/OrK6dkxCMtkUFcgiIiIicbK2spKtV6yNbMzOovPNF5F/3nDtUpGiVCCL\niIiIxMmqDRtoU1kd0ZZz3nA6nH9CkhJJfWx2T2ERERERaZzS8nLaVNUokPXgj5SnAllEREQkTlaV\nl5NTWRXRlpnbJklppL5UIIuIiIjESWl5ea0lFhm5rZOURupLBbKIiIhInJRWVNQqkK1NTpLSSH2p\nQBYRERGJk1UbNtRag6wCOfWpQBYRERGJk9KKCnJqLrFooyUWqU4FsoiIiEicRFuDbLpJL+WpQBYR\nERGJk1VRtnnTDHLqU4EsIiIiEidrytbTqjoQ0Wa5WoOc6lQgi4iIiMRJ6+/n1mrTTXqpTwWyiIiI\nSBx8u2IF/Z9/N6Ktsn0eWT27JCmR1JcKZBEREZE4ePKxYgb8sCSire35J2CZmUlKJPWlAllEREQk\nxj5fvJi9/js2oq2sQzu2uPiUJCWShlCBLCIiIhJj//fgU+yxcGVEW5erziIjT1u8pQMVyCIiIiIx\n9MHsnxj4/HsRbWt6dqbHWccmKZE0lApkERERkRhxd16/5z9sv3xtRHuvGy/AsrOSlEoaSgWyiIiI\nSIy89sVXHD1qckRb6fa96Hz8YUlKJI2hAllEREQkBiqrq5l2xyP0WLshon27Wy/FMlRypRP9aYmI\niIjEwH/Hf8BxE76MaFv9m11pf8i+SUokjaUCWURERKSJ1lZUsPqux8mrrP65LWCwy11XYWZJTCaN\noQJZREREpIkef2EkQ0t+iGgrG3YgObttn6RE0hQqkEVERESaYE5pKZ3/8VxEUVXeOptf/eUPScsk\nTaMCWURERKQJHnvgCfadvTSizc4fTlb3zklKJE2VdgWymV1rZp+Y2WozW2xmr5jZjvU47gQzm25m\n683sczM7IhF5RUREpPma8ONs9n8m8pHSazq1Y6crzk5SIomFtCuQgf7AA8A+wKFANjDOzOp8NPq9\niQAAIABJREFUdqOZ7Q88BzwK7AG8BrxqZrvGP66IiIg0R1WBAG/c8a9aDwXpfuOFZOTmJCmVxELa\nPdLF3YeEvzazM4ElQCHwQR2HXQqMcfd7Q69vMrNBwCXARXGKKiIiIs3YExM/5MTRn0a0le7Qm21P\nGZqkRBIr6TiDXFMHwIEVmxizH/B2jbaxoXYRERGRBlm+fj0r7vgPHTdURrTveNeVeihIM5DWf4IW\n3FjwH8AH7v7NJob2ABbXaFscahcRERFpkHuffp7jPpsV0VZ26D607VeQpEQSS2m3xKKGh4BdgQOS\nHURERERahvE//cTu/3o5YpaxolU2O999VdIySWylbYFsZv8EhgD93X3hZoYvArrXaOseaq/TiBEj\nyM/Pj2grKiqiqKiogWlFRESkOVhfWUnx3f/m6vmRKztzLjmZ7F41Sw2JleLiYoqLiyPaSktL4/Z+\n5u5xO3m8hIrjYcBAd/+hHuP/B7Rx92FhbZOAz9291k16ZlYATJkyZQoFBfqvEhEREQm6ZexbHH7+\nnXRbV/5z27qendntk/8jI6d1EpO1PCUlJRQWFgIUuntJLM+ddjPIZvYQUAQcDawzs40/rpW6+4bQ\nmKeA+e5+XajvPmC8mV0OvBE6vhA4N6HhRUREJG19tmgRFQ88F1EcA2xz5xUqjpuZdLxJ7wKgPTAe\nWBD2cWLYmN6E3YDn7h8BpwDnAdOA44Bhm7mxT0RERASAsspKrn3iOU7/NPLGvOr+BbQd3C9JqSRe\n0m4G2d03W9S7+8FR2l4CXopLKBEREWnW/jhhAme98D7ZgV+WplZnZdLn7isJbqolzUk6ziCLiIiI\nJMy42bOZ/9+R7DN3eUR7xwtPotV2vZOUSuIp7WaQRURERBJl0bp1/P6FV3jmva8j2n3LbnS+4szk\nhJK40wyyiIiISBTVgQCnjBrFOaM/pdP6ioi+nndfSUZemyQlk3hTgSwiIiISxZ8+/JCySVM5/qu5\nEe15Rx9E3qD9kpRKEkFLLERERERqGDd7Nnd9MInXx06L7GiXS5fbLk1OKEkYzSCLiIiIhJm1ahUn\njxrFeZNnsu2KdRF9Xa4/n6weXZKUTBJFBbKIiIhIyNqKCo559VU6zF/KhZNnRvS1LtiF9mcOq+NI\naU60xEJEREQECLhzxpgxfLNkKcVjptGqOvBLZ2YmXf92FZaZmbyAkjCaQRYREREBbps8mZdnzuS3\nJT9QOH9FRF/++SfQ+tc7JCmZJJoKZBEREWnxXvruO26aNImtVq7jygnTI/qy+mxJp2vOSVIySQYt\nsRAREZEWadG6dUycN49XZs6keMYMzJ3b3pxGm6rqiHHd/nENGbk5SUopyaACWURERH42a9UqiqdP\nZ1V5edR+i9ZmRoYZrTIy2G+LLTh8m23IsGgjk6cqEOCLpUv5aMGCnz9+KC2NGHPytNnsN2dZRFv7\ns46lzQF7JjKqpAAVyCIiIgIEi+O9n3mGFRs2NOk8O3TsyPm77073vDxaZWTQKjOTVpmZtA792ioz\n8+f27IwMsjIyyM7IIDv0OjvsdaYZVs9iu7yqikXr1rFg3ToWrF3L9ytXMn3FCqYvX85Xy5ZRVlVV\n57E9V5dxzfjIx0ln9e5B55suaNLXQtKTCmQRERGhOhDgrDffbHJxDDBz5UqunDAhBqmCwgvmrPAC\nOiODykCAdZWVrK2spKK6evMnq8Ofxn1B24rI47veezUZbXObGl/SUIMLZDNrDewDbA3kAkuBqe7+\nY4yziYiISILcV1LCxHnzkh0jqspAgMpAADYxA9xY7Vq1Ymibdhw8a3Fk+6lDyT3wNzF/P0kP9S6Q\nzewA4DLgKCAbKAXWA52A1mb2A/AI8LC7r4lDVhEREYmDGcuXc93EiRFtW7Zty6Ctt97ssQ64Ow5M\nW7KEL5ct29whSbVDx47s27Mn+22xBfttsQW/7tKF8vGfsjBsjOW1ofOfL0laRkm+ehXIZjYSKACe\nAw4DPnP39WH92wL9gSLgcjM73d3fikNeERERiaGyykrOGDOG8tDyBHNnt0WreHSvHdktq0PDTrZl\nBz7P7sjY2bNZtG4dlR6gqjpAVSD4URkIBNsCoXb3OHxG0Cozg045OXRp04be7drRu117erdrx/Yd\nOtC+devgoKXrYeksNjCLsrcnRx6/Ux8y27eNSzZJD/WdQX4DON7dK6N1uvsPwA/AU2a2K9AzRvlE\nREQkTlasX8/Rr77KJ4sWAZBVHeC//5vEb+atgKffZ1EjztkdOD2mKWOnLPSxOdnb9Y53FElx9SqQ\n3f3f9T2hu38DfNPoRCIiIhJ389asYfCLL/L18uU/tx3z9dxgcdzCtdpuq2RHkCRr9C4WZtYK6EaN\np/G5+5ymhhIREZH4mb58OYe/+CJz10TeMnT89AVJSpRacrTvcYvXmF0sdgAeB/av2UVwrX5mDHKJ\niIhIHExesIChL79cazu33QMZ7PXT0oi2zG6dsFbZiYyXVNY2l/anDiVnn18nO4okWWNmkJ8EqoAj\ngYUEi2IRERFJcaN/+IHhI0eyvsZ2abt06MAr42fiYTfNZbTLY6spz5OR0zrRMUWSrjEF8h5AobvP\niHUYERERiY8nvvySc8eNo7rGzhF7d+/Oi9MWUjH2w4j2vCMHqjiWFitj80Nq+QboEusgIiIiEnsB\nd66fOJGzx46tVRwP7tOHkYurqHj69Yh2a5tLxz/8NpExRVJKYwrka4C7zOxAM+tsZu3DP2IdUERE\nRBpnQ1UVp4waxe0ff1yr77Rdd+XZ0gzW3vl4ZEd2Fj2euo3sbXslKKVI6mnMEou3Q7++U6NdN+mJ\niIikiKVlZQx79VU+WlB7Z4qrfvMbbliygaXX/qNWX7cHryd3wF6JiCiSshpTIB8U8xQiIiISMzOW\nL2foyy/zQ2lpRHumGQ8eeiinLVrLot//FWosuej8l0tpd+yhiYwqkpIaXCC7+4R4BBEREZGmGz9n\nDse+9hqryssj2tu1asULRx3FgPkrWXjOTRB6tPRGHa85mw7nn5DIqCIpqzH7IA/YVL+7v9/4OCIi\nItJYT331FeeOG0dlIBDR3rtdO9447jh2mLuUBaf9ES+viOjPv+BEOl5xZgKTiqS2xiyxGB+lLfz/\naOK6BtnM+gNXAYVAT+AYdx+5ifEDgfdqNDvQ092XxC2oiIhIgrg7N0+axK2TJ9fqK+zendePPZZO\ns+az4KQr8XXrI/rbnTKUzn++BDNLVFyRlNeYArljjdfZwJ7ArcD1TU60eXnANOAx4OV6HuPAjsDP\nz9RUcSwiIs3Bhqoqzhk7luemT6/VN2z77Xl2yBCyZsxmwfARBFZFPlo676gD6XrvVSqORWpozBrk\n0ijNb5lZBXAvwZnduHH3N4E3AaxhV/RSd18dn1QiIiKJt3LDBoa9+ioT582r1Xd5YSF3DRxI1dez\nohbHbQ7am+7/uhHL1OZTIjU1Zh/kuiwGdorh+WLJgGlmtsDMxpnZ/skOJCIi0hQL1q5l4P/+V6s4\nzjDjwUMO4Z6DDqLqmx9YcPwfCKyMnB9qM6CQHk/ehrVulcjIImmjMTfp7V6zieBa4D8SXPqQahYC\n5wOfAa2Bc4HxZra3u6diXhERkU36fuVKBr3wArNXRxa+bbOz+b+jjmLItttS/vX30Yvj/gX0+O8d\nZOTmJDKySFppzBrkaQTX9NZc3jAZOLvJiWLM3b8Dvgtrmmxm2wEjgDOSk0pERKRxpi5ezOCXXmJJ\nWVlEe8+8PEYffzx7dOtG+ZczWXDCCAIrIldF5vQroMczd6o4FtmMxhTI29R4HSC4vndDDPIkyifA\nAZsbNGLECPLz8yPaioqKKCoqilcuERGROr303XecPno0ZVVVEe3bd+jAuOHD2aZDBzZ88iULi64m\nsHptxJicA/ak5zOaOZb0VFxcTHFxcURbaWm02+Jiw7zGU3QadRKzDu6+KgZ5Gvq+ATazzVsdx40D\nVrv78Dr6C4ApU6ZMoaCgIAZJRUREGi/gzi11bOO2Z7duvHn88XTLy6NswmcsOv1avCxyzipnv770\nLL6bjLw2iYosEnclJSUUFhYCFLp7SSzP3Zg1yNcAs939/0KvnweGm9lCYIi7fx7LgFHePw/Ynl+W\neGxrZn2BFe4+18z+Cmzh7meExl8G/Ah8DeQQXIN8EDAonjlFRERiYXV5Ob8dPZqRs2bV6juwd29e\nO+YY2rduzboxE1n0u5uhojJizM8zxyqOReqtMUssLgBOBTCzQQQLzcHAicDdwGExSxfdXgQf/OGh\nj3tC7U8RXAPdA+gdNr5VaMwWQBnwBXCInvgnIiKpbsby5Rz32mtMX7GiVt9Zu+3Gvw49lNZZWax5\ncRxLLrm91uOjcwftR/fHbiWjTetERRZpFhpTIPcA5oZ+fyTwvLuPM7PZwMexClYXd5/AJranc/ez\nary+m2DhLiIikjZe+u47zhwzhrWVkTPCmWb8/aCDuGTPPTEzSp96jWVX3QM1lky2PeZguj10I5bd\nmG/1Ii1bY66alQRnaOcSnDm+IdRuxPkx0yIiIs1dVSDAdRMncvenn9bq65STwwtHH83BW22Fu7Pi\nzsdY+bcna41rd9qRdP3blXoIiEgjNaZAfhl4zsxmAp2BMaH2PYHvYxVMRESkpVmybh0njxrFe3Pn\n1urr27UrLw8bxrYdOuCVVSy94m7WFI+uNS7/ghPp/OdL9PhokSZoTIE8AphNcBb5anffuI9MT+DB\nGOUSERFpUSYvWMDwkSOZv3Ztrb4zfvUrHjr0UHKzswmsLWPR2Tey/r1Pao3reOWZdLz6bBXHIk3U\n4ALZ3SuBv0Xpehb4XZMTiYiItCDuzoNTp3L5+PFUBgIRfdkZGdx/8MGc37cvZkbV4uUsPOVqKr74\nLvIkGRl0ueMP5J91bAKTizRfsVy53xO4Fbg9hucUERFptlZt2MA5Y8fy8syZtfp6tWvHi0cfzT49\newJQMfMnFp58FVVzFkaMszat6f7vm8k7on9CMou0BLq1VUREJAk+XbiQk0aN4scoTwM7qHdv/nfk\nkXTLywNg/aSpLDrrBgIrV0eMy+icT89n7iRnr18lJLNIS6ECWUREJIHcnftLSrhqwoRaSyoArtl7\nb/7Srx9ZGcEdTVc/PZKl19wLVZF7HGf12ZKe/7ubVtv1rnUOEWkaFcgiIiIJsqysjN+NG8dr39fe\n9KlzmzY8NXgwQ7fbDgCvqmL5jf+k9D8v1Rrbes9d6PHsnWR17Rj3zCItUb0LZDO7dzNDujYxi4iI\nSLP19k8/cfro0Sxct65W3wFbbknx0KH0bt8egOpVa1h87s2sH197L+Tcwf3o/vBNenS0SBw1ZAZ5\nz3qM0eObRUREwpRXVXH9Bx9wz2efRe3/49578+cDDiA79FCPiu9ms+j066icVXsv5A6Xnkqn68/D\nMup8oKyIxEC9C2R3PyieQURERJqbGcuXU/TGG0xbsqRWX5c2bfjvkCEM3mabn9vWjnyPJZf+FV+3\nPmKstW5F179fTbsTDo97ZhHRGmQREZGYc3ce+eILRrz3Huurqmr1H96nD08ecQQ9QrtUeFUVK257\nhFX/LK41NrNrJ3o8fbt2qhBJIBXIIiIiMbSpG/FaZWZy54ABXFpQQEboaXdVS1ey+Lxb2PBBSe3x\nv96BHk//lexe3eOeW0R+oQJZREQkRt6aPZvTx4xhUZQb8Xbt3JniI49k966/3NO+4ZMvWXTuLVQv\nqL0Eo93JR9DlrivIaNM6rplFpDYVyCIiIk1UXlXFdRMncu+UKVH7L95jD+4eOJA22dkAeCDAqvuf\nZcUdj0F15P7GZGfR5fbLaH/GMCw0yywiidWQbd7OBka6+7I45hEREUkr05cv55Q6bsTr2qYNjw8e\nzJGhvY0BqpasYMnFf4m6hVtmz670ePxWrTcWSbKGzCCfBjxkZiXAawSL5enxiSUiIpLaqgMB/j5l\nCjd88AHlNWeBgcF9+vBE2I14AGUTPmPJhbdSvXRFrfE5B+xJ90duIatbp7jmFpHNa8g2bwebWUdg\nKHA0cL2ZLQZGEiyYP3D32s/MFBERaWa+XbGCs958k48WLKjV1zozk7sGDuSSPff8+UY8r6hkxd1P\nsOq+Z8A98oCMDDpeeSYdLz8dC+2FLCLJ1aA1yO6+EngGeMbMWgEHEyyWnwXamNloggXzGHevfYeC\niIhIGqsOBLivpITrP/iADVG2b/tV6Ea8X4fdiFfx7Y8svvBWKr6cWWt8Zo8udH/4JtocUJ9ncYlI\nojT6Jj13rwDeDH1cZGZ7ESyWbwR2AW6NSUIREZEU8N2KFZw9diyT5s+v1WfAZYWF3N6vX8SNeKWP\nvMiKv/wbL6+odUzuIfvS7Z/XkdmlY7yji0gDxWwXC3f/DPgMuMnMsmN1XhERkWSqDgS4v6SE6+qY\nNd6+QweeGDyYfr16/dxWNX8xS35/O+sn1t7bmKxMOt9wPvkXnqRHRoukqLhs8+bulfE4r4iISCJ9\nv3IlZ735Jh/UMWt8aUEBt/fvT+7GWWN31r4wlmXX3kdg9dpax2Tv1IfuD91I6913jHd0EWkC7YMs\nIiJSQ8CdB0pKuHbixKiPit42P58nBg9mQO/eP7dVzlvM0ivuZv27H0c9Z/4FJ9Lp+vPIyNGDP0RS\nnQpkERGRMN+tWMG548bx/rx5Uft/v+ee/LV/f/JatQKCa41XP/Eqy299GF+3vtb4rC270fWB68jt\nXxjX3CISOzErkM2sAzDE3Z+L1TlFREQSpaK6mrs++YS/TJ4cdV/jbfLzefzwwzlwq61+OWbmTyz9\nw51s+OTLqOdsO3wQXe4YQWZ+u7jlFpHYi+UM8tbAfwEVyCIiklY+nD+fc8eN45vly6P2X7zHHtwx\nYABtN84aV1Sy6sFiVt7zVNQdKjJ7dKHrXZeTd0T/uOYWkfjQEgsREWmxSsvLufb99/nX559H7e/T\nvj2PDx7MQWGzxmXjP2XZtf+g8vs5UY9p99uj6HzzhZo1FkljKpBFRKTFcXdenjmT37/zDgvX1X6u\nVYYZfygo4E8HHPDzrHHVgiUsu/GfrBv5XtRzZvXZgq73Xq21xiLNgApkERFpUeauXs0l77zDyFmz\novYXdO/OI4MGUdijBxBaTvHv51n5t6fwsto34ZGRQf6FJ9Lp6nPIyM2JZ3QRSZB6F8hmdulmhmzZ\nxCz1zdEfuAooBHoCx7j7yM0ccyBwD/ArYA5wm7s/FeeoIiKSQqoDAf41bRrXTpzI2sra2/XnZmVx\na79+XFpQQFboAR5lEz4LLqeY+VPUc7Yu2IWud11B6747xTW7iCRWQ2aQR9RjTPQFWbGVB0wDHgNe\n3txgM+sDjAIeAk4BDgX+Y2YL3P2t+MUUEZFU8cnChVz09ttMWbw4av/gPn3416BB9MnPB6Bixo8s\n/9NDlL09Oer4jE75dL7hfNqdOlRPwxNphupdILv7NvEMUl/u/ibwJoCZWT0OuRD4wd2vDr3+1sz6\nESz4VSCLiDRjy9ev59qJE/nPF1/gUfq75eZy38EHc9JOO2FmVC1Zwco7H2P1M6MgEKh9gBntf3sU\nna4/j8xO+XHPLyLJ0RLWIO8LvF2jbSzw9yRkERGRBAi489iXX/LH999nxYYNUcec8+tfc9eAAXRq\n04ZA2QZW/ev/WPnAs1Ef9gHQeo+d6XLnCHIKdo1ndBFJAfUqkM3sZHf/Xz3H9ga2cvdJTUoWOz2A\nmv+nthhob2at3b08CZlERCROpixaxEVvv80nixZF7d+lUyceOvRQDtxqK7y6mtX/G8OK2x+leuHS\nqOMzu3ai07Xn0O6UoVhmZjyji0iKqO8M8oVmdjPwBPC6u08P7zSzfOAA4DRgEHBOTFOKiIhsxsoN\nG7jhgw/417RpUZdT5GVnc9N++/GHwkKyzVjzytusvOuJOvcztjat6XBxER0uLiKjbW58w4tISqlX\ngezuA83saOD3wF/NbB3BWdgNQEeCs7TLgCeB3dw9+l0QybEI6F6jrTuwenOzxyNGjCA/P3KNWVFR\nEUVFRbFNKCIijRZw5+mvv+bqCRNYuj768ojhO+7IvQceSK927Vj3xvssvutxKqb/EP2EZrQ7+Qg6\nXfs7snp2jWNyEamv4uJiiouLI9pKS0vj9n7mHu3n7E0cYNYF6Efw0dJtCBbGU4Gp7h7ljob4MbMA\nm9nmzczuAI5w975hbc8BHdx9SB3HFABTpkyZQkFBQaxji4hIjExbsoSL336bDxcsiNq/Y8eOPHDI\nIQzaemvKxn3Iijsfo+LLmXWer83Aveh8y8W03m37eEUWkRgpKSmhsLAQoNDdS2J57gbfpOfuy4BX\nYxmiIcwsD9ge2LiDxbZm1hdY4e5zzeyvwBbufkao/2HgYjO7E3gcOAQYDkQtjkVEJPWVlpdz06RJ\n/HPqVAJRJnraZGVxw777cnlhIYH3S5h//u2Ul0yPcqagVr/egU7XnUfuIftQvw2SRKQ5S8ddLPYC\n3gM89HFPqP0p4GyCyz16bxzs7rPNbCjBXSsuBeYB57h7zZ0tREQkxbk7z06fzpXjx7O4rCzqmGO2\n356/DxhAlw8+Z9kRF1L++bd1nq/VLtvS8ZpzyBvSX4WxiPyswQWyma2EqPc/OME1yd8DT7r7E03M\nFpW7TwDq3JXd3c+K0vY+wSfviYhImvpq6VIufucd3p83L2r/dh06cH//AfT7bCarhlzC4llz6zxX\n9g5b0+mqs8gbdpAe9CEitTRmBvnPwPXAGOCTUNvewGDgQWAb4F9mluXuj8YkpYiItFiry8v504cf\ncl9JCdVRllPkZGVx4267c963i1l74rUsXbCkznNlb9OLjledSdvjDtWWbSJSp8YUyP2AG9z94fBG\nMzsfOMzdjzezLwguZ1CBLCIijRJw58mvvuK6iRPrXE5xevvO3DRzGXbfnZSujT4GgoVxh8tOo91J\nh2NZ6bi6UEQSqTH/ShwOXBOl/R1+WQ88GrijsaFERKRlmzR/Ppe9+y5TFkfZNdSdoavKuXXmctpP\neB0Cgajr/gBa/Wp7Ol52GnlHH6gZYxGpt8YUyCuAo6j9qOajQn0AecCaJuQSEZEWaN6aNVw9YQLF\nM2bU6mtdWc2w7xZy+YxFdPl+/ibPk7NvXzpcdpp2pRCRRmlMgXwrwTXGB/HLGuTfENw27YLQ60HA\nhKbHExGRlmB9ZSV/++wz7vj4Y8qqqiL6tl6xllOmzebkr+eRV7aJ5ztlZJB3RH/yLzyRNvvsHufE\nItKcNWYf5EfN7BvgEuC4UPO3wEB3/zA05p66jhcREdnI3Xnxu++4cvx45qz55T8eMwMBDv5+EadO\nnU2/2Us3eQ5rm0v7U4eSf+5wsrfeIt6RRaQFaNSdCu4+CZgU4ywiItKCTF28mMvee4+JYdu2bbt8\nDcd/OYdjv5pLt3WbmC0GsrbqSf65x9PulKFktm8b77gi0oI0qkA2s0zgGGCXUNPXwEh3r45VMBER\naZ6WrFvHDZMm8Z8vvsCBtuWVDJ0+n+O/nEPBgpWbPb7NQXuTf9Yx5A7aTztSiEhcNOZBIdsT3KVi\nS4JLKwCuBeaa2VB3nxXDfCIi0kxUVFfzz6lT+dOHH7J2Qzn7zF3G8V/OYfC3C2lTten5lYyO7Wl3\nyhDyTx9G9ra9EpRYRFqqxvzofT8wC9jX3VcAmFln4JlQ39DYxRMRkXTn7oz64QeufO89Wk//kd9/\nM48hM+bTfe2ml1AAtN7rV+SfeQx5Rx9ERpvWCUgrItK4AnkgYcUxgLsvN7M/onXJIiIS5oulS7mz\n+CW6vvMpD02fT5+V6zZ7TGbXTrQ98TDaFw2h1U7bJCCliEikxhTI5UC7KO1tgYqmxRERkeZg4Zff\nMvrfz9F1/BT+vLh08wdkZZJ32P60KxpC7iH7YtlaWywiydOYf4FGAY+Y2Tn8sg/yPsDDwMhYBRMR\nkfTh7lR89T2lr7/HvJfGkT9nMQfW47hWu+1AuxMOo+3ww8jq1ineMUVE6qUxBfKlwFPAR0Bl2HlG\nApfFKJeIiKQ4DwQo/+xr1r7xPutGTaBqzkIA8jdzXFafLWl3/KG0Pe5QWu3YJ+45RUQaqjEPClkF\nDDOzHYCdQ83T3f37mCYTEZGUU716LevHf0rZ25Mpe2cy1UtWbP4gYH2HtnQefhgdTzic1nvuosc/\ni0hKa/QiL3efCcyMYRYREUkx7k7FjB8pe/sjyt6ezIZPvoTNbMm20ZK81szZZ1f2O3M42x52AJaZ\nGee0IiKxUa8C2czure8J3f3yxscREZFkC6wtY/2kqT8XxVXzFtf72Ln5uYzdsSeL+/Xl4jNP4qQt\n9OhnEUk/9Z1B3rOe47yxQUREJDkCG8op/+xr1k8soWziFMpLpkN1/R+M+l2XdozdsSfjdtyCDTv0\n5u4DD+S4HXbQMgqR/2/vzuPjKu97j39+oxlJlm1tyAvG2KCA7eDYxnZDsSGxwU1oQtqmudkMTZOb\n3qxkM21JmhctDX1BU8pyk5vSrIRwG3zLvdkoJKVhcwibAWMbg5EhBlvebSRb8ibN8rt/nCN7NJ6x\nNCNpFuv7fr3mpZnnPOecnySO5uuHZ54jFWtQAdndLxnpQkREpDg8kaBnbRtHHnuOI489x9HVG/Ce\nwa/S2VMV4elpLTzaOpFVrZPY0jyO8dXVXHvhhXxhwQJqdftnEalw+ismInKK8944PS9s4ujqFzjy\n2+c58sRa/ODhvI6xvX4Mj7ZOYtWbJvHktBaOVAdvHxEzPjV3LtcvXszEsWNHonwRkaJTQBYROcUk\n39jP0Wdf5OjTL3D0mQ30rN2IH83zPk6xKLtmnMmPJ43lwbMm8ErLeMiYMvGO6dO5ZelS5kyYMIzV\ni4iUngKyiEgFc3fir2zh6OoNHF0dBOL4q1vzP5AZNfNmUnvxfJ6YPoEVXbvZ3Hs0a9eZzc3csmQJ\n725t1TxjETklKSCLiFQIdye5Yw896zfRs66NnnVtHH3uJVKdXQUdLzbrbOouXsCYty1ooYe4AAAb\nKklEQVSgdvF8Vh/u5ksPP8zqXVuy9m+qreXvFy/mM/PmEdOSbSJyClNAFhEpQ+5OYtvuY0G4Z/0m\neta3kdq3v+BjxmZMp/aCOYx520LGXDSf6KTTAGjv6uLLv1nFypdfzrpflRmfOf98/n7xYk4bM6bg\n84uIVAoFZBGREnN3Elt2Hg/DL2yiZ/0mUh0HCj6mjamhZsF51L71LdReMIfa35tNVVN9vz6H43Fu\nWr2am555hiOJRNbjvPOss7h16VJmt7QUXIuISKVRQBYRKaHettfY/el/oHfD0G5MWnX6hCAIXzCH\n2gveQs3sc7BY9j/x7s7dGzfylcceY1t3d9Y+M5qauHXpUs0zFpFRSQFZRKSE3rjhu3mH40j9OKrn\nzqBm3ozgg3VvnUNs6qRB7fv0zp186eGHeWrnzqzbG2pquG7RIq6aP59qzTMWkVFKAVlEpISOrn7h\npNsjjeOpmTeTmrkzqZkbBOLoWVPyHtXd3t3NVx57jH976aXs5+lbz/iii2ipq8vr2CIipxoFZBGR\nEkkdPEzqjf7zjGsvXkDtwvPCUDyD6LTThzTF4Ug8zs3PPsvXn36awznmGS+bNo3bLrlE6xmLiIQq\nMiCb2VXAXwGTgXXA5939mRx9Pwr8EHCg713mqLtriERESiq+9cRpDqfffRORMTVDPra78+9tbVyz\nahXtOeYZn9PYyC1Ll/JHb3qT5hmLiKSpuIBsZh8CbgE+CawGVgAPmNkMd9+XY7cDwAyOB2Qf8UJF\nRAaQyAjIVRObhyUcP7trF1965BEe37496/b66mr+btEiPjd/PjXRinsbEBEZcZX4l3EF8B13vwvA\nzD4NXA58HLgpxz7u7nuLVJ+IyKDEt+7q9zo6fcqQjrf38GG++thj/OCFF7KOAhjwiblz+YeLLmLi\n2LFDOpeIyKmsogKymcWAhcCNfW3u7mb2ILDoJLuOM7PXgQiwBviqu2f/pIqISJEktu7o9zp25uSC\njpNMpfj2unVc+9vfsr+nJ2ufpWeeyf+85BLmTZxY0DlEREaTigrIQAtQBezOaN8NzMyxTxvB6PJ6\noAH4a+AJMzvP3Xfk2EdEZMRlzkGOTjs972M8sX07Vz30EGv37Mm6vbWhgZuXLuW955yjecYiIoNU\naQE5b+7+FPBU32szexLYCHwKuK5UdYmIJDKmWMTyCMi7Dh3iy6tWcVeOZdvGxmJce+GFrFi4UPOM\nRUTyVGl/NfcBSSBzRfxJwK4Tu5/I3RNm9jxwzkB9V6xYQUNDQ7+25cuXs3z58sFVKyKSg7uf8CG9\n6PSBA3I8meRf1q7luscfp6u3N2uf5bNm8c9LlnDG+PHDUquISKmtXLmSlStX9ms7cOBAjt5DV1EB\n2d3jZvYcsAy4F8CC/2e4DPjmYI5hZhFgDnD/QH1vu+02FixYUHjBIiI5pPZ3k+o+1K8tdubJA/Kq\n9nY+99BDbNiXfcGe2aedxreWLWPptGnDVqeISDnINkC5Zs0aFi5cOCLnq6iAHLoVuDMMyn3LvNUB\ndwKY2V3ANnf/avj6bwmmWLwKNALXANOA7xe9chGRUOboMZEI0Ry3i97e3c1fr1rFypdfzrq9vrqa\nr110EVedfz4x3R5aRGTIKi4gu/s9ZtYCXE8wtWItcFnaMm5TgfTbRTUB3yW4qUgn8BywyN2zv9OI\niBTBCR/QmzIBi/X/k7zn0CG+u349/7R6NQfj8azH+ejs2Xz97W9nspZtExEZNhUXkAHc/Xbg9hzb\nLs14fTVwdTHqEhEZrBPmH4dLvKXceWjLFr63fj0/f/VV4qlU1v3PnziRby1bxkVnnDHitYqIjDYV\nGZBFRCpdfEv/gByfMoF/fPppvrd+Pa+d5IMnjTU13HDxxXxq3jyqIpGRLlNEZFRSQBYRKYHMEeTb\ndm/jm489lrO/AX8xZw43vu1tTKirG+HqRERGNwVkEZESiLf3D8hbG8Zk7VcbjfLBGTP4woIFLJxc\n2J32REQkPwrIIiJF5u4k2vsv3b69of+o8JyWFj45dy5XnnceTbW1xSxPRGTUU0AWESmy5J4O/EhP\nv7ZtDcEqFB857zyumj+fCyZP1q2hRURKRAFZRKTIMkePeyPG7nG1VJnx/csuo1prGYuIlJQ+Ai0i\nUmSZayDvaKgjFTHObmhQOBYRKQMKyCIiRZbYsqPf6231wfzjmc3NpShHREQyKCCLiBRZ5gjytsYw\nIDc1laIcERHJoIAsIlJkmXOQtzVoBFlEpJwoIIuIFFnmXfTaw4A8SwFZRKQsKCCLiBSRJ5Mktu/u\n17ZdI8giImVFAVlEpIgSO/dBPNGvrb2xjoaaGibqFtIiImVBAVlEpIgSGR/QOxKt4o26GmY2NenG\nICIiZUIBWUSkiDJXsNjeMAbMNL1CRKSMKCCLiBRR5ghye3iLaQVkEZHyoYAsIlJEmQFZayCLiJQf\nBWQRkSI64SYhWuJNRKTsKCCLiBTRCSPIDXUYcI5GkEVEyoYCsohIkXhvnMSOvf3atjXUcVZDA7XR\naImqEhGRTArIIiJFkti+B9z7tbU31mn+sYhImVFAFhEpksz5x101Ubpqq7WChYhImVFAFhEpksTW\nHf1eb9MtpkVEypICsohIkcS3ZF/BQgFZRKS8KCCLiBRJon1Xv9fb+m4SojnIIiJlRQFZRKRITlwD\neQzjYjGmjBtXoopERCQbBWQRkSJJZE6xaBzLzOZmzKxEFYmISDYKyCIiRZA60kNyb0e/tvaGOs0/\nFhEpQwrIIiJFkGjfeULb9gatgSwiUo4UkEVEiiBzBYuOMdUcro5qBFlEpAxVZEA2s6vM7DUzO2Jm\nT5nZWwfo/wEz2xj2X2dm7ypWrSIiAImMD+i1N2qJNxGRclVxAdnMPgTcAlwHzAfWAQ+YWUuO/ouB\nu4HvAecDvwB+bmbnFadiERGIt2dfA/ncxsZSlCMiIidRcQEZWAF8x93vcveXgU8Dh4GP5+j/BeBX\n7n6ru7e5+98Ba4DPFadcEZEsK1g01DFt/HjGVleXqCIREcmlogKymcWAhcBDfW3u7sCDwKIcuy0K\nt6d74CT9RUSG3YlrIGsFCxGRclVRARloAaqA3Rntu4HJOfaZnGd/EZFhlzkHeVvDWAVkEZEyVWkB\nWUSk4iS7DpLa392vrb1RS7yJiJSraKkLyNM+IAlMymifBOzKsc+uPPsfs2LFChoaGvq1LV++nOXL\nlw+qWBERgMTWE//c7KgfoxFkEZFBWrlyJStXruzXduDAgRE7X0UFZHePm9lzwDLgXgAL7tG6DPhm\njt2ezLL9HWH7Sd12220sWLBgSDWLiCS27uj3ete4WnqjVQrIIiKDlG2Acs2aNSxcuHBEzldRATl0\nK3BnGJRXE6xqUQfcCWBmdwHb3P2rYf9vAI+a2dXA/cBygg/6faLIdYvIKBXPGEHe1lDHmGiUqePH\nl6giERE5mYoLyO5+T7jm8fUEUyXWApe5+96wy1Qgkdb/STO7ArghfLwC/Im7v1TcykVktDrhA3qN\ndcxoaiJiVqKKRETkZCouIAO4++3A7Tm2XZql7SfAT0a6LhGRbE5Y4q2+jlmaXiEiUra0ioWIyAjL\nNoKs+cciIuVLAVlEZAS5u24SIiJSYRSQRURGUKrjAH7oSL+29saxWgNZRKSMVeQcZBEZmq7/8ys6\nb/4hVlUFVVVYtAoikeBrVeRYO9EqrCoS9KmKBK8jae3RKiwSfk0/VvjaYtHj26JVWKwKqqLYsed9\n/cO2vufVMSwWDfavjmHRKFYdxWIxrDp6Yp9YNKijDGWOHifM2DW+lhkaQRYRKVsKyCKjUGp/N4kt\nOwfuWEmiVUFojkahL0yHAdqqY0GIjuUO2cfCeCyGxcJjxWLBsapjWE0NkdpqrKY6eN33PP3Rb3sN\nVlNN4vX+ayDvrB/DpPp6xldXl+gHJSIiA1FAFhmNkslSVzD8Ekk8kcRLXccAtjXoFtMiIuWuPP+f\npIiMKE+mSl3CqLWtQUu8iYiUO40gi4xC496zhOoZ0/FEEpIpPJmEZDLjdSpoC59n7ZtKa08kj/dP\nJPFE4viobjIJ8cTxPonk8W2JxPG2ePDa4wk8Hofe4KvHk6fMqPemCfXMU0AWESlrCsgio1CsdSqx\n1qmlLiMvnkzi8UQQtOMJvDd+7CuJBH4sTId9+ranh+3eeBDAe9PaEsf70hsnFe6b6o2T7I1DPE4k\nnsB74nhPL360J+jf04sf7Q2eHw3aSZ18ZH5Ty3h+PnsqH1RAFhEpawrIIlIRrCpcDaO2Jq/93J32\n7m7W7d3Luj17WLd3Lxv2ddLlvSQiKRKpFPHa4GsilSKeAoiFj0BdNMrU8eODx7hxx5+PH88Z48Yx\nddw4JtTVBSPhfUG6pxfvibNv/37e8W93k4gYr7aMJxmJaA6yiEiZU0AWkVPG0USCl95441gQ7nt0\nHj06pOMeTiTY1NnJps7OnH3qolFmNDczs6mJGU1NzGxuZmZzM7vH1/Di5MZj/WqqqphWXz+kekRE\nZGQpIItIxTnU23sssLZ1dPByRwfr9+7l5Y4Okl6adSwOJxKs3bOHtXv2nLTfuU1NVJXpms0iIhJQ\nQBaRspRMpdja1UVbGIL7wnBbZyfburtLXV7BNL1CRKT8KSCLSMn0JpNs7eritQMHjj1e6eykrbOT\nVzo76RnGlSsaamqYN2FC8Jg4kanjxhGrqiJqRjQSIRaJ9Pva9zzhzs6DB9l28CDburuPP8LXOw8d\nIpXHqPXslpZh+55ERGRkKCCLyIhJheEyPQD3PTYfOMD2gwfzCpeD9abGxn5heN6ECUyvr8fMCj5e\nLolUip0HD/LK/v1sCke42zo6aOvo4PWurn7fX311NX8+e3ZBNYiISPEoIIvIkKXcWbN7N6va2/nd\n/v1sDkPwlq6uYR0FTmfAtPr64MNwTU28+bTTmDdhAnMmTCjqbZyjkQhn1tdzZn09l06b1m9bTyLB\nq/v309bRQXdvL5dMm6YP6ImIVAAFZBEpSHdvL79+/XXu37yZ+zdvZvfhwyNynoaaGmamrQoxs6mJ\nGc3NnNvYyJhYbOADlFBNNMrslhZNqxARqTAKyCIyaK92dnL/5s3ct3kzq9rbiQ9wY4zBaqyp4eyG\nBs5uaKC1oaFfGJ5QV1fw1AgREZFCKCCLSE7xZJLfbt/Ofb/7Hfe/9hptHR0FHaemqupYAM72aKqt\nHebKRURECqeALCI5PbVzJ5fec8+g+89oamLxlCm0Njb2C8CTx44lolFgERGpEArIIpLToilTaKqt\nzXknulgkwpIzz+Ty1lYub23lXK3xKyIipwAFZBHJKRqJ8K6zz+bujRuPtU2qq+Pdra28p7WVP5g+\nnfqamhJWKCIiMvwUkEXkpN7T2kpbRwfvCUeJF06erOkSIiJySlNAFpGT+vCsWSx/85tLXYaIiEjR\nREpdgIiUNy2xJiIio40CsoiIiIhIGgVkEREREZE0CsgiIiIiImkUkEVERERE0lRUQDazJjP7sZkd\nMLNOM/u+mY0dYJ9HzSyV9kia2e3FqllktFm5cmWpSxCpOLpuRMpLRQVk4G7gzcAy4HLg7cB3BtjH\nge8Ck4DJwOnANSNYo8iopjd6kfzpuhEpLxWzDrKZzQIuAxa6+/Nh2+eB+83sr9x910l2P+zue4tR\np4iIiIhUtkoaQV4EdPaF49CDBCPEvz/Avlea2V4ze8HMbjSzMSNWZYUrx1GMYtQ03OcYjuMVeox8\n9xts/3L8b6OclNvPp1j1lNu1U27XTSHHHm3K7eeja2dk96uUa6eSAvJkYE96g7sngY5wWy4/Bv4M\nWArcCHwE+N8jU2LlK7c/VKCAPNL7KSAPj3L7+ehNfmT3q5Q3+UpQbj8fXTsju1+lXDsln2JhZv8I\nfPkkXZxg3nFB3P37aS9fNLNdwINmdra7v5Zjt1qAjRs3FnrainXgwAHWrFlT6jL6KUZNw32O4The\nocfId7/B9h/ufqeacvu+i1VPuV075XbdDLZvuf33U0zl9r3r2hnZ/Ybz2knLabWDLmCQzN2H+5j5\nFWB2GnDaAN02E4z83uzux/qaWRVwFHi/u/9ikOerAw4Cl7n7r3P0uYJg5FlEREREytuV7n73cB6w\n5CPI7v4G8MZA/czsSaDRzOanzUNeBhjwdB6nnE8wKr3zJH0eAK4EXicI4CIiIiJSXmqBswhy27Aq\n+QhyPszsl8BE4DNANXAHsNrdPxJunwI8BHzE3Z81s1bgCuCXBCF8HnArsNXdLy3BtyAiIiIiZa7k\nI8h5ugL4FsHqFSng/wFfTNseA2YAdeHrXuAPwj5jgXbg/wI3FKleEREREakwFTWCLCIiIiIy0ipp\nmTcRERERkRGngCwiIiIikkYBuQBmNtXMHjGzF81srZm9v9Q1iVQKM/upmXWY2T2lrkWkEpjZe8zs\nZTNrM7O/KHU9IpViKO83moNcADObDEx09/VmNgl4DjjX3Y+UuDSRsmdmbwfGAx919w+Wuh6Rchau\n9/8SsAToJni/WeTunSUtTKQCDOX9RiPIBXD3Xe6+Pny+G9gHNJe2KpHK4O6/IbhZj4gM7AJgQ/i+\nc4hg2dJ3lrgmkYowlPcbBeQhMrOFQMTdt5e6FhEROeVMAdLfX3YAZ5SoFpFRY1QEZDN7m5nda2bb\nzSxlZn+cpc9VZvaamR0xs6fM7K2DOG4z8CPgEyNRt0ipjdS1IzIa6PoRKUw5XDujIiAT3CRkLfBZ\ngttM92NmHwJuAa4juBX1OuABM2tJ6/NZM3vezNaYWY2ZVQM/A25093xudS1SSYb92ilO2SJlYcjX\nD8GI8dS012eEbSKnsuG4doZk1H1Iz8xSwHvd/d60tqeAp939i+FrI7jr3jfd/aYcx1kJbHT364tQ\ntkjJDde1E/ZbClzl7h8Y2apFykOh10/ah/SWEnxI7xlgsT6kJ6PFUN97Cn2/GS0jyDmZWQxYCDzU\n1+bBvxoeBBbl2Oci4APAe9NGxmYXo16RclHItRPu92vg34F3mdlWM/v9ka5VpNwM9vpx9yTwl8Cj\nwBrgZoVjGc3yee8ZyvtNdHjKrWgtQBWwO6N9NzAz2w7u/jj62Ynkfe0AuPs7RrIokQox6OvH3e8D\n7itSXSLlLp9rp+D3m1E/giwiIiIikk4BOVjDOAlMymifBOwqfjkiFUPXjkjhdP2IFKYo186oD8ju\nHie4M9GyvrZwsvcy4IlS1SVS7nTtiBRO149IYYp17YyKebRmNhY4B7CwqdXM5gEd7t4O3ArcaWbP\nAauBFUAdcGcJyhUpG7p2RAqn60ekMOVw7YyKZd7MbAnwCCeupfcjd/942OezwDUEQ/Rrgc+7+7NF\nLVSkzOjaESmcrh+RwpTDtTMqArKIiIiIyGCN+jnIIiIiIiLpFJBFRERERNIoIIuIiIiIpFFAFhER\nERFJo4AsIiIiIpJGAVlEREREJI0CsoiIiIhIGgVkEREREZE0CsgiIiIiImkUkEVERERE0iggi8io\nYGaPmNmtefSfbmYpM5s7zMddEh63frD7lJu07yFpZj8tdT0nE9aZMrOOUtciIpVDAVlERos/Bf42\nj/5bgcnABjhpsM33uACeZ/9y5MAM4GN9DWZ2Z/gzuj2zs5n9S7jtjiLWCMHv8EtFPqeIVDgFZBEZ\nFdx9v7sfyqO/u/sed0+FTUYQCm0oxz3F7HX3rrTXTvAPiw+bWU1fY/h8ObClyPXh7nuAA8U+r4hU\nNgVkERkVMqdCmNlrZvY3ZvYDM+sysy1m9om07cemWJjZdODhcFNnOLXgjhzH/TMzeyY85k4z+7GZ\nTciz1pSZfdLM/sPMDpnZS2Z2oZm9KTzfQTN73MzOTtun1cx+bma7zKzbzFab2bKM437WzDaZ2ZGw\n3z1p295vZuvN7LCZ7TOz/zKzMfnUHXoeaAfel9b2PoJw/HxGPTnPmW3qipn9LH0EeqDfoYhIoRSQ\nRWQ0uxp4BjgfuB34VzM7N21731SIrcB/C5+fC5wOfDHHMaPAtcBc4E+A6cAPC6jtWuBOYB6wEbgb\n+DZwA7CQYCT7W2n9xwH3A5eE38+vgHvNbCqAmS0EvhEedwZwGfCbcNvk8PjfB2YBS4CfkjFaPkgO\n3AF8PK3t4wQ/g2PHG8ZzDvQ7FBHJW7TUBYiIlND97v7t8Pk/mdkKgoD5SthmEEy3SPuQV+a0gn7c\n/c60l6+b2ZeAp82szt0P51HbHe7+EwAzuwl4Eviauz8Ytn2DIIj2nXc9sD5t/+vM7H3AHxMEx2nA\nwfB7PkQwyrsu7Hs6UAX8zN3bw7YX86g104+Br5vZmQQDMYuBDxH8bPsM1zkH+h2KiORNI8giMpq9\nkPF6FzBxKAc0s4Vmdm/4v/u7gEfDTdOGUNvu8OuGjLZaMxsXnnesmd0cTsfoNLNugpHZvvP+mmCa\nw2tmdpeZXZE2hWId8BCwwczuMbP/YWaNedZ7jLvvA+4D/jvBh/jud/fMVSSG65zD/jsUEVFAFpHR\nLJ7x2hnC30UzqwP+E9gPXAH8HsEqFwDVQ6jNT9LWV+8tBFM6vgJcTDA1Y0Pfed39ILAA+DCwA/ga\nsM7M6t095e7vBP6QYBT388DL4dzrQv2QIBz/OfCDzI05ztmWds4UJ063iGU5z7D+DkVEQH9EREQG\nqzf8WnWSPrOAZuBv3P1xd98ETBqm8w+0NNxi4E53v9fdXwT2AGf1O0AQSh92968QBOizgEvTtj/p\n7l8D5hMEzz+lcP9JEM6jwH/l6pRxzt60c+4lmIYBgJlFgLcMoR4RkUHTHGQRkcHZQhBS/8jMfgkc\nybK821aCkPcFM/s2MIfgQ3GZCvnwW7Z90tteAd5nZveFr6+n/4fiLgdaCT6Y1wlcHm5vM7MLgGUE\nQXYPcCHQArxUQJ1AEMbNbFb4/IRwP4hzPgzcYmbvBn5H8GG8gqd9iIjkQyPIIjJaZIa0bCOyOfu4\n+w7gOuDrBPNc/9cJOwdzbz8GvJ9g2sA1wF8O4jyD2T5Q29UEwfdx4BcEI7hr0rbvJ1hu7SGCEPpJ\n4MPuvhHoAt5OsApGG0G4vtrdc478Doa7HwyndmQz0DnvAH4UPh4lCMkPZxxjsD8nEZG8WJZ/2IuI\niORkZksIwmqzu5f9TTjM7GPAre7eXOpaRKQyaIqFiIgUqt3M/sPdryx1IbmEq3lUAUdKXYuIVA6N\nIIuISF7CW0efEb48GN7OuSyZWWv4NOnuRb/VtYhUJgVkEREREZE0+pCeiIiIiEgaBWQRERERkTQK\nyCIiIiIiaRSQRURERETSKCCLiIiIiKRRQBYRERERSaOALCIiIiKSRgFZRERERCSNArKIiIiISJr/\nD0GzKAMYNVU/AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21b19dc3d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(2, 1, figsize=(8, 8))\n",
"\n",
"masses = np.arange(0.08, 5.0, 0.02)\n",
"\n",
"ax[0].set_xlabel(\"initial mass [Msun]\")\n",
"ax[0].set_ylabel(\"log(T / K)\")\n",
"\n",
"ax[0].semilogx(model_props[:,0], model_props[:,1], '-', c='#008b8b', lw=3)\n",
"ax[0].semilogx(masses, tr, '-', c='#dc143c', lw=3)\n",
"\n",
"ax[1].set_xlabel(\"initial mass [Msun]\")\n",
"ax[1].set_ylabel(\"log(L / Lsun)\")\n",
"\n",
"ax[1].semilogx(model_props[:,0], model_props[:,2], '-', c='#008b8b', lw=3)\n",
"ax[1].semilogx(masses, lr, '-', c='#dc143c', lw=3)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There are clear discrepancies, particularly in the low-mass regime. However, we note there are significant differences in relaxed effective temperatures starting around 1.5 solar masses. Luminosities tend to trace the relaxed models quite well until approximately 0.4 Msun. Since these are logarithmic values, noticeable differences are quite sizeable when it comes to model adjustments during runtime. It's quite likely that corrections will exceed tolerances in the allowed parameter adjustments during a model's evolution.\n",
"\n",
"### Effective temperature\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"tp1 = np.array([line for line in model_props if line[0] < 0.23])\n",
"tp2 = np.array([line for line in model_props if 0.23 <= line[0] < 1.5])\n",
"\n",
"tpoly1 = np.polyfit(tp1[:,0], tp1[:,1], 2)\n",
"tpoly2 = np.polyfit(tp2[:,0], tp2[:,1], 3)"
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f21b1190d90>]"
]
},
"execution_count": 70,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArEAAAFqCAYAAAANywJcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3XecVNX9//HXWdpKBxVUQBGwYDAqRMROExWUosSIvWFJ\nM+SbxF+iiVF/P803zQSjsSURgpJgAyyIDXtJBAQLqPSOILIgZVl2z++PWWWHJrPs7p3ZfT0fj3no\nnHPunc/w2Lv3zeXcc0OMEUmSJCmX5CVdgCRJkpQpQ6wkSZJyjiFWkiRJOccQK0mSpJxjiJUkSVLO\nMcRKkiQp5xhiJUmSlHMMsZIkSco5hlhJkiTlHEOsJEmSck5GITaEcHUIYVoIoaD09UYI4bSv2aZJ\nCOHOEMKSEMLGEMLMstuEEG4MIZRs9fqwvF9IkiRJ1V/tDMcvBK4DPgECcAkwLoRwZIxxxtaDQwh1\ngOeBZcBZwBLgAGD1VkPfB3qV7hNgc4Z1SZIkqQbJKMTGGJ/aqumGEMI1QDdgmxALXA40BbrFGItL\n2xZsZ9zmGOOKTGqRJElSzVXuObEhhLwQwrlAfeDNHQw7s7TvrhDCshDCeyGEn4cQtv7cg0IIi0MI\ns0MIo0IIbcpblyRJkqq/TKcTEELoRCqY5gNrgUExxpk7GN4O6AmMAk4HOgB/Lf3cW0rHvEVqWsJH\nwL7Ar4FXQgidYozrMq1PkiRJ1V+IMWa2QQi1gf2BJsBgYChw0vaCbAjhI6AecGAs/aAQwjDgJzHG\nVjvYfxNgPjAsxviPHYzZEzgVmAdszOgLSJIkqSrkA22BiTHGzyp65xlfiY0xbgbmlL6dGkLoClwL\nXLOd4UuBTTE9Kc8A9gkh1C7d19b7LwghfEzqqu2OnAo8mGntkiRJqnLnAw9V9E4zDrHbkUfqauv2\nvA4M2artEGDp9gIsQAihIdAeGLmTz5wHMGrUKDp27JhRsdXBsGHDuP3225Mu4ytVVU9Ff87u7q+8\n22e6XSbjd2Vstv38VJVs/N5VUVO2HTe7s4/KOnYqelx1k23f23NO5W5XkeecGTNmcMEFF0Bpbqto\nGYXYEMKtwARSKww0IpWsTwb6lPaPBBbFGH9Ruslfge+FEIYDdwAHAz8H/lRmn78DniA1haAVcBOp\nJbZG76SUjQAdO3akc+fOmXyFaqFJkyZZ9b2rqp6K/pzd3V95t890u0zG78rYbPv5qSrZ+L2roqZs\nO252Zx+VdexU9LiKsn79ekaNGsXQoUMJIXz9BpUk244dzzmVu11Fn3NKVcrUz0yvxLYARpC6AasA\nmA70iTG+WNrfmjJrvMYYF4UQTgVuB6YBi0v//7dl9tma1CXmPYEVwGukluSq8LkT1cWQIVtf3E5W\nVdVT0Z+zu/sr7/aZbpfJ+Gz72cgm2fhnUxU1Zdtxszv7qKxjJxt/NqZMmcIll1zCe++9x3/nzuWY\nIUOYW1DAvDVrCMCofv2qrJZs+/PxnFO52+XSOSfjG7uyQQihMzB58uTJWfW3QykX9O/fn/Hjxydd\nhpRzKvPYWV9UxLuffspbCxcy4s9/ZvqYMVBSsmXABRfAEUcAUL92bb649tpEr85Ku2LKlCl06dIF\noEuMcUpF778i5sRKkqQMFBQW8sqiRUxasICXFi5k2vLllEybBs8+Cyu28+yfceOgY0eoW5f1mzez\ncsMG9q5fv+oLl7KIIVaqYZL+5x8pV+3usbN47Voe++QTHv34Y15dvJiSL/8ldPNmGD4cli7d/ob7\n7JO6Elu37ldNcwsKDLGq8QyxUg1jiJXKZ1ePnTmrV/PgjBnM+Owz1mzaxNpNm1i1cSPvr1y5/Q1q\n14Z99902xOblQa9eND79dNrtuSdtGzembZMmtG3cmFYNG+7mt5FynyFWkqTdVLh5M2NnzeK+6dN5\nYcGCzHfQuze8++5X82DbdOzI9b//PQNPPpkW9es7/1XaDkOsJEnltHjtWv46bRr3TpvGig0b0jvX\nrYPZs+GTT6BFCzjxxLTuurVqcey++9Jj//3p3qYNf1u+nGlTp3LTTTcxYMAAg6v0NQyxkiRl6M0l\nSxg+ZQqPfPwxm79cRWDdOpgzZ8tr6VL4ct5r69Zw4ok0qVePM9u35+yDDqJP27bUr1Pnq312vuMO\nGjRoQF5eXgLfSMo9hlhJknZBcUkJY2fN4vf//S9vbT1/9aWX4KmndrhtWLyYx089ldMPO4y6tWpt\nd0yjRo0qsFqp+jPESpK0E5uKixn5wQf873/+w6zVq7c/qGXLne4jxkjxJ59Q9/DDK6FCqWYyxEqS\ntB0bN29m+Guv8ZsRI/i8SZPUlIDt2KN2bc4980xGjhhBcXFxWl/9+vU58cQT6d27tw/nkSqYIVaS\npDI+XbWKHw8fziMPP0zhzJmpFQOOPXabENumUSN+cNRRXH744TTfYw8+6NKF9957j+OOO46TTz6Z\nk08+mWOOOYZ69eol9E2k6s0QK0mq8UpKSpj47LP86k9/4p0XX4SiovQBM2akbtIKgaNatOCnRx/N\n4IMPpk6Z+a2PPPIILVu2pG6ZhxJIqjyGWElSjVYSIz0HD+blxx/f8aDVqzmqpITbzjmHPm3bbnf5\nqzZt2lRilZK2ZoiVJNVYLy5YwE9ffpkpzZrtcExenToc2707d552GkcceGAVVidpZwyxkqQa56NV\nq/jJSy/x5Jw5qYZDDoHmzWHVqtT7WrXY88gj+f6ll/KTiy+moY95lbKOIVaSVO1t3LiR/Px8Vm/c\nyM1vvskdU6dueUgBQF4eHHccvPMOB5xyCrf/+McMOvLI5AqW9LUMsZKkamvhwoXccMMNTJs2je+P\nGMEvXntt28fDljqkf39u+8MfGHjQQT7yVcoBhlhJUrWzbt06brvtNv7whz+wceNGAIb+7newnaur\nLerX5+bjj+fyww+nto98lXKGIVaSVG3EGBkzZgz/8z//w+LFi9M7n30WDj8cSpfFqlurFj/u0oWf\nH3MMjV3LVco5hlhJUrUwe/Zsvvvd7/Lss89uf8CaNbB8Oey3HwM6dOCP3bvTrmnTqi1SUoUxxEqS\nqoUbb7xx+wE2Lw+6dYNTTuHgNm0Y3rMnp7pUlpTzDLGSpJwXY6TrFVfw0NixxHXrtnQcdBAMGEB+\nq1b8sls3fnL00dQt85QtSbnLECtJymmL1q7lymefZcLcuTBgADz0EDRpkvr/Tp3oc+CB3NW7N+2d\nOiBVK4ZYSVJOijEy4oMP+NGkSRQUFqYajzwSCgvhyCPZq1kz/tyzJ0MOPdQls6RqyBArScoZMUZC\nCCxft44rn32W8bNnpw8IAbp14/yOHflTjx7sVb9+MoVKqnSGWElS1tu8eTPXX389GzZsoPcPf8jl\nEyeycjsPLdi3QQPu6dOHM9u3T6BKSVXJECtJympLly7l3HPP5ZVXXgHgjjVroFOnbcZddNhh/Kln\nT5rl51d1iZISYIiVJGWt119/ncGDB7Ns2bItjQ8/DK1bQ+mNWi3q1+e+Pn3o36FDQlVKSoLP15Mk\nZaV77rmHHj16pAdYSN24tXAhAAM7dOD9Sy4xwEo1kFdiJUlZpaioiB/84Afcc88923Y2bQoXXkiD\n9u35c8+eXNapkysPSDWUIVaSlFWmTZvG/X/727YdBx8M553Ht9q146EzzuCgZs2qvjhJWcPpBJKk\nrFESIy8UF1MyaFB6R48ecPnl/Kx7d14/7zwDrCSvxEqSssOqDRu4eMIEnpwzB7p2hWXL4M034Tvf\nocVxxzGqb19Oads26TIlZQlDrCQpcVOWL+fsceOYt2bNlsYzzoBjjqF31678s29f9mnQILkCJWUd\nQ6wkKVF/f+89vvv88xQWF6e1h7w8fj1oENd360atPGe/SUpniJUkVbmSkhJWrFrFr6dO5e5p07bp\n33uPPRh9xhn0OuCABKqTlAv8q60kqUoVFRXxnQsuoF3nztz91lvb9B+3335MvegiA6yknTLESpKq\nzMaNG+l1xhk8Mno06xcuhAcegKKir/p/2Lkzk77zHVo1apRckZJygiFWklQl1q5dS+eTTuLVZ5/d\n0jhnDvz73+xRuzYP9uvHn3v2pG6tWskVKSlnOCdWklTpVn72Gd884QSWzpyZ3lGnDi1OPJFnzzuP\nI1q0SKY4STnJECtJqlRzFy3iyBNPZM28eekd+fl0/vnPefanP2XPPfZIpDZJucsQK0mqNAvWrOGo\ngQO3DbANGnDu73/PyKFDqeP0AUnl4JxYSVKlmLJ8Occ8+CAFp58Oe+65paNJE2568EFGX321AVZS\nuRliJUkV7uk5czjpX/9i2bp10KQJXHUVNG1KXvPmPPTkk/xqwICkS5SU45xOIEmqUPdOm8Z3n3+e\n4hi3NDZrxoHXXceIfv048fDDkytOUrVhiJUkVYgYI796/XX+73YeYNCjTRseHTCAZvn5CVQmqToy\nxEqSdltRcTFXP/ccf3///W36LjjsMP526qmu/yqpQhliJUm7Zd2mTZz5wANMmjoV2rdP67uhWzdu\nPv54QggJVSepujLESpLKbdWGDfT5+9+Z/Otfw+rVcMklcMgh5IXAX3v35sojjki6REnVlKsTSJLK\nZckXX3D8ffcx+eabYeVK2LwZHniAup98wuMDBhhgJVUqQ6wkKWOzV6/m2PvvZ+ZvfgOffrqlY/Nm\nDnj9dfodeGByxUmqEZxOIEnKyAcrV9Jz5Eg+vf12WLo0re+Adu14+bnnqOVNXJIqWUZXYkMIV4cQ\npoUQCkpfb4QQTvuabZqEEO4MISwJIWwMIczcepsQwvdCCHNDCBtCCG+FEI4uz5eRJFWuycuWcdLI\nkXx6xx2waFFaX5sDDuC1l19m3333Tag6STVJptMJFgLXAZ2BLsCLwLgQQsftDQ4h1AGeB/YHzgIO\nBoYCi8uM+Q7wB+BG4ChgGjAxhLBXhrVJkirR64sX03PMGFa9/DLMm5fWt1+rVrzy0ku0bt06meIk\n1TgZTSeIMT61VdMNIYRrgG7AjO1scjnQFOgWYywubVuw1ZhhwD0xxpGQutoL9AMuA36bSX2SpMrx\n4oIFnPnYY6zfvBlOOAE+/xxefRWAlvvsw0uTJtG2bdtki5RUo5T7xq4QQl4I4VygPvDmDoadWdp3\nVwhhWQjhvRDCz0MIeaX7qEPqiu4LX24QY4ykrt4eW97aJEkV5/n58+n3ZYAFCAHOPJMDBw+mefPm\nvPD88xx00EHJFimpxsn4xq4QQidSwTQfWAsMijHO3MHwdkBPYBRwOtAB+Gvp594C7AXUApZvtd1y\n4JBMa5MkVaxn581jwNixbPwywJbq36ED/x42jILPPqNly5YJVSepJivP6gQzgSOAJsBgYGQI4aQd\nBNk8UoH0ytIrrFNDCK2Bn5AKsZKkLPXM3LkMHDuWwuLitPZvH3wwD/brR51atcg3wEpKSMYhNsa4\nGZhT+nZqCKErcC1wzXaGLwU2lQbYL80A9gkh1AZWAsXA1r8FWwLLvq6WYcOG0aRJk7S2IUOGMGTI\nkF35KpKkHZi4gwB77qGH8s++famd5zLjkrYYPXo0o0ePTmsrKCio1M+siHVi84B6O+h7Hdg6UR4C\nLC0Nw4QQJgO9gPGl70Pp++Ff98G33347nTt3LmfZkqTteX7+fAaMHUvhnDnQpg2UBtbzOnZkxOmn\nG2AlbWN7FxGnTJlCly5dKu0zM10n9tYQwokhhANCCJ1CCLcBJ5Oa80oIYWQI4dYym/wVaB5CGB5C\nOCiE0A/4OfCXMmP+CAwNIVwUQjgUuJvUzWIPlP9rSZLK48UFCzjz8ccpnDYN7rwTxoyB4mIuPOww\nRhpgJWWRTK/EtgBGAPsCBcB0oE+M8cXS/tbAV7P/Y4yLQginAreTWv91cen//7bMmDGla8LeTGoa\nwbvAqTHGFeX6RpKkcnll4ULOfOwxNn70ETz4IMQIkyfTunZt/vqDH1DLACspi2S6TuwVX9Pfcztt\nbwPHfc12dwF3ZVKLJKnivLVkCX0fe4z18+fDP/4BZVYjWPT22zw4ahRXXnllghVKUjr/Wi1JNdy7\nn37K6Y8+yrolS+D++6GwMK3/8ssvZ+jQoQlVJ0nbZ4iVpBpsxmefccrDD7N6xQq47z744ou0/kGD\nBnH33XeTuudWkrKHIVaSaqjZq1fTa8wYVq5fDyNGpB4lW0aPHj146KGHqF27IhaykaSKZYiVpBpo\n8dq19B4zhqXr1n31GFn22OOr/qOOOoqxY8eSn5+fYJWStGOGWEmqYVauX88pDz/MvDVrtjS2bcsR\nv/41+7VqRYcOHZgwYQKNGzdOrkhJ+hr+G5Ek1SBrCgs5/dFHmbFqVVr7kS1aMOmcc1hz7rkUFxfT\n0sfJSspyhlhJqiE2FBXR//HHeWf58rT2Q5o359nBg2man0/T/fdPqDpJyozTCSSpBigqLuacJ57g\n5UWL0tr3b9SI5wYPZu/69ROqTJLKxxArSdVcSYxcMXEiT86ZA8XFX7W3qF+f5779bdo491VSDjLE\nSlI1d93LLzPyww9hzhz4/e9h2TKa1KvHs4MHc3Dz5kmXJ0nlYoiVpGrsd//5D79/5x1Ytiz1ONmV\nK+Guu7itTRuOaNEi6fIkqdwMsZJUTT3w/vv87JVXUg8xuP9+2Lgx1bFhAz8eMoQpU6YkW6Ak7QZD\nrCRVQ0/Nns0VEyfC+vWpAFtQkNbfp08fvvnNbyZUnSTtPkOsJFUz7yxbxjlPPEFxYSH8/e/w6adp\n/ccffzz/+te/fJyspJxmiJWkamTu6tX0e+wx1hcWwoMPwvz5af2HHXYY48ePZ48yj5iVpFxkiJWk\nauKzDRs4/bHH+HT9eigpgRjT+lu1asUzzzxDc1ckkFQNGGIlqRrYUFTEgLFj+ejLx8nWqQMXX8y+\n3bsD0LRpUyZOnEibNm2SK1KSKpAToiQpx5XEyEUTJvD64sVp7Ye3bMkrEyZw+223ccopp/CNb3wj\noQolqeIZYiUpx13/6qs88vHHaW2tGjbk6bPPpml+PjfddFNClUlS5XE6gSTlsH+89x6/+c9/0toa\n163LhLPPpnWjRglVJUmVzxArSTnq5YULueq559Laaufl8eiAARy+994JVSVJVcMQK0k56JPPP+es\nceMo+uwzeO21r1YiuKt3b3ofcEDC1UlS5XNOrCTlmFUbNnDGY4+xatWq1NO4Pv0UVq5k2E03MdSn\ncEmqIbwSK0k5pKi4mG8/8QQfL1+e/jSu119n4d13U1hYmGyBklRFDLGSlEN+/NJLvDh3Lowatc3T\nuD744APWr1+fUGWSVLUMsZKUI+6fPp2/TJkCjz4KM2ak9bVu3ZqJEyfSrFmzhKqTpKpliJWkHPDa\nokV89/nnYcIE+O9/0/qaNm3KM88849O4JNUohlhJynIL1qzh7PHjKVq+HF55Ja0vPz+fJ5980qdx\nSapxDLGSlMXWFxUxaNw4Pl2/HvbeGy6/HOrVA6BWrVr8+9//5vjjj0+4SkmqeoZYScpSMUaumDiR\nKcuXb2k86CCOvekmWrRowb333kv//v2TK1CSEuQ6sZKUpf74zjuMnjkzre3gZs14+vzz4aqraNq0\naUKVSVLyDLGSlIVeXLCAn201/7Vx3bqMHzSIpvn5kJ+fUGWSlB2cTiBJWWbBmjV854knKCl9lCxA\nAB7q149DmjdPrjBJyiKGWEnKIhs3b6b/qFGsXLYsrf2m44+nX/v2CVUlSdnHECtJWSLGyNDx45l2\n221w552wYgUA/du35/pu3RKuTpKyiyFWkrLEHf/9L6Ouuw4WLYLPP4e77mL/tWsZ2bcveSEkXZ4k\nZRVDrCRlgdcWLuRHV1wBs2ZtafziC/IffZRGdeokV5gkZSlDrCQlbPkXX3DquecS33svrb1x8+Y8\n8dhj5OX5q1qStuZvRklKUFFxMUefey7r33gjrb1u/fpMeu45Dj744IQqk6TsZoiVpAQNvP56Fj71\nVFpbXp06PDV+PJ07d06oKknKfoZYSUrIuFmzeLpxYzjooC2NeXn8Y9QoevfqlVxhkpQDDLGSlIBZ\nn3/ORU8/DXXrwmWXQadOANz4pz9x0TnnJFydJGU/HzsrSVVsfVERZ48fz5pNm1INtWvDBRfwvcaN\n+fU11yRbnCTlCEOsJFWhGCPXPPcc00sfZPCl8zp14o6+fROqSpJyj9MJJKkK3Tt9OiM//DCt7Rt7\n7sm9p5xC8IEGkrTLvBIrSVVgxYoVzC8u5ocvvpjW3qhuXR4dMIAGdesmVJkk5SavxEpSJZs+fToH\nH3IIp1xzDZuKi9P6/n7qqRzSvHlClUlS7jLESlIlmjlzJr1792b155+zeuxYeOYZiBGAH3fpwuBD\nDkm4QknKTYZYSaokc+bMoVevXqwoexPXCy/Af/7DCa1a8ZuTTkquOEnKcYZYSaoECxcupFevXixZ\nsiS9o1079j7+eP595pnUqVUrmeIkqRowxEpSBVu8eDE9evRg3rx56R3770+47DLGnHUW+zVsmEht\nklRdZBRiQwhXhxCmhRAKSl9vhBBO28n4i0MIJSGE4tL/loQQ1m815h9l+r58PV3eLyRJSdq8eTN9\n+vRh9uzZ6R377QeXX86tvXvTff/9kylOkqqRTK/ELgSuAzoDXYAXgXEhhI472aYA2KfM64DtjJkA\ntCwzZkiGdUlSVqhduza33HILeWWnCrRsCUOH0v/ww/lZ167JFSdJ1UhGITbG+FSM8ZkY4+wY46wY\n4w3AF0C3nW8WV8QYPy19rdjOmMKtxhRkUpckZZPCjh0pueACqFUL9t4brrySdq1aMeL008nzgQaS\nVCHK/bCDEEIecA5QH3hzJ0MbhhDmkQrMU4BfxBg/3GpM9xDCcuBzUld3b4gxripvbZKUlPdXrOCK\niROhUye49FLYZx/ymzfnkf79aZqfn3R5klRtZBxiQwidSIXWfGAtMCjGOHMHwz8CLgOmA02AnwJv\nhBAOizF+ecvuBOBRYC7QHrgNeDqEcGyMpYspSlIOKCgs5Kzx41m/eXOqoXQN2Lt69eKoli0TrEyS\nqp/yXImdCRxBKpQOBkaGEE7aXpCNMb4FvPXl+xDCm8AM4CrgxtIxY8ps8kEI4T1gNtAdmFSO+iSp\nysUYuWTCBD75/PO09iu/+U0uPfzwhKqSpOor4xAbY9wMzCl9OzWE0BW4FrhmV7YNIUwFOuxkzNwQ\nwsrSMTsNscOGDaNJkyZpbUOGDGHIEO8Lk1S5Vq5cSWFhIa1atQLgt//5D2NnzUob862WLflzz55J\nlCdJVWr06NGMHj06ra2goHJvcQq7+y/2IYQXgPkxxst2YWwe8AHwVIzxJzsY0xqYDwyIMT65gzGd\ngcmTJ0+mc+fO5S9eksrh008/pXfv3hQWFvLSSy8xo6iIUx5+mJIyv0+b5+cz5cILOWCrv2hLUk0x\nZcoUunTpAtAlxjilovef0ZXYEMKtpOawLgAaAecDJwN9SvtHAotijL8off9LUtMJZgFNgZ8B+wP3\nl/Y3IDWt4FFgGamrr/8LfAxM3L2vJkkVb9myZfTq1YsPP0zdn3pyjx6suvhiSurU+WpMAEafcYYB\nVpIqUabrxLYARpCaF/s8qbVi+8QYXyztb01qndcvNQPuBT4EngIaAseWmT9bDHwTGEfqJrD7gP8C\nJ8UYizL+NpJUiZYsWUL37t2/CrAAn3z0EZ/9859p424+/nj6tG1bxdVJUs2S0ZXYGOMVX9Pfc6v3\nPwZ+vJPxG4EdPvFLkrLFokWL6NmzJ5988kl6R/PmMGjQV2/PaNeOX3Tb2dLZkqSKUO51YiWpppg/\nfz49e/Zkzpw56R177QVXXQVNmwLQrkkTRvbt6wMNJKkKGGIl6Wtcd9112wbYvfdOBdjSea8t69dn\n3MCBNPOBBpJUJTKdEytJNc4999zDt771rS0NLVrA1Vd/FWAPad6cN887j057751QhZJU8xhiJelr\nNG7cmDNuuw1atYJ99kkF2MaNAThuv/14fcgQDiydUiBJqhpOJ5CknSguKWHYpEnc8e67MHQoxAgN\nGwIw6KCDeLBvX/Yos7yWJKlqGGIlaQc2FBVxwdNP89iXKxI0aPBV3w+OOorbe/SgVp7/oCVJSTDE\nStIOLF+/nlcXLdqm/bcnncRPjj6a4CoEkpQYLyFI0g60bdKEp846i/q1U3/fr5OXx4P9+vHTrl0N\nsJKUMEOsJO3E0fvuy5gzz6R5fj4TBw/mvI4dky5JkoTTCSTpa/Vr3565Q4fSuF69pEuRJJXySqwk\n7QIDrCRlF0OsJEmSco4hVpIkSTnHECtJkqScY4iVJElSzjHESpIkKecYYiVJkpRzDLGSJEnKOYZY\nSZIk5RxDrCRJknKOIVaSJEk5xxArSZKknGOIlSRJUs4xxEqSJCnnGGIlSZKUcwyxkiRJyjmGWEmS\nJOUcQ6wkSZJyjiFWkiRJOccQK0mSpJxjiJUkSVLOMcRKkiQp5xhiJUmSlHMMsZIkSco5hlhJkiTl\nHEOsJEmSco4hVpIkSTnHECtJQHFJSdIlSJIyYIiVVKMtWrSIe0aM4KiRI3lq9uyky5Ek7aLaSRcg\nSUnZuHEjAwYNYso778CJJ9L/00/5e9++XNypU9KlSZK+hiFWUo0UY+TKq65KBViAV1+lZOlSLtmw\ngQhcYpCVpKzmdAJJNdIdf/kL/xw5Mr1x9Wr2b9qUU9u2TaQmSdKuM8RKqnHmzp3LsGHD0hvr1aPZ\nVVfx/EUXsW/DhskUJknaZYZYSTXOg8uWUXLuuVCnzldt+eedx3Pf/z4HNWuWYGWSpF3lnFhJNcp9\n06fzy9dfhyOPhBYtYMQI8jp35okbb6TLPvskXZ4kaRcZYiXVGI9/8glXP/fclob99oMf/YhRZ51F\n7wMOSK4wSVLGnE4gqUZ4ZeFChjz5JCUxprUP79ePId/4RkJVSZLKyxArqdqbvmIF/ceOpbC4OK39\n+m7d+EHnzglVJUnaHYZYSdXavIICTnvkEQoKC9Parzj8cG45/viEqpIk7S5DrKRqa9aKFXxzwACW\nLl2a1j6wQwf+esophBASqkyStLsMsZKqpSVr19Jl0CDWvvwy/PnPMG8eACe2bs1D/fpRO89ff5KU\nyzL6LR5f2i6NAAAXDklEQVRCuDqEMC2EUFD6eiOEcNpOxl8cQigJIRSX/rckhLB+O+NuDiEsCSGs\nDyE8F0LoUJ4vI0kAK9avp8v3vsea119PNaxZA3ffTZtZsxg/cCB7lFkfVpKUmzK9FLEQuA7oDHQB\nXgTGhRA67mSbAmCfMq+0dWxCCNcB3weuBLoC64CJIYS6GdYmSazasIHjbruNZQ89lNYeatdm1OWX\n0zQ/P6HKJEkVKaN1YmOMT23VdEMI4RqgGzBjx5vFFTvZ7bXALTHGJwFCCBcBy4GBwJhM6pNUsxUU\nFtLj/vuZNXw4bLUSwV/vu4+Tjj46ocokSRWt3JPCQgh5IYRzgfrAmzsZ2jCEMC+EsCCEMDaEcFiZ\nfRxI6ursC1+2xRjXAG8Dx5a3Nkk1z9pNmzj13/9m+h//mJo+UMbV117LVRdemFBlkqTKkHGIDSF0\nCiGsBQqBu4BBMcaZOxj+EXAZ0B84v/Tz3ggh7Ffavw8QSV15LWt5aZ8kfa31RUWc8dhjvP3QQ1/d\nwPWl404+mTt+//tkCpMkVZryXImdCRxBav7qX4GRIYRDtzcwxvhWjHFUjHF6jPFV4CxgBXBVeQuW\npLI2bt7MgLFjeWXRIjjhBCjz9K1Wbdow7pFHqF3bJ2xLUnWT8W/2GONmYE7p26khhK6k5rVesyvb\nhhCmAl+uPrAMCEBL0q/GtgSmft3+hg0bRpMmTdLahgwZwpAhQ75uU0nVQOHmzZw9bhzPz5+fasjP\nh4suosFrr1HywguMHzuWvfbaK9kiJakGGD16NKNHj05rKygoqNTPDHGr54hnvIMQXgDmxxgv24Wx\necAHwFMxxp+Uti0BfhdjvL30fWNSgfaiGOPDO9hPZ2Dy5MmT6ewjI6UaqbikhG8/8QSPf/JJWnvz\n/Hwmfec7tCwpoWXLlglVJ0maMmUKXbp0AegSY5xS0fvP6EpsCOFWYAKwAGhEap7ryUCf0v6RwKIY\n4y9K3/8SeAuYBTQFfgbsD9xfZrd/IrXKwSxgHnALsAgYV94vJan6++Xrr28TYJvUq8ezgwfzzb33\nTqgqSVJVyXQ6QQtgBLAvqfVfpwN9Yowvlva3BjaXGd8MuJfUTVqfA5OBY8veCBZj/G0IoT5wD6mg\n+ypweoxxU+ZfR1JN8OjHH3Pb22+ntTWsU4dnzj6bLvt4T6gk1QSZrhN7xdf099zq/Y+BH+/Cfn8N\n/DqTWiTVTB+sXMnFEyaktdXOy+OJQYPott9+O9hKklTd+PBwSTlj9caNDBo3jnULFsArr0DpnP4/\n9ehB9/33T7g6SVJVct0ZSTmhJEYufPppPlm8GB54AFatgoULueBXv+K7Rx6ZdHmSpCrmlVhJOeHm\nN97gyVmz4MEHUwEW4N13mf7rX7Ns2bJki5MkVTlDrKSsN37WLG5680145hn4+OO0vj322IPmzZsn\nVJkkKSmGWElZ7aNVq7jw6adh2jSYNCmtr2XLljz66KPUq1cvoeokSUkxxErKWms3bWLQ2LGsmTcP\n/v3vtL7atWvzyCOP0KpVq2SKkyQlyhArKSuVxMjFEyYwY8UKGDUKiorS+ocPH84JJ5yQUHWSpKQZ\nYiVlpd+8/XbqiVy1asHgwdCgwVd9l19+OVdffXWC1UmSkuYSW5KyzjNz53LDa69taWjXjibXXcf+\njz9O/bp1ufPOOwkhJFegJClxhlhJWWX26tUMefJJYpm2vBAYc+GFnPiTn7B27Vpv5JIkGWIlZY/i\nkhLOf+opVhcWprXfesIJ9GnbFkgtqSVJknNiJWWNu6dN4+2lS9PaBh98MD/r2jWhiiRJ2coQKykr\nLPniC37x6qtpbQc1a8Y/TjvN+a+SpG0YYiVlhR+9+CJrnn4aliz5qu3eU06hYd26CVYlScpWhlhJ\niXtq9mweHjECJk6EO++E99/n4m98g+777590aZKkLGWIlZSodZs2cfldd8HYsamGTZtg5EgOnDo1\n2cIkSVnNECspUcMefZTld98NJSVbGmOkXZs2yRUlScp6hlhJiXljzhzuGzYM1q9Pa//Zz37GhRde\nmFBVkqRcYIiVlIiizZvpd/bZsHx5WnuPU0/l1ltvTagqSVKuMMRKSsSlN9/M6nffTWtr0a4d4x5+\nmFq1aiVUlSQpVxhiJVW5pV98wfjmzeGkk75qy2vYkJefeYZGjRolWJkkKVcYYiVVuR9NmsTazZvh\nzDPh29+GunX5w9//zqEHHZR0aZKkHFE76QIk1SwT5sxhzEcfbWno2pVvDxrEj7797eSKkiTlHK/E\nSqoy64uK+O7zz6e1Nc/P584BAxKqSJKUqwyxkqrMzW++ybw1a9Lafnfyyexdv35CFUmScpUhVlKV\neG/FCv7wzjtpbSe1bs2lnTolVJEkKZc5J1ZSpRo9ejSTJk1i2vHHs7nMU7nq5OVx9ymnEEJIsDpJ\nUq4yxEqqNC+//DKXXHIJmzZtghdegIsuggYNALiua1c67rlnwhVKknKV0wkkVYoPP/yQgQMHpgIs\nwJw5MHw4rF9Ph6ZN+cUxxyRboCQppxliJVW4pUuXcvrpp7N69er0jkMPhfr1+espp7BHnTrJFCdJ\nqhYMsZIq1Nq1a+nXrx8LFixI7/jGN2DAAM7v2JHeBxyQTHGSpGrDECupwhQVFXHOOecwderU9I79\n94fzzmPPBg34Y/fuidQmSapeDLGSKsz8+fOZPHlyeuOee8Kll1InP59H+/enRemNXZIk7Q5DrKQK\n06FDB0Y8+SR5e++damjQAK64Aho25L4+fTi5TZtkC5QkVRuGWEkVZvm6dVzz7ruUfO970KEDXHop\n7LUX13frxsU+1ECSVIFcJ1ZShdhQVMSAsWOZv2ZN6grslVdCCHznkEO4+fjjky5PklTNeCVW0m4r\niZGLJ0zg7aVLtzSGQLd99+Ufp51Gnk/lkiRVMEOspN32y9de4+GPP05ra9u4MWMHDnQ9WElSpTDE\nSsrY6tWrmT59OgAPvP8+t779dlp/47p1efKss2jpSgSSpErinFhJGSksLGTQoEG88847/PKuu7hh\nxYq0/loh8HD//nxjr70SqlCSVBN4JVbSLispKeGyyy7jpZde4osvvuC6Sy6haKursHf27k2ftm2T\nKVCSVGMYYiXtsuuvv56HHnpoS0NJCTzzDGzcCMD/fOtbXHXEEQlVJ0mqSQyxknbJ8OHD+c1vfpPe\nWLduai3Y/HwGdOjA/550UjLFSZJqHEOspK913333ce2116Y35uXBhRdC69Yc1aIFD/btS608f6VI\nkqqGZxxJOzV58mSuuuqqbTvOPhsOPZRWDRvyxKBBNKhbt+qLkyTVWIZYSTvVuXNn/s/Pf57eePrp\n0LUrDerU4cmzzqJVo0bJFCdJqrEMsZJ2atm6dbx9xBFw2mmpht69oWdP8kLgX2ecwZEtWiRboCSp\nRnKdWEk79MzcuVz09NOs2LABevWCAw9MvYA/du/OGe3bJ1yhJKmmMsRK2kZRcTE3vPYav/3vf9M7\n2rUjLwRuPeEEfti5czLFSZKEIVbSVuauXs2Qp57i7aVLt+lr3agRo/v144TWrROoTJKkLQyxkgCY\nNWsW72zcyNWTJlFQWLhNf//27fn7aaex5x57JFCdJEnpMrqxK4RwdQhhWgihoPT1RgjhtF3c9twQ\nQkkI4bGt2v9R2l729XQmdUnaPe9MncrhXbowZMgQCtatS+urk5fHn3r0YOzAgQZYSVLWyHR1goXA\ndUBnoAvwIjAuhNBxZxuFENoCvwNe2cGQCUBLYJ/S15AM65JUThPefptju3dn45o18P77MGIEFBUB\n0KFpU9487zyu7dKFEELClUqStEVGITbG+FSM8ZkY4+wY46wY4w3AF0C3HW0TQsgDRgG/AubuYFhh\njHFFjPHT0ldBJnVJylyMkf+dMIF+p57K5jVrtnTMnAnPP895HTsy5aKL6LLPPskVKUnSDpR7ndgQ\nQl4I4VygPvDmTobeCCyPMf5jJ2O6hxCWhxBmhhDuCiE0L29dkr7e2k2bOGvECP7P+ecTC9L/zph3\n4IH89dZbGdW3L418CpckKUtlfGNXCKETqdCaD6wFBsUYZ+5g7AnApcARO9nlBOBRUldp2wO3AU+H\nEI6NMcZM65O0c1OXL+fsUaOY+5vfwOefp/Xt0a4dL7/wAke3bZtMcZIk7aLyrE4wk1QobQIMBkaG\nEE7aOsiGEBoCI4GhMcbPt91NSoxxTJm3H4QQ3gNmA92BSeWoT9J2xBi5Y+pUfvLSSxTddResXJnW\nv2f79kx/4w328wlckqQckHGIjTFuBuaUvp0aQugKXAtcs9XQ9sABwBNhyx0heQAhhE3AITHGbebI\nxhjnhhBWAh34mhA7bNgwmjRpktY2ZMgQhgzxvjCprJIYueyZZxjxwQephoED4d574YsvAGjdoQNT\n3niDvffeO8EqJUm5avTo0YwePTqtraCgcm9xCrv7L/YhhBeA+THGy7Zqr0sqiJb1/4CGwA+BT0oD\n8db7aw3MBwbEGJ/cwWd2BiZPnjyZzj41SNqpGCM/fPFF/jJ1anrHp59S5/772a9ZM9587TX23Xff\nZAqUJFVLU6ZMoUuXLgBdYoxTKnr/GV2JDSHcSmoO6wKgEXA+cDLQp7R/JLAoxviLGOMm4MOttl8N\nxBjjjNL3DUjd+PUosIxU6P1f4GNgYvm/lqQv3fLmm9sGWOAnffty+dCh1K9XzwArSco5mU4naAGM\nAPYFCoDpQJ8Y44ul/a2Bba6u7kQx8E3gIqApsIRUeP1VjLEow9okbeWuqVO58Y030trq5OXxcP/+\nDOiw9T+USJKUOzIKsTHGK76mv+fX9F+61fuNwC498UtSZv41cybff+GFtLYAjOzb1wArScp55V4n\nVlL2mjh3Lhf+85/E2bPT2v/SqxfnHnpoQlVJklRxDLFSNfPWkiUMvPdeNt95J/ztbzBvHgA3HXcc\n3z3qqGSLkySpghhipWrkg5UrOXX4cDbecQcUFEBREfztb5zTsCG/PPbYpMuTJKnCGGKlamJ+QQHd\nf/tb1gwfDuvWbenYuJHPHnmELcs1S5KU+8rzxC5JWebTdes44ZZbWHnHHbBpU1pf165dGTNmzA62\nlCQpN3klVspxawoLOe6Xv2TRn/+8TYA98eSTef7552nevHlC1UmSVDkMsVIO27h5MwPHjmX25Mmw\nOX2J5lNOPZWJEybQqFGjhKqTJKnyGGKlHDa3oIDpK1dCv35w9NFftZ8xaBBPjh/PHnvskWB1kiRV\nHkOslMM67rknr517Lq2bNIHBg6nXuTNnDRnC42PGULdu3aTLkySp0hhipRx36J578saQIRzTqhWv\njBvHw6NGUbu292xKkqo3z3RSNdCmcWPePO88l9GSJNUYXomVqgkDrCSpJjHESpIkKecYYiVJkpRz\nDLGSJEnKOYZYSZIk5RxDrCRJknKOIVaSJEk5xxArSZKknGOIlSRJUs4xxEqSJCnnGGIlSZKUcwyx\nkiRJyjmGWEmSJOUcQ6wkSZJyjiFWkiRJOccQK0mSpJxjiJUkSVLOMcRKkiQp5xhiJUmSlHMMsZIk\nSco5hlhJkiTlHEOsJEmSco4hVpIkSTnHECtJkqScY4iVJElSzjHESpIkKecYYiVJkpRzDLGSJEnK\nOYZYSZIk5RxDrCRJknKOIVaSJEk5xxArSZKknGOIlSRJUs4xxEqSJCnnGGIlSZKUcwyxkiRJyjmG\nWEmSJOUcQ6wkSZJyjiFWkiRJOccQK0mSpJyTUYgNIVwdQpgWQigofb0RQjhtF7c9N4RQEkJ4bDt9\nN4cQloQQ1ocQngshdMikLkm7bvTo0UmXIOUkjx0pu2R6JXYhcB3QGegCvAiMCyF03NlGIYS2wO+A\nV7bTdx3wfeBKoCuwDpgYQqibYW2SdoEnYql8PHak7JJRiI0xPhVjfCbGODvGOCvGeAPwBdBtR9uE\nEPKAUcCvgLnbGXItcEuM8ckY4/vARcB+wMBMapMkSVLNUe45sSGEvBDCuUB94M2dDL0RWB5j/Md2\n9nEgsA/wwpdtMcY1wNvAseWtrbrLtqsBVVVPRX/O7u6vvNtnul0m47PtZyObZOOfTVXUlG3Hze7s\no7KOnWz82cgm2fbn4zmncrfLpXNOxiE2hNAphLAWKATuAgbFGGfuYOwJwKXAFTvY3T5ABJZv1b68\ntE/bkfQPzdb8hVK52+XSL5Rslo1/NobYyt3OEFsxsu3Px3NO5W6XS+ec2uXYZiZwBNAEGAyMDCGc\ntHWQDSE0BEYCQ2OMn+92penyAWbMmFHBu80NBQUFTJkyJekyvlJV9VT05+zu/sq7fabbZTJ+V8Zm\n289PVcnG710VNWXbcbM7+6isY6eix1U32fa9PedU7nYVec4pk9Pyd7mADIQY4+7tIITngFkxxmu2\naj8CmAIUA6G0+csrv8XAIaX/Pxs4MsY4vcy2LwFTY4zDdvCZ5wEP7lbhkiRJqgrnxxgfquidludK\n7NbygHrbaZ8BHL5V2/8DGgI/BBbGGDeHEJYBvYDpACGExsAxwJ07+cyJwPnAPGDj7hQvSZKkSpEP\ntCWV2ypcRiE2hHArMAFYADQiFSRPBvqU9o8EFsUYfxFj3AR8uNX2q4EYYyw7D+BPwA0hhFmkQukt\nwCJg3I7qiDF+BlR4opckSVKFeqOydpzpldgWwAhgX6CA1NXTPjHGF0v7WwObM9lhjPG3IYT6wD1A\nU+BV4PTSECxJkiRtY7fnxEqSJElVrdzrxEqSJElJMcRKkiQp51TbEBtCaB1CmBRC+CCE8G4IYXDS\nNUm5IITwWAhhVQhhTNK1SLkihHBGCGFmCOGjEMLlSdcj5YLdPd9U2zmxIYR9gBYxxukhhJbAZOCg\nGOOGhEuTsloI4SRSq49cHGM8J+l6pGwXQqhFajWek4G1pM43x1bCg36kamV3zzfV9kpsjHHZlw9Q\niDEuB1YCzZOtSsp+McZXgC+SrkPKIV2B90vPO+uApyldelLSju3u+abahtiyQghdgLwY4+Kka5Ek\nVTv7AWXPL0uAVgnVItUYWRNiQwgnhhDGhxAWhxBKQgj9tzPmeyGEuSGEDSGEt0IIR+/CfpuTWtt2\naGXULSWpso4bqabwGJIyly3HTdaEWKAB8C7wXWCbibohhO8AfwBuBI4CpgETQwh7lRnz3RDC1BDC\nlBBCvRBCXeBx4NYY49tV8SWkKlbhx03VlC1ljd0+hkhdeW1d5n2r0japuqqI42a3ZeWNXSGEEmBg\njHF8mba3gLdjjNeWvg/AQmB4jPG3O9jPaGBGjPHmKihbSlRFHTel47oD34sxfrtyq5ayR3mPoTI3\ndnUndWPXf4HjvLFLNcHunnt253yTTVdidyiEUAfoArzwZVtMpe/ngWN3sM3xwLeBgWWuMn2jKuqV\nskF5jpvS7Z4D/g2cHkJYEEI4prJrlbLRrh5DMcZi4H+Al4ApwO8NsKqpMjn37O75pvbul1sl9gJq\nAcu3al8OHLK9DWKMr5M730+qDBkfNwAxxlMqsygph+zyMRRjfBJ4sorqkrJZJsfNbp1vcuJKrCRJ\nklRWroTYlUAx0HKr9pbAsqovR8oJHjfS7vEYkjJXZcdNToTYGGMRqSeg9PqyrXSScC/gjaTqkrKZ\nx420ezyGpMxV5XGTNXNGQwgNgA5AKG1qF0I4AlgVY1wI/BF4IIQwGfgPMAyoDzyQQLlSVvC4kXaP\nx5CUuWw5brJmia0QwsnAJLZdb2xEjPGy0jHfBX5G6pL0u8APYozvVGmhUhbxuJF2j8eQlLlsOW6y\nJsRKkiRJuyon5sRKkiRJZRliJUmSlHMMsZIkSco5hlhJkiTlHEOsJEmSco4hVpIkSTnHECtJkqSc\nY4iVJElSzjHESpIkKecYYiVJkpRzDLGSJEnKOYZYSZIk5RxDrCRJknLO/wfjAzhvt9CW4AAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21b13e8cd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(1, 1, figsize=(8, 4))\n",
"\n",
"ax.semilogx(tp1[:,0], tp1[:,1], '-', c='#008b8b', lw=3)\n",
"ax.semilogx(tp2[:,0], tp2[:,1], '-', c='#008b8b', lw=3)\n",
"ax.semilogx(tp1[:,0], tpoly1[0]*tp1[:,0]**2 + tpoly1[1]*tp1[:,0] + tpoly1[2], '--', c='black', lw=3)\n",
"ax.semilogx(tp2[:,0], tpoly2[0]*tp2[:,0]**3 + tpoly2[1]*tp2[:,0]**2 + tpoly2[2]*tp2[:,0] + tpoly2[3], '--', c='black', lw=3)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Luminosity\n",
"\n",
"Above 1.5 Msun, there appear to be very little deviations of the true model sequence from the initial seed model sequence. We can thus leave this parameteriztion alone. Below 1.5 Msun, we can alter the shape of the relationship down to 0.23 Msun. In addition, we can prescribe a new shape to the relationship for objects with masses below 0.23 Msun."
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"p1 = np.array([line for line in model_props if line[0] < 0.23])\n",
"p2 = np.array([line for line in model_props if 0.23 <= line[0] < 1.5])\n",
"\n",
"poly1 = np.polyfit(p1[:,0], p1[:,2], 2)\n",
"poly2 = np.polyfit(p2[:,0], p2[:,2], 2)"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f21b195dc90>]"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArMAAAFqCAYAAAAJPtJhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3Xl4VdW9//H3IsyzgICgiFgncCRaBUVUiqhQQAZraFW0\nrdr2WosdbO3P1utte28H69Vaf7WKFX8qgwNDBRQcURGtiUgRBFFkEiLIKHOS9fsjERLGADk5Zyfv\n1/Pkqee7197ne3jYnE931l47xBiRJEmSkqhGuhuQJEmSDpZhVpIkSYllmJUkSVJiGWYlSZKUWIZZ\nSZIkJZZhVpIkSYllmJUkSVJiGWYlSZKUWIZZSZIkJZZhVpIkSYmV0jAbQvhFCOHtEML6EEJ+CGFs\nCOH4cuw3OIQwN4SwOYTwXgjh0lT2KUmSpGRK9ZXZbsBfgLOBrwG1gCkhhHp72yGE0BV4AngQOB0Y\nD4wLIXRMca+SJElKmBBjrLw3C6EF8Blwfozx9b2MGQXUjzH2LVV7E3g3xvj9yulUkiRJSVDZc2ab\nAhFYvY8xXYAXdqk9X1KXJEmSdqi0MBtCCMD/Aq/HGOfsY2hrIH+XWn5JXZIkSdqhZiW+1/1AR+Dc\nijxoCKE50Av4BNhSkceWJElShagLtAeejzF+XpEHrpQwG0K4D7gM6BZjXL6f4SuAVrvUWpXU96QX\n8PihdShJkqRK8E2Kb/SvMCkPsyVBth/QPca4uBy7vAn0AO4tVetZUt+TTwAee+wxTjrppEPoNHmG\nDRvG3Xffne42yqiMnlLxHod6zIPd/0D3K+/4ih5X1WTa566sfir6fSrieAdzjFSdN+Udm2l/fypT\npn326nruZNp3TnnGzp07l29961tQktsqUkrDbAjhfiAH6AtsDCF8ecV1XYxxS8mYEcCyGONtJdvu\nAV4JIdwCTCzZPxv47l7eZgvASSedROfOnVPzQTJUkyZNMu4zV0ZPqXiPQz3mwe5/oPuVd3xFj6tq\nMu1zV1Y/Ff0+FXG8gzlGqs6b8o7NtL8/lSnTPnt1PXcy7TvnAMdW+JTQVN8AdiPQGHgF+LTUzxWl\nxhxFqZu7YoxvAkOA64GZwACg335uGquWcnJy0t3Cbiqjp1S8x6Ee82D3P9D9yjs+E/9uZJJM+/Op\nrH4q+n0q4ngHc4xUnTcHc+zqJtP+fKrruZNp3zkHc+yKVKnrzKZCCKEzkJubm5tR/29RSoK+ffsy\nYcKEdLchJYrnjXTg8vLyyM7OBsiOMeZV5LEre51ZSZIkqcIYZqVqLNN+ZSglgeeNlFkMs1I15pey\ndOA8b6TMYpiVJElSYhlmJUmSlFiGWUmSJCWWYVaSJEmJZZiVJElSYhlmJUmSlFiGWUmSJCWWYVaS\nJEmJZZiVJElSYhlmJUmSlFiGWUmSJCWWYVaSJEmJZZiVJElSYhlmJUmSlFiGWUmSJCWWYVaSJEmJ\nZZiVJElSYhlmJUmSlFiGWUmSJCWWYVaSJEmJZZiVJElSYhlmJUmSlFiGWUmSJCWWYVaSJEmJZZiV\nJElSYhlmJUlKkA8+/5wLRo1i/urV6W5FygiGWUmSEmJbYSHfnDSJV5cu5YxHH+Xv771HjDHdbUlp\nZZiVJCkh7pg+nbz8fAA2FRRww9SpPDhrVpq7ktLLMCtJUgJMW7KE/3nrrTK1k5o141sdO6apIykz\nGGYlScpw67Zu5apJkyg9oaBWjRo83rs39WvVSltfUiYwzEqSlOH+48UXWbxhQ/GL7dsB+M1553FG\nq1Zp7ErKDIZZSZIy2BNz5/LYnDnFL6ZPh7vvpkvDhvz4zDPT25iUIQyzkiRlqI/WruXGqVMhRnjp\nJRg7FlauZO1f/8r6devS3Z6UEQyzkiRloG2FheQ8+ywbtm6FSZNg8uQd2+bOnk3v3r3ZunVrGjuU\nMoNhVpKkDPSrN97gXytWwAsvwCuv7Lb90ksvpXbt2pXfmJRhDLOSJGWYFxYt4vdvv138onNnaNq0\nzPZ77rmH22+/nRBCGrqTMothVpKkDJK/cSPfmjhxZ6F5c2p+73u0POIIatSowSOPPMIPf/jD9DUo\nZZia6W5AkiQVK4qRqyZNIn/TpjL1Pw4cSO9rr2XWrFkMHDgwTd1JmckwK0lShvj9228zddGiMrXe\nHTpwc+fOhBA47rjj0tSZlLmcZiBJUgZ4Y9kybn/99TK1tg0b8sgllzg3VtoHw6wkSWn2+ebNXDFq\nFIVx5wNra4TA471706J+/TR2JmU+w6wkSWlUFCPn/+hHfHr77VBqisGvunSh+1FHpbEzKRkMs5Ik\npVHOb37DnAcfhM2b4YEHYP58LjjqKP7POeekuzUpEQyzkiSlyf88+ihj/vM/ix9XC7B9O/zjH/z2\nxBPJquFXtFQenimSJKXBhBdf5Bff+Q4UFpapX/2DH9D1tNPS1JWUPIZZSZIq2b/ff5+B/fsXX4kt\n5ZxBg3jk7rvT1JWUTIZZSZIq0YoVKzivRw8KvviiTL1Nt268NmqUy3BJB8gwK0lSJXrt889Zf8QR\nZWp1O3Ui79lnqZmVlaaupORKaZgNIXQLIUwIISwLIRSFEPruZ3z3knGlfwpDCC1T2ackSZXho7Vr\n+e5LL0FODpx/PgDhqKN4fvx4WjVunObupGRK9eNsGwAzgeHAM+XcJwLHAxt2FGL8rOJbkySp8mwp\nKGDwhAms27oVatSAr38dWrbkf773Pc4/9th0tyclVkrDbIzxOeA5gHBgk4BWxhjXp6YrSZIq322v\nvca7n5W9NjNk6FB+euGFaepIqhoycc5sAGaGED4NIUwJIXRNd0OSJB2KqZ98wt25uWVqJzVrxgM9\ne3rDl3SIMi3MLgduAAYCA4AlwCshhNPT2pUkSQfp882buWby5DK1OllZjPn612lYu3aaupKqjlTP\nmT0gMcb5wPxSpRkhhGOBYcA16elKkqQDl5eXx+TJk3mnUyeWb9xYZtsfunfn5MMPT1NnUtWSUWF2\nL94Gzt3foGHDhtGkSZMytZycHHJyclLVlyRJe7RkyRL69OnD8uXLoXNnGDwYahZ/5fZq356bzjgj\nzR1KqTNy5EhGjhxZprZu3bqUvV+IXz4POsVCCEVA/xjjhAPcbwqwPsY4aC/bOwO5ubm5dO7cuQI6\nlSTp4G3YsIHzzjuPWbNm7Sx26ABDh9KiWTNmXXMNRzRsmL4GpTTIy8sjOzsbIDvGmFeRx07pldkQ\nQgPgKxTf1AXQIYRwGrA6xrgkhPDfQJsY4zUl428GFgLvA3WB7wIXAj1T2ackSRWhoKCAb3zjG2WD\nLEAIUKsWD/XqZZCVKliqpxmcCbxM8dqxEbirpD4CuA5oDRxVanztkjFtgE3ALKBHjHFaivuUJOmQ\nxBi5+eabmbzLzV4cfjhcfTU3ZmfT7ytfSU9zUhWW6nVmX2UfKybEGK/d5fUfgT+msidJklLh3nvv\n5f777y9bbNAArruOc449lv91PVkpJTJtaS5JkhJnxYoV/OIXvyhbrFkThg6l9dFH83S/ftSpmYR7\nrqXkMcxKknSIWrduzV9Gjiy+Evulb3yDWh068FTfvrRxnqyUMoZZSZIO0YqNG/nPFSvgP/6jeI7s\nxRfD6adz70UXcW7btuluT6rS/J2HJEmHYEtBAZePG8eSDRugRQv44Q+hTh2+c8op3HDaaeluT6ry\nDLOSJB2kGCM3TJnCjOXLdxbr1qXbkUfy1699jRDC3neWVCGcZiBJ0kH647/+xaNz5pSpHd24MU/3\n7UvtrKw0dSVVL4ZZSZIOQGFhIQATFizg59PKLoPesFYt/nn55Rxev346WpOqJcOsJEnlNH36dE49\n9VTGvv4635w4kdIPhA/A4717c8rhh6erPalaMsxKklQOixYton///syZM4eBPXvyxezZZbb/tls3\n+vqEL6nSGWYlSdqPDRs20KdPH1auXAlA3LIFhg+Hjz4C4KqOHfn5V7+azhalasswK0nSPhQWFjJk\nyBBm73IlluOOg/bt6dKmDX+/+GJXLpDSxDArSdI+3HrrrTz77LNliy1bwre+RbumTRnbrx91fVSt\nlDaGWUmS9uKhhx7irrvuKlusXx+uvZbGTZowccAAWpV+hK2kSmeYlSRpD2KMjB07tmwxKwuuuYas\nww/nqb59OdmVC6S0M8xKkrQHIQR+9be/UfO883YWBw6EDh34W8+e9GzfPm29SdrJST6SJO3BJ+vW\n0e+f/6SgXz9o0QLWr4ezzuIXZ5/Nd049Nd3tSSphmJUkaRdrtmzhsqefJn/TpuLCuecC8M2TTuI3\npa/USko7pxlIklTK1oICBowfz9zVq8vUL2rXjocvuYQaLsElZRTDrCRJJQqLirhq0iReWbKkTL1T\n8+Y83bcvtbOy0tSZpL0xzEqSqr3FixcTY+RHL7/Mk/Pnl9l2RIMGTBo4kKZ166apO0n74pxZSVK1\nNnv2bLp27UrHiy/mrbPOKl5+q0Sj2rWZOGAA7Ro3TmOHkvbFK7OSpGorPz+fPn36sGHDBt56+ml4\n+GHYvBmAWjVqMLZfP85o1SrNXUraF8OsJKla2rx5M/3792fRokU7i/Pnw8svE4BHL7uMHkcfnbb+\nJJWPYVaSVO3EGLnuuuuYMWNG2Q1HHw09e3LPRRdx5Yknpqc5SQfEMCtJqnbuuOMORo0aVbZ42GEw\ndCi/7NaNmzp3Tk9jkg6YYVaSVK089thj3HnnnWWLderAdddxw7nn8l8lD0iQlAyGWUlStRIbNiSU\nXmarRg246ioGn38+f+3Rg+BDEaREMcxKkqqN/I0buXPVKuIPflA8rQCgXz8u7tWLx3r3JquGX4tS\n0rjOrCSpWli7ZQuXPP00C9auhdat4aab4L336DJoEM/4dC8psfy/oJKkKu+Lbdu47JlnmPnZZzuL\njRpxSv/+TBwwgAa1a6evOUmHxDArSarSNm/fTr9x43jz00/L1I9p0oTnBw3iMB9TKyWaYVaSVGVt\nKyxk0IQJvLR4cZn6EQ0aMHXwYI5o2DBNnUmqKM6ZlSRVSaPGjGH4qlW8sGlTmXrzevV4YfBgjm3a\nNE2dSapIhllJUpXz/JQpDBkyhFinDgwdCsccA0CTOnWYMmgQHVu0SG+DkiqM0wwkSVXKrH//m69f\nfjmxsBA2bYIHHoB336VhrVo8N3AgnVu1SneLkiqQYVaSVGUsXbaMrj16sL301ILCQmp++inPDhjA\nOW3apK85SSlhmJUkVQlr163j9PPPZ+PKlWXqNU47jYkPP0z3o45KU2eSUskwK0lKvG3btnFqjx58\n/vHHZerh6KN56oknuLhkzqykqscwK0lKtBgjPYcNY0lubtkNLVowYswYLu/YMT2NSaoUhllJUmLF\nGPnZq68yrV07OOusnRsaNOD+UaO46qtfTV9zkiqFYVaSlEgxRn7x2mv86Z13ICsLBg+Gnj2hVi1+\n+/DDfK9Hj3S3KKkSGGYlSYkTY+TWadP4/dtv7yyGQI1evfjLc89x2xVXpK85SZXKhyZIkhIlxshP\nXnmFP+8yRzYAj1xyCVd16pSexiSlhWFWkpQYMUZ+9PLL3JuXV6YegIcNslK1ZJiVJCVCUYx8d9w4\nHl6wAELYUQ/AI5deytUGWalacs6sJCnjFRYVcc3TT/PwjTfC2LFQVARAjRB49LLLDLJSNeaVWUlS\nRisoKuKqceMY9eMfw2efFf988QU1hgzh8f79ufLEE9PdoqQ08sqsJCljbSss5MqxYxl1222wePHO\nDf/+Nxfm5RlkJXllVpKUmbYUFDBo3Dgm/u53MG9emW3NW7Xi4T/9KU2dScokhllJUsbZuG0b/caN\n48V77oF33y2zrVHTpkx76SXatWuXpu4kZRLDrCQpo6zfupU+Y8fy2j/+AdOnl9lWt149pkyeTMeO\nHdPUnaRMk9I5syGEbiGECSGEZSGEohBC33Lsc0EIITeEsCWEMD+EcE0qe5QkZY41W7Zw8VNP8drS\npXDssVC37o5tNWvVYuwzz3DOOeeksUNJmSbVN4A1AGYC3wfi/gaHENoDzwIvAqcB9wAPhRB6pq5F\nSVImWLVpExeNGcNby5cXFzp0gBtvJDRqRAiBxx97jEsuuSS9TUrKOCmdZhBjfA54DiCEUitc7933\ngI9jjD8reT0vhHAeMAyYmpouJUnptmzDBno++SRzV68uU2953HEMnzqVtR9+yBVXXJGm7iRlskyb\nM3sO8MIuteeBu9PQiySpEixYs4aeTz7JJ+vXl6m3adiQFwcP5sTmzeHss9PUnaRMl2lhtjWQv0st\nH2gcQqgTY9yahp4kSSny75Urufipp1ixcWOZ+tGNG/PiFVdwbNOmaepMUlJkWpiVJFUT05cto/cz\nz7B282aosfMWjhOaNWPqoEEc1bhxGruTlBSZFmZXAK12qbUC1u/vquywYcNo0qRJmVpOTg45OTkV\n26Ek6ZA9v3AhA8aPZ9PChTByJFx9NbRuzRktW/L8oEEcXr9+uluUdJBGjhzJyJEjy9TWrVuXsvcL\nMe53kYGKeaMQioD+McYJ+xjzP8ClMcbTStWeAJrGGC/byz6dgdzc3Fw6d+5c0W1LkirY6A8+4KpJ\nk9i+ZAk88ABs3gz163P6L3/Jy7fcQtNSy3FJqhry8vLIzs4GyI4x5lXksVO9zmyDEMJpIYTTS0od\nSl4fVbL9v0MII0rt8reSMb8PIZwQQvg+MAj4cyr7lCRVjvvffZecZ59l+9Kl8Pe/FwdZgE2bWPiH\nP7B0wYL0NigpcVK9zuyZwLtALsXrzN4F5AH/WbK9NXDUl4NjjJ8AvYGvUbw+7TDg2zHGXVc4kCQl\nSIyR/5w+nR+8+CIxP784yG7aVGbM2WefzVe+8pU0dSgpqVK9zuyr7CMwxxiv3UNtGpCdyr4kSZWn\nsKiIH770EvfPnAn5+fC3v8EuqxdcdNFFjBs3jrpOMZB0gDLtBjBJUhWytaCAqydPZsy8ebBmTXGQ\n/eKLMmO6devGhAkTqFevXpq6lJRkqZ5mIEmqpr7Yto0+Y8cWB1mAxo2LH1FbSteuXZk4cSINGjRI\nQ4eSqgLDrCSpwq3atImLxozhhUWLdhazsqj5rW9xziWXANClSxcmT55Mo0aN0tSlpKrAMCtJqlCL\n16/nvFGj+NeKFWXqDWvVYvIVVzBtwgR+/etf89xzz9HYByNIOkTOmZUkVZi5n3/OxU89xdING8rU\nW9Srx+SBAzmzdWsA7rjjjjR0J6kqMsxKkirE9GXL6DN2LGu2bClTb9eoEVMHD+b4Zs3S1Jmkqsxp\nBpKkQzZhwQJ6PPlkcZBduRJKni7ZsXlzpg8ZYpCVlDKGWUnSIXlw1iwuHz+eLQUFsGAB/O//woQJ\nfLV1a1678kraeoOXpBQyzEqSDkqMkV+/8QbXT5lCUYwwZw4MHw7btsHrr9Nt1iwO8yEIklLMMCtJ\nOmAFRUV8d8oU7nzzzeLCzJkwYgQUFOwYc9cf/8ioUaPS1KGk6sIbwCRJB2Tjtm1c8c9/MmnhwuLC\nW2/B00/vmCf7pYEDBzJw4MA0dCipOjHMSpLK7bONG+kzduzONWRffhkmTdpt3NChQ3nwwQepWdOv\nGUmp5TQDSVK5LFizhq4jR+4MsuvWwYsv7jbupptuYvjw4QZZSZXCMCtJ2q+3ly+n6xNP8NHatTuL\nTZrQ8IYbqF2nzo7Sbbfdxj333EONGn69SKoc/msjSdqnZz/6iAtHj2bl5s1l6kc3bszbv/oVo0eN\nombNmtx111389re/JYSQpk4lVUf+DkiStFd/f+89vvfCC8VLb5VyesuWTBowgCMaNuSk/v2ZN28e\nHTp0SFOXkqozw6wkaTcxRn71xhv8ZsaM3bZ97eijebpvXxqXml5gkJWULoZZSVIZ2wsL+e6UKYx4\n//3iQkEBlNzMdVXHjjzUqxe1s7LS2KEk7eScWUnSDhu2baPP2LE7g+y8efD738OKFfzynHMYceml\nBllJGcUwK0kCYMXGjVwwejRTPvmkuPD22/Dww7B2LYc9/jjf79DBm7skZRzDrCSJD9esoesTT5CX\nn1/8JK/nnoMnn4SiIgDWrFhBnz592LBhQ5o7laSynDMrSdXcm59+St+xY1m1eTNs3w6jR8N77+02\n7oQTTqBWrVpp6FCS9s4rs5JUjT09fz4Xjh5dHGQ3bIC//W2PQfbWW2/l8ccfp27dumnoUpL2ziuz\nklQNxRi5OzeXn7zyCjtWkJ0xAxYvLjMuKyuL++67jxtvvLHSe5Sk8jDMSlI1U1hUxI9efpn73n23\n7IYePTh81SpW5uUB0LhxY8aMGUOvXr3S0KUklY/TDCSpGtm4bRuXjx+/e5AFrj/9dOa99BKnnnoq\n7du3Z/r06QZZSRnPK7OSVE2s2LiRPs88Q25+/m7b/rtbN2796lcJIfDss89Sp04dWrZsmYYuJenA\nGGYlqRp4f9Uqej/zDIvWry9Tr52VxSOXXELOSSftqB111FGV3Z4kHTTDrCRVcS8tXsyA8eNZt3Ur\nLFwIbdtC7docVrcu4/r143zDq6QEM8xKUhU2YvZsvjNlCgWFhfDqqzBpEpx+Ou1vvJHnBg3ihGbN\n0t2iJB0Sw6wkVUExRn79xhv814wZsHVr8dO8vlw/9t13+fbatQZZSVWCqxlIUhWztaCAqyZNKg6y\n+flw7727PQjhjttu4709PBxBkpLGK7OSVIWs3ryZy8ePZ9rSpZCbC08/XfyI2lJCCNxxxx2ccsop\naepSkiqOYVaSqoiP167lsmeeYd7q1fDaazBhwm5jmjZtyuOPP85ll12Whg4lqeI5zUCSqoC3ly+n\nyxNPFAdZgFNPhYYNy4w544wzeOeddwyykqoUw6wkJdz4BQu4YPRoPtu0aWexSROaf/vbhBAAuP76\n65k+fTrHHntsmrqUpNRwmoEkJdhf8vK4+aWXiLvUT2nRgonXX8+otm1p3bo1V111VVr6k6RUM8xK\nUgIVxcitr77Kn955Z7dtPY8+mif79qVJnTr89Kc/TUN3klR5nGYgSQmztaCAIf/8J3965BGIZa/J\nXnvyyUwcMIAmdeqkpzlJqmSGWUlKkLVbtnDBAw8w+pZbYMQIyMvbse3Oc89leK9e1MrKSmOHklS5\nnGYgSQmxZP16uv7sZywdMQK2bCkujh1L1rHHMvzKK7nm5JPT26AkpYFXZiUpAV6fP58TevRg6QMP\n7AyyAFu30nHqVK7u1Cl9zUlSGhlmJSnD/Wb4cM4/6yw27+Fmr9Zt2/KXP/xhxxJcklTdGGYlKYP9\nIy+P22+5hbh+/W7b+l1xBXNnz6Z79+5p6EySMoNhVpIyUIyR37/1Fte99BIMHFhmW1b9+vx9xAjG\njR5N06ZN09ShJGUGbwCTpAxTWFTED196iftnziwudOwI2dmQm0ur7Gxef+opvtK+fVp7lKRMYZiV\npAyyaft2hkycyPgFC8pu6NePi3v2ZOJvfkNNl96SpB0Ms5KUZkuXLqVNmzas3rKFr48dy4zly3cb\nc9ellzIsO9sbvSRpF86ZlaQ0KSgo4M9//jMnnHACf7jvPs4dOXK3IFs7K4tRffpwy5lnGmQlaQ8M\ns5KUBq+//jqdO3fmxz/+MZs2beK2n/+c+YsWlRnTtE4dpgwaxDdOPDFNXUpS5jPMSlIlys/PZ+jQ\noXTr1o1///vfO+px82YYP37H6yMbNeL1nBy6H3VUOtqUpMRIeZgNIfwghLAwhLA5hDAjhHDWPsZe\nE0IoCiEUlvxvUQhhU6p7lKRUKyws5L777uOEE05gxIgRex7UoAEUFnJKixa8OWQInVq0qNwmJSmB\nUnoDWAjhG8BdwPXA28Aw4PkQwvExxlV72W0dcDzw5eSwmMoeJakybNu2jbvvvpt169btvvGII+Dy\ny+GYY7jwqKMY278/TerUqfwmJSmBUn1ldhjwQIzx0RjjB8CNwCbgun3sE2OMK2OMn5X8rExxj5KU\ncvXq1ePee+8tW6xTB/r2hZtvhmOO4coTT2TywIEGWUk6ACkLsyGEWkA28OKXtRhjBF4Auuxj14Yh\nhE9CCItDCONCCB1T1aMkVaael1xC27PPLn5xxhnws59Bt26QlcUt2dk83rs3dWq6YqIkHYhU/qvZ\nAsgC8nep5wMn7GWfeRRftZ0FNAF+CkwPIXSMMX6aqkYlKdU2bNvGwPHjWXbRRcVB9thjd2z7U/fu\n/Pisvd5OIEnah4xazSDGOCPG+FiMcVaM8TVgALASuCHNrUnSXsUYmTx5Mjk5ORQUFOy2/bONG7lw\n9GimLloEzZrtCLI1a9Tg/112mUFWkg5BKq/MrgIKgVa71FsBK8pzgBhjQQjhXeAr+xs7bNgwmjRp\nUqaWk5NDTk5O+bqVpIMwY8YMfv7zn/Pqq68C0L17d2688cYd2xevX0/PJ59k/po1ZfZrUKsWT/Xt\nyyXHHFOp/UpSqo0cOZKRI0eWqe3x5tcKEoqnsabo4CHMAN6KMd5c8joAi4F7Y4x/LMf+NYD3gYkx\nxp/sZUxnIDc3N5fOnTtXXPOStA9z5szhl7/8JePGjStTb9GiBR9++CFNmzblg88/p+dTT7F0w4ay\nY+rVY9KAAZx1xBGV2bIkpU1eXh7Z2dkA2THGvIo8dqqnGfwZ+G4I4eoQwonA34D6wCMAIYRHQwi/\n+3JwCOH2EELPEMIxIYQzgMeBdsBDKe5Tkspl8eLFXHfddZxyyim7BVmAVatW8cADD5C7YgXdRo3a\nLci2b9yYN3JyDLKSVEFSettsjHFMCKEFcCfF0wtmAr1KLbd1JFB6gtlhwN+B1sAaIBfoUrKslySl\n3YQJE/jHP/6xx23t2rXjzjvv5Mjzz+fCMWPYsG1bme2dmjdnyuDBtGnYsDJalaRqIeU3gMUY748x\nto8x1osxdokxvlNq20UxxutKvb4lxnhMydg2McavxxhnpbpHSSqv66+/nvbt25epNW/enLvvvpt5\n8+bR7Lzz6D1u3G5B9qutW/PqlVcaZCWpgmXUagaSlOlq167Nf/3XfwHQoEEDfvWrX/Hxxx/zox/9\niKc+/pjLx41ja2FhmX16tGvHi1dcQfN69dLRsiRVaa7OLUkHKCcnh0WLFvGd73yHVq1asfyLL7jh\n2WcZ9cFllmuqAAAQdElEQVTuM6IGHHccT/gwBElKGf91laQDlJWVxS9/+UsKioq4Ny+P//P667tN\nKwC49uST+fvFF1Ozhr8Ek6RUMcxK0kGY8emnfO+FF5j52Wd73H5LdjZ/uuACilcklCSlimFWkg7A\n6s2b+cVrr/HgrFnsaZXuw+rW5Q/nn8+3TznFICtJlcAwK0nlUBQjI2bP5mfTprFq8+Y9jhnaqRO/\nP/98WjZoUMndSVL1ZZiVpHIY/cEHXPf883vcdnKLFtz/ta/R7cgjK7krSZJ3JUhSOQw+4QROb9my\nTK1BrVr8sXt38q66yiArSWlimJWkcqhZowb/92tf2/F64HHHMffaa/nJWWdRKysrjZ1JUvXmNANJ\nKqdz2rThjq5d+Wrr1lzaoUO625EkYZiVpAPy665d092CJKkUpxlIkiQpsQyzkiRJSizDrCRJkhLL\nMCtJkqTEMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTEMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJ\nkqTEMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTEMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTE\nMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTEMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTEMsxK\nkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTEMsxKkiQpsQyzkiRJSizDrCRJkhLLMCtJkqTEMsxKkiQp\nsQyzkiRJSizDrCRJkhLLMCtJkqTESnmYDSH8IISwMISwOYQwI4Rw1n7GDw4hzC0Z/14I4dJU9yhJ\nkqRkSmmYDSF8A7gL+DVwBvAe8HwIocVexncFngAeBE4HxgPjQggdU9mnJEmSkinVV2aHAQ/EGB+N\nMX4A3AhsAq7by/gfApNjjH+OMc6LMf4KyAP+I8V9SpIkKYFSFmZDCLWAbODFL2sxxgi8AHTZy25d\nSraX9vw+xkuSJKkaS+WV2RZAFpC/Sz0faL2XfVof4HhJkiRVY65mIEmSpMSqmcJjrwIKgVa71FsB\nK/ayz4oDHL/DsGHDaNKkSZlaTk4OOTk55WpWkiRJh27kyJGMHDmyTG3dunUpe79QPI01RQcPYQbw\nVozx5pLXAVgM3Btj/OMexo8C6sUY+5WqvQG8F2P8/l7eozOQm5ubS+fOnVPxMSRJknQI8vLyyM7O\nBsiOMeZV5LFTeWUW4M/AIyGEXOBtilc3qA88AhBCeBRYGmO8rWT8PcArIYRbgIlADsU3kX03xX1K\nkiQpgVIaZmOMY0rWlL2T4ukCM4FeMcaVJUOOBApKjX8zhDAE+G3Jz4dAvxjjnFT2KUmSpGRK9ZVZ\nYoz3A/fvZdtFe6g9DTyd6r4kSZKUfK5mIEmSpMQyzEqSJCmxDLOSJElKLMOsJEmSEsswK0mSpMQy\nzEqSJCmxDLOSJElKLMOsJEmSEsswK0mSpMQyzEqSJCmxDLOSJElKLMOsJEmSEsswK0mSpMQyzEqS\nJCmxDLOSJElKLMOsJEmSEsswK0mSpMQyzEqqEmKMFBQVpbsNSVIlq5nuBiRpVzFG5q9Zw3MLFzJ1\nwQLyV65k8xdfsGXjRrZu2kRBCIRjj2VrYSHbCgvZWljI9pIge2SjRnRq3pzD8vNpU6sWZ3ToQJcT\nTqB9mzZkZWWl+ZNJkiqaYVZSRvhi2zZeXrKEyR9/zJgRI/g8Nxfy82HNmt0HH3EE3HLLHo+zdMMG\nlm7YAA8/DHPn7twQAnWaNKFxixa0P+YY+l12GbfdfDMhhBR9IklSZTDMSqpU69ato1GjRoQQmPP5\n50xeuJDnFi7ktWXL2FZYWDxo4UL44IO9H2Tr1v2/0YYNZV/HyNa1a1m5di0rFyzgX/Pn89c6dTi3\nbVvOK/k5rWVLatZw9pUkJYlhVlJKffbZZ0ybNo1p06bx4ssvM/f99xk8fDhvbtvGkl0D55datdr3\nQcsTZr/4Yt/bjzuO5Rs38tT8+Tw1fz4ADWrVokubNpzbpg3nHXkk5xxxBA1r197/e0mS0sYwK6lC\nbdy4kX/+85+88sorvPDyy3xUEhRLGzNtGnTqtPeD7CXM1qlXj3oNGtCkWTMeHDSI2llZ1Cn1s72o\niA9Wr+b9Vav4S7NmbCgooHBvofb443fvfft2Xli0iBcWLQKgXaNGLLrhhv1/aElS2hhmJVWI7YWF\nvPvZZ0yZM4fbhwyBGPc+OD9/j2G2Zo0anNe2LeefdhrL69Wje3Y2J598Mu3ataNRo0bUrLn/f7JO\na9kSgDs/+giALzZv5q0FC3j7ww+Z9fHHzP34Y+bNnMmWdu32e6xz2rTZ7xhJUnoZZiUdkMLCQrKy\nsli3dSszPv2U15ct441ly5ixfDmbCwqKB7VuDcuX7/0g+fk7/rNdo0Zc2qEDl7Rvz0Xt2tG4Tp3i\nDT17Vki/DevVo8cpp9DjlFN21GKMLFi7lteXLi3u/9NPmbd69W77nte2bYX0IElKHcOspH2KMZI7\nezbDR49m6nPPsX7LFpoOG8aHe1pl4EsdOpQNs3XqwNFHQ4cO1D3+eM49+2wuO/54Lj3mGE5s1qzS\nVxQIIXDcYYdx3GGHcW1JyP1s40aml4Tz15ctIzc/3zArSQlgmJVUxtotW5ixZAlPP/ccr06dyicz\nZrB95cqdA0Jg5ZIl0LDh3g9y/PGwejV06ECzTp248Jxz6NauXUavGNCyQQP6H3cc/Y87DoBN27dT\nx3VpJSnjGWalamzNli3k5eeTW+rno/fegwcf3PuKATEWL5t15pl73HxSs2acd+WVnPfjH3Ne27Yc\n06RJItdyrV+rVrpbkCSVg2FWqmZWbNzIfe++y+gPPmDB2rW7D2jVCr6c+7o3JWG2Vo0anNW6dfE6\nrUceSdc2bWher15qGpckaQ8Ms1I1Mffzz/nD9Ok8/sYbbG/RYu8D69YtnvP64Ydl640b0/yMM+h8\nwQX07tWLc485hlNatKBOOVYYkCQpVfwWkqqwGCOTZs/m9uHDefell2DePGjUCG69Ffbxq/+sjh0p\nXLCAw48/ni49enBFv34MvPBC6vqrd0lShjHMSlXQx598wm8eeoinxo5lwwcfQFHRzo2ff168NFbr\n1gDUzsri1BYtyG7dmuxWrchu1Yq2Q4cSiopoWbJmqyRJmcowK1UhG7dt49ejR3PX1Vfvc1zWnDkM\n7dmT6089ldNbtqS2d+1LkhLKMCtVES8vXszACRNYs3Ej1K8PmzbteWAIDDniCB7q1atyG5QkKQUy\nb7FHSQfllBYt2FJQAFlZcNJJZbaFWrU4uXt3/vrAA+SvWMGjw4enqUtJkiqWV2alKqJF/fpcd/LJ\n/HXmTOjUCebOpXnnzgy94gpuHzqUJo0apbtFSZIqnFdmpSpk2JlnkhUCl/Xpw4uzZ7Ny2jT+dNNN\nBllJUpXllVmpCjm2aVMWXX89bQ2vkqRqwiuzUhVjkJUkVSeGWUmSJCWWYVaSJEmJZZiVJElSYhlm\nJUmSlFiGWUmSJCWWYVaSJEmJZZiVJElSYhlmJUmSlFiGWUmSJCWWYVaSJEmJZZiVJElSYhlmJUmS\nlFgpC7MhhMNCCI+HENaFENaEEB4KITTYzz6vhBCKSv0UhhDuT1WPUnU3cuTIdLcgJY7njZRZUnll\n9gngJKAH0Bs4H3hgP/tE4O9AK6A1cATwsxT2KFVrfilLB87zRsosNVNx0BDCiUAvIDvG+G5J7SZg\nYgjhJzHGFfvYfVOMcWUq+pIkSVLVkqors12ANV8G2RIvUHzl9ez97PvNEMLKEMK/Qwi/CyHUS1GP\niZeJVwcqo6dUvMehHvNg9z/Q/co7PhP/bmSSTPvzqax+Kvp9KuJ4B3OMVJ03B3Ps6ibT/nyq67mT\nad85B3PsipSqMNsa+Kx0IcZYCKwu2bY3jwPfAi4AfgdcBfy/1LSYfJn2jwoYZlO9n2G2YmTan091\n/UI+2GNU1S/kJMi0P5/qeu5k2nfOwRy7Ih3QNIMQwn8Dt+5jSKR4nuxBiTE+VOrl+yGEFcALIYRj\nYowL97JbXYC5c+ce7Nsm1rp168jLy0t3G2VURk+peI9DPebB7n+g+5V3fEWPq2oy7XNXVj8V/T4V\ncbyDOUaqzpvyjs20vz+VKdM+e3U9dzLtO6c8Y0vltLrlbqCcQoyx/INDaA4038+wjym+ovqnGOOO\nsSGELGALMCjGOL6c71cf+ALoFWOcupcxQyi+oitJkqTM9s0Y4xMVecADujIbY/wc+Hx/40IIbwJN\nQwhnlJo32wMIwFsH8JZnUHy1d/k+xjwPfBP4hOKwLEmSpMxSF2hPcW6rUAd0ZfaADhzCJKAl8D2g\nNvAw8HaM8aqS7W2AF4GrYozvhBA6AEOASRQH5tOAPwOLY4wXpaRJSZIkJVpKluYqMQS4j+JVDIqA\np4CbS22vBRwP1C95vQ34WsmYBsAS4EngtynsUZIkSQmWsiuzkiRJUqql8glgkiRJUkoZZiVJkpRY\nVT7MhhCODCG8HEJ4P4QwM4QwKN09SUkRQngmhLA6hDAm3b1ISRBC6BNC+CCEMC+E8O109yMlxaF8\n31T5ObMhhNZAyxjjrBBCKyAXOC7GuDnNrUkZL4RwPtAIuCbGeEW6+5EyWcl66nOA7sAGir9vusQY\n16S1MSkBDuX7pspfmY0xrogxzir573xgFdAsvV1JyRBjnEbxg0sk7d9Xgdkl3zsbKV5q8uI09yQl\nwqF831T5MFtaCCEbqBFjXJbuXiRJVU4boPT3y6dA2zT1IlUbGRdmQwjdQggTQgjLQghFIYS+exjz\ngxDCwhDC5hDCjBDCWeU4bjNgBPDdVPQtpVuqzh2pOvD8kQ5OJpw7GRdmKX5gwkzg+xQ/yraMEMI3\ngLuAX1P8uNv3gOdDCC1Kjfl+COHdEEJeCKFOCKE2MBb4XYzxQB6nKyVJhZ87ldO2lBEO+fyh+Ers\nkaVety2pSVVZRZw7hySjbwALIRQB/WOME0rVZgBvxRhvLnkdKH5a2L0xxj/s5TgjgbkxxjsroW0p\n7Srq3CkZdwHwgxjj4NR2LWWGgz1/St0AdgHFN4D9C+jqDWCqLg71u+dgv28y8crsXoUQagHZwItf\n1mJxGn8B6LKXfc4FBgP9S11x6lQZ/UqZ4mDOnZL9pgKjgUtDCItDCGenulcp05T3/IkxFgI/Bl4B\n8oA/GWRVnR3Id8+hfN/UrJh2K00LIAvI36WeD5ywpx1ijG+QvM8pVbQDPncAYow9U9mUlBDlPn9i\njM8Cz1ZSX1KmO5Bz56C/bxJ1ZVaSJEkqLWlhdhVQCLTapd4KWFH57UiJ4bkjHTzPH+ngVMq5k6gw\nG2PcTvETVXp8WSuZSNwDmJ6uvqRM57kjHTzPH+ngVNa5k3FzSUMIDYCvAKGk1CGEcBqwOsa4BPgz\n8EgIIRd4GxgG1AceSUO7Usbw3JEOnuePdHAy4dzJuKW5QgjdgZfZfa2yETHG60rGfB/4GcWXqWcC\nN8UY36nURqUM47kjHTzPH+ngZMK5k3FhVpIkSSqvRM2ZlSRJkkozzEqSJCmxDLOSJElKLMOsJEmS\nEsswK0mSpMQyzEqSJCmxDLOSJElKLMOsJEmSEsswK0mSpMQyzEqSJCmxDLOSJElKLMOsJEmSEssw\nK0mSpMT6/4+JBUmymXVnAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f21b18b3590>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(1, 1, figsize=(8, 4))\n",
"\n",
"ax.semilogx(p1[:,0], p1[:,2], '-', c='#008b8b', lw=3)\n",
"ax.semilogx(p2[:,0], p2[:,2], '-', c='#008b8b', lw=3)\n",
"ax.semilogx(p1[:,0], poly1[0]*p1[:,0]**2 + poly1[1]*p1[:,0] + poly1[2], '--', c='black', lw=3)\n",
"ax.semilogx(p2[:,0], poly2[0]*p2[:,0]**2 + poly2[1]*p2[:,0] + poly2[2], '--', c='black', lw=3)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Implementation\n",
"\n",
"These new fits better represent the relaxed models, but will they work when implemented as seed values? "
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"log(T) and log(L) Coefficients for the lowest mass objects: \n",
"[-1.27192877 0.9650018 3.36316571] [-14.33705482 5.09735054 -0.6592411 ]\n",
"\n",
"\n",
"log(T) and log(L) Coefficients for low mass objects: \n",
"[ 0.11365404 -0.38799192 0.45719128 3.45458154] [-0.45439653 1.7710227 0.06103889]\n"
]
}
],
"source": [
"print \"log(T) and log(L) Coefficients for the lowest mass objects: \\n\", tpoly1, poly1\n",
"print \"\\n\\nlog(T) and log(L) Coefficients for low mass objects: \\n\", tpoly2, poly2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The new parameterization had no influence over model convergence."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## UPDATE\n",
"\n",
"Error appears to have been due to a value (JCORE) being read or set to zero erroneously. Since it is used to define an array index later in the routine (STARIN), a memory reference error was thrown and SEGFAULT initiated. A temporary fix has been issued."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
arcana261/notes | jupyter/logistic_regression.ipynb | 1 | 166287 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"id": "indian-inquiry",
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import math\n",
"from scipy import optimize\n",
"from scipy.special import expit"
]
},
{
"cell_type": "code",
"execution_count": 2,
"id": "naked-desktop",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" x1 x2 y\n",
"count 1.000000e+02 1.000000e+02 100.000000\n",
"mean -7.910339e-17 -3.885781e-16 0.600000\n",
"std 1.000000e+00 1.000000e+00 0.492366\n",
"min -1.828813e+00 -1.916760e+00 0.000000\n",
"25% -7.567373e-01 -9.709414e-01 0.000000\n",
"50% 7.136900e-02 7.858797e-02 1.000000\n",
"75% 7.486940e-01 7.070312e-01 1.000000\n",
"max 1.756768e+00 1.756865e+00 1.000000\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>x1</th>\n",
" <th>x2</th>\n",
" <th>y</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.454739</td>\n",
" <td>1.002172</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>-1.341640</td>\n",
" <td>0.528167</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>-0.075407</td>\n",
" <td>0.790305</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>-0.851656</td>\n",
" <td>-0.771617</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.501142</td>\n",
" <td>1.051400</td>\n",
" <td>1</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" x1 x2 y\n",
"0 0.454739 1.002172 1\n",
"1 -1.341640 0.528167 0\n",
"2 -0.075407 0.790305 1\n",
"3 -0.851656 -0.771617 0\n",
"4 0.501142 1.051400 1"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data = pd \\\n",
" .read_csv('data/logistic_regression.txt', names=['x1', 'x2', 'y']) \\\n",
" .sample(frac=1)\n",
"data.reset_index(inplace=True, drop=True)\n",
"\n",
"for column in data.columns:\n",
" if column == 'y':\n",
" continue\n",
" data[column] = (data[column] - data[column].mean()) / data[column].std()\n",
"\n",
"print(data.describe())\n",
"data.head()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"id": "ambient-uncle",
"metadata": {},
"outputs": [],
"source": [
"def draw_train_set(data):\n",
" ax = data[data['y'] == 0].plot.scatter(x='x1', y='x2', c='red')\n",
" data[data['y'] == 1].plot.scatter(x='x1', y='x2', c='blue', ax=ax)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"id": "annual-connecticut",
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAeiElEQVR4nO3dbbBdVXkH8P/fvJArSQDJrfIWrlimigwFchJFrYOCTGAcAoiU64wSjRNR0Rk+2FKdast0bNUP2BZbzBiGaEtAqELUaOBiHdpxkNwgSAIGAyaSmJoraAQNJsGnH/Y+5uTcffZ522uvtfb+/2bO3HPP2ffc5+y3Z73ttWlmEBER6eQlvgMQEZGwKVGIiEguJQoREcmlRCEiIrmUKEREJNdM3wG4sGDBAhsbG/MdhohINDZt2vRLMxvNeq+SiWJsbAyTk5O+wxARiQbJHZ3eU9OTiIjkUqIQEZFcShQiIpJLiUJERHIpUYiISC4liqJNTQEbNyY/RUQqQImiSGvXAiefDLztbcnPtWt9RyQiMjQliqJMTQErVgD79gF79yY/V6xQzUJEoqdEUZTt24HZsw9/bdas5HURkYgpURRlbAzYv//w1w4cSF53SF0i9aTtLmVSoijK6CiwejUwMgLMn5/8XL06ed0RdYnUk7a7lI1VvBVqo9Ewb3M9TU0lzU1jY06TxNRUcpLYt+/QayMjwI4dTv+tpErazJn/V9tdXCC5ycwaWe+pRlG00VFg8WLnR626RMrV2tTjs0Qf03ZX81h1KFFEylOXSC21JoaFC4Hly/0Nbhtmu5d54lbzWLUoUUTKQ5dILbWPen7hhekn6jJL9INu9zJP3BopXj2VvB9FKXw1UrcYHwfOP997GJXWbOpp7RNoV3ZNrt/t3nribn6PFSuSz3Cxz2Sts2Yy1T4aJyWKQaxdmxxps2cnxcvVq5Oj14PRUR18LmU19cyaBcycmfw8cMBPTa6f7V72iVvNotWjpqd+qV5dK1lNPWvWJKOMJiaSn57KCD0r+8StZtHqUY2iX6pX106npp5YNnfzxL1iRXm1IDWLVovXREHyZgBvB7DHzE7PeP9cAHcD+Gn60tfM7PrSAsyienUtxd7E5+PEHfs6k0N8Nz3dAmBpl2X+x8zOTB9+kwSgerVEq6RLfKSCvNYozOx+kmM+YxiI6tUiUiO+axS9OIfkIyS/TfK1nRYiuZLkJMnJqTI6llU8kwDpamhxIfRE8RCAk83szwH8K4C7Oi1oZqvMrGFmjVGdvKWGdDW0uBJ0ojCz35jZ8+nz9QBmkVzgOSyR4GjUtrgUdKIg+QqSTJ8vQRLvM36jEglPTJMFAmoii43v4bFrAZwLYAHJnQA+BWAWAJjZTQAuB/BBkgcB7ANwpVVxXnSRIcU0ajugiQ2kR7ofhUhFNE/ArRfVhXYC1v00wpV3PwpdmS1SETGM2tbEBnFSohCpkNCvhh4bmz4T7wsvhNlEJocE3ZktIv4V3fHc3tpdwdbvylGiEJGOir42Y/t24KUvPfy1kZFwR2dJQolCRKaZmgLuuaf4azNiGp0lhyhRSDQ09r4czVrEZZdN708Y9toMzakZJyUKiYKmpyhH6xXev/3t9PeLKP2Pj8d14ydRopABlVm61/QU5cm6whsAjjyy2NJ/FebUrFMNV4lC+lZ26T626SliltWHMGcO8LWvqfTfqm41XCUK6YuP0r06QMuT1Ydw883ABRfEXfovUh1ruEoU0hcfpXt1gJYrrw+hTs0trVq/dx1ruEoUFVf0ge2rdK8O0HJl9SHUrbmlqf17P/RQ/Wq4ShQV5uLA9lm6r0IHaKzq2NwCZH/va68Fbrih3GPAd01OiaKiXB7YKt3XTx2bW4DO3/vss8s7BkKoyWlSwIpyPUtn6JPPDavZFh3qLKxlq+uAgrzvXcYx0Frgax7LK1YkswSXuV+qRlFRdT2wixBCCS4kzaRZdnNLCHwPpAilJqcbF1VYDDeyCU2oN9bxVcNpvxvdDTckzS51q2n5Wv9l7o95Ny5SjaLC1JfQv1BKcK181XA6deTWLUkA/gZS+K7RNPm+Z/bNAN4OYI+ZnZ7xPgH8M4CLAPwOwHIze6jcKONW9b6EooXWZOejjbpZev7Vr3Q3uhCEcOdC3zWKWwAszXn/QgCnpo+VAP69hJikxkIpwTWVXcNprb0sWzZ99lj1c/nhe2i41xqFmd1PcixnkWUAvmxJR8oDJI8meZyZ7S4nQqmjEEpwTWXWcLJqL7NmJcmytZ9LtYn6CX147AkAnm75fWf62rREQXIlkloHFi5cWEpwUl2hNNk1azjtgxJcxJY1pHpkBLjjDuCYY/wnTfEn9ETRMzNbBWAVkIx68hyOSGHKquF0qr2cdZYSRN357qPoZheAk1p+PzF9TaRWymijDq1/RsIReo1iHYBrSN4G4HUA9qp/QsSdkPpnJBy+h8euBXAugAUkdwL4FIBZAGBmNwFYj2Ro7DYkw2Pf6ydSkfoIpX9GwuF71FPuJWDpaKcPlxSOiIhkCL2PQkREPFOiEBGRXEoUIg75vuGMSBGUKEQc0XTlUhVKFCIO1PXWoVJNShQiDoQ4XbnIoJQoRBwIbbpykWEoUYg4oOkwpEpCn8JDhuHr/o0CQNNhSHWoRlFVGnITBN83nAE0RFeGp0RRRRpyIymVF6QIShQu+SrKachNEHyX5FVekKIoUbjisyinITfehVCSV3lBiqJE4YLvopyG3Hjle/M3qbwQDt+1y2EpUbgQQlFufBzYsQOYmEh+jufO6C4FCmHzAyovhCKE2uWwmNzyoVoajYZNTk76C2BqKtkj2u9Sv2OHjtIaCG3zxzpKOta4W4W2L+QhucnMGlnvqUbhgsuiXOx12BoIrSQfwhDdflWhFA6EU7sclmoULhVdJFq7Nmnsnj07aXxevTq6JqXQSoku4wntu8YiplJ4NzF9l2BrFCSXktxKchvJ6zLeX05yiuTD6eP9PuIcWJFFuVB6SIcQWinRdTwxluSLNkgFuCqlcCC82uXAzMzLA8AMAE8COAXAbACPADitbZnlAG7s97MXLVpkXu3ZY/bgg8nPojz4oNlRR5kBhx7z5yevR2DPHrORkcPDHxkpdhXFHE8V3Xprsk6POir5eeutvf1dFbeNi1NC0QBMWodzqs8axRIA28zsKTPbD+A2AMs8xlMMV8XUyMc6hlZKDC2eqhmmAlyZUniL2GuXPhPFCQCebvl9Z/pau3eQ/BHJO0me1OnDSK4kOUlycqqKl8JGfvSEludCi6dqhk3EGt0dltBHPX0DwJiZnQHgXgBrOi1oZqvMrGFmjVFfJ0/XxdSIj57Q8lxo8VRNp0Q8d27vfRaxl8KrxOc047sAtNYQTkxf+yMze6bl1y8B+GwJcQ2ujGLq6Gi0R05o026HFk+VNBPxihVJWenAgeT5okVRD9qrLW/DY0nOBPAEgPOQJIiNAN5lZltaljnOzHanzy8F8Ndm9vpun+11eGxzCGvz6NDRIDXWHCI8d26SJGIYJlpXecNjvdUozOwgyWsAbEAyAupmM9tC8nokve/rAHyU5MUADgJ4FskoqLB1K6ZqcH00tKmG16wAb9yY1CRaE0WzVVbrNny64K5MFbhgri6yNpWaqQYX04VndZVXo1CiKIuOlGhkbapZs4CZM5Xjh6FWWbeGrQEHe2V2rWjgfjSyNtWBA1FfFB+EiAftBc/1LANKFGXRwP1oZG2qdsrxg9GQ1+KVMbuPEkVZXAzc10yyTrRvqjlzsmsYyvESgjIaK5QoylRk3Tu0GfYqpnVT/exnwC236OI8CVMZjRXqzI6ROsa90HBZCVURAwWCvI5ChtCsa2pQeqkivijeGSXPMLieZUBNTzFSx3gQqthF1M93qmLrZ8zb1OVAASWKGFV0RruYDtIqniT7+U4VuI/WNFXcpkVRH0XMKlTvj+mi9Sp2EfX7nTZuTE6oe/ceem3+/KTzf/Fi9/EWrYrbtF+64K6qKjIoPbbSaRWvnez3OxUxjXhIQt+mebXtMmriShTiXegHabsqdhH1+52yWj+b04jH2HQT8jbNaxIrrbms0z1SY354v2e29CXGeyQ37wc9f35/94MO2SDfqXkv6Mcei28btgtxm+YdG0UfN8i5Z7aGx4p3WTe5Cb1vvoo3PRrkO1VpGvEQt2neSHigvHWuRCFBCPEg7aaK11UM+p1CbrrpR2jbtNt6LWudq49CglGRvvlaquiIbe/y1muZ61zDY0WkMBUasR2UvPVa1DrXFB7SGx3lQYh5M4TWdFMVeeu1jHXutemJ5FKSW0luI3ldxvtHkLw9ff8HJMc8hFkPuiw1CNoMEiJvTU8kZwB4AsDbAOwEsBHAuJk91rLMhwCcYWZXk7wSwKVm9pfdPltNT33SZalB0GYIS8w1u0GEemX2EgDbzOwpM9sP4DYAy9qWWQZgTfr8TgDnkWSJMdZDbFe8VZQ2Qzhc1exims+slc9EcQKAp1t+35m+lrmMmR0EsBfAsVkfRnIlyUmSk1OxbYVuXO9dVRnbGDlthjC4mlIm5mbF3ERBcj7JV2W8foa7kAZjZqvMrGFmjdEq1RPL2LsiH9sYaymtXeSboTJc1Oxim8+sXcdEQfIKAD8G8F8kt5BsnRPylgL+9y4AJ7X8fmL6WuYyJGcCOArAMwX87ziUuXcVeZvWEsVcSssS6WaoFBc1u9ibFfNqFB8HsMjMzgTwXgBfIXlp+l4R/QQbAZxK8pUkZwO4EsC6tmXWAbgqfX45gO9aFS/86KTsvSuyK95iL6V1EtlmqBwXNbvYmxXzrqOYYWa7AcDMHiT5FgDfJHkSgKFP1mZ2kOQ1ADYAmAHgZjPbQvJ6JJNTrQOwGkmC2gbgWSTJpD5i37sc0x1hxZWip5SJcT6zVh2Hx5L8PoB3m9mTLa/NA3AXgDeZ2RGlRDiASg2PLeKu6RWl4aQSm5CH3A56ZfYHAbyE5GnNaxvM7DmSS1G3kr1PMc6WN6g+j6LYS2lSP7Feud71gjuSmwF8BcBnAcxJfzbM7Bz34Q2mUjWKuhjiXqghl9JEYjHsBXevQzLy6PtIOqB/DuCNxYUntTdkr7Q6f0Xc6iVRHACwD8AIkhrFT83sD06jknqJfeygSMX1kig2IkkUiwH8BYBxknc4jUrqRaO7RILWS6JYYWafNLMDZrbbzJZh+vUOIoPTJckiQet6Pwozm9YrbGZfcROO1FadRnd1oE55GUQZ+41uhSrhGB1N9vbt2+O/vLpPVZuKRMpR1n6jROFKVWaqK1NNz5ZVnYpE3Cpzv1GicKGmJ7xMvSbMGp8tNehLBlHmfqNEUbQan/Cm6SdhOtzrQ6/cadCXDKLM/UaJomgqHib6TZiO9voYKnca9CWDKHO/UaIomoqHiX4TpoO9PqbKne5DIYMoa7/pOjxW+qSZ6hKDJMyCh8jGNg15rBPGiV9l7DdKFC7omoDBE2aBe70qdyLFUKJwRcVD7wlTlTuRYihRiFueE6YqdyLDU6KQylPlrj40DYobXkY9kXwZyXtJ/iT9eUyH5V4k+XD60ESEItJRDEOhY+VreOx1AO4zs1MB3Jf+nmWfmZ2ZPi4uL7waC/3qNBFM301jGgodI1+JYhmANenzNQAu8RSHtFKRTCKQtZvqOle3ut4z28k/JX9tZkenzwngV83f25Y7COBhAAcB/JOZ3ZXzmSsBrASAhQsXLtqxY0fhcVfa1FRy1LVedDAyklzFo8ZeCUSn3XTTJmDRIu2+wxj2ntmD/tMJkpszHstal7MkU3XKViengb8LwOdJvqrT/zOzVWbWMLPGqPaM/qlIJhHotJs+/7ymQXHJ2agnMzu/03skf0HyODPbTfI4AHs6fMau9OdTJL8H4CwAT7qIt/Z0dZpEIG83XbxYQ6Fd8dVHsQ7AVenzqwDc3b4AyWNIHpE+XwDgjQAeKy3CutHMdBKBbrvp6GiSMLTbFstXH8WxAL4KYCGAHQCuMLNnSTYAXG1m7yf5BgBfBPAHJAnt82a2upfPbzQaNjk57Q6u0gsNRJcIaDctXl4fhZdE4ZoShYhIf7x0ZouISDUoUYiISC4lChERyaVEIRIZzbIiZVOikDjV9GypWVbEByUKccPliTyUs2XJyUoT34kvShRSPJcn8lDOlh6SlWZZEV+UKKRYrk/kIZwtPSUrzbIivihRSLFcn8hDOFt6SlaaZUV8UaKQYrk+kYdwtvSYrMbHk6mzJyaSn+Pjzv+liBKFFKyME3kIZ8uPf9xbstLEd1I2Z9OMS42Nj2fP91zkTG6jo37OlGvXJv0Rs2cDZsDHPgZ84AM6a0ulqUbRqqZj851oL/aGMqR1GO2d2C+8AHz6076jEnFOiaKpCieyUIUypHVYIYy4EvFAiQKozoksVFkn2Bkz4jvBhjDiSsQDJQpAJUXXsk6wzz8PPPSQl3AGFsKIq5pT67AfShSASoqujY4CN9ww/fVrr43viA9hxFVNqXXYHy+JguQ7SW4h+Yf09qedlltKcivJbSSvcxaQSorunX02MG/e4a/FWmvT+NTSqXXYL181is0ALgNwf6cFSM4A8AUAFwI4DcA4ydOcRaSSoltjY8DBg4e/plpb1MpsBlLrsF9eEoWZPW5mW7sstgTANjN7ysz2A7gNwDKngbksKda9cVW1tkopuxlIrcN+hdxHcQKAp1t+35m+Fh81riY61drqnkTzBLhufDQDqZzhl7NEQXKC5OaMh5NaAcmVJCdJTk4FdFCpcbVNFS/Ec8XzuumUo3w1A6l12B9nicLMzjez0zMed/f4EbsAnNTy+4npa53+3yoza5hZYzSkYoYaVztTEu3M87rJy1E+m4E0jsCPkJueNgI4leQrSc4GcCWAdZ5j6p8aV7NNTQHr1wMz26YbUxJNeCxgdMtRagYaToCtiV35Gh57KcmdAM4B8C2SG9LXjye5HgDM7CCAawBsAPA4gK+a2RYf8Q5FR9V0zeLqRz4CPPfc4e8piSY8FjB6yVF1aQYq+qQea0srzcx3DIVrNBo2OTnpO4zDFTlzasymppIjZN++w1+fOxd48cUkiVb1rNOv5ky1s2YlSaKkdZO1iUZGkoRQp123daLg/fuHX/2hr1eSm8ws87q2kJueqkWNq4ms4uq8ecCNN1a7aDoIT8V215XgGJpeXHQRxdxdqftRSLmymlQOHgQuukhJNIun+250uqXIsIoupbvSPKm3lv6bJ/VB10XM3ZWqUbQrorgTQ5HJF/XZRKPoSnBMg9xcnNRj3vWVKFoV0dMUa29VmerSEyqHcdH04qpM5uqkHuuur87spn57mrI6p0PvrRLxqOjDo4xmrNbDHKj2eBR1Zvein+JOp1pDzL1VEpYKNl8WWUovqxmr2fw2MVHvhgIliqZeGyXz9tCYe6tkOl8n6wo3X/bc9NJl3ZdZJoupb8UVJYqmXos7eXtozL1VcjhfJ+sanJW6dpL3sO7LLJOpoUB9FNN1uzCul4ZWXVwXN599TRs3JifIvXsPvTZ/flIEX7zY7f8OQR/rvqzrEevS9ag+in50K+70UmvQxXVx81mEDKX50lezWx/rvqwRRGoo0AV3g3F1NZKEwff0qKtXTy8ql7mP+bwqrs91X9b1iHU/5NX0JJKl7HmW2psrfTVfhtDO4mmOq7rLa3pSjUIkS5lFyE4leB/FVhdzV/Srue5/+MPk97POKuf/SkfqoxDppIy+ptBGOYXSRzIxAVxyCXDFFZUbIhwjJQoRn0IbexlCz21oyVPU9CTiVSgl+Fa+e25DaP6Sw6hGIdUT0/QXIZTgO8Xla4h3iMmz5pQopFpinP4i1ilFXQk1efYjpsJKD7wMjyX5TgB/B+A1AJaYWeZYVpLbATwH4EUABzsN3Wqn4bE1FcLQTilOrDMcxHJ3pjYhXpm9GcBlAO7vYdm3mNmZvSYJqbHQOoZlODHOcDBoR3zgNRAvicLMHjezrT7+t1SY2rbFt0EKKxE0l4beR2EA7iG5ieTKvAVJriQ5SXJyKtCsLI5VoW1b4tZvYSWSocDOEgXJCZKbMx7L+viYN5nZ2QAuBPBhkm/utKCZrTKzhpk1RnViqC91DItP/RZWImkudXYdhZmdX8Bn7Ep/7iH5dQBL0Fu/htRZWTPFiWTp5zqUSJpLg216InkkyXnN5wAuQNIJLiIStl474iNpLvWSKEheSnIngHMAfIvkhvT140muTxd7OYD/JfkIgAcBfMvMvuMjXhERZyJoLtU04yIiEuR1FCLFCnwcukjMlCgkfhGMQxeJmRKFxC2ScegiMVOikLhFMg5dJGZKFBK3SMahi8RMiULiFsk4dJGY6Q53Ej/fd2QTqTglCqkGTdsh4oyankREJJcShYiI5FKiEBGRXEoUIiKSS4lCRERyKVGIiEguJQoRyaYZeSWlRCEi02lGXmmhRCEih9OMvNJGiUJEDqcZeaWNr3tmf47kj0n+iOTXSR7dYbmlJLeS3EbyupLDFKknzcgrbXzVKO4FcLqZnQHgCQB/074AyRkAvgDgQgCnARgneVqpUYrUkWbklTZeJgU0s3tafn0AwOUZiy0BsM3MngIAkrcBWAbgMfcRitScZuSVFiHMHvs+ALdnvH4CgKdbft8J4HWdPoTkSgArAWDhwoVFxidST5qRV1LOEgXJCQCvyHjrE2Z2d7rMJwAcBPCfw/4/M1sFYBUANBoNG/bzREQk4SxRmNn5ee+TXA7g7QDOM7OsE/suACe1/H5i+pqIiJTI16inpQD+CsDFZva7DottBHAqyVeSnA3gSgDryopRREQSvkY93QhgHoB7ST5M8iYAIHk8yfUAYGYHAVwDYAOAxwF81cy2eIpXRKS2fI16+tMOr/8cwEUtv68HsL6suEREZDpmdw/EjeRzALb6jqNHCwD80ncQPYglTiCeWBVn8WKJNcQ4TzazzGFuIQyPdWGrmTV8B9ELkpMxxBpLnEA8sSrO4sUSayxxNmmuJxERyaVEISIiuaqaKFb5DqAPscQaS5xAPLEqzuLFEmsscQKoaGe2iIgUp6o1ChERKYgShYiI5KpEoojpRkgk30lyC8k/kOw4PI7kdpKPpleuT5YZY/r/e40zhHX6MpL3kvxJ+vOYDsu9mK7Ph0mWNh1Mt3VE8giSt6fv/4DkWFmxtcXRLc7lJKda1uH7PcV5M8k9JDd3eJ8k/yX9Hj8ieXbZMaZxdIvzXJJ7W9bnJ8uOsWdmFv0DwAUAZqbPPwPgMxnLzADwJIBTAMwG8AiA0zzE+hoAfwbgewAaOcttB7DA4zrtGmdA6/SzAK5Ln1+Xtf3T9573EFvXdQTgQwBuSp9fCeD2QONcDuDGsmPLiPXNAM4GsLnD+xcB+DYAAng9gB8EGue5AL7pe3328qhEjcLM7rFkbigguRHSiRmL/fFGSGa2H0DzRkilMrPHzSz4q8Z7jDOIdZr+zzXp8zUALvEQQye9rKPW+O8EcB5JlhgjEM627MrM7gfwbM4iywB82RIPADia5HHlRHdID3FGoxKJos37kJQm2mXdCOmEUiIajAG4h+Sm9KZMIQplnb7czHanz/8PwMs7LDeH5CTJB0heUk5oPa2jPy6TFnj2Aji2lOgyYkh12pbvSJtz7iR5Usb7IQhlv+zFOSQfIfltkq/1HUwn0UzhUfaNkIbRS6w9eJOZ7SL5J0hm2f1xWkIpTEFxliIv1tZfzMxIdhrzfXK6Tk8B8F2Sj5rZk0XHWmHfALDWzH5P8gNIakFv9RxTzB5Csk8+T/IiAHcBONVvSNmiSRQW0Y2QusXa42fsSn/uIfl1JE0DhSaKAuIMYp2S/AXJ48xsd9rEsKfDZzTX6VMkvwfgLCTt8i71so6ay+wkORPAUQCecRxXu65xmllrTF9C0jcUoihuemZmv2l5vp7kv5FcYGahTRZYjaanqt0IieSRJOc1nyPprM8cOeFZKOt0HYCr0udXAZhWGyJ5DMkj0ucLALwRwGMlxNbLOmqN/3IA3+1Q2HGpa5xt7fwXI7lPTIjWAXhPOvrp9QD2tjRNBoPkK5p9USSXIDkfl11A6I3v3vQiHgC2IWmTfDh9NEeQHA9gfctyFwF4Akkp8hOeYr0USZvp7wH8AsCG9liRjDx5JH1s8RFrL3EGtE6PBXAfgJ8AmADwsvT1BoAvpc/fAODRdJ0+CmBFifFNW0cArkdSsAGAOQDuSPfjBwGc4mk9dovzH9P98REA/w3g1Z7iXAtgN4AD6T66AsDVAK5O3yeAL6Tf41HkjC70HOc1LevzAQBv8BFnLw9N4SEiIrkq0fQkIiLuKFGIiEguJQoREcmlRCEiIrmUKEREJJcShUiJSH6H5K9JftN3LCK9UqIQKdfnALzbdxAi/VCiEHGA5OJ08rw56ZX2W0iebmb3AXjOd3wi/YhmrieRmJjZxvTmSP8AYATAf5hZiNOwiHSlRCHizvVI5lB6AcBHPcciMjA1PYm4cyyAuQDmIZnPSSRKShQi7nwRwN8iuT/KZzzHIjIwNT2JOEDyPQAOmNmtJGcA+D7JtwL4ewCvBjCX5E4ks9hu8BmrSDeaPVZERHKp6UlERHIpUYiISC4lChERyaVEISIiuZQoREQklxKFiIjkUqIQEZFc/w+FUoP/lbNFpQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"draw_train_set(data)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"id": "fossil-causing",
"metadata": {},
"outputs": [],
"source": [
"def extract(data, start, end):\n",
" m = data.shape[0]\n",
" view = data[start:(end - 1)]\n",
" \n",
" dropped_view = view\n",
" if 'y' in data.columns:\n",
" dropped_view = dropped_view.drop('y', axis=1)\n",
" if 'y^' in data.columns:\n",
" dropped_view = dropped_view.drop('y^', axis=1)\n",
" X = dropped_view.to_numpy()\n",
" y = None\n",
" if 'y' in data.columns:\n",
" y = view['y'].to_numpy().reshape(view.shape[0], 1)\n",
" return X, y\n",
"\n",
"def expand(data, p, min_p=0):\n",
" p = p + 1\n",
" m = data.shape[0]\n",
" n = data.shape[1]\n",
" result = data.copy()\n",
" \n",
" pv = [0] * n\n",
" while True:\n",
" r = 1\n",
" sumof = 0\n",
" for i in range(0, n):\n",
" if data.columns[i] in ['y', 'y^']:\n",
" continue\n",
" pv[i] = pv[i] + r\n",
" r = pv[i] // p\n",
" pv[i] = pv[i] % p\n",
" if pv[i] < min_p:\n",
" sumof = 0\n",
" break\n",
" sumof = sumof + pv[i]\n",
" if r > 0:\n",
" break\n",
" if sumof < 2:\n",
" continue\n",
" toadd = None\n",
" name = ''\n",
" for i in range(0, n):\n",
" if pv[i] < 1 or data.columns[i] in ['y', 'y^']:\n",
" continue\n",
" name = name + data.columns[i]\n",
" if pv[i] > 1:\n",
" name = name + '^' + str(pv[i])\n",
" temp = data[data.columns[i]].pow(pv[i])\n",
" if toadd is None:\n",
" toadd = temp\n",
" else:\n",
" toadd = toadd.add(temp)\n",
" \n",
" result[name] = toadd\n",
" \n",
" result.insert(0, 'x0', [1] * m)\n",
" \n",
" return result\n",
" \n",
"\n",
"def cost_fn(theta, X, y, lamb):\n",
" # Note: np.multiply performs element-wise multiplication instead of matrix multiplication\n",
" # Note: np.matmul performs matrix multiplication\n",
" # Note: expit is the sigmoid function\n",
" m = X.shape[0]\n",
" n = X.shape[1]\n",
" Theta = theta.reshape(n, 1)\n",
" \n",
" h = expit(np.matmul(X, Theta))\n",
" \n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
" result = result[0,0]\n",
" result = result + (lamb / (2 * m)) * (np.sum(np.multiply(Theta, Theta)) - math.pow(Theta[0,0], 2))\n",
" \n",
" return result\n",
"\n",
"def gradient_fn(theta, X, y, lamb):\n",
" m = X.shape[0]\n",
" n = X.shape[1]\n",
" Theta = theta.reshape(n, 1)\n",
" \n",
" h = expit(np.matmul(X, Theta))\n",
" result = (np.matmul(X.T, (h - y)) / m)\n",
" \n",
" lamb_vector = np.ones((n, 1))\n",
" lamb_vector[0, 0] = 0\n",
" \n",
" result = result + (lamb / m) * np.multiply(lamb_vector, Theta)\n",
" \n",
" return result.reshape(n)\n",
"\n",
"def solve(X, y, lamb):\n",
" n = X.shape[1]\n",
" result = optimize.minimize(\n",
" lambda theta: cost_fn(theta, X, y, lamb),\n",
" jac=lambda theta: gradient_fn(theta, X, y, lamb),\n",
" x0=np.array([0] * n),\n",
" method='BFGS')\n",
" return result.x.reshape(n, 1)\n",
"\n",
"def predict(X, theta):\n",
" return (expit(np.matmul(X, theta)) >= 0.5).reshape(X.shape[0]).astype(int)\n",
"\n",
"def accuracy(X, y, theta):\n",
" return np.sum((y.reshape(X.shape[0]) == predict(X, theta)).astype(int)) / X.shape[0]\n",
"\n",
"def f1score(X, y, theta):\n",
" yh = predict(X, theta)\n",
" y = y.reshape(X.shape[0])\n",
" tp = np.sum(np.logical_and(yh == 1, y == 1).astype(int))\n",
" fp = np.sum(np.logical_and(yh == 1, y == 0).astype(int))\n",
" fn = np.sum(np.logical_and(yh == 0, y == 1).astype(int))\n",
" return tp / (tp + ((fp + fn) / 2))\n",
"\n",
"def check_gradient_inner(n, cost_fn, gradient_fn):\n",
" EPSILON = 1e-5\n",
" theta = np.random.rand(n)\n",
" result = np.zeros((n,))\n",
" for i in range(0, n):\n",
" theta[i] = theta[i] + EPSILON\n",
" cost_plus = cost_fn(theta)\n",
" theta[i] = theta[i] - 2 * EPSILON\n",
" cost_minus = cost_fn(theta)\n",
" theta[i] = theta[i] + EPSILON\n",
" estimated_grad = (cost_plus - cost_minus) / (2 * EPSILON)\n",
" real_grad = gradient_fn(theta)\n",
" result[i] = (estimated_grad - real_grad[i]) / real_grad[i]\n",
" return result\n",
"\n",
"def check_gradient(data, lamb):\n",
" m = data.shape[0]\n",
" expanded = expand(data, 0)\n",
" X, y = extract(expanded, 0, m + 1)\n",
" n = X.shape[1]\n",
" return check_gradient_inner(\n",
" n,\n",
" lambda theta: cost_fn(theta, X, y, lamb),\n",
" lambda theta: gradient_fn(theta, X, y, lamb),\n",
" )\n",
"\n",
"def select_model(data, max_p):\n",
" m = data.shape[0]\n",
"\n",
" df = pd.DataFrame(index=range(0, max_p + 1), columns=['power',\n",
" 'cost', 'accuracy', 'f1',\n",
" 'cost(minp=p)', 'accuracy(minp=p)', 'f1(minp=p)'])\n",
" for p in range(0, max_p + 1):\n",
" expanded = expand(data, p)\n",
" Xtrain, ytrain = extract(expanded, 0, math.ceil(m*0.8))\n",
" Xcv, ycv = extract(expanded, math.ceil(m*0.8), m + 1)\n",
" theta = solve(Xtrain, ytrain, 0)\n",
" cost = cost_fn(theta, Xcv, ycv, 0)\n",
" acc = accuracy(Xcv, ycv, theta)\n",
" f1 = f1score(Xcv, ycv, theta)\n",
" \n",
" expanded = expand(data, p, p)\n",
" Xtrain, ytrain = extract(expanded, 0, math.ceil(m*0.8))\n",
" Xcv, ycv = extract(expanded, math.ceil(m*0.8), m + 1)\n",
" theta = solve(Xtrain, ytrain, 0)\n",
" cost_minp_eq_p = cost_fn(theta, Xcv, ycv, 0)\n",
" acc_minp_eq_p = accuracy(Xcv, ycv, theta)\n",
" f1_minp_eq_p = f1score(Xcv, ycv, theta) \n",
" \n",
" df.loc[p] = [p, cost, acc, f1, cost_minp_eq_p, acc_minp_eq_p, f1_minp_eq_p]\n",
" \n",
" ax = df.plot.line(x='power', y='cost')\n",
" df.plot.line(x='power', y='cost(minp=p)', ax=ax)\n",
" \n",
" ax = df.plot.line(x='power', y='accuracy')\n",
" df.plot.line(x='power', y='accuracy(minp=p)', ax=ax)\n",
" \n",
" ax = df.plot.line(x='power', y='f1')\n",
" df.plot.line(x='power', y='f1(minp=p)', ax=ax)\n",
" \n",
" df.sort_values(by=['cost'], inplace=True)\n",
" df.reset_index(inplace=True, drop=True)\n",
" df.sort_values(by=['accuracy'], ascending=False, inplace=True)\n",
" \n",
" return df\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 22,
"id": "scientific-afghanistan",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([-2.0490901e-11, 9.0191873e-11, -1.2285678e-11])"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"check_gradient(data, 0)"
]
},
{
"cell_type": "code",
"execution_count": 23,
"id": "confused-neighbor",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([-4.33928864e-10, 3.20162180e-12, 9.89222765e-12])"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"check_gradient(data, 1000)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"id": "automated-pierre",
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>power</th>\n",
" <th>cost</th>\n",
" <th>accuracy</th>\n",
" <th>f1</th>\n",
" <th>cost(minp=p)</th>\n",
" <th>accuracy(minp=p)</th>\n",
" <th>f1(minp=p)</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2</td>\n",
" <td>0.084683</td>\n",
" <td>0.95</td>\n",
" <td>0.941176</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>5</td>\n",
" <td>0.163753</td>\n",
" <td>0.95</td>\n",
" <td>0.941176</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>7</td>\n",
" <td>0.166304</td>\n",
" <td>0.95</td>\n",
" <td>0.941176</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>6</td>\n",
" <td>0.189854</td>\n",
" <td>0.95</td>\n",
" <td>0.941176</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>0.196743</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>9</td>\n",
" <td>0.252572</td>\n",
" <td>0.95</td>\n",
" <td>0.941176</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>10</td>\n",
" <td>0.629281</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>3</td>\n",
" <td>NaN</td>\n",
" <td>1.0</td>\n",
" <td>1.0</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>4</td>\n",
" <td>NaN</td>\n",
" <td>0.95</td>\n",
" <td>0.941176</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>8</td>\n",
" <td>NaN</td>\n",
" <td>0.9</td>\n",
" <td>0.888889</td>\n",
" <td>0.196746</td>\n",
" <td>0.85</td>\n",
" <td>0.842105</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" power cost accuracy f1 cost(minp=p) accuracy(minp=p) f1(minp=p)\n",
"2 2 0.084683 0.95 0.941176 0.196746 0.85 0.842105\n",
"5 5 0.163753 0.95 0.941176 0.196746 0.85 0.842105\n",
"7 7 0.166304 0.95 0.941176 0.196746 0.85 0.842105\n",
"6 6 0.189854 0.95 0.941176 0.196746 0.85 0.842105\n",
"1 1 0.196743 0.85 0.842105 0.196746 0.85 0.842105\n",
"0 0 0.196746 0.85 0.842105 0.196746 0.85 0.842105\n",
"9 9 0.252572 0.95 0.941176 0.196746 0.85 0.842105\n",
"10 10 0.629281 0.85 0.842105 0.196746 0.85 0.842105\n",
"3 3 NaN 1.0 1.0 0.196746 0.85 0.842105\n",
"4 4 NaN 0.95 0.941176 0.196746 0.85 0.842105\n",
"8 8 NaN 0.9 0.888889 0.196746 0.85 0.842105"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAEGCAYAAAB1iW6ZAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAgLUlEQVR4nO3de3zU9Z3v8dcngRBQSAQCSEIIWhTCNRAvFRWr1VVbsXvqDS9HpFv32Fptq27V7nHP4bRnXd3j2a7SddVq20e9FXW7tKW13q/UEoeLXOQihiHIJYQMILeQ5LN/zEyMIcAQZuY3M3k/Hw8ezu83v/x+nx/Bd375/ubz/Zm7IyIi2S8v6AJERCQ5FOgiIjlCgS4ikiMU6CIiOUKBLiKSI3oEdeCBAwd6RUVFUIcXEclK77///lZ3L+nsvcACvaKigpqamqAOLyKSlcxs3cHe05CLiEiOUKCLiOQIBbqISI4IbAy9M/v376euro69e/cGXYp0UFhYSFlZGT179gy6FBE5iIwK9Lq6Ovr27UtFRQVmFnQ5EuPuNDQ0UFdXx4gRI4IuR0QOIqOGXPbu3cuAAQMU5hnGzBgwYIB+cxLJcBkV6IDCPEPp+yKS+TIu0EVEclVLq/Pj3y9nSV0kJftXoCfZokWLmDdvXtBliEgGWr1lJ4++9TGrN3+akv0r0JNMgS4iBxNaFwFg0vDjUrJ/BXonfvnLXzJ+/HgmTJjAddddR21tLeeeey7jx4/nvPPOIxwOAzBnzhzGjh3LhAkTOPvss2lqauKee+7h2WefZeLEiTz77LMBn4mIZJJQuJH+xxRQMaBPSvafUR9bbO9//3YZyz/ZkdR9Vg7txz9cMuaQ2yxbtowf/ehHvPvuuwwcOJBt27Zx/fXXt/15/PHHueWWW/jNb37DrFmzePHFFyktLSUSiVBQUMCsWbOoqanhoYceSmrtIpL9QuFGqoYVp+xDBrpC7+DVV1/l8ssvZ+DAgQD079+f+fPnc/XVVwNw3XXX8fbbbwMwZcoUZsyYwaOPPkpLS0tgNYtI5ovsbmJt/a6UDbdABl+hH+5KOhM8/PDDvPfee/z+979n8uTJvP/++0GXJCIZamE4AkBVeXHKjqEr9A7OPfdc5syZQ0NDAwDbtm3jjDPO4JlnngHgySef5KyzzgLgo48+4rTTTmPWrFmUlJSwfv16+vbty86dOwOrX0QyUyjcSJ7BhLLilB0jY6/QgzJmzBh++MMfMnXqVPLz86mqquLBBx/khhtu4P7776ekpIQnnngCgDvuuIPVq1fj7px33nlMmDCB8vJy7r33XiZOnMhdd93FlVdeGfAZiUgmCIUbGTWkH8f0Sl3sJrRnM7sQ+AmQDzzm7vd2ss0VwP8CHFjs7lcnsc60it8Abe/VV189YLsXXnjhgHX9+/dnwYIFKatNRLJPS6uzKBzhryeVpvQ4hw10M8sHZgPnA3XAAjOb6+7L220zErgLmOLujWY2KFUFi4hkm1Wbd7KrqYVJ5am7IQqJjaGfCqxx97Xu3gQ8A1zaYZtvArPdvRHA3bckt0wRkewVvyGaCYFeCqxvt1wXW9feScBJZvaOmf05NkRzADO70cxqzKymvr6+axWLiGSZeEPR8BQ1FMUl61MuPYCRwDnAdOBRMyvuuJG7P+Lu1e5eXVLS6UOrRURyTijcyKTy1DUUxSUS6BuAYe2Wy2Lr2qsD5rr7fnf/GFhFNOBFRLq1eENRVYqHWyCxQF8AjDSzEWZWAFwFzO2wzW+IXp1jZgOJDsGsTV6ZIiLZKV3j55BAoLt7M3Az8CKwAvi1uy8zs1lmNi222YtAg5ktB14D7nD3hlQVnck6m20xPu/Lkbj44ouJRCJJrCwxV111FatXr077cUVyVSjcSH6eMWFYUcqPldAYurvPc/eT3P1Ed/9xbN097j439trd/fvuXunu49z9mVQWnck6C/T77ruPb33rW0e0n3nz5lFcXJzEyhJz0003cd9996X9uCK5KtpQ1Jc+Banv41TrfyeSOX3uqlWr6NWrV9tkXzNmzOCmm27i9NNP54QTTuD1119n5syZjB49mhkzZrTVUFFRwdatW6mtrWX06NF885vfZMyYMVxwwQXs2bMHgHPOOYdbb72ViRMnMnbsWP7yl78kdH61tbWMGjWKa665htGjR3PZZZexe/duAM466yxefvllmpubk/g3KtI9xRuK0jHcApnc+v+HO2HTB8nd55BxcNEBTa6fk+zpc5944gkmTZr0uWM0NjYyf/585s6dy7Rp03jnnXd47LHHOOWUU1i0aBETJ0783ParV6/m6aef5tFHH+WKK67g+eef59prrwVg9+7dLFq0iDfffJOZM2eydOlSXnvtNb73ve8dcG59+vTh3XffBWDlypX87Gc/Y8qUKcycOZOf/vSn3H777eTl5fGFL3yBxYsXM3ny5K7+TYsI7RqKhhen5Xi6Qu8g2dPnbty4kY4f0bzkkkswM8aNG8fgwYMZN24ceXl5jBkzhtra2gP2MWLEiLaQnzx58ue2mT59OgBnn302O3bsIBKJ8KUvfYlFixYd8Cce5gDDhg1jypQpAFx77bVt5wQwaNAgPvnkkyP4WxORzoTCjUB6bohCJl+hH+ZKOhMkMn1u79692b59++fW9erVC4C8vLy21/HlzoY62m+Tn5/fNuQCHPC5VjNL6Aq9s6+L27t3L7179z7whEXkiITWRRhwTAHl/VPbUBSnK/QOkj197ujRo1mzZk3K6o0/5u7tt9+mqKiIoqKihK7Qw+Ew8+fPB+Cpp57izDPPbHtv1apVjB07NmU1i3QXC8ONVJUfl/KGorjMvUIPSLKnz73kkku47bbbcPeUfFMLCwupqqpi//79PP744wl/3cknn8zs2bOZOXMmlZWV3HTTTQBs3ryZ3r17M2TIkKTXKtKdNO5qYu3WXVxWXZa+g7p7IH8mT57sHS1fvvyAdbnglltu8Zdeeinp+506daovWLDgiL/u448/9jFjxnT63gMPPOCPPfZYp+/l6vdHJBVeWbHJh//gdz7/o61J3S9Q4wfJVQ25pMHdd9/d9rHATFdcXHzAXPAicuRC6yLk5xnjy1LfUBSnIZc0GDx4MNOmTTv8hkfo9ddf79LXVVRUsHTp0k7fu+GGG46iIhGJC4UbGX18ehqK4jLuCj36G4VkGn1fRBLX0uosXp++hqK4jAr0wsJCGhoaFB4Zxt1paGigsLAw6FJEssLKTel5QlFHGTXkUlZWRl1dHXr4ReYpLCykrCyNd+tFsli6G4riMirQe/bsyYgRI4IuQ0TkqITCjQw8toBh/dPboJdRQy4iIrlgYTiS1oaiOAW6iEgSbdvVxMdbd1FVXpz2YyvQRUSSaGFA4+egQBcRSar4E4rS2VAUp0AXEUmi0LpI2huK4hToIiJJ0tzSyuK69DcUxSnQRUSSZOXmnewOoKEoToEuIpIkoXAECOaGKCjQRUSSZuG6YBqK4hToIiJJEkrzE4o6UqCLiCRBw6f7qG3YHdhwCyjQRUSSYmHb+HlxYDUo0EVEkiAUbqRHnjG+rDiwGhToIiJJEH1CUT96F+QHVkNCgW5mF5rZSjNbY2Z3dvL+DDOrN7NFsT9/k/xSRUQyU3NLK4vXbw90uAUSmA/dzPKB2cD5QB2wwMzmuvvyDps+6+43p6BGEZGM9uGmnezZ38Kk4cHdEIXErtBPBda4+1p3bwKeAS5NbVkiItkjyBkW20sk0EuB9e2W62LrOvq6mS0xs+fMbFhnOzKzG82sxsxq9Jg5EckVoXCEgcf2ouy4YBqK4pJ1U/S3QIW7jwdeAn7R2Ubu/oi7V7t7dUlJSZIOLSISrFC4kUnlxYE1FMUlEugbgPZX3GWxdW3cvcHd98UWHwMmJ6c8EZHMtvXTfaxr2B34+DkkFugLgJFmNsLMCoCrgLntNzCz49stTgNWJK9EEZHMtTDgCbnaO+ynXNy92cxuBl4E8oHH3X2Zmc0Catx9LnCLmU0DmoFtwIwU1iwikjE+ayhK/xOKOkrokRruPg+Y12HdPe1e3wXcldzSREQyX2hdI5VD+1HYM7iGojh1ioqIdFFzSytL6rZnxHALKNBFRLos3lBUFXCHaJwCXUSki0IZ0lAUp0AXEemi0LpGSvoG31AUp0AXEemiUDiSEQ1FcQp0EZEu2PrpPsLbgn1CUUcKdBGRLgiti42fZ0CHaJwCXUSkC0LhCD3yjHGlwTcUxSnQRUS6IBRuZEyGNBTFKdBFRI7Q/pZWltRFqMqg8XNQoIuIHLEPN+5k7/7WjBo/BwW6iMgR+6yhqDjYQjpQoIuIHKFQuJFBfXtRWpwZDUVxCnQRkSMUfULRcRnTUBSnQBcROQL1O/exftseJg0vDrqUAyjQRUSOwMIMm5CrPQW6iMgRCIUj9Mw3xmZQQ1GcAl1E5AiEwo1UDi3KqIaiOAW6iEiC4g1FmfZxxTgFuohIgtoaijJw/BwU6CIiCWtrKMqwDtE4BbqISIJC4UYG9+vF0KLCoEvplAJdRCRBmdpQFKdAFxFJQFtDUYaOn4MCXUQkIZ+NnxcHW8ghKNBFRBIQCjfSM98YMzTzGoriFOgiIglYuC7CmAxtKIpLKNDN7EIzW2lma8zszkNs93UzczOrTl6JIiLB2t/SypINkYweP4cEAt3M8oHZwEVAJTDdzCo72a4vcCvwXrKLFBEJ0oqNO2JPKCoOupRDSuQK/VRgjbuvdfcm4Bng0k62+z/APwF7k1ifiEjgQusyd4bF9hIJ9FJgfbvluti6NmY2CRjm7r8/1I7M7EYzqzGzmvr6+iMuVkQkCKFwhCH9ChmaYU8o6uiob4qaWR7wAHDb4bZ190fcvdrdq0tKSo720CIiaREKN2b8cAskFugbgGHtlsti6+L6AmOB182sFjgdmKsboyKSC7bs3EtdY2Y3FMUlEugLgJFmNsLMCoCrgLnxN919u7sPdPcKd68A/gxMc/ealFQsIpJGoXURAKpyIdDdvRm4GXgRWAH82t2XmdksM5uW6gJFRIK0MNxIQX4eY0v7BV3KYfVIZCN3nwfM67DunoNse87RlyUikhlC4UbGlPajV4/MbSiKU6eoiMhBNDW3sqRue1aMn4MCXUTkoFZs3MG+5sx9QlFHCnQRkYPIhhkW21Ogi4gcRCgc4fiiQo4vyuyGojgFuojIQYTWNWbNcAso0EVEOrVlx142RPZQVV4cdCkJU6CLiHTis/FzXaGLiGS1UDhCQX4eY4ZmfkNRnAJdRKQToXXZ01AUp0AXEemgqbmVJRuyp6EoToEuItLB8o07aMqihqI4BbqISAdtTyjKkoaiOAW6iEgHoXBjVjUUxSnQRUQ6WBiOZN1wCyjQRUQ+Z3MWNhTFKdBFRNr5bPxcV+giIlktFHtCUTY1FMUp0EVE2gmFI4zNsoaiOAW6iEhMU3MrH2RhQ1GcAl1EJGbZJ9ujDUVZOH4OCnQRkTahcARAV+giItkuFG5kaFEhQ4oKgy6lSxToIiIxC9c1UpWlwy2gQBcRAWDT9r18sn1v1g63gAJdRARo94SiLOwQjVOgi4gQ7RAt6JHHmKFFQZfSZQp0ERGiV+jjSoso6JG9sZi9lYuIJMm+5haWbtiR1cMtkGCgm9mFZrbSzNaY2Z2dvP8/zOwDM1tkZm+bWWXySxURSY1ln+ygqSX7nlDU0WED3czygdnARUAlML2TwH7K3ce5+0TgPuCBZBcqIpIq2TzDYnuJXKGfCqxx97Xu3gQ8A1zafgN339Fu8RjAk1eiiEhqLQxHKC3uzeB+2dlQFNcjgW1KgfXtluuA0zpuZGbfBr4PFADndrYjM7sRuBGgvLz8SGsVEUmJULiRyVl+dQ5JvCnq7rPd/UTgB8DfH2SbR9y92t2rS0pKknVoEZEu27h9DxuzvKEoLpFA3wAMa7dcFlt3MM8AXzuKmkRE0ia0LgJk//g5JBboC4CRZjbCzAqAq4C57Tcws5HtFr8CrE5eiSIiqRMKN9KrRx6Vx2ffE4o6OuwYurs3m9nNwItAPvC4uy8zs1lAjbvPBW42sy8D+4FG4PpUFi0ikiy50FAUl8hNUdx9HjCvw7p72r2+Ncl1iYik3L7mFpZt2MGMKRVBl5IU2f8jSUSki5ZuiDcUFQddSlIo0EWk21rYNsNi9t8QBQW6iHRj8YaiQVneUBSnQBeRbisUbsyJjyvGKdBFpFv6rKGoOOhSkkaBLiLdUltDUY6Mn4MCXUS6qXhD0egcaCiKU6CLSLcUCjcyviw3GoricudMREQSFG8oyqXhFlCgi0g3FG8oqlKgi4hkt7aGouHFwRaSZAp0Eel2+hb24NxRgxjUNzcaiuISmpxLRCSXXHlKOVeekntPTdMVuohIjlCgi4jkCAW6iEiOUKCLiOQIBbqISI5QoIuI5AgFuohIjlCgi4jkCAW6iEiOUKCLiOQIBbqISI5QoIuI5AgFuohIjlCgi4jkiIQC3cwuNLOVZrbGzO7s5P3vm9lyM1tiZq+Y2fDklyoiIody2EA3s3xgNnARUAlMN7PKDpstBKrdfTzwHHBfsgsVEZFDS+QK/VRgjbuvdfcm4Bng0vYbuPtr7r47tvhnoCy5ZYqIyOEk8sSiUmB9u+U64LRDbP8N4A+dvWFmNwI3ApSXd+1pIZue/S77Nyzu0tceLQNK+vaiV4/8QI4vIjliyDi46N6k7zapj6Azs2uBamBqZ++7+yPAIwDV1dXelWPU79zLrsieLtd4tBp2NTG2tIh8s8BqEBHpTCKBvgEY1m65LLbuc8zsy8APganuvi855R1o3N88nKpdH9abq+qZ/sRfuLJoGPd+fXxgdYiIdCaRQF8AjDSzEUSD/Crg6vYbmFkV8O/Ahe6+JelVZoizTyrhW+ecyOzXPuL0EwbwtarSoEuSLLd3fwvvrNnKS8s388qHWyjIz2PqySVMPamEM04cQN/CnkGXKFnksIHu7s1mdjPwIpAPPO7uy8xsFlDj7nOB+4FjgTkWHYoIu/u0FNYdmO99+SQWfNzI3f/xAePKijix5NigS5IsE9ndxKsfbuGl5Zt5Y1U9u5taOLZXD845uYSm5lb+c+EGnnovTI88Y/Lw49oCvvL4fpiG+uQQzL1LQ9lHrbq62mtqagI59tHatH0vF//rWwzq24vffHsKhT11k1QOra5xNy8t38xLyzfz3sfbaGl1BvfrxfmVgzm/cginn9C/7WZ7U3MroXAjb6yq542V9SzfuAOI3pA/a+RApp5UwlkjS+h/TEGQpyQBMbP33b260/cU6F3z+sotzHhiAdNPLecf/9u4oMuRDOPurNi4k5eWb+ZPyzex7JNoKI8cdCwXjImG+PjSIvLyDn/FvWXHXt5cvZU3VtXz1up6Irv3Ywbjy4qZelL06n3isGLyE9iXZD8Feor80x8/5N9e/4ifXDWRSydqPL27a25pZUFtY1uI1zXuwQwmlx/XFuIjBh5zVMdoaXU+2LCdN1bW88aqLSxaH6HVoah3T86MXb1PPamEwf0Kk3RWkmkU6CnS3NLKVY/8mRUbd/Db75zJCRpP73Z2NzXz5qr4Tc3NRHbvp6BHHmd9YSDnVw7mvNGDKenbK2XHj+xu4u01W2MBX8+WndEPmI0a0rct3CdXHKfeiRyiQE+hjdv3cPFP3mJIUW/+41tnaDy9G2j4dB+vrNjCn5Zv5q3V9exrbqWod0/OGzWIC8YM5qyRJRzTK6ktHglxdz7ctJM3VtXz5qp6FtRuY3+L06cgnzNOHBAL+EGUD+iT9tokeRToKfbayi3c8MQCrjmtnB//tcbTc1Ht1l1tNzVr1m2j1aG0uDfnVw7mgsrBnDKiPz3zM2vy0l37mpn/UQNvrKrn9VVbWL8t2pA3YuAxnD1yIFNPLuH0EwbQpyD9P3yk6xToaXDvHz7k4Tc+4sHpVVwyYWjQ5chRco+OVf9pWTTEV27eCcDo4/u1hfiYodnzMUJ3p7ZhN2+s3MIbq+qZv7aBvftbKcjP49QR/Zl6UglXVA+jqI8+957pFOhpsD82nr5y005++50zj/rmlwTjo/pP+fk7tby8YjMbt+8lz+DUEf05v3IIF1QOZlj/3Biu2Lu/hQW123hzVXTsffWWT3n/78/XRyGzgAI9TT6J7OHif32LoUW9eUHj6Vnp/XXbuOax95h6UgnnVw7h3FGDukXI1e/cl9Kbt5I8CvQ0evXDzcz8eQ3Xnl7Oj76m8fRs09rq7GtupXeBfhhLZjpUoGfWXZwccO6owfzt2Sfwqz+H+d2ST4IuR45QXp4pzCVrKdBT4Pa/OplJ5cXc+fwH1G7dFXQ5ItJNKNBToGd+Hg9ePYn8POPbT4XYu78l6JJEpBtQoKdIaXFv/t/lE1j2yQ7+77wVQZcjIt2AAj2Fvlw5mG+eNYJfzl/HvA82Bl2OiOQ4BXqK/d2Fo6gqL+YHzy1hXYPG00UkdRToKdYzP48Hp1eRFxtP39es8XQRSQ0FehqUHdeHf758Aks37OAf530YdDkikqMU6GlyfuVgvnHmCH7+bi1/0Hi6iKSAAj2NfnDhKCYMK+bvnl9CuGF30OWISI5RoKdRQY88HppehQE3P63xdBFJLgV6mg3r34f7L5/AkrrtGk8XkaRSoAfgr8YMYeaU6Hj6H5duCrocEckRCvSA3HnRKCaUFXHHc4tZv03j6SJy9BToASnokcdDV08C4OanQjQ1twZckYhkOwV6gIb178P9l01gcd127v2DxtNF5Ogo0AN24dghzDijgsff+Zg/LdN4uoh0nQI9A9x18SjGlxVx+xyNp4tI1yUU6GZ2oZmtNLM1ZnZnJ++fbWYhM2s2s8uSX2Zu69Ujn4emT8Idbn56ocbTRaRLDhvoZpYPzAYuAiqB6WZW2WGzMDADeCrZBXYX5QP6cN9l41m8PsJ9f9R4uogcuUSu0E8F1rj7WndvAp4BLm2/gbvXuvsSQJeWR+Giccdz/ReH89jbH/PS8s1BlyMiWSaRQC8F1rdbroutO2JmdqOZ1ZhZTX19fVd2kfPu/spoxpb24/Y5i6lr1Hi6iCQurTdF3f0Rd6929+qSkpJ0Hjpr9OqRz+yrJ9Ha6nzn6YXsb9EvPSKSmEQCfQMwrN1yWWydpMjwAcdw79fHszAc4f4XVwZdjohkiUQCfQEw0sxGmFkBcBUwN7VlyVfGH89//+JwHnlzLS9rPF1EEnDYQHf3ZuBm4EVgBfBrd19mZrPMbBqAmZ1iZnXA5cC/m9myVBbdXdx98WjGDO3HbXMWsyGyJ+hyRCTDmbsHcuDq6mqvqakJ5NjZpHbrLr764NucNPhYnv3bL9IzX71gIt2Zmb3v7tWdvad0yHAVA4/h3q+P4+QhfWlpDeaHr4hkhx5BFyCH99XxQ/nq+KFBlyEiGU5X6CIiOUKBLiKSIxToIiI5QoEuIpIjFOgiIjlCgS4ikiMU6CIiOUKBLiKSIwJr/TezemBdF798ILA1ieVkA51z96Bz7h6O5pyHu3un848HFuhHw8xqDjaXQa7SOXcPOufuIVXnrCEXEZEcoUAXEckR2RrojwRdQAB0zt2Dzrl7SMk5Z+UYuoiIHChbr9BFRKQDBbqISI7IukA3swvNbKWZrTGzO4OuJ9XMbJiZvWZmy81smZndGnRN6WBm+Wa20Mx+F3Qt6WBmxWb2nJl9aGYrzOyLQdeUamb2vdi/6aVm9rSZFQZdU7KZ2eNmtsXMlrZb19/MXjKz1bH/Hpes42VVoJtZPjAbuAioBKabWWWwVaVcM3Cbu1cCpwPf7gbnDHAr0YeSdxc/Af7o7qOACeT4uZtZKXALUO3uY4F84Kpgq0qJnwMXdlh3J/CKu48EXoktJ0VWBTpwKrDG3de6exPwDHBpwDWllLtvdPdQ7PVOov+jlwZbVWqZWRnwFeCxoGtJBzMrAs4Gfgbg7k3uHgm0qPToAfQ2sx5AH+CTgOtJOnd/E9jWYfWlwC9ir38BfC1Zx8u2QC8F1rdbriPHw609M6sAqoD3Ai4l1f4F+DugNeA60mUEUA88ERtmeszMjgm6qFRy9w3APwNhYCOw3d3/FGxVaTPY3TfGXm8CBidrx9kW6N2WmR0LPA981913BF1PqpjZV4Et7v5+0LWkUQ9gEvBv7l4F7CKJv4Znoti48aVEf5gNBY4xs2uDrSr9PPq58aR9djzbAn0DMKzdcllsXU4zs55Ew/xJd38h6HpSbAowzcxqiQ6pnWtmvwq2pJSrA+rcPf6b13NEAz6XfRn42N3r3X0/8AJwRsA1pctmMzseIPbfLcnacbYF+gJgpJmNMLMCojdR5gZcU0qZmREdW13h7g8EXU+quftd7l7m7hVEv7+vuntOX7m5+yZgvZmdHFt1HrA8wJLSIQycbmZ9Yv/GzyPHbwS3Mxe4Pvb6euA/k7XjHsnaUTq4e7OZ3Qy8SPSu+OPuvizgslJtCnAd8IGZLYqtu9vd5wVXkqTAd4AnYxcqa4EbAq4npdz9PTN7DggR/STXQnJwCgAzexo4BxhoZnXAPwD3Ar82s28QnUL8iqQdT63/IiK5IduGXERE5CAU6CIiOUKBLiKSIxToIiI5QoEuIpIjFOgiIjlCgS6SRLGJpkQCoUCXnGVmFbH5xZ+MzTH+XKwz8bzYJFgfxOar7mVmp5jZC7Gvu9TM9phZgZkVmtna2PoTzeyPZva+mb1lZqNi639uZg+b2XvAfQGesnRzCnTJdScDP3X30cAO4PtE56i+0t3HEe2Wvolop+LE2NecBSwFTgFO47PZLR8BvuPuk4HbgZ+2O04ZcIa7fz+VJyNyKPr1UHLdend/J/b6V8D/JDop1KrYul8A33b3fzGzj8xsNNF59x8gOkd5PvBWbLbLM4A50alHAOjV7jhz3L0lxecickgKdMl1Hee2iAADDrLtm0SfhrUfeJnolXw+cAfR32Yj7j7xIF+76yjrFDlqGnKRXFfe7vmcVwM1QIWZfSG27jrgjdjrt4DvAvPdvZ5o8J8MLI3NQf+xmV0O0VkwzWxCms5BJCEKdMl1K4k+h3UFcBzw/4nOZDjHzD4g+lSkh2Pbvkf06TFvxpaXAB/4ZzPYXQN8w8wWA8vI8ccfSvbRbIuSs2KP7Ptd7CHEIjlPV+giIjlCV+giIjlCV+giIjlCgS4ikiMU6CIiOUKBLiKSIxToIiI54r8AObpxIgHEu0gAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAEGCAYAAABrQF4qAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAy4UlEQVR4nO3deXxV9Z3/8dcnO4QACYQtgSwIyA7mAgoacOtgraCOa13RCkzLTOfXcfzpdJufnbb+Zjoznc7PFlBRcSkqasu0tNYFCCgKN7KvJiGBhC2QsBOyfX5/3Jt4DUtu4N577vJ5Ph55cO9Z7v2ckHxy7vec8z6iqhhjjIlecU4XYIwxJris0RtjTJSzRm+MMVHOGr0xxkQ5a/TGGBPlEpwuoK2ePXtqbm6u02UYY0xEKS4uPqSqmeeaF3aNPjc3F7fb7XQZxhgTUUSk4nzzbOjGGGOinDV6Y4yJctbojTEmyoXdGL0xpn0NDQ1UVlZSV1fndCkmxFJSUsjOziYxMdHvdazRGxOBKisrSUtLIzc3FxFxuhwTIqrK4cOHqaysJC8vz+/12h26EZEFInJQRDafZ76IyK9EpERENorIFT7zHhKRL7xfD/ldlTHmgurq6ujRo4c1+RgjIvTo0aPDn+T8GaN/CZh6gfk3AYO8XzOB33gLygB+DEwAxgM/FpH0DlVnjDkva/Kx6WL+39tt9KpaBNRcYJHpwEL1+BToLiJ9gb8C3lfVGlWtBd7nwn8wTAT5tOwwxRW1TpdhjPFDIM66yQL2+Dyv9E473/SziMhMEXGLiLu6ujoAJZlgOnmmkVmvFPPt14o509jkdDnGmHaExemVqjpfVV2q6srMPOcVvCaMvOnew9HTDRw4dobfr9/rdDkmijU2NjpdQlQIRKOvAvr7PM/2TjvfdBPBGpqaeX7lLsblpjOsb1fmrSiludnuUhaLbr31VgoKChg+fDjz588H4M9//jNXXHEFo0eP5vrrrwfgxIkTzJgxg5EjRzJq1CjefvttALp06dL6WosXL+bhhx8G4OGHH2b27NlMmDCBJ554gjVr1nDVVVcxduxYJk6cyI4dOwBoamri8ccfZ8SIEYwaNYr//u//5qOPPuLWW29tfd3333+f2267LQTfjfAWiNMrlwBzRGQRngOvR1V1n4i8B/zM5wDs14CnAvB+xkF/3LiPqiOneXr6cE6caeS7i9bz4faD3Dist9Olxaz/8z9b2Lr3WEBfc1i/rvz4luEXXGbBggVkZGRw+vRpxo0bx/Tp03nssccoKioiLy+PmhrPob2f/OQndOvWjU2bNgFQW9v+sZ3Kyko++eQT4uPjOXbsGCtXriQhIYEPPviAf/qnf+Ltt99m/vz5lJeXs379ehISEqipqSE9PZ1vf/vbVFdXk5mZyYsvvsgjjzxy6d+QCNduoxeR3wJTgJ4iUonnTJpEAFWdCywFvg6UAKeAGd55NSLyE2Ct96WeVtULHdQ1YU5VmbuilEG9unDtkF40q/Jv7+1g3opSa/Qx6Fe/+hXvvvsuAHv27GH+/PkUFha2nt+dkZEBwAcffMCiRYta10tPb//kuzvvvJP4+HgAjh49ykMPPcQXX3yBiNDQ0ND6urNnzyYhIeEr7/fAAw/w6quvMmPGDFavXs3ChQsDtMWRq91Gr6r3tjNfge+cZ94CYMHFlWbCTdEXh9i+/zi/uHM0cXFCHMJj1+Tz4yVbcJfX4MrNcLrEmNTenncwLF++nA8++IDVq1fTuXNnpkyZwpgxY9i+fbvfr+F7mmDb88JTU1NbH//whz/k2muv5d1336W8vJwpU6Zc8HVnzJjBLbfcQkpKCnfeeWfrH4JYFhYHY01kmLu8lD5dU5g2ul/rtDtd2aR3TmTuijIHKzOhdvToUdLT0+ncuTPbt2/n008/pa6ujqKiInbt2gXQOnRz44038uyzz7au2zJ007t3b7Zt20Zzc3PrJ4PzvVdWlueEvZdeeql1+o033si8efNaD9i2vF+/fv3o168f//Iv/8KMGTMCt9ERzBq98cuGPUdYXXaYR6/OIynhyx+bzkkJPHhVLh9sO0DJweMOVmhCaerUqTQ2NjJ06FCefPJJrrzySjIzM5k/fz633347o0eP5u677wbgBz/4AbW1tYwYMYLRo0ezbNkyAJ555hm+8Y1vMHHiRPr27Xve93riiSd46qmnGDt27FfOwvnWt77FgAEDGDVqFKNHj+b1119vnXfffffRv39/hg4dGqTvQGQRz8hL+HC5XGo3Hgk/33ntc4q+qOaTJ68jLeWrYUo1J+uZ+MyHTBvdj3+9Y7RDFcaWbdu2WRO7gDlz5jB27FgeffRRp0sJinP9/4tIsaq6zrW87dGbdpUfOsmfNu/jgStzzmryABmpSdzt6s+766o4cMzSFI2zCgoK2LhxI/fff7/TpYQNa/SmXc+tLCMhLo6HJ+Wed5lvXZNPU7OyYNWu0BVmzDkUFxdTVFREcnKy06WEDWv05oKqj5/hreJK/rogi15pKeddrn9GZ24e1Y/XPtvNsbqGEFZojGmPNXpzQQtXl9PQ1Mxj1+S3u+yswnxOnGnk9c92h6AyY4y/rNGb8zp5ppGFqyv4q2F9yM/s0u7yI7K6cc2gnixYtcvCzowJI9bozXktWusJL5s1uf29+RazCgdy8PgZfrfOYo2MCRfW6M05NTQ188LKMsbnZTB2gP/3i5l0WQ+G9+vKvKIyCzszYUVVue666zh2zP9coCVLlvDMM88Esapz27RpU2vIWyBYozfn9IeNe9l7tI7ZHdibB89l7bMmD6Ss+iQfbDsQpOpMrAhkTPHSpUsZPXo0Xbt29XudadOm8eSTTwasBn+NHDmSyspKdu8OzPEua/TmLKrKvBVlDOmdxrVDenV4/a+P6EP/jE7MXVFKuF2QZwIn0mKKX3vtNaZPnw5AeXk5l19+OQ8//DCDBw/mvvvu44MPPmDSpEkMGjSINWvWAJ7IhTlz5rTW9Xd/93dMnDiR/Px8Fi9eDHhyfwoLC7n55psZMmQIs2fPprm52a/vYcu2ulwuBg8ezB/+8IfWebfccstXwuAuhaX9mLMs31nN9v3H+fc7R1/U/SkT4uN47Jp8fvT7LbgrahlnYWfB9acnYf+mwL5mn5Fw04WHLCItpvjjjz9m3rx5re9RUlLCW2+9xYIFCxg3bhyvv/46q1atYsmSJfzsZz/jd7/73Vl17du3j1WrVrF9+3amTZvGHXfcAcCaNWvYunUrOTk5TJ06lXfeeYc77riDu+++u/UPk6/vfe97PPjgg4Dnj86aNWsoLS3l2muvpaSkhJSUFFwuF8888wxPPPFEu9+v9lijN2eZt6KUvt1SuMUnvKyj7izoz3++v5N5K0qt0UepSIsprqmpIS0trfU98vLyGDlyJADDhw/n+uuvR0QYOXIk5eXl56zr1ltvJS4ujmHDhnHgwJdDk+PHjyc/3zPMee+997Jq1SruuOMO3njjjXa39a677iIuLo5BgwaRn5/P9u3bGTNmDL169WLv3sDcwc0avfmK9XuO8GlZDT+4eehXwss6qlNSPA9NzOWXH3zBFweOM6h3WvsrmYvTzp53MERiTHFCQgLNzc3ExXl+rn2vnI2Li2t9HhcXd95jA77r+A5Ltv3k2/Lcnz36861bV1dHp06dLrit/rIxevMV84tK6ZqSwD3jB1zyaz10VS6dEuOZV2QRxtEmEmOKhwwZQllZcH4W16xZw65du2hubuaNN97g6quvBuCNN95g/fr1Z321NHmAt956i+bmZkpLSykrK2PIkCEA7Ny5kxEjRgSkPmv0ptWuQyf50+b9PHBVDl2SL/3DXnpqEneP68/v11ex7+jpAFRowkUkxhTffPPNLF++PMDfCY9x48YxZ84chg4dSl5eXofuUztgwADGjx/PTTfdxNy5c0lJ8USNLFu2jJtvvjkwBapqu1/AVGAHntsFPnmO+TnAh8BGYDmQ7TPvX4EtwDbgV3ijkc/3VVBQoMYZT72zUQd9f6keOHY6YK+5+/BJzX/qj/rTP24N2Gsa1a1b7ft5Id/5znf0+eef/8q0vXv36g033BDw91q2bJnefPPNF7XuQw89pG+99dZZ0+vq6nTChAna0NBwzvXO9f8PuPU8fbXdPXoRiQeeBW4ChgH3isiwNov9AlioqqOAp4Gfe9edCEwCRgEjgHHA5Iv7k2SCqfr4GRYXV/LXV2RfMLyso/pndOYbo/ry+me7OXraws5M8J0vprhv37489thjHbpgyim7d+/mmWeeCdhtEP15lfFAiaqWAYjIImA6sNVnmWHA97yPlwG/8z5WIAVIAgTPTcXtKpow9PInnvCymYUdu0DKHzML8/n9+r289lkF355yWcBf3xhfxcXF55131113Bfz9pkyZ0u4B4vPxPebga9CgQQwaNOjii2rDnzH6LGCPz/NK7zRfG4DbvY9vA9JEpIeqrsbT+Pd5v95T1W2XVrIJtBNnGlm4upypw/uQ1zO1/RU6aHg/T9jZix+XU9dgYWeBonYxWky6mP/3QB2MfRyYLCLr8AzNVAFNInIZMBTIxvPH4ToRuabtyiIyU0TcIuKurq4OUEnGX4vW7OZYXWNQ9uZbzJ48kGoLOwuYlJQUDh8+bM0+xqgqhw8fbj1g6y9/hm6qgP4+z7O903zffC/ePXoR6QL8taoeEZHHgE9V9YR33p+Aq4CVbdafD8wHzz1jO7QF5pI0NDXzwqpdTOhgeFlHTRzYg5FZ3ZhfVMadrv7Ex3X8ilvzpezsbCorK7Edo9iTkpJCdnZ2h9bxp9GvBQaJSB6eBn8P8E3fBUSkJ1Cjqs3AU8AC76zdwGMi8nM8Y/STgV92qEITVEvW72Xf0Tp+dvvIoL6PJ+wsnzmvr+P9rQeYOqJPUN8v2iUmJrZegWpMe9odulHVRmAO8B6eUyTfVNUtIvK0iEzzLjYF2CEiO4HewE+90xcDpcAmPOP4G1T1fwK7CeZiqSrzikoZ0juNKYMzg/5+U4f3YUBGZws7MybE/Dp3R1WXAkvbTPuRz+PFeJp62/WagFmXWKMJkuU7qtl54AT/cdfFhZd1lCfsLI8f/n4La8trGZ9nGTjGhIJdGRvD5q4opd8lhpd11J2u/vRITWLuitKQvacxsc4afYxat7uWz3bV8Og1+STGh+7HICXRE3b20faD7Nh/PGTva0wss0Yfo+atKKNbp0TuGde//YUD7IErc+iUGM98CzszJiSs0cegsuoTvLd1Pw9cmUNqAMLLOsrCzowJLWv0Mei5lbtIjI/joYm5jtXwrWvyUOCFlbscq8GYWGGNPsYcPF7H259XckdBNplpye2vECTZ6Z25ZVRffrtmN0dPWdiZMcFkjT7GvPSxN7zsmuDFHfhrZuFATtY38epnFU6XYkxUs0YfQ06caeSVTyu4aUQfcoMQXtZRw/p1pXBwpoWdGRNk1uhjyKI1uzle18iswoFOl9Jq9uR8Dp04wzufW9iZMcFijT5G1Dc28/zKXVyZn8Ho/t2dLqfVVfk9GJXdjedWltHUbLEIxgSDNfoYsWTDXvYfq2P25PDZmwdv2FnhQHYdOsn7W/c7XY4xUckafQxoblbmF5VyeZ80JocgvKyjpo7oQ06PzvxmRZmFnRkTBNboY8DynQfZeeAEsybnhyS8rKPi44THrslnw54jfLarxulyjIk61uhjwNzlZWR178Q3RoUuvKyj7ijIpkdqEvMs7MyYgLNGH+WKK2pZU17Do1fnhTS8rKNSEuN5eGIuy3ZUs33/MafLMSaqhO9vvgmI+UWldOuUyN0OhJd11ANX5dA5KZ75KyzszJhAskYfxUqrT/CXrQd48Cpnwss6qnvnJO4ZN4AlG/ZSdcTCzowJFGv0Uey5ojKSHA4v66hHvWFnC1ZZ2JkxgeJXoxeRqSKyQ0RKROTJc8zPEZEPRWSjiCwXkWyfeQNE5C8isk1EtopIbgDrN+dx8Fgd73xexZ2ubHp2cS68rKOyundi2uh+FnZmTAC12+hFJB54FrgJGAbcKyLD2iz2C2Chqo4CngZ+7jNvIfBvqjoUGA8cDETh5sJe/KScxuZmvnW18+FlHTWzMJ9T9U288mm506UYExX82aMfD5Soapmq1gOLgOltlhkGfOR9vKxlvvcPQoKqvg+gqidU9VRAKjfndbyugVc/reCmEX3DIryso4b27cqUIZm89ImFnRkTCP40+ixgj8/zSu80XxuA272PbwPSRKQHMBg4IiLviMg6Efk37yeErxCRmSLiFhF3dXV1x7fCfMVvW8LLJkfe3nyLWYUDOXSinrc/r3S6FGMiXqAOxj4OTBaRdcBkoApoAhKAa7zzxwH5wMNtV1bV+arqUlVXZmb4XaIfSeobm3lh1S4mDuzBqOzuTpdz0a7Mz2B0djeeK7KwM2MulT+NvgrwPQk72zutlaruVdXbVXUs8H3vtCN49v7Xe4d9GoHfAVcEoG5zHr9fX8WBY2eYFWbhZR0lIsyePJDyw6d4b4uFnRlzKfxp9GuBQSKSJyJJwD3AEt8FRKSniLS81lPAAp91u4tIy276dcDWSy/bnIsnvKyMy/ukUTiop9PlXLKvDe9Dbo/OzFtRamFnxlyCdhu9d098DvAesA14U1W3iMjTIjLNu9gUYIeI7AR6Az/1rtuEZ9jmQxHZBAjwXMC3wgDw0faDfHHwBLMnDwzL8LKOio8THivMZ0PlUT4ts7AzYy6WhNueksvlUrfb7XQZEenOuZ+w90gdy/9xSljn2nREXUMTV//fjxjerxsvPzLe6XKMCVsiUqyqrnPNi45uYCiuqGFteS3fuia8w8s6KiUxnhmT8lixs5pt+yzszJiLET0dIcbNW1FG986REV7WUfdP8IadFVnYmTEXwxp9FCg5eIL3tx3gwStz6JwU/uFlHdWtcyL3jveEnVXW2vV2xnSUNfooEInhZR316NV5CPCChZ0Z02HW6CPcgWN1vLuuirtc/ekRQeFlHdWveyemjenHojV7qD1Z73Q5xkQUa/QR7sWPveFl1+Q5XUrQzSzM53RDE69+WuF0KcZElOgb0I0hx+saeO3TCm4a2ZecHpEXXtZRl/fpyrVDMnnh413srrGx+lCIE+HRa/IY3DvN6VJC4kxjE79eVsoDV+VEVLx3e6zRR7CPSw5x/EwjD16Z43QpIfPdGwbz3UXr+LjkkNOlxIRDJ+vZf6wuZq5hWFxcyX99+AWpyfHMLIzsGBFf1ugjmLu8lqSEOMYM6O50KSEzpn93VvzjtU6XETOeXVbCv723g237jjG0b1enywmqpmblOe8pvO7yWmYWOlxQANkYfQRzV9QyKqsbyQlnJT8bExD3T8ghNSmeeStKnS4l6P6yZT/lh0/Rp2sKxRW1UZWvZI0+QtU1NLFl71FcuRlOl2KiWMs1DP+zcV9UX8OgqsxdUUpOj85857rLOHyynvLD0bO91ugj1IY9R2hoUlw56U6XYqLcIzFwDcOnZTVsqDzKY9fkMyHPs/PkLo+eID1r9BHKXVELQIE1ehNksXANw7yiUnp2SeKOgmwuy+xC15QEir2/Y9HAGn2EKq6oZWBmKumpSU6XYmLArMKBnG5o4pUovIZh275jLN9RzcMTc0lJjCcuTijISW/dmYoG1ugjUHOzUlxRiyvHxudNaAzpk8Z1l/eKyhu2zy8qo3NSPPf7nKbsys2g5OCJqPkEY40+ApVUn+Do6QYKcm3YxoTOrMJ8ak7W81Zx9NywvbL2FEs27OWecQPo3vnLT8ctQ6LRMnxjjT4Cucs9P3x2INaE0vi8DMb07x5VN2xfsKocAR5tEyEyOrs7ifESNcM3fjV6EZkqIjtEpEREnjzH/BwR+VBENorIchHJbjO/q4hUisj/C1ThscxdUUOP1CTyekZ/7IEJHy03bN9dc4o/bd7ndDmX7Mipehat3c200f3I6t7pK/M6JcUzvF83iiui48ybdhu9iMQDzwI3AcOAe0VkWJvFfgEsVNVRwNPAz9vM/wlQdOnlGvB8nCzISY+K+8KayHLjsN7k90xl3oqyiL+g6JXVFZyqb2Lm5PxzznflpLOh8ihnGiP/mIQ/e/TjgRJVLVPVemARML3NMsOAj7yPl/nOF5ECPDcM/8ull2uqj5+h4vApXDY+bxzQcsP2TVVHWV162OlyLlpdQxMvfVLOlCGZXN7n3NEOrtx06hub2VwV+bew9KfRZwF7fJ5Xeqf52gDc7n18G5AmIj1EJA74d+DxC72BiMwUEbeIuKurq/2rPEa1fJQssDNujENuG5tFzy7JzI3gWzsuLq7k8Ml6Zk8+f3BZy+9YNAzfBOpg7OPAZBFZB0wGqoAm4NvAUlW94GF6VZ2vqi5VdWVmZgaopOjUEmQ2Iiu6A6ZM+EpJjOeRq3Mp2lnNlr1HnS6nw5qaledWljG6f/fWq2DPJTMtmZwenVtPfohk/jT6KsD3jtPZ3mmtVHWvqt6uqmOB73unHQGuAuaISDmecfwHReSZANQds9wVtYzOtiAz46z7vGFnkXjD9j9v3k/F4VPMLsxv9zhXQU56VASc+dPo1wKDRCRPRJKAe4AlvguISE/vMA3AU8ACAFW9T1UHqGounr3+hap61lk7xj+n65vYXHXUhm2M47p1SuSbEwbwh4372BNBN4FpCS/L65nK14b3aXd5V05GVASctdvoVbURmAO8B2wD3lTVLSLytIhM8y42BdghIjvxHHj9aZDqjWkbKo/Q2GxBZiY8PHJ1HnESWWFnq8sOs6nKE14WH9f+WWvjvCc9rI3wgDO/xuhVdamqDlbVgar6U++0H6nqEu/jxao6yLvMt1T1zDle4yVVnRPY8mNLsQWZmTDSt1snpo/J4o21kRN2Nm9FGT27JHH7FW3PJzm3gZld6NYpkeIIH6e3K2MjiLu8hst6dbEgMxM2Wm7YvnB1+Iedbd17jBU7q5kxKY+URP+OcX0ZcBYDe/TGeV8GmdnevAkfg3uncf3lvXh5dTmn68P7wqL5RaWkJsVz/4SO3WO5ICed0uqTEfOp5Vys0UeIkuoTHKtrtGEbE3ZmTR5Izcl6FhfvaX9hh1TWnuJ/Nu7j3vED6NY5sUPruqIg4MwafYRoDTKzWweaMDMuN50rBnRn/soyGpuanS7nnF5YtQvBcwC5o0b3j/yAM2v0EaIlyCy3R2enSzHmK0SEWZMHsqfmNH/avN/pcs5Se7KeRWv2MG1MP/q1CS/zR0pi5AecWaOPEO5yCzIz4evGod6ws6LSsLu46JVPKzjd0MSswvPHHbQn0gPOrNFHgIPH69hdY0FmJnzFxQkzC/PZXHWMT8Io7KwlvOy6y3sxpE/aRb+OKzfDG3AWeZEPYI0+IrScw2tXxJpwduvYLDLTkpm7otTpUlq9VVxJzcl6ZhWeO4rYXy0nQURq7o01+gjgrqgl2YLMTJhLSYznkUl5rPziUFjs+TY2NfNcURlj+ndn/AXCy/yRmZZMbo/OEXtA1hp9BPAEmXW3IDMT9r45YQBdkhPCIuzsz1v2s7vmFLMntx9e5o+CnAw+j9CAM2v0Ye50fRNbqo7ajcBNRPgy7Gyvo2Fnqsq8FWXk90zlxmHth5f5w5WbzuGT9ew6dDIgrxdK1ujDnAWZmUjzyKQ84uOE51c6t1e/utQbXlboX3iZP1p+ByNx+MYafZizIDMTafp0S+HWMVm84d5DjUOxAb9ZUUrPLsncNta/8DJ/RHLAmTX6MNcSZNa9swWZmcgxszCfuoZmFq4uD/l7b9l7lJVfHOKRq3P9Di/zRyQHnFmjD2MWZGYi1aDeadwwtBcvf1LOqfrGkL73/KIyUpPiua+D4WX+aAk4c+qTysWyRh/GvjhoQWYmcs2aPJDaUw285b7gLaMDak/NKf6wcR/fnDCAbp06Fl7mj3G5LTcMj6zhG2v0YazlI+I4CzIzEWhcbgYFOek8F8KwsxdW7SJOLi68zB+jsrt5A84ia/jGGn0YKy6vpWeXJHIsyMxEqFmF+VTWnmZpCMLOak7Ws2jtbqaPyaJvt46Hl/kjJTGeEVndIu6ArF+NXkSmisgOESkRkbNu7i0iOSLyoYhsFJHlIpLtnT5GRFaLyBbvvLsDvQHRzF1hQWYmst0wtDf5manMXR78sLNXVldQ19DMzEuMO2iPKyedjVWRFXDWbqMXkXjgWeAmYBhwr4gMa7PYL4CFqjoKeBr4uXf6KeBBVR0OTAV+KSLdA1R7VGsNMrN8GxPB4uKEWYX5bN13jFUlh4L2Pqfrm3h5dTnXX96Lwb0vPrzMHwU5kRdw5s8e/XigRFXLVLUeWARMb7PMMOAj7+NlLfNVdaeqfuF9vBc4CGQGovBo1xpkZlfEmgh369gseqUlM29F8C6gWlzsOWd/1uSLjyL2VyQGnPnT6LMA33uEVXqn+doA3O59fBuQJiI9fBcQkfFAEnBWtJ2IzBQRt4i4q6ur/a09qrUGmfXr5nQpxlyS5IR4Hrk6j1UlwQk7a2xqZv7KMq4Y0J1xIdgxisSAs0AdjH0cmCwi64DJQBXQOoAlIn2BV4AZqnrW4XdVna+qLlV1ZWbaDj94LpQand2dpAQ7Xm4iX0vYWTAijP+0eT97ak4za/LAkB3PKsjJoDiCAs786SJVQH+f59neaa1Uda+q3q6qY4Hve6cdARCRrsAfge+r6qeBKDrana5vYsveYzZsY6JG15RE7pswgKWb9rH7cODCzlSVeUWlnvCyob0D9rrtGZebTs3JesoiJODMn0a/FhgkInkikgTcAyzxXUBEeopIy2s9BSzwTk8C3sVzoHZx4MqObuv3eILMQvEx1JhQeeRqb9jZqsCN1X9SepjNVceYWZhPXIDCy/zRcre3SDnNst1Gr6qNwBzgPWAb8KaqbhGRp0VkmnexKcAOEdkJ9AZ+6p1+F1AIPCwi671fYwK8DVGn5SbEVwywRm+iR++uKdw2Nos33Xs4fOJMQF5z7opSMtOSue2KwIWX+SO/Zxe6d06MmAunEvxZSFWXAkvbTPuRz+PFwFl77Kr6KvDqJdYYc9wVtQyyIDMThWYW5vOmu5KXV1fwvRsHX9Jrba7yhJf976mXh/ymPHFxQsGA9Ig5IGtH+sJMc7PyeUWt3QjcRKXLeqVxw9DeLFx96WFn84vK6JKcwDcnDAhQdR1TkJtOWYQEnFmjDzNfBpnZhVImOv3NlHyOnGrgzbV72l/4PPbUnOKPm4IXXuaPlosZIyHgzBp9mGkZ87NoYhOtCnIycOWk89zKXRcddvb8yjJPeNmk4ISX+SOSAs6s0YcZtwWZmRgwa/JAqo6c5o+b9nV43ZqT9bzh3sOtY7Lo0y0lCNX5J5ICzqzRhxl3RY0FmZmod/3lvbisVxfmrijr8EVHC1eXhyS8zB/jcjPYWHmUuobwDjizRh9GDh6rY0/NacufN1EvLk6YWZjPtn3HWPmF/2Fnp+ubePmTcm4Y2otBQQ4v80dBTjr1TeEfcGaNPoy47UbgJoZMH9OP3l2TmVfkfyzCm+491J5qYHYIwsv80RpwFuYHZK3RhxF3uSfIbLgFmZkYkJwQzyOT8vi45DCbKtvfI25saua5lWUU5KTjCpNPvT27JJPXMzXskyyt0YeR4ooaRve3IDMTO+6dMIC05ATm+rFXv3TzfiprTzMrDMbmfRXkpPP57vAOOLOOEiZagszstEoTS7qmJHLflTn8adM+Kg6fPyBMVZm3opSBmancEMLwMn+4csI/4MwafZhoCTKzK2JNrJkxKZeEuDieW3n+sLNVJYfYsvcYswoHhjS8zB+REHBmjT5MuMstyMzEppaws7fclRw6T9jZvBVl9EpLZvrYfiGurn2REHBmjT5MWJCZiWWPFeZT39TMwk/Kz5q3ueooq0oO8cjVeSEPL/NHJAScWaMPA83Nyue7a8PmTAJjQu2yXl24cWhvXl5dwckzXw07m1dURpqD4WX+cOVmUFZ9MmDxy4FmjT4M7Dx4nON1jXYg1sS0WZMHcvR0A2/4hJ3tPnyKP27cyzevHEDXFGfCy/zROk4fpnv11ujDQMs5uHYg1sSygpx0xuWm88KqXTR4w86eX1VGfJw4Gl7mj5FZ3UiKj7NGb86vuKKWnl2SGZBhQWYmts0q9IadbdzH4RNneNO9h9vGZtG7q3PhZf7wBJx1Ddtxer8avYhMFZEdIlIiIk+eY36OiHwoIhtFZLmIZPvMe0hEvvB+PRTI4qOFu6IGlwWZGcN1l/diUK8uzF1RysurK7zhZeERd9AeV24Gm8I04KzdRi8i8cCzwE3AMOBeERnWZrFf4LkB+CjgaeDn3nUzgB8DE4DxwI9FxMYnfBzwBpnZsI0xX4adbd9/nN8sL+HGYb25rFcXp8vySzgHnPmzRz8eKFHVMlWtBxYB09ssMwz4yPt4mc/8vwLeV9UaVa0F3gemXnrZ0aNlfN6CzIzxmD4mi95dk2loUmZPDq+4gwsJ54Azfxp9FuB7z69K7zRfG4DbvY9vA9JEpIef6yIiM0XELSLu6upqf2uPCu6KGgsyM8ZHUkIcP75lOI9MyouoW2qGc8BZoA7GPg5MFpF1wGSgCvB7oEpV56uqS1VdmZmZASopMhRX1DLGgsyM+Yqvj+zLj25pO0Ic/lw56RRX1IRdwJk/3aUK6O/zPNs7rZWq7lXV21V1LPB977Qj/qwby07VN3qCzGx83pio4MpNp/ZUA6XV4RVw5k+jXwsMEpE8EUkC7gGW+C4gIj1FpOW1ngIWeB+/B3xNRNK9B2G/5p1m8ASZNTVr693kjTGRrWWoqTjMcm/abfSq2gjMwdOgtwFvquoWEXlaRKZ5F5sC7BCRnUBv4KfedWuAn+D5Y7EWeNo7zfBl2p0FmRkTHQZmppLeOTHsxukT/FlIVZcCS9tM+5HP48XA4vOsu4Av9/CND3dFLYN7d6Fb5/C9tNsY4z8RoSAnPeyukLUjgA5pCTKLpLMKjDHtK8jJoOxQeAWcWaN3iAWZGROdwjHgzBq9Q9ZakJkxUSkcA86s0TukuLzGgsyMiUIpifGMzO7G2vLwOe/EGr1D3BW1jMu1IDNjopErJ53NVcfCJuDMGr0DDhyro7L2tOXbGBOlWgLONoVJwJk1egd8eaMRO+PGmGjUGnAWJufTW6N3gLuihpTEOIb36+p0KcaYIOjRJZn8nqlhc4WsNXoHFFfUMjq7O4nx9u03Jlq1XDgVDgFn1mlCzILMjIkN4RRwZo0+xNbvtiAzY2JBOAWcWaMPsZa7z1iQmTHRLZwCzqzRh5i7opYhvdMsyMyYKOcJOMsIi1sLWqMPoaZmZV1FLQU2Pm9MTHDlprPr0EkOORxwZo0+hHYeOM7xMxZkZkysaPlddzr3xhp9CLV8hLMDscbEhhFhEnBmjT6EistryExLpn9GJ6dLMcaEQEvAmdvhgDO/Gr2ITBWRHSJSIiJPnmP+ABFZJiLrRGSjiHzdOz1RRF4WkU0isk1Engr0BkQSd0UtrhwLMjMmloRDwFm7jV5E4oFngZuAYcC9IjKszWI/wHMv2bF4bh7+a+/0O4FkVR0JFACzRCQ3QLVHlP1HLcjMmFgUDgFn/uzRjwdKVLVMVeuBRcD0Nsso0BLc0g3Y6zM9VUQSgE5APXDskquOQG7vRRMWZGZMbAmHgDN/Gn0WsMfneaV3mq9/Bu4XkUo8NxH/W+/0xcBJYB+wG/iFqp41WCUiM0XELSLu6urqjm1BhHCX11qQmTExqEeXZPIzUx0dpw/Uwdh7gZdUNRv4OvCKiMTh+TTQBPQD8oB/EJH8tiur6nxVdamqKzMzM0AlhZfiilrG9LcgM2NikSsnneLdtTQ3OxNw5k/XqQL6+zzP9k7z9SjwJoCqrgZSgJ7AN4E/q2qDqh4EPgZcl1p0pDl5ppGt+47ZaZXGxChXTgZHTjVQduiEI+/vT6NfCwwSkTwRScJzsHVJm2V2A9cDiMhQPI2+2jv9Ou/0VOBKYHtgSo8cG/Z4gszsilhjYlPL775T4/TtNnpVbQTmAO8B2/CcXbNFRJ4WkWnexf4BeExENgC/BR5WTwjzs0AXEdmC5w/Gi6q6MRgbEs7cFbWIWJCZMbEqv2cqGalJjuXeJPizkKouxXOQ1Xfaj3webwUmnWO9E3hOsYxp7opaBvdKo1snCzIzJhaJCFcMSHfsClk7MhhkTc3K5xZkZkzMczLgzBp9kO3Yf5wTFmRmTMxzMuDMGn2QtdxdZpxdKGVMTBuZ3Y2khDhHzqe3Rh9k7opaeqUlk51uQWbGxLLkhHhGZXVz5ICsNfogc5fX4sq1IDNjjOc0y81VR0MecGaNPoj2H62j6sjp1psEG2Nimysng4YmZWNlaAPOrNEHUWuQmR2INcbgE3BWEdpxemv0QeQur6VTYjzDLMjMGANkpCaRn5lKcYivkLVGH0TuihpG9+9mQWbGmFZOBJxZBwqSk2ca2bbvuAWZGWO+womAM2v0QbLeG2TmsitijTE+nAg4s0YfJO5yb5CZHYg1xvhoCThba40+8rkrahjSO42uKRZkZoz5kohQkJPeetV8KFijD4KmZmXd7iN2I3BjzDm5ctIpP3yK6uOhCTizRh8ErUFmNj5vjDmHlt4QqoAza/RBUNx6oZSdcWOMOduILE/AWaiGb6zRB4EFmRljLiTUAWfW6IPAgsyMMe0JZcCZX41eRKaKyA4RKRGRJ88xf4CILBORdSKyUUS+7jNvlIisFpEtIrJJRFICuQHhZt/R01QdOW3DNsaYCwplwFm7jV5E4vHc5PsmYBhwr4gMa7PYD/DcNHwscA/wa++6CcCrwGxVHQ5MARoCVn0YarkIwg7EGmMupOWsvLUhuBGJP3v044ESVS1T1XpgETC9zTIKtCR3dQP2eh9/DdioqhsAVPWwqoY2iDnEiis8QWZD+1qQmTHm/DJSkxiYmRqSM2/8afRZwB6f55Xeab7+GbhfRCqBpcDfeqcPBlRE3hORz0XkiXO9gYjMFBG3iLirq6s7tAHhxl1Rw5j+3S3IzBjTLldOBsUVwQ84C1Q3uhd4SVWzga8Dr4hIHJAAXA3c5/33NhG5vu3KqjpfVV2q6srMzAxQSaHXGmRmwzbGGD8U5KZz9HQDpdXBDTjzp9FXAf19nmd7p/l6FHgTQFVXAylATzx7/0WqekhVT+HZ27/iUosOVy1BZnZFrDHGH67WG5EEd/jGn0a/FhgkInkikoTnYOuSNsvsBq4HEJGheBp9NfAeMFJEOnsPzE4Gtgaq+HBjQWbGmI7I65lKj9SkoCdZJrS3gKo2isgcPE07HligqltE5GnArapLgH8AnhOR/4XnwOzDqqpArYj8B54/FgosVdU/BmtjnGZBZsaYjhARrghBwFm7jR5AVZfiGXbxnfYjn8dbgUnnWfdVPKdYRrWWILNbx/ZzuhRjTARx5aTz/tYDVB8/Q2ZaclDew04NCZDt+495gszsQiljTAe4cj09I5inWVqjD5CW/yQ7EGuM6YgRWV1JSojDHcQLp6zRB4i7vJbeXS3IzBjTMckJ8YzODm7AmTX6ACmuqMWVk2FBZsaYDivIyWDL3uAFnFmjD4CWIDMbtjHGXAxXTjoNTcqGPUeC8vrW6APAgsyMMZeiIMgXTvl1emUkOHKqno9++QgDm3aF/L37NjXzZjKMeD8dsKEbY0zHpAO/Sz1C9eeD4doXA/76UdPo4+KE7p0T6XQmPuTv3Yl4uqYkEGdN3hhzkTK7JNHYKTgXW0ZNo++aksh1fx/4v4TGGBMKWZwdCxwoNkZvjDFRzhq9McZEOWv0xhgT5azRG2NMlLNGb4wxUc4avTHGRDlr9MYYE+Ws0RtjTJQTzx3/woeIVAMVl/ASPYFDASonUsTaNsfa9oJtc6y4lG3OUdXMc80Iu0Z/qUTEraoup+sIpVjb5ljbXrBtjhXB2mYbujHGmChnjd4YY6JcNDb6+U4X4IBY2+ZY216wbY4VQdnmqBujN8YY81XRuEdvjDHGhzV6Y4yJclHT6EVkqojsEJESEXnS6XqCTUT6i8gyEdkqIltE5LtO1xQqIhIvIutE5A9O1xIKItJdRBaLyHYR2SYiVzldU7CJyP/y/lxvFpHfikiK0zUFmogsEJGDIrLZZ1qGiLwvIl94/w3IjaijotGLSDzwLHATMAy4V0SGOVtV0DUC/6Cqw4Arge/EwDa3+C6wzekiQui/gD+r6uXAaKJ820UkC/g7wKWqI4B44B5nqwqKl4CpbaY9CXyoqoOAD73PL1lUNHpgPFCiqmWqWg8sAqY7XFNQqeo+Vf3c+/g4nl/+YN2JLGyISDZwM/C807WEgoh0AwqBFwBUtV5VjzhaVGgkAJ1EJAHoDOx1uJ6AU9UioKbN5OnAy97HLwO3BuK9oqXRZwF7fJ5XEgNNr4WI5AJjgc8cLiUUfgk8ATQ7XEeo5AHVwIve4arnRSTV6aKCSVWrgF8Au4F9wFFV/YuzVYVMb1Xd5328H+gdiBeNlkYfs0SkC/A28PeqeszpeoJJRL4BHFTVYqdrCaEE4ArgN6o6FjhJgD7OhyvvuPR0PH/k+gGpInK/s1WFnnrOfQ/I+e/R0uirgP4+z7O906KaiCTiafKvqeo7TtcTApOAaSJSjmd47joRedXZkoKuEqhU1ZZPa4vxNP5odgOwS1WrVbUBeAeY6HBNoXJARPoCeP89GIgXjZZGvxYYJCJ5IpKE58DNEodrCioRETzjtttU9T+cricUVPUpVc1W1Vw8/8cfqWpU7+mp6n5gj4gM8U66HtjqYEmhsBu4UkQ6e3/OryfKD0D7WAI85H38EPD7QLxoQiBexGmq2igic4D38ByhX6CqWxwuK9gmAQ8Am0RkvXfaP6nqUudKMkHyt8Br3p2YMmCGw/UElap+JiKLgc/xnF22jiiMQxCR3wJTgJ4iUgn8GHgGeFNEHsUT135XQN7LIhCMMSa6RcvQjTHGmPOwRm+MMVHOGr0xxkQ5a/TGGBPlrNEbY0yUs0ZvjDFRzhq9MSHgDecyxhHW6E3MEZFcb7b7a95898XeqzCv9waHbfJmhSeLyDgRece73nQROS0iSSKSIiJl3ukDReTPIlIsIitF5HLv9JdEZK6IfAb8q4ObbGKcNXoTq4YAv1bVocAx4Ht48sHvVtWReK4a/xs8V2WO8a5zDbAZGAdM4Mu00PnA36pqAfA48Guf98kGJqrq94K5McZciH2cNLFqj6p+7H38KvBDPEFaO73TXga+o6q/FJFSERmK574H/4EnHz4eWOlND50IvOWJZQEg2ed93lLVpiBvizEXZI3exKq22R9HgB7nWbYIz93LGoAP8Oz5xwP/iOdT8RFVHXOedU9eYp3GXDIbujGxaoDPvVe/CbiBXBG5zDvtAWCF9/FK4O+B1apajecPwhBgs/ceALtE5E7wpIqKyOgQbYMxfrFGb2LVDjz32d0GpAP/iScV8i0R2YTnDlZzvct+hudOP0Xe5xuBTfplIuB9wKMisgHYQpTfxtJEHkuvNDHHe+vFP3hvPG1M1LM9emOMiXK2R2+MMVHO9uiNMSbKWaM3xpgoZ43eGGOinDV6Y4yJctbojTEmyv1/DTE5ekggrZ0AAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAEGCAYAAABrQF4qAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAA1BElEQVR4nO3deXyV1bnw/d+VmUDIzBgyIQiIyBAStEVQq9XaSsXWOmD1ONKn9j3nOe371L49x1bP6du+PbbH9nSgtKUqUK3a1qp1qAMKtmSHMMqokDkQCNmEQMic6/1j72AMQ3Zg733v4fp+Pvl4Z93TdUdyZe211r2WqCrGGGMiV4zTARhjjAksS/TGGBPhLNEbY0yEs0RvjDERzhK9McZEuDinAxgoKytL8/PznQ7DGGPCysaNGw+ravbp9oVcos/Pz6e8vNzpMIwxJqyISPWZ9lnTjTHGRDhL9MYYE+Es0RtjTIQLuTZ6Y0x46erqoq6ujvb2dqdDiQpJSUnk5OQQHx/v8zmW6I0x56Wuro6UlBTy8/MREafDiWiqSlNTE3V1dRQUFPh83qBNNyKyQkQOicj2M+wXEfmpiOwVkW0iMrvfvjtF5EPv150+R2WMCRvt7e1kZmZakg8CESEzM3PIn558aaN/Arj2LPuvAyZ5v+4HfukNKAP4DlACFAPfEZH0IUVnjAkLluSD51x+1oMmelVdC7jPcsgi4Cn1KAXSRGQs8GngDVV1q+oR4A3O/gfDhBFXRRMbq484HYYxxgf+GHUzHqjt932dt+xM5acQkftFpFxEyhsbG/0Qkgmkju4evrJ6E1/7/Sa6e3qdDscYfvrTnzJ16lRuuukmLr30UhITE3nsscecDitkhERnrKouB5YDFBUV2UooIe7V9xtwt3YC8PbuQ1xz0RiHIzLR7he/+AVvvvkmCQkJVFdX88ILLzgdUkjxR42+HpjQ7/scb9mZyk2YW1laTX5mMmNGJrGy9IxvXRsTFEuXLqWiooLrrruO1atXM3fu3CENPYwG/qjRvwg8KCLP4Ol4PaqqB0TkdeD/7dcBew3wLT/czzho5/4WNlYf4d+un0prRw///eYHVB1uJT9ruNOhmRDwyEs72Lm/xa/XnDZuJN/53EVn3L9s2TJee+011qxZQ1ZWll/vHSl8GV75NLAeuFBE6kTkHhFZKiJLvYe8AlQAe4FfA/8LQFXdwH8AG7xfj3rLTBhb5aomKT6GL86ZwC3FE4iLEVa7rFZvTCgbtEavqrcOsl+Br55h3wpgxbmFZkJNS3sXL2yu54ZLxpGaHE8q8Xz6ojE8W17H16+5kKT4WKdDNA47W83bOMfmujE++/Omek509nDHvPyTZUvm5XG0rYuXtu53LjBjzFmFxKgbE/pUlZWl1VySk8rFOakny+cVZnDBqBGsKq3mi0UTznIFYwKvoaGBoqIiWlpaiImJ4fHHH2fnzp2MHDnS6dAcZYne+MRV6WbvoeP81xdmfKxcRFhSkst3X9rJtrpmZuSkOROgiWpVVVUnt+vq6pwLJERZ043xycrSalKHxfO5S8adsm/xnByGxceyyoZaGhOSLNGbQR1qaef17Q3cXJRz2g7XkUnxfH7WeP6yZT9HT3Q5EKEx5mws0ZtBPbOhlu5e5faSvDMes2ReLh3dvTy3sfaMxxhjnGGJ3pxVd08vv3fVMH9S1llfirpoXCqzc9NY7aqht9dmsTAmlFiiN2f15q5DNLS0c8e8M9fm+9xxaR6Vh1v5x76mIERmjPGVJXpzVqtd1YxLTeLKKaMGPfa66WPJGJ7AytKqwAdmjPGZJXpzRhWNx1n34WFuK8klLnbwfypJ8bHcXDSBN3Ye5MDRtiBEaIyHL9MUt7W1sWDBAnp6eny+7rJly3jqqaf8He6gXn75ZR5++GG/Xc/G0ZszWu2qIT5WuHmu7y9C3V6Sy6/W7uNpVw3/es2FAYzOmI/4Mk3xihUrWLx4MbGxvk/VsXTp0sEPCoDrr7+ef//3f+ehhx4iOTn5vK9nNXpzWm2dPTxXXsu108cyKiXJ5/MmZCSzcHI2T2+opcsWJTFB4Os0xatXr2bRokUAvPPOOyxYsIBFixZRWFjIQw89xOrVqykuLubiiy9m3759AHz3u989+clg4cKFfPOb36S4uJjJkyezbt06AJ544gkWLVrEwoULmTRpEo888ojPsS9cuJB//ud/ZubMmUyfPp2ysjLA8yLiwoULefnll8/rZ9PHavTmtF7aup+W9m6WlOQO+dw7Ls3j7ifK+duOg1w/Y2wAojMh69WHoOF9/15zzMVw3Q/OuNuXaYo7OzupqKggPz//ZNnWrVvZtWsXGRkZFBYWcu+991JWVsZPfvIT/ud//ofHH3/8lOt0d3dTVlbGK6+8wiOPPMKbb74JQFlZGdu3byc5OZm5c+dy/fXXU1RUxPz58zl27Ngp13nsscf41Kc+BcCJEyfYsmULa9eu5e6772b79u0AFBUVsW7dOm6++WZff1JnZInenNYqVzWTR4+guCBjyOcumDyKnPRhrCytskRvQsLhw4dJS0v7WNncuXMZO9bz73PixIlcc801AFx88cWsWbPmtNdZvHgxAHPmzPnYtAtXX301mZmZJ4957733Tibqwdx6q2eC4Msvv5yWlhaam5tJS0tj1KhR7N/vn8kCLdGbU2ytbWZb3VH+Y9FF57TifGyMcHtJHv/fa7v58OAxJo1OCUCUJiSdpebtpGHDhtHe3v6xssTExJPbMTExJ7+PiYmhu7v7tNfpOyY2NvZjxwz8Pen73pca/ZnObW9vZ9iwYYM/nA8s0ZtTrCytZnhCLJ+fddq13H1yc1EO//3GB6wqreaRRdP9GJ0xQ5eenk5PTw/t7e0kJfne5+SrN954A7fbzbBhw3jhhRdYscKzDIcvNfo//OEPXHHFFbz33nukpqaSmuqZHfaDDz5g+nT//O741BkrIteKyB4R2SsiD51mf56IvCUi20TkHRHJ6bfvhyKyQ0R2ichP5VyqiCZojrR28tLW/dw4ezwpSee+7mbmiEQ+c/EY/ripntaO09eOjPG3hoYGcnJy+PGPf8x//ud/kpOTQ0uLZ2nDa665hvfeey8g9y0uLuamm25ixowZ3HTTTRQVFfl8blJSErNmzWLp0qX89re/PVm+Zs0arr/+ev8EqKpn/QJigX1AIZAAbAWmDTjmOeBO7/aVwErv9mXA373XiMWzJOHCs91vzpw5apyz/N19mvfNl3XXgaPnfa3yqibN++bLurq02g+RmVC1c+dOp0PwycaNG3XJkiV+v+7vfvc7/epXv3pO5y5YsEA3bNhwSnlDQ4NeeeWVZzzvdD9zoFzPkFd9qdEXA3tVtUJVO4FngEUDjpkGvO3dXtNvvwJJ3j8QiUA8cHAIf4dMEPX2Kqtd1czNT2fKmPNfqGF2bjpTx47kqfVVfRUCYxwze/ZsrrjiiiG9MOWUmpoafvSjH/nter4k+vFA/ykJ67xl/W0FFnu3bwRSRCRTVdfjSfwHvF+vq+qugTcQkftFpFxEyhsbG4f6DMZP3tt7mKqmEyzxYV4bX4gId8zLY3fDMTbVHPHLNY05H3ffffeQXpjyxV133cXPfvazczr3nXfeOW0zz9y5c5k5c+Z5RvYRf70w9Q1ggYhsBhYA9UCPiFwATAVy8PxxuFJE5g88WVWXq2qRqhZlZ2f7KSQzVCtLq8kakcC108f47ZqLZo4jJTGOlettUZJIZp/Ygudcfta+JPp6oP878Dnesv433q+qi1V1FvBtb1kzntp9qaoeV9XjwKvApUOO0gRcfXMbb+06yJfmTiAxzn81nuGJcSyePZ5X3m+g6XiH365rQkdSUhJNTU2W7INAVWlqahryyCFfhlduACaJSAGeBH8LcFv/A0QkC3Crai/wLWCFd1cNcJ+IfB8QPLX9x4cUoQmKp101KHBr8dDfhB3Mknl5PLm+mmfL6/jKwol+v75xVk5ODnV1dViza3AkJSWRk5Mz+IH9DJroVbVbRB4EXsczcmaFqu4QkUfx9PK+CCwEvi8iCqwFvuo9/Xk8o3Dex9Mx+5qqvjSkCE3AdXb38syGWq6aMoqc9POfQGmgSaNTmFeYwWpXNfdfXkhsjI2wjSTx8fEUFBQ4HYY5C59emFLVV4BXBpQ93G/7eTxJfeB5PcAD5xmjCbDXdzRw+HiH3zphT+eOefl89febePeDQ1w5ZXTA7mOMOZXNXmlYWVpNbkYyl08KXEf4NReNJjsl0TpljXGAJfoot6fhGGWVbpbMyyUmgE0q8bEx3Dp3Au980Eit+0TA7mOMOZUl+ii3qrSahLgYvjjH98VFztWtJbnEiLDaVRPwexljPmKJPood7+jmz5vr+eyMsaQPTwj4/camDuNTU0fxbHkt7V2h/3aiMZHCEn0Ue2FzPcc7urkjgJ2wA90xLx93ayevbj8QtHsaE+0s0UcpVWVVaTXTx49k5oS0oN33somZFGYNt05ZY4LIEn2UKq8+wu6GY9wxL++cFhc5VzExwm0luWyqaWbH/qNBu68x0cwSfZRaub6alKQ4PnfJuKDf+4tzJpAUH8OqUuuUNSYYLNFHocPHO3h1+wG+MCeH5ITgLzKWmhzPDZeM44XN9bS0dwX9/sZEG0v0UegPG2rp6tGAvgk7mDvm5dPW1cOfNtY5FoMx0cISfZTp6VV+76rhExdkMjF7hGNxXJyTyiUT0ljlqrFZD40JMEv0UWbN7kPUN7cFdUjlmSwpyWXvoeOUVridDsWYiGaJPsqsLK1m9MhEPjXV+YnFPnfJOFKHxbOq1IZaGhNIluijSHVTK2s/bOTW4lziYp3/X58UH8vNRTm8vqOBgy3tTodjTMRy/rfdBM3vXTXEiARkcZFzdXtJHt29yjNltYMfbIw5J5boo0R7Vw9/KK/l0xeNZvTIoS1DFkj5WcO5fHI2T5fV0N3T63Q4xkQknxK9iFwrIntEZK+IPHSa/Xki8paIbBORd0Qkp9++XBH5m4jsEpGdIpLvx/iNj/667QDNJ7ocHVJ5JktKcmloaefNXYecDsWYiDRooheRWODnwHXANOBWEZk24LDHgKdUdQbwKPD9fvueAv5LVacCxYD9NjtgZWk1E7OHc2lhptOhnOLKKaMYl5pknbLGBIgvNfpiYK+qVqhqJ/AMsGjAMdOAt73ba/r2e/8gxKnqGwCqelxVbdWJINtef5Qttc0sCfK8Nr6Ki43htpJc3tt7mH2Nx50Ox5iI40uiHw/07ymr85b1txVY7N2+EUgRkUxgMtAsIn8Skc0i8l/eTwgfIyL3i0i5iJTbSvL+t6q0mmHxsSyePbSV44Pp5rkTiI8VVtv8N8b4nb86Y78BLBCRzcACoB7owbP4+Hzv/rlAIXDXwJNVdbmqFqlqUXZ24NYtjUZH27p4YUs9n5/lGbMeqkalJHHt9LE8v7GWtk5blMQYf/Il0dcD/deZy/GWnaSq+1V1sarOAr7tLWvGU/vf4m326QZeAGb7IW7joz9urKO9qzckO2EHWlKSS0t7Ny9t3e90KMZEFF8S/QZgkogUiEgCcAvwYv8DRCRLRPqu9S1gRb9z00Skr5p+JbDz/MM2vuhbXGR2bhoXjUt1OpxBFRdkMHn0CJ4qrbL5b4zxo0ETvbcm/iDwOrALeFZVd4jIoyJyg/ewhcAeEfkAGA18z3tuD55mm7dE5H1AgF/7/SnMaf1jXxMVh1vDojYPICLcMS+P7fUtbK2zRUmM8RefJiNX1VeAVwaUPdxv+3ng+TOc+wYw4zxiNOdoVWk16cnxfObisU6H4rPPzxrPD17dzcr11UFd4tCYSGZvxkaohqPt/G3nQW6eO4Gk+FMGOoWslKR4bpw9npe27edIa6fT4RgTESzRR6iny2roVeX24vBotulvybw8Ort7ed4WJTHGLyzRR6Cunl6eLqth4eRscjOTnQ5nyKaMGcnc/HRWuarp7bVOWWPOlyX6CPTGzoMcOtYRNp2wp7NkXh7VTSdYt/ew06EYE/Ys0UegVaXVjE8bxsILRzkdyjm7dvoYskYksHK9zX9jzPmyRB9h9h46xj/2NXH7vFxiY0JvXhtfJcbF8qW5E3h790Hqm9ucDseYsGaJPsKsKq0hITaGm4smDH5wiLu1OBcFnnbZ/DfGnA9L9BHkRGc3f9xYx2cuHkPWiESnwzlvOenJXDVlFM9sqKGz2xYlMeZcWaKPIH/Zsp9jHd1h3Qk70JJ5eRw+3slrOxqcDsWYsGWJPkKoKivXVzNlTApz8tKdDsdvLp+UTW5GMqusU9aYc2aJPkJsrm1m54EW7rg0NBcXOVcxMcKSebmUVbnZ03DM6XCMCUuW6CPEqvXVjEiM4/MzB64JE/6+OGcCCXExttSgMefIEn0EcLd28vK2A9w0ezzDE32apy6spA9P4LMzxvKnTXUc7+h2Ohxjwo4l+gjwbHktnT293B5BnbAD3TEvj9bOHv68uX7wg40xH2OJPsz19iqrXdWUFGQweXSK0+EEzMwJaUwfP5JV66ttURJjhsgSfZh798NGat1t3HFp5Nbm4aNFSfYcPEZ59RGnwzEmrPiU6EXkWhHZIyJ7ReSh0+zPE5G3RGSbiLwjIjkD9o8UkToR+Zm/Ajceq9ZXk52SyDXTxjgdSsDdcMl4UpLibP4bY4Zo0J47EYkFfg5cjWex7w0i8qKq9l/79THgKVV9UkSuBL4P3NFv/38Aa/0XtgHY39zG23sO8bUrLiAhLvI/nA1LiOULc3J4an01W2qbnQ4nKsQIfPv6aVw9bbTToQTF4eMdfHX1Jh5ZdBFTxox0Ohy/8WWIRjGwV1UrAETkGWARH1/kexrwr97tNcALfTtEZA6edWRfA4rOP2TTZ92HjajC5y4Z53QoQfPA5RNp7eimq8fa6YPBVdHED1/bzVVTRhETxpPk+WrFe5W4Kt28tHV/1CX68UBtv+/rgJIBx2wFFgM/AW4EUkQkEzgC/AhYAnzqTDcQkfuB+wFyc3N9jT3quSrcZI1I4IJRI5wOJWjGpCbxwy9c4nQYUeOFzfX8yx+28PbuQ3wqwmv1x9q7WOl9V8NV4XY4Gv/y1+f9bwALRGQzsACoB3qA/wW8oqpnXRNOVZerapGqFmVnZ/sppMjnqnRTXJARUW/CmtDy2RljGZ82jGXv7nM6lIB7uqyGY+3dXDYxk611zbR39Tgdkt/4kujrgf5z3uZ4y05S1f2qulhVZwHf9pY1A5cCD4pIFZ52/C+LyA/8EHfUqztygvrmNorzM5wOxUSwuNgY7ptfQHn1EcqrIquW219Hdw+/fa+SSwszuXd+AV09yqaayBnd5Uui3wBMEpECEUkAbgFe7H+AiGSJSN+1vgWsAFDV21U1V1Xz8dT6n1LVU0btmKHr+2hZUpjpcCQm0t08dwLpyfERXav/y+b9HGzpYOnCiRTlZyASWc03gyZ6Ve0GHgReB3YBz6rqDhF5VERu8B62ENgjIh/g6Xj9XoDiNV6uyibSkuO5MIJfkjKhITkhjjsvy+fNXYf44GDkTSzX26ssW7uPaWNHcvmkLEYmxTNt7EhclU1Oh+Y3PrXRq+orqjpZVSeq6ve8ZQ+r6ove7edVdZL3mHtVteM013hCVR/0b/jRy1XpZm5+RlSMhDDOu/PSfIbFx/KrdyucDsXv3th1kIrGVh5YUHiyv6ukIJPNNc10dEdGO33kD76OQA1H26luOkFJgbXPm+BIH57Al+ZO4C9b6tkfQWv4qirL3t3HhIxhXH/x2JPlJYUZdHT3sq3uqIPR+Y8l+jDU95GypMDa503w3Du/AAV++16l06H4TVmlm801zdw3v5C42I/SYd8gB1dFZDTfWKIPQ65KNymJcUwbFzkvdJjQl5OezA2XjOPpshqaT3Q6HY5fLHt3HxnDE/jinAkfK08fnsCUMSm4KiOjQ9YSfRhyVTRRlJ9OrLXPmyB7YEEhJzp7ImK+od0NLazZ08hdl+UzLCH2lP3FBRlsrD5CV0/4L0xviT7MNB7rYF9jqw2rNI6YMmYkV1yYzRP/qAr7F4p+9W4FyQmxfPkMM7+WFGRyorOH9+vDv53eEn2YKfN+lLSOWOOUpQsm0tTayXPltYMfHKLqjpzgxa37uWVuLmnJCac9prigr50+/JtvLNGHmbLKJpITYpk+PtXpUEyUKi7IYFZuGsvXVdAdps0av1lXieDpYD6T7JREJmYPpywCxtNbog8zrko3c/LSiY+1/3XGGSLC0gUTqXW38cr2BqfDGbIjrZ38YUMtN8wcx7i0YWc9tqQwk/KqI/T0hvdsqZYtwsiR1k52NxyzZhvjuKunjmZi9nCWvbMv7JZ2fHJ9FW1dPSxdMHHQY0sKMjjW0c3O/S1BiCxwLNGHkbIqm9/GhIaYGOGByyey80AL6z487HQ4PjvR2c2T/6jiU1NH+bTGct+7KuE+HYIl+jDiqnCTGBfDjBxrnzfOWzRrHKNHJobVZGfPbqjlyIkun2rz4Fn/IC8zmdIw75C1RB9GXJVNzM5NJzHu1DG/xgRbYlws93yygH/sa2JbXbPT4Qyqq6eXX6+rpCgvnaIhTO9dUpDBhio3vWHcTm+JPky0tHex80DLySFfxoSCW4tzSUmKC4ta/V+3HaC+uc3n2nyfkoJMjrZ1sSeMZ+60RB8myqvcqHomWzImVKQkxXPHvDxe3d5A5eFWp8M5o77JyyaNGsGVU0YN6dy+37lwnvfGEn2YcFW4SYiNYXZuutOhGPMx//SJAuJjY1i+NnSnMH7ng0Z2NxzjgQUThzy1d056MuPThoX1vDeW6MNEaaWbSyakkhRv7fMmtGSnJPKFOTn8cWMdh1ranQ7ntJa9s4+xqUnccMm4czq/pCCDskp32A0l7eNToheRa0Vkj4jsFZFTlgIUkTwReUtEtonIOyKS4y2fKSLrRWSHd9+X/P0A0eB4Rzfb64/atMQmZN0/v5Du3l5W/L3K6VBOsbnmCK5KN/d8soCEuHOr25YUZtDU2sneQ8f9HF1wDPrUIhIL/By4DpgG3Coi0wYc9hie9WBnAI8C3/eWnwC+rKoXAdcCj4tImp9ijxqbqj1v5ln7vAlV+VnDuW76WFaXVtPS3uV0OB+z7N19pA6L59bi3HO+xkfj6cOz+caXP2/FwF5VrVDVTuAZYNGAY6YBb3u31/TtV9UPVPVD7/Z+4BCQ7Y/Ao4mrsonYGLH2eRPSli6YyLGObn7vqnE6lJP2NR7nbzsP8uVL8xieGHfO18nLTGb0yMSITvTjgf7T1NV5y/rbCiz2bt8IpIjIx9oZRKQYSABOGYclIveLSLmIlDc2Nvoae9RwVbi5eHzqef1DNSbQLs5J5RMXZLLivcqQWWt1+bsVJMTGcOdl+ed1HRGhpCATV0VTWLbT+6sz9hvAAhHZDCwA6oGT/6dFZCywEvgnVT1lujtVXa6qRapalJ1tFf7+2jp72FrXbM02JiwsXTCRQ8c6+POmeqdD4WBLO3/eXM/NRRPIGpF43tcrLsjg0LEOqppO+CG64PIl0dcD/dfZyvGWnaSq+1V1sarOAr7tLWsGEJGRwF+Bb6tqqT+Cjiaba47Q1aPMs45YEwY+eUEWF40byfK1FY7P+LjivUq6e3u5b36hX643L4zH0/uS6DcAk0SkQEQSgFuAF/sfICJZItJ3rW8BK7zlCcCf8XTUPu+/sKNHaaWbGIGifGufN6FPRPjKwolUHG7ljZ3OTWF8tK2L1a4arp8xjtzMZL9cc2L2CLJGJJxc/CecDJroVbUbeBB4HdgFPKuqO0TkURG5wXvYQmCPiHwAjAa+5y2/GbgcuEtEtni/Zvr5GSJaWWUTF41LJSUp3ulQjPHJddPHkpeZzC/frXCsPXu1q5rjHd08cLl/avPg+SNWXJARlh2yPrXRq+orqjpZVSeq6ve8ZQ+r6ove7edVdZL3mHtVtcNbvkpV41V1Zr+vLQF7mgjT0d3D5ppmm9/GhJXYGOG++YVsrW12ZNbH9q4eVrxXxfxJWX5fia2kIJP65jZq3eHVTm9vxoawrbVH6ejutYVGTNj5wpwcskYkODLZ2Z821XP4eAdfGeLkZb44uY5smNXqLdGHMFdFEyJYjd6EnaT4WP7pEwW8+0FjUFdn6ulVlq/dx4ycVC6d6P8BDBeOTiEtOT7sOmQt0YcwV6Xb+w/r9KvUGxPKlpTkMTwhll+tDV6t/vUdDVQ1nWDpgomIDG3yMl/ExAhz88Ovnd4SfYjq6ullY/UR5tmygSZMpSbHc1tJLi9vOxCUNu2+qYgLsobz6YvGBOw+JQUZ1LhPcOBoW8Du4W+W6EPU+/VHaevqsWYbE9bu+WQhMQK/WRf4KYzX72tiW91R7ptfSOwQpyIeir7KVzgNs7REH6Jc3tEKluhNOBuTmsTnZ47nD+W1NB3vCOi9fvnuPrJGJLJ49sAZWvxr6tiRpCTGhdU6spboQ5SrsokLRo3wy6vbxjjpgQWFtHf18uT66oDdY3v9UdZ9eJi7P5kf8DUbYmOEovx0XJXh0yFriT4Edff0Ul51xIZVmohwwagUrp42mqfWV3Giszsg91j27j5GJMZxe0leQK4/UElhJhWNrRw6FpoLrQxkiT4E7TzQwvGObkqsI9ZEiKULJtJ8ootnymoHP3iIqptaeeX9A9xekkvqsOC8Qd5XCdtQeSQo9ztfluhDUF8nj9XoTaSYk5dOcX4Gv32vkq6eUyawPS+/XldBXEwMd3+ywK/XPZvp41NJTogNm+YbS/QhqLTCTX5mMqNHJjkdijF+s3RhIfXNbby0db/frnn4eAfPlddx46zxQf19iY+NYU5e+slBE6HOEn2I6e1VNlS5bX1YE3GuuHAUF45O4Vd+nOzsib9X0dnTy/0L/Dd5ma9KCjLYc/AY7tbOoN97qCzRh5jdDcc42tZlC42YiCMiPLCgkD0Hj7Fmz6Hzvt7xjm6eWl/FNdNGMzF7hB8iHJqSMBpPb4k+xPS1+VlHrIlEn7tkHOPThrHsnfN/geqZshpa2rtZGoDJy3wxIyeVxLiYsGint0QfYlwVbnLShzE+bZjToRjjd/GxMdzzyQLKqtxsrD73ESud3b38Zl0lJQUZzMp1ZlGexLhYZuemW43eDI2qUlbltrdhTUS7pXgCacnx5zWF8V+21NPQ0s7Shc7U5vuUFGaw80ALR9u6HI1jMD4lehG5VkT2iMheEXnoNPvzROQtEdkmIu+ISE6/fXeKyIferzv9GXyk2XvoOO7WTlsf1kS05IQ4vnxpPm/sPMjeQ8eGfH5vr/KrtRVMGZPCwsnZAYjQdyUFmahCeVVo1+oHTfQiEgv8HLgOmAbcKiLTBhz2GJ51YWcAjwLf956bAXwHKAGKge+IiC1+egalfePnrSPWRLi7LssnKT6GZe8Ova3+rd2H2HvoeMCmIh6KWblpJMTGhPy0xb7U6IuBvapaoaqdwDPAogHHTAPe9m6v6bf/08AbqupW1SPAG8C15x92ZHJVNDFmZBK5Gf5ZzNiYUJUxPIEvFU3gL1vqhzzd77J39zE+bRifnTE2QNH5Lik+lksmpIb8QiS+JPrxQP/3luu8Zf1tBRZ7t28EUkQk08dzEZH7RaRcRMobGxt9jT2iqCquSjclhRmO11KMCYZ75xfSq/DbdZU+n7PB24l73/wC4mJDo4uxpCCT7fs905aEKn/9pL4BLBCRzcACoB7o8fVkVV2uqkWqWpSd7Wybm1Oqmk7QeKzDXpQyUWNCRjKfnTGWp8tqOHrCt87MZe/sIz05npvnTghwdL4rKcygp1fPaxRRoPmS6OuB/j/VHG/ZSaq6X1UXq+os4NvesmZfzjUefR/9bMSNiSYPXD6R1s4eVpZWDXrsnoZjvLX7EHdelk9yQlzgg/PRnLx04mIkpJtvfEn0G4BJIlIgIgnALcCL/Q8QkSwR6bvWt4AV3u3XgWtEJN3bCXuNt8wM4Kp0kzUikYnZw50OxZigmTZuJAsmZ/O7v1fR3nX2RoBfrd3HsPhY7rw0PzjB+Sg5IY7p41NDukN20ESvqt3Ag3gS9C7gWVXdISKPisgN3sMWAntE5ANgNPA977lu4D/w/LHYADzqLTP9qCquiiZKCqx93kSfpQsm0tTayXMb6854TH1zGy9u2c+X5k4gfXhCEKPzTUlhBtvqmmnr9LnFOqh8aqNX1VdUdbKqTlTVviT+sKq+6N1+XlUneY+5V1U7+p27QlUv8H79LjCPEd7qjrSx/2i7Das0UWleYQaXTEjj12sr6D7DFMa/XVeJAvfOD95UxEMxryCTrh5lU01ottOHRrd1lCv1tu1ZR6yJRiLCVxYUUuM+wavbG07Z33yik2c21HDDJePISQ/NocdF+enECCHbfGOJPgSUVbpJS45n0qjgz8BnTCi4etoYCrOGs+zdfadMYfzU+mpOdPbwgANTEfsqJSmei8aF7nh6S/QhwFXppjg/g5gYa5830Sk2Rrj/8kJ27G/hvb2HT5a3dfbwxD+quOLCbKaMGelghIMrKchgc23zoJ3KTrBE77ADR9uocZ+waYlN1Ltx9nhGpSR+bLKz5zbW4m7tdGwq4qEoLsigs7uXrbXNTodyCkv0DutbiszWhzXRLjEulrs/WcDf9zbxft1Runt6Wb62glm5aWHxfklxQQYSou30lugd5qpsIiUpjqljQ/tjqTHBcFtJLimJcSx7dx9/ff8AdUfaQmLyMl+kJSdw4eiUkJyf3hK9w/ra52Otfd4YRibFc/u8PF7dfoAf/e0DJmYP5+qpo50Oy2fzCjPZWH2ErjMME3WKJXoHHTrWTkVja1h8LDUmWO7+RD5xMTHUuE/wwOUTw2qQQklBBm1dPWyrO+p0KB9jid5BZSfnn7eOWGP6jBqZxG0lueRlJrNo1jinwxmSud5KW6itI2uJ3kGuCjfDE2KZPs7a543p7+HPTuON/72AxLhYp0MZkqwRiVwwasTJQRahwhK9g1yVTczJzwiZebWNCRUxMUJCXHj+XpQUZFBe5T7jdA5OCM+fZARwt3bywcHjNqzSmAhTUphJa2cPOw+0OB3KSZboHXKyfd4SvTERZV5fO30INd9YoneIq7KJpPgYZuSkOR2KMcaPRo1MoiBreEh1yFqid4irws3s3PSwbYc0xpxZcX4GZZVuenp18IODwLKMA46e6GJXQ4tNS2xMhCopzKClvZvdDaHRTu9ToheRa0Vkj4jsFZGHTrM/V0TWiMhmEdkmIp/xlseLyJMi8r6I7BKRb/n7AcLRhio3qthCI8ZEqL53Y0JlOoRBE72IxAI/B64DpgG3isi0AYf9G54lBmfhWVP2F97yLwKJqnoxMAd4QETy/RR72HJVNpEQG8PMCWlOh2KMCYDxacPISR8WMh2yvtToi4G9qlqhqp3AM8CiAcco0PfWTyqwv1/5cBGJA4YBnUBofJZxUFmlm5kT0kiKD6+XQYwxvispyKSsyn3KQipO8CXRjwdq+31f5y3r77vAEhGpA14BvuYtfx5oBQ4ANcBjp1scXETuF5FyESlvbGwc2hOEmeMd3Wzf32LNNsZEuJKCDNytnXx46LjTofitM/ZW4AlVzQE+A6wUkRg8nwZ6gHFAAfB1ETllPTBVXa6qRapalJ2d7aeQQlN5lacn3jpijYlsfZW5UFhe0JdEXw9M6Pd9jresv3uAZwFUdT2QBGQBtwGvqWqXqh4C/g4UnW/Q4cxV6SYuRpidl+Z0KMaYAMrNSGbMyCRKQ6BD1pdEvwGYJCIFIpKAp7P1xQHH1ABXAYjIVDyJvtFbfqW3fDgwD9jtn9DDk6uiiRk5qSQnxDkdijEmgESEkkLPeHqn2+kHTfSq2g08CLwO7MIzumaHiDwqIjd4D/s6cJ+IbAWeBu5Sz5P9HBghIjvw/MH4napuC8SDhIO2Ts881TYtsTHRoaQgk8ZjHVQebnU0Dp+qlar6Cp5O1v5lD/fb3gl84jTnHcczxNIAm2qO0N2rttCIMVHiZDt9pZvC7BGOxWFvxgaRq6KJGIGivHSnQzHGBEFh1nCyRiQ63iFriT6ISivdTB+fSkpSvNOhGGOCQEQoKcjA5XA7vSX6IGnv6mFLbbNNS2xMlCkpzODA0XbqjrQ5FoMl+iDZUttMZ3evjZ83Jsr0/c6XOth8Y4k+SMoq3YjA3Hyr0RsTTSaNGkF6cjwuB8fTW6IPEldlE1PGjCQ12drnjYkmMTHC3PwMRxcisUQfBJ3dvWysPmLt88ZEqZLCTGrdbexvdqad3hJ9ELxf30x7Vy/zbCIzY6JSXyXPqfnpLdEHQal3Tupi64g1JipNHTuSlKQ4x5pvLNEHQVmlm8mjR5AxPMHpUIwxDoiNEYrzMxxbiMQSfYB19/RSXuW2aQ+MiXIlhRlUHG7lUEt70O9tiT7AduxvobWzx8bPGxPl+ppunRhmaYk+wPra5GxFKWOi2/RxIxmeEOtIO70l+gBzVbgpzBrOqJQkp0MxxjgoLjaGOfkZjoy8sUQfQD29SlmV22rzxhjAM8zyg4PHcbd2BvW+lugDaHdDC8fau60j1hgDcPJdmrIgN9/4lOhF5FoR2SMie0XkodPszxWRNSKyWUS2ichn+u2bISLrRWSHiLwvIlHThtE3lMo6Yo0xABePTyMpPubkuzXBMugKUyISi2dJwKuBOmCDiLzoXVWqz7/hWWLwlyIyDc9qVPkiEgesAu5Q1a0ikgl0+f0pQpSrsokJGcMYlzbM6VCMMSEgIS6G2bnpQR9540uNvhjYq6oVqtoJPAMsGnCMAiO926nAfu/2NcA2Vd0KoKpNqtpz/mGHvt5epazSbbV5Y8zHlBRksruhhaMnglfn9SXRjwdq+31f5y3r77vAEhGpw1Ob/5q3fDKgIvK6iGwSkf9znvGGjQ8PHefIiS6byMwY8zElhRmowoaq4NXq/dUZeyvwhKrmAJ8BVopIDJ6moU8Ct3v/e6OIXDXwZBG5X0TKRaS8sbHRTyE5q2+s7LxCq9EbYz4yc0IaCXExQR1P70uirwcm9Ps+x1vW3z3AswCquh5IArLw1P7XquphVT2Bp7Y/e+ANVHW5qhapalF2dvbQnyIEuSrdjE1NIifd2ueNMR9Jio9l5oS0oLbT+5LoNwCTRKRARBKAW4AXBxxTA1wFICJT8ST6RuB14GIRSfZ2zC4AdhLhVBVXhZuSggxExOlwjDEhpqQgg+31RznWHpx2+kETvap2Aw/iSdq78Iyu2SEij4rIDd7Dvg7cJyJbgaeBu9TjCPBjPH8stgCbVPWvAXiOkFJxuJXDxzsosWYbY8xplBRk0qtQXn0kKPcbdHglgKq+gqfZpX/Zw/22dwKfOMO5q/AMsYwaH42ft45YY8ypZuelERcjlFW6ueLCUQG/n70ZGwCuyiayUxIpyBrudCjGmBCUnBDHjJxUXBXB6ZC1RO9nfe3zxdY+b4w5i5LCTLbVHeVEZ3fA72WJ3s9q3W00tLQzz5ptjDFnUVyQQXevsqm6OeD3skTvZ6Un55+3jlhjzJkV5aUTIwRlPL0lej9zVbjJGJ7ApFEjnA7FGBPCUpLimT4+NSjj6S3R+5mrsonifGufN8YMrqQggy21zbR3BXYKMEv0flTf3EbdkTZbaMQY45OSgkw6u3vZUtsc0PtYovejvsUEbKERY4wv5uZnIPLRuzeBYonej1wVbkYmxTFlzMjBDzbGRL3U5HimjBkZ8A5ZS/R+5Kr0jJ+PjbH2eWOMb0oKMthUc4TO7t6A3cMSvZ8cammn8nCrLTRijBmSeYUZtHf18n59c8DuYYneT0q9Q6SsI9YYMxTF3sphINeRtUTvJ2WVTYxIjGPaWGufN8b4LmN4ApNHjwjoeHpL9H7iqnAzJy+duFj7kRpjhqa4IIONVW66ewLTTm9ZyQ+ajnfw4aHj1mxjjDknJQWZtHb2sH1/S0Cub4neD8r62uetI9YYcw76KollARpm6dPCIyJyLfATIBb4jar+YMD+XOBJIM17zEPexUr6798JfFdVH/NP6B/XfKKTtx+/m4k9lYG4/FmN6unl2USY9XY6YEMrjTFDMwp4IbmZxg2T4fLf+f36gyZ6EYkFfg5cjWex7w0i8qJ3Vak+/4ZnicFfisg0PKtR5ffb/2PgVb9FfRoxMUJacjzDOmIDeZsziGVkUhwxluSNMecoOyWB7mHxAbm2LzX6YmCvqlYAiMgzwCI+vsi3An3DTVKB/X07ROTzQCXQ6od4z2hkUjxX/ov//xIaY0wwjPd+BYIvbfTjgdp+39dxajzfBZaISB2e2vzXAERkBPBN4JHzjtQYY8w58Vdn7K3AE6qaA3wGWCkiMXj+APy3qh4/28kicr+IlItIeWNjo59CMsYYA7413dQDE/p9n+Mt6+8e4FoAVV0vIklAFlACfEFEfoino7ZXRNpV9Wf9T1bV5cBygKKiIj2H5zDGGHMGviT6DcAkESnAk+BvAW4bcEwNcBXwhIhMBZKARlWd33eAiHwXOD4wyRtjjAmsQZtuVLUbeBB4HdiFZ3TNDhF5VERu8B72deA+EdkKPA3cpapWMzfGmBAgoZaPi4qKtLy83OkwjDEmrIjIRlUtOt0+ezPWGGMinCV6Y4yJcCHXdCMijUD1eVwiCzjsp3DCRbQ9c7Q9L9gzR4vzeeY8Vc0+3Y6QS/TnS0TKz9ROFami7Zmj7XnBnjlaBOqZrenGGGMinCV6Y4yJcJGY6Jc7HYADou2Zo+15wZ45WgTkmSOujd4YY8zHRWKN3hhjTD+W6I0xJsJFTKIXkWtFZI+I7BWRh5yOJ9BEZIKIrBGRnSKyQ0T+2emYgkVEYkVks4i87HQswSAiaSLyvIjsFpFdInKp0zEFmoj8b++/6+0i8rR3RtyIIiIrROSQiGzvV5YhIm+IyIfe/6b7414Rkej7LXd4HTANuNW7pGEk6wa+rqrTgHnAV6Pgmfv8M54J9qLFT4DXVHUKcAkR/uwiMh74v4AiVZ2OZx3qW5yNKiCewDu9ez8PAW+p6iTgLe/35y0iEj39ljtU1U6gb7nDiKWqB1R1k3f7GJ5f/kCtRBYyRCQHuB74jdOxBIOIpAKXA78FUNVOVW12NKjgiAOGiUgckEy/5UkjhaquBdwDihcBT3q3nwQ+7497RUqi92W5w4glIvnALMDlcCjB8Djwf4Beh+MIlgKgEfidt7nqNyIy3OmgAklV64HH8KxzcQA4qqp/czaqoBmtqge82w3AaH9cNFISfdTyrsv7R+BfVLXF6XgCSUQ+CxxS1Y1OxxJEccBs4JeqOgtoxU8f50OVt116EZ4/cuOA4SKyxNmogs+7podfxr9HSqL3ZbnDiCMi8XiS/GpV/ZPT8QTBJ4AbRKQKT/PclSKyytmQAq4OqFPVvk9rz+NJ/JHsU0ClqjaqahfwJ+Ayh2MKloMiMhbA+99D/rhopCT6k8sdikgCno6bFx2OKaBERPC02+5S1R87HU8wqOq3VDVHVfPx/D9+W1Ujuqanqg1ArYhc6C26CtjpYEjBUAPME5Fk77/zq4jwDuh+XgTu9G7fCfzFHxf1Zc3YkKeq3SLSt9xhLLBCVXc4HFagfQK4A3hfRLZ4y/4fVX3FuZBMgHwNWO2txFQA/+RwPAGlqi4ReR7YhGd02WYicDoEEXkaWAhkiUgd8B3gB8CzInIPnunab/bLvWwKBGOMiWyR0nRjjDHmDCzRG2NMhLNEb4wxEc4SvTHGRDhL9MYYE+Es0RtjTISzRG9MEHgn5zLGEZboTdQRkXzv3O6rvfO7P+99C/Mq78Rh73vnCk8Ukbki8ifveYtEpE1EEkQkSUQqvOUTReQ1EdkoIutEZIq3/AkRWSYiLuCHDj6yiXKW6E20uhD4hapOBVqAf8UzP/iXVPViPG+NfwXPW5kzvefMB7YDc4ESPpotdDnwNVWdA3wD+EW/++QAl6nqvwbyYYw5G/s4aaJVrar+3bu9Cvh3PBNpfeAtexL4qqo+LiL7RGQqnnUPfoxnfvhYYJ139tDLgOc807IAkNjvPs+pak+An8WYs7JEb6LVwLk/moHMMxy7Fs/qZV3Am3hq/rHA/43nU3Gzqs48w7mt5xmnMefNmm5MtMrtt/bqbUA5kC8iF3jL7gDe9W6vA/4FWK+qjXj+IFwIbPeuAVApIl8Ez6yiInJJkJ7BGJ9YojfRag+edXZ3AenAf+OZFfI5EXkfzwpWy7zHuvCs9LPW+/024H39aEbA24F7RGQrsIMIX8bShB+bvdJEHe/Siy97F542JuJZjd4YYyKc1eiNMSbCWY3eGGMinCV6Y4yJcJbojTEmwlmiN8aYCGeJ3hhjItz/D66bPok68QzMAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"select_model(data, 10)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"id": "matched-distinction",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Index(['x0', 'x1', 'x2', 'y', 'x1^2', 'x1x2', 'x1^2x2', 'x2^2', 'x1x2^2',\n",
" 'x1^2x2^2'],\n",
" dtype='object')\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: divide by zero encountered in log\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n",
"<ipython-input-5-be07fd130d69>:71: RuntimeWarning: invalid value encountered in matmul\n",
" result = (np.matmul(y.T, np.log(h)) + np.matmul(1 - y.T, np.log(1 - h))) / (-m)\n"
]
},
{
"data": {
"text/plain": [
"array([[10.99806814],\n",
" [ 4.09906074],\n",
" [ 4.35988893],\n",
" [-2.19265142],\n",
" [ 8.45894967],\n",
" [ 2.16723751],\n",
" [-1.31700181],\n",
" [ 2.78205894],\n",
" [-3.50965323]])"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"P = 2\n",
"expanded = expand(data, P)\n",
"X, y = extract(expanded, 0, data.shape[0] + 1)\n",
"Xtrain, ytrain = extract(expanded, 0, math.ceil(data.shape[0] * 0.8))\n",
"Xcv, ycv = extract(expanded, math.ceil(data.shape[0] * 0.8), data.shape[0] + 1)\n",
"theta = solve(X, y, 0)\n",
"print(expanded.columns)\n",
"del expanded\n",
"theta"
]
},
{
"cell_type": "code",
"execution_count": 11,
"id": "fitting-lindsay",
"metadata": {},
"outputs": [],
"source": [
"def plot_model(data, P, theta, step, sensitivity=0.2):\n",
" if P < 2:\n",
" xmin = data['x1'].min()\n",
" xmax = data['x1'].max()\n",
" count = math.ceil((xmax - xmin) / step)\n",
" Xplot = pd.DataFrame(index=range(0, count), columns=['x'])\n",
" Xplot['x1'] = np.arange(xmin, xmax, step)\n",
" if P == 1:\n",
" Xplot['x2'] = -(theta[0,0] + theta[1,0] * Xplot['x1']) / (theta[2,0] + theta[3,0] * Xplot['x1'])\n",
" elif P == 0:\n",
" Xplot['x2'] = -(theta[0,0] + theta[1,0] * Xplot['x1']) / (theta[2,0])\n",
" ax = Xplot.plot.line(x='x1', y='x2',c='g')\n",
" else:\n",
" x1min = data['x1'].min()\n",
" x1max = data['x1'].max()\n",
" x2min = data['x2'].min()\n",
" x2max = data['x2'].max()\n",
" x1count = math.ceil((x1max - x1min) / step)\n",
" x2count = math.ceil((x2max - x2min) / step)\n",
" Xplot = pd.DataFrame(index=range(0, x1count * x2count), columns=['x1', 'x2'])\n",
" for i in range(0, x1count):\n",
" x1 = x1min + step * i\n",
" for j in range(0, x2count):\n",
" x2 = x2min + step * j\n",
" Xplot.loc[i * x1count + j] = [x1, x2]\n",
" Xplot = expand(Xplot, P)\n",
" X, _ = extract(Xplot, 0, Xplot.shape[0] + 1)\n",
" Xplot['y^'] = (np.abs((np.matmul(X, theta)) - 0) < sensitivity).reshape(X.shape[0]).astype(int)\n",
" ax = Xplot[Xplot['y^'] == 1].plot.scatter(x='x1', y='x2', c='green')\n",
" \n",
" ax = data[data['y'] == 0].plot.scatter(x='x1', y='x2', c='red', ax=ax)\n",
" data[data['y'] == 1].plot.scatter(x='x1', y='x2', c='blue', ax=ax)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"id": "documented-brook",
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"<ipython-input-11-846deff93970>:28: RuntimeWarning: invalid value encountered in less\n",
" Xplot['y^'] = (np.abs((np.matmul(X, theta)) - 0) < sensitivity).reshape(X.shape[0]).astype(int)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAtjElEQVR4nO2de3Bcd33oP1+tdqW1FEcB74WQh5XQtA0Nqe3IaSmUR2unToaJnRBo1HtLgsUNaXE6cYdpQ0K5lCF06OPaA6HFvpVLoEW44ULsUnNDTC5tmd4UK3aCnZiAQ+WxXbdZg63Gsiztrn73j7Mr7x6dPfvQee/3M6PZ19nVd885e76/71uMMSiKoihKPbrCFkBRFEWJNqooFEVRFFdUUSiKoiiuqKJQFEVRXFFFoSiKorjSHbYAfrBs2TIzODgYthiKoiix4ZlnnjlljMk5vZZIRTE4OMj4+HjYYiiKosQGETla7zV1PSmKoiiuqKJQFEVRXFFFoSiKoriiikJRFEVxRRWFoiiK4ooqCq/J52HfPutWURQlAaii8JKxMVi+HNautW7HxsKWSFEUZdGoovCKfB5GRmB6GiYnrduREbUsFEWJPaoovGJiAjKZ2ufSaet5RVGUGKOKwisGB2F2tva5QsF63kc0JNKZ6HFXgkQVhVfkcjA6CtksLF1q3Y6OWs/7hIZEOhM97krQSBJHoQ4NDZnQej3l85a7aXDQVyWRz1sXienpC89ls3D0qK//VikT0GF2/L963BU/EJFnjDFDTq+pReE1uRysXt3SrzY/lWffiX3kp/KOj53QkEiwVLt6wlzRx+m4q3ssOSSye2ycGDs4xsjuETKpDLOlWUZWjTC6f3T+8ej6UYavG17wvpBCIh3J2JiVwJbJwMwMzM1Z+76yqh8ZgTVrglnRL+a4B2kFVe+z2VnLCzu88DRWYoJaFCGSn8ozsnuE6eI0kzOTTBeneeS7j9Q8Htk14mhZhBAS6UjsWc/nzy+8UAe5om/3uAdpBWmmePJQRdEuHtjVE2cmyKQyrtukU2kmzkw4vjY8bPmm9+61bnXF5j1Orh47QVtyrR73oC/ccXKPKc2hrqd28MiuHhwYZLo47brN+eJ5BgcG676ey6kV4SdOrp50Grq7rdtCIRxLrpXjXrlwVwfAKxduP+RWt2jyUIuiVTxenpk596yzRq8r/uLk6nn00XhZckFfuNUtmjzUomgVD5dnE2cmWJJZwuTMZN1tulPdTJyZINenv7KwGB62gtX2QHBcLnyVC/fISHBWUL19psSTUBWFiOwA3gm8bIy5zuH1twO7gH8tP/VVY8zHAxPQCQ+XZ4MDg8yWZl23mS5O05/pb/mzFW+Ju4svjAt33PeZcoGwXU+fB9Y12OafjDEryn/hKgnw1K7O9eUYXT9KtjvL0p6l9KR6SEu6ZpveVC/HJo81rKtQlEa0UeKjKEAEKrNFZBD4uotF8SFjzDtb+cxAKrM9TErPT+WZODNBf6afFdtW1FgZKUmRSWUa1lUoiqIshrhXZr9JRJ4TkW+IyM/V20hE7hGRcREZzweRsO3h8izXl2P1ZatZtmTZguB1yZSaqqtQFNBqaMUfoq4o9gPLjTE/D3wGeLzehsaY7caYIWPMUC6mtnUluO2GW12F0tlos0DFLyKtKIwx/2mMOVu+vwdIi8iykMXyDS/qKpTORKuhFT+JtKIQkdeKiJTv34gl74/DlcpftK5CaYe4VUOriyxehKooRGQM+H/Az4jIcREZEZF7ReTe8iZ3AIdE5Dng08CdJuzou48043qq1FUoSjVxqoZWF1n8CLWOwhjjmr5jjHkEeCQgcUJH6yqUdgmjqK4dql1kYXTfVdoj0q6nTkPrKpTFEIcmkXFzkSkWoddR+EGoE+48QOsqlKSSz8Pll9e6yTIZOH5cLYqwiXsdRcehdRVKlPA68GxfmyZwrZo4VFFEGK2rUMLG68DzxAQssZ3S2ay6nqKOKooI00xwW+sqFD/I5+Gb3/S+NiNO2VnKBVRRRBh7cLs31UtKUjXbmDnDqXOnOiK4rbn3wVCxIm6/vbabPiw+8KyzKuKJBrNjQCW4fXr6NBt2bqip3k5Lmq6uLnq7exMd3PZoqKDSgHzeUhJ2BVEhm7UyqhZ7Yfewp6biERrMjjmV4PYVF1+xoMVHwRSYKc0EHtwOcnWv7SmCo96M8L4+b1f/SWh53kkWriqKGHF29izZVNZ1myCC20FX1mrufXA4xRB6e+GrX41ubUYYdFp1uSqKGDE4MEiJkus2fge3w1jdawA0OJxiCDt2wE03xXv17yWdaOGqoogZYTcNDGN1rwHQYHGr8O4kd0s11d+7Ey1cVRQxopm6imwmW+N68vqHHdbqPg7tKZKEUwyh09wtFezfe//+zrNwVVHEiFbrKvz4YYe5uk9CADSudKK7BZy/9+bNsGVLsL+BsC05VRQxotm6CoDDE6d438aSLz9sXd13Hp3oboH633vVquB+A1Gw5EJtM660zvB1w6y5ak3duoruVDfbxrfxiS8/wYz5OnDx/GuVH7ZX6Y1JXtlrnn8tnZpQ4Pa9g/gNRKUtu1oUMcStrmK6OM3D33mYmYu+D6XaFuWd8MP2giis4KJERWkG7W6JAmEnUkTFklOLIsZU6iqmSxeURaYrY7mj+k7B+o2wawekCvRIP6OjqcT/sBdLVFZwTnKFYeHYK+K3bLHcLp1kaQ0PW8c/jP0fFUtOLYoYMzgwCFL7XJd0XQh4v3EnbF5O9903c+DwaY0lNEFUVnDVhGXh1AvkdpKSqBBWIkXYFk2FsGdm7xCRl0XkUJ3XRUQ+LSJHROR7IrIqaBmjjD24ne3OsvXmrVBdStF3CnndOMtyyevp5QdRWcFVCCPbqJJhc+BA9JRmJxKF5JGwXU+fx5qJ/YU6r98MXFP++wXgL8q3Spnq4PbgwOB8rcXkzOT8NtlMlgMnD3BJ9hIGBwbJ9XXYcrAFojZ7umLhVDfp8zIpwU61q2lmBubmal/XOFc4hJ08EqqiMMb8o4gMumyyHviCsVrcPi0iAyJyqTHmZDASxoNcX67m4m8PcE/NTrFh5wYdn9okYfqk7QRp4TjFZ9Jpy90RBaWphEfUYxSXAceqHh8vP7cAEblHRMZFZDyf9CqgBuj41MUTleK+IH3UTvGZbBYef1xrZjqdsF1PnmGM2Q5sB2seRcjihIaT68lOpcOsuqDiQVAWTj3rZeXK8BWmEi5RtyhOAFdUPb68/JxSh8GBwQWuJzs6PjV+BGHhRCXDRokeUbcodgObROTLWEHsSY1PNKaZDrOnzp2aD4CrZaFUiFJ8RokOoSoKERkD3g4sE5HjwP8A0gDGmM8Be4BbgCPAOeB94UgaH5pxPQGs3LYy8eNTlfYIO8NGiR5hZz25Xp3K2U4fDEicRNBMh9mCKUAJZkozAIzsGmHNVWvUslAUxZGoxyiUFrEX4fWkekhL2vU9QYxPVRQlvkQ9RqG0QXURXn+mnxXbVuA2QVWD24qiuKGKIqFUivDyU/nQx6d2MtquXEkC6npKOM2OTz1w8gD7TuzTQjwP0XblSlIQK16cLIaGhsz4+HjYYkSC/FSe5VuXu9ZWpCRFJpXRFh8eks9byqG6R1M2a1U3q2WhRBERecYYM+T0mloUCaeZ8ana4sN7otiuXFHaRWMUHUCj8alOaIuPxRG1duWKshjUougQ3Man2pkuTtOf6Q9IsmSi7TCUJKEWRZJxSLlxGp9qpzfVy9nZs+Sn8trmYxFoOwwlKahFkVTqpNw4jU+1M8cc+0/uZ/nW5az94lqWb13O2CFN2WmHKLQrr0ys6/Du+8oi0KynJNIg5Wbs0Bgju0ZIp9LMFmcpzBUomQsVed10k+5O17iost1Zjt5/VC2LmFE9sW521nJ/6UwJxQnNegqLsJZyDVJuhq8b5uj9R9n7m3vZdeeuBfGInnQPXVJ7amibj9YJeyUfxrxtJZmoovCLMKutmki5qQS3V166ckFwe7Y0u6CxoLb5aI0oFNtpiq7iFaoo/CDspVyLKTf2Fh5mzoBZuM2pc6e0ersJwj78FTRFNzqEbV0uFlUUfhCFpdzwsBWTaDDs2KnFR0+6h66uhafGym0rNbjdBFE4/KApulEhCtblYtFgth/EqH+DU4uPnq4eZuZmXN+nwe36RO3wx7UxYVzlriZq54IbGswOGj+Xch7bsPYWH9nuLB9520fIprKu79Pgdn2itpKPQopuqyRhFQ7RsS4Xi1oUfuL1ksjHXMfq4jqgYSPBTCrD8c3HW7YoorZK9FOeqH3XuBCnVXgj4vRdImtRiMg6EXlRRI6IyAMOr98tInkRebb89/4w5GwbL5dyPkdIK1lQlTkWjRoJtjPDImqrRL/lieNK3mvaMYCTsgqH6FmX7RKaRSEiKeAHwFrgOLAPGDbGvFC1zd3AkDFmUyufHbpF4cdSct8+64o2OXnhuaVLrWD16tXe/A8bFSvj9PRp3vOV9zA5c+F/L+1ZymN3PMYl2UuaavERtZVV1ORJIu0awEk8NnGwLqNqUdwIHDHG/MgYMwt8GVgfojze4NcyNYRcR7dai6nZKTbs3NB0FlTUVolRkydpLMYATsoqvJq4W5dhKorLgGNVj4+Xn7PzLhH5noh8RUSuqPdhInKPiIyLyHg+iaWwIf967K4mpxkWh/OH69ZZRC2nP2ryJI3FKuIms7uVgIh61tPfAYPGmOuBJ4FH621ojNlujBkyxgzlwlLbfi9TQ/r1NDNOtVgqutZZRG2VGDV5kkY9Rdzf33zMIu6r8CQRZoziTcDHjDG/Vn78YQBjzB/V2T4F/MQYc3Gjzw4tRpFE5yrNjVO1U6/OImq+2qjJkyQqMYp02lISIyOWMtYGhdEkqjGKfcA1InKViGSAO4Hd1RuIyKVVD28FDgcoX+skdJlqz4LqSfWQlrTre+rVWURtlRg1eZJEtQH8zDPWTyHstiZKe4Q2uMgYUxSRTcATQArYYYx5XkQ+DowbY3YDvyMitwJF4CfA3WHJ2zSNptXEdAlbPU61P9PPim0roFR/+yQ0EYzpoYoUuZz1t2+fZUlUG9sVr6zu2+gT6oQ7Y8weYI/tuY9W3f8w8OGg5Vo0lV+HnZgPB6jUWOSn8g3rKNqps4gSTodKp9W1jyYPxJuoB7OTQ1RainpAM8HtbCbLxJkJ8lP52HWcdTpUd90VrWLBuJFQr2yk8LNDrSqKoEhQ4v7gwOCCeRV2zhfPx3acqtOhKhQSoeNDRVNe/cPvLgPa6ykoEpYRleRxqk6Hyo7PRfGK0jReXVqimvXUWfhhe4c4DaXdcaoHTh6IvCvKfqh6e50tDPWvK1EgCGeFWhRB41UqTYQC4051Fr2pXkqmRGGuMP9cSlJkUhkyqQyzpVlG148yfF10/Q/Vh2rv3tqagJjlISgJJgiLQhVFHImgG6vaFVUoFdiybgv3/f19FEyh7nvi4oqqoOmySlSxFze2s5BxUxShpscqbVKxNSOUlF5dZzE4MMjEmQm6U90UivUVBVgZVHFRFPWynjsZVZ7RoFH51mLRGEUciWhSevVMi/5Mf8OWH9PF6QWxjTgRYojIN1r5TlGbL+IFcT6mfnYZUEURR2KQlH529mzDcaq9qV6OTR6bD27H6UeaxItkK98pQWVB8yTxmHqFxijiTITt/mYaCVYHt8/tX4/83SjZnu6wY/MNiWCIaNG0+p1CmKPlK0k8pq2i6bFJJcId7ZoZpzo/0+InaQpf+wtmz3fHYnWaoNrJeVr9Tl60EY8SUT+mbtZ2EJa4KgrFNxrVWsxzZhBStVed7vRcZH6kdiIaIloUrX4nJ+/nyAjccEM8XTdRPqZuLrGg3GWqKBRfqR6nWrftx8AElGqXc69Mn2f/9Ff9F7ANYhAiapl2vlOS2ohH9Zi6xYKCjBOpolACwdUV1XcK1m+E7nPQM2nd3rqRzf/03yJbwZ3EvkXtfKeK9/Ps2Wi7bpohisfUzSUWpLtM6yiUwKiutTg9fZoNOzdcCHa/cSdc/S3LDTUwYSkPspGus0hiXUW73ynKrptWiNoxbbRfg9rnalEogVJxRV1x8RULM6L6TsFl42UlEf86i04iqq6buOO2X4Pc52pRKKFQqbOYLtVPn+1N9XJ29iz5qfx8xXdUrQvF/+rgTsVtvwa1z1VRKBcIsC5jcGAQxH2bOebYf3I/b/v822LTSNALIlwe05CouW6Sgtt+DWKfh+p6EpF1IvKiiBwRkQccXu8RkZ3l1/9FRAZDELMzCLgstZk6i7nSHJuf2GzVWsxMMl2cZmTXSGQD3F6g1cFKFAmtMltEUsAPgLXAcWAfMGyMeaFqm98GrjfG3CsidwK3GWN+vdFnd0xltleEWJZacSudnj7Ne77yHiZnLpT69qX7AJgqTM0/t7RnKY/d8RiXZC9JnCtKq4OjRZwtu3aIamX2jcARY8yPjDGzwJeB9bZt1gOPlu9/BfhVEWngsFBaJsSyVLc6i9JcacFzU7NTbNi5IXbjVZsh6tXBnYRfll2c+plVE6aiuAw4VvX4ePk5x22MMUVgEni104eJyD0iMi4i4/m4HYVG+H12RSC30e6KynZn2XrzVrAZvPNtP6pcUYfzhyM/Na8ZInAYFPwrZIuzW9FVUYjIUhF5vcPz1/snUnsYY7YbY4aMMUO5JNmJQZxdEcltrG75cfT+o6x67SqWZJa4vqdYKrLif67lHZ/8Pa58+IZYWxgROQwdjx+WXdy77dbNehKR9wBbgZdFJA3cbYzZV37588CqRf7vE8AVVY8vLz/ntM1xEekGLgZ+vMj/Gx+qz66K43pkxMqH8/rqEZHcxlxfribuULftR5nC994Fu0aZTc1CKcNdR+5lzV+tiW3sIiKHoaPxw7KL4KyxlnCzKB4EbjDGrADeB3xRRG4rv+ZFnGAfcI2IXCUiGeBOYLdtm93AXeX7dwBPmST2Ra9H0E7riHWjtbujelI9pCV9YYOpZbBrFIpLYGYAiksoPP45Drx0PDSZvSBih6Hj8MOyi7tb0a2OImWMOQlgjPmuiLwD+LqIXMECz3HrGGOKIrIJeAJIATuMMc+LyMeBcWPMbmAUS0EdAX6CpUw6h7ifXR5Q3fajP9PPim0roFR+sdJ1tljlnuoqWM8ryiLw2rKrKB/7XOu4LAbcFMUrIvJ6Y8xLAMaYkyLyduBx4Oe8+OfGmD3AHttzH626fx54txf/K5bE/ezyiIo7Kj+Vx8xVrVEcus5SSnPFlecClU9JJl4XssXZrejmevotoEtE3lB5whjzCrAOeL/fgillotjS0i8aZHdNnJmoDW47dJ3tfdcHOVbcn4gsKCV5xNWt2LDgTkQOAV8E/hjoLd8OGWPe5L947aEFdzFkbMyynDIZ6s1CrTtedWrZfNfZVP/p+fGqndLyQ1G8YLEFd7+AlXn0z1gB6H8D3uydeErH02TuYN22H1VdZ53qLPJTefJTebUyFKVNmmkKWACmgSyWRfGvxpg5X6VSOosWcgftMy3sbT+c2Da+jU9+55NqZShKmzRjUezDUhSrgV8GhkXkMV+lUjqLFrO7mhqvWma6OM3D33m4oxoLKorXNKMoRowxHzXGFIwxJ40x61lY76Ao7dNm4nrDOgsg05VZ0JU2nUpz4OQBdUUpSpOE1j3WTzSYHVPabNdZ6UDbn+nnhu031AS7e1O9lEyJwlxh/rmUpCIZ8O60bqWKN3h13kS1e6yi1JLLWWf7xERLTXAqrqhrc9e23VgwbMsizg3jlPAI6rxRi8IvdHnYOk2kyDZD9ejUiTMTrP3iWteAd9gzLnQOhdIOXp83alEEjS4PL9Bsi3QP22tWLIxcX47BgcGGAe+wZ1zoHAqlHYI8b1RReE3c+wl7SSsK06ezPteXY8sv/zU9//4W+gtXOY5cDdsVpS29lHYI8rxRReE1ujy0aFVh+nTWj43B5nW3k/nSP1D4sx9yf//T9Gf6Xd8TdFaUzqFQ2iHI80ZjFF6jDmeLffssS2KyKjawdKnVs2r1auf3VGIU1Q0QF9HbyvlQGMz9yznfc6zu+8LKitKwltIOmvUUR3R5aNGOheBxA0Rn40546Pr/tbANSBVhtQGJa8M4JVyCOG/UovALXR56biG0iptxx5J8021Ast1ZHnzLg9oGREk0bhaFKgrFX0JWmI10Vd2OtDZ6u3s5Xzw//zjbneXo/UdjO3JVUey4KYpmmgIqSvt4Pf2lRRoNi6m0ARnZNUI6lWamOMPc3BwFc6GS260NSFi1F4oSJGpRKAq1bUBWbFtRU3uR7rL6R8WhDUinox7f9olcMFtEXiUiT4rID8u3l9TZriQiz5b/tBGh4huVIr1lS5bVjlsF63EM2oB0Olrn6h9hZT09AHzLGHMN8K3yYyemjTEryn+3BideB9NsJXVCWTBuFehJ95DpztR5h4V2pA0W+2mqda7+EpaiWA88Wr7/KLAhJDmUanRJ5tjyozRXinwbkE7C6TTVOld/CUtRvMYYc7J8/9+B19TZrldExkXkaRHZ4PaBInJPedvxvC4jWkeXZMDCGRf1OtDacXJFHc4fVgvDY+qdpv392gbFT3zLehKRvcBrHV56qPqBMcaISL2f4XJjzAkRuRp4SkQOGmNectrQGLMd2A5WMHsRoncmLYwjTTrV41YrHWiXZJY0HLlaTbFUZOW2lfR292qw20PqnaZnz1qpz/ZU6A47dX3DN0VhjFlT7zUR+Q8RudQYc1JELgVervMZJ8q3PxKRbwMrAUdFoSwS7UxXQ64vV5Py2sj1ZKdgClCCmdIMACO7Rlhz1RpNo10kbqfp6tXuqdBK+4TletoN3FW+fxewy76BiFwiIj3l+8uANwMvBCZhp6GtR+ri5I7adOMm1xGsdtKpNBNnJnxvA5J0Gp2m2gbFH0KpoxCRVwN/C1wJHAXeY4z5iYgMAfcaY94vIr8EbAPmsBTaVmPMaDOfr3UUi0AT0etSPRAp15dzHcFqJ5PK8Ol1n2bzE5u19sID9DT1Hm3hoSg+M3ZobL66e7Y4S2GuQMmU5l/vppt0d7pGmWgbECVKaAsPRfGZ6gC4U6PBnnTPgvdoGxAlLqiiUBSPqATA81N5x1qMagsDLtReqCtKiTo6j0JRPKbZWgytvVDigloUiuID7dRiNFt7oYFcJWjUolDiSQx6UlUaDeb6co6tQewUTIGZ0oxro0HtsqKEgSoKxR/8vJBH5WrZwne0u6Oarb2objSoXVaUsND0WMV7KmPlMhmrjNbLEahu802D9MO0+R1bqb2wz7x48PVf45P//R1Mn73Q/S7bP8s/PJVh9WpPvpXSwURuHoWSYPxe9kahTegivmPFHXVt7toaC6M31btgip492P2J597P9EyxZpvpmSL9uVOefj1FsaOKQvEWvy/kUehJ5dF3HL5umKP3H2Xvb+5l15276M/0u27ffdFpMrf9FnSfg55J6D5H7+0f5Fhxv2ZKKb6iWU+Kt/h9Ia80+wmzTaiH39Gt9sLObGkWrhuD5XvgzCAMTFDoP82GnTu1FkPxFbUoFG8Jorng8LAVk9i717r1Kv7RCg8+6Ol3tAe7nVxR8yNZ+07BZePQd0prMZRA0GC24g9Oyf5JKACoDmLPzMBDD8EHPuDZ96kEu53agPSl+wCYKkzVfX9a0nR1dekcDKVltClgsyThQhZV/MyECooAM67yU3mWb11ekxXVm+pFRFwzpexo40GlWTTrqRmikpufRJJSABBgxpVTG5AdG3Ysuhajgs7FUFpBLQqITm5+Utm3z1LAk1XtK/r74amniFUBQAjniX0GRvVz7dRijK4fBQMju0c0AK7UoBZFI6KQm59knLKEzp6F/ftDEadtQpgCWN0GxP5cO7UYGx/fyMjukQUB8LhYFjHo3JJIVFFANHLzk0wuB1u2LHx+8+b4/eKjkHFVLU6LtRiprhRdUvuzr+eeihrqHQ6PUBSFiLxbRJ4Xkbny+NN6260TkRdF5IiIPOCbQDov2n9WrYKLLqp9Lq5WW8QGM1csjJWXrmyqFsO+TWUuxtovrmX51uWMHYreFTgpYa64EpZFcQi4HfjHehuISAr4LHAz8AZgWETe4JtEEVspJo7BQSjWtp9Qq81bWqrFqKKZWgyn4HeQbiD1DodLKJXZxpjDACLittmNwBFjzI/K234ZWA+84JtguZx/q8ROT72NQkV1B9DsSNZCoVD3M+xzMUZWjTC6f7Q2IH5wONBsZ/UOh0uUYxSXAceqHh8vPxc/1LlqUc9q0whlfdrYN26uqNJciTkz5/p++1yMR777SG1A/Eu/z8iICdQNpN7hcPFNUYjIXhE55PC33qf/d4+IjIvIeD5KFxx1rtZi9++rEq3PIvfNomsxppbBiSHrtorU5Ovp6q6d/51Ow4HDp30NiKt3ODxCraMQkW8DHzLGLCh6EJE3AR8zxvxa+fGHAYwxf9TocyPVwsOphmDpUutsj1MNgR9o/Up9PNw3bdViHLwTdo1CahZKGVi/Ed64E4D0+dfBlqMUZi54rrt7Zun+3Z+iZ+l/am1GTIlrHcU+4BoRuUpEMsCdwO6QZWodda46k8/Dnj3QbQuTaYTSwsPobau1GF3nXmMpieISmBmwbnftmLcsTO/LcOvGmnbnxXe+l/M9x2JZmxE0cfS0hpUee5uIHAfeBPy9iDxRfv51IrIHwBhTBDYBTwCHgb81xjwfhryLQp2rC6m4VO67D155pfY1VaIWAS4w7LUY2bPXWpZENamC1docKyCeWfFV2Lwc3rvGui1bGxWcajPi2DbE64t6XD2t2sIjKDo966mCk0sFrJYepVI8mwX6RaWRYnWWmM/7Jj+V58qHb+D8n3zfsiQqdJ+zFELfKXpTvZRMicJc/cwpe+sQp8ypqLumvO5jGXVPa1xdT8kiYkVaoeHkUrnoInjkEY1Q2gkhepvry7HjNz5F+rZ7IW25lrp7Zknfdi9LXzVLtjvL1pu3LqjFsGOvzajJnJrs432f/XMOT0R3hKsfOShxrgXRCXdKsDi5VIpFuOUWVaJO+FnbU4fh64ZZ81drOPCRF+HMICuvzcCSP2PizH0MDgwycWaCJZklNfUZTVMOks+kCqz8fD8f+dOX+MDdSxcE2asD72FQuahXr/4rF/V2D0ecw5WqKOx44SJSN1N9tPAuFuT6ctx0ffUxydVcuBu1CnFkatmFIHkRZoA/2HwpD5/4WXb8xqci1dXWj4t6nE99dT1V40WkKa7RqiDRhPhY41SfsenGTa6tQwArGG4PkncVOH/qNXW72jZqJeJXBpFfOShxPfU1mF2h1UhTvVGfUY5WKYqH2N1EbmNcAcui2HLUMUjes9TKfpspzcy/ZB/rag+Ij6SfZPRjb/a1jUj1zxyS7SjQYHYztBJpqmc1xDlapUSLGCTb2+szGnax7TtlFe5V1V+wfiP0nWKmNFOjJKBBK5HJPh75yErfGx5UclD27u1sR4EqigrNOiXd0iHiHK1SFhLWxTrm7ktX19TQN8h86KdJ3bWupv4i05Uh03VhkbVsCoZOWLeOnBmErtr03MqazOt6De3Co4riAs06Jd2sBi2uSw5hXawTclWqLuI7ev9RPnPzZ+YfP/u7T5K58jnLwijTJV2kuqy4xp0H4egWePIL1u2vH3T4BwMTUKrtUXV+tsj+c19l+dblns7WUEeBxigW0ihjqZk4hGY9xZswY00d0hts7NAYI7tGSKfSFEoFq3U58Ptf2sj3//Q8S6qMhXPdsHwznOqzfcjBX7dai6QKUErTfdsHSP/8/67pW5XtznL0/qOLSrXtlNCjW4xC02PtNMpbbybHLYTcd8VD/Eiib5aouC99XuxUz82orplYt+7VZB65HQoXfE6FFAyecVAUb9wJV3/LckMNTNAzMI3dSVJpJXJJ9pIFQfd6j+3EOa3VK9SiaBe1GpJL2EvIEFp3OP7/oKYSVeOw7+taFDbSXZYrqrq1SKNWIq20Fkn6T97NolBFoShOBH2xtl+Fwroqha0kYX7fz6agODPNB2/vZecbZf6ink6lmS3OUpgrUDIX5mJ0042IUDD1e1A1ouKqAlytjqhUkHuJKgpFaYegLtZhruDtRCVGks/DgQOcOX+Gfx0c4PLXr2xYq9GXtkyOqSq3Vatku7M8+JYH+eR3PumJFRInVFEoSlSJwgo+ivI0UJ75qTzLty6vCVz3pnoRkYVDmFqkt7uX88XzTW/vRcA8CmjBnaJElajlXkYhxbuJFOFFj3mtQ6Yr49x+xAWn2Rvg0G6kweMooxaFooRJVFbwTnKFFbltwf3V1phXF5qZtWHHHjAfXT+6oMFhHNxX6npSOou4paeEneUUNTxUnvZ6jeqAuNPjLeu2cN/f37eogHg7LrAouK9UUSidQ5QCw60QN+XmNx4qz0YZS9WPJ85MsPaLa9ubtVGmL93HsilDLn+OiYHGab0AS3uW8tgdj9XUe7Qq+2KVTOQUhYi8G/gYcC1wozHG8aouIhPAK0AJKNb7EnZUUXQoUXXjKO0RgvJ0CpK3yn891MX2x+eYTUGmBBvXw843ur8nCu6rKCqKa4E5YBvwoQaKYsgY09LMRFUUHUpUUjuVWNOKu8pez7FsyupPtaR44fOaKRhcNmVVn1cskDDcV5Fr4WGMOQwgImH8eyWpRKX9hRJrnNqLfPStH3V8bK/nGDxjtRyhSlHUbUFS5s6DMLqLGgvk66tSFOeKzm9wYeLMhC9xjqj3ejLAN0XEANuMMdvrbSgi9wD3AFx55ZUBiadECm3Ko3hErq929Gu9x/mpfM3sjYkBSM/Vfla6ZD3vxLIpS0ksKV6wQnbsgp/+qQInsq2Nm50uTtOf6W/pPc3iWx2FiOwVkUMOf+tb+Ji3GGNWATcDHxSRt9bb0Biz3RgzZIwZyumFoXOJ66xJJZbY6zmmLs5y4BObKPZmmOyBc2m497Y0d75jk+N8juum+iwLpIpCCv7wqveRTWVbkqU31cvZ2bMefrsLhJr1JCLfxiVGYdv2Y8BZY8yfNtpWYxSKogTJguyjfJ7Thw8wMcCC9iPVGUvHXzrAil/cgFQlYJhslh+/8AxX/k1rNSB+xigiW5ktIn0iclHlPnATcChcqRRFURZiHwtLLsclb72JldfftGBUbPXjldffhNgq4WV0lGWD19afEljn8ej6Ud/qMMLKeroN+AyQA84Azxpjfk1EXgf8pTHmFhG5Gvha+S3dwJeMMQ838/lqUSiKEivqpAJ3dB2F36iiUBRFaY1Yup4UpSXyeauOImazpRUlDqiiUOLP2JhVkb12rXU7Nha2RIqSKFRRKPGmiZbUiqIsDlUUSryJ2jwHRUkgqiiUeKNtOxTFd1RRKPEmChPZFCXhRL3Xk6I0ZngY1qzReQ6K4hOqKJRkkMupglAUn1DXk6IoiuKKKgpFURTFFVUUiqIoiiuqKBRFURRXVFEoiqIorqiiUBRFUVxRRaEoijPakVcpo4pCUZSFaEdepQpVFIqi1KIdeRUbqigURalFO/IqNkJRFCLyJyLyfRH5noh8TUQG6my3TkReFJEjIvJAwGIqSmeiHXkVG2FZFE8C1xljrgd+AHzYvoGIpIDPAjcDbwCGReQNgUqpKJ2IduRVbITSFNAY882qh08DdzhsdiNwxBjzIwAR+TKwHnjBfwkVpcPRjrxKFVHoHrsR2Onw/GXAsarHx4FfqPchInIPcA/AlVde6aV8itKZaEdepYxvikJE9gKvdXjpIWPMrvI2DwFF4G8W+/+MMduB7QBDQ0NmsZ+nKIqiWPimKIwxa9xeF5G7gXcCv2qMcbqwnwCuqHp8efk5RVEUJUDCynpaB/wecKsx5lydzfYB14jIVSKSAe4Edgclo6IoimIRVtbTI8BFwJMi8qyIfA5ARF4nInsAjDFFYBPwBHAY+FtjzPMhyasoitKxhJX19FN1nv834Jaqx3uAPUHJpSiKoixEnMMD8UZEXgFeDFuOJlkGnApbiCaIi5wQH1lVTu+Ji6xRlHO5McYxzS0K6bF+8KIxZihsIZpBRMbjIGtc5IT4yKpyek9cZI2LnBW015OiKIriiioKRVEUxZWkKortYQvQAnGRNS5yQnxkVTm9Jy6yxkVOIKHBbEVRFMU7kmpRKIqiKB6hikJRFEVxJRGKIk6DkETk3SLyvIjMiUjd9DgRmRCRg+XK9fEgZSz//2bljMI+fZWIPCkiPyzfXlJnu1J5fz4rIoG1g2m0j0SkR0R2ll//FxEZDEo2mxyN5LxbRPJV+/D9Icm5Q0ReFpFDdV4XEfl0+Xt8T0RWBS1jWY5Gcr5dRCar9udHg5axaYwxsf8DbgK6y/c/BXzKYZsU8BJwNZABngPeEIKs1wI/A3wbGHLZbgJYFuI+bShnhPbpHwMPlO8/4HT8y6+dDUG2hvsI+G3gc+X7dwI7Iyrn3cAjQcvmIOtbgVXAoTqv3wJ8AxDgF4F/iaicbwe+Hvb+bOYvERaFMeabxuoNBdYgpMsdNpsfhGSMmQUqg5ACxRhz2BgT+arxJuWMxD4t/89Hy/cfBTaEIEM9mtlH1fJ/BfhVEZEAZYToHMuGGGP+EfiJyybrgS8Yi6eBARG5NBjpLtCEnLEhEYrCxkas1YQdp0FIlwUiUXsY4Jsi8kx5KFMUico+fY0x5mT5/r8Dr6mzXa+IjIvI0yKyIRjRmtpH89uUFzyTwKsDkc5BhjL1juW7yu6cr4jIFQ6vR4GonJfN8CYReU5EviEiPxe2MPWITQuPoAchLYZmZG2CtxhjTojIf8Hqsvv98grFMzySMxDcZK1+YIwxIlIv53t5eZ9eDTwlIgeNMS95LWuC+TtgzBgzIyIfwLKCfiVkmeLMfqxz8qyI3AI8DlwTrkjOxEZRmBgNQmoka5OfcaJ8+7KIfA3LNeCpovBAzkjsUxH5DxG51BhzsuxieLnOZ1T26Y9E5NvASiy/vJ80s48q2xwXkW7gYuDHPstlp6Gcxphqmf4SKzYURWIx9MwY859V9/eIyJ+LyDJjTNSaBSbD9ZS0QUgi0iciF1XuYwXrHTMnQiYq+3Q3cFf5/l3AAmtIRC4RkZ7y/WXAm4EXApCtmX1ULf8dwFN1Fjt+0lBOm5//Vqw5MVFkN/DecvbTLwKTVa7JyCAir63EokTkRqzrcdALhOYIO5ruxR9wBMsn+Wz5r5JB8jpgT9V2twA/wFpFPhSSrLdh+UxngP8AnrDLipV58lz57/kwZG1Gzgjt01cD3wJ+COwFXlV+fgj4y/L9XwIOlvfpQWAkQPkW7CPg41gLG4Be4LHyefxd4OqQ9mMjOf+ofD4+B/xf4GdDknMMOAkUyufoCHAvcG/5dQE+W/4eB3HJLgxZzk1V+/Np4JfCkLOZP23hoSiKoriSCNeToiiK4h+qKBRFURRXVFEoiqIorqiiUBRFUVxRRaEoiqK4oopCUQJERP6PiJwRka+HLYuiNIsqCkUJlj8BfjNsIRSlFVRRKIoPiMjqcvO83nKl/fMicp0x5lvAK2HLpyitEJteT4oSJ4wx+8rDkT4BZIG/NsZEsQ2LojREFYWi+MfHsXoonQd+J2RZFKVt1PWkKP7xaqAfuAirn5OixBJVFIriH9uAP8Caj/KpkGVRlLZR15Oi+ICIvBcoGGO+JCIp4J9F5FeAPwR+FugXkeNYXWyfCFNWRWmEdo9VFEVRXFHXk6IoiuKKKgpFURTFFVUUiqIoiiuqKBRFURRXVFEoiqIorqiiUBRFUVxRRaEoiqK48v8BLsFfouqFJOAAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_model(data, P, theta, 0.05, sensitivity=1)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"id": "dominant-phone",
"metadata": {},
"outputs": [],
"source": [
"def select_lambda(Xtrain, ytrain, Xcv, ycv, begin, end, step):\n",
" m = data.shape[0]\n",
" \n",
" count = math.ceil((end - begin) / step)\n",
" df = pd.DataFrame(index=range(0, count), columns=['lambda', 'cost', 'accuracy', 'f1'])\n",
" \n",
" for i in range(0, count):\n",
" lamb = begin + i * step\n",
" theta = solve(Xtrain, ytrain, lamb)\n",
" cost = cost_fn(theta, Xcv, ycv, 0)\n",
" acc = accuracy(Xcv, ycv, theta)\n",
" f1 = f1score(Xcv, ycv, theta)\n",
" df.loc[i] = [lamb, cost, acc, f1]\n",
" \n",
" df.plot.line(x='lambda', y='cost')\n",
" df.plot.line(x='lambda', y='accuracy')\n",
" df.plot.line(x='lambda', y='f1')\n",
" df.sort_values(by=['cost'], inplace=True)\n",
" print(df)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"id": "spiritual-central",
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" lambda cost accuracy f1\n",
"0 1 0.124022 0.95 0.941176\n",
"1 2 0.149835 0.95 0.941176\n",
"2 3 0.167398 0.95 0.941176\n",
"3 4 0.181364 0.95 0.941176\n",
"4 5 0.19325 0.95 0.941176\n",
".. ... ... ... ...\n",
"994 995 0.745111 0.4 0.571429\n",
"995 996 0.745159 0.4 0.571429\n",
"996 997 0.745207 0.4 0.571429\n",
"997 998 0.745254 0.4 0.571429\n",
"998 999 0.745301 0.4 0.571429\n",
"\n",
"[999 rows x 4 columns]\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAEGCAYAAAB1iW6ZAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAjzUlEQVR4nO3deXxddZ3/8dcne7M1zdK9adoS6IKUJbQssiODqDA6KgUHWRyZRdxHB0YHtczPcUZn1FF+KjLAiEhH+SlWrDICigulNLUV6EY32iRdkmbfbtbP7497U25DSm7bm5zce9/Px+M+cs853977OT3lzTffc873mLsjIiKJLy3oAkREJD4U6CIiSUKBLiKSJBToIiJJQoEuIpIkMoL64tLSUq+oqAjq60VEEtKGDRsOu3vZSNsCC/SKigqqq6uD+noRkYRkZnuPtU1DLiIiSUKBLiKSJBToIiJJIrAx9JH09fVRW1tLKBQKupQxkZOTw+zZs8nMzAy6FBFJQhMq0GtraykoKKCiogIzC7qcuHJ3Ghsbqa2tZd68eUGXIyJJaEINuYRCIUpKSpIuzAHMjJKSkqT97UNEgjehAh1IyjAfksz7JiLBm1BDLiIiicrd6ekfpLOnn47Iq7NngI6ePjp6BsLrQ+H1ly+cytI5RXGvQYEeZ5s2bWL//v1cc801QZciIjHqHxiko6ef9lA/baE+2kOR9919tA8t9/TTHuqjLbKtsyf8ag/109kbDuv+wdieL1FWkK1ATwSbNm2iurpagS4yjnr7B2np7qWtu4+Wrj5au/uODuZQH23d/a+F87BtXb0Do35HTmYaBTmZFORkUJCdQX5OBqX5ueRlZ5AfeeVlZ1CQk0FeVtT77Azys9PJz84kLzudvKwM0tLGZvhVgT6C733ve3zlK1/BzDjjjDO45557uO222zh8+DBlZWU8+OCDlJeX86Mf/YgvfOELpKenM3nyZJ566inuvvtuuru7+f3vf89dd93F9ddfH/TuiCQEd6e9p5/WSCC3dPXR0t175H1rdx+tI63rHj2QszLSKMzJoHAokHMymVaYc+T9a+uHliM/J4V/5mdnkJUx4U45vs6EDfQv/GwzW/a3xfUzF88s5HPvWPKGbTZv3sw///M/89xzz1FaWkpTUxM333zzkdcDDzzARz7yER5//HFWrlzJk08+yaxZs2hpaSErK4uVK1dSXV3NN7/5zbjWLpJI3J2Onn6aOntp6uyluauXxo7Iz85emjt7aerso6mzh+auPlq6wiH9RiMW2RlpFOVmUjQpi8mTMplTnMubJmUyeVImRbnhn5NzsyiKrCuc9FpIZ2ekj9/OB2jCBnpQnnnmGd7znvdQWloKQHFxMWvXruXHP/4xADfddBOf/vSnAbjwwgu55ZZbeO9738u73vWuwGoWGWvuTluon8MdPTS093C4o+dIWA9/NXf10tzZR+/A4IiflZWeRnFeFlPysijOy2Rm0SSm5GYdHcyTMikati4nMzVC+WRM2EAfrSc9EXz7299m3bp1/PznP+ecc85hw4YNQZckErOhXvThjt4jIT3yz14aOnro7R85oItyMynODQf0nOJcls4uojg/68i6kqHwzs2iOD+LvKx0XcI7RiZsoAfl8ssv553vfCef+MQnKCkpoampiQsuuIBVq1Zx00038cgjj3DRRRcBsGvXLpYvX87y5cv5xS9+QU1NDQUFBbS3twe8F5Lqunr7Odga4mBbiENtIQ629kR+hjjUHjoS2KG+14d0mkFJfjal+dmUFWSzYGo+ZQXZlEWWSyPbSvLDwxsZ6RN/bDlVKNCHWbJkCZ/5zGe45JJLSE9P56yzzuIb3/gGt956K1/+8pePnBQF+NSnPsWOHTtwd6644gqWLl1KeXk5X/rSlzjzzDN1UlTizt1p7OzlQEs4rA+2hTh0VHCH37eH+l/3ZwuyM5g2OYdphdmcW1FMaX7WkYCO/jklN4v0MboKQ8aWucd23WS8VVVV+fAHXGzdupVFixYFUs94SYV9lBPXNzDIwdYQdS3d7G/ppq65m7qW1177W7pf16tOTzOmFmQzrTCH6YXhwJ42Ofx+emHOkfd52eq/JQMz2+DuVSNt0xEWGUcDg86B1m72NXaxt6mLmqaucFhHgvtQW+h1V3qU5mcza8okFk4v4IqFU5lVNIkZRZOYEQnqkvxs9agFUKCLxF2ob4B9TV3sbexiX1MX+xo72dvUxb7GLmqbu4+6+iMjzZhRlMOsokmcv6CE2UWTmDVlErOKcplZlMPMokm6ukNiFlOgm9nVwNeBdOB+d//SsO1fBS6LLOYCU9296EQKcvekPQMe1PCWxF//wCC1zd3sPtzBrvrO8M+GTvY2dnKoreeotgXZGZSX5LJwRgFXLZnO3JJcyovDr5lFk9S7lrgZNdDNLB24F3gLUAusN7PV7r5lqI27fzyq/YeBs06kmJycHBobG5NyCt2h+dBzcnKCLkWOQ1uoj90Nneyq7zgS3rsaOtjb2HVUT7s4L4v5pXm8+ZQy5pbkHgntuSV5TMnNTLp/zzIxxdJDXwbsdPfdAGa2CrgO2HKM9jcAnzuRYmbPnk1tbS0NDQ0n8scnvKEnFsnE0907wM76DrYdbGP7wXa2H2pn+8F26ttf621npBnlJbksKMvn8kVTWVCWz4KyPOaX5jMlLyvA6kXCYgn0WUBN1HItsHykhmY2F5gHPHMixWRmZuppPjKmBgadVxs72X6wnW0H23klEt6vNnYyNCKWnZFG5bR83lxZSuXUAhaU5bFgaj7lxblk6pprmcDifVJ0BfCYu484U46Z3Q7cDlBeXh7nrxY5Wt/AIDsOdfDy/lY217Xy8v42tuxvo7sv/M8zzaCiJI/TphVw7dKZLJxewKnTC6goydO4tiSkWAK9DpgTtTw7sm4kK4APHeuD3P0+4D4IX4ceY40io+rtH2T7wXZeqms9EuBbD7YfuV09NyudJTMLuf7cOSyZWcjC6YVUTsvXFSSSVGIJ9PVApZnNIxzkK4Abhzcys4XAFGBtXCsUGcHB1hAb9zWzsaaFP+5t5qW6Vnoi4V2Qk8HpMydzywUVLJlZyOmzJqvXLSlh1EB3934zuwN4kvBliw+4+2YzWwlUu/vqSNMVwCrXtXkSZ739g7xU1xoO8H0t/HFfMwdaww/bzkpP4/RZhdx03lzOLC/ijFlFzCmepKtKJCXFNIbu7muANcPW3T1s+fPxK0tSWahvgE01Lbywp4l1exrZsLf5yO3us6dMoqqimLPmFHH23CksmlGQMnNdi4xGd4pK4EJ9A2zY28y63Y08v6eJTTUt9PYPYgYLpxey4txyls8r5py5U5haqOv4RY5FgS7jzt3Zfqid371ymN/uaOCFPU309A+SZrBk5mTef95cls8vYVlFMZNzM4MuVyRhKNBlXBzu6OH3O8IB/vsdh4/csHPK1HxuXF7ORZWlVFUUU5ijABc5UQp0GRPuzo76Dp7aeointhxiY00L7jAlN5MLTynl4soy3lxZysyiSUGXKpI0FOgSN30Dg6x/tYmnttTz1NZD7GvqAuCM2ZP52BWnctnCMk6fOZk0XT4oMiYU6HJS+gYGWburkZ+/eIBfbj5Ia3cfWRlpXLighL++ZD5XLJzG9Mk6kSkyHhToctz6BwZZt6eJJ148wC9fPkBzVx/52RlcuWgqV58+g4sqS/V0HJEA6L86iYm781JdK49tqGXNSwc43NFLblY6Vy6axtvPmMHFp5bpNnqRgCnQ5Q3Vt4X4ycY6HttQy476DrIy0njLomm8Y+kMLj1tqkJcZAJRoMvr9A0M8qsth/hhdQ2/faWBQYezy4v44jvfxNvOmMHkSbq0UGQiUqDLEQdau3n0hRpWvbCP+vYeZkzO4W8vXcC7zp7NgrL8oMsTkVEo0FOcu/PcrkYeXruXX209xKA7l5xaxr+cN5dLT5uqGQpFEogCPUX19A/w+MY6vvu7Peys72BKbiZ/ddE83rdsLuUluUGXJyInQIGeYlq7+vj+ur089NyrNLT3sHhGIf/+nqW87YwZOsEpkuAU6CniUFuI+367m1Uv7KOzd4CLKkv56nvP5MJTSjR3uEiSUKAnufq2EN96dhePrNvHwKDzjjNm8MGL57Nk5uSgSxOROFOgJ6mG9h6+8+wuHn5+L/2Dzl+cPYsPX17JnGKNj4skKwV6kmkP9fGt3+zigT/sobd/kHeeNZsPX34KFaV5QZcmImNMgZ4k+gcGeXR9DV/71Ss0dvZy7dKZfOzKSubr+nGRlKFAT3DuzjPb6vnimq3sauhk2bxiHnzbIs6YXRR0aSIyzhToCWxvYyd3/3Qzz77SwLzSPL5z0zlctXiarloRSVEK9ATU0z/Afc/u5pu/3klGmvHZty3i/edXkJWRFnRpIhIgBXqCeW7XYT77+MvsbujkbW+awT+9fbEeICEiAMTUpTOzq81su5ntNLM7j9HmvWa2xcw2m9kP4lumdPT0848/eYkbv7uO/gHnoVvP5d73na0wF5EjRu2hm1k6cC/wFqAWWG9mq919S1SbSuAu4EJ3bzazqWNVcCpau6uRTz32J+pauvngRfP45FWn6TZ9EXmdWIZclgE73X03gJmtAq4DtkS1+SBwr7s3A7h7fbwLTUWhvgG+9IttPPTcq8wtyeWHf30+51YUB12WiExQsQT6LKAmarkWWD6szakAZvYHIB34vLv/cvgHmdntwO0A5eXlJ1JvythZ386HHtnI9kPt3Hz+XP7hrQvJzdIpDxE5tnglRAZQCVwKzAZ+a2ZvcveW6Ebufh9wH0BVVZXH6buTirvz2IZa7v7pZnKz0nno1nO59DSNYInI6GIJ9DpgTtTy7Mi6aLXAOnfvA/aY2SuEA359XKpMEV29/Xz2Jy/z4411nD+/hK+tOJNphTrpKSKxiSXQ1wOVZjaPcJCvAG4c1uZx4AbgQTMrJTwEszuOdSa9mqYubn94A9sPtvHxK0/ljstP0dOCROS4jBro7t5vZncATxIeH3/A3Teb2Uqg2t1XR7ZdZWZbgAHgU+7eOJaFJ5O1uxr5u0c2MDDoPHjrMi45tSzokkQkAZl7MEPZVVVVXl1dHch3TxTuzsPP7+ULP9vCvNI8vvv+KuZpVkQReQNmtsHdq0bapssmAjI46Nzz8y08+IdXuXLRVL56/ZkU5GQGXZaIJDAFegBCfQN88od/4ucvHeC2C+fx2bctIk3j5SJykhTo46y1u4/bv1fNuj1NfOaaRXzw4vlBlyQiSUKBPo4Od/Twl/evY1dDB19fcSbXnTkr6JJEJIko0MdJfVuIG+9fR21zFw/esow3V5YGXZKIJBkF+jg40NrNjd9dx6G2EP996zKWzy8JuiQRSUIK9DF2oLWb67/zPE2dvTz8gWWcM1eTa4nI2FCgj6HGjh7ed/86miNhflb5lKBLEpEkpkAfI22hPm5+8AXqmrt5+APLFeYiMub0EMox0N07wF89VM22A+18+y/PYdk8DbOIyNhTDz3OBgadj6zayPq9TfznirO4bKGmvhWR8aEeepx9cc1WfrXlEJ9/xxLesXRm0OWISApRoMfRw2tf5b9+v4dbLqjg5gsqgi5HRFKMAj1OfrO9ns+t3swVC6fyT29fHHQ5IpKCFOhxsLexk488upHTphfynzecpQdTiEggFOgnqbt3gL/5/h8xM+676RzysnWeWUSCofQ5Ce7OP/7kJbYdbOOBW85lTnFu0CWJSApTD/0kfH/dPn6ysY6PXXEql52myxNFJFgK9BO0/WA79zyxhUtOLePDl58SdDkiIgr0ExHqG+CjqzZSmJPBV96zVE8bEpEJQWPoJ+DffrmdbQfbefCWcykryA66HBERQD304/bsKw088Ic93Hz+XN3WLyITigL9OLSF+vj0Y3+icmo+d12zKOhyRESOElOgm9nVZrbdzHaa2Z0jbL/FzBrMbFPk9VfxLzV4X/rFNhrae/jKe5aSk5kedDkiIkcZdQzdzNKBe4G3ALXAejNb7e5bhjX9H3e/YwxqnBDW7mrkB+v2cfvF81k6pyjockREXieWHvoyYKe773b3XmAVcN3YljWxdPcOcNePX2RuSS4fv/LUoMsRERlRLIE+C6iJWq6NrBvuL8zsRTN7zMzmjPRBZna7mVWbWXVDQ8MJlBuMbzyzg1cbu/iXd72JSVkaahGRiSleJ0V/BlS4+xnAr4D/HqmRu9/n7lXuXlVWVhanrx5bew53cv/v9vCus2dxwYLSoMsRETmmWAK9Dojucc+OrDvC3RvdvSeyeD9wTnzKC97Kn20mKyONO9+6MOhSRETeUCyBvh6oNLN5ZpYFrABWRzcwsxlRi9cCW+NXYnCe3nqIX29v4KNXVDK1ICfockRE3tCoV7m4e7+Z3QE8CaQDD7j7ZjNbCVS7+2rgI2Z2LdAPNAG3jGHN46Knf4CVT2xhQVmenj4kIgkhplv/3X0NsGbYuruj3t8F3BXf0oL18Nq97G3s4nu3LSMrQ/dficjEp6QaQVuoj2/+eicXVZZy8amJcfJWRESBPoLv/nY3LV19/MPVOhEqIolDgT5MfXuI+3+3h7efMYPTZ00OuhwRkZgp0If5xtM76RsY5O+vOi3oUkREjosCPUpdSzePvrCP68+dQ0VpXtDliIgcFwV6lO88uwsz+NBleqSciCQeBXpEfVuIVetrePc5s5lZNCnockREjpsCPeK7v9vNwKDzt5eody4iiUmBDjR29PD95/dx3dKZlJfkBl2OiMgJUaAD/712L6H+Af7usgVBlyIicsJSPtBDfQM88vxerlg4lVOmFgRdjojICUv5QF+9aT+Nnb3cduG8oEsRETkpKR3o7s4Df9jDwukFnL+gJOhyREROSkoH+tpdjWw72M5tF87DzIIuR0TkpKR0oD/whz2U5GVx7Zkzgy5FROSkpWyg17V08/S2elYsm0NOph78LCKJL2UD/YfrawBYcW55wJWIiMRHSgb6wKDzo+oa3nxKKXOKdSORiCSHlAz0377SwP7WEDcsU+9cRJJHSgb6oy/soyQviysXTQu6FBGRuEm5QK9vC/H0tnrefc5sPfxZRJJKyiXaTzftZ2DQee+5c4IuRUQkrlIu0B/fVMfS2ZNZUJYfdCkiInEVU6Cb2dVmtt3MdprZnW/Q7i/MzM2sKn4lxs/O+nY272/jujNnBV2KiEjcjRroZpYO3Au8FVgM3GBmi0doVwB8FFgX7yLj5fGN+0kzePvSGUGXIiISd7H00JcBO919t7v3AquA60Zodw/wr0AojvXFjbvz0z/VceEppUwtyAm6HBGRuIsl0GcBNVHLtZF1R5jZ2cAcd//5G32Qmd1uZtVmVt3Q0HDcxZ6MP+5rpqapmz/XcIuIJKmTPilqZmnAfwCfHK2tu9/n7lXuXlVWVnayX31cnnjxAFkZafzZ6dPH9XtFRMZLLIFeB0Rf4zc7sm5IAXA68BszexU4D1g9kU6Mujv/u/kQF1eWkp+dEXQ5IiJjIpZAXw9Umtk8M8sCVgCrhza6e6u7l7p7hbtXAM8D17p79ZhUfAJermujrqWbq5aody4iyWvUQHf3fuAO4ElgK/BDd99sZivN7NqxLjAentx8kPQ0063+IpLUYhp/cPc1wJph6+4+RttLT76s+Prl5oMsqyimOC8r6FJERMZM0t8purO+g531HVytk6EikuSSPtD/d8tBAK5aouEWEUluSR/ov9nWwJKZhcyYPCnoUkRExlRSB3prdx8b9jVz6Wnje827iEgQkjrQn9t5mIFB59LTpgZdiojImEvqQH/2lQYKcjI4a05R0KWIiIy5pA10d+fZVxp48ymlZKQn7W6KiByRtEm3o76DA60hLjlV4+cikhqSNtB/s70egEt0QlREUkTSBvrvdhzm1Gn5ulxRRFJGUgZ638Ag1a82c8GC0qBLEREZN0kZ6C/WttLdN8DyecVBlyIiMm6SMtCf390IwDIFuoikkKQM9HV7mjhtWgEl+dlBlyIiMm6SLtDD4+dNLJ+v3rmIpJakC/SX6lrp6h3gvPklQZciIjKuki7Q1+1uAjR+LiKpJ+kC/Y/7mplXmkepxs9FJMUkVaC7Oxv3tWgyLhFJSUkV6HUt3Rzu6OHM8qKgSxERGXdJFeibaloAOGvOlGALEREJQFIF+sZ9LWRnpLFwRkHQpYiIjLukCvRNNS2cPmsymZr/XERSUEzJZ2ZXm9l2M9tpZneOsP1vzOwlM9tkZr83s8XxL/WN9fYP8nJdq06IikjKGjXQzSwduBd4K7AYuGGEwP6Bu7/J3c8E/g34j3gXOpptB9vo6R/UCVERSVmx9NCXATvdfbe79wKrgOuiG7h7W9RiHuDxKzE2L9a2ArB0dtF4f7WIyISQEUObWUBN1HItsHx4IzP7EPAJIAu4fKQPMrPbgdsBysvLj7fWN7TlQBuFORnMnqIHWohIaorb2UN3v9fdFwD/AHz2GG3uc/cqd68qK4vvo+G2Hmhj0YxCzCyunysikihiCfQ6YE7U8uzIumNZBfz5SdR03AYGnW0H2lk0o3A8v1ZEZEKJJdDXA5VmNs/MsoAVwOroBmZWGbX4NmBH/Eoc3d7GTrr7Blg8U4EuIqlr1DF0d+83szuAJ4F04AF332xmK4Fqd18N3GFmVwJ9QDNw81gWPdzWA+0ALFYPXURSWCwnRXH3NcCaYevujnr/0TjXdVy2HGglI804ZWp+kGWIiAQqKW6p3HqgnQVl+eRkpgddiohIYJIi0LcdaGOR5m8RkRSX8IHe2dPP/tYQldMU6CKS2hI+0Hc3dAKwoCwv4EpERIKV8IG+q6EDQCdERSTlJXyg76zvID3NKC9WD11EUlvCB/quhg7mFueSlZHwuyIiclISPgV3NXQwv0zDLSIiCR3o/QODvHq4iwVTNdwiIpLQgb6/JUTvwCALStVDFxFJ6EDf19QFwJzi3IArEREJXkIHek3zUKDroRYiIokd6E1dZKQZMyYr0EVEEjvQm7uZWTSJ9DQ9pUhEJLEDvalLwy0iIhEJHei1zV3MmaIToiIikMCB3tXbz+GOXl3hIiISkbCBXtvcDeiSRRGRIQkb6DVD16BP0Ri6iAgkcKAfbAsB6JJFEZGIhA30Q209mEFpflbQpYiITAgJG+gN7SFK8rLJSE/YXRARiauETcNDbT1MK8wOugwRkQkjpkA3s6vNbLuZ7TSzO0fY/gkz22JmL5rZ02Y2N/6lHu1QW4ipBQp0EZEhowa6maUD9wJvBRYDN5jZ4mHNNgJV7n4G8Bjwb/EudLj69h6mFeaM9deIiCSMWHroy4Cd7r7b3XuBVcB10Q3c/dfu3hVZfB6YHd8yj9Y/MMjhjh710EVEosQS6LOAmqjl2si6Y/kA8IuRNpjZ7WZWbWbVDQ0NsVc5zOGOXtxhqnroIiJHxPWkqJn9JVAFfHmk7e5+n7tXuXtVWVnZCX9PfXv4GnT10EVEXpMRQ5s6YE7U8uzIuqOY2ZXAZ4BL3L0nPuWNrLGjF4CSfAW6iMiQWHro64FKM5tnZlnACmB1dAMzOwv4DnCtu9fHv8yjNXeFA31KbuZYf5WISMIYNdDdvR+4A3gS2Ar80N03m9lKM7s20uzLQD7wIzPbZGarj/FxcdHc1QfAlFzdJSoiMiSWIRfcfQ2wZti6u6PeXxnnut5Qa1cvZlA4ST10EZEhCXmnaHNXH5MnZerRcyIiURI00Hs13CIiMkxCBnpLVx9FOiEqInKUhAx09dBFRF4vIQO9LdRHYU5M53NFRFJGQgZ6d+8AudkKdBGRaAkZ6F29A+RlpQddhojIhJJwgT446HT1DjApSz10EZFoCRfoof4BAHLVQxcROUrCBXpXbzjQNeQiInK0xAv0nnCga8hFRORoiRfoff2AhlxERIZLvEDv1Ri6iMhIEi/Qe4YCXUMuIiLREi/QezXkIiIykoQL9O4+DbmIiIwk4QK9U0MuIiIjSrhAPzLkkq0euohItIQL9PLiXK5eMp3cTAW6iEi0hBu3uGrJdK5aMj3oMkREJpyE66GLiMjIFOgiIkkipkA3s6vNbLuZ7TSzO0fYfrGZ/dHM+s3s3fEvU0RERjNqoJtZOnAv8FZgMXCDmS0e1mwfcAvwg3gXKCIisYnlpOgyYKe77wYws1XAdcCWoQbu/mpk2+AY1CgiIjGIZchlFlATtVwbWSciIhPIuJ4UNbPbzazazKobGhrG86tFRJJeLIFeB8yJWp4dWXfc3P0+d69y96qysrIT+QgRETmGWMbQ1wOVZjaPcJCvAG482S/esGHDYTPbe4J/vBQ4fLI1JBjtc2rQPqeGk9nnucfaYO4+6p82s2uArwHpwAPu/n/MbCVQ7e6rzexc4CfAFCAEHHT3JSdYbCz1VLt71Vh9/kSkfU4N2ufUMFb7HNOt/+6+BlgzbN3dUe/XEx6KERGRgOhOURGRJJGogX5f0AUEQPucGrTPqWFM9jmmMXQREZn4ErWHLiIiwyjQRUSSREIF+mizPiYqM5tjZr82sy1mttnMPhpZX2xmvzKzHZGfUyLrzcz+M/L38KKZnR3sHpw4M0s3s41m9kRkeZ6ZrYvs2/+YWVZkfXZkeWdke0WghZ8gMysys8fMbJuZbTWz85P9OJvZxyP/rl82s0fNLCcZj7OZPWBm9Wb2ctS64z62ZnZzpP0OM7v5eGpImECPcdbHRNUPfNLdFwPnAR+K7NudwNPuXgk8HVmG8N9BZeR1O/Ct8S85bj4KbI1a/lfgq+5+CtAMfCCy/gNAc2T9VyPtEtHXgV+6+0JgKeF9T9rjbGazgI8AVe5+OuF7WVaQnMf5IeDqYeuO69iaWTHwOWA54YkRPzf0P4GYuHtCvIDzgSejlu8C7gq6rjHa158CbwG2AzMi62YA2yPvvwPcENX+SLtEehG+d+Fp4HLgCcAI3z2XMfyYA08C50feZ0TaWdD7cJz7OxnYM7zuZD7OvDa5X3HkuD0B/FmyHmegAnj5RI8tcAPwnaj1R7Ub7ZUwPXRSZNbHyK+YZwHrgGnufiCy6SAwLfI+Wf4uvgZ8GhiadrkEaHH3/shy9H4d2efI9tZI+0QyD2gAHowMM91vZnkk8XF29zrgK4SfmXCA8HHbQHIf52jHe2xP6pgnUqAnPTPLB/4f8DF3b4ve5uH/XSfNNaZm9nag3t03BF3LOMoAzga+5e5nAZ289is4kJTHeQrh5yfMA2YCebx+WCIljMexTaRAj9usjxORmWUSDvNH3P3HkdWHzGxGZPsMoD6yPhn+Li4ErjWzV4FVhIddvg4UmdnQlBTR+3VknyPbJwON41lwHNQCte6+LrL8GOGAT+bjfCWwx90b3L0P+DHhY5/Mxzna8R7bkzrmiRToR2Z9jJwRXwGsDrimuDAzA/4L2Oru/xG1aTUwdJb7ZsJj60Pr3x85U34e0Br1a11CcPe73H22u1cQPpbPuPv7gF8DQ8+lHb7PQ38X7460T6ierLsfBGrM7LTIqisIP/kraY8z4aGW88wsN/LvfGifk/Y4D3O8x/ZJ4CozmxL57eaqyLrYBH0S4ThPOFwDvALsAj4TdD1x3K83E/5V7EVgU+R1DeGxw6eBHcBTQHGkvRG+4mcX8BLhKwgC34+T2P9LgSci7+cDLwA7gR8B2ZH1OZHlnZHt84Ou+wT39UygOnKsHyc8Q2lSH2fgC8A24GXgYSA7GY8z8Cjh8wR9hH8b+8CJHFvgtsj+7wRuPZ4adOu/iEiSSKQhFxEReQMKdBGRJKFAFxFJEgp0EZEkoUAXEUkSCnRJKmbWEafP+byZ/X0M7R4ys3eP1k5kPCjQRUSShAJdkpKZ5ZvZ02b2RzN7ycyui6yviMxF/pCZvWJmj5jZlWb2h8j808uiPmapma2NrP9g5M+bmX3TwvPyPwVMjfrOu81sfWTe7/sid0aKjBsFuiSrEPBOdz8buAz496iAPQX4d2Bh5HUj4bt1/x74x6jPOIPwHDPnA3eb2UzgncBphOfkfz9wQVT7b7r7uR6e93sS8PYx2jeREWWM3kQkIRnwRTO7mPD0vLN4berSPe7+EoCZbSb8AAI3s5cIz2c95Kfu3g10m9mvCT9w4GLgUXcfAPab2TNR7S8zs08DuYTn/94M/GzM9lBkGAW6JKv3AWXAOe7eF5nVMSeyrSeq3WDU8iBH/zcxfF6MY86TYWY5wP8lPCdHjZl9Pur7RMaFhlwkWU0mPN96n5ldBsw9gc+4zsLPvywhPIHYeuC3wPUWfhbqDMLDOfBaeB+OzGuvK19k3KmHLsnqEeBnkWGUasKz/R2vFwlP81oK3OPu+83sJ4TH1bcQnhp2LYC7t5jZdwnPKHiQcPiLjCvNtigikiQ05CIikiQU6CIiSUKBLiKSJBToIiJJQoEuIpIkFOgiIklCgS4ikiT+P1BUQJ33FVGuAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAEGCAYAAAB1iW6ZAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAbEUlEQVR4nO3dfZRcdZ3n8fenbjVmEhjMEwhJmkTNIgESAm14cHSSxczgAwRExiCrJAJZjjK6M4Oc4CoiuOrsDuP6kPHY6yDrY4aFwYlsBAmEDaNBEhwEkhCIEEwjjDEJiUgi3cl3/6jbTaXp0FWderq3P69z+tD31q+qfrdv88ntb/3u76eIwMzMsq/Q7A6YmVltONDNzHLCgW5mlhMOdDOznHCgm5nlRLFZbzxu3LiYPHlys97ezCyTHnzwwd9GxPiBHmtaoE+ePJm1a9c26+3NzDJJ0tMHeswlFzOznHCgm5nlhAPdzCwnmlZDN7N86+7upquriz179jS7K5k0YsQIJk6cSFtbW8XPcaCbWV10dXVx2GGHMXnyZCQ1uzuZEhFs27aNrq4upkyZUvHzXHIxs7rYs2cPY8eOdZgPgSTGjh1b9V83DnQzqxuH+dAN5WeXuZLLms3bue/xrSBx3swJTBk3qtldMjNrCZkL9J8/vYOvrNxEBPxuTzefPvv4ZnfJzKwlZK7k8p//9A089fl3Me7QQ+jeu6/Z3TGzYa6np6fZXeiTuUDvlRREz16vtmRmB3buuedyyimncPzxx9PZ2QnAHXfcwcknn8yMGTM488wzAXjhhRdYuHAhJ554ItOnT+fWW28F4NBDD+17rVtuuYUFCxYAsGDBAi6//HJOPfVUrrrqKh544AFOP/10Zs6cyRlnnMHGjRsB2Lt3L1deeSUnnHAC06dP5ytf+Qr33HMP5557bt/r3nXXXZx33nk1Od7MlVx6FQsFevY50M2y4DM/XMf6X++q6WtOO/qPBy253njjjYwZM4bdu3fz5je/mXnz5nHZZZexatUqpkyZwvbt2wG4/vrrOfzww3nkkUcA2LFjx6Dv39XVxU9/+lOSJGHXrl3cd999FItFVqxYwSc+8QluvfVWOjs72bx5Mw899BDFYpHt27czevRoPvzhD7N161bGjx/PN7/5TT70oQ8d/A+ELAd6IvY60M3sVXz5y1/mtttuA2DLli10dnbytre9rW9s95gxYwBYsWIFS5cu7Xve6NGjB33tCy64gCRJANi5cycXX3wxTzzxBJLo7u7ue93LL7+cYrG43/t94AMf4Dvf+Q4LFy5k9erVfOtb36rJ8WY20JOCXEM3y4hmDF649957WbFiBatXr2bkyJHMnj2bk046iccee6zi1ygfOth/TPioUS+PsPvUpz7FnDlzuO2229i8eTOzZ89+1ddduHAhZ599NiNGjOCCCy7oC/yDldkaerHgK3QzO7CdO3cyevRoRo4cyWOPPcb999/Pnj17WLVqFU899RRAX8ll7ty5LFmypO+5vSWXI488kg0bNrBv376+K/0DvdeECRMAuOmmm/r2z507l69//et9H5z2vt/RRx/N0UcfzWc/+1kWLlxYs2POcKC7hm5mB3bWWWfR09PDcccdx+LFiznttNMYP348nZ2dvOc972HGjBm8733vA+CTn/wkO3bs4IQTTmDGjBmsXLkSgC984Qu8+93v5owzzuCoo4464HtdddVVXH311cycOXO/US+XXnop7e3tTJ8+nRkzZvC9732v77GLLrqISZMmcdxxx9XsmBXRnFDs6OiIg1ng4pyv/itjRx3CNxfOqmGvzKxWNmzYUNOwypsrrriCmTNncskllxywzUA/Q0kPRkTHQO0zXUP3FbqZZdEpp5zCqFGjuOGGG2r6upkN9LZCwTV0M8ukBx98sC6vm9kaum8sMmt9zSrp5sFQfnaZDfRiInr2ediiWasaMWIE27Ztc6gPQe986CNGjKjqeZktuXjYollrmzhxIl1dXWzdurXZXcmk3hWLqpHZQE8KBbpdcjFrWW1tbVWttmMHr6KSi6SzJG2UtEnS4gEeP0bS3ZIelnSvpOr+WRkCX6Gbme1v0ECXlABLgHcA04ALJU3r1+zvgG9FxHTgOuDzte5of66hm5ntr5KSyyxgU0Q8CSBpKTAPWF/WZhrw1+n3K4Ef1LCPAyoWxNbf/YHP/2hDVc8TpZWOjn3dYXXqmZlZc1QS6BOALWXbXcCp/dr8AngP8CXgPOAwSWMjYlt5I0mLgEUA7e3tQ+0zACdMOJwfPfocN/1kc1XP+0PPPnbt6eZz5514UO9vZtZqavWh6JXAVyUtAFYBzwB7+zeKiE6gE0q3/h/MG1761tdz6VtfX/Xzzvj83XT3uFRjZvlTSaA/A0wq256Y7usTEb+mdIWOpEOB8yPi+Rr1saaSxFMGmFk+VTLKZQ0wVdIUSYcA84Fl5Q0kjZPU+1pXAzfWtpu141kazSyvBg30iOgBrgDuBDYAN0fEOknXSTonbTYb2CjpceBI4L/Vqb8HrTTc0SUXM8ufimroEbEcWN5v3zVl398C3FLbrtVHaaUjX6GbWf5kdi6XofJapGaWV8Mv0F1DN7OcGoaBLnq8uLSZ5dCwC3SvdGRmeTXsAr0t8UpHZpZPwy7QE5dczCynhl2gt/lOUTPLqWEX6InnUTeznBp2gV4sFOh2ycXMcmj4BbpvLDKznBp2ge5hi2aWV8Mu0IsF0bVjNy95TnQzy5lhF+htSemQNzy7q8k9MTOrrWEX6H9+/OsAvMC0meXOsAv0YkEAnkLXzHJn+AV6WnLxSBczy5thF+hJ3xW6Sy5mli/DLtB7Sy6+QjezvBl+gZ6UAt1j0c0sb4ZfoBdKh9zjD0XNLGeGXaD31tA9bNHM8mbYBXpb4hq6meXTsAv0vit0l1zMLGeGXaD31dB9hW5mOTP8Ar2v5OIaupnly/ALdN/6b2Y5NewCPfGNRWaWUxUFuqSzJG2UtEnS4gEeb5e0UtK/SXpY0jtr39Xa6J0+1zV0M8ubQQNdUgIsAd4BTAMulDStX7NPAjdHxExgPvAPte5orbw8ysU1dDPLl2IFbWYBmyLiSQBJS4F5wPqyNgH8cfr94cCva9nJWuqtof94/b/z7K49B2w3d9qRzDn2iEZ1y8zsoFUS6BOALWXbXcCp/dpcC/xY0l8Co4C3D/RCkhYBiwDa29ur7WtNSOItbxzLxude4NmdAwf6zt0v8cvfvOBAN7NMqSTQK3EhcFNE3CDpdODbkk6IiP3qGhHRCXQCdHR0NK2I/d1LT3vVxy/6xv3s6XZJxsyypZIPRZ8BJpVtT0z3lbsEuBkgIlYDI4BxtehgMySFgj80NbPMqSTQ1wBTJU2RdAilDz2X9WvzK+BMAEnHUQr0rbXsaCO1FeQbj8wscwYN9IjoAa4A7gQ2UBrNsk7SdZLOSZv9DXCZpF8A3wcWRERmL3GTgjzXi5llTkU19IhYDizvt++asu/XA2+pbdeap5jIJRczy5xhd6doJYqFgu8kNbPMcaAPoFiQF5E2s8xxoA8gKchX6GaWOQ70ARQTD1s0s+xxoA+gWJDnejGzzHGgDyApeJSLmWWPA30AbYlr6GaWPQ70ASSFgm8sMrPMcaAPoFgQPb7138wyxoE+gGIi9gXsc9nFzDLEgT6A3kUw/MGomWVJreZDz5Viuu7oVbf8gqSw/795Y0a1sfgdx/UtZWdm1ioc6AOYMfG1HDN2JGs279hv/+7uvWz//UvMn9XOG8Yf2qTemZkNzIE+gNPfMJb/9/E5r9i//JFn+fB3f+4RMGbWklxDr0LSV1v3CBgzaz0O9Cq0JaVA901HZtaKHOhV6P2AtNslFzNrQQ70KvQOZ/QVupm1Igd6FYquoZtZC3OgV6GY1tA9ysXMWpEDvQrFtIbukouZtSIHehV6hy16vVEza0UO9CoUPWzRzFqYA70KvSUXT9plZq3IgV4Fj3Ixs1bmQK9C363/HuViZi3IgV6FtsSjXMysdVUU6JLOkrRR0iZJiwd4/IuSHkq/Hpf0fM172gL6Rrk40M2sBQ06fa6kBFgCzAW6gDWSlkXE+t42EfFXZe3/EphZh742Xd+t/x62aGYtqJL50GcBmyLiSQBJS4F5wPoDtL8Q+HRtutdaeoct3ry2i7VP7xik9csksfAtkzm5fXS9umZmVlGgTwC2lG13AacO1FDSMcAU4J4DPL4IWATQ3t5eVUdbwahDisw+djy/2v4i65/dVfHzNv/294wZ2eZAN7O6qvWKRfOBWyJi70APRkQn0AnQ0dGRuUJ0oSBuWjir6ud1fPYu193NrO4q+VD0GWBS2fbEdN9A5gPfP9hO5U2xUGCvhzqaWZ1VEuhrgKmSpkg6hFJoL+vfSNKbgNHA6tp2MfuSguj2zUhmVmeDBnpE9ABXAHcCG4CbI2KdpOsknVPWdD6wNCJ8KdpPMZHHrptZ3VVUQ4+I5cDyfvuu6bd9be26lS/Fgjz/i5nVne8UbYBioUCPx66bWZ050BsgKbjkYmb150BvgLbEJRczqz8HegMkBXmGRjOrOwd6AxQLBc+hbmZ150BvAA9bNLNGcKA3QFIQ3S65mFmdOdAboOhRLmbWAA70BigmBY9yMbO6c6A3QLEg31hkZnXnQG8A31hkZo1Q6/nQbQBtSYFnd+5h0bfWAvDB0yfzJ1PHNblXZpY3DvQGmH3seDY8u4tfbX+RX259gcNGtDnQzazmHOgNMO+kCcw7aQIAf/o/VrLXNxmZWR24ht5gnkrXzOrFgd5gpal0HehmVnsO9AZLfIVuZnXiQG+wtkSuoZtZXTjQG8xX6GZWLw70BnMN3czqxYHeYJ5K18zqxYHeYElBdLuGbmZ14EBvME+la2b14kBvsGJS8GIXZlYXDvQGK12hu+RiZrXnQG8wL3ZhZvXiQG+w0mIXDnQzq72KAl3SWZI2StokafEB2vyFpPWS1kn6Xm27mR9e7MLM6mXQ6XMlJcASYC7QBayRtCwi1pe1mQpcDbwlInZIOqJeHc66tkT0uIZuZnVQyXzos4BNEfEkgKSlwDxgfVmby4AlEbEDICJ+U+uO5kVSENt//xIX3/hAs7vyCq8pFrjm7GlMHD2y2V0xsyGoJNAnAFvKtruAU/u1+Q8Akn4CJMC1EXFH/xeStAhYBNDe3j6U/mbenGOP4NFndvH87u5md2U/f+jey2PP/Y53nPg6B7pZRtVqxaIiMBWYDUwEVkk6MSKeL28UEZ1AJ0BHR8ewLCSfedyRnHnckc3uxits2f4ib/3vK/2BrVmGVfKh6DPApLLtiem+cl3AsojojoingMcpBbxlRDERgD+wNcuwSgJ9DTBV0hRJhwDzgWX92vyA0tU5ksZRKsE8WbtuWr0lhVKgdzvQzTJr0ECPiB7gCuBOYANwc0Ssk3SdpHPSZncC2yStB1YCH4+IbfXqtNVesVD6Vdi71yNwzLKqohp6RCwHlvfbd03Z9wH8dfplGdRbcvFdrGbZ5TtFDSjdwQoOdLMsc6AbUFZycaCbZZYD3YCXr9C7XUM3yywHugFQKAjJV+hmWeZAtz5tBU/ta5ZlDnTrkxREj0suZpnlQLc+xYJ8hW6WYQ5061NMPFe7WZY50K1PUvAC1mZZ5kC3Pl7A2izbHOjWp5i4hm6WZbWaD91yoFgQqx7fyvzO1a/ari0p8Ml3TePY1x3WoJ6ZWSV8hW59LuiYxOvHH8q+4IBfL/Xs474nfsv9T3oyTbNW4yt06/OROW/kI3Pe+Kptdu7uZsZnfuzSjFkL8hW6VaVvVkbfgGTWchzoVpXE0+yatSwHulWlLfE0u2atyoFuVUkv0F1yMWtBDnSriiTP+WLWohzoVjXP+WLWmhzoVrWi53wxa0kOdKta4jlfzFqSA92q1uY5X8xakgPdqlZa2ciBbtZqHOhWtaLXHjVrSQ50q1pplItr6GatxoFuVUsKottX6GYtp6JAl3SWpI2SNklaPMDjCyRtlfRQ+nVp7btqraJYEHtdQzdrOYNOnyspAZYAc4EuYI2kZRGxvl/Tf4qIK+rQR2sxpRq6Sy5mraaSK/RZwKaIeDIiXgKWAvPq2y1rZcVEPPDUds7/2k9Z9fjWZnfHzFKVBPoEYEvZdle6r7/zJT0s6RZJkwZ6IUmLJK2VtHbrVgdBVv1FxyRmTHotD215nns3+jyatYpafSj6Q2ByREwH7gL+90CNIqIzIjoiomP8+PE1emtrtP902jF8+5JTOWxE0aNdzFpIJYH+DFB+xT0x3dcnIrZFxB/SzW8Ap9Sme9bKih7tYtZSKgn0NcBUSVMkHQLMB5aVN5B0VNnmOcCG2nXRWlXi0S5mLWXQUS4R0SPpCuBOIAFujIh1kq4D1kbEMuCjks4BeoDtwII69tlahO8YNWstgwY6QEQsB5b323dN2fdXA1fXtmvW6oqJPHzRrIX4TlEbssQrF5m1FAe6DVlboeAaulkLcaDbkJWu0F1yMWsVDnQbMi90YdZaHOg2ZF7owqy1ONBtyDxJl1lrcaDbkJUWuvAVulmrcKDbkCUF0e2Si1nLcKDbkBULvkI3ayUOdBuyYuJb/81aiQPdhqxYED17/aGoWauoaC4Xs4EkBfH0thd515fv229/+5iRLHn/yRQKalLPzIYnB7oN2fknT2RP99799j297UV+9Ohz7O7ey6jX+NfLrJH8f5wN2Zw3HcGcNx2x375//NenuP729a6tmzWBa+hWU8W0zOLaulnjOdCtpopJKdA9nNGs8RzoVlO9V+hea9Ss8RzoVlNJofQr5XnSzRrPgW411ZaWXDxpl1njOdCtppLeD0VdcjFrOAe61dTLo1wc6GaN5kC3mir21tB9hW7WcA50q6kk6R3l4hq6WaM50K2meksuvkI3azwHutVUb8nFNXSzxnOgW00VPWzRrGkc6FZTHrZo1jwVBbqksyRtlLRJ0uJXaXe+pJDUUbsuWpa0+U5Rs6YZNNAlJcAS4B3ANOBCSdMGaHcY8DHgZ7XupGXHy1foLrmYNVol86HPAjZFxJMAkpYC84D1/dpdD/wt8PGa9tAypbeGfu2y9dzw48eb3Buz1vTRM6dy9oyja/66lQT6BGBL2XYXcGp5A0knA5Mi4v9KOmCgS1oELAJob2+vvrfW8qaMG8X7T23n+RdfanZXzFrW4X/UVpfXPegViyQVgL8HFgzWNiI6gU6Ajo4OF1lzqC0p8LnzTmx2N8yGpUo+FH0GmFS2PTHd1+sw4ATgXkmbgdOAZf5g1MyssSoJ9DXAVElTJB0CzAeW9T4YETsjYlxETI6IycD9wDkRsbYuPTYzswENGugR0QNcAdwJbABujoh1kq6TdE69O2hmZpWpqIYeEcuB5f32XXOAtrMPvltmZlYt3ylqZpYTDnQzs5xwoJuZ5YQD3cwsJxTRnPt7JG0Fnh7i08cBv61hd7LAxzw8+JiHh4M55mMiYvxADzQt0A+GpLURMaxuXPIxDw8+5uGhXsfskouZWU440M3MciKrgd7Z7A40gY95ePAxDw91OeZM1tDNzOyVsnqFbmZm/TjQzcxyIlOBXuli1VkjaZKklZLWS1on6WPp/jGS7pL0RPrf0el+Sfpy+nN4OF0xKpMkJZL+TdLt6fYUST9Lj+2f0imbkfSadHtT+vjkpnZ8iCS9VtItkh6TtEHS6Xk/z5L+Kv29flTS9yWNyON5lnSjpN9IerRsX9XnVtLFafsnJF1cTR8yE+iVLladUT3A30TENEoLhHwkPbbFwN0RMRW4O92G0s9gavq1CPha47tcMx+jNC1zr78FvhgRbwR2AJek+y8BdqT7v5i2y6IvAXdExJuAGZSOPbfnWdIE4KNAR0ScACSU1lTI43m+CTir376qzq2kMcCnKS3zOQv4dO8/AhWJiEx8AacDd5ZtXw1c3ex+1elY/wWYC2wEjkr3HQVsTL//OnBhWfu+dln6orT61d3AfwRuB0Tp7rli/3NOaT7+09Pvi2k7NfsYqjzew4Gn+vc7z+eZl9ckHpOet9uBP8/reQYmA48O9dwCFwJfL9u/X7vBvjJzhc7Ai1VPaFJf6ib9E3Mm8DPgyIh4Nn3oOeDI9Pu8/Cz+J3AVsC/dHgs8H6VFVWD/4+o75vTxnWn7LJkCbAW+mZaZviFpFDk+zxHxDPB3wK+AZymdtwfJ93kuV+25PahznqVAzz1JhwK3Av8lInaVPxalf65zM8ZU0ruB30TEg83uSwMVgZOBr0XETOD3vPwnOJDL8zwamEfpH7OjgVG8siwxLDTi3GYp0AdbrDrTJLVRCvPvRsQ/p7v/XdJR6eNHAb9J9+fhZ/EW4Jx0YfGllMouXwJeK6l3Ja3y4+o75vTxw4FtjexwDXQBXRHxs3T7FkoBn+fz/HbgqYjYGhHdwD9TOvd5Ps/lqj23B3XOsxTor7pYdZZJEvCPwIaI+Puyh5YBvZ9yX0yptt67/4PpJ+WnATvL/qzLhIi4OiImRmlh8fnAPRFxEbASeG/arP8x9/4s3pu2z9SVbEQ8B2yRdGy660xgPTk+z5RKLadJGpn+nvcec27Pcz/Vnts7gT+TNDr96+bP0n2VafaHCFV+4PBO4HHgl8B/bXZ/anhcf0LpT7GHgYfSr3dSqh3eDTwBrADGpO1FacTPL4FHKI0gaPpxHMTxzwZuT79/PfAAsAn4P8Br0v0j0u1N6eOvb3a/h3isJwFr03P9A2B03s8z8BngMeBR4NvAa/J4noHvU/qcoJvSX2OXDOXcAh9Kj38TsLCaPvjWfzOznMhSycXMzF6FA93MLCcc6GZmOeFANzPLCQe6mVlOONAtVyS9UKPXuVbSlRW0u0nSewdrZ9YIDnQzs5xwoFsuSTpU0t2Sfi7pEUnz0v2T07nIb5L0uKTvSnq7pJ+k80/PKnuZGZJWp/svS58vSV9VaV7+FcARZe95jaQ16bzfnemdkWYN40C3vNoDnBcRJwNzgBvKAvaNwA3Am9Kv91O6W/dK4BNlrzGd0hwzpwPXSDoaOA84ltKc/B8Ezihr/9WIeHOU5v3+I+DddTo2swEVB29ilkkCPifpbZSm553Ay1OXPhURjwBIWkdpAYKQ9Ail+ax7/UtE7AZ2S1pJacGBtwHfj4i9wK8l3VPWfo6kq4CRlOb/Xgf8sG5HaNaPA93y6iJgPHBKRHSnszqOSB/7Q1m7fWXb+9j//4n+82IccJ4MSSOAf6A0J8cWSdeWvZ9ZQ7jkYnl1OKX51rslzQGOGcJrzFNp/cuxlCYQWwOsAt6n0lqoR1Eq58DL4f3bdF57j3yxhvMVuuXVd4EfpmWUtZRm+6vWw5SmeR0HXB8Rv5Z0G6W6+npKU8OuBoiI5yX9L0ozCj5HKfzNGsqzLZqZ5YRLLmZmOeFANzPLCQe6mVlOONDNzHLCgW5mlhMOdDOznHCgm5nlxP8Hg/Jwk0HQ5TIAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAEGCAYAAABrQF4qAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAdUElEQVR4nO3df5QdZZ3n8ffn3tudRkhifjRMTCckOGEgMyAwTdDJjIIKBNaZjD/WDePuoMsxukfcWVfGDesMYDyM7jk64o+IRjfLjqJZF11sNYcsP4LuKGg6wIAJBpogpjsgTQARBJLu/u4fVd2pNB363nR133srn9c59+TWU1W3n+rqfPrpp556ShGBmZkVV6neFTAzs8nloDczKzgHvZlZwTnozcwKzkFvZlZwlXpXYLS5c+fGokWL6l0NM7Omsm3bticion2sdQ0X9IsWLaK7u7ve1TAzayqSHjnUuqq6biStkLRTUo+kNWOsP17SrZLulXS7pI7MukFJ96SvrsM7BDMzO1zjtugllYF1wLlAL7BVUldE7Mhs9ingnyLif0p6I/AJ4N+l656PiNPyrbaZmVWrmhb9MqAnInZFxD5gI7By1DZLgdvS91vGWG9mZnVSTR/9fGB3ZrkXOGvUNv8CvA34LPBWYLqkORGxF2iT1A0MAJ+MiBsnXGszsxzs37+f3t5eXnjhhXpXpWptbW10dHTQ0tJS9T55XYy9DPiCpHcDPwL6gMF03fER0SfpBOA2SfdFxEPZnSWtBlYDLFy4MKcqmZm9vN7eXqZPn86iRYuQVO/qjCsi2Lt3L729vSxevLjq/arpuukDFmSWO9Ky7BffExFvi4jTgY+mZU+n//al/+4CbgdOH6Py6yOiMyI629vHHB1kZpa7F154gTlz5jRFyANIYs6cOTX/BVJN0G8FlkhaLKkVWAUcNHpG0lxJw591ObAhLZ8ladrwNsByIHsR18ysrpol5IcdTn3H7bqJiAFJlwKbgTKwISK2S1oLdEdEF3A28AlJQdJ184F095OBL0saIvml8slRo3Vy87t9A3zp9qRH6KR5M7jwlHmT8WXMzJpOVX30EbEJ2DSq7IrM+xuAG8bY7yfAKROsY1We3zfI57f0EAEz2ioOejNrGp/73Oe49tprWbp0KXv27OGuu+7i6quv5rLLLsvl8xvuztjDNeeYaTz8iX/FP2y6n6/fecgbxMzMGs4Xv/hFbrnlFlpbW3nkkUe48cYbc/38wk1qJsHgkJ+aZWbN4f3vfz+7du3iggsu4Prrr+fMM8+saehkNQrToh9Wlhjy4xHNrEYf+952dux5JtfPXPqqGVz553/4stt86Utf4qabbmLLli3MnTs3168/rHAt+nJJbtGbmWUUrkVfkhiK5MaCZhs2ZWb1M17Lu5kVrkVfSsPdvTdmZonCtejL6a+uwQhKuEVvZs3jscceo7Ozk2eeeYZSqcQ111zDjh07mDFjxoQ+t3BBXyol4T44FLSU61wZM7Mq/PKXvxx539vbm/vnF67rppx23XjkjZlZonhBn2nRm5lZAYNeIy36OlfEzJpCNNlf/4dT38IFfTm9/jrkpDezcbS1tbF3796mCfvh+ejb2tpq2q9wF2NHum6a5MSZWf10dHTQ29tLf39/vatSteEnTNWicEE/POrGLXozG09LS0tNT2pqVgXsunGL3swsq3BBX/LFWDOzgxQv6N11Y2Z2kMIF/cgUCA56MzOgyqCXtELSTkk9ktaMsf54SbdKulfS7ZI6MusulvRg+ro4z8qPpeQ+ejOzg4wb9JLKwDrgAmApcJGkpaM2+xTwTxFxKrAW+ES672zgSuAsYBlwpaRZ+VX/pYaHVzbLuFgzs8lWTYt+GdATEbsiYh+wEVg5apulwG3p+y2Z9ecDN0fEkxHxFHAzsGLi1T60kRb90GR+FTOz5lFN0M8HdmeWe9OyrH8B3pa+fyswXdKcKvdF0mpJ3ZK6J3rjwoGgd4vezAzyuxh7GfAGSXcDbwD6gMFqd46I9RHRGRGd7e3tE6rIcNeNZ680M0tUc2dsH7Ags9yRlo2IiD2kLXpJxwBvj4inJfUBZ4/a9/YJ1HdcHnVjZnawalr0W4ElkhZLagVWAV3ZDSTNlTT8WZcDG9L3m4HzJM1KL8Kel5ZNmpLnozczO8i4QR8RA8ClJAF9P/CtiNguaa2kv0g3OxvYKekB4Djg6nTfJ4GPk/yy2AqsTcsmjYPezOxgarRhiJ2dndHd3X3Y+/+45wne9dWf8pZT5/F7M2qbyvPE46bzzjMXjL+hmVmDkbQtIjrHWle42SsXzn4Fx06fxpZfPF7TfvsGh5DkoDezwilc0C+Y/Qp+9tE317zfpzbv5Iu390xCjczM6qtwc90crlJJDIXvqDWz4nHQp8qe3tjMCspBn/L4ezMrKgd9angeewe9mRWNgz7lRxCaWVE56FNlt+jNrKAc9KmyH0FoZgXloE+NtOjddWNmBeOgT43MkeMWvZkVjIM+5Ra9mRWVgz5V9pOpzKygHPSp0sjF2DpXxMwsZw76VCUN+gEnvZkVjIM+VfKzZs2soBz0qQN99HWuiJlZzhz0KU9qZmZFVVXQS1ohaaekHklrxli/UNIWSXdLulfShWn5IknPS7onfX0p7wPIi581a2ZFNe4TpiSVgXXAuUAvsFVSV0TsyGz2dyQPDb9W0lJgE7AoXfdQRJyWa60ngee6MbOiqqZFvwzoiYhdEbEP2AisHLVNADPS9zOBPflVcWqUfMOUmRVUNUE/H9idWe5Ny7KuAv6tpF6S1vwHM+sWp106P5T0Z2N9AUmrJXVL6u7v76++9jkqewoEMyuovC7GXgRcFxEdwIXA1ySVgEeBhRFxOvCfgW9ImjF654hYHxGdEdHZ3t6eU5Vqc2AcvYPezIqlmqDvAxZkljvSsqxLgG8BRMQdQBswNyJejIi9afk24CHgxIlWejKUPE2xmRVUNUG/FVgiabGkVmAV0DVqm18BbwKQdDJJ0PdLak8v5iLpBGAJsCuvyudp+GLsLx77bZ1rYmaWr3FH3UTEgKRLgc1AGdgQEdslrQW6I6IL+DDwFUkfIrkw++6ICEmvB9ZK2g8MAe+PiCcn7WgmoGPWUQA8+Pizda6JmVm+xg16gIjYRHKRNVt2Reb9DmD5GPt9G/j2BOs4JebNPIr26dPqXQ0zs9z5ztiMssSgJzUzs4Jx0GeUS/JcN2ZWOA76jCTonfRmViwO+oxKSQx6dKWZFYyDPqNUksfRm1nhOOgzypKfMGVmheOgz/DFWDMrIgd9hi/GmlkROegzyr4Ya2YF5KDPcIvezIrIQZ+RBL2b9GZWLA76jGQKBAe9mRWLgz6jUnbQm1nxOOgzSvLFWDMrHgd9RsUXY82sgBz0GSXfMGVmBeSgz3CL3syKyEGfUfLwSjMroKqCXtIKSTsl9UhaM8b6hZK2SLpb0r2SLsysuzzdb6ek8/OsfN4qDnozK6BxnxkrqQysA84FeoGtkrrS58QO+zvgWxFxraSlJM+XXZS+XwX8IfAq4BZJJ0bEYN4HkoeyxP7B4IX9h65epSQqZf8hZGbNo5qHgy8DeiJiF4CkjcBKIBv0AcxI388E9qTvVwIbI+JF4GFJPenn3ZFD3XPXWinR9/TznPT3Nx1ym5lHtfDP/+Ucpre1TGHNzMwOXzVBPx/YnVnuBc4atc1VwP+V9EHgaODNmX3vHLXv/NFfQNJqYDXAwoULq6n3pHjfG17N8XOOJhi7+2Z73zP84L5Heeq5/Q56M2sa1QR9NS4CrouIT0t6HfA1SX9U7c4RsR5YD9DZ2Vm3TvLFc4/mP5z96kOuv/HuPn5w36MMhvvxzax5VBP0fcCCzHJHWpZ1CbACICLukNQGzK1y36ZRLgnAQzDNrKlUc1VxK7BE0mJJrSQXV7tGbfMr4E0Akk4G2oD+dLtVkqZJWgwsAX6WV+WnWiUN+gGPzDGzJjJuiz4iBiRdCmwGysCGiNguaS3QHRFdwIeBr0j6EMmF2XdHRADbJX2L5MLtAPCBRh1xU43hFv2AJ8QxsyZSVR99RGwiGTKZLbsi834HsPwQ+14NXD2BOjaMSnm468ZBb2bNwwPCa1CSu27MrPk46GtQKSXfriGPujGzJuKgr4H76M2sGTnoa+A+ejNrRg76Goy06D2O3syaiIO+BpWSW/Rm1nwc9DUYHnXjoDezZuKgr4H76M2sGTnoa+ApEMysGTnoa1BOx9G7RW9mzcRBXwO36M2sGTnoa1DyNMVm1oQc9DU4MLyyzhUxM6tBXk+YOiIM3zB1/U8f4cc9Txy0ToL3vf7VnNIxsx5VMzM7JAd9DV55VAt/tmQuj/7mBXb++rcHret5/Fk6Zr3CQW9mDcdBX4NKucTXLhn9XPTE0ituct+9mTUk99HnpFySR+OYWUOqKuglrZC0U1KPpDVjrP+MpHvS1wOSns6sG8ysG/2s2cJoKZc8vt7MGtK4XTeSysA64FygF9gqqSt9fCAAEfGhzPYfBE7PfMTzEXFabjVuUG7Rm1mjqqZFvwzoiYhdEbEP2AisfJntLwK+mUflmkmlJAY87tLMGlA1QT8f2J1Z7k3LXkLS8cBi4LZMcZukbkl3SvrLQ+y3Ot2mu7+/v7qaNxi36M2sUeV9MXYVcENEDGbKjo+ITuCvgGskvXr0ThGxPiI6I6Kzvb095ypNDffRm1mjqibo+4AFmeWOtGwsqxjVbRMRfem/u4DbObj/vjDcojezRlVN0G8FlkhaLKmVJMxfMnpG0knALOCOTNksSdPS93OB5cCO0fsWQaUkBv3QcDNrQOOOuomIAUmXApuBMrAhIrZLWgt0R8Rw6K8CNkZENu1OBr4saYjkl8ons6N1iiRp0ftirJk1nqrujI2ITcCmUWVXjFq+aoz9fgKcMoH6NY2Ku27MrEH5zticVHwx1swalIM+J+WSGHAfvZk1IAd9TioluUVvZg3JQZ+Tckns98VYM2tADvqcuEVvZo3K89HnpFIu8dyLA+zqf7am/eZOn8aMtpZJqpWZmYM+N0e3lnmo/zne+Okf1rTfgtlH8f8+8sZJqpWZmYM+N2suOJlzTjq2pn2+e88efvLQE+NvaGY2AQ76nPzezDZWnjbmpJ6HtPOx3/KjB5pztk4zax6+GFtHw3fTHjxrhJlZvhz0dVQpJ99+j9Yxs8nkoK+jckkAniPHzCaVg76OWsoOejObfA76OqqU0q4bz5FjZpPIQV9HlbRF76kTzGwyOejraLhF71kvzWwyOejrqDLSR+8WvZlNHgd9HVWGR924RW9mk6iqoJe0QtJOST2S1oyx/jOS7klfD0h6OrPuYkkPpq+Lc6x70xseR+9RN2Y2mcadAkFSGVgHnAv0AlsldWUf8h0RH8ps/0Hg9PT9bOBKoBMIYFu671O5HkWTaim568bMJl81LfplQE9E7IqIfcBGYOXLbH8R8M30/fnAzRHxZBruNwMrJlLhIim768bMpkA1QT8f2J1Z7k3LXkLS8cBi4LZa9pW0WlK3pO7+/iNnkq8Wd92Y2RTI+2LsKuCGiBisZaeIWB8RnRHR2d7ennOVGtdwi/7e3qe5c9deHtn7XJ1rZGZFVM00xX3AgsxyR1o2llXAB0bte/aofW+vvnrFNvOo5MlSV3x3OwDHTKvw84+dX88qmVkBVdOi3woskbRYUitJmHeN3kjSScAs4I5M8WbgPEmzJM0CzkvLDDi1YyZdly7nG+89i3/9xx08++KAZ7I0s9yN26KPiAFJl5IEdBnYEBHbJa0FuiNiOPRXARsjM7l6RDwp6eMkvywA1kbEk/keQvOSxKkdrwTg7l89DcD+wSHKpXL9KmVmhVPVE6YiYhOwaVTZFaOWrzrEvhuADYdZvyOGZ7I0s8niO2MbxMgInEGPqTezfDnoG8TwXbL7PabezHLmoG8Qw3fJ7neL3sxy5qBvECPz3rhFb2Y5c9A3iBY/hMTMJomDvkH4ISRmNlkc9A1i5LGC7qM3s5w56BuEx9Gb2WRx0DeIA103btGbWb4c9A3iQNeNW/Rmli8HfYM4MDe9W/Rmlq+q5rqxyTf8oPCrf3A/M4/qqXNtXurtZ3TwzjMXjL+hmTUct+gbxJLjpvPmk48bmaO+kezY8ww33nOoRxCYWaNzi75BHDOtwlcv7qx3Nca0av0dHt9v1sTcordxtZRL7PNoILOm5aC3cbWUS75IbNbEHPQ2rpay3HVj1sQc9DauirtuzJpaVUEvaYWknZJ6JK05xDbvlLRD0nZJ38iUD0q6J3295KHi1vhayyW36M2a2LijbiSVgXXAuUAvsFVSV0TsyGyzBLgcWB4RT0k6NvMRz0fEaflW26ZSpSRPtmbWxKpp0S8DeiJiV0TsAzYCK0dt815gXUQ8BRARj+dbTaunlkrJUzOYNbFqgn4+sDuz3JuWZZ0InCjpx5LulLQis65NUnda/pdjfQFJq9Ntuvv7+2upv02BFrfozZpaXjdMVYAlwNlAB/AjSadExNPA8RHRJ+kE4DZJ90XEQ9mdI2I9sB6gs7PTTccG01IueVZNsyZWTYu+D8hOctKRlmX1Al0RsT8iHgYeIAl+IqIv/XcXcDtw+gTrbFOsUnbXjVkzqybotwJLJC2W1AqsAkaPnrmRpDWPpLkkXTm7JM2SNC1TvhzYgTWV1rLYPzREhMPerBmN23UTEQOSLgU2A2VgQ0Rsl7QW6I6IrnTdeZJ2AIPA30bEXkl/AnxZ0hDJL5VPZkfrWHOolEtEwDW3PEhJetltX3vCbM46Yc4U1czMqqFGa6V1dnZGd3d3vathGZvue5RLv3EX1Tzl8DULXsl3P7B88itlZgeRtC0ixpwZ0bNX2rguPGUePVdfOO527/v6NnY/+bspqJGZ1cJBb1UplV6+ywagtVLyMEyzBuS5biw3rR6dY9aQHPSWm5ayb6wya0QOestNS9ldN2aNyEFvuWkpl9g34KA3azQOestNqyc/M2tIDnrLjaczNmtMDnrLTfJs2WComjurzGzKOOgtN62V5Mdpvx8kbtZQHPSWm5ZyclOV++nNGouD3nLTUk5+nDbd+yg79jxT59qY2TAHveVm7jHTAPjIt+/lPdf9rM61MbNhDnrLzVtOnceWy87m7Wd08NsXBupdHTNLOegtN5JYPPdojp0xzcMszRqIg95y15JObtZozzowO1I56C1309JhlvvcqjdrCFUFvaQVknZK6pG05hDbvFPSDknbJX0jU36xpAfT18V5Vdwal4dZmjWWcR88IqkMrAPOBXqBrZK6ss9+lbQEuBxYHhFPSTo2LZ8NXAl0AgFsS/d9Kv9DsUbRmg6z3DcwBNPqXBkzq6pFvwzoiYhdEbEP2AisHLXNe4F1wwEeEY+n5ecDN0fEk+m6m4EV+VTdGlXL8B2y7roxawjVBP18YHdmuTctyzoROFHSjyXdKWlFDftawRzUojezusvrmbEVYAlwNtAB/EjSKdXuLGk1sBpg4cKFOVXJ6qXVF2PNGko1Lfo+YEFmuSMty+oFuiJif0Q8DDxAEvzV7EtErI+IzojobG9vr6X+1oCGW/TuujFrDNUE/VZgiaTFklqBVUDXqG1uJGnNI2kuSVfOLmAzcJ6kWZJmAeelZVZgw3Pe/PKJ59jV/+zIa/eTv/PYerM6GLfrJiIGJF1KEtBlYENEbJe0FuiOiC4OBPoOYBD424jYCyDp4yS/LADWRsSTk3Eg1jiOaUt+rN7/9btesu7zF53On7/mVVNdJbMjmhqthdXZ2Rnd3d31roZNwOBQcNsvHud3+w7Md/P8vkHWfOc+/v4tS7nkTxfXsXZmxSRpW0R0jrUur4uxZiPKJXHu0uMOKhsOeo/EMZt6ngLBpsTISBwHvdmUc9DblCiXRLkk9g0O1rsqZkccB71NmdZyyS16szpw0NuUaa046M3qwUFvU6alXPLdsmZ14KC3KTOtUuJFt+jNppyD3qZMa6XkOerN6sBBb1MmuRjrUTdmU803TNmUaa2U+OcHn+Dcf/xhvati1pBOmjeDz190eu6f66C3KfOe5Yu45f5f17saZg1rwayjJuVzHfQ2Zd52RgdvO6Oj3tUwO+K4j97MrOAc9GZmBeegNzMrOAe9mVnBOejNzArOQW9mVnAOejOzgnPQm5kVXMM9HFxSP/DIYe4+F3gix+o0Ax/zkcHHfGSYyDEfHxHtY61ouKCfCEndh3oKelH5mI8MPuYjw2Qds7tuzMwKzkFvZlZwRQv69fWuQB34mI8MPuYjw6Qcc6H66M3M7KWK1qI3M7NRHPRmZgVXmKCXtELSTkk9ktbUuz55kbRA0hZJOyRtl/Q3aflsSTdLejD9d1ZaLkmfS78P90o6o75HcHgklSXdLen76fJiST9Nj+t/SWpNy6elyz3p+kV1rfgESHqlpBsk/ULS/ZJedwSc5w+lP9c/l/RNSW1FO9eSNkh6XNLPM2U1n1dJF6fbPyjp4lrqUIigl1QG1gEXAEuBiyQtrW+tcjMAfDgilgKvBT6QHtsa4NaIWALcmi5D8j1Ykr5WA9dOfZVz8TfA/Znl/wZ8JiJ+H3gKuCQtvwR4Ki3/TLpds/oscFNEnAS8huT4C3ueJc0H/iPQGRF/BJSBVRTvXF8HrBhVVtN5lTQbuBI4C1gGXDn8y6EqEdH0L+B1wObM8uXA5fWu1yQd63eBc4GdwLy0bB6wM33/ZeCizPYj2zXLC+hIf/jfCHwfEMndgpXR5xvYDLwufV9Jt1O9j+Ewjnkm8PDouhf8PM8HdgOz03P3feD8Ip5rYBHw88M9r8BFwJcz5QdtN96rEC16DvzADOtNywol/VP1dOCnwHER8Wi66jHguPR9Eb4X1wAfAYbS5TnA0xExkC5nj2nkeNP1v0m3bzaLgX7gf6RdVl+VdDQFPs8R0Qd8CvgV8CjJudtG8c811H5eJ3S+ixL0hSfpGODbwH+KiGey6yL5FV+IcbKS3gI8HhHb6l2XKVYBzgCujYjTgec48Oc8UKzzDJB2Pawk+SX3KuBoXtrFUXhTcV6LEvR9wILMckdaVgiSWkhC/vqI+E5a/GtJ89L184DH0/Jm/14sB/5C0i+BjSTdN58FXimpkm6TPaaR403XzwT2TmWFc9IL9EbET9PlG0iCv6jnGeDNwMMR0R8R+4HvkJz/op9rqP28Tuh8FyXotwJL0qv1rSQXdLrqXKdcSBLw34H7I+IfM6u6gOEr7xeT9N0Pl/91evX+tcBvMn8iNryIuDwiOiJiEcl5vC0i3gVsAd6Rbjb6eIe/D+9It2+6Vm9EPAbslvQHadGbgB0U9DynfgW8VtIr0p/z4WMu9LlO1XpeNwPnSZqV/iV0XlpWnXpfpMjxYseFwAPAQ8BH612fHI/rT0n+rLsXuCd9XUjSN3kr8CBwCzA73V4kI5AeAu4jGdFQ9+M4zGM/G/h++v4E4GdAD/C/gWlpeVu63JOuP6He9Z7A8Z4GdKfn+kZgVtHPM/Ax4BfAz4GvAdOKdq6Bb5Jcg9hP8pfbJYdzXoF/nx57D/CeWurgKRDMzAquKF03ZmZ2CA56M7OCc9CbmRWcg97MrOAc9GZmBeegtyOCpGdz+pyrJF1WxXbXSXrHeNuZTQUHvZlZwTno7Ygi6RhJt0q6S9J9klam5YvSeeCvk/SApOslvVnSj9P5v5dlPuY1ku5Iy9+b7i9JX1DyTIRbgGMzX/MKSVvTOdfXp3eBmk0ZB70daV4A3hoRZwDnAJ/OBO/vA58GTkpff0VyZ/JlwH/NfMapJHPwvA64QtKrgLcCf0DyPIS/Bv4ks/0XIuLMSOZcPwp4yyQdm9mYKuNvYlYoAv5B0utJpkGez4EpYh+OiPsAJG0neTBESLqPZD7xYd+NiOeB5yVtIXkQxOuBb0bEILBH0m2Z7c+R9BHgFSRzr28HvjdpR2g2ioPejjTvAtqBP46I/eksmW3puhcz2w1lloc4+P/K6HlDDjmPiKQ24Iskc5bslnRV5uuZTQl33diRZibJfPf7JZ0DHH8Yn7FSybNN55BMvLYV+BHwb5Q863YeSbcQHAj1J9JnCngkjk05t+jtSHM98L20O6abZObEWt1LMpXuXODjEbFH0v8h6bffQTL97h0AEfG0pK+QzM74GMkvBbMp5dkrzcwKzl03ZmYF56A3Mys4B72ZWcE56M3MCs5Bb2ZWcA56M7OCc9CbmRXc/weNQL75e+YvAgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"select_lambda(Xtrain, ytrain, Xcv, ycv, 0, 1000, 1)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"id": "magnetic-simon",
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 3.65125582],\n",
" [ 1.05866988],\n",
" [ 1.1372875 ],\n",
" [-0.63801386],\n",
" [ 2.19595738],\n",
" [ 0.49927364],\n",
" [-0.41689667],\n",
" [ 0.64177321],\n",
" [-1.05491053]])"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lamb = 1\n",
"theta = solve(X, y, lamb)\n",
"data['y^'] = (np.matmul(X, theta) >= 0.5).astype(int).reshape(X.shape[0])\n",
"theta"
]
},
{
"cell_type": "code",
"execution_count": 16,
"id": "favorite-belief",
"metadata": {},
"outputs": [],
"source": [
"def draw_learning_curve(data, P, lamb, start=None, end=None):\n",
" df = [] # m, cv, train\n",
" expanded = expand(data, P)\n",
" \n",
" start = start or 0\n",
" end = end or data.shape[0]\n",
" \n",
" for m in range(start, end + 1): \n",
" Xtrain, ytrain = extract(expanded, 0, math.ceil(m*0.8))\n",
" Xcv, ycv = extract(expanded, math.ceil(m*0.8), m + 1)\n",
" if ycv.shape[0] < 1:\n",
" continue\n",
" \n",
" theta = solve(Xtrain, ytrain, lamb)\n",
" cost_train = cost_fn(theta, Xtrain, ytrain, 0)\n",
" cost_cv = cost_fn(theta, Xcv, ycv, 0)\n",
" \n",
" df.append([m, cost_cv, cost_train])\n",
" \n",
" df = pd.DataFrame(df, columns=['m', 'cv', 'train'])\n",
" ax = df.plot.line(x='m', y='cv')\n",
" df.plot.line(x='m', y='train', ax=ax)\n"
]
},
{
"cell_type": "code",
"execution_count": 17,
"id": "artistic-election",
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAEGCAYAAAB1iW6ZAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABHiElEQVR4nO2dd5xU5fX/38/MzvZe2cruwtI7C2JBEXuD2DUxUVNMLNGYauovMc10Tb5qNEaNRsXeEDSKIooFlt5ZFhZYYHvvU57fH3dmd7axbXan7Hm/XvNi59bDzJ3PPfc855xHaa0RBEEQ/B+Ttw0QBEEQPIMIuiAIQoAggi4IghAgiKALgiAECCLogiAIAUKQt06cmJios7OzvXV6QRAEv2TTpk2VWuuk3tZ5TdCzs7MpKCjw1ukFQRD8EqXU4b7WSchFEAQhQBBBFwRBCBBE0AVBEAIEr8XQBUEQhoLVaqWkpITW1lZvmzKihIaGkpGRgcViGfA+IuiCIPgVJSUlREVFkZ2djVLK2+aMCFprqqqqKCkpIScnZ8D7SchFEAS/orW1lYSEhIAVcwClFAkJCYN+ChFBFwTB7whkMXcxlP+jCLofsulwNTtK6rxthiAIPoYIuh/yw5e288s3d3nbDEEQfAwZFPUzWtrtHKpsIjKkDa31mHj0FARhYIiH7mfsK2vAoaG+1UZFQ5u3zRGEMclTTz3FrFmzmD17Npdffjnjx4/H4XAA0NTURGZmJlarddTtEg/dz9hzor7j7wPljSRHh3rRGkHwLr96cxe7j9f3v+EgmJYWzf+7bHqf63ft2sVvfvMbPvnkExITE6murubmm2/mww8/5Oyzz2blypVccMEFg8of9xTiofsZu4/XYzEbYZbC8kYvWyMIY4/333+fq6++msTERADi4+O59tpref755wFYsWIF1157rVdsEw/dz9hzop45mbHsLW2gsLzB2+YIglc5mSc9mixbtoyf/OQnVFdXs2nTJpYuXeoVO8RD9yMcDs3e0gampUaTlxxJYZl46IIw2ixdupQXX3yRqqoqAKqrq4mMjGTBggXcddddXHrppZjNZq/YJh66H3G0ppnGNhtTU6Npsdp5f2+5t00ShDHH9OnT+elPf8pZZ52F2Wxm7ty5PPnkk1x77bVcffXVrF271mu2iaD7Ea4B0Wlp0TS02nihoITqpnbiI4K9bJkgjC1uvPFGbrzxxi7LrrrqKrTWXrLIQEIufsTuEw2YFExKiWJiSiRgZLoIgiCACLpfsft4PblJkYRazOQli6ALgtAVEXQ/Ys+JeqalRgOQFhNGmMUsmS6CIHQggu4n1LVYOVbbwlSnoJtMionJkeKhC4LQgQi6n+AaEJ2aGtWxLE8EXRAEN0TQ/QT3DBcXE1MiOVHXSkPr6PeMEATB9xBB9xP2nKgnMTKY5KjO3i0Tk2RgVBBGm9raWh566KFB73fxxRdTW1vreYPcEEH3E3afqO+In7vISzHCL9LTRRBGj74E3WaznXS/VatWERsbO0JWGYig+wE2u4P9ZY09BD0zLozgIBNFIuiCMGrcc889FBUVMWfOHBYsWMDixYtZtmwZ06ZNA+ALX/gC8+fPZ/r06Tz66KMd+2VnZ1NZWUlxcTFTp07lG9/4BtOnT+f888+npaXFI7YNqFJUKXUh8ABgBh7TWt/Xbf1NwJ+AY85F/6e1fswjFgocrGyi3eboSFl0EWQ2kZsYIR66MHZZfQ+U7vDsMcfNhIvu63P1fffdx86dO9m6dStr167lkksuYefOneTk5ADw+OOPEx8fT0tLCwsWLODKK68kISGhyzEKCwt57rnn+Ne//sU111zDyy+/zA033DBs0/sVdKWUGXgQOA8oATYqpd7QWu/utunzWus7hm2R0ANXv+fuHjrAxORItpXUjrJFgiC4WLhwYYeYA/z973/n1VdfBeDo0aMUFhb2EPScnBzmzJkDwPz58ykuLvaILQPx0BcCB7TWBwGUUiuA5UB3QRdGiD2l9QSbTeQmRfRYl5ccxVs7TtDSbics2Dsd3gTBa5zEkx4tIiI6f5dr167lvffe49NPPyU8PJwlS5bQ2traY5+QkJCOv81ms8dCLgOJoacDR93elziXdedKpdR2pdRLSqnM3g6klLpFKVWglCqoqKgYgrljk4r6NpKjQ7CYe35deSmRaA1FFY0crW7mRy9tZ/LPVrPhULUXLBWEwCcqKoqGht4rtOvq6oiLiyM8PJy9e/fy2Wefjaptnuq2+CbwnNa6TSn1TeA/QI8O71rrR4FHAfLz873blsyPqGuxEhPW+3RWE509XX762k52HavDZFI4HJp3d5eyMCd+NM0UhDFBQkICp59+OjNmzCAsLIyUlJSOdRdeeCH//Oc/mTp1KpMnT2bRokWjattABP0Y4O5xZ9A5+AmA1rrK7e1jwB+Hb5rg4mSCnp0QQajFxJ4T9dywaDy3LpnAt5/bIh66IIwgzz77bK/LQ0JCWL16da/rXHHyxMREdu7c2bH8+9//vsfsGoigbwTylFI5GEJ+HfBF9w2UUqla6xPOt8uAPR6zUKCuxdrhiXcnOMjEq7edTlx4MONijKKjU3LieWhtEY1tNiJDpOW9IIwV+o2ha61twB3AOxhC/YLWepdS6l6l1DLnZncqpXYppbYBdwI3jZTBY5G6FivRoX3PID41NbpDzAEW5sRjd2g2Ha4ZDfMEQfARBuS+aa1XAau6LfuF298/Bn7sWdMEF3UtVmLC+xb07swfH0eQSbHhUBVnTUoaQcsEwTtorVFKeduMEWUosx9JpaiP02q102Zz9BlD743w4CBmpMdIHF0ISEJDQ6mqqvL6dG8jidaaqqoqQkND+9/YDQmw+jj1zk6K0YMQdDDi6E+sL6bVaifUIvnpQuCQkZFBSUkJgZ76HBoaSkZGxqD2EUH3cepbDEEfjIcORhz9kXUH2XKkllMnJPS/gyD4CRaLpUtlptCJhFx8nLohCnp+djxKIWEXQRhDiKD7OEMV9JgwC1PHRbOhuKr/jQVBCAhE0H2coQo6GGGXTYdraLc5PG2WIAg+iAi6j1PXPHRBPyUnnlargx3H6jxtliAIPogIuo9T12LMghIVOvjx6wXOXi4SRxeEsYEIuo9T12IlItjca6fF/kiMDGFCUgQbDkkcXRDGAiLoPs7JGnMNhIU5CRQU12B3BG4RhiAIBiLoPk5di3XQRUXuzMuKpaHNxuGqJg9aJQiCLyKC7uPUtw7PQ3c17apoaPOUSYIg+Cgi6D5O/TBDLklRxlRXFY0i6IIQ6Iig+zjDjaEnRhqCXikeuiAEPCLoPs5wBT0uPBiTgsrGdg9aJQiCLyKC7sNY7Q6a2+3DEnSzSZEQGSIxdEEYA4ig+zCusv/hZLmAEXaplBi6IAQ8Iug+zHD6uLiTGBksgi4IYwARdB/GU4KeFCUhF0EYC4ig+zCeCrkkRYZQ2dge0FN2CYIggu7TDHW2ou4kRobQbndQ32rzhFmCIPgoIug+jKcEvaO4SMIughDQiKD7MJ4bFHUWF8nAqCAENCLoPkxdi5Uwi5ngoOF9TYlRwYAIuiAEOiLoPsxwq0RdJEVKyEUQxgIi6D6M0Tp38DMVdScuPBizSYmHLggBjgi6D+MpD91kUsRHBFPZIP1cBCGQGZCgK6UuVErtU0odUErdc5LtrlRKaaVUvudMHLvUtdg8IuhghF2kha4gBDb9CrpSygw8CFwETAOuV0pN62W7KOAu4HNPGzlWqR/mbEXuJEZJPxdBCHQG4qEvBA5orQ9qrduBFcDyXrb7NfAHoNWD9o1pPBVyAWc/FxkUFYSAZiCCng4cdXtf4lzWgVJqHpCptX7rZAdSSt2ilCpQShVUVFQM2tixhM3uoLHNgyGXKCn/F4RAZ9iDokopE/BX4Hv9bau1flRrna+1zk9KShruqQOaBmeZvidj6O12B/UtUv4vCIHKQAT9GJDp9j7DucxFFDADWKuUKgYWAW/IwOjA0Vrzwb5ybHZHxzJPVYm6cFWLysCoIAQuAxH0jUCeUipHKRUMXAe84Vqpta7TWidqrbO11tnAZ8AyrXXBiFgcgGw5WsvNT2xk1c7SjmWeFnRXPxcZGBWEwKVfQdda24A7gHeAPcALWutdSql7lVLLRtrAscCeE/UAbDlS07HMU61zXSRKtaggBDwDKkPUWq8CVnVb9os+tl0yfLPGFoVljQBsO1rbsczzIRfp5yIIgY5UivoA+8saANh1vB6rM47uaUGX8n9BCHxE0H2A/WWNxIRZaLM52FdqiLunBd1kUiREBEvIRRACGBF0L1Pd1E5lYxvL56QBsK2kFjCqRIODTIRazB47V6JzKjpBEAITEXQv4wq3LJ2STFy4pSOO7skqURdJUv4vCAGNCLqXKXQK+qSUKGZnxrK9pA6A+lbPC3piZIiEXAQhgBFB9zL7yxqJCgkiNSaU2Rmx7C9roKnNNiIeemJUMFVS/i8IAYsIupfZX9ZAXkokSilmZ8bg0LDzWN3IhFyk/F8QAhoRdC9TWN7IpJQoAGZlxALGwGhdi5Xo0OHPVuSOq1q0olEaYgYaD7xXyDWPfOptMwQvI4LuRSob26huaifPKeiJkSFkxIWxraSOuuaRiaEDVMjMRQHHlqM1bDhUTW2zfLdjGRF0L7K/Y0A0smPZ7MxYth6ppcGDrXNdSD+XwKW0znjqcg2qC2MTEXQvsr+0M8PFxeyMGI7VtqC15/q4uJB+LoFLufM7dW8fIYw9RNC9yP7yRqJDg0h2es4As51xdPBclaiL2DCLlP8HIG02O9VNRqjFVZgmjE1E0L1IYVkDk1KiUEp1LJuRHoPJ+dbTgm4yKWMqOhH0gKK83vg+g4NMbD1aJ2mpYxgRdC+htWZ/WWPHgKiLiJCgjhCMpwUdpPw/ECmrN+LniycmUtnYxok6yWIaq4ige4mKhjbqWqxdBkRdzMqIASAmfGQEXWLogUWZ00M/f3oKIHH0sYwIupfY7+yBPqmbhw6wKDcBi1mRHBXq8fNKP5fAo9TpoS+ZnEyw2cRWiaOPWTxbuSIMGFfKYl4vHvrlc9NZlJtAfESwx8+bEBFMVZOEXAKJ8vpWgoNMJEeFMDUtWjz0MYx46F6isLyB2HALSZEhPdYppUiLDRuR88aEW2i3OWi12kfk+MLoU1rfSkp0CEop5mTEsKOkDrvDcwOjHxdWstltekTBdxFB9xL7SntmuIwGroHW2mbrqJ5XGDnK6lsZF22E52ZlxNLUbqeootEjx263Objjuc388o1dHjmeMLKIoHsBrbWzh0vPcMtIExtmhHFcMyIJ/k9ZfRvJTkGfnRkLwFYPhV0+2FdObbOVXcfraW6Xpm6+jgi6F2i1OmhotY1YWOVkdHroEkcPBLTWXTz03MQIokKCusTRHQ7N4x8foriyadDHf3XzMQDsDs22o9JWwNcRQfcCnp4vdDDEOlMhxUMPDBrabDS320mJNsZiTCbFrMyYLhWjf3l3H/eu3M1PXt0xqGPXNrfz/t5yrpyXAcCmw9Ues1sYGUTQvUB9qyGm0aGjL+gdHroIekBQ5iwiSonuTHGdnRHL3hMNtFrtvL71GA9+UMT4hHA+KaoalCiv3H6CdruDm0/PJi85koLDMjDq64igewFveuiuYqU6GRQNCFxFRV0EPTMWm0OzYsMRfvjSdhbmxPPG7WcQF27h/94/MOBjv7rlGJNTopieFk1+dhybD9fg8GD2jOB5RNC9QL1T0D3dTXEgRIUEYTYpCbkECK6ionHdPHSAX765m6SoEB7+0jxiwi18fXEuH+yrYOex/mPhxZVNbDpcw+Xz0lFKMX98PPWtNgrLPZM9I4wMIuhewJseulKK6NAgaltkUDQQcPVxcffQx8WEkhIdQniwmX99JZ8EZ63Dl08dT1Ro0IC89Fe3HEMpWD4nDYD88XEAFEgc3acRQfcCHR66h6eYGyix4cHUybyiAUFZfSvRoUGEBZu7LP/TVbN5+msLmZoa3bEsOtTCzadl8/au0o5K5d7QWvPqlmOcPiGR1BgjE2t8QjiJkcFsKpY4ui8zIEFXSl2olNqnlDqglLqnl/XfUkrtUEptVUp9rJSa5nlTAweXmHoj5OI6r6QtBgZl9a2Mi+nZ8+fMSUnMHx/fY/nNp+cQHmzmwQ/69tI/P1TNkepmLp+b3rHMCLvEycCoj9Ovi6iUMgMPAucBJcBGpdQbWuvdbps9q7X+p3P7ZcBfgQtHwN4e2B0ah9ZYzP7zsFHfaiUi2Ow1m2NF0AOG0vq2LuGW/oiLCObLi8bzr48OUl7fhlKgFFhtmorGNsrrW2lqtxNmMXPhjHFd9s0fH887u8oob2gdkcZxwvAZyDP/QuCA1voggFJqBbAc6BB0rXW92/YRwKgNhf965W52Ha/jxW+dNlqnHDZ1LVaveedg5KIXVw2+yETwPcrrW8lLThzUPrecmcv+sgYa24wnRa3BbFJMS4tmyeQkkqNCyc+OIyKkqzzMzzbi6JsP13DhjFTP/AcEjzIQQU8Hjrq9LwFO6b6RUup24LtAMLDUI9YNgC1Ha9l7oh6t9aj3RRkq9S1WrwyIuogJs0gvlwDA7tCUN7R1FBUNlITIEJ64eeGgzzcjLYaQIBMFxSLovorHnvm11g9qrScAPwJ+1ts2SqlblFIFSqmCiooKj5y3uLKJNpvDr2bhqWuxeqWoyEVsmIX6VqvkFPswDofm9mc288mByj63qWpqw+7QXVIWR5LgIBOzM2Ilju7DDMRDPwZkur3PcC7rixXAw72t0Fo/CjwKkJ+fP2w1qW1u70gBLKlpJilqcJ6Kt6hvtZHuhT4uLqLDLGgNDa22EZkVSRg+JTUtvLXjBIXlDbx915mYTD2fPsvqehYVjTTzs+N47KODtFrthFrM/W7/9KfF/PHtfdi1RmtwaM0V8zL4/RUzR8HascdAPPSNQJ5SKkcpFQxcB7zhvoFSKs/t7SVAoedM7JviquaOv4/WtIzGKT1CfYuV6DDvzS0SGy4dF32dAxVGWuH+skbe3lXa6za95aCPNPOz4rDa9YAn0XihoIT4yGC+uDCLL586ngXZ8Ty/8QglNc397ywMmn4FXWttA+4A3gH2AC9orXcppe51ZrQA3KGU2qWU2ooRR79xpAx2x717nD9dIL4QQwekuMiHKSo3ru302DD+vqaw1/BYR5VoL2mLI8V8Z4HR69uO97ttZWMbO47VcfX8DH526TR+cvFU/nDVLJRSPP3Z4ZE2dUwyoBi61nqV1nqS1nqC1vq3zmW/0Fq/4fz7Lq31dK31HK312VrrUemGX1zVhFJGOXuJn3jodoemoc3m3Ri6dFz0eYoqGkmMDOYHF0xmb2kD/9vd00svq2/FpIxpBUeLuIhgbjotm2c/P8IT6w+ddNuPC434/5mTkjqWpceGccH0FFZsOCr91UcA/0ne7oXiyibSYsLISYrwG0FvaPVe2b+LWJm1yOcpqmgkNymSS2elkpMYwQNrDqB1Vy+9rL6VpKgQgka5nuHnl07j/Gkp3LtyN6t3nOhzu3X7K4iPCGZGWkyX5TedlkNdi5XXtvTv5QuDw78FvaqZ8QnhZMSF+U3Ipc6LjblcSAtd3+dAeSMTkiIJMpu44+yJ7DlRz7u7y7psM9iiIk9hNin+fv1c5mXFcdfzW9lwqGd/F4dDs66wkjMmJvYY0F2QHcf0tGie/ORQj5uUMDz8WtAPVzWRnRhBRlw4JTUtfpGG583GXC5cN5N6EXSfpLqpnZpmKxOSIgCjQdb4hHAeWFPYRQDL61u9IugAoRYzj30ln4y4ML7xVAFHqro6VLtP1FPZ2MZZbuEWF0opbjotm/1ljXxSVDVaJo8J/FbQ65qt1DRbyXZ66O02B5WNbd42q1/qnX1cvCnooRYzoRaTlP/7KK4JnicmG3POBplN3H72RHYdr2fFxs4av1K3qee8QVxEMP+5eSHtNgd/eXdfl3XrCo06k8WTeq9ivWx2GgkRwf3G4YXB4beC7ipdz06IIDMuHPCP1MXOkIv30hbBmCxaBkV9kwPOnuMTkjonEb9yXgaL8xL5f6/vYvORGlqtdmqbrYOuEvU0mfHh3HhaNm9sO96lg+O6/RVMTY3us+dLqMXMF0/JYs3ecg5LGwqP4f+CnhhBRpxRpOMPcfR6HxgUdZ1fBkV9k6LyRkKCTF2Kz8wmxd+vm0tKTAi3/ncTu44bk1R4K+TizjfPzCUiOIj739sPQGObjYLiGs7swzt3ccOi8ZiV4oE1o1K2MibwX0GvNMQ7Kz6c9A5B9yMP3Ytpi2BMRSceum/iynDpPpgYFxHMIzfkU9di5db/bgZ8Q9DjIoL56unZrNpRyq7jdXxaVIXNoXuNn7uTEh3Kt86awCubj/H+3rKTbisMDL8V9MNVTaTFhBJqMRMeHERCRLB/eOgtVoJMivDg/sumR5LYMBF0X6Wooqkjft6daWnR/PGq2ZQ3GONFo1lUdDK+tjiX6NAg/vZuIev2VxAebCa/l37s3fn2OROZnBLFj1/ZIdejB/BbQT9U1cT4hIiO90bqon946NFhFq93howRQfdJWq12jtY0d2S49May2Wl866wJhAebSfNiTyB3YsIsfGNxLu/tKeP1rcc4NTeB4KD+5SUkyMyfr55NZWM7v165u9/thZPjt4J+uKqZ7EQ3QY8P9wtBr2+1eT1+Dka1qMTQfY9DlU1o3XVAtDfuuWgKBT87l8gQ7w6uu3PzGTnEhVuob7Vx1uSTh1vcmZkRw61nTeClTSV8sLd8BC0MfPxS0OtarFQ3tZOdEN6xLCMujGN+kItutM71/o8wJsxCi9VOm83ubVMEN1wpi/0JOkB4sPevI3ciQ4K4bclEzCbFkknJg9rXFXq555Xt8uQ4DPxS0F1pTl1DLuG02x0dsUVfpd7LsxW5iJGOiz5JUbnRnyj3JCEXX+bri3NY98OzyXJztgZCSJCZ3185k7L6Nt7a3nc7AeHk+KWgu9rm5iR2jaGD76cuervToguXDXUSdvEpDlQ0khEXNqBe476IUmrIvf7nZsYSHxHM5iMygcZQ8UtBP+xsm5sV3+kFZPpJ6mJ9q2946K4GXeKh+xZFzh4uYxGlFPOyYkXQh4FfCvqhqibGRYcS5pb6l+GsFvVlD11rTZ2PeOiuFroyMOpZjlY3Yx/iOI7DoTlY2cjEMSroAHOz4jhY0SRtKYaIXwq6keHSNUYXajGTGBnC0Wrf9dBbrQ6sdu31oiJwC7mIh+4xmtpsnPOXD/neC1uH1EXwWG0LrVYHE/rIQR8LzM2KBYzJ34XB46eC3kR2Qs9Bo4y4MEpqfddD94VOiy5iw4xBUWmh6znKG9potzt4betxnvykeND7DybDJVCZnRGLScEWmYh6SPidoDe0WqlsbO+Sg+7C14uLfKUxF0BUaBBKQZ082nqMKme3z/TYMH771h4+Pzi41rBFFcbY0MmKigKdiJAgpoyLZvORWm+b4pf4naAfdma4ZPeSFpURF87x2pYhxzBHGl9pzAVgMimiQ6Va1JNUNRk3xz9dPYus+HBuf3YLpXWtA96/qKKRuHALCZHe7aDobeZmxbL1aK3P/o59Gb8T9EOVPXPQXWTGh2G1647Z0H0NV4qgL8TQwVktKoLuMaqdgj4+IYJHvjyf5nYbtz6ziXabY0D7Hygbuxku7szLiqOxzdbRRlgYOH4n6J1FRb176OC7qYu+5KGD9HPxNC5BT4gIJi8lij9dNZstR2p5fACTOBQUV7OhuJpTcvtvaBXozBsfByDpi0PA7wT95tNzWH3X4l7Lnn29uMgX5hN1R3qie5bKxjYigs0dRUGXzErlnCnJ/N/7Byhv6Pupsc1m555XdpAeG8ZtSyaOlrk+S3ZCOHHhFjbLwOig8TtBjwgJYmpqdK/rXBVqPuuhO6ef84VeLmAIuswr6jmqm9qJjwzusuynl0ylzWbnz+/s62MveHhtEQfKG/nN5TOI8KFmW95CKcXcrDjx0IeA3wn6yQi1mEmKCuFote966JEhQQSZfeNjlxi6Z6luaic+ouuAZm5SJDedls2Lm0rYeayuxz4Hyht46IMils1O4+zJg2toFcjMy4qlqKJJWlMMEt9QFg+SHhvG8Tof9dBbfaPTogtXDH0oRTBCT6oa20mMCO6x/Nvn5BEfHsyv3tzV5bN2ODT3vLyD8BAzv7hs2mia6vPMyzLi6FuOipc+GAJO0NNiQzlR66NZLj7SadFFbFgwdoemsc3mbVMCAsND7yno0aEWvnf+ZDYW1/DWjhOUN7Ty9s5SfvjydgoO1/DTi6eSOMZTFbszK9MoMJJ89MHhO+6ih0iNCeP9veVorb0+K1B3fKV1rosYt34uUT6SSumvaK2pamrrEUN3ce2CTJ7+7DDfWbEVmzO/Oths4qr5GVw1P2M0TfULIkOCmJQSxRaJow+KgBP0tNgwWq0OaputxPXiLXmTuhYrmfGD6xM9krj3c8n0si3+TkObDatdk9DHNWc2Kf545SweX3+I6WnRzM2KY0Z6NCFB/tkmdzSYNz6ON7cex+HQPSbMFnpnQCEXpdSFSql9SqkDSql7eln/XaXUbqXUdqXUGqXUeM+bOjDSnJPmHqv1vTh6Q6vNZ4qKQFroepLqRlcOet+hk5kZMfzt2jl8fXEu88fHiZj3w/ysOBrabOwprfe2KX5Dv4KulDIDDwIXAdOA65VS3UdwtgD5WutZwEvAHz1t6EBJdaYunhhEyfVo4Sutc124Qi4i6MPHVfbfV8hFGDxn5CUC8OH+Ci9b4j8MxENfCBzQWh/UWrcDK4Dl7htorT/QWrtyBT8DvBYUdHnoJ3ws08Vmd9DYZvOJxlwuOjouSmrYsHE15uor5CIMnpToUKamRrN2nwj6QBmIuqQDR93elwCnnGT7rwGre1uhlLoFuAUgKytrgCYOjsTIECxmxXEfy3RpaDUySXzKQ5eQi8dwlf33luUiDJ2zJyfxyLqDzpTfkfvtPP3ZYV4qOEqr1UGrzU6b1cHl89L5wfmT/Sp+79G0RaXUDUA+8Kfe1mutH9Va52ut85OSkjx56g5MJsW4mFCO+1gMvaPs34di6KEWE8FBJmpbpIXucKlq6j+GLgyeJZOTsTs06wsrR/Q8j310kPKGNrITw5mTGcvU1CgeXlvED17ajs0+sOZqvsBAPPRj0CUJIsO5rAtKqXOBnwJnaa3bPGPe0EiNCfO5kIuvNeYCo8Q6NswyItV4WmsueuAjLpg+jrvPm+Tx4/sa1U3thAebu0yLKAyfeVmxRIUG8cG+ci6amToi56hqbONwVTM/vmgK3zxrAmBcv/94/wB/fXc/9a1W/nH9XL+YuHsggr4RyFNK5WAI+XXAF903UErNBR4BLtRal3vcykGSFhPKxmLfyl/tmK0o3HcEHUau4+KeEw3sLW3gaHUzXz0jx6duZCNBVWObhFtGgCCzicV5iXy4v2LEaku2Oqe7m+usTgXD2bnznDxiwy384vVd3PTEBr50yngiQsxEBAeRGBXik62O+xV0rbVNKXUH8A5gBh7XWu9SSt0LFGit38AIsUQCLzo/8CNa62UjaPdJSYsNo6z+BHaHxuwj8a/Oxly+JWypsWF8VFjJ058d5ksLszwWL1xXaAxkNbXbefbzI9y6ZIJHjuurVDW1y4DoCLFkUjKrdpSy50QD09I6G/MVljWgFExMjhrW8bccqcVsUsxMj+mx7iunZhMTZuH7L27js4PVXda9eccZzMzouY83GVDKhdZ6FbCq27JfuP19roftGhapsWHYHJqKhjbGObNevI0vzSfqzm+Wz+DHr27n56/t5OVNJfz28hlMTxv+RbpufwWTU6JIjArmifWH+OoZ2T3yrm12h880Khsu1U3tpET7xrUWaJw12RhvW7u/vEPQy+pbufqRT0mLCWPVXYuHdfwtR2uYmhrVZ7hs+Zx0zsxLorKxjcY2G/WtNr7xVAGvbCnxOUEPjF9TN1ypi77UpMsVQ/eltEWArIRw/vu1U7j/2jmU1DRz2T8+ZvWOE8M6ZnO7jYLiGs6anMQtZ06gvKGN17ce77LNk+sPMffX73KgvGFY5/IV+urjIgyflOhQprmlL2qt+cFL26lttrKntJ7aYcyLa3doth2tY25m3Em3i3NOWjI3K46zJiWxdHIyb2474XPT5AWkoKfGOIuLfCh1sa7FisWsCPPBgRWlFF+Ym86a7y4hKSqE1TtLh3W8zw5W0W53cGZeEmfmJTJlXBT/WncQh/Pif3tnKb9auZuGVhvPfH7EE/8Fr6K1pqpRQi4jyZLJSWw6XENdi5WnPj3Muv0VXD43Ha3pEQoZDIXlDTS22ZibFTuo/ZbPSaOysY1PiwY3EfhIE5CCnt5RLepDHnqLkUfraw3D3IkJtzB5XDQHK4c3l+O6/ZWEWkzkZ8ehlOKbZ+VSWN7IB/vK2XKkhu88v4XZGbGcOzWZV7cco9Vq99D/wDs0ttlotzvEQx9BXOmLT31SzO9W7WHJ5CTuu3ImoRYTnx0cuqhucXZznJd1cg+9O2dPSSYqJIjXt/ZI+PMqASno0WFBhAebfaqfi6+V/fdFbmIEByuahtUj/cP9FSzKTehI87p0VhppMaH89d39fP0/BSRHhfLYjfl85dRsaput/G93mafM9wodc4lKC9wRw5W++Jd39xMREsQfr5pFSJCZ/PHxwxT0GuLCLb3OUXwyQi1mLpgxjrd3lvqUQxKQgq6UIjXGt/qi17faiPIDQZ+QFEFzu53S+qF9dkermzlU2cSZeZ2FYxazia+ekcOu4/XYteaJmxeQGBnCGRMTSY8N44WNR09yRN+nym1yaGFkcKUvAvz+ipkkRxnjZIty49lb2tBxUx0sW47UMjcrbkhPzsvnpNHQZmPtPq9nanfgWyN0HiQt1rvFRat2nGDl9uPUNFmpaW7nYGUTi3ITvGbPQMl15tYerGjqGIsYDK5GSmdO6loJfN3CLHafqOdLp2R15O+aTIpr8jP523v7OVrd7FOthQdDVaOU/Y8G3z1vMudPG8cF08d1LDt1gvGb2nCoigtnDK7wqK7FSmF5I8tmpw3JnlNzE0iMDOH1rccHfe6RIiA9dIC0mDCOe6HjYqvVzo9f2c5tz2xm65FarHYHGXHhLJ+dxrfOzB11ewZLblIEAAcrhhZHX7e/gvTYMCY4j+MiMiSIv14zh/nj47ssvzo/A6XghQL/9dKrm4zCaBH0kWViciRfmJveZdnM9FjCLOYhDYxuL6kFuhYUDYYgs4lLZ6WyZm85Da2+0Q8pYD301NhQKhraaLPZR63v9IHyBm5/Zgv7yhq4bckEvnveJL/Lsx4XHUp4sJmiiqZB72u1O/ikqIrLZqcN+BE2LTaMsyYl8WJBCd85d5LPFIINho6Qi7TOHXWCg4zB96Fkm2w+XItSMDtz6Lnky+ek8eQnxbyzq8wnZp7yL7UZBGnOcEFZ3ci3lTlc1cR9q/dy2T/WU9nYxn++upAfXjjF78QcjPGH3KQIDlYOXtA3H66hsc3GWZMSB7XftfmZlNa3ss5P+15XN7YTZjETHhyw/pFPsyg3gX1lDR0tjAfKlqM1TEqOGtb0i3MyY8mKD/eZbBf/U5wBkuZMXRyp4iKtNe/sKuXL//6cs/60ln99dJAlk5NYdddizpo0Mp0kR4vcxMghhVzWFVZgNilOmzg4QT9nagoJEcGs2OifOelVUlTkVVxjUxsODTzsorV2DojGDuvcSikumZXK+gOVPjHZuv8Jut0Kxzb3u1lq7MhOdPHwh0V88+lNFJU38t3zJrH+R0t5+Ib5AVH+nZsUwbHalkGlYzkcmtU7S5mfFTfofjXBQSaWz0lnzZ5yn0oBGyhVTe0SbvEiszJiCA828+kg0hcPVTZR12IdtqADnJITj0PDdmeTL2/if4L+4R/g8Qtg9xsn3cwVcuky0YXDAQfWwM6XO18H18Igc67f2VXKn97Zx2Wz0/joR0u585w8n+kZ4wlykyLR2rjoB8rHByo5WNHE9acMbbrpeeNjsTk0B8qHV9TkDaqb2iRl0YtYzCbysweXj77ZWVA01AFRd1xtA7aIoA+BU2+H1Nnw4o2w9bk+NwsLNhMbbuk60cX6++G/V8BLX+18PbUcnrwEynYP6PS7j9dz9/NbmZUew5+umuWXg3j9kZvoynTpR9DbGqF8L2jNfz4pJjEymIuH2LN6yjij6dLeUv/r7VLd2E68TGzhVRblxrO/rJHKAcTRC4qr+d2qPYyLDmWiB1rgxoRbmJAUwebD3m/Z7X+jOGFx8OXXYMUX4bVvQXsjLPxGr5umxYR1ThZ9Yht88DuYugyW/qxzo8PrYc298M8zYNGtMOsaOLYJDn8KJRsgcTJc/EeIy6aioY2v/2cj0aEW/vWVfL9oeD9oKgvJDRtA6mLhu/DGndBwHFt0FvnVs1ky7xpChjgQnJMYQUiQiT0n/GuGd601lRJy8TquOPrnB6u5ZFbfTsXrW4/xgxe3kx4XxuM3LfBYu+i5WXG8v7d8xHq2DxT/E3SAkEj44gvw0s2w6vvQUgtnfh+6fZBpsaGU1LSAtQVeuQXCE+CyByDcLRc6aTJM+wKs+RV8+iB8+n/G8sgUSM+HQx/CQ6eil/6cO7bOorq5nZe+dRrJARAr70HlAXj4dMK1g8fCF7D38DWgJ3b9XFtq4Z2fwtb/QtIUOOM7FK9/hW+Y3yJo+5twfBLMvg5mXQsxA0/jMpsUk8dFsbe0D0GvdQ6Yxo7MXLRDpandTrtN+rh4m5npMcSGW/j96j1kxYf3aGvrcBgzEP3tvf2ckhPPI1+eT2y4576zuVmxvLSphCPVzYxPiOh/hxHCPwUdwBIK1zwFr98OH/wGqg/CZfdDUOejb2pMmDHyveZeqNgLN7zSVcxdhMcbQj//ZmO7jAUQn2sIWe1RWHk36p0f8yPHRPYs+DUzemmE7/doDSu/A0GhMOd6Fm14hnOPfAL/+AfEuBVzVOyDpkpY/D0460c0O8xcsTqbiyYG84epxbD9BePzXvNryDnTEPcpl0JodF9n7mDKuCje29OLl7NthfE9O2yQPt+4AU9bBlFunpgyg3n0L+fqRin79wUsZhNP3ryQ25/ZzJUPf8LPL5vGDadkYXdo3tpxgofXFrG3tIEr5qVz3xWzCA7ybLTZ1dxr85EaEfQhY7bA5Y9AXA58eB/UFMO1/4UI4/ErLTaMme1b4LOHYOE3YeI5Jz9e2hzj5U5sJnzpRcrXP032uz9m7uYvgflrcPZPer85+CvbnoPij+DSv0H+V/lr6zW0bX2J38TtQ1mbO7dLnQNL7oH0eQC8+vlh6lttXL14AWSfDfk3Q/Uh2P68cczXboWgu2HyxTDjSoju9jiszGAygymIefHtvNDUTkVDm/EEpLUx7vHeLyF7sfH97XoN3v258ep+nPGnweSLjFf86FTlVjmrRCXk4n3mZMay8ttncPcLW/n5aztZu7ecAxWNHK5qJi85kvuvncPyOQMvehsMk1KiiAg2s+VILZfP9V6BkRpOV73hkJ+frwsKCjx3wB0vwWu3GYIx70aoPUL5kb2Elm8lNC6d4Ns/Bsvge5O42HS4mq8+/C5vzfyIjAPPQGgMnHUPJLlNgBwaC2lze4R+fJ6mKvi/fEjMg5vfBpOJJ9cf4pdv7mbDT87pM7ykteaC+9dhMZtY+e0zev5QtIaSjYa473wFWvrPE97imEj0/KuYsPg640a84VHjRvCFhzufvqoPQeH/jPETFy21cOA9KHcObidNgbzzjVfWIuPmPwK8t7uMrz9VwGu3n86czNgROYcwOBwOzUNrjQmeZ6THcPvZEzlvaorH4uV98cV/fUZ9q5WV3x7eDEr9oZTapLXO722df3vo7sy8CmLHG4Ola34FYfGER2TynmMu6af/PxYMQ8zBaMBURyQ1Z/2WjHO+BW/fA2//qOeG48+A834FGb1+3r7Juz+Htnq49H4wGY+iriZdRRVNfQr6p0VV7C9r5I9Xzerd61EKMhcarwvvgyOfgbu3rzVoOzjs4LDRUlZI0IfPMmHLfbDlPmObU++A837dYRcA8Tlwyjd7nu/8Xxtiv/9t2LcaPnsYPvk7hMRAxnwjph+dYfwbnwMJeRCR2PsNWGuoK4GyXdBSY/wfXGE4N6ql06LPYTIp7liax5cXZRMdFmRcm3YblO6FuPEQMrw5SPtiblYs//zwIC3t9i7T2X1SVElsWHCX+VBHisARdIDMBXD3TrC1QmgMNdXNfOePH3CfTmPBMA/t+uHGRwZD7Ay48U0o3W4MuLo4sQ3W/QkeOwemXgZLf9HVg/dFDn0EW5+BM74LKdM6Fnc06aps7Oho150VG48SG24ZWLc6swVyTu65hM2AWzbkc3F6Cz+fcBCi04wb9WCIzzGylRbdCq31Rp1B4TtQuhNKd0BTt/YCobGQMBGC3To9WluNsYK2uq7bRqdD9hmQdaoRckqeJn1cRpMtzxi1IwkTjWs1eTokTzWSJHohJtxi/D63/Bc++QfUHjZWxI6HlBmQMr3zFZ9rhP6GwbysOOwOzfaSWk5xZt0crWzgN4+/TJRu5MIZ47h2YRbhFrNxvqhx/Rxx8ASWoIPxWO58NE+NCSUmzMInRVVct3B42RGuH268a2RcKSMf3p2sRTDni/DpQ4ZnuPctmH6FkYGTPHVY5x8RHHZY9QOIy4Yzf9BlVVpMGKEWU5+56M3tNt7dXcbl89I9mr45ZVwU66st8JU7h3+w0Ghj8HTass5l1laoP2Z48lWFULkfqorA7tZPOygEZl7p/LHPgJBoOPKpMcZQ9L4RQgIwh7AsdALhweMJL3LA+NMDa1zFl/jk/+B/P4WYLOeTntt1GTve+K6Spxo3aBct1bD5aWiuhIyFxu+wsdx46irbBftXg3YY2waFGhlvSVM6/3U/llIQk2nc1E29D6jOyYzFhIPybe9A0V4o2UTy0U2ssjidvv3OF8Alf4UFX/PQh9NJ4Am6G0FmE8tmp/FCwdFhzxhU02Q0YOprZvAOQqJgyY8g/6vw6T9gw2Ow8yUj//3M7/e8CXiTna9AxR646omuHirGY2t2QkSfuejv7i6jxWpn+RB7SffFlNRoPiqspN3m8HgmAmBkRyVMMF555w58v5Rpxg9Qa2Pw/fhmOLaZ1m0fcZ1pDTy/2tguaaqRHuvCHATjZhqCkrnQ8Mq0hvYmaK2FoLCOQXyhD9b9Cd7/DUxbDlc8BqYgw9su320UBJbvhvI9xriKo1s/lbzz4Yy7jaeq7qE1a4vxJOYS+Io9UPxx5w27NyzhxhNC4iRD+F3/OmwkbH+ez8OeIWlbNZgstCbOYEX7mcTkncrli+dSWN7Ivz86xJGaZi6tncYXPf9JBbagg9Fv++nPDvPmtuPcsGj8kI8z6FndI5PgvHvhtLs6B/f2vAE5Z8Hpd8KEcwY2eOpwwIZH4PhWIwUwd4lnBl3tNlj7e8MDnfaFXjeZkBTJzuN1va57Y+txUmNCWZDtWY90amp0RwuA0Yg5DhqljLBOfA7MuJJ7j22gvrGJV5eHwuGP4egGaHcbJ2ith88fNR75wfD62pvA4dY/O3GSITjjTzNEPy7H/wbWXRQ8AR/9xagXGDez85U42biZDgat4YPfGoI+61pY/lBnaqrrO5hySef2divY3CpFTeaTJ0JYwnrPbGuth8rCroPuDptxE6l0PtUd3WA4au6YgiiNOIU/t5zKfT/6Hj98eR/vlZax7sqzITKEvFz49QIH//mkmPPmdO3r7ikCXtBnpscwOSWKlzaVDEvQh9yAKSIBzvk5nPZt2PQEfPZP+O+VhpAuus3I4OjrQm8og1e/CQc/MDyD7SuMH//CWwyPPzJ56D/87Sugugiue7bPR8gJSRGs3nmiR0/5mqZ2PtxfwdfOyPF45sDUccaA1d7S+l4Fva7FyrajtRysaOTimaleL/CqbmonISoCxi+E8af2vpGtDU5sh6OfG/USodGGsIfFGWGBw5/C7tdg83+M7cPijXz7tLnGNi7MFsg8xRDIwXzvVUXw1veg4UTnMmWGxIlOwZ1t/Bs1bng3ks8eNpIF0ucb4rr5qc5BcGU2noqSp3WGR5KmGqLsHrt22I2Qyt63YO9KQ0TnfcU5YN/P07HZ4plsptBoYxC9P9qbOgXe1gqTL2bL9kaef30X5xc18Ob249y2ZAKJbnPNWswmvr545FJqA17QlVJcnZ/Bb97aw4HyBiYmD22Eu3q45d1hscaj36LbYMeLhsf2+m1Ghsn8myD/a10LeArfhVe/ZVw0lz0As66DXa8a3vqq7xuv4Cinp5JreO7TLzfO0x+2dlj7B0MwJl/c52a5SZE4NByuamZSSufntnpnKTaHZtkcz4ZbwGgBEBxk6tHT5YH3Cnl927EuMf3H1xfz7DdOISOuM1ykteb5jUfZUFzNH66chaWfVgSNbTa+8u/PuXRWGl89I2dQttY0tVNU0cjszH68raAQY8A+s4+h+TPuNp7EynfDsQKj9cSxzfDRms4YrzuR44xw0YSlkDbPGAPpS4j3rDRqAUxmo9DLha3duMnsfr1zWXiC4WiMm+n8d4bhWQcN4Lr/+H547/8ZyQBXPm7s47AbN7DSHZ3hkRNbjZuXC3NI16wTW6vhGZuDIfdsWPJjwzvvw+nwKsERPTz8eVnGDeX7L24jMiSIWxZPGFWTAl7QAZbPSef3q/fyYkEJP754aIOT1U3t5CUPv5EPQSEw9waY8yWjrcDnj8JHfzUeU7uTPB2uehySpxjv51xvvI5tgqMbjR9LdZHxfvdrhnc05RKYeQ1EpXQexxJh5Ji7fvRbnoK6I3DZ307qkbnm/lx/oLKLoL++9RgTkiKYlur5kEiQ2cSklMguPV3e31vWUbJ9xdx056S+8M2nN3HtI5+x4pZFZMaH02q184vXd/JCQQkAs9JjuOn0k4v0e7vL2Hykls1HailvaONHF04ecOHJYx8fpMVq58ZTs4f8/+3AZDIEdNwM4wYPxgCuza1baHsjHPwQDrwLe940sjfASMtMnQXjZjk97hkQP8EIqX3yd+PGfc1TvbdNaK034sel2w3hLdsJGx/rPK8pyBD1xDxjf9fL4jbmcvAD4/qdcaVR6Ofykk1mY7/EPOCKzu3bGqFyn9HYrWJP1xCVKch40pl47oilF44kk8dFEWoxUdNs5XvnTTIybUaRMSHoSVEhnD05mVe2HOMHF0we0kxCg46h94dShledu8QYZNv1qvEDdhEWZ/ywewvHpM83Xi60Ngbptj5nxPV2vtxzn4SJhqczdRms+7MRs51w8srZaWnRLMqN53er9jA1NZpFuQmcqGthQ3E1d587acSaEE0ZF83afUZ6YavVzq/e3M2EpAie/topXQZKn/36Im749+dc88in/OWa2dy3ei/bS+q4c+lECg7XcP+aQi6fm3HSH9XK7SdIjQll6ZRk/vlhEdVNbfzu8pn9XiM1Te08ub6Yi2emkpcyQsJjCe36/YfFwtwvGS+7zSnC24102eNboeDfbjcABWjjye/C33dpidGF0GhDQN3DRXYbVB0wxL1sl/PfnbBvVddsIHdmXQdfeGhgqX8hkT2v4QDBYjYxJzOWfaUN3DzIJz5PMCBBV0pdCDwAmIHHtNb3dVt/JnA/MAu4Tmv9Uo+DeJmr8zN4b08Z6worWDolpf8d3Ghpt9NitRs56CNBXLbx2D1UlOr8gVzwWyPFzj0/vuGEkdHywW+NF8AV/+o3Xmo2KR65IZ8rHl7PN5/exMu3nsYHe8vRmiHPlD4QpowzxjwqGtpYseEIh6ua+W83MQeYmRHDc98wRP2L//qcyJAgHv3yfM6fPo7dx+u55B8f8Y/3C/nZpdN6PU9di5V1+yv48qnj+dklU0mMDOGBNYVUNbZzz0VTTirU//74EM1WO3cuzfPo/33AmIOMXHhnCwbAEOLqIqenvcvwzN1TNgdz7OQpxsu9DsDhgKZyo7+R+5ODJcwI/fhiWMQL3HfFLFptdiJDRt9f7veMSikz8CBwHlACbFRKvaG1dm8gfgS4Cfj+SBjpCZZOSSYhIpgXC0oGLegd/Tr8oRowKMTw+ruT/1Xjh7jjRaM6s58iHxcx4RaevHkhlz+0npuf3EBokJnZmbFkJ45cAyJXKGfNnjIeXHuAi2eO44y83qe1m5YWzYpbFvHouoPcumRCR5hoWlo01+Zn8p9Pi/nSovHk9GLve7vLaLc7uHRWKkop7j5vEomRwfzyzd2s2VvO5JQoLpmVymWz07rsX9vczpOfFHPxjFQmj/OhsIA5yJlDPXnwBVkDwWQyBk5HoCAmkBjJ30Z/DOSWuhA4oLU+qLVuB1YAy9030FoXa623A72M4PgGFrOJL8xN5709ZR1VnwPFtX2cB9tteoXYTFj83R5FRP2RGR/OYzcuoKKhjcLyRo/nnndnilPQf/XmbhSKn17Su4ftYlJKFH++enaHmLv47vmTsJhN3Ld6T6/7rdx+nPTYsC49WL58ajaf3rOUXy2bTkyYhb+9t59z/rKW363aQ0u7MT3e4x8forHNxrfPmTiM/6UgeJ6BCHo6cNTtfYlz2aBRSt2ilCpQShVUVIz+DO/XLsjEatf8++ODg9qvWsq7mZMZyz+un8e8rNgRyW5xJz4imJToEFqsdu5YOpH02KH14UmOCuW2JRN4Z1dZj+nJ6pqtfFRY2eGdd9kvOpQbT8vmhW+dyqf3nMO1C7J4dN1BLrh/Hat3nOCJ9cVcNGNcxyxLguArjGrQS2v9qNY6X2udn5SUNJqnBgxP7rLZaTz+cTEVDf1PVeWio4/LGJ9m7LxpKbxy2+ld8mpHinlZceQmRfD1xcMbWPr64lzSYkL52Ws7qW/tLOZ5Z5eRenmy2W0AxsWE8vsrZrLilkWYTYpbn9lMQ5uNO8/xUuxcEE7CQAT9GOA+82+Gc5lf8t3zJtFud/DgBwcGvE+noI9dD320+es1c3j99tO7FDQNhVCLmT9fPZviyiZu++9mrHYjKrhyxwljZpsBTlayKDeB1Xct5q5z8vjeeZOYOgIpm4IwXAYi6BuBPKVUjlIqGLgOeGNkzRo5chIjuCY/g2c+P8zR6ub+d8CoEg0yKaJDx0SWp08QFmwmKtQzObynTUzk91fM5OMDlfzklR1UN7Wz/kAll/QSbjkZoRYzd583iW+Ldy74KP0KutbaBtwBvAPsAV7QWu9SSt2rlFoGoJRaoJQqAa4GHlFK7RpJo4fLnefkoZTigTWFA9q+pqmduIhgr07+KgyPq/MzufOcPF7cVMLNT27E7tBcMvPk4RZB8DcG5HJqrVcBq7ot+4Xb3xsxQjF+QWpMGDeeOp5/f3yIb56Z229hSFVTu3+kLAon5e5z8yipaeaVzcfITghnui82/xKEYTBmKwFuXTKR8OAg/vK//f1u6/EqUcErKKW474pZXL8wk7vPG7lKV0HwFmNW0OMjgrnptGze3lVKZePJM15E0AOH4CATv79iFstHqH2pIHiTMSvoAAtyjF7eReW9T+LgoqqxTQRdEASfZ0wL+gTnvJlFfUyzBmC1O6hvtYmgC4Lg84xpQXfNm1nUxzRrADXNMqu7IAj+wZgWdJNJkZsYeVJBlypRQRD8hTEt6AATkvsR9EZnY66I0W1ULwiCMFhE0JMiKKlpodVq73V9dUfIRTx0QRB8GxH0pEi0hkOVvQ+MSh8XQRD8BRF0Zw/tvsIuVa6QyyjPDSgIgjBYxrygu2aiKSrv20OPDbcMaR5SQRCE0WTMq1RYsJn02LA+PfTq5nbi/X2mIkEQxgRjXtDByHQ5WNmHoDdK2b8gCP6BCDpGpktReRMOh+6xTvq4CILgL4igYwyMtljtlNa39lhX1dQ+pucSFQTBfxBBp+9MF4dDU9PcTpzE0AVB8ANE0IEJya5Ml66C3tBqw+7QEnIRBMEvEEEHkiJDiAoN6tF1sarJ6JMuIRdBEPwBEXSMmWwmJPXs6SKNuQRB8CdE0J30JuhVTdI6VxAE/0EE3cmE5AjK6ttoaLV2LKtpcnVaFEEXBMH3EUF34sp0OegWRxcPXRAEf0IE3UlvqYvVTe2EB5sJtZi9ZZYgCMKAEUF3Mj4hnCCT6iHokrIoCIK/IILuxGI2kZUQ3qXrogi6IAj+RJC3DfAlJiRF8u6eMvJ/8y4hQWYqGts4bUKCt80SBEEYECLobnx76UQy4sJoszloszpotzu4fG6at80SBEEYECLobszKiGVWRqy3zRAEQRgSA4qhK6UuVErtU0odUErd08v6EKXU8871nyulsj1uqSAIgnBS+hV0pZQZeBC4CJgGXK+UmtZts68BNVrricDfgD942lBBEATh5AzEQ18IHNBaH9RatwMrgOXdtlkO/Mf590vAOUop5TkzBUEQhP4YiKCnA0fd3pc4l/W6jdbaBtQBPdJDlFK3KKUKlFIFFRUVQ7NYEARB6JVRzUPXWj+qtc7XWucnJSWN5qkFQRACnoEI+jEg0+19hnNZr9sopYKAGKDKEwYKgiAIA2Mggr4RyFNK5SilgoHrgDe6bfMGcKPz76uA97XWPWdcFgRBEEaMfvPQtdY2pdQdwDuAGXhca71LKXUvUKC1fgP4N/C0UuoAUI0h+oIgCMIoorzlSCulKoDDQ9w9Eaj0oDmeQuwaHGLX4PFV28SuwTEcu8ZrrXsdhPSaoA8HpVSB1jrf23Z0R+waHGLX4PFV28SuwTFSdkm3RUEQhABBBF0QBCFA8FdBf9TbBvSB2DU4xK7B46u2iV2DY0Ts8ssYuiAIgtATf/XQBUEQhG6IoAuCIAQIPi/oSqlMpdQHSqndSqldSqm7nMvjlVLvKqUKnf/GjbJdoUqpDUqpbU67fuVcnuPsCX/A2SPeK5OSKqXMSqktSqmVvmKXUqpYKbVDKbVVKVXgXObV79FpQ6xS6iWl1F6l1B6l1KnetkspNdn5Oble9Uqp73jbLqdtdzuv+Z1KqeecvwVfuL7uctq0Syn1HeeyUf+8lFKPK6XKlVI73Zb1aocy+Lvzc9uulJo3nHP7vKADNuB7WutpwCLgdmc/9nuANVrrPGCN8/1o0gYs1VrPBuYAFyqlFmH0gv+bszd8DUaveG9wF7DH7b2v2HW21nqOWw6ut79HgAeAt7XWU4DZGJ+bV+3SWu9zfk5zgPlAM/Cqt+1SSqUDdwL5WusZGNXj1+Hl60spNQP4Bka779nApUqpiXjn83oSuLDbsr7suAjIc75uAR4e1pm11n71Al4HzgP2AanOZanAPi/aFA5sBk7BqP4Kci4/FXjHC/ZkOC+apcBKQPmIXcVAYrdlXv0eMRrJHcKZIOArdnWz5XxgvS/YRWer7HiM1iErgQu8fX0BVwP/dnv/c+CH3vq8gGxgZ3/XE/AIcH1v2w3l5Q8eegfOqe3mAp8DKVrrE85VpUCKF+wxK6W2AuXAu0ARUKuNnvDQe+/40eB+jIvZ4Xyf4CN2aeB/SqlNSqlbnMu8/T3mABXAE84Q1WNKqQgfsMud64DnnH971S6t9THgz8AR4ATG3Aeb8P71tRNYrJRKUEqFAxdjdID1le+xLzsGMt/EgPEbQVdKRQIvA9/RWte7r9PGrW3U8y+11nZtPBJnYDzqTRltG7qjlLoUKNdab/K2Lb1whtZ6HsZj5u1KqTPdV3rpewwC5gEPa63nAk10eyz31vUF4IxFLwNe7L7OG3Y5Y7/LMW6EaUAEPcMLo47Weg9G2Od/wNvAVsDebRuvfY+jZYdfCLpSyoIh5s9orV9xLi5TSqU616dieMleQWtdC3yA8agZq4ye8NB77/iR5nRgmVKqGGO6wKUYMWJv2+Xy7tBal2PEgxfi/e+xBCjRWn/ufP8ShsB72y4XFwGbtdZlzvfetutc4JDWukJrbQVewbjmfOH6+rfWer7W+kyMOP5+vP95uejLjoHMNzFgfF7QlVIKoz3vHq31X91WufdgvxEjtj6adiUppWKdf4dhxPX3YAj7Vd6yS2v9Y611htY6G+NR/X2t9Ze8bZdSKkIpFeX6GyMuvBMvf49a61LgqFJqsnPROcBub9vlxvV0hlvA+3YdARYppcKdv03X5+XV6wtAKZXs/DcLuAJ4Fu9/Xi76suMN4CvObJdFQJ1baGbwjObAxRAHF87AeDzZjvEYtRUjPpaAMfBXCLwHxI+yXbOALU67dgK/cC7PBTYABzAek0O8+NktAVb6gl3O829zvnYBP3Uu9+r36LRhDlDg/C5fA+J8xK4IjJm/YtyW+YJdvwL2Oq/7p4EQb19fTrs+wri5bAPO8dbnhXEDPgFYMZ4Av9aXHRgJCw9ijL/twMgeGvK5pfRfEAQhQPD5kIsgCIIwMETQBUEQAgQRdEEQhABBBF0QBCFAEEEXBEEIEETQBUEQAgQRdEEQhABBBF0QMBq/OfuhP6mU2q+UekYpda5Sar2zh/VCb9soCP0hgi4InUwE/oLRZG0K8EWMSuXvAz/xol2CMCBE0AWhk0Na6x1aawdGe4I12iil3oHR31oQfBoRdEHopM3tb4fbewdGm11B8GlE0AVBEAIEEXRBEIQAQbotCoIgBAjioQuCIAQIIuiCIAgBggi6IAhCgCCCLgiCECCIoAuCIAQIIuiCIAgBggi6IAhCgPD/AffCmO/mHDqmAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"draw_learning_curve(data, P, lamb, start=20)"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "bright-firewall",
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.2"
}
},
"nbformat": 4,
"nbformat_minor": 5
}
| gpl-2.0 |
balarsen/pymc_learning | Tests/Sum of Poisson.ipynb | 1 | 129769 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pymc as mc\n",
"import seaborn\n"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"bkg = 4\n",
"cts = 20\n",
"\n",
"realbkg = mc.Uniform('bkg', 1, 1000)\n",
"obsbkg = mc.Poisson('obsbkg', realbkg, observed=True, value=bkg)\n",
"\n",
"realcts = mc.Uniform('cts', 0, 1000)\n",
"obscts = mc.Poisson('obscts', realbkg + realcts, observed=True, value=cts)\n",
"\n",
"model = mc.MCMC((realbkg, obsbkg, realcts, obscts))\n",
"map = mc.MAP(model)\n",
"map.fit()"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" [-----------------100%-----------------] 40000 of 40000 complete in 3.9 secPlotting bkg\n",
"Plotting cts\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/balarsen/miniconda3/envs/python3/lib/python3.5/site-packages/numpy/core/fromnumeric.py:225: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future\n",
" return reshape(newshape, order=order)\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"bkg:\n",
" \n",
"\tMean SD MC Error 95% HPD interval\n",
"\t------------------------------------------------------------------\n",
"\t5.022 2.199 0.039 [ 1.234 9.279]\n",
"\t\n",
"\t\n",
"\tPosterior quantiles:\n",
"\t\n",
"\t2.5 25 50 75 97.5\n",
"\t |---------------|===============|===============|---------------|\n",
"\t1.691 3.436 4.682 6.238 10.249\n",
"\t\n",
"\n",
"cts:\n",
" \n",
"\tMean SD MC Error 95% HPD interval\n",
"\t------------------------------------------------------------------\n",
"\t15.891 5.111 0.094 [ 6.715 26.781]\n",
"\t\n",
"\t\n",
"\tPosterior quantiles:\n",
"\t\n",
"\t2.5 25 50 75 97.5\n",
"\t |---------------|===============|===============|---------------|\n",
"\t6.727 12.284 15.628 19.055 26.836\n",
"\t\n",
"None\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAz8AAAIDCAYAAAAqmqAhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xd4FNX6B/DvlvQASYAAUgygdC9BioKioqDCpSnCFctF\nUEEEwQvys4s0QdErXARFBAmIShUUKYKCIIQWIPSWEEpII6RuytbfHzGb3Wwvs7Ob+X6eh4fszOyc\nd2fP7p535sw5MoPBYAAREREREVENJxc7ACIiIiIiIl9g8kNERERERJLA5IeIiIiIiCSByQ8RERER\nEUkCkx8iIiIiIpIEJj9ERERERCQJTH6IiIiIiEgSmPwQEREREZEkMPkhIiIiIiJJ8Fryo1arMWDA\nABw+fNi47MiRI3jyySfRqVMnPPHEE0hMTPRWcUREJAHWfluuX7+OkSNHolOnTujfvz/27dtn9pz9\n+/djwIABiI+PxwsvvIBr166ZrV++fDkeeOABdO7cGe+++y7Ky8t98lqIiEh8Xkl+1Go1Jk2ahEuX\nLhmX3bp1C2PHjsWAAQPwyy+/4PHHH8err76KrKwsbxRJREQ1nLXfFgAYN24cYmNjsX79egwcOBDj\nx49HZmYmACAjIwPjxo3DkCFDsH79ekRHR2PcuHHG527fvh2LFi3CjBkzkJCQgOTkZMydO9enr4uI\niMTjcfKTkpKCYcOG4fr162bLjx49CqVSiZEjR6JJkyYYM2YMgoODkZyc7GmRRERUw9n6bUlMTMS1\na9cwffp0tGjRAqNHj0Z8fDzWrVsHAFizZg3uuusuvPDCC2jZsiVmz56N9PR045WjlStXYsSIEXjw\nwQfRoUMHTJs2DevWrePVHyIiifA4+Tl06BC6d++O1atXw2AwGJdHRUUhPz8fO3bsAADs3LkTJSUl\naNWqladFEhFRDWfrt+XEiRNo3749QkJCjMs6d+6M48ePG9d37drVuC40NBTt2rXDsWPHoNfrcfLk\nSXTp0sW4Pj4+HhqNBufOnfPBqyIiIrEpPd3B8OHDrS7v0qULnnnmGUyYMAFyuRx6vR6zZ89GXFyc\np0USEVENZ+u3JScnB7GxsWbL6tata+xSnZ2dbbG+Xr16yMrKQmFhIcrLy83WKxQKREVFITMzEx07\ndvTyqyAiIn/jcfJji0qlwrVr1zBhwgQ89NBD+O233zBjxgx07NgRzZs3F6pYIiKqwUpLSxEcHGy2\nLDg4GGq1GgBQVlZmc31ZWZnxsa3nExFRzSbYUNdLliwBAIwdOxZt27bFxIkT0bFjR6xYscLpfZh2\ndSAiIgoJCbFIVNRqNUJDQx2ur0x6rK0PCwtzOgb+NvlG27ZtIZPJ0LZtW7FDIaIaRLArP2fOnEGb\nNm3MlrVt29Zi1B57ZDIZCgtLodPpvR2e1ykUctSuHcZ4BcJ4hcV4hRWo8fqjBg0aWPyO3Lx5E/Xr\n1zeuz8nJsVjftm1bREdHIyQkBDdv3jT2QNDpdMjPzzc+3xn++tvkz/XMndgKCgqN/+flqfwqNl/x\n59gA/46PsbknEGLzlGDJT2xsrMUPVGpqKpo0aeLSfnQ6PbRa/zr49jBeYTFeYTFeYQVavP6oY8eO\nWLJkCdRqtfFKTlJSknEQg44dO+Lo0aPG7UtLS3HmzBlMmDABMpkMd911F5KSkoyDIhw7dgxBQUEW\nJ+sc8ef3sibG5ovXUxOPm6/4c3yMzT3+HJunBEt+hg4dimeffRYJCQl4+OGH8fvvv+Ovv/7Cxo0b\nhSqSiIhquG7duqFRo0Z466238Oqrr+KPP/7AyZMnMWfOHADAkCFDsGzZMixZsgS9evXCF198gaZN\nmxqTnWeeeQZTp07FHXfcgdjYWEybNg3Dhg0zGz1OTAkJX0OlKkZERCRGjBgtdjgkAaxzJDVeTX5k\nMpnx744dO2LBggWYP38+5s+fj+bNm2PJkiVo2bKlN4skIqIazvS3RS6XY9GiRXjnnXcwZMgQNGvW\nDAsXLkTDhg0BAI0bN8aCBQswa9YsLFq0CHfffTcWLlxofH6/fv2Qnp6OqVOnQqPR4LHHHsMbb7zh\n89dkS/fuPaHVaqFUCnZuksgM6xxJjVdr+tmzZ80e9+rVC7169fJmEUREJDHVf1uaNm2KlStX2ty+\nZ8+e2LZtm831L7/8Ml5++WWvxedNrVrx5n7yLdY5khrBRnsjIiIiIiLyJ0x+iIiIiIhIEtjBk4iI\nyE+cPn0CGo0GQUFBaN/+H2KHQxLAOkdSw+SHiIjITyQnJ0GlUiEiIoINUfIJ1jmSGiY/REREfuKZ\nZ0aKHQJJDOscSQ3v+SEiIiIiIklg8kMBQavT49d9l3H+ap7YoRARERFRgGK3NwoIOw5fww87LwIA\nvp7yEJQK5u1ERERE5BomPxQQEk9lGv9Wa/RMfoioRlq7dhVKSlQID4/A0KHPih0OSQDrHEkNkx8K\nCAaxAyByYP2fKTh3JQ+vPnEXomuFiB0OBag772wDtbocwcGsQ+QbrHMkNUx+KODIZGJHQGROq9Pj\n18QrAICV289jwlMcLpbcEx/fWewQSGJY50hqvNZ3SK1WY8CAATh8+LBxWUZGBl5++WXEx8fjscce\nw9atW71VHBGR3zCYXJrMzi8VLxAiIiKyyyvJj1qtxqRJk3Dp0iXjMp1Oh9GjRyMkJAQbN27EqFGj\nMGXKFLNtiJxlMLDjGxERERF5xuNubykpKZg8ebLF8t27dyMrKwurV69GeHg44uLisHfvXhw7dgx3\n3HGHp8USERHVOGlpqdBqtVAqlYiLayF2OCQBrHMkNR4nP4cOHUL37t3x+uuvo2PHjsblhw8fxr33\n3ovw8HDjsi+++MLT4oiI/BCvTJJ3/PnnTqhUxYiIiERc3GixwyEJYJ0jqfE4+Rk+fLjV5deuXUOT\nJk3w2WefYdOmTYiJicH48ePRu3dvT4skIiKqkYYPfwEVyTRHdiHfYJ0jqRFsspSSkhJs2LABhYWF\nWLx4MQYNGoSJEyfi9OnTQhVJRCQSNhrIO4KDgxEcHILg4GCxQyGJYJ0jqRFsqGuFQoHo6GhMmzYN\nANC2bVscOXIEq1evxvTp013YT2BMZlkZJ+MVSlXjMihIDqXSv+MOtOPLeD1j2ulNBljUT3+L15FA\niZP8z9tTZ0GtV1gsl8lkCApSQKPROT2ATUFhkfH/ye/PMS7X6/Xo3+c+PPLQg94JmogkRbDkp379\n+pDLzX9AmzdvjgsXLri0n9q1w7wZluAYrzAUiqrkJyoqAmEhgTFFVaAc30qM1z0arc74t1whR3R0\nhNXt/CVeIqHcyNNAcVt32xsEOb8vvSzY+H9eRDfjcp2mHOcvXGTyQ0RuEawFGR8fj6+++goGgwGy\nv2elTElJQePGjV3aT2FhKXQ6vRAhepVCIUft2mGMVyCmMebnq1AW7N/JT6AdX8brGbVJ8qPX6ZGX\npzJb72/xOlIZL/neli0bUVpairCwMPTrN1jscEgCWOdIagRrQf7zn//EokWL8OGHH+LFF1/E3r17\nsXfvXqxbt86l/eh0emi1zjUWli37GseOJWHBgsVW17/22hjcfXcXjBz5sksxWHP06BHUq1cPzZrF\nmS13JV5/ECjxmvaS0GkN0Mr9P2YgcI5vJcbrZhwmMRgAmzH5S7zkv6KiohEWFo6QkBCxQyGJYJ0j\nqfFq8lN5hQcAIiMjsWzZMnz44YcYMGAAbrvtNsybNw9t2rTxZpF2YxDSxIljsWDBYovkh4ikiAMe\nkHf06MGuXORbrHMkNV5Nfs6ePWv2uGXLlli5cqU3iyAiIiIiInJLjRvSR6PR4OOPZ6J37/vx9NNP\nYNeunVa3S0+/jgEDHsW33y4BAJSXl2POnBl4/PGH8OST/8TmzZvw4IP3IDMz0+K5Q4cOBABMmPAK\nvv12CbZu3YzRo0dh/PjxePTRh7BjxzaUlKjw0UfTMGDAo+jVqzueffYp7N2727iPvLw8fPDB23js\nsQcxaNDjWLx4oXFddnYW3nzzP+jd+34MHToI3367xOnRcYhIDPx8knN69uxq/N2xZfz40Zgw4RWv\nl7106WL07NnV7jbHjiWhZ8+uOH78qFP71Gg0WLDgc+zYsc0bIRIRCa7GJT+nTp2ATCbDsmWrMGjQ\nEHz44btIT79utk1+fj4mT56A3r0fM97/M2/eXJw+fRKff74Q06Z9hO+/X2Ez4ViyZAUAYNasTzB8\n+PMAgJMnk9GqVSssWbIc3brdi3nzPsX169cwb94ifPfdWnTs2AkffzwLWq0WAPD225Nx61YuFi78\nBtOnz8GWLb9gw4a1AIB3352CunXrYfnyH/Duu1OxY8c2rFixTJDjFZDYw4j8GKsneSI7OwsajQZq\ntdrr+5bJZA67hrdu3RaLF3+LVq2c66Kem3sTa9Z8b/xto8CTnZ2FzMwbyM7OEjsUIp/w7yGz3FC/\nfiwmT34LCoUCzZrdjsTEv7B58yaMGTMOAFBaWoIpUyaiffv2mDhx8t/LSrF9+xZ89tkCtG3bHgDw\n+utT8MYbE6yWERUVBQCoVas2QkNDAQByuRyvvPIKVCoNtFo9OnXqjOHDn0fz5i0AAE8//Sw2b96E\nvLxbKCgowJkzp7Bmzc9o2LAhAGDKlHdQWlqCpKTDyMrKwtdfJ0Amk6FJk6YYN+51fPTRhxgx4kXh\nDpyf45UvIpKCrVs3IScnCwqFOD/P4eHhaNeug9Pb87s58G3dugkqVTEiIiIxYsRoscMhElyNS37u\nuKMVFIqqCdZatWqDtLTLxsfr1q2GTqdD585Vl/6vXEmDVqtFmzbtjMs6dLjLpS/16OhoBAcHQ6XS\nAAAef/yf2LNnNzZt2oCrV9Nw/nzF/VA6nR7Xrl1B7dq1jYkPANx//wMAgPXr16CgIB+PPlp1A6LB\noIdGo0FhYSFq167tdExE5HtsCpIjKpUKM2a8jz17/kRoaCgeeeRRjB07HiEhoRg48CkcOHDA7ArN\nwYOJePvtyXjssX/izTffBVDRy+HLLxfgwoVzqFMnCv/617PYv38vmjZtjP/7v/fslp+Y+BcWL16E\nq1evoEGDBhgx4kU8/vg/AVR0e5sw4RUsWLAY8fF3o7y8HAsWfI79+/ciPz8PjRrdhv79B2P48OeQ\nmZmBYcMGQSaT4aOPpmHZsiUIb9RJuANHghg48CkYDHrIZDWuMxCRVTUu+ak+M7nBoEdQUNWsaq1b\nt8G//vUspk17D/369UezZnHGZMk02XH1bFZwsPkQkTNmfIDTp0/iscf64YknnkJMTD2MHTsKAKBU\n2j7sOp0Ot98ehzlz/msRQ2RkpEsx1VhsXZLfYWc3ct66dT+ie/f7MXPmx7hyJQ1ff70QOTlZmDVr\nLqKjY6BUBhmTn+PHj+Ldd6fg0Uf7GhOfq1fT8Prrr6Jt2/aYPn028vPz8dVXC1BcrELTpvbn0jMY\nDJg7dzZGj34VdevWw3ffJWD27Olo1ao1WrS4A4D5qKnz53+KI0cOYfz4/yAmJgYHDuzHl1/+D1FR\nUejT53HMmjUX7747BS+88BIeeKAXZi74XqCjRkKJjo4ROwQin6pxyU9qaorZ4zNnTqNLl6qZobt1\n646HHnoEW7b8gs8++wTz5y9CkyZNoVQG4fz5s+jUqTMA4Ny5s24Pm11SosLOnduxZMkKtG5d0W86\nMfGvv9ca0KRJMxQWFiInJxv168cCANau/RFHjx7BoEFPIjMzE1FRUQgPr5gl/vDhA9i69Ve8//50\nt+IhIqExIyfnNW/eArNnfwoAuOee7pDJZFiw4L+4fDnV2FUaAM6dO4M33/wPHn64D956633j8oSE\nZYiMrIXPPluA4OBgAEDTprcbT7DZI5PJ8Pbb76Nr13sBALfd1hhPP/0Ejh1LMiY/pifekpOPoWvX\ne/Dww70BAPHxdyMsLAxRUdFQKpVo1aq1cT933tnKk8NCROQTNe4aZ2ZmBubN+xRXrqRh+fJvcPHi\neQwePMRiu9dem4QTJ47h9993/D2rcX/Mm/cpzpw5hVOnTmL+/IofJlv5T2hoGFJTU6BSFVusCw4O\nQVhYGHbv/h2ZmRk4eDARn38+FwCgVqvRvHkL3H13F8yePR2pqZdw9OgRrFqVgHvuuRfdut2LRo0a\nYdq095CaegnJycfwySezERYW5rM5jIjIffyUkiMPPfSI2eMHH+wFg8GA5OSqEdYyMzMwefJrMBiA\n//zn/8y2P3YsCd2732dMfICKrtqNGt3mVPn/+Ee88e/bbqu4UlRUVGR1206duuDnn3/ClCkTsX79\nGmRk3MCIES+ie/f7nCqLiMjf1Ljkp3v3+1BYWIBRo57Fzp2/4eOPP0fduvUAmF/Kb9q0GYYOfRoL\nF85DaWkpxo17HXfccSdef30cPvjgLfTp0xcAzLrMmXrqqX9h0aL5+PbbbyzWKZVKvP/+DOza9Tue\nf34YFi6chxdeeAl169bDxYvnAQDvvz8dYWFhGDNmFGbM+ACDBw/B4MFPQS6X/93lDRgzZiTef/8t\n3Hff/Zg48Q1vH6qAwvPqRFRT1K1b1+xxZbejoqIi7N69A7du5SIj4wbatm0PrVaDpUsXm22fn5+H\nqKhoi/3GxDjXfSkkJNT4d+XvounVHtPfytdffwOjR7+KjIwMzJ//KYYNG4SxY0fh0qWLTpVF/m/3\n7h3Yvv0X7N69Q+xQiHyiRnV7GzXKdJSSGRbr//e/r8wev/rqRLz66kQAwN69uzFlyjvGrmVnz57G\nt98qUadOlNWyxowZZxxBDgAGDBhotv7++x8wDmJQqV+/Aca/69ath1mz5lrdd6NGt+GTTz63uo6I\n/BsTdXKksLDQ7HFubi6AiiRIo9HAYNCjfv1YfPLJPHz99SL8+ON36NPncWM36vr1Y5Gfn2ex37w8\ny2WeUiqVeP75kXj++ZHIzs7Cvn17sXz5Ekyf/h5WrFjt9fLI9yqHVpfLFY43JqoBatyVH3d9++0S\nzJ//KdLTr+PChXNYtOh/6NnzQbOR40hEbFESUQ2RmLjP7PHOndsgl8vRqVNn9OnTD3Xr1keTJk0h\nl8sxcuRLqF+/AT7+eAb0ej2AivtuEhP3QaPRGPdx8eJ5ZGTc8Gqc5eXlGD78Sfz443cAgNjYBnji\niafQu/djxgnA5XI2IwJdnz79MGDAEPTp00/sUIh8gt9af5s6dRYyMm5g1KhnMWnSeDRp0hRvvml/\nuFAiIgDgVCfkinPnzuDjj2fi6NEjWLlyOZYt+xr9+w9C48ZNLLYNCQnFpEn/h4sXL2DVqooJtv/9\n71FQqYoxefJr2L//L2zfvgXvvDMFMpncK8lIZRe4kJAQtG7dFsuXf4P161fj+PGj2LRpA7Zs2Yxe\nvSruW6ochTQp6TDOnDnlcdlEREKrEd3e8orKMX9dMlo1jcIzvd0bbeb22+Mwb94iL0dGQjDwMhD5\nMQ54QPbIZDKMHPkyzp6tGMktIiISzz47AiNHvmyxXaXu3e/DQw89goSEb9Cr1yNo0qQpPvtsARYt\n+h/ef/9NREfH4PnnRyIhYSnCw8Mdlm9tmely07/ffPM9LFmyCD/+uAq5ubmIjo7GwIFP4MUXxwAA\nwsMj8PTTz2HTpg3Yv/8v1GvJgRCIyL95LflRq9UYMmQIPvjgA3Tt2tVsXXFxMfr27YvJkydj8ODB\n3irSaOX287iaVYyrWcUY8kBLhASzqxoREfmfPXsO2V2vUhVj9uxPLZKUGTPmGP9OSjoMpTIIX321\nzLisuLgY8+bNRVxcnM19jxo1utq9sZYxderU2exxWFgYJkyYjAkTJtvc77hxEzFuXMX9syMmfGhz\nO/JPKlUxDAYDZDIZIiI4nyDVfF5JftRqNSZNmoRLly5ZXf/JJ5/g5s2b3ijKqpsFZca/9ex/QkQi\n4jcQeWLduu+hUhUjIiISI0ZYJioAcP78OSxd+hXGjBmP1q3bID8/H6tXr0Lt2nXQrx/v2yDXOFPn\niGoSj5OflJQUTJ5s+4zQkSNHcPDgQdSrV8/TokjC2KAkf8b6Sd7Su3df6HQ6u4PtPPPM89BqNdi0\naT2ysjIRFhaOu+/ujKlTpyM6Ohp5eSofRkyBzpk6R1STeJz8HDp0CN27d8frr7+Ojh07mq3TaDSY\nOnUqpk6divfe4+ABRP7sh9/O43xaLkb1a4uwkBpxO6AoeM8PeaJx46ZObffvf4/Cv/89ymyZUskx\njMh1ztY5oprC4xbO8OHDba778ssv0a5dO/To0cPTYkjiDOzOKKiC4nJ8v/0cACCmViiG975T5IiI\niIiIvE+w07uXLl3CmjVr8PPPP3u0H4XC8Zks0/tClUq5KGe/KuN0Jl5/EGjxmt78K9Z77IpAO74a\nXVVymXFLxePrIp1pci6zPAPvb/E6EihxEhERuUqw5Of999/HhAkTEBMT49F+atcOc7iN6Q91VFQ4\nwkODPCqzuiuZhUhNL0DP+MZQOmgUOBOvPwmUeE2Tnzp1vP8eCyVQjm+ZrurvIKUC0dER4gXjAn85\nvmVqrfFvuVxu8/j5S7zkvw4fToRaXY7g4BB07dpd7HBIAljnSGoESX5u3LiBY8eO4fz585g9ezYA\noKysDFOnTsWWLVvw9ddfO72vwsJS6HR6u9uYrs/PL0G5l+9XGD93FwDgWkYhBtwXZ3UbhUKO2rXD\nnIrXH/hTvFm3SvDDzou4766G6Nq2gdVtKmc2B4R5j73Nn46vM4qLq0ZM1Gh1fn/DtL8d33J1Vfao\n1+ktjp+/xetIZbzkezduXEdJSYnD+XqIvIV1jqRGkBZkw4YNsWPHDrNlzz33HEaMGIH+/fu7tC+d\nTg+t1n5jwbTHiVarh1YhTOPit0NX0feeZna3cSZef+IP8X7643Fk3SrB0Qs5WPZWfYfbC/kee5s/\nHF9nmDbIDXpDQMQM+M/xrR6DrZj8JV7yX4MGDRU7BJIY1jmSGkGSH7lcjqZNzUcPUSgUiImJQWxs\nrBBF+lR+cTmOX7qJLq1jERkWGN2v/FnWrRKxQyAiIiIiCfBq8lN9Rmpn1wWaOd8dRXZ+KfafysQ7\nz3UWOxxB6fR6GAxweK8T1SA16LNKREREZMqryc/Zs2dtrvv999+9WZQoKnvXZeeXAgAuXS8QLxgf\n0Gj1+GDpQai1esx86R5R537hSNfkzww2pjm9mlWEWuHBqB/N+2eIiIj8gX/fNe4knqgWxpHz2cjK\nq0j0dh1LR797bxc5IvIJZppeceFaPuasOgoA+OatXiJHQ4EiIeFrqFTFiIiIxIgRo8UOhySAdY6k\npkYkP75qq0ktx9Ka3ASvFXmEKjbHKdBsO3jV+Hd2Xika1K8tYjQUKLp37wmtVgulskb8PFMAYJ0j\nqWFNdwEb4EREJKRWrdqKHQJJDOscSU2NuIud3d5qPr7FREREROSpGpH8kED86FKXH4VCZIG3SRER\nEQWGGtHtjQ0PIs/w6qmwytU6XM0sRK0QhdihkJ87ffoENBoNgoKC0L79P8QOhySAdY6kpkYkPyQQ\nf2oQM8MVFA+vsKZ9exgA8NpT/0CnO+qJHA35s+TkJKhUKkRERLAhSj7BOkdSUyOSn0A9a11SpsGV\nzCK0bhYNuTxAX4QI2FCnQLXs17NYMLGn2GGQH3vmmZFih0ASwzpHUlMjkp9ANW35YeTkl2HQ/c0x\n6P7mYofj15jvEBEREZGnasSAB4F6JSAnvwwAsOmvyx7vq6RMg6TzOShX6zzel1GAHlchGQwG/LI/\nDVsPXBE7FK8K1KunfsnOseRhJiIiEhev/NQQn61OxuWMQnRuXR/jnrhL7HBqrJOpufhpTyoAoMVt\ntdG6WbTIEZHf+fukARNKIiIi/+OVKz9qtRoDBgzA4cOHjcuOHz+Op59+Gp06dULfvn2xdu1at/Z9\n4Vo+Dp7JgsHO5R02MoDLGYUAgKTzOd7baQ08rgUqNVZsP48TKbluPf96jsr4d0ZuibfCEp3px4sX\n/IjEs3btKiQkfI21a1eJHQpJBOscSY3HV37UajUmTZqES5cuGZfdvHkTo0ePxjPPPINPPvkEp06d\nwttvv43Y2Fg8+OCDTu+7uESNmQlHAAByuQxd28R6Gi5J3De/nMbptDzsPpaOZW89LHY4VIMFandc\nEtedd7aBWl2O4OAQsUMhiWCdI6nxKPlJSUnB5MmTLZbv3LkT9evXx+uvvw4AaNasGQ4cOIDNmze7\nlPxk3ao6s37oTJYgyc/1nGKkZRTh3vYNoFQ4uBDG1ox4vHToT6fleWdHNYzp1dMaeMFPcM5+NfAq\nNTkSH99Z7BBIYljnSGo8Sn4OHTqE7t274/XXX0fHjh2Nyx944AG0a9fOYvuioiJPihPEB0sPAQBy\nC8ssRlzT6vTYm3xDjLD8g0mDzr/abExCyY/514eFiIiITHiU/AwfPtzq8ttuuw233Xab8XFubi62\nbNmCCRMmuF2WWqt3+7nO+O3wNYvkZ0/yDXz32wVByyXyB7znx4s44AEREZHfEnyo6/Lycrz22muI\njY3Fv/71L7f3czI1F0t/PePFyKqzbPIdPpttvqCGtGY0Wh3OXcmDVucgoTR5uWwQk69pdXps3JuK\nxFOZYodC5DNpaam4dOkC0tJSxQ6FJIJ1jqRG0KGuS0pKMHbsWFy9ehU//PADQkI8u5lu38lMjBnU\nwWK5aU6iVMqhVLqe0xkMsHheaIjCYrvq21Q+VijM/3eVOzG7u6//rT+B4xdvok+3HLzQt43N7RTy\nqv3I5TKXYtTq9MgtKEODmHCnnwPYid3kPVa4+R47XZYdcrnM7G9b+/C0Pvia6euQyVx7r11xs6AM\n+09moHuHhqgfFWZ3251J1/HzvjQAwD/uqIs6kVXfH/52fBVK85umlEo5ZFZOlsjg3c+6UPzluErR\nn3/uhEpVjIiISMTFjRY7HJIA1jmSGsGSn+LiYrz00ku4fv06EhIS0LRpU6/sNzo6wmKZ6Q91nTrh\niAgLcnm/MpnMYt+hIeb7kVvZpvrj2rXtN+hssfa63OVoX8cv3gQA7Dh0FRP+1clifV5hGaYtPYDr\n2cXGZWFhwS7F+NbCv3A6NRf/93wX9Ixv7PTzbJVhmnRERUUg0o332Nmy7AkLCzb+HR4RYtzHoTOZ\nOHY+G88RVmheAAAgAElEQVQ81ga1wqu2sVcfDAYDEn49A70BGNm/ndXGspB0egNu5peiQUw4yk0u\nAgYFKbxaH01N+mIfbuaXYseRa/huWl+7215KL6x6oFRajcndzxtQcQU0O68UjetHur2PSkGlGuPf\nSoUc0dERCAqyPHkik1t+hxCZGj78BVRca68ZPQ3I/7HOkdQIkvwYDAaMHz8e6enp+O677xAXF+e1\nfeflqSyW6Uy6b+Xnl0Bd5vrLMhgMFvtWq7Vmj/VWtql8rFDIUbt2GAoLS83icZa11+UuV/ZlLd6F\nG04i5XqB2bKyUrVxv6k3CpB4KhOP3XM76tUJhU6vx8INJ6FUyPHK4A6Qy2Q4nVoxj84nK4+gw+1R\nHseu11d1vMvPV0FT5nny484xLy1VG/8uUZUb9zFj6UEAQM6tEox78i6n6sOJlJtYv6tiiPi42Ah0\nalXfYfkarR6nLueiVZMot5J8Uws3nMTBM1l4qX87tG8RU1WGRufV+mjqZn4pAKCgWO2wDI2m6vNX\nVFiKvNCqZMLTzxsAzPnuKM6k3cLYwR3QvUNDAMDe5BtQlWnwWLdmLiWjqrKq5Een0yMvTwWNRmex\nncHgfL3T6w24cC0ftzeshbAQ385HXXl8yfeCg4Mdb0TkRaxzJDWC/KKuXbsWhw4dwpdffonIyEjc\nvFlxpSEoKAh16tTxaN9aKwMfmN6srdXqrW7jiMHKvi2GrzUYLLap/linc698d57jjX1ptTrodOYv\ntLKBakqvr3rtHy6rmMz2ZOotzHzpHvx1IgNHzlVMrtq1TSw63WneiHctHhvbmoSoc/M9drosO0yT\nMNNjUunohRyzZfbqQ8bNEpO/VbirRV2H5a/cdg67j9/AbfUiMPOle1wN38zBM1kAgG82n8Gn43oY\nlxus1HMhOCrD7HNt4zi6+3kDgDNptwAAX248ha5tYpGeU4wlv1TcVxhTKxR3O5GMGuMwiaHyu8TW\nxMzOxGswGLDpr8v4eV8amjWIxIcjuzkdCxEREdnmteRHJpMZz5T+9ttvMBgMeOWVV8y26dq1K1as\nWOH0Pn16k71E7+hPyyxCUye6/Vg7PDduVpzBLlCVG5cVlWisbOldNfGtcvY17T5eMfR65bE3dauw\nDFGRIWZdBAOZreRBKBm5VcloSnqBS8mPGTthF6rUyCsqR3Qt2/c/LvzpJFJvFCKvqOJzdTWr2Oa2\nRERE5BqvJT9nz541/v3NN994a7ducK/BZKiRTWrHND44w+8NgfrulKt1yCsqQ706ll2ITHtVedrO\nTzqfg4U/nUTn1vUx7om7PNpXzUidXHP80k0UqNSON7TBlbdvesJhfD7+fqvrCkvUSDqf43YcFPi2\nbNmI0tJShIWFoV+/wWKHQxLAOkdS49uO5D5SUqbFydRcdGgRg4hQz+8NEZvBYPD5zfDV2Svdxyfo\nA4Zeb8CbX+3HrcJyvPvvzmh5m2ddPu1Z+NNJAPBKw1mKb+f/1p3w3s4cfFQLim0nWabdKkmaoqKi\nERYW7vHoqETOYp0jqfHr5Mfd5v4XG07g3NV83NGkDt55rrNzT3KizWFtk6tZRWjWoJZL8bli0U8n\ncSWrCG8/1xlRka59MZWptbiSWYQ7m0QFfFeoQIy+QFWOW4UVXZdW/34J7zzvZF0kAOaft0B8/4nc\n0aPHg2KHQBLDOkdSUyMmc6jeMDp3NR8AcKnaiGXVZeRW3Tfh7vnWT3887uYzHcstKMOR8znIyS/D\nmj8uufz8uT8cx8ffH8NPe4WduMyTi1Kmo2RJTaA06H19741VNWSC4eoKVGrHkw0TERGR1/h18uNO\nk8uV5yz66VTV85x4orXmV3Gp/cZ7SZkGe5JvIL+43O521uj0VY2iIgflWHM5o2KelF8Tr0Cn12P3\nsXRcuJbv8n4c8aRtvGGPZWKmKtNg/Z8pOH81r6oM94twyaGzWViz6xLUVoYptlAz2+NmVv12AZMW\n7jOb80kSPHlvnayslzMKMfmLfZj93VFjgukPeSYREVFN5tfd3pzlSnshO68ERSUatGxcB5m3Shw/\nwUOLNp7CmbQ8xNQOwaev3md3WyHv7fkjKR0//H5RkH2bshb9rBVHcHvDWnju0dYW63ILyiyWrdx+\nHofOZuPXxCtY9tbDFuuFaiCWa3T4atNpAIBCLsOQB1tabLPhT5NkTQIN1d+PXgcALNx4CrNH3yty\nNP7LnTr5zeYz0BsMuJxRCJ3eAKVCAtk0OZSdnQW9Xge5XIHY2AZih0MSwDpHUlMjkh9nlam1eGvx\nAQDAW8/eXW2t49aLO23dM2kVVy9uFZajXK3D+j9TENeoFnp0aGS23dwfjqFQpcY7z3c2TmjozbZ1\n4ulMq8utNbe83aZPuVGIlBuF+Gf3OLtD/FY6dDbbyxE4x3TkuzNpeRhi0g1arzfgREou9FZauWXV\nJsN115YDV5BbWIbhj9wJpcK/LsoWqly/cunIiZSbKNfosevodTz9yJ12750LqLTAg2BzrMyxRdKy\ndesmqFTFiIiIxIgRo8UOhySAdY6kxq+TH2fbEM5uZzqPxx9Hr/v8NoJN+y5jZ1LFmfQurWPN1p29\nUpEkbTlwBU8+0MLiClBANf5ssHZvw4mUXBEisc7evS1bD17B+j8tu+gZDAa8/81B9wo0eY9v5Krw\n14kMAEDDmHD06dLUvX26SSZCDZu3tmqEtY++S8JXkx/yeQzOKFNrERrsm6/KhG3nfFIO+a+BA5+C\nwaCHTOZfJ0Co5mKdI6nx6+THrXt+XHqSzFiKted5Ozk6d6XqHhaNjZucf028gitZRZg0LN5suadX\nY1x5LUI1g1NvFKK0XCvo6HjeUv14WUt8KuUWen5VxHT442se3l9TrtYhJFjh0nMcz3MlbHKk1vjn\nTf9/Hk/Hiu3nMbhnCwzoESdYOZXfPyVl3rmKSIErOjpG7BBIYljnSGpqRJrvbmLg6ys/pnGmZRTZ\n3O5U6i0UejDhonXOv1ihbmVZ/PNpfPjtYePM9QHPyiF1934k0+TD02o5Z9VRD/fgH8S8+b/ySljC\ntvMwGICfrAzM4XEZZl9AEriBjIiIyA/UiOTHHQaDCF3JTNo3joZ49nZTSIh7Niq5Gus5k1HcAp0n\n75NZ/TPZkbNJua0hkq9k2U6sASAlvSDgulfVxJGuXXlJP++7jKMXPJ/AloiISOr8utubNdZGRHOn\nXVSoUkNtcoO7vw8x62nbz5WuWTWwnWmTVqeHqlSDOpEhricyXuwqab4r53by9uJEzHzpXpe7uM1a\nmWSxTIx7fjyReqMA9cp1qB3i2mv3V46+fzbuvQwAWDTpAZ/df0Ti2L17B8rLyxASEoqHHuojdjgk\nAaxzJDV+feVHyJHIzleb78bxPQ/ishedo7mGvFmWNa42m/2lmW0wGDBn1VFMXrgfl9ILvH+5zZX9\nuZF95xaWY8+JGy4/z2rxJsFavf/NK6W4xtZn8mpWET5cdhjj5+5ya/4sv2FyUJ1990vLnZh/SgIy\nMzPxyiuvoHPnznjkkUeQkJBgXHfmzBkMGzYM8fHxGDp0KE6fPm323M2bN6NPnz7o1KkTxo8fj7w8\n/7oSrdFooFarodFIdwJo8i3WOZIaryQ/arUaAwYMwOHDh43Lrl+/jpEjR6JTp07o378/9u3b5/J+\nrTYIPGig2j0r74PcR6gE6/DZLEH26yxfpI32RmJz118nMpB6oxB6gwHLfj3r3k68FJbpbuRW6qlG\nq8fGvZb3neh0/p20C+Hgmar6flGASXt9xVq3R+m9m+6ZOHEiIiIi8NNPP+Gdd97BvHnzsHPnTpSW\nlmL06NHo2rUrNmzYgPj4eIwZMwZlZRXziZ04cQLvvfceXnvtNaxevRoFBQV4++23RX415vr06YcB\nA4agT59+YodCEsE6R1LjcfKjVqsxadIkXLp0yWz5uHHjEBsbi/Xr12PgwIEYP348MjOtzzXjK850\n7SlX63Als0iQxrZZLC72jxLszLuVHXtUlh9c1ikt12Lpr2fwx98TdNry7daq+16qvx1eeRmOdmJ6\n5t+0ulmpG9sPXcXP+9K8EVXAOJV6y/i3UJP/eoun3xfOnhgR+nspEBQWFiI5ORljx45Fs2bN8Mgj\nj6Bnz544cOAAtmzZgrCwMEyZMgUtWrTAu+++i4iICGzbtg0AsGrVKvTt2xcDBw5Eq1atMHfuXPz5\n559IT08X+VUREZGveJT8pKSkYNiwYbh+3byRmZiYiGvXrmH69Olo0aIFRo8ejfj4eKxbt86jYIVU\n2aSYseIIpi0/jD+Pe6c7kdVC/JzgYQrcjv1pTyr2nczEd79dcHoCUoXcjY+CzLOreWZjfdlo1P55\nPB0fLD2EX/anuV2Oc7FURWMtzygp1+K6h0NwU3VVB5o5jfNCQ0MRFhaG9evXQ6vVIjU1FUePHkXb\ntm2RnJyMzp07m21/991349ixYwCA48ePo2vXrsZ1DRs2RKNGjZCcnOzT10BEROLxKPk5dOgQunfv\njtWrV5s13k6cOIH27dsjJCTEuKxz5844fvy4J8UBcNzY9PTM6I2bKgDAiu3nrezbo127zqS8c1fz\nbI7u5VcEOkaunPlPuVFo/FvrZLcwhcJ/riyYRpKw7Tyu5xRDo7X+3heWqPG/dSesrnOXrXr++Vrn\nG4gGgwHHLuTgckah441doNebByfUR9IXF5r8/GKW3woODsYHH3yAH3/8ER07dkS/fv3wwAMPYMiQ\nIcjOzkZsrPkE0nXr1kVWVkVXyZycHIv19erVE71XgimVqhjFxUVQqXiygXyDdY6kxqNhg4YPH251\nubUfGNMfIHKdVmdAwtZzeLF/O6/uV2+lTS10m8wfRxaTu9MS9WLL27zbm/PP23bwqnfKd+LFuDI/\n09ELN7Hwp5MAgIX/eQBhIZ6PULb459M4ffkWWt5W2+N9+Rvj++/gDAuvEFVISUnBww8/jBdffBEX\nLlzAjBkz0L17d5SVlSE4ONhs2+DgYKjVFfOmOVrvCoVCmPGC1q37HipVMSIiIvHii6+4FZNQsTnD\nV0m9XC6DUumd1+kPx80WX8QW6HXOFsbmnkCIzVOCjJlaWlrqtR+Y6pRKORRyOQwGA3Yfu4E9yTdw\n1aQ7TvUvQ9PHCqX9b+Xqz7UYUltmuY0xJmcqi8nuHF1pUCpkUFQra9+pTIwZ3MFiW7nC9mt2ZNaK\nI/hnj9vxr4fvtBqnsQwbPzQV70fVExQKucPyFQrbP1q237+qVp+95wPmP76Otq0kl8vM3hOZEz+s\nFc+xXR9Mx+WyVnfkpl3tTGP2wo+6q883fR0ymfPvjy37T2UY/y4sUaNWRLCdrR3vW6mUGwc6SE7J\nNS5XyB3XN3fIrRwDe+WYHb+/t5VbG7nCZF+m9XT1rovo1raBw5ajs/XZU/74o1cpMTER69atw549\nexAcHIx27dohMzMTX375JZo1a2bxO6NWqxEaGgoACAkJsbveFbVrh7n/Iux46qkh0Gq1UCqViI6O\ncGsfQsXmDIVC7pMe3qFhwW4fH1vEPG6OCBlboNc5Rxibe/w5Nk8JkvyEhISgoKDAbJm7PzDVRUVF\nQKmQY90fF5GwxXKErjp1ws0em36Qb6nsD+NY/UMfXG3+FLlcZvWLwXSZvcpi2tiNjLR/LOpEhSO4\nzPJ+FWvlh4UFO9zGnl/3X8ErQ+KNj5UKy7lTwsKt/9BER0cgNDTI+DgiwvEPUkREiM1tqi+vfCwz\nOXZ16oSjTmQIbDFtHEZFRaC2kw3vOlFVdUepkDt8HeFWXofMJOa8wjKT/Sssto2ICDFbXykkJMjj\nH3VXn29aH4OCbL/2yuU6nd5uA9k0IY+OjnAqnujoCGxLTMPhM1l49al/mK2rY+NzZateeio0zPI9\nsFeOPKjqq7TyvQ4Ksj0HUXR0hNl7vjc5A3uTMxBlp14DQO064YiODre7TU13+vRpxMXFmZ1ga9u2\nLb766it06dIFOTnmk8HevHkT9evXBwDExsbi5s2bFuur91RwRmFhKXQCdEWuU6e+8e+8PJVLz1Uo\n5KhdO0yw2Jyh0+l9ModGWana5eNjiz8cN1t8EVug1zlbGJt7AiE2TwmS/DRo0MBi9DfTHyBPnE+9\nifNX85CwxfoM9fn5JWaPTT/IRUVl1Te3uS0AaDTmc2oUFKvxw7YzVp/nTGUxXZ6ZXWQ3loL8EpSq\nLef0MI1xw58pyM4rRVyjWnZfhzNMn6PVWZZbVqqxut+8PBVKS6vOpKpUjn+QVKpym9tUX56dU4Qg\npRwGk/55BQUl0GtsD2SgNbk/Jj9fBZ3a8dwFWq0eBSZ1R6fTO3wdpSWWr8OAqvpgejlHq9VZbFtS\nUtWNzLSulZdXHOsDp92/D8HVOlBcXPXZ0Ghsv/a8PBWSL93Ewg0n8fg9zfDkgy2tbldeXvX+LN10\nEteyivGff3V0GPPCdRX3FRUlmHexKygstfqcEivvgTdYq+/2yilUVX0GKt/r6t8f1fdl7XtC76Bf\nW0F+CYJlwp9X99YPjBBiY2Nx5coV45lqAEhNTUXTpk0RHx+PxYsXm21/7NgxjB07FgAQHx+PpKQk\nDB48GACQkZGBzMxMdOxov25ao9Ppzb5r/ImYsfmqa6Zeb/D6a+R76j5/jo+xucefY/OUICdoOnbs\niDNnzph1L0hKSkJ8fLydZznnra8S8a2NxAeAxaAAWq3e+M9RBlv9Ta5+czUAfL/jotXnVe67srJU\n/jNl+qOwfKvt11DxOgzQWal0lftNzy7Gxr2Xsf9UpsV9H9bKdsQ0Zms/Xqavq/rzTA+TTu+47Mof\nLWvb3cw3b+SO/Ww3zly+ZRaTaazW/pkOeqHTGWy+H2YMBrPBEQwGOHyezsaPr7E+VBvKunqcpvUr\nPafYYttFP52yHa8Dto5NuY3R7/Qmr/1qVhEST2VCbaXxrtXq8dmPx1Gm1mHj3stm+9ZodDh3JQ+5\n+aVmn8PDZ7OReasEC9efdBhzpbNXzCeetPZZAMzrkqv/7NEbLN9bu/szeb2Gv7e19v1hui+rg7M4\naDlqdO69Vlf/+dvZPlMPP/wwlEol3nvvPaSlpeGPP/7A4sWL8e9//xuPPvooioqK8NFHHyElJQUz\nZ85ESUkJHn/8cQAV96lu2rQJ69atw7lz5/Dmm2+iV69eaNy4scivioiIfEWQKz/dunVDo0aN8NZb\nb+HVV1/FH3/8gZMnT2LOnDlCFFcjyWD/fvqi0qqrGbcKRZ7l3oun+iZ9YT4Zrlqjx3/XHEftcMdd\n12wxGAyOR4uTwfXX4cUznCqTLo5C3S+86+h1rP7jksPtiks1+HLjKYzs18ZiXfVEu1yjq7g/TS7H\nkfM5+HJjRcLWqkkdi+fmFNi/8uoO/xs6w3luDfzBEQ8QGRmJ5cuX46OPPsLQoUMRExODcePGYejQ\noQCAxYsXY+rUqVizZg1at26NJUuWGLtcx8fHY/r06Zg/fz4KCgpw//33Y8aMGWK+HAuHDydCrS5H\ncHAIunbtLnY4JAGscyQ1Xkt+TBuXcrkcixYtwjvvvIMhQ4agWbNmWLhwIRo2bOit4mzzoG1w/mqe\n44084nxwbOJUUWvMz0LPW5uMBjHhUJVqER6qxOgB7aolN1V/q8o0+GhlEurVCcV/htnv2uL1Y+5n\nb+LK3y7YXHezwLJbmbUrrGt2mSdPbyzch9oRwZj+Yjds2JNqXG79oof3D4gvD3FJmQZlah1ialu5\nX89HgRSVaBAb7Zuy/FnLli2xdOlSq+vuuusubNiwweZzBw8ebOz25o9u3LiOkpIShIdL+94u8h3W\nOZIaryU/Z8+aDz7QtGlTrFy50lu7d5pp9yFXffz9MbPH3p5V3tX2kb3SfX3GW2Vl8AVr63wxjPXl\njCJczqi6Z+r+uxqhffMYky2qjvTmfWnIvFWCzFslZs/xFkFOxItwOWP2d0fdep6qTAtVmRYXrhU4\nDNvRsfL3eawmL9yPco0O/e69HQPui0NIkALpOcW4cL0Ad5nUv8rj4NTVxmocVafl285hxov3uBQ3\nBZZBg4aKHQJJDOscSY3/jmfqpv9tsH9fgSuEvxJkm6ftX283JH87fM2pdc7MF+PtpFJVZntAA9PE\nzKVj4kyIjrZx82V6I4H0dLJfNwp0vImD9b8nXfdOLHacv5qHk6m5Drf7NfGKRb0q//seqC0HrmDN\n390H3196CCu3n8e6P1OM2zl75N15l9NzvD+4AxERkZTUuOSn3MoIae6yd7VDaAa435OmtFyLKV/u\n92Y4gth3MsPxRk6wbHdbb1Z6OyE4cSkXdt8lB8XZavx6IzdM9GCkOHeZxm01CXZwPK5l275qu/K3\n89bLdCawv2Xnl+Lj74/h8zXJSL1R6HD7NXbuj9p1LN3s8aGz2RbbCJWAenJ1m4iISOpqXPJjj7ev\nOLjMm20hOy9l9/F0FBR7PqFsdZfSC5Bb7ab16o3Ib7ecw+o/LEfEq+5mQSmW/mo5T5N3uH6gU9IL\nkZJu/lrW7LqEtbsu2WzEHr9002qjV6vTY/UfF/HboSsux+Ety36tul8nJ78US36xHKLdq6p9tqwO\nZObgfbE3zPOZNOtXYV15p1PSq+YeO5Fy086WFVIzHCdInnD36+j9pYe8GwgREZGECDLam78KpJGh\nikvUuGrnTLg9Qo3L/tHKJItlM1ccsVi2/ZDtLnJAxfuQVyTyCHVWLPypqsvkpesFuHS9orHculmU\nzedUT+AMBuCPo+n4db8TiY+NCimTOdc4t8c0kZi3NhkZuSV2tvYRB5mKEAm7rfJv+MPxILIiIeFr\nqFTFiIiIxIgRo72234//uwCZucJ3m1TLwuGfM0SRLULVOSJ/JankRyjVrwyUlmsRFqJEcanjyTVt\n4dld/5GdZ32CTVsuXc+3u76kTIPQEPsfvXlrT7hUpi1bD17xSeIjg/mVVWsXcdQOkvLqc/sI6cg5\nyyt23pKeo8L/fbkfNx0O7W2Z/XIka+revafZBK7ekn6zGMW1hR8sI6yW423IvwhV54j8FWu6F2w7\neBVBQQoMf7wt1u26hF/2p2FUv7ZoUj/SbDtftWs8LccXV8i8eeO2M4Ms+IqjrkwXr+fjk++PoX3z\nGHRuXV/weNbuSnG8kUT4sp44TnyIrGvVqq3YIZDEsM6R1Ejqnh+hrN2dgu93XMDp1Fz8vC8NBoNl\ndyhvszcimKrUs4EafNFEXLHd+g3s3ubr27wcnblf+NMp6PQGnEjJtfke+mK4cG+Tyaonzf6TkBIR\nERFVktaVH4HblFez7M8j443Rnw6czoRGp0fjepE2t9lxxP49N1JVWu69kQDdpXNiuG2Nn893Y5PJ\n50uIOZWIiCqVl5WhuNg73zMKhRxKpR5FRSqL7+iIiEjxB0siIq+SVvJTA3wt9KhdAa5ApTZreB+7\nWDVwwA+/XxC8fK1O7/Tlprxi64M++GK+G29bsf28qIMqJJ3PxtWsYvTvcTuClAqr27h67oHNHRLD\n6dMnoNFoEBQUhPbt/yF2OH5JrgzCX2fzsX/KPO/sUAbIZbKKgWJMvieK8rIw441/o2uXbt4px0+x\nzpHUSCr5YWOm5vtig+2BAnLyRbwP4+/KZzp31E97UkUKxvvETHwOnsnC4p9PAwDkchkG3d9ctFiI\nPJWcnASVSoWIiAg2RG2QyeSoc3sPwcvRh6VCpxO/x4DQWOdIavw7+alhtw34xXDDfsDbPQhy8kpR\nptYiNFhpMVePv7hV6PvEy5mJPANdoUqNFduq7h87mZrL5IcC2jPPjBQ7BJIY1jmSGkEHPMjMzMQr\nr7yCzp0745FHHkFCQoKQxVHAcD37sddl6ae9l/HeNwe9ck+VN+j1lnHcKixH1i3fJr+/Jqb5tDwx\nCDlflJ9UJyIiIvIiQa/8TJw4EU2aNMFPP/2Eixcv4o033kDjxo3Ru3dvIYs1k19cjoJiNW5vWMvn\nQ3+dv2Z/vhfynluF5dj012WxwwAAnLqca3X5218f8HEktP9UBgpVGjzWranLz02/KfyEkERERORb\ngiU/hYWFSE5OxqxZs9CsWTM0a9YMPXv2xIEDB5xOft5c+JfHcUz6Yh8AYMrT8agdGeLx/lxxNu2W\nT8sLFMu2uD5ogzN568/70lwPxgnf77zo0vY6nX9cMpDClYvq1cL0NWflleCbzRVDzkfXCvG748EB\npIiIiHxPsG5voaGhCAsLw/r166HVapGamoqjR4+iXbt2Tu9DrfHejYa/HrjitX2RZ/xhyGkh6ax0\neyPfy8krNf594XpgXIUtLtWIHQKJbO3aVUhI+Bpr164SOxSSCNY5khrBrvwEBwfjgw8+wPTp07Fi\nxQrodDo8+eSTePLJJ4UqkmowfztrHwiOX7rpeKMajFWGAtGdd7aBWl2O4GDf9lQg6WKdI6kR9J6f\nlJQUPPzww3jxxRdx4cIFzJgxAz169ED//v2FLNYm9jIhIiJ/Fh/fWewQSGJY50hqBEt+EhMTsW7d\nOuzZswfBwcFo164dMjMz8eWXX4qS/MhkMiiUgg5uZ1mmPHDSLeXfx0ZVqvHPIZID51CSD+07lWn2\nWCarqssKRdXnXS6TQaHwbiVSevB9olTKPbrnx5OynWF67IiIiGoSwZKf06dPIy4uDsHBwcZlbdu2\nxeLFi4Uq0q6gIAXq1A7zaZmB1ICIjo4AAHywdJfIkVgnD6BEknwnt8B8/iSFQm6sy5GRxcblISFK\nhIcHw5sqy3H3uZ7MSeVJ2URERFImWPITGxuLK1euQKvVQqmsKCY1NRVNmjQRqki7tBodCgtLHW/o\nRUnnsn1anify8iqG9U3L8MOrPrA+dw5RdVqt3liXi4urEqPyci1UKrVXy6osxx03MgtEK9sZCoUc\ntX18sogqpKWlGn834+JaiB0OSQDrHEmNYMnPww8/jLlz5+K9997DK6+8gtTUVCxevBiTJ08Wqki7\nDAYDdDq9KGUHAq3Wz48Ncx9ygsFgMNZl0yHH9QJ8/j35zJy/mida2eTf/vxzJ1SqYkRERCIubrTY\n4Vn/AzQAACAASURBVJAEsM6R1AiW/ERGRmL58uX46KOPMHToUMTExGDcuHEYOnSoUEUSEVklg3/l\nzxy9kGwZPvwFVNRWdvUl32CdI6kRdLS3li1bYunSpUIW4TzOKEhU4/kyp8jJd78brYHZD9lgep8s\nkS+wzpHUBM4d+R46ffkWiko4gSCRVHk74Vi6+Yzbz92TnOHFSIiIiMhZkkl+AGDVjgtih0BuMvhV\npyUKBNVzHW/XoKw896/8HL2Q48VIiIiIyFmCdnvzN9eyix1v5IHcAt+OJudNCdvOYcTjbcQOg0g4\nzJ8pAGzZshGlpaUICwtDv36DxQ6HJIB1jqRGUld+hLY6gK8s/Xn8htgh2HWrsFzsECgQmCQ41W/z\n83buU+DlobOJACAqKhoxMXURFRUtdigkEaxzJDWSuvJDRNJhcYsPBxmgANCjx4Nih0ASwzpHUsMr\nP0RUY9i6N6y4VIPNiVd8HA0RERH5G175IaIa79DZbLFDICIiIj/A5IeIiMhPZGdnQa/XQS5XIDa2\ngdjhkASwzpHUMPkhoy82nBQ7BCLPGCrm87l4vQCr/7godjRELtu6dRNUqmJERERixIjRYodDEsA6\nR1LD5IeMOPcIBTpVmRbnruZj7g/HxA6FyC0DBz4Fg0EPmYy35JJvsM6R1DD5IaIaQ28wYNexdLHD\nIHJbdHSM2CGQxLDOkdQwzSeiGiVIwa81IiIisk7QVoJarca0adPQrVs33H///fj888+FLI6IJC6v\nqBzZeSVih0FERER+StBubzNnzsShQ4ewbNkyFBcX4z//+Q8aN26MYcOGCVksEUlYyo1CsUMgctvu\n3TtQXl6GkJBQPPRQH7HDIQlgnSOpESz5KSgowIYNG7B8+XJ06NABADBq1CgkJycz+SEiIrJCo9FA\nrVZDLleIHQpJBOscSY1gyU9SUhJq1aqFLl26GJe9/PLLQhVHREQU8Pr06Sd2CCQxrHMkNYLd83Pt\n2jU0btwYGzduRN++fdG7d28sWrQIBoNBqCKJiIiIiIhsEuzKT0lJCdLS0rB27VrMmTMHOTk5eP/9\n9xEeHo4XXnhBqGKJiGo8pVLYEe0UHDGPiIhqKMGSH4VCAZVKhc8++wwNGzYEAKSnp+OHH35g8kNE\n5IHo6AixQyCBqFTFMBgMkMlkiIiIFDsckgDWOZIawZKf2NhYhISEGBMfAGjevDkyMzOFKpKISBLy\n8lSC7l+hkKN27TBByyDr1q37HipVMSIiIjFixGixwyEJYJ0jqREs+YmPj0d5eTmuXLmC22+/HQCQ\nkpKCxo0bC1UkEZEkaLV6sUMggfTu3Rc6nQ4KBUfeIt9gnSOpESz5iYuLw4MPPoi33noLU6dORU5O\nDpYsWYJx48YJVSQREVFAa9y4qdghkMSwzpHUCDrJ6aeffoqZM2fi2WefRVhYGJ577jk8++yzQhZJ\nRERERERklaDJT2RkJObMmYM5c+YIWQwREREREZFDgiY/RERE5LzDhxOhVpcjODgEXbt2FzsckgDW\nOZIaJj9ERER+4saN6ygpKUF4eLjYoZBEsM6R1DD5ISIi8hODBg0VOwSSGNY5khpO401ERERERJLA\n5IeIKMAYDAaxQyAiIgpITH6IiAKMhpOcEhERuYX3/BARBZjgIM7EXlMlJHwNlaoYERGRGDFitNjh\nkASwzpHUMPkhIiLyE92794RWq4VSyZ9n8g3WOZIa1nQiIiI/0apVW7FDIIlhnSOp4T0/REREREQk\nCUx+iIiIiIhIEnzW7W306NGoW7cuZs+e7asiiYiIAsrp0yeg0WgQFBSE9u3/IXY4JAGscyQ1Prny\n8+uvv2LPnj2+KIqIiChgJScn4fDhRCQnJ4kdCkkE6xxJjeBXfgoKCjB37lz84x88m0BERGTPM8+M\nFDsEkhjWOZIawZOfjz/+GIMGDUJ2drbQRREREREREdkkaLe3xMREJCUlYdy4cUIWQ0RERERE5JBg\nyY9arcaHH36IqVOnIjg4WKhiiIiIiIiInCJYt7cFCxagQ4cO6NGjh1BFEBFJklIp7Fg1CgVnQRDL\n2rWrUFKiQnh4BIYOfVbscEgCWOdIagRLfrZs2YLc3Fx06tQJAKDRaAAA27dvx9GjR4UqloioxouO\njhA7BBLInXe2gVpdjuDgELFDIYlgnSOpESz5+e6776DVao2P586dCwCYMmWKUEUSEUlCXp5K0P0r\nFHLUrh0maBlkXXx8Z7FDIIlhnSOpESz5adSokdnjiIiKM5VNmzYVqkgiohovJEgBrVYvdhhEREQB\niR27iYgCyID74sQOgYiIKGAJPs9PpdmzZ/uqKCKiGiskSCF2CCSgtLRUaLVaKJVKxMW1EDsckgDW\nOZIanyU/RETkOZlM7AhISH/+uRMqVTEiIiIRFzda7HBIAljnSGqY/BARBRCDQewISEjDh78AwACA\nWS75BuscSQ2THyIiIj/BScHJ11jnSGo44AERUQBhtzciIiL3Mfkh8rH2zWPEDoECGHMfIiIi97Hb\nG5GPvTKoPc5fzccXG06KHQoR+ZktWzaitLQUYWFh6NdvsNjhkASwzpHUMPkh8jEZZLi7VX2xw6BA\nxX5vNVpUVDTCwsIREhIidigkEaxzJDVMfshvDLwvDj/vSxM7DMEFKdnb1JEOzWNw6vItscMg8rke\nPR4UOwSSGNY5khq2wshvDO5Z8ydX69K6PpMfJygVPEa28LoPERGR+9jCIPKhLm1i7a6vE8khR8k+\nTvNDRETkPiY/RD50Kb3A+HezBpEW61s0qu3LcCgAGTjLKdRqNaZNm4Zu3brh/vvvx+eff25cd+bM\nGQwbNgzx8fEYOnQoTp8+bfbczZs3o0+fPujUqRPGjx+PvLw8X4dvV3Z2FjIzbyA7O0vsUEgiWOdI\nagIm+QkOCphQ7ep7bzOxQ/BLL/6zrdgh+NwdjeuIHYLf4j39tgWxSyBmzpyJxMRELFu2DJ9++inW\nrFmDNWvWoLS0FKNHj0bXrl2xYcMGxMfHY8yYMSgrKwMAnDhxAu+99x5ee+01rF69GgUFBXj77bdF\nfjXmtm7dhA0bfsTWrZvEDoUkgnWOpEbQAQ+ysrIwa9YsHDx4EKGhoejbty8mTZrk9GzCCrkMOn3F\nWc6oyBBk55UKGa5XzRlzL95afMBi+ZMPtMDWA1cFK7d/j9uxef8Vwfbvrj5dmmLHkWs21zeICfdh\nNOJp1STK+PeQB1uiqESDw+eyRYzIP8mY/ZANBQUF2LBhA5YvX44OHToAAEaNGoXk5GQoFAqEhYVh\nypQpAIB3330Xe/bswbZt2zB48GCsWrUKffv2xcCBAwEAc+fORa9evZCeno7GjRuL9ppMDRz4FAwG\nPWQyJrnkG6xzJDWC1vQJEyagvLwc33//Pf773/9i165dmD9/vtPPXzv7n8a/A60pZKvxppAL++Xy\n5AMtzR7XjwoVtDxnDe99p931IUEKAMDtDWv5IhzRdG5dNcR1WIgSYwd3sNjmnnYNfBmSKJo3sv8+\nB9LnfVivO7y2L2cGw5B6p7ekpCTUqlULXbp0MS57+eWXMWvWLCQnJ6Nz585m29999904duwYAOD4\n8ePo2rWrcV3Dhg3RqFEjJCcn+yZ4J0RHxyAmph6iozkZMvkG6xxJjWAt8dTUVJw4cQKzZ89Gy5Yt\n0blzZ0yYMAGbN292eh+mIz49GO8fZ+Wc0aZZlOONfGTmS/eKHYJD3drGokn9CADA+Cfucmsfn792\nvzdDcsoDHW9zetsPR3bFF6/3dOqKRvMangA6JYCyn0c6e+e7qe3t0fh8/H1e2VdNdu3aNTRu3Bgb\nN25E37590bt3byxatAgGgwHZ2dmIjTUfVKRu3brIyqq4lyEnJ8difb169ZCZmemz+ImISFyCdXur\nX78+lixZgpiYqjMJBoMBRUVFTu9DJpNh+ovdkJZRhHvbN8CaXZeECNXr+nRtand91zaxOHIu2ydn\ncANhWOVXBlVd/ahbx/UrVbNH34s6Eb4fJU3uQgO9WQMmNKYc3bMfCLlP/x5xePIB68Ozd2/fEImn\nXWtQvzygHcJD/5+9Ow+LquzfAH7PwszAADKCoKK4oAiCMoiIG5mGpuZWprlU5hJWprb5M7PCpUTD\nNHN7TctKy9dCX/fSVkuzcsdELMUNF4REjXVgZn5/EKMjM8DADGfg3J/r4tI558ycex4e4HznPOc5\nLhVuFx1S988MlicvLw/nz5/Hl19+ifnz5yMzMxNvvvkm3NzcUFBQUGZYtUKhgE6nA4AK19tC5oTX\nXpVmspStNvxMOSOZTAq5gH9Hy/ueOgNnzsdsVVMbslWXw4ofDw8PdO9+59N4o9GI9evXo2vXrja9\nTvNGnmjSoGRWrOE9WwleAPWLDsBXv5V/zY7MylFx6dKJg0MxqncQXly6z87phOeqlEMqAXILimts\nn4INA3Ly61LeGNMRm/aeRcp555rNCii/+Jn0cBh+O1W7r4N6emBbm4sfL/fy766+/MX7IJEASoWs\nOtFqPZlMhtzcXLz77rto2LAhAODy5cv4/PPP0aJFizKFjE6ng0pV8qGKUqksd70tPD1dq/gOyrd9\n+3YUFBRApVJh4MCBVXoNS9lcXMTdb6rKw10FjUYtdAyH9TfAcX3OWTBb1Thztupy6IQHd3vnnXeQ\nmpqKTZs22fS8u6u8gBoeDiSTSjCqdxDW7T5tMY81crnU4k0aX3xMa/oEybtexX+IekU2wfeH021I\njDKfUMnlUkwd1h5Lvky26XUqq1NbP/yecmd6TGuFX3mfnFX3UzWZTCLIJ3PW3qsllc0nlUoglVW/\nqHq8TxBaN/XC/RH+Fouf5x4OQ4tGnli17STOpN+y8Aol7p50xJ6MVkrWsJb1ER3aEAdPZ9p9n/Ym\nk1rvd5aWK+RS6IoNVl+voj7iUYNnN53xE79Svr6+UCqVpsIHAFq0aIFr164hOjoamZnmfScrKwsN\nGjQwPTcrK6vM+nuHwlXG7dv50Outfz+rKjc3H/n5+dDrjcjOzrXpuTKZFJ6erhazFRXpgbp7LOMw\n/+QU2Px9sKfyvqf24qg+JzRmq5rakK26aqT4SUxMxLp16/Dee+8hMDCw4ifc5e436enhuF9A/bo0\nx1cHzpdZ3jG0kVnxo7IyLMW3vhuu38gDALRv4wd317IHKo39PGz6BGnSMK3Nxc+9r6/RqNGjY7Ny\nix8fL1dk3azaTHodgs2LH0vXtDzeL7jc913dT9U8PV2h0agRP6EzZq8pO8NedUx/siMWfHrI4jqV\nygW+GlersxC2buqFvy7dhEwqqfR7dHGRwdW1/DMApYbHBuGLb/+0uM7NTQmNRo2+3Vri+q1CJH3/\nl9l6Px8PBAc2wJsTOmPPbxfww6FLuJxZ9uerY4gfXhkdiRkr9+PMpZtWs9ja9gqF5V89LnIZNBo1\nlFbWV8a7U+/Dy0t+qvLzK+vBri0sfl/96rtZXL5w6n24cPU2PthyAv/kFZVZX1EfcYZPn52BVqtF\nYWEhLly4gGbNmgEAzp49iyZNmkCr1WLVqlVm2x89ehTPPvus6bmHDx/GkCFDAABXr17FtWvXEB4e\nbnMOvd6A4nKK2ap64IF+pv9X9fUtZRP7RBlV5ajvszPlcFSfcxbMVjXOnK26HP7x3ty5c/HJJ58g\nMTERsbGxNj//9u18ZGfnIjs7F67yqn0i/tzDZWfUutdjPQMx88lIdAltaLZc42Z+EJaXb3lseOsm\n9TAnrgveerozUKxHzj/5WDI1Bo2870zhfPt2gem9ZGfnVjhqKjenAGqVbQeB2dm5aB/oDQBo3sgD\n2dm5uHmz/KLRaMMn++GtvM0e59/THiU3YLzn9QyGcj9NurtNsrNz8ej9gWhewWxgd7t1q6SPBDYs\ne9PQ6mrV0AMLnu1icd0DHfyh11tuO5lUgjfGR6N/l2Z47cnIMu/x7q+7FRXpkZ9fWKlsYc2tT6wR\n0MDt3+99Hh6MalJmvenTzGI9+kQ2QUMrU43rioqRn1eIN8d0tLoNAItt/9bT0Va3t/aLp4GXCtnZ\nuSjSVX3YZAMPBR6937YPWarCXSG1+D2Mad+ozLIRD7RGi8b10KG1D/5vVAeLr2fptSytr4mv27ed\n97YCzZs3R48ePfDqq68iNTUVP//8M1avXo1Ro0ahT58++OeffzBv3jycPXsWb731FvLy8tC3b18A\nwMiRI7F161YkJSUhNTUV06dPR8+ePZ1mmmsiInI8hxY/y5Ytw8aNG7F48WL069ev4idYUFp5Fhcb\n4O2pwth+wRgS08Km14gMalDhNgaDEYGN6+HpgW3Nlt9b9Vo7BejppkBEG18E+Lmb8nq4uqD5XUP1\nSpeXfr0yIgJymRT3hTfCe5O749XR5gdFxcUGzH/G8oG3NcXFBkwcFIpnBofipeFa077KZ/kA/t52\nfml4OAIbm9+Y01CJU6IGvbHcDPe2S//OzfDmmCir25f3fHszGAyQ3zM9eWxkE8wZ1wleagXUrubF\nabd2DfHSY+FYNLk7NB6qkoPehp5l3qO1zEZjSXtV5NXRHdDEp2zB8cKwcLwwLByNvdWm15dJJLhf\naz4znUFvPYP5dkbTNuV9iGDpNRp7Wzgroik5kzvygbJTn0e09sHgbi1QXGyo1qfUxcUG9It23M2E\nAxt7Yv7Ezlbbr3NbvzLL+ncpOUOh1xvg76PGO892Qdcw8w9aKvpelNeH7P3lbEMd7rVw4UI0a9YM\no0ePxowZM/D4449j9OjRcHd3x6pVq3Do0CEMHToUJ06cwOrVq03X9Gi1WsyZMwfLly/HqFGj4OXl\nhXnz5gn8boiIqCY5bNjb2bNnsXLlSkycOBERERFm46x9fHyq/Lox/04vvOXnc5V+jj1vmGi465jg\nmcGhOPZXFjKy88spyO7s+97rHEKaabDshRgo/r0Q1dPCmH51BbM/Wbp5qKtSjk42zQglweDuLXAo\n9TouZ1n/5DmspTfOXTOfrS+4mcbCq5lTVXEIU0XXSJSy1G72IpFI4Ko0vz5rVO8g0/+fHhiKN9b8\nZnrcsL4bwlp42+0aJGvX3AQ1tXzWp/Ss372e7BuMfSeuorgShdXd7t66tHCxJjjAC6kXrQ+NA4D4\nsVHIKyhGfU9VmQlMJg9tb/p/dX9kHXmT1CExLeGrsX4WrL5nxRfP+9RzxYQBbdEtrCG27T+PQd2a\n2zFh3efu7o758+dj/vz5Zda1a9cOmzdvtvrcIUOGmIa9OaPc3BwYjUZIJBKo1fY/m010L/Y5EhuH\nnfn57rvvYDAYsHLlSsTExCAmJgbdu3dHTEyMo3ZpEmLhgLzUkO4tENG6csWXpeOnDkF3ntvKvx7i\nBoXijTEd4aq0fIB/92tYmuFKYWUGnvKmbvb2vHNNSEU3i7S237s19XXH4O4tMOPxyPI3ROmwtjsa\neasxfVSE1e1bNPJE51DrhVjPDtaHm0wf3cF0/5/yuLveKRCnDG1vNtSwuqRSSbnFm7+PGmum90Sf\nqKaIDGqAPhVMc26rgd2aw99HjXArRY0t+nduZvq/tX5XHhe5DO9O6oZOIZYvDp/66J3rJqx9X1UK\neaWKg8qWLstfug8fvdqrklub8/l3WvWZT1Tc7+/+nWJpsoZpIyOgdJGhd0fbvv8hzetj+ugOCGle\n9uaCHdtUfMaa6p6kpM/x6aerkZT0udBRSCTY50hsHHbmJy4uDnFxcY56+TLGPxSCD3eewn3hjXHj\nn4Iy6+fFdcb5a7fRsY0vDp2+jqN/ZVl4lRLN/DxwIeMfxA0MLbOuTYAGU4a2h5vKvgdxpWaNjcK+\nE1cRG1n2Og0AmD4qAgU6PZYklUxg0NhHjUHdmmPb/vOmg7nKeuqhtjiUcg1j+rYBALhU5poqC4VU\nm4B7is27Kr7Xn4w0fQof1KQe/rxrZrGeEf54ok8bq7tq0cgTc8ZHo1hvQHLa31i26QSAkuur/rIy\nQ5m2tQ8C/NzxyopfzJY/+WAb/Pf7vzAqNggff5Va7ls0eyuV2EYqkWCEhWFc9uCmlGPuhJJrZ8bN\n/77M+peGh2PRF5W7O33f6AAcO5MFL3clWjcxH75o7USJ4Z5iV+OhRFNfd/xuYSpqpUKG5S/eh7OX\nb5nOCHq5K3Azx/J1cuWfnKncT46Hm6LKwx3fefbOtPuDu7fA1n3Wzyb7aVxx6sK/s+ZZ+BkIaabB\n0hdiLM7yqLSx0Hx2SBhOnruBR+8PxKFaMOsd2VdsbD/o9XrIZJyammoG+xyJTY1Nde1o3do1QvtA\nb7i7umDxl2UPBhvWdzNdsB0d4geDwYg1O05ZfK0Zj3fA37cL0OjfaxZeHqHFki+T0b19IwAlB9iV\nZnbmp+IhRwF+HhhVzg0x2wRoYDQaMTK2NVQKGQL8PODfQI3WTb3QzMrzZFamTh7aqzV6RTQ2HTyW\nmd7WQtzKDJq6X9sY2/afB2A+/OjlERH48ehlbPjuLyvPtEwuk6JTiB8mD5fhVFoWht4XiOX/O4E/\nzt3AAgvXRN075Gn8QyHo1q4RYsIbQSaVIunHs8jJLzvbliWOHD5lcX8Awlv74L/flwwHa9/qTl97\naXg4lm/5A33uOrsQ1rLyZ4RUCjlmje1kYx7b3r+rUm6WadIj7fD2p4ctblve2aeoYF+b75Nzryce\nbIN1u0+ja1hDDOzaHH+cu4HPvrE8O95DXZqVW/yEtvDGj8euAIDViR/uLXymj4rAD0cvY2DX5jbl\njgr2RVSw7VMvU93g72/fs8dEFWGfI7GpM8UPUPIpMFByd/U/0m4AKBmadi+JRIKuYY2sFj8KF5mp\n8AGA0Ob1za7NsYWtB4+Vek2JxGx4jUwqRaiFYTOlpBIJEp/tiuvZeVi59aTVA3+phQP90mtOHv73\nmqbKFHAPdWmOeu5Ks8keAMBFLjUfkmZj0/SJboaoIB8UFxvw0mNaq9vdffudxj5qdGtXUrTK/p24\n4JURWsxae9C2ndcgP40b4p+KgkQC+Hrduc4mrKU3lr9wH6Q23F+oskp/du4V2rzsENKI1g2waW8a\nAGBYz0B0KGdCkfoe1s9GBvhaH1se3sobzw4Jw6HU6ziYWrUbnvaM8EfPiDvD7/zqu1ktfuQyKVa+\n1APPLtprcX2HIB+M6dsGHm4K+HhV7h4DbQI0Zc+KEhERkaDqRPFz7zj7dnd98nxfeON7N6+SqhQ+\nQMXX/FTGlKHtsfx/J8wO5GzlXU8F73oq+Glcyz3roW3lg2Nn7gwJXPBMF1zI+MfUptbeg6+XK67f\nzMdT/YLhIpdazaq+6/ocn0oMG6yKu8/W3DtZAVBydq0i/Ts3Q69yrkdylAc7lcxS1szKDX0dUfgA\nwKP3B+KHI5dNj+MGtsWVv/PQy8Lwy8Y+arz+ZEfIpBKrOSsj0MIHE6UkEgmign1xO1dntfgJvevn\n/LFerbDx+zPVmjhAqZBhRK9W2PjDmZJZ+hp5YuvPaegdFQCJRIIeWk6HTEREVNvVieJnZKz59Rbu\nri54cXg4sm7mo2u7hlaedYc9Lia3pmcHf/ycfBVA5Q66LdG29sGyF+6DUlH98bhPD2yL5f/7AxFW\nPq2PbNPAVPwYUTJz1d3XNlnLMHtcJ/x9uwCNfcqfoKBFI0/cH+GPm/8UIraj5euaqsvd1QUKFyl0\nRQY8EtPS4jZDe7TEN4fSEdSknsXrKkJb1C/zvgt1eofkvVurJtYLAmtG9w7C5p/S8FS/4Crv994z\nP51Dy/+5adnYs5Kve6fY1bayfZbHe2u9sf2DcfriTTRr6IGHYgJhKCq5H9CDnQLQObRhuROFAMCL\nw8Oxbvdpq0PR+nQKwH3axqZJLl4eYX0yDyJHOHjwAHS6QigUSkRF2XarA6KqYJ8jsam1xc/0URFY\nte0kYq3MrtSuEtdCvP10NJLP/m26lscRmjf0RPxTUXBTyeFm4w1L72aPwgcAfDVumD2uk9WpmL3v\nOuD3tTC8p1cHfyT9eBYA0PauIVFKhazCwqfUkw9an+TAHqRSCRY+1w23cgrh38Dy0KqHujRH/87N\n8P2Ry6bix0/jiozskps7ermbH0S/9ngkvvjhDO53wKf/Ea19cPSvLJtvaFvqgcgm6NnB3+KwRaHJ\nZVIsntwdWbfyy9wjCigZmvbD0ctW78vjIr/T78Na1kdM+8aIad8YcrkU9dyVyM6+czPUigofoOT3\nwt0THVhS1anZHeHR+wOR9ONZDOlu273NqPa6ciUdeXl5cHOz36yVROVhnyOxcZ6/8jZqE6DBu5O6\nVeuC9EbearNrexylOkODalqbAC/07RSAgiI9oi1MUa1SyPFwTAucPJ+N8Q+1tfAKzsHd1cVsCmxL\nJBIJOrZpYLoO5JUREfjm0CXU91CW6RdNfd3xcjnXGVXH+Ifa4tDp6whrYf26rYrYo/BxU8mRV1Bc\n8YY2qqdWWC1MRvcJQq/IJmhsZXry6LZ+2PnrBej1Bkwa0s7u2Zxd/87N0DWsIbzclRVvTHXC4MHD\nhI5AIsM+R2JTa4sfoOZn4hIDiUSC4b1albvNwG4tMLBb3fgkup67EonPdoXRaIR3PZXDpqwuj5tK\nbrdr06rj7We6Yf4nvzv0TOi9pBIJ/Ms5Y+gil+LtCdEwwmiasEJsWPgQERHZT60ufojswdvG+yPV\nVa2aeiFxUrcq3zfHUUomeeAHHURERFR94vwolYiIiIiIRIdnfoiIiJzEJ598gNzcHKjV7hgzJk7o\nOCQC7HMkNix+iIiInESXLjEoLi6GXM4/z1Qz2OdIbBza03U6HWbNmoVvvvkGKpUK48aNw9ixYx25\nSyIiolorKChE6AgkMuxzJDYOLX4WLFiAlJQUrFu3Dunp6Zg+fTr8/f3Rp08fR+6WiIiIiIioDIdN\neJCfn4+kpCS8/vrrCA4ORmxsLCZMmID169c7apdERERERERWOezMT2pqKvR6PbTaOzeGjIyMxKpV\nqxy1SyIicgJZWVnw8fEROkatdPJkMoqKiuDi4oLQ0PZCxyERYJ8jsXFY8ZOZmQkvLy+zC+i8PVyu\nUAAAIABJREFUvb1RWFiI7OxsaDQaR+2aiIgENHToULRv3x7Dhg1DTEwMb0htg+PHDyM3NxdqtZoH\nolQj2OdIbBxW/OTn50OhUJgtK32s0+kctVsiIhLYd999hx9//BGff/455syZg4cffhhDhw5Fw4YN\nhY7m9EaN4qRAVLPY50hsHFb8KJXKMkVO6WNXV9dKv45MVjvuw1qak3kdg3kdi3kdq7bmrSq5XI7Y\n2FjExsZi7969mD17NlatWoWuXbti2rRpCAwMtFNSIiIi2zis+PHz88PNmzdhMBgglZb8Ic3KyoJK\npYKnp2elX8fTs/KFkjNgXsdiXsdiXseqbXmrKjMzE1u3bsWWLVugUqnwzDPP4KGHHsKBAwcwadIk\nfP3110JHJCIikXJY8RMSEgK5XI5jx46hQ4cOAIBDhw4hLCzMUbskIiInMGDAAPTr1w+JiYkICblz\nD5HY2Fjs2rVLwGRERCR2Dit+VCoVBg8ejPj4eMybNw8ZGRlYu3Yt5s+f76hdEhGRE/jxxx9x5MgR\nhISEIDs7GwcOHED//v0BAIsWLRI4nXP78svPkJeXCzc3NYYNGy10HBIB9jkSG4fe5HTGjBmYPXs2\nxowZAw8PD0ydOhWxsbGO3CUREQls0aJFSE9PR7du3VBUVITNmzfj5MmTmDZtmtDRnF7r1sHQ6Qqh\nUCiFjkIiwT5HYuPQ4kelUiEhIQEJCQmO3A0RETmRAwcOYMeOHQAAX19frFq1CkOGDGHxUwlabaTQ\nEUhk2OdIbGrH1ENERFRrFBUVoaCgwPRYr9cLmIaIiOgOh575ISIi8RkwYABGjRqFBx98EBKJBHv2\n7MFDDz0kdCwiIiIWP0REZF+TJ09GmzZt8Pvvv0Mmk+G5555Dr169hI5VK5w/n4bi4mLI5XI0b95S\n6DgkAuxzJDYsfoiIyO66du2Kdu3awWg0AgCuXLmCxo0bC5zK+e3d+y1yc3OgVrujefM4oeOQCLDP\nkdiw+CEiIrtas2YN3n///TI3tN63b59AiWqPkSOfAmAEIBE4CYkF+xyJjVNOeKDT6fDaa68hKioK\nMTExWLt2raB5vv32WwQHByMkJMT079SpUwEAKSkpGD58OLRaLYYNG4aTJ0+aPXfHjh3o3bs3IiIi\n8PzzzyM7O9thOXU6HQYOHIiDBw+alqWnp2Ps2LGIiIjAgAEDsH//frPn/PLLLxg4cCC0Wi2eeuop\nXLp0yWz9xx9/jPvuuw+RkZGYOXMmCgsLHZr3rbfeKtPWn332mWl9Re25cOFCdOnSBdHR0UhMTLRL\nzoyMDEyZMgXR0dHo0aMH5s+fD51OB8A527e8vM7YvhcvXsT48eMRERGBXr164cMPPzStc8b2rSiz\nM7Zxqbi4OMyYMcP0uLq/v6xl3bBhA3bv3o19+/aZfVHFFAoFFAolFAqF0FFIJNjnSGycsvhZsGAB\nUlJSsG7dOsTHx2PZsmXYs2ePYHnOnDmDXr16Yf/+/di/fz/27duHt99+G/n5+YiLi0NUVBQ2b94M\nrVaLiRMnmmY5Sk5Oxuuvv47Jkydj48aNuHXrltmBhz3pdDq89NJLOHPmjNnySZMmwdfXF5s2bcKg\nQYPw/PPP49q1awCAq1evYtKkSRg6dCg2bdoEjUaDSZMmmZ67e/durFixAnPnzsUnn3yC48eP2+1g\nzFretLQ0vPLKK9i3b5+prR999FEAFbfnRx99hJ07d2LFihVYunQptm/fbpfCecqUKSgsLMTnn3+O\nRYsW4YcffsCSJUsAAM8995zTtW95eZ2tfY1GI+Li4uDj44OtW7di1qxZWLlyJXbu3AnAOdu3oszO\n1saldu7ciZ9++sn0uLq/v8rL2qhRIzRq1MguuYmIiOzJ6Yqf/Px8JCUl4fXXX0dwcDBiY2MxYcIE\nrF+/XrBMZ8+eRevWrVG/fn14e3vD29sb7u7u2LlzJ1xdXTFt2jS0bNkSM2fOhFqtxtdffw0A+Oyz\nz9CvXz8MGjQIQUFBSExMxN69e3H58mW75xs+fDjS09PNlh84cACXLl3CnDlz0LJlS8TFxUGr1SIp\nKQkA8MUXX6Bdu3Z46qmnEBgYiISEBFy+fNl0JmbdunUYM2YMevTogbCwMMyePRtJSUnV/vTcWt7S\ndW3btjW1s7e3N5TKkhuvVdSe69atw9SpUxEREYFOnTrhlVdeqXa/SUtLQ3JyMhISEhAYGIjIyEhM\nmTIFO3bswK+//or09HSnat/y8gLO175ZWVlo27Yt4uPjERAQgPvuuw9dunTB4cOHnbJ9K8oMOF8b\nA8CtW7eQmJiI9u3bm5ZV9/dXeVkjIiIwc+ZM7NmzB3v37jV9ERERCc3pip/U1FTo9XpotVrTssjI\nSCQnJwuW6ezZs2jRokWZ5cnJyYiMNL85WIcOHXD06FEAwLFjxxAVFWVa17BhQzRq1AjHjx+3a77f\nf/8dXbp0wcaNG00XF5fmCw0NNR14ASVteezYMdP6u/OpVCq0bdsWR48ehcFgwIkTJ9CxY0fTeq1W\ni6KiIqSmpjokb05ODjIyMtC8eXOLzyuvPa9fv46rV6+a5Y2MjMSVK1eQlZVV5awNGjTA6tWrUb9+\nfbPl//zzD44fP+507Wspr9FoxD///OO07bto0SK4ubkBAA4fPoxDhw6hU6dOTtm+1jIfPHgQ0dHR\nTtnGQMnZ9MGDByMwMNC0rDq/vyrKeuzYMVy8eBHr1q3DmjVrsGbNGrOhgWTdrl1bsGnTBuzatUXo\nKCQS7HMkNk434UFmZia8vLwgl9+J5u3tjcLCQmRnZ0Oj0dR4pnPnzuHnn3/GypUrYTAY0K9fP0ye\nPBnXr19HUFCQ2bbe3t6moVyZmZnw9fU1W+/j42MatmMvI0eOtLjc0v69vb2RkZEBALh+/brFfBkZ\nGbh9+zYKCwvN1stkMnh5eeHatWsIDw+3e960tDRIJBKsXLkSP/30E7y8vDB27FgMGTLE6vspbc/M\nzExIJBKz9T4+PjAajbh27Rp8fHyqlNXDwwPdu3c3PTYajVi/fj26dOnilO1rLW/Xrl2dsn3v1qtX\nL1y9ehX3338/+vTpg3nz5jld+1aUOTk52ena+MCBAzh8+DC2b9+O+Ph40/Lq/P6qKOu6deuqlJUA\nLy8NXF3dzIp+IkdinyOxcbriJz8/v8xFd6WPSy/arklXrlxBQUEBlEollixZgvT0dNP1PgUFBRaz\nluasaL2jWWvLyuQrHfdfk/nT0tIglUoRGBiIJ554Ar///jveeOMNuLu7IzY2tty8+fn5ZfI6ot+8\n8847OHXqFJKSkrB27Vqnb9933nkHqampSEpKwh9//OHU7bt06VJkZWVh1qxZmDdvXq3ov6WZ4+Pj\n8fbbbyMsLMyp2lin02HWrFmIj48vs9/q/P6qKGtGRgZee+01pKen47PPPsP//d//ISEhAX5+flV6\nH2LStWsPoSOQyLDPkdg4XfGjVCrL/KEvfezq6lrjeRo3bozffvvNNGVrcHAwDAYDpk2bhujoaItZ\nVSoVAOvvpXS9oymVSty6dcvmfJ6enlYPunQ6ncO+D0OGDEGvXr1MbR0UFITz589jw4YNiI2NLbc9\nSz+x0ul0ZbLbK29iYiLWrVuH9957D61atXL69r03b6tWrZy6fUNDQwEAr776Kl555RU8+uijuH37\ntsU8gPDte3fmGTNmYNq0aZg+fbpTtfHSpUsRFhaGrl27lllX0e+n6mSNj4/H0KFDsWrVKmg0GkRH\nR2P69On4+OOPq/Q+iIiI7MXprvnx8/PDzZs3YTAYTMuysrKgUqnK3DOipty738DAQBQWFsLHxweZ\nmZlm67KystCgQQMAgK+vb5mx+llZWWWGkjiKn59fufnKW6/RaKBUKs3y6/V63Lx50/R8R7i3rVu2\nbInr168DKL89/fz8YDQazdaXDs2xR97SGcMSExMRGxsLwLnb11JewPna9++//8a3335rtqxVq1Yo\nKipCgwYNnLJ9y8ucm5vrVG28a9cufPfdd4iIiEBERAS2b9+O7du3o0OHDhX23+pkvX79Ovr37w+J\nRAKZTIaJEyfixo0bVXoPRERE9uR0xU9ISAjkcrnpomYAOHToEMLCwgTJs2/fPkRHR5vNEJWSkgKN\nRoOOHTviyJEjZtsfPXoUERERAEousC6dAQoomZrXntcbVCQ8PBwpKSlmn94ePnzYNJlEeHi4Wf78\n/HykpKQgIiICEokE7dq1M8t/9OhRuLi4IDg42CF533//fYwdO9Zs2alTp0yTTVhrT61WC19fXzRu\n3Nhs/aFDh9CoUaNqX4+ybNkybNy4EYsXL0a/fv1My521fa3ldcb2TU9Px+TJk80Owk+cOAFvb29E\nRkbi5MmTTte+1jLXr18fn376qVO18fr167F9+3Zs27YN27ZtQ69evdCrVy9s3boV4eHhpskNSlXm\n91dlskokEuTn50MiKblp4pUrV6qUX4yuX8/AtWtXcP16htBRSCTY50hsZLNmzZoldIi7yeVyXL16\nFRs2bEC7du1w4sQJLFy4EK+88gpatmxZ43m8vb3xxRdfIDU1Fa1bt0ZycjLeeustjB8/HoMGDcKH\nH36IjIwMNG7cGCtWrEBqairmzJkDuVyOBg0aYP78+WjQoAGkUini4+PRpk0bjBgxwmF5ly1bhkce\neQT+/v5o3LgxduzYgaNHjyIwMBBJSUnYtWsX3n77bbi7u6NJkyZ49913IZPJUK9ePSQkJMBoNOLl\nl18GUDJ71qJFi9CyZUvk5OTgzTffRN++fdGzZ0+H5HVzc8P7778PV1dX+Pj4YOfOnfjoo4/w1ltv\nwc/Pr8L2LCwsxKpVqxAaGmqaInns2LFmMwfa6uzZs3j55ZcxceJE9OnTB3l5eaavVq1aOV37lpfX\nx8fH6drX19cXP/30E/bt24fQ0FCcOHECb731Fp599ln07dvX6dq3osydO3d2qjb28PBAvXr1TF8/\n/fQTFAoFHnnkEQQEBFTr91d5WT08PPDmm2/i2rVrOHv2LBITEzF16lS0adOmWm3vTAoKimAwGCve\n0EZJSZ8jOfkILlw4B602suIn3EUqlcDVVWEx21ff7YNO2cSeUR0u7fA2FOvyIVe4oWXk4Brff2Fu\nNrqF+aJJk6Y1vu9S5X1P7cVRfU5ozFY1tSFbdUmMd8817CQKCgowe/Zs7N69Gx4eHpgwYQKeeOIJ\nwfKcPXsW8+bNw7Fjx6BWqzFixAg899xzAEo+8Y2Pj0daWhratGmD2bNnm32yvGXLFixZsgS3bt1C\n9+7dMXfuXNSrV89hWUNCQvDpp5+apqi9dOkSXnvtNSQnJyMgIAAzZ85E586dTdv//PPPePvtt5GR\nkYEOHTpgzpw58Pf3N61fvXo1Pv74YxQVFeHBBx/EG2+8Yde7QN+b9/vvv8eSJUtw4cIF+Pv748UX\nXzQbtlVeexoMBiQmJmLz5s2QSqUYPnw4XnzxxWrl++CDD7B48WKzZUajERKJBKdOncLFixcxc+ZM\np2nfivI6W/sCJcOl5s6diwMHDsDV1RWPP/444uLiADhv/y0vszO2canSm5QmJCQAqN7vr4qypqWl\n4cCBAzAYDIiOji4zs1xtl52di+JiQ8Ub2vy6N2A0GiCRSKHR1K/4CXeRy6XQaNQWs015LQE5ntH2\njOpw334wHgU5f0Pl7o3YuJqfKv3W9TRMeywUnaO71Pi+S5X3PbUXR/U5oTFb1dSGbNXllMUPERHV\nXqU3mr3X3fcNqu2c+cCAxY99iKX4qQ5nzsdsVVMbslX7deyQhYiIyGThwoWm/xcVFeHMmTOIioqq\nU8UPERHVTix+iIjIrjZu3Gj2+M8//8SKFSsESkNERHQHix8iInKooKAgnD17VugYtcKPP36DwsIC\nKJUq3H9/b6HjkAiwz5HYsPghIiK7+uyzz8wep6amQq2u/jhtMSgqKoJOp4NUKhM6CokE+xyJDYsf\nIiKyqz/++MPssUajwaJFiwRKU7v07t1f6AgkMuxzJDYsfoiIyK5Kp9ImIiJyNix+iIjIroYOHQqJ\nRGJ1fVJSUg2mISIiuoPFDxER2VXnzp2RlZWFxx57DC4uLti6dSuysrIwatQooaM5vdzcHNONidVq\nd6HjkAiwz5HYsPghIiK7+u2338zO7rRr1w6PPPIIOnXqJGCq2iEp6XPk5uZArXbHmDFxQschEWCf\nI7Fh8UNERHaVk5ODK1euoHHjxgCACxcuwGBwrjuFO6vY2H7Q6/WQyTjzFtUM9jkSGxY/RERkV88/\n/zwefvhhhIWFwWg04q+//sI777wjdKxawd+/qdARSGTY50hsWPwQEZFdDRgwANHR0Thy5AiUSiW0\nWi28vLyEjkVERASp0AGIiKhuKS4uxv/+9z98//33iIyMxH//+18UFxcLHYuIiIjFDxER2de8efNw\n9epVnDhxAhKJBEePHsWcOXOEjlUrHDx4APv3/4iDBw8IHYVEgn2OxIbD3oiIyK6OHDmCLVu2YMiQ\nIXB3d8eKFSswcOBAoWPVCleupCMvLw9ubm5CRyGRYJ8jsWHxQ0REdiWVmg8qKC4uLvemp3TH4MHD\nhI5AIsM+R2LD4oeIiOwqJiYGb775JnJycrBlyxYkJSWhZ8+eQsciIiJi8UNERPb1wgsvICkpCTdv\n3sR3332H/v37Y8SIEULHIiIiYvFDRET2NW7cOKxduxbDhnE4DRERORcWP0REZFc5OTnIzs6GRqMR\nOkqt88knHyA3NwdqtTvGjIkTOg6JAPsciY1TFz9GoxE3buTCYDAKHcWpSKUS1K+vZtvcg+1iGdvF\nOraNZVKpBN7e7lV+vl6vR8+ePdG0aVMolUrT8qSkJHvEq9O6dIlBcXEx5HKn/vNMdQj7HImNU/d0\niUQCqVTCg5J7SKUSto0FbBfL2C7WsW0sk0qrNzPbq6++aqck4hMUFCJ0BBIZ9jkSG6cufoiIqPbY\nuHEjHnvsMXTq1EnoKERERBZJK96EiIioYv/9739N/x83bpyASYiIiCzjmR8iIrILo/HO0MEbN24I\nmKT2OnkyGUVFRXBxcUFoaHuh45AIsM+R2LD4ISIiu5NIqnfdkFgdP34Yubm5UKvVPBAVmKuHD977\naDtkn37l0P3czrqIz9e8Dw8PT4fuxxr2ORIbFj9ERGQXRqMRBQUFMBqNMBgMpv+XcnV1FTBd7TBq\n1FihI9C/FK6eULSIdfh+VPgVxcXFDt+PNexzJDYsfoiIyC5Onz6NiIgIU8Gj1WohkUhgNBohkUhw\n6tQpgRMSEZHYsfghIiK7SE1NFToCERFRuTjbGxERERERiQLP/BARETmJL7/8DHl5uXBzU2PYsNFC\nxyERYJ8jsanymR+dToeBAwfi4MGDVrdJSUnB8OHDodVqMWzYMJw8ebKquyMiIqrzWrcORkhIGFq3\nDhY6CokE+xyJTZXO/Oh0Orz00ks4c+aM1W3y8/MRFxeHwYMHY/78+diwYQMmTpyIb7/9FiqVqsqB\niYiI6iqtNlLoCCQy7HMkNjaf+Tl79iyGDx+O9PT0crfbuXMnXF1dMW3aNLRs2RIzZ86EWq3G119/\nXeWwREREREREVWVz8fP777+jS5cu2Lhxo9n9G+6VnJyMyEjzTxM6dOiAo0eP2p6SiIiIiIiommwe\n9jZy5MhKbXf9+nUEBQWZLfP29i53qBwREZGYnT+fhuLiYsjlcjRv3lLoOCQC7HMkNg6b7a2goAAK\nhcJsmUKhgE6nc9QuiYiIarW9e79Fbm4O1Gp3NG8eJ3QcEgH2ORIbhxU/SqWyTKGj0+lsnuxAJuOt\niO5V2iZsG3NsF8vYLtaxbSxjewhn5MinABgBSAROQmLBPkdi47Dix8/PD5mZmWbLsrKy0KBBg0q/\nhkQiwa+//oro6Gh7x6sTPD1dhY7glNgulrFdrGPbkLO4d8QEkaOxz5HYOKz4CQ8Px+rVq82WHT16\nFM8884xNr5ObW4Ds7Fx7Rqv1ZDIpPD1dcft2PvR6g9BxnAbbxTK2i3VsG8tK26U2iIuLg7e3NxIS\nEgCU3F9u1qxZ+PPPP9G6dWvMmjULoaGhpu137NiBJUuWICsrC926dcPcuXOh0WiEik9ERDXMrsVP\nVlYWPDw8oFQq8eCDD2LRokWYN28eHnvsMWzYsAF5eXno16+fTa+p1xtRXMyDEkv0egPbxgK2i2Vs\nF+vYNrXTzp078dNPP+Hhhx8GUPH95ZKTk/H6669jzpw5CA4Oxty5czFjxgz85z//EfidEBFRTanW\nwG6JxHx8aPfu3fHVV18BANzd3fGf//wHhw4dwtChQ3HixAmsXr2aNzglIqJqu3XrFhITE9G+fXvT\nsoruL/fZZ5+hX79+GDRoEIKCgpCYmIi9e/fi8uXLQr2NMnbt2oJNmzZg164tQkchkWCfI7Gp1pmf\nU6dOmT1OTU01e9yuXTts3ry5OrsgIiIqY8GCBRg8eDCuX79uWlbe/eWGDBmCY8eOYeLEiaZ1DRs2\nRKNGjXD8+HH4+/vXWPbyeHlp4OrqBqVSKXQUEgn2ORIbh13zQ0RE5AgHDhzA4cOHsX37dsTHx5uW\nV3R/uczMTPj6+pqt9/HxwbVr1xwfupK6du0hdAQSGfY5EhsWP0REVGvodDrMmjUL8fHxZWapquj+\ncva8/5wzTgde3tTtnMTYeUkggVwuhVxe9vvm7NPxO3M+Zqua2pCtulj8EBFRrbF06VKEhYWha9eu\nZdZVdH85e91/DnDu6dEtZXNxkQmQhCpDIgW8vNTQaNRWt3Hm/gY4dz5mqxpnzlZddar4+eijD3D0\n6GEsXbrK4vrJkyeiQ4eOGDv26RpORkRE9rBr1y78/fffiIiIAAAUFRUBAHbv3o0BAwaUe385X19f\nZGVllVl/71C4ynDU9OjXr1+DXm+ATCaFr29Dm55b3tTtRUV6oO4ey9RqRgNw82YuJJKy19zUxHT8\njupzQmO2qqkN2aqrThU/QNkZ6IiIqO5Yv349iouLTY8TExMBANOmTcPvv/9u8f5yzz77LABAq9Xi\n8OHDGDJkCADg6tWruHbtGsLDw23O4ajp0bdv34Lc3Byo1e4YMyauSq9hKZvRHuHIIYwouaVHef3J\nkdPxO6rPOQtmqxpnzlZdda74ISKiuqtRo0Zmj9XqkqFCTZs2hUajsXh/ub59+wIARo4ciSeffBLh\n4eEICwvDvHnz0LNnT6eZ6Q0ABg16FEajARKJ8423p7qJfY7Eps719KKiIixY8BZiY7tjxIiH8cMP\n31rc7vLldAwc2Adr15Z8SlhYWIj58+eib9/78cgjD2HHjq3o0SPa6ixA+/btxbhxo9GrVzf07dsT\ns2bNREFBgWn97t27MHr0o4iN7Y5nnx2Pv/46bVq3a9d2PP74MDzwQDc8/fSTOH78qGndsGGDsHLl\nUgwe3Bfjxz+BI0cOYdiwQVi4cD769r0fn3/+qT2aiYiozqno/nJarRZz5szB8uXLMWrUKHh5eWHe\nvHkCpzan0dRH/fo+0GjqCx2FRIJ9jsSmzp35+eOPZLRo0RIfffQZ9u//GbNmzURQUDD8/ZuYtrl5\n8yZefnkKYmMfNF3/8957iTh58gQWL16O4uJiJCTMgdFoeaDA5cvpeOONV/Hyy6+iY8doXLp0AXPm\nvIFt2zZj+PBR+O23A5g/fy5efPH/EBkZhS+//C+mT38JX3yxFXv2fIXFixMxbdoMhISEYufObXjl\nlSnYsGEzfHxKxqV/883XeO+9FTAYDLh9+xauXbuKoiIdPvxwPVxcXBzfiEREtURCQoLZ44ruLzdk\nyBDTsDciIhKfOnfmp0EDX7z88qsICGiGkSMfR3h4BHbs2Gpan5+fh2nTpiI0NBRTp77877J87N69\nCy+9NB0hIaFo1y4cL7wwzeo+jEYjXnzx/zBgwGA0bNgQUVHRiIyMwrlzaQCAbds2o3fvvhg06GH4\n+zfB88+/gNjYPrh9+xaSkjZi+PCR6NOnH5o2DcAzzzyPwMDW2LTpC9PrP/hgf7Ro0RKBga0AlFzH\n9PjjT8Hfvwl8ff0c0WxERERERHVenTvz06pVEGSyO1N6BgUF4/z5c6bHSUkbodfrERkZZVp24cJ5\nFBcXIzi4rWlZWFg7q2d+mjRpChcXF3z66UdISzuLc+fScP58Gh58sD8A4OLFCxgy5FHT9nK5HM89\nN/XffZ3DuHHmFxSGhrbDhQvnTY8bNjQf025tGRER1S0//vgNCgsLoFSqcP/9vYWOQyLAPkdiU+fO\n/Nx7AySj0WA2VKxNm2DMnj0PGzd+hosXz//7HNm/2xrvep71uXH++utPPPHEY7hw4Ry02g6YMeNN\nPPBAH9N6udx6TalQKMvMSGcwGGAw6O/aRnHv0zjcjYhIBIqKiqDT6UxTeBM5GvsciU2dO/OTlnbW\n7HFKykl07NjJ9LhTpy64//4HsGvXdrz77jtYsmQFmjRpCrncBadPn0JERCQAIDX1lNVps/fs+Qpa\nbQe88cZc07JLly6iRYuWAIAmTQJw5sxfpnUGgwGPPfYw4uPnIiCgGf74IxndusWY1p88eQJabYfq\nv3kiIqrVevfuL3QEEhn2ORKbOnfm59q1q3jvvYW4cOE8Pv54Df766zSGDBlaZrvJk19CcvJRfPfd\nN3B1dUX//gPw3nsLkZLyB/744wSWLFkIALBU/3h61sPZs3/h1KmTuHjxApYuXYzU1BTTncMfffQx\n7NmzC199tQOXL6fj/fffBWBEUFAwHntsNDZt+gK7d+/CpUsXsXLlUpw9+xcGDuQFuEREREREjlTn\nzvx06dINt2/fwrhxo9GokT8WLFgMb28fAOY3QG3aNADDho3A8uXvoWvX7pg06QUsXJiAF16YBHd3\ndzz88DCsXr3C4nCzYcNG4MyZ03jxxUlQKJQID4/A2LFP47vv9gAAwsMj8PLLr+Ljj9fgxo2/0aZN\nCBYsWAyFQoFevWKRnf031qxZhRs3stC6dRssXrwcTZsG/PvqvEkrEREREZEjSIzlXdwzcm3FAAAg\nAElEQVQiMIlEgj17foBWG+nwff3884+Iiupsuh/EqVMnMWnS0/jmm5/NJlBwBnK5FBqNGtnZuXX2\n7rtVwXaxjO1iHdvGstJ2Iesc1Wdyc3NgNBohkUigVrvb9Nzy+vOU1xKQ4xltz6gO9+0H41GQ8zdU\n7t6IjftQ6DgO88+lX/HBW89YvM9OTfyOclSfExqzVU1tyFbt17FDljph7drV+OWXfXj88aeQm5uD\nFSveR0xMD6crfIiIqO5KSvocubk5UKvdMWZMXMVPIKom9jkSGxY//4qPfxuLF7+DceNGw8XFBTEx\n92Py5BeFjkVERCISG9sPer2eH7xRjWGfI7Fh8fOvZs2a4733Vggdg4iIRMzfv6nQEUhk2OdIbOrc\nbG9ERERERESWsPghIiIiIiJR4LA3IiIiJ3Hw4AHodIVQKJSIiuoidBwSAfY5EhsWP0RERE7iypV0\n5OXlwc3NTegoJBLscyQ2LH6IiIicxODBw4SOQCLDPkdiY/M1PzqdDq+99hqioqIQExODtWvXWt32\nm2++wUMPPYSIiAiMHj0aKSkp1QpLRERERERUVTYXPwsWLEBKSgrWrVuH+Ph4LFu2DHv27Cmz3Zkz\nZ/DKK69g4sSJ2LZtG4KDgxEXF4fCwkK7BCciIiIiIrKFTcVPfn4+kpKS8PrrryM4OBixsbGYMGEC\n1q9fX2bbffv2oXXr1hg0aBCaNm2Kl156CVlZWThz5ozdwhMREREREVWWTdf8pKamQq/XQ6vVmpZF\nRkZi1apVZbb18vLCmTNncOTIEURERGDTpk3w8PBAQEBA9VMTERHVQZ988gFyc3OgVrtjzJg4oeOQ\nCLDPkdjYVPxkZmbCy8sLcvmdp3l7e6OwsBDZ2dnQaDSm5f3798f333+PUaNGQSaTQSqV4oMPPoCH\nh4f90hMREdUhXbrEoLi42OzvLJEjsc+R2NjU0/Pz86FQKMyWlT7W6XRmy2/evImsrCzEx8cjPDwc\nGzZswKuvvor//e9/qF+/fjVjExER1T1BQSFCRyCRYZ8jsbGp+FEqlWWKnNLHrq6uZssXLlyINm3a\nYOTIkQCAOXPmoF+/fti8eTMmTJhQ6X3KZBLI5TbPy1CnyWRSs3+pBNvFMraLdWwby9geRERUV9lU\n/Pj5+eHmzZswGAyQSkv+OGZlZUGlUsHT09Ns25MnT+LJJ580PZZIJAgODsaVK1dsCqhWq6DRqG16\njlh4erpWvJEIsV0sY7tYx7YhIiISB5uKn5CQEMjlchw7dgwdOnQAABw6dAhhYWFltvX19S0zs9u5\nc+fQvn17mwLm5hYgOzvXpufUdTKZFJ6errh9Ox96vUHoOE6D7WIZ28U6to1lpe1CNe/kyWQUFRXB\nxcUFoaG2/b0kqgr2ORIbm4oflUqFwYMHIz4+HvPmzUNGRgbWrl2L+fPnAyg5C+Th4QGlUolhw4bh\ntddeQ1hYGCIiIvDFF1/g6tWrGDJkiE0B9Xojiot5UGKJXm9g21jAdrGM7WId24acxfHjh5Gbmwu1\nWs0DUaoR7HMkNjZP7TFjxgzMnj0bY8aMgYeHB6ZOnYrY2FgAQPfu3TF//nwMGTIE/fv3R35+Plat\nWoWMjAyEhITg008/5WQHREREVowaNVboCCQy7HMkNjYXPyqVCgkJCUhISCizLjU11ezx0KFDMXTo\n0KqnIyIiIiIishNO6UNERERERKLA4oeIiIiIiESBt/MlIiJyEl9++Rny8nLh5qbGsGGjhY5DIsA+\nR2LD4oeIiMhJtG4dDJ2uEAqFUugoJBLscyQ2LH6IiIichFYbKXQEEhn2ORIbXvNDRERERESiwOKH\niIiIiIhEgcPeiIiInMT582koLi6GXC5H8+YthY5DIsA+R2LD4oeIiMhJ7N37LXJzc6BWu6N58zih\n45AIsM+R2LD4ISIichIjRz4FwAhAInASEgv2ORIbFj9EREROQqFQCB2BRIZ9jsSGxQ8REZFAln/w\nEVLSrtrltaQSCeRyGYqL9TAYjWbrsnMlUHnaZTdERLUaix8iIiKBXMm4gXyvLg7fj8rL4bsgIqoV\nWPwQERE5iVauaZBLilFslONMPmfeIsfbtWsL8vPz4erqiv79hwgdh8jhWPwQERE5iQKDEjKJHHqj\nTOgoJBJeXhq4urpBqVQKHYWoRrD4ISIichLphf5CRyCR6dq1h9ARiGqUVOgARERERERENYHFDxER\nERERiQKHvRERETkJN2keJBIjjEYJ8gxuQschEbh+PQMGgx5SqQy+vn5CxyFyOBY/RERETqKV2zko\npEXQGVyQnBMqdBwSga++2orc3Byo1e4YMyZO6DhEDsfih4iIyEmczguEBEYYIRE6ConEoEGPwmg0\nQCLhlRAkDix+iIiInEShQSV0BBIZjaa+0BGIahTLfCIiIiIiEgUWP0REREREJAo2Fz86nQ6vvfYa\noqKiEBMTg7Vr11rd9vTp0xg1ahTCw8MxaNAg/Pbbb9UKS0REVJc1U11CS9dzaKa6JHQUEokff/wG\nu3dvx48/fiN0FKIaYXPxs2DBAqSkpGDdunWIj4/HsmXLsGfPnjLb5eTkYPz48WjdujV27NiB3r17\n4/nnn8eNGzfsEpyIiKiukUoMkEkMkEoMQkchkSgqKoJOp0NRUZHQUYhqhE0THuTn5yMpKQkffvgh\ngoODERwcjAkTJmD9+vXo06eP2babN2+GWq3G7NmzAQCTJ0/GTz/9hD/++AP33Xef/d4BERFRHXEu\nv5nQEUhkevfuL3QEohplU/GTmpoKvV4PrVZrWhYZGYlVq1aV2fbgwYPo1auX2bIvv/yyijGJiIiI\niIiqx6Zhb5mZmfDy8oJcfqdm8vb2RmFhIbKzs822vXTpEjQaDd588010794dI0aMwJEjR+yTmoiI\niIiIyEY2D3tTKBRmy0of63Q6s+V5eXlYs2YNnnzySaxZswY7duzA+PHj8fXXX8PPz6/S+5TJJJDL\nOSnd3WQyqdm/VILtYhnbxTq2jWVsD+G4SIoAGAFIUGR0EToOiUBubg6MRiMkEgnUaneh4xA5nE3F\nj1KpLFPklD52dXU1Wy6TyRASEoLnn38eABAcHIz9+/dj69atiIuLq/Q+1WoVNBq1LTFFw9PTteKN\nRIjtYhnbxTq2DTmLEPWfUEiLoDO4IDknVOg4JAJJSZ8jNzcHarU7xoyp/PEZUW1lU/Hj5+eHmzdv\nwmAwQCot+WQwKysLKpUKnp6eZts2aNAALVu2NFvWvHlzXL161aaAubkFyM7Otek5dZ1MJoWnpytu\n386HXs8ZgUqxXSxju1jHtrGstF2o5p3LD4AERhghEToKiURsbD/o9XrIZDKhoxDVCJuKn5CQEMjl\nchw7dgwdOnQAABw6dAhhYWFlttVqtTh48KDZsrS0NAwcONCmgHq9EcXFPCixRK83sG0sYLtYxnax\njm1DzuIfvYfQEUhk/P2bCh2BqEbZNLBbpVJh8ODBiI+Px4kTJ/Dtt99i7dq1GDNmDICSs0CFhYUA\ngBEjRuD06dNYtmwZLl68iCVLliA9PR2DBg2y/7sgIiIiIiKqgM1Xtc6YMQNhYWEYM2YM5s6di6lT\npyI2NhYA0L17d3z11VcAgMaNG+PDDz/E999/j4EDB2Lv3r1YvXo1fH197fsOiIiIiIiIKsGmYW9A\nydmfhIQEJCQklFmXmppq9jgiIgKbN2+uejoiIiIRaaS4BplED71Rhqu6hkLHIRE4ePAAdLpCKBRK\nREV1EToOkcPZXPwQERGRY3jIc+AiKUaRUY6ruoq3J6quK1fSkZeXBzc3N6GjENUIFj9ERERO4s+8\nVkJHIJEZPHiY0BGIahTvZEdERERERKLA4oeIiIiIiESBxQ8REREREYkCr/khIiJyEu3dT0IhLYLO\n4ILknFCh45AIfPLJB8jNzYFa7Y4xY+KEjkPkcCx+iIiInER6QWNIJQYYjByYQTWjS5cYFBcXQy7n\nISGJA3s6ERGRk7hRrBE6AolMUFCI0BGIahSLHyIiIiKBGA3AN999D3cPjzLrZFIJ3NVK5OQWQm8w\nVms/7m5q3BfTvVqvQVQXsPghIiIiEojavwM2HfwbQKFD91N8/WsWP0Rg8UNEROQ0fFyyIJMYoDdK\nkVXkI3QcqgEyuQJqTSOH70eX42lx+cmTySgqKoKLiwtCQ9s7PAeR0Fj8EBEROQk/RaZptjcWP1QT\njh8/jNzcXKjVahY/JAosfoiIiJzEyVxefE41a9SosUJHIKpRnEuTiIiIiIhEgcUPERERERGJAosf\nIiIiIiISBV7zQ0RE5CRC1KfhIilGkVGOU7lthI5DIvDll58hLy8Xbm5qDBs2Wug4RA7H4oeIiMhJ\n3CjSQCbRQ2+UCR2FRKJ162DodIVQKJRCRyGqERz2RkREtUpGRgamTJmC6Oho9OjRA/Pnz4dOpwMA\npKenY+zYsYiIiMCAAQOwf/9+s+f+8ssvGDhwILRaLZ566ilcunRJiLdgVYbOF1cKGyFD5yt0FBIJ\nrTYSnTp1hVYbKXQUohrB4oeIiGqVKVOmoLCwEJ9//jkWLVqEH374AUuWLAEAPPfcc/D19cWmTZsw\naNAgPP/887h27RoA4OrVq5g0aRKGDh2KTZs2QaPRYNKkSUK+FSIiqmEsfoiIqNZIS0tDcnIyEhIS\nEBgYiMjISEyZMgU7duzAr7/+ivT0dMyZMwctW7ZEXFwctFotkpKSAABffPEF2rVrh6eeegqBgYFI\nSEjA5cuXcfDgQYHfFRER1RQWP0REVGs0aNAAq1evRv369c2W//PPPzh+/DhCQ0OhVN65diEyMhLH\njh0DACQnJyMqKsq0TqVSoW3btjh69GjNhK+EevJb0Mhvop78ltBRSCTOn0/DmTN/4vz5NKGjENUI\nTnhARES1hoeHB7p37256bDQasX79enTp0gWZmZnw9TW/Vsbb2xsZGRkAgOvXr5dZ7+PjY1rvDJqp\n0qGQFkFncEFyTj2h45AI7N37LXJzc6BWu6N58zih4xA5nM3Fj06nw6xZs/DNN99ApVJh3LhxGDt2\nbLnPSU9Px8CBA/HBBx+YfepGRERUHe+88w5OnTqFpKQkrF27FgqFwmy9QqEwTYZQUFBQ7npbyGT2\nGTghkZg//iMn2C6vS1SGBJDLy/bbJ54YB6PRCIlEYnF9eUp/Duz182BPzFY1tSFbddlc/CxYsAAp\nKSlYt24d0tPTMX36dPj7+6NPnz5WnzNr1iwUFBRUKygREdHdEhMTsW7dOrz33nto1aoVlEolbt0y\nHy6m0+mgUqkAAEqlskyho9Pp4OnpafO+PT1dqx78LkqlHNDfeWwAp7gmx5DJpNBo1BbWWFpmG3v9\nPDgCs1WNM2erLpuKn/z8fCQlJeHDDz9EcHAwgoODMWHCBKxfv95q8bNt2zbk5eXZJSwREREAzJ07\nFxs3bkRiYiJiY2MBAH5+fjhz5ozZdllZWWjQoIFpfWZmZpn1ISEhNu//9u186PWGKqa/o7CwmAPQ\nqUbo9QZkZ+fa9TVlMik8PV3t9vNgT8xWNbUhW3XZ9Cs3NTUVer0eWq3WtCwyMhKrVq2yuH12djbe\nffddfPjhhxgwYED1khIREQFYtmwZNm7ciMWLF6N3796m5eHh4Vi9ejV0Op1peNvhw4fRsWNH0/oj\nR46Yts/Pz0dKSgomT55scwa93oDi4uofGBiN1X4Josoxwi591hJ7/Tw4ArNVjTNnqy6bBs9lZmbC\ny8sLcvmdmsnb2xuFhYXIzs4us/38+fPx8MMPo1WrVtVPSkREonf27FmsXLkScXFxiIiIQFZWlumr\nU6dOaNSoEV599VWcOXMGH3zwAU6cOIFHH30UADB06FAcOXIEq1evxpkzZzBjxgwEBASgU6dOAr+r\nO1q5piHY7U+0cuXMW1Qzdu3agk2bNmDXri1CRyGqETYPe7N0sSiAMuOof/nlFxw9ehRz586tVkCZ\nzPYL8Oo6Z74YTUhsF8vYLtaxbSxz5vb47rvvYDAYsHLlSqxcuRIATBdrnzp1CsuXL8fMmTMxdOhQ\nBAQEYPny5WjYsCEAwN/fH0uXLsXbb7+NFStWoEOHDli2bJmQb6eMAoMSMokceiOv/aGa4eWlgaur\nm9kU8UR1mU3Fj7WLRQHA1fXOGLzCwkLMmjUL8fHxZYolW6nVKisX6FFdvhitOtgulrFdrGPb1B5x\ncXGIi7M+HW9AQADWrVtndX1MTAy+/vprR0Szi/RCf6EjkMh07dpD6AhENcqm4sfPzw83b96EwWCA\nVFryyWBWVhZUqv9v7/7Doirz/oG/5wcwgLAiCZlhWW4yyhMDiGbrjy4jzdbCNO3XlmmGmQnPdm3f\n1LVG0xT7ZV25GfrssqmbXxUtrTTFb9tamyWghiugoqZQiqCiAgMDM+f7hw+jI8zIwDD3gfv9uq6u\nnHvOnPOem3vuM5+Zc84YnK6Wk5+fj5KSEsycORPKVQc0P/fccxg7dizmzZvX4m1WV9d6/QS9jk7N\nJ6OJxH5pHvvFNfZN87x1UikREZHaeFT8GI1G6PV67N+/H/Hx8QCA3NxcxMTEOC0XGxuLHTt2OLXd\nd999eOONNzB48GCPAtpsSqc94aqtOvPJaG3Bfmke+8U19g0REZEcPCp+DAYDkpOTYTabsWjRIpSV\nlSEzMxPp6ekALn8LFBISgoCAAERFRTV5fEREBLp16+ad5ERERJ1MkLYGGo0CRdGgxh4kOg5J4MyZ\nMtjtNmi1OkRERIqOQ9TuPD6rdfbs2YiJicGkSZOwYMECpKWlOX5jYciQIdi2bVuzj9Nc+zPWRERE\n5KRP0HEYg4+gT9Bx0VFIEtu2bcamTf8X27ZtFh2FyCc8/mk1g8GAxYsXY/HixU3uKyoqcvm4wsJC\nTzdFREQklUM1t0MDBQr4gSH5xkMPPQJFsUOjUe9VHom8ib8rTUREpBJ1doPoCCSZsDCejkByYZlP\nRERERERSYPFDRERERERS4GFvREREKnGLoQQ6TQNsih4napteNZXI2775Jht1dbUICDDgnnvuEx2H\nqN2x+CEiIlIJrcYOncYOBfzdKfKN+vp6WK1WaLU60VGIfILFDxERkUoct9wiOgJJ5r77HhAdgcin\neM4PERERERFJgcUPERERERFJgYe9ERERqYSfph6AAkCDesVPdBySQHV1FRRFgUajQXBwF9FxiNod\nix8iIiKVMAYfhr+2Hla7H/Kr+ouOQxLIyvoE1dVVCA7ugkmTUkTHIWp3LH6IiIhU4rilFzRQoEAj\nOgpJIilpNGw2G3Q6Xu2N5MDih4iISCUu2UJERyDJ9OzJ35MiufCCB0REREREJAUWP0REREREJAUe\n9kZERKQSPfxPQ6exwabocMp6o+g4JIGcnN2wWuvg7x+AxMTBouMQtTsWP0RERCoRoq+Cn6YB9Yoe\np6yi05AMfv21FDU1NQgKChIdhcgnWPwQERGpxOGaPqIjkGSSkyeIjkDkUzznh4iIiIiIpMDih4iI\niIiIpMDih4iIiIiIpMBzfoiIiFTizi4H4a+th9Xuh/yq/qLjUCdirbdiw8ZPm7SfLT8Ju90GrVaH\n8O69PFqnVqdBcJA/qmussNsUAECPHjdiyN28ahypF4sfIiIilSitvQlajR12hQdmkHcFRg3Dpr1V\nTdq7B/4GWo0Cu6JBeUlDK9Zc73SrS/VWFj+kaix+iIiIVOJcQ5joCNRJ6fwCEOgX0KS9CuGOfweG\ntH07fg2Gtq+EqB15/NGS1WrFnDlzkJiYiKFDhyIzM9Plst988w3Gjh2LuLg4JCcn4+uvv25TWCIi\nIiIiotbyuPhZsmQJCgoKsHr1apjNZixbtgw7duxostyhQ4cwc+ZMTJgwAVu2bMHEiRORmpqKQ4cO\neSU4ERERERGRJzwqfiwWC7KysjB37lxER0cjKSkJU6dOxZo1a5os+8UXX2Dw4MF48sknERUVhSef\nfBKDBg3Ctm3bvBaeiIioM7nBrwKR/mdwg1+F6CgkCY45ko1H5/wUFRXBZrPBZDI52hISEpCRkdFk\n2Ycffhj19fVN2quqmp5sR0RERECkf7njam8V9TeIjkMS4Jgj2XhU/JSXl6Nr167Q6688LDw8HHV1\ndTh//jzCwq6cqHnbbbc5PfbIkSP44Ycf8MQTT7QxMhERUed0sNooOgJJhmOOZONR8WOxWODv7+/U\n1njbarW6fNy5c+cwc+ZMJCQk4N577/UooE6ngV7PS35eTafTOv2fLmO/NI/94hr7pnnsDyIi6qw8\nKn4CAgKaFDmNtwMDA5t9TEVFBSZPngyNRoP333/f44DBwQaEhQV7/DgZhIY23+eyY780j/3iGvuG\niIhIDh4VP5GRkaisrITdbodWe/mTwYqKChgMBoSGhjZZvqysDE8//TR0Oh1Wr17tdFhcS1VX1+L8\n+WqPH9eZ6XRahIYG4uJFC2w2u+g4qsF+aR77xTX2TfMa+4WIiKiz8aj4MRqN0Ov12L9/P+Lj4wEA\nubm5iImJabKsxWLB1KlT4efnh1WrVqFbt26tCmizKWho4JuS5thsdvZNM9gvzWO/uMa+IbUwBh+C\nn6YB9YoehdV9RcchCXDMkWw8Kn4MBgOSk5NhNpuxaNEilJWVITMzE+np6QAufwsUEhKCgIAAfPTR\nRygtLcWqVatgt9tRUVHhWEeXLl28/0yIiIg6uHP1YdBpbLApOtFRSBIccyQbj4ofAJg9ezbmz5+P\nSZMmISQkBGlpaUhKSgIADBkyBOnp6Rg7dix27NiB2tpaTJw40enxY8eOxeLFi72TnoiIqBMps0aI\njkCS4Zgj2Xhc/BgMBixevLjZAqaoqMjxb/6YKRERERERqQmvZ0pERERERFLw+JsfIiIiah+/0V+A\nFgrs0OBCw29ExyEJcMyRbFj8EBERqcQthlL4a+thtfshv4pvRKn9ccyRbFj8EBERqcR/qqJFRyDJ\ncMyRbFj8EBERqYQdvNww+RbHHMmGFzwgIiIiIiIpsPghIiIiIiIp8LA3IiIilegTeAx6TQMaFD2K\nLbeJjkMS4Jgj2bD4ISIiUolaewB0Gj1sCs/DIN/gmCPZsPghIiJSidK6nqIjkGQ45kg2POeHiIiI\niIikwOKHiIiIiIikwMPeiIiIVCJIWwONRoGiaFBjDxIdhyTAMUey6RDf/OTl5SAiIhQREaHIy8sR\nHYeIiKhd9Ak6DmPwEfQJOi46CkmCY45kw29+iIiIVOJQze3QQIECjegoJAmOOZINix8iIiKVqLMb\nREcgyXDMkWw6xGFvREREREREbcXih4iIiIiIpMDD3oiIiFTiFkMJdJoG2BQ9TtRGiY5DEuCYI9mw\n+CEiIlIJrcYOncYOBXbRUUgSHHMkGxY/REREKnHccovoCCQZjjmSDc/5ISIiIiIiKfCbHyIiIiLy\nisqLFsxd+Ha7bycmug8ee2Rsu2+HOh+Pix+r1Yp58+YhOzsbBoMBU6ZMweTJk5tdtqCgAPPmzcPh\nw4fx29/+FvPmzUP//v3bHJqIiKgz8tPUA1AAaFCv+ImOQxLw9pgz3DICv7Z5LdfXcDAXjz3igw1R\np+PxYW9LlixBQUEBVq9eDbPZjGXLlmHHjh1NlrNYLEhJSUFiYiI2bdoEk8mEadOmoba21ivBO7K8\nvBxERIQiIiIUeXk5ouOQQBwLvsO+po7AGHwYsSEFMAYfFh2FJMExR7LxqPixWCzIysrC3LlzER0d\njaSkJEydOhVr1qxpsuyXX36JwMBAvPzyy7jtttvw5z//GcHBwfjqq6+8Fl7NOtIbLV9n7Uh94w2d\n4fl2hudA1BEct/TC4erbcNzSS3QUkgTHHMnGo+KnqKgINpsNJpPJ0ZaQkID8/Pwmy+bn5yMhIcGp\nLT4+Hvv27Wtl1I7t6jePRUWFouN0eB31zXhRUWGHzC0zEWOto45vartLthBctIXiki1EdBSSBMcc\nycaj4qe8vBxdu3aFXn/lVKHw8HDU1dXh/PnzTsueOXMGERERTm3h4eEoKytrQ1zytY7yJiwvLwfd\nunWBRqNBbq56c1LLdJRxdz2d5XkQERF1Fh5d8MBiscDf39+prfG21Wp1aq+trW122WuXc28gCgtD\nYLcrAAYCAIqKQuHtK3QXFRXij3+cAQBYuvQviI42emGdoXDODMftEyci0Zbno9NpERoK/PhjEdLS\nXnDkBtCq59E0q7bZ+7ZvP4fRo5NatH53fepuey3lrn8LC0Ngs7Vsne3xt2+6jStZm/7tAdd9751s\njePl4kUtbDZ3OZ23B1wZT//93y+7zNkevDFGLj+20O1zaEnftCVLax/rrefvvM6WjyedTov77mvz\nJomIiFRHoyiK0tKFv/rqKyxcuBDfffedo+3o0aMYM2YMfvzxR4SGhjrap02bhr59++Kll15ytL39\n9ts4duwYPvzww5aF07Q0GREReVPL9wxyOn++Gg0N9jav588L3sYpv3jH7R7+p6HT2GBTdDhlvbHN\n6+/Idq54FrVVZ2HoEo6klL+KjtNpddQxF1GXi3Tz/3F5v16vRVhYsNdeq97EbK3TmK3N6/Fk4cjI\nSFRWVsJut0OrvfxJZEVFBQwGg1Ph07hseXm5U1tFRQW6d+/exshERESdU4i+Cn6aBtQrepzy5EAJ\nolbimCPZeFT8GI1G6PV67N+/H/Hxlz+pys3NRUxMTJNlY2NjsXLlSqe2ffv24fnnn2/x9n74Aaiu\nroXN5vojyMLCAsehX3/848tYuvQtAMD7738Io7Ffi7flap2erKc9HtfcfTqdBsHBBrd909osrdUe\n2/N0nVf3y3/+c9Cnz98b2rsPly1bDptNcdoGAJ+OdW+vo63rdPVa8vQ1Kcq1WYDW/T2vpdNpABi8\nkpE8c7imj+gIJBmOOZKNR8WPwWBAcnIyzGYzFi1ahLKyMmRmZiI9PR3A5W92QkJCEBAQgFGjRuHd\nd9/FokWL8Oijj2Lt2rWoqanB6NGjW7y9QYOA8+dtbr92s9kuANgDAOjVq8zx74ctzn8AABFpSURB\nVDvuuACTqcGTp+dgMt2Bxx/feVVLy9ZzdRZPtu/ucc3dd/lrP/d909osrdUe2/P073B1v/zXf7Xu\nbyhSa8edO85/l4swmRKctnH5JHzvjtmWav/ne/1crl5L7rL5+rXlzrVZEhISvdKnen37ntNFREQk\nikfFDwDMnj0b8+fPx6RJkxASEoK0tDQkJV0+CX7IkCFIT0/H2LFj0aVLF3z00Ucwm81Yv349+vbt\ni5UrV8Jg8O6niQkJiThz5qLj9pNPPu3V9fvCtc9BreukjichIRHnzlWp9vhdb+O4JyIiInc8uuCB\nCDK8YfOUmk9GE4n90jx3/ZKXl4PRo+8FAGzb9v+QkJAoIqIwHDPN89ZJpZ1Ze13wgK7gBQ/Inepf\ncqC1Vbu8X4PLV6602exoyxvdwTE9kfrCtDasoSk173s6QrY2r8cLWYiog+I3JUTqcmeXg/DX1sNq\n90N+VX/RcUgCHXXMBfds2Yd1fm3cTnXNgTaugdSGxQ8REZFKlNbeBK3GDrvC867INzjmSDYsfoiI\niFTiXEOY6AgkGY45kg3LfCIiIiIikgKLHyIiIiIikgIPeyMiIlKJG/wqoNPYYVO0qKi/QXQckgDH\nHMmG3/wQEZFUrFYr5syZg8TERAwdOhSZmZmiIzlE+pfjpoDTiPQvFx2FJMExR7LhNz9ERCSVJUuW\noKCgAKtXr0ZpaSleeeUV9OzZEyNHjhQdDQerjaIjkGQ45kg2LH6IiEgaFosFWVlZ+Otf/4ro6GhE\nR0dj6tSpWLNmjSqKHyJSl4ry0zhwIN+r69TrtQgNDcTFixbHD4nefnsfBAUFeXU71DwWP0REJI2i\noiLYbDaYTCZHW0JCAjIyMgSmIiK1OlF/G8z/853X16sBoPzvv+uqKzFlTH+MH5vs9e1QUyx+iIhI\nGuXl5ejatSv0+iu7v/DwcNTV1eH8+fMIC+NvnhDRFaERt7f7NiyXeL6VL7H4ISIiaVgsFvj7+zu1\nNd62Wq0tXo9O553rBWk0zreNwYfgp2lAvaJHYXVfr2yDyB2OOfE0Gh12ZGfj11On23U7ZWWncfx0\nDQyBwW7CADqtFja7/cpXUx66dPYkNn3yt9Y92A1vzbuqL37Cwtz8gSTHvmke+6V57BfX2DfyCAgI\naFLkNN4ODAxs8XpCQ1u+rDsZ78/3yno6pXd4CBDJZLLoANLgpa6JiEgakZGRqKyshN1ud7RVVFTA\nYDAgNDRUYDIiIvIFFj9ERCQNo9EIvV6P/fv3O9pyc3MRExMjMBUREfkKix8iIpKGwWBAcnIyzGYz\nDhw4gJ07dyIzMxOTJk0SHY2IiHxAoyhKK09nIiIi6nhqa2sxf/58bN++HSEhIZg6dSqeeuop0bGI\niMgHWPwQEREREZEUeNgbERERERFJgcUPERERERFJgcUPERERERFJgcUPERERERFJgcUPERERERFJ\nQZXFj9VqxZw5c5CYmIihQ4ciMzNTdCQhysrKkJqaikGDBmH48OFIT0+H1WoFAJSWlmLy5MmIi4vD\nmDFj8O9//1twWjFSUlIwe/Zsx+2CggJMnDgRJpMJEyZMwMGDBwWm8z2r1Yr58+dj4MCBGDJkCJYu\nXeq4T/a+OX36NJ5//nkkJCTg3nvvxccff+y4T8a+sVqtePDBB5GTk+Nou9688v333+PBBx+EyWTC\nM888g5KSEl/HFkrN+yZ3+wu1uHa+VgN3c6Zo7uYsUVozb4jMtn//fjz22GOIi4vD6NGjsWHDBiHZ\nXOVrVFVVhaFDh+Kzzz4TkKz5bKdOncJzzz0Hk8mEUaNGYdu2barJlpubi3HjxiEuLg4PP/wwdu/e\n7dE6VVn8LFmyBAUFBVi9ejXMZjOWLVuGHTt2iI7lc6mpqairq8Mnn3yCd999F//85z/x/vvvAwBe\neOEFREREYOPGjXjooYfw4osv4vTp04IT+9aXX36JXbt2OW5bLBakpKQgMTERmzZtgslkwrRp01Bb\nWyswpW8tXLgQu3fvxt/+9je8/fbbWL9+PdavX8++AZCWlobg4GB8+umnmDNnDt577z3s3LlTyr6x\nWq146aWXUFxc7NQ+Y8YMl/PKqVOnMGPGDIwfPx4bN25EWFgYZsyYISK+MGreN7nbX6jBtfO1Wria\nM9XA1ZwlSmvmDZHZKioqkJKSgrvuugubN2/GzJkzsXDhQvzrX//yaTZX+a725ptvoqKiwsepLmsu\nm81mQ0pKCgICAvDZZ59hypQpePnll13m92W2c+fOYfr06XjwwQfx+eef4/7778cLL7yAsrKylq9Y\nUZmamhrlzjvvVHJychxtH374ofLUU08JTOV7R48eVaKjo5WzZ8862r744gtl2LBhyu7du5W4uDil\ntrbWcd8zzzyjfPDBByKiClFZWakMHz5cmTBhgjJr1ixFURRlw4YNSlJSktNyI0eOVD799FMREX2u\nsrJS6d+/v9NrZ8WKFcqcOXOUrKwsqfvmwoULSt++fZUjR4442mbOnKksWLBAur4pLi5WkpOTleTk\nZCU6OlrZs2ePoiiK8v3337udV9577z2nedhisSjx8fGOx3d2at43udtfqEFz87UauJszRXM3Z4nQ\n2nlDZLa1a9cqDzzwgNOyr776qvKnP/3JZ9nc5WuUk5OjjBw5UhkyZIjP9zuusu3cuVNJTExUqqur\nHcvOmDFDWb9+vfBs2dnZyl133eW07MCBA5Xt27e3eN2q++anqKgINpsNJpPJ0ZaQkID8/HyBqXyv\ne/fuWLlyJbp16+bUfunSJfz000/o378/AgICHO0JCQnYv3+/r2MKs2TJEiQnJ+P22293tOXn5yMh\nIcFpufj4eOzbt8/X8YTIy8tDSEgIBgwY4Gh77rnn8MYbb+Cnn36Sum8MBgMCAwOxceNGNDQ04Nix\nY9i7dy+MRqN0fbNnzx4MHjwY69atg3LVb1zn5+e7nVfy8/ORmJjouM9gMKBfv36dtp+upeZ9U3P7\nC0VRcOnSJYGprmhuvlYDd3OmaK7mrH79+gnJ09p5Q2S2YcOGYfHixU2W9/XrwlU+AKivr4fZbIbZ\nbIafn59Pc7nLlpOTg7vuugtBQUGOtmXLlmHChAnCs3Xt2hWVlZXIzs4GAOzcuRM1NTW44447Wrxu\nvdfTtlF5eTm6du0Kvf5KtPDwcNTV1eH8+fMICwsTmM53QkJCMGTIEMdtRVGwZs0aDB48GOXl5YiI\niHBaPjw83LOv/Dqw3bt3Iy8vD59//jnMZrOj/cyZM00Gf3h4uM+/phWlpKQEPXv2xGeffYaMjAzU\n19dj3LhxmD59uvR94+/vj9deew2vv/46Vq1aBZvNhnHjxmH8+PHIzs6Wqm8ef/zxZtuvN6+cOXOm\nyf033HCDNPOOmvdNrvYXd999t7BMjVzN12rgbs7UaDRCs7mas8aNGyckT2vnDV9wle2mm27CTTfd\n5Lh99uxZbN26Fampqb6KBsB1PgBYvnw5+vXrJ+y16ipbSUkJbr75ZrzzzjvYvHkzunXrhhdffBFJ\nSUnCsw0YMABPPPEEUlNTodVqYbfbsXjxYtx6660tXrfqih+LxQJ/f3+ntsbbajt505fefPNNFBYW\nIisrC5mZmc32kQz9Y7VaMW/ePJjN5iZ9UFtbK22/AEBNTQ1+/vlnbNiwAenp6SgvL8drr72GoKAg\n6fsGAI4ePYoRI0bg2WefxeHDh7FgwQIMHjyYffO/XM29jf0gez91pH3Tm2++iaKiImzcuFFoDnfz\ntRo0N2e++uqrCAoKwjPPPCM6XrNz1t13340xY8aIjuZwvXlDLerq6jBz5kxERETg0UcfFR0HAFBc\nXIz169djy5YtoqM0UVNTg02bNuGBBx5ARkYGfvjhB6SlpWH9+vXo37+/0GzV1dUoKSlBamoq7rnn\nHuzYsQMLFixAbGwsevfu3aJ1qK74CQgIaPKiabwdGBgoIpJwb731FlavXo333nsPffr0QUBAAC5c\nuOC0jNVqhcFgEJTQdz744APExMQ0+ymJq7EjQ78AgE6nQ3V1Nd555x3ceOONAIBffvkFn3zyCXr3\n7i113+zevRtZWVnYtWsX/P390a9fP5w+fRrLly9Hr169pO6bRtebV1y9vkJDQ32WUaSOsm+6en8h\n+jAzd/O1GriaM9euXSu8+HE3Z6mp+OkI70dqamowffp0nDx5EmvXrnU6RE+kV199FampqU1Ob1AD\nnU6HsLAwzJ8/HwBgNBqRm5uLdevW4fXXXxeabeXKlQCA6dOnA4Dj8PVVq1a1+Ntl1RU/kZGRqKys\nhN1uh1Z7+ZSkiooKGAwGaXayV1uwYAHWrVuHt956y/F1Y2RkZJNDcioqKtC9e3cREX1q69atOHv2\nLOLi4gBcPl4WALZv344xY8agvLzcaXlZ+gUAIiIiEBAQ4NiJA0Dv3r1x+vRpDBo0SOq+OXjwIG69\n9VanTyiNRiM++ugjDBgwQOq+aXS9eSUyMrLZfjIajT7LKFJH2Dc1t78Qyd18vXfvXpHRALifM0Vz\nNWdlZGQITNWU2t+PVFVVYerUqSgtLcXHH3+MqKgo0ZEAAL/++iv27duHQ4cOOc5Lqq2thdlsxtat\nW7FixQqh+bp37+6Y5xr17t0bhw8fFpToioKCAkRHRzu1GY1Gjw5VV90FD4xGI/R6vdPJcrm5uYiJ\niRGYSoxly5Zh3bp1WLp0KUaPHu1oj42NRUFBgdOnkHl5eU4n4nZWa9asweeff44tW7Zgy5YtGDFi\nBEaMGIHNmzcjNja2ycnX+/btk6JfAMBkMqGurg4nTpxwtB09ehQ333wzTCZTkzcbMvVNREQETpw4\ngYaGBkfbsWPHEBUVJX3fNLrevBIbG+vUTxaLBQUFBdL0k9r3Ta72FyK5m6/VwNWc2bNnT4GpLnM1\nZ918880CUzWl5vcjiqLgxRdfxC+//II1a9YI/yb0ajfeeCOys7OxefNmx+sjIiICaWlpWLhwoeh4\nMJlMOHLkiNOFBtT02ri20PH0taG64sdgMCA5ORlmsxkHDhzAzp07kZmZiUmTJomO5lNHjx7F8uXL\nkZKSgri4OFRUVDj+GzhwIHr06IFZs2ahuLgYK1aswIEDB/DII4+Ijt3uevTogaioKMd/wcHBCA4O\nRlRUFEaNGoVLly5h0aJFOHr0KBYuXIiamhrVvBFob7feeiuGDx+OWbNmoaioCN9++y1WrlyJJ554\nAiNHjpS6b0aMGAG9Xo+5c+fi559/xtdff42MjAw8/fTT0vdNo+vNK+PHj8fevXuxcuVKFBcXY/bs\n2ejVqxcGDhwoOLlvqHnf5G5/IZK7+VoN3M2Zormbs9REze9HNmzYgD179mDhwoXo0qWL4zVx7WF6\nImi1WqfXRlRUFHQ6Hbp169bkAhIi/P73v4fdbse8efNw8uRJ/OMf/8C3336rivOlJkyYgF27duHj\njz9GSUkJ/v73v+O7777z7HXb9itxe5/FYlFmzZqlxMXFKcOGDVNWrVolOpLPZWRkKNHR0U7/9e3b\nV4mOjlYURVFOnDih/OEPf1DuvPNOZcyYMcru3bsFJxZj1qxZTr8bkZ+frzz88MNKbGysMnHiRKWw\nsFBgOt+7dOmS8sorryjx8fHK7373O+Uvf/mL4z7Z+6a4uFiZMmWKMmDAAGXkyJFO84qsfXPtb06c\nPHnS7byya9cuZdSoUYrJZFKmTJmilJaW+jqyUGrdN11vf6EW187XauBuzhTN3Zwlkqfzhq+zNf5u\n07PPPtvkdREdHS30t7ma+52fRiNGjBD6+3LXZisuLnb8Xe+//34lOztbNdm+/vprJTk5WYmLi1PG\njRvn8ZjTKMo1Fx0nIiIiIiLqhFR32BsREREREVF7YPFDRERERERSYPFDRERERERSYPFDRERERERS\nYPFDRERERERSYPFDRERERERSYPFDRERERERSYPFDRERERERSYPFDRERERERSYPFDRERERERSYPFD\nRERERERS+P/ctJx44JYsawAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x116fc3fd0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAz8AAAIDCAYAAAAqmqAhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XlcVOX+B/DPLMywiSCCmmnmjhvgGqalpHX1unVNyzaz\nulRm2rX8qW1WmplmpaamZup1yzWt1BYrtcwtRDDFDURFBUGRZVhm/f3BdWTgwGxn5swwn/fr1Ss4\nc+Y83znzjDzfeTaZyWQygYiIiIiIqJaTSx0AERERERGROzD5ISIiIiIin8Dkh4iIiIiIfAKTHyIi\nIiIi8glMfoiIiIiIyCcw+SEiIiIiIp/A5IeIiIiIiHwCkx8iIiIiIvIJTH6IiIiIiMgniJb8JCQk\nYOrUqebfT548iZEjRyImJgYjRozAiRMnxCqKiIh8hFarxeDBg3HkyBHzsczMTIwZMwaxsbEYNGgQ\n9u/fb/GcP//8E4MHD0ZMTAyeeeYZXLp0yeLxlStX4r777kOXLl3w5ptvoqyszC2vhYiIpCdK8rNj\nxw7s27fP/HtJSQkSEhLQrVs3bN26FTExMXjhhRdQWloqRnFEROQDtFotJk6ciHPnzlkcf/nllxEZ\nGYktW7ZgyJAhGDduHLKysgAAV69excsvv4zhw4djy5YtCAsLw8svv2x+7o8//ohFixZh+vTpWLVq\nFZKTkzFnzhy3vi4iIpKO08lPfn4+5syZg06dOpmP7dixAwEBAZg0aRKaN2+ON998E0FBQfjhhx+c\nLY6IiHxAWloaRo4ciczMTIvjBw4cwKVLl/D++++jefPmSEhIQExMDDZv3gwA2LhxIzp27IhnnnkG\nLVq0wIcffojLly+be45Wr16N0aNH4/7770eHDh3w3nvvYfPmzez9ISLyEU4nPx999BGGDh2KFi1a\nmI+lpKSgS5cuFud17twZSUlJzhZHREQ+4PDhw4iLi8OGDRtgMpnMx1NSUtC+fXuo1WrzsS5duuDY\nsWPmx7t162Z+zN/fH+3atUNSUhKMRiOOHz+Orl27mh+PiYmBTqfDqVOn3PCqiIhIak4lPwcOHEBi\nYqLFkAIAuHbtGiIjIy2OhYeHIzs725niiIjIR4waNQqTJ0+2SHIAICcnp8a/L0J/f+rXr4/s7GwU\nFBSgrKzM4nGFQoHQ0FDzsDkiIqrdHE5+tFot3n33XUybNg0qlcrisdLS0irHVCoVtFqto8URERGh\npKSkxr8vNf39uTXvlH+fiIh8l8PJz4IFC9ChQwf07NmzymNqtbrKHxKtVgt/f3+7yqg41IGIiMja\n35eaHr+V9Ag9HhAQYHMM/NtENYmKioJMJkNUVJTUoRCRAKWjT9y5cyeuX7+O2NhYAIBOpwNQvpLO\noEGDkJOTY3F+bm4uIiIi7CpDJpOhoKAEBoPR0TDdRqGQIyQkgPG6CON1LcbrWt4arydq0KBBldXf\nKv59adCggeDfn6ioKISFhUGtViM3Nxd33303AMBgMODmzZt2/X3i3ybXqQ3x5ucXmP+fl6eRMrwq\nasP99WSM17XE+tvkcPKzZs0a6PV68++3lgqdNGkSDh8+jGXLllmcn5SUhBdffNHucgwGI/R6z39D\nbmG8rsV4XYvxupa3xeuJoqOjsWzZMmi1WnNPTmJionkRg+joaBw9etR8fklJCU6ePInx48dDJpOh\nY8eOSExMNC+KkJSUBD8/P7Rt29auOLztvWS8rlVdvJ76GmrL/fVUjNezOZz8NGrUyOL3oKAgAECT\nJk0QFhaGTz75BDNnzsSjjz6K9evXo7i4GAMGDHAuWiIi8mndu3dHo0aNMGXKFIwdOxa//vorjh8/\njlmzZgEAhg8fjq+++grLli1D37598fnnn6NJkybmZOfxxx/HtGnT0LJlS0RGRuK9997DyJEjqyys\nQMCqVUuh0RQhKCgYo0cnSB0Okd1Yh0mIw8lPTYKDg/HFF19g2rRp2LhxI9q0aYNly5bZPeeHiIhI\nJpOZf5bL5Vi0aBHeeOMNDB8+HE2bNsXChQvRsGFDAEDjxo2xYMECfPDBB1i0aBE6d+6MhQsXmp8/\ncOBAXL58GdOmTYNOp8NDDz2E119/3e2vyRvExfWGXq+HUumSpgKRy7EOkxCZycNnbublabyiK06p\nlCMsLIjxugjjdS3G61reGi9Vz9veS8brGkLxRke3xdWrV9Co0R1ITvas/aNqw/31ZIzXtcT62+T0\nJqdERERERETegMkPERERERH5BA6CJCK7pF7IQ35RGXq0a2AxF4OIapcTJ1Kg0+ng5+eH9u07SR0O\nkd1Yh0kIkx8islmBRos565MAACo/BTq3tm/vLiLyHsnJidBoNAgKCmLDkbwS6zAJYfJDRDbLzis2\n/3z0TA6TH6Ja7PHHx0gdApFTWIdJCOf8EBERERGRT2DyQ0Q28+yF8YmIiIhqxuSHiBzCpQ6IiIjI\n23DODxEREVWxadNaFBdrEBgYhBEjnpA6HCK7sQ6TECY/REREVEWrVm2h1ZZBpVJLHQqRQ1iHSQiT\nHyIiB+gNRpRqDQgO8JM6FCKXiInpInUIRE5hHSYhnPNDRGQno8mE91YewX8W/IEruRqpwyEiIiIb\nMfkh8kLrfj6Dd1ccRl5hmXRB+PCKB9fzS3E5RwOD0YT1u89IHQ4RERHZiMPeiLxMmdaA3YmZAIC1\nP5/BuH91lCYQLnsNgLeBaq+MjHTo9XoolUo0a9Zc6nCI7MY6TEKc7vm5ePEinnvuOcTGxiI+Ph7L\nly83PzZjxgy0bdsWUVFR5v+vXbvW2SKJfJrBeLu5fT2/VMJIfBcTHvIFe/fuxk8/fY+9e3dLHQqR\nQ1iHSYhTPT8mkwkJCQmIjo7G9u3bkZGRgYkTJ6Jhw4b45z//ifT0dLz++ut4+OGHzc8JDg52Omgi\n3+YhTW8fHvZG5AtGjXoG5f/e8MNO3ol1mIQ41fOTm5uLdu3aYdq0aWjatCnuu+8+xMXFITExEQCQ\nlpaGdu3aITw83PyfWs3lBolE4+Z/z00mD0m8JMY/o+QLVCoVVCo1VCqV1KEQOYR1mIQ4lfxERETg\nk08+QWBgIAAgMTERR44cQY8ePVBUVITs7Gw0a9ZMjDiJSIiEuYjMh1MApoBERETeSbQFD+Lj43H1\n6lX06dMHDz74IFJSUiCTybB48WLs27cPoaGhGDNmDIYNGyZWkUQkIRNTAADsBSIiIvImoiU/CxYs\nQG5uLqZNm4YPPvgAHTp0gFwuR4sWLfDUU0/h8OHDePvttxEcHIx+/fqJVSyRb2PLW3JMAam22rlz\nG0pKShAQEICBA/nFJXkf1mESIlry0759ewDA1KlTMWnSJEyePBnx8fEICQkBALRu3RoZGRlYv369\nXcmPQiHOVkR6vQ47dnyPoUMftn5yJVeuXMaFCxmIi7u32nNuxSlWvK7GeF3LlfFWvKZMBiiVzpdh\na7wVH5fLZaKU7Qip64NScTvrlMms3wep47WXt8RJrhUaGoaAgEDO1SWvxTpMQpxKfq5fv46kpCSL\nZKZly5bQ6XTQaDQIDQ21OL958+Y4dOiQXWWEhAQ4E6LZtm3bsHr1CjzzzJN2P3fChBno3r07Bg58\n0Oq5YsXrLozXtVwRr59aa/5ZqZAjLCxItGtbi7fOjRLzz2qVn6hlO0Kq+lBmvP2zn5/C5vvgbfWX\nfFvPnvdLHQKRU1iHSYhTyU9mZiZeeeUV7Nu3DxEREQCA48ePo169evjvf/+LpKQkrFixwnx+amoq\n7r77brvKKCgogcFgtH6iFYWFJTAaTcjL09j9XJ3OgNJSXY3PVSjkCAkJEC1eV2O8ruXKeDUlOvPP\neoPRoTpdma3xFhbe3leoTFvzZ8KVpK4P+fnF5p/1OoPV+yB1vPa6FS8REVFt41Ty07FjR3To0AFT\np07F1KlTkZmZiY8//hgvvfQSoqOjsXTpUqxYsQL9+vXD77//jm+//RarV6+2qwyDwQi93vbGwo8/\n7sR///sVsrOz0KpVG0yc+H8oKirCBx+8BwDo2bMrNm78FkVFhZg790OcPXsGISF1MWTIw3jmmeer\nXG/mzPeQlJSIY8eOIjHxL7zxxjSMGDEEzz33AjZsWIeHHhqAV1+dhJUrl+P777cjOzsbdeuGYujQ\nf2HMmH//7zUY8OWXX2Dnzu9QVlaKbt3uwaRJUxESUhc6nQ4LF87D7t0/AAB69IjDhAmTzMMFXc3e\n+ys1xlue8JiZIOr1rcVbseFuMopbtiOkqg96w+2ZPiaTyeYYvK3+kvsdP56M1atXYPbszxy+RlJS\nIsaPfxELFixB165dqz2vd+9uePbZBPPfKmu+/347MjLOY9y4Vx2OjYhIak4N7JbL5Vi0aBECAwPx\n2GOP4e2338bTTz+NJ598Eh07dsT8+fOxbds2DB48GGvXrsXcuXPRqVMnsWKv4tChA5g1azoeffQJ\nrFr1Ndq0icLkyRPRsWM0xo9/DZGRDbB9+4+IiIjAjBnT0Lp1W6xZsxlTpryNtWv/i4MH/6xyzQkT\nXkOHDh3x2GNP4IMP5piP//13Cr76ag1GjBiFXbu+x8aNX2PmzJnYtGkbxoz5N776ainOnj0NAFi2\nbDF+/HEn3nrrXSxZshJ5eTcwZ86HAIAvvvgcp0+n4uOPF2D+/CXQaDR4550pLrtHRETkub77bhvO\nnz/v9HVkMuuroSxZsgKDB1c/CfzatWxkZV3BtWvZAIBVq5ajoCDf6diI3KVyHSYCRFjwICIiAvPn\nzxd8LD4+HvHx8c4WYbNvv92K/v3/gSFDyhc1GDfuVahUfigsLEBwcDDkcgX+PJWPHw//jctXLqN3\n7/vRoEEDNGzYEJ99tgh33HFHlWsGBQVDqfRDQEAg6tSpA42mCADw6KOPo1Gj8vOvXcvGW2+9ix49\neiAvT4OhQ/+Fr75aivPn09GqVRt8//02jBv3H3Trdg8AYNKkN/Drrz+jrKwU33yzCV9+uRrNm7cA\nALz55nsYNKgf0tPTzMeIPJIvrzTHzV6pFmjXrkONj+/atR0aTRGCgoIxenSCm6IiEg/rMAkRbbU3\nT3Dx4gUMG/aI+XelUomxYydYnLNlbzoAIOiu+7Fq1XJs374VPXv2wkMPDURYWD2by2rQoJH559jY\nLjh9+iQ++eQTnDp1BqdPn0Je3g0YDAbcvHkT+fn5aN26rfn8u+5qhjFj/o309DTodDq8+OKzMFVq\nTF26dJHJD1E1dh64gOuFZXg0vgXkPp2FkbfR6/VYsWIZfv75B1y/novGje/EqFFPYcCAQZg58z3s\n2vU9AOC++7pj6tR3MGDAIPz88w9Yu/a/uHTpAgICAtGjxz146aUJqF+/fo1lZWScx5o1K5CcfAyB\ngUEYMGAQEhLGQi4vH/RRedjbxo3rsX37Fly9ehV169ZFt249MHr0swgMDMKIEUOQnZ2FXbu+xw8/\n7MDGjd+iYcOGrr1ZRE4aMuQRmExGyGRcwZJuq1XJj1Jp+8up16IPvpj+Evbt+w379/+OV18di0mT\n3sCgQUOtPlcmk0Glur1s4vffb8P8+Z/i0UdHom/fBzB27AS88soLAAA/v+pjMhgM/9sIdjn8/f0t\n46sXbvNrId/i650ONwpK8fUvZwEAdQKUGBTXzP1B2DCkiEjIu+++iUOH/sTo0c+hXbsOOHBgP2bO\nfA8qlQrPPPM8bt7Mw5kzp/Hhhx/jjjsa4/jxZMyYMQ3PPpuA6OhYXLt2DQsXfob33nsTCxYsqbYc\nk8mEzz//FGPGPI+xY1/Cjh27sHbtKkRGNsC//jWiyvk///wDvvhiAcaN+w9atGiJCxcy8Pnn5fOO\n3nhjGmbOnIPXX5+ANm2iMGbM81YTLyJPYM+X2uQ7alXyc+edTXHu3Fnz70ajEY8++jCmTZtucZ7R\noEfuqZ1QKjti5MjHMXLk4/j44w+xd++vgsmPtbHT27ZtxXPPJWDcuBeRl6dBXl4+8vJuACgfNle3\nbijOnTtr7sk5e/Y0Jk+eiLVrN0MmkyE//yZatCiflJqXl4dZs97H+PGvoXHjO526H1T7+WIbvKjC\nancXswsFz8m5WYJNe9LQI6oBurSJED8IX89AySHp6WnYu/dXvPrqJAwfPhIA0LlzV1y9egVHj/6F\nBx54EKGhYfDzUyEqqnzvvOTkbQgICMATT4w2f8FXt25dpKaesFreiBGjMHr0swgLC0Lr1h2wZ89v\nOHr0iGDyk5ychDvuaGx+LDo6FgEBASgoKAAAtGrVBiqVCqGhoebYiIi8Ua1Kfh555FFMnDgOnTpF\no1OnGGzatB6ACa1bt0Vubg4KCwug1lyHX2AYSm6cx6efzsYLL4xDcbEGx44l4f77+wpe198/AJmZ\nF5GXlwcAVYaohYTUxZEjh5CR8Q9cvZqDRYsWwmAwQKvVmuP68svFqF+/PkJDwzBv3lx07NgJAQEB\nGDz4YcyZMxP/939vIjQ0DAsWfIpr17Jxxx2NXXqviBzhCW3+ijHIqhnytmBLCjJzNPjr1DV8NcX6\nvMPzVwuwdV86HuzWBB2bs9eVXCMl5RhkMhnuu6+PxfEZMz6q9jkxMV2wbNliPPXUSPTp8wDuuede\ndOvWAz16xFktr1OnGIvfGzW6A4WFRYLnxsZ2xfbtW/Hss0/gvvv64p577kX//v+w/qKIiLxMrUp+\noqNj8dprU7By5Ze4ceM62rSJwkcffQqVSoXOnbuhceM7cWbvJ2hy71g06vwkSot/R0LCaCgUCsTH\nP4jRo58TvO7gwUMxa9Z0XLhwATNmfFSlJ+jVV1/Dhx9Ox7BhwxAaGob4+P4IDAwwr/b25JPPQKPR\nYNq0N6DX63Hvvb3x6quTAACvvPIqFi6ch7ffngy9Xo+YmM74+ON5Nq3UQ54hO68YKeeuo2fHhgjy\n95M6HLfxiBpaTRCZOfbtPzR91V8AgBPnb9iULPlklxs57dZKafYMxenQoSM+/ngevv56HTZsWIc1\na1aiXr16ePrpZzF8+KPVPk8mkyEgIKDKMZNJeKn1Bx7oD8CEb77ZjJUrv8Ty5UsQGhqK+PgHEBvb\nBX369Lc5ZiJPsWdP+eJSarU/6zCZ1arkBwAGDhyMgQMHVzkeEhKC5ctX49lZv5qPzZ0uvEpdZb17\n90Hv3n3Mv+/bd9ji8aZNm2HZshUICwtCXp6myj4eSqUSL788AS+/bLn4AgCo1f6YOHEyJk6cbFMs\n5HmmLjkIADiRcQOvjoiWOBpyCxd1gRlNJsiZWNVawcF1AAA3b+ahfv3bwzEvXsxAfn4+OnYU/vej\nW7d70K3bPSgrK8PRo0ewadPXmDdvLtq374S2baNEi++BBx7EAw88iOJiDQ4fPohFi+Zj27Zv0KyZ\nfZuTE3kKnU4HrVYLuVwhdSjkQbj8BXm8azdLcPRMDgxGDxhzVYOUtOtSh+ATTLhdDzwhTTiRkSfK\ndc5cuokJ837Hpj3nRLkeeZ5OnWJgMpnwxx/7LI4vWjQf8+fPBQDzSmy3LFw4D//+92gAgFqtRlxc\nL4wdOwEmkwnZ2VdFi23atKl4883yEQmBgUHo0+cBjB8/ESaTCe3aRQvGRuTp+vcfiMGDh6N//4FS\nh0IepNb1/FDtM+WLAwCAUp0RPds3kDga8ii1qJfko7VHYQKw6+BFjOjTUupwyAVatmyFvn37YdGi\n+SgtLUGrVm1w4MB+HDiwHx98MBtAee9QXt51HDz4J1q1ao2uXbtj48Z1+OCDd/HggwOg0+mwbt1/\nUbduXXTu3K3asirPTbWmc+dumDt3FhYunIe4uHtRUJCPFSuWoUmTpmjZspU5trNnT+PYsaOIimoP\ntVpt5apERJ6HyQ95jc2/nmXyQx6x6IIr1NKXRZW88850fPXVUmza9DXy82/irrvuxowZH6FXr/sB\nlA/dPnjwT7zxxut47rkX8MQTo/HOO9Oxfv0avPXW/0Emk6FTp1jMn78EderUqbac6uaNVjwuk8nM\nvw8d+i/o9Xps374F27ZthlqtRteuPfDSS69AoSgfMjRq1JNYsOATvPbaK/jss0XVDtMjIvJkTH7I\nZx06mY0fDl3EqH6t0LpJqNThOMi9PR+e1kB316sv1eqxfvdZ3NWwDuI7cwl6cpxSqURCwlgkJIwV\nfLx58xZYs2ajxbFbc3FsFRvbpcrcVABV9gWqfM7w4SPNS3ADgEZTBJPJBI2mCEFBwejX7yH06/eQ\nzXEQSe1WHZbJZAgKCpY6HPIQTH68iNFowomMG7gjPAjhdf2tP8EL/Z5yBbv/ysTTD7VBi8Z1XVrW\nkm/L98mYtfaobSt8kQVPGHHmrhC+/SMDv6dcxe8pV3FPu4YelwQSucLmzevMic/o0QlSh0NkN9Zh\nEsLkx4vsOXYZa346AwC1trG+YucpAMAHqxOrvEY2OAmQZthb2pV8889avcH9ARBJoF+/ATAYDOZh\nb77g1737sP2HfZArbGseyWSAyk8JrU5v/rfpZkGh+f//eWtWtc8t0eRj1rT/Q2homNNxkzBfrMNk\nHZMfL7Lt9/NSh0AkuYqrvUmx3JvJ5BmrzBG5WuPGTaQOwe1On01DXkAslKoA6ydXpLr9o0mmMv8/\nP7h7tU8pyE9CUVERkx8X8sU6TNZx3UryGmxwlrN3FSdyXuW6x3eAiIjIO/lMz0/OzRKcuiDOfhwk\nDTY4q3L7vBsmXkREROTFnOr5uXjxIp577jnExsYiPj4ey5cvNz+WmZmJMWPGIDY2FoMGDcL+/fud\nDtYZk784gBW7Tkkag7M8YYI5keQsRr3xQ0HkKkeOHMD+/Xtw5MgBqUMhcgjrMAlxuOfHZDIhISEB\n0dHR2L59OzIyMjBx4kQ0bNgQ//znPzF27FhERUVhy5Yt2L17N8aNG4ddu3ahYcOGYsbvU/ilO0nO\nAzLwih8Dt4VToSAOOyRfceVKJoqLixEYGCh1KEQOYR0mIQ4nP7m5uWjXrh2mTZuGwMBANG3aFHFx\ncUhMTER4eDgyMzOxadMmqNVqJCQk4MCBA9i8eTPGjRsnZvxE5E5s+Au6tY8EUW0ydOgIqUMgcgrr\nMAlxeNhbREQEPvnkE3M2nZiYiL/++gvdu3dHcnIy2rdvD7VabT6/S5cuOHbsmPMR+zC2rQjwpLlP\nNVdIg9HommI95waYHUrNljoEIiIisoEoq73Fx8fjySefRExMDB588EHk5OQgMjLS4pzw8HBkZ7OB\nQFRZmc6Am0VlTl/nWl4xtDrX7kFja97x1c5UTJj3By5kFYoeQ3ZesejXtMba9w5HT+e4JQ4iIiJy\njiirvS1YsAC5ubl49913MXPmTJSUlEClUlmco1KpoNVq7b62QuG61biVSvGufStOV8ZbkVwhg9yJ\nriB3x+sIoffHVfFWLEtvMMJgNEHtZ/+maLeuY+v9NZpMmLbkMK7llWDGv3ugaYM61suocE2ZrLzM\nlLRcfLz+GO6oH4RZL8bZHbet8VZ8XC6XVfsZ+iPlKgBg4TfH8ckrveyOpyZf/3LW/HN2XonVz7G9\nn3Oh8yt+1BQKeZUkUFbDvbj1nIr/dyQGd/LkfxeIiIicIUry0759ewDAlClT8Prrr+ORRx5BQUGB\nxTlarRb+/v52XzskxM6NxuwQFhYk+jVdGa9CfrtBMnbuXkx4NBY9O93h1DVdGa+zhN4fV8V7qyyd\n3oixs3+BpkSHxZMfQN1gtZVnCl/nFmvxZl3X4FpeCQBg429p+OCle62WIVPe/tgqlQqEhQVh+fe/\nAwCu5GqcqtfW4q2Te7vXRa1WWi2ruEwv+ufMWGHekVIht3r9Jd+ehKZEh3ee7wE/pfWEVuh6ygqJ\ncN26gdAZLHvYVH7W7wVge/11xb9NRPZatWopNJoiBAUFY/ToBKnDIbIb6zAJcTj5uX79OpKSktCv\nXz/zsZYtW0Kn0yEiIgJpaWkW5+fm5iIiIsLucgoKSmAwuGbuQF6eRrRrKRRyhIQECMZ7MbsQC7Yc\nx70dGmLYfc0dLqPiHIriUj0+XHUE/32rXw3PcCxeT1H5/TGZXFcfbpV19EwOsq6XN/DX/5CKRx9o\n5dB1bL2/Bfkl5p/1egO+2n4cF7MLkTCkPQLUwh/PAo22wnOMyMvTWCQEjtRrW+MtLCw1//zjwQu4\nmlOEiY/GQC4X7oU0mUx2xaM3GC16toRUnEpkMBqtXn9/yhUAwNZfzuDB7k2txiB0PYP+dqE384ur\n3COdTl9jHPZ+3sT8t8kRt+Il3xYX1xt6vR5Kpc9sCUi1DOswCXG4NmRmZuKVV17Bvn37zEnN8ePH\nER4eji5dumD58uXQarXm4W+JiYno2rWr3eUYDEbo9a5pnLviukLxzv36GPIKy7B1XzoG9WwmannO\nvgYx729JmR5qlcKp4XgVCcXlqvpw65oHT2SZj+n09pdV+Xxr8eorNITzi7T4Zl86AGDzb2kY1U84\n8dJVvJ7JVH79CuOwnLk/1uKt3HBPSbuOHX9mYMA9dwmebzLZHs/Pf13Cpt/S8PRDbdCrUyObnmPP\n9fMKy2w6V+icistbG/RG6Cst5mA0mmy6tq3111X/5hHZo3XrKKlDIHIK6zAJcXhgd8eOHdGhQwdM\nnToVaWlp2Lt3Lz7++GO89NJL6NatGxo1aoQpU6bg3LlzWLp0KY4fP45HHnlEzNglU6YzoKDY9vlL\neYXOT2YHrE+6ltL5qwWYMP8PfLYx2WVl1JRTaUp1dr0n1Tl4wr2LclScO1KqvT2U6sp12775z9do\nkV9UhnyN86/dUZv2pOGqjfHWZP3us9AbjPhqZ6oIUbmYB644R0RERNY5nPzI5XIsWrQIgYGBeOyx\nx/D222/j6aefxpNPPgm5XI7FixcjJycHw4cPx3fffYeFCxd67QanOr3R3LA2GI14a9lBTFywH9dc\nvOqUy5YKdoEl209AbzDi7/M3XFZGdVvMlJTp8drC/fjPgj+QL8KqaR6vwo3IzS/Fawv/lDCYcm8u\nO+S2skwVMg+h0Xau3oTUJJT5cB16IiIir+DUIMiIiAjMnz9f8LEmTZpg9erVzlzeIxhNJry38giy\nbxTjvWe7o0Srx/WC8gb21n3peHFoB5eUe+L8DXz+zXHEd26MEX1alh90UwPr6nUNdh26iPuj70CL\nxnVteo4P/p+mAAAgAElEQVTOyXk4Wp0BByoMObPHsXO50OrKy/8t6TKG9XZ8XpW7ifGOGr1g49HC\nYi1S0q4jumV9BAf4iXbdyq/89MU8LN72t1PXzL5RjAb1HNsNXG8w4tDJbDSJDLZp5T4iT3biRAp0\nOh38/PzQvn0nqcMhshvrMAnheqZW5N4swZVcDQxGE9ZXWGLX1eZuOIYyrQG7Dl68fdAFjVyd3oji\nUr3FsZmrE/FHylV8sDpR9PKqs3VfOlb9cLrKcZu+xff8tr/9anjdUr5cR8ue+/UxLN+RivmbU5yO\nQVZDyvjRuiQUFOucur4zey79kpiJ5TtS8e6KIy7vgSJyteTkRBw5cgDJye77W0AkJtZhEsLlL6yo\nzc0Xg8GIN5YeRF5hKWb++x7UCylfilxTKRlyh5+OXHJ7mdb8dOQSHrNztTd7VaxftXnk1MVrRQCA\nc5fzLY7vP34V2XklGNqrWbXPLdMZABOgVtm/71JF7ri/vyVddn0hRG7y+ONjpA6ByCmswySEPT/W\nVGidStU2vVHwv+WFRW69nbl4E9k3iqHVGfHN7+lOXcvdDXed3oiSMtcnaeZ77wCD0YRFW49jybcn\n7B+aVumGGk0mnDh/Q7TFMzzBzaIyLN+Riu//zMCvicJJQ5nWgMlfHMDri/ZX6aF0J1nF96M2fyNC\nRERUy7Hnxx4SZT+Jp3PQv1sT0a9bceK2vW3z81cL4K9SoFG4+zdj1BuMeHPZQRSV6PBhwj0uLctg\ndLyluz/5Mg6eLF89rkvrCHRtGwmgfCjfqh9Oo0CjxSN9WpjPr+k92Jt0Gat/OgMAmPuy9Y1QPZnJ\nZMJ3f2Yg42qh+diZSzcFzz14Msu8r9HeY5fRpW1keU8QERERkQNqRfKzctcpXMsrxvhHOsFfJe5L\n8sYveY0mU4177RiNJmhKdQ5PIbqQVYjpq/4CAMyf0FvUCey2SL2Qh9z88h6ZHQcv4O6GIS4ry5l8\n90bB7V6aiktRp18pwL7k8o03w0LUNl1r6z7neuY8ycmMPGz7/bxN51bMPdOuFGDTnrTqT/YwJjhe\nfzbtOYfubRvgroZcNIGIiEhMXpv8aHUG7DhwAUql3NyQ3HHgAobf38LKM51T02RrW2z89Rz+dX9z\nq7vYOyo3vwQfrE5EizvqYty/OlZ53GQy4aN1R5FxtRDPObhS3R8pV80/p18pQKcW4VXKkIk0Ds4k\n8JuxYovY1dmpC3r7ikpuT8i/kX97WJ3QLTMYjSjQODeBX1R23m+h0y/nCuwJZMN9Pnomp+r1Jfh2\n4pejmS4fgrfr4EXsOngRX02Jd2k5RDXZtGktios1CAwMwogRT0gdDpHdWIdJiNcmPzsOXMB3f2ZY\nHHNmfkZ1Kq7YJINMeI8PO/xw+CJC66jxoAuGsQHAmp/OIL9Ii6NnclBQrEVIoMrica3OiLOZ5ZPO\nv9h6e+WtP//Owog+LVA32LaeiJpczC5y6TfWFg1emScv9Ww9LmtnLNhyHClp1y2OXc4pciIm6Qnu\nX+Wpb+H/VJxr9ePhqotzVJe76Q1G/JKYiSYNgnF/V/cPESVyRqtWbaHVlkGlcv7vApEUWIdJiNcu\neFC5QVjZiYwbVVaWskWpVo/3Vh7B/M0pVZaqFWtSf/oV++Pal3zFPPehopIyPXYdvICMrAIAgKZC\nr4K9OcFH65LsjkvIeyuPiHIdAEg5V/F9Ln8DKiagJzPysHxHqmjlicFkMuH81QLB9wuwrx4J1fNP\nNiZbLd9TmEwmXMgqtDhmMIgXn7sW2si64diGxr8lXcaGX8/h4/XHUFxqfw/e5j1pHvV+km+JiemC\n7t17Iiami9ShEDmEdZiEeG3Pj5BbTYS0K/mY+/UxAMDHY3ual3C2xmA0YtfBi7iQVYgLKETa5QIE\nBVjeImeHvQGwe0hYqVZf7R5Da346Y94c9Ksp8Va/QK+p58rRBh7gurUg5m8R2Bemwku4IjSESkSO\nvN9Hz+Ri4TfHXRCN99HqjFWSYaPQIhLV3WYvb/gfO5tr/rlAo4Xazq+bdh68gOZ3hKBz6wiRIyMi\nIvJNtSr5uaXi3ID0KwXVJj8frklEs4YhGNWvFX46cglb96ZZJCZavQGBptu36GZRGfYlu38fD61e\nYJjQ/9xKfNzJ2aF/zpQMWE6CdzVHehY27xVhUr6XN/prYs8wxawbJTU+bt9tksFgNEIhv52B6A1G\nl82/gwnwU1qWpf5f2SVlesxZn4TwEH+MfbhDjV+IOPOlBBEREVny6OTnXOZNpF28gZiW9auuXlZD\no7Tit/U1tY3OZubjbGY+/hl3F74W6FmpXMTF7CJczPbu+Ra1g/clBo4kUbn5NTf8q+PMKmOVXcwu\nRJC/H8Lr2tZ7Kraf/xJv89vLOUX49+w9AIAPX7gHOTdL8PnW44gMDRStjMoU8tvvhE5vBPzKk59d\nhy4gI6sQGVmFSL9agBZ31K32Ghz2RlLJyEiHXq+HUqlEs2bNpQ6HyG6swyTEo5Of/3y6FwCQMKQd\n7mnX0ObnWexHaEPDQVddz4qVFmt+kRZlWoPdO8+7a7sgqTZldTVvbAtaxiyr5njFU2QWy2M7Kjuv\nGKFBarvrKFC+l9OtJc3nje+FOoEqUXr9CoqlWb0uqcIQtM+3HDevOpfpwgUkquvRqTgfLOt6cY3J\nD5FU9u7dDY2mCEFBwWjWLEHqcIjsxjpMQjw6+bnlj5SrtiU/Au0yZxrKRqOp+sQIwOlLN/Hmlwfx\n0YtxUNqzdkQtykrcNeG8InfnPn+nX4feaEJMy/pVHhOcvyIxo9GEvKIyZN0oxtwNxxAe4o/ZL8XZ\nPdds91+Z5p8nzP8DY4d1gL/a/iSqsj1J1oeOfvdnBjo2r2f1PEd7xwSX23aCLbf25Pkb6Nkussrx\n5TtScW/HRqLGQySGUaOegbh9yUTuxTpMQrwi+ZHLq1bamqqxRc+PTcsNC58zd8Mxq8+9UVCGK7nF\nkMtlCAhyzVKKYiYYYvSaVLyEO3thbhSU4WzmTbuGAeUXleHitSK0axZmMdfDVlk3is2rq709uivu\nbmS5oeqeY7bNAbP7PTSZHM7yFm49juQKq8Rdr2YJ+NybJVCpFFWWQ68QhMVvi7b9jYmPRjsWlBWV\nb883+9LxjQ0bu+YXaXExuxClWgOa3yHOZreO7FElVCVNMFnU1S+2pqBjs/sQoFJ6Ze8l+R6Vqrp/\nG4i8A+swCXEq+cnOzsYHH3yAQ4cOwd/fHwMGDMDEiROhUqkwY8YMrFmzBjKZzLzp5VtvvYUnnrB/\nkymF3Y0Ri+zHKmvLZluzL/kKfknMhFwGvD4qFm2bhjl1Pe/knm9Vpq/8Cw/3vtvm8yd/cQBavREj\n+rTAgHvuAlCeEK35+UyVcy9dqzr86daeSABwMuNGleTn2Llci9+3/3He5tgqy80XZ5+qZBvqc9aN\nYryx9CAAYPHE+6FUVk0MvaV9/u6K8tXkenfy/N6Ta3kluKuB6/bAIiIiopo5lfyMHz8eoaGhWLdu\nHW7evIk33ngDCoUCkyZNQnp6Ol5//XU8/PDD5vODg4MdKkew56fGBQ9us6UBd6OgzPpJNfglsXx4\nkNEEzF6XhEmPxSCqmfUhO7YTL7EQe5iaK4e9nbl0U/D4ifM3qn1O5W/tb62Ut2lPmjn5WbnrlGCC\n8N8fT1U5VvGbe6F6WLmCbf/jPBrUq3kCfcUQS7X6Gs8VS+VO/5+O3F5I4NzlfES3qjqkz9t6J35P\nuSpp+ct3nMS1PNuG4dnzufG294GIiMiTOZz8pKenIyUlBfv370e9euUN/fHjx2P27NmYNGkS0tLS\n8PzzzyM8PNzpIAUbnTWQ2Zn9iL108/6/s2pMfqQceequhlReYRnC6tQ8DNBkMuHgiWyEVnPerLVH\nBY+fybR/k9iKzlb3fIF7U3FKT8VVBI+eycG239ORmePc3JFqY3HjZKrq6r/g8EIfaogv++4ELl3T\nYNKoGKvnHjl1zaZr3ppDyISGvMHOndtQUlKCgIAADBw4TOpwiOzGOkxCHN7gIiIiAsuWLTMnPkB5\nY6mwsBBFRUXIzs5Gs2bNxIix6jLX1RBqT9zU2NCrI3JDRPxmq+0BekqjasqSAygurblXI/F0DpZ9\nfxJz1ie5Karqnb6YJ3jcoudHVr5HzdXrGny+9bjDiY9N9UPsN1Kky92a/1Tb5dwswYET2cjMKcIW\nB/dtOnspv8rbuPz7k3Zfx0M+0uSDQkPDUK9eOEJDfXEoN9UGrMMkxOGenzp16qBXr17m300mE9as\nWYOePXsiPT0dMpkMixcvxr59+xAaGooxY8Zg2DDHsm7h3Me2TQG37k3HgB531Xj9Wtu4qLTk96Vr\nRVZ7YyozmkwoKtYhJMi+SYM6vRGz1x/Fu2O6V3tOxc1oxVZSpkeA2vbq/dG6JISHVL03GVmF5p9l\nMhnW/Hgae45dESXGmqRfLXB6Lpqz7M2/cm6WICI0wDXBuJnecHuVx5tFji05Pnt9UpUVArPzSlCm\nM9h9rSu5GhxPv45enRohyN/PoXiI7NWz5/1Sh0DkFNZhEiLaam+zZ8/GqVOnsHnzZvz999+Qy+Vo\n0aIFnnrqKRw+fBhvv/02goOD0a9fP7GKrJbBcLvVZrBhKeIjqbYNWbGV9RKdWMDBQT//lYmvfzmL\nZg3tm2y96Ju/kXQ2B/8ZEY0OzcuHMBbY2BiUakPYHQcysHVvOp54sLXF8cycIny+9TiKy4R7pK4L\nzP2qOL9IJoPDiU/i6RzEtoqwOfksKTPguz8zHCpLiMmBpT7t3VxzwZYUvP9cD7ue46kqzh0zitwL\nl3OzxO4vXN768hAA4MCJrBq/UCAiIqKaiZL8zJkzB6tXr8Znn32Gli1bomXLloiPj0dISPnKWK1b\nt0ZGRgbWr1/vUPIjk8mqrEYl1BskA6BUyiFXWD4otJJVRdUtBeyoP//OQrNGdfCPHncJ7gMjl1d9\nPRV9W2nFMIWNc56USrnFfVEq5OZyvv7lLADLnozqrlHRrd6ZTzYm479v9YNOb0RihR4bhUJWpdya\nrmfBBdNa5HIZtuwtXyJ5zU+WK7ot/OZvmyekC7FWj24RelmpF/IwdekBfDk5HnKFw6NNHaZUyi2W\n+q5YpRRyORT/i0lRITZ7l3zOzNHYfI8qs3denyspFDL4Ofg6KhO6he8sP1zlWE33reLn/2J2kcP3\n2B4KCeooERGROzid/EyfPh0bNmzAnDlzLBKbW4nPLc2bN8ehQ4ccKkOlUiIsLMjimFAD4NZ5KpXl\ny6r8XHdY9/NZdG3fCO8vr/qa1eqqr6eizXss5xj42zjMJSwsyOK+hIYGom6wfcPcaopr+/4MbK+0\n90qd4ACEhQVV26Cv6XqV3ycxlFWzKa1MVr6vjTOCbdzHSaEQbshrdUaEhQWhTh1xN9i0RWhoEJQV\n3iO1+nadCq7jj5CQ8uFqt/4PAEo/+zc0dfSz5ueCuuCoOnUCUDfE3/y7Uun4xq623sOa7luexrKn\nVYp/z8g3XbuWDaPRALlcgcjIBlKHQ2Q31mES4lSL4/PPP8eGDRvw6aefon///ubj8+fPR1JSElas\nWGE+lpqairvvtn1/lop0Wj3y8iwbjAZD1UauVqvHweTLyM27PefHTyGv8lx3+XTdUdwsrDqUqqhY\nizPpuYgIs21+RGmpzqbz8vI00Fdo/N+8WQyjzr6llGu6V1t+O1flWGFRCfLyNDAKvB/WrqfT2j/3\nwZqd1Q0VMwEGJ4cv5dywrR4J9fbdkpenQVGhuD2NtjhwLBPnMvPxj3uawl+lRFnZ7TpVVFiKgoIS\nhIQEoKCgxPzZ0jqwDLejnzWdm5b8tkVhYSn8KgxM0zpRT8uqGWJZWU337ZcKy5JbO1csCoXcIhEm\n37Rr13ZoNEUICgrG6NEJUodDZDfWYRLicPKTlpaGxYsX44UXXkBsbCxyc29v9ti3b18sXboUK1as\nQL9+/fD777/j22+/xerVqx0qy2gyWTTqAeHJ2Ocu5+PgyWyLY706NaryXHcpriZpOXwyG4dPZuO1\nR2PQ/m7r+wHV1JiuSK83WtwXvcFo92u393yDoep7Y+v1xJ5LUSMZnF7ZYtNvtq36VdPbpdcbYTC6\nvz7OXle+ot7WfelYOqmPRYwGo9Gc8Bgq1Blb611Fjn7WHCjKZQwGo8WXK/bOfarI1kUr7LlvUv17\nRr5nyJBHYDIZIZNxGCR5J9ZhEuJw8vPLL7/AaDRi8eLFWLx4MYDyRoJMJkNqairmz5+PefPmYd68\neWjcuDHmzp2LTp06iRa4kNz8qt+o2zpfRgord6Vizth7Rb6qe1uRnnt3qTq/J9u2aIM7c1NnEgyX\nqLRSIpEvCgsTc7NuIvdjHSYhDic/CQkJSEiovgsxPj4e8fHxjl7eKl9qdDu636Uv3SNrZJCJvplt\ndbIrLLVe2YqdqegWFemWOKqTV6R1ad3IvGb/Kn+Jp1237Lkj5BarvUkYCBEREYmK/YASck2b6naj\nTexV7Mh5v6dchVYn7bClyonP6Ys3USbi/Kt3vqq6mpm3sVjpjj0/REREtQaTHxcSq8l0IuOG9ZME\nSn1/5V/IyCoQKQrnmEwmlNg4+dsVHO09cwWph1FVvhc7DlzA7HVHpQnGQ1V8j85k5ksYCZF09uz5\nGT/++B327PlZ6lCIHMI6TEKY/LiQtTbujYIy/J5iff5F2mXbE5jzVy338am8bLY1Wgd2n6/JF9v/\nhslkwudbj2PC/N9xNvOmqNcn+xWX6qGrtDrfWTbwyYtkZWXhxRdfRJcuXfDAAw9g1apV5sdOnjyJ\nkSNHIiYmBiNGjMCJEycsnvv999+jf//+iI2Nxbhx45CXl+fu8L2GTqeDVquFTmfbiqNEnoZ1mIR4\nZfJTXKpD2hXP6NFw1oqdpyx+/+HQRYkiKbfs+5OiXu9w6jVkZBUi6Wwu9IbyJIiktTsxE3+kXJU6\nDI/lSb2EJGzChAkICgrCN998gzfeeAOfffYZdu/ejZKSEiQkJKBbt27YunUrYmJi8MILL6C0tHwI\ncEpKCt566y288sor2LBhA/Lz8zF16lSJX43n6t9/IAYPHo7+/QdKHQqRQ1iHSYhXJj/vr/pL6hBE\ndeBEFmatPYpL14qwUWAvHXdyxcTz0grD3QqL+e2LJ08hybhagDyBval8jSe/R76uoKAAycnJeOml\nl9C0aVM88MAD6N27Nw4ePIidO3ciICAAkyZNQvPmzfHmm28iKCgIP/zwAwBg7dq1GDBgAIYMGYLW\nrVtjzpw52Lt3Ly5fvizxqyIiInfxyuTnWl6J1CHYxNZG5LLvTuLMpZs+M+9i0x73J3j8Nt+6lHM5\neGf5Yby2cD/01WxaS66h4949NvP390dAQAC2bNkCvV6P9PR0HD16FFFRUUhOTkaXLl0szu/cuTOS\nksr3uTp27Bi6detmfqxhw4Zo1KgRkpOT3foaiIhIOl6Z/NRWmlLnFgTQVLOpqtQqf4m+62D50L5U\nuxZyqD08NRHbtPus+Wdf7/1x17Lot7zw8R6bz0294NtzVFQqFd555x18/fXXiI6OxsCBA3Hfffdh\n+PDhuHbtGiIjLZeSDw8PR3Z2+ebXOTk5VR6vX78+srKy3Ba/N9FoilBUVAiNxv7l64k8AeswCXF4\nnx9v4UujV6YuOVjlmMvb2TYUUN17UOCjQ+BKRVxWWkzHznrWXjtSSvfgOYVz1idh+eS+lstx+5i0\ntDTEx8fjueeew5kzZzB9+nTExcWhtLQUKpXK4lyVSgWtVgsAVh+3h0LhHd8d3orTkXg3b14HjaYI\nQUHBeO65F8UOTZAz8YpSvhuLlQFQKuVQKt1XqNT3117OxuvuOuxr99fdxIrTq5KfC1mFCAlSWT/R\nRxWVSJdMeH47TAZPSYWX70iVOgSXkXoZb7Es+07chT/EpinVIzjAT+owJHHgwAFs3rwZ+/btg0ql\nQrt27ZCVlYXFixejadOmVRIZrVYLf39/AIBara7xcXuEhAQ4/iIk4Ei8jzwyHHq9HkqlEmFhQS6I\nqnpS3d+AAPe1MWQyoG7dQLffW8A36i8gXR32lfvrrbwm+Um9kIc565OgkNvXyi4stv8bvdqkuMyA\n35I4mdfzk7Pa4d+z90gdgtNkkMForB1JXG104sQJNGvWzKIHJyoqCl988QW6du2KnBzLHszc3FxE\nREQAACIjI5Gbm1vl8cpD4WxRUFACgxfMjVMo5AgJCXAo3rp1I8w/5+VpxA5NkDPxiqGkxH1tBpMJ\nyM8vdtu9BaS/v/ZyNl5312Ffu7/uditeZ3lF8nM49Zp5nLvBzkbJ4dRreH6Q57+hrnL+agHOX5V4\nCA/bkT7DWEt6fjz9VfhyMh8ZGYkLFy6Yv80FgPT0dDRp0gQxMTFYsmSJxflJSUl46aWXAAAxMTFI\nTEzEsGHDAABXr15FVlYWoqOj7Y7DYDBC70ULVTBeG8t1Y5EmAHq9RK+T9cGlGK9n845BfnBuieSE\nOXvEC4Qs/HTkEvYl17xRq1bvmXNcqHo+3LaGzgvqqy+/P/Hx8VAqlXjrrbeQkZGBX3/9FUuWLMHT\nTz+NBx98EIWFhZg5cybS0tIwY8YMFBcX4x//+AcAYNSoUdi+fTs2b96MU6dOYfLkyejbty8aN24s\n8asiIiJ38YqeH/Jcf6ffwN/pNa/atmCL9Bub+nJj0RGe3vPhSnO+PiZ1CDbw3RodHByMlStXYubM\nmRgxYgTq1auHl19+GSNGjAAALFmyBNOmTcPGjRvRpk0bLFu2zDynJyYmBu+//z7mzZuH/Px89OrV\nC9OnT5fy5Xi0I0cOQKstg0qlRrducVKHQ2Q31mESwuSHfILWh7pzxVJbFi+ojXx52BsAtGjRAsuX\nLxd8rGPHjti6dWu1zx02bJh52BvV7MqVTBQXFyMwMFDqUIgcwjpMQpj8EFEVJpMJyWnXpQ6DquHr\nyQ+5x9ChI6QOgcgprMMkxKk5P9nZ2Rg/fjx69OiB+++/H7NmzTIvI5qZmYkxY8YgNjYWgwYNwv79\n+0UJmGoHX93g1Fv8epQrBHoymQ8PeyMiInKGU8nP+PHjUVZWhnXr1uGTTz7Bb7/9hnnz5gEAxo4d\ni8jISGzZsgVDhgzBuHHjuIs2mXnHvArf9dORS1KHQDVh7kNEROQQh4e9paenIyUlBfv370e9evUA\nlCdDs2fPRu/evZGZmYlNmzZBrVYjISHBvDHduHHjRAueiMgXMfchIiJyjMPJT0REBJYtW2ZOfG4p\nLCxEcnIy2rdvD7VabT7epUsXHDvGb/uJiJwl46QfcoNVq5ZCoylCUFAwRo9OkDocIruxDpMQh5Of\nOnXqoFevXubfTSYT1qxZg7i4OOTk5FTZMTs8PBzZ2dmOR0pERAC44AG5R1xcb4vNZIm8DeswCRGt\nNsyePRupqanYvHkzVqxYAZVKZfG4SqUyL4ZARESOUyrlUCpct0e1woXXJu/RunWU1CEQOYV1mISI\nkvzMmTMHq1evxmeffYaWLVtCrVYjPz/f4hytVmveaI6IiBxXLyyICQoREZEDnE5+pk+fjg0bNmDO\nnDno168fAKBBgwY4d+6cxXm5ubmIiIhwtjgiIp9382Yx5HLXjX1TKOQICQlw2fWJiIik4lTy8/nn\nn2PDhg349NNP0b9/f/Px6OhoLFu2DFqt1jz8LTExEV27dnUuWiIigsFghNHIiT/kWidOpECn08HP\nzw/t23eSOhwiu7EOkxCHk5+0tDQsXrwYL7zwAmJjY5Gbm2t+rHv37mjUqBGmTJmCsWPH4tdff8Xx\n48cxa9YsUYImIvJlXO2N3CE5OREajQZBQUFsOJJXYh0mIQ4nP7/88guMRiMWL16MxYsXAyhf8U0m\nkyE1NRULFy7Em2++ieHDh6Np06ZYuHAhGjZsKFrgRERE5DqPPz5G6hCInMI6TEIcTn4SEhKQkFD9\nmulNmzbF6tWrHb08ERERERGRqLhcEBERERER+QQmP0RERERE5BO45S0RERFVsWnTWhQXaxAYGIQR\nI56QOhwiu7EOkxAmP0RERFRFq1ZtodWWQaVSSx0KkUNYh0kIkx8iIiKqIiami9Qh1G4mE1JSkpGV\nleWW4qKjY6BU+lYSwDpMQpj8EBEREblZUIP2+PLnSwCuuLysotwMzP0/NWJjY1xeFpGnY/JDRERE\n5GYKPzVCG7R0T2FGvXvKIfICTH6IiIioioyMdOj1eiiVSjRr1lzqcIjsxjpMQpj8EBERURV79+6G\nRlOEoKBgNGtW/abmRJ6KdZiEMPkhIiKiKkaNegaACYBM4kiIHMM6TEKY/BAREVEVKpVK6hCInMI6\nTELkUgdARERERETkDkx+iIiIiIjIJ3DYGxEREVWxc+c2lJSUICAgAAMHDpM6HCK7sQ6TENF6frRa\nLQYPHowjR46Yj82YMQNt27ZFVFSU+f9r164Vq0giIiJykdDQMNSrF47Q0DCpQyFyCOswCRGl50er\n1WLixIk4d+6cxfH09HS8/vrrePjhh83HgoODxSiSiIiIXKhnz/ulDgEAsP/gIeze86dbyjpzOhXK\n5g9bP5G8gqfUYfIsTic/aWlpeO2116p97Pnnn0d4eLizxRAREZEP+n3/IVxAtFvKUrdxTzlEJB2n\nh70dPnwYcXFx2LBhA0wmk/l4UVERsrOz0axZM2eLICIiIiIicprTPT+jRo0SPJ6eng6ZTIbFixdj\n3759CA0NxZgxYzBsGCecERERebpr17JhNBoglysQGdlA6nCI7MY6TEJcttpbeno65HI5WrRogaee\negqHDx/G22+/jeDgYPTr189VxRIR1XpKpWt3KVAouAsCAbt2bYdGU4SgoGCMHp0gdThEdmMdJiEu\nS36GDRuG+Ph4hISEAABat26NjIwMrF+/nskPEZETwsKCpA6BfMCQIY/AZDJCJmMyTN6JdZiEuHSf\nn1uJzy3NmzfHoUOHXFkkEVGtl5encen1FQo5QkICXFoGeb6wsHpSh0DkFNZhEuKy5Gf+/PlISkrC\nipXnIPYAACAASURBVBUrzMdSU1Nx9913u6pIIiKfoNcbpQ6BiIjIK7msH7Bv3744cuQIVqxYgUuX\nLmHdunX49ttv8fzzz7uqSCIiIiIiomqJ2vMjk8nMP3fs2BHz58/HvHnzMG/ePDRu3Bhz585Fp06d\nxCySiIiIXGDPnp9RVlYKtdofffr0lzocIruxDpMQUZOf1NRUi9/j4+MRHx8vZhFERETkBjqdDlqt\nFnK5QupQiBzCOkxCXLrgAREREXmn/v0HSh0CkVNYh0kI1/4jIiIiIiKfwOSHiIiIiIh8Aoe9ERER\nURUaTRFMJhNkMhmCgoKlDofIbqzDJITJDxEREVWxefM6aDRFCAoKxujRCVKHQ2Q31mESwuSHiIiI\nqujXbwAMBgMUCq6URd6JdZiEMPkhIiKiKho3biJ1CEROYR0mIVzwgIiIiIiIfAKTHyIiIiIi8gkc\n9kZERERVHDlyAFptGVQqNbp1i5M6HCK7sQ6TECY/REREVMWVK5koLi5GYGCg1KEQOYR1mIQw+SEi\nIqIqhg4dIXUIRE5hHSYhnPNDREREREQ+gckPEQCFXAalgh8HIiIiotqMrT0iADKZDDKZ1FEQERER\nkSuJkvxotVoMHjwYR44cMR/LzMzEmDFjEBsbi0GDBmH//v1iFEXkEnJ+DUBEZGHVqqVYtOgTrFq1\nVOpQiBzCOkxCnG7yabVaTJw4EefOnbM4/vLLLyMyMhJbtmzBkCFDMG7cOGRlZTlbHHmBkEA/qUOw\nmwzidfuM+1dH0a5F9ps4MlrqEIhqhbi43ujTpz/i4npLHQqRQ1iHSYhTq72lpaXhtddeq3L8wIED\nuHTpEjZu3Ai1Wo2EhAQcOHAAmzdvxrhx45wpklykQb1AZN8oFuVagf5+KCjWiXItd2l+RwjOXc4X\n5VomkyiXIQd1aB4udQhEtULr1lFSh0DkFNZhEuJUz8/hw4cRFxeHDRs2wFShxZeSkoL27dtDrVab\nj3Xp0gXHjh1zpjhyobHDOnhlj41Yhva6W7S+n3bNwkS6EhERERGJyankZ9SoUZg8ebJFkgMAOTk5\niIyMtDgWHh6O7OxsZ4ojF2oSGYxPX+klyrVMAEb2bSnKtdyljoiJX4Baic//c59o1yMiIiIicbhk\nk9OSkhKoVCqLYyqVClqt1hXFkQiUSvFm/MsADLq3GQbd2wxPz9gt2nVdSSHiMtdKpRxhan/RrieV\nFo1DkHa5QOow7CZmXfZUrn6NYn4eyHudOJECnU4HPz8/tG/fSepwiOzGOkxCXJL8qNVq5Odbzp/Q\narXw9/f+BmFtFRYWJNq15HKZqNdzh5CQAIi11rW3vfbqKBUKqUNwiDfc//p1/ZGbX+rw873hNZL3\nS05OhEajQVBQEBuO5JVYh0mIS5KfBg0aVFn9LTc3FxEREa4ojkSQl6cR7VoGo0nU67lDQUEJygfs\nOS8vTyP6N+fhIf64XuB4Y9kReoOh2sfUfgoEB/i5PSZbeEPdc3ZDXVe/RoVCXv6FAPm0xx8fI3UI\nRE5hHSYhLhnbEB0djZMnT1oMc0tMTERMTIwriiMR6PVG6PVGcS5mMol7PRfwVynQqcXtVcEMBiP+\ndV8LUa6t1xthMIj72k0iJWb26NYmEg91b2JxLKZlfUx4pBM+e6UXXn/MMz/PnlzvbhnSq5lTz7/1\n+XLVf2LXXyIiIk/hkuSne/fuaNSoEaZMmYJz585h6dKlOH78OB555BFXFEcEAGgcYftQIKERbv26\n3IlnB0ah9Z11EXWXZ63YJt4uRLZ5on9rxHe5E/dF32FxfPwjnRDdsj7UKoVYowR9Up1AlfWTiIiI\nSHSiJT+yCi0huVyORYsWIScnB8OHD8d3332HhQsXomHDhmIVRx7M2T6K6Bb279OikMvsGkoktBeP\nXC5Dr06NMOXJLpg0KhaRYZ407Md9mYafUo4HutxZ5X4q5JYxyJzMfoL8XTLq1uVa3BEidQhERETk\nINFaH6mpqRa/N2nSBKtXrxbr8uQmTRsE42J2kVPXuKtBHaeeP2ZgFDbtOYf9x7Osnjv58VgoFHJE\nhgVg3qZkp8qtgpuVWiSJ7e+uZ/GYs+lY6yahSDqb6+RVhD07MApf7Uy1fqJUWLfIC2zatBbFxRoE\nBgZhxIgnpA6HyG6swySE65l6kAYe0NPwf6Ninb7GEw+2dur5IUEqPPVgG5vObdM0DC0b10VIoAqh\nwWrrTyCr5BV6dEKCbg/P6lSpR87Znh9XDC2MDC3/DDWqHyj6tYl8TatWbREV1QGtWrWVOhQih7AO\nk5Bal/z063qnxe+zX4qTKBL7OduYrGjy444lMYH+zm32+cyAtgiRaD6DPcPebLrVlc65q2EdDOrZ\nzK6YxNItKtL6SSKpeG+CA/zwyvCOGNm3Je6PsZz/I5c7V1/7dm7s1POJyLViYrqge/eeiInpInUo\nRA5hHSYhtS75qax+Xel6Uzq3tm9p7+oa5Esn9bG77BaN69r9HEfcGRGMMQNuf6MSHOBc8uSMgffc\n5dLrB6qV8FdJs/dN6ztDMXFktFvKkleqiLGtIvCPHk2hkFv+c+Fs8lP5eqJww9SoEX1bCh6vF6JG\n08hg1wdAREREDqt1yY/M7etiuVaDsIAqPRr3RTfC3Y2km3TdN9byG/ueHRsiukU4urSJQEyr+hJF\nVd4z88G/e+D9Z7vj7kbOzTsCgLpBnrMiV1CAEh2a278QhCNsTWqczH1cSq10XZLaukkopj/Xvcrc\nto9ejMM7Y7q5rFwiIiJyXq1LfnxBgFqJt0d3ddn133mm5msP63036tf1BwA8+WBrKORyTBgRjZcf\n7lil18DdGoUH4c7IYPzrfuf37Hnun1EiRCSOlm7qyQNsT2rEHKYptsYRQegeFYm7GtbBsF53V3l8\nyL3NnLx+MKZVSnQUcrnk9Z9ITBkZ6Th37gwyMtKlDoXIIazDJMQ715r1Qe3vrocT528AsK13q/Ky\nxDWJaWnZW9OsYdVepQE9miKvqAxNI+ugTqAK05/vgUKNFvVD3TOsUCGXwWC0fYksox3nVicyLBCz\nXrgHU5YcBGDjPKEKEoZ1xNJtx52Oo7xs9zWqZZ7cpYPyhRJSL+TVeI5MJsOLQzsAAH5JzKzyeJ/Y\nxvh2f4YrwsPi1+7H7r8u4WRGntU4b5n1Yhz+PH4Vd0YEY9G2v10SF5G99u7dDY2mCEFBwWjWLEHq\ncIjsxjpMQmpd8lNbv3jtE3OHOfmxhT2N5fAQf6vnqFUKJAxuf/t3PwXUDiY+93ZsaHUZ64rhNwoP\nhNEEZN8otjinpmFpBoP4awnbckcfvq+5+efBvZtbTX6eGdAWK3edcjIyoF2zMJzMsK2hbY2tvRc1\nndaldQQSz+SIEk9lLwxtj1fn/yEck8Cx1k1CzT9PfDQaTSLrWB3SOOmxGBSW6PDF9hN2x6f2U+D/\n2bvzuKjK/Q/gn1mYYRhABhAUl0gEQVEGSRFzSS+amAtqmlq5ZVi53RZvqd1wSzTMsnzZNTMrNdPQ\nNJfKvP3Sq9db7phIpVaKC4LhwjrAzO8PY2ScM8BsnBn5vF+vXjnnnJnzmWce4HznnPM8jySEIu96\nCU7/UbfnBPmpkNy9FQpulVm9PyJnGTVqHG6Py36P/mGlex77MAnhZW92GixwSU0VCYBpwzrUXxgb\nDelh+T04Q4cwx9wXNPJv4RbX+fuKM+x1UnxLq7YPaCRceIY2se6epcd6m7dFQjvTSYXH96/bUJ8e\ndRw1z0tp+bsThced11Ap5ZAAmDykfZ1etzbWjibYIsgbU4e1x+Qh0Yi+P6BO93JFhfqjc1QwunVo\namtMIrenUCigUCihULjO/Y9E1mAfJiH3XPHj4+W40cbqMnJTv841H+xqwwPRKdLyMMXNG9/Zh1j3\nUNg7vHVNmvibz7diMFg+KzOhv/B9NkIto1Javqm9ZbAPhj8UhqT4lvD9q0/YMq+MSdRaPp+QQLVV\nw20Dlr+LmuGA+ZaeHtjW5HGrEMv3DTVrrDb+u3rhUhOJRIKXRmpr3e754TFYNr074trUPPphRHP7\n72uy1LNiwxsjro31w4WPT4rEm5MftC/UX5TVRgpUKmRQe95zJ96JiIhc3j1X/HRrb/s3tV3aBZs8\nvu+ub9+fFJi8U1mHoY9rugCr1tF+3fw6vgArz8BY+qb97mZQeEjRpmXNxUxSl/swvFdrpI7vjDH9\n2uC5IdFWZQFMP7vaPopZT1g/j4Cll1TVcFbFZjUUnfMnxhsPxq0ZMrxtqL/wrqo/kNRtCPQpVpwl\nvXvCVWeRSCTQ+NTeh8Oa1T764pCerRHevBE6RQYhLMQXz4/QwlvlgT4PtHBEVCIiIqqDe+6rR5mV\n37xXV9u9L706NkfW7wV1vpchIbpJrdtUH5hA6Cb9ZoFqs2VVBnS9Dz9mXUW7+/3xf8cu1imT+7Bc\naaSldIG3lweUHnUbzljjo8RD2rsn1KxbUVn9LFVtA0142fJNvoOK25rOptWFXCZF+rQe+Pm3fLS/\n37GFhTPK90mD2+GXi7dw/Odc7D1+yan7qsnEAVE48nMeRieafzFydxpPhQz/HNcJFRV6AECrEF+8\nPa0bR4gjl7Vr11aUlJRApVKhf/9kseMQWY19mIS47ZkfXwde3maNCXUc/njq0PaI/WvOm5oObaof\n+FQvfhIfaI62oRrBs01VhvYIw6JnEtC8seUCyZKxSZFQqzzwsJX3qDhKoIV7XarIZRK0CvGFVCLB\nxAGml2/5+SihtvtSvboVC9VrCmcco0oAKOTCP4ZDut++F8th9y/V8gZaBPsgrk2Q3ZOXAqhr89rM\nx0uBxM4tHTapbmJcc5ue1zW6KaYO6yB471bfTrWf0WHhQ67Mz08Df/8A+PlZf8kwkStgHyYhbnvm\nZ+nUbthx4Hds3f9bve63rpcjxUbcub+h5sveqhU/1Y60H0kINbkx2/TeE9PX6NKuCdbu/qVOuaqE\nN2+E9fOScPNGsfGb6Po0Y1Qsvj18AQ9GN8Xcjw6ZrZdIJHjl8Y4oKq1AI7VCtPuhnHwMD4kEWJjS\nBWcu3jAbWeyRhFCENWuEltUm03yybwTW7v6lTiPm1aRlkDfOXy20+fm1ufuytzo9x4azV3c/oy6X\noQoZ3ScCh3++iuuFOsH1gx4MxZcHfsewnq0E1wsJCVSjX3xLfP3DeZsyEYmta9eeYkcgsgv7MAlx\n6TM/XSxcNhbdyh9SiQQDHwzFomcSzGZat0b1e1IetON+IVtVjVgW4OsJ32rFjjWH+rbeH2LNXEC2\nEjqcNRiAxn4qjE6MMLuvqjq5TGosAB1f+9T5iNzaZ1jN39cTnaOCzZZLpRK0DfU3ObvRq2NzLH4m\nAeMtDAwhhrtv3JfLpHW+XHBUYjj8fZWYMSrWIYVmXUeqEzLryTj06thM8N6twd3ux5uTH8QjCaFW\nvWaQlcPB16Wf99SGWPWaREREdIdTi589e/YgMjISUVFRxv9Pnz69zs9/eUwnzJ8YbzKk7tAerYzz\nzUgkErODC6GDh/H9Iy0WSN4qBd54JgGvPx1vNjKZLQfcEon5pKE1ub+pL9Kf7YoFE+NN9ufsMw5i\nMtjw7pxRePhXu5Hdw8KlZ6aXvdmX4uHO5pdBVX/NqlEBn6rl0srGfiqXulyq+txGrUJ8sfiZBJP1\n1aNOG9YBTQO8MPmvwSf6PNACS557sNaR+KouIX0u2XTQCke2QmAjFZ7s2watBUadq+vAB+ZPtG7z\n2k5+zRgVizEPt7E+BxEREQFw8mVvZ86cQe/evbFgwQLjN8FKZd0PIOQyKe5r4mNy8NQvvqXVwwl3\n7xCC7h1CMGHRd4LrA22crFPIu3/vAU8rL72xNNcLOdfQnmH4I7cQLYLUCGwk3AesGe2tNiN6tUa/\nzi2R8f1ZHPjJ/JK1SYPaYfhDYQ7tj/Wh+sATHVoF1FgkaMMDoQ238OVADQf+Tw9sizJdJRp5m762\ny39J4OCATQO8RLsE1JXodDqkpaVh586dUCgUGDZsGJ5//nkAQFZWFubMmYNffvkF4eHhmDNnDtq1\nuzNB844dO7Bs2TLk5+fjwQcfxPz586HR8H4AIVev5kKvr4RUKkNQkPnZaSJXxz5MQpx65ufs2bMI\nDw+Hv78/AgICEBAQAG/v2ufOsYejDgsCfJV4KPbuEcJq56tWuMy38vfS5TESJ5wW81Z54J9jH8C4\nJMtnWkwu36rhc63LUMcSiQSNvJUW40ulEqcWPvJqlzk2r8McVvawc/A5M1Vt584c8WuhpollG5IF\nCxbg4MGD+PDDD7FkyRJs2rQJmzZtQklJCVJSUtCpUyds2bIFWq0WkyZNQmlpKQAgMzMTr776KqZO\nnYqNGzfixo0bmDlzpsjvxnV99dU2bNnyGb76apvYUYhswj5MQpz6l/Ts2bN48EHHTBBYE1suo7Jk\neK8wHPzpClIGtTOZgNQujj4SrKMxD7fB4G7344XlB8zWOWqULJvY2RyO/Lxr3Vf1y95q2M6ae02c\nMYJcXbqYh1yK4Q+F4decGxj5t3D8V+DskzM44j26xtcJzmeprcYlRaKJvxcUdRze/V5248YNbNmy\nBR999BGio29fBjlhwgScOHECMpkMKpUKM2bMAADMnj0b+/btw9dff43k5GSsX78eSUlJGDRoEAAg\nPT0dvXr1wsWLF9GsmfVfdt3rBg16FAaDHhKJS98eTGQR+zAJcWrx89tvv+E///kP3nvvPej1evTr\n1w/Tpk2Dh4eIB961SIq/D0nxdyZ5fP3peKzeeVrwhnRXJ5FI4HfXt+Vd2gUjNNgH/rXMaeRMtpQu\nLnEyzY4MESb3kdR97iBbWSpuk7rchySn7NGULZ9xTc9xic/fBtGt7kwC2yW69gFVLBWxPWLunbO4\n9jpy5Ah8fHzwwAMPGJc9/fTTAIDXXnsNcXGmA1Z07NgRx44dQ3JyMo4fP45JkyYZ1zVp0gRNmzbF\niRMnWPwI0GiEJzEmchfswyTEacXPpUuXUFpaCqVSiWXLliEnJwcLFixAWVkZZs2aVefXuXvSUg8P\nKWRS02XVL0eS3XXjutzCjex3nlvzNi2CfTBnQmeL66s/N75dE8FJVmuaN6X686tfLieXSUzWyWTV\n3qNUUuv7Elrv563Ac0Pa//V6UpP/321Ij1b4Yt85k/dQ2z6FCF0qVlN+y/uo9v5lUpuy3P1qdXkN\nabV2l0olFj9LieTuz+v2v/85rhN+zLqCR7qGGteb9lfb2vVud1/GNq5/pNnr1tRutfWHmlRvE+lf\n/bb6xy6v4+dVfbTDu8nlMsH2NetfEtva0xGfgZAmAWq8ntIFkAAhjb1x82aJTTmclc8SeyaLdrYL\nFy6gWbNm2Lp1K1auXIny8nIMHToUzz77LK5evYqICNO50QICAnDmzBkAQF5eHoKCgkzWBwYG4sqV\n+jkLSkRE4nNa8RMSEoIffvgBvr6374WIjIyEXq/HP/7xD8ycObPON+36+qpMttX4qc3+MFd/7Odn\nOuGnRnPn8QujO2Lpp0dNnyuXmmxjLY1Gjbee74kjp3PR/8H74eNlfgDn4WHazDHhgfjzZhk6tw02\n2Xf199HIzwsanztnZ7pqm+PdzScBAIN6tq41s9B6qdT8vfr6Ct9jMmFwe7Ro4ot3Nh0HAKhUCpva\n6b6mvjj1258myxK0zaGxcObJ0j7kJp+xF7zsnORUIrG8r+rybt2Z90WhkEOlEj5A9/CQCb5e5/Yh\n6Nw+5K5t7/QHX1+VXf2vSpNgX2jDG+P4r3kAgKZBPmav26iRFzQa4c+7qh9Y6g81UavvnF309Lzd\nTxQ2vse3n++Ji3mFSGgfgqEvbzcu12jUgiPyKRV3DbNtw8+zWuXhkM/AkuqvXVv76qXCRYcz87mb\n4uJi/P777/j888+xaNEi5OXl4bXXXoOXlxdKS0uhUJj+jCoUCuh0t3+Oa1tvDVcuEKuz54sNMQjl\ndcjEywS5XHpP9AdXxrzO5aicTr3srarwqRIWFoaysjJcv369zqPr3LxZYnI5TMH1IrMzPxUVlcZ/\n37hebLKuoKDI+O9AH/MD18oKvck21iooKEKA2gNJ8S3h46XAzZslqKw0nTRUV15h/Pe8pzojtKmv\nyfON76Pa825cLwaqvS8AeHtaN+gq9FDJJbVmFlr/t7jmxuUymRS+virBvFWKi+8cEJSU6Gxqp4Fd\n78P5KzcR2sQXndsGwUMug6Sy0uJrWVqu1+urbVOMMk/7uq7BYHlf1VX/pr6ivBIlJcIHSeXlpu+p\npvZtF+qHvcdyAACe0rrlENKssRoX84oQ4OuJgoIiNFLfKQhv3So1e90bN4ohh/BnffNmSa39wZKi\nojLjv0v/6ifV+/zNWyUoKKhbseqv9oC/WoPCWyUI9vdC7p+3f56vXy8yKYCr2rdMV2Hy/Aorfp6T\nurTE/szLeOExrV2/A+qiLj9vAHDzVpngcmfnu1tVXlckk8lQVFSEN998E02a3J4L7uLFi/j0009x\n//33mxUyOp0Onp63v2xRKpU1rreGq7aPJbbk3b59O0pLS+Hp6YmBAwc6IZVl1fN6enoAwj8aZAVf\nX5VdX3SJyda8YvXhhtK+7sppxc/+/fvx4osvYt++fcbhrbOysuDn52fVsKKVlXqTC+ErKvQw3F34\nVauOKir0eLxPBDbs+RWP/a01KiruHGhUlJsfdBgMMNnGWnc/t7JSb7as+nX8lZUGy/ur/j4EtvP9\n66xSXfJW32behM44f/UWOkcF1ymvcV21gkOvryF3DZRyGV4YobWYrabc1fXq2Bxrdp0GAEgl9n1m\ndclRxa/apVjR9/vjRpFw8ePvoxR8PaH2jYtojHFJkfD3UULt6WHze3lhhBY/ZOWic1TQ7Z+Lah1N\nqJ/V+Fn/dUBe0zaW6PV39qs33N6vybKa+nwNTN+PXvCmIMPdN8kY6r6v4Q+1xqM9wyCRSBzSn+qi\ntvYtt7CuvvK5g6CgICiVSmPhAwD3338/rly5gvj4eOTl5Zlsn5+fj8aNGxufm5+fb7b+7kvh6sKW\nLwrEUNfCW0hRUQlKSkpQWWmotwJcKG9paXm97Pted/NmiV1fdInBnv4L1H8ftjdvfXPXvPZyWvET\nGxsLlUqF2bNnY/LkyTh//jzS09ONN6Zao/plb3W5Qfxvcc3RrUNTk/lHgNsHZnczO3hyhjruI+o+\nDc5cvAEAUHo47hRk8yBvpw9t7Gw9tSFoHKCGr6fM6nmehNT1U2/krcTUYe2Rf6MUCdFN8PUP5wW3\nG967dZ33LZFIHHIDu8ZHiX7xLY2PRRpU0JThrv87iLMGhuCcOe5Hq9WirKwMf/zxB+677/bgNGfP\nnkXz5s2h1WqxcuVKk+2PHTuGZ5991vjcI0eOIDk5GQBw+fJlXLlyBTExMVbnsOWLAjHZkvdvf7sz\nPEp9v9fqeat/mUK2q6jQ2/VFl5hszStWH24o7euunFb8qNVqrF69GgsXLsSjjz4KtVqNkSNHYsKE\nCVa/ltC1/rW5u/CxpNyFKt1HEu5DeaUeLYO84amw7qN5eXQsFn96zKF57q92eV5kS3EnAZRKJeiu\nbYaCgqJ6/wGNDW8suPzJvhFo01Lj9hNP1jQpqa0ccqhiMsOshU3u2lHLJj6O2LNo3Lgb1ZvQ0FD0\n7NkTr7zyClJTU5GXl4dVq1Zh8uTJ6Nu3L5YsWYKFCxfisccew4YNG1BcXIx+/foBAEaNGoUxY8Yg\nJiYG0dHRWLhwIXr16sWR3oiIGhCn3vMTFhaG1atX2/06Pl4eKPjrWvjbc7zYdoQg9M14YCPXuc5R\n4SHDiF51P4NQXRsnFCfNG3tj8pD2KK+sREQLP4e/vpgccYwpkUgQEug6N6Jbe+D8XHI0Dpy8jBFW\nnLWqPcTt/9V1ctiaGEyGBK+dXCbBsB5hNu2L3MuSJUuwYMECPP7441CpVHjiiSfw+OOPAwBWrlyJ\n1NRUbNq0CW3atMGqVauM9/RotVrMmzcPy5Ytw40bN9CtWzfMnz9fzLdCRET1zC2mC396QFssXHcE\nEc39zAY7AOr+LfPdl72FNvHBkw9HWNiaACCujfBZD3J/D0QG4YFI6+91qNFfP2IhgWoc+/X2vRUq\npW0TcwY2UiHveimAuhVQkwa1g5edA2GIzSUuXXQD3t7eWLRoERYtWmS2rn379tiyZYvF5yYnJxsv\ne6OaFRUVwmAwQCKRQK1270unqWFiHyYhbnGk0KyxN96e2h1yWe0HQDUdIwU2ujOiz7PJ0ejk6AM/\nchuN/Ww749cjJgTb9v8GqUTilhPf1pcBCaG4fK0YIYFeNp9dHZ8UiWWbM9EulJPUEYkhI+NTFBUV\nQq32xtixKWLHIbIa+zAJcYviB7Dtvp+7+Xgp8I9RsfjzVikeqMczGtUP/jwVtn0LTo4xoOt9OPZr\nPp4Z3M6m53urPPDm5AchlcDlzjIM7Ho/9mdegY+XB8KbNxInxF9fPigVMkwZ2t6ulwr0U2H+U/HW\n79yN8Z4fciWJiUmorKyETMa/W+Se2IdJiGsdvdWDyPvq/8b9gQ+G4o/cW2gS4IVgf6963z/dMbRH\nGIbaeV+It8q+CVadJaCRJ5ZOfRAKuVRwRDxftfAErQ7Fy7aI7hnNmrUQOwKRXdiHScg9Ufy4+nXy\nKqUcM0bFih2DGoCquaCEOGKIcFdTvRBVKtz//bn67zIiIiJ35/5HCyJIGdQWCg8pRv4tXOwoRK6l\nni/b6tu5BUKb+CC6lT/a8t4gIiIiqsU9ceanvnVp2wSdIoMER54jckV+3vVwyZsIlB4yvDauk9gx\nHIb3/JArOXToIHS6MigUSnTqlCB2HCKrsQ+TEBY/NnLFwqdViC/OXbqJ+4Lde6JHcpwRvVrjvz9d\nwdMD24odhYjczKVLOSguLoaXF+9VJffEPkxC7onip1fHZlj7zc8AAIWH6xUl9eXvw2Nw/Nd8xLQO\nEDsKuYh+8S3RL76l2DHIDvfqWTtyfYMHDxc7ApFd2IdJyD1R/PSMCYHaU44m/l4ueUamvnir+eiL\nQQAAIABJREFUPNCtQ1OxY1AD06jawbm/j2cNW5I17m/qg/5dQsUbtpyIiOgedE8UP1IpJ5wkEku7\nUH/01IagTFeJrtFNxI5zz5DLpIirx/nIiIiIGoJ7ovghIvFIJBKM7RcpdgwiIiKiWrH4ISJyEV7K\nO7+Su7Tl2WwS18cfv4+iokKo1d4YOzZF7DhEVmMfJiEsfkh0gY08kX+jVOwYRKJTeMgw84mOuHyt\nGN3a8/49EldCQndUVFRALuehArkn9mES4tTeoNPpMGfOHHz77bfw9PTEhAkTMH78eGfuktzQC49p\n8dm/f+X9IkQAwpv7Iby5n9gxiBARESV2BCK7sA+TEKcWP4sXL0ZWVhbWrl2LnJwcvPzyy2jWrBn6\n9u3rzN2Sm2ni74W/D48ROwYRERER3eOcNi50SUkJMjIy8OqrryIyMhKJiYmYOHEi1q1b56xdEhER\nERERWeS0Mz/Z2dmorKyEVqs1LouLi8PKlSudtUsiInIB+fn5CAwMFDsG2enUqUyUl5fDw8MD7dp1\nEDsOkdXYh0mI04qfvLw8+Pn5mdxkFhAQgLKyMhQUFECj0Thr10REJKJhw4ahQ4cOGD58OLp37w6J\nRCJ2JLLBiRNHUFRUBLVazQNHckvswyTEacVPSUkJFAqFybKqxzqdzlm7JSIikf373//G999/j08/\n/RTz5s3DkCFDMGzYMDRpwkFN3Mno0RygiNwb+zAJcVrxo1QqzYqcqscqlarOryOTOe22JIeqysm8\nzsG8zsW8zuWueW0ll8uRmJiIxMRE7N27F3PnzsXKlSvRtWtXzJgxA2FhYQ5KSkREZB2nFT/BwcG4\nfv069Ho9pNLbf0jz8/Ph6ekJX1/fOr+Or2/dCyVXwLzOxbzOxbzO5W55bZWXl4dt27Zh69at8PT0\nxDPPPINHHnkEBw8exOTJk/H111+LHZGIiBoopxU/UVFRkMvlOH78ODp27AgAOHz4MKKjo521SyIi\ncgEDBgxAUlIS0tPTERV1Z56NxMRE7Nq1S8RkRETU0Dmt+PH09MTgwYORmpqKhQsXIjc3F2vWrMGi\nRYuctUsiInIB33//PY4ePYqoqCgUFBTg4MGD6N+/PwBg6dKlIqejuvr88/UoLi6Cl5caw4c/LnYc\nIquxD5MQp05yOnPmTMydOxdjx46Fj48Ppk+fjsTERGfukoiIRLZ06VLk5OTgwQcfRHl5ObZs2YJT\np05hxowZYkcjK4SHR0KnK4NCoRQ7CpFN2IdJiFOLH09PT6SlpSEtLc2ZuyEiIhdy8OBB7NixAwAQ\nFBSElStXIjk5mcWPm9Fq48SOQGQX9mES4h5DDxERkdsoLy9HaWmp8XFlZaWIaYiIiO5w6pkfIiJq\neAYMGIDRo0fj4YcfhkQiwe7du/HII4+IHYuIiIjFDxEROdbUqVPRpk0b/Pjjj5DJZHjuuefQu3dv\nsWORlX7//RwqKiogl8sRGtpK7DhEVmMfJiEsfoiIyOG6du2K9u3bw2AwAAAuXbqEkJAQkVORNfbu\n3YOiokKo1d4IDU0ROw6R1diHSQiLHyIicqgPPvgA77zzjtmE1vv37xcpEdli1KhxAAwAJCInIbIN\n+zAJcckBD3Q6HWbNmoVOnTqhe/fuWLNmjah59uzZg8jISERFRRn/P336dABAVlYWRowYAa1Wi+HD\nh+PUqVMmz92xYwf69OmD2NhYTJkyBQUFBU7LqdPpMHDgQBw6dMi4LCcnB+PHj0dsbCwGDBiAAwcO\nmDznv//9LwYOHAitVotx48bhwoULJus/+ugj9OjRA3FxcZg9ezbKysqcmnfBggVmbb1+/Xrj+tra\nc8mSJUhISEB8fDzS09MdkjM3NxfTpk1DfHw8evbsiUWLFkGn0wFwzfatKa8rtu/58+fx1FNPITY2\nFr1798bq1auN61yxfWvL7IptXCUlJQUzZ840Prb395elrBs2bMA333yD/fv3m/xH7kWhUEChUEKh\nUIgdhcgm7MMkxCWLn8WLFyMrKwtr165Famoqli9fjt27d4uW58yZM+jduzcOHDiAAwcOYP/+/Xj9\n9ddRUlKClJQUdOrUCVu2bIFWq8WkSZOMoxxlZmbi1VdfxdSpU7Fx40bcuHHD5MDDkXQ6HV544QWc\nOXPGZPnkyZMRFBSEzZs3Y9CgQZgyZQquXLkCALh8+TImT56MYcOGYfPmzdBoNJg8ebLxud988w1W\nrFiB+fPn4+OPP8aJEyccdjBmKe+5c+fw0ksvYf/+/ca2fvTRRwHU3p4ffvghdu7ciRUrVuDdd9/F\n9u3bHVI4T5s2DWVlZfj000+xdOlS/N///R+WLVsGAHjuuedcrn1ryutq7WswGJCSkoLAwEBs27YN\nc+bMwXvvvYedO3cCcM32rS2zq7VxlZ07d2Lfvn3Gx/b+/qopa9OmTdG0aVOH5CYiInIklyt+SkpK\nkJGRgVdffRWRkZFITEzExIkTsW7dOtEynT17FuHh4fD390dAQAACAgLg7e2NnTt3QqVSYcaMGWjV\nqhVmz54NtVqNr7/+GgCwfv16JCUlYdCgQYiIiEB6ejr27t2LixcvOjzfiBEjkJOTY7L84MGDuHDh\nAubNm4dWrVohJSUFWq0WGRkZAIBNmzahffv2GDduHMLCwpCWloaLFy8az8SsXbsWY8eORc+ePREd\nHY25c+ciIyPD7m/PLeWtWte2bVtjOwcEBECpvD05WW3tuXbtWkyfPh2xsbHo3LkzXnrpJbv7zblz\n55CZmYm0tDSEhYUhLi4O06ZNw44dO/C///0POTk5LtW+NeUFXK998/Pz0bZtW6SmpqJly5bo0aMH\nEhIScOTIEZds39oyA67XxgBw48YNpKeno0OHDsZl9v7+qilrbGwsZs+ejd27d2Pv3r3G/4iIiMTm\ncsVPdnY2KisrodVqjcvi4uKQmZkpWqazZ8/i/vvvN1uemZmJuDjTCbQ6duyIY8eOAQCOHz+OTp06\nGdc1adIETZs2xYkTJxya78cff0RCQgI2btxovLm4Kl+7du2MB17A7bY8fvy4cX31fJ6enmjbti2O\nHTsGvV6PkydP4oEHHjCu12q1KC8vR3Z2tlPyFhYWIjc3F6GhoYLPq6k9r169isuXL5vkjYuLw6VL\nl5Cfn29z1saNG2PVqlXw9/c3WX7r1i2cOHHC5dpXKK/BYMCtW7dctn2XLl0KLy8vAMCRI0dw+PBh\ndO7c2SXb11LmQ4cOIT4+3iXbGLh9Nn3w4MEICwszLrPn91dtWY8fP47z589j7dq1+OCDD/DBBx+Y\nXBpI7mHXrq3YvHkDdu3aKnYUIpuwD5MQlxvwIC8vD35+fpDL70QLCAhAWVkZCgoKoNFo6j3Tb7/9\nhv/85z947733oNfrkZSUhKlTp+Lq1auIiIgw2TYgIMB4KVdeXh6CgoJM1gcGBhov23GUUaNGCS4X\n2n9AQAByc3MBAFevXhXMl5ubi5s3b6KsrMxkvUwmg5+fH65cuYKYmBiH5z137hwkEgnee+897Nu3\nD35+fhg/fjySk5Mtvp+q9szLy4NEIjFZHxgYCIPBgCtXriAwMNCmrD4+PujWrZvxscFgwLp165CQ\nkOCS7Wspb9euXV2yfavr3bs3Ll++jIceegh9+/bFwoULXa59a8ucmZnpcm188OBBHDlyBNu3b0dq\naqpxuT2/v2rLunbtWpuykmvx89NApfIy+QKCyJ2wD5MQlyt+SkpKzG5Mq3pcddN2fbp06RJKS0uh\nVCqxbNky5OTkGO/3KS0tFcxalbO29c5mqS3rkq/quv/6zH/u3DlIpVKEhYXhySefxI8//oh//vOf\n8Pb2RmJiYo15S0pKzPI6o9+88cYbOH36NDIyMrBmzRqXb9833ngD2dnZyMjIwE8//eTS7fvuu+8i\nPz8fc+bMwcKFC92i/1ZlTk1Nxeuvv47o6GiXamOdToc5c+YgNTXVbL/2/P6qLWtubi5mzZqFnJwc\nrF+/Hv/4xz+QlpaG4OBgm94HiaNr155iRyCyC/swCXG54kepVJr9oa96rFKp6j1PSEgIfvjhB+OQ\nrZGRkdDr9ZgxYwbi4+MFs3p6egKw/F6q1jubUqnEjRs3rM7n6+tr8aBLp9M57XNITk5G7969jW0d\nERGB33//HRs2bEBiYmKN7Vn1rY5OpzPL7qi86enpWLt2Ld5++220bt3a5dv37rytW7d26fZt164d\nAOCVV17BSy+9hEcffRQ3b94UzAOI377VM8+cORMzZszAyy+/7FJt/O677yI6Ohpdu3Y1W1fb7yd7\nsqampmLYsGFYuXIlNBoN4uPj8fLLL+Ojjz6y6X0QERE5isvd8xMcHIzr169Dr9cbl+Xn58PT09Ns\nzoj6cvd+w8LCUFZWhsDAQOTl5Zmsy8/PR+PGjQEAQUFBZtfq5+fnm11K4izBwcE15qtpvUajgVKp\nNMlfWVmJ69evG5/vDHe3datWrXD16lUANbdncHAwDAaDyfqqS3MckbdqxLD09HQkJiYCcO32FcoL\nuF77Xrt2DXv27DFZ1rp1a5SXl6Nx48Yu2b41ZS4qKnKpNt61axf+/e9/IzY2FrGxsdi+fTu2b9+O\njh071tp/7cl69epV9O/fHxKJBDKZDJMmTcKff/5p03sgIiJyJJcrfqKioiCXy403NQPA4cOHER0d\nLUqe/fv3Iz4+3mSEqKysLGg0GjzwwAM4evSoyfbHjh1DbGwsgNs3WFeNAAXcHprXkfcb1CYmJgZZ\nWVkm394eOXLEOJhETEyMSf6SkhJkZWUhNjYWEokE7du3N8l/7NgxeHh4IDIy0il533nnHYwfP95k\n2enTp42DTVhqT61Wi6CgIISEhJisP3z4MJo2bWr3/SjLly/Hxo0b8dZbbyEpKcm43FXb11JeV2zf\nnJwcTJ061eQg/OTJkwgICEBcXBxOnTrlcu1rKbO/vz8++eQTl2rjdevWYfv27fjyyy/x5Zdfonfv\n3ujduze2bduGmJgY4+AGVery+6suWSUSCUpKSiCR3J5Y8NKlSzblJ3FdvZqLK1cu4erVXLGjENmE\nfZiEyObMmTNH7BDVyeVyXL58GRs2bED79u1x8uRJLFmyBC+99BJatWpV73kCAgKwadMmZGdnIzw8\nHJmZmViwYAGeeuopDBo0CKtXr0Zubi5CQkKwYsUKZGdnY968eZDL5WjcuDEWLVqExo0bQyqVIjU1\nFW3atMHIkSOdlnf58uUYOnQomjVrhpCQEOzYsQPHjh1DWFgYMjIysGvXLrz++uvw9vZG8+bN8eab\nb0Imk6FRo0ZIS0uDwWDAiy++COD26FlLly5Fq1atUFhYiNdeew39+vVDr169nJLXy8sL77zzDlQq\nFQIDA7Fz5058+OGHWLBgAYKDg2ttz7KyMqxcuRLt2rUzDpE8fvx4k5EDrXX27Fm8+OKLmDRpEvr2\n7Yvi4mLjf61bt3a59q0pb2BgoMu1b1BQEPbt24f9+/ejXbt2OHnyJBYsWIBnn30W/fr1c7n2rS1z\nly5dXKqNfXx80KhRI+N/+/btg0KhwNChQ9GyZUu7fn/VlNXHxwevvfYarly5grNnzyI9PR3Tp09H\nmzZt7Gp7V1JaWg693lD7hiKTSiVQqRQ25c3I+BSZmUfxxx+/QauNq/0JDiCUd//BH3BNXz9XTDjC\nuSNfokJXArnCC63iBosdBwBQWpiPXh1bomnTJjb3BzHY03+B+u/D9uatb+6a114SQ/Wxhl1EaWkp\n5s6di2+++QY+Pj6YOHEinnzySdHynD17FgsXLsTx48ehVqsxcuRIPPfccwBuf+ObmpqKc+fOoU2b\nNpg7d67JN8tbt27FsmXLcOPGDXTr1g3z589Ho0aNnJY1KioKn3zyiXGI2gsXLmDWrFnIzMxEy5Yt\nMXv2bHTp0sW4/X/+8x+8/vrryM3NRceOHTFv3jw0a9bMuH7VqlX46KOPUF5ejocffhj//Oc/HTpT\n8t15v/vuOyxbtgx//PEHmjVrhueff97ksq2a2lOv1yM9PR1btmyBVCrFiBEj8Pzzz9uV7/3338db\nb71lssxgMEAikeD06dM4f/48Zs+e7TLtW1teV2tf4PblUvPnz8fBgwehUqnwxBNPICUlBYDr9t+a\nMrtiG1epmqQ0LS0NgH2/v2rLeu7cORw8eBB6vR7x8fFmI8u5u4KCIlRU6GvfUGRyuRQajdqmvAUF\nf8Jg0EMikUKj8a/9CQ4glHfRm+/gl3Jxrv6wxZ73n0Jp4TV4egcgMcU1hni/fjkbcyd2Q2ys1ub+\nIAZ7+i9Q/33Y3rz1zV3z2sslix8iInJfVRPN3q36vEHuzt0OFtw5L4sf+zXU4qe+Ma9zOar4cbnR\n3oiIyL0tWbLE+O/y8nKcOXMGnTp1uqeKHyIick8sfoiIyKE2btxo8viXX37BihUrREpDRER0B4sf\nIiJyqoiICJw9e1bsGGSl77//FmVlpVAqPfHQQ33EjkNkNfZhEsLih4iIHGr9+vUmj7Ozs6FW23+d\nNtWv8vJy6HQ6SKUysaMQ2YR9mISw+CEiIof66aefTB5rNBosXbpUpDRkqz59+osdgcgu7MMkhMUP\nERE5VNVQ2kRERK6GxQ8RETnUsGHDIJFILK7PyMioxzRERER3sPghIiKH6tKlC/Lz8/HYY4/Bw8MD\n27ZtQ35+PkaPHi12NLJCUVGhcZJktdpb7DhEVmMfJiEsfoiIyKF++OEHk7M77du3x9ChQ9G5c2cR\nU5G1MjI+RVFRIdRqb4wdmyJ2HCKrsQ+TEBY/RETkUIWFhbh06RJCQkIAAH/88Qf0etefPZxMJSYm\nobKyEjIZR8oi98Q+TEJY/BARkUNNmTIFQ4YMQXR0NAwGA3799Ve88cYbYsciKzVr1kLsCER2YR8m\nISx+iIjIoQYMGID4+HgcPXoUSqUSWq0Wfn5+YsciIiKCVOwARER0b6moqMAXX3yB7777DnFxcfjs\ns89QUVEhdiwiIiIWP0RE5FgLFy7E5cuXcfLkSUgkEhw7dgzz5s0TOxZZ6dChgzhw4HscOnRQ7ChE\nNmEfJiG87I2IiBzq6NGj2Lp1K5KTk+Ht7Y0VK1Zg4MCBYsciK126lIPi4mJ4eXmJHYXIJuzDJITF\nDxEROZRUanpRQUVFRY2TnpJrGjx4uNgRiOzCPkxCWPwQEZFDde/eHa+99hoKCwuxdetWZGRkoFev\nXmLHIiIiYvFDRESO9fe//x0ZGRm4fv06/v3vf6N///4YOXKk2LGIiIhY/BARkWNNmDABa9aswfDh\nvOSEiIhcC4sfIiJyqMLCQhQUFECj0Ygdhezw8cfvo6ioEGq1N8aOTRE7DtmptLQExcXFUColKC4u\nRkWF3mn7UqlULnGfH/swCXHp4sdgMODPP4ug1xvEjuJSpFIJ/P3VbJu7sF2EsV0sY9sIk0olCAjw\ntvn5lZWV6NWrF1q0aAGlUmlcnpGR4Yh4VE8SErqjoqICcrlLHypQHXhpmuOND7+BBN9AIpXAoDfA\nWb/xim9dw4ynh+Ghnj2ctIe6Yx8mIS7dGyQSCaRSCQ9K7iKVStg2AtguwtgulrFthEml9n1j+8or\nrzgoCYkpIiJK7AjkIApPbyju61Y/O7t2ARWVrjGpMfswCXHp4oeIiNzHxo0b8dhjj6Fz585iRyEi\nIhIkrX0TIiKi2n322WfGf0+YMEHEJERERMJ45oeIiBzCYLhz6eCff/4pYhJyhFOnMlFeXg4PDw+0\na9dB7DhEVmMfJiEsfoiIyOFcYaQnss+JE0dQVFQEtVrNA0dyS+zDJITFDxEROYTBYEBpaSkMBgP0\ner3x31VUKpWI6chao0ePFzsCkV3Yh0kIix8iInKIn3/+GbGxscaCR6vVQiKRwGAwQCKR4PTp0yIn\nJCKiho7FDxEROUR2drbYEYiIiGrE0d6IiIiIiKhB4JkfIiIiMvP55+tRXFwELy81hg9/XOw4RFZj\nHyYhNp/50el0GDhwIA4dOmRxm6ysLIwYMQJarRbDhw/HqVOnbN0dERER1aPw8EhERUUjPDxS7ChE\nNmEfJiE2nfnR6XR44YUXcObMGYvblJSUICUlBYMHD8aiRYuwYcMGTJo0CXv27IGnp6fNgYmIiMj5\ntNo4sSMQ2YV9mIRYfebn7NmzGDFiBHJycmrcbufOnVCpVJgxYwZatWqF2bNnQ61W4+uvv7Y5LBER\nERERka2sLn5+/PFHJCQkYOPGjSbzN9wtMzMTcXGmFXfHjh1x7Ngx61MSERERERHZyerL3kaNGlWn\n7a5evYqIiAiTZQEBATVeKkdERESu4fffz6GiogJyuRyhoa3EjkNkNfZhEuK00d5KS0uhUChMlikU\nCuh0OmftkoiIiBxk7949KCoqhFrtjdDQFLHjEFmNfZiEOK34USqVZoWOTqezerADmYxTEd2tqk3Y\nNqbYLsLYLpaxbYSxPQgARo0aB8AAQCJyEiLbsA+TEKcVP8HBwcjLyzNZlp+fj8aNG9f5NSQSCf73\nv/8hPj7e0fHuCb6+KrEjuCS2izC2i2VsGyJzd1+9QeRu2IdJiNOKn5iYGKxatcpk2bFjx/DMM89Y\n9TpFRaUoKChyZDS3J5NJ4eurws2bJais1Isdx2WwXYSxXSxj2wirahd3kJKSgoCAAKSlpQG4Pb/c\nnDlz8MsvvyA8PBxz5sxBu3btjNvv2LEDy5YtQ35+Ph588EHMnz8fGo1GrPhERFTPHFr85Ofnw8fH\nB0qlEg8//DCWLl2KhQsX4rHHHsOGDRtQXFyMpKQkq16zstKAigoelAiprNSzbQSwXYSxXSxj27in\nnTt3Yt++fRgyZAiA2ueXy8zMxKuvvop58+YhMjIS8+fPx8yZM/Gvf/1L5HdCRET1xa4LuyUS02so\nu3Xrhq+++goA4O3tjX/96184fPgwhg0bhpMnT2LVqlWc4JSIiOx248YNpKeno0OHDsZltc0vt379\neiQlJWHQoEGIiIhAeno69u7di4sXL4r1Nlzarl1bsXnzBuzatVXsKEQ2YR8mIXad+Tl9+rTJ4+zs\nbJPH7du3x5YtW+zZBRERkZnFixdj8ODBuHr1qnFZTfPLJScn4/jx45g0aZJxXZMmTdC0aVOcOHEC\nzZo1q7fs7sLPTwOVygtKpVLsKEQ2YR8mIU6754eIiMgZDh48iCNHjmD79u1ITU01Lq9tfrm8vDwE\nBQWZrA8MDMSVK1ecH9oNde3aU+wIRHZhHyYhLH6IiMht6HQ6zJkzB6mpqWYjOdU2v5wj559zl+HA\n3W04d6G8UimHKXY3MpkEcrn9fe5e6L+uzF3z2ovFDxERuY13330X0dHR6Nq1q9m62uaXc9T8c4D7\nDY/uznk9PT2AMhHDkNW8vT2h0agd9nru3H/dgbvltVeDKX4qKirw1Vc7MHBgsthRiIjIRrt27cK1\na9cQGxsLACgvLwcAfPPNNxgwYECN88sFBQUhPz/fbP3dl8LVhbsMj27PcO5Xr15BZaUeMpkUQUFN\nnJTQlFDe0tLyetk3OU5hoWOmKbF3OoL67sPuNn2Cu+a1V4Mpfr799mt88skaFj9ERG5s3bp1qKio\nMD5OT08HAMyYMQM//vij4Pxyzz77LABAq9XiyJEjSE6+/Xfg8uXLuHLlCmJiYqzO4W7Do9uSd/v2\nrSgqKoRa7Y2xY1OclExY9bx6vaFe9032c/Q0Jbb+vInVhxvC7wd31mCKH4OBvzyJiNxd06ZNTR6r\n1bcvrWnRogU0Go3g/HL9+vUDAIwaNQpjxoxBTEwMoqOjsXDhQvTq1YsjvVkwaNCjMBj0kEjc434A\noruxD5OQe674+eabXfjkkw+Rm3sF4eFt8MIL/0BhYSHS0uYBAHr06IxNm75EYeEtvPlmGn799Rf4\n+jbCoEFDMG7cRMHX/O23c3j33bfw00+ZqKioQFRUW7z88my0bBkKADh9+hTeffct/PJLNoKCgvHU\nU8/gb3/rAwD46adMrFjxDn799WdoNP4YPXoMkpOHAQAWLpwLAPjll5/x55/XsGLFBxg1aijGjZuI\nL774HO3ba5GWtsTJLUZEdG+oml8uNTUVmzZtQps2bUzml9NqtZg3bx6WLVuGGzduoFu3bpg/f77I\nqV2XRuNvcd1H6zbg0E/nHL5PqUQCuVyGiopK6P/60vLatWvwCot2+L7o3ldTH6aG654qfn744SAW\nLZqP55//B+LiOuHzzz/Dyy+/gE2btmHatBfx2Wfr8MEHa9GoUSO88soLiInRIjV1Ic6f/x2zZ/8D\nkZFt0aWL6U20BoMBr7zyAjp3TsCMGTNRWHgLS5cuxnvvvYu0tDdRUFCA55+fgn79HsHMma/hp58y\n8frrcxAaej/kcjmmT38WI0c+YVy3dOliBAQEoHv3hwDcLtbS0t6Ev38AmjdvAQA4cOA/+Ne/1qCy\nsrK+m5CIyK2kpaWZPK5tfrnk5GTjZW9ku/MXr6DEL6Fe9uXlVy+7IaIG4p4qfr78cgv69OmHQYOG\nAACmTPk7FAoP3Lp1E97e3pBKZdBoNACAK1cuoXv3nggODkaTJk3w9tsrEBISYvaaZWVlSE5+FEOH\nPgql8va3h/36DcCGDWsBAHv2fINGjRrh739/CQDQokVL3Lp1E2Vlpdi161tERLTB008/a1z3xx+/\n49NPPzEWP1FR7dC1azeTfSYnDzMWQkRERERE5Bj3VPFz/vwfSE5+1PhYLpfjueemC247ZswE/Otf\ny7Ft2xZ07doNDz/cX/D0qKenJ5KTh+Grr3YgO/s0/vjjd/zySzb8/QMBABcu/IHw8DYmzxkxYjQA\n4MMP30fbtu1N1kVHd8C2bXe+lWzSxPT6dUvLiIiI6tP333+LsrJSKJWeeOihPmLHIbIa+zAJuafu\nAJPL617LjR49Bps2bcMTT4zF5cuX8Pe/P4cdO7aZbVdSUoKJE5/Enj27cd9992PixGdMCqqa9qlQ\nKCGRmE7OptfroddXVttGcffTBJcRERHVp/Lycuh0OuNw4kTuhn2YhNxTZ36aN2+JM2eAg0atAAAg\nAElEQVR+NT7W6/V47LEhSE01vaFVp9PhvffexeOPj8GIEaMxYsRoLFmShr17v8OAAYNNtj127Aiu\nXbuGdes+NxYyP/zwXwAG4z4PHjxg8pzU1JmIjGyHli3vw/HjR03W/fTTCbRseZ+j3jIREZFT9OnT\nX+wIRHZhHyYh99SZn0cffQy7d+/CV1/twMWLOXjnnTcBGBAREQmVSoVbt27i4sUcyGQyZGYex1tv\nvYHz5/9AdnYWjh8/hoiISLPX9PVthJKSYuzd+x2uXLmM7du3YsuWz42zhD/8cBJu3bqJFSuWISfn\nAnbt2o79+/ehc+cuGDLkUZw58wvef38FLlw4j6++2oEvvtiMoUNH1HPLEBERERHRPXXmJyYmFi++\n+Ao++ugD/PnnNbRpE4XFi9+CQqFAx46d0KxZc4wZ8xjee2815s1Lw9KlbyAlZSxkMhl69+6LsWOf\nMnvN6Oj2GD/+aSxd+gZ0ujKEhYXjxRdfwaJF83HtWj4CAgKxePHbWLZsCTIyNiEkpBnmzHkdYWGt\nAQBvvPE2li9/G599th7BwcGYNu0FJCUNsPge7r5MjoiIiIiIHENicOHZPyUSCXbv/j9otXFiR3Ep\ncrkUGo0aBQVFDWpG3tqwXYSxXSxj2wiraheyzF36jD19vKioEAaDARKJBGq1t8m6eYvfwu+GGEdG\nvWfsef8plBZeg6d3ABJTVosdp97dunYBk5JaILF3b7tfy97f0TX1YWdwt78p7prX7tdxQBYiIiK6\nx2RkfIqiokKo1d4YOzZF7DhEVmMfJiEsfoiIiMhMYmISKisrIZPJxI5CZBP2YRLC4oeIiIjMNGvG\nybbJvbEPk5B7arQ3IiIiIiIiS1j8EBERERFRg8DL3oiIiMjMoUMHodOVQaFQolOnBLHjEFmNfZiE\nsPghIiIiM5cu5aC4uBheXl5iRyGyCfswCWHxQ0RERGYGDx4udgQiu7APkxCr7/nR6XSYNWsWOnXq\nhO7du2PNmjUWt/3222/xyCOPIDY2Fo8//jiysrLsCktERERERGQrq4ufxYsXIysrC2vXrkVqaiqW\nL1+O3bt3m2135swZvPTSS5g0aRK+/PJLREZGIiUlBWVlZQ4JTkREREREZA2rip+SkhJkZGTg1Vdf\nRWRkJBITEzFx4kSsW7fObNv9+/cjPDwcgwYNQosWLfDCCy8gPz8fZ86ccVh4IiIiIiKiurLqnp/s\n7GxUVlZCq9Ual8XFxWHlypVm2/r5+eHMmTM4evQoYmNjsXnzZvj4+KBly5b2pyYiIiKn+vjj91FU\nVAi12htjx6aIHYfIauzDJMSq4icvLw9+fn6Qy+88LSAgAGVlZSgoKIBGozEu79+/P7777juMHj0a\nMpkMUqkU77//Pnx8fByXnoiIiJwiIaE7KioqTP7mE7kT9mESYlVvKCkpgUKhMFlW9Vin05ksv379\nOvLz85GamoqYmBhs2LABr7zyCr744gv4+/vbGZuIiIicKSIiSuwIRHZhHyYhVhU/SqXSrMipeqxS\nqUyWL1myBG3atMGoUaMAAPPmzUNSUhK2bNmCiRMn1nmfMpkEcrnV4zLc02Qyqcn/6Ta2izC2i2Vs\nG2FsDyIiuldZVfwEBwfj+vXr0Ov1kEpv/3HMz8+Hp6cnfH19TbY9deoUxowZY3wskUgQGRmJS5cu\nWRVQrfaERqO26jkNha+vqvaNGiC2izC2i2VsGyIioobBquInKioKcrkcx48fR8eOHQEAhw8fRnR0\ntNm2QUFBZiO7/fbbb+jQoYNVAYuKSlFQUGTVc+51MpkUvr4q3LxZgspKvdhxXAbbRRjbxTK2jbCq\ndqGG7dSpTJSXl8PDwwPt2ln3t5vIFbAPkxCrih9PT08MHjwYqampWLhwIXJzc7FmzRosWrQIwO2z\nQD4+PlAqlRg+fDhmzZqF6OhoxMbGYtOmTbh8+TKSk5OtClhZaUBFBQ9KhFRW6tk2AtguwtgulrFt\niMydOHEERUVFUKvVPHAkt8Q+TEKsHv5i5syZmDt3LsaOHQsfHx9Mnz4diYmJAIBu3bph0aJFSE5O\nRv/+/VFSUoKVK1ciNzcXUVFR+OSTTzjYARERkRsYPXq82BGI7MI+TEKsLn48PT2RlpaGtLQ0s3XZ\n2dkmj4cNG4Zhw4bZno6IiIiIiMhBOKQPERERERE1CCx+iIiIiIioQeCUt0RERGTm88/Xo7i4CF5e\nagwf/rjYcYisxj5MQlj8EBERkZnw8EjodGVQKJRiRyGyCfswCWHxQ0RERGa02jixIxDZhX2YhPCe\nHyIiIiIiahBY/BARERERUYPAy96IiIjIzO+/n0NFRQXkcjlCQ1uJHYfIauzDJITFDxEREZnZu3cP\niooKoVZ7IzQ0Rew4RFZjHyYhLH6IiIjIzKhR4wAYAEhETkJkG/ZhEsLih4iIiMwoFAqxIxDZhX2Y\nhHDAAyIiIiIiahBY/BARERERUYPAy96IiIjIzK5dW1FSUgKVSoX+/ZPFjkNkNfZhEsLih4iIiMz4\n+WmgUnlBqVSKHYXIJuzDJITFDxEREZnp2rWn2BGI7MI+TEJ4zw8RERERETUILH6IiIiIiKhB4GVv\nREREZObq1Vzo9ZWQSmUICgoWOw6R1diHSQiLHyIiIjLz1VfbUFRUCLXaG2PHpogdh8hq7MMkhMUP\nERERmRk06FEYDHpIJLxCntwT+zAJYfFDREREZjQaf7EjENmFfZiEsBQmIiIiIqIGgcUPERERERE1\nCFYXPzqdDrNmzUKnTp3QvXt3rFmzxuK2P//8M0aPHo2YmBgMGjQIP/zwg11hiYiIqH58//23+Oab\n7fj++2/FjkJkE/ZhEmJ18bN48WJkZWVh7dq1SE1NxfLly7F7926z7QoLC/HUU08hPDwcO3bsQJ8+\nfTBlyhT8+eefDglOREREzlNeXg6dTofy8nKxoxDZhH2YhFg14EFJSQkyMjKwevVqREZGIjIyEhMn\nTsS6devQt29fk223bNkCtVqNuXPnAgCmTp2Kffv24aeffkKPHj0c9w6IiIjI4fr06S92BCK7sA+T\nEKuKn+zsbFRWVkKr1RqXxcXFYeXKlWbbHjp0CL179zZZ9vnnn9sYk4iIiIiIyD5WXfaWl5cHPz8/\nyOV3aqaAgACUlZWhoKDAZNsLFy5Ao9HgtddeQ7du3TBy5EgcPXrUMamJiIiIiIisZPVlbwqFwmRZ\n1WOdTmeyvLi4GB988AHGjBmDDz74ADt27MBTTz2Fr7/+GsHBwXXep0wmgVzOQemqk8mkJv+n29gu\nwtgulrFthLE9CACKigphMBggkUigVnuLHYfIauzDJMSq4kepVJoVOVWPVSqVyXKZTIaoqChMmTIF\nABAZGYkDBw5g27ZtSElJqfM+1WpPaDRqa2I2GL6+qto3aoDYLsLYLpaxbYjMZWR8iqKiQqjV3hg7\ntu5/t4lcBfswCbGq+AkODsb169eh1+shld7+ZjA/Px+enp7w9fU12bZx48Zo1aqVybLQ0FBcvnzZ\nqoBFRaUoKCiy6jn3OplMCl9fFW7eLEFlpV7sOC6D7SKM7WIZ20ZYVbtQw5aYmITKykrIZDKxoxDZ\nhH2YhFhV/ERFRUEul+P48ePo2LEjAODw4cOIjo4221ar1eLQoUMmy86dO4eBAwdaFbCy0oCKCh6U\nCKms1LNtBLBdhLFdLGPbEJlr1qyF2BGI7MI+TEKsurDb09MTgwcPRmpqKk6ePIk9e/ZgzZo1GDt2\nLIDbZ4HKysoAACNHjsTPP/+M5cuX4/z581i2bBlycnIwaNAgx78LIiIiIiKiWlh9V+vMmTMRHR2N\nsWPHYv78+Zg+fToSExMBAN26dcNXX30FAAgJCcHq1avx3XffYeDAgdi7dy9WrVqFoKAgx74DIiIi\nIiKiOrDqsjfg9tmftLQ0pKWlma3Lzs42eRwbG4stW7bYno6IiIhEcejQQeh0ZVAolOjUKUHsOERW\nYx8mIVYXP0RERHTvu3QpB8XFxfDy8hI7CpFN2IdJCIsfIiIiMjN48HCxIxDZhX2YhHAmOyIiIiIi\nahBY/BARERERUYPA4oeIiIiIiBoE3vNDREREZj7++H0UFRVCrfbG2LEpYschshr7MAlh8UNERERm\nEhK6o6KiAnI5DxXIPbEPkxD2BiIiIjITEREldgQiu7APkxDe80NERERERA0Cix8iIiIiImoQeNkb\nERERmTl1KhPl5eXw8PBAu3YdxI5DZDX2YRLC4oeIiIjMnDhxBEVFRVCr1TxwJLfEPkxCWPwQERGR\nmdGjx4sdgcgu7MMkhPf8EBERERFRg8Dih4iIiIiIGgQWP0RERERE1CDwnh8iIiIy8/nn61FcXAQv\nLzWGD39c7DhEVmMfJiEsfoiIiMhMeHgkdLoyKBRKsaMQ2YR9mITwsjciInIrubm5mDZtGuLj49Gz\nZ08sWrQIOp0OAJCTk4Px48cjNjYWAwYMwIEDB0ye+9///hcDBw6EVqvFuHHjcOHCBTHeglvQauPQ\nuXNXaLVxYkchsgn7MAlh8UNERG5l2rRpKCsrw6effoqlS5fi//7v/7Bs2TIAwHPPPYegoCBs3rwZ\ngwYNwpQpU3DlyhUAwOXLlzF58mQMGzYMmzdvhkajweTJk8V8K0REVM9Y/BARkds4d+4cMjMzkZaW\nhrCwMMTFxWHatGnYsWMH/ve//yEnJwfz5s1Dq1atkJKSAq1Wi4yMDADApk2b0L59e4wbNw5hYWFI\nS0vDxYsXcejQIZHfFRER1Rfe80NERG6jcePGWLVqFfz9/U2W37p1CydOnEC7du2gVN65vj8uLg7H\njx8HAGRmZqJTp07GdZ6enmjbti2OHTtmspxu+/33c6ioqIBcLkdoaCux4xBZjX2YhLD4ISIit+Hj\n44Nu3boZHxsMBqxbtw4JCQnIy8tDUFCQyfYBAQHIzc0FAFy9etVsfWBgoHE9mdq7dw+KigqhVnsj\nNDRF7DjkJhQqX6zdvBsZX/3X7teSSCSQy6WoqNDDYDCYrS8vL8PjQ/qgd88egs9nHyYhVhc/Op0O\nc+bMwbfffgtPT09MmDAB48ePr/E5OTk5GDhwIN5//31+u0ZERA7zxhtv4PTp08jIyMCaNWugUChM\n1isUCuNgCKWlpTWut4ZM5h5XjVfltCXvk09OgMFgMB6AVieRSADzY1EiKL0aAV59Yf1PlbCymtYV\nXcfV3Fyz/lmlpj7sDPb8vInBXfPay+riZ/HixcjKysLatWuRk5ODl19+Gc2aNUPfvn0tPmfOnDko\nLS21KygREVF16enpWLt2Ld5++220bt0aSqUSN27cMNlGp9PB09MTAKBUKs0KHZ1OB19fX6v37eur\nsj24CGzLq7a4RqmUAyW25yFyFC+1EhqNpb5quQ87U8P4/eC+rCp+SkpKkJGRgdWrVyMyMhKRkZGY\nOHEi1q1bZ7H4+fLLL1FcXOyQsERERAAwf/58bNy4Eenp6UhMTAQABAcH48yZMybb5efno3Hjxsb1\neXl5ZuujoqKs3v/NmyWorNTbmL7+yGRS+PqqHJ63rKzCYa9FZI/iojIUFBSJHQOA837enMVd89rL\nquInOzsblZWV0Gq1xmVxcXFYuXKl4PYFBQV48803sXr1agwYMMC+pERERACWL1+OjRs34q233kKf\nPn2My2NiYrBq1SrodDrj5W1HjhzBAw88YFx/9OhR4/YlJSXIysrC1KlTrc5QWalHRYXrHyxUcXRe\nofsviMRQqTe43M9iQ//94OqsKn7y8vLg5+cHufzO0wICAlBWVoaCggJoNBqT7RctWoQhQ4agdevW\njklLREQN2tmzZ/Hee+9h0qRJ+P/27j4sqjrvH/h7YIBBhBsloXJzS70FlGRgRBcFvdcQL10Nukt3\ne1ozzdptzbWtFNtEFx/Qtsz1KfMyfonVWmzbg5vl0+W2laWYigmYgKKsiYwLxsPAwMz39wc3E8Oc\nAYaHOWc479d1deV858yc93z4zsz5zJxzJiYmBkaj0Xbd2LFjccstt2Dp0qX47W9/i8OHD+PMmTPI\nzMwEANx77714/fXXsWPHDvz85z/H5s2bMWTIEIwdO1auh6NoH3/8PkwmE/z9/TF9eqrccYhcxjlM\nUlze7U3qYFEADvtRf/nllzh58iQyMjK6FdDb2z0HqXkSTztAzV1YF2msi3OsjTQl1+PQoUOwWq3Y\ntm0btm3bBgC2A5oLCgqwZcsWPP/887j33nsxZMgQbNmyBTfffDMAYPDgwdi0aRNWr16NrVu3IjY2\nFps3b5bz4ShacPAA+Pv3szt1OJEn4RwmKS41P84OFgUAf/8f98FraGjAihUrkJ6e7tAsuSogQNfO\ngWzqprYD1DqLdZHGujjH2niOBQsWYMEC56esHTJkCLKzs51en5iYiE8++aQ3ovU548dPkjsCUbdw\nDpMUl5qfsLAwVFVVwWq1wsur+ZNBo9EInU5nd7acvLw8XL58GQsXLrTbL/ixxx5DamoqVqxY0el1\n1tbWK+ZANqXwtAPU3IV1kca6OMfaSOupg0qJiIiUxqXmJzIyElqtFqdOnUJsbCwAIDc3F1FRUXbL\nRUdHY//+/XZjU6ZMwerVqxEfH+9SQItFeQeyKYXaDlDrLNZFGuviHGtDRESkDi41PzqdDikpKUhP\nT8eaNWtQXl6OrKws28GkRqMRgYGB8PPzw2233eZw+9DQUAwcOLBnkhMREVGvuXatHFarBV5e3ggN\nDZM7DpHLOIdJistHtaalpSEqKgpz5sxBRkYGFi1aZPuNhYSEBOzbt0/ydhqNpntJiYiIyG327fsA\n7733V+zb94HcUYi6hHOYpLj0zQ/Q/O3P2rVrsXbtWofrCgsLnd6uoKDA1VURERGRTO6++z4IYYVG\no9yz/xG1h3OYpLjc/BAREVHfN2AAd1Mnz8Y5TFLYChMRERERkSqw+SEiIiIiIlXgbm9ERETk4MiR\nA2hoqIefnw7/8z9T5I5D5DLOYZLC5oeIiIgcNDY2wmw2w8vLW+4oRF3COUxS2PwQERGRgylTpssd\ngahbOIdJCo/5ISIiIiIiVWDzQ0REREREqsDd3oiIiMhBbW0NhBDQaDQICOgvdxwil3EOkxQ2P0RE\nROQgJ+ct1NbWICCgP+bMWSB3HCKXcQ6TFDY/RERE5CApaRosFgu8vXmmLPJMnMMkhc0PERERORg8\n+Da5IxB1C+cwSeEJD4iIiIiISBXY/BARERERkSpwtzciIiJycPz4UZjNDfD19UNcXLzccYhcxjlM\nUtj8EBERkYMrV8pQV1eHfv36yR2FqEs4h0kKmx8iIiJykJIyS+4IRN3COUxSeMwPERERERGpApsf\nIiIiIiJSBTY/RERERESkCjzmh4iIiBy88cZrqK2tQUBAf8yZs0DuOEQu4xwmKWx+iIiIyEF8fCKa\nmpqg1XJTgTwT5zBJ4WwgIiIiByNGRModgahbOIdJisvH/JjNZixbtgxxcXFITExEVlaW02WPHDmC\n1NRUxMTEICUlBYcPH+5WWCIiIiIioq5yuflZt24d8vPzkZ2djfT0dGzevBn79+93WO7cuXNYuHAh\nZs2ahQ8//BCzZ8/GU089hXPnzvVIcCIiIiIiIle4tNubyWRCTk4Odu7ciYiICERERGD+/PnYvXs3\nkpOT7Zbdu3cv4uPj8eCDDwIAHnzwQRw+fBj79u1DeHh4zz0CIiIi6nFnz+ahsbERPj4+GDVqtNxx\niFzGOUxSXGp+CgsLYbFYoNfrbWMGgwHbt293WPaee+5BY2Ojw3hNTU0XYhIREZE7nT59ArW1tQgI\nCOCGI3kkzmGS4lLzU1FRgeDgYLuzZoSEhKChoQGVlZUYMGCAbXzo0KF2tz1//jy++uorPPDAA92M\nTERERL3tgQfmyh2BqFs4h0mKy7u9+fr62o21XDabzU5v95///AcLFy6EwWDAXXfd5VJAb28NtFr+\nFmtr3t5edv+nZqyLNNbFOdZGGutBRER9lUvNj5+fn0OT03LZ399f8jZGoxFz586FRqPBxo0bXQ4Y\nEKDDgAEBLt9ODYKCpGuudqyLNNbFOdaGiIhIHVxqfsLCwlBVVQWr1Qovr+ZPBo1GI3Q6HYKCghyW\nLy8vx69//Wt4e3sjOzvbbre4zqqtrUdlZa3Lt+vLvL29EBTkjx9+MMFiscodRzFYF2msi3OsjbSW\nuhAREfU1LjU/kZGR0Gq1OHXqFGJjYwEAubm5iIqKcljWZDJh/vz58PHxwa5duzBw4MAuBbRYBJqa\nuFEixWKxsjYSWBdprItzrA2Ro3fffRN1dbXo1y8As2Y9KHccIpdxDpMUl5ofnU6HlJQUpKenY82a\nNSgvL0dWVhYyMzMBNH8LFBgYCD8/P7z66qsoKyvDrl27YLVaYTQabffRv3//nn8kREREKrZz11v4\n9rtLdmMaDeDro4W5sQlCuHZ/wQFe8PLSwGqtwuI/Ztpdd/VaBfyHRnc3MlGv+u//joDZ3ABfXz+5\no5CCuNT8AEBaWhpWrlyJOXPmIDAwEIsWLUJSUhIAICEhAZmZmUhNTcX+/ftRX1+P2bNn290+NTUV\na9eu7Zn0REREBAAoKb2CG/3HSl/pKz3cnhsAIABoALT5zNKfn2GSB9DrDXJHIAVyufnR6XRYu3at\nZANTWFho+/e+ffu6l4yIiIiIiKgH8XymRERERESkCi5/80NERER9339pb8ALAlZocKPpv+SOQ+Sy\nixdL0NTUBK1Wi9tvHyp3HFIINj9ERETk4Ke6Mvh6NcJs9UFeDZsfUh4vby0+PXQYBUWXJK8PC9bA\n20sDi1WgvMrFM360IYTA9CkTMeFn47p1PyQ/Nj9ERETk4NuaCLkjELXLR9cfGPa/uOLk+qs1Ftu/\nrVrvbq3LarXgWO43bH76ADY/RERE5MCK7m0sEsmNc5ik8IQHRERERESkCmx+iIiIiIhIFbjbGxER\nETkY7l8CraYJTUKLIhPPlEWeh3OYpLD5ISIiIgf1Vj94a7SwCB43QZ6Jc5iksPkhIiIiB2UNg+WO\nQNQtnMMkhcf8EBERERGRKrD5ISIiIiIiVeBub0REROSgn1cdNBoBITSos/aTOw6RyziHSQqbHyIi\nInIwvN8F+Ho1wmz1QV7NKLnjELmMc5ikeETzc+LEcUybdhcAYN++QzAY4mRORERE1LedqxsGDQQE\nNHJHIeoSzmGS4hHNDxEREblXg1UndwSibuEcJik84QEREREREakCmx8iIiIiIlIF7vZGREREDn6q\nuwxvTRMsQovS+tvkjkPkMs5hksLmh4iIiBx4aazw1lghYJU7ClGXcA6TFDY/RERE5OCC6adyRyDq\nFs5hksJjfoioQydOHEdoaBBCQ4Nw4sRxueMQERERdQmbHyIiIiIiUgWXmx+z2Yxly5YhLi4OiYmJ\nyMrKcrpsfn4+Zs+eDb1ej1mzZuHs2bPdCkvNn8APHNgfGo0G2dlvdOnT+Laf4vNTfSIiastH0wgf\njRk+mka5oxB1CecwSXG5+Vm3bh3y8/ORnZ2N9PR0bN68Gfv373dYzmQyYcGCBYiLi8N7770HvV6P\nxx9/HPX19d0KXFhYoKoNdTYmREQkh8iA7xAdmI/IgO/kjkLUJZzDJMWl5sdkMiEnJwd//OMfERER\ngaSkJMyfPx+7d+92WPYf//gH/P398eyzz2Lo0KF4/vnnERAQgE8++aTHwvdVrRuewsKCLt2uLzRK\nnvR4PClrZ3V1HlL39cX5RJ7ngmkIvqsdigumIXJHIeoSzmGS4lLzU1hYCIvFAr1ebxszGAzIy8tz\nWDYvLw8Gg8FuLDY2FidPnuxiVHJFT31DptSNsN7K1duP1931bL2bZG6ucv5+clDqXCZSqmpLIH6w\nBKHaEih3FKIu4RwmKS41PxUVFQgODoZW++MZskNCQtDQ0IDKykq7Za9du4bQ0FC7sZCQEJSXl3cj\nLpHruNHbu1ypb0/8LTz179lebiU9ppaGmYiIqC9y6Xd+TCYTfH197cZaLpvNZrvx+vp6yWXbLte+\nsSgoCITVKgCMBQCUlobZ/l1YGIS+eMK65sfl7PHCdvnixVCn17VXp9b33/Z2HS/rvnq3XXdh4Tks\nXvwkAOD3v3/WIZe3txeCgoAffvCCxeL8ftp7DJ1dtrCwwJZlw4YtAJzfrvWyUrl7U+vHU1AQCIul\n8+trfx46nyOt/04bNmxBRESk02U7+/g7W8O2f5f21t0658aNWzFiRESnsrSXre067Zdrb450/jnZ\nG5zVl4iIqK/RCCFEZxf+5JNPsGrVKnz++ee2seLiYsyYMQNff/01goKCbOOPP/44wsPD8fTTT9vG\n/vznP6OkpARbt27tXDhNZ5MREVFP6vw7gzpVVtaiqUlZvxr/fMaf8b1PbI/d3y2+V+GtscAivPG9\n+eYeu9++7uBr81Bfcx26/iFIWrBT7jiq1pNz2Gq1IDqoCIt/9xuny2i1XhgwIECRrw9SPDVvt+/H\nlYXDwsJQVVUFq9UKL6/mTyKNRiN0Op1d49OybEVFhd2Y0WjEoEGDuhmZiIiIelugtgY+miY0Ci2+\nd2WnDSKF4BwmKS41P5GRkdBqtTh16hRiY5s/XcrNzUVUVJTDstHR0dixY4fd2MmTJ/HEE090en1f\nfQXU1tbDYnH+EWRBQT4WLfotAGDx4mexYcOLAJp3Y4mMHCm5XNvr2tP2dgCcrq/1de2to7377Ew2\nb28NAgJ0HdbGnbr7mHpCZ+vS1bkgJ1fmYdvH07ou33571uljl7suvbH+ju6zM3NGCXPbmfYeX3fn\nDKDr7fikcN/VDZc7AlG3cA6TFJeaH51Oh5SUFKSnp2PNmjUoLy9HVlYWMjMzATR/sxMYGAg/Pz9M\nnToVL7/8MtasWYNf/vKXePvtt1FXV4dp06Z1en3jxgGVlZZ2v4rT60fg/vsP2i6npU1tdW2T0+Va\nX9eetrdrPhj5GAAgOXkg0tIO2i3fmXVYLDds9zFixI3/G/3xsl7ffrbmr/06rlJf/vEAABArSURB\nVI07tX1MBkNcl+rdHZ2tS9usHdVbCTqqr7N5D9jX5c47nT8Puvoc6Sm9sf6O/tadmTPtvQbIPX/a\ne3zdnTNERER9kUvNDwCkpaVh5cqVmDNnDgIDA7Fo0SIkJSUBABISEpCZmYnU1FT0798fr776KtLT\n0/HOO+8gPDwcO3bsgE7n2Z8mGgxxuHbthx69D7nP7qQ2PfE3dDdPzEy9j/OCiIjINS43PzqdDmvX\nrsXatWsdrissLLS7fOedd+K9997rejryGNwII1IWPieV4ZnnV+Dfle75ht7q5Y+An7hlVUSqowHw\n9bFcrF7/ivNlvDTw8/NBQ0MjhLV7hyX8fNJ4jB/HM2/2BpebH+p53Egh6h298dzi85Vc4u0P/yFx\ncqfoktH9z8LXqxFmqw/yakbJHYfIZT05hzVe3ug38kEUt/dZhhU9tse45l9H2fz0EjY/RERE5KCs\n/lZ4aaywCh4DRp6Jc5iksPkhIiIiB/9pGiB3BKJu4RwmKWyFiYiIiIhIFdj8EBERERGRKnC3NyIi\nInJwk48R3horLMILxsab5I5D5DLOYZLCb36IiEhVzGYzli1bhri4OCQmJiIrK0vuSIoU5luBW/2u\nIsy3Qu4oRF3COUxS+M0PERGpyrp165Cfn4/s7GyUlZVhyZIlGDx4MJKTk+WOpihnayPljkDULZzD\nJIXNDxERqYbJZEJOTg527tyJiIgIREREYP78+di9ezebHyJSjDOFJXh2+bpeXYfGC/Dx0WJ05FD8\n8n/v6dV1KQmbHyIiUo3CwkJYLBbo9XrbmMFgwPbt22VMRURkz394Cq67aV0+5065aU3KwOaHiIhU\no6KiAsHBwdBqf3z7CwkJQUNDAyorKzFgAH8XhIjU5eLFYry95123rCs8fARi9dFuWZczbH6IiEg1\nTCYTfH197cZaLpvN5k7fj7d3584XpNF0PpvSRAacg4+mCY1Ci4LacLnjELmMc7hzmm6Zir3fNrll\nXSfzP8bYMTFdum1nX3c7ovjmZ8CAALkjKBZrI411kca6OMfaqIefn59Dk9Ny2d/fv9P3ExTUuWX/\n39ZVnQ9HfcNLKXInIKJ28FTXRESkGmFhYaiqqoLVarWNGY1G6HQ6BAUFyZiMiIjcgc0PERGpRmRk\nJLRaLU6d+vEA39zcXERFRcmYioiI3IXNDxERqYZOp0NKSgrS09Nx5swZHDx4EFlZWZgzZ47c0YiI\nyA00QgghdwgiIiJ3qa+vx8qVK/Hpp58iMDAQ8+fPx8MPPyx3LCIicgM2P0REREREpArc7Y2IiIiI\niFSBzQ8REREREakCmx8iIiIiIlIFNj9ERERERKQKbH6IiIiIiEgVFNn8mM1mLFu2DHFxcUhMTERW\nVpbckWRRXl6Op556CuPGjcOkSZOQmZkJs9kMACgrK8PcuXMRExODGTNm4IsvvpA5rTwWLFiAtLQ0\n2+X8/HzMnj0ber0es2bNwtmzZ2VM535msxkrV67E2LFjkZCQgA0bNtiuU3ttrl69iieeeAIGgwF3\n3XUX3njjDdt1aqyN2WzGzJkzcfz4cdtYR68rX375JWbOnAm9Xo9HHnkEly9fdndsWXnae9PBgwcR\nERGByMhI2/8XLVokdywHXZmLcpLKu2rVKodav/nmmzKm9LxtiPbyKrG+ly5dwrx58xATE4PJkydj\n586dtuuUWN/28iqxvq31+LaeUKA//elPIiUlRRQUFIgDBw6I2NhY8emnn8ody+1mz54tFixYIIqK\nikRubq5ITk4W69evF0IIMXPmTPHcc8+J4uJisX37dqHX68X3338vc2L32rt3rwgPDxdLly4VQghR\nV1cnJkyYINavXy+Ki4vFqlWrxIQJE4TJZJI5qfu88MILYurUqeLMmTPi6NGj4mc/+5nYs2cPayOa\nn09PP/20KC0tFQcPHhR6vV4cOHBAlbVpaGgQTz75pIiIiBDHjh2zjd99991OX1euXLki9Hq9yMrK\nEkVFReL3v/+9mDlzplwPQRae9t60bds28Zvf/EZcv35dGI1GYTQaRXV1tdyx7HRlLsrJWd65c+eK\nHTt22OpsNBpFfX29jEk9bxuivbxKq6/VahVTp04Vzz33nCgtLRX//Oc/hcFgEHv37hVCKK++HeVV\nWn1b641tPcU1P3V1dWL06NHi+PHjtrGtW7eKhx9+WMZU7ldcXCwiIiLE9evXbWN79+4VEydOFEeP\nHhUxMTF2E/ORRx4RmzZtkiOqLKqqqsSkSZPErFmzbE+Id999VyQlJdktl5ycLP7+97/LEdHtqqqq\nxKhRo+yeO6+99ppYtmyZyMnJUXVtbty4IcLDw8X58+dtYwsXLhQZGRmqq01RUZFISUkRKSkpdhtw\nX375ZbuvK6+88ord67DJZBKxsbF2G4B9mSe+Nz3zzDPi5ZdfljuGU12di3JxllcIISZOnCi++OIL\nGdPZ87RtiPbyCqG8+l67dk0sXrxY1NbW2sZ+97vfiZUrVyqyvu3lFUJ59W3RW9t6itvtrbCwEBaL\nBXq93jZmMBiQl5cnYyr3GzRoEHbs2IGBAwfajVdXV+P06dMYNWoU/Pz8bOMGgwGnTp1yd0zZrFu3\nDikpKRg2bJhtLC8vDwaDwW652NhYnDx50t3xZHHixAkEBgZizJgxtrHHHnsMq1evxunTp1VdG51O\nB39/f/ztb39DU1MTSkpK8M033yAyMlJ1tTl27Bji4+OxZ88eiFa/cZ2Xl9fu60peXh7i4uJs1+l0\nOowcObLP1qktT3xvKi4uxh133CF3DKe6Ohfl4ixvTU0NysvLcfvtt8sXrg1P24aQyiuEQHV1tWLr\n+/LLL6Nfv34Amt9/c3NzMXbsWMXWt23e48ePY9y4cYqsb4ve2tZTXPNTUVGB4OBgaLVa21hISAga\nGhpQWVkpYzL3CgwMREJCgu2yEAK7d+9GfHw8KioqEBoaard8SEgIysvL3R1TFkePHsWJEyfw5JNP\n2o1fu3ZN1XW5fPkyBg8ejPfffx/Tpk1DUlIStm7dCiGE6mvj6+uL5cuX469//Suio6Mxffp0TJw4\nEffee6/qanP//fdjyZIldm/MADp8XZGq00033dRn69SWJ743XbhwAf/6178wdepUTJkyBS+99BIa\nGxvljmXT1bkoF2d5S0pKoNFosG3bNkyaNAkpKSl4//33ZUrZzNO2IZzlHT9+vCLr29rkyZPx0EMP\nQa/XIzk5WZH1ba0lb0xMDJKTk1FcXKzI+vbmtp6240Xcy2QywdfX126s5XLLgW9qtH79ehQUFCAn\nJwdZWVmSNVJDfcxmM1asWIH09HSHGtTX16u2LgBQV1eHixcv4t1330VmZiYqKiqwfPly9OvXT/W1\nAZo/BZ88eTLmzZuH7777DhkZGYiPj2dt/o+z196WOqi9Tp723nTlyhXU19fDz88PGzduRFlZGVat\nWoWGhgYsW7ZM7njt6mguKk1JSQm8vLwwbNgwPPzwwzh27BheeOEF9O/fH0lJSXLHA+B52xDr169H\nYWEhcnJy8O233yq6vps2bYLRaMSKFSuwZs0axc/flrzp6elYvXo1oqKiFFff3t7WU1zz4+fn5/AA\nWi77+/vLEUl2L774IrKzs/HKK69g+PDh8PPzw40bN+yWMZvN0Ol0MiV0n02bNiEqKgrjx493uM7Z\n3FFDXQDA29sbtbW1eOmll3DzzTcDAP7973/jrbfewh133KHq2hw9ehQ5OTn47LPP4Ovri5EjR+Lq\n1avYtm0bhgwZouratOjodcXZ8ysoKMhtGeXkae9Nt956K77++mvb3yciIgJWqxXPPfcc0tLSoNFo\nZE7onKe9x6WmpmLy5Mm2Wo8YMQIXL17E22+/rYiNc0/bhmibd/jw4Yqu76hRowAAS5cuxTPPPIP7\n7rsPP/zwg90ySqpvS960tDQ8++yzWLJkieLq29vbeorb7S0sLAxVVVWwWq22MaPRCJ1Op5o32dYy\nMjLwxhtv4MUXX7RNwrCwMFRUVNgtZzQaMWjQIDkiutXHH3+MQ4cOISYmBjExMfjoo4/w0UcfITY2\nVtV1AYDQ0FD4+fnZGh8AuOOOO3D16lWEhoaqujZnz57F7bffbvdpUWRkJK5cuaL62rTo6Pmj9ueX\nJ743tc01bNgwNDQ0oKqqSqZEneOJc61trYcOHYpr167JlOZHnrYNIZUXUF59r1+/joMHD9qNDR8+\nHI2NjRg0aJDi6tte3traWsXVt7e39RTX/ERGRkKr1dodGJabm4uoqCgZU8lj8+bN2LNnDzZs2IBp\n06bZxqOjo5Gfn2/X+Z44ccLuQNy+avfu3fjoo4/w4Ycf4sMPP8TkyZMxefJkfPDBB4iOjnY44O3k\nyZOqqAsA6PV6NDQ0oLS01DZWXFyMn/zkJ9Dr9fjmm2/slldTbUJDQ1FaWoqmpibbWElJCW677TbV\n16ZFR68r0dHRdnUymUzIz89XTZ087b3p888/x7hx49DQ0GAby8/PR3BwMAYMGCBjso552nvcX/7y\nF8ydO9durKCgQPaTTXjaNoSzvEqsb1lZGRYuXGi3EX7mzBmEhITAYDDg7Nmziqqvs7wDBw7Erl27\nFFffXt/W65Fz0fWw5cuXixkzZoi8vDxx4MABYTAYxIEDB+SO5VZFRUVi5MiRYuPGjaKiosLuP4vF\nImbMmCEWL14szp8/L7Zv3y5iY2NlP0e/HJYuXWo7/WF1dbUYP368WL16tSgqKhIZGRkiISGhT/9e\nS1uPP/64+NWvfiUKCgrEZ599JuLj48Xu3btFdXW1iI+PV21tqqurRUJCgliyZIm4cOGCOHTokBg3\nbpx45513VF2b8PBw2+l6O3pdKSsrE9HR0eK1114T58+fF4sWLRKpqalyxnc7T3pvqqmpEZMmTRJ/\n+MMfRElJiThy5IhITEwUO3fulDuaJFfmohK0zpuXlydGjRolXn/9dXHp0iXx5ptvitGjR4vTp0/L\nls/TtiHay6vE+losFnHfffeJefPmiaKiInHkyBExYcIEkZ2dLSwWi/jFL36hqPq2l1eJ9W2rp7f1\nFNn8mEwmsXTpUhETEyMmTpwodu3aJXckt9u+fbuIiIiw+y88PFxEREQIIYQoLS0VDz30kBg9erSY\nMWOGOHr0qMyJ5dH6CSFE85vQPffcI6Kjo8Xs2bNFQUGBjOncr7q6WixZskTExsaKCRMmiC1bttiu\nU3ttioqKxKOPPirGjBkjkpOT7V5X1Fqbtr9VcunSpXZfVz777DMxdepUodfrxaOPPirKysrcHVlW\nnvbe1DLnY2NjRWJiot3rgdK4Ohfl1jbvoUOHxN133y2io6PF9OnTZW+KPW0boqO8SquvEM2/nbNw\n4UIxZswYkZiYKLZv3267Tonzt728Sqxvaz29racRotXJ6omIiIiIiPooxR3zQ0RERERE1BvY/BAR\nERERkSqw+SEiIiIiIlVg80NERERERKrA5oeIiIiIiFSBzQ8REREREakCmx8iIiIiIlIFNj9ERERE\nRKQKbH6IiIiIiEgV2PwQEREREZEqsPkhIiIiIiJV+P8AASIrI8950gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x115587ef0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"model.sample(40000, burn=3000, thin=10)\n",
"mc.Matplot.plot(model)\n",
"print(model.summary())"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Warning: Stochastic b2's value is neither numerical nor array with floating-point dtype. Recommend fitting method fmin (default).\n",
"Warning: Stochastic b1's value is neither numerical nor array with floating-point dtype. Recommend fitting method fmin (default).\n"
]
}
],
"source": [
"bkg = 4\n",
"cts = 20\n",
"\n",
"realbkg = mc.Uniform('bkg', 1, 1000)\n",
"obsbkg = mc.Poisson('obsbkg', realbkg, observed=True, value=bkg)\n",
"\n",
"realcts = mc.Uniform('cts', 0, 1000)\n",
"\n",
"@mc.stochastic\n",
"def obscts(realbkg=realbkg, realcts=realcts, observed=True, value=cts):\n",
" return mc.Poisson('b1', realbkg) + mc.Poisson('b2', realcts)\n",
"\n",
"\n",
"model = mc.MCMC((realbkg, obsbkg, realcts, obscts))\n",
"map = mc.MAP(model)\n",
"map.fit()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" [-----------------54% ] 21971 of 40000 complete in 40.1 sec"
]
}
],
"source": [
"model.sample(40000, burn=3000, thin=10)\n",
"mc.Matplot.plot(model)\n",
"print(model.summary())"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda env:python3]",
"language": "python",
"name": "conda-env-python3-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| bsd-3-clause |
rohinkumar/AngDiameterTest | Basics.ipynb | 1 | 1647161 | null | gpl-2.0 |
computational-class/cjc2016 | code/selenium.ipynb | 2 | 1962 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-20T14:58:07.401040",
"start_time": "2017-05-20T14:58:07.332376"
},
"collapsed": true
},
"outputs": [],
"source": [
"from selenium import webdriver\n",
"import selenium.webdriver.support.ui as ui\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-20T14:58:22.971511",
"start_time": "2017-05-20T14:58:20.826559"
},
"collapsed": true
},
"outputs": [],
"source": [
"browser = webdriver.Firefox() # 打开Firefox浏览器\n"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-20T14:58:53.289422",
"start_time": "2017-05-20T14:58:52.792826"
},
"collapsed": true
},
"outputs": [],
"source": [
"browser.get(\"http://xwb100.cn/login/login.php\") \n",
"#打开网址手工登陆 #新微榜加入了用户注册界面,包含验证码 \n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
},
"latex_envs": {
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 0
},
"toc": {
"toc_cell": false,
"toc_number_sections": true,
"toc_threshold": 6,
"toc_window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
nkmk/python-snippets | notebook/re_character_type_process.ipynb | 1 | 4913 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import re"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<re.Match object; span=(0, 3), match='abc'>\n"
]
}
],
"source": [
"p = re.compile('[a-z]+')\n",
"print(p.fullmatch('abc'))"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"None\n"
]
}
],
"source": [
"print(p.fullmatch('abc123'))"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"match\n"
]
}
],
"source": [
"s = 'abc'\n",
"\n",
"if p.fullmatch(s):\n",
" print('match')\n",
"else:\n",
" print('no match')"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"no match\n"
]
}
],
"source": [
"s = 'abc123'\n",
"\n",
"if p.fullmatch(s):\n",
" print('match')\n",
"else:\n",
" print('no match')"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<re.Match object; span=(0, 3), match='abc'>\n"
]
}
],
"source": [
"p = re.compile('[a-z]+$')\n",
"print(p.match('abc'))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"None\n"
]
}
],
"source": [
"print(p.match('abc123'))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<re.Match object; span=(3, 6), match='abc'>\n"
]
}
],
"source": [
"p = re.compile('[a-z]+')\n",
"print(p.search('123abcABC'))"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"None\n"
]
}
],
"source": [
"print(p.search('123ABC'))"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['abc', 'xyz']\n"
]
}
],
"source": [
"p = re.compile('[a-z]+')\n",
"result = p.findall('123abcABCxyz')\n",
"print(result)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'list'>\n"
]
}
],
"source": [
"print(type(result))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'str'>\n"
]
}
],
"source": [
"print(type(result[0]))"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[]\n"
]
}
],
"source": [
"print(p.findall('123ABC'))"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"abcxyz\n"
]
}
],
"source": [
"s_result = ''.join(p.findall('123abcABCxyz'))\n",
"print(s_result)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"6\n"
]
}
],
"source": [
"print(len(s_result))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"2\n"
]
}
],
"source": [
"print(len('🇯🇵'))"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
ankdesh/DeepLearning-UdacityCapston | notebooks/TFRecord/Create hdf5 file.ipynb | 1 | 135326 | {
"cells": [
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import h5py\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import glob\n",
"from PIL import Image\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"IMG_FOLDER_NAME = '../data/FullImageDataSet/train_sample/'\n",
"OUTPUT_H5File = 'trainFile.hdf5'\n",
"IMAGE_SIDE = 100"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(100, 100, 3)\n",
"uint8\n"
]
},
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7fb7c8e85810>"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP4AAAD/CAYAAADRymv0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvd3LdUtyH/arXvt5zswosS0rkiZYaEZnRiiQm1wFgiGW\nsTCxAlauhEMINr5NiMEhxNZ9IM5NyB+QgPBNYnKjgEmiCDkKBAIOxGAsy7IxEVESjWILjz0f5332\nXl25qK9f9Vp7P++Zj0cD8/Y5+332XqtXf1RX1a+6urqXqCo+pA/pQ/r+SuP3uwEf0of0Ib19+iD4\nH9KH9H2YPgj+h/QhfR+mD4L/IX1I34fpg+B/SB/S92H6IPgf0of0fZi+LcEXkX9DRH5DRH5TRP7j\n71SjPqQP6UP67ib5VtfxRWQA+E0AfwLA/wPgbwL4M6r6G9+55n1IH9KH9N1I3w7i/6sA/r6q/paq\nXgH81wB+7jvTrA/pQ/qQvpvp2xH8PwLg/6Lfv+3XPqQP6UP6Hk+X73YFIvIhJvhD+pB+n5Kqytn1\nb0fw/28AP06/f8yvHdKPf/GL+OLHX4RC8YUvfhFf+ImfwMAFGzYA1i4FoAOAKKZOTExAFVBAZEAg\nAARTFQrSJQpI3FVAxPJDrMwpUQMgqsBUCBTm2lAoBEYa8VIVohP/y9/4Vfz0H/9pu+qFq0x/BvaM\nClQHVAXQAcXA2DeMaYaUqmLOHfvtin3eoJiYOqFzh+qOud+wzx27Tsw5IWPg8vSE54+e8dnP/QA+\n+wM/AMFwGlk9gg1DNgiG9UcVwMSv/E9/HX/iT/4pzNSz1XHN/5BtHyrYdINM8atouQRqNUvdmVCo\nACriv2P4gv4DQnym2XZrv+Wa0Qr8jV/+6/jjf/Jns7lZk04AEypZC1SBgYENw/su+ZCqQFXtA3/W\n/+63K16+8U188vVv4Ktf/Sq++k++iq+9vOAb1yt2nZChGFCI7pA5sW0btm0DRCBjQAQYUAwn6z/4\nzX+Aj7/0Zeh0Egug6uOqO4Adih37DtwmMHfBPgXYvesAMCZkTMimwDaLzlOgO4xWY4OMgTEEYwjm\nrpj7xJzAVEG45kSAbROMi+BrX/9n+Kdf/SpkWMP+4a///VUUM307gv83AXxZRL4A4P8F8GcA/Ntn\nGb/48U/gX/+ZnwY0BI6UENsDWj8l8pzqK0oSHCNLXsmBgWoJv4grE2NvrkOiPZXZy7FWiQ5jKLH2\nqYhrAPsk08tajn00+uf3VXr3e7+Wv0o0Wa6zkFe9a8kl4NIK8MdUXdCoKNEll+SzutShmt2kMeRv\noa6VPq3BvT1eJsSEuq5bG7RV1IGgl+/luI5Uqj7VkWgjl6o6f+hC1ipI1Vsi1e/oKxAKAwlAKlLj\n4nxpz43leeQvIZqKt6VgMrLGWAB/6Id+ED/8R37YFNa2fXcEX1V3Efn3AfwyrI//par+3dPMA5Ax\njFhE+CBmIHYoxE7u6LCNdJ85xB3JMuyyNAKlsNP9UplAM4ZcqK1oSbZUkmZJDWVIb8hvH6vVhAhq\nVoIGXKgNpiH3gOiIC6SExNoLoIglrt+sH1MnRNU+C6lZeXWxq1SCwKzEVlAJTmUZLnAp+pAcsT4C\nTSfRN/WKRbToj+pvqQATHuN8FuLhimDkpaaj468joqaQTuxzYk7FNEMAMq29Q0L4FGYoKhQ7CaSL\nHSnupKZOQ37YWARtQ/cE6TYXzlT0zlsp/NFFbxsEGAqMUaMTwg/Pn2pTFYotxyWI8hpefltzfFX9\nHwD81Gv5vvDlLwGbWAcnoNMZVkmQpAS3Y1N8Y7SqK5JMUiwTMhJmqtO5nta44Nq3aQVLX/z4Y1cQ\nXegZTSTsZh3N/ArmUJlmeos6H2sqP3WlIXOa6ezWhURjHXFSEVEDdU5MK9IZV/Dxxz+ZuRa8a5Rk\nxkzKBtNS6yODpiIs7LGWzBAXlODXOOnyvaG2K6wvfPzlHMs22jIATIhPKULZm4IYpSS184SQ0tYJ\nTJ8GqSqmqpvLCt0BmUa7ocAQASQU24RLM4Z0VaYA/tAP/iBRlxVY6nBjq5nDnkI/w5UeSipoqQCm\nQr1qETPvRxoJVrA470gqaFPEAsXMsXhd6IE3cO4BwBe+9DEKz4t1/Ef7yhgWwroAMgBGB7rA93R5\nYElKiI+mLe36Fz7+CVLPvWbREO0SSBbO0OyqNkphlqpUnswuUvVL60brXJjSgcrxbzTx4y/95IEY\nsiD/WW+qW6Vks2Tp4xHC77jdy1naK/Rv0Id/A4qf+NKXl6f4i1SVebEmDzF+A5o6fFV5/CSJZ/3r\nAxWK6LQzQsIJ4A//0B92P9FZ8kFV4uTSoaftS/In06xjFFQjAJSO+udNeXj3bQRfvee9Lff1UqEH\nnPBFxEfd6bKu53kVDeH0oEGoEOUf56hfKBhCEYZy/V3L5ZipmGbkX5TiCPhQt0pY6EswGytnJeJz\n9vdLrbNeupfcjQ2yH05SCwZbNC8r11XBpBKNIs7KX6YrdC3oEtSXleZRS1iFIq6InKEmfEJ+fC5p\nG1o3geIObc8uZyO9r2QaRrHse7iDi+3aI+mxsr8HBP+Q7tFNYiYfjhPN+XnePxH+MsQq6fHSIsjv\nJxQlVCupCbl1NQnDmqDGrqZKQszyETaQqxh+OObKobQ6/pz1jYXGzfIDc0lXrOmMWtGya6pQEFUc\nKcVoeApmYRkLp54MVgpENbAUts/bTbnFlC8cbqxVrZ3KF3xCLQKQC8X77l+EfRY0tgvRtI0LK8VA\n74nz8aCk1X9tWp+rInqW2dfzpEI6aetJejvExz3zCAATOIRfi1HkjsBzDWt5TRSawNMTycf8/L1W\nrpJLOaUce6etW8fyYPnwZ2nBYmSsIdZtynJWd6DUIUn7JrClz/BoL006KeOoaM+boKSw9VBciYzc\nHYbmg/DlXHWYtHEMZThxj0s0hH6YzyCtSFJuQX37O1BLkM6fYl4NlWn5Re4Aa8DXKqNnVo+3LnRk\nrHzpUZ3Xc2FPMs+QmpLm6j5Nb4P47weuaMzoiCN0qwu/tr/pCb+L8us99nWvAyL09yH3U+OWMkKz\nuEXQWf1MUUUZxH7clNNupYF83sWQJ7q4MlO5hPy31Bc5PLTQa6ksgVtWSoXi76LVKHLKI4rV8diF\nPiwAzxGrBghlEejLwuIKQMoTX7UJRR6E8AxqqxSRUkl24bfVHGmjXJZAt52q7dHXdSTJv9BAqkru\n40dC/72A+M1eiyTB3HLoLDh70Nromd+z2PsVnt95HyUkgKgvMz1AcqArnGLRDl3hlX6t7rJ71jqL\nqU1UO8LW8IegKE6dO6vlcwIpuZQJtxQ4qPsgKGtDzjtYCrvj/N32nZLcZ+9dOhblyEoCSYsIP+Kx\nSX0cubNuRtCOnDmOPseXsDRcCaQiCuUQCiB4XFsV2VlVCq4Cu8FPUltOPeMYX6b83kL8I3ydsHhR\nZmHMYqAa7ddMGs59aM6j1JA6PveePGkDBb+wNb5q/0JVryPNtG7c9UQSEnpHl7uKLvwdfnL6VBZD\nMVIsIzYToNHe/9LXs9beV9CupNrNO0qD+9MS980F/ESwmqXgS3slYgtR0soKgQpTX4kW3lcX+kD8\nHv1QFC0ltMIBWxUC6PH5R0na8neMZf/vUXoz515fpfe/ytdKe+nhKouK9gHQpYuP5HPJF57dfMQH\ntzkUW0uQhSfQK+cSzgFmRrsefay5qVkEguEWxgDOh80bWUuFC4NT885lKWjLCBahK/EcK5SSWo65\nO1Ny6yjGEJ0NQ1lISznax713WykDIzJTdFU9EYnoIqkTEdI7MTFlNoUMoEK+z4SH7s1YJ5WwKqre\nc7USg7cQI4qJz/pcxLk0K8Rpq0qFmAIif+yRvkt6E8EXFZIU/+dE6IOYbLZ0UkSqdeJk/mUQ369h\n7dH2/Dl7x0CcsGhyegzPSbQcPxP9lOr9eE1XL1ox7Z5FUpqXXEnYqPQG6CtPRsNQ884+AnqgN4/i\nWXMfduYA6dJyyAkLdMT0+yq1hOnC4TsMEvGnx/Erpk8dRysPXp+4hhVaugvFMCDILQ4C3zMBQ+0I\nFkoSSQ5SlpSBa6ux3oV5lQRT07Pna9IuuVT5PYP4ZUJxh1jgJZmZux3EE2IOwsz8nVCjR6E9/y30\ng0057fnaPJ+kdeXEOwEBER18EDAlv6xbGfVxFcBTnoNkOq5J1QMtoc+1bVdIhQQ8AtRmykDblbiD\nYE9yGrHK5URZrZLKt1YFWam4pNUNWAWdhgUsP8P3UTxly4Aa6O9aJcVPqsbsT1gZwh0qKzHm9qsX\nQQHMQ7uBjAUgXs7WSa1/xdo+W5bhCwC6vHeu43bfT78P6/jFqcUqxYacNDSuFn6uQr+WLaKnU9vM\nIT5sKzxRu5bM7TcjwGFp7bRd8Qwv+a3opiX0WIWeFCNtAmp82JqpySTJXIu1ZU5VK6BiDiLDWR+O\n13hprvfm7GohnUhn03vpRIWeXLlfFqtvE0JF7uDzOIDKO3KMjkRlfgBdc1pleUi0NwElpVZrdSzz\nvb19R04YEIcpHc8dT6fPh2/n6c2cexEwYQxQRg7vtkpNF9gicGEpJ14sl2TBLhSFQFzRwhwSdccP\nun6mBNCv1dU+d+9dPRf+sBZqProEKaEjv+XkGqMo8cCV6C7hsmBpV9DYFUWLjeitXkG71UpjwiUv\nvWOj4agz41ZaRiE0vb5EQA1U73xihbEgPRB+EWKV4K1C6aqjLK96OJmV6qtdibHio67Qbfpg99LR\ntyi57sFCt8TOL2RTiAGWu9Lpr9Kn1nfSGwl+oVbbWXQkhSe7qm3wV9vRrnergeO2qai1HXzjVAUH\n8/Wf3ugU3DVy65jYH0Ct9WizUAQsufGf7TofhByM+t4gQodsRtMCTIDgnpHX0mEfDJ71MHOyLXGk\nUov2SYvirD1ciK4XqjyoM64mxeCW0H2L5HEq4aT1df/ngKj5TBjvkqTO7hz8U/FQ94kE+TVXUIgg\noU8C2nFeZLsQYNbYs0CicfcrZHojUz8Yg7FWnKaEagvRcn6MJR+VmjXkjhTtfkRuAzngukCwEqBr\nIZMHDVoMmFYcaYZDvdbAHBpNs776aEqC6zlwwIHnaUZICEU9yvb37pHqyA6sLoqVb+7jvbcdi2/9\njKwItD3WsCLf6p5qKzB6xgFreyVbHVum7dAUVqaLWiTesRQht8G73oIT/cOjz+vygLS/q1+YLfx7\n3RGES68/LHnXeSkckopXp1Rv49VH7J9mTujEN0Ipak9+v4e8vghgQ0ssOXkzbwlgL1D8UmdsDpBY\nRKXXj6PZX3ypWSWXM0RsU6toforZQ/iPiH1PaDTQI9tSrMbCzkwCADqDftEPKyiUgGbjQyMr2Dez\nqsJaBi2q570T6sGfiUCYs3DkdWl1nRpU71ZlHl9N6OccmHNA5wY/6gkNdtPpBscIrXFg/o2owWxv\nmQM5/TqsyUuSOSyMxlns72oePa/b651Eozg1ashoq0EjptHfE8t565meAef0M/7qMSNYSQCB7kBj\npxw318y09lnFlfCvTJj5uOwmeMRUjRFZ8E8QWqj0cPLBPfcy0UFeMr+VvRQXQmXq3dHPrmlwlbev\n1rhpHkxLPe257Ld2KT3hnVzCDvrqOjZL90OJNMlXyl+OzLOj3uNa62teO1oeTYFHl6b4eQkm+Kot\nHJE+UnSAO4oxgBmdCOuIw3VI+OleKGh13m+qsBGs07zoR8pfIgKQPS21jyAVhwt9Rp0+SL/vb9LR\nVXt+6lSa/gwNz/NH5e9T9vIM1RWIdE5jRu3ljpyVS8+80hr+dei9vh8VLM9qrSz1L7ydAS/J64/b\n++2ku5uR+Npip9lF1zJKTVet021Wy+DAdnGhh/ietND+rEahhP62Z0sBUzpcMOIK6sP1KvW17tD9\nU0/z9wDiv096XexPzLjDfX2tkMVI+LSK5hEx6x7P26OmQ24ODBGQI/O1Kkrge2JGebQT8pWUVhEz\nFhXvqBuBIv5racH7pR6B9l6NO712KEKzmYT6SkphVZfVHiCQNejYTBU0PM/xOLdY3PZExApEnIDQ\nxL6Jt08jhMO9s9Yjv94xyu5e5fT7KPjE9CWJ7S7PdyUESYLRTCNLL64GHJX/NZTvFqgNV20jPSNi\nzcVzHhpFPODjWsK0ysLMN6EP89KmAfFdi0j304LMdVlRS533lJD2/lOoLj/ZPqljXZgWdDoMShYY\nkhXjWFuAc/swOe4qFl6bMFabnTfa3GTpX1tnRym2JIkH9UAwp9o5d2QHF0tUu3g5EdCMFmQ+iJbE\nZpl0F7gi6G53Rvv3S7r8zUrfM72hV39NWoSgS/V7MWUpkCV09VkATYZPZhFr3XfwsPFNxKjdEbgA\nxTua/n4S2OxqX66V0JfwRyUR5yA4OmyOfasSrQ9bE7gTRFpQJ4fElY1k3jpuO7GSFWyWoP0KyVlX\nCvUjULFr77PEBi8XxEqNTbrw6hvit6lK1qN+kGZF4HW28fo4Yor4qwPNUfilfV/POjgV34fpxLhp\npCh/yeNy3ljwC+UDzAttQuO/FsZZZXaPr9K/9eXVSDEeREK8VSexCVxoH3Vwq4Loay/ckkAhaV4T\nUFnMGb2J9UR9TzF39DkTh1NAPJDF6Rd64gDWiyI+q4fbw8KXBXojmmP3McoxWoeFnl1gzCBrLe5p\n3AgHLM1ZopXZ9bYhoO7migwr3bBQ/HsKtzNN6y4rSBroGht1BVu+gHOY7EuE5bCtRpwHZ52nN3bu\nsTZkXXhEIvsiNSWLdGIVHBMP4uOU87VHynfdniuG3OzY61F3q8KhvhZkuql/b6iPqaPHiXpI2hAT\nvQ8XPEjpdNXHjHn6LDTXn1fX1LeWaOpTlTxqAH3oRy6jvmetAowhKdhVTsid32uL8go7Nrfyq1sX\nkadZW/7oAIdYdYHnFaQV0SMQLNTz98Q6Pst2Nci0Py/AGCEUveucVlPQu3kvoONQxDlWdc2/NPik\nMzXZ8N/SByIPaOCnvGozbOQ0z6lonA1wsy0J+aQMJxbQe106c27WMzQy4XhUzbYD/cCIM6MiQFjb\nnWX5b6lf128UJRc+i2ImQvW1vBD2/JQQigugaFdHq+0Rqx4l8KjcdK2htVQddj9P8nzUy+SoNmZZ\nOtpdbfcVzUp9T232Rmfu9fF6mChf7+BaYmWXToa8cS5gITqSg3O0N7jmR402p9yncUynwy6fp1q0\neDhXn7JNayKTNSyHDHhxRpRgm0583n9X5XMQSbaOGlbmZE1VmHpWx0Qr4IFqaVWTwmPl/oCJxRDw\nLAePoLjQqwthvHZMMJe2R7VmlSlmdnt6/qBm5yZFvNyk2t1V+GHy6gqn2IyVBY0DLfvGxjIlxavs\nd6hTVbInj9KbevVjCUuaU6OYJC+djGaGby8swpoxxLnXtyJwMXktx6xEeqylHjFzWPJHZUAddEFN\npSGdRRpiZqU0wEuRjUkc8jvqa/zf+tbUHgkaB9TIMjCi/Uo277zVLR0QlaPl7qWDYj1jcI/jJ63P\nCsxWH+JdjCHEFARL22FtDAKhd6+7UDt7eRJ30j03Uc8g2+kcTKRd0xzP4OgYmxa2HnxWAf9WFjuG\nH6Q3PIHH/0p19Ei6yFia75BWPm0FhCTceZbaEW+ICQ2/svGdhlXlzfzrcvetJKbPIaXCi7qpfU34\n1/IIWRi9UULf0etTpG+pn1Ejm3Xqwv24QHa89sTGccX4s5C048llOuJSWxqCMBXYXiqCx/JiHytX\nHeE7ELqutTwcOUM19Mdjg1KqYGveMRsiLmAFC0kBezyab4f4UiZMw5zU+p2Tk+TMI61A5VxlIKUg\naDtMsXvLV8RnTVzomMQ/VnvXMrmfXpGUuxGAJ89qVxA51tymRY8F20XTGZ9XY+tV5aVFtRltWRTR\ng9Y7Aj/IQOUc2tIZqLLGPxrXeFdCFMTqrtk7vlQZINAktzevRZrGOGhqlyii4hOyx1nSwbfiiiHb\nvtByBcjQ38y/6pVbvb39Z+nNlvNix1Cb79xxpbOJqrSOw5pb/fmzLSNtXrt43hrPvI+puTxkc/TX\nH+rHLh85u46EWisiLb8qmFMzx+jDL208NkbzWa7RWfWgcu/0KNsSfoRQJbo05xHgOC6i2LkcYSEk\n3QBbPDEM8CnoRSA7RHQJSkrB5E8zgLrAS5j1kZccumSd3PMpMzu2oVND+QCkLtAcQ7GWs+bsRM5T\nfRPUXufRN9qkw6QL1u1akEW3C35pzYdMubJt7q4qeMxNDQoSu9fgjWqhteyj9VFtWb38x0TMR0J+\nAjZLl2WpmEVXEE495mVdpFKXJ6sS4ZJOU9lKWR3ZESWi93t9gqQN/GmdYI3RyGg3SUXW2gMGls5r\nWbtUhNz0ilVjXC1iUnJBzQFHCFHPsZdoXApGsoGxglAKLPJPVYvsi6lAID/x7JGG/K16Gc6/pMXp\n05XeNIDnEUOpYBksJ/yrQk/lyFrPmd82fmcti4A00clPO/8uHjxE0p0x/XrtXDCkfXFinKxXr/zQ\n5q/+txsIjs4pqEB6FLM+R25oC1AjkTr2KmWgiVYq9Si2k6gQNARAFudUjXUX4HtWyfn4apIw7snS\nzvPDXuEKeL3G7bBdle11XllS/Wf2vqZCj/P0GqOj+G7l8OF9yBOWDv6Ns/ZHvSt6HNMbCb72dhwh\nM28c+ORTJN74ssDeWk0ykEhEaMmJZcGtuUd4vr/kP3FGLSuLq7EA3szxXqnpKb1LVwXycKgQznv9\nu79hiDzsKfRHlRrKWhvtSaCXOPX+WfJSN/ma8g1Ff3Y5lldQ78SsF3II9QGLwPe+xZgovGgXLt5V\nyrXlVuWUx+D/c0jO5ody9z6EozDX77OvVkf2oVV2Lwampzcz9YHQep1QMcRnxlkI6KO5Mg8c+0nb\n+fNUTy+cvcCdyLUpaFS1MRCHddjQtn6RltQiAKS/8JGUUxOMI8P2Xp94glOEmx872xVzyohCd6zN\n0kVoNLQsoKAhiH7ZBg06tRq7U4ofbu0HVGcT1o78ve9ZXJQQbdSgxSwZdtqTS6OEOYVjwA7iMHPe\nxr9enBHTgdM3DTOmZAMllUlnUztpCaLQ4RGMc9IoSfYdQc+m8CdsTwfxlmufEnr6G2cK3nU89PRG\nZ+55+EQyGQk/LT+s+BMeStGSj1Mvr/9d/QZZkxNkaIhCEbkpi2yFh9+GZhUAmMjtlL4mzAEkmmix\nA1nHahb60c5TrYip0Tia38WuwxrAAdCsh12ChTgWSJLR2tmPeJusJjOXIzDK6PGTknk5Sg+wOWkJ\nPpJORT2krNfpyGsqAY/5bbzhJgOOUpePKl9sVTzphbBj2AoI5eaXZSB2Ok4FMAegG1Q3TL0AUAvF\nHd6PVD6T6A8SKHLseQtDyyhqHDWmVgNtA9CcMTqjWeMmtz5eOWYTqjeoDmjs1gx6JKp52zZjyTmB\n25wYsqxonKQ3W85jfc4aM0hxbyE8lyfmAe+4gNLQhIL504uNMAyh54rp2S6gT6C4I0uwV6qY0lAN\nBcNcV8QUwtyJ0491PgB9lqmN6bKtS7/q+2oplPBH0MmENGtLGmVA1xq2HlCt22tCdVVbs+1OF1HQ\nsmppgtjnkGvieUNpGCZER7ZjKLBr9SE3/5BFxWNowjys5ozYdcSfw9+c63gfSocO2OyU1hRuQGlL\nvyQSh99DVVLJxtx+hnMyItES7OrojSxL4FZR+GaoP3TQCOLoND8zZKpizgkVO6b1UXo7514KTQ9g\nXHwdy2PmabWxJKIpFWnihFYKa+UIkX2kAM/uaftTP1LZBqPeefBul8Jss99jCHROZEBGIDShQReu\nVeC9ERJs5Nrej4LW8ExToMwE7/1e6BYHouaklmoS/vIYUZIKUr+ptfZJGktdkN7bY8H36L5UrkQn\nDQVDCuJsaZkb2YoLJU9vsQn9kh0SYAxgzqRrd/sVP/a33fAnrIu6r/T+3k4VUpQhA/6iEAFPKc7T\nmwl+8EvRNhq2eN5DUBXYGuraRWkak8h7voBNX11TtuFeV9I7sVahK1by56INj2mcZbOgybCDHwAt\nTV6d8nq6rImGMesMnKhRZnkIfXWgGpfOyzX4JPJ6reIDVcIfqPq6El1HIdg3qha6ag7VUHjohHwg\ngGv5ZlzwXDv6VMJ+frTbUp838nC4Cvh5PT7tzj4BgDHAL+voy43Vdwg74Za6ku/DF0FHooM4OLaI\n+5imVaYPhwjAe2zLFZEfE5FfFZG/IyJ/W0T+A7/+gyLyyyLy90TkfxSRP3i/kPjHOiGyUcfrkzjk\n/bKIal5tJ6FltGiKW3OgeM20HiP2yaWPT5O8NbIyUp8PP0ypMGKATcO8cjDqoRBxs29Fj1Cg3OQE\ntAQ2LQ933PgupV5yp5Mkb6xWBP/2ftI+Vs02L9h20B1n6uK8lUo7+LQ9fRT6tb5+AAfNsVPP9nGK\n+boduioNFLNXugH+hgWJ/iPYdmlTKPGpVOf99D778W8A/qKq/ssA/jUA/56I/EsA/hKAX1HVnwLw\nqwD+8v0ipIRMNkA2M+GFtdmqBBZyN7pT3mQE7Z9QFavmLry+N5SvJBZ60v6fVn/kc90R8+naE88W\nDWMNmcUm+8tCD/rOqwzf4RRMD3Q9yweOpn/Xfx/W2LXdPQ/Zx1pGmOdoUlBvKWqtRFGjoKZ7iu4R\nh5WY5Kck2duf8lnCLjIgI4ReFp50kMy/NKbNUCB+zEF+XfJfFXxV/R1V/Vv+/WsA/i6AHwPwcwB+\n0bP9IoB/61E51kbWgitS0wd8X3L56ID6BzNqMV/zWyFrLm/xYZJngHNOjWOnYo51akreT41BelcS\nawAchDJWGvLJrPJcgQZBu2IMy+hYZi4LIcDDzPGcJoBpuogEcW7zNxSxkCAAEv5ThS7FJ+3e/aTt\ne0XbKXr/X7cCjneFCd62wGph2tI8e5+E5NJwoX23ZnShpboyF196LBqGQDOhGfXr92us/Knm+CLy\nRQD/CoD/DcCPqupXAFMOIvIjDx8m5VnTSTlk6CQvbc9DJS68qf2i37HuJ54/hFuorqYyT4Q15rWH\nxq8X198T8Z6/T5Ny1WKx80M4Y+6aS4tqfRNQjHzG/FrtwWi+Ik3MHt7wWn9gAU2v9KGRjdUQyndl\nrpqdtpnELRctAAAgAElEQVT9oazjU/VcXePs0VpjnvKvHJXBitFd6JF/3z9psgS/s/Cwx57bnk7S\nmIELLUkL1n9X4a9+1dn5oQibxUORgRHsE+z0Gh++t+CLyD8H4L8F8BdU9WsiB4Prbk2/9iv/PeIF\nFz/+8ZfxhS/9JGmuXkBfsEIf12XNOLbWkvL1a8GW9HAT+LMGu5NprZSJ/DDpof0PamoKq92Xpd0n\nyYT0pB4SeDhCJ7NL4V+F5d43dXSR7FN75qi3j+1cRLh/pbH29kYEZfBue1oXH4/w3xI4zpMqL6d/\npz0B19TcsIIEmTNlx20/lBtzcoyigxdCzbY8wpud2KmHEvjWzkD2YqTf+8f/GP/0q/+ky8Sd9F6C\nLyIXmND/VVX9Jb/8FRH5UVX9ioh8HsDv3nv+p3/mT4H2YFngShCq0Woh3sY3u9AXCEiLNONlYKXs\nay1c4tLbuvNeCM6l6XL9faCFzDK2Fd/DaXAqsmxZAclZikL6Q96FpavlK6XkzvfAqfe1eHrp7Y72\njUaKOKK6WxApNLFeziVnzEEIPPqBFaIWxCS937mcyNYkfwfuWgttak0BNvzJVQelFp+NuccfMH15\ntb/6EP239EM/9EP4/L/4eQzZMCD4zb/3G+eNxfsftvlfAfh1Vf0v6Np/B+DP+fc/C+CX1oc4WWSZ\n5jSkOcXZ5Qyi4Erk1BULesQA5V/Wj1RIzvGoOObjbl4sfx91jjv0SOBPLImlG/ZDDvcO+ZsjCWXC\nJo2K6c9bsvgJkvSdaas3R8w5ths4XdlYy2pkqnFOczxvu8A/ICmzTf045grQ4WENdRKCFP2pvixs\nkXZ2dxJnHTmdcDp6DbnEqtFHbf1rGiadBdwAqh4R3oxqHPE7exIepVcRX0T+KIB/B8DfFpH/w6iE\nXwDwVwD8NRH58wB+C8DP3y0DOBm4aFotnLDpo64o0uYkPdCs7jv9i5iVqJpnpbYGLncfr/bcI17M\n+xgRGT2IHWoiftLgvgLxqD+vpuyr4GFx4syhLLSr7VDRjLLcC/mStoZMN7hJGvzO5rc2d0vqd+Ll\nhsMnCrJd1uPds9Ubzt7sEhaunDPTkmPe13w49Av7JtcVE6uEMrTxZyVKy9h8/5QPjoROcRdBX/O/\np/ItvSr4qvq/Atju3P6Z154H4LHh4fApwSoGi99h5qWuzxyNdr2F6T/oRCkhP9LQHWYSTLwWqVid\nbcvj/KeUEyNKSWJlSVFRutayHeXHiz5XnkDMo40+zf/b2ivtCb8WQJcIFc+S6LUgIF0Y8r73OAOM\nuKhsgS551z7Vv9yilKh2qwQmaesaRevJrD3k0cC1q72+CoFaXxdNTkxFtfDOat1HgJId9Mm11PfV\nm4/ld8e3bEEnFmN8WoF4Nb3N7rxFAeXPnJB35MxoLMTSkh6W/6LcOv+MSWWWgjGzH6qQA+d1PKLO\n6TLTa8kh4I6izVdBZfYjRHYsoO8PlbdGd1FsfqLqRHzzhmKIvU55qeVTptef0eWTiBnoTt/Pnm2U\nOPO3nPDUAs6Z8bg2D7RcwaQr4gNNkE59qork0544kIedd8Gz5+N0XBZcwtw1TvztVtqnSW+0LVdS\nKBJlcY+fSwubCUVaNsnICKCIneYFTIrY+amMxisE3W0vXs1zno49Ojs//5EgNx/IK+mshSvD9/yC\nQWiXW4+/xfSaUipTn9qj1TmODWjPLchbgsxK6oTWd5pz9Ob798W5dwoGYWDcUVK8a4/dUrVEOiBK\n8fueL0DrUepi3a3aVX2tJsJro/omgj8xkUtYAEisG4dX+GYl9Rt3z5hwTXsQVilGMbOrQLaVo2v9\nVHAKbQzW0QBbqz04EE80u8ZWTkV6ek9xNyfDhRZrE9PmJKbWpYkrAx2G4a6qoIuyIM8BVR8kprmA\nxjLauiKXZL9Y4bPYNjFXehRFU10H3K2e2nQrGUeR/jQ2nVHPhToa4nYDEcp0WQRAxbSgWNuGR3Kc\ns41pWIYspFYGzcE8R20F16S9AHFcWEbCvp8ifxvBd423nlmnQNsuelhKUQp8SIRaUwxsSIbXEaGZ\ny6tP1YkZSBSD1YSTLQfxv6AAGLJgztpz1OSkeBoFot0R/dVNTGtvMNRZXYK61bSP/+sMdKJVciSy\nHzWDLOFelXW0PBBbW3nHOIiOgqvWOh4aUS7Fe8jefy1joACa0HeUTksHHgy11GZjECGyQKk6caUB\nqIrbl7OUX0RSNlBJqU4FnoeAKoGKuFCnp56J5LsB7fAGhCJIK1aE2hthvWUVP0pv8yYd4ferFEom\n68fuLwC14yiyxnKI/9Yjm3shZRlIDVtDMx4Zhq40u0pr251i81xfzhBdFl5qxl16F2oZOwnihRqE\ncRC4X5Y0U4JDMJrTpQE9fS0lU3PadKsmHQUlldLpEe1c17kPPUEycX691/1HVBHpKBYtibVqti1k\n3ail/Tv9bTvqlnFhpBcGnDMtqcF6RjNxYS5U75GQIdxzoqH0aaHV+PoqsT0tLjj60VqnjQ8d0AFB\nLhlGNx6kt9mWO+yQgMPpJQCZN4UkdlfctLKDGEQj8MdLCIIrIHGMUihCpRKIp2NwshWJaMXEvByW\nwpPo0fCQ8jxK2blsOt8LhLfTgQRDB/htNd2mDF0urANTvAsjhejZGb+V64zMjkHuIau/bC+cvs6I\nxqdF4XhGZXFIefsr4DPGhpS81vN5J5UPrwgte91PNaALSrxAJ6nkyMlCnwq/+lllxdizovRcysrX\nW6be5Il0PAf54+CQXKpn+qTWnN7PnRSf9VhI6YiI0TjM+3X3Ih6nN3tpph0A4Z2SQuPSsuu74gQb\npDlzg+3bUhFAMLhodr9UvoNVs8agVtl5O4VfqU49lXT21gLAaq6XQATLysHpV4czoCwc9hUkpUqr\nB7JErAgruN5XUrWhGFPoy6opuqCV1H51PbJwWHlbqu1UYFgawhSp0pui4U1UraJYHZHMy00Wt8xq\niqwkgIW8xX3L9GrpswaSeqfr+YoMUQTMhPArpsIRn4hWFadPQU/GyfrniE9TXGl1UztTnpB49lp6\nwzP3usBm/LMLRmMOCIBhClspkGfR7L5MWuhDmjSZ/8ycokvqGpi1SBf6+tuFIrt2ghQP9K0UWrcg\nI+3z/HvLjdr+9iAVXj05NO7QtOpM5GISaw2ON3tRArEser+nZEEout2wtuUBxRbwrckLYz7nb+sB\nyXfd3Jb1qQcVF+Lft+6oJRLzdXqeae5D1FxEqhBfomPtqoHwrtUF5fMq94u5EsfQsiJeg3u81Rw/\ntS2pLuVTwZw4kmfJIDW71htOAaQ252dPt8SyGz8JemhZNJB+KV/qSqBZEN6aA5G7RJ+PQSD+nfac\npsKXEtQy8oM/AlSr7wF9RYNExCiX9Wq0wsejqtdGw7Q/FoAPBFx7UqIhVAGQ0ytSUCk27XuNSwvK\n0V53Iv8SVtd26EVuEh7uVW94lMo96n2QsONIkUfLGTPC0qn328GnqgSKnjv8d4qyYviUpOiXoBTJ\ne4W0enoTwd9v1yJI2WR5X3UHMKBDEK8vynXOacIPaNuAU8svjpJUHx+EMOe0ww5GaU1mHUbxJKuu\nQ91xNkexaly+nzHJet2uHU9uaUq/WpAXTw4pif6oYkqqzaUQe1aWrixfCVG5V2dMtISPLAqA+3hP\n+Z2VGeMRfofDXDjay9ZI/pXW9ox2Uz+EMoTfS0n05IM+DoczlEbkbdGV135bWbUX5bzHtGzoyjlb\n4+O7UkVQylKdMBEIlkvkLvQCq5wVy730Nst515urJV9ayygpTRNKVe2wQnEH0IA5SOII6gjSyVEQ\nz2vLLIRBCDUwp9pZ5nGYQS7x1fz6YPQdhL6YcE3nh0Scj3pNaar9jBDNvFfgRIIWMS4Rnc5AIhyR\np2gKjnvJQh8GQYpDr5dXL2R59pikFPZJ21uA5kkqgTqvTEG8EvlaFknrIFDQVk4m5pzkYPaeupDG\n2PCpQIfGUz0SZwK03+jAlGhCvhxhkOrqW8MSyHvRn4Aqqf7WW7sd+DxyNbyKuaZ/P72J4H/y9W9g\nbBvG8JD/9PhKDiYwANkgQzFlQkaEWSjEj0OKleZEeRFIKIuy2zxJclo691yAmS9jXf9g0C28m5aY\nhOat60ut9EzgcQ2oRIPSxGXECtMv+F4LSqnF/Vf8NwEVTIm3xnCtmqgB5TaT6cvKjfRPIN7B5+DE\nEOonoGDMWuWyZudxM0aVFM5BKTTDPlchuYWyPMRGpUY9Pm0Mn7l4vyIUXIo8BSECQIfz0UhEV7IC\nqpkh7t7eQF4vMPW+V9YtpKLA2hcAGYsys+MDvBrWwj3v6K41vYngf/PrX8fl8oTL5QlAECGEPlDY\nBV8u9n3s2IZgbGGau/CLEyjRXni0GnKGadV07CRdfbCp2wq186YuCMZCbwxRqZbVmo/gjsVwL70W\nrlsYUd/zyGxHfJ8wldhkg4TaXk1bBTaeSUV11s74KxWKelRMq/DDlmbD78MFPehxleMrPX6o5L1H\n40TiFPqpZgGSP8hYpxQAv2ikgnnCYmSq0zHb9+pfviQHnsZGsPtzLXexSRVpuabwA7B4RG/nwYw9\npjcR/G/8s6/h6fKcgh+oaV31dUgZEFwc9QdkbNg2wXYJCDNv6aD1VxGBbhdgm644gDD/U9umKMcy\nUDhOeEaII+K5wRBLjxkt1UzpEKKicttvSNqcQeIRhvM9OQSrrMmZWsIPYo0uhdqw1OPRQnxY6JH5\nFMyYtC6frHkSHs1kVFZISzpYEkpn//fihPNRO3ndfx0y6762Z6xNFj2aK0sohEeivfevo4Lzkx2Z\nnSPfD3HwVh0DqtgJ7IZHVhqWSFm1/CB1yGWkrAwl1lO3LEKh3OOkY3ozwb9sT7iMS+uQusAbhez0\nXWCDDDuFd3sa2J7EQ5AVMuwFFGMbifb7dsG+mZVQ0ViCMQa2sWHbtsXc66wNoNCQ9C7gZaVgBLI/\nIOi5Mqfyo7qTZTBy9Fgtx3qCORPtyfIwsZ9gbGLxCaUgEAsMa+UvTJOoEvnCqqoIzFABctK/aFMX\nZkkzOcxsLkxDyTYaciaFmbjI9khJLQnC0pVEfuT4nzkM4d1ootOiv3i/hANWCrFTg2TyHpck8ESF\nvnNAnF52zgGolHgP16L42qpNTPqVeOt7QPA/+fo3sI0NQ+rwwJhVaxyxLQMh/OJHcG9PgvEskGFa\nTYbg8mTCHO88u2xPuKTgSwr+Ngaenp/xDEDUBonCs9GZir8xLtcwHq3dc+45nZZj4SigmZyPEiNT\nVpAVOmrCBZ3mGG3dPPtLLHFo0oIWTfjtfpflE8M06o42+QOLjB8TLaM08NdQYAzraIgojd5sMqMk\nmYUfZZU1my/44ywJ8uYaihWlpINQyzrM8iV8KT5eWiW07pGSqU4GOM6iUSceoT6w3r2X3kTwr+/e\n4aoxvtypge7cuzjqmyKQi2BcABkKDMW2DTw9X3B5ukCGobr5DkjwYdfHtuEz+w6ommNxsykExpkj\nkMjVrpfQd1B7jbirX4Bv1Uj7NLcG/85cOpvCXEp/Uo3GdKQ91yHQGNCZOBDr1KmwmrOPUlkh6+z3\naHmsbetdEkU5pM8UtQthwEcVfW9MNFcCyA1apzQ0ZRJCFOWVykpD4966PuG8uAII0Z+ufKLMVBfK\nVJZ4kp4l2yEMLwF0Vf7RT+jdZcE1vY3gv7zDvE3se2nLMJdU4XvnBYoNkAty7u/Wv2ym0bangefn\nZzx/dIFsA7Kx4G+IJbshA9tlA6Z5Vi+XCy5PTxgXW1k4bJMF629kG9tgpgApjjK9wvl6v5uCQFck\nGnkWIyDm+MVmJ8yt0coKfYo669laZgujoJDJCqH1EkK+KE8SMU1nStZN3Uu2rudD2xNlG2J1i6KQ\nX0pfkdLVQHmqUwBDO0fUVYexw3Gl3l0LBCT82Y4D1CYf1ZkPJKjLeJbIL7VqSPOqMALt/VkXCVBV\n3b0bI/49hPhz32spwgdiTkB1T0/rPoF9F8wpUAyoDoxNzAgYhvqXpw36mRt0dyG+DOzbFdft4rq1\n3lBy2S7pyf3osx/hMyJ4Gr6bSaSI5vOsGg43rVy9SjO7grCMaykNBEpCa73BqBGlX8syU4E4cFjC\nSQfb0yCymXVCDB0WZ0W/Wf0CwWAfhPproa1a2HtHTZjmVOhuW0pHMJYG6lc/TNCJFvGacKdSYYo9\nkMxJykDVzmLgORaDs63SROyG5Px2k3o1OMRGx850qIfFhXPANjix446xPbwm4oAwxmbXI7TWC4nI\nN5V4frhCkTo/IUpblYAIyhMcASjwFaTgr+lvStZccSliCzSW330rOu/lnzF1GnZxiOQu0ekxCjrV\nDWUhi+V+epvIvf1Wmg0A1CKp5j4xXThv+8T1RXG9mbNE58C4DHPkbabVn543YD5D5w3b04Zx2YAx\nzISHIAJ1RDZsl4uXDUCAy+WC7emCiyDRJDZDdNOoBN3e1Mta3NmX0L+uxlcTwxBIK9I1em7pVQ8m\n8TcdxyCrpvfZjBcSRDcV05gUSYZYBV8VHqnmzlAA6vI7dWJ3wd+klKAhiqL2SCDRXfy1yyn2qRw6\nXbz7dI2Xz4SYmRBY1H0/VvAIYRYAMlIQo28R4srxDrUmXu5R1ZmBTUHLmB7OfKus93G44AoA30qW\n0whXshM0xodEPCI+/vGaa0xfdVHsc5bPJgJ5nL/U5SP/y51XoVQV8cbwZn1OdYCbtsMzIpdeSW/0\ntlxNusT6rb3St15SOKAYYh/rqHmogxECOUUtr8Uvz1CJbiUY40IA3Qf2fcftdsO+764VSzN2e72b\nX4HQaIpd2r+aWSqO2lA1Hgob9fVBKIEStwziajAzlsCVuE9IpDSXnYrdIx51MxvR2rq0pTGJKyIo\n5rQ3+SqmZ5n2joOhjignAg+mVdoAJ1drpSQsmbZ5q7Uvrms6TQ1c3To4Wx1x2y/PrpNQjTUR4mXS\nVCw+t9eMLu1tsHuaaJ/KBtVulSwwxw6Jvlo+u6wghD/ekdd7E8qn/BPehuZlte25NZZSxT9Ibyf4\nQA5iMYSjrQ/SGMDmynIOxTYKlSBK54y41ocjdm6bjI0/AnWLYt937LuhXEwraq15ZUw4AeknyFJh\n6xYl9IlHIfCEUAdKxDpyq9P/aWhZf49YQ0KuZUFYiLKZ8/tuS2+bt2fYWmiVxcyS3ni4taAwv6hH\nW4xSenqCJrUaHVTJzlIPhIS+aFRAQP2SGGGmgZWxoeb/a0sCCSNwK0jKs7V6U4+jvFs7IuUYy1p9\n+TMdZmJTolL0fYxCxXQN1hVUzt3TAh4Q2F6VyHEstW7ZtKywJTqW+/Lz6UcWypudsksDm7prN8QO\ncgkS9adEWO7ECC+rWwMiEfrjx3lpBQL1ebspFk3LYhaTNYKeC6osv3PNWpYntQ8VsAhHQIJr6q7y\nlmyL5POyWHzv2p4U2ZyYu+J2CyVnpv6Tr5CM6XH8OT3odZt5P7Gr4rYD+65hrdqccgrwZE8NcS8T\nd6AVSB5mBTLgZaFVnnFQEFnsnktgLFTn9JaWp6Q9nL0c8GV6vQttemPCQgjlnwqmxq+7W8PyU1JG\ny6gS6perVFwpURvzbooyRKYbjZ3xis9Jo+nRYniU3gjxgVUg4xMOFBsrF+oAWLHOB0kGpgu8hScO\nn411MRV/hgIjQmju4Ce4jEADBIJXDu4KJMZUeYXuWH4Bqt9Vd/WwEiSLMIfdlQOhOs+Xiw8c8efE\n7bbjerW/+77bPbkA44IxBJv2jRvM/CHwt91WX263sCDU/Ql1Ft0Wjrgl/DRVqCMT4EqQ+D8FLJ2q\ngsLzmcuNtXkrRo2iCF0pRvWhRKPu4obyjmc0ZwhZBN0sOtqUTgy+upXQLbsQ4hkBUSnwupbkbSHE\nFxL+9m9dRSqgEPAoUxqApJNQB3yy7GY/Xk1vJPg1NGmeO+In2ytr1AZqNlgK02ph5+ggLVd+0mLF\nmEbwumwVnMzhlOZhqCsk/F3Rk/ZlhtYDkiOE24U2kG7GBz7PlQpqKocPs1D9F91RV55z7thvO64v\nV3zy7orr1fwaVtQzZCjGAC4zykYKD2BKY58TL9cd1+uO68vE9eqWw27z/I8+umD/zAXzo2eIAtt2\nwbYJEKHS0UYX+lRpvmwYeyRq3joxdbff6s49nblipVOAzeI8Zvh9NFRFKBOtlYmsMSaByO88pmFY\nV5sryXJd82lXADEaOaWonCX4ORtHRjeEzCaitT91zy0Vq0NhkZI16spaLh50hQz1+BeNJYrH6Y3O\n1Tf0gbjZTYgfjptiljgQX6BzN+bwZbUxN8+vUB3QaVoOEf2HAfGX/ggEQ2YuBdqqEbFBOH+aoNMK\n6qrA4y8p1ACulk2y+QRXJPSwgI6O4pLPRsndgGCxn2lB2AqA+TGu1xs+efcOX//6N/Hu5Yp9320Z\nTz4L2YBtE9wuGwmNANOPiNKJ277j3Scv+OSbL3j55IZ37264vdxwu94gIvjs557xuc99hNvnPoO5\nTzx/9BGenwXbpRoejrK0Zrz/tUmmlrUUuy9bDsTuM3HFv6kJ6LhskMsGHTbPnhKrJTWOHIwzVX0Z\n0CyG3NFN45XyReNWFEYcBO+A63WpTSSZGeJX5GkI7ZZqG0K3Onjp0IjTTXx1JRORemXWxwpT8BPx\nvW4Q3SB+XqNl7/CzpjcS/ElCv4MFP9Awtk3mZhMAmBtU3PExBKoXmqLbWj9kA12swVVbh/VgvUL+\ng3b1376UgjTbVkhgs2tRqqyBUQJgPzRNgsKC7pQbWWChE3RFfHrOf8Wy1L7vuN5uePfJC775jW/i\nk3fvcNt3jE2wPQ08fXTB075h33cMGW5GW+zEVFtmuu07vvnuBd/4+jfx7huuAN5dcX25QgBcXz6L\n/XbDnI54HiQlGnPoEPoSwmz4hC/f7rjNG3a9+aLZRCx/hfk/APNHYGCbF2yq6fU159osB2+s9yM2\n6ylmHo4hGSfRhZ9n0yXGYbVVs8vHAISAAySKDeUTpRHhszWNSKUuoLoXwaThL+tlRR8bu7oUNozt\ncan35p2Uv6Q3E/ww7zW/mzIIb2rMGXOJTOFaLzoy0vQp6fM/Umhtv+te5CuUtyAfbc+W8KdwJ1r1\nfDgMyKudT0vh8IggrZnwROc6LLVfz/7TiAUwM32/7T7Hv5mpP3cMDFrVsCVNa4dgqo3KPhW32w23\n2w0vL1e8vKPPJ+/w7t0LRIDtYvskLs8XXF6ecHl+wvM+MbbpW6OltS38HwBIyfm0ZN+xY8fEjkDC\n9ONoCH7tW5MNGcobp8sODIyc+cX0pRRvrOGXU1RaW4q45DTtl90/obRd11VCWGmueFmh1zBLmhUx\nMUjHY4ypxtn8bBEy0zxiq6Cbh7cnD1m9rxn7b3TKrgJawt/dMawh/eOCki6ukAXvFIc2lcPGq4q/\na8/duTPCyUOZOdAm49fhzWP0jxRg/prwu2MrNmnweNorrCTN1kFowHpr1f11tigJ0nThvplpfr3e\nMHXHhi0F3j67FzzSx7CHU/DlhqsL/Lt3L3h594J3717wySefALBw6ctHF1xeLnh694znj264zR2b\nDt8E1a0ZOGKWHlVfJvTYCtyw635wdg2PXNuKMmZqq0BMI1jAz7CVhox4DSQUpDDOVI7Iz2k6WSmJ\nsVMrMD99D0ZNvRoUJHovZqG0anwqRC/LaDYFuMRiKf/HlAgJff6lucyD9HamPmpeJlBbD40L6kfi\npYAbUcIC4NgECYKWRZxLNJEhorRkcNw5SmGEfeity6QsZijBzaFgky4eYVfOHT3tj6T1QEVVsRxk\nsposkY3n+bMchC7YEa+w72ZZyZQUwhDyONtdFdgV2PeJ227K4uXlipdPXnB9d8Xtap95uwGA3X93\nxbvnGy4fXfF0veKj29XOSxDbeRnr3Ymqipw+qVp8gFklV9zUrBJWvsOF3IZIMHc7onpsF4xNLYR7\nCMa2QTdg2wB4tGaSMxWtKx7IqdAboh84IMfdh2Q1AGu4sszOY4HYmnP8EwzXaOY6zpHjBK/d0sk2\niRv2DoiS4Y54xImZ3kjw3S+pJR6ta2TmD6dFCnScMpSI7/dBOrJHaFgYbx7MUZcd7A6WlEaFGr8C\nAXhVlsXbfjMSl6H3iA71QDZNkVMVBMKdRHFVE9xsZuGfijn3NKPn7o6zISkAqopd3THogU5TFXOf\nKYzXlyte3r3g5eUF15erIfPNhPPmiuHin4+uV1xvV2z7gGySUlIKstqcTj5H/Ov1its0i6FGwAUf\nApkKwcDcgX0C26Y2pdg2jG2kQ1Fk2IoFjQ7gSiZKDgFNRdDHkwcnrEcltA4rCyh9fzyIg4YvglHJ\niuSKk29zdYqVyGNh7SxR4MQxCq/a+J7eyNSfuQkFqk2c0mQPve3SwPuL2wkjoRRQbMZyXCZyJRt3\n9y5MxaB3ljdni67P9llbYC4H1bZQ2jARpZqbRTdDouO65DVp49YOgmiJVkLCKbqHAvAIRSHPOmoz\nR5agSGshpwgvJvy3680cefvu81DBPieu+47rfsXL9Yrr7YbbvrvC2TDGyPGB07sCZXz/gIYv4obr\nfsNtv2UfhrjYO0EFgrkr5g6MYUK/PdlH4aHDY2DEcmHM1c94IIQ+LREaaBfSFrOxBPA0ACALIFzU\nDcpqQNumpbaz0IVcQQUET7Xxlv49CozGCq8oUANfMfOBt3Tupa3bJCAJmzHRKADvnvhUwgBwYl5V\nbY2wCK0dc74QAClHoj/TRJwYaVWjB6WyCKjkv3qCNIvA80fWMo7C3y0MZ3g/jVh3zU0bGvsRElHU\nPfIKOPLr9J2Ttx23FzPtr9cb9qshve4VOWZr/eZAfLldXXB3mz6EQAlKuLz6MsNjjj9xve42vdhv\nFnGoClHBJiOlSlQwL8C8SAr+Zb/g4srV0H/abk63YBRYUE+I5TS0Xdlqso4BOYjjXyc/A02uXND4\nxyvD0kcU/ihSGuuUP5URHBTbGC8eH12VUwl9BL2ZvFAQ0IP0ZohfWi08vgd9Foaa/W4ZyJtNmkFF\nSO1XjBoAACAASURBVHeERgwCrxrYy0nGVK7AkcaGt15XyNogygum0WSEM8GulkfV3RWYM/rFOXnw\n6KfwdulPfxOh/JxqKKlK+wayIJ8aALENdCpsP8Ntx367Yb/uKfSF9rayopjYdeK63zCu17b5aZ8T\nQ2cu7R2Sk0xd8PdYfbhd/djrWaZ+CCkEcxfMm2CMDdvYPA5AAT9+bbvYkm6zfpC4ShZcKGAGnWWg\n4hKbzksXUhFocGQ4F8MRCSijr/iuOx/n4Kpia82yenPiV2wP9zHLnpUAsZXM0PWK3L/xJh0E+ikq\nAo9tZcCI5BFZSO+AoYDfj3m8ncMfgQxsFrhSGLXG3KwFr28qORxVEHvoeam0mQJCTAPO48MZzDKr\nr/k65pjrhSBHOckngTlU9pnQx+XYjqkzkdSW7nYLsx2j5sz+zJy+p32OKmOfmDf77DcT/OknF7Gy\nnh54c9134HrD9XYjh+KOsVltY8iipLR9LLQ4nIkv+aILof+MJgM6rpgDJfjhfB2C7bLhEhaJo+qk\nejVfWglXut0or6VfXegv2DBA7FLMwyYhHNGJuWoGUaJs5Q/3We1ZDzQsCG9TztFj2W9AxccprAZF\nExXzgYm/cVU9OOj95vrvLfhi4VX/O4DfVtU/LSI/COC/AfAFAP8ngJ9X1a+ePzzT2mriQkwvdI/0\nmv11EyH2n7Pwl8BJXadPHkywCH8xSVgjApDJGKZXallH+m6QcR/DdOsHpbQUskQa/mzdnhErLZ3m\nIHIHXzj6yKMf6L8p0m8QHJPWDu3h3vcdM9D+FnN7stAcwRTmHMR+g14Hrjfzygfib3OHyNZ1OAFs\nKDCzMGb6FPIQCaDOZHTBnwLsQ7GJnZw03U8k28Dl+YL92c5c6HSpqYXm1VCeobiV+CGEupB5RfsY\n38CrHH2fx2cXxZVNWAYSoxkgJjn29o+mVVlxHHEvolEXEKLmFMtrvG55afD9NB7e7ekvAPh1+v2X\nAPyKqv4UgF8F8JfvP9rX7e+mk0MvSCfmXAppWhGlUoBqbbMVTUIHPCBLmE0+cCot5GhpExktJ8Us\nJgHVK5zr0yWvNJla1c8ZsDn53CcwYyeis7129AMIed+5B/96NTM/lIfakuAYAtmGP7Nj32/mlb/t\n2G8m9BoORbagEDhMiM/bokPxxPKerypcX8x5+PJiqwvvPrF4gpdP3vmKg/khbjElSR9DkTTBJP9d\niPeI8npndHJK5vsH0Pkh4itmBkcdeaTKCkGn4KVk/eOejWZiaismneBlubxfei/EF5EfA/CzAP4T\nAH/RL/8cgD/m338RwP8MUwYn6YGwA6mlI+8ynU1CKH3qPDoS+jPUR0fNVAAix3lw1OjCX1bKneTj\npctgcDFr18O/sS7z3KHM8qv+YwQPJI2DRjQEjPMlDrqZOSduLmBX/+y3G+bN5/YCyAYXfMEuCtUd\nc7fnb1f36u/8aqqFOCn0k4QfeSRaBPRcrzeI+pkBQU+1U382TDtDUTZMAXABxtOGp9sTbjdTdHnG\nwepgiBWWdu09hX8R1OKr4qH1U+97qrr4vnCBJrUmuHTZpgSLwIMqPJGlshJO7czT9L6m/n8O4D8C\n8Afp2o+q6lcAQFV/R0R+5O7THKyzpHSUKA9HsvfyEJtMJvTc1VWLSqK/H+0dZ+9HfiKwxPv1ol1e\nU9sXAUKxZvLhMB4NZ7T4zdrsTig28aJsYswQ0tao5SMKW8pzU19noGCs8xuCDz9VJ9q/z4nr7Ybr\n9QXX6wtuN9vYoxpvLOodyVUBv7TvNi24hV9BL7WaEH1J7745FnXWVKScijbFEAXmmDmm0NhApC70\nCryInbz8tOH55dkcjGHdRJx8DgZZGskrZQXoMmCrqNW1AI8YMEG9X2BRArG0eDL+vGpVCn9FDLIA\nILANOEezsXSFL3UnM0jqp9fSq4IvIv8mgK+o6t8SkZ9+kPUV+ApyBFO7CbpogyNvkw3HRiQFUXTh\nD2FyQR/x2VLQE3Fhplsb8jb6MeikEFhxcKtP1twZ/cMM7kGDZI5yvVJ9Xhk0iUTE0qnmoHMEzhhy\n8gFMtXDYcJTuOnG7OeK7qb3vsQknNjuREMHP4ZuAqFTo7e2GOZ/S5I62JdY5SoUSyhdYTp8quPAD\nijHLclMohs1aMMW2oGAI8A7YnjYz92+hdFgZK0rM+9SjxvKcVaUPQo5RWmkIL74fE4WAqM6z0W3m\n9ocDGLUH2ksIfR3cSYTN1kk1kT7R/8fS/z6I/0cB/GkR+VkAnwXwz4vIXwXwOyLyo6r6FRH5PIDf\nvVfAP/ztr7lXGfgDn3vCH/jcM0L9xfZI05joNEqa6OlYKclbCb8PXi7LBNLH0tmxnNKxIei1Waja\n0IUgqwJOxvXMHOve7pp66FL2EYkagYJIuWQHE6a9PlrhYyloOgU6B+xUF8mDO0J4Tejj5FkgDju0\nrb08dbBGzb0EL481m76SsSKTz+/Dqah+CGp8x3Tn7xZdDIVl0Z4j9nlsgOxyepRaoR/VyfSi4Qrx\nbpCiDCukAkpL19/w5mvzyx/GTtcfC7ZEXytY7UxYpbqzlJ57IrwF/+h3fxe/9//9IxQn30+vCr6q\n/gKAXwAAEfljAP5DVf13ReQ/A/DnAPwVAH8WwC/dK+PjH/sBzN3OcbP461q+OYpIXandXTinSWVE\nzq1C7t1sGoOFPhwp9yTWnxVC2lgfJfPqVeOmiqr2MU8eSqo14ePTHYeg3dSDO8r26aG6c0dbF1ab\nm+sUEzDvW2yT3a8WQbfvtzTz4y1FEstE4uv5WuMx3cTPefY+MS/u4GMDJoogQUznnhbz1xgqdrWI\nPVEX/Gkn48om2PatxS0o0SI86uHbsBLrrcudt+pSCnx8F77PEiuZ7/6Id2Ru2iWzBT+VPSBA+vIo\nJKVZtsxEyTe0yedf+JEfxuc//6MpW7/+d9gX39O3s47/nwL4ayLy5wH8FoCfv5cxNRotDQWR1E0p\n70YiS+noQuo16IUnMxRCUYNHwRiRmgdeK/9BscRYJ6rWoD7SG4dConB29GjoaXqrS6ufbZhiJIpi\nLldAOMt2C9u1l4jEjj9jlrlPzK0iFhXAfrN19JfrO5vj7zc7mWYA2GwubUf7m59jqGKbwWgC3Sva\n73a94fa827r6Nj2GAsWoMfXIOX7/KOWb4qG9iPcsFU12JQsjnZlxhoMRozziitj5lj6A0OVE3Rjj\nZg0QnRFjpR6CHHEn2jiUlLwUj9+x/JhvAvFJDwQMLLxQy5LqCpFcvVRV9P9QdUufSvBV9dcA/Jp/\n/z0AP/N+T4qhxnBTL0ylRReHWRrdjaOcxZfpNuFttUXuLvSKgenn83ndWT4JnZsH29LMchIhnxc9\nWibdjJNUEA2nQ2sP+ItC1DYli+2Mm8EgIhWw1Gz7OKFIs546MESAKdAdFqq7mwLw4vKwCkyF7jvm\nPjCHIfrcxbfdfoJP3n1isff7FRMbdPNXlz0Jtk0womO7CX846uR2w+3lxZYDn59xe3rCvm2Y2+an\n8vrUZobA1yaifd+xz5t9dMeutllHdPjG7WmrCAJsGHastw6oeKDS1cKM5y1WFSZEaZqC4X4OX6GI\nxTWS+AbAILRXf72AD4Me6I/0ZYi4cg0eExtUH5omjAlYnSPtWyqSUCzuoxDNtq+KJGcwKu5UrGfz\n/oP0RiG76FR1L5Gh/UjzjOeRSsSKz4hP2EPxR4E6fbcQL50lrgEDE1bNH9xQdkZo+N6F6Eib+x/y\noFkiNjbi8QAmDBPqyIbchYgcM+Y6tk68bbkBXer0sklC7wpNgk6KjNDbNzP59x24Xq94ub7g3cuL\nxd3P3VZBLgNysZeZbJvmIRuidkCGwoOf9h27r7tfPYR33p6gT/46Chnw1yWhe/RD6O0cgan+liUB\n4gzGXSbi3UYi052SBhhxbLq6hRNlQwrxlQhT1oB/Fpd3smaMcAh+1OmIEYdvlLxaRJ5AYjeswYVo\nxu3nMiPI+rwHIVGHmkyUSafVHxDiI4BMEOG8ykLfTchDeqNNOj0iqo6aCgMmiFRimM8GyqPesBJ7\n98P8r3/5w4Qjc4gtqGxGXBS+Zd8i/p/N7vb9PCmQGj7dwloym1Ma1dxJ12CHVU0ogPgnBlZrsNH6\n0dvBdVV4r8fax9ZescMvtmEx8Ntl89N1zK0u08z3COpTj/rbA3X38Nr7EpcLvZA5roH6M+qNpUP3\nCwyLF8A+bVsxBPHNVgk3V/al+Ekz1t9mNfGnUlteDl5ga4qKKMu+gwagC4oXB+eeg+YQWCr81Em7\n3opphXCL7rJCS2+E+EXM0JBplbR160XoUIIcAn+Y3iff94U5HtdKobXZa1uDV9mqJXHskiRxT4Se\nASX7TP3x/tc72NZPCD0L/0nTtT/cef7Oc6RYVf2orTS3LfIuX9s1LGBn8w0w2wajqtiqgOwVg6Dq\np+nsy5uKVH0DkGLQPBszlvIizNfODACmH4YqfmCvIs5nVPHXT8UBo7H7TFavdXmN+oCgIycPzkKq\n8B/1GFyUIiOBD2tySgDM0h5/IASQdbOcsM/7JwKeFuRDA68K1e+AV/87kez0T/UgGXoLWSBbY9jU\nmShmdlRsMdYAD2DIZQY0cGCDf3iZ5p5yiJzfeurWQ7uqzqI5Vw5T8n3rK0doMWUt54R1g/iWlgMx\nRb5hyD+zDvNQfx25KQDFtgk2sbcO3247dtc2cyqGo/fU+pt9A3wapzkM4cnPJbzQcWIqewzb4DNk\nAGKHbMqwwKtNN1yw4QkbLjKsXWO4v8fKr6nekfZ5Kei/HIIuQM2ztTKfy6fQt1qZsjJOs2F9EWaX\n/NAEMUYLosX4adixuhgSNLaQOqvilUn+G+3Os8GtjTiskQGkBtf+b4W7IXYf1d8gif97qgStjPVy\nvazoxN5Ta08n2xEb6In+/MOkTWD5kXtPs4IIh2Q5KLV5xYNnczoRLXZPcjjmDKkD8c0KmGHliOZx\n5NsQXIadZDyHYActxYXgh9DrJGaLfhrY00GB5I+wvPZ+xIFtAGMM6ADGZrHuGBsgAxdsuOiGDRs2\nHdi2kUoixCH8PDGqTM+uFkO103hDvG3qkUKxNMx5PJ//5WCwEt0aB8oJhfouTbcgNfxJi5CnkeLl\nBh+2JT0GJ1kffe/0Roh/geiEYDfPMGtbMQeSDls/thUnZxxMTLX1ZYGdHR7bQwd1usryj29sCgfX\nkHAUmhdW/PXT0FglGKnsFZqvmPZS1+E5XD92mJkglsC4z9auCfhpOUA4aOwZGCMKeypK2Fmgt2Hz\n3thUo0PtCHafHRtQ2OvF5q55Ak6Z6Jp02LaBpyf/XAa2i2Bz5TlGnIFm4zfntOOzfNPO9XbzpSla\n63alNXU2tM9ViF0hm72+/HIZeHq2Y7ym+CbaYZuyNt2w4YILnnCRZ3z00ROenzc8Xdyxlst1cSCF\nLHPhUIT2HxuMNhbDfUmGKC6bKBuCLadcVE4esE/sQC3+Fl+qlglbmZi0tOxtjLNHgFiJse3UgFjs\nRTZmULnRR6mYidg9qoKIKnyU3lTw4z3muXdJXBOK2hx+iB2ZrCUw4W2WoRBs2NUcQ5CBDUAGjCQ9\nxYnqSBJHOrnQjyHYyDQQNxn3GUyKmoxIeGzXIJplkiD0xwfCejjB22fNeLGhtbaH13s1PO13Brig\n5tb16i1DyO1ir8Wc046rttcpGzrP2GwzCtFu+47rzc7Lu/kGG3HUvWybCdTTwOVp4DKAzQUgwp7D\nEbnD0P7ldsW7q4X9zjlL8N0kzaPAHP3jHX91rNbAZRv4zOWCzzxfsD2JrXiM8mUPbBBc8DSe8TQ+\nwkfPH+Gjz1xwuQi2iBeYatMUdUcg8UTivAT/RZCR5B6O4Z9Q2eo+GZ5ANLtRBy3nuTpJ3xAd7RZz\nbj+jQcZIKxQy4+wX9//6WQBiL8cA4MLvPMB8R3wuYQmTRfM9sZwnujm5/GCINHVcU2mZ6kPooES4\nYwf23rx4CUPMx0Los542Pi7s/nOcODyKjOs9mreBj74UysFPlCbmcpP2uRzUcSMf1bpDxrJTYK1l\n6YPD64z/ggF8HTzLU9T8PjbyEDIN9+Y/0WcbFkQzoRjbgGx+rPWIMul47xlr5toqzfBbtdFL2VA3\nacWO3LpsA0+XDZenkeHCO9QdaBtELngaT3janvF8ecLz0wWXi531t4D7qYUW6jJXUOBO3bASKT4k\nhH7meBSXyCJ8HE1SNcVt56O2FMt+iCNHimwY8eIMSBgyBTZS/NP6XWZW8s6j9HZzfF5/PoqGpQBa\nNFlA2o5URPOUxrNcnNS1QmqUwijl7HmZkIupeOhN/XufwA8IT/08e6I/Gea+nNxjJ2F8PDpPgDiO\neSYKVB519RpHkZs3X3C5mNl92QTbkHSajc03O21mjtt0wv/j+mespeOkbYmDtVsS9TKI4UpgbPaZ\nBqyAbBDZcBlPuIwnPF8ueHq64LJt2EbsxZjNxDeeqP0MRDEwMvJI1PbvzmOlppkh0XjuTIz7KC6/\nTiC5JhE2V61wXa6hntP+T/YsLM9H6Y0QP2ZJK3kYkji4oeeURPBwegSo1wAcHHtVg2vZYn74tXxY\nK7cxOgfzZC5qX7RxManUO/saPQ5l9SJWHbY+XMx7InwLJ8Y9sND7FCOQLqdALPgXd6DBYufHGC78\n4u8rcGtMeQvwnufnNcEna63Y26dhsQ4e07NhU47tMqDx/rOxAWPDRZ5wGRc8bYb2myP+YLM3QIIH\nJoZ8wcKw6hrBFtqrty2QyGem9Wz7cj7Whxr0LEdISLwD8pxLQs6rDysUHOs9S28i+G2lBEBBN/32\nv0H6xIb0npan88zUWcyDYxtAQqE05Aq+U1bc8vSJzl4riMIIKUqEhX+zYjpww50+SH9O+b8U6FBs\ntS888x+WEJFm5xBD922Yx/yyDWzbZkcawnwD4UkPwY8ya+//nqG5MU4h7LMpJU1ls8mWsRmh0dNp\nFYpm22xL9XbBJob4l+2CcRn5go22AWsZk+Q9VgSndOx4aj61/kyWIajpKvHPKoRrfZE/rckw5wGw\nsB9t4dUyeTSHP7GkT9KbHbbZkWxh7JSUphrSvFpPPg0PPYQUgJxZFFV/cAEPcrXsJL8srXzkLVnN\nSb3PBBVWzEZ8QpL/Zc0Qba/K+n9+FuEMZO8NCaYvU1zzCCw2Dkz4S+i3y0iPuW7qjtcQfm8so33G\n49/SdA/HZkbpEQ1tCW9g5HJrDGih99g2bJcLZFwwtgsu4wnbuGAbm71JN9qTZmCZ+qTbyupBiVnk\nCTBn5a9Yv+TglfUgoeGX8dA7Dx4sQWpo4/ElWypLb6v2vp3ze98CfpY+zZl733JKsRc+A2UA2FDv\nuC/jphC9zold99aXFVBEK/c+a9JDY9D1/H2z6EyNnJroDUG4x+RQoghFArgsL2McmHEOXBBlhJOz\nzPZE8bCmspZ6h1xtZ50USFP7GnJlZatDjLfNVlrGJvlJ4YopxCRTn87Z75YIt9desBKGDq988LFc\nho6hcEYqnrHV9ORoMRG1AumVucHaHKsj8ZZdhRuhESyGieLbE0Y4VkSfAq3q5IPnMznfSrU2pmOn\nOaWa9Zqgr+mNEB9gM1d8XZlVq4Szif/1vCIp/jBnUB2mGXl4Ta8fVXzeEtf3RWD0sXk0zqdJyihI\nlBGqawkGST8FQHvVLYMuBde4k5Ms5+0UH+8VWplhjqNM8vj4llbEMpgr2xD0LaPoTDFtW51jn6G1\ntu7ploYf9jljng8M2RaBD8Gu/ePMtOX9B2TGizKi/x6pt7lfwNsXb88lSWtjzOLLtOdQfDhKx+vn\nlZ6OTT8SA0Zl9ALJKlutrsJnvJZ4WTp4l7eDnzxxAjrvl95mjg+Pu9bQs0AYGxXoUvN7+zbKLFb3\n/kYek1lPOSEAm4o1H+JclO6gBN/qdgPlXefPzXzUBN68djJ28R7Bej1YFm3/kLAfGSdsiRKqCvPv\n8BTsW2a3o6kt8dfc3uf3m3vUI6ZCXKPFve1igT63ZPY61Tej91gpZUvr6K2YbogrjTgXMM7oxxiQ\nOXAJwYfkWrtsA2Ns3kZTRDbmIeohfx6N6B9ZSRjjAum76ZhRlC08TUUUrWLLzkvKsVU1R/ExOb/H\n1KOhebfUzAo5KjWpZvTnWC5eQa63EXyJ7ZGxdlamujraRyRbJUnkKqHnKcGaakDS/M9bpRTYPPLW\ngdXDp0H6/mT9iwz8WAeehDgYEmcDSdnpOd7BWMKvaVDES0E4wCisAT/hio7I8sCdMSw0NwU7hN+C\nY6wkxeVi9yLf2He3VFzY+YRfWf0QpBjS8tC0OOwEIXtr79htqVC2EFyEnWdBNmOk0Fc0IYgmXixN\nh8IUM4VOkzXfE51ATVbYOhBpzSEiO0rJm2IPoS/5u4fAZZWvtXXAyuCe+J7Z+LmSJaD2crzGx2+0\nO+9MDBhPIzYaSbkYpIiwYsQv0a9Op9iHcLPpDzaj/MsKy8vPtkOWb5+ZDqptsGNfNlCe304OdjDW\nXNfyafw5Hb3m1iv3/MEwYEUUzq1A26Njb7gCoHm0y5Ttx3czm6yBQCpV1As6EvXrSFFeZoxtwekH\nmEjE36fgtk/IvkOHQObEvtfxWupCWoen9ncnsGsu6UekjxDtkIxu1qdqJV6qkvu3ACsan8P4rmN2\nPpZJP/qubdzZF3VPjWSt5425k95M8C08F5AG6/WC43MdKYlkFcfsgh6MUHiAVAm8CkCOv1wNAFmH\nZ809aUuzvJek9Lc+Qp7fszqKNIbYYQXcK92/s+MMJMTZCEZ8d5WqeXl3f+VW8xM4MSRDVxcaAe5g\nc6caz/+93phCxAswmVXzw86+ePWV1oGa8TZe3AQ6BLgNPPkxW/uuuFw0Z0DNmQt/NVjMdUhwCufL\nfD6jrobJhIAg6hysnfZ4CH2z70CGOV+AnZFLGmhhhdxcRX/TYdoY7thuhryDnXrGRkt6I8HfnaAW\nY5+o20hXrFonTwQeyvKfP0V0rpK6p79WAmg1IBDfB0igUOfyw3bHaMHKUKcKIIa/Yuu7WiCSQNfh\n4oK8bbowC5UVTBJo7vP25GHtT9m02rfgNh71bSFj87mzrd/X2Qdi+yzCB+CWgQRbx3b7QOc4RDOr\nIMdd25ar7uNTV0oT2AG9KXaxUN3L5QmX7YYxdmzbxHaZhZA+6IG+fDn5i1d4VMpAkt62tNRIRxii\nC6Aedx9+HUVnhgVo16DrVAp3EX+xjDSWd/mBoqbwNxGAAU8rtygxwEl6G8Eft0IoASB20p3xdnTK\nD2WQCWichNcRXWLElNAIRexkVCnv/xgl+PFqLXEJP77dVZmyFTNzkN33NKtWzetzYrIJ6O1o6wfg\nxhUP93x1so0haUgdz/mmWvTdrnGsNcz55BtNtrHhMi64bBdctidsm+3HDxqPIdjGxGW7YNsupiDE\nD930gz7tE6Z54Z/78cy/oCihV/4L3Ka9U++qgm3fcd13Uy66QXUDdMMYF1wuO8Y2gRF72BabSATx\nmjUR02A0EcxVDvVJfew7SEWSPgPxfSPi0xFvL+xoLxNm5ycNsDoZQ7Im7rJJW9WYzt+jnmdLAv6a\nPCGAY+h7ReAjvRnih3Y1TVUmPptJ+c7vpuE4oilGp0ynQnrWkqMGXkYuSrez9duRVUBnH7p1uLyq\n7sJ1FaHfPA/nvKbklPrPlZ21otfI5VPI7G7LaZjlwY7nwhTfwyR3eIup05DNgnY2E35bq585Hqqh\nHOyttdu4QGR3wYcfna75As1Jgq8wEuwaR/BpLSUCLvzmdJy6m1F4Ay63W+7KE/i23Msznj/asXkc\ngJHHlHiKmcQ1F/pY6qWlzqLfQlWy6OK4twCn8ou4O1rqgFRrAtl5rAAO/CVUZ8hE/HaHpKmoWpYm\ntI8v1s0S/M4lZ3zU09vE6ktp+joAMWwqE4R+goqjGcjQ10DgMG9Qwt/mfF0VKBNNWD3wbG1tcJD+\nnvAj6499261BVLJGuBX1K//4p+o4a0138DBi5WuyQ9Co+7EGj1AQfnxVzK2LicQto62sotaD5DKA\nVlfYwaqO5HXWvRLtKyQrxqUOmNBUg1MdR2fsuBTcbv7Sj+uO62Zv3onyaQgapdI1j8CHMrvEQUeC\n1IvJ3x1ry5A5EiuALaeNheZ1IOzAlMhbVm7U2VquVUVjoeb8paaUrizrFsz374f2wJsdthnUm1DE\n64cC9X3zY4ZuhnaNIxa1rU9384Z4krUvMRrbDvnbtTf5Zz2xkkCOzalyiNxNkQfxeQrB57LYX4Um\nKFgZJUQHGCKG0KywzML0kKcBUysbI6yI1aEXMByx4u4lL+GPFvt5BG0uGcJvfzVQf5bzsGLzq2vs\nS1xpmOopnH/evNtuQn/bdtyu9facM/5m6q43yv6IKSDSSpgw56Jt628wQUWUKR50KeuAOcwuDgzY\nmwG4BM7BfElJzpaAqR+LgyPGumUTh6xXdMAbBfDEvxSX7mQPxEeciw4gTnk5a3swxboez4KWeZNY\n7AHXJI6moCkd0iAsv3iNholsy2m32vpZjrhViTAWWj+WgVzrDyeVf7dDPIVM3K4MBcRuWpZD0Oy4\nAjIQp7nETkVgxfoKs7bxiEMiuEfethlmPE1uZCXsQi3l04AnbvvMo8JSoWRfFmvCB62iGYtOMaih\nP5WcdF0pEnoqytdTV3OcMmcbNs0yy4fF/NGKJ7rx+RJK/Hui0FqdUbYgz7d4RfLfbJNOUtAZitw/\nKAVQee7oxBjJ+t2kJn4ehYdbEuvoXFYMXjDTPZQ/9kyzhHAeHRRHwrsemh/fu/Ze1cHJc9xpgIQ/\nLgk7tU9aHMJfQg/+3gRfINhRTtbyuyyRJfmxsGw6yDPoIDBTZC/hCkEMrg9rZp/TnH57HPYx/VQi\nrWeSBFV3yvBUevNXlzjSOYTeKGThcUR/nsPFz5CBBTZ+L/r8Ff7S1q7X0HtNZQHfT2+ySWfhSJiQ\nuAefUf8g9J1Jl0LP+xbVhEZtQpf43DBmNeXo6nvQnC2MqIvLOGn38uwB8dNqAJXHDCvUP0IcXNoC\ngwAAIABJREFU/5gMl1deojXkPVavazSk75/hB2DkgRlh7oel0WA6mloIVfV1QQgNHZtimhQqcolw\n3+PFnhPXq79dt70sM0qrlZwspiE+yy+jAFG+2CTzc5tl+UsD1hRPkUK6tbYyAsVL9HYV3+c3KZpG\nla0ob7DwvVeQ620Q//9v7+1irWuS86Cneu19vvlm4vgX2zImJgglASOCLCFMImSELREJKb7CwoqQ\nf+AOJVFAyD83KHckUoQskRsrEEVRhOwkCjZSEMGyIq5QEiWAY8e2mMHjiSPPeDIwUYLnPXt1FxdV\nT1V1r7XPOV8835kXzdvft9+z91q9enV3/XZVdXUV5oQsi6TzmYaQWBfWD4ftSD01fIc5BNlNTLnW\nnZ+puBky/y7XrQSf7ztjtgwbOC+UkOeQooGqIrGNh37pwhAEiGApMYSIv+pGPk2W1vwY8XYg9IVp\nCAASf9lNyQShNeMOSvsKzUhBANXIZ6y+ZBDMSQzCHV3NsNc6Lq1jjyOzNFBoNjbas9Qy6hIDQOyQ\njKUZcz66dJ3tLlgkfijjhbE7oUlhZL7scVE2DSvSdlFTYKMJ7emFOn0vfTqh6mQ79+vU8orptQ1B\nkuFyavJ4oCojj7J3bdI5SVnnTP7MhZnzn0ntkqwRQL87aQWCAbxZXWUfZXkkCfugd09P1IxCRNHo\nW2FwwT81M8SH9AzcMuK1A8okHgiftL0wiF88amdObJFeFvOpO5OakqjMgzbaLzvyQPlXQZWEsjbh\nbzDs8HX+vnfsTvh7L8TvfWg0PsqYgoNqhGPQa4GbKDPqJPHbIAT18JOTfTJQ1fBOaJ0AX3Ll8uI+\ny684Xp1SuYW7tr/MVelQnduXqPnAq0l8AbSFdd5s9Vo2N1SELirk2ZALh406VG8bUnVFSu2n5mKC\nNwzImXlFJtDJ8txh153i/pzPe0GnAS1kEZUo7blMSalfJCq/S36IqUFIRCiSoeugEy+iV4UqqK/v\nReeKEuMoxFI3NrjmNirRi7XLDD7rHFkMoBMvYEtAMjYSfzfC56Gb0ym7Plg79UcxHIeqe5F4wnlp\nEE9Mmv2hIA4pHXPogmvpt4I5/eYbkYhkRQGwG2eizOc5OEAyroIS9S1F00nBQVx/bn/+K0n8Ntnu\njF5c4lP9cmSsavOhrJKaKqn/rUQfFu6D+f/YbAnaDBnHO0n8R+49/bpvfQMCCSg/SYSSbziz5ocl\nvEr9RCAyhgHFKEQ/HyCafDLYay6O5yUGsUaIVqkeGV1LKB4pvcl4yWwIz8zrx6QZ3AdQwy3YOq81\ntMkI37uiN671KfUHrp0bjhAwihY1lx6RqCQgK8nkCkLV70U1mKZmwgxNjSEdAoVwzwSAS5bs2xFn\nitKXS6SosvaiMvckemO2T0v9V/LjbwjeKTTsYSKWyeaCnA6VeTKCLc+WkUDaOu+Tbb5IQYe9XWbb\nk5axcGsnhFwmZLtP89WTQto5fXBlOiQi9jHjzdkGzwGwwzPSEEQ/fpPaXlW/C6lUYqwbIOIniUHZ\nzIK0VKddi/Pv0jSy92z+YdacujaG91M9/z9gS0Idnr6rD3RJwo+DOplRSM0Pb3swCkB5aG4MMqV+\nDDEs9BLnL4gUBAmmYN75WcFLYZXQopBowQwz+Ida7VJ7FvTh7YTc135jGCsZcAqfKa9E+Bfk8Qjd\niF9d/CtloUtDTQKv2vHBa0TkDUKXJMoiWSaJL/FIEPOEBSczNvXOATGRvSZnPvLjtc9V2vN1cvIp\nNXVpAKj8MqW+DIsYI9GJZj47jrl4NXJs9dVVnBdDZelSbqetE1EQOZiP+6RbEv2UsFMFMqS8uzAE\nxw2eNDT6QMfwU4B6+PdHV4wtbRY8KEVrX0mUrcLdK5QloRF9lfwVdLzmwU2hiuc7BrUMvr+uo8qa\nMDdWzTkIAxAVV1fpQ2wMhrmqX4j7b4WqL5puFtGBOV94AmeOYJMQNAfLKRBr0ULrgTxNeL/6qKM3\nVu9sXiiNi1qYOF9VKY7L/jFtQBF6X3BspGjWSnILJyrM58g8ytq+1E+kY7ir7WsvcsXpqYRBy9wu\n604uzwNbkCLY/X0lr14wXjLV+mFaxQ0T8W9bw1DJMxDJoJtLuOZ9GTn+ydC31xN6XbJvOa6E3cws\nw1vEuw7QGu+erkFEKxENF20peChoqPpAWPPjSTIiAbg1usInduMF03tix2ZC9Inf2b/nyiut8bek\nWDflWDnheKt455oI8E0wCI7LRyb1fiX44xuSgJfXqwN5Jc+7RVB2EHuDJdkDZQDJkWphjEECC6e3\nnYOz3vX+OvEPDHQd6LBlFN+Y/K6sacucGC/RbAuAiXMhV0N9mSpif0CuUUu/pz1RPgdqOfy0ZPhp\nWwtpXxOn5H4L68xwPFEV22TU/dy/SvhF2QjThSaT5hTzI5z7+CMp8eM/Xs/7FWGMyHVqN/uxQE+c\neZRngZU4tSCwaTsI+8UM81UjqcJvesEz5ZVU/UxVRLRe6c6QeEbKAFYIOj1YVgNUQeyVmyO5uVYA\n1rcTW+Z2a9/OGQUZWSxSEAZAEo4eG7IaUpibEM/jzekXXyeJa3yJ9X4SvxYW4y1o7nYMiUzJz/lc\nZptHb7HeHF9TxrSs8QNGfmBpMOSG5bCODZfrhq4bmo44mdeWAL6rEmq7+Zrl5icDH2qHfvZ9jzW+\n0rpfRW/BjGB9rFK1oUXK1zV+mF0dThoE7DCq0p4w4ZtLHw7CV+cfK/OMIsaOuD+/YisZUqolVTNV\noNS/V17JnccNOXlk0hQI8UQv05B8sjYFitRY1fozmVnUvxdxxkX2pzAqLKQS7gsard2q0UqBTDIn\nf6ldCaJHOPBtfen+eSi2krlQ/Llp9cmLc0eAFWEKX6oZHiwYiI8peR9ozLPN4uqHnNpYWhNgM6K/\nXu0zcDENhV6IZpl8AfGDMhXaBMNPwFRwvW/Gvd47BrciT4YhIEhaF+LnyIuADQYFEnydAAoFa2v1\n+Rym0edkehmQtga9X/VYVgFpTNkYbLvjOFBAx7Jj9Ly8iPBF5CsB/BkA/woM5X4QwC8D+AkA3wLg\nVwB8j6p+/nwIWpa+rlipJVmIECyNfwxFK02IgtuqCUcmW6B6HkN3TcmkHVtDIOE0TTq7Peapcqg6\nV6+6CNuKdwlMMgj7WLQI1qmsQk8kQWVIQWiOiJpgLHFyqW6Xv3NPAdsXkbYPZtbR8nwg1tqlZa5C\n0Aenk1CrI9ttQ77ICQyeyfd6aXh474L333+AXCxjLsRCtw2cphmODvTdI/f2ZPqqZuDrt46xd08T\nTrUHiPPNg+hc60m+Bu4Iz7MZCBUanOcZDIWeAmhi8sUWIEjpzXmtShGZLkGkcCNcAZbWViU0DNF8\nLDuSOCM+xgr+p8n+5RL/xwD8VVX990XkAuBjAH4UwM+o6p8UkR8C8CMAfvjsYcUtOmMdbIBe/Dsl\niAIy/MOJsWutDcsI0woARDCk2YeSXBXNjU8Y5kVo1a9NDCiEp4X7N6pySmU5oULi5yTTM0T52hpZ\njD3DJYf6UiOWMv7u2gY15Ehg6fPEE6BDfRMbT7jp1Cze2hXS1fMZGmsYyKzFjXEOPIpOBD0CbeyU\n25CE2oyYY+0v4HT2kZl8VIE2GrBlqC+axHl3Cj+JR4AmA7IJrtcNH33/AYDietvx3n4xeKPHvOlQ\njF0tNr8rbo8jAnKgO7qv8bV3TzoybMmgydgNRgPCjjM5yQAUduQ64O5GwGfLNZXAVIRrsoY519N2\n6Qmo9Xl/+NxGxiVZd376mwI/7CPaoB4lySVE9mhmVSjfchFSbSX3y7OELyK/HcC/parfb4igO4DP\ni8h3A/gOr/bnAPx13CF8YI/BwZErN+Vx5c/Jl2RvAlcDUyWsxz8PEWcAaZQJS6kHbjBQLOYhVYLs\nnuZ0Vvk3YrqDzU/ED7ab/rJokvvXiEqj/Ka6vAbYBKgUrhdVmZPMiwFLgGbWnQHIcKBrC+epwO0i\nohngZIIWmfZayU1n9dglJO0JGTOgXtc0N8GGsOyJQOO7M7WmaArg0vCRj1whTXDddzzuG1Q6AE/N\n5unD+m4M7vEN0LYODPEDNjp63zF8jY9hxC0YEVxEQ5pE5z1bzzA4BS0pwqUcsZM0bJbgkeGSfBS8\nqMyddgFK9CHAEKbQYoqu4lnhv9SYaPlXJPHH78Q52rACHYlqIhPuhH77DOG/ZHfe7wTwWRH5syLy\nt0Xkx0XkowC+QVU/DQCq+usAvv5+E1SX6g48e70ikWqyzZRnzTCTxpRp44WNfnrT9PRq9j1bbJUy\nRafVv1Ol+yNdq9Vo1rvFJQqNcVKe533xD9V+ahRNLIHWpg1bpNKyawikck3DKTG7IlMfCIDYaFIC\nKbR+0Xw+/dZwop91zRy7MZyt5Wm8l+uGbRPIZvdqFt+tYUr6WfV1neCYf6d02+xzxSmdYcIRsN2Z\nsSZT5pjOcJOArTALQVM1hqetfOVyAkiWT30y3srJX1zk95pneQnhXwB8G4A/rarfBuCfwCT7C0cC\nmGgfSxUJ7pqW6QWvlqZD3QrVCwXZkmRCCk/PJ5IcrOVRbVafACc2zBNvF/Tk4qHSVPW8us4fMht/\nvK7pa3+yn2aNJtFvKMEozGisgdaosmfWhBAS3gCRTGPpISrsXC1DKpuIHtd5EPjBnFta9u2o6wbZ\nkOf1lXP70iZBgsdk1wjbxgrMieIXRr+CjUyjEP0EMCo/IpUmF/UscUTqzQXo07ZoRTADXfp3hpqp\nkZZPED2frQLwacp/yRr/7wP4lKr+Lf/9l2GE/2kR+QZV/bSIfCOAz9xr4Jd/7R8FMn3Vx97DV7//\nkWdeKaA2sKK+3Z5nlEQSUufAK8vHVaPKIBUItw3Wdz1J3U/xvlUGIFVqVMC4FCZCuEvSEHQloML4\nKEXh6bGxWRJK0fColcTL9ktMJVdpUGGKq0UTququD0n9jDz67wd8+VCOzeauPrpSJ+epuKsOHr4r\nwMWXbTI2QC+WLFS6aRlbw2gtzvEbSgalkZ57OpijSNRcjfv3IIrCTSv5BJFL0mtoGDPsDW/EHyvw\nW2E+CQWqDQXunFqfcima2YyLDgAgYb6iY2Ean/nMp/Ebn/2Mv/JpqfQs4Tthf0pEfpeq/jKA7wTw\n8/75fgB/AsD3Afipe2387m/+Cs+uJei7ZWU9f1lBUmSMJZcDpvLjqNkAOZmoyE70a1nBCc3Af9bQ\n0uCpshUdxn3+nL2Zn3C0FPY02zDAnkE3n1zkrhO9qfoMjgpJGdLYiF5kBPFDRhoOKT3jCO1UBTnv\ncdourfuF0TaeaxfrTVq7/V+31kuzNfGlSe4m1AswFF0A7ZaTv41hJ/d4Dv8+UoewVN2lLwXxY6MX\nv3PeJjU7rThFVB6IP+E3wzVYsdsBVBGjndGkXENLVhSP59KVr7J+02ZQELr2I9Cj4I3f+rp/5uvx\nVV//dRaT0IBf+ru/gHvlpVb9PwLgL4jIFcAnAPwALEjyJ0XkBwF8EsD33Hu4Sq4whPgPGxd/IyYU\naF4tpT710uDtK01WS1m0P3PkSRWr71x6vJZ7JExN676GUDWQw9PsQFjW1ZFE1vqu282qLkCvSAai\n0EPAqTBDW2MijXLGAKna/ONOTH2gbXZarcDat6Selv7KTsOl0Yon7PjRW5FnHoWWOOOU+GQsG5oA\n2xhQdEAbhjZIA8YGbJv6IR8NTPVt2sd87Hd1SRZSD+LP2PiCYzj5XqAcAloAnr1APaG6WNnGATcK\nns74p8tfxw9vIJhCbU+yut751OaJA/cFmpUXEb6q/u8A/vWTW9/1kudFBNP58KKg1dcuoLA+j1hC\nWjehKbENIDpL/tU0Th9/+T0HZ0TPXtL9KDECR5jDxAenNije0WtQyT7GRF3giEU+NToj+WSNR/rT\ny7BE4Cp4c6m82ac1d11qWNN5KEYfdIN5Guph920f/G7EP8z9Jg1+eq2fqScZ+qquFqT6b+qaYjij\n2rx+R9MGuHfAjskWaIPH9W9oHakZKVX9VeIbpzE3Ws5P2nLvaVIz/KTMHYUNtRiz0hdKdDhMErrA\n9B78nYffuacFhuRAutS5133vqz6P2a+YgQeh4nLfuAbBzxwQcH9mrFNcA4DkXAiSmUzrtKpild/T\n91JllcY690VLZRuDIYBXDrW34pb57+HRXlVLQdQ/mvkdQ0WLMMl+JY0rYmMOpTHX3WVU2W0Svp1+\n0+I/SQIpp+H0PtCGog3XZjTX090z3Xb1KHrxtX2V+AedKtf8dGsxRqEBaGq9oTpsEt/iNijxLQ4h\nnJOZvrsw10kKah5NsS6PVhwgO0hFUaNOKpQy4wrDeL1qMd0ciJIwQ8BnqSn8pVONxMpFRNyjaOJe\n2afwVHmlWP15k0KdBgR4ynCVhM7iaZ9c8ktCJAX9RO+8ybfnf2DAxNLDWrIvvJdtxbVl3RgjqifF\nnnzmV6WWMz+jqVJO1dX5A4l/TEE1Q83q3xUewEPjn/3dTMHGBtsdp8Omyva1exbbGv+O8q4xLNNt\nbI4xqcw4e1PJK4t2aa91/orZtRmp0xfRXDoPuvDaiHZbs3h9BSOVi3ZU1/jUYKp2pEW74oavdWIn\nYUIoVNY1g+2MwSrkxGU7wxWgXWNmBbOKRvRdWJrM1e75mAND76ubAF6R8Ocdd8AUR1l6WcNbZ492\noFPWLQyg/k4OXivI4fls24sCs4SeGwx0mCY15LDf57gkEdTrTUwveAcNV7PbLFBmAeCkno+U+t1T\nVwpI9PMYGkwiG+FbsuzhhBOqc/3ocK0gj8bqvhQwiS8wPxwg9L/LxGLze4jTWZK2ptYzX99DLYfA\naAhbRONhHyIeUFWOAStzWqGRJ/auRH8UQAF9gUdZ+nWJxzBZXIifNWYAfC6CqaddnsqGoAd4JkJV\nXC8vk9QqIn6nyh9JLYe4KsHJ7pdXU/XnvwUYEWRcuV+ijbr0Tws1fdSFwMuiZnJfFY4wE9UzelAh\n/oUnT0XJwQ/od6wdqnqRpHM9KeqmBOUf4Edi9TaGE2J3oxv1jaNU0piRSpzsXJx06wxFh51Yy/Z3\n5rhXX0OTlzfM7jxBruu9C9kXJ76Ao0f+uQ1GRfyMQ/jJPp4INJj7It1PsbtoKiBhzEr0ur42HiKF\n4he41Pmkr/VJ45kE7J6hv6xP+N9plsQPyRRz7HxqOS649H47LK9zko5zyVi7CpEAmBXhRHivmZ/i\nI+adqgZZAEYyhkBvEv0KT1TFc3mtXwnlY3pm/e7Miz3V5b4msVekzN/+/kUiAsU4eYrfqcoOJ3z1\nfW2xP6/0XXxEs48f6Salu65nWmqBb4Udin0M3DqlvXq4NDzKphB/Yb0ovzTm2/+6PWDyMoivPXyL\nLiV9JABd5rbCNf6iEP3yyX/uUUVBEpWsRimKxOUJfLq2cWRJk1io2sJiU0r8XdssPEmOdYbCBCk3\nIX0xrPq/1ZIqX0NuWrCOprGvTjsJBDGINVVC0QPc9c3JIdEjZiot+ifU75fvWVlZDhoaCdX7nbHc\njMp3FPCxzRJY4jdHAt+uzAHVzUtHNCpjBGIOI4pNEFLVeKap0JsMN/DRyCYT8zDi3tH6htYt5HeM\njr1b4ouu3QnfT3T1vfSbS2caDWPDjGsSQMkUQFcgDPaDUkocP0TdGKnTPEJ9l0P4Kw8iI+BUjZ91\ng8057FOix/QpjbOFVziXCQYQiKEFnqnZwftR4/zF4TGJPHWcLV6pgy44dXsNka6MLbngc5rGK6Xe\nKhI4iG/ixcEEYpeRJnIKxDeDGKnX1X4gh6ComsjZClor7PuAAE9zx5kdwYHDMSTLz397aVMDUFTF\nin4A7qaq6Z+sDe5KP3aZfnvnio7WTLZZOhmuKNuv15CE38h7YcTf3Wq/946t72jdGFEfdm0f3VV9\nI3zXxzOZZqzxW7zTtBKLCYgTcX03IOE0fO1te8wHpDWL6MOYqbmCsbhrY09N1JiNe8EACiTr90nC\nLyi5mqV0vVhKMI5oYtZn66usGeUuKg9d4Zio1Wqq7Ifxe1PBKBjxV9s/7WaU11vjh6Vep14ZYicp\ncLrse+w1QtqnKfkRklyiIXAWUVH+iV4dOeOkeanZGCbEWivqctPWWmmwczQ4qHT8W5nh/KLcY7/0\nOjQY3ldMm58qI6EwEQWaFsaI6B9PngkDnn8gWAi/uz0ht/lKVfNJ/M63dCi0w7UJGNMYu9kifCOO\nNo3dctP6utoJnAgqth9UaZ+61e25el/WgK4zmNSQ72psloBqzt1aqHFw+bRimEjRIiqsJMd8xMxc\n4k5xK9EPuC3MjLjnMStzebW8+gCQx2PDJEEACQVxk6Bi+rldtGwbndaSlPTO9qoLyTW0QznK65My\nsdFsZJIucnx+tR2fG6HY+9RfJpXuTqeSNFKdto+t7PP4q7IOXDadJKLZo0PViXI+oVZEk/Cd+Lsb\n+DZoJN2YXXpOmE748OOzaSdgENBla9CtQbYBbFUVFtRTeg8TUnB+jdx8Tr09zuTZb8IEzm8Wxlyf\nkBO+XAXC0ifatqZXTurAKgiOI8o5cg0BDkNYlmHx4Kznyita9XMyrbQCwSQQDWfUAGO864YTKvsR\nHkqpz511EWK56kRrfwrxV/Uu6lZJXjk95UYl6FLX15RkSDp7nouab9FqQIPW8+hqu+pRDsoNMgsb\n8XE2ATaxe2ZrU0/YoW5th4Xob7AtsBeBXBrQEWvQvQ/c9h23/Qa5pWGx947H2w2P+45bH9iZ4qsB\n26XhcrXddtu2ZRBPDQraFbfdDINsf4yOy3XD9bJhexBsInkMFsguy/mKE+Qkxl7UmSSCRKdZzXZ4\nZArto7Tn9mVxibHqaNzWvEqMrJf++XVpkUSfDxI16zAq+pnG4nrGpLgk/gYjgIARmqkp3S+v6s7T\nIuEs5dJmGVIcac0bjdj0kRtZuPXUXBn0Fzeq/b4WomHpSOhIY9faM12RI/80zOvI4OE1KEQ1+Zer\n3Im0Ns6MIVsIH7lXfhVbRCDzqfc8ADJOYrTgl601XMQ3vqhiE/s0V+uD+DdAroL2IGi9oQ2xTLdq\nqvjoisf9hu1xw4Cp/eqE/+bxEY+3Pd15ArRLw/W9Cx4errheL7hcLrg03xysliRj3DoeHzvePN7w\nm7cbHh9vuO07xuh4eLjg4eGC9/QB77WrpeEyQLkWwrlBAsANYGuOxdZaUbEdPsWwxjRtmS1HYu7N\nm5xmRFUBhiSsT3lEZQxJyOf6HZdbGsQfWoLM9VjUcSwyB5XlS2SpVgA897Dswaja8FPllQjfi1tL\nq+xOo0YhDOkA7NTWVPnn09lbkCaNf0UIoAoEyTktUnm+4Jf9XwEmgxElh7j0pSo/K2Req+YdoEU5\nrO58kxkrNdYhM6snEg/FFEAzeER0eUXzIJfNJd4GJ3xRt7qLre09tFauDVtvZry7AWi2QUc7cNtv\naI/NXXhmi+69483thttt9/PpbXnTtoaHqxHv9XrBZducYZNYPQ/+7YY3bx7xm194gy+8ecTtZhK/\nv/eA0a9oW8Pl4WoELIBt1jHbSqxikCp3xRmAkpTTnQQ/M1oE0cskWpOx0Mhq7QgY8JOIkLaIyU5Q\nJP+qJhzzOZJVJBkfcJbYxJ2SQHh3oGrRkrIRi1yD4WnHUq49XV6J8B10glwyc1ILVU42i1TckKmm\n0siXEjLVnKr6Z24sFBhX5c+5L/8GAIX/ZxGS9kz0dq+yB7YcKUGmW1kz+446H1QHuVNPyQAq8ZeD\nJFwqkPsrBrTBXYjMX+gMUiwH3tYGtq2bFb4BdEQOzQMrqqq7jzzAQvtwo15JqHHZcNk2c+lJhalA\nh+fCv91we7zh8fERt8cbxhhxnt7t1vGw2280Y+B5xHVmZgpCKRqZAEWyowRTJUimJCgTgUlcm8sq\n4v0dz1HS9MBR1kxo7X8idg0+MJVYsmqsWcj89CTOTX1MWugmWn+yi69E+OfrNQWTD+RkTye/TIRa\nuHZI+Vl1o5EvCFeOn2rXXTfQkLPbu+zCtI7X8yk1IUebL4oUSGt+5f0V4DEiaSfCIy3usUmmdz8B\ndiTR+xwqNSemOJOByH3ny6etDVw2S3IhngobMCLr3bLYUtNUuFV/7+i7xfDLJtjEDse4XjZcXcXf\nwrCXc1sPwbgF8d9sI1AzF+B+2/23aW8cVue4Q4qzVZneA9o/ytwp6g/Cs0J95ewLPLNWyGY1h/vC\nRCTczlUDJNNnFt24VgiZOGD0WzQZSKRZS89AGUvBp7ANgPjK+xMmnZbXidyj+iISA6nyMQk3ySol\nqs2ShASnZGzle7FuhipexewZlOvEzPdnrcP+pMa3Tij7m87HU1N/rX2KdLr8Msob7mLbd5Oc+94x\nukZueQusGehkSso8piO0hRZTZ0Q7Wku/e7E0q1reegHQJf37o1viSGixKzRKeikRezZ2czIMqG/h\nHZ4DPw679ISa6UHoaK3kB9gtw24/HHPt72I4bxpXYnKp5g9UIiFboGBYRecMn0mHm5zjjp8CMM9+\n1Cv2hZXpu8SZBEs2WXB76YW4YY+azT1cYbv3/Q/H8moSX+U8RprbV9PamgNg74PDhpsnE0lS0lt7\nemg7WOJpeV4lino6awvWscpZvc+ajIh9nzSKyqE1lxqzvPL3uXXcCH/Hbd/Rb7ulunaCsSVABqkI\nUkJFFl0nmiYC9Rz3W4mtj6d0oI95Pobvx1fPWW958zZctuaag6v41XgafR/QbsRvRG+aQ2Vm3a/t\n0j0Xv8b24NHNnsEzM5rPee4LcLiroibErNt2Z42xSsMBveP4kvJlFVPnJbXTlO7lFhzPSeBVrcMd\nLTKI/977lwRzq5B/Bq1fR+ILz2OTSQ22kps25vuF6l0vIjGrq1l2KmPzXVtSwEiJn5/6m8877QWx\n1FIU92hzui9ZQ2t/KfGXsrImQbUraHL2QIai3u879ttuavK+GzHsmsdGd7O2q3B3HtBh0rI1Yx4c\nb3MjWvWOxEgV0E6jmKvPLrktFbql2brIhq1xXd+CEFdZE2TncQZhsOoK7QNjH9hvA7e3Cu4CAAAg\nAElEQVSbRTqq+SSh1AbcrhH77oXbdPMjRfLH0i0MfAm2Nm1zlYTwwqGDDxatj9gjKBaehaNTQwuL\nfIy76A/BiLSgpgbhpjJCqFC7OOLSimG0P81i5355JYnfjbh5ai6AecZb2eiSse61nq4fsXWxaRLG\nPIbUU/oWopcKwsJRC6mxN6Ins/3SogLLSrZK8RxPNVCp1Hmwf8Oar4b4++jmA789Yr/tlme+Iw+Q\n5I66phgqsT7uagk1hliPiFx140tagdVDSLVoDGqquhOfmVWbE/1WEmW0IzKGZZkqMCC01g1jMH0f\n2G8dt9sOQDCGxwD0PAq7Dw1TBpDuu/hQ8lftkDPuY1jToYjfy776LVEcE08nHMvTE8xSI6wgL0yl\nMNbSOcSanURf/k0vxvym1AIQz2vB1ZcQPfBahC8jdwtRIBZuSeLP+m2qXz/k/LbfuQVYA7ShbRYb\nPoleqlo1s/qUtqmursRftOLjEP3ftNin1Kxtxru5L+EwD9Qi1N1qJtVvuxnG9tsNos0I/7bbmn8s\nuWZUMillS7tHYw0qV8ULIg4Uo4fMwMuz6UwqZQLMTYqdoI6xjljyTmSlVQDM8efEf3s0iT883Zfu\ntjTYO3MDUMqmik/XoSyEH7O5EKJM63rM3wvYj8DV6aqc1DrSd8KQT5Wd+gtTmFuT8gT/nbtYDIy8\nQ02iMJLnyqsR/pzZ1f35DJyoEVPhqsvIPnVlgdtAyQ1tuPM0MEGTN/+iSbBCwCxdByXdfLU+N/OC\ncm8KQEmCCHcbmYsAGdCDkLhMitG7SfbHx0fsjzc0bNCB43HR5f1x+s1QdD+brnOcrlvKdCDhCErR\n0RC76Hx3XfO1dVuI/xAnpiBXmZhLYrBmv/aB297RbjsAYFyS8Mdtx947+iBMlt2ZlXGVBa7bgkFC\nmF24/N4OsM7YzKNcrwu0FQ3iVVHT8WgxaKWQ1ulzVpKVZiARdVMh7JBLA5vexN9iI79bXpHwkbrm\nQe2vUl+RfvpEoOQJdo1bOUma62ac4VK+XuYk1bfO2gcws/+KNDI9Z7fZx2mwyJW2R1lN3LtoF6Iu\nCQVhFSYW0T/dbZ1/u6VLrKFDhoRxbIyRDBTGRO3MO8EQhbTh+wUVeawTJgkarNSyXUKlBeEL1EJ9\nSfSSwTqtIOHk756IH6lZwMfGGP594PbohK9upfGjsPe9+xp/1lAMDWYDn9l8zoxr1cinmF3LsnwM\nLvdpRn0WNTQklH+NCVikZor/lekg4Fsers2XnlFgkOhnSRZTnYaqIvGfpvxXDODh2p0dMqtqtbwW\nWM1SBCAbdwFajEnOTLT81CJh2H5tbfLjToBhGXGrrjgOQ0L2c/YoUEUZqdUcHp5VNKXvNqrY9THM\nt07j3u3xhk02iAr6zf3ufYQq3fw8O3SBdsEQAH3A9uFKvK8DRpit2VZdkVBBDfkzoajxCMbUZ6Tg\nFCA6qblFRjqsNvfbh/dGYcS/d8i+w/bmW9pN7QPD/ftjKKpgFEHsAsxlxgTcO6USnkKDMZOgWtwr\n4D00bETv3yjuKeHJVBdvQpU/U/eomfNDuYjEURK/ZShaG6jaVFlaqqCeuHRWXs+qbxCLEdqJoGOe\n4JivMk1VTYyB5/QwcKVGM4iQQaQErRMbExrNzmR7OmVFVRAtLsfyL01J2Vmev5vPVmaP0FU0nk4E\n866T8Pcdt8ebhby6VtR9LaxjQIaahVsF0A0YzQk/2w0lSzWy5PKsusY5I/FL6bETeROu7blJiok3\nUuIPDo5RZVKOw/J3CUWyRyLuN0AxMHQz8usW508DX0j10kbz+IFJo5sESy2VEJVTANsIBsQZgdgA\nDOikycnSjl2bsaTCr5qQCc+j8Kl65LJ58oRJ5CZv9mtZYEWrqmNp5by83iYdISHmHvW8nWsXiCwb\nbXwiZXqizJjeH6MeYwfiFnJ67vFGJQVMyMWHtFxwy6rWWietSjKgo7sR89pMnZBc4tlZ8QP744C2\njgYNiTjqiaPOWWjgs5wZlEqI9zHm3lJcwaL4Rnk/x8Xpremw+LcytFi3+gm15LaepYdn4vEwzOjJ\nGOiet4QuTt2NITBKMe0Elmf/ynP3vC8r8a9ayAEIQATyzHGiA9WaMxPveTnuDZg3ZB2t7C7PtZVn\nz9sv4LLfoREsO1MrE3i6u1FeJwOPiEsCLUE1GoRAIb/ungKq6rgSfyG8JxncPQeHE/XCN9b2qxQ+\ncmJ7+I6OcKc7KQEmSaHnrZghDBbJdjP3l26GnrFpJ4je/zLQbggGjx/n/Pu/3RfOsW035jGZVij7\nZMgbJfacUReF6ClJyQzt0A0j/C2Inzn94UE+Fr3WsUHEx9U944/HInAjynbJwza3rVl/JggKVp34\naTqoGGZ/o71niGg11JHohwzXmDRiKw79W2Tf/d4VIeKEMu3E43InlduX0P1rSfwNlkppjY43ylc/\njBG6wU5USaKnEWwdjfmVmb+PG3kSGVtNzIayH8BPkCVZr8R8lNUzc6jJLVYFMi26fAOh4apeIAnS\nokuDlUsvAjoAqxIBO/R7j25nDbGtMSraWmpsxsi3Bntvy/x33G5rR2INoAHbRXxHXvcps/lSnzLz\nquSySlWMsXTXFnpHqpr2UXTAtwi3TdG2AWkDij0Ykzl0BECLdSkj+0yjMRBYrn3B9brh+rDhcmlo\nW8EF36QVEQUTQQJcdgmBWdZ+4ocNiqcUmrSAqpMXlICm0ZmLtTGQZj1RiIdzCAOopDkuSSxDhyok\nzjNMDixMlywWm0HsylMbAg1tCeS4ybFMVuyT8kpW/c1pvB6E7ROnA6q7IaWfqBs2ekFsOFFgXneC\ncf+ZvJPzFv7dQIJiC2DFImEPkrzx5QBPw1Fy22AN4lW4QSQVQyCNdZXorQW7NspSzNTnDa0ZOGSo\nWe7hPsyuFvByU+y3AZE91D3Og7o7zjIbuQvw1uzM+QGM5lF8rqHsfiTW0B3SFO0qGLs64Rshhna2\nGTKNhfDHMKYjw2w4CpPw6rGDQzvP6zRpvykgO4beLNBoANoJo2ZaCMRTgLmvv/DP1hqu1w0P1w2X\nixjhixlATfpvELG9BsZYzB1KYqNaHJAnxbQGaVuc6Htg/FOZNc3QLdQYGNmebE57o1T30HQG3DQA\ncMLn+6UJIlkpmaIY3EqWh+wK7U2uMYuQ8PFkeR3C161Ib7sk04x1l/gtXRNIiU8uTTyctQYSf1Xv\nTObT7lzBzkfSczCDmSraOnNTmDc1leiBk7vkeg/lk4Ge853a32Rqkga2MUv13hneaotiAnpgR0cH\ndGBXO0mnD8H1Nozwm7iaLUCz/vUxcPM4eVGFjNz7DzRo06lf6vOsSvfiDV/4ghHptm9o2+YuP4Hl\nUxgY+25Guj1tFbQzxOxRcxAflhP+GNxqC0CaLxdM4l+upuqbml+B53M6bW0lPtD/r8GkErgy/Y1I\nw6NIKM/UL9RcZvjHeQ+ioSGIh64L3HPK/SehPRRfvaBcR2hHVdOU+pHlwhPlVQh/aAO332oZZJLA\nCJ3qzCcPIDnaTMKgeqvaYtJk+a+m4a7GPl3+zj+K0WWd6fLEgfi9PxEptuwRJ25WLqYw6Rn6QjnZ\nRl2NH8PTY/U9ToxlEyodiu6xCztk23G5dFwuV19CCK6XhsulRXzUwMCNiS+HQoYagfYyUa4hiCqa\nDkA7Rr+h7w1vVDH2HZc3G7bLBe2y2Rl6W3OEV+i+Q3vH/mZgvwF9hycREUwqN8jcDLl5HqDCpJds\niu2CSPN1ufAU3WWNmxw91b9KoMLJ12k7BbUxPUGOsCDErUWaajKKtK/msi6MnKD3wxmF/7visnek\nvKfYt8S0sCHzJrA5JFnK3/vllbblUl22zjDSKsMoXSpqTkRI40g2QCLGYnedZaiVyiDyb8wr5a3M\nU/X0GMo/d+ZUp+8c13wlwBRSZh4NaS7sAGR4dF/BCWOU8wkwoGIbdboH4OwXS7rR3H6wX8wa7vua\nMETR0QNJm4fRxoEMDbBAGxgD8F16tsPuBvSBftst197lgu1yMcK/NFDbxLDkHf02sO/A6IkDfEfS\n64gxMwlHLN0uwHYVbBdxSb/FMqfCePL3TzCRYpspQCr7JPhuYf0VoEu7AU9Sey3csuuATOKu+A/M\nW0KqCCH2U5NAkfzZg+MyPtjOseNLeSVVX+feg52euecq0RsA5hlfP5WLri63qb14wLsS01q697JB\nsNWprWOdRJ0zuDCgyCS/14lTY5r3u0WWG2a6uV4veO+9K263B1ub9x7I1Yclrgh/ujM51YGuYpF9\nNID6yTfazPpMUTWYy69MJYlBu9XtTdBloEuHisNnCJrv4JML0CJkw0S4jIHRrd7qXiWcE/eLxFNY\noE5k+3ErvsOcWXx1cybDMOia3HQiypSgkxaAI/zNDnMOPwojiTnO5loIt3qPAsfxWmwODDc1yGKW\n2HxEY5KCpOPaGkvAzp9oLyfllQ7UsL/kfZVThUtC+IvXKiNIaV9Vo2AewCnxCxDRXQwnnaoELS+q\n+AHoRS840aI0EK32a61TvleNkq4yMSSn8kIrP/3WD+9d8N5HHtD7Dfve0PseVuvbDuju6n9bkMcl\nad997jwlNppZ+kVoiESGD9eRDQDwQzG6HabBk3RUGnQo2jDrexuAbO63b3DCV9+Gi8gVqJpTLvmq\nmF96RZrAiH4T2/tP1527K23bcUrQ0BDZCIm/algHaJReFCaR/Toy/IOTKekT4Ylxl13MqCJUTLct\nW1vujZqCOFaOKMvf+uplI9nLhNirZtmdSBa1iykdZ0LHdG1tJf+VOxJ/AhaOVV46SYenyvtm38C5\nbphuZQ31feqVLn0VM2RdLhseHq7Y9/fw0fc/iv0rbni4NOz7jjG4HXfgDfPZ9YGd21jVjUCZtC4s\n3Gllc+lVCN/iKgQYRtyDhqjdwny7Ah12WJbCogGH2wja6JA2wKPwmipELWUXPOaAiA8gTQkIfgeo\np9kX8ezBwHUTXDcLGYYyBiDdoqpaIgIRrSmYgiwZ92xxQcGtGesSLuclwnYJxZxOuAUju1KfC6LX\ncnPmgtUoqZNA9AbECJ7hACP4mgazea68Ypbde2xrIemyYywB4qHmwVnPVbRDu6413Pdp1sn/IFXO\nJf8d7uOPryKORL+wJP+5teaEf0Hv7+FjH92B0fHew8UMbN3TXY+OL3zhDX7zCxtue8fuRsB9t+AX\nFVubA0b4Sj2ZRE/CH4Aw5bZTZ0j1Euhkpx5k30cT07C7aRuy0efOFCm+j4A5A5YVaPilyzzz/ibA\npQGXJrhutj8AwETwWigsJacT/YHMz6EV6vikQWZ/Dpqk8p8k+gwitXmRsqyZe5AMypjAKrEtWCnm\npEyK8JnaPTKB6M3LxNmrSnwOSKdrhdPKQgCllk0YnXRPaUFkIHl11TWe7S0rnc1hbeze/YKME9Gj\nuOdi4UMhrAUJbC2+XTZcrle8NxSj79Cx43oR9HGNwyxvvVu9h4sTvp2Cc7sZ8YdBjjnvtPshHXZP\nZaTEd8Jnz8wIaRitXTF2BboAG9BwdQL3a3GcFhmKEX6L9j2pRy/6Pi33rp1UiZes3RmVn/RjgUzO\nZGRg23huQeoNETbLd6jaeX8zyTi8HBsl5f25XroUXXCJioVrTmkoRMzlIUeg90Xi/amZeKfCwK/w\n/Z5TuxpL2OoOfgnxv5rEr1NahpufMosrs503MdBgNw9vFcBHt98HIf2XlZWspyKx8s86lFRVDhXf\ncbjoYIiwbQ3X68WQd7wH0R23q1h8++i49Rv2vuP6sOG929VVfctl9+gprYZvcb3dbDlAZqC+6FaM\nTLYxxGPIiUk8tJNagkB3hbaBrall6hXNM1IaXDWzdjcZ2Dxk2IjCt6yGLltV0zkXgc1JMkRzbXpE\n3z5gB2wOXEqEj5Kh0QgARh9YUNOq+AVGHOXNJPyfK9VNV7ePVAFHDSqdC5rvFZvpKTxXJIlaOQ6r\nXKNCbazNV58vk/bACwlfRP4YgP/I3/1zAH4AwMcA/ASAbwHwKwC+R1U/f/o8/w3xVj4gkc5KYJUA\nVHHC6IeZ0BdleWIK4sCYb69TVCUAa8z9sMCiI8PhI9kfg3q1CRV5n8MuqmUFIxz5HVewbQK9bhhj\nw+gXC3n1E2jbrmjd6lyvW5xme9sHHm6Wz673HX3vePOm4XIBHm92pFVXBtb6P3bAumllKhYX4Sft\nmCHN7APdOfHYBDqan25LBpA6r0oaAkN/ELgxayzzIeAioDL9oSa7u6cgu+2Wl2DbdqvTBP3aoLqh\nbotVTYk/baJJEM4wDwydJf5TRZwwA/eKxLePFM3FgFnDCgI96CHwOaq4MiHWJAlnTpWq/tPKaC3P\nEr6IfBOAPwzg96jqo4j8BIDvBfAvA/gZVf2TIvJDAH4EwA+ftrFKX/Uww0Jg9dv6dAnzm/QE72Bh\nz0SxqvqUlhST/zeZS04TmQvmy6l6LJf05HuisjciM9FrvPjYySQF76f4XvZNsF0bVDZDqKFQsf2u\n27bhqs3y8+nAw1Dsu32GJ+t8uAreXIHHm+DNTbCPhq4eVusbZbAL0OwsP1Xm9TPVGmqWefr+VT2A\nn7vjOD/NZJO4xjN862s4Ey7qW4BtnENaBOskE7DmIuJ/KG7d8g6+eXODyM0SjGyCMTbkBiEB931k\njH7SoqB6XlZSWZHlhMMHjB0XhWHj1e+fOJhSQ2J1M72OMSph2Ycvf8q7CvEHzackXPAme/hceamq\nvwH4mBirfh/Ar8EI/Tv8/p8D8Ndxl/ArTzWkTssmr64dJhqctbG629IdmLVLM+XZ1C94sWoax9CH\nw7JsqqDzzcVQk7hTiJ5XtDYlMcDIzc7e+g63thmBAz2WBbH1zaVbV8GmDX0oLlfbytt7w9gbLpvi\negHe3ATXXXDrF3S1k2vRPUJwb8BuklyHYN8VW7PU13036Z07yzr6uJlko2bmW3vpa+bJNhGi5OkY\nnOSLlF+kvXg8u2tOwwOTbnvH4+MNrT36xqKGMa7IWcYk5aFlqRUTPsN4wphKSzoBcGbwRMZKyCvd\nuUvPY9WKy3oumfJ7LlXzKeiBYDKC3DexPP4SjeVZwlfVfyAifwrArwL4fwH8NVX9GRH5BlX9tNf5\ndRH5+nttpMSfBzkLWypgJ8Tnn9y3Bxzn63y4Va5OysFUo8pq10bUAfwyBnpSnn+QuGjwa87NuenG\nEdfXw1zz2+l4ZuQBNlgeQ5N4sc142Gc0wdYs4WaTKy4bcO0Ne7/kefejZ8rrvWHsEjvn+u5GwltH\nvw2Mnaf4qG+k2SPxhgJmIxBYmG1dwJa/JpFHrMWNPnOi6xl3weB9h8rYB26yo8kO8Q07NBbSHhB2\nCzJbXaThPeSSVZjk/SkOCDNRJjMvSrrWuouLkFGr8LBePqu1xZjR6Z1n5Rm95W55iar/VQC+G7aW\n/zyAvygif+ikL3cx/e996nMOCuCrvuJ9fOVve9+fIJ+vXdcEltYFANdI59L+3stTxvt/QhaUCDsR\nv86oeuxduV4BTEvuCyBQ5FP2U1x15D3NNnm/NWN/CktTtbkp3ZJtihO++g4vi31Ha9AGbO2C67Xh\nYVzQ9WrZe7kfoMPi/3eB7rZvQLsf2hGE3/0wj4wdePP46P7+sk4VicjDyJQc1MU5VniObe/zCChB\n2IYLixgX0HfFo+4QuWG7NPT9YgyP5KeuSRTiD8J1Lht7BCbMSjypiBMwLmoA95rE5iVl92bAx3Lu\nTKDX6CVdHyoXJEaWL1ywh/v9FcA//I3P4rOf+SxeUl6i6n8XgE+o6ucAQET+CoDfB+DTlPoi8o0A\nPnOvgW/9lq/Frmo7xwaw99l1wuCRUYgnLKBEgiYhFYkg/MQ+ZI8cMbex8uYs9r1I+ddyAuS9gFVh\nAjN8KE0Kdy6W6LQROFAK0Ag2JfP3t4WEI1IF0Y+Q+pyssFx7a43ji/icYnTypQKkoSmwqWCgYejF\nj6gCvWVQz9PHLfWW6NPy4g3/cA395vaIN49v0EeP+WZ7Nioxut6p2ztTgu0fIJEGIkd4tbkI7Fh0\nd9+qexuGYh87mtxwfbjk4aEFqBVOZEKAZ3hUwkB8i4T41mmZ8INhtQDV6Fnea1GvLXTAmQGIgzCV\nawlTTwbl2tzaLv/T+gvlL0VWkH3iHBRf83Vfi6/9uq8JIfdLv/hLuFdeQvi/CuDbReQjAN4A+E4A\nfxPAPwbw/QD+BIDvA/BT9xpo9FEW/GWZaJJGGsaskyAkz3mjESQ1yfKbax6Fb2nFISnBpBkImW5x\ns5CY7xA9f09+9+KiY2SWYH1YEogRTZbSPJmU+GOJJCm91BP3pqUayB2J2gStS2wPDUs7gIsIbGkA\nv+/74YfEjjlLqy22TvdY+NEHtPs5eL1H3x73N3hzu1p6rK7oXfF467jtFr47umJ/9PRgmrBvyjgM\net9zsoQ7iGDaQlNBU0sg2rR5mrEdkIaH/cH27OsROoyVIL7Yjj9nkkS6/JPu4slaXsR6BSSZr5T6\nA7HehiYTr9JJA08K7oSQyDGEUGFYdPTHtUAoeI5hdqsykXU+zstL1vh/Q0T+EoC/A+Dmf38cwFcA\n+EkR+UEAnwTwPU+0kQLL/zvCq3KxYuUECid3QimqOooxjPX18KOokXzdQc/iuw56mf95ekLpJxBS\n/wsBUF/LXKRNPGKOSUq1md9aJPdzkyE2ZpYZ0NHAsydDKVKXdJKeDBVlFm2T8A3AEOjGVDsaJ97w\nexyl5SR76Yrrnnn/elfcbgOP+0B3T8B+UeybeQOMGXa07Q1as2Ceps1Taofq5sTP8VmHdcD3B4B5\n0wu+JKONds7ACmqGWAQJCdjdczSbv8hiptO7lIAsG3VApg6ataPmSXMaiV8EmbAjhnun8NZpF++U\nF1n1VfWPA/jjy+XPwZYBzz9PYgamDwdUXS81AmLit9zJBJyOUClEp3uyXPggU/PBSnatdvLoq7j7\nvAuMJoJhO1wQkY4MnlEyL4nz5IcS3ZuluCq9aOouNJD1NXD1OxSQrunHN6ucaVse3y8uoQXqQT6b\nPS0Dlw5cO+J4rd6Bm8cI3DxT0H4B9guglpcDqrvPSbe4hNGtp04oadjjtttUiUcncBVT6uiiUVHS\n5u7EhElqjnluYCsMIJoLKfyykuznANH4qNZrWv6WdibK/uB4WlH/zO+1llfblptx1bmW5VZRr4TJ\n6CGuEp8Rj7LS07yuAmXiCSfMXIETCJ61m5UiiEPmYA3Rs16/kAVQ268uCLFA5aZm1RekqhnOSdd8\nNjEFkYm9mWHQPBV0ZDpheztMdWNaRgtJ33xlIUXCekgNtgFchuUGIOFfrorrTXG7KPbLwL4l4VuO\nvhuG7ui6h21hHxtELzBUvABoENlACTwtaTi/y7LPryKkbBB9UYEp3YNB5BRX5RI+1HzjOSSFFVHf\nU9flRRM50HlqttwZOR8wU6rFn6LJTNrwuhx5GdN4nUQckWQBoMErVz4lWw0Uh8w1T44jW5IFelSS\nkvifCWhkxQN3OHJnKY9kBNesXVTe/hKi1/pyNuVWfEr/hs3y46lAWzOpKT2IPmLiYQYoAG68yg6L\np75usA01EeI+AJWG0Zoh4shAvKZ1zB0qG7oKdoWH/5px77ID/aK4Xoz4u0t8EvkYgq439NHRh530\n08aGvW9Q2AdMtaKemXmYrm8n/tp+fMurTy3J5yi8NYVhFB2ZS4EE7+zlWe1A9XOU6ymQpN6nknIC\nczKKfLLEGGBC3UMfVlke338LCuwrEb5Oc2N/NT7JzW0yxKU93XRmDDPCZrJIdRVKiuWUal7lAZUD\nZ4fWHlJKe9/ieVmgUikofwYwtCLPXSsCJ2VqN6LPpokq7UuDNIXqxQgBXPdvsR5vaqkymw/CxjMQ\nGSud8KFGzc1dQQyf1+aE7+toqcTvJ+JaGI+tzxtaWPl1AONiqbv2y8DDVdF3YH/wLMADGKNZ+K0K\nxrhi6I69N+y7rfVHPTfRQ15V4cZFdY2l4b2HBzw8XHF9uGDbtrDcE158bjqFh1K+suiFz1oa+COZ\nB7zyLfnXkebA4DXfJgcjYSV6dZfloeXod7ZH1Eif2GSQ1Cre3gZVXzSTF2ghdKFFOjkCs9YKTAJB\n7Jjn3IFUeWaQJ4gw4sawmkY7hLkeAZomr4IAJ9lXTgm4UjaBJ8st36LpSkxuD49WGcgyMDzklHHz\n2ZK7+VQgHp0jalQp8JNmqHlQNabGpE7B3tGhlj/PEl24UXCzGRptg26bx8oaM2zDLeye7rv7hpeB\nHQ0Xg4VLVmU24Gsa/HgqrhHh5iHH79kuwbFj74K9A8P32QPMGb8Z8YPuRU8Ntisu1wve/9hH8P77\n7+N6fQimZDDwcGOfRnr70s6RgWCpo82/VsKX6btrrJMCkIw14AxjUmQo9rBiTchp9O7eByWjQCH4\npQOFfdE4qWf3cLJ0KOUVz86jdCbJulpfiJ8hnnm8tAY8IoQzGEC2y0I/sDoDSCbJtr3e0ruqoAeD\nOtysBsjT13tHU9JLqcrVdW0iNB73yw9a1IlcU3ZBxrvSQ2GpMNAUZvU3AhF1+zftI3TS++/mhGre\n/G7POQMaW4NuW3HpCdoQO4/P89bLsE0zDRtULjkJCpDaIlGo5ncj/AtEroB8xBjd6Ogd2Lsd8NFd\n6jXZ0HwdIrqFe7bvA/3W0dqG9z76Hj7ykfdwvVwmiW+MwogoThMqUjKNqCnlw16wCIoJVqEOFiFW\nNcCFsZsBthIflwazul/fYt4uIjy1XSobhQNo1q/6fmVib4dxbyJUl0KuX8ZUcwxxDkbMYBlcMoKz\nUgMbAiS+zAipf/LUSsHn9fJeHVbqCnlN7j3wVNFZgaAaV6296cGS6Y1UJ+2WM4RQLZxTlrgBomBu\nH7WFSWsbhmyubdn+mwigcYqxUFOTKEc3t0X+0M3I5csYw0+9tXW6iLpRsFmqrq5oqtjUWF4TW0ZA\nSfzWod4UfdvQmmUmYrbdnHmEik1v0Qqwp8mhFiEfLxOfc5ga3ZkWV6AYSwyyFQUyQTkAABssSURB\nVHZVsoF430z09/B2xrFZZxXM2HGvvE7OPWI1HBiF6CWMfYX4JbkjiV7KaDOwoQywzBAnqvBjRPWX\nEuKLBkbgGZJUbWFW1F9YXFLY/xy3y5awqvswQjJoILsI3M+vbu8qe93CY0JNAKCPPrQtRj4CGVMA\nKqz+ePMAnHLiUbbP0TZ3Qdqg+uiekHOEpOSJP6J2ys6mfoIv1V0IxHcABmPb/OBf2XC5Xgrhc45o\n3LO5NHMGE10kvbGv0/oYC2oEaCmo7DNpcRXB0nqdpCylsenvWpI1VBlZ+YKWMSQPz96Ep+yF+P1K\nEt8lReCq5oRyJAJUaU2aCuZ4MndTlpMCkYlJxJwmylVLb4jaF4+lcPza0eBazDBTnjkqFXGNjM/S\nYGeoqAGyFalFdSjnx8bqbjrPyy91nloZXsyvKwB0+LmqLwC6bIBLfBsqmQTbNbhZdCVfIzlen2fL\nlFSPQBcgTujJawJBU4W2kf0MYqJG4mqrr9+3YafeXK5+iEdoRZIwAVfiy7yTKpYQXSNyY0ZwW8YK\nriTIM8oip7GPFKIMz0HRXs9sTZzLmBlG6ikN3skckmlJ6Ss1sdW/dF5eSeKjsr+UvMWNZ9dTZzLk\nrhQj4aKKCjCApfs/FappM8bi65xwAQcceHLSVqVBAGgFyrKlT5ZPDHO9F9104vfcg8IxUgR7HhZV\nrlN91E1dWiqT5/hmHT10mO8R9aPNQFKkUZR9KumqdSSBiCcOi3mv7Tvh03aggG0lhgcFpvHR+j4W\ndyE83LoehOKGMt0gsKPGeHIPjWXJ6VMuU4zkyp3M+gjXCSti3gsop7FO3LT2/DAn+Vfit5a/+Ure\nb9FcjEAVq3bi3VzanrWzp8qrSXxOVlo1M+HjKfXNX+6XwjPWpwx5U9WbpnrV6+6+myghmNCjLHBf\nrDDoDHhZkITfyAS4W48BQVJrk3idcJuY37su62vPJwYbvDQNSvU/u6Vp+CIrjblMJkcrtHXHJR74\nHLmKephwagxwqSawXYfB7tWicm2uXM33rL6CDQ0XiLiK3wT15MI8rakQrVKa5yEdDA+AWlIQ869L\nAIV1zkHocNCKAk7wuswv4wsklYwD2oVKOmMC3/XiUt3aL3js9ZJtkuhBm/3IT4i8Un8mX6BK1XuF\ngC01k/cfp5Xt3xECVuvsRrgLVo5f/84l+qIzAjAOgfdnXYG4IcuDtFD7sz49LWIBsisVgVMCU9rS\nyWWeED4TG6r8HWbIy6VaMojmSpojm45QUfms/WXMAdf+jBqiRV2R+eHV9hCUzS5m7NssgAkXYwhh\n1DNBkrrJ+kkXJwk+5JAO3yuwSnBdgXEKF14fWok08YoEH/0UMr7SXgB+xu05g/AzeD+Vt0ni2y4Q\n+y6mKvIAxlMnmwp41lPaKRtyA0fWnzKXqlqgR6GT5CmEeO3XzIkDmCdGH7KqjLuZuXRKVe+HU12u\nc8l8joCh1ZrtVNaha+9kAe3yw3zgKQW5TZmtpXmQkt6JvsQapLKcTAXeRRIqI+xI9Plxza4GvIi7\ntgJuCuW5fGCwVs4Ro1fFJWbDhk1MzechapxH21+UjFAh7r8v7fm/9eRdzpufDhDaCcdLOCtyPT2c\nIUYzRZsoMw6RZEI2PjnanQqEgdolif40KEbgu+O6IDxfBw0O8pz8ifI6h2bCgkQhw63HzKZm3yPp\noxKoHpOuLQhexI6YEt9mK8J7Gxi0ga4W1NI03SixdkrJXy4k3RQubPjpCApxf3T02KRrSD0p/MRz\nCiCz4vC78R3jSE1yBxYNMvHmYuOYeIaIb/WWvEHEU86xtWH9T6mqlTkWNYBEsorJaiDK4JPhcOMb\nyhZaACJqLjjmghUkwxGzxEvsJHRCEep/VVZz7qkNcOValyJJRQLBRu7ujGIolxOp+Pt2JHSFe0Q8\nwEsskClO5Cn4kl3xuIAhnn4MU6HET/oTZ/7D4WY7IMnozlSJZBo2xq1pIoFqXBc3AvPcQdWxaI2C\nWaU4L68UsrsgdvMAjwp2De+ycXYld+eAGdFFK6kRvrpmQL9tC8KkdEIwgSghPCn5UMS+BLITRcmm\nCODmxBTt1kkuNgwjyioTSEjrmnohfjZZCDGfrWqoE3DFJQEyGYQTSJ1/tci/dAcuUmKgSD4JO4O6\n5KqTqL7yFpikFxkhOYEaMpseC3p3NOa0z4NFvjcTaeSyhOG8sTIQAZppFJTOWjQte5cGfgXkrdO+\nP1+dOa1QQEwGbQCD4c3h6ZBk0uy745MZRM0oG2feRSFBr3qYuJZD2GYkKwR5eCpxwd25yRDZ+4Gn\nyqsZ98iEQiUSzMCgMagYdAhkqjAMNInfcnxVXTpIuXrskty5lSaxAxd/jo1GXTblow0f71qpDEBk\negeXygdaP7yDlfyiJHOx207JaPNzAHJJRQmrkbckeUZwRBDJrV3+Fr72OD2U+hxDML3sSuoI1CY0\n6gSTL4arbJuGzEKia/sCNCHDLiWHHJGg1IFS5WYPFRPrJr35fSlVtUxVhuX66NRtDYJoM+fB8V0k\nhOTEgJZ5fRoL2cET4ijllYx7DfTj2uQlB56FFQHXELnWsEgkJNLFtXWMXFPhgC5rxcPPnNTy0kDg\npbXp3Sndbe4VES9/6OadHpGtO4ZJtVSeQp9qds5d3qqo4yRW+mrtUv+UkDSyQIPdMcZd+80NUZK/\npj0O3pfVE5Ato0FKnhlD2GqIldIvwNXtMqK0PcwESPgnuyizXxga194z0ZMouSkJvpRKyRyCoeBE\nYEswBo0wcdGBJsixToLA510o7BJESQ/Pq+4VLija4L3yepF7AArlFuMbfb70Ibv66DH3E5EHpL0B\nLaJpFmXl81QJ/WyquvpNaytlJTXfPLzK+3SqKWTfglEE8eoMu3hckKE2rE/toC5P+O7alRRFQtHk\n7xNu/WXEXxCOLtPa4EfnujCRU08syhhipiYBlIY5m2caI6v9QBOukv2j9K9hsGRayjVwzvxSZxWC\nhfA4R2egIowmQmUXOefWTxWFHDS7bEUA8HgtDW7iDMKNm2SNPkEoa4jEuuDpBf+13ni+vF6sfoyB\ndmoJCWHEb0csUu3haaxDKwI8/6IkyaeJfibumbR5v/yM1lMRzSdPge0Im8Sq2a7PgwLh4lzfX3Ew\n+JJWiTw/Mm39rHiggaXTAyKwdNjUe6Ugr7D+2i8p8yG5no1O1LoKahAqaxu2GYkjtVmiMVKzfzKn\n5YpWXBrS8Oa9KabG+rZqS6kzvWg2wPLksUxPyHG+U68oQqf69rVco/1jwAKiGpdkG3DAiXxPMDdJ\nWsnx4S7zWsvrRe4Fx0twKAfhJk9eY6n9n20Ea9uplkL0Dtie6FyRrKsbKqKKo9qx9afnmdK1XnIV\ncG1q4UMTbh3UNy5nwj8QOsTUZEwM7zVnFJRY5SNm4KJvrjIs1olQXQbvsDqchIVajASi5zikSC5/\nUL1PYYySeCY3+/j1siwpfhFjWAi7JNEA5U3l/UediFMbhFuQLRit5q48wi4wbSw6bZnuqT9RyccY\nmhzqy6tiXHs+M1ksN6ffNQbgvLwO4dcJKHw4EjsSlCUwJoARxKgJEC+LsoYAhf/zIiXhpOjJrN21\nBfr7YvX3Am5bkWTeZnxWc5Ys8WdCbKr6Guvg80K2JTFHgcnOCLiTVCmtpx5XxJeZ+MH1OUOLz3tB\n78xwa7TNnK2p2RHOdWu+FVgweSFS1ZdgbJOaf8C3l5SiVjOmAa4ZPqc9+jMVWie6UnznOw66RjD3\nApT6Es1Nbff7QqnxdJ9fKYBnBDCMtzf30VPiS6iqdPnwO5DM4qANVEhzGoXSghWQ3Ly4DK19jT6c\nTVOk1BKgkgHbncgidD2Z2p/6W9v2Plav2vncJSIkAqVudLZZYyoyo759b+U7LfNCHyiOav6c1CHf\n6P8p55tRcNUMNqan2H5dktmzmSwkd2qK23p8nNqC2dTQLkBM2iuJXudtIJMGNbHLIHD2xYBxInIV\nk9S+R1a5VYMwcwYpM/wqE04mNRN9ZQvzswswqIJEz54XQK+Wcw8xaQSbhWGqM4VI5zy8IuPOK+/m\nOvQwhQhjlMRHCvEbgKvFdd70QGkD1BmrEx/IV65zfsNnvDwpwuAZ9oHreld2Fo/lndlDINA8GzkL\nUmzhgiW2HwjDFesXg1El4eSchoDRJizMdpoyJudQqvt8X1KIOOOkwhYu2upaLHhBak2HBJkEPITX\nBEZTiUQahG0kBk2gxPkDBSLhAWlBkNRcFqCW3+mOnRc/UaTyl3wftzS3GPkR0Hll4VJ+rWL7qr1w\nqXeq2r4dEr+uj2T+T53DEljQSeoDKBJitvIfhisgyw/Dz5qTLLtUtzrapJ4aVKY+LMMq/4n/nn3L\nM6A1nvGnnSDpR64b+yh0q87QiKBkbijIUCzd6+o85qNIGZsDmeeAVuoVkTyvf5X8MxTZF1+r+8Kf\nYbgZkmwwjLV6KFAF6bkGd+ZNyyYJtIFpsX00ztBlaIQMixMq6VXK2IBqDnP8IwOa4J/LzQWA8TWj\nLFPKxpD8nZXVydJUxagj6SajqfoWaT3uF+Gm9dZdQWLllfz4LJWY/Z+K9EWUTkSiSSyxnn1yAT97\nXOOVIrP6XZjldDLOE+VA/AR2NQoSk0rEXBC3JsMIVlA2qcQjwQBcoj3Rh/s9JdbfH8UagZavX2A1\n8eEkGhr3yKkiE1CZi1DcGJ/hOfKUUr5Gvkzd887H7UKwTvgDR3atQfTuOotw3NpqITuFe1fuWATC\n8Lxe93mi3Do+iKIHRVDWVDe4ZiBiwf3KRuqcHqX/WuHtMO5BizTLwZhhi5iTqhIHPtUnhdVJWlwq\n6zvzxyL5oxAEqwolByjee9qgXiO+KiezvxXYOVJnNFwPC5b1YUp90kelYSmfVShNHRaAVt7oX1jc\nvTdkgPyy4FtF+nUPRMQEVHsIYVTCZjlAHpOlICOuNoBK/BJwiwMvg8EkEQMeohvGzSSaiXRKfQFD\nZTyiVHR2h07FdUE92oLqEWrQfJvgyMDr12pDFEhofqyTWapqQzlL+ZHp2vS6t0Xi2xh0njlyw9Bb\niZ1erxibqto3ieoy6joprHseLvuyEpP5pHZBifTB3mE4PMuJyUXklQ52tifaY6DJQd174vnzJA/e\nL3XiRNYRcK0685ba0RjV5ApxOIZRg100DaDu0b9bijWf/LWQU84CJf1E+oFtpeeJbkcQs15pQcuT\nQfMaMml9cpqLeBvxuGCrYKXvKgWW/t8p9YXPrO+B1zLuxb9a2KF9YjVaid/rT+v0kzV2bT+Rr/K/\nL0KRI6dfbk/x6C8puvwSSak4EZN/C4Fwj7kUZnkWeHSvc9NpvyfqpFeaiKJ5fzC9JqW0Ynl/RFfC\n4jVAqa/JdGLPQE5krPFBzUDjHQtv9PlXhK3A5+EQo38YZbm2EP80I3Ve+SokOI4sZpkC/nIY67yu\nDaEo68CWtu5idt3SzME8g4yvmIgj1+tUb+eV7vD4aW7STQR4SdGCfLEWLCr+aswjaBlNGP1cEXd+\nSXw5SIGCHOfLivk5riiraYxvJ6LI9Ld0QAuA1cZen5sMnEColBJDc8+55/SbTH5BAMcxRGKMaEXK\nlHG504Kv081ndMkOSU6xZLz77Mo6sj9/IB6nMKkx8aFqh7AoQscZWKzWiyU/9gTk9KZNwF1xDb6k\nKKAg8RN6cbdoXUMKZAstaszxbLMK/hLELNNz2UCtXKdKAx5PlVcL2TVtzwGl3JKb3HL4Pn1tALRD\nATTxXeZPEP+quIXVn3ngD+v7mavq1Arr6lRn+ju9XKuwjYoZdEQk1UCag/LJ7caBaMtHgDmyLd9N\npmXIT+mIWSoWIkz2KMEUZsvyHYLDLH1btCSIAzy01PF/lTvosmMxV8fpXIl+7sfsyuW4KS1zMw0E\neRCmCEb0QUvzJNUqCE7kqY+neUoMixUofiXF0gZ7hhAEAmCIxjbb1Xek/mppgtgvMeHfMidxuyLJ\nWp4meuCVU29VMpsCVwq3UikDqmt+yUm6VyaCAnBm1AvV/KmGantBIMf3LCyi3H9u4g899ctLrBwR\ny5FVsvPx9gn0ktfj90RHkhoKqaAwm2Aa97oc/CQbXkl1VsXn7xGkVefHpW0Kr9nmcKY9Va1JZTbo\nRe/Kc8lyV4gFG6w6T9xzZST7D0xGVoORBqJwSWLS35OxOKnrPNXTPGf05okRfOrywhQTzWewvTUS\nH0CRfYVXSSJ2ZaORDaISf6mToWIfSi9fUgwe90gfeOrW6XtDQ/MHCyEkcdlhFBHCLFbflkgVqZYB\nPTNVk8yPedVJa6QilDw6G54JJF97Tx5VgHLZEfI+mNx5Xyv55mckrpTmQ2maNr3kTYWWvPyLLUfm\nXgLuUnXeu+44NaIX560JP2pjCoR3Ip8KELrAq65Pr+ccgxrdIQ7mbKJegHuvuzuPZL9KIQK6aAWT\nxD/7AEs76wXcoYTny/SIHp+WerP0uC4T0nYwE/Fpx+dsEBMhVDecuM87PG6nRK3T95SB61uLCKI6\nXAX0Msazecg1dfZ56kHp58xc2L4TC8Qlosb9Nebi3giJVRPe1GmWlNz3PHYzWh39ANWwHCHBWD37\n9cr9fotW/aMwbIG7JQHU5YRUxkjRLiHmJb9GP/TeQEt5xbPzEjiHaeEoLXNiuV5G5cgg9Zn6l7rU\nUT1Yfp+V5Z4U3HkB9wz30mQln/UbW+cjpmHm2/7UnYmpQSDTvehb9j2kzTo/lKQo6242UxSoZDLZ\npwMB3pXGZ7eW+V9U+5CUJAVyoIM002kC3DI0kSlfkZiW75whY9+Y8CWMe1Pr2RfOCYOdAicIS01Q\nZCy/X5EKu9kIOb2PDCEmJg2EfGplrHOKMr+nZHJPE/8rufOI+HoCAARhx3citTMDSoD01h1kCx8u\nn/V3va4nz+SdSkunOB/ilmhxxtASM3T6SQDm0VCV0yjZ/0lP2a+0QMtE/1o2utR5Eqkz4NdIX+7t\nIHITV8nMxoEbLRFsktMRUulQKtG3Sg8lZigt+0eDLN9LbercgXactSR6ySkuTIG1ZG0AhFvMjOQa\nvtYhgnBuw9B5mIMT3JfsF4me5wTEssIFyhTyW77UvJLxJpVTKNTSnrn/RSmLCcrLSoxPFAGO2610\nmQnO0henz4f3e3lKlVvk08mo73RO159FRU9uh7pP4Yy/hVtI7s2rTn9eMlcrEdZHp/EtrzuDOAoR\nFd1i+veeK3SKkjuww7KZRTEZxs+GShlc35RSf33/yvmrE3bW2Mhr5/0h2ZFnsT3Urtlms3qCbJ5a\nzONsDGUzT9PVqxD+b/yj37yPCJxwOevqSugk9qcw9gWM5AXlk5/4+NMVVsw/6dIZH5qAWHhXxpef\ntVXUnxV9/OcnP/HxxLx1R0jtruLYxgtKjXVf21xvHLQUACtZCYBf+cT/iZCpsWY9Ev8cGstG67W8\nXtt/cjwn9VKrtLHOmXnt/v/9uX8Yz1Utal26TUKAWkFRxu53jGzJ8GdI5vvLOi0Y1Zlm9BLYvgrh\nf/bzXwBQgKaIfdWTX0/LpEWmHitnMifXzKWdqP1bYwCf/PjHU6Usf1GQYX5b8v5ckzEASZf++hxQ\n6umRMLKkFCBh62T7sKd+5f86YVRs8FQ813ZLvPhiV4l3lr4Yncn87KSd8A9HVRlWkscnP/HxILSE\nO6bvWom9JMhgV4GcX3HVW3RuZ13Bn5ZpXuepD4xT4HOf+1z+KJ94l87EP79fiuJaGFaUWb7HEe+F\nRBZOlW8oa/2XYP6rxurPP0joNrIw4BepJ8EgUESj/bMm5Yg5kTrl/3Q9rcE38U9Ik7ld0tVxtGeq\nwFyTa/z4r6oI6sprCXm9N6Z1rXtUa9cez72fpVpFMAlUBCqe1jnWpMnJmpy2jKl+qTOz9rMBVAkv\nkAoXfqsAKESVgTZJCU9hhHrdFWqV6KOViYGvVg3H6xBi9XQIndbfwWdRh5Eznt/u5wCa805kredY\n3Stvy0USUEHws3Iuu4+A17j/W5Pw90tyZb49kGmlsKqC4j77uU+MPhI9qzVxvvhdZ+AFXpy1s1NZ\nNZn1XoaZ1qac+PlyCn/MGZMq0a9IaS2c9EnvzJ8+M9azUNZTlXj+fY+4FtGyXD9rdVb76901cu+L\ng7Uz8d8fR3niJXvQf0tdenK71bvyrrwrH2bRO079D53w35V35V15+8qrGPfelXflXXm7yjvCf1fe\nlS/D8qETvoj8ARH5RRH5ZRH5oQ/7fR+0iMg3i8jPisjPi8jPicgf8etfLSJ/TUR+SUT+JxH5yi91\nX2sRkSYif1tEftp/v+39/UoR+Ysi8vd8rv+N/x/0+Y+JyN8Vkf9DRP6CiDy87X1+aflQCV8s1cp/\nDeDfBfCtAL5XRH7Ph/nOf4qyA/hPVfVbAfybAP4T7+MPA/gZVf3dAH4WwI98Cft4Vv4ogF8ov9/2\n/v4YgL+qqv8SgN8L4BfxFvdZRL4JwB8G8G2q+q/CPGDfi7e4zx+oRH6yD+ED4NsB/I/l9w8D+KEP\n851fhD7/9wC+C4aY3+DXvhHAL36p+1b6+M0A/mcA/zaAn/Zrb3N/fzuAj59cf5v7/E0APgngq2FE\n/9NvO158kM+Hrer/swA+VX7/fb/2VhYR+ecB/GsA/lcYcD8NAKr66wC+/kvXs0P5rwD855gdyW9z\nf38ngM+KyJ/15cmPi8hH8Rb3WVX/AYA/BeBXAfwagM+r6s/gLe7zBynvjHteROS3AfhLAP6oqv5j\nHKMz3gq/p4j8ewA+rar/G54PRntbygXAtwH406r6bQD+CUz7eyvnGABE5KsAfDeAb4FJ/4+JyB/C\nW9znD1I+bML/NQC/o/z+Zr/2VhURucCI/s+r6k/55U+LyDf4/W8E8JkvVf+W8vsB/EER+QSA/w7A\nvyMifx7Ar7+l/QVM0/uUqv4t//2XYYzgbZ1jwNT6T6jq51S1A/grAH4f3u4+v7h82IT/NwH8iyLy\nLSLyAOA/gK2V3rby3wL4BVX9sXLtpwF8v3//PgA/tT70pSiq+qOq+jtU9V+AzefPqup/COB/wFvY\nXwBw1fhTIvK7/NJ3Avh5vKVz7OVXAXy7iHxEbAvcd8KMqW9zn19cXiNk9w/ALLoNwH+jqv/lh/rC\nD1hE5PcD+F8A/Bxy68WPAvgbAH4SwD8HM/J8j6r+P1+qfp4VEfkOAP+Zqv5BEfkavMX9FZHfC+DP\nALgC+ASAHwCw4e3u838BY643AH8HwH8M4CvwFvf5peVdyO678q58GZZ3xr135V35MizvCP9deVe+\nDMs7wn9X3pUvw/KO8N+Vd+XLsLwj/HflXfkyLO8I/115V74MyzvCf1felS/D8o7w35V35cuw/H/e\nbwJEQs2BqQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb7c8fddc90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Read img files from Folder\n",
"imgs = []\n",
"for imgFile in glob.glob(IMG_FOLDER_NAME + \"/*.png\"):\n",
" img = Image.open(imgFile)\n",
" img = img.resize((IMAGE_SIDE, IMAGE_SIDE))\n",
" img_raw = np.asarray(img)\n",
" imgs.append(img_raw)\n",
"print imgs[0].shape\n",
"print imgs[0].dtype\n",
"plt.imshow(imgs[0])"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Write to H5 file\n",
"h5file = h5py.File(OUTPUT_H5File,\"w\")\n",
"dataset = h5file.create_dataset('cacheName', data=np.array(imgs))\n",
"#dataset = h5file.create_dataset('cacheName', (len(imgs), 3, IMAGE_SIDE, IMAGE_SIDE), dtype='uint8')\n",
"#for i,img in enumerate(imgs):\n",
"# h5file[i] = img\n",
"h5file.close()"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Read hdf5 file and display image\n",
"h5file_read = h5py.File(OUTPUT_H5File)\n",
"readData= h5file_read.get('cacheName')"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"img = Image.fromarray(readData[0])"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7fb7c8dca250>"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP4AAAD/CAYAAADRymv0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvd3LdUtyH/arXvt5zswosS0rkiZYaEZnRiiQm1wFgiGW\nsTCxAlauhEMINr5NiMEhxNZ9IM5NyB+QgPBNYnKjgEmiCDkKBAIOxGAsy7IxEVESjWILjz0f5332\nXl25qK9f9Vp7P++Zj0cD8/Y5+332XqtXf1RX1a+6urqXqCo+pA/pQ/r+SuP3uwEf0of0Ib19+iD4\nH9KH9H2YPgj+h/QhfR+mD4L/IX1I34fpg+B/SB/S92H6IPgf0of0fZi+LcEXkX9DRH5DRH5TRP7j\n71SjPqQP6UP67ib5VtfxRWQA+E0AfwLA/wPgbwL4M6r6G9+55n1IH9KH9N1I3w7i/6sA/r6q/paq\nXgH81wB+7jvTrA/pQ/qQvpvp2xH8PwLg/6Lfv+3XPqQP6UP6Hk+X73YFIvIhJvhD+pB+n5Kqytn1\nb0fw/28AP06/f8yvHdKPf/GL+OLHX4RC8YUvfhFf+ImfwMAFGzYA1i4FoAOAKKZOTExAFVBAZEAg\nAARTFQrSJQpI3FVAxPJDrMwpUQMgqsBUCBTm2lAoBEYa8VIVohP/y9/4Vfz0H/9pu+qFq0x/BvaM\nClQHVAXQAcXA2DeMaYaUqmLOHfvtin3eoJiYOqFzh+qOud+wzx27Tsw5IWPg8vSE54+e8dnP/QA+\n+wM/AMFwGlk9gg1DNgiG9UcVwMSv/E9/HX/iT/4pzNSz1XHN/5BtHyrYdINM8atouQRqNUvdmVCo\nACriv2P4gv4DQnym2XZrv+Wa0Qr8jV/+6/jjf/Jns7lZk04AEypZC1SBgYENw/su+ZCqQFXtA3/W\n/+63K16+8U188vVv4Ktf/Sq++k++iq+9vOAb1yt2nZChGFCI7pA5sW0btm0DRCBjQAQYUAwn6z/4\nzX+Aj7/0Zeh0Egug6uOqO4Adih37DtwmMHfBPgXYvesAMCZkTMimwDaLzlOgO4xWY4OMgTEEYwjm\nrpj7xJzAVEG45kSAbROMi+BrX/9n+Kdf/SpkWMP+4a///VUUM307gv83AXxZRL4A4P8F8GcA/Ntn\nGb/48U/gX/+ZnwY0BI6UENsDWj8l8pzqK0oSHCNLXsmBgWoJv4grE2NvrkOiPZXZy7FWiQ5jKLH2\nqYhrAPsk08tajn00+uf3VXr3e7+Wv0o0Wa6zkFe9a8kl4NIK8MdUXdCoKNEll+SzutShmt2kMeRv\noa6VPq3BvT1eJsSEuq5bG7RV1IGgl+/luI5Uqj7VkWgjl6o6f+hC1ipI1Vsi1e/oKxAKAwlAKlLj\n4nxpz43leeQvIZqKt6VgMrLGWAB/6Id+ED/8R37YFNa2fXcEX1V3Efn3AfwyrI//par+3dPMA5Ax\njFhE+CBmIHYoxE7u6LCNdJ85xB3JMuyyNAKlsNP9UplAM4ZcqK1oSbZUkmZJDWVIb8hvH6vVhAhq\nVoIGXKgNpiH3gOiIC6SExNoLoIglrt+sH1MnRNU+C6lZeXWxq1SCwKzEVlAJTmUZLnAp+pAcsT4C\nTSfRN/WKRbToj+pvqQATHuN8FuLhimDkpaaj468joqaQTuxzYk7FNEMAMq29Q0L4FGYoKhQ7CaSL\nHSnupKZOQ37YWARtQ/cE6TYXzlT0zlsp/NFFbxsEGAqMUaMTwg/Pn2pTFYotxyWI8hpefltzfFX9\nHwD81Gv5vvDlLwGbWAcnoNMZVkmQpAS3Y1N8Y7SqK5JMUiwTMhJmqtO5nta44Nq3aQVLX/z4Y1cQ\nXegZTSTsZh3N/ArmUJlmeos6H2sqP3WlIXOa6ezWhURjHXFSEVEDdU5MK9IZV/Dxxz+ZuRa8a5Rk\nxkzKBtNS6yODpiIs7LGWzBAXlODXOOnyvaG2K6wvfPzlHMs22jIATIhPKULZm4IYpSS184SQ0tYJ\nTJ8GqSqmqpvLCt0BmUa7ocAQASQU24RLM4Z0VaYA/tAP/iBRlxVY6nBjq5nDnkI/w5UeSipoqQCm\nQr1qETPvRxoJVrA470gqaFPEAsXMsXhd6IE3cO4BwBe+9DEKz4t1/Ef7yhgWwroAMgBGB7rA93R5\nYElKiI+mLe36Fz7+CVLPvWbREO0SSBbO0OyqNkphlqpUnswuUvVL60brXJjSgcrxbzTx4y/95IEY\nsiD/WW+qW6Vks2Tp4xHC77jdy1naK/Rv0Id/A4qf+NKXl6f4i1SVebEmDzF+A5o6fFV5/CSJZ/3r\nAxWK6LQzQsIJ4A//0B92P9FZ8kFV4uTSoaftS/In06xjFFQjAJSO+udNeXj3bQRfvee9Lff1UqEH\nnPBFxEfd6bKu53kVDeH0oEGoEOUf56hfKBhCEYZy/V3L5ZipmGbkX5TiCPhQt0pY6EswGytnJeJz\n9vdLrbNeupfcjQ2yH05SCwZbNC8r11XBpBKNIs7KX6YrdC3oEtSXleZRS1iFIq6InKEmfEJ+fC5p\nG1o3geIObc8uZyO9r2QaRrHse7iDi+3aI+mxsr8HBP+Q7tFNYiYfjhPN+XnePxH+MsQq6fHSIsjv\nJxQlVCupCbl1NQnDmqDGrqZKQszyETaQqxh+OObKobQ6/pz1jYXGzfIDc0lXrOmMWtGya6pQEFUc\nKcVoeApmYRkLp54MVgpENbAUts/bTbnFlC8cbqxVrZ3KF3xCLQKQC8X77l+EfRY0tgvRtI0LK8VA\n74nz8aCk1X9tWp+rInqW2dfzpEI6aetJejvExz3zCAATOIRfi1HkjsBzDWt5TRSawNMTycf8/L1W\nrpJLOaUce6etW8fyYPnwZ2nBYmSsIdZtynJWd6DUIUn7JrClz/BoL006KeOoaM+boKSw9VBciYzc\nHYbmg/DlXHWYtHEMZThxj0s0hH6YzyCtSFJuQX37O1BLkM6fYl4NlWn5Re4Aa8DXKqNnVo+3LnRk\nrHzpUZ3Xc2FPMs+QmpLm6j5Nb4P47weuaMzoiCN0qwu/tr/pCb+L8us99nWvAyL09yH3U+OWMkKz\nuEXQWf1MUUUZxH7clNNupYF83sWQJ7q4MlO5hPy31Bc5PLTQa6ksgVtWSoXi76LVKHLKI4rV8diF\nPiwAzxGrBghlEejLwuIKQMoTX7UJRR6E8AxqqxSRUkl24bfVHGmjXJZAt52q7dHXdSTJv9BAqkru\n40dC/72A+M1eiyTB3HLoLDh70Nromd+z2PsVnt95HyUkgKgvMz1AcqArnGLRDl3hlX6t7rJ71jqL\nqU1UO8LW8IegKE6dO6vlcwIpuZQJtxQ4qPsgKGtDzjtYCrvj/N32nZLcZ+9dOhblyEoCSYsIP+Kx\nSX0cubNuRtCOnDmOPseXsDRcCaQiCuUQCiB4XFsV2VlVCq4Cu8FPUltOPeMYX6b83kL8I3ydsHhR\nZmHMYqAa7ddMGs59aM6j1JA6PveePGkDBb+wNb5q/0JVryPNtG7c9UQSEnpHl7uKLvwdfnL6VBZD\nMVIsIzYToNHe/9LXs9beV9CupNrNO0qD+9MS980F/ESwmqXgS3slYgtR0soKgQpTX4kW3lcX+kD8\nHv1QFC0ltMIBWxUC6PH5R0na8neMZf/vUXoz515fpfe/ytdKe+nhKouK9gHQpYuP5HPJF57dfMQH\ntzkUW0uQhSfQK+cSzgFmRrsefay5qVkEguEWxgDOh80bWUuFC4NT885lKWjLCBahK/EcK5SSWo65\nO1Ny6yjGEJ0NQ1lISznax713WykDIzJTdFU9EYnoIqkTEdI7MTFlNoUMoEK+z4SH7s1YJ5WwKqre\nc7USg7cQI4qJz/pcxLk0K8Rpq0qFmAIif+yRvkt6E8EXFZIU/+dE6IOYbLZ0UkSqdeJk/mUQ369h\n7dH2/Dl7x0CcsGhyegzPSbQcPxP9lOr9eE1XL1ox7Z5FUpqXXEnYqPQG6CtPRsNQ884+AnqgN4/i\nWXMfduYA6dJyyAkLdMT0+yq1hOnC4TsMEvGnx/Erpk8dRysPXp+4hhVaugvFMCDILQ4C3zMBQ+0I\nFkoSSQ5SlpSBa6ux3oV5lQRT07Pna9IuuVT5PYP4ZUJxh1jgJZmZux3EE2IOwsz8nVCjR6E9/y30\ng0057fnaPJ+kdeXEOwEBER18EDAlv6xbGfVxFcBTnoNkOq5J1QMtoc+1bVdIhQQ8AtRmykDblbiD\nYE9yGrHK5URZrZLKt1YFWam4pNUNWAWdhgUsP8P3UTxly4Aa6O9aJcVPqsbsT1gZwh0qKzHm9qsX\nQQHMQ7uBjAUgXs7WSa1/xdo+W5bhCwC6vHeu43bfT78P6/jFqcUqxYacNDSuFn6uQr+WLaKnU9vM\nIT5sKzxRu5bM7TcjwGFp7bRd8Qwv+a3opiX0WIWeFCNtAmp82JqpySTJXIu1ZU5VK6BiDiLDWR+O\n13hprvfm7GohnUhn03vpRIWeXLlfFqtvE0JF7uDzOIDKO3KMjkRlfgBdc1pleUi0NwElpVZrdSzz\nvb19R04YEIcpHc8dT6fPh2/n6c2cexEwYQxQRg7vtkpNF9gicGEpJ14sl2TBLhSFQFzRwhwSdccP\nun6mBNCv1dU+d+9dPRf+sBZqProEKaEjv+XkGqMo8cCV6C7hsmBpV9DYFUWLjeitXkG71UpjwiUv\nvWOj4agz41ZaRiE0vb5EQA1U73xihbEgPRB+EWKV4K1C6aqjLK96OJmV6qtdibHio67Qbfpg99LR\ntyi57sFCt8TOL2RTiAGWu9Lpr9Kn1nfSGwl+oVbbWXQkhSe7qm3wV9vRrnergeO2qai1HXzjVAUH\n8/Wf3ugU3DVy65jYH0Ct9WizUAQsufGf7TofhByM+t4gQodsRtMCTIDgnpHX0mEfDJ71MHOyLXGk\nUov2SYvirD1ciK4XqjyoM64mxeCW0H2L5HEq4aT1df/ngKj5TBjvkqTO7hz8U/FQ94kE+TVXUIgg\noU8C2nFeZLsQYNbYs0CicfcrZHojUz8Yg7FWnKaEagvRcn6MJR+VmjXkjhTtfkRuAzngukCwEqBr\nIZMHDVoMmFYcaYZDvdbAHBpNs776aEqC6zlwwIHnaUZICEU9yvb37pHqyA6sLoqVb+7jvbcdi2/9\njKwItD3WsCLf6p5qKzB6xgFreyVbHVum7dAUVqaLWiTesRQht8G73oIT/cOjz+vygLS/q1+YLfx7\n3RGES68/LHnXeSkckopXp1Rv49VH7J9mTujEN0Ipak9+v4e8vghgQ0ssOXkzbwlgL1D8UmdsDpBY\nRKXXj6PZX3ypWSWXM0RsU6toforZQ/iPiH1PaDTQI9tSrMbCzkwCADqDftEPKyiUgGbjQyMr2Dez\nqsJaBi2q570T6sGfiUCYs3DkdWl1nRpU71ZlHl9N6OccmHNA5wY/6gkNdtPpBscIrXFg/o2owWxv\nmQM5/TqsyUuSOSyMxlns72oePa/b651Eozg1ashoq0EjptHfE8t565meAef0M/7qMSNYSQCB7kBj\npxw318y09lnFlfCvTJj5uOwmeMRUjRFZ8E8QWqj0cPLBPfcy0UFeMr+VvRQXQmXq3dHPrmlwlbev\n1rhpHkxLPe257Ld2KT3hnVzCDvrqOjZL90OJNMlXyl+OzLOj3uNa62teO1oeTYFHl6b4eQkm+Kot\nHJE+UnSAO4oxgBmdCOuIw3VI+OleKGh13m+qsBGs07zoR8pfIgKQPS21jyAVhwt9Rp0+SL/vb9LR\nVXt+6lSa/gwNz/NH5e9T9vIM1RWIdE5jRu3ljpyVS8+80hr+dei9vh8VLM9qrSz1L7ydAS/J64/b\n++2ku5uR+Npip9lF1zJKTVet021Wy+DAdnGhh/ietND+rEahhP62Z0sBUzpcMOIK6sP1KvW17tD9\nU0/z9wDiv096XexPzLjDfX2tkMVI+LSK5hEx6x7P26OmQ24ODBGQI/O1Kkrge2JGebQT8pWUVhEz\nFhXvqBuBIv5racH7pR6B9l6NO712KEKzmYT6SkphVZfVHiCQNejYTBU0PM/xOLdY3PZExApEnIDQ\nxL6Jt08jhMO9s9Yjv94xyu5e5fT7KPjE9CWJ7S7PdyUESYLRTCNLL64GHJX/NZTvFqgNV20jPSNi\nzcVzHhpFPODjWsK0ysLMN6EP89KmAfFdi0j304LMdVlRS533lJD2/lOoLj/ZPqljXZgWdDoMShYY\nkhXjWFuAc/swOe4qFl6bMFabnTfa3GTpX1tnRym2JIkH9UAwp9o5d2QHF0tUu3g5EdCMFmQ+iJbE\nZpl0F7gi6G53Rvv3S7r8zUrfM72hV39NWoSgS/V7MWUpkCV09VkATYZPZhFr3XfwsPFNxKjdEbgA\nxTua/n4S2OxqX66V0JfwRyUR5yA4OmyOfasSrQ9bE7gTRFpQJ4fElY1k3jpuO7GSFWyWoP0KyVlX\nCvUjULFr77PEBi8XxEqNTbrw6hvit6lK1qN+kGZF4HW28fo4Yor4qwPNUfilfV/POjgV34fpxLhp\npCh/yeNy3ljwC+UDzAttQuO/FsZZZXaPr9K/9eXVSDEeREK8VSexCVxoH3Vwq4Loay/ckkAhaV4T\nUFnMGb2J9UR9TzF39DkTh1NAPJDF6Rd64gDWiyI+q4fbw8KXBXojmmP3McoxWoeFnl1gzCBrLe5p\n3AgHLM1ZopXZ9bYhoO7migwr3bBQ/HsKtzNN6y4rSBroGht1BVu+gHOY7EuE5bCtRpwHZ52nN3bu\nsTZkXXhEIvsiNSWLdGIVHBMP4uOU87VHynfdniuG3OzY61F3q8KhvhZkuql/b6iPqaPHiXpI2hAT\nvQ8XPEjpdNXHjHn6LDTXn1fX1LeWaOpTlTxqAH3oRy6jvmetAowhKdhVTsid32uL8go7Nrfyq1sX\nkadZW/7oAIdYdYHnFaQV0SMQLNTz98Q6Pst2Nci0Py/AGCEUveucVlPQu3kvoONQxDlWdc2/NPik\nMzXZ8N/SByIPaOCnvGozbOQ0z6lonA1wsy0J+aQMJxbQe106c27WMzQy4XhUzbYD/cCIM6MiQFjb\nnWX5b6lf128UJRc+i2ImQvW1vBD2/JQQigugaFdHq+0Rqx4l8KjcdK2htVQddj9P8nzUy+SoNmZZ\nOtpdbfcVzUp9T232Rmfu9fF6mChf7+BaYmWXToa8cS5gITqSg3O0N7jmR402p9yncUynwy6fp1q0\neDhXn7JNayKTNSyHDHhxRpRgm0583n9X5XMQSbaOGlbmZE1VmHpWx0Qr4IFqaVWTwmPl/oCJxRDw\nLAePoLjQqwthvHZMMJe2R7VmlSlmdnt6/qBm5yZFvNyk2t1V+GHy6gqn2IyVBY0DLfvGxjIlxavs\nd6hTVbInj9KbevVjCUuaU6OYJC+djGaGby8swpoxxLnXtyJwMXktx6xEeqylHjFzWPJHZUAddEFN\npSGdRRpiZqU0wEuRjUkc8jvqa/zf+tbUHgkaB9TIMjCi/Uo277zVLR0QlaPl7qWDYj1jcI/jJ63P\nCsxWH+JdjCHEFARL22FtDAKhd6+7UDt7eRJ30j03Uc8g2+kcTKRd0xzP4OgYmxa2HnxWAf9WFjuG\nH6Q3PIHH/0p19Ei6yFia75BWPm0FhCTceZbaEW+ICQ2/svGdhlXlzfzrcvetJKbPIaXCi7qpfU34\n1/IIWRi9UULf0etTpG+pn1Ejm3Xqwv24QHa89sTGccX4s5C048llOuJSWxqCMBXYXiqCx/JiHytX\nHeE7ELqutTwcOUM19Mdjg1KqYGveMRsiLmAFC0kBezyab4f4UiZMw5zU+p2Tk+TMI61A5VxlIKUg\naDtMsXvLV8RnTVzomMQ/VnvXMrmfXpGUuxGAJ89qVxA51tymRY8F20XTGZ9XY+tV5aVFtRltWRTR\ng9Y7Aj/IQOUc2tIZqLLGPxrXeFdCFMTqrtk7vlQZINAktzevRZrGOGhqlyii4hOyx1nSwbfiiiHb\nvtByBcjQ38y/6pVbvb39Z+nNlvNix1Cb79xxpbOJqrSOw5pb/fmzLSNtXrt43hrPvI+puTxkc/TX\nH+rHLh85u46EWisiLb8qmFMzx+jDL208NkbzWa7RWfWgcu/0KNsSfoRQJbo05xHgOC6i2LkcYSEk\n3QBbPDEM8CnoRSA7RHQJSkrB5E8zgLrAS5j1kZccumSd3PMpMzu2oVND+QCkLtAcQ7GWs+bsRM5T\nfRPUXufRN9qkw6QL1u1akEW3C35pzYdMubJt7q4qeMxNDQoSu9fgjWqhteyj9VFtWb38x0TMR0J+\nAjZLl2WpmEVXEE495mVdpFKXJ6sS4ZJOU9lKWR3ZESWi93t9gqQN/GmdYI3RyGg3SUXW2gMGls5r\nWbtUhNz0ilVjXC1iUnJBzQFHCFHPsZdoXApGsoGxglAKLPJPVYvsi6lAID/x7JGG/K16Gc6/pMXp\n05XeNIDnEUOpYBksJ/yrQk/lyFrPmd82fmcti4A00clPO/8uHjxE0p0x/XrtXDCkfXFinKxXr/zQ\n5q/+txsIjs4pqEB6FLM+R25oC1AjkTr2KmWgiVYq9Si2k6gQNARAFudUjXUX4HtWyfn4apIw7snS\nzvPDXuEKeL3G7bBdle11XllS/Wf2vqZCj/P0GqOj+G7l8OF9yBOWDv6Ns/ZHvSt6HNMbCb72dhwh\nM28c+ORTJN74ssDeWk0ykEhEaMmJZcGtuUd4vr/kP3FGLSuLq7EA3szxXqnpKb1LVwXycKgQznv9\nu79hiDzsKfRHlRrKWhvtSaCXOPX+WfJSN/ma8g1Ff3Y5lldQ78SsF3II9QGLwPe+xZgovGgXLt5V\nyrXlVuWUx+D/c0jO5ody9z6EozDX77OvVkf2oVV2Lwampzcz9YHQep1QMcRnxlkI6KO5Mg8c+0nb\n+fNUTy+cvcCdyLUpaFS1MRCHddjQtn6RltQiAKS/8JGUUxOMI8P2Xp94glOEmx872xVzyohCd6zN\n0kVoNLQsoKAhiH7ZBg06tRq7U4ofbu0HVGcT1o78ve9ZXJQQbdSgxSwZdtqTS6OEOYVjwA7iMHPe\nxr9enBHTgdM3DTOmZAMllUlnUztpCaLQ4RGMc9IoSfYdQc+m8CdsTwfxlmufEnr6G2cK3nU89PRG\nZ+55+EQyGQk/LT+s+BMeStGSj1Mvr/9d/QZZkxNkaIhCEbkpi2yFh9+GZhUAmMjtlL4mzAEkmmix\nA1nHahb60c5TrYip0Tia38WuwxrAAdCsh12ChTgWSJLR2tmPeJusJjOXIzDK6PGTknk5Sg+wOWkJ\nPpJORT2krNfpyGsqAY/5bbzhJgOOUpePKl9sVTzphbBj2AoI5eaXZSB2Ok4FMAegG1Q3TL0AUAvF\nHd6PVD6T6A8SKHLseQtDyyhqHDWmVgNtA9CcMTqjWeMmtz5eOWYTqjeoDmjs1gx6JKp52zZjyTmB\n25wYsqxonKQ3W85jfc4aM0hxbyE8lyfmAe+4gNLQhIL504uNMAyh54rp2S6gT6C4I0uwV6qY0lAN\nBcNcV8QUwtyJ0491PgB9lqmN6bKtS7/q+2oplPBH0MmENGtLGmVA1xq2HlCt22tCdVVbs+1OF1HQ\nsmppgtjnkGvieUNpGCZER7ZjKLBr9SE3/5BFxWNowjys5ozYdcSfw9+c63gfSocO2OyU1hRuQGlL\nvyQSh99DVVLJxtx+hnMyItES7OrojSxL4FZR+GaoP3TQCOLoND8zZKpizgkVO6b1UXo7514KTQ9g\nXHwdy2PmabWxJKIpFWnihFYKa+UIkX2kAM/uaftTP1LZBqPeefBul8Jss99jCHROZEBGIDShQReu\nVeC9ERJs5Nrej4LW8ExToMwE7/1e6BYHouaklmoS/vIYUZIKUr+ptfZJGktdkN7bY8H36L5UrkQn\nDQVDCuJsaZkb2YoLJU9vsQn9kh0SYAxgzqRrd/sVP/a33fAnrIu6r/T+3k4VUpQhA/6iEAFPKc7T\nmwl+8EvRNhq2eN5DUBXYGuraRWkak8h7voBNX11TtuFeV9I7sVahK1by56INj2mcZbOgybCDHwAt\nTV6d8nq6rImGMesMnKhRZnkIfXWgGpfOyzX4JPJ6reIDVcIfqPq6El1HIdg3qha6ag7VUHjohHwg\ngGv5ZlzwXDv6VMJ+frTbUp838nC4Cvh5PT7tzj4BgDHAL+voy43Vdwg74Za6ku/DF0FHooM4OLaI\n+5imVaYPhwjAe2zLFZEfE5FfFZG/IyJ/W0T+A7/+gyLyyyLy90TkfxSRP3i/kPjHOiGyUcfrkzjk\n/bKIal5tJ6FltGiKW3OgeM20HiP2yaWPT5O8NbIyUp8PP0ypMGKATcO8cjDqoRBxs29Fj1Cg3OQE\ntAQ2LQ933PgupV5yp5Mkb6xWBP/2ftI+Vs02L9h20B1n6uK8lUo7+LQ9fRT6tb5+AAfNsVPP9nGK\n+boduioNFLNXugH+hgWJ/iPYdmlTKPGpVOf99D778W8A/qKq/ssA/jUA/56I/EsA/hKAX1HVnwLw\nqwD+8v0ipIRMNkA2M+GFtdmqBBZyN7pT3mQE7Z9QFavmLry+N5SvJBZ60v6fVn/kc90R8+naE88W\nDWMNmcUm+8tCD/rOqwzf4RRMD3Q9yweOpn/Xfx/W2LXdPQ/Zx1pGmOdoUlBvKWqtRFGjoKZ7iu4R\nh5WY5Kck2duf8lnCLjIgI4ReFp50kMy/NKbNUCB+zEF+XfJfFXxV/R1V/Vv+/WsA/i6AHwPwcwB+\n0bP9IoB/61E51kbWgitS0wd8X3L56ID6BzNqMV/zWyFrLm/xYZJngHNOjWOnYo51akreT41BelcS\nawAchDJWGvLJrPJcgQZBu2IMy+hYZi4LIcDDzPGcJoBpuogEcW7zNxSxkCAAEv5ThS7FJ+3e/aTt\ne0XbKXr/X7cCjneFCd62wGph2tI8e5+E5NJwoX23ZnShpboyF196LBqGQDOhGfXr92us/Knm+CLy\nRQD/CoD/DcCPqupXAFMOIvIjDx8m5VnTSTlk6CQvbc9DJS68qf2i37HuJ54/hFuorqYyT4Q15rWH\nxq8X198T8Z6/T5Ny1WKx80M4Y+6aS4tqfRNQjHzG/FrtwWi+Ik3MHt7wWn9gAU2v9KGRjdUQyndl\nrpqdtpnELRctAAAgAElEQVT9oazjU/VcXePs0VpjnvKvHJXBitFd6JF/3z9psgS/s/Cwx57bnk7S\nmIELLUkL1n9X4a9+1dn5oQibxUORgRHsE+z0Gh++t+CLyD8H4L8F8BdU9WsiB4Prbk2/9iv/PeIF\nFz/+8ZfxhS/9JGmuXkBfsEIf12XNOLbWkvL1a8GW9HAT+LMGu5NprZSJ/DDpof0PamoKq92Xpd0n\nyYT0pB4SeDhCJ7NL4V+F5d43dXSR7FN75qi3j+1cRLh/pbH29kYEZfBue1oXH4/w3xI4zpMqL6d/\npz0B19TcsIIEmTNlx20/lBtzcoyigxdCzbY8wpud2KmHEvjWzkD2YqTf+8f/GP/0q/+ky8Sd9F6C\nLyIXmND/VVX9Jb/8FRH5UVX9ioh8HsDv3nv+p3/mT4H2YFngShCq0Woh3sY3u9AXCEiLNONlYKXs\nay1c4tLbuvNeCM6l6XL9faCFzDK2Fd/DaXAqsmxZAclZikL6Q96FpavlK6XkzvfAqfe1eHrp7Y72\njUaKOKK6WxApNLFeziVnzEEIPPqBFaIWxCS937mcyNYkfwfuWgttak0BNvzJVQelFp+NuccfMH15\ntb/6EP239EM/9EP4/L/4eQzZMCD4zb/3G+eNxfsftvlfAfh1Vf0v6Np/B+DP+fc/C+CX1oc4WWSZ\n5jSkOcXZ5Qyi4Erk1BULesQA5V/Wj1RIzvGoOObjbl4sfx91jjv0SOBPLImlG/ZDDvcO+ZsjCWXC\nJo2K6c9bsvgJkvSdaas3R8w5ths4XdlYy2pkqnFOczxvu8A/ICmzTf045grQ4WENdRKCFP2pvixs\nkXZ2dxJnHTmdcDp6DbnEqtFHbf1rGiadBdwAqh4R3oxqHPE7exIepVcRX0T+KIB/B8DfFpH/w6iE\nXwDwVwD8NRH58wB+C8DP3y0DOBm4aFotnLDpo64o0uYkPdCs7jv9i5iVqJpnpbYGLncfr/bcI17M\n+xgRGT2IHWoiftLgvgLxqD+vpuyr4GFx4syhLLSr7VDRjLLcC/mStoZMN7hJGvzO5rc2d0vqd+Ll\nhsMnCrJd1uPds9Ubzt7sEhaunDPTkmPe13w49Av7JtcVE6uEMrTxZyVKy9h8/5QPjoROcRdBX/O/\np/ItvSr4qvq/Atju3P6Z154H4LHh4fApwSoGi99h5qWuzxyNdr2F6T/oRCkhP9LQHWYSTLwWqVid\nbcvj/KeUEyNKSWJlSVFRutayHeXHiz5XnkDMo40+zf/b2ivtCb8WQJcIFc+S6LUgIF0Y8r73OAOM\nuKhsgS551z7Vv9yilKh2qwQmaesaRevJrD3k0cC1q72+CoFaXxdNTkxFtfDOat1HgJId9Mm11PfV\nm4/ld8e3bEEnFmN8WoF4Nb3N7rxFAeXPnJB35MxoLMTSkh6W/6LcOv+MSWWWgjGzH6qQA+d1PKLO\n6TLTa8kh4I6izVdBZfYjRHYsoO8PlbdGd1FsfqLqRHzzhmKIvU55qeVTptef0eWTiBnoTt/Pnm2U\nOPO3nPDUAs6Z8bg2D7RcwaQr4gNNkE59qork0544kIedd8Gz5+N0XBZcwtw1TvztVtqnSW+0LVdS\nKBJlcY+fSwubCUVaNsnICKCIneYFTIrY+amMxisE3W0vXs1zno49Ojs//5EgNx/IK+mshSvD9/yC\nQWiXW4+/xfSaUipTn9qj1TmODWjPLchbgsxK6oTWd5pz9Ob798W5dwoGYWDcUVK8a4/dUrVEOiBK\n8fueL0DrUepi3a3aVX2tJsJro/omgj8xkUtYAEisG4dX+GYl9Rt3z5hwTXsQVilGMbOrQLaVo2v9\nVHAKbQzW0QBbqz04EE80u8ZWTkV6ek9xNyfDhRZrE9PmJKbWpYkrAx2G4a6qoIuyIM8BVR8kprmA\nxjLauiKXZL9Y4bPYNjFXehRFU10H3K2e2nQrGUeR/jQ2nVHPhToa4nYDEcp0WQRAxbSgWNuGR3Kc\ns41pWIYspFYGzcE8R20F16S9AHFcWEbCvp8ifxvBd423nlmnQNsuelhKUQp8SIRaUwxsSIbXEaGZ\ny6tP1YkZSBSD1YSTLQfxv6AAGLJgztpz1OSkeBoFot0R/dVNTGtvMNRZXYK61bSP/+sMdKJVciSy\nHzWDLOFelXW0PBBbW3nHOIiOgqvWOh4aUS7Fe8jefy1joACa0HeUTksHHgy11GZjECGyQKk6caUB\nqIrbl7OUX0RSNlBJqU4FnoeAKoGKuFCnp56J5LsB7fAGhCJIK1aE2hthvWUVP0pv8yYd4ferFEom\n68fuLwC14yiyxnKI/9Yjm3shZRlIDVtDMx4Zhq40u0pr251i81xfzhBdFl5qxl16F2oZOwnihRqE\ncRC4X5Y0U4JDMJrTpQE9fS0lU3PadKsmHQUlldLpEe1c17kPPUEycX691/1HVBHpKBYtibVqti1k\n3ail/Tv9bTvqlnFhpBcGnDMtqcF6RjNxYS5U75GQIdxzoqH0aaHV+PoqsT0tLjj60VqnjQ8d0AFB\nLhlGNx6kt9mWO+yQgMPpJQCZN4UkdlfctLKDGEQj8MdLCIIrIHGMUihCpRKIp2NwshWJaMXEvByW\nwpPo0fCQ8jxK2blsOt8LhLfTgQRDB/htNd2mDF0urANTvAsjhejZGb+V64zMjkHuIau/bC+cvs6I\nxqdF4XhGZXFIefsr4DPGhpS81vN5J5UPrwgte91PNaALSrxAJ6nkyMlCnwq/+lllxdizovRcysrX\nW6be5Il0PAf54+CQXKpn+qTWnN7PnRSf9VhI6YiI0TjM+3X3Ih6nN3tpph0A4Z2SQuPSsuu74gQb\npDlzg+3bUhFAMLhodr9UvoNVs8agVtl5O4VfqU49lXT21gLAaq6XQATLysHpV4czoCwc9hUkpUqr\nB7JErAgruN5XUrWhGFPoy6opuqCV1H51PbJwWHlbqu1UYFgawhSp0pui4U1UraJYHZHMy00Wt8xq\niqwkgIW8xX3L9GrpswaSeqfr+YoMUQTMhPArpsIRn4hWFadPQU/GyfrniE9TXGl1UztTnpB49lp6\nwzP3usBm/LMLRmMOCIBhClspkGfR7L5MWuhDmjSZ/8ycokvqGpi1SBf6+tuFIrt2ghQP9K0UWrcg\nI+3z/HvLjdr+9iAVXj05NO7QtOpM5GISaw2ON3tRArEser+nZEEout2wtuUBxRbwrckLYz7nb+sB\nyXfd3Jb1qQcVF+Lft+6oJRLzdXqeae5D1FxEqhBfomPtqoHwrtUF5fMq94u5EsfQsiJeg3u81Rw/\ntS2pLuVTwZw4kmfJIDW71htOAaQ252dPt8SyGz8JemhZNJB+KV/qSqBZEN6aA5G7RJ+PQSD+nfac\npsKXEtQy8oM/AlSr7wF9RYNExCiX9Wq0wsejqtdGw7Q/FoAPBFx7UqIhVAGQ0ytSUCk27XuNSwvK\n0V53Iv8SVtd26EVuEh7uVW94lMo96n2QsONIkUfLGTPC0qn328GnqgSKnjv8d4qyYviUpOiXoBTJ\ne4W0enoTwd9v1yJI2WR5X3UHMKBDEK8vynXOacIPaNuAU8svjpJUHx+EMOe0ww5GaU1mHUbxJKuu\nQ91xNkexaly+nzHJet2uHU9uaUq/WpAXTw4pif6oYkqqzaUQe1aWrixfCVG5V2dMtISPLAqA+3hP\n+Z2VGeMRfofDXDjay9ZI/pXW9ox2Uz+EMoTfS0n05IM+DoczlEbkbdGV135bWbUX5bzHtGzoyjlb\n4+O7UkVQylKdMBEIlkvkLvQCq5wVy730Nst515urJV9ayygpTRNKVe2wQnEH0IA5SOII6gjSyVEQ\nz2vLLIRBCDUwp9pZ5nGYQS7x1fz6YPQdhL6YcE3nh0Scj3pNaar9jBDNvFfgRIIWMS4Rnc5AIhyR\np2gKjnvJQh8GQYpDr5dXL2R59pikFPZJ21uA5kkqgTqvTEG8EvlaFknrIFDQVk4m5pzkYPaeupDG\n2PCpQIfGUz0SZwK03+jAlGhCvhxhkOrqW8MSyHvRn4Aqqf7WW7sd+DxyNbyKuaZ/P72J4H/y9W9g\nbBvG8JD/9PhKDiYwANkgQzFlQkaEWSjEj0OKleZEeRFIKIuy2zxJclo691yAmS9jXf9g0C28m5aY\nhOat60ut9EzgcQ2oRIPSxGXECtMv+F4LSqnF/Vf8NwEVTIm3xnCtmqgB5TaT6cvKjfRPIN7B5+DE\nEOonoGDMWuWyZudxM0aVFM5BKTTDPlchuYWyPMRGpUY9Pm0Mn7l4vyIUXIo8BSECQIfz0UhEV7IC\nqpkh7t7eQF4vMPW+V9YtpKLA2hcAGYsys+MDvBrWwj3v6K41vYngf/PrX8fl8oTL5QlAECGEPlDY\nBV8u9n3s2IZgbGGau/CLEyjRXni0GnKGadV07CRdfbCp2wq186YuCMZCbwxRqZbVmo/gjsVwL70W\nrlsYUd/zyGxHfJ8wldhkg4TaXk1bBTaeSUV11s74KxWKelRMq/DDlmbD78MFPehxleMrPX6o5L1H\n40TiFPqpZgGSP8hYpxQAv2ikgnnCYmSq0zHb9+pfviQHnsZGsPtzLXexSRVpuabwA7B4RG/nwYw9\npjcR/G/8s6/h6fKcgh+oaV31dUgZEFwc9QdkbNg2wXYJCDNv6aD1VxGBbhdgm644gDD/U9umKMcy\nUDhOeEaII+K5wRBLjxkt1UzpEKKicttvSNqcQeIRhvM9OQSrrMmZWsIPYo0uhdqw1OPRQnxY6JH5\nFMyYtC6frHkSHs1kVFZISzpYEkpn//fihPNRO3ndfx0y6762Z6xNFj2aK0sohEeivfevo4Lzkx2Z\nnSPfD3HwVh0DqtgJ7IZHVhqWSFm1/CB1yGWkrAwl1lO3LEKh3OOkY3ozwb9sT7iMS+uQusAbhez0\nXWCDDDuFd3sa2J7EQ5AVMuwFFGMbifb7dsG+mZVQ0ViCMQa2sWHbtsXc66wNoNCQ9C7gZaVgBLI/\nIOi5Mqfyo7qTZTBy9Fgtx3qCORPtyfIwsZ9gbGLxCaUgEAsMa+UvTJOoEvnCqqoIzFABctK/aFMX\nZkkzOcxsLkxDyTYaciaFmbjI9khJLQnC0pVEfuT4nzkM4d1ootOiv3i/hANWCrFTg2TyHpck8ESF\nvnNAnF52zgGolHgP16L42qpNTPqVeOt7QPA/+fo3sI0NQ+rwwJhVaxyxLQMh/OJHcG9PgvEskGFa\nTYbg8mTCHO88u2xPuKTgSwr+Ngaenp/xDEDUBonCs9GZir8xLtcwHq3dc+45nZZj4SigmZyPEiNT\nVpAVOmrCBZ3mGG3dPPtLLHFo0oIWTfjtfpflE8M06o42+QOLjB8TLaM08NdQYAzraIgojd5sMqMk\nmYUfZZU1my/44ywJ8uYaihWlpINQyzrM8iV8KT5eWiW07pGSqU4GOM6iUSceoT6w3r2X3kTwr+/e\n4aoxvtypge7cuzjqmyKQi2BcABkKDMW2DTw9X3B5ukCGobr5DkjwYdfHtuEz+w6ommNxsykExpkj\nkMjVrpfQd1B7jbirX4Bv1Uj7NLcG/85cOpvCXEp/Uo3GdKQ91yHQGNCZOBDr1KmwmrOPUlkh6+z3\naHmsbetdEkU5pM8UtQthwEcVfW9MNFcCyA1apzQ0ZRJCFOWVykpD4966PuG8uAII0Z+ufKLMVBfK\nVJZ4kp4l2yEMLwF0Vf7RT+jdZcE1vY3gv7zDvE3se2nLMJdU4XvnBYoNkAty7u/Wv2ym0bangefn\nZzx/dIFsA7Kx4G+IJbshA9tlA6Z5Vi+XCy5PTxgXW1k4bJMF629kG9tgpgApjjK9wvl6v5uCQFck\nGnkWIyDm+MVmJ8yt0coKfYo669laZgujoJDJCqH1EkK+KE8SMU1nStZN3Uu2rudD2xNlG2J1i6KQ\nX0pfkdLVQHmqUwBDO0fUVYexw3Gl3l0LBCT82Y4D1CYf1ZkPJKjLeJbIL7VqSPOqMALt/VkXCVBV\n3b0bI/49hPhz32spwgdiTkB1T0/rPoF9F8wpUAyoDoxNzAgYhvqXpw36mRt0dyG+DOzbFdft4rq1\n3lBy2S7pyf3osx/hMyJ4Gr6bSaSI5vOsGg43rVy9SjO7grCMaykNBEpCa73BqBGlX8syU4E4cFjC\nSQfb0yCymXVCDB0WZ0W/Wf0CwWAfhPproa1a2HtHTZjmVOhuW0pHMJYG6lc/TNCJFvGacKdSYYo9\nkMxJykDVzmLgORaDs63SROyG5Px2k3o1OMRGx850qIfFhXPANjix446xPbwm4oAwxmbXI7TWC4nI\nN5V4frhCkTo/IUpblYAIyhMcASjwFaTgr+lvStZccSliCzSW330rOu/lnzF1GnZxiOQu0ekxCjrV\nDWUhi+V+epvIvf1Wmg0A1CKp5j4xXThv+8T1RXG9mbNE58C4DHPkbabVn543YD5D5w3b04Zx2YAx\nzISHIAJ1RDZsl4uXDUCAy+WC7emCiyDRJDZDdNOoBN3e1Mta3NmX0L+uxlcTwxBIK9I1em7pVQ8m\n8TcdxyCrpvfZjBcSRDcV05gUSYZYBV8VHqnmzlAA6vI7dWJ3wd+klKAhiqL2SCDRXfy1yyn2qRw6\nXbz7dI2Xz4SYmRBY1H0/VvAIYRYAMlIQo28R4srxDrUmXu5R1ZmBTUHLmB7OfKus93G44AoA30qW\n0whXshM0xodEPCI+/vGaa0xfdVHsc5bPJgJ5nL/U5SP/y51XoVQV8cbwZn1OdYCbtsMzIpdeSW/0\ntlxNusT6rb3St15SOKAYYh/rqHmogxECOUUtr8Uvz1CJbiUY40IA3Qf2fcftdsO+764VSzN2e72b\nX4HQaIpd2r+aWSqO2lA1Hgob9fVBKIEStwziajAzlsCVuE9IpDSXnYrdIx51MxvR2rq0pTGJKyIo\n5rQ3+SqmZ5n2joOhjignAg+mVdoAJ1drpSQsmbZ5q7Uvrms6TQ1c3To4Wx1x2y/PrpNQjTUR4mXS\nVCw+t9eMLu1tsHuaaJ/KBtVulSwwxw6Jvlo+u6wghD/ekdd7E8qn/BPehuZlte25NZZSxT9Ibyf4\nQA5iMYSjrQ/SGMDmynIOxTYKlSBK54y41ocjdm6bjI0/AnWLYt937LuhXEwraq15ZUw4AeknyFJh\n6xYl9IlHIfCEUAdKxDpyq9P/aWhZf49YQ0KuZUFYiLKZ8/tuS2+bt2fYWmiVxcyS3ni4taAwv6hH\nW4xSenqCJrUaHVTJzlIPhIS+aFRAQP2SGGGmgZWxoeb/a0sCCSNwK0jKs7V6U4+jvFs7IuUYy1p9\n+TMdZmJTolL0fYxCxXQN1hVUzt3TAh4Q2F6VyHEstW7ZtKywJTqW+/Lz6UcWypudsksDm7prN8QO\ncgkS9adEWO7ECC+rWwMiEfrjx3lpBQL1ebspFk3LYhaTNYKeC6osv3PNWpYntQ8VsAhHQIJr6q7y\nlmyL5POyWHzv2p4U2ZyYu+J2CyVnpv6Tr5CM6XH8OT3odZt5P7Gr4rYD+65hrdqccgrwZE8NcS8T\nd6AVSB5mBTLgZaFVnnFQEFnsnktgLFTn9JaWp6Q9nL0c8GV6vQttemPCQgjlnwqmxq+7W8PyU1JG\ny6gS6perVFwpURvzbooyRKYbjZ3xis9Jo+nRYniU3gjxgVUg4xMOFBsrF+oAWLHOB0kGpgu8hScO\nn411MRV/hgIjQmju4Ce4jEADBIJXDu4KJMZUeYXuWH4Bqt9Vd/WwEiSLMIfdlQOhOs+Xiw8c8efE\n7bbjerW/+77bPbkA44IxBJv2jRvM/CHwt91WX263sCDU/Ql1Ft0Wjrgl/DRVqCMT4EqQ+D8FLJ2q\ngsLzmcuNtXkrRo2iCF0pRvWhRKPu4obyjmc0ZwhZBN0sOtqUTgy+upXQLbsQ4hkBUSnwupbkbSHE\nFxL+9m9dRSqgEPAoUxqApJNQB3yy7GY/Xk1vJPg1NGmeO+In2ytr1AZqNlgK02ph5+ggLVd+0mLF\nmEbwumwVnMzhlOZhqCsk/F3Rk/ZlhtYDkiOE24U2kG7GBz7PlQpqKocPs1D9F91RV55z7thvO64v\nV3zy7orr1fwaVtQzZCjGAC4zykYKD2BKY58TL9cd1+uO68vE9eqWw27z/I8+umD/zAXzo2eIAtt2\nwbYJEKHS0UYX+lRpvmwYeyRq3joxdbff6s49nblipVOAzeI8Zvh9NFRFKBOtlYmsMSaByO88pmFY\nV5sryXJd82lXADEaOaWonCX4ORtHRjeEzCaitT91zy0Vq0NhkZI16spaLh50hQz1+BeNJYrH6Y3O\n1Tf0gbjZTYgfjptiljgQX6BzN+bwZbUxN8+vUB3QaVoOEf2HAfGX/ggEQ2YuBdqqEbFBOH+aoNMK\n6qrA4y8p1ACulk2y+QRXJPSwgI6O4pLPRsndgGCxn2lB2AqA+TGu1xs+efcOX//6N/Hu5Yp9320Z\nTz4L2YBtE9wuGwmNANOPiNKJ277j3Scv+OSbL3j55IZ37264vdxwu94gIvjs557xuc99hNvnPoO5\nTzx/9BGenwXbpRoejrK0Zrz/tUmmlrUUuy9bDsTuM3HFv6kJ6LhskMsGHTbPnhKrJTWOHIwzVX0Z\n0CyG3NFN45XyReNWFEYcBO+A63WpTSSZGeJX5GkI7ZZqG0K3Onjp0IjTTXx1JRORemXWxwpT8BPx\nvW4Q3SB+XqNl7/CzpjcS/ElCv4MFP9Awtk3mZhMAmBtU3PExBKoXmqLbWj9kA12swVVbh/VgvUL+\ng3b1376UgjTbVkhgs2tRqqyBUQJgPzRNgsKC7pQbWWChE3RFfHrOf8Wy1L7vuN5uePfJC775jW/i\nk3fvcNt3jE2wPQ08fXTB075h33cMGW5GW+zEVFtmuu07vvnuBd/4+jfx7huuAN5dcX25QgBcXz6L\n/XbDnI54HiQlGnPoEPoSwmz4hC/f7rjNG3a9+aLZRCx/hfk/APNHYGCbF2yq6fU159osB2+s9yM2\n6ylmHo4hGSfRhZ9n0yXGYbVVs8vHAISAAySKDeUTpRHhszWNSKUuoLoXwaThL+tlRR8bu7oUNozt\ncan35p2Uv6Q3E/ww7zW/mzIIb2rMGXOJTOFaLzoy0vQp6fM/Umhtv+te5CuUtyAfbc+W8KdwJ1r1\nfDgMyKudT0vh8IggrZnwROc6LLVfz/7TiAUwM32/7T7Hv5mpP3cMDFrVsCVNa4dgqo3KPhW32w23\n2w0vL1e8vKPPJ+/w7t0LRIDtYvskLs8XXF6ecHl+wvM+MbbpW6OltS38HwBIyfm0ZN+xY8fEjkDC\n9ONoCH7tW5MNGcobp8sODIyc+cX0pRRvrOGXU1RaW4q45DTtl90/obRd11VCWGmueFmh1zBLmhUx\nMUjHY4ypxtn8bBEy0zxiq6Cbh7cnD1m9rxn7b3TKrgJawt/dMawh/eOCki6ukAXvFIc2lcPGq4q/\na8/duTPCyUOZOdAm49fhzWP0jxRg/prwu2MrNmnweNorrCTN1kFowHpr1f11tigJ0nThvplpfr3e\nMHXHhi0F3j67FzzSx7CHU/DlhqsL/Lt3L3h594J3717wySefALBw6ctHF1xeLnh694znj264zR2b\nDt8E1a0ZOGKWHlVfJvTYCtyw635wdg2PXNuKMmZqq0BMI1jAz7CVhox4DSQUpDDOVI7Iz2k6WSmJ\nsVMrMD99D0ZNvRoUJHovZqG0anwqRC/LaDYFuMRiKf/HlAgJff6lucyD9HamPmpeJlBbD40L6kfi\npYAbUcIC4NgECYKWRZxLNJEhorRkcNw5SmGEfeity6QsZijBzaFgky4eYVfOHT3tj6T1QEVVsRxk\nsposkY3n+bMchC7YEa+w72ZZyZQUwhDyONtdFdgV2PeJ227K4uXlipdPXnB9d8Xtap95uwGA3X93\nxbvnGy4fXfF0veKj29XOSxDbeRnr3Ymqipw+qVp8gFklV9zUrBJWvsOF3IZIMHc7onpsF4xNLYR7\nCMa2QTdg2wB4tGaSMxWtKx7IqdAboh84IMfdh2Q1AGu4sszOY4HYmnP8EwzXaOY6zpHjBK/d0sk2\niRv2DoiS4Y54xImZ3kjw3S+pJR6ta2TmD6dFCnScMpSI7/dBOrJHaFgYbx7MUZcd7A6WlEaFGr8C\nAXhVlsXbfjMSl6H3iA71QDZNkVMVBMKdRHFVE9xsZuGfijn3NKPn7o6zISkAqopd3THogU5TFXOf\nKYzXlyte3r3g5eUF15erIfPNhPPmiuHin4+uV1xvV2z7gGySUlIKstqcTj5H/Ov1its0i6FGwAUf\nApkKwcDcgX0C26Y2pdg2jG2kQ1Fk2IoFjQ7gSiZKDgFNRdDHkwcnrEcltA4rCyh9fzyIg4YvglHJ\niuSKk29zdYqVyGNh7SxR4MQxCq/a+J7eyNSfuQkFqk2c0mQPve3SwPuL2wkjoRRQbMZyXCZyJRt3\n9y5MxaB3ljdni67P9llbYC4H1bZQ2jARpZqbRTdDouO65DVp49YOgmiJVkLCKbqHAvAIRSHPOmoz\nR5agSGshpwgvJvy3680cefvu81DBPieu+47rfsXL9Yrr7YbbvrvC2TDGyPGB07sCZXz/gIYv4obr\nfsNtv2UfhrjYO0EFgrkr5g6MYUK/PdlH4aHDY2DEcmHM1c94IIQ+LREaaBfSFrOxBPA0ACALIFzU\nDcpqQNumpbaz0IVcQQUET7Xxlv49CozGCq8oUANfMfOBt3Tupa3bJCAJmzHRKADvnvhUwgBwYl5V\nbY2wCK0dc74QAClHoj/TRJwYaVWjB6WyCKjkv3qCNIvA80fWMo7C3y0MZ3g/jVh3zU0bGvsRElHU\nPfIKOPLr9J2Ttx23FzPtr9cb9qshve4VOWZr/eZAfLldXXB3mz6EQAlKuLz6MsNjjj9xve42vdhv\nFnGoClHBJiOlSlQwL8C8SAr+Zb/g4srV0H/abk63YBRYUE+I5TS0Xdlqso4BOYjjXyc/A02uXND4\nxyvD0kcU/ihSGuuUP5URHBTbGC8eH12VUwl9BL2ZvFAQ0IP0ZohfWi08vgd9Foaa/W4ZyJtNmkFF\nSO1XjBoAACAASURBVHeERgwCrxrYy0nGVK7AkcaGt15XyNogygum0WSEM8GulkfV3RWYM/rFOXnw\n6KfwdulPfxOh/JxqKKlK+wayIJ8aALENdCpsP8Ntx367Yb/uKfSF9rayopjYdeK63zCu17b5aZ8T\nQ2cu7R2Sk0xd8PdYfbhd/djrWaZ+CCkEcxfMm2CMDdvYPA5AAT9+bbvYkm6zfpC4ShZcKGAGnWWg\n4hKbzksXUhFocGQ4F8MRCSijr/iuOx/n4Kpia82yenPiV2wP9zHLnpUAsZXM0PWK3L/xJh0E+ikq\nAo9tZcCI5BFZSO+AoYDfj3m8ncMfgQxsFrhSGLXG3KwFr28qORxVEHvoeam0mQJCTAPO48MZzDKr\nr/k65pjrhSBHOckngTlU9pnQx+XYjqkzkdSW7nYLsx2j5sz+zJy+p32OKmOfmDf77DcT/OknF7Gy\nnh54c9134HrD9XYjh+KOsVltY8iipLR9LLQ4nIkv+aILof+MJgM6rpgDJfjhfB2C7bLhEhaJo+qk\nejVfWglXut0or6VfXegv2DBA7FLMwyYhHNGJuWoGUaJs5Q/3We1ZDzQsCG9TztFj2W9AxccprAZF\nExXzgYm/cVU9OOj95vrvLfhi4VX/O4DfVtU/LSI/COC/AfAFAP8ngJ9X1a+ePzzT2mriQkwvdI/0\nmv11EyH2n7Pwl8BJXadPHkywCH8xSVgjApDJGKZXallH+m6QcR/DdOsHpbQUskQa/mzdnhErLZ3m\nIHIHXzj6yKMf6L8p0m8QHJPWDu3h3vcdM9D+FnN7stAcwRTmHMR+g14Hrjfzygfib3OHyNZ1OAFs\nKDCzMGb6FPIQCaDOZHTBnwLsQ7GJnZw03U8k28Dl+YL92c5c6HSpqYXm1VCeobiV+CGEupB5RfsY\n38CrHH2fx2cXxZVNWAYSoxkgJjn29o+mVVlxHHEvolEXEKLmFMtrvG55afD9NB7e7ekvAPh1+v2X\nAPyKqv4UgF8F8JfvP9rX7e+mk0MvSCfmXAppWhGlUoBqbbMVTUIHPCBLmE0+cCot5GhpExktJ8Us\nJgHVK5zr0yWvNJla1c8ZsDn53CcwYyeis7129AMIed+5B/96NTM/lIfakuAYAtmGP7Nj32/mlb/t\n2G8m9BoORbagEDhMiM/bokPxxPKerypcX8x5+PJiqwvvPrF4gpdP3vmKg/khbjElSR9DkTTBJP9d\niPeI8npndHJK5vsH0Pkh4itmBkcdeaTKCkGn4KVk/eOejWZiaismneBlubxfei/EF5EfA/CzAP4T\nAH/RL/8cgD/m338RwP8MUwYn6YGwA6mlI+8ynU1CKH3qPDoS+jPUR0fNVAAix3lw1OjCX1bKneTj\npctgcDFr18O/sS7z3KHM8qv+YwQPJI2DRjQEjPMlDrqZOSduLmBX/+y3G+bN5/YCyAYXfMEuCtUd\nc7fnb1f36u/8aqqFOCn0k4QfeSRaBPRcrzeI+pkBQU+1U382TDtDUTZMAXABxtOGp9sTbjdTdHnG\nwepgiBWWdu09hX8R1OKr4qH1U+97qrr4vnCBJrUmuHTZpgSLwIMqPJGlshJO7czT9L6m/n8O4D8C\n8Afp2o+q6lcAQFV/R0R+5O7THKyzpHSUKA9HsvfyEJtMJvTc1VWLSqK/H+0dZ+9HfiKwxPv1ol1e\nU9sXAUKxZvLhMB4NZ7T4zdrsTig28aJsYswQ0tao5SMKW8pzU19noGCs8xuCDz9VJ9q/z4nr7Ybr\n9QXX6wtuN9vYoxpvLOodyVUBv7TvNi24hV9BL7WaEH1J7745FnXWVKScijbFEAXmmDmm0NhApC70\nCryInbz8tOH55dkcjGHdRJx8DgZZGskrZQXoMmCrqNW1AI8YMEG9X2BRArG0eDL+vGpVCn9FDLIA\nILANOEezsXSFL3UnM0jqp9fSq4IvIv8mgK+o6t8SkZ9+kPUV+ApyBFO7CbpogyNvkw3HRiQFUXTh\nD2FyQR/x2VLQE3Fhplsb8jb6MeikEFhxcKtP1twZ/cMM7kGDZI5yvVJ9Xhk0iUTE0qnmoHMEzhhy\n8gFMtXDYcJTuOnG7OeK7qb3vsQknNjuREMHP4ZuAqFTo7e2GOZ/S5I62JdY5SoUSyhdYTp8quPAD\nijHLclMohs1aMMW2oGAI8A7YnjYz92+hdFgZK0rM+9SjxvKcVaUPQo5RWmkIL74fE4WAqM6z0W3m\n9ocDGLUH2ksIfR3cSYTN1kk1kT7R/8fS/z6I/0cB/GkR+VkAnwXwz4vIXwXwOyLyo6r6FRH5PIDf\nvVfAP/ztr7lXGfgDn3vCH/jcM0L9xfZI05joNEqa6OlYKclbCb8PXi7LBNLH0tmxnNKxIei1Waja\n0IUgqwJOxvXMHOve7pp66FL2EYkagYJIuWQHE6a9PlrhYyloOgU6B+xUF8mDO0J4Tejj5FkgDju0\nrb08dbBGzb0EL481m76SsSKTz+/Dqah+CGp8x3Tn7xZdDIVl0Z4j9nlsgOxyepRaoR/VyfSi4Qrx\nbpCiDCukAkpL19/w5mvzyx/GTtcfC7ZEXytY7UxYpbqzlJ57IrwF/+h3fxe/9//9IxQn30+vCr6q\n/gKAXwAAEfljAP5DVf13ReQ/A/DnAPwVAH8WwC/dK+PjH/sBzN3OcbP461q+OYpIXandXTinSWVE\nzq1C7t1sGoOFPhwp9yTWnxVC2lgfJfPqVeOmiqr2MU8eSqo14ePTHYeg3dSDO8r26aG6c0dbF1ab\nm+sUEzDvW2yT3a8WQbfvtzTz4y1FEstE4uv5WuMx3cTPefY+MS/u4GMDJoogQUznnhbz1xgqdrWI\nPVEX/Gkn48om2PatxS0o0SI86uHbsBLrrcudt+pSCnx8F77PEiuZ7/6Id2Ru2iWzBT+VPSBA+vIo\nJKVZtsxEyTe0yedf+JEfxuc//6MpW7/+d9gX39O3s47/nwL4ayLy5wH8FoCfv5cxNRotDQWR1E0p\n70YiS+noQuo16IUnMxRCUYNHwRiRmgdeK/9BscRYJ6rWoD7SG4dConB29GjoaXqrS6ufbZhiJIpi\nLldAOMt2C9u1l4jEjj9jlrlPzK0iFhXAfrN19JfrO5vj7zc7mWYA2GwubUf7m59jqGKbwWgC3Sva\n73a94fa827r6Nj2GAsWoMfXIOX7/KOWb4qG9iPcsFU12JQsjnZlxhoMRozziitj5lj6A0OVE3Rjj\nZg0QnRFjpR6CHHEn2jiUlLwUj9+x/JhvAvFJDwQMLLxQy5LqCpFcvVRV9P9QdUufSvBV9dcA/Jp/\n/z0AP/N+T4qhxnBTL0ylRReHWRrdjaOcxZfpNuFttUXuLvSKgenn83ndWT4JnZsH29LMchIhnxc9\nWibdjJNUEA2nQ2sP+ItC1DYli+2Mm8EgIhWw1Gz7OKFIs546MESAKdAdFqq7mwLw4vKwCkyF7jvm\nPjCHIfrcxbfdfoJP3n1isff7FRMbdPNXlz0Jtk0womO7CX846uR2w+3lxZYDn59xe3rCvm2Y2+an\n8vrUZobA1yaifd+xz5t9dMeutllHdPjG7WmrCAJsGHastw6oeKDS1cKM5y1WFSZEaZqC4X4OX6GI\nxTWS+AbAILRXf72AD4Me6I/0ZYi4cg0eExtUH5omjAlYnSPtWyqSUCzuoxDNtq+KJGcwKu5UrGfz\n/oP0RiG76FR1L5Gh/UjzjOeRSsSKz4hP2EPxR4E6fbcQL50lrgEDE1bNH9xQdkZo+N6F6Eib+x/y\noFkiNjbi8QAmDBPqyIbchYgcM+Y6tk68bbkBXer0sklC7wpNgk6KjNDbNzP59x24Xq94ub7g3cuL\nxd3P3VZBLgNysZeZbJvmIRuidkCGwoOf9h27r7tfPYR33p6gT/46Chnw1yWhe/RD6O0cgan+liUB\n4gzGXSbi3UYi052SBhhxbLq6hRNlQwrxlQhT1oB/Fpd3smaMcAh+1OmIEYdvlLxaRJ5AYjeswYVo\nxu3nMiPI+rwHIVGHmkyUSafVHxDiI4BMEOG8ykLfTchDeqNNOj0iqo6aCgMmiFRimM8GyqPesBJ7\n98P8r3/5w4Qjc4gtqGxGXBS+Zd8i/p/N7vb9PCmQGj7dwloym1Ma1dxJ12CHVU0ogPgnBlZrsNH6\n0dvBdVV4r8fax9ZescMvtmEx8Ntl89N1zK0u08z3COpTj/rbA3X38Nr7EpcLvZA5roH6M+qNpUP3\nCwyLF8A+bVsxBPHNVgk3V/al+Ekz1t9mNfGnUlteDl5ga4qKKMu+gwagC4oXB+eeg+YQWCr81Em7\n3opphXCL7rJCS2+E+EXM0JBplbR160XoUIIcAn+Y3iff94U5HtdKobXZa1uDV9mqJXHskiRxT4Se\nASX7TP3x/tc72NZPCD0L/0nTtT/cef7Oc6RYVf2orTS3LfIuX9s1LGBn8w0w2wajqtiqgOwVg6Dq\np+nsy5uKVH0DkGLQPBszlvIizNfODACmH4YqfmCvIs5nVPHXT8UBo7H7TFavdXmN+oCgIycPzkKq\n8B/1GFyUIiOBD2tySgDM0h5/IASQdbOcsM/7JwKeFuRDA68K1e+AV/87kez0T/UgGXoLWSBbY9jU\nmShmdlRsMdYAD2DIZQY0cGCDf3iZ5p5yiJzfeurWQ7uqzqI5Vw5T8n3rK0doMWUt54R1g/iWlgMx\nRb5hyD+zDvNQfx25KQDFtgk2sbcO3247dtc2cyqGo/fU+pt9A3wapzkM4cnPJbzQcWIqewzb4DNk\nAGKHbMqwwKtNN1yw4QkbLjKsXWO4v8fKr6nekfZ5Kei/HIIuQM2ztTKfy6fQt1qZsjJOs2F9EWaX\n/NAEMUYLosX4adixuhgSNLaQOqvilUn+G+3Os8GtjTiskQGkBtf+b4W7IXYf1d8gif97qgStjPVy\nvazoxN5Ta08n2xEb6In+/MOkTWD5kXtPs4IIh2Q5KLV5xYNnczoRLXZPcjjmDKkD8c0KmGHliOZx\n5NsQXIadZDyHYActxYXgh9DrJGaLfhrY00GB5I+wvPZ+xIFtAGMM6ADGZrHuGBsgAxdsuOiGDRs2\nHdi2kUoixCH8PDGqTM+uFkO103hDvG3qkUKxNMx5PJ//5WCwEt0aB8oJhfouTbcgNfxJi5CnkeLl\nBh+2JT0GJ1kffe/0Roh/geiEYDfPMGtbMQeSDls/thUnZxxMTLX1ZYGdHR7bQwd1usryj29sCgfX\nkHAUmhdW/PXT0FglGKnsFZqvmPZS1+E5XD92mJkglsC4z9auCfhpOUA4aOwZGCMKeypK2Fmgt2Hz\n3thUo0PtCHafHRtQ2OvF5q55Ak6Z6Jp02LaBpyf/XAa2i2Bz5TlGnIFm4zfntOOzfNPO9XbzpSla\n63alNXU2tM9ViF0hm72+/HIZeHq2Y7ym+CbaYZuyNt2w4YILnnCRZ3z00ROenzc8Xdyxlst1cSCF\nLHPhUIT2HxuMNhbDfUmGKC6bKBuCLadcVE4esE/sQC3+Fl+qlglbmZi0tOxtjLNHgFiJse3UgFjs\nRTZmULnRR6mYidg9qoKIKnyU3lTw4z3muXdJXBOK2hx+iB2ZrCUw4W2WoRBs2NUcQ5CBDUAGjCQ9\nxYnqSBJHOrnQjyHYyDQQNxn3GUyKmoxIeGzXIJplkiD0xwfCejjB22fNeLGhtbaH13s1PO13Brig\n5tb16i1DyO1ir8Wc046rttcpGzrP2GwzCtFu+47rzc7Lu/kGG3HUvWybCdTTwOVp4DKAzQUgwp7D\nEbnD0P7ldsW7q4X9zjlL8N0kzaPAHP3jHX91rNbAZRv4zOWCzzxfsD2JrXiM8mUPbBBc8DSe8TQ+\nwkfPH+Gjz1xwuQi2iBeYatMUdUcg8UTivAT/RZCR5B6O4Z9Q2eo+GZ5ANLtRBy3nuTpJ3xAd7RZz\nbj+jQcZIKxQy4+wX9//6WQBiL8cA4MLvPMB8R3wuYQmTRfM9sZwnujm5/GCINHVcU2mZ6kPooES4\nYwf23rx4CUPMx0Los542Pi7s/nOcODyKjOs9mreBj74UysFPlCbmcpP2uRzUcSMf1bpDxrJTYK1l\n6YPD64z/ggF8HTzLU9T8PjbyEDIN9+Y/0WcbFkQzoRjbgGx+rPWIMul47xlr5toqzfBbtdFL2VA3\nacWO3LpsA0+XDZenkeHCO9QdaBtELngaT3janvF8ecLz0wWXi531t4D7qYUW6jJXUOBO3bASKT4k\nhH7meBSXyCJ8HE1SNcVt56O2FMt+iCNHimwY8eIMSBgyBTZS/NP6XWZW8s6j9HZzfF5/PoqGpQBa\nNFlA2o5URPOUxrNcnNS1QmqUwijl7HmZkIupeOhN/XufwA8IT/08e6I/Gea+nNxjJ2F8PDpPgDiO\neSYKVB519RpHkZs3X3C5mNl92QTbkHSajc03O21mjtt0wv/j+mespeOkbYmDtVsS9TKI4UpgbPaZ\nBqyAbBDZcBlPuIwnPF8ueHq64LJt2EbsxZjNxDeeqP0MRDEwMvJI1PbvzmOlppkh0XjuTIz7KC6/\nTiC5JhE2V61wXa6hntP+T/YsLM9H6Y0QP2ZJK3kYkji4oeeURPBwegSo1wAcHHtVg2vZYn74tXxY\nK7cxOgfzZC5qX7RxManUO/saPQ5l9SJWHbY+XMx7InwLJ8Y9sND7FCOQLqdALPgXd6DBYufHGC78\n4u8rcGtMeQvwnufnNcEna63Y26dhsQ4e07NhU47tMqDx/rOxAWPDRZ5wGRc8bYb2myP+YLM3QIIH\nJoZ8wcKw6hrBFtqrty2QyGem9Wz7cj7Whxr0LEdISLwD8pxLQs6rDysUHOs9S28i+G2lBEBBN/32\nv0H6xIb0npan88zUWcyDYxtAQqE05Aq+U1bc8vSJzl4riMIIKUqEhX+zYjpww50+SH9O+b8U6FBs\ntS888x+WEJFm5xBD922Yx/yyDWzbZkcawnwD4UkPwY8ya+//nqG5MU4h7LMpJU1ls8mWsRmh0dNp\nFYpm22xL9XbBJob4l+2CcRn5go22AWsZk+Q9VgSndOx4aj61/kyWIajpKvHPKoRrfZE/rckw5wGw\nsB9t4dUyeTSHP7GkT9KbHbbZkWxh7JSUphrSvFpPPg0PPYQUgJxZFFV/cAEPcrXsJL8srXzkLVnN\nSb3PBBVWzEZ8QpL/Zc0Qba/K+n9+FuEMZO8NCaYvU1zzCCw2Dkz4S+i3y0iPuW7qjtcQfm8so33G\n49/SdA/HZkbpEQ1tCW9g5HJrDGih99g2bJcLZFwwtgsu4wnbuGAbm71JN9qTZmCZ+qTbyupBiVnk\nCTBn5a9Yv+TglfUgoeGX8dA7Dx4sQWpo4/ElWypLb6v2vp3ze98CfpY+zZl733JKsRc+A2UA2FDv\nuC/jphC9zold99aXFVBEK/c+a9JDY9D1/H2z6EyNnJroDUG4x+RQoghFArgsL2McmHEOXBBlhJOz\nzPZE8bCmspZ6h1xtZ50USFP7GnJlZatDjLfNVlrGJvlJ4YopxCRTn87Z75YIt9desBKGDq988LFc\nho6hcEYqnrHV9ORoMRG1AumVucHaHKsj8ZZdhRuhESyGieLbE0Y4VkSfAq3q5IPnMznfSrU2pmOn\nOaWa9Zqgr+mNEB9gM1d8XZlVq4Szif/1vCIp/jBnUB2mGXl4Ta8fVXzeEtf3RWD0sXk0zqdJyihI\nlBGqawkGST8FQHvVLYMuBde4k5Ms5+0UH+8VWplhjqNM8vj4llbEMpgr2xD0LaPoTDFtW51jn6G1\ntu7ploYf9jljng8M2RaBD8Gu/ePMtOX9B2TGizKi/x6pt7lfwNsXb88lSWtjzOLLtOdQfDhKx+vn\nlZ6OTT8SA0Zl9ALJKlutrsJnvJZ4WTp4l7eDnzxxAjrvl95mjg+Pu9bQs0AYGxXoUvN7+zbKLFb3\n/kYek1lPOSEAm4o1H+JclO6gBN/qdgPlXefPzXzUBN68djJ28R7Bej1YFm3/kLAfGSdsiRKqCvPv\n8BTsW2a3o6kt8dfc3uf3m3vUI6ZCXKPFve1igT63ZPY61Tej91gpZUvr6K2YbogrjTgXMM7oxxiQ\nOXAJwYfkWrtsA2Ns3kZTRDbmIeohfx6N6B9ZSRjjAum76ZhRlC08TUUUrWLLzkvKsVU1R/ExOb/H\n1KOhebfUzAo5KjWpZvTnWC5eQa63EXyJ7ZGxdlamujraRyRbJUnkKqHnKcGaakDS/M9bpRTYPPLW\ngdXDp0H6/mT9iwz8WAeehDgYEmcDSdnpOd7BWMKvaVDES0E4wCisAT/hio7I8sCdMSw0NwU7hN+C\nY6wkxeVi9yLf2He3VFzY+YRfWf0QpBjS8tC0OOwEIXtr79htqVC2EFyEnWdBNmOk0Fc0IYgmXixN\nh8IUM4VOkzXfE51ATVbYOhBpzSEiO0rJm2IPoS/5u4fAZZWvtXXAyuCe+J7Z+LmSJaD2crzGx2+0\nO+9MDBhPIzYaSbkYpIiwYsQv0a9Op9iHcLPpDzaj/MsKy8vPtkOWb5+ZDqptsGNfNlCe304OdjDW\nXNfyafw5Hb3m1iv3/MEwYEUUzq1A26Njb7gCoHm0y5Ttx3czm6yBQCpV1As6EvXrSFFeZoxtwekH\nmEjE36fgtk/IvkOHQObEvtfxWupCWoen9ncnsGsu6UekjxDtkIxu1qdqJV6qkvu3ACsan8P4rmN2\nPpZJP/qubdzZF3VPjWSt5425k95M8C08F5AG6/WC43MdKYlkFcfsgh6MUHiAVAm8CkCOv1wNAFmH\nZ809aUuzvJek9Lc+Qp7fszqKNIbYYQXcK92/s+MMJMTZCEZ8d5WqeXl3f+VW8xM4MSRDVxcaAe5g\nc6caz/+93phCxAswmVXzw86+ePWV1oGa8TZe3AQ6BLgNPPkxW/uuuFw0Z0DNmQt/NVjMdUhwCufL\nfD6jrobJhIAg6hysnfZ4CH2z70CGOV+AnZFLGmhhhdxcRX/TYdoY7thuhryDnXrGRkt6I8HfnaAW\nY5+o20hXrFonTwQeyvKfP0V0rpK6p79WAmg1IBDfB0igUOfyw3bHaMHKUKcKIIa/Yuu7WiCSQNfh\n4oK8bbowC5UVTBJo7vP25GHtT9m02rfgNh71bSFj87mzrd/X2Qdi+yzCB+CWgQRbx3b7QOc4RDOr\nIMdd25ar7uNTV0oT2AG9KXaxUN3L5QmX7YYxdmzbxHaZhZA+6IG+fDn5i1d4VMpAkt62tNRIRxii\nC6Aedx9+HUVnhgVo16DrVAp3EX+xjDSWd/mBoqbwNxGAAU8rtygxwEl6G8Eft0IoASB20p3xdnTK\nD2WQCWichNcRXWLElNAIRexkVCnv/xgl+PFqLXEJP77dVZmyFTNzkN33NKtWzetzYrIJ6O1o6wfg\nxhUP93x1so0haUgdz/mmWvTdrnGsNcz55BtNtrHhMi64bBdctidsm+3HDxqPIdjGxGW7YNsupiDE\nD930gz7tE6Z54Z/78cy/oCihV/4L3Ka9U++qgm3fcd13Uy66QXUDdMMYF1wuO8Y2gRF72BabSATx\nmjUR02A0EcxVDvVJfew7SEWSPgPxfSPi0xFvL+xoLxNm5ycNsDoZQ7Im7rJJW9WYzt+jnmdLAv6a\nPCGAY+h7ReAjvRnih3Y1TVUmPptJ+c7vpuE4oilGp0ynQnrWkqMGXkYuSrez9duRVUBnH7p1uLyq\n7sJ1FaHfPA/nvKbklPrPlZ21otfI5VPI7G7LaZjlwY7nwhTfwyR3eIup05DNgnY2E35bq585Hqqh\nHOyttdu4QGR3wYcfna75As1Jgq8wEuwaR/BpLSUCLvzmdJy6m1F4Ay63W+7KE/i23Msznj/asXkc\ngJHHlHiKmcQ1F/pY6qWlzqLfQlWy6OK4twCn8ou4O1rqgFRrAtl5rAAO/CVUZ8hE/HaHpKmoWpYm\ntI8v1s0S/M4lZ3zU09vE6ktp+joAMWwqE4R+goqjGcjQ10DgMG9Qwt/mfF0VKBNNWD3wbG1tcJD+\nnvAj6499261BVLJGuBX1K//4p+o4a0138DBi5WuyQ9Co+7EGj1AQfnxVzK2LicQto62sotaD5DKA\nVlfYwaqO5HXWvRLtKyQrxqUOmNBUg1MdR2fsuBTcbv7Sj+uO62Zv3onyaQgapdI1j8CHMrvEQUeC\n1IvJ3x1ry5A5EiuALaeNheZ1IOzAlMhbVm7U2VquVUVjoeb8paaUrizrFsz374f2wJsdthnUm1DE\n64cC9X3zY4ZuhnaNIxa1rU9384Z4krUvMRrbDvnbtTf5Zz2xkkCOzalyiNxNkQfxeQrB57LYX4Um\nKFgZJUQHGCKG0KywzML0kKcBUysbI6yI1aEXMByx4u4lL+GPFvt5BG0uGcJvfzVQf5bzsGLzq2vs\nS1xpmOopnH/evNtuQn/bdtyu9facM/5m6q43yv6IKSDSSpgw56Jt628wQUWUKR50KeuAOcwuDgzY\nmwG4BM7BfElJzpaAqR+LgyPGumUTh6xXdMAbBfDEvxSX7mQPxEeciw4gTnk5a3swxboez4KWeZNY\n7AHXJI6moCkd0iAsv3iNholsy2m32vpZjrhViTAWWj+WgVzrDyeVf7dDPIVM3K4MBcRuWpZD0Oy4\nAjIQp7nETkVgxfoKs7bxiEMiuEfethlmPE1uZCXsQi3l04AnbvvMo8JSoWRfFmvCB62iGYtOMaih\nP5WcdF0pEnoqytdTV3OcMmcbNs0yy4fF/NGKJ7rx+RJK/Hui0FqdUbYgz7d4RfLfbJNOUtAZitw/\nKAVQee7oxBjJ+t2kJn4ehYdbEuvoXFYMXjDTPZQ/9kyzhHAeHRRHwrsemh/fu/Ze1cHJc9xpgIQ/\nLgk7tU9aHMJfQg/+3gRfINhRTtbyuyyRJfmxsGw6yDPoIDBTZC/hCkEMrg9rZp/TnH57HPYx/VQi\nrWeSBFV3yvBUevNXlzjSOYTeKGThcUR/nsPFz5CBBTZ+L/r8Ff7S1q7X0HtNZQHfT2+ySWfhSJiQ\nuAefUf8g9J1Jl0LP+xbVhEZtQpf43DBmNeXo6nvQnC2MqIvLOGn38uwB8dNqAJXHDCvUP0IcXNoC\ngwAAIABJREFU/5gMl1deojXkPVavazSk75/hB2DkgRlh7oel0WA6mloIVfV1QQgNHZtimhQqcolw\n3+PFnhPXq79dt70sM0qrlZwspiE+yy+jAFG+2CTzc5tl+UsD1hRPkUK6tbYyAsVL9HYV3+c3KZpG\nla0ob7DwvVeQ620Q//9v7+1irWuS86Cneu19vvlm4vgX2zImJgglASOCLCFMImSELREJKb7CwoqQ\nf+AOJVFAyD83KHckUoQskRsrEEVRhOwkCjZSEMGyIq5QEiWAY8e2mMHjiSPPeDIwUYLnPXt1FxdV\nT1V1r7XPOV8835kXzdvft9+z91q9enV3/XZVdXUV5oQsi6TzmYaQWBfWD4ftSD01fIc5BNlNTLnW\nnZ+puBky/y7XrQSf7ztjtgwbOC+UkOeQooGqIrGNh37pwhAEiGApMYSIv+pGPk2W1vwY8XYg9IVp\nCAASf9lNyQShNeMOSvsKzUhBANXIZ6y+ZBDMSQzCHV3NsNc6Lq1jjyOzNFBoNjbas9Qy6hIDQOyQ\njKUZcz66dJ3tLlgkfijjhbE7oUlhZL7scVE2DSvSdlFTYKMJ7emFOn0vfTqh6mQ79+vU8orptQ1B\nkuFyavJ4oCojj7J3bdI5SVnnTP7MhZnzn0ntkqwRQL87aQWCAbxZXWUfZXkkCfugd09P1IxCRNHo\nW2FwwT81M8SH9AzcMuK1A8okHgiftL0wiF88amdObJFeFvOpO5OakqjMgzbaLzvyQPlXQZWEsjbh\nbzDs8HX+vnfsTvh7L8TvfWg0PsqYgoNqhGPQa4GbKDPqJPHbIAT18JOTfTJQ1fBOaJ0AX3Ll8uI+\ny684Xp1SuYW7tr/MVelQnduXqPnAq0l8AbSFdd5s9Vo2N1SELirk2ZALh406VG8bUnVFSu2n5mKC\nNwzImXlFJtDJ8txh153i/pzPe0GnAS1kEZUo7blMSalfJCq/S36IqUFIRCiSoeugEy+iV4UqqK/v\nReeKEuMoxFI3NrjmNirRi7XLDD7rHFkMoBMvYEtAMjYSfzfC56Gb0ym7Plg79UcxHIeqe5F4wnlp\nEE9Mmv2hIA4pHXPogmvpt4I5/eYbkYhkRQGwG2eizOc5OEAyroIS9S1F00nBQVx/bn/+K0n8Ntnu\njF5c4lP9cmSsavOhrJKaKqn/rUQfFu6D+f/YbAnaDBnHO0n8R+49/bpvfQMCCSg/SYSSbziz5ocl\nvEr9RCAyhgHFKEQ/HyCafDLYay6O5yUGsUaIVqkeGV1LKB4pvcl4yWwIz8zrx6QZ3AdQwy3YOq81\ntMkI37uiN671KfUHrp0bjhAwihY1lx6RqCQgK8nkCkLV70U1mKZmwgxNjSEdAoVwzwSAS5bs2xFn\nitKXS6SosvaiMvckemO2T0v9V/LjbwjeKTTsYSKWyeaCnA6VeTKCLc+WkUDaOu+Tbb5IQYe9XWbb\nk5axcGsnhFwmZLtP89WTQto5fXBlOiQi9jHjzdkGzwGwwzPSEEQ/fpPaXlW/C6lUYqwbIOIniUHZ\nzIK0VKddi/Pv0jSy92z+YdacujaG91M9/z9gS0Idnr6rD3RJwo+DOplRSM0Pb3swCkB5aG4MMqV+\nDDEs9BLnL4gUBAmmYN75WcFLYZXQopBowQwz+Ida7VJ7FvTh7YTc135jGCsZcAqfKa9E+Bfk8Qjd\niF9d/CtloUtDTQKv2vHBa0TkDUKXJMoiWSaJL/FIEPOEBSczNvXOATGRvSZnPvLjtc9V2vN1cvIp\nNXVpAKj8MqW+DIsYI9GJZj47jrl4NXJs9dVVnBdDZelSbqetE1EQOZiP+6RbEv2UsFMFMqS8uzAE\nxw2eNDT6QMfwU4B6+PdHV4wtbRY8KEVrX0mUrcLdK5QloRF9lfwVdLzmwU2hiuc7BrUMvr+uo8qa\nMDdWzTkIAxAVV1fpQ2wMhrmqX4j7b4WqL5puFtGBOV94AmeOYJMQNAfLKRBr0ULrgTxNeL/6qKM3\nVu9sXiiNi1qYOF9VKY7L/jFtQBF6X3BspGjWSnILJyrM58g8ytq+1E+kY7ir7WsvcsXpqYRBy9wu\n604uzwNbkCLY/X0lr14wXjLV+mFaxQ0T8W9bw1DJMxDJoJtLuOZ9GTn+ydC31xN6XbJvOa6E3cws\nw1vEuw7QGu+erkFEKxENF20peChoqPpAWPPjSTIiAbg1usInduMF03tix2ZC9Inf2b/nyiut8bek\nWDflWDnheKt455oI8E0wCI7LRyb1fiX44xuSgJfXqwN5Jc+7RVB2EHuDJdkDZQDJkWphjEECC6e3\nnYOz3vX+OvEPDHQd6LBlFN+Y/K6sacucGC/RbAuAiXMhV0N9mSpif0CuUUu/pz1RPgdqOfy0ZPhp\nWwtpXxOn5H4L68xwPFEV22TU/dy/SvhF2QjThSaT5hTzI5z7+CMp8eM/Xs/7FWGMyHVqN/uxQE+c\neZRngZU4tSCwaTsI+8UM81UjqcJvesEz5ZVU/UxVRLRe6c6QeEbKAFYIOj1YVgNUQeyVmyO5uVYA\n1rcTW+Z2a9/OGQUZWSxSEAZAEo4eG7IaUpibEM/jzekXXyeJa3yJ9X4SvxYW4y1o7nYMiUzJz/lc\nZptHb7HeHF9TxrSs8QNGfmBpMOSG5bCODZfrhq4bmo44mdeWAL6rEmq7+Zrl5icDH2qHfvZ9jzW+\n0rpfRW/BjGB9rFK1oUXK1zV+mF0dThoE7DCq0p4w4ZtLHw7CV+cfK/OMIsaOuD+/YisZUqolVTNV\noNS/V17JnccNOXlk0hQI8UQv05B8sjYFitRY1fozmVnUvxdxxkX2pzAqLKQS7gsard2q0UqBTDIn\nf6ldCaJHOPBtfen+eSi2krlQ/Llp9cmLc0eAFWEKX6oZHiwYiI8peR9ozLPN4uqHnNpYWhNgM6K/\nXu0zcDENhV6IZpl8AfGDMhXaBMNPwFRwvW/Gvd47BrciT4YhIEhaF+LnyIuADQYFEnydAAoFa2v1\n+Rym0edkehmQtga9X/VYVgFpTNkYbLvjOFBAx7Jj9Ly8iPBF5CsB/BkA/woM5X4QwC8D+AkA3wLg\nVwB8j6p+/nwIWpa+rlipJVmIECyNfwxFK02IgtuqCUcmW6B6HkN3TcmkHVtDIOE0TTq7Peapcqg6\nV6+6CNuKdwlMMgj7WLQI1qmsQk8kQWVIQWiOiJpgLHFyqW6Xv3NPAdsXkbYPZtbR8nwg1tqlZa5C\n0Aenk1CrI9ttQ77ICQyeyfd6aXh474L333+AXCxjLsRCtw2cphmODvTdI/f2ZPqqZuDrt46xd08T\nTrUHiPPNg+hc60m+Bu4Iz7MZCBUanOcZDIWeAmhi8sUWIEjpzXmtShGZLkGkcCNcAZbWViU0DNF8\nLDuSOCM+xgr+p8n+5RL/xwD8VVX990XkAuBjAH4UwM+o6p8UkR8C8CMAfvjsYcUtOmMdbIBe/Dsl\niAIy/MOJsWutDcsI0woARDCk2YeSXBXNjU8Y5kVo1a9NDCiEp4X7N6pySmU5oULi5yTTM0T52hpZ\njD3DJYf6UiOWMv7u2gY15Ehg6fPEE6BDfRMbT7jp1Cze2hXS1fMZGmsYyKzFjXEOPIpOBD0CbeyU\n25CE2oyYY+0v4HT2kZl8VIE2GrBlqC+axHl3Cj+JR4AmA7IJrtcNH33/AYDietvx3n4xeKPHvOlQ\njF0tNr8rbo8jAnKgO7qv8bV3TzoybMmgydgNRgPCjjM5yQAUduQ64O5GwGfLNZXAVIRrsoY519N2\n6Qmo9Xl/+NxGxiVZd376mwI/7CPaoB4lySVE9mhmVSjfchFSbSX3y7OELyK/HcC/parfb4igO4DP\ni8h3A/gOr/bnAPx13CF8YI/BwZErN+Vx5c/Jl2RvAlcDUyWsxz8PEWcAaZQJS6kHbjBQLOYhVYLs\nnuZ0Vvk3YrqDzU/ED7ab/rJokvvXiEqj/Ka6vAbYBKgUrhdVmZPMiwFLgGbWnQHIcKBrC+epwO0i\nohngZIIWmfZayU1n9dglJO0JGTOgXtc0N8GGsOyJQOO7M7WmaArg0vCRj1whTXDddzzuG1Q6AE/N\n5unD+m4M7vEN0LYODPEDNjp63zF8jY9hxC0YEVxEQ5pE5z1bzzA4BS0pwqUcsZM0bJbgkeGSfBS8\nqMyddgFK9CHAEKbQYoqu4lnhv9SYaPlXJPHH78Q52rACHYlqIhPuhH77DOG/ZHfe7wTwWRH5syLy\nt0Xkx0XkowC+QVU/DQCq+usAvv5+E1SX6g48e70ikWqyzZRnzTCTxpRp44WNfnrT9PRq9j1bbJUy\nRafVv1Ol+yNdq9Vo1rvFJQqNcVKe533xD9V+ahRNLIHWpg1bpNKyawikck3DKTG7IlMfCIDYaFIC\nKbR+0Xw+/dZwop91zRy7MZyt5Wm8l+uGbRPIZvdqFt+tYUr6WfV1neCYf6d02+xzxSmdYcIRsN2Z\nsSZT5pjOcJOArTALQVM1hqetfOVyAkiWT30y3srJX1zk95pneQnhXwB8G4A/rarfBuCfwCT7C0cC\nmGgfSxUJ7pqW6QWvlqZD3QrVCwXZkmRCCk/PJ5IcrOVRbVafACc2zBNvF/Tk4qHSVPW8us4fMht/\nvK7pa3+yn2aNJtFvKMEozGisgdaosmfWhBAS3gCRTGPpISrsXC1DKpuIHtd5EPjBnFta9u2o6wbZ\nkOf1lXP70iZBgsdk1wjbxgrMieIXRr+CjUyjEP0EMCo/IpUmF/UscUTqzQXo07ZoRTADXfp3hpqp\nkZZPED2frQLwacp/yRr/7wP4lKr+Lf/9l2GE/2kR+QZV/bSIfCOAz9xr4Jd/7R8FMn3Vx97DV7//\nkWdeKaA2sKK+3Z5nlEQSUufAK8vHVaPKIBUItw3Wdz1J3U/xvlUGIFVqVMC4FCZCuEvSEHQloML4\nKEXh6bGxWRJK0fColcTL9ktMJVdpUGGKq0UTququD0n9jDz67wd8+VCOzeauPrpSJ+epuKsOHr4r\nwMWXbTI2QC+WLFS6aRlbw2gtzvEbSgalkZ57OpijSNRcjfv3IIrCTSv5BJFL0mtoGDPsDW/EHyvw\nW2E+CQWqDQXunFqfcima2YyLDgAgYb6iY2Ean/nMp/Ebn/2Mv/JpqfQs4Tthf0pEfpeq/jKA7wTw\n8/75fgB/AsD3Afipe2387m/+Cs+uJei7ZWU9f1lBUmSMJZcDpvLjqNkAOZmoyE70a1nBCc3Af9bQ\n0uCpshUdxn3+nL2Zn3C0FPY02zDAnkE3n1zkrhO9qfoMjgpJGdLYiF5kBPFDRhoOKT3jCO1UBTnv\ncdourfuF0TaeaxfrTVq7/V+31kuzNfGlSe4m1AswFF0A7ZaTv41hJ/d4Dv8+UoewVN2lLwXxY6MX\nv3PeJjU7rThFVB6IP+E3wzVYsdsBVBGjndGkXENLVhSP59KVr7J+02ZQELr2I9Cj4I3f+rp/5uvx\nVV//dRaT0IBf+ru/gHvlpVb9PwLgL4jIFcAnAPwALEjyJ0XkBwF8EsD33Hu4Sq4whPgPGxd/IyYU\naF4tpT710uDtK01WS1m0P3PkSRWr71x6vJZ7JExN676GUDWQw9PsQFjW1ZFE1vqu282qLkCvSAai\n0EPAqTBDW2MijXLGAKna/ONOTH2gbXZarcDat6Selv7KTsOl0Yon7PjRW5FnHoWWOOOU+GQsG5oA\n2xhQdEAbhjZIA8YGbJv6IR8NTPVt2sd87Hd1SRZSD+LP2PiCYzj5XqAcAloAnr1APaG6WNnGATcK\nns74p8tfxw9vIJhCbU+yut751OaJA/cFmpUXEb6q/u8A/vWTW9/1kudFBNP58KKg1dcuoLA+j1hC\nWjehKbENIDpL/tU0Th9/+T0HZ0TPXtL9KDECR5jDxAenNije0WtQyT7GRF3giEU+NToj+WSNR/rT\ny7BE4Cp4c6m82ac1d11qWNN5KEYfdIN5Guph920f/G7EP8z9Jg1+eq2fqScZ+qquFqT6b+qaYjij\n2rx+R9MGuHfAjskWaIPH9W9oHakZKVX9VeIbpzE3Ws5P2nLvaVIz/KTMHYUNtRiz0hdKdDhMErrA\n9B78nYffuacFhuRAutS5133vqz6P2a+YgQeh4nLfuAbBzxwQcH9mrFNcA4DkXAiSmUzrtKpild/T\n91JllcY690VLZRuDIYBXDrW34pb57+HRXlVLQdQ/mvkdQ0WLMMl+JY0rYmMOpTHX3WVU2W0Svp1+\n0+I/SQIpp+H0PtCGog3XZjTX090z3Xb1KHrxtX2V+AedKtf8dGsxRqEBaGq9oTpsEt/iNijxLQ4h\nnJOZvrsw10kKah5NsS6PVhwgO0hFUaNOKpQy4wrDeL1qMd0ciJIwQ8BnqSn8pVONxMpFRNyjaOJe\n2afwVHmlWP15k0KdBgR4ynCVhM7iaZ9c8ktCJAX9RO+8ybfnf2DAxNLDWrIvvJdtxbVl3RgjqifF\nnnzmV6WWMz+jqVJO1dX5A4l/TEE1Q83q3xUewEPjn/3dTMHGBtsdp8Omyva1exbbGv+O8q4xLNNt\nbI4xqcw4e1PJK4t2aa91/orZtRmp0xfRXDoPuvDaiHZbs3h9BSOVi3ZU1/jUYKp2pEW74oavdWIn\nYUIoVNY1g+2MwSrkxGU7wxWgXWNmBbOKRvRdWJrM1e75mAND76ubAF6R8Ocdd8AUR1l6WcNbZ492\noFPWLQyg/k4OXivI4fls24sCs4SeGwx0mCY15LDf57gkEdTrTUwveAcNV7PbLFBmAeCkno+U+t1T\nVwpI9PMYGkwiG+FbsuzhhBOqc/3ocK0gj8bqvhQwiS8wPxwg9L/LxGLze4jTWZK2ptYzX99DLYfA\naAhbRONhHyIeUFWOAStzWqGRJ/auRH8UQAF9gUdZ+nWJxzBZXIifNWYAfC6CqaddnsqGoAd4JkJV\nXC8vk9QqIn6nyh9JLYe4KsHJ7pdXU/XnvwUYEWRcuV+ijbr0Tws1fdSFwMuiZnJfFY4wE9UzelAh\n/oUnT0XJwQ/od6wdqnqRpHM9KeqmBOUf4Edi9TaGE2J3oxv1jaNU0piRSpzsXJx06wxFh51Yy/Z3\n5rhXX0OTlzfM7jxBruu9C9kXJ76Ao0f+uQ1GRfyMQ/jJPp4INJj7It1PsbtoKiBhzEr0ur42HiKF\n4he41Pmkr/VJ45kE7J6hv6xP+N9plsQPyRRz7HxqOS649H47LK9zko5zyVi7CpEAmBXhRHivmZ/i\nI+adqgZZAEYyhkBvEv0KT1TFc3mtXwnlY3pm/e7Miz3V5b4msVekzN/+/kUiAsU4eYrfqcoOJ3z1\nfW2xP6/0XXxEs48f6Salu65nWmqBb4Udin0M3DqlvXq4NDzKphB/Yb0ovzTm2/+6PWDyMoivPXyL\nLiV9JABd5rbCNf6iEP3yyX/uUUVBEpWsRimKxOUJfLq2cWRJk1io2sJiU0r8XdssPEmOdYbCBCk3\nIX0xrPq/1ZIqX0NuWrCOprGvTjsJBDGINVVC0QPc9c3JIdEjZiot+ifU75fvWVlZDhoaCdX7nbHc\njMp3FPCxzRJY4jdHAt+uzAHVzUtHNCpjBGIOI4pNEFLVeKap0JsMN/DRyCYT8zDi3tH6htYt5HeM\njr1b4ouu3QnfT3T1vfSbS2caDWPDjGsSQMkUQFcgDPaDUkocP0TdGKnTPEJ9l0P4Kw8iI+BUjZ91\ng8057FOix/QpjbOFVziXCQYQiKEFnqnZwftR4/zF4TGJPHWcLV6pgy44dXsNka6MLbngc5rGK6Xe\nKhI4iG/ixcEEYpeRJnIKxDeDGKnX1X4gh6ComsjZClor7PuAAE9zx5kdwYHDMSTLz397aVMDUFTF\nin4A7qaq6Z+sDe5KP3aZfnvnio7WTLZZOhmuKNuv15CE38h7YcTf3Wq/946t72jdGFEfdm0f3VV9\nI3zXxzOZZqzxW7zTtBKLCYgTcX03IOE0fO1te8wHpDWL6MOYqbmCsbhrY09N1JiNe8EACiTr90nC\nLyi5mqV0vVhKMI5oYtZn66usGeUuKg9d4Zio1Wqq7Ifxe1PBKBjxV9s/7WaU11vjh6Vep14ZYicp\ncLrse+w1QtqnKfkRklyiIXAWUVH+iV4dOeOkeanZGCbEWivqctPWWmmwczQ4qHT8W5nh/KLcY7/0\nOjQY3ldMm58qI6EwEQWaFsaI6B9PngkDnn8gWAi/uz0ht/lKVfNJ/M63dCi0w7UJGNMYu9kifCOO\nNo3dctP6utoJnAgqth9UaZ+61e25el/WgK4zmNSQ72psloBqzt1aqHFw+bRimEjRIiqsJMd8xMxc\n4k5xK9EPuC3MjLjnMStzebW8+gCQx2PDJEEACQVxk6Bi+rldtGwbndaSlPTO9qoLyTW0QznK65My\nsdFsZJIucnx+tR2fG6HY+9RfJpXuTqeSNFKdto+t7PP4q7IOXDadJKLZo0PViXI+oVZEk/Cd+Lsb\n+DZoJN2YXXpOmE748OOzaSdgENBla9CtQbYBbFUVFtRTeg8TUnB+jdx8Tr09zuTZb8IEzm8Wxlyf\nkBO+XAXC0ifatqZXTurAKgiOI8o5cg0BDkNYlmHx4Kznyita9XMyrbQCwSQQDWfUAGO864YTKvsR\nHkqpz511EWK56kRrfwrxV/Uu6lZJXjk95UYl6FLX15RkSDp7nouab9FqQIPW8+hqu+pRDsoNMgsb\n8XE2ATaxe2ZrU0/YoW5th4Xob7AtsBeBXBrQEWvQvQ/c9h23/Qa5pWGx947H2w2P+45bH9iZ4qsB\n26XhcrXddtu2ZRBPDQraFbfdDINsf4yOy3XD9bJhexBsInkMFsguy/mKE+Qkxl7UmSSCRKdZzXZ4\nZArto7Tn9mVxibHqaNzWvEqMrJf++XVpkUSfDxI16zAq+pnG4nrGpLgk/gYjgIARmqkp3S+v6s7T\nIuEs5dJmGVIcac0bjdj0kRtZuPXUXBn0Fzeq/b4WomHpSOhIY9faM12RI/80zOvI4OE1KEQ1+Zer\n3Im0Ns6MIVsIH7lXfhVbRCDzqfc8ADJOYrTgl601XMQ3vqhiE/s0V+uD+DdAroL2IGi9oQ2xTLdq\nqvjoisf9hu1xw4Cp/eqE/+bxEY+3Pd15ArRLw/W9Cx4errheL7hcLrg03xysliRj3DoeHzvePN7w\nm7cbHh9vuO07xuh4eLjg4eGC9/QB77WrpeEyQLkWwrlBAsANYGuOxdZaUbEdPsWwxjRtmS1HYu7N\nm5xmRFUBhiSsT3lEZQxJyOf6HZdbGsQfWoLM9VjUcSwyB5XlS2SpVgA897Dswaja8FPllQjfi1tL\nq+xOo0YhDOkA7NTWVPnn09lbkCaNf0UIoAoEyTktUnm+4Jf9XwEmgxElh7j0pSo/K2Req+YdoEU5\nrO58kxkrNdYhM6snEg/FFEAzeER0eUXzIJfNJd4GJ3xRt7qLre09tFauDVtvZry7AWi2QUc7cNtv\naI/NXXhmi+69483thttt9/PpbXnTtoaHqxHv9XrBZducYZNYPQ/+7YY3bx7xm194gy+8ecTtZhK/\nv/eA0a9oW8Pl4WoELIBt1jHbSqxikCp3xRmAkpTTnQQ/M1oE0cskWpOx0Mhq7QgY8JOIkLaIyU5Q\nJP+qJhzzOZJVJBkfcJbYxJ2SQHh3oGrRkrIRi1yD4WnHUq49XV6J8B10glwyc1ILVU42i1TckKmm\n0siXEjLVnKr6Z24sFBhX5c+5L/8GAIX/ZxGS9kz0dq+yB7YcKUGmW1kz+446H1QHuVNPyQAq8ZeD\nJFwqkPsrBrTBXYjMX+gMUiwH3tYGtq2bFb4BdEQOzQMrqqq7jzzAQvtwo15JqHHZcNk2c+lJhalA\nh+fCv91we7zh8fERt8cbxhhxnt7t1vGw2280Y+B5xHVmZgpCKRqZAEWyowRTJUimJCgTgUlcm8sq\n4v0dz1HS9MBR1kxo7X8idg0+MJVYsmqsWcj89CTOTX1MWugmWn+yi69E+OfrNQWTD+RkTye/TIRa\nuHZI+Vl1o5EvCFeOn2rXXTfQkLPbu+zCtI7X8yk1IUebL4oUSGt+5f0V4DEiaSfCIy3usUmmdz8B\ndiTR+xwqNSemOJOByH3ny6etDVw2S3IhngobMCLr3bLYUtNUuFV/7+i7xfDLJtjEDse4XjZcXcXf\nwrCXc1sPwbgF8d9sI1AzF+B+2/23aW8cVue4Q4qzVZneA9o/ytwp6g/Cs0J95ewLPLNWyGY1h/vC\nRCTczlUDJNNnFt24VgiZOGD0WzQZSKRZS89AGUvBp7ANgPjK+xMmnZbXidyj+iISA6nyMQk3ySol\nqs2ShASnZGzle7FuhipexewZlOvEzPdnrcP+pMa3Tij7m87HU1N/rX2KdLr8Msob7mLbd5Oc+94x\nukZueQusGehkSso8piO0hRZTZ0Q7Wku/e7E0q1reegHQJf37o1viSGixKzRKeikRezZ2czIMqG/h\nHZ4DPw679ISa6UHoaK3kB9gtw24/HHPt72I4bxpXYnKp5g9UIiFboGBYRecMn0mHm5zjjp8CMM9+\n1Cv2hZXpu8SZBEs2WXB76YW4YY+azT1cYbv3/Q/H8moSX+U8RprbV9PamgNg74PDhpsnE0lS0lt7\nemg7WOJpeV4lino6awvWscpZvc+ajIh9nzSKyqE1lxqzvPL3uXXcCH/Hbd/Rb7ulunaCsSVABqkI\nUkJFFl0nmiYC9Rz3W4mtj6d0oI95Pobvx1fPWW958zZctuaag6v41XgafR/QbsRvRG+aQ2Vm3a/t\n0j0Xv8b24NHNnsEzM5rPee4LcLiroibErNt2Z42xSsMBveP4kvJlFVPnJbXTlO7lFhzPSeBVrcMd\nLTKI/977lwRzq5B/Bq1fR+ILz2OTSQ22kps25vuF6l0vIjGrq1l2KmPzXVtSwEiJn5/6m8877QWx\n1FIU92hzui9ZQ2t/KfGXsrImQbUraHL2QIai3u879ttuavK+GzHsmsdGd7O2q3B3HtBh0rI1Yx4c\nb3MjWvWOxEgV0E6jmKvPLrktFbql2brIhq1xXd+CEFdZE2TncQZhsOoK7QNjH9hvA7e3Cu4CAAAg\nAElEQVSbRTqq+SSh1AbcrhH77oXbdPMjRfLH0i0MfAm2Nm1zlYTwwqGDDxatj9gjKBaehaNTQwuL\nfIy76A/BiLSgpgbhpjJCqFC7OOLSimG0P81i5355JYnfjbh5ai6AecZb2eiSse61nq4fsXWxaRLG\nPIbUU/oWopcKwsJRC6mxN6Ins/3SogLLSrZK8RxPNVCp1Hmwf8Oar4b4++jmA789Yr/tlme+Iw+Q\n5I66phgqsT7uagk1hliPiFx140tagdVDSLVoDGqquhOfmVWbE/1WEmW0IzKGZZkqMCC01g1jMH0f\n2G8dt9sOQDCGxwD0PAq7Dw1TBpDuu/hQ8lftkDPuY1jToYjfy776LVEcE08nHMvTE8xSI6wgL0yl\nMNbSOcSanURf/k0vxvym1AIQz2vB1ZcQPfBahC8jdwtRIBZuSeLP+m2qXz/k/LbfuQVYA7ShbRYb\nPoleqlo1s/qUtqmursRftOLjEP3ftNin1Kxtxru5L+EwD9Qi1N1qJtVvuxnG9tsNos0I/7bbmn8s\nuWZUMillS7tHYw0qV8ULIg4Uo4fMwMuz6UwqZQLMTYqdoI6xjljyTmSlVQDM8efEf3s0iT883Zfu\ntjTYO3MDUMqmik/XoSyEH7O5EKJM63rM3wvYj8DV6aqc1DrSd8KQT5Wd+gtTmFuT8gT/nbtYDIy8\nQ02iMJLnyqsR/pzZ1f35DJyoEVPhqsvIPnVlgdtAyQ1tuPM0MEGTN/+iSbBCwCxdByXdfLU+N/OC\ncm8KQEmCCHcbmYsAGdCDkLhMitG7SfbHx0fsjzc0bNCB43HR5f1x+s1QdD+brnOcrlvKdCDhCErR\n0RC76Hx3XfO1dVuI/xAnpiBXmZhLYrBmv/aB297RbjsAYFyS8Mdtx947+iBMlt2ZlXGVBa7bgkFC\nmF24/N4OsM7YzKNcrwu0FQ3iVVHT8WgxaKWQ1ulzVpKVZiARdVMh7JBLA5vexN9iI79bXpHwkbrm\nQe2vUl+RfvpEoOQJdo1bOUma62ac4VK+XuYk1bfO2gcws/+KNDI9Z7fZx2mwyJW2R1lN3LtoF6Iu\nCQVhFSYW0T/dbZ1/u6VLrKFDhoRxbIyRDBTGRO3MO8EQhbTh+wUVeawTJgkarNSyXUKlBeEL1EJ9\nSfSSwTqtIOHk756IH6lZwMfGGP594PbohK9upfGjsPe9+xp/1lAMDWYDn9l8zoxr1cinmF3LsnwM\nLvdpRn0WNTQklH+NCVikZor/lekg4Fsers2XnlFgkOhnSRZTnYaqIvGfpvxXDODh2p0dMqtqtbwW\nWM1SBCAbdwFajEnOTLT81CJh2H5tbfLjToBhGXGrrjgOQ0L2c/YoUEUZqdUcHp5VNKXvNqrY9THM\nt07j3u3xhk02iAr6zf3ufYQq3fw8O3SBdsEQAH3A9uFKvK8DRpit2VZdkVBBDfkzoajxCMbUZ6Tg\nFCA6qblFRjqsNvfbh/dGYcS/d8i+w/bmW9pN7QPD/ftjKKpgFEHsAsxlxgTcO6USnkKDMZOgWtwr\n4D00bETv3yjuKeHJVBdvQpU/U/eomfNDuYjEURK/ZShaG6jaVFlaqqCeuHRWXs+qbxCLEdqJoGOe\n4JivMk1VTYyB5/QwcKVGM4iQQaQErRMbExrNzmR7OmVFVRAtLsfyL01J2Vmev5vPVmaP0FU0nk4E\n866T8Pcdt8ebhby6VtR9LaxjQIaahVsF0A0YzQk/2w0lSzWy5PKsusY5I/FL6bETeROu7blJiok3\nUuIPDo5RZVKOw/J3CUWyRyLuN0AxMHQz8usW508DX0j10kbz+IFJo5sESy2VEJVTANsIBsQZgdgA\nDOikycnSjl2bsaTCr5qQCc+j8Kl65LJ58oRJ5CZv9mtZYEWrqmNp5by83iYdISHmHvW8nWsXiCwb\nbXwiZXqizJjeH6MeYwfiFnJ67vFGJQVMyMWHtFxwy6rWWietSjKgo7sR89pMnZBc4tlZ8QP744C2\njgYNiTjqiaPOWWjgs5wZlEqI9zHm3lJcwaL4Rnk/x8Xpremw+LcytFi3+gm15LaepYdn4vEwzOjJ\nGOiet4QuTt2NITBKMe0Elmf/ynP3vC8r8a9ayAEIQATyzHGiA9WaMxPveTnuDZg3ZB2t7C7PtZVn\nz9sv4LLfoREsO1MrE3i6u1FeJwOPiEsCLUE1GoRAIb/ungKq6rgSfyG8JxncPQeHE/XCN9b2qxQ+\ncmJ7+I6OcKc7KQEmSaHnrZghDBbJdjP3l26GnrFpJ4je/zLQbggGjx/n/Pu/3RfOsW035jGZVij7\nZMgbJfacUReF6ClJyQzt0A0j/C2Inzn94UE+Fr3WsUHEx9U944/HInAjynbJwza3rVl/JggKVp34\naTqoGGZ/o71niGg11JHohwzXmDRiKw79W2Tf/d4VIeKEMu3E43InlduX0P1rSfwNlkppjY43ylc/\njBG6wU5USaKnEWwdjfmVmb+PG3kSGVtNzIayH8BPkCVZr8R8lNUzc6jJLVYFMi26fAOh4apeIAnS\nokuDlUsvAjoAqxIBO/R7j25nDbGtMSraWmpsxsi3Bntvy/x33G5rR2INoAHbRXxHXvcps/lSnzLz\nquSySlWMsXTXFnpHqpr2UXTAtwi3TdG2AWkDij0Ykzl0BECLdSkj+0yjMRBYrn3B9brh+rDhcmlo\nW8EF36QVEQUTQQJcdgmBWdZ+4ocNiqcUmrSAqpMXlICm0ZmLtTGQZj1RiIdzCAOopDkuSSxDhyok\nzjNMDixMlywWm0HsylMbAg1tCeS4ybFMVuyT8kpW/c1pvB6E7ROnA6q7IaWfqBs2ekFsOFFgXneC\ncf+ZvJPzFv7dQIJiC2DFImEPkrzx5QBPw1Fy22AN4lW4QSQVQyCNdZXorQW7NspSzNTnDa0ZOGSo\nWe7hPsyuFvByU+y3AZE91D3Og7o7zjIbuQvw1uzM+QGM5lF8rqHsfiTW0B3SFO0qGLs64Rshhna2\nGTKNhfDHMKYjw2w4CpPw6rGDQzvP6zRpvykgO4beLNBoANoJo2ZaCMRTgLmvv/DP1hqu1w0P1w2X\nixjhixlATfpvELG9BsZYzB1KYqNaHJAnxbQGaVuc6Htg/FOZNc3QLdQYGNmebE57o1T30HQG3DQA\ncMLn+6UJIlkpmaIY3EqWh+wK7U2uMYuQ8PFkeR3C161Ib7sk04x1l/gtXRNIiU8uTTyctQYSf1Xv\nTObT7lzBzkfSczCDmSraOnNTmDc1leiBk7vkeg/lk4Ge853a32Rqkga2MUv13hneaotiAnpgR0cH\ndGBXO0mnD8H1Nozwm7iaLUCz/vUxcPM4eVGFjNz7DzRo06lf6vOsSvfiDV/4ghHptm9o2+YuP4Hl\nUxgY+25Guj1tFbQzxOxRcxAflhP+GNxqC0CaLxdM4l+upuqbml+B53M6bW0lPtD/r8GkErgy/Y1I\nw6NIKM/UL9RcZvjHeQ+ioSGIh64L3HPK/SehPRRfvaBcR2hHVdOU+pHlwhPlVQh/aAO332oZZJLA\nCJ3qzCcPIDnaTMKgeqvaYtJk+a+m4a7GPl3+zj+K0WWd6fLEgfi9PxEptuwRJ25WLqYw6Rn6QjnZ\nRl2NH8PTY/U9ToxlEyodiu6xCztk23G5dFwuV19CCK6XhsulRXzUwMCNiS+HQoYagfYyUa4hiCqa\nDkA7Rr+h7w1vVDH2HZc3G7bLBe2y2Rl6W3OEV+i+Q3vH/mZgvwF9hycREUwqN8jcDLl5HqDCpJds\niu2CSPN1ufAU3WWNmxw91b9KoMLJ12k7BbUxPUGOsCDErUWaajKKtK/msi6MnKD3wxmF/7visnek\nvKfYt8S0sCHzJrA5JFnK3/vllbblUl22zjDSKsMoXSpqTkRI40g2QCLGYnedZaiVyiDyb8wr5a3M\nU/X0GMo/d+ZUp+8c13wlwBRSZh4NaS7sAGR4dF/BCWOU8wkwoGIbdboH4OwXS7rR3H6wX8wa7vua\nMETR0QNJm4fRxoEMDbBAGxgD8F16tsPuBvSBftst197lgu1yMcK/NFDbxLDkHf02sO/A6IkDfEfS\n64gxMwlHLN0uwHYVbBdxSb/FMqfCePL3TzCRYpspQCr7JPhuYf0VoEu7AU9Sey3csuuATOKu+A/M\nW0KqCCH2U5NAkfzZg+MyPtjOseNLeSVVX+feg52euecq0RsA5hlfP5WLri63qb14wLsS01q697JB\nsNWprWOdRJ0zuDCgyCS/14lTY5r3u0WWG2a6uV4veO+9K263B1ub9x7I1Yclrgh/ujM51YGuYpF9\nNID6yTfazPpMUTWYy69MJYlBu9XtTdBloEuHisNnCJrv4JML0CJkw0S4jIHRrd7qXiWcE/eLxFNY\noE5k+3ErvsOcWXx1cybDMOia3HQiypSgkxaAI/zNDnMOPwojiTnO5loIt3qPAsfxWmwODDc1yGKW\n2HxEY5KCpOPaGkvAzp9oLyfllQ7UsL/kfZVThUtC+IvXKiNIaV9Vo2AewCnxCxDRXQwnnaoELS+q\n+AHoRS840aI0EK32a61TvleNkq4yMSSn8kIrP/3WD+9d8N5HHtD7Dfve0PseVuvbDuju6n9bkMcl\nad997jwlNppZ+kVoiESGD9eRDQDwQzG6HabBk3RUGnQo2jDrexuAbO63b3DCV9+Gi8gVqJpTLvmq\nmF96RZrAiH4T2/tP1527K23bcUrQ0BDZCIm/algHaJReFCaR/Toy/IOTKekT4Ylxl13MqCJUTLct\nW1vujZqCOFaOKMvf+uplI9nLhNirZtmdSBa1iykdZ0LHdG1tJf+VOxJ/AhaOVV46SYenyvtm38C5\nbphuZQ31feqVLn0VM2RdLhseHq7Y9/fw0fc/iv0rbni4NOz7jjG4HXfgDfPZ9YGd21jVjUCZtC4s\n3Gllc+lVCN/iKgQYRtyDhqjdwny7Ah12WJbCogGH2wja6JA2wKPwmipELWUXPOaAiA8gTQkIfgeo\np9kX8ezBwHUTXDcLGYYyBiDdoqpaIgIRrSmYgiwZ92xxQcGtGesSLuclwnYJxZxOuAUju1KfC6LX\ncnPmgtUoqZNA9AbECJ7hACP4mgazea68Ypbde2xrIemyYywB4qHmwVnPVbRDu6413Pdp1sn/IFXO\nJf8d7uOPryKORL+wJP+5teaEf0Hv7+FjH92B0fHew8UMbN3TXY+OL3zhDX7zCxtue8fuRsB9t+AX\nFVubA0b4Sj2ZRE/CH4Aw5bZTZ0j1Euhkpx5k30cT07C7aRuy0efOFCm+j4A5A5YVaPilyzzz/ibA\npQGXJrhutj8AwETwWigsJacT/YHMz6EV6vikQWZ/Dpqk8p8k+gwitXmRsqyZe5AMypjAKrEtWCnm\npEyK8JnaPTKB6M3LxNmrSnwOSKdrhdPKQgCllk0YnXRPaUFkIHl11TWe7S0rnc1hbeze/YKME9Gj\nuOdi4UMhrAUJbC2+XTZcrle8NxSj79Cx43oR9HGNwyxvvVu9h4sTvp2Cc7sZ8YdBjjnvtPshHXZP\nZaTEd8Jnz8wIaRitXTF2BboAG9BwdQL3a3GcFhmKEX6L9j2pRy/6Pi33rp1UiZes3RmVn/RjgUzO\nZGRg23huQeoNETbLd6jaeX8zyTi8HBsl5f25XroUXXCJioVrTmkoRMzlIUeg90Xi/amZeKfCwK/w\n/Z5TuxpL2OoOfgnxv5rEr1NahpufMosrs503MdBgNw9vFcBHt98HIf2XlZWspyKx8s86lFRVDhXf\ncbjoYIiwbQ3X68WQd7wH0R23q1h8++i49Rv2vuP6sOG929VVfctl9+gprYZvcb3dbDlAZqC+6FaM\nTLYxxGPIiUk8tJNagkB3hbaBrall6hXNM1IaXDWzdjcZ2Dxk2IjCt6yGLltV0zkXgc1JMkRzbXpE\n3z5gB2wOXEqEj5Kh0QgARh9YUNOq+AVGHOXNJPyfK9VNV7ePVAFHDSqdC5rvFZvpKTxXJIlaOQ6r\nXKNCbazNV58vk/bACwlfRP4YgP/I3/1zAH4AwMcA/ASAbwHwKwC+R1U/f/o8/w3xVj4gkc5KYJUA\nVHHC6IeZ0BdleWIK4sCYb69TVCUAa8z9sMCiI8PhI9kfg3q1CRV5n8MuqmUFIxz5HVewbQK9bhhj\nw+gXC3n1E2jbrmjd6lyvW5xme9sHHm6Wz673HX3vePOm4XIBHm92pFVXBtb6P3bAumllKhYX4Sft\nmCHN7APdOfHYBDqan25LBpA6r0oaAkN/ELgxayzzIeAioDL9oSa7u6cgu+2Wl2DbdqvTBP3aoLqh\nbotVTYk/baJJEM4wDwydJf5TRZwwA/eKxLePFM3FgFnDCgI96CHwOaq4MiHWJAlnTpWq/tPKaC3P\nEr6IfBOAPwzg96jqo4j8BIDvBfAvA/gZVf2TIvJDAH4EwA+ftrFKX/Uww0Jg9dv6dAnzm/QE72Bh\nz0SxqvqUlhST/zeZS04TmQvmy6l6LJf05HuisjciM9FrvPjYySQF76f4XvZNsF0bVDZDqKFQsf2u\n27bhqs3y8+nAw1Dsu32GJ+t8uAreXIHHm+DNTbCPhq4eVusbZbAL0OwsP1Xm9TPVGmqWefr+VT2A\nn7vjOD/NZJO4xjN862s4Ey7qW4BtnENaBOskE7DmIuJ/KG7d8g6+eXODyM0SjGyCMTbkBiEB931k\njH7SoqB6XlZSWZHlhMMHjB0XhWHj1e+fOJhSQ2J1M72OMSph2Ycvf8q7CvEHzackXPAme/hceamq\nvwH4mBirfh/Ar8EI/Tv8/p8D8Ndxl/ArTzWkTssmr64dJhqctbG629IdmLVLM+XZ1C94sWoax9CH\nw7JsqqDzzcVQk7hTiJ5XtDYlMcDIzc7e+g63thmBAz2WBbH1zaVbV8GmDX0oLlfbytt7w9gbLpvi\negHe3ATXXXDrF3S1k2vRPUJwb8BuklyHYN8VW7PU13036Z07yzr6uJlko2bmW3vpa+bJNhGi5OkY\nnOSLlF+kvXg8u2tOwwOTbnvH4+MNrT36xqKGMa7IWcYk5aFlqRUTPsN4wphKSzoBcGbwRMZKyCvd\nuUvPY9WKy3oumfJ7LlXzKeiBYDKC3DexPP4SjeVZwlfVfyAifwrArwL4fwH8NVX9GRH5BlX9tNf5\ndRH5+nttpMSfBzkLWypgJ8Tnn9y3Bxzn63y4Va5OysFUo8pq10bUAfwyBnpSnn+QuGjwa87NuenG\nEdfXw1zz2+l4ZuQBNlgeQ5N4sc142Gc0wdYs4WaTKy4bcO0Ne7/kefejZ8rrvWHsEjvn+u5GwltH\nvw2Mnaf4qG+k2SPxhgJmIxBYmG1dwJa/JpFHrMWNPnOi6xl3weB9h8rYB26yo8kO8Q07NBbSHhB2\nCzJbXaThPeSSVZjk/SkOCDNRJjMvSrrWuouLkFGr8LBePqu1xZjR6Z1n5Rm95W55iar/VQC+G7aW\n/zyAvygif+ikL3cx/e996nMOCuCrvuJ9fOVve9+fIJ+vXdcEltYFANdI59L+3stTxvt/QhaUCDsR\nv86oeuxduV4BTEvuCyBQ5FP2U1x15D3NNnm/NWN/CktTtbkp3ZJtihO++g4vi31Ha9AGbO2C67Xh\nYVzQ9WrZe7kfoMPi/3eB7rZvQLsf2hGE3/0wj4wdePP46P7+sk4VicjDyJQc1MU5VniObe/zCChB\n2IYLixgX0HfFo+4QuWG7NPT9YgyP5KeuSRTiD8J1Lht7BCbMSjypiBMwLmoA95rE5iVl92bAx3Lu\nTKDX6CVdHyoXJEaWL1ywh/v9FcA//I3P4rOf+SxeUl6i6n8XgE+o6ucAQET+CoDfB+DTlPoi8o0A\nPnOvgW/9lq/Frmo7xwaw99l1wuCRUYgnLKBEgiYhFYkg/MQ+ZI8cMbex8uYs9r1I+ddyAuS9gFVh\nAjN8KE0Kdy6W6LQROFAK0Ag2JfP3t4WEI1IF0Y+Q+pyssFx7a43ji/icYnTypQKkoSmwqWCgYejF\nj6gCvWVQz9PHLfWW6NPy4g3/cA395vaIN49v0EeP+WZ7Nioxut6p2ztTgu0fIJEGIkd4tbkI7Fh0\nd9+qexuGYh87mtxwfbjk4aEFqBVOZEKAZ3hUwkB8i4T41mmZ8INhtQDV6Fnea1GvLXTAmQGIgzCV\nawlTTwbl2tzaLv/T+gvlL0VWkH3iHBRf83Vfi6/9uq8JIfdLv/hLuFdeQvi/CuDbReQjAN4A+E4A\nfxPAPwbw/QD+BIDvA/BT9xpo9FEW/GWZaJJGGsaskyAkz3mjESQ1yfKbax6Fb2nFISnBpBkImW5x\ns5CY7xA9f09+9+KiY2SWYH1YEogRTZbSPJmU+GOJJCm91BP3pqUayB2J2gStS2wPDUs7gIsIbGkA\nv+/74YfEjjlLqy22TvdY+NEHtPs5eL1H3x73N3hzu1p6rK7oXfF467jtFr47umJ/9PRgmrBvyjgM\net9zsoQ7iGDaQlNBU0sg2rR5mrEdkIaH/cH27OsROoyVIL7Yjj9nkkS6/JPu4slaXsR6BSSZr5T6\nA7HehiYTr9JJA08K7oSQyDGEUGFYdPTHtUAoeI5hdqsykXU+zstL1vh/Q0T+EoC/A+Dmf38cwFcA\n+EkR+UEAnwTwPU+0kQLL/zvCq3KxYuUECid3QimqOooxjPX18KOokXzdQc/iuw56mf95ekLpJxBS\n/wsBUF/LXKRNPGKOSUq1md9aJPdzkyE2ZpYZ0NHAsydDKVKXdJKeDBVlFm2T8A3AEOjGVDsaJ97w\nexyl5SR76Yrrnnn/elfcbgOP+0B3T8B+UeybeQOMGXa07Q1as2Ceps1Taofq5sTP8VmHdcD3B4B5\n0wu+JKONds7ACmqGWAQJCdjdczSbv8hiptO7lIAsG3VApg6ataPmSXMaiV8EmbAjhnun8NZpF++U\nF1n1VfWPA/jjy+XPwZYBzz9PYgamDwdUXS81AmLit9zJBJyOUClEp3uyXPggU/PBSnatdvLoq7j7\nvAuMJoJhO1wQkY4MnlEyL4nz5IcS3ZuluCq9aOouNJD1NXD1OxSQrunHN6ucaVse3y8uoQXqQT6b\nPS0Dlw5cO+J4rd6Bm8cI3DxT0H4B9guglpcDqrvPSbe4hNGtp04oadjjtttUiUcncBVT6uiiUVHS\n5u7EhElqjnluYCsMIJoLKfyykuznANH4qNZrWv6WdibK/uB4WlH/zO+1llfblptx1bmW5VZRr4TJ\n6CGuEp8Rj7LS07yuAmXiCSfMXIETCJ61m5UiiEPmYA3Rs16/kAVQ268uCLFA5aZm1RekqhnOSdd8\nNjEFkYm9mWHQPBV0ZDpheztMdWNaRgtJ33xlIUXCekgNtgFchuUGIOFfrorrTXG7KPbLwL4l4VuO\nvhuG7ui6h21hHxtELzBUvABoENlACTwtaTi/y7LPryKkbBB9UYEp3YNB5BRX5RI+1HzjOSSFFVHf\nU9flRRM50HlqttwZOR8wU6rFn6LJTNrwuhx5GdN4nUQckWQBoMErVz4lWw0Uh8w1T44jW5IFelSS\nkvifCWhkxQN3OHJnKY9kBNesXVTe/hKi1/pyNuVWfEr/hs3y46lAWzOpKT2IPmLiYQYoAG68yg6L\np75usA01EeI+AJWG0Zoh4shAvKZ1zB0qG7oKdoWH/5px77ID/aK4Xoz4u0t8EvkYgq439NHRh530\n08aGvW9Q2AdMtaKemXmYrm8n/tp+fMurTy3J5yi8NYVhFB2ZS4EE7+zlWe1A9XOU6ymQpN6nknIC\nczKKfLLEGGBC3UMfVlke338LCuwrEb5Oc2N/NT7JzW0yxKU93XRmDDPCZrJIdRVKiuWUal7lAZUD\nZ4fWHlJKe9/ieVmgUikofwYwtCLPXSsCJ2VqN6LPpokq7UuDNIXqxQgBXPdvsR5vaqkymw/CxjMQ\nGSud8KFGzc1dQQyf1+aE7+toqcTvJ+JaGI+tzxtaWPl1AONiqbv2y8DDVdF3YH/wLMADGKNZ+K0K\nxrhi6I69N+y7rfVHPTfRQ15V4cZFdY2l4b2HBzw8XHF9uGDbtrDcE158bjqFh1K+suiFz1oa+COZ\nB7zyLfnXkebA4DXfJgcjYSV6dZfloeXod7ZH1Eif2GSQ1Cre3gZVXzSTF2ghdKFFOjkCs9YKTAJB\n7Jjn3IFUeWaQJ4gw4sawmkY7hLkeAZomr4IAJ9lXTgm4UjaBJ8st36LpSkxuD49WGcgyMDzklHHz\n2ZK7+VQgHp0jalQp8JNmqHlQNabGpE7B3tGhlj/PEl24UXCzGRptg26bx8oaM2zDLeye7rv7hpeB\nHQ0Xg4VLVmU24Gsa/HgqrhHh5iHH79kuwbFj74K9A8P32QPMGb8Z8YPuRU8Ntisu1wve/9hH8P77\n7+N6fQimZDDwcGOfRnr70s6RgWCpo82/VsKX6btrrJMCkIw14AxjUmQo9rBiTchp9O7eByWjQCH4\npQOFfdE4qWf3cLJ0KOUVz86jdCbJulpfiJ8hnnm8tAY8IoQzGEC2y0I/sDoDSCbJtr3e0ruqoAeD\nOtysBsjT13tHU9JLqcrVdW0iNB73yw9a1IlcU3ZBxrvSQ2GpMNAUZvU3AhF1+zftI3TS++/mhGre\n/G7POQMaW4NuW3HpCdoQO4/P89bLsE0zDRtULjkJCpDaIlGo5ncj/AtEroB8xBjd6Ogd2Lsd8NFd\n6jXZ0HwdIrqFe7bvA/3W0dqG9z76Hj7ykfdwvVwmiW+MwogoThMqUjKNqCnlw16wCIoJVqEOFiFW\nNcCFsZsBthIflwazul/fYt4uIjy1XSobhQNo1q/6fmVib4dxbyJUl0KuX8ZUcwxxDkbMYBlcMoKz\nUgMbAiS+zAipf/LUSsHn9fJeHVbqCnlN7j3wVNFZgaAaV6296cGS6Y1UJ+2WM4RQLZxTlrgBomBu\nH7WFSWsbhmyubdn+mwigcYqxUFOTKEc3t0X+0M3I5csYw0+9tXW6iLpRsFmqrq5oqtjUWF4TW0ZA\nSfzWod4UfdvQmmUmYrbdnHmEik1v0Qqwp8mhFiEfLxOfc5ga3ZkWV6AYSwyyFQUyQTkAABssSURB\nVHZVsoF430z09/B2xrFZZxXM2HGvvE7OPWI1HBiF6CWMfYX4JbkjiV7KaDOwoQywzBAnqvBjRPWX\nEuKLBkbgGZJUbWFW1F9YXFLY/xy3y5awqvswQjJoILsI3M+vbu8qe93CY0JNAKCPPrQtRj4CGVMA\nKqz+ePMAnHLiUbbP0TZ3Qdqg+uiekHOEpOSJP6J2ys6mfoIv1V0IxHcABmPb/OBf2XC5Xgrhc45o\n3LO5NHMGE10kvbGv0/oYC2oEaCmo7DNpcRXB0nqdpCylsenvWpI1VBlZ+YKWMSQPz96Ep+yF+P1K\nEt8lReCq5oRyJAJUaU2aCuZ4MndTlpMCkYlJxJwmylVLb4jaF4+lcPza0eBazDBTnjkqFXGNjM/S\nYGeoqAGyFalFdSjnx8bqbjrPyy91nloZXsyvKwB0+LmqLwC6bIBLfBsqmQTbNbhZdCVfIzlen2fL\nlFSPQBcgTujJawJBU4W2kf0MYqJG4mqrr9+3YafeXK5+iEdoRZIwAVfiy7yTKpYQXSNyY0ZwW8YK\nriTIM8oip7GPFKIMz0HRXs9sTZzLmBlG6ikN3skckmlJ6Ss1sdW/dF5eSeKjsr+UvMWNZ9dTZzLk\nrhQj4aKKCjCApfs/FappM8bi65xwAQcceHLSVqVBAGgFyrKlT5ZPDHO9F9104vfcg8IxUgR7HhZV\nrlN91E1dWiqT5/hmHT10mO8R9aPNQFKkUZR9KumqdSSBiCcOi3mv7Tvh03aggG0lhgcFpvHR+j4W\ndyE83LoehOKGMt0gsKPGeHIPjWXJ6VMuU4zkyp3M+gjXCSti3gsop7FO3LT2/DAn+Vfit5a/+Ure\nb9FcjEAVq3bi3VzanrWzp8qrSXxOVlo1M+HjKfXNX+6XwjPWpwx5U9WbpnrV6+6+myghmNCjLHBf\nrDDoDHhZkITfyAS4W48BQVJrk3idcJuY37su62vPJwYbvDQNSvU/u6Vp+CIrjblMJkcrtHXHJR74\nHLmKephwagxwqSawXYfB7tWicm2uXM33rL6CDQ0XiLiK3wT15MI8rakQrVKa5yEdDA+AWlIQ869L\nAIV1zkHocNCKAk7wuswv4wsklYwD2oVKOmMC3/XiUt3aL3js9ZJtkuhBm/3IT4i8Un8mX6BK1XuF\ngC01k/cfp5Xt3xECVuvsRrgLVo5f/84l+qIzAjAOgfdnXYG4IcuDtFD7sz49LWIBsisVgVMCU9rS\nyWWeED4TG6r8HWbIy6VaMojmSpojm45QUfms/WXMAdf+jBqiRV2R+eHV9hCUzS5m7NssgAkXYwhh\n1DNBkrrJ+kkXJwk+5JAO3yuwSnBdgXEKF14fWok08YoEH/0UMr7SXgB+xu05g/AzeD+Vt0ni2y4Q\n+y6mKvIAxlMnmwp41lPaKRtyA0fWnzKXqlqgR6GT5CmEeO3XzIkDmCdGH7KqjLuZuXRKVe+HU12u\nc8l8joCh1ZrtVNaha+9kAe3yw3zgKQW5TZmtpXmQkt6JvsQapLKcTAXeRRIqI+xI9Plxza4GvIi7\ntgJuCuW5fGCwVs4Ro1fFJWbDhk1MzechapxH21+UjFAh7r8v7fm/9eRdzpufDhDaCcdLOCtyPT2c\nIUYzRZsoMw6RZEI2PjnanQqEgdolif40KEbgu+O6IDxfBw0O8pz8ifI6h2bCgkQhw63HzKZm3yPp\noxKoHpOuLQhexI6YEt9mK8J7Gxi0ga4W1NI03SixdkrJXy4k3RQubPjpCApxf3T02KRrSD0p/MRz\nCiCz4vC78R3jSE1yBxYNMvHmYuOYeIaIb/WWvEHEU86xtWH9T6mqlTkWNYBEsorJaiDK4JPhcOMb\nyhZaACJqLjjmghUkwxGzxEvsJHRCEep/VVZz7qkNcOValyJJRQLBRu7ujGIolxOp+Pt2JHSFe0Q8\nwEsskClO5Cn4kl3xuIAhnn4MU6HET/oTZ/7D4WY7IMnozlSJZBo2xq1pIoFqXBc3AvPcQdWxaI2C\nWaU4L68UsrsgdvMAjwp2De+ycXYld+eAGdFFK6kRvrpmQL9tC8KkdEIwgSghPCn5UMS+BLITRcmm\nCODmxBTt1kkuNgwjyioTSEjrmnohfjZZCDGfrWqoE3DFJQEyGYQTSJ1/tci/dAcuUmKgSD4JO4O6\n5KqTqL7yFpikFxkhOYEaMpseC3p3NOa0z4NFvjcTaeSyhOG8sTIQAZppFJTOWjQte5cGfgXkrdO+\nP1+dOa1QQEwGbQCD4c3h6ZBk0uy745MZRM0oG2feRSFBr3qYuJZD2GYkKwR5eCpxwd25yRDZ+4Gn\nyqsZ98iEQiUSzMCgMagYdAhkqjAMNInfcnxVXTpIuXrskty5lSaxAxd/jo1GXTblow0f71qpDEBk\negeXygdaP7yDlfyiJHOx207JaPNzAHJJRQmrkbckeUZwRBDJrV3+Fr72OD2U+hxDML3sSuoI1CY0\n6gSTL4arbJuGzEKia/sCNCHDLiWHHJGg1IFS5WYPFRPrJr35fSlVtUxVhuX66NRtDYJoM+fB8V0k\nhOTEgJZ5fRoL2cET4ijllYx7DfTj2uQlB56FFQHXELnWsEgkJNLFtXWMXFPhgC5rxcPPnNTy0kDg\npbXp3Sndbe4VES9/6OadHpGtO4ZJtVSeQp9qds5d3qqo4yRW+mrtUv+UkDSyQIPdMcZd+80NUZK/\npj0O3pfVE5Ato0FKnhlD2GqIldIvwNXtMqK0PcwESPgnuyizXxga194z0ZMouSkJvpRKyRyCoeBE\nYEswBo0wcdGBJsixToLA510o7BJESQ/Pq+4VLija4L3yepF7AArlFuMbfb70Ibv66DH3E5EHpL0B\nLaJpFmXl81QJ/WyquvpNaytlJTXfPLzK+3SqKWTfglEE8eoMu3hckKE2rE/toC5P+O7alRRFQtHk\n7xNu/WXEXxCOLtPa4EfnujCRU08syhhipiYBlIY5m2caI6v9QBOukv2j9K9hsGRayjVwzvxSZxWC\nhfA4R2egIowmQmUXOefWTxWFHDS7bEUA8HgtDW7iDMKNm2SNPkEoa4jEuuDpBf+13ni+vF6sfoyB\ndmoJCWHEb0csUu3haaxDKwI8/6IkyaeJfibumbR5v/yM1lMRzSdPge0Im8Sq2a7PgwLh4lzfX3Ew\n+JJWiTw/Mm39rHiggaXTAyKwdNjUe6Ugr7D+2i8p8yG5no1O1LoKahAqaxu2GYkjtVmiMVKzfzKn\n5YpWXBrS8Oa9KabG+rZqS6kzvWg2wPLksUxPyHG+U68oQqf69rVco/1jwAKiGpdkG3DAiXxPMDdJ\nWsnx4S7zWsvrRe4Fx0twKAfhJk9eY6n9n20Ea9uplkL0Dtie6FyRrKsbKqKKo9qx9afnmdK1XnIV\ncG1q4UMTbh3UNy5nwj8QOsTUZEwM7zVnFJRY5SNm4KJvrjIs1olQXQbvsDqchIVajASi5zikSC5/\nUL1PYYySeCY3+/j1siwpfhFjWAi7JNEA5U3l/UediFMbhFuQLRit5q48wi4wbSw6bZnuqT9RyccY\nmhzqy6tiXHs+M1ksN6ffNQbgvLwO4dcJKHw4EjsSlCUwJoARxKgJEC+LsoYAhf/zIiXhpOjJrN21\nBfr7YvX3Am5bkWTeZnxWc5Ys8WdCbKr6Guvg80K2JTFHgcnOCLiTVCmtpx5XxJeZ+MH1OUOLz3tB\n78xwa7TNnK2p2RHOdWu+FVgweSFS1ZdgbJOaf8C3l5SiVjOmAa4ZPqc9+jMVWie6UnznOw66RjD3\nApT6Es1Nbff7QqnxdJ9fKYBnBDCMtzf30VPiS6iqdPnwO5DM4qANVEhzGoXSghWQ3Ly4DK19jT6c\nTVOk1BKgkgHbncgidD2Z2p/6W9v2Plav2vncJSIkAqVudLZZYyoyo759b+U7LfNCHyiOav6c1CHf\n6P8p55tRcNUMNqan2H5dktmzmSwkd2qK23p8nNqC2dTQLkBM2iuJXudtIJMGNbHLIHD2xYBxInIV\nk9S+R1a5VYMwcwYpM/wqE04mNRN9ZQvzswswqIJEz54XQK+Wcw8xaQSbhWGqM4VI5zy8IuPOK+/m\nOvQwhQhjlMRHCvEbgKvFdd70QGkD1BmrEx/IV65zfsNnvDwpwuAZ9oHreld2Fo/lndlDINA8GzkL\nUmzhgiW2HwjDFesXg1El4eSchoDRJizMdpoyJudQqvt8X1KIOOOkwhYu2upaLHhBak2HBJkEPITX\nBEZTiUQahG0kBk2gxPkDBSLhAWlBkNRcFqCW3+mOnRc/UaTyl3wftzS3GPkR0Hll4VJ+rWL7qr1w\nqXeq2r4dEr+uj2T+T53DEljQSeoDKBJitvIfhisgyw/Dz5qTLLtUtzrapJ4aVKY+LMMq/4n/nn3L\nM6A1nvGnnSDpR64b+yh0q87QiKBkbijIUCzd6+o85qNIGZsDmeeAVuoVkTyvf5X8MxTZF1+r+8Kf\nYbgZkmwwjLV6KFAF6bkGd+ZNyyYJtIFpsX00ztBlaIQMixMq6VXK2IBqDnP8IwOa4J/LzQWA8TWj\nLFPKxpD8nZXVydJUxagj6SajqfoWaT3uF+Gm9dZdQWLllfz4LJWY/Z+K9EWUTkSiSSyxnn1yAT97\nXOOVIrP6XZjldDLOE+VA/AR2NQoSk0rEXBC3JsMIVlA2qcQjwQBcoj3Rh/s9JdbfH8UagZavX2A1\n8eEkGhr3yKkiE1CZi1DcGJ/hOfKUUr5Gvkzd887H7UKwTvgDR3atQfTuOotw3NpqITuFe1fuWATC\n8Lxe93mi3Do+iKIHRVDWVDe4ZiBiwf3KRuqcHqX/WuHtMO5BizTLwZhhi5iTqhIHPtUnhdVJWlwq\n6zvzxyL5oxAEqwolByjee9qgXiO+KiezvxXYOVJnNFwPC5b1YUp90kelYSmfVShNHRaAVt7oX1jc\nvTdkgPyy4FtF+nUPRMQEVHsIYVTCZjlAHpOlICOuNoBK/BJwiwMvg8EkEQMeohvGzSSaiXRKfQFD\nZTyiVHR2h07FdUE92oLqEWrQfJvgyMDr12pDFEhofqyTWapqQzlL+ZHp2vS6t0Xi2xh0njlyw9Bb\niZ1erxibqto3ieoy6joprHseLvuyEpP5pHZBifTB3mE4PMuJyUXklQ52tifaY6DJQd174vnzJA/e\nL3XiRNYRcK0685ba0RjV5ApxOIZRg100DaDu0b9bijWf/LWQU84CJf1E+oFtpeeJbkcQs15pQcuT\nQfMaMml9cpqLeBvxuGCrYKXvKgWW/t8p9YXPrO+B1zLuxb9a2KF9YjVaid/rT+v0kzV2bT+Rr/K/\nL0KRI6dfbk/x6C8puvwSSak4EZN/C4Fwj7kUZnkWeHSvc9NpvyfqpFeaiKJ5fzC9JqW0Ynl/RFfC\n4jVAqa/JdGLPQE5krPFBzUDjHQtv9PlXhK3A5+EQo38YZbm2EP80I3Ve+SokOI4sZpkC/nIY67yu\nDaEo68CWtu5idt3SzME8g4yvmIgj1+tUb+eV7vD4aW7STQR4SdGCfLEWLCr+aswjaBlNGP1cEXd+\nSXw5SIGCHOfLivk5riiraYxvJ6LI9Ld0QAuA1cZen5sMnEColBJDc8+55/SbTH5BAMcxRGKMaEXK\nlHG504Kv081ndMkOSU6xZLz77Mo6sj9/IB6nMKkx8aFqh7AoQscZWKzWiyU/9gTk9KZNwF1xDb6k\nKKAg8RN6cbdoXUMKZAstaszxbLMK/hLELNNz2UCtXKdKAx5PlVcL2TVtzwGl3JKb3HL4Pn1tALRD\nATTxXeZPEP+quIXVn3ngD+v7mavq1Arr6lRn+ju9XKuwjYoZdEQk1UCag/LJ7caBaMtHgDmyLd9N\npmXIT+mIWSoWIkz2KMEUZsvyHYLDLH1btCSIAzy01PF/lTvosmMxV8fpXIl+7sfsyuW4KS1zMw0E\neRCmCEb0QUvzJNUqCE7kqY+neUoMixUofiXF0gZ7hhAEAmCIxjbb1Xek/mppgtgvMeHfMidxuyLJ\nWp4meuCVU29VMpsCVwq3UikDqmt+yUm6VyaCAnBm1AvV/KmGantBIMf3LCyi3H9u4g899ctLrBwR\ny5FVsvPx9gn0ktfj90RHkhoKqaAwm2Aa97oc/CQbXkl1VsXn7xGkVefHpW0Kr9nmcKY9Va1JZTbo\nRe/Kc8lyV4gFG6w6T9xzZST7D0xGVoORBqJwSWLS35OxOKnrPNXTPGf05okRfOrywhQTzWewvTUS\nH0CRfYVXSSJ2ZaORDaISf6mToWIfSi9fUgwe90gfeOrW6XtDQ/MHCyEkcdlhFBHCLFbflkgVqZYB\nPTNVk8yPedVJa6QilDw6G54JJF97Tx5VgHLZEfI+mNx5Xyv55mckrpTmQ2maNr3kTYWWvPyLLUfm\nXgLuUnXeu+44NaIX560JP2pjCoR3Ip8KELrAq65Pr+ccgxrdIQ7mbKJegHuvuzuPZL9KIQK6aAWT\nxD/7AEs76wXcoYTny/SIHp+WerP0uC4T0nYwE/Fpx+dsEBMhVDecuM87PG6nRK3T95SB61uLCKI6\nXAX0Msazecg1dfZ56kHp58xc2L4TC8Qlosb9Nebi3giJVRPe1GmWlNz3PHYzWh39ANWwHCHBWD37\n9cr9fotW/aMwbIG7JQHU5YRUxkjRLiHmJb9GP/TeQEt5xbPzEjiHaeEoLXNiuV5G5cgg9Zn6l7rU\nUT1Yfp+V5Z4U3HkB9wz30mQln/UbW+cjpmHm2/7UnYmpQSDTvehb9j2kzTo/lKQo6242UxSoZDLZ\npwMB3pXGZ7eW+V9U+5CUJAVyoIM002kC3DI0kSlfkZiW75whY9+Y8CWMe1Pr2RfOCYOdAicIS01Q\nZCy/X5EKu9kIOb2PDCEmJg2EfGplrHOKMr+nZHJPE/8rufOI+HoCAARhx3citTMDSoD01h1kCx8u\nn/V3va4nz+SdSkunOB/ilmhxxtASM3T6SQDm0VCV0yjZ/0lP2a+0QMtE/1o2utR5Eqkz4NdIX+7t\nIHITV8nMxoEbLRFsktMRUulQKtG3Sg8lZigt+0eDLN9LbercgXactSR6ySkuTIG1ZG0AhFvMjOQa\nvtYhgnBuw9B5mIMT3JfsF4me5wTEssIFyhTyW77UvJLxJpVTKNTSnrn/RSmLCcrLSoxPFAGO2610\nmQnO0henz4f3e3lKlVvk08mo73RO159FRU9uh7pP4Yy/hVtI7s2rTn9eMlcrEdZHp/EtrzuDOAoR\nFd1i+veeK3SKkjuww7KZRTEZxs+GShlc35RSf33/yvmrE3bW2Mhr5/0h2ZFnsT3Urtlms3qCbJ5a\nzONsDGUzT9PVqxD+b/yj37yPCJxwOevqSugk9qcw9gWM5AXlk5/4+NMVVsw/6dIZH5qAWHhXxpef\ntVXUnxV9/OcnP/HxxLx1R0jtruLYxgtKjXVf21xvHLQUACtZCYBf+cT/iZCpsWY9Ev8cGstG67W8\nXtt/cjwn9VKrtLHOmXnt/v/9uX8Yz1Utal26TUKAWkFRxu53jGzJ8GdI5vvLOi0Y1Zlm9BLYvgrh\nf/bzXwBQgKaIfdWTX0/LpEWmHitnMifXzKWdqP1bYwCf/PjHU6Usf1GQYX5b8v5ckzEASZf++hxQ\n6umRMLKkFCBh62T7sKd+5f86YVRs8FQ813ZLvPhiV4l3lr4Yncn87KSd8A9HVRlWkscnP/HxILSE\nO6bvWom9JMhgV4GcX3HVW3RuZ13Bn5ZpXuepD4xT4HOf+1z+KJ94l87EP79fiuJaGFaUWb7HEe+F\nRBZOlW8oa/2XYP6rxurPP0joNrIw4BepJ8EgUESj/bMm5Yg5kTrl/3Q9rcE38U9Ik7ld0tVxtGeq\nwFyTa/z4r6oI6sprCXm9N6Z1rXtUa9cez72fpVpFMAlUBCqe1jnWpMnJmpy2jKl+qTOz9rMBVAkv\nkAoXfqsAKESVgTZJCU9hhHrdFWqV6KOViYGvVg3H6xBi9XQIndbfwWdRh5Eznt/u5wCa805kredY\n3Stvy0USUEHws3Iuu4+A17j/W5Pw90tyZb49kGmlsKqC4j77uU+MPhI9qzVxvvhdZ+AFXpy1s1NZ\nNZn1XoaZ1qac+PlyCn/MGZMq0a9IaS2c9EnvzJ8+M9azUNZTlXj+fY+4FtGyXD9rdVb76901cu+L\ng7Uz8d8fR3niJXvQf0tdenK71bvyrrwrH2bRO079D53w35V35V15+8qrGPfelXflXXm7yjvCf1fe\nlS/D8qETvoj8ARH5RRH5ZRH5oQ/7fR+0iMg3i8jPisjPi8jPicgf8etfLSJ/TUR+SUT+JxH5yi91\nX2sRkSYif1tEftp/v+39/UoR+Ysi8vd8rv+N/x/0+Y+JyN8Vkf9DRP6CiDy87X1+aflQCV8s1cp/\nDeDfBfCtAL5XRH7Ph/nOf4qyA/hPVfVbAfybAP4T7+MPA/gZVf3dAH4WwI98Cft4Vv4ogF8ov9/2\n/v4YgL+qqv8SgN8L4BfxFvdZRL4JwB8G8G2q+q/CPGDfi7e4zx+oRH6yD+ED4NsB/I/l9w8D+KEP\n851fhD7/9wC+C4aY3+DXvhHAL36p+1b6+M0A/mcA/zaAn/Zrb3N/fzuAj59cf5v7/E0APgngq2FE\n/9NvO158kM+Hrer/swA+VX7/fb/2VhYR+ecB/GsA/lcYcD8NAKr66wC+/kvXs0P5rwD855gdyW9z\nf38ngM+KyJ/15cmPi8hH8Rb3WVX/AYA/BeBXAfwagM+r6s/gLe7zBynvjHteROS3AfhLAP6oqv5j\nHKMz3gq/p4j8ewA+rar/G54PRntbygXAtwH406r6bQD+CUz7eyvnGABE5KsAfDeAb4FJ/4+JyB/C\nW9znD1I+bML/NQC/o/z+Zr/2VhURucCI/s+r6k/55U+LyDf4/W8E8JkvVf+W8vsB/EER+QSA/w7A\nvyMifx7Ar7+l/QVM0/uUqv4t//2XYYzgbZ1jwNT6T6jq51S1A/grAH4f3u4+v7h82IT/NwH8iyLy\nLSLyAOA/gK2V3rby3wL4BVX9sXLtpwF8v3//PgA/tT70pSiq+qOq+jtU9V+AzefPqup/COB/wFvY\nXwBw1fhTIvK7/NJ3Avh5vKVz7OVXAXy7iHxEbAvcd8KMqW9zn19cXiNk9w/ALLoNwH+jqv/lh/rC\nD1hE5PcD+F8A/Bxy68WPAvgbAH4SwD8HM/J8j6r+P1+qfp4VEfkOAP+Zqv5BEfkavMX9FZHfC+DP\nALgC+ASAHwCw4e3u838BY643AH8HwH8M4CvwFvf5peVdyO678q58GZZ3xr135V35MizvCP9deVe+\nDMs7wn9X3pUvw/KO8N+Vd+XLsLwj/HflXfkyLO8I/115V74MyzvCf1felS/D8o7w35V35cuw/H/e\nbwJEQs2BqQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fb7c8eb1350>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(img)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
nkmk/python-snippets | notebook/numpy_flip_image.ipynb | 1 | 1762 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"from PIL import Image"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'numpy.ndarray'>\n"
]
}
],
"source": [
"img = np.array(Image.open('data/src/lena.jpg'))\n",
"print(type(img))"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(225, 400, 3)\n"
]
}
],
"source": [
"print(img.shape)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"Image.fromarray(np.flipud(img)).save('data/dst/lena_np_flipud.jpg')"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"Image.fromarray(np.fliplr(img)).save('data/dst/lena_np_fliplr.jpg')"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"Image.fromarray(np.flip(img, (0, 1))).save('data/dst/lena_np_flip_ud_lr.jpg')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
RTHMaK/RPGOne | scipy-2017-sklearn-master/notebooks/09 Review of Scikit-learn API.ipynb | 3 | 5524 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%load_ext watermark\n",
"%watermark -d -u -a 'Andreas Mueller, Kyle Kastner, Sebastian Raschka'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# SciPy 2016 Scikit-learn Tutorial"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# A recap on Scikit-learn's estimator interface"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Scikit-learn strives to have a uniform interface across all methods. Given a scikit-learn *estimator*\n",
"object named `model`, the following methods are available (not all for each model):\n",
"\n",
"- Available in **all Estimators**\n",
" + `model.fit()` : fit training data. For supervised learning applications,\n",
" this accepts two arguments: the data `X` and the labels `y` (e.g. `model.fit(X, y)`).\n",
" For unsupervised learning applications, `fit` takes only a single argument,\n",
" the data `X` (e.g. `model.fit(X)`).\n",
"- Available in **supervised estimators**\n",
" + `model.predict()` : given a trained model, predict the label of a new set of data.\n",
" This method accepts one argument, the new data `X_new` (e.g. `model.predict(X_new)`),\n",
" and returns the learned label for each object in the array.\n",
" + `model.predict_proba()` : For classification problems, some estimators also provide\n",
" this method, which returns the probability that a new observation has each categorical label.\n",
" In this case, the label with the highest probability is returned by `model.predict()`.\n",
" + `model.decision_function()` : For classification problems, some estimators provide an uncertainty estimate that is not a probability. For binary classification, a decision_function >= 0 means the positive class will be predicted, while < 0 means the negative class.\n",
" + `model.score()` : for classification or regression problems, most (all?) estimators implement\n",
" a score method. Scores are between 0 and 1, with a larger score indicating a better fit. For classifiers, the `score` method computes the prediction accuracy. For regressors, `score` computes the coefficient of determination (R<sup>2</sup>) of the prediction.\n",
" + `model.transform()` : For feature selection algorithms, this will reduce the dataset to the selected features. For some classification and regression models such as some linear models and random forests, this method reduces the dataset to the most informative features. These classification and regression models can therefore also be used as feature selection methods.\n",
" \n",
"- Available in **unsupervised estimators**\n",
" + `model.transform()` : given an unsupervised model, transform new data into the new basis.\n",
" This also accepts one argument `X_new`, and returns the new representation of the data based\n",
" on the unsupervised model.\n",
" + `model.fit_transform()` : some estimators implement this method,\n",
" which more efficiently performs a fit and a transform on the same input data.\n",
" + `model.predict()` : for clustering algorithms, the predict method will produce cluster labels for new data points. Not all clustering methods have this functionality.\n",
" + `model.predict_proba()` : Gaussian mixture models (GMMs) provide the probability for each point to be generated by a given mixture component.\n",
" + `model.score()` : Density models like KDE and GMMs provide the likelihood of the data under the model."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Apart from ``fit``, the two most important functions are arguably ``predict`` to produce a target variable (a ``y``) ``transform``, which produces a new representation of the data (an ``X``).\n",
"The following table shows for which class of models which function applies:\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<table>\n",
"<tr style=\"border:None; font-size:20px; padding:10px;\"><th>``model.predict``</th><th>``model.transform``</th></tr>\n",
"<tr style=\"border:None; font-size:20px; padding:10px;\"><td>Classification</td><td>Preprocessing</td></tr>\n",
"<tr style=\"border:None; font-size:20px; padding:10px;\"><td>Regression</td><td>Dimensionality Reduction</td></tr>\n",
"<tr style=\"border:None; font-size:20px; padding:10px;\"><td>Clustering</td><td>Feature Extraction</td></tr>\n",
"<tr style=\"border:None; font-size:20px; padding:10px;\"><td> </td><td>Feature Selection</td></tr>\n",
"\n",
"</table>\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
twosigma/beakerx | test/ipynb/groovy/accessible_URL_arguments.ipynb | 2 | 1081 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### http://{path}?bar=200&foo=300"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"beakerx.urlArg(\"bar\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"beakerx.urlArg(\"foo\")"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Groovy",
"language": "groovy",
"name": "groovy"
},
"language_info": {
"codemirror_mode": "groovy",
"file_extension": ".groovy",
"mimetype": "",
"name": "Groovy",
"nbconverter_exporter": "",
"version": "2.4.3"
},
"toc": {
"base_numbering": 1,
"nav_menu": {},
"number_sections": false,
"sideBar": false,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": false,
"toc_position": {},
"toc_section_display": false,
"toc_window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
bmilius-nmdp/check_glstring | docs/glstring_class.ipynb | 1 | 9625 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# glstring\n",
"## examples using the GlString class"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"gls = HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03^HLA-B*08:01+HLA-B*44:01/HLA-B*44:02^HLA-C*01:02^HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n",
"ver = 3.23.0\n"
]
}
],
"source": [
"from glstring.glstring import *\n",
"\n",
"gls = (\"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03^\"\n",
" \"HLA-B*08:01+HLA-B*44:01/HLA-B*44:02^\"\n",
" \"HLA-C*01:02^\"\n",
" \"HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\")\n",
"\n",
"ver = \"3.23.0\"\n",
"\n",
"print('gls =', gls)\n",
"print('ver =', ver)"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03^HLA-B*08:01+HLA-B*44:01/HLA-B*44:02^HLA-C*01:02^HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n"
]
}
],
"source": [
"g = GlString(gls, ver)\n",
"print(g.gls)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3.23.0\n"
]
}
],
"source": [
"print(g.ver)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"[GlString('HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03', '3.23.0'),\n",
" GlString('HLA-B*08:01+HLA-B*44:01/HLA-B*44:02', '3.23.0'),\n",
" GlString('HLA-C*01:02', '3.23.0'),\n",
" GlString('HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92', '3.23.0')]"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g.locus_blocks()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03\n",
"HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
"HLA-C*01:02\n",
"HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n"
]
}
],
"source": [
"for locus_block in g.locus_blocks():\n",
" print(locus_block.gls)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"'HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03'"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g.locus_blocks()[0].gls"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"'3.23.0'"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g.locus_blocks()[0].ver"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"[GlString('HLA-A*01:01/HLA-A*01:02+HLA-A*24:02', '3.23.0'),\n",
" GlString('HLA-A*01:03+HLA-A*24:03', '3.23.0'),\n",
" GlString('HLA-B*08:01+HLA-B*44:01/HLA-B*44:02', '3.23.0'),\n",
" GlString('HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92', '3.23.0')]"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g.genotypes()"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02\n",
"HLA-A*01:03+HLA-A*24:03\n",
"HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
"HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n"
]
}
],
"source": [
"for genotype in g.genotypes():\n",
" print(genotype.gls)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"----------------------------------------\n",
"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03\n",
" > HLA-A*01:01/HLA-A*01:02+HLA-A*24:02\n",
" > HLA-A*01:03+HLA-A*24:03\n",
"----------------------------------------\n",
"HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
" > HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
"----------------------------------------\n",
"HLA-C*01:02\n",
"----------------------------------------\n",
"HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n",
" > HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n"
]
}
],
"source": [
"for locus_block in g.locus_blocks():\n",
" print('-' * 40)\n",
" print(locus_block.gls)\n",
" for genotype in locus_block.genotypes():\n",
" print(' >', genotype.gls)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"----------------------------------------\n",
"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03\n",
"> HLA-A*01:01/HLA-A*01:02+HLA-A*24:02\n",
" > HLA-A*01:01/HLA-A*01:02\n",
" > HLA-A*24:02\n",
"> HLA-A*01:03+HLA-A*24:03\n",
" > HLA-A*01:03\n",
" > HLA-A*24:03\n",
"----------------------------------------\n",
"HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
"> HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
" > HLA-B*08:01\n",
" > HLA-B*44:01/HLA-B*44:02\n",
"----------------------------------------\n",
"HLA-C*01:02\n",
"----------------------------------------\n",
"HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n",
"> HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n",
" > HLA-DRB5*01:01~HLA-DRB1*03:01\n",
" > HLA-DRB1*04:07:01/HLA-DRB1*04:92\n"
]
}
],
"source": [
"for locus_block in g.locus_blocks():\n",
" print('-'*40)\n",
" print(locus_block.gls)\n",
" for genotype in locus_block.genotypes():\n",
" print('>', genotype.gls)\n",
" for genotype_block in genotype.genotype_blocks():\n",
" print(' >', genotype_block.gls)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"----------------------------------------\n",
"HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03\n",
"-> HLA-A*01:01/HLA-A*01:02+HLA-A*24:02|HLA-A*01:03+HLA-A*24:03\n",
"--> HLA-A*01:01/HLA-A*01:02+HLA-A*24:02\n",
"--> HLA-A*01:03+HLA-A*24:03\n",
"----------------------------------------\n",
"HLA-B*08:01+HLA-B*44:01/HLA-B*44:02\n",
"----------------------------------------\n",
"HLA-C*01:02\n",
"----------------------------------------\n",
"HLA-DRB5*01:01~HLA-DRB1*03:01+HLA-DRB1*04:07:01/HLA-DRB1*04:92\n"
]
}
],
"source": [
"for locus_block in g.locus_blocks():\n",
" print('-'*40)\n",
" print(locus_block.gls)\n",
" for genotype_list in locus_block.genotype_lists():\n",
" print('->', genotype_list.gls)\n",
" for genotype_list_block in genotype_list.genotype_list_blocks():\n",
" print('-->', genotype_list_block.gls)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| lgpl-3.0 |
timothydmorton/usrp-sciprog | day4/Newton-Method.ipynb | 1 | 13770 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Optimization\n",
"\n",
"We're often interested in the best-fitting model to some data. On Day 3, we introduced the concept of a likelihood and least-squares fitting. For linear models, we can do that in one step because the problem is uniquely determined. Today we will introduce how to fit functions that have non-linear parameters.\n",
"\n",
"\n",
"## Gradients!\n",
"\n",
"We will assume the we know the likelihood $\\mathcal{L}$ (it's often Gaussian), which means that we have a function that is maximized with the choice of good parameters. The function we normally work with is\n",
"\n",
"$$\n",
"f(x) = - \\log\\mathcal{L}(x\\mid\\mathcal{D})\n",
"$$\n",
"\n",
"which we then minimize. The log is there to remove the exponentials in many likelihoods. For example, for the ordinary least-squares solution, $f=\\chi^2$.\n",
"\n",
"> Mind the sign!\n",
"> It's *very* common to write down a model, optimize it, and then get some nonsense fit from the Minimum-Likelihood™ parameters.\n",
"\n",
"The variable $x$ stands for the parameter we want to find the optimal value for. Notice that we don't require it to have any specific relation (for instance linear). Instead, we will demand that $f(x)$ represents a well-behaved function: we can expect derivatives of $f$ to exist everywhere in the region of interest. We can thus write down the **Taylor series** expansion for $f$ about some point $x_0$:\n",
"\n",
"$$\n",
"f (x) = f (x_0) + g(x_0) (x - x_0) + \\frac{1}{2} H(x_0) (x - x_0)^2 + \\mathcal{O}((x-x_0)^3)\n",
"$$\n",
"\n",
"where $g$ is the gradient, i.e. $g \\equiv df(x)/dx$, and the **Hessian** $H$ is $H \\equiv d^2 f(x) / dx^2$.\n",
"\n",
"Although we don't know anything a priori about the convergence of this series, it is clear that as the distance $x - x_0$ becomes smaller, the higher-order terms become less important.\n",
"\n",
"The first term of the above series is constant, so it will not tell much about where to look for a minimum. The second term is proportional to the gradient, telling in which direction the function is decreasing fastest, but it doesn't tell us what step size to take.\n",
"\n",
"A first-order gradient descent method thus is typically a fixed-point iteration of the kind\n",
"\n",
"$$\n",
"x_{t+1} = x_t - \\lambda_t g(x_t)\n",
"$$\n",
"\n",
"At iteration $t$, it goes downhill by a certain amount $\\lambda_t$, which yet needs to be determined; setting it properly may require experience in the dark arts.\n",
"\n",
"\n",
"The third, or quadratic term describes a parabolic behavior and is therefore the lowest-order term to predict a minimum. Unlike $g$, we can expect $H$ to be roughly constant over small regions because it's variations are of higher-order (and in the case of a true parabola: identically zero).\n",
"\n",
"Thus second-order gradient descent (also called **Newton methods**) have fixed-point iterations of the form\n",
"\n",
"$$\n",
"x_{t+1} = x_t - H^{-1}(x_t) g(x_t)\n",
"$$\n",
"\n",
"We'll see why in a minute. This means that the optimal step size for a quadratic approximation of the function $f$ is given by the inverse curvature of $f$. That sounds intuitive enough, but let's have a picture anyway."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"# two parabolae\n",
"f = lambda x, c: c*x**2\n",
"c = 1, 0.5\n",
"\n",
"# initial point\n",
"x_ = -0.75\n",
"y_ = [ f(x_, ci) for ci in c ]\n",
"\n",
"# compute gradient and hessian\n",
"g = [ 2*c[i]*x_ for i in range(2) ]\n",
"H = [ 2*c[i] for i in range(2) ]\n",
"\n",
"# Newton step\n",
"x__ = [ x_ - 1/H[i]*g[i] for i in range(2) ]\n",
"y__ = [ f(xi, ci) for xi, ci in zip(x__, c) ]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"hide_input": "true"
},
"outputs": [],
"source": [
"# plotting\n",
"x = np.linspace(-1,1,100)\n",
"fig, axes = plt.subplots(1, 2, figsize=(12,6))\n",
"axes[0].plot(x, f(x, c[0]))\n",
"axes[1].plot(x, f(x, c[1]))\n",
"axes[0].axis('off')\n",
"axes[1].axis('off')\n",
"axes[0].scatter([x_, x__[0]], [y_[0], y__[0]], c=['k', 'w'], ec='k', s=100, zorder=10)\n",
"axes[0].plot([x_, x_, x__[0]], [y_[0], y__[0], y__[0]], c='k')\n",
"axes[1].scatter([x_, x__[1]], [y_[1], y__[1]], c=['k', 'w'], ec='k', s=100, zorder=10)\n",
"axes[1].plot([x_, x_, x__[1]], [y_[1], y__[1], y__[1]], c='k')\n",
"axes[0].text(0,0.25,'$f(x)=x^2,\\,H=2$', ha='center', size=16)\n",
"axes[1].text(0,0.25,'$f(x)=x^2/2,\\,H=1$', ha='center', size=16)\n",
"axes[0].text(x_/2, x__[0]-0.01, '$\\Delta x$', ha='center', va='top', size=16)\n",
"axes[1].text(x_/2, x__[1]-0.01, '$\\Delta x$', ha='center', va='top', size=16)\n",
"axes[0].text(x_-0.01, y_[0]/2, '$\\Delta y$', ha='right', va='center', size=16)\n",
"axes[1].text(x_-0.01, y_[1]/2, '$\\Delta y$', ha='right', va='center', size=16)\n",
"axes[0].set_ylim(-0.2,1.1)\n",
"axes[1].set_ylim(-0.2,1.1)\n",
"fig.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Despite having different slopes at the starting position (filled circle), the Newton scheme performs only a single step (open circle) to move to the exact minimum, from any starting position, *if the function is quadratic*. This is even more useful because \n",
"\n",
"> Any smooth function close to its minimum looks like a quadratic function!\n",
"\n",
"That's a consequence of the Taylor expansion because the first-order term $g$ vanishes close to the minimum, so all deviations from the quadratic form are of order 3 or higher in $x-x_0$.\n",
"\n",
"So, why doesn't everyone compute the Hessian for optimization. Well, it's typically expensive to compute a second derivative. And in $d$ dimensions (one for each parameter), the Hessian is a matrix with $d(d+1)/2$ elements. This is why there are several **quasi-Newton methods** like [BFGS](https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm), that accumulate information from previous iterations into an estimate of $H$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Newton's Method for finding a root\n",
"\n",
"[Newton's method](https://en.wikipedia.org/wiki/Newton's_method) was initially designed to find the root of a function, not its minimum. So, let's find out how these two are connected.\n",
"\n",
"The central idea is to approximate $f$ by its tangent at some initial position $x_0$:\n",
"\n",
"$$\n",
"y = f(x_0) + g(x_0) (x-x_0)\n",
"$$\n",
"\n",
"As we can see in this animation from Wikipedia, the $x$-intercept of this line is then closer to the root than the starting position $x_0$:\n",
"\n",
"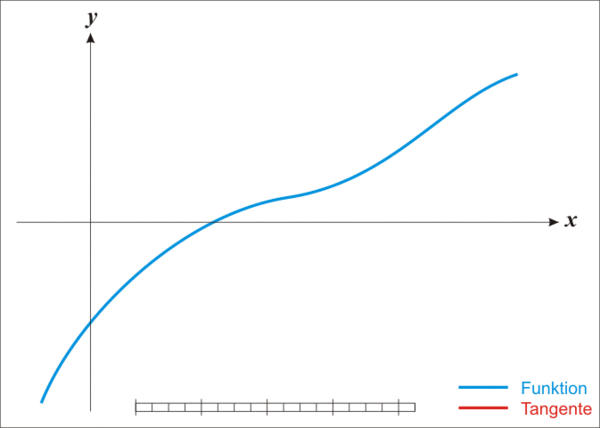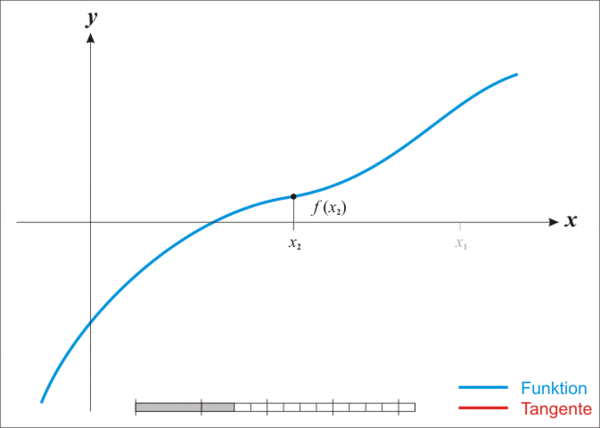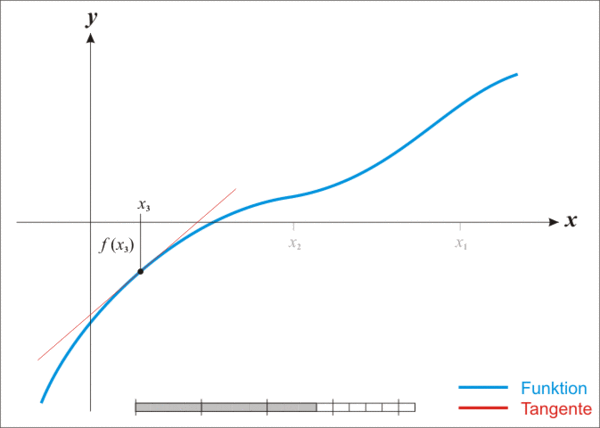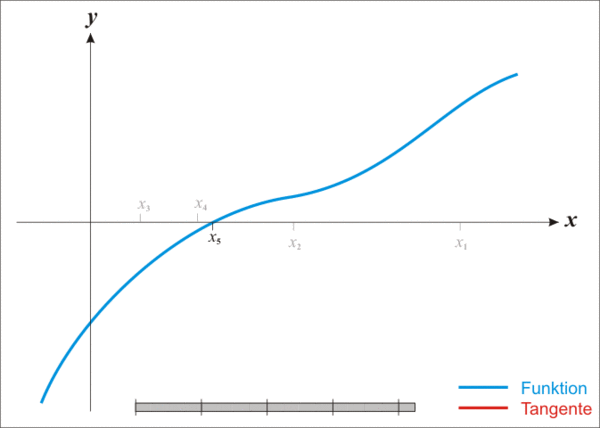\n",
"\n",
"That is, we need to solve the linear relation\n",
"\n",
"$$\n",
"f(x_0) + g(x_0) (x-x_0) = 0\n",
"$$\n",
"\n",
"for $x$ to get the updated position. In 1D: $x_1 = x_0 - f(x_0)/g(x_0)$. Repeating this sequence\n",
"\n",
"$$\n",
"x_{t+1} = x_t - \\frac{f(x_t)}{g(x_t)}\n",
"$$\n",
"\n",
"will yield a fixed point, which is the root of $f$ *if one exists in the vicinity of $x_0$*."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"def newtons_method(f, df, x0, tol=1E-6):\n",
" x_n = x0 \n",
" while abs(f(x_n)) > tol:\n",
" x_n = x_n - f(x_n)/df(x_n)\n",
" return x_n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Minimizing a function\n",
"\n",
"As the maximum and minimum of a function are defined by $f'(x) = 0$, we can use Newton's method to find extremal points by applying it to the first derivative. That's the origin for the Newton update formula above:\n",
"\n",
"$$\n",
"x_{t+1} = x_t - H^{-1}(x_t) \\ g(x_t)\n",
"$$\n",
"\n",
"Let's try this with a simply function with known minimum:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# define a test function\n",
"def f(x):\n",
" return (x-3)**2 - 9\n",
"\n",
"def df(x):\n",
" return 2*(x-3)\n",
"\n",
"def df2(x):\n",
" return 2."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true,
"jupyter": {
"outputs_hidden": false
}
},
"outputs": [],
"source": [
"root = newtons_method(f, df, x0=0.1)\n",
"print (\"root {0}, f(root) = {1}\".format(root, f(root)))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true,
"jupyter": {
"outputs_hidden": false
}
},
"outputs": [],
"source": [
"minimum = newtons_method(df, df2, x0=0.1)\n",
"print (\"minimum {0}, f'(minimum) = {1}\".format(minimum, df(minimum)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There is an important qualifier in the statement about fixed points: **a root needs to exist in the vicinity of $x_0$!** Let's see what happens if that's not the case:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"jupyter": {
"outputs_hidden": false
}
},
"outputs": [],
"source": [
"def g(x):\n",
" return (x-3)**2 + 1\n",
"dg = df # same derivatives for f and g\n",
"newtons_method(g, dg, x0=0.1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As long as you don't interrupt the execution of this cell (Tip: click \"Interrupt Kernel\"), `newtons_method` will not terminate and come back with a result.\n",
"\n",
"With a little more defensive programming we can make sure that the function will terminate after a given number of iterations:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"def newtons_method2(f, df, x0, tol=1E-6, maxiter=100000):\n",
" x_n = x0 \n",
" for _ in range(maxiter):\n",
" x_n = x_n - f(x_n)/df(x_n)\n",
" \n",
" if abs(f(x_n)) < tol:\n",
" return x_n\n",
" \n",
" raise RuntimeError(\"Failed to find a minimum within {} iterations \".format(maxiter))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"jupyter": {
"outputs_hidden": false
}
},
"outputs": [],
"source": [
"newtons_method2(g, dg, x0=0.1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Using scipy.optimize\n",
"\n",
"scipy comes with a pretty feature-rich [optimization package](https://docs.scipy.org/doc/scipy/reference/optimize.html), for one- and multi-dimensional optimization. As so often, it's better (as in faster and more reliable) to leverage exisiting and battle-tested code than to try to implement it yourself.\n",
"\n",
"### Exercise 1:\n",
"\n",
"Find the minimum of `f` with `scipy.optimize.minimize_scalar`. Look up the various arguments to function in the documentation (either online or by typing `scipy.optimize.minimize_scalar?`) and choose appropriate inputs. When done, visualize your result to confirm its correctness."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Exercise 2:\n",
"\n",
"To make this more interesting, we'll create a new multi-dimensional function that resembles `f`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def h(x, p):\n",
" return np.sum(np.abs(x-3)**p, axis=-1) - 9"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In 2D, find the minimum of `h` for `p=2` with `scipy.optimimze.minimize`. Note that you have not been given a derivative of `h`. You can choose to compute it analytically, or see if `minimize` has options that allow you to work without.\n",
"\n",
"When done, visualize your result to confirm its correctness."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| mit |
jobovy/misc-notebooks | apogee/apogee-lsf-groupings.ipynb | 1 | 1532175 | null | bsd-3-clause |
vvishwa/deep-learning | batch-norm/Batch_Normalization_Exercises.ipynb | 1 | 39009 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Batch Normalization – Practice"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Batch normalization is most useful when building deep neural networks. To demonstrate this, we'll create a convolutional neural network with 20 convolutional layers, followed by a fully connected layer. We'll use it to classify handwritten digits in the MNIST dataset, which should be familiar to you by now.\n",
"\n",
"This is **not** a good network for classfying MNIST digits. You could create a _much_ simpler network and get _better_ results. However, to give you hands-on experience with batch normalization, we had to make an example that was:\n",
"1. Complicated enough that training would benefit from batch normalization.\n",
"2. Simple enough that it would train quickly, since this is meant to be a short exercise just to give you some practice adding batch normalization.\n",
"3. Simple enough that the architecture would be easy to understand without additional resources."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This notebook includes two versions of the network that you can edit. The first uses higher level functions from the `tf.layers` package. The second is the same network, but uses only lower level functions in the `tf.nn` package.\n",
"\n",
"1. [Batch Normalization with `tf.layers.batch_normalization`](#example_1)\n",
"2. [Batch Normalization with `tf.nn.batch_normalization`](#example_2)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The following cell loads TensorFlow, downloads the MNIST dataset if necessary, and loads it into an object named `mnist`. You'll need to run this cell before running anything else in the notebook."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting MNIST_data/train-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/train-labels-idx1-ubyte.gz\n",
"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"import tensorflow as tf\n",
"from tensorflow.examples.tutorials.mnist import input_data\n",
"mnist = input_data.read_data_sets(\"MNIST_data/\", one_hot=True, reshape=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Batch Normalization using `tf.layers.batch_normalization`<a id=\"example_1\"></a>\n",
"\n",
"This version of the network uses `tf.layers` for almost everything, and expects you to implement batch normalization using [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We'll use the following function to create fully connected layers in our network. We'll create them with the specified number of neurons and a ReLU activation function.\n",
"\n",
"This version of the function does not include batch normalization."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"\"\"\"\n",
"DO NOT MODIFY THIS CELL\n",
"\"\"\"\n",
"def fully_connected(prev_layer, num_units):\n",
" \"\"\"\n",
" Create a fully connectd layer with the given layer as input and the given number of neurons.\n",
" \n",
" :param prev_layer: Tensor\n",
" The Tensor that acts as input into this layer\n",
" :param num_units: int\n",
" The size of the layer. That is, the number of units, nodes, or neurons.\n",
" :returns Tensor\n",
" A new fully connected layer\n",
" \"\"\"\n",
" layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)\n",
" return layer"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We'll use the following function to create convolutional layers in our network. They are very basic: we're always using a 3x3 kernel, ReLU activation functions, strides of 1x1 on layers with odd depths, and strides of 2x2 on layers with even depths. We aren't bothering with pooling layers at all in this network.\n",
"\n",
"This version of the function does not include batch normalization."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"\"\"\"\n",
"DO NOT MODIFY THIS CELL\n",
"\"\"\"\n",
"def conv_layer(prev_layer, layer_depth):\n",
" \"\"\"\n",
" Create a convolutional layer with the given layer as input.\n",
" \n",
" :param prev_layer: Tensor\n",
" The Tensor that acts as input into this layer\n",
" :param layer_depth: int\n",
" We'll set the strides and number of feature maps based on the layer's depth in the network.\n",
" This is *not* a good way to make a CNN, but it helps us create this example with very little code.\n",
" :returns Tensor\n",
" A new convolutional layer\n",
" \"\"\"\n",
" strides = 2 if layer_depth % 3 == 0 else 1\n",
" conv_layer = tf.layers.conv2d(prev_layer, layer_depth*4, 3, strides, 'same', activation=tf.nn.relu)\n",
" return conv_layer"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Run the following cell**, along with the earlier cells (to load the dataset and define the necessary functions). \n",
"\n",
"This cell builds the network **without** batch normalization, then trains it on the MNIST dataset. It displays loss and accuracy data periodically while training."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Batch: 0: Validation loss: 0.69066, Validation accuracy: 0.10020\n",
"Batch: 25: Training loss: 0.40348, Training accuracy: 0.07812\n",
"Batch: 50: Training loss: 0.32874, Training accuracy: 0.10938\n",
"Batch: 75: Training loss: 0.32664, Training accuracy: 0.07812\n",
"Batch: 100: Validation loss: 0.32607, Validation accuracy: 0.09900\n",
"Batch: 125: Training loss: 0.32351, Training accuracy: 0.14062\n",
"Batch: 150: Training loss: 0.32545, Training accuracy: 0.15625\n",
"Batch: 175: Training loss: 0.32736, Training accuracy: 0.10938\n",
"Batch: 200: Validation loss: 0.32522, Validation accuracy: 0.11260\n",
"Batch: 225: Training loss: 0.32507, Training accuracy: 0.14062\n",
"Batch: 250: Training loss: 0.32610, Training accuracy: 0.09375\n",
"Batch: 275: Training loss: 0.32387, Training accuracy: 0.18750\n",
"Batch: 300: Validation loss: 0.32564, Validation accuracy: 0.11260\n",
"Batch: 325: Training loss: 0.32367, Training accuracy: 0.14062\n",
"Batch: 350: Training loss: 0.32777, Training accuracy: 0.06250\n",
"Batch: 375: Training loss: 0.32563, Training accuracy: 0.12500\n",
"Batch: 400: Validation loss: 0.32574, Validation accuracy: 0.11000\n",
"Batch: 425: Training loss: 0.32619, Training accuracy: 0.04688\n",
"Batch: 450: Training loss: 0.32667, Training accuracy: 0.10938\n",
"Batch: 475: Training loss: 0.32398, Training accuracy: 0.20312\n",
"Batch: 500: Validation loss: 0.32535, Validation accuracy: 0.09240\n",
"Batch: 525: Training loss: 0.32837, Training accuracy: 0.04688\n",
"Batch: 550: Training loss: 0.32466, Training accuracy: 0.20312\n",
"Batch: 575: Training loss: 0.32340, Training accuracy: 0.12500\n",
"Batch: 600: Validation loss: 0.32493, Validation accuracy: 0.11260\n",
"Batch: 625: Training loss: 0.32785, Training accuracy: 0.15625\n",
"Batch: 650: Training loss: 0.32530, Training accuracy: 0.14062\n",
"Batch: 675: Training loss: 0.32741, Training accuracy: 0.12500\n",
"Batch: 700: Validation loss: 0.32513, Validation accuracy: 0.09860\n",
"Batch: 725: Training loss: 0.32644, Training accuracy: 0.10938\n",
"Batch: 750: Training loss: 0.32451, Training accuracy: 0.14062\n",
"Batch: 775: Training loss: 0.32561, Training accuracy: 0.04688\n",
"Final validation accuracy: 0.09900\n",
"Final test accuracy: 0.10090\n",
"Accuracy on 100 samples: 0.11\n"
]
}
],
"source": [
"\"\"\"\n",
"DO NOT MODIFY THIS CELL\n",
"\"\"\"\n",
"def train(num_batches, batch_size, learning_rate):\n",
" # Build placeholders for the input samples and labels \n",
" inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])\n",
" labels = tf.placeholder(tf.float32, [None, 10])\n",
" \n",
" # Feed the inputs into a series of 20 convolutional layers \n",
" layer = inputs\n",
" for layer_i in range(1, 20):\n",
" layer = conv_layer(layer, layer_i)\n",
"\n",
" # Flatten the output from the convolutional layers \n",
" orig_shape = layer.get_shape().as_list()\n",
" layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])\n",
"\n",
" # Add one fully connected layer\n",
" layer = fully_connected(layer, 100)\n",
"\n",
" # Create the output layer with 1 node for each \n",
" logits = tf.layers.dense(layer, 10)\n",
" \n",
" # Define loss and training operations\n",
" model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\n",
" train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)\n",
" \n",
" # Create operations to test accuracy\n",
" correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))\n",
" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\n",
" \n",
" # Train and test the network\n",
" with tf.Session() as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
" for batch_i in range(num_batches):\n",
" batch_xs, batch_ys = mnist.train.next_batch(batch_size)\n",
"\n",
" # train this batch\n",
" sess.run(train_opt, {inputs: batch_xs, labels: batch_ys})\n",
" \n",
" # Periodically check the validation or training loss and accuracy\n",
" if batch_i % 100 == 0:\n",
" loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,\n",
" labels: mnist.validation.labels})\n",
" print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))\n",
" elif batch_i % 25 == 0:\n",
" loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys})\n",
" print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))\n",
"\n",
" # At the end, score the final accuracy for both the validation and test sets\n",
" acc = sess.run(accuracy, {inputs: mnist.validation.images,\n",
" labels: mnist.validation.labels})\n",
" print('Final validation accuracy: {:>3.5f}'.format(acc))\n",
" acc = sess.run(accuracy, {inputs: mnist.test.images,\n",
" labels: mnist.test.labels})\n",
" print('Final test accuracy: {:>3.5f}'.format(acc))\n",
" \n",
" # Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.\n",
" correct = 0\n",
" for i in range(100):\n",
" correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],\n",
" labels: [mnist.test.labels[i]]})\n",
"\n",
" print(\"Accuracy on 100 samples:\", correct/100)\n",
"\n",
"\n",
"num_batches = 800\n",
"batch_size = 64\n",
"learning_rate = 0.002\n",
"\n",
"tf.reset_default_graph()\n",
"with tf.Graph().as_default():\n",
" train(num_batches, batch_size, learning_rate)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With this many layers, it's going to take a lot of iterations for this network to learn. By the time you're done training these 800 batches, your final test and validation accuracies probably won't be much better than 10%. (It will be different each time, but will most likely be less than 15%.)\n",
"\n",
"Using batch normalization, you'll be able to train this same network to over 90% in that same number of batches.\n",
"\n",
"\n",
"# Add batch normalization\n",
"\n",
"We've copied the previous three cells to get you started. **Edit these cells** to add batch normalization to the network. For this exercise, you should use [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization) to handle most of the math, but you'll need to make a few other changes to your network to integrate batch normalization. You may want to refer back to the lesson notebook to remind yourself of important things, like how your graph operations need to know whether or not you are performing training or inference. \n",
"\n",
"If you get stuck, you can check out the `Batch_Normalization_Solutions` notebook to see how we did things."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**TODO:** Modify `fully_connected` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def fully_connected(prev_layer, num_units, is_training):\n",
" \"\"\"\n",
" Create a fully connectd layer with the given layer as input and the given number of neurons.\n",
" \n",
" :param prev_layer: Tensor\n",
" The Tensor that acts as input into this layer\n",
" :param num_units: int\n",
" The size of the layer. That is, the number of units, nodes, or neurons.\n",
" :returns Tensor\n",
" A new fully connected layer\n",
" \"\"\"\n",
" layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)\n",
"\n",
" layer = tf.layers.batch_normalization(layer, training=is_training)\n",
" layer = tf.nn.relu(layer)\n",
" return layer"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**TODO:** Modify `conv_layer` to add batch normalization to the convolutional layers it creates. Feel free to change the function's parameters if it helps."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def conv_layer(prev_layer, layer_depth, is_training):\n",
" \"\"\"\n",
" Create a convolutional layer with the given layer as input.\n",
" \n",
" :param prev_layer: Tensor\n",
" The Tensor that acts as input into this layer\n",
" :param layer_depth: int\n",
" We'll set the strides and number of feature maps based on the layer's depth in the network.\n",
" This is *not* a good way to make a CNN, but it helps us create this example with very little code.\n",
" :returns Tensor\n",
" A new convolutional layer\n",
" \"\"\"\n",
" strides = 2 if layer_depth % 3 == 0 else 1\n",
" conv_layer = tf.layers.conv2d(prev_layer, layer_depth*4, 3, strides, 'same', activation=tf.nn.relu)\n",
" conv_layer = tf.layers.batch_normalization(conv_layer, training=is_training)\n",
" conv_layer = tf.nn.relu(conv_layer)\n",
" return conv_layer"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**TODO:** Edit the `train` function to support batch normalization. You'll need to make sure the network knows whether or not it is training, and you'll need to make sure it updates and uses its population statistics correctly."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Batch: 0: Validation loss: 0.69055, Validation accuracy: 0.09860\n",
"Batch: 25: Training loss: 0.62911, Training accuracy: 0.10938\n",
"Batch: 50: Training loss: 0.54283, Training accuracy: 0.15625\n",
"Batch: 75: Training loss: 0.48776, Training accuracy: 0.07812\n",
"Batch: 100: Validation loss: 0.46307, Validation accuracy: 0.11260\n",
"Batch: 125: Training loss: 0.44106, Training accuracy: 0.10938\n",
"Batch: 150: Training loss: 0.41721, Training accuracy: 0.07812\n",
"Batch: 175: Training loss: 0.39374, Training accuracy: 0.07812\n",
"Batch: 200: Validation loss: 0.38370, Validation accuracy: 0.08680\n",
"Batch: 225: Training loss: 0.37264, Training accuracy: 0.09375\n",
"Batch: 250: Training loss: 0.36432, Training accuracy: 0.09375\n",
"Batch: 275: Training loss: 0.35929, Training accuracy: 0.06250\n",
"Batch: 300: Validation loss: 0.35560, Validation accuracy: 0.09240\n",
"Batch: 325: Training loss: 0.35081, Training accuracy: 0.03125\n",
"Batch: 350: Training loss: 0.35347, Training accuracy: 0.12500\n",
"Batch: 375: Training loss: 0.35275, Training accuracy: 0.06250\n",
"Batch: 400: Validation loss: 0.34188, Validation accuracy: 0.11760\n",
"Batch: 425: Training loss: 0.30678, Training accuracy: 0.23438\n",
"Batch: 450: Training loss: 0.25516, Training accuracy: 0.37500\n",
"Batch: 475: Training loss: 0.22896, Training accuracy: 0.48438\n",
"Batch: 500: Validation loss: 0.20522, Validation accuracy: 0.50360\n",
"Batch: 525: Training loss: 0.20960, Training accuracy: 0.54688\n",
"Batch: 550: Training loss: 0.21292, Training accuracy: 0.46875\n",
"Batch: 575: Training loss: 0.15521, Training accuracy: 0.50000\n",
"Batch: 600: Validation loss: 0.15440, Validation accuracy: 0.67700\n",
"Batch: 625: Training loss: 0.15890, Training accuracy: 0.62500\n",
"Batch: 650: Training loss: 0.15213, Training accuracy: 0.64062\n",
"Batch: 675: Training loss: 0.15449, Training accuracy: 0.65625\n",
"Batch: 700: Validation loss: 0.15554, Validation accuracy: 0.69280\n",
"Batch: 725: Training loss: 0.14911, Training accuracy: 0.75000\n",
"Batch: 750: Training loss: 0.16774, Training accuracy: 0.68750\n",
"Batch: 775: Training loss: 0.11901, Training accuracy: 0.71875\n",
"Final validation accuracy: 0.78440\n",
"Final test accuracy: 0.77810\n",
"Accuracy on 100 samples: 0.78\n"
]
}
],
"source": [
"def train(num_batches, batch_size, learning_rate):\n",
" # Build placeholders for the input samples and labels \n",
" inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])\n",
" labels = tf.placeholder(tf.float32, [None, 10])\n",
" \n",
" #boolean to hold if network is training\n",
" is_training = tf.placeholder(tf.bool)\n",
" # Feed the inputs into a series of 20 convolutional layers \n",
" layer = inputs\n",
" for layer_i in range(1, 20):\n",
" layer = conv_layer(layer, layer_i, is_training)\n",
"\n",
" # Flatten the output from the convolutional layers \n",
" orig_shape = layer.get_shape().as_list()\n",
" layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])\n",
"\n",
" # Add one fully connected layer\n",
" layer = fully_connected(layer, 100, is_training)\n",
"\n",
" # Create the output layer with 1 node for each \n",
" logits = tf.layers.dense(layer, 10)\n",
" \n",
" # Define loss and training operations\n",
" model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\n",
" with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):\n",
" train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)\n",
" \n",
" # Create operations to test accuracy\n",
" correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))\n",
" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\n",
" \n",
" # Train and test the network\n",
" with tf.Session() as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
" for batch_i in range(num_batches):\n",
" batch_xs, batch_ys = mnist.train.next_batch(batch_size)\n",
"\n",
" # train this batch\n",
" sess.run(train_opt, {inputs: batch_xs, labels: batch_ys, is_training:True})\n",
" \n",
" # Periodically check the validation or training loss and accuracy\n",
" if batch_i % 100 == 0:\n",
" loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,\n",
" labels: mnist.validation.labels,\n",
" is_training:False})\n",
" print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))\n",
" elif batch_i % 25 == 0:\n",
" loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys, is_training:False})\n",
" print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))\n",
"\n",
" # At the end, score the final accuracy for both the validation and test sets\n",
" acc = sess.run(accuracy, {inputs: mnist.validation.images,\n",
" labels: mnist.validation.labels,\n",
" is_training:False})\n",
" print('Final validation accuracy: {:>3.5f}'.format(acc))\n",
" acc = sess.run(accuracy, {inputs: mnist.test.images,\n",
" labels: mnist.test.labels,\n",
" is_training:False})\n",
" print('Final test accuracy: {:>3.5f}'.format(acc))\n",
" \n",
" # Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.\n",
" correct = 0\n",
" for i in range(100):\n",
" correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],\n",
" labels: [mnist.test.labels[i]],\n",
" is_training:False})\n",
"\n",
" print(\"Accuracy on 100 samples:\", correct/100)\n",
"\n",
"\n",
"num_batches = 800\n",
"batch_size = 64\n",
"learning_rate = 0.002\n",
"\n",
"tf.reset_default_graph()\n",
"with tf.Graph().as_default():\n",
" train(num_batches, batch_size, learning_rate)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With batch normalization, you should now get an accuracy over 90%. Notice also the last line of the output: `Accuracy on 100 samples`. If this value is low while everything else looks good, that means you did not implement batch normalization correctly. Specifically, it means you either did not calculate the population mean and variance while training, or you are not using those values during inference.\n",
"\n",
"# Batch Normalization using `tf.nn.batch_normalization`<a id=\"example_2\"></a>\n",
"\n",
"Most of the time you will be able to use higher level functions exclusively, but sometimes you may want to work at a lower level. For example, if you ever want to implement a new feature – something new enough that TensorFlow does not already include a high-level implementation of it, like batch normalization in an LSTM – then you may need to know these sorts of things.\n",
"\n",
"This version of the network uses `tf.nn` for almost everything, and expects you to implement batch normalization using [`tf.nn.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/nn/batch_normalization).\n",
"\n",
"**Optional TODO:** You can run the next three cells before you edit them just to see how the network performs without batch normalization. However, the results should be pretty much the same as you saw with the previous example before you added batch normalization. \n",
"\n",
"**TODO:** Modify `fully_connected` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.\n",
"\n",
"**Note:** For convenience, we continue to use `tf.layers.dense` for the `fully_connected` layer. By this point in the class, you should have no problem replacing that with matrix operations between the `prev_layer` and explicit weights and biases variables."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [],
"source": [
"def fully_connected(prev_layer, num_units, is_training):\n",
" \"\"\"\n",
" Create a fully connectd layer with the given layer as input and the given number of neurons.\n",
" \n",
" :param prev_layer: Tensor\n",
" The Tensor that acts as input into this layer\n",
" :param num_units: int\n",
" The size of the layer. That is, the number of units, nodes, or neurons.\n",
" :returns Tensor\n",
" A new fully connected layer\n",
" \"\"\"\n",
" layer = tf.layers.dense(prev_layer, num_units, activation=tf.nn.relu)\n",
" gamma = tf.Variable(tf.ones([num_units]))\n",
" beta = tf.Variable(tf.zeros([num_units]))\n",
"\n",
" pop_mean = tf.Variable(tf.zeros([num_units]), trainable=False)\n",
" pop_variance = tf.Variable(tf.ones([num_units]), trainable=False)\n",
"\n",
" epsilon = 1e-3\n",
" \n",
" def batch_norm_training():\n",
" batch_mean, batch_variance = tf.nn.moments(layer, [0])\n",
"\n",
" decay = 0.99\n",
" train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))\n",
" train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))\n",
"\n",
" with tf.control_dependencies([train_mean, train_variance]):\n",
" return tf.nn.batch_normalization(layer, batch_mean, batch_variance, beta, gamma, epsilon)\n",
" \n",
" def batch_norm_inference():\n",
" return tf.nn.batch_normalization(layer, pop_mean, pop_variance, beta, gamma, epsilon)\n",
"\n",
" batch_normalized_output = tf.cond(is_training, batch_norm_training, batch_norm_inference)\n",
" return tf.nn.relu(batch_normalized_output)\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**TODO:** Modify `conv_layer` to add batch normalization to the fully connected layers it creates. Feel free to change the function's parameters if it helps.\n",
"\n",
"**Note:** Unlike in the previous example that used `tf.layers`, adding batch normalization to these convolutional layers _does_ require some slight differences to what you did in `fully_connected`. "
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def conv_layer(prev_layer, layer_depth, is_training):\n",
" \"\"\"\n",
" Create a convolutional layer with the given layer as input.\n",
" \n",
" :param prev_layer: Tensor\n",
" The Tensor that acts as input into this layer\n",
" :param layer_depth: int\n",
" We'll set the strides and number of feature maps based on the layer's depth in the network.\n",
" This is *not* a good way to make a CNN, but it helps us create this example with very little code.\n",
" :returns Tensor\n",
" A new convolutional layer\n",
" \"\"\"\n",
" strides = 2 if layer_depth % 3 == 0 else 1\n",
"\n",
" in_channels = prev_layer.get_shape().as_list()[3]\n",
" out_channels = layer_depth*4\n",
" \n",
" weights = tf.Variable(\n",
" tf.truncated_normal([3, 3, in_channels, out_channels], stddev=0.05))\n",
" \n",
" bias = tf.Variable(tf.zeros(out_channels))\n",
"\n",
" conv_layer = tf.nn.conv2d(prev_layer, weights, strides=[1,strides, strides, 1], padding='SAME')\n",
" conv_layer = tf.nn.bias_add(conv_layer, bias)\n",
" gamma = tf.Variable(tf.ones([out_channels]))\n",
" beta = tf.Variable(tf.zeros([out_channels]))\n",
"\n",
" pop_mean = tf.Variable(tf.zeros([out_channels]), trainable=False)\n",
" pop_variance = tf.Variable(tf.ones([out_channels]), trainable=False)\n",
"\n",
" epsilon = 1e-3\n",
" \n",
" def batch_norm_training():\n",
" # Important to use the correct dimensions here to ensure the mean and variance are calculated \n",
" # per feature map instead of for the entire layer\n",
" batch_mean, batch_variance = tf.nn.moments(conv_layer, [0,1,2], keep_dims=False)\n",
"\n",
" decay = 0.99\n",
" train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))\n",
" train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))\n",
"\n",
" with tf.control_dependencies([train_mean, train_variance]):\n",
" return tf.nn.batch_normalization(conv_layer, batch_mean, batch_variance, beta, gamma, epsilon)\n",
" \n",
" def batch_norm_inference():\n",
" return tf.nn.batch_normalization(conv_layer, pop_mean, pop_variance, beta, gamma, epsilon)\n",
"\n",
" batch_normalized_output = tf.cond(is_training, batch_norm_training, batch_norm_inference)\n",
" return tf.nn.relu(batch_normalized_output)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**TODO:** Edit the `train` function to support batch normalization. You'll need to make sure the network knows whether or not it is training."
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Batch: 0: Validation loss: 0.69116, Validation accuracy: 0.08680\n",
"Batch: 25: Training loss: 0.61918, Training accuracy: 0.09375\n",
"Batch: 50: Training loss: 0.57291, Training accuracy: 0.14062\n",
"Batch: 75: Training loss: 0.54827, Training accuracy: 0.12500\n",
"Batch: 100: Validation loss: 0.51580, Validation accuracy: 0.08680\n",
"Batch: 125: Training loss: 0.47078, Training accuracy: 0.12500\n",
"Batch: 150: Training loss: 0.41947, Training accuracy: 0.09375\n",
"Batch: 175: Training loss: 0.37808, Training accuracy: 0.06250\n",
"Batch: 200: Validation loss: 0.37041, Validation accuracy: 0.11000\n",
"Batch: 225: Training loss: 0.37841, Training accuracy: 0.04688\n",
"Batch: 250: Training loss: 0.39858, Training accuracy: 0.09375\n",
"Batch: 275: Training loss: 0.38057, Training accuracy: 0.15625\n",
"Batch: 300: Validation loss: 0.40183, Validation accuracy: 0.11000\n",
"Batch: 325: Training loss: 0.44106, Training accuracy: 0.01562\n",
"Batch: 350: Training loss: 0.42878, Training accuracy: 0.07812\n",
"Batch: 375: Training loss: 0.45432, Training accuracy: 0.15625\n",
"Batch: 400: Validation loss: 0.44503, Validation accuracy: 0.32180\n",
"Batch: 425: Training loss: 0.30620, Training accuracy: 0.48438\n",
"Batch: 450: Training loss: 0.07195, Training accuracy: 0.87500\n",
"Batch: 475: Training loss: 0.34081, Training accuracy: 0.53125\n",
"Batch: 500: Validation loss: 0.11314, Validation accuracy: 0.81720\n",
"Batch: 525: Training loss: 0.48202, Training accuracy: 0.40625\n",
"Batch: 550: Training loss: 0.17013, Training accuracy: 0.73438\n",
"Batch: 575: Training loss: 0.02425, Training accuracy: 0.96875\n",
"Batch: 600: Validation loss: 0.03587, Validation accuracy: 0.94600\n",
"Batch: 625: Training loss: 0.01194, Training accuracy: 0.96875\n",
"Batch: 650: Training loss: 0.01723, Training accuracy: 0.96875\n",
"Batch: 675: Training loss: 0.00529, Training accuracy: 0.98438\n",
"Batch: 700: Validation loss: 0.02844, Validation accuracy: 0.96120\n",
"Batch: 725: Training loss: 0.01406, Training accuracy: 0.95312\n",
"Batch: 750: Training loss: 0.01881, Training accuracy: 0.96875\n",
"Batch: 775: Training loss: 0.01447, Training accuracy: 0.96875\n",
"Final validation accuracy: 0.96460\n",
"Final test accuracy: 0.96360\n",
"Accuracy on 100 samples: 0.99\n"
]
}
],
"source": [
"def train(num_batches, batch_size, learning_rate):\n",
" # Build placeholders for the input samples and labels \n",
" inputs = tf.placeholder(tf.float32, [None, 28, 28, 1])\n",
" labels = tf.placeholder(tf.float32, [None, 10])\n",
" \n",
" # boolean variable if network is training\n",
" is_training = tf.placeholder(tf.bool)\n",
" # Feed the inputs into a series of 20 convolutional layers \n",
" layer = inputs\n",
" for layer_i in range(1, 20):\n",
" layer = conv_layer(layer, layer_i, is_training)\n",
"\n",
" # Flatten the output from the convolutional layers \n",
" orig_shape = layer.get_shape().as_list()\n",
" layer = tf.reshape(layer, shape=[-1, orig_shape[1] * orig_shape[2] * orig_shape[3]])\n",
"\n",
" # Add one fully connected layer\n",
" layer = fully_connected(layer, 100, is_training)\n",
"\n",
" # Create the output layer with 1 node for each \n",
" logits = tf.layers.dense(layer, 10)\n",
" \n",
" # Define loss and training operations\n",
" model_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\n",
" train_opt = tf.train.AdamOptimizer(learning_rate).minimize(model_loss)\n",
" \n",
" # Create operations to test accuracy\n",
" correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(labels,1))\n",
" accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))\n",
" \n",
" # Train and test the network\n",
" with tf.Session() as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
" for batch_i in range(num_batches):\n",
" batch_xs, batch_ys = mnist.train.next_batch(batch_size)\n",
"\n",
" # train this batch\n",
" sess.run(train_opt, {inputs: batch_xs, labels: batch_ys, is_training:True})\n",
" \n",
" # Periodically check the validation or training loss and accuracy\n",
" if batch_i % 100 == 0:\n",
" loss, acc = sess.run([model_loss, accuracy], {inputs: mnist.validation.images,\n",
" labels: mnist.validation.labels,\n",
" is_training:False})\n",
" print('Batch: {:>2}: Validation loss: {:>3.5f}, Validation accuracy: {:>3.5f}'.format(batch_i, loss, acc))\n",
" elif batch_i % 25 == 0:\n",
" loss, acc = sess.run([model_loss, accuracy], {inputs: batch_xs, labels: batch_ys,\n",
" is_training:False})\n",
" print('Batch: {:>2}: Training loss: {:>3.5f}, Training accuracy: {:>3.5f}'.format(batch_i, loss, acc))\n",
"\n",
" # At the end, score the final accuracy for both the validation and test sets\n",
" acc = sess.run(accuracy, {inputs: mnist.validation.images,\n",
" labels: mnist.validation.labels, is_training:False})\n",
" print('Final validation accuracy: {:>3.5f}'.format(acc))\n",
" acc = sess.run(accuracy, {inputs: mnist.test.images,\n",
" labels: mnist.test.labels, is_training:False})\n",
" print('Final test accuracy: {:>3.5f}'.format(acc))\n",
" \n",
" # Score the first 100 test images individually. This won't work if batch normalization isn't implemented correctly.\n",
" correct = 0\n",
" for i in range(100):\n",
" correct += sess.run(accuracy,feed_dict={inputs: [mnist.test.images[i]],\n",
" labels: [mnist.test.labels[i]], is_training:False})\n",
"\n",
" print(\"Accuracy on 100 samples:\", correct/100)\n",
"\n",
"\n",
"num_batches = 800\n",
"batch_size = 64\n",
"learning_rate = 0.002\n",
"\n",
"tf.reset_default_graph()\n",
"with tf.Graph().as_default():\n",
" train(num_batches, batch_size, learning_rate)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once again, the model with batch normalization should reach an accuracy over 90%. There are plenty of details that can go wrong when implementing at this low level, so if you got it working - great job! If not, do not worry, just look at the `Batch_Normalization_Solutions` notebook to see what went wrong."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.