Id
stringlengths 1
6
| PostTypeId
stringclasses 7
values | AcceptedAnswerId
stringlengths 1
6
⌀ | ParentId
stringlengths 1
6
⌀ | Score
stringlengths 1
4
| ViewCount
stringlengths 1
7
⌀ | Body
stringlengths 0
38.7k
| Title
stringlengths 15
150
⌀ | ContentLicense
stringclasses 3
values | FavoriteCount
stringclasses 3
values | CreationDate
stringlengths 23
23
| LastActivityDate
stringlengths 23
23
| LastEditDate
stringlengths 23
23
⌀ | LastEditorUserId
stringlengths 1
6
⌀ | OwnerUserId
stringlengths 1
6
⌀ | Tags
list |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
755 | 2 | null | 726 | 56 | null | I don't know about famous, but the following is one of my favourites:
>
Conducting data analysis is like
drinking a fine wine. It is important
to swirl and sniff the wine, to unpack
the complex bouquet and to appreciate
the experience. Gulping the wine
doesn’t work.
-Daniel B. Wright (2003), see [PDF of Article](http://www.baomee.info/pdf/MakeFriends/1.pdf).
Reference:
Wright, D. B. (2003). Making friends with your data: Improving how statistics are conducted and reported1. British Journal of Educational Psychology, 73(1), 123-136.
| null | CC BY-SA 3.0 | null | 2010-07-27T09:44:12.930 | 2013-02-25T00:40:34.507 | 2013-02-25T00:40:34.507 | 183 | 183 | null |
757 | 2 | null | 73 | 4 | null | I find [lattice](http://cran.r-project.org/web/packages/lattice/index.html) along with the companion book "Lattice: Multivariate Data Visualization with R" by Deepayan Sarkar invaluable.
| null | CC BY-SA 2.5 | null | 2010-07-27T09:51:19.900 | 2010-07-27T09:51:19.900 | null | null | 439 | null |
758 | 2 | null | 723 | 9 | null | This is a method using Monte Carlo to show whether a result is correct.
Our Null Hypothesis H_0 is that our dataset does not have an interesting clustering. Our alternative hypothesis H_1 is that our dataset contains an interesting clustering.
Hereby we think of interesting as, more interesting than the clustering structure of a random dataset with the same row and column margins. Of course other constraints could be chosen, but to loose constraints will make our result too general, and to narrow constraints will fix the clustering to much, therefore making our result insignificant automatically. The margins, as we will see, are a good choice because of the methods existing for randomizing with it.
Let's define as our test statistic the clustering error (squared in-cluster distance), T from Π_0. The value for our original dataset is t.
We don't know anything about this distribution, except that we can draw samples from it. Which makes it a good candidate for Monte Carlo.
Now we draw n (i.i.d) random samples from Π_0 and calculate the empirical p-value with the formula p_emp = 1 / (n+1) * (Σ_i=1-n I(t_i >= t) + 1)
The random sampling can be done by swap randomization. In simple words, a square is searched with on two opposite corners an 1 and on the other two corners a 0. Then the corners are flipped. This is keeping the column and row margins. The procedure is repeated enough times until the dataset is randomized enough (this will take some experiments). More info about this can be found in [Assessing Data Mining Results via Swap Randomization by Gionis et. al.](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.76.3286&rep=rep1&type=pdf)
One method to do this is defining the distribution of your data and taking the clustering error as test-statistic t.
For example, if we consider all data sets with the same row and column margins as being our data distribution, than we can take n random matrices Xi from this distribution and calculate the clustering error for them. Then we can calculate the emperical p-value by the formula
| null | CC BY-SA 2.5 | null | 2010-07-27T10:00:23.720 | 2010-07-27T10:00:23.720 | null | null | 190 | null |
759 | 2 | null | 725 | 3 | null | I am afraid there is no; during my little adventure with such data we have just converted it to a data frame form, added some extra attributes made from neighborhoods of pixels and used standard methods. Still, packages [ripa](http://cran.r-project.org/web/packages/ripa/index.html) and [hyperSpec](http://cran.r-project.org/web/packages/hyperSpec/index.html) might be useful.
For other software, I've got an impression that most of sensible applications are commercial.
| null | CC BY-SA 2.5 | null | 2010-07-27T10:07:42.560 | 2010-07-27T10:07:42.560 | null | null | null | null |
760 | 2 | null | 575 | 22 | null | I am currently writing a paper in which I have the pleasure to conduct both between and within subjects comparisons. After discussion with my supervisor we decided to run t-tests and use the pretty simple `Holm-Bonferroni method` ([wikipedia](http://en.wikipedia.org/wiki/Holm%E2%80%93Bonferroni_method)) for correcting for alpha error cumulation. It controls for familwise error rate but has a greater power than the ordinary Bonferroni procedure.
Procedure:
- You run the t-tests for all comparisons you want to do.
- You order the p-values according to their value.
- You test the smallest p-value against alpha / k, the second smallest against alpha /( k - 1), and so forth until the first test turns out non-significant in this sequence of tests.
Cite Holm (1979) which can be downloaded via the link at [wikipedia](http://en.wikipedia.org/wiki/Holm%E2%80%93Bonferroni_method).
| null | CC BY-SA 2.5 | null | 2010-07-27T10:24:44.870 | 2010-07-27T13:08:54.103 | 2010-07-27T13:08:54.103 | 442 | 442 | null |
761 | 2 | null | 665 | 21 | null | I like this from Steve Skienna's [Calculated Bets](http://books.google.com/books?id=UvWGgaE4ZA8C&lpg=PA86&ots=RXQyDddYcu&dq=In%20summary%2C%20probability%20theory%20enables%20us%20to%20find%20the%20consequences%20of%20a%20given%20ideal%20world%2C%20while%20statistical%20theory%20enables%20us%20to%20to%20measure%20the%20extent%20to%20which%20our%20world%20is%20ideal.&pg=PA86#v=onepage&q&f=false) (see the link for complete discussion):
>
In summary, probability theory enables us to find the consequences of a given ideal world, while statistical theory enables us to to measure the extent to which our world is ideal.
| null | CC BY-SA 2.5 | null | 2010-07-27T10:26:36.600 | 2010-07-27T10:26:36.600 | null | null | 251 | null |
762 | 2 | null | 575 | 7 | null | Have a look at the [multcomp](http://cran.r-project.org/web/packages/multcomp/index.html)-package and its vignette [Simultaneous Inference in General Parametric Models](http://cran.r-project.org/web/packages/multcomp/vignettes/generalsiminf.pdf). I think it should do what wan't and the vignette has very good examples and extensive references.
| null | CC BY-SA 2.5 | null | 2010-07-27T11:04:03.853 | 2010-07-27T11:04:03.853 | null | null | 214 | null |
763 | 2 | null | 562 | 11 | null | The final year of the NetFlix Prize competition (2009) seemed to me to have sharply changed the general community-wide presumption against combining multiple learning algorithms.
For instance, my formal training (university courses) and later on-the-job oversight/mentoring taught us to avoid algorithm combination unless we had an explicit reason to do so--and "to improve resolution of my current algorithm", wasn't really deemed a good reason. (Others might have a different experience--of course i'm inferring a community-wide view based solely on my own experience, though my experience in coding poorly-performing ML algorithms is substantial.)
Still, there were a few "patterns" in which combining algorithms in one way or another was accepted, and actually improved performance. For me, the most frequent example involved some ML algorithm configured in machine mode (assigning a class label to each data point) and in which there were more than two classes (usually many more). When for instance, using a supervised-learning algorithm to resolve four classes, and we would see excellent separation except for let's say Class III versus Class IV. So out of those six decision boundaries, only one resolved below the required threshold. Particularly when classes III and IV together accounted for a small percent of the data, adding an additional algorithm optimized just on the resolution of those two classes, was a fairly common solution to this analytical problem type. (Usually that 'blind spot' was an inherent limitation of the primary algorithm--e.g., it was a linear classifier and the III/IV decision boundary was non-linear.
In other words, when we had a reliable algorithm suited to the processing environment (which was usually streaming data) and that performed within the spec except for a single blind spot that caused it to fail to resolve two (or more) classes that accounted for a small fraction of the data, then it was always better to 'bolt-on' another specialized algorithm to catch what the main algorithm was systematically missing.
Lastly, on this topic, i would like to recommend highly Chapter 17, Combining Multiple Learners, in [Introduction to Machine Learning](http://www.cmpe.boun.edu.tr/~ethem/i2ml2e/), 2d, by Ethem Alpaydin, MIT Press, 2010. Note that this is the second edition published a few months ago; the first edition was published in 2004 and i doubt it has the same coverage of this topic. (Actually i recommend the entire text, but that chapter in particular since it relates to Shane's Question.)
In 25 pages, the author summarizes probably every ML algorithm-combination scheme whose utility has been demonstrated in the academic literature or practice--e.g., bagging, boosting, mixture of experts, stacked generalization, cascading, voting, error-correcdting,....
| null | CC BY-SA 2.5 | null | 2010-07-27T11:04:08.207 | 2010-08-04T07:39:52.463 | 2010-08-04T07:39:52.463 | 438 | 438 | null |
764 | 1 | 772 | null | 16 | 6585 | I have commonly heard that LME models are more sound in the analysis of accuracy data (i.e., in psychology experiments), in that they can work with binomial and other non-normal distributions that traditional approaches (e.g., ANOVA) can't.
What is the mathematical basis of LME models that allow them to incorporate these other distributions, and what are some not-overly-technical papers describing this?
| Linear Mixed Effects Models | CC BY-SA 2.5 | null | 2010-07-27T11:29:20.193 | 2010-08-07T17:52:12.747 | 2010-08-07T17:52:12.747 | null | 445 | [
"mixed-model"
]
|
765 | 2 | null | 283 | 17 | null | A model is saturated if and only if it has as many parameters as it has data points (observations). Or put otherwise, in non-saturated models the degrees of freedom are bigger than zero.
This basically means that this model is useless, because it does not describe the data more parsimoniously than the raw data does (and describing data parsimoniously is generally the idea behind using a model). Furthermore, saturated models can (but don't necessarily) provide a (useless) perfect fit because they just interpolate or iterate the data.
Take for example the mean as a model for some data. If you have only one data point (e.g., 5) using the mean (i.e., 5; note that the mean is a saturated model for only one data point) does not help at all. However if you already have two data points (e.g., 5 and 7) using the mean (i.e., 6) as a model provides you with a more parsimonious description than the original data.
| null | CC BY-SA 2.5 | null | 2010-07-27T11:56:42.250 | 2010-07-27T12:32:15.423 | 2010-07-27T12:32:15.423 | 442 | 442 | null |
766 | 2 | null | 270 | 3 | null | Most statistical packages have a function to calculate the natural logarithm of the factorial directly (e.g. the lfactorial() function in R, the lnfactorial() function in Stata). This allows you to include the constant term in the log-likelihood if you want.
| null | CC BY-SA 2.5 | null | 2010-07-27T12:10:34.937 | 2010-07-27T12:10:34.937 | null | null | 449 | null |
767 | 2 | null | 577 | 235 | null | Your question implies that AIC and BIC try to answer the same question, which is not true. The AIC tries to select the model that most adequately describes an unknown, high dimensional reality. This means that reality is never in the set of candidate models that are being considered. On the contrary, BIC tries to find the TRUE model among the set of candidates. I find it quite odd the assumption that reality is instantiated in one of the models that the researchers built along the way. This is a real issue for BIC.
Nevertheless, there are a lot of researchers who say BIC is better than AIC, using model recovery simulations as an argument. These simulations consist of generating data from models A and B, and then fitting both datasets with the two models. Overfitting occurs when the wrong model fits the data better than the generating. The point of these simulations is to see how well AIC and BIC correct these overfits. Usually, the results point to the fact that AIC is too liberal and still frequently prefers a more complex, wrong model over a simpler, true model. At first glance these simulations seem to be really good arguments, but the problem with them is that they are meaningless for AIC. As I said before, AIC does not consider that any of the candidate models being tested is actually true. According to AIC, all models are approximations to reality, and reality should never have a low dimensionality. At least lower than some of the candidate models.
My recommendation is to use both AIC and BIC. Most of the times they will agree on the preferred model, when they don't, just report it.
If you are unhappy with both AIC and BIC and have free time to invest, look up Minimum Description Length (MDL), a totally different approach that overcomes the limitations of AIC and BIC. There are several measures stemming from MDL, like normalized maximum likelihood or the Fisher Information approximation. The problem with MDL is that its mathematically demanding and/or computationally intensive.
Still, if you want to stick to simple solutions, a nice way for assessing model flexibility (especially when the number of parameters are equal, rendering AIC and BIC useless) is doing Parametric Bootstrap, which is quite easy to implement. [Here is a link](http://www.ejwagenmakers.com/2004/PBCM.pdf) to a paper on it.
Some people here advocate for the use of cross-validation. I personally have used it and don't have anything against it, but the issue with it is that the choice among the sample-cutting rule (leave-one-out, K-fold, etc) is an unprincipled one.
| null | CC BY-SA 4.0 | null | 2010-07-27T12:31:57.280 | 2019-08-26T17:08:49.033 | 2019-08-26T17:08:49.033 | 7290 | 447 | null |
768 | 2 | null | 665 | 5 | null | In probability theory, we are given random variables X1, X2, ... in some way, and then we study their properties, i.e. calculate probability P{ X1 \in B1 }, study the convergence of X1, X2, ... etc.
In mathematical statistics, we are given n realizations of some random variable X, and set of distributions D; the problem is to find amongst distributions from D one which is most likely to generate the data we observed.
| null | CC BY-SA 2.5 | null | 2010-07-27T12:36:47.457 | 2010-07-27T12:36:47.457 | null | null | null | null |
769 | 1 | null | null | 2 | 585 | When does data analysis cease to be statistics ?
Are the following examples all applications of statistics ?: computer vision, face recognition, compressed sensing, lossy data compression, signal processing.
| What types of data analysis do not count as statistics? | CC BY-SA 2.5 | null | 2010-07-27T12:46:48.420 | 2010-07-27T16:00:22.087 | null | null | 327 | [
"mathematical-statistics"
]
|
770 | 1 | null | null | 6 | 345 | During every machine learning tutorial you'll find, there is the common "You will need to know x amount of stats before starting this tutorial". As such, using your knowledge of stats, you will learn about machine learning.
My question is whether this can be reversed. Can a computer science student learn statistics through studying machine learning algorithms? Has this been tested, at all? Are there examples where this is the case already?
| Is it possible to use machine learning as a method for learning stats, rather than vice-versa? | CC BY-SA 2.5 | null | 2010-07-27T12:53:30.250 | 2011-02-14T23:04:02.267 | 2010-09-17T20:31:31.940 | null | 453 | [
"machine-learning",
"teaching"
]
|
771 | 2 | null | 770 | -1 | null | I think that learning machine learning requires only an elementary subset of statistics; too much may be dangerous, since some intuitions are in conflict. Still, the answer to the question can it be reversed is no.
| null | CC BY-SA 2.5 | null | 2010-07-27T13:02:58.047 | 2010-07-27T13:02:58.047 | null | null | null | null |
772 | 2 | null | 764 | 16 | null | One major benefit of mixed-effects models is that they don't assume independence amongst observations, and there can be a correlated observations within a unit or cluster.
This is covered concisely in "Modern Applied Statistics with S" (MASS) in the first section of chapter 10 on "Random and Mixed Effects". V&R walk through an example with gasoline data comparing ANOVA and lme in that section, so it's a good overview. The R function to be used in `lme` in the `nlme` package.
The model formulation is based on Laird and Ware (1982), so you can refer to that as a primary source although it's certainly not good for an introduction.
- Laird, N.M. and Ware, J.H. (1982) "Random-Effects Models for Longitudinal Data", Biometrics, 38, 963–974.
- Venables, W.N. and Ripley, B.D. (2002) "Modern Applied Statistics with S", 4th Edition, Springer-Verlag.
You can also have a look at the ["Linear Mixed Models"](http://cran.r-project.org/doc/contrib/Fox-Companion/appendix-mixed-models.pdf) (PDF) appendix to John Fox's "An R and S-PLUS Companion to Applied Regression". And [this lecture by Roger Levy](http://idiom.ucsd.edu/~rlevy/lign251/fall2007/lecture_14.pdf) (PDF) discusses mixed effects models w.r.t. a multivariate normal distribution.
| null | CC BY-SA 2.5 | null | 2010-07-27T13:07:38.643 | 2010-07-27T13:07:38.643 | null | null | 5 | null |
773 | 2 | null | 283 | 20 | null | As everybody else said before, it means that you have as much parameters have you have data points. So, no goodness of fit testing. But this does not mean that "by definition", the model can perfectly fit any data point. I can tell you by personal experience of working with some saturated models that could not predict specific data points. It is quite rare, but possible.
Another important issue is that saturated does not mean useless. For instance, in mathematical models of human cognition, model parameters are associated with specific cognitive processes that have a theoretical background. If a model is saturated, you can test its adequacy by doing focused experiments with manipulations that should affect only specific parameters. If the theoretical predictions match the observed differences (or lack of) in parameter estimates, then one can say that the model is valid.
An example: Imagine for instance a model that has two sets of parameters, one for cognitive processing, and another for motor responses. Imagine now that you have an experiment with two conditions, one in which the participants ability to respond is impaired (they can only use one hand instead of two), and in the other condition there is no impairment. If the model is valid, differences in parameter estimates for both conditions should only occur for the motor response parameters.
Also, be aware that even if one model is non-saturated, it might still be non-identifiable, which means that different combinations of parameter values produce the same result, which compromises any model fit.
If you wanna find more information on these issues in general, you might wanna take look at these papers:
Bamber, D., & van Santen, J. P. H. (1985). How many parameters can a model have and still be testable? Journal of Mathematical Psychology, 29, 443-473.
Bamber, D., & van Santen, J. P. H. (2000). How to Assess a Model's Testability and Identifiability. Journal of Mathematical Psychology, 44, 20-40.
cheers
| null | CC BY-SA 2.5 | null | 2010-07-27T13:09:54.817 | 2010-07-27T13:09:54.817 | null | null | 447 | null |
774 | 2 | null | 770 | 8 | null | I really wouldn't suggest using machine learning in order to learn statistics. The mathematics employed in machine learning is often different because there's a real emphasis on the computational algorithm. Even treatment of the same concept will be different.
A simple example of this would be to compare the treatment of linear regression between a basic statistics textbook and a machine learning textbook. Most machine learning texts give a heavy treatment to concepts like "[gradient descent](http://en.wikipedia.org/wiki/Gradient_descent)" and other optimzation techniques, while a statistics textbook will typically just cover [ordinary least squares](http://en.wikipedia.org/wiki/Ordinary_least_squares) (if even that).
Lastly, machine learning generally doesn't cover the same material when it comes to things like model comparison, sampling, etc. So while some of the basic models are the same, the conceptual frameworks can be very different.
| null | CC BY-SA 2.5 | null | 2010-07-27T13:14:19.160 | 2010-07-27T13:14:19.160 | null | null | 5 | null |
775 | 1 | 777 | null | 10 | 8324 | What is the difference between operations research and statistical analysis?
| Operations research versus statistical analysis? | CC BY-SA 3.0 | null | 2010-07-27T13:14:54.837 | 2014-02-04T05:06:46.563 | 2012-02-23T10:41:34.117 | null | 460 | [
"operations-research"
]
|
776 | 2 | null | 769 | 3 | null | This may be slightly controversial, but certainly most of the examples that you give are not statistics (some of these would more properly fall under machine learning):
Statistics usually covers the scenario where you are making inferences something when you only have a subset of the data (hence the use of things like [the p-value](https://stats.stackexchange.com/questions/31/what-is-the-meaning-of-p-values-and-t-values-in-statistical-tests)). The goal is to come to a deeper understanding of the underlying process that generates the data.
In the examples that you provide, the goal is to perform some kind of action; whether the model itself is an accurate depiction of the underlying process is completely irrelevant so long as the predictions are accurate. See [my related question](https://stats.stackexchange.com/questions/6/the-two-cultures-statistics-vs-machine-learning) about the difference between machine learning and statistics.
| null | CC BY-SA 2.5 | null | 2010-07-27T13:25:13.050 | 2010-07-27T13:25:13.050 | 2017-04-13T12:44:24.667 | -1 | 5 | null |
777 | 2 | null | 775 | 13 | null | Those are entire academic discplines so I do not think you can expect much more here than pointers to further, and more extensive, documentation as e.g. Wikipedia on [Operations Research](http://en.wikipedia.org/wiki/Operations_research) and [Statistics](http://en.wikipedia.org/wiki/Statistics).
Let me try a personal definition which may be grossly simplifying:
- Operations Research is concerned with process modeling and optimisation
- Statistical Modeling is concerning with describing the so-called 'data generating process': find a model that describes something observed, and then do estimation, inference and possibly prediction.
| null | CC BY-SA 2.5 | null | 2010-07-27T13:35:21.463 | 2010-07-27T13:35:21.463 | null | null | 334 | null |
778 | 2 | null | 672 | 15 | null | I'm sorry, but there seems to be some confusion here:
Bayes' theorem is not up for discussion of the neverending Bayesian-[Frequentist](http://en.wikipedia.org/wiki/Probability_interpretations#Frequentism) debate. It is a theorem that is consistent with both schools of thought (given that it is consistent with Kolmogorov's probability axioms).
Of course, Bayes' theorem is the core of Bayesian statistics, but the theorem itself is universal. The clash between frequentists and Bayesians mostly pertains to how prior distributions can be defined or not.
So, if the question is about Bayes' theorem (and not Bayesian statistics):
Bayes' theorem defines how one can calculate specific conditional probabilities. Imagine for instance that you know: the probability of somebody having symptom A, given that they have disease X p(A|X); the probability of somebody in general having disease X p(X); the probability of somebody in general having symptom A p(A). with these 3 pieces of information you can calculate the probability of somebody having disease X, given that they have sympotm A p(X|A).
| null | CC BY-SA 2.5 | null | 2010-07-27T13:39:35.543 | 2011-02-02T19:09:56.450 | 2011-02-02T19:09:56.450 | 509 | 447 | null |
779 | 1 | null | null | 9 | 3152 | I've heard that a lot of quantities that occur in nature are normally distributed. This is typically justified using the central limit theorem, which says that when you average a large number of iid random variables, you get a normal distribution. So, for instance, a trait that is determined by the additive effect of a large number of genes may be approximately normally distributed since the gene values may behave roughly like iid random variables.
Now, what confuses me is that the property of being normally distributed is clearly not invariant under monotonic transformations. So, if there are two ways of measuring something that are related by a monotonic transformation, they are unlikely to both be normally distributed (unless that monotonic transformation is linear). For instance, we can measure the sizes of raindrops by diameter, by surface area, or by volume. Assuming similar shapes for all raindrops, the surface area is proportional to the square of the diameter, and the volume is proportional to the cube of the diameter. So all of these ways of measuring cannot be normally distributed.
So my question is whether the particular way of scaling (i.e., the particular choice of monotonic transformation) under which the distribution does become normal, must carry a physical significance. For instance, should heights be normally distributed or the square of height, or the logarithm of height, or the square root of height? Is there a way of answering that question by understanding the processes that affect height?
| Normal distribution and monotonic transformations | CC BY-SA 2.5 | null | 2010-07-27T13:49:41.073 | 2013-03-16T00:54:30.960 | 2013-03-16T00:54:30.960 | 805 | 463 | [
"data-transformation",
"normality-assumption"
]
|
780 | 2 | null | 775 | 9 | null | Operations Research (OR), sometimes called "Management Science", consists of three main topics, Optimization, Stochastic Processes, Process and Production Methodologies.
OR uses statistical analysis in many contexts (for example discrete event simulations) but they should not be considered the same, additionally one of the main topics in OR is optimization (linear, and nonlinear) which can make it more clear why these two fields should be considered different
There is [another exchange website for OR](http://www.or-exchange.com/questions) if you are interested
| null | CC BY-SA 2.5 | null | 2010-07-27T13:55:18.623 | 2010-07-27T19:10:25.243 | 2010-07-27T19:10:25.243 | 172 | 172 | null |
781 | 2 | null | 712 | 3 | null | One approach would be to use Bloom filters. Check [SAFELINK](http://www.uni-due.de/soziologie/schnell_forschung_safelink_software.php) project website for [programs](http://www.uni-due.de/methods/bloom/index-en-bloom.html) in Java and Python. Paper explaining method is [here](http://dx.doi.org/10.1186/1472-6947-9-41).
There is also an interesting approach to anaonymization of strings in the context of [record linkage](http://en.wikipedia.org/wiki/Record_linkage) using n-grams developed by [ANU Data Mining Group](http://datamining.anu.edu.au/projects/linkage.html). The paper with description and sample Python code is available [here](http://www.biomedcentral.com/1472-6947/4/9/).
| null | CC BY-SA 3.0 | null | 2010-07-27T13:59:02.623 | 2011-04-30T18:31:33.180 | 2011-04-30T18:31:33.180 | 22 | 22 | null |
782 | 2 | null | 779 | 4 | null | I think you missunderstood (half of) the use statistician make of the normal distribution but I really like your question.
I don't think it is a good idea to assume systematically normality and I admit it is done sometime (maybe because the normal distribution is tractable, unimodal ...) without verification. Hence your remark about monotonic map is excellent !
However the powerfull use of normality comes when you construct yourself new statistics such as the one that appears when you apply the empiriral counter part of expectation: the empirical mean. Hence empirical mean and more generally smoothing is what makes normality appear everywhere...
| null | CC BY-SA 2.5 | null | 2010-07-27T14:02:37.327 | 2010-07-27T15:44:37.567 | 2010-07-27T15:44:37.567 | 223 | 223 | null |
783 | 2 | null | 726 | 53 | null | >
... surely, God loves the .06 nearly as much as the .05. Can there be any
doubt that God views the strength of evidence for or against the null as a
fairly continuous function of the magnitude of p? (p.1277)
Rosnow, R. L., & Rosenthal, R. (1989). Statistical procedures and the justification of knowledge in psychological science. American Psychologist, 44(10), 1276-1284. [pdf](https://web.archive.org/web/20140330070045/http://socrates.berkeley.edu/%7Emaccoun/PP279_Rosnow.pdf).
| null | CC BY-SA 4.0 | null | 2010-07-27T14:03:52.940 | 2022-11-23T09:59:13.570 | 2022-11-23T09:59:13.570 | 362671 | 442 | null |
784 | 2 | null | 614 | 5 | null | [Street-Fighting Mathematics](https://mitpress.mit.edu/books/street-fighting-mathematics). The Art of Educated Guessing and Opportunistic Problem Solving by Sanjoy Mahajan from MIT. Available under a Creative Commons Noncommercial Share Alike license.
Available as a free download on the MIT Press website (but not from the [author's website](http://streetfightingmath.com/)).
| null | CC BY-SA 3.0 | null | 2010-07-27T14:04:13.360 | 2016-10-06T19:41:41.493 | 2016-10-06T19:41:41.493 | 122650 | 22 | null |
785 | 2 | null | 726 | 25 | null | >
The statistician cannot evade the responsibility for understanding the
process he applies or recommends.
-– Sir Ronald A. Fisher
| null | CC BY-SA 2.5 | null | 2010-07-27T14:10:31.507 | 2010-12-03T04:02:46.950 | 2010-12-03T04:02:46.950 | 795 | 447 | null |
786 | 2 | null | 726 | 31 | null | >
The death of one man is a tragedy.
The death of millions is a statistic.
-- Kurt Tucholsky, in: Französischer Witz, 1925
| null | CC BY-SA 3.0 | null | 2010-07-27T14:14:10.623 | 2015-12-05T15:54:52.310 | 2015-12-05T15:54:52.310 | 36678 | 460 | null |
787 | 2 | null | 726 | 6 | null | >
Statistics are the triumph of the
quantitative method, and the
quantitative method is the victory of
sterility and death.
~ Hillaire Belloc in The Silence of the Sea
| null | CC BY-SA 2.5 | null | 2010-07-27T14:20:42.650 | 2010-07-27T14:20:42.650 | null | null | 460 | null |
788 | 2 | null | 726 | 2 | null | >
A witty statesman said, you might
prove anything by figures.
~ Thomas Carlyle, Chartism (1839) ch. 2
| null | CC BY-SA 2.5 | null | 2010-07-27T14:25:39.673 | 2010-07-27T14:25:39.673 | null | null | 460 | null |
789 | 2 | null | 614 | 5 | null | [Statistical Analysis with the General Linear Model](http://psy.otago.ac.nz/miller/index.htm#GLMBook)
It covers basic linear models (ANOVA, ANCOVA, multiple regression). I can tell by personal experience that it is really really good book to get into the general framework of linear models, which are very useful in many advanced approaches (e.g., hierarchical modeling).
| null | CC BY-SA 3.0 | null | 2010-07-27T14:38:34.183 | 2014-06-20T06:34:29.530 | 2014-06-20T06:34:29.530 | 930 | 447 | null |
790 | 1 | null | null | 4 | 6855 | I am looking at a scientific paper in which a single measurement is calculated using a logarithmic mean
>
'triplicate spots were combined to
produce one signal by taking the
logarithmic mean of reliable spots'
Why choose the log-mean?
Are the authors making an assumption about the underlying distribution?
That it is what...Log-Normal?
Have they just picked something they thought was reasonable... i.e. between a a mean and a geometric mean?
Any thoughts?
| Why (or when) to use the log-mean? | CC BY-SA 2.5 | null | 2010-07-27T14:46:49.640 | 2022-02-11T14:00:06.143 | 2022-02-11T14:00:06.143 | 11887 | 228 | [
"distributions",
"mean",
"logarithm",
"geometric-mean"
]
|
791 | 2 | null | 770 | 3 | null | I really dont think so, as there are fundamental aspects in statistics that are simply overlooked in machine learning. For instance, in statistics, when fitting a model to data, the discrpeancy function that is used (e.g., G^2, RMSEA) is essential because they have different statistical properties. In machine learning, it just doesnt matter, so it is not covered at all.
Of course one could argue that you could learn those things later, but IMHO, it is better to undestand and care about some issues, and possibly in the future not care about them, then the other way around.
cheers
| null | CC BY-SA 2.5 | null | 2010-07-27T14:52:19.113 | 2010-07-27T14:52:19.113 | null | null | 447 | null |
792 | 2 | null | 779 | 4 | null | Simply CLT (nor any other theorem) does not state that every quantity in the universe is normally distributed. Indeed, statisticians often use monotonic transformations to improve normality, so they could use their favorite tools.
| null | CC BY-SA 2.5 | null | 2010-07-27T15:03:28.010 | 2010-07-27T15:03:28.010 | null | null | null | null |
793 | 2 | null | 790 | 3 | null | >
Are the authors making an assumption
about the underlying distribution?
You are making an assumption whether you choose to use it or whether you choose against using it.
For Power Law distributions it usually makes sense to look at the logarithms.
| null | CC BY-SA 2.5 | null | 2010-07-27T15:04:58.067 | 2010-07-27T15:04:58.067 | null | null | 3807 | null |
794 | 2 | null | 726 | 45 | null | >
The subjectivist (i.e. Bayesian)
states his judgements, whereas the
objectivist sweeps them under the
carpet by calling assumptions
knowledge, and he basks in the
glorious objectivity of science.
I.J. Good
| null | CC BY-SA 2.5 | null | 2010-07-27T15:05:38.800 | 2010-07-27T15:05:38.800 | null | 7620 | 7620 | null |
795 | 1 | null | null | -3 | 2133 | I have data compiled by someone else where score averages have been computed over time- averages range from 0-100. The original scores have negative values in many cases and the average would have been negative also, raw average ranges from -30 to 90. How is this 'normalization' accomplished?
Thanks
| Normalization of series | CC BY-SA 2.5 | null | 2010-07-27T15:08:11.493 | 2010-07-27T15:36:41.480 | null | null | 474 | [
"mean"
]
|
796 | 2 | null | 305 | 38 | null | I would like to oppose the other two answers based on a paper (in German) by [Kubinger, Rasch and Moder (2009)](http://www.psycontent.com/content/t5726m72644gq457/).
They argue, based on "extensive" simulations from distributions either meeting or not meeting the assumptions imposed by a t-test, (normality and homogenity of variance) that the welch-tests performs equally well when the assumptions are met (i.e., basically same probability of committing alpha and beta errors) but outperforms the t-test if the assumptions are not met, especially in terms of power. Therefore, they recommend to always use the welch-test if the sample size exceeds 30.
As a meta-comment: For people interested in statistics (like me and probably most other here) an argument based on data (as mine) should at least count equally as arguments solely based on theoretical grounds (as the others here).
---
Update:
After thinking about this topic again, I found two further recommendations of which the newer one assists my point. Look at the original papers (which are both, at least for me, freely available) for the argumentations that lead to these recommendations.
The first recommendation comes from Graeme D. Ruxton in 2006: "If you want to compare the central tendency of 2 populations based on samples of unrelated data, then the unequal variance t-test should always be used in preference to the Student's t-test or Mann–Whitney U test."
In:
Ruxton, G.D., 2006. [The unequal variance t-test is an underused
alternative to Student’s t-test and the Mann–Whitney U test](http://beheco.oxfordjournals.org/content/17/4/688.full).
Behav. Ecol. 17, 688–690.
The second (older) recommendation is from Coombs et al. (1996, p. 148): "In summary, the independent samples t test is generally acceptable in terms of controlling Type I error rates provided there are sufficiently large equal-sized samples, even when the equal population variance assumption is violated. For unequal-sized samples, however, an alternative that does not assume equal population variances is preferable. Use the James second-order test when distributions are either short-tailed symmetric or normal. Promising alternatives include the Wilcox H and Yuen trimmed means tests, which provide broader control of Type I error rates than either the Welch test or the James test and have greater power when data are long-tailed." (emphasis added)
In:
Coombs WT, Algina J, Oltman D. 1996. [Univariate and multivariate omnibus hypothesis tests selected to control type I error rates when population variances are not necessarily equal](http://rer.sagepub.com/content/66/2/137.full.pdf). Rev Educ Res 66:137–79.
| null | CC BY-SA 2.5 | null | 2010-07-27T15:14:22.937 | 2010-10-19T15:28:42.237 | 2010-10-19T15:28:42.237 | 442 | 442 | null |
797 | 2 | null | 779 | 6 | null | Very good question. I feel that the answer depends on the whether you can identify the underlying process that gives rise to the measurement in question. If for example, you have evidence that height is a linear combination of several factors (e.g., height of parents, height of grandparents etc) then it would be natural to assume that height is normally distributed. On the other hand if you have evidence or perhaps even theory that the log of height is a linear combination of several variables (e.g., log parents heights, log of grandparents heights etc) then the log of height will be normally distributed.
In most situations, we do not know the underlying process that drives the measurement of interest. Thus, we can do one of several things:
(a) If the empirical distribution of heights looks normal then we use a the normal density for further analysis which implicitly assumes that height is a linear combination of several variables.
(b) If the empirical distribution does not look normal then we can try some transformation as suggested by [mbq](https://stats.stackexchange.com/users/88/mbq) (e.g. log(height)). In this case we implicitly assume that the transformed variable (i.e., log(height)) is a linear combination of several variables.
(c) If (a) or (b) do not help then we have to abandon the advantages that CLT and an assumption of normality give us and model the variable using some other distribution.
| null | CC BY-SA 2.5 | null | 2010-07-27T15:19:43.983 | 2010-07-27T15:25:00.930 | 2017-04-13T12:44:37.420 | -1 | null | null |
798 | 1 | 862 | null | 118 | 265258 | I'm interested in finding as optimal of a method as I can for determining how many bins I should use in a histogram. My data should range from 30 to 350 objects at most, and in particular I'm trying to apply thresholding (like Otsu's method) where "good" objects, which I should have fewer of and should be more spread out, are separated from "bad" objects, which should be more dense in value. A concrete value would have a score of 1-10 for each object. I'd had 5-10 objects with scores 6-10, and 20-25 objects with scores 1-4. I'd like to find a histogram binning pattern that generally allows something like Otsu's method to threshold off the low scoring objects. However, in the implementation of Otsu's I've seen, the bin size was 256, and often I have many fewer data points that 256, which to me suggests that 256 is not a good bin number. With so few data, what approaches should I take to calculating the number of bins to use?
| Calculating optimal number of bins in a histogram | CC BY-SA 3.0 | null | 2010-07-27T15:21:48.417 | 2022-11-17T19:53:13.150 | 2016-06-03T00:57:01.100 | 28666 | 476 | [
"rule-of-thumb",
"histogram"
]
|
799 | 2 | null | 764 | 9 | null | The main advantage of LME for analysing accuracy data is the ability to account for a series of random effects. In psychology experiments, researchers usually aggregate items and/or participants. Not only are people different from each other, but items also differ (some words might be more distinctive or memorable, for instance). Ignoring these sources of variability usually leads to underestimations of accuracy (for instance lower d' values). Although the participant aggregation issue can somehow be dealt with individual estimation, the item effects are still there, and are commonly larger than participant effects. LME not only allows you to tackle both random effects simultaneously, but also to add specificy additional predictor variables (age, education level, word length, etc.) to them.
A really good reference for LMEs, especially focused in the fields of linguistics and experimental psychology, is
[Analyzing Linguistic Data: A Practical Introduction to Statistics using R](http://rads.stackoverflow.com/amzn/click/0521709180)
cheers
| null | CC BY-SA 2.5 | null | 2010-07-27T15:26:34.537 | 2010-07-27T15:26:34.537 | null | null | 447 | null |
800 | 2 | null | 795 | 1 | null | The question is a bit unclear. But, perhaps the normalization you are looking for is this:
Normalized Score = 100 * (Raw Score - min(Raw_score)) / (max(Raw Score) - min(Raw Score))
| null | CC BY-SA 2.5 | null | 2010-07-27T15:27:18.890 | 2010-07-27T15:27:18.890 | null | null | null | null |
801 | 2 | null | 798 | 6 | null | I'm not sure this counts as strictly good practice, but I tend to produce more than one histogram with different bin widths and pick the histogram which histogram to use based on which histogram fits the interpretation I'm trying to communicate best. Whilst this introduces some subjectivity into the choice of histogram I justify it on the basis I have had much more time to understand the data than the person I'm giving the histogram to so I need to give them a very concise message.
I'm also a big fan of presenting histograms with the same number of points in each bin rather than the same bin width. I usually find these represent the data far better then the constant bin width although they are more difficult to produce.
| null | CC BY-SA 4.0 | null | 2010-07-27T15:30:31.073 | 2020-01-24T17:34:43.113 | 2020-01-24T17:34:43.113 | -1 | 210 | null |
802 | 2 | null | 779 | 5 | null | The rescaling of a particular variable should, when possible, relate to some comprehensible scale for the reason that it helps make the resulting model interpretable. However, the resulting transformation need not absolutely carry a physical significance. Essentially you have to engage in a trade off between the violation of the normality assumption and the interpretability of your model. What I like to do in these situations is have the original data, data transformed in a way that makes sense, and the data transformed in a way that is most normal. If the data transformed in a way that makes sense is the same as the results when the data is transformed in a way that makes it most normal, I report it in a way that is interpretable with a side note that the results are the same in the case of the optimally transformed (and/or untransformed) data. When the untransformed data is behaving particularly poorly, I conduct my analyses with the transformed data but do my best to report the results in untransformed units.
Also, I think you have a misconception in your statement that "quantities that occur in nature are normally distributed". This only holds true in cases where the value is "determined by the additive effect of a large number" of independent factors. That is, means and sums are normally distributed regardless of the underlying distribution from which they draw, where as individual values are not expected to be normally distributed. As was of example, individual draws from a binomial distribution do not look at all normal, but a distribution of the sums of 30 draws from a binomial distribution does look rather normal.
| null | CC BY-SA 2.5 | null | 2010-07-27T15:35:14.460 | 2010-07-27T15:35:14.460 | null | null | 196 | null |
803 | 2 | null | 795 | 4 | null | Or more generically,
`Index = ( ((RawValue - Min(Raw))/(Max(Raw)-Min(Raw)) * (Max(Out)-Min(Out) ) + Min(Out)`
Where `Raw` is the input vector, `Out` is the output vector, and `RawValue` is the value in question. Srikant's answer is the same for an output range of 0 to 100.
To convert back, rearrange to get:
`RawValue = (((Index - Min(Out))*(Max(Raw)-Min(Raw)) / (Max(Out)-Min(Out)) + Min(Raw)`
| null | CC BY-SA 2.5 | null | 2010-07-27T15:36:41.480 | 2010-07-27T15:36:41.480 | null | null | 257 | null |
804 | 2 | null | 305 | 13 | null | Of course, one could ditch both tests, and start using a Bayesian t-test (Savage-Dickey ratio test), which can account for equal and unequal variances, and best of all, it allows for a quantification of evidence in favor of the null hypothesis (which means, no more of old "failure to reject" talk)
This test is very simple (and fast) to implement, and there is a paper that clearly explains to readers unfamiliar with Bayesian statistics how to use it, along with an R script. You basically can just insert your data send the commands to the R console:
[Wetzels, R., Raaijmakers, J. G. W., Jakab, E., & Wagenmakers, E.-J. (2009). How to Quantify Support For and Against the Null Hypothesis: A Flexible WinBUGS Implementation of a Default Bayesian t-test.](http://www.ruudwetzels.com/articles/Wetzelsetal2009_SDtest.pdf)
there is also a tutorial for all this, with example data:
[http://www.ruudwetzels.com/index.php?src=SDtest](http://www.ruudwetzels.com/index.php?src=SDtest)
I know this is not a direct response to what was asked, but I thought readers might enjoy having this nice alternative
| null | CC BY-SA 4.0 | null | 2010-07-27T15:43:51.857 | 2021-11-06T11:36:47.957 | 2021-11-06T11:36:47.957 | 11887 | 447 | null |
805 | 1 | null | null | 2 | 1738 | I am attempting to calculate the standard error (SE) for the positive predictive value (PPV), negative predictive value (NPV), and diagnostic odds ratio (DOR) that I have obtained using the rates of true positives, false positives, true negatives, and false negatives in a sample. I am able to get 95% CIs but not SE.
Thank you!
| How do I calculate the SE for PPV, NPV, and DOR? | CC BY-SA 2.5 | null | 2010-07-27T15:43:55.057 | 2010-08-13T13:35:40.603 | 2010-08-13T13:35:40.603 | 8 | null | [
"error",
"standard-error"
]
|
806 | 1 | 829 | null | 6 | 10198 | Lately, there have been numerous questions about [normalization](http://en.wikipedia.org/wiki/Normalization_%28statistics%29)
What are some of the situations where you never ever ever should normalize your data, and what are the alternatives?
| When should normalization never be used? | CC BY-SA 2.5 | null | 2010-07-27T15:56:38.297 | 2010-09-27T23:40:16.273 | null | null | 59 | [
"normality-assumption"
]
|
807 | 2 | null | 769 | 1 | null | A statistic is any sample estimation of a population characteristic is it not? Thus, I would suggest so long as inference from a characterized sample to a population is taking place what is occurring is, at least in part, statistics. Under my definition machine learning would be a discipline that makes use of statistics. For example, under many examples of machine learning it seems like part of what is happening is an attempt to take information provided to the system (a sample) in order to guess from which distribution (a population) it arose.
| null | CC BY-SA 2.5 | null | 2010-07-27T16:00:22.087 | 2010-07-27T16:00:22.087 | null | null | 196 | null |
808 | 2 | null | 726 | 10 | null | >
A statistical analysis, properly conducted, is a delicate dissection of uncertainties, a surgery of suppositions.
-- M.J. Moroney
| null | CC BY-SA 2.5 | null | 2010-07-27T16:04:42.707 | 2010-10-02T17:12:07.793 | 2010-10-02T17:12:07.793 | 795 | 482 | null |
809 | 2 | null | 726 | 3 | null | >
An argument over the meaning of words
is a matter of law, an argument
grounded in empirical data and
quantitative estimates is an argument
about science.
~ Razib Khan (though he is not a statistician or famous)
| null | CC BY-SA 2.5 | null | 2010-07-27T16:14:26.303 | 2010-07-27T16:14:26.303 | null | null | null | null |
810 | 2 | null | 798 | 26 | null | If you use too few bins, the histogram doesn't really portray the data very well. If you have too many bins, you get a broken comb look, which also doesn't give a sense of the distribution.
One solution is to create a graph that shows every value. Either a dot plot, or a cumulative frequency distribution, which doesn't require any bins.
If you want to create a frequency distribution with equally spaced bins, you need to decide how many bins (or the width of each). The decision clearly depends on the number of values. If you have lots of values, your graph will look better and be more informative if you have lots of bins. [This wikipedia page](http://en.wikipedia.org/wiki/Histogram#Number_of_bins_and_width) lists several methods for deciding bin width from the number of observations. The simplest method is to set the number of bins equal to the square root of the number of values you are binning.
[This page from Hideaki Shimazaki](http://toyoizumilab.brain.riken.jp/hideaki/res/histogram.html) explains an alternative method. It is a bit more complicated to calculate, but seems to do a great job. The top part of the page is a Java app. Scroll past that to see the theory and explanation, then keep scrolling to find links to the papers that explain the method.
| null | CC BY-SA 3.0 | null | 2010-07-27T16:17:43.867 | 2012-12-23T06:12:04.710 | 2012-12-23T06:12:04.710 | 25 | 25 | null |
811 | 2 | null | 726 | 15 | null | >
It is the mark of a truly intelligent
person to be moved by statistics.
George Bernard Shaw
| null | CC BY-SA 2.5 | null | 2010-07-27T16:18:28.013 | 2010-07-27T16:18:28.013 | null | null | null | null |
812 | 1 | 904 | null | 11 | 3856 | There are a lot of references in the statistic literature to "functional data" (i.e. data that are curves), and in parallel, to "high dimensional data" (i.e. when data are high dimensional vectors). My question is about the difference between the two type of data.
When talking about applied statistic methodologies that apply in case 1 can be understood as a rephrasing of methodologies from case 2 through a projection into a finite dimensional subspace of a space of functions, it can be polynomes, splines, wavelet, Fourier, .... and will translate the functional problem into a finite dimensional vectorial problem (since in applied mathematic everything comes to be finite at some point).
My question is: can we say that any statistical procedure that applies to functional data can also be applied (almost directly) to high dimension data and that any procedure dedicated to high dimensional data can be (almost directly) applied to functional data ?
If the answer is no, can you illustrate ?
EDIT/UPDATE with the help of Simon Byrne's answer:
- sparsity (S-sparse assumption, $l^p$ ball and weak $l^p$ ball for $p<1$) is used as a structural assumption in high dimensional statistical analysis.
- "smoothness" is used as a structural assumption in functional data analysis.
On the other hand, inverse Fourier transform and inverse wavelet transform are transforming sparcity into smoothness, and smoothness is transformed into sparcity by wavelet and fourier transform. This make the critical difference mentionned by Simon not so critical?
| What is the difference between functional data analysis and high dimensional data analysis | CC BY-SA 2.5 | null | 2010-07-27T16:19:42.880 | 2019-12-03T03:18:34.650 | 2019-12-03T03:18:34.650 | 11887 | 223 | [
"data-mining",
"curve-fitting",
"signal-processing",
"functional-data-analysis",
"wavelet"
]
|
813 | 2 | null | 726 | 97 | null | >
Statistical thinking will one day be
as necessary a qualification for
efficient citizenship as the ability
to read and write.
--H.G. Wells
| null | CC BY-SA 2.5 | null | 2010-07-27T16:23:12.707 | 2010-07-27T16:23:12.707 | null | null | null | null |
814 | 2 | null | 726 | 9 | null | >
These days the statistician is often
asked such questions as "Are you a
Bayesian?" "Are you a frequentist?"
"Are you a data analyst?" "Are you a
designer of experiments?". I will
argue that the appropriate answer to
ALL of these questions can be (and
preferably should be) "yes", and that
we can see why this is so if we
consider the scientific context for
what statisticians do.
--G.E.P. Box
| null | CC BY-SA 2.5 | null | 2010-07-27T16:26:53.157 | 2010-07-27T16:26:53.157 | null | null | null | null |
815 | 2 | null | 779 | 5 | null | I must admit that I do not really understand your question:
- your raindrops example is not very satisfying since this is not illustrating the fact that the Gaussian behaviour comes from the "average of a large number of iid random variables".
- if the quantity $X$ that you are interested in is an average $\frac{Y_1+\ldots+Y_N}{N}$ that fluctuates around its mean in a Gaussian way, you can also expect that $\frac{f(Y_1)+\ldots+f(Y_N)}{N}$ has a Gaussian behaviour.
- if the fluctuation of $X$ around its mean are approximately Gaussian and small, then so are the fluctuation of $f(X)$ around its mean (by Taylor expansion)
- could you cite some true examples of (real life) Gaussian behaviour coming from averaging: this is not very common! Gaussian behaviour is often used in statistics as a first rough approximation because the computations are very tractable. As physicists uses the harmonic approximation, statisticians uses the Gaussian approximation.
| null | CC BY-SA 2.5 | null | 2010-07-27T16:34:22.917 | 2010-07-27T16:34:22.917 | null | null | 368 | null |
816 | 2 | null | 806 | 4 | null | Of course one should never try to blindly normalize data if the data does not follow a (single) normal distribution.
For example one might want to rescale observables $X$ to all be normal with $(X-\mu)/\sigma$, but this can only work if the data is normal and if both $\mu$ and $\sigma$ are the same for all data points (e.g. $\sigma$ doesn't depend on $\mu$ in a particular $X$ range).
| null | CC BY-SA 2.5 | null | 2010-07-27T16:34:55.863 | 2010-09-27T23:40:16.273 | 2010-09-27T23:40:16.273 | 159 | 56 | null |
817 | 2 | null | 779 | 5 | null | Vipul, you're not being totally precise in your question.
>
This is typically justified using the
central limit theorem, which says that
when you average a large number of iid
random variables, you get a normal
distribution.
I'm not entirely sure this is what you're saying, but keep in mind that the raindrops in your example are not iid random variables. The mean calculated by sampling a certain number of those raindrops is a random variables, and as the means are calculated using a large enough sample size, the distribution of that sample mean is normal.
The law of large numbers says that the value of that sample mean converges to the average value of the population (strong or weak depending on type of convergence).
The CLT says that the sample mean, call it XM(n), which is a random variable, has a distribution, say G(n). As n approaches infintity, that distribution is the normal distribution. CLT is all about convergence in distribution, not a basic concept.
The observations you draw (diameter, area, volume) don't have to be normal at all. They probably won't be if you plot them. But, the sample mean from taking all three observations will have a normal distribution. And, the volume won't be the cube of the diameter, nor will the area be the square of the diameter. The square of the sums is not going to be the sum of the squares, unless you get oddly lucky.
| null | CC BY-SA 2.5 | null | 2010-07-27T16:37:40.463 | 2010-07-27T16:37:40.463 | null | null | 62 | null |
818 | 2 | null | 73 | 2 | null | We mostly use:
- ggplot - for charts
- stats
- e1071 - for SVMs
| null | CC BY-SA 2.5 | null | 2010-07-27T16:37:42.413 | 2010-08-09T08:15:05.380 | 2010-08-09T08:15:05.380 | 509 | 480 | null |
819 | 2 | null | 805 | 3 | null | The PPV and NPV are proportions. You know the numerator and denominator, which both are positive integers, so you can calculate the proportion. Your goal, I presume, is to quantify how well you have determined those values. If your sample size is huge, then those values are likely to be very close to their true population values. If the sample size is small, then there is more random variability and those values are more likely to be far from their true value.
The confidence intervals you calculated tell you what you want to know. Given a bunch of assumptions, you can be 95% confident that the confidence interval includes the population value.
What about the standard error? The problem is that the uncertainty of a proportion is not symmetrical. The asymmetry is very noticeable when the proportion is far from 0.50 and the sample size is small. Since the confidence interval is not symmetrical around the observed proportion, trying to express this uncertainty as a single plus/minus standard error won't be very informative. It makes more sense to report the confidence interval.
If you really want to calculate a standard error, even knowing it isn't very helpful, here is the formula to compute an approximate standard error from p (the proportion) and n (sample size; the denominator):

| null | CC BY-SA 2.5 | null | 2010-07-27T16:40:37.527 | 2010-07-27T16:40:37.527 | 2017-03-09T17:30:36.287 | -1 | 25 | null |
820 | 1 | 822 | null | 0 | 140 | I am building a web application for used book trading and I am adding a feature to propose other book that would be interesting when they view an offer.
Currently the data that I store are the following (they are updated each time someone visit an offer) :
ISBN (book of the offer)
SessId (a unique id that everyone has when visiting the website)
NumberOfVisit (The number of time someone has view an offer of that book)
I also have access to some user update data which categorize the book by subject and course. It isn't necessarily up-to-date and precise, but it's nonetheless data.
What are the approach to list the most interesting books for a book ?
| How can I link item by relevance? | CC BY-SA 2.5 | null | 2010-07-27T16:42:39.070 | 2010-08-07T17:52:01.997 | 2010-08-07T17:52:01.997 | null | 488 | [
"algorithms"
]
|
821 | 2 | null | 820 | 1 | null | You probably want to look at [recommender systems](http://en.wikipedia.org/wiki/Recommender_system).
| null | CC BY-SA 2.5 | null | 2010-07-27T16:46:45.040 | 2010-07-27T16:46:45.040 | null | null | null | null |
822 | 2 | null | 820 | 2 | null | There are many,many ways to do this....I'd suggest googling for some search terms to get started, such as "market basket analysis", or having a look at Toby Segaran's "Programming Collective Intelligence" if you know python (even if you don't - it is pretty easy to understand).
| null | CC BY-SA 2.5 | null | 2010-07-27T16:50:45.797 | 2010-07-27T16:50:45.797 | null | null | 247 | null |
823 | 2 | null | 726 | -3 | null | >
Let’s be clear: the work of science
has nothing whatever to do with
consensus. Consensus is the business
of politics. Science, on the contrary,
requires only one investigator who
happens to be right, which means that
he or she has results that are
verifiable by reference to the real
world. In science consensus is
irrelevant. What is relevant is
reproducible results. The greatest
scientists in history are great
precisely because they broke with the
consensus.
There is no such thing as consensus
science. If it’s consensus, it isn’t
science. If it’s science, it isn’t
consensus. Period.
Michael Crichton
| null | CC BY-SA 2.5 | null | 2010-07-27T16:50:51.430 | 2010-07-27T16:50:51.430 | null | null | 25 | null |
824 | 2 | null | 672 | 25 | null | Bayes' theorem is a relatively simple, but fundamental result of probability theory that allows for the calculation of certain conditional probabilities. Conditional probabilities are just those probabilities that reflect the influence of one event on the probability of another.
Simply put, in its most famous form, it states that the probability of a hypothesis given new data (P(H|D); called the posterior probability) is equal to the following equation: the probability of the observed data given the hypothesis (P(D|H); called the conditional probability), times the probability of the theory being true prior to new evidence (P(H); called the prior probability of H), divided by the probability of seeing that data, period (P(D); called the marginal probability of D).
Formally, the equation looks like this:
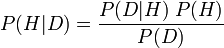
The significance of Bayes theorem is largely due to its proper use being a point of contention between schools of thought on probability. To a subjective Bayesian (that interprets probability as being subjective degrees of belief) Bayes' theorem provides the cornerstone for theory testing, theory selection and other practices, by plugging their subjective probability judgments into the equation, and running with it. To a frequentist (that interprets probability as [limiting relative frequencies](http://en.wikipedia.org/wiki/Frequency_%28statistics%29)), this use of Bayes' theorem is an abuse, and they strive to instead use meaningful (non-subjective) priors (as do objective Bayesians under yet another interpretation of probability).
| null | CC BY-SA 2.5 | null | 2010-07-27T16:56:35.273 | 2010-07-27T17:15:57.083 | 2017-03-09T17:30:36.300 | -1 | 39 | null |
825 | 1 | 827 | null | 28 | 9273 | I have R-scripts for reading large amounts of csv data from different files and then perform machine learning tasks such as svm for classification.
Are there any libraries for making use of multiple cores on the server for R.
or
What is most suitable way to achieve that?
| Any suggestions for making R code use multiple processors? | CC BY-SA 2.5 | null | 2010-07-27T17:04:37.710 | 2010-10-14T18:01:00.103 | 2010-10-14T18:01:00.103 | 930 | 480 | [
"r",
"parallel-computing",
"multicore"
]
|
826 | 2 | null | 643 | 5 | null | I like to demonstrate sampling variation and essentially the Central Limit Theorem through an "in-class" exercise. Everybody in the class of say 100 students writes their age on a piece of paper. All pieces of paper are the same size and folded in the same fashion after I've calculated the average. This is the population and I calculate the average age. Then each student randomly selects 10 pieces of paper, writes down the ages and returns them to the bag. (S)he calculates the mean and passes the bag along to the next student. Eventually we have 100 samples of 10 students each estimating the population mean which we can describe through a histogram and some descriptive statistics.
We then repeat the demonstration this time using a set of 100 "opinions" that replicate some Yes/No question from recent polls e.g. If the (British General) election were called tomorrow would you consider voting for the British National Party. Students them sample 10 of these opinions.
At the end we've demonstrated sampling variation, the Central Limit Theorem, etc with both continuous and binary data.
| null | CC BY-SA 3.0 | null | 2010-07-27T17:06:17.613 | 2011-06-02T08:09:07.907 | 2011-06-02T08:09:07.907 | 2116 | 215 | null |
827 | 2 | null | 825 | 16 | null | If it's on Linux, then the most straight-forward is [multicore](http://cran.r-project.org/web/packages/multicore/index.html). Beyond that, I suggest having a look at [MPI](http://www.stats.uwo.ca/faculty/yu/Rmpi/) (especially with the [snow](http://cran.r-project.org/web/packages/snow/index.html) package).
More generally, have a look at:
- The High-Performance Computing view on CRAN.
- "State of the Art in Parallel Computing with R"
Lastly, I recommend using the [foreach](http://cran.r-project.org/web/packages/foreach/index.html) package to abstract away the parallel backend in your code. That will make it more useful in the long run.
| null | CC BY-SA 2.5 | null | 2010-07-27T17:06:30.563 | 2010-07-27T17:06:30.563 | null | null | 5 | null |
828 | 2 | null | 825 | 5 | null | Shane is correct. Both [multicore](http://cran.r-project.org/package=multicore) and [Rmpi](http://cran.r-project.org/package=Rmpi) are winners.
Slightly broader coverage of the topic is in the [CRAN Task View on High-Performance Computing](http://cran.r-project.org/web/views/HighPerformanceComputing.html). This also links to a fairly recent survey article on [Parallel Computing with R](http://www.jstatsoft.org/v31/i01/) from JSS.
Lastly, a few hands-on examples and tips are in the Intro to HPC with R tutorial I give once in a while -- see my [presentations page](http://dirk.eddelbuettel.com) for the most recent copy from last week at useR.
| null | CC BY-SA 2.5 | null | 2010-07-27T17:12:15.030 | 2010-07-27T17:12:15.030 | null | null | 334 | null |
829 | 2 | null | 806 | 3 | null | Whether one can normalize a non-normal data set depends on the application. For example, data normalization is required for many statistical tests (i.e. calculating a z-score, t-score, etc.) Some tests are more prone to failure when normalizing non-normal data, while some are more resistant ("robust" tests).
One less-robust statistic is the mean, which is sensitive to outliers (i.e. non-normal data). Alternatively, the median is less sensitive to outliers (and therefore more robust).
A great example of non-normal data when many statistics fail is bi-modally distributed data. Because of this, it's always good practice to visualize your data as a frequency distribution (or even better, test for normality!)
| null | CC BY-SA 2.5 | null | 2010-07-27T17:15:37.367 | 2010-07-27T17:15:37.367 | null | null | 491 | null |
830 | 2 | null | 825 | 3 | null | Both Shane and Dirk's responses are spot on.
Nevertheless, you might wanna take a look at a commercial version of R, called [Revolution R](http://www.revolutionanalytics.com/) which is built to deal with big datasets and run on multiple cores. This software is free for academics (which might be your case, I dont know)
| null | CC BY-SA 2.5 | null | 2010-07-27T17:18:36.487 | 2010-07-27T17:18:36.487 | null | null | 447 | null |
831 | 2 | null | 790 | 1 | null | In the case of log-normally distributed data .... the geometric mean is a better measure of central tendancy than the arithmetic mean. I mean I would guess they look at the paper and have seen a log-normal distribution.
Spots ... makes me think its referring to probes from a microarray .. in which case they do tend to do log-normally distributed (can't find the reference though sorry).
| null | CC BY-SA 2.5 | null | 2010-07-27T17:19:27.563 | 2010-07-27T17:19:27.563 | null | null | 494 | null |
832 | 2 | null | 643 | 2 | null | If you use Stata, you can use the -clt- command that creates graphs of sampling distributions, see
[http://www.ats.ucla.edu/stat/stata/ado/teach/clt.htm](http://www.ats.ucla.edu/stat/stata/ado/teach/clt.htm)
| null | CC BY-SA 2.5 | null | 2010-07-27T17:37:35.300 | 2010-07-27T17:37:35.300 | null | null | null | null |
833 | 2 | null | 812 | 18 | null | Yes and no. At the theoretical level, both cases can use similar techniques and frameworks (an excellent example being Gaussian process regression).
The critical difference is the assumptions used to prevent overfitting (regularization):
- In the functional case, there is usually some assumption of smoothness, in other words, values occurring close to each other should be similar in some systematic way. This leads to the use of techniques such as splines, loess, Gaussian processes, etc.
- In the high-dimensional case, there is usually an assumption of sparsity: that is, only a subset of the dimensions will have any signal. This leads to techniques aiming at identifying those dimensions (Lasso, LARS, slab-and-spike priors, etc.)
UPDATE:
I didn't really think about wavelet/Fourier methods, but yes, the thresholding techniques used for such methods are aiming for sparsity in the projected space. Conversely, some high-dimensional techniques assume a projection on to a lower-dimensional manifold (e.g. principal component analysis), which is a type of smoothness assumption.
| null | CC BY-SA 2.5 | null | 2010-07-27T17:44:35.993 | 2010-07-28T11:37:58.753 | 2010-07-28T11:37:58.753 | 495 | 495 | null |
834 | 1 | null | null | 10 | 13137 | I've heard that AIC can be used to choose among several models (which regressor to use).
But i would like to understand formally what it is in a kind of "advanced undergraduated" level, which I think would be something formal but with intuition arising from the formula.
And is it possible to implement AIC in stata with complex survey data?
| What is AIC? Looking for a formal but intuitive answer | CC BY-SA 4.0 | null | 2010-07-27T17:46:25.223 | 2019-09-12T13:05:52.073 | 2019-09-12T13:05:52.073 | 11887 | 498 | [
"stata",
"aic",
"intuition"
]
|
835 | 2 | null | 726 | 12 | null | [Data is the sword of the 21st century, those who wield it well, the Samurai.](http://googleblog.blogspot.com/2009/02/from-height-of-this-place.html)
| null | CC BY-SA 2.5 | null | 2010-07-27T17:57:48.807 | 2010-07-27T17:57:48.807 | null | null | 62 | null |
836 | 2 | null | 834 | 4 | null | It is a heuristic, and as such, has been subjected to extensive testing. So when to trust it or not is not simple clear-cut and always-true decision.
At a rough approximation, it trades off goodness of fit and number of variables ("degrees of freedom"). Much more, as usual, [at the Wikipedia article about AIC](http://en.wikipedia.org/wiki/Akaike_information_criterion).
| null | CC BY-SA 2.5 | null | 2010-07-27T18:14:44.467 | 2010-07-27T18:14:44.467 | null | null | 334 | null |
837 | 1 | 858 | null | 2 | 7702 | I am creating multiple logistic regression models using lrm from Harrell's Design package in R. One model I would like to make is the model with no predictors. For example, I want to predict a constant c such that:
```
logit(Y) ~ c
```
I know I how to compute c (divide the number of "1"s by the total), what I would like is to use `lrm` so I can manipulate it as a model in a consistent way with the other models I am making. Is this possible, and if so how?
I have tried so far:
```
library(Design)
data(mtcars)
lrm(am ~ 1, data=mtcars)
```
which gives the error:
```
Error in dimnames(stats) <- list(names(cof), c("Coef", "S.E.", "Wald Z", :
length of 'dimnames' [1] not equal to array extent
```
and I have tried:
```
lrm(am ~ ., data=mtcars)
```
But this uses all the predictors, rather then none of the predictors.
| R lrm model with no predictors | CC BY-SA 3.0 | null | 2010-07-27T18:25:40.277 | 2013-08-09T00:48:47.660 | 2013-08-09T00:47:53.890 | 7290 | 501 | [
"r",
"logistic"
]
|
838 | 2 | null | 834 | 5 | null | Basically one needs a loss function in order to optimize anything. AIC provides the loss function which when minimized gives a "optimal"* model which fits the given data. The AIC loss function (2k-2*log(L)) tries to formulate the bias variance trade off that every statistical modeler faces when fitting a model to finite set of data.
In other words while fitting a model if you increase the number of parameters you will improve the log likelihood but will run into the danger of over fitting. The AIC penalizes for increasing the number of parameters thus minimizing the AIC selects the model where the improvement in log likelihood is not worth the penalty for increasing the number of parameters.
- Note that when I say optimal model it is optimal in the sense that the model minimizes the AIC. There are other criteria (e.g. BIC) which may give other "optimal" models.
I don't have any experience with stata so cannot help you with the other part of the question.
| null | CC BY-SA 2.5 | null | 2010-07-27T18:28:36.730 | 2010-07-27T18:28:36.730 | null | null | 288 | null |
839 | 2 | null | 743 | 5 | null | Though it is not generally labeled as Bayesian search theory, such methods are pretty widely used in oil exploration. There are, however, important differences in the standard examples that drive different features of their respective modeling problems.
In the case of lost vessel exploration (in Bayesian search theory), we are looking for a specific point on the sea floor (one elevation), with a distributions modeling the likelihood of its resting location, and another distribution modeling the likelihood of finding the boat were it at that depth. These distributions are then guide search, and are continuously updated through the results of the guided search.
Though similar, oil exploration is fraught with complicating features (multiple sampling depths, high sampling costs, variable yields, multiple geological indicators, drilling cost, etc.) that necessitate methods that go beyond what is considered in the prior example. See [Learning through Oil and Gas Exploration](http://www.nek.lu.se/ryde/NordicEcont09/Papers/levitt.pdf) for an overview of these complicating factors and a way to model them.
So, yes, it may be said that the oil exploration problem is different in magnitude, but not kind from lost vessel exploration, and thus similar methods may be fruitfully applied. Finally, a quick literature search reveals many different modeling approaches, which is not too surprising, given the complicated nature of the problem.
| null | CC BY-SA 2.5 | null | 2010-07-27T18:33:51.930 | 2010-07-27T18:39:12.480 | 2010-07-27T18:39:12.480 | 39 | 39 | null |
840 | 2 | null | 73 | 2 | null | I work with both R and [MATLAB](http://en.wikipedia.org/wiki/MATLAB) and I use [R.matlab](http://cran.r-project.org/web/packages/R.matlab/index.html) a lot to transfer data between the two.
| null | CC BY-SA 2.5 | null | 2010-07-27T18:33:56.767 | 2010-08-09T08:13:30.967 | 2010-08-09T08:13:30.967 | 509 | 288 | null |
841 | 1 | 844 | null | 17 | 6126 | I have $N$ paired observations ($X_i$, $Y_i$) drawn from a common unknown distribution, which has finite first and second moments, and is symmetric around the mean.
Let $\sigma_X$ the standard deviation of $X$ (unconditional on $Y$), and $\sigma_Y$ the same for Y. I would like to test the hypothesis
$H_0$: $\sigma_X = \sigma_Y$
$H_1$: $\sigma_X \neq \sigma_Y$
Does anyone know of such a test? I can assume in first analysis that the distribution is normal, although the general case is more interesting. I am looking for a closed-form solution. Bootstrap is always a last resort.
| Comparing the variance of paired observations | CC BY-SA 2.5 | null | 2010-07-27T18:38:02.297 | 2011-03-13T20:31:13.040 | 2011-02-10T07:50:44.253 | 223 | 30 | [
"distributions",
"hypothesis-testing",
"standard-deviation",
"normal-distribution"
]
|
842 | 2 | null | 825 | 5 | null | I noticed that the previous answers lack some general HPC considerations.
First of all, neither of those packages will enable you to run one SVM in parallel. So what you can speed up is parameter optimization or cross-validation, still you must write your own functions for that. Or of course you may run the job for different datasets in parallel, if it is a case.
The second issue is memory; if you want to spread calculation over a few physical computers, there is no free lunch and you must copy the data -- here you must consider if it makes sense to predistribute a copy of data across computers to save some communication. On the other hand if you wish to use multiple cores on one computer, than the multicore is especially appropriate because it enables all child processes to access the memory of the parent process, so you can save some time and a lot of memory space.
| null | CC BY-SA 2.5 | null | 2010-07-27T18:39:32.153 | 2010-07-27T18:39:32.153 | null | null | null | null |
843 | 2 | null | 798 | 3 | null | If I need to determine the number of bins programmatically I usually start out with a histogram that has way more bins than needed. Once the histogram is filled I then combine bins until I have enough entries per bin for the method I am using, e.g. if I want to model Poisson-uncertainties in a counting experiment with uncertainties from a normal distribution until I have more than something like 10 entries.
| null | CC BY-SA 2.5 | null | 2010-07-27T18:47:25.880 | 2010-07-27T18:47:25.880 | null | null | 56 | null |
844 | 2 | null | 841 | 5 | null | You could use the fact that the [distribution of the sample variance](http://en.wikipedia.org/wiki/Variance#Distribution_of_the_sample_variance) is a chi square distribution centered at the true variance. Under your null hypothesis, your test statistic would be the difference of two chi squared random variates centered at the same unknown true variance. I do not know whether the difference of two chi-squared random variates is an identifiable distribution but the above may help you to some extent.
| null | CC BY-SA 2.5 | null | 2010-07-27T18:48:54.927 | 2010-07-27T18:48:54.927 | null | null | null | null |
845 | 2 | null | 841 | 7 | null | If you want to go down the non-parametric route you could always try the squared ranks test.
For the unpaired case, the assumptions for this test (taken from [here](http://www.stat.wvu.edu/~xiawang/courses/stat551/hwk/hw14.pdf)) are:
- Both samples are random samples from their respective populations.
- In addition to independence within each sample there is mutual independence between
the two samples.
- The measurement scale is at least interval.
These [lecture notes](http://www.stat.wvu.edu/~xiawang/courses/stat551/hwk/hw14.pdf) describe the unpaired case in detail.
For the paired case you will have to change this procedure slightly. Midway down [this page](http://www.itl.nist.gov/div898/software/dataplot/refman1/auxillar/signrank.htm) should give you an idea of where to start.
| null | CC BY-SA 2.5 | null | 2010-07-27T19:02:09.860 | 2010-07-28T00:08:20.203 | 2010-07-28T00:08:20.203 | 8 | 8 | null |
846 | 1 | 851 | null | 2 | 553 | I'm working on regression models in STATISTICA application and I need to know what is Fisher-Snedecor distribution for and how to analyze my regression model in this distribution.
What the significance level means? What is v1 and v2? I need an explanation and little tutorial on real data.
| Regression output and Fisher-Snedecor distribution | CC BY-SA 3.0 | null | 2010-07-27T19:10:53.667 | 2014-12-01T17:25:36.057 | 2014-12-01T17:25:36.057 | 503 | 503 | [
"regression"
]
|
847 | 1 | null | null | 0 | 148 | Google Website Optimizer (GWO) is a tool provided by Google to do [A/B](http://en.wikipedia.org/wiki/A/B_testing) and [MVT](http://en.wikipedia.org/wiki/Multivariate_testing) experiments on websites.
This has been an unanswered question for a long time so I thought I'd ask it here and see if I can get any help. Here is some documentation (clues) that Google has published about the statistics used:
- All about statistics
- Fractional versus Full Factorial analysis
Example Data ([summary pdf](http://dl.dropbox.com/u/2511052/gwoTestResults/WebOptimizer-summary.pdf)):
- XML
- CSV
I (as well as many others) are interested in discovering the math used by Google, because no one has been able to reproduce their calculations yet.
Thank you in advance for any help that you can provide.
| What statistical model is used to calculate the test results for GWO? | CC BY-SA 3.0 | null | 2010-07-27T19:12:53.037 | 2013-09-16T22:37:44.463 | 2013-09-16T22:37:44.463 | 22468 | 500 | [
"computational-statistics",
"model"
]
|
848 | 2 | null | 805 | 0 | null | As an addition to Harvey's response if you have a small sample of data then there are alternatives to the standard error approximation formula shown above. I would recommend using software, one example would be to use the `binom.test` function in R, to calculate these confidence intervals rather than doing it "by hand".
| null | CC BY-SA 2.5 | null | 2010-07-27T19:19:46.097 | 2010-07-27T19:19:46.097 | null | null | null | null |
849 | 2 | null | 612 | 29 | null | Principal Components Analysis (PCA) and Common Factor Analysis (CFA) are distinct methods. Often, they produce similar results and PCA is used as the default extraction method in the SPSS Factor Analysis routines. This undoubtedly results in a lot of confusion about the distinction between the two.
The bottom line is, these are two different models, conceptually. In PCA, the components are actual orthogonal linear combinations that maximize the total variance. In FA, the factors are linear combinations that maximize the shared portion of the variance--underlying "latent constructs". That's why FA is often called "common factor analysis". FA uses a variety of optimization routines and the result, unlike PCA, depends on the optimization routine used and starting points for those routines. Simply there is not a single unique solution.
In R, the factanal() function provides CFA with a maximum likelihood extraction. So, you shouldn't expect it to reproduce an SPSS result which is based on a PCA extraction. It's simply not the same model or logic. I'm not sure if you would get the same result if you used SPSS's Maximum Likelihood extraction either as they may not use the same algorithm.
For better or for worse in R, you can, however, reproduce the mixed up "factor analysis" that SPSS provides as its default. Here's the process in R. With this code, I'm able to reproduce the SPSS Principal Component "Factor Analysis" result using this dataset. (With the exception of the sign, which is indeterminant). That result could also then be rotated using any of Rs available rotation methods.
```
# Load the base dataset attitude to work with.
data(attitude)
# Compute eigenvalues and eigen vectors of the correlation matrix.
pfa.eigen<-eigen(cor(attitude))
# Print and note that eigen values are those produced by SPSS.
# Also note that SPSS will extract 2 components as eigen values > 1 = 2
pfa.eigen$values
# set a value for the number of factors (for clarity)
factors<-2
# Extract and transform two components.
pfa.eigen$vectors [ , 1:factors ] %*%
+ diag ( sqrt (pfa.eigen$values [ 1:factors ] ),factors,factors )
```
| null | CC BY-SA 2.5 | null | 2010-07-27T19:22:33.407 | 2010-07-27T19:27:45.063 | 2010-07-27T19:27:45.063 | 485 | 485 | null |
850 | 2 | null | 837 | 0 | null | Try creating a dummy variable with so many ones as the number of rows in mtcars and put it formula instead of one.
| null | CC BY-SA 2.5 | null | 2010-07-27T19:28:38.133 | 2010-07-27T19:28:38.133 | null | null | null | null |
851 | 2 | null | 846 | 5 | null | The Fisher Snedecor distribution is another name for the [F-distribution](http://en.wikipedia.org/wiki/F-distribution). The F-distribution comes from the ratio of two chi-squared variables.
In regression, you use the F-distribution in the [ANOVA](http://en.wikipedia.org/wiki/Analysis_of_variance) table. This table gives you information about which variables/covariates should be in your model.
The v1 and v2 are called the degrees of freedom. In simple linear regression,o.e.
Y = a + bx + epsilon
we have a single extra variable. So v1 = p = 1 and v2 = n-p-1 = n-2.
I don't use STATISTICA, so I can't give you more detailed information.
| null | CC BY-SA 2.5 | null | 2010-07-27T19:34:06.107 | 2010-07-27T19:34:06.107 | null | null | 8 | null |
852 | 1 | null | null | 5 | 1272 | The coefficient on a logged explanatory variable when the dependent variable also is in log form is an elasticity (or the percentage change in the dependent variable if the explanatory variable changes by one percent). Suppose I estimate a regression without logging the dependent variable but I use a log link in a General Linear Model (and family gaussian) while the explanatory variable remains in log form. Is the coefficient on that explanatory variable still an elasticity?
| Elasticities Using GLM | CC BY-SA 2.5 | null | 2010-07-27T19:52:26.970 | 2010-11-02T04:32:16.943 | 2010-11-02T04:32:16.943 | 159 | null | [
"econometrics",
"generalized-linear-model"
]
|
853 | 2 | null | 847 | 1 | null | It sounds like they simply use Choice Modeling. You would use conditional logistic regression to analyze it.
The people from JMP (SAS) have a nice (free) book about Design of Experiments and Choice Modeling.
| null | CC BY-SA 2.5 | null | 2010-07-27T19:55:30.113 | 2010-07-27T19:55:30.113 | null | null | 74 | null |
854 | 2 | null | 192 | 2 | null | I would use Fisher's Exact Test, even for large N. I wouldn't know why not. Any performance argument predates today's fast computers.
| null | CC BY-SA 2.5 | null | 2010-07-27T19:58:44.973 | 2010-07-27T19:58:44.973 | null | null | 506 | null |
855 | 2 | null | 806 | 2 | null | I thought this was too obvious, until I saw this [question](https://stats.stackexchange.com/questions/795/normalization-of-series)!
When you normalise data, make sure you always have access to the raw data after normalisation. Of course, you could break this rule if you have a good reason, e.g. storage.
| null | CC BY-SA 2.5 | null | 2010-07-27T20:05:20.027 | 2010-07-27T20:05:20.027 | 2017-04-13T12:44:52.277 | -1 | 8 | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.