Id
stringlengths 1
6
| PostTypeId
stringclasses 7
values | AcceptedAnswerId
stringlengths 1
6
⌀ | ParentId
stringlengths 1
6
⌀ | Score
stringlengths 1
4
| ViewCount
stringlengths 1
7
⌀ | Body
stringlengths 0
38.7k
| Title
stringlengths 15
150
⌀ | ContentLicense
stringclasses 3
values | FavoriteCount
stringclasses 3
values | CreationDate
stringlengths 23
23
| LastActivityDate
stringlengths 23
23
| LastEditDate
stringlengths 23
23
⌀ | LastEditorUserId
stringlengths 1
6
⌀ | OwnerUserId
stringlengths 1
6
⌀ | Tags
sequence |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
537 | 2 | null | 534 | 15 | null | Your example is that of a [controlled experiment](http://en.wikipedia.org/wiki/Controlled_experiment). The only other context that I know of where a correlation can imply causation is that of a [natural experiment](http://en.wikipedia.org/wiki/Natural_experiment).
Basically, a natural experiment takes advantage of an assignment of some respondents to a treatment that happens naturally in the real world. Since assignment of respondents to treatment and control groups is not controlled by the experimenter the extent to which correlation would imply causation is perhaps weaker to some extent.
See the wiki links for more information controlled / natural experiments.
| null | CC BY-SA 2.5 | null | 2010-07-23T02:42:39.580 | 2010-07-23T02:42:39.580 | null | null | null | null |
538 | 2 | null | 534 | 46 | null | Correlation is not sufficient for causation. One can get around the Wikipedia example by imagining that those twins always cheated in their tests by having a device that gives them the answers. The twin that goes to the amusement park loses the device, hence the low grade.
A good way to get this stuff straight is to think of the structure of Bayesian network that may be generating the measured quantities, as done by Pearl in his book [Causality](http://rads.stackoverflow.com/amzn/click/052189560X). His basic point is to look for hidden variables. If there is a hidden variable that happens not to vary in the measured sample, then the correlation would not imply causation. Expose all hidden variables and you have causation.
| null | CC BY-SA 3.0 | null | 2010-07-23T04:49:41.213 | 2013-12-24T23:44:38.263 | 2013-12-24T23:44:38.263 | 556 | 260 | null |
539 | 1 | 4183 | null | 64 | 56374 | In answering [this question on discrete and continuous data](https://stats.stackexchange.com/questions/206/discrete-and-continuous) I glibly asserted that it rarely makes sense to treat categorical data as continuous.
On the face of it that seems self-evident, but intuition is often a poor guide for statistics, or at least mine is. So now I'm wondering: is it true? Or are there established analyses for which a transform from categorical data to some continuum is actually useful? Would it make a difference if the data were ordinal?
| Does it ever make sense to treat categorical data as continuous? | CC BY-SA 2.5 | 1 | 2010-07-23T06:17:10.517 | 2022-12-14T06:46:23.663 | 2017-07-24T11:31:19.080 | 11887 | 174 | [
"categorical-data",
"data-transformation",
"ordinal-data",
"continuous-data"
] |
540 | 2 | null | 534 | 14 | null | In my opinion the APA Statistical Task force summarised it quite well
>
''Inferring causality from nonrandomized
designs is a risky enterprise.
Researchers using nonrandomized
designs have an extra obligation to
explain the logic behind covariates
included in their designs and to alert
the reader to plausible rival
hypotheses that might explain their
results. Even in randomized
experiments, attributing causal
effects to any one aspect of the
treatment condition requires support
from additional experimentation.''
- APA Task Force
| null | CC BY-SA 2.5 | null | 2010-07-23T06:17:56.740 | 2010-07-23T06:17:56.740 | null | null | 183 | null |
541 | 2 | null | 539 | 21 | null | If there are only two categories, then transforming them to (0,1) makes sense. In fact, this is commonly done where the resulting dummy variable is used in regression models.
If there are more than two categories, then I think it only makes sense if the data are ordinal, and then only in very specific circumstances. For example, if I am doing regression and fit a nonparametric nonlinear function to the ordinal-cum-numeric variable, I think that is ok. But if I use linear regression, then I am making very strong assumptions about the relative difference between consecutive values of the ordinal variable, and I'm usually reluctant to do that.
| null | CC BY-SA 2.5 | null | 2010-07-23T06:22:04.313 | 2010-07-23T06:22:04.313 | null | null | 159 | null |
542 | 2 | null | 499 | 7 | null | In the social science context where I come from, the issue is whether you are interested in (a) prediction or (b) testing a focused research question.
If the purpose is prediction then data driven approaches are appropriate.
If the purpose is to examine a focused research question then it is important to consider which regression model specifically tests your question.
For example, if your task was to select a set of selection tests to predict job performance, the aim can in some sense be seen as one of maximising prediction of job performance.
Thus, data driven approaches would be useful.
In contrast if you wanted to understand the relative role of personality variables and ability variables in influencing performance, then a specific model comparison approach might be more appropriate.
Typically when exploring focussed research questions the aim is to elucidate something about the underlying causal processes that are operating as opposed to developing a model with optimal prediction.
When I'm in the process of developing models about process based on cross-sectional data I'd be wary about:
(a) including predictors that could theoretically be thought of as consequences of the outcome variable. E.g., a person's belief that they are a good performer is a good predictor of job performance, but it is likely that this is at least partially caused by the fact that they have observed their own performance.
(b) including a large number of predictors that are all reflective of the same underlying phenomena. E.g., including 20 items all measuring satisfaction with life in different ways.
Thus, focused research questions rely a lot more on domain specific knowledge.
This probably goes some way to explaining why data driven approaches are less often used in the social sciences.
| null | CC BY-SA 2.5 | null | 2010-07-23T06:49:38.953 | 2010-07-23T06:49:38.953 | null | null | 183 | null |
543 | 2 | null | 10 | 10 | null | In addition to what has already been said above about summated scales, I'd also mention that the issue can change when analysing data at the group-level. For example, if you were examining
- life satisfaction of states or countries,
- job satisfaction of organisations or departments,
- student satisfaction in subjects.
In all these cases each aggregate measure (perhaps the mean) is based on many individual responses (e.g., n=50, 100, 1000, etc.). In these cases the original Likert item begins to take on properties that resemble an interval scale at the aggregate level.
| null | CC BY-SA 2.5 | null | 2010-07-23T07:13:03.533 | 2010-07-23T07:13:03.533 | null | null | 183 | null |
544 | 2 | null | 539 | 18 | null | It is common practice to treat ordered categorical variables with many categories as continuous. Examples of this:
- Number of items correct on a 100 item test
- A summated psychological scale (e.g., that is the mean of 10 items each on a five point scale)
And by "treating as continuous" I mean including the variable in a model that assumes a continuous random variable (e.g., as a dependent variable in a linear regression). I suppose the issue is how many scale points are required for this to be a reasonable simplifying assumption.
A few other thoughts:
- Polychoric correlations attempt to model the relationship between two ordinal variables in terms of assumed latent continuous variables.
- Optimal scaling allows you to develop models where the scaling of a categorical variable is developed in a data driven way whilst respecting whatever scale constraints you impose (e.g., ordinality). For a good introduction see De Leeuw and Mair (2009)
### References
- De Leeuw, J., & Mair, P. (2009). Gifi methods for optimal scaling in R: The package homals. Journal of Statistical Software, forthcoming, 1-30. PDF
| null | CC BY-SA 3.0 | null | 2010-07-23T07:27:31.830 | 2013-08-13T03:53:08.900 | 2013-08-13T03:53:08.900 | 183 | 183 | null |
545 | 2 | null | 481 | 1 | null | The problem (dilemma) you face appears to be the one of selecting an optimal (or otherwise good) sampling interval for revising your forecasts. To start with, see [link text](http://books.google.com.au/books?id=XXFNW_QaJYgC&pg=PA42) of Brown's famous book, which would also qualify as a good reference. It all boils down to "balancing the risk of not noticing a change quickly against the inherent variability of the data and the cost of revising plans frequently". If you are not prepared to revise your forecast (and the decisions that motivated it) daily, you don't really need to use the (noisiest) daily data. An important point, often lost in the contemporary forecasting literature, is that forecasts are only necessary to assist with making a decision (unless one also knows how to derive fun from them).
| null | CC BY-SA 2.5 | null | 2010-07-23T08:15:23.430 | 2010-07-23T08:15:23.430 | null | null | 273 | null |
546 | 2 | null | 423 | 44 | null | Another one from [xkcd](http://xkcd.com/388/):
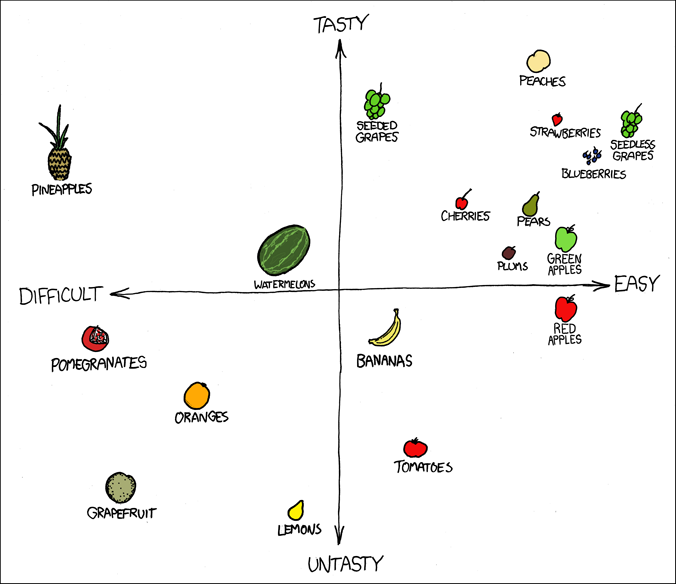
| null | CC BY-SA 2.5 | null | 2010-07-23T08:18:52.737 | 2010-08-11T09:20:21.947 | 2017-03-09T17:30:36.260 | -1 | 183 | null |
547 | 2 | null | 534 | 16 | null | There is also a problem with the opposite case, when lack of correlation is used as a proof for the lack of causation. This problem is nonlinearity; when looking at correlation people usually check Pearson, which is only a tip of an iceberg.
| null | CC BY-SA 2.5 | null | 2010-07-23T08:33:04.260 | 2010-07-23T08:33:04.260 | null | null | null | null |
548 | 1 | 559 | null | 9 | 3252 | In an answer to [this question about treating categorical data as continuous](https://stats.stackexchange.com/questions/539/does-it-ever-make-sense-to-treat-categorical-data-as-continuous), optimal scaling was mentioned. How does this method work and how is it applied?
| How can I use optimal scaling to scale an ordinal categorical variable? | CC BY-SA 2.5 | null | 2010-07-23T10:51:52.960 | 2010-07-23T16:30:41.750 | 2017-04-13T12:44:51.217 | -1 | 266 | [
"categorical-data",
"data-transformation",
"optimal-scaling"
] |
549 | 2 | null | 539 | 6 | null | In an analysis of ranking by frequency, as with a Pareto chart and associated values (eg how many categories make up the top 80% of product faults)
| null | CC BY-SA 2.5 | null | 2010-07-23T13:28:55.297 | 2010-07-23T13:28:55.297 | null | null | 270 | null |
550 | 2 | null | 155 | 12 | null | I have used the drunkard's walk before for random walk, and the drunk and her dog for cointegration; they're very helpful (partially because they're amusing).
One of my favorite common examples is the [Birthday Paradox](http://mathworld.wolfram.com/BirthdayProblem.html) ([wikipedia entry](http://en.wikipedia.org/wiki/Birthday_problem)), which illustrates some important concepts of probability. You can simulate this with a room full of people.
Incidentally, I strongly recommend Andrew Gelman's ["Teaching Statistics: A Bag of Tricks"](http://www.stat.columbia.edu/~gelman/bag-of-tricks/) for some examples of creative ways to teach statistical concepts (see the [table of contents](http://www.stat.columbia.edu/~gelman/bag-of-tricks/contents.pdf)). Also look at his paper about the course that he teaches on teaching statistics: ["A Course on Teaching Statistics at the University Level"](http://www.stat.columbia.edu/~gelman/research/published/teachcourse3.pdf). And on ["Teaching Bayes to Graduate Students in Political Science, Sociology,
Public Health, Education, Economics, ..."](http://www.stat.columbia.edu/~gelman/research/published/teachingbayes.pdf).
For describing Bayesian methods, using an unfair coin and flipping it multiple times is a pretty common/effective approach.
| null | CC BY-SA 2.5 | null | 2010-07-23T13:58:07.597 | 2010-07-23T16:25:03.033 | 2010-07-23T16:25:03.033 | 5 | 5 | null |
551 | 2 | null | 298 | 97 | null | I always tell students there are three reasons to transform a variable by taking the natural logarithm. The reason for logging the variable will determine whether you want to log the independent variable(s), dependent or both. To be clear throughout I'm talking about taking the natural logarithm.
Firstly, to improve model fit as other posters have noted. For instance if your residuals aren't normally distributed then taking the logarithm of a skewed variable may improve the fit by altering the scale and making the variable more "normally" distributed. For instance, earnings is truncated at zero and often exhibits positive skew. If the variable has negative skew you could firstly invert the variable before taking the logarithm. I'm thinking here particularly of Likert scales that are inputed as continuous variables. While this usually applies to the dependent variable you occasionally have problems with the residuals (e.g. heteroscedasticity) caused by an independent variable which can be sometimes corrected by taking the logarithm of that variable. For example when running a model that explained lecturer evaluations on a set of lecturer and class covariates the variable "class size" (i.e. the number of students in the lecture) had outliers which induced heteroscedasticity because the variance in the lecturer evaluations was smaller in larger cohorts than smaller cohorts. Logging the student variable would help, although in this example either calculating Robust Standard Errors or using Weighted Least Squares may make interpretation easier.
The second reason for logging one or more variables in the model is for interpretation. I call this convenience reason. If you log both your dependent (Y) and independent (X) variable(s) your regression coefficients ($\beta$) will be elasticities and interpretation would go as follows: a 1% increase in X would lead to a ceteris paribus $\beta$% increase in Y (on average). Logging only one side of the regression "equation" would lead to alternative interpretations as outlined below:
Y and X -- a one unit increase in X would lead to a $\beta$ increase/decrease in Y
Log Y and Log X -- a 1% increase in X would lead to a $\beta$% increase/decrease in Y
Log Y and X -- a one unit increase in X would lead to a $\beta*100$ % increase/decrease in Y
Y and Log X -- a 1% increase in X would lead to a $\beta/100$ increase/decrease in Y
And finally there could be a theoretical reason for doing so. For example some models that we would like to estimate are multiplicative and therefore nonlinear. Taking logarithms allows these models to be estimated by linear regression. Good examples of this include the Cobb-Douglas production function in economics and the Mincer Equation in education. The Cobb-Douglas production function explains how inputs are converted into outputs:
$$Y = A L^\alpha K^\beta $$
where
$Y$ is the total production or output of some entity e.g. firm, farm, etc.
$A$ is the total factor productivity (the change in output not caused by the inputs e.g. by technology change or weather)
$L$ is the labour input
$K$ is the capital input
$\alpha$ & $\beta$ are output elasticities.
Taking logarithms of this makes the function easy to estimate using OLS linear regression as such:
$$\log(Y) = \log(A) + \alpha\log(L) + \beta\log(K)$$
| null | CC BY-SA 3.0 | null | 2010-07-23T14:43:14.180 | 2016-03-10T09:17:17.420 | 2016-03-10T09:17:17.420 | 20921 | 215 | null |
552 | 2 | null | 486 | 29 | null | AIC = -2Ln(L)+ 2k
where L is the maximised value of Likelihood function for that model and k is the number of parameters in the model.
In your example -2Ln(L)+ 2k <0 means that the log-likelihood at the maximum was > 0
which means that the likelihood at the maximum was > 1.
There is no problem with a positive log-likelihood. It is a common misconception that the log-likelihood must be negative. If the likelihood is derived from a probability density it can quite reasonably exceed 1 which means that log-likelihood is positive, hence the deviance and the AIC are negative. This is what occurred in your model.
If you believe that comparing AICs is a good way to choose a model then it would still be the case that the (algebraically) lower AIC is preferred not the one with the lowest absolute AIC value. To reiterate you want the most negative number in your example.
| null | CC BY-SA 2.5 | null | 2010-07-23T14:53:50.583 | 2010-07-23T14:53:50.583 | null | null | 215 | null |
553 | 2 | null | 276 | 11 | null | The trivial answer is that more data are always preferred to less data.
The problem of small sample size is clear. In linear regression (OLS) technically you can fit a model such as OLS where n = k+1 but you will get rubbish out of it i.e. very large standard errors. There is a great paper by Arthur Goldberger called Micronumerocity on this topic which is summarized in chapter 23 of his book A Course in Econometrics.
A common heuristic is that you should have 20 observations for every parameter you want to estimate. It is always a trade off between the size of your standard errors (and therefore significance testing) and the size of your sample. This is one reason some of us hate significance testing as you can get an incredibly small (relative) standard error with an enormous sample and therefore find pointless statistical significance on naive tests such as whether a regression coefficient is zero.
While sample size is important the quality of your sample is more important e.g. whether the sample is generalisable to the population, is it a Simple Random Sample or some other appropriate sampling methodology (and have this been accounted for during analysis), is there measurement error, response bias, selection bias, etc.
| null | CC BY-SA 2.5 | null | 2010-07-23T15:02:40.983 | 2010-07-23T15:20:15.537 | 2010-07-23T15:20:15.537 | 215 | 215 | null |
554 | 2 | null | 155 | 12 | null | I like to demonstrate sampling variation and essentially the Central Limit Theorem through an "in-class" exercise. Everybody in the class of say 100 students writes their age on a piece of paper. All pieces of paper are the same size and folded in the same fashion after I've calculated the average. This is the population and I calculate the average age. Then each student randomly selects 10 pieces of paper, writes down the ages and returns them to the bag. (S)he calculates the mean and passes the bag along to the next student. Eventually we have 100 samples of 10 students each estimating the population mean which we can describe through a histogram and some descriptive statistics.
We then repeat the demonstration this time using a set of 100 "opinions" that replicate some Yes/No question from recent polls e.g. If the (British General) election were called tomorrow would you consider voting for the British National Party. Students them sample 10 of these opinions.
At the end we've demonstrated sampling variation, the Central Limit Theorem, etc with both continuous and binary data.
| null | CC BY-SA 2.5 | null | 2010-07-23T15:09:02.370 | 2010-07-23T15:09:02.370 | null | null | 215 | null |
555 | 1 | 557 | null | 103 | 15497 | ANOVA is equivalent to linear regression with the use of suitable dummy variables. The conclusions remain the same irrespective of whether you use ANOVA or linear regression.
In light of their equivalence, is there any reason why ANOVA is used instead of linear regression?
Note: I am particularly interested in hearing about technical reasons for the use of ANOVA instead of linear regression.
Edit
Here is one example using one-way ANOVA. Suppose, you want to know if the average height of male and females is the same. To test for your hypothesis you would collect data from a random sample of male and females (say 30 each) and perform the ANOVA analysis (i.e., sum of squares for sex and error) to decide whether an effect exists.
You could also use linear regression to test for this as follows:
Define: $\text{Sex} = 1$ if respondent is a male and $0$ otherwise.
$$
\text{Height} = \text{Intercept} + \beta * \text{Sex} + \text{error}
$$
where: $\text{error}\sim\mathcal N(0,\sigma^2)$
Then a test of whether $\beta = 0$ is a an equivalent test for your hypothesis.
| Why is ANOVA taught / used as if it is a different research methodology compared to linear regression? | CC BY-SA 4.0 | null | 2010-07-23T15:17:56.770 | 2021-10-27T06:02:33.423 | 2021-10-27T06:02:33.423 | 44269 | null | [
"regression",
"anova"
] |
556 | 2 | null | 206 | -4 | null | Discrete data can take on only integer values whereas continuous data can take on any value. For instance the number of cancer patients treated by a hospital each year is discrete but your weight is continuous. Some data are continuous but measured in a discrete way e.g. your age. It is common to report your age as say, 31.
| null | CC BY-SA 2.5 | null | 2010-07-23T15:18:34.053 | 2010-07-23T15:18:34.053 | null | null | 215 | null |
557 | 2 | null | 555 | 61 | null | As an economist, the analysis of variance (ANOVA) is taught and usually understood in relation to linear regression (e.g. in Arthur Goldberger's A Course in Econometrics). Economists/Econometricians typically view ANOVA as uninteresting and prefer to move straight to regression models. From the perspective of linear (or even generalised linear) models, ANOVA assigns coefficients into batches, with each batch corresponding to a "source of variation" in ANOVA terminology.
Generally you can replicate the inferences you would obtain from ANOVA using regression but not always OLS regression. Multilevel models are needed for analysing hierarchical data structures such as "split-plot designs," where between-group effects are compared to group-level errors, and within-group effects are compared to data-level errors. [Gelman's paper](http://dx.doi.org/10.1214%2F009053604000001048) [1] goes into great detail about this problem and effectively argues that ANOVA is an important statistical tool that should still be taught for it's own sake.
In particular Gelman argues that ANOVA is a way of understanding and structuring multilevel models. Therefore ANOVA is not an alternative to regression but as a tool for summarizing complex high-dimensional inferences and for exploratory data analysis.
Gelman is a well-respected statistician and some credence should be given to his view. However, almost all of the empirical work that I do would be equally well served by linear regression and so I firmly fall into the camp of viewing it as a little bit pointless. Some disciplines with complex study designs (e.g. psychology) may find ANOVA useful.
[1] Gelman, A. (2005). Analysis of variance: why it is more important than ever (with discussion). Annals of Statistics 33, 1–53. [doi:10.1214/009053604000001048](http://dx.doi.org/10.1214%2F009053604000001048)
| null | CC BY-SA 3.0 | null | 2010-07-23T15:35:55.653 | 2013-09-30T15:35:44.163 | 2013-09-30T15:35:44.163 | 30872 | 215 | null |
558 | 1 | null | null | 17 | 1027 | I am trying to get a global perspective on some of the essential ideas in machine learning, and I was wondering if there is a comprehensive treatment of the different notions of loss (squared, log, hinge, proxy, etc.). I was thinking something along the lines of a more comprehensive, formal presentation of John Langford’s excellent post on [Loss Function Semantics](http://hunch.net/?p=269).
| Comprehensive overview of loss functions? | CC BY-SA 2.5 | null | 2010-07-23T16:15:33.137 | 2022-11-27T20:48:05.443 | 2017-08-29T15:23:29.323 | 53690 | 39 | [
"references",
"loss-functions"
] |
559 | 2 | null | 548 | 7 | null | The general idea is that you should scale the categorical variable in such way that the resulting continuous variables will be just the most useful. So, it is always coupled with some regression or learning procedure and so the fitting of the model is accompanied by optimization (or trying various possibilities) of ordinal variables scaling.
For some more practical issues, consult the docks of R [aspect](http://cran.r-project.org/web/packages/aspect/index.html) and [homals](http://cran.r-project.org/web/packages/homals/index.html) packages.
| null | CC BY-SA 2.5 | null | 2010-07-23T16:30:41.750 | 2010-07-23T16:30:41.750 | null | null | null | null |
560 | 2 | null | 507 | 22 | null | I use the Gelman-Rubin convergence diagnostic as well. A potential problem with Gelman-Rubin is that it may mis-diagnose convergence if the shrink factor happens to be close to 1 by chance, in which case you can use a Gelman-Rubin-Brooks plot. See the ["General Methods for Monitoring Convergence of Iterative Simulations"](http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.55.1675) paper for details. This is supported in [the coda package](http://cran.r-project.org/web/packages/coda/index.html) in R (for "Output analysis and diagnostics for Markov Chain Monte Carlo simulations"). `coda` also includes other functions (such as the Geweke’s convergence diagnostic).
You can also have a look at ["boa: An R Package for MCMC Output Convergence
Assessment and Posterior Inference"](http://www.jstatsoft.org/v21/i11/paper).
| null | CC BY-SA 3.0 | null | 2010-07-23T16:36:50.980 | 2015-03-20T07:04:21.643 | 2015-03-20T07:04:21.643 | 183 | 5 | null |
561 | 2 | null | 534 | 21 | null | At the heart of your question is the question "when is a relationship causal?" It doesn't just need to be correlation implying (or not) causation.
A good book on this topic is called Mostly Harmless Econometrics by Johua Angrist and Jorn-Steffen Pischke. They start from the experimental ideal where we are able to randomise the "treatment" under study in some fashion and then they move onto alternative methods for generating this randomisation in order to draw causal influences. This begins with the study of so called natural experiments.
One of the first examples of a natural experiment being used to identify causal relationships is Angrist's 1989 paper on ["Lifetime Earnings and the Vietnam Era Draft Lottery."](http://www.irs.princeton.edu/pubs/pdfs/251.pdf) This paper attempts to estimate the effect of military service on lifetime earnings. A key problem with estimating any causal effect is that certain types of people may be more likely to enlist, which may bias any measurement of the relationship. Angrist uses the natural experiment created by the Vietnam draft lottery to effectively "randomly assign" the treatment "military service" to a group of men.
So when do we have a causality? Under experimental conditions. When do we get close? Under natural experiments. There are also other techniques that get us close to "causality" i.e. they are much better than simply using statistical control. They include regression discontinuity, difference-in-differences, etc.
| null | CC BY-SA 2.5 | null | 2010-07-23T16:49:47.407 | 2010-07-23T16:49:47.407 | null | null | 215 | null |
562 | 1 | 566 | null | 13 | 6132 | This is a fairly general question:
I have typically found that using multiple different models outperforms one model when trying to predict a time series out of sample. Are there any good papers that demonstrate that the combination of models will outperform a single model? Are there any best-practices around combining multiple models?
Some references:
- Hui Zoua, Yuhong Yang "Combining time series models for forecasting" International Journal of Forecasting 20 (2004) 69– 84
| When to use multiple models for prediction? | CC BY-SA 2.5 | null | 2010-07-23T16:51:11.790 | 2012-03-24T02:28:14.880 | 2012-03-23T03:44:56.367 | 9007 | 5 | [
"time-series",
"modeling",
"model-comparison"
] |
563 | 1 | null | null | 44 | 14907 | Instrumental variables are becoming increasingly common in applied economics and statistics. For the uninitiated, can we have some non-technical answers to the following questions:
- What is an instrumental variable?
- When would one want to employ an instrumental variable?
- How does one find or choose an instrumental variable?
| What is an instrumental variable? | CC BY-SA 2.5 | null | 2010-07-23T16:53:20.117 | 2018-01-24T21:54:03.920 | 2010-11-23T17:06:45.300 | 8 | 215 | [
"regression",
"econometrics",
"instrumental-variables"
] |
564 | 1 | null | null | 53 | 99562 | Difference in differences has long been popular as a non-experimental tool, especially in economics. Can somebody please provide a clear and non-technical answer to the following questions about difference-in-differences.
What is a difference-in-difference estimator?
Why is a difference-in-difference estimator any use?
Can we actually trust difference-in-difference estimates?
| What is difference-in-differences? | CC BY-SA 3.0 | null | 2010-07-23T16:57:50.063 | 2019-08-05T09:47:24.193 | 2014-11-24T13:37:12.850 | 26338 | 215 | [
"regression",
"econometrics",
"difference-in-difference"
] |
565 | 2 | null | 562 | 2 | null | The most spectacular example is the [Netflix challenge](http://www.netflixprize.com/), which made really boosted blending popularity.
| null | CC BY-SA 2.5 | null | 2010-07-23T17:02:28.887 | 2010-07-23T17:02:28.887 | null | null | null | null |
566 | 2 | null | 562 | 8 | null | Sometimes this kind of models are called an ensemble. For example [this page](http://wapedia.mobi/en/Machine_learning_ensemble) gives a nice overview how it works. Also the references mentioned there are very useful.
| null | CC BY-SA 2.5 | null | 2010-07-23T17:05:52.033 | 2010-07-23T17:05:52.033 | null | null | 190 | null |
567 | 2 | null | 170 | 20 | null | I've often found the Engineering Statistics Handbook useful. It can be found [here](http://www.itl.nist.gov/div898/handbook/).
Although I've never read it myself, I hear [Introduction to Probability and Statistics Using R](https://rdrr.io/cran/IPSUR/f/inst/doc/IPSUR.pdf) is very good. It's a full ~400 page ebook (also available as an actual book). As a bonus, it also teaches you R, which of course you want to learn anyways.
| null | CC BY-SA 4.0 | null | 2010-07-23T17:11:35.127 | 2021-05-31T03:49:17.623 | 2021-05-31T03:49:17.623 | 287839 | 92 | null |
568 | 2 | null | 31 | 8 | null | In statistics you can never say something is absolutely certain, so statisticians use another approach to gauge whether a hypothesis is true or not. They try to reject all the other hypotheses that are not supported by the data.
To do this, statistical tests have a null hypothesis and an alternate hypothesis. The p-value reported from a statistical test is the likelihood of the result given that the null hypothesis was correct. That's why we want small p-values. The smaller they are, the less likely the result would be if the null hypothesis was correct. If the p-value is small enough (ie,it is very unlikely for the result to have occurred if the null hypothesis was correct), then the null hypothesis is rejected.
In this fashion, null hypotheses can be formulated and subsequently rejected. If the null hypothesis is rejected, you accept the alternate hypothesis as the best explanation. Just remember though that the alternate hypothesis is never certain, since the null hypothesis could have, by chance, generated the results.
| null | CC BY-SA 2.5 | null | 2010-07-23T17:29:50.730 | 2010-07-23T17:29:50.730 | null | null | 92 | null |
569 | 2 | null | 562 | 4 | null | Following up on Peter's response on ensemble methods:
- This is covered in "The Elements of Statistical Learning" (see page 288, for example).
- Witten and Frank "Data Mining: Practical Machine Learning Tools and Techniques" covers this in section 7.5, including a discussion of Bagging, Randomization, Boosting, Additive regression, Additive logistic regression, Option trees, Logistic model trees, and Stacking.
- This is covered in Chapter 14 of Christopher M. Bishop "Pattern Recognition and Machine Learning", including Bayesian Model Averaging, Boosting, Committees, Tree-based Models, and Conditional Mixture Models.
| null | CC BY-SA 2.5 | null | 2010-07-23T17:32:44.140 | 2010-07-23T17:32:44.140 | null | null | 5 | null |
570 | 1 | 3798 | null | 14 | 1152 | I'm curious if there are graphical techniques particular, or more applicable, to structural equation modeling. I guess this could fall into categories for exploratory tools for covariance analysis or graphical diagnostics for SEM model evaluation. (I'm not really thinking of path/graph diagrams here.)
| What graphical techniques are used in Structural Equation Modeling? | CC BY-SA 2.5 | null | 2010-07-23T17:59:27.367 | 2013-02-25T06:23:08.783 | 2010-07-27T00:49:21.897 | 251 | 251 | [
"structural-equation-modeling",
"data-visualization"
] |
571 | 2 | null | 534 | 8 | null | One useful sufficient condition for some definitions of causation:
Causation can be claimed when one of the correlated variables can be controlled (we can directly set its value) and correlation is still present.
| null | CC BY-SA 2.5 | null | 2010-07-23T18:29:41.240 | 2010-07-23T18:29:41.240 | null | null | 217 | null |
572 | 2 | null | 555 | 24 | null | I think Graham's second paragraph gets at the heart of the matter. I suspect it's not so much technical than historical, probably due to the influence of "[Statistical Methods for Research Workers](http://en.wikipedia.org/wiki/Ronald_Fisher)", and the ease of teaching/applying the tool for non-statisticans in experimental analysis involving discrete factors, rather than delving into model building and associated tools. In statistics, ANOVA is usually taught as a special case of regression. (I think this is similar to why biostatistics is filled with a myriad of eponymous "tests" rather than emphasizing model building.)
| null | CC BY-SA 2.5 | null | 2010-07-23T18:42:05.440 | 2010-07-23T18:54:03.763 | 2010-07-23T18:54:03.763 | 251 | 251 | null |
573 | 1 | null | null | 11 | 1784 | In "[Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations](http://dx.doi.org/10.1145/1553374.1553453)" by Lee et. al.([PDF](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.149.802&rep=rep1&type=pdf)) Convolutional DBN's are proposed. Also the method is evaluated for image classification. This sounds logical, as there are natural local image features, like small corners and edges etc.
In "[Unsupervised feature learning for audio classification using convolutional deep belief networks](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.154.380&rep=rep1&type=pdf)" by Lee et. al. this method is applied for audio in different types of classifications. Speaker identification, gender indentification, phone classification and also some music genre / artist classification.
How can the convolutional part of this network be interpreted for audio, like it can be explained for images as edges?
| How to understand a convolutional deep belief network for audio classification? | CC BY-SA 3.0 | null | 2010-07-23T19:45:45.270 | 2017-11-09T12:58:33.937 | 2017-11-09T12:58:33.937 | 128677 | 190 | [
"classification",
"unsupervised-learning",
"intuition",
"deep-belief-networks"
] |
574 | 2 | null | 212 | 0 | null | Assuming there is some training involved, you may use some kind of cross-validation, or bootstrap of a train set.
If not, stick to the Srikant solution. I would do it even simpler, just assuming that the number of error is Poisson distributed.
| null | CC BY-SA 2.5 | null | 2010-07-23T20:07:51.003 | 2010-07-23T20:07:51.003 | null | null | null | null |
575 | 1 | 762 | null | 20 | 24177 | What is the preferred method for for conducting post-hocs for within subjects tests? I've seen published work where Tukey's HSD is employed but a review of Keppel and Maxwell & Delaney suggests that the likely violation of sphericity in these designs makes the error term incorrect and this approach problematic. Maxwell & Delaney provide an approach to the problem in their book, but I've never seen it done that way in any stats package. Is the approach they offer appropriate? Would a Bonferroni or Sidak correction on multiple paired sample t-tests be reasonable? An acceptable answer will provide general R code which can conduct post-hocs on simple, multiple-way, and mixed designs as produced by the `ezANOVA` function in the `ez` package, and appropriate citations that are likely to pass muster with reviewers.
| Post-hocs for within subjects tests? | CC BY-SA 3.0 | null | 2010-07-23T20:14:05.327 | 2022-11-29T18:53:35.480 | 2013-07-16T15:46:47.513 | 17230 | 196 | [
"r",
"repeated-measures",
"multiple-comparisons",
"post-hoc",
"sphericity"
] |
576 | 2 | null | 564 | 6 | null | [Wikipedia has a decent entry on this subject](http://en.wikipedia.org/wiki/Difference_in_differences), but why not just use linear regression allowing for interactions between your independent variables of interest? This seems more interpretable to me. Then you might read up on [analysis of simple slopes (in the Cohen et al book free on Google Books)](http://books.google.com/books?id=fuq94a8C0ioC&lpg=PP1&dq=applied%20multiple%20regression%20correlation%20analysis%20for%20the%20behavioral%20sciences&pg=PA271#v=onepage&q=simple%20slopes&f=false) if your variables of interest are quantitative.
| null | CC BY-SA 2.5 | null | 2010-07-23T20:42:43.260 | 2010-07-23T20:42:43.260 | null | null | 36 | null |
577 | 1 | 767 | null | 283 | 236285 | The AIC and BIC are both methods of assessing model fit penalized for the number of estimated parameters. As I understand it, BIC penalizes models more for free parameters than does AIC. Beyond a preference based on the stringency of the criteria, are there any other reasons to prefer AIC over BIC or vice versa?
| Is there any reason to prefer the AIC or BIC over the other? | CC BY-SA 2.5 | null | 2010-07-23T20:49:12.340 | 2022-11-29T18:45:04.257 | 2018-12-14T20:24:18.153 | 196 | 196 | [
"modeling",
"aic",
"cross-validation",
"bic",
"model-selection"
] |
578 | 2 | null | 527 | 2 | null | If you have no way of knowing the true concentration, the simplest approach would be a correlation. A step beyond that might be to conduct a simple regression predicting the outcome on method 2 using method 1 (or vice versa). If the methods are identical the intercept should be 0; if the intercept is greater or less than 0 it would indicate the bias of one method relative to another. The unstandardized slope should be near 1 if the methods on average produce results that are identical (after controlling for an upward or downward bias in the intercept). The error in the unstandardized slope might serve as an index of the extent to which the two methods agree.
It seems to me that the difficulty with statistical methods here that you are seeking to affirm what is typically posed as a null hypothesis, that is, that there are no differences between the methods. This isn't a death blow for using statistical methods so long as you don't need a p value and you can quantify what you mean by "equivalent" and can decide how much deviation the two methods can have from one another before you no longer consider them equivalent. In the regression approach I detailed above, you might consider the methods equivalent if confidence interval around the slope estimate included 1 and the CI around the intercept included 0.
| null | CC BY-SA 2.5 | null | 2010-07-23T21:18:52.370 | 2010-07-23T21:18:52.370 | null | null | 196 | null |
579 | 2 | null | 577 | 10 | null | Indeed the only difference is that BIC is AIC extended to take number of objects (samples) into account. I would say that while both are quite weak (in comparison to for instance cross-validation) it is better to use AIC, than more people will be familiar with the abbreviation -- indeed I have never seen a paper or a program where BIC would be used (still I admit that I'm biased to problems where such criteria simply don't work).
Edit: AIC and BIC are equivalent to cross-validation provided two important assumptions -- when they are defined, so when the model is a maximum likelihood one and when you are only interested in model performance on a training data. In case of collapsing some data into some kind of consensus they are perfectly ok.
In case of making a prediction machine for some real-world problem the first is false, since your training set represent only a scrap of information about the problem you are dealing with, so you just can't optimize your model; the second is false, because you expect that your model will handle the new data for which you can't even expect that the training set will be representative.
And to this end CV was invented; to simulate the behavior of the model when confronted with an independent data. In case of model selection, CV gives you not only the quality approximate, but also quality approximation distribution, so it has this great advantage that it can say "I don't know, whatever the new data will come, either of them can be better."
| null | CC BY-SA 3.0 | null | 2010-07-23T21:23:18.427 | 2014-04-11T11:31:10.767 | 2014-04-11T11:31:10.767 | 17230 | null | null |
581 | 1 | 588 | null | 21 | 27139 | I am currently using Viterbi training for an image segmentation problem. I wanted to know what the advantages/disadvantages are of using the Baum-Welch algorithm instead of Viterbi training.
| What are the differences between the Baum-Welch algorithm and Viterbi training? | CC BY-SA 4.0 | null | 2010-07-23T22:12:36.750 | 2018-10-03T16:53:01.837 | 2018-10-03T16:53:01.837 | null | 99 | [
"machine-learning",
"hidden-markov-model",
"image-processing",
"viterbi-algorithm",
"baum-welch"
] |
582 | 2 | null | 577 | 7 | null | As you mentioned, AIC and BIC are methods to penalize models for having more regressor variables. A penalty function is used in these methods, which is a function of the number of parameters in the model.
- When applying AIC, the penalty function is z(p) = 2 p.
- When applying BIC, the penalty function is z(p) = p ln(n), which is based on interpreting the penalty as deriving from prior information (hence the name Bayesian Information Criterion).
When n is large the two models will produce quite different results. Then the BIC applies a much larger penalty for complex models, and hence will lead to simpler models than AIC. However, as stated in [Wikipedia on BIC](http://en.wikipedia.org/wiki/Bayesian_information_criterion):
>
it should be noted that in many
applications..., BIC simply reduces to
maximum likelihood selection because
the number of parameters is equal for
the models of interest.
| null | CC BY-SA 2.5 | null | 2010-07-23T23:38:20.190 | 2010-07-23T23:43:40.540 | 2010-07-23T23:43:40.540 | 108 | 108 | null |
583 | 2 | null | 577 | 103 | null | Though AIC and BIC are both [Maximum Likelihood estimate](http://en.wikipedia.org/wiki/Maximum_likelihood) driven and penalize free parameters in an effort to combat overfitting, they do so in ways that result in significantly different behavior. Lets look at one commonly presented version of the methods (which results form stipulating normally distributed errors and other well behaving assumptions):
- ${\bf AIC} = -2 \ln\left(\text{likelihood}\right) + 2k$
and
- ${\bf BIC} = -2\ln\left(\text{likelihood}\right) + k\ln(N)$
where:
- $k$ = model degrees of freedom
- $N$ = number of observations
The best model in the group compared is the one that minimizes these scores, in both cases. Clearly, AIC does not depend directly on sample size. Moreover, generally speaking, AIC presents the danger that it might overfit, whereas BIC presents the danger that it might underfit, simply in virtue of how they penalize free parameters (2*k in AIC; ln(N)*k in BIC). Diachronically, as data is introduced and the scores are recalculated, at relatively low N (7 and less) BIC is more tolerant of free parameters than AIC, but less tolerant at higher N (as the natural log of N overcomes 2).
Additionally, AIC is aimed at finding the best approximating model to the unknown data generating process (via minimizing expected estimated [K-L divergence](http://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence)). As such, it fails to converge in probability to the true model (assuming one is present in the group evaluated), whereas BIC does converge as N tends to infinity.
So, as in many methodological questions, which is to be preferred depends upon what you are trying to do, what other methods are available, and whether or not any of the features outlined (convergence, relative tolerance for free parameters, minimizing expected K-L divergence), speak to your goals.
| null | CC BY-SA 4.0 | null | 2010-07-24T00:07:06.830 | 2022-06-07T21:34:59.793 | 2022-06-07T21:34:59.793 | 126931 | 39 | null |
584 | 2 | null | 581 | 1 | null | Forward-backward is used when you want to count 'invisible things'. For example, when using E-M to improve a model via unsupervised data. I think that Petrov's paper is an example. In the technique I'm thinking of, you first train a model with annotated data with fairly coarse annotations (e.g. a tag for 'Verb'). Then you arbitrarily split the probability mass for that state in two slightly unequal quantities, and retrain, running forward-backward to maximize likelihood by redistributing mass between the two states.
| null | CC BY-SA 2.5 | null | 2010-07-24T00:44:43.103 | 2010-07-24T00:44:43.103 | null | null | 240 | null |
585 | 2 | null | 526 | 5 | null | You can certainly get different results simply because you train on different examples. I very much doubt that there's an algorithm or problem domain where the results of the two would differ in some predictable way.
| null | CC BY-SA 2.5 | null | 2010-07-24T00:46:15.330 | 2010-07-24T00:46:15.330 | null | null | 240 | null |
586 | 2 | null | 558 | 8 | null | The [Tutorial on Energy-Based Learning](https://web.archive.org/web/20100701041534/http://yann.lecun.com/exdb/publis/) by LeCun et al. might get you a good part of the way there. They describe a number of loss functions and discuss what makes them "good or bad" for energy based models.
| null | CC BY-SA 4.0 | null | 2010-07-24T01:41:28.650 | 2022-11-23T11:32:12.237 | 2022-11-23T11:32:12.237 | 362671 | 251 | null |
587 | 2 | null | 577 | 88 | null | My quick explanation is
- AIC is best for prediction as it is asymptotically equivalent to cross-validation.
- BIC is best for explanation as it is allows consistent estimation of the underlying data generating process.
| null | CC BY-SA 2.5 | null | 2010-07-24T03:58:58.333 | 2010-07-24T03:58:58.333 | null | null | 159 | null |
588 | 2 | null | 581 | 28 | null | The Baum-Welch algorithm and the Viterbi algorithm calculate different things.
If you know the transition probabilities for the hidden part of your model, and the emission probabilities for the visible outputs of your model, then the Viterbi algorithm gives you the most likely complete sequence of hidden states conditional on both your outputs and your model specification.
The Baum-Welch algorithm gives you both the most likely hidden transition probabilities as well as the most likely set of emission probabilities given only the observed states of the model (and, usually, an upper bound on the number of hidden states). You also get the "pointwise" highest likelihood points in the hidden states, which is often slightly different from the single hidden sequence that is overall most likely.
If you know your model and just want the latent states, then there is no reason to use the Baum-Welch algorithm. If you don't know your model, then you can't be using the Viterbi algorithm.
Edited to add: See Peter Smit's comment; there's some overlap/vagueness in nomenclature. Some poking around led me to a chapter by Luis Javier Rodrıguez and Ines Torres in "Pattern Recognition and Image Analysis" (ISBN 978-3-540-40217-6, pp 845-857) which discusses the speed versus accuracy trade-offs of the two algorithms.
Briefly, the Baum-Welch algorithm is essentially the Expectation-Maximization (EM) algorithm applied to an HMM; as a strict EM-type algorithm you're guaranteed to converge to at least a local maximum, and so for unimodal problems find the MLE. It requires two passes over your data for each step, though, and the complexity gets very big in the length of the data and number of training samples. However, you do end up with the full conditional likelihood for your hidden parameters.
The Viterbi training algorithm (as opposed to the "Viterbi algorithm") approximates the MLE to achieve a gain in speed at the cost of accuracy. It segments the data and then applies the Viterbi algorithm (as I understood it) to get the most likely state sequence in the segment, then uses that most likely state sequence to re-estimate the hidden parameters. This, unlike the Baum-Welch algorithm, doesn't give the full conditional likelihood of the hidden parameters, and so ends up reducing the accuracy while saving significant (the chapter reports 1 to 2 orders of magnitude) computational time.
| null | CC BY-SA 3.0 | null | 2010-07-24T04:22:01.467 | 2018-02-27T19:30:29.797 | 2018-02-27T19:30:29.797 | 132399 | 61 | null |
589 | 2 | null | 411 | 9 | null | Computational issues are the strongest argument I've heard one way or the other. The single biggest advantage of the Kolmogorov distance is that it's very easy to compute analytically for pretty much any CDF. Most other distance metrics don't have a closed-form expression except, sometimes, in the Gaussian case.
The Kolmogorov distance of a sample also has a known sampling distribution given the CDF (I don't think most other ones do), which ends up being related to the Wiener process. This is the basis for the Kolmogorov-Smirnoff test for comparing a sample to a distribution or two samples to each other.
On a more functional-analysis note, the sup norm is nice in that (as you mention) it basically defines uniform convergence. This leaves you with norm convergence implying pointwise convergence, and so you if you're clever about how you define your function sequences you can work within a RKHS and use all of the nice tools that that provides as well.
| null | CC BY-SA 2.5 | null | 2010-07-24T04:54:53.943 | 2010-07-24T04:54:53.943 | null | null | 61 | null |
590 | 1 | 611 | null | 4 | 375 | In some papers, for example in ["The Geometric Density with Unknown Location Parameter"](http://www.jstor.org/stable/2239262) by Klotz, a Geometric Distribution is called a Geometric Density.
For me, this claim looks erroneous, however Klotz is a serious statistician and a professor in the field.
My question is, to what extend is it legitimate to call a Geometric Distribution a Geometric Density?
| To what extent can we call a Geometric Distribution a Geometric Density | CC BY-SA 2.5 | null | 2010-07-24T09:09:14.243 | 2010-08-03T19:39:42.083 | 2010-07-25T10:09:23.647 | 190 | 190 | [
"distributions",
"discrete-data"
] |
591 | 2 | null | 558 | 5 | null | The loss function is given by the problem. It could be anything. For example, you could also penalize the used CPU time and space.
In reinforcement learning, the loss function is an unknown non-deterministic function.
You cannot redefine it without changing the problem.
| null | CC BY-SA 2.5 | null | 2010-07-24T09:33:01.940 | 2010-07-24T09:33:01.940 | null | null | 200 | null |
592 | 2 | null | 421 | 5 | null | It is a bit old, but I have found Chris Chatfield's book,
[Statistics for Technology: A Course in Applied Technology](http://rads.stackoverflow.com/amzn/click/0412253402)
to be an excellent introduction.
It was how I first learned about statistics from a conceptual point of view.
| null | CC BY-SA 2.5 | null | 2010-07-24T09:52:52.377 | 2010-08-11T08:38:27.217 | 2010-08-11T08:38:27.217 | 509 | 57 | null |
593 | 2 | null | 575 | 5 | null | I recall some discussion on this in the past; I'm not aware of any implementation of Maxwell & Delaney's approach, although it shouldn't be too difficult to do. Have a look at "[Repeated Measures ANOVA using R](https://web.archive.org/web/20100124203354/http://gribblelab.org/2009/03/09/repeated-measures-anova-using-r/)" which also shows one method of addressing the sphericity issue in [Tukey's HSD](http://en.wikipedia.org/wiki/Tukey%27s_range_test).
You might also find [this description of Friedman's test](http://www.r-statistics.com/2010/02/post-hoc-analysis-for-friedmans-test-r-code/) of interest.
| null | CC BY-SA 4.0 | null | 2010-07-24T12:09:08.743 | 2022-11-29T18:53:35.480 | 2022-11-29T18:53:35.480 | 362671 | 5 | null |
594 | 1 | 599 | null | 18 | 698 | The E-M procedure appears, to the uninitiated, as more or less black magic. Estimate parameters of an HMM (for example) using supervised data. Then decode untagged data, using forward-backward to 'count' events as if the data were tagged, more or less. Why does this make the model better? I do know something about the math, but I keep wishing for some sort of mental picture of it.
| E-M, is there an intuitive explanation? | CC BY-SA 2.5 | null | 2010-07-24T19:25:59.147 | 2015-10-05T23:56:07.353 | 2015-10-05T23:56:07.353 | 12359 | 240 | [
"expectation-maximization",
"intuition"
] |
595 | 2 | null | 492 | 7 | null | You could use the (fast :) ) discrete wavelet transform. The package wavethresh under R will do all the work.
Anyway, I like the solution of @James because it is simple and seems to go straigh to the point.
| null | CC BY-SA 2.5 | null | 2010-07-24T19:43:24.270 | 2010-08-03T19:40:40.863 | 2010-08-03T19:40:40.863 | 223 | 223 | null |
596 | 1 | 1722 | null | 4 | 996 | E-M provides a way to improve the estimation of a generative model with unannotated data. Is there anything out there that works the same way for discriminative models (e.g. perceptrons)?
For example, consider averaged perceptron tagger. It would be handy to be able to throw the entire Gigaword through some process of unsupervised model improvement.
EDIT:
So, I was pleasantly surprised to note that this site has the ambition of dealing with machine learning, but I'm learning by experiment what vocabulary is generic and what is very domain-specific. Apologies.
Consider a sequence classification problem, like part-of-speech tagging or named entity extraction. You can train a generative model (e.g. an HMM). That's a probability model, and you can apply E-M. However, the number of states grows prohibitive if you want to look at many features, and so the fashion tends toward things like CRFs (batch) or Perceptron (online).
For example, [this](https://aclanthology.org/E09-1087/) paper talks about unsupervised learning in for a perceptron POS tagger, but the details are that they add the output of several pre-existing taggers to the training set of their model.
| Something like E-M for discriminative models? | CC BY-SA 4.0 | null | 2010-07-24T19:50:48.730 | 2022-11-24T03:18:28.493 | 2022-11-24T03:14:16.043 | 362671 | 240 | [
"machine-learning",
"expectation-maximization"
] |
597 | 2 | null | 558 | 6 | null | Well, there's [this](http://docs.google.com/viewer?a=v&q=cache%3acfjRh4vE38kJ%3abooks.nips.cc/papers/files/nips16/NIPS2003_LT21.pdf+passive-aggressive+machine+learning&hl=en&gl=us&pid=bl&srcid=ADGEEShVh5WierOOrVz8pTpfOPVUCm8HIqkUCm1rxCsUPm5UUapNONytwRMjMq63zcOye0L3djRjQCZW6YN_r12SvIEaWCtbx3b5La7EJ8nQuoWm2Jw8n8DuLEjS19K56fh8DZLOfrHu&sig=AHIEtbRBrb7Q7Lx6LSh_fKEFXyWaxW0RVw) and [that](http://portal.acm.org/citation.cfm?id=1248547.1248566). Two papers by Cramer and others discussing loss in the context of online learning algorithms.
| null | CC BY-SA 2.5 | null | 2010-07-24T19:55:30.013 | 2010-07-24T19:55:30.013 | null | null | 240 | null |
598 | 2 | null | 3 | 7 | null | Few more on top of already mentioned:
- KNIME together with R, Python and Weka integration extensions for data mining
- Mondrian for quick EDA
And from spatial perspective:
- GeoDa for spatial EDA and clustering of areal data
- SaTScan for clustering of point data
| null | CC BY-SA 4.0 | null | 2010-07-24T20:15:20.653 | 2022-11-27T23:25:03.597 | 2022-11-27T23:25:03.597 | 362671 | 22 | null |
599 | 2 | null | 594 | 12 | null | Just to save some typing, call the observed data $X$, the missing data $Z$ (e.g. the hidden states of the HMM), and the parameter vector we're trying to find $Q$ (e.g. transition/emission probabilities).
The intuitive explanation is that we basically cheat, pretend for a moment we know $Q$ so we can find a conditional distribution of Z that in turn lets us find the MLE for $Q$ (ignoring for the moment the fact that we're basically making a circular argument), then admit that we cheated, put in our new, better value for $Q$, and do it all over again until we don't have to cheat anymore.
Slightly more technically, by pretending that we know the real value $Q$, we can pretend we know something about the conditional distribution of $Z|\{X,Q\}$, which lets us improve our estimate for $Q$, which we now pretend is the real value for $Q$ so we can pretend we know something about the conditional distribution of $Z|\{X,Q\}$, which lets us improve our estimate for $Q$, which... and so on.
Even more technically, if we knew $Z$, we could maximize $\log(f(Q|X,Z))$ and have the right answer. The problem is that we don't know $Z$, and any estimate for $Q$ must depend on it. But if we want to find the best estimate (or distribution) for $Z$, then we need to know $X$ and $Q$. We're stuck in a chicken-and-egg situation if we want the unique maximizer analytically.
Our 'out' is that -- for any estimate of $Q$ (call it $Q_n$) -- we can find the distribution of $Z|\{Q_n,X\}$, and so we can maximize our expected joint log-likelihood of $Q|\{X,Z\}$, with respect to the conditional distribution of $Z|\{Q_n,X\}$. This conditional distribution basically tells us how $Z$ depends on the current value of $Q$ given $X$, and lets us know how to change $Q$ to increase our likelihood for both $Q$ and $Z$ at the same time for a particular value of $Q$ (that we've called $Q_n$). Once we've picked out a new $Q_{n+1}$, we have a different conditional distribution for $Z|\{Q_{n+1}, X\}$ and so have to re-calculate the expectation.
| null | CC BY-SA 3.0 | null | 2010-07-24T20:23:06.997 | 2013-05-15T04:27:01.810 | 2013-05-15T04:27:01.810 | 805 | 61 | null |
600 | 2 | null | 411 | 12 | null | Mark,
the main reason of which I am aware for the use of K-S is because it arises naturally from Glivenko-Cantelli theorems in univariate empirical processes. The one reference I'd recommend is A.W.van der Vaart "Asymptotic Statistics", ch. 19. A more advanced monograph is "Weak Convergence and Empirical Processes" by Wellner and van der Vaart.
I'd add two quick notes:
- another measure of distance commonly used in univariate distributions is the Cramer-von Mises distance, which is an L^2 distance;
- in general vector spaces different distances are employed; the space of interest in many papers is polish. A very good introduction is Billingsley's "Convergence of Probability Measures".
I apologize if I can't be more specific. I hope this helps.
| null | CC BY-SA 2.5 | null | 2010-07-24T20:36:13.223 | 2010-07-24T20:36:13.223 | null | null | 30 | null |
602 | 1 | 1733 | null | 4 | 361 | Do you know any good heuristics for finding optimal value of ν in case of ν-SVM classification? In this particular problem I have a radial basis kernel, if it helps.
| Heuristics for optimizing ν-SVM? | CC BY-SA 2.5 | null | 2010-07-24T22:29:40.557 | 2010-08-16T09:23:45.913 | null | null | null | [
"machine-learning",
"svm"
] |
603 | 2 | null | 526 | 3 | null | >
Usually of course the difference is
unnoticeable, and so goes my question
-- can you think of an example when the result of one type is
significantly different from another?
I am not sure at all the difference is unnoticeable, and that only in ad hoc example it will be noticeable. Both cross-validation and bootstrapping (sub-sampling) methods depend critically on their design parameters, and this understanding is not complete yet. In general, results within k-fold cross-validation depend critically on the number of folds, so you can expect always different results from what you would observe in sub-sampling.
Case in point: say that you have a true linear model with a fixed number of parameters. If you use k-fold cross-validation (with a given, fixed k), and let the number of observations go to infinity, k-fold cross validation will be asymptotically inconsistent for model selection, i.e., it will identify an incorrect model with probability greater than 0. This surprising result is due to Jun Shao, "Linear Model Selection by Cross-Validation", Journal of the American Statistical Association, 88, 486-494 (1993), but more papers can be found in this vein.
In general, respectable statistical papers specify the cross-validation protocol, exactly because results are not invariant. In the case where they choose a large number of folds for large datasets, they remark and try to correct for biases in model selection.
| null | CC BY-SA 2.5 | null | 2010-07-24T22:54:13.430 | 2010-07-24T22:54:13.430 | null | null | 30 | null |
604 | 1 | null | null | 7 | 776 | I am puzzled by something I found using Linear Discriminant Analysis. Here is the problem - I first ran the Discriminant analysis using 20 or so independent variables to predict 5 segments. Among the outputs, I asked for the Predicted Segments, which are the same as the original segments for around 80% of the cases. Then I ran again the Discriminant Analysis with the same independent variables, but now trying to predict the Predicted Segments. I was expecting I would get 100% of correct classification rate, but that did not happen and I am not sure why. It seems to me that if the Discriminant Analysis cannot predict with 100% accuracy it own predicted segments then somehow it is not a optimum procedure since a rule exist that will get 100% accuracy. I am missing something?
Note - This situation seems to be similar to that in Linear Regression Analysis. If you fit the model $y = a + bX + \text{error}$ and use the estimated equation with the same data you will get $\hat{y}$ [$= \hat{a} + \hat{b}X$]. Now if you estimate the model $\hat{y} = \hat{a} + \hat{b}X + \text{error}$, you will find the same $\hat{a}$ and $\hat{b}$ as before, no error, and R2 = 100% (perfect fit). I though this would also happen with Linear Discriminant Analysis, but it does not.
Note 2 - I run this test with Discriminant Analysis in SPSS.
| Why prediction of a predicted variable from a discriminant analysis is imperfect | CC BY-SA 3.0 | null | 2010-07-24T23:09:05.870 | 2011-05-03T09:00:53.737 | 2011-05-03T09:00:53.737 | 183 | 165 | [
"regression",
"discriminant-analysis"
] |
605 | 2 | null | 604 | 1 | null | This is quite normal in case of machine learning -- it does not need to be optimal, it must be general.
| null | CC BY-SA 2.5 | null | 2010-07-24T23:25:48.150 | 2010-07-24T23:25:48.150 | null | null | null | null |
606 | 2 | null | 490 | 20 | null | A very popular approach is penalized logistic regression, in which one maximizes the sum of the log-likelihood and a penalization term consisting of the L1-norm ("lasso"), L2-norm ("ridge"), a combination of the two ("elastic"), or a penalty associated to groups of variables ("group lasso"). This approach has several advantages:
- It has strong theoretical properties, e.g., see this paper by Candes & Plan and close connections to compressed sensing;
- It has accessible expositions, e.g., in Elements of Statistical Learning by Friedman-Hastie-Tibshirani (available online);
- It has readily available software to fit models. R has the glmnet package which is very fast and works well with pretty large datasets. Python has scikit-learn, which includes L1- and L2-penalized logistic regression;
- It works very well in practice, as shown in many application papers in image recognition, signal processing, biometrics, and finance.
| null | CC BY-SA 2.5 | null | 2010-07-25T02:37:06.947 | 2010-07-25T02:37:06.947 | null | null | 30 | null |
607 | 2 | null | 6 | 227 | null | I think the answer to your first question is simply in the affirmative. Take any issue of Statistical Science, JASA, Annals of Statistics of the past 10 years and you'll find papers on boosting, SVM, and neural networks, although this area is less active now. Statisticians have appropriated the work of Valiant and Vapnik, but on the other side, computer scientists have absorbed the work of Donoho and Talagrand. I don't think there is much difference in scope and methods any more. I have never bought Breiman's argument that CS people were only interested in minimizing loss using whatever works. That view was heavily influenced by his participation in Neural Networks conferences and his consulting work; but PAC, SVMs, Boosting have all solid foundations. And today, unlike 2001, Statistics is more concerned with finite-sample properties, algorithms and massive datasets.
But I think that there are still three important differences that are not going away soon.
- Methodological Statistics papers are still overwhelmingly formal and deductive, whereas Machine Learning researchers are more tolerant of new approaches even if they don't come with a proof attached;
- The ML community primarily shares new results and publications in conferences and related proceedings, whereas statisticians use journal papers. This slows down progress in Statistics and identification of star researchers. John Langford has a nice post on the subject from a while back;
- Statistics still covers areas that are (for now) of little concern to ML, such as survey design, sampling, industrial Statistics etc.
| null | CC BY-SA 3.0 | null | 2010-07-25T03:29:41.460 | 2017-11-06T11:17:18.020 | 2017-11-06T11:17:18.020 | 79114 | 30 | null |
608 | 1 | null | null | 28 | 1690 | In a [question](https://stats.stackexchange.com/questions/577/is-there-any-reason-to-prefer-the-aic-or-bic-over-the-other) elsewhere on this site, several answers mentioned that the AIC is equivalent to leave-one-out (LOO) cross-validation and that the BIC is equivalent to K-fold cross validation. Is there a way to empirically demonstrate this in R such that the techniques involved in LOO and K-fold are made clear and demonstrated to be equivalent to the AIC and BIC values? Well commented code would be helpful in this regard. In addition, in demonstrating the BIC please use the lme4 package. See below for a sample dataset...
```
library(lme4) #for the BIC function
generate.data <- function(seed)
{
set.seed(seed) #Set a seed so the results are consistent (I hope)
a <- rnorm(60) #predictor
b <- rnorm(60) #predictor
c <- rnorm(60) #predictor
y <- rnorm(60)*3.5+a+b #the outcome is really a function of predictor a and b but not predictor c
data <- data.frame(y,a,b,c)
return(data)
}
data <- generate.data(76)
good.model <- lm(y ~ a+b,data=data)
bad.model <- lm(y ~ a+b+c,data=data)
AIC(good.model)
BIC(logLik(good.model))
AIC(bad.model)
BIC(logLik(bad.model))
```
Per earlier comments, below I have provided a list of seeds from 1 to 10000 in which AIC and BIC disagree. This was done by a simple search through the available seeds, but if someone could provide a way to generate data which would tend to produce divergent answers from these two information criteria it may be particularly informative.
```
notable.seeds <- read.csv("http://student.ucr.edu/~rpier001/res.csv")$seed
```
As an aside, I thought about ordering these seeds by the extent to which the AIC and BIC disagree which I've tried quantifying as the sum of the absolute differences of the AIC and BIC. For example,
```
AICDiff <- AIC(bad.model) - AIC(good.model)
BICDiff <- BIC(logLik(bad.model)) - BIC(logLik(good.model))
disagreement <- sum(abs(c(AICDiff,BICDiff)))
```
where my disagreement metric only reasonably applies when the observations are notable. For example,
```
are.diff <- sum(sign(c(AICDiff,BICDiff)))
notable <- ifelse(are.diff == 0 & AICDiff != 0,TRUE,FALSE)
```
However in cases where AIC and BIC disagreed, the calculated disagreement value was always the same (and is a function of sample size). Looking back at how AIC and BIC are calculated I can see why this might be the case computationally, but I'm not sure why it would be the case conceptually. If someone could elucidate that issue as well, I'd appreciate it.
| How can one empirically demonstrate in R which cross-validation methods the AIC and BIC are equivalent to? | CC BY-SA 2.5 | null | 2010-07-25T05:08:20.333 | 2010-08-03T22:58:09.447 | 2017-04-13T12:44:35.347 | -1 | 196 | [
"r",
"aic",
"cross-validation",
"bic"
] |
609 | 2 | null | 411 | 10 | null | As a summary, my answer is : if you have an explicit expression or can figure out some how what your distance is measuring (what "differences" it gives weigth to), then you can say what it is better for. An other complementary way to analyse and compare such test is the minimax theory.
At the end some test will be good for some alternatives and some for others. For a given set of alternatives it is sometime possible to show if your test has optimal property in the worst case: this is the minimax theory.
---
Some details
Hence You can tell about the properties of two different test by regarding the set of alternative for which they are minimax (if such alternative exist) i.e. (using the word of Donoho and Jin) by comparing their "optimal detection boudary" [Link](https://projecteuclid.org/journals/annals-of-statistics/volume-32/issue-3/Higher-criticism-for-detecting-sparse-heterogeneous-mixtures/10.1214/009053604000000265.full).
Let me go distance by distance:
- KS distance is obtained calculating supremum of difference between empirical cdf and cdf. Being a suppremum it will be highly sensitive to local alternatives (local change in the cdf) but not with global change (at least using L2 distance between cdf would be less local (Am I openning open door ?)). However, the most important thing is that is uses the cdf. This implies an asymetry: you give more importance to the changes in the tail of your distribution.
- Wassertein metric (what you meant by Kantorovitch Rubinstein ? ) http://en.wikipedia.org/wiki/Wasserstein_metric is ubiquitous and hence hard to compare.
- For the particular case of W2 it has been uses in Link and it is related to the L2 distance to inverse of cdf. My understanding is that it gives even more weight to the tails but I think you should read the paper to know more about it.
- For the case of the L1 distance between density function it will highly depend on how you estimate your dentity function from the data... but otherwise it seems to be a "balanced test" not giving importance to tails.
---
To recall and extend the comment I made which complete the answer:
I know you did not meant to be exhaustive but you could add Anderson darling statistic (see [http://en.wikipedia.org/wiki/Anderson%E2%80%93Darling_test](http://en.wikipedia.org/wiki/Anderson%E2%80%93Darling_test)). This made me remind of a paper fromo Jager and Wellner (see [Link](https://projecteuclid.org/journals/annals-of-statistics/volume-35/issue-5/Goodness-of-fit-tests-via-phi-divergences/10.1214/0009053607000000244.full)) which extands/generalises Anderson darling statistic (and include in particular higher criticism of Tukey). Higher criticism was already shown to be minimax for a wide range of alternatives and the same is done by Jager and Wellner for their extention. I don't think that minimax property has been shown for Kolmogorov test. Anyway, understanding for which type of alternative your test is minimax helps you to know where is its strength, so you should read the paper above..
| null | CC BY-SA 4.0 | null | 2010-07-25T07:18:44.263 | 2022-08-03T22:46:15.427 | 2022-08-03T22:46:15.427 | 79696 | 223 | null |
610 | 2 | null | 492 | 9 | null | It sounds dodgy to me as the trend estimate will be biased near the point where you splice on the false data. An alternative approach is a nonparametric regression smoother such as loess or splines.
| null | CC BY-SA 2.5 | null | 2010-07-25T09:13:59.517 | 2010-07-25T09:13:59.517 | null | null | 159 | null |
611 | 2 | null | 590 | 6 | null | Heuristic answer: Without much mathematic you could say that a continuous variable has a density with respect to the Lebesgue measure, and a discrete random variable has a density with respect to the counting measure.
Developped answer: The concept of density is much wider than you may think. A density of a probability measure $P$ can be defined with respect to a measure $\lambda$ that dominates $P$ by the Radon Nikodym Theorem (see [http://en.wikipedia.org/wiki/Radon%E2%80%93Nikodym_theorem](http://en.wikipedia.org/wiki/Radon%E2%80%93Nikodym_theorem)). Here density should be understood as a density with respect to the counting measure defined on the mentionned countable set. I agree that it is not extremely rigorous not to mention the reference when talking about a density (but who mention density wrt lesbesgue measure?), but it pose no problem while reading the paper in question so ....
---
Additional Annex Notes
I have seen a certain number of machine learning notes (I won't do delation) where the reference measure is not the counting measure and we see things such as $P(X=x|Y=y)$ with X being a continuous variable (with a density wrt Lebesgues) (to apply Bayes principle and derive the Bayes rule). I guess people want to be pedagogic and do not want to bother students with technical details ;) My conclusion would be that even great mathematician can commit abuse of wording or of notation (it is not the case in the paper you mention because the authors of a paper in AoP may have mathematical background), it is not a problem as along as it is understood by everyone...
| null | CC BY-SA 2.5 | null | 2010-07-25T12:36:23.680 | 2010-08-03T19:39:42.083 | 2010-08-03T19:39:42.083 | 223 | 223 | null |
612 | 1 | 136936 | null | 70 | 56577 | I have tried to reproduce some research (using PCA) from SPSS in R. In my experience, `principal()` [function](http://www.personality-project.org/r/html/principal.html) from package `psych` was the only function that came close (or if my memory serves me right, dead on) to match the output. To match the same results as in SPSS, I had to use parameter `principal(..., rotate = "varimax")`. I have seen papers talk about how they did PCA, but based on the output of SPSS and use of rotation, it sounds more like Factor analysis.
Question: Is PCA, even after rotation (using [varimax](https://en.wikipedia.org/wiki/Varimax_rotation)), still PCA? I was under the impression that this might be in fact Factor analysis... In case it's not, what details am I missing?
| Is PCA followed by a rotation (such as varimax) still PCA? | CC BY-SA 3.0 | null | 2010-07-25T14:31:31.773 | 2018-03-08T17:58:40.510 | 2015-12-15T20:37:16.417 | 12615 | 144 | [
"r",
"spss",
"pca",
"factor-analysis",
"factor-rotation"
] |
613 | 2 | null | 130 | 11 | null | I have been a heavy R user for the past 6-7 years. As a language, it has several design limitations. Yet, for work in econometrics and in data analysis, I still wholeheartedly recommend it. It has a large number of packages that would be relevant to you for econometrics, time series, consumer choice modeling etc. and of course excellent visualization, good algebra and numerical libraries etc. I would not worry too much about data size limitations. Although R was not designed for "big data" (unlike, say, SAS) there are ways around it. The availability of packages is what makes the difference, really.
I've only read Clojure's language specs, and it's beautiful and clean. It addresses in a natural way issues of parallelization and scale. And if you have some basic java or OOP knowledge, you can benefit from the large number of high-quality java libraries.
The issue I have with Clojure is that is a recent one-man (R.Hickey) operation, therefore 1) very risky 2) very immature 3) with niche adoption. Great for enthusiasts, early adopters, CS/ML people who want to try new things. For a user who sees a language as a means to an end and who needs very robust code that can be shared code with others, established languages seem a safer choice. Just know who you are.
| null | CC BY-SA 2.5 | null | 2010-07-25T14:33:25.313 | 2010-07-25T14:33:25.313 | null | null | 30 | null |
614 | 1 | null | null | 40 | 10561 | There have been a few questions about statistical [textbooks](https://stats.stackexchange.com/questions/tagged/textbook), such as the question [Free statistical textbooks](https://stats.stackexchange.com/questions/170/free-statistical-textbooks). However, I am looking for textbooks that are Open Source, for example, having an [Creative Commons](http://creativecommons.org/) license. The reason is that in course material in other domains, you still want to include some text about basic statistics. In this case, it would be interesting to reuse existing material, instead of rewriting that material.
Therefore, what Open Source textbooks on statistics (and perhaps machine learning) are available?
| Open Source statistical textbooks? | CC BY-SA 2.5 | null | 2010-07-25T14:53:50.473 | 2016-10-06T19:43:59.697 | 2017-04-13T12:44:21.160 | -1 | 107 | [
"references",
"open-source"
] |
615 | 2 | null | 612 | 2 | null | Thanks to the chaos in definitions of both they are effectively a synonyms. Don't believe words and look deep into the docks to find the equations.
| null | CC BY-SA 2.5 | null | 2010-07-25T14:56:32.433 | 2010-07-25T14:56:32.433 | null | null | null | null |
616 | 2 | null | 614 | 7 | null | The ["Statistics"](http://en.wikibooks.org/wiki/Statistics) book on wikibooks
| null | CC BY-SA 2.5 | null | 2010-07-25T15:25:13.873 | 2010-07-25T15:32:14.903 | 2010-07-25T15:32:14.903 | 5 | 5 | null |
617 | 2 | null | 614 | 10 | null | [Multivariate statistics with R](http://www.opentextbook.org/2009/04/03/multivariate-statistics-with-r/)
| null | CC BY-SA 2.5 | null | 2010-07-25T15:32:59.290 | 2010-07-25T15:32:59.290 | null | null | 5 | null |
618 | 2 | null | 36 | 28 | null | I've always liked this one:
source: [http://pubs.acs.org/doi/abs/10.1021/ci700332k](http://pubs.acs.org/doi/abs/10.1021/ci700332k)
| null | CC BY-SA 2.5 | null | 2010-07-25T18:02:06.573 | 2010-07-25T18:10:35.387 | 2010-07-25T18:10:35.387 | 54 | 54 | null |
619 | 2 | null | 524 | 4 | null | I have a depressing and not-very-specific anecdote to share here. I spent some time as a co-worker of a statistical MT researcher. If you want to see a really big, complex, model, look no further.
He was putting me through NLP bootcamp for his own amusement. I am, in general, the sort of programmer who lives and dies by the unit test and the debugger. As a young person at Symbolics, I was struck by the aphorism, 'programming is debugging an empty editor buffer.' (Sort of like training a perceptron model.)
So, I asked him, 'how do you test and debug this stuff.' He answer was, "You get it right the first time. You think it through (in his case, often on paper) very carefully, and you code it very carefully. Because when you get it wrong, the chances of isolating the problem are very slim."
| null | CC BY-SA 2.5 | null | 2010-07-25T20:08:35.907 | 2010-07-25T20:08:35.907 | null | null | 240 | null |
620 | 2 | null | 614 | 4 | null | [R programming wiki book](http://en.wikibooks.org/wiki/R_Programming)
| null | CC BY-SA 2.5 | null | 2010-07-25T22:04:16.257 | 2010-07-25T22:04:16.257 | null | null | 253 | null |
621 | 2 | null | 614 | 4 | null | Some googling found [Statistics & Probability on CollegeOpenTextbooks.org](http://collegeopentextbooks.org/textbook-listings/textbooks-by-subject/statisticsandprobability). Still, be aware that most of CC-ed material is share-aliked (so you must also publish your work on CC) or at least attributed (so you must add info that certain part was copied and from whom). The same works with GFDL (both SA & A), it is even worse since in principle you should print it along with the document.
| null | CC BY-SA 3.0 | null | 2010-07-25T23:56:43.840 | 2016-10-06T19:43:59.697 | 2016-10-06T19:43:59.697 | 122650 | null | null |
622 | 1 | 628 | null | 67 | 29552 | I see these terms being used and I keep getting them mixed up. Is there a simple explanation of the differences between them?
| What is the difference between a partial likelihood, profile likelihood and marginal likelihood? | CC BY-SA 2.5 | null | 2010-07-26T09:12:21.093 | 2022-05-17T12:52:26.377 | 2022-05-17T12:52:26.377 | 11887 | 159 | [
"estimation",
"maximum-likelihood",
"likelihood",
"profile-likelihood"
] |
623 | 2 | null | 175 | 5 | null | Garbage in, garbage out....
Implicit in getting the full benefit of linear regression is that the noise follows a normal distribution. Ideally you have mostly data and a little noise.... not mostly noise and a little data. You can test for normality of residuals after the linear fit by looking at the residuals. You can also filter input data before the linear fit for obvious, glaring errors.
Here are some types of noise in garbage input data that do not typically fit a normal distribution:
- Digits missing or added with hand-entered data (off by a factor of 10 or more)
- Wrong or incorrectly converted units (grams vs kilos vs pounds; meters, feet, miles, km), possibly from merging multiple data sets (Note: The Mars Orbiter was thought to be lost in this way, so even NASA rocket scientists can make this mistake)
- Use of codes like 0, -1, -99999 or 99999 to mean something non-numeric like "not applicable" or "column unavailable" and just dumping this into a linear model along with valid data
Writing a spec for what is "valid data" for each column can help you tag invalid data. For instance, a person's height in cm should be in a range, say, 100-300 cm. If you find 1.8 for height that's a typo, and while you can assume it was 1.8 m and alter it to 180 -- I'd say it is usually safer to throw it out and best to document as much of the filtering as possible.
| null | CC BY-SA 4.0 | null | 2010-07-26T09:46:48.410 | 2020-09-18T08:21:19.847 | 2020-09-18T08:21:19.847 | 22047 | 87 | null |
624 | 1 | 625 | null | 3 | 460 | In engineering, we usually have Handbooks that pretty much dictate the state of the practice. These books are usually devoid of theory and focus on the applied methodology. Is there a forecasting Handbook out there? that solely focuses on the technique and not the background?
| Forecasting handbooks | CC BY-SA 2.5 | null | 2010-07-26T11:53:11.027 | 2010-09-30T21:25:14.480 | 2010-09-30T21:25:14.480 | 930 | 59 | [
"forecasting"
] |
625 | 2 | null | 624 | 4 | null | There are two that I know of:
- Handbook of economic forecasting. Relatively theoretical. Not for undergraduates. A narrow look at forecasting --- specifically about economic forecasting.
- Principles of forecasting. Simpler, broader. Widely used by forecasting practitioners. Often reflects the idiosyncratic opinions of the editor which are presented as established facts.
Alternatively, you could use an intro textbook. [My own textbook](http://robjhyndman.com/forecasting) is often used as a sort of handbook by forecasting practitioners working in a business environment.
| null | CC BY-SA 2.5 | null | 2010-07-26T12:01:58.983 | 2010-07-26T12:20:12.410 | 2010-07-26T12:20:12.410 | 159 | 159 | null |
626 | 2 | null | 125 | 16 | null | "[Bayesian Core: A Practical Approach to Computational Bayesian Statistics](http://amzn.to/2kxDAo2)" by Marin and Robert, Springer-Verlag (2007).
"Why?": the author explain the why of the bayesian choice and the how very well. It's a practical book, but written by one of the finest bayesian thinkers alive. It's not exhaustive. Other books have that objective. It picks up a few topics that are relevant, useful, and illuminating the foundations.
About "choice": if you really want to delve into bayesian foundation, Xi'an' "The Bayesian Choice" is clear, deep, essential.
| null | CC BY-SA 4.0 | null | 2010-07-26T12:38:40.610 | 2018-12-20T11:35:42.960 | 2018-12-20T11:35:42.960 | 7224 | 30 | null |
627 | 2 | null | 170 | 17 | null | I really like [The Little Handbook of Statistical Practice](https://web.archive.org/web/20100731030727/http://www.tufts.edu/%7Egdallal/LHSP.HTM) by Gerard E. Dallal
| null | CC BY-SA 4.0 | null | 2010-07-26T12:53:22.357 | 2023-06-02T11:54:01.243 | 2023-06-02T11:54:01.243 | 362671 | 236 | null |
628 | 2 | null | 622 | 67 | null | The likelihood function usually depends on many parameters. Depending on the application, we are usually interested in only a subset of these parameters. For example, in linear regression, interest typically lies in the slope coefficients and not on the error variance.
Denote the parameters we are interested in as $\beta$ and the parameters that are not of primary interest as $\theta$. The standard way to approach the estimation problem is to maximize the likelihood function so that we obtain estimates of $\beta$ and $\theta$. However, since the primary interest lies in $\beta$ partial, profile and marginal likelihood offer alternative ways to estimate $\beta$ without estimating $\theta$.
In order to see the difference denote the standard likelihood by $L(\beta, \theta|\mathrm{data})$.
Maximum Likelihood
Find $\beta$ and $\theta$ that maximizes $L(\beta, \theta|\mathrm{data})$.
Partial Likelihood
If we can write the likelihood function as:
$$L(\beta, \theta|\mathrm{data}) = L_1(\beta|\mathrm{data}) L_2(\theta|\mathrm{data})$$
Then we simply maximize $L_1(\beta|\mathrm{data})$.
Profile Likelihood
If we can express $\theta$ as a function of $\beta$ then we replace $\theta$ with the corresponding function.
Say, $\theta = g(\beta)$. Then, we maximize:
$$L(\beta, g(\beta)|\mathrm{data})$$
Marginal Likelihood
We integrate out $\theta$ from the likelihood equation by exploiting the fact that we can identify the probability distribution of $\theta$ conditional on $\beta$.
| null | CC BY-SA 4.0 | null | 2010-07-26T14:40:27.763 | 2018-11-10T16:48:52.343 | 2018-11-10T16:48:52.343 | 165856 | null | null |
631 | 1 | 28567 | null | 56 | 42285 | What is an estimator of standard deviation of standard deviation if normality of data can be assumed?
| Standard deviation of standard deviation | CC BY-SA 2.5 | null | 2010-07-26T16:10:45.817 | 2017-12-14T19:07:13.493 | 2017-11-25T22:29:39.437 | 128677 | null | [
"estimation",
"standard-deviation",
"normality-assumption"
] |
632 | 2 | null | 631 | 5 | null | Assume you observe $X_1,\dots,X_n$ iid from a normal with mean zero and variance $\sigma^2$. The (empirical) standard deviation is the square root of the estimator $\hat{\sigma}^2$ of $\sigma^2$ (unbiased or not that is not the question). As an estimator (obtained with $X_1,\dots,X_n$), $\hat{\sigma}$ has a variance that can be calculated theoretically. Maybe what you call the standard deviation of standard deviation is actually the square root of the variance of the standard deviation, i.e. $\sqrt{E[(\sigma-\hat{\sigma})^2]}$? It is not an estimator, it is a theoretical quantity (something like $\sigma/\sqrt{n}$ to be confirmed) that can be calculated explicitely !
| null | CC BY-SA 3.0 | null | 2010-07-26T16:23:25.073 | 2012-06-08T12:25:22.157 | 2012-06-08T12:25:22.157 | 4856 | 223 | null |
633 | 1 | 634 | null | 6 | 5522 | I have a data set of about 3,000 field observations.
The data collected is divided into 20 variables (real numbers), 30 boolean variables, and 10 or so look up variables and one "answer" variable
We have about 20,000 objects in the field, and i'm trying to produce an "answer" for the 20,000 objects based on the 3,000 observations.
What are some of the available methods that incorporate booleans and look up tables?
any suggestions on how i should proceed?
EDIT
the answer variable is a boolean as well
EDIT 2
a sample of the variable data:
- Age of specimen
- length, area, volume
- time since last inspection
- height
- design life
Lookup table
- material type
- coating type
- design standard
- design effectiveness
a sample of the boolean
- is it inspected?
- is it in bad shape
- does it need repairs soon
the answer variable which is my f(x) is:
- is it useable
| Incorporating boolean data into analysis | CC BY-SA 2.5 | null | 2010-07-26T17:29:19.477 | 2010-11-02T18:47:07.033 | 2010-10-17T19:07:16.110 | 930 | 59 | [
"modeling",
"categorical-data",
"model-selection",
"binary-data"
] |
634 | 2 | null | 633 | 8 | null | You are decribing "[categorical variables](http://www.oswego.edu/~srp/stats/variable_types.htm)" (represented in R a factors). These can be incorporated into almost any statistical model by being assigned levels. You would need to give more detail about your particular problem in order to be advised on a particular method.
Edit
If the response variable has two possible outcomes, you might consider [binomial](http://en.m.wikipedia.org/wiki/Binomial_regression) or [logistic](http://en.wikipedia.org/wiki/Logistic_regression) regression.
Note: If you're not familiar with the different kinds of variables in statistics, I suggest reading the first few chapters of Andrew Gelman's "[Data Analysis Using Regression and Multilevel/Hierarchical Models](http://www.stat.columbia.edu/~gelman/arm/)" which covers this in a very understandable manner.
| null | CC BY-SA 2.5 | null | 2010-07-26T17:46:45.127 | 2010-07-26T18:25:45.280 | 2010-07-26T18:25:45.280 | 5 | 5 | null |
635 | 2 | null | 480 | 17 | null | Implementations of RF differ slightly. I know that Salford Systems' [proprietary implementation](http://salford-systems.com/products/randomforests/overview.html) is supposed to be better than the [vanilla one](http://cran.r-project.org/web/packages/randomForest/) in R. A description of the algorithm is in [ESL by Friedman-Hastie-Tibshirani, 2nd ed, 3rd printing](http://www-stat.stanford.edu/~tibs/ElemStatLearn/download.html). An entire chapter (15th) is devoted to RF, and I find it actually clearer than the original paper. The tree construction algorithm is detailed on p.588; no need for me to reproduce it here, since the book is available online.
| null | CC BY-SA 3.0 | null | 2010-07-26T17:50:21.780 | 2011-08-21T20:53:14.543 | 2011-08-21T20:53:14.543 | 740 | 30 | null |
636 | 2 | null | 633 | 1 | null | Try Random Forest; from my experience it may perform well on such kind of data, and gives you a some additional interesting information, like variable importance and object similarity measure.
| null | CC BY-SA 2.5 | null | 2010-07-26T17:50:37.240 | 2010-07-26T18:21:26.337 | 2010-07-26T18:21:26.337 | null | null | null |
637 | 2 | null | 633 | 4 | null | It sounds like you are trying to predict your boolean response, yes?
This is called classification.
Logistic Regression is the obvious choice here, but there are other methods too. You can't do traditional regression, because the response is not a real number.
The lookup variables are called nominals, and can be dealt with in regression by using "dummy" variables.
For example, if your lookup variable is type=[steel, aluminum, plastic] (N=3), then your dummy variables would look like this:
IsSteel = [1,0]
IsAlum = [1,0]
There would only be two (N-1) dummy variables, as IsSteel=0 AND IsAlum=0 represents "IsPlastic"=1
But any good stats program should handle this.
If you need a book, I recommend Multivariate Data Analysis by Hair.
| null | CC BY-SA 2.5 | null | 2010-07-26T18:22:33.917 | 2010-07-26T18:22:33.917 | null | null | 74 | null |
638 | 1 | 644 | null | 10 | 2346 | Provided a sample size "N" that I plan on using to forecast data. What are some of the ways to subdivide the data so that I use some of it to establish a model, and the remainder data to validate the model?
I know there is no black and white answer to this, but it would be interesting to know some "rules of thumb" or usually used ratios. I know back at university, one of our professors used to say model on 60% and validate on 40%.
| Calculating ratio of sample data used for model fitting/training and validation | CC BY-SA 3.0 | null | 2010-07-26T18:24:35.737 | 2016-08-03T22:15:51.213 | 2016-08-03T22:15:51.213 | 22468 | 59 | [
"machine-learning",
"modeling",
"sample",
"validation"
] |
641 | 1 | 646 | null | 5 | 7900 | Sites like eMarketer offer general survey results about internet usage.
Who else has a big set of survey results, or regularly releases them?
- Preferably marketing research focused.
Thanks!
| Where is a good place to find survey results? | CC BY-SA 2.5 | null | 2010-07-26T19:20:53.477 | 2015-12-04T16:03:27.630 | 2010-09-16T12:42:31.387 | null | 74 | [
"dataset",
"survey"
] |
642 | 2 | null | 641 | 2 | null | government websites usually .... I use the [RITA](http://www.rita.dot.gov/) a lot
| null | CC BY-SA 2.5 | null | 2010-07-26T19:23:19.133 | 2010-07-26T19:23:19.133 | null | null | 59 | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.