licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | code | 17027 | push!(LOAD_PATH, "..")
@static if ENV["JULIA_JUSTRELAX_BACKEND"] === "AMDGPU"
using AMDGPU
AMDGPU.allowscalar(true)
elseif ENV["JULIA_JUSTRELAX_BACKEND"] === "CUDA"
using CUDA
CUDA.allowscalar(true)
end
using Test, Suppressor
using GeoParams
using JustRelax, JustRelax.JustRelax2D
using ParallelStencil, ParallelStencil.FiniteDifferences2D
const backend_JR = @static if ENV["JULIA_JUSTRELAX_BACKEND"] === "AMDGPU"
@init_parallel_stencil(AMDGPU, Float64, 2)
AMDGPUBackend
elseif ENV["JULIA_JUSTRELAX_BACKEND"] === "CUDA"
@init_parallel_stencil(CUDA, Float64, 2)
CUDABackend
else
@init_parallel_stencil(Threads, Float64, 2)
CPUBackend
end
using JustPIC, JustPIC._2D
# Threads is the default backend,
# to run on a CUDA GPU load CUDA.jl (i.e. "using CUDA") at the beginning of the script,
# and to run on an AMD GPU load AMDGPU.jl (i.e. "using AMDGPU") at the beginning of the script.
const backend = @static if ENV["JULIA_JUSTRELAX_BACKEND"] === "AMDGPU"
JustPIC.AMDGPUBackend
elseif ENV["JULIA_JUSTRELAX_BACKEND"] === "CUDA"
CUDABackend
else
JustPIC.CPUBackend
end
import JustRelax.@cell
# Load script dependencies
using Printf, Statistics, LinearAlgebra, CellArrays, StaticArrays
# -----------------------------------------------------------------------------------------
## SET OF HELPER FUNCTIONS PARTICULAR FOR THIS SCRIPT --------------------------------
function copyinn_x!(A, B)
@parallel function f_x(A, B)
@all(A) = @inn_x(B)
return nothing
end
@parallel f_x(A, B)
end
import ParallelStencil.INDICES
const idx_j = INDICES[2]
macro all_j(A)
return esc(:($A[$idx_j]))
end
@parallel function init_P!(P, ρg, z)
@all(P) = abs(@all(ρg) * @all_j(z)) * <(@all_j(z), 0.0)
return nothing
end
function init_phases!(phases, particles, xc_anomaly, yc_anomaly, r_anomaly, sticky_air,top, bottom)
ni = size(phases)
@parallel_indices (i, j) function init_phases!(
phases, px, py, index, xc_anomaly, yc_anomaly, r_anomaly, sticky_air, top, bottom
)
@inbounds for ip in JustRelax.JustRelax.cellaxes(phases)
# quick escape
JustRelax.@cell(index[ip, i, j]) == 0 && continue
x = JustRelax.@cell px[ip, i, j]
y = -(JustRelax.@cell py[ip, i, j]) - sticky_air
if top ≤ y ≤ bottom
@cell phases[ip, i, j] = 1.0 # crust
end
# thermal anomaly - circular
if ((x - xc_anomaly)^2 + (y + yc_anomaly)^2 ≤ r_anomaly^2)
JustRelax.@cell phases[ip, i, j] = 2.0
end
if y < top
@cell phases[ip, i, j] = 3.0
end
end
return nothing
end
@parallel (@idx ni) init_phases!(
phases,
particles.coords...,
particles.index,
xc_anomaly,
yc_anomaly,
r_anomaly,
sticky_air,
top,
bottom,
)
end
# Initial thermal profile
@parallel_indices (i, j) function init_T!(T, y, sticky_air, top, bottom, dTdz, offset)
depth = -y[j] - sticky_air
if depth < top
T[i + 1, j] = offset
elseif top ≤ (depth) < bottom
dTdZ = dTdz
offset = offset
T[i + 1, j] = (depth) * dTdZ + offset
end
return nothing
end
function circular_perturbation!(T, δT, xc_anomaly, yc_anomaly, r_anomaly, xvi, sticky_air)
@parallel_indices (i, j) function _circular_perturbation!(
T, δT, xc_anomaly, yc_anomaly, r_anomaly, x, y, sticky_air
)
depth = -y[j] - sticky_air
@inbounds if ((x[i] - xc_anomaly)^2 + (depth[j] + yc_anomaly)^2 ≤ r_anomaly^2)
# T[i + 1, j] *= δT / 100 + 1
T[i + 1, j] = δT
end
return nothing
end
nx, ny = size(T)
@parallel (1:(nx - 2), 1:ny) _circular_perturbation!(
T, δT, xc_anomaly, yc_anomaly, r_anomaly, xvi..., sticky_air
)
end
function init_rheology(CharDim; is_compressible = false, steady_state=true)
# plasticity setup
do_DP = true # do_DP=false: Von Mises, do_DP=true: Drucker-Prager (friction angle)
η_reg = 1.0e16Pa * s # regularisation "viscosity" for Drucker-Prager
Coh = 10.0MPa # yield stress. If do_DP=true, τ_y stand for the cohesion: c*cos(ϕ)
ϕ = 30.0 * do_DP # friction angle
G0 = 6.0e11Pa # elastic shear modulus
G_magma = 6.0e11Pa # elastic shear modulus perturbation
soft_C = NonLinearSoftening(; ξ₀=ustrip(Coh), Δ=ustrip(Coh) / 2) # softening law
pl = DruckerPrager_regularised(; C=Coh, ϕ=ϕ, η_vp=η_reg, Ψ=0.0, softening_C = soft_C) # plasticity
if is_compressible == true
el = SetConstantElasticity(; G=G0, ν=0.25) # elastic spring
el_magma = SetConstantElasticity(; G=G_magma, ν=0.25)# elastic spring
β_rock = 6.0e-11
β_magma = 6.0e-11
else
el = SetConstantElasticity(; G=G0, ν=0.5) # elastic spring
el_magma = SetConstantElasticity(; G=G_magma, ν=0.5) # elastic spring
β_rock = inv(get_Kb(el))
β_magma = inv(get_Kb(el_magma))
end
if steady_state == true
creep_rock = LinearViscous(; η=1e23 * Pa * s)
creep_magma = LinearViscous(; η=1e18 * Pa * s)
creep_air = LinearViscous(; η=1e18 * Pa * s)
else
creep_rock = DislocationCreep(; A=1.67e-24, n=3.5, E=1.87e5, V=6e-6, r=0.0, R=8.3145)
creep_magma = DislocationCreep(; A=1.67e-24, n=3.5, E=1.87e5, V=6e-6, r=0.0, R=8.3145)
creep_air = LinearViscous(; η=1e18 * Pa * s)
β_rock = 6.0e-11
β_magma = 6.0e-11
end
g = 9.81m/s^2
rheology = (
#Name="UpperCrust"
SetMaterialParams(;
Phase = 1,
Density = PT_Density(; ρ0=2650kg / m^3, α=3e-5 / K, T0=0.0C, β=β_rock / Pa),
HeatCapacity = ConstantHeatCapacity(; Cp=1050J / kg / K),
Conductivity = ConstantConductivity(; k=3.0Watt / K / m),
LatentHeat = ConstantLatentHeat(; Q_L=350e3J / kg),
ShearHeat = ConstantShearheating(1.0NoUnits),
CompositeRheology = CompositeRheology((creep_rock, el, pl)),
Melting = MeltingParam_Caricchi(),
Gravity = ConstantGravity(; g=g),
Elasticity = el,
CharDim = CharDim,
),
#Name="Magma"
SetMaterialParams(;
Phase = 1,
Density = PT_Density(; ρ0=2650kg / m^3, T0=0.0C, β=β_magma / Pa),
HeatCapacity = ConstantHeatCapacity(; Cp=1050J / kg / K),
Conductivity = ConstantConductivity(; k=1.5Watt / K / m),
LatentHeat = ConstantLatentHeat(; Q_L=350e3J / kg),
ShearHeat = ConstantShearheating(0.0NoUnits),
CompositeRheology = CompositeRheology((creep_magma, el_magma)),
Melting = MeltingParam_Caricchi(),
Gravity = ConstantGravity(; g=g),
Elasticity = el_magma,
CharDim = CharDim,
),
#Name="Sticky Air"
SetMaterialParams(;
Phase = 1,
Density = ConstantDensity(ρ=1kg/m^3,),
HeatCapacity = ConstantHeatCapacity(; Cp=1000J / kg / K),
Conductivity = ConstantConductivity(; k=15Watt / K / m),
LatentHeat = ConstantLatentHeat(; Q_L=0.0J / kg),
ShearHeat = ConstantShearheating(0.0NoUnits),
CompositeRheology = CompositeRheology((creep_air,)),
Gravity = ConstantGravity(; g=g),
CharDim = CharDim,
),
)
end
function main2D(; nx=32, ny=32)
init_mpi = JustRelax.MPI.Initialized() ? false : true
igg = IGG(init_global_grid(nx, ny, 1; init_MPI = init_mpi)...)
# Characteristic lengths
CharDim = GEO_units(;length=12.5km, viscosity=1e21, temperature = 1e3C)
#-------JustRelax parameters-------------------------------------------------------------
# Domain setup for JustRelax
sticky_air = nondimensionalize(1.5km, CharDim) # thickness of the sticky air layer
ly = nondimensionalize(12.5km,CharDim) + sticky_air # domain length in y-direction
lx = nondimensionalize(15.5km, CharDim) # domain length in x-direction
li = lx, ly # domain length in x- and y-direction
ni = nx, ny # number of grid points in x- and y-direction
di = @. li / ni # grid step in x- and y-direction
origin = nondimensionalize(0.0km,CharDim), -ly # origin coordinates of the domain
grid = Geometry(ni, li; origin=origin)
εbg = nondimensionalize(0.0 / s,CharDim) # background strain rate
(; xci, xvi) = grid # nodes at the center and vertices of the cells
#---------------------------------------------------------------------------------------
# Physical Parameters
rheology = init_rheology(CharDim; is_compressible=true, steady_state=false)
cutoff_visc = nondimensionalize((1e16Pa*s, 1e24Pa*s),CharDim)
κ = (4 / (rheology[1].HeatCapacity[1].Cp * rheology[1].Density[1].ρ0))
dt = dt_diff = (0.5 * min(di...)^2 / κ / 2.01) # diffusive CFL timestep limiter
# Initialize particles -------------------------------
nxcell, max_xcell, min_xcell = 20, 40, 15
particles = init_particles(backend, nxcell, max_xcell, min_xcell, xvi...)
subgrid_arrays = SubgridDiffusionCellArrays(particles)
# velocity grids
grid_vx, grid_vy = velocity_grids(xci, xvi, di)
# temperature
pT, pPhases = init_cell_arrays(particles, Val(2))
particle_args = (pT, pPhases)
# Circular temperature anomaly -----------------------
x_anomaly = lx * 0.5
y_anomaly = nondimensionalize(-5km,CharDim) # origin of the small thermal anomaly
r_anomaly = nondimensionalize(1.5km, CharDim) # radius of perturbation
anomaly = nondimensionalize((750 + 273)K, CharDim) # thermal perturbation (in K)
init_phases!(pPhases, particles, x_anomaly, y_anomaly, r_anomaly, sticky_air, nondimensionalize(0.0km,CharDim), nondimensionalize(20km,CharDim))
phase_ratios = PhaseRatio(backend_JR, ni, length(rheology))
phase_ratios_center!(phase_ratios, particles, grid, pPhases)
# Initialisation of thermal profile
thermal = ThermalArrays(backend_JR, ni) # initialise thermal arrays and boundary conditions
thermal_bc = TemperatureBoundaryConditions(;
no_flux = (left=true, right=true, top=false, bot=false),
)
@parallel (@idx ni .+ 1) init_T!(
thermal.T, xvi[2],
sticky_air,
nondimensionalize(0e0km,CharDim),
nondimensionalize(15km,CharDim),
nondimensionalize((723 - 273)K,CharDim) / nondimensionalize(15km,CharDim),
nondimensionalize(273K,CharDim)
)
circular_perturbation!(
thermal.T, anomaly, x_anomaly, y_anomaly, r_anomaly, xvi, sticky_air
)
thermal_bcs!(thermal, thermal_bc)
temperature2center!(thermal)
# STOKES ---------------------------------------------
# Allocate arrays needed for every Stokes problem
stokes = StokesArrays(backend_JR, ni) # initialise stokes arrays with the defined regime
pt_stokes = PTStokesCoeffs(li, di; ϵ = 1e-4, CFL = 1 / √2.1)
# ----------------------------------------------------
args = (; T=thermal.Tc, P=stokes.P, dt=dt)
pt_thermal = PTThermalCoeffs(
backend_JR, rheology, phase_ratios, args, dt, ni, di, li; ϵ=1e-5, CFL=0.8 / √2.1
)
# Pure shear far-field boundary conditions
stokes.V.Vx .= PTArray(backend_JR)([
εbg * (x - lx * 0.5) / (lx / 2) / 2 for x in xvi[1], _ in 1:(ny + 2)
])
stokes.V.Vy .= PTArray(backend_JR)([
(abs(y) - sticky_air) * εbg * (abs(y) > sticky_air) for _ in 1:(nx + 2), y in xvi[2]
])
flow_bcs = VelocityBoundaryConditions(;
free_slip = (left=true, right=true, top=true, bot=true),
free_surface = true,
)
flow_bcs!(stokes, flow_bcs)
compute_viscosity!(stokes, phase_ratios, args, rheology, cutoff_visc)
ϕ = @zeros(ni...)
compute_melt_fraction!(
ϕ, phase_ratios.center, rheology, (T=thermal.Tc, P=stokes.P)
)
# Buoyancy force
ρg = @zeros(ni...), @zeros(ni...) # ρg[1] is the buoyancy force in the x direction, ρg[2] is the buoyancy force in the y direction
for _ in 1:5
compute_ρg!(ρg[2], phase_ratios, rheology, (T=thermal.Tc, P=stokes.P))
@parallel init_P!(stokes.P, ρg[2], xci[2])
end
# Arguments for functions
args = (; T=thermal.Tc, P=stokes.P, dt=dt, ΔTc=thermal.ΔTc)
@copy thermal.Told thermal.T
# Time loop
t, it = 0.0, 0
T_buffer = @zeros(ni.+1)
Told_buffer = similar(T_buffer)
dt₀ = similar(stokes.P)
for (dst, src) in zip((T_buffer, Told_buffer), (thermal.T, thermal.Told))
copyinn_x!(dst, src)
end
grid2particle!(pT, xvi, T_buffer, particles)
@copy stokes.P0 stokes.P
thermal.Told .= thermal.T
P_init = deepcopy(stokes.P)
Tsurf = thermal.T[1, end]
Tbot = thermal.T[1, 1]
local ϕ, stokes, thermal
while it < 1
# Update buoyancy and viscosity -
args = (; T=thermal.Tc, P=stokes.P, dt=Inf, ΔTc=thermal.ΔTc)
compute_ρg!(ρg[end], phase_ratios, rheology, (T=thermal.Tc, P=stokes.P))
compute_viscosity!(stokes, phase_ratios, args, rheology, cutoff_visc)
# Stokes solver -----------------
solve!(
stokes,
pt_stokes,
di,
flow_bcs,
ρg,
phase_ratios,
rheology,
args,
dt,
igg;
kwargs = (;
iterMax = 100e3,
free_surface = true,
nout = 5e3,
viscosity_cutoff = cutoff_visc,
)
)
tensor_invariant!(stokes.ε)
dt = compute_dt(stokes, di, dt_diff, igg)
# --------------------------------
compute_shear_heating!(
thermal,
stokes,
phase_ratios,
rheology, # needs to be a tuple
dt,
)
# Thermal solver ---------------
heatdiffusion_PT!(
thermal,
pt_thermal,
thermal_bc,
rheology,
args,
dt,
di;
kwargs =(;
igg = igg,
phase = phase_ratios,
iterMax = 150e3,
nout = 1e3,
verbose = true,
)
)
for (dst, src) in zip((T_buffer, Told_buffer), (thermal.T, thermal.Told))
copyinn_x!(dst, src)
end
subgrid_characteristic_time!(
subgrid_arrays, particles, dt₀, phase_ratios, rheology, thermal, stokes, xci, di
)
centroid2particle!(subgrid_arrays.dt₀, xci, dt₀, particles)
subgrid_diffusion!(
pT, T_buffer, thermal.ΔT[2:end-1, :], subgrid_arrays, particles, xvi, di, dt
)
# ------------------------------
compute_melt_fraction!(
ϕ, phase_ratios.center, rheology, (T=thermal.Tc, P=stokes.P)
)
# Advection --------------------
# advect particles in space
advection!(particles, RungeKutta2(), @velocity(stokes), (grid_vx, grid_vy), dt)
# advect particles in memory
move_particles!(particles, xvi, particle_args)
# check if we need to inject particles
inject_particles_phase!(particles, pPhases, (pT, ), (T_buffer,), xvi)
# update phase ratios
phase_ratios_center!(phase_ratios, particles, grid, pPhases)
particle2grid!(T_buffer, pT, xvi, particles)
@views T_buffer[:, end] .= Tsurf
@views T_buffer[:, 1] .= Tbot
@views thermal.T[2:end - 1, :] .= T_buffer
thermal_bcs!(thermal, thermal_bc)
temperature2center!(thermal)
thermal.ΔT .= thermal.T .- thermal.Told
vertex2center!(thermal.ΔTc, thermal.ΔT)
@show it += 1
t += dt
end
finalize_global_grid()
return ϕ, stokes, thermal
end
@testset "thermal stresses" begin
@suppress begin
ϕ, stokes, thermal = main2D(; nx=32, ny=32)
nx_T, ny_T = size(thermal.T)
@test Array(thermal.T)[nx_T >>> 1 + 1, ny_T >>> 1 + 1] ≈ 0.5369 rtol = 1e-2
@test Array(ϕ)[nx_T >>> 1 + 1, ny_T >>> 1 + 1] ≈ 9.351e-9 rtol = 1e-1
end
end
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | code | 2551 | @static if ENV["JULIA_JUSTRELAX_BACKEND"] === "AMDGPU"
using AMDGPU
elseif ENV["JULIA_JUSTRELAX_BACKEND"] === "CUDA"
using CUDA
end
using JustRelax, Test
import JustRelax.JustRelax2D as JR2
import JustRelax.JustRelax3D as JR3
import JustRelax: AMDGPUBackendTrait, CUDABackendTrait
const bk = JustRelax.backend
const env_backend = ENV["JULIA_JUSTRELAX_BACKEND"]
const DeviceTrait = @static if env_backend === "AMDGPU"
AMDGPUBackendTrait
elseif env_backend === "CUDA"
CUDABackendTrait
else
CPUBackendTrait
end
const backend = @static if env_backend === "AMDGPU"
AMDGPUBackend
elseif env_backend === "CUDA"
CUDABackend
else
CPUBackend
end
const myrand = @static if env_backend === "AMDGPU"
AMDGPU.rand
elseif env_backend === "CUDA"
CUDA.rand
else
rand
end
A, M, V = @static if env_backend === "AMDGPU"
ROCArray, ROCMatrix, ROCVector
elseif env_backend === "CUDA"
CuArray, CuMatrix, CuVector
else
Array, Matrix, Vector
end
@testset "Traits" begin
# test generic arrays
@test bk(A) === DeviceTrait()
@test bk(M) === DeviceTrait()
@test bk(V) === DeviceTrait()
@test bk(myrand(2)) === DeviceTrait()
@test bk(myrand(2,2)) === DeviceTrait()
@test bk(myrand(2,2,2)) === DeviceTrait()
# test PTArray
if env_backend !== "AMDGPU" && env_backend !== "CUDA"
@test PTArray() === A
else
@test true === true
end
@test PTArray(backend) === A
@test_throws ArgumentError PTArray(bk(rand()))
@test_throws ArgumentError PTArray(bk("potato"))
@test_throws ArgumentError PTArray(backend, bk(rand()))
# test error handling
@test_throws ArgumentError bk(rand())
@test_throws ArgumentError bk("potato")
# test JR structs
## 2D
ni = 2, 2
stokes2 = JR2.StokesArrays(backend, ni)
thermal2 = JR2.ThermalArrays(backend, ni)
@test bk(stokes2.V) === DeviceTrait()
@test bk(stokes2.τ) === DeviceTrait()
@test bk(stokes2.R) === DeviceTrait()
@test bk(stokes2.P) === DeviceTrait()
@test bk(stokes2) === DeviceTrait()
@test bk(thermal2) === DeviceTrait()
## 3D
ni = 2, 2, 2
stokes3 = JR3.StokesArrays(backend, ni)
thermal3 = JR3.ThermalArrays(backend, ni)
@test bk(stokes3.V) === DeviceTrait()
@test bk(stokes3.τ) === DeviceTrait()
@test bk(stokes3.R) === DeviceTrait()
@test bk(stokes3.P) === DeviceTrait()
@test bk(stokes3) === DeviceTrait()
@test bk(thermal3) === DeviceTrait()
end
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | code | 5867 | @static if ENV["JULIA_JUSTRELAX_BACKEND"] === "AMDGPU"
using AMDGPU
elseif ENV["JULIA_JUSTRELAX_BACKEND"] === "CUDA"
using CUDA
end
using JustRelax, Test
import JustRelax.JustRelax2D as JR2
import JustRelax.JustRelax3D as JR3
const env_backend = ENV["JULIA_JUSTRELAX_BACKEND"]
const backend = @static if env_backend === "AMDGPU"
AMDGPUBackend
elseif env_backend === "CUDA"
CUDABackend
else
CPUBackend
end
const BackendArray = PTArray(backend)
@testset "2D allocators" begin
ni = nx, ny = (2, 2)
stokes = JR2.StokesArrays(backend, ni)
@test size(stokes.P) == ni
@test size(stokes.P0) == ni
@test size(stokes.∇V) == ni
@test size(stokes.EII_pl) == ni
@test typeof(stokes.P) <: BackendArray
@test typeof(stokes.P0) <: BackendArray
@test typeof(stokes.∇V) <: BackendArray
@test stokes.V isa JustRelax.Velocity
@test stokes.U isa JustRelax.Displacement
@test stokes.ω isa JustRelax.Vorticity
@test stokes.τ isa JustRelax.SymmetricTensor
@test stokes.τ_o isa JustRelax.SymmetricTensor
@test stokes.ε isa JustRelax.SymmetricTensor
@test stokes.ε_pl isa JustRelax.SymmetricTensor
@test typeof(stokes.EII_pl) <: BackendArray
@test stokes.viscosity isa JustRelax.Viscosity
@test stokes.R isa JustRelax.Residual
R = stokes.R
@test R isa JustRelax.Residual
@test isnothing(R.Rz)
@test size(R.Rx) == (nx-1, ny)
@test size(R.Ry) == (nx, ny-1)
@test size(R.RP) == ni
@test typeof(R.Rx) <: BackendArray
@test typeof(R.Ry) <: BackendArray
@test typeof(R.RP) <: BackendArray
@test_throws MethodError JR2.Residual(10.0, 10.0)
visc = stokes.viscosity
@test size(visc.η) == ni
@test size(visc.η_vep) == ni
@test size(visc.ητ) == ni
@test typeof(visc.η) <: BackendArray
@test typeof(visc.η_vep) <: BackendArray
@test typeof(visc.ητ) <: BackendArray
@test_throws MethodError JR2.Viscosity(10.0, 10.0)
tensor = stokes.τ
@test size(tensor.xx) == (nx, ny)
@test size(tensor.yy) == (nx, ny)
@test size(tensor.xy) == (nx + 1, ny + 1)
@test size(tensor.xy_c) == (nx, ny)
@test size(tensor.II) == (nx, ny)
@test typeof(tensor.xx) <: BackendArray
@test typeof(tensor.yy) <: BackendArray
@test typeof(tensor.xy) <: BackendArray
@test typeof(tensor.xy_c) <: BackendArray
@test typeof(tensor.II) <: BackendArray
@test_throws MethodError JR2.StokesArrays(backend, 10.0, 10.0)
end
@testset "2D Displacement" begin
ni = nx, ny = (2, 2)
stokes = JR2.StokesArrays(backend, ni)
stokes.V.Vx .= 1.0
stokes.V.Vy .= 1.0
JR2.velocity2displacement!(stokes, 10)
@test all(stokes.U.Ux.== 10)
JR2.displacement2velocity!(stokes, 5)
@test all(stokes.V.Vx.==2.0)
end
@testset "3D allocators" begin
ni = nx, ny, nz = (2, 2, 2)
stokes = JR3.StokesArrays(backend, ni)
@test size(stokes.P) == ni
@test size(stokes.P0) == ni
@test size(stokes.∇V) == ni
@test size(stokes.EII_pl) == ni
@test typeof(stokes.P) <: BackendArray
@test typeof(stokes.P0) <: BackendArray
@test typeof(stokes.∇V) <: BackendArray
@test stokes.V isa JustRelax.Velocity
@test stokes.U isa JustRelax.Displacement
@test stokes.ω isa JustRelax.Vorticity
@test stokes.τ isa JustRelax.SymmetricTensor
@test stokes.τ_o isa JustRelax.SymmetricTensor
@test stokes.ε isa JustRelax.SymmetricTensor
@test stokes.ε_pl isa JustRelax.SymmetricTensor
@test typeof(stokes.EII_pl) <: BackendArray
@test stokes.viscosity isa JustRelax.Viscosity
@test stokes.R isa JustRelax.Residual
R = stokes.R
@test R isa JustRelax.Residual
@test size(R.Rx) == (nx-1, ny, nz)
@test size(R.Ry) == (nx, ny-1, nz)
@test size(R.Rz) == (nx, ny, nz-1)
@test size(R.RP) == ni
@test typeof(R.Rx) <: BackendArray
@test typeof(R.Ry) <: BackendArray
@test typeof(R.Rz) <: BackendArray
@test typeof(R.RP) <: BackendArray
@test_throws MethodError JR3.Residual(1.0, 1.0, 1.0)
visc = stokes.viscosity
@test size(visc.η) == ni
@test size(visc.η_vep) == ni
@test size(visc.ητ) == ni
@test typeof(visc.η) <: BackendArray
@test typeof(visc.η_vep) <: BackendArray
@test typeof(visc.ητ) <: BackendArray
@test_throws MethodError JR3.Viscosity(1.0, 1.0, 1.0)
tensor = stokes.τ
@test size(tensor.xx) == ni
@test size(tensor.yy) == ni
@test size(tensor.xy) == (nx + 1, ny + 1, nz )
@test size(tensor.yz) == (nx , ny + 1, nz + 1)
@test size(tensor.xz) == (nx + 1, ny , nz + 1)
@test size(tensor.xy_c) == ni
@test size(tensor.yz_c) == ni
@test size(tensor.xz_c) == ni
@test size(tensor.II) == ni
@test typeof(tensor.xx) <: BackendArray
@test typeof(tensor.yy) <: BackendArray
@test typeof(tensor.xy) <: BackendArray
@test typeof(tensor.yz) <: BackendArray
@test typeof(tensor.xz) <: BackendArray
@test typeof(tensor.xy_c) <: BackendArray
@test typeof(tensor.yz_c) <: BackendArray
@test typeof(tensor.xz_c) <: BackendArray
@test typeof(tensor.II) <: BackendArray
@test_throws MethodError JR3.StokesArrays(backend, 10.0, 10.0)
end
@testset "3D Displacement" begin
ni = nx, ny, nz = (2, 2, 2)
stokes = JR3.StokesArrays(backend, ni)
stokes.V.Vx .= 1.0
stokes.V.Vy .= 1.0
stokes.V.Vz .= 1.0
JR3.velocity2displacement!(stokes, 10)
@test all(stokes.U.Ux.==10.0)
JR3.displacement2velocity!(stokes, 5)
@test all(stokes.V.Vx.==2.0)
end
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 979 | # Authors
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl)'s development is coordinated by a group of *principal developers*,
who are also its main contributors and who can be contacted in case of
questions about [JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl). In addition, there are *contributors* who have
provided substantial additions or modifications. Together, these two groups form
"The JustRelax.jl Authors".
## Principal Developers
* [Albert de Montserrat](https://github.com/albert-de-montserrat),
Institute for Geophysics, ETH Zurich, Switzerland
* [Pascal Aellig](https://github.com/aelligp),
Institute for Geosciences, Johannes Gutenberg University Mainz, Germany
## Contributors
The following people contributed major additions or modifications to [JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) and
are listed in alphabetical order:
* Sidney Beeler
* Lukas Fuchs
* Boris Kaus
* Patrick Sanan
* Hendrik Ranocha
* Ludovic Räss
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 5362 | # Contributor Covenant Code of Conduct
## Our Pledge
We as members, contributors, and leaders pledge to make participation in our
community a harassment-free experience for everyone, regardless of age, body
size, visible or invisible disability, ethnicity, sex characteristics, gender
identity and expression, level of experience, education, socio-economic status,
nationality, personal appearance, race, religion, or sexual identity
and orientation.
We pledge to act and interact in ways that contribute to an open, welcoming,
diverse, inclusive, and healthy community.
## Our Standards
Examples of behavior that contributes to a positive environment for our
community include:
* Demonstrating empathy and kindness toward other people
* Being respectful of differing opinions, viewpoints, and experiences
* Giving and gracefully accepting constructive feedback
* Accepting responsibility and apologizing to those affected by our mistakes,
and learning from the experience
* Focusing on what is best not just for us as individuals, but for the
overall community
Examples of unacceptable behavior include:
* The use of sexualized language or imagery, and sexual attention or
advances of any kind
* Trolling, insulting or derogatory comments, and personal or political attacks
* Public or private harassment
* Publishing others' private information, such as a physical or email
address, without their explicit permission
* Other conduct which could reasonably be considered inappropriate in a
professional setting
## Enforcement Responsibilities
Community leaders are responsible for clarifying and enforcing our standards of
acceptable behavior and will take appropriate and fair corrective action in
response to any behavior that they deem inappropriate, threatening, offensive,
or harmful.
Community leaders have the right and responsibility to remove, edit, or reject
comments, commits, code, wiki edits, issues, and other contributions that are
not aligned to this Code of Conduct, and will communicate reasons for moderation
decisions when appropriate.
## Scope
This Code of Conduct applies within all community spaces, and also applies when
an individual is officially representing the community in public spaces.
Examples of representing our community include using an official e-mail address,
posting via an official social media account, or acting as an appointed
representative at an online or offline event.
## Enforcement
Instances of abusive, harassing, or otherwise unacceptable behavior may be
reported to
[Albert de Montserrat](https://github.com/albert-de-montserrat),
[Pascal Aellig](https://github.com/aelligp),
or any other of the principal developers responsible for enforcement listed in
[AUTHORS.md](AUTHORS.md).
All complaints will be reviewed and investigated promptly and fairly.
All community leaders are obligated to respect the privacy and security of the
reporter of any incident.
## Enforcement Guidelines
Community leaders will follow these Community Impact Guidelines in determining
the consequences for any action they deem in violation of this Code of Conduct:
### 1. Correction
**Community Impact**: Use of inappropriate language or other behavior deemed
unprofessional or unwelcome in the community.
**Consequence**: A private, written warning from community leaders, providing
clarity around the nature of the violation and an explanation of why the
behavior was inappropriate. A public apology may be requested.
### 2. Warning
**Community Impact**: A violation through a single incident or series
of actions.
**Consequence**: A warning with consequences for continued behavior. No
interaction with the people involved, including unsolicited interaction with
those enforcing the Code of Conduct, for a specified period of time. This
includes avoiding interactions in community spaces as well as external channels
like social media. Violating these terms may lead to a temporary or
permanent ban.
### 3. Temporary Ban
**Community Impact**: A serious violation of community standards, including
sustained inappropriate behavior.
**Consequence**: A temporary ban from any sort of interaction or public
communication with the community for a specified period of time. No public or
private interaction with the people involved, including unsolicited interaction
with those enforcing the Code of Conduct, is allowed during this period.
Violating these terms may lead to a permanent ban.
### 4. Permanent Ban
**Community Impact**: Demonstrating a pattern of violation of community
standards, including sustained inappropriate behavior, harassment of an
individual, or aggression toward or disparagement of classes of individuals.
**Consequence**: A permanent ban from any sort of public interaction within
the community.
## Attribution
This Code of Conduct is adapted from the [Contributor Covenant][homepage],
version 2.0, available at
https://www.contributor-covenant.org/version/2/0/code_of_conduct.html.
Community Impact Guidelines were inspired by [Mozilla's code of conduct
enforcement ladder](https://github.com/mozilla/diversity).
[homepage]: https://www.contributor-covenant.org
For answers to common questions about this code of conduct, see the FAQ at
https://www.contributor-covenant.org/faq. Translations are available at
https://www.contributor-covenant.org/translations.
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 2480 | # Contributing
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) is an open-source project and we are very happy to accept contributions
from the community. Please feel free to [open issues](https://github.com/PTsolvers/JustRelax.jl/issues/new) or submit patches (preferably
as [pull requests](https://github.com/PTsolvers/JustRelax.jl/pulls)) any time. For planned larger contributions, it is often
beneficial to get in contact with one of the principal developers first (see
[AUTHORS.md](AUTHORS.md)).
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) and its contributions are licensed under the MIT license. As a contributor, you certify that all your
contributions are in conformance with the *Developer Certificate of Origin
(Version 1.1)*, which is reproduced below.
## Developer Certificate of Origin (Version 1.1)
The following text was taken from
[https://developercertificate.org](https://developercertificate.org):
Developer Certificate of Origin
Version 1.1
Copyright (C) 2004, 2006 The Linux Foundation and its contributors.
1 Letterman Drive
Suite D4700
San Francisco, CA, 94129
Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.
Developer's Certificate of Origin 1.1
By making a contribution to this project, I certify that:
(a) The contribution was created in whole or in part by me and I
have the right to submit it under the open source license
indicated in the file; or
(b) The contribution is based upon previous work that, to the best
of my knowledge, is covered under an appropriate open source
license and I have the right under that license to submit that
work with modifications, whether created in whole or in part
by me, under the same open source license (unless I am
permitted to submit under a different license), as indicated
in the file; or
(c) The contribution was provided directly to me by some other
person who certified (a), (b) or (c) and I have not modified
it.
(d) I understand and agree that this project and the contribution
are public and that a record of the contribution (including all
personal information I submit with it, including my sign-off) is
maintained indefinitely and may be redistributed consistent with
this project or the open source license(s) involved.
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 4225 | <h1> <img src="./docs/src/assets/logo.png" alt="JustRelax.jl" width="50"> JustRelax.jl </h1>
[](https://ptsolvers.github.io/JustRelax.jl/dev/)
[](https://github.com/PTsolvers/JustRelax.jl/discussions/)
[](https://doi.org/10.5281/zenodo.10212422)

[](https://buildkite.com/julialang/justrelax-dot-jl)
[](https://codecov.io/gh/PTsolvers/JustRelax.jl)
[](https://opensource.org/licenses/MIT)
<p align="center"><img src="./docs/src/assets/logo.png" alt="JustRelax.jl" width="200"></p>
:warning: This Package is still under active development
- The API is still subject to change.
- The benchmarks and miniapps are working and provide the user with an insight into the capabilities of the package.
Need to solve a very large multi-physics problem on many GPUs in parallel? Just Relax!
`JustRelax.jl` is a collection of accelerated iterative pseudo-transient solvers using MPI and multiple CPU or GPU backends. It's part of the [PTSolvers organisation](https://ptsolvers.github.io) and
developed within the [GPU4GEO project](https://www.pasc-ch.org/projects/2021-2024/gpu4geo/). Current publications, outreach and news can be found on the [GPU4GEO website](https://ptsolvers.github.io/GPU4GEO/).
The package relies on other packages as building blocks and parallelisation tools:
* [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl)
* [ImplicitGlobalGrid.jl](https://github.com/omlins/ImplicitGlobalGrid.jl)
* [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl)
* [JustPIC.jl](https://github.com/JuliaGeodynamics/JustPIC.jl)
The package serves several purposes:
* It provides a collection of solvers to be used in quickly developing new applications
* It provides some standardization so that application codes can
- more easily handle local material properties through the use of [GeoParams.jl]((https://github.com/JuliaGeodynamics/GeoParams.jl))
- more easily switch between a pseudo-transient solver and another solvers (e.g. an explicit thermal solvers)
* It provides a natural repository for contributions of new solvers for use by the larger community
We provide several miniapps, each designed to solve a well-specified benchmark problem, in order to provide
- examples of usage in high-performance computing
- basis on which to build more full-featured application codes
- cases for reference and performance tests
## Installation
`JustRelax.jl` is a registered package and can be added as follows:
```julia
using Pkg; Pkg.add("JustRelax")
```
However, as the API is changing and not every feature leads to a new release, one can also do `add JustRelax#main` which will clone the main branch of the repository.
After installation, you can test the package by running the following commands:
```julia
using JustRelax
julia> ]
pkg> test JustRelax
```
The test will take a while, so grab a :coffee: or :tea:
## Miniapps
Available miniapps can be found in the [miniapps folder](miniapps) and will be updated regularly. The miniapps are designed to be simple and easy to understand, while still providing a good basis for more complex applications. The miniapps are designed to be run on a single node, but can be easily extended to run on multiple nodes using [ImplicitGlobalGrid.jl](https://github.com/omlins/ImplicitGlobalGrid.jl) and [MPI.jl](https://github.com/JuliaParallel/MPI.jl).
## Benchmarks
Current (Blankenback2D, Stokes 2D-3D, thermal diffusion, thermal stress) and future benchmarks can be found in the [Benchmarks](miniapps/benchmarks).
## Funding
The development of this package is supported by the [GPU4GEO](https://ptsolvers.github.io/GPU4GEO/) [PASC](https://www.pasc-ch.org) project.
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 1088 | # Security Policy
We take security issues seriously. We appreciate all efforts
to responsibly disclose any security issues and will make every
effort to acknowledge contributions.
## Supported Versions
The current stable release following the interpretation of
[semantic versioning (SemVer)](https://julialang.github.io/Pkg.jl/dev/compatibility/#Version-specifier-format-1)
used in the Julia ecosystem is supported with security updates.
## Reporting a Vulnerability
To report a security issue, please use the GitHub Security Advisory
["Report a Vulnerability"](https://github.com/PTsolvers/JustRelax.jl/security/advisories/new)
tab.
We will send a response indicating the next steps in handling your report.
After the initial reply to your report, we will keep you informed of the
progress towards a fix and full announcement, and may ask for additional
information or guidance.
Please report security bugs in third-party modules directly to the person
or team maintaining the module.
Public notifications of vulnerabilities will be shared in community channels
such as Slack.
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 1903 | ```@meta
CurrentModule = JustRelax
```# JustRelax.jl
Need to solve a very large multi-physics problem on many GPUs in parallel? Just Relax!
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) is a collection of accelerated iterative pseudo-transient solvers using MPI and multiple CPU or GPU backends. It's part of the [PTSolvers organisation](https://ptsolvers.github.io) and
developed within the [GPU4GEO project](https://www.pasc-ch.org/projects/2021-2024/gpu4geo/). Current publications, outreach and news can be found on the [GPU4GEO website](https://ptsolvers.github.io/GPU4GEO/).
The package relies on other packages as building blocks and parallelisation tools:
* [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl) - device agnostic parallel kernels
* [ImplicitGlobalGrid.jl](https://github.com/omlins/ImplicitGlobalGrid.jl) - (GPU-aware) distributed parallelisation (MPI)
* [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl) - Material physics
* [JustPIC.jl](https://github.com/JuliaGeodynamics/JustPIC.jl) - Particle-in-cell advection
The package serves several purposes:
* It provides a collection of solvers to be used in prototyping new applications
* It provides some standardization so that application codes can
- more easily handle local material properties through the use of [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl)
- more easily switch between a pseudo-transient solver and another solvers (e.g. an explicit thermal solvers)
* It provides a natural repository for contributions of new solvers for use by the larger community
We provide several miniapps, each designed to solve a well-specified benchmark problem, in order to provide
- examples of usage in high-performance computing
- basis on which to build more full-featured application codes
- cases for reference and performance tests
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 12433 | # Blankenbach benchmark
Thermal convection benchmark from [Blankenbach et al., 1989](https://academic.oup.com/gji/article/98/1/23/622167)
## Initialize packages
Load [JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) necessary modules and define backend.
```julia
using JustRelax, JustRelax.JustRelax2D, JustRelax.DataIO
const backend_JR = CPUBackend
```
For this benchmark we will use particles to track the advection of the material phases and their information. For this, we will use [JustPIC.jl](https://github.com/JuliaGeodynamics/JustPIC.jl)
```julia
using JustPIC, JustPIC._2D
const backend = CPUBackend # Options: CPUBackend, CUDABackend, AMDGPUBackend
```
We will also use [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl) to write some device-agnostic helper functions:
```julia
using ParallelStencil
@init_parallel_stencil(Threads, Float64, 2) #or (CUDA, Float64, 2) or (AMDGPU, Float64, 2)
```
and will use [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl/tree/main) to define and compute physical properties of the materials:
```julia
using GeoParams
```
## Script
### Model domain
```julia
nx = ny = 51 # number of cells per dimension
nit = 6e3
igg = IGG(
init_global_grid(nx, ny, 1; init_MPI= true)...
) # initialize MPI grid
ly = 1.0 # domain length in y
lx = ly * ar # domain length in x
ni = nx, ny # number of cells
li = lx, ly # domain length in x- and y-
di = @. li / ni # grid step in x- and -y
origin = 0.0, 0.0 # origin coordinates
grid = Geometry(ni, li; origin = origin)
(; xci, xvi) = grid # nodes at the center and vertices of the cells
dt = dt_diff = 0.9 * min(di...)^2 / 4.0 # diffusive CFL timestep limiter
```
### Rheology
```julia
rheology = (
SetMaterialParams(;
Phase = 1,
Density = PT_Density(; ρ0 = 1, α = 1, β = 0.0),
HeatCapacity = ConstantHeatCapacity(; Cp = 1.0),
Conductivity = ConstantConductivity(; k = 1.0),
CompositeRheology = CompositeRheology((LinearViscous(; η = 1),)),
RadioactiveHeat = ConstantRadioactiveHeat(0.0),
Gravity = ConstantGravity(; g = 1e4),
),
)
```
### Initialize particles
```julia
nxcell = 24 # initial number of perticles per cell
max_xcell = 35 # maximum number of perticles per cell
min_xcell = 12 # minimum number of perticles per cell
particles = init_particles(
backend, nxcell, max_xcell, min_xcell, xvi..., di..., ni...
) # particles object
subgrid_arrays = SubgridDiffusionCellArrays(particles) # arrays needed for subgrid diffusion
# velocity grids
grid_vx, grid_vy = velocity_grids(xci, xvi, di) # staggered velocity grids
```
and we want to keep track of the temperature `pT`, temperature of the previous time step `pT0`, and material phase `pPhase`:
```julia
pT, pT0, pPhases = init_cell_arrays(particles, Val(3))
particle_args = (pT, pT0, pPhases)
```
### Temperature anomaly
```julia
xc_anomaly = 0.0 # origin of thermal anomaly
yc_anomaly = 1 / 3 # origin of thermal anomaly
r_anomaly = 0.1 / 2 # radius of perturbation
```
Helper function to initialize material phases with [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl)
```julia
function init_phases!(phases, particles)
ni = size(phases)
@parallel_indices (i, j) function init_phases!(phases, index)
@inbounds for ip in JustRelax.cellaxes(phases)
# quick escape if the ip-th element of the [i,j]-th cell is empty
JustRelax.@cell(index[ip, i, j]) == 0 && continue
# all particles have phase number = 1.0
JustRelax.@cell phases[ip, i, j] = 1.0
end
return nothing
end
@parallel (@idx ni) init_phases!(phases, particles.index)
end
init_phases!(pPhases, particles, lx, yc_anomaly, r_anomaly)
```
or we can use the alternative one-liners
```julia
@views pPhase.data[!isnan.(particles.index.data)] .= 1.0
```
or
```julia
map!(x -> isnan(x) ? NaN : 1.0, pPhase.data, particles.index.data)
```
and finally we need the phase ratios at the cell centers:
```julia
phase_ratios = PhaseRatio(backend_JR, ni, length(rheology))
phase_ratios_center(phase_ratios, particles, grid, pPhases)
```
### Stokes and heat diffusion arrays
Stokes arrays object
```julia
stokes = StokesArrays(backend_JR, ni)
```
and the correspondent heat diffusion one
```julia
thermal = ThermalArrays(backend_JR, ni)
```
### Initialize thermal profile and viscosity fields
To initialize the thermal profile we use [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl) again
```julia
@parallel_indices (i, j) function init_T!(T, y)
T[i, j] = 1 - y[j]
return nothing
end
@parallel (@idx size(thermal.T)) init_T!(thermal.T, xvi[2]) # cell vertices
@parallel (@idx size(thermal.Tc)) init_T!(thermal.Tc, xci[2]) # cell centers
```
and we define a rectangular thermal anomaly at $x \in [0, 0.05]$, $y \in [\frac{1}{3} - 0.05, \frac{1}{3} + 0.05]$
```julia
function rectangular_perturbation!(T, xc, yc, r, xvi)
@parallel_indices (i, j) function _rectangular_perturbation!(T, xc, yc, r, x, y)
@inbounds if ((x[i]-xc)^2 ≤ r^2) && ((y[j] - yc)^2 ≤ r^2)
T[i, j] += .2
end
return nothing
end
ni = size(T)
@parallel (@idx ni) _rectangular_perturbation!(T, xc, yc, r, xvi...)
return nothing
end
xc_anomaly = 0.0 # center of the thermal anomaly
yc_anomaly = 1/3 # center of the thermal anomaly
r_anomaly = 0.1/2 # half-width of the thermal anomaly
rectangular_perturbation!(thermal.T, xc_anomaly, yc_anomaly, r_anomaly, xvi)
```
We initialize the buoyancy forces and viscosity
```julia
ρg = @zeros(ni...), @zeros(ni...)
η = @ones(ni...)
args = (; T = thermal.Tc, P = stokes.P, dt = Inf)
compute_ρg!(ρg[2], phase_ratios, rheology, args)
compute_viscosity!(stokes, 1.0, phase_ratios, args, rheology, (-Inf, Inf))
```
where `(-Inf, Inf)` is the viscosity cutoff.
### Boundary conditions
```julia
flow_bcs = VelocityBoundaryConditions(;
free_slip = (left = true, right=true, top=true, bot=true),
)
thermal_bc = TemperatureBoundaryConditions(;
no_flux = (left = true, right = true, top = false, bot = false),
)
thermal_bcs!(thermal, thermal_bc)
thermal.Told .= thermal.T
```
### Pseuo-transient coefficients
```julia
pt_stokes = PTStokesCoeffs(li, di; ϵ=1e-4, CFL = 1 / √2.1)
pt_thermal = PTThermalCoeffs(
backend_JR, rheology, phase_ratios, args, dt, ni, di, li; ϵ=1e-5, CFL = 1e-1 / √2.1
)
```
### Just before solving the problem...
We need to allocate some arrays to be able to do the subgrid diffusion of the temperature field at the particles level:
```julia
T_buffer = @zeros(ni.+1) # without the ghost nodes at the x-direction
Told_buffer = similar(T_buffer) # without the ghost nodes at the x-direction
dt₀ = similar(stokes.P) # subgrid diffusion time scale
# copy temperature to buffer arrays
for (dst, src) in zip((T_buffer, Told_buffer), (thermal.T, thermal.Told))
copyinn_x!(dst, src)
end
# interpolate temperatyre on the particles
grid2particle!(pT, xvi, T_buffer, particles)
pT0.data .= pT.data
```
where
```julia
function copyinn_x!(A, B)
@parallel function f_x(A, B)
@all(A) = @inn_x(B)
return nothing
end
@parallel f_x(A, B)
end
```
In this benchmark we want to keep track of the time `trms`, the rms-velocity `Urms`
$U_{rms} = \sqrt{\int_{\Omega} (V_x^2 + V_y^2 ) d\Omega}$
and the Nusselt number at the top of the model `Nu_top`
$Nu_{top} = \int \frac{\partial T}{\partial x} dx$
And we will store their time history in the vectors:
```julia
Urms = Float64[]
Nu_top = Float64[]
trms = Float64[]
```
We further need two buffer arrays where to interpolate the velocity field at the vertices of the grid cells
```julia
# Buffer arrays to compute velocity rms
Vx_v = @zeros(ni.+1...)
Vy_v = @zeros(ni.+1...)
```
### Advancing one time step
1. Solve stokes
```julia
solve!(
stokes,
pt_stokes,
di,
flow_bcs,
ρg,
phase_ratios,
rheology,
args,
Inf,
igg;
kwargs = (;
iterMax = 150e3,
nout = 200,
viscosity_cutoff = (-Inf, Inf),
verbose = true
)
)
# calculate adaptive time step
dt = compute_dt(stokes, di, dt_diff)
```
2. Heat diffusion solver
```julia
heatdiffusion_PT!(
thermal,
pt_thermal,
thermal_bc,
rheology,
args,
dt,
di;
kwargs = (;
igg = igg,
phase = phase_ratios,
iterMax = 10e3,
nout = 1e2,
verbose = true,
)
)
```
3. Subgrid diffusion at the particle level
```julia
for (dst, src) in zip((T_buffer, Told_buffer), (thermal.T, thermal.Told))
copyinn_x!(dst, src)
end
subgrid_characteristic_time!(
subgrid_arrays, particles, dt₀, phase_ratios, rheology, thermal, stokes, xci, di
)
centroid2particle!(subgrid_arrays.dt₀, xci, dt₀, particles)
subgrid_diffusion!(
pT, T_buffer, thermal.ΔT[2:end-1, :], subgrid_arrays, particles, xvi, di, dt
)
```
4. Advect particles
```julia
# advect particles in space
advection!(particles, RungeKutta2(), @velocity(stokes), (grid_vx, grid_vy), dt)
# advect particles in memory
move_particles!(particles, xvi, particle_args)
# check if we need to inject particles
inject_particles_phase!(particles, pPhases, (pT, ), (T_buffer, ), xvi)
# update phase ratios
phase_ratios_center(phase_ratios, particles, grid, pPhases)
```
5. Interpolate `T` back to the grid
```julia
# interpolate fields from particle to grid vertices
particle2grid!(T_buffer, pT, xvi, particles)
@views T_buffer[:, end] .= 0.0
@views T_buffer[:, 1] .= 1.0
@views thermal.T[2:end-1, :] .= T_buffer
flow_bcs!(stokes, flow_bcs) # apply boundary conditions
temperature2center!(thermal)
```
6. Update buoyancy forces and viscosity
```julia
args = (; T = thermal.Tc, P = stokes.P, dt=Inf)
compute_viscosity!(stokes, 1.0, phase_ratios, args, rheology, (-Inf, Inf))
compute_ρg!(ρg[2], phase_ratios, rheology, args)
```
7. Compute Nusselt number and rms-velocity
```julia
# Nusselt number, Nu = ∫ ∂T/∂z dx
Nu_it = sum( ((abs.(thermal.T[2:end-1,end] - thermal.T[2:end-1,end-1])) ./ di[2]) .*di[1])
push!(Nu_top, Nu_it)
# Compute U rms
# U₍ᵣₘₛ₎ = √ ∫∫ (vx²+vz²) dx dz
Urms_it = let
JustRelax.JustRelax2D.velocity2vertex!(Vx_v, Vy_v, stokes.V.Vx, stokes.V.Vy; ghost_nodes=true)
@. Vx_v .= hypot.(Vx_v, Vy_v) # we reuse Vx_v to store the velocity magnitude
sqrt(sum( Vx_v.^2 .* prod(di)) )
end
push!(Urms, Urms_it)
push!(trms, t)
```
### Visualization
We will use [Makie.jl](https://github.com/MakieOrg/Makie.jl) to visualize the results
```julia
using GLMakie
```
### Fields
```julia
# Make particles plottable
p = particles.coords
ppx, ppy = p
pxv = ppx.data[:]
pyv = ppy.data[:]
clr = pT.data[:]
idxv = particles.index.data[:];
# Make Makie figure
fig = Figure(size = (900, 900), title = "t = $t")
ax1 = Axis(fig[1,1], aspect = ar, title = "T [K] (t=$(t/(1e6 * 3600 * 24 *365.25)) Myrs)")
ax2 = Axis(fig[2,1], aspect = ar, title = "Vy [m/s]")
ax3 = Axis(fig[1,3], aspect = ar, title = "Vx [m/s]")
ax4 = Axis(fig[2,3], aspect = ar, title = "T [K]")
# grid temperature
h1 = heatmap!(ax1, xvi[1], xvi[2], Array(thermal.T[2:end-1,:]) , colormap=:lajolla, colorrange=(0, 1) )
# y-velocity
h2 = heatmap!(ax2, xvi[1], xvi[2], Array(stokes.V.Vy) , colormap=:batlow)
# x-velocity
h3 = heatmap!(ax3, xvi[1], xvi[2], Array(stokes.V.Vx) , colormap=:batlow)
# particles temperature
h4 = scatter!(ax4, Array(pxv[idxv]), Array(pyv[idxv]), color=Array(clr[idxv]), colormap=:lajolla, colorrange=(0, 1), markersize=3)
hidexdecorations!(ax1)
hidexdecorations!(ax2)
hidexdecorations!(ax3)
Colorbar(fig[1,2], h1)
Colorbar(fig[2,2], h2)
Colorbar(fig[1,4], h3)
Colorbar(fig[2,4], h4)
linkaxes!(ax1, ax2, ax3, ax4)
save(joinpath(figdir, "$(it).png"), fig)
fig
```
### Final model
Temperature field

And time history of the rms-velocity and Nusselt number

| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 7175 | # ShearBand benchmark
Shear Band benchmark to test the visco-elasto-plastic rheology implementation in [JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl)
## Initialize packages
Load [JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) necessary modules and define backend.
```julia
using JustRelax, JustRelax.JustRelax2D, JustRelax.DataIO
const backend_JR = CPUBackend
```
We will also use [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl) to write some device-agnostic helper functions:
```julia
using ParallelStencil
@init_parallel_stencil(Threads, Float64, 2) #or (CUDA, Float64, 2) or (AMDGPU, Float64, 2)
```
and will use [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl/tree/main) to define and compute physical properties of the materials:
```julia
using GeoParams
```
## Script
### Model domain
```julia
nx = ny = 64 # number of cells per dimension
igg = IGG(
init_global_grid(nx, ny, 1; init_MPI= true)...
) # initialize MPI grid
ly = 1.0 # domain length in y
lx = ly # domain length in x
ni = nx, ny # number of cells
li = lx, ly # domain length in x- and y-
di = @. li / ni # grid step in x- and -y
origin = 0.0, 0.0 # origin coordinates
grid = Geometry(ni, li; origin = origin)
(; xci, xvi) = grid # nodes at the center and vertices of the cells
dt = Inf
```
### Physical properties using GeoParams
```julia
τ_y = 1.6 # yield stress. If do_DP=true, τ_y stand for the cohesion: c*cos(ϕ)
ϕ = 30 # friction angle
C = τ_y # Cohesion
η0 = 1.0 # viscosity
G0 = 1.0 # elastic shear modulus
Gi = G0/(6.0-4.0) # elastic shear modulus perturbation
εbg = 1.0 # background strain-rate
η_reg = 8e-3 # regularisation "viscosity"
dt = η0/G0/4.0 # assumes Maxwell time of 4
el_bg = ConstantElasticity(; G=G0, Kb=4)
el_inc = ConstantElasticity(; G=Gi, Kb=4)
visc = LinearViscous(; η=η0)
pl = DruckerPrager_regularised(; # non-regularized plasticity
C = C,
ϕ = ϕ,
η_vp = η_reg,
Ψ = 0
)
```
### Rheology
```julia
rheology = (
# Low density phase
SetMaterialParams(;
Phase = 1,
Density = ConstantDensity(; ρ = 0.0),
Gravity = ConstantGravity(; g = 0.0),
CompositeRheology = CompositeRheology((visc, el_bg, pl)),
Elasticity = el_bg,
),
# High density phase
SetMaterialParams(;
Density = ConstantDensity(; ρ = 0.0),
Gravity = ConstantGravity(; g = 0.0),
CompositeRheology = CompositeRheology((visc, el_inc, pl)),
Elasticity = el_inc,
),
)
```
### Phase anomaly
Helper function to initialize material phases with [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl)
```julia
function init_phases!(phase_ratios, xci, radius)
ni = size(phase_ratios.center)
origin = 0.5, 0.5
@parallel_indices (i, j) function init_phases!(phases, xc, yc, o_x, o_y, radius)
x, y = xc[i], yc[j]
if ((x-o_x)^2 + (y-o_y)^2) > radius^2
JustRelax.@cell phases[1, i, j] = 1.0
JustRelax.@cell phases[2, i, j] = 0.0
else
JustRelax.@cell phases[1, i, j] = 0.0
JustRelax.@cell phases[2, i, j] = 1.0
end
return nothing
end
@parallel (@idx ni) init_phases!(phase_ratios.center, xci..., origin..., radius)
end
```
and finally we need the phase ratios at the cell centers:
```julia
phase_ratios = PhaseRatio(backend_JR, ni, length(rheology))
init_phases!(phase_ratios, xci, radius)
```
### Stokes arrays
Stokes arrays object
```julia
stokes = StokesArrays(backend_JR, ni)
```
### Initialize viscosity fields
We initialize the buoyancy forces and viscosity
```julia
ρg = @zeros(ni...), @zeros(ni...)
η = @ones(ni...)
args = (; T = thermal.Tc, P = stokes.P, dt = Inf)
compute_ρg!(ρg[2], phase_ratios, rheology, args)
compute_viscosity!(stokes, 1.0, phase_ratios, args, rheology, (-Inf, Inf))
```
where `(-Inf, Inf)` is the viscosity cutoff.
### Boundary conditions
```julia
flow_bcs = VelocityBoundaryConditions(;
free_slip = (left = true, right = true, top = true, bot = true),
no_slip = (left = false, right = false, top = false, bot=false),
)
stokes.V.Vx .= PTArray(backend_JR)([ x*εbg for x in xvi[1], _ in 1:ny+2])
stokes.V.Vy .= PTArray(backend_JR)([-y*εbg for _ in 1:nx+2, y in xvi[2]])
flow_bcs!(stokes, flow_bcs) # apply boundary conditions
update_halo!(@velocity(stokes)...)
```
### Pseuo-transient coefficients
```julia
pt_stokes = PTStokesCoeffs(li, di; ϵ=1e-4, CFL = 1 / √2.1)
```
### Just before solving the problem...
In this benchmark we want to keep track of τII, the total time `ttot`, and the analytical elastic solution `sol`
```julia
solution(ε, t, G, η) = 2 * ε * η * (1 - exp(-G * t / η))
```
and store their time history in the vectors:
```julia
τII = Float64[]
sol = Float64[]
ttot = Float64[]
```
### Advancing one time step
1. Solve stokes
```julia
solve!(
stokes,
pt_stokes,
di,
flow_bcs,
ρg,
phase_ratios,
rheology,
args,
dt,
igg;
kwargs = (;
iterMax = 150e3,
nout = 200,
viscosity_cutoff = (-Inf, Inf),
verbose = true
)
)
```
2. calculate the second invariant and push to history vectors
```julia
tensor_invariant!(stokes.ε)
push!(τII, maximum(stokes.τ.xx))
it += 1
t += dt
push!(sol, solution(εbg, t, G0, η0))
push!(ttot, t)
```
## Visualization
We will use [Makie.jl](https://github.com/MakieOrg/Makie.jl) to visualize the results
```julia
using GLMakie
```
## Fields
```julia
# visualisation of high density inclusion
th = 0:pi/50:3*pi;
xunit = @. radius * cos(th) + 0.5;
yunit = @. radius * sin(th) + 0.5;
fig = Figure(size = (1600, 1600), title = "t = $t")
ax1 = Axis(fig[1,1], aspect = 1, title = L"\tau_{II}", titlesize=35)
ax2 = Axis(fig[2,1], aspect = 1, title = L"E_{II}", titlesize=35)
ax3 = Axis(fig[1,2], aspect = 1, title = L"\log_{10}(\varepsilon_{II})", titlesize=35)
ax4 = Axis(fig[2,2], aspect = 1)
heatmap!(ax1, xci..., Array(stokes.τ.II) , colormap=:batlow)
heatmap!(ax2, xci..., Array(log10.(stokes.EII_pl)) , colormap=:batlow)
heatmap!(ax3, xci..., Array(log10.(stokes.ε.II)) , colormap=:batlow)
lines!(ax2, xunit, yunit, color = :black, linewidth = 5)
lines!(ax4, ttot, τII, color = :black)
lines!(ax4, ttot, sol, color = :red)
hidexdecorations!(ax1)
hidexdecorations!(ax3)
save(joinpath(figdir, "$(it).png"), fig)
fig
```
### Final model
Shear Bands evolution in a 2D visco-elasto-plastic rheology model

| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 251 | # Field advection
## Particles-in-Cell
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) relies on [JustPIC.jl](https://github.com/JuliaGeodynamics/JustPIC.jl) for advections of particles containing material information.
## Upwind
## WENO5
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 928 | # Selecting the backend
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) supports three backends: the default CPU backend, and two GPU backends for Nvidia and AMD GPUs. The default CPU backend is selected upon loading JustRelax:
```julia
using JustRelax
```
The GPU backends are implemented as extensions, and can be selected upon loading the appropriate GPU package before loading JustRelax. If running on Nvidia GPUs, use the [CUDA.jl](https://github.com/JuliaGPU/CUDA.jl) package:
```julia
using CUDA, JustRelax
```
and if running on AMD GPUs, use the [AMDGPU.jl](https://github.com/JuliaGPU/AMDGPU.jl) package:
```julia
using AMDGPU, JustRelax
```
Two and three dimensional solvers are implemented in different submodules, which also need to be loaded. To access the two-dimensional module:
```julia
using JustRelax.JustRelax2D
```
and for the three-dimensional module:
```julia
using JustRelax.JustRelax3D
```
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 3538 | # Flow boundary conditions
Supported boundary conditions:
1. Free slip
$\frac{\partial u_i}{\partial x_i} = 0$ at the boundary $\Gamma$
2. No slip
$u_i = 0$ at the boundary $\Gamma$
3. Free surface
$\sigma_z = 0 \rightarrow \tau_z = P$ at the top boundary
## Defining the boundary conditions
We have two ways of defining the boundary condition formulations:
- `VelocityBoundaryConditions`, and
- `DisplacementBoundaryConditions`.
The first one is used for the velocity-pressure formulation, and the second one is used for the displacement-pressure formulation. The flow boundary conditions can be switched on and off by setting them as `true` or `false` at the appropriate boundaries. Valid boundary names are `left` and `right`, `top` and `bot`, and for the 3D case, `front` and `back`.
For example, if we want to have free free-slip in every single boundary in a 2D simulation, we need to instantiate `VelocityBoundaryConditions` or `DisplacementBoundaryConditions` as:
```julia
bcs = VelocityBoundaryConditions(;
no_slip = (left=false, right=false, top=false, bot=false),
free_slip = (left=true, right=true, top=true, bot=true),
free_surface = false
)
bcs = DisplacementBoundaryConditions(;
no_slip = (left=false, right=false, top=false, bot=false),
free_slip = (left=true, right=true, top=true, bot=true),
free_surface = false
)
```
The equivalent for the 3D case would be:
```julia
bcs = VelocityBoundaryConditions(;
no_slip = (left=false, right=false, top=false, bot=false, front=false, back=false),
free_slip = (left=true, right=true, top=true, bot=true, front=true, back=true),
free_surface = false
)
bcs = DisplacementBoundaryConditions(;
no_slip = (left=false, right=false, top=false, bot=false, front=false, back=false),
free_slip = (left=true, right=true, top=true, bot=true, front=true, back=true),
free_surface = false
)
```
## Prescribing the velocity/displacement boundary conditions
Normally, one would prescribe the velocity/displacement boundary conditions by setting the velocity/displacement field at the boundary through the application of a background strain rate `εbg`.
Depending on the formulation, the velocity/displacement field is set as follows for the 2D case:
### Velocity formulation
```julia
stokes.V.Vx .= PTArray(backend)([ x*εbg for x in xvi[1], _ in 1:ny+2]) # Velocity in x direction
stokes.V.Vy .= PTArray(backend)([-y*εbg for _ in 1:nx+2, y in xvi[2]]) # Velocity in y direction
```
Make sure to apply the set velocity to the boundary conditions. You do this by calling the `flow_bcs!` function,
```julia
flow_bcs!(stokes, flow_bcs)
```
and then applying the velocities to the halo
```julia
update_halo!(@velocity(stokes)...)
```
### Displacement formulation
```julia
stokes.U.Ux .= PTArray(backend)([ x*εbg*lx*dt for x in xvi[1], _ in 1:ny+2]) # Displacement in x direction
stokes.U.Uy .= PTArray(backend)([-y*εbg*ly*dt for _ in 1:nx+2, y in xvi[2]]) # Displacement in y direction
flow_bcs!(stokes, flow_bcs)
```
Make sure to initialize the displacement according to the extent of your domain. Here, lx and ly are the domain lengths in the x and y directions, respectively.
Also for the displacement formulation it is important that the displacement is converted to velocity before updating the halo. This can be done by calling the `displacement2velocity!` function.
```julia
displacement2velocity!(stokes, dt) # convert displacement to velocity
update_halo!(@velocity(stokes)...)
```
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 3737 | # Pseudo-transient iterative method
The pseudo-transient method consists in augmenting the right-hand-side of the target PDE with a pseudo-time derivative (where $\psi$ is the pseudo-time) of the primary variables. We then solve the resulting system of equations with an iterative method. The pseudo-time derivative is then gradually reduced, until the original PDE is solved and the changes in the primary variables are below a preset tolerance.
## Heat diffusion
The pseudo-transient heat-diffusion equation is:
$\widetilde{\rho}\frac{\partial T}{\partial \psi} + \rho C_p \frac{\partial T}{\partial t} = \nabla \cdot (\kappa\nabla T) = -\nabla q$
We use a second order pseudo-transient scheme were continuation is also done on the flux, so that:
$\widetilde{\theta}\frac{\partial q}{\partial \psi} + q = -\kappa\nabla T$
## Stokes equations
For example, the pseudo-transient formulation of the Stokes equations yields:
$\widetilde{\rho}\frac{\partial \boldsymbol{u}}{\partial \psi} + \nabla\cdot\boldsymbol{\tau} - \nabla p = \boldsymbol{f}$
$\frac{1}{\widetilde{K}}\frac{\partial p}{\partial \psi} + \nabla\cdot\boldsymbol{v} = \beta \frac{\partial p}{\partial t} + \alpha \frac{\partial T}{\partial t}$
## Constitutive equations
A pseudo-transient continuation is also done on the constitutive law:
$\frac{1}{2\widetilde{G}} \frac{\partial\boldsymbol{\tau}}{\partial\psi}+ \frac{1}{2G}\frac{D\boldsymbol{\tau}}{Dt} + \frac{\boldsymbol{\tau}}{2\eta} = \dot{\boldsymbol{\varepsilon}}$
where the wide tile denotes the effective damping coefficients and $\psi$ is the pseudo-time step. These are defined as in [Räss et al. (2022)](https://gmd.copernicus.org/articles/15/5757/2022/):
$\widetilde{\rho} = Re\frac{\eta}{\widetilde{V}L}, \qquad \widetilde{G} = \frac{\widetilde{\rho} \widetilde{V}^2}{r+2}, \qquad \widetilde{K} = r \widetilde{G}$
and
$\widetilde{V} = \sqrt{ \frac{\widetilde{K} +2\widetilde{G}}{\widetilde{\rho}}}, \qquad r = \frac{\widetilde{K}}{\widetilde{G}}, \qquad Re = \frac{\widetilde{\rho}\widetilde{V}L}{\eta}$
where the P-wave $\widetilde{V}=V_p$ is the characteristic velocity scale for Stokes, and $Re$ is the Reynolds number.
### Physical parameters
| Symbol | Parameter |
| :------------------------------- | :--------------------: |
| $T$ | Temperature |
| $q$ | Flux |
| $\boldsymbol{\tau}$ | Deviatoric stress |
| $\dot{\boldsymbol{\varepsilon}}$ | Deviatoric strain rate |
| $\boldsymbol{u}$ | Velocity |
| $\boldsymbol{f}$ | External forces |
| $P$ | Pressure |
| $\eta$ | Viscosity |
| $\rho$ | Density |
| $\beta$ | Compressibility |
| $G$ | Shear modulus |
| $\alpha$ | Thermal expansivity |
| $C_p$ | Heat capacity |
| $\kappa$ | Heat conductivity |
### Pseudo-transient parameters
| Symbol | Parameter |
| :------------------- | :---------------------------: |
| $\psi$ | Pseudo time step |
| $\widetilde{K}$ | Pseudo bulk modulus |
| $\widetilde{G}$ | Pseudo shear modulus |
| $\widetilde{V}$ | Characteristic velocity scale |
| $\widetilde{\rho}$ | Pseudo density |
| $\widetilde{\theta}$ | Relaxation time |
| $Re$ | Reynolds number |
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 660 | # Installation
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) is a registered package and can be added as follows:
```julia
using Pkg; Pkg.add("JustRelax")
```
or
```julia-repl
julia> ]
(@v1.10) pkg> add JustRelax
```
!!! info "Install from a specific branch"
However, as the API is changing and not every new feature leads to a new release, one can also clone the main branch of the repository:
```julia
add JustRelax#main
```
After installation, you can test the package by running the following commands:
```julia-repl
using JustRelax
julia> ]
(@v1.10) pkg> test JustRelax
```
The test will take a while, so grab a ☕️ or 🍵
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 163 | # List of all functions
Here an overview of all functions:
```@autodocs
Modules = [JustRelax, JustRelax.JustRelax2D, JustRelax.JustRelax3D, JustRelax.DataIO]
```
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 228 | # Material physics
[JustRelax.jl](https://github.com/PTsolvers/JustRelax.jl) is fully integrated with [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl/tree/main) to perform all the material physics computations.
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 3239 | # Using GeoParams.jl to define the rheology of the material phases
We will use the same physical parameters as the ones defined in [Hummel et al 2024](https://doi.org/10.5194/se-15-567-2024).
The thermal expansion coefficient $\alpha$ and heat capacity $C_p$ are the same for all the material phases
```julia
α = 2.4e-5 # 1 / K
Cp = 750 # J / kg K
```
The density of all the phases is constant, except for the oceanic lithosphere, which uses the pressure and temperature dependent equation of state $\rho = \rho_0 \left(1 - \alpha (T-T_0) - \beta (P-P_0) \right)$, where $\rho_0 = \rho (T=1475 \text{C}^{\circ})=3200 \text{kg/m}^3$.which corresponds to the `PT_Density` object from [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl):
```julia
density_lithosphere = PT_Density(; ρ0=3.2e3, α = α, β = 0e0, T0 = 273+1474)
```
We will run the case where the rheology is given by a combination of dislocation and diffusion creep for wet olivine,
```julia
using GeoParams.Dislocation
using GeoParams.Diffusion
disl_wet_olivine = SetDislocationCreep(Dislocation.wet_olivine1_Hirth_2003)
diff_wet_olivine = SetDiffusionCreep(Diffusion.wet_olivine_Hirth_2003)
```
and where plastic failure is given by the formulation from [Duretz et al, 2021](https://doi.org/10.1029/2021GC009675)
```julia
# non-regularized plasticity
ϕ = asind(0.1)
C = 1e6 # Pa
plastic_model = DruckerPrager_regularised(; C = C, ϕ = ϕ, η_vp=η_reg, Ψ=0.0)
```
Finally we define the rheology objects of [GeoParams.jl](https://github.com/JuliaGeodynamics/GeoParams.jl)
```julia
rheology = (
SetMaterialParams(;
Name = "Asthenoshpere",
Phase = 1,
Density = ConstantDensity(; ρ=3.2e3),
HeatCapacity = ConstantHeatCapacity(; Cp = Cp),
Conductivity = ConstantConductivity(; k = 2.5),
CompositeRheology = CompositeRheology( (LinearViscous(; η=1e20),)),
Gravity = ConstantGravity(; g=9.81),
),
SetMaterialParams(;
Name = "Oceanic lithosphere",
Phase = 2,
Density = density_lithosphere,
HeatCapacity = ConstantHeatCapacity(; Cp = Cp),
Conductivity = ConstantConductivity(; k = 2.5),
CompositeRheology = CompositeRheology(
(
disl_wet_olivine,
diff_wet_olivine,
plastic_model,
)
),
),
SetMaterialParams(;
Name = "oceanic crust",
Phase = 3,
Density = ConstantDensity(; ρ=3.2e3),
HeatCapacity = ConstantHeatCapacity(; Cp = Cp),
Conductivity = ConstantConductivity(; k = 2.5),
CompositeRheology = CompositeRheology( (LinearViscous(; η=1e20),)),
),
SetMaterialParams(;
Name = "StickyAir",
Phase = 4,
Density = ConstantDensity(; ρ=1), # water density
HeatCapacity = ConstantHeatCapacity(; Cp = 1e34),
Conductivity = ConstantConductivity(; k = 3),
CompositeRheology = CompositeRheology((LinearViscous(; η=1e19),)),
),
)
```
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 3791 | # Model setup
As described in the original [paper](https://doi.org/10.5194/se-15-567-2024), the domain consists of a Cartesian box of $\Omega \in [0, 3000] \times [0, -660]$ km, with two 80 km thick oceanic plates over the asthenospheric mantle.
We will use [GeophysicalModelGenerator.jl](https://github.com/JuliaGeodynamics/GeophysicalModelGenerator.jl) to generate the initial geometry, material phases, and thermal field of our models. We will start by defining the dimensions and resolution of our model, as well as initializing the `Grid2D` object and two arrays `Phases` and `Temp` that host the material phase (given by an integer) and the thermal field, respectively.
```julia
nx, nz = 512, 218 # number of cells per dimension
Tbot = 1474.0 # [Celsius]
model_depth = 660 # [km]
air_thickness = 10 # [km]
Lx = 3000 # model length [km]
x = range(0, Lx, nx);
z = range(-model_depth, air_thickness, nz);
Grid2D = CartData(xyz_grid(x,0,z))
Phases = zeros(Int64, nx, 1, nz);
Temp = fill(Tbot, nx, 1, nz);
```
In this model we have four material phases with their respective phase numbers:
| Material | Phase number |
| :---------------- | :----------: |
| asthenosphere | 0 |
| oceanic lithosphere | 1 |
| oceanic crust | 3 |
| sticky air | 4 |
We will start by initializing the model as asthenospheric mantle, with a thermal profile given by the half-space cooling model with an age of 80 Myrs.
```julia
add_box!(
Phases,
Temp,
Grid2D;
xlim = (0, Lx),
zlim = (-model_depth, 0.0),
phase = LithosphericPhases(Layers=[], Phases=[0]),
T = HalfspaceCoolingTemp(Tsurface=20, Tmantle=Tbot, Age=80,Adiabat=0.4)
)
```

Next we add a horizontal 80 km thick oceanic lithosphere. Note that we leave a 100 km buffer zone next to the vertical boundaries of the domain, to facilitate the sliding of the oceanic plates.
```julia
add_box!(
Phases,
Temp,
Grid2D;
xlim = (100, Lx-100), # 100 km buffer zones on both sides
zlim = (-model_depth, 0.0),
phase = LithosphericPhases(Layers=[80], Phases=[1 0]),
T = HalfspaceCoolingTemp(Tsurface=20, Tmantle=Tbot, Age=80, Adiabat=0.4)
)
```

As in the original paper, we add a 8km thick crust on top of the subducting oceanic plate.
```julia
# Add right oceanic plate crust
add_box!(
Phases,
Temp,
Grid2D;
xlim = (Lx-1430, Lx-200),
zlim = (-model_depth, 0.0),
Origin = nothing, StrikeAngle=0, DipAngle=0,
phase = LithosphericPhases(Layers=[8 72], Phases=[2 1 0]),
T = HalfspaceCoolingTemp(Tsurface=20, Tmantle=Tbot, Age=80, Adiabat=0.4)
)
```

And finally we add the subducting slab, with the trench located at 1430km from the right-hand-side boundary.
```julia
add_box!(
Phases,
Temp,
Grid2D;
xlim = (Lx-1430, Lx-1430-250),
zlim = (-80, 0.0),
Origin = nothing, StrikeAngle=0, DipAngle=-30,
phase = LithosphericPhases(Layers=[8 72], Phases=[2 1 0]),
T = HalfspaceCoolingTemp(Tsurface=20, Tmantle=Tbot, Age=80, Adiabat=0.4)
)
```

```julia
surf = Grid2D.z.val .> 0.0
@views Temp[surf] .= 20.0
@views Phases[surf] .= 3
```

```julia
li = (abs(last(x)-first(x)), abs(last(z)-first(z))) .* 1e3 # in meters
origin = (x[1], z[1]) .* 1e3 # lower-left corner of the domain
Phases = Phases[:,1,:] .+ 1 # +1 because Julia is 1-indexed
Temp = Temp[:,1,:].+273 # in Kelvin
```
| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.3.2 | 400eb2287ceaccfcb37bb7db095ecd914493ce75 | docs | 8204 | # 2D subduction
Model setups taken from [Hummel et al 2024](https://doi.org/10.5194/se-15-567-2024).
# Model setup
We will use [GeophysicalModelGenerator.jl](https://github.com/JuliaGeodynamics/GeophysicalModelGenerator.jl) to generate the initial geometry, material phases, and thermal field of our models.
# Initialize packages
Load JustRelax necessary modules and define backend.
```julia
using CUDA # comment this out if you are not using CUDA; or load AMDGPU.jl if you are using an AMD GPU
using JustRelax, JustRelax.JustRelax2D, JustRelax.DataIO
const backend_JR = CUDABackend # Options: CPUBackend, CUDABackend, AMDGPUBackend
```
For this benchmark we will use particles to track the advection of the material phases and their information. For this, we will use [JustPIC.jl](https://github.com/JuliaGeodynamics/JustPIC.jl)
```julia
using JustPIC, JustPIC._2D
const backend = CUDABackend # Options: JustPIC.CPUBackend, CUDABackend, JustPIC.AMDGPUBackend
```
We will also use [ParallelStencil.jl](https://github.com/omlins/ParallelStencil.jl) to write some device-agnostic helper functions:
```julia
using ParallelStencil
@init_parallel_stencil(CUDA, Float64, 2)
```
### Helper function
We first define a helper function that will be useful later on
```julia
function copyinn_x!(A, B)
@parallel function f_x(A, B)
@all(A) = @inn_x(B)
return nothing
end
@parallel f_x(A, B)
end
```
# Script
## Model domain
```julia
nx, ny = 256, 128 # number of cells in x and y directions
ni = nx, ny
di = @. li / ni # grid steps
grid = Geometry(ni, li; origin = origin)
(; xci, xvi) = grid # nodes at the center and vertices of the cells
```
## Physical properties using GeoParams
For the rheology we will use the `rheology` object we created in the previous section.
## Initialize particles
```julia
nxcell = 40 # initial number of particles per cell
max_xcell = 60 # maximum number of particles per cell
min_xcell = 20 # minimum number of particles per cell
particles = init_particles(
backend, nxcell, max_xcell, min_xcell, xvi...
)
)
subgrid_arrays = SubgridDiffusionCellArrays(particles)
# velocity staggered grids
grid_vxi = velocity_grids(xci, xvi, di)
```
We will like to advect two fields, the temperature `pT` and the material phases of each particle `pPhases`. We will initialize these fields as `CellArray` objects:
```julia
pPhases, pT = init_cell_arrays(particles, Val(2))
particle_args = (pT, pPhases)
```
# Assign particles phases anomaly
Now we assign the material phases from the arrays we computed with help of [GeophysicalModelGenerator.jl](https://github.com/JuliaGeodynamics/GeophysicalModelGenerator.jl)
```julia
phases_device = PTArray(backend)(phases_GMG)
phase_ratios = PhaseRatio(backend, ni, length(rheology))
init_phases!(pPhases, phases_device, particles, xvi)
phase_ratios_center!(phase_ratios, particles, grid, pPhases)
```
## Temperature profile
We need to copy the thermal field from the [GeophysicalModelGenerator.jl](https://github.com/JuliaGeodynamics/GeophysicalModelGenerator.jl) object to the `thermal` that contains all the arrays related to the thermal field.
```julia
Ttop = 20 + 273
Tbot = maximum(T_GMG)
thermal = ThermalArrays(backend, ni)
@views thermal.T[2:end-1, :] .= PTArray(backend)(T_GMG)
thermal_bc = TemperatureBoundaryConditions(;
no_flux = (left = true, right = true, top = false, bot = false),
)
thermal_bcs!(thermal, thermal_bc)
@views thermal.T[:, end] .= Ttop
@views thermal.T[:, 1] .= Tbot
temperature2center!(thermal)
```
## Stokes arrays
Stokes arrays object
```julia
stokes = StokesArrays(backend, ni)
pt_stokes = PTStokesCoeffs(li, di; ϵ=1e-4, Re=3π, r=1e0, CFL = 1 / √2.1) # Re=3π, r=0.7
```
## Buoyancy forces and lithostatic pressure
```julia
ρg = ntuple(_ -> @zeros(ni...), Val(2))
compute_ρg!(ρg[2], phase_ratios, rheology_augmented, (T=thermal.Tc, P=stokes.P))
stokes.P .= PTArray(backend)(reverse(cumsum(reverse((ρg[2]).* di[2], dims=2), dims=2), dims=2))
```
## Viscosity
```julia
args0 = (T=thermal.Tc, P=stokes.P, dt = Inf)
viscosity_cutoff = (1e17, 1e24)
compute_viscosity!(stokes, phase_ratios, args0, rheology, viscosity_cutoff)
```
## Boundary conditions
We we will use free slip boundary conditions on all sides
```julia
# Boundary conditions
flow_bcs = VelocityBoundaryConditions(;
free_slip = (left = true , right = true , top = true , bot = true),
)
```
## Pseuo-transient coefficients
```julia
pt_thermal = PTThermalCoeffs(
backend, rheology_augmented, phase_ratios, args0, dt, ni, di, li; ϵ=1e-5, CFL=1e-3 / √3
)
```
## Just before solving the problem...
Because we have ghost nodes on the thermal field `thermal.T`, we need to copy the thermal field to a buffer array without those ghost nodes, and interpolate the temperature to the particles. This is because [JustPIC.jl](https://github.com/JuliaGeodynamics/JustPIC.jl) does not support ghost nodes yet.
```julia
T_buffer = @zeros(ni.+1)
Told_buffer = similar(T_buffer)
dt₀ = similar(stokes.P)
for (dst, src) in zip((T_buffer, Told_buffer), (thermal.T, thermal.Told))
copyinn_x!(dst, src)
end
grid2particle!(pT, xvi, T_buffer, particles)
```
## Advancing one time step
1. Interpolate fields from particle to grid vertices
```julia
particle2grid!(T_buffer, pT, xvi, particles)
@views T_buffer[:, end] .= Ttop
@views T_buffer[:, 1] .= Tbot
@views thermal.T[2:end-1, :] .= T_buffer
thermal_bcs!(thermal, thermal_bc)
temperature2center!(thermal)
```
2. Solve stokes
```julia
t_stokes = @elapsed begin
out = solve!(
stokes,
pt_stokes,
di,
flow_bcs,
ρg,
phase_ratios,
rheology_augmented,
args,
dt,
igg;
kwargs = (
iterMax = 150e3,
nout = 1e3,
viscosity_cutoff = viscosity_cutoff,
free_surface = false,
viscosity_relaxation = 1e-2
)
);
end
println("Stokes solver time ")
println(" Total time: $t_stokes s")
println(" Time/iteration: $(t_stokes / out.iter) s")
```
3. Update time step
```julia
dt = compute_dt(stokes, di) * 0.8
```
4. Thermal solver and subgrid diffusion
```julia
heatdiffusion_PT!(
thermal,
pt_thermal,
thermal_bc,
rheology_augmented,
args,
dt,
di;
kwargs = (
igg = igg,
phase = phase_ratios,
iterMax = 50e3,
nout = 1e2,
verbose = true,
)
)
subgrid_characteristic_time!(
subgrid_arrays, particles, dt₀, phase_ratios, rheology_augmented, thermal, stokes, xci, di
)
centroid2particle!(subgrid_arrays.dt₀, xci, dt₀, particles)
subgrid_diffusion!(
pT, thermal.T, thermal.ΔT, subgrid_arrays, particles, xvi, di, dt
)
```
5. Particles advection
```julia
# advect particles in space
advection!(particles, RungeKutta2(), @velocity(stokes), grid_vxi, dt)
# advect particles in memory
move_particles!(particles, xvi, particle_args)
# check if we need to inject particles
inject_particles_phase!(particles, pPhases, (pT, ), (T_buffer, ), xvi)
# update phase ratios
phase_ratios_center!(phase_ratios, particles, grid, pPhases)
```
6. **Optional:** Save data as VTK to visualize it later with [ParaView](https://www.paraview.org/)
```julia
Vx_v = @zeros(ni.+1...)
Vy_v = @zeros(ni.+1...)
velocity2vertex!(Vx_v, Vy_v, @velocity(stokes)...) # interpolate velocity from staggered grid to vertices
data_v = (; # data @ vertices
T = Array(T_buffer),
τII = Array(stokes.τ.II),
εII = Array(stokes.ε.II),
Vx = Array(Vx_v),
Vy = Array(Vy_v),
)
data_c = (; # data @ centers
P = Array(stokes.P),
η = Array(stokes.viscosity.η_vep),
)
velocity_v = ( # velocity vector field
Array(Vx_v),
Array(Vy_v),
)
save_vtk(
joinpath(@__DIR__, "vtk_" * lpad("$it", 6, "0")),
xvi,
xci,
data_v,
data_c,
velocity_v
)
```
### Final model
Solution after 990 time steps

| JustRelax | https://github.com/PTsolvers/JustRelax.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 682 | using LaserFields
using Documenter
DocMeta.setdocmeta!(LaserFields, :DocTestSetup, :(using LaserFields); recursive=true)
makedocs(;
modules=[LaserFields],
authors="Johannes Feist <[email protected]> and contributors",
repo="https://github.com/jfeist/LaserFields.jl/blob/{commit}{path}#{line}",
sitename="LaserFields.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://jfeist.github.io/LaserFields.jl",
edit_link="main",
assets=String[],
),
pages=[
"Home" => "index.md",
],
)
deploydocs(;
repo="github.com/jfeist/LaserFields.jl",
devbranch="main",
)
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 362 | module LaserFields
using SpecialFunctions
using DelimitedFiles
using DataInterpolations
export LaserField, LaserFieldCollection, make_laserfield
export E_field, A_field, E_fourier, A_fourier
export start_time, end_time, envelope, Teff
include("constants.jl")
include("typedef.jl")
include("fielddefs.jl")
include("make_field.jl")
include("precompile.jl")
end | LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 655 | const GAUSSIAN_TIME_CUTOFF_SIGMA = 3.5*sqrt(log(256))
const au_as = 1/24.188843265903884 # attosecond in a.u.
const au_wcm2toel2 = 1/3.5094455205784296e16 # W/cm^2 in a.u. for electric field squared
const au_wcm2 = 1.5536611487396207e-16 # W/cm^2 in a.u
const au_m = 1/5.29177210903e-11 # m in a.u.
const au_cm = 1/5.29177210903e-9 # cm in a.u.
const au_nm = 1/5.29177210903e-2 # nm in a.u.
const au_c = 137.0359990836958 # c (speed of light) in a.u. == 1/alpha
const au_eV = 1/27.211386245935508 # eV in a.u.
const au_m_He = 7294.299386612553 # m of He nucleus in a.u.
const au_m_n = 1838.6836617324586 # m of neutron in a.u.
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 6713 | macro _laserfield_struct(Name,args...)
nfreefields = 5
defs = Any[]
for arg in args
if arg isa Symbol
nfreefields += 1
push!(defs, :($(arg)::$(Symbol(:T,nfreefields))))
elseif arg isa Expr && arg.head == :(::)
push!(defs, arg)
else
throw(ArgumentError("invalid argument to new_lf_field"))
end
end
DerivT = :LaserField
if Name isa Expr && Name.head == :(<:)
DerivT = Name.args[2]
Name = Name.args[1]
end
Ts = Symbol.(:T,1:nfreefields)
esc(quote
Base.@kwdef struct $(Name){$(Ts...)} <: $(DerivT)
is_vecpot::Bool
E0::T1
ω0::T2
t0::T3
ϕ0::T4
chirp::T5
$(defs...)
end
end)
end
# laser field with a Gaussian envelope with std dev σ
@_laserfield_struct GaussianLaserField σ
_envelope(lf::GaussianLaserField,tr) = (env = lf.E0 * exp(-tr^2/(2*lf.σ^2)); (env, -env * tr/lf.σ^2))
# F[exp(-z*t^2)] = exp(-w^2/4z)/sqrt(2z) (for real(z)>0)
_envelope_fourier(lf::GaussianLaserField,ω) = (z = 0.5/lf.σ^2 - 1im*lf.chirp; lf.E0 * exp(-ω^2/4z) / sqrt(2z))
start_time(lf::GaussianLaserField) = lf.t0 - GAUSSIAN_TIME_CUTOFF_SIGMA*lf.σ
end_time( lf::GaussianLaserField) = lf.t0 + GAUSSIAN_TIME_CUTOFF_SIGMA*lf.σ
Teff(lf::GaussianLaserField,n_photon) = lf.σ * sqrt(π/n_photon)
@_laserfield_struct SinExpLaserField T exponent
"returns the result of the integral Int(exp(i*(a*t+b*t**2)),{t,-T/2,T/2}) / sqrt(2π)"
function expiatbt2_intT(a,b,T)
iszero(b) && return sqrt(2/π)/a * sin(a*T/2)
t1 = inv(sqrt(complex(b))) # b might be negative
zz1 = (1+1im)/4 * t1 # = (1+1im)/(2*sqrt(4b))
z34 = (-1+1im)/sqrt(8) * t1 # == (-1)**(3/4) / sqrt(4b)
# the sign(b) is surprisingly not given by mathematica - not sure yet why it misses it,
# but it's necessary for agreement with the numerical fourier transform
sign(b) * (erf(z34*(a-b*T)) - erf(z34*(a+b*T))) * zz1 * cis(-a^2/4b)
end
function _envelope(lf::SinExpLaserField,tr)
trel = tr/lf.T
if abs(trel) > 0.5
(0., 0.)
else
lf.E0 .* (cospi(trel)^lf.exponent,
-lf.exponent*π/lf.T * cospi(trel)^(lf.exponent-1) * sinpi(trel))
end
end
function _envelope_fourier(lf::SinExpLaserField,ω)
isinteger(lf.exponent) || error("sin_exp fourier transform only implemented for integer exponents")
# rewrite the _envelope as a sum of exponentials, which are easy to Fourier transform over a limited time interval
# cos(πt/T)^n = 1/2^n (exp(iπt/T)+ exp(-iπt/T))^n = 1/2^n sum_k=0^n binomial(n,k) exp(i(n-2k)πt/T)
n = Int(lf.exponent)
wd = π/lf.T
res = 0im
for k = 0:n
res += binomial(n,k) * expiatbt2_intT((n-2k)*wd - ω, lf.chirp, lf.T)
end
return lf.E0/2^n * res
end
start_time(lf::SinExpLaserField) = lf.t0 - lf.T/2
end_time( lf::SinExpLaserField) = lf.t0 + lf.T/2
Teff(lf::SinExpLaserField,n_photon) = lf.T * gamma(0.5 + n_photon*lf.exponent) / (sqrt(π)*gamma(1 + n_photon*lf.exponent))
abstract type FlatTopLaserField <: LaserField end
@_laserfield_struct LinearFlatTopLaserField<:FlatTopLaserField Tflat Tramp
@_laserfield_struct Linear2FlatTopLaserField<:FlatTopLaserField Tflat Tramp
start_time(lf::FlatTopLaserField) = lf.t0 - lf.Tflat/2 - lf.Tramp
end_time( lf::FlatTopLaserField) = lf.t0 + lf.Tflat/2 + lf.Tramp
function _envelope(lf::FlatTopLaserField,tr)
# for linear field, the peak time is the middle of the interval
if abs(tr) > lf.Tflat/2 + lf.Tramp
(0., 0.)
elseif abs(tr) > lf.Tflat/2
trel = (lf.Tramp + lf.Tflat/2 - abs(tr))/lf.Tramp
lf.E0 .* (ramponfunc(lf,trel), -sign(tr)*ramponfuncpr(lf,trel) / lf.Tramp)
else
(lf.E0, 0.)
end
end
ramponfunc(::LinearFlatTopLaserField,trel) = trel
ramponfuncpr(::LinearFlatTopLaserField,trel) = 1.
ramponfunc(::Linear2FlatTopLaserField,trel) = sin(π/2*trel)^2
ramponfuncpr(::Linear2FlatTopLaserField,trel) = sin(π*trel) * π/2
function _envelope_fourier(lf::LinearFlatTopLaserField,ω)
lf.chirp == 0 || error("Fourier transform of 'linear' field with chirp not implemented!")
return lf.E0 * sqrt(8/π) * sinc(ω*lf.Tramp/2π) * sinc(ω*(lf.Tramp+lf.Tflat)/2π) * (lf.Tramp+lf.Tflat)/4
end
function _envelope_fourier(lf::Linear2FlatTopLaserField,ω)
lf.chirp == 0 || error("Fourier transform of 'linear2' field with chirp not implemented!")
return lf.E0 * sqrt(2π^3) * cos(ω*lf.Tramp/2) * sinc(ω*(lf.Tramp+lf.Tflat)/2π) * (lf.Tramp+lf.Tflat)/ (2π^2 - 2*lf.Tramp^2*ω^2)
end
Teff(lf::LinearFlatTopLaserField,n_photon) = lf.Tflat + 2*lf.Tramp / (1+2*n_photon)
Teff(lf::Linear2FlatTopLaserField,n_photon) = lf.Tflat + 2*lf.Tramp * gamma(0.5+2n_photon) / (sqrt(π)*gamma(1+2n_photon))
@_laserfield_struct InterpolatingLaserField duration datafile::String Efun Afun start_time end_time
function InterpolatingLaserField(datafile; is_vecpot)
# print('# Reading laser_field from file:', datafile)
data = readdlm(datafile)
ndims(data) == 2 && size(data,2) == 2 || error("Laser field datafile '$datafile' must contain two columns: time and field")
tt, ff = eachcol(data)
# print('# Number of data points found:', len(tt))
issorted(tt) || error("Laser field datafile '$datafile' must be sorted by time")
# analyze the data we have read to guess some information about the field
start_time = tt[1]
end_time = tt[end]
if is_vecpot
Afun = CubicSpline(ff,tt)
Efun = t -> -DataInterpolations.derivative(Afun,t)
else
Efun = CubicSpline(ff,tt)
Afun = t -> -DataInterpolations.integral(Efun,start_time,t)
end
# guess the parameters of the field - note that this is just a simple estimation, not anything rigorous
TX = Inf
E0 = 0.
Eprev = Efun(tt[1])
t0 = 0.
lastzerocrossing = -Inf
for t in LinRange(tt[1],tt[end],20*length(tt))
E = Efun(t)
if abs(E) > E0
E0 = abs(E)
t0 = t
end
if sign(E) != sign(Eprev)
TX = min(TX,2*(t-lastzerocrossing))
lastzerocrossing = t
# @show t, lastzerocrossing, TX
Eprev = E
end
end
ω0 = 2π / TX
duration = tt[end] - tt[1]
chirp = 0.
ϕ0 = 0.
InterpolatingLaserField(; is_vecpot,E0,ω0,t0,duration,chirp,ϕ0,datafile,Efun,Afun,start_time,end_time)
end
start_time(lf::InterpolatingLaserField) = lf.start_time
end_time( lf::InterpolatingLaserField) = lf.end_time
E_field(lf::InterpolatingLaserField,t) = (start_time(lf) <= t <= end_time(lf)) ? lf.Efun(t) : 0.
A_field(lf::InterpolatingLaserField,t) = (start_time(lf) <= t <= end_time(lf)) ? lf.Afun(t) : 0.
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 3799 |
"""Get a value from one of several possibly defined parameters, or a default value if none are defined.
Makes sure that at most one of the options are specified, and that at least one is given if there is no default value.
sample use: `x = @select_param args (x => args.x, x_squared => sqrt(x_squared), 0.)`
This makes it possible to call a function with either `x`, `x_squared`, or neither, and in the last case, `x` is set to 0.
"""
macro select_param(nt,options)
@assert options.head ∈ (:block,:tuple)
params = []
default = nothing
for arg in options.args
if arg isa Expr && arg.head == :call
ex = arg.args
@assert ex[1] == :(=>) && length(ex) == 3
push!(params, ex[2] => ex[3])
elseif !(arg isa LineNumberNode)
@assert isnothing(default) "Cannot have more than one default argument"
default = arg
end
end
parnamestr = join(first.(params),", ")
checkexpr(head,par) = Expr(head, :(haskey($nt,$(QuoteNode(first(par))))), last(par))
ifexpr = currif = checkexpr(:if, params[1])
for par in params[2:end]
push!(currif.args, checkexpr(:elseif, par))
currif = currif.args[end]
end
if isnothing(default)
push!(currif.args, :(error("ERROR: You need to specify one out of: ($($parnamestr))!")))
else
push!(currif.args, default)
end
esc(quote
if sum(haskey.(Ref($nt),$(first.(params)))) > 1
error("ERROR: Cannot specify more than one out of: ($($parnamestr))\npassed arguments: $($nt)")
end
$ifexpr
end)
end
# General function to make a laser field with the parameter conventions from fortran laserfields library
make_laserfield(args...; kwargs...) = LaserField(args...; kwargs...)
LaserField(d) = LaserField(; d...)
function LaserField(; form::String, is_vecpot::Bool, pargs...)
args = values(pargs)
if form == "readin"
return InterpolatingLaserField(args.datafile; is_vecpot=is_vecpot)
end
E0 = @select_param args (E0 => args.E0, intensity_Wcm2 => sqrt(args.intensity_Wcm2 * au_wcm2toel2))
ω0 = @select_param args (ω0 => args.ω0, omega => args.omega, lambda_nm => 2π*au_c / (args.lambda_nm * au_nm))
ϕ0 = @select_param args (ϕ0 => args.ϕ0, phase_pi => π*args.phase_pi, 0.)
chirp = @select_param args begin
chirp => args.chirp
linear_chirp_rate_w0as => ω0 * args.linear_chirp_rate_w0as / au_as
0.
end
t0 = @select_param args (t0 => args.t0, peak_time => args.peak_time, peak_time_as => args.peak_time_as * au_as)
duration = @select_param args (duration => args.duration, duration_as => args.duration_as * au_as)
Tramp = @select_param args (Tramp => args.Tramp, rampon => args.rampon, rampon_as => args.rampon_as * au_as, 0.)
kwargs = Dict(pairs((; is_vecpot, ϕ0, E0, ω0, t0, chirp)))
if form in ("gaussian","gaussianF")
# convert from FWHM of field to standard deviation of field
kwargs[:σ] = duration / sqrt(log(256))
return GaussianLaserField(; kwargs...)
elseif form in ("gaussian2","gaussianI")
# convert from FWHM of intensity to standard deviation of field
kwargs[:σ] = duration / sqrt(log(16))
return GaussianLaserField(; kwargs...)
elseif form in ("sin2","sin4","sin_exp")
kwargs[:T] = duration
kwargs[:exponent] = form=="sin2" ? 2 : (form=="sin4" ? 4 : args.form_exponent)
return SinExpLaserField(; kwargs...)
elseif form in ("linear","linear2")
kwargs[:Tflat] = duration
kwargs[:Tramp] = Tramp
lftype = form=="linear" ? LinearFlatTopLaserField : Linear2FlatTopLaserField
return lftype(; kwargs...)
else
error("Unknown laser field form '$form'")
end
end
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 2026 | using SnoopPrecompile
@precompile_setup let
general_args = (is_vecpot=true,E0=1.5,ω0=0.12,t0=500.,chirp=0.,ϕ0=0.8π)
test_fields = [
GaussianLaserField(; general_args...,σ=100.),
SinExpLaserField(; general_args...,T=800.,exponent=2),
SinExpLaserField(; general_args...,T=800.,exponent=4),
SinExpLaserField(; general_args...,T=800.,exponent=7),
LinearFlatTopLaserField(; general_args...,Tflat=400.,Tramp=150),
Linear2FlatTopLaserField(;general_args...,Tflat=400.,Tramp=150),
]
lfc = LaserFieldCollection(test_fields)
@precompile_all_calls begin
ts = LinRange(0,1000,1001)
for lf in (test_fields..., lfc)
lf.(ts)
A_field.(lf,ts)
try
envelope.(lf,ts)
catch
end
end
test_fields_fourier = filter(test_fields) do lf
try
E_fourier(lf,1.)
return true
catch
return false
end
end
ts = LinRange(0,10000,10001)
ωs = LinRange(0,0.2,1001)[2:end]
for lf in test_fields_fourier
EF = E_fourier.(lf,ωs)
AF = A_fourier.(lf,ωs)
E = E_field.(lf,ts)
A = A_field.(lf,ts)
end
lf = LaserField(form="gaussianI",is_vecpot=true,intensity_Wcm2=1e14,lambda_nm=45.,
peak_time_as=0,duration_as=1000.,ϕ0=0.3π,linear_chirp_rate_w0as=1e-4)
ts = LinRange(-100,100,2001)
A_field.(lf,ts)
A_fourier.(lf,ωs)
A_fourier.(lf,ωs)
lf = make_laserfield(form="gaussianI", is_vecpot=true, phase_pi=1, duration_as=100.,
peak_time_as=400, intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
lf = GaussianLaserField(; is_vecpot=true, ϕ0=π, E0=1., ω0=1., t0=0., σ=1., chirp=0.)
ts = start_time(lf):TX(lf)/100:end_time(lf)
lf.(ts)
end
end | LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 3402 | abstract type LaserField end
Base.Broadcast.broadcastable(lf::LaserField) = Ref(lf)
TX(lf::LaserField) = 2π/lf.ω0
(lf::LaserField)(t) = E_field(lf,t)
envelope(lf::LaserField,t) = _envelope(lf,t-lf.t0)[1]
function E_field(lf::LaserField,t)
tr = t - lf.t0
env, envpr = _envelope(lf,tr)
ϕt = lf.ϕ0 + lf.ω0*tr + lf.chirp*tr^2
osc = sin(ϕt)
if lf.is_vecpot
# dϕ/dt = ω0 + 2 chirp tr
oscpr = (lf.ω0 + 2lf.chirp*tr)*cos(ϕt)
return -(env * oscpr + envpr * osc) / lf.ω0
else # describes electric field directly
return env * osc
end
end
function A_field(lf::LaserField,t)
lf.is_vecpot || error("laser field is not given as a vector potential, cannot get A(t) analytically!")
tr = t - lf.t0
env, _ = _envelope(lf,tr)
osc = sin(lf.ϕ0 + lf.ω0*tr + lf.chirp*tr^2)
# Divide out derivative of oscillation to ensure peak amplitude of E0 for electric field
return env*osc / lf.ω0
end
"""Return the fourier transform of the envelope of the laser field.
We write the whole pulse as
f(t) = (env(t) exp(i*(phi0 + ω0*tr + chirp*tr^2)) + c.c. ) / 2im, where tr = t-tpeak
For the fourier transform of the envelope, we include the chirp term
exp(i chirp (t-tpeak)^2) in the envelope, so that its fourier transform is a complex function.
However, for unchirped pulses, the result will be purely real."""
function _envelope_fourier end
function E_fourier(lf::LaserField,ω)
# analytically determine the fourier transform of the defined laser fields
# determined as Int exp(-i*ω*t) E(t) dt
# with tr = t-tpeak, the whole pulse is
# f(t) = env(t) sin (phi0 + ω0*tr + chirp*tr^2)
# = (env(t) exp(IU*(phi0 + ω0*tr + chirp*tr^2)) - c.c. ) / 2im
# for the fourier transform, we include the chirp term exp(i chirp tr^2) in the envelope.
# this part is transformed in lf_envelope_fourier.
# exp(IU*phi0) is just a constant prefactor, and the linear phase ω0*tr just gives a shift in frequency,
# F[f(t) exp(im ω0 t)](ω) = F[f(t)](ω-ω0)
# complex conjugation of the transformed function gives complex conjugation + reversal of the argument in the transform, so
# F[conjg(f(t) exp(im ω0 t))](ω) = conjg(F[f(t) exp(IU ω0 t)](-ω)) = conjg(F[f(t)](-ω-ω0))
ELFT = ( _envelope_fourier(lf, ω-lf.ω0) * cis(lf.ϕ0)
- (_envelope_fourier(lf,-ω-lf.ω0) * cis(lf.ϕ0))') / 2im
# the fourier transform of the part was determined as if it was centered around t=0
# shift in time now -- just adds a phase exp(-im*ω*t0), as F[f(t-a)] = exp(-im*ω*a) F[f(t)]
ELFT *= cis(-ω*lf.t0)
if lf.is_vecpot
# if this laser field was defined as a vector potential, we need to multiply
# with -im*ω to get the fourier transform of the electric field:
# E = -dA/dt --> F[-dA/dt] = -iω F[A]
# in addition, we need to take into account that A0 = E0 / lf.ω0
ELFT *= -1im * ω / lf.ω0
end
return ELFT
end
A_fourier(lf::LaserField,ω) = E_fourier(lf,ω) / (-1im*ω)
struct LaserFieldCollection{T} <: LaserField
lfs::T
end
start_time(lf::LaserFieldCollection) = minimum(start_time, lf.lfs)
end_time(lf::LaserFieldCollection) = maximum(end_time, lf.lfs)
TX(lf::LaserFieldCollection) = minimum(TX, lf.lfs)
for f in (:E_field, :A_field, :E_fourier, :A_fourier, :envelope)
@eval $f(lf::LaserFieldCollection, t) = sum(Base.Fix2($f,t), lf.lfs)
end
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | code | 6028 | using LaserFields
using Test
@testset "LaserFields.jl" begin
using LaserFields
using LaserFields: GaussianLaserField, SinExpLaserField, LinearFlatTopLaserField, Linear2FlatTopLaserField, InterpolatingLaserField
general_args = (is_vecpot=true, E0=1.5, ω0=0.12, t0=500., chirp=0., ϕ0=0.8π)
test_fields = [
GaussianLaserField(; general_args..., σ=100.),
SinExpLaserField(; general_args..., T=800., exponent=2),
SinExpLaserField(; general_args..., T=800., exponent=4),
SinExpLaserField(; general_args..., T=800., exponent=7),
LinearFlatTopLaserField(; general_args..., Tflat=400., Tramp=150),
Linear2FlatTopLaserField(;general_args..., Tflat=400., Tramp=150),
]
@testset "General arguments" for lf in test_fields
@test lf.is_vecpot == true
@test lf.E0 == 1.5
@test lf.ω0 == 0.12
@test lf.t0 == 500
@test lf.chirp == 0.0
@test lf.ϕ0 == 0.8π
end
@testset "LaserFieldCollection" begin
lfc = LaserFieldCollection(test_fields)
@test lfc isa LaserFieldCollection
@test length(lfc.lfs) == 6
@test lfc(500.) == sum(lf(500.) for lf in test_fields)
@test E_field(lfc, 300.) == sum(E_field(lf, 300.) for lf in test_fields)
@test A_field(lfc, 300.) == sum(A_field(lf, 300.) for lf in test_fields)
@test E_fourier(lfc, 1.) == sum(E_fourier(lf, 1.) for lf in test_fields)
@test A_fourier(lfc, 1.) == sum(A_fourier(lf, 1.) for lf in test_fields)
@test start_time(lfc) == minimum(start_time, test_fields)
@test end_time(lfc) == maximum(end_time, test_fields)
end
@testset "read-in field vecpot" begin
lf = InterpolatingLaserField("laserdat.dat", is_vecpot=true)
@test lf.is_vecpot == true
@test lf.E0 == 0.15985607526339093
@test lf.ω0 == 0.16132596121126513
@test lf.t0 == 353.37042585063125
@test lf.duration == 700.0
@test lf.ϕ0 == 0.0
@test lf.chirp == 0.0
@test lf.datafile == "laserdat.dat"
@test start_time(lf) == 0.0
@test end_time(lf) == 700.0
end
@testset "read-in field e-field" begin
lf = InterpolatingLaserField("laserdat.dat", is_vecpot=false)
@test lf.is_vecpot == false
@test lf.E0 == 0.996830886761803
@test lf.ω0 == 0.16009446532415655
@test lf.t0 == 343.63364005991866
@test lf.duration == 700.0
@test lf.ϕ0 == 0.0
@test lf.chirp == 0.0
@test lf.datafile == "laserdat.dat"
@test start_time(lf) == 0.0
@test end_time(lf) == 700.0
end
@testset "LaserField" begin
@testset "working" begin
lf = LaserField(form="gaussianI", is_vecpot=true, phase_pi=1, duration_as=100.,
peak_time_as=400, intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
@test lf isa GaussianLaserField
@test lf.is_vecpot == true
@test lf.σ == 100. * LaserFields.au_as / sqrt(log(16.))
@test lf.t0 == 400. * LaserFields.au_as
@test lf(lf.t0) == lf.E0
@test lf.ϕ0 ≈ π
end
@testset "overspecified parameters" begin
@test_throws ErrorException LaserField(form="gaussianI", is_vecpot=true, phase_pi=0.5, duration=10., duration_as=100.,
peak_time_as=400, intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
@test_throws ErrorException LaserField(form="gaussianI", is_vecpot=true, phase_pi=0.5, duration_as=100.,
peak_time=0., peak_time_as=400, intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
@test_throws ErrorException LaserField(form="gaussianI", is_vecpot=true, phase_pi=0.5, duration_as=100.,
peak_time_as=400, E0=0.3, intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
end
@testset "missing parameters" begin
@test_throws ErrorException LaserField(form="gaussianI", is_vecpot=true, phase_pi=0.5,
peak_time_as=400, intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
@test_throws ErrorException LaserField(form="gaussianI", is_vecpot=true, phase_pi=0.5, duration_as=100.,
intensity_Wcm2=1e14, lambda_nm=12., linear_chirp_rate_w0as=0.)
@test_throws ErrorException LaserField(form="gaussianI", is_vecpot=true, phase_pi=0.5, duration_as=100.,
peak_time_as=400, lambda_nm=12., linear_chirp_rate_w0as=0.)
end
end
@testset "Teff" begin
refTs = Dict("gaussianI" => [ 1064.4670194312, 752.69184778925, 614.5703202121, 532.23350971561, 476.04412305096 ],
"gaussianF" => [ 752.69184778925, 532.23350971561, 434.56684093796, 376.34592389463, 336.61402755334 ],
"sin2" => [ 375, 273.4375, 225.5859375, 196.38061523438, 176.19705200195 ],
"sin4" => [ 273.4375, 196.38061523438, 161.18025779724, 139.94993409142, 125.37068761958 ],
"linear" => [ 1066.6666666667, 1040, 1028.5714285714, 1022.2222222222, 1018.1818181818 ],
"linear2" => [ 1075, 1054.6875, 1045.1171875, 1039.2761230469, 1035.2394104004 ])
for (form, Teffs) in refTs
for (n_photon, T) in enumerate(Teffs)
lf = LaserField(form=form, is_vecpot=true, duration=1000., rampon=100., E0=1., omega=1., t0=0.)
@test Teff(lf,n_photon) ≈ T
end
end
end
end
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | docs | 2414 | # LaserFields
[](https://jfeist.github.io/LaserFields.jl/stable/)
[](https://jfeist.github.io/LaserFields.jl/dev/)
[](https://github.com/jfeist/LaserFields.jl/actions/workflows/CI.yml?query=branch%3Amain)
[](https://codecov.io/gh/jfeist/LaserFields.jl)
`LaserFields.jl` is a library to describe the time-dependent electric fields of
a laser pulse. It implements the same pulse shapes and most of the features of
the [laserfields library](https://github.com/jfeist/laserfields) written in
Fortran. Please see the documentation of that library for the parameter
meanings, conventions used, etc. In particular, the "main" constructor
`LaserField(; kwargs...)` accepts the same parameters as the Fortran library
parameter files as keyword arguments, and returns an instance of a subtype of
the abstract base type `LaserField` depending on the parameters. E.g., to create
a Gaussian pulse with a duration (defined as the FWHM of the intensity) of 6 fs,
a wavelength of 800 nm, a peak intensity of 1e14 W/cm^2, and with the peak at
time t=7fs, one should call
```julia
lf = LaserField(form="gaussianI", is_vecpot=true, lambda_nm=800,
intensity_Wcm2=1e16, duration_as=6000, peak_time_as=7000)
```
Given a `LaserField` instance `lf`, the functions `E_field(lf,t)`,
`E_fourier(lf,ω)`, `A_field(lf,t)`, and `A_fourier(lf,ω)` can be used to obtain,
respectively, the electric field as a function of time, its Fourier transform
(implemented for most pulse shapes), the vector potential as a function of time,
and its Fourier transform. Calling the instance as a function, `lf(t)` returns
the electric field, i.e., is equivalent to `E_field(lf,t)`. The notebooks in the
`examples` folder show some ways to use the library, including how to define a
set of fields through a YAML configuration file.
The "effective" duration of the pulse for n-photon processes can be obtained as
`Teff(lf,n_photon)`, which is the integral over the pulse intensity envelope to
the n-th power (i.e., electric field envelope to the (2n)th power) over the
pulse, see, e.g., https://doi.org/10.1103/PhysRevA.77.043420 (Eq. 14).
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 0.1.4 | 76fae9f07d0a30cd8e979df6cfd538ee1e80a0b2 | docs | 189 | ```@meta
CurrentModule = LaserFields
```
# LaserFields
Documentation for [LaserFields](https://github.com/jfeist/LaserFields.jl).
```@index
```
```@autodocs
Modules = [LaserFields]
```
| LaserFields | https://github.com/jfeist/LaserFields.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 505 | using Documenter, NeuralNetDiffEq
makedocs(
sitename = "NeuralNetDiffEq.jl",
authors="#",
clean = true,
doctest = false,
modules = [NeuralNetDiffEq],
format = Documenter.HTML(#analytics = "",
assets = ["assets/favicon.ico"],
canonical="#"),
pages=[
"Home" => "index.md",
"Tutorials" => Any[
],
]
)
deploydocs(
repo = "github.com/SciML/NeuralNetDiffEq.jl.git";
push_preview = true
)
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 2097 | module NeuralNetDiffEq
using Reexport, Statistics
@reexport using DiffEqBase
using Flux, Zygote, DiffEqSensitivity, ForwardDiff, Random, Distributions
using DiffEqFlux, Adapt, CuArrays
import Tracker, Optim
abstract type NeuralNetDiffEqAlgorithm <: DiffEqBase.AbstractODEAlgorithm end
struct TerminalPDEProblem{G,F,Mu,Sigma,X,T,P} <: DiffEqBase.DEProblem
g::G
f::F
μ::Mu
σ::Sigma
X0::X
tspan::Tuple{T,T}
p::P
TerminalPDEProblem(g,f,μ,σ,X0,tspan,p=nothing) = new{typeof(g),typeof(f),
typeof(μ),typeof(σ),
typeof(X0),eltype(tspan),
typeof(p)}(
g,f,μ,σ,X0,tspan,p)
end
Base.summary(prob::TerminalPDEProblem) = string(nameof(typeof(prob)))
function Base.show(io::IO, A::TerminalPDEProblem)
println(io,summary(A))
print(io,"timespan: ")
show(io,A.tspan)
end
struct KolmogorovPDEProblem{ F, G, Phi, X , T , D ,P,U0, ND} <: DiffEqBase.DEProblem
f::F
g::G
phi::Phi
xspan::Tuple{X,X}
tspan::Tuple{T,T}
d::D
p::P
u0::U0
noise_rate_prototype::ND
KolmogorovPDEProblem( f, g, phi , xspan , tspan , d, p=nothing, u0=0 , noise_rate_prototype= nothing) = new{typeof(f),typeof(g),typeof(phi),eltype(tspan),eltype(xspan),typeof(d),typeof(p),typeof(u0),typeof(noise_rate_prototype)}(f,g,phi,xspan,tspan,d,p,u0,noise_rate_prototype)
end
Base.summary(prob::KolmogorovPDEProblem) = string(nameof(typeof(prob)))
function Base.show(io::IO, A::KolmogorovPDEProblem)
println(io,summary(A))
print(io,"timespan: ")
show(io,A.tspan)
print(io,"xspan: ")
show(io,A.xspan)
println(io , "μ")
show(io , A.f)
println(io,"Sigma")
show(io , A.g)
end
include("ode_solve.jl")
include("pde_solve.jl")
include("pde_solve_ns.jl")
include("kolmogorov_solve.jl")
include("stopping_solve.jl")
export NNODE, TerminalPDEProblem, NNPDEHan, NNPDENS, KolmogorovPDEProblem, NNKolmogorov, NNStopping
end # module
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 2429 | struct NNKolmogorov{C,O,S,E} <: NeuralNetDiffEqAlgorithm
chain::C
opt::O
sdealg::S
ensemblealg::E
end
NNKolmogorov(chain ; opt=Flux.ADAM(0.1) , sdealg = EM() , ensemblealg = EnsembleThreads()) = NNKolmogorov(chain , opt , sdealg , ensemblealg)
function DiffEqBase.solve(
prob::Union{KolmogorovPDEProblem,SDEProblem},
alg::NNKolmogorov;
abstol = 1f-6,
verbose = false,
maxiters = 300,
trajectories = 1000,
save_everystep = false,
use_gpu = false,
dt,
dx,
kwargs...
)
tspan = prob.tspan
sigma = prob.g
μ = prob.f
noise_rate_prototype = prob.noise_rate_prototype
if prob isa SDEProblem
xspan = prob.kwargs.data.xspan
d = prob.kwargs.data.d
u0 = prob.u0
phi(xi) = pdf(u0 , xi)
else
xspan = prob.xspan
d = prob.d
phi = prob.phi
end
ts = tspan[1]:dt:tspan[2]
xs = xspan[1]:dx:xspan[2]
N = size(ts)
T = tspan[2]
#hidden layer
chain = alg.chain
opt = alg.opt
sdealg = alg.sdealg
ensemblealg = alg.ensemblealg
ps = Flux.params(chain)
xi = rand(xs ,d ,trajectories)
#Finding Solution to the SDE having initial condition xi. Y = Phi(S(X , T))
sdeproblem = SDEProblem(μ,sigma,xi,tspan,noise_rate_prototype = noise_rate_prototype)
function prob_func(prob,i,repeat)
SDEProblem(prob.f , prob.g , xi[: , i] , prob.tspan ,noise_rate_prototype = prob.noise_rate_prototype)
end
output_func(sol,i) = (sol[end],false)
ensembleprob = EnsembleProblem(sdeproblem , prob_func = prob_func , output_func = output_func)
sim = solve(ensembleprob, sdealg, ensemblealg , dt=dt, trajectories=trajectories,adaptive=false)
x_sde = reshape([],d,0)
# sol = solve(sdeproblem, sdealg ,dt=0.01 , save_everystep=false , kwargs...)
# x_sde = sol[end]
for u in sim.u
x_sde = hcat(x_sde , u)
end
y = phi(x_sde)
if use_gpu == true
y = y |>gpu
xi = xi |> gpu
end
data = Iterators.repeated((xi , y), maxiters)
if use_gpu == true
data = data |>gpu
end
#MSE Loss Function
loss(x , y) =Flux.mse(chain(x), y)
cb = function ()
l = loss(xi, y)
verbose && println("Current loss is: $l")
l < abstol && Flux.stop()
end
Flux.train!(loss, ps, data, opt; cb = cb)
chainout = chain(xi)
xi , chainout
end #solve
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 2924 | struct NNODE{C,O,P,K} <: NeuralNetDiffEqAlgorithm
chain::C
opt::O
initθ::P
autodiff::Bool
kwargs::K
end
function NNODE(chain,opt=Optim.BFGS(),init_params = nothing;autodiff=false,kwargs...)
if init_params === nothing
if chain isa FastChain
initθ = DiffEqFlux.initial_params(chain)
else
initθ,re = Flux.destructure(chain)
end
else
initθ = init_params
end
NNODE(chain,opt,initθ,autodiff,kwargs)
end
function DiffEqBase.solve(
prob::DiffEqBase.AbstractODEProblem,
alg::NeuralNetDiffEqAlgorithm,
args...;
dt,
timeseries_errors = true,
save_everystep=true,
adaptive=false,
abstol = 1f-6,
verbose = false,
maxiters = 100)
DiffEqBase.isinplace(prob) && error("Only out-of-place methods are allowed!")
u0 = prob.u0
tspan = prob.tspan
f = prob.f
p = prob.p
t0 = tspan[1]
#hidden layer
chain = alg.chain
opt = alg.opt
autodiff = alg.autodiff
#train points generation
ts = tspan[1]:dt:tspan[2]
initθ = alg.initθ
if chain isa FastChain
#The phi trial solution
if u0 isa Number
phi = (t,θ) -> u0 + (t-tspan[1])*first(chain(adapt(typeof(θ),[t]),θ))
else
phi = (t,θ) -> u0 + (t-tspan[1]) * chain(adapt(typeof(θ),[t]),θ)
end
else
_,re = Flux.destructure(chain)
#The phi trial solution
if u0 isa Number
phi = (t,θ) -> u0 + (t-tspan[1])*first(re(θ)(adapt(typeof(θ),[t])))
else
phi = (t,θ) -> u0 + (t-tspan[1]) * re(θ)(adapt(typeof(θ),[t]))
end
end
try
phi(t0 , initθ)
catch err
if isa(err , DimensionMismatch)
throw( throw(DimensionMismatch("Dimensions of the initial u0 and chain should match")))
else
throw(err)
end
end
if autodiff
dfdx = (t,θ) -> ForwardDiff.derivative(t->phi(t,θ),t)
else
dfdx = (t,θ) -> (phi(t+sqrt(eps(t)),θ) - phi(t,θ))/sqrt(eps(t))
end
function inner_loss(t,θ)
sum(abs2,dfdx(t,θ) - f(phi(t,θ),p,t))
end
loss(θ) = sum(abs2,inner_loss(t,θ) for t in ts) # sum(abs2,phi(tspan[1],θ) - u0)
cb = function (p,l)
verbose && println("Current loss is: $l")
l < abstol
end
res = DiffEqFlux.sciml_train(loss, initθ, opt; cb = cb, maxiters=maxiters, alg.kwargs...)
#solutions at timepoints
if u0 isa Number
u = [first(phi(t,res.minimizer)) for t in ts]
else
u = [phi(t,res.minimizer) for t in ts]
end
sol = DiffEqBase.build_solution(prob,alg,ts,u,calculate_error = false)
DiffEqBase.has_analytic(prob.f) && DiffEqBase.calculate_solution_errors!(sol;timeseries_errors=true,dense_errors=false)
sol
end #solve
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 1417 | struct NNPDEHan{C1,C2,O} <: NeuralNetDiffEqAlgorithm
u0::C1
σᵀ∇u::C2
opt::O
end
NNPDEHan(u0,σᵀ∇u;opt=Flux.ADAM(0.1)) = NNPDEHan(u0,σᵀ∇u,opt)
function DiffEqBase.solve(
prob::TerminalPDEProblem,
alg::NNPDEHan;
abstol = 1f-6,
verbose = false,
maxiters = 300,
save_everystep = false,
dt,
trajectories)
X0 = prob.X0
ts = prob.tspan[1]:dt:prob.tspan[2]
d = length(X0)
g,f,μ,σ,p = prob.g,prob.f,prob.μ,prob.σ,prob.p
data = Iterators.repeated((), maxiters)
#hidden layer
opt = alg.opt
u0 = alg.u0
σᵀ∇u = alg.σᵀ∇u
ps = Flux.params(u0, σᵀ∇u...)
function sol()
map(1:trajectories) do j
u = u0(X0)[1]
X = X0
for i in 1:length(ts)-1
t = ts[i]
_σᵀ∇u = σᵀ∇u[i](X)
dW = sqrt(dt)*randn(d)
u = u - f(X, u, _σᵀ∇u, p, t)*dt + _σᵀ∇u'*dW
X = X .+ μ(X,p,t)*dt .+ σ(X,p,t)*dW
end
X,u
end
end
function loss()
mean(sum(abs2,g(X) - u) for (X,u) in sol())
end
iters = eltype(X0)[]
cb = function ()
save_everystep && push!(iters, u0(X0)[1])
l = loss()
verbose && println("Current loss is: $l")
l < abstol && Flux.stop()
end
Flux.train!(loss, ps, data, opt; cb = cb)
save_everystep ? iters : u0(X0)[1]
end #pde_solve
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 2691 | struct NNPDENS{C1,C2,O} <: NeuralNetDiffEqAlgorithm
u0::C1
σᵀ∇u::C2
opt::O
end
NNPDENS(u0,σᵀ∇u;opt=Flux.ADAM(0.1)) = NNPDENS(u0,σᵀ∇u,opt)
function DiffEqBase.solve(
prob::TerminalPDEProblem,
pdealg::NNPDENS;
verbose = false,
maxiters = 300,
trajectories = 100,
alg,
pabstol = 1f-6,
save_everystep = false,
kwargs...)
X0 = prob.X0
tspan = prob.tspan
d = length(X0)
g,f,μ,σ = prob.g,prob.f,prob.μ,prob.σ
p = prob.p isa AbstractArray ? prob.p : Float32[]
data = Iterators.repeated((), maxiters)
#hidden layer
opt = pdealg.opt
u0 = pdealg.u0
σᵀ∇u = pdealg.σᵀ∇u
p1,_re1 = Flux.destructure(u0)
p2,_re2 = Flux.destructure(σᵀ∇u)
p3 = [p1;p2;p]
ps = Flux.params(p3)
re1 = p -> _re1(p[1:length(p1)])
re2 = p -> _re2(p[(length(p1)+1):(length(p1)+length(p2))])
re3 = p -> p[(length(p1)+length(p2)+1):end]
function F(h, p, t)
u = h[end]
X = h[1:end-1]
_σᵀ∇u = re2(p)([X;t])
_p = re3(p)
_f = -f(X, u, _σᵀ∇u, _p, t)
vcat(μ(X,_p,t),[_f])
end
function G(h, p, t)
X = h[1:end-1]
_p = re3(p)
_σᵀ∇u = re2(p)([X;t])'
vcat(σ(X,_p,t),_σᵀ∇u)
end
function F(h::Tracker.TrackedArray, p, t)
u = h[end]
X = h[1:end-1].data
_σᵀ∇u = σᵀ∇u([X;t])
_f = -f(X, u, _σᵀ∇u, p, t)
Tracker.collect(vcat(μ(X,p,t),[_f]))
end
function G(h::Tracker.TrackedArray, p, t)
X = h[1:end-1].data
_σᵀ∇u = σᵀ∇u([X;t])'
Tracker.collect(vcat(σ(X,p,t),_σᵀ∇u))
end
noise = zeros(Float32,d+1,d)
prob = SDEProblem{false}(F, G, [X0;0f0], tspan, p3, noise_rate_prototype=noise)
function neural_sde(init_cond)
map(1:trajectories) do j #TODO add Ensemble Simulation
predict_ans = Array(concrete_solve(prob, alg, init_cond, p3;
save_everystep=false,
sensealg=TrackerAdjoint(),kwargs...))[:,end]
(X,u) = (predict_ans[1:(end-1)], predict_ans[end])
end
end
function predict_n_sde()
_u0 = re1(p3)(X0)
init_cond = [X0;_u0]
neural_sde(init_cond)
end
function loss_n_sde()
mean(sum(abs2, g(X) - u) for (X,u) in predict_n_sde())
end
iters = eltype(X0)[]
cb = function ()
save_everystep && push!(iters, u0(X0)[1])
l = loss_n_sde()
verbose && println("Current loss is: $l")
l < pabstol && Flux.stop()
end
Flux.train!(loss_n_sde, ps, data, opt; cb = cb)
save_everystep ? iters : re1(p3)(X0)[1]
end #pde_solve_ns
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 2387 | struct NNStopping{C,O,S,E} <: NeuralNetDiffEqAlgorithm
chain::C
opt::O
sdealg::S
ensemblealg::E
end
NNStopping(chain ; opt=Flux.ADAM(0.1) , sdealg = EM() , ensemblealg = EnsembleThreads()) = NNStopping(chain , opt , sdealg , ensemblealg)
function DiffEqBase.solve(
prob::SDEProblem,
alg::NNStopping;
abstol = 1f-6,
verbose = false,
maxiters = 300,
trajectories = 1000,
save_everystep = false,
dt,
kwargs...
)
tspan = prob.tspan
sigma = prob.g
μ = prob.f
g = prob.kwargs.data.g
u0 = prob.u0
ts = tspan[1]:dt:tspan[2]
N = size(ts)[1]
T = tspan[2]
m = alg.chain
opt = alg.opt
sdealg = alg.sdealg
ensemblealg = alg.ensemblealg
prob = SDEProblem(μ,sigma,u0,tspan)
ensembleprob = EnsembleProblem(prob)
sim = solve(ensembleprob, sdealg, ensemblealg, dt=dt,trajectories=trajectories,adaptive=false)
payoff = []
times = []
iter = 0
# for u in sim.u
un = []
function Un(n , X )
if size(un)[1] >= n
return un[n]
else
if(n == 1)
ans = first(m(X[1])[1])
un = [ans]
return ans
else
ans = max(first(m(X[n])[n]) , n + 1 - size(ts)[1])*(1 - sum(Un(i , X ) for i in 1:n-1))
un = vcat( un , ans)
return ans
end
end
end
function loss()
reward = 0.00
for u in sim.u
X = u.u
reward = reward + sum(Un(i , X )*g(ts[i] , X[i]) for i in 1 : size(ts)[1])
un = []
end
return 10000 - reward
end
dataset = Iterators.repeated(() , maxiters)
cb = function ()
l = loss()
un = []
println("Current loss is: $l")
end
Flux.train!(loss, Flux.params(m), dataset, opt; cb = cb)
Usum = 0
ti = 0
Xt = sim.u[1].u
for i in 1:N
un = []
Usum = Usum + Un(i , Xt)
if Usum >= 1 - Un(i , Xt)
ti = i
break
end
end
for u in sim.u
X = u.u
price = g(ts[ti] , X[ti])
payoff = vcat(payoff , price)
times = vcat(times, ti)
iter = iter + 1
# println("SUM : $sump")
# println("TIME : $ti")
end
sum(payoff)/size(payoff)[1]
end #solve
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 3390 | using Test, Flux, StochasticDiffEq
println("Kolmogorov Tests")
using DiffEqDevTools , NeuralNetDiffEq
using Distributions
#Using SDEProblem for the Algorithm.
# For a diract delta take u0 = Normal(0 , sigma) where sigma --> 0
u0 = Normal(1.00 , 1.00)
xspan = (-2.0 , 6.0)
tspan = (0.0 , 1.0)
g(u , p , t) = 2.00
f(u , p , t) = -2.00
d = 1
sdealg = EM()
prob = SDEProblem(f , g , u0 , (0.0 , 1.0) ; xspan = xspan , d = d)
opt = Flux.ADAM(0.01)
m = Chain(Dense(1, 5, elu),Dense(5, 5, elu) , Dense(5 , 5 , elu) , Dense(5 , 1))
ensemblealg = EnsembleThreads()
sol = solve(prob, NNKolmogorov(m,opt , sdealg,ensemblealg) , verbose = true, dt = 0.01,
abstol=1e-10, dx = 0.0001 , trajectories = 100000 , maxiters = 500)
# using Plots
#
# x_val = collect(xs)
# x_val= reshape(x_val , 1 , size(x_val)[1])
# y_val = m(x_val)
# y_val = reshape(y_val , 800001 , 1)
# x_val = collect(xs)
# plot(x_val , y_val,linewidth=3,title="Solution to the linear ODE with a thick line",
# xaxis="Time (t)",yaxis="u(t) (in μm)",label="My Thick Line!")
# # plot(x_val , y_val)
# plot!(x_val , analytical(x_val),linewidth=3,title="Solution to the linear ODE with a thick line",
# xaxis="Time (t)",yaxis="u(t) (in μm)",label="My Thick Line!")
#
## The solution is obtained taking the Fourier Transform.
analytical(xi) = pdf.(Normal(3 , sqrt(1.0 + 5.00)) , xi)
##Validation
xs = -5:0.00001:5
x_1 = rand(xs , 1 , 1000)
err_l2 = Flux.mse(analytical(x_1) , m(x_1))
@test err_l2 < 0.01
##
##Using the KolmogorovPDEProblem.
function phi(xi)
y = Float64[]
for x in xi
y = push!(y , 1.77*x -0.015*x^3)
end
y = reshape(y , size(xi)[1] , size(xi)[2] )
return y
end
xspan2 = (-6.0 , 6.0)
tspan2 = (0.0 , 1.0)
#f = mu and g = sigma
g2(u , p , t) = 0.5*u
f2(u , p , t) = 0.5*0.25*u
d2 = 1
sdealg2 = EM()
prob2 = KolmogorovPDEProblem(f2 , g2, phi , xspan2 , tspan2, d2)
opt2 = Flux.ADAM(0.01)
m2 = Chain(Dense(1, 16, elu) , Dense(16 , 32 , elu),Dense(32 , 16 , elu), Dense(16 , 1))
sol = solve(prob2, NeuralNetDiffEq.NNKolmogorov(m2,opt2 , sdealg2, ensemblealg), verbose = true, dt = 0.01,
dx = 0.0001 , trajectories = 1000 , abstol=1e-6, maxiters = 300)
function analytical2(xi)
y = Float64[]
a = 1.77*exp(0.5*(0.5)^2*1.0)
b = -0.015*exp(0.5*(0.5*3)^2*1.0)
for x in xi
y = push!(y , a*x + b*x^3)
end
y = reshape(y , size(xi)[1] , size(xi)[2] )
return y
end
xs2 = -5.00:0.01:5.00
x_val2 = rand(xs2 , d2 , 50)
errorl2 = Flux.mse(analytical2(x_val2) , m2(x_val2))
println("error_l2 = ", errorl2, "\n")
@test errorl2 < 0.4
##Non-Diagonal Test
f_noise = (du,u,p,t) -> du.=1.01u
g_noise = function (du,u,p,t)
du[1,1] = 0.3u[1]
du[1,2] = 0.6u[1]
du[1,3] = 0.9u[1]
du[1,4] = 0.12u[2]
du[2,1] = 1.2u[1]
du[2,2] = 0.2u[2]
du[2,3] = 0.3u[2]
du[2,4] = 1.8u[2]
end
Σ = [1.0 0.3 ; 0.3 1.0]
uo3 = MvNormal([0.0 ; 0.0], Σ)
sdealg3= EM()
xspan3 = (-10.0 , 10.0)
tspan3 = (0.0 , 1.0)
d3 = 2
prob = SDEProblem(f_noise , g_noise , uo3 , (0.0 , 1.0) ; xspan = xspan3 , d = d3 , noise_rate_prototype=zeros(2,4))
opt = Flux.ADAM(0.01)
m3 = Chain(Dense(d3, 32, elu) ,Dense(32 , 64 , elu), Dense(64 , 1))
sol3 = solve(prob, NeuralNetDiffEq.NNKolmogorov(m3,opt , sdealg3 , EnsembleThreads()), verbose = true, dt = 0.001,
abstol=1e-6, dx = 0.001, trajectories = 1000,maxiters = 200)
println("Non-Diagonal test working.")
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 2097 | using Test, Flux, Optim
println("NNODE Tests")
using DiffEqDevTools , NeuralNetDiffEq
using Random
Random.seed!(100)
# Run a solve on scalars
linear = (u,p,t) -> cos(2pi*t)
tspan = (0.0f0, 1.0f0)
u0 = 0.0f0
prob = ODEProblem(linear, u0 ,tspan)
chain = Flux.Chain(Dense(1,5,σ),Dense(5,1))
opt = Flux.ADAM(0.1, (0.9, 0.95))
sol = solve(prob, NeuralNetDiffEq.NNODE(chain,opt), dt=1/20f0, verbose = true,
abstol=1e-10, maxiters = 200)
opt = BFGS()
sol = solve(prob, NeuralNetDiffEq.NNODE(chain,opt), dt=1/20f0, verbose = true,
abstol=1e-10, maxiters = 200)
# Run a solve on vectors
linear = (u,p,t) -> [cos(2pi*t)]
tspan = (0.0f0, 1.0f0)
u0 = [0.0f0]
prob = ODEProblem(linear, u0 ,tspan)
chain = Flux.Chain(Dense(1,5,σ),Dense(5,1))
opt = BFGS()
sol = solve(prob, NeuralNetDiffEq.NNODE(chain,opt), dt=1/20f0, abstol=1e-10,
verbose = true, maxiters=200)
#Example 1
linear = (u,p,t) -> @. t^3 + 2*t + (t^2)*((1+3*(t^2))/(1+t+(t^3))) - u*(t + ((1+3*(t^2))/(1+t+t^3)))
linear_analytic = (u0,p,t) -> [exp(-(t^2)/2)/(1+t+t^3) + t^2]
prob = ODEProblem(ODEFunction(linear,analytic=linear_analytic),[1f0],(0.0f0,1.0f0))
chain = Flux.Chain(Dense(1,128,σ),Dense(128,1))
opt = ADAM(0.01)
sol = solve(prob,NeuralNetDiffEq.NNODE(chain,opt),verbose = true, dt=1/5f0, maxiters=200)
@test sol.errors[:l2] < 0.5
#=
dts = 1f0 ./ 2f0 .^ (6:-1:2)
sim = test_convergence(dts, prob, NeuralNetDiffEq.NNODE(chain, opt))
@test abs(sim.𝒪est[:l2]) < 0.1
@test minimum(sim.errors[:l2]) < 0.5
=#
#Example 2
linear = (u,p,t) -> -u/5 + exp(-t/5).*cos(t)
linear_analytic = (u0,p,t) -> exp(-t/5)*(u0 + sin(t))
prob = ODEProblem(ODEFunction(linear,analytic=linear_analytic),0.0f0,(0.0f0,1.0f0))
chain = Flux.Chain(Dense(1,5,σ),Dense(5,1))
opt = ADAM(0.01)
sol = solve(prob,NeuralNetDiffEq.NNODE(chain,opt),verbose = true, dt=1/5f0)
@test sol.errors[:l2] < 0.5
#=
dts = 1f0 ./ 2f0 .^ (6:-1:2)
sim = test_convergence(dts, prob, NeuralNetDiffEq.NNODE(chain, opt))
@test abs(sim.𝒪est[:l2]) < 0.5
@test minimum(sim.errors[:l2]) < 0.1
=#
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 7816 | using Flux, Zygote, LinearAlgebra, Statistics
println("NNPDEHAN_tests")
using Test, NeuralNetDiffEq
# one-dimensional heat equation
x0 = [11.0f0] # initial points
tspan = (0.0f0,5.0f0)
dt = 0.5 # time step
time_steps = div(tspan[2]-tspan[1],dt)
d = 1 # number of dimensions
m = 10 # number of trajectories (batch size)
g(X) = sum(X.^2) # terminal condition
f(X,u,σᵀ∇u,p,t) = 0.0 # function from solved equation
μ_f(X,p,t) = 0.0
σ_f(X,p,t) = 1.0
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hidden layer size
opt = Flux.ADAM(0.005) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = [Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d)) for i in 1:time_steps]
alg = NNPDEHan(u0, σᵀ∇u, opt = opt)
ans = solve(prob, alg, verbose = true, abstol=1e-8, maxiters = 200, dt=dt, trajectories=m)
u_analytical(x,t) = sum(x.^2) .+ d*t
analytical_ans = u_analytical(x0, tspan[end])
error_l2 = sqrt((ans-analytical_ans)^2/ans^2)
println("one-dimensional heat equation")
# println("numerical = ", ans)
# println("analytical = " ,analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 0.1
# high-dimensional heat equation
d = 30 # number of dimensions
x0 = fill(8.0f0,d)
tspan = (0.0f0,2.0f0)
dt = 0.5
time_steps = div(tspan[2]-tspan[1],dt)
m = 30 # number of trajectories (batch size)
g(X) = sum(X.^2)
f(X,u,σᵀ∇u,p,t) = 0.0
μ_f(X,p,t) = 0.0
σ_f(X,p,t) = 1.0
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hidden layer size
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = [Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d)) for i in 1:time_steps]
alg = NNPDEHan(u0, σᵀ∇u, opt = opt)
ans = solve(prob, alg, verbose = true, abstol=1e-8, maxiters = 150, dt=dt, trajectories=m)
u_analytical(x,t) = sum(x.^2) .+ d*t
analytical_ans = u_analytical(x0, tspan[end])
error_l2 = sqrt((ans - analytical_ans)^2/ans^2)
println("high-dimensional heat equation")
# println("numerical = ", ans)
# println("analytical = " ,analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
#Black-Scholes-Barenblatt equation
d = 30 # number of dimensions
x0 = repeat([1.0f0, 0.5f0], div(d,2))
tspan = (0.0f0,1.0f0)
dt = 0.25
time_steps = div(tspan[2]-tspan[1],dt)
m = 30 # number of trajectories (batch size)
r = 0.05
sigma = 0.4
f(X,u,σᵀ∇u,p,t) = r * (u .- sum(X.*σᵀ∇u))
g(X) = sum(X.^2)
μ_f(X,p,t) = 0.0
σ_f(X,p,t) = Diagonal(sigma*X)
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hide layer size
opt = Flux.ADAM(0.001)
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
σᵀ∇u = [Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d)) for i in 1:time_steps]
alg = NNPDEHan(u0, σᵀ∇u, opt = opt)
ans = solve(prob, alg, verbose = true, abstol=1e-8, maxiters = 150, dt=dt, trajectories=m)
u_analytical(x, t) = exp((r + sigma^2).*(tspan[end] .- tspan[1])).*sum(x.^2)
analytical_ans = u_analytical(x0, tspan[1])
error_l2 = sqrt((ans .- analytical_ans)^2/ans^2)
println("Black Scholes Barenblatt equation")
# println("numerical ans= ", ans)
# println("analytical ans = " , analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
# Allen-Cahn Equation
d = 10 # number of dimensions
x0 = fill(0.0f0,d)
tspan = (0.3f0,0.6f0)
dt = 0.015 # time step
time_steps = div(tspan[2]-tspan[1], dt)
m = 20 # number of trajectories (batch size)
g(X) = 1.0 / (2.0 + 0.4*sum(X.^2))
f(X,u,σᵀ∇u,p,t) = u .- u.^3
μ_f(X,p,t) = 0.0
σ_f(X,p,t) = 1.0
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hidden layer size
opt = Flux.ADAM(5^-4) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = [Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d)) for i in 1 : time_steps]
alg = NNPDEHan(u0, σᵀ∇u, opt = opt)
ans = solve(prob, alg, verbose = true, abstol=1e-8, maxiters = 150, dt=dt, trajectories=m)
prob_ans = 0.30879
error_l2 = sqrt((ans - prob_ans)^2/ans^2)
println("Allen-Cahn equation")
# println("numerical = ", ans)
# println("prob_ans = " , prob_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
#Hamilton Jacobi Bellman Equation
d = 20 # number of dimensions
x0 = fill(0.0f0,d)
tspan = (0.0f0, 1.0f0)
dt = 0.2
ts = tspan[1]:dt:tspan[2]
time_steps = length(ts)-1
m = 20 # number of trajectories (batch size)
λ = 1.0f0
g(X) = log(0.5 + 0.5*sum(X.^2))
f(X,u,σᵀ∇u,p,t) = -λ*sum(σᵀ∇u.^2)
μ_f(X,p,t) = 0.0
σ_f(X,p,t) = sqrt(2)
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 12 + d #hidden layer size
opt = Flux.ADAM(0.03) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = [Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d)) for i in 1 : time_steps]
alg = NNPDEHan(u0, σᵀ∇u, opt = opt)
ans = solve(prob, alg, verbose = true, abstol=1e-8, maxiters = 150, dt=dt, trajectories=m)
T = tspan[2]
MC = 10^5
W() = randn(d,1)
u_analytical(x, t) = -(1/λ)*log(mean(exp(-λ*g(x .+ sqrt(2.0)*abs.(T-t).*W())) for _ = 1:MC))
analytical_ans = u_analytical(x0, tspan[1])
error_l2 = sqrt((ans - analytical_ans)^2/ans^2)
println("Hamilton Jacobi Bellman Equation")
# println("numerical = ", ans)
# println("analytical = " , analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.5
# Nonlinear Black-Scholes Equation with Default Risk
d = 20 # number of dimensions
x0 = fill(100.0f0,d)
tspan = (0.0f0,1.0f0)
dt = 0.125 # time step
m = 20 # number of trajectories (batch size)
time_steps = div(tspan[2]-tspan[1],dt)
g(X) = minimum(X)
δ = 2.0f0/3
R = 0.02f0
f(X,u,σᵀ∇u,p,t) = -(1 - δ)*Q(u)*u - R*u
vh = 50.0f0
vl = 70.0f0
γh = 0.2f0
γl = 0.02f0
function Q(u)
Q = 0
if u < vh
Q = γh
elseif u >= vl
Q = γl
else #if u >= vh && u < vl
Q = ((γh - γl) / (vh - vl)) * (u - vh) + γh
end
end
µc = 0.02f0
σc = 0.2f0
μ_f(X,p,t) = µc*X #Vector d x 1
σ_f(X,p,t) = σc*Diagonal(X) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hidden layer size
opt = Flux.ADAM(0.008) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
σᵀ∇u = [Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d)) for i in 1:time_steps]
alg = NNPDEHan(u0, σᵀ∇u, opt = opt)
ans = solve(prob, alg, verbose = true, abstol=1e-8, maxiters = 100, dt=dt, trajectories=m)
prob_ans = 57.3 #60.781
error_l2 = sqrt((ans - prob_ans)^2/ans^2)
println("Nonlinear Black-Scholes Equation with Default Risk")
# println("numerical = ", ans)
# println("prob_ans = " , prob_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 8135 | using Flux, Zygote, StochasticDiffEq
using LinearAlgebra, Statistics
println("NNPDENS_tests")
using Test, NeuralNetDiffEq
println("one-dimensional heat equation")
x0 = Float32[11.] # initial points
tspan = (0.0f0,5.0f0)
dt = 0.5 # time step
d = 1 # number of dimensions
m = 10 # number of trajectories (batch size)
g(X) = sum(X.^2) # terminal condition
f(X,u,σᵀ∇u,p,t) = Float32(0.0)
μ_f(X,p,t) = zero(X) #Vector d x 1
σ_f(X,p,t) = Diagonal(ones(Float32,d)) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hidden layer size
opt = Flux.ADAM(0.005) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
ans = solve(prob, pdealg, verbose=true, maxiters=200, trajectories=m,
alg=EM(), dt=dt, pabstol = 1f-6)
u_analytical(x,t) = sum(x.^2) .+ d*t
analytical_ans = u_analytical(x0, tspan[end])
error_l2 = sqrt((ans-analytical_ans)^2/ans^2)
println("one-dimensional heat equation")
# println("numerical = ", ans)
# println("analytical = " ,analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 0.1
println("high-dimensional heat equation")
d = 50 # number of dimensions
x0 = fill(8.0f0,d)
tspan = (0.0f0,2.0f0)
dt = 0.5
m = 50 # number of trajectories (batch size)
g(X) = sum(X.^2)
f(X,u,σᵀ∇u,p,t) = Float32(0.0)
μ_f(X,p,t) = zero(X) #Vector d x 1
σ_f(X,p,t) = Diagonal(ones(Float32,d)) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hidden layer size
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=m,
alg=EM(), dt=dt, pabstol = 1f-6)
u_analytical(x,t) = sum(x.^2) .+ d*t
analytical_ans = u_analytical(x0, tspan[end])
error_l2 = sqrt((ans - analytical_ans)^2/ans^2)
println("high-dimensional heat equation")
# println("numerical = ", ans)
# println("analytical = " ,analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
println("Black-Scholes-Barenblatt equation")
d = 30 # number of dimensions
x0 = repeat([1.0f0, 0.5f0], div(d,2))
tspan = (0.0f0,1.0f0)
dt = 0.2
m = 30 # number of trajectories (batch size)
r = 0.05f0
sigma = 0.4f0
f(X,u,σᵀ∇u,p,t) = r * (u - sum(X.*σᵀ∇u))
g(X) = sum(X.^2)
μ_f(X,p,t) = zero(X) #Vector d x 1
σ_f(X,p,t) = Diagonal(sigma*X) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 10 + d #hide layer size
opt = Flux.ADAM(0.001)
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=m,
alg=EM(), dt=dt, pabstol = 1f-6)
u_analytical(x, t) = exp((r + sigma^2).*(tspan[end] .- tspan[1])).*sum(x.^2)
analytical_ans = u_analytical(x0, tspan[1])
error_l2 = sqrt((ans .- analytical_ans)^2/ans^2)
println("Black Scholes Barenblatt equation")
# println("numerical ans= ", ans)
# println("analytical ans = " , analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
# Allen-Cahn Equation
d = 10 # number of dimensions
x0 = fill(0.0f0,d)
tspan = (0.3f0,0.6f0)
dt = 0.015 # time step
m = 20 # number of trajectories (batch size)
g(X) = 1.0 / (2.0 + 0.4*sum(X.^2))
f(X,u,σᵀ∇u,p,t) = u .- u.^3
μ_f(X,p,t) = zero(X) #Vector d x 1
σ_f(X,p,t) = Diagonal(ones(Float32,d)) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 20 + d #hidden layer size
opt = Flux.ADAM(5^-3) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=m,
alg=EM(), dt=dt, pabstol = 1f-6)
prob_ans = 0.30879
error_l2 = sqrt((ans - prob_ans)^2/ans^2)
println("Allen-Cahn equation")
# println("numerical = ", ans)
# println("prob_ans = " , prob_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
# Hamilton Jacobi Bellman Equation
d = 30 # number of dimensions
x0 = fill(0.0f0,d)
tspan = (0.0f0, 1.0f0)
dt = 0.2
m = 30 # number of trajectories (batch size)
λ = 1.0f0
#
g(X) = log(0.5f0 + 0.5f0*sum(X.^2))
f(X,u,σᵀ∇u,p,t) = -λ*sum(σᵀ∇u.^2)
μ_f(X,p,t) = zero(X) #Vector d x 1 λ
σ_f(X,p,t) = Diagonal(sqrt(2.0f0)*ones(Float32,d)) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 256 #hidden layer size
opt = Flux.ADAM(0.1) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
@time ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=m,
alg=EM(), dt=dt, pabstol = 1f-4)
T = tspan[2]
MC = 10^5
W() = randn(d,1)
u_analytical(x, t) = -(1/λ)*log(mean(exp(-λ*g(x .+ sqrt(2.0)*abs.(T-t).*W())) for _ = 1:MC))
analytical_ans = u_analytical(x0, tspan[1])
error_l2 = sqrt((ans - analytical_ans)^2/ans^2)
println("Hamilton Jacobi Bellman Equation")
# println("numerical = ", ans)
# println("analytical = " , analytical_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
# Nonlinear Black-Scholes Equation with Default Risk
d = 20 # number of dimensions
x0 = fill(100.0f0,d)
tspan = (0.0f0,1.0f0)
dt = 0.125 # time step
m = 20 # number of trajectories (batch size)
g(X) = minimum(X)
δ = 2.0f0/3
R = 0.02f0
f(X,u,σᵀ∇u,p,t) = -(1 - δ)*Q(u)*u - R*u
vh = 50.0f0
vl = 70.0f0
γh = 0.2f0
γl = 0.02f0
function Q(u)
Q = 0
if u < vh
Q = γh
elseif u >= vl
Q = γl
else #if u >= vh && u < vl
Q = ((γh - γl) / (vh - vl)) * (u - vh) + γh
end
end
µc = 0.02f0
σc = 0.2f0
μ_f(X,p,t) = µc*X #Vector d x 1
σ_f(X,p,t) = σc*Diagonal(X) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, x0, tspan)
hls = 256 #hidden layer size
opt = Flux.ADAM(0.008) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
@time ans = solve(prob, pdealg, verbose=true, maxiters=100, trajectories=m,
alg=EM(), dt=dt, pabstol = 1f-6)
prob_ans = 57.3
error_l2 = sqrt((ans - prob_ans)^2/ans^2)
println("Nonlinear Black-Scholes Equation with Default Risk")
# println("numerical = ", ans)
# println("prob_ans = " , prob_ans)
println("error_l2 = ", error_l2, "\n")
@test error_l2 < 1.0
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 1325 | using Test, Flux , StochasticDiffEq , LinearAlgebra
println("Optimal Stopping Time Test")
using NeuralNetDiffEq
d = 1
r = 0.04f0
beta = 0.2f0
T = 1
u0 = fill(80.00 , d , 1)
sdealg = EM()
ensemblealg = EnsembleThreads()
f(du,u,p,t) = (du .= r*u)
sigma(du,u,p,t) = (du .= Diagonal(beta*u))
tspan = (0.0 , 1.0)
N = 50
dt = tspan[2]/49
K = 100.00
function g(t , x)
return exp(-r*t)*(max(K - maximum(x) , 0))
end
prob = SDEProblem(f , sigma , u0 , tspan ; g = g)
opt = Flux.ADAM(0.1)
m = Chain(Dense(d , 5, tanh), Dense(5, 16 , tanh) , Dense(16 , N ), softmax)
sol = solve(prob, NeuralNetDiffEq.NNStopping( m, opt , sdealg , ensemblealg), verbose = true, dt = dt,
abstol=1e-6, maxiters = 20 , trajectories = 200)
##Analytical Binomial Tree approach for American Options
function BinomialTreeAM1D(S0 , N , r , beta)
V = zeros(N+1)
dT = T/N
u = exp(beta*sqrt(dT))
d = 1/u
S_T = [S0*(u^j)* (d^(N-j)) for j in 0:N]
a = exp(r*dT)
p = (a - d)/(u - d)
q = 1.0 - p
V = [max(K - x , 0) for x in S_T]
for i in N-1:-1:0
V[1:end-1] = exp(-r*dT).*(p*V[2:end] + q*V[1:end-1])
S_T = S_T*u
V = [max(K - S_T[i] , V[i]) for i in 1:size(S_T)[1]]
end
return V[1]
end
real_sol = BinomialTreeAM1D(u0[1] , N , r , beta)
error = abs(sol - real_sol)
@test error < 0.5
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | code | 868 | using SafeTestsets
const GROUP = get(ENV, "GROUP", "All")
const is_APPVEYOR = Sys.iswindows() && haskey(ENV,"APPVEYOR")
const is_TRAVIS = haskey(ENV,"TRAVIS")
@time begin
if GROUP == "All" || GROUP == "NNODE"
@time @safetestset "NNODE" begin include("NNODE_tests.jl") end
end
if !is_APPVEYOR && (GROUP == "All" || GROUP == "NNPDEHan")
@time @safetestset "NNPDEHan" begin include("NNPDEHan_tests.jl") end
end
if GROUP == "All" || GROUP == "NNPDENS"
@time @safetestset "NNPDENS" begin include("NNPDENS_tests.jl") end
end
if GROUP == "All" || GROUP == "NNKOLMOGOROV"
@time @safetestset "NNKolmogorov" begin include("NNKolmogorov_tests.jl") end
end
if GROUP == "All" || GROUP == "NNSTOPPINGTIME"
@time @safetestset "NNStopping" begin include("Stopping_tests.jl") end
end
if !is_APPVEYOR && GROUP == "GPU"
end
end
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | docs | 10182 | # NeuralNetDiffEq
[](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
[](https://travis-ci.org/SciML/NeuralNetDiffEq.jl)
[](https://ci.appveyor.com/project/ChrisRackauckas/neuralnetdiffeq-jl)
[](https://coveralls.io/github/JuliaDiffEq/NeuralNetDiffEq.jl?branch=master)
[](http://codecov.io/github/JuliaDiffEq/NeuralNetDiffEq.jl?branch=master)
The repository is for the development of neural network solvers of differential equations such as physics-informed
neural networks (PINNs) and deep BSDE solvers. It utilizes techniques like deep neural networks and neural
stochastic differential equations to make it practical to solve high dimensional PDEs efficiently through the
likes of scientific machine learning (SciML).
# Examples
## DeepBSDE Solver
## Solving a 100 dimensional Hamilton-Jacobi-Bellman Equation
In this example we will solve a Hamilton-Jacobi-Bellman equation of 100 dimensions.
The Hamilton-Jacobi-Bellman equation is the solution to a stochastic optimal
control problem. Here, we choose to solve the classical Linear Quadratic Gaussian
(LQG) control problem of 100 dimensions, which is governed by the SDE
`dX_t = 2sqrt(λ)c_t dt + sqrt(2)dW_t` where `c_t` is a control process. The solution
to the optimal control is given by a PDE of the form:
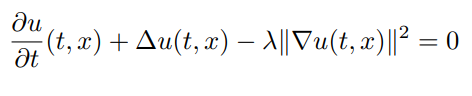
with terminating condition `g(X) = log(0.5f0 + 0.5f0*sum(X.^2))`. To solve it
using the `TerminalPDEProblem`, we write:
```julia
d = 100 # number of dimensions
X0 = fill(0.0f0,d) # initial value of stochastic control process
tspan = (0.0f0, 1.0f0)
λ = 1.0f0
g(X) = log(0.5f0 + 0.5f0*sum(X.^2))
f(X,u,σᵀ∇u,p,t) = -λ*sum(σᵀ∇u.^2)
μ_f(X,p,t) = zero(X) #Vector d x 1 λ
σ_f(X,p,t) = Diagonal(sqrt(2.0f0)*ones(Float32,d)) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, X0, tspan)
```
As described in the API docs, we now need to define our `NNPDENS` algorithm
by giving it the Flux.jl chains we want it to use for the neural networks.
`u0` needs to be a `d` dimensional -> 1 dimensional chain, while `σᵀ∇u`
needs to be `d+1` dimensional to `d` dimensions. Thus we define the following:
```julia
hls = 10 + d #hidden layer size
opt = Flux.ADAM(0.01) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
```
And now we solve the PDE. Here we say we want to solve the underlying neural
SDE using the Euler-Maruyama SDE solver with our chosen `dt=0.2`, do at most
100 iterations of the optimizer, 100 SDE solves per loss evaluation (for averaging),
and stop if the loss ever goes below `1f-2`.
```julia
@time ans = solve(prob, pdealg, verbose=true, maxiters=100, trajectories=100,
alg=EM(), dt=0.2, pabstol = 1f-2)
```
## Solving the 100 dimensional Black-Scholes-Barenblatt Equation
In this example we will solve a Black-Scholes-Barenblatt equation of 100 dimensions.
The Black-Scholes-Barenblatt equation is a nonlinear extension to the Black-Scholes
equation which models uncertain volatility and interest rates derived from the
Black-Scholes equation. This model results in a nonlinear PDE whose dimension
is the number of assets in the portfolio.
To solve it using the `TerminalPDEProblem`, we write:
```julia
d = 100 # number of dimensions
X0 = repeat([1.0f0, 0.5f0], div(d,2)) # initial value of stochastic state
tspan = (0.0f0,1.0f0)
r = 0.05f0
sigma = 0.4f0
f(X,u,σᵀ∇u,p,t) = r * (u - sum(X.*σᵀ∇u))
g(X) = sum(X.^2)
μ_f(X,p,t) = zero(X) #Vector d x 1
σ_f(X,p,t) = Diagonal(sigma*X) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, X0, tspan)
```
As described in the API docs, we now need to define our `NNPDENS` algorithm
by giving it the Flux.jl chains we want it to use for the neural networks.
`u0` needs to be a `d` dimensional -> 1 dimensional chain, while `σᵀ∇u`
needs to be `d+1` dimensional to `d` dimensions. Thus we define the following:
```julia
hls = 10 + d #hide layer size
opt = Flux.ADAM(0.001)
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
```
And now we solve the PDE. Here we say we want to solve the underlying neural
SDE using the Euler-Maruyama SDE solver with our chosen `dt=0.2`, do at most
150 iterations of the optimizer, 100 SDE solves per loss evaluation (for averaging),
and stop if the loss ever goes below `1f-6`.
```julia
ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=100,
alg=EM(), dt=0.2, pabstol = 1f-6)
```
# API Documentation
## Solving High Dimensional PDEs with Neural Networks
To solve high dimensional PDEs, first one should describe the PDE in terms of
the `TerminalPDEProblem` with constructor:
```julia
TerminalPDEProblem(g,f,μ_f,σ_f,X0,tspan,p=nothing)
```
which describes the semilinear parabolic PDE of the form:
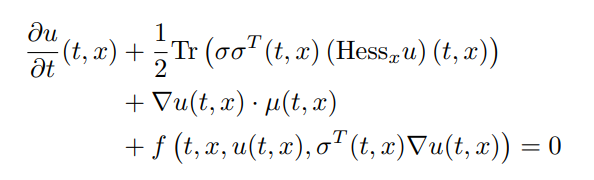
with terminating condition `u(tspan[2],x) = g(x)`. These methods solve the PDE in
reverse, satisfying the terminal equation and giving a point estimate at
`u(tspan[1],X0)`. The dimensionality of the PDE is determined by the choice
of `X0`, which is the initial stochastic state.
To solve this PDE problem, there exists two algorithms:
- `NNPDENS(u0,σᵀ∇u;opt=Flux.ADAM(0.1))`: Uses a neural stochastic differential
equation which is then solved by the methods available in DifferentialEquations.jl
The `alg` keyword is required for specifying the SDE solver algorithm that
will be used on the internal SDE. All of the other keyword arguments are passed
to the SDE solver.
- `NNPDEHan(u0,σᵀ∇u;opt=Flux.ADAM(0.1))`: Uses the stochastic RNN algorithm
[from Han](https://www.pnas.org/content/115/34/8505). Only applicable when
`μ_f` and `σ_f` result in a non-stiff SDE where low order non-adaptive time
stepping is applicable.
Here, `u0` is a Flux.jl chain with `d` dimensional input and 1 dimensional output.
For `NNPDEHan`, `σᵀ∇u` is an array of `M` chains with `d` dimensional input and
`d` dimensional output, where `M` is the total number of timesteps. For `NNPDENS`
it is a `d+1` dimensional input (where the final value is time) and `d` dimensional
output. `opt` is a Flux.jl optimizer.
Each of these methods has a special keyword argument `pabstol` which specifies
an absolute tolerance on the PDE's solution, and will exit early if the loss
reaches this value. Its defualt value is `1f-6`.
## Solving ODEs with Neural Networks
For ODEs, [see the DifferentialEquations.jl documentation](http://docs.juliadiffeq.org/dev/solvers/ode_solve#NeuralNetDiffEq.jl-1)
for the `nnode(chain,opt=ADAM(0.1))` algorithm, which takes in a Flux.jl chain
and optimizer to solve an ODE. This method is not particularly efficient, but
is parallel. It is based on the work of:
[Lagaris, Isaac E., Aristidis Likas, and Dimitrios I. Fotiadis. "Artificial neural networks for solving ordinary and partial differential equations." IEEE Transactions on Neural Networks 9, no. 5 (1998): 987-1000.](https://arxiv.org/pdf/physics/9705023.pdf)
## Solving Kolmogorov Equations with Neural Networks
A Kolmogorov PDE is of the form :
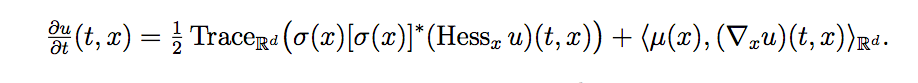
Considering S be a solution process to the SDE:
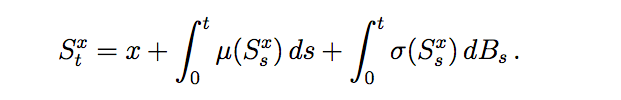
then the solution to the Kolmogorov PDE is given as:
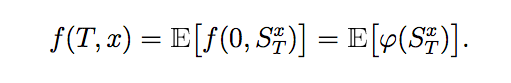
A Kolmogorov PDE Problem can be defined using a `SDEProblem`:
```julia
SDEProblem(μ,σ,u0,tspan,xspan,d)
```
Here `u0` is the initial distribution of x. Here we define `u(0,x)` as the probability density function of `u0`.`μ` and `σ` are obtained from the SDE for the stochastic process above. `d` represents the dimenstions of `x`.
`u0` can be defined using `Distributions.jl`.
Another was of defining a KolmogorovPDE is using the `KolmogorovPDEProblem`.
```julia
KolmogorovPDEProblem(μ,σ,phi,tspan,xspan,d)
```
Here `phi` is the initial condition on u(t,x) when t = 0. `μ` and `σ` are obtained from the SDE for the stochastic process above. `d` represents the dimenstions of `x`.
To solve this problem use,
- `NNKolmogorov(chain, opt , sdealg)`: Uses a neural network to realise a regression function which is the solution for the linear Kolmogorov Equation.
Here, `chain` is a Flux.jl chain with `d` dimensional input and 1 dimensional output.`opt` is a Flux.jl optimizer. And `sdealg` is a high-order algorithm to calculate the solution for the SDE, which is used to define the learning data for the problem. Its default value is the classic Euler-Maruyama algorithm.
## Related Packages
- [ReservoirComputing.jl](https://github.com/MartinuzziFrancesco/ReservoirComputing.jl) has an implementation of the [Echo State Network method](https://arxiv.org/pdf/1710.07313.pdf) for learning the attractor properties of a chaotic system.
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 1.6.0 | 9c7d79b65a2e24e658d58b4cfe254ecfd58b660a | docs | 10042 | # NeuralNetDiffEq
The repository is for the development of neural network solvers of differential equations such as physics-informed
neural networks (PINNs) and deep BSDE solvers. It utilizes techniques like deep neural networks and neural
stochastic differential equations to make it practical to solve high dimensional PDEs efficiently through the
likes of scientific machine learning (SciML).
# Examples
## DeepBSDE Solver
## Solving a 100 dimensional Hamilton-Jacobi-Bellman Equation
In this example we will solve a Hamilton-Jacobi-Bellman equation of 100 dimensions.
The Hamilton-Jacobi-Bellman equation is the solution to a stochastic optimal
control problem. Here, we choose to solve the classical Linear Quadratic Gaussian
(LQG) control problem of 100 dimensions, which is governed by the SDE
`dX_t = 2sqrt(λ)c_t dt + sqrt(2)dW_t` where `c_t` is a control process. The solution
to the optimal control is given by a PDE of the form:
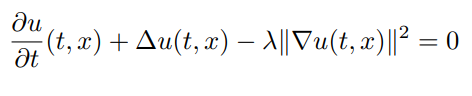
with terminating condition `g(X) = log(0.5f0 + 0.5f0*sum(X.^2))`. To solve it
using the `TerminalPDEProblem`, we write:
```julia
d = 100 # number of dimensions
X0 = fill(0.0f0,d) # initial value of stochastic control process
tspan = (0.0f0, 1.0f0)
λ = 1.0f0
g(X) = log(0.5f0 + 0.5f0*sum(X.^2))
f(X,u,σᵀ∇u,p,t) = -λ*sum(σᵀ∇u.^2)
μ_f(X,p,t) = zero(X) #Vector d x 1 λ
σ_f(X,p,t) = Diagonal(sqrt(2.0f0)*ones(Float32,d)) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, X0, tspan)
```
As described in the API docs, we now need to define our `NNPDENS` algorithm
by giving it the Flux.jl chains we want it to use for the neural networks.
`u0` needs to be a `d` dimensional -> 1 dimensional chain, while `σᵀ∇u`
needs to be `d+1` dimensional to `d` dimensions. Thus we define the following:
```julia
hls = 10 + d #hidden layer size
opt = Flux.ADAM(0.01) #optimizer
#sub-neural network approximating solutions at the desired point
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
# sub-neural network approximating the spatial gradients at time point
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
```
And now we solve the PDE. Here we say we want to solve the underlying neural
SDE using the Euler-Maruyama SDE solver with our chosen `dt=0.2`, do at most
100 iterations of the optimizer, 100 SDE solves per loss evaluation (for averaging),
and stop if the loss ever goes below `1f-2`.
```julia
@time ans = solve(prob, pdealg, verbose=true, maxiters=100, trajectories=100,
alg=EM(), dt=0.2, pabstol = 1f-2)
```
## Solving the 100 dimensional Black-Scholes-Barenblatt Equation
In this example we will solve a Black-Scholes-Barenblatt equation of 100 dimensions.
The Black-Scholes-Barenblatt equation is a nonlinear extension to the Black-Scholes
equation which models uncertain volatility and interest rates derived from the
Black-Scholes equation. This model results in a nonlinear PDE whose dimension
is the number of assets in the portfolio.
To solve it using the `TerminalPDEProblem`, we write:
```julia
d = 100 # number of dimensions
X0 = repeat([1.0f0, 0.5f0], div(d,2)) # initial value of stochastic state
tspan = (0.0f0,1.0f0)
r = 0.05f0
sigma = 0.4f0
f(X,u,σᵀ∇u,p,t) = r * (u - sum(X.*σᵀ∇u))
g(X) = sum(X.^2)
μ_f(X,p,t) = zero(X) #Vector d x 1
σ_f(X,p,t) = Diagonal(sigma*X) #Matrix d x d
prob = TerminalPDEProblem(g, f, μ_f, σ_f, X0, tspan)
```
As described in the API docs, we now need to define our `NNPDENS` algorithm
by giving it the Flux.jl chains we want it to use for the neural networks.
`u0` needs to be a `d` dimensional -> 1 dimensional chain, while `σᵀ∇u`
needs to be `d+1` dimensional to `d` dimensions. Thus we define the following:
```julia
hls = 10 + d #hide layer size
opt = Flux.ADAM(0.001)
u0 = Flux.Chain(Dense(d,hls,relu),
Dense(hls,hls,relu),
Dense(hls,1))
σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu),
Dense(hls,hls,relu),
Dense(hls,hls,relu),
Dense(hls,d))
pdealg = NNPDENS(u0, σᵀ∇u, opt=opt)
```
And now we solve the PDE. Here we say we want to solve the underlying neural
SDE using the Euler-Maruyama SDE solver with our chosen `dt=0.2`, do at most
150 iterations of the optimizer, 100 SDE solves per loss evaluation (for averaging),
and stop if the loss ever goes below `1f-6`.
```julia
ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=100,
alg=EM(), dt=0.2, pabstol = 1f-6)
```
# API Documentation
## Solving High Dimensional PDEs with Neural Networks
To solve high dimensional PDEs, first one should describe the PDE in terms of
the `TerminalPDEProblem` with constructor:
```julia
TerminalPDEProblem(g,f,μ_f,σ_f,X0,tspan,p=nothing)
```
which describes the semilinear parabolic PDE of the form:
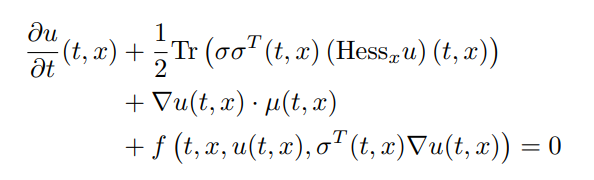
with terminating condition `u(tspan[2],x) = g(x)`. These methods solve the PDE in
reverse, satisfying the terminal equation and giving a point estimate at
`u(tspan[1],X0)`. The dimensionality of the PDE is determined by the choice
of `X0`, which is the initial stochastic state.
To solve this PDE problem, there exists two algorithms:
- `NNPDENS(u0,σᵀ∇u;opt=Flux.ADAM(0.1))`: Uses a neural stochastic differential
equation which is then solved by the methods available in DifferentialEquations.jl
The `alg` keyword is required for specifying the SDE solver algorithm that
will be used on the internal SDE. All of the other keyword arguments are passed
to the SDE solver.
- `NNPDEHan(u0,σᵀ∇u;opt=Flux.ADAM(0.1))`: Uses the stochastic RNN algorithm
[from Han](https://www.pnas.org/content/115/34/8505). Only applicable when
`μ_f` and `σ_f` result in a non-stiff SDE where low order non-adaptive time
stepping is applicable.
Here, `u0` is a Flux.jl chain with `d` dimensional input and 1 dimensional output.
For `NNPDEHan`, `σᵀ∇u` is an array of `M` chains with `d` dimensional input and
`d` dimensional output, where `M` is the total number of timesteps. For `NNPDENS`
it is a `d+1` dimensional input (where the final value is time) and `d` dimensional
output. `opt` is a Flux.jl optimizer.
Each of these methods has a special keyword argument `pabstol` which specifies
an absolute tolerance on the PDE's solution, and will exit early if the loss
reaches this value. Its defualt value is `1f-6`.
## Solving ODEs with Neural Networks
For ODEs, [see the DifferentialEquations.jl documentation](http://docs.juliadiffeq.org/dev/solvers/ode_solve#NeuralNetDiffEq.jl-1)
for the `nnode(chain,opt=ADAM(0.1))` algorithm, which takes in a Flux.jl chain
and optimizer to solve an ODE. This method is not particularly efficient, but
is parallel. It is based on the work of:
[Lagaris, Isaac E., Aristidis Likas, and Dimitrios I. Fotiadis. "Artificial neural networks for solving ordinary and partial differential equations." IEEE Transactions on Neural Networks 9, no. 5 (1998): 987-1000.](https://arxiv.org/pdf/physics/9705023.pdf)
## Solving Kolmogorov Equations with Neural Networks
A Kolmogorov PDE is of the form :
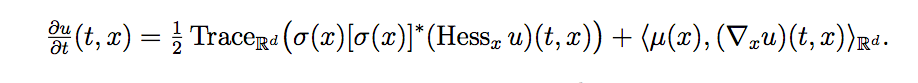
Considering S be a solution process to the SDE:
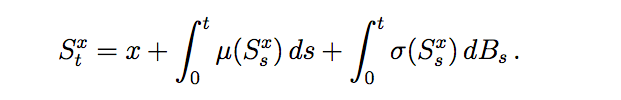
then the solution to the Kolmogorov PDE is given as:
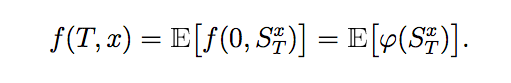
A Kolmogorov PDE Problem can be defined using a `SDEProblem`:
```julia
SDEProblem(μ,σ,u0,tspan,xspan,d)
```
Here `u0` is the initial distribution of x. Here we define `u(0,x)` as the probability density function of `u0`.`μ` and `σ` are obtained from the SDE for the stochastic process above. `d` represents the dimenstions of `x`.
`u0` can be defined using `Distributions.jl`.
Another was of defining a KolmogorovPDE is using the `KolmogorovPDEProblem`.
```julia
KolmogorovPDEProblem(μ,σ,phi,tspan,xspan,d)
```
Here `phi` is the initial condition on u(t,x) when t = 0. `μ` and `σ` are obtained from the SDE for the stochastic process above. `d` represents the dimenstions of `x`.
To solve this problem use,
- `NNKolmogorov(chain, opt , sdealg)`: Uses a neural network to realise a regression function which is the solution for the linear Kolmogorov Equation.
Here, `chain` is a Flux.jl chain with `d` dimensional input and 1 dimensional output.`opt` is a Flux.jl optimizer. And `sdealg` is a high-order algorithm to calculate the solution for the SDE, which is used to define the learning data for the problem. Its default value is the classic Euler-Maruyama algorithm.
## Related Packages
- [ReservoirComputing.jl](https://github.com/MartinuzziFrancesco/ReservoirComputing.jl) has an implementation of the [Echo State Network method](https://arxiv.org/pdf/1710.07313.pdf) for learning the attractor properties of a chaotic system.
## Citation
If you use NeuralNetDiffEq.jl or are influenced by it's ideas for expanding it, please cite:
```
@article{DifferentialEquations.jl-2017,
author = {Rackauckas, Christopher and Nie, Qing},
doi = {10.5334/jors.151},
journal = {The Journal of Open Research Software},
keywords = {Applied Mathematics},
note = {Exported from https://app.dimensions.ai on 2019/05/05},
number = {1},
pages = {},
title = {DifferentialEquations.jl – A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia},
url = {https://app.dimensions.ai/details/publication/pub.1085583166 and http://openresearchsoftware.metajnl.com/articles/10.5334/jors.151/galley/245/download/},
volume = {5},
year = {2017}
}
```
| NeuralNetDiffEq | https://github.com/SciML/NeuralNetDiffEq.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 7452 |
module BasicPOMCP
#=
Current constraints:
- action space discrete
- action space same for all states, histories
- no built-in support for history-dependent rollouts (this could be added though)
- initial n and initial v are 0
=#
using POMDPs
using Parameters
using ParticleFilters
using CPUTime
using Colors
using Random
using Printf
using POMDPLinter: @POMDP_require, @show_requirements
using POMDPTools
import POMDPs: action, solve, updater
import POMDPLinter
using MCTS
import MCTS: convert_estimator, estimate_value, node_tag, tooltip_tag, default_action
using D3Trees
export
POMCPSolver,
POMCPPlanner,
action,
solve,
updater,
NoDecision,
AllSamplesTerminal,
ExceptionRethrow,
ReportWhenUsed,
default_action,
BeliefNode,
LeafNodeBelief,
AbstractPOMCPSolver,
PORollout,
FORollout,
RolloutEstimator,
FOValue,
D3Tree,
node_tag,
tooltip_tag,
# deprecated
AOHistoryBelief
abstract type AbstractPOMCPSolver <: Solver end
"""
POMCPSolver(#=keyword arguments=#)
Partially Observable Monte Carlo Planning Solver.
## Keyword Arguments
- `max_depth::Int`
Rollouts and tree expension will stop when this depth is reached.
default: `20`
- `c::Float64`
UCB exploration constant - specifies how much the solver should explore.
default: `1.0`
- `tree_queries::Int`
Number of iterations during each action() call.
default: `1000`
- `max_time::Float64`
Maximum time for planning in each action() call.
default: `Inf`
- `tree_in_info::Bool`
If `true`, returns the tree in the info dict when action_info is called.
default: `false`
- `estimate_value::Any`
Function, object, or number used to estimate the value at the leaf nodes.
default: `RolloutEstimator(RandomSolver(rng))`
- If this is a function `f`, `f(pomdp, s, h::BeliefNode, steps)` will be called to estimate the value.
- If this is an object `o`, `estimate_value(o, pomdp, s, h::BeliefNode, steps)` will be called.
- If this is a number, the value will be set to that number
Note: In many cases, the simplest way to estimate the value is to do a rollout on the fully observable MDP with a policy that is a function of the state. To do this, use `FORollout(policy)`.
- `default_action::Any`
Function, action, or Policy used to determine the action if POMCP fails with exception `ex`.
default: `ExceptionRethrow()`
- If this is a Function `f`, `f(pomdp, belief, ex)` will be called.
- If this is a Policy `p`, `action(p, belief)` will be called.
- If it is an object `a`, `default_action(a, pomdp, belief, ex)` will be called, and if this method is not implemented, `a` will be returned directly.
- `rng::AbstractRNG`
Random number generator.
default: `Random.GLOBAL_RNG`
"""
@with_kw mutable struct POMCPSolver <: AbstractPOMCPSolver
max_depth::Int = 20
c::Float64 = 1.0
tree_queries::Int = 1000
max_time::Float64 = Inf
tree_in_info::Bool = false
default_action::Any = ExceptionRethrow()
rng::AbstractRNG = Random.GLOBAL_RNG
estimate_value::Any = RolloutEstimator(RandomSolver(rng))
end
struct POMCPTree{A,O}
# for each observation-terminated history
total_n::Vector{Int} # total number of visits for an observation node
children::Vector{Vector{Int}} # indices of each of the children
o_labels::Vector{O} # actual observation corresponding to this observation node
o_lookup::Dict{Tuple{Int, O}, Int} # mapping from (action node index, observation) to an observation node index
# for each action-terminated history
n::Vector{Int} # number of visits for an action node
v::Vector{Float64} # value estimate for an action node
a_labels::Vector{A} # actual action corresponding to this action node
end
function POMCPTree(pomdp::POMDP, b, sz::Int=1000)
acts = collect(actions(pomdp, b))
A = actiontype(pomdp)
O = obstype(pomdp)
sz = min(100_000, sz)
return POMCPTree{A,O}(sizehint!(Int[0], sz),
sizehint!(Vector{Int}[collect(1:length(acts))], sz),
sizehint!(Array{O}(undef, 1), sz),
sizehint!(Dict{Tuple{Int,O},Int}(), sz),
sizehint!(zeros(Int, length(acts)), sz),
sizehint!(zeros(Float64, length(acts)), sz),
sizehint!(acts, sz)
)
end
struct LeafNodeBelief{H, S} <: AbstractParticleBelief{S}
hist::H
sp::S
end
POMDPs.currentobs(h::LeafNodeBelief) = h.hist[end].o
POMDPs.history(h::LeafNodeBelief) = h.hist
# particle belief interface
ParticleFilters.n_particles(b::LeafNodeBelief) = 1
ParticleFilters.particles(b::LeafNodeBelief) = (b.sp,)
ParticleFilters.weights(b::LeafNodeBelief) = (1.0,)
ParticleFilters.weighted_particles(b::LeafNodeBelief) = (b.sp=>1.0,)
ParticleFilters.weight_sum(b::LeafNodeBelief) = 1.0
ParticleFilters.weight(b::LeafNodeBelief, i) = i == 1 ? 1.0 : 0.0
function ParticleFilters.particle(b::LeafNodeBelief, i)
@assert i == 1
return b.sp
end
POMDPs.mean(b::LeafNodeBelief) = b.sp
POMDPs.mode(b::LeafNodeBelief) = b.sp
POMDPs.support(b::LeafNodeBelief) = (b.sp,)
POMDPs.pdf(b::LeafNodeBelief{<:Any, S}, s::S) where S = float(s == b.sp)
POMDPs.rand(rng::AbstractRNG, s::Random.SamplerTrivial{<:LeafNodeBelief}) = s[].sp
# old deprecated name
const AOHistoryBelief = LeafNodeBelief
function insert_obs_node!(t::POMCPTree, pomdp::POMDP, ha::Int, sp, o)
acts = actions(pomdp, LeafNodeBelief(tuple((a=t.a_labels[ha], o=o)), sp))
push!(t.total_n, 0)
push!(t.children, sizehint!(Int[], length(acts)))
push!(t.o_labels, o)
hao = length(t.total_n)
t.o_lookup[(ha, o)] = hao
for a in acts
n = insert_action_node!(t, hao, a)
push!(t.children[hao], n)
end
return hao
end
function insert_action_node!(t::POMCPTree, h::Int, a)
push!(t.n, 0)
push!(t.v, 0.0)
push!(t.a_labels, a)
return length(t.n)
end
abstract type BeliefNode <: AbstractStateNode end
struct POMCPObsNode{A,O} <: BeliefNode
tree::POMCPTree{A,O}
node::Int
end
mutable struct POMCPPlanner{P, SE, RNG} <: Policy
solver::POMCPSolver
problem::P
solved_estimator::SE
rng::RNG
_best_node_mem::Vector{Int}
_tree::Union{Nothing, Any}
end
function POMCPPlanner(solver::POMCPSolver, pomdp::POMDP)
se = convert_estimator(solver.estimate_value, solver, pomdp)
return POMCPPlanner(solver, pomdp, se, solver.rng, Int[], nothing)
end
Random.seed!(p::POMCPPlanner, seed) = Random.seed!(p.rng, seed)
function updater(p::POMCPPlanner)
P = typeof(p.problem)
S = statetype(P)
A = actiontype(P)
O = obstype(P)
return UnweightedParticleFilter(p.problem, p.solver.tree_queries, rng=p.rng)
# XXX It would be better to automatically use an SIRParticleFilter if possible
# if !@implemented ParticleFilters.obs_weight(::P, ::S, ::A, ::S, ::O)
# return UnweightedParticleFilter(p.problem, p.solver.tree_queries, rng=p.rng)
# end
# return SIRParticleFilter(p.problem, p.solver.tree_queries, rng=p.rng)
end
include("solver.jl")
include("exceptions.jl")
include("rollout.jl")
include("visualization.jl")
include("requirements_info.jl")
end # module
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 657 | abstract type NoDecision <: Exception end
Base.showerror(io::IO, nd::NoDecision) = print(io, """
Planner failed to choose an action because the following exception was thrown:
$nd
To specify an action for this case, use the default_action solver parameter.
""")
struct AllSamplesTerminal <: NoDecision
belief
end
Base.showerror(io::IO, ast::AllSamplesTerminal) = print(io, """
Planner failed to choose an action because all states sampled from the belief were terminal.
To see the belief, catch this exception as ex and see ex.belief.
To specify an action for this case, use the default_action solver parameter.
""")
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 1758 | function POMDPLinter.requirements_info(solver::AbstractPOMCPSolver, problem::POMDP)
println("""
Since POMCP is an online solver, most of the computation occurs in `action(planner, state)`. In order to view the requirements for this function, please, supply an initial beleif to `requirements_info`, e.g.
@requirements_info $(typeof(solver))() $(typeof(problem))() initialstate(pomdp)
""")
end
function POMDPLinter.requirements_info(solver::AbstractPOMCPSolver, problem::POMDP, b)
policy = solve(solver, problem)
requirements_info(policy, b)
end
POMDPLinter.requirements_info(policy::POMCPPlanner, b) = @show_requirements action(policy, b)
@POMDP_require action(p::POMCPPlanner, b) begin
tree = POMCPTree(p.problem, b, p.solver.tree_queries)
@subreq search(p, b, tree)
end
@POMDP_require search(p::POMCPPlanner, b, t::POMCPTree) begin
P = typeof(p.problem)
@req rand(::typeof(p.rng), ::typeof(b))
s = rand(p.rng, b)
@req isterminal(::P, ::statetype(P))
@subreq simulate(p, s, POMCPObsNode(t, 1), p.solver.max_depth)
end
@POMDP_require simulate(p::POMCPPlanner, s, hnode::POMCPObsNode, steps::Int) begin
P = typeof(p.problem)
S = statetype(P)
A = actiontype(P)
O = obstype(P)
@req gen(::P, ::S, ::A, ::typeof(p.rng))
@req isequal(::O, ::O)
@req hash(::O)
# from insert_obs_node!
@req actions(::P)
AS = typeof(actions(p.problem))
@req length(::AS)
@subreq estimate_value(p.solved_estimator, p.problem, s, hnode, steps)
@req discount(::P)
end
@POMDP_require estimate_value(f::Function, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int) begin
@req f(::typeof(pomdp), ::typeof(start_state), ::typeof(h), ::typeof(steps))
end
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 4313 | struct PORollout
solver::Union{POMDPs.Solver,POMDPs.Policy,Function}
updater::POMDPs.Updater
end
struct SolvedPORollout{P<:POMDPs.Policy,U<:POMDPs.Updater,RNG<:AbstractRNG}
policy::P
updater::U
rng::RNG
end
struct FORollout # fully observable rollout
solver::Union{POMDPs.Solver,POMDPs.Policy}
end
struct SolvedFORollout{P<:POMDPs.Policy,RNG<:AbstractRNG}
policy::P
rng::RNG
end
struct FOValue
solver::Union{POMDPs.Solver, POMDPs.Policy}
end
struct SolvedFOValue{P<:POMDPs.Policy}
policy::P
end
"""
estimate_value(estimator, problem::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int)
Return an initial unbiased estimate of the value at belief node h.
By default this runs a rollout simulation
"""
function estimate_value end
estimate_value(f::Function, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int) = f(pomdp, start_state, h, steps)
estimate_value(n::Number, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int) = convert(Float64, n)
function estimate_value(estimator::Union{SolvedPORollout,SolvedFORollout}, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int)
rollout(estimator, pomdp, start_state, h, steps)
end
@POMDP_require estimate_value(estimator::Union{SolvedPORollout,SolvedFORollout}, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int) begin
@subreq rollout(estimator, pomdp, start_state, h, steps)
end
function estimate_value(estimator::SolvedFOValue, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int)
POMDPs.value(estimator.policy, start_state)
end
function convert_estimator(ev::RolloutEstimator, solver, pomdp)
policy = MCTS.convert_to_policy(ev.solver, pomdp)
SolvedPORollout(policy, updater(policy), solver.rng)
end
function convert_estimator(ev::PORollout, solver, pomdp)
policy = MCTS.convert_to_policy(ev.solver, pomdp)
SolvedPORollout(policy, ev.updater, solver.rng)
end
function convert_estimator(est::FORollout, solver, pomdp)
policy = MCTS.convert_to_policy(est.solver, UnderlyingMDP(pomdp))
SolvedFORollout(policy, solver.rng)
end
function convert_estimator(est::FOValue, solver, pomdp::POMDPs.POMDP)
policy = MCTS.convert_to_policy(est.solver, UnderlyingMDP(pomdp))
SolvedFOValue(policy)
end
"""
Perform a rollout simulation to estimate the value.
"""
function rollout(est::SolvedPORollout, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int)
b = extract_belief(est.updater, h)
sim = RolloutSimulator(est.rng,
steps)
return POMDPs.simulate(sim, pomdp, est.policy, est.updater, b, start_state)
end
@POMDP_require rollout(est::SolvedPORollout, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int) begin
@req extract_belief(::typeof(est.updater), ::typeof(h))
b = extract_belief(est.updater, h)
sim = RolloutSimulator(est.rng,
steps)
@subreq POMDPs.simulate(sim, pomdp, est.policy, est.updater, b, start_state)
end
function rollout(est::SolvedFORollout, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int)
sim = RolloutSimulator(est.rng,
steps)
return POMDPs.simulate(sim, pomdp, est.policy, start_state)
end
@POMDP_require rollout(est::SolvedFORollout, pomdp::POMDPs.POMDP, start_state, h::BeliefNode, steps::Int) begin
sim = RolloutSimulator(est.rng,
steps)
@subreq POMDPs.simulate(sim, pomdp, est.policy, start_state)
end
"""
extract_belief(rollout_updater::POMDPs.Updater, node::BeliefNode)
Return a belief compatible with the `rollout_updater` from the belief in `node`.
When a rollout simulation is started, this function is used to create the initial belief (compatible with `rollout_updater`) based on the appropriate `BeliefNode` at the edge of the tree. By overriding this, a belief can be constructed based on the entire tree or entire observation-action history.
"""
function extract_belief end
# some defaults are provided
extract_belief(::NothingUpdater, node::BeliefNode) = nothing
function extract_belief(::PreviousObservationUpdater, node::BeliefNode)
if node.node==1 && !isdefined(node.tree.o_labels, node.node)
missing
else
node.tree.o_labels[node.node]
end
end
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 3162 | function POMDPTools.action_info(p::POMCPPlanner, b; tree_in_info=false)
local a::actiontype(p.problem)
info = Dict{Symbol, Any}()
try
tree = POMCPTree(p.problem, b, p.solver.tree_queries)
a = search(p, b, tree, info)
p._tree = tree
if p.solver.tree_in_info || tree_in_info
info[:tree] = tree
end
catch ex
# Note: this might not be type stable, but it shouldn't matter too much here
a = convert(actiontype(p.problem), default_action(p.solver.default_action, p.problem, b, ex))
info[:exception] = ex
end
return a, info
end
action(p::POMCPPlanner, b) = first(action_info(p, b))
function search(p::POMCPPlanner, b, t::POMCPTree, info::Dict)
all_terminal = true
nquery = 0
start_us = CPUtime_us()
for i in 1:p.solver.tree_queries
nquery += 1
if CPUtime_us() - start_us >= 1e6*p.solver.max_time
break
end
s = rand(p.rng, b)
if !POMDPs.isterminal(p.problem, s)
simulate(p, s, POMCPObsNode(t, 1), p.solver.max_depth)
all_terminal = false
end
end
info[:search_time_us] = CPUtime_us() - start_us
info[:tree_queries] = nquery
if all_terminal
throw(AllSamplesTerminal(b))
end
h = 1
best_node = first(t.children[h])
best_v = t.v[best_node]
@assert !isnan(best_v)
for node in t.children[h][2:end]
if t.v[node] >= best_v
best_v = t.v[node]
best_node = node
end
end
return t.a_labels[best_node]
end
solve(solver::POMCPSolver, pomdp::POMDP) = POMCPPlanner(solver, pomdp)
function simulate(p::POMCPPlanner, s, hnode::POMCPObsNode, steps::Int)
if steps == 0 || isterminal(p.problem, s)
return 0.0
end
t = hnode.tree
h = hnode.node
ltn = log(t.total_n[h])
best_nodes = empty!(p._best_node_mem)
best_criterion_val = -Inf
for node in t.children[h]
n = t.n[node]
if n == 0 && ltn <= 0.0
criterion_value = t.v[node]
elseif n == 0 && t.v[node] == -Inf
criterion_value = Inf
else
criterion_value = t.v[node] + p.solver.c*sqrt(ltn/n)
end
if criterion_value > best_criterion_val
best_criterion_val = criterion_value
empty!(best_nodes)
push!(best_nodes, node)
elseif criterion_value == best_criterion_val
push!(best_nodes, node)
end
end
ha = rand(p.rng, best_nodes)
a = t.a_labels[ha]
sp, o, r = @gen(:sp, :o, :r)(p.problem, s, a, p.rng)
hao = get(t.o_lookup, (ha, o), 0)
if hao == 0
hao = insert_obs_node!(t, p.problem, ha, sp, o)
v = estimate_value(p.solved_estimator,
p.problem,
sp,
POMCPObsNode(t, hao),
steps-1)
R = r + discount(p.problem)*v
else
R = r + discount(p.problem)*simulate(p, sp, POMCPObsNode(t, hao), steps-1)
end
t.total_n[h] += 1
t.n[ha] += 1
t.v[ha] += (R-t.v[ha])/t.n[ha]
return R
end
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 3083 | function D3Trees.D3Tree(p::POMCPPlanner; title="POMCP Tree", kwargs...)
@warn("""
D3Tree(planner::POMCPPlanner) is deprecated and may be removed in the future. Instead, please use
a, info = action_info(planner, b)
D3Tree(info[:tree])
Or, you can get this info from a POMDPTools History
info = first(ainfo_hist(hist))
D3Tree(info[:tree])
""")
if p._tree == nothing
error("POMCPPlanner has not constructed a tree yet, run `action(planner, belief)` first to construct the tree.")
end
return D3Tree(p._tree; title=title, kwargs...)
end
function D3Trees.D3Tree(t::POMCPTree; title="POMCP Tree", kwargs...)
lenb = length(t.total_n)
lenba = length(t.n)
len = lenb + lenba
children = Vector{Vector{Int}}(undef, len)
text = Vector{String}(undef, len)
tt = fill("", len)
link_style = fill("", len)
style = fill("", len)
ba_children = [Set{Int}() for i in 1:lenba]
for (ha_o, c) in t.o_lookup
ha, o = ha_o
push!(ba_children[ha], c)
end
min_V = minimum(t.v)
max_V = maximum(t.v)
for b in 1:lenb
children[b] = t.children[b] .+ lenb
text[b] = @sprintf("""
o: %s
N: %-10d""",
b==1 ? "<root>" : node_tag(t.o_labels[b]),
t.total_n[b]
)
tt[b] = """
o: $(b==1 ? "<root>" : node_tag(t.o_labels[b]))
N: $(t.total_n[b])
$(length(t.children[b])) children
"""
link_width = max(1.0, 20.0*sqrt(t.total_n[b]/t.total_n[1]))
link_style[b] = "stroke-width:$link_width"
end
for ba in 1:lenba
children[ba+lenb] = collect(ba_children[ba])
text[ba+lenb] = @sprintf("""
a: %s
N: %-7d\nV: %-10.3g""",
node_tag(t.a_labels[ba]), t.n[ba], t.v[ba])
tt[ba+lenb] = """
a: $(tooltip_tag(t.a_labels[ba]))
N: $(t.n[ba])
V: $(t.v[ba])
$(length(ba_children[ba])) children
"""
link_width = max(1.0, 20.0*sqrt(t.n[ba]/t.total_n[1]))
link_style[ba+lenb] = "stroke-width:$link_width"
rel_V = (t.v[ba]-min_V)/(max_V-min_V)
if isnan(rel_V)
color = colorant"gray"
else
color = weighted_color_mean(rel_V, colorant"green", colorant"red")
end
style[ba+lenb] = "stroke:#$(hex(color))"
end
return D3Tree(children;
text=text,
tooltip=tt,
style=style,
link_style=link_style,
title=title,
kwargs...
)
end
Base.show(io::IO, mime::MIME"text/html", t::POMCPTree) = show(io, mime, D3Tree(t))
Base.show(io::IO, mime::MIME"text/plain", t::POMCPTree) = show(io, mime, D3Tree(t))
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | code | 5964 | using BasicPOMCP
using Test
using POMDPs
using POMDPModels
using NBInclude
using D3Trees
using Random
using POMDPTools
using POMDPLinter: @requirements_info, @show_requirements, requirements_info
using ParticleFilters: n_particles, particles, particle, weights, weighted_particles, weight_sum, weight
import POMDPs:
transition,
observation,
reward,
discount,
initialstate,
updater,
states,
actions,
observations
struct ConstObsPOMDP <: POMDP{Bool, Symbol, Bool} end
updater(problem::ConstObsPOMDP) = DiscreteUpdater(problem)
initialstate(::ConstObsPOMDP) = BoolDistribution(0.0)
transition(p::ConstObsPOMDP, s::Bool, a::Symbol) = BoolDistribution(0.0)
observation(p::ConstObsPOMDP, a::Symbol, sp::Bool) = BoolDistribution(1.0)
reward(p::ConstObsPOMDP, s::Bool, a::Symbol, sp::Bool) = 1.
discount(p::ConstObsPOMDP) = 0.9
states(p::ConstObsPOMDP) = (true, false)
actions(p::ConstObsPOMDP) = (:the_only_action,)
observations(p::ConstObsPOMDP) = (true, false)
@testset "POMDPTools" begin
pomdp = BabyPOMDP()
test_solver(POMCPSolver(), BabyPOMDP())
end;
@testset "type stability" begin
pomdp = BabyPOMDP()
solver = POMCPSolver(rng = MersenneTwister(1))
planner = solve(solver, pomdp)
b = initialstate(pomdp)
tree = BasicPOMCP.POMCPTree(pomdp, b, solver.tree_queries)
node = BasicPOMCP.POMCPObsNode(tree, 1)
r = @inferred BasicPOMCP.simulate(planner, rand(MersenneTwister(1), initialstate(pomdp)), node, 20)
end;
@testset "belief dependent actions" begin
pomdp = ConstObsPOMDP()
function POMDPs.actions(m::ConstObsPOMDP, b::LeafNodeBelief)
@test currentobs(b) == true
@test history(b)[end].o == true
@test history(b)[end].a == :the_only_action
@test mean(b) == 0.0
@test mode(b) == 0.0
@test only(support(b)) == false
@test pdf(b, false) == 1.0
@test pdf(b, true) == 0.0
@test rand(b) == false
@test n_particles(b) == 1
@test only(particles(b)) == false
@test only(weights(b)) == 1.0
@test only(weighted_particles(b)) == (false => 1.0)
@test weight_sum(b) == 1.0
@test weight(b, 1) == 1.0
@test particle(b, 1) == false
# old type name - this can be removed when upgrading versions
@test b isa AOHistoryBelief
return actions(m)
end
solver = POMCPSolver(rng = MersenneTwister(1))
planner = solve(solver, pomdp)
b = initialstate(pomdp)
tree = BasicPOMCP.POMCPTree(pomdp, b, solver.tree_queries)
node = BasicPOMCP.POMCPObsNode(tree, 1)
@inferred BasicPOMCP.simulate(planner, rand(MersenneTwister(1), initialstate(pomdp)), node, 20)
end;
@testset "simulation" begin
pomdp = BabyPOMDP()
solver = POMCPSolver(rng = MersenneTwister(1))
planner = solve(solver, pomdp)
solver = POMCPSolver(max_time=0.1, tree_queries=typemax(Int), rng = MersenneTwister(1))
planner = solve(solver, pomdp)
b = initialstate(pomdp)
a, info = action_info(planner, b)
println("time below should be about 0.1 seconds")
etime = @elapsed a, info = action_info(planner, b)
@show etime
@test etime < 0.2
@show info[:search_time_us]
sim = HistoryRecorder(max_steps=10)
simulate(sim, pomdp, planner, updater(pomdp))
end;
@testset "d3t" begin
pomdp = BabyPOMDP()
solver = POMCPSolver(max_time=0.1, tree_queries=typemax(Int), rng = MersenneTwister(1))
planner = solve(solver, pomdp)
b = initialstate(pomdp)
a, info = action_info(planner, b, tree_in_info=true)
d3t = D3Tree(info[:tree], title="test tree")
# inchrome(d3t)
show(stdout, MIME("text/plain"), d3t)
solver = POMCPSolver(max_time=0.1, tree_queries=typemax(Int), rng=MersenneTwister(1), tree_in_info=true)
planner = solve(solver, pomdp)
a, info = action_info(planner, b)
d3t = D3Tree(info[:tree], title="test tree (tree_in_info solver option)")
end;
@testset "Minimal_Example" begin
@nbinclude(joinpath(dirname(@__FILE__), "..", "notebooks", "Minimal_Example.ipynb"))
end;
@testset "consistency" begin
# test consistency when rng is specified
pomdp = BabyPOMDP()
solver = POMCPSolver(rng = MersenneTwister(1))
planner = solve(solver, pomdp)
hist1 = simulate(HistoryRecorder(max_steps=1000, rng=MersenneTwister(3)), pomdp, planner)
solver = POMCPSolver(rng = MersenneTwister(1))
planner = solve(solver, pomdp)
hist2 = simulate(HistoryRecorder(max_steps=1000, rng=MersenneTwister(3)), pomdp, planner)
@test discounted_reward(hist1) == discounted_reward(hist2)
end;
@testset "requires" begin
# REQUIREMENTS
solver = POMCPSolver()
pomdp = TigerPOMDP()
println("============== @requirements_info with only solver:")
requirements_info(solver)
println("============== @requirements_info with solver and pomdp:")
requirements_info(solver, pomdp)
@show_requirements POMDPs.solve(solver, pomdp)
end;
@testset "errors" begin
struct TerminalPOMDP <: POMDP{Int, Int, Int} end
POMDPs.isterminal(::TerminalPOMDP, s) = true
POMDPs.actions(::TerminalPOMDP) = [1,2,3]
solver = POMCPSolver()
planner = solve(solver, TerminalPOMDP())
@test_throws AllSamplesTerminal action(planner, Deterministic(1))
let ex = nothing
try
action(planner, Deterministic(1))
catch ex
end
@test sprint(showerror, ex) == """
Planner failed to choose an action because all states sampled from the belief were terminal.
To see the belief, catch this exception as ex and see ex.belief.
To specify an action for this case, use the default_action solver parameter.
"""
end
end
@testset "FORollout" begin
struct TestMDPSolver1 <: Solver end
POMDPs.solve(::TestMDPSolver1, m::MDP) = FunctionPolicy(s->first(actions(m)))
solver = POMCPSolver(estimate_value=FORollout(TestMDPSolver1()))
m = BabyPOMDP()
planner = solve(solver, m)
@test action(planner, initialstate(m)) in actions(m)
end
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.3.11 | 6bd8e6c1eb1c9fe993907c6eb1e9df02b8b23b04 | docs | 5621 | # BasicPOMCP
[](https://github.com/JuliaPOMDP/BasicPOMCP.jl/actions/workflows/CI.yml)
[](https://codecov.io/gh/JuliaPOMDP/BasicPOMCP.jl)
This package implements the PO-UCT online tree search algorithm for [POMDPs.jl](https://github.com/JuliaPOMDP/POMDPs.jl). PO-UCT is the most useful component of the POMCP algorithm described in \[1\]. The other component of POMCP, re-use of particles in the tree for belief updates, is not implemented for reasons described in the [Belief Update](#belief-update) section below.
> \[1\] Silver, D., & Veness, J. (2010). Monte-Carlo Planning in Large POMDPs. In *Advances in neural information processing systems* (pp. 2164–2172). Retrieved from http://discovery.ucl.ac.uk/1347369/
Problems should be specified using the [POMDPs.jl](https://github.com/JuliaPOMDP/POMDPs.jl) interface. For more information, see the [POMDPs.jl documentation](http://juliapomdp.github.io/POMDPs.jl/latest/).
This package replaces the deprecated [POMCP.jl package](https://github.com/JuliaPOMDP/POMCP.jl). It has fewer features, but is much simpler.

## Installation
```julia
using Pkg
Pkg.add("BasicPOMCP")
```
## Usage
```julia
using POMDPs, POMDPModels, POMDPSimulators, BasicPOMCP
pomdp = TigerPOMDP()
solver = POMCPSolver()
planner = solve(solver, pomdp)
for (s, a, o) in stepthrough(pomdp, planner, "s,a,o", max_steps=10)
println("State was $s,")
println("action $a was taken,")
println("and observation $o was received.\n")
end
```
A minimal example showing how to implement a problem for the solver to use is here: https://github.com/JuliaPOMDP/BasicPOMCP.jl/blob/master/notebooks/Minimal_Example.ipynb
## Solver Options
Solver options are set with keyword arguments to the `BasicPOMCP` constructor. The options are described in the docstring which can be accessed with `?POMCPSolver`.
The output of `?POMCPSolver` is printed below, but may not be up to date.
> POMCPSolver(#=keyword arguments=#)
>
> Partially Observable Monte Carlo Planning Solver.
>
> ## Keyword Arguments
>
> - `max_depth::Int`
> Rollouts and tree expension will stop when this depth is reached.
> default: `20`
>
> - `c::Float64`
> UCB exploration constant - specifies how much the solver should explore.
> default: `1.0`
>
> - `tree_queries::Int`
> Number of iterations during each action() call.
> default: `1000`
>
> - `max_time::Float64`
> Maximum time for planning in each action() call.
> default: `Inf`
>
> - `tree_in_info::Bool`
> If `true`, returns the tree in the info dict when action_info is called.
> default: `false`
>
> - `estimate_value::Any`
> Function, object, or number used to estimate the value at the leaf nodes.
> default: `RolloutEstimator(RandomSolver(rng))`
> - If this is a function `f`, `f(pomdp, s, h::BeliefNode, steps)` will be called to estimate the value.
> - If this is an object `o`, `estimate_value(o, pomdp, s, h::BeliefNode, steps)` will be called.
> - If this is a number, the value will be set to that number
> Note: In many cases, the simplest way to estimate the value is to do a rollout on the fully observable MDP with a policy that is a function of the state. To do this, use `FORollout(policy)`.
>
> - `default_action::Any`
> Function, action, or Policy used to determine the action if POMCP fails with exception `ex`.
> default: `ExceptionRethrow()`
> - If this is a Function `f`, `f(pomdp, belief, ex)` will be called.
> - If this is a Policy `p`, `action(p, belief)` will be called.
> - If it is an object `a`, `default_action(a, pomdp, belief, ex)` will be called, and if this method is not implemented, `a` will be returned directly.
>
> - `rng::AbstractRNG`
> Random number generator.
> default: `Random.GLOBAL_RNG`
## Belief Update
This solver does not reuse decision-making simulations for the belief update as in the original Silver and Veness paper. We have found that unweighted particle filtering approach to be unuseful in practice because
1. The number of particles that comprise the next belief is small because only the particles in the branch corresponding to the actual action and observation can be used,
2. Even in the Silver and Veness paper, domain-specific particle reinvigoration must be used, and
3. The computation time required to run a standard weighted particle filter is small compared to the amount of time needed to plan with POMCP, so reusing the simulations gives minimal benefit.
Instead, a custom belief updater, or an updater from [ParticleFilters.jl](https://github.com/JuliaPOMDP/ParticleFilters.jl) should be used.
## Tree Visualization
The search tree can be visualized with [D3Trees.jl](https://github.com/sisl/D3Trees.jl) after running the `action_info()` as in the example below. **Note: tree_in_info must be set to true either as a solver option or as a keyword argument to action_info() for this to work** (it is disabled by default because it can use a lot of memory).
```julia
using POMDPs
using BasicPOMCP
using POMDPModels
using POMDPTools
using D3Trees
using Random
pomdp = BabyPOMDP()
solver = POMCPSolver(tree_queries=1000, c=10.0, rng=MersenneTwister(1))
planner = solve(solver, pomdp)
a, info = action_info(planner, initialstate(pomdp), tree_in_info=true)
inchrome(D3Tree(info[:tree], init_expand=3))
```
This should produce the image at the top of the README.
| BasicPOMCP | https://github.com/JuliaPOMDP/BasicPOMCP.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 389 | using Documenter
using FFTA
makedocs(
sitename = "FFTA",
format = Documenter.HTML(),
pages = ["Development Tools" => "dev.md"],
modules = [FFTA]
)
# Documenter can also automatically deploy documentation to gh-pages.
# See "Hosting Documentation" and deploydocs() in the Documenter manual
# for more information.
deploydocs(
repo = "github.com/dannys4/FFTA.jl.git"
)
| FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 1280 | module FFTA
using Primes, DocStringExtensions, Reexport, MuladdMacro, LinearAlgebra
@reexport using AbstractFFTs
import AbstractFFTs: Plan
include("callgraph.jl")
include("algos.jl")
include("plan.jl")
#=
function fft(x::AbstractMatrix{T}) where {T <: Real}
M,N = size(x)
y1 = similar(x, Complex{T})
y2 = similar(x, Complex{T})
g1 = CallGraph{Complex{T}}(size(x,1))
g2 = CallGraph{Complex{T}}(size(x,2))
for k in 1:N
@views fft!(y1[:,k], x[:,k], 1, 1, FFT_FORWARD, g1[1].type, g1, 1)
end
for k in 1:M
@views fft!(y2[k,:], y1[k,:], 1, 1, FFT_FORWARD, g2[1].type, g2, 1)
end
y2
end
function bfft(x::AbstractVector{T}) where {T <: Real}
y = similar(x, Complex{T})
g = CallGraph{Complex{T}}(length(x))
fft!(y, x, 1, 1, FFT_BACKWARD, g[1].type, g, 1)
y
end
function bfft(x::AbstractMatrix{T}) where {T <: Real}
M,N = size(x)
y1 = similar(x, Complex{T})
y2 = similar(x, Complex{T})
g1 = CallGraph{Complex{T}}(size(x,1))
g2 = CallGraph{Complex{T}}(size(x,2))
for k in 1:N
@views fft!(y1[:,k], x[:,k], 1, 1, FFT_BACKWARD, g1[1].type, g1, 1)
end
for k in 1:M
@views fft!(y2[k,:], y1[k,:], 1, 1, FFT_BACKWARD, g2[1].type, g2, 1)
end
y2
end =#
end
| FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 11040 | fft!(::AbstractVector{T}, ::AbstractVector{T}, ::Int, ::Int, ::Direction, ::AbstractFFTType, ::CallGraph{T}, ::Int) where {T} = nothing
@inline function direction_sign(d::Direction)
Int(d)
end
function (g::CallGraph{T})(out::AbstractVector{T}, in::AbstractVector{U}, start_out::Int, start_in::Int, v::Direction, t::AbstractFFTType, idx::Int) where {T,U}
fft!(out, in, start_out, start_in, v, t, g, idx)
end
"""
$(TYPEDSIGNATURES)
Cooley-Tukey composite FFT, with a pre-computed call graph
# Arguments
`out`: Output vector
`in`: Input vector
`start_out`: Index of the first element of the output vector
`start_in`: Index of the first element of the input vector
`d`: Direction of the transform
`g`: Call graph for this transform
`idx`: Index of the current transform in the call graph
"""
function fft!(out::AbstractVector{T}, in::AbstractVector{U}, start_out::Int, start_in::Int, d::Direction, ::CompositeFFT, g::CallGraph{T}, idx::Int) where {T,U}
root = g[idx]
left_idx = idx + root.left
right_idx = idx + root.right
left = g[left_idx]
right = g[right_idx]
N = root.sz
N1 = left.sz
N2 = right.sz
s_in = root.s_in
s_out = root.s_out
w1 = convert(T, cispi(direction_sign(d)*2/N))
wj1 = one(T)
tmp = g.workspace[idx]
@inbounds for j1 in 0:N1-1
wk2 = wj1
g(tmp, in, N2*j1+1, start_in + j1*s_in, d, right.type, right_idx)
j1 > 0 && @inbounds for k2 in 1:N2-1
tmp[N2*j1 + k2 + 1] *= wk2
wk2 *= wj1
end
wj1 *= w1
end
@inbounds for k2 in 0:N2-1
g(out, tmp, start_out + k2*s_out, k2+1, d, left.type, left_idx)
end
end
"""
$(TYPEDSIGNATURES)
Discrete Fourier Transform, O(N^2) algorithm, in place.
# Arguments
`out`: Output vector
`in`: Input vector
`N`: Size of the transform
`start_out`: Index of the first element of the output vector
`stride_out`: Stride of the output vector
`start_in`: Index of the first element of the input vector
`stride_in`: Stride of the input vector
`d`: Direction of the transform
"""
function fft_dft!(out::AbstractVector{T}, in::AbstractVector{T}, N::Int, start_out::Int, stride_out::Int, start_in::Int, stride_in::Int, d::Direction) where {T}
tmp = in[start_in]
@inbounds for j in 1:N-1
tmp += in[start_in + j*stride_in]
end
out[start_out] = tmp
wk = wkn = w = convert(T, cispi(direction_sign(d)*2/N))
@inbounds for d in 1:N-1
tmp = in[start_in]
@inbounds for k in 1:N-1
tmp += wkn*in[start_in + k*stride_in]
wkn *= wk
end
out[start_out + d*stride_out] = tmp
wk *= w
wkn = wk
end
end
function fft_dft!(out::AbstractVector{Complex{T}}, in::AbstractVector{T}, N::Int, start_out::Int, stride_out::Int, start_in::Int, stride_in::Int, d::Direction) where {T<:Real}
halfN = N÷2
wk = wkn = w = convert(Complex{T}, cispi(direction_sign(d)*2/N))
tmpBegin = tmpHalf = in[start_in]
@inbounds for j in 1:N-1
tmpBegin += in[start_in + stride_in*j]
iseven(j) ? tmpHalf += in[start_in + stride_in*j] : tmpHalf -= in[start_in + stride_in*j]
end
out[start_out] = convert(Complex{T}, tmpBegin)
iseven(N) && (out[start_out + stride_out*halfN] = convert(Complex{T}, tmpHalf))
@inbounds for d in 1:halfN
tmp = in[start_in]
@inbounds for k in 1:N-1
tmp += wkn*in[start_in + k*stride_in]
wkn *= wk
end
out[start_out + d*stride_out] = tmp
wk *= w
wkn = wk
end
@inbounds for k in halfN+1:N-1
out[start_out + stride_out*k] = conj(out[start_out + stride_out*(N-k)])
end
end
function fft!(out::AbstractVector{T}, in::AbstractVector{U}, start_out::Int, start_in::Int, d::Direction, ::DFT, g::CallGraph{T}, idx::Int) where {T,U}
root = g[idx]
fft_dft!(out, in, root.sz, start_out, root.s_out, start_in, root.s_in, d)
end
"""
$(TYPEDSIGNATURES)
Power of 2 FFT, in place
# Arguments
`out`: Output vector
`in`: Input vector
`N`: Size of the transform
`start_out`: Index of the first element of the output vector
`stride_out`: Stride of the output vector
`start_in`: Index of the first element of the input vector
`stride_in`: Stride of the input vector
`d`: Direction of the transform
"""
function fft_pow2!(out::AbstractVector{T}, in::AbstractVector{U}, N::Int, start_out::Int, stride_out::Int, start_in::Int, stride_in::Int, d::Direction) where {T, U}
if N == 2
out[start_out] = in[start_in] + in[start_in + stride_in]
out[start_out + stride_out] = in[start_in] - in[start_in + stride_in]
return
end
m = N ÷ 2
fft_pow2!(out, in, m, start_out , stride_out, start_in , stride_in*2, d)
fft_pow2!(out, in, m, start_out + m*stride_out, stride_out, start_in + stride_in, stride_in*2, d)
w1 = convert(T, cispi(direction_sign(d)*2/N))
wj = one(T)
@inbounds for j in 0:m-1
j1_out = start_out + j*stride_out
j2_out = start_out + (j+m)*stride_out
out_j = out[j1_out]
out[j1_out] = out_j + wj*out[j2_out]
out[j2_out] = out_j - wj*out[j2_out]
wj *= w1
end
end
function fft!(out::AbstractVector{T}, in::AbstractVector{U}, start_out::Int, start_in::Int, d::Direction, ::Pow2FFT, g::CallGraph{T}, idx::Int) where {T,U}
root = g[idx]
N = root.sz
s_in = root.s_in
s_out = root.s_out
fft_pow2!(out, in, N, start_out, s_out, start_in, s_in, d)
end
"""
$(TYPEDSIGNATURES)
Power of 4 FFT, in place
# Arguments
`out`: Output vector
`in`: Input vector
`N`: Size of the transform
`start_out`: Index of the first element of the output vector
`stride_out`: Stride of the output vector
`start_in`: Index of the first element of the input vector
`stride_in`: Stride of the input vector
`d`: Direction of the transform
"""
function fft_pow4!(out::AbstractVector{T}, in::AbstractVector{U}, N::Int, start_out::Int, stride_out::Int, start_in::Int, stride_in::Int, d::Direction) where {T, U}
ds = direction_sign(d)
plusi = ds*1im
minusi = ds*-1im
if N == 4
out[start_out + 0] = in[start_in] + in[start_in + stride_in] + in[start_in + 2*stride_in] + in[start_in + 3*stride_in]
out[start_out + stride_out] = in[start_in] + in[start_in + stride_in]*plusi - in[start_in + 2*stride_in] + in[start_in + 3*stride_in]*minusi
out[start_out + 2*stride_out] = in[start_in] - in[start_in + stride_in] + in[start_in + 2*stride_in] - in[start_in + 3*stride_in]
out[start_out + 3*stride_out] = in[start_in] + in[start_in + stride_in]*minusi - in[start_in + 2*stride_in] + in[start_in + 3*stride_in]*plusi
return
end
m = N ÷ 4
@muladd fft_pow4!(out, in, m, start_out , stride_out, start_in , stride_in*4, d)
@muladd fft_pow4!(out, in, m, start_out + m*stride_out, stride_out, start_in + stride_in, stride_in*4, d)
@muladd fft_pow4!(out, in, m, start_out + 2*m*stride_out, stride_out, start_in + 2*stride_in, stride_in*4, d)
@muladd fft_pow4!(out, in, m, start_out + 3*m*stride_out, stride_out, start_in + 3*stride_in, stride_in*4, d)
w1 = convert(T, cispi(direction_sign(d)*2/N))
wj = one(T)
w1 = convert(T, cispi(ds*2/N))
w2 = convert(T, cispi(ds*4/N))
w3 = convert(T, cispi(ds*6/N))
wk1 = wk2 = wk3 = one(T)
@inbounds for k in 0:m-1
@muladd k0 = start_out + k*stride_out
@muladd k1 = start_out + (k+m)*stride_out
@muladd k2 = start_out + (k+2*m)*stride_out
@muladd k3 = start_out + (k+3*m)*stride_out
y_k0, y_k1, y_k2, y_k3 = out[k0], out[k1], out[k2], out[k3]
@muladd out[k0] = (y_k0 + y_k2*wk2) + (y_k1*wk1 + y_k3*wk2)
@muladd out[k1] = (y_k0 - y_k2*wk2) + (y_k1*wk1 - y_k3*wk3) * plusi
@muladd out[k2] = (y_k0 + y_k2*wk2) - (y_k1*wk1 + y_k3*wk3)
@muladd out[k3] = (y_k0 - y_k2*wk2) + (y_k1*wk1 - y_k3*wk3) * minusi
wk1 *= w1
wk2 *= w2
wk3 *= w3
end
end
function fft!(out::AbstractVector{T}, in::AbstractVector{U}, start_out::Int, start_in::Int, d::Direction, ::Pow4FFT, g::CallGraph{T}, idx::Int) where {T,U}
root = g[idx]
N = root.sz
s_in = root.s_in
s_out = root.s_out
fft_pow4!(out, in, N, start_out, s_out, start_in, s_in, d)
end
"""
$(TYPEDSIGNATURES)
Power of 3 FFT, in place
# Arguments
out: Output vector
in: Input vector
N: Size of the transform
start_out: Index of the first element of the output vector
stride_out: Stride of the output vector
start_in: Index of the first element of the input vector
stride_in: Stride of the input vector
d: Direction of the transform
plus120: Depending on direction, perform either ±120° rotation
minus120: Depending on direction, perform either ∓120° rotation
"""
function fft_pow3!(out::AbstractVector{T}, in::AbstractVector{U}, N::Int, start_out::Int, stride_out::Int, start_in::Int, stride_in::Int, d::Direction, plus120::T, minus120::T) where {T, U}
if N == 3
@muladd out[start_out + 0] = in[start_in] + in[start_in + stride_in] + in[start_in + 2*stride_in]
@muladd out[start_out + stride_out] = in[start_in] + in[start_in + stride_in]*plus120 + in[start_in + 2*stride_in]*minus120
@muladd out[start_out + 2*stride_out] = in[start_in] + in[start_in + stride_in]*minus120 + in[start_in + 2*stride_in]*plus120
return
end
# Size of subproblem
Nprime = N ÷ 3
ds = direction_sign(d)
# Dividing into subproblems
fft_pow3!(out, in, Nprime, start_out, stride_out, start_in, stride_in*3, d, plus120, minus120)
fft_pow3!(out, in, Nprime, start_out + Nprime*stride_out, stride_out, start_in + stride_in, stride_in*3, d, plus120, minus120)
fft_pow3!(out, in, Nprime, start_out + 2*Nprime*stride_out, stride_out, start_in + 2*stride_in, stride_in*3, d, plus120, minus120)
w1 = convert(T, cispi(ds*2/N))
w2 = convert(T, cispi(ds*4/N))
wk1 = wk2 = one(T)
for k in 0:Nprime-1
@muladd k0 = start_out + k*stride_out
@muladd k1 = start_out + (k+Nprime)*stride_out
@muladd k2 = start_out + (k+2*Nprime)*stride_out
y_k0, y_k1, y_k2 = out[k0], out[k1], out[k2]
@muladd out[k0] = y_k0 + y_k1*wk1 + y_k2*wk2
@muladd out[k1] = y_k0 + y_k1*wk1*plus120 + y_k2*wk2*minus120
@muladd out[k2] = y_k0 + y_k1*wk1*minus120 + y_k2*wk2*plus120
wk1 *= w1
wk2 *= w2
end
end
function fft!(out::AbstractVector{T}, in::AbstractVector{U}, start_out::Int, start_in::Int, d::Direction, ::Pow3FFT, g::CallGraph{T}, idx::Int) where {T,U}
root = g[idx]
N = root.sz
s_in = root.s_in
s_out = root.s_out
p_120 = convert(T, cispi(2/3))
m_120 = convert(T, cispi(4/3))
if d == FFT_FORWARD
fft_pow3!(out, in, N, start_out, s_out, start_in, s_in, d, m_120, p_120)
else
fft_pow3!(out, in, N, start_out, s_out, start_in, s_in, d, p_120, m_120)
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 3624 | @enum Direction FFT_FORWARD=-1 FFT_BACKWARD=1
@enum Pow24 POW2=2 POW4=1
abstract type AbstractFFTType end
# Represents a Composite Cooley-Tukey FFT
struct CompositeFFT <: AbstractFFTType end
# Represents a Radix-2 Cooley-Tukey FFT
struct Pow2FFT <: AbstractFFTType end
# Represents a Radix-3 Cooley-Tukey FFT
struct Pow3FFT <: AbstractFFTType end
# Represents a Radix-4 Cooley-Tukey FFT
struct Pow4FFT <: AbstractFFTType end
# Represents an O(N²) DFT
struct DFT <: AbstractFFTType end
"""
$(TYPEDSIGNATURES)
Node of a call graph
# Arguments
`left`: Offset to the left child node
`right`: Offset to the right child node
`type`: Object representing the type of FFT
`sz`: Size of this FFT
"""
struct CallGraphNode
left::Int
right::Int
type::AbstractFFTType
sz::Int
s_in::Int
s_out::Int
end
"""
$(TYPEDSIGNATURES)
Object representing a graph of FFT Calls
# Arguments
`nodes`: Nodes keeping track of the graph
`workspace`: Preallocated Workspace
"""
struct CallGraph{T<:Complex}
nodes::Vector{CallGraphNode}
workspace::Vector{Vector{T}}
end
# Get the node in the graph at index i
Base.getindex(g::CallGraph{T}, i::Int) where {T} = g.nodes[i]
"""
$(TYPEDSIGNATURES)
Check if `N` is a power of `base`
"""
function _ispow(N, base)
while N % base == 0
N = N/base
end
return N == 1
end
"""
$(TYPEDSIGNATURES)
Check if `N` is a power of 2 or 4
"""
function _ispow24(N::Int)
N < 1 && return nothing
while N & 0b11 == 0
N >>= 2
end
return N < 3 ? Pow24(N) : nothing
end
"""
$(TYPEDSIGNATURES)
Recursively instantiate a set of `CallGraphNode`s
# Arguments
`nodes`: A vector (which gets expanded) of `CallGraphNode`s
`N`: The size of the FFT
`workspace`: A vector (which gets expanded) of preallocated workspaces
`s_in`: The stride of the input
`s_out`: The stride of the output
"""
function CallGraphNode!(nodes::Vector{CallGraphNode}, N::Int, workspace::Vector{Vector{T}}, s_in::Int, s_out::Int)::Int where {T}
if iseven(N)
pow = _ispow24(N)
if !isnothing(pow)
push!(workspace, T[])
push!(nodes, CallGraphNode(0, 0, pow == POW2 ? Pow2FFT() : Pow4FFT(), N, s_in, s_out))
return 1
end
end
if N % 3 == 0
if _ispow(N, 3)
push!(workspace, T[])
push!(nodes, CallGraphNode(0, 0, Pow3FFT(), N, s_in, s_out))
return 1
end
end
if isprime(N)
push!(workspace, T[])
push!(nodes, CallGraphNode(0,0, DFT(),N, s_in, s_out))
return 1
end
Ns = [first(x) for x in collect(factor(N)) for _ in 1:last(x)]
if Ns[1] == 2
N1 = prod(Ns[Ns .== 2])
elseif Ns[1] == 3
N1 = prod(Ns[Ns .== 3])
else
# Greedy search for closest factor of N to sqrt(N)
Nsqrt = sqrt(N)
N_cp = cumprod(Ns[end:-1:1])[end:-1:1]
N_prox = abs.(N_cp .- Nsqrt)
_,N1_idx = findmin(N_prox)
N1 = N_cp[N1_idx]
end
N2 = N ÷ N1
push!(nodes, CallGraphNode(0,0,DFT(),N,s_in,s_out))
sz = length(nodes)
push!(workspace, Vector{T}(undef, N))
left_len = CallGraphNode!(nodes, N1, workspace, N2, N2*s_out)
right_len = CallGraphNode!(nodes, N2, workspace, N1*s_in, 1)
nodes[sz] = CallGraphNode(1, 1 + left_len, CompositeFFT(), N, s_in, s_out)
return 1 + left_len + right_len
end
"""
$(TYPEDSIGNATURES)
Instantiate a CallGraph from a number `N`
"""
function CallGraph{T}(N::Int) where {T}
nodes = CallGraphNode[]
workspace = Vector{Vector{T}}()
CallGraphNode!(nodes, N, workspace, 1, 1)
CallGraph(nodes, workspace)
end
| FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 5936 | import Base: *
import LinearAlgebra: mul!
abstract type FFTAPlan{T,N} <: Plan{T} end
struct FFTAInvPlan{T,N} <: FFTAPlan{T,N} end
struct FFTAPlan_cx{T,N} <: FFTAPlan{T,N}
callgraph::NTuple{N, CallGraph{T}}
region::Union{Int,AbstractVector{<:Int}}
dir::Direction
pinv::FFTAInvPlan{T}
end
struct FFTAPlan_re{T,N} <: FFTAPlan{T,N}
callgraph::NTuple{N, CallGraph{T}}
region::Union{Int,AbstractVector{<:Int}}
dir::Direction
pinv::FFTAInvPlan{T}
flen::Int
end
function AbstractFFTs.plan_fft(x::AbstractArray{T}, region; kwargs...)::FFTAPlan_cx{T} where {T <: Complex}
N = length(region)
@assert N <= 2 "Only supports vectors and matrices"
if N == 1
g = CallGraph{T}(size(x,region[]))
pinv = FFTAInvPlan{T,N}()
return FFTAPlan_cx{T,N}((g,), region, FFT_FORWARD, pinv)
else
sort!(region)
g1 = CallGraph{T}(size(x,region[1]))
g2 = CallGraph{T}(size(x,region[2]))
pinv = FFTAInvPlan{T,N}()
return FFTAPlan_cx{T,N}((g1,g2), region, FFT_FORWARD, pinv)
end
end
function AbstractFFTs.plan_bfft(x::AbstractArray{T}, region; kwargs...)::FFTAPlan_cx{T} where {T <: Complex}
N = length(region)
@assert N <= 2 "Only supports vectors and matrices"
if N == 1
g = CallGraph{T}(size(x,region[]))
pinv = FFTAInvPlan{T,N}()
return FFTAPlan_cx{T,N}((g,), region, FFT_BACKWARD, pinv)
else
sort!(region)
g1 = CallGraph{T}(size(x,region[1]))
g2 = CallGraph{T}(size(x,region[2]))
pinv = FFTAInvPlan{T,N}()
return FFTAPlan_cx{T,N}((g1,g2), region, FFT_BACKWARD, pinv)
end
end
function AbstractFFTs.plan_rfft(x::AbstractArray{T}, region; kwargs...)::FFTAPlan_re{Complex{T}} where {T <: Real}
N = length(region)
@assert N <= 2 "Only supports vectors and matrices"
if N == 1
g = CallGraph{Complex{T}}(size(x,region[]))
pinv = FFTAInvPlan{Complex{T},N}()
return FFTAPlan_re{Complex{T},N}(tuple(g), region, FFT_FORWARD, pinv, size(x,region[]))
else
sort!(region)
g1 = CallGraph{Complex{T}}(size(x,region[1]))
g2 = CallGraph{Complex{T}}(size(x,region[2]))
pinv = FFTAInvPlan{Complex{T},N}()
return FFTAPlan_re{Complex{T},N}(tuple(g1,g2), region, FFT_FORWARD, pinv, size(x,region[1]))
end
end
function AbstractFFTs.plan_brfft(x::AbstractArray{T}, len, region; kwargs...)::FFTAPlan_re{T} where {T}
N = length(region)
@assert N <= 2 "Only supports vectors and matrices"
if N == 1
g = CallGraph{T}(len)
pinv = FFTAInvPlan{T,N}()
return FFTAPlan_re{T,N}((g,), region, FFT_BACKWARD, pinv, len)
else
sort!(region)
g1 = CallGraph{T}(len)
g2 = CallGraph{T}(size(x,region[2]))
pinv = FFTAInvPlan{T,N}()
return FFTAPlan_re{T,N}((g1,g2), region, FFT_BACKWARD, pinv, len)
end
end
function AbstractFFTs.plan_bfft(p::FFTAPlan_cx{T,N}) where {T,N}
return FFTAPlan_cx{T,N}(p.callgraph, p.region, -p.dir, p.pinv)
end
function AbstractFFTs.plan_brfft(p::FFTAPlan_re{T,N}) where {T,N}
return FFTAPlan_re{T,N}(p.callgraph, p.region, -p.dir, p.pinv, p.flen)
end
function LinearAlgebra.mul!(y::AbstractVector{U}, p::FFTAPlan{T,1}, x::AbstractVector{T}) where {T,U}
fft!(y, x, 1, 1, p.dir, p.callgraph[1][1].type, p.callgraph[1], 1)
end
function LinearAlgebra.mul!(y::AbstractArray{U,N}, p::FFTAPlan{T,1}, x::AbstractArray{T,N}) where {T,U,N}
Rpre = CartesianIndices(size(x)[1:p.region-1])
Rpost = CartesianIndices(size(x)[p.region+1:end])
for Ipre in Rpre
for Ipost in Rpost
@views fft!(y[Ipre,:,Ipost], x[Ipre,:,Ipost], 1, 1, p.dir, p.callgraph[1][1].type, p.callgraph[1], 1)
end
end
end
function LinearAlgebra.mul!(y::AbstractArray{U,N}, p::FFTAPlan{T,2}, x::AbstractArray{T,N}) where {T,U,N}
R1 = CartesianIndices(size(x)[1:p.region[1]-1])
R2 = CartesianIndices(size(x)[p.region[1]+1:p.region[2]-1])
R3 = CartesianIndices(size(x)[p.region[2]+1:end])
y_tmp = similar(y, axes(y)[p.region])
rows,cols = size(x)[p.region]
for I1 in R1
for I2 in R2
for I3 in R3
for k in 1:cols
@views fft!(y_tmp[:,k], x[I1,:,I2,k,I3], 1, 1, p.dir, p.callgraph[1][1].type, p.callgraph[1], 1)
end
for k in 1:rows
@views fft!(y[I1,k,I2,:,I3], y_tmp[k,:], 1, 1, p.dir, p.callgraph[2][1].type, p.callgraph[2], 1)
end
end
end
end
end
function *(p::FFTAPlan{T,1}, x::AbstractVector{T}) where {T<:Union{Real,Complex}}
y = similar(x, T <: Real ? Complex{T} : T)
LinearAlgebra.mul!(y, p, x)
y
end
function *(p::FFTAPlan{T,N1}, x::AbstractArray{T,N2}) where {T<:Union{Real, Complex}, N1, N2}
y = similar(x, T <: Real ? Complex{T} : T)
LinearAlgebra.mul!(y, p, x)
y
end
function *(p::FFTAPlan_re{T,1}, x::AbstractVector{T}) where {T<:Union{Real, Complex}}
if p.dir == FFT_FORWARD
y = similar(x, T <: Real ? Complex{T} : T)
LinearAlgebra.mul!(y, p, x)
return y[1:end÷2 + 1]
else
x_tmp = similar(x, p.flen)
x_tmp[1:end÷2 + 1] .= x
x_tmp[end÷2 + 2:end] .= iseven(p.flen) ? conj.(x[end-1:-1:2]) : conj.(x[end:-1:2])
y = similar(x_tmp)
LinearAlgebra.mul!(y, p, x_tmp)
return y
end
end
function *(p::FFTAPlan_re{T,N}, x::AbstractArray{T,2}) where {T<:Union{Real, Complex}, N}
if p.dir == FFT_FORWARD
y = similar(x, T <: Real ? Complex{T} : T)
LinearAlgebra.mul!(y, p, x)
return y[1:end÷2 + 1,:]
else
x_tmp = similar(x, p.flen, size(x)[2])
x_tmp[1:end÷2 + 1,:] .= x
x_tmp[end÷2 + 2:end,:] .= iseven(p.flen) ? conj.(x[end-1:-1:2,:]) : conj.(x[end:-1:2,:])
y = similar(x_tmp)
LinearAlgebra.mul!(y, p, x_tmp)
return y
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 1493 | using Test, Random
function padnum(m,x)
digs = floor(Int, log10(m))
digs_x = floor(Int, log10(x))
v = fill(' ', digs-digs_x)
for d in digits(x)[end:-1:1] push!(v, '0' + d) end
String(v)
end
Random.seed!(1)
@testset verbose = true "FFTA" begin
@testset verbose = true "1D" begin
@testset verbose = false "Complex" begin
include("onedim/complex_forward.jl")
include("onedim/complex_backward.jl")
x = rand(ComplexF64, 100)
y = fft(x)
x2 = bfft(y)/length(x)
@test x ≈ x2 atol=1e-12
end
@testset verbose = false "Real" begin
include("onedim/real_forward.jl")
include("onedim/real_backward.jl")
x = rand(Float64, 100)
y = fft(x)
x2 = bfft(y)/length(x)
@test x ≈ x2 atol=1e-12
end
end
@testset verbose = false "2D" begin
@testset verbose = true "Complex" begin
include("twodim/complex_forward.jl")
include("twodim/complex_backward.jl")
x = rand(ComplexF64, 100, 100)
y = fft(x)
x2 = bfft(y)/length(x)
@test x ≈ x2
end
@testset verbose = true "Real" begin
include("twodim/real_forward.jl")
include("twodim/real_backward.jl")
x = rand(Float64, 100, 100)
y = fft(x)
x2 = bfft(y)/length(x)
@test x ≈ x2
end
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 242 | using FFTA, Test
test_nums = [8, 11, 15, 16, 27, 100]
@testset "backward" begin
for N in test_nums
x = ones(ComplexF64, N)
y = bfft(x)
y_ref = 0*y
y_ref[1] = N
@test y ≈ y_ref atol=1e-12
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 256 | using FFTA, Test
test_nums = [8, 11, 15, 16, 27, 100]
@testset verbose = true " forward" begin
for N in test_nums
x = ones(ComplexF64, N)
y = fft(x)
y_ref = 0*y
y_ref[1] = N
@test y ≈ y_ref atol=1e-12
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 362 | using FFTA, Test, LinearAlgebra
test_nums = [8, 11, 15, 16, 27, 100]
@testset "backward" begin
for N in test_nums
x = ones(Float64, N)
y = brfft(x, 2*(N-1))
y_ref = 0*y
y_ref[1] = 2*(N-1)
if !isapprox(y_ref, y, atol=1e-12)
println(norm(y_ref - y))
end
@test y_ref ≈ y atol=1e-12
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 255 | using FFTA, Test
test_nums = [8, 11, 15, 16, 27, 100]
@testset verbose = true " forward" begin
for N in test_nums
x = ones(Float64, N)
y = rfft(x)
y_ref = 0*y
y_ref[1] = N
@test y ≈ y_ref atol=1e-12
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 242 | using FFTA, Test
test_nums = [8, 11, 15, 16, 27, 100]
@testset "backward" begin
for N in test_nums
x = ones(ComplexF64, N, N)
y = bfft(x)
y_ref = 0*y
y_ref[1] = length(x)
@test y ≈ y_ref
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 241 | using FFTA, Test
test_nums = [8, 11, 15, 16, 27, 100]
@testset " forward" begin
for N in test_nums
x = ones(ComplexF64, N, N)
y = fft(x)
y_ref = 0*y
y_ref[1] = length(x)
@test y ≈ y_ref
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 239 | using FFTA, Test
test_nums = [8]
@testset "backward" begin
for N in test_nums
x = ones(Float64, N, N)
y = brfft(x, 2(N-1))
y_ref = 0*y
y_ref[1] = N*(2(N-1))
@test y_ref ≈ y atol=1e-12
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | code | 240 | using FFTA, Test
test_nums = [8, 11, 15, 16, 27, 100]
@testset " forward" begin
for N in test_nums
x = ones(Float64, N, N)
y = rfft(x)
y_ref = 0*y
y_ref[1] = length(x)
@test y ≈ y_ref
end
end | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | docs | 3317 | # FFTA: Fastest Fourier Transform in my Apartment
## A library by Danny Sharp
[](https://github.com/dannys4/FFTA.jl/actions)
[](https://dannys4.github.io/FFTA.jl/stable/)
[](https://codecov.io/gh/dannys4/FFTA.jl)
This is a *pure Julia* implementation of FFTs, with the goal that this could supplant other FFTs for applications that require odd Julia objects. Currently this supports `AbstractArray{T,N}` where `N` in `{1,2}` (i.e. `AbstractVector` and `AbstractMatrix`). If you're looking for more performance, checkout `FFTW.jl`. Regardless of `T`, `one(::Type{T})` must be defined. Additionally, if `T<:Real`, then `convert(::Type{T}, Float64)` has to be defined. Otherwise, `convert(::Type{T},ComplexF64)` must be defined.
Some ideas outside the feature requests in Issues:
- Make the code more readable
- Use `StaticArrays` for the workspace in small cases
- Strictly generate code for certain cases
- Create a SIMD type for Complex numbers
- E-Graphs for the call-graph
- Other performance left on the table....
Interface:
- `fft(x::AbstractVector)`-- Forward FFT
- `fft(x::AbstractMatrix})`-- Forward FFT
- `bfft(x::AbstractVector})`-- Backward FFT (unscaled inverse FFT)
- `bfft(x::AbstractMatrix})`-- Backward FFT (unscaled inverse FFT)
NOTE: Currently, my C++ code is actually faster than this, so "Fastest Fourier Transform in my Apartment" is a bit of a misnomer.
## Why use this?
There's a lot of FFT packages out there, no doubt. Many are great. Some, like mine, are "good enough". Many aren't so great. As far as I know, though, very few are as generic as FFTA. Does that matter? Yes. One of the main draws of Julia is the fact that a lot of functions "just work" with types from other packages. FFTA aims to abide by this philosophy. For example, have you ever wanted to generate what an FFT looks like symbolically? Well, now you can.
```julia
using FFTA, Symbolics
N = 16
@variables x_a[1:N]::Complex
x = collect(x_a)
y = simplify.(fft(x))
```
Now, if you have a signal afterward that you want to substitute in, you can call `map(y_el -> substitute(y_el, Dict(x .=> signal)), y)`. Make no mistake-- it's almost certainly more efficient to just plug your type into `FFTA.fft` than using substitution. But this is an example of how `FFTA` integrates wonderfully and gracefully with the Julia ecosystem. If you want high precision FFTs, use `Complex{BigFloat}`. If you want to use an `SVector` from `StaticArrays` because your data is small, then use that! If you want to use `SizedArray{Complex{BigFloat}}`, be my guest. These are opportunities that won't be provided to you in almost any other package out there.
As of this commit, you can do
```julia
julia> import FFTA, FFTW
julia> N = 64
julia> @btime FFTA.fft(x) setup=(x = @SVector rand(N));
698.611 ns (8 allocations: 2.11 KiB)
julia> @btime FFTW.fft(x) setup=(x = @SVector rand(N));
5.433 μs (34 allocations: 4.70 KiB)
```
It's painfully obvious that this example is cherry-picked. Nonetheless, the user can finally take the speedups so much of the Julia community has worked so hard on and propogate them into the FFT.
| FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | docs | 205 | # Development Documentation
Here is the documentation for key parts of the development side of the package.
```@docs
CallGraphNode
CallGraph
CallGraphNode!
fft!
fft_dft!
fft_pow2!
fft_pow3!
fft_pow4!
``` | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 0.2.4 | a1f6c69af58d058e5f5a21256ccc390f547042f0 | docs | 59 | # FFTA.jl
Documentation for FFTA.jl
```@docs
fft
bfft
``` | FFTA | https://github.com/dannys4/FFTA.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | code | 212 | using Pkg, Revise
Pkg.activate(".")
using PlotlyJS, PlotlyGeometries
fig = plot()
fig.plot.layout = blank_layout()
display(fig)
add_ref_axes!(fig, [0, 0, 0], [2, 1, 1])
add_arrows!(fig, [0, 0, 0], [1, 0, 0], 1) | PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | code | 1029 | using PlotlyJS
using PlotlyGeometries
# create a simple cuboid (random color)
c1 = cuboids([0, 0, 0], [1, 2, 3]; opc=0.2)
# translate the cube
gtrans!(c1, [2, 4, 6])
# rotate cube (rotation according to axis)
grot!(c1, 45, [0, 0, 1])
# create fig with PlotlyJS (use blank_layout() to easily create a blank layout)
fig = plot(c1, blank_layout())
# add reference axes
add_ref_axes!(fig, [0, 0, 0], 1)
# show figure
display(fig)
# create ellipsoid
e1 = ellipsoids([0, 5, 0], [3, 1, 1], "purple"; opc=0.1)
# rotate ellipsoid (Tait–Bryan angles)
grot!(e1, [10, 20, 30])
# add elipsoid to figure
addtraces!(fig, e1)
# create sphere
s1 = spheres([3, -2, 0], 2, "coral"; opc=0.1)
addtraces!(fig, s1)
# add line
l1 = lines([2, 4, 6], [0, 5, 0], "orange"; style="dash")
addtraces!(fig, l1)
# add arrow and text
add_arrows!(fig, [2, 4, 8], [0, 0, -1], 1/4, "black")
add_text!(fig, [2, 4, 8.5], "this is a cube")
add_arrows!(fig, [0, 6, 2], [0, -1, -1], 1/4, "black")
add_text!(fig, [0, 6, 2.5], "this is an ellipsoid")
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | code | 784 | using PlotlyJS
using PlotlyGeometries
# create two triangles
pts = []
push!(pts, [0, 0, 0])
push!(pts, [0, 1, 0])
push!(pts, [1, 0, 0])
p1 = polygons(pts, "aqua"; opc=0.5)
for p in pts
p[3] += 1
end
p2 = polygons(pts, "aqua"; opc=0.5)
fig = plot([p1, p2], blank_layout())
display(fig)
add_ref_axes!(fig)
# create a set of rectangles
pts = []
# first side
push!(pts, [0, 0, 0])
push!(pts, [1, 0, 0])
push!(pts, [1, 0, 1])
push!(pts, [0, 0, 1])
# second side
push!(pts, [0, 0, 0])
push!(pts, [0, 1, 0])
push!(pts, [0, 1, 1])
push!(pts, [0, 0, 1])
# third side
push!(pts, [0, 1, 0])
push!(pts, [1, 0, 0])
push!(pts, [0, 1, 1])
push!(pts, [1, 0, 1])
p3 = polygons(pts, 4, "yellow"; opc=0.5)
addtraces!(fig, p3)
for n = 0:360
set_view!(fig, n, 90)
sleep(0.1)
end
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | code | 303 | module PlotlyGeometries
using PlotlyJS
using Combinatorics
using LinearAlgebra
using BatchAssign
export cuboids, cubes, squares, ellipsoids, spheres, lines, polygons,
grot!, gtrans!, sort_pts, sort_pts!,
add_ref_axes!, add_arrows!, add_text!, blank_layout, set_view!
include("api.jl")
end
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | code | 26963 | """
cuboids(origin::Vector{<:Real}, dimension::Vector{<:Real}, color::String=""; opc::Real=1)
Creates a 3D box mesh centered at the given origin with specified dimensions and color.
# Arguments
- `origin::Vector{<:Real}`: A vector of three Reals specifying the center of the box.
- `dimension::Vector{<:Real}`: A vector of three Reals specifying the dimensions (width, height, depth) of the box.
- `color::String`: A string specifying the color of the box.
# Keywords
- `opc`: (optional) A Real specifying the opacity of the box. Default is 1.
"""
function cuboids(origin::Vector{<:Real}, dimension::Vector{<:Real}, color::String=""; opc::Real=1)
@assert length(origin) == 3
@assert length(dimension) == 3
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
x1 = origin[1] - dimension[1] / 2
x2 = origin[1] + dimension[1] / 2
y1 = origin[2] - dimension[2] / 2
y2 = origin[2] + dimension[2] / 2
z1 = origin[3] - dimension[3] / 2
z2 = origin[3] + dimension[3] / 2
x = [x1, x1, x2, x2, x1, x1, x2, x2]
y = [y1, y2, y2, y1, y1, y2, y2, y1]
z = [z1, z1, z1, z1, z2, z2, z2, z2]
i = [7, 0, 0, 0, 4, 4, 6, 6, 4, 0, 3, 2]
j = [3, 4, 1, 2, 5, 6, 5, 2, 0, 1, 6, 3]
k = [0, 7, 2, 3, 6, 7, 1, 1, 5, 5, 7, 6]
return mesh3d(x=x, y=y, z=z,
i=i, j=j, k=k,
flatshading=true,
color=color,
opacity=opc,
lighting=attr(
diffuse=0.1,
specular=1.2,
roughness=1.0,
),
)
end
"""
cubes(origin::Vector{<:Real}, side::Real, color::String=""; opc::Real=1)
Creates a 3D cube mesh centered at the given origin with specified dimensions and color.
# Arguments
- `origin::Vector{<:Real}`: A vector of three Reals specifying the center of the cube.
- `side::Real`: Side length of the cube.
- `color::String`: A string specifying the color of the cube.
# Keywords
- `opc`: (optional) A Real specifying the opacity of the cube. Default is 1.
"""
function cubes(origin::Vector{<:Real}, side::Real, color::String=""; opc::Real=1)
@assert length(origin) == 3
@assert side > 0
return cuboids(origin, [side, side, side], color; opc=opc)
end
"""
squares(origin::Vector{<:Real}, side::Real, color::String="", mode::String="z"; opc::Real=1)
Creates a 2D square mesh centered at the given origin with the specified side length and color.
# Arguments
- `origin::Vector{<:Real}`: A vector of three Reals specifying the center of the square.
- `side::Real`: A Real specifying the side length of the square.
- `color::String`: A string specifying the color of the square.
- `mode`::String: (optional) A string specifying the orientation of the square ("x", "y", or "z"). Default is "z".
# Keywords
- `opc`: (optional) A Real specifying the opacity of the square. Default is 1.
"""
function squares(origin::Vector{<:Real}, side::Real, color::String="", mode::String="z"; opc::Real=1)
@assert length(origin) == 3
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
if mode == "x"
x = [origin[1], origin[1], origin[1], origin[1]]
y = [origin[2] - side / 2, origin[2] + side / 2, origin[2] + side / 2, origin[2] - side / 2]
z = [origin[3] - side / 2, origin[3] - side / 2, origin[3] + side / 2, origin[3] + side / 2]
i = [0, 2]
j = [1, 3]
k = [2, 0]
elseif mode == "y"
x = [origin[1] - side / 2, origin[1] - side / 2, origin[1] + side / 2, origin[1] + side / 2]
y = [origin[2], origin[2], origin[2], origin[2]]
z = [origin[3] - side / 2, origin[3] + side / 2, origin[3] + side / 2, origin[3] - side / 2]
i = [0, 2]
j = [1, 3]
k = [2, 0]
else
x = [origin[1] - side / 2, origin[1] - side / 2, origin[1] + side / 2, origin[1] + side / 2]
y = [origin[2] - side / 2, origin[2] + side / 2, origin[2] + side / 2, origin[2] - side / 2]
z = [origin[3], origin[3], origin[3], origin[3]]
i = [0, 2]
j = [1, 3]
k = [2, 0]
end
return mesh3d(x=x, y=y, z=z, i=i, j=j, k=k,
color=color,
opacity=opc,
lighting=attr(
diffuse=0.1,
specular=1.2,
roughness=1.0
),
)
end
"""
ellipsoids(origin::Vector{<:Real}, par::Vector{<:Real}, color::String=""; opc::Real=1, tres=61, pres=31, ah::Real=0)
Creates a 3D ellipsoid mesh.
# Arguments
- `origin::Vector{<:Real}`: The center of the ellipsoid.
- `par::Vector{<:Real}`: Parameters of the ellipsoid (a, b, c).
- `color::String`: The color of the ellipsoid.
# Keywords
- `opc`: The opacity of the ellipsoid. Default is 1.
- `tres`: The resolution of the mesh grid (theta). Default is 61.
- `pres`: The resolution of the mesh grid (phi). Default is 31.
- `ah`: alphahull value. Default is 0.
"""
function ellipsoids(origin::Vector{<:Real}, par::Vector{<:Real}, color::String=""; opc::Real=1, tres=61, pres=31, ah::Real=0)
@assert length(origin) == 3
@assert length(par) == 3
@assert all(par .> 0)
@assert tres > 0
@assert pres > 0
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
phi = LinRange(0, 360, pres)
tht = LinRange(0, 180, tres)
x = sind.(tht) .* cosd.(phi') .* par[1] .+ origin[1]
y = sind.(tht) .* sind.(phi') .* par[2] .+ origin[2]
z = cosd.(tht * ones(length(phi))') .* par[3] .+ origin[3]
x = x[:]
y = y[:]
z = z[:]
return mesh3d(x=x, y=y, z=z,
alphahull=ah,
flatshading=true,
color=color,
opacity=opc,
lighting=attr(
diffuse=0.1,
specular=2.0,
roughness=0.5
),
)
end
"""
spheres(origin::Vector{<:Real}, r::Real, color::String=""; opc::Real=1, tres=60, pres=30, ah::Real=0)
Creates a 3D sphere mesh.
# Arguments
- `origin::Vector{<:Real}`: The center of the ellipsoid.
- `r::Real`: Radius of the sphere.
- `color::String`: The color of the ellipsoid.
# Keywords
- `opc`: The opacity of the ellipsoid. Default is 1.
- `tres`: The resolution of the mesh grid (theta). Default is 60.
- `pres`: The resolution of the mesh grid (phi). Default is 30.
- `ah`: alphahull value. Default is 0.
"""
function spheres(origin::Vector{<:Real}, r::Real, color::String=""; opc::Real=1, tres=60, pres=30, ah::Real=0)
@assert length(origin) == 3
@assert r > 0
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
return ellipsoids(origin, [r, r, r], color; opc=opc, tres=tres, pres=pres, ah=ah)
end
"""
lines(pt1::Vector{<:Real}, pt2::Vector{<:Real}, color::String; opc::Real=1, style="")
Creates a 3D line between two points.
# Arguments
- `pt1::Vector{<:Real}`: Starting point of the line.
- `pt2::Vector{<:Real}`: Ending point of the line.
- `color::String`: The color of the line.
# Keywords
- `opc`: The opacity of the line. Default is 1.
- `style`: The line style (e.g., "solid", "dash"). Default is "".
"""
function lines(pt1::Vector{<:Real}, pt2::Vector{<:Real}, color::String=""; opc::Real=1, style="")
@assert length(pt1) == 3
@assert length(pt2) == 3
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
x = [pt1[1], pt2[1]]
y = [pt1[2], pt2[2]]
z = [pt1[3], pt2[3]]
return scatter3d(x=x, y=y, z=z,
mode="lines",
line=attr(
color=color,
dash=style,
),
showlegend=false,
flatshading=true,
opacity=opc,
)
end
"""
polygons(pts::Vector, color::String; opc::Real=1, ah::Real=0)
Creates a polygon mesh from a set of points (form around the mid point of the set of points).
# Arguments
- `pts::::Vector`: List of points defining the polygon.
- `color::String`: The color of the polygon.
# Keywords
- `opc`: The opacity of the polygon. Default is 1.
- `ah`: alphahull value. Default is 0.
"""
function polygons(pts::Vector, color::String=""; opc::Real=1, ah::Real=0)
@assert all(length.(pts) .== 3)
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
for vec in pts
for num in vec
@assert isreal(num)
end
end
N = length(pts)
pts_copy = sort_pts(pts)
@all x y z = []
for i in eachindex(pts_copy)
push!(x, pts_copy[i][1])
push!(y, pts_copy[i][2])
push!(z, pts_copy[i][3])
end
mid = zeros(3)
for n in eachindex(pts_copy)
for m in 1:3
mid[m] += pts_copy[n][m]
end
end
mid .= mid ./ N
push!(x, mid[1])
push!(y, mid[2])
push!(z, mid[3])
a = 0:1:length(pts)
i = []
j = []
k = []
for n = 0:length(a)-2
push!(i, a[mod(n + 0, length(a) - 1)+1])
push!(j, a[mod(n + 1, length(a) - 1)+1])
push!(k, a[end])
end
return mesh3d(x=x, y=y, z=z,
i=i, j=j, k=k,
alphahull=ah,
color=color,
opacity=opc,
lighting=attr(
diffuse=0.1,
specular=1.2,
roughness=1.0
),
)
end
"""
polygons(pts::Vector, ng::Int, color::String; opc::Real=1, ah::Real=0)
Creates a group of polygons from a set of points and a specified number of vertices per polygon.
# Arguments
- `pts::Vector`: List of points defining the mesh.
- `ng::Int`: Number of vertices per polygon.
- `color::String`: The color of the mesh.
# Keywords
- `opc`: The opacity of the mesh. Default is 1.
- `ah`: alphahull value.
"""
function polygons(pts::Vector, ng::Int, color::String=""; opc::Real=1, ah::Real=0)
@assert all(length.(pts) .== 3)
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
for vec in pts
for num in vec
@assert isreal(num)
end
end
@assert ng > 0
N = length(pts)
@all x y z i j k = []
Ng = floor(Int, N / ng)
for p = 1:Ng
ptsg = []
for m = 1:ng
push!(ptsg, pts[(p-1)*ng+m])
end
sort_pts!(ptsg)
for i in eachindex(ptsg)
push!(x, ptsg[i][1])
push!(y, ptsg[i][2])
push!(z, ptsg[i][3])
end
mid = zeros(3)
for n in eachindex(ptsg)
for m in 1:3
mid[m] += ptsg[n][m]
end
end
mid .= mid ./ ng
push!(x, mid[1])
push!(y, mid[2])
push!(z, mid[3])
a = 0:1:length(ptsg)
for n = 0:length(a)-2
push!(i, a[mod(n + 0, length(a) - 1)+1] + (p - 1) * (ng + 1))
push!(j, a[mod(n + 1, length(a) - 1)+1] + (p - 1) * (ng + 1))
push!(k, a[end] + (p - 1) * (ng + 1))
end
end
return mesh3d(x=x, y=y, z=z,
i=i, j=j, k=k,
alphahull=ah,
color=color,
opacity=opc,
lighting=attr(
diffuse=0.1,
specular=1.2,
roughness=1.0
),
)
end
"""
gtrans!(geo::GenericTrace, dis::Vector{<:Real})
Translates a 3D geometry by a specified displacement vector.
# Arguments
- `geo::GenericTrace`: The geometry to translate.
- `dis::Vector{<:Real}`: A vector of three Reals specifying the translation distances for the x, y, and z axes.
"""
function gtrans!(geo::GenericTrace, dis::Vector{<:Real})
@inbounds for n in eachindex(geo.x)
geo.x[n] += dis[1]
geo.y[n] += dis[2]
geo.z[n] += dis[3]
end
end
"""
grot!(geo::GenericTrace, rotang::Vector{<:Real}, center::Vector{<:Real}=[0])
Rotates a 3D geometry around a specified center point. (Tait–Bryan rotation)
# Arguments
- `geo::GenericTrace`: The 3D geometry to be rotated, which must have `x`, `y`, and `z` coordinates.
- `rotang::Vector{<:Real}`: A vector of three Tait–Bryan rotation angles in degrees for rotations around the x, y, and z axes respectively.
- `center::Vector{<:Real}`: The center point of rotation. Default is `[0]`, which means the rotation center will be set at the geometric center of the object.
"""
function grot!(geo::GenericTrace, rotang::Vector{<:Real}, center::Vector{<:Real}=[0])
@assert length(rotang) == 3
alpha = rotang[1]
beta = rotang[2]
gama = rotang[3]
Rx = [1 0 0;
0 cosd(alpha) -sind(alpha);
0 sind(alpha) cosd(alpha)]
Ry = [cosd(beta) 0 sind(beta);
0 1 0;
-sind(beta) 0 cosd(beta)]
Rz = [cosd(gama) -sind(gama) 0;
sind(gama) cosd(gama) 0;
0 0 1]
R = Rz * Ry * Rx
pos = []
for n in eachindex(geo.x)
push!(pos, [geo.x[n], geo.y[n], geo.z[n]])
end
if center == [0] # rotation center set at the geometry center
center = sum(pos) ./ length(pos)
else
@assert length(center) == 3
end
@inbounds for n in eachindex(geo.x)
vec = R * (pos[n] - center)
geo.x[n] = vec[1] + center[1]
geo.y[n] = vec[2] + center[2]
geo.z[n] = vec[3] + center[3]
end
end
"""
grot!(geo::GenericTrace, ang::Real, axis::Vector{<:Real}, origin::Vector{<:Real}=[0])
Rotates the geometry by the specified angle `ang` around the axis `axis` and origin `origin`.
# Arguments
- `geo::GenericTrace`: The geometry to be rotated.
- `ang::Real`: The rotation angle.
- `axis::Vector{<:Real}`: The rotation axis.
- `origin::Vector{<:Real}=[0]`: The rotation origin. Defaults to the center of the geometry if not specified.
"""
function grot!(geo::GenericTrace, ang::Real, axis::Vector{<:Real}, origin::Vector{<:Real}=[0])
@assert length(axis) == 3
pos = []
for n in eachindex(geo.x)
push!(pos, [geo.x[n], geo.y[n], geo.z[n]])
end
axis_norm = axis ./ norm(axis)
vrot = similar(pos)
if origin == [0] # rotation center set at the geometry center
origin = sum(pos) ./ length(pos)
else
@assert length(origin) == 3
end
v = similar(origin)
for n in eachindex(vrot)
v .= (pos[n] .- origin)
vrot[n] = cosd(ang) * v + sind(ang) * cross(axis_norm, v) + (1 - cosd(ang)) * dot(axis_norm, v) * axis_norm
pos[n] = vrot[n] .+ origin
end
geo.x = getindex.(pos, 1)
geo.y = getindex.(pos, 2)
geo.z = getindex.(pos, 3)
end
"""
sort_pts(pts::Vector)
Sorts points in place based on their angular position relative to the centroid.
# Arguments
- `pts::Vector`: List of points to be sorted.
"""
function sort_pts(pts::Vector)
@assert all(length.(pts) .== 3)
N = length(pts)
ang = zeros(length(pts))
mid = zeros(3)
for n in eachindex(pts)
for m in 1:3
mid[m] += pts[n][m]
end
end
mid .= mid ./ N
c = collect(combinations(1:N, 3))
thtr = 0
phir = 0
vec = similar(mid)
for n in eachindex(c)
vec .= cross(pts[c[n][2]] .- pts[c[n][1]], pts[c[n][3]] .- pts[c[n][1]])
if norm(vec) == 0
continue
else
vec .= vec ./ norm(vec)
thtr = acosd(vec[3])
phir = atand(vec[2], vec[1])
break
end
end
Ry = [
cosd(thtr) 0 -sind(thtr);
0 1 0;
sind(thtr) 0 cosd(thtr)
]
Rz = [
cosd(phir) sind(phir) 0;
-sind(phir) cosd(phir) 0;
0 0 1
]
R = Ry * Rz
pts_rot = similar(pts)
mid_rot = R * mid
for n in eachindex(pts)
pts_rot[n] = R * pts[n]
ang[n] = atan(pts_rot[n][2] - mid_rot[2], pts_rot[n][1] - mid_rot[1])
end
pts_rot .= pts[sortperm(ang)]
return pts_rot
end
"""
sort_pts!(pts::Vector)
Sorts points in place based on their angular position relative to the centroid.
# Arguments
- `pts::Vector`: List of points to be sorted.
"""
function sort_pts!(pts::Vector)
@assert all(length.(pts) .== 3)
N = length(pts)
ang = zeros(length(pts))
mid = zeros(3)
for n in eachindex(pts)
for m in 1:3
mid[m] += pts[n][m]
end
end
mid .= mid ./ N
c = collect(combinations(1:N, 3))
thtr = 0
phir = 0
vec = similar(mid)
for n in eachindex(c)
vec .= cross(pts[c[n][2]] .- pts[c[n][1]], pts[c[n][3]] .- pts[c[n][1]])
if norm(vec) == 0
continue
else
vec .= vec ./ norm(vec)
thtr = acosd(vec[3])
phir = atand(vec[2], vec[1])
break
end
end
Ry = [
cosd(thtr) 0 -sind(thtr);
0 1 0;
sind(thtr) 0 cosd(thtr)
]
Rz = [
cosd(phir) sind(phir) 0;
-sind(phir) cosd(phir) 0;
0 0 1
]
R = Ry * Rz
pts_rot = similar(pts)
mid_rot = R * mid
for n in eachindex(pts)
pts_rot[n] = R * pts[n]
ang[n] = atan(pts_rot[n][2] - mid_rot[2], pts_rot[n][1] - mid_rot[1])
end
pts .= pts[sortperm(ang)]
return nothing
end
"""
add_ref_axes!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}=[0, 0, 0], r::Real=1)
Adds reference axes (x, y, z) to a plot.
# Arguments
- `plt::PlotlyJS.SyncPlot`: The plot to which the axes will be added.
- `origin::Vector{<:Real}`: The origin point of the axes.
- `r::Real`: The length of the reference axes.
"""
function add_ref_axes!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}=[0, 0, 0], r::Real=1)
@assert length(origin) == 3
@assert r > 0
cx = cone(x=[r + origin[1]], y=[origin[2]], z=[origin[3]], u=[r / 10], v=[0], w=[0],
colorscale=[[0, "red"], [1, "red"]],
showscale=false)
cy = cone(x=[origin[1]], y=[r + origin[2]], z=[origin[3]], u=[0], v=[r / 10], w=[0],
colorscale=[[0, "green"], [1, "green"]],
showscale=false)
cz = cone(x=[origin[1]], y=[origin[2]], z=[r + origin[3]], u=[0], v=[0], w=[r / 10],
colorscale=[[0, "blue"], [1, "blue"]],
showscale=false)
lx = scatter3d(x=[origin[1], r + origin[1]], y=[origin[2], origin[2]], z=[origin[3], origin[3]],
line=attr(color="red"),
mode="lines",
showlegend=false)
ly = scatter3d(x=[origin[1], origin[1]], y=[origin[2], r + origin[2]], z=[origin[3], origin[3]],
line=attr(color="green"),
mode="lines",
showlegend=false)
lz = scatter3d(x=[origin[1], origin[1]], y=[origin[2], origin[2]], z=[origin[3], r + origin[3]],
line=attr(color="blue"),
mode="lines",
showlegend=false)
addtraces!(plt, cx)
addtraces!(plt, cy)
addtraces!(plt, cz)
addtraces!(plt, lx)
addtraces!(plt, ly)
addtraces!(plt, lz)
relayout!(plt, scene=attr(
annotations=[
attr(
showarrow=false,
x=origin[1] + 1.1 * r,
y=origin[2],
z=origin[3],
text="x",
font=attr(color="red")
),
attr(
showarrow=false,
x=origin[1],
y=origin[2] + 1.1 * r,
z=origin[3],
text="y",
font=attr(color="green")
),
attr(
showarrow=false,
x=origin[1],
y=origin[2],
z=origin[3] + 1.1 * r,
text="z",
font=attr(color="blue")
),
]
))
return nothing
end
"""
add_ref_axes!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, r::Vector{<:Real})
Adds reference axes (x, y, z) to a plot.
# Arguments
- `plt::PlotlyJS.SyncPlot`: The plot to which the axes will be added.
- `origin::Vector{<:Real}`: The origin point of the axes.
- `r::Vector{<:Real}`: The lengths of the reference axes.
"""
function add_ref_axes!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, r::Vector{<:Real})
@assert length(origin) == 3
@assert length(r) == 3
@assert all(r .> 0)
csize = minimum([r[1] / 10, r[2] / 10, r[3] / 10])
cx = cone(x=[r[1] + origin[1]], y=[origin[2]], z=[origin[3]], u=[csize], v=[0], w=[0],
colorscale=[[0, "red"], [1, "red"]],
showscale=false)
cy = cone(x=[origin[1]], y=[r[2] + origin[2]], z=[origin[3]], u=[0], v=[csize], w=[0],
colorscale=[[0, "green"], [1, "green"]],
showscale=false)
cz = cone(x=[origin[1]], y=[origin[2]], z=[r[3] + origin[3]], u=[0], v=[0], w=[csize],
colorscale=[[0, "blue"], [1, "blue"]],
showscale=false)
lx = scatter3d(x=[origin[1], r[1] + origin[1]], y=[origin[2], origin[2]], z=[origin[3], origin[3]],
line=attr(color="red"),
mode="lines",
showlegend=false)
ly = scatter3d(x=[origin[1], origin[1]], y=[origin[2], r[2] + origin[2]], z=[origin[3], origin[3]],
line=attr(color="green"),
mode="lines",
showlegend=false)
lz = scatter3d(x=[origin[1], origin[1]], y=[origin[2], origin[2]], z=[origin[3], r[3] + origin[3]],
line=attr(color="blue"),
mode="lines",
showlegend=false)
addtraces!(plt, cx)
addtraces!(plt, cy)
addtraces!(plt, cz)
addtraces!(plt, lx)
addtraces!(plt, ly)
addtraces!(plt, lz)
relayout!(plt, scene=attr(
annotations=[
attr(
showarrow=false,
x=origin[1] + 1.1 * r[1],
y=origin[2],
z=origin[3],
text="x",
font=attr(color="red")
),
attr(
showarrow=false,
x=origin[1],
y=origin[2] + 1.1 * r[2],
z=origin[3],
text="y",
font=attr(color="green")
),
attr(
showarrow=false,
x=origin[1],
y=origin[2],
z=origin[3] + 1.1 * r[3],
text="z",
font=attr(color="blue")
),
]
))
return nothing
end
"""
add_arrows!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, dir::Vector{<:Real}, len::Real=1.0, color::String=""; opc::Real=1, endpoint::Bool=true, asize::Real=len)
Creates a 3D arrow starting from a point and pointing in a given direction.
# Arguments
- `plt::PlotlyJS.SyncPlot`: The plot to which the axes will be added.
- `origin::Vector{<:Real}`: The starting point of the arrow.
- `dir::Vector{<:Real}`: The direction vector of the arrow.
- `len::Real`: length of the arrow
- `color::String`: The color of the arrow.
# Keywords
- `opc`: The opacity of the arrow. Default is 1.
- `asize` Size factor of the arrow cone. Default is `len`.
"""
function add_arrows!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, dir::Vector{<:Real}, len::Real=1.0, color::String=""; opc::Real=1, endpoint::Bool=true, asize::Real=len)
@assert length(origin) == 3
@assert length(dir) == 3
@assert len > 0
@assert asize > 0
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
dir_norm = dir / norm(dir) * len
if endpoint == true
c = cone(x=[origin[1] + dir_norm[1]], y=[origin[2] + dir_norm[2]], z=[origin[3] + dir_norm[3]], u=[dir_norm[1]/len*asize], v=[dir_norm[2]]/len*asize, w=[dir_norm[3]/len*asize],
colorscale=[[0, color], [1, color]],
opacity=opc,
showscale=false)
l = scatter3d(x=[origin[1], origin[1] + dir_norm[1]], y=[origin[2], origin[2] + dir_norm[2]], z=[origin[3], origin[3] + dir_norm[3]],
line=attr(color=color, width=2 *dir_norm),
mode="lines",
opacity=opc,
showlegend=false)
else # origin at center
c = cone(x=[origin[1] + dir_norm[1] / 2], y=[origin[2] + dir_norm[2] / 2], z=[origin[3] + dir_norm[3] / 2], u=[dir_norm[1]/len*asize], v=[dir_norm[2]/len*asize], w=[dir_norm[3]/len*asize],
colorscale=[[0, color], [1, color]],
opacity=opc,
showscale=false)
l = scatter3d(x=[origin[1] - dir_norm[1] / 2, origin[1] + dir_norm[1] / 2], y=[origin[2] - dir_norm[2] / 2, origin[2] + dir_norm[2] / 2], z=[origin[3] - dir_norm[3] / 2, origin[3] + dir_norm[3] / 2],
line=attr(color=color, width=2 * dir_norm),
mode="lines",
opacity=opc,
showlegend=false)
end
addtraces!(plt, c)
addtraces!(plt, l)
return nothing
end
"""
add_text!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, text::String, color::String="")
Add text to plot.
# Arguments
- plt::PlotlyJS.SyncPlot: Plot to add text.
- origin::Vector{<:Real}: origin of the text.
- text::String:: text to be added.
- color::String=: color of the text.
"""
function add_text!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, text::String, color::String="")
if color == ""
@all r g b = round(Int, rand() * 255)
color = "rgb($r, $g, $b)"
end
addtraces!(plt, scatter3d(x=[origin[1]], y=[origin[2]], z=[origin[3]],
mode="text", text=[text], textposition="middle center",
textfont=attr(
color=color,
),
showlegend=false,
))
return nothing
end
"""
blank_layout()
Return blank layout.
"""
function blank_layout()
layout = Layout(
scene=attr(
xaxis=attr(
visible=false,
showgrid=false
),
yaxis=attr(
visible=false,
showgrid=false
),
zaxis=attr(
visible=false,
showgrid=false
),
aspectmode="data",
),
)
return layout
end
"""
set_view!(plt::PlotlyJS.SyncPlot, az::Real, el::Real, r::Real=1)
Set az/el (deg) view of the plot.
# Arguments
- plt::PlotlyJS.SyncPlot: plot to be modified.
- az::Real: az value.
- el::Real: el value.
- r::Real=1: distance.
"""
function set_view!(plt::PlotlyJS.SyncPlot, az::Real, el::Real, r::Real=1.25 * sqrt(3))
if el == 90
el -= 0.01
elseif el == -90
el += 0.01
end
x = r * cosd(el) * cosd(az)
y = r * cosd(el) * sind(az)
z = r * sind(el)
plt.plot.layout.scene_camera = attr(eye=attr(x=1.25, y=1.25, z=1.25))
plt.plot.layout.scene_camera[:eye][:x] = x
plt.plot.layout.scene_camera[:eye][:y] = y
plt.plot.layout.scene_camera[:eye][:z] = z
react!(plt, plt.plot.data, plt.plot.layout)
return nothing
end
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | code | 120 | using PlotlyGeometries
using PlotlyJS
using Test
@testset "PlotlyGeometries.jl" begin
# Write your tests here.
end
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | docs | 1292 | # PlotlyGeometries.jl
[](https://github.com/akjake616/PlotlyGeometries.jl/actions/workflows/CI.yml)
`PlotlyGeometries.jl` is a Julia package designed for creating and manipulating 3D geometrical shapes and visualizations using [`PlotlyJS.jl`](https://github.com/JuliaPlots/PlotlyJS.jl). This package provides a variety of functions to easily generate and customize 3D shapes like boxes, spheres, ellipsoids, lines, and arrows, as well as utility functions for transformations and visual enhancements.I hope this package will be useful for those trying to create better illustrations for their academic research using Julia :wink:
<p align="center">
<img alt="PlotlyGeometries.jl" src="./media/illus.gif" width="50%" height="auto" />
</p>
## Installation
To install `PlotlyGeometries.jl`, use the following command in the Julia REPL:
```julia
using Pkg
Pkg.add("PlotlyGeometries")
```
## Learn by Examples
Please refer to the examples to get familiar with some basic usages:
- `ex_basics.jl`: Some basic geometry creation/transformation stuff.
- `ex_polygons.jl`: Use polygons to build geometries.
## Usage
Please refer to the [user manual](./docs/MANUAL.md) in the docs folder.
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 2.2.1 | 139a0771a670243a80e7903d04f620dd14cc8377 | docs | 8492 | # Manual for PlotlyGeometries.jl
## Overview
This manual contains the API provided by `PlotlyGeometries.jl`. Outputs of the functionalities are mostly traces to be added on Plotly plots. In order to use this module, `PlotlyJS.jl` should be installed first.
## API
### Geometry Creation
#### cuboids
```julia
cuboids(origin::Vector{<:Real}, dimension::Vector{<:Real}, color::String=""; opc::Real=1)
```
Creates a 3D box mesh centered at the given origin with specified dimensions and color.
##### Arguments
- `origin::Vector{<:Real}`: A vector of three Reals specifying the center of the box.
- `dimension::Vector{<:Real}`: A vector of three Reals specifying the dimensions (width, height, depth) of the box.
- `color::String`: A string specifying the color of the box.
##### Keywords
- `opc`: (optional) A Real specifying the opacity of the box. Default is 1.
#### cubes
```julia
cubes(origin::Vector{<:Real}, side::Real, color::String=""; opc::Real=1)
```
Creates a 3D cube mesh centered at the given origin with specified dimensions and color.
##### Arguments
- `origin::Vector{<:Real}`: A vector of three Reals specifying the center of the cube.
- `side::Real`: Side length of the cube.
- `color::String`: A string specifying the color of the cube.
##### Keywords
- `opc`: (optional) A Real specifying the opacity of the cube. Default is 1.
___
#### squares
```julia
squares(origin::Vector{<:Real}, side::Real, color::String="", mode::String="z"; opc::Real=1)
```
Creates a 2D square mesh centered at the given origin with the specified side length and color.
##### Arguments
- `origin::Vector{<:Real}`: A vector of three Reals specifying the center of the square.
- `side::Real`: A Real specifying the side length of the square.
- `color::String`: A string specifying the color of the square.
- `mode`::String: (optional) A string specifying the orientation of the square ("x", "y", or "z"). Default is "z".
##### Keywords
- `opc`: (optional) A Real specifying the opacity of the square. Default is 1.
___
#### ellipsoids
```julia
ellipsoids(origin::Vector{<:Real}, par::Vector{<:Real}, color::String=""; opc::Real=1, tres=61, pres=31, ah::Real=0)
```
Creates a 3D ellipsoid mesh.
##### Arguments
- `origin::Vector{<:Real}`: The center of the ellipsoid.
- `par::Vector{<:Real}`: Parameters of the ellipsoid (a, b, c).
- `color::String`: The color of the ellipsoid.
##### Keywords
- `opc`: The opacity of the ellipsoid. Default is 1.
- `tres`: The resolution of the mesh grid (theta). Default is 61.
- `pres`: The resolution of the mesh grid (phi). Default is 31.
- `ah`: alphahull value. Default is 0.
___
#### spheres
```julia
spheres(origin::Vector{<:Real}, r::Real, color::String=""; opc::Real=1, tres=60, pres=30, ah::Real=0)
```
Creates a 3D sphere mesh.
##### Arguments
- `origin::Vector{<:Real}`: The center of the ellipsoid.
- `r::Real`: Radius of the sphere.
- `color::String`: The color of the ellipsoid.
##### Keywords
- `opc`: The opacity of the ellipsoid. Default is 1.
- `tres`: The resolution of the mesh grid (theta). Default is 60.
- `pres`: The resolution of the mesh grid (phi). Default is 30.
- `ah`: alphahull value. Default is 0.
___
#### lines
```julia
lines(pt1::Vector{<:Real}, pt2::Vector{<:Real}, color::String; opc::Real=1, style="")
```
Creates a 3D line between two points.
##### Arguments
- `pt1::Vector{<:Real}`: Starting point of the line.
- `pt2::Vector{<:Real}`: Ending point of the line.
- `color::String`: The color of the line.
##### Keywords
- `opc`: The opacity of the line. Default is 1.
- `style`: The line style (e.g., "solid", "dash"). Default is "".
___
#### polygons
```julia
polygons(pts::Vector, color::String; opc::Real=1, ah::Real=0)
```
Creates a polygon mesh from a set of points (form around the mid point of the set of points).
##### Arguments
- `pts::::Vector`: List of points defining the polygon.
- `color::String`: The color of the polygon.
##### Keywords
- `opc`: The opacity of the polygon. Default is 1.
- `ah`: alphahull value. Default is 0.
```julia
polygons(pts::Vector, ng::Int, color::String; opc::Real=1, ah::Real=0)
```
Creates a group of polygons from a set of points and a specified number of vertices per polygon.
##### Arguments
- `pts::Vector`: List of points defining the mesh.
- `ng::Int`: Number of vertices per polygon.
- `color::String`: The color of the mesh.
##### Keywords
- `opc`: The opacity of the mesh. Default is 1.
- `ah`: alphahull value.
___
### Geometry Manipulation
#### translation
```julia
gtrans!(geo::GenericTrace, dis::Vector{<:Real})
```
Translates a 3D geometry by a specified displacement vector.
##### Arguments
- `geo::GenericTrace`: The geometry to translate.
- `dis::Vector{<:Real}`: A vector of three Reals specifying the translation distances for the x, y, and z axes.
___
#### rotation (according to Tait–Bryan angle)
```julia
grot!(geo::GenericTrace, rotang::Vector{<:Real}, center::Vector{<:Real}=[0])
```
Rotates a 3D geometry around a specified center point. (Tait–Bryan rotation)
##### Arguments
- `geo::GenericTrace`: The 3D geometry to be rotated, which must have `x`, `y`, and `z` coordinates.
- `rotang::Vector{<:Real}`: A vector of three Tait–Bryan rotation angles in degrees for rotations around the x, y, and z axes respectively.
- `center::Vector{<:Real}`: The center point of rotation. Default is `[0]`, which means the rotation center will be set at the geometric center of the object.
___
#### rotation (according to axis)
```julia
grot!(geo::GenericTrace, ang::Real, axis::Vector{<:Real}, origin::Vector{<:Real}=[0])
```
Rotates the geometry by the specified angle `ang` around the axis `axis` and origin `origin`.
##### Arguments
- `geo::GenericTrace`: The geometry to be rotated.
- `ang::Real`: The rotation angle.
- `axis::Vector{<:Real}`: The rotation axis.
- `origin::Vector{<:Real}=[0]`: The rotation origin. Defaults to the center of the geometry if not specified.
___
### Additional Features
#### sort points
```julia
sort_pts(pts::Vector)
```
Sorts points based on their angular position relative to the centroid.
##### Arguments
- `pts::Vector`: List of points to be sorted.
___
#### inplace sort points
```julia
sort_pts!(pts::Vector)
```
Sorts points in place based on their angular position relative to the centroid.
##### Arguments
- `pts::Vector`: List of points to be sorted.
___
#### add reference axis
```julia
add_ref_axes!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}=[0, 0, 0], r::Real=1)
```
Adds reference axes (x, y, z) to a plot.
##### Arguments
- `plt::PlotlyJS.SyncPlot`: The plot to which the axes will be added.
- `origin::Vector{<:Real}`: The origin point of the axes.
- `r::Real`: The length of the reference axes.
___
```julia
add_ref_axes!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, r::Vector{<:Real})
```
Adds reference axes (x, y, z) to a plot.
##### Arguments
- `plt::PlotlyJS.SyncPlot`: The plot to which the axes will be added.
- `origin::Vector{<:Real}`: The origin point of the axes.
- `r::Vector{<:Real}`: The lengths of the reference axes.
___
#### add arrows
```julia
add_arrows!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, dir::Vector{<:Real}, len::Real=1.0, color::String=""; opc::Real=1, endpoint::Bool=true, asize::Real=len)
```
Creates a 3D arrow starting from a point and pointing in a given direction.
##### Arguments
- `plt::PlotlyJS.SyncPlot`: The plot to which the axes will be added.
- `origin::Vector{<:Real}`: The starting point of the arrow.
- `dir::Vector{<:Real}`: The direction vector of the arrow.
- `len::Real`: length of the arrow
- `color::String`: The color of the arrow.
##### Keywords
- `opc`: The opacity of the arrow. Default is 1.
- `asize` Size factor of the arrow cone. Default is `len`.
___
#### add texts
```julia
add_text!(plt::PlotlyJS.SyncPlot, origin::Vector{<:Real}, text::String, color::String="")
```
Add text to plot.
##### Arguments
- plt::PlotlyJS.SyncPlot: Plot to add text.
- origin::Vector{<:Real}: origin of the text.
- text::String:: text to be added.
- color::String=: color of the text.
___
#### blank layout
```julia
blank_layout()
```
Return blank layout for easy use.
___
#### set view angle
```julia
set_view!(plt::PlotlyJS.SyncPlot, az::Real, el::Real, r::Real=1.25 * sqrt(3))
```
Set az/el (deg) view of the plot.
##### Arguments
- plt::PlotlyJS.SyncPlot: plot to be modified.
- az::Real: az value.
- el::Real: el value.
- r::Real=1: distance.
___
| PlotlyGeometries | https://github.com/akjake616/PlotlyGeometries.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 699 | using GraphSignals
using Documenter
makedocs(;
modules=[GraphSignals],
authors="Yueh-Hua Tu",
repo="https://github.com/yuehhua/GraphSignals.jl/blob/{commit}{path}#L{line}",
sitename="GraphSignals.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://yuehhua.github.io/GraphSignals.jl/stable",
assets=String[],
),
pages=[
"Home" => "index.md",
"Manual" =>
[
"FeaturedGraph" => "manual/featuredgraph.md",
"Sparse graph strucutre" => "manual/sparsegraph.md"
]
],
)
deploydocs(repo="github.com/yuehhua/GraphSignals.jl")
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 195 | module GraphSignalsCUDAExt
using SparseArrays
using CUDA, CUDA.CUSPARSE
using GraphSignals
include("linalg.jl")
include("sparsematrix.jl")
include("sparsegraph.jl")
include("random.jl")
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 667 | function GraphSignals.adjacency_matrix(adj::CuSparseMatrixCSC{T}, ::Type{S}) where {T,S}
GraphSignals._dim_check(adj)
return CuMatrix{S}(collect(adj))
end
function GraphSignals.adjacency_matrix(adj::CuSparseMatrixCSC)
GraphSignals._dim_check(adj)
return CuMatrix(adj)
end
function GraphSignals.adjacency_matrix(adj::CuMatrix{T}, ::Type{S}) where {T,S}
GraphSignals._dim_check(adj)
return CuMatrix{S}(adj)
end
function GraphSignals.adjacency_matrix(adj::CuMatrix)
GraphSignals._dim_check(adj)
return adj
end
degrees(adj::CuSparseMatrixCSC, ::Type{T}=eltype(adj); dir::Symbol=:out) where {T} =
degrees(CuMatrix{T}(adj); dir=dir)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 359 | GraphSignals.random_walk(sg::GraphSignals.SparseGraph{B,T}, start::Int, n::Int=1) where {B,T<:CuSparseMatrixCSC} =
random_walk(collect(sg.S), start, n)
GraphSignals.neighbor_sample(sg::GraphSignals.SparseGraph{B,T}, start::Int, n::Int=1; replace::Bool=false) where {B,T<:CuSparseMatrixCSC} =
neighbor_sample(collect(sg.S), start, n; replace=replace)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 385 | function GraphSignals.SparseGraph(A::CuSparseMatrixCSC{Tv}, edges::AnyCuVector{Ti}, directed::Bool) where {Tv,Ti}
E = maximum(edges)
return SparseGraph{directed,typeof(A),typeof(edges),typeof(E)}(A, edges, E)
end
GraphSignals.SparseGraph(A::CuSparseMatrixCSC, directed::Bool, ::Type{T}=eltype(A)) where {T} =
SparseGraph(A, order_edges(A, directed=directed), directed, T)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 1570 | sparsecsc(A::AnyCuMatrix) = CuSparseMatrixCSC(A)
SparseArrays.rowvals(S::CuSparseMatrixCSC, col::Integer) = rowvals(S)[SparseArrays.getcolptr(S, col)]
SparseArrays.rowvals(S::CuSparseMatrixCSC, I::UnitRange) = rowvals(S)[SparseArrays.getcolptr(S, I)]
GraphSignals.rowvalview(S::CuSparseMatrixCSC, col::Integer) = view(rowvals(S), SparseArrays.getcolptr(S, col))
GraphSignals.rowvalview(S::CuSparseMatrixCSC, I::UnitRange) = view(rowvals(S), SparseArrays.getcolptr(S, I))
# TODO: @allowscalar should be removed.
SparseArrays.getcolptr(S::CuSparseMatrixCSC, col::Integer) = CUDA.@allowscalar S.colPtr[col]:(S.colPtr[col+1]-1)
SparseArrays.nonzeros(S::CuSparseMatrixCSC, col::Integer) = GraphSignals._nonzeros(S, col)
SparseArrays.nonzeros(S::CuSparseMatrixCSC, I::UnitRange) = GraphSignals._nonzeros(S, I)
SparseArrays.nzvalview(S::CuSparseMatrixCSC, col::Integer) = _nzvalview(S, col)
SparseArrays.nzvalview(S::CuSparseMatrixCSC, I::UnitRange) = _nzvalview(S, I)
GraphSignals.colvals(S::CuSparseMatrixCSC; upper_traingle::Bool=false) =
GraphSignals.colvals(S, size(S, 2); upper_traingle=upper_traingle)
GraphSignals.colvals(S::CuSparseMatrixCSC, n::Int; upper_traingle::Bool=false) =
GraphSignals._colvals(S, n; upper_traingle=upper_traingle)
GraphSignals.get_csc_index(S::CuSparseMatrixCSC, i::Integer, j::Integer) = _get_csc_index(S, i, j)
GraphSignals.order_edges(S::CuSparseMatrixCSC; directed::Bool=false) = _order_edges(S; directed=directed)
GraphSignals.order_edges!(edges, S::CuSparseMatrixCSC, ::Val{false}) = _order_edges!(edges, S, Val(false))
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 2648 | module GraphSignals
using LinearAlgebra
using SparseArrays
using ChainRulesCore
using ChainRulesCore: @non_differentiable
using Distances
using FillArrays
using Functors: @functor
using Graphs, SimpleWeightedGraphs
using Graphs: AbstractGraph, AbstractSimpleGraph
using MLUtils
using SimpleWeightedGraphs: AbstractSimpleWeightedGraph
using StatsBase
using NNlib
using NearestNeighbors
import Graphs: adjacency_matrix, laplacian_matrix
@static if !isdefined(Base, :get_extension)
using Requires
function __init__()
@require CUDA = "052768ef-5323-5732-b1bb-66c8b64840ba" include("../ext/GraphSignalsCUDAExt.jl")
end
end
export
# featuredgraph
AbstractFeaturedGraph,
NullGraph,
FeaturedGraph,
ConcreteFeaturedGraph,
graph,
matrixtype,
node_feature,
edge_feature,
global_feature,
has_graph,
has_node_feature,
has_edge_feature,
has_global_feature,
# graph
adjacency_list,
# sparsegraph
AbstractSparseGraph,
SparseGraph,
SparseSubgraph,
incident_edges,
edge_index,
# graphdomains
positional_feature,
has_positional_feature,
# linalg
laplacian_matrix,
normalized_laplacian,
scaled_laplacian,
laplacian_matrix!,
normalized_laplacian!,
scaled_laplacian!,
# subgraph
FeaturedSubgraph,
subgraph,
mask,
# random
random_walk,
neighbor_sample,
# neighbor_graphs
kneighbors_graph,
# tokenizer
node_identifier,
identifiers
include("positional.jl")
include("graph.jl")
include("linalg.jl")
include("sparsematrix.jl")
include("sparsegraph.jl")
include("graphdomain.jl")
include("graphsignal.jl")
include("featuredgraph.jl")
include("neighbor_graphs.jl")
include("subgraph.jl")
include("random.jl")
include("dataloader.jl")
include("tokenizer.jl")
# Non-differentiables
@non_differentiable nv(x...)
@non_differentiable ne(x...)
@non_differentiable GraphSignals.to_namedtuple(x...)
@non_differentiable adjacency_list(x...)
@non_differentiable GraphSignals.adjacency_matrix(x...)
@non_differentiable is_directed(x...)
@non_differentiable has_graph(x...)
@non_differentiable has_node_feature(x...)
@non_differentiable has_edge_feature(x...)
@non_differentiable has_global_feature(x...)
@non_differentiable SparseGraph(x...)
@non_differentiable neighbors(x...)
@non_differentiable incident_edges(x...)
@non_differentiable order_edges(x...)
@non_differentiable aggregate_index(x...)
@non_differentiable kneighbors_graph(x...)
@non_differentiable GraphSignals.orthogonal_random_features(x...)
@non_differentiable GraphSignals.laplacian_matrix(x...)
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 1491 | function MLUtils.numobs(fg::AbstractFeaturedGraph)
obs_size = 0
if has_node_feature(fg)
nf_obs_size = numobs(node_feature(fg))
obs_size = check_obs_size(obs_size, nf_obs_size, "node features")
end
if has_edge_feature(fg)
ef_obs_size = numobs(edge_feature(fg))
obs_size = check_obs_size(obs_size, ef_obs_size, "edge features")
end
if has_global_feature(fg)
gf_obs_size = numobs(global_feature(fg))
obs_size = check_obs_size(obs_size, gf_obs_size, "global features")
end
if has_positional_feature(fg)
pf_obs_size = numobs(positional_feature(fg))
obs_size = check_obs_size(obs_size, pf_obs_size, "positional features")
end
return obs_size
end
function check_obs_size(obs_size, feat_obs_size, feat::String)
if obs_size != 0
msg = "inconsistent number of observation between $feat ($feat_obs_size) and others ($obs_size)"
@assert obs_size == feat_obs_size msg
end
return feat_obs_size
end
function MLUtils.getobs(fg::AbstractFeaturedGraph, idx)
nf = has_node_feature(fg) ? getobs(node_feature(fg), idx) : node_feature(fg)
ef = has_edge_feature(fg) ? getobs(edge_feature(fg), idx) : edge_feature(fg)
gf = has_global_feature(fg) ? getobs(global_feature(fg), idx) : global_feature(fg)
pf = has_positional_feature(fg) ? getobs(positional_feature(fg), idx) : positional_feature(fg)
return ConcreteFeaturedGraph(fg, nf=nf, ef=ef, gf=gf, pf=pf)
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 13037 | const MATRIX_TYPES = [:adjm, :normedadjm, :laplacian, :normalized, :scaled]
const DIRECTEDS = [:auto, :directed, :undirected]
_string(s::Symbol) = ":$(s)"
abstract type AbstractFeaturedGraph end
"""
FeaturedGraph(g, [mt]; directed=:auto, nf, ef, gf, pf=nothing,
T, N, E, with_batch=false)
A type representing a graph structure and storing also arrays
that contain features associated to nodes, edges, and the whole graph.
A `FeaturedGraph` can be constructed out of different objects `g` representing
the connections inside the graph.
When constructed from another featured graph `fg`, the internal graph representation
is preserved and shared.
# Arguments
- `g`: Data representing the graph topology. Possible type are
- An adjacency matrix.
- An adjacency list.
- A Graphs' graph, i.e. `SimpleGraph`, `SimpleDiGraph` from Graphs, or `SimpleWeightedGraph`,
`SimpleWeightedDiGraph` from SimpleWeightedGraphs.
- An `AbstractFeaturedGraph` object.
- `mt::Symbol`: Matrix type for `g` in matrix form. if `graph` is in matrix form, `mt` is
recorded as one of `:adjm`, `:normedadjm`, `:laplacian`, `:normalized` or `:scaled`.
- `directed`: It specify that direction of a graph. It can be `:auto`, `:directed` and
`:undirected`. Default value is `:auto`, which infers direction automatically.
- `nf`: Node features.
- `ef`: Edge features.
- `gf`: Global features.
- `pf`: Positional features. If `nothing` is given, positional encoding is turned off. If an
array is given, positional encoding is assigned as given array. If `:auto` is given,
positional encoding is generated automatically for node features and `with_batch` is considered.
- `T`: It specifies the element type of graph. Default value is the element type of `g`.
- `N`: Number of nodes for `g`.
- `E`: Number of edges for `g`.
- `with_batch::Bool`: Consider last dimension of all features as batch dimension.
# Usage
```
using GraphSignals, CUDA
# Construct from adjacency list representation
g = [[2,3], [1,4,5], [1], [2,5], [2,4]]
fg = FeaturedGraph(g)
# Number of nodes and edges
nv(fg) # 5
ne(fg) # 10
# From a Graphs' graph
fg = FeaturedGraph(erdos_renyi(100, 20))
# Copy featured graph while also adding node features
fg = FeaturedGraph(fg, nf=rand(100, 5))
# Send to gpu
fg = fg |> cu
```
See also [`graph`](@ref), [`node_feature`](@ref), [`edge_feature`](@ref), and [`global_feature`](@ref).
"""
mutable struct FeaturedGraph{T,Tn<:AbstractGraphSignal,Te<:AbstractGraphSignal,Tg<:AbstractGraphSignal,Tp<:AbstractGraphDomain} <: AbstractFeaturedGraph
graph::T
nf::Tn
ef::Te
gf::Tg
pf::Tp
matrix_type::Symbol
function FeaturedGraph(graph::SparseGraph, nf, ef, gf, pf, mt::Symbol)
check_matrix_type(mt)
check_features(graph, nf, ef, pf)
nf = NodeSignal(nf)
ef = EdgeSignal(ef)
gf = GlobalSignal(gf)
pf = NodeDomain(pf)
new{typeof(graph),typeof(nf),typeof(ef),typeof(gf),typeof(pf)}(graph, nf, ef, gf, pf, mt)
end
function FeaturedGraph{T,Tn,Te,Tg,Tp}(graph, nf, ef, gf, pf, mt
) where {T,Tn,Te,Tg,Tp}
check_matrix_type(mt)
check_features(graph, nf, ef, pf)
graph = T(graph)
nf = NodeSignal(Tn(nf))
ef = EdgeSignal(Te(ef))
gf = GlobalSignal(Tg(gf))
pf = NodeDomain(Tp(pf))
new{T,typeof(nf),typeof(ef),typeof(gf),typeof(pf)}(graph, nf, ef, gf, pf, mt)
end
end
@functor FeaturedGraph
function FeaturedGraph(graph, mat_type::Symbol; directed::Symbol=:auto, T=eltype(graph), N=nv(graph), E=ne(graph),
nf=nothing, ef=nothing, gf=nothing, pf=nothing, with_batch::Bool=false)
@assert directed ∈ DIRECTEDS "directed must be one of $(join(_string.(DIRECTEDS), ", ", " or "))"
dir = (directed == :auto) ? is_directed(graph) : directed == :directed
if pf == :auto
A = nf[1, ntuple(i -> Colon(), length(size(nf))-1)...]
pf = generate_grid(A, with_batch=with_batch)
end
nf = NodeSignal(nf)
ef = EdgeSignal(ef)
gf = GlobalSignal(gf)
pf = NodeDomain(pf)
return FeaturedGraph(SparseGraph(graph, dir, T), nf, ef, gf, pf, mat_type)
end
## Graph from JuliaGraphs
FeaturedGraph(graph::AbstractGraph; kwargs...) =
FeaturedGraph(graph, :adjm; T=Float32, kwargs...)
## Graph in adjacency list
FeaturedGraph(graph::AbstractVector{T};
ET=eltype(graph[1]), kwargs...) where {T<:AbstractVector} =
FeaturedGraph(graph, :adjm; T=ET, kwargs...)
## Graph in adjacency matrix
FeaturedGraph(graph::AbstractMatrix{T}; N=nv(graph), nf=nothing, kwargs...) where T =
FeaturedGraph(graph, :adjm; N=N, nf=nf, kwargs...)
function FeaturedGraph(fg::FeaturedGraph;
nf=node_feature(fg), ef=edge_feature(fg), gf=global_feature(fg),
pf=positional_feature(fg))
nf = NodeSignal(nf)
ef = EdgeSignal(ef)
gf = GlobalSignal(gf)
pf = NodeDomain(pf)
return FeaturedGraph(graph(fg), nf, ef, gf, pf, matrixtype(fg))
end
"""
ConcreteFeaturedGraph(fg; nf=node_feature(fg), ef=edge_feature(fg),
gf=global_feature(fg), pf=positional_feature(fg))
This is a syntax sugar for construction for `FeaturedGraph` and `FeaturedSubgraph` object.
It is an idempotent operation, which gives the same type of object as inputs.
It wraps input `fg` again but reconfigures with `kwargs`.
# Arguments
- `fg`: `FeaturedGraph` and `FeaturedSubgraph` object.
- `nf`: Node features.
- `ef`: Edge features.
- `gf`: Global features.
- `pf`: Positional features.
# Usage
```jldoctest
julia> using GraphSignals
julia> adjm = [0 1 1 1;
1 0 1 0;
1 1 0 1;
1 0 1 0];
julia> nf = rand(10, 4);
julia> fg = FeaturedGraph(adjm; nf=nf)
FeaturedGraph:
Undirected graph with (#V=4, #E=5) in adjacency matrix
Node feature: ℝ^10 <Matrix{Float64}>
julia> ConcreteFeaturedGraph(fg, nf=rand(7, 4))
FeaturedGraph:
Undirected graph with (#V=4, #E=5) in adjacency matrix
Node feature: ℝ^7 <Matrix{Float64}>
```
"""
ConcreteFeaturedGraph(fg::FeaturedGraph; kwargs...) = FeaturedGraph(fg; kwargs...)
## dimensional checks
function check_num_nodes(graph_nv::Real, N::Real)
msg = "number of nodes must match between graph ($graph_nv) and features ($N)"
graph_nv == N || throw(DimensionMismatch(msg))
end
function check_num_edges(graph_ne::Real, E::Real)
msg = "number of edges must match between graph ($graph_ne) and features ($E)"
graph_ne == E || throw(DimensionMismatch(msg))
end
# generic fallback
check_num_nodes(graph_nv::Real, feat) = check_num_nodes(graph_nv, size(feat, 2))
check_num_edges(graph_ne::Real, feat) = check_num_edges(graph_ne, size(feat, 2))
check_num_nodes(g, feat) = check_num_nodes(nv(g), feat)
check_num_edges(g, feat) = check_num_edges(ne(g), feat)
function check_matrix_type(mt::Symbol)
errmsg = "matrix_type must be one of $(join(_string.(MATRIX_TYPES), ", ", " or "))"
mt ∈ MATRIX_TYPES || throw(ArgumentError(errmsg))
end
function check_features(graph, nf, ef, pf)
check_num_edges(ne(graph), ef)
check_num_nodes(nv(graph), nf)
check_num_nodes(nv(graph), pf)
return
end
## show
function Base.show(io::IO, fg::FeaturedGraph)
direct = is_directed(fg) ? "Directed" : "Undirected"
println(io, "FeaturedGraph:")
print(io, "\t", direct, " graph with (#V=", nv(fg), ", #E=", ne(fg), ") in ", matrixrepr(fg))
has_node_feature(fg) && print(io, "\n\tNode feature:\tℝ^", nf_dims_repr(fg.nf), " <", typeof(fg.nf), ">")
has_edge_feature(fg) && print(io, "\n\tEdge feature:\tℝ^", ef_dims_repr(fg.ef), " <", typeof(fg.ef), ">")
has_global_feature(fg) && print(io, "\n\tGlobal feature:\tℝ^", gf_dims_repr(fg.gf), " <", typeof(fg.gf), ">")
has_positional_feature(fg) && print(io, "\n\tPositional feature:\tℝ^", pf_dims_repr(fg.pf), " <", typeof(fg.pf), ">")
end
matrixrepr(fg::FeaturedGraph) = matrixrepr(Val(matrixtype(fg)))
matrixrepr(::Val{:adjm}) = "adjacency matrix"
matrixrepr(::Val{:normedadjm}) = "normalized adjacency matrix"
matrixrepr(::Val{:laplacian}) = "Laplacian matrix"
matrixrepr(::Val{:normalized}) = "normalized Laplacian"
matrixrepr(::Val{:scaled}) = "scaled Laplacian"
## Accessing
matrixtype(fg::FeaturedGraph) = fg.matrix_type
Graphs.is_directed(fg::AbstractFeaturedGraph) = is_directed(graph(fg))
function Base.setproperty!(fg::FeaturedGraph, prop::Symbol, x)
if prop == :graph
check_num_nodes(x, fg.nf)
check_num_edges(x, fg.ef)
check_num_nodes(x, fg.pf)
elseif prop == :nf
x = NodeSignal(x)
check_num_nodes(fg.graph, x)
elseif prop == :ef
x = EdgeSignal(x)
check_num_edges(fg.graph, x)
elseif prop == :gf
x = GlobalSignal(x)
elseif prop == :pf
x = NodeDomain(x)
check_num_nodes(fg.graph, x)
end
setfield!(fg, prop, x)
end
"""
graph(fg)
Get referenced graph in `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
graph(fg::FeaturedGraph) = fg.graph
"""
node_feature(fg)
Get node feature attached to `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
node_feature(fg::FeaturedGraph) = node_feature(fg.nf)
"""
edge_feature(fg)
Get edge feature attached to `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
edge_feature(fg::FeaturedGraph) = edge_feature(fg.ef)
"""
global_feature(fg)
Get global feature attached to `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
global_feature(fg::FeaturedGraph) = global_feature(fg.gf)
"""
positional_feature(fg)
Get positional feature attached to `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
positional_feature(fg::FeaturedGraph) = positional_feature(fg.pf)
"""
has_graph(fg)
Check if `graph` is available or not for `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
has_graph(fg::FeaturedGraph) = fg.graph != Fill(0., (0,0))
"""
has_node_feature(::AbstractFeaturedGraph)
Check if `node_feature` is available or not for `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
has_node_feature(fg::FeaturedGraph) = has_node_feature(fg.nf)
"""
has_edge_feature(::AbstractFeaturedGraph)
Check if `edge_feature` is available or not for `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
has_edge_feature(fg::FeaturedGraph) = has_edge_feature(fg.ef)
"""
has_global_feature(::AbstractFeaturedGraph)
Check if `global_feature` is available or not for `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
has_global_feature(fg::FeaturedGraph) = has_global_feature(fg.gf)
"""
has_positional_feature(::AbstractFeaturedGraph)
Check if `positional_feature` is available or not for `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
has_positional_feature(fg::FeaturedGraph) = has_positional_feature(fg.pf)
## Graph property
"""
nv(fg)
Get node number of graph in `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
Graphs.nv(fg::FeaturedGraph) = nv(graph(fg))
"""
ne(fg)
Get edge number of in `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
Graphs.ne(fg::FeaturedGraph) = ne(graph(fg))
to_namedtuple(fg::AbstractFeaturedGraph) = to_namedtuple(graph(fg))
Graphs.vertices(fg::FeaturedGraph) = vertices(graph(fg))
"""
edges(fg)
Returns an iterator over an edge list for graph in `fg`.
# Arguments
- `fg::FeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
Graphs.edges(fg::FeaturedGraph) = edges(graph(fg))
Graphs.neighbors(fg::FeaturedGraph; dir::Symbol=:out) = neighbors(graph(fg); dir=dir)
Graphs.neighbors(fg::FeaturedGraph, i::Integer; dir::Symbol=:out) = neighbors(graph(fg), i, dir=dir)
Graphs.has_edge(fg::FeaturedGraph, i::Integer, j::Integer) = has_edge(graph(fg), i, j)
incident_edges(fg::FeaturedGraph) = incident_edges(graph(fg))
## Graph representations
"""
adjacency_list(fg)
Get adjacency list of graph in `fg`.
# Arguments
- `fg::AbstractFeaturedGraph`: A concrete object of `AbstractFeaturedGraph` type.
"""
adjacency_list(fg::FeaturedGraph) = adjacency_list(graph(fg))
adjacency_matrix(fg::FeaturedGraph, ::Type{T}=eltype(graph(fg))) where {T} =
adjacency_matrix(graph(fg), T)
degrees(fg::AbstractFeaturedGraph, ::Type{T}=eltype(graph(fg)); dir::Symbol=:out) where {T} =
degrees(graph(fg), T; dir=dir)
## sample
StatsBase.sample(fg::AbstractFeaturedGraph, n::Int) =
subgraph(fg, sample(vertices(fg), n; replace=false))
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 2041 | """
adjacency_list(adj)
Transform a adjacency matrix into a adjacency list.
"""
function adjacency_list(adj::AbstractMatrix{T}) where {T}
n = size(adj,1)
@assert n == size(adj,2) "adjacency matrix is not a square matrix."
A = (adj .!= zero(T))
if !issymmetric(adj)
A = A .| A'
end
indecies = collect(1:n)
ne = Vector{Int}[indecies[view(A, :, i)] for i = 1:n]
return ne
end
adjacency_list(adj::AbstractVector{<:AbstractVector{<:Integer}}) = adj
GraphSignals.nv(g::AbstractMatrix) = size(g, 1)
GraphSignals.nv(g::AbstractVector{T}) where {T<:AbstractVector} = size(g, 1)
function GraphSignals.ne(g::AbstractMatrix, directed::Bool=is_directed(g))
g = Matrix(g) .!= 0
if directed
return sum(g)
else
return div(sum(g) + sum(diag(g)), 2)
end
end
function GraphSignals.ne(g::AbstractVector{T}, directed::Bool=is_directed(g)) where {T<:AbstractVector}
if directed
return sum(length, g)
else
e = 0
for i in 1:length(g)
for j in g[i]
if i ≤ j
e += 1
end
end
end
return e
end
end
GraphSignals.is_directed(g::AbstractMatrix) = !issymmetric(Matrix(g))
function GraphSignals.is_directed(g::AbstractVector{T}) where {T<:AbstractVector}
edges = Set{Tuple{Int64,Int64}}()
for (i, js) in enumerate(g)
for j in Set(js)
if i != j
e = (i,j)
if e in edges
pop!(edges, e)
else
push!(edges, (j,i))
end
end
end
end
!isempty(edges)
end
function remove_self_loops!(adj::AbstractVector{<:AbstractVector{<:Integer}})
N = nv(adj)
for i in 1:N
deleteat!(adj[i], adj[i] .== i)
end
return adj
end
function remove_self_loops(adj::AbstractVector{T}) where {T<:AbstractVector{<:Integer}}
N = nv(adj)
new_adj = T[adj[i][adj[i] .!= i] for i in 1:N]
return new_adj
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 718 | abstract type AbstractGraphDomain end
struct NullDomain <: AbstractGraphDomain
end
domain(::NullDomain) = nothing
positional_feature(::NullDomain) = nothing
has_positional_feature(::NullDomain) = false
pf_dims_repr(::NullDomain) = 0
check_num_nodes(graph_nv::Real, ::NullDomain) = nothing
struct NodeDomain{T} <: AbstractGraphDomain
domain::T
end
@functor NodeDomain
NodeDomain(::Nothing) = NullDomain()
NodeDomain(d::AbstractGraphDomain) = d
domain(d::NodeDomain) = d.domain
positional_feature(d::NodeDomain) = d.domain
has_positional_feature(::NodeDomain) = true
pf_dims_repr(d::NodeDomain) = size(d.domain, 1)
check_num_nodes(graph_nv::Real, d::NodeDomain) = check_num_nodes(graph_nv, size(d.domain, 2))
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 1934 | abstract type AbstractGraphSignal end
struct NullGraphSignal <: AbstractGraphSignal
end
signal(::NullGraphSignal) = nothing
node_feature(::NullGraphSignal) = nothing
edge_feature(::NullGraphSignal) = nothing
global_feature(::NullGraphSignal) = nothing
has_node_feature(::NullGraphSignal) = false
has_edge_feature(::NullGraphSignal) = false
has_global_feature(::NullGraphSignal) = false
nf_dims_repr(::NullGraphSignal) = 0
ef_dims_repr(::NullGraphSignal) = 0
gf_dims_repr(::NullGraphSignal) = 0
check_num_nodes(graph_nv::Real, ::NullGraphSignal) = nothing
check_num_edges(graph_nv::Real, ::NullGraphSignal) = nothing
struct NodeSignal{T} <: AbstractGraphSignal
signal::T
end
@functor NodeSignal
NodeSignal(::Nothing) = NullGraphSignal()
NodeSignal(::NullGraphSignal) = NullGraphSignal()
NodeSignal(s::NodeSignal) = s
signal(s::NodeSignal) = s.signal
node_feature(s::NodeSignal) = s.signal
has_node_feature(::NodeSignal) = true
nf_dims_repr(s::NodeSignal) = size(s.signal, 1)
check_num_nodes(graph_nv::Real, s::NodeSignal) = check_num_nodes(graph_nv, size(s.signal, 2))
struct EdgeSignal{T} <: AbstractGraphSignal
signal::T
end
@functor EdgeSignal
EdgeSignal(::Nothing) = NullGraphSignal()
EdgeSignal(::NullGraphSignal) = NullGraphSignal()
EdgeSignal(s::EdgeSignal) = s
signal(s::EdgeSignal) = s.signal
edge_feature(s::EdgeSignal) = s.signal
has_edge_feature(::EdgeSignal) = true
ef_dims_repr(s::EdgeSignal) = size(s.signal, 1)
check_num_edges(graph_ne::Real, s::EdgeSignal) = check_num_edges(graph_ne, size(s.signal, 2))
struct GlobalSignal{T} <: AbstractGraphSignal
signal::T
end
@functor GlobalSignal
GlobalSignal(::Nothing) = NullGraphSignal()
GlobalSignal(::NullGraphSignal) = NullGraphSignal()
GlobalSignal(s::GlobalSignal) = s
signal(s::GlobalSignal) = s.signal
global_feature(s::GlobalSignal) = s.signal
has_global_feature(::GlobalSignal) = true
gf_dims_repr(s::GlobalSignal) = size(s.signal, 1)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 9132 | function adjacency_matrix(adj::AbstractMatrix{T}, ::Type{S}) where {T,S}
_dim_check(adj)
return Matrix{S}(adj)
end
function adjacency_matrix(adj::AbstractMatrix)
_dim_check(adj)
return Array(adj)
end
adjacency_matrix(adj::Matrix{T}, ::Type{T}) where {T} = adjacency_matrix(adj)
function adjacency_matrix(adj::Matrix)
_dim_check(adj)
return adj
end
function _dim_check(adj)
m, n = size(adj)
(m == n) || throw(DimensionMismatch("adjacency matrix is not a square matrix: ($m, $n)"))
end
"""
degrees(g, [T=eltype(g)]; dir=:out)
Degree of each vertex. Return a vector which contains the degree of each vertex in graph `g`.
# Arguments
- `g`: should be a adjacency matrix, `SimpleGraph`, `SimpleDiGraph` (from Graphs) or
`SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: result element type of degree vector; default is the element type of `g` (optional).
- `dir`: direction of degree; should be `:in`, `:out`, or `:both` (optional).
# Examples
```jldoctest
julia> using GraphSignals
julia> m = [0 1 1; 1 0 0; 1 0 0];
julia> GraphSignals.degrees(m)
3-element Vector{Int64}:
2
1
1
```
"""
function degrees(g, ::Type{T}=eltype(g); dir::Symbol=:out) where {T}
adj = adjacency_matrix(g, T)
if issymmetric(adj)
d = vec(sum(adj, dims=1))
else
if dir == :out
d = vec(sum(adj, dims=1))
elseif dir == :in
d = vec(sum(adj, dims=2))
elseif dir == :both
d = vec(sum(adj, dims=1)) + vec(sum(adj, dims=2))
else
throw(ArgumentError("dir only accept :in, :out or :both, but got $(dir)."))
end
end
return T.(d)
end
"""
degree_matrix(g, [T=eltype(g)]; dir=:out, squared=false, inverse=false)
Degree matrix of graph `g`. Return a matrix which contains degrees of each vertex in its diagonal.
The values other than diagonal are zeros.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `dir::Symbol`: The way to calculate degree of a graph `g` regards its directions.
Should be `:in`, `:out`, or `:both`.
- `squared::Bool`: To return a squared degree vector or not.
- `inverse::Bool`: To return a inverse degree vector or not.
# Examples
```jldoctest
julia> using GraphSignals
julia> m = [0 1 1; 1 0 0; 1 0 0];
julia> GraphSignals.degree_matrix(m)
3×3 LinearAlgebra.Diagonal{Int64, Vector{Int64}}:
2 ⋅ ⋅
⋅ 1 ⋅
⋅ ⋅ 1
```
"""
function degree_matrix(g, ::Type{T}=eltype(g);
dir::Symbol=:out, squared::Bool=false, inverse::Bool=false) where {T}
d = degrees(g, T, dir=dir)
squared && (d .= sqrt.(d))
inverse && (d .= safe_inv.(d))
return Diagonal(T.(d))
end
safe_inv(x::T) where {T} = ifelse(iszero(x), zero(T), inv(x))
@doc raw"""
normalized_adjacency_matrix(g, [T=float(eltype(g))]; selfloop=false)
Normalized adjacency matrix of graph `g`, defined as
```math
D^{-\frac{1}{2}} \tilde{A} D^{-\frac{1}{2}}
```
where ``D`` is degree matrix and ``\tilde{A}`` is adjacency matrix w/o self loop from `g`.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `selfloop`: Adding self loop to ``\tilde{A}`` or not.
"""
function normalized_adjacency_matrix(g, ::Type{T}=float(eltype(g));
selfloop::Bool=false) where {T}
adj = adjacency_matrix(g, T)
selfloop && (adj += I)
inv_sqrtD = degree_matrix(g, T, dir=:both, squared=true, inverse=true)
return inv_sqrtD * adj * inv_sqrtD
end
"""
laplacian_matrix(g, [T=eltype(g)]; dir=:out)
Laplacian matrix of graph `g`, defined as
```math
D - A
```
where ``D`` is degree matrix and ``A`` is adjacency matrix from `g`.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `dir::Symbol`: The way to calculate degree of a graph `g` regards its directions.
Should be `:in`, `:out`, or `:both`.
"""
Graphs.laplacian_matrix(g, ::Type{T}=eltype(g); dir::Symbol=:out) where {T} =
degree_matrix(g, T, dir=dir) - adjacency_matrix(g, T)
@doc raw"""
normalized_laplacian(g, [T=float(eltype(g))]; dir=:both, selfloop=false)
Normalized Laplacian matrix of graph `g`, defined as
```math
I - D^{-\frac{1}{2}} \tilde{A} D^{-\frac{1}{2}}
```
where ``D`` is degree matrix and ``\tilde{A}`` is adjacency matrix w/o self loop from `g`.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `dir::Symbol`: The way to calculate degree of a graph `g` regards its directions.
Should be `:in`, `:out`, or `:both`.
- `selfloop::Bool`: Adding self loop to ``\tilde{A}`` or not.
"""
function normalized_laplacian(g, ::Type{T}=float(eltype(g));
dir::Symbol=:both, selfloop::Bool=false) where {T}
L = adjacency_matrix(g, T)
if dir == :both
selfloop && (L += I)
inv_sqrtD = degree_matrix(g, T, dir=:both, squared=true, inverse=true)
L .= I - inv_sqrtD * L * inv_sqrtD
else
inv_D = degree_matrix(g, T, dir=dir, inverse=true)
L .= I - inv_D * L
end
return L
end
@doc raw"""
scaled_laplacian(g, [T=float(eltype(g))])
Scaled Laplacien matrix of graph `g`, defined as
```math
\hat{L} = \frac{2}{\lambda_{max}} \tilde{L} - I
```
where ``\tilde{L}`` is the normalized Laplacian matrix.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
"""
function scaled_laplacian(g, ::Type{T}=float(eltype(g))) where {T}
adj = adjacency_matrix(g, T)
# @assert issymmetric(adj) "scaled_laplacian only works with symmetric matrices"
E = eigen(Symmetric(Array(adj))).values
return T(2. / maximum(E)) .* normalized_laplacian(adj, T) - I
end
"""
transition_matrix(g, [T=float(eltype(g))]; dir=:out)
Transition matrix of performing random walk over graph `g`, defined as
```math
D^{-1} A
```
where ``D`` is degree matrix and ``A`` is adjacency matrix from `g`.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `dir::Symbol`: The way to calculate degree of a graph `g` regards its directions.
Should be `:in`, `:out`, or `:both`.
"""
function transition_matrix(g, ::Type{T}=float(eltype(g)); dir::Symbol=:out) where {T}
inv_D = degree_matrix(g, T; dir=dir, inverse=true)
A = adjacency_matrix(g, T)
return inv_D * A
end
"""
random_walk_laplacian(g, [T=float(eltype(g))]; dir=:out)
Random walk normalized Laplacian matrix of graph `g`, defined as
```math
I - D^{-1} A
```
where ``D`` is degree matrix and ``A`` is adjacency matrix from `g`.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `dir::Symbol`: The way to calculate degree of a graph `g` regards its directions.
Should be `:in`, `:out`, or `:both`.
"""
random_walk_laplacian(g, ::Type{T}=float(eltype(g)); dir::Symbol=:out) where {T} =
SparseMatrixCSC(I - transition_matrix(g, T, dir=dir))
"""
signless_laplacian(g, [T=eltype(g)]; dir=:out)
Signless Laplacian matrix of graph `g`, defined as
```math
D + A
```
where ``D`` is degree matrix and ``A`` is adjacency matrix from `g`.
# Arguments
- `g`: Should be a adjacency matrix, `FeaturedGraph`, `SimpleGraph`, `SimpleDiGraph` (from Graphs)
or `SimpleWeightedGraph`, `SimpleWeightedDiGraph` (from SimpleWeightedGraphs).
- `T`: The element type of result degree vector. The default type is the element type of `g`.
- `dir::Symbol`: The way to calculate degree of a graph `g` regards its directions.
Should be `:in`, `:out`, or `:both`.
"""
signless_laplacian(g, ::Type{T}=eltype(g); dir::Symbol=:out) where {T} =
degree_matrix(g, T, dir=dir) + adjacency_matrix(g, T)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 2322 | """
kneighbors_graph(X, k, metric; include_self=false, weighted=false)
kneighbors_graph(X, k; include_self=false, weighted=false)
Generate `k`-nearest neighborhood (kNN) graph from their node features.
It returns a `FeaturedGraph` object, which contains a kNN graph and
node features `X`.
# Arguments
- `X::AbstractMatrix`: The feature matrix for each node with size `(feat_dim, num_nodes)`.
- `k`: Number of nearest neighbor for each node in kNN graph.
- `metric::Metric`: Distance metric to measure distance between any two nodes.
It aceepts distance objects from Distances.
- `include_self::Bool`: Whether distance from node to itself is included in nearest neighbor.
- `weighted::Bool`: Whether distance could be the edge weight in kNN graph.
# Usage
```jldoctest
julia> using GraphSignals, Distances
julia> nf = rand(Float32, 10, 1024);
julia> fg = kneighbors_graph(nf, 5)
FeaturedGraph:
Directed graph with (#V=1024, #E=5120) in adjacency matrix
Node feature: ℝ^10 <Matrix{Float32}>
julia> fg = kneighbors_graph(nf, 5, Cityblock())
FeaturedGraph:
Directed graph with (#V=1024, #E=5120) in adjacency matrix
Node feature: ℝ^10 <Matrix{Float32}>
julia> nf = rand(Float32[0, 1], 10, 1024);
julia> fg = kneighbors_graph(nf, 5, Jaccard(); include_self=true)
FeaturedGraph:
Directed graph with (#V=1024, #E=5120) in adjacency matrix
Node feature: ℝ^10 <Matrix{Float32}>
```
"""
function kneighbors_graph(X::AbstractMatrix, k::Int, metric::Metric;
include_self=false, weighted=false)
searchtree = NearestNeighbors.BallTree(X, metric)
search_k = include_self ? k : k+1
idxs, dists = NearestNeighbors.knn(searchtree, X, search_k, false)
include_self || remove_self_loops!(idxs)
if weighted
N = length(idxs)
g = SimpleWeightedGraph(N)
for i in 1:N
for j in 1:k
add_edge!(g, i, idxs[i][j], dists[i][j])
end
end
else
g = idxs
end
return FeaturedGraph(g, nf=X)
end
function kneighbors_graph(X::AbstractArray{T,3}, k::Int, metric::Metric; kwargs...) where {T}
X = reshape(mean(X, dims=3), size(X)[1:2]...)
return kneighbors_graph(X, k, metric; kwargs...)
end
kneighbors_graph(X::AbstractArray, k::Int; kwargs...) = kneighbors_graph(X, k, Euclidean(); kwargs...)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 1003 | """
generate_grid(A, with_batch=false)
Returns grid coordinates for tensor `A`.
# Arguments
- `A::AbstractArray`: The tensor to reference to.
- `with_batch::Bool`: Whether to consider last dimension as batch. If `with_batch=true`,
the last dimension is not consider as a component of coordinates.
# Usage
```jldoctest
julia> using GraphSignals
julia> A = rand(3, 4, 5);
julia> coord = GraphSignals.generate_grid(A);
julia> size(coord)
(3, 3, 4, 5)
julia> coord = GraphSignals.generate_grid(A, with_batch=true);
julia> size(coord)
(2, 3, 4)
```
"""
function generate_grid(A::AbstractArray; with_batch::Bool=false)
dims = with_batch ? size(A)[1:end-1] : size(A)
N = length(dims)
colons = ntuple(i -> Colon(), N)
coord = similar(A, N, dims...)
for i in 1:N
ones = ntuple(x -> 1, i-1)
coord[i, colons...] .= reshape(1:dims[i], ones..., :)
end
return coord
end
@deprecate generate_coordinates(A, with_batch=false) generate_grid(A, with_batch=false)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 2899 | """
random_walk(g, start, n=1)
Draw random walk samples from a given graph `g`. The weights for each edge on graph
are considered to be proportional to the transition probability.
# Arguments
- `g`: Data representing the graph topology. Possible type are
- An adjacency matrix.
- An `FeaturedGraph` or `SparseGraph` object.
- `start::Int`: A start point for a random walk on graph `g`.
- `n::Int`: Number of random walk steps.
# Usage
```julia
julia> using GraphSignals
julia> adjm = [0 1 0 1 1;
1 0 0 0 0;
0 0 1 0 0;
1 0 0 0 1;
1 0 0 1 0];
julia> fg = FeaturedGraph(adjm);
julia> random_walk(adjm, 1)
1-element Vector{Int64}:
5
julia> random_walk(fg, 1, 3)
3-element Vector{Int64}:
5
4
4
julia> using Flux
julia> fg = fg |> gpu;
julia> random_walk(fg, 4, 3)
3-element Vector{Int64}:
1
1
1
```
See also [`neighbor_sample`](@ref)
"""
random_walk(A::AbstractMatrix, start::Int, n::Int=1) =
[sample(1:size(A, 1), Weights(view(A, :, start))) for _ in 1:n]
random_walk(x::AbstractVector, n::Int=1) = [sample(1:length(x), Weights(x)) for _ in 1:n]
random_walk(sg::SparseGraph, start::Int, n::Int=1) = random_walk(sg.S, start, n)
random_walk(fg::FeaturedGraph, start::Int, n::Int=1) = random_walk(graph(fg), start, n)
"""
neighbor_sample(g, start, n=1; replace=false)
Draw random samples from neighbors from a given graph `g`. The weights for each edge on graph
are considered to be proportional to the transition probability.
# Arguments
- `g`: Data representing the graph topology. Possible type are
- An adjacency matrix.
- An `FeaturedGraph` or `SparseGraph` object.
- `start::Int`: A vertex for a random neighbor sampling on graph `g`.
- `n::Int`: Number of random neighbor sampling.
- `replace::Bool`: Sample with replacement or not.
# Usage
```julia
julia> using GraphSignals
julia> adjm = [0 1 0 1 1;
1 0 0 0 0;
0 0 1 0 0;
1 0 0 0 1;
1 0 0 1 0];
julia> fg = FeaturedGraph(adjm);
julia> neighbor_sample(adjm, 1)
1-element Vector{Int64}:
4
julia> neighbor_sample(fg, 1, 3)
3-element Vector{Int64}:
5
4
2
julia> using Flux
julia> fg = fg |> gpu;
julia> neighbor_sample(fg, 4, 3, replace=true)
3-element Vector{Int64}:
1
5
5
```
See also [`random_walk`](@ref)
"""
neighbor_sample(A::AbstractMatrix, start::Int, n::Int=1; replace::Bool=false) =
sample(1:size(A, 1), Weights(view(A, :, start)), n; replace=replace)
neighbor_sample(x::AbstractVector, n::Int=1; replace::Bool=false) = sample(1:length(x), Weights(x), n; replace=replace)
neighbor_sample(sg::SparseGraph, start::Int, n::Int=1; replace::Bool=false) =
neighbor_sample(sg.S, start, n; replace=replace)
neighbor_sample(fg::FeaturedGraph, start::Int, n::Int=1; replace::Bool=false) =
neighbor_sample(graph(fg), start, n; replace=replace)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 11771 | abstract type AbstractSparseGraph <: AbstractGraph{Int} end
"""
SparseGraph(A, directed, [T])
A sparse graph structure represents by sparse matrix.
A directed graph is represented by a sparse matrix, of which column
index as source node index and row index as sink node index.
# Arguments
- `A`: Adjacency matrix.
- `directed`: If this is a directed graph or not.
- `T`: Element type for `SparseGraph`.
"""
struct SparseGraph{D,M,V,T} <: AbstractSparseGraph
S::M
edges::V
E::T
end
function SparseGraph{D}(A::AbstractMatrix{Tv}, edges::AbstractVector{Ti}, E::Integer) where {D,Tv,Ti}
@assert size(A, 1) == size(A, 2) "A must be a square matrix."
return SparseGraph{D,typeof(A),typeof(edges),typeof(E)}(A, edges, E)
end
function SparseGraph(
A::AbstractMatrix{Tv},
edges::AbstractVector{Ti},
directed::Bool,
::Type{T}=eltype(A)
) where {Tv,Ti,T}
E = length(unique(edges))
spA = (Tv === T) ? SparseMatrixCSC{Tv,Ti}(A) : SparseMatrixCSC{T,Ti}(A)
return SparseGraph{directed}(spA, edges, E)
end
SparseGraph(A::SparseMatrixCSC, directed::Bool, ::Type{T}=eltype(A)) where {T} =
SparseGraph(A, order_edges(A, directed=directed), directed, T)
SparseGraph(A::AbstractMatrix, directed::Bool, ::Type{T}=eltype(A)) where {T} =
SparseGraph(sparsecsc(A), directed, T)
function SparseGraph(
adjl::AbstractVector{T},
directed::Bool,
::Type{Te}=eltype(eltype(adjl))
) where {T<:AbstractVector,Te}
n = length(adjl)
colptr, rowval, nzval = to_csc(adjl)
spA = SparseMatrixCSC(n, n, UInt32.(colptr), UInt32.(rowval), Te.(nzval))
return SparseGraph(spA, directed)
end
SparseGraph(g::G, directed::Bool=is_directed(G), ::Type{T}=eltype(g)) where {G<:AbstractSimpleGraph,T} =
SparseGraph(g.fadjlist, directed, T)
SparseGraph(g::G, directed::Bool=is_directed(G), ::Type{T}=eltype(g)) where {G<:AbstractSimpleWeightedGraph,T} =
SparseGraph(SimpleWeightedGraphs.weights(g)', directed, T)
function to_csc(adjl::AbstractVector{T}) where {T<:AbstractVector}
ET = eltype(adjl[1])
colptr = ET[1, ]
rowval = ET[]
for nbs in adjl
r = sort!(unique(nbs))
push!(colptr, colptr[end] + length(r))
append!(rowval, r)
end
nzval = ones(ET, length(rowval))
return colptr, rowval, nzval
end
@functor SparseGraph{true}
@functor SparseGraph{false}
struct SparseSubgraph{G<:AbstractSparseGraph,T} <: AbstractSparseGraph
sg::G
nodes::T
end
@functor SparseSubgraph
SparseArrays.sparse(sg::SparseGraph) = sg.S
SparseArrays.sparse(ss::SparseSubgraph) = sparse(ss.sg)[ss.nodes, ss.nodes]
Base.collect(sg::AbstractSparseGraph) = collect(sparse(sg))
Base.show(io::IO, sg::SparseGraph) =
print(io, "SparseGraph{", eltype(sg), "}(#V=", nv(sg), ", #E=", ne(sg), ")")
Base.show(io::IO, ss::SparseSubgraph) =
print(io, "subgraph of ", ss.sg, " with nodes=$(ss.nodes)")
Graphs.nv(sg::SparseGraph) = size(sparse(sg), 1)
Graphs.nv(ss::SparseSubgraph) = length(ss.nodes)
Graphs.ne(sg::SparseGraph) = sg.E
# Graphs.ne(ss::SparseSubgraph) =
Graphs.is_directed(::SparseGraph{G}) where {G} = G
Graphs.is_directed(::Type{<:SparseGraph{G}}) where {G} = G
Graphs.is_directed(ss::SparseSubgraph) = is_directed(ss.sg)
Graphs.is_directed(::Type{<:SparseSubgraph{G}}) where {G} = is_directed(G)
function Graphs.has_self_loops(sg::AbstractSparseGraph)
for i in vertices(sg)
isneighbor(graph(sg), i, i) && return true
end
return false
end
function has_all_self_loops(sg::AbstractSparseGraph)
for i in vertices(sg)
isneighbor(graph(sg), i, i) || return false
end
return true
end
Base.eltype(sg::SparseGraph) = eltype(sparse(sg))
Base.eltype(ss::SparseSubgraph) = eltype(ss.sg)
Graphs.has_vertex(sg::SparseGraph, i::Integer) = 1 <= i <= nv(sg)
Graphs.has_vertex(ss::SparseSubgraph, i::Integer) = (i in ss.nodes)
Graphs.vertices(sg::SparseGraph) = 1:nv(sg)
Graphs.vertices(ss::SparseSubgraph) = ss.nodes
Graphs.edgetype(::AbstractSparseGraph) = Tuple{Int, Int}
Graphs.has_edge(sg::SparseGraph, i::Integer, j::Integer) = j ∈ outneighbors(sg, i)
Graphs.has_edge(ss::SparseSubgraph, i::Integer, j::Integer) =
(i in ss.nodes && j in ss.nodes && has_edge(ss.sg, i, j))
Base.:(==)(sg1::SparseGraph, sg2::SparseGraph) =
sg1.E == sg2.E && sg1.edges == sg2.edges && sg1.S == sg2.S
Base.:(==)(ss1::SparseSubgraph, ss2::SparseSubgraph) =
ss1.nodes == ss2.nodes && ss1.sg == ss2.sg
graph(sg::SparseGraph) = sg
graph(ss::SparseSubgraph) = ss.sg
subgraph(sg::AbstractSparseGraph, nodes::AbstractVector) = SparseSubgraph(graph(sg), nodes)
function to_namedtuple(sg::SparseGraph)
es, nbrs, xs = collect(edges(sg))
return (N=nv(sg), E=ne(sg), es=es, nbrs=nbrs, xs=xs)
end
edgevals(sg::SparseGraph) = sg.edges
edgevals(sg::SparseGraph, col::Integer) = view(sg.edges, SparseArrays.getcolptr(sparse(sg), col))
edgevals(sg::SparseGraph, I::UnitRange) = view(sg.edges, SparseArrays.getcolptr(sparse(sg), I))
"""
neighbors(sg, i)
Return the neighbors of vertex `i` in sparse graph `sg`.
# Arguments
- `sg::SparseGraph`: sparse graph to query.
- `i`: vertex index.
"""
Graphs.neighbors(sg::SparseGraph{false}; dir::Symbol=:out) = rowvals(sparse(sg))
Graphs.neighbors(sg::SparseGraph{false}, i::Integer; dir::Symbol=:out) = outneighbors(sg, i)
function Graphs.neighbors(sg::SparseGraph{true}, i::Integer; dir::Symbol=:out)
if dir == :out
return outneighbors(sg, i)
elseif dir == :in
return inneighbors(sg, i)
elseif dir == :both
return unique!(append!(inneighbors(sg, i), outneighbors(sg, i)))
else
throw(ArgumentError("dir must be one of [:out, :in, :both]."))
end
end
Graphs.outneighbors(sg::SparseGraph) = map(i -> outneighbors(sg, i), vertices(sg))
Graphs.outneighbors(sg::SparseGraph, i::Integer) = rowvalview(sparse(sg), i)
Graphs.inneighbors(sg::SparseGraph) = map(i -> inneighbors(sg, i), vertices(sg))
function Graphs.inneighbors(sg::SparseGraph, i::Integer)
mask = map(j -> isneighbor(sg, i, j), vertices(sg))
return findall(mask)
end
function noutneighbors(sg::SparseGraph, i)
Base.depwarn("noutneighbors will be deprecated in the next release.", :noutneighbors)
return length(SparseArrays.getcolptr(SparseMatrixCSC(sparse(sg)), i))
end
isneighbor(sg::SparseGraph, j, i) = any(j .== outneighbors(sg, i))
"""
dsts(sg::SparseGraph)
Returns all the destination vertex of each edge from graph `sg`.
For undirected graph, the same edge is considered once only.
"""
dsts(sg::SparseGraph{true}) = rowvals(sparse(sg))
"""
srcs(sg::SparseGraph)
Returns all the source vertex of each edge from graph `sg`.
For undirected graph, the same edge is considered once only.
"""
srcs(sg::SparseGraph{true}) = colvals(sparse(sg))
function dsts(sg::SparseGraph{false})
# For undirected graph, upper traingle of matrix is considered only.
S = sparse(sg)
res = Int[]
for j in vertices(sg)
r = rowvalview(S, j)
r = view(r, r .≤ j)
append!(res, r)
end
return res
end
srcs(sg::SparseGraph{false}) = colvals(sparse(sg), upper_traingle=true)
"""
incident_edges(sg, i)
Return the edges incident to vertex `i` in sparse graph `sg`.
# Arguments
- `sg::SparseGraph`: sparse graph to query.
- `i`: vertex index.
"""
incident_edges(sg::SparseGraph{false}) = edgevals(sg)
incident_edges(sg::SparseGraph{false}, i) = edgevals(sg, i)
function incident_edges(sg::SparseGraph{true}, i; dir=:out)
if dir == :out
return incident_outedges(sg, i)
elseif dir == :in
return incident_inedges(sg, i)
elseif dir == :both
return append!(incident_inedges(sg, i), incident_outedges(sg, i))
else
throw(ArgumentError("dir must be one of [:out, :in, :both]."))
end
end
incident_outedges(sg::SparseGraph{true}, i) = edgevals(sg, i)
function incident_inedges(sg::SparseGraph{true,M,V}, i) where {M,V}
inedges = V()
for j in vertices(sg)
mask = isneighbor(sg, i, j)
edges = edgevals(sg, j)
append!(inedges, edges[findall(mask)])
end
return inedges
end
Base.getindex(sg::SparseGraph, ind...) = getindex(sparse(sg), ind...)
# Base.getindex(ss::SparseSubgraph, ind...) =
edge_index(sg::SparseGraph, i, j) = sg.edges[get_csc_index(sparse(sg), j, i)]
# edge_index(ss::SparseSubgraph, i, j) =
"""
Transform a CSC-based edge index `edges[eidx]` into a regular cartesian index `A[i, j]`.
"""
function get_cartesian_index(sg::SparseGraph, eidx::Int)
r = rowvals(sparse(sg))
idx = findfirst(x -> x == eidx, edgevals(sg))
i = r[idx]
j = 1
while idx > noutneighbors(sg, 1:j)
j += 1
end
return (i, j)
end
"""
aggregate_index(sg; direction=:undirected, kind=:edge)
Generate index structure for scatter operation.
# Arguments
- `sg::SparseGraph`: The reference graph.
- `direction::Symbol`: The direction of an edge to be choose to aggregate. It must be one of `:inward` and `:outward`.
- `kind::Symbol`: To aggregate feature upon edge or vertex. It must be one of `:edge` and `:vertex`.
"""
function aggregate_index(sg::SparseGraph, kind::Symbol=:edge, direction::Symbol=:outward)
if !(kind in [:edge, :vertex])
throw(ArgumentError("kind must be one of :edge or :vertex."))
end
if !(direction in [:inward, :outward])
throw(ArgumentError("direction must be one of :outward or :inward."))
end
return aggregate_index(sg, Val(kind), Val(direction))
end
@deprecate aggregate_index(sg::SparseGraph{true}, ::Val{:edge}, ::Val{:inward}) dsts(sg)
@deprecate aggregate_index(sg::SparseGraph{true}, ::Val{:edge}, ::Val{:outward}) srcs(sg)
@deprecate aggregate_index(sg::SparseGraph{false}, ::Val{:edge}, ::Val{:inward}) dsts(sg)
@deprecate aggregate_index(sg::SparseGraph{false}, ::Val{:edge}, ::Val{:outward}) srcs(sg)
@deprecate aggregate_index(sg::SparseGraph{true}, ::Val{:vertex}, ::Val{:inward}) outneighbors(sg)
@deprecate aggregate_index(sg::SparseGraph{true}, ::Val{:vertex}, ::Val{:outward}) inneighbors(sg)
@deprecate aggregate_index(sg::SparseGraph{false}, ::Val{:vertex}, ::Val{:inward}) outneighbors(sg)
@deprecate aggregate_index(sg::SparseGraph{false}, ::Val{:vertex}, ::Val{:outward}) inneighbors(sg)
## Graph representations
adjacency_list(sg::SparseGraph) = map(j -> outneighbors(sg, j), vertices(sg))
adjacency_matrix(sg::AbstractSparseGraph, T::DataType=eltype(sg)) =
adjacency_matrix(sparse(sg), T)
degrees(sg::SparseGraph, T::DataType=eltype(sg); dir::Symbol=:out) =
degrees(sparse(sg), T; dir=dir)
## Edge iterator
struct EdgeIter{G,S}
sg::G
start::S
function EdgeIter(sg::SparseGraph)
if ne(sg) == 0
start = (0, (0, 0))
else
S = SparseMatrixCSC(sparse(sg))
j = 1
while 1 > length(SparseArrays.getcolptr(S, 1:j))
j += 1
end
i = rowvals(S)[1]
e = collect(edgevals(sg))[1]
start = (e, (i, j))
end
return new{typeof(sg),typeof(start)}(sg, start)
end
end
graph(iter::EdgeIter) = iter.sg
Graphs.edges(sg::SparseGraph) = EdgeIter(sg)
Base.length(iter::EdgeIter) = nnz(sparse(graph(iter)))
function Base.iterate(iter::EdgeIter, (el, i)=(iter.start, 1))
next_i = i + 1
if next_i <= ne(graph(iter))
car_idx = get_cartesian_index(graph(iter), next_i)
next_el = (next_i, car_idx)
return (el, (next_el, next_i))
elseif next_i == ne(graph(iter)) + 1
next_el = (0, (0, 0))
return (el, (next_el, next_i))
else
return nothing
end
end
function Base.collect(iter::EdgeIter)
g = graph(iter)
return edgevals(g), rowvals(sparse(g)), colvals(sparse(g))
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 3964 | sparsecsc(A::AbstractMatrix) = sparse(A)
SparseArrays.getcolptr(S::SparseMatrixCSC, col::Integer) = S.colptr[col]:(S.colptr[col+1]-1)
SparseArrays.getcolptr(S::SparseMatrixCSC, I::UnitRange) = S.colptr[I.start]:(S.colptr[I.stop+1]-1)
SparseArrays.rowvals(S::SparseMatrixCSC, col::Integer) = _rowvals(S, col)
SparseArrays.rowvals(S::SparseMatrixCSC, I::UnitRange) = _rowvals(S, I)
rowvalview(S::SparseMatrixCSC, col::Integer) = _rowvalview(S, col)
rowvalview(S::SparseMatrixCSC, I::UnitRange) = _rowvalview(S, I)
_rowvals(S, col) = rowvals(S)[SparseArrays.getcolptr(S, col)]
_rowvalview(S, col) = view(rowvals(S), SparseArrays.getcolptr(S, col))
SparseArrays.nonzeros(S::SparseMatrixCSC, col::Integer) = _nonzeros(S, col)
SparseArrays.nonzeros(S::SparseMatrixCSC, I::UnitRange) = _nonzeros(S, I)
SparseArrays.nzvalview(S::SparseMatrixCSC, col::Integer) = _nzvalview(S, col)
SparseArrays.nzvalview(S::SparseMatrixCSC, I::UnitRange) = _nzvalview(S, I)
_nonzeros(S, col) = nonzeros(S)[SparseArrays.getcolptr(S, col)]
_nzvalview(S, col) = view(nonzeros(S), SparseArrays.getcolptr(S, col))
"""
colvals(S, [n]; upper_traingle=false)
Returns column indices of nonzero values in a sparse array `S`.
Nonzero values are count up to column `n`. If `n` is not specified,
all nonzero values are considered.
# Arguments
- `S::SparseCSC`: Sparse array, which can be `SparseMatrixCSC` or `CuSparseMatrixCSC`.
- `n::Int`: Maximum columns to count nonzero values.
- `upper_traingle::Bool`: To count nonzero values in upper traingle only or not.
"""
colvals(S::SparseMatrixCSC; upper_traingle::Bool=false) =
colvals(S, size(S, 2); upper_traingle=upper_traingle)
colvals(S::SparseMatrixCSC, n::Int; upper_traingle::Bool=false) =
_colvals(S, n; upper_traingle=upper_traingle)
function _colvals(S, n::Int; upper_traingle::Bool=false)
if upper_traingle
ls = [count(rowvalview(S, j) .≤ j) for j in 1:n]
pushfirst!(ls, 1)
cumsum!(ls, ls)
l = ls[end]-1
else
colptr = collect(SparseArrays.getcolptr(S))
ls = view(colptr, 2:(n+1)) - view(colptr, 1:n)
pushfirst!(ls, 1)
cumsum!(ls, ls)
l = length(rowvals(S))
end
return _fill_colvals(rowvals(S), ls, l, n)
end
function _fill_colvals(tmpl::AbstractVector, ls, l::Int, n::Int)
res = similar(tmpl, l)
for j in 1:n
fill!(view(res, ls[j]:(ls[j+1]-1)), j)
end
return res
end
"""
Transform a regular cartesian index `A[i, j]` into a CSC-compatible index `spA.nzval[idx]`.
"""
get_csc_index(S::SparseMatrixCSC, i::Integer, j::Integer) = _get_csc_index(S, i, j)
function _get_csc_index(S, i::Integer, j::Integer)
idx1 = SparseArrays.getcolptr(S, j)
row = view(rowvals(S), idx1)
idx2 = findfirst(x -> x == i, row)
return idx1[idx2]
end
"""
Order the edges in a graph by giving a unique integer to each edge.
"""
order_edges(S::SparseMatrixCSC; directed::Bool=false) = _order_edges(S; directed=directed)
_order_edges(S::SparseMatrixCSC; directed::Bool=false) = _order_edges!(similar(rowvals(S)), S, Val(directed))
order_edges!(edges, S::SparseMatrixCSC, ::Val{false}) = _order_edges!(edges, S, Val(false))
order_edges!(edges, S, ::Val{true}) = _order_edges!(edges, S, Val(true))
function _order_edges!(edges, S, ::Val{false})
@assert issymmetric(S) "Matrix of undirected graph must be symmetric."
k = 1
for j in axes(S, 2)
idx1 = SparseArrays.getcolptr(S, j)
row = rowvalview(S, j)
for idx2 in 1:length(row)
idx = idx1[idx2]
i = row[idx2]
if i < j # upper triangle
edges[idx] = k
edges[get_csc_index(S, j, i)] = k
k += 1
elseif i == j # diagonal
edges[idx] = k
k += 1
end
end
end
return edges
end
function _order_edges!(edges::T, S, ::Val{true}) where {T}
edges .= T(1:length(edges))
edges
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 4234 | """
FeaturedSubgraph(fg, nodes)
Construct a lightweight subgraph over a `FeaturedGraph`.
# Arguments
- `fg::AbstractFeaturedGraph`: A base featured graph to construct a subgraph.
- `nodes::AbstractVector`: It specifies nodes to be reserved from `fg`.
# Usage
```
julia> using GraphSignals
julia> g = [[2,3], [1,4,5], [1], [2,5], [2,4]];
julia> fg = FeaturedGraph(g)
FeaturedGraph:
Undirected graph with (#V=5, #E=5) in adjacency matrix
julia> subgraph(fg, [1,2,3])
FeaturedGraph:
Undirected graph with (#V=5, #E=5) in adjacency matrix
Subgraph: nodes([1, 2, 3])
```
See also [`subgraph`](@ref) for syntax sugar.
"""
struct FeaturedSubgraph{G<:AbstractFeaturedGraph,T} <: AbstractFeaturedGraph
fg::G
nodes::T
end
@functor FeaturedSubgraph
ConcreteFeaturedGraph(fsg::FeaturedSubgraph; nf=node_feature(fsg.fg),
ef=edge_feature(fsg.fg), gf=global_feature(fsg.fg),
pf=positional_feature(fsg.fg), nodes=fsg.nodes) =
FeaturedSubgraph(
ConcreteFeaturedGraph(fsg.fg; nf=nf, ef=ef, gf=gf, pf=pf),
nodes
)
"""
subgraph(fg, nodes)
Returns a subgraph of type `FeaturedSubgraph` from a given featured graph `fg`.
It constructs a subgraph by reserving `nodes` in a graph.
# Arguments
- `fg::AbstractFeaturedGraph`: A base featured graph to construct a subgraph.
- `nodes::AbstractVector`: It specifies nodes to be reserved from `fg`.
"""
subgraph(fg::AbstractFeaturedGraph, nodes::AbstractVector) = FeaturedSubgraph(fg, nodes)
subgraph(fsg::FeaturedSubgraph, nodes::AbstractVector) = FeaturedSubgraph(fsg.fg, nodes)
## show
Base.show(io::IO, fsg::FeaturedSubgraph) =
print(io, fsg.fg, "\n\tSubgraph:\tnodes(", fsg.nodes, ")")
graph(fsg::FeaturedSubgraph) = graph(fsg.fg)
Graphs.vertices(fsg::FeaturedSubgraph) = fsg.nodes
function Graphs.edges(fsg::FeaturedSubgraph)
sg = graph(fsg.fg)
S = SparseMatrixCSC(sparse(sg))
nodes = collect(fsg.nodes)
sel = map(x -> x in nodes, colvals(S))
sel .&= map(x -> x in nodes, rowvals(S))
return sort!(unique!(collect(edgevals(sg))[sel]))
end
Graphs.adjacency_matrix(fsg::FeaturedSubgraph) = view(adjacency_matrix(fsg.fg), fsg.nodes, fsg.nodes)
has_node_feature(fsg::FeaturedSubgraph) = has_node_feature(fsg.fg)
node_feature(fsg::FeaturedSubgraph) = node_feature(fsg.fg)
has_edge_feature(fsg::FeaturedSubgraph) = has_edge_feature(fsg.fg)
edge_feature(fsg::FeaturedSubgraph) = edge_feature(fsg.fg)
has_global_feature(fsg::FeaturedSubgraph) = has_global_feature(fsg.fg)
global_feature(fsg::FeaturedSubgraph) = global_feature(fsg.fg)
has_positional_feature(fsg::FeaturedSubgraph) = has_positional_feature(fsg.fg)
positional_feature(fsg::FeaturedSubgraph) = positional_feature(fsg.fg)
Graphs.neighbors(fsg::FeaturedSubgraph) = mapreduce(i -> neighbors(graph(fsg), i), vcat, fsg.nodes)
incident_edges(fsg::FeaturedSubgraph) = mapreduce(i -> incident_edges(graph(fsg), i), vcat, fsg.nodes)
repeat_nodes(fsg::FeaturedSubgraph) = mapreduce(i -> repeat_nodes(graph(fsg), i), vcat, fsg.nodes)
## Linear algebra
degrees(fsg::FeaturedSubgraph, T::DataType=eltype(graph(fsg.fg)); dir::Symbol=:out) =
degrees(fsg.fg, T; dir=dir)[fsg.nodes]
degree_matrix(fsg::FeaturedSubgraph, T::DataType=eltype(graph(fsg.fg)); dir::Symbol=:out) =
degree_matrix(fsg.fg, T; dir=dir)[fsg.nodes, fsg.nodes]
normalized_adjacency_matrix(fsg::FeaturedSubgraph, T::DataType=eltype(graph(fsg.fg)); selfloop::Bool=false) =
normalized_adjacency_matrix(fsg.fg, T; selfloop=selfloop)[fsg.nodes, fsg.nodes]
laplacian_matrix(fsg::FeaturedSubgraph, T::DataType=eltype(graph(fsg.fg)); dir::Symbol=:out) =
laplacian_matrix(fsg.fg, T; dir=dir)[fsg.nodes, fsg.nodes]
normalized_laplacian(fsg::FeaturedSubgraph, T::DataType=eltype(graph(fsg.fg));
dir::Symbol=:both, selfloop::Bool=false) =
normalized_laplacian(fsg.fg, T; selfloop=selfloop)[fsg.nodes, fsg.nodes]
scaled_laplacian(fsg::FeaturedSubgraph, T::DataType=eltype(graph(fsg.fg))) =
scaled_laplacian(fsg.fg, T)[fsg.nodes, fsg.nodes]
"""
mask(fg, m)
A syntax sugar for masking graph.
Returns a `FeaturedSubgraph`.
"""
mask(fg::AbstractFeaturedGraph, m::AbstractVector) = subgraph(fg, m)
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 4136 | orthogonal_random_features(nvertex::Int, dims::Vararg{Int}) =
orthogonal_random_features(Float32, nvertex, dims...)
orthogonal_random_features(::Type{T}, g, dims::Vararg{Int}) where {T} =
orthogonal_random_features(T, nv(g), dims...)
orthogonal_random_features(g, dims::Vararg{Int}) =
orthogonal_random_features(float(eltype(g)), nv(g), dims...)
function orthogonal_random_features(::Type{T}, nvertex::Int, dims::Vararg{Int}) where {T}
N = length(dims) + 2
orf = Array{T,N}(undef, nvertex, nvertex, dims...)
for cidx in CartesianIndices(dims)
G = randn(T, nvertex, nvertex)
A = qr(G)
copyto!(view(orf, :, :, cidx), A.Q)
end
return orf
end
function laplacian_matrix(::Type{T}, g, dims::Vararg{Int}) where {T}
L = laplacian_matrix(g, T)
U = eigvecs(L)
return repeat(U, outer=(1, 1, dims...))
end
laplacian_matrix(g, dims::Vararg{Int}) = laplacian_matrix(float(eltype(g)), g, dims...)
"""
node_identifier([T], g, dims...; method=GraphSignals.orthogonal_random_features)
Constructing node identifier for a graph `g` with additional dimensions `dims`.
# Arguments
- `T`: Element type of returning objects.
- `g`: Data representing the graph topology. Possible type are
- An adjacency matrix.
- An adjacency list.
- A Graphs' graph, i.e. `SimpleGraph`, `SimpleDiGraph` from Graphs, or `SimpleWeightedGraph`,
`SimpleWeightedDiGraph` from SimpleWeightedGraphs.
- An `AbstractFeaturedGraph` object.
- `dims`: Additional dimensions desired following after first two dimensions.
- `method`: Available methods are `GraphSignals.orthogonal_random_features` and
`GraphSignals.laplacian_matrix`.
# Usage
```jldoctest
julia> using GraphSignals
julia> adjm = [0 1 1 1;
1 0 1 0;
1 1 0 1;
1 0 1 0];
julia> batch_size = 10
10
julia> node_id = node_identifier(adjm, batch_size; method=GraphSignals.orthogonal_random_features);
julia> size(node_id)
(4, 4, 10)
```
See also [`identifiers`](@ref) for node/edge identifiers.
"""
node_identifier(::Type{T}, g, dims...; method=orthogonal_random_features) where {T} =
method(T, g, dims...)
node_identifier(g, dims...; method=orthogonal_random_features) =
method(float(eltype(g)), g, dims...)
"""
identifiers([T], g, dims...; method=orthogonal_random_features)
Returns node identifier and edge identifier.
# Arguments
- `T`: Element type of returning objects.
- `g`: Data representing the graph topology. Possible type are
- An adjacency matrix.
- An adjacency list.
- A Graphs' graph, i.e. `SimpleGraph`, `SimpleDiGraph` from Graphs, or `SimpleWeightedGraph`,
`SimpleWeightedDiGraph` from SimpleWeightedGraphs.
- An `AbstractFeaturedGraph` object.
- `dims`: Additional dimensions desired following after first two dimensions.
- `method`: Available methods are `GraphSignals.orthogonal_random_features` and
`GraphSignals.laplacian_matrix`.
# Usage
```jldoctest
julia> using GraphSignals
julia> V, E = 4, 5
(4, 5)
julia> batch_size = 10
10
julia> adjm = [0 1 1 1;
1 0 1 0;
1 1 0 1;
1 0 1 0];
julia> node_id, edge_token = identifiers(adjm, batch_size);
julia> size(node_id)
(8, 4, 10)
julia> size(edge_id)
(8, 10, 10)
```
See also [`node_identifier`](@ref) for generating node identifier only.
"""
function identifiers(::Type{T}, g, dims...; method=orthogonal_random_features) where {T}
fg = FeaturedGraph(g)
node_id = node_identifier(T, g, dims...; method=method)
node_token = vcat(node_id, node_id)
el = to_namedtuple(fg)
xs_id = NNlib.gather(node_id, batched_index(el.xs, size(node_id)[end]))
nbr_id = NNlib.gather(node_id, batched_index(el.nbrs, size(node_id)[end]))
edge_token = vcat(xs_id, nbr_id)
return node_token, edge_token
end
identifiers(g, dims...; method=orthogonal_random_features) =
identifiers(float(eltype(g)), g, dims...; method=method)
function batched_index(idx::AbstractVector, batch_size::Integer)
b = copyto!(similar(idx, 1, batch_size), collect(1:batch_size))
return tuple.(idx, b)
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
|
[
"MIT"
] | 0.9.2 | 6108a8e889648f0d3951d40b2eb47e9d79fb4516 | code | 3911 | @testset "dataloader" begin
vdim = 3
edim = 5
gdim = 7
pdim = 11
V = 4
E = 5
obs_size = 100
batch_size = 10
nf = rand(vdim, V, obs_size)
ef = rand(edim, E, obs_size)
gf = rand(gdim, obs_size)
pf = rand(pdim, V, obs_size)
y = rand(30, obs_size)
adjm = [0 1 1 1;
1 0 1 0;
1 1 0 1;
1 0 1 0]
@testset "numobs, getobs" begin
fg = FeaturedGraph(adjm; nf=nf, ef=ef, gf=gf, pf=pf)
@test numobs(fg) == obs_size
@test getobs(fg) == fg
for idx in (2, 2:5, [1, 3, 5])
idxed_fg = getobs(fg, idx)
@test graph(idxed_fg) == graph(fg)
@test node_feature(idxed_fg) == node_feature(fg)[:, :, idx]
@test edge_feature(idxed_fg) == edge_feature(fg)[:, :, idx]
@test global_feature(idxed_fg) == global_feature(fg)[:, idx]
@test positional_feature(idxed_fg) == positional_feature(fg)[:, :, idx]
end
fg = FeaturedGraph(adjm; nf=nf, ef=ef)
@test numobs(fg) == obs_size
@test getobs(fg) == fg
for idx in (2, 2:5, [1, 3, 5])
idxed_fg = getobs(fg, idx)
@test graph(idxed_fg) == graph(fg)
@test node_feature(idxed_fg) == node_feature(fg)[:, :, idx]
@test edge_feature(idxed_fg) == edge_feature(fg)[:, :, idx]
@test global_feature(idxed_fg) == global_feature(fg)
@test positional_feature(idxed_fg) == positional_feature(fg)
end
fg = subgraph(FeaturedGraph(adjm; nf=nf, ef=ef), [1, 3, 4, 5])
@test numobs(fg) == obs_size
@test getobs(fg) == fg
for idx in (2, 2:5, [1, 3, 5])
idxed_fg = getobs(fg, idx)
@test graph(idxed_fg) == graph(fg)
@test node_feature(idxed_fg) == node_feature(fg)[:, :, idx]
@test edge_feature(idxed_fg) == edge_feature(fg)[:, :, idx]
@test global_feature(idxed_fg) == global_feature(fg)
@test positional_feature(idxed_fg) == positional_feature(fg)
end
end
@testset "shuffleobs" begin
fg = FeaturedGraph(adjm; nf=nf, ef=ef, gf=gf, pf=pf)
shuffled_obs = shuffleobs(fg)
@test shuffled_obs isa MLUtils.ObsView
@test shuffled_obs.data isa FeaturedGraph
end
@testset "splitobs" begin
fg = FeaturedGraph(adjm; nf=nf, ef=ef, gf=gf, pf=pf)
train, test = splitobs(fg, at=0.7)
@test train isa MLUtils.ObsView
@test test isa MLUtils.ObsView
@test length(train) == 0.7 * obs_size
@test length(test) == 0.3 * obs_size
end
@testset "DataLoader" begin
fg = FeaturedGraph(adjm; nf=nf, ef=ef, gf=gf, pf=pf)
loader = DataLoader((fg, y), batchsize = batch_size)
@test length(loader) == obs_size ÷ batch_size
obs, next = iterate(loader)
batched_x, batched_y = obs
@test batched_x isa FeaturedGraph
@test node_feature(batched_x) == node_feature(fg)[:, :, 1:batch_size]
@test edge_feature(batched_x) == edge_feature(fg)[:, :, 1:batch_size]
@test global_feature(batched_x) == global_feature(fg)[:, 1:batch_size]
@test positional_feature(batched_x) == positional_feature(fg)[:, :, 1:batch_size]
@test batched_y == y[:, 1:batch_size]
obs, next = iterate(loader, next)
batched_x, batched_y = obs
@test batched_x isa FeaturedGraph
@test node_feature(batched_x) == node_feature(fg)[:, :, (batch_size+1):2batch_size]
@test edge_feature(batched_x) == edge_feature(fg)[:, :, (batch_size+1):2batch_size]
@test global_feature(batched_x) == global_feature(fg)[:, (batch_size+1):2batch_size]
@test positional_feature(batched_x) == positional_feature(fg)[:, :, (batch_size+1):2batch_size]
@test batched_y == y[:, (batch_size+1):2batch_size]
end
end
| GraphSignals | https://github.com/yuehhua/GraphSignals.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.